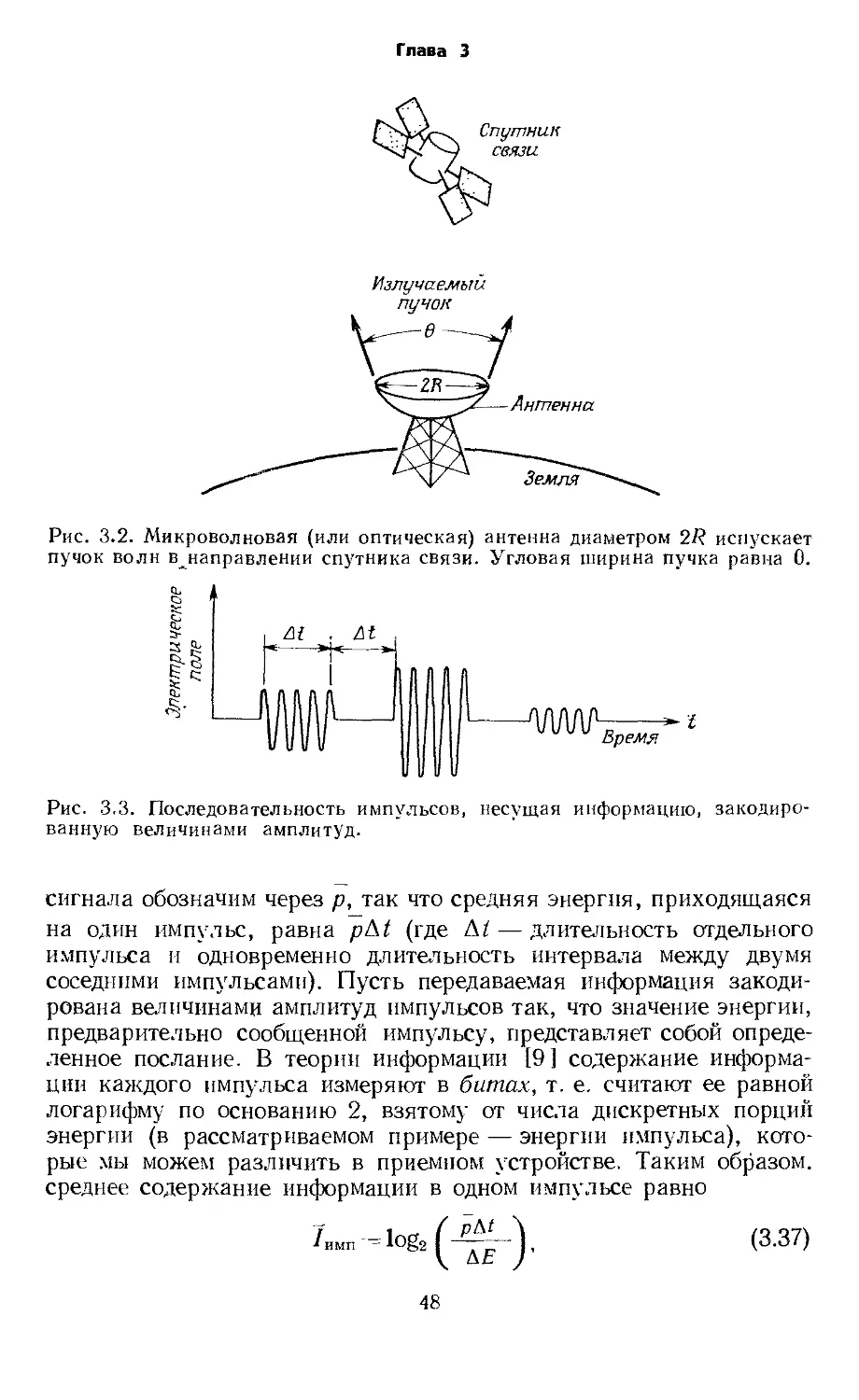
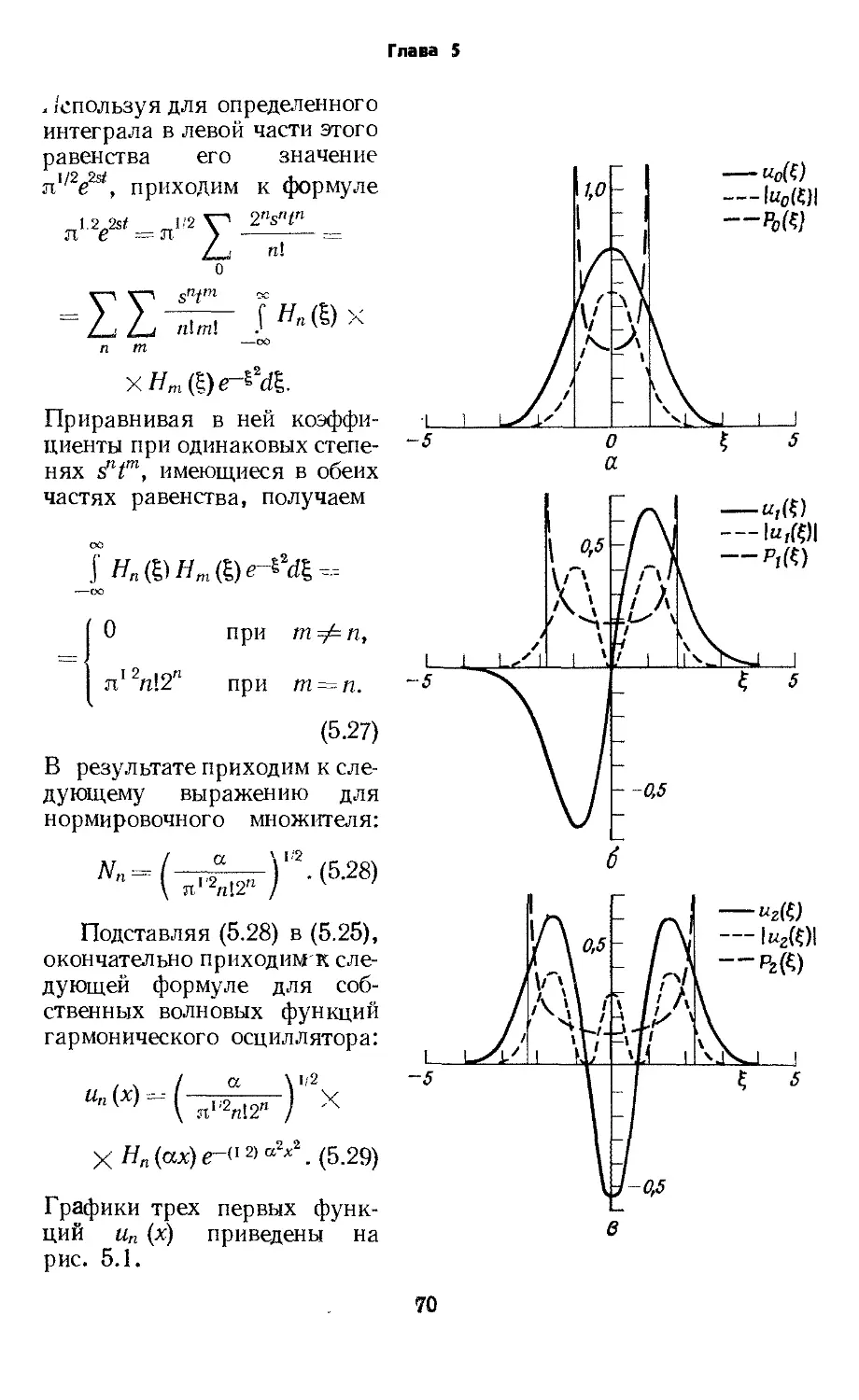
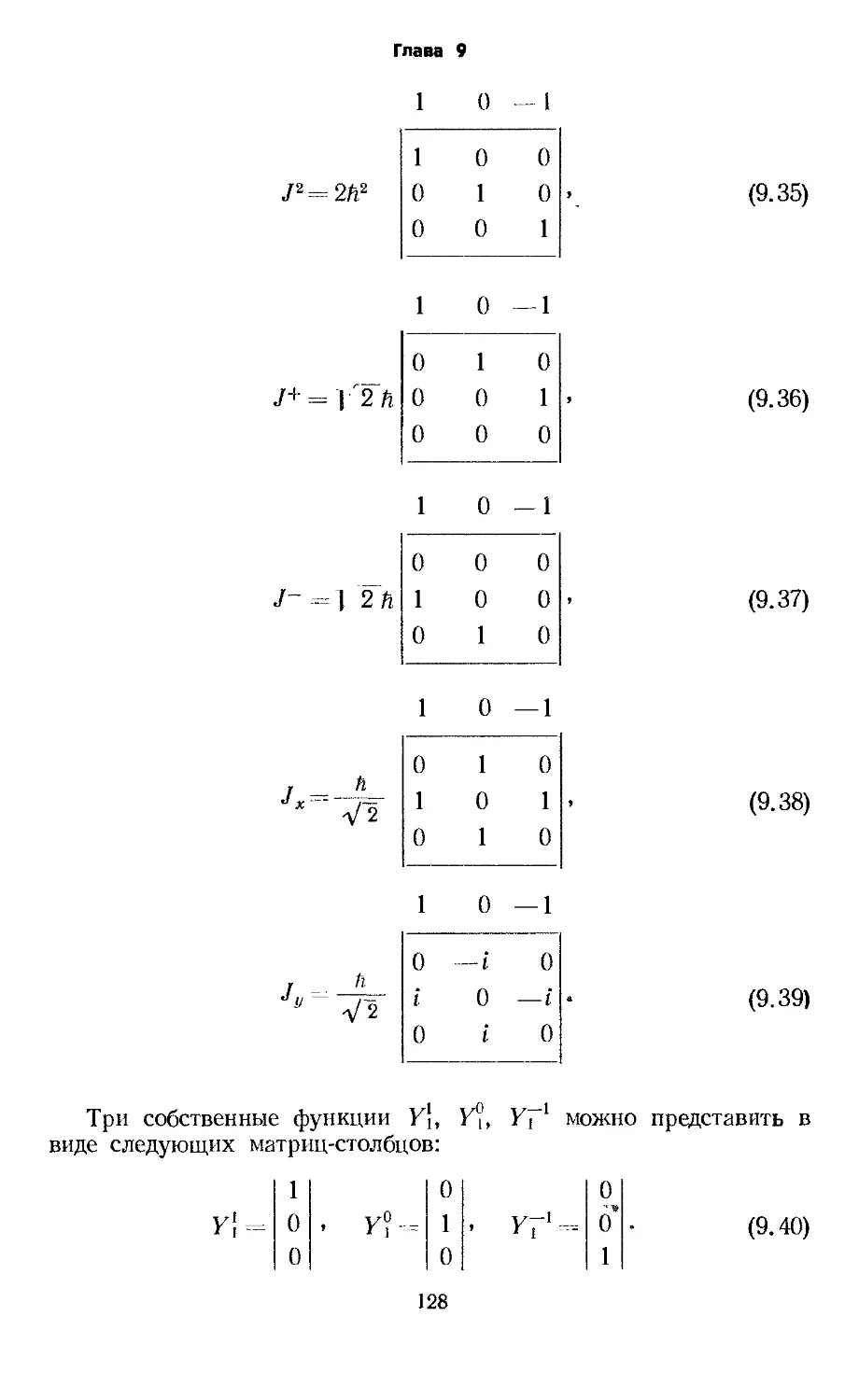
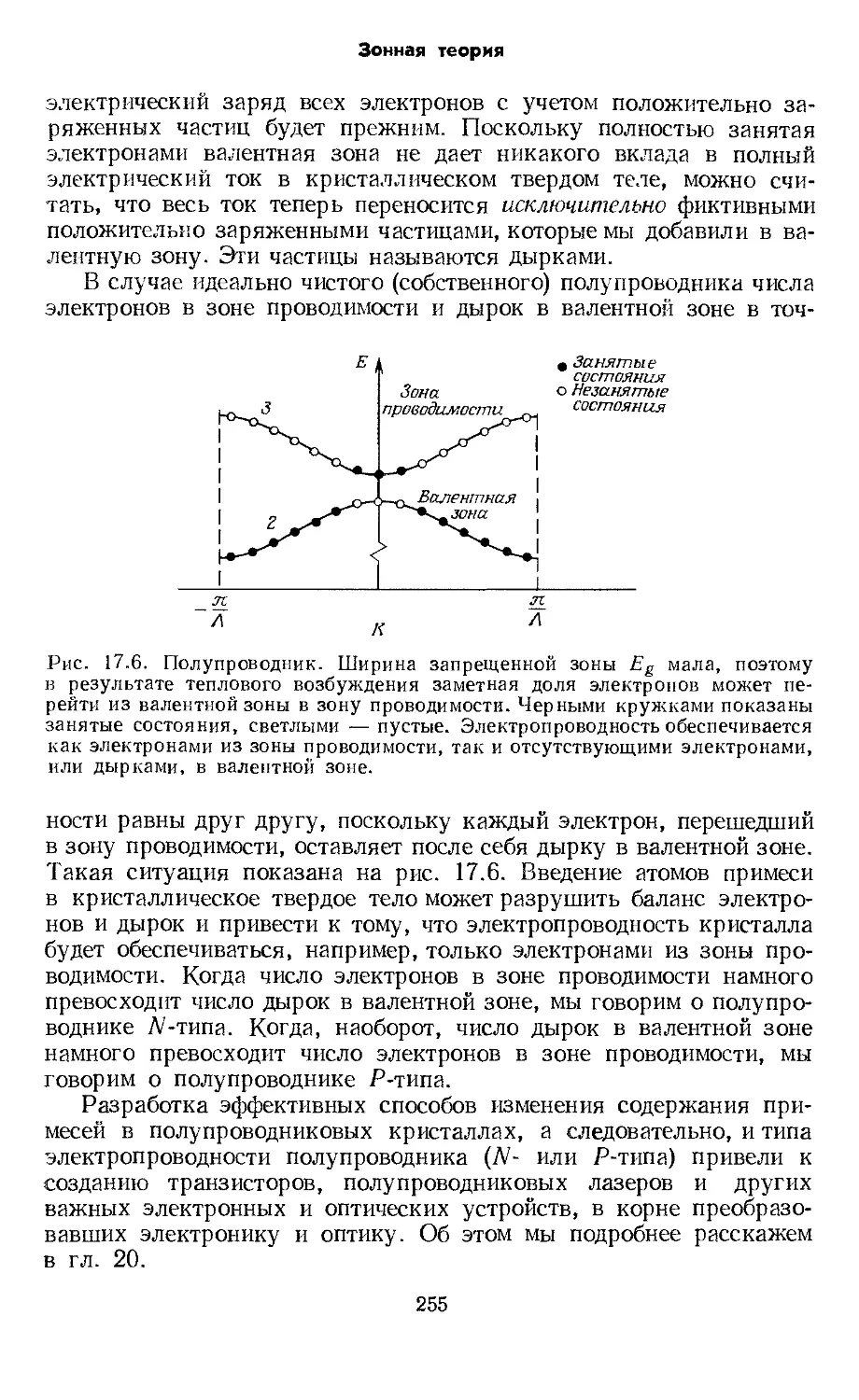
Text
Ап 1пйос1исйоп *о ТИеогу
апс! Арр1юа1юп5
оГ ОиагЛит МесЬапгсз
ЛМ\'О\; УАШУ
СаП1'огП1а
ЛоЬп иЧ1еу & 5оп?
Уогк СЫсЬез1ег
Тогоп1о 81
1982
~'^.« ,•■ I
ВМ1
ю
О
А. Ярив
Введение в теорию
и приложения
квантовой механики
Перевод с английского
д-ра физ.-мат. наук. проф. В, В. Толмачева
МОСКВА «МИР» 1984
ББК 22.314
Я 73
УДК 530.145
Ярив А.
Я73 Введение в теорию и приложения квантовой механики.
Пер. с англ.— М.: Мир, 1984.— 360 с, ил.
Киша ученого из США содержит сжатое и вместе с тем четкое изложение
оенпв квантовой механики. Большое внимание уделяется прикладным вопросам,
11 частности квантован теории полупроводниковых транзисторов и полупроводни-
полупроводниковых лазеров.
Книга рассчитана на студентов н асиирапгоп, интересующихся вопросами
практического применения квантовой механики.
1704020000—061 г ББК 22.314
я 84 61-85. ч. 1 5т,
Редакция литературы по физике
Соруп^М .С) 1982 Ьу ЛоЬп \\Ч1еу & Зопк, 1пс. ЛИ
Кехегуес!. АиПюп/ей 1гап51аНоп Сгот Еп^
ПхЬ 1ап^иа^е ейШоп риЬНхЬес! Ьу ЛоЬп \\*Пеу
& 5оп5, 1пс.
С) Перевод на русский язык, «Мир», 1984
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
Предлагаемая вниманию читателей книга посвящена основам
квантовой физики. По замыслу автора, она должна стать первой
книгой для приступающих к изучению этой дисциплины. Книга
выгодно отличается от традиционных учебников квантовой меха-
механики. Она отражает взгляд автора, специалиста по прикладной
физике, электронике и оптике, на современную квантовую теорию.
Как указывает автор в своем предисловии, книга написана на
основе вводного, точнее сказать, ознакомительного курса кванто-
квантовой механики, читавшегося ряд лет в Калифорнийском техноло-
технологическом институте в США студентам младших курсов, собираю-
собирающимся специализироваться по прикладной физике. Таким образом,
книга адресована неподготовленному читателю, желающему, од-
однако, понять основные принципы квантовой механики, ознако-
ознакомиться с ее важнейшими достижениями и приложениями и, самое
главное, осмыслить возможности ее использования в областях фи-
физики, которые принято называть прикладными.
Автор отобрал из всего круга вопросов, рассматриваемых кван-
квантовой механикой, только самый необходимый теоретический мате-
материал и, не вдаваясь в сложную математическую теорию, ярко изло-
изложил ее основы на примере нескольких простых, главным образом,
одномерных модельных задач (потенциальная яма, барьер, одно-
одномерный осциллятор, одномерная электромагнитная мода, лазер
Фабри—Перо, одномерный кристалл).
Особенно удачны разделы, относящиеся к взаимодействию элек-
электромагнитного излучения с веществом. Здесь много оригинального.
Так, рассматривая теорию атома водорода, автор здесь же весьма
уместно обсуждает эффект Доплера для излучающего атома водо-
водорода. С единых позиций очень четко изложена теория поглощения
и усиления электромагнитных волн, распространяющихся в атом-
атомной среде. Чрезвычайно доходчиво написаны и разделы, посвя-
посвященные весьма сложной теории квантования электромагнитного
поля, где автор рассматривает не трехмерный ящик, как это обычно
делают, а простой одномерный ящик.
Книга особенно ценна тем, что в ней на высоком теоретическом
уровне освещены важнейшие современные прикладные аспекты
квантовой физики, в частности теория лазеров и мазеров и твердо-
твердотельная полупроводниковая электроника. Очень удачно объяснены
основные принципы работы лазера, который рассматривается просто
Предисловие переводчика
как одномерный эталон Фабри—Перо, заполненный средой с ин-
инверсной населенностью уровней. Прекрасно описаны принципы
работы полупроводникового диода с РЛ^-переходом, РЛФ-тран-
зистора и полупроводникового инжекционного лазера для оптиче-
оптических линий связи.
Конечно, изложение не всегда достаточно строго. Отдельные
положения предлагается принять на веру, но это делается очень
разумно, с большим педагогическим тактом, так что у читателя
вовсе не создается впечатления, что ему что-то важное недосказали.
В русском издании по возможности исправлены отдельные не-
недочеты английского оригинала, в частности ошибки в математиче-
математических формулах, некоторая непоследовательность терминологии и не-
нечеткость отдельных утверждений.
Книгу настоятельно следует рекомендовать студентам — буду-
будущим физикам и инженерам-физикам, а также инженерам-электрон-
инженерам-электронщикам и инженерам-оптикам, которые хотят углубить свои теоре-
теоретические знания. Книга, несомненно, будет полезна и преподава-
преподавателям, ведущим курсы общей физики и квантовой механики в вузах.
Читатели всех этих категорий найдут для себя в книге много по-
полезного и ценного.
В. В. Толмачев
ПРЕДИСЛОВИЕ АВТОРА
В Калифорнийском технологическом институте в США послед-
последние десять лет наметилась тенденция, которая привела к созданию
нового направления в подготовке студентов и аспирантов. Это на-
направление получило название прикладной физики. В настоящее
время в институте создана особая специальность, носящая то же
название; ее могут по своему желанию выбрать студенты и аспи-
аспиранты.
По прикладной физике специализируются те студенты или сту-
студентки, которые хотели бы приложить свои знания не к раскрытию
и выявлению тайн природы, а к решению технических проблем и
технологических задач.
До сих пор почти все аспиранты, собирающиеся заниматься
прикладной физикой, слушали обычные курсы физики. В физи-
физическом образовании, которые они получали, будучи студентами,
большое место отводилось атомной теории рассеяния, физике эле-
элементарных частиц, теории относительности, что отражало в основ-
основном круг интересов физических кафедр, преподававших физику
этим студентам.
Изучение упомянутых вопросов, разумеется, осуществлялось
в ущерб таким разделам физики, как атомная и молекулярная
спектроскопия, взаимодействие излучения с веществом, электрон-
электронные свойства кристаллов, хотя именно эти разделы лежат в основе
новейших прикладных дисциплин, посвященных изучению лазе-
лазеров, полупроводниковой электроники, оптической связи, т. е. того
круга вопросов, которые играют все более и более важную роль
при разработке новой техники.
В основу настоящей книги легли записи лекций по новому ввод-
вводному курсу, который читается в настоящее время в Калифорний-
Калифорнийском технологическом институте для студентов, специализирую-
специализирующихся по прикладной физике. По замыслу, этот курс студенты
должны прослушать перед традиционным курсом квантовой меха-
механики. Мы стремились не только осветить в едином курсе формаль-
формальные основы квантовой теории и те физические эксперименты, для
объяснения которых была предложена теория, но и познакомить
студентов с важнейшими приложениями современной квантовой
физики.
Две практические темы освещены в этой книге, а именно
устройство и принцип действия полупроводниковых транзисторов
Предисловие автора
и лазеров. К рассмотрению транзисторов мы обратились по той
простой причине, что они представляют собой основные элементы
различных современных электронных приборов и устройств, вклю-
включая электронные вычислительные машины. Довольно большое вни-
внимание уделено описанию лазеров. Это объясняется тем, что лазеры
оказали огромное революционизирующее воздействие на многие
области современной науки и техники, включая исследования по
термоядерному синтезу, атомной и молекулярной спектроскопии,
технике оптической связи, осуществляемой с помощью стеклянных
оптических волокон, и т. д.
Предполагается, что после настоящего вводного курса студент
прослушает одно- или двухгодичный традиционный курс кванто-
квантовой механики.
Надеемся, что раннее знакомство студентов с приложениями
квантовой механики пробудит у них интерес к этой области науки,
что, несомненно, принесет свои плоды, если студент действительно
решит в дальнейшем заниматься прикладной физикой.
Автор хотел бы выразить благодарность Руфине Стрэттон
и своей жене Франсис за аккуратную перепечатку и редактирование
рукописи, а также Джону Стефану Смиту, который внимательно
прочитал корректуры, проявив при этом творческий подход и сде-
сделав ряд ценных критических замечаний.
Амнон Ярив,
Пасадена, Калифорния
ГЛАВА 1
ПОЧЕМУ ПОЯВИЛАСЬ КВАНТОВАЯ МЕХАНИКА
В конце XIX и в самом начале XX вв. стало ясно, что сущест-
существовавшая в то время физическая наука нуждалась в коренном
пересмотре. Все большее число вновь открываемых физических
явлений и многие эксперименты было невозможно объяснить, хотя
бы качественно, на основе тех законов физики, которые были сфор-
сформулированы в то время. Особенно большие проблемы возникли
при попытках интерпретировать явления, относящиеся к «малень-
«маленьким» частицам — электронам и атомам, а также к их взаимодейст-
взаимодействию с электромагнитными полями.
Сначала эти дыры физики пытались залатать с помощью произ-
произвольно вводимых гипотез и постулатов. Однако, по мере того как
число таких допущений росло, становилось все более ясным, что
физика нуждается в полном коренном пересмотре, в особенности
те ее разделы, которые касаются малых систем. В результате поя-
появилась квантовая механика — одно из самых выдающихся до-
достижений человеческого разума.
В настоящей главе речь идет о становлении квантовой механики
и одновременно кратко излагаются некоторые важнейшие резуль-
результаты классической физики. Описываются также отдельные физи-
физические явления, которые, как показала история, была не в состоя-
состоянии объяснить классическая физика.
§ 1.1. Ньютонова механика
и классическая электромагнитная теория
Ньютонова механика. В классической нерелятивистской фи-
физике предполагается, что частицы движутся под действием механи-
механических сил. Закон движения отдельной частицы имеет вид
A.1)
т.
где т — масса частицы, Р — сила, V — скорость. С помощью этого
закона и закона всемирного тяготения, например, возможно пра-
правильно описать движение небесных тел или точно предсказать тра-
траектории артиллерийских снарядов.
Один из главных аспектов ньютоновой механики состоит в ее
детерминизме. Если известны положение и скорость частицы в не-
некоторый момент времени и если мы знаем силы, действующие на
9
Глава 1
нее, то поведение частицы во все последующие моменты времени
точно предопределено, т. е. детерминировано.
Электромагнитная теория. Электрическое Е (г, I) и магнитное
В (г, I) поля описываются в классической электромагнитной тео-
теории уравнениями Максвелла, которые в пустом пространстве в си-
системе СИ имеют вид *)
го1Е--- <!*-, A.2а)
го!В = ——~, A.26)
с2 (К К
где с — скорость света в пустоте. Используя векторное тождество
(Ну го1 А = — \2А + цгас! (Ну А, а также уравнение (Ну Е ^ О,
справедливое в пустом пространстве, из A.2а) и A.26) выводим
уравнение
У2Е 1- ^ = 0 A.3)
с2 дР
и в точности такое же уравнение для поля В (г, /). Уравнение A.3)
имеет решение
Е-Ке1Е0<Гм<й^к-г)), A.4)
в котором
к со, с A.5)
Выражение A.4) описывает поле, представляющее собой пло-
плоскую волну, распространяющуюся со скоростью с в направлении
вектора к. В этом случае покоящийся наблюдатель будет регистри-
регистрировать поле, колеблющееся с частотой V = со/2л. (Единицей ча-
частоты является герц, равный одному колебанию в секунду.) Длина
волны дается формулой
Х~*?- = Л-. A.6)
к V
Итак, в классической физике существовали две формальные
теории для описания физических явлений. Первая — механика —
имела дело с частицами. Вторая — электромагнитная теория —
описывала волны электромагнитного излучения. Предполагалось,
что оба класса явлений различны, хотя и связаны друг с другом
законом для силы Лоренца
2) Здесь с2 = ((Хоб,,), где щ и е0 — соответственно магнитная проницае-
проницаемость и электрическая постоянная пустого пространства.
10
Почему появилась квантовая механика
Это силаче которой поля Е и В действуют на частицу, обладающую
электрическим зарядом е и движущуюся со скоростью V.
§ 1.2. Излучение абсолютно черного тела
Одной из "главных нерешенных проблем, которой занимались
физики на рубеже XIX—XX вв., была проблема излучения
абсолютно черного тела. Идеальное «абсолютно черное тело» — это
V, ГЦ
Рис. 1.1. Частотная зависимость спектральной интенсивности / (л) (мощ-
(мощность в расчете на единицу площади и единицу частоты) для излучения
абсолютно черного тела при температурах Т= 1000 и 1500 К- Штриховая
кривая соответствует зависимости, описываемой законом Рэлея—Джинса
1см. A.7)].
тело, которое полностью поглощает падающее на него излучение
любых длин волн. Многие обычные вещества, например сажа,
являются прекрасными поглотителями в широкой области спектра.
Рассуждения, основанные на классической термодинамике,
показывали, что спектральная интенсивность I (\>) испущенного
излучения (измеряемая в единицах Вт/м2 на единичный частотный
интервал) должна быть одинаковой для всех абсолютно черных
тел, нагретых до одинаковой заданной температуры. Это предска-
предсказание подтверждается экспериментом. На рис. 1.1 показаны со-
соответствующие экспериментальные кривые. Спектральная интен-
интенсивность достигает максимума при некоторой частоте \т, а по обе
стороны от максимума падает до нуля. Частота максимума, так
же как и его высота, увеличивается с ростом температуры.
11
Глава 1
Все предпринятые до 1900 г. попытки теоретически предсказать
форму экспериментальной кривой спектральной интенсивности
излучения абсолютно черного тела на основе известных тогда фун-
фундаментальных законов классической физики оказались безрезуль-
безрезультатными. Используя классическую статистическую термодинамику
и законы механики и электромагнитной теории, можно было только
получить так называемую формулу Рэлея—Джинса
^ A.7)
в которой константа к = 1,3807-10—23 Дж/'К называется констан-
константой Больцмана. Кривая, описываемая законом Рэлея—Джинса,
приведена на рис. 1.1. За исключением области очень малых ча-
частот, закон Рэлея—Джинса совершенно не согласуется с экспери-
экспериментом. Он предсказывает (как легко убедиться, интегрируя по
всем частотам спектральную интенсивность), что полная интенсив-
интенсивность излученной энергии неограниченно возрастает. В действи-
действительности полная излучаемая интенсивность конечна.
Макс Планк 11 ] в 1900 г. разрешил проблему излучения абсо-
абсолютно черного тача, постулировав, что обмен энергией между ато-
атомами и испущенным ими электромагнитным излучением происхо-
происходит дискретными порциями энергии и что наименьшая порция энер-
энергии при заданной частоте V равна
<В--кх, A.8)
где Н — некоторая постоянная. Только целые кратные энергии
Нх могут передаваться при взаимодействии атомов и излучения.
С помощью своего постулата Планк вывел формулу для спектраль-
спектральной интенсивности теплового равновесного электромагнитного из-
излучения абсолютно черного тела
/(у) = _*Е*. 41 , A.9)
с< ь —~ *
которая дала блестящее согласие с экспериментом при условии,
что постоянной к приписывалось значение
к -6,62377-10~34 Дж-с.
Константу к, численное значение которой мы привели с учетом
данных самых последних экспериментов, называют постоянной
Планка.
Идея о том, что энергия электромагнитного поля квантуется,
а не принимает непрерывные значения, явилась новым и очень
глубоким добавлением к классической физике.
При определенных обстоятачьствах волны электромагнитного
излучения лучше представлять себе как потоки частиц — фото-
фотонов, движущихся со скоростью света с и обладающих энергией Нх.
12
Почему появилась квантовая механика
§ 1.3. Теплоемкость твердых тел
и фотоэлектрический эффект
Существовали и другие физические явления, которые не могла
объяснить классическая физика; к ним относились, в частности,
результаты экспериментов по определению теплоемкости твер-
1,0
0,9
0,8
0,7
\ 16
^ °'5
Ь ОА
0,3
0,2
о л
о
7,0
0,9
0,8
0,1
\ ом
0,3
0,1
0,1
О
—
|
4
1
V
-
—
*-*
—
V
. I
Алюминий, !
| Т=396К 1
_
I
„
\ \
\ Г"
!
\ \
\
"Г
100
гоо
7, К
300
4С0
4--
А
/
-
/
/
—
::|г
Т
ш
1
...
ь
=309 К
■
.О—
юо
гоо
300
т, к
Рис. 1.2. Экспериментальные данные (точки) и теоретические кривые для
дебаевской модели, относящиеся к теплоемкости алюминия и меди. (Из
статьи [3].)
дых тел. На рис, 1.2 приведены соответствующие эксперименталь-
экспериментальные кривые. При низких температурах теплоемкость С пропор-
пропорциональна Г3. При высоких температурах теплоемкость С стре-
стремится к постоянному значению.
Согласно классической статистической термодинамике, каждый
атом в кристалле следует рассматривать как осциллятор со сред-
средней энергией теплового возбуждения, равной величине кТ/2 в рас-
13
Глава 1
чете на одну степень свободы. Полная энергия единицы объема кри-
кристалла, таким образом, равна
8 = шит,
где N — плотность кристалла (число атомов на 1 м3). Тогда для
теплоемкости Сг, = дё/дТ получаем формулу
С = ЗЫк. A.10)
Как видим, согласно этой классической формуле, теплоемкость
не зависит от температуры в противоречии с экспериментом.
Противоречие классической теории с экспериментом удалось
разрешить Эйнштейну 12 ] и Дебаю 13 I, которые применили план-
ковское условие квантования A.8) к механическим колебаниям
осцилляторов кристаллической решетки. Весьма существенный ре-
результат,- который был получен при применении постулата Планка
к атомным осцилляторам в твердом теле, заключался в утвержде-
утверждении, что средняя равновесная энергия теплового возбуждения
осциллятора не равна «классическому» значению кТ, а дается фор-
формулой
Г . A.11)
1 Х
Обратите внимание, что, согласно этой формуле, Ш » кТ при
кТ у>> Ну. Использование формулы A.11) для разрешения про-
проблемы теплоемкости твердых тел привело к прекрасному согласию
с экспериментом, как видно на рис. 1.2.
Фотоэлектрический эффект. Непосредственным подтверждением
справедливости идеи квантования энергии электромагнитного поля
может служить фотоэлектрический эффект. Когда свет, имеющий
частоту V, падает на твердое тело, с поверхности твердого тела в
вакуум испускаются электроны, если только выполнено условие
/гл'>ф, где ф — константа, характерная для данного вещества
(а часто также и для физической природы его поверхности). Если
Ну>ц>, испускаемые электроны имеют кинетическую энергию Т,
определяемую соотношением
Эксперименты показывают, что эта формула выполняется не-
независимо от интенсивности падающего электромагнитного излуче-
излучения. Последняя определяет только число испущенных твердым те-
телом электронов в единицу времени.
Объяснение фотоэлектрического эффекта дал Эйнштейн в 1905 г.,
введя в физику представление о фотонах — частицах электромаг-
электромагнитного поля, переносящих каждая энергию Ну. Он предположил,
что электроны в твердом теле удерживаются от испускания в ва-
вакуум энергетическим барьером, имеющим высоту ц. Попадающий
14
Почему появилась квантовая механика
в твердое таю фотон может передать свою энергию Ну какому-ни-
какому-нибудь электрону, находящемуся вблизи поверхности. Когда /п><Сф,
этой энергии недостаточно для преодоления потенциального барьера
и электрон не может вылететь из твердого тела. Когда Ну^хр, из-
избыток энергии Т = Ну—ф проявляется как кинетическая энергия
электрона, покидающего поверхность твердого тела.
§ 1.4. Импульс фотона и комптоновское рассеяние
Разительные успехи применения постулата Планка для объяс-
объяснения частотной зависимости интенсивности излучения абсо-
абсолютно черного тела и температурной зависимости теплоемкости
твердых тат показали, что электромагнитное излучение можно
считать состоящим из отдачьных частиц, или корпускул — фото-
фотонов, обладающих каждый энергией й<в (Ну = На»).1) Дальнейшее
подтверждение корпускулярной природы электромагнитного из-
излучения дали эксперименты по фотоэлектрическому эффекту.
Поэтому естественно возник в то время вопрос: не обладает ли фо-
фотон, как и всякая частица, импульсом, так же как и энергией?
Классическое рачятивистское соотношение между энергией Е
и импульсом р для частицы имеет вид
A.12)
где га — масса покоя частицы, с — скорость света в пустом про-
пространстве, V-—скорость частицы. Для фотона в формуле A.12)
надо положить V = с. И так как энергия фотона конечна (Ж = Ну),
его масса покоя га должна равняться нулю. Тогда из формулы A.12)
получаем формулу
& = рс. A,13)
Используя теперь соотношение Ж = йа> и о = кс, отсюда полу-
получаем
* А^ A.14)
с "к с
Формулу A.4) для плоской электромагнитной волны
можно переписать, вводя в нее энергию и импульс фотона, в сле-
следующем виде:
Е,-Еое-1Ш~р-г)П A.15)
*) Часто в квантовой механике используют так называемую «перечерк-
«перечеркнутую» постоянную Планка 1г~к/2п.
15
Глава 1
Идея приписывания импульса р переносчику электромагнит-
электромагнитного поля — фотону, конечно, нуждается в экспериментальной
проверке. Наиболее простую и убедительную проверку утвержде-
утверждения, что фотон действительно обладает импульсом, дают экспери-
эксперименты по рассеянию коротковолнового электромагнитного излуче-
излучения (обычно рентгеновских лучей) на электронах — так называе-
называемому комптоновскому рассеянию.
Падающий
фотон
Е =р, с, импульс = р7
Р1
Рис. 1.3. Комптоновское рассеяние электромагнитного излучения па элек-
электронах.
В эксперименте по комптоновскому рассеянию электромагнит-
электромагнитное излучение с длиной волны Х± (К± = сЛ^) падает на электроны.
С помощью спектрометра измеряют длину волны К2 электромаг-
электромагнитного излучения, рассеянного электронами в некотором направ-
направлении, составляющем угол 6 с направлением падающего пучка.
Предположим, что элементарный акт комптоновского рассея-
рассеяния состоит в рассеянии одного фотона с энергией р±с и импуль-
импульсом рх на электроне, который первоначально покоился, как пока-
показано на рис. 1.3.
Приравнивая друг другу полные энергии (суммы энергий элек-
электрона и фотона) до и после акта рассеяния и обозначая через ре
импульс рассеянного электрона, получаем соотношение
р1с+тс^р2с^(р2е + т2с2у2с. A.16)
Закон сохранения импульса дает еще одно соотношение
Р1 = Р, + Рг- A-17)
Применяя теорему косинусов к треугольнику импульсов A.17),
получаем соотношение
р.- р? + р|-2р1ргсо5в. A.17а)
16
Почему появилась квантовая механика
Простые преобразования соотношения A.16) и соотношения A.17а)
позволяют получить формулу
е
Р\
тс= 2 81ГГ
Вспомним теперь, что импульс фотона и длина волны излуче-
излучения связаны соотношением р — Н/К. Таким образом, последнюю
формулу можно представить в виде
Л2 — Л!— 51ГР -4лАе51П2 , A-18)
тс 2 2
где так называемая комптоновская длина волны электрона опреде-
определяется соотношением
Кс = П,тсх4-\0~и м.
Эксперименты по комптоновскому рассеянию прекрасно сог-
согласуются с теоретической формулой A.18). Особенно замечательно,
то, что экспериментальный сдвиг длины волны АК действительно
не зависит от длины волны падающего излучения. Поскольку вы-
вывод формулы A.18) основан на предпосылке, что фотон обладает
импульсом, связанным с его энергией соотношением р = Ж'с, экс-
экспериментальное подтверждение формулы A.18) можно считать также
и подтверждением указанного предположения.
Числовой пример. Пусть падающее излучение имеет длину волны
% — 1 мкм A мкм = 10~е м). Положив 6 --^ я в формуле A.18),
получим
Это очень малый относительный сдвиг, и его трудно измерить. Если
же эксперименты производить с рентгеновским излучением с дли-
длиной волны К — 1 А A А = 10~~10 м), относительный сдвиг длины
волны рассеянного излучения равен
и его легко измерить экспериментально.
§ 1.5. Волновая природа частиц
В предыдущих параграфах мы рассказали о том, как классиче-
классической физике под давлением неоспоримых экспериментальных фак-
фактов пришлось принять идею о корпускулярной природе электро-
электромагнитного излучения. С этой идеей очень хорошо согласовыва-
согласовывалось открытие того, что и частицы — электроны — также ведут
«двойную жизнь» и при определенных обстоятельствах проявляют
себя как волны.
17 ] Научно-техническая библпоте
Тамбовского ВАМИ -^
Глава 1
В 1924 г. Луи де Бройль высказал предположение, что с элек-
электроном, обладающим импульсом р, следует связывать волну с дли-
длиной волны
\ = Ыр. A.19)
Первые эксперименты, наиболее ярко продемонстрировавшие
двойственную корпускулярно-волновую природу электронов, были
произведены Дэвиссоном и Джермером [4 ]. В своих эксперимен-
экспериментах эти исследователи бомбардировали кристалл никеля моно-
моноэнергетическим пучком электронов. Они обнаружили, что, вместо
того чтобы рассеиваться более или менее однородно по всем направ-
направлениям, электроны рассеивались только в некоторых строго опре-
определенных направлениях. Последние можно было предсказать с по-
помощью брэгговской теории дифракции электромагнитных волн
на кристаллах, в частности с помощью теории дифракции рентге-
рентгеновских лучей, сделав предположение, что с электроном, обладаю-
обладающим кинетической энергией Ж и импульсом р, связана волна
я)) (г, ()^С(ГИ:?'-рг)т, A.20)
где С — некоторая постоянная. Оказалось, что длина волны X,,
электрона совпадает с длиной волны, предсказанной де Бройлем:
К ^=—А=.. A.21)
р -уЧтё
В A.20) использовано обозначение й = Н/2п, а в A.21) Ш — р2/2от
(нерелятивистская формула).
Дифракция электронов наблюдается в направлениях, для ко-
которых падающий электронный пучок удовлетворяет условию
Брэгга
<Ьт6=--/(У2), A.22)
в котором / — 1, 2, 3 . . . , й — расстояние между двумя соседними
атомными плоскостями, 6 — угол падения, показанный на рис. 1.4.
При выполнении условия Брэгга A.22) вторичные электронные
волны, рассеянные от соседних атомных плоскостей кристалла в на-
направлении 6, находятся в фазе друг с другом и складываются
(рис. 1.4, б).
Самое существенное в обсуждаемом представлении об электро-
электронах как о волнах состояло в том, что волновые свойства приписы-
приписывались единственному электрону, причем считалось, что он испы-
испытывает рассеяние одновременно на всех атомах кристалла. Такое
описание электронов было в корне отлично от господствовавшего
в то время представления о них, как о бильярдных шариках.
Числовой пример. Из A.21) для длины электронной волны по-
получаем формулу
I 1а) = —Ыи, A.23)
У<?(эВ)
18
Почему появилась квантовая механика
так что при энергии <§ электрона порядка нескольких электрон-
вольт *) длина волны Ке имеет порядок нескольких ангстрем. При
такой длине волны можно наблюдать дифракцию электронов на
кристаллах с типичными межатомными расстояниями порядка
3—5 А.
Падающие электроны (Е, р)
Рассеянные
электроны (Е,р')
Рис. 1.4. а рассеяние электронов на кристалле; б — сильное рассеяние
наблюдается только тогда, когда разность хода АОВ двух рассеянных лу-
лучей оказывается равной целому числу электронных длин волн Хе. Так как
АОВ = 2 й 5ш в, это интерференционное условие приводит непосредствен-
непосредственно к условию Брэгга A-22).
Если вместо электронов использовать нейтроны, то для них
справедлива формула
"" A.24)
-У^(эВ)
из которой следует, что только очень «медленные» нейтроны с энер-
энергией, скажем, порядка 1 '40 эВ могут использоваться в дифракцион-
дифракционных экспериментах на кристаллах. Действительно, именно мед-
медленные нейтроны широко применяются в настоящее время при
исследованиях структуры кристаллов [5 I.
х) 1 эВ = 1.602-10~-10 Дж — это энергия, до которой ускоряется перво-
первоначально покоившийся электрон, пройдя разность потенциалов, равную 1 В.
19
Глава 1
§ 1.6. Атом водорода и теория Бора
В качестве последнего примера безуспешных попыток класси-
классической физики дать полную теорию физических явлений рассмот-
рассмотрим атом водорода. Согласно классической модели Резерфорда
[6], атом водорода состоит из одного электрона, вращающегося
вокруг положительно заряженного тяжелого малого атомного
ядра—протона. Эта классическая модель не смогла объяснить два
основных экспериментальных факта: а) стабильность атома водо-
водорода, б) структуру излучаемого им электромагнитного спектра.
Остановимся на указанных недостатках классической модели Ре-
Резерфорда подробнее.
Электрон, движущийся по искривленной орбите, обладает уско-
ускорением, а следовательно, должен непрерывно излучать электромаг-
электромагнитные волны. Поскольку при этом он излучает и энергию, радиус
его орбиты должен все время уменьшаться до тех пор, пока элек-
электрон не упадет на ядро. Простой расчет, основанный на законах
классической физики (см. задачу 2 в конце настоящей главы), по-
показывает, что характерное время жизни электрона, движущегося
на водоро до подобной орбите, равно 100 с. Экспериментально,
однако, хорошо известно, что атом водорода, находящийся в ос-
основном состоянии, удивительно стабилен, т. е. его время жизни
представляется бесконечным.
Теперь рассмотрим спектр электромагнитного излучения атома
водорода. Частота излучения в классической электромагнитной
теории должна совпадать с частотой орбитального движения элек-
электрона. По мере того как электронная орбита сжимается, частота
обращения непрерывно возрастает. Таким образом, спектр излу-
излучения, испущенного возбужденным атомом водорода, казалось бы,
должен быть непрерывным, т. е. в нем должны быть представлены
все частоты. Эксперименты, однако, показывают, что спектр излу-
излучения атома водорода, наоборот, состоит из семейств дискретных
линий. Частоты одной такой группы линий, называемой серией
Бальмера, эмпирически можно описать формулой
/но(эВ)- 13,64(-1—-1-), A.25)
в которой п = 3, 4, 5.
Бор [7| в 1913 г. предложил теорию, объясняющую оба этих
экспериментальных факта: стабильность атома водорода и диск-
дискретный характер его спектра излучения. Он постулировал, что
возможное орбитальное движение электрона в атоме водорода
должно удовлетворять дополнительному условию: момент коли-
количества движения электрона должен равняться целому кратному
величины Н, т. е.
1^пП (л=1. 2, 3, ... ). A.26)
20
Почему появилась квантовая механика
Выведем важные следствия из условия Бора A.26). Рассмотрим
движение электрона на таких круговых орбитах, для которых
момент количества движения квантуется согласно условию Бора
A.26). Пусть радиус электронной орбиты равен а, и пусть ядро
имеет электрический заряд е = \е\.
Приравнивая кулоновскую силу притяжения электрона к ядру
центростремительной силе, получаем
4ле0о2
/<в = — I
\ а I
или —— — т<А2а,
где введено удобное обозначение
4яе0
Условие Бора A.26) в случае круговых орбит принимает вид
таРа^пП, A.28)
так как / = та>а2.
Комбинируя A.27) с A.28), получаем для радиусов квантован-
квантованных боровских орбит
а„ -^—п2 апп2 (п 1,2,. . ), A.29)
где а„ = радиус а, соответствующий целому числу п: величина
ао= Н2/е2м -—- 0,53-100 м, имеющая размерность длины, называется
боровским радиусом.
Числа ап дают значения радиусов допустимых электронных ор-
орбит. Угловую частоту обращения электрона на орбите п можно
найти из A.28) и A.29):
4
ПН т'М /, ОАч
со„= -=—— . A.30)
тап 11 п
Полная энергия электрона, движущегося на орбите п, равна по
определению сумме кинетической и потенциальной (кулоновской)
энергий:
Еп -■- — (а>па,гУ A-31)
2 ап
Из этой формулы с учетом A.29) и A.30) получаем окончательную
формулу для допустимых значений энергии атома водорода
те4 Е
Еп-'- тт~ =-■—-—^—» A.32)
где Е„ = те% 2Й2 = 13,64 эВ.
21
Глава 1
Состояние с наименьшей энергией соответствует значению
л = 1. Для него, согласно A.29), орбита имеет самый малый ра-
радиус. Самая большая энергия Е =-= 0 получится, если положить
в A.32) п = оо, т. е. считать, что электрон и протон удалены друг
от друга на бесконечно большое расстояние. Энергия ионизации
атома водорода, которая по определению представляет собой наи-
наименьшую энергию, необходимую для удаления электрона с орбиты
Е3=~Ев/9-
-п-3
Рис. 1.5. Энергетические уровни атома водорода в теории Бора.
п ^ 1 на бесконечность, равна Еа —- 13,64 эВ. Диаграмма энерге-
энергетических уровней Еп для различных п представлена на рис. 1.5.
С появлением теории Бора атомная физика начала бурно раз-
развиваться. Из предсказываемой теорией дискретности энергетиче-
энергетических уровней атомов непосредственно вытекала дискретность на-
наблюдаемых спектров электромагнитного излучения, испускаемого
возбужденными атомами. Действительно, согласно Бору, излуче-
излучение испускается всякий раз, как только атом переходит с некото-
некоторого возбужденного состояния на нижележащее по энергии состоя-
состояние. Серия Бальмера, например, возникает в результате переходов
атомов водорода с возбужденных состояний п — 3, 4, 5, ... в со-
состояние п — 2. Требуя, чтобы энергия испущенного фотона была
равна энергии, теряемой атомом, из A.32) получаем формулу для
частоты излучения, испускаемого при переходе из состояний п > 3
в состояние п
— о.
2:
йсо (эВ) = 13,64 Л_!___!_\
\ 2* я* /
Это выражение в точности совпадает с эмпирической формулой
A.25).
Теория Бора позволила также понять причину наблюдаемой
стабильности атома водорода в основном состоянии. Поскольку
для состояний с наименьшей допустимой энергией квантовое число
22
Почему появилась квантовая механика
п = 1, атом, находящийся в этом состоянии, не может терять энер-
энергию путем переходов в нижележащие состояния, т. е. должен быть
стабилен.
Свою теорию Бор развил на основе произвольно принятого им
постулата A.26). Его условие A.26) квантования момента количе-
количества движения электрона в атоме не следовало из какой-либо бо-
более общей теории пли из каких-то более фундаментальных сообра-
соображений. Оно было изобретено Бором исключительно для атома во-
водорода. В последующем остро ощущавшаяся физиками неудовлетво-
неудовлетворенность постулативным характером теории Бора расчистила до-
дорогу для появления новой теории — квантовой механики.
В 1924 г. де Бройль предложил свое знаменитое соотношение
р =-- к/К [см. A.19)], связывающее длину волны К и импульс р
частицы. Используя это соотношение, де Бройль показал, что
боровское условие квантования момента количества движения
/ = пН [см. A.26)] эквивалентно требованию, чтобы длина Ь„
боровской орбиты удовлетворяла условию
(п = 1, 2, 3 . . .), т. е. вмещала в себя целое число электронных
длин волн.
Такого рода условие для отбора дискретных длин волн часто
появляется в классической математической физике при рассмотре-
рассмотрении сферических и цилиндрических задач или в теории распростра-
распространения и дифракции волн. Оно непосредственно вытекает из требо-
требования однозначности физически допустимых решений волновых
уравнений. Решение должно принимать свое первоначальное зна-
значение, когда координатный азимутальный угол изменяется на це-
целое кратное 2л.
С появлением теории Бора окончательно стало ясно, что такие,
казалось бы, различные физические явления, как дифракция элек-
электронов на кристаллах, комптоновское рассеяние, спектр излуче-
излучения атома водорода, объясняются волновой природой электрона.
Задачи
1. Покажите, что для атома водорода выполняется соотношение:
Кинетическая энергия — — Полная энергия =
— — 1/2 (Потенциальная энергия).
2. Оцените время жизни классической частицы с массой т и -зарядом — I1,
вращающейся по круговой орбите радиусом г вокруг массивного ядра
с зарядом е.
Указание. Вычислите время жизни по формуле
Полная энергия
Излученная мощность
и найдите в каком-нибудь учебнике формулу для мощности излучения
ускоренно движущегося электрического заряда.
23
Глава 1
3. Покажите, что условие квантования Бора A.26) момента количества
движения электрона эквивалентно требованию, чтобы на длине электрон-
электронной орбиты укладывалось целое число длин волн.
4. Покажите, что в пределе п 1 частота
V -=. Еп+г " Еп
к
перехода я -Ь 1 -»- я стремится к классической частоте вращения элек-
электрона по круговой орбите.
5. По какому-либо учебнику разберите вывод формулы A.9).
6. Работа выхода для алюминия равна 4,25 эВ. Вычислите максимальную
кинетическую энергию электронов, испускаемых поверхностью алюми-
алюминиевого образца, который облучается ультрафиолетом с длиной волны
X = 2100 А.
7. Чему равна максимальная энергия, теряемая фотоном с начальной энер-
энергией Лм —= 10 кэВ, который сталкивается с покоящимся электроном?
Чему равна скорость электрона после столкновения?
8. Самые малые детали предмета, которые еще можно .рассмотреть с помощью
микроскопа, имеют размер порядка длины волны излучения, используе-
используемого и микроскопе. Каков предел теоретической разрешающей способ-
способности электронного микроскопа, работающего на электронах, ускоряе-
ускоряемых до энергии 150 кэВ? В каком отношении она находится с разрешаю-
разрешающей способностью оптического микроскопа, работающего на видимом
свете D000 А<^<7000 А)?
9. С помощью рис. 1.4 покажите, что условие Брэгга можно записать в
виде формулы
р' —р-Б/-^-, A.33)
а
где ^ единичный вектор, нормальный к параллельным атомным плоско-
плоскостям, от которых происходит отражение волны. Можно поэтому считать,
что неличина 2л A является квазиимпульсом, а формула A.33) представ-
представляет собгй гакон сохранения импульса электронов в кристалле.
ГЛАВА 2
ОПЕРАТОРЫ
Математические операторы широко используются в квантовой
механике, поэтому необходимо знать их основные свойства. В на-
настоящей главе мы кратко напомним читателю основные определения
и теоремы из математической теории операторов.
§ 2.1. Математические свойства операторов
Определения. Оператором, вообще говоря, называют опреде-
определенный набор правил, с помощью которых из любой функции можно
построить другую вполне определенную функцию. Например, рас-
рассмотрим математический оператор
Л = 1+ —•
дх
Он преобразует произвольную функцию / (х) в новую функцию:
А[(х)^[(х) + ^, B.1)
которую мы обозначаем А[ (х), выписывая символ оператора пе-
перед символом функции.
Операторы будем обозначать большими буквами с «крышеч-
«крышечками» над ними. Операторы, с которыми мы будем встречаться
в настоящей книге, содержат величины г, \, т. е. пространствен-
пространственные координаты и производные по ним; иными словами, мы будем
рассматривать ниже только операторы, действующие в простран-
пространстве функций, зависящих от г.
В качестве второго примера рассмотрим следующий математи-
математический оператор:
А =-. — х, B.2)
дх к '
в результате действия которого на произвольную функцию / (х)
получаем
^ У( ^)(х). B.3)
^[хЦх)] +Г{х)(. ^
дх дх \ дх
Результат последнего преобразования можно выразить оператор-
операторным равенством
-?-х=-1+х-2-. B.4)
дх дх
25
Глава 2
Любое операторное равенство, примером которого служит ра-
равенство B.4), означает, что при действии на произвольную функцию
/ (х) оператора, стоящего в левой части такого равенства, полу-
получается в точности та же функция, как и при действии на нее опера-
оператора, стоящего в правой части операторного равенства. В настоя-
настоящей книге нам будут нужны только так называемые линейные опе-
операторы, т. е. такие операторы, которые удовлетворяют для любых
функций / (а) и д (а) и для любого числа с соотношениям
Суммой операторов А -|- В называют оператор, действие ко-
которого на произвольную функцию / (а) равно сумме действий на
нее отдельных операторов, т. е.
§ 2.2. Собственные функции
и собственные числа операторов
С каждым линейным оператором А (х, д;дх) 1) можно связать
набор чисел а„ и набор функций и„ (х), которые удовлетворяют
уравнению
А
(х, —\ип(х) апип(х). B.5а)
Числа ап называются собственными числами оператора А, а функ-
функции ип (а) — его собственными функциями. Набор чисел а„ может
быть дискретным или непрерывным.
Рассмотрим, например, оператор рх = — Игд!дх. Чтобы найти
его собственные числа и собственные функции, необходимо решить
уравнение
— Щ — и„ (а) ^ рир (а). B.56)
дх
Решением уравнения B.56) является функция
ир{х) = е1""\ B.6)
причем число р может принимать любые значения, включая ком-
комплексные числа. Таким образом, собственные числа р могут быть
любыми числами.
') Отметим некоторую нечеткость используемого автором обозначения.
Величины х и д/дх нельзя рассматривать как аргументы оператора. Своим обо-
обозначением автор хочет подчеркнуть, что оператор А получается в резуль-
результате комбинирования символов х и д/дх.— Прим. перев.
26
Операторы
Однако, если дополнительно к уравнению B.56)Потребовать
выполнение граничного условия, заключающегося в том, что функ-
функция ир (х) пространственно периодична с периодом Ь, то получим
следующее ограничение на выбор чисел р:
~ = п~ (л = 0, ±1, ±2,. . .)• B.7а)
Таким образом, для собственных функций получаем формулу
ип(х)-<?пС1лЦх; B.76)
теперь собственные числа принимают только дискретные дейст-
действительные значения.
Это важное замечание. Как видим, собственные числа и собст-
собственные функции определяются не только математической природой
оператора, но и граничными условиями, налагаемыми на функции.
Очевидным образом обобщим уравнение B.5а) на все трехмер-
трехмерное пространство, сделав замену
^^!) B.8)
дх \ дх ду дг
где 1, }, к — единичные векторы в направлении осей х, у, г соот-
соответственно. Уравнение для отыскания собственных чисел и собст-
собственных функций, аналогичное B.56), имеет вид
— 1П\и1тп (г) - аьппЫшп (г), B.9)
или
— 1ЬA-~+1~-+к~) п1тп (Г) аЦтпЩтп (О, B.10)
\ дх ду дг I
где &1тп — собственные числа, являющиеся в рассматриваемом
случае векторами.
Предположим, что собственные функции щтп можно искать
в виде произведений
Щтп (х, у, г) = /г (х) §„ (у) рп (г). B11)
Подставляя B.11) в B.10), приходим к трем самостоятельным урав-
уравнениям
^шпрп, B.12)
дх ду дг
в которых щ, ат и ап — некоторые постоянные числа. Таким об-
образом, возможное решение уравнений B.12) имеет вид
1+апг), B.13)
где С — произвольная постоянная.
27
Глава 2
Подставляя B.13) в B.10), приходим к уравнению
— Иг\Щтп (х, у, г) =-. П (ш, + \ат + 1ш„) щтп, B.14)
из которого следует, что собственные числа уравнения B.9) даются
выражениями
а^п^П^щ + Щт + кпп). B.15)
Если теперь потребовать, чтобы собственные функции щтп удов-
удовлетворяли периодическим граничным условиям по х, у и г с перио-
периодами А, В и С соответственно, то получим аналогичную B.7а)
формулу
/2л . . /л2я . . «2л \ /о 1с\
+]+к^ B.16)
в которой /, т, п — произвольные целые числа, независимо про-
пробегающие значения 0, ±1, ± 2, .... Формула B.16) показыва-
показывает, что собственными числами являются векторы, имеющие дей-
действительные дискретные компоненты.
§ 2.3, Эрмитовы операторы
Операторы, соответствующие физическим величинам в кван-
квантовой механике (в основном только они и рассматриваются в этой
книге), обладают следующим свойством:
У*(Аё)Л3г^[А[Уёй% B.17)
где / (г) и §■ (г) — две произвольные функции г), 2).
Оператор, обладающий свойством B.17), называется эрмито-
эрмитовым.
Легко показать, что, например, оператор — 1д/дх является эр-
эрмитовым (см. задачу 1 в конце настоящей главы), т. е. для любых
функций / и§, таких, что /&->- 0 при х -*- оо, выполняется соот-
соотношение
') Предполагается, что функции /(г) и § (г) при | г | —>- оо стремятся к
нулю так же быстро, как и волновые функции, описывающие физические
состояния квантовой системы.
2) Когда здесь и ниже в тексте в интеграле не указаны пределы интег-
интегрирования, подразумевается, что он берется по полной области задания
функций.
28
Операторы
Эрмитово сопряженные операторы. Для любого данного линей-
линейного оператора А всегда существует другой оператор В, называе-
называемый эрмитово сопряженным оператором оператору А:
\ /* (г)Ад (г) йЧ = ^ Ш С")]* 8 (г) Л, B.19)
где / и §■ — две произвольные функции. Для эрмитово сопряжен-
сопряженного оператора используется обозначение
которое словами читается «А с крестом».
Таким образом, формулу B.19) можно записать в виде
(' /* (г)Ад (г) Л - 5 [Л+ / (г)]* д (г) Л. B.20)
Сравнивая B.20) с B.17), видим, что оператор А эрмитов в том
случае, когда эрмитово сопряженный ему оператор совпадает с ним
самим. Иными словами, любой эрмитов оператор А удовлетворяет
условию
Л+ А. B.21)
§ 2.4. Ортогональность собственных функций
эрмитова оператора и действительность
его собственных чисел
Теорема. Любые две собственные функции и„ и и,„ любого эр-
эрмитова оператора А удовлетворяют условию
,и;(г)«т(г)Л = 0 (тфп), B.22)
если только не равны друг другу соответствующие им собственные
числа ап и ат. Собственные числа ап любого эрмитова оператора А
действительны.
Когда две функции и„ и ит удовлетворяют условию B.22), их
называют ортогональными друг другу.
Доказательство. Поскольку ип (г) и ит (г) являются собствен-
собственными функциями оператора А, они удовлетворяют соотношениям
Лит атит,
Аип а„ип,
а следовательно,
5 итАипйлг ^ а„ \ и*типс13г,
B:23)
5 и*пАи„43г = ат \ ипитйАг.
29
Глава 2
Так как оператор А эрмитов, можно воспользоваться его свой-
свойством B.17) для преобразования левой части второго соотношения
B.23) и написать
5 (Аип )"итйАг = ат \ ипитс13г.
Взяв комплексное сопряжение от обеих частей последнего равен-
равенства, получаем
5 ит Аипй3г ^ ат \ итипй3г. B.24)
Вычитая теперь B.24) из первого соотношения B.23), приходим
к формуле
{ап^а'т)^итипй3г^. Г2.25)
Рассматривая формулу B.25) при п = т, находим
(ап—а'п)$\и„?(?г -..-0.
Входящий в эту формулу интеграл отличен от нуля, следовательно,
ап = ап. Другими словами, собственные числа любого эрмитова
оператора являются действительными числами.
Из формулы B.25) при п ф т и при условии ап Ф ат (т. е.
при условии ап Ф а*т), заключаем, что интеграл в левой части
формулы B.25) должен равняться нулю. Таким образом, функции
ип и ит ортогональны, т. е. удовлетворяют условию B.22).
Когда имеются две (или больше) собственные функции, соот-
соответствующие одному и тому же собственному значению (т. е. ат —
= ап), то для таких функций мы не можем доказать ортогональ-
ортогональность вышеописанным способом. Оказывается, однако, что в та-
таком случае всегда можно выбрать линейные комбинации функций
и„, которые будут ортогональны друг другу. Это утверждение мы
приводим здесь без доказательства.
§ 2.5. Нормировка собственных функций
Поскольку уравнения вида B.5а) для отыскания собственных
функций и собственных чисел линейны (так как они составлены
для линейных операторов), собственные функции из этих уравне-
уравнений можно найти только с точностью до произвольных постоянных
множителей. Эти множители определяют, исходя из дополнитель-
дополнительного условия
$ипи^г=1, B.26)
которое называется условием нормировки. Соответствующие мно-
множители будем называть нормировочными константами или мно-
множителями.
30
Операторы
Условия ортогональности B.22) и нормировки B.26) можно
записать в виде одного условия, так называемого условия ортонор-
мировки:
^и"питс13г ~дпт, B.27)
где Ьпт — дельта-символ Кронекера, равный 1 при т = п и О
при п Ф т.
§ 2.6. Полнота набора собственных функций
Важное свойство бесконечного набора всех собственных функ-
функций ип (г) произвольного эрмитова оператора А (удовлетворяющих
уравнению Аип ~ апип) состоит в том, что по ним можно разло-
разложить произвольную функцию я]; (г) рассматриваемого функциональ-
функционального пространства, т. е. представить ее в виде
!>(г) = ЕМ«(г). B-28)
п
Разумеется, существуют определенные ограничения, налагае-
налагаемые на функции ф (г), и, в частности, их поведение на бесконеч-
бесконечности. Однако мы не будем здесь на них подробно останавливаться,
предположив, что все функции я|) (г), которые рассматриваются
в квантовой механике, «хорошие» т. е. подчиняются указанным
ограничениям.
Коэффициенты разложения Ь-ь в B.28) (вообще говоря, ком-
комплексные числа) можно найти, умножая B.28) на функции и* (г)
и интегрируя. Таким образом, получаем соотношение
Г Щ (г) я]; (г) й\ = Е Ь„ \ ш (г) ип (г) /г.
п
Используя условия ортонормировки B.27), отсюда непосредст-
непосредственно выводим формулу для коэффициентов разложения в B.28):
6/ = .ГыГ(г)Ч>(г)а3г. B.29)
Можно представить себе, что в некотором абстрактном смысле
коэффициенты 6, являются «проекциями» функции я]; (г) на функ-
функции и.{ (г). Таким образом, набор всех функций ип (г) можно мы-
мыслить как набор «единичных базисных векторов» в некотором бес-
бесконечномерном пространстве. Саму функцию я]; (г) можно считать
некоторым «вектором» в этом пространстве, а формулу B.28) рас-
рассматривать как формулу разложения «вектора» по «базисным еди-
единичным векторам» ип (г).
Формально разложение B.28) эквивалентно разложению
трехмерного вектора Т по единичным базисным векторам е; неко-
некоторой декартовой системы координат в трехмерном пространстве.
31
Глава 2
Проекция вектора Т на направление единичного вектора е; равна
скалярному произведению: 7\- = (Т-е;).
Следуя указанной аналогии, можно считать, что интеграл B.29)
есть «скалярное произведение» «векторов» «,- (г) и я|) (г). Условие
B.27) тогда выступает как аналог условия ортонормировки
(е*.е/) = 6,/ B.31)
единичных базисных векторов декартовой системы координат.
Пример. Разложение по собственным функциям оператора. Со-
Согласно B.28), произвольную функцию я|) (г) можно разложить по
собственным функциям любого эрмитова оператора А. Возьмем,
например, оператор — 1д/дх, собственные функции которого, рас-
рассматриваемые на ограниченном интервале — Ы2<^х<^Ь12, даются
формулой B.76):
\3пЬ)х . B.32)
Здесь мы ввели множители 1/1/ Ь, чтобы удовлетворить условию
нормировки B.26).
Непосредственно легко убедиться, что функции ип ортого-
ортогональны друг другу в смысле условия B.22), в котором интегриро-
интегрирование должно производиться от — Ы2 до Ы2. Функции ип (х)
можно использовать для разложения произвольной функции гр (.V),
заданной на интервале — Ы2<^х<^Ы2.
Таким образом, приходим к формулам
B.33)
\
у1 -1-2
которые представляют собой не что иное, как формулы разложе-
разложения функции я]; (х) в ряд Фурье, или формулы фурье-преобразова-
ния.
§ 2.7. Дираковские обозначения
Дирак предложил очень удобные обозначения для интегралов
от волновых функций, которые постоянно встречаются в кванто-
квантовой механике. Эти обозначения очень упрощают работу с указан-
указанными интегралами и позволяют без труда формально проводить
многие важные доказательства.
Рассмотрим, например, интеграл
32
Операторы
в котором / и ^ — две функции, описывающие квантовые состоя-
состояния. Используя дираковские обозначения, представим этот интег-
интеграл угловыми скобками с вертикальной чертой между* значками
функций:
B-34)
В соответствии с английским названием скобки (бракет) Дирак
предложил называть индивидуальные функции / и § в B.34) «бра-
вектором» и «кет-вектором» и обозначать следующим образом:
/*-></1,
Условимся обозначать интеграл B.34) бра-^и кет-векторами, на-
написанными друг за другом.
Результат действия оператора А на функцию ^ в дираковских
обозначениях записывают так:
а потому имеем простую запись
Условие ортонормировки B.27) в дираковских обозначениях
записывается в виде
(ип\ит) = (п\т) = ЬПт, B.35)
а «проекция» B.29) функции я|) (г) на функцию «,- (г) — в виде
Ь^-AцЩ. B.36)
Разложение B.28) произвольной функции | я];), описывающей
квантовое состояние, теперь представляется следующим образом:
«) = Е \п){пЩ. B.37а)
Формальная интерпретация по Дираку формулы B.37а) состоит
в следующем. Действуя на произвольную функцию состояния
|я])) оператором ^ |«)(м|, получаем снова функцию |я])). Другими
п
словами, следует считать, что этот оператор-единичный:
Е\п)(п\ = Т, B-376)
где / — обозначение единичного оператора.1) Напомним, что на-
набор функций \п) — это полный набор ортонормированных функ-
функций. Формулой B.376) мы будем часто пользоваться.
*) Единичным оператором называют оператор, оставляющий неизмен-
неизменной любую функцию, на которую он действует, т. е. // = / .где ^ — произ-
произвольная функция.
2 Заказ № 683 33
Глава 2
Чтобы немного попрактиковаться в использовании дираков-
ских обозначений, перепишем в них важные формулы B.19) и B.20).
В дираковских обозначениях формула B.19) записывается
в виде
B.38)
а формула B.20) — в виде
<1\А\ё) = (ЛЧ\ё). B.39)
Исключительное удобство дираковских обозначений можно
прочувствовать, если провести с их помощью формальное дока-
доказательство утверждения
«если А=В*, то В = А* », B.40)
из которого непосредственно вытекает, что
(А* )* А. B.41)
Предлагаем читателю проделать это самостоятельно.
Задачи
1. Покажите с помощью интегрирования по частям, что оператор —1д/дх
эрмитов.
2. Докажите, что операторы, соответствующие физическим величинам,
должны быть эрмитовыми.
3. Докажите утверждения B.40) и B.41), используя дираковские обозначе-
обозначения.
4. Найдите трехмерные собственные функции оператора «\7. Выпишите
формулу разложения произвольной функции / (г) по указанным собствен-
собственным функциям.
5. Покажите, что оператор ( (А^ — А) эрмитов для произвольного опера-
оператора А.
ГЛАВА 3
ОСНОВНЫЕ ПОСТУЛАТЫ КВАНТОВОЙ МЕХАНИКИ
В классической физике неявно предполагается, что движение
микрочастицы можно описать точно. Считается, что можно точно
измерить как координаты, так и компоненты вектора скорости
частицы в любой момент времени г, не оказывая при этом на ча-
частицу никакого возмущающего действия.
В квантовой механике, напротив, учитывается, что любой акт
измерения существенно влияет на микросистему и сильно изменяет
ее состояние. Возмущения, вносимые измерительным прибором,
пренебрежимо малы только для «больших» (классических) систем.
Для «малых» (квантовых) систем, таких, как электрон, атомное
ядро, атом, принципиально важно учитывать возмущения, вноси-
вносимые измерительными приборами.
Чтобы пояснить это, рассмотрим какой-нибудь эксперимент,
с помощью которого можно было бы сфотографировать электрон,
вращающийся на орбите в атоме водорода. Мы уже знаем [см.
A.29)], что радиус такой орбиты порядка 1 А. Следовательно, нам
нужен такой метод фотографирования, при котором можно было бы
о
различить детали, имеющие размеры порядка 1 А. И здесь следует
считаться с одним из основных результатов электромагнитной тео-
теории (точнее, теории дифракции), а именно с тем, что предельное
разрешение деталей предмета, рассматриваемого с помощью лю-
любого оптического прибора, приблизительно равно длине волны
используемого электромагнитного излучения. Таким образом, для
фотографирования электрона на водородной орбите частота излу-
излучения должна превышать предельную частоту
.-^-^- = 8.10- Г.
Значит, энергия одного фотона такого излучения должна быть
равна огромной величине
Ну =1,95-10-15 Дж=1,23-104 эВ.
Итак, мы пришли к неутешительному выводу: чтобы измерить
положение электрона, энергия связи которого с протоном в атоме
водорода имеет порядок 10 эВ [см. A.32)], нам необходимо бомбар-
бомбардировать этот электрон «снарядами» (фотонами) с энергией порядка
10* эВ. Измерение положения электрона с помощью такого фотона
2* 35
■ лава л
вызовет, очевидно, огромные возмущения скорости электрона.
Чем с большей точностью требуется узнать положение электрона,
тем меньше должна быть длина волны используемого электромаг-
электромагнитного излучения и тем больше будет неопределенность конечной
скорости подвергающегося измерению электрона.
На первый взгляд положение вещей кажется совершенно без-
безнадежным. Если «малые» системы столь дачикатны, а измеритель-
измерительные средства столь грубы, то вообще возможно ли что-либо узнать
об этих системах? Квантовая механика дает на этот вопрос утвер-
утвердительный ответ, хотя она и признает, что существуют такие во-
вопросы в отношении микросистем, на которые физик принципиально
не может ответить. Тем не менее она утверждает, что все же можно
получить большую полезную и интересную информацию, произ-
производя физические эксперименты даже с очень малыми системами.
Эта информация довольно необычна с точки зрения классической
физики.
Сам математический аппарат квантовой механики, выглядя-
выглядящий на первый взгляд очень странно, прекрасно приспособлен к
описанию физических измерений над очень малыми системами.
Он основывается на небольшом числе физических постулатов (не-
доказываемых положений). Некоторые философские стороны этих
постулатов до сих пор дискутируются в физической литературе
(см., например, [8])г.
В настоящей книге мы примем следующую точку зрения. Оп-
Оправданием для использования квантовой механики служит вовсе
не то, что мы догматически верим в ее какую-то особую внутреннюю
непогрешимость, а лишь то, что она проста, непротиворечива и ус-
успешно объясняет эксперименты. По-видимому, ею следует поль-
пользоваться, пока не будет создана более успешная физическая тео-
теория.
§ 3.1. Основные постулаты квантовой механики
Постулат 1. Каждой физической величине (импульсу, коорди-
координате, энергии, моменту количества движения и т. д.) соответствует
свой эрмитов оператор. При единичном акте измерения этой физи-
физической величины мы получаем одно из чисел из набора ап (дискрет-
(дискретного или непрерывного). Это — набор собственных чисел эрмитова
оператора, соответствующего данной физической величине.
Таким образом, чтобы описать возможные результаты изме-
измерений данной физической величины, необходимо решить математи-
математическую задачу на отыскание собственных чисел и собственных
функций для оператора физической величины [типа задачи B.5а) ].
При этом мы находим как возможные экспериментальные значе-
значения ап рассматриваемой физической величины, так и соответст-
соответствующие им собственные функции и„ (г).
36
основные постулаты квантовой механики
Пусть оператор А соответствует физической величине А, а
оператор В — физической величине В. Процедуре последователь-
последовательного измерения сначала величины А, а потом величины В соответст-
соответствует оператор В А. Процедуре измерения этих величин в обратном
порядке соответствует оператор АВ. Поскольку измерения сильно
возмущают систему, две указанные процедуры могут дать неодина-
неодинаковые результаты.
Согласно сформулированному выше постулату 1, процедуры
измерения величин А я В действительно влияют друг на друга
(результат измерения величин А и В зависит от порядка, в котором
проводятся эти измерения над системой) в том случае, когда вы-
выполняется условие
АВ — ВАфО. C.1)
Величину А В—В А в квантовой механике называют коммутатором
операторов А и В и обозначают квадратными скобками
[А, В]=АВ—ВА. (аЗ)
В гл. 1 мы уже видели, что для устранения недостатков класси-
классической физики в нее была произвольно введена величина /г. Поэ-
Поэтому неудивительно, как мы вскоре убедимся, что взаимное влияние
друг на друга физических величин А и В характеризуется комму-
коммутатором [А, В], равным по порядку величины Й.,
Постулат 2. Физическая система описывается волновой функ-
функцией я]; (г) *), которая содержит всю мыслимую информацию о со-
состоянии системы в некоторый момент времени. Будем считать, что
волновая функция нормирована следующим образом:
)>*3(гI|:(г)аяг=1. C.3)
Если я]; (г) = ип (г), где ип (г)—одна из собственных фун кций опера-
тора]Л (удовлетворяющая уравнению Аип = апип), то измерение
для нее величины А для состояния я|) (г) даст значение ап.
Если я]; (г) не совпадает с какой-либо собственной функцией
и„ (г) оператора А, то вероятность того, что при измерении вели-
величины А будет получено значение а..,, равна
т. е. она равна квадрату модуля «проекции» функцин я]; (г) на функ-
функцию ип (г). [См. текст после формулы B.29) ].
') В настоящей гл. 3 мы везде опускаем временной аргумент волновой
функцин и обозначаем ее простоя]' (г). Следует, однако, помнить, что все наши
рассуждения относятся к некоторому выделенному моменту времени ( = 10,
Функция ф (г), входящая в C.4), обозначает на самом деле функцию г[' (г, @),
причем здесь /0 — просто параметр, характеризующий функцию я)) (г), За-
Зависимость волновых функций гр от времени I мы еще будем подробно обсуж-
обсуждать в гл. 10.
37
Глава 3
В справедливости формулы C.4) можно убедиться, рассматри-
рассматривая разложение функции я]) (г) по собственным функциям и„ (г)
оператора А:
Умножим обе части разложения C.5) на м* (г) и проинтегри-
проинтегрируем по всему пространству. Используя условие ортонормировки.
B.27), получаем
&Л =- Г ы* (г) 1]) (г) ^г; C.6>
поэтому формулу C.4) можно записать в виде
Р*{ап) = \Ьп?, C.7>
так что вероятность экспериментального наблюдения конкретного
значения ап измеряемой величины А равна \Ьп\2, т. е. равна квад-
квадрату амплитуды вероятности обнаружения нашей системы в со-
состоянии и„.
Из C.4) непосредственно следует, что если я|) (г) = ип (г), то
вероятность Р^ (а{) обнаружения значения щ при измерении ве-
величины А для системы, находящейся в состоянии я|) (г), равна еди-
единице при I = п и нулю при I Ф п. Другими словами, когда волно-
волновая функция я]; (г) равна одной из собственных функций опера-
оператора Л, например функции ип (г), тогда при измерении величины А
с достоверностью получаем значение ап.
§ 3.2. Среднее значение физической величины
Рассмотрим очень большое число идентичных систем, или ан-
ансамбль систем, каждая из которых описывается одной и той же
волновой функцией я]з (г). Согласно постулату 2 (см. §3.1), вероят-
вероятность того, что при единичном акте измерения величины А полу-
получится ее значение ап, равна
Я* (ап) = I Ьп |2 = | Г ип (г) г|; (г) сРг |2. C.8).
Среднее значение величины А, которое получается в резуль-
результате серии измерений, производимых над индивидуальными систе-
системами ансамбля, равно сумме произведений чисел ап на вероятно-
вероятности их появления Р-ф (ап), т. е. дается формулой
п
ф(ап) = 3:ап\Ьпр, C.9)
п
которую также можно записать в виде
(А) = Г г|;* (г)Ау (г) йЧ. C.10>
38
Основные постулаты квантовой механики
Доказательство формулы (ЗЛО). Воспользуемся разложением
C.5) и представим формулу C.10) в виде
(А) = Г X X ЬпЪцСпАиЛ. C.11)
■ П 1
Учитывая, что Л «г = щщ, используя условие ортонормировки
B.27) и переставляя порядок суммирований и интегрирования,
отсюда получаем формулу
(А) -1 X Ь;&,а*6„< = I а„ | Ь„ |2, C.12)
П I П
которая в точности совпадает с формулой C.9).
Будем называть среднее (А) средним по ансамблю значением
величины А, или (квантовомеханическим) математическим ожи-
ожиданием величины А.
§ 3.3, Конкретный вид квантовомеханических
операторов
В § 3.1 мы сформулировали основные постулаты квантовой ме-
механики, согласно которым физическим величинам сопоставляются
операторы, а возможным результатам физических измерений —•
собственные числа этих операторов.
Мы еще не сформулировали, однако, никаких правил, которым
надо следовать, чтобы сопоставить конкретные операторы конкрет-
конкретным физическим величинам.
Разумеется, сопоставлять операторы физическим величинам
нужно так, чтобы в пределе больших (классических) систем соот-
соотношения между квантовомеханическими операторами превращались
в соотношения между соответствующими классическими величинами.
Чтобы удовлетворить этому требованию, предположим, что в кван-
квантовой механике математические формулы, определяющие те или
иные операторы, имеют в точности такой же вид, как в классиче-
классической физике.
В качестве примера рассмотрим оператор момента количества
д вижения частицы. В классической физике имеем соотношение
1 = [г-р] C.13)
связывающее момент количества движения 1 с импульсом р и ко-
координатой г частицы. В квантовой механике поэтому следует счи-
считать, что оператор момента количества движения дается формулой
Мг-р], C.14)
т. е. формулами
1х = УРг—гру и т. д.
39
Глава 3
По-видимому, самый простой способ сопоставить оператор х
координате х частицы — это считать, что он просто сводится к ум-
умножению на х функции, на которую он действует, т. е.
жф(г). C.15)
Аналогично можно определить операторы у и г для координат у
и 2 частицы. Правильность такого определения операторов х, у
и 2 подтверждается в § 3.4.
Рассмотрим теперь другой пример и найдем оператор энергии
одномерного гармонического осциллятора с константой жесткости
пружины К и массой М. Переписывая для операторов соответст-
соответствующую формулу классической физики, получаем
к = -^-^ — Кх, C.16)
где х обозначает оператор отклонения колеблющейся точечной
частицы массой М от ее положения равновесия.
Нам остается сопоставить оператор рх импульсу рх. В § 1,5
отмечалось, что наблюдаемые волновые свойства частицы можно
описать, сопоставляя частице с импульсом рх волну
г|ф-, *) = Се"^°-/>*х>Л C.17)
[здесь мы снова приводим формулу A.20), предполагая, что ча-
частица движется вдоль координатной осп х]. Функция я|' (х, I)
должна быть функцией состояния с точно определенным значением
импульса рх, поэтому, согласно постулату 1 (см. § 3.1), она должна
быть собственной функцией оператора рх, соответствующей собст-
собственному числу рх.
Отбрасывая зависимость волновых функций от времени (она
сейчас для нас несущественна), видим, что уравнение на отыскание
собственных функций и собственных чисел оператора рх импульса
рх должно иметь вид
р^^ = р^!\ C.18)
Отсюда непосредственно следует, что оператор рх должен иметь
следующую форму:
р^_/й 3 C.19)
дх
Соответственно оператор импульса частицы в трехмерном про-
пространстве имеет следующий вид:
р=—/Йу. C-20)
40
Основные поступапы квантовой механики
§ 3.4. Перестановочное соотношение
для операторов координаты и импульса.
Коммутирующие операторы и их собственные функции
Поскольку координата и импульс являются самыми главными
физическими величинами, характеризующими частицу в класси-
классической механике, важно знать, коммутируют ли между собой их
квантовомеханические операторы. Используя формулы C.15) и
C,20), непосредственно получаем
^?) = Ш; C.21)
дх дх
поскольку функция / (х) произвольная, отсюда приходим к пере-
перестановочному соотношению
[х, р*] Ап,
или к более общему соотношению
[п, р/] = ;й6,-Л C.22)
где гх = .г и т. д.
Как видим, операторы координаты и импульса частицы не ком-
коммутируют. Измерения координаты и импульса частицы оказы-
оказывают сильные взаимные влияния и мешают друг другу. Указан-
Указанные величины нельзя измерить одновременно с произвольно задан-
заданной точностью.
Взаимно коммутирующие операторы. Когда два каких-либо опе-
оператора, например А я В, коммутируют, они обладают одинаковым
набором собственных функций, т. е, собственные функции опера-
оператора А являются собственными функциями оператора В, и наоборот.
Докажем это утверждение. Так как ВА = АВ, то АВиь -
----- ВАиь = АЬиь == ЪАиь, где иь — собственная функция опера-
оператора В, соответствующая собственному числу Ь. Таким образом,
функция Л«й является собственной функцией оператора В с собст-
собственным числом Ъ. Если имеется только одна собственная функция
оператора В, соответствующая собственному числу Ь, то Аи:, —
= сиь, где с—некоторое число. Иными словами, функция иь
является в этом случае также и собственной функцией оператора Д.
Если же теперь имеется не одна, а несколько собственных функций,
соответствующих собственному числу Ь, то из вышеприведенного
рассуждения следует, что функция Аиь является линейной комби-
комбинацией этих собственных функций. Таким образом, можно построить
такую линейную комбинацию указанных вырожденных функций
оператора В, т. е. функций, соответствующих одному и тому же
41
Глава 3
собственному числу, которая будет также и собственной функцией
оператора А.
Доказательство обратного утверждения, состоящего в том, что
если два эрмитовых оператора имеют одинаковый набор собствен-
собственных функций, то они коммутируют — предоставляем провести чи-
читателю в виде упражнения.
Теперь мы сможем лучше понять, почему две физические вели-
величины, соответствующие двум коммутирующим операторам, можно
измерить с произвольно заданной точностью так, чтобы процедура
измерения одной величины не мешала процедуре измерения другой.
Сначала произведем измерение какой-нибудь физической ве-
величины, например В, соответствующей оператору В. Согласно ос-
основным постулатам квантовой механики (см. § 3.1), в результате
измерения мы должны получить одно из собственных чисел, ска-
скажем число Ъ, оператора В. Система после такого измерения ока-
окажется в собственном состоянии щ„ соответствующем собственному
числу Ь. Поскольку операторы А и В обладают одинаковым набо-
набором собственных функций, проводимое непосредственно после из-
измерения величины В измерение другой физической величины А
с достоверностью даст значение с, которое является собственным
числом оператора А, соответствующим собственной функции иь,
т. е. Аиъ — сиь. Если мы после этого еще раз измерим первую фи-
физическую величину В, то получим опять значение Ь. Таким обра-
образом, возможно одновременно измерять с произвольно заданном:
точностью значения физических величин А и В.
Мы можем теперь также лучше понять причину того, почему две
физические величины, соответствующие двум некоммутирующим ме-
между собой операторам, нельзя измерить одновременно с произ-
произвольно заданной точностью. Возьмем, например, два (некоммути-
рующих друг с другом) оператора А и В. После измерений физи-
физической величины, соответствующей оператору А, система перейдет
в какое-то собственное состояние этого оператора А, скажем в со"
стояние фд4) (это собственное состояние, которое соответствует
измеренному собственному числу а). Поскольку операторы А \\ В
не коммутируют друг с другом, указанная собственная функция,
вообще говоря, не будет собственной функцией оператора В. Но
мы можем разложить функцию <р^л> по собственным функциям иь
оператора В:
Следовательно, при измерении физической величины В, произво-
производимом после измерения физической величины А, можно получить
42
Основные постулаты квантовой механики
любое значение из набора собственных чисел Ь, каждое с соответст-
соответствующей вероятностью \сь\-. Другими словами, процедура измере-
измерения величины А вносит неопределенность в процедуру измерения
величины В. Результат измерения величины В теперь не достове-
достоверен — его можно предсказать лишь с некоторой вероятностью.
Когда операторы А и В коммутируют, они обладают одинако-
одинаковым набором собственных функций, и тогда в разложении функции
■фа4' (х) остается только одно слагаемое, соответствующее, скажем,
Ъ = Ь'. В этом случае измерение величины В, производимое после
измерения величины А, даст определенное значение V величины В,
ибо | сь- \' = 1 \\\сь |2 = 0 при Ъ Ф Ъ'.
§ 3.5. Физический смысл волновой функции
Согласно C.12), среднее значение (А) некоторой физической
величины А можно найти, вычисляя интеграл
<Л)-|>*(г)ЛяНг)Л, C.23)
в котором я); обозначает функцию состояния системы.
Используем формулу C.23) для вычисления среднего значения
вектора координаты г. Поскольку оператор г сводится к умноже-
умножению функции на г, имеем формулу
Ф-Л^МриРг. C.24)
Вспоминая определение среднего значения некоторого случай-
случайного вектора 5 (г), характеризуемого данной функцией распреде-
распределения Р (г) [такой, что | Р (г) й3г = 1 ], можем написать формулу
5ср=1Р(гM(г)Л. C.25)
Сравнивая C.25) и C.24), видим, что величина |т]; (г)|2 (Рг есть
вероятность найти частицу внутри бесконечно малого объема й3г
около точки г. В этом состоит физический смысл волновой функции.
§ 3.6. Собственные функции оператора энергии.
Стационарное уравнение Шредингера
В квантовой механике собственные функции и собственные
числа оператора энергии играют особенно важную роль. Это свя-
связано с тем, что часто физические измерения, производимые над си-
системой, сводятся в конечном счете к измерениям энергии (или ча-
частоты электромагнитного излучения), теряемой или приобретаемой
.43
Глава 3
системой при ее переходе из одного состояния в другое. Оператор
энергии — гамильтониан — для одной частицы имеет вид
* гУ(г),
2т
где V (г) — функция потенциальной энергии частицы. Поэтому
собственные функции и собственные числа энергии частицы сле-
следует находить, решая уравнение
)Мг)=Е"*(г)" (а26)
Оператор р равен — 1Н\. Уравнение C.26) называется стацио-
стационарным уравнением Шредингера. Функция иЕ (г) — волновая функ-
функция, описывающая систему, пребывающую в состоянии с энергией Е.
§ 3.7. Соотношение неопределенностей
В § 3.3 мы показали, что импульс и координату частицы нельзя
измерить одновременно с произвольно заданной точностью. При-
Причина этого состоит в том, что операторы рх и х не коммутируют друг
с другом.
Чтобы найти количественную меру взаимных помех, которые
вносят друг в друга процедуры измерения указанных физических
величин, рассмотрим движение частицы в одномерном случае в ог-
ограниченной области размером порядка Ах. Математически можно
выразить это утверждение, считая, что частица описывается вол-
волновой функцией
1]\(л-)-с-^2(Дл»2. C.27)
1Функция C.27) не нормирована. Нормировочный множитель не
существен для дальнейших рассуждений ]. Распределение вероят-
вероятностей значений координаты х частицы, таким образом, пропорцио-
пропорционально функции Р (х) = |я]) (л:)|2=ехр [—л:2/(Ал:J], которая
очень быстро убывает при \х\ > Ах. График указанной функции
представлен на рис. 3.1, а. Вероятность обнаружения при измере-
измерении значения импульса р у нашей частицы, согласно C.4), дается
формулой
Р(р)=\у(р)\2 = \\Ц(х)ир(х)йх\\ ' C.28)
где ир (х) обозначает собственную функцию оператора импульса,
которая в свою очередь дается формулой C.18):
«Р(*Ь е'рх1Н. C.29)
44
Основные постулаты квантовой механики
(Здесь снова мы опускаем несущественный для нас нормировочный
множитель.) Интеграл в C.28) можно вычислить:
Ф (Р) = I
Щ> (х) их = I ет
их =
Рис. 3.1. а — гауссово распределение вероятностей Р (х) значений коорди-
координаты х частицы; б — распределение вероятностей Р (р) значений импульса р
той же самой частицы [см. C.27) и C.31).]
причем последний интеграл в C.30) является просто некоторой
константой, не зависящей от р. Таким образом,
,а»„
График функции распределения вероятностей значений импульса
частицы приведен на рис. 3.1, б. Согласно C.31), область измене-
изменения значений импульса частицы ограничена интервалом
Й/Ах.
C.32)
45
Глава 3
Если величину Ах считать мерой неопределенности положения
частицы, а величину Ар — мерой разброса ее импульса, то можно
утверждать, что
Ар Ах —п. C.33)
Всякая попытка локализовать более точно частицу (т. е. сделать
меньше неопределенность Ах) приводит к возрастанию неопреде-
неопределенности Ар импульса частицы, и наоборот.
Существует известный дуализм при описании частицы в коор-
координатном (х) и импульсном (р) пространствах. Появившаяся у нас
функция (р (р), задаваемая в импульсном пространстве, полностью
аналогична волновой функции я|) (л), задаваемой в координатном
пространстве. Поэтому функцию <р (р) можно рассматривать как
волновую функцию в импульсном пространстве. Согласно C.30),
функция ф (р) определяется формулой
оо
ф(Р>= $У(х)е-""пAх, C.34)
так что функция ф (р/Й) является фурье-образом функции я]) (х).
Так как исходная функция и ее фурье-образ содержат в себе одну
и ту же информацию, можно с равным успехом всю квантовую ме-
механику развивать в импульсном пространстве в точности так же,
как мы ее развиваем сейчас в координатном пространстве.
Имеется еще одно важное соотношение неопределенностей, свя-
связывающее неопределенность значения энергии частицы с длитель-
длительностью временного интервала А^, в течение которого проводится
измерение. Предположим, что мы производим измерение скорости
частицы за время, пока она проходит определенное расстояние Ь.
Длительность по времени такого измерения равна
Аг =
Кроме того,
Аи — Ар/т,
так что
ЛЯ --= А (р2/2т) = (р/т) Ар,
АЕАг~АрЬ=АрАх;
а тогда из C.33) непосредственно следует соотношение
АЕАг ~ Н, C.35)
т. е. искомое соотношение неопределенностей.
Соотношение C.35) выражает следующее. Чем выше желаемая
точность измерения энергии системы, тем больше должен быть
временной интервал, необходимый для проведения этого измере-
измерения.
46
Основные постулаты квантовой механики
Можно с удовлетворением отметить, что мерой неопределенности
в соотношениях C.33) и C.35) служит та же самая постоянная
Планка й, которую он ввел в своей теории излучения абсолютно
черного тела.
§ 3.8. Соотношения неопределенностей
для электромагнитных полей
Хотя соотношения неопределенностей мы вывели только для
электронов, они справедливы также для любых микрочастиц.
В частности, соотношения неопределенностей проявляются, на-
например, для системы фотонов, т. е. для электромагнитного поля.
Рассмотрим, например, антенну, предназначенную для испуска-
испускания несущего информацию электромагнитного пучка СВЧ-диапа-
зона, посылаемого с Земли к спутнику связи, как показано на
рис. 3.2. Конечность угла 6, характеризующего угловую ширину
испускаемого пучка электромагнитных волн, объясняется тем, что
фотоны (которые здесь рассматриваются как частицы) первона-
первоначально находились в ограниченной пространственной области раз-
размером
Дх~ 21?,
равным диаметру «чаши» антенны. Согласно соотношению неопре-
неопределенностей C.32), такая неопределенность Ах приводит к неопре-
неопределенности импульса фотона
Др~ Й/2Д.
Угол 6, характеризующий угловую ширину пучка, таким образом,
равен
е^_^ * =.-—^, (З.зб)
р 2ПBпП:"к) 4д#
где мы использовали формулу A.14), согласно которой р = 2лй/Я,-
Разумеется, это хорошо известный результат. В классической
электромагнитной теории формула C.36) выражает известное свой-
свойство фурье-преобразования, связывающего функцию распределе-
распределения поля в плоскости антенны и функцию углового распределения
излучаемого поля в удаленных от антенны областях пространства.
Свойства фурье-преобразования, разумеется, также лежат и в ос-
основе соотношений неопределенностей в квантовой механике, как
это непосредственно ясно из вышеприведенного их вывода [см.
текст до и после формулы C.34)].
Еще один пример. Рассмотрим следующее из квантовой меха-
механики ограничение на величину скорости, с которой можно пере-
передавать информацию с помощью импульсов электромагнитного поля.
В частности, рассмотрим информацию, которую несет последова-
последовательность импульсов, показанная на рис. 3.3. Среднюю мощность
47
Глава 3
Спутник
связи
Излучаемый
пучок
Рис. 3.2. Микроволновая (или оптическая) антенна диаметром 2^? испускает
пучок волн в^направлении спутника связи. Угловая ширина пучка равна 0.
Время
Рис. 3,3. Последовательность импульсов, несущая информацию, закодиро-
закодированную величинами амплитуд.
сигнала обозначим через р, так что средняя энергия, приходящаяся
на один импульс, равна рА1 (где А1— длительность отдельного
импульса и одновременно длительность интервала между двумя
соседними импульсами). Пусть передаваемая информация закоди-
закодирована величинами амплитуд импульсов так, что значение энергии,
предварительно сообщенной импульсу, представляет собой опреде-
определенное послание. В теории информации [9 ] содержание информа-
информации каждого импульса измеряют в битах, т. е. считают ее равной
логарифму по основанию 2, взятому от числа дискретных порций
энергии (в рассматриваемом примере — энергии импульса), кото-
которые мы можем различить в приемном устройстве. Таким образом,
среднее содержание информации в одном импульсе равно
C.37)
48
Основные постулаты квантовой механики
где АЕ обозначает величину энергетического разрешения, т. е.
наименьшую разность энергий импульсов, которую можно изме-
измерить. Поскольку измерение энергии данного импульса произво-
производится за интервал времени, равный А1, энергетическое разреше-
разрешение АЕ можно определить из соотношения неопределенностей
C.35). Следовательно, АЕ ■—• Н1А1. Подставляя это значение в фор-
формулу C.37), получаем
Средняя скорость передачи информации, по определению, равна
среднему содержанию информации, умноженному на среднее число
\12Аг импульсов в секунду:
Очевидно, скорость С можно увеличить, если уменьшить длитель-
длительность Л* отдельного импульса и интервала между ними. В пределе
А1 можно сделать равным по порядку величины частоте колеба-
колебаний /~ используемых электромагнитных волн. Тогда из C.38) по-
получаем формулу
НЫИ]' <з-з9а>
где В = (АО обозначает ширину полосы. Формула Шенона [9],
полученная в теории информации на основе классических (не кван-
квантовых) рассуждений, имеет вид
С -= [1ое-2 A + р/Мощность шумов)] В. C.396)
Формула C.39а) описывает устанавливаемый квантовой меха-
механикой фундаментальной предел для скорости передачи информа-
информации. Величина ПсоВ имеет размерность мощности, и по аналогии
с C.396) ее можно считать шумом, загрязняющим мощность сиг-
сигнала р. Поскольку при выводе формулы C.396) мы пользовались
соотношением неопределенностей, мы должны заключить, что мощ-
мощность шумов /гсоБ имеет не классическую, а квантовомеханическую
природу.
Задачи
1. Считая, что функция ^ (г, с) пр;> г —»- оо ведет себя как 1 'гп, найти значе-
значения п, при которых интеграл
берущийся по бесконечно большой замкнутой поверхности, обращается
в нуль.
49
Глава 3
2. Докажите, что два эрмитовых оператора А и В коммутируют, если они
обладают одним и тем же набором собственных функций.
3. Докажите, что для собственных функций щ гамильтониана ^ = р2/2т +
+ V (г) (удовлетворяющих уравнению д%щ = Ецц) справедлива формула
н
„ I • * V ■ « , "/»<"■
Указание. Сначала вычислите коммутатор [^, л"].
4. Покажите, что
Указание. Сначала вычислите производную (д"/дхп)(хи).
5. На каком этапе рассуждения, приводящего к соотношению неопределен-
неопределенностей C.33), мы неявно использовали некоммутативность операторов
импульса и координаты?
ГЛАВА 4
ОДНОМЕРНЫЕ ЗАДАЧИ НА ОТЫСКАНИЕ
СОБСТВЕННЫХ ЧИСЕЛ ЭНЕРГИИ
Среди задач на отыскание собственных чисел задача на отыска-
отыскание собственных функций и собственных чисел оператора энергии
(или гамильтониана) имеет особое значение. Полная энергия изо-
изолированной системы постоянна, поэтому она является важнейшей
характеристикой системы. Кроме того, энергетические уровни си-
системы (т. е. собственные числа ее энергии) нужны для выяснения,
например, структуры химической связи, электронной структуры
кристаллов, электрических и оптических свойств атомов и моле-
молекул, скоростей химических реакций и т. д. Структура квантовых
энергетических уровней системы, таким образом, имеет самое не-
непосредственное отношение к тому, какими наблюдаемыми свойст-
свойствами обладает вещество (например, к его цвету) и к возможности
его использования в современной технике.
В настоящей главе займемся решением нескольких простых
одномерных задач на отыскание собственных чисел энергии ча-
частицы. Для каждой из них будем решать стационарное уравнение
Шредннгера
Г + V (х) \ иЕ (х) _ ЕиЕ (х), D.1)
в котором оператор энергии (гамильтониан) р2' 2т -'- V (х) равен
сумме кинетической и потенциальной энергий частицы. Решая
уравнение D.1), найдем собственные числа энергии Е и энергетиче-
энергетические собственные функции иР (х). Здесь V (х) — функция потен-
потенциальной энергии частицы.
§ 4.1. Бесконечная потенциальная яма
Рассмотрим частицу массой т, движущуюся в одномерной по-
потенциальной яме, т. е. в поле, потенциал которого равен нулю на
интервале — а<ах<аа и бесконечности вне этого интервала, как
показано на рис. 4.1.
Уравнение для отыскания собственных чисел энергии имеет
вид D.1), причем в этом уравнении, согласно C.20), для оператора
р следует использовать его явное выражение — Ш&'&х. Таким
образом, нам надо решить уравнение
( - -?- ~^Г т V (х) ) иЕ (х) _- ЕиЕ (х). D.2)
\ 2т их1 I
51
Глава 4
Решение уравнения D.2) в области — а<ах<.а, в которой V (х)=0,
имеет вид
иЕ = соз кх или иЕ = зш кх, D.3)
причем
к = ^'2тЕ!Ж. D.4)
Вне области — а<:х<а функция иЕ (х) должна равняться
нулю. Это непосредственно следует из D.2), поскольку в указанной
*-х
Рис. 4.1. Бесконечная потенцпальнгя яма и две первые (п - О, 1) собст-
собственные функции связанной частицы.
области потенциал Г (л*) имеет бесконечно большую величину.
Чтобы функция иЕ (х) обращалась в нуль при .V -- ~ а, должно
выполняться условие
2.7
D.5)
где п —■ 0, 1, 2, 3, . в случае четного решения (оно дается коси-
косинусом), и
= 2п1 — \.
D.6)
где п = 1, 2, 3, ... в случае нечетного решения (оно дается сину-
синусом).
Четные и нечетные решения, таким образом, записываются со-
соответственно в виде
D.7)
D.8)
52
Одномерные задачи
решения мы выписали с нормировочными множителями Bа)~1'2,
а
значения которых находятся из условия | и% (х) с1х---I.
—а
Формула для энергии
Е^-^— D.9)
с учетом D.5) и D.6) принимает вид
Еу-^Р^^-, D.10)
Вта1
где / -= 1, 2, 3 Нечетные значения / соответствуют четным
решениям. Наименьшую энергию имеет четное решение (даваемое
косинусом) с п - 0 (или / = 1). Следующим по энергии располо-
расположено нечетное решение с п = 1 (или / = 2). Согласно D.5) и D.6),
четные и нечетные решения чередуются по мере возрастания энер-
энергии.
§ 4.2. Конечная потенциальная яма
Рассмотрим следующую задачу. Предположим, что частица
движется в потенциальной яме, ограниченной потенциальными
барьерами конечной высоты V, как показано на рис. 4.2. Поскольку
такая потенциальная яма симметрична [т. е. для нее V (х) =
= Г I— .г) I, решения уравнения Шредингера
) D.11)
йх-
должмы обладать либо нечетной симметрией (удовлетворять усло-
условию иЕ (—х) = — ис (.*)], либо четной симметрией [удовлетво-
[удовлетворять условию иЕ (х) = иЕ (— х) ] *). При построении решений
удобно рассматривать два следующих случая.
Случай 1. Е<аУ. Во внутренней области \\х\ < а решение
уравнения D.11) можно представить в виде
иЕ (X) = соз кьх, ив (х) == $1П кох, D.12)
где
" . D.13)
В области ||л:|>а решение имеет вид]
иЕ[(х) = Се-к1х\ D.14)
') Связь симметрии собственной функции с симметрией потенциала
V (х) более полно обсуждается в гл. 5 настоящей книги.
53
Глава 4
где
D.15)
Возможное другое решение ехр (кх) следует отбросить из физиче-
физических соображений, ибо оно не удовлетворяет условию конечности
интеграла 1]иЕ(х)\гйх. Поскольку потенциал V (х) и вторая
производная решения и'Е (х) везде конечны, первая производная
решения ы'е (х) и само решение иЕ (х) должны быть всюду непре-
непрерывными функциями, включая точки х = ± а- Используя это ус-
условие непрерывности для четного решения и его производной в
точке х = а, получаем
СО5 коа = Се~™, D.16а)
а также —/гозт/гоа=—кСг~ш . D.166)
-« . . ^ со Следовательно, имеем урав-
нение
-а а ^ D.17а)
Рис. 4.2. Конечная потенциальная яма.
Рассмотрев аналогично нечетное решение, придем к уравнению
— %а. D.176)
Константы к0 и к, определяемые формулами D.13) и D.15),
должны удовлетворять одному из уравнений D.17а) или D.176).
Из уравнений D.13) и D.15) непосредственно получаем уравнение
D.18)
й2
представляющее собой уравнение окружности радиусом }
на плоскости с осями ка и кф,.
Таким образом, теперь нам необходимо решить систему уравне-
уравнений D.18) и {4.17) относительно к0 и к. На рис. 4.3 иллюстрируется
процедура графического отыскания неизвестных величин к0 и х.
Решения лежат в верхней полуплоскости (так как х>0) и
даются пересечениями кривой, задаваемой уравнением D.17а), с
окружностью, задаваемой уравнением D.18). Первые три решения
нумеруются числами п = О, 2, 4. Соответствующие им собственные
функции обозначим и0, и2, и4.
54
Одномерные задачи
Рис. 4.3. Графическое нахождение значений величин х и А,, для собственных
функций частицы, движущейся в одномерной прямоугольной потенциальной
яме. Указанные значения соответствуют точкам пересечения (жирные точки)
кривой D.17а) (в случае четных решений) или кривой D.176) (в случае не-
нечетных решений) с окружностью, описываемой уравнением D.18). Радиус
окружности вычисляется по формуле -^ЪпУ (а/Л). (Для конкретной задачи
следует рассматривать только одну какую-нибудь окружность.)
1 \
! Ч
!
:
[
1
Г
У
п ~ 1
1
^
-а а
Рис. 4.4. Собственные функции для первых трех связанных состояний ча-
частицы в конечной потенциальной яме.
55
Глава 4
Константы х и к0 для нечетных решений находятся аналогично
и даются координатами точек пересечений окружности D.18) с
кривой, задаваемой уравнением D.176). Первые два решения за-
занумеруем числами п = 1, 3. Соответствующие собственные функции
обозначим ц„ и3.
Из формы кривых на рис. 4.3 видно, что число связанных со-
состояний (число пересечений кривых) возрастает с увеличением вы-
высоты потенциальных барьеров. Если значение константы Г лежит
в пределах
5 — < л/2тУаЧН2 <EЧ-1)—. D.19)
то имеется точно 5 + 1 связанных состояний частицы в потенци-
потенциальной яме. Номер я состояния равен, таким образом, числу ну-
нулей функции ип (х). Графики первых трех собственных функций
при н — 0, 1,2 приведены на рис. 4.4. Из рис. 4.3 видно, что чем
больше номер п, тем меньше значение х, а следовательно, тем
глубже проникает соответствующая функция и„ (а) в область
\
Энергия собственного состояния ип (х), согласно D.13), равна
с —— «
2т
где кт — значение к0 для решения ип (х).
Заметим, что сейчас рассматриваются только решения в слу-
случае Е<^У. Классическая частица с энергией Е<^У не может про-
проникнуть внутрь барьера, т, е. оказаться в области |х|>а. В кван-
квантовой механике, наоборот, имеется плотность вероятностей! иЕ (х)|2,
которая отлична от нуля при |х|>а. Квантовомеханическая ча-
частица пробирается туда, куда соответствующая классическая ча-
частица боится ступить.
Случай 2. Е> V. В этом случае энергия частицы больше высоты
потенциального барьера и величина х = A,'й) 1 2т (V—Е) ста-
становится мнимой, так что решение D,12) — D.14) должно даваться
теперь синусоидальной функцией иЕ (х) всюду. Следовательно,
плотность вероятности отлична от нуля во всей бесконечной об-
области, частица не будет связанной. Теперь физически разумно го-
говорить о частице, приближающейся к яме по одному из направле-
направлений, и искать вероятность того, пройдет она через потенциальное
поле или отразится от него. Подробно случаи Е>\~ рассматривается
в следующем параграфе.
§ 4.3. Конечным потенциальный барьер
Рассмотрим теперь частицу, падающую слева на потенциальный
барьер высотой V и шириной а, изображенный на рис. 4.5, а. Фор-
Формулы, которые мы здесь получим, применимы также к случаю по-
56
Одномерные задачи
\х=а
Рис. 4.5. а — вид потенциального барьера V (х); и — типичное распределе-
распределение вероятностей | ые (х) |2 при Е <С V. В области внутри барьера (при О <С
<С х <С а) кривая соответствует случаю ~ла "> 1, когда она имеет вид силь
затухающей экспоненты \ив (х) |2 :»" ехр (— 2у,х).
сильно
тенциальной ямы, изображенной на рис. 4.2, если константу V
заменить на — V. Сначала рассмотрим случай Е<^У, при котором
соответствующая классическая частица должна была бы повер-
повернуться назад в точке х = 0. Решением уравнения Шредингера
D.2) является функция
иЕ (х) -=
■\-Аё~1кх при
г КХ +СеКХ при
—1к (л;—а)
D.20)
при х>а,
для которой
'-Е) .
D.21)
Выражение D.20) записано для падающей волны ехр (Игх) единич-
единичной амплитуды. Волна А ехр (— 1кх) является отраженной (собст-
(собственное число импульса, равное — Нк, для нее отрицательно). При
х>а функция иЕ (х) описывает частицу, которая движется направо.
Вид функции | иЕ (х)]2 в случае Е<: V показан на рис. 4.5, б. Тре-
57
Глава 4
буя выполнения условий непрерывности функций иЕ (х) и иЕ (х)
на стенках барьера при д- = 0 и л — а, получаем систему четырех
линейных уравнений для определения неизвестных коэффициентов
А, В, С, Е>, входящих в D.20). Разрешая эту систему, приходим
к формуле
^D.22)
2Ык сЬ ум (к2 — у.2) 5Ь ум
Вероятность туннелирования частицы сквозь барьер, т. е. вероят-
вероятРис. 4.6. Коэффициенты прозрачности и отражения для прямоугольного
потенциального барьера.
ность найти ее за барьером (при л>а), дается квадратом модуля
5ГГ
4(П,\')(\ ~~Е:
D.23)
Отметим, что при Е<сУ прозрачность барьера Т (Е) всегда меньше
единицы.
Когда энергия падающей частицы больше высоты барьера, т. е.
когда О!7, константа к становится чисто мнимой, и вместо фор-
формулы D.23) получаем формулу
,= 1 -и-
D.24)
Поведение коэффиццента прозрачности Т (Е) в обоих случаях
(при Е<сУ и при Е^>У) схематически показано на рис. 4.6. На нем
приведен также коэффициент отражения 7? — | А !'2. В качестве
упражнения предоставляем читателю доказательство соотношения
7?-г
D.25)
58
Одномерные задачи
Формулы D.23) и D.24) позволяют сделать два важных вывода.
1. Если энергия падающей частицы меньше высоты потенци-
потенциального барьера, т. е. Е<У (когда направление движения клас-
классической частицы меняется наА обратное при х = 0), то все же
имеется конечная, отличная от нуля вероятность проникновения
(туннелирования) частицы через барьер.* Вероятность эта дается
формулой D.23). В пределе малой вероятности туннелирования
[когда [2т (V—Е)]1'2 (а/к) ^:. 1] из формулы D.23) приближенно-
получаем
2. Если Е>У, то коэффициент прозрачности Т (Е) имеет ряд
максимумов, равных единице. Два таких максимума, соответст-
соответствующих некоторым двум значениям энергии Е2 и Е}, показаны на
рис. 4.6. Они соответствуют условию, что сдвиг фазы для частицы,
проходящей в области барьера путь туда и обратно, равный
(а!к) \гЪт (Е—V), равен целому кратному 2л. Для каждого ука-
указанного максимума отраженные от стенок барьера волны при х -- О
и при х — а интерферируют и гасят друг друга, и частица не испы-
испытывает отражения от барьера. В этом случае квантовомеханическнй
потенциальный барьер по своему действию напоминает оптический
интерферометр, или эталон Фабри — Перо [101. Это оптическое
устройство, которое в простейшем исполнении состоит из пластинки
прозрачного твердого тела со строго параллельными плоскими гра-
гранями. Кривая зависимости коэффициента прозрачности от частоты
для эталона Фабри—Перо описывается функцией D.24) , а соответ-
соответствующие математические вычисления идентичны приведенным
в данном параграфе.
В заключение отметим, что в случае «перевернутого» барьера,
показанного штриховой кривой на рис. 4.5, в формуле D.24) нужно
заменить V на — | У|. Получаемая при этом вместо барьера потен-
потенциальная яма идентична рассмотренной в § 4.2, но теперь мы имеем
дело со случаем Е>У, а потому решение для положительных Е
не нормируемо (всюду дается синусоидальной функцией). В § 4.2
были рассмотрены только «связанные» решения. Для «несвязанных»
решений энергия Е может принимать произвольные положитель-
положительные значения. Другими словами, возможно построить решение
уравнения Шредингера, имеющее вид D.20) и удовлетворяющее
граничным условиям при любой положительной энергии Е. Для
связанных решений, рассмотренных в § 4.2, имеется только конеч-
конечное число допустимых дискретных собственных чисел энергии Е.
Таким образом, приходим к выводу, что полный спектр собствен-
собственных чисел энергии Е потенциальной ямы является частично ди-
дискретным, а частично непрерывным.
59
Глава 4
§ 4.4. Физические явления,
объясняемые туннелированием частиц
сс-Распад атомных ядер. Распад атомных ядер, сопровождаю-
сопровождающийся испусканием а-частиц, можно рассматривать как квантовое
туннельное явление. Ядро до акта распада можно представлять
Рис. 4.7. Зависимость потенциальной энергии взаимодействия ос-частицы
B = 2) и «дочернего» ядра с электрическим зарядом G,—2) е от расстояния г.
При больших расстояниях (г 10~14 м) кривая соответствует обычному
кулоновскому отталкиванию. При малых расстояниях доминируют ядерные
силы притяжения.
как сферическую потенциальную яму, внутри которой содержится
одна а-частица (ядро атома гелия). Кривая зависимости потен-
потенциальной энергии а-частицы от расстояния г от центра масс дочер-
дочернего атомного ядра схематически показана на рис. 4.7. Поведение
кривой при больших г определяется кулоновским отталкиванием
электрических зарядов одного знака, а при малых г<;7? (где,
Я ~~ 10~12 см) преобладающую роль играют ядерные силы притя-
притяжения. Можно считать, что частица, энергия Е которой меньше
максимальной высоты потенциального барьера, находится в по-
потенциальной яме и «отскакивает» то от одной, то от другой ее стенки;
при этом существует очень малая вероятность туннелирования ча-
частицы через барьер, т. е. частичного ее ухода из ямы при каждом
«ударе» о стенку.
Вероятность туннелирования ы-частицы з единицу времени из
ямы (обратная величина среднего времени жизни распадающе-
распадающегося ядра) равна числу столкновений частицы со стенками ямы в
единицу времени, умноженному на вероятность туннелирования
60
Одномерные задачи
при одном акте отражения. Частота соударений а-частицы со стен-
стенкой по порядку величины равна
V р " йк йл
СО
где V — средняя скорость частицы в яме. Согласно D.5), можно
считать, что к ?х л'/?. Вероятность туннелирования при одном
столкновении дается формулой D.26):
та
Диэлектрик
'Металл'
. „Металл,
V
Как мы видим, скорость распа-
распада определяется, главным обра-
образом экспоненциальным множи-
множителем в коэффициенте прозрач-
прозрачности Т (Е). Его конкретное
значение очень чувствительно
к точной форме барьера и может
различаться на много порядков
для различных атомных ядер.
Гуннелирование электронов в
твердых телах. Квантовое тунне- Рис- 4-8- Схематическое изображе-
лирование проявляется также в ние «санДвича» металл-днэлек-
• ,-, трик—металл. Когда приложено
физике твердого тела. Предста- напряжение, через «сандвич» течет
ВИМ, что имеются два проводни- постоянный ток. Электроны пересе-
ка, показанные на рис.4 4 8 (они кают слой диэлектрика в результате
могут быть сверхпроводниками квантового туннелирования.
или полупроводниками), разде-
ленные тонким (~ Ю А) слоем диэлектрика. Если на такой «сандвич»
наложить напряжение, то через него потечет электрический ток.
Этот ток создается электронами, туннелнрующими из одного ме-
металла в другой через потенциальный барьер, образованный слоем
диэлектрика х). Туннельная природа этого электрического тока
подтверждается его экспоненциальной зависимостью от толщины
диэлектрического слоя в согласии с формулой D.26).
Читателю, знакомому с электромагнитной теорией, можно ука-
указать на точную формальную аналогию явления туннелирования
электронов с явлением распространения электромагнитных волн
в волноводах ниже критической частоты. (См., например, [11].)
') Этот потенциальный барьер образуется по следующим физическим
причинам. При установлении контакта между различными по своим снойст
вам материалами химические потенциалы "электронов выравниваются за
счет перетекания электрического заряда от одного материала к другому. Та-
Таким образом, в месте расположения контакта возникает градиент потенциала.
61
Глава 4
Задачи
1. Найдите решение ид (х) для потенциальной ямы вида
оо при х<0,
У(х) =
показанной на рис. 4.9.
О при 0<х<а,
Уо при
а
а
,
V
X
х- а х = 0
Рис. 4.9.
2. а. Проведите полностью выкладки, приводящие к формуле D.22) для О.
б. Докажите соотношение D.25).
3. Используя какой-нибудь учебник, разберитесь с аналогией между явле-
явлением туннелирования электрона и явлением распространения колеба-
колебаний в волноводе при частоте ниже пороговой.
4. Математически сформулируйте одномерную задачу о пропускании и от-
отражении частицы, падающей на два потенциальных барьера, каждый
из которых имеет вид, показанный на рис. 4.5, о, и которые разделены
расстоянием й.
Указание. Полезно использовать матричный формализм для описания
действия отдельной ямы на собственную функцию. Следует рассмотреть
матрицу, связывающую друг с другом амплитуды падающей и отражен-
отраженной волн, взятые на какой-нибудь плоскости, с этими амплитудами нз
другой плоскости.
о. Используйте матричный формализм из задачи 4 для описания распростра-
распространения частицы через произвольный ряд прямоугольных барьеров.
6. Оцените время жизни частицы массой т, находящейся в потенциальной
яме, показанной на рис. 4.9.
Указание. В этой задаче связанная частица не имеет истинных собствен-
собственных функций, так как она постоянно «вытекает» из ямы вследствие тун-
туннелирования через стенки. Чтобы приближенно оценить время жизни,
надо сначала предположить, что V = оо, и построить собственные функ-
функции захваченной ямой частицы. Можно считать, что частица падает на
границу х = •— а со скоростью V ~ Нк/т и отражается от нее, а частота
соударений со стенкой равна я/а.
ГЛАВА 5
ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
В настоящей главе мы подробно опишем решение задачи на оты-
отыскание собственных чисел и собственных функций энергии для
одномерного квантового гармонического осциллятора. Идеализи-
Идеализированный гармонический осциллятор — это точечная масса, при-
прикрепленная к идеальной пружинке, причем по предположению
трение совершенно отсутствует. Возвращающая сила такой пру-
пружинки считается строго пропорциональной ее удлинению.
В квантовой теории очень многих физических явлений мы фак-
фактически имеем дело с квантовой теорией простого одномерного гар-
гармонического осциллятора. В качестве примеров можно назвать,
в частности, квантовое рассмотрение мод электромагнитного из-
излучения, колебаний кристаллической решетки твердого тела и даже
электрических колебаний радиотехнического колебательного
7? ^-контура.
Поэтому задача о квантовом гармоническом осцилляторе имеет
фундаментальное значение для всей квантовой механики. Матема-
Математическая теория этой задачи изумительно элегантна, и ее надо
очень хорошо усвоить, чтобы вполне овладеть такими важными
разделами науки, как квантовая оптика, квантовая теория флук-
флуктуации, шумов и теория когерентности.
Без знакомства с квантовым гармоническим осциллятором ни-
никак не обойтись.
§ 5.1. Четность
Прежде чем заняться непосредственно квантовой теорией гар-
гармонического осциллятора, поговорим сначала подробнее о понятии
четности, которое мы уже использовали в § 4.1.
Рассмотрим стационарное уравнение Шредингера для частицы,
Движущейся в потенциальном поле V (г):
>Е(г)~У(г)иЕ(г)=ЕиЕ(г). E.1)
1т
Пусть потенциальная функция V (г) симметрична относительно
так называемого преобразования инверсии, т. е. пусть она удовлет-
удовлетворяет условию
Г(—г)=-1'(г). E.2)
63
Глава 5
Следовательно, справедливо непосредственно вытекающее из
E.1) и E.2) уравнение
- -^ У2% (- г) + V (г) иЕ (- г) = ЕиЕ( - г); E.3)
таким образом, функция иЕ (— г) тоже является собственной функ-
функцией того же самого гамильтониана, что и собственная функция
иЕ (г), и соответствует тому же самому собственному числу Е.
Предположим теперь, что существует только одна собственная
функция, соответствующая каждому собственному числу Е (т. е.
будем считать, что все собственные числа Е невырождены). Тогда
при любом Е функции иЕ (г) и иЕ (— г) будут линейно зависимыми
и для них можно написать соотношение
иЕА-г) = ЪиЕ(г), E.4)
в котором % — некоторое число.
Введем теперь в рассмотрение оператор четности Р, который
по определению действует на любую функцию / (г) следующим об-
образом:
иначе говоря, оператор совершает преобразование инверсии Фор-
Формулу E.4) можно тогда записать следующим образом:
РиЕ (г) =,иЕ(—г) = %иЕ (г). E.5а)
Отсюда непосредственно приходим к соотношению
Р2иЕ (г) - %2иЕ (г) = иЕ (г). E.56)
(Два раза действуя оператором Р, мы превращаем функцию иР (г)
саму в себя.) Из E.56) непосредственно следует, что
^2=1 (или К= +1). E.6)
Рассмотрим, например, сначала случай К = 1. Из E.4) тогда
следует, что
т. е. функция иЕ (г) остается инвариантной при преобразовании
инверсии. Тогда говорят, что функция иЕ (г) обладает четной чет-
четностью. Во втором случае, когда % = — 1, имеем соотношение
М—«•)=— иЕ(г), E.7)
показывающее, что функция иЕ (г) обладает нечетной четностью.
Итак, мы доказали следующее утверждение. В потенциальном
поле с центральной симметрией собственные функции стационар-
стационарного уравнения Шредингера должны обладать либо четной, либо
нечетной четностями.
64
Гармонический осциллятор
Вышеприведенное доказательство, разумеется, неприменимо
в тех случаях, когда система собственных функций иЕ (г) стацио-
стационарного уравнения Шредингера вырождена (т. е. когда одной и той
же энергии Е соответствует более одной собственной функции).
Оказывается, однако, что в этих случаях всегда возможно по-
построить такие линейные комбинации исходных собственных функ-
функций ив (г), которые будут обладать точными значениями четности
(т. е. не будут меняться или будут только изменять знак при пре-
преобразовании инверсии г ->- — г). На доказательстве этого утвержде-
утверждения мы здесь останавливаться не будем.
Заметим в заключение, что имеется очень много физических
задач, в которых потенциальная функция V (г) не обладает цен-
центральной симметрией [т. е. V (— г) Ф V (г) ]. В этих случаях собст-
собственные функции стационарного уравнения Шредингера не будут
обладать точно определенными четностями.
§ 5.2. Решение задачи о гармоническом
осцилляторе
Стационарное уравнение Шредингера для одномерного гармони-
гармонического осциллятора с возвращающей силой Кх имеет вид
4- — Кх 2и = Ей. E.8)
2т Ох2 ' 2
Используя замену
Й2 \ й / т Йш -
уравнение E.8)^легко привести к виду
^- + (Я-Е2)« = 0. E.9)
При больших I2 > Я функция и ведет себя как ехр (—12/2),
так что естественно попытаться искать точное решение в виде
и(Б) = Я(Б)в~"ЕЧ E-10)
где Я (|) —[некоторая функция |.
Подставляя E.10) в E.9), приходим к уравнению
-~ 2Б-^ + (Ь-1)Я = 0. E.11)
Предположим теперь, что функцию Я можно представить в виде
следующего ряда:
+ а2Г+ • • .), E.12)
где ао^в— первый ненулевой член разложения. Подставляя E.12)
3 Заказ Л*> 683 65
Глава 5
в E.11) и приравнивая нулю коэффициенты при одинаковых сте-
степенях 5, получаем уравнения
5(8— 1)ао = 0.
E+ 1)8^ = О,
E + 2)E+1)о2-B5+1 —Ь)ао = О,
+^)аV+^—{2!!^-2V+1-К)ао~0. E.13)
Поскольку а0 Ф О, из первого уравнения в E.13) следует, что
либо 5 = 0, либо 5 = 1. Из второго уравнения в E.13) заключаем,
что либо 5 — 0, либо а± = 0, либо 5 = ах = 0. Последнее урав-
уравнение в E.13) показывает, как коэффициент ао+2 можно вычис-
вычислить по предыдущему коэффициенту аи. Разложение E.12), таким
образом, естественно распадается на сумму двух разложений:
1) разложения, содержащего а„ с четными целочисленными значе-
значениями индекса V (оно начинается с а0); 2) разложения, содержащего
а„ с нечетными значениями индекса V (оно начинается с ах).
Рассмотрим сначала случай 5 =-- 0. Так как а0 ф 0, имеется
лишь единственная возможность оборвать бесконечный ряд из
коэффициентов аи с четным V. Надо потребовать, чтобы величина %
удовлетворяла соотношению
при некотором V. Поскольку V — четное число, согласно E.14),
К будет принимать значения
а, = 2»+1 = 1, 5, 9 E.15а)
Как видно из E.13), при таком выборе % мы не можем оборвать
бесконечный ряд коэффициентов а„ с нечетными V. Поэтому единст-
единственная возможность оставить в разложении Я E) конечное число
членов •— это потребовать, чтобы а± — 0. Тогда мы вообще выбьем
почву из-под ног ряда из а„ с нечетными V.
Аналогично можно рассмотреть случай 5=1 и заключить,
что можно оборвать ряд из а„ с четными V и вообще отбросить ряд
из ар с нечетными V, так как ах — 0. Тогда величина % должна при-
принимать значения
^ = 2^ + 3 = 3, 7, И E.156)
Получающийся полином Нп E) имеет нечетную степень (поскольку
полином четной степени умножается на 5).
Учитывая E.14) и E.15а, б), приходим к выводу, что возмож-
возможные значения "К даются формулой
66
Гармонический осциллятор
в которой /? = 0, 1, 2, 3, .... С использованием соотношения
% = 2Е/Нсо последняя формула приводит к следующим дискретным
значениям собственных чисел энергии гармонического осцилля-
осциллятора:
E.16)
Согласно E.16), квантовый гармонический осциллятор, даже
когда он находится в состоянии с наименьшей энергией (при п = 0),
обладает отличной от нуля энергией Ню/2. Наименьшая возможная
энергия классического гармонического осциллятора, конечно, равна
нулю. Это существенное различие квантового и классического ос-
осцилляторов является следствием соотношения неопределенностей.
В самом деле, если классический осциллятор обладает нулевой
энергией, то его импульс р и координата х одновременно равны
нулю. Но этого не может быть в квантовой механике, так как,
согласно соотношению неопределенностей, АрАх > Н. Если не-
неопределенности Ар и Ах распределены между импульсом р и коор-
координатой х таким образом, что полная энергия Ео минимальна и со-
соотношение неопределенностей удовлетворяется, то мы получаем
как раз значение Ео = Ню/2.
Докажем это. Полную энергию нашего гармонического осцил-
осциллятора в основном состоянии можно представить выражением
Е = —
которое с учетом соотношения неопределенностей АрАх = К/2 за-
запишем в виде
Е =
' / КП* (АрJ
' /
2 \
Минимизируя последнее выражение по Ар, получаем
^мин ~ Н(д.
Полиномы Эрмита. Как мы убедились, решениями обыкновен-
обыкновенного дифференциального уравнения E.11), соответствующими зна-
значениям % = 2я + 1, являются полиномы степени п. Полиномы
четны, если число п четное, и нечетны, если число п нечетное. По-
Полагая К = 2п + 1 в E.11), получаем дифференциальное уравнение
для полиномов Н„ E), называемых в математике полиномами Эр-
Эрмита:
^Ё 2Б-^- + 2пЯ„ = 0. E.17)
й\
67
Глава 5
Эти полиномы, оказывается, очень легко построить, разлагай
функцию е ^ 6 в ряд по степеням 5:
О (I, з) = е^-^ = «-*+** = \ Л-Ж. 5». E.18)
/ * п!
Функцию О (|, 5) называют поэтому производящей функцией.
Покажем, что полиномы Нп (^), построенные с помощью разло-
разложения E.18), удовлетворяют дифференциальному уравнению E.17).
Для этого выведем два важных рекуррентных соотношения.
Дифференцируя ряд E.18) по \, придем к формуле
с
56=2<Л
п! 1_а п\
11=0
в которой штрихом обозначена производная полинома Эрмита по
его аргументу. Приравнивая коэффициенты при одинаковых сте-
степенях 5, придем к первому рекуррентному соотношению
НпA)=.2пНп^{1). E.19)
Второе рекуррентное соотношение получим, дифференцируя ряд
E.18) по §:
оо
~~ " " ""'-. E.20)
п!
Используя формулу E.18) для разложения экспоненты, стоящей
в левой части E.20), получаем
отсюда непосредственно следует искомое второе рекуррентное со-
соотношение
1Нп (Щ -.= ±- Нп+1 (|) + пН„^ (I). E.21)
Из первого соотношения E.19) получаем
Я*=2л/С, E.21а)
поэтому второе соотношение E.21) можно представить в виде
; -~- B%Нп)^Н'п+1 = 2\Нп + 2Нп-Н'п+1.
68
Гармонический осциллятор
Полученное соотношение можно преобразовать, используя E.19)
и E.21а), к виду обыкновенного дифференциального уравнения
Н"п (I) - 21Н'п (I) + 2пИп {I) = 0, E.22)
которое в точности совпадает с дифференциальным уравнением
E.17).
Таким образом, в качестве основных формул, определяющих
полиномы Эрмита Н„ E), можно использовать либо уравнение
E.17), либо формулу E.18), либо рекуррентные соотношения E.19)
и E.21).
Из формулы E.18) сразу получаем еще одну формулу, опреде-
определяющую полиномы Эрмита:
Нп (I) = -|1 (е^<-1>2) |._« = е1а (-1)" -^
==еБ*(_1)»_^!_в-41. E.23)
Используя ее для вычисления первых трех полиномов Эрмита,
получим для них простые выражения:
/Ш = 1, #1© = 2Б, Я»© = 4Е«-2. E.24)
Как видно, полиномы Эрмита определены таким образом, что
коэффициент при наибольшей степени | в полиноме Нп E) равен 2".
Некоторые полезные интегралы. Согласно E.10), собственные
функции гармонического осциллятора имеют вид
ип (х) = Ыпе-М2)а***Нп (ах), E.25)
причем входящий сюда нормировочный множитель следует выби-
выбирать, исходя из условия
оо
| ипипйх = 1.
—оо
Подставляя в это условие формулу E.25), получаем
]ипипс1х = Ы2п ]е~А*Н2п(ах)их ==-^- I е-Ев//&) # = 1. E.26)
—оо —оо СС —оо
Появившийся в E.26) интеграл легче всего вычислить с помощью
производящей функции E.18). В самом деле, рассмотрим интеграл
п=0 т—0
69
Глава 5
. кпользуя для определенного
интеграла в левой части этого
равенства его значение
я1/2ем, приходим к формуле
п\
8'Н
Приравнивая в ней коэффи-
коэффициенты при одинаковых степе-
степенях з"Г\ имеющиеся в обеих
частях равенства, получаем
О при тфп,
я'2/г!2" при т = п.
E.27)
В результате приходим к сле-
следующему выражению для
нормировочного множителя:
Подставляя E.28) в E.25),
окончательно приходимк сле-
следующей формуле для соб-
собственных волновых функций
гармонического осциллятора:
Графики трех первых функ-
функций ип (х) приведены на
рис. 5.1.
■|_
-5
1,0
\
- I
О
а
к *
Гармонический осциллятор
Рис. 5.1. Волновые функции гармонического осциллятора. Сплошные кри-
кривые изображают функции а~|/2 ип (ах), где ах= |, при п = О, 1, 2, 3 и 1(Ь
пунктирные кривые — функции оГ1ипип для тех же значений п. Штрихо-
Штриховые кривые изображают функции распределений вероятностей для соответст-
соответствующего классического гармонического осциллятора, энергия которого
равна энергии квантового осциллятора. Вертикальными прямыми обозна-
обозначены границы классического движения, (Из статьи [12].)
71
Глава 5
Используем теперь производящую функцию E.18) для вычис-
вычисления интеграла
со
\ и„ (йит1йх) их.
—со
Начнем с рассмотрения интеграла
0A, з)е-^ -%-[0& 1)г-?*Ы. E-30)
который с учетом E.18) можно представить в виде
со
Г
3
п\т\
п т
х
E.31)
«•эо
Интеграл в правой части последнего равенства, очевидно,
можно представить в виде суммы Двух определенных интегралов,
которые легко вычислить. Сохраняя порядок слагаемых, прихо-
приходим к формуле
- я1'2 (8 + 0 ё*
/1=0
Приравнивая теперь коэффициенты при одинаковых степенях
&Чт и используя формулу E.29), окончательно имеем следующую
формулу:
а1—! 1
\ 2 /
при Ш —
-«(-) при т.
2 /
О в остальных случаях.
С помощью формулы E.32) можно вывести еще одну полезную
формулу для интеграла, содержащего функции ип и ит. Возьмем
следующее соотношение (см. задачу 3 к гл. 3), справедливое для
72
Гармонический осциллятор
двух произвольных одночастичных волновых функций:
оо
щ (х)хщ(х)их — \ щ—Ш-йх. E.33)
их (ЕI Е *\ 1 дх,
—оо —оо
Подставим в это соотношение собственные функции гармониче-
гармонического осциллятора. Тогда с учетом формулы E.32) получим
оо
] ип (х) хит (х) их =
—оо
1 / П+ 1 \1.2 / Й , , ,.12 , ,
— {———| —Л/ (п + 1) при т = п+1,
при т = п—1.
1/2 ' * ^
2тсо в остальных случаях,
О E.34)
причем при выводе мы учли, что в E.33) Еп+1—Еп = йсо.
Приведем без доказательства формулу еще для одного опреде-
определенного интеграла:
оо
] ип (х) хгит (х) их =
—оо
С 2и+ I
—! при т = п,
2«2 *
E.35)
2а2
О в остальных случаях.
Вывод этой формулы мы предоставляем читателю в качестве по-
полезной задачи.
§ 5.3. Операторы уничтожения и рождения
Рассмотрим два новых оператора с и с+, определяемые форму"
лами
1 « а « , I д
О, = 7~~ ^ '*
а дх
E.36)
-у2 V2 а
73
Глава 5
в которых а4
Переходя в этих формулах от переменной х к переменной | =
= ах, получаем совсем простые соотношения:
(У F'37)
Выясним теперь, как действует оператор а на собственную функ-
функцию и„ (ах) гармонического осциллятора. Очевидно, в силу E.37),
аип (ах) = -^ (& + -|-) NпНп © <г**2 =
E.38)
Используя выражение E.28) для нормировочного множителя
Ып, а также рекуррентное соотношение E.19), находим
-^ Н'п (I) е-? * = п12Ып^Нп _х (I) е-е*,
так что окончательно имеем следующую простую формулу:
аип — м1/2и„_1.
Рассуждая аналогично, придем еще к одной простой формуле:
аЧ = (п+1)'\+, E.39)
Формулы E.38) и E.39) утверждают следующее. В результате
действия оператора а на собственную функцию ип получаем со-
соседнюю с ней по энергии собственную функцию ип_!. Отвечающая
ей энергия на один квант /гсо меньше энергии, отвечающей функ-
функции ип. По указанной причине оператор а в квантовой механике
называют (осцилляторным) оператором уничтожения. Оператор а +
называют оператором рождения, так как он преобразует функцию
ип в функцию ип+1, соответствующую энергии, которая на один
квант /гсо больше энергии, отвечающей функции и„.
Из E.36) непосредственно вытекает, что операторы й и й ' не
эрмитовы. Действительно, они представляются суммами с ком-
комплексными коэффициентами двух эрмитовых операторов х и рх.
Поэтому, в частности, операторы йий" нельзя рассматривать как
квантовые операторы каких-либо физических величин.
74
Гармонический осциллвтор
Вычислим коммутатор операторов а и а+. Используя опреде-
определяющие их формулы E.36), имеем
а
Согласно C.22), правая часть в последней формуле равна единице:
[а, а+] = 1. E.40)
Обращая формулы E.36), можно выразить операторы "х и рх
через операторы а и а+. Приходим к простым соотношениям:
E.41)
Подставляя их в формулу для гамильтониана
2т
и используя наши обозначения а4 — тЮК1, со = \ Щт, получаем
формулу
Каа
а),
которую с использованием перестановочного соотношения E.40)
можно представить в виде
E.42)
Таким образом, мы получили самое удобное выражение для га-
гамильтониана квантового гармонического осциллятора, которым
будем неоднократно пользоваться дальше в этой книге.
Оператор а* а коммутирует с оператором <?§. Его собственные
числа даются целыми числами п. Чтобы в этом убедиться, обра-
обратимся к соотношениям E.39). Тогда получим
аг аип = а+ 1 п и„_1 = пип.
В заключение настоящего параграфа отметим, что с найденными
здесь собственными функциями квантового гармонического осцил-
осциллятора приходится часто встречаться при исследованиях самых
различных, даже чисто классических физических явлений. В ча-
частности, например, эти функции появляются в теории распростра-
75
Глава 5
нения света вдоль оптического волокна, показатель преломления
которого квадратично зависит от расстояния от оси волокна, т. е.
Решение волнового уравнения для распространяющихся мод элек-
электромагнитного поля вдоль такого волокна формально аналогично
решению уравнения для квантового гармонического осциллятора.
Такие оптические волокна используются в настоящее время в оп-
оптических линиях связи [13].
Задачи
1. Используя метод производящей функции, вычислите интеграл
для собственных волновых функций ип и ит квантового гармонического
осциллятора.
2. Докажите, что операторы а и а+ эрмитово сопряжены друг другу.
3. а. Убедитесь, что перестановочное соотношение [а, сЛ ] = 1 не противоре-
противоречит соотношению а = й/йа^ ■
б. Покажите, что
где «о — волновая функция основного состояния гармонического осцил-
осциллятора, а / (а+) — произвольный полином по а+.
4. Выведите формулы E.33) — E.35), пользуясь операторами рождения
и уничтожения и формулами E.39). Убедитесь, что
(а*)"
ГЛАВА 6
КВАНТОВОМЕХАНИЧЕСКИЙ МОМЕНТ
КОЛИЧЕСТВА ДВИЖЕНИЯ
Предварительное изучение операторов компонент момента ко-
количества движения частицы и их собственных функций, которому
посвящена настоящая глава, необходимо для теории движения
электрона в сферически-симметричном потенциальном поле (т. е.
поле, удовлетворяющем условию V (г) = V (г), где г = |г|) и для
квантовомеханической теории вращения молекул.
§ 6.1. Операторы момента количества
движения частицы
Удобно выразить операторы компонент момента количества
движения частицы через производные по сферическим координатам,
которые изображены на рис. 6.1. Сферические координаты г, Э,
Ф точки связаны с ее декартовыми координатами х, у, г соотноше-
соотношениями
х=г зтЭеозф,
*/ = гзтЭзтф, F.1)
г = г соз Э.
Подставляя в известную в классической физике формулу
1 = [г-р], F.2)
определяющую вектор момента количества движения частицы, вы-
выражение для оператора импульса р = — Шу, получаем следую-
следующие выражения для операторов декартовых компонент момента
количества движения квантовой частицы:
Ь = УРг—гру= —»А (у — г-!
<6-3)
\ ду дх I
Эти выражения для операторов 1Х, 1У, 1г легко преобразовать к
сферическим координатам, хотя соответствующие вычисления до-
77
Глава 6
вольно громоздки. Кратко рассмотрим основные этапы этих вы-
вычислений на примере преобразования оператора
Очевидно,
дг
д дг
дг дг
дг
д
ду
дв д дц>
дв дг ~т~ Лр дг '
F.4)
где д/дг, д/д<р и д/дв обозначают частные производные по сфериче-
сферическим координатам, т. е.
д
дг
д
дг
д
дв
дВ
Учитывая, что г2 = х2 + у2 + г2, получаем формулу
г дг г
дг ~~ г '
F.5)
а из равенства соз Э = г/г — еще одну
формулу
(б.б)
дг г
Наконец, очевидно, что
Рис. 6.1. Сферические —— = 0.
(г, в, ф) и декартовы (х, у, г) дг
координаты точки г.
Подставляя F.5) и F.6) в F.4), приходим к результату
д г, д з'тв д
„ д зт в
- = соз Э —
дг дг г
дв
F.7)
Аналогично рассуждая, найдем выражение для производной
дц> уд зт ф сов в д
д д дг _д__дв
дг ду
дв ду
дц> ду г
сов ф д
гвтв дц>
дг
дв
F.8)
Подставляя формулы F.8) и F.7) в первую формулу F.3) и исполь-
используя формулы F.1), после элементарных алгебраических преобра-
преобразований окончательно получаем
д д
58 дф
F.9)
78
Квантовомеханический момент количества движения
Проводя аналогичные вычисления, можно вывести также фор-
формулы
/Ли=»й(—созф-^+аеемшр-^-). (б.Ю)
\ оо оф /
1г=-Ш^~. F.11)
Используя F.9) — F.11), после довольно неприятных вычис-
вычислений получаем формулу для оператора квадрата момента коли-
количества движения:
!
апе)+
F.12)
Таким образом, мы нашли исходные выражения для операто-
операторов компонент момента количества движения частицы и для опера-
оператора квадрата момента количества движения в сферических коор-
координатах.
§ 6.2. Собственные функции
и собственные числа оператора г-компоненты
момента количества движения
Согласно F.11), имеем следующее простое выражение для опе-
оператора г-компоненты момента количества движения:
4=— 1й—, F.13)
дф
поэтому нам необходимо решить следующее уравнение для отыска-
отыскания собственных функций и собственных чисел оператора /г:
^ F.14)
где и (ф) — собственная функция, а 1г — соответствующее ей соб-
собственное число.
Общее решение уравнения F.14) имеет вид
и(ф)=е<;/Л)'гф, F.15)
и поскольку функция и (ф) должна быть однозначной функцией
угла ф, необходимо потребовать выполнение дополнительного ус-
условия
и(ф + 2л) = и(ф); F.16)
в силу этого ограничения, набор чисел 1г может быть только ди-
дискретным:
1г = Нт, F.17)
где т= 0, ± 1, ±2, ....
79
Глава 6
Подставляя F.17) в F.15), приходим к следующей окончатель-
окончательной формуле для искомых собственных функций:
ит(ф) = BяГ1/Утф. F.18)
Выше мы говорили об условии квантования F.17) в связи с бо-
ровским постулатом A.26). Теперь это условие квантования мы по-
получили как непосредственное следствие формальной квантовоме-
ханической теории, тогда как в гл. 1 мы его приняли просто как
некоторое постулативное допущение.
§ 6.3. Собственные функции
и собственные числа оператора
момента количества движения
Согласно F.12), уравнение для нахождения собственных функ-
функций и собственных чисел оператора квадрата момента количества
движения I2 имеет вид
F.19)
где Рй2 обозначает собственное число рассматриваемого опера-
оператора, а Кц — соответствующую этому числу собственную функ-
функцию; операторы I2 и /2 коммутируют между собой ([1, 12] = 0),
так как оператор 1г = — шд/д<р, очевидно, коммутирует с опера-
оператором д2/дф2. Следовательно, функцию Ур (Э, ф) можно считать
одновременной собственной функцией операторов I2 и 1г. Это дейст-
действительно будет так *), если ее представить в следующем виде:
У (Э ф) = Bп)~~1!2Р т (Э) е'тф7" F*20)
причем здесь индекс р указывает на зависимость вида функции
•Ррт F) от собственного числа Й2Р оператора I2. В силу F.11),
имеем
У^рт@» ф)==ЙтУрт(Э, ф), F.21)
причем т = 0, ±1, ± 2, .... Подставляя выражение F.20) в
уравнение F.19), получаем обыкновенное дифферещиальное урав-
уравнение, содержащее только производные по Э; оно имеет следующий
видЛ
1) Формулу F.20) можно также вывести и по-другому, применяя к диф-
дифференциальному уравнению F.19) так называемый метод разделения пере-
переменных.
80
Квантовомеханический момент количества движения
В последнем уравнении F.22) удобно использовать замену не-
независимой переменной ш = еоз Э, после чего оно преобразуется
к виду
^[^1/*Ц)=О. F.23)
Уравнение F.23) можно также представить следующим образом:
■^-__а«_^.+ /_Р__ «? )Р = От F.24)
йю2 1-^ш2 6т \ 1— ю2 A—ш2J /
Как мы видим, функция Р может быть сингулярной при т =
= ± 1. Исследуем ее поведение в окрестности точки т = 1. В этой
окрестности уравнение F.24) можно приближенно заменить урав-
уравнением
^!^„_1_^^__^_Р = 0. F.25)
4*11 Ш Л/1\*1 \/
Ли2 1 — хи бхю 4A — ту
Подобно E.12), предположим, что решение последнего уравне-
уравнения имеет вид
^J+ • . . ], F.26)
причем без ограничения общности можно считать, что а0 ф 0. Под-
Подставим F.26) в F.25) и приравняем нулю коэффициенты при раз-
различных целых степенях A—т). Равенство нулю коэффициента при
степени A—ш)^^.'дает соотношение
а0
(а(а-1)+а—^
из которого непосредственно следует, что
а = ±|т|/2.
Таким образом, существуют два независимых решения Р в ок-
окрестности точки т = 1: для одного а = — | т |/2 (оно стремится
к бесконечности при т -*■ 1), для другого а = | т |/2 (оно стремится
к нулю при т -> 1).
Обозначим первое решение символом Р^\ а второе — симво-
символом Рр1'. Эти решения можно представить в виде следующих раз-
разложений:
A—а»ГГт1/2 [«; + «; A - т) +. . . ]. F.27)
— 1.
F.28)
Аналогично можно рассмотреть окрестность точки т = — 1.
Теперь решение следует искать в виде разложения
81
Глава 6
причем, как легко показать, снова а = ± \т\12. Соответственно
строим два независимых решения:
РИ=A+шIт12[Ь0 + М1+ш)+ • • -1,
Р^1) = A+юГ1т1/2[^ + ь;A+ш)+ . . . ]. F.29)
Точки ш=1, —1 соответствуют углам 0 = 0, п. Решения
РЦ' и Р^1) расходятся соответственно при ш=1 и при го = — 1,
и их следует отбросить. Таким образом, нам необходимо искать
такое решение полного дифференциального уравнения F.24), ко-
которое около точки ш = 1 приближенно совпадает с функцией
Ро!) (ш) и около точки ш = — 1 приближенно совпадает с функ-
функцией Ро~1) (ш). Можно предположить, что искомое решение имеет
следующий вид:
F.30)
Из F.24) легко получить дифференциальное уравнение для
функции 2рт (о>):
A_а*)-^_2(|т| + 1)а;-^- + [р-|т|(|т| + 1)]2 = 0. F.31)
Решение уравнения F.31) будем искать в виде разложения
2(а;) = 5>*рА F.32)
о
Подставляя F.32) в F.31) и приравнивая нулю коэффициенты при
разных степенях щ, получаем соотношения
(й + 2)(й+1H*+,, = [(й + |тВ(й + |т| + 1)-р]сь. F.33)
Чтобы функция Ъ (ш) оставалась конечной в области — 1 ^ ш < 1
(соответствующей области 0 ^ Э ^ л), разложение F.32) должно
обрываться на некотором значении к. Из F.33) видим, что такое
обрывание произойдет, если предположить, что константа р, остав-
оставшаяся пока неопределенной, равна одному из следующих чисел:
Р = /(/+1), F.34а)
где 1 = к + \т\. F.346)
Тогда разложение F.32) оборвется на члене а^, ибо соотно-
соотношение F.33) гарантирует нам, что коэффициент а/е+2, а также и все
последующие коэффициенты аи равны нулю. При этом разложение
должно содержать либо четные, либо нечетные степени к, но ни-
никоим образом не может включать в себя и те и другие степени.
Четное решение получаем, если положим а0 Ф- 0 и аг = 0.
Нечетное решение получается при а0 — 0, аг Ф- 0. В обоих случаях
82
Квантовомеханический момент количества движения
показатель наивысшей степени в оборванном разложении Ъ (а)
дается одной и той же формулой к — I—| т \.
Итак, решения дифференциального уравнения F.31), удовлет-
удовлетворяющие физическому условию конечности при хю = + 1, харак-
характеризуются целыми числами т, которые принимают значения т =
= О, ±1, ± 2, . . . , и положительным целым числом /, которое
принимает значения / = 0, 1, 2, .... Из формулы F.346) непо-
непосредственно следует, что, поскольку к — неотрицательное целое
число, то
| т К /. F.35)
Решения уравнения F.24) обозначают Р™ (да) и называют присое-
присоединенными функциями Лежандра. Для каждого значения / имеется
2/ + 1 решений, соответствующих т = — /, — / + 1, . . . , 0, . . .
Решение исходного уравнения F.19), записанное в виде F.20),
дается теперь формулой
у? (е, ф)== ы!и_ РГ(е)в'тф, (б.зб)
где М[т — нормировочный множитель, который надо еще вычис-
вычислить. После замены т = еоз Э функция РТ (ш>) превращается в
функцию РТ (Э).
Собственное число оператора квадрата момента количества дви-
движения I2 равно р/г2, причем мы показали, что Р принимает только
дискретные значения F.34). Поэтому окончательно имеем формулы
Э, Ф). F.37)
Таким образом, абсолютная величина момента количества дви-
движения частицы может принимать только дискретный набор значе-
значений, равных |- / (/ + 1) /г, причем / = 0, 1, 2, .... У частицы,
находящейся в одном из таких собственных состояний, г-компо-
нента момента количества движения может быть равна тй, где
т — одно из целых чисел — /,..., 0, ...,/.
Обращаясь к формулам F.9), F.10) и F.36), находим
D) = Иг //, т зт ф 1- с1§ Э соз ф /, т\ = 0
и аналогично
так что для собственных состояний V точные значения имеют
операторы /2 и Р, а средние значения двух остальных операторов,
83
Глава б
1Х и 1у, равны нулю. Это еще одно проявление взаимной некомму-
некоммутативности операторов компонент момента количества движения.
Акт измерения величины /2 уничтожает какую-либо информа-
информацию о величинах 1Х и 1У.
Вектор 1 можно представить себе наглядно как проведенный
из начала координат вектор, имеющий длину |. / (/+ 1) й и ле-
лежащий на некоторой конической поверхности, так что его проек-
проекция на ось г всегда равна тН (рис. 6.2). Этот рисунок не нужно
понимать буквально, он просто нужен нам, чтобы легче запомнить
т=2
т --0
Рис. 6.2. Геометрическое изображение пяти собственных состояний момента
количества движения частицы при / = 2.
соотношения, существующие в квантовой механике, между ком-
компонентами вектора момента количества движения.
Нормировка функций V? @, ф)- Условие нормировки функций
V? имеет следующий вид:
г (в, ФI2<ш=1,
F.38)
где интегрирование ведется по поверхности единичной сферы и
где ёп — 31п 8 йЭЛр обозначает дифференциал телесного угла.
Условие нормировки F.38) следует из того, что величина
\УТ F, ц>)\2йп дает вероятность найти частицу внутри бесконечно
малого телесного угла *Й2, построенного около направления Э, ф,
проведенного из начала координат. Подставляя в F.38) формулу
84
Квантовомеханический момент количества движения
[РТ (Э)]2 япвсЮЛр = 1, F.39)
F.36), приходим к условию
Я2Я
3) 2л
о о
которое после тривиального интегрирования по ф с использова-
использованием замены т = еоз 6 можно записать совсем просто
1
I Мш |2 I [РТ И]2 йхю = \. F.40)
В учебниках по математике можно отыскать формулу
[ 2 </+ ""В1 при / = /',
1 Р?()РрЬ \ <2/+') С- И)' F.41)
0 при 1ф1',
используя которую для интеграла F.40), приходим к следующей
окончательной формуле для нормировочного множителя:
так что
У? (в, ф) = (_ 1)т Л /(И+1)(/
отсюда непосредственно следует, что
Значения четностеи для функций УГF» ф)- Чтобы найти зна-
значения четностеи для функций Ут @, ф), необходимо подейство-
подействовать на любую функцию УТ (б, ф) оператором четности. Действие
оператора четности (или инверсии) сводится к замене 8 ->■ я—0,
Ф -> Ф + я, т. е.
РУ1Ф, Ч>) = У?(п-в, ф + я). F.43)
Учитывая, что
У?ф, у) ее Р7(ш)еш\
находим
УТ (я—в, ф + я) ее РТ (-ш) е1т<9е1тп: F.44)
Принимая теперь во внимание, что функция РТ (о>) равна произ-
произведению ф ункции A — ю2I т |/2 и некоторого полинома степени
85
Глава 6
Рис. 6.3. Полярные диаграммы, показывающие угловую зависимость вели-
величин | У™|2 для волновых сферических функций У^, У\, У\, У~^1. Обратите
внимание на симметрию полярных диаграмм относительно оси г.
I — |т|, содержащего только четные или только нечетные сте-
степени т, получаем соотношение
Поэтому, согласно F.44), имеем
КГ (я-в, ф + я)=(-1)'У7(е, ф).
F.45)
Видим, что функция У~Т @, ф) имеет определенную (четную
или нечетную) четность в зависимости от того, четно или нечетно
целое число /.
Следует подчеркнуть, что наш выбор оси г был совершенно про-
произвольным, ибо нигде в рассуждениях мы не использовали ничего,
что могло бы выделить какие-то специфические направления оси г.
Таким образом, истинный физический смысл формулы F.17) со-
состоит в утверждении, что процедура измерения компоненты момента
количества движения в любом направлении должна давать значе-
значения тп. При этом нельзя одновременно измерить компоненты век-
вектора 1 в двух ортогональных направлениях х и у, поскольку опе-
операторы соответствующих компонент момента количества движе-
движения частицы не коммутируют друг с Другом и с оператором компо-
компоненты вдоль оси 2.
86
Квантовомеханический момент количества движения
Мишень
Магнит
Движущиеся атомы
Диафрагмы
Атомная печка
Рис. 6.4. Эксперимент Штерна—Герлаха.
Вычислим, например, коммутатор операторов 1Х и 1У. Исполь-
Используя формулы F.3) и C.22), получаем
F.46)
[4, ГЛ = [[ур*—гру), [грх—хрг)]
= Иг [руХ — рху] = Шг.
Аналогично рассуждая, можно вывести формулы
\1в, /г] = Ш;, F.47)
[4, 1Х]=~-ШУ. F.48)
Чтобы запомнить формулы F.46) — F.48), удобно воспользо-
воспользоваться мнемоническим правилом, а именно записать простое фор-
формальное соотношение
[Г, 1] = Ш. F.49)
Приведем в заключение явные выражения для некоторых пер-
первых собственных функций оператора момента количества движе-
движения частицы:
Уо= ( ) * («-состояние),
у/'
'/г . _ е'*
51П0—т=^
7
ч-Шл~«-
ГГ'=(^-УШ" е
-|ф
(р-состояния). F.50)
87
Глава 6
Функции с числами / = О, 1, 2, 3 обозначаются латинскими бук-
буквами 5, р, й, I соответственно. Угловая зависимость приведенных
четырех сферических функций Уо, У\, У?, УТ1 схематично пока-
показана на рис. 6.3 в виде соответствующих полярных диаграмм.
Задачи
1. Проведите подробный вывод формул F.9) — F.11).
2. Убедитесь, что [I2, &] = [Г2, 1У) = 0.
3. Рассмотрите атом с орбитальным моментом количества движения Ь (его
обозначим буквой Ь, а не 1, чтобы подчеркнуть то обстоятельство, что
момент количества движения атома может быть суммой моментов коли-
количества движения более чем одного электрона). Считайте, что атом обладает
магнитным моментом цд., связанным с вектором момента количества дви-
движения Ь формулой цд. = §РЬ (здесь §Р — некоторая константа, о которой
пойдет речь в гл. 18). Пусть теперь пучок атомов с одним и тем же зна-
значением (Ь2) = Ь {Ь + 1) Й2 движется вдоль оси х со скоростью у0 через
неоднородное магнитное поле с индукцией В = е2 (Во + кг) (рис. 6.4).
Предполагая, что энергия взаимодействия атома с полем В (В = |Хо")
описывается формулой та = — (цд., В), а сила, на него действующая,—
формулой Р = — Ум, рассчитайте разрешенные квантовой механикой
возможные траектории атомов в области, занятой магнитным полем.
Соответствующий эксперимент был произведен в 1921 г. Штерном и Гер-
лахом [14—16] (прекрасное описание этого эксперимента имеется в
книге [17]).
ГЛАВА 7
ЧАСТИЦА В СФЕРИЧЕСКИ-СИММЕТРИЧНОМ
ПОТЕНЦИАЛЬНОМ ПОЛЕ И АТОМ ВОДОРОДА
В первой части настоящей главы будут изложены некоторые об-
общие положения квантовомеханической теории в отношении ча-
частицы, движущейся в сферически-симметричном потенциальном
поле, т. е. в поле с потенциалом V (г), величина которого в любой
точке зависит только от расстояния г точки до некоторого центра.
Во второй части главы в качестве важного частного случая такого
движения частицы будет рассмотрен атом водорода, для которого
потенциал V (г) описывает кулоновское притяжение, действующее
между электроном и ядром.
§ 7.1. Частица в сферически-симметричном
потенциальном поле
Рассмотрим частицу массой те, движущуюся под влиянием
сил сферически-симметричного потенциального поля V (г). Ста-
Стационарное уравнение Шредингера C.25) для такой частицы имеет
вид
(^ )> 6> Ч?) = Еив(г, 6, Ф), G.1)
причем в сферических координатах справедливо следующее выра-
выражение для лапласиана:
г2 дг \ дг I ' г2 81П 6 д8 \ д8 / ' г2 81п2 6 дф2
G.2)
Подставляя G.2) в G.1), приходим к уравнению
2те I./* дг \ дг /^ г28ш6 дВ
+ У(г)]иЕ(г, 6, ц>) = ЕиЕ(г, 6, Ф). G.3)
Согласно F.11), оператор квадрата орбитального момента коли-
количества движения частицы в сферических координатах записывается
следующим образом:
!в/«\ 1*л G-4)
е ае \
89
Глава 7
поэтому уравнению G.3) можно придать следующий более удоб-
удобный вид:
дг
= ЕиЕ(г, Э, ф). G.5)
Из уравнения G.5) непосредственно видно, что гамильтониан
частицы в сферически-симметричном поле коммутирует с операто-
оператором I2, т. е.
{т, Г2] = 0. G.6)
Кроме того, напомним, что, как было показано в § 6.3,
[Га. /г] = 0. G.7)
Следовательно, операторы I2, /г и Ж коммутируют друг с другом
и потому имеют общий набор собственных функций. Таким образом,
решения уравнения Шредингера G.5) можно искать в виде
иЕ(г, Э, ф) = Л„,(г)К?|(в, Ф), G.8)
причем, согласно F.37),
ГУ? (в, ф) = / (/ + 1) Н2У? (в, Ф), G.9)
07F, ф) = тАКГ(в, Ф) G.10)
и функция Яы зависит только от радиуса г. Через п обозначено
квантовое число, нумерующее состояния, различным образом за-
зависящие от г. Подставляя G.8) в G.5), учитывая, что
12(е, ф)цЕ(г, е, ф) = /(/+1)/г2кГ(е, у)Кп1(г),
и сокращая правую и левую части уравнения G.5) на УТ, получаем
так называемое радиальное уравнение Шредингера:
= Еп1Яы(г), G.11)
так что новое квантовое число п нумерует различные решения
уравнения G.11).
Чтобы продвинуться дальше, необходимо задаться определен-
определенной формой потенциальной функции V (г).
Итак, мы показали, что угловая зависимость (от 6, ср) энергети-
энергетических собственных функций дается собственными функциями
У7 F. ф) момента количества движения. Отсюда следует, в ча-
частности, что квадрат момента количества движения и проекция
его на ось г являются интегралами движения для частицы, движу-
90
Частица в сферически-симметричном поле
щейся в сферически-симметричном потенциальном поле. Поскольку
в случае сферически-симметричного потенциала V (г) направление
оси 2 ничем не выделено, проекцию 1 на любое направление и его
абсолютную величину можно измерить с произвольно заданной
высокой точностью.
§ 7.2. Атом водорода
Задачу об атоме водорода можно рассматривать как частный
случай задачи о движении частицы в сферически-симметричном
потенциале. Для атома водорода потенциал V (г) обусловлен ку-
лоновским взаимодействием между атомным ядром с зарядом Те 1)
и электроном с зарядом —е. Потенциальная энергия взаимодейст-
взаимодействия, таким образом, теперь определяется формулой
У(г).
4пе0г г
е2м=—-, G.12)
4П80
здесь г — расстояние между электроном и ядром атома.
При записи формулы G.12) для V (г) произвольный начальный
уровень отсчета энергии выбран так, что энергия взаимодействия
считается равной нулю, когда электрон удален на бесконечное
расстояние от ядра.
Радиальное уравнение Шредингера G.11) для атома водорода
принимает следующий вид:
& ^+4^1 „,и - ад,М.
G.13)
Массу ядра считаем бесконечной, поэтому кинетическая энергия
ядра равна нулю (поправку на конечность массы ядра рассмотрим
в § 7.3). Согласно принятому нами выбору начального уровня от-
отсчета, энергии связанных состояний электрона в атоме водородз
должны быть отрицательными, т. е.
ЕП1 = — I ЕП1 |.
Введем сокращенные обозначения
2\ЕП1\) ай2
G.14)
2) Здесь фактически автор рассматривает не атом водорода, а так назы-
называемый водородоподобный атом. Для атома водорода 2=1,— Прим. черев,
91
Глава 7
с помощью которых радиальное уравнение Шредингера G.13)
можно записать в следующем простом виде:
Сначала посмотрим, как ведут себя решения уравнений G.15)
в окрестности сингулярных точек р = 0ир = оо.В окрестности
р = оо уравнение G.15) можно приближенно заменить уравнением
**._-!-Я = 0,
йр2 4
решения которого имеют вид
Решение е для собственных функций, разумеется, недопу-
недопустимо, так как при р ->■ оо оно неограниченно возрастает.
Рассуждая в точности так же, как выше при получении формулы
E.12), предположим, что
И%1 (р) = р Ь (р) в , ('.1ч)
где Ь (р) — некоторый полином:
причем а0 ф. 0. Число 5 положительно (когда 5<0, решение /?
обращается в бесконечность при р -*- 0, что недопустимо).
Подставляя G.16) в G.15), приходим к уравнению
р^+р[2(8+1)р]^
ар* ар
G.18)
Чтобы последнее уравнение удовлетворялось при р = 0, необхо-
необходимо потребовать выполнения равенства
так что либо
8=1, G.19)
либо
5=-(/ + 1).
Так как / > 0, значение 5 = — (/ + 1) не подходит; его использо-
использование в G.16) привело бы к решению /? (р), которое обращалось
бы в бесконечность при р = 0. Используя другое значение 8=1,
из уравнения G.18) получаем уравнение
^ -р]~- + ^~1-1)Ь= 0. G.20)
92
Частица в сферически-симметричном поле
Теперь подставим разложение G.17) в G.20) и приравняем нулю
коэффициенты при различных цечых степенях р. Так, придем к
формулам
1+\ — К
а — а
21 + 2
1 + 2 —К
а2 =
4/4-6
и в общем случае — к формуле
G.21)
У+ (* + 1)^+2/ + 2)
Разложение G.17) должно обрываться на некотором конечном
значении V. Если бы этого не происходило, то из G.21) мы сразу
получили бы, что ау+1 -»- а^х при V -*■ оо, а потому Ь (р) -*- ер
при р -*■ оо, т. е. решение Яп% (р) обращалось бы тогда в бесконеч-
бесконечность при р -»- оо, а это недопустимо. Чтобы разложение G.17)
обрывалось, скажем, на (V + 1)-м члене, необходимо, согласно
G.21), потребовать выполнения условия
Я = г + /+1 = п, G.22)
где п — некоторое положительное целое число. Наименьшее зна-
значение V равно нулю, следовательно,
п>1+\. G.23)
Полином Ь (р) в формуле G.17), построенный описанным обра-
образом, обозначим символом Ьп[ (р). Целое число п назовем «главным»
квантовым числом. Из G.16) и G.19), а также из того факта, что
Ь (р) является полиномом степени V = п—/—1, заключаем, что
решение КП[ (р) можно представить в виде произведения функции
е 2 на полином (по р) степени п—1.
Полагая К = п в уравнении G.20), приходим к дифференци-
дифференциальному уравнению
р-^+[2(/+1)-р]-^- + (л-/-1I„| = 0. G.24)
В математической литературе предпочитают иметь дело с функ-
функциями Ьрч (р), которые называют присоединенными полиномами Ла-
герра и которые удовлетворяют дифференциальному уравнению
= 0. G.25)
Сопоставление G.24) с G.25) приводит к простому соотношению
= ед(р). G.26)
93
Глава 7
Наконец, теперь все готово, чтобы выписать полностью формулу
для решения Кп{ (р). Используя G.16) и G.26), а также вспоминая,
что 8 = 1, получаем
Кп1 (р) = Ы1йе'р 2 р'Ьщ (р) = Ли~Р У^!1 (Р), G.27)
где ИП1 — нормировочный множитель, значение которого следует
еще вычислить.
Собственные числа. Чтобы найти собственное число энергии
(т. е. просто энергию) состояния п, I, т, обратимся к последней
формуле B.14). Полагая в ней К = п, получим формулу для значе-
значений энергии
т 72р4 22е2
| р т<г ем ем /728)
где йо=__(^ = 5,2917-10-11 м,
е2м = -^— = 2,3098 • 1О^28 кг • м3 • с-2;
4.ТСЕ0
величина а0 называется боровским радиусом.
Как видим, мы пришли в точности к формуле Бора [см. A.32)]
для уровней энергии атома водорода, которую он получил, пред-
предположив, что момент количества движения электронов в атоме
квантуется и принимает значения, равные целым кратным вели-
величины Н.
Используя формулу G.28), чтобы преобразовать выражение
G.14) для величины а„, получаем
22
а
пав
подставляя это значение ап в аргумент р = апг радиальной волно-
волновой функции, приходим к формуле
'' 1—г)'1%! р-г). G.29)
\ па0 / \ па0 )
Нормировочный множитель. Собственную функцию
ишт(г, 6, ф) = Мг/е-р|2рВД11(р)КГ(е, ф) G.30)
надо нормировать условием
оо Я2Я
I I Л
(г, 9, Ф) р г2 з1п 9 й«Шф = 1. G.31)
94
Частица в сферически-симметричном попе
Учтем, что мы уже отнормировали 1см. F.38) ] сферические функ-
функции У (Э, ф) условием
я 2я
111 у? F, ф) Р 51п &ш<р=1. G.32)
о о
Поэтому для вычисления нормировочного множителя N нам ос-
остается потребовать, чтобы интеграл по г в G.31) был равен единице.
1 ' I
10
2г/а0
гг/а0
15
15
гг/а0
Рис. 7.1. Графики радиальных волновых функций ЯП1 (г) при п — 1, 2, 3
и /== 0, 1, 2.
Используя соотношение р = апг, это требование можно записать
в виде
а! о
G.33)
95
Глава 7
Таблица 7.1. Некоторые низколежащие нормированные водородоподобиые
функции.
Буквы слева представляют собой общепринятые обозначения состояний;
5 обозначает состояния с /=0| р — состояния с 1=1, Л — состояния с / = 2
и т. д.
5 : «2оо = C2л)'
ао ) \ "о
«210 = (зад- (А-K2 -Щ- е~гг12а'° см е
ао
р: «21±1 = F4яГ'"^
ао / ао
(г/а'K12 (
иаоо= ^ 0) 27-18
81 (ЗпI2
5/2 /■
1.2 1 ^
е
«310= у .Г Гв--^-)-^* °со5е
±1ф
81я^ V «о ) %
B/) Ф
а: 11320= К ^' е °Cсо520—
81 (бI/2 ;2
B/а;K'
3'2
«32 ±о=
162л
Если теперь воспользоваться табличным значением появив-
появившегося в G.33) определенного интеграла:
^^|- G.34)
96
Частица в сферически-симметричном попе
то легко получить следующее выражение для нормировочного мно-
множителя:
/ 2п[(п + 1)\Г \
па0
где использовано обозначение а„ = 27,/па0.
Итак, мы можем теперь, исходя из G.30), выписать оконча-
окончательные полные выражения для водородных волновых функций
г, 6, ш) =17 ) ~1^—^И-Ь-1'2е~~2г'п"°1—-'— А х
па0 " " °
Х^Ц^г)У7ф, Ф). G.36)
Графики некоторых радиальных волновых функций /?г/(г) пока-
показаны на рис. 7.1.
В заключение этого параграфа приведем в табл. 7.1 явные вы-
выражения для некоторых нормированных собственных функций
атома водорода низких порядков. Величина йо, встречающаяся
в формулах в табл. 7.1, связана с боровским радиусом а0 соотно-
соотношением
где Мц — масса ядра. С помощью поправочного множителя
1 + те1Мп учитывается конечность массы ядра, которое до сих
пор считалось имеющим бесконечную массу. Указанную поправку
мы подробно обсудим в следующем параграфе.
§ 7.3. Поправка на конечность массы ядра
в теории атома водорода
В теории атома водорода, изложенной в предыдущем параграфе,
считалось, что атомное ядро имеет бесконечно большую массу.
Это предположение было сделано неявно, когда мы пренебрегли
оператором кинетической энергии р%/2М атомного ядра в гамиль-
гамильтониане G.13) (здесь рм означает оператор импульса атомного
ядра).
Теперь обобщим теорию § 7.2. Рассмотрим двухчастичную си-
систему, составленную из двух точечных частиц с массами т1 и т2.
Эти частицы расположены друг от друга на расстоянии | гж — г2|,
где г1 и г2 — радиус-векторы масс т, и т2, проведенные из неко-
некоторой общей начальной точки в пространстве. Гамильтониан та-
такой двухчастичной системы имеет вид
.М~- -■7^-У?-^-^4 1/(!г1-гг|). G.37)
2т1 2т2
Лапласиану? составлен из производных по координатам частицы Ь
4 Заказ №№3 97
Глава 7
лапласиан щ — из производных по координатам частицы 2. Потен-
Потенциал взаимодействия по предположению зависит только от скаляр-
скалярного расстояния |г,—г2| между частицами.
Нам необходимо теперь решить следующую задачу на отыска-
отыскание собственных функций и собственных чисел:
(г„ г2). G.38)
В этой задаче мы перейдем от переменных Г], г2 к новым перемен-
переменным г и К, связанным с исходными переменными соотношениями
т1х1 + т2х2 = МХ и т. д.,
х1—х2 = х и т. д., G.39)
М =т1-г-т2.
Вектор К (с компонентами X, V, 2.) характеризует положение
центра масс системы, а вектор г (с компонентами х, у, г) характе-
характеризует относительное векторное расстояние между обеими части-
частицами. Из формул G.39) непосредственно следует, что
G.40)
Подставляя G.40) в G.37), приходим к следующему уравнению
Шредингера:
^) (г, К), G.41)
где [I — так называемая приведенная масса, определяемая фор-
формулой
-1 = _!_ + _!_, G.42)
и Е — собственное число энергии, а VЕ — соответствующая ему
собственная функция. Для решения задачи на собственные функ-
функции и собственные числа G.41), записанной в координатах г, К,
можно использовать метод разделения переменных. Предположим,
что решение 11Е (г, К) представляет собой следующее произведение
функций:
(/Е(г, К)-«(гIР(Ю, G.43)
причем одна функция зависит от г, а другая — от К, Подставляя
G.43) в G.41) и деля правую и левую части равенства на иШ, по-
получаем соотношение
А2 1 „
Ж Г (К) 2ц и (г)
98
Частица в сферически-симметричном попе
Так как соотношение, G.44) должно выполняться при всех зна-
значениях переменных г и К, зависящее от К слагаемое в левой части
G.44) должно быть равно некоторой постоянной, скажем, Е', а
зависящее от г слагаемое — другой постоянной Е":
-— 4—ч%№ (К)---= Ё. G.45)
2Л1 ГТК)
-у?н(гН-У(г) = Е" G-46)
2и. и (г)
Кроме того, чтобы удовлетворялось соотношение G.44), необхо-
необходимо потребовать выполнения равенства
Е' + Е" = Е. G.47)
Таким образом, уравнение G.41) задачи на отыскан несобственных
функций и собственных чисел, которое имело независимыми пе-
переменными гх и г2, свелось к двум простым уравнениям G.45) и
G.46), каждое из которых относится к своей независимой перемен-
переменной Р или г. Решением первого уравнения G.45) является функция
IV (К) етк, G.48)
для которой К — некоторый произвольный действительный вектор.
Константа Е' определяется выражением
Е' -^-. G.49)
2М
По аналогии с C.18) функцию № (К) будем идентифицировать
с собственной функцией импульса, соответствующей собственному
числу импульса центра масс, равному Щ. Постоянная Е', таким
образом, представляет собой кинетическую энергию полной массы
М, помещенной в центр масс, т. е. в точку, характеризуемую век-
вектором Р.
Второе уравнение G.46) совпадает по форме с уравнением G.1).
Это уравнение Шредингера для частицы с массой ц, движущейся
в потенциальном поле со сферически-симметричным потенциалом
V (г). В частном случае водородоподобного атома с зарядом ядра
Ъе следует положить
У(г) = —2е?„/г.
Решение уравнения G.46) идентично с решением, приведенным
в § 7.2, так что можно использовать формулу G.25) для собствен-
собственных чисел, заменив только в ней тс на ^:
Е»^^Г^1^^^2^., G.50)
2Гг2п2 2а'п2
О
где ао = —^ -= а0 A + -^-■'] ■ G.51)
4*
Глава 7
Чтобы найти значение приведенной массы ц, надо воспользо-
воспользоваться формулой G.42) и подставить в нее вместо тг массу элек-
электрона те, а вместо пи — массу ядра Мк. В случае атома водорода
«энергетический» поправочный множитель 1 4- те/М^: равен
1 + 1/1836 — 1,000545. Относительное изменение энергии кван-
квантовых переходов атома водорода, таким образом, имеет величину
порядка 5-10~4; оно легко обнаруживается экспериментально
в атомной спектроскопии.
Полная энергия Е атома водорода равна сумме G.47) кинети-
кинетической энергии Е' (движения центра масс) и (внутренней) энергии
возбуждения Е":
р
(п =
Энергия
Н2К2
2/И
= 1, 2. .
отдачи
72 2
^ ем
2а'0п2
. .)• G-52)
и доплеровское
Рис. 7.2. Лтом водорода, нахо-
находящийся в квантовом состоянии
я( и обладающий импульсом
АК{ в системе центра масс, испус-
испускает фотон с импульсом Йк и пе-
смещение. Возбужденный атом
водорода (или другой возбужден-
возбужденный атом) может испускать элек-
электромагнитное излучение, если
в нем происходит квантовый пе-
переход в состояние с меньшей энер-
энерС 52
р
масс после испускания фотона
равен йК2-
реходит в квантовое состояние п2. гиеи. Согласно формуле G.52),
Импульс атома в системе центра энергия, высвобождаемая 'в таком
процессе излучения, например при
квантовом переходе из состояния
п1 в состояние пг, включает в себя
кинетическую энергию /г2/B/2М поступательного движения центра
масс атома.
Рассмотрим атом, первоначально находившийся в квантовом
состоянии пх и имевший импульс центра масс, равный ЛК^- Пусть
в нем произошел квантовый переход с уровня ^ на уровень п2.
Предположим, что в этом элементарном акте импульс центра масс
атома изменяется и становится равным йК2, а излучаемый фотон
имеет энергию /гсо и импульс Нк. Описанный элементарный процесс
представлен'на рис. 7.2. Поскольку полная энергия изолирован-
изолированной системы сохраняется, имеет место равенство
2Л1
+ "' "" 2М
G.53)
В силу закона сохранения импульса для изолированной системы
в указанном элементарном процессе имеем еще одно векторное
равенство
К! = К2 + к. G.54)
100
Частица в сферически-симметричном попе
Следовательно,
G.55)
где а — угол между векторами к и К1.
Разрешая совместно уравнения G.53) и G.55) относительно /ш
(энергии испущенного фотона), получаем
Ны — И (соо + Асо),
соо = Е"х ~ Еп* , Дю= —(аМ^сова—Л2). G.56)
Замечая, что НК^^Му, к = со/с, где у — начальная скорость
атома, отсюда имеем формулу
Дсо=со{—сова 1 G.57)
\ с 2/Ис2 / ч ;
и поэтому при Дсо ? соо приходим к приближенной формуле
G.58)
Второе слагаемое в скобках представляет собой доплеровское
смещение частоты излучения, испущенного атомом, компонента ско-
скорости которого в направлении испущенного излучения равна,
V сов а. Третье слагаемое в скобках в G.58) (равное йсоо/2Мс2 и бе-
берущееся со знаком минус) часто игнорируют. Однако оно представ-
представляет собой важную поправку на энергию отдачи атома для испу-
испускаемой частоты и отражает тот факт, что даже в случае V — О
(атом вначале покоится) наличие не равного нулю импульса у ис-
испущенного фотона обязательно приводит к появлению энергии от-
отдачи атома, т. е. атом приобретает скорость после испускания фо-
фотона. Энергию отдачи атома надоТвычесть из энергии испущенного
фотона.
В эффекте Мессбауэра (см., например, [16]) импульс отдачи,
обусловленный испусканием у-излучения атомными ядрами кри-
кристалла, передается всему кристаллу. Поэтому поправка на энер-
энергию отдачи — йсо2/2Мс2 становится чрезвычайно малой, так как
в ней М обозначает массу всего кристалла. В результате испус-
испускаются очень узкие линии.
Вырождение энергетических уровней. Энергия покоящегося
атома водорода (К = 0) зависит только от главного квантового
числа п г):
Еп-— М
2а'0п2
') Ниже мы увидим, что эта формула, строго говоря, неверна, так как
надо учитывать наличие спина у электрона в атоме водорода и связанные
с ним поправки на так называемую «тонкую структуру» атомных уровней.
101
Глава 7
Одному и тому же значению главного квантового числа п со-
соответствует целый набор квантовых уровней с различными значе-
значениями квантового числа / = 0, 1, 2, . . . , п—1, так что полное
число уровней с энергией Е„ равно
ЕB/+1) = п2. G.59)
1 = 0
Каждому / соответствуют 2/ + 1 квантовых уровней с различ-
различными значениями т = — I, . . . , I. Так, для п = 2 имеем сле-
следующий набор уровней: п1т = 2x0, 2р1, 2рО, 2р,—1, где 5 обозна-
обозначает уровень со значением / = 0, а р — уровни со значением / = 1.
Линейные комбинации собственных функций. Рассмотрим в ка-
качестве примера волновые функции 2р-состояний атома водорода
«21т {г, 6. ф), приведенные в табл. 7.1:
и211 - Сге^г/2Чт Эе'ф, G.60)
и21_! _-,Сге~г'2а° 8Ш ве^ф, G.61)
иш - \ 2 Сге~ г/2°° соз Э. G.62)
Поскольку эти три функции вырождены (т. е. описываемые ими
квантовые состояния имеют одну и ту же энергию Е), любые но-
новые ортонормированные линейные комбинации указанных функ-
функций также будут собственными функциями первоначального га-
гамильтониана, соответствующими той же самой энергии Е.
Нас сейчас интересует следующий набор новых собственных
функций, принимающих только действительные значения:
4 + «21-1) = ~ Сге~ г;2оо яп в(V* + в"*41) -
/2
I 2ру) ^ -^~ (%-%_,) ^-^ Сгеа* яп
I 2рг) = ипо = | 2" Се" фа° г. G.63)
Указанные функции представляют собой собственные функции
гамильтониана Ш и оператора Р, но они не являются собственными
функциями оператора \г. Новым волновым собственным функциям
G.63) соответствуют распределения вероятностей |к(г)|2, сильно
отличающиеся от распределений вероятностей для функций «2ц>
«21-1 и «2Ю- Полярные диаграммы, изображающие распределения
102
Частица в сферически-симметричном поле
\иг,,!\госгге~''/ао%тгв
Рис. 7.3. а и б — полярные диаграммы, изображающие распределение ве-
вероятностей, для собственных функций м91+1 и ыО10 атома водорода; в, г и
д — полярные диаграммы, изображающие распределение вероятностей для
линейных комбинаций G.63). Вероятности сконцентрированы соответст-
соответственно около осей х, у, г.
103
Глава 7
вероятностей для функций G.63), показаны на рис. 7.3. Видно, что
для состояния 12рх), например, электронная плотность концентри-
концентрируется около оси х.
Указанные линейные комбинации вырожденных собственных
функций атома водорода описывают состояния атома в кристалле
или в молекуле. Волновые функции такого типа как бы подстраи-
подстраиваются под локальную пространственную симметрию кристалла
или молекулы. Именно по этой причине следует образовывать со-
соответствующие линейные комбинации собственных функций. При-
Пример такой «гибридизации» атомных волновых функций рассма-
рассматривается в следующем параграфе.
§ 7.4. Гибридизация волновых функций
и химическая связь в молекулах
Волновые собственные функции с более сложными пространст-
пространственными свойствами симметрии можно построить, образуя линей-
линейные комбинации стандартных собственных функций атома водо-
водорода, в которые включаются
как 5-функция (/ = 0), так и
р-функции (/ = 1).
Рассмотрим, например, мо-
молекулу метана СН4. Атом угле-
углерода в молекуле метана хими-
химически связан с четырьмя атома-
атомами водорода четырьмя тетра-
эдрическими химическими свя-
связями с так называемыми «ва-
«валентными» углами Н—С—Н
между связями, равными 109°28',
как показано на рис. 7.4. Эта
тетраэдрическая симметрия мо-
молекулы метана должна влиять на
^ГмК„ТчУеРсак„е°сЛве„КзУ„Лв неТ электронные волновые функции
атома углерода. Каждой из че-
четырех химических связей углерода должна соответствовать своя
электронная волновая функция %1; Хг> Хз> 5С4> причем
XI - -~ B5 + 2рх + 2ру + 2Рг),
Ъ. = -т=- B5- 2рх - 2ру + 2рг),
1
■у/4
1
/Ос Оп |_О#-* Ол \
"" ~ТГ (""~ 4>* + *Ру— *Рг),
G.64)
104
Частица в сферически-симметричном поле
где символами 2рх, и- г обозначены собственные волновые функции
\2рх,у, г.). определяемые формулами G.63). Волновые функции %и
%2> %з> Ул называются гибридизоеанными орбиталями. Химическая
связь в молекуле СН4 осуществляется за счет того, что каждый из
четырех внешних электронов конфигурации 2«22р2 атома углерода
помещается на одну из гибридизованных орбиталей %г, %2, %8, уЛ,
Пользуясь формулами G.64), легко убедиться, что функции
%1> %2> Хз> Ул ортогональны друг другу и что каждая из них имеет
распределение вероятностей с максимумами по направлениям
н
Рис. 7.5. Тетраэдральная гибридизация орбиталей конфигурации 2«22р2
атома углерода позволяет понять природу химических связей С—С и С—Н
в молекуле этана С2Нв.
A, 1, 1), (—1, — 1, 1), A, — 1, — 1), (— 1, 1, —1) соответственно
(направления указываются относительно положения атома угле-
углерода С, помещенного в начало координат).
Пространственная направленность гибридизованных волновых
функций (орбиталей) позволяет понять химическую связь не только
в молекуле метана, но и в других молекулах. В молекуле этана
С2Не, например, каждый из двух атомов углерода С пребывает
в состоянии, подобном состоянию атома углерода в молекуле ме-
метана (см. рис. 7.4). Отличие состоит лишь в том, что теперь две гиб-
ридизованные орбитали направлены вдоль одной общей оси С—С
(ось г'), как показано на рис. 7.5. Остальные три гибридизоваиные
орбитали каждого атома С идут на образование тетраэдрнческих
химических связей с соседними атомами водорода, находящимися
в своих основных состояниях, характеризуемых 15-орбиталями.
Более полное обсуждение теории химических связей в молеку-
молекулах и соответствующих выигрышей в энергии, которые делают
устойчивыми химические связи, читатель найдет в любом учебнике
физической химии (см., например, [19, гл. 61).
105
Глава 7
Задачи
1. Покажите, что гибридизованные волновые функции ЗС1( у.г, Хз. 7.4. давае-
даваемые формулами G.64), действительно имеют геометрические направления,
показанные на рис. 7.4.
2. Убедитесь, что орбитали ул, у_2, '/з. Х4 ортогональны.
3. Вычислите и сравните друг с другом значения энергий перехода п :— 2 -*-
_*. п = 1 для атома водорода, для атома дейте.>ия (протон + нейтрон +
+ электрон) и для иона (Не3)+ B протона + нейтрон + электрон).
4. Вычислите поправки на энергию отдачи атомного ядра для энергий пе-
перехода п = 2 -»- п = 1 для водородоподобных атомов из задачи 3.
5. Вычислите квантовомеханическое среднее значение {\1г)п1 для состояния
п1 атома водорода. Убедитесь, что имеет место равенство
Здесь символ ( )обозначает квантовомеханическое среднее значение
физической величины, заключенной в скобках (см. § 3.2).
ГЛАВА 8
СИСТЕМЫ ТОДЖЕСТВЕННЫХ ЧАСТИЦ
В классической физике путем мгновенного одновременного из-
измерения положения и импульса каждой частицы системы тождест-
тождественных частиц в некоторый момент времени / возможно «пометить»
частицы, а затем проследить за последующим движением каждой
из них. Таким образом, можно предсказать положение и импульс
каждой частицы в любой момент времени 1'~>1.
В квантовой механике такие одновременные измерения положе-
положений и импульсов частиц системы невозможны. В квантовой теории
постулируется, что нельзя различить никакие две конфигурации
системы тождественных частиц, которые отличаются друг от друга
только перестановкой двух (или большего числа) частиц. Ниже
мы убедимся, что такого рода ограничение приводит к новым и
необычным физическим свойствам квантовых систем тождествен-
тождественных частиц.
§ 8.1. Система из двух частиц
Рассмотрим систему, состоящую из двух невзаимодействующих
тождественных частиц 1 и 2, для которых по отдельности справед-
справедливы уравнения
(8.1)
где я])а и % — любые две собственные функции некоторого одно-
частичного гамильтониана Ж. Используемое обозначение, напри-
например % A), указывает, что учитывается зависимость волновой функ-
функции частицы 1 как от ее пространственных координат, так и от спи-
спиновой координаты х). Поскольку сейчас мы предполагаем, что ча-
частицы не взаимодействуют друг с другом, гамильтониан полной
двухчастичной системы имеет вид
Ж(\, 2)^ЖA) + ЖB). (8.2)
Из (8.1) и (8.2) непосредственно следует, что функция я]з A, 2) =
') Читателю, пожалуй, здесь стоит заглянуть вперед в § 9.8 и 18.2,
чтобы немного узнать о спине.
107
Глава 8
= а|>а B) я]^ A) является решением полного уравнения Шредингера
двухчастичной системы
ЖA, 2I1.A, 2) = (Е1+ЕЩA, 2),
соответствующим собственному числу Ех + ^2- Решениями этого
уравнения с тем же самым собственным числом будут также и функ-
функции
Возникает естественный вопрос: какое из этих четырех решений
правильное? Попытаемся ответить на него.
Рассмотрим оператор перестановки Р12 полных наборов коор-
координат обеих частиц, т. е. оператор, который при действии на про-
произвольную двухчастичную функцию переставляет в ней аргументы
частиц 1 и 2. Из (8.1) и (8.2) непосредственно следует, что
РиШ{\, 2) = Ж(\, 2)Р12, (8.3)
т. е. операторы Р12 и <ЖA, 2) коммутируют друг с другом. Следо-
Следовательно, указанные два оператора имеют общий набор собствен-
собственных функций. Пусть я]) A, 2) — некоторая собственная функция
оператора Р12, т. е.
Р12яИ1, 2) = Яя|)A, 2), (8.4а)
где Я — собственное число оператора Р12. Из (8.4а) непосредст-
непосредственно получаем, что
2)=<фA, 2), (8.46)
ибо действуя по очереди два раза оператором перестановки на
функцию, мы возвращаемся к исходной функции. Второе равен-
равенство в (8.46) показывает, что
поэтому'функция я|>A, 2) должна быть либо симметричной (при
% = 1), либо антисимметричной (при Я, = — 1) по отношению
к перестановке в ней аргументов обеих частиц. Обозначая симво-
символом я])8 симметричную функцию и символом % антисимметричную
функцию, запишем уравнения
Ри%A. 2)=-1Ы1, 2). (8.5)
Для двухчастичной системы, составленной из двух тождествен-
тождественных невзаимодействующих частиц, одна из которых находится в со-
108
Системы тождественных частиц
стоянии „ч|>с, а другая — в состоянии \|>,.,, имеются как симметрич-
симметричная, так и антисимметричная собственные функции соответственно:
- -^- №„A) % B) + <фа B) % A)],
-^№«A)^B) -ф„С2
(8.6а)
(8-66)
Эксперименты показывают, что системы, составленные из тож-
тождественных частиц с полуцелым спином (т. е. 5, = A/2)/? , C/2) /?,
E/2) Н, . . .), например из электронов, протонов или нейтронов,
описываются антисимметричными (относительно перестановок аргу-
аргументов отдельных частиц) волновыми функциями. Частицы такого
типа называют фермионами.
Системы, состоящие, например, из фотонов, а-частиц и любых
других тождественных частиц с целым спином (для них вг = О, Л,
2/г, . . .), описываются симметричными , волновыми функциями.
Соответствующие частицы называются бозонами.
Волновые функции системы, состоящей более чем из двух фер-
миопов, можно строить так же, ■ как мы строили выше двухэлек-
тронную функцию я])о. Функция должна изменять знак при пере-
перестановке аргументов любых двух частиц и обращаться в нуль,
когда какие-либо две частицы занимают одно и то же квантовое
одночастичное, состояние. Такую нормированную волновую функ-
функцию можно записать компактно в виде так называемого слэтеров-
ского детерминанта:
я|JB).
(8.7)
где числа 1, . . . , N, заключенные в скобки, обозначают полные
наборы координат отдельных частиц, а индексы 1, . . . , N —
различные одночастичные собственные состояния.
При перестановке в детерминанте (8.7) координат любых двух
частиц знак функции»-;^ изменяется, поскольку мы переставляем
два столбца детерминанта. Кроме того, если в детерминанте (8.7)
какие-то две одночастичные собственные функции одинаковы, т. е.
эти два собственных состояния имеют одинаковые наборы собствен-
собственных квантовых чисел (с учетом также и спинового квантового числа),
109
Глава 8
то волновая функция ч|з„ — 0. Это случается по той причине, что при
наличии двух идентичных состояний в детерминанте (8.7) появятся
две одинаковые строки, а такой детерминант равен нулю.
Разложение детерминанта (8.7) содержит Л/1 слагаемых, каждое
из которых представляет собой произведение Л/ одночастнчных вол-
волновых функций. Каждое из Л/! этих слагаемых соответствует од-
одной определенной последовательности расположения номеров N
частиц. Таким образом, Л/! произведений в сумме (8.7) соответст-
соответствуют всем Л/1 перестановкам N частиц по N состояниям. Типичное
произведение имеет вид: ^(З) ф2 D) . . . -ф^ (т). В нем частица
3 помещена в состояние 1, частица 4 — в состояние 2 н т. д.
Антисимметрия многофермнонных волновых функций прояв-
проявляется, в частности, в том, что собственная функция % обращается
в нуль, когда какие-либо две частицы занимают одно и то же
состояние. Это утверждение часто называют «принципом запрета
Паули».
Подчеркнем, что принцип Паули является непосредственным
следствием постулата об антисимметрии фермионной волновой функ-
функции. Принятие этого положения в квантовой маханике не приводит
ни к каким внутренним противоречиям.
Симметричные собственные функции, предназначенные для опи-
описания систем бозонов, можно строить по аналогии со слэтеров-
скими детерминантами, только нужно в разложении слэтеровского
детерминанта заменить все появляющиеся знаки минус на знаки
плюс. Поэтому, в частности, можно строить симметричные волно-
волновые функции, в которых две (или даже все) одночастичные волно-
волновые функции одинаковы. Это легко видеть на примере простой
двухбозонной системы, описываемой функцией (8.6а). Функция я]^
не обращается в нуль, если в ней положить а = [1
Принцип антисимметрии и симметрии многочастичных волно-
волновых функций приводит к очень глубоким физическим следствиям.
Рассмотрим, например, энергию многофермионной системы в пре-
предельном случае нулевой температуры. Согласно квантовой стати-
статистике, с которой мы подробно познакомимся в гл. 15, при нулевой
температуре частицы распределятся по доступным для них состоя-
состояниям таким образом, чтобы полная энергия системы была наи-
наименьшей при условии выполнения принципа запрета Паули. При
Т = 0 самой низкой энергией обладает невырожденное состояние
системы фермионов (т. е. состояние, для которого только одна соб-
собственная функция сопоставляется каждому собственному числу);
оно строится следующим образом. Поместим одну частицу в состоя-
состояние я]H с самой низкой энергией Ео. Поскольку в системе фермионов
никакие две частицы не могут находиться в одном и том же кванто-
квантовом состоянии, вторую частицу мы можем поместить только в сле-
следующее по энергии состояние, скажем с энергией Ег. Третью ча-
частицу нужно поместить еще выше и т. д. Таким образом построим
ПО
Системы тождественных частиц
состояние, которое при пренебрежении энергией взаимодействия
частиц между собой имеет полную энергию
Для системы из N бозонов при температуре Т =-- 0 состояние
с наименьшей энергией получается, если все бозоны поместить в
одночастичное состояние с самой низкой энергией, т. е. в так на-
называемое основное состояние.
Из сказанного, в частности, сразу следует, что система N бо-
бозонов имеет намного меньшую энергию, чем система N фермионов.
Учитывать указанное важное свойство фермионов совершенно
необходимо, чтобы понять, в частности, поведение электронов в кри-
кристаллах, являющихся диэлектриками, проводниками и полупро-
полупроводниками, о чем пойдет речь в гл. 17.
Другое важное свойство фермионов следует даже из внешнего
вида функции (8.66). Оно заключается в том, что, когда аргументы
1 и 2 функции я])о совпадают, она обращается в нуль. Таким обра-
образом, вероятность найти два фермиона близко один от другого очень
мала. (Высказанное утверждение мы уточним в следующем пара-
параграфе, где будет показано, что вероятность найти два электрона
в одной и той же точке пространства при условии, что их спины па-
параллельны, равна нулю.) Таким образом, фермионы как бы стре-
стремятся оттолкнуть друг друга, в то время как бозоны стремятся
собраться вместе.
Квантовостатическне различия в поведении систем фермионов
и бозонов будут еще раз подробно обсуждаться в гл. 15 и 16.
§ 8.2. Атом гелия •>
Проиллюстрируем теперь соображения о симметрии многочас-
многочастичных волновых функций систем тождественных частиц, изло-
изложенные в предыдущем параграфе, в частном случае системы, со-
состоящей из двух электронов, которые движутся в сферически-
симметричном потенциальном поле атомного ядра с зарядом Ъе
и массой М. (Для атома гелия 1 = 2.) Полный гамильтониан такой
двухэлектронной системы имеет вид
Последнее слагаемое представляет собой энергию кулоновского
отталкивания обоих электронов друг от друга (поэтому эта энергия
берется с знаком плюс), величина г12 обозначает расстояние между
электронами, ц — приведенную [массу A/ц = \1те + 1/М), ё*м =
== е2/4зте0.
') Здесь, как п и случае атом;! водород;!, правильнее говорить о гелно-
подобном атоме.— Прим. перев.
111
Глава 8
В нулевом приближении полностью пренебрегаем энергией
взаимодействия е~м1г12. Тогда наша задача на отыскание собствен-
собственных функций и собственных чисел сведется к простой задаче:
= ЕЪ(гг, г2) ^ 52), (8.9)
где &', обозначает спиновое состояние /-го электрона (г = 1, 2).
Так как гамильтониан в (8.9) является суммой двух одноэлек-
тронных водородоподобных гамильтонианов, один из которых со-
содержит величины \/[ и Гл а другой — величины у2 и га, прост-
пространственную двухчастичную волновую функцию можно взять в виде
произведения двух водородных волновых функций, подробно опи-
описанных в гл. 7. Таким образом, приходим к функции
я]) (г,, г2, 5р 52) --"„,,,„, (^«„^(г^х («,. «а). (8-10)
причем
(|г ^ —^■)"»■'■-(Г|) *-"*'■"■(Г1)> (8Л1)
Е«, ^т7^' (8Л2)
2а0П1
Здесь % (в1, 52) обозначает спиновую волновую функцию. Полная
энергия Е системы в состоянии, описываемом функцией я]) (гг, г2,
«!, 52), равна сумме одночастичных энергий
Е = ЕЩ + Еп. (8.13)
Основное состояние я]H A, 2) гелиоподобного атома мы получим*
если положим в приведенных формулах п1 = 1 и п.2 = 1. Обозна-
Обозначив кратко функцию и100 как и1$, из (8.10) имеем
2)^^о(", г2, 8,, ^) = ииA)и1ВB)%(81, 52). (8.14)
Чтобы функция я1H A, 2) была антисимметричной относительно
перестановки полных наборов координат обоих электронов, спино-
спиновая функция % (в1г 52)Тдолжна быть антисимметричной относительно
перестановки ее аргументов 5Х н 5,. Таким образом, приходим к
формуле
=ы1вA)и1,B)|аA)РB)аB)РA)], (8.15)
■у/2
которая имеет в точности вид формулы (8.66), только теперь ^
обозначают спиновые волновые функциид" соответствующие двум
возможным проекциям спина (ть ^ 1/2 и /?г$ =--?— 1/2) на ось г.
В нулевом приближении энергия основного состояния вычис-
112
Системы тождественных частиц
ляется по формулам (8.12) и (8.13), в которых надо положить п1 =
= п2=1; таким образом, получаем
Е0^—1Чм1а0. (8.16)
Поправка первого порядка к нулевой энергии Ео. Поправку
первого порядка к энергии основного состояния можно вычислить,
если с помощью нулевой волновой функции (8.15) рассчитать сред-
среднее значение энергии взаимодействия е|,/г12, которой до сих пор
мы пренебрегали. Эту поправку первого порядка следует добавить
к нулевой энергии Ео.
Используя общую формулу C.10), получаем
г12
(8.17)
где г12 = |г2—гж |. Формальное обоснование использования фор-
формулы (8.17) для расчета поправки первого порядка к энергии Ео
будет дано в^гл.^П.
Как указано в табл. 7.1, имеет место формула
и подобная формула для и1$ B). Подставляя эти выражения для
одночастичных волновых функций в (8.17), приходим к следующей
формуле для поправки первого порядка к нулевой энергии:
Появившийся здесь определенный интеграл вычисляется элемен-
элементарно (см. задачу 8.3). В результате приходим к простой формуле
.4
АЕ —
так что
|) ^Г4У (8.19)
Энергия ионизации атома гелия (т. е. энергия, необходимая
для удаления'одного электрона из основного состояния атома на
бесконечность) равна разности энергии — 22е2Лг/2йё одноэлектрон-
113
Глава 8
ной системы, возникающей в результате ионизации атома гелия,
и начальной энергии (8.19):
А) "^B—г)- (8-20)
»' 2а0 У *)
2% а0
Сравнение энергий ионизации, рассчитанных по формуле (8.20),
с экспериментальными ее значениями для нескольких гелиоподоб-
ных атомов проводится в табл. 8.1.
Таблица 8.1
Экспериментальные Значения по формуле
Конфигурация значения энергии Еио„, эВ (8.20)
Не G = 2) 2-1,584 20,43
1,1+ G - 3) 75,0;« 71,52
Ве++ G ■= 4) 153,<)(И) 149,84
С4+ B 6) ,492,0 И 388,24
Как показывает сопоставление формул (8.20) и G.28), взаимо-
взаимодействие между двумя электронами можно учесть, заменяя заряд
атомного ядра Ъ на эффективный заряд \ 7.B. — 5/4). Это легко
понять, так как распределение заряда электрона 1 налагается на
распределение зарядов электрона 2 и атомного ядра. Поэтому вто-
второй электрон частично экранирует (т. е. уменьшает) эффективный
заряд атомного ядра, действующего на первый электрон. В точно-
точности такое же влияние на заряд ядра оказывает другой электрон.
Возбужденные состояния. Чтобы рассчитать энергию волно-
волновой функции первого возбужденного состояния атома гелия, нужно
поместить один электрон в основное состояние и18 (л = 1), а дру-
другой — в первое возбужденное состояние «25 (п = 2, I = 0).
Тогда можно образовать следующие четыре антисимметричные вол-
волновые функции из указанных пространственных и спиновых одно-
электронных волновых функций:
^ (8.21)
1
1
Т
1 .
—— [щ,
2
2
A)«
2) —ы18B)ыг4A)|[аA)РB)-;-аB)Р
2,B) — М2)ы«A)]аA)аB).
&B)-«иB)«25A)]РA)РB).
114
AI. (8-
(8.
(8.
22)
23)
24)
Системы тождественных частиц
Индексом 5 обозначена симметричная по пространственным ко-
координатам собственная функция, а индексом и — антисимметрич-
антисимметричные функции. Полные собственные функции (зависящие как от
пространственных, так и от спиновых координат), разумеется,
всегда антисимметричны относительно перестановки координат
частиц 1 и 2.
Состояние я]),.; называют синглетным, оно характеризуется ну-
нулевым значением полного спинового момента количества движения
E = 0). В этом состоянии спины обоих электронов антипарал-
лельны друг другу. Такое состояние называют еще парасоспюя-
нием. Для каждого из состояний я]за1, "фа2, я|)оз, которые называются
триплетными, квантовое число полного спинового момента коли-
количества движения равно единице (з = 1). Проекции полного спина
для указанных состояний на ось г соответственно равны т., = 0,
1 и — 1.
Таким образом, три рассматриваемые собственные функции от-
отличаются друг от друга только ориентацией вектора полного спи-
спинового момента количества движения относительно оси г. Для
каждого из рассматриваемых состояний спины обоих электронов
параллельны друг другу. Все указанные состояния вместе назы-
называются ортосостояниями.
Если в полном гамильтониане (8.8) пренебречь потенциальной
энергией взаимодействия е2м/г12, то состояния я|M, я|)а1, я|)а2, я|)о3
станут вырожденными. Энергия каждого из них тогда будет равна
^о ^г., + Я28, (8.25)
где
2а0п~
Энергию Е{1) в первом приближении можно получить, добав-
добавляя к энергии (8.25) поправку, аналогичную (8.17), учитывающую
межэлектронное взаимодействие. Фактически нужно вычислить
среднее значение полного гамильтониана (8.8) для функций нуле-
нулевого порядка (8.21) — (8.24). Для «парафункций» имеем формулу
Е\п - Я^я^г^гг, (8.26)
а для триплетных «ортофункций» — формулу
Е? - ,Г.|\|'о^М3г 1Й3г2. (8.27)
В результате несложных вычислений приходим к следующим
окончательным выражениям:
<1! + А, (8.28)
А-С^—А, (8.29)
115
Глава 8
в которых
О = |'К A) -^ и% B)^г/г2, (8.30)
е2
А = ГГыи (П «й B) — - «ь B) щ, A) 4 3г,А>- (8.31)
Как видим, энергия синглетного состояния превышает энергию
триплетных состояний на величину 2А. Это объясняется тем, что
функция % принимает максимальные значения при гх — г2, тогда
как функции %, напротив, при гг — г2 равны нулю. В состоянии,
описываемом функцией я1M, электроны расположены ближе друг
к другу, поэтому вклад от кулоновского отталкивания (е2м1гл^
для этого состояния имеет большую величину.
Задачи
1. Получите формулы (8.28) и (8.29).
2. Покажите, что квантовые числа проекции полного спинового момента
количества движения для трех триплетных состояний (8.22) — (8,24) со-
соответственно равны т$ = 0, 1 и — 1.
3. Вычислите определенный интеграл, входящий в правую часть формулы
(8.18).
4. Выпишите в явном виде детерминант для волновой функции трех элек-
электронов. Возьмите следующие три одночастичных собственных состояния:
и1\ 1/2), и2 I — 1/2) и и2 I '/2), где ± 1/2 обозначают проекции спина те
на ось г, а щ — пространственные волновые функции.
5. Рассмотрите систему N электронов, заключенных в ящике объемом V,
ограниченном бесконечными потенциальными барьерами.
а. Найдите значение энергии самого высокого занятого одноэлектрон-
ного состояния, т. е. энергию Ферми при Т = 0 К-
б. Получите выражение для полной минимальной энергии системы, под-
подчиняющейся принципу Паули.
в. Вычислите значения энергии по формулам, которые вы получите в
п. «а» и «б», полагая, что /V = 1022, V = 1 см3.
Указание. Если электрон находится в ящике объемом V = а-Ь-с, то
энергетические собственные функции электрона имеют вид
Щгп СС51П / / X 1 51П И у 151П 1п 2 1,
где /, г, п — три произвольных целых числа. Собственные числа энергии
состояний равны
Приведенные функции ицп удовлетворяют уравнению Шредингера для
свободного электрона и обращаются в нуль на непроницаемых стенках
ящика. Подробно об этом рассказано в § 15.5.
ГЛАВА 9
МАТРИЧНАЯ ФОРМУЛИРОВКА КВАНТОВОЙ МЕХАНИКИ
В гл. 6 и 7 мы решили несколько конкретных задач на стацио-
стационарное уравнение Шредингера и нашли собственные числа энергии
(разрешенные энергии) и соответствующие энергетические собст-
собственные функции. В настоящей главе мы покажем, как решать по-
подобные задачи н находить собственные числа и собственные функ-
функции, используя матричный метод.
Два основных подхода квантовой механики — метод дифферен-
дифференциального уравнения Шредингера и матричный метод Гейзенберга
[20 ] — формально эквивалентны и часто используются одновре-
одновременно.
Прежде чем приступить непосредственно к изложению матрич-
матричной формулировки квантовой механики, кратко напомним основы
математической теории матриц.
§ 9.1. Основы алгебры матриц
Мы считаем, что читатель уже знаком с основными определе-
определениями и основными операциями матричного исчисления. Поэтому
наш обзор основ матричной алгебры будет кратким.
Элемент Ы, матрицы АВ, являющейся произведением матриц
А и В, вычисляется по формуле
(АВ)а -^АьпВга, (9.1)
т
так что, например,
(АВС)к1 = ЕЕ АктВ1?1ПСп1-
т п
Единичная матрица. Единичной называется такая квадратная
матрица /, произведение которой с любой другой квадратной мат-
матрицей той же размерности дает ту же самую матрицу, т. е.
В1 ^В, 1В~В. (9.2)
Отсюда следует, что /м = 6И, где би — символ Кронекера, рав-
равный 1 при к = I и равный 0 при к -ф I.
Обратная матрица. Обратной матрицей В~1 для квадратной
матрицы В называется такая матрица, которая, будучи умножен-
умноженной на эту матрицу, дает единичную матрицу; иначе говоря, для
117
Глава 9
любой матрицы В, для которой существует обратная матрица,
имеем соотношения
В^В^ВВ-1 I. (9.3)
Обратная матрица произведения матриц равна произведению
обратных матриц, взятых в обратном порядке:
(АВ)-1 =В~1А-1. (9.4)
Элементы обратной матрицы А~г вычисляются по правилу
/ л—1\ Алгебраическое дополнение Ац, ,„ -.
(■Д )ы — : (У • о)
Детерминант Л
Обратите внимание на обратный порядок индексов к и / в правой
части формулы (9.5).
Эрмитово сопряжение матриц. Эрмитовы матрицы. Эрмитово
сопряженной для матрицы А матрицей, обозначаемой Л+ , назы-
называется такая матрица, элементы которой вычисляются по правилу
(А*)ы--=Аш. (9.6)
где звездочка обозначает обычное комплексное сопряжение.
Матрица называется эрмитовой, когда эрмитово сопряженная
ей матрица совпадает с ней самой, т. е. когда
Л+^Л. (9.7)
Используя (9.6), равенство (9.7) можно записать как равенство
матричных элементов:
Аы--Ак. (9.8)
Для эрмитовой матрицы операции транспонирования (пере-
(перестановки столбцов со строками) эквивалентна взятию комплекс-
комплексного сопряжения (вместо каждого элемента берется комплексно-
сопряженная величина). Эрмитовыми, следовательно, могут быть
только квадратные матрицы.
Из (9.8) непосредственно следует, в частности, что матричные
элементы Акк эрмитовой матрицы, лежащие на ее главной диаго-
диагонали, являются действительными числами.
Унитарные матрицы. Унитарной называется квадратная мат-
матрица, для которой эрмитово сопряженная ей матрица равна обрат-
обратной матрице, т. е.
А*---А-1. (9.9)
Из (9.9) непосредственно следует, что для любой унитарной
матрицы А выполняется соотношение АА^ = /. Для матричных
элементов унитарной матрицы имеем соотношение
{АА%1 = 2 АкпА1г = ^ АкпА)п =бы. (9.10)
п п
При преобразовании мы использовали формулу (9.6).
118
Матричная формулировка квантовой механики
§ 9.2. Преобразования квадратных матриц
Матрица А', полученная из квадратной матрицы А с помощью
операции
Л' 5Л5-1, (9.11)
называется преобразованной матрицей А; квадратная матрица 5
задает преобразование.
Матричные равенства инвариантны относительно любого пре-
преобразования входящих в них матриц. Например, возьмем типич-
типичное матричное равенство, содержащее сумму и произведения мат-
матриц:
АВ + СЛЕ Р.
С помощью матрицы 5 это равенство можно преобразовать следую-
следующим образом:
так как 5-15 = /. Согласно (9.11), полученное матричное равен-
равенство можно записать в виде следующего равенства для преобразо-
преобразованных матриц:
А'В'\СВ'Е' -Р'. (9.12)
Оно имеет в точности такой же вид, как и равенство (9.11) для ис-
исходных матриц.
§ 9.3. Диагонализация квадратной матрицы
Особенно интересно такое преобразование исходной матрицы А',
для которого преобразованная матрица А имеет диагональный вид,
т. е. все недиагональные матричные элементы преобразованной
матрицы А равны нулю.
Ниже в § 9.6 мы объясним, каким образом в матричной форму-
формулировке квантовой механики диагональные элементы Акк преобра-
преобразованной диагональной матрицы А и матричные элементы 8Ы мат-
матрицы преобразования 5 связаны с решениями стационарного урав-
уравнения Шредингера или вообще любого другого уравнения на оты-
отыскание собственных чисел и собственных функций.
Итак, предположим, что преобразованная матрица А диаго-
нальна. Неизвестные нам пока диагональные матричные элементы
матрицы А обозначим Акк = Ак, так что
Умножая справа на матрицу 5 матричное соотношение
'З = Л, получаем соотношение
8А' ~А8.
119
Глава 9
Вычислив матричный элемент к1 для этого соотношения, полу-
получим следующие равенства:
Считая, что рассматриваемые квадратные матрицы являются
матрицами N >: N. т. е. имеют размерность М, получим из (9.13)
для каждого фиксированного значения к алгебраическую систему N
линейных однородных уравнений относительно неизвестных
5А1 8км (необходимо для каждого фиксированного значе-
значения индекса к заставить индекс / пробегать значения от 1 до М).
Указанная алгебраическая система линейных однородных уравне-
уравнений имеет нетривиальные решения в том и только том случае, когда
детерминант матрицы, составленный из коэффициентов этой ал-
алгебраической системы, обращается в нуль, т. е. когда
ЩАт1^Акдш\^0. (9.14)
Разрешая это алгебраическое уравнение степени N (которое
имеет N корней Ак при к = 1, . . . , Ы), получаем N диагональных
элементов искомой диагональной матрицы А. Эти диагональные
элементы Аг Аи называются собственными числами исход-
исходной матрицы А'. '■
Р- После решения уравнения (9.14) элементы E&п матрицы преоб-
преобразования можно найти следующим образом. Каждое найденное
собственное число Ак надо подставить обратно в алгебраическую
систему уравнений (9.13). Получающуюся при этом однородную
алгебраическую систему линейных однородных" уравнений следует
разрешить и найти из нее величины 5/е1, 5/г2, • • • , 5;гЛг, которые,
однако, определяются таким образом только с точностью до умно-
умножения их всех на один и тот же произвольный множитель. Так сле-
следует поступить с каждым из N корней Ак; в результате мы построим
всю матрицу Зьт- Произвольные множители, появляющиеся при
решении однородных систем уравнений, следует фиксировать, по-
потребовав, чтобы матрица 5 была унитарной 1), т. е. потребовав,
согласно § 9.4, чтобы выполнялись соотношения (9.10):
') В § 9-3 исходная матрица А' неявно предполгиаотся эршггоиой.—
Прим. перев.
120
Матричная формулировка квантовой механики
§ 9.4. Представление операторов
физических величин матрицами
В матричной формулировке квантовой механики оператору А
произвольной физической величины при фиксировании произволь-
произвольного полного набора ортонормированных функций ит (г), или,
как говорят, представления, сопоставляется матрица А, произ-
произвольный элемент кт которой вычисляется по формуле
\п^П(ик\А \ит). (9.15)
Будем считать, что переменная г в (9.15) обозначает здесь не только
координаты частицы, но также и ее спиновую координату. Соот-
Соответственно интегрирование по <Рг обозначает как интегрирование
по пространственным переменным, так и суммирование по спино-
спиновой координате.
Подчеркнем, что представление оператора А матрицей А за-
зависит от выбора произвольного набора ортонормированных функ-
функций ит (г), а потому не единственно. Оператор А, кроме рассмат-
рассматриваемого, может иметь и другие представления.
Выбрав другой полный набор ортонормированных функций
ьп (г), получим еще одно представление, например А', оператора А.
В этом случае имеем равенства
Представим теперь оператор А, используя в качестве базисного
набора его собственные функции г|)„ (которые удовлетворяют урав-
уравнению Лг|)„ = Л„г|)„). Матрица, соответствующая этому набору
функций, диагональна, причем ее диагональными элементами яв-
являются собственные числа рассматриваемого оператора. Действи-
Действительно, имеем равенства
№Мт*г = Ая6ят. (9.166)
Матрица преобразования. Функции набора уп можно разложить
по функциям набора ик:
При написании второго равенства в (9.17) мы воспользовались фор-
формулой B.37а). Обратное разложение функций ик по функциям у„
имеет вид
:«*>
Следовательно,
121
Глава 9
Величины 5Й„ можно рассматривать как элементы некоторой
матрицы 5. Эту матрицу назовем матрицей преобразования, пере-
переводящего набор функций ьп в набор функций ик.
Определенная формулами (9.19) матрица 5 является унитарной
матрицей. Докажем это. Покажем, что, действительно, 55+ = /,
где / — единичная матрица. В самом деле,
155+ \ы .=-■= 2^ 8кп 5^ .-= ^ 5Ая5*„ --- ^ (ик | с„> Ф„ \ Щ) =•- (ик! щ) Л,,,.
п п т
При преобразованиях мы воспользовались формулой B.376):
§ 9.5. Преобразования матриц оператора
данной физической величины
В предыдущем параграфе мы рассмотрели два произвольных
матричных представления оператора А (одно с использованием
набора функций Vп и другое — набора функций и„):
= Е «*„»„•
Матрицу А можно построить, исходя из матрицы А', н наоборот,
если воспользоваться преобразованием матриц:
А 8А8~1 8А8*,
А'--^8*А8, (9.21)
где 5 — унитарная матрица преобразования, определенная фор-
формулой (9.19).
Чтобы доказать первую формулу (9.21), необходимо в первую
формулу (9.20) вместо функций ы* и щ подставить их разложе-
разложения (9.18):
Ак1 ^ | и;Аи^г у , ^ «, А % ^ ^Зг ^
Если матрица А' эрмитова, то эрмитова и матрица А. Другими
словами, матрицы сохраняют свою эрлштовость при унитарном
преобразовании. Чтобы это доказать, необходимо убедиться в спра-
122
Матричная формулировка квантовой механики
ведливости равенства Аы = Ац, для матрицы А, которая опреде-
определяется первой формулой (9.21). Имеем очевидные соотношения:
где мы воспользовались определением эрмитовой матрицы, поло-
положив А'тп = (А'т1)*. Беря комплексное сопряжение последнего ра-
равенства и меняя в нем индексы т и п, получаем
т. е., согласно (9.8), приходим к выводу, что матрица А действи-
действительно эрмитова.
Укажем важное следствие, непосредственно вытекающее из
полученного результата. Собственные числа эрмитовой матрицы
являются'действительными числами. Действительно, при любом
унитарном преобразовании эрмитовой матрицы получается эрми-
эрмитова матрица, элементы которой должны удовлетворять соотноше-
соотношению (9.8), а потому ее диагональные элементы должны быть дейст-
действительными числами. Это утверждение относится равным образом
и к диагональной эрмитовой матрице, диагональные элементы ко-
которой являются ее собственными числами.
Другое важное следствие, которым мы воспользуемся в настоя-
настоящей главе, состоит в следующем. Эрмитовы матрицы, получаю-
получающиеся друг из друга унитарным преобразованием, имеют одинако-
одинаковые собственные числа.
§ 9.6. Отыскание собственных функций
и собственных чисел оператора физической величины
с использованием матричного метода
Процедура отыскания собственных функций и собственных чи-
чисел эрмитова оператора А произвольной физической величины
сводится к решению дифференциального уравнения
Аи„~А„и„. (9.22)
Функции и„ называются собственными функциями оператора А,
действительные числа А„ — его собственными числами.
В качестве примера задачи на отыскание собственных чисел
и собственных функций, которую мы уже решили, упомянем за-
задачу E.8). Собственные функции ип дифференциального уравнения
E.8) даются формулой E.29), а собственные числа, согласно
E.16),— формулой Е„ — й<а (п -4- 1/2). Другой пример—за-
пример—задача F.37) на отыскание собственных функций и собственных чи-
123
Глава 9
сел оператора!2. Собственными функциями этого оператора являются
функции УР F, гр), а его собственные числа равны НН (I '- 1).
Они находятся из решения дифференциального уравнения
РуТ(е, ф)=--й2/(/-ь1)кГ(е, ф). (9,23)
Задачу на отыскание собственных функций и собственных чи-
чисел эрмитова оператора А любой физической величины можно
решить и иначе, а именно* матричным методом.
Будем исходить из представления оператора А матрицей А',
задаваемого с помощью некоторого полного ортонормированного,
а в остальном произвольного набора функций юк (г). Матричные
элементы матрицы А' следует вычислять по формуле
Аы=\ г^Л^сРг.
Диагонализуя матрицу А' с использованием метода, описанного
в § 9.3, построим диагональную матрицу
А=--8А'8~\
диагональные элементы которой, согласно формуле (9.166) и § 9.5,
как раз и являются искомыми собственными числами оператора А.
В результате описанной в § 9.3 процедуры диагонализации мы най-
найдем также и матрицу 5, которая преобразует матрицу А' в матрицу
А. Согласно (9.18), матричные элементы матрицы 5 можно исполь-
использовать для вычисления собственных функций щ оператора А'
по формулам
и, -= V 5Г V .
п
Функции ик действительно будут собственными функциями опера-
оператора А, поскольку матричное представление Ак, = ] щАщсРг
диагонально.
Описанную процедуру отыскания собственных функции и соб-
собственных чисел эрмитова оператора произвольной физической ве-
величины часто используют в атомной физике и атомной спектроско-
спектроскопии, поскольку она очень удобна для применения численных ме-
методов расчета на современных ЭВМ.
§ 9.7. Матричные элементы матриц операторов
момента количества движения
В качестве иллюстрации применения идей, изложенных выше,
вычислим матричные элементы для операторов момента количества
движения. Они необходимы для проведения важной квантовомеха-
нической процедуры сложения моментов количества движения,
в частности для сложения орбитального и спинового магнитных
моментов частицы.
124
Матричная формулировка квантовой механики
Пусть 5 обозначает векторный оператор момента количества
движения некоторой физической системы. Определим так называе-
называемые «поднимающий» и «опускающий» операторы ^+ и ^~ форму-
формулами г)
/ 1хиу, Зу = -^-{)+—)-), (9.24)
так что /+ = (/~)+. Эти операторы удовлетворяют следующим
перестановочным соотношениям:
[/=*=, /2] = +/г/±, []2, /±] = 0, [[/+, /~] = 2й/г. (9.25)
Эти соотношения легко вывести, используя формулы F.46) —
F.48). Так, например, первое перестановочное соотношение (9.25)
доказывается следующим образом:
[■/*, /*]=[ Ох ± и у), /«]=[/„ /*] ±»О у. У Л=
Установим теперь результат действия операторов У± на одно"
временные собственные функции V1!1 (Э, ф)^операторов Р и Уг.
Очевидно, имеем формулы
при написании которых мы воспользовались равенством /гУ/1 =';
= НтУ1/1 и первым перестановочным соотношением (9.25). Согласно
последней формуле, функции )±У'Р являются собственными функ-
функциями оператора Зг с собственными числами Н (т+1). Тем самым
мы доказали, что указанные функции должны быть пропорцио-
пропорциональны функциям К^-1'. Таким образом, можно написать
(в, Ф) = КСйУ7±' F. Ф). (9- 26)
где Ст — некоторые константы, подлежащие определению.
Рассмотрим теперь матричные элементы операторов З2, Уг и У*
для набора функций V? (Э, ф). Используя формулы F.37) и (9.26),
х) В этом параграфе мы обозначаем операторы момента количества дви-
движения прописными, а не строчными буквами, как в гл. 6. Этим мы хотим
подчеркнуть, что наши рассуждения применимы к любой системе частиц, а
не только к системе, составленной из одной частицы.
125
Глава 9
получаем следующие формулы для указанных матричных элемен-
элементов:
я 2п
об
6/, /'«т. т-,
'»г!/ш, /'т' "П/ЛО/, /'От, т',
+ЙСт, (9.27)
(О/т; /, яг+1
Последние две формулы для операторов У* написаны на основании
формулы (9.26). Доказательство соотношения С~+1 = (С%) * пре-
предоставляем читателю (задача 8 в конце настоящей главы).
Чтобы найти теперь выражения для констант Ст, вычислим
т-й диагональный элемент третьего перестановочного соотноше-
соотношения (9.25):
(/+/-_ /-/+)„. ,„ -= 2Й (J)т. т =• 2Н2т,
где мы опустили индексы / в обозначениях матричных элементов,
так как, согласно формулам (9.27), матричные элементы всех опе-
операторов момента количества движения между состояниями с раз-
различными / равны нулю. Поэтому во всех формулах, приводимых
ниже, индекс /, имеющий постоянное значение, не выписывается
хотя и подразумевается. Раскрывая матричный элемент, стоящий
в левой части последней формулы, получаем
/ . \^т, т' » т', т •!т, т' »т', т) — " т, т—1 » т—1, т~Т
т'
— Гт, т+1 /++,. т - 2Н2т, (9.28)
так что с использованием двух последних формул (9.27) оконча-
окончательно имеем следующее соотношение:
которое, очевидно, можно записать иначе:
|Ст-.|2-|Ст|2 = 2т. (9.29)
Чтобы найти величины | Ст|2, используем операторное соотно-
соотношение
(/ + ) (9.30)
и вычислим для него т-й диагональный элемент для обеих сторон
равенства.
126
Матричная формулировка квантовой механики
Матричные элементы для операторов З2 и )? находятся непо-
непосредственно по формулам (9.27), так что в результате получаем
формулу
2* т'
йV и± /,2(Ст_,С;_, -!- С;пСт). (9.31)
Комбинируя (9.31) и (9.29), находим
где предполагается, что произвольные фазовые множители у вол-
волновых функций У? выбраны таким образом, чтобы определяемы6
формулами (9.27) величины Ст были действительными положитель-
положительными числами. Подставляя найденные значения величин Ст в
(9.26), приходим к важным формулам
—ЗТГ\ ут+'
„_ т ,^ '^_ 'т_{ (9.32)
или к формулам
0~Iпк I. т+1 = 0+\, т+1; /т -= А I Щ+1) — т(т + 1), (9.33)
которые мы и хотели вывести.
Используя формулы (9.27) и (9.33), можно построить любые
матрицы, соответствующие операторам момента количества движе-
движения, в пространстве функций Кт (Э, ср). Поскольку матричные эле-
элементы между функциями с различными / обращаются в нуль,
можно ограничиться рассмотрением «субматриц», соответствую-
соответствующих многообразиям с постоянным индексом /. (Термин многообра-
многообразие используется, чтобы характеризовать различные подпростран-
подпространства, составленные из 2/ -г 1 собственных функций У^1 (Э, ср)
с фиксированным индексом / и с индексом т, пробегающим цело-
целочисленные значения, заключенные в интервале — / ^ пг < /).
Рассмотрим, например, случай / — 1. В этом случае имеем следую-
следующие матрицы 3 У 3:
т 1 0-1
(9.34)
1
0
0
0
0
0
0
0
-1
127
^ =
Глава
1
2/г2
1
0
0
1
уТй
0
0
0
1
1~А
0
1
0
1
й
0
1
0
1
й
/
0
1
0
9
0
0
1
0
0
1
0
0
0
0
0
1
0
1
0
1
0
1
1)
1
_1
0
0
1
_1
0
1
0
1
0
0
0
— 1
0
1
0
— 1
0
— 1
0
(9.35)
(9.36)
(9.37)
(9.38)
(9.39)
Три собственные функции У\, У°и У{ ' можно представить в
виде следующих матриц-столбцов:
(9.40)
1
О
О
О
1
О
. УТ1^-
0
О
1
128
Матричная формулировка квантовой механики
Уравнение
в виде
ЗгУ
п
1
1
0
0
— —
0
0
0
0
0
1
0
0
1
= —П
0
0
1
— — й У\ , например, теперь записывается
(9.41)
Как видим, уравнения F.37) для собственных функций и собствен-
собственных чисел операторов I2 и 1г удовлетворяются, если в этих уравне-
уравнениях операторы заменить на матрицы (9.34) — (9.38), а собствен-
собственные функции — на матрицы-столбцы (9.40).
§ 9.8. Спиновый момент количества движения
Развивая математическую теорию операторов момента количе-
количества движения и их собственных функций, мы исходили до сих пор
из дифференциальных уравнений задачи F.37) на отыскание собст-
собственных функций и собственных чисел:
(е, ф) А2/(Л-1)УГ(е, Ф;>,
Так как операторы момента количества движения были опреде-
определены формулами, содержащими производные по пространственным
координатам 6, ср, решения УТ F, ф) могли быть только однознач-
однозначными функциями, задаваемыми в обычном трехмерном простран-
пространстве. Это обстоятельство, как было показано в § 6.2, приводит
к тому, что квантовые числа гп и / принимают только целочислен-
целочисленные значения.
Если же теперь в качестве исходного пункта математической
теории операторов момента количества движения взять перестано-
перестановочные соотношения F.49):
[С, Ь]---1ЙЬ,
то указанные ограничения на значения квантовых чисел т и /
больше не будут иметь места.
Именно так обстоит дело для частицы, имеющей помимо орби-
орбитального момента количества движения I. = [г-р] и собственный
момент количества движения, который не затрагивает пространст-
пространственных координат частиц. Операторы этого момента количества
движения коммутируют с любым гамильтонианом, который содер-
содержит только переменные г и р, а потому они будут интегралами
движения любого такого гамильтониана. Такой собственный
«внутренний» момент количества движения, обозначаемый 8, на-
называют спиновым, чтобы отличить его от орбитального момента
количества движения Ь. Экспериментально установлено, "что- как
Заказ № №3
129
Глава 9
спин электрона, так и спин протона равен половине (я = 1/2), сле-
следовательно, их проекции равны /и5 = ± 1/2 (принимают только
по два значения).
В теории спинового момента количества движения с самого на-
начала выставляется требование, чтобы его отдельные операторы
удовлетворяли перестановочным соотношениям F.49). Поэтому
процедура вычисления матриц для операторов спинового момента
идентична описанной в предыдущем параграфе процедуре построе-
построения матриц для операторов орбитального момента количества дви-
движения. Следует только учесть, что спиновое квантовое число 5
может принимать не только целые, но также и полуцелые число-
числовые значения.
Таким образом, полные собственные функции, описывающие
состояния частицы, зависят от координат частицы г и от коорди-
координаты, которая является проекцией спинового момента количества
движения частицы на произвольно направленную ось г:
4> = 1>(г, е, Ф, 5г).
Оператор полного момента количества движения частицы равен
сумме операторов орбитального и спинового моментов количества
движения:
]^Ь+8. (9.42)
Можно теперь воспользоваться описанным в § 9.7 матричным
формализмом и представить операторы спинового момента коли-
количества движения частицы и их собственные функции соответствую-
соответствующими квадратными матрицами и матрицами-столбцами. Собствен-
Собственные функции записываются следующими столбцами:
т, =-- -
(9 43)
а операторы — следующими квадратными матрицами:
(9.44)
Три квадратные матрицы (9.44) (с опущенным множителем /г/2)
130
Матричная формулировка квантовой механики
называются матрицами Паули и обозначаются соответственно сим-
символами ах, оу и а2, так что матрицы спиновых моментов количества
движения даются формулами
1 1 1
х-~ 2 х, у~~ 2 "' г~~ 2 г"
Операторы 5* = 5* ± [§у предстаапяются следующими матри-
матрицами:
5+ ,--П
5- --- П
(9.45)
Обратите внимание на то, что операторы 5Х, 5,;, 5г эрмитовы, а
операторы 5
и 5 таковыми не являются [поскольку
§ 9.9. Сложение моментов количества движения
Рассмотрим две независимые квантовые системы с квантовыми
числами их полных моментов количества движения, соответственно
равными ]\ и /2. Наборы операторов, описывающих эти две различ-
различные системы, коммутируют друг с другом. Обозначим символами
а'-'1 и ру/ собственные функции соответственно операторов З'и 3 ъ
И
31,
Рассмотрим теперь собственные функции комбинированной си-
системы, составленной из двух указанных квантовых систем, зада-
задаваемые произведениями функций «/,''Э/?2- При заданных значениях
квантовых чисел ]г и /2 всего имеется B]\ + 1) B/2 + 1) таких соб-
собственных функций. Указанные комбинированные собственные функ-
функции являются одновременными собственными функциями операто-
операторов З'и 31, Iг и /2г.
Рассмотрим еще набор собственных функций я])/1 нашей комби-
комбинированной квантовой системы, составленной из двух независи-
независимых систем, для которых матрицы операторов 3?, 31, Р, }г диаго-
нальны.
Оператор ^ определяется* как сумма операторов ^ г и 12:
3-3н-32. (9.46)
Собственные числа операторов З2 и ]г, согласно основным посту-
постулатам квантовой механики, дают возможные экспериментальные
131
Глава 9
значения квадрата полного момента количества движения 3 =
= 3! + 3 2 комбинированной системы и его г-компоненты 1 г.
Поскольку на два вышеуказанных набора собственных функ-
функций «натянуто» одно и то же пространство и поскольку каждый на-
набор состоит из ортиормированных функций, оба набора собствен-
собственных функций должны быть связаны друг с другом некоторым уни-
унитарным преобразованием.
Найдем формулы этого преобразования, или, другими словами,
произведем квантовомеханическое сложение моментов количества
движения обеих систем.
Собственные функции яр™ операторов "з], У-2, З2, Уг, таким об-
образом, можно представить в виде линейных комбинаций функций
^Т = И И (л4т1т2! Л/У™) аТ1 Р'Г- (9*47)
в которых (/]/2т1т21/1/2/'") обозначают коэффициенты разложе-
разложения. Согласно (9.20), эти коэффициенты можно рассматривать
как элементы унитарной матрицы преобразования от набора функ-
функций яр™ к набору функций ат'Рт% Очевидно, что в правую часть
разложения (9.47) входят только такие функции а^'Р/"-, Для
которых т1 -г /л2 = т. В этом легко убедиться, если подейство-
подействовать на правую и левую части (9.47) оператором 3г = 3 Хг + /2г-
Таким образом, разложение (9.47) можно также представить в сле-
следующем виде:
Укажем еще на одно свойство коэффициентов разложения, вхо-
входящих в формулу (9.47). Оно состоит в том, что
(Щ/21Л/2 (/. + 4) (/, + /2) ) = 1, (9- 49)
так как
гЫ1+/2 = а/1р'2 (9.50)
Действительно, из формулы (9.48) непосредственно видно, что
при т = /п^ + т2 = /г + /2 в разложении (9.48) имеется только
одно слагаемое 1).
х) При этом тг может принимать только одно значение, ибо должны
одновременно выполняться два неравенства тг <; /], т2 = т—т1 — 1г +
+ /2—т1 ^ /2 (а следовательно, два неравенства тг <; )и т1 ~^ /]), из
которых заключаем, что т1 = /V— Прим. перев.
132
Матричная формулировка квантовой механики
Итак, при фиксированных ]\ и /2 максимальное значение собст-
собственного числа /, очевидно, равно ]г + /2, причем каждому значе-
значению / соответствует 2/ + 1 собственных функций, нумеруемых
целым или полуцелым числом т из интервала — / ^ т ^ / в за-
зависимости от того, целое или полуцелое число /. При фиксирован-
фиксированных ]\ и /2 число всех собственных функций я]?/1 должно равняться
числу собственных функций а™'|3™2, т. е. равняться числу
B/1+1) B/2-г 1); отсюда получаем, что наименьшее значение, кото-
которое может принимать собственное число /, равно \]\—/2|. Дейст-
вительно, в этом легко убедиться, так как
X ) = BД+1)B/2-М).
! = I 1,-11 I
Коэффициенты разложения, появившиеся в формуле (9.47), на-
называются коэффициентами Клебша—Гордана. В книге Кондона
и Шортли [21 ] приведены таблицы значений этих коэффициентов
для некоторых значений /х и /2.
Собственные функции операторов 3], з\, З2 и )г (где 3 =
= 3! + 12) в простейших случаях легко построить, используя в ка-
качестве исходной функцию (9.50). Например, произведем сложение
моментов количества движения двух систем с ]\ = /2 = 1. Нам
необходимо построить 3-3 = 9 функций я]з™. В качестве исходной
возьмем функцию
1Ц = «}Р1. (9.51)
Применим к обеим частям (9.51) оператор )~~ = /Г "'г У^- Исполь-
Используя (9.32), получим тогда, например, что
- 244 = V 2~ (а%\ + а|р?), (9.52)
Аналогично строятся остальные функции гр§, я|>2 ', %2, соответст-
соответствующие / = 2. Функцию я|)! можно найти, замечая, что, согласно
формуле (9.48),
чЬ1 — /1/-уОК1 I 11Гу1Ки /О с;4Л
Ш — ШХтр "| с/СС .р \^« ^ /
где аи () — числа, которые необходимо определить. Требуя, чтобы
величина (я|)| | я|)',) равнялась единице и предполагая, что а и Ъ —
действительные числа, получаем соотношение
а2 + ^-1. (9.55)
|)|
Из условия, что величина <я|)| | -ф^> должна быть равна нулю, полу-
получаем еще одно соотношение
а + Ь^-0. (9.56)
133
Гяааа 9
Системе двух уравнений (9.59) и (9.56) удовлетворяют числа
причем надо взять либо верхние, либо нижние знаки. Беря (произ-
(произвольно) верхние знаки в (9.57), получаем
Действуя на функцию я])]1 оператором У~ ~ /Г + Уг". построим
две оставшиеся функции я]з° и -ф^1. Аналогично построим последнюю
оставшуюся функцию я]$.
Задачи
1. Известно, что произвольную функцию / можно разложить по двум произ-
произвольным полным наборам функций %)п и ип:
Известны коэффициенты разложения функций %)п по функциям щ:
"п = Е 8кпик-
к
Очевидно, что интеграл $ [*[(Рг не должен зависеть от того, с помощью
какого разложения по наборам функций {юп или ип) он вычисляется. Дока-
Докажите, что унитарность матрицы 5 вытекает из этого требования.
2. Докажите, что след квадратной матрицы А, определяемый формулой
5р А ,_- ^ Акк,
к
инвариантен относительно любого унитарного преобразования этой мат-
матрицы, т. е. убедитесь, что
5рЛ =^5
где 5 — любая унитарная матрица.
3. Докажите, что (АВ)'( = В'Ы'Г.
4. Докажите, что из условия Ак1= $ ю^Ау^г ~ А[к, в котором Vп —
какой-нибудь набор ортонормированных функций, следует эрмнтовость
оператора А.
5. Докажите, что матрица произведения операторов равна произведению
матриц этих операторов.
в. Проверьте справедливость утверждения из задачи 5 на примере матрич-
матричных элементов оператора х2:
Они были вычислены в задаче 1 из гл. 5.
7. Докажите, что любые две матрицы коммутируют, если существует неко-
некоторое преобразование, которое одновременно приводит эти матрицы к
диагональному виду, и что это условие является необходимом и доста-
достаточным.
134
Матричная формулировка квантовой механики
8. Докажите, что С^ц_, = (С+)*, где С~+1 и С+ — константы, определя-
определяемые формулами (9.27).
9. Докажите, что функция (\/-у/2) (аРф\—а1^) является собственной функ-
функцией оператора З2, где 3 = Зг -у- Л2.
Чему равно соответствующее этой функции собственное число указан-
указанного оператора?
10. Постройте набор собственных функций ф"? для /^ = 1/2 и /2 = 1, ис-
используя описанную в § 9.9 процедуру сложения двух моментов количества
движения.
11. Покажите, что в случае спина, равного 1/2 ($ = 1/2),
ЬхЬу -г 5(/5л; -■= 0.
12. Убедитесь, что собственные векторы (9.40) ортогональны друг к дру-
другу и нормированы на единицу. Используя матричное представление,
убедитесь, что они являются собственными функциями оператора Л2.
13. а. Докажите, что для состояния ф5> определяемого формулой (8.21),
квантовое число 5 спинового момента количества движения равно нулю,
б. Докажите, что для состояний фа1> фаз и фа8, даваемых формулами
(8.22) —(8.24), квантовое число спинового момента количества движения
равно единице, т. е. 5 = 1, а квантовое число проекции спина т8 — 0, 1
и — 1 соответственно. (Спиновые квантовые числа 5 и твопределяются
соотношениями
В КОТОРЫХ 5 = 5! + $2.)
14. Докажите формулу (9.21), используя дираковские обозначения. (На-
(Напомним, что 2 I щК1'п I = I•)
ГЛАВА 10
ПОЛНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
До сих пор мы рассматривали только такие квантовомеханиче-
ские задачи, в которых основные величины, характеризующие ча-
частицу, а именно энергия или волновая функция -ф (х), не зависели
от времени. Собственные функции частицы с энергиями Еп мы на-
находили из решения стационарного уравнения Шредингера
( --^ V2 + У (•")) ип (г) - Е,:ип (г). A0.1)
Так, мы убедились, в частности в § 2.2, что для свободной частицы
[т. е. при V (г) = 0 ] решениями стационарного уравнения Шре-
Шредингера A0.1) [см. B.6)] являются функции вида
и (г, р)-Се1<рг)Т\ A0.2)
где С — произвольные постоянные.
Кроме того, мы узнали также, что для объяснения результатов
некоторых важных экспериментов, например, по дифракции элек-
электронов на кристаллах, необходимо использовать зависящие от
времени волновые функции [см. A.20I, которые соответствуют
реальным волнам:
ф(г, 0 = Се'<р-г):П-шл. A0.3)
Таким образом, стационарное уравнение Шредингера не в со-
состоянии объяснить весь имеющийся экспериментальный материал.
Поэтому необходимо его обобщить таким образом, чтобы оно опи-
описывало бы также и временные эффекты.
Угадать вид нового уравнения Шредингера нетрудно. Заметим,
что функция A0.3) удовлетворяет следующему уравнению:
~^ЬУ*+У{Г' 1))^{Г' /) = 1'А-|-*<г' '), (Ю.4)
или уравнению
Ж(г, »Ау, /I>(г, /) = ---=»А-|-ф(г, О- (Ю.5)
Получаем как раз искомое дифференциальное уравнение, которое
называется полным уравнением Шредингера. Правомерность исполь-
использования последнего подтверждается следующими соображениями.
Когда гамильтониан в A0.5) явно не зависит от времени, из пол-
полного уравнения Шредингера получаются все результаты, которые
136
Полное уравнение Шредингера
следуют из стационарного уравнения Шредингера. б. Теория, ос-
основанная на полном уравнении Шредингера A0.5), прекрасно
согласуется с экспериментом, в. В пределе, когда постоянная
Планка Ь. стремится к нулю, теория согласуется с результатами
классической физики.
Непосредственной подстановкой легко убедиться, что в частном
случае, когда гамильтониан Ш не зависит явно от времени, общее
решение уравнения A0.5) имеет вид
яK(г, о=1ад.(г)г^й. (Ю.6)
п
где ип — собственные функции гамильтониана Ж, соответствую-
соответствующие энергиям Еп. Они находятся из решения соответствующего
стационарного уравнения Шредингера
Жип{г)^Епип[(г). A0.7)
Подчеркнем, что коэффициенты а;1 в разложении A0.6) не за-
зависят от времени.
Вероятность Рп найти квантовую систему в момент времени I
в состоянии ип с энергией Еп равна
§ 10.1. Вероятностная интерпретация
временной волновой функции
Рассмотрим физическую интерпретацию зависящей от времени
волновой функции г|з (г, г). Она совершенно аналогична интерпре-
интерпретации не зависящей от времени волновой функции ■ф (г) (см. § 3.1).
Теперь, однако, надо рассмотреть вероятность Р (г, I) найти ча-
частицу внутри бесконечно малого объема й3г в любой данный момент
времени I. Постулируем, что эта вероятность равна
Р.(г, 0 = 1 ЧЧг
Поскольку вероятность найти частицу вообще в каком-то месте
в пространстве в момент времени I равна единице, должно, оче-
очевидно, выполняться условие нормировки
11 -ф (г, /)|ай8г=1,
а следовательно, условие
— Лф(г, 0РЛ--0.] A0.9)
Последнее соотношение, обеспечивающее сохранение вероятно-
вероятности, получается непосредственно из полного уравнения Шредин-
Шредингера A0.4) следующим образом. Очевидно,
137
Глава 10
Подставляя сюда вместо производных д^/дг и д\$*,д1 их выражения,
полученные из уравнения A0.4), приходим к соотношению
— |' I ф |2 й3г =-. — I' (ф*уая|5—фу2^*) &*• (Ю. 10)
й1 'у 2т \,
Интеграл, стоящий в правой части, преобразуем, используя
теорему Грина х) Тогда получим
2т -у
2т у
A0.11)
Поскольку функция 1|) обращается в нуль на бесконечности,
последний интеграл, берущийся по бесконечно удаленной замкну-
замкнутой поверхности А, равен нулю. Таким образом, мы непосредст
венно получаем доказываемое соотношение A0.9).
§ 10.2. Эволюция во времени средних значений
операторов физических аеличин
Среднее значение (или математическое ожидание) физической
величины дается формулой C.12):
<Л)-/-ф*(г, *Мф(г, Ц&г, A0.12)
в которой А обозначает квантовомеханический оператор данной
физической величины. Как видим, среднее (А), вообще говоря,
является функцией времени I.
Вычислим производную по времени I от величины (А). При
этом будем исходить непосредственно из уравнения Шредингера
A0.5), которое с использованием дираковских обозначений можно
х) Согласно теореме Грина, для любых двух функций /(г) и § (г) имеет
место интегральное соотношение $ (/у2^ — 8Ъ2() ^3|" = $ (/У§ — 8у1)'п^а'
г а
в котором А — замкнутая поверхность, ограничивающая произвольный
объем V, п — единичный вектор нормали к поверхности, направленный
наружу, (Рг и йа — соответственно бесконечно малые элементы объема н по-
поверхности.
138
Полное уравнение Шредингера
записать в виде:
гй 01
Кроме этого уравнения, имеем сопряженное ему уравнение
A0.13)
A0Л4)
Формула A0.12) в дираковских обозначениях запишется следую-
следующим образом:
<1>|Л|1>>. A0.15)
Дифференцируя формулу A0.15) по времени, получаем соот-
соотношение
а
которое кратко можно записать в виде
IА | ф) + (Ф | А | ■ф) + (ф | А | ■ф) —
4|^), A0.16)
A0.17)
Мы пришли, таким образом, к искомой формуле, описывающей
временную эволюцию среднего значения оператора физической
величины.
Выведем теперь из формулы A0.17) важное следствие.
Теорема Эренфеста. Согласно теореме Эренфеста, в квантовой
механике справедливы классические уравнения движения
т — р, —— = —уК, (,10.18)
если только входящие в них классические величины понимать как
средние значения квантовых операторов соответствующих физиче-
физических величин. [В A0.18) V (г) — функция потенциальной энергии. ]
Доказательство. Воспользуемся формулой A0.17) для вычис-
вычисления производной по времени от среднего значения оператора
х. Тогда получим соотношение
139
Глава 10
Появившийся здесь оператор у2х, очевидно, можно понимать как
оператор ху2—2 (д/дх); следовательно,
й (х) 1К Г . * д
77 \^*И Г <Р*>-
й/ т 3 дх т
При получении последнего равенства мы воспользовались тем, что
оператор импульса рх = — Ш (д/дх). Кроме того, мы учли оче-
очевидное перестановочное соотношение [У(г), х] = 0.
Итак, мы убедились в справедливости первого доказываемого
уравнения A0.18).
Чтобы получить второе уравнение A0.18), обратимся снова
к формуле A0.17) и используем ее теперь для вычисления произ-
производной по времени от среднего значения оператора рх. Тогда по-
получим соотношение
При преобразованиях мы учли очевидное перестановочное соотно-
соотношение [у2, д/дх] = 0.
Итак, мы убедились в справедливости также и второго доказы-
доказываемого уравнения A0.18).
Задачи
1. Предположим, что функция ф (г, 1) при г -> оо убывает как 1/г™. Какое
ограничение на значения числа п. налагает требование сходимости интег-
интеграла A0.11), берущегося по бесконечно удаленной замкнутой поверхно-
поверхности?
2. Докажите, что если зависящая от времени волновая функция ф (г, I)
дается интегралом
2яй
и если она удовлетворяет полному уравнению Шредингера, то функция
Ф (р, I) удовлетворяет уравнению
140
Полное уравнение Шредингера
в котором оператор V (г'йур) получается из функции V (г) с помощью за-
замены в ней радиус-вектора г на оператор г'йур, т. е. с помощью замены
в этой функции каждой координаты х; на оператор Шд/др1. Оператор ур
означает градиент по импульсным переменным.
Указание. Убедитесь сначала, что имеет место равенство
оо
Г дФ {рхП , IX
е ф -- —-
др г Й
— оо
для любой функции Ф, удовлетворяющей условию Ф (— оо) = Ф (+оо) ^0.
ГЛАВА 11
ТЕОРИЯ ВОЗМУЩЕНИЙ
В предшествовавших главах мы рассмотрели несколько при-
примеров конкретных задач на отыскание собственных чисел и собст-
собственных функций квантовомеханических операторов физических
величин.
Особый интерес при этом мы проявили к задаче на нахождение
собственных чисел энергии, т. е. к решению стационарного урав-
уравнения Шредингера
Л&Ф-т "= Ьтит.
В настоящей главе мы установим, какое влияние оказывают
малые возмущения, добавляемые к нулевому гамильтониану Жо,
на его собственные числа Ет и собственные функции ит.
С такими возмущениями приходится часто встречаться на прак-
практике, выясняя, например, как действуют на ту или иную атомную
систему внешние электромагнитные или постоянные магнитное
и электрическое поля или столкновения ее с другими атомами и мо-
молекулами, если только, разумеется, указанные физические эффекты
не включены уже в нулевой гамильтониан Жо рассматриваемой
атомной системы.
Поскольку уравнение Шредингера редко удается решить точно,
излагаемые в этой главе методы теории возмущений широко ис-
используются в квантовой механике.
§ 11.1. Стационарная теория возмущений
Рассмотрим следующую задачу. Пусть нам дан нулевой гамиль-
гамильтониан Ж(, и известны все его собственные функции ит и собствен-
собственные числа Ет, т. е. пусть нам известны все решения стационарного
уравнения Шредингера
Ш(,ит^ Е,„ит. (П.1)
Выясним, какими будут новые собственные функции и собствен-
собственные числа, если теперь мы добавим к гамильтониану Жо некоторое
малое возмущение^', т. е. перейдем от гамильтонианаЖ() к гамиль-
гамильтониану Жо -г Ж'.
Один из методов решгния указанной задачи состоит в диагона-
лизации матрицы оператора Жо + Ж' путем отыскания подходя-
142
Теория возмущений
щего набора базисных функций. Процедура днагонализации под-
подробно описана выше в § 9.3. Метод диагонализации часто приме-
применяется на практике.
Вместе с тем, когда М' .< Жо, можно использовать другой ме-
метод — метод теории возмущений, который позволяет вычислять
поправки к собственным функциям ит и собственным числам Ет
вплоть до любого требуемого порядка. Выводом общих формул для
таких поправок мы и займемся в настоящем параграфе.
Поправки первого порядка. Представим полный гамильтониан
в виде Шь + №', где X — некоторый параметр, принимающий
значения из интервала 0 ^ А, ^ 1. Он как бы «включает» (при
X — 1) или «выключает» (при X = 0) малое возмущение. Будем ис-
искать собственные числа Ш и собственные функции \]э гамильтониана
Жя -|- ХШ', используя основное уравнение
фъ + Ш')Ъ^ХРЪ (П.2)
представим интересующие нас величины разложениями по целым
положительным степеням параметра X:
Г - Шо + Х^г + X2 И72 + ... A1.3)
Подставляя разложения A1.3) в исходное уравнение A1.2),
получаем
(Жо + ХЖ) (Ч-'о Ч- Ц1 + Щ\ + .)^(Ш0^, ХШ^Л2№2+ . .) х
Приравнивая коэффициенты при Х°, X1 и А,2 в обеих частях пос-
последнего равенства, получаем соответственно уравнения
5^о*1 + ^Чо - «^1 + ^\%, A1.4а)
Первое уравнение A1.4а) идентично с уравнением A1.1), поэ-
поэтому в нулевом приближении имеем следующее решение:
»7о = ^га, (П.46)
где ит и Ет — некоторая собственная функция и соответствующее
ей собственное число нулевого гамильтониана Ж(), т. е. гамильто-
гамильтониана, в который превращается полный гамильтониан в отсутст-
отсутствие возмущения.
143
Глава И
Займемся вторым уравнением A1.4а). Разложим функцию
в ряд по функциям «„:
п
и подставим этот ряд во второе уравнение A1.4а). Придем тогда
к равенству
Е *№„+*Ч. - ^ Е <'Ч+*>«•
п п
умножая которое на ик и интегрируя, а также используя условие
ортонормировки (и„ | «(,) = 6*„, получим уравнение
Ека^ + Ж'кт^Ета^^$кт, A1.6)
из которого при кф т непосредственно следует, что
ар=-.-^-, A1.7)
и при к-~= т
^1-Жпт. (П.8)
Таким образом, формула A1.8) позволяет опредачить величину
Шг — поправку первого порядка к энергии Ет. Это важнейший
результат квантовомеханическои теории возмущений.
Остается вычислить коэффициенты а^. Их мы найдем из усло-
условия, что поправленная волновая функция первого порядка г]з =
= ит + Я, ■ф! должна быть нормирована на единицу:
.Г К + *• Е а>пУ К -н я. Е а<4) л- =
П 5
A1.9)
>1
п
Пренебрегая в последней формуле членами второго порядка, по-
получаем сразу, что йщ' = 0.
Таким образом, собственные функции и собственные числа с
учетом поправки первого порядка даются формулами:
-~^ик, A1.10а)
к • т
. A1.106)
Поправки второго порядка. Теперь найдем выражения для по-
поправок второго порядка Ш2 и $2. Поправку второго порядка г|з2
к волновой функции представим в виде ряда:
144
Теория возмущений
и подставим этот ряд в третью формулу A1.4а):
Е <№«„ + *' Е а>п = Е *№,«„ + В^Ч1, I Г2«т.
Подставляя в последнее равенство также и разложение A1.5) для
функции гр1, умножая его на ин и интегрируя, придем к следую-
следующему уравнению:
+ 1Г,а<>> + Ш,ртк. A1.11)
Полагая в этом уравнении к = т, получим формулу
гг - е <>*;„- «^=е <1}^п -»- ая>*;Вт-
Подставляя сюда явные выражения A1.7) для а',1' и A1.8) для И^,
убеждаемся, что последние два слагаемых в правой части формулы
взаимно уничтожаются. В результате приходим к важной формуле
-|_ A1.12)
для поправки второго порядка к энергии.
Рассмотрим теперь уравнение A1.11) при к Ф т. Используя
формулы A1.7) и A1.8), а также формулу с$ = 0, находим
кп
Ет - Еп) (Ет - Ек) (Ет - Ек)*
причем здесь к =/= т. Чтобы найти величину а„\ необходимо" снова
рассмотреть условие нормировки A1.9). С точностью до поправок
второго порядка это условие можно записать в виде
Используя, кроме того, формулу а„ = 0, отсюда получаем, что
2 /__>■■" 2 1^, (Е„ - Еп)*
п п ■ т
145
Глааа 11
Таким образом, полагая X = 1, получаем следующие выражения
для собственных функций и энергий с учетом поправок второго
порядка:
Ч -= и
т + /
1и Ет-
-Ек
к • т п т
<л |2
(Ет - Еп) (Ет - Ек)
«* —
(Е„-Ек)* !
-ит ,
A1.14)
A1.15)
Обратите внимание, что, согласно A1.12), поправка второго
порядка к энергии всегда стремится увеличить энергетические
разности \Ет—Е„\. В квантовой механике словами об этом гово-
говорят так: «Энергетические уровни стремятся растолкнуть друг
друга».
§ 11.2. Временная теория возмущений
Временная теория возмущений используется в качестве основ-
основного орудия при изучении вызываемых возмущениями квантовых
переходов, т. е. переходов системы с одного энергетического уровня
на другой.
Уже отмечалось выше [см. A0.6) I, что для системы с не зави-
зависящим явно от времени гамильтонианом общее решение полного
уравнения Шредингера
^ A1.16)
можно представить разложением
Ч1 (г, *) - Е апип (г)
A1.17)
в котором ап — произвольные коэффициенты и ип — собственные
функции гамильтониана (удовлетворяющие уравнению Жйип =
= Епип).
Если наша система в некоторый начальный момент времени,
скажем в момент времени /, обладала энергией Ет, то следует счи-
считать, что
ат~ 1, а„ —0 при пфт\ A1.18)
таким образом, система будет обладать той же самой энергией Ет
и во все последующие моменты времени.
146
Теория аозмущений
Предположим теперь, что рассматриваемую систему каким-то
образом возмутили, и ее гамильтониан изменился. Пусть вместо
нулевого гамильтониана Жй мы теперь имеем, например, гамиль-
гамильтониан
Ж(()^Ж0 + Ж A). A1.19)
Зависящую от времени волновую функцию яр (/) нужно находить
теперь как решение следующего полного уравнения Шредингера:
\Ж0 + Ж (/)] * ■-= Ш 4г ■ (И -20)
Используя полноту набора функций и„, волновую функцию
1|1 (г, /), рассматриваемую в каждый конкретный момент времени /,
можно разложить по функциям ип:
г|-(г, {)^%а„(()ип(г)е-'Еп(П. A1.21)
п
Так как теперь наш новый гамильтониан явно зависит от вре-
времени, коэффициенты разложения а„ (/) в A1.21) в отличие от ко-
коэффициентов ап в A1.17) являются функциями времени I. Это об-
обстоятельство чрезвычайно существенно.
Предположим, что при измерении невозмущенной энергии в не-
некоторый момент времени /, скажем в момент времени / = 0, мы по-
получили значение Ет. Тогда следует предположить, что в момент
времени / — 0
ат@)=--1, а„@)^0 прилет. A1.22)
Поскольку коэффициенты ап (I) изменяются со временем, по-
последующее измерение энергии, произведенное, скажем, в момент
времени /, может дать любое ее значение Ек. Вероятность такого
события равна | а*. (/) | 2; следовательно, вероятность обнаружить
систему в момент времени / в состоянии к при условии, что в началь-
начальный момент / — 0 она находилась в состоянии т, равна \ак A)\2.
Таким образом, решая полное уравнение Шредингера, мы мо-
можем узнать, как в результате действия возмущения Ж' @
изменяется со временем / вероятность найти систему в различных
собственных состояниях ип оператора Жй.
Итак, чтобы описать временную эволюцию системы, надо найти
коэффициенты ап (/).
Для этого подставим разложение A1.21) в A1.20). Тогда полу-
получим соотношение
— — ) Оп(^0+ Ж) ипе '■ ■
147
Глава 11
Умножая его на ик и интегрируя, а также используя условие ор-
тонормировки, приходим к выражению
ак=—-^У апМы @е'акп*, A1.23)
А / 1
п
где «циклическая частота» перехода п ->- к определяется соотноше-
соотношением
„ _ Ек-Еп
До сих пор не было сделано никаких приближений. Решение си-
системы уравнений A1.23) математически полностью эквивалентно
решению исходного полного уравнения Шредингера.
Так же, как в § 11.1, введем теперь параметр А,, «включающий»
и «выключающий» возмущение Ш'■ Полный гамильтониан будет
теперь равен сумме
Коэффициенты ап (/) можно представить следующими разло-
разложениями:
а ^а<°>
п п
подставляя которые в A1.23), придем к уравнению
Приравнивая коэффициенты при одинаковых степенях к в ле-
левой и правой частях равенства, получим уравнения
A1.24)
Решением нулевой системы уравнений, представленной первой
строкой в A1.24), служат функции а[0)= сопб!. Следовательно, ве-
величины а/гО)@ должны совпадать с начальными значениями для
148
Теория аозмущений
искомых коэффициентных функций аи (/). Поэтому выбираем их
следующим образом:
а<о) = 1, а<о) = о при пч-т,
так как достоверно известно, что при / = О система находилась
в состоянии с энергией Ет.
Систему уравнений первого приближения, представленную вто-
второй строкой в A1.24), таким образом, можно записать в следую-
следующем виде:
а? —±-Ж'ктеШ^, A1.25)
причем величина |й4° (/)|2дает в первом приближении вероятность
найти систему в момент времени I в состоянии к при условии, что
в начальный момент г — 0 она находилась в состоянии т.
Гармоническое периодическое возмущение. Рассмотрим кон-
конкретный пример возмущающего гамильтониана, который изменяется
со временем по простому гармоническому закону:
Ж @ = Не~ш + (Я4) еш. A1.26а)
Два слагаемых в формуле A1.26а) необходимо брать, чтобы
обеспечить эрмитовость возмущающего гамильтониана. Подставляя
A1.26а) в A1.25) и интегрируя по времени от 0 до /, при к Ф т
получаем
I («О,
V A1.266)
соАга -(- со
Нижний предел интегрирования мы взяли равным нулю, чтобы
автоматически учесть начальное условие: а*1* @) = 0 при к Ф т-
Ограничимся рассмотрением случая, когда частота со близка
к абсолютной величине частоты перехода т -*■ к, т. е. к величине
щт\, так что /гсо ^ | Еь — Ет\. Тогда, согласно A1.266), для
вероятности перехода из состояния т в состояние к за время от О
до / получаем следующую приближенную формулу:
а(»).2~_М^1
~1Г Aй'<т ± СО) П
1г ^-. A1.27)
± соJ
В этой формуле следует брать знак минус, если ыкт ^ со, и
знак плюс, если соАт ^ — со. Перекрестные члены со знаменате-
149
Глава 11
«лем вида (соАш — со) ((акт—со) мы отбросили, так как при со сн
г-, I св;,т | их вклад пренебрежимо мал.
Первое слагаемое в правой части формулы A1.266) доминирует
над вторым, когда йсо = Ек— Ет и когда, следовательно, Ек>Ет.
Наоборот, второе слагаемое в A1.266) доминирует над первым,
когда йсо -т^ Ет—Ек и, следовательно, когда Ек<^Ет. Таким
образом, гармоническое периодическое возмущение может вызы-
вызывать квантовые переходы как вниз, так и вверх по энергии из состоя-
состояния т в состояние к. Энергия состояния к отличается от энергии
состояния т на величину, приблизительно равную йсо.
Выведем теперь формулу для вероятности перехода из состоя-
состояния т в континуальную группу состояний, близких по энергии
к состоянию к, предположив ради определенности, что Ек^>Ет.
Обозначим р (&>/;„,) плотность таких конечных состояний, т. е.
число состояний, приходящихся на единичный частотный интервал.
Поскольку теперь щт = со, в формуле A1.27) надо взять знак
минус. Так приходим к следующей формуле:
51П2 Г— @)*,„ - СО) П
А^рЫ^и. A1.28)
А_
-у(СО|;т— С0I
Если величина | Н'кт\г слабо зависит от конечного состояния к,
то ее можно вынести из-под знака интеграла. Тогда в подынтеграль-
подынтегральном выражении останется произведение следующих двух множи-
множителей:
Г 1
51П2 — (С0Ага— СО)/
1
~ (С0;гт — Ш)
На рис. 11.1 приведены графики функций § (соАт) и р (соАт).
В качестве независимой переменной взята величина соА,„. Интер-
Интервал, на котором в основном сосредоточена функция
зил2 — (шЛт — ш)(\
В («,„„ 0 =-- -^ --1—. A1.29)
]
равен по порядку величины 2пИ. Его можно сделать сколь угодно
150
Теория возмущений
малым, увеличивая время наблюдения /. Площадь под графиком
указанной функции равна
Г • 1
I (СЙЬп A)) ' I
12 -1 -*- - °-< A1.30)
51П-
— @)
г
Рассмотрим случай, когда время / достаточно велико, чтобы
величина 2п/{, характеризующая «ширину» функции § (щт, (),
Рис. 11.1. Кривые, соответствующие множителям в подынтегральном выра-
выражении в A1.28): функция плотности конечных состояний р (ш/,т) и функция
вероятности перехода § (шьт, 0 = 51П2 (('/г) (ш/гт— (о) I]' [A/2) (о)^т—ш)]2.
была много меньше, чем «ширина» Лео функции р (со*т). Интеграл
в A1.28) тогда можно приближенно вычислить; это дает
р(со)
51П2
(«;..„, - @) (
Г ' Т
— («;гт — и)
»кт
2л
1'т
р(со)
A1.31)
"Ага
так как в рассматриваемом случае из-под знака интеграла можно
вынести функцию р (»Ат), взяв ее в точке щ,п = со.
Вероятность квантового перехода т ->- ^ в единицу времени
дается формулой
тп-+к
2л
A1.32)
здесь р (/;) обозначает плотность конечных состояний по энергии Е
151
Глава 11
1так что р (со) = Нр(Е)\. Знак минус в формуле A1.32) следует
взять при Ек<^Ет, когда доминирующим оказывается второе
слагаемое в правой части формулы A1.266).
Формула A1.32) справедлива также и для вероятности пере-
перехода из состояния \т) в одно единственное состояние | к), принад-
принадлежащее континууму состояний. Тогда формулу следует предста-
представить в виде
^ ^ A1.33)
Когда Ек—Ет ^ — йсо, в аргументе б-функции величину йсо
следует добавлять, а не вычитать. При выводе формулы A1.33)
мы использовали тот факт, что при достаточно больших / функцию
51П2 (хИ2)!(х/2)'г можно заменить на 2л(Ь{х), так как .V принимает
непрерывные значения.
Формулу A1.32) часто называют «золотым правилом» Ферми.
Используя эту формулу, всегда следует помнить, что она дает ве-
вероятность перехода из одного состояния т в континуум состояний к,
принадлежащих единичному интервалу энергий вблизи энергии
состояния к. В тех случаях, когда мы имеем дело с единственным
состоянием к, необходимо пользоваться исходной формулой A1.27).
Возмущение, задаваемое ступенчатой функцией времени. Инте-
Интересно рассмотреть другой частный случай, когда возмущение пред-
представляет собой «ступенчатую» функцию времени, т. е. когда
0 при I ^ О,
Н' при *>0. (П-34)
Такое возмущение можно рассматривать также и как предельный
случай гармонического периодического возмущения при со -»- 0.
Будем исходить из системы уравнений первого приближения,
представленной второй строкой в A1.24). Учитывая начальное ус-
условие а(п @) = Ьпт (предполагается, что в начальный момент си-
система была в состоянии т) и рассуждая так же, как при выводе
формулы A1.32), приходим к формуле
^«н* -= ~ I Нш |2 б (Ет - Ек) ~ -±-1 Н'кт |* б (уя -V,). A1.35)
Как мы видим, полученное выражение очень похоже на выра-
выражение A1.33) и совпадает с последним при со = 0. Теперь из-за
наличия 6-функций требуется, чтобы энергия Ек конечного состоя-
состояния была в точности равна энергии Ет начального состояния.
Следует отметить, что формула A1.35), так же как и формула
A1.33), относится к случаю перехода в единственное состояние к,
в данном случае принадлежащее континууму состояний. Чтобы
получить вероятность перехода из начального состояния \т) в
152
Теория аозмущений
группу конечных состояний \к), надо просуммировать или проин-
проинтегрировать вероятности ^т к по конечным состояниям.
Пределы применимости «золотого правила» Ферми. Укажем
в заключение два условия применимости выведенных выше формул
A1.31) и A1.33). Первое состоит в том, что величина* 2пН должна
быть мала по сравнению с «шириной» 2яАу функции плотности
конечных состояний р (щт). Второе условие состоит в том, что
величина | аУ (О!2 Должна быть много меньше единицы, так как
только в этом случае мы можем ограничиться первым порядком
теории возмущений и пренебречь членами более высокого порядка.
С учетом A1.27) второе условие можно представить неравенством
—^- ?; —• A1.36)
Таким образом, формула теории возмущений первого порядка дает
хорошее приближение только при достаточно малом времени /
когда вероятность перехода из начального состояния т в состоя
ние к еще остается много меньше единицы.
Объединяя оба вышеуказанных условия, приходим к единому
условию
|/4п| <*•-!-<~Ау,
устанавливающему пределы применимости формул A1.33) и A1.35)
и «золотого правила» Ферми. В случаях когда последнее условие
не выполняется, надо использовать другие методы. Об этом мы рас-
расскажем в § 13.1.
§ 11.3. Формализм матрицы плотности
Формализм матрицы плотности, которому посвящен данный
параграф, широко используется в настоящее время при описании
временной эволюции больших квантовых систем, состоящих из
большого числа идентичных частиц. С его помощью очень удобно
производить усреднения по ансамблю частиц.
Формализмом матрицы плотности мы воспользуемся в гл. 13
для описания физических явлений поглощения и дисперсии элек-
электромагнитного излучения, взаимодействующего со средой, имеющей
атомное строение.
Рассмотрим волновую функцию г]з (г, /) изолированной отдель-
отдельной атомной системы. Эта функция удовлетворяет уравнению
Шредингера
«Ж@Ч>(г, О-'Й-^!^1. (П.37)
153
Глааа 11
и ее можно разложить по произвольному полному набору ортонор-
мированных функций ип (г):
1- (г. О -= Е Си (() ип (г) = X С„ | л), A1.38)
причем (п\т) — Ь„т.
Из A1.38) непосредственно находим
С„=|""ХГ. О^ = <«!*>• (И.39)
Среднее значение какой-либо физической величины Л в состоянии
г|з (г, /) вычисляется по формуле A0.12):
(А) = ]' г^Л^г - - <г|; | Л | Ц->. A1.40)
С использованием формулы B.376) отсюда получаем
<Л>- 1.1,(У\т)(т\А\пХп\у)=:2121С'тСпАта. A1.41)
л т п т
Формула A1.41) относится к изолированной отдельной атомной си-
системе (которую в дальнейшем будем называть просто «атомом»).
На практике, однако, в большинстве реальных физических экс-
экспериментов мы имеем дело не с единственной атомной системой,
а с системами, состоящими из огромного числа одинаковых атомов,
т. е., как правило, с ансамблем идентичных атомных систем. Для
них мы измеряем не саму величину ( А), а величину (А), усреднен-
усредненную по ансамблю одинаковых систем. Соответствующее среднее
будем обозначать чертой сверху:
A1.42)
п т
Удобно ввести величину
рпга = С~С^ A1.43)
. A1.44)
используя которую получаем вместо A1.42) формулу
Щ ХХрщпЛт„ = Х(рЛ)т„. 5р(рЛ). A1.45)
п т п
Непосредственно из формулы A1.44) и определения операции
умножения матриц видно, что величины рпт можно рассматривать
как матричные элементы пт для оператора
(П-46)
который называется оператором плотности.
Согласно A1.43), имеем очевидное соотношение рш„ = р*пт,
так что оператор (.> эрмитов.
154
Теория возмущений
Часто бывает необходимым рассматривать дифференциальное
уравнение, которому удовлетворяет оператор о (^). Составим это
уравнение. Дифференцируя по времени / формулу A1.46), полу-
получаем
^ - (П.47а)
Уравнение Шредингера A1.37) можно записать в виде
\Ъ)--}^Зв\У). (П.476}
Используя эрмитовость оператора Ж, из уравнения A1.476) можно
получить еще одно уравнение х)
^^ A1.47в)
Подставляя A1.47в) и A1.476) в A1.47а), приходим к уравнению
01 Л Л
где квадратные скобки обозначают коммутатор операторов. Таким
образом, с использованием A1.46) окончательно приходим к диф-
дифференциальному уравнению
ф ' \М, р| A1.48)
01 Ш
для оператора плотности р.
На практике обычно приходится иметь дело не с уравнением
A1.48), а с системой уравнений:
—р-^-= \Ж, р]пт-'~ Релаксационные члены, A1.49)
01 Иг
где в правые части добавлены феноменологически так называемые
релаксационные члены, чтобы учесть диссипативные свойства ан-
ансамбля систем.
ь) Уравнение A1.47в) в силу* эрмитовости оператора^ означает, что
Л
где/ —произвольная функция. Последнее равенство очевидно в силу A1.476).
155
Глава 11
Как применять уравнения A1.49), мы объясним на примере
в гл. 13, в которой уравнения A1.49) будут использованы при рас-
рассмотрении явлений поглощения и дисперсии электромагнитных
волн в средах с атомной структурой.
Задачи
1. Согласно формуле A1.27) и рис. 11.1, переход между двумя состояниями
к и т под влиянием электрического поля, осциллирующего с частотой со,
происходит при условии, что Еь—Ет = со -г б, причем энергетическая
величина б может иметь самое большее величину порядка 2я//, где I —
время наблюдения.
Означает ли этот результат, что закон сохранения энергии нарушается?
Согласуется ли он с принципом неопределенностей для энергии и времени
ее измерения?
2. Рассмотрите электрическое поле с круговой поляризацией
Ех = Е0со5 со/,
которое взаимодействует с атомами водорода, первоначально находив-
находившимися в состоянии | п, I, т) с т=0, и вызывает их переходы в состояние
\п, /', т').
Какому условию должны удовлетворять квантовые числа п', /'. т' и п,
I, т, чтобы переходы действительно имели место, если: а) Еп' > Еп
и б) ЕП' < Е„?
3. Решите задачу 2, при обратном направлении круговой поляризации, т. е.
считая, что
Ех — Е0со& со/,
Еу = — Е0&1п со/.
4. Решите задачу 2, считая, что поле линейно-поляризовано в направлении
оси г, т. е.
Е — гЕ0со& со/.
5. а. Покажите, что линейно-поляризованное электрическое поле, напри-
например поле
Е — хЕ0со5 со/,
можно представить в виде суммы двух полей, поляризованных по кругу
в противоположных направлениях в плоскости ху.
б. В чем заключаются так называемые «правила отбора», т. е. условия,
которым должны удовлетворять квантовые числа п, I, т и п'', /', т , чтобы
был возможен переход между состояниями | п, /, т) и | п , /', т ) под
действием линейно-поляризованного поля, описываемого формулой из
п. «а»?
ГЛАВА 12
ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ
С АТОМНОЙ СИСТЕМОЙ
В настоящей главе рассматривается взаимодействие отдельной
атомной системы с электромагнитным полем. Излагается теория
спонтанных и индуцированных переходов под действием электро-
электромагнитного поля. В следующей главе мы используем полученные
здесь результаты для объяснения явлений поглощения и усиления
электромагнитного излучения атомной средой. Материал настоя-
настоящей главы нужен также для понимания принципов работы лазеров.
§ 12.1. Некоторые сведения
из электромагнитной теории
Уравнения Максвелла, описывающие распространяющееся
электромагнитное поле, имеют вид
ПЛЕ - — , ШУ V р,
д(
A2.1)
го!Н Л-—, сП\'В О,
д1
где ^ — плотность объемного электрического тока. Другие обозна-
обозначения были уже объяснены в гл. 1. В однородной изотропной среде
поля В и Б связаны с полями Н и Е соотношениями
О = еЕ, A2.2)
где [х и е — соответственно магнитная и диэлектрическая прони-
проницаемости среды.
Взяв операцию ротора от обеих частей первого уравнения в первой
строке A2.1), а затем используя первое уравнение из второй строки
A2.1), а также соотношения A2.2), в случае 1=0 приходим к
уравнению
ГО I ГО1 Е — — 116 .
Вспоминая векторное тождество го! го! А = — У2А -г
-гйгас1 сНуА, справедливое в декартовых координатах, и учитывая
условие сНу Е = 0, справедливое при р = 0, последнее уравнение
157
Глааа 12
можно записать в виде
У2Е^е-^-=О. A2.3)
Уравнение A2.3) имеет важное решение вида
Е = Еое~'"((>)(~-к-г>, A2.4)
где к = со \ [хе, которое описывает плоскую волну, распростра-
распространяющуюся вдоль направления произвольного вектора к, с длиной
волны
A2.5)
и частотой колебаний
у = со/2зт. A2.6)
Фазовая скорость распространения этой волны дается соотноше-
соотношением
— - —. A2.7)
в котором п — \ (,и/|ы0) (е'е0) — показатель преломления среды,
ас~ (Моео)~ — скорость света в пустом пространстве.
Рассматривая уравнения Максвелла A2.1), можно показать,
с учетом равенства сПу Е = 0, что функция A2.4) действительно
удовлетворяет этим уравнениям, но при условии, что вектор Ео
перпендикулярен вектору к, вдоль которого распространяется
рассматриваемая плоская электромагнитная волна. Магнитное
поле Н волны A2.4) рассчитываем с помощью первого уравнения
из второй строки A2.1):
Н= 1,^Г[е,-Е01е"'(ш'"кг>, A2.8)
где ей — единичный вектор, направленный вдоль вектора к. Век-
Вектор Н, таким образом, перпендикулярен как вектору Е, так и век-
вектору к.
Советуем читателю вывести формулу A2.8) следующим образом.
В уравнениях Максвелла положите, что го! а — [у-а] и сПу а =
= (У-а), а операцию набла V и производную д/дг замените со-
соответственно на Иг и — ш, что формально правильно для волн вида
A2.4), A2.5). Тогда получается алгебраическая система уравнений,
решение которых приводит к формулам A2.8). В правильности
формулы A2.8) можно убедиться и иначе, рассмотрев какой-нибудь
158
Взаимодействие излучения с системой
частный случай, скажем, направив вектор Ео вдоль оси х. а за-
затем использовать уравнение
. с дН
ГО1 Е -=■ —
д1
для расчета магнитного поля Н.
Взаимное расположение векторов Е, Н и к в плоской гармони-
гармонической электромагнитной волне показано на рис. 12.1.
Рис. 12.1. Взаимное расположение направлений векторов Е, Н и к для мо-
монохроматической плоской волны с длиной волны "к = 2л/к.
Энергия электромагнитного поля. Возьмем скалярное произве-
произведение первого уравнения в первой строке A2.1) с Н, а первого
уравнения второй строки в A2.1) — с Е и вычтем второе уравнение
из первого; тогда получим
-[е(Е-Е)+ц(Н.Н)].
2 д(
Воспользуемся теперь векторным тождеством
сНу[А-В] (В-го1А) —(А-го1В)
и преобразуем левую часть в полученном соотношении. Тогда при-
придем к уравнению
-сН\[Е-Н]- — д—
2 д1
[е(Е-Е) + ц(Н-Н)].
Применив к нему теорему Гаусса1)
5(И\-Ай8г= С (А-п)
Г 5
A2.9)
A2.10)
]) В наш гературеэту теорему называют теоремой Гаусса — Остро-
Остроградского. — Прим. перве.
159
Глааа 12
окончательно получим уравнение
, A2.11)
где V — произвольный объем, 5 — ограничивающая его поверх-
поверхность, п — внешняя единичная нормаль к поверхности 5, йа —
бесконечно малый элемент площади поверхности 5.
Величина [Е-Н] называется вектором Пойнтинга1). Этот век-
вектор характеризует величину потока энергии электромагнитного
поля через единичную площадку. Вектор [Е-Н] имеет направле-
направление потока. Таким образом, интеграл в A2.11) по поверхности 5,
взятый со знаком минус, равен полному потоку энергии, втекаю-
втекающей в объем V.
В силу закона сохранения энергии для среды без энергетических
потерь величина интегрального потока притекающей энергии
должна быть равна скорости увеличения запасенной энергии. Та-
Таким образом, полная электромагнитная энергия, запасенная в
объеме V, должна определяться формулой
#= —.|" [е(Е-Е)-г|1(Н-Н)]сCг. A2.12)
2 V
§ 12.2. Квантование мод электромагнитного поля
Рассмотрим теперь моды электромагнитного поля простого пло-
плоского резонатора, представленного на рис. 12.2. Внутри резонатора,
имеющего две параллельные идеально проводящие стенки, имеется
электромагнитное поле, заполняющее все пространство между
стенками. Пусть электрическое поле какой-то моды электромаг-
электромагнитного поля направлено параллельно оси у. Поскольку величина
Еу должна равняться нулю на абсолютно проводящих стенках
резонатора, т. е. при г = 0 и при г = Ь, возьмем электрическое
поле электромагнитной моды в виде
Е/ = Ц 2/Уе р1 ({) ап кгг, A2.13а)
где V — полный объем резонатора, или объем, занятый модой,
)—единичный вектор в направлении оси у. Моду вида A2.13а)
можно считать суперпозицией двух бегущих плоских электромаг-
электромагнитных волн вида A2.4). Чтобы поле Е действительно обращалось
в нуль на стенках, т. е. при г.=,Ь, должно выполняться равенство
к[ = Ы1Ь, где / — некоторое целое число. Оно равно целому числу
полуволн, укладывающихся на длине Ь резонатора. Магнитное
поле Н рассматриваемой электромагнитной моды должно быть
') В отечественной литературе этот вектор чисто называют вектором
Умова—Пойнтинга.— Прим. перев.
160
Взаимодействие излучения с системой
максимально на стенках резонатора и перпендикулярно электри-
электрическому полю Е. Для него можно использовать выражение
СО5 к,1Х,
где I — единичный вектор в направлении оси х и со/ =
Яг
A2.136)
-1/2
Рис. 12.2. Мода электромагнитного поля, устанавливающегося в плоском
резонаторе между двумя абсолютно отражающими параллельными стенками,
расположенными на расстоянии Ь друг от друга. Чтобы электрическое поле
Еу обращалось в нуль при г = 0 и при г = Ь, на расстоянии Ь должно укла-
укладываться целое число полуволн, т. е. I. = / (к/2), или к^ = /я.
Если подставить A2.13а) и A2.136) в первое уравнение в первой
строке уравнений Максвелла A2.1), то получим уравнение
Рг
A2.14)
Подстановка в первое уравнение второй строки уравнений Мак-
Максвелла A2.1) дает уравнение
= --^-. A2.15)
Комбинируя уравнения A2.14) и A2.15), приходим к уравнениям
Общее решение уравнения для Ц1 имеет вид
щ
A2.16)
Используя A2.13а) и A2.136) и формулы A2.12), для энергии
моды получаем
Ж, =
1
I
[е (Е/ • Е/) + ц (Н, • Н,)] с1Ч -
A2.17)
6 Заказ № 683
161
Глааа 12
Сравним это выражение с выражением E.8) для гамильтониана
гармонического осциллятора:
2/п
A2.18)
где со2 = К т. Как мы видим, классический гамильтониан <?;/ элек-
электромагнитной моды, даваемый выражением A2.17), совпадает
с квантовым гамильтонианом A2.18), если сделать в A2.17) замену
р1 -> р И Ц1 -*■ X И ПОЛОЖИТЬ ГП = 1.
Квантование электромагнитной моды можно, таким образом,
осуществить, рассматривая формально моду как гармонический
осциллятор и считая р/ и <# парой сопряженных операторов им-
импульса и координаты 1), которые удовлетворяют, подобно опера-
операторам р и х в случае точечной частицы, перестановочным соотно-
соотношениям
[Р/, Рт\\Я1, Чт\-0, A2.19)
[<?/, рт\ - 1ПЬ,.т. A2.20)
Формальная аналогия величин р, и ^/ с величинами р и х осно-
основана, разумеется, не только на сходстве гамильтонианов A2.17)
и A2.18). Уравнения движения, которым удовлетворяют обе пары
сопряженных величин, тоже совершенно одинаковы. Уравнения
Гамильтона для величин р и х с учетом A2.18) имеют вид
йр
—
дх
рм __ р С12 21)
й1 др т
Уравнения Гамильтона для величин р/ и цг с учетом A2.17) имеют
вид
йР1 дк-1
A2.22)
Они совпадают с уравнениями A2.14) и A2.15), которые выше мы
вывели из уравнений Максвелла.
г) Начиная с этого момента, мы будем считать величины р; и сц опера-
операторами и обозначать их р, и щ.
162
Взаимодействие излучения с системой
Итак, мы установили формальное соответствие величин р/ и <#
для электромагнитной моды с величинами р и х для гармонического
осциллятора.
Электромагнитные операторы рождения и уничтожения. В точ-
ночти так же, как для гармонического осциллятора (см. § 5.3),
полезно ввести оператор уничтожения щ и оператор рождения а}
для электромагнитной моды, определяемые формулами
A2-23)
или обратными формулами
(й/+а/). A2.24а)
В отличие от операторов р/ и ^г операторы а/ и а! не эрмитовы,
но они эрмитово сопряжены друг другу.
Подставляя выражения A2.24а) в формулы A2.13а) и A2.136)
для полей Е/ и Н/, приходим к формулам
(а\ ~ сц) яп кг, A2.246)
(а\ + сц)
как видим, электрическое и магнитное поля электромагнитной моды
описываются квантовомеханическими операторами.
Используя перестановочные соотношения A2.19), A2.20) и фор-
формулы A2.23), выведем перестановочные соотношения для операто-
операторов уничтожения и рождения:
[а,, ат~\ = Щ, а^]=0,
[а/,ат] = б/,т. A2.25)
Модовый гамильтониан A2.17) можно записать через опера-
операторы а* и щ:
163
Глава 12
Используя последнее перестановочное соотношение из A2.25), за-
заменим (ца\ на 1 ~г Щсц; в результате окончательно получим
Ж-1 =--= йсо,
I а\ щ + — \ ■ A2.26)
Формальная аналогия между электромагнитной модой и гармо-
гармоническим осциллятором позволяет сразу построить для нее собст-
собственные функции | п/), которые, как и их аналоги ип в § 5.3, удов-
удовлетворяют следующим уравнениям:
ец\п1) = {п1)Ч*\гц—1). A2.27)
Таким образом, уравнение на собственные числа и собственные
функции энергии электромагнитной моды принимает вид
п\
A2.28)
Следовательно, энергия электромагнитной моды может прини-
принимать только значения из набора чисел
М A2.29)
иными словами, энергия электромагнитной моды квантуется.
Квантование энергии электромагнитных мод было постулиро-
постулировано Планком в 1900 г. (см. § 1.2). Мы пришли к этому квантова-
квантованию, применив основные постулаты квантовой механики к электро-
электромагнитному полю.
Квантование бегущих волн. Вместо рассмотрения стоячих волн,
каковыми являются электромагнитные моды, и их квантования,
описываемого формулами A2.246), можно обратиться к бегущим
плоским электромагнитным волнам и с помощью их квантования
получить для какой-либо одной такой волны формулы
». л/^УЫ*)е'1кГ~ак-,Л1)е1кг1 A2.30)
и (г, 0 = [ ]^^Шк*
здесь вектор к характеризует направление распространения волны,
а'вектор е^х. перпендикулярный вектору к,— направление элек-
электрического поля. Два направления поляризации, возможные для
данного вектора к, обозначены индексом К (X — 1, 2). Магнитное
164
Взаимодействие излучения с системой
поле Нк/ направлено вдоль векторного произведения [еы-к/к],
а потому оно перпендикулярно и вектору к, и электрическому
полю Еь?..
§ 12.3. Излучение абсолютно черного тела
В § 1.2 мы уже говорили о том, с какими непреодолимыми труд-
трудностями столкнулась классическая физика при попытках объяс-
объяснить экспериментально полученную кривую спектральной плот-
плотности теплового равновесного электромагнитного излучения. По-
Постараемся теперь понять основные закономерности теплового излу-
излучения, используя те сведения, которые мы уже имеем.
Рассмотрим поле теплового равновесного электромагнитного из-
излучения при температуре Т, заключенное в кубическом ящике со
стороной ребра, равной Ь.
Обобщая на трехмерный случай формулу A2.13а), запишем
электрическое поле, соответствующее отдельной электромагнитной
моде в таком ящике, в виде
Ерщ ОС 51П {кхХ) 51П (куу) 51П (кгг) СО5 ю/.
Это поле обращается в нуль на стенках ящика при условии, что
кх = р - , ку—1 - , кг = т - , A2.31)
где р, I, т — произвольные положительные целые числа. Подстав-
Подставляя приведенное выражение для электрического поля в волновое
уравнение A2.3), получаем соотношение
к2 = со2цг = ~ (р2 + Р + т2). A2.32)
Следовательно, каждая тройка целых чисел р, I, т определяет
некоторую электромагнитную моду в рассматриваемом кубическом
ящике, частота которой дается формулой A2.32).
Теперь нам надо найти плотность распределения электромаг-
электромагнитных мод по частотам (число мод, приходящихся на единичный
интервал частоты). Начнем с разбиения воображаемого фиктивного
пространства с координатными осями кх, ку, к2 на элементарные
объемы. Согласно A2.31), отдельная электромагнитная мода за-
задается тройкой положительных целых чисел р, I, т (изменение
знака одного из них не дает новой независимой электромагнитной
моды, так как поле полученной моды отличается только знаком
от поля моды с положительными целыми р, I, т). Таким образом,
каждой электромагнитной моде в фиктивном пространстве кх, ку,
к2 можно сопоставить малый объем с1кхс1куAкг = (п/ЬK. Этот
объем надо поместить на конце вектора, проведенного из начала
координат в точку с координатами (рп/Ь, 1п/Ь, пт-!Ь) (рис. 12.3).
165
Глава 12
Чтобы найти число Мк электромагнитных мод, вектор к кото-
которых в рассматриваемом фиктивном пространстве кх, к,.., к- имеет
абсолютную величину, заключенную в интервале от 0 до к, надо
разделить объем всего к-пространства, занимаемого этими модами
[равный A/8) D 3) лка] на объем (л/,K, приходящийся на одну
моду. (Множитель 1.8 введен по той причине, что компоненты кх,
ку, к2 принимают только положительные значения, а потому надо
рассматривать лишь один октант пространства кх, ку, к,.) Затем
полученный результат следует умножить на 2, чтобы учесть два
независимых возможных направления поляризации электромагнит-
электромагнитной волны, характеризуемой вектором к.
Элементарный.
объем
Рис. 12.3. Каждой тройке положительных целых чисел р, /, т соответствует
волновой вектор к с компонента ми р (пЛ), I (п/Ц, т (п/1_), выходящий и*
начала координат. Каждой моде соответствует кубический элементарный
объем (л/Ця, расположенный вблизи конца этого вектора. Один из таких
объемов, помещенный в начало координат, показан на рисунке.
Таким образом, приходим к следующей формуле:
Зл2
A2.33)
где V ~- Ь3 — объем ящика. Используя теперь формулу A2.32)
и соотношение (не = (п2 с2) (где п — показатель преломления),
имеем еще одну формулу
к2 = со2ие = пг. A2.34)
с2
Используя A2.34), формулу A2.33) можно представить в виде
где А\, — число электромагнитных мод с частотами, заключенными
в интервале от 0 до данной частоты V.
166
Взаимодействие излучения с системой
Таким образом, приходим к следующей формуле для плотности
распределения электромагнитных мод, т. е. для числа мод, прихо-
приходящихся на единичный объем и на единичный интервал частоты:
, A2,35)
ик ' V ах с*
Средняя тепловая энергия одной электромагнитной моды, имею-
имеющей частоту V, дается формулой (вывод ее приведен ниже):
Я A2.36)
еНукт -1
Чтобы получить вклад в спектральную плотность энергии теп-
теплового электромагнитного излучения абсолютно черного тела, ко-
который вносят электромагнитные моды с частотами, заключенными
от V до V т <Л>, надо ^Ср умножить на р (г). Тогда получим для
спектральной плотности энергии теплового электромагнитного из-
излучения абсолютно черного тела (в расчете па единичный интервал
частоты) следующую формулу:
р(у)= М^ . A2.37)
Если мы хотим получить выражение для спектральной интен-
интенсивности / (у) этого теплового излучения (измеряемой в ваттах на
квадратный метр на единицу частоты), то р (V) следует умножить
на скорость света *) с/п и произвести усреднение по всему конти-
континуальному множеству направлений распространения мод. В ре-
результате придем к формуле
/(У)= 2л/п'3 . A2.38)
с2(е^Г_,)
Формула для средней тепловой энергии электромагнитной моды.
Выведем теперь формулу для средней тепловой энергии одной
моды электромагнитного поля, т. е. формулу для Еср.
Энергия электромагнитной моды, находящейся в квантовом
состоянии п, равна
Еп Ям [п —
(я т- -1-) . A2.39)
') Для электромагнитной моды, распространяющейся в заданном на-
направлении, справедливо следующее соотношение;
Спектральная интенсивность = Скорость распространения
энергии '.-. Плотность энергии.
167
Глава 12
Вероятность того, что эта мода при тепловом равновесии будет на-
находиться в состоянии л, дается формулой Больцмана [см. A6.2) ]:
„—Е кТ
р(л) = -|—? A2.40)
5=0
Таким образом, средняя энергия теплового возбуждения моды
равна
оо X йш (п + 1:2) ехр ( — Рйш (п -и 1,2))
Еср = X Епр G1) -= — ,
A2.41)
где В ^ (кТ)^1. Сумма в знаменателе с точностью до несуществен
ного множителя является суммой геометрической прогрессии и
дается формулой
Дифференцируя это соотношение по В, получаем еще одну формулу
Подставляя обе полученные формулы в числитель и знаменатель
выражения A2.41), сразу приходим к результату
2 ' е«и Ы _ ]
Слагаемое йсо/2 представляет собой так называемую «энергию
нулевых колебаний» данной электромагнитной моды (энергия ее
самого низкого, или основного, состояния, для которого п - 0).
Энергию нулевых колебаний нельзя отобрать у системы, т. е.
она не может быть использована. Отбрасывая нулевую энергию,,
приходим к формуле
йш . A2.43)
1 еЫ> кГ _ )
Именно эту формулу мы использовали выше |см. A2.36) I. При
высоких температурах, когда кТ ^- На, из формулы A2.43) полу-
получаем приближенную формулу
с,с\-, = к! ,
хорошо известную из классической статистической физики х).
г) Речь идет о теореме о равномерном распределении энергии по степе-
степеням свободы, согласно которой на одну осцилляторную степень свободы
приходится энергия кТ,2~т кТ/2 = к Т.— Прим. перев.
168
Взаимодействие излучения с системой
§ 12.4. Индуцированные переходы атомной системы
в столкновительном режиме
Когда на атомную систему, находящуюся в возбужденном энер-
энергетическом состоянии, действует электромагнитное излучение, в ней
имеют место переходы в ниже- и вышерасположенные энергети-
энергетические состояния, причем скорость переходов прямо пропорцио-
пропорциональна плотности энергии падающего электромагнитного поля.
Ниже мы рассчитаем эту скорость, пользуясь полуклассической тео-
теорией, согласно которой возбужденные атомы рассматриваются
квантовомеханически, а поле электро-
электромагнитного излучения — классически. $
Пусть наша атомная система в момент
времени / = О (момент, с которого мы на- р 1
чали наблюдение) находилась в состоянии ~?
2 и пусть ее нижерасположенное по энер- р 124 Л
гии состояние 1 отделено от состояния 2 тических уровня "атом-
энергетическим интервалом Е2—Ег == ной системы, рассмат-
=йо>21» как показано на рис. 12.4. риваемые при выводе
Пусть электрическое поле падающего Формулы для скорости
■> г ^ —» индуцированных пере-
на среду электромагнитного излучения ХОДов. (Другие энерге-
в точке г, в которой расположена атомная тические уровни не по-
система, дается формулой казаны.) При I = 0 си-
система находилась в со-
Е(г, /)-=Е0(г)со5<о*. A2.44) стоянии 2.
Поскольку потенциальная энергия электрона в электрическом
поле Е определяется формулой
V- —е(Е-г), A2.45)
для гамильтониана взаимодействия атомной системы с электромаг-
электромагнитным полем имеем следующее выражение:
Ж (I) = е-М- (еш + е-ш), A2.46)
при написании которого мы предположили, что электрическое поле
поляризовано в направлении оси у.
Как видим, гамильтониан взаимодействия A2.46) имеет стан-
стандартный вид A1.26а). Поэтому можно непосредственно восполь-
воспользоваться формулой A1.32) для скорости переходов вниз B ->- 1)
или вверх A ->■ 2) 1):
1) Используя здесь формулу A 1.32), мы ограничиваемся (см. текст в
конце § 11.2) рассмотрением только тех случаев, когда атомная система ис-
испытывает много столкновений с другими атомами, прежде чем в ней произой-
произойдет хотя бы один индуцированный электромагнитным полем переход с уровня
на уровень. Это предположение оправдано для большинства обычных экспе-
экспериментов, в которых используются слабые электромагнитные поля. В тех
169
Глава 12
\гЬ (Е.-Е.-Псл), A2.47)
2А
причем здесь
еу12= е\ и\ущйх. A2.48)
Когда разность энергий Е2—Ег уровней точно неизвестна (при-
(причины такого положения вещей объясняются в конце настоящего
параграфа), следует пользоваться функцией формы линии § (Е),
определяемой соотношением
§ (Е) АЕ = Вероятность найти значение Ег — Е1г
заключенное между Е и Е + а"Е, A2.49)
при этом, очевидно, I § (Е) йЕ = 1. Тогда формула для скорости
Н^инд индуцированных электромагнитным полем переходов по-
получается интегрированием формулы A2.47) по всем возможным
значениям Е2—Ег с весовой функцией § (Е2—Е^):
инд = — .I о (Е, — Ег — Ы) § (Ег—Ех) А (Е, — Ех) -^
2П
В этой формуле можно перейти от функции § (Е) к аналогичной
функции § (х), зависящей от частоты, используя очевидное опреде-
определяющее последнюю функцию соотношение § (х) их = § (Е) й (Нх)
(закон сохранения вероятности). Так, придем к формуле
Ц?„ил~ Ё<?21!'2*2^). A2.50)
Обычно электромагнитное поле характеризуют не величиной Ео,
а интенсивностью /%, (измеряется в единицах Вт/м2), причем
, Энергия
1~
Скорость распространения энергии =
Объем
гГп~Ет. с спе„Ег.,
A2.51)
случаях, когда индуцированные электромагнитным полем переходы, про-
пропорциональные квадрату амплитуды поля, осуществляются намного чаще,
чем столкновения между атомами, формулу A1.32) использовать нельзя.
О том, что нужно делать в этом случае, мы поговорим в § 13.1.
170
Взаимодействие излучения с системой
Поэтому формулу A2.50) можно представить окончательно в виде:
В следующем параграфе мы покажем, что матричный элемент
у12 связан с временем жизни /Спонт атомной системы (относительно
спонтанного перехода 2 -»- 1) формулой
'споит
так что формулу для скорости индуцированных переходов можно
записать также в виде
"У Л- A2.526)
Формулы A2.52а), A2.526) играют важную роль в теории яв-
явлений поглощения и дисперсии света в атомных средах. Поговорим
о некоторых следствиях из этих формул.
Скорость индуцированных переходов с уровня 2 на уровень 1
пропорциональна интенсивности падающего на атомную систему
электромагнитного излучения. Но она пропорциональна также
и квадрату матричного элемента е2у212 [формула A2.48) ]. Следо-
Следовательно, если собственные функции их \\ и2 атомной системы имеют
одну и ту же четность, т. е. если их произведение и1и.1 оказывается
четной функцией, то ?/,2 = 0 и скорость И7„нд индуцированных
переходов обращается в нуль. Такие невозможные по нашей фор-
формуле переходы называются «дипольно-запрещенными».
В качестве примера дипольно-запрещенного квантового пере-
перехода укажем переход атома водорода из состояния п. = 3, 1 = 2
в его основное состояние п = 0, / = 0. Согласно § 6.3, четность
состояния электрона в атоме водорода определяется четностью
квантового числа /.
Согласно A2.52а), A2.526), скорость №т1Д индуцированных пе-
переходов зависит от § (у). Это обстоятельство требует пояснений.
До сих пор мы рассматривали разность энергий состояний Е2—Е1
как точно определенную квантовую величину, поскольку энергии
Е; — собственные числа дифференциального стационарного урав-
уравнения Шредингера. В реальных атомных системах, однако, всегда
существует механизм, который делает собственные числа энергии,
а потому и разность Е„—Е1г неопределенными, так что разность
энергий Е2—Ег на самом деле не имеет точного значения. Один
из наиболее распространенных механизмов связан с тем, что столк-
столкновения с другими атомами или спонтанные переходы в нижерас-
нижерасположенные состояния могут изменять время жизни атома, находя-
находящегося на уровне 1 или 2. Согласно соотношению неопределенно-
171
Глава 12
стей C.35), это приводит к размазыванию разности энергий Ег—Е1
на интервал
АЕ—К'т, A2.53)
где т — время жизни атомной системы. Таким образом, для изоли-
изолированных атомов энергетическая ширина АЕ функции формы спек-
спектральной линии § (Е) определяется формулой A2.53).
§ 12.5. Спонтанные электромагнитные переходы
атомной системы
Как указывалось в предыдущем параграфе, атом под влиянием
электромагнитного излучения испытывает индуцированные пере-
переходы на другие энергетические уровни со скоростью, которая, со-
согласно формуле A2.52а), A2.526), пропорциональна интенсивности
падающего на него электромагнитного излучения.
В настоящем параграфе мы учтем, что, кроме индуцированных
электромагнитным полем переходов, атом может совершать пере-
переходы на ниже расположенные уровни также и при полном отсутст-
отсутствии внешнего электромагнитного излучения. Такие переходы на-
называются «спонтанными», поскольку их скорость не зависит от
интенсивности /V поля электромагнитного излучения.
К выводу о существовании такого рода переходов атомных
систем впервые пришел Эйнштейн [22 ] в 1916 г. Он рассуждал
следующим образом.
Представим себе большую систему, состоящую из идентичных
атомов, или ансамбль атомов; система находится в тепловом равно-
равновесии с тепловым электромагнитным излучением абсолютно чер-
черного тела при некоторой температуре Т. Средние числа атомов,
занимающих некоторые уровни, скажем 2 и 1, т. е. два собственных
состояния атома (ниже будем их называть населенностями) должны
соответствовать формуле Больцмана A6.3). Предполагая, что
квантовое вырождение уровней одинаково, т. е. ^2 — ёи из этои
формулы получаем
Если Е2^>ЕЪ то Ы2<^А'1. С другой стороны, полное число ато-
атомов, совершающих переходы с уровня 2 на уровень 1 за данный
промежуток времени, при тепловом равновесии должно быть равно
числу атомов, совершающих обратные переходы с уровня 1 на уро-
уровень 2. Это следует из того, что числа N2 и Nг не должны меняться
с течением времени. Указанное разумное требование не будет про-
противоречить неравенству К2<^Ы1 только в том случае, если допу-
допустить, что скорость переходов отдельного атома вниз B —>- 1) больше
172
Взаимодействие излучения с системой
скорости его переходов вверх A —>- 2). Поэтому Эйнштейн посту-
постулировал следующие формулы для скорости переходов:
11-"',^=- Вр(у). A2.55)
Согласно этим формулам, скорость переходов вниз B -*■ 1) равна
сумме скорости индуцированных переходов Вр (г) [которая про-
пропорциональна плотности электромагнитного излучения р (л>) ] и ско-
скорости спонтанных переходов А. Скорость переходов вверх равна
только скорости индуцированных переходов Вр (г). Приравнивая
числа атомов, совершающих переходы вверх и вниз в данный про-
промежуток времени, приходим к соотношению
N. [Вр (V) 4 А] „--- А^Вр (V), A2.56)
так что
Л/2 ВрЫ -Ъ-в.ьт ^^ A25?)
Л'] Д[) (V) 4- А
где использовано, что Нх — Е2—Ег. Формула A2.57) должна со-
согласовываться с формулой Планка для спектральной плотности
энергии теплового электромагнитного излучения. Если мы сопо-
сопоставим формулу A2.57) с формулой A2.37):
Р(У) „, ^'Т* - "'
то сразу получим знаменитое соотношение Эйнштейна
,4 8лп3/гув
В ~ с3
A2.58)
Скорость спонтанных переходов А отдельного атома называют
эйнштейновским коэффициентом А.
Предположим теперь, что каким-то образом в начальный мо-
момент времени нам удалось перевести значительное число атомов
среды в возбужденное состояние 2, хотя в нормальных условиях,
т. е. при тепловом равновесии, населенность этого уровня прене-
пренебрежимо мала. Если отсутствует внешнее электромагнитное излу-
излучение [т. е. если р (у) = 0 ], то, согласно формулам A2.55), среднее
число атомов, совершающих переход 2 -*■ 1 в единицу времени,
равно N2А. Таким образом, средняя населенность возбужденных
атомов N2, находящихся в состоянии 2, должна убывать по закону
173
Глава 12
поэтому
Ы2 ({) = Ы2 @) е~м = N.2 @)
Таким образом, коэффициент Эйнштейна А равен обратному вре-
времени жизни 4понт возбужденного атома относительно спонтанного
перехода.
В следующем параграфе мы пока-
; жем, что каждый спонтанный пе-
переход сопровождается испуска-
испусканием одного фотона с частотой V =:=
её (Е2—Е^/Н. Это дает возможность
проследить за эволюцией населенно-
населенности Л'2 атомного уровня 2, а сле-
следовательно, измерить среднее время
4понт- Метод состоит в том, что большое
число атомов переводят в возбужден-
возбужденное состояние, а затем определяют вре-
временную зависимость интенсивности
спонтанного излучения. Такая зави-
зависимость интенсивности излучения от
времени изображена на рис. 12.5.
Бремя, мс
Рис. 12.5. Населенность воз-
возбужденного состояния, реги-
регистрируемая по изменению
интенсивности испущенного
электромагнитного излучения.
§ 12.6. Квантовомеханический вывод формулы
для скорости спонтанных переходов
Займемся теперь строгим выводом формулы для скорости
спонтанных переходов атомной системы из возбужденного состо-
состояния | 2) в нижерасположенное состояние | 1).
Предположим, что атом эффективно взаимодействует только
с одной модой электромагнитного излучения. Формулу для ско-
скорости переходов под действием одной электромагнитной моды не-
необходимо просуммировать по всем модам; тогда мы найдем полную
скорость спонтанных переходов из состояния | 2) в состояние | 1).
Таким образом, наша полная квантовомеханическая система
теперь состоит из единственного атома и единственной моды элек-
электромагнитного излучения /, как показано на рис. 12.6.
До перехода атом находился в возбужденном состоянии 12),
а мода / электромагнитного излучения — в состоянии | щ). Началь-
Начальное состояние полной системы обозначим символом
Н 2) |
A2.59)
После перехода атом оказывается в нижнем состоянии | 1), а мода /
приобретает квант излучения и переходит в состояние | щ + 1).
174
Взаимодействие излучения с системой
Таким образом, конечное состояние полной системы следует обо-
обозначить символом
11, 71/+1) = | 1>|и/+1). A2.60)
Энергии начального и конечного состояний определяются выра-
выражениями
Рис. 12.6. Схематическое изображение квантовомеханической системы, рас-
рассматриваемой при выводе формулы для скорости спонтанных переходов.
Первоначально атом находится в состоянии | 2), а мода электромагнитного
излучения / — в состоянии | п/). Атом перехолит в нижерасположепное со-
состояние | 1), а мода излучения — в вышерасположенное состояние \гц + 1).
так что
Е1 — Е{ = Е2—Е1 — Нщ. A2.61)
Гамильтониан взаимодействия атома с электромагнитной мо-
модой определяется формулой A2.45):
Ж~-еЕ1и(г. 1)у, A2.62)
в которой предполагается, что мода электромагнигного поля ли-
линейно-поляризована вдоль оси у и что она распространяется вдоль
оси г. Теперь подставим формулу A2.30) в A2.62). Тогда получим
Ж' =- — 1е
—Л-г
A2.63)
Поскольку наша полная квантовомеханическая система включает
в себя также и поле электромагнитной моды, гамильтониан X'
теперь явно не зависит от времени.
175
Глава 12
Скорость переходов можно вычислить по формуле A1.33):
2—Е, — йсо,). A2.64)
Чтобы преобразовать формулу A2.64), необходимо воспользоваться
соотношениями
(щ + 11 а] | «/> = V и/ + 1,
<п,+11 а, |«!>-■=--О,
<1|г/|2) = г/12. A2.65)
Тогда из A2.64) сразу получаем
2-Ег-Пщ), A2.66)
где верхний индекс указывает, что рассматривается переход, воз-
возникающий за счет взаимодействия атома с электромагнитной мо-
модой /.
Обычно величину И7(/) разбивают на два слагаемых:
117(/) — 117(/) -X \У/Ц)
Первое слагаемое
Ц7<<)д = ^^11 ^ |* „/6 (Е2_Е!-йю,) A2.67)
дает скорость индуцированных переходов, так как оно пропорцио-
пропорционально плотности энергии (я/йсо/ /I/) рассматриваемой моды элек-
электромагнитного излучения. Второе слагаемое
^оет= -^^14/12 ^(Ъ-^-Йй),) A2.68)
дает скорость спонтанных переходов, так как оно не зависит от
энергии электромагнитной моды.
Заметим, что
Г(/)
_ _П/> A2.69)
т. е. отношение скорости индуцированных переходов к скорости
спонтанных переходов (обе скорости для моды /) равно щ — числу
квантов (фотонов) рассматриваемой моды электромагнитного из-
излучения.
При /1/ — 0, т. е. когда мода находится в своем основном со-
состоянии, скорость индуцированных переходов 1^д обращается
в нуль, и полная скорость переходов оказывается равной а
176
Взаимодействие излучения с системой
Чтобы найти полную скорость спонтанных переходов, надо про-
просуммировать формулу A2.68) по всем электромагнитным модам.
Число мод, приходящихся на единичный интервал частоты в ящике
объемом V, дается, согласно A2.35), выражением
Следовательно, полная скорость спонтанных переходов равна
вспоит - Г К&онтр (V/) <Ч = _^1^М Х° . A2.70)
о екс*
При выводе формулы A2.70) мы воспользовались соотношением
Е2—Е1 = к\0.
Чтобы получить более точное выражение, следует, конечно,
учесть различные направления поляризации электрического поля
различных электромагнитных мод. Поэтому матричный элемент
|г/12|2 в A2.70) надо заменить выражением
тогда окончательная формула для скорости спонтанных переходов
принимает следующий вид:
Гаюит - —^ - „ ° (I х1г | * +14/м | * + I гв |2).
'споит о&НС
A2.71)
Напомним, что скорость Испоит обозначают также буквой А,
как в A2.58).
Пример. Время жизни атома водорода относительно спонтан-
спонтанного перехода |2р) -> | 1 5). В качестве примера вычислим время
жизни атома водорода относительно спонтанного перехода из воз-
возбужденного состояния п -= 2, / = 1 (т. е. из состояния 12р)) в со-
состояние я = 1, / = 0 (т. е. в состояние | 15».
Верхнее состояние л — 2, 1=1 трехкратно вырождено; для
него квантовое число т может принимать три значения: т = 1,
0, — 1. Эти три верхних состояния можно выбрать следующим об-
образом 1см. G.63) I:
2
• е
1 2 1 32л
I У) =-" — («211 —«21-1) =" =~ ( ) б у,
I 2 1 32л ^ а° I
\г) = и,10--= ( ) ге г.
I чо, \ °0 /
177
Глава 12
Основное состояние атома водорода описывается функцией
1е~гга'. A2.73)
\ л
Скорость спонтанных переходов дается формулой A2.71):
депонт = ""'""/ (I*и 12 -1 У* 12 Ч-12ц |*). A2.74)
Скорость переходов зависит, вообще говоря, от того, в каком из
трех верхних вырожденных состояний (п = 2) первоначально на-
находился рассматриваемый атом водорода. Для определенности
предположим, что первоначально атом находился, например, в воз-
возбужденном состоянии |д:). Матричные элементы перехода тогда
можно вычислить, используя формулы A2.72) и A2.73):
У12 = < 1 I у I х) ее |' хуе~~дгг 12а"йЧ.-.. О, A2.75)
г*. - <11 г | х) ее |" гхе-~гг '2а сРг О,
%, -=(\\Х\Х)= — — | Г4е~3" 2С"С(Г ^ 51 '
I 32 -Ч
1281 2
243 г г
A2.76)
Эти выражения для х12, у12, г12 следует подставить в A2.74), учи-
учитывая [см. G.50) ], что для рассматриваемого перехода в атоме
водорода
кх(п2п 1)
кхо(п2п 1),
откуда \>0 — 3,288-1013 22. В результате получим
Гспс„т-6,27-10824.
2-*1
Для атома водорода B=1) мы имеем
<с™,„т-Испоит-1,60-Ю-в с. A2.77)
Если бы мы взяли состояние | у) или | г} в качестве начального
возбужденного состояния, то получили бы в точности то же число
A2.77), ибо соответствующие матричные элементы равны друг
ДРУгу:
<г|г|1)-<у|4/|1>-<*|*|1>.
Поэтому время A2.77) характеризует время жизни относительно
спонтанного перехода атома водорода в возбужденном состоянии
п = 2, 1= I.
178
Взаимодействие излучения с системой
Задачи
1. Докажите, что времена жизни относительно спонтанного перехода для
состояний \у) и | г) [см. A2.12)] равны времени жизни для состояния | х).
2. Вычислите время жизни атома водорода относительно перехода
п = 3, I ■-- 2 -»- п ~- 2, / = 1.
3. Убедитесь, что выражение A2.67) для скорости индуцированных перехо-
переходов согласуется с выражением A2.50).
4. а. Вычислите времена жизни относительно переходов п -*■ п—1 и п -*■ п—2
для электрона, движущегося в потенциальном поле одномерного осцил-
осциллятора V — A/2) то)(уС2. Считайте, что /гсоо = 1 эВ и что осциллятор на-
находится в состоянии п -•= 3.
б. Чему равно время жизни для состояния п относительно спонтанного
перехода п -*■ п—2, если потенциальная энергия дается выражением
V (х) ^ A/2) тш--А-24- Ьх3, где Ь =-- 2-1029 эВ-м?
6. Выведите формулу A2.38) для интенсивности равновесного теплового
электромагнитного излучения абсолютно черного тела, пользуясь извест-
известным выражением для спектральной плотности энергии такого излучения.
6. Проквантунте энергию простого электрического колебательного контура
состоящего из индуктивности Ь и параллельно включенной с ней емко-
емкости С. В частности, ответьте на вопросы:
а. Что играет роль канонически сопряженных координаты и импульса
в данном случае?
б. Какой вид примет гамильтониан, выраженный через сопряженные
координату и импульс, если записать его с помощью операторов уничто-
уничтожения а У и рождения с?
Указание. При решении задачи вы должны получить формулы
аг --
где / (() и V @ — соответственно мгновенные значения тока и напряже-
напряже2 = (ЬСI
ния в контуре, причем ш2 = ()
7. а. Используя результаты задачи 6, получите выражения для среднеквад-
среднеквадратичного значения напряжения и тока, учитывая вклад нулевых коле-
колебаний для «проквантованного» контура НС. Вычислите их для случая
^. = 2,53-10 Гн и С = Ю-2 Ф.
б. Предполагая, что решения задач 6 и 7а пригодны также и для элек-
электрического колебательного контура, содержащего сопротивление К,
включенное последовательно с I и С, покажите, что средняя диссипируе-
мая в контуре мощность равна
Р « ПыВ,
где В = (НС) — ширина резонансной полосы этого контура (или, что
то же самое, обратное время релаксации).
ГЛАВА 13
ПОГЛОЩЕНИЕ, УСИЛЕНИЕ И ДИСПЕРСИЯ
ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ АТОМНОЙ СРЕДОЙ
Электромагнитное излучение, распространяющееся в матер и
альной среде, взаимодействует с атомами (или молекулами) среды
и заставляет их переходить из одних квантовых состояний (или
уровней) в другие состояния (или уровни). Это взаимодействие
проявляется при обычных условиях в явлении поглощения элек-
электромагнитного излучения средой и в явлении дисперсии электро-
электромагнитного излучения (т. е. в зависимости фазовой скорости рас-
распространяющейся в среде электромагнитной волны от ее частоты).
В состояниях, сильно отличающихся от состояния теплового рав-
равновесия, когда в среде создается так называемая «инверсная на-
населенность» уровней атомов, интенсивность падающего на среду
электромагнитного излучения при прохождении среды может уве-
увеличиваться (будет наблюдаться «отрицательное поглощение», или
усиление, электромагнитных волн). Такое явление имеет место
в активных средах лазерных усилителей и генераторов.
Как уже обсуждалось в § 11.2, взаимодействие атома с гармони-
гармоническим по времени возмущением, каковым является электрическое
поле падающего на него электромагнитного излучения, может за-
заставить атом совершать переходы между двумя квантовыми состоя-
состояниями, скажем между состояниями п и т. Это возможно, когда
энергия фотона /гсо падающего электромагнитного излучения почти
равна разности энергий | Еп — Ет' двух указанных атомных со-
состояний.
В теории явлений поглощения, усиления и дисперсии электро-
электромагнитного излучения в атомной среде следует различать следую-
следующие два предельных случая.
1. В первом предельном случае говорят о так называемом бес-
столкновительном режиме, при котором отдельный квантовый
переход в атоме совершается за время, много меньшее, чем время
между последовательными столкновениями этого атома с другими
атомами («столкновением» мы называем любое серьезное возмуще-
возмущение атома его окружением). Поскольку время одного перехода
в атоме, как будет показано в § 13.1, имеет порядок ли ц.Е0 (где
[I — матричный элемент оператора электрического дипольного мо-
момента для данного перехода, Ео — амплитуда электрического поля),
взаимодействие атома с электромагнитным излучением происходит
в бесстолкновительном режиме, если выполняется неравенство
180
Поглощение, усиление и дисперсия
Благодаря появлению лазеров, дающих электромагнитное из-
излучение очень высокой интенсивности, т. е. с большими значениями
Ео, в настоящее время можно добиться выполнения этого неравен-
неравенства в лабораторных условиях.
2. Во втором случае речь идет о так называемом столкновитель-
ном режиме, в котором столкновения доминируют. Тогда выпол-
выполняется обратное неравенство
л Л ...
цЕ0
С указанным особенно важным предельным случаем мы встре-
встречаемся в большинстве обычных экспериментов, а также во многих
природных явлениях, в которых проявляется поглощение и диспер-
дисперсия света. Столкновительный режим осуществляется также и внутри
лазерного резонатора, где имеет место взаимодействие между ато-
атомами н полем электромагнитного излучения. Подробно столкнови-
столкновительный режим рассматривается в § 13.2—13.4.
§ 13.1. Временная эволюция
двухуровневого атома
в бесстолкновительном режиме
Большинство встречающихся на практике задач, касающихся
взаимодействия поля электромагнитного излучения с атомами, изу-
изучается с помощью методов теории возмущений. Однако имеется
одна простая модельная задача, которую можно решить точно,
без каких-либо приближении. Это задача об изолированном, а
следовательно, ни с чем не сталкивающемся атомном объекте
(атоме, молекуле или отдельном электроне), который по предполо-
предположению может находиться только в двух квантовых состояниях,
обозначаемых 1 и 2, и который взаимодействует с полем классиче-
классической монохроматической электромагнитной волны.
Реальные атомы, разумеется, имеют бесконечное множество
энергетических уровней. Однако они все же очень хорошо моде-
моделируются с помощью указанной простой двухуровневой модели,
если только какой-то один атомный переход оказывается (почти)
в резонансе *) с частотой приложенного электромагнитного поля.
Собственные функции обоих уровней модельного атомного
объекта обозначим через ил и ы,, невозмущенный гамильтониан —
через Жо, а соответствующие его невозмущенные собственные
') Под «резонансом» здесь пон имаем условие, что энергия фотона Лео
падающего электромагнитного нзл учения с хорошим приближением равна
энергии перехода | Ег—Е± \.
181
Глава 13
энергии — через Еу и Е2, так что
(г) = Еупу (г),
A3.1)
Жйщ. (г) ■= Е2Щ. (г),
где под г подразумеваются как пространственные, так и спиновая
координаты электрона. При наличии гармонического электриче-
электрического поля
возмущающий гамильтониан, согласно A2.46), имеет вид
Ж' = — (хЕ0со5со/, " A3.2)
где [х — проекция векторного оператора ег электрического диполь-
ного момента атома на направление электрического поля. Полный
гамильтониан дается суммой Жо + Ж'. (Для рассматриваемого
сейчас электрического дипольного перехода, происходящего под
действием электромагнитного поля, поляризованного, скажем, по
направлению оси у, следует считать, что [I = еу.)
При наличии возмущения Ж' волновые функции будут линей-
линейными комбинациями функций и1 и и2.
г|з @ аг @ иг е^1ь)'1 ~ а, @ ше'10"', A3.3)
где со1-2 = ЕЪ2:!Н и а1A) и а2 (/) — функции, которые нужно
отыскивать. Волновая функция ф (I) должна удовлетворять ура в
нению Шредингера Ш^ ~ 1Щ\ которое в данном случае записы-
записывается в виде
( х0 И|^ (еш 4- е~1тГ)\ «А-^- A3.4)
Заметим, что при Ео ~ 0 волновая функция A3.3) представляет
собой решение уравнения A3.4), если считать функции а, (/) и
иг (I) константами.
Подставим выражение A3.3) для функции гр (г) в уравнение
A3.4), умножим обе части уравнения на и2 и проинтегрируем. Тогда,
используя условия ортонормировки
<1|2)-0, <1|1)-=<2|2)-1 A3.5)
и условие
\1и -_•= \1Ш = О,
которое выполняется в том случае, когда каждая функция их и и2
имеет точно определенную четность (тогда г/ц = г/22 = 0, согласно
§ 6.3), получаем уравнение
182
Поглощение, усиление и дисперсия
Ограничимся рассмотрением случая, когда приложенная ча-
частота со почти равна частоте перехода, т. е. когда со.,—ы1 г= о.
Тогда первое слагаемое в скобках в правой части уравнения A3.6)
будет колебаться примерно с частотой 2со, и среднее от него по вре-
времени, значительно превышающему период колебаний 2л/со, равно
нулю. Таким образом, в уравнении A3.6) следует оставить только
второе, «медленное» слагаемое в скобках, т. е. ехр М (со2—а>г—со) I ].
Таким образом, приходим к следующему приближенному урав-
уравнению:
^_и^_ ахе-ш. A3.7а)
2 * '
й ахе.
Ш 2
Рассуждая аналогично, можно получить еще одно приближенное
уравнение:
/й-^-^-М^о.е'". A3.76)
Ш 2 ^
Здесь использованы сокращенные обозначения:
Д == СО — (Юо — СО!).
Величина Л характеризует «рассогласование» частот.
Полученную систему приближенных уравнений A3.7а, б)
легко разрешить относительно функций аг {I) и а2 (О- Поясним
основные этапы процедуры построения решения.
Прежде всего предположим, что решение системы A3.7а, б)
можно искать в виде
01.2@-^1.2*"^, A3.8)
где следует взять либо индекс 1, либо индекс 2. Подставим A3.8)
в A3.7а). Чтобы все члены в получаемом уравнении имели одина-
одинаковую временную зависимость, должно выполняться соотношение
52-5! — Д. A3.9)
Сократив все члены полученного уравнения на одинаковые вре-
временные экспоненциальные множители, получим алгебраическую
однородную линейную систему двух уравнений относительно не-
неизвестных Аг и А 2. Эта система имеет нетривиальное решение
только в том случае, если ее детерминант равен нулю. Приравни-
Приравнивая детерминант нулю, находим
■ /А /V
(-Л ± СО ).
2
183
Глава 13
Отсюда с учетом A3.9) имеем формулу
! —; ( Д -4- (д) )а A*3.10)
Здесь
= — , ш = I/ Д': + 4У':. A3.11)
2А
Окончательно для неизвестной функции аг (I) приходим к выра-
выражению
^ +АТе8^ , A3.12)
причем здесь А~\~ и АТ — пока произвольные константы.
Если в начальный момент времени (при / = 0) атомная система
находилась в нижнем состоянии, то, согласно A3.3), следует счи-
считать, что ах @) = 1 и а2 @) = 0. Тогда из A3.12) получаем соотно-
соотношение
АТ + АТ=1. A3.13)
Подставим теперь выражение A3.12) для функции ау (I) в пра-
правую часть уравнения A3.76) и решим получившееся уравнение от-
относительно а2 (/). Таким образом, мы выразим функцию аг (I) че-
через константы А^ и А\~. Требуя выполнения начального условия
а2 @) = 0, придем еще к одному соотношению
А^ -^Л_ =-.0. A3.14)
Л —
Решая систему уравнений A3.13) и A3.14) относительно А\ и АХ,
получаем формулы
'А 1+^ A3.15)
2ш' 2ш'
Подстановка A3.15) н A3.10) в A3.12) дает окончательные вы-
выражения для искомых функций:
а»(г)^ — 1—- 51 п ( \е , A3.17)
которые и являются решением системы уравнений A3.7 а, б).
В случае точного резонанса, когда со = и„—«!, очевидно,
Л = 0 и О = 2ю'. Тогда из A3.16) и A3.17) имеем
A3.18)
184
Поглощение, усиление и дисперсия
так что вероятности |а1(<)|2 и |а2(/)|2 найти систему в состоя-
состояниях 1 и 2 соответственно будут в случае точного резонанса осцил-
осциллировать между нулем и единицей по простому гармоническому
закону с частотой
2А
Графики функций \аг (/)|2 и \а2 (I) |2 приведены на рис. 13 1.
Колебательный характер зависимости от времени / функций
сх @ и а2 ({), которые в случае точного резонанса зависят от вре-
времени по простому гармони-
гармоническому закону, характерен
для любой системы двух свя-
связанных линейных осциллято-
осцилляторов.
Простое осцилляторное
поведение атома сильно на-
нарушается, когда его взаимо-
взаимодействие с электромагнитным
полем прерывается упругими
и неупругими столкновения-
столкновениями с другими атомами. Об
этом мы подробнее поговорим
в § 13.4.
Рис. 13.1. Зависимость от времени I
вероятности | а1 @12 найти атом в ниж-
нижнем состоянии п вероятности | о2 (О 12
найти атом в верхнем состоянии. На
атом действует поле Е0со5 со/, частота
со которого удовлетворяет условию точ-
точного резонанса со = со2—со,.
Решив для рассматривае-
рассматриваемой модельной двухуров-
двухуровневой атомной системы пол-
полное уравнение Шредингера
и отыскав волновую функ-
функцию г|1 (/), описывающую атомную систему при наличии возмущаю-
возмущающего электромагнитного излучения, мы можем теперь рассчитать
средние значения нужных физических величин.
Для описания процессов испускания и поглощения электро-
электромагнитного излучения атомом надо вычислить среднее значение
| яр* (/) |п)' @ сРг оператора электрического дипольного момента \х.
Пользуясь выражением A3.3) для функции ч|; (/), а также учитывая,
что A | и | 1) -- B| ц | 2) = 0, приходим к простой формуле
\ц) = \1п\ (/) а.> (г) в Ы: "' -г Компл. сопр. A3.19)
Представим теперь, что у нас имеется образец, содержащий N
атомов, которые первоначально (при / — 0) находились в своих
основных состояниях, описываемых собственной функцией иг.
Пусть на этот образец начинает действовать переменное электри-
электрическое поле ^0со5 со/. Тогда для суммарного электрического ди-
дипольного момента образца имеем очевидную формулу
р{1) ■- N \ц/ - Ы\Ш\ (/) а2 (/)е1<11)'"~Ш2)<-г Компл. сопр. A3.20)
185
Глааа 13
Такой «гигантский» диполь подобен многоэлементной излучаю-
излучающей антенне, и, когда число N достаточно велико, излучение этой
«антенны» (на частоте со2—С01) можно легко зарегистрировать.
В самом деле, пусть возмущающее поле внезапно выклю-
выключается при { = я/2^. Тогда, согласно формулам A3.18),
л2о гг, *()ия,а
I 2 I 2
и электрический момент излучающего диполя приобретает вполне
детектируемое максимальное возможное значение
р(/) ^ _. _^11_ е1 <«■-»-■)' _|_ компл сопр. ___ Д'и 51П!(«!—озо) /].
A3.21)
Особое состояние образца, когда его /V атомов «приготавли-
«приготавливаются» с помощью мощного электромагнитного излучения таким
образом, чтобы фазы электрических дипольных моментов отдель-
отдельных атомов оказались когерентными между собой, впервые изучил
Дикке [23]. который назвал его «сверхнзлучающим состоянием»,
В заключение настоящего параграфа полезно еще раз напом-
напомнить читателю, что здесь мы занимались только бесстолкновшпель-
ным режимом. Режим этот может быть экспериментально осущест-
осуществлен, однако, только в тех случаях, когда интенсивность поля
излучения достаточно велика. Тогда атом будет успевать совер-
совершить достаточное число осцилляции между состояниями 1 и 2,
прежде чем испытает хотя бы одно «столкновение» н «забудет»
свою начальную фазу. Другими словами, мы считаем, что выпол-
выполняется неравенство \кЕ0'Н > 1/тстолк. Когда выполняется противо-
противоположное неравенство иЕ0 'К <; 1,'тСТОЛк. надо рассматривать
столкновнтельный режим и, согласно критерию из § 11.2, для
его изучения можно использовать теорию возмущений. Столкно-
вительный режим осуществляется в большинстве обычных экспе-
экспериментов, а также в резонаторах лазеров.
§ 13.2. Поглощение и усиление
электромагнитного излучения атомными системами
в столкновительном режиме
Как было показано в § 12.4, атом под действием приложенного
электромагнитного поля вынужден совершать переходы между
своими собственными состояниями. Если атом первоначально на-
находился в одном таком собственном состоянии, которое для опреде-
определенности будем называть состоянием 2, то скорость вынужденных,
186
Поглощение, усиление и дисперсия
или индуцированных, переходов в состояние 1 с энергией
согласно формуле A2.52а), равна
(у)
К'инд — 'V.
8л/гс/Лспонт
где Я, — длина волны электромагнитного излучения, 4пош — время
жизни атома относительно спонтанного перехода 2-> 1, Д.— ин-
интенсивность электромагнитного излучения, ^ (л1) —функция формы
излучаемой линии.
Здесь следует особо заметить, что уже само понятие функции
формы линии имеет смысл лишь для столкновительного режима,
к которому только и относятся все приводимые ниже рассуждения
настоящего параграфа.
Посмотрим теперь, что произойдет, когда плоская электромаг-
электромагнитная волна с интенсивностью Д. (измеряемой в единицах Вт.'м2)
н частотой V проходит через среду с плотностью населенности на
уровнях 2 и 1, равной соответственно Л/» и Nг (число соответствую-
соответствующих атомов в 1 м3). Число переходов вниз B —>■ 1) в единицу вре-
времени, совершаемых атомами, содержащимися в единице объема
среды, равно
а число противоположных переходов (вверх) равно
Таким образом, избыток числа переходов вверх над числом перехо-
переходов вниз равен
При каждом перехоме вниз A -*■ 2) электромагнитная волна те
ряет один фотон, а при каждом переходе вверх B-* 1) приобретает
один фотон. Полная теряемая электромагнитной волной мощность
в единице объема среды дается, таким образом, формулой
Потерн мощности должны приводить к уменьшению интенсивности
проходящей через среду электромагнитной волны, как показано
на рис. 13.2.
Здесь изображен кубический бесконечно малый объем Айг ве-
вещества, плотности населенностей уровней обозначены через К2
и Л',. Электромагнитная волна с интенсивностью Д. (г) падает нор-
нормально на грань кубика (с координатой г) и выходит через проти-
противоположную грань (с координатой г — йг), имея интенсивность
/у (г 4 ^г). При стационарных условиях (когда д,дг — 0) полный
187
Глааа 13
прирост мощности электромагнитной волны, заключенной между
обеими гранями рассматриваемого кубического объема, равен
[/л. (г -' йг) — 1Х (г)] А = ^
йг
Этот прирост должен равняться мощности — (Л^— ЛГ2) ШтщН\Айг,
которую теряют атомы, заключенные в объеме Айг. Таким обра-
образом, приходим к уравнению
йг
A3.24)
Подставляя в правую часть этого уравнения явное выражение
Рис. 13.2. Баланс мощности излучения для бесконечно малого объема ве-
вещества. Мощность (Л/2—Nх) К7^/гVЛйг, передаваемая полем электромагнит-
электромагнитного излучения атомам вещества, должна быть равна уменьшению мощности
проходящей волны. При ЛГ2<;ЛГ1 мощность электромагнитной волны по-
поглощается, и волна должна затухать по мере прохождения через слой ве-
вещества.
A2.526) для скорости переходов №инд, получим уравнение
а/у
йг
(V)
■Л-
A3.25)
Отсюда следует, что электромагнитное излучение по мере прохож-
прохождения через среду затухает по закону
]х{х)- 1хф)е~а\ A3.26)
где
A3.27а)
/У (у)
ОГШ"/спонт
Для среды, находящейся в тепловом равновесии, N г =
Ы2е(Е'~~Е'):кт, так что для нее Л^1>Л^2 [и а>0. Такие термо-
188
Поглощение, усиление и дисперсия
динамические равновесные среды поглощают проходящее через них
электромагнитное излучение, причем коэффициент поглощения дается
формулой A3.27а).
Однако во многих специальных случаях можно «накачать»
среду, т. е. перевести в ней значительную часть атомов с более
низкого уровня 1 на более высокий уровень 2, так чтобы выполня-
выполнялось обратное неравенство Лг2>Лгг. Согласно формуле A3.27а),
Падающая
волна
Усиливающая среда ('Лгг>Лг,)
Прошедшая
волна
Падающая
волна
Поглощающая среда
Прошедшая
волна
Рис. 13.3. Усиление распространяющейся электромагнитной волны в среде
с инверсной (о) и ее поглощение в среде с обычной (б) населенностью уров-
уровней. Атомы в верхнем состоянии 2 с энергией Е2 обозначены черными круж-
кружками, атомы в нижнем состоянии 1 с энергией Ег — светлыми кружками.
это приведет к тому, что коэффициент поглощения а изменит знак.
Проходящая через среду электромагнитная волна будет тогда не
поглощаться, а усиливаться.
Именно так и происходит усиление электромагнитных волн
в лазерных усилителях, впервые предложенных в оптическом ва-
варианте Шавловом и Таунсом в 1958 г. [241. Условие А^2>А^г на-
называют условием инверсной населенности. Коэффициент усиления
определяется формулой
т ^ ^ а = (#2 _ дг1} —/ЩМ—. A з.27б)
Различие между поглощающими (А^1>А^2) и усиливающими
(N1<^N.^) средами иллюстрируется на рис. 13.3.
189
Глааа 13
§ 13.3. Электрическая поляризация среды,
электрическая восприимчивость
и диэлектрическая проницаемость
В предыдущем параграфе мы, используя формулу временной
теории возмущений для скорости индуцированных переходов, опи-
описали поглощение (или усиление) электромагнитного излучения
при прохождении через среду, имеющую атомную структуру.
Взаимодействие электромагнитного излучения с атомами среды
проявляется также и в изменении фазовой скорости электромаг-
электромагнитной волны, проходящей через среду. Это изменение в электро-
электромагнитной теории учитывают, полагая, что скорость света в среде
равна с п, где с — скорость света в пустом пространстве и п =
-- \ е е0 — показатель преломления среды (е — ее диэлектриче-
диэлектрическая проницаемость). В настоящем параграфе мы выведем формулу
для диэлектрической проницаемости е, непосредственно рассмат-
рассматривая атомное строение среды.
Физический механизм, приводящий к замедлению распростра-
распространения электромагнитных волн в среде по сравнению с пустотой,
состоит в следующем. Переменное электрическое поле электро-
электромагнитной волны, проходящей через среду, с определенной силой
воздействует на электроны и атомные ядра атомов (и молекул)
среды, заставляя их колебаться с частотой падающей волны. Ко-
Колеблющиеся электрические заряды испускают электромагнитное
излучение в точности той же частоты, что и частота падающей на
среду электромагнитной волны. Полное электромагнитное поле
в среде оказывается, таким образом, когерентной суперпозицией
указанных полей. В результате фазовая скорость волны в среде
имеет иную величину, чем в пустоте.
Чтобы учесть эффекты, обусловленные колебаниями электронов
и атомных ядер под действием распространяющейся электромаг-
электромагнитной волны, выпишем уравнения Максвелла для среды, по пред-
предположению лишенной свободных электрических зарядов:
го! Е ,
01
ГО1 Н —-
61
н представим вектор электрического смещения в виде суммы
0 = 8оЕ + Р=--рЕ, A3.28)
где е — диэлектрическая проницаемость среды, Р — вектор элек-
электрической поляризации среды (формально определяемый как элек-
электрический днпольный момент единицы объема среды). Электриче-
Электрическая поляризация среды непосредственно связана с ее атомным
строением.
190
Поглощение, усиление и дисперсия
В классической электромагнитной теории вектор электриче-
электрической поляризации определяется формулой
г-*о 1-' "Г
в которой р.{ — электрические дипольные моменты различных ато-
атомов, нумеруемых индексом г; суммирование производится по всем
атомам, содержащимся в объеме V. В квантовой механике приме-
применяется формула
РA)^К (р,A)), A3.29)
в которой N — число атомов в единице объема среды и и (/) — век-
векторный оператор электрического дипольного момента отдельного
атома. В случае когда атом обладает единственным электроном,
следует считать, что ц, (I) — — ег, где г — векторный оператор
радиус-вектора, выходящего из атомного ядра и оканчивающегося
на электроне.
Дисперсию среды, возникающую из-за наличия магнитных ди-
польных моментов у атомов (и молекул) среды, здесь рассматривать
не будем.
В § 13.4 будет показано, что в рамках линейной теории погло-
поглощения и дисперсии электрическое поле
Е (О =--- Ео со5 со/ - Ке (Еоеш) A3.30)
(здесь используются простые скалярные обозначения) индуцирует
в каждом атоме колеблющийся электрический дипольный момент,
среднее значение которого по ансамблю атомов равно
(|1@)-Цосо5(со/—ф). A3.31)
Тогда, согласно A3.29), для поляризации (электрического ди-
дипольного момента единицы объема) получаем формулу
Р @ - N ф ({)) =-- Л^10со5(<о/ —ф) --:-. Ке (Р0<?'ш(), A3.32)
в которой
Р0 = Л^0<Г"{. A3.33)
Здесь Ео и Ро — комплексные амплитуды соответственно электри-
электрического поля и индуцированной полем поляризации. Начальный
момент отсчета времени мы выбрали так, чтобы сделать амплитуду
Ео действительной. Амплитуда Ро при этом все равно оказывается,
вообще говоря, комплексной. Наличие отличной от нуля фазы ц
у амплитуды Ро означает, что колебания функции Р (/) запазды-
запаздывают по сравнению с колебаниями функции Е (I), причем сдвиг
по времени равен величине ц ю, как показано на рис. 13.4.
191
Гпааа 13
В следующем параграфе мы покажем, что индуцированный элек-
электрический дипольный момент отдельного атома и0 пропорционален
электрическому полю Ео. Этой пропорциональностью можно вос-
воспользоваться, чтобы ввести важную физическую константу среды
%а (со) с помощью выражения
A3.34)
или выражения
РA)^Пе(гоХаЕоеш). A3.35)
Комплексная постоянная %а называется электрической воспри-
восприимчивостью среды; она характеризует величину электрической
поляризуемости среды.
ЕA) = Ео еоз шЪ
1
Рис. 13.4. Электрическое поле Е (I) и индуцированная поляризация Р (I)
в атомной среде. Обратите внимание на запаздывание функции Р (I) по от-
отношению к функции Е (О-
Если представить уЛ в виде
Ъ, = %а — 1Ха, A3-36)
считая %а и 1а действительными величинами, то формулу A3.35)
можно записать следующим образом:
Р @ = ШаЕ0 СО5 о/ + ШаЕ0 51П (ОЛ A3.37)
Поскольку электрическое поле описывается выражением Е {г) ==
-— Ео соз со/, действительное значение полной электрической вос-
восприимчивости %а (т. е. отсутствие чисто мнимой компоненты,
%а" = 0) означает, что колебания функций Р (/) и Е (/) происходят
в фазе. Комплексную восприимчивость %а можно связать с ком-
комплексной диэлектрической проницаемостью е, воспользовавшись
основными определяющими формулами
Е0 = гЕ0. A3.38)
Здесь %ь характеризует остаточную (фоновую) поляризацию среды,
а %а представляет собой вклад изучаемых нами атомных переходов.
192
Поглощение, усиление и дисперсия
Полная диэлектрическая проницаемость среды определяется
формулой A3.28). С учетом A3.38) имеем
~-^-%а), A3.39)
гь I
где ь'ь == е0 A 4~ %ь) — фоновая диэлектрическая проницаемость;
она вычисляется с учетом всех источников электрической поляри-
поляризации среды, кроме рассматриваемых атомных переходов, обозна-
обозначаемых индексом а.
Физический смысл электрической восприимчивости %«(ю)-
В § 12.1 было показано, что плоская монохроматическая элек-
электромагнитная волна, распространяющаяся в среде с диэлек-
диэлектрической проницаемостью е, описывается формулой
Е(г, 1) = Е0аов(аи — к'г)-=Ке[Е^ы-к'*], A3.40)
в которой
к' = а\ \пё. A3.41)
Отсюда с помощью формулы A3.39) непосредственно получаем при-
приближенное выражение
к' -. со | цг = со | \аеь [ 1 + (ео/е,;) %а (со)] -
^ со \ ^[1 +(го/2гь)ум(а)}, A3.42)
где при написании последнего равенства использовано то обстоя-
обстоятельство, что обычно е0 1%а \12еь <^ 1. Вводя в рассмотрение вели-
величину к = со] \хеь и выражая %а (со) через величины ум и у^ с по-
помощью A3.36), приходим к формуле
к-7^^, A3.43)
в которой и = (еь/е0)|/2 — фоновый показатель преломления (фак-
(фактически это просто показатель преломления для электромагнит-
электромагнитной волны, частота которой сильно отличается от частоты рассмат-
рассматриваемого атомного перехода).
Влияние электрической поляризации атомов среды на распро-
распространение электромагнитной волны в такой среде легче всего по-
понять, подставляя A3.43) в A3.40). Так мы придем к формуле
Е(г, 0 = Ке{ { [ ^ ^)\
^41 A3-44)
Из этой формулы видно, что учет влияния величины у'а просто
сводится к изменению величины константы к, которую теперь надо
7 Заказ № 6КЗ 193
Глааа 13
умножить на множитель A — %^/2п2). Таким образом, скорость
электромагнитной волны уменьшается в соответствии с этим мно-
множителем. Величина %'а определяет затухание [когда %'а (со)>0]
или нарастание [когда у"а (со)<;0] распространяющейся в среде
электромагнитной волны.
Как непосредственно видно из A3.44), фазовая скорость распро-
распространения электромагнитной волны дается формулой
?— , A3.45)
Оф13
к [1 + х'а (со) ,'2п2] п[1+ъ'а (со) /2«2] « (ш>
в которой
п(со) = пA+Ха(«)/2«2)- A3.46)
Как видим, в случае сред с нормальной населенностью (УУ1>УУ2)
при у'а (со)>0 взаимодействие замедляет волну с частотой со<;соо.
Для волны с частотой со>соо фазовая скорость увеличивается.
В средах с инверсной населенностью (Л^1<:Л^2) величина %'а (со)
изменяет знак и фазовая скорость электромагнитной волны оказы-
оказывается больше, чем с!п при со<;соо и меньше при со>соо.
Нам теперь остается только получить формулу для комплекс-
комплексной электрической восприимчивости %а (со).
§ 13.4. Вывод формулы для комплексной
электрической восприимчивости с использованием
формализма матрицы плотности
В настоящем параграфе мы воспользуемся формализмом мат-
матрицы плотности, описанным в § 11.3, и с его помощью выведем
формулу для электрической восприимчивости ансамбля атомов
(спинов, ионов и т. д.), взаимодействующих с гармоническим пе-
периодическим электромагнитным полем.
Предположим, что в указанном взаимодействии участвуют
только два атомных уровня с энергиями Ег и Ег, как показано
на рис. 13.5. Это допущение совершенно законно, если угловая ча-
частота со поля приближенно совпадает с угловой частотой атомного
перехода со ^ (Е2—Е^/Н.
При учете только двух атомных уровней матрица плотности
сводится к простой матрице размерности 2 X 2, с четырьмя мат-
матричными элементами р11; р12, р21, р22.
Предположим, что гамильтониан Ж' ($) описывает электромаг-
электромагнитное взаимодействие электрического дипольного типа и что его
можно взять в виде
A3.47)
где [X — оператор проекции вектора электрического дипольного
194
Поглощение, усиление и дисперсия
момента, атома на направление электрического поля Е (/). Сначала
будем считать, что поле Е (г) не квантовано и что его напряжен-
напряженность можно рассматривать как обычную классическую величину.
Диагональные матричные элементы электрического дипольного
момента \а будем предполагать равными нулю:
= О
A3.48)
Они равны нулю потому, что средние значения оператора электри-
электрического днпольного момента для состояний с точно определенной
четностью обращаются в нуль.
Фазы собственных функций 12) и
| 1) без ограничения общности вы-
б
берем таким образом, чтобы вы- «
поднялось соотношение Ц
Полный гамильтониан двух-
двухуровневой системы возьмем в виде
Уровень 2
■Ег
Уровень 1
Другие
уровни
Рис. 13.5. Двухуровневая атом-
атомная система, взаимодействующая
с полем электромагнитного из-
излучения, частота со которого
практически равна частоте атом-
атомного перехода 2-<->-1, так что
1\щ?^Ет- Р-\. Остальные уров-
уровни, не участвующие во взаимо-
взаимодействии и не учитываемые в из-
излагаемой теории, изображены
штриховыми линиями.
где Жо — гамильтониан системы
в отсутствие возмущающего пе-
переменного электрического поля
|т. е. при ^ (/) = 0] и Ж' — га-
гамильтониан взаимодействия атома
с электромагнитным полем, оп-
определяемый выражением A3.47).
Релаксационные эффекты, . или
«эффекты столкновений», мы не включаем в гамильтониан Ж, так
как учитываем их феноменологически с помощью формализма мат-
матрицы плотности.
Наша задача состоит в вычислении усредненного по ансамблю
атомов электрического [дипольного момента (и), индуцированного
у одного атома электрическим полем Е (/).
В качестве базисных функций для составления матриц опера-
операторов }х и р возьмем (энергетические) собственные функции ип не-
невозмущенного гамильтониана Жо, удовлетворяющие уравнению
Ж-'Ф-п = Е,и„, причем п = 1, 2. Используя формулы A1.45) и
A3.49), находим
А>1 Р22
=и(р12+р21).A3.51)
195
Глава 13
Уравнение, описывающее изменение матричных элементов опера-
оператора рс течением времени, получаем из A1.49)
.. _}-5П Р1. A3.52)
си Ь.
В выбранных базисных функциях ип операторы Ж0Р и -М'р пред-
представляются следующими произведениями матриц:
Е1 0 \/ РИ Р12 \
о Р Г A3-53)
О Е2 ) \ р21 р22 )
О [х \ / Рп р12 \
п '- A354)
}х 0 ) \ р21 р22 )
так что вместо операторного уравнения A3.52) имеем следующие
скалярные уравнения:
~1Г- " — ^оРг! + » -^~- (Рп -
A3.55)
й / ч . 2м/? (I) ( * \
—-- (Ри—Р22) = 1 —"-Ф21—Рги»
при написании которых использовано обозначение
со0==(Е2 — ^1)/й,
а также свойство эрмитовости оператора р, в силу которого р12 =ргь
Рассмотрим теперь подробнее средние по ансамблю. Согласно
формуле A1.43), имеем для среднего значения элемента матрицы
плотности выражение
N
, N
N -1
т •
причем суммирование ведется по всем N атомам ансамбля. Из
A3.56) непосредственно видно, что если внезапно выключить поле
Е (г), то недиагональные (п Ф т) матричные элементы рпт матрицы
плотности начнут релаксировать к нулевым значениям. Происхо-
Происходит это по той простой причине, что отдельные слагаемые С^С^т
в сумме A3.56), относящиеся к различным атомам, представляют
собой комплексные числа, фазы которых сильно различаются от
атома к атому; к тому же они еще и резко изменяются случайным
образом после каждого «столкновения». Таким образом, сумма
A3.56) при п Ф т обращается в нуль уже после нескольких атом-
атомных столкновений.
Исходя из тех сведений, которыми мы располагаем, нетрудно
качественно понять причины резкого изменения фазы волновой
функции при отдельном атомном столкновении.
196
Поглощение, усиление и дисперсия
Представим себе атом, находящийся в квантовом состоянии
п, описываемом волновой функцией и„ (г) ехр (— 1ЕпИИ). Предпо-
Предположим далее, что на этот атом во время «столкновения» действует
поле кулоновских сил другого атома, который оказался где-то
поблизости. Пусть длительность столкновения равна т, а взаимо-
взаимодействие приводит к изменению энергии АЕ„, причем АЕп можно
вычислить, используя общие формулы из § 11.1. В течение времен-
временного интервала, на котором происходит столкновение, волновая
функция атома приблизительно равна
ы„(г)ехр/ —
й
После «выключения» столкновения она, очевидно, дается выраже-
выражением
и„ (г) ехр / — г —^— / — г го
\ й
в котором
й
Таким образом, действие отдельного столкновения на волновую
функцию сводится к умножению ее на фазовый множитель ехр (—ир),
как мы н полагали.
Поскольку столкновения происходят случайно, отсюда непо-
непосредственно следует, что средние от сумм в A3.56) с п фт, взятые
по ансамблю атомов, обращаются в нуль.
Прибегая к аналогичным рассуждениям, можно показать, что
диагональные матричные элементы рпп матрицы плотности будут
@)
релаксировать к их равновесным значениям р„„.
Приведенные соображения можно облечь в правильную мате-
математическую форму, если чисто феноменологически ввести в урав-
уравнения A3.55) и A3.56) так называемые релаксационные члены *):
— — —1С00р21+1 (ри — р22) . A0.01)
Ри — Ргг)= 1 ; фг1 — 921
Ь
йг
A3.58*
') Здесь мы пользуемся обозначениями, введенными Ф. Блохом в 1946 г.
[25]. Впрочем, время релаксации населенностей уровней Тх здесь мы обо-
обозначаем т.
197
Глааа 13
Так называемое время поперечной релаксации обозначено Т2. Оно
постоянно и характеризует время, за которое индивидуальные
атомы ансамбля «забывают» фазовую когерентность, существовав-
существовавшую в момент выключения поля Е (I). Диагональные матричные
элементы рХ1 и р22, согласно A3.58), восстанавливают их равно-
равновесные значения в процессе, характеризуемом постоянной вре-
времени т.
В частном случае простого гармонического периодического поля
в системе уравнений A3.57) и A3.58) удобно перейти к новым не-
неизвестным функциям
а12 @ = аа, @ = р12@ е~ш, A3.59)
так что уравнение A3.55) теперь примет вид
X
д& 2й
X (Рц — Р22) е . A3.60)
Поскольку величины сц и рA медленно изменяются на временах
порядка существенного изменения экспонент ехр (± ко^), т. е.
времени 2л/со, слагаемое с экспонентой ехр (т{) в A3.60) оказы-
оказывается несинхронизованным с остальными слагаемыми в этом урав-
уравнении (оно колеблется с другой частотой). Следовательно, среднее
от него по времени, превышающему 2л/со, равно нулю. Пренебре-
Пренебрегая этим слагаемым в A3.60), приходим к уравнению
A3.61)
Уравнение A3.58) теперь записывается в виде
A3.62)
причем в A3.62) мы сократили экспоненциальный временной мно-
множитель.
При исследовании стационарного режима с помощью уравнений
A3.61) и A3.62) все производные по времени в них следует прирав-
приравнять к нулю. Складывая и вычитая затем уравнение A3.61) с ком-
198
Поглощение, усиление и дисперсия
плексно-сопряженньш уравнением, получаем
- -=г- (сг21—с4) — » (соо—со) (сг21 + <гя) +» -
A3.63а)
— I (соо—») 0*21 — о-2)) ~— (ст21 — ОгО = 0.
'2
Из уравнения A3.62) непосредственно находим еще одно соот-
соотношение
П<0>
A3.636)
Алгебраическая система трех уравнений A3.63а) и A3.636) для
(ст21—С21), (с?21 + 021) и (рХ1—р22) решается без труда. Так, на-
например, получаем
= 2Пт а21 =
о
о
о
—1(@0—(О)
120
О
0 — -Г1
— 7Т' —1@H—со) 120
1(С00 — О)) —^2"' О
так что
1т с21 =
(Ри — Р22)о
A3.64)
Кроме того, имеем формулу
Кеа21 =
(ш — ш0J Т\ + 4^2Г2^:
A3.65)
В формулах A3.64) и A3.65) использовано удобное сокращенное
обозначение О = цЕ0/2й.
199
Гпааа 13
Вспомним теперь нашу основную формулу A3.51). Ее можно
представить в виде
<Ц @) = И (Ри + Р21) = Н-'К*"""* + <&«""") = 2ц Ке (апе~ш) =
= 2ц [(Ке 021) со5 со/ + Aт а21) зш со/]. A3.66)
Электрический дипольный момент единицы объема, таким обра-
образом, равен
Р @ = N <ц @) = -^^-^-^ х
V (ш0 — м) Г2#0 СОВ С0< -|- Ер 5Ш С0< Л 3 671
1 + (со — сооJ Т\ -|- 4{22Г21;
причем входящие сюда плотности населенностей атомных уровней
у атомов ансамбля следует считать равными следующим величинам:
Л/1 =Л'Р11, Л/2 =А'Р22.
Сравнивая A3.67) с A3.37), приходим к следующим окончатель-
окончательным формулам:
|л2Г2(лг<0)-Лг20)) 1
%а (<») =
-|- (со — со„J Т\ +
A3.68а)
еой 1 + (со — сооJ Ц + 4Й27'2т
Графики функций %'а (со) и /^ (со) для ансамбля атомов пока-
показаны на рис. 13.6. Они характеризуют поведение ансамбля атомов
в слабых полях. Функциональная зависимость вида %"а (со) ^_ [14-
4- (со—содJ?!] называется лоренцееой. Полушириной кривой
атомного резонанса условно называют ширину кривой на высоте,
равной половине максимальной. Полуширина определяется фор-
формулой
ДЮ--2/7У A3.686)
^Согласно общей формуле A3.44), среда, в кшорой возникает
индуцированный электрический дипольный момент, должна пог-
поглощать электромагнитное излучение; коэффициент поглощения
определяется формулой
а(со) = —. A3.68в)
200
Поглощение, усиление и дисперсия
Подставляя сюда выражение A3.68а) для %"а (со) и считая, что
Ц*1,|окончательно получаем следующую формулу:
ос (со) —
A3.69)
Итак, теперь мы имеем две разные формулы для коэффициента
поглощения электромагнитного излучения атомной средой. Первая
формула, A3.27), была выведена, исходя из «золотого правилам
ш-ш0
(в единицах
Рис. 13.6. Графики действительной %а и мнимой ха частей комплексной элек-
электрической восприимчивости при пренебрежимо малом насыщении
О2Е27>/Й2 .г 1).
Ферми; функция формы линии § (V) для данного атомного перехода
в ней считалась заранее заданной. Вторая формула, A3.69), полу-
получена с помощью модели, в которую феноменологически введены
два параметра — «столкновительные» времена Т2 и т.
Поскольку обе формулы, A3.27) и A3.69), относятся к одной
и той же физической величине — коэффициенту поглощения среды
а (со), мы должны согласовать их друг с другом. Используем, кроме
того, для преобразования формулы A3.27) формулу A2.71), со-
согласно которой для времени жизни атома относительно спонтан-
спонтанного перехода имеем выражение
/-> — 2«3^2 I У12 Р М3 2п3|Л2Ш3
депонт — 7 = >
екс2 е/ге3
причем здесь \1г = ег \у12\2-
В результате сравнения двух указанных формул для коэффи-
коэффициента поглощения мы получаем следующее выражение для функ-
функции формы линии:
——, A3.70)
201
Глааа 13
которое справедливо в рассматриваемом случае столкновительного
режима.
Полуширина функции формы линии § (V) обозначена Д\>. Из
A3.70) непосредственно видим, что полуширина связана с атомным
столкновительным временем Т2 соотношением
Лт=1/зтТ2. A3.71)
Теорию, развитую в настоящем параграфе, можно с успехом
применять к объяснению результатов большого числа различных
экспериментов, в которых имеет место взаимодействие электро-
электромагнитного излучения со средой, в частности взаимодействие света
со средами, имеющими атомную структуру. В следующей главе
мы применим эту теорию к специальному, но важному случаю собст-
собственных колебаний в лазерных резонаторах.
Задачи
1. Сравните рассуждения, приводящие к формулам A3.68а, б, в), с рассуж-
рассуждениями Блоха (см. статью 125]), когда он рассматривает поглощение
и дисперсию электромагнитного излучения в случае магнитного резо-
резонанса.
2. Выведите обе формулы A3.68а),
3. Покажите, что далеко от области насыщения (когда {22Т2т 1) конец
вектора %а (со) + 1%а (со) описывает окружность при изменении частоты со.
4. В бесстолкновительной теории взаимодействия электромагнитного излу-
излучения с двухуровневой атомной системой (см. § 13.1) обмен энергией ме-
между атомом и электромагнитным полем совершается периодически в ту
и другую сторону, так что после усреднения по времени реальная пере-
передача энергии отсутствует. В столкновительной теории [см. A3.23)] энер-
энергия либо поглощается средой, либо переходит от среды к излучению в за-
зависимости от знака разности населенностей уровней N1—Ыг. В чем при-
причина этого различия? (Постарайтесь не проводить математические вы-
выкладки, которые здесь сложны и громоздки, а попытайтесь придумать
простое объяснение «на пальцах».)
ГЛАВА 14
СОБСТВЕННЫЕ ОПТИЧЕСКИЕ КОЛЕБАНИЯ ЛАЗЕРА
Идея использовать среды с инверсной населенностью атомных
уровней для усиления и генерации электромагнитных волн незави-
независимо была высказана в 1953—1955 гг. несколькими группами иссле-
исследователей в США и СССР [26—30 ].
В 1960 г. по предложению Шавлова и Таунса [24] Мейман [31]
создал первый лазер на кристалле рубина. Слово 1азег образовано
из первых букв английских слов ЬщМ Атр1Шса1юп Ьу 51лти1а{ес1
Егшззюп о! КасНаШп AщЬ{—свет, атр1Шса{юп — усиление, зИ-
ти1а*ес1 — стимулированный, егшйзюп — испускание, гасНаШп —
излучение). Таким образом, название «лазер» нужно расшифро-
расшифровывать как «усиление света методом стимулированного испускания
электромагнитного излучения».
Появление лазеров ознаменовало революцию в оптике, ибо все
физические источники света, использовавшиеся в оптике до появ-
появления лазеров, не были когерентными, т. е. не были монохроматич-
ными. Высокая степень когерентности лазерного электромагнит-
электромагнитного излучения позволила сегодня манипулировать со светом почти
так же, как с радиоволновым и микроволновым электромагнитным
излучением.
§ 14.1. Лазерный электромагнитный генератор
В гл. 13 было уже показано, что при инверсной населенности
уровней, когда в верхнем квантовом состоянии Е2 атомной системы
находится больше атомов, чем в состоянии Еъ среда способна уси-
усиливать проходящее через нее электромагнитное излучение. Уси-
Усиление происходит в результате стимулированного испускания из-
излучения инверсной средой при условии, что частота этого излуче-
излучения приблизительно равна частоте атомного перехода (Е2—Е^/Н.
Если такую среду с инверсной населенностью поместить внутри
устройства, в котором могут возбуждаться электромагнитные моды,
т. е. внутри электромагнитного резонатора, то в последнем могут
возникнуть устойчивые колебания электромагнитного поля. Для
возникновения таких колебаний необходимо, чтобы величина мощ-
мощности стимулированного излучения превосходила мощность не-
неизбежных потерь в резонаторе.
Рассмотрим устройство, схематически показанное на рис. 14.1.
Среда с инверсной населенностью помещена в так называемый эта-
203
Гпааа 14
лон Фабри—Перо 1), т. е. в оптический резонатор, образованный
двумя плоскими (или немного искривленными) параллельными
зеркалами с коэффициентами отражения Е.г и ^2. В среде с инверс-
инверсной населенностью происходит экспоненциальное нарастание ин-
интенсивности электромагнитной волны с частотой V, которое харак-
характеризуется коэффициентом усиления [см. A3.27)]
V)
A4.1)
В этой формуле § (V) — нормированная на единицу функция формы
■—Зеркала
Рис. 14.1. Лазерный генератор. Среда с инверсной населенностью (Л'Э>Л^1)
помещена между двумя плоскопараллельными зеркалами с коэффициентами
отражения /?г и Ка-
Калинин для перехода 2-»-1, % — длина волны, соответствующая
частоте V, в пустом пространстве, А^2 и А\ — плотности населен-
ностей соответственно верхнего и нижнего уровней атомных систем
в инверсной лазерной среде.
Направим теперь внутрь резонатора, заполненного средой с ин-
инверсной населенностью, электромагнитную волну с интенсивностью
/, распространяющуюся перпендикулярно зеркалам. После одного
полного прохождения волной пути вперед и назад между зеркалами
интенсивность ее станет равной
/ад^*-04', A4.2)
где а — коэффициент поглощения среды, характеризующий не-
неизбежные оптические потери в ней, а /?1/?2—'множитель, учиты-
учитывающий уменьшение интенсивности электромагнитной волны при
отражении на каждом из двух зеркал, ограничивающих резонатор.
Для поддержания электромагнитных колебаний в резонаторе не-
необходимо, чтобы интенсивность 1К1К2ехр [2 {у—а)/] после од-
одного прохождения волной пути в одном и обратном направлении
между зеркалами была равна начальной интенсивности /. Иначе
г) Эталон, или интерферометр, Фабри—Перо назван в честь ученых,
впервые предложивших это устройство. См. [32].
204
Собственные оптические колебания лазера
говоря, при установившемся устойчивом колебательном режиме
должно выполняться соотношение
Отсюда находим пороговое значение коэффициента усиления:
A4.3)
Сред
Зеркало 2
Рис. 14.2. Схема лазерного генератора. Среда с инверсной населенностью
атомных уровней, которая характеризуется следующей частотной зависи-
зависимостью комплексного волнового числа:
V 2п2 ) сг
2п2 2
помещена между двумя отражающими зеркалами.
Лазер Фабри—Перо. Уточним теперь проведенное выше рас-
рассуждение и найдем более строгие условия возбуждения колебаний
в лазерном резонаторе. Выясним, что происходит не с интенсив-
интенсивностью электромагнитной волны, «болтающейся» между двумя зер-
зеркалами в эталоне Фабри—Перо, а с электрическим полем этой
волны.
Эталон Фабри—Перо содержит среду с инверсной населен-
населенностью уровней (рис. 14.2). Предположим, что бегущая плоская
электромагнитная волна, описываемая формулой *)
Е (г, I) = Еьё(ш ~~ ,
падает на резонатор слева. Волновое число электромагнитной волны
в среде, заполняющей резонатор, определяется формулой A3.43):
-^-, A4.4)
2п2
*) Физически существующее действительное электрическое поле, за-
зависящее от пространственных координат и времени, следует вычислять по
формуле Е (г, 1) = Ке [Е{вс <ш'—йг>]. в тексте мы опустили символ Ке<
чтобы упростить обозначения.
205
Глава 14
где а — коэффициент поглощения среды, обусловленного всеми дру-
другими механизмами потерь энергии, кроме переходов 2 ♦->■ 1. По-
Поглощению, связанному с этими переходами, соответствует вели,
чина ха. Волновое число к = соя/с характеризует распространение
в данной среде электромагнитной волны, частота которой сильно
отличается от частоты используемого в лазере атомного перехода.
Величина %а (со) = %а (со) — 1%'а (со) обозначает комплексную
электрическую восприимчивость среды, обусловленную рассмат-
рассматриваемым атомным переходом.
Обозначим через 1Х отношение амплитуды прошедшего через
левое зеркало электрического поля к амплитуде падающего на него
поля, а через 12 — ту же величину для правого зеркала. Отноше-
Отношения амплитуд отраженного внутрь лазерной среды электрического
поля к амплитудам падающего электрического поля для левого
и правого зеркал обозначим соответственно гу и г2.
Множитель, характеризующий изменение поля волны при одно-
однократном прохождении ею резонатора, равен ехр (— Иг'1), где к'
определяется формулой A4.4), а I — длина резонатора. Склады-
Складывая поля многократно отраженных волн в выходной плоскости ре-
резонатора, найдем полное электрическое поле на выходе
-т'1+ . . . ). A4.5)
Это выражение представляет собой геометрическую прогрессию,
сумма которой равна (будем считать, что '2к1
Мое*'1 о2ее
1Е, A4.6)
причем при выводе мы воспользовались формулой A4.4), записан-
записанной в следующем сокращенном виде:
к'=к + Ак + Цу—сс)/2,
где
4№). A4.8)
л2 8яп2*спонт
Зависимость коэффициента пропускания \Е{/Ес\2 эталона
Фабри—Перо от частоты показана на рис. 14.3а. Когда среда в эта-
эталоне Фабри—Перо между двумя зеркалами не обладает ни погло-
поглощающими (а = 0), ни усиливающими (у = 0) свойствами, коэффи-
коэффициент пропускания \Е(/Е1\2 принимает равное единице макси-
максимальное значение при бесконечном наборе эквидистантных частот,
разделенных частотным интервалом АV = с/2п1. Эти равные еди-
206
Собственные оптические колебания лазера
нице максимумы коэффициента пропускания наблюдаются при вы-
выполнении условия Ы \= (со/с) п1] = /гаг, где т — произвольное
целое число. Указанные частоты называют частотами продольных
собственных электромагнитных колебаний эталона Фабри—Перо.
Если для среды, заключенной между двумя зеркалами эталона,
выполняется условие у—сх2>0, то коэффициент пропускания при
указанных выше резонансных частотах оказывается больше еди-
единицы, т. е. выполняется неравенство |Е(| 2>|Е,-|. Все устройство
тогда начинает работать как когерентный усилитель электромаг-
электромагнитного излучения. Когда разность у—а оказывается настолько
большой, что выполняется равенство
-"Л 1к+Ак (ш)] 1еь (ш)~а] ' = 1, A4.9)
знаменатель в формуле A4.6) обращается в нуль и коэффициент
пропускания | Е(/Ес ]2 эталона Фабри—Перо неограниченно воз-
возрастает. Физически это означает, что на выходе эталона может
появиться конечная прошедшая волна Е{ при исчезающе малой
волне Е{ на входе; иными словами, внутри лазерного резонатора воз-
возбуждается лазерное собственное колебание. Указанные особенности
коэффициента пропускания проявляются в виде ряда бесконечно
высоких максимумов нулевой ширины, показанных на рис. 14.3а.
Частоты, при которых наблюдаются эти максимумы, представляют
собой частоты собственных оптических колебаний лазера.
Условие A4.9) для нахождения частот собственных колебаний
лазера имеет очень простой физический смысл. Оно состоит в тре-
требовании, что волна, прошедшая в резонаторе путь туда и обратно
между зеркалами, должна вернуться к начальной плоскости, имея
те же самые амплитуду и фазу, с точностью до добавления к фазе
целого кратного 2я. Такое условие обеспечивает интерференцион-
интерференционное усиление многократно отраженных от зеркал резонатора волн,
а следовательно, возбуждение внутри резонатора устойчивого поля
электромагнитного излучения.
Разобьем комплексное условие A4.9) возбуждения в лазере
собственных электромагнитных колебаний на «амплитудную» и «фа-
«фазовую» части. Тогда придем к формуле
для порогового значения коэффициента усиления у (со) и к формуле
A4.11)
в которой т = 1, 2, 3 . . . , для частот собственных колебаний ла-
лазера. Амплитудное условие A4.10) можно переписать также в виде
формулы для порогового значения коэффициента усиления:
■у (со) = ее -кг/г. A4.12)
207
3 *
1
1
I
Усиливающая среда-( _ у, ~ '
В Р' - 1,035
Прозрачная среда — С еу! -1,00
Поглощающая 0 ^9
1,5
2,0
2,5 3,0 3,5
в (в единииах л)
4,5
Рнс. 14.3а. Зависимость коэффициента пропускания | Е</Ес |2 лазера Фабри—Перо [см. A4.6)] от величины сдвига
фазы 0=2 {Ы—тл), где т — целое число, для волны, прошедшей одни раз путь туда и обратно между зеркалами.
/? г гхг2 = 0,9. Коэффициент усиления интенсивности волны прн однократном' прохождении через резонатор
(без отражении) равен ехр (у[) [он эквивалентен множителю ехр (у—а) в формуле A4.6)]. Кривые и н Е, для ко-
которых ехр (у1) > 1, таким образом, относятся к поглощающей среде, кривая С, для которой ехр (у1) = 1,— к про-
прозрачной среде, а кривые А и В, для которых ехр (у1) > 1, — к усиливающей среде. Заметьте, что прн ехр (у1) > 1
максимумы коэффициента пропускания становятся больше единицы, а прн ехр (у1) < 1 они меньше единицы. Это
справедливо прн всех значениях К. Когда ехр (у[) = 1 (т. е. коэффициент усиления прн однократном прохож-
прохождении волной резонатора компенснрует потерн на зеркалах), коэффициент пропускания становится бесконечным и
в резонаторе возбуждаются собственные электромагнитные колебания.
о
■■О
Усиливающая среда—<^^
Прозрачная среда — С
Поглощающая среда —
Г1 _.07П
едГ1 ~т0<330
2,0-
2,5
3,0 3,5
9(в единицах .я)
г»
о
О»
э
а
х
X
а
п
X
X
а
ш
X
X
а
а
ш
■о
ш
Рис. 14.36. Зависимость коэффициента отражения | ЕГ1Е112 для лазера Фабри—Перо от величины сдвига фазы
6. Обратите внимание на то, что, когда ехр (у/) > 1, максимумы кривой \ЕГ/Е{\2 становятся больше единицы, т. е.
имеет место усиление волны при отражении. Усиление волны прн отражении становится бесконечным при усло-
условии ехр (у/) = 1. (Заметьте, что только кривая С достигает осн абсцисс.)
Глава 14
Как видим, оно совпадает с условием A4.3), если положить гггг =
= > #1#2- Используя формулы A4.1) и A4.12), можно вычислить
критическое (пороговое) значение плотности инверсной населенно-
населенности атомных уровней, необходимой для возбуждения собственных
колебаний в лазерном резонаторе:
ее -
A4.13)
Разрешенные
моды
Коэффициент
усиления у(\')
Уровень
потерь
Спектр
выходной
мощности
б
Рис. 14.4. а — неоднородно уширенная вследствие эффекта Доплера линия
6328 А атома Ые и положения частот разрешенных продольных мод в лазер-
лазерном резонаторе; б — зависимость интенсивности (квадрата амплитуды)
собственных мод гелий-неонового лазера от частоты. Для указанных шести
мод коэффициент усиления имеет достаточную величину, чтобы могли воз-
возбудиться собственные колебания (см. [33]).
Частоты собственных колебаний лазера. Фазовое условие A4.11)
возбуждения собственных колебаний в лазерном резонаторе удов-
удовлетворяется для бесконечного набора частот ут. Значения этих
частот можно вычислить, подставляя формулу A4.7) для Л& в фор-
формулу A4.11). Так получаем уравнение
2ЛV„
= тл.
A4.14)
Напомним читателю, что к = 2пп\/с. Из A4.14) видим, что при
1 %а Ь>) 1 С 1 частоты собственных колебаний лазера даются про-
простой формулой
ут^т—с—. A4.15)
т 2п1 К '
210
Собственные оптические колебания лазера
В лазере возбуждаются собственные колебания электромагнит-
электромагнитного поля при частотах, точно (или приближенно) равных \т, при
условии, что коэффициент усиления среды лазера на этих частотах
превышает пороговое значение A4.12). Кривые зависимости ко-
коэффициента усиления у (V) и квадрата амплитуды колебаний от
частоты для широко распространенного в настоящее время гелий-
неонового лазера с длиной волны 0,6328 мкм показаны на рис. 14.4.
Охладитель
Внешнее 1 Руби?
зеркало " степ.
Лампа-вспышка
. Внешнее зеркало
т (частично пропускающее
I излучение)
Выходной
пучок
Накопительный
конденсатор
Источник
напряжения
Рис. 14.5. Типичный импульсный рубиновый лазер с двумя внешними зер-
зеркалами, накачиваемый лампой-вспышкой.
30
^ 15
^ го
оГ /5
| 10
5
0
Рис. 14.6. Энергетические уровни, используемые в рубиновом лазере.
При возбуждении собственных колебаний в резонаторе лазер
отбирает энергию от среды с инверсной населенностью и излучает
энергию в оптическом диапазоне, поэтому, если не производить
«накачку», т. е. не переводить новые атомы на верхний уровень 2,
инверсная населенность начинает уменьшаться и возникшие в ла-
лазере собственные колебания прекратятся. Это произойдет в тот
момент, когда инверсная населенность атомных уровней упадет
211
Глава 14
ниже критического значения, вычисленного по формуле A4.3).
Если атомы среды в резонаторе лазера все время «накачивать» на
уровень 2, то можно поддерживать непрерывные колебания. Таким
образом, лазеры могут быть двух типов: с импульсным и непрерыв-
непрерывным режимом работы. В импульсном режиме работает, например,
рубиновый лазер.
Рубиновый лазер. Первым материалом, в котором удалось по-
получить лазерную генерацию [31], был рубин/В рубиновом лазере
Электрический
вход
_ги1_
Оптические
Усилитель Пороговый
/ аетектор
Инжекционнып
лазер на
двойной
гетероструктуре
Модулятор
_л_п_
Электрически
выход
Рис. 14.7. Схема оптической волоконной линии связи Передаваемая инфор-
информация закодирована в виде двоичных электрических импульсов. Эти импульсы
модулируют непрерывную световую волну, генерируемую полупроводни-
полупроводниковым инжекционным лазером. Таким образом, электрические импульсы
как бы «воспроизводятся» формой огибающей интенсивности световой полны,
которая по стеклянной оптической волоконной линии поступает в приемное
устройство. Оптический детектор на выходе преобразует световые импульсы
опять в электрические. Затем информация, поступившая в виде электриче-
электрических импульсов, декодируется (см., например, книгу [32]).
используются переходы ионов Сг3+, которые являются примесями
в кристалле А12О3. Схема типичного рубинового лазера изображена
на рис. 14.5, а на рис. 14.6 представлена соответствующая схема
энергетических уровней иона Сг3+. Накачка совершается путем
облучения кристалла рубина интенсивной вспышкой света (с по-
помощью мощной импульсной лампы, подобной применяемой при
фотографировании). Ионы Сг3+ поглощают свет и переходят на
полосы 4/72 и 4/71 1). Затем ионы Сг3+ очень быстро (за время по-
порядка 10~7 с) переходят на верхний лазерный уровень 2Е. По-
Поскольку (спонтанное) время жизни этого уровня сравнительно ве-
велико (порядка 3-Ю с), при накачке световой вспышкой большая
часть (> 0,5) атомов переходит с основного уровня на верхний ла-
лазерный уровень 2Е. Собственные колебания в рубиновом лазере
возбуждаются, когда разность населенностей Ы^е — А^л. становится
настолько большой, что усиление начинает перекрывать неизбеж-
неизбежные потери в рубиновом резонаторе.
') Используются обычные в атомной спектроскопии обозначения атом-
атомных уровней: *Р8, *Р1г 2Е, М2.
212
Собственные оптические колебания лазера
В настоящее время лазеры все шире и шире используются в
науке и технике. Благодаря исключительной монохроматичности
излучения лазеры незаменимы при проведении особенно тщатель-
тщательных спектроскопических измерений энергии атомных и молекуляр-
молекулярных переходов, а также для создания стандартов частоты. Высокая
монохроматичность лазерного излучения позволяет также использо-
использовать лазеры для генерирования несущей волны в оптических ли-
линиях связи. Каналы связи, которые можно создать с помощью мо-
модулированных информацией световых пучков, передаваемых по
стеклянным оптическим волокнам (толщиной меньше человеческого
волоса), начинают играть все большую роль в современных линиях
связи. Схематически оптическая система связи с использованием
инжекционного лазера показана на рис. 14.7.
Благодаря пространственной когерентности лазерного излуче-
излучения, в силу которой испущенная лазером электромагнитная волна
имеет почти идеально плоский волновой фронт, излучение лазера
можно сфокусировать в объем порядка %3. Интенсивность электро-
электромагнитного поля в этом объеме будет очень высокой. Такое интен-
интенсивное электромагнитное излучение можно использовать для по-
получения чрезвычайно горячей плазмы, настолько горячей, что в
ней может начаться термоядерная реакция. Кроме того, благодаря
высокой интенсивности излучения, испускаемого лазерами, в нем
удается возбуждать высокие гармоники (вторую, третью н т. д.
до девятой), которые заставляют валентные электроны атомов ко-
колебаться в сильно нелинейных режимах. Указанное физическое яв-
явление в настоящее время интенсивно изучается в новой области
науки, называемой нелинейной оптикой. Существует еще один
важный тип лазеров — полупроводниковый лазер непрерывного
действия (рис. 14.7). Такой лазер незаменим при создании оптиче-
оптических линий связи. Подробно устройство полупроводникового ла-
лазера описано в гл. 21.
Задачи
1. Выведите формулу для отношения интенсивностей отраженной и падаю-
падающей воли в эталоне Фабри—Перо.
2. Постройте кривую зависимости коэффициента отражения | ЕГ1Е{\ от ча-
частоты для эталона Фабри—Перо. Рассмотрите интервал частот, который
включает два минимума (или два максимума). Считайте, что коэффициент
усиления активной среды не зависит от частоты. Примите, что г2х = г| =
= 0,8 и что: а) е<?-«>1 = 1,0 и б) е№-«>/= 1,1.
3. Выведите формулу для зависимости полуширины (ширина на половине
максимума) коэффициента пропускания эталона Фабри—Перо от ча-
частоты V. Учтите, что гг = г2 = -\/Я. и что полуширина мала по сравне-
сравнению с шириной частотного интервала между модами (с/2) пй (т. е. «< 1).
Ответ: Полуширина равна с/2п1Р, где Р = яУ#/( 1 — /?) — доброт-
добротность резонатора.
213
Глава 14
4. Изобразите примерно ход кривой зависимости коэффициента пропуска-
пропускания эталона Фабри—Перо {у — а = Ак = 0) от частоты. Воспользуй-
Воспользуйтесь соотношением
'ЖЧ- Гггг= 1.
В чем качественное различие случаев B(г " 1 (высокая добротность)
11Л^1 ~ 1 (обычная добротность)?
5. а. Выведите формулу 5ля комплексного коэффициента отражения Ег/Ес
для эталона Фабри—Перо, который изображен на рис. 14.1.
б. Убедитесь, что условие A4.9) для возбуждения собственных колеба-
колебаний лазера вытекает из требования Ег/Е{ = оо (при этом произведение
у (со) I должно оставаться конечным).
в. Как качественно изменится формула A4.15) для частот собственных элек-
электромагнитных колебаний лазера, если в формуле A4.15) мы не будем пре-
пренебрегать слагаемым [%'а ^)]/2п2? Можете использовать лоренцеву форму
A3.66) для функции %о (^)- Покажите, что частоты собственных колеба-
колебаний будут «затягиваться» резонансной атомной частотой со0.
7. Обсудите качественно, как величина затягивания частоты зависит от
ширины бV = 1/Т2 лоренцевой функции электромагнитного отклика %'а (\).
ГЛАВА 15
КВАНТОВАЯ СТАТИСТИКА
Необходимость использования статистических методов при опи-
описании квантовомеханических систем тождественных частиц обус-
обусловлена теми же причинами, которые привели и к созданию клас-
классической статистической физики.
Если мы имеем квантовую систему, состоящую из большого
числа N одинаковых частиц, то в принципе возможно проследить
ее временную эволюцию путем решения соответствующего уравне-
уравнения Шредингера
Н(ри <&. - ■ ■ . Рк, Як, О*(Л. *. • ■ ■ . <7л'> Ц^Ш^-; A5.1)
от
при этом должно быть задано начальное состояние системы, описы-
описываемое начальной волновой функцией г}) (дъ д2, . . . , <7д?> 0)- Ука-
Указанная процедура, однако, оказывается совершенно практически
неосуществимой даже в тех случаях, когда число частиц /V мало,
поскольку начальные условия мы никогда не знаем с такой сте-
степенью точности, чтобы можно было решать уравнение A5,1), В слу-
случаях же больших значений N г) не стоит даже и пытаться вычислять
многочастичную волновую функцию.
Вместо этого полезно обратиться к статистическим свойствам
больших ансамблей, составленных из тождественных малых си-
систем, сделав допущение, что статистика ансамбля позволяет на-
надежно предсказывать среднее поведение отдельной малой системы.
§ 15.1. Три вида индивидуальных
квантовых частиц
Рассмотрим квантовомеханическую систему.^составленную из
N слабо взаимодействующих друг с другом частиц, заключенных
в объеме V. Этими «частицами» могут быть атомы, электроны, атом-
атомные ядра, протоны, гармонические осцилляторы, фотоны и т. д.
или конгломераты этих частиц.
Будем предполагать, что плотность частиц в системе достаточно
мала, чтобы с хорошим приближением энергию системы можно
было считать равной сумме энергий индивидуальных частиц.
1) Чтобы представить невероятно огромную величину числа N в прак-
практически интересных случаях, напомним читателю, что плотность электронов
в зоне проводимости типичного металла имеет порядок 1023 см~3.
215
Глава 15
Микроскопические энергетические состояния системы /V частиц
мы будем характеризовать, приписывая каждой частице 5 системы
определенное квантовое состояние т}I5), причем
<7>I# = е;я#, A5.2)
где -М (р$, д$) — гамильтониан для частицы 5, заключенной в ящике
объемом V. Таким образом, т]),-5' представляет собой одночастичную
энергетическую собственную функцию для частицы 5, находящейся
в 1-м квантовом состоянии с собственным числом энергии, равным е;.
Полная энергия системы частиц, таким образом, равна
^=Х>*ег, A5.3)
где щ — число частиц с энергией е(- в рассматриваемом состоянии
системы /V частиц.
Вообще говоря, имеется не одна возможность распределения
/V частиц системы по энергетическим уровням е,-, дающая одну и ту
же полную энергию системы Е. (Правильнее сказать, не энергию Е,
а энергию в интервале Е ± 6Е, где 6Е — разрешение наших из-
измерительных приборов.) Каждое такое распределение, которое
в принципе описывается одной собственной функцией системы N
частиц, называется различимым микроскопическим распределением.
Фундаментальный постулат квантовой статистики заключается
в утверждении, что при тепловом равновесии разные различимые
микроскопические распределения частиц по состояниям, обладающие
одной и той же (в пределах ошибки ЬЕ) полной энергией, имеют
одинаковую вероятность.
Основное, чем мы займемся в настоящей главе,— это отыскание
наиболее вероятных распределений частиц (пъ п2, . . . , п8, . . .)
для тепловой равновесной системы /V частиц. Для этого нужно
знать вероятность для данной системы /V частиц с энергией Е, найти
пг частиц с энергией еь п2 частиц с энергией е2 и т. д. при условии,
что полная энергия системы, определяемая формулой A5,3), ос-
остается постоянной и равной Е.
Вообще говоря, данному, как мы будем говорить, «макроскопи-
«макроскопическому состоянию» (пх, п2, . . . , Па, . . .) соответствует несколько
микроскопически различных распределений, поэтому из сформули-
сформулированного выше основного постулата квантовой статистики сразу
вытекает, что вероятность наблюдать данное макроскопическое
состояние (п1г п2, . . . , п$, . . .) пропорциональна числу микроско-
микроскопических распределений, имеющих энергию Е, равную энергии
рассматриваемого макроскопического состояния. Таким образом,
приходим к заключению, что наиболее вероятное макроскопическое
216
Квантовая статистика
состояние (пъ п2, ■ ■ ■ , п$, . . .) —это такое состояние, которому
соответствует самое большое число реализующих его микроскопи-
микроскопически различимых распределений.
Общий план подхода к сформулированной задаче состоит в сле-
следующем.
Сначала выведем формулу для Р (пи п2, . . . , пв, . . .) — числа
микроскопически различимых распределений, соответствующих дан-
данному макроскопическому состоянию (пъ п2, . . . , пъ, . . .), а затем
найдем то макроскопическое состояние (пъ п2, ■ ■ ■ , п$, - - .)> для
которого Р принимает максимальное значение при условии, что
полное число частиц в системе и полная энергия системы остаются
постоянными. Соответствующее распределение частиц системы по их
энергетическим уровням — это наиболее вероятное распределение
для данной системы, находящейся в состоянии теплового равно-
равновесия.
Частицы, которыми мы сейчас будем заниматься, могут быть
трех типов.
А. Идентичные различимые частицы. Два примера систем та-
таких частиц: 1) система из очень тяжелых точечных материальных
частиц, которые заключены внутри очень большого ящика; 2) ан-
ансамбль гармонических осцилляторов.
Б. Идентичные неразличимые частицы с полу целым спином —
фермионы (полный спин каждой такой частицы равен й/2, Зй/2,
5й/2 и т. д.). Примеры: электроны, протоны. Как отмечалось в § 8.1,
эти частицы подчиняются принципу запрета Паули, согласно ко-
которому никакие две частицы не могут занимать одно и то же кван-
квантовое состояние. Иначе говоря, любая полная ^-частичная собст-
собственная функция такой системы частиц всегда антисимметрична
(изменяет знак при перестановке ее аргументов, относящихся к лю-
любым двум частицам). Такое ограничение, как будет показано дальше,
приводит к важному особому типу квантовой статистики частиц.
В. Идентичные неразличимые частицы с целым спином — бо-
бозоны. Примеры: фотоны, фононы, атомные ядра с четным числом
нуклонов и атомы с четным числом элементарных частиц. Прин-
Принцип запрета Паули неприменим к системам, построенным из бо-
бозонов, поэтому вполне возможно, что две или более частиц в системе
будут находиться в одном и том же одночастичном состоянии.
Любые А^-частичные собственные функции системы таких частиц
симметричны (не меняют знака при перестановках аргументов, от-
относящихся к любым двум частицам).
Прежде чем приступить к выводу вероятностных законов рас-
распределений частиц по их состояниям при тепловом равновесии,
нам необходимо ответить на вопрос: какие мыслимые распределения
частиц действительно микроскопически различимы, а какое нет?
Ответ оказывается различным в зависимости от того, с какого вида
частицами, А, Б или В, мы имеем дело.
217
Глава 15
Чтобы пояснить этот момент, рассмотрим простейшую систему,
состоящую из двух тождественных частиц с двумя разрешенными
собственными состояниями (рис. 15.1).
В случае А мы можем занумеровать частицы номерами 1 и 2,
поскольку, хотя частицы и тождественны, они различимы (по своим
положениям, например). Все четыре показанных расположения,
таким образом, микроскопически различимы для частиц вида А.
Иначе можно сказать, что имеются четыре различных энергетиче-
(/) (г) \з) й)
г 1 1 г
Тождественные
различимые »
частицы в
Тождественные
неразличимые частицы
с пзлуцелым спином
к
Тождественна 'с
перазли чимые
частицы с целым
спином
Рис, 15.1. Различные возможные расположения и соответствующие собствен-
собственные функции двух частиц, которые могут находиться в двух состояниях.
ских состояния двухчастичной системы с указанными на рис. 15.1
собственными функциями. В случае Б (фермионы) возможно только
расположение 2. Расположения 1 и 4 запрещены принципом запрета
Паули, поскольку в них две тождественные ферми-частицы зани-
занимают одно и то же квантовое состояние. Расположение 3 тоже
следует отбросить, поскольку его невозможно отличить от располо-
расположения 2. (Оба этих расположения описываются одной и той же
собственной функцией, которая является антисимметричной ком-
комбинацией одночастичных функций, так что оба этих расположения
надо считать за одно. Единственное, что можно сказать: одна ча-
частица занимает верхнее энергетическое состояние, а другая — ниж-
нижнее состояние. Но нам не известно, какая именно частица нахо-
находится в данном состоянии.) Расположения 1 и 4 разрешены для
частиц вида В, поскольку бозоны не подчиняются принципу Паули.
В случае В расположения 2 и 3, однако, тоже дают одно состояние
(описываемое симметричной комбинацией одночастич ых функций).
218
Квантовая статистика
§ 15,2. Комбинаторика квантовых
многочастичных систем
Теперь все подготовлено, чтобы заняться отысканием наиболее
вероятных распределений частиц по их состояниям для систем ча-
частиц различных видов.
Наша система содержит N тождественных частиц со следующим
спектром разрешенных энергетических уровней для каждой ча-
частицы:
Эти энергетические уровни могут быть вырождены, так что, вообще
говоря, с каждым энергетическим уровнем может быть связано бо-
более одного одночастичного квантового состояния.
При выводе законов распределений частиц по их состояниям
воспользуемся следующим приемом. Разделим все одночастичные
состояния с энергиями, простирающимися от—оо до оо, на энер-
энергетические «интервалы». В интервал 5, например, пусть входят все
одночастичные квантовые состояния, энергии которых лежат вну-
внутри определенного энергетического интервала Ае5 около энергии еЕ.
(Величину Аеь выберем произвольно. Ее можно взять равной пре-
предельному разрешению наших приборов бе.) Число одночастичных
квантовых состояний в «интервале» 5 обозначим §&.
Макроскопическое состояние (п1г п2, . . . , п5, . . .) ^-частичной
системы будем характеризовать теперь, задавая числа частиц п1г
п2, • • . , «5, • • • из N частиц системы в соответствующих энергети-
энергетических «интервалах». Вообще говоря, имеется много микроскопи-
микроскопических способов распределения N частиц по «интервалам», приво-
приводящих к одному и тому же макроскопическому состоянию (пи
п2, . . . , п5, . . .). Индивидуальное микроскопическое распределе-
распределение частиц по одночастичным состояниям считается различимым,
если ему соответствует своя ^-частичная собственная функция.
Согласно основному постулату квантовой статистики, сформу-
сформулированному выше, при тепловом равновесии любые два микроско-
микроскопически различимых распределения частиц, имеющие одну и ту же
полную энергию Е (в пределах ЬЕ), одинаково вероятны. Вероят-
Вероятность найти систему с п1 частицами в «интервале 1», п2 частицами
в «интервале 2» и т. д., следовательно, пропорциональна числу
микроскопически различимых распределений, которые соответст-
соответствую тодному и тому же макроскопическому состоянию (пъ п2, ...
. . ., Пц, . . .). Обозначим это число Р (пъ п2, . . . , п$,. . .) или просто
Р (л,).
Следующая наша задача — рассчитать Р (пь) поочередно для
систем, состоящих из указанных трех основных видов частиц.
Тождественные различимые частицы. Определим число микро-
микроскопически различимых распределений N частиц системы по их
219
Глава 15
состояниям, характеризуемых тем, что пг частиц попадает в «ин-
«интервал 1», п2 частиц — в «интервал 2» и т. д.
Найдем сначала число способов, которыми можно выбрать пг час-
частиц из полного числа N частиц для помещения их в «интервал 1», игно-
игнорируя на первых порах способы распределения этих частиц по кван-
квантовым состояниям в указанном энергетическом «интервале». Первую
частицу можно выбрать наугад из N частиц, вторую частицу сле-
следует выбирать уже из N—1 частиц и т. д., так что полное число
различных способов выбора пг частиц из N частиц для помещения
их в «интервал 1» равно
'т . A5.4)
(Л/ — «1)!
При получении результата A5.4) мы считали различными спо-
способы, отличающиеся перестановками-' пг частиц данной группы.
Так, например, последовательности трех частиц 1, 4, 7 и 7, 4, 1
мы учитывали как различные. Учтем теперь, что мы не должны
различать внутренний порядок частиц в энергетическом «интер-
«интервале». Поэтому разделим выражение A5.4) на пг\, т. е. на число
перестановок п1 частиц между собой. В результате получим сле-
следующее число способов выбора п1 частиц из N частиц:
™A5.5)
и,! (К' - щ)\
Число одночастичных квантовых состояний, принадлежащих
«интервалу 1», выше мы обозначили §г. Первую частицу из п1 можно
поместить в любое из §г состояний «интервала 1». Вторую частицу
тоже можно поместить в любое из §г состояний. Так как ча:тицы
различимы, можно заполнять одно и то же состояние любым числом
частиц. Полное число различимых микроскопических распределе-
распределений п1 частиц по одночастичным состояниям «интервала 1», таким
образом, равно |^'. Умножая на него число A5.5), получаем сле-
следующую формулу для полного числа микроскопически различимых
размещений пг частиц из полного их числа N по §г состояниям энер-
энергетического «интервала 1»:
ЛИЛ
Р1 = ± . A5.6)
Число различимых микроскопических размещений п2 из остав-
оставшихся N—пг частиц в энергетическом «интервале 2» дается ана-
аналогичной формулой
Р2= ("-"■>**■ . A5.7)
«г! ('V — «1 — п2)\
220
Квантовая статистика
Итак, в случае А полное число различимых микроскопических
распределений Ы- частиц системы, соответствующих данному мак-
макроскопическому состоянию, с п1 частицами в «интервале 1», я2
частицами в «интервале 2» и т. д. равно
Р (п5) = Р (пъ п2 пв, . . . ) =
Тождественные неразличимые частицы с полуцелым спином —
фермионы. Поскольку теперь частицы неразличимы, нельзя уста-
установить, какая именно частица занимает данное одночастичное со-
состояние. Можно лишь определить, попадает ли данная частица
в «интервал 1» или нет. Каждое состояние имеет свою собственную
одночастичную функцию, поэтому в силу принципа запрета Паули
(которому подчиняются частицы с полуцелым спином) оно не мо-
может быть заполнено более чем одной частицей. Если бы частицы
были различимы, то задачу о размещении п5 частиц по @6 состоя-
состояниям мы стали бы решать следующим образом. Сначала мы поме-
поместили бы одну какую-нибудь первую частицу в любое состояние
из & состояний данного энергетического «интервала 5». Существует
§\; способов так поступить. Потом стали бы размещать вторую ча-
частицу. Но, поскольку теперь никакие две частицы не могут зани-
занимать одного и того же одночастичного состояния, вторую частицу
можно поместить только в одно из (^—1) оставшихся мест. Таким
образом (для фермпонов) всего получаем
размещений (в силу принципа запрета Паули ^ > п$). При полу-
получении последней формулы мы различали, однако, разные переста-
перестановки п6 частиц между собой. Число таких перестановок равно п5!.
Поскольку частицы неразличимы, указанные перестановки не
должны приводить к различным распределениям (им ведь соответст-
соответствует одна и та же собственная функция). Следовательно, полное
число различных микроскопических распределений п8 частиц в энер-
энергетическом интервале в равно
Р = &(&—!)• - • (& — я* + 1) = &1
а полное число микроскопических распределений, соответствующих
макроскопическому состоянию с числом п1 частиц в «интервале 1»,
221
Глава 15
числом п2 частиц в «интервале 2» и т. д., равно
Р(п,) = Р{пъ гц, . . . ,л5, . . )
П
5=1
П
5=1
A5.10)
Тождественные неразличимые частицы с целым спином — бо-
бозоны. В этом случае, так же как в случае Б, неразличимость ча-
частиц ие позволяет установить, какая из частиц находится в дан-
Стенка
Частицы Разбиения
о о I о I 1о6ооГооо|оо| |оо
2 10 4 3 1 О г
Стенка
Рис 15.2. Схема, позволяющая определить число различных способов рас-
распределения п$ неразличимых частиц (кружки) по ^8 состояниям (каждое со-
состояние ограничено двумя вертикальными черточками или вертикальной
черточкой и стенкой) энергетического интервала. На этом рисунке ге5 = 14,
ном энергетическом «интервале», какая из них занимает данное
одночастичное квантовое состояние. Однако теперь не нужно на-
накладывать никаких ограничений на полное число частиц, занимаю-
занимающих любое данное одночастичное состояние. На языке квантовой
механики это означает, что более одной частицы могут иметь одну
и ту же одночастичную собственную функцию.
Число различных размещений п& частиц по ^5 состояниям в
энергетическом «интервале 5» можно легко найти, обращаясь к
рис. 15.2 134, гл. 101. Каждый кружок представляет частицу, а
вертикальные черточки — разбиение. Пространство между двумя
соседними вертикальными черточками или вертикальной черточ-
черточкой и стенкой представляет одно одночастичное состояние. Про-
Проводя &—1 вертикальных черточек, мы получаем §-$ одночастичных
состояний данного энергетического «интервала 5». Число кружков
равно п5 и равно числу частиц в данном энергетическом интервале.
На рис. 15.2 ^ = 8и /г5 = 14. Если н5 кружков и ^ь—1 вертикаль-
вертикальных черточек были бы различимы, то число всех расположений
кружков и вертикальных черточек равнялось бы числу перестано-
перестановок (и5 -[ ^5—1) объектов между собой, т.е. («5-г §\,—1)! Пос-
Поскольку, однако, кружки и вертикальные черточки неразличимы,
перестановки вертикальных черточек между собой [число которых
равно (§;<.— 1)П и перестановки кружков между собой [число ко-
которых равно п<Д] не приведут к различным расположениям.
222
Квантовая статистика
Число различимых размещений пв частиц в «интервале 5», таким
образом, равно
Р,= &1±1Ь=Ж-, A5.11)
так что полное число различных микроскопических распределе-
распределений, соответствующих данному макроскопическому состоянию, ха-
характеризуемому заданием последовательности чисел пи п2, • • .
. ., п.,, . . . в рассматриваемом случае определяется формулой
Р (п.) = Р (пи щ п5, . . . ) =
E)
«81 («■* — 1I
5=1
§ 15.3. Статистики Максвелла — Больцмана,
Ферми —Дирака и Бозе — Эйнштейна
В предыдущем параграфе мы подсчитали для системы из N ча-
частиц, каким числом микроскопически различимых способов можно
распределить п1 частиц в энергетическом «интервале 1», п2 частиц —
в энергетическом «интервале 2» и т. д. Мы вывели формулы для
этого числа
Р (п4) = Р (пъ щ, . . . , щ, . . . )
в случаях А — тождественных различимых частиц, Б — фермио-
нов, В — бозонов.
Согласно нашему постулату, при тепловом равновесии равно-
равновероятны все микроскопически различимые распределения с фик-
фиксированным полным числом частиц и с фиксированной одной и той
же полной энергией. Следовательно, наиболее вероятно то макро-
макроскопическое состояние (пъ п2 «5, , . .), для которого число
микроскопически различимых распределений Р (пъ п2, . . ., п5, . . .)
максимально. Наша следующая задача — найти это распределе-
распределение, т. е. найти числа пи п2, . . . , п5, . . . , для которых число
Р (пь) максимально, при выполнении дополнительных условий по-
постоянства числа частиц
Х A5.13)
5=1
и постоянства энергии
со
^ е8пв = Е= СОП81. A5.14)
5=1
Оказывается, удобнее находить максимум не величины Р, а
логарифма этой величины 1и Р. Разыскивать максимум любой
223
Глава 15
функции О (п^ п2» ■ • •) при дополнительных условиях /(«1, п2, ...) =
= 0 и §■ (пъ п2, . . .) = 0 можно с помощью метода неопределен-
неопределенных множителей Лагранжа. В соответствии с этим методом нужно
построить новую функцию
Р{пъ пъ . , . , а, Р) С(пи п2 . . . ) —
гц, . ) A5.15)
и найти ее максимум без каких-либо дополнительных условий,
считая переменные пъ п2 а, р независимыми. Так прихо-
приходим к уравнениям
-^--0, A5.16)
^ , -^- = 0, A5.17)
да
причем уравнения A5.16) выполняются при всех 5.
Используя метод неопределенных множителей Лагранжа в на-
нашей задаче, находим
С-1пР(п5),
'-Aл)-*
так что
18&пО"Е]' A5Л8)
Случай А. Тождественные различимые частицы. В этом случае
для Р имеем формулу A5.8). Поэтому для функции Т7 (формула
A5.18)] имеем явное выражение
5=1
Е
224
Квантовая статистика
Предположим, что все пв > 1. Тогда, используя формулу Стир-
линга 1) для каждого 5, получаем уравнение
ЯР
= 1п&— 1пп5—а— ре,=-О. A5.20)
дп8
Условия A5.17) дают нам просто дополнительные условия A5.13)
и A5.14).
Случай Б. Фермионы. Согласно выражению A5.10) для Р, имеем
формулу
—/О!]}.
5=1
Используя формулу Стирлинга, последнее выражение для 1п Р
можно представить приближенной формулой
Е {& — (п81пп5— п5) —
5=1
««) 1П (Вш— «•)— (^5— «5I | =
&! —л, 1пп,—(#,—л,) 1п(&—«
5=1
Рассматривая теперь функцию
находим уравнения
для каждого 5. При выводе мы предположили, что ^5—п5 > 1.
Случай В. Бозоны. Повторяя слово в слово рассуждение, при-
приводящее к формуле A5.21), но взяв теперь в качестве исходного
выражение A5.12), приходим к уравнениям
э,) — 1пя8—а— ре5 = О, A5.22)
справедливым при всех 5.
Собирая вместе формулы A5.20) — A5.22), получаем следую-
следующие законы тепловых равновесных распределений. В случае ста-
статистики Максвелла-—Больцмана имеем
^ A5'23)
х) Согласно формуле Стирлинга, !п и! ~ п !п п—п при п ); !.
Заказ № 683 225
Глава 15
в случае статистики Ферми—Дирака
«5 = —^^ A5.24)
и в случае статистики Бозе — Эйнштейна
п$ = ——^ . A5.25)
§ 15.4. Смеси частиц нескольких различных видов
Обобщение наших рассуждений на смеси, т. е. на системы, со-
содержащие частицы нескольких типов, проводится без труда. Для
определенности рассмотрим систему, содержащую ./V тождествен-
тождественных частиц вида А и М тождественных частиц вида В. Частицы
каждого типа могут быть либо бозонами, либо фермионами, либо
подчиняться статистике Максвелла—Больцмана. Число различи-
различимых микроскопических распределений N частиц подсистемы А
равно РA) («!,..., пв, . . .), а соответствующее число для М ча-
частиц подсистемы В равно Р'2'^, . . . , тк, , . .). Числа РA) и
РB) определяются формулами A5.8), A5.10) и A5.12) в зависимости
от вида рассматриваемых частиц.
Полное число различимых микроскопических распределений
частиц всей смеси в данном макроскопическом состоянии, характе-
характеризуемом последовательностью чисел (пи п2, . . . , п8, . . .) для
частиц вида А и последовательностью чисел (ти т2, ■ ■ . , тк, . . .)
для частиц вида В, равно
Р(п$, тк) = Р(Х){пъ ... п„ . . . )РB)К> • • .,т*,. • • )•
Чтобы найти наиболее вероятное распределение отдельных частиц
по их состояниям в рассматриваемой смеси, необходимо отыскать
максимум 1п Р (я5, тк) при дополнительных условиях
Е«5 = #, A5.26)
5=1
Ет,.--М, A5.27)
Х>5е5+1>?е?. = Е, A5.28)
5=1 ?. = 1
где е5 и е?_ — соответственно одночастичные собственные числа
энергии для частиц^вида А и В. Числа е5, в^ задают теперь новые
энергетические «интервалы».
226
Квантовая статистика
Применим метод неопределенных множителей Лангража и бу-
будем действовать так же, как при выводе формулы A5.20). Рассмот-
Рассмотрим функцию
Р^Ы РA)(«1> п2, . . . ) + 1пЯ(аК, пи,. . .) —
4A, "
и составим для нее уравнения
дР
дР
дР
A5.29)
= 0, A5.30)
-■■=,0, A5.31)
= 0, _^_ = 0, _^_ = 0, A5.32)
да.х да.2 д$
причем уравнения A5.30) должны выполняться при всех 5, а
A5.31) — при всех к. Из A5.30) получаем
дР д !п Р,
а из A5.31)
—«1—рр8-=°. A5.33)
дР д !п Р2 о п Пг ол\
а2—ре^ = О. Aо.34)
дт%
Формулы A5.33) и A5.34) идентичны по виду с формулами,
полученными для систем, состоящих из частиц какого-нибудь од-
одного вида. Поэтому мы приходим к законам распределений A5.23)—
A5.25). Единственное различие состоит в том, что теперь для ча-
частиц вида А мы должны использовать параметр аи а для частиц,
вида В — параметр а2. Но оба указанных распределения все равно
характеризуются одним и тем же параметром р. (Дальше мы по-
покажем, что параметр C очень просто связан с температурой.)
В качестве примера рассмотрим систему частиц, для которой
частицы подсистемы А подчиняются статистике Максвелла^—Больи-
мана, а частицы подсистемы В — статистике Ферми—Дирака.
Наиболее вероятные распределения частиц по их состояниям в
тепловой равновесной смеси частиц обоих видов даются теперь
формулами
п, = ^ A5.35)
8* 227
Глава 15
для частиц вида А (тождественных различимых частиц) и
т -^ A5.36)
для частиц вида В (фермионов).
§ 15.5. Определение значения параметра р
в законах распределений частиц
Чтобы пользоваться законами распределений A5.23) — A5.25),
необходимо знать значения констант а и C, которые появляются
в формулах. Необходимо при этом использовать дополнительные
условия A5.13) и A5.14), вытекающие, впрочем, непосредственно
из уравнений A5.17).
В предыдущем параграфе мы уже убедились, что параметр р
более важен, чем параметр а, поскольку одно и то же значение C
входит в законы распределений разных видов частиц в том случае,
когда система является смесью, т. е. содержит частицы более од-
одного вида, тогда как значения параметра а оказываются различ-
различными для частиц разных видов. Поэтому сначала займемся пара-
параметром C.
Чтобы найти его значение, рассмотрим газ, составленный из N
массивных атомов с нулевым спином. Из-за большой массы эти ча-
частицы практически неподвижны. Пусть объем V, в котором заклю-
заключены частицы, велик. Поэтому эти частицы можно рассматривать
как различимые и невзаимодействующие.
Распределение таких частиц по одночастичным состояниям под-
подчиняется закону Максвелла—Больцмана A5.23):
п —&—.. A5.37)
Назовем энергетическим «интервалом» 5 группу энергетических
собственных состояний, энергии которых попадают в малый «ин-
«интервал» Ае5 около энергии е5. Число состояний в этом «интервале»
равно
Л~"~'О^-е5/2Ле5, A5.38)
где V — объем того пространства, в котором движутся частицы,
т — масса каждой частицы.
Когда плотность частиц достаточно велика, можно использо-
использовать формулу A5.38) и заменить суммирование
■ = Ы A5.39)
1-1-*
5=1 5=1
228
Квантовая статистика
интегрированием
4яУтBтI'2 _а °? „ „
N = е * е е й& =
А3 о
4я1/тBтI2 „ ,„ / с, х
= в 1и 1 I 1, 110.411)
А \ 2 /
где используемая Г-функция формально определяется интегралом
оо
Г(х) = У е~иих~1 Аи. A5.41)
о
Полная энергия системы N частиц дается формулой
4пУшBтI'2
_а
/I8 О
4пУтBтI'2 „ ,.„
А8 ' ■
Разделив A5.46) на A5.48), получим
® _ й г C/2) 2_
Е ~Р Г E/2) ™ 3
так что
^ 2 Я
6 ~ 3 N
A5.42)
^ /
Р,
A5.43)
Мы предположили, что наши частицы достаточно тяжелые,
чтобы их можно было считать различимыми. Следовательно, к ним
можно применить результаты классической статистической физики.
Средняя энергия, приходящаяся на одну частицу, при тепловом
равновесии, таким образом, равна (см., например, [35])
Е№ = C/2) кТ, A5.44)
где Т — температура, так что
Щ = кТ, A5.45)
здесь к — постоянная Больцмана.
Значение параметра р для фермионов мы найдем теперь, исполь-
используя следующее мысленное построение. Предположим, что система
является смесью и содержит, кроме фермионов, Л^ массивных
частиц, описываемых законом распределения Максвелла^—Больц-
Максвелла^—Больцмана. При равновесии энергия подсистемы тяжелых частиц пусть
равна Ег, а фермионов Е, так что полная энергия всей системы
равна Е + Ег.
В § 15.4 мы показали, что в смеси из нескольких видов частиц
для^каждого вида частиц получается свой закон распределения
229
Глава 15
[см. формулы A5.23) — A5.25) в зависимости от вида частиц]
с единым общим значением параметра р.
Значение параметра р для подсистемы тяжелых частиц, подчи-
подчиняющейся статистике Максвелла—Больцмана, можно определить
способом, в точности совпадающим с только что описанным. При-
Приходим поэтому к формуле A5.45), согласно которой р = (кТ)'1.
Поскольку, согласно § 15.4, для обоих видов частиц в тепловой
равновесной смеси значение параметра р одинаково, непосредст-
непосредственно заключаем, что параметр р и для системы фермионов равен
(кТ)-К
Подобные рассуждения можно провести для смеси, состоящей
из тяжелых частиц и бозонов, и прийти к заключению, что пара-
параметр р для частиц любого вида равен (кТ)-1.
Чтобы закончить вывод формул для законов статистических
распределений, нужно еще определить значения параметров а,
входящих в формулы A5.23) — A5.25). Для этого, однако, необ-
необходимо конкретизировать физическую природу частиц. Важнейшие
примеры систем частиц, для которых можно определить параметр
а, мы рассмотрим в следующей главе.
Вывод формулы A5.38) для @я. Энергетические собственные
функции и свободной частицы массой /л, движущейся в прямо-
прямоугольном ящике с непроницаемыми стенками, должны удовлетворять
уравнению Шредингера
к2
2т \ дх* ' ду2
-^-)«=е«. A5-46)
в котором е — собственные числа энергии частицы. Кроме того,
функции и должны обращаться в нуль на стенках ящика.
Соответствующие решения указанной задачи можно предста-
представить в виде
(, ■ях \ . I ли \ . / лг \
I I 51П I Ш ~^- 1 51П / П I =
~ з!п (кхх) 81П (куу) 81П (кгг), A5.47)
где кх = 1п/а, ку = тп/Ь, кг = ля/с и а, Ь, с — длины ребер
ящика. Числа /, т, п — произвольные неотрицательные целые
числа х). Таким образом, с каждым квантовым состоянием частицы
можно связать свой вектор
где 1, ,|, к — единичные векторы декартовых осей. Энергии рассмат-
г) Считая /, т, п отрицательными, мы не получаем новых независимых
решений.
230
Квантовая статистика
риваемых состояний можно найти, подставляя A5.47) в A5.46).
Для них получаем формулу
*шп=^(Ы +*2 + ф|1ЯЯ- -Щ^- A5.48)
Так как изменение каждого из чисел /, т, п на единицу приводит
к новым собственным состояниям щтп, с каждым собственным
состоянием в пространстве кх, ку, кг можно связать малый объем
Таким образом, число собственных состояний, параметр к =
= Л/ кх -\- к% + к\ для которых пробегает значения от 0 до к,
равно
№У«»Ю>_^_»У_. A5.49)
п3/У 6л2
Здесь 4пк8/3 — объем в пространстве кх, ку, кг шара радиусом к.
Множитель 1/8 появляется потому, что нужно учитывать только
положительные значения кх, ку, кг. Объем п8/У приходится на
каждое отдельное Состояние.
Число состояний, параметр к для которых лежит в интервале
от к до к -\- йк, равно
*"(*> *»?A5.50)
йк 6п2
поэтому, используя соотношения гк = Нгкг12т и йк = тдя,к1Кгк,
получаем формулу для числа состояний в интервале Ае5:
ё$ = ~~^- е';2Ае5, A5.51)
т. е. формулу A5.38).
Задачи
1. Проведите полностью вывод формулы A5.22).
2. Выведите формулы A5.23) —A5.25).
3. По какому-нибудь учебнику разберите вывод формулы A5.50): Е/N =
= C/2) кТ.
231
ГЛАВА 16
КОНКРЕТНЫЕ ПРИМЕРЫ СТАТИСТИЧЕСКИХ ЗАКОНОВ
РАСПРЕДЕЛЕНИИ ЧАСТИЦ
В предыдущей главе мы вывели формулы для статистических
законов распределения квантовых частиц по их состояниям. Эти
формулы содержат, однако, неизвестный параметр а, значение ко-
которого нужно определять особо в каждом конкретном случае.
О том, как это сделать, пойдет речь в настоящей главе. Будут рас-
рассмотрены два важных примера систем частиц — вырожденный элек-
электронный газ и фотонный газ.
§ 16.1. Распределение Максвелла — Больцмана
Для частиц, подчиняющихся статистике Максвелла—Больцмана,
подставляя Р = (кТ)'1 и Г C/2) = \ я/2 в формулу A5.40) и раз-
разрешая ее относительно а, получаем
2п3'2Уш BтI 2
3 2
где N — число частиц, т — масса одной частицы, V — объем, в ко-
котором заключена система частиц.
Согласно формуле A5.23), доля атомов с энергией ег (или, бо-
более точно, доля атомов из энергетического «интервала» /) дается
формулой
5
в которую а не входит. Отношение населенностей двух уровней,
скажем I и /, при тепловом равновесии, таким образом, равно
-Ь- = Л-е-Рг*,)*т ^ A6.3)
и в)
Это известная формула Больцмана.
§ 16.2. Распределение Ферми — Дирака
Согласно формуле A5.24), функция распределения тождествен-
тождественных неразличимых частиц с полуцелым спином (фермионов) имеет
вид
" —. A6.4)
232
Конкретные примеры статистических законов
Подставляя сюда значение р = {кТ)~~х и вводя новую величину
|Л=— акТ,
которая называется химическим потенциалом, формулу A6.4) пред-
представим в виде
л,= ^ . A6.5)
& /е ц\/кт
Если мы теперь используем индекс 5 для нумерации таких «ин-
«интервалов», которые содержат по одному состоянию (а не совокуп-
0.5
\
\
/нд)<<!
т=о
\
\
/НО) е
Рис. 16.1. Функция распределения Ферми—Дирака при абсолютном нуле
температуры и при малой конечной температуре. Ширина переходной об-
области между областями / (е) = I и / (е) ^ 0 порядка_/гГ.
ность §8 вырожденных состояний, соответствующих энергетиче-
энергетическому уровню е5, как до сих пор), то в формуле A6.5) следует по-
положить §3 = 1. Тогда получаем
!. A6.6)
(Т)]/1кТ + 1
Функция / (е) дает закон распределения Ферми—Дирака, ко-
который характеризует вероятность того, что в тепловой равновес-
равновесной системе одночастичное квантовое состояние е занято фермио-
ном. Следовательно, / (е) ^ 1.
На рис. 16.1 приведены графики функций / (е) при Г = 0 и
при некоторой конечной малой температуре Т. Если Т = 0, то
функция / (е) равна единице при е-<(л и нулю при е>(л. Другими
словами, при нулевой температуре все одночастичные состояния
с энергией, меньшей значения химического потенциала (Л @), за-
заняты, а все состояния с энергией, превышающей (Л @), не заняты.
При отличной от нуля температуре переход от занятых к незанятым
состояниям «размазан» на энергетическую область шириной по-
порядка кТ, как показано на рис. 16.1.
При энергиях е, удовлетворяющих условию &—(Л ^> кТ, имеем
Полученная простая экспонен ииальная зависимость вероятности
233
Глава 16
наблюдать занятое фермионом состояние в точности совпадает
с законом Больцмана A6.3), так что в рассматриваемом предельном
случае больших энергий фермионы ведут себя, как классические
частицы.
Найдем теперь значение химического потенциала (л @) при ну-
нулевой температуре Т = 0. Рассмотрим в качестве примера свобод-
свободный электронный газ, заключенный в объеме V, которым с успе-
успехом можно моделировать электроны проводимости в металле.
Число одноэлектронных состояний, лежащих в интервале с1ь-,
согласно формуле A5.51), равно
^1_е^е. A6.7)
Дополнительный множитель 2 появляется здесь из-за того, что
каждая пространственная волновая функция электрона описы-
описывает не одно, а два квантовых состояния, одно (с т$ = 1/2) со спи-
спином, направленным вверх, и другое (с /п8 = — 1/2) со спином,
направленным вниз. Число занятых электронами состояний из
энергетического интервала йг равно произведению полного числа
§■ (е) (Ы всех таких состояний, лежащих в интервале йе, на вероят-
вероятность / (е) заполнения каждого из них. Поскольку полное число
электронов фиксировано и равно Ы, имеем
Г $ (е) /
о
поэтому, используя формулы A6.6) и A6.7), окончательно получаем
простое соотношение
\ е12
е12 д&. A6.8)
А3 3
о
Когда температура равна нулю, / (е) = 1 при е<(л и / (е) = 0
при е>(л, так что определенный интеграл в последней формуле
легко вычислить:
Подставляя значение интеграла в A6.8), приходим к следующей
формуле:
Химический потенциал [А @), часто называемый энергией
234
Конкретные примеры статистических законов
Ферми, играет важную роль в теории металлов и в теории полу-
полупроводников.
Поведение многих металлов можно объяснить, используя при-
приближенную модель свободного электронного газа. Согласно этой
модели, при очень низких температурах все электронные состоя-
состояния в металле до энергии е = [л заполнены, а все состояния выше
Энергии е = (Л не заняты. При более высоких температурах уровни
из энергетического интервала кТ около уровня Ферми (Л заняты
частично. Все это показано на рис. 16.2.
Рис. !6.2. Зависимость плотности состояний д (е) и плотности электронов
д (е) [ (е) от энергии. При нулевой температуре состояния до энергии ц @)
заполнены. Штриховая кривая изображает плотность заполненных состоя-
состояний при температуре Т ■»':. |1 @)//г.
Рассмотрим теперь числовой пример и вычислим значение хи-
химического потенциала (энергию Ферми) для металла с плотностью
электронов 1029 м~8. Подставляя это значение плотности в фор-
формулу A6.9), находим
ц @) = 1,257- Ю-18 Дж-= 7,85 эВ.
Здесь полезно обратить внимание читателя на то, что именно
вследствие наличия принципа запрета Паули энергетические
уровни электронов- в металле даже при Т = 0 заполнены вплоть
до уровня со столь большой энергией е « 7,85 эВ. [В системе бо-
бозонов, в которой любое одночастичное состояние может быть за-
занято любым числом частиц, при нулевой температуре все частицы
находились бы в нижнем состоянии е = 0 (конденсация). ] Элек-
Электроны металла вблизи границы заполненных состояний имеют
скорость уъ, которая при нулевой температуре Т = 0 находится
из очевидного условия
причем в рассмотренном выше числовом примере ур = 1,67-108 см/с.
Следует подчеркнуть, что такими огромными скоростями элек-
235
Глава 16
троны металла обладают даже при нулевой температуре и что их
существование можно объяснить только с позиций квантовой ме-
механики.
Укажем еще на одно простое, но важное свойство химического
потенциала (л (Т). Оно состоит в следующем. Химический потен-
потенциал характеризует увеличение полной энергии системы при до-
добавлении к ней одной дополнительной частицы, т. е.
A6.10)
Такая наглядная физическая интерпретация химического по-
потенциала непосредственно вытекает из закона распределения
Ферми—Дирака A6.6). Действительно, поскольку состояния до
уровня энергии \х(Т) заняты [мы пренебрегаем малой «переходной»
областью шириной кТ вблизи (л(Т) ], добавляемую частицу можно
поместить только на уровень (л(Т).
В качестве полезной задачи предлагаем читателю убедиться,
что при Т = 0 справедливо соотношение
** аЕ ^@) A6.11)
в котором Е = } вд (е) йг обозначает энергию ^-частичной си-
о
стемы (при нулевой абсолютной температуре).
Таким образом, если два образца с различными значениями хи-
химических потенциалов привести в контакт друг с другом, то ча-
частицы будут перетекать из образца с большим значением (Л в обра-
образец с меньшим (Л. Равновесие установится только после того, как
химический потенциал примет единое значение в обоих образцах.
В противном случае всегда можно уменьшить энергию системы пу-
путем переноса частиц из областей с высоким значением химического
потенциала в области с низким его значением.
Представление об общем характере зависимости химического
потенциала (Л (Т) от температуры можно получить непосредственно
из формулы A6.8), рассматривая ее теперь при температурах Т Ф 0.
Не будем останавливаться, однако, на подробном выводе, по-
поскольку интересующийся читатель легко может найти его в каком-
либо учебнике (например, в [5]), а просто приведем окончательную
формулу
[Н)*] (Ш2)
Отметим еще одно важное проявление принципа запрета Паули
для электронов металла. Рассмотрим электронную теплоемкость
металлов.
236
Конкретные примеры статистических законов
Если бы электроны были классическими частицами, то на каж-
каждый из них приходилась бы полная тепловая энергия ЗкТ/2, так
что энергия единицы объема металлического образца с объемной
плотностью электронов Ы/У равнялась бы V — C/2 ){№ IV) кТ, а по-
потому электронная теплоемкость единицы объема образца С =
= д1ЛдТ была бы равна C/2)(Ы/У)к.
Эта формула, однако, неверна, так как дает значения, примерно
на два порядка превышающие экспериментальные данные для
большинства металлов при комнатных температурах.
Причины такого расхождения классической теории с экспери-
экспериментом легко понять, если взглянуть на рис. 16.2. Действительно,
полная энергия системы электронов определяется интегралом
основной вклад в который дают полностью занятые электронами
состояния [/ (е) = 1 ] с энергиями, меньшими химического потен-
потенциала. Следовательно, вклад всех этих состояний во внутреннюю
энергию II системы N электронов практически постоянен, и элек-
электронная теплоемкость С = 6Е1АТ практически равна нулю.
Основной вклад в электронную теплоемкость С металла дает,
таким образом, очень небольшая доля, порядка кТ/\ь электронов,
энергии которых отличаются от химического потенциала (Л на ве-
величину порядка кТ. Эти электроны приближенно можно рассмат-
рассматривать как классические частицы, на каждую из которых прихо-
приходится тепловая энергия C/2) кТ. Вклад энергий таких электронов
в полную энергию единицы объема системы, таким образом, равен
так что для электронной теплоемкости металла имеем следующее
приближенное выражение:
с_ йЕ _ йЕ' о / N \ ,_ кТ
ат ат \ V I |л@)
Точная формула для теплоемкости электронной системы имеет
следующий вид (см. [5}):
п л2 / N \ , кТ лк ,оч
С = / )к . AЬ.13)
2 I V I |л@) К '
В рассмотренном выше числовом примере при Т = 300 К имеем
кТ/ц, @) = 1/300. Именно на такой порядок величины различаются
экспериментальные и рассчитанные по классической теории зна-
значения электронной теплоемкости.
237
Глава 16
§ 16.3. Распределение Бозе — Эйнштейна
Рассмотрим теперь подробнее закон распределения Бозе—Эйн-
Бозе—Эйнштейна A5.25). Чтобы найти а в этом случае, мы должны нало-
наложить, как и в случае других распределений частиц, условие по-
постоянства числа частиц системы. Вычисления в общем случае, од-
однако, оказываются довольно громоздкими. (Мы не будем их здесь
проводить.) Вместо этого ограничимся простым частным случаем
системы бозонов, на котором все существенное легко проследить.
Рассмотрим равновесное тепловое электромагнитное излучение.
Им мы уже занимались в гл. 12, но там мы считали, что «частицами»
системы являются электромагнитные моды (осцилляторы), которые
вследствие их различимости подчиняются закону распределения
Максвелла—Больцмана A6.2).
Теперь мы примем другую точку зрения и будем полагать, что
Поле излучения состоит из фотонов, а не из электромагнитных мод,
или осцилляторов.
Одночастичные состояния возьмем, впрочем, такие же, как для
электромагнитных мод:
■ф(г) ^ е'кг. A6.14)
Эти состояния мы подробно рассмотрели в § 12.2.
Частица (фотон) в состоянии к имеет энергию Н\ (причем V =
= кс!2п). Каждый фотон, кроме того, характеризуется своим век-
вектором распространения, или волновым вектором к, и единичным
спином 5=1, проекция которого может принимать два значения
/л5 = + 1. Квантовые числа тх = + 1 описывают два состояния
с противоположными направлениями круговой поляризации фо-
фотона, обладающего данным волновым вектором к. Фотоны являются
неразличимыми частицами, так как имеют целочисленный спин
E ). Поэтому они подчиняются закону распределения Бозе—
Эйнштейна A5.25):
A6.15)
еа+Е5,ЛГ _ ! -
в который мы подставили р = (кТ)~~1.
Напомним, что параметр а появился у нас [см. формулу A5.18) ]
вследствие учета условия сохранения полного числа частиц N си-
системы.
Полное число фотонов (частиц) в электромагнитном излучении,
однако, не фиксировано и может быть каким угодно. (Это очень
тонкое обстоятельство, которое заслуживает, чтобы на нем оста-
остановиться подробнее. Если рассматривать электромагнитные моды
как «частицы» системы, мы должны просто сказать, что при увели-
увеличении энергии поля электромагнитного теплового излучения
увеличивается и энергия, запасенная в каждой из электромаг-
238
Конкретные примеры статистических законов
нитных мод. При этом полное число мод остается, конечно, неиз-
неизменным. Если, напротив, рассматривать фотоны как частицы си-
системы, то увеличение ее энергии неизбежно приведет к увеличению
числа фотонов, соответствующих каждой данной электромагнитной
моде. Число фотонов, таким образом, в тепловом электромагнитном
излучении не может сохраняться.)
Поскольку теперь число частиц (фотонов) не фиксировано, со-
совершенно бессмысленно учитывать дополнительное условие A5.13),
приведшее к появлению параметра а в законах распределений,
так что в формуле A6.15) в случае фотонов следует просто положить
а — 0. Тогда закон распределения для фотонов примет следующий
простой вид:
п== 1? . A6.16)
В законе A6.16) ^ означает число фотонных состояний к, ча-
частоты которых лежат в интервале д.\ около частоты V. Число таких
состояний дается формулой A2.35):
Ё5 с3
Число частиц (фотонов) в интервале бх, таким образом, согласно
формуле A6.16), равно
П. — • б\.
' с3 (еНу'кт - 1)
Умножим последнюю формулу на энергию Ьу отдельного фо-
фотона. Получим тогда (после деления на полный объем системы V)
окончательную формулу для спектральной плотности энергии теп-
теплового равновесного электромагнитного излучения абсолютно чер-
черного тела в интервале частот от V до V + д.\:
<ь,, A6.17)
)
в полном согласии с формулой A2.37).
Задачи
1. Докажите, что в равновесной смеси, составленной из трех видов частиц,
температуры подсистем частиц одинаковы.
2. Выведите формулу для энергии Ферми двумерного электронного газа,
заключенного в прямоугольнике со сторонами а и Ь.
3. Убедитесь, что распространяющиеся в произвольном направлении две
тлоскополяризованные электромагнитные волны с взаимно ортогональ-
ортогональными поляризациями можно рассматривать и как две волны с противо-
противоположно направленными круговыми поляризациями.
239
Глава 16
Указание. Покажите, что каждую плоскополяризованную электромаг-
электромагнитную волну можно представить как линейную комбинацию двух волн
с противоположными круговыми поляризациями.
4. Убедитесь в справедливости формулы A6.11).
5. Выведите формулу A6.17) для спектральной плотности энергии тепло-
теплового равновесного излучения абсолютно черного тела
р (V) г-=.
рассматривая в качестве «частиц» электромагнитные моды, а не фотоны.
Указание. Ответьте на основной вопрос: являются ли электромагнитные
моды различимыми?
ГЛАВА 17
ЗОННАЯ ТЕОРИЯ ЭЛЕКТРОНОВ
В КРИСТАЛЛИЧЕСКИХ ТВЕРДЫХ ТЕЛАХ
В предыдущих главах мы изучили некоторые одночастичные
и двухчастичные квантовые системы. В частности, мы занимались
атомом водорода (гл. 7), частицей в потенциальной яме (гл. 4),
а из двухчастичных систем — атомом гелия (§8.2). В предыдущей
главе мы обсуждали статистические свойства свободного электрон-
электронного газа в металлах.
В настоящей главе будет подробно рассмотрена задача об элек-
электроне, движущемся в пространственно-периодическом потенци-
потенциальном поле. Эта задача нужна для понимания электрических
свойств кристаллических твердых тел, обладающих правильной
кристаллической решеткой.
Впервые в настоящей главе мы начинаем знакомство с вопро-
вопросами физики твердого тела. Речь пойдет о теории запрещенных
энергетических зон и о теории так называемых зон Бриллюэна.
В этих теориях существенно учитывается пространственная перио-
периодичность кристаллической решетки. Впрочем, материал этой главы
полезен и для понимания других разделов физики, где приходится
иметь дело с распространением волн в периодических структурах,
или в пространственно ограниченных задачах и в пространственно
ограниченных системах, например при исследованиях распростра-
распространения акустических волн в кристаллах [5] или электромагнитных
волн в волноводах.
§ 17.1. Модель Кронига — Пенни
Характерные свойства волновых функций электрона в кри-
кристалле можно уяснить с помощью простой одномерной модели
Кронига—Пенни. Потенциальное поле, принимаемое в этой модели,
показано на рис. 17.1. Изображен график функции потенциальной
энергии V (х) электрона. Волновые функции электрона опреде-
определяются путем решения следующего уравнения Шредингера:
"" . = [Е-У(х)]у(х). A7.1)
2т ах2
Прежде чем приступить к отысканию решений этого уравнения,
укажем на некоторые общие свойства волновых функций в перио-
периодической среде. Согласно математической теореме Флоке (которую
в физике твердого тела называют теоремой Блоха [36]), любое ре-
241
Глава 17
шение волнового уравнения для периодической среды можно пред-
представить в следующем виде:
Цк(г)=ик(г)е{к-\ A7.2)
где ик (г) — периодическая функция с тем же периодом, что и
среда. В одномерном случае формула A7.2) принимает вид
ук(х) = ик(х)е1Кх, A7.3)
причем
ик(х + А) = ик(х), {ПА)
где Л — пространственный период.
г
* —-л -
г
Эк
1
• .г — »
г
сп »
а„ ■ - —
2
/
Рис. 17.1. Одномерный периодический потенциал.
Чтобы доказать, что волновую функцию -ф (х) действительно
можно представить в блоховской форме A7.3), введем в рассмотре-
рассмотрение оператор трансляции ТА, определяемый формулой
ТА{(х) = [(х + А), A7.5)
где I (х) — произвольная функция.
Докажем, что оператор ТА коммутирует с гамильтонианом Ш>
Пусть ч)з (х) — собственная функция гамильтониана Ж, удовлетво-
удовлетворяющая уравнению Жър (х) — Е^ (х), где Е — собственное число
энергии электрона. Используя A7.5), можно тогда написать
Следовательно,
так что операторы 1иГЛ действительно коммутируют друг с дру-
другом, поскольку функции 4)) (х) образуют полный набор.
Два коммутирующих между собой оператора обладают одина-
одинаковым набором собственных функций, поэтому функции яр (х) можно
242
х) ---- Жу (х + Л) = Еу (х + Л).
Зонная теория
выбрать так, чтобы они были и собственными функциями оператора
ТА (см. гл. 3).
Найдем эти функции. Пусть с обозначает соответствующее соб-
собственное число. Тогда имеем уравнение
ТлУ(х) = У(х+Л) = сЧр(х), A7.6а)
где с — некоторая константа. Далее,
1M (х + & А) = св<ф (х), (П.66)
где д — произвольное целое число. Чтобы найти с, необходимо на-
наложить определенные граничные условия на функции гр (х). Обычно
[5] используется граничное условие
где Ь = Л^Л — длина нашего одномерного кристалла. Тогда в
силу A7.66) имеем соотношение
Ц(х), A7.7)
так что
с"=1, с^<Ряе", A7.8)
причем @ = О, I, 2, . . . , N — 1. Таким образом, функция, удов-
удовлетворяющая A7.6а) и A7.7), имеет вид
%(х) = е12пехШАиЁ(х), A7.9)
где ие (х) — периодическая функция с периодом Л. Используя со-
сокращенное обозначение
2^ ^^ A7.10)
где § = 0, + 1, +2 собственные функции оператора тран-
трансляции ТА можно записать в виде
Ук(х) = е1Кхик(х), A7.11)
а это как раз и есть теорема Блоха. (Величину К будем называть
константой распространения волновой функции. ]
Теперь все подготовлено, чтобы приступить к решению уравне-
уравнения Шредингера
^^0. A7.12)
Так как потенциал V (х) равен постоянной Уо в областях 1 и нулю
в областях 2, решение уравнения A7.12) в каждой области пред-
243
Глава 17
ставляет собой суперпозицию двух соответствующих линейно не-
независимых экспоненциальных решений:
к11х-пА) + Ьпе-к11х-пА) в области 1, A7.13)
* 1х~пА) + йпе-{к* (х~пА) в области 2, A7.14)
г|> (х) =
причем
-\/2тЕ
A7.15)
A7.16)
Наша следующая задача — найти коэффициенты а„, Ъп и с„,
йп, которые определяют вид искомой функции -ф (х). Требуя, чтобы
•ф (х) и (Щ (хIйх были непрерывными при х = пА, приходим к
уравнениям
= сп+1е-^А + с1п+1е1к*А, A7.17)
кгап—кгЬп = 1
Эти же граничные условия при х= пА + 1 = (п + 1)Л —5 дают
A7.18)
Уравнения A7.17) и A7.18) можно записать в матричном виде:
Сп+1
V /
A7.19)
\
Сп+Х
А
лп+г
Ъп
+1
. A7.20)
244
Ъп
=
А В
СО
ап+1
Ьп+1
Зонная теория
Умножая эти уравнения (слева и справа) на соответствующие мат-
матрицы, можно, очевидно, прийти к соотношению
A7.21)
связывающему величины а„+1, Ьп+1 с величинами а„, Ьп. В этом
соотношении
А = е
A7.22)
Гсоз к4 + 4г (—- -~"Ь1
Матрицу с элементами А, В, С, О назовем трансформационной
матрицей. Из A7.22) непосредственно видно, что
АО—ВС=\,
т. е. что эта матрица имеет равный единице детерминант.
Используя формулу A7.21), можно вычислить все пары коэффи-
коэффициентов ап, Ьп для любой элементарной ячейки, если известна
одна какая-нибудь их пара в некоторой ячейке. Определив таким
образом коэффициенты ап, Ъп, с помощью A7.19) можно найти сп,
йп по известным ап-1г Ъп-\.
Рассмотрим решение 1M (х) в области 1, принадлежащей п-й эле-
элементарной ячейке [см. A7.13)]:
1M (х) = а„Л (*-"
Заменяя х на х + Л, отсюда получим
Л (*-«
е
> 1 и
"Г °А1
С другой стороны, функция 1M (х) должна удовлетворять теореме
Блоха и иметь форму A7.11):
245
Глава 17
Сопоставляя обе формулы для 1M (%), приходим к заключению,
что имеет место соотношение
Ьп+1
—1КА
Используя A7.21) и производя замену п
в виде
I
А В
С В
Ьп
^= €
—;кл
ап
Ьп
A7.23)
п, запишем A7.23)
A7.24)
Уравнение A7.24) имеет вид уравнения на отыскание собствен-
ных чисел и собственных функций: Аип = апип. Матрицу с эле-
элементами А, В, С, В можно рассматривать как матрицу двумерного
трансляционного оператора А, а столбцы (а„, Ь„) — как собствен-
собственные векторы. Множитель е~1кА дает, таким образом, собственное
число матрицы.
Вычитая правую часть A7.24) из левой части, приходим к мат-
матричному уравнению
А-е~1КА
В
С
—1'КЛ
Ьп
= 0.
A7.25)
Мы получили однородную алгебраическую систему двух урав-
уравнений относительно двух неизвестных ап и Ьп. Она имеет нетриви-
нетривиальное решение в том и только в том случае, когда ее детерминант
обращается в нуль. Вычисляя этот детерминант с использованием
формул A7.22), получаем уравнение для отыскания собственных
чисел
1^ ||^]2}12. A7.26)
в котором индекс 1 (или 2) слева следует брать при выборе знака
«плюс» (или «минус») справа. Собственные векторы, соответствую-
соответствующие собственным числам A7.26), можно рассчитать, подставляя
A7.26) в A7.25). Так, получим формулу
а0
Ьо
В
A7.27)
в которой N — нормировочный множитель, выбираемый из усло-
условия | Щ>*с1х = 1. Когда известны коэффициенты а0 и Ьо, мы мо-
246
Зонная теория
жем подставить их в формулы A7.23) и A7.13) и найти для соб-
собственной функции 1MК (х) для области 1 в п-й элементарной ячейке
следующее явное выражение:
ч])к (х) = N [(о/» {х~пА) + V"*1 {х-пА)) е~1К {х~пА)'] е1кх. A7.28)
Полученное выражение для функции ч|з (х) согласуется с теоремой
Блоха A7.11), поскольку функция, заключенная в квадратные
скобки, периодична с периодом Л. Константу распространения К
находим из уравнения A7.26), из которого непосредственно следует,
что
соз(/СЛ) = A/2)(Л+1>). A7.29)
Это дисперсионное соотношение описывает распространение волно-
волновой функции в одномерном периодическом потенциальном поле.
Используя явные выражения A7.22) для величин А и й, получаем
соз(КЛ) = соз(/г20 сп (кг5) + зт(/г2*) зЬ (М) ( *' 2 ) - A7.30)
V 2/г1й2 /
Исследуем теперь подробнее дисперсионное соотношение A7.30).
Правая его часть, согласно A7.15) и A7.16), есть функция энергии
частицы Е = Й2й|/2/л. При любом данном значении энергии Е мы
можем, таким образом, вычислить правую часть A7.30) и затем
рассчитать из A7.30) значение /СЛ (с точностью до добавления
к нему целого кратного 2л). При этом следует различать два случая.
а. Энергия имеет такую величину, что
A7.31)
Тогда, как это непосредственно следует из A7.29), величина /Сока-
/Соказывается действительным числом, а функция ч|зк (х), согласно
A7.28), описывает модулированную распространяющуюся волну.
Эти области значений Е называют разрешенными зонами.
б. Энергия имеет такую величину, что
A/2)(Л+Я)>1. A7.32)
Тогда сов к А 2> 1, поэтому величина К должна быть комплексной.
Но, поскольку A/2) (А + Щ — действительное число, имеем
A7.33)
причем т = + л, + 2л [Формула A7.33) выводится очень
просто. Предоставляем это сделать читателю. ] В рассматриваемом
случае экспоненциальный множитель в формуле A7.28) имеет вид
ехр AКх) = ётш Л ехр (-1К{\ х),
247
Глава 17
а потому функция 4'к (х) экспоненциально затухает. Внутри боль-
большого кристалла она должна обратиться в нуль. (Решения, содер-
содержащие ехр (| /С; 1 х), следует вообще отбросить, так как они беспре-
беспредельно возрастают, т. е. нефизичны.)
Энергетические интервалы, для которых A/2)(Л + /))>■■ 1 и
для которых величина К принимает комплексные значения, назы-
называются запрещенными зонами. Электроны, обладающие такими
«запрещенными» энергиями, не могут существовать внутри боль-
большого кристалла. Практически такие электроны можно обнаружить
только вблизи поверхности кристалла или какого-либо нарушения
кристаллической структуры, на расстояниях порядка двух-трех
расстояний КТ1-
Типичные кривые зависимости Е от К. (и от /0), получаемые
из дисперсионного соотношения A7.30), показаны на рис. 17.2а.
Заметим, что константа затухания Ж принимает максимальное
значение в середине запрещенной зоны.
Условие /СЛ = /таг, которое, согласно A7.33), определяет гра-
границу запрещенной зоны, формально эквивалентно одномерному
условию Брэгга в теории дифракции рентгеновских лучей (см. [5]).
Когда указанное условие выполняется, отражения волновой функ-
функции %рк (х) от соседних элементарных ячеек происходятУв фазе
друг с другом. Следовательно, отраженные волны усиливают друг
друга, поскольку разность фаз, приобретаемая при прохождении
волной рассматриваемого пространственного интервала туда и
обратно, равна 2/СЛ = 2гаг. При выполнении указанного условия
функция *|эк (х) испытывает отражение и не может «проникнуть»
внутрь кристалла, поскольку она экспоненциально затухает в нем
с постоянной A7.33).
В результате полного отражения бегущей волны, которое на-
наблюдается при /СЛ = /гаг, образуется стоячая волна. (Напомним,
что стоячая волна возникает при интерференции волн е не .)
Одному и тому же значению К. = пгп/А соответствуют два незави-
независимых решения в виде стоячих волн (одно из них четное, другое —
нечетное). Экстремумы одной из указанных функций лежат внутри
потенциальных барьеров, поэтому соответствующая собственная
энергия Е2 будет больше собственной энергии, отвечающей второй
функции, которая внутри барьеров имеет узлы. Таким образом,
каждому значению К. = /гат/Л соответствуют две собственные
функции, которым отвечают две различные энергии. Указанные
энергии Ег и Е2 на рис. 17.2а определяют «потолок» и «дно» запре-
запрещенной зоны. Примерное поведение обеих собственных функций
на краях запрещенной зоны показано на рис. 17.26.
Область — л</СЛ < п называется первой зоной Бриллюэна г).
*) Бриллюэн внес большой вклад в разработку основ теории распростра-
распространения волн в периодических средах. См., например, его книгу [37].
248
N3
(О
Вторая
запрещенная зона
Третья зона
Бриллюэна
|
^
>, (" \ Первая Т
<^-\запрещтная зона^
^ 'половина \
е= второй —*\
зоны Бриллюэна I
\втпорои
Первая зонд Бриллюэна ^ зоны Вриллюзна
Третья зона:
Бриллюэна
-л
О
КА
а
Зп
■о
Рис. 17.2а. Зависимость Е от А"Л для электронов в модели Кронига—Пенни.
Глава 17
Две области, я<г /СЛ<2л и — 2л</СЛ< — п, рассматриваемые
вместе, называются второй зоной Бриллюэна и т. д.
Поскольку из дисперсионного соотношения A7.30) величину
/СЛ можно найти только с точностью до слагаемого 2лт, где т —
произвольное целое число, функция я|;к (х), определяемая форму-
формулой A7.28), не должна изменяться, если в ней К заменить на
К + т Bя/Л). Поэтому можно ограничить область изменения ве-
величины К интервалом —я/Л</С<я/Л и рассмотреть диспер-
дисперсионную кривую (рис. 17.2а) в этом интервале. Для этого надо сдви-
сдвинуть все кривые, изображенные сплошными линиями, горизон-
У(х) V; !
кг/ П I >-^о1 Ь-/ I
I
'Ой
_^
X
Рис. 17.26. Примерные графики собственной функции ^ (нечетная симмет-
симметрия) и собственной функции г]J (четная симметрия) при энергии, лежащей
на границе запрещенной зоны, т. е. при К& = /ля, К1 = 0. Внутри потен-
потенциальных барьеров функция ^х имеет узлы, а функция г]}2 — экстремумы.
Собственная энергия Ег для функции фх, таким образом, меньше собствен-
собственной энергии Е2 для функции ■фг-
тально на соответствующие отрезки 2пЦА (где / — некоторое це-
целое число). В результате получим диаграмму так называемых при-
приведенных энергетических зон, показанную на рис. 17.3.
Примерный график определяемой формулой A7.28) волновой
функции \рк (х) для электрона, энергия которого лежит в первой
запрещенной зоне (/("Л = я 4- 1/0), показан на рис. 17.4. Обра-
Обратите внимание на изменение фазы функции [ехр (г/СЛ) = — 1 ]
в каждой элементарной ячейке. В основном функция ч|?к (х) изме-
изменяется примерно синусоидально в областях 2 и экспоненциально
в областях 1. Огибающая этой функции описывается затухающей
экспонентой ехр (— КьХ), так что функция быстро убывает по мере
проникновения внутрь кристалла, поэтому ее связывают с «поверх-
«поверхностным» электронным состоянием.
§ 17.2. Кристаллическое твердое тело,
содержащее большое число электронов
В предыдущем параграфе мы занимались одномерной задачей
об электроне, движущемся в периодическом потенциальном поле.
Решив уравнение Шредингера, мы нашли одночастичные собствен-
собственные функции [см. A7.28)]:
Цк(х) = ик(х)е!Кх A7.34)
и одночастичные собственные энергии Ек.
250
Зонная теория
Е Л
Рис. [7.3, Приведенные зоны. Нумерация соответствует рис. 17.2а.
,ч_
кг
г
О
к,
1
2
Рис. 17.4. Волновая функция электрона, энергия которого лежит в первой
запрещенной зоне.
251
Глава 17
Если пренебречь взаимодействием между электронами кристал-
кристаллического твердого тела, результаты этой задачи можно применить
к реальному кристаллу, содержащему большое число электронов.
Для этого нужно поочередно помещать в каждое состояние К, на-
начиная с самого низкоэнергетического, по одному электрону, пока
так не будут размещены все электроны, имеющиеся в кристалле.
Как мы уже показали при выводе формулы A7.10), для одно-
одномерного кристалла, имеющего N элементарных ячеек, разрешены
следующие значения константы распространения К-
причем §■ = 0, ±1, ± 2, . . . , так что два соседних значения К
разделены интервалом А/С = 2п1Ь.
Занягпыь
• состояния
о Незанятые
состояния
Рис. 17.5. В диэлектриках (к числу которых относятся собственные полу-
полупроводники при очень низких температурах) все энергетические состояния
валентной зоны заняты электронами (черные кружки), а все энергетические
состояния всех зон, расположенных выше валентной зоны, пусты. Из этих
зон только одна (зона проводимости) показана на рисунке.
Разрешенные значения К изображены черными кружками на
рис. 17.5. На каждое состояние в зоне Бриллюэна приходится
отрезок длиной 2п1Ь, так что всего имеется
2п/А
Д/С
Л
разрешенных значений К в каждой зоне Бриллюэна. Однако каж-
каждому значению К сопоставляется два спиновых состояния элек-
электрона (с т$ = ± 1/2), поэтому всего в каждую зону Бриллюэна
можно поместить 2Ы электронов. (Напомним, что N — число эле-
элементарных ячеек в кристалле.)
252
Зонная теория
Если бы число валентных *) электронов, приходящихся на одну
элементарную ячейку кристалла, было равно 2, первая зона Брил-
Бриллюэна оказалась бы полностью заполненной. Когда это число равно
■единице, зона будет заполнена лишь наполовину. Вообще при чет-
четном числе электронов, приходящихся на одну элементарную
ячейку кристалла, получаем полностью заполненные зоны; при
нечетном числе валентных электронов самая верхняя зона будет
заполнена только наполовину.
Предположим теперь, что к кристаллу с четным числом элек-
электронов в элементарной ячейке, т. е. к кристаллу, у которого самая
верхняя зона Бриллюэна заполнена, а следующая за ней более
высокая зона — пуста (рис. 17.5), приложено внешнее электриче-
электрическое поле. Оказывается, что в таком кристалле электрический ток
возникнуть не сможет. Этот удивительный факт непосредственно
следует из симметрии самой верхней заполненной зоны. Дейст-
Действительно, в заполненной зоне каждому электрону, движущемуся
вправо (/B>0), всегда соответствует электрон, движущийся влево
(/("<; 0) с равной и противоположной скоростью2). Таким образом,
сумма обеих скоростей, а потому и вклад этих двух электронов в об-
общий электрический ток в кристалле, равны нулю, следовательно,
кристалл оказывается диэлектриком.
Если же верхняя зона Бриллюэна заполнена лишь частично, то
приложенное электрическое поле нарушает точный баланс электро-
электронов с положительными и отрицательными значениями константы
распространения К.- В таком кристалле можно возбудить электри-
электрический ток, и кристалл оказывается металлом.
Итак, приходим к заключению, что радикально различная элек-
электропроводность кристаллических твердых тел определяется исклю-
исключительно физической структурой кристалла, а именно числом ва-
валентных электронов, приходящихся на одну элементарную ячейку.
Примером кристаллического твердого тела, обладающего ме-
металлическими свойствами, может служить натрий. Кристалл нат-
натрия имеет объемноцентрированную кубическую решетку. Зоны
Бриллюэна содержат по два состояния на каждый атом натрия,
так как элементарная ячейка кристалла содержит один атом №.
Атом натрия имеет один валентный 35-электрон. Поэтому самая
верхняя зона Бриллюэна заполнена только наполовину, и кристалл
натрия оказывается хорошим проводником.
Примером кристаллического твердого тела, являющегося ди-
диэлектриком, может служить хлорид натрия №С1. Элементарная
*) Предполагается, что «внутренние» электроны атомов сильно связаны
•с ними и не играют существенной роли в процессах электропроводности в
кристаллическом твердом теле.
2) Для более полного объяснения необходимо ввести в рассмотрение
групповую скорость электронов, о которой пойдет речь в следующем па-
параграфе.
253
Глава 17
ячейка этого кристалла содержит один атом Ыа и один атом С!_
Таким образом, на каждую элементарную ячейку приходится 28,
т. е. четное число электронов. Следовательно, самая верхняя зона
Бриллюэна заполнена электронами полностью, и кристалл ЫаС1
представляет собой диэлектрик.
Для кристаллов с четным числом электронов, приходящихся
на элементарную ячейку, самую верхнюю целиком заполненную-
электронами зону Бриллюэна называют валентной зоной, а сле-
следующую за ней зону — зоной проводимости. Энергетический за-
зазор между экстремальными энергиями этих зон, т. е. наименьшее
энергетическое «расстояние» между зонами, называют шириной
запрещенной зоны Е8.
Однако наше утверждение о том, что валентная зона полностью
занята электронами, а зона проводимости совершенно пуста, строго
справедливо только при нулевой температуре. Из закона распреде-
распределения Ферми—Дирака A6.6) непосредственно видно, что при ко-
конечных температурах некоторая доля электронов все же будет пе-
переходить в зону проводимости. Каждый такой перешедший в зону
проводимости электрон оставляет в валентной зоне незанятое со-
состояние — дырку.
Приложенное внешнее электрическое поле сможет вызвать элек-
электрический ток в таком кристалле, так как теперь зоны в нем не бу-
будут целиком заполненными или совершенно пустыми. Кристаллы,
у которых ширина Ее запрещенной зоны мала, так что через нее
может быть переброшено достаточное число электронов, называются
полупроводниками. Примерами хорошо известных и широко при-
применяемых полупроводников могут служить кристаллы кремния 51
(Ее = 1,1 эВ) и арсенида галлия ОаАз (Е6 = 1,45 эВ).
Электропроводность чистых, без примесей, или нелегирован-
нелегированных полупроводников в отличие от металлов определяется возбуж-
возбуждением электронов через запрещенную зону, а потому сильно за-
зависит от температуры и обращается в нуль при Т = О, так как,
согласно закону распределения Ферми—Дирака A6.6), при нуле-
нулевой температуре валентная зона должна быть целиком заполненной,
а зона проводимости — совершенно пустой.
Как уже говорилось выше, при наложении электрического поля
в полупроводнике возникает электрический ток, обусловленный
несбалансированным движением отдельных электронов в зоне
проводимости и в валентной зоне. Поскольку число занятых элек-
электронами состояний в валентной зоне обычно на много порядков
больше числа незанятых, можно представить себе всю картину
следующим образом.
Будем считать, что все состояния валентной зоны заняты элек-
электронами, но, что, кроме электронов, в валентной зоне имеется еще
некоторое число фиктивных положительно заряженных частиц,
в точности равное числу вакантных состояний. При этом полный
254
Зонная теория
электрический заряд всех электронов с учетом положительно за-
заряженных частиц будет прежним. Поскольку полностью занятая
электронами валентная зона не дает никакого вклада в полный
электрический ток в кристаллическом твердом теле, можно счи-
считать, что весь ток теперь переносится исключительно фиктивными
положительно заряженными частицами, которые мы добавили в ва-
валентную зону. Эти частицы называются дырками.
В случае идеально чистого (собственного) полупроводника числа
электронов в зоне проводимости и дырок в валентной зоне в точ-
с Занятые
состояния
о Незапятые
состояния
' Л
к
Л
Рис. 17.6. Полупроводник. Ширина запрещенной зоны Её мала, поэтому
в результате теплового возбуждения заметная доля электронов может пе-
перейти из валентной зоны в зону проводимости. Черными кружками показаны
занятые состояния, светлыми —пустые. Электропроводность обеспечивается
как электронами из зоны проводимости, так и отсутствующими электронами,
или дырками, в валентной зоне.
ности равны друг другу, поскольку каждый электрон, перешедший
в зону проводимости, оставляет после себя дырку в валентной зоне.
Такая ситуация показана на рис. 17.6. Введение атомов примеси
в кристаллическое твердое тело может разрушить баланс электро-
электронов и дырок и привести к тому, что электропроводность кристалла
будет обеспечиваться, например, только электронами из зоны про-
проводимости. Когда число электронов в зоне проводимости намного
превосходит число дырок в валентной зоне, мы говорим о полупро-
полупроводнике Л7-типа. Когда, наоборот, число дырок в валентной зоне
намного превосходит число электронов в зоне проводимости, мы
говорим о полупроводнике Р-типа.
Разработка эффективных способов изменения содержания при-
примесей в полупроводниковых кристаллах, а следовательно, и типа
электропроводности полупроводника (УУ- или Р-типа) привели к
созданию транзисторов, полупроводниковых лазеров и других
важных электронных и оптических устройств, в корне преобразо-
преобразовавших электронику и оптику. Об этом мы подробнее расскажем
в гл. 20.
255
Глава 17
§ 17.3. Движение электрона в кристаллическом
твердом теле
Классическую картину движения точечного электрона нельзя
непосредственно использовать при рассмотрении квантовомехани-
ческого электрона, описываемого блоховскои собственной функцией
1>к (х, г) = ик (х) е1 (^~ЕкЩ . A7.35)
Это связано с тем обстоятельством, что функция г|5к (х, г) «разма-
«размазана» по всему объему кристалла и не локализована. Точечный
Рис. 17.7. а — пространственное распределение вероятностей для локали-
локализованного при / = О электрона; б — соответствующая функция распреде-
распределения | а^ |2 в импульсном пространстве.
электрон можно описать только «пакетом», или линейной комбина-
комбинацией собственных функций г|5к (х, ^),
Предположим, что -ф (х, 0) представляет собой волновую функ-
функцию электрона в какой-то момент времени, который без ограниче-
ограничения общности будем считать нулевым, I = 0. Пусть, далее, функция
■ф (х, 0) локализована в пределах области с характерным размером 6,
как показано на рис. 17.7. Поскольку функции ик (х) образуют
полный ортонормированный набор состояний (см. § 2.6), то для
256
Зонная теория
функции г); (х, 0) можно написать разложение
Ц(х, 0) = Еакик(х)еКх. A7.36)
к
При этом
ь
ак= Г $ (х, 0) и*к (х) ё~1Кх их, A7.37)
б
где ^ — длина рассматриваемого здесь одномерного «кристалла».
Распределение вероятностей, описываемое функцией ак, показано
на рис. 17.7, б. Оно сосредоточено около среднего значения Ко-
Волновая функция -ф (х, г) при ^^>0 должна удовлетворять
полному уравнению Шредингера Ж"§ = ш д^1д1, а также началь-
начальному условию г); (х, I) |(=0 = г); (х, 0), где функция г); (х, 0) опреде-
определяется выражением A7.36). Поэтому эту волновую функцию можно
представить следующим рядом:
к ...... A7-38)
Разлагая энергию Ек в окрестности Ко, получаем приближен-
приближенную формулу
(К-Ко),
Л» ' ак
подстановка которой в A7.38) дает
$ (х. 0=1 аКо+АКиКо+АК (х) ехр {» Г(К0 + АК) х —
A7.39,
где А/С = К—Ко- Если наблюдатель будет двигаться с такой ско-
скоростью, чтобы для него фаза волны
хАК 1—^-ЛК* A7.40)
в A7.39) представлялась постоянной (здесь мы обозначили
йЕкШК\Ко просто как ёЕк/ёК), то он будет «видеть» неизменную
функцию| г); (х, {)\. Такой наблюдатель должен двигаться со ско-
скоростью
^ ^^«п, A7-41)
9 Заказ № 683 ' 257
Глава 17
Скорость VI■Р называется групповой скоростью электронного вол-
волнового пакета. Она представляет собой скорость перемещения ка-
какой-либо точки огибающей для функции | -ф (х, I) | 2, показанной
на рис. 17.7, а. В большинстве случаев, когда мы просто говорим
о скорости электрона в кристалле, мы на самом деле имеем в виду
групповую скорость его волны.
Выведем еще одно важное соотношение. Приравняем работу
— её'ьТХ)(И, произведенную над электроном за время 6.1 внешним
приложенным электрическим полем <§Г, приросту энергии элек-
электрона 6ЕК (здесь считаем, что е=|е|):
4^. A7.42)
* с1Ек йК.
йК
Используя соотношения угр = A Ъ) йЕк16К, отсюда получаем
уравнение
йК её
6.1 П
или в общем случае
а
{ПАЗ)
= Внешняя сила. A7.44)
си
Таким образом, приходим к заключению, что в отношении дейст-
действующих на него внешних сил электрон (точнее пакет электронных
волн) ведет себя так, как если бы он обладал импульсом пК. Вели-
Величина пК называется квазиимпульсом. Ускорение электронного вол-
волнового пакета при действии на него внешнего поля равно
ск>гр 1 й
а/ па
/ йк_\ 1. ЙХ.Л1, A7.45)
\ ак ) а йК'~ си
откуда, используя уравнение движения A7.43), непосредственно
получаем
—и__ =—е^ I л_ =, , A7.4Ь)
а \ А2 йК2 I Эффективная масса
так что эффективная масса электрона равна
те-пЧ-^-У\ A7.47)
Движение электрона в кристалле под действием внешних сил
происходит так, как если бы его эффективная масса была обратно
пропорциональна кривизне дисперсионной кривой (кривая зави-
зависимости Ек от К). Эффективные массы элементарных носителей
электрического тока для некоторых широко распространенных по-
полупроводниковых кристаллов приведены в табл. 19.1 на стр. 291.
258
Зонная теория
§ 17.4. Изменение электропроводности
полупроводников путем введения примесей
На характер распределения электронов по состояниям в полу-
полупроводниковом кристалле можно существенно повлиять путем вве-
введения в кристалл посторонних атомов примеси. Этот процесс на-
называется легированием.
Атом примеси в кристаллической решетке часто замещает атом
основной решетки. Образуя химические связи с соседними атомами,
примесные атомы теряют или приобретают электроны, так что в ре-
результате у них оказывается столько же валентных электронов,
сколько и у основных атомов кристалла.
Так, например, если добавлять пятивалентные атомы мышьяка
Аз в кристалл кремния (валентность 51 равна 4), то «лишний» (пя-
(пятый) электрон мышьяка переходит к кристаллу. Поскольку все
состояния валентной зоны кристалла кремния уже заполнены (см.
рис. 17.5), дополнительные электроны должны разместиться в зоне
проводимости. Такие примеси называются примесями Л^-типа (или
отрицательного типа).
Если атом примеси обладает меньшим числом валентных элек-
электронов, чем атом основной решетки, то «чужой» атом — например
2п в 51 — может образовать химические связи с соседними атомами,
отбирая валентный электрон у атомов кристалла. Остающаяся при
этом вакансия, называемая дыркой, может принять участие в пере-
переносе электрического тока, о чем мы будем говорить ниже. Такой
вид примеси называется «примесью Р-типа» (или положительною
типа).
Основное различие между примесной и обсуждавшейся выше
собственной электропроводностью (которая обусловлена тепловым
возбуждением электронов из валентной зоны в зону проводимости
через запрещенную зону в идеально чистом кристалле) состоит в
том, что при примесной электропроводности число электронов не
равно числу дырок. Количественную теорию примесной электро-
электропроводности мы изложим в гл. 19.
Электрический ток в полупроводниках. Процесс возникновения
электрического тока в примесном полупроводнике Л^-типа схема-
схематически показан на рис. 17.8. На рис. 17.8, а изображены занятые
состояния в /(-пространстве, существовавшие до приложения элек-
электрического поля. На рис. 17.8, б изображено положение в обычном,
физическом пространстве при I = 0 единственного электрона из
зоны проводимости. Предположим, что к кристаллу в нулевой мо-
момент I = 0 прикладывается электрическое поле. Это поле обуслов-
обусловливает изменение величины К. у рассматриваемого электрона, ко-
которое, согласно A7.43), происходит со скоростью
йК её
Л ~~ ~ п
9* 259
Глава 17
В результате в момент времени Д^ мы имеем распределение занятых
состояний, изображенное на рис. 17.8, в.
Поскольку валентная зона полностью заполнена, ее электроны
не дают никакого вклада в электрический ток. Как уже говорилось,
это обусловлено тем, что каждому электрону с положительной груп-
групповой скоростью (Ш) (с1Е1йК) соответствует электрон (при — К)
с равной и противоположно направленной групповой скоростью.
1=0
*~ К
Сила, действующая
на электроны
6
I
-■! + —»/ I
Рис. 17.8. Протекание электрического тока в полупроводнике Л^-типа. а —
электрон при I = О находится на дне зоны проводимости {К =0); б — тот
же электрон при { = 0 находится в пространственной точке х = 0; в —
к моменту { = Д^ электрон в /^-пространстве смещается в точку, где диспер-
дисперсионная кривая имеет положительный наклон; г — электрон в обычном
пространстве смещается вправо, так как с'гр = A/А) йЕк/с1К> 0. Отсюда
следует, что электрон имеет положительную эффективную массу.
Электрический ток создается, таким образом, только электронами
зоны проводимости. Поскольку единственный электрон из зоны
проводимости, показанный на рис. 17.8, а, движется в направле-
направлении положительных К, он имеет положительную групповую ско-
скорость и в обычном, физическом пространстве сдвигается направо,
как показано на рис. 17.8, г. Электрон, таким образом, ускоряется
в направлении приложенной к нему силы, т. е. имеет положитель-
положительную массу. Это согласуется с формулой A7.47), которая связывает
элективную массу электрона с кривизной энергетической зоны
Е (К) в /(-пространстве.
260
Зонная теория
Соответствующие кривые для полупроводника Р-типа представ-
представлены на рис. 17.9. На рис. 17.9, а одно состояние на «потолке»
валентной зоны не занято в начальный момент I = 0. Ситуация
совершенно не изменится, если считать, что вакансия в валентной
зоне заполнена одним добавочным электроном и одной положи-
положио
Сила, действующая
на электроны
~<±>
р
■*-®
п
Рис. 17.9. Полупроводник Р-типа. а — в валентной зоне при г = 0 не за-
занято одно электронное состояние; б — соответствующая дополнительная
положительная частица (дырка), способная свободно передвигаться, зани-
занимает положение х— 0 при { = 0; в — под действием внешнего электрического
поля распределение электронов в валентной зоне перестраивается и дырка
сдвигается вправо в Л'-пространстве в область, где Vгр = A/Н) (йЕ/йК) <0;
г — поскольку групповая скорость отрицательна, в обычном физическом
пространстве дырка смещается влево. Этот процесс можно представить как
движение положительно заряженного носителя электрического тока (дырки),
обладающей положительной эффективной массой
причем в Я'-пространстве и в реальном физическом пространстве дырка за-
занимает место электронной вакансии.
тельно заряженной частицей — дыркой, причем как в реальном
физическом, так и в /(-пространстве электрон и положительно за-
заряженная частица неразлучно следуют друг за другом. Таким об-
образом, валентная зона теперь оказывается целиком заполненной
и поэтому не дает никакого вклада в полный электрический ток.
Иначе говоря, весь возникающий в таком кристалле электрический
261
Глава 17
ток можно считать обусловленным движением фиктивного поло-
положительного заряда — дырки.
Движение дырки в /(-пространстве под действием электриче-
электрического поля показано на рис. 17.9, в. Добавленный электрон и его
«тень» в виде дырки движутся, согласно A7.43), в положительном
/(-направлении. Поскольку теперь, однако, наклон йЕ:йК, а сле-
следовательно, и групповая скорость электрона ь?р отрицательны,
перемещение дырки (которая должна сопровождать электрон) в.
реальном, физическом пространстве происходит в левую сторону,
в направлении приложенного электрического поля. Дырка обла-
обладает положительным зарядом и ее ускорение совпадает по направ-
направлению с силой еШ', следовательно масса дырки положительна.
Масса дырки, таким образом, равна взятой со знаком минус массе
связанного с дыркой электрона:
Разработка эффективных способов изменения электропровод-
электропроводности полупроводников путем легирования их примесями Ы- и
Р-типа лежит в основе создания транзисторов и интегральных элек-
электронных схем. Подробнее этот вопрос обсуждается в гл. 19.
Задачи
1. Выведите формулы A7.22) для матричных элементов А, В, С, О.
2. Выведите формулу A7.33).
3. (Необходимо умение работы на ЭВМ.) Решите численно задачу на отыска-
отыскание собственных чисел и собственных функций для электронов, движу-
движущихся в периодическом потенциале Кронига—Пенни при 5 = ( — 4 А,
Уо = 5 В. Считайте, что Е = Л2к2/2т, а затем найдите численное значе-
значение константы распространения К путем численного решения трансцен-
трансцендентного уравнения A7.30). Найдите соответствующий собственный век--
тор (с0) Ьв) из уравнения A7.27). Проведите вычисления с некоторым
шагом для значений К из интервала 0 <; К ^ л/Л (считайте, что Л =
= 5 + I = 8 А).
4. Приписав импульс М,- электрону в кристаллическом твердом теле, по-
покажите, что классическое соотношение
Мощность = Сила X Скорость
остается справедливым и в квантовой механике, если скоростью элек-
электрона считать его групповую скорость.
ГЛАВА 18
ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И АТОМНЫХ ЯДЕР
С МАГНИТНЫМ ПОЛЕМ.
МАГНИТНЫЙ РЕЗОНАНС. МАЗЕРЫ
Электроны и атомные ядра обладают магнитными дипольными
моментами. Дипольные магнитные моменты электронов обуслов-
обусловлены их орбитальным движением вокруг ядер, а также их собст-
собственным вращением (спином). Дипольные магнитные моменты атом-
атомных ядер обусловлены только спином ядер.
Все упомянутые магнитные дипольные моменты могут взаимо-
взаимодействовать с внешними магнитными полями, а также друг с дру-
другом; в результате изменяются наблюдаемые энергетические уровни
системы. Физические явления, в которых проявляется взаимо-
взаимодействие атомных и ядерных дипольных магнитных моментов с внеш-
внешними магнитными полями, относятся к явлениям магнитного ре-
резонанса. Исследованиями магнитного резонанса в настоящее время
занимается большое число химиков и физиков.
Некоторые физические приборы, например СВЧ мазерный уси-
усилитель, атомные часы на основе водородного мазера, были бы не-
немыслимыми, если бы мы не знали теории взаимодействия атомных
и ядерных магнитных дипольных моментов с внешними магнит-
магнитными полями.
§ 18.1. Орбитальный магнитный момент электрона
Эксперименты показывают, что частоты электромагнитного из-
излучения, испущенного возбужденными атомами водорода, нахо-
находящимися в магнитном поле, сдвигаются по сравнению с их значе-
значениями в нулевом поле. Кроме того, магнитное поле вызывает рас-
расщепление некоторых спектральных линий.
Чтобы объяснить результаты этих экспериментов, необходимо
уточнить уравнение Шредингера, учтя в нем влияние внешнего
магнитного поля. Это можно сделать, добавив к гамильтониану
системы в нулевом магнитном поле новое слагаемое, которое опи-
описывает дополнительную энергию электрона, обусловленную взаи-
взаимодействием с внешним магнитным полем. Математически строгий
вывод выражения для возмущающего гамильтониана довольно
формален, и мы займемся им немного позже.
Начнем изложение с менее формального, но, к сожалению, не-
нестрогого вывода. Его преимущество состоит в том, что в нем отчет-
отчетливо выявляется связь гамильтониана возмущения с работой, про-
производимой над электроном возмущающим внешним магнитным
полем,
263
Глава 18
Рассмотрим электрон, движущийся по некоторой замкнутой
орбите С. Работа, производимая электрическим полем над элек-
электроном (с зарядом — е, причем е = |е.), который, двигаясь по ор-
орбите, совершает полный оборот, равна
IV = — е\ (Е-д&) = — е [(го1 Е-п)да. A8.1)
С 5
При написании последнего равенства мы использовали известную-
теорему Стокса из векторного анализа:
С(го1А-п)аа= |(А-Ж>), A8.2)
5 С
которая связывает контурный интеграл (по контуру С) от произ-
произвольного векторного поля А с поверхностным интегралом (по по-
поверхности 5, натянутой на контур С) от ротора этого поля. В A8.2)
п представляет собой единичный вектор, нормальный к поверхно-
поверхности 5, йа—-элемент площади поверхности 5. Дифференциал д& —
векторное приращение пути вдоль контура С. Для преобразования
правой части соотношения A8.1) воспользуемся уравнением Мак-
Максвелла
го*Е = ?5-; A8.3)
тогда получим
ИР = е— {(В • п) йа = -р- [епг2В (Щ. A8.4)
При написании последнего равенства мы предположили, что элек-
электрон движется по круговой орбите радиусом г в однородном маг-
магнитном поле, причем В обозначает компоненту поля, нормальную-
к плоскости орбиты. Электрон с импульсом р и массой т совершает
один оборот за время
„1 2лг 2г\тт
V р
Поэтому работа, произведенная полем над электроном за время й1г
равна работе A8.4), совершенной за один оборот, умноженной на
число оборотов, происходящих за время 6.1, т. е. на множитель (И'Т:
^^^. A8.5)
<И д
(И 2шт 2т <И 2т
Здесь йВ = {йВ1й1) 6,1 — изменение В за время сИ.
Полное изменение энергии электрона при включении магнит-
магнитного поля В получим интегрированием A8.5) по полю от 0 до В:
^-В. A8.6)
2т
264
Взаимодействие с магнитным полем
Учитывая, что В здесь обозначает компоненту магнитного поля,
нормальную круговой орбите электрона, можно теперь написать
следующее выражение для гамильтониана, соответствующего энер-
энергии Д№:
Л^=,^-([г.р]-В) = -^A-В)=-(А/-В). A8.7)
2т 2т
в котором 1 = 1г - р ] — оператор орбитального момента количества
движения электрона.
Поскольку энергия взаимодействия дипольного магнитного
момента |и с магнитным полем с индукцией В равна —(|л-В), из
формулы A8.7) непосредственно заключаем, что оператор орби-
орбитального магнитного момента электрона имеет вид
р,= --^1. A8.8)
2
Оператор орбитального магнитного момента обычно записывают
немного в другом виде:
"' A89)
где р = еН/2т — так называемый магнетон Бора, численно равный
9,272-10~24 Дж-м2/Вб.
Полный гамильтониан электрона, движущегося в сферически-
симметричном потенциальном поле и одновременно в однородном
магнитном поле с индукцией В, равен сумме гамильтониана G.5)
в нулевом поле и магнитного гамильтониана A8.7):
2т \ г* дг \ дг )) ^ 2тг-~
т. е.
Ж = Жо~'~ — ((-В) = Жо~-^-В1г> A8.10)
Л Гг
где ось г без ограничения общности мы считаем направленной вдоль
поля В.
Собственные числа энергии Е„[т гамильтониана A8.10) можно
получить, решая уравнение
<?ёЧп1т = Еп1тип1т ■
Выше мы показали [см. G.1) ], что операторы Жо и 1г коммутируют
друг с другом. Они обладают, следовательно, общим набором соб-
собственных функций иП1т (г, 6, ф). (Обратите внимание, что здесь
т — квантовое число, а не масса электрона.) Пользуясь соотно-
соотношениями 1ги,Пт = Нтитт и Жф-пы = Е„1ип[т, уравнение на
265
Глава 18
отыскание собственных чисел и собственных функций гамильто-
нианаХA8.10) можно записать в следующем виде:
Хф-тт -г — В1гип[т = (Е„[ -г пфВ\ и,йт,
й
так что
о -\—— В12 1 ип[т = (Еп1 -- пфВ) и„1,п — Епыипит
причем
Еп1т = Е,п т§В, A8.11)
где т = — /, — I -\- 1, . . . , /.
Согласно формуле A8.11) г), данный квантовый уровень с энер-
энергией Е,а, существовавший в нулевом магнитном поле, расщепляется
полем В на 2/ -}- 1 отдельных подуровней, нумеруемых квантовым
числом т. Имевшееся в сферически-симметричном потенциальном
поле B1 Ч~ 1)-кратное орбитальное вырождение уровня с энергией
Е„1 снимается при включении магнитного поля.
Численный пример. С помощью лабораторного магнита легко
создать магнитное поле, равное, скажем, 4 Вб/м2 A Вб.м2 = 10* Гс).
В поле В = 1 Вб/м2 расщепление уровней, т. е. расстояние между
уровнями с соседними значениями т (|Ат| == 1), равно
6Е = р = 9,272.10-24 Дж.
Это так называемое «зеемановское расщепление» уровней чаще
всего теперь изучают, помещая образец в электромагнитное СВЧ-
поле с частотой Н\ ~ 8Е, которое вызывает переходы между рас-
расщепленными магнитным полем уровнями. Требуемая частота элек-
электромагнитного СВЧ-поля в рассматриваемом примере должна быть
равна
V =.--Н. = 9>2720~- = 1,399• 1010 Гц.
/г 6,626- Ю-84
Она действительно лежит в СВЧ-диапазоне.
При исследовании магнитного резонанса изучают зеемановское
расщепление уровней в атомах и молекулах, измеряя поглощение
и дисперсию переменного электромагнитного поля в среде, содер-
содержащей исследуемые атомы. Подробнее об этом мы расскажем в
§ 18.3.
Формально строгий квантовомеханический вывод выражения
для гамильтониана электрона в магнитном поле. Формальный кван-
квантовомеханический вывод выражения для гамильтониана A8.10)
*) Формула A8.11) имеет точно такой же вид и в системе СГС Надо
только считать, что Р = 9,272-10~21, а поле В выразить в гауссах.
266
Взаимодействие с магнитным полем
начинается с рассмотрения гамильтониана электрона, движущегося
в магнитном поле с векторным потенциалом А:
X =^ _!_ (р—еАJ — V = Жо -г -^- [сК\' А -1- (А ■ §гай) ] — — А2,
2/» 2т 2т
причем здесь
2т
= го1А,
(хотя последняя формула нам и сейчас не понадобится, мы ее все
же приводим.)
Дальше рассмотрим только случай однородного магнитного
поля В = ег В. Векторный потенциал А этого магнитного поля
возьмем в виде
При таком выборе векторного потенциала приведенный выше га-
гамильтониан можно записать так:
ду дх
Используя определение оператора момента количества движения
электрона 1 = [г-р] = — Ш [г-у], полученное выражение для
гамильтониана можно представить следующим образом:
Ж =^3^о-т — 1В+ -^- =Ш0+ — (Г-В) + -^1 (х2 ~у*), A8.12)
й 2т А 8т
где р г= П | е \12т.
Если отбросить теперь в A8.12) слагаемое с суммой х2 — у-,
то получится в точности формула A8.10). Последнее слагаемое в га-
гамильтониане A8.12) называют диамагнитным. Им обычно прене-
пренебрегают в тех случаях, когда квантовое число / момента количества
движения электрона или квантовое число 5 его спина не равны
одновременно нулю. Для этих случаев легко показать, что отноше-
отношение диамагнитного слагаемого к слагаемому (р/й) A-В) имеет по-
порядок (еВ1Ш) (г2), т. е. пренебрежимо мало для экспериментально
доступных в лабораторных условиях магнитных полей В, скажем
до полей порядка Юа Вб'см2.
267
Глава 18
§ 18.2. Спиновый момент количества движения
В предыдущем параграфе было показано, что с орбитальным
моментом количества движения частицы всегда связан соответст-
соответствующий магнитный дипольный момент, причем, согласно формуле
A8.9), операторы обоих моментов пропорциональны друг другу.
Мы вывели также формулу A8.11) для расщепления уровней энер-
энергии электрона в магнитном поле, из которой, в частности, следует,
что основное состояние атома водорода с п = 0 не должно рас-
расщепляться в магнитном поле, поскольку для него квантовое число /,
а следовательно, и квантовое число т равны нулю.
Однако эксперименты, произведенные еще на заре квантовой
механики, показали, что уровень п = 0 атома водорода расщеп-
расщепляется в магнитном поле на два подуровня, причем величина рас-
расщепления пропорциональна величине магнитного поля. В 1926 г.
на основе этих экспериментов Уленбек и Гаудсмит [38, 39 ] были
вынуждены принять допущение, что электрон обладает собствен-
ным, или спиновым, моментом количества движения.
Соответствующий спиновому моменту количества движения
оператор обозначим 8. Оказывается, он обладает только двумя соб-
собственными состояниями: | 1/2) (спин «вверх») и | — 1/2) (спин
«вниз»). Компоненты векторного оператора 8 удовлетворяют в точ-
точности таким же перестановочным соотношениям, как и компоненты
векторного оператора 1.
Другими словами, они имеют вид перестановочных соотноше-
соотношений F.49):
[$, 5]^гй8. A8.13)
Эксперименты показали также, что собственные числа опера-
оператора 5г, т. е. разрешенные значения проекции на ось г спинового
момента количества движения, соответствующие состояниям | 1/2)
и |— 1/2), равны Й/2 и — Й/2, так что
±-—) =
Уравнения A8.14), A8.15) идентичны уравнениям F.37), только
теперь квантовое число /, которое принимало значения / = О, 1,
2, . . . , следует заменить на 5 = 1/2, а квантовое число т — на
квантовое число тв = ± 1/2.
Оператор дипольного магнитного момента (х5, как показывают
эксперименты, связан с оператором спинового момента количества
268
Взаимодействие с магнитным полем
движения 8 соотношением:
М,= — 8 = —2р —. A8.16)
те Н
Сравнивая формулы A8.16) и A8.8), видим, что постоянный
множитель в соотношении для щ и 8 в два раза больше множителя
в соотношении для ц{ и 1. Этот факт известен в квантовой механике
как спиновая магнитная аномалия.
Полное собственное состояние электрона на орбите в атоме во-
водорода теперь нужно характеризовать тройкой квантовых чисел п,
I, т, нумерующих орбитальные волновые функции ы„/от, и, кроме
того, спиновым квантовым числом ш5, которое принимает два зна-
значения: 1/2 и — 1/2. Полная собственная функция электрона в атоме
водорода записывается, таким образом, в виде
%11тт$ = И„1т (г) | ГПВ), |/П5>= + -~
Энергия атома водорода, находящегося в основном состоянии
(п = 1, / = 0, т = 0) и помещенного во внешнее магнитное поле,
дается собственными числами гамильтониана Ж = <Ж0 + Bр/Й) Взг:
о п ~т~ хЭ5г
и1001т$) = Ет1Пв ]тв) = (Ео + 2р/л5В) и1001пи). A8.17)
Так как /п5 = ± 1/2, основное состояние атома водорода с энер-
энергией Ео в магнитном поле с магнитной индукцией В расщепляется
на следующие два подуровня:
Энергетическое расстояние между этими уровнями равно
A8.19)
Такое предсказываемое квантовой теорией расщепление блестяще
подтверждается экспериментом.
Как уже говорилось выше, существование собственного, или
спинового, момента количества движения у электрона сначала было
постулировано на основе непосредственных экспериментальных
данных (см. [38, 39]). Немного позже, в 1928 г., Дирак [40] в своей
релятивистской квантовомеханической теории доказал, что элек-
электрон должен обладать спином. Нейтроны и протоны тоже обладают
внутренним моментом количества движения 5 = 1/2. Об этом пой-
пойдет речь в следующем параграфе.
269
Глава 18
§ 18.3. Спины атомных ядер
и ядерный магнитный резонас
Эксперименты показали, что, подобно электронам, атомные
ядра тоже обладают собственными, или спиновыми, моментами ко-
количества движения и связанными с ними магнитными дипольными
моментами.
В полной аналогии с A8.14) и A8.15) введем в рассмотрение
оператор I спинового момента количества движения атомного ядра
с собственными функциями | /, т}), удовлетворяющий перестано-
перестановочным соотношениям F.49):
[Г, |] = Ш- A8.20)
Таким образом,
/г|/, т,) = Пт,\1, т,), A8.21)
Г2|/, т/> = Йг/(/+1)|/, т,). A8.22)
Проекция спинового момента количества движения атомного
ядра на направление произвольной оси г равна Нт,, где т, может
принимать одно из следующего набора значений: —/, — /-М,
. . . , /. Ядерные спиновые состояния, таким образом, харак-
характеризуются безразмерными квантовыми числами / и т,. Для атом-
атомного ядра с нечетным массовым числом А спиновое квантовое
число / принимает полуцелые значения (т. е. равно 1/2, 3/2 и т. д.),
а для атомных ядер с четным массовым числом А квантовое число /
принимает целые значения. Например, ядра 0м и О18 имеют спин
/ = 0, а ядро О17 — спин / = 5/2. Протоны и нейтроны тоже имеют
спины / = 1/2.
В полной аналогии с A8.16) векторный оператор магнитного
момента атомного ядра пропорционален его спиновому моменту,
т. е. имеет место формула
!^^ A8-23)
к
р
в которой Шр — масса протона. Положительная константа |3Л, =
= еН/2тр называется ядерным магнетоном. Его численное значе-
значение в СИ равно 5,049-10~27 Дж-м2/Вб. (В системе СГС ядерный
магнетон р# = 5,049-10"~24 эрг- Гс.) Значения константы #л,
найденные из экспериментов, приведены в табл. 18.1, в которую
также включены значения спина / для нескольких важнейших
атомных ядер. Положительное значение §^ означает, что вектор
магнитного момента ядра и вектор его спинового момента количе-
количества движения направлены в одну сторону.
Гамильтониан взаимодействия атомного ядра с внешним маг-
магнитным полем В имеет вид
■ В) = - ~ ЫЫ1 • В). A8,24)
270
Взаимодействие с магнитным полем
Таблица /Л'./ Магнитные моменты и частоты ядерного магнитного резонанса
(Я.МР) для некоторых атомных ядер
2
0
1
6
8
14
Атом
Нейтрон
Н (протон)
С
О
А
1
1
2
12
13
16
17
18
28
29
30
I
1.2
1 2
1
0
1.2
0
5/2
0
0
1/2
0
«Л' '
— 1.913
2.79268
0.85738
Ч),7022
— 1,893
—0,5548
Частота ЯМР при поле
1 Вб м!. 10- Гц
29, 167
42.576
6,536
10,705
5,772
8,458
Данные взяты из работы: УаНап Д55ос1а4ез, Ь'МК ТаЫе, 44Ь ее]. (Ра1о ЛНо. СаШогша).
Его собственные числа легко рассчитать; имеем
, т,\1г\1, т,> =
A8.25)
причем без ограничения общности предполагаем, что магнитное
поле направлено вдоль оси г.
Формула A8.25) показывает, что в результате взаимодействия
магнитного момента ядра с магнитным полем, создаваемым электро-
электронами атома в месте расположения атомного ядра, уровни атомного
ядра расщепляются на 2/ + 1 подуровней. Расстояние между
двумя соседними подуровнями равно
Л* = 1Ял1Р*В- A8.26)
Изучением переходов между магнитно-расщепленными энерге-
энергетическими подуровнями атомного ядра занимаются при исследо-
исследованиях ядерного магнитного резонанса (ЯМР). Экспериментально
ядерный магнитный резонанс впервые наблюдали Блох [41 ] и
Парселл [42 ]. (Упомянутые работы, посвященные этим эксперимен-
экспериментам, написаны очень доступно.)
В типичном эксперименте по ЯМР образец, содержащий иссле-
исследуемые атомные ядра, помещают между двумя полюсами электро-
электромагнита и одновременно подвергают действию радиочастотного
переменного магнитного поля с частотой V, которое направлено
перпендикулярно постоянному магнитному полю В, создаваемому
электромагнитом. Когда частота приложенного магнитного поля V
271
Глава 13
попадает почти в резонанс с частотой A8.26), начинается сильное
поглощение радиочастотной мощности в результате возбуждения
индуцированных переходов между расщепленными зеемановскпми
ядерными подуровнями.
Индуктивная катушки.
' создающая магнитное
Рч-поле
Высокочас-
Высокочастотный
E-50МГц)
генератор
тока
Т
у ( /) Вольтметр
, К\У постоянного
I ~ I напряжения
Рис. 18.1. Схема лабораторной установки для исследования ядерного маг-
магнитного резонанса. Радиочастотный (РЧ) генератор возбуждает ток, который,
протекая но катушке, создает внутри ее переменное магнитное поле. Когда
при постепенном изменении постоянного магнитного поля оно проходит
через резонанс, поглощение РЧ-энергии в образце приводит к резкому па-
падению» добротности <2 резонансного контура ЬСХ, что в свою очередь вызы-
вызывает падение РЧ-напряжения Уф Выпрямляющий диод преобразует напря-
напряжение Уг( в постоянное напряжение. Таким образом, поглощение радиоча-
радиочастотной мощности магнитными моментами атомных ядер регистрируется по
изменению постоянного напряжения и поэтому очень легко наблюдается.
Экспериментальная установка для наблюдения ЯМР схемати-
схематически показана на рис. 18.1. Чтобы получить представление о по-
порядках величин резонансных частот в ЯМР, рассмотрим протоны.
(Ампула с водой или глицерином содержит огромное число прото-
протонов.) Принимая, что в A8.26) магнитное поле В — 1 Вб'м2 A0* Гс),
и используя данные из табл. 18.1, получаем
V =
2-2,79268-5,049-10-~27-1
6,6257-Ю-34
Метод ЯМР в настоящее время очень широко применяется в хи-
химии и в физике твердого тела. Успехами он обязан обнаружив-
обнаружившейся чрезвычайно чувствительности резонансной частоты по-
поглощения — частоты зеемановского расщепления уровней атомного
ядра — к физическим условиям и симметрии окружения атомного
ядра. Эта чувствительность объясняется тем обстоятельством, что
полное магнитное поле, которое «чувствуется» атомным ядром, скла-
складывается из внешнего поля, поля других атомных ядер (если у них
272
Взаимодействие с магнитным полем
/ -^ 0) и поля, создаваемого электронами, окружающими атомное
ядро. Ничтожные изменения электронного окружения ядра, про-
происходящие, например, при образовании химических связей в мо-
Рис. 18.2. Экспериментальная кривая ядерного парамагнитного резонанса
для ядер водорода в этиловом спирте СН8СН2ОН. Самый большой пик со-
соответствует трем протонам метильной группы СН8, следующий пик — про-
протонам групп СН2 и самый маленький — протону группы ОН [43]. (Рису-
(Рисунок взят из книги [44].)
лекулах, вызывают отчетливые наблюдаемые сдвиги резонансных
линий. Один из примеров использования метода ЯМР в химии по-
показан на рис. 18.2.
§ 18.4. Сверхтонкое взаимодействие
Ядерные дипольные магнитные моменты «чувствуют» магнит-
магнитные поля, создаваемые (орбитальными и спиновыми) магнитными
моментами окружающих электронов, и, наоборот, электроны «чув-
«чувствуют» магнитные поля атомных ядер. Описывающий эти взаимо-
взаимодействия гамильтониан имеет вид
. — ■<*
п
причем оператор
A8.27)
A8.28)
обозначает оператор полного (орбитального и спинового) момента
количества движения. Гамильтониан A8.27) часто называют га-
гамильтонианом сверхтонкого взаимодействия.
Гамильтониан A8.27) конструируется следующим образом.
В гамильтониан взаимодействия Ш = — (,ич- ■ В,,) подставляют Ве —
индукцию магнитного поля, создаваемого в месте расположения
атомного ядра движущимися вокруг него по орбитам (и обладаю-
273
Глава 18
щими спином) электронами. Используя закон Бно—Савара, можно
написать простую формулу
3 •» A8.29)
для магнитного поля, которое создается в центре орбиты радиусом
/? электроном с полным моментом количества движения 3. В этой
формуле и о — магнитная проницаемость пустого пространства.
В результате такого рассуждения приходим с точностью до кон-
константы А к выражению A8.27) для гамильтониана Жэл.-т-
Полный магнитный гамильтониан атома или молекулы во внеш-
внешнем магнитном поле В равен сумме гамильтонианов для зееманов-
ских расщеплений и гамильтониана взаимодействия магнитных
моментов ядер и электронов:
А, ^
Противоположные знаки первых двух слагаемых в A8.30)
объясняются различием формул A8.9) и A8.23). Для магнитного
момента электрона имеем формулу
к=-еЛ-^-' A8-31)
в которой @^ — так называемый й'-фактор Ланде, равный 1 для
исключительно орбитального движения E — 0) и 2 для исключи-
исключительно спинового движения (Ь = 0). Общая точная формула для
ё'-фактора имеет следующий вид х):
Чтобы рассчитать энергетические уровни электрон-ядерной си-
системы, необходимо найти собственные числа гамильтониана Ш;.
Они получаются в результате непосредственной диагонализации
матрицы какого-либо матричного представления этого гамильто-
гамильтониана с помощью процедуры, описанной в § 9.6. Удобным набором
базисных функций для матричного представления служат функ-
м, м,
ции %р^ ■/г|)/ '.
Аналитическое исследование двух предельных случаев, а именно
очень слабого и очень сильного магнитного поля, производится
особенно просто.
В пределе нулевого поля (В = 0) следует рассмотреть оператор
Р=Г-г1, A8.33)
]) Вывод этой формулы читатель найдет в каком-либо учебнике, на-
например, в [45].
274
Взаимодействие с магнитным полем
являющийся суммой операторов ядерного и электронного момен-
моментов количества движения. Для него аналогично A8.14) и A8.15)
имеем уравнения
Р2|.Р, тр) = Л*Р(Р+1)\Р, тР) A8.34)
Рг\Р, тР) = Пте\Р. тр), A8.35)
Функций | Р, тР) можно представить в виде линейных комбинаций
функций-произведений:
/
I РI ,, *—' , Р, тР, т., т , * ^ ' / •
Л1 ^=— / 1 I ^
где аъ, Мрз т/, т} — коэффициенты разложения, причем в разло-
разложение входят только слагаемые с \МР — М71 = \М^\ < /. Таким
образом, функции | Р, тР) [являются собственными функциями
операторов З2, I2, Р2 и Рг, но не операторов ^г и 1г.
Теперь воспользуемся операторным соотношением
р2 = A + 5J 12-4-32+2(Г-3),
из которого следует очевидная формула
(Г- 3) = — (Р2— I2— 3*). A8.36)
причем
32\Р, тР)^Н^^~1)\Р, те),
\2\р, тР)^П2'1A + 1) \Р, тР),
так что
(Р, тр\\-3\Р, тр) = -?^-[Р{Р+1)-1{1 + 1)^У + 1)]. A8.37)
Таким образом, в нулевом магнитном поле гамильтониан элек-
электрон-ядерного сверхтонкого взаимодействия (Л/й2) A-3) имеет сле-
следующие расщепленные уровни энергии:
Е(Р. тР)\в^ ^[Р(Р г 1)-/(/-Ь 1)-/(/ + 1)|. A8.38)
В обратном предельном случае сильного магнитного поля можно
считать малым возмущением слагаемое (Л/Й2) A-Л) в A8.20). Пре-
Предельный случай сильных магнитных полей называют случаем Па-
шена—Бака. Нулевые собственные функции момента количества
движения можно теперь взять в виде
^т, ^/ф*1/. A8.39)
275
Глава 18
В случае сильного магнитного поля моменты Л и I никак не свя-
связаны друг с другом, так что теперь «хорошими» квантовыми чис-
числами оказываются т, и т^, а не Р и тР.
Используем функции A8.39) в качестве базисных волновых
функций и обратимся к общим формулам A1.116) первого порядка
теории возмущений, чтобы вычислить собственные числа полного
- Г-1
>'=А
± Г = о±™
Рис. 18.3. Расщепление энергии основного состояния 251/2 (и = 0, / = 0)
атома водорода в результате сверхтонкого взаимодействия электрона с яд-
ядром и взаимодействия с внешним магнитным полем. В нулевом поле расщеп-
расщепление равно Ну = А, где у= 1,420405-108 Гц (К = 21,121 см). В водород-
водородном мазере используется вынужденный переход «2» -*- «1».
гамильтониана A8.30). В качестве гамильтониана возмущения
возьмем гамильтониан
так что имеем формулу
1, т,, ^, т^) =
/,—
и+
-Г" .„ *г«г г \'ху х I 'у"у)
из которой получаем
Е{1, т,, ^, т^)-=@^$Вт^—^^хВт,-'^ Ат^т^, A8.40)
поскольку все диагональные матричные элементы операторов 1Х,
^а-. 1У, Л; равны нулю.
276
Взаимодействие с магнитным полем
В качестве примера случая, когда необходимо производить од-
одновременный учет влияния эффектов внешнего магнитного поля
и магнитного сверхтонкого взаимодействия, рассмотрим основной
энергетический уровень атома водорода, находящегося в своем
основном орбитальном состоянии 2.$1/2 (п = 0, / = 0). Для него
/ т= 8 = 1/2. Кроме того, из табл. 18.1 видим, что / = 1/2. В пре-
пределе нулевого поля В = 0 хорошими квантовыми числами являются
Р и тР. Поскольку Р = I + 3, квантовое число Р может принн-
атомов Диафрагма
водорода
Кварцевый
баллончик,
покрытый
тефлоном
Селектор состояний
1_ Приемный
7=^ виток
СБЧ-
резонатор
Рис. 18.4. Принципиальная схема водородного мазера. Пучок атомов водо-
водорода с т;= 1/2 выделяется неоднородным магнитным полем (селектором
состояний) и направляется в отверстие СВЧ-резонатора. Стимулированное
излучение, обусловленное переходом | 1, 0)-»-| 0, 0) (мы используем кван-
квантовые числа, применяемые для обозначения уровней в нулевом магнитном
поле, так как внутри резонатора В = 0), действует на помещенный в резо-
резонатор приемный виток, подсоединенный к регистрирующей аппаратуре.
мать только два значения: 1 и 0. Из формулы A8.38) тогда имеем
I —А
1^=1 4
Е(Р,
Е(Р,
ЗА
A8.41)
Оба этих энергетических уровня при В = 0 показаны на рис. 18.3.
Экспериментальное значение константы А, измеренное методом
магнитного резонанса [46], равно
Гц.
Указанной частоте соответствует длина волны
Я = —=«21,121 см.
V
Это — известная «21-сантиметровая водородная линия», которая
испускается атомами водорода в межзвездном пространстве; в на-
настоящее время она широко используется в радиоастрономии при
проведении астрофизических исследований.
277
Глава 18
На рис. 18.3 представлена также область больших магнитных
полей, описываемая формулой A8.40). Обратите внимание на ис-
использование различных квантовых чисел в случае слабых (Р, тР)
и сильных {т}, т,) магнитных полей. Энергетические уровни при
ненулевых полях рассчитываются по формуле A8.40) (в которой
надо положить / = 5 = 1/2, / = 1/2, А/П = 1,420405-109).
Водородный мазер. Расщепленные сверхтонким взаимодействием
уровни атома водорода в нулевом магнитном поле, показанные на
рис. 18.3, были использованы для создания мазера [47], принци-
принципиальная схема которого показана на рис. 18.4. Пучок атомарного
водорода, испускаемый высокочастотным электрическим газовым
разрядом, направляется в область с сильно неоднородным магнит-
магнитным полем (селектор состояний). Сила, действующая на магнитный
дипольный момент атома в неоднородном магнитном поле, пропор-
пропорциональна проекции магнитного момента на направление гради-
градиента поля. Таким образом, атомы водорода в двух верхних состоя-
состояниях \Р, тР) = | 1,1), | 1, 0), для которых в сильных полях /^ =
= 1/2, отделяются от атомов водорода в двух нижних состояниях,
для которых в сильном магнитном поле т} = — 1 '2. Пучок выде-
выделенных атомов водорода через отверстие впускается в СВЧ-резона-
тор с резонансной частотой V = 1,420405-109 Гц. Высокочастотное
магнитное поле в резонаторе вызывает индуцированные переходы
атомов водорода из состояния | Р, тР) = 11, 0), обозначенного сим-
символом «2» на рис. 18.3, в состояние ' Р, тР) — | 0, 0), обозначенное
символом «1». Испускаемое при этом атомами электромагнитное
излучение когерентно складывается с излучением, имеющимся
в резонаторе. Если радиационные потери в резонаторе малы (ре-
(резонатор с высокой добротностью О) и если пучок возбужденных
атомов водорода достаточно интенсивный, то мощность излучения,
испущенного в процессе стимулированного испускания, больше
теряемой мощности.
Тогда в резонаторе возникнут самоподдерживающиеся электро-
электромагнитные колебания. Такое устройство получило название «ма-
«мазер» (по первым буквам английского выражения М1сго\\'а\-е АтрН-
КсаИоп Ьу 51итш1а1ей Егшззюп о! КасНаНоп, что означает — уси-
усиление микроволн путем вынужденного излучения).
Колебания электромагнитного поля в мазере исключительно
стабильны по частоте. Это объясняется рядом причин: а) сравни-
сравнительно малой зависимостью населенностей верхнего B) и нижнего
A) уровней от слабого магнитного поля, связанной с тем, что
йЕ%]1йВ~ 0 (рис. 18.3); б) большим временем жизни атомов в со-
состоянии 2 относительно спонтанных переходов в состояние 1; в) вы-
высокой добротностью С1 СВЧ-резонатора. Вследствие высокой ста-
стабильности частоты водородный мазер применяется для создания
стандарта времени — «атомных часов», у которых стабильность
частоты составляет 1 : 1014.
278
Взаимодействие с магнитным полем
Излучение с частотой 1420,405 МГц («21-сантиметровая линия»),
испускаемое нейтральным водородом, находящимся в межзвездном
пространстве в нашей Галактике, было впервые обнаружено
в 1951 г. Эваном и Парселлом [48]. Это электромагнитное излуче-
излучение порождается спонтанными переходам» (с временем жизни
Приближение Удаление
33'
+ 100
Рис, 18.5. Форма линии, испускаемой межзвездными атомами водорода на
разных долготах относительно центральной плоскости нашей Галактики
(из работы [8]).
^спонт —■ 11 миллионов лет) атомов водорода из состояния | Р, тР) =
— | 1,0) в состояние \Р, тР) = | 0, 0). Возбуждение верхних со-
состояний атомов водорода происходит в результате действия на них
теплового фонового равновесного электромагнитного излучения
Т = 3,5 К, существующего в межзвездном пространстве.
Наблюдение линии с длиной волны 21 см позволило радиоастро-
радиоастрономам открыть спиральную структуру нашей Галактики, Частота
(V — 1420,405 МГц) линии излучения покоящегося атома водорода
смещается вследствие эффекта Доплера в сторону больших или
меньших частот в зависимости от того, движется ли излучающий
атом к наблюдателю или от него. Доплеровское смещение равно
279
Глава 18
где V — компонента скорости атома в направлении к наблюдателю.
Примеры экспериментально зарегистрированных спектров пока-
показаны на рис. 18.5.
§ 18.5. Электронный парамагнитный резонанс
В исследованиях по электронному парамагнитному резонансу
{ЭПР) изучают переходы между расщепленными постоянным маг-
магнитным полем электронными подуровнями. Эти переходы индуци-
индуцируются высокочастотным электромагнитным полем, обычно СВЧ-
диапазона. Кроме того, на образец действует большое постоянное
магнитное поле, которое расщепляет энергетические уровни.
В качестве простой иллюстрации теории ЭПР рассмотрим элек-
электрон, находящийся в своем основном состоянии п = / = 0. При
наличии магнитного поля В, направленного по оси г, гамильтониан
электрона имеет следующий вид:
^, A8.42)
" ' л
где Шй — гамильтониан в нулевом поле В = 0. Собственные функ-
функции электрона можно представить в виде произведений орбиталь-
орбитальных и спиновых функций:
A8.43)
где гг100 обозначает орбитальную функцию основного состояния
(п = 1, / = 0, т = 0). Согласно формулам A8.18), энергия состоя-
состояний | ± 1/2) определяется формулой
на
~
В$г
A8'44)
б которой Ео = {и100\ Ж(\ и100) — энергия электрона в нулевом
магнитном поле В = 0. Расщепление уровней в магнитном поле
показано на рис. 18.6.
Если кроме постоянного магнитного поля В на электрон дейст-
действует переменное магнитное поле
В@ = В1соз(о^, A8.45)
то, согласно общей формуле теории возмущений A1.33), перемен-
переменное поле может вызвать индуцированные переходы между состоя-
состояниями | ± 1/2). Это произойдет в том случае, если частота поля со
удовлетворяет условию резонанса Йсо = Е_{., —Е110 = 2рВ и воз-
возмущающий гамильтониан имеет ненулевой матричный элемент
между состояниями | 1/2) и |— Г2)|.
280
Взаимодействие с магнитным полем
Чтобы обеспечить выполнение последнего требования, напра-
направим поле В @ вдоль оси х, т. е. перпендикулярно постоянному
магнитному полю. Тогда гамильтониан магнитного взаимодействия
с переменным полем принимает вид
A8.46)
Гамильтониан A8.46) следует добавить к гамильтониану A8.42),
чтобы получить полный гамильтониан. Подставляя A8.45) в A8.46).
"е „1/г~Е,/г~грв
3=0
-в
*-*^в>
Рис. 18.6. Энергетические уровни электронного спина во внешнем магнитном
поле.
запишем гамильтониан взаимодействия с радиочастотным магнит-
магнитным полем В! @ в виде
< @ - -2- Ва (еш + е~ш).
A8.47)
Скорость перехода одного атома из состояния | — 1/2) в состоя-
состояние | 1/2) и из состояния | 1/2) в состояние |-— 1/2) определяется
«золотым правилом» Ферми A1.33):
II- XV'
2Я
бBрВ —Й<о). A8.48)
Отметим, что если бы мы направили поле В @ по оси г (т. е.
параллельно постоянному магнитному полю), то не смогли бы воз-
возбудить переходы между атомными уровнями, поскольку
<1.'2|%| — 1/2) = 0.
Матричный элемент в A8.48) легко вычислить, используя фор-
формулы (9.24):
1 / Л ф ■
— E +~г
A8.49)
281
Глава 18
СБЧ-
СВЧ- волновод
генератор^
Полюс
магнита
Кристаллы ческии
детектор
Амперметр
Рис. 18.7а. Типичная схема установки для наблюдения электронного пара-
парамагнитного резонанса. Исследуемый образец помещают в СВЧ-волновод,
где он подвергается действию высокочастотного поперечного магнитного
поля. Направленное по оси г постоянное магнитное поле создается магнитом
(на рисунке показан один его полюс). Передаваемая по волноводу мощность
измеряется на его выходе измерителем мощности, состоящим из кристалли-
кристаллического детектора и амперметра постоянного тока.
Держатель
образца
пасппйстранст.сл
Т
Рис. 18.76. Электромагнитное поле СВЧ-волны, распространяющейся в вол-
волноводе. На парамагнитный кристалл, помещенный внутри волновода вблизи
стенки, влияет гармонически осциллирующее магнитное поле проходящей
волны. Как показано на рисунке, около стенки это поле перпендикулярно
направленному по оси г постоянному магнитному полю, создаваемому элек-
электромагнитом, изображенным на рис. !8.7а.
и формулы (9.32):
A8.50)
тогда формула A8.48) преобразуется к виду
Вт6BрВ- /ко).
A8.51)
Взаимодействие с магнитным полем
В экспериментах по электронному парамагнитному резонансу
(ЭПР) образец, содержащий исследуемые электроны, помещают
внутрь СВЧ-волновода (или резонатора), где он подвергается дейст-
действию переменного магнитного поля В^оз а>1. Постоянное магнитное
поле создается электромагнитом, показанным на рис. 18.7а. Обычно
частоту поддерживают постоянной, а чтобы достичь резонанса,
изменяют величину постоянного поля. Поле внутри волновода
показано на рис. 18.76.
При подходе к резонансной области, где 2|ЗВ = /гсо, возникают
индуцированные переменным магнитным полем переходы, что при-
приводит к поглощению энергии из СВЧ-поля со скоростью (Вт/с):
Р = (Ыг—ЫДШе>У, A8.52)
где 47 — скорость индуцированных переходов на один атом, опре-
определяемая формулой A8.51), N2 и Nг — числа электронов (в еди-
единице объема) соответственно на верхнем | 1/2) и нижнем |— 1/2}
уровнях, V — объем образца. В экспериментах наблюдают поглоще-
поглощение в довольно широкой области около резонансного значения по-
постоянного магнитного поля В. Это связано главным образом с прост-
пространственной неоднородностью приложенного постоянного магнитного
поля по объему образца, которая приводит к тому, что резонансные
условия для атомов, находящихся в различных местах образца,
выполняются при несколько различных значениях приложенного
постоянного магнитного поля. Указанные неоднородности магнит-
магнитного поля могут быть связаны с несовершенством конструкции маг-
магнита н с вариациями окружения для различных атомов образца.
Так, например, соседние атомы могут обладать собственными маг-
магнитными моментами и создавать собственные магнитные поля.
Чтобы количественно учесть указанное размытие резонансной
кривой, введем функцию формы линии § |2|3 (В—Во) ]. Вероятность
того, что данный атом в действительности «видит» поле из интервала
от В до В — сШ, когда номинальное значение приложенного поля
равно В(), равна §■ [2р (В—Во) ] й BрВ). Следовательно, должно
выполняться условие нормировки
поскольку атом обязательно «видит» какое-то поле из всего беско-
бесконечного интервала от — оо до оо. Функция § [2Р {В—Во) ] имеет
колоколообразную форму с максимумом при В — Во и с характер-
характерной шириной, равной среднеквадратичному отклонению В от но-
номинального значения Во, усредненному по объему образца (и ум-
умноженному на 2Р).
Усредненную скорость переходов №ср для одного атома можно
вычислить, умножая A8.51) на § [2р (В—Во) ] и интегрируя. Тогда
283
Глава 18
приходим к формуле
т
2Й
A8.53)
так что кривая зависимости поглощения от приложенного магнит-
магнит100
Рис. 18.8. Зависимость производной поглощенной мощности от приложен-
приложенного магнитного поля, полученная с помощью типичной СВЧ-установки для
исследования ЭПР.
ного поля Во при фиксированной частоте со уширяется вследствие
влияния функции §. На рис. 18.8 показана экспериментальная кри-
кривая зависимости производной поглощенной мощности по полю
от приложенного постоянного магнитного поля. Она получена с по-
помощью установки, принципиальная схема которой показана на
рис. 18.7а.
Задачи
1. Вычислите спонтанное время жизни для сверхтонкого перехода
О ) —>■ | Р, тр) = | 0, 0) для атома водорода, находящегося
п = 1, / = 0 B5у2) в нулевом магнитном поле.
в основном состоянии
284
Взаимодействие с магнитным лолем
Указание. Повторите рассуждение из § 12.6, но возьмите вместо возму-
возмущающего гамильтониана A2.63) магнитный дипольный гамильтониан
«+-«,) со5 к[г,
который вызывает магнитные дипольные переходы. Считайте, что
| 1 П\_ ! /„-12о1-2 , „1/2о-12Ч
| 1, V)— .— \а] 2 р, 2 —а, 2Р| 2 ),
1П П\ —!—~(п— 1'2о1 2 „12о —124
' -/2 ^ 12 Р1.2 — те1 2Р1 2 )'
где а^" — электронные и р^" — ядерные спиновые собственные функции.
Ответ: 1Спонт = Ю миллионов лет!
2. Рассчитайте уровни сверхтонкого расщепления для основного состояния
атома водорода B5],2), показанные на рис. 18.3. Их можно найти путем
диагонализации гамильтониана A8.30) в подходящем матричном пред-
представлении. Проверьте себя по книге Рамсея [44].
3. Выведите формулу A8.29).
4. Выведите приближенную формулу для порядка величины отношения
«диамагнитного» слагаемого к «парамагнитному» слагаемому (р//г) A-В)
в магнитном гамильтониане A8.11), заменив (х2 + у2) средним значением
(х2 -г У2), вычисленным для основного состояния атома водорода. При
каких значениях В это отношение будет меньше 10~3?
ГЛАВА 19
ПЕРЕНОС ЗАРЯДОВ В ПОЛУПРОВОДНИКАХ
Трудно дать однозначный ответ на вопрос о том, что оказало
большее влияние на развитие мировой цивилизации во второй по-
половине XX века - достижения ядерной физики или успехи физики
полупроводников, которые привели, в частности, к созданию сов-
современных ЭВМ, изменивших полностью наши способы хранения
и обработки информации. Лично я отдаю предпочтение физике по-
полупроводников *).
Поэтому целесообразно закончить книгу главами, посвящен-
посвященными некоторым вопросам физики полупроводников, имеющими
прикладное значение. К тому же это даст нам возможность объеди-
объединить отдельные основные концепции, которые до сих пор были ос-
освещены несколько фрагментарно. Имеются в виду такие понятия,
как электронные энергетические состояния, энергетические зоны,
групповая скорость электронной волны в кристаллах, статистика
Ферми—Дирака.
§ 19,1. Носители зарядов
в собственных полупроводниках
Важнейшей задачей физики полупроводников является расчет
концентрации носителей зарядов в полупроводниковом кристалле.
Рассмотрим, например, полупроводниковый кристалл с энергети-
энергетическими зонами, изображенными на рис. 19.1. На этом рисунке
указаны химический потенциал ц, и ширина запрещенной зоны Ег
В качестве нулевого уровня энергии произвольно выбран потолок
валентной зоны.
Вероятность того, что в кристалле при тепловом равновесии
электронное состояние с энергией е занято электроном, определяется
законом распределения Ферми—Дирака A6.6) 2):
1- . A9.1)
1) Опасность всемирного «ядерного пожара», возможно, заставляет не-
некоторых физиков думать иначе и отдавать предпочтение ядерной физике.
2) В настоящей главе мы используем следующие обозначения, приня-
принятые в современной литературе по физике полупроводников: Е — напряжен-
напряженность электрического поля, Е& — ширина запрещенной зоны, е — энергия
электрона.
286
Перенос зарядов в полупроводниках
Предположим теперь, что энергия е электронов в зоне проводи-
проводимости связана с константой распространения К электронной волны,
как и для свободных электронов, параболической зависимостью
2т,
в которой те — эффективная масса электрона, определяемая фор-
формулой A7.47). Тогда воспользовавшись выражением A6.7), можно
Зона
проводимости
Валентная
■зона
Г Лу
а
Рис. 19.1. а — энергетические зоны полупроводника с малой концентрацией
электронов (черные кружки) в зоне проводимости и дырок (светлые кружки)
в валентной зоне; б — график функции распределения Ферми—Дирака
/ (е). Обратите внимание, что масштаб оси ординат на рисунках а и б одина-
одинаков.
вывести следующую формулу для плотности электронных состояний
в зоне проводимости (число состояний, приходящихся на единицу
энергии и на единицу объема):
""'?(е—ЕЛФ. A9.2)
Аналогично получаем формулу для плотности электронных состоя-
состояний в валентной зоне
2л2
~еI2.
A9.3)
в которой через тп мы обозначили эффективную массу электрона
в валентной зоне. При нашем выборе нулевого уровня энергии
(см. рис. 19.1) электроны в валентной зоне обладают отрицатель-
отрицательными энергиями, поэтому величина — е в формуле A9.3) поло-
положительна.
Наша следующая задача — найти концентрацию п электронов
в зоне проводимости и концентрации) /; дырок в валентной зоне.
287
Глава 19
Определять концентрации п и р нужно по той причине, что именно
электроны в зоне проводимости и дырки в валентной зоне являются
носителями зарядов, т. е. ответственны за электрический ток в по-
полупроводниковом кристалле, к которому приложено электрическое
поле.
Концентрация электронов. Число с1п электронов в зоне прово-
проводимости (в расчете на 1 м3), энергии которых заключены в энерге-
энергетическом интервале от е до е -\- йг, равно произведению плотности
состояний и вероятности заполнения отдельного состояния элек-
электроном, т. е. йп = Опр (е) / (е) йг, так что концентрация электро-
электронов в зоне проводимости (число электронов в 1 м3) определяется
выражением
п= 5°Япр
Е&
Ниже будет показано, что химический потенциал ц обычно
располагается внутри запрещенной зоны, так что выполняется ус-
условие (е—(я) 2> кТ при в^>ЕЁ. Таким образом, можно приближенно
заменить закон распределения Ферми—Дирака A9.1) следующей
зависимостью:
Пг)~е*^\ A9.4)
где р = (кТ)~1. Тогда выражение для концентрации п можно пред-
представить в виде
Вводя теперь новую переменную и = р (е—Ее), интеграл в
A9.5) можно преобразовать совсем к простому виду
1 ( 2", \
2л2 \ А2 )
32 еЗ(М-^«,) °°
1 ? —и I
и е йи.
2л2 V А2 ) Р32 о
Появившийся здесь определенный интеграл легко берется; он ра-
равен | л/2, так что для концентрации электронов в собственном
полупроводниковом кристалле получаем
п = 2 (-^^K 2ё~ (Е*-И кт = Ыпре- (Е^ кт, A9.6)
где Л^ пр — так называемая эффективная плотность состояний в зоне
проводимости, которая по определению равна
. A9.7)
288
Перенос зарядов в полупроводниках
Пример. Для кристалла кремния при Т = 300 К, для которого
пге = 0,2 пг (см. ниже табл. 19.1), получаем Ыпр = 2,2-1018 см~3.
Концентрация дырок. Число дырок (в 1 м3) в энергетическом
интервале, простирающемся от е до е -г с?е, в валентной зоне равно
по определению числу незанятых элек-
электронами состояний в этом интервале д&.
Вероятность того, что состояние е не за-
занято электроном, равна единице минус
вероятность того, что состояние е занято
электроном. Обозначим указанную [ве-
[вероятность //, (е):
Ые) = !-/>) = 1— '
Температура, К
1200 800 600 500 400
Е-Ц
е-ц) кТ
„3 (е
+ 1
10"
> (8-ц)
+ 1
где при переходе к последнему прибли- с юк
женному равенству мы воспользовались ;$а~
тем, что \1—е ^> кТ. "Щ-
Рис. 19.2. Кривая зависимости \е. (прI12 от
Т~ в кремнии для концентрации носителей
заряда, соответствующей собственной про-
проводимости. Точками изображены экспери- да«
ментальные значения. Сплошная прямая со-
соответствует закону
\
\
\
\
Сравнение теории и эксперимента дает, та-
таким образом, Ее= 1,21 эВ (из работы [50]).
0,001
0,002
-', /г'
Рассуждая совершенно так же, как при выводе формулы A9.6),
можно написать следующее выражение для концентрации дырок
в собственном полупроводниковом кристалле:
так что
причем
р = 2
A9.8)
A9.9)
обозначает так называемую эффективную плотность состояний
в валентной зоне.
Заказ № 683
289
Глава 19
Перемножив формулы A9.6) и A9.9), получим для произведе-
произведения концентраций электронов и дырок простое соотношение
=4 р^)'^тйГ *-*«"". A9-10)
Из этого соотношения выпал химический потенциал ц, поэтому
можно считать, что произведение концентраций электронов и ды-
дырок и для идеального чистого и для примесного полупроводника
дается формулой A9.10) и равно константе, которая для данного
полупроводника зависит только от температуры.
Эксперименты хорошо согласуются с формулой A9.10), как
видно из рис. 19.2, на котором изображена кривая зависимости
Ы (пРI2 от обратной температуры Г-
Собственные полупроводники. В идеально чистом, или, как
еще говорят, собственном полупроводнике п — р, поскольку каж-
каждый электрон, перешедший в зону проводимости, оставляет вакант-
вакантное место (дырку) в валентной зоне. Так происходит потому, что,
как мы уже говорили в § 17.2, число валентных электронов у ато-
атомов, образующих кристаллическую решетку, точно равно числу
электронов, необходимому для полного заполнения валентной зоны
кристалла. Таким образом, электроны могут попасть в зону про-
проводимости только путем теплового возбуждения из валентной зоны
(тепловое возбуждение описывается законом распределения
Ферми—Дирака A6.6)]. Из формулы A9.10) непосредственно по-
получаем, что в идеально чистом, или собственном, полупроводнике 1)
р, -ф^=Ъ (^K2 К'",K Vе» *г . A9.11)
Значение химического потенциала (д для собственного полупровод-
полупроводника можно найти, приравняв концентрации пир, которые опре-
определяются формулами A9.6) и A9.9). В результате получаем формулу
ц=,-^в—. А/гТЧп-^-, A9.12)
2 ' 4 те К '
из которой видно, что химический потенциал в собственном полу-
полупроводнике практически совпадает с серединой запрещенной зоны.
Численный пример. Чтобы получить представление о порядке ве-
величин концентраций носителей зарядов в собственном полупровод-
полупроводнике, рассмотрим, например, кристаллы ОаА8 при Т = 300 К- Ис-
Используя данные, приведенные в табл. 19.1 (ш(, = 0,07 т, /пЛ =
= 0,6 т, Е8 = 1,43 эВ), получаем
„/ 2л/г-300 \32/пПт. пс о,34 / 1,43с \ „ п.г 1Г.В -
пг=-=2| I @,07 0,6 м2) ехр [ — | =-2,246- 10е см~Л
V Л2 / Н \ 2/г-ЗОО /
*) Индекс 1 обозначает собственный полупроводник.— Прим. перев.
290
Перенос зарядов в полупроводниках
Таблица 19.1. Некоторые основные параметры полупроводниковых кристаллов
Кристалл
Ал мал
Се
3!
1пАв
1пЗЬ
1пР
СаАк
Ширина запре
ЗОНЫ. 'г>'.
г-ок
5,4
0,75
1,20
0,36
0,26
1,29
1,52
ЩСННоН
Г = ЗОЛ К
0,67
1,11
0.34
0,16
1,35
1,43
те т
0,1
0,2
0,024
0,012
0,073
0,07
тн т
0,04
0,16
0,41
0,25
0,2
0,6
16,0
12,0
12,5
15,9
12,1
11,5
Таким образом, концентрации носителей заряда (электронов
и дырок) в собственном полупроводнике на много порядков меньше,
чем в металлах (в которых она порядка 1022 см" 3 или больше).
Следовательно, электропроводность собственного полупроводника
с шириной запрещенной зоны Е& порядка 1 эВ очень мала, если
только не рассматривать предельного случая очень высоких темпе-
температур. Экспериментально измеряемая электропроводность даже
самых чистых полупроводников в большинстве случаев на-
намного превышает собственную электропроводность, т. е. она опре-
определяется имеющимися в ничтожных количествах примесными ато-
атомами.
Чтобы получить нужное значение электропроводности, кри-
кристаллы, используемые в полупроводниковых устройствах, спе-
специально легируют (т. е. вводят определенное количество примесей).
Постараемся выяснить, как наличие атомов примесей влияет
на электропроводность полупроводникового кристалла.
§ 19.2. Энергии ионизации примесных атомов
в полупроводниковом кристалле
Выясним теперь, что произойдет, если атом примеси займет
место атома совершенной кристаллической решетки полупровод-
полупроводникового кристалла. Для определенности возьмем, например, атомы
мышьяка (Аз) в кристалле германия (Ое).
Атом Ое имеет четыре валентных электрона 48Чр-. В кристалле
Ое из четырех собственных функций этих электронов образуется
четыре тетраэдрические хр-орбитали, о чем мы подробно говорили
в § 7.4. Схематически тетраэдрические орбитали изображены на
рис. 19.3. С помощью указанных орбиталей в кристалле образуются
тетраэдрические химические связи между соседними атомами и весь
1.Л0* 291
Глава 19
Связывающая
орбитосль
Рис. 19.3. Тетраэдрические связывающие орбитали и основной элемент
структуры решетки германия.
а
постоянная
решетки
Рис. 19.4. Фундаментальная (примитивная) элементарная ячейка кристал-
кристаллической решетки алмаза. Четыре тетраэдрические связывающие орбитали,
изображенные на рис. 19.3, здесь показаны как черные стержни.
кристалл приобретает кристаллическую структуру типа алмаза,
показанную на рис. 19.4.
Рассмотрим теперь, что происходит, когда примесный атом
мышьяка Аз замещает в кристаллической решетке один атом гер-
германия. Атом мышьяка имеет пять валентных электронов D524р3).
Четыре из этих электронов пойдут на образование четырех тетра-
эдрических химических связей с соседними четырьмя атомами гер-
германия. Пятый электрон оказывается «лишним» и создает очень
рыхлую химическую связь с ионным остовом А8+, как показано
на рис. 19.5. Атом мышьяка, обладающий дополнительным элек-
электроном (по сравнению с атомом германия, место которого он зани-
занимает), называется донорным, а соответствующий примесный полу-
292
Перенос зарядов в полупроводниках
проводник — полупроводником А^-типа (по-англинскн пе§а1К'е —
отрицательный).
Задача отыскания волновых функций и энергий «лишнего» (пя-
(пятого) электрона подобна задаче для атома водорода, подробно рас-
рассмотренной в гл. 7. Ионный остов Аз+ играет роль протона атома
водорода, а пятый электрон подобен единственному электрону
в атоме водорода 1).
Избыточный электрон,
отданный атолюм
мышьяка
Ионизованный,
донорный атом
Кристалл
германия
Рис. 19.5. Четыре из пяти валентных электронов примесного атома /У-типа
(в данном случае атома мышьяка) идут па образование четырех тетраэдри-
ческих химических связей с соседними атомами германия. Пятый электрон
атома мышьяка рыхло связан с ионным остовом Ак+. Энергия, необходимая
для удаления на бесконечность пятого электрона с орбиты, связывающей
электрон с родительским атомом, т. е. энергия ионизации атома примеси,,
равна Ео (см. рис. 19.6).
Имеются, однако, два основных различия между нашей задачей
и задачей об атоме водорода, рассмотренной в гл. 7: 1) эффективная
масса те электрона, движущегося в кристалле, отлична от массы т
свободного электрона; 2) электрон в кристалле, движется в среде
со статической диэлектрической проницаемостью е, превышающей
диэлектрическую проницаемость пустого пространства е0, в котором
движется электрон в атоме водорода. Таким образом, на электрон
в кристалле силы кулоновского взаимодействия влияют меньше,
чем на электрон в атоме водорода.
*) Такая простая модель, строго говоря, незаконна, так как в силу ко-
конечных пространственных размеров четырех связывающих электронных
орбиталей положительно заряженный остов мышьяка нельзя аппроксими-
аппроксимировать точечным зарядом, как ядро в атоме водорода. Модель, однако, ока-
оказывается полезной для описания высоких энергетических уровней, а также
для расчета порядка величины энергии ионизации донорного атома.
Ю Заказ .V» 683
293
Глава 19
Отсюда следует, что мы можем использовать непосредственно
формулы из § 7.2, заменив в них е0 и т на е и те. Тогда энергию
ионизации донорного атома в кристалле можно вычислить по фор-
формуле G.28), которая с учетом поправок принимает вид
= 13,64 -2^-эВ. A9.13а)
о
2DлеJЛ2 2DлеоJк* (е/е0)
Для полупроводников отношение те!т обычно имеет порядок
0,1, а отношение е/е0 — порядок 10 (см. табл. 19.1). Поэтому энер-
энергия ионизации донорного примесного атома в полупроводниковом
кристалле составляет малую долю [(тс/т) (ео/еJ ^ 10~8] от энер-
энергии ионизации атома водорода. Типичные значения энергии иони-
ионизации донорных примесных атомов в полупроводниках 10—20 мэВ.
Например, экспериментально измеренная энергия ионизации атома
Аз в германии равна 12 мэВ.
Заметим, что радиус орбиты находящегося в основном состоя-
состоянии «лишнего» электрона донорной примеси в кристалле опреде-
определяется формулой
Л24ле Й24ле0 е/е0 е/г0
теег те1 те/т те, т
в которой а0 — боровский радиус, равный 5,2917-10"1 м.
В приведенном выше примере с атомом мышьяка в германии
имеем ао ^ 100 а0, так что донорные электроны «скитаются» по
большому числу элементарных ячеек кристалла.
На диаграммах энергетических зон полупроводника основное
состояние «лишнего» электрона, отдаваемого атомом примеси кри-
кристаллу, расположено на расстоянии Ев ниже дна зоны проводи-
проводимости, т. е. попадает в запрещенную зону.
Таким образом, зона проводимости играет для примесного
атома ту же роль, какую непрерывный спектр, лежащий выше
порога ионизации, играет для атома водорода. Если увеличить
каким-либо образом на Ев энергию электрона в примеси, находя-
находящегося в основном водородоподобном состоянии га = 1, то он пе-
перейдет на дно зоны проводимости, где его волновая функция уже
не локализована около данного донорного атома.
Примесный атом, обладающий меньшим числом валентных элек-
электронов, чем атомы полупроводника, называется акцепторным. При-
Примером акцепторной примеси могут служить атомы трехвалентного
индия в кристалле германия (или кремния). При образовании хи-
химической связи между атомом примеси и атомом кристалла при-
примесь отбирает электрон из валентной зоны кристалла, где остается
вакантное место — дырка. Возникающая положительно заряжен-
294
Перенос зарядов в полупроводниках
ная дырка может притянуться к отрицательному ионному остову
1п~~; при этом выделяется «водородная» энергия ионизации
^ . 1Г= ^_=. . __ A9
2 DдбJ /]2 ° '" — *9 ' '* ' ' *'*
где /мЛ — эффективная масса дырки. Физически процесс «иониза-
«ионизации» акцепторного атома заключается в перемещении электрона
с потолка валентной зоны на связан-
связанное СОСТОЯНИе акцепторного атома. Ис- Зта проводимости ^
пользуя формальную аналогию между I Ев
Электронами И ДЫркаМИ, МОЖНО пред- Запрещенная зона ^
ставить себе указанный процесс как X. ^
х_ . 5±
изъятие дырки с локализованной ор-
биты ОСНОВНОГО СОСТОЯНИЯ, Образуемого Валентная зона \
ею около отрицательно заряженного
акцепторного иона И помещение ее Рис- 19-6- Энергетические
в валентную зону кристалла (напомним, в^опупр^в^дьшк'овом™^
что на наших энергетических диаграм- сталлё. Основное состоя-
мах энергия дырок увеличивается при нне донорной примеси ле-
перемещении их вниз). Энергия, за- жпт |1иже Дна золы ПР°-
трачиваемая на указанный процесс, ь°Д1Ва°а™цепТорноТСп°пЯи11еИ
равна ЕА. Основное состояние акцеп- СИС1_ выше потолка ва-
торного атома изображается линией, лентной зоны на расстоя-
расположенной выше потолка валентной ни" ^а-
зоны на расстоянии ЕА от нее.
Основные состояния донорных и акцепторных атомов, таким
образом, попадают внутрь запрещенной зоны, как показано на
рис. 19.6.
§ 19.3. Концентрации носителей зарядов
в примесных полупроводниках
Для создания новых полупроводниковых приборов с необходи-
необходимыми электрическими характеристиками исключительно важно
уметь управлять концентрациями подвижных носителей зарядов
(электронов и дырок).
Рассмотрим сначала так называемый полупроводник уУ-типа,
т. е. полупроводник, в который введены донорные атомы с кон-
концентрацией Ыо (число атомов примеси в 1 см3). Пусть Ео обозна-
обозначает энергию ионизации донорного атома (рис. 19.7). Вероятность
того, что донорный атом нейтрален, т. е. что его «лишний» электрон
находится в нем в основном состоянии, дается функцией"распреде-
функцией"распределения Ферми—Дирака
—Ц-. A9.14)
/(Е2)
/К 2/ 1-гехр[Р(Е2-М)]
10* 295
Глава 19
в которой х= р (Е2—ц), р = (кТ)-1 и Е2 = Еп—Ев обозначает
энергию основного состояния электрона в донорном атоме, отсчи-
отсчитываемую от потолка валентной зоны. Концентрация ионизован-
ионизованных донорных атомов равна разности полной концентрации Nо
и концентрации Ыо[ (Е2) нейтральных донорных атомов в кри-
кристалле
I- A9.15)
= ^-^—=N0-—-^ . A916)
Предположим теперь, что п ^> р (обоснованность этого предпо-
предположения будет показана в конце наших рассуждений). Тогда, по-
поскольку пр = гй = соп§1 [см. A9.10)],
имеем неравенство п > и,-. Поэтому
большая часть электронов появляется
в зоне проводимости в результате ио-
ионизации донорных атомов. Следова-
Следовательно,
п^А^. A9.17)
Рис. 19.7. Диаграмма энер- С ДРУ™Й стороны, концентрация п оп-
гетических уровней. ределяется также формулой A9.6):
п^МПр<?^-Ее). A9.18)
Сопоставляя ее с формулой A9.15), получаем соотношение
из которого непосредственно следует, что
поэтому
Формула A9.20) принимает особенно простой вид при высоких
и низких температурах.
«Высокие» температуры. В этом предельном случае, с которым
чаще всего приходится встречаться на практике,
г^^!. A9.21)
Л'пр
Поэтому корень в A9.20) можно разложить в ряд Тейлора и сохра-
296
Перенос зарядов в полупроводниках
нить только первые два члена разложения. Так, приходим к про-
простому соотношению
*» = -%>-**'. A9.22)
из которого непосредственно получается следующая приближенная
формула для химического потенциала:
\1 = Ей-кТ1п-Ц?*-. A9.23)
Подставляя A9.22) в A9.18), приходим еще к одной формуле
п^Ы„ре'^Ее~!^-^Ее = Ы1}. A9.24)
"пр
Таким образом, в пределе «высоких» температур практически
все донорные атомы ионизованы и концентрация электронов в зоне
проводимости практически равна концентрации Л^с донорных
атомов.
Теперь покажем справедливость сделанного в самом начале
допущения п ^> п,-. Согласно численному примеру, приведенному
в конце § 19.1, т ^ 10е см~3. Так как п = А^>, сделанное выше
предположение справедливо, если концентрация донорных атомов
Л^д>108 см~~3. Указанное условие действительно всегда выпол-
выполняется на практике.
Численный пример. Интересно оценить, как влияют примеси
на положение химического потенциала в кремнии. Предположим,
что ЫПр = 2,2-1018 см~3 (см. пример в § 19.1), и примем типичные
значения концентрации донорных атомов Мв = 1018 см~
ное значение температуры Т = 300 К- Тогда
^-=0,14 эВ,
и, согласно формуле A9.23), химический потенциал расположен
на 0,14 эВ ниже дна зоны проводимости. Напомним, что химиче-
химический потенциал в идеально чистом собственном полупроводнике,
согласно A9.12), должен лежать примерно на Ее/2 ^ 0,55 эВ ниже
дна зоны проводимости. Таким образом, примесь в рассматривае-
рассматриваемом случае приводит к существенному сдвигу химического потен-
потенциала [I из его среднего положения в идеально чистом кристалле
вверх на величину 0,41 эВ. Вычисленное положение химического
потенциала ц, а также другие энергии показаны на рис. 19.8. Ве-
Вероятность / (Е%) пребывания донорного атома в неионизованном
состоянии равна
/ (Е2) = = ! = 0,026.
297
Глава 19
Таким образом, 97,4 % донорных атомов ионизованы. Каждый иони-
ионизованный донорныи атом отдает свой электрон в зону проводимости,
следовательно, п ~ М%, как и предполагалось выше.
Зона проводимости
0,091 зВ 2
Валентная зона.
а
б
Рис. 19.8. а — положение уровня Ферми (химического потенциала ц) и энер-
энергия ионизации донорного атома для кремния, в который введена примесь
атомов мышьяка Л'д ~ 1016 см—3; б — функция распределения Ферми —
Дирака.
«Низкие» температуры. Пусть теперь температура настолько
низка, что выполняется обратное неравенство
В этом предельном случае из формулы A9.20) получаем соотно-
соотношение
а из формулы A9.18) находим
A9.25)
A9.26)
в которой Ев = Ее—Е2 обозначает энергию ионизации донорного
примесного атома.
Разрешая A9.25) относительно химического потенциала [д, по-
получаем
" A9.27)
298
Перенос зарядов в полупроводниках
§ 19.4. Рассеяние электронов
в полупроводниковом кристалле
В гл. 17 было показано, что при наличии внешнего электриче-
электрического поля Е движение электрона в кристалле описывается урав-
уравнением
^ = — еЕ, A9.28)
в котором те — эффективная масса электрона, е — абсолютная ве-
величина его заряда (е = |е|) и угр — его групповая скорость.
В идеально совершенной жесткой кристаллической решетке движе-
движение носителей ничем не стеснено и электропроводность кристалла
имеет бесконечно большую величину.
В реальном кристалле движение отдельного электрона постоянно
прерывается из-за действия большого числа различных физиче-
физических механизмов. Каждое отклонение АУ (г) потенциального поля
кристалла от идеально периодического поля (возмущение) может
привести к рассеянию электронов.
Квантовомеханический процесс рассеяния мы должны рассмат-
рассматривать как переход электрона из начального блоховского состояния
%с(П=«к(г)е'Кг A9.29)
в конечное блоховское состояние
^к'(г) = «к'(г)с/к'г A9.30)
под действием возмущения АУ (г). Скорость рассеяния, таким об-
образом, пропорциональна, согласно «золотому правилу» Ферми
A1.32), квадрату матричного элемента:
]1к>|2. A9.31)
Рассеивающее возмущение АУ (г) может появиться в силу дей-
действия разнообразных физических механизмов. К ним нужно в пер-
первую очередь отнести следующие: 1. Колебания кристаллической
решетки. Рассеяние на колебаниях решетки сопровождается ис-
испусканием и поглощением фононов, как показано на рис. 19.9, а
и б. Рассеивающийся электрон либо отбирает энергию от фонона,
либо отдает ее ему. 2. Рассеяние на ионизованном или нейтральном
атоме примеси или на другом дефекте кристаллической решетки,
например на вакансии (рис. 19.10).
В подавляющем большинстве случаев рассеяние происходит
практически упруго, поскольку масса объектов, на которых рас-
рассеиваются электроны (дефекты решетки, примесные атомы, сами
атомы решетки), во много раз больше массы электрона (или дырки).
Роль столкновений сводится, таким образом, к хаотизации направ-
направлений движения носителя заряда (электрона или дырки) в кри-
299
Глава 19
сталле, тогда как энергия носителей остается практически постоян-
постоянной. Таким образом, можно считать, что траектория движения
электрона (или дырки) в кристалле представляет собой некоторую
сложную ломаную линию, состоящую из прямолинейных отрезков,
причем в отсутствие электрического поля среднее смещение частицы
К'(г')
к (О
К'(е')
а.'
а
и (с)
е=е' + Ьсорон Сохранение
энергии
К = К'+кфт Сохранение
импульса
К(е)
К (г)
Рис. 19-9. а — рассеяние электрона, сопровождающееся испусканием фо-
фонона. Электрон с квазиимпульсом К и энергией е рассеивается в состояние
с квазиимпульсом К' и энергией е', испуская при этом фонон с волновым
вектором кфон. б—рассеяние электрона сопровождается поглощением фонона.
Все происходит так же, как на рисунке а, только теперь фонон поглощается
(соответственно изменен знак у вектора кфон). Импульсы сталкивающихся
частиц (электрона и фонона) пропорциональны векторам К и кфо„. Законы
сохранения импульса изображаются векторными треугольниками.
в течение любого интервала времени равно^нулю. Средняя длина
отдельных отрезков ломаной равна средней длине свободного про-
пробега
/ = %т, A9.32)
где т = й^расс — среднее время между двумя последовательными
столкновениями носителя заряда, ют — тепловая скорость носи-
носителя
V
2кТ
те
Типичная траектория хаотического движения частицы в кристалле
показана на рис. 19.11, а.
300
Перенос зарядов в полупроводниках
Когда к кристаллу приложено внешнее электрическое поле, оно
ускоряет электрон (или дырку) между каждыми двумя последова-
последовательными актами их рассеяния, так что появляется среднее смеще-
смещение частицы в направлении силы, на нее действующей, как пока-
показано на рис. 19.11, б. Если среднее время между двумя последова-
Рис. 19.10. Рассеяние электрона в кристаллической решетке кремния на
ионизованном атоме примеси замещения (Ав+) и на локализованном дефекте
решетки|(показана вакансия).
тельными столкновениями обозначить т, то дрейфовая скорость
электрона будет равна
о,^ ——т„= — ц„Е, A9.33)
A9.34)
где нижние индексы пае относятся к электрону (здесь мы следуем
общепринятым обозначениям). Константа цп называется подвиж-
подвижностью электрона.
Аналогичные формулы можно написать для движения дырки:
A9.35)
ехр
301
Глава 19
Полный электрический ток, протекающий через единицу площади
полупроводника в единицу времени, таким образом, равен
I = — пеюе + реьи = (епцп + еру.р) Е,
где пир обозначают соответственно концентрации электронов и ды-
дырок в полупроводниковом кристалле. Используя известную фор-
Ж {электрическое
поле)
Среднее
смещение
Рис. 19.11. Хаотическое тепловое движение электрона, прерываемое актами
рассеяния, а — поле не приложено, среднее смещение электрона равно
нулю; б — под действием приложенного электрического поля электрон сме-
смещается в среднем в направлении действующей на него силы.
мулу закона Ома I = оЕ, где о
сти, получаем
~^ «Л» ,
коэффициент электропроводно-
A9.36)
те тн
Численный пример. Экспериментальные значения подвижностеи
носителей зарядов в некоторых полупроводниках приведены в
табл. 19.2. Используя указанные в таблице значения подвижностеи
и значения эффективных масс из табл. 19.1, находим для кристалла
кремния:
и для кристалла антимонида индия 1п5Ь:
с.
302
Перенос зарядов в полупроводниках
Таблица 19.2. Экспериментально измеренные значения подвижностеи электронов
и дырок при комнатной температуре в некоторых кристаллах а)
Подвижность, см2/(В-с)
Кристалл
Электроны Дырки
Алмаз 1 800 1 200
5! 1 600 600
Се 4 500 2 000
ОаЛ$ 7 000 300
Си 35 —
АвС1 50 —
1п5п 33 000 —
1пЛ$ 78 000 —
1пР 4 600 —
а) Чтобы получить подвижность в СИ [т. е. в м2.(В-с)]/ нужно приведенные в таблице
числа разделить на 10*.
Среднее расстояние, которое проходит электрон между двумя по-
последовательными столкновениями в кристалле кремния, таким
образом, равно
V—
V те
т„ ^ 2-10-» ■ 1,8- 10-ы = 3,6-10~8 м = 360А.
§ 19.5. Диффузия и рекомбинация
Как мы видели выше, частота столкновений носителей зарядов
с нерегулярностями кристалла в полупроводниках чрезвычайно
велика. Это приводит к важному следствию, а именно, оказывается,
что при рассмотрении изменений на масштабах, значительно пре-
превышающих среднюю длину свободного пробега носителей (как мы
только что показали, она равна нескольким сотням ангстрем),
перенос носителей происходит по законам диффузии.
Чтобы вывести уравнение диффузии, обратимся к рис. 19.12
и рассмотрим баланс носителей, пересекающих некоторую произ-
произвольную плоскость, скажем площадку с координатой х0 и площадью
А, за время, равное времени среднего свободного пробега т. Число
частиц, пересекающих площадку в направлении слева направо
за время т, равно
^(о~), A9.37а)
303
Глава 19
а число частиц, пересекающих за это время площадку в направле-
направлении справа налево, равно
м -- ' ' М A9.376)
Здесь / — средняя длина свободного пробега, п (х) — концентра-
концентрация носителей, A12) Ап — полное число частиц, пересекающих
площадку А за время т. С помощью множителя 1/2 учитывается то
I —
Хп + 1и
Рис. 19.12. Диффузия носителей зарядов в режиме, когда доминируют столк-
столкновения. Средняя длина свободного пробега обозначена /.
обстоятельство, что в среднем только половина частиц движется
к данной плоскости с какой-либо одной стороны. Средняя концен-
концентрация частиц, которые пересекают плоскость х0 слева направо,
берется при значении координаты х0 — 112, а частиц, пересекающих
ее справа налево,— при значении координаты х0 + И2. Полное
число частиц, пересекающих рассматриваемую плоскость в направ-
направлении слева направо за время т, таким образом, равно
2 дх
Обозначим буквой / поток частиц. По определению он равен пол-
полному числу частиц, пересекающих единицу площади за единицу
времени. Разделив последнюю формулу на хА, находим
/^ ?__*!_ =_о_*!_, A9.38)
2т дх дх
где введен коэффициент диффузии В, который определяется фор-
формулой
A9.39)
2т
Коэффициенты диффузии электронов и дырок обозначим соответст-
соответственно Оп и Б},.
Соотношение Эйнштейна. Как коэффициент диффузии
И
2т„
304
Перенос зарядов в полупроводниках
так и подвижность
для определенного типа носителей зарядов, в данном случае для
электронов, зависят от одной и той же величины — среднего вре-
времени свободного пробега т„. Используя эти формулы и очевидные
соотношения
приходим
к важному
2
г-
2 2
ЧкТ
тпе
соотношению
Оп
кТ
A9.40)
A„ е
Это известное соотношение Эйнштейна. Оно связывает коэффи-
коэффициент диффузии и подвижность для любого типа носителей зарядов,
если перенос совершается практически в условиях теплового рав-
равновесия. Соотношение Эйнштейна играет важную роль в теории
протекания электрического тока через РЫ-переход, излагаемой
в следующей главе.
Интересно проверить, насколько хорошо выполняется соотно-
соотношение Эйнштейна, например для кристалла кремния. Из табл. 19.2
берем значение подвижности электронов в кремнии цп =
— 0,16 м2/(В-с). Вычисляя по этой подвижности с помощью соот-
соотношения Эйнштейна коэффициент диффузии электронов, находим
Вп = кТц„/е = 41,2-10~4 м2/с. Экспериментальные значения ко-
коэффициента диффузии лежат в пределах от 4-Ю"^3 до 5-10~3 м2/с.
Дрейф так называемых неосновных носителей электрического
тока в полупроводниках и их диффузия впервые были продемонстри-
продемонстрированы в классических экспериментах Хайнеса и Шокли(рис. 19.13)
Рекомбинация электронов и дырок. Выше мы получили явные
выражения для тепловых равновесных концентраций электронов
(п) и дырок (р) с энергиями, лежащими соответственно в зоне про-
проводимости и в валентной зоне.
Обратим теперь внимание на динамический характер теплового
равновесия. В кристалле, находящемся в тепловом равновесии,
постоянно происходят процессы аннигиляции электронов и дырок
и их рождения. Основной процесс аннигиляции показан на
рис. 19.14, а. Он состоит в том, что электрон из зоны проводимости
переходит в незаполненное состояние в валентной зоне. При этом
населенности электронного и дырочного уровней уменьшаются
каждая на одну частицу. Такой процесс аннигиляции называется
электронно-дырочной рекомбинацией.
305
Глава 19
Хз Коллектор
К осциллографу
Рис. 19.13. Прямоугольной формы «пакет» дырок инжектируется через ле-
левый контакт (эмиттер) в стержень из германия Л/-типа. Инжектированное
облако носителей заряда дрейфует затем под действием приложенного к
стержню электрического поля со скоростью ~ор = ЦРЕ. Когда облако под-
подходит к правому контакту (коллектору) в момент времени C, часть зарядов
попадает в коллектор и дает сигнал на экране осциллографа. Диффузионное
расплывание инжектированного в германий облака электрического заряда
показано на рисунках а—г. Подвижность дырок рассчитывают по измерен-
измеренному времени прибытия (я облака к правому контакту по формуле AР =
= х3/^3Е. Диффузия приводит к размытию пакета дырок по мере его продви-
продвижения от эмиттера к коллектору. Это размытие проявляется в изменении
формы импульсов тока коллектора, регистрируемого при разных положе-
положениях х коллектора. (Такой эксперимент впервые был произведен Хайнесом
и Шокли [51 ]).
306
Перенос зарядов в полупроводниках
Процесс аннигиляции фактически представляет собой спонтан-
спонтанный переход (см. гл. 12). Поэтому время жизни электрона относи-
относительно этого процесса называется временем рекомбинации тг. [Оно
подобно спонтанному времени жизни тСПО11Т. ] Для времени реком-
рекомбинации можно вывести формулу, повторяя слово в*слово рассуж-
рассуждения, приведшие к формуле A2.71). Если, например, в полупро-
полупроводнике Р-типа концентрация п(х) электронов в точке х по какой-то
причине не равна равновесному значению пр, то в отсутствие внеш-
внешних воздействий следует ожидать, что она будет релаксировать
к своему равновесному значению по закону
дп __ __ » - пр A9.41)
До рекомбинации
с
После рекомбинаци и
Зона,
проводимости
Валентная зона
а
Рис. 19.14. Переход электрона из состояния а в зоне проводимости в неза-
незаполненное состояние Ь в валентной зоне приводит к одновременной анниги-
аннигиляции электрона и дырки. Процесс называется электронно-дырочной реком-
рекомбинацией. В рассматриваемом примере до рекомбинации (а) имеются три
электрона и две дырки, после рекомбинации (б) — два электрона и одна
дырка.
Вводя в рассмотрение так называемую избыточную электронную
плотность яиаб = п — пр, этот закон запишем в виде
д(
так что
«изб @ = пт6 @) е
A9.42)
Уравнение переноса носителей заряда. Теперь мы в состоянии
изучить, как изменяются концентрации п (х, г) электронов и р (х, {)
дырок в самых общих ситуациях.
Рассмотрим сначала бесконечно малый объем (IV, показанный
на рис. 19.15. Пусть поток (т. е. число частиц, проходящих через
единицу площади в единицу времени) электронов или дырок в на-
307
Глава 19
правлении х равен / (л% /). Общий баланс всех изменений, которые
происходят в объеме йУ за единицу времени, можно выразить сле-
следующими словами: «Увеличение числа частиц внутри объема йУ
за единицу времени равно сумме избытка приходящих частиц (оп-
(определенного типа) над уходящими частицами (того же самого типа)
и скорости, с которой частицы (этого типа) рождаются внутри
объема V за вычетом скорости, с которой они уничтожаются». За-
Запишем это утверждение математически:
дп{х'
Ц + Сйх—Шх, A9.43)
где Си/? — соответственно скорости рождения и уничтожения
х * их
Рис. 19.15. Бесконечно малый объем, используемый для вывода уравнения
переноса носителей A9.45). Разность О—Я представляет собой результирую-
результирующую скорость рождения частиц в единице объема.
частиц (число частиц, родившихся или исчезнувших в 1 м3 за 1 с),
/ — поток частиц (число частиц в расчете на 1 м2 в 1 с). Поскольку
а/
дх
уравнение A9.43) можно переписать в виде г)
их,
д( дх '
A9.44)
Если использовать уравнение A9.44), например, для электро-
электронов, то поток частиц / следует представить как сумму «дрейфового»
и «диффузионного» потоков:
„ „ дп
1 = — пипЬ —ип ;
дх
В трехмерном случае уравнение A9.44) принимает вид
дп ,. , , _ „
д(
308
Перенос зарядов в полупроводниках
тогда A9.44) можно преобразовать к виду
дп д
д( дх
Соответствующее уравнение для дырок имеет вид
др _ д
д( дх
A9.45)
A9.46)
(Конечно, скорости О и Я для электронов и дырок не обязательно
совпадают).
X
Рис. 19.16. Решение стационарного диффузионного уравнения A9.48) для
плотности электронов в полубесконечном полупроводниковом кристалле
Р-типа.
В том случае, когда электроны являются неосновными носите-
носителями, в свободном от электрического поля полупроводнике Р-типа
следует положить Е — О и использовать формулу A9.41):
О— Я= —
п (х) — щ
так что в стационарном режиме {д!дг = 0) из уравнения A9.45)
получаем уравнение
„ д2п п (х) — пр
дх2
A9.47)
Вводя избыточную плотность электронов пи3б = п (х) — пр, урав-
уравнение A9.47) можно преобразовать к виду
«изб
Общее решение последнего уравнения имеет вид
A9.48)
* + Ве~хЬп; A9.49)
здесь ^п — так называемая «диффузионная длина» для избыточ-
избыточных неосновных носителей (в данном случае электронов) — опре-
определяется формулой
Ьп
A9.49а)
309
Глава 19
Диффузия в полубесконечное пространство. С этим случаем
диффузии мы встретимся в следующей главе при изучении РМ-пе-
рехода.
Пусть избыточная концентрация носителей на некоторой пло-
плоскости, скажем при х = О, все время поддерживается постоянной
и равной, например, п,гаг, @). Тогда константу А в формуле A9.49)
следует положить равной нулю, поскольку ее ненулевое значение
повело бы к физически недопустимому решению, экспоненциально
возрастающему при увеличении х. Таким образом, распределение
концентрации во всей области х>0 дается формулой
«изб(х) = «изо@)<Г*Ч A9.50)
Отсюда видно, что функция п (х) очень быстро достигает значения
пр, которое она имеет внутри материала, как показано на рис. 19.16.
Задачи
1. Используя значение электропроводности меди при комнатной темпера-
температуре, оцените величину среднего времени между столкновениями для
носителей электрического тока.
2. Предположите, что в полупроводнике имеется незначительное количе-
количество донор пых атомов. Какова энергия Ферми такого кристалла при
Т -- 0 К?
3. Стерженек арсенида галлия вырастили из расплава, содержащего 100 г
СаАк и Ю г 2п.
а. Найдите концентрацию атомов цинка.
б. Вычислите энергию ионизации акцепторного атома 2п (считайте,
что е = 12 е0).
в. Определите положение уровня Ферми в случаях «низких» и «высоких»
температур.
г. Вычислите концентрации п и р.
4. Рассмотрите устройство, изображенное на рис. 19.17. На кристалл крем-
кремния Л'-типа действует электрическое поле Ег= Уо!1 и одновременно магнит-
магнитное поле Во, направление которого показано на рисунке.
а. Убедитесь, что вольтметр показывает напряжение
V = ц -^ В А
где ц — подвижность электронов,
б. Убедитесь, что
еу _
/Во пс
где / — полный электрический ток, Еу — У1й — поперечное электриче-
электрическое поле, А — площадь сечения, нормального к оси г.
Указание. В кристалле возникает поперечное электрическое поле Еу
(направленное по оси у). Оно определяется из условия, что сила, дейст-
действующая на дрейфующий электрон со стороны электрического поля, равна
по величине и противоположна по направлению силе, действующей со
стороны магнитного поля.
310
Перенос зарядов в полупроводниках
в. Найдите, чему равно поперечное электрическое поле, возникающее
в образце СаАк при / = 1 см, Во = 1 Вб/м2, Уо = 103 В и ц = 0,7 м2/(Вс).
5. Получите выражение для плотности поверхностных зарядов (Кл/м2),
которые появляются на верхней (или нижней) плоских гранях образца
в устройстве, показанном на рис. 19.17.
6. Стерженек германия длиной 1 см, подвижность электронов в котором
ип -= 4500 см2/(В-с), подсоединен к источнику с напряжением V,, =
= 100 В.
а. Сколько времени потребуется электрону для дрейфа через всю длину
стерженька?
б. Сколько столкновений испытывает в среднем один электрон при та-
таком дрейфе?
Рис. 19.17.
п. Чему равна полная энергия, полученная электроном от поля во время
этого дрейфа и отданная кристаллической решетке?
7. Рассмотрите идеально чистый кристалл СаАк при Т = 77 К, в котором
ц„ = \№ см2/(Вс) и цр = 10* см2/(Вс).
а. Приняв, что коэффициент поглощения света материалом образца
а --- 10 см, рассчитайте электропроводность образца непосредственно
после окончания облучения его импульсом света с интенсивностью, рав-
равной 1 Дж/см2. (Считайте, что каждый поглощенный фотон создает одну
электронно-дырочную пару и что произведение коэффициента поглощения
на типичный размер кристалла много меньше единицы.) ,
б. Пусть образец подвергается непрерывному облучению светом с ин-
интенсивностью 10 Вт/см2. Какова стационарная электропроводность об-
образца при условии, что время электронно-дырочной рекомбинации хг
равно 10~7 с?
п. Можно ли использовать экспериментальную схему, описанную в
п. а, чтобы измерить время рекомбинации тг?
8. а. Докажите, что электрон с эффективной массой те вращается по круго-
круговой орбите, перпендикулярной направлению однородного магнитного
поля В, с угловой скоростью <0цикл = еВ/те, называемой частотой цик-
циклотронного резонанса.
б. Объясните, как путем одновременного измерения частоты циклот-
циклотронного резонанса и поперечного напряжения (см. задачу 4) найти время
рассеяния трасс.
ГЛАВА 20
ПОЛУПРОВОДНИКИ С РЛГ-ПЕРЕХОДОМ.
ПЕРЕНОС ЗАРЯДОВ ЧЕРЕЗ РЛ^Р-ПЕРЕХОД
Как показывает само название книги, автор стремился не только
дать изложение основных положений квантовой физики, вытекаю-
вытекающих из ее фундаментальных постулатов, но и осветить важнейшие
прикладные аспекты квантовой теории. Исходя из этой концепции,
мы уже говорили в предыдущих главах о таких важных прикладных
вещах, как лазеры и водородные мазеры.
В настоящей главе мы воспользуемся изложенным в предыду-
предыдущих главах теоретическим материалом, чтобы объяснить принцип
работы полупроводникового транзистора. Это устройство, изобре-
изобретенное Бардином, Браттейном и Шокли [52, 53] в 1946 г., следует
отнести к числу самых выдающихся прикладных достижений совре-
современной науки.
Действительно, благодаря транзисторам, в частности, возникла
вся современная электроника на интегральных схемах, которая со-
совершила революцию в способах хранения и использования инфор-
информации с помощью современных ЭВМ. Многочисленные применения
ЭВМ для управления работой станков и ходом технологических
процессов также покоятся на этой основе.
Прежде чем переходить к рассмотрению работы транзистора,
необходимо сначала понять механизм переноса электрических за-
зарядов через контактную область, разделяющую полупроводники
Р- и Л^-типа, или через так называемый РМ-переход.
§ 20.1. Распределение концентраций
носителей зарядов и потенциала в Р/У-переходе
Существует множество способов изготовления РМ-переходов.
Обычный метод основан на использовании диффузии акцепторных
атомов внутрь полупроводника Л^-типа. В этом случае диффузион-
диффузионный слой, в котором концентрация акцепторных атомов Л^л больше
концентрации донорных атомов Мв, представляет собой полупро-
полупроводник Р-типа. РМ-переход возникает вблизи плоскости, в кото-
которой МА = Мо.
На рис. 20.1, а изображен идеализированный контакт между
двумя полупроводниками с резкой границей раздела при х = О,
слева от которой (при х<0) существует избыток акцепторных ато-
атомов NА над донорным атомами Мв, а справа (при х>0) — избы-
избыток донорных атомов над акцепторными.
312
Полупроводники с /"Л'-переходом
Чтобы понять, что происходит на поверхности контакта (х = 0),
представим себе, что Р- и Л^-стороны контакта сначала были раз-
разделены, а затем их привели в соприкосновение друг с другом.
В первый момент после установления контакта в Р-области (при
х<0) подвижными носителями электрического тока являются
дырки, а в Л^-области (при х>0)— электроны. В момент сопри-
соприкосновения областей начинается диффузия, в результате которой
часть дырок переходит из Р- в Л^-область, а часть электронов —
из М- в Р-область. Электроны, переместившиеся справа налево
в Р-область, оставляют зону шириной Ь, содержащую только по-
положительно заряженные донорные ионы, что показано на рис. 20.1 ,а
и в. Точно так же дырки, которые переходят из области х<0 в об-
область л:>0, оставляют зону шириной а, содержащую только от-
отрицательно заряженные акцепторные ионы. Перетекание электри-
электрического заряда прекращается в тот момент, когда электростатиче-
электростатический потенциальный барьер, создаваемый заряженным слоем
— а<^х<сЬ, становится достаточно высоким, чтобы подавить всякое
дальнейшее перемещение электронов и дырок через плоскость
х = 0. Такой электростатический потенциальный барьер показан
на рис. 20.1, д. Он называется диффузионным потенциалом. Об-
Область — а<^х<^Ь называется обедненным слоем, поскольку су-
существующее в нем электрическое поле вымывает оттуда все под-
подвижные свободные носители — электроны и дырки.
Поскольку весь образец находится в состоянии теплового рав-
равновесия, во всех его точках должно установиться одно и то же,
единое по всему образцу значение химического потенциала ц, по-
показанное горизонтальной штриховой линией на рис. 20.1, е. Далеко
от плоскости контакта х = 0 химический потенциал должен, од-
однако, занять то положение относительно краев зон, которое он
имеет в объеме вР-и Л^-областях кристалла. Последнее требование
следует примирить с условием постоянства химического потенциала
ц по всему кристаллу. Это условие может быть выполнено, если
предположить, что края зоны проводимости и валентной зоны в об-
области вблизи контакта х = 0 искривлены, как показано на
рис. 20.1, е. Поскольку края зон характеризуют энергию электро-
электронов, форма краев должна быть зеркальным отражением кривой
электростатического потенциала еУ (х), показанной на рис. 20.1, д.
Контактная разность потенциалов <р. В области контакта по-
полупроводников Р- и N -типов полная плотность электрического
тока, создаваемого дырками (т. е. число дырок в единицу времени
в расчете на единицу площади), равна сумме «диффузионного» и
«дрейфового» токов (см. § 19.5):
313
Л/у,
1
Глава
1
-а х
С
1
1
1
-я
+
-г
-г
0
20
|
+
ь
ь
; 1
ь^
-а
Д7на проводимости
Р ""V
р^ -
ч. N
Валентная зона
е
Рис. 20.1. РЛ^-переход в полупроводнике, а — область (—а<х<:0) не-
нескомпенсированных ионизованных акцепторных атомов и область @ < х < 6)
нескомпенсированных ионизованных доноров; б — профиль легирования
(зависимость разности Ыд—Л^д от х); в — распределение нескомпенсиро-
ванного электрического заряда, создаваемого ионизованными примесными
атомами в обедненном слое; г — распределение электрического поля
= — | р (*) их, йЕ1йх = р/е
)■•
314
Полупроводники с /"Л'-переходом
где мы воспользовались определением подвижности:
ОМ
г" ах
Плотность тока электронов рассчитывается аналогично
1е(х) = —Д, — 4- пцп —. B0.2)
дх ах
При тепловом равновесии и электрический ток, создаваемый дыр-
дырками, и электрический ток, создаваемый электронами, должны быть
равны нулю в любой плоскости х. Следовательно, с учетом формулы
B0.1), получаем
п * _ „.. ау
е
кТ
X
ау
ах
Н1л
1
Р
'" ах
ар
Ох
а
ах
ИЛИ
А\Г 1 Аг, А
1п р,
где мы использовали соотношение Эйнштейна A9.40), согласно
которому Ор/[1р = кТ/е. Интегрируя последнее уравнение по х
от хл до х2, приходим к формуле
кТ ,..ГР(*1I B0.3)
так что
—е B0.4)
Возьмем теперь в качестве точки Х\ точку х = — а, в которой
концентрация дырок рр равна ее значению в глубине Р-области,
а в качестве точки х2 — точку х = Ь, в которой р = рп (т. е. кон-
концентрация дырок равна ее равновесному значению в глубине Л^-об-
ласти). Тогда, согласно B0.3), для контактной разности потенциа-
потенциалов на РЛ^-переходе получим значение
<р = У(Ь) — У(—а)= 1п-^-. B0.5)
е Рп
д—распределение электростатического потенциала \еУ (х) — —е | Е{х)йх,
—а
диффузионный потенциал <р — (кТ/е) 1п («„Рр/«|) = (кТ/е) 1п (Л^Л^/п^)],
е — зонная диаграмма.
315
Глава 20
Рассуждая аналогично, но исходя из формулы B0.2), для кон-
контактной разности потенциалов находим выражение
<р= —1п-^=-. B0.6)
е пр
Складывая формулы B0.6) и B0.5) и используя соотношение
A9.10), согласно которому пррп = п|, а также формулу A9.24)
для предельного случая «высоких» температур, согласно которой
пп « Л^р и Рр» МА, приходим к следующему простому выраже-
выражению:
B07)
Зависимость концентрации электронов от х описывается фор-
формулой, аналогичной B0.4):
п(х2) ^ се[У (хй)-^У (х.ЦкТ ^ B0 8)
П (*!>
в которой противоположный знак показателя экспоненты по срав-
сравнению с B0.4) учитывает то обстоятельство, что электрон притяги-
притягивается к областям с большими значениями электростатического
потенциала У (х).
Полагая хл = — а и х2 = 6 в формулах B0.4) и B0.8), прихо-
приходим к простым соотношениям
пр = п{—а) = п (Ь) е~щ = ппе~е<р. B0.9)
Если на рассматриваемый переход наложить внешнее напря-
напряжение Кг, то потенциальный барьер на РЛ^-переходе станет рав-
равным ф—Уа. При этом условимся считать знак напряжения Уа
положительным, когда Р-область соединена с положительным по-
полюсом источника, а Л^-область — с отрицательным полюсом. Тогда
через РЛ^-переход может течь электрический ток. [Положительное
напряжение будем называть отпирающим, а отрицательное — за-
запирающим. ]
§ 20.2. РЛ-переход с приложенным внешним напряжением
Условие теплового равновесия нарушается, когда к контактной
области приложено внешнее напряжение \'а. Получающиеся энер-
энергетические диаграммы с искривленными зонами показаны на
рис. 20.2, а—в для случаев Уа = 0 (а), Уа>0 (б) и Уа<0 (в).
Знак напряжения Уа выбирается в соответствии с соглашением,
приведенным в конце § 20.1. При наложении напряжения Уа на
полупроводник с РЛ^-переходом контактная разность потенциалов
316
Полупроводники с РЛ'-переходом
а: =0
Рис. 20.2. Искривление краев зон и потенциальный барьер в РЛ?-переходе
в отсутствие напряжения (а), с приложенным отпирающим (б) и запирающим
(в) напряжением.
Ф становится равной ф—Уа. Соответственно высота барьера умень-
уменьшается до значения ф — \Уа\ в случае отпирающего напряжения
(Уа>0) и возрастает до значения ф -|- | Уа | в случае запирающего
напряжения (Уа<^0), как показано на рис. 20.2, бив.
Отметим, что разность химических потенциалов для Р- и ^-ча-
^-частей полупроводника равна еУа. Действительно, химический по-
потенциал представляет собой энергию, на которую увеличивается
энергия системы при добавлении к ней одного электрона, а энергия,
затрачиваемая на перенос электрона из Р-области в Л^-область,
равна еУа.
317
Глава 20
Изменение высоты потенциального барьера от значения ср до
значения ф—Уа должно сопровождаться, как будет показано не-
немного ниже, изменением ширины а^-Ъ обедненного слоя
(рис. 20.2, б и в).
Чтобы рассчитать распределение носителей тока в области
РЛ^-перехода, снова будем исходить из формулы B0.1). Согласно
этой формуле, плотность тока, обусловленного дырками, равна
"ч ' " их " " их
Поскольку теперь Уа Ф 0, плотность дырочного тока /Л (х) нельзя
считать равной нулю. Однако очень простые оценки (см. задачу 3)
показывают, что
В
V
B0.10)
т. е. дрейфовая и диффузионная слагающие дырочного тока в от-
отдельности на много порядков больше полного дырочного тока.
Поэтому с очень большой точностью можно считать, как и выше,
что
О * =_р^_^_. B0.11)
их их
Следовательно, можно использовать непосредственно соотношение
B0.9), нужно только всюду заменить <р на <р—Уа'
Мы видим, таким образом, что концентрации неосновных носителей
(электронов в Р-области и дырок в Л^-области) на границах обед-
обедненного слоя отличаются от их значения в глубине материала на
один и тот же множитель ехр (Уа[кТ). Избыточные концентрации
неосновных носителей на границах обедненного слоя, таким обра-
образом, определяются следующими выражениями:
Ризб(Ь) = р(Ь)—рп^Рп{еУакт— 1), B0.13а)
„ ,/ п\~п( п\ „ — „ (реХ/акГ П С90 ИбЪ
Заметим, что ризб ф) = 0 при Уа = 0, тогда как ризб (Ь) ^ 0 при
Vа й: 0. Аналогично ведет себя и величина пИЗб (— «)• Следует
помнить, что границы х = — аих = 6 обедненного слоя не фикси-
фиксированы, а изменяются в зависимости от Уа.
Соотношения B0.13а и б) называются основными законами РЫ-
перехода. Они постоянно используются в инженерных расчетах.
318
Полупроводники с РЛ'-переходом
Протекание тока через РЛ'-переход. Теперь у нас все подготов-
подготовлено, чтобы получить выражение для полного тока через РМ-пе-
реход. В области х > Ь электрическое поле равно нулю [так как
V (х) = сопб1 ], так что распределение концентрации дырок опре-
определяется только диффузией. Используя непосредственно формулу
A9.49), получаем в области х > Ъ распределение
риз6(х) = риз6 (&)в-(*- Ь) Ь» = Рп (ееУ"кт - 1) е{х-ЬIь» B0.14)
и аналогично в области х^ —а—распределение
птб(х) = птб(~а)е{х+а)Ьп = пр(е^кт~1)е^а)Ьп. B0.15)
Распределение электронов и дырок в области РМ-перехода пока-
показано на рис. 20.3.
При стационарном режиме полный электрический ток через
РМ-переход одинаков во всех сечениях х. Поэтому его можно
найти, рассматривая, например, границу х = Ь обедненного слоя.
Ток этот слагается из дырочной и электронной компонент. Первая
из них дается формулой
еВрА
B0.16)
причем мы здесь воспользовались тем, что "йрт&'йх = йр'йх, и со-
соотношением B0.14). Электронную компоненту тоже следует вычис-
вычислять при х = Ь. Если в обедненном слое, т. е. в области
— а < х < Ь, не происходит рекомбинации электронов и дырок,
то число электронов, пересекающих плоскость х = Ь за данный
промежуток времени, равно числу электронов, пересекающих пло-
плоскость х — — а за тот же промежуток времени. Тогда, согласно
B0.15)
йп
их
еВпА
,б(-с)-
B0.17)
Таким образом, полный электрический ток через РЛ^-переход
описывается выражением
или 1^1игс(?У°!кт—1), B0.18)
где так называемый шок насыщения определяется формулой
^-+^^\. B0.19)
319
Глава 20
р
_____
4- + +
+ + +
N
/{рай зоны
проводимости
Рис. 20.3. Распределение носителей зарядов при отпирающем напряжении
на РЛ'-переходе. а — область контакта и обедненный слой с пространствен-
пространственным электрическим зарядом; б — зонная диаграмма; в — распределение
концентрации^дырок р (х) = р„ + рп (ееУакТ — 1) е~^х~Ь) ьр. [Обратите вни-
внимание на то, что согласно основному закону РЛ'-перехода р (Ь) = раее " .
При х>6 функция р (х) экспоненциально уменьшается до значения рп];
г — распределение концентрации электронов п (х) = п. -\- п„ (е а ■—
Формула B0.18) описывает основное, выпрямляющее свойство
РЛ'-перехода. При отпирающем напряжении (Уо>0) ток через
переход имеет большую величину и сопротивление Уа11 перехода
мало. Когда к РЛ^-переходу приложено запирающее напряжение
(Уа<;0), ток становится равным току насыщения — /нас, который
очень мал по сравнению с прямым током. В результате импеданс
перехода при запирающем напряжении имеет очень большую ве-
величину.
320
Полупроводники с ЯЛ'-переходом
Именно благодаря такой вольтамперной характеристике полу-
полупроводниковые диоды находят столь многочисленные применения,
в том числе, например, в логических электронных схемах или в
СВЧ-смесителях.
Полученная экспериментально вольтамперная характеристика
типичного РЛ^-перехода показана на рис. 20.4.
1)
1
1нас ^^^
Т Запирающее
налряжени е
)
Отпирающее
напряжение
Рис. 20.4. Экспериментальная вольтамперная характеристика типичного
РЛ'-перехода.
Электрическое поле в переходе. Электрическая емкость перехода.
Во многих случаях при использовании полупроводниковых диодов
с РМ-переходами, например в солнечных батареях, оптических
детекторах, параметрических СВЧ-усилителях и т. д., необходимо
знать распределение электрического поля в обедненном слое пере-
перехода.
Используя уравнение Максвелла (Ну Е = р/е и определение
электрического потенциала Е = — йУ/йх, путем непосредственного
рассмотрения рис. 20.3 получаем уравнение
B0.20)
их2 в
в области —а<сх<;0 и уравнение
B0.21)
ах- е
в области 0<Сх<С Ь, где е — статическая (низкочастотная) диэлек-
диэлектрическая проницаемость полупроводника. Обедненный слой пол-
полностью лишен носителей зарядов, так что его электрический заряд
создается ионизованными акцепторными атомами в области
— а<^х<^0, где р = — еМА,и ионизованными донорными атомами
в области 0<Сх<;Ь, где р = — еЫо (предполагаем, что все при-
примесные атомы в обедненном слое ионизованы). Плотность электри-
электрического заряда вне обедненного слоя равна нулю.
321
Глава 20
Граничные условия для уравнений B0.20) и B0.21) имеют вид
йУ ^0,
1
= 0, B0.22)
Е йУ
х=ь йх
т. е. мы требуем, чтобы электрическое поле обращалось в нуль на
границах обедненного слоя. Кроме того, в качестве граничного
условия потребуем непрерывности функции V (х) при х = 0.
Кроме указанных, должно выполняться еще одно граничное
условие: а именно, полное падение напряжения на обедненном слое
должно быть равно заданной величине:
Уф)—У(—а)=ч — Уа. B0.23)
Решение дифференциальных уравнений B0.20) и B0.21) с гра-
граничными условиями B0.22) имеет вид
V (х) --- -^- (х2 + Чах) B0.24)
в области — а<;х<;0 и
V (х) ■=- — -^- (х2 — 2Ьх) B0.25)
в области 0<;х<;Ь.
Используя условие непрерывности потенциала при х -- 0, по-
получаем соотношение
ЫАа = ЫоЬ, B0.26)
которое показывает, что обедненный слой имеет положительный
заряд Моае на Л^-стороне (при —а<^х<^Щ, создаваемый ионизо-
ионизованными донорными атомами, и равный ему отрицательный заряд
— МдЬе на Р-стороне (при 0<Сх<;Ь), создаваемый ионизованными
акцепторными атомами.
Согласно условию B0.23), имеем
Тогда, используя соотношение B0.26), получаем следующие фор-
формулы для определения границ обедненного слоя:
^га) B0-28)
322
Полупроводники с ЯЛ'-перекодом
Дифференцируя B0.24) и B0.25), получаем электрическое поле
Е = МА{х + а) B0.29а)
в области —а<;х<;0 и
Е --= — Мо ф—х) B0.296)
8
в области 0<;х<;Ь. Электрическое поле имеет максимальную ве-
величину на границе Р- и Л^-областей, т. е. при х = 0, где
Р 2 (ф - Уа)
*-*макс — »
а -А- Ь
так что при Уо<с0 (запирающее напряжение) вблизи границы пе-
перехода могут существовать очень сильные поля (порядка 105 В/см).
Полный заряд, приходящийся на единицу площади, по одну
сторону от обедненного слоя можно вычислить по формуле
согласно B0.27) и B0.28), он зависит от приложенного напряжения
Уа. Таким образом, электрическая емкость единицы площади РЫ-
перехода равна
С^ в^ йа
Благодаря нелинейному характеру зависимости С от Уа диоды
с РЛ^-переходами нашли применение в параметрических СВЧ-уси-
лителях [54 ].
§ 20.3. Транзистор с Р;УР-переходом
Транзистор с РЛ^Р-переходом схематически изображен на
рис. 20.5. Транзистор изготовляется из одного монокристалла,
обычно кремния, в который контролируемым образом тем или иным
способом вводятся примеси Р- и Л^-типов; в результате образуется
«сандвич» Р—N—Р, показанный на рис. 20.5.
Транзистор можно рассматривать как два РЛ^-перехода, сое-
соединенные «лицом к лицу» через общую переходную область В,
которую называют базой. Будем считать, что, когда напряжение
УВЕ положительно, на левый РЛ^-переход наложено отпирающее
напряжение. Будем также предполагать, что, когда напряжение
УВ(: положительно, на правый РЛ^-переход наложено запирающее
напряжение. Конец транзистора, соединенный с положительным
323
Глава 20
полюсом напряжения УВЕ, называется эмиттером (обозначается Е),
а противоположный конец, соединенный с отрицательным полю-
полюсом напряжения Увс,— коллектором (обозначается С). Смысл та-
такой терминологии выяснится ниже, когда мы станем описывать
работу транзистора.
Если рассматривать транзистор как устройство с двумя входами
и одним выходом и токами IЕ, Iв и 1^, то в стационарном режиме
для него должно удовлетворяться соотношение
1е + 1в = 1о B0.31)
т. е. полный ток, втекающий в устройство или вытекающий из него,
равен нулю.
1с
(Выход)
Рис. 20.5. Транзистор с РАФ-переходом и схема его включения.
Прежде чем перейти к математическому описанию процессов,
происходящих в транзисторе, полезно сначала чисто качественно
понять его работу. Объясним, например, действие транзистора в ка-
качестве усилителя мощности. В этом случае напряжения УВЕ и Увс
положительны; соответствующая схема показана на рис. 20.5.
Отпирающее напряжение УВЕ на эмиттерном переходе создает
большой положительный ток IЕ через этот переход, о чем мы уже
говорили в § 20.2. Поскольку эмиттер обычно легирован сильнее,
чем база, ток в нем переносится в основном дырками, движущимися
в направлении от Е к В. Попав в базу В, дырки становятся, однако,
неосновными носителями. Если толщина базы достаточно мала, то
большинство инжектированных в нее дырок сможет продиффун-
дировать к коллекторному переходу, к которому приложено боль-
большое запирающее напряжение У'вс. Под действием этого напряже-
напряжения все дошедшие до коллекторного перехода дырки беспрепятст-
беспрепятственно попадут в коллекторную область С, и возникнет коллек-
коллекторный ток 1с.
Для читателей, не очень хорошо знакомых с электроникой,
дадим несколько более подробное объяснение. Дырки, которые
под действием напряжения, приложенного к обедненному слою В,
попадают на коллектор С, создают избыточный положительный
заряд в этой области. Этот заряд начинает притягивать через внеш-
внешний проводник из батареи ]/2 электроны, которые стремятся ском-
324
Полупроводники с /-Л'-переходом
пенсировать возникший положительный заряд. Таким образом,
возникает коллекторный ток /с.
Небольшая часть дырок, инжектированных эмиттером в базу,
не вынесет, однако, такого путешествия и прорекомбинирует с элек-
электронами, которые являются в базе основными носителями. Следо-
Следовательно, будет выполняться неравенство 1Е>1^. При каждом
акте рекомбинации исчезают один электрон и одна дырка. По-
Поскольку, однако, в стационарном режиме число электронов, имею-
имеющихся в базе, должно оставаться неизменным, прорекомбиниро-
вавшие электроны должны непрерывно восполняться. Таким об-
образом, возникнет ток базы Iв. Направление тока Iв, показанное
на рис. 20.5, соответствует общепринятому. В рассматриваемой
ситуации электроны должны втекать в базу (чтобы заменить про-
рекомбинировавшие электроны), так что /в<;0.
В транзисторе толщина базы обычно очень мала, поэтому боль-
большая часть дырок, инжектированных в нее эмиттером, собирается
коллектором, на который подано запирающее напряжение. Пред-
Предположим, например, что из 21 инжектированной дырки 20 попало
в коллектор и испытало рекомбинацию в базе. Тогда имеем (в еди-
единицах тока)
/^21, /с = 20, /в--1.
Схему включения транзистора, показанную на рис. 20.5, на-
называют схемой с общей базой, поскольку здесь входная и выход-
выходная цепи имеют общую электрическую базу. Хотя входной и вы-
выходной токи в схеме на рис. 20.5 почти равны друг другу, мы полу-
получаем большое усиление мощности, поскольку выходной импеданс
2Ь может превышать входное сопротивление /?,- во много раз. Это
объясняется тем, что в рассматриваемом случае к эмиттерному пе-
переходу приложено отпирающее напряжение, поэтому в соответст-
соответствии с вольтамперной характеристикой (рис. 20.4) небольшие из-
изменения напряжения АУВ приводят к большим изменениям тока
Л/г. Если на коллекторный переход подано запирающее напряже-
напряжение, то картина будет обратной. Следовательно, имеем
АУс ... АУЕ
Поскольку мощность на входе транзистора есть величина по-
порядка 12ЕЯ(, а мощность на выходе—порядка /с-^, а 1Е =г Iс,
транзистор работает как усилитель мощности.
В приведенном описании работы транзистора эмиттерный ток
рассматривался как вынуждающее действие, а токи 1С и Iв как
отклики системы на это действие. Можно, однако, рассматривать
ток базы Iв как входной (вынуждающее действие), а ток коллек-
коллектора /с — как выходной (отклик). В приведенном примере прирост
325
Глава 20
АУВ тока базы обусловливает прирост тока коллектора А/с —-
= —20 Л/в. Поэтому транзистор можно использовать и как уси-
усилитель тока. В таком случае слабый входной ток питает базу, а
усиленный ток выходит с коллекторного конца.
Электрические токи в транзисторе. Приведенное выше качествен-
качественное описание работы транзистора показывает, насколько важна
взаимная связь токов эмиттера, базы и коллектора. Чтобы полу-
получить связывающие их формулы, обратимся снова к рис. 20.5. Пред-
Предположим, что благодаря введению большого количества примесей
в области эмиттера и коллектора по сравнению с областью базы
(р+ ;;>~ п) токи, протекающие через оба перехода, в основном соз-
создаются дырками. Начнем с того, что найдем распределение кон-
концентрации дырок в области базы. Поскольку в этой области
@<;х<;ш) нет электрического поля, общее решение диффузион-
диффузионного уравнения для избыточной концентрации дырок в соответст-
соответствии с формулой A9.49) имеет вид
Константы А и В следует определить из граничных значений,
Рте, @) и р113б (ш), которые даются формулами B0.13).
Используя формулы B0.13) в сочетании с последней формулой,
получаем условия
1"Т
Справедливость последнего приближенного равенства следует из
того, что е\'2 Ъ кТ. Разрешая два приведенных выше уравнения
относительно А и В и подставляя найденные значения в выражение
для р„зб (х), получим для области 0<х<ш формулу
Плотность дырочного тока, текущего через базу, таким образом,
равна
1к(х) ^ОреА-^-
"_ 1) сЬ ^^1^ ^_ сп ^Ц , B0.32)
1 ' 1 I
причем в этой и последующих формулах А означает площадь кон-
контакта, нормальную к направлению протекающего тока. Ток из
эмиттера в базу, таким образом, равен
/, ^ МО) = ^- П^кт- 1)с№ ^--; -—V
Ьр \ (-,, 5П (Ш/Ьр) I
B0.33а)
Вычисленные токи показаны на рис. 20.6.
326
Полупроводники с ЯЛ переходом
Теперь поучительно подробнее рассмотреть два предельных слу-
случая. Пусть сначала ширина ш базы много больше диффузионной
длины Ьр (ш ,, Ьг). Этот случай показан на рис. 20.7, а. При та-
таких условиях эмиттерный и коллекторный переходы оказываются
практически независимыми друг от друга. Распределение дырок
р (х) и дырочный ток /р =- — еОрйрШх подчиняются законам
B0.14) и B0.16) для отдельного перехода. Ток коллектора не за-
'е
1Л ——
т
Б \
(р>) !
1
1—*'1/,@}
1 В
1
х = О
1
• 1
ек 1 |
1
14 х=ш
1
! с
| №*)
I
т
в
Рис. 20.6. а — края валентной зоны и зоны проводимости для типичного
транзистора с РЛ'Р-переходом; б — реальное расположение эмиттера, базы
и коллектора и приложенные напряжения; в — обычное обозначение транзи-
транзистора па электронных схемах.
висит от тока эмиттера. При таких условиях устройство нельзя
использовать как транзистор.
Случай, когда и.' X Ьр, представлен на рис. 20.7, б. При таких
условиях доля инжектированных эмиттером дырок, которые ре-
комбинируют в области базы, пренебрежимо мала, так что распре-
распределение концентрации рп (х) приближенно изображается прямой
линией.
Если бы график функции р„{х) представлял собой прямую ли-
линию, то ток эмиттера—ЬРеАйр!йх^х=^ и ток коллектора
—ОреАйр/йх |х=и1 в точности были бы равны друг Другу. Однако функ-
функция рп(х) несколько отклоняется от строго линейной зависимости,
а именно наклон при х — ш оказывается немного меньше наклона
327
Глава 20
при х = 0. Таким образом, ток коллектора немного меньше тока,
инжектируемого эмиттером в базу. Разность этих двух токов равна
току базы.
При типичных значениях напряжения, т. е. при условии
— еУ!> кТ, и для транзисторов с узкой базой (ш < Ьр) получаем
из B0.33а) следующую приближенную формулу (с точностью до
квадратичных членов по ш!Ьр):
B0.336)
р+
п
р+
Рис. 20.7. а — транзистор с широкой базой (ш . > Ьр) [распределения кон-
концентрации рп (х) неосновных носителей около эмиттерного и коллекторного
переходов не зависят друг от друга]; б — транзистор с узкой базой [теперь
рекомбинация дырок в базе не играет существенной роли, что приводит
почти к линейной зависимости рп (х). Ток коллектора практически равен
току эмиттера].
Тогда ток коллектора в том же приближении, что и в B0.336),
дается формулой
еУ':кт. B0.34)
Ток базы получается как разность токов:
т т т _ РреАрпш „еу,1кт _
ерпАш
2т,
р
B0.35)
причем при записи последнего равенства мы воспользовались со-
соотношениями Ьп, Р = Оп,рт:г 1см. A9.496) ].
Интересно и поучительно получить формулу B0.35) для тока
базы, используя другие, физически более наглядные рассуждения.
328
Полупроводники с ЯЛ'-лереходом
Ток базы переносится электронами, приходящими в область базы
на место электронов, потерянных в результате рекомбинации с дыр-
дырками при протекании дырочного тока через базу. Число таких
рекомбинаций за единицу времени равно
дг Полное число избыточных дырок в базе
^ рскомб ^^ ' ' "
ни
= А [ Ризб(л')- их. B0.36)
3 1
В предельном случае очень узкой базы (ш С ^Р) формула для
Ризб (х), приведенная перед формулой B0.32), представляет собой
почти линейную зависимость, описывающую изменение рИЗб (х)
от значения (р„ ееУ11кт —1) при х = 0 до значения — р„ при
х = ш. Таким образом, выполняя интегрирование в B0.36), по-
получаем
Лг _ рпАхю ( еУ, кТ о\ _ РпАш е1/, кт
'"'рскомб— Vе ^/ = ^ '
2тг 2тг
так как \еУг > кТ. Используя соотношение Iв = — еЛ^Скомб,
отсюда сразу приходим к формуле B0.35).
Важным техническим параметром, характеризующим транзи-
транзистор, является коэффициент усиления по току эмиттера:
п_ а/с __ \1с
01Е >Е
который связывает изменение выходного тока (коллектора) с выз-
вызвавшим его изменением входного тока (эмиттера). Используя фор-
формулы B0.33а) и B0.34), приходим к следующей формуле для ко-
коэффициента усиления:
а = ! B0.37)
Если, например, отношение ы>/Ьр = 0,2, то коэффициент усиления
а = 0,98, т. е. 98 % дырок, инжектированных эмиттером в базу,
поступает на коллектор.
Если транзистор используется как усилитель тока, то входной
ток дожен питать базу, а выходным будет ток коллектора. В этом
случае полезно рассмотреть параметр
Р= 'с = /с а _ «,/ 1у \2
1 в /с— Iв а— 1 \ ш /
B0.38)
Для рассмотренного выше примера р = — 50.
11 Заказ № 683 329
а '" *
с*3,
ад
о
-т. Г ~ %
а:\ I ».■_.*.,. ^» .... % •%..%. ,.
С - * л * Г . . .
1%Ж(
* Ч-> G
Г**"-
. *■ ■
...-.-« «7-,'-1-
'Яг А;
1 Г
{.._.
Рис. 20.8. Фотография современной интегральной схемы большого размера, изготовленной на основе мо-
монокристалла кремния. (Фотография любезно предоставлена автору С Л. Милом из Калифорнийского тех-
но.юпнц-скпго имст|п\т;О
Полупроводники с РЛ-переходом
Здесь автору снова невольно вспоминаются те трудности, ко-
которые он испытывал, еще будучи студентом, когда стремился по-
понять физический механизм процесса, характеризуемого коэффи-
коэффициентом усиления C. Здесь может помочь следующее рассуждение.
Рассмотрим один электрон, приходящий в область базы из источ-
источника тока. Этот дополнительный электрон немного понижает по-
потенциальный барьер в обедненном слое А (рис. 20.6, о), облегчая,
таким образом, инжекцию дырок из области Е в область В. В рас-
рассмотренном примере это приведет к появлению 49 дополнительных
дырок, которые начнут диффундировать через базу в коллектор,
тем самым увеличивая ток /с. Но 50-я дырка испытает рекомби-
рекомбинацию с электроном, т. е. уничтожит его, так что восстановится
начальное распределение потенциала. В результате из-за поступ-
поступления на базу только одного электрона на коллектор попадает 50
дырок, т. е. C = — 50. Современная интегральная электронная
схема, изготовленная на основе монокристалла кремния, показана
на рис. 20.8. Важный тип транзистора — так называемый полевой
транзистор — обсуждается в задаче 8.
Задачи
1. Найдите распределение ноля и потенциала для РМ~перехода, в котором
избыточная концентрация примесей изменяется линейно с расстоянием й
от значения Л'р в Л'-области до значения Ы\ в Р-области.
2. Покажите, что внутри обедненного слоя полупроводника при нулевом
напряжении справедливо соотношение р (х) п (х) —- щ. Проведя термоди-
термодинамическое рассмотрение, покажите, что, когда внешнее напряжение
отсутствует (Уа = 0), полный ток через РМ-переход равен нулю. Оце-
Оцените порядки величин и продемонстрируйте справедливость неравенства
B0.10).
3. Покажите, что при наличии приложенного напряжения Уа концентра-
концентрации носителей электрического тока п. (х) и р (х) в обедненном слое удов-
удовлетворяют соотношению
П(х)р(Х) ■- пУГакТ.
4. Выведите формулу для толщины обедненного слоя, электрической емко-
емкости и высоты барьера при отличном от нуля напряжении, приложенном
к контакту металла с полупроводником (Л'-типа), у которого уровень
Ферми лежит точно посредине запрещенной зоны.
5. Покажите, что при А'р > Л^ концентрация N,4 (х), где х — положение
края обедненного слоя со стороны Р-области, дается формулой
в которой С — электрическая емкость единицы площади перехода, Vа —
приложенное внешнее напряжение. Поскольку х зависит от Уа, вышепри-
вышеприведенная формула показывает, что величину Ыа (х) можно определить,
измеряя зависимость С от Vа.
6. Изобразите на рисунке, подобном рис. 20-6, различные кривые для тран-
транзистора с Л'РЛ'-переходом. Качественно объясните, как он работает.
И* 331
Глава 20
7. Выведите формулу для параметра а для транзистора с РЛ'Р-переходом
с учетом ненулевой электронной составляющей эмиттерного тока /д.
Другими словами, считайте, что вкладом электронов, проходящих через
обедненный слой А справа налево, нельзя пренебречь по сравнению с
вкладом дырок, движущихся слева направо.
8. Рассмотрите работу показанного на рис. 20.9 устройства (полевого тран-
транзистора на контакте металл—полупроводник). Легированный (Л'-типа)
слой толщиной I (порядка 2 мкм) выращивается .методом эпитаксии (в виде
монокристалла) на диэлектрической подложке, обладающей той же кри-
Источник
Сток
Полупроводник
М-типа
Рис. 20 9.
сталлической структурой. Сильно легированные (металлизированные)
области Л'-типа, называемые «источником» и «стоком», служат электро-
электродами. Из-за наличия обедненного слоя толщиной ш электронный ток мо-
может течь только по каналу шириной й. Так как 1У зависит от напряжения
У со на контакте металл—полупроводник, полный ток /,$д определяется
запирающим напряжением Уев-
Считая известной концентрацию примесей Л'д и электропроводность
Л'-областей, используйте результаты задачи 4, чтобы получить формулу
для крутизны вольтампернои характеристики
для рассматриваемого полевого транзистора.
ГЛАВА 21
ПОЛУПРОВОДНИКОВЫЙ ИНЖЕКЦИОННЫЙ ЛАЗЕР
В настоящее время на наших глазах совершается революция
в технике связи. Передача информации (телефонные разговоры,
телевизионные программы, ЭВМ с периферийными устройствами
и т. д.), осуществляемая в настоящее время с помощью электриче-
электрических сигналов, распространяющихся по металлическим проводам,
уступает место передаче информации с помощью световых импуль-
импульсов, распространяющихся по стеклянным волокнам толщиной
меньше человеческого волоса. Огромные неоспоримые преимущества
этого вида связи состоят в следующем:
1. Потери мощности сигнала чрезвычайно малы (меньше
1 дБ/км). 2. Число создаваемых информационных каналов потен-
потенциально чрезвычайно велико, так как можно использовать очень
короткие импульсы (длительностью меньше 100 с), каждый из
которых передает один бит информации и которые можно включать
и выключать с огромной скоростью A010 бит/с). 3. Диаметр оптиче-
оптического стеклянного волокна очень мал A0—100 мкм).
Реальное осуществление связи с помощью оптических волокон
стало возможным лишь после того, как в 1962 г. был изобретен
полупроводниковый инжекционный лазер. Этот, пока что единст-
единственный лазер накачивается электрическим током, поэтому его
легко вводить в электронные схемы, используемые в современных
линиях связи. Кроме того, длины волн @,8 мкм<Я,<;1,6 мкм)
излучения такого лазера попадают в оптимальную область для пе-
передачи по оптическому стеклянному волокну (малые потери, малая
дисперсия групповой скорости сигнала).
Сведения из физики полупроводников, которые читатель уже
получил из предыдущих глав, вполне достаточны для качественного
понимания принципов работы полупроводникового инжекцион-
ного лазера. С количественной теорией можно познакомиться по
литературе, приведенной в конце книги.
§ 21.1. Поглощение света
и оптическое стимулированное излучение
в полупроводниковом кристалле
В сильно легированном полупроводнике уровень Ферми должен
сдвигаться либо в зону проводимости, если примесь донорная,
либо в валентную зону, если примесь акцепторная. Такие полу-
«33
Глава 21
проводники называются вырожденными. Их зонная структура по-
показана на рис. 21.1.
В согласии с законом распределения Ферми—Дирака
B1.1)
при Т = О К все электронные состояния с энергией ниже ЕР за-
заняты, а все состояния с энергией выше Ер свободны, как показано
Рис. 21.1. а — энергетические зоны вырожденного полупроводника У-типа
при Т = О К; б — энергетические зоны вырожденного полупроводника
Р-типа при Т = О К- Заштрихованы области, полностью заполненные элек-
электронами. Светлые кружки обозначают незанятые состояния.
на рис. 21.1. Таким образом, вырожденный полупроводник ведет
себя как металл, электропроводность которого не обращается в нуль
при нулевой температуре. Незанятые состояния в валентной зоне
мы называем дырками. Они ведут себя как электроны, с той лишь
разницей, что их заряд положителен (так как дырка на самом деле
есть «недостающий» электрон). Энергия дырки на энергетической
диаграмме отсчитывается по направлению вниз.
Чтобы понять, почему энергия дырки возрастает при смещении
на энергетической диаграмме сверху вниз, обратимся к рис. 21.1, б.
Когда мы говорим, что дырка возбуждается и переходит из состоя-
состояния А в состояние В, которое на энергетической диаграмме распо-
расположено ниже состояния А, мы на самом деле имеем в виду электрон,
который переходит из состояния В в состояние А, а этот процесс
требует затрат положительной энергии.
Межзонные переходы и поглощение света полупроводником.
Как и в обычных лазерах, усиление электромагнитного излучения
в полупроводниковом лазере представляет собой эффект, обратный
эффекту поглощения. Таким образом, чтобы добиться усиления,
334
Полупроводниковый инжекционный лазер
необходимо «перевернуть» занятые и незанятые состояния. Кроме
того, необходимо хорошо понимать физическую природу происхо-
происходящих электронных переходов.
Гамильтониан взаимодействия электрона в полупроводнике
с оптическим электрическим полем
ё(г, 0=^#о*(в>'~копт'Г)-1"Компл. сопр., B1.2)
направленным по предположению вдоль оси х, имеет вид
Х- ^ 1^. (У (и/-копт-) + Компл_ сопр_) B1 3)
Чтобы с помощью формулы A1.32) временной теории возмущений
найти скорость перехода электрона из валентной зоны (состояние
в ней обозначаем буквой V) в зону проводимости (состояние в ней
обозначаем буквой с) под действием электрического поля & (г, /),
необходимо вычислить следующий матричный элемент:
Ж ^_^[и;к(г)иск(г)хе'(к''к^К"")ТA\ B1.4)
где мы использовали формулу A7.35) для электронных волновых
функций. Из-за сильных осцилляции фазового множителя
с(к ~к~к»»т)'г в B1.4) значения матричного элемента Жас очень малы,
за исключением случаев, когда с хорошим приближением выпол-
выполняется условие
к'-к-ко,,,, B1.5)
В оптическом диапазоне копт ~= 2п,"К —. 105 см, в то время как
для электронов, если только не рассматривать области непосредст-
непосредственно вблизи границ зон, |к'— к|~ к ^ 10ч см. Поэтому можно
считать, что кот = 0, после чего приведенное выше условие для
переходов, идущих с заметной скоростью, примет вид
к'^к. B1.6)
Таким образом, переходы в основном имеют место между началь-
начальными и конечными состояниями с одним и тем же вектором к. Это
условие назовем условием сохранения квазиимпульса.
Вычислим теперь коэффициент поглощения а (со) плоской
электромагнитной волны с угловой частотой со, распространяю-
распространяющейся в нелегированном (собственном) полупроводнике, зонная
диаграмма которого показана на рис. 21.2. Как мы только что ви-
видели, квазиимпульс сохраняется, поэтому на диаграмме переход
изображается вертикальной стрелкой. Пусть образец находится
в тепловом равновесии, а уровень Ферми расположен посредине
запрещенной зоны, далеко от границ валентной зоны и зоны
проводимости, так что все уровни в валентной зоне заполнены,
335
Глава 21
а все уровни в зоне проводимости -— пустые. Удобнее всего
исходить из формулы A1.32) для вероятности перехода из состоя-
состояния а в состояние Ь в единицу времени:
й
Согласно рис. 21.2, для перехода, обозначенного вертикальной
стрелкой,
р р й^2 / 1 | _}
" 2 \ тс ' га
Отнесенную к единице времени вероятность одного перехода можно,
Зона проводимости
Рис. 21.2. Поглощение фотона в полупроводнике в результате перехода
электрона из занятого состояния (а) в валентной зоне в пустое^состояние (Ъ)
в зоне проводимости.
таким образом, вычислить по формуле
й
где
т = -
2т
Йсо
B1.8)
обозначает приведенную массу электрона. Полное число N пере-
переходов, совершающихся в единицу времени в кристалле объемом V,
получим, умножая B1.8) на р (к), т. е. на число электронных со-
состояний в единичном интервале к (при фиксированном объеме V),
а затем интегрируя по всем значениям к. Используя формулу
A5.50), получаем
336
Полупроводниковый инжекционный лазер
Вводя новую переменную интегрирования
2т
последний интеграл можно представить в виде
B1.10)
где Нгкг12т = Йсо—Е^. Коэффициент поглощения определяется
формулой
, ч Поглощенная мощность в единице объема Л'Аш/К
а (со) — — ,
Падающая на единицу площади мощность 8 п^2/2
B1.11)
где п — показатель преломления полупроводникового кристалла,
с — скорость света в пустоте, <§Г0 — амплитуда электрического
поля. Используя B1.10), непосредственно получаем
схо((о)==К(/гсо — Е/2, B1.12)
причем коэффициент К рассчитывается по конкретным данным для
каждого данного полупроводникового электронного перехода. Для
арсенида галлия (ОаАз), например, имеем
Яв=1,5 эВ.
тс = 0,065 те,
где те — масса свободного электрона, поэтому
К = 6-103 см-1/
Таким образом, для частоты, при которой энергия фотона превы-
превышает ширину запрещенной зоны Ее, скажем на 0,01 эВ, коэффи-
коэффициент поглощения а0 (со) = 6-103-10 = 600 см-1.
Предположим теперь, что нам как-то удалось «приготовить»
полупроводниковый кристалл таким образом, что все его состоя-
состояния, расположенные вплоть до некоторого уровня в зоне проводи-
проводимости, оказались заполнены электронами, а все состояния, распо-
расположенные выше некоторого уровня в валентной зоне,— пустыми.
Энергетическая диаграмма такого кристалла показана на рис. 21.3.
При Т = 0 К все состояния зоны проводимости вплоть до «квази-
«квазиуровня» Ферми Ер, заполнены, а все состояния валентной зоны
выше «квазиуровня» Ферми Ер незаполнены. Расчет зависимости
337
Глава 21
коэффициента поглощения а от энергии фотона Йсо для такого кри-
кристалла проводится в точности так же, как расчет коэффициента
а0 (<°) 1см. B1.11)]. Но, так как теперь верхние состояния запол-
заполнены, а нижние незаполнены, коэффициент поглощения меняет
знак. Иными словами, излучение должно теперь усиливаться, а не
поглощаться. Таким образом, для полупроводника, энергетиче-
энергетическая диаграмма которого изображена на рис. 21.3, получаем
— ао(и>)^—К (На — ЕеУ^
при
при
при Ны>Ерс—Ер^ B1.13)
т
77
Рис. 21.3. Полупроводник с вырожденными электронной и дырочной насе-
ленностями. В противоположность рис. 21.2 для частоты и коэффициент
поглощения отрицателен, и возникает эффект усиления. Черные кружки
изображают занятые электронами состояния, светлые кружки — незанятые
состояния.
причем в области Ее<сН(»<сЕр — ЕР имеем усиление, а в области
На>^>Ер —ЕР — поглощение.
Вышеприведенные соображения впервые высказал Думке [55],
первым предсказавший осуществимость лазера на полупроводни-
полупроводниках и оценивший их возможности. Согласно приведенным выше
соображениям, в арсениде галлия, например для которого
/№—Ее = 0,01 эВ, коэффициент, стоящий в показателе экспо-
экспоненты (т. е. коэффициент а0, входящий в формулу / — 10е~а'г),
равен 600 см. Поэтому коэффициент усиления для такого полу-
полупроводника с инверсной населенностью должен быть равен 600 см.
Это обстоятельство убедительно говорит в пользу создания лазе-
338
Полупроводниковый инжекционный лазер
ров на основе полупроводников с сильным оптическим поглоще-
поглощением.
Пока что мы рассмотрели случай нулевой температуры. При
отличной от нуля температуре в выражении для скорости переходов
вверх величину B1.9) нужно умножить на вероятность того, что
нижний уровень а занят, а верхний уровень Ь свободен, поскольку
переход не может начаться из пустого состояния и закончиться
в уже занятом состоянии. Указанный множитель равен
Д, (Еа) У — /с (Еь)]. Чтобы получить результирующую скорость
переходов вверх (поглощение), нужно вычесть из скорости перехо-
переходов вверх (а -*- Ь) скорость обратных переходов вниз (Ь -*~ а). Мат-
Матричный элемент имеет тот же вид, и интегрирование в выражении
для скорости обратного перехода производится так же, как и для
прямого перехода 1см. B1.9)], только теперь, при ненулевых тем-
температурах, необходимо умножить скорость на множитель
/г (Еь) [1 —Д, (Еа)], который дает вероятность того, что верхний
уровень Ь (в зоне проводимости) занят, а нижний уровень а (в ва-
валентной зоне) — незанят.
Избыток числа переходов вверх (поглощение) над числом пе-
переходов вниз (усиление), совершаемых за одну секунду, теперь
дается формулой B1.9), в которую входят упомянутые множители,
представляющие собой вероятности занятости и незанятости уров-
уровней :
\ 2т
-Е„— /ко 1 кЫк =
' ё }
о \ 2т /
-Й<о) кЧк, B1.14)
/
Й2А2
где Еь-Еа = Е„+ Л1_=йю. B1.14а)
в 2т
Из формулы B1.14) вытекает ряд важных следствий.
Условием усиления электромагнитного излучения является не-
неравенство Nа^ь<^Ыь а, которое, согласно B1.14), выполняется
при условии
!ЛЕь)-1„(Е^>0. B1.15)
Используем в этом неравенстве формулу закона распределения
Ферми—Дирака B1.1) с «квазиуровнями» Ферми ЕР в валент-
валентной зоне и Ер в зоне проводимости. Тогда придем к заключению,
что должно выполняться следующее неравенство:
Ерс-ЕРп>П(о. B1.16)
339
Глава 21
Оно представляет собой так называемое условие Бернарда—
Дураффурга для инверсной населенности в полупроводниковом
кристалле. Отметим, что при тепловом равновесии ЕР = ЕР< и
полупроводник, таким образом, либо прозрачен, либо поглощает
свет на всех частотах.
а
Рис. 21.4. Построение кривой зависимости коэффициента усиления у (<о) от со.
Штриховые кривые на рисунках виг соответствуют более высокой степени
возбуждения. В этом случае точка 1 смещается вправо, что приводит к уве-
увеличению 1'макс и частоты, на которой максимум наблюдается.
Вернемся к формуле B1.14). Интегрирование в ней можно про-
провести так же, как в B1.11); в результате получается совсем простая
формула
так что для коэффициента усиления у (со) — — а (со) имеем
у(в>) = ао(в>)\?с(Еь)—Ь(Еа)], B1.17)
причем энергии Еа и Еь удовлетворяют условию B1.14).
Из формулы B1.17) видим, что максимальное усиление, кото-
которое можно получить с данным полупроводниковым кристаллом на
частоте со, численно равно а0 (со) — коэффициенту поглощения
этого полупроводника при нулевой температуре. Чтобы получить
максимальное усиление, необходимо возбудить кристалл таким
образом, чтобы выполнялись условия Д. (Еь) = 1 и Д, (Еа) = 0.
Тогда верхний лазерный уровень (лежащий в зоне проводимости)
340
Полупроводниковый инжекционный лазер
заполнен [Д (Еь) = 1 ], а нижний уровень (лежащий в валентной
зоне) незаполнен [Д (Еа) = 0].
Величина а0 (со), т. е. коэффициент поглощения собственного
полупроводника при нулевой температуре, не зависит от темпера-
температуры и от характера населенности уровней. Отсюда следует, что
—*\ I-*— Активный слой
I I
Ш"'/,> -у/^:у,
Рис. 21.5. Вырожденный РЛ'-переход: а — при нулевом приложенном на-
напряжении; б — при отпирающем напряжении Уа ~ Ее/е. Область, содер-
содержащая и электроны и дырки, называется активным слоем. Волнистая стрелка
изображает процесс рекомбинации электрона с дыркой в активном слое,
приводящий к испусканию фотона с энергией Йсо = ЕР —ЕР .
гс ^V
зависимость коэффициента усиления у (со) от температуры и спо-
способов возбуждения уровней должна содержаться в множителе
[/г (Еь)-—Д (Еа) ], входящем в формулу B1.17). Справедливость
этого заключения можно оценить, обращаясь к рис. 21.4, где пред-
представлен график функции B1.17). Он позволяет сделать два вывода.
Во-первых, при усилении возбуждения уменьшается число носи-
носителей тока в обеих зонах, а потому увеличивается максимально
возможное усиление уывкс, как показано штриховыми кривыми
на рис. 21.4, в и г. Во-вторых, при повышении температуры уши-
341
Глава 21
ряется переходная область функции распределения Ферми—Ди-
Ферми—Дирака, что, согласно рис. 21.4, г, приводит к уменьшению ум,1КС.
Лазер на РЛ-переходе. Впервые лазерное действие полупровод-
полупроводниковых кристаллов было продемонстрировано на кристалле арсе-
нида галлия с вырожденным РА^-переходом. При инжекции силь-
сильного тока в таком переходе около обедненного слоя возникает об-
область с вырожденной населенностью как электронов, так и дырок.
На рис. 21.5 показан вырожденный РМ-переход. При нулевом
приложенном напряжении (или при малых напряжениях), как
видно из рис. 21.5, а, условие Ер—Ер >/гсо не выполняется и уси-
усиление отсутствует. Если приложенное к переходу отпирающее на-
напряжение примерно равно по величине напряжению Е&е, как
показано на рис. 21.5, б, то образуется активный слой с вырожден-
вырожденной населенностью как электронов, так и дырок. При частоте со
выполняется условие усиления Цы<^Ер —Ер^ и электромагнит-
электромагнитное излучение с частотой со, заключенное в пределах активного
слоя, усиливается.
Толщину активного слоя можно определить, оценив расстояние,
которое электрон, инжектированный в Р-область, может пройти
(в результате диффузии) до акта рекомбинации с дыркой, т. е. до
перехода в валентную зону. Поскольку коэффициент диффузии
^ ^ 10 см2/с, время рекомбинации /,^10^8с, для толщины актив-
активного слоя получаем ]' Ш, ~ 10~4 см. Как видим, толщина
этого слоя очень мала.
Сначала для создания РА^-переходов в кристаллах ОаАз ис-
использовалась диффузия акцепторных атомов, например атомов
цинка, в А^-область кристалла ОаАз. При этом диффузия атомов 2п
происходила из нанесенного на поверхность кристалла слоя с очень
высоким значением концентрации акцепторов (ЫА --- 10го см^3),
а ^-область предварительно легировалась атомами донорной при-
примеси, концентрация которых имела порядок 1018 см~3. В качестве
донорной примеси чаще всего использовался теллур Те.
Теперь кристаллы ОаАз для полупроводниковых лазеров вы-
выращивают методом эпитаксии, а именно наращивают поочередно
различным образом легированные слои на подложку; таким образом
получается так называемая двойная гетероструктура ОаАз'ОаА1Аз.
Подробнее об этом мы расскажем несколько ниже. На рис. 21.6
схематически изображен полупроводниковый лазер с РА'-перехо-
дом. Оптический резонатор, который необходим для поддержания
оптических колебаний в полупроводниковом лазере, образуется
двумя отполированными противоположными гранями кристалла.
У кристаллов ОаАз часто используются грани (ПО) — естественные
плоскости спайности.
В современных полупроводниковых инжекционных лазерах
используется сложная многослойная структура, выращенная ме-
342
Полупроводниковый инжекционный лазер
тодом эпитаксии из жидкой или газообразной фазы. В такой струк-
структуре активным слоем служит слой кристалла ОаАз, в котором про-
происходит генерация света в результате стимулированной электронно-
дырочной рекомбинации. Слой ОаАз заключен между двумя вы-
выращенными одновременно с ним слоями кристалла Оа^^А^Аз.
В кристалле Оа^^А^Аз доля х атомов галлия замещена атомами
алюминия. По сравнению с ОаАз кристалл Оа^-Д^Аз характе-
характеризуется большей шириной запрещенной зоны и меньшим показа-
показателем преломления. Полупроводниковый лазер на двойной гетеро-
структуре показан на рис. 21.7. Вся структура представляет со-
собой единый кристалл.
Отполированная
грань
Р-область,
легированная 2п
Ы-область
Отполированная
грань
Лазерный
пучок ,
Переход
Рис. 21.6. Полупроводниковый лазер с РЛ'-переходом на основе кристалла
ОаАз. Две параллельные плоскости спайности кристалла служат отражате-
отражателями лазерного резонатора.
Основная причина использования в полупроводниковом лазере
ограничивающих слоев Оа^-Д^Аз заключается в следующем.
Слой ОаАз имеет больший показатель преломления, чем слой
Оа^^А^Аз, поэтому лазерное излучение, распространяющееся
в ОаАз, испытывает полное внутреннее отражение от границ раз-
раздела с соседними слоями. В результате лазерное излучение не мо-
может выйти за пределы активного слоя, типичная толщина кото-
которого составляет 2000 А; описанная система исключает дифракцион-
дифракционные потери. Такая пространственная ограниченность генерируе-
генерируемого светового пучка увеличивает интенсивность лазерного света,
а следовательно, и величину лазерного усиления.
Распространение света в плоскопараллельном слое, показатель
преломления которого больше показателя преломления окруже-
окружения, можно математически описать, используя теорию мод в диэ-
диэлектрическом волноводе. Знать поведение этих мод совершенно
необходимо, чтобы полностью понять принцип работы инжекцион-
ного лазера. Подробности читатель может найти в соответствующей
литературе, указанной в конце книги.
343
Глава 21
Грань
A10)
Золото
Распределение
интенсивности
лазерного
излучения
Лазерное
излучение
• Электроны
о Дырки
Рис. 21.7. Полупроводниковый лазер на двойной гетероструктуре
СаА$/СаА1А$. Электроны и дырки инжектируются в активный слой кри-
кристалла ОаАз из слоев Са^яА^Аз соответственно Л'- и Р-типа. Излучение
с частотой, близкой к \'= Е^/Н, усиливается в результате стимулированной
электронно-дырочной рекомбинации.
I
\
100
80
60
'
о
0,2330
Ц2370 0,1410
Энергия фотонов, эВ
0,2450
Рис. 21.8. Спектр инфракрасного излучения, испускаемого лазерным дио-
диодом из 1пЗЬ, к которому приложено отпирающее напряжение выше и ниже
порога генерации, Т = 1,7 К- Широкий спектр ниже порога обусловлен
спонтанной рекомбинацией электронов и дырок. Ширина узкой линии выше
порога генерации определяется только разрешающей способностью спектро-
спектрометра. Масштаб по оси ординат для линии, генерируемой выше порога,
уменьшен, чтобы линия уместилась вместе со спектром излучения, испу-
испускаемого ниже порога. В действительности площадь, ограничиваемая этой
линией, много больше площади, ограничиваемой «допороговой» кривой.
344
Полупроводниковый инжекционный лазер
Рекомбинационная эффективность полупроводникового лазер-
лазерного перехода определяется величиной вероятности того, что ин-
инжектированный в переход носитель заряда испытает рекомбина-
рекомбинацию, сопровождающуюся излучением фотона. Для некоторых хо-
хороших полупроводниковых материалов (ОаАз, Оа1пА5Р, СаА1Аз)
рекомбинационная эффективность достигает 50 %. Из рис. 21.5, б
видно, что энергия фотона, которую он получает при электронно-
дырочной рекомбинации, практически равна ширине запраценной
Электрический
модулирующий
сигнал
Оптическое
волокно
Активный
слой 0аА5
Рис. 21.9. Полупроводниковый лазер на двойной гетероструктуре
СаА5/ОаА1А5, модулируемый электрическими сигналами, которые включают
и выключают лазер. Эта модуляция превращается в серию оптических им-
импульсов, которые распространяются по оптическому волокну и достигают
приемного устройства.
зоны Ее. Поскольку приложенное к переходу отпирающее напря-
напряжение ]/а при больших токах, необходимых для превышения по-
порога генерации лазерных колебаний, практически равно Ее/е, от-
отношение энергии испущенного фотона к энергии, затраченной
(источником тока) на перенесение одного электрона по цепи, почти
равно единице. Таким образом, полупроводниковый инжекцион-
ный лазер представляет собой очень эффективный преобразователь
электрической энергии в световую.
Типичный спектр выходящего светового пучка ниже и выше
порога генерации показан на рис. 21.8.
Наконец, на рис. 21.9 схематически изображен диодный полу-
полупроводниковый лазер на двойной гетероструктуре, сигнал от ко-
которого распространяется по стеклянному волокну оптической ли-
линии связи.
345
Глава 21
Задачи
1. Несколько идеализированная модель диэлектрического волновода для
диодного лазера на двойном гетеропереходе изображена на рис. 21.10.
Электромагнитные моды (или электромагнитное излучение с частотой
со/2п) удовлетворяют следующему скалярному волновому уравнению:
' =0.
7 ~ 3/ оо О*СЕ. 1--^А*-т-/\5
х-О,3м км
ОаА$
Рис. 21.10. Двумерный плоский вол- Рис. 21.11. Типичный волновод для
новоя- лазера на двойной гетероструктуре
СаАз/СаА1Л$.
Предположив, что решение этого уравнения имеет вид
Е, =-- А [в ( ч >и (х),
найдите функцию // (х) и константу распространения Р/. Покажите, что
для достаточно малых значений параметра (й/к) л/п2 п2 может сущест-
существовать только ограниченная в пространстве мода (т. е. мода, экспонен-
экспоненциально убывающая с ростом х).
Указание. Эта задача формально эквивалентна рассмотренной в § 4.2
задаче об электроне, движущемся в конечной потенциальной яме. Гра-
Граничные условия также аналогичны использованным в § 4.2, а именно
Еу и дЕу/дх должны быть непрерывны на поверхности раздела и обра-
обращаться в нуль при х = ± оо,
2. а. Найдите модовую функцию /0 (х) и константу распространения Рй
моды самого низкого порядка для волновода, показанного на рис. 21.11.
б. Нарисуйте график модовой функции /0 (х).
в. Какая доля энергии моды распространяется внутри активного слоя?
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1. РШпск М.— Апп. РЬу<=., 4, 553 A901).
2. ЕтвШп А.— Апп. РНуз., 22, 180 A907).
3. ВеЬуе Р.— Апп. РЬуз., 39, 789 A912).
4. Оаг'ыюп С, Сегтег I,— ЫаШге, 119, 558 A927).
5. КИШ С. 1п*го<к1сНоп Ю ЗоПй 31а1е РЬузкз, 5 1Ь. ей. (Л. \УПеу & Зопз,
Не\у Уогк, 1974). [Имеется перевод: Киттель Ч. Введение в физику
твердого тела.— М.: Наука, 1963.]
6. ЯиНгефгё Е.— РЬП. Ма§., 21, 669 A911).
7. ВоНг И.— РЬН. Ма§., 26, 476 A913).
8. ВоНт О. (Эиап1шп ТЬеогу (Ргеп11се-На11, Еп§1е\\'оой С1Шз., N. Л., 1955).
[Имеется перевод: Бом Д. Квантовая теория.— М,: Наука, 1965.]
9. ЗНаппоп С. Е., ЧХ/еауег Ш. ТИе Ма4ЬетаНса1 ТЬеогу оГ Соттип1са41оп
(ип1уегз|4у оГ ИПпеш Ргезз, игЬапа, III., 1949).
10. Вот М., и;'о// Е. Рппар1е8 оГ Ор^сз, Згй ей. (Рег^атоп, Неш Уогк,
1965). [Имеется перевод: Борн М., Вольф Э. Основы оптики.— М.:
Наука, 1970.]
11. Цато 5., ШШппегу /. /?., Уап Вигег Т. Ие1й& апс! Шауез 1П Соттипг-
са4юп Е1ес4гоп1С8 (ЛоЬп ШЛеу & Зопз, Не\\- Уогк, 1965).
12. Ье1'§Н1оп /?. В- Рг1пс1р1е8 оГ Мос1егп РЬу81С8 (МсО^аVV-Н^1I, Неш Уогк,
1959).
13. Уаг1г А. 1п4гойис41Оп 4о Ор41са1 Е1ес4гопгс8, 2пй ей. (НоН КгпеЬаг4
апй №ш8(оп, Ыеш Уогк, 1976).
14 81егп О,— 2. РЬу31к, 7, 249 A921).
15. ОеПасН Ш., 81ет О,— 2. РЬувгк, 9, 349 A922).
16. Оег1асН Ш., 81егп О,— Апп.'РЬуз., 74, 673 A924).
17. [ЦсМтеуег Р. К. Кеппагй Е. И. 1п4гойисиоп 4о Мойегп РЬукгсз. (Мс-
Огаш-НШ, Ыеш Уогк, 1933).
18. Вготт Р. С. ТИе РЬуисв оГ ЗоПйв (Веп]'агпш, Ыеда Уогк, 1967).
19. Кагр1ия /И., Роггег /?. N. А4отк апй Мо1еси1е$ (Веп]'ат1п, Меп1о Рагк,
СаПЬ, 1970).
20. НеЫепЬег^ Ш. ТЬе РИув1са1 Рг1пс1р1е8 оГ РиапШт ТЬеогу (Ш1Уег$Ну
оГ СЬ1са§о Ргекк, 1930). [Имеется перевод: Гейзенберг В. Физические
принципы квантовой теории.— М.: ГТТИ, 1932.]
21. Сопйоп Е. V., 8когИеу О. И. ТЬе ТЬеогу о{ А1огшс Зрес1га (СатЬгг^е
ишуегейу Ргезз, Ыеш Уогк, 1959). [Имеется перевод : Кондон Е.,
Шортли Г. Теория атомных спектров.— М.: ИЛ, 1949.]
22. ЕшиШп Л.— РЬуз. Ье11., 18, 121 A917).
23. тске Я. Н.~- РЬук- Кеу., 93, 99 A954).
24. 8сНаШоы> А. I., Тошпеа С. Н.— РЬуз. Ке\-., 112, 1940 A958).
25. В1осН Р., Нап&еп Ж'. Ш., Раскагй Н. М.— РЬуз. Кеу., 70, 960 A946).
26. ШеЬег /.— ЩЕ Тгапз. Рго{. Огоир оп Е1ес1гоп Оеугсез, 3, 1 A953).
27. Оогйоп /. Р., 2,ещег Н. /., Тохюпеа С. Н.— РЬуз. Кеу., 95, 282 A954).
28. Согйоп 1. Р., 1ещег Н. /., Тошпеи С. Я,— РЬуз. Кеу., 99, 1264 A955).
29. Басов И. Г., Прохоров А. М.— ЖЭТФ, 27, 431 A954).
30. Басов Н. Г., Прохоров А. М.— ЖЭТФ, 28, 249 A955).
31. Ма(тап Т. Н.— На1иге. 187, 493 A960).
32. РаЬгу С, Рет1 Л,—Апп. Опт. РИуз., 16, 115 A899).
33. Рог к Я. /-., НетоИ В. /?., Ко^еШк П.— Арр1. Ор!.. 3, 1471 A964).
347
Цитированная литература
34. То1тап Я. С. ТЬе Рппар1е5 оГ 54аН841са1 МесЬашсз (ОхГогс!
Ргевв, ОхГогё, 1959).
35. КИМ С. Е1етеп1агу 51аИ8Иса1 РЬузкз (ЛоЬп \УПеу & Зопк, Не™ Уогк,.
1967). [Имеется перевод предыдущего издания: Киттель Ч, Элементар-
Элементарная статистическая физика.— М.; ИЛ, 1960.]
36. В1осН Р.— 2. РЬуик, 52, 555 A928).
37. ВгШошп Ь. \Уауе Ргора^аиоп ш РепосПс 31гис4уге$ (МсОгаш-Н1П,.
Ме\у Уогк, 1946).
38. УЫепЬеск О. П., Ооий&тН 5,— На1игич88., 13, 953 <1925).
39. УЫепЬеск О. Е., СоийятИ 5,— НаШге, 117, 264 A926).
40. О1гас Р. А. М.~- Ргос. Коу. Зое, А117, 610 A928).
41. В1осН Р., Нап&еп Ш. Ш., Раскагё Н. М.~- РЬуз Кеу., 69, 127 A946).
42. РигсеИ Е, М., Тоггеу, Роипй Н. V.— РЬуз. Кеу., 69, 37 A946).
43. АгпоЫ /. Г., ВкагтаН 5. 5., Раскагй М. Е.— ,]. СЬегп. РЬуз., 19. 507
A951).
44. Яатжу N. Р. Мис1еаг Мотеп1в (Л. Ц/Пеу & Зопз, Ке\у Уогк, 1953).
45. }аг'^ А. Риап4ит Е1ес4гоп1С8, 1$4. ей (ЛоЬп ШЛеу & Зопк, N6%- Уогк,
1967).
46. Иа}е /., Ие1жп Е., ИаЫ I.— РЬуз. Кеу., 71, 914 A947).
47. К1еррпег В., СоЫепЬещ N.. Яатяеу И.— РЬуз. Кеу., 126, 603 A962)
48. Ехюеп Н. I., РигсеИ Е. М.— На1иге, 168, 356 A951).
49. Кегг Р., Шеягегкоиг О, Са1асНс 34гис4иге. Уо1. 5 (Шгу. оГ СЬ1са§о Рге$5г
1964).
50. Мопп Р. /., МаИа /. Р.— РЬуз. Кеу., 96, 28 A954).
51. Наупея й. Я., 8Носк1еу 1Г,— РЬуз. Кеу., 75, 631 A949).
52. Вагйееп /., ВгаИат Ш. Н.— РЬуз. Кеу., 75, 1208 A949).
53. ЗНосЫеу Ш.~- Ве11 Зу81ет ТесЬ. Л., 28 A949).
54. Непокага М.— т: НапсШисЬ йег РЬузгк. 23 (Зрг1п§егЛ'ег1ай, ВегПп,
1969).
55. Битке Ш. Р.— РЬуз. Ке\'., 127, 1559 A962).
ЛИТЕРАТУРА, РЕКОМЕНДУЕМАЯ
ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
С, Сегтег I. Н. ТЬе 8саНепп§ оГ е1ес4гоп8 Ьу а $ш§1е сгукЫ оГ
пгскеЬ— Ка4иге, 119, 558 A927): ОШгасНоп оГ е1ес4гоп8 Ьу а сгу$Ы
оГ шскеК— РЬуз. Кеу., 30, 705 A927).
йе Вго^Не Ь. 1пуе$41§аНоп8 оп 4Ье 4Ьеогу оГ ^иап^а.— Апп. РЬу$., 3, 22 A925),
Е'м&Шп А. Оп а ЬеипзНс рот4 оГ уге^ сопсегпт§ 4Ье §епегаНоп апй 4гап8-
ГогтаНоп оГ П^Ы.— Апп. РЬуз., 17, 132 A905).
ЕшягеШ А., 1п[е1A I. ТИе Еуо1иНоп о? РЬузгсз (Ыеи' Уогк, 31топ & ЗсЬиз-
4ег, 1961). [Имеется перевод: Эйнштейн А., Инфельд Л. Эволюция фи-
физики,—М.: ГИТТЛ, 1956.]
Сатош) О. Мг. Тотркшз т \Уопс!ег1апс! апй Мг. Тотрк1п8 Ехр1оге$ 4Ье
А4от.—1п: Сатош О. Мг. Тотрктз 1п РарегЬаск (Ке\у Уогк, СатЬ-
г!Й§е Ш1Уег$Ну Рге$$, 1965).
Огау Р. Е., СатрЬеИ I., ЗеаНе I. Е1ес4готс Ргтсгр1е$ (Не%- Уогк, ЛоЬп
ШЛеу & Золе, 1969).
Напаек Т., 8сктт1оии А. /.., 8ег1ея О. ТЬе $рес4гит оГ а4огп1с Ьуйго^еп.—
ЗсгепШк Атег1сап, 240, N0. 3 A979).
МШег 8. Е., МагсаНН Е. А, /., Ы Т. КезеагсЬ 4о\уагй ор41са1 4гап8ГП1881Оп
8у81ет8,— Ргос. ШЕЕ, 61, 1703 A973).
8VеИо О. ]. Рппар1е8 оГ ^а8е^8 (Неш Уогк, Р1епит Рге88, 1976). [Имеется
перевод: Звелто О. Физика лазеров.— М.: Мир, 1979.]
5ге 5. М. РИу81С8 оГ Зет1сопйис4ог Оеу1се8(Не\у Уогк, \УПеу-1п1ег8С1елсе,
1969).
Ткотаоп О. Р., Яе1й А. ОгГГгасНоп оГ са4Ьойе гаув Ьу а 4Ып Шт.— На4иге,
119, 890 A927).
Ткотжп Р. Ехрептеп48 оп 4Ье (ИГГгасйоп оГ са4Ьойе гаув.— Ргос. Коу. Зое,
А117, 600 A928); А119, 651 A928).
КеН А. ТЬе АХИг&сХ'юп оГ са4Ьос!е гаув Ьу 4Ь1п се11и1о1й ГПтв.— Ргос. Коу.
Зое, А119, 663 A928).
У&п йег Ие1 А. ЗоПй 34а4е РЬу8гса1 Е1ес4гошс8 (Е§1ешоой СПГЬ, N. ^ .у
РгепПсе На11, 1976).
Уапг А. 1п4гос!исНоп 4о Ор41са1 Е1ес4гоп1С8 (Не\у Уогк, НоН, КшеЬаг4,
ШтвЮн, 1976).
Теория диэлектрических волноводов изложена в книге:
Уагю А. С^иапШт Е1ес4гопк$, 2пй ей. (Ые^- Уогк, }. ШЛеу & Зопз, 1975).
[Имеется перевод. Ярив А. Квантовая электроника.— М.: Сов. радио.
1980).
Дополнительную информацию о полупроводниковых лазерах можно
почерпнуть в книгах:
Ратяк М. В., Сааеу Н. С. Не4его$4шс4иге Ьазегз (№%■ Уогк, Асайегшс
Ргезв, 1978). [Имеется перевод : Кейси X., Паниш М. Лазеры на гете-
роструктурах.— М.: Мир, 1981.]
Випег /. К. 5егшсопёис1ог Ьазегз (Неш Уогк, ШЕЕ Ргезз, 1980).
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютно черное тело 11
Акт измерения 36
Алгебра матриц 117
Альфа-распад 60
Альфа-частица 60
Ансамбль систем 28, 154. 196
Антенна 47
Атом акцепторный 291
— водорода 20, 91
— гелиоподобный, возбужденное со-
состояние 114
основное состояние 112
— гелия 111
—двухуровневый 181
— донор ный 292
Атомная среда 180
Бегущие электромагнитные волны
160, 164
Бит 48
Бозоны 109, 217, 222, 225
Боровские орбиты 21
Боровский радиус 21, 94
Валентная зона 254
Валентные электроны 253
Вектор Пойнтинга 160
— электрической поляризации 190
Вероятность квантового перехода
151, 152
— нахождения частицы 43
— туннелирования 58
— экспериментального наблюдения
значения величины 38
Взаимодействие сверхтонкое 273
— электромагнитного излучения с
атомной системой 157
средой 180
Возмущение гармоническое периоди-
периодическое 149
— ступенчатое 152
Волна плоская электромагнитная 10,
15, 158
Волновая природа частиц 17
электрона 23
— функция 37, 136
вероятностная интерпретация
43, 137
в импульсном пространстве 46
— - физический смысл 43, 137
Волновод для лазера с гетерострук-
турой 346
Волновое уравнение 76, 158
— число комплексное 193
Волновые функции двухэлектронные
108
Восприимчивость электрическая
среды 192
Время жизни атома водорода 177
возбужденного атома 174
классической частицы 23
спонтанное 171, 177
для сверхтонкого перехода
284
— релаксации населенностей уров-
уровней 197
поперечное 198
Вырождение энергетических уров-
уровней атома водорода 101
Вырожденные населенности в полу-
полупроводнике 338
Гамильтониан во внешнем магнит-
магнитном поле 265
— гелиоподобного атома 111
— двухчастичной системы 97, 107
— для сферически-симметричного
поля 89
— модовый 163
— электромагнитного поля 161, 164
Гармонический осциллятор 63
Гауссово распределение 45
Гелий-неоновый лазер 211
Германий 291
Гетероструктура двойная 342
Гибридизация волновых функций 104
Главное квантовое число 93
Двухуровневая атомная система 195
Дельта-символ Кронекера 31
Детерминант слэтеровский 109
Детерминизм 9
350
Предметный указатель
Диагонализация квадратной ыат-
р ицы 119
Дипольный момент магнитный 263,
270
электрический 191
— переход для атома водорода, мат-
матричные элементы 178
Дираковские обозначения 32
Дисперсионное соотношение в мо-
модели Кронига—Пенни 247
Дисперсия среды 180
Дифракция брэгговская электронов
и нейтронов 18
— электромагнитных волн 47
Диффузия в полубесконечное про-
пространство 310
— носителей зарядов в полупровод-
полупроводниках 304
Диэлектрик 253
Диэлектрическая проницаемость
193
комплексная 192
Длина волны дебройлевская 18
комптоновская 17
— свободного пробега средняя
300
Доплеровское смещение 100, 279
— уширение линии 2Ю
Емкость РЛ'-перехода 321
Закон Рэлея—Джинса 12
Законы РЛ'-перехода 318
Золотое правило Ферми 152
Зона проводимости 254
Зоны Бриллюэна 248, 250
— запрещенные 248
— энергетические приведенные 250
Квазиимпульс электрона в кристалле
24, 258, 333
Квантование бегущих волн 164
— электромагнитных мод 160
— энергии электрического колеба-
колебательного контура 179
электромагнитного поля 12,
14
Квантовая механика 9, 23
— статистика 215
— физическая величина 36
Квантовое состояние системы 36
Квантовомеханическое представле-
представление 121
Когерентность 213
Коммутатор 37
Комптоновское рассеяние 15
Константа распространения волно-
волновой функции в кристалле 243
Контактная разность потенциалов
РЛ'-перехода 313
Континуум состояний 152
Концентрация дырок в собственном
полупроводнике 289
— электронов в собственном полу-
полупроводнике 288
и дырок в примесном полупро-
полупроводнике 295
Коэффициент диффузии 304
— отражения лазера Фабри — Перо
209
— прозрачности потенциального
барьера 58
— пропускания лазера Фабри—Перо
208
— усиления, пороговое значение 205
— — среды с инверсной населен-
населенностью 189
Коэффициенты излучения Эйнштей-
Эйнштейна 173
— Клебша—Гордана 133
Кремний 254, 291
Излучение абсолютно черного тела
11, 165
— спонтанное, интенсивность 174
— электромагнитное равновесное
тепловое 238
Измерение положения 35
Импульс фотона 15
Импульсное пространство 46
Инверсная населенность 203
Индуцированные переходы 169
Информация 48
— скорость передачи 49
Лазер гелий-неоновый 211
— инжекционный 212, 345
— полупроводниковый 342
— рубиновый 212
— Фабри—Перо 205
Лазерное собственное колебание
207
Лазерный генератор 203
— диод 344
— усилитель 189
Лапласиан 89
Легирование 259, 262
351
Предметный указатель
Магнитный дипольный момент атом-
атомного ядра 270
орбитальный электрона 265
спиновый электрона 263
Мазер водородный 278
Матрица единичная 117
— квадратная 119
— обратная 117
— плотности 153, 194
-- преобразования 122
— трансформационная 245
— унитарная 118
— эрмитова 118
.Матрицы операторов момента коли-
количества движения 127. 128
Матричный метод Гейзенберга 117
Металл 253
Метод Лагранжа неопределенных
множителей 224
— разделения переменных 98
Модель Кронига—Пенни 241
— Резерфорда 20
Моды электромагнитного поля 160
средняя тепловая энергия
167
Момент количества движения 39, 77
— — — коммутационные соотноше-
соотношения 86
матрицы 124, 126, 127
орбитальный 129
собственные функции и
числа 83
Моментов количества движения сло-
сложение 131
Мощность шумов 49
Напряжение на РЛ'-переходе, запи-
запирающее и отпирающее 317
Населенность уровней 172
инверсная 203
условие Бернирда—Дураф-
фурга 340
Неразличимые частицы 221, 222
Несвязанные решения 59
Носители зарядов в полупроводни-
полупроводниках 286, 295
неосновные 318, 324
Нулевые колебания 168
Ньютонова механика 9
Одномерные задачи 51
Оператор единичный 33
— импульса 40
— перестановки 108
— плотности 154
— рождения 73, 163
— трансляции 242
— уничтожения 73, 163
— четности 64
— энергии 43
Операторы 25
— квантовомеханические, представ-
представление матрицами 121
— коммутирующие 41
— линейные 26
— момента количества движения
частицы 39, 77
— рождения и уничтожения элек-
электромагнитные 163
— эрмитово сопряженные 29
— эрмитовы 28
Орбитали гибридизованные 105
— связывающие 292
Ортосостояния 115
Парасостояния 115
Перестановочные соотношения для
мод электромагнитного ноля 162,
163
момента количества движе-
движения 125
операторов координаты и
импульса 41
рождения и уничтоже-
уничтожения 75
Переходы квантовые спонтанные и
индуцированные 157, 172
— межзонные в полупроводниках
332
Периодический потенциал 242
Поглощение излучения средой
180
—света в полупроводниках 331
Подвижность дырок 301, 303
— электронов 301, 303
Показатель преломления среды 158,
190
Полиномы Лагранжа присоединен-
присоединенные 93
— Эрмита 67
рекуррентные соотношения
68
Полуклассическая теория 169
Полупроводник 254
— примесный 295
электропроводность 259
— собственный 254, 286, 290
352
Предметный указатель
электропроводность 291
— Л'-типа 255, 293
— Р-типа 255, 312
Полупроводники с РЛ'-переходом
312, 314
Полуширина линии 200
Поляризация среды 190
— электромагнитного поля круговая
156
Поправка на конечность массы ядра
97
Поправки теории возмущений вто-
второго порядка 143
первого порядка 144
Постоянная Больцмана 12, 229
Постоянная Планка 12, 15, 47
Постулаты квантовой механики 36,
37
Потенциальная яма 51, 53
Потенциальное поле сферически-
симметричное 89
Потенциальный барьер 55
Преобразование инверсии 63
Преобразованная матрица 119
Приведенная масса 98
Примеси в полупроводниках 255,
259, 292
Принцип запрета Паули ПО, 218,
221
Производящая функция 68
Процедура измерения 137
Работа выхода 24
Различимые частицы 219
Разрешенные зоны 247
Распределение Бозе—Эйнштейна
238
— вероятностей 45, 105
значений импульса 45
координаты 44
— Максвелла—Больцмана 232
— Ферми—Дирака 232, 286, 332
Распространение электромагнитной
волны 193
Рассеяние электронов 19
в полупроводниковом кри-
кристалле 299
Режим бесстолкновительный 180
— столкновительный 181
Рекомбинация в базе транзистора
327
— электронов и дырок 305
Релаксационные члены 197
Релаксация 155
Рубиновый лазер 212
Ряд Фурье 32
Сандвич металл—диэлектрик — ме-
металл 61
Свободный электронный газ 234. 235
Связанные решения 59
Серия Бальмера 22
Символ Кронекера 117
Симметрия волновых функций 108
Система из двух частиц 107
Системы тождественных частиц 107
Скорость групповая электрона 258
— индуцированных и спонтанных
переходов 176
— носителя тепловая 300
— передачи информации 49
— света 158, 190
— фазовая 158
Слэтеровский детерминант 109
Собственные колебания лазера 210
Собственные функции 26, 110
гармонического осциллятора 70
линейные комбинации 102
момента количества движения
85
нормировка 30
оператора импульса 26, 27,
40, 44
энергии 43
ортогональность 29
полнота набора 31, 121
— разложение по ним 31
спиновые 270
с учетом поправок второго по-
порядка 146
— первого порядка 144
Собственные числа 26, 83
гармонического осциллятора 67
момента количества движения
29, 80
с учетом поправок второго по-
порядка 146
первого порядка 144
эрмитова оператора 30
эрмитовой матрицы 120, 123
Собственный полупроводник 254,
286, 290
Соотношение де Бройля—Эйнштейна
23, 173, 304
— неопределенностей 44, 67
для координаты и импульса 46
электромагнитных полей
47
энергии и времени 46
Состояние сверхизлучаюшее
Дикке 186
— синглетное 115
— системы квантовое 37
— триллетное 115
353
Предметный указатель
Спектр дискретный 59
— непрерывный 59
— электромагнитного излучения
атома водорода 20
Спектральная интенсивность 11
Спиновый момент количества дви-
движения 129
электрона 268
ядра 270
Среднее значение физической вели-
величины 38
— по ансамблю 39, 154, 196
Статистика Бох—Эйнштейна 223,
225
— Максвелла — Больцмана 223, 224,
232
— Ферми -Дирака 223, 225
Статистические законы распределе-
распределений частиц 232
Стимулированное излучение полу-
полупроводников 332
Столкновения атомные 180
— в формализме матрицы плотности
196
Сферические координаты 59, 77, 78
Теорема Блоха 241
— Гаусса 159
— Гаусса—Остроградского 159
— Грина 138
— о равновесном распределении
энергии 168
— Стокса 264
— Флокс 241
— Эренфеста 139
Теория Бора 20, 22, 23
— возмущений временная 142, 146
стационарная 142
— информации 48
— электромагнитная 10, 157
Тепловое движение хаотическое 302
— равновесие 229
— — электромагнитных мод 167
Теплоемкость 137
— твердых тел 13
Тождественные частицы 107
Транзистор полевой 330
— с РЛЛпереходом 329
Туннелирование частиц 60
— электронов в твердых телах 59, 61
Усиление излучения средой 180
Усилитель СВЧ параметрический 323
— электромагнитного излучения 207
Условие Бора 20, 23
— Брэгга 18, 248
— нормировки 30
— ортонормировки 31
Уравнение Шредингера полное 136
радиальное 90, 91
стационарное 44
Уравнения Максвелла Ю, 157,
190
— переноса носителей зарядов 307
Уровни энергетические 51
Фермионы 109, 217, 221, 225
Форма Линии 201
лоренцева 200
Формализм матрицы плотности 153
194
Формула Больцмана 172, 232
— для комплексной электрической
восприимчивости 200
энергии атома водорода 21
— Планка 12, 173
— Рзлея—Джинса 12
— Стирлинга 225
— Шенона 49
Фотон 12, 14, 16
фотоны как частицы 238
Фотоэлектрический эффект 13
Функции водородоподобные 96
— Лежандра 83
Функция потенциальной энергии
44
— формы линии 170, 201
Фурье-образ функции 46
Фурье-преобразование 32, 47
Химическая связь 104, 273
Химический потенциал 233, 234,
236, 290, 297
Центр масс 98
Четность 63, 64
Эволюция средних значений 138
Эксперимент Штерна и Герлаха 87
Эксперименты Дэвиссона и Джер-
мера 18
Электронный газ 234, 235
354
Предметный указатель
— парамагнитный резонанс 230
Элементарная ячейка 252, 292
Энергетические уровни 51
Энергия ионизации акцепторного
атома 295
атома водорода 22
донорного атома 294
— нулевых колебаний моды 168
осциллятора 67
— одномерного гармонического ос-
осциллятора 40
— отдачи ядра 100
— Ферми 116, 235
— фотона 16
— электромагнитного поля 159
Эталон Фабри—Перо 59, 204, 205,
213, 214
Эффект Доплера 210
— Мессбауэра 101
Эффективная масса дырки 262
электрона 258
Ядерный магнетон 270
— магнитный резонанс 270, 272
ОГЛАВЛЕНИЕ
Предисловие переводчика 5
Предисловие автора 7
Глава 1. Почему появилась квантовая механика , 9
§ 1.1. Ньютонова механика и классическая электромагнитная теория 9
§ 1.2. Излучение абсолютно черного тела 11
§ 1.3. Теплоемкость твердых тел и фотоэлектрический эффект 13
§ 1.4. Импульс фотона и комлтоповское рассеяние 15
§ 1.5. Волновая природа частиц 17
§ 1.6. Атом водорода и теория Бора 20
Задачи 23
Глава 2. Операторы . .... . 25
§2.1. Математические свойства операторов 25
§ 2.2. Собственные функции и собственные числа оператора 26
§ 2.3. Эрмитовы операторы 28
§ 2.4. Ортогональность собственных функций эрмитова оператора и
действительность его собственных чисел 29
§ 2.5. Нормировка собственных функций 30
§ 2.6. Полпота набора собственных функций 31
§ 2.7. Дираковские обозначения 32
Задачи 34
Глава 3. Основные постулаты квантовой механики . . 35
§ 3.1. Основные постулаты квантовой механики 36
§ 3.2. Среднее значение физической величины 38
§ 3.3. Конкретный вид квантовомеханических операторов 39
§ 3.4. Перестановочное соотношение для операторов координаты и
импульса. Коммутирующие операторы и их собственные функ-
функции 41
§ 3.5. Физический смысл волновой функции 43
§ 3.6. Собственные функции оператора энергии. Стационарное урав-
уравнение Шредиигера 43
§ 3.7. Соотношение неопределенностей 44
§ 3.8. Соотношения неопределенностей для электромагнитных полей 47
Задачи 49
Глава 4. Одномерные задачи на отыскание собственных чисел энергии 51
§ 4.1. Бесконечная потенциальная яма 51
§ 4.2. Конечная потенциальная яма 53
§ 4.3. Конечный потенциальный барьер 56
§ 4.4. Физические явления, объясняемые туииелироваиием частиц 60
Задачи 62
Глава 5. Гармонический осциллятор 63
§ 5.1. Четность 63
§ 5.2. Решение задачи о гармоническом осцилляторе 65
356
Оглавление
§ 5.3. Операторы уничтожения и рождения 73
Задачи 76
Глава 6. Квантовомеханический момент количества движения 77
§ 6.1. Операторы момента количества движения частицы 77
§ 6.2. Собственные функции и собственные числа оператора г-ком-
нонеиты момента количества движения 79
§ 6.3- Собственные функции и собственные числа оператора квадрата
момента количества движения 80
Задачи 88
Глава 7. Частица в сферически-симметричном потенциальном лоле
и атом водорода ... . . ... . 89
§ 7.1. Частица в сферически-симметричном потенциальном ноле 89
§ 7.2. Атом водорода 91
§ 7.3. Поправка на конечность массы ядра в теории атома водорода 97
§ 7.4. Гибридизация волновых функций и химическая связь в моле-
молекулах 104
Задачи 106
Глава 8. Системы тождественных частиц . 107
§ 8.1. Система из двух частиц 107
§ 8.2. Атом гелия 111
Задачи 11(>
Глава 9. Матричная формулировка квантовой механики . 117
§ 9.1. Основы алгебры матриц 117
§ 9.2. Преобразование квадратных матриц 119
§ 9.3. Диагоиализация квадратной матрицы 119
§ 9.4. Представление операторов физических величин матрицами 121
§ 9.5. Преобразования матриц оператора данной физической вели-
величины 122
§ 9.6. Отыскание собственных функций н собственных чисел опера-
оператора физической величины с использованием матричного ме-
метода 123
§ 9.7. Матричные элементы матриц операторов момента количества 124
движения
§ 9.8. Спиновый момент количества движения 129
§ 9-9. Сложение моментов количества движения 131
Задачи 134
Глава 16. Полное уравнение Шредингера . . . . 136
§ 10.1. Вероятностная интерпретация временной волновой функции 137
§ 10.2. Эволюция во времени средних значений операторов физиче-
физических величин 138
Задачи 140
Глава 11. Теория возмущений 142
§ 11.1. Стационарная теория возмущений 142
§ 11.2. Временная теория возмущений 146
§ 11.3. Формализм матрицы плотности 153
Задачи 156
Глава 12. Взаимодействие электромагнитного излучения с атомной си-
системой . ж . . . . 157
§ 12.1. Некоторые сведения из электромагнитной теории 157
§ 12.2. Квантование мод электромагнитного поля 160
357
Оглавление
§ 12.3. Излучение абсолютно черного тела 1Н5
§ 12.4. Индуцированные переходы атомной системы в столкиовитель-
ном режиме 169
§ 12.5. Спонтанные электромагнитные переходы атомной системы 172
§ 12.6. Квантовомехаиический вывод формулы для скорости спон-
спонтанных переходов 174
Задачи 179
Глава 13. Поглощение, усиление и дисперсия электромагнитного излу-
излучения атомной средой , 180
§ 13.1. Временная эволюция двухуровневого атома в бесстолкновм-
телытом режиме 181
§ 13.2. Поглощение и усиление электромагнитного излучения атом-
атомными системами в столкновителыюм режиме 186
§ 13.3. Электрическая поляризация среды, электрическая восприим-
восприимчивость и диэлектрическая проницаемость 190
§ 13.4. Вывод формулы для комплексной электрической восприим-
восприимчивости с использованием формализма матрицы плотности 194
Задачи 202
Глава 14. Собственные оптические колебания лазера . 203
§ 14.1. Лазерный электромагнитный генератор 203
Задачи 213
Глава 15. Квантовая статистика .... . . 215
§ 15.1. Три вида индивидуальных квантовых частиц 215
§ 15.2. Комбинаторика квантовых многочастичиых систем 219
§ 15.3. Статистики Максвелла—Больцмаиа, Ферми—Дирака и
Бозе—Эйнштейна 228
§ 15.4. Смеси частиц нескольких различных видов 226
§ 15.5. Определение параметра Р в законах распределений частиц 228
Задачи 231
Глава 16. Конкретные примеры статистических законов распределений
частиц . . . ... 232
§ 16.1. Распределение Максвелла—Больцмана 232
§ 16.2. Распределение Ферми—Дирака 232
§ 16.3. Распределение Бозе—Эйнштейна 238
Задачи 239
Глава 17. Зонная теория электронов в кристаллических твердых телах 241
§ 17.1. Модель Кронига—Пении 2И
§ 17.2. Кристаллическое твердое тело, содержащее большое число
электронов 250
§ 17.3. Движение электрона в кристаллическом твердом теле 250
§ 17.4. Изменение электропроводности полупроводников путем вве-
введения примесей 259
Задачи 262
Глава 18. Взаимодействие электронов и атомных ядер с магнитным ло-
лем. Магнитный резонанс. Мазеры , . . . 263
§ 18.1. Орбитальный магнитный момент электрона 263
§ 18.2. Спиновый момент количества движения 268
§ 18.3. Спины атомных ядер и ядерный магнитный резонанс 270
§ 18.4. Сверхтонкое взаимодействие 273
§ 18.5. Электронный парамагнитный резонанс 280
Задачи , 284
358
Оглавление
Глава 19. Перенос зарядов, в полупроводниках . . 286
§ 19.1. Носители зарядов в собственных полупроводниках 286
§ 19.2. Энергии ионизации примесных атомов в полупроводниковом
кристалле 291
§ 19.3. Концентрации носителей зарядов в примесных полупровод-
полупроводниках 295
§ 19.4. Рассеяние электронов п полупроводниковом кристалле 299
§ 19.5. Диффузия и рекомбинация 303
Задачи ' 310
Глава 20. Полупроводники с ЯЛ-переходом. Перенос зарядов через
ЯЛ^Я-лереход . . 312
§ 20.1. Распределение концентраций носителей зарядов и потенциала
в РЛ/-нереходе 312
§ 20.2. РТУ-нереход с приложенным внешним напряжением ЗК>
§ 20.3. Транзистор с РАФ-переходом 323
Задачи 331
Глава 21. Полупроводниковый инжекционный лазер . . 333
§ 21.1. Поглощение света и оптическое стимулированное излучение
в полупроводниковом кристалле 333
Задачи 346
Цитированная литература 347
Литература, рекомендуемая для .дальнейшею чтения 319
Предметный указатель 350