Text
Л.В.ЕРШОВ Р.Б.РАЙХМИСТ
ПОСТРОЕНИЕ ГРАФИ КО О ФУНКЦИЙ
Л.В.ЕРШОВ
Р.Б.РАЙХМИСТ
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
КНИГА ДЛЯ УЧИТЕЛЯ
МОСКВА „ПРОСВЕЩЕНИЕ1* 1984
Б БК 22.14 Е80
. ' »
Рецензенты:
учителя математики — Т. И. ТФУШАНИНА «S.JH. №М (г. Меснвф,
Ершов Л. В., Райхмист Р. Б.
Е80 Построение графиков функций: Кн. для учителя. — М.: Просвещение, 1984" — 80 с., ил.
Пособие предназначено учителям математики средних школ. Оно содержит теоретический материал* общую схему исследования функций, которая иллюстрируется многочисленными примерами, а также рассматривается построение графиков сложных унк-ций средствами элементарной математики и предлагается методика построения эскизов графиков функций без проведения полного исследования.
с 4306010400—591 ББК 22.14
103(03)—84 140-84 - ч .512
©Издательство «Просвещение^ 1(184 г.
Глава I
§ 1. ФУНКЦИЯ. ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Пусть D и Е — числовые множества, а х и у — соответственно их элементы. ' \
Определение. Если каждому х£ Е ставится в соответствие по некоторому закону только одно значение у 6 Е, то говорят, что между переменными х и у существует функциональная зависимость, и называют х независимой переменной или аргументом, а у — зависимой переменной или функцией.
Символическая запись функции: у — f (х), или х-^ у. Множество D называют областью определения функции и обозначают D ([), а множество Е — областью изменения функции.
Функция может быть, задана различными способами: аналитическим, табличным, описательным, 'графическим. „
К основным элементарным функциям относятся следующие:
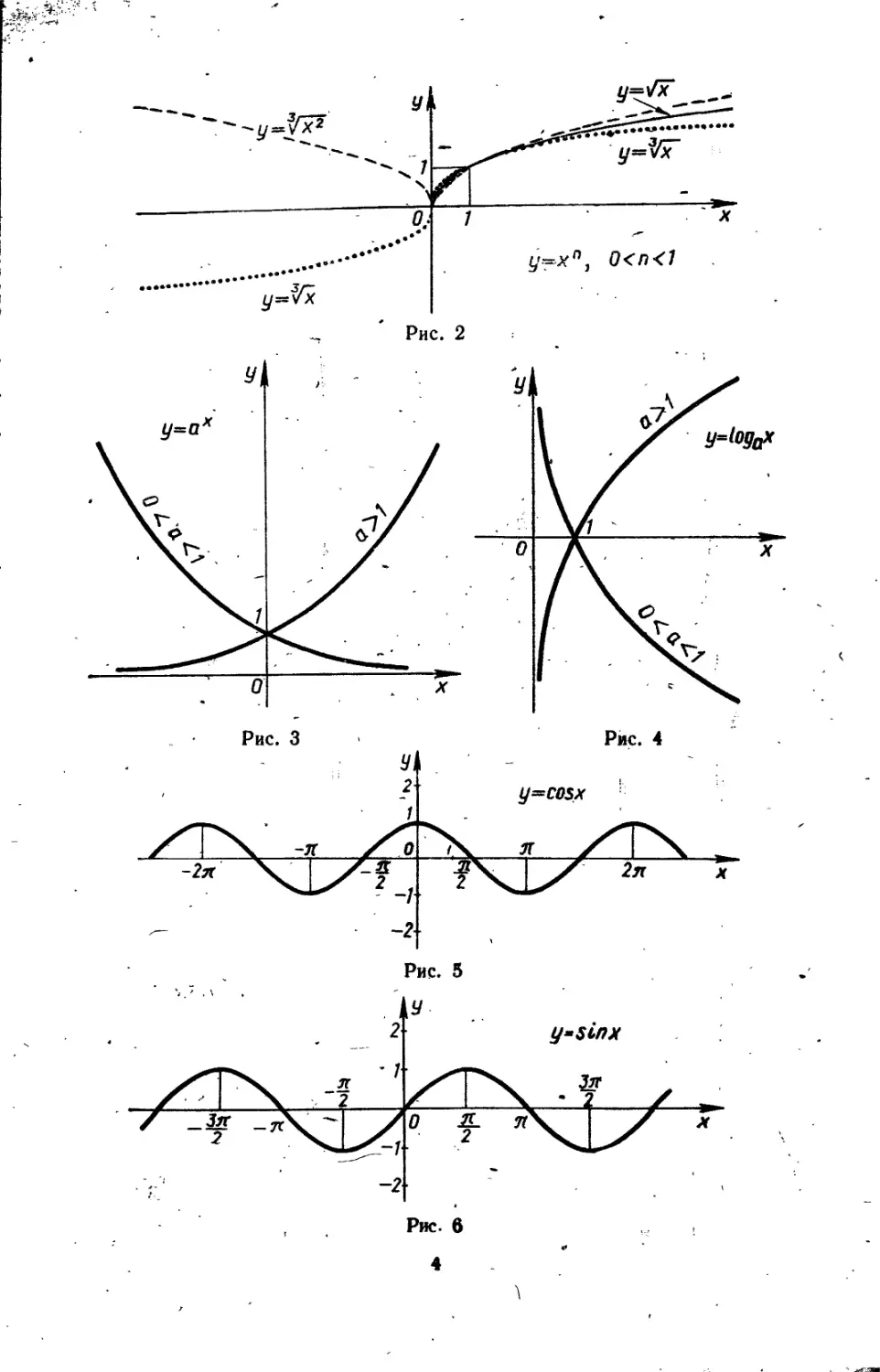
1. Степенная функция у = х", где п — действительное число, большее ну- у,
ля (рис. 1, 2). i
2. Показательная функция у = ах, \ где а>0; а=/=-1 (рис. 3). \
3. Логарифмическая функция у== ЧД — logax, где а > 0, а =#1 (рис. 4). Ц
4. Тригонометрические функции: \
у = sin х, у = cos х, у— tg х, у =ctg х \ (рис. 5, 6, 7, 8). \
5. Обратные тригонометрические \ функции: у = arcsin х, у = arccos х, \ 1 у = arctg х, у = arcctg х (рис. 9, 10, у
11, 12). ~7Ъ
Основные элементарные функции { могут соединяться между собой с по- / мощью арифметических действий (ело- / жения, вычитания, умножения и деле- ъ / ния), а также с помощью операции взя-тия функции от функции (суперпозиций-функций). Особо выделим два важных | частных случая: I
1. Линейная функция у = kx + Ь. . ”2. Квадратичная функция у = ах2 4-4- 6х + с (а 0). Ри
3
Рис. 5
y*sinx
Рис. 6
4
5
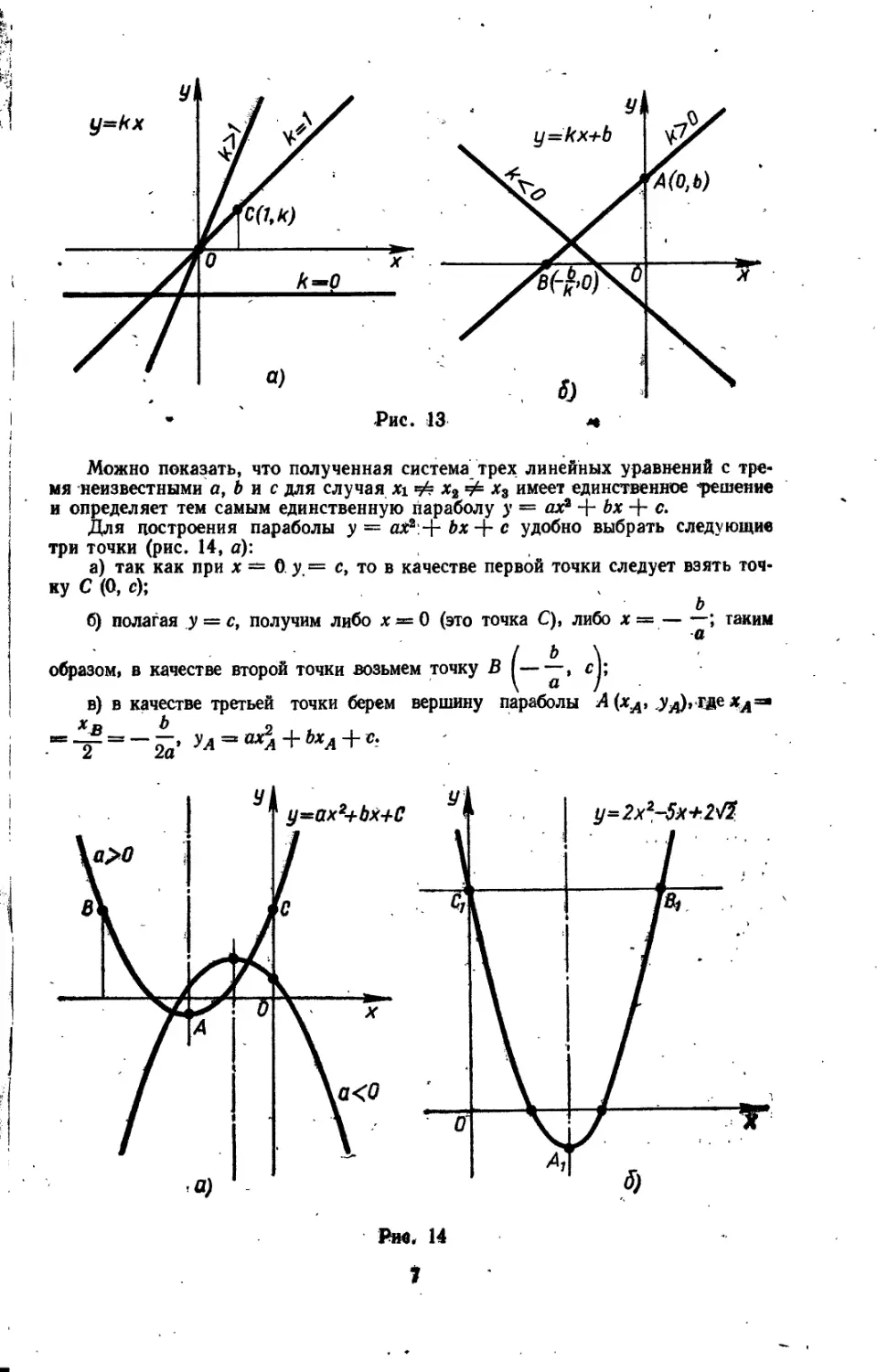
Замечание 1. График линейной функции — прямую линию удобно строить по двум точкам: точке А с координатами х = 0, у — b и точке В с
координатами у = 0, х = —— (/г т^ 0) (рис. 13, б). В случае Ъ = 0 прямая к
проходит чёрез начало координат, и для построения графика следует взять еще одну точку, например точку С (1, k). В случае k = 0 прямая параллельна оси абсцисс (рис. 13, а).
Замечание 2. Покажем один из многих приемов построения графика квадратичной функции — параболы^ Этот способ основывается на том факте, что три различные точки, принадлежащие параболе, определяют ее единственным образом.
Пусть нам даны три различные точки, принадлежащие графику квадратичной функции: Mi (xi, >), М2 (х2, у2), М »(хъ Уз)- Очевидно,, что xl^ х2=£ х3, в противном случае найдутся, хотя бы две точки параболы, лежащие на прямой, параллельной оси ординат, чего быть не может.
Так как по условию точки принадлежат графику квадратичной функции, то их координаты удовлетворяют уравнению у — ах2 + Ьх + с, т. е.
yi = axl + bxi + с, уа = axl + bx2 + б, Уз = ал|.+ Ьх3 + с.
6
Можно показать, что полученная система трех линейных уравнений с тремя неизвестными а, b и с для случая xi х2 ¥= х3 имеет единственное ^решение и определяет тем самым единственную параболу у = ах2 + Ьх + с.
Для построения параболы у = at2:+Z>x+<? удобно выбрать следующие три точки (рис. 14, а):
а) так как при х = 0 у = с, то в качестве первой точки следует взять точку С (0, с);
b
б) полагая у = с, получим либо х = 0 (это точка С), либо х = — —; таким
-а
' , ’ О [ b \
образом, в качестве второй точки возьмем точку В I —
в) в качестве третьей точки берем вершину параболы А (хА, уд), где Хд="
X D Ь 9
= ^ = 0J^+*^ + c-
46 £ЛЛ
Рио. 14
I
, Пример. Построить график функции у — 2х3 — 5х 4- 2)/^2. Отметим три точки: Cf (0, 2^2), ВЛ--, 2^2], ddp 37Т ®етви паРаболы нап-5
равлены вверх. Парабола симметрична относительно прямой х ~ — (рис. 14, б).
§ 2. общие свойства функции
Четность и нечетность
Определение. .Функция у = f (х) называется четной, если для любого значения х, взятого из области определения функции, значение —х также принадлежит области определения и выполняется равенство f (х) =f (—х).
Согласно определению график четной функции симметричен относительно оси ординат (рис. 15).
Примеры четных функций: у = х2 (см. рис. 1), у =-/х* (см. рис. 2), у = cos х (см. рис. 6).'
Определен и,е. Функция у = f (х) называется нечетной,. если для любого-значения х, взятого.’из области.определения функции, значение — х также принадлежит области определения и выполняется равенство f (х) — —f (—х).Т
• Из определения следует, чтд график нечетной функции симметричен относительно начала координат' (рис. 16).
8
Примеры нечетных функций: (см. рис. 1), у—.у^х
(см. рис. 2), у = sin х (см. рис. 5), у — tg х (см. рис. 7), у = — arctg х (см. рис. 11), у — arcsin х (см; рис. 9).
Замечание. При построении графиков четных и нечетных функций достаточно построить только правую ветвь графика — для положительных значений аргумента. Левая ветвь достраивается симметрично относительно оси у для четной функции и кососимметрично (т. е. симметрично относительно начала координат) для нечетной.
Примеры функций, не являющихся ни четными, ни нечетными: у = ж8 — х, у = х — 2,- у = sin (2х — 1).
Периодичность ,
Определение. Функция у = f (х) называется периодической, если существует такое число Т Ф 0, что для любого значения, х, взятого из области определения, .значения х 4- 7\ х — Т также принадлежат области определения и выполняется равенство /(х) = f (х 4- Т) (рис. 17).
Число Т называется периодом функции. Заметим, что всякая периодическая функция имеет бесконечное число периодов. В самом деле, числа, вида пТ при любом целом .я также являются периодами функции f (х), .так как
f (х + пТ) = f [(х + (п - 1)7} 4- 7’] =
: =/[х4-4«-1)71 = /[(х4-(я-2)7)4-Т] = . ‘ =... =/(х). .
' Примеры периодических функций! у = sin х (см. рис. 5), у = cos х (см. рис. 6), у = tg х (см. рис. 7), у = ctg х (см. рис. 8). Отметим, что периодическую функцию достаточно исследовать в пределах одного периода. ч
Примеры непериодических функций:’ у — х3, у — arcctg х, у = е*, у = sin (х2 4- 1).
Нули функции
Определение. Нулем функции называется то действительное значение х, при котором значение функции равно нулю.
Для того чтобы найти нули функции, следует решить уравнение/(х) = 0. Действительные корни этого уравнения являются, нулями функции у — f (х), и наоборот. Графически нули функции
2 Заказ G9U
9
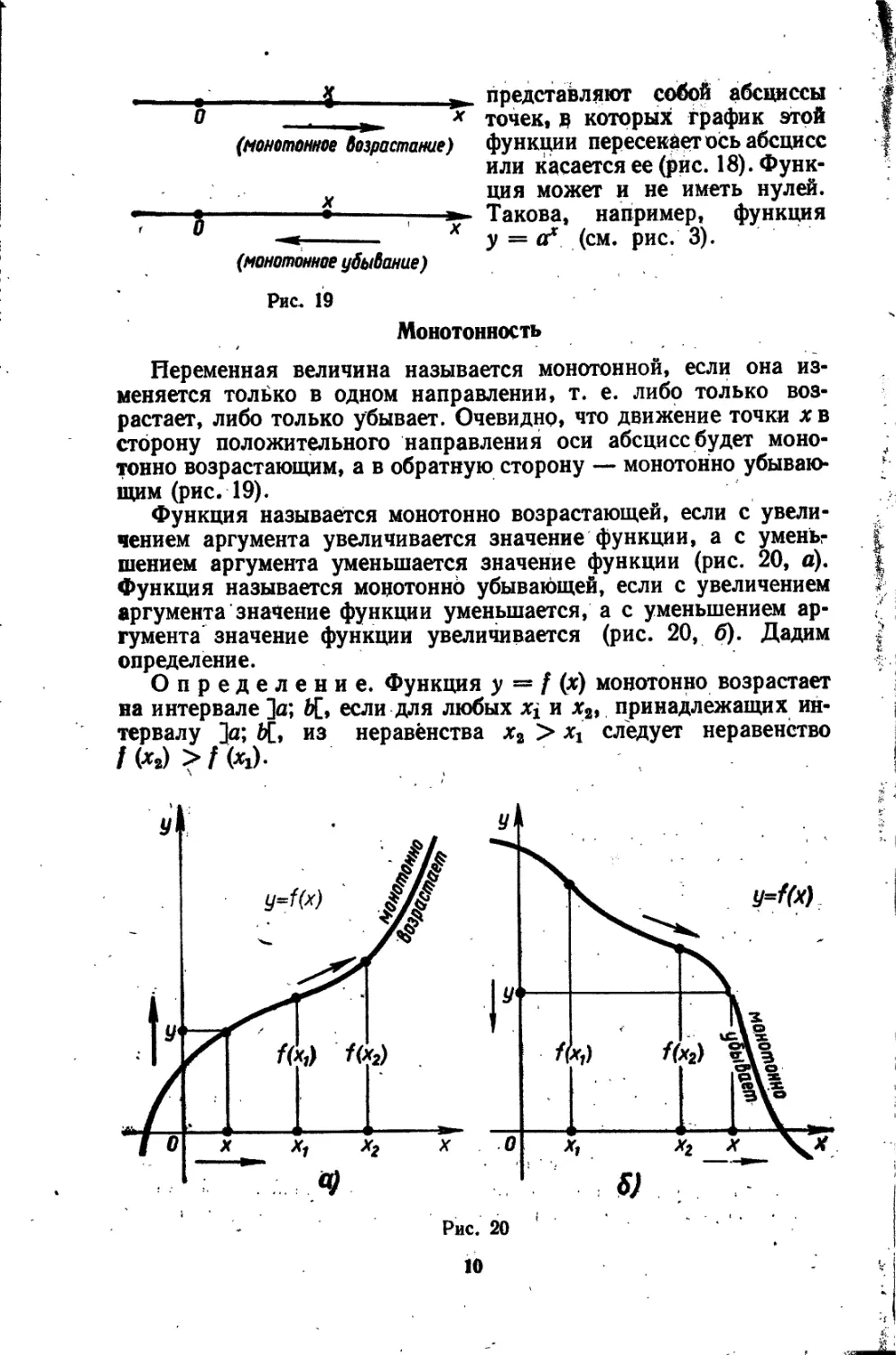
t |__________ж представляют собой абсциссы
О ж * точек, р которых график этой
(монотонное возрастание) функции пересекаетесь абсцисс или касается ее (рис. 18). Функция может и не иметь нулей. Такова, например, функция у = а* (см. рис. 3).
(монотонное убывание)
Рис. 19
Монотонность
Переменная величина называется монотонной, если она изменяется только в одном направлении, т. е. либо только возрастает, либо только убывает. Очевидно, что движение точки х в сторону положительного направления оси абсцисс будет моно- ; тонко возрастающим, а в обратную сторону — монотонно убываю- • щим (рис. 19).
Функция называется монотонно возрастающей, если с увеличением аргумента увеличивается значение функции, а с умень- J шением аргумента уменьшается значение функции (рис. 20, а). ।
Функция называется монотонно убывающей, если с увеличением > аргумента значение функции уменьшается, а с уменьшением аргумента значение функции увеличивается (рис. 20, б). Дадим | определение. |
Определение. Функция у = / (х) монотонно возрастает на интервале ]а; 6[, если для любых Xj и х3, принадлежащих интервалу ]а; Ц, из неравенства х2 > хг следует неравенство / (*2) > / (*i)-
Рис. 20
10
Функция у = f (х) монотонно убывает на интервале ]а; 6[, если для любых х2 и х2, принадлежащих интервалу ]о;. Й[»'из неравенства х2 > х2 следует неравенство f (х2) < f (х^.
Естественно, что интервал ]а; &[ предполагаемся взятым из области определения функции.
Изучим интервалы монотонного возрастания и убывания основных элементарных функций.
1. у = kx + & (см. рис. 13, б). Функция монотонно возрастает на всей числовой оси при Jt > 0 и монотонно убывает на всей - числовой оси при k < 0.
2. у = ах® + Ьх 4- с (см. рис. 14). При а > 0 функция моно-' тонно убывает на интервале ]—оо; хл[ и монотонно возрастает на интервале ]хл;’ 4-оо[ (хл — абсцисса вершины параболы).
При а < 0 функция монотонно возрастает на интервале ]—оо; хл[ и, монотонно убывает на интервале ]хл; +оо[.
3. у — хп (см, рис. 1, 2). При нечетном п > 1 функция монотонно возрастает,на всей числовой оси (например, у = л?). При четном п > Г функция - монотонно убывает на интервале ]—оо; 0[и монотонно возрастает на интервале ]0; +оо[ (например, у = х2). При 0 < п = — < 1 (р, q — нечетные числа), функция монотонно возрастает на всей числовой оси (например, у — у х).
При 0 < п = — < 1 и р четном, q нечетном (например, у= х8) <7 ’
функция монотонно убывает на интервале ]—оо; 0[ и монотонно возрастает на ]0; 4-°°[-
При 0 < п = — < 1 и q четном, р нечетном (например, у—У^) Я
функция монотонно возрастает на интервале ]0; 4-оо[.
4. у = 0х (см. рис. 3). При а > 1 функция монотонно. возрастает на всей числовой оси. При 0 < а < 1 функция монотонно убывает jja всей числовой оси.
5. у ==loge х (см. рис. 4). При а > 1 функция монотонно возрастает на интервале ]0;-4-оо[; при 0 < а < Г функция монотонно убывает на интервале ]0; 4-оо[,
в. у = tg х (см. рис.. 7)i На интервале j—функция монотонно возрастает. Так как tg -х — функция периодическая с периодом л, то она монотонно возрастает на любом интервале вида J—4- nk; 4- л^С где k = 0, ±1, ±2, ... .
7./у = arctg х (см. рис,- 11). Функция монотонно ' возрастает на всей Числовой оси.
Выпуклость и вогнутость
Определение. Функция у = f (х) называется вогнутой в точке х = а, если касательная к графику функции в точке
2* II
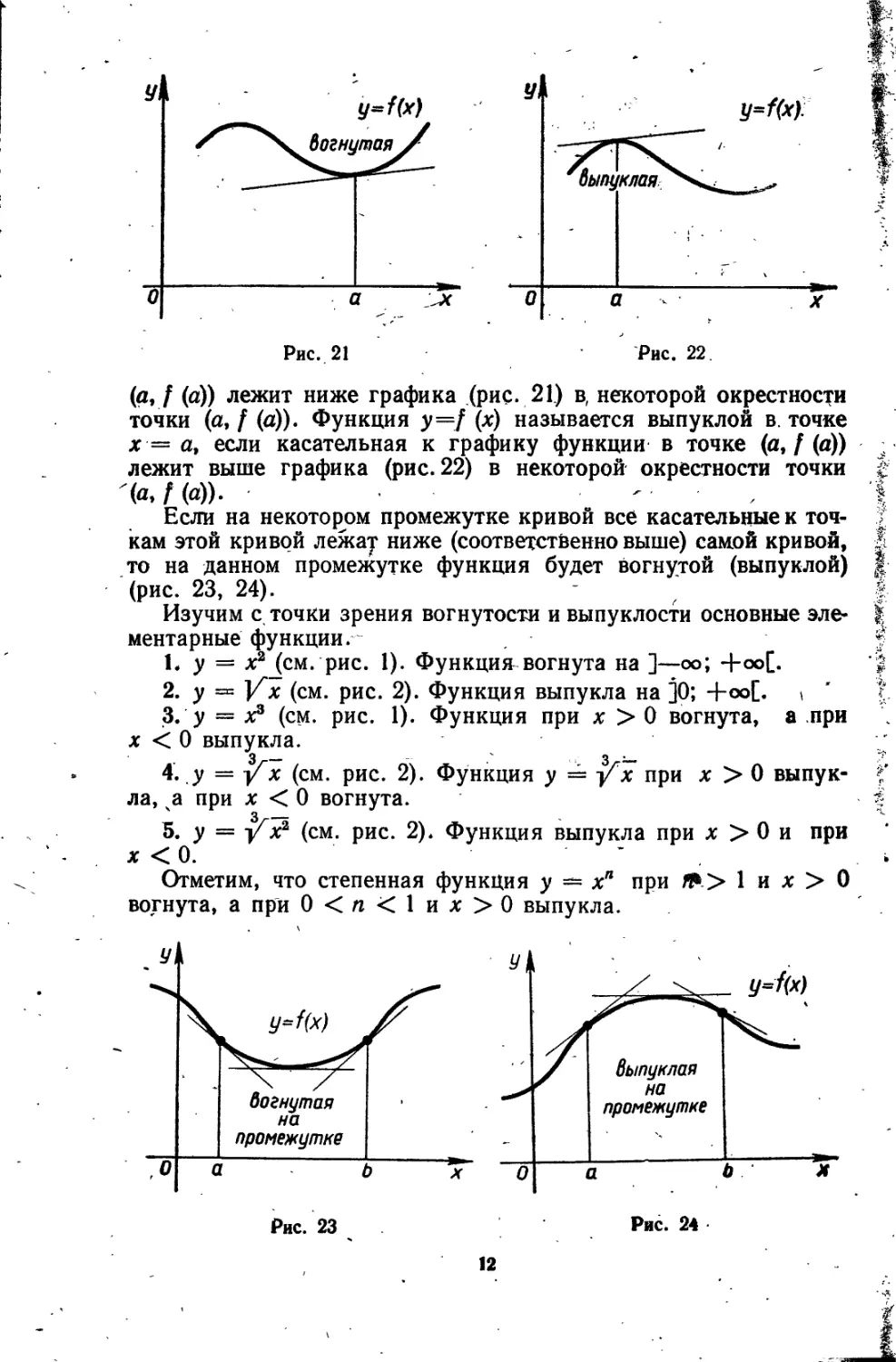
(a, f (а)) лежит ниже графика (рис. 21) в, некоторой окрестности точки (a, f (а)). Функция у=/ (х) называется выпуклой в. точке х — а, если касательная к графику функции в точке (а, / (а)) лежит выше графика (рис. 22) в некоторой окрестности точки (а./(а))- ' ,
Если на некотором промежутке кривой все касательные к точкам этой кривой лежау ниже (соответственно выше) самой кривой, то на данном промежутке функция будет вогнутой (выпуклой) (рис. 23, 24).
Изучим с точки зрения вогнутости и выпуклости основные элементарные функции.
1. у = х2 (см. рис. 1). Функция вогнута на ]—оо; +<»[.
2. у = ]/х (см. рис. 2). Функция выпукла на ]0; 4-оо[. (
3. у = х8 (см. рис. 1). Функция при х > 0 вогнута, а при х < 0 выпукла.
4. у — у/гх (см. рис. 2). Функция у = frx при х > 0 выпук- f ла, а при х < 0 вогнута. f
5. у = уЛх2 (см. рис. 2). Функция выпукла при х > 0 и при х < 0. ’ i
Отметим, что степенная функция у = х" при 1 и х > 0 вогнута, а при 0<п<1их>0 выпукла.
в. у, = а* (см. рис. 3). Функция вогнута на ]—оо; 4-оо[. -
7. у = log3 х (см. рис. 4). Функция выпукла на. ]0; 4-.оо[ при а > 1 и вогнута на ]0; 4-°°1 при 0 < а < 1.
8. у = tg х (см. рис. 7). Функция вогнута на |зтй; —+ «М и выпукла на j—у + л/г; где k = 0, ±1, ±2, '
9. у = arctgx (см; рис. ’11). Функция выпукла на ]0; 4-оо[ и вогнута на’]—об; 0(7.
10. у «в ахг 4- Ьх -|- с (см. рис. 14). Функция вогнута при а > 0 на ]—оо; 4-°°[ и выпукла при а '< 0 на ]—оо; 4-°о[.
Экстремумы
Точка х0 называется точкой локального максимума (или просто максимума) для функции f (х), если значение функции в этой точке больше, чем значения функции в ближайших соседних точках (рис. 25). Точка х0 называется точкой локального минимума (или просто минимума) для функции f (х), если значение функции в этой точке меньше, чем значения функции в ближайших соседних точкам (рис. 25).
Для обозначения максимума или минимума существует общий термин «экстремум» (латинское слово: крайний). Дадим теперь определение. Пусть функция у — f (х) определена на отрезке [а; 6].
Опр е д е л е н и е. Функция у = / (х) имеет Локальный максимум в точке х0 € [а; &]» если существует окрестность точки х0, целиком содержащаяся в [а; &] и такая, что для любого х, принадлежащего этой окрестности, выполняется неравенство /(Х)</(ХО).
Под окрестностью точки Хо понимают интервал длиной 2е с
13
центром в точке х0, т. е. ]л% — в; хл + «С. где в — произвольное положительное число.
Функция у = f (ж) имеет локальный минимум в точке Хо € £ [а; 6], если существует окрестность точки х0, целиком содержащаяся в [а; о] и такая, что для любого х, принадлежащего этой окрестности, выполняется неравенство f (ж) > f (х0)-
Замечание. Приращение функции Д/ (х) = f (х) — J (ха) в некоторой окрестности точки экстремума не меняет знак, т. е. положительно, если в точке х0 минимум, и отрицательно, если- в точке х0 — максимум. Этот факт следует из определения экстремума. Не все основные элементарные функции обладают экстремальными точками.
Степенная функция у — х" имеет минимум в точке х = 0 при п = 2fe > 1 (например, у = х2) (см. рис. 1) и при 0 < л = — < 1, причём р — четное 3
число, а 4 — нечетное число (например, у = (см. рис. 2).
Квадратичная функция у = ах2 + 6х 4- с (см. рис. 14) имеет минимум в b b
точке хл— — — при а >0 и, имеет максимум в точке хА= — — при а <0.
л
Функция у => sin х (см. рис. 5) имеет максимумы (у = 1) в точках х„= —4* л
4- 2лл, где л = 0, sl± 1, ±2,...', и минимумы (у == —1) в точках х*==— ~ 4-
4-2лЛ, где ft=Q, ±1, ±2, ... .
Функция у = сое х (см. рис. 6) имеет максимумы (у = 1)> в. точках хя == — 2лпг где л = 0, sfal, ±2, и минимумы (у = —1) в точках х* = я 4- 2лй, где Л = 0, ±1, ±2,... .
S 3. ПРЕДЕЛ ФУНКЦИИ, НЕПРЕРЫВНОСТЬ
Предел функции
Функция у = f (ж) имеет предел, равный А .при х -> а, если с приближением значения аргумента ж к числу а значение функции f (ж) как угодно близко приближается к числу А. Обозначение! lim / (ж) = А.
Х-*а ' '
В самой точке х = а функция может и не быть определена. Такова, например, функция у = в точке ж = 0. Как известно, lim = 1, хотя в точке ж = 0 значение функции не определено. *-»о х
Дадим определение предела функции.
Определение. Число А называется пределом функции у = f (x) в точке ж = а, если для любого е > 0 найдется такое число б > 0, что для всех ж, удовлетворяющих неравенству 0 < | ж — а | <6, выполняется неравейство \f (ж) -г- А | < 8.
В определении предела функции не указывается, каким образом аргумент ж,стремится к числу а. Если предел функции в точке а существует, то он не зависит, стало быть, от способа при-
14
ближения аргумента х в точке а. Пусть „ д+0
переменная величина х обозначает движу- •
щуюся, точку на реи абсцисс. Тогда дви-ярение этой точки к а может происходить ---*-*-
справа или слёва. Результат движения точ- а '*
ки справа к а будем обозначать а + 0, а ре-
зультат движения слева к а будем обо- Рис. 26
значать а — 0, где знаки +0 и —0 играют роль указателей направления движения точки к а. В обоих случаях, естественно, результатом движения точек будет число а (рис. 26). Дадим определение для общей ситуации.
Определение. Число В называется правым пределом функциц f (*) ПРИ стремлении х к точке а справа (т. е. по значе- , ниям х > а), если для любого е > 0 найдется такое 6 > 0, что для всех х, удовлетворяющих неравенству 0 < х — а < б, выполняется неравенство |/ (х) — А | < 8. Правый предел символически обозначают. так: lim f (х) = f (а + 0) = В.
Число С называется левым пределом функции f (х) при стремлении х к точке а слева (т. е. по значениям х < а), если для любого е > 0 найдется такое 6 > 0, что для всех х, удовлетворяющих неравенству —б < х — а < 0, выполняется неравенство \f (X) - С I < 8.
Обозначение левого предела: lim f (х) = f (а — 0) = с.
Из определения предела функции вытекает следующее утверждение. Если предел функции в точке а существует, то существуют и равны между собой левый и правый пределы функции в этой точке. Beptto й'обратное. Если левый и правый пределы функции в точке а существуют и равны числу А, то предел функции в точке а существует и тоже равен А.
Рассмотрим, однако, функцию у == в окрестности Точки
х = 0. Для такой функции в точке х =' 0 не существует никакого конечного предела. В этом случае вводят специальное определение предела.
Определение. Говорят, что limf(a) = oo, если для х-+а
любого числа D > 0 найдется такое число б > 0, что для всех х, удовлетворяющих неравенству 0 < [ х — а\ < б, выполняется неравенство j/(x)| > D. *
Функция f (х) при х, стремящемся к а, называется -бесконечно большой. Вместо записи lim f (х) = оо употребляется и такая «-►а
запись: f(x).->oo при х-+а (f(x) стремится к бесконечности, когда х стремится к.а).
По существу, тем самым к множеству R действительных чисел присоеди-. няют число, большее любого действительного числа, так что окрестность отвечающей ему бесконечно удаленной точки оси ординат есть множество чи~ сея у. для которых | у| > Ь, где О—любое положительное число. {Окрестность
45 '
бесконечно удаленной точки оси ординат и саму эту точку можно наглядно . представить себе, если вообразить, что концы оси у соединены. Тогда точка & соединения и будет бесконечно удаленной точкой.) Неравенство |у[ >D рас- д падается на два неравенства: у > D и у < —В, что графически означает на-личие двух полуокрестностей. Таким образом, бесконечно удаленная точка оси у раздваивается на две точки, которые обозначают -f-oo и —со. Аналогично бесконечно удаленная точка оси х раздваивается на две точки +оо и —со, имеющие каждая свою полуокрестность.
Очень важным понятием в теории пределов является понятие ’ бесконечно малой.
Определение.. Функция а (х) называется бесконечно ,. малой при х, стремящемся к а, если lim а(х) == 0.
Таковы, например/ функции sin х, хг, tg х, arcsiji х, arctgx
^1рй х 0; loga х при х -> 1; qos х при х ->
Особо выделим понятие функции, бесконечно малой на бесконечности.
Определение. Функция а (х) называется бесконечно ।, ' малой на бесконечности, если lim а (х) = От (’
Х->ОО ' .. ,7.
Согласно определению значения функции а (х) по абсолютной •< величине становятся и продолжают оставаться меньше любого | наперед заданного положительного.числа, как только значения ? аргумента по абсолютной величине становятся достаточно большими. - ?
, . Непрерывность
Если при постепенном изменении аргумента функция также меняется постепенно, то говорят, что функциц непрерывна. При этом малому изменению аргумента отвечает малое изменение функции. Дадим определение.
Определение. Функция у = f (х) называется непре-рывной в точке х0,-если она определена в некоторой окрестности этой точки (включая саму точку) и предел функции в точке х0 существует и равен значению функции в самой этой'точке, т. ,е.
1im/(x) = A = f (х0) = /[limx]. ".
х->х0 х-*х9
Из определения следует,, что приращение функции А/ (х) — — f (х)— / (х0) стремится к нулю при приращении аргумента Ах, стремящемся к нулю, т. е. lim [/ (х) — f (х0)] — lim Ду = 0.
' z , Дх-ьО Дх->0
Функция у = /(х) называется непрерывной на интервале, - если она определена на этом интервале и непрерывна в каждой точке интервала.
Геометрически непрерывность функции на интервале означает, чзо график этой функции ria данном интервале есть сплошная линия без скачков и разрывов. Другими словами, отдельные точки на графике непрерывной (иа .интервале) функции можно (!!!) (на данном интервале) соединять сплошной линией.
< -
16
Если в каких-либо точках интервала функция неявляется непрерывной, то такие точки называются точками разрыва. _ . ' .. ' sinx .... - . .....
Примеры. 1. ,, Функция у =--------непрерывна на всей числовой оси,
кроме точки х =О, в которой функция не определена. Таким образом, точка sinx
х = 0 есть точка разрыва функции у = —, так как в определении непрерывной в точке функции участвует значение функции в данной точке, а оно в точке х = 0 не определено.
2х
2. Точкой разрыва функции у=“-------- служит точка х = 0, в которой
2Т+1 • '
пределы функции слева и справа существуют» но не равны -между собой» т. е. предел функции в точке х = 0 не существует. 4
Действительно, '
X 2_
2* 1 2*
lim —7— = lim —-----------т*=1; lim ------------«0.
х-*0-|-0 X Х-+04-0 _ £. х-*о—о _L
2* +1 14-2 х * 2* +1
3» Точками разрыва функции у ---------- будут точки х = 1 и х = — 1,
в которых значения функции не определены, и, следовательно, не выполняется определение непрерывности функции в точке.
Замечание. Элементарные функции непрерывны во всех точках, где они определены. Отсюда следует, что точками разрыва элементарных функций могут служить только точки, в которых эти функции не определены (пример 3).
§ 4. АСИМПТОТЫ ч
Определение. Если расстояние б от точки М кривой у — f (х) Д° некоторой определенной прямой при х -> х0 и неограниченном удалении точки М от начала координат стремится к нулю, то эта прямая называется асимптотой кривой. -
Различают вертикальные, горизонтальные и наклонные асимптоты.
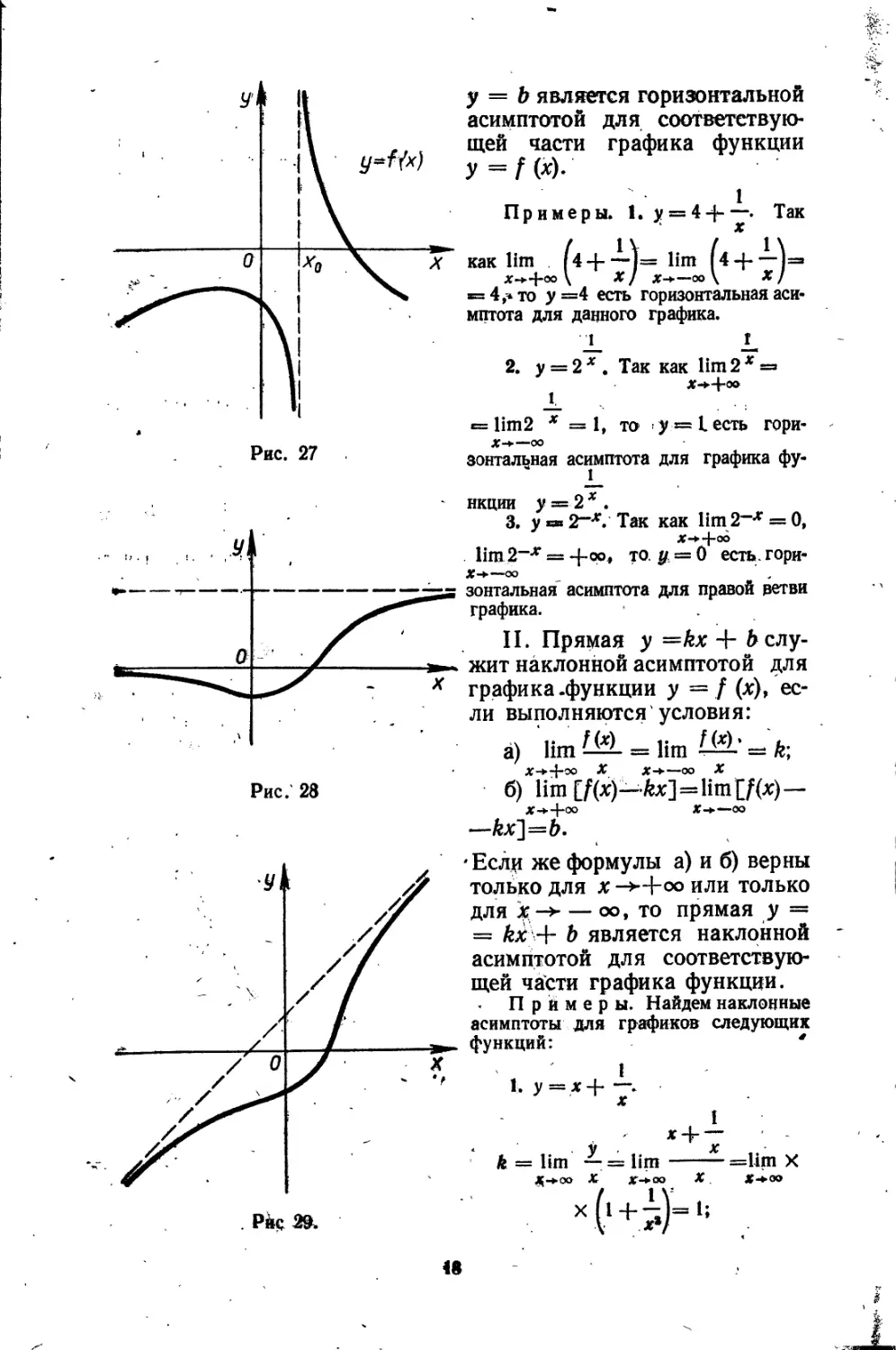
Если в определении асимптоты х0 — конечное число, то соответствующая асимптота называется вертикальной (рис. 27). При этом в точке хь хотя бы один из пределов (левый или правый) должен равняться +оо или —со. Поэтому вертикальные "асимптоты следует искать в точках разрыва функции.
Если в определении асимптоты х0 есть 4-оо или —оо, то соответствующая асимптота будет либо горизонтальной (рис. 28), либо наклонной (рис. 29).
’ I. Прямая у= Ь служит горизонтальной асимптотой для графика функции у — f (х), если lim./ (х) == lim f (х) = Ь. Если же равен числу В' только один ИЗ этих пределов, то прямая
17
у — b является горизонтальной асимптотой для соответствующей части графика функции У = f (х).
1
Примеры. 1. у = 4-^~- Так как lim -f- —\= lim ^4 4-’Ц=8 Х->4"°0 \ X / —оо \ X /
== 4,< то у =4 есть горизонтальная асимптота для данного графика.
2_ L
2. у = 2 х . Так как lim 2 х »
1 х»4-оо
= lim2 х = 1, то у = 1 есть гори-00
зонтальная асимптота для графика фу-
нкции у = 2 х .
3. у«®2“х. Так как lim 2“* = О, Х->-|~оо
lim 2-х = + оо, то. у = 0 есть гори-Х->—оо зонтальная асимптота для правой ветви графика.
II. Прямая у =kx + Услужит наклонной асимптотой для графика .функции у = / (х), если выполняются условия:
a) lim = lim == k\ X х-¥—оо X
б) lim [f(x)—Ax]=lim[f(x)— X->~J-oo —оо
—kx]=b.
•Если же формулы а) и б) верны только для х ->-|-оо или только для Х.-> — оо, то прямая у = = Ах -Ь b является наклонной асимптотой для соответствующей части графика функции.
Примеры. Найдем наклонные асимптоты для графиков следующих функций: *
1. у = х+р
I х 4г ~
k == lim — = lim---=lim X
^-►оо X х-*оо X. Х-*оо
x(l+i)=1;
<8
/ 1 \ 1
b = lim (у —kx) = lim lx + — — л I = lim ~ = O. X-*cd ' X->oo \ X J X->co X
Прямая y — x служит наклонной асимптотой для графика функции у=»х4-~*
»<-!» i-llm Х->4-оо X Х-*4~оо х(х+1) х-»+оо х(х;+1)
/I х I (х — 1) • \
61 = lim (у — krx) = lim —1——— — х|=»
Х-*4-оо \ X 4“ 1 /
^Пт (ЧЧ-2-
х 4“ 1 ж->4*оо \ Х4-1;/ ;
Прямая у = х — 2 является наклонной асимптотой для правой ветви графика данной функции. ... У |х|(х— 1) (—х)(х—1) -
fea = lim — = lim — ----— = lim ---------———— If
X-*—-oo X X->—оо X (X — 1) X-*—oo ?(*+)
. .. . x /|x|(x— 1) \ (—X) (x — 1)+x (x + 1)
/>,= Inn (у—M = lim ' + x = lim -—-----; ; '-J = 2.
X->—~oo \ X 4- 1 / oo *+l
Прямая у =—x -^-2 является наклонной асимптотой для левой ветви графика |х|(х— 1) функции у =-------------.
§ В. ПРОИЗВОДНАЯ. ЭКСТРЕМУМ
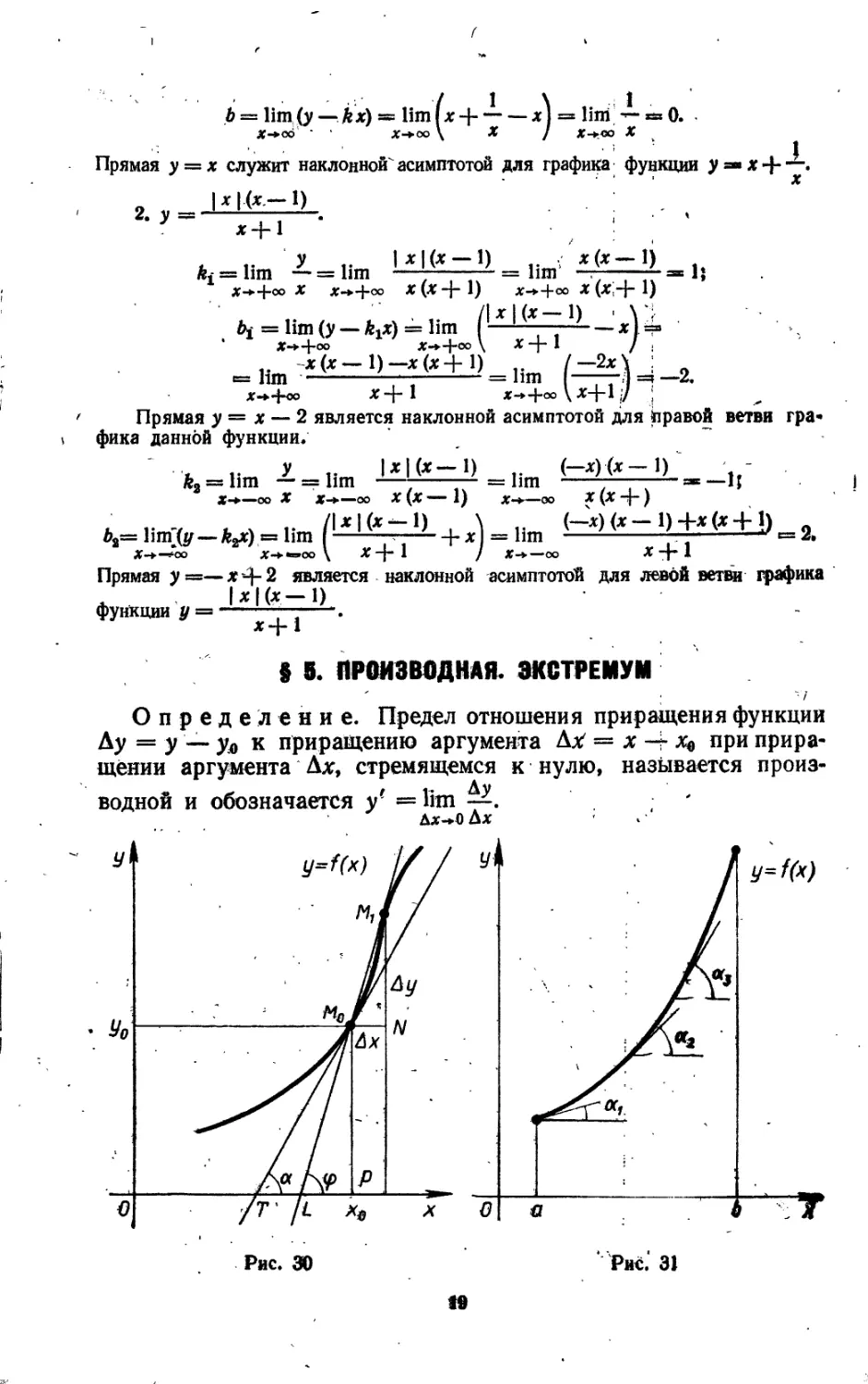
Определение. Предел отношения приращения функции Ду = у — ул к приращению аргумента Ax' = х Ч- х^ при приращении аргумента Дх, стремящемся к нулю, называется производной и обозначается у' = Вт —. '
Ах-»оДх
Рис. 30 Рис.' 31
ЙО
При этом подразумевается, что указанный предел существует. Геометрически производная функции у = f (х) в точке х0 равна угловому коэффициенту касательной к кривой у = f (х) в точке (х0, Уо) (рис. 30), или, что то же самое, тангенсу угла наклона указанной касательной к оси х, т. е. tg а (рис. 30). :
Дадим определение касательной. Касательной к кривой У — f (*) в точке Мо называется предельное положение МйТ секущей Л1оЛ11» когда точка' Мг вдоль по кривой стремится к совпадению с ТОЧКОЙ Мо. :
Из ДЛТ12И0У следует, что — = tg <р, где tg ф— угловой Дх :
коэффициент секущей. Угловой же коэффициент касательной получается отсюда путем перехода к пределу при Дх ->- 0:
tg а = lim tg <р = lim = у'(х0).
В последующем изложении нам потребуется довольно большое число, теорем.из курса математического анализа, доказательства которых мы опускаем.
•Отметим, что если функция в точке х0 ймёет производную, то в этой точке функция непрерывна.
Если функция имеет производную во всех точках некоторого интервала, то она непрерывна на данном интервале. Таким образом, чтобы доказать непрерывность функции на некотором интервале, часто бывает удобно вычислить производную этой функ-. ции и показать, что она существует на данном интервале. Однако, если производная в точке не существует, это не означает, что функция в этой точке обязательно разрывна. Непрерывная в точке функция. может и не иметь в этой точке производной. Такова, например, функция у = | х| в точке х = 0. Функция у = у^х в точке х = 0 непрерывна, хотя lim у' =
*-*о
1 “1
= lim—х . = оо, т. е. производная функции не существует вточ-
*->•0 3
ке х = 0. Следующее утверждение позволяет судить о монотонности функции на интервале..
Пусть у — f (х) имеет производную на интервале. Тогда,' если на всем интервале:
1) Г (х) > 0, то f (х) монотонно возрастает на интервале (рис. 31);
2) f (х) < О, то f (х) монотонно убывает на интервале (рис. 32);
3) f (х) 9 0, то f (х) == const на интервале (рис. 33). Условие/' (х) >0(tga>0) в каждой точке интервала означает геометрически, что' касательная к кривой в любой ее точке образует с положительным направлением оси абсцисс острый угол (рис. 31).
Условие /' (х) < 0 (tg a < 0) в каждой точке интервала озна-
20
Рис. 32
Рис. 33
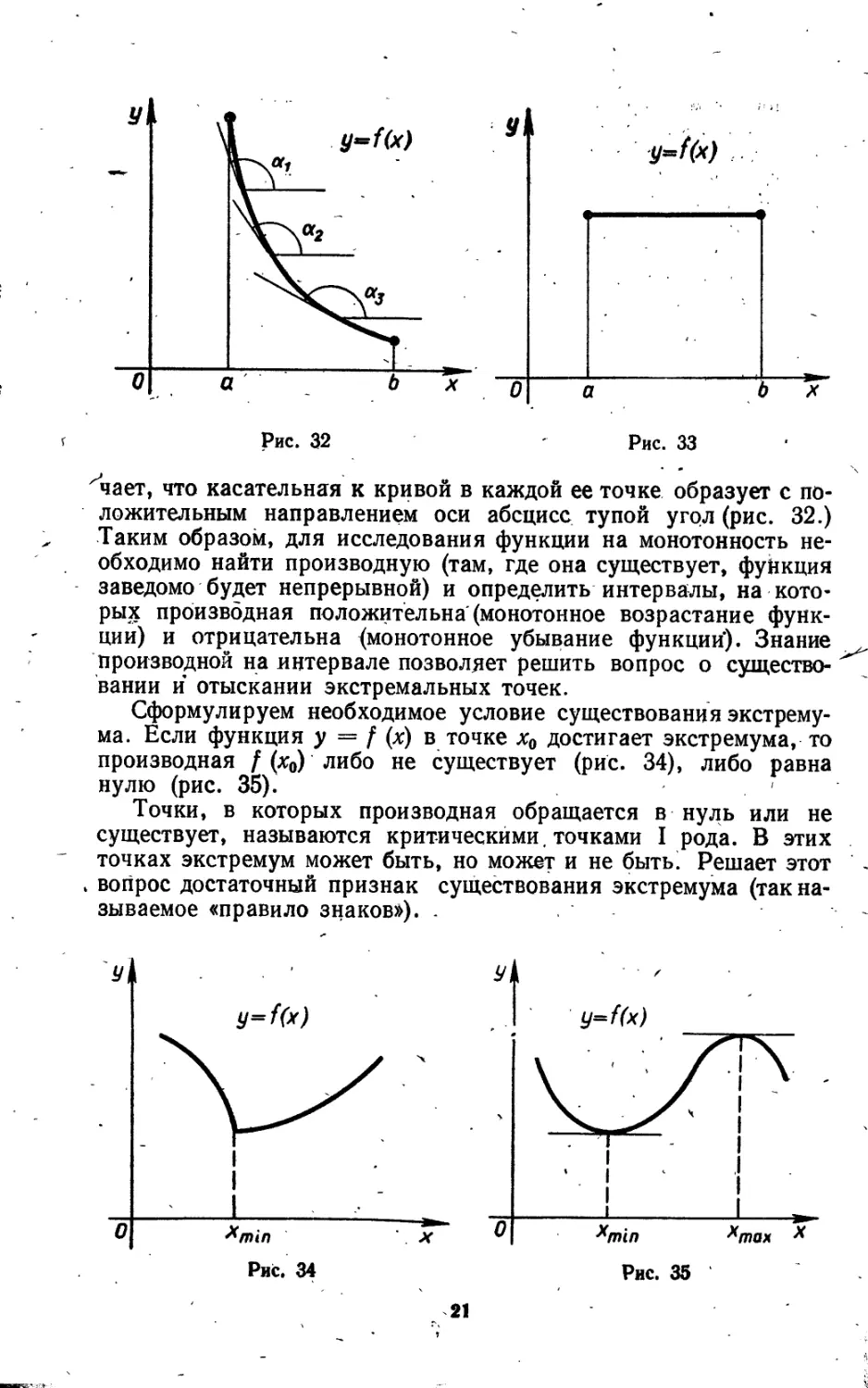
'чает, что касательная к кривой в каждой ее точке образует с положительным направлением оси абсцисс тупой угол (рис. 32.) Таким образом, для исследования функции на монотонность необходимо найти производную (там, где она существует, функция заведомо будет непрерывной) и определить интервалы, на которых производная положительна (монотонное возрастание функции) и отрицательна (монотонное убывание функции'). Знание производной на интервале позволяет решить вопрос о существовании и отыскании экстремальных точек.
Сформулируем необходимое условие существования экстремума. Если функция у = f (х) в точке х0 достигает экстремума, то производная f (х0) либо не существует (рис. 34), либо равна нулю (рис. 35).
Точки, в которых производная обращается в нуль или не существует, называются критическими. точками I рода. В этих точках экстремум может быть, но может и не быть. Решает этот . вопрос достаточный признак существования экстремума (так называемое «правило знаков»). .
Пусть функция у = f (х) определена и непрерывна в некоторой окрестности точки х0, включая саму точку, и производная f (х) существует в окрестности этой точки, за исключением, быть может, самой точки х0.
Тогда, если:
1) f (х) > 0 (знак +) при х <х0 и f (х < 0) (знак —) при х > х0, то функция в точке х0 достигаем максимума: .
2) f (х) < 0 (знак —) при х < х0 и f (х) > 0 (знак +) при х > Хо, то функция в точке х0 достигает минимума;
3) f (х) не меняет знак, то экстремума нет.-
Таким образом, точка максимума отделяет промежуток монотонного возрастания функции от участка монотонного убывания, а точка минимума отделяет. промежуток монотонного убывания от участка монотонного возрастания (если двигаться в положительном направлении оси абсцисс).
Схема применения производной для отыскания интервалов монотонности и экстремумов будет следующая:
1) находим производную f (х);
2) находим интервалы знакопостоянства производной f (х) (интервалы монотонности функциц f (х)), т. е. решаем неравенства?/' (х) > 0 и /' (х) < 0;
3) находим критические точки I рода, т. е. точки, в которых fr (х)' Либо равна нулю, либо не существует;
с помощью достаточного признака исследуем функцию в критических точках I рода на экстремум;
5) вычисляем значения функции в экстремальных точках.
• ' „ . 1 .
Примеры 1. у = —----.
2х
Находим производную: у' =
Решаем неравенства:
—2х
a) у' > 0, или > 0, откуда х < 0; таким образом, при х < 0 про-
изводная положительна (знак +);
-^-2х
б) у'<0, или —------откуда х>0, т. е. при х>0 производная
(х2 + 1)а
. отрицательна (знак —).
Приравнивая к нулю производную, находим критическую точку I рода: 2х
у' - - 7^7/ = °’ 0ТКУда х - °-
Удобно рисовать следующую схему (рис. 36) (стрелками f и\> обозначим монотонное возрастание и убывание функции на соответствующих интер-> валах). Из схемы (рис. 36) следует, что в точке х = 0 функция имеет максимум (производная меняет знак с + на —). Кроме того, на интервале ]—оо; 0[ функция монотонно возрастает, а на интервале ]0; +оо] монотонно убывает.
Вычисляем значение функции в точке максимума:
при * = *Шах = 0 У = Ум»= . 1 , , - 1» «* max г 4
2. у = (х* — 4х + 3)».
22
Знаку': Поведение Функции у:
I
Рис. 36
Находим производную: = 2 (ха — 4х + 3) (2х — 4).
Решаем неравенства:
а) У' > 0, или 2 (х2 — 4х + 3) (2х4) > 0.
(х —1) (х — 2) (х — 3) > 0 и окончательно получим: 1 < х < 2, х > 3. Такимобразом, на интервалах]!; 2[U]3; +оо[ производная положительна (знак +); -
б) у' < 0, или 2 (х3 — 4х + 3) (2х — 4) < 0, откуда х < 1, 2 < х < 3 * т. е. на интервалах ]—оо; 1 [ |J]2; 3[ производная отрицательна (знак —).
Приравнивая к нулю производную, находим критические точки I рода: у' = 2 (х3 — 4х + 3) (2х — 4) =* 0, откуда Xi = 1, х2 = 2, х2 = 3.
Рисуем схему (рис. 37), из которой следует/ что в точке х = 1 функция имеет минимум, в точке х = 2 — максимум, в точке х = 3 — минимум*
Кроме того, на интервалах ]—<»; 1 [ U ]2; 3[ функция монотонно убывает, а на интервалах ]1; 2 [(J]3; +оо[ монотонно возрастает.
Значения функции в экстремальных точках:
при х = xmln =1 у - ymln = 0;
при х = хшах = 2 у = Утлх = 1} ПР" * = *min = 3 У = Утш =°-
3. у = у-*2 — 1. ч 2х
Находим производную: у' — ~ —
Зу(х2—I)2
Решаем неравенства: 2
у >0, или т 1 — >0, откуда х>0, хч4>1: зуй5- I)2
' У < 0, или г -----------' < 0, откуда х < 0, Xijt—1,
3/(х2—I)2
Знак у': Поведение функции у:
Производная равна нулю .в точке х = 0 и не существует в точках х — — 1, х = + 1.
Таким образом, имеем три критические точки I рода: xi = —1, х2 = О, х5 = + 1. Рисуем схему (рис. 38), из которой следует, что в точке х2~ О функция имеет минимум, а в точках Xi = —1 и х3 = I экстремума нет. Кроме ' того, на интервалах*]—оо; --1 [(J] — 1; 0£ функция монотонно убывает, а на интервалах ]0; +1 [UB; +о°[ функция монотонно возрастает,
Находим значение функции в экстремальной точке:4 при х = xmln =0 у = ymln = -1.
§ 6. ВЫПУКЛОСТЬ И ВОГНУТОСТЬ. ТОЧКИ ПЕРЕГИБА
Если первая производная у' существует на некотором интервале X, то тем самым каждому х из этого интервала ставится в соответствие производная данной функции. Это однозначное соответствие является новой функцией х-> ff (х). Может оказаться, что для указанной новой -функции в некоторой точке х0 б X существует производная. Тогда эта производная называется второй производной от первоначальной функции в упомянутой точке и обозначается символом у " (х0) или f" (х0).
Применение второй производной к выяснению выпуклости (вогнутости) графика функции на интервале основано на следующей теореме из курса математического анализа.
Т е о р ем а. Если вторая производная f" (х) существует на интервале ]а; &L и не меняет знака на этом интервале, то
1) при f" (х) > 0 (знак +) функция f (х) вогнута на интервале ]а; Ь[; _ -
2) при f" (х) < 0 (знак —) функция f (х) выпукла на интервале ]а;Я. ' . - . .
Из теоремы следует, что для нахождения интервалов выпуклости и вогнутости функции нужно найти вторую производную и решить неравенства:
а) Г (х) < 0, б) Г (х) >0.
24
Определение. Точка
Л40(х0, f(x0)) кривой у — f (х) назы- y^f(x)
вается ее точкой перегиба, если' /
она отделяет интервал, на кото- / ;~
ром функция выпукла, от интер- /
вала, на котором она вогнута '/ X У
(рис. 39). /
Сформулируем необходимый /________________[__________м
признак существования точки пе-у 0 х0 X
региба. '
Если функция в точке х0 име-
ет перегиб, то вторая производная Рис’ 39
в этой точке либо не существует, либо равна нулю.
Точки,-в которых вторая производная обращается в нуль или не существует, называются критическими точками II рода. В этих точках перегиб может быть, а может и не быть. Решает этот вопрос достаточный признак существования точки перегиба (так называемое «правило дождя»).
Пусть функция определена и непрерывна в некоторой окрест-' ности точки х0, включая саму точку. Пусть далее вторая производная в этой точке равна нулю или не существует.
Тогда, если:
1) Г <х) < 0 йри х < х0, 1) Г (х) > 0 при х < х0,
2) f (х) > 0 при х > х0 2) f" (х) < 0 при х > Хо,
то точка Мо (хо, / (хо)) будет точкой перегиба кривой у — f (х). Схема применения второй производной для отыскания интервалов выпуклости и вогнутости и точек перегиба совершенно аналогична схеме отыскания экстремумов и интервалов монотонности, только вместо первой производной рассматривается вторая.
l.i
Примеры. 1. у = ..—
х2 + 1 „ 2(3х2—1) Л Находим вторую производную: у = . Решаем неравенства:
. „ ’ 2(3х2— 1) Л 1. i
>°’или "(7+1)»'> ’откудаж<-л 2(3х«—1) л 1 1
ф у <0, ИЛИ (х^+1)3 1 ткула
Приравнивая к нулю вторую производную, находим критические точки II ро-
-°’ тую Vf-
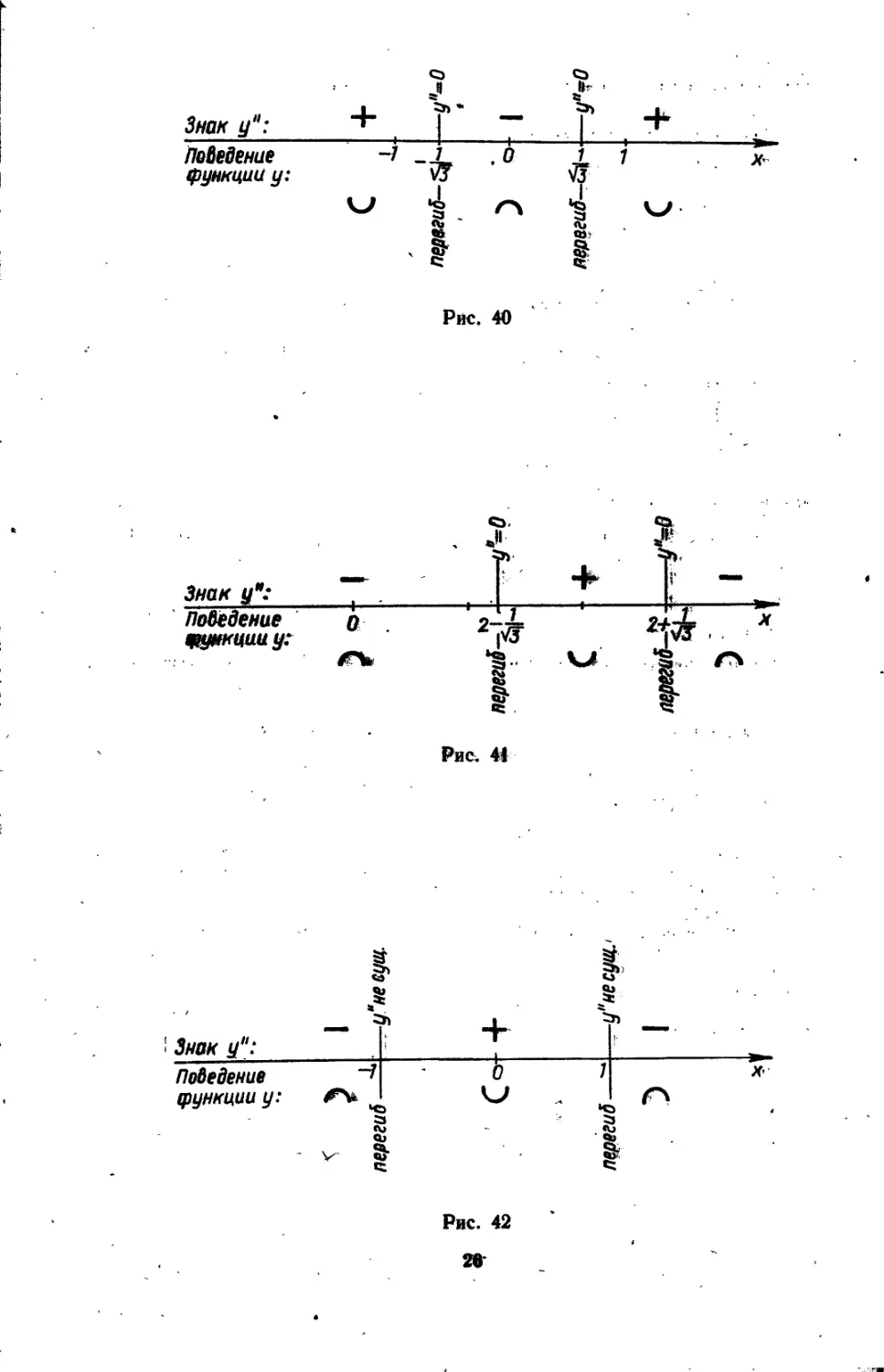
1 1 Из схемы (рис. 40) следует, что в точках Xf == — -7==, функция име-
у 3 уЗ
+<» Функ-
ет перегибы. Кроме того, на интервалах
3 Заказ 6912
25
Знак у": Поведение функции у:
Рис. 40
Знак у": г
Поведение о
Ч&ккцииу:
•3//g* Поведение функции у:
Рис. 42
20
ция вогнута, а на интервале
Т: гНвыпукла-
3
Ординаты точек перегиба: у^ = у2 = — * 4 • ;
2. у = (х2 —4х + 3)2. ’ ,
Находим вторую ^производную: у" = 121 х? — 4х + ~). Решаем неравенства. \ о J
2) у” > 0, или 12 (х* — 4х -f- •—) > 0, откуда х > 2 + —^==, х < 2 — Z7~-
Таким образом, на интервалах j— оо, 2 — U j 2 + функ-
ция вогнута, на интервале 12 — -—==; 2-|- —;=[ функция выпукла. Приравнивая J У 3 • г 3 L
к нулю вторую производную, находим критические точки II рода: у" «= 12 (х2 — -4х+^)=°> 0ТКУда ^ = 2-F5=: *i = 2+yT’
1 1
Из схемы (рис. 41) следует, что в точках х^ =2 —^==; д^=2 функция имеет перегибы.
Ординаты точек перегиба: у± = (х% — 4х^ + 3)? =« Уа = (^2 “ 4х2 + 3)?=»
4
JT. • ' " '
& у =х^/’х2— I/ . 2 х« + 3
Находим вторую производную: у” =»— ~ . Решаем неравенства:
(х*- 1Р
2 х2 4- 3 а), у" > 0, или — — ------5“ > 0, откуда —1 < х < 1|
(х*-1)Т
2 х2 4- 3
б) уп <0, или — — -------g- <0, откуда х < — 1;,х> 1.
(х2 —1)F
В точках Xi — —1, х2 — + 4 вторая производная не существует (знаменатель обращается в нуль); сама же функция в этих точках существует, непрерывна и принимает значение, .равное нулю.
Учитывая, что ни в одной точке действительной оси вторая производная в нуль не обращается, критическими точками II рода будут только точки *1 == 1, *2 = + 1.
Из схемы {рис. 42) следует, что в точках xi = —1, х2 = 1 функция имеет перегибы.
Кроме того, на интервалах ]—оо; —1 [(J]l; +«>[ функция выпукла, а на z интервале ]—I; 1[ вогнута. Ординаты точек перегиба: yi= у2 — 0-
3*
Глава l|
$ 7. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ ПРИ ПОСТРОЕНИИ ГРАФИКОВ
‘ Метода математического анализа позволяют строить достаточно точный график заданной функции, если только удается Хорошо изучить свойства этой функции.
Изучение свойств функции при построении графика целесообразно проводить по следующей схеме:
I. Нахождение области определения и точек разрыва; вычисление значений функции (или соответствующих пределов) в граничных точках области определения.
II. Определение четности или нечетности, периодичности функции.
III. Определение нулей функции и интервалов знакопостоян-ства.
IV. Нахождение асимптот. - . '
V. Исследование функций на экстремум, определение интервалов монотонности.
VI. Нахождение точек перегиба и интервалов выпуклости и вогнутости.
Полезно каждый этап исследования функции по данной схеме сопровождать, соответствующим построением.
Отметим, что эта далеко не полная схема позволяет тем не менее успешно строить графики подавляющего большинства функций, встречающихся на практике в школе, техникуме и техническом вузе.
$ 8. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ОБЩЕЙ СХЕМЫ
Для иллюстрации указанной схемы рассмотрим примеры по-строения графиков функций следующих классов:
А. Степенные функции, заданные или в виде произведения
многочленов, или в виде многочленов третьей и выше степени.
У
В. Дробно-рациональные функции. Так называются функции вида
_ где и Q (х) — многочлены от х.
Q (*)
С. Сумма (разность) функций.
D. Сложные функции. Так называются функции вида у =
» ф (х)], где ф и f — любые из элементарных функций.
Примеры.
1. у = х (х 4- 1) (х — 1).
28
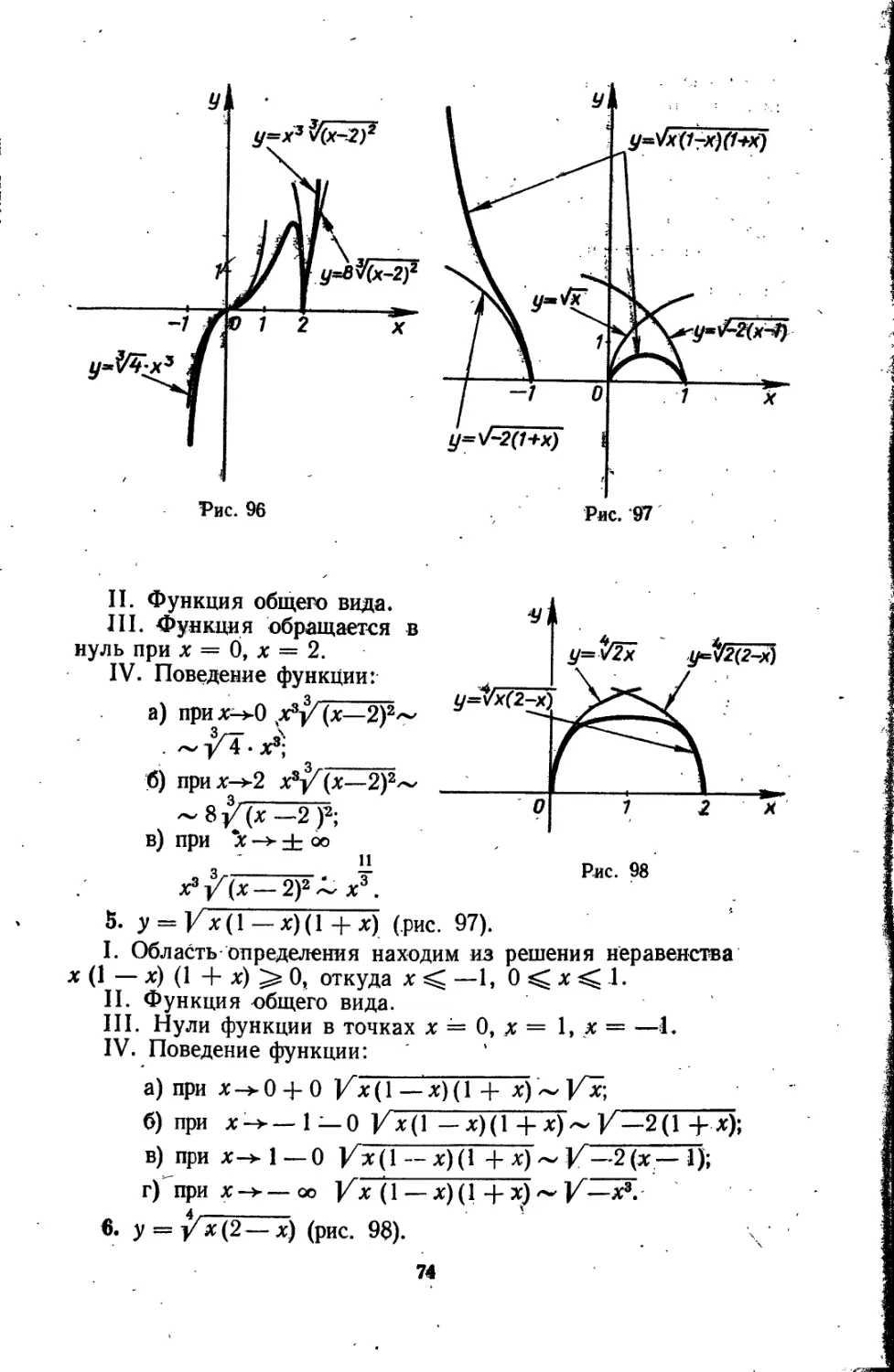
I. Область определения — вся числовая ось. Точек разрыва нет. Граничные значения функции;
limx(x.-|-1) (х—1) = + оо, limx(x4-l)(x—1)=—<х>.
X-*—оо
II. Функция непериодическая, нечетная.
III. Функция имеет три нуля: х = 0, х = —1, х — 1.
Для нахождения интервалов знакопостоянства решаем неравенство х (х + 1)(х — 1) > 0.
Его решением служит объединение -двух интервалов: ]-1;0[и]1;+«€
.Таким . образом, функция положительна на. интервалах ]—1; О +<»[-и отрицательна на интервалах
]—оо; — I[U]O; 1[ (последнее следует из нечетности функции).
IV. Найдем угловой коэффициент наклонной асимптоты?
^limZ^lim^^-^t-U^oo. Х->оо X Х->оо X
Таким образом, наклонных, а следовательно, и горизонтальных асимптот нет. Вертикальных асимптот также не имеется (нет точек разрыва).
V. Найдем производную функции: у' = Зх2 —1.
Решаем неравенства: а) у' >0, или Зх2—1 > 0, откуда х < — ^==, х >р=;б) /= °.или Зх2—1 <0, откуда — у=. < х <
' Таким образом, на интервалах 1—оо; — ^Luful-^=; +<»Гпроиз-водная пгмюжительна, на интервале ^==; производная отрицательна.
, Приравнивая к нулю производную, находим критические точки I рода: у'= Зх2—1 . = 0, откуда х = х =—p-L..
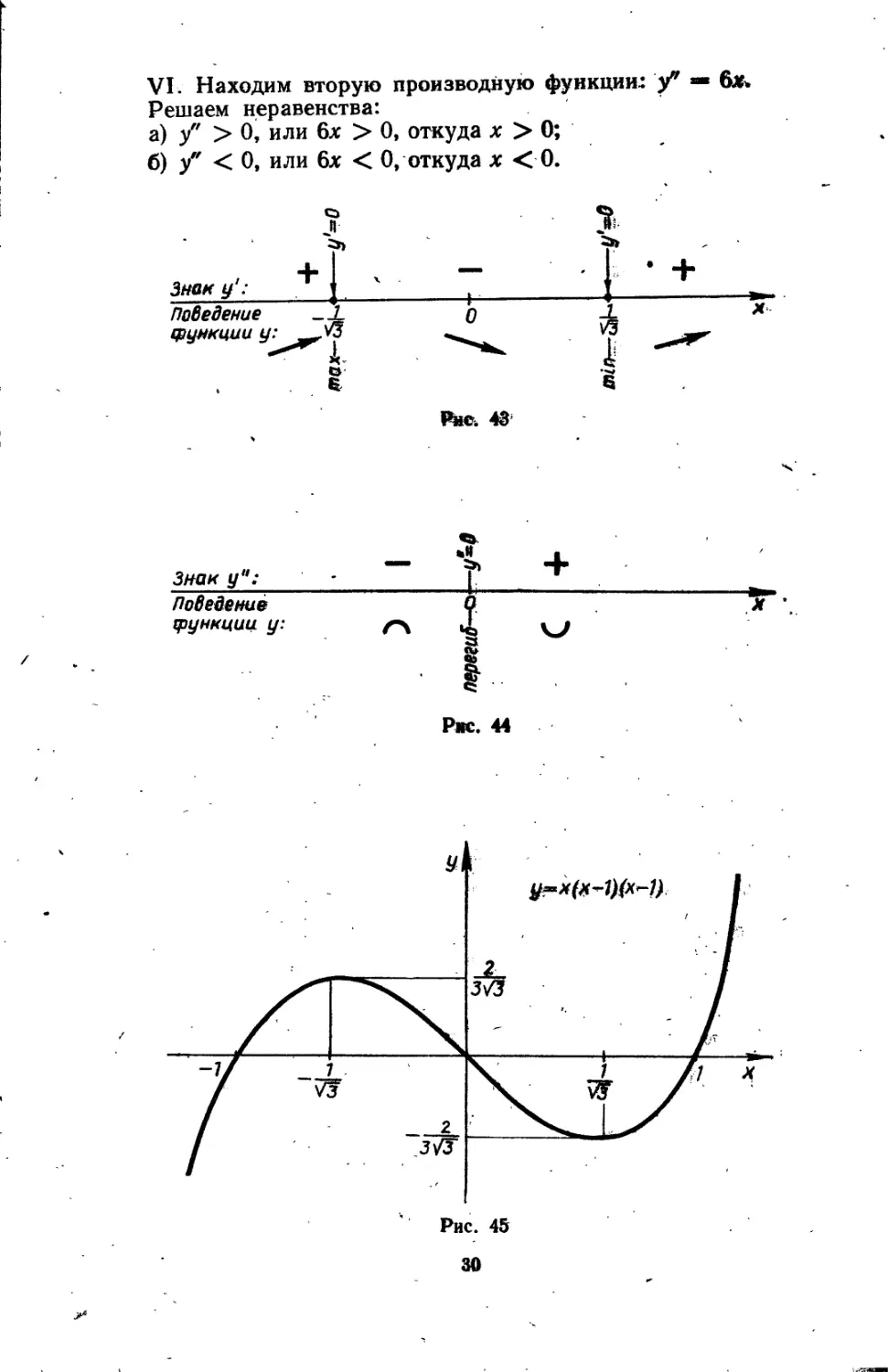
Рисуем схему (рис. 43), из которой следует, что в точке х =
в — —= функция имеет максимум, а в точке х = — мини-
мум.
Отметим, кроме того, что на интервалах —оо;
u]-J=; 4-oof функция монотонно возрастает, а на интервале ]— функция монотонно убывает.
Значения функции в экстремальных точках:
1 2 1 2
При Яшах ХЗ” Ушах — 3 ’ ПР** У~3~ 3 j/'З ’
29
VI. Находим вторую производную функции: у? « Решаем неравенства:
а) у" > 0, или 6х > 0, откуда х > 0;
б) у" < 0, или 6х < 0, откуда х < 0.
Знак у': Поведение функции у:
Знак у": Поведение Функции у:
Rife 4а
30
Приравнивая к нулю вторую производную, найдем критическую точку II рода: у" == = 6х = 0, откуда х — 0.
Рисуем схему (рис. 44), из которой следует, что в точке х = 0 функция имеет перегиб (это также следует из нечетности функции). Кроме того, на интервале ]—оо; 0[функция выпукла, а на интервале ]0; +оо[ вогнута. Ордината точки перегиба: упер = 0.
График функции представлен на рис. 45. При построении пользуемся симметрией графика относительно начала координат.
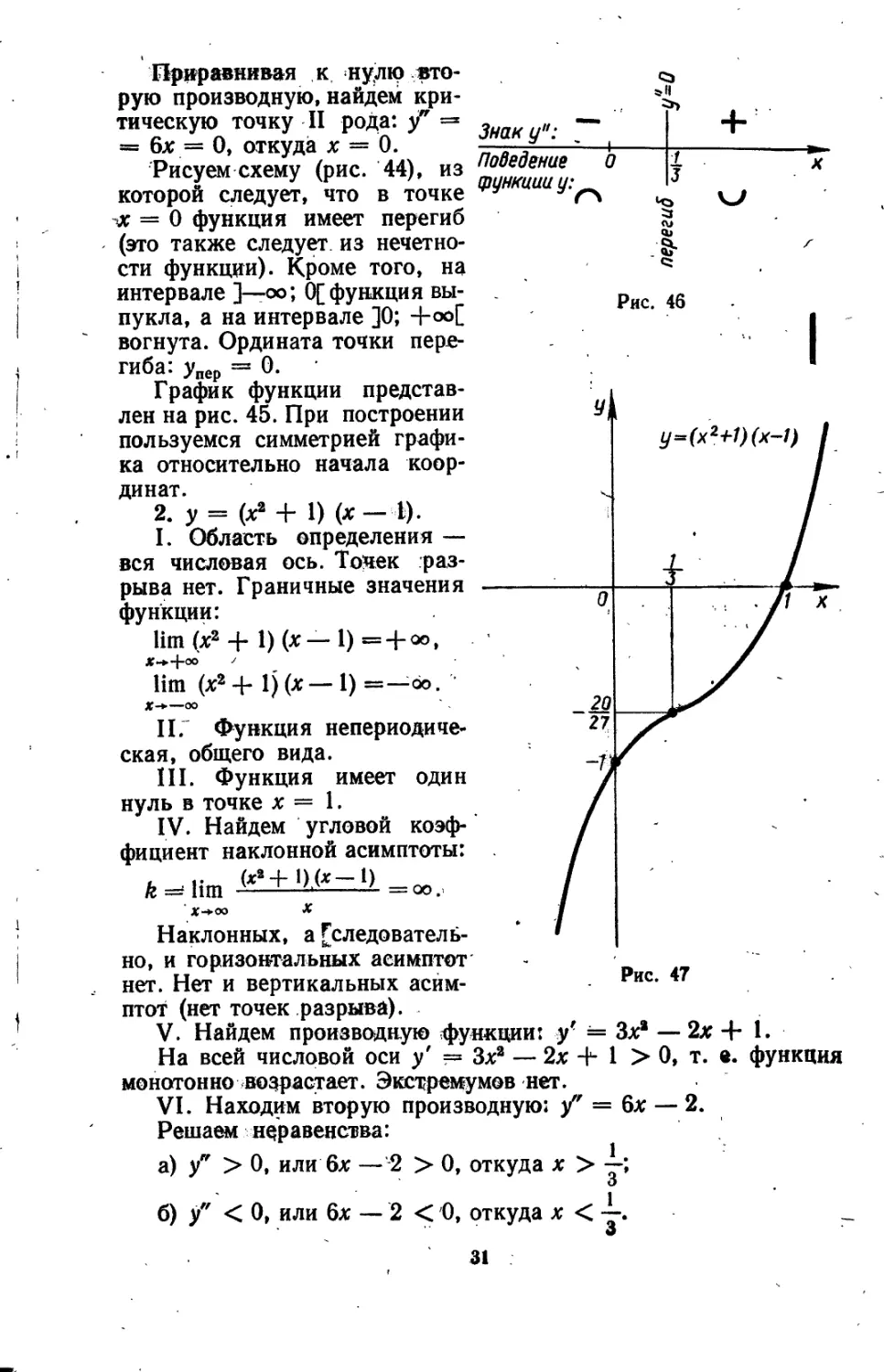
2. у = (х2 + 1) (х - I).
I. Область определения — вся числовая ось. Точек разрыва нет. Граничные значения функции:
lim (х2 4- 1) (х — 1) = + оо,
lim (х2 4-1) (х — 1) =—оо. Х->—оо
II. ' Функция непериодическая, общего вида.
III. Функция имеет один нуль в точке х = 1.
IV. Найдем угловой коэф-' фициент наклонной асимптоты:
^lin „оо.
Х->оо %
Наклонных, а [следователь-
Рис. 46
Знак у": Поведение о
функиии у:
но, и горизонтальных асимптот -
нет. Нет и вертикальных асим- Рис’ 47
птот (нет точек разрыва).
V. Найдем производную функции: у' = Зх2 — 2х 4- 1.
На всей числовой оси у' = Зх2 — 2х 4- 1 > 0, т. е. функция монотонно возрастает. Экстремумов нет.
VI. Находим вторую производную: у" = 6х — 2.
Решаем неравенства:
а) у" > 0, или 6х — 2 > 0, откуда х > —; 3
б) у" < 0, или 6х — 2 < 0, откуда х < —.
3
31
Приравнивая к нулю вторую производную, найдем критическую точку II рода: у" = 6х — 2, откуда х = —.
- Из схемы (рис. 46) следует, что в точке х — — -функция имеет 3
перегиб. На интервале —оо; — функция выпукла, а на интер-J 31
1 1 ч Г вале у, +оо вогнута.
20
Ордината точки перегиба: упер — —
График функции представлен на рисе 47.
- 3i у = х* — 2х®—1.
I. Область определения — вся числовая ось. Точек разрыва нет. Граничные значения функции:
„ lim (х4 — 2х® — 1) e +оо; lim (х* — 2х® — 1) = -|-оо.
X-b-f-OO «-►—оо
II. Функция общего вида, непериодическая.
III. Нахождение нулей функции и интервалов знакопостоян-ства 'в данном случае затруднительно. Поэтому переходим к следующему пункту.
IV. Найдем угловой коэффициент наклонной асимптоты: k =iim = оо.
Асимптот нет. . ~
V. Найдем производную функции: у* — 4х® — 6х*.
Решаем неравенства:
а) у' > 0. или 4х® — 6х2 * > 0, откуда х > у.
Таким образом, на интервале +°°£ производная положительна. ' . - •
б) у' < 0, или 2х2 (2х — 3) <0, откуда х < 0, 0 < х < у. 1 Г 1 з г
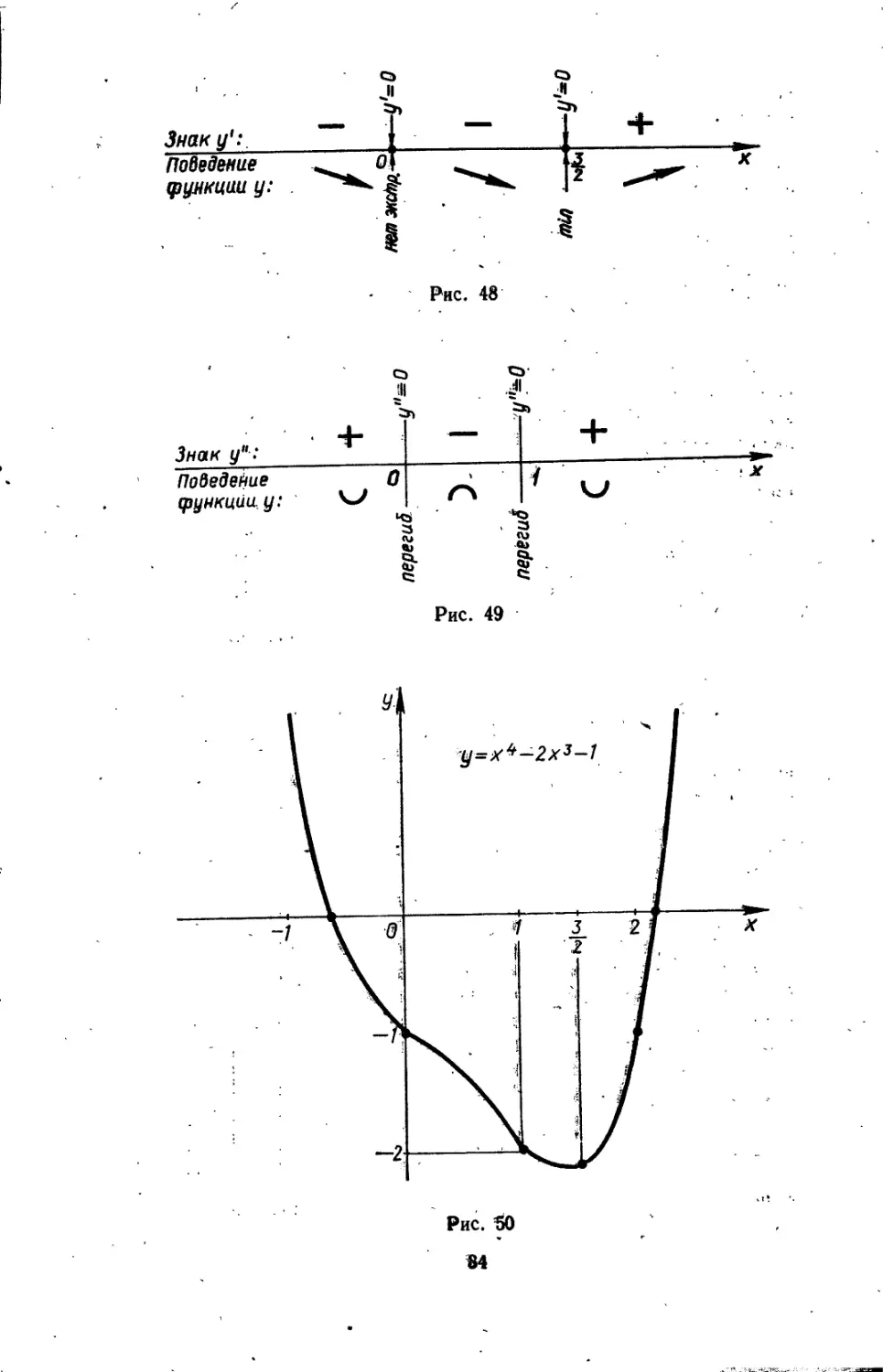
На интервала* —оо; 0 U Ю;у производная отрицательна. Приравнивая к нулю производную, находим критические точки I рода: - у' = 4№ — бх8 = 0, откуда х = 0, х = —. ’
3
Из схемы (рис. 48) следует, что в точке х =— функция имеет
1 r 1 3 Г 4
минимум. Отметим, что на интервалах — оо; 0.1 (J 0; -Н функция
монотонно убывает, а на интервале +оо£ монотонно возрас-
тает, .
82
Ордината точки минимума: ymln' = —2^.
VI. Находим вторую производную: у" = 12х* — 12х.
Решаем неравенства:
а) у" > 0, или 12х* — 12х > 0, откуда х < 0, хч> 1.
Таким образом, на интервалах ]—со; О [U]l; +«>[ вторая производная положительна.
б) У" < 0; или 12х* — 12х < 0, откуда 0 < х < 1, т., е. на интервале ]0; 1[ вторая производная отрицательна. Приравнивая к нулю вторую производную, находим критические точки II рода: у" = 12лг — 12х = 0, откуда х = 0, х = 1. ,
Из схемы (рис. 49) следует, что в точках х = 0 их = 1 функция имеет перегибы. На интервалах ]—со; O [Q11; Ч-оо[ функция вогнута,- а на интервале ]0; 1[ выпукла.
Ординаты точек перегиба: при х = 0 упер « —1; при х — 1 Упер — —2- График функции представлен на рис. 50.
4. у=_1л»4-х-Ь4.
О
I. Область определения—вся числовая ось. Точек разрыва нет. Граничные значения функции: lim (—tx®4- х + 4^ =—оо;
*-►+<» \ « /
lira {—+ Л + 4)’“ +°°.
со \ О. /
II. Функция общего вида, непериодическая.
III. Нахождение нулей функции и интервалов знакопостоян-ства в данном случае затруднительно.
IV. Найдем углово'й коэффициент наклонной асимптоты:
k = lim - .... " = —оо.
Х-ьоо X
Асимптот нет. ,
V. Найдем производную функции: у' = — х* + 1.
Решаем неравенства:
а) у' > 0, или —х* 4-1 >0, откуда —1 < х. < 1;
б) у' < 0, или —х4 4- 1 < 0, откуда х <—1; х > 1.
Приравнивая к нулю производную, находим критические точки 1рода: у' = —х? + 1 == 0, откуда х = —1, х = 1.
Из схемы (рис. 51) следует, что в точке х = —1 функция имеет минимум, а в точке х=1—максимум. На интервалах ]—со; —4-со[ функция монотонно убывает, а на интервале ]—1; 1[ монотонно возрастает.
Ординаты экстремальных точек:
при х = — 1 ymln = 31; Гфи х = 1 утах = 4-1.
О : О ' ’
’ VI. Находим вторую производную: у" = 4л8.
На интервале ]—оо; 0[ вторая производная положительна, а на интервале ]0; 4-оо[ отрицательна. В точке х = 0 (критическая
83
Знак у': Поведение функции у:
Рис. 48
Знак у": Поведение функции у:
точка II рода) вторая производная обращается в нуль. Из схемы (рис. 52) следует, что в точке х = 0 функция имеет перегиб, на интервале 0 [ функция вогнута, а на интервале ]0; +оо] выпукла. Ордината точки перегиба упер = 4.
График функции представлен на рис. 53. .
б.у = 2±±1.
J 3 — х
I. Область определения — вся числовая ось, кроме точки х = 3, в которой функция имеет разрыв.
Граничные значения функции:
lim 2;
X -»—оо 3 — X 1? 2х + 1 ж ---------— =*4-оо; х->з—о з—х
lim ---оо-
г->3+0 3 — х
lim 3i±l=-2.
x-*-|-oo 3 — X
Отсюда следует, что имеется вертикальная асимптота х = 3 и горизонтальная асимптота У = -2- .
II. Функция общего вида, непериодическая.
III. Функция имеет один нуль в точке х =—-.
2
Для нахождения интервалов знакопостоянства решаем неравенства:
а) У > 0. или > О, ’ 3—х
откуда — -i < х < 3;
б) у < 0, или 1 < 0, от-' л ’ з—х
куда х < — 1; х > 3.
У У . Sh Ji. Знак у':______iii
Поведение -Ц о Г?
функции I
•1 I
Рис . 51
Знак у*< ПабейбншГ функции у:
Рис. т
Функция положительна на интервале j—у; з£ и отрицательна на интервалах|—оо; —~[U]3; + оо£.
IV. Найдем параметры наклонной асимптоты:
k - lim 2*t 1. = 0; b = lim (у — kx) = lim 2.
X->oo X (3 — X) X->oo X->oo 3 — x
Наклонных асимптот нет, есть вертикальная х = 3 и гори* < зонтальная у = —2.
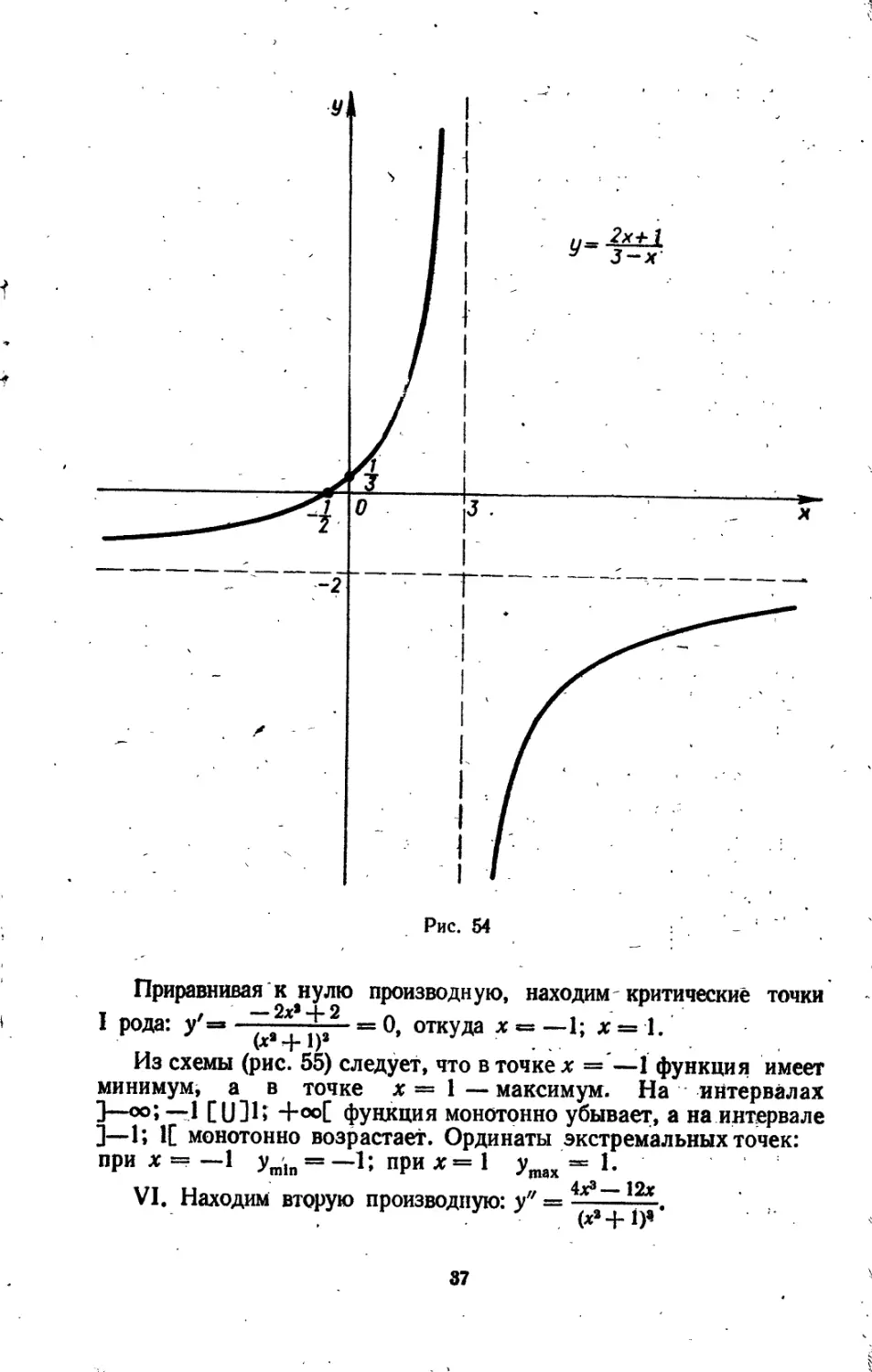
V. Найдем производную функции: у' = ——.
Производная положительна всюду, где функция определена. Таким образом, функция монотонно возрастает на интервале ]-—оо, 3; [ (J ]3; +<»[, экстремумов нет.
VI. Находим вторую производную: у"— ——• >
Решаем неравенства:
14
а) у" > 0, или > 0» откУДа х < 3;
б) У"<0, или (-Д-ф <0>-откуда х>0. _
Вторая производная в нуль нигде не обращается, точек перегиба, нет. На интервале ]—оо; 3[ функция вогнута, а на интервале ]3; 4-оо[ выпукла.
График функции представлен на рис. 54.
6. у = — «8+1
I. Область определения — вся числовая ось. Точек разрыва нет. 9 v 2х
Граничные значения: lim ----=0; lim ----------- 0.
F - X-+ooJK»4-l X—ooX»4-l
II. Функция непериодическая, нечетная.
III. Функция имеет один нуль в точке-х “ 0.
Функция положительна на интервале ]0; +оо[ и отрицательна на интервале]—оо; 0Q.
IV. Найдем параметры наклонной асимптоты: k == lim'-........—- - 0; b = lira—= 0.
' х-*оо X (х* -j- 1-) х-»оо X21-
Таким образом, имеется горизонтальная асимптота у = 0.
V. Найдём производную функции: у' =--------.
' ’ (х2 -|- I)2
Решаем неравенства: >
а) у' > 6, или > °’ откуда — f < х < 1;
(х?4-1)2
б) У' < 0, или ' < 0» откуда х < —1; х > 1.
Приравнивая к нулю производную, находим'критические точки _ . — -I- 2 л « -
I рода: у'= " = °» откуда х = —1; х = 1.
Из схемы (рис. 5о) следует, что в точке х = —1 функция имеет
минимум, а в точке х=1—максимум. На интервалах ]—<»;—1 [U]1; +<»[ функция монотонно убывает, а на интервале ]—Г, 1[ монотонно возрастает. Ординаты экстремальных точек: при х == —1 ymln = —1; прих=1 утах = 1-
VI. Находим вторую производную: у" =
4л3—12х
(*»+!)*•
87
Решаем неравенства:
а) у" > 0, или
б) у" < О, или
——— >0, откуда — КЗ<х<0; х>У~3;
(Х3 + I)3 »
***~ *?£ < о, откуда 0 < х < КЗ; х <— КЗ?
(Х*+ I)3
Приравнивая к нулю вторую производную, находим критические точки II рода:
4хЗ-12х
У (х* + I)3
= 0, откуда х = 0; х = -1' 3: х = КЗ. •
Из схемы (рис. 56) следует, что в точках х = 0, х = —КЗ, х = КЗ; функция имеет перегибы; на интервалах ]—КЗ; 0[[| Ц]КЗ; -р де>[ функция вогнута, а на интервала^ ]0; K.3CU1 — оо; — /3 [выпукла. Ординаты точек перегиба:
при X =г0 упер = 0; при х = — V 3 упер = — 5-; при Х = УЗ
Упер ” 2 '
График функции прёдставлен на рис. 57
Знак у': Подедение tpyfiKuuh у:
Рис. 55
Поведение фунхцииу;
Рис. 56
1
X
Пт —-— = — оо; X->.2-—0 X2 4
Пт —-— — — оо; я->2—ox2 — 4.
Jhn< —— = 0.
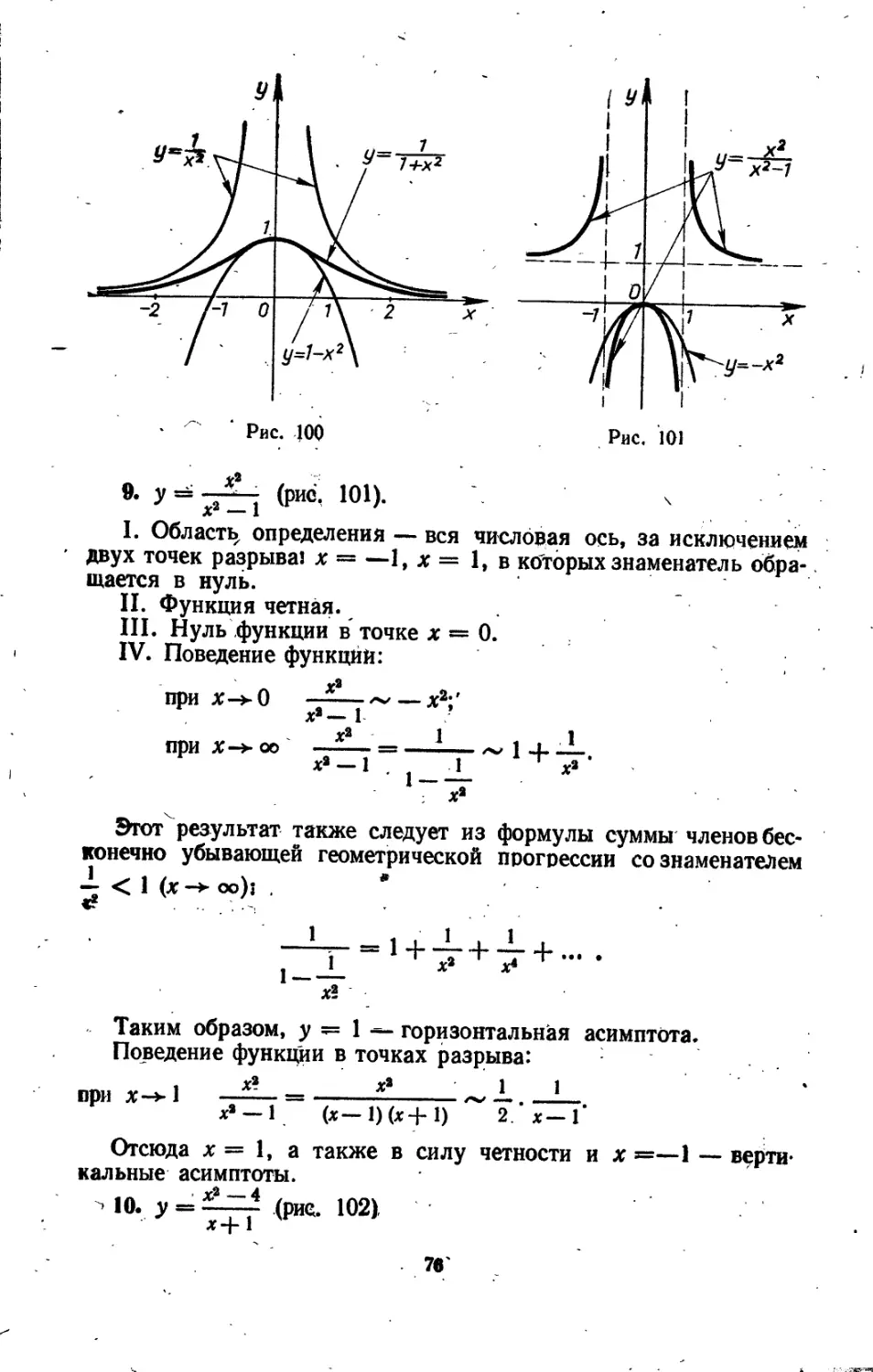
I. Область определения — вся числовая ось, креме точек » 2 и х — —2, в которых функция терпит разрывы. '
Граничные значения функции:
lim —— = 0; ж-*—со х? — 4
Hm « Н х->-2-}-0Х2—4 lim —— = х->2-Ь0Х?~ 4
Отсюда следует, что имеются две вертикальные асимптоты х = 2 и х = —2 и горизонтальная у = 0.
II. Функция непериодическая, нечетная.
III. Функция имеет один нуль в точке х = 0.
Для нахождения интервалов знакопостоянства решаем неравенство:
у' > 0, или —-— > 0, откуда —2 < х < 0 их >2. х2 — 4
Функция положительна на интервалах ]—2; 0 [J]2; 4-оо[ и отрицательна (в силу нечетности) на интервалах^]—оо; —2[ UJO; 2[. t
IV. Найдем параметры наклонной асимптоты:
k = lim — = lim--------= 0; b =.lim(y— kx) — lim —-— = 0.
X-*x X x-.ooX(X2 —4) X-.cc X-.00X?— 4
Наклонных асимптот нет, есть горизонтальная асимптота у=0.
V. Найдем производную функции: у' —-----х * '
(х2 — 4)2
Производная отрицательна на всей числовой оси, кроме точек х — 2 и х — —2, где она не существует (fi этих точках и сама функция не существует). .Функция монотонно убывает всюду, где она определена.
VI. Находим вторую производную: у" — 2*** ~^2\
39
Решаем неравенства:
а) у" > О, или > 0. откуда —2 < х < 0; х > 2;.
б) у" < 0, или -* < 0, откуда х < —2; 0 < х < 2.
(х*. — 4)s
Приравнивая к нулю вторую производную, находим критическую точку II рода: х — 0.
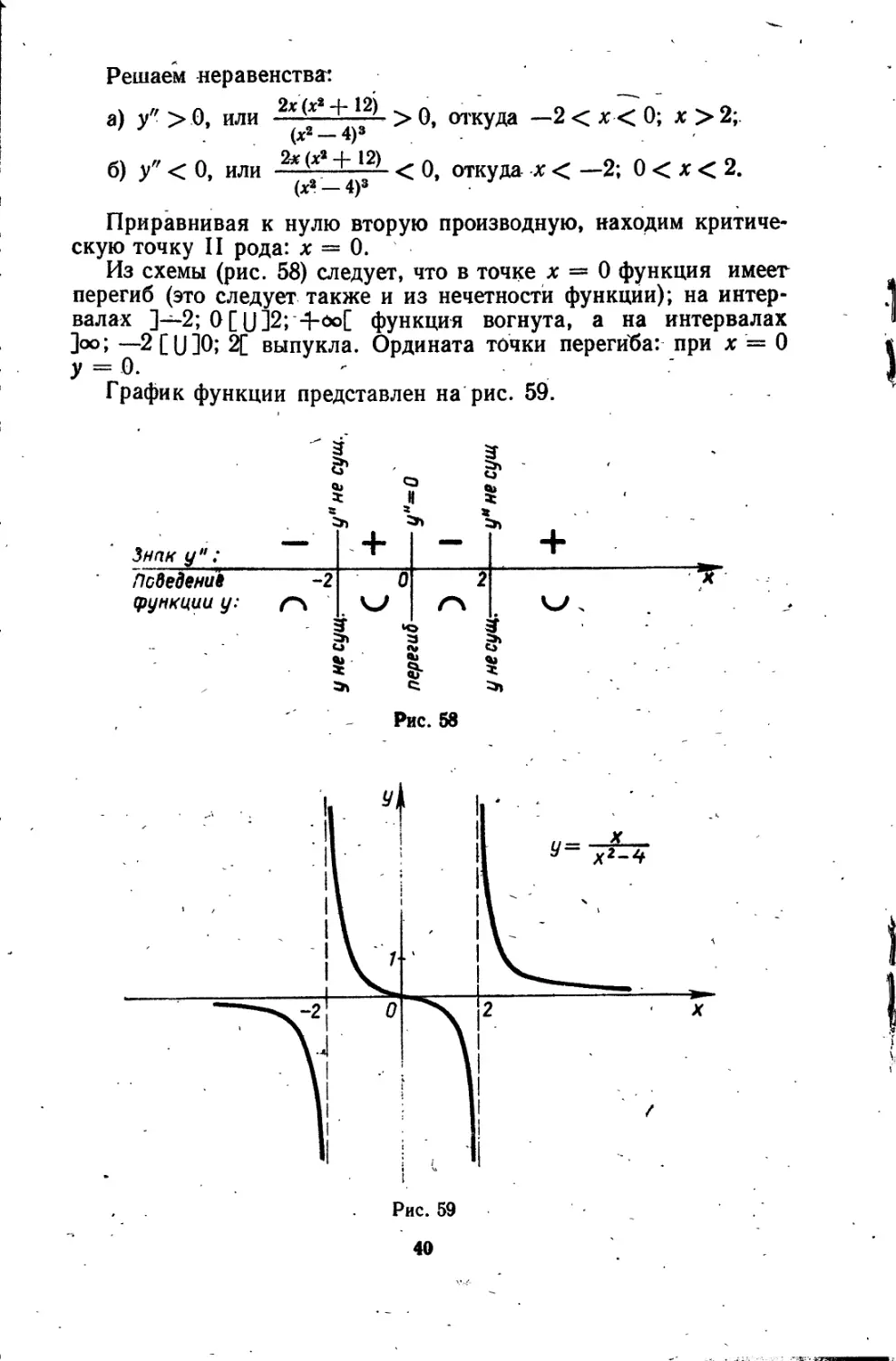
Из схемы (рис. 58) следует, что в точке х = 0 функция имеет перегиб (это следует также и из нечетности функции); на интервалах ]—2; 0[(JJ2;+<эо[ функция вогнута, а на интервалах ]оо; —2 [ (J ]0; 2[ выпукла. Ордината точки перегиба: при х = 0 у = 0.
График функции представлен на рис. 59.
Знак у" ; ПсЬедениЬ Функции у;
Рис. 58
40
lim --------= — оо;
i—о 2 (x-f- 1)»
lim ——— = 4-oo. ^+oo2(x+l)»
8. у =---------. v
I. Область определения — вся числовая ось, кроме точки х = —1, в которой функция терпит разрыв. Граничные значения функции:
lim ——— = Ц- оо; х^-оо2(х+1)«
lim —— = — оо х^_1+о2(х+ 1)1
Отсюда следует, что имеется вертикальная асимптота х = —1.
II. Функция непериодическая, общего вида.
III. Функция имеет один нуль в точке х — 0. Функция положительна при х > 0 и отрицательна при х < 0.
IV. Найдем параметры наклонной асимптоты:
/г — lim — = lim---—-----= —;
JC-+0O X Х-*оо 2х (Х 4" I)* 2
ft = lim (у— £x) = lim[——-------xl==—1. „
JC-.OO х->оо [2 (х -j- 1)? 2 J
Уравнение наклонной асимптоты: у = х — 1. ..
V. Найдем производную функции: у' =
Решаем неравенства:
а) у' > 0, или откуда х < —3; —1 < х < 0; *>0;
' б) у' < 0, или х < о, откуда —3 < х < —I.
' 7 2(х+1)”
Приравнивая к нулю производную, находим критические точ-. ки I рода: х — 0, х — —3.
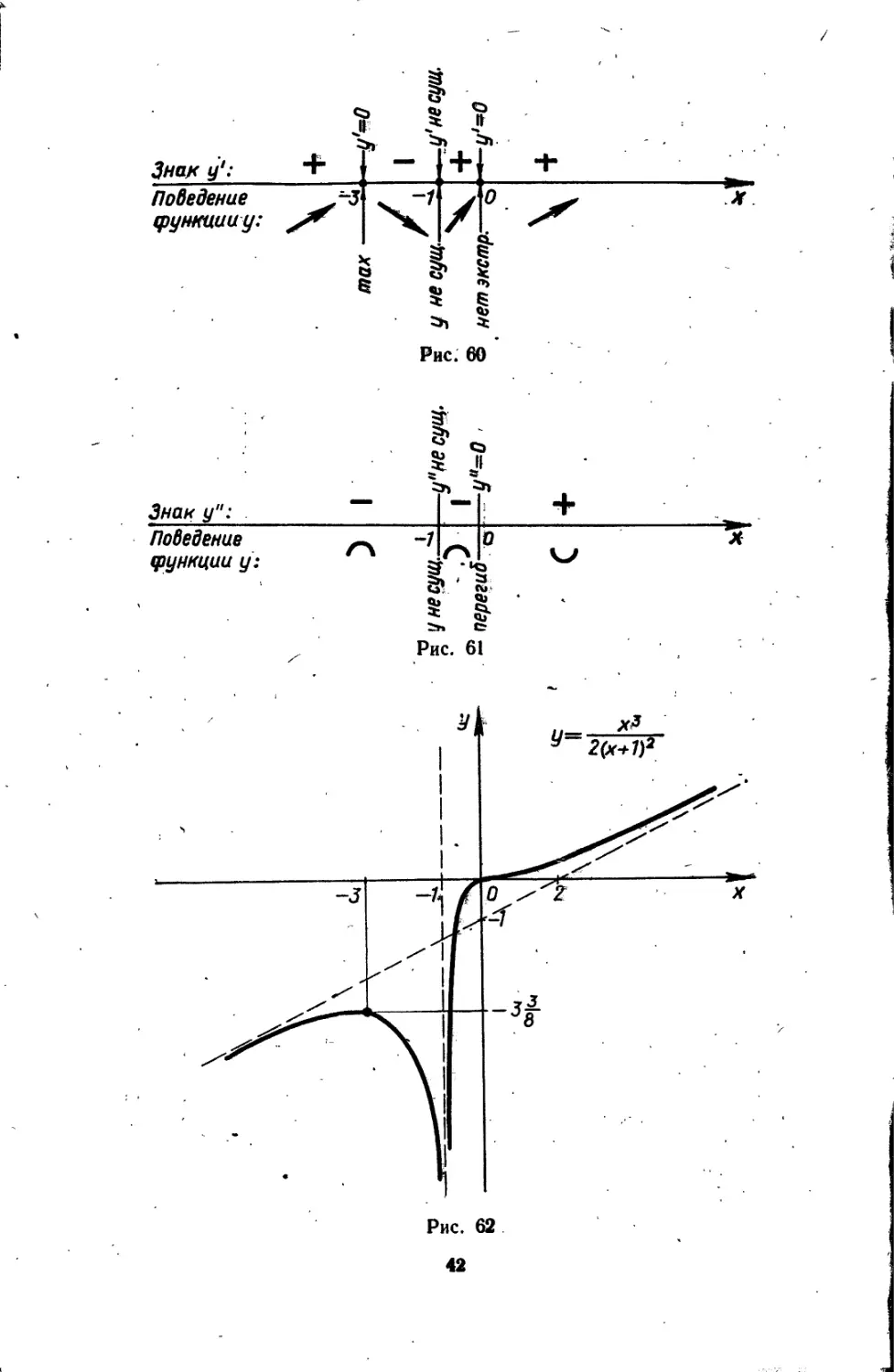
Из схемы (рис. 60) следует, что в точке х = —3 функция имеет максимум, в точке х == 0 экстремума. нет. На интервалах [—оь; —3 [(J]—1; О[иЮ; +°°[ функция монотонно возрастает, на интервале ]—3; —1[ монотонно убывает.
Ордината точки максимума: утах = — 3
Зх
VI. Находим вторую производную: у" = —:-----.
(•^ 4“ О •
Вторая производная положительна на интервале ]0; -?оо[ И отрицательна на интервалах]—оо; —1-CU3— U 0 [. Критическая точка II рода: х = 0. -
Из схемы (рис. 61) следует, что в точке х = 0 функция имеет перегиб; на интервалах]—оо; —1 [J]—1; 0[ функция выпукла, на интервале ]0; +оо[ вогнута. Ордината точки перегиба: у„ер = О»
График функции представлен на рис. 62.
41
Знак у": Поведение функции у:
3HW у1: Поведение функиииу:
Рис. 60
42
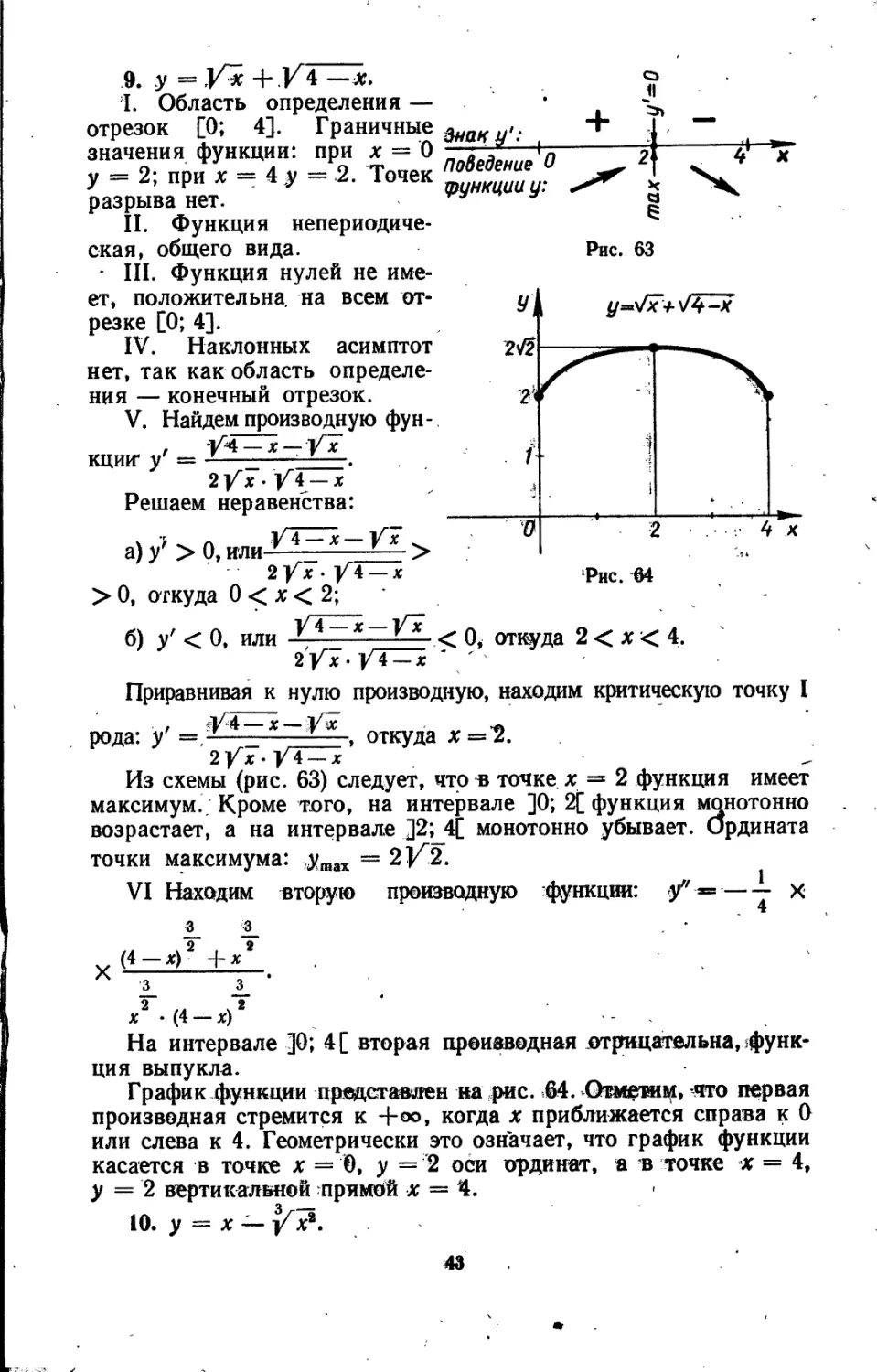
9. у = У~х + .К4 —х.
I. Область определения — отрезок [0; 4]. Граничные значения функции: при х = 0 у — 2; при х — 4 у = .2. Точек разрыва нет.
II. Функция непериодическая, общего вида.
• III. Функция нулей не имеет, положительна, на всем отрезке [0; 4].
IV. Наклонных асимптот нет, так как область определения — конечный отрезок.
V. Найдем производную фун-
Знаку': ( Поведение О функции у:
Рис. 63
2 Ух • У4 — х
Решаем неравенства:
\ 7 л У 4 — х — ’У х .
а) у > 0, нли^—=— >
2Ух • У4 — х
> 0, откуда 0 < х < 2;
б) у' < 0, или У4 * 0, откуда 2 < х < 4.
2 Ух • уТ^х ' ' '
Приравнивая к нулю производную, находим критическую точку I
. 4/4—х — 1/^
рода: у = -————— . откуда х =2.
2 Ух • УГ^х
Из схемы (рис. 63) следует, что в точке, х = 2 функция имеет максимум.. Кроме того, на интервале ]0; 2[ функция монотонно возрастает, а на интервале ]2; 4[ монотонно убывает. Ордината точки максимума: утах = 2J/2.
VI Находим вторую производную функции: -у" =--- х
4
з з
2 2
(4-х)* 2 +х
'3 3
2 2
х • (4 — х) - .
На интервале ДО; 4[ вторая производная отрицательна, .функция выпукла.
График.функции представлен на рис. .64. Отметим, что первая производная стремится к Н-оо, когда х приближается справа к О или слева к 4. Геометрически это означает, что график функции касается в точке х = 0, у = 2 оси ординат, а в точке х = 4, у = 2 вертикальной примой х — 4.
10. у = х — уСх’.
43
1. Область определения — вся числовая ось. Точек разрыва' нет.
Граничные значения функции:
11m у <= Мт (х—frx*) = — оо;
Х-»>—оо X-**—ОО
lim у = Нт (х—frx*) = Мтх /1 — \ = + °°>
«-»+«> «*+“ *-+“ \ уТ/
II. Функция непериодическая, общего вида.
III. Нули функции в точках х = 0 и х = 1. -
Функция положительна при х > 1 и отрицательна на интер*' валах ]—оо; 0 [ U J0; ![•
IV. Параметры наклонной асимптоты:
fe — lim = 1; b=lim(x—>/x*—x)« — oo.
X-+OO X Х-Ф00
Наклонных асимптот нет.
о
V. Найдем производную функции: у' = 1--5.
3-/х
Решаем неравенства:
а) у' > 0, или 1
б) у' < 0, или 1
2 я
— ^=>0’ откуда х<0; х>—\
—°* ^уда 0< х<
Приравнивая к нулю производную, находим критическую точку II рода:
—= откуда х = ^.
Зух
Кроме того, критической точкой I рода будет служить точка х = 0, в которой не существует производная.
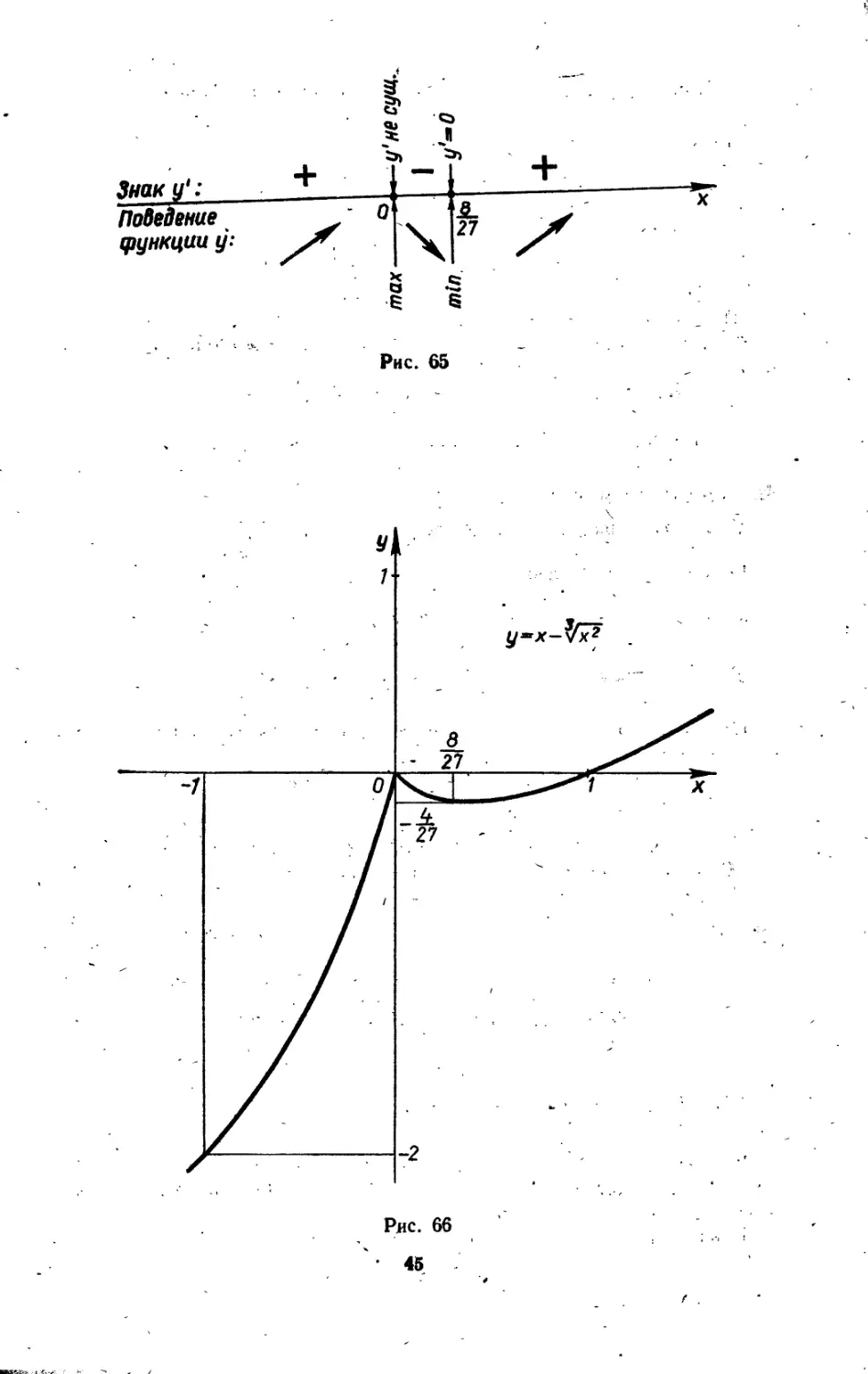
Из -схемы (рис. 65) следует, что в точке х = 0 функция имеет маквимум, в точке х = ^ — минимум; на интервалах J— <»;0 • (jj^; +°°^ функция монотонно возрастает, на интервале |0; монотонно убывает. Ординаты экстремальных точек:
"Ри *~0утах~0; при х»^ут1п=-±.
2 1
VI. Находим вторую производную функции: у" = — • —.
т 4 х
Вторая производная всюду положительна, кроме точки х = О, где она не существует. Поэтому функция вогнута на интервалах ]—<х>; 0CU30; Ч-ооС- '
График функции представлен на рис. 66.
44
11. у = V*2 —3*4-2.
I. Область определения — вся- числовая ось. Точек разрыва нет.
Граничные значения функции:
lim у/^х2— Зх 4- 2 = 4-0©; lim yfx2 — Зх 4- 2 = 4t 00.
ОО Х“++<5О
II. Функция непериодическая, общего вида.
III. Нули функции в точках х — 2; х = 1.
Функция положительна на интервалах ]—оо; Г[ Ц]2; 4-оо[ и отрицательна наинтёрвале ]1; 2[. '
IV. Параметры наклонной асимптоты: v
k — lim -ТЬ-2_ — 0; b = lim yfx2 — Зх 4- 2 = 00.
Х-юо X Х-юо
Наклонных асимптот нет.
1 2х__3
V. Найдем производную функции: у' —-----......
3 / (х* — 3x4-2)»
Решаем неравенства: .
а) у' > 0, или 4- --------------> 0, откуда х > -2-, х^ 2;
3 ?/(х»-Зх4-2)» 2 7
б) у' < 0, или Л------------- < о, откуда х < х 4= 1.
3 2
Приравнивая к нулю производную, найдем критическую точку тт 3 .
II рода:х = —.
Кроме того, имеются еще две критические точки I рода: х = 1 и х = 2. В этих точках производная не существует.,
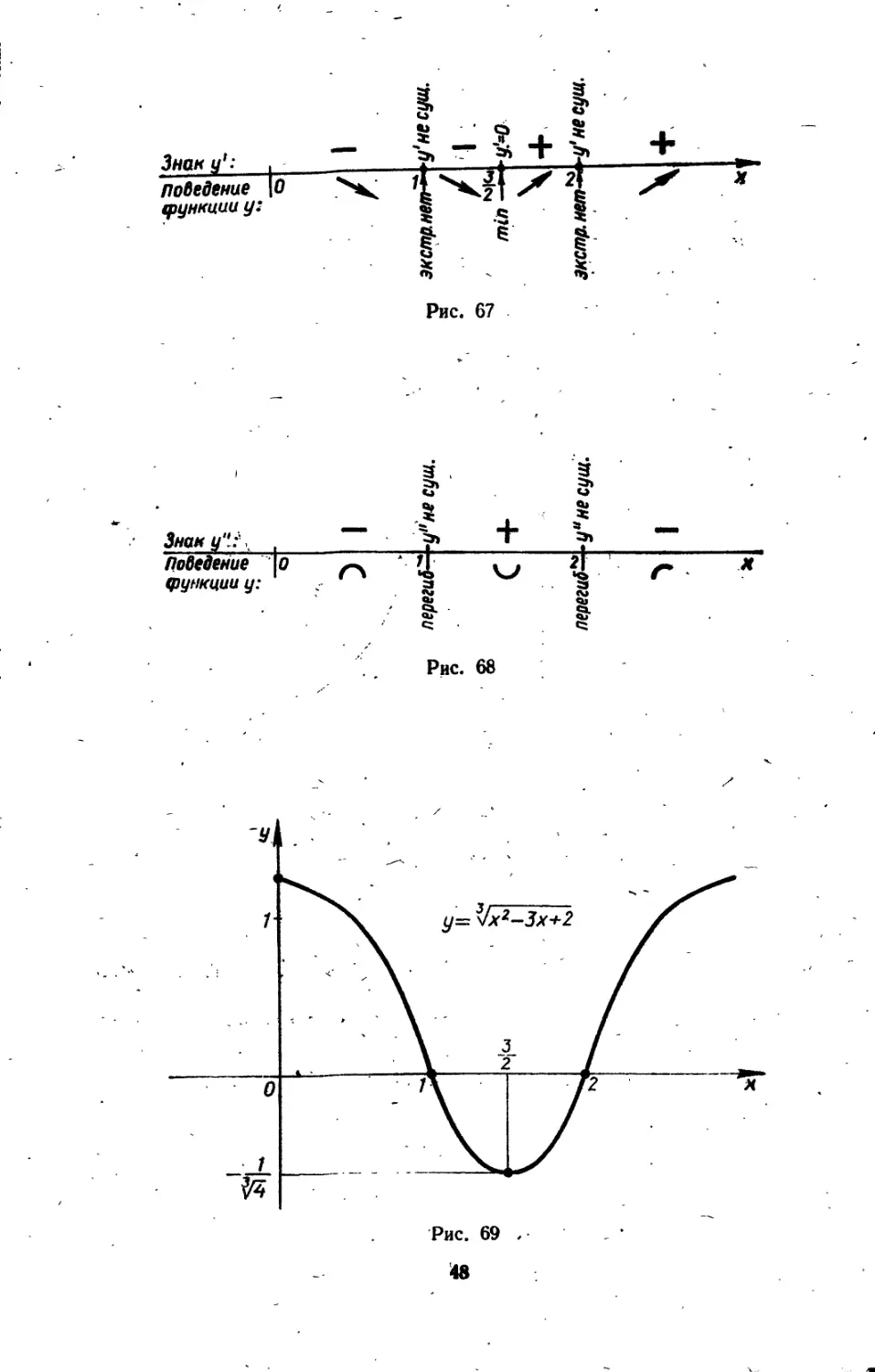
. Из схемы (рис. 67) следует, что функция монотонно убывает на интервалах —оо; 1 и монотонно возрастает на ин-
з име-
2
т-Х-. В точ-
]3 Г 1 Г 3
2 J 2; 4-оо . Таким образом, в точке х = —
ется минимум. Ордината точки минимума: ymIn = ках х = 1, х = 2 экстремумов нет.
VI. Находим вторую производную: у"
Решаем неравенства:
2 х» —3x4-3
9 т’
(х* —Зх-р2)
а) у" > 0, или — | > °, откуда г< X < 2;
б) У" < 0, или — у • < 0, откуда х < 1; х > 2.
4Г
Вторая производная в нуль нигде не обращается, однако в точках х — 1 и х = 2 она не существует. Эти точки являются критическими точками IГ рода. Из схемы (рис. 68) следует, что на интервалах,]—оо; l[|Jj2; °°Е функция выпукла, а на интервале ]1; 2[ вогнута. В точках х — Д' и х = 2 функция имеет' перегибы. Ординаты точек перегиба: при х = 1 Упер = 0; при х = 2 упер = 0.
График функции представлен на рис. 69.
- 12. у =
I. Область определения — вся числовая ось, кроме точки х = 1, в которой функция терпит разрыв. Граничные значения функции:
: _i_ 1 ' 1 1
lim е*-1 = 1; lime*";1 — 0; -limex~l— + оо; lim ex~l = 1. X-*—оо X->1—0 Х->1-|-& Х-ь-роо =
Отсюда следует, что х — 1 есть вертикальная асимптота.
II. Функция общего вида, непериодическая.
III. Нулей функция не имеет, положительна на всей числовой оси, кроме точки х = 1.
IV. Параметры наклонной асимптоты: 1 ' 1 ) ГЛ t—i
k = lim -— = 0; b — lim & = 1.
i * . - • . X->OO X X-kOO
Имеется горизонтальная асимптота у = 1.
V. Найдем производную функции: у' = —
Производная отрицательна на всей числовой оси, кроме точ-
ки х == 1. Следовательно, функция монотонно убывает всюду, где она определена. '
VI. Находим вторую производную: у" = • е*”1.
Решаем неравенства: 2х—1 (х - 1)« 2х—1 (х - 1)*
а) у" > 0, или
•б) у" < 0, или
2х— 1 (х-4)*
• е* * >0, откуда х>—;х=^1 *
4 ~—। 1
.е <0, откуда х<—. .
1
х—t ’
' Приравнивая к нулю вторую производную, найдем крйтичес-кую точку II рода: х = у.
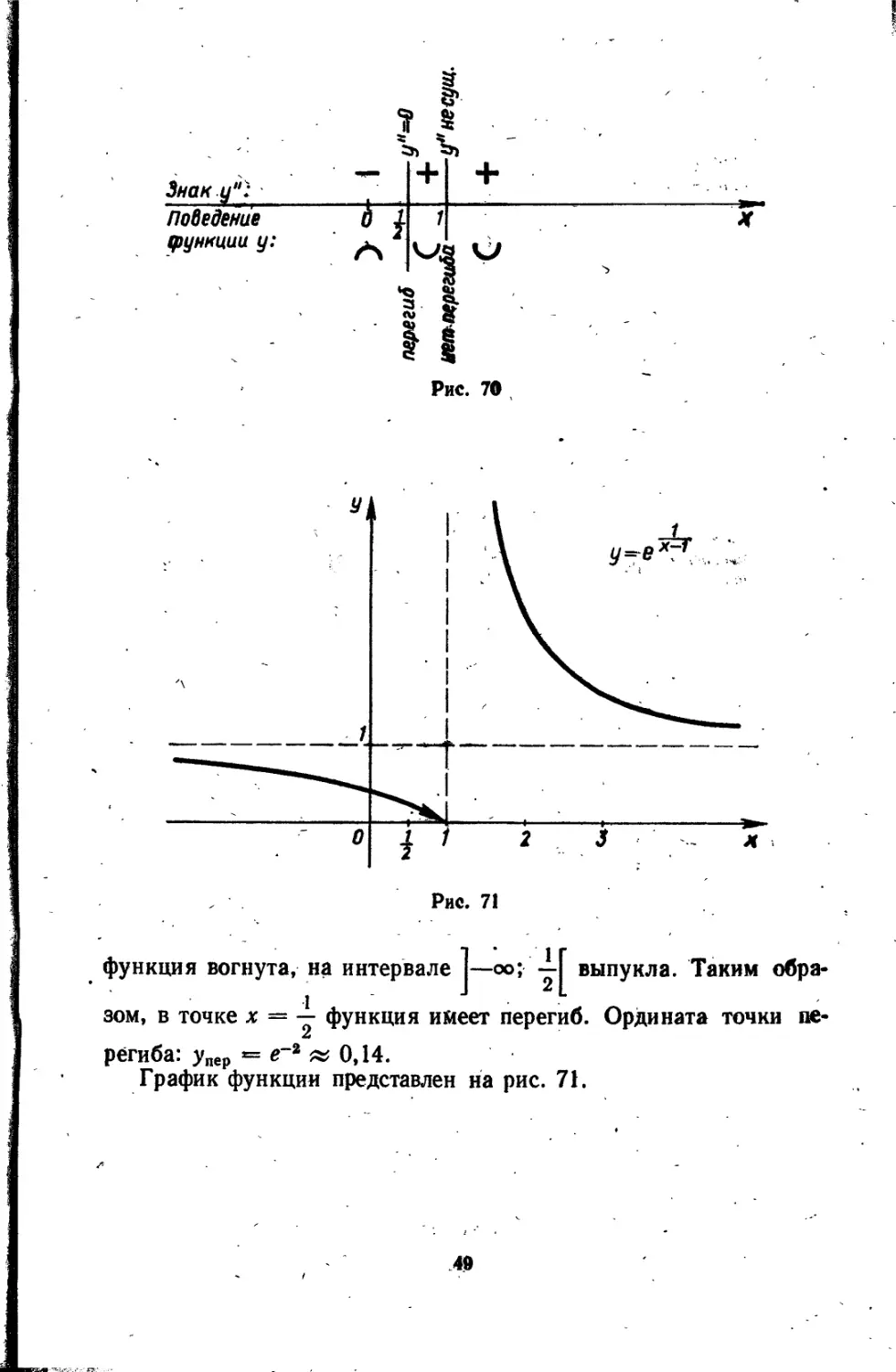
Из схемы (рис. 70) следует, что на интервалах 1—; 1 f (j] Ь +<ю|
12 | j I
Знак у1: ।
поведение |0 функции у:
Рис. 67
Знак у”: t
Поведение [о функции у:
Рис. 68
48
Знак у"I поведение функции у:
Рис. 79 ,
функция вогнута, на интервале j—оо; выпукла. Таким обра-
зом, в точке х = у функция имеет перегиб. Ордината точки перегиба: упер = в-2 ~ 0,14.
График функции представлен на рис. 71.
49
Глава III
$ 9. ОПЕРАЦИИ НАД ГРАФИКАМИ ФУНКЦИЙ
В этой главе мы рассмотрим графики функций вида у = /[ф(х)], где <р (х) — любая из-основных элементарных функций, а / — любая из следующих операций над ними: прибавление к функции какого-либо числа, умножение функции на число, деление единицы на функцию, возведение функции в положительную степень, извлечение корня из функции, нахождение показательной функции от функции, логарифмирование функции, нахождение модуля функции, нахождение тригонометрических функций от функций.
Все указанные операции можно проводить непосредственно над графиками основных элементарных функций (понимая под этим выполнение операций над соответствующими координатами), поскольку эти графики известны. Как правило.графикфункции-у=/[ф(х)] трудно, а порой и просто невозможно построить, используя общую схему исследования функции (гл. П). В то же время эскиз такого графика легко нарисовать с помощью упрощенной схемы исследования, если использовать операции над графиками.
Схема построения графика указанной сложной функции следующая:
1) строим график функции ух = <р($;
•2) отмечаем на этом графике характерные точки, т. е. нули и точки разрыва, находим граничные точки или соответствующие пределы и одну-две промежуточные точки;
3) производим заданные операции над ординатами выбранных точек, вычисляем соответствующие пределы и отмечаем полученные точки и предельные значения на рисунке, начерченной под графиком функции yj = <р(х) так, чтобы ось yi была продолжением оси у;
4) соединяем полученные точки сплошной (в силу непрерывности элементарных функций всюду, где они определены) линией и учитываем'(если она есть) симметрию графика относительно точки или прямой.
На самом деле полученные точки можно соединять не сплошной, а даже плавной линией, так как рассматриваемые в этой главе элементарные функции недифференцируемы лишь в отдельных, Rak правило, хорошо известных точках. Так, например, функция у = | х | не имеет производной в точке х = 0, функция у = у^х2—I ; це имеет производной в точках х = 1 и х = —1, й, следовательно, в этих точках указанные функции недифференцируемы.
50
1
На практике, екажем, для вычисления площади фигуры, ограниченной некоторой замкнутой кривой, или объема тела вращения и т. п. вполне достаточно построить эскиз графика. Впрочем, при необходимости такой эскиз всегда можно уточнить с помощью методов, рассмотренных в предыдущей главе,.
Проиллюстрируем приведенную выше схему построения
эскизов графиков сложных функций на примерах.
Уд
ак
*2
-ак-
Mi
ЛА
К'
Рис. 72
Xf. х
О
i 10. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ ВИДА у= У (Ал:+Ь)
Как известно, график функции yi = АхН- йгестыпрямаяьлиния. .
Замечание. График функции ух = (рис.симметричен
точки Л4в1 —О I. i Д ействительно; пурть = — — 4- «> *, = \ к ) ; k
относительно
b
«= — — — а.
k 9
.Тогда
где а—любое положительное число.
/ ь V
У1М == +1> = k I — — 4- al 4- b == akf
\ к J
! b \
\ к J
Итак, У1 (*f) = —Уа (x2)- Таким образом, точка Mi симметрична точке М2 „ / ь Л относительно точки МОт.
\ k I
о 1 \«
lim [2<----лфь—©©г
-♦•4-00 \ 3 /
1-У = (2
L Область определения— ы:я. действительная осы Граничные значения:
/ 1 \з
lim [2— —х) = 4- оо; X-.-—оо\ 3 / 3
II. Здесь у! = 2 — -i-x, у = yf . О
Строим график функции yi — 2.— у*" -
Отмечаем на этом графике характерные точки —, точки пересечения с осями координат и одну промежуточнуюточку; Возводим в куб ординаты этих точек:
а) Мх (6; 0): ух = 0, отсюда у = yf — 0, получаем точку Ni (6; 0);
51
о " X
• Рис. 73 . Рис. 74 х
б) Mg (0; ,2)j yi — 2, отсюда у « у® = 8, получаем точку Na (0; 8); в) A4g (3.; 1): yi — 1, отсюда У = У® = 1, получаем точку N3(&, 1).
Наносим подученные точки на нижний рисунок, соединяем их плавной линией и учитываем симметрию графика относительно точки Ni (6, 0).
. Действительно, функция yi = 2 — 2-х симметрична относительно точки Mi (6, 0), поэтому функция у = у® симметрична относительно Точки Nj (6, 0).
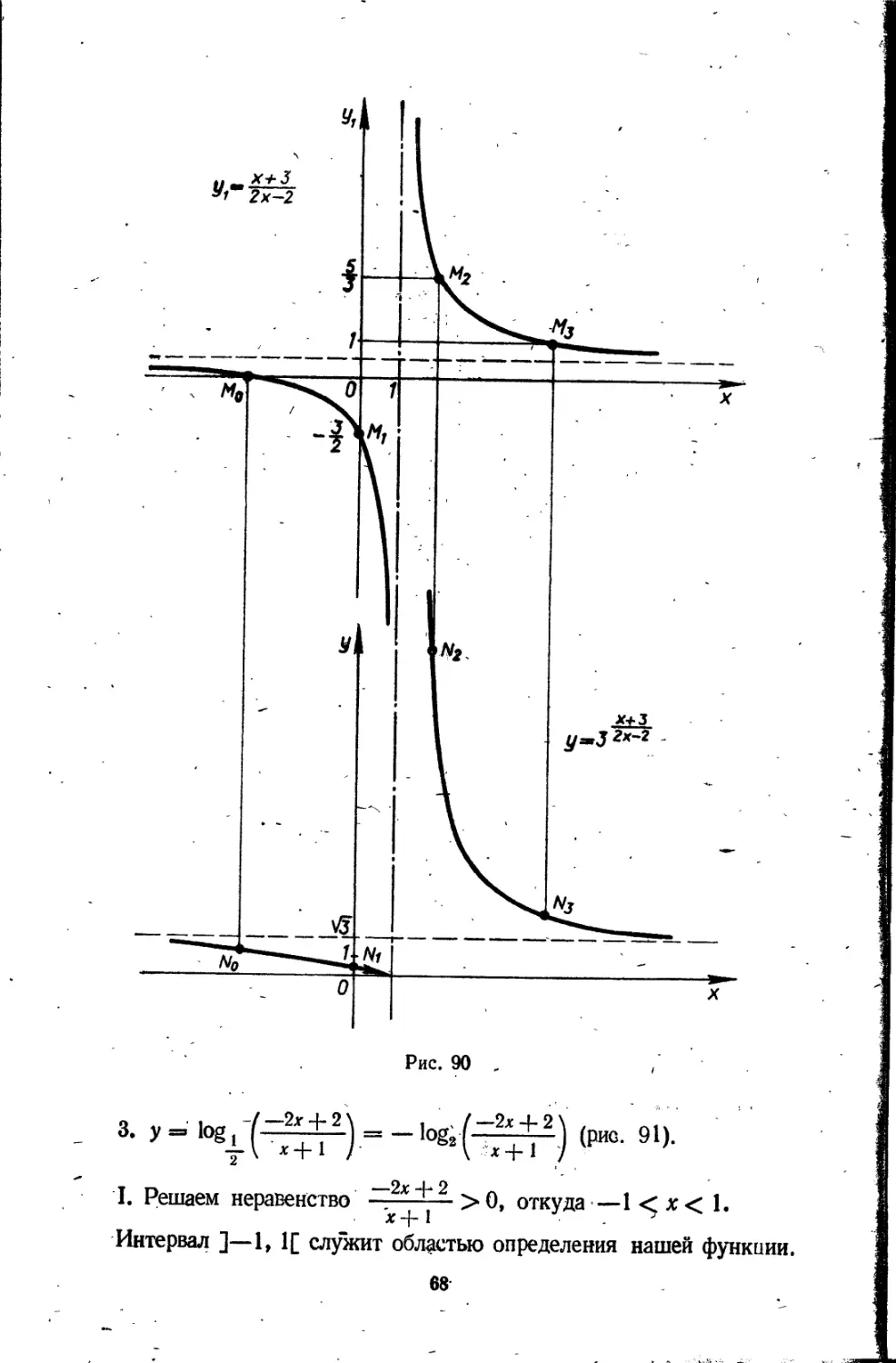
2, у = У 2 — 2х (рис, 74).
I. Решаем неравенство 2 — 2x^0, откуда —оо < х 1. Этот
полуинтервал является областью определения нашей функции.
Граничное значения:
lim У 2 — 2х — 4- оо; при х = 1 у = 0. X. -ь —оо
И. Здесь yi = 2 — 2х, у = Vyi*
62
Отмечаем на графике функции yi == 2 — 2х характерные точки пересечения с осями координат и одну промежуточную точку: Mi (1; 0), М2 (0; 2), Ма (—1; 4).
Производим извлечение квадратного корня из ординат этих точек:
a) Mi (I; 0): у£ — 0, отсюда у — Vyi = 0» получаем точку Ni(l; 0); б) Ма (0; 2): у£ = 2, отсюда у = Vyi =“ V*i получаем точку JV4(0;V2);
в) Mt (—1; 4): yi = 4, отсюда у=РЛуги2, получаем точку
Na(— 1; 2). ? 'г
Наносим полученные точки на нижний рисунок и соединяем их плавной линией, учитывая, что при х -*• —оо у -> 4-оо.
3. у = |/ух —4 (рис< 75)-
О
Рис. 76
I. Область определения—вся действительная ось.
Граничные значения!
Л-оо^ Тх—У == — во;
/3 7“| Г"
lim у тх— т= + оо.
^Ж-*-{-оо г *
II. ЗдесьXi=^x— у =
Отмечаемна графике.функции
~х — у характерные точки: Aft(l; 0), Afa(3; 1), Ms (% 2), Af4fO; —
\ :2/
Извлекаем корень кубический из ординат этих точек.
а) ЛС&(1;- 0): У1 = 0, отсюда
У = у У1 = 0, получаем . точку А (-1; 0);
i6) Л^З; 1): yi = 1, отсюда У = Т^У1в 1, получаем точку ЛЦ(3; I);
в) Л1^(5; 2): yt = 2, отсюда
3/*— 3 z-—
у j/fy1 == у 2, получаем точку
ЛГ8(5; ^2);
г) Л1^0; -1): У!=-|. 3z— 1
' отсюда у =-------у У1 =-— з^г, получаем точку Nt (0; — \
к ^7
Наносим полученные точки на нижний рисунок, соединяем их -плавной линией и учитываем симметрию графика относительно точки Ni (1, 0).
4. у = з~2Х+1 (рис. 76).
I. Область определения —/?.
Граничные значения: .
lim 3~^+1 = + <х>; lim 3~^+‘ = lim 3^ = 0.
5S4
- Ось х, таким образом, является горизонтальной! асимптотой для правой части графика.
П. Здесь ух — —2х 4- 1, у = Зу*.
Отмечаем на графике функции ух. =—2x4-1 характерные точки:
МоМ-;0)„ Afti(O; 1), Л12(1; -1). \ /
Возводим основание 3 в степень с показателем, равньш ординате указанной точки:
0J: У1 = отсюда у = Зу* = 1, получаем
1): У1 ='Н отсюда у = Зу,= 3,. получаем
—0: У1 — —Ъ отсюда у = Зу* = —получаем
з
точку
точку
точку
Наносим полученные точки на нижний рисунок»» соединяем их плавной линией, учитывая, что при х->—оо- у-> -В ои-и что ось х является горизонтальной! асимптотой для. правой части графика.
5. у = 1g (2 — Зх) (рис. 77).
I. Решаем неравенство 2 — Зх > 0, откуда х .
Этот интервал*—область определения нашей функции.
Граничные значения:
lim 1g (2 — Зх) = + .оо; lim lg (2 — Зх) = — оо.
2
Таким образом, х = — есть вертикальная асимптота,
'II. Здесь у1; = 2 — Зх, у = 1g yt.
Отмечаем на графике функции у = 2 — Зх характерные точки: лЦу; 1), Мг (0; 2), ю).
a) Afj p-;-Й: yi = 1; отсюда» у. = lg yi = О» получаем* точку
\3 )
б) М2 (0; 2): ух = 2, отсюда у = Igyi = 1g,2, получаем точку AM0;lg2); .
(8 \ /
— у; 101: ух = 10, отсюда у == lg yi = 1; получаем точку
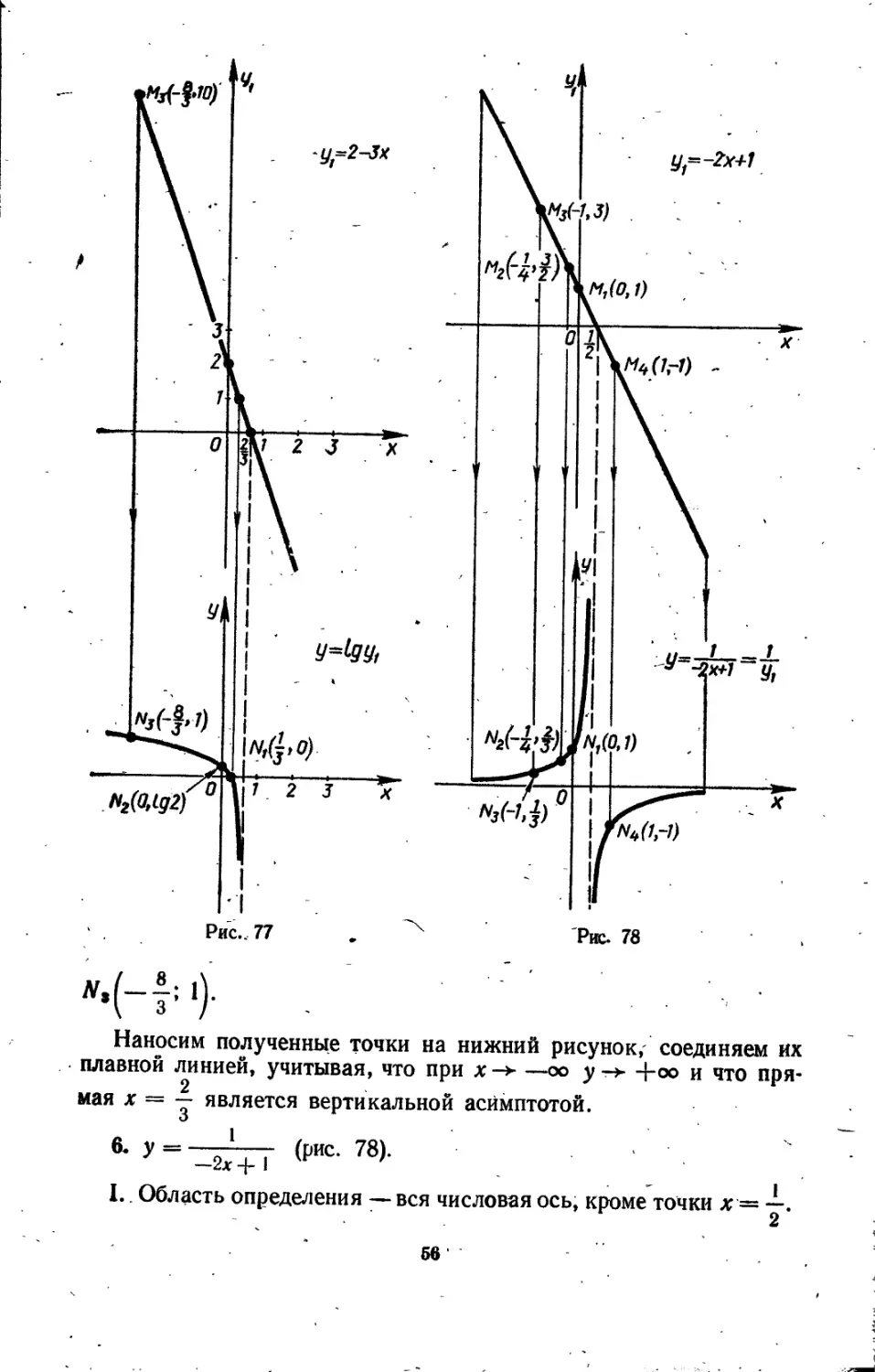
Наносим полученные точки на нижний рисунок, соединяем их плавной линией, учитывая, что при х -> —оо у -> +<х> и что пря-2 ...
мая х = — является вертикальной асимптотой.
6- У = ' А (Рис- 78).
1
I.. Область определения — вся числовая ось, кроме точки х = —.
56
---5----- 4- оо; lim -1—
—2х+1 1 2x4-1
т Т
0.
оо;
Граничные значений: lira —= 0; l*m »-r—оо —2х + 1 1
**Т” >• lim .--5——
i х->4“°о —2х -р 1
Таким образом*, имеется горизонтальная асимптота у = 0 и вёр-1 . 7
тикальная асимптота х — —.
II. Здесь у£ = —2х + 1, у = —.' _
У1
Отмечаем на графике функции yi = —2х + 1 характерные точки:
Х(0; 1), лЦ-1; {), м3(-1; з), м4(1; -П-
a) Afi (0; 1): yt = 1, отсюда У = — = 1, получаем точку Vi
AMO; 1); ;
(1 3 \ 3 12
— —; —j: yt = —, отсюда у = — — —, получаем точку
Ч 4 3/ в) Л«.(—1; 3): Уг=3, да у = — = —, получаем Л 3 ч,; 4 .
Наносим полученные
на нижний рисунок, соединяем -их плавной линией; учитываем при этом, что ‘ у = 0 — горизонтальная асимптота, X — —— 2 вертикальная асимптота и что график симметричен относительно точки х ——. 2
7. у = | j —2х (рис. 79).
I. Область определения — вся числовая ось.
4
II. Здесь ух =? — — 2х, у — О
отсю-
точку
Рис. 79
точки
Строим график функции ух = Д-2.
57
Рассмотрим какую-нибудь точку графика у. == -4 — 2х с положительной ординатой. Так как абсолютная величина (модуль) поло- ' жительной ординаты точки графика у( = — *—2х есть она сама, то эта ордината, а также все ординаты левой части графика yt = = 4- — 2х просто совпадают с соответствующими ординатами гра-14 I --------------2х|.
Рассмотрим теперь какую-нибудь точку графика уt = 4. — 2х с отрицательной ординатой. Поскольку модуль отрицательной ординаты точки графика yt = 4- — 2х есть число положительное, равное значению отрицательной ординаты, взятому со знаком «минус», то эта ордината должна откладываться на графике вверх (в положительном направлении оси у). Таким образом, правую часть графика, для которой у! < 0, получаем отражениём относительно оси х.
8. у = sin (2х + 3) (рис. 80).
I. Область определения — вся числовая ось.
II. Здесь у£ -= 2х + 3, у = sin уг
Отметим, что функция у sinyt периодична е периодом 2л. Поэтому рассматриваем отрезок осй: 0^yj^2n. На этом отрезке выбираем 5 характерных точек: у\ = 0, у8 = —, у8 — л, У4 = — л, 2 2
у, = 2л.
На графике функции у2 = 2х + 3 находим точки с соответствующими ординатами. Таким образом, получаем следующие характерные точки графика у j = 2х3:
/_3-1-А \
Af а (— о), М21 =--— , М.
Ц 2 . / 2 \ 2 2 / б) * 8\ 2 /
/ „ 3
/-3 + —л „
2 ’ 2 Г \ 2 ’
СЗ \
——; 01: у! — 0, отсюда y = siny1 — 0, получаем точку
\ 2 )
б) ; — j: yi = —, отсюда у = sin У1 = L получаем точ*
(л \
—3+ 2 I
—1J;
r—3 ~|" 2л
м
58
в) *»( 3^"; л): У^я, отсюда у «<>sin yt « О, полу-лг ~Ь я • nV
чаем точку AM-—<и)«
г) У1=3
Зя • Зя
г® —, отсюда у = sin— •« 2 2
== — 1, получаем точку
= 2л, отсюда у *= sin 2л. — О, получаем точку N* о).
Полученные точки наносим на нижний рисунок и соединяем плавной линией. Оставшуюся часть графика можно достроить, пользуясь периодичностью функции у = = sin (2х + 3) с периодом л.
§ 11. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС, ДЕФОРМАЦИЯ И ОТРАЖЕНИЕ
Рис. 80
Простейшие операции над графиками такие, как параллельный перенос, деформация (растяжение и сжатие) и отражение удобно производить не по указанной выше схеме, а по следующим простым правилам.
1. у = /(х)+& (параллельный перенос вдоль оси ординат). Сначала строим график функции у == / (х) и затем переносим его параллельно самому себе вверх (Ь > 0) или вниз (Ь < 0) на | b | единиц. Проще, однако, опустить (Ь > 0) или соответственно поднять (Ь < 0) ось х на | b | единиц.
2. у = f (х — а) (параллельный перенос вдоль оси абсцисс).
Строим график функции у = f (х) и переносим его параллельно самому себе вправо (а > 0) или влево (а < 0) на | а| единиц. Вместо этого можно перенести ось у влево (а > 0) или соответственно вправо (а < 0) на | а| единиц.
3, у = .—Jf (х) (отражение относительно оси абсцисс). Строим график функции у = f (х) и зёркально отражаем его относительно оси х. ч >
4. у = / (-—л) (отражение относительно оси ординат). Строим график функции у = f (х) и зеркально отражаем его относительно оси ординат.
59
5. у = Af (x)t (А > 0) (деформация графика вдоль оси. ординат). *
Строим график функции у — f (х) и увеличиваем его ординаты^ в А раз при А > 1 (растяжение графика) или уменьшаем его ординаты в ~ раз при 0<А<1 (сжатие графика).
в, у = / (Лх), (Л > 0) (деформация графика вдоль оси абсцисс).
§ 12. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ ВИДА y=f(ax*+bx+c)
Как известно, графиком функции yi = ах® 4-. Ьх 4- с служит парабола, симметричная относительно прямой х =« — —.
2а
1. у = (х® — 4х 4-3)®.
I. Область определения — вся числовая ось.
Граничные значения: lim (х®— 4х 4-3)®=-4" оо,
II. ух = х® — 4х 4- 3, у = yf.
Строим график функции ух = х® — 4х 4- 3. Отмечаем на этом графике характерные точки — вершину параболы, точки пересечения параболы с осяйи координат и одну промежуточную точку:
(4; 3.) М3 (1; 0), Mt (0; 3).
В силу симметрии графика относительно прямой х = 2 Для построения эскиза достаточно трех точек: Л40, Л4Х, Afa.
Возводим в квадрат ординаты этих точек:
a) Afo (2;.—1): ух = —1, отсюда у = у 2 = 1, получаем точку No (2; 1)Г
б) Mi (3; 0)j yi 0, отсюда у = 0, получаем точку Ni (3; 0); в) М3 (4; 3): ух — 3, отсюда' у = 9, получаем точку N3 (4; 9).
Наносим полученные точки на нижний рисунок, соединяем их плавной линией и учитываем граничные значения и симметрию относительно прямой х = 2.
2. у = у^х2-}- 1 (рис. 81).
. I.- Область определения — вся числовая ось.
Граничные значения:
Нт Их* 4-1.- 4-оо •
Функция четная, т. е. график ее симметричен относительно оси ординат. - -
И- У1 = ^4- 1.
На графике функции yt *=> х2 4- 1 отмечаем выбранные точки: Л40 (0; 1), Л4х (1;'2), М2 (2; 5).
Извлекаем корень кубический из ординат этих точек:
3/—
а) Мо(0; .1): yt = 1, отсюда У = УУ1=“1, получаем точку лго(О; 1); . -
З у— з
б) Mj(l; 2): Ух = 2, отсюда У = у 2, получаем точку (1; у 2);
3 у— з
в) М2(2; 5): yi =;5, отсюда у = у 5, получаем точку N't (2; у 5).
График можно дополнить точкой N3 (0,1; уГ 1,01).
3. у = г**-2*-3 (рис. 82).
I. Область определения — вся числовая ось.
Граничные значения: lim 2*’-2*-3 = 4- <ж>.
Х-*оо
II. Ух = ха —2х —3, у = 2У*.
Отмечаем точки награфике функции yi = х2 — 2х— 3.
У М9 (1; -4), Mi (2; —3), М2 (3; 0).
Возводим основание 2 в степень с показателем, равным ординате указанной точки. При этом точке Ма (1; —4) графика функции Ух — х3 — 2х 3 будет соответствовать точка No (1; -4) графика функции у = 2У‘, точке Л4Х (2; —3) —точка Wj ^2; точке М3 (3; 0) —точка Na (3; 1). Наносим точки No, Nu N2 на нижний
рисунок и соединяем их плавной кривой. Ввиду симметрии графика функции yi = х2 — 2х — 3 относительно прямой х = 1 искомый график также будет симметричен относительно этой прямой.
4. у = log2 (—х2 4- 2х 4- 8) (рис. 83).
I. Область определения: —х? 4* 2х 4- 8> 0, откуда —2<х<4. Граничные значения:
lim ' log2 (—х2 4* 2х 4- 8) = —оо; lim loga (—х24-2х 4- 8)=—оо. 2-f-0 Х-4—0
Имеются две вертикальные асимптоты: х = —2; х = 4.
II. ух = —х2 4- 2х 4- 8, у = log2 ух. -• -Выбранные точки графика функции yi = —х2 4- 2х 4- 8: .
: Мо (1; 9), Мх (2; 8), (1 + 2^2; 1).\
Соответствующие точки- графика искомой функции:
(1; log, 9), Л/х (2; 3), Nt (1 4- 2^2; 0).
61
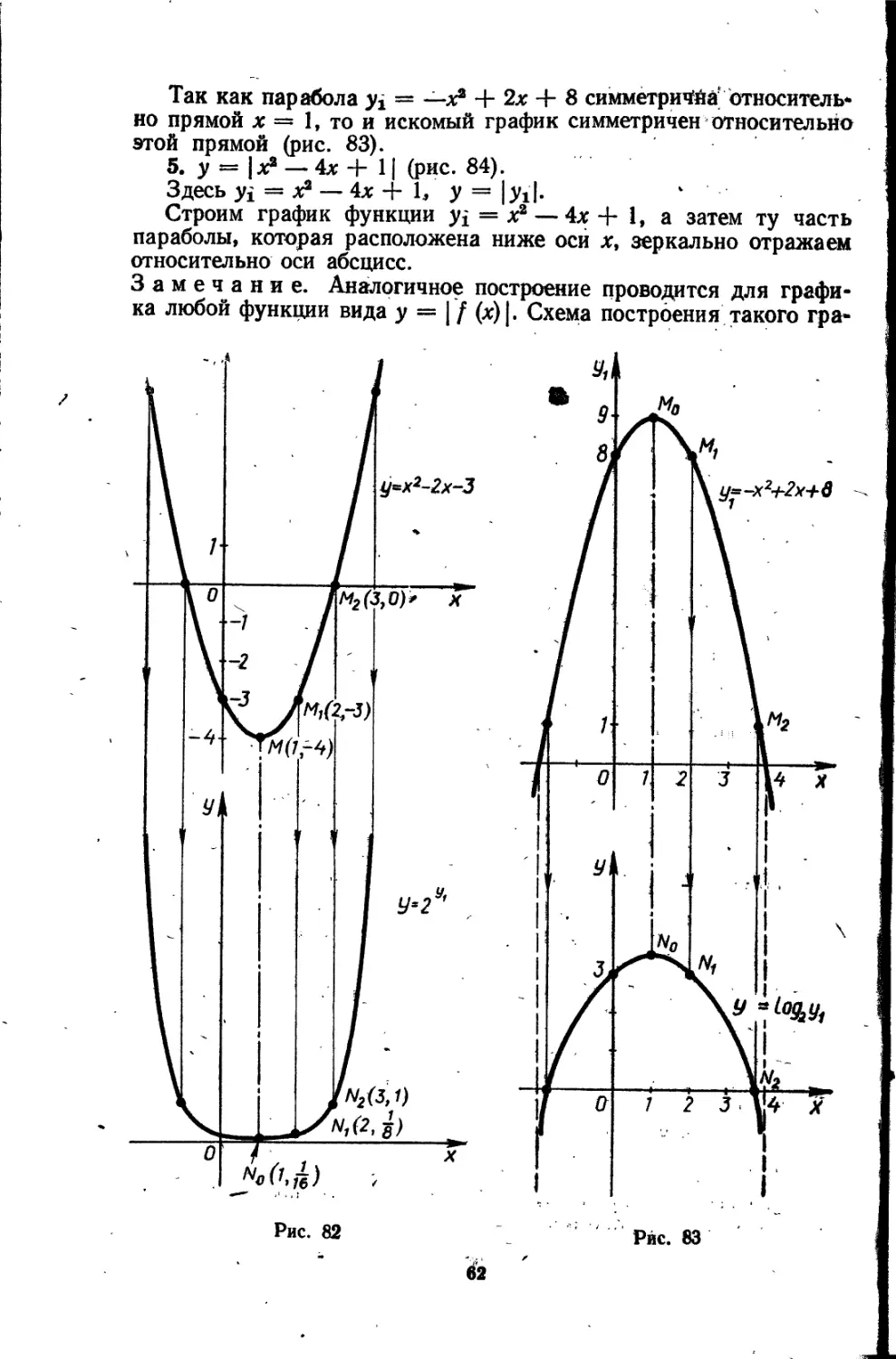
Так как парабола у£ = —х8 + 2х + 8 симметрична относительно прямой х = 1, то и искомый график симметричен относительно этой прямой (рис. 83).
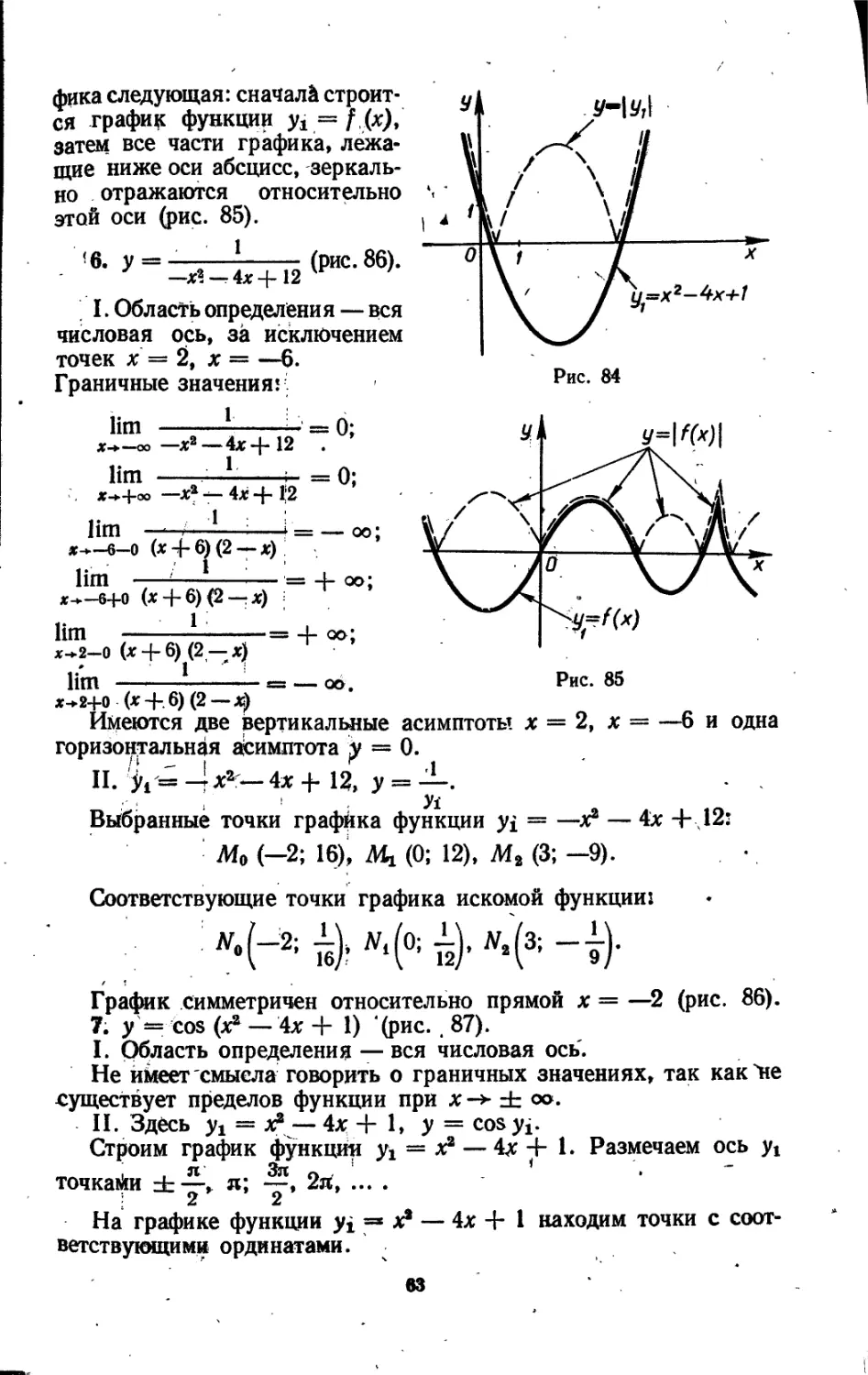
5. у = (х8 — 4х + 11 (рис. 84).
Здесь yi = х8 — 4х + 1, у = |yi|. ‘
Строим график функции yj = х8 — 4х + 1, а затем ту часть параболы, которая расположена ниже осй х, зеркально отражаем относительно оси абсцисс.
Замечание. Аналогичное построение проводится для графика любой функции вида у — | f (х)|. Схема построения такого гра-
фика следующая: сначала строится график функции yi = f (х), затем все части графика, лежащие ниже оси абсцисс, зеркально отражаются относительно этой оси (рис. 85).
!6. у = ----------(рис. 86).
' —х? — 4x4-12 '
I. Область определения — вся числовая ось, за исключением точек х' — 2, х = —6. Граничные значения! ;
Рис. 84
lim --------------L = 0;
оо —х2 — 4х 4-12
lim -----—--------г- = 0;
-►+«> —х2 — 4х -|- 1'2
1 оо;
асимптоты х = 2, х = —6 и одна
lim _
ж—в—о (х 4- 6) (2 — х) lim —’—5—:— = -х-.-6+о (х4-6)(2—-х) ' lim ———------------- 4-
*-►2—0 (х 4- 6) (2 — х) lim --------5----— = — оо.
х-,24-0 (х 4-. 6) (2 — ж)
Имеются две вертикальные горизонтальная асимптота у = 0.
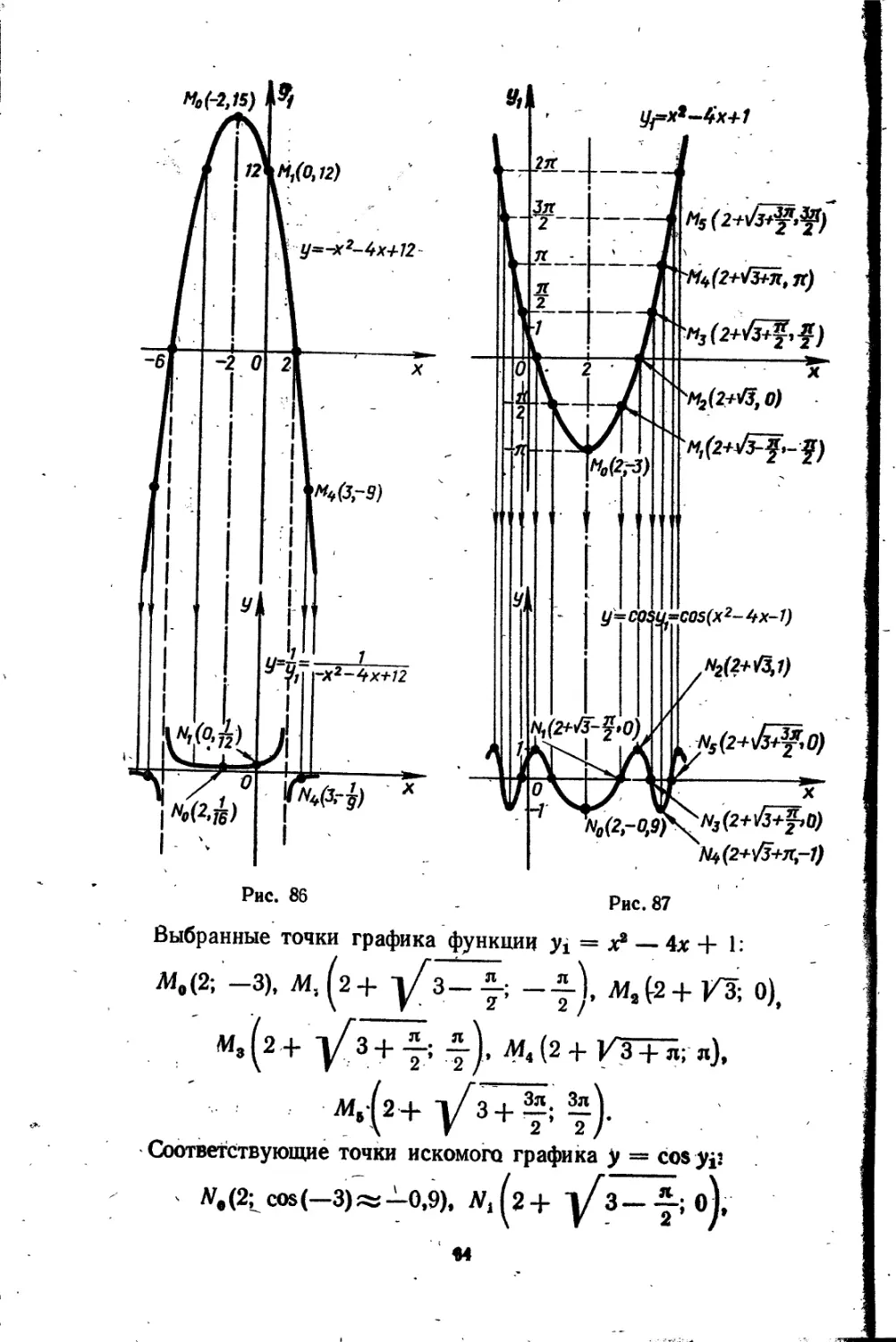
II. У1 — —г &— 4х 4-12, у = —.
Выбранные точки графйка функции yi = —х* — 4х 4- ,12: Мо (—2; 16), Mt (0; 12), (3; —9).
Соответствующие точки графика искомой функции:
ЛГ0(—2; N^O; -Ц, N./3; — Д.
Ц 16/’ \ 12/ \ 9/
График симметричен относительно прямой х = —2 (рис. 86). 7; у — cos (х2 — 4х 4- 1) ‘(рис.. 87).
I. Область определения — вся числовая ось.
Не имеет смысла говорить о граничных значениях, так как'не существует пределов функции при х -> ± оо.
II. Здесь ух — х8— 4х 4* 1, у = cos yv
Строим график функции ух = х8 — 4х 4- 1. Размечаем ось yt точками ±—, л; —, 2rt......
; ^2 2
На графике функции yi = х* — 4х 4- 1 находим точки с соответствующими ординатами. •
S3
ft.
у^=х*—4х+1
Рис. 87
Выбранные точки графика функции yi = х2 — 4х + 1:
Л10(2; -3), A1s(2+ —2-), М3(2+]/3; 0),
М8 (2 + j/3 + -2-), (2 + V3TS; л),
Л1,(2 + у<3+^;
Соответствующие точки искомого графика у = cosyj’ ^(2L cos(—3) я» —0,9), Nt (г 4- l/3 ~ V! °)*
<M
I
^(2 + ГЗ; 1),
N3 ^2 + у 3 + ^-; о), JV4(2+ l^a + л; -1), ;
' И; _'
ЛГв(2 + Уз +—j °1 '
Точки Ni, N3, N3, N3> N6 наносим иа нижний рисунок, соединяем пиарной кривой и учитываем симметрию графика относительно. Прямой х == 2.
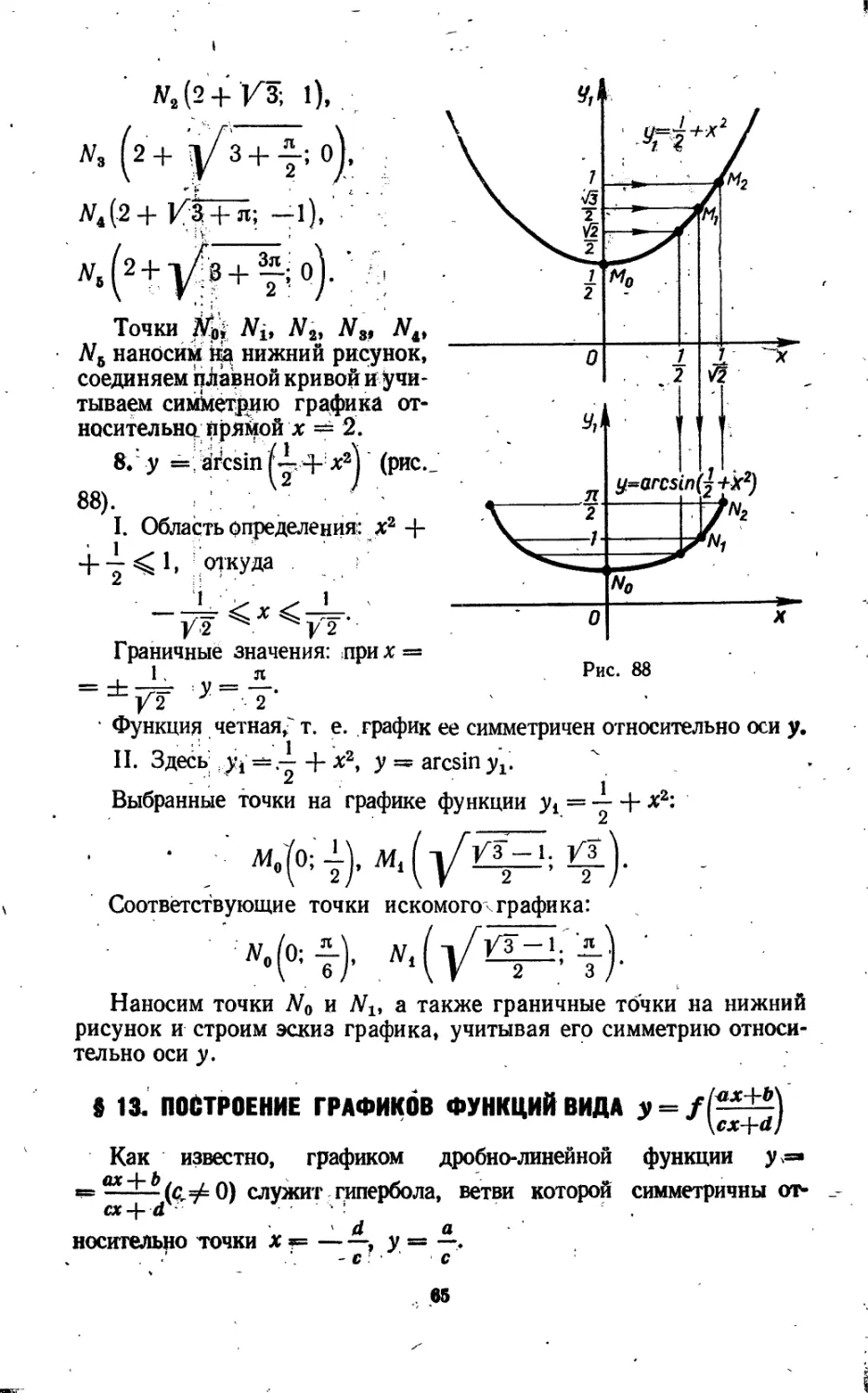
8.у =, arcsin /i+х2У (рис._ 88). 2
I. Область определения: х2 4--j--j < 1, откуда
1 / 1 ---7=- < X < —г=.
У .2 ^]/2 '
Граничные значения: при х =
, 1. л Рис. 88
±/2‘ У 2’
Функция четная/ т. е. график ее симметричен относительно оси у.
II. Здесь >1=.-^ + х2, yssarcsinyp
.2 1
Выбранные точки на графике функции yt = — + х2:
Л^УЦр.1; 1^.).
Соответствующие точки искомого^графика:
Наносим точки No и Nlt а также граничные точки на нижний рисунок и строим эскиз графика, учитывая его симметрию относительно оси у.
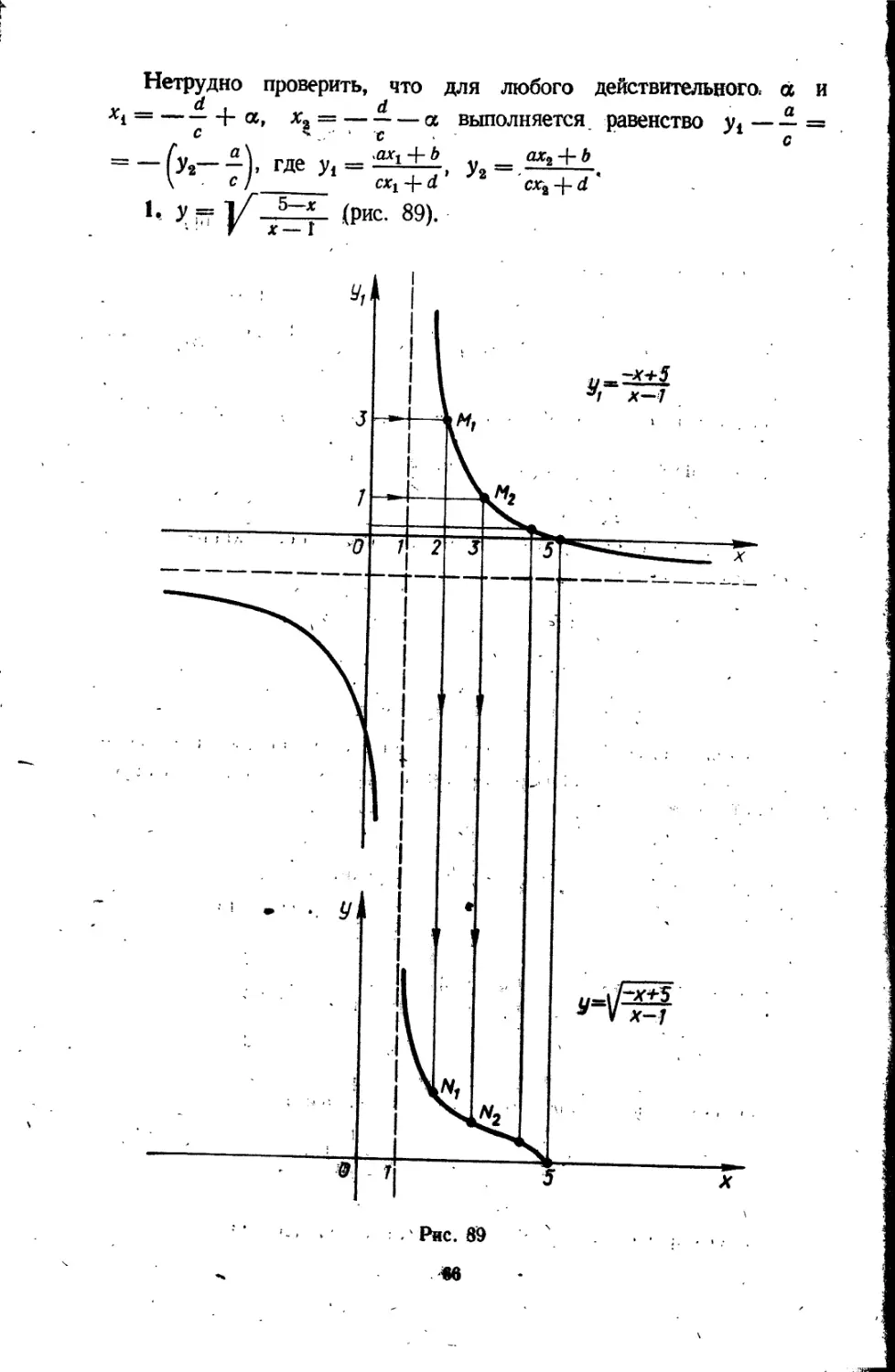
« 13. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ ВИДА y =
\cx-j-dj
Как известно, графиком дробно-линейной функции у^
= (с> о) служит гипербола, ветви которой симметричны от*
cx-f- d -
da
носительно точки х ₽----» № —•
- С : С
Нетрудно проверить, что для любого действительного» а и d d а
= — — + а, х2 = — — — а выполняется, равенство yt-------------------=
С '* . 1 с С
«6
I. Область определения!
—> 0, откуда 1 < х < 5.
Х-7- 1 Х^=\
графике функции yi = -----Л44 (2; 3),
у — 1
Граничные значения: lim 1/~J?—оо, у = 0 при х = 5.
x—i-l-o К X — 1
Имеется вертикальная асимптота х = 1.
п.У1 = *21 •» у = УЗч; при 1+° у^ +
Выбранные точки на
М2(3; 1>. ' -
Соответствующие точки искомого графика у = Vyi: (2; К 3),
ЛМЭ; 1). . •
График функции представлен на рис. 89.
2. у = 32х~2 (рйс. 90).
I. Область определения — вся ^числовая ‘ось, кроме х— 1. Граничные значения:
*4-3 х-ЬЗ
lim З2*-2 = V~3‘ lim З2*-2 = 0;
Х->—оо Х->1 — 0
ж-рз жН-3 _
lim 32х—2==+’Оо; lim32j(-2 =/3;
*-►14-0 х+<х>
Отсюда следует, что прямая х = 1 является вертикальной асимптотой для графика нашей функции, а прямая у = КЗ — горизонтальной асимптотой.
II. Здесь у, = у = 3*
Строим график дробно-линейной функции:
при х->- <» у£-> у; при, 1 — ух — оо; при х->- 1 + 0
У1-> + оо. • ; g
Выбранные точки на графике функции <
Мв(-3; 0), AfJO; Nd* |), Ms(5; 1).
Соответствующие им точки искомого графика:
^(-3; 1), -ЦЛ N^2-,-9V3), ^(5; 3).
\ 6 V э /
х-ЬЗ
График функции у = з2*-2 ^редставлен на рис. 90.
«7
3. у » log ,7 = — bg2(- (рис. 91).
-1Д x+1 / к *+l /
I. Решаем неравенство . >0, откуда —1 < х< 1.
Интервал ]—1, 1[ служит областью определения нашей функции.
68
. ••
:кинэьвнб эгшышекЦ
Таким образом, прямые ,х = 1 и х — —1 являются вертикальными асимптотши. тт —2#4- 2 ,
П. У1 = —ТТ“’ У = — 10&У1-
х -J- 1
Строим график дробно-линейной функции: при х -> оо у£->- —оо; при х->-— 1 —0 у1-> —оо; при х->—1 + 0 у£-> + оо.
Выбранные точки на графике функции у. = ~2х~^~2:
*4-1
м»(т: 4)’ 4 Мг(0; 2)> 4
. \ Q \ О / \ О /
- Соответствующие точки графика функции у — —log2yi’ . aJI; 1), aUI; ol tf2(0; -1), nJ- 1;' -2).
График искомой функции представлен на рис. 91.
4. y=Jg—.
Здесь = y = tgy,'
Строим график дробно-линейной функции у4 =
Отметим, что при х->оо yj-> 1; при х-*—2 — 0у->-}-<»; при — 2-f-Oyt-*—оох.
Те значения х, для которых значения yt =---- будут равны
' х 2 *
±у! ^"2"? •••» являются точками разрыва нашей функции,
а соответствующие прямые, как легко показать, служат вертикальными асимптотами. При x->±ooy->tglsal,7..
Для упрощения построения эскиза графика у = tg-- абсцис-
х 2
еы характ ерных точек можно не вычислять. Достаточно разметить ось yj О.” « < Зл ,
, ±—, •••» спроектировать их на линию yt=
х ' 2 г
= -—- и полученные таким образом точки графика функции yt = х • 2
=----- спроектировать в свою очередь на ось х нижнего рисунка.
y-f-2 .
Вычисляя значения тангенса от ординат характерных точек М9, Mt, М9, Mit Mit ..., получим ординаты точек искомого гра--фика: N9, Ni, N9, Ns, Nt, N6, ... .
Глава IV
$ 14. ЭСКИЗИРОВАНИЕ ГРАФИКОВ ФУНКЦИЙ
Под эскизированием графика функции мы будем понимать построение эскиза (наброска) графика функции без проведения полного исследования функции По общей схеме (гл. П), однако такого эскиза, который достаточно точно отражает основные элементы поведения функции, а именно поведение функции в окрестностях граничных точек и точек разрыва, в нулях и на бесконечности.
Для дальнейшего нам . потребуется понятие эквивалентности функций.
Определение. Бесконечно малые при х-*а(или бесконечно большие) функции а(х) и Р(х) называются эквивалентными (а(х)~ ~Р(х)) при х-+а, если lim£^ = 1.
ж-*аР(х)
(Число а может быть конечным или бесконечным.)
Геометрически тот факт, что а (х) Р (х) при х -> а, означает, что в некоторой, вообще говоря, достаточно малой окрестности точки х = а графим функции а (х) может быть заменен на график эквивалентной ей функции Р (х) с точностью тем большей, чем меньше выбранная окрестность (рис. 92).
Рассмотрим примеры эквивалентных функций. При х -> О имеем:
>inx_|,
1. sinx~x, так как lim *-►0
2. tg х ~ х, lim == 1. х-*0 х
При х-> 4-оо имеем:
1. х(х— 3)(Х4-1)~*®, lim х(х —3) (х-|-1) _ । »-+°о X3
И
2. Х’ рЧх —2)2~х\
lim t
Ж-*4-00 . 11
3 X
При х -> 4- 1 имеем:
/
71
1. -———— ---------, так как lim I-=----:-—-
(х—1)(х —2) х—1 х-и \(х—1) (х —2) х — 1
3 —- -
2. х3у/Г(х — I)2 ~ ^(х— I)2, lim-? = 1.
При х 2 имеем:
х _ 2
(х— 1) (х — 2) х—2’
(х о* \
------.--1= 1,
(х — 1) (х — 2) х —2/
Схема эскизирования графика функции выглядит следующим образом:
I. Нахождение области определения, граничных точек области определения и точек разрыва.
II. Определение четности (нечетности), периодичности функций. . ’ „
III. Определение нулей функции.
/ IV. Исследование поведения функции в окрестностях граничных точек, точек разрыва, в нулях и на бесконечности. Необходимо каждый этап исследования функции по этой схеме сопровождать соответствующим построением-
$ 15. ПРАКТИЧЕСКОЕ ПОСТРОЕНИЕ ЭСКИЗОВ ГРАФИКОВ ФУНКЦИЙ
1. у — х2 (х — 2) (х 4- 1) (рис. 93).
I. Область определениявся ч II. Функция общего вида.
III. Функция обращается в нуль при х = 0, х = 2, х = —1.
IV. Поведение функции в нулях:
а) при х —>• О х2(х — 2) (х + + 1) 2Х2;
б) при х -> —1 х®(х — 2) (х + + 1) 3 (х + 1);
в) при х->2 х2(х'—2)(х + + 1) ~ 12 (х - 2)-.
Поведение функции на бесконечности:
при х ->• + оо х 2(х — 2)(х + 1) ~ х4;
при х-> —оо х®(х — 2) (х + 1) ~
-~х*.
Наносим полученные результаты на рис.-93 и отдельные части (!!!)
72
I
графика (в силу непрерывности) соединяем сплошной линией. Идея эскизирования графиков как раз и состоит в.том, чтобы соединять сплошной линией не отдельные точки графика, а отдельные его части (куски). При необходимости полученный эскиз всегда можно уточнить с помощью методов главы II.
2. у = (х _ I)2 (х + I)4 (х — 2)3 (рис. 94). •
I. Область определения — вся числовая ось, точек разрыва нет.
II. Функция общего вида.
III. Нули функции в точках х = 1, х — —1,-х = 2.
IV. Поведение функции:
а) при х —— 1 (х — 1)2(х4- 1)4(х — 2)3~—108 (х 4- I)4;
б) при х —> 1 (х — I)2 (х + J)4 (х — 2)3 — —16 (х — I)2;
в) при х —> 2 (х — I)2 (х + I}4 (х — 2)3 ~ 81 (х — 2)3;
г) при х -> ± оо (х — I)2 (х + I)4 (х — 2)3 ~ х*.
3. у = х2 (х + 1) у^х — 2 (рис. ,95).
I. Область определения — вся числовая ось, точек разрыва нет.
II. Функция общего вида...
III. Нули функции в точках х0, х = —1, х = 2.
IV. Поведение функции: . '
а) при х — 1 х2(х4- 1)у^х —2~ — y^3(x-f- 1);
б) при х->-0 х2 (х 1) yGc — 2 ~ — у^2 х2;
в) при х->2 х2(х4- l)y^x —2~ 12^ —2;
3/.— 4
г) при х->± оо х2(х 4-1) ух— 1 ~х .
4. у = х3 у' (х — 2)2 (рис. 96).
I. Область определения — вся числовая ось, точек разрыва нет.
73
Рис. 96
В
II. Функция общего вида.
III. Функция обращается нуль при х = б, х = 2.
IV. Поведение функции:
а) при х->0 х3}/' (х—2)2^ Sr-r s'* . ~ у 4 • х3;
б) при х->2 х3-^(х—2)2^ ~8у>(х —2)2;
в) при X -> ± ОО п xpfrtx — 2)2~х3.
5. у — У х (1 — х) (1 + х) (рис. 97).
I. Область определения находим из решения неравенства
х (1 — х) (1 + х) О, откуда х С —1» О С х 1.
II. Функция общего вида.
III. Нули функции в точках х = 0,х = 1, х = —1.
IV. Поведение функции:
а) при х-> 0 4- О J/x(l — х)(1 + х) ~ У~х\
б) при х— 1 — 0 ]/х(1 — х)(1 + х) ~ У —2(1 4- х);
в) при х-> 1 — О Ух(1 — х)(1 4- х) ~ V—2(х — 1);
г) при х->— оо Кх (1 —х)(1 4-х)~ V— х8.
в. у = Vх х(2— х) (рис. 98).
74
I. Область- определения находим из решения неравенства х (2 — х) 0, откуда 0<х<2.
II. Функция общего вида.
III. Нули функции в точках х — 0, х — 2.
IV. Поведение функции:
а) при х->9-^-0- х(2— х)~
б) при х->2—О?; v4х(2 — х) ~ ~^2- 2— х.
7. у = x^tn (х — 1) (рис. 99).
I. Область определения находим из решения неравенства х — 1 >0, откуда х > 1.
II. Функция общего вида-.
III. Нуль функции в1 точке х = 2.
IV. Поведение функции:
при х -> 2 х2 in (х — 1) ~ 41п (х — Г)’;
при х->1 + 0 х8 In (х — 1) ~ In (х — 1) -> —<ю.
Отсюда следует, что х = 1 — вертикальная асимптота.
Поведение функции на бесконечности:
при х-> + оо х2 In (х—1) ~ х2 In х. Заметим, что при х >е х2 In х > х2.
Таким образом, наша функция на бесконечности растет быстрее, чем х2.
8' У = (рие’ 100)-
I. Область определения — вся числовая ось.
II. Функция четная.
III. Нулей функция не имеет.
IV. Поведение функции: при х->оо ~
Таким образом, у = 0 есть горизонтальная асимптота.
Рассмотрим поведение функции при х-> 0. Так как при х-> 0 можно' считать | —х2 [ < I, то по формуле суммы членов бесконечно убывающей геометрической прогрессии со знаменателем (—х2) получим: 7
1 + (—хг) 4- (—х2)2 + (—х2)3 + ... =--!---= —.
' ' 1 — (—х2) 1 + х2
Ограничиваясь первыми двумя членами прогрессии, найдем, что
—— ~ 1 — х2 при х—> 0.
1 + х* '
I. Облает^ определения — вся числовая ось, за исключением • двух точек разрыва! х — —1, х = 1, в которых знаменатель обра-. щается в нуль. _
II. Функция четная.
III. Нуль функции в' точке х = 0.
IV. Поведение функции:
при х->0 —-—~ — х2;'
х*— 1 х2 1 1
при оо -----------= —-----~ 1 4- —.
F X» - 1 . , 1 X»
1-----
X*
Этот результат также следует из формулы суммы членов бесконечно убывающей геометрической прогрессии со знаменателем 1 < 1 (х -> <ю);
Таким образом, у - 1 — горизонтальная асимптота. Поведение функции в точках разрыва: . х? х* 1 1
при 1 ----------------------~ .
и х» —1 (х—1)(х-Ь1) 2. х—1
Отсюда х = 1, а также в силу четности и х ==—1 — вертикальные асимптоты.
> 10. у - (рис. 102).
1
76'
I. Область определения — вся числовая ось, кроме точки разрыва х = —1, в которой знаменатель обращается в нуль.
II. Функция общего вида.
III. Нули функции в точках х = 2, X = 2.
IV. Поведение функции:
при х->— 2 —
*+•
-<1=аМ2>~4(х+2); ^~А(х-2); x-f-1 3V ’ . №-4 -3
при х->2
Отсюда х — —1 — вертикальная асимптота.
Поведение функции на бесконечности: .
х2 — 4
\ X/1 1
-j-=(x——'j х-
1 \ Х)
х(1—±+-L—±.+ ...) = x—i-2+-LL... .
\ X X2 х3 / XX2
ГГ\ х2 —— 4
Таким образом, при х->оо ---~х—**
Отсюда, следует, что у = х — 1 есть наклонная асимптота.
11 . у = х (рис 103).
I. Область определени я находим из решения системы неравенств:
s-i— > 0, - рткуда 0 х < 2. 2 — х^О,
II. Функция общего вида.
III. Нуль функции в точке х.= 0.
IV. Поведение функции: ________________________i. _ з_ . при х-*-0 4-0 х 1/ —~ -=-х2 ; . - у 2 —х /2
при х -> 2 — 0 х 1/ —— ~ 2 2 •. : —► 4- оо. v У 2 — х /2=ж
77
Отсюда следует, что х — = 2 — вертикальная- асимптота.
12. y = x.-f- — (рис. 104); X
I. Область определения — вся числовая ось, за исклю* чением точки разрыва х = 0.
II. Функция нечетная.
III. Нулей функция не имеет. •
IV. Поведение функции: при х->0 х + — ~ — (х = 0 — вер-X X
тикальная асимптота); при оо х 4.1 /V %,.
X
Поэтому у —х— наклонная асимптота.
УПРАЖНЕНИЯ
Построить графики функций.
1. у = X* (1 — X1 2).
2. у — (1 — х2) (2 + х).
3, у = х3 —Зх + 2.
4. у = х3 + 2х + 3.
5, у =.(х2 — Зх) (х — I)3.
6. у = У х (4 — х2).
7, у.^уТ2 (х-2).
8. у = у^х(1 — х2).
9. У = ^(1 — *) (2 + 4
10. у = /х + '3(х — 2).
1
16, у =-------------------
У х2 + 2х —3
18; у
л— 1
х2 — 9’
2О.< у =
х + 2 х2 — Г
78
x2+l _
zi. 23. 3 • x*-f-x4-l ’ ' (2x4-1) x
(x + 3) (2-x) ‘
x2 — 3
25. У~ *+!’
07 X3
>=н/
29. (x-l)(x-2)
У~ x+1' ’ I
31. у=.2-|-У4 —x.
1
33. у = 2^x .
35. 2х
У <2*4-Г
_ 3* —2*
37. У~3Х— 2*‘
39. /1
41. y=lg(x? —2|x|4-3).
43. y= lg(l — Igx).
45 у = 1g (x8 — 4x).
47. _ 1
У~ Iglg* ’
49. у = sin (x2— 1).
/ 1 \COSX'
51. у=(т)- •
53. 1
У — ~ -
0,5 4- cos x
55. . *+ 1 у = arctg — X,— 1
57. у = arcctg (tg x).
24.
26.
x3
y = (I _ X)(i 4- X») *
У = — •
32. у = 3 X\
34. *y-=----—.
У 2х — 1
42. у — log 1 (x2 - 1).
T . '
44. у = lg(/x — 1). *
1
46. у =-----------
1
48. у =--------------
IgTcos (x + 1)]
SO. y=tg —.
x
54. y= arcsm—. x
56. у = arccos (2T).
. 2x
58. y = arcsm------.
1 +#3
- 79
ОГЛАВЛЕНИЕ
Глава! ....... 3
§ 1. Функция. Основные элементарные функции . » * 4 s • . — '
§ 2. Общие свойства функции ......f * s s 4 , 8
§ 3. Предел функции, непрерывность ............. 14
§ 4. Асимптоты 17
§ 5. Производная. Экстремум 19
§ 6. Выпуклость и вогнутость. Точки перегиба . ....... . 24
Г л а в а II . . ...» . . . л . ..............................., , 28
§ 7. Общая схема исследования функций при построении графиков, —
' § ^Практическое применение общей схемы . . . ...... . —
Главами! ......... 50 J
§ 9. Операций над графиками функций .......... . —
§ 10. Построение графиков функций вида у =* / (hx + b) , . . . 51 i
§ Н. Параллельный перенос, деформация и отражение . . , . , 59
§ 12. Построение графиков функций вида у = f (ах2 + Ьх + с) . . . 60
§ 13. Построение графиков функций вида у — f .... 65
+ dj
Глава IV ......................... 71 J
§ 14. Эскизирование графиков функций ............ — J
§ 15. Практическое построение эскизов графиков функций .... 72
< . . . j
Леонид Викторович Ершов j
Рудольф Борисович Райхмист
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ ।
. I
Зав. редакцией Хабиб Р. А. |
Редактор Антонова Л. В. ’
Обложка художника Николаева Б. Л, Художественный редактор Карасик Ё. Н. Технические редакторы Махова Н. Н„ Новоселова В. В.
Корректор В. Ф. Малышева.
ИБ № 8106 , ,
Сдано в набор 17.41.83. Подписано к печати 08.06.84. Формат 60 x90*/ie- Бум. типограф. № 3 Гарант, литерат. Печать высокая. Усл. печ. л. 5,0. Усл, кр.-отт. 5,25. Уч.-изд. л. 4,SL Тираж 157 000 экз. Заказ 5912. Цена 10 коп.
Ордена Трудовогд Красного Знамени издательство :< Просвещение» Государственного ко- j
митета РСФСР по делам издательств, полиграфии и книжной торговли. 129846, Москва, з
3-Й проезд Марьиной рощи, 41. 5
(Отпечатано с матриц Саратовского ордена Трудового Красного Знамени полиграфического комбината Росглавполиграфпрома Государственного комитета РСФСР по делам изда« < телъств, полиграфии и книжной торговли в областной типографии управления изда* тельств, полиграфии и книжной торговли Ивановского облисполкома, 153628, г. Иваново.
ул, Типографская, 6.
10 к.