•1
X
■Г
•" г
/
и
л--
АПОЛЛОНИИ
ПЕРГСКИЙ
/	■••■■' Г/
¡5*
г
л 1
КОНИЧЕСКИЕ
СЕЧЕНИЯ
И^ТМиМФ
V- ф
?■’.■ ?
«■	X *	Л-
/■*
Г.. .
>
У”
< Г
л
9м
аь
я*
Л‘ -
%
£
1
4
г
V

АПОЛЛОНИИ ПЕРГСКИИ
КОНИЧЕСКИЕ
СЕЧЕНИЯ
Под общей редакцией А.А. Панферова, С.В. Кирбятъева.
перевод сделан с древнегреческого текста,
изданного ИЛ. Гейбергом (I.L. Heiberg).
Москва
ЮСТИЦИНФОРМ
2019

УДК 514
ББК 22.1518
П16
Авторский коллектив
Вступительная статья 				Кирбятьев С_В.
Предисловие фер Ээке (перевод)	[Антонов Т В._
Предисловие к переводу	Кирбятьев С В
Книги 1-1У (дословный перевод)
Книги 1-1У (текст)

Чертежи и примечания

Набор формул

Антонов Т. В.
КирбятьевС.В , [Мануйлов К В
КирбятьевС.В.
Маламашина А.И.
Аполлоний Пергский
П16	Конические сечения / под общ. ред. А.А. Панферова, СВ Кирбятьева — М : Юстицин-
форм, 2019 - 448 с.
1БВЫ 978-5-7205-1459-4
Книга представляет собой первый в России перевод первых четырех книг «Кони¬
ческих сечений» великого древнегреческого математика Аполлония Пергского Труд
Аполлония, поднявший изучение парабол, гипербол и эллипсов на новый уровень,
послужил также основой для создания новых разделов геометрии и оказался тем ма¬
тематическим аппаратом, который использовал Исаак Ньютон при создании теории
движения небесных тел.
«Конические сечения» неоднократно переводились на арабский язык, латынь и на
все основные современные европейские языки. Но русского издания, за исключени¬
ем первых двадцати теорем, переведенных И Ягодинским в 1928 году, еще не было.
Книга адресована историкам математики, преподавателям и всем интересующим¬
ся историей математики
л»
Ключевые слова геометрия, Аполлоний, парабола, гипербола, эллипс.
УДК 514
ББК 22.151
»БВИ 978-5-7205-1459-4
© ОАО «НИИ ТМ и МФ», 2019
© Оформление ООО «Юстицинформ», 2019

APOLLONIUS
FROM PERGE
CONIC SECTIONS
Editors by A.A. Panferov, S.V. Kirbyatyev
Moscow
YUSTITSINFORM
2019

yflK 514
55K22 1518
ni6
Writing team
Introductory article

Preface of fer Eeke (translation)
Preface to the translation

Books l-IV (literal translation) _
Books l-IV (text)

Drawings and notes

Set of formulas
Kirbyatyev S.V.
Antonov T. V |
Kirbyatyev S V.
¡Antonov TV. |

Kirbyatyev S.V.,[Manuilov K V.
Kirbyatyev S.V.
Malamashina A.I.
Apollonius from Perge
n 16	Conic sections / ed. by A.A. Panferov, S V Kirbyatyev. — M: Yustitsinform, 2019. — 448 pp
ISBN 978-5-7205-1459-4
The book represents the first translation of the first four books of «'Conic sections» by the
great Ancient Greek mathematician Apollonius from Perge in Russia. Apollonius’s work which
has lifted studying of parabolas, hyperboles and ellipses to new level has formed also a basis
for creation of new sections of geometry, and it was the mathematical apparatus which was
used by Isaac Newton in the course of creation of his celestial motion theory.
«Conic sections» were translated repeatedly into Arabic, into Latin and into all main
modem European languages But the Russian edition didn’t exist yet, except for the first
twenty theorems translated by I. Yagodinsky in 1928.
The book is addressed to historians of mathematics, lecturers and to all interested in
mathematics history.
Keywords, geometry, Apollonius, parabola, hyperbole, ellipse.
YAK 514
BBK 22.151
ISBN 978-5-7205-1459-4
© JSC «Research Institute of Exact Mechanical Engineering», 2019
© Design LLC «Yustitsinform», 2019

ОГЛАВЛЕНИЕ
Вступительная статья

1.	Конические сечения до Аполлония	‘-3
2.	Аполлонии и его «Конические сечения»	 20
3. Другие сочинения Аполлония

4. От греков до арабов
Влияние Аполлония на
пейскую науку

25
28
30
Введение к первому переводу с древнегреческого на французский язык
Предисловие

1.	О переводе

2.	О терминологии Аполлония

Древнегреческий алфавит

Свойства про
порпии

64
65
68
68
Книга 1
Письмо к Евдему	69
Определения 1	72
Предложения	75
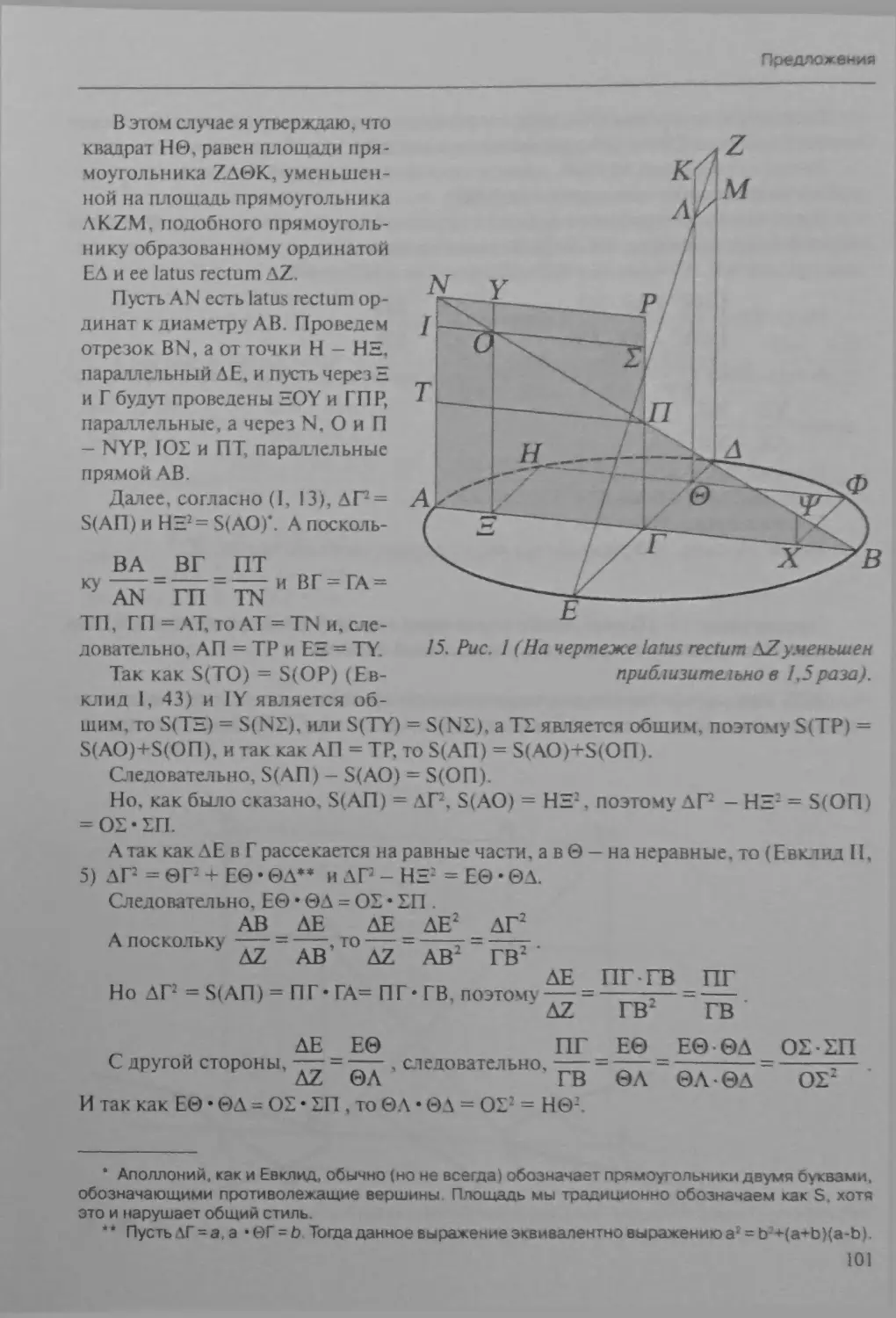
Предложение 1. Прямая, соединяющая вершину конуса с любой точкой
конической поверхности, лежит на ней	75
Предложение 2. Прямая, соединяющая две любые точки конической по¬
верхности, кроме вершины, лежит внутри конической поверхности,
а ее продолжения — вне	76
Предложение 3. Сечение конуса плоскостью, проходящей через верши¬
ну, есть треугольник	77
Предложение 4. Сечение конуса плоскостью, параллельной основанию,
есть круг	77
Предложение 5. Другое сечение, дающее круг и называемое противопо¬
ложным 	78
Предложение 6. Отрезки между точками конической поверхности, па¬
раллельные отрезкам, перпендикулярным основанию осевой пло¬
скости, делятся ею пополам

Предложение 7. Диаметр и ординаты конического сечения

Предложение 8. Условие того, что коническое сечение простирается в
бесконечность	84
Предложение 9. Если сечение конуса не противоположное и не парал¬
лельно основанию, то оно не окружность	85
Предложение 10. Конические сечения являются выпуклыми	кривыми	86
Предложение 11. Определение и уравнение параболы. Latus rectum	86
Предложение 12. Определение и уравнение гиперболы	90
Предложение 13. Определение и уравнение эллипса	95
80
82
•I«
к
5

Оглавление
98
5?
та.
та
ЙЕ
та
Предложение 14. Определение и основное свойство противолежащих
сечений
Предложение 15. Ордината, проведенная через середину диаметра
эллипса, есть сопряженный диаметр

Предложение 16. Прямая, проведенная через середину диаметра
противолежащих параллельно ординатам к нему, есть сопряженный
диаметр

Определения II

Предложение 17. Прямая, проведенная через вершину параллельно
ординате, лежит вне сечения (то есть, является касательной)

Предложение 18 Прямая, проведенная параллельно касательной или
секущей через точку, лежащую внутри конического сечения, есть
секущая

Предложение 19 Прямая, проведенная параллельно ординате через
точку, лежащую внутри конического сечения, есть секущая

Предложение 20. Квадраты ординат параболы относятся как абсциссы....
Предложение 21. Отношения квадратов ординат к абсциссам и другим
отрезкам диаметра у гиперболы и эллипса

Предложение 22. Прямая, соединяющая две точки параболы или гипер-
лы, пересечется с диаметром

Предложение 23. Прямая, соединяющая две точки эллипса между сопря¬
женными диаметрами, пересечется с ними вне сечения

Предложение 24. Касательная к параболе или гиперболе пересекается
с диаметром

Предложение 25. Касательная к эллипсу в точке между сопряженными
диаметрами, пересечется с их продолжениями

Предложение 26. Прямая, параллельная диаметру параболы или гипер¬
болы, пересекается с сечением только в одной точке

Предложение 27 Если отрезок пересекается внутри параболы с диаме¬
тром, то, продолженный в любую сторону, он с ней пересечется

Предложение 28. Если внутри гиперболы проведен отрезок, параллель¬
ный касательной к противолежащему сечению, то продолженный
в любую сторону, он пересечется с гиперболой

Предложение 29 Если прямая, проходящая через центр противолежащих,
пересекает одно из сечений, то она пересекает и другое сечение

Предложение 30 Отрезок, проведенный через центр до пересечения
с эллипсом или противолежащими, делится центром пополам

Предложение 31 Если из точки на диаметре, находящейся слева от цен¬
тра, провес
то ее продолжение попадет внутрь сечения

Предложение 32 Между касательной и сечением не лежит никакая
прямая
Предложение 33. Если прямая, пересекающая параболу, отделяет на ди¬
аметре вне кривом отрезок, равный абсциссе, то эта прямая - каса¬
тельная

100
102
104
104
105
105
106
107
108
109
НО
111
111
112
113
114
115
116
117
та
та
к
•Ж
та
•а
Й»
ЙЕ
та
та
»Ж
та
та
и
та
сти прямую, встречающуюся с правой ветвью гиперболы.
119
6

Оглавление
•ж
122
124
125
127
128
129
м
132
133
134
Предложение 34. Если прямая, пересекающая гиперболу или эллипс, делит
диаметр в определенном отношении, то эта прямая - касательная		120
Предложение 35. Касательная к параболе отделяет на диаметре отрезок,
равный абсциссе (обратное Предложению 33)	121
Предложение 36. Касательная к гиперболе и эллипсу делит диаметр в
том же отношении, что и ордината, проведенная из точки касания
(обратное Предложению 34)

Предложение 37. Соотношения между квадратом ординаты гиперболы
или эллипса и отрезками, отсекаемыми на диаметре ординатой и ка¬
сательной

Предложение 38. Те же соотношения для сопряженною диаметра

Предложение 39. Очевидное следствие из Предложения 37

Предложение 40. Очевидное следствие из Предложения 38

Предложение 41. Сумма и разность площадей равноугольных параллело¬
граммов, построенных на радиусе и ординате гиперболы

Предложение 42. Равенство площадей треугольника и параллелограмма,
составленных из прямых, параллельных касательной, ординате и ди¬
аметру параболы

Предложение 43. Соотношение между площадями трех треугольников,
составленных из диаметров и прямых, параллельных ординате и ка¬
сательной гиперболы или эллипса

Предложение 44. Продолжение Предложения 43 для противолежащих

Предложение 45. Аналогичное свойство по отношению к сопряженному
диаметру

Предложение 46. Все диаметры параболы параллельны, а отрезки, па¬
раллельные касательной к вершине (по Аполлонию), есть ординаты... 137
Предложение 47. Отрезки, пардтлельные касательной к гиперболе или
эллипсу, есть ординаты к диаметру, проходящему через точку касания
Предложение 48. Продолжение Предложения 47 для противолежащих

Предложение 49. Доказывается, что отрезок, удовлетворяющий некото¬
рому условию, есть latus rectum

Предложение 50. То же для гиперболы и эллипса

Предложение 51. То же для противолежащих

Предложение 52. Построение конуса, сечение которого есть парабола с
заданным Lr и прямым углом между ординатами и диаметром

Предложение 53. Построение параболы с произвольным углом между ор¬
динатами и диаметром

Предложение 54. Построение № 52 для гиперболы

Предложение 55. Построение № 53 для гиперболы

Предложение 56. Построение № 52 для эллипса (диаметр больше, чем 1_г)

Предложение 57. То же построение, но диаметр меньше, чем Lr

Предложение 58. Построение № 53 для эллипса

Предложение 59. Построение противолежащих, если заданы Lr, диаметр
(Lt) и угол между ординатами и диаметром

135
ни
•а
138
139
»а
139
140
142
•а
144
146
147
149
151
152
153
154
7

Оглавление
Предложение 60. Построение сопряженных гипербол
Дословный перевод книги 1

154
157
Книга 11
Препожен ия

Препожение 1 Если прямые, проведенные из центра гиперболы, отсе¬
кают отрезки касательной, квадраты которых равны четверти площа¬
ди эйдоса,тоони не имеют с кривой общих точек (асимптоты)

Препожение 2. Нельзя провести другие асимптоты под меньшим углом..
Препожение 3 Касательная пересекается с асимптотами и делится точ¬
кой касания пополам, а квадраты отрезков равны четверти площади
эйдоса

Препожение 4. Построение гиперболы, проходящей через данную точку
при заданных асимптотах

Препожение 5. Прямая, касающаяся параболы или гиперболы в точке пе¬
ресечения кривой и диаметра, параллельна ординате к этому диаметру....
Препожение 6 То же для эллипса

Препожение 7 Прямая, проходящая через точку касания и середину се¬
кущей. параллельной касательной, есть диаметр

Препожение 8 Если прямая пересекается с гиперболой в двух точках,
то отрезки, отсекаемые асимптотами, будут равны

Препожение 9 Если прямая пересекающаяся с асимптотами, рассека¬
ется гиперболой пополам, то она есть касательная

Препожение 10 Площадь прямоугольника, ограниченного отрезками,
на которые делит гипербола секущую, ограниченную асимптотами,
равна четвертой части площади эйдоса
Препожение 11 Прямая, пресекающая стороны угла, дополнительного
к углу между асимптотами, пересечется с гиперболой только в одной
точке, а произведение отрезков, на которые ее делят асимптоты, рав¬
но квадрату параллельного ей радиуса
Препожение 12. Произведение двух произвольных отрезков от любой
точки гиперболы до асимптот не зависит от выбора точки, если от¬
резки попарно параллельны
Предложение 13 Прямая, параллельная асимптоте, пересекается с кри¬
вой только в одной точке

Предложение 14 Асимптоты неограниченно сближаются с кривой

Предложение 15 Асимптоты противолежащих совпадают

Предложение 16 Отрезки прямой между противолежащими и асимпто¬
тами равны, если она пересекает сто
образованному асимптотами

Предложение 17 Асимптоты противолежащих и сопряженных им сече¬
ний являются общими 	.

Предложение 18 Прямая, пересекающаяся с одним из сопряженных се¬
чении. пересекается с каждым из сечений, лежащих рядом, только в
одной точке

«К»
ЙЙЕ
М
»!•
к
о
й
•Л
•Л
•ж
• >
»1».
роны угла, дополнительного к
199
199
200
201
202
203
203
204
204
205
205
206
207
208
209
209
210
211
211
8

Оглавление
212
214
215
Ле
КС
•Ж
Предложение 19. Касательная к сопряженному сечению делится точкой
касания пополам	212
Предложение 20. Две прямые, проведенные из центра так, что каждая
параллельна касательной к конечной точке другой, есть сопряжен¬
ные диаметры

Предложение 21. У сопряженных диаметров касательные пересекаются
на одной из асимптот

Предложение 22. Произведение отрезков из (11, 10) равно квадрату па¬
раллельного им радиуса

Предложение 23. Произведение отрезков секущей, ограниченных сосед¬
ними сопряженными сечениями, равно удвоенному квадрату парал¬
лельного им радиуса	216
Предложение 24. Две прямые, пересекающие параболу в двух точках
каждая, пересекутся друг с другом	216
Предложение 25. То же для гиперболы	217
Предюжение 26. Две секущие, не проходящие через центр эллипса, не
делят друг друга пополам	217
Предложение 27. Касательные к концам диаметра эллипса параллельны ..218
Предложение 28. Прямая, рассекающая две параллельные секущие по¬
полам, есть диаметр	218
Предюжение 29. Прямая, проведенная от точки пересечения двух касатель¬
ных к середине отрезка, соединяющего точки касания, есть диаметр	219
Предюжение 30. Диаметр, проведенный от точки пересечения двух ка¬
сательных, делит пополам отрезок, соединяющий точки касания
(Предложение, обратное № 29)	219
Предложение 31. Касательные к концам диаметра гиперболы параллель¬
ны. Если же это не диаметр, то они пересекутся в той стороне от сое¬
диняющей их прямой, где находится центр	220
Предложение 32. Касательные или секущие к противолежащим пересека¬
ются внутри угла, дополнительного к углам, содержащим сечения	221
Предложение 33. Касательная или секущая к одному противолежащему
не имеет общих точек со вторым	221
Предложение 34. Прямая, проходящая через точку касания одного из
противолежащих и середину секущей другого, параллельную каса¬
тельной, есть диаметр	  222
Предложение 35. Если диаметр разбивает секущую пополам, то каса¬
тельная к другому противолежащему, проходящая через конец диа¬
метра, параллельна секущей	222
Предложение 36. Если секущие противолежащих параллельны, то пря¬
мая, соединяющая их середины, есть диаметр			223
Предюжение 37. Если прямая, проведенная не через центр, рассекает
противолежащие сечения, то отрезки, проведенные из центра парал¬
лельно ей и через ее середину, есть сопряженные диаметры	223
еж
еЖ
еж
•Ж
еж
9

Оглавление
Предложение 38. Прямая, соединяющая точку пересечения касатель¬
ных к противолежащим и середину отрезка между точками касания,
и прямая, проходящая через центр параллельно ему, - сопряженные
диаметры...	224
Предложение 39. Прямая, проведенная через точку пересечения каса¬
тельных к противолежащим и центр, проходит через середину отрез¬
ка между точками касания	225
Предложение 40. Если через точку пересечения двух касательных к про¬
тиволежащим провести прямую, параллельную отрезку, соединя¬
ющему точки касания, то прямые между точками пересечения ее с
кривыми и серединой этого отрезка есть касательные	225
Предюжение 41. Две прямые, проходящие не через центр противолежа¬
щих, не могут делить друг друга пополам	226
Предюжение 42. То же для дзя противолежащих и сопряженных	227
Предюжение 43. Два диаметра противолежащих, проведенные к середи¬
не некоторой секущей и пар&тлельноей. являются сопряженными. ... 227
Предюжение 44. Построение диаметра заданного конического сечения.... 228
Предюжение 45. Нахождение центра эдтипса и гиперболы	228
Предюжение 46 Построение оси параболы	229
Предюжение 47. Построение оси гиперболы и эллипса	230
Предюжение 48. Сечения не могут иметь других осей	230
Предюжение49. Построение касательной к коническому сечению из
точки, находящейся вне его	232
Предюжение 50. Построение касательной, образующей заданный угол с
осью	236
Предюжение 51. Построение касательной к параболе и гиперболе, кото¬
рая образует с диаметром, проведенным через точку касания, угол,
равный заданному острому углу	240
Предюжение 52. В эдзипсе угол, образованный касательной и радиу¬
сом, проведенным к точке касания не меньше угла, дополнительно¬
го к углу, образованному прямыми, соединяющими конец малой оси
и концы большой оси	242
Предюжение 53. Построение касательной к эллипсу, которая образует с ди¬
аметром, проведенным через точку касания, заданный ос трый угол	244
Дословный перевод книги II	247
м.
•I»
♦Л
»а
м
с?
.о
ЛК.
с»
кв»
•а
Книга III
Предложение 1. Площади треугольников, образованных двумя касатель¬
ными и диаметрами. проведенными через точки касания, равны	275
Предложение 2 Площади треугольника и четырехугольника, образо¬
ванных диаметрами, касательными и параллельными им прямыми,
равны	 276
Предложение 3 Площади двух четырехугольников, образованных ди¬
аметрами, и прямыми, проведенными из двух точек кривой парал¬
лельно касатетьным через точки пересечения диаметров с кривой,
равны	    278
••«44*
»Л
10

Оглавление
* г
0
Предложение 4. Предложение I для противолежащих сечений	279
Предложение 5. Площадь треугольника равна сумме двух других (гипер¬
бола)	279
Предложение 6.	Повторение Предложения 2...	280
Предложение 7.	Предложение Здля противолежащих сечений	281
Предложение 8. Если через точки пересечения диаметров со второй ги¬
перболой будут проведены прямые, параллельные касательным, то
площади четырехугольников, образованных диаметрами, касатель¬
ными и параллельными им прямыми, равны	282
Предложение 9. Еще одно равенство площадей четырехугольников (ги¬
пербола) 	283
Предложение 10. Вариант Предложения 7	283
Предложение 11. Повторение Предюжения 5	284
Предложение 12. Еще одно равенство площадей четырехугольников
(гипербола)	285
Предложение 13. Площади треугольников, образованных двумя каса¬
тельными к смежным сопряженным гиперболам и диаметрами, про¬
веденными к точкам касания, равны	285
Предложение 14. Если к двум смежным сопряженным гиперболам про¬
ведены касательные, а через точки касания диаметры, то площадь
треугольника, образованного этими диаметрами и прямой, пардл-
лельной одной из касательных равна сумме площадей двух других
треугольников	286
Предложение 15. Если к гиперболе проведены две касательные, а через
точки касания диаметры, то площадь треугольника, образованно¬
го одним из диаметров и прямыми, проведенными из некоторой точ¬
ки на сопряженном сечении параллельно касательным равна сумме
площадей двух других треугольников	287
Предложение 16. Квадрат отношения отрезков касательных равен отно¬
шению произведения двух отрезков к квадрату третьего	289
Предложение 17. Квадрат отношения отрезков касательных равен отно¬
шению произведений отрезков, на которые разбивают друг друга па¬
раллельные им секущие

Предложение 18. Предложение 16 для проти
Предложение 19. Предложение 17 для противолежащих

Предложение 20. Отношение произведения отрезков, на которые каса¬
тельная разбивает прямые, проведенные между противолежащими
парддлельно прямой, соединяющей точки касания, к квадрату отрез¬
ка касательной есть постоянная величина	294
Предложение 21. Предыдущее отношение равно отношению произведе¬
ний отрезков двух прямых, параллельных, одна — касательной, а дру¬
гая - прямой, соединяющей точки касания	295
Предложение 22. В случае противолежащих 1д и Ьг относятся как произ¬
ведения отрезков, на которые ордината и прямая, параллельная диа¬
метру, делят друг друга	 296
•Л
291
292
293
яс
лежащих

Оглавление
с».
о
О.
Предложение 23 Квадрат отношения отрезков касательных к противо¬
лежащим равен отношению произведении отрезков двух пересекаю¬
щихся параллельных им прямых, на которые они делят друг друга . ...
Предложение 24. Если прямые, параллельные сопряженным диаметрам,
пересекаются между четырьмя сечениями, то произведение отрезков
одной прямой плюс произведение отрезков другой, умноженное на
квадрат отношения этих диаметров, равно удвоенному квадрату по¬
ловины диаметра, находящегося в числителе

Предложение 25 Предложение 24 в случае, если точка пересечения, ле¬
жит внутри одного из противолежащих

Предложение 26 Предложение 24 в случае, если точка пересечения, ле¬
жит внутри одного из сопряженных

Предложение 27. Предложение 24 для эллипса

Предложение 28. Отношение сумм квадратов секущих, параллельных со¬
пряженным диаметрам, равно отношению квадратов этих диаметров
Предложение 29. Аналогичная теорема для отрезков, отделяемых асим¬
птотами ,
Предложение 30 Прямая, проведенная параллельно одной из асимптот
от пересечения касательных до се кушей, соединяющей точки каса¬
ния, делится гиперболой пополам

Предложение 31 Предложение 30 для противолежащих

Предложение 32 Если проведена секущая, соединяющая точки касания,
а через точку пересечения касательных параллельная ей прямая, то
отрезок, проведенный из середины секущей параллельно одной и з
асимптот, делится гиперболой пополам

Предложение 33. Предложение 32 для противолежащих

Предложение 34. Если от точки на асимптоте проведена касательная, а
через точку касания прямая, пардллельная этой асимптоте, то отре¬
зок. проведенный от точки асимптоты, делится гиперболой попо¬
лам. если он пардллелен второй асимптоте

Предложение 35. Если отточки на асимптоте проведена секущая, то от¬
резки, образующиеся при этом, относятся как отрезки, на которые
секущая внутри сечения делится прямой, параллельной асимптоте и
проведенной из точки касания

Предложение 36 Предложение 35, если вместо секущей проведена пря¬
мая, пересекающая оба противолежащих

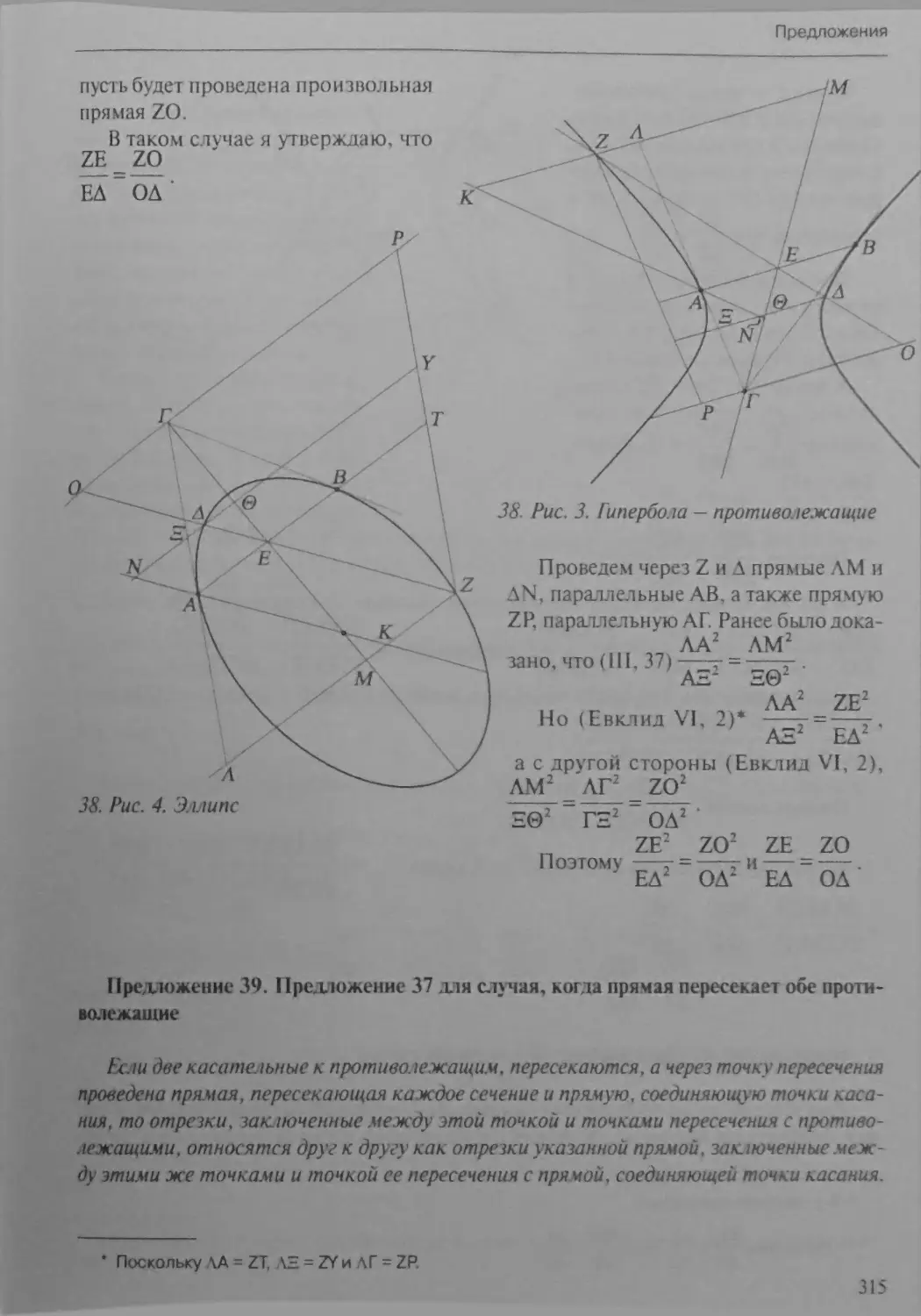
Предложение 37 Отношение между отре зками, на которые секущая,
проведенная из точки пересечения касательных, разбивается кривой
и прямой, соединяющей точки касания

Предложение 38 Отношение между отрезками, на которые прямая, про¬
веденная из произвольной точки сечения через середину секущей,
соединяющей точки касания, разбивается кривой и этой секущей

Предложение 39 Предложение 37 для случая, когда прямая пересекает
обе противолежащие

Предложение 40 Предложение 38 - частный случай

297
298
300
301
302
....304
304
305
306
307
308
»г»
309
«1».
309
•II
311
312
»1«
314
•Л
315
316
12

Оглавление
Предложение 41. Отношения отрезков, на которые три касательные к
параболе делят друг друга, равны	 318
Предложение 42. Произведение отрезков параллельных касательных, отсе¬
каемых третьей касательной, равно четвертой части плошали эйдоса	319
Предложение 43. Произведение отрезков, отсекаемых касательной на
асимптотах - постоянная величина	.	32!
Предложение 44. Прямые, проходящие через точки пересечения каса¬
тельных с асимптотами, параллельны прямой, соединяющей точки
касания	  321
Предложение 45. Углы между прямыми, соединяющими фокус эллипса
или гиперболы с точками пересечения произвольной касательной и
перпендикуляров, проведенных от концов оси, будут прямыми	322
Предложение 46 Углы, образованные теми же прямыми с касательны¬
ми, будут равны

Предложение 47. Прямая, проведенная из точки пересечения тех же пря¬
мых к точке касания, будет перпендикулярна касательной

Предложение 48. Прямые, проведенные отточки касания к фокусам, об¬
разуют равные углы с касательной
Предложение 49. Если от одного из фокусов проводится перпендикуляр
к касательной, то прямые, проведенные отточки их пересечения к
концам оси, образуют прямой угол

Предложение 50. Прямая, проведенная от центра сечения к касательной,
равна половине оси, если она параллельна прямой, соединяющей
фокус и точку касания

Предложение 51. Разность расстояний от фокусов до произвольной точ¬
ки на противолежащих равна длине оси

Предложение 52. Сумма расстояний от фокусов до произвольной точки
на эллипсе равна длине оси

Предложение 53. Если через концы диаметра провести касательные, то
произведение отрезков, отсекаемых на них прямыми, проведенными
из тех же точек через какую-нибудь точку на сечении, равно площа¬
ди эйдоса

Предложение 54. Соотношение, которое словами кратко не описать

Предложение 55. Подобное соотношение для противолежащих

Предложение 56. Предложение 54 для противолежащих

Дословный перевод книги III

¿IE
О
323
324
325
326
326
327
328
СЕ
СЕ
329
330
322
333
335
Книга IV
Письмо к Атталу
Предложение 1. Предложение, обратное (III, 37). Если из точки А прове¬
дены две касательные и секущая, пересекающаяся с сечением в двух
точках, то прямая, проведенная через точку касания, пересечется с
кривой в другой точке касания, если она делит секущую в том же от¬
ношении, что и в (III, 37)	 365
Предложение 2. Предложение I для гиперболы
13

Оглавление
м.
О
Предложение 3. Предложение 1 для гиперболы (другой вариант)	366
Предложение 4. Предложение 1 для противолежащих, если точка расположе¬
на внутри угла, дополнительного к углу, ограниченному асимптотами	367
Предложение 5 Если выполняются условия Предложения 1, а точка А
лежит на асимптоте, то проведенная прямая параллельна асимптоте.
Предложение, обратное (III, 35)	 367
Предложение 6 Если из одной точки проведены две касательные и, па¬
раллельно асимптоте, отрезок, разделенный кривой пополам, то
прямая, проведенная через точку касания и конец отрезка, пересе¬
чется с гиперболой в другой точке касания	368
Предложение 7. Предложение 6, если точка АЗ лежит вне угла между
асимптотами	369
Предложение 8, Если выполняются условия Предложения 6, а точка А
лежит на асимптоте, то проведенная прямая параллельна этой асим¬
птоте Предложение, обратное (III, 34)		 	 369
Предложение 9. Если из точки А проведены две секущие, то прямая, де¬
лящая их в том же отношении, что и в (III, 37), пересечет кривую в
точках касания прямых, проведенных из А. Другое Предложение, об¬
ратное (III, 37)	 370
Предложение 10. Предложение 9 для гиперболы	370
Предложение 11. Предложение 9 для гиперболы (другой вариант)	371
Предложение 12 Предложение 9, если точка А лежит вне угла между
асимптотами		371
Предложение 13 Если выполняются условия Предложения 9, а точка А лежит
на асимптоте, то прямая, проведенная через точки деления секущих, па¬
раллельна этой асимптоте и пересечется с кривой в точке касания	372
Предложение 14 Если из точки А, лежащей на асимптоте, проведены ка¬
сательная и две секущие, одна из которых удовлетворяет условию
Предложения I. а другая - Предложения 6, то проведенная прямая
параллельна этой асимптоте и пересечется с кривой в точке касания	373
Предложение 15. Предложение 4 для случая, когда прямая, удовлетво¬
ряющая соотношению, пересекает оба противолежащих, а А лежит
внутри угла, образованного асимптотами	374
Предложение 16. То же самое, если точка А лежит внутри дополнитель¬
ного угла	374
Предложение 17. Предложение 5 для противолежащих	375
Предложение 18 Предложение 12 если прямая, проведенная из точки А,
пересекает оба противолежащих, а А лежит внутри угла, обра зован¬
ного асимптотами	375
Предложение 19 То же самое, если точка А лежит внутри дополнитель¬
ного утла	376
Предложение 20 Предложение 13, если две прямые пересекают оба про¬
тиволежащих и удовлетворяют условию Предложения 1	377
Предложение 21 Предложение 14 для противолежащих	377
Предложение 22 То же самое, если точка А лежит внутри дополнитель¬
ного угла.. 		378
»!•
»!•
• • • •
к • 1 •
»Ж
«
14

Оглавление
Предложение 23. Если из точки Д проведены две касательные и. парал¬
лельно асимптотам, два отрезка, которые делятся кривыми пополам.
то прямая, проведенная через их концы, пройдет через точки касания ...378
Предложение 24. Два конических сечения не могут частично совпадать.... 379
Предложение 25. Два конических сечения не могут пересечься более чем
в четырех точках	379
Предложение 26. Если два конических сечения касаются друг друга в од¬
ной точке, то они могут иметь кроме этого не более двух общих точек....381
Предложение 27. Два конических сечения, касающиеся друг друга в двух
точках, не имеют других общих точек

Предложение 28. Предложение 27 для эллипсов

Предложение 29. Предложение 27 для случая, когда общая точка нахо¬
дится между точками касания

Предложение 30. Парабола не может касаться другой параболы более
чем в одной точке

Предложение 31. Парабола не может касаться гиперболы в двух точках,
находясь вне нее

Предложение 32. Парабола не может касаться эллипса с внутренней сто¬
роны в двух точках

Предложение 33. Гипербола не может касаться гиперболы в двух точках
Предложение 34. Если эллипсы касаются друг друга в двух точках и их
центры совпадают, то прямая, соединяющая точки касания, прохо¬
дит через центр

Предложение 35. Конические сечения не могут пересекаться более чем в
двух точках, если выпуклости дуг, заключенные между точками пере¬
сечения являются разнонаправленными

Предложение 36. Если коническое сечение имеете одним из противоле¬
жащих две общие точки и выпуклости дуг между ними однонаправле-
ны, то его продолжения не пересекутся с другим проти
Предложение 37. Если коническое сечение имеет общую точку с одним из
противолежащих, то оно не будет иметь с другим более двух общих точек ...388
Предложение 38. Коническое сечение имеете противолежащими не бо¬
лее четырех общих точек	388
Предложение 39. Если коническое сечение касается изнутри одного из
противолежащих, то оно не будет иметь общих точек с другим	389
Предложение 40. Если коническое сечение касается каждого из противо¬
лежащих в одной точке, то оно не имеет с ними других общих точек	389
Предложение 41. Если гиперболы пересекаются в двух точках, имея
между ними про
не имеют общих точек

Предложение 42. Если гипербола пересекается с обоими противолежа¬
щими, то сечение, противолежащее ей, не имеет ни с одним из них
двух общих точек

Предложение 43. Если гипербола рассекает каждое из противолежащих
в двух точках, а дуги между ними имеют противоположные выпукло¬
сти, то сечение, противолежащее ей не будет иметь общих точек ни с
одним из этих противолежащих

382
383
383
БК
4 • •
КС
ЛЖ
тивоположные выпуклости, то их противолежащие
•А
384
384
385
385
386
387
387
390
390
391
15

Оглавление
Предложение 44. Если две гиперболы пересекаются в четырех точках, то
их противолежащие не имеют общих точек	393
Предложение 45. Если гипербола пересекается в двух точках с одним
противолежащим, имея одинаково направленные выпуклости, а со
вторым у нее одна общая точка, то сечение, противолежащее ей, не
будет иметь общих точек ни с одним из этих противолежащих	394
Предложение 46. Если пшербола имеете одним из противолежащих три об¬
щие точки, то их противолежащие будут иметь только одну общую точку	394
Предложение 47. Если пшербола касается одного противолежащего се¬
чения, а другое рассекает в двух точках, то сечение, противолежащее
ей, не будет иметь с ними общих точек

Предложение 48. Если гиперболы пересекаются в двух точках, а в одной
касаются, то их противолежащие не имеют общих точек

Предложение 49. Если гиперболы касаются друг друга в одной точке и пе¬
ресекаются в другой, то их противолежащие не имеют общих точек ....
Предложение 50. Если гиперболы касаются друг друга в одной точке, то
их противолежащие имеют не больше двух общих точек	399
Предложение 51. Если гипербола касается обоих противолежащих, то ее
проги вал ежа шее не имеете ними общих точек (частный случай № 43). .. 400
Предложение 52. Если одни противолежащие касаются друт их в одной
точке каждое, имея одинаково направленные выпуклости в точках
касания, то они не имеют других общих точек

Предложение 53 Если две гиперболы касаются друг друга в двух точках,
то их противолежащие не имеют общих точек

Предложение 54. Если две гиперболы касаются друг друга, имея в точке
касания противоположно направленные выпуклости, то их противо¬
лежащие не имеют общих точек

Предложение 55. Две пары противолежащих сечений пересекаются не
более чем в четырех точках

Предложение 56 Если гипербола соприкасается с другой гиперболой в
одной точке, то они пересекаются не более чем в двух других точках...
Предложение 57. Если противолежащие сечения касаются противолежа¬
щих сечений в двух точках, то они не будут иметь других общих точек....406
Дословный перевод книги IV
Распределение предложений по темам
Предложения, на которые было больше трех ссылок
Приложения
•э
•Ж
•к
о:
о
•Л
МЛ
но
•II
•и
О!«
• >
о
<•
• а
о
I
Теоремы Евклида, на которые есть ссылки в тексте
Шкала времен жизни геометров
395
396
• ?
' *
• ••«
•1«
397
400
401
402
402
404
408
428
429
430
Новая теорема в отношении учения о конических сечениях Якоба Бернулли... 435
Латинский текст и чертежи	435
Перевод	440
Список литературы444
16

ВСТУПИТЕЛЬНАЯ СТАТЬЯ
История математики, и в частности история конических сечений, подробно опи¬
сана во множестве превосходных сочинении, поэтому вроде бы и нет нужды повто¬
рять во вступительной статье то, что легко можно найти в уже написанных книгах1
Однако изучение этих книг требует немало времени, да и значительную их часть со¬
ставляет материал, не относящийся к истории конических сечений. Поэтому мы ре¬
шили поместить здесь небольшой популярный очерке кратким описанием истории
возникновения и развития учения о конических сечениях. Даты рождения и смер¬
ти древнегреческих математиков мы приводим лишь для ориентировки, поскольку
хотя некоторые из них и известны точно, например год гибели Архимеда, но боль¬
шей частью они очень условны, а то и просто выдуманы.
1.	КОНИЧЕСКИЕ СЕЧЕНИЯ ДО АПОЛЛОНИЯ
Восемь книг «Коник» Аполлония Пергского не были первым в истории трудом,
посвященным коническим сечениям. Его предшественниками были Менехм. Ев¬
клид и Аристей, но их книги не дошли до нас подобно тому, как не сохранились
книги геометров — предшественников Евклида. И подобно тому, как их открытия
были собраны, систематизированы и развиты в «Началах» Евклида, так и результа¬
ты исследований конических сечений были собраны и развиты в «Кониках» Апол¬
лония. И как «Начала» — итоговая на то время книга по элементарной геометрии,
так и «Коники» — итоговая книга по коническим сечениям. Эти книги сделали не¬
актуальными предыдущие сочинения, и на них постепенно перестали ссылаться и
перестали их читать и переписывать.
Но с чего начиналась история изучения конических сечений? Как они были от¬
крыты и что заставило эллинских математиков признать достойными исследования
кривые, которые нельзя начертить с помощью циркуля и линейки?
Вначале, как это обычно бывает в математике, была задача, которую не удава¬
лось решить известными на то время методами. Именно так появились, например,
производные, интегралы, мнимые числа и многое другое. Сначала эти нововведе¬
ния вызывали протест, а мнимая единица вообще считалась порождением дьяво¬
ла. но постепенно с ними смирялись, и они входили в обиход. В данном случае та¬
кой задачей была одна из трех знаменитых задач древности, не решаемых с помо¬
щью циркуля и линейки, — задача об удвоении куба: дан куб, и надо построить куб
вдвое большего объема2). По этому поводу даже были сочинены две легенды. Они
известны нам из комментария Евтокия Аскалонского (480—540) к сочинению Архи¬
меда «О шаре и цилиндре». Согласно Евтокию, легенды изложены в письме Эратос¬
фена (276-194 гг. до н.э.) царю Птолемею (письмо, впрочем, считается подложным;
перевод письма см. (1, с. 472—475]). По одной легенде, надо было увеличить вдвое
1	Например, [3], [4], [6], [8], [12], [17], [18], [20], [21], [23]. Здесь и далее указаны позиции из
списка литературы см. 444 с.
2	Подробное описание этих трех задач есть во всех общих трудах по истории математики, а так¬
же в отдельных брошюрах и книгах, например: [13], [14], [22]
17

Вступительная статья
’г г
мавзолей сына Миноса, Главка. Согласно другой, через примерно тысячу лет, уже
во времена Платона (428-348 гг. до н.э.), чтобы избавиться от чумы, жители Делоса
должны были по указанию оракула увеличить объем жертвенника вдвое. Было что-
нибудь подобное в реальности или не было, но задача считалась важной, и Платон
даже сетовал, что государство не понуждает математиков более активно занимать¬
ся ею, да и вообще стереометрией1).
Но почему она считалась столь важной? Во-первых, потому, что задача была ин¬
тересной сама по себе, и многие математики на протяжении столетий предлагали
новые и новые способы ее решения. А во-вторых, она появилась как естественное
продолжение предыдущего развития геометрии. После открытия пифагорейцами
несоизмеримости стороны квадрата и его диагонали началась геометризация ариф¬
метики, поскольку, хотя иррациональные и рациональные числа несоизмеримы, но
изобразить на чертеже сторону и диагональ квадрата можно без труда. Дело здесь,
собственно, не в изображении на чертеже, чертеж - лишь вспомогательное сред¬
ство2), а в том, что множество длин отрезков обладает большей полнотой, чем мно¬
жество рациональных чисел. Сложение теперь можно трактовать как приложение
отрезков друг к другу, а умножение - как составление прямоугольника (это даже не
называлось умножением, так как слово «умножение» относилось лишь к перемно¬
жению целых чисел (11, кн 7, Опр. 16]). Возведению в квадрат соответствовало по¬
строение квадрата, а чтобы извлечь квадратный корень из числа, изображаемого в
вше прямоугольника, надо было преобразовать его в квадрат равной площади. Тог¬
да сторона квадрата и есть корень'). Далее, надо было определять и сравн и вать пло¬
щади разных многоугольников. Любой многоугольник можно разбить на треуголь¬
ники. а площадь треугольника равна половине площади прямоугольника, постро¬
енного на его основании и высоте. Таким способом мы можем сравнивать площади
любых многоугольников. Следовательно, надо уметь складывать площади прямоу¬
гольников, к которым мы сводим площадь многоугольника. Для этого приведем их
к одному основанию (см. комментарий к 1.60), тогда сложение площадей сведет¬
ся к сложению высот. По-гречески это называлось парабола (приложение). Если же
теперь преобразовать получившийся прямоугольник а* *Ь в квадрат ххх (как это де¬
лается, см. комментарий к 1,11), что равносильно решению уравнения х2 ~ а*Ь. или
а/х=х/Ь. то можно сравнивать площади многоугольников как площади квадратов.
Для этого надо уметь строить квадраты, плошади которых образуют натуральный
ряд. Пусть имеется квадрат а*а и надо построить квадрат ххх, например, удвоен¬
ной плошали. Дзя этого строим прямоугольник дх/>. где Ь = 2а. Если преобразовать
его в равновеликий квадратххх. то задача решена. Отношение Ь:аУ как это видно из
построения и из уравнения, показывает, во сколько раз увеличилась площадь ква¬
драта Таким образом, площадь любого многоугольника выражалась через плошадь
С»
•II
•II.
1 Платон «Государство», кн. 7 {528).
‘ « когда они вдобавок пользуются чертежами и делают отсюда выводы, их мысль обращена
не на чертеж а на те фигуры подобием которых он служит. Выводы свои они делают только для
четырехугольника самого по себе и его диагонали, а не для той диагонали, которую они начерти¬
ли Так и во всем остальном* Платон «Государство», кн 6(510) См об этом также [15, с 20,21].
• Кроме геометризации были и другие возможности выхода из кризиса, см.: [6, с. 78].
18

1. Конические сечения до Аполлония
Л1».
квадрата, и только не удавалось свести к квадрату площадь круга. Отсюда и появи¬
лась знаменитая задача о квадратуре круга.
Следующий естественный шаг — определение объемов много! ранников. Дчя это¬
го надо свести их объемы к объемам параллелепипедов, а те — к кубам. И опять не¬
обходимо построить натуральный ряд, но уже из объемов кубов. Первый шаг — уд¬
воение куба. Итак, пусть а — ребро заданного куба. Тогда х’ = 2а , следовательно,
х = Ч 2 а. То есть задача сводится к извлечению кубического корня из двух, или. если
требуется увеличить объем в п раз, то из и. А вот это проделать с помощью цирку¬
ля и линейки никак не получалось1). После нескольких неудавшихся попыток было
решено, что и не получится (доказано это было только в XIX веке П. Ваннелем). И
тогда стали изобретать иные способы решения. Одним из таких способов было при¬
менение различных механических устройств, а другим — использование кривых ли¬
ний, которые и стали новым объектом исследования математиков2 3).
Сначала Гиппократ Хиосский (470—410 гг. до н.э.) заметил, что если у квадратов
мы имеем пропорцию для одного среднего геометрического а/х = х/Ь, то у кубов —
для двух: а/х —х/у =у/Ь, где отношение Ь:а равно на этот раз увеличению объема
куба. Это позволяло решить задачу, но Гиппократ задачу все же не решил. Архит Та-
рентский (428-348 гг. до н.э.) показал, что решение может быть получено как ре¬
зультат пересечения конуса, цилиндра и тора без дырки’). Но, как писал Эратосфен
в письме Птолемею «они доказали лишь возможность такого построения, выпол¬
нить же его на самом деле и дать практический способ не смогли» [ 1, с. 473]. «Они»
— это Архит и Евдокс Книдский (408—355 гг. до н.э.). Решение Евдокса до нас не до¬
шло, Архит же не смог выполнить построения, поскольку линия пересечения была
линией двоякой кривизны. Это стимулировало поиски решения с помощью таких
кривых, которые, в отличие от линии Архита, можно было бы начертить на плоско¬
сти. Они были найдены учеником Евдокса Менехмом (380—320 гг. до н.э.)4). Кри¬
вые получались при пересечении конуса плоскостью и поэтому их назвали объем¬
ными или телесными (отереоС) местами (прямые же и круги — это плоские места). И
хотя труды Менехма до нас недошли, мы знаем его решение из описания Евтокия.
Заключалось оно в следующем. Из пропорции для двух средних легко получить, что
х2 = ау, у2 -Ьх,ху = аЬ, а это уравнения двух парабол и гиперболы. Если мы возьмем
первые два выражения, то решением будет абсцисса пересечения двух парабол, оси
которых перпендикулярны, если первое и последнее, или второе и последнее — аб¬
сцисса пересечения параболы и гиперболы. Но тут надо было еще выяснить, суще¬
ствуют ли такие непрерывные кривые.
Менехм первым установил, что кривые эти появляются в результате пересечения
конуса плоскостью под углом в 90 градусов к образующей и что их три вида («триа¬
да Менехма»). А поскольку коническая поверхность непрерывна, то и линия ее пе-
•Л
•I»
•Ж
• •
1	А вот вавилоняне умели извлекать кубические корни, но приближенно Для них был характерен
лее практический подход к математике, связанный с вычислениями положения небесных светил
2	Все решения древнегреческих математиков в изложении Евтокия см.: в [1, с. 459-479], а также
в (13, с. 92-125], где кроме древнегреческих, приведены еще и решения Виета, Декарта и Ньютона.
3	Решение Архита подробно рассмотрено в [1, с. 471,3, с. 209-211; 8, с. 106, 13, с. 98-102].
4	Он был из города Алопеконнес в Малой Азии, но Менехмом Алопеконнесским его что-то ни¬
кто не называет.
•ю
19

Вступительная статья
ресечения с плоскостью тоже непрерывна. При этом вид кривой зависит от величи¬
ны угла при вершине конуса, поэтому они получили следующие названия: сечение
тупоугольного конуса, прямоугольного, остроугольного. Эти названия оставались в
употреблении, пока Аполлоний не заменил их теми, что употребляются сейчас (ги¬
пербола, парабола, эллипс). Но и Архимед еще пользовался старыми наименовани¬
ями. Так как Менехм решил задачу об удвоении куба с помощью парабол и гипер¬
бол, то он, конечно, знай! способ их построения на плоскости, то есть, по сути, знал
их уравнения. Строить же эти кривые как сечения конуса было очень неудобно, и
действительно, мы видим, что греческие геометры обращаются с ними большей ча¬
стью как с плоскими кривыми, описываемыми соответствующими сюмптомами. как
называли это они, или уравнениями, как говорим мы (уравнений они все же не пи¬
сали). Тот же подход мы видим и в современных курсах аналитической геометрии.
Между тем исследование новых кривых продолжалось: Аристей Старший (око¬
ло 300 г. до н.э.) написал пять книг о конических сечениях, Евклид (325—265 гг.
до н.э.) - четыре. Коническими сечениями занимались также Трасидей и Ни котел
Киренские1), Конон Самосский (280-220 гг. до н.э.) и многие другие. Конические
сечения сделались модной темой. И хотя все их сочинения утеряны, но из работ Ар¬
химеда (287-212 гг. до н.э.) и ссылок в его работах видно, что известно к тому вре¬
мени было уже немало2).
2.	АПОЛЛОНИЙ И ЕГО «КОНИЧЕСКИЕ СЕЧЕНИЯ»
Аполлонии Пергский жил в 111-11 вв. до н.э. Годы его жизни точно неизвестны, и
разброс у разных авторов довольно велик: 265-170 гг. до н.э. (Веселовский [ 1, с. 443]),
250-170 гг до н.э. (Розенфельд [18, с. 172]), а Кольман даже приводит в двух местах
своей книги различные даты: 262-200 гг. до н.э. и 265-170 гг. до н.э. |8, с. 171 и 2311.
В зарубежной литературе, как правило, приводятся даты 262-190 гг. до н.э. Полу¬
чается, что жил он от 62 до 95 лет. О жизни Аполлония почти ничего не известно.
Родился он в Перге в Малой Азии'). Жил долгое время в Александрии Египетской,
бывал в Пергаме и Эфесе, где встречазся со своими знакомыми математиками Ев-
демом, Атталом и Филонидом; в Азександрию к нему приезжал Навкрат. О том, кто
эти люди и чем конкретно занимались, ничего не известно, кроме того, что все они,
по-видимому, были математиками4).
Они упоминаются только в письме-предисловии Аполлония к четвертой книге Есть предпо¬
ложение, что Никотел - это на самом деле Никомед (280-210 гг. до н.э )
■ См [1,с 28]. Поскольку Архимед излагал только собственные открытия, то он не доказывал
того, что на тот момент было уже известно, а либо ссылался на «Начала теории конических сечений* *,
не указывая, впрочем, автора, либо ни на что не ссылался, а просто писал, что это уже известно.
1 Несмотря на схожее название. Перга - не Пергам. Перга недалеко от Антальи, а Пергам - на
северо-западе Турции
* Есть только разные предположения. Так, Розенфельд пишет, что Аттал - ученик Евдема [7, с.
172], а Лурье и Кольман, что он был царем Пергама [9, с 100; 10, с. 173] Лурье также приводит
весьма интересные, но чисто гипотетические соображения о политических взглядах Аполлония и о
его полемике с Архимедом Впрочем, Рожанский [17, с. 172], пишет, ссылаясь на Фрэзера (Fraser
Р М Ptolemaic Alexandria), что Аттал Аполлония, вовсе не царь Пергама.
20
•ю

2 Аполлоний и его «Конические сечения
• Л
Из писем, которыми Аполлоний сопровождал отсылаемые труды, следует, что
помимо всего прочего, он занимался в Александрии коническими сечениями,
можно, читал лекции на эту тему, поскольку, когда его посетил там Навкрат и попро¬
сил записать их, Аполлоний, по его словам, «как можно скорее написал этот труд в
восьми книгах и передал ему без всякой отделки». Но ведь ясно, что груд такого объ¬
ема и сложности не напишешь вот так, сходу. В это же время Аполлоний приезжал
в Пергам к Евдему, который тоже проявил большой интерес. Поэтому Аполлоний
стал высылать ему книги в уже обработанном виде, по мере их готовности. Вторую
книгу привез его сын, которого тоже звали Аполлоний. В письме просьба обсудить
написанное «с теми, которые сведуши в этих предметах». К третьей книге, тоже по¬
сланной Евдему, письма нет. Затем Евдем умер, и остальные пять книг были посла¬
ны опять же в Пергам, но уже Атталу.
«Конические сечения» Аполлония состоят из восьми книг. Первые четыре дошли
до нас на древнегреческом языке, пятая, шестая и седьмая — в переводе Сабита ибн
Корры (836—901 гг.) (чтобы сделать с них перевод, Э. Галлей изучил арабский язык),
а восьмая книга не была переведена на арабский язык, так как греческий текст был
утерян уже тогда. Ее восстановил Галлей (1656-1742 гг.). но насколько близко к ори¬
гиналу. судить трудно. В итоге в 1710 году появилось первое полное издание восьми
книг «Конических сечений».
Первые четыре книги содержат, как пишет Аполлоний в сопроводительном пись¬
ме, изложение начал теории конических сечений, а в следующих четырех рассма¬
триваются более специальные вопросы. Аполлоний писал сводный труд (особен¬
но это относится к первым четырем книгам), поэтому в него вошли не только его
собственные открытия, но и какое-то количество материала или заимствованного
или переработанного и обобщенного. Иногда даже утверждают, что в первых четы¬
рех книгах Аполлоний просто собрал все известное до него. Папп Александрийский
(290—350 гг.) в VII книге «Математического собрания» писал: «Аполлоний допол¬
нил четыре книги Евклида о конических сечениях и добавил к ним четыре другие,
образуя восемь книг» [цит. по: 18, с. 32 ]. В наше время Веселовский [1, с. 28] пишет,
что Аполлоний в первых четырех книгах просто «резюмирует труды предшествую¬
щих ему авторов». Наиболее последовательно эту точку зрения проводит Пауль фер
Ээке в предисловии к своему переводу Аполлония на французский язык (1921 г.).
Это предисловие мы приводим в нашей книге полностью, поскольку, несмотря
на некоторую тяжеловесность слога и иногда, может быть, излишнюю обстоятель¬
ность, в нем содержится немало ценного материала, ранее не публиковавшегося на
русском языке, как о текстах Аполлония и истории их издания, так и о нем самом.
Но с его оценкой первых четырех книг Аполлония трудно согласиться. Так. фер
Ээке пишет, что «четыре первые книги не открывают нам нового направления гео¬
метрии, представляя собой упорядоченную компиляцию более ранних знаний о ко¬
нических сечениях» и что «из предисловия к первой книги Конических сечений следу¬
ет, что Аполлоний и не претендовал на что-то большее». Но как раз из предисловий
и следует, что Аполлоний вовсе не считал свой труд просто упорядоченной компи¬
ляцией. Конечно, оценивать значимость первых четырех книг можно по-разному,
но далее следуют еше более сильные утверждения. Как известно, все древнегрече¬
ские авторы считают Аполлония первым, кто стал рассматривать конические сече-
21
НС
ЛИ

Вступительная статья
О
ния на произвольном конусе с круговым основанием. Но фер Ээке отказывает ему
и в этом! Откуда же тогда Аполлоний это заимствовал? Оказывается, «он первым
применил этот исключительный способ получения на основе некоего специально¬
го трактата, посвященного кривым второго порядка». Заметим, способ все-таки ис¬
ключительный! Но что же это за трактат, кто его автор? Это неизвестно, посколь¬
ку способ был изложен «в каком-нибудь не дошедшем до нас труде». То есть ни об
авторе, ни о труде его никто ничего не знает, но первооткрыватель все-таки он. А
что же тогда сделал Аполлоний? Ну, возможно, он придумал названия, хотя и это,
по мнению фер Ээке, еще не факт: «Однако можно допустить с некой долей веро¬
ятности, что именно Аполлонию мы обязаны самими наименованиями параболы,
гиперболы и эллипса». Словом, гиперкритицизм во всем его великолепии! Но все-
таки надо заметить, что большинство авторов, пишущих об Аполлонии, ничего по¬
добного вышеприведенным взглядам не высказывают.
Содержание первых четырех книг описано довольно подробно в любой книге по
истории математики, особенно в 1181 и 128], поэтому обрисуем его лишь в самом об¬
щем виде, но все же немного подробнее, чем это делает сам Аполлоний.
Первая книга начинается с определений. Сначала дается определение конуса и
конической поверхности. И уже в первом определении мы видим отличие от того,
что писали раньше. Ведь конус определялся у Евклида как тело, получающееся в ре¬
зультате вращения прямоугольного треугольника вокруг одного из катетов. Ясно, что
и наклонные конусы, и вторая часть конической поверхности таким определени¬
ем исключаются из рассмотрения1). А из определения Аполлония они появляются
сами собой, да и диаметры Аполлоний определяет, уже заранее зная, что гипербола
имеет две ветви, о чем до него никто не упоминал. Затем вводится понятие сопря¬
женного диаметра, но о сопряженных гиперболах не говорится ничего до послед¬
него Предложения2) первой книги.
Первые десять Предложений касаются некоторых свойств прямых и плоскостей,
пересекающих конус, и служат подготовкой к Предложениям 11 -13, в которых да¬
ется классификация конических сечений в зависимости от угла, под которым про¬
водится секущая плоскость.
Принципиальным отличием от предыдущих авторов было то, что все три вида
сечений получаются при пересечении плоскостью одного и того же конуса, прямо¬
го или наклонного. До этого, как уже говорилось, параболу получали как пересече¬
ние прямоугольного прямого конуса плоскостью, перпендикулярной образующей,
гиперболу - тупоугольного, а эллипс - остроугольного. В Предложениях 11-13 вы¬
водятся и уравнения кривых в косоугольных координатах, причем начало координат
можно поместить в любой точке кривой, а вид уравнения от этого не меняется. Но
координаты Аполлония отличаются от координат Декарта тем, что начало их обя¬
зательно должно лежать на кривой, а не в произвольной точке плоскости, то есть
они привязаны к кривой, а не задают плоскость. Исходя из вида уравнений, Апол-
»Ж»
•У11
»Ж»
Тем не менее в работе Архимеда *0 коноидах и сфероидах» наклонный конус присутствует
П.с 179]
‘ Мы пишем это слово везде с заглавной буквы, чтобы не путать с предложением в граммати¬
ческом смысле
22

2 Аполлоний и его «Конические сечения»
лоний вводит новые названия конических сечений: парабола, гипербола, эллипс1).
В Предложении 14 дается определение и основное свойство полной гиперболы, за¬
ключающееся в том, что ее ветви имеют одинаковые параметры и общий диаметр.
Аполлоний называет гиперболой одну ветвь, а обе — противолежащими сечениями,
или просто противолежащими. Даже если бы Аполлоний на этом и остановился,
его труд все равно был бы выдающимся, поскольку это был новый подход, откры¬
вающий новые возможности для исследования, но он конечно же не остановился.
На этом рассмотрение конусов заканчивается и, кроме трех задач на пост{
в конце первой книги, Аполлоний рассматривает конические сечения исключитель¬
но как планиметрические кривые, описываемые соответствующими уравнениями.
После 16-го Предложения Аполлоний добавляет еще три определения: он гово¬
рит, что центр - это середина диаметра, и зачем-то опять дает определение сопря¬
женного диаметра. Но главный пункт здесь, ради чего все и затеяно, — это постули¬
рование длины сопряженного диаметра, сделанное, впрочем, без каких-либо обо¬
снований. Получается, что Аполлоний уже знал о сопряженных гиперболах, ведь без
них говорить о длине сопряженного диаметра не имеет смысла. И эти сопряженные
гиперболы тоже были в древнегреческой математике чем-то совершенно новым.
Оставшаяся часть первой книги посвящена доказательству разных свойств ди¬
аметров, ординат, абсцисс и касательных. Здесь же несколько теорем о площадях,
ими отсекаемых. В расположении этих теорем трудно увидеть какой-то ясный план:
темы начинаются и бросаются, но все они будут продолжены в следующих книгах
Декарт считал, что никакого плана и не было [3, с. 340, 341; 28, с. 63]. Но Цейтен
полагает, что план был, и главной целью первой книги было доказательство того,
что конические сечения, рассматривавшиеся Аполлонием, тождественны тем се¬
чениям, которые рассматривались до него, то есть сечениям, перпендикулярным
образующим конуса. Ну а попутно он доказывал и некоторые другие свойства [21,
с. 1361. Завершают первую книгу задачи на построение: дано коническое сечение и
надо построить для него конус, затем построение противолежащих и, наконец, по¬
строение сопряженных гипербол.
Во второй книге продолжаются все темы, начатые в первой, кроме площадей и
свойств ординат, и добавляются новые: асимптоты и сопряженные гиперболы, а
также теоремы о параллельности касательных к противолежащим. Они составля¬
ют более половины книги.
В третьей книге Аполлоний возвращается к теме площадей и посвящает им пер¬
вые пятнадцать теорем. Причем речь идет всегда о площадях различных многоу¬
гольников, но никогда об отсекаемых сегментах кривых, которыми занимался Ар¬
химед. Аполлоний не рассматривает здесь свойств диаметров и ординат и пересече¬
ния прямых и кривых. Нет и задач на построение, зато много внимания уделяется,
как и в первых двух книгах, противолежащим, а также сопряженным гиперболам.
Новая тема третьей книги - фокусы. Разумеется, Аполлоний так их не называет. Он
их вообще никак не называет. Для него это просто «точки, возникшие в результате
приложения». Фокусам, впрочем, посвящено лишь семь теорем, при этом Аполло¬
ний ничего не пишет о фокусе параболы и его свойствах. Возможно, из-за того, что
фокус у него определяется как точка Ена оси АВ, для которой выполняется соотно¬
шение ЛЕЕВ = % Ьг-и, а для параболы такое определение не подходит, поскольку у
23

Вступительная статья
Ж
нее нет ограниченной оси. Тут подошло бы определение фокуса с помощью дирек¬
трисы, но о директрисе у Аполлония нет ни слова. Возможно, он не придавал этим
точкам того значения, которое они приобрели потом1), ведь до орбит небесных тел
было еще далеко.
Четвертая книга посвящена двум основным темам. Первая - продолжение темы,
начатой в 3-й книге - то, что сейчас называется теоремами о полюсах и полярах и
относится к проективной геометрии (первые 23 теоремы). Вторая - подробное рас¬
смотрение пересечений конических сечений между собой (теоремы 24-57). О во¬
просах, связанных с этой темой, Аполлоний рассказывает в письме к 4-й книге.
В отличие от Евклида. Аполлоний вкратце указывает в своих письмах-предисло¬
виях. что он сделал нового, а что изложил «более полным и более общим способом,
чему других писавших об этом». Но из предшественников упоминает только Евкли¬
да и Конона, да и то лишь в связи с не вполне удачными их работами. В то же время,
как уже было сказано, из писем Аполлония мы узнаем имена математиков, о которых
более ничего не известно2). Очевидно, круг математиков Античности был гораздо
шире списка из двух десятков постоянно упоминаемых имен выдающихся ученых.
Труден ли Аполлоний для понимания? Вот что пишет об этом ван дер Варден:
«Аполлоний виртуозно владеет геометрической алгеброй, но не менее виртуозно
умеет скрывать свой первоначальный ход мыслей. Из-за этого-то его книгу и трудно
понимать: рассуждения его элегантны и кристально ясны, но что его привело имен-
но к таким рассуждениям, а не к иным каким-нибудь, - об этом можно лишь дога¬
дываться» [3,с. 338, 339]. Но практически тоже самое писали и об Архимеде 110, с.
115-117] и даже о Евклиде: «Евклид нигде не посвящает читателя в тот анализ, ко¬
торым добыто доказательство; оно всегда излагается догматически в законченной
синтетической форме и нередко производит на “противоположную сторону” впе¬
чатление искусно построенной, но неожиданной аргументации речи адвоката» (24,
с. 138,139].То есть упреки в трудности относятся, скорее, не к Аполлонию, а ко всей
древнегреческой математике Трудны же для понимания у Аполлония лишь некото¬
рые теоремы, доказательство которых представляет собой длинную цепь преобра¬
зований. так что трудно понять, куда же тебя ведут и уж совсем непонятно, как же
он до этого додумался, да еше не используя алгебраические обозначения. При этом
встречаются неизвестно откуда взявшиеся, совсем не очевидные положения, кото¬
рые Аполлоний не доказывает, а иногда тщательно доказываются и вполне очевид¬
ные. Следуя греческой традиции, Аполлоний вначале всегда приводит чисто сло¬
весную формулировку; без каких-либо обозначений, которая независимо от длины
должна состоять всего из одной фразы вида «если.. то...». Без привычки ее иногда
трудно понять, но без всякого ущерба для понимания можно и пропустить, посколь-
ку далее следует это же утверждение, но уже в привычной нам форме. Надо сказать,
нам, в отличие от Аполлония, отнюдь не всегда удавалось обойтись одной фразой.
Является ли труд Алотюния полным и всеохватывающим? Разумеется, нет, ведь
в нем отсутствуют теоремы, доказанные Архимедом, ничего нет о директрисе, о фо-
ж*
М
Подробнее о названиях см. в примечаниях к Предложениям 11-13.
5 Попытки некоторых авторов привязать их к известным в истории личностям не имеют ника¬
ких оснований
24

3. Другие сочинения Аполлония
кусе параболы и т.д. Тем не менее это был конечно же энциклопедический свод зна¬
ний о конических сечениях, ставший уже тогда классическим. Какова была реакция
на его появление, мы не знаем, не считая того, что он вытеснил из употребления все
труды предшественников. Первые комментарии, которые нам известны, появились
лишь пятьсот лет спустя.
3. ДРУГИЕ СОЧИНЕНИЯ АПОЛЛОНИЯ
»1*
Аполлоний написал не только «Конические сечения», но из всех прочих его со¬
чинений до наших дней сохранилось лишь одно - «Об отсечении отношения». Про
остальные мы знаем лишь по описаниям и упоминаниям более поздних греческих
и арабских авторов. Многое из того, что известно об этих комментариях и о сочи¬
нениях Аполлония, а также об истории появления и издания текстов Аполлония на
арабском Востоке и в Европе можно прочитать в Предисловии фер Ээке, помешен¬
ном в данной книге.
Мы же ограничимся тем, что приведем здесь список этих сочинений, сопрово¬
ждаемый примечаниями к некоторым из его пунктов (надо иметь в виду, что пере¬
воды названий книг у разных авторов несколько различаются, а названия некото¬
рых из них и вовсе неизвестны).
№
Название
1.
Об отсечении отношения.
2.
Об отсечении площади.
3.
Две книги об определенном сечении.
4.
О точках касания.
5.
О плоских [геометрических] местах.
6.
О наклонениях.
7.
Сравнение додекаэдра и икосаэдра.
8.
Общее рассуждение.
9
О винте (букв. «Об улитке»).
10.
О неупорядоченных иррациональностях.
11.
Быстрое получение результатов (букв. «Ускоряющее роды»).
12.
Трактаты по астрономии, в которых было доказано, что движение планет можно опи¬
сать с помощью эпициклов и деферентов, определялось расстояние до Луны, Солнца
и планет. Теория движения Луны.
13.
Трактат по катоптрике.
14
Трактат о зажигательных зеркалах
«О наклонениях»
В русскоязычной литературе |18, с. 20; 1, с. 519; 8, с. 175] название этой работы
переводится как «Вставки». Вставка - это отрезок определенной длины, который пе-
25

Вступительная статья
ресекает какую-то линию, а его продолжение проходит через заданную точку, вокруг
которой он вращается. Если линия, например, представляет собой прямую, то конец
отрезка описывает кривую, называемую конхоидой Никомеда. Никомед (280-210 гг.
до н.э.) использовал вставки для решения задач об удвоении куба и о трисекции угла.
«Сравнение додекаэдра и икосаэдра»
Книга XIV«Начал» Евклида написана, как известно, Гипсиклом (190-120 гг. до
н.э.). В сопроводительном письме к ней говорится о книге Аполлония «Сравне¬
ние додекаэдра и икосаэдра». Это первое известное нам упоминание сочинений
Аполлония, хотя и вряд ли прижизненное. Гипсикл пишет: «Василия из Тира, о
мой Протарх, прибывши в Александрию и сойдясь с моим отцом вследствие об¬
щих математических интересов, провел у него большую часть времени своего пре¬
бывания И вот однажды, когда они разбирали написанную Аполлонием книгу
о сравнении вписанных в одну и ту же сферу додекаэдра и икосаэдра, - в каком
именно отношении они друг к другу находятся, - Василия с моим отцом приш¬
ли к мнению, что это не было правильно изложено Аполлонием, и они сами на¬
писали исправленный текст, как я мог услышать от моего отца. Позднее и мне са¬
мому попалась в руки другая изданная Аполлонием книга, содержащая некоторое
доказательство, касающееся вышеизложенного, и я сам с большим воодушевле¬
нием занялся исследованием этой задачи. Теперь с изданной Аполлонием книгой
можно, по-видимому, всем ознакомиться, так как она находится в обращении, как
кажется, в позднейшей более тщательно написанной редакции; сам же я, напи¬
савши в виде комментария все, что мне показалось нужным, решил обратиться к
тебе» 111. книга XIV, с. 142]
«Общее рассуждение»
Это трактат по геомегрии с изложением иного подхода, нежели у Евклида. Прокл
Диадох (412-485 гг.) в своей работе [15] неоднократно упоминает о нем. сравнивая
Евктида и Аполлония (подробнее см. у фер Ээке).
«О винте (букв. «Об улитке»)»
О сочинении Аполлония Прокл упоминает в связи с рассуждением о том. какие
линии являются простыми, а какие нет. Он считал, что винтовая линия, в отличие
от прямой и окружности, не яатяется простой (15, с. 113]. Работа Аполлония о вин¬
товой линии была, возможно, единственным в то время сочинением на эту тему. В
сочинении Архимеда с похожим названием речь идет не о винтовой линии, а о пло¬
ской спирати. Встречаются утверждения, что Архимед «открыл так называемую вин¬
товую линию и дат ее применение к построению винтового двигателя» [7, с. 21,42].
Винтовой насос он, конечно, построил, но о винтовой линии Архимед либо не пи¬
сал, либо работа до нас не дошла.
•11
«Быстрое получение результатов»
Буквальный перевод названия этой работы - «Ускоряющее роды» вызывает не¬
которое недоумение: математические труды никогда не имели подобных названий,
пусть и употребленных в переносном смысле С.Я. Лурье считал это название отра-
26

3 Друг ие сочинения Аполлония
женнем полемики между Аполлонием и Архимедом, возникшей из-за разного под¬
хода к вычислению числа и к способам записи больших чисел. По его мнению, за¬
дача Архимеда об исчислении быков и коров имела тот же источник [ 10, с. 202-206].
»!•
•Ж
»1«
«Трактаты по астрономии, в которых было доказано, что движение планет можно
описать с помощью эпициклов и деферентов, определялось расстояние до Луны, Солн¬
ца и планет. Теория движения Луны»
Сколько было трактатов и как они назывались — неизвестно. Известно, что по¬
сле Аполлония теория эпициклов сменила теорию сфер Евдокса, с помошью кото¬
рой объяснялось попятное движение планет. Сферы имели общий центр, совпада¬
ющий с центром Земли. Изначально их было 27, затем, по мере уточнения наблю¬
дений, пришлось добавлять еще и, наконец, стало уже 56 сфер, по нескольку на
каждую планету. Комбинируя их вращения, можно было получить реальное дви¬
жение планет и Солнца. Но теория сфер противоречила другим наблюдениям. На¬
пример, поскольку планеты находятся все время на одном и том же расстоянии от
Земли, их блеск должен быть постоянным. Но он же меняется! Изменяется также
угловой размер Луны, из-за чего солнечные затмения бывают полными, а бывают
кольцеобразными и т.д. Эти недостатки теории привели к тому, что она была заме¬
нена теорией эпициклов. Клавдий Птолемей (100—170) писал, что доказали пригод¬
ность эпициклов для объяснения движения планет «различные математики, а так¬
же Аполлоний Пергский» и далее приводит доказательства, ссылаясь уже только на
Аполлония 116. с. 373-375]. Пытался ли Аполлоний создать теорию, описывающую
конкретные результаты наблюдений, мы не знаем. Это сделали потом Гиппарх Ни-
кейский (190-120 гг. до н.э.) для Солнца и Луны и Птолемей для планет [16, с. 432—
438]. Поскольку неизвестно, кто такие эти «различные математики», то считается,
что эпициклы в науку ввел Аполлоний. Впрочем, ван дер Варден палагает. что это
были еще пифагорейцы.
Интересно, что Аполлоний, автор «Конических сечений», занимался эпицикла¬
ми, но даже не пытался представить орбиты планет в виде эллипсов. Что ему поме¬
шало? Историк античной науки и философии И.Д. Рожанский считает, что поме¬
шала «неуклонная приверженность к догме кругового движения небесных тел» [17,
с. 142]. Скорее всего, он прав, ведь даже спустя 1800 лет Галилеи (1564-1642) отвер¬
гал эллиптические траектории планет.
«Трактат по катоптрике» и «Трактат о зажигательных зеркалах»
Об этих трактатах написано в предисловии фер Ээке. Однако Тумер утвержда¬
ет, что на самом деле сочинение «О зажигательных зеркалах* принадлежит Диоклу
(240-180 гг. до н.э.) [18, с. 107]. Знал ли Аполлоний об оптических свойствах фоку¬
сов? В «Кониках» об этом ни слова, но это и неудивительно: в математических тру¬
дах писать о технических применениях считалось неуместным. В любом случае, за¬
жигательные зеркала — это зеркала параболические, но как раз о фокусе парабаты
Аполлоний ничего и не пишет. Об оптических свойствах фокуса парабаты писал
Диокл, который также сообщает, что этим вопросом занимался Досифей, извест¬
ный нам лишь тем, что Архимед посылал ему свои сочинения. А что же сам Архи¬
мед? Архимед сжег зеркалами римский флот и написал «Катоптрику». Считается,

Вступительная статья
что она содержала изложение всех достижений греческой геометрической оптики,
в том числе и описание зажигательных зеркал 110, с. 117; 17, с. 3331. Но книга до нас
не дошла1), а легенда о сожжении флота ничего не доказывает, поскольку совсем не
обязательно знать оптические свойства параболы, чтобы сжечь зеркалами корабль,
да и располагать воинов с зеркалами по параболе тоже не обязательно. Достаточ¬
но просто свести солнечные зайчики в одно место, что и было неоднократно про¬
демонстрировано в наше время.
4.	ОТ ГРЕКО
ДО АРАБО
•ж
о
Какова была дальнейшая судьба трудов Аполлония, что писали о них современ¬
ники1’ Что-то, наверное, писали, но до нас ничего не дошло. Единственный исто¬
рик математики, которого мы знаем из тех времен и чьи сочинения сохранились хотя
бы в отрывках, Евдем Родосский (370-300 гг. до н.э.) умер до рождения Аполлония.
Если бы после него были другие историки, то должны были сохраниться какие-ни¬
будь упоминания их трудов у поздних авторов. Но ничего этого нет, так что, скорее
всего, их и не было. Но вот после Аполлония проныо пятьсот лет, и наступила пора
комментаторов и составителей математических сборников, Паппа, Прокла, Евто-
кия. Серен Атинойскии кроме комментария, недошедшего до нас, написал книги
«О сечении цилиндра» и «О сечении конуса», где доказал, что эллипсы, получаю¬
щиеся при сечении плоскостью конуса и цилиндра однотипны. О комментаторах и
их трудах можно прочитать в предисловии фер Ээке.
Ну а что же было дальше? Дальше, как известно, наступил упадок греческой ма¬
тематики, да и не только математики. В Александрии были разгромлены Музейон
и Серапеум. Конечно, что-то еше делалось, культурная традиция продолжалась: в
Александрии около 500 г. была основана Школа медицины и философии, действо¬
вала Афинская академия, но математикой там уже почти не занимались. Почему-то,
когда говорят об упадке математических исследований, ссылаются обычно на рим¬
лян. которые, как считается, не проявляли интереса к математике в силу чересчур
практического склада ума Может, и не проявляли, но ведь римляне же не запреща¬
ли заниматься математикой грекам. Скорее, тут сыграло свою роль принятие хри¬
стианства и борьба с язычеством в любых его проявлениях. Но дело было не только
в религии. Нельзя забывать, что племена, сокрушившие Римскую империю на за¬
паде и поселившиеся в ней, были уж очень далеки от науки. Каким же образом в та¬
кой ситуации могли уцелеть рукописи, для кого они представляли интерес? Храни¬
телем и продолжателем греческой учености стал Восток, с которого, кстати, и полу¬
чила в свое время первые знания эллинская наука. На Востоке, в отличие от Запада,
христиане не были гонителями языческой учености Напротив, епископы Север Се-
бохт (’’ - 667). известный как Север Математик, возглавлявший Сирийскую ученую
академию, и его ученик Яков Эдесский писали трактаты по математике и филосо¬
фии. Уже в IV—VI вв начался перевод греческих текстов на арамейский язык. По-
|Ц
с»
»1»
’ В XVI в Гонгава опубликовал перевод с арабского неизвестного греческого автора Текст при¬
писали тогда Архимеду, но сейчас его авторство не является общепризнанным [ 10, с. 117].
28

4 От греков до арабов
еле разгона в 529 г. Афинской академии ученые и философы продолжили свою де¬
ятельность при дворе Хосрова I (501-579), где занимались в том числе и перевода¬
ми текстов.
единственным источником. Только в библиотеке Гондишапурекой академии на¬
считывалось около 400 000 книг. Впоследствии, после заключения мира с Византи¬
ей, некоторые ученые вернулись, причем мирным договором предусматривалось,
что они не будут подвергаться преследованиям. Ну а затем наступила эпоха арабов,
которые продолжили традицию. Александрийская школа в 718 г. переезжает в Ан¬
тиохию, а в середине IX в. — в Харран, на границе нынешних Сирии и Турции, где
начинают преподавать математику и астрономию. К концу VIH в. был переведено
большое количество греческих математических текстов. Переводили также и с си¬
рийского языка, с персидского, переводили индийские тексты, часть которых была
написана греками-эмигрантами. В начале IX в. был основан в Багдаде Дом мудро¬
сти. Для него в Византии покупали древнегреческие сочинения, которые все-таки
большей частью там не уничтожались, а хранились в монастырях. Книги привози¬
лись из завоеванных стран, а однажды после поражения, нанесенного аль-Мамуном
византийскому императору, из библиотек Византии было вывезено по одному эк¬
земпляру каждой из хранившихся там книг; почти все они были переведены на араб¬
ский язык. Знания, полученные от греческих и индийских математиков, усваива¬
лись, комментировались и совершенствовались.
Но вернемся к сочинениям Аполлония. В середине IX в. обработку его «Кони¬
ческих сечений» сделали три брата Бану Муса 119, с. 23]. Один из них - ал-Хасан
написал также «Книгу об удлиненной круговой фигуре», в которой был, возможно,
впервые предложен способ вычерчивания эллипса с помощью веревки и двух ко¬
лышков. Изобретение этого способа приписывали потом в Европе разным ученым.
К трудам Аполлония неоднократно обращался выдающийся ученый Сабит ибн Кор¬
ра (836-901). В составленном его праправнуком списке трудов прадеда есть упоми¬
нание о работе Сабита ибн Корры над одной из книг Аполлония: «Его “Усовершен¬
ствование первой книги сочинения Аполлония о сечении в определенном отноше¬
нии1'. Это сочинение состоит из двух книг. Сабит усовершенствовал первую из них
очень хорошо, прокомментировал, разъяснил и растолковал ее, а вторую он не усо¬
вершенствовал, и она непонятна» {19. с. 31]. Но самое ценное, что сделал Сабит ибн
Корра для сохранения наследия Аполлония, — это перевод «Конических сечений»,
которые Галлей перевел затем на латынь. Внук Сабита ибн Коры, Ибрахим ибн Си¬
наи, написал комментарии к «Коникам», не дошедшие до нас. Наряду с перевода¬
ми и комментариями писались и самостоятельные трактаты о конических сечениях.
Тем не менее в геометрии какого-то особого продвижения не было. Зато продвиже¬
ние было в другом: на Востоке появилась алгебра, развитие которой привело евро¬
пейцев к созданию аналитической геометрии.
Тем временем в Европе началось Возрождение, и античные знания, сохранен¬
ные и обогащенные усилиями правителей и ученых Востока, в том числе и теория
конических сечений, стали понемногу в нее возвращаться. Как это происходило с
«Кониками» Аполлония, подробно описано у фер Ээке.
29

Вступительная статья
5.	ВЛИЯНИЕ АПОЛЛОНИЯ НА ЕВРОПЕЙСКУЮ НАУКУ
Л»
•I»
Сначала европейские ученые, подобно математикам Востока, занимались пере¬
водом и изучением «Конических сечений», и в этот период ничего существенно но¬
вого в теории сечений сделано не было. Но вместе с геометрией европейцы полу¬
чили с Востока и алгебру. И если у греков произошла, как мы знаем, геометризация
алгебры, то есть числа выражались через длины отрезков, то в Европе с этого вре¬
мени начался процесс алгебраизании геометрии, то есть отрезки и кривые выража¬
лись через числа и уравнения. Средствами алгебры решали задачи на деление отрез¬
ков, построение треугольников и т.д.
Наконец, в первой половине XVII века был сделан решающий шаг: кривые ли¬
нии, и в первую очередь конические сечения, а затем и линии высших порядков ста¬
ли выражать и исследовать с помощью уравнений. Впервые это было сделано в ра¬
боте Пьера де Ферма (1601-1665) «Введение в изучение плоских и телесных мест» и
в «Геометрии» Рене Декарта (1596-1650). «Геометрия» Декарта была опубликована
в 1637 г. и сразу приобрела широкую известность. Ферма написал свой труд немно¬
го раньше, но при жизни он не был опубликован. Для написания уравнений кри¬
вых, естественно, необходимо было ввести систему координат, и это не было чем-то
совершенно новым ни в математике, ни в астрономии. Как мы знаем, Аполлоний
для исследования конических сечений постоянно использовал системы координат
(большей частью косоугольных), в которых осями служили обычно диаметры и се¬
кущие В этих координатах Аполлоний и выводил уравнения кривых, при этом ока¬
залось, что вид уравнений не зависел от выбора начальной точки, находившейся
где-нибудь на кривой1). Эти координатные оси были неразрывно связаны с иссле¬
дуемыми кривыми Примерно так же было первоначально и у европейских матема¬
тиков И Декарт, и Ферма писали еще об абсциссах, как об «отрезках диаметра», да
и привычную для нас систему «декартовых координат» в «Геометрии» Декарта мы
почти нигде не увидим вторую ось он на чертежах не изображал. Тем не менее коор¬
динатные оси теперь не были привязаны к конкретной кривой, а заключали в себе
пространство, в котором находились геометрические объекты. Это наряду с приме¬
нением алгебры сразу расширило возможности координатного метода, что Декарт
и продемонстрировал в своей «Геометрии», получив теперь уже настоящие уравне¬
ния различных кривых и решив ряд задач. Так появилась алгебраическая геометрия,
которую Исаак Ньютон (1643-1727) назвал аналитической. Ферма, как и Декарт,
тоже является основателем аналитической геометрии. Он первый провел класси¬
фикацию кривых в зависимости от порядка их уравнения, установил, что уравне¬
ние первого порядка определяет прямую, а уравнение второго порядка — кониче¬
ское сечение Но алгебра, которой он пользовался, была устарелой по сравнению с
алгеброй Декарта, что, по мнению А П. Юшкевича привело к тому, что сочинение
Декарта имело гораздо большее влияние [5, с. 2911. Впрочем, и Декарта понимали с
трудом и обычно его «Геометрия» печаталась вместе с обширными комментариями.
С»
О
Напомним, что уравнения Аполлония можно увидеть только в осовремененных переводах. Сам
же он, как и другие древнегреческие математики, их не писал, а выражал все словами.
30

5 Влияние Аполлония на европейскую науку
•Г*
Таким образом, подобно тому, как труды Архимеда явились предтечей матема¬
тического анализа, так и координатный метод, примененный Аполлонием в «Ко¬
нических сечениях», послужил основой для создания аналитической геометрии.
Впрочем, благодаря Аполлонию свойства конических сечений были и без того
уже достаточно изучены, поэтому нового добавилось не так уж много, и математи¬
ки занимались в основном кривыми высших порядков. Ньютон впервые дал совре¬
менную классификацию алгебраических кривых и исследовал во «Всеобщей ариф¬
метике» кривые третьего порядка. Тем не менее работа по переводу учения о кони¬
ческих сечениях на аналитический язык продолжалась, и в конце XIX века оно. как
и вся аналитическая геометрия, приняло полностью современную форму.
Другим принципиально новым достижением начиная с XVI века явилось ак¬
тивное применение конических сечений в естествознании. Сначала Галилео Гали¬
лей доказал, что брошенное тело летит по параболе1), что совершенно расходилось
с предшествовавшими представлениями, затем Иоганн Кеплер (1571 — 1630), изучая
результаты наблюдений, установил, что орбита Марса — эллипс. А это уже настоль¬
ко порывало с многовековой традицией, что даже Галилей так и не согласился с тем,
что планеты движутся по эллиптическим траекториям. Но, как известно, Ньютон
это доказал с помощью закона всемирного тяготения, после чего конические сече¬
ния получили широчайшее применение в небесной механике. Ну а ныне исполь¬
зование конических сечений настолько разнообразно, что трудно представить, что
когда-то это был раздел математики, практически не имеющий применения.
Мы уже упоминали, что Ньютон внес большой вклад в исследование алгебраи¬
ческих кривых, тем не менее он считал алгебраические методы чуждыми геометрии
и в своей знаменитой книге «Математические начала натуральной философии» ис¬
пользовал именно геометрические доказательства вполне в духе Аполлония, кото¬
рого он, кстати, тщательно изучал. Обычно считается, что Ньютон не использовал
уже созданные им методы математического анализа, поскольку опасался, что кни¬
га будет непонятна читателям, но возможно, что он, как и Готфрид Лейбниц (1646—
1716), полагал, что следует создать чисто геометрический анализ. В XIX веке эту
идею активно пропагандировали и развивали Якоб Штейнер (1796—1863) и Ми¬
шель Шаль (1793—1880) [23, с. 182 и далее]. В известной мере таким анализом мож¬
но считать проективную геометрию, в которой они видели возрождение синтетиче¬
ского направления в геометрии. Ее основы были заложены еше Жераром Дезаргом
(1591 — 1661) в связи с развитием им учения о перспективе2). Но идеи Дезарга пони¬
мал, пожалуй, только Блез Паскаль (1623—1662), написавший «Полный труд о ко¬
нических сечениях», в котором на основе своей знаменитой 3-й леммы вывел по¬
ложения Аполлония и получил новые результаты, но труд не был издан, а рукопись
утеряна. В итоге интерес к методам проективной геометрии возродился только че¬
рез сто лет. Во времена Аполлония проективной геометрии как отдельного раздела
математики еше не было, но поскольку из его теории следует, что коническое сече-
1	Это верно, если линии силы тяжести параллельны, то есть решение Галилея приближенное.
2	Заметим, что Дезарг был дружен с Декартом, но тот холодно относился к геометрическим ме¬
тодам. Над развитием проективной геометрии в XIX веке работали многие выдающиеся ученые:
Монж, Понселе, фон Штаудт и другие
31

Вступительная статья
ние любого вида можно рассматривать как соответствующую проекцию окружно¬
сти, то ясно, что теория конических сечений Аполлония и проективная геометрия
тесно связаны между собой. К проективной геометрии с большим или меньшим ос¬
нованием ныне относят многие теоремы Аполлония. Таковы, например, теоремы
о полюсах и полярах (111,30-40), (IV, 1-23) и некоторые другие1). Таким образом,
«Конические сечения» послужили отправной точкой для развития двух новых раз¬
делов математики: аналитической и проективной геометрии.
Исходя из вышесказанного, мы можем заключить, что влияние трудов Аполло¬
ния на мировую науку было весьма значительным. Иногда это влияние было явным
и очевидным, а иногда опосредованным. Вот что, пишет об этом Б.А. Розенфельд:
♦Несомненно, что Ж Л. Лагранж, который сам называл свое дифференциальное ис¬
числение “алгебраическим” и находился под очевидным влиянием Аполлония, не
мог не читать латинский перевод “Конических сечен ий", появившийся в 1710 г. Ла¬
гранж создал свою теорию условного экстремума, отправляясь от результатов этой
книги» [18, с. 149].
•I»
О
Инициатором и вдохновителем перевода «Конических сечении» Аполлония на
русский язык был математик К.В. Мануйлов (1945-2016). Он же сделал и первич¬
ную обработку перевода первых четырех книг «Конических сечении». Константин
Викторович был ревностным сторонником и неутомимым пропагандистом изучения
классического наследия и считал большим упущением недостаточное знание тех ве¬
ликих трудов, на которых покоится здание науки. Преодолению данного недостат¬
ка могло бы помочь издание классиков точных наук, и мы видим, чго сейчас в Рос¬
сии, после долгого перерыва, этот процесс заметно активизировался. Константин
Викторович полагал, что, обратившись к классике, современная наука много выи¬
грает, и даже, возможно, сможет решить некоторые проблемы, оставшиеся ей в на¬
следство от предыдущих эпох, «потому что в основополагающих сочинениях име¬
ются не только те семена, которые развились и принесли плоды, но в них покоят¬
ся и бесчисленные иные семена, которые еще ждут своего развития» (А. Эттинген).
о:
Кирбятьев С. В.
2017г.
Подробно о связи теории Аполлония с проективной геометрией написано в [18, с. 79-1001
32

<
ВВЕДЕНИЕ К ПЕРВОМУ ПЕРЕВОДУ
<
С ДРЕВНЕГРЕЧЕСКОГО НА ФРАНЦУЗСКИЙ ЯЗЫК
Работа опубликована под эгидой Бельгийского университетского фонда. Дескле
де Броуэр, Брюгге, Кэо Буа, 1921. Введение и примечания: Паульфер Ээке, горный
инженер, генеральный инспектор.
«Qui Archimède et 4poUomum intellegit,
recenlorium summorum vivontm inventa
parents mirabitur
l^ibnr
Тот, кто понимает Архимеда и Аполлония,
будет более скромно восхищаться
достижениями великих современников.
Лейбниц
I
История лишь очень немногое донесла до нас личности и обстоятельствах жиз¬
ни Аполлония Пергского; только часть его обширных трудов дошла до наших дней.
Евтокий Аскалонский, геометр V в., которому принадлежит комментарий к Ко¬
ническим сечениям Аполлония, говорит, что некий Гераклид составил биографию
Архимеда, в которой он среди прочего упоминает, что Аполлоний родился в Перге,
малоазиатском городе Памфилии, в эпоху царствования Птолемея Эвергета, египет¬
ского царя, пришедшего к власти в 247 г. до н.э. С другой стороны, из пассажа Пто¬
лемея Хенна1), от которого дошли лишь фрагменты, помещенные в ценный для нас
сборник отрывков из старых работ, составленный в IX в. Фотием2, патриархом кон-
стагп инопольским, узнаем что Аполлоний подолгу жил в Египте, где у учеников Ев¬
клида изучал математику в Музее Александрии и где позднее он сам достиг большой
известности как знаток геометрии и астрономии в правление Птолемея Филопато-
ра. Если считать, что этот последний умер на семнадцатый год правления, в 205 г. до
н.э., можно заключить, что Аполлоний появился примерно через 40 лет после Архи¬
меда, непосредственно предшествуя великому астроному Гиппарху'). Наконец, по-
’ ПТОЛЕМЕЙ, сын Гефестиона, называемый Хенн, - мифограф, живший во времена Траяна и
Адриана, составил компиляцию под названием: Новая история для многознающих в 7 книгах, от
которых до нас дошли лишь отрывки, сохраненные Фотием. Они были опубликованы вслед за Ко¬
ионом и Партением в издательстве TEUCHER в Лейпциге в 1802 г.
2	Работа ФОТИЯ, известная как Мириобиблион, или Библиотека, впервые была напечатана в
Аугсбурге в 1501 г., согласно греческому тексту, носит следующее название. Описание и пере¬
числение прочитанных нами книге числе 270, содержание которых пожелал знать наш друг Тара-
сий Пассаж, относящийся к Аполлонию, можно найти в издании Photii Bibliotheca ex recogmtione
I. BEKKER Berolini, 1824, 2 vol., 4, p. 151.
Гиппарх Никейский, ум около 125 г. до н.э. Из 8 написанных им работ до нас дошли две. Звезд¬
ный каталог и Комментарий к феноменам Евдокса и Арата, первая публикация. Vittorio, Флорен¬
ция, 1567 г, инфолио
33

Введение к первому переводу с древнегреческого на французский язык
еле недавнего хронологического исследования, проведенного Кронером (Сгопеп),
считается, что Аполлоний умер в 170 г. до н.э.* 1)
Евтокий в том месте своего комментария, где он излагает новые концепции,
предложенные Аполлонием, о способе создания конических сечений, рассказыва¬
ет нам. что он прочел в книге 6 не дошедшей до наших дней работы Гемина Родос¬
ского2) Геометрические сочинения, что современники Аполлония называли его «ве-
ЙЕ
•Э
ликим геометром* в знак восхищения его великолепными доказательствами теорем
о конических сечениях3).
Витрувий в своем Трактате об архитектуре упоминает Аполлония в числе вели¬
ких ученых мужей Античности: «Но такие гении очень редки; мало людей вроде Ари¬
старха Самосского, Филолая и АрхитаТарентского, Аполлония Пергского, Эратос¬
фена Киренского, Архимеда и Скопина Сиракузского, которые сумели с помощью
расчетов и знания тайн природы сделать большие открытия в механике и гномони¬
ке и оставили потомству об этом научные труды»4). Великин астроном Галлей даже
замены в предисловии к своему изданию опубликованного впервые греческого тек¬
ста Аполлония, что вышеприведенный пассаж Витрувия ссылается на имя Аполло¬
ния даже прежде Архимеда5). Однако маловероятно, чтобы Витрувий желал обозна¬
чить здесь некое превосходство. В самом деле, не следует забывать, что гений Апол¬
лония проявился лишь в чисто умозрительной сфере геометрии формы; в то время
как гении Архимеда, одновременно и более глубокий, и более универсальный, соз¬
дал работы, не имеющие равных с точки зрения научного прогресса, не только в об¬
ласти геометрии измерений, о «полезности каковых в каждодневной жизни» он упо¬
минает, нои в области механики и гидростатики, которые он открыл и для которых
он по праву считается первым инженером0).
Из предисловий к работам Аполлония мы знаем, что он поддерживал связи со
всеми крупными геометрами своего времени. Евдему, с которым он сдружился во
время своего пребывания в Пергаме, он посвятит две первые книги Конических се-
чений, Айалу, посте смерти Евдема, он посвятит четыре последние. Также из его
предисловий мы узнаем, что во время путешествия в Эфес он познакомился с гео¬
метром Филон идом, а также что под влиянием геометра Навкрата, с которым они
встретились в Атександрии, Аполлоний переписал свои труды по коническим сече-
' См Sitzungsb d. Berliner Akad , 1900, pp. 942-950.
1 Гемин Родосский, греческий геометр и астроном (70-е гг до н.э ), написал трактат под назва¬
нием Геометрические сочинения, который не сохранился, но во времена Евтокия еще существо¬
вал Этот последний донес до нас прозвание Аполлония «великий геометр». Прокп использовал
трактат Гемина в своем комментарии на Начала Евклида От Гемина остался трактат Введение в
астрономию изданный впервые на греческом языке, с латинской версией Hildenc, Altorf, 1590, in-
8, второе издание, с французским переводом аббата Алма (HALMA), вслед за Царским каноном
Птолемея под названием Table chronologique des règnes etc Paris, 1819, in-4*.
3	См. Комментарий Евтокия в выше приведенном издании Аполлония: Heiberg, Vol. Il, p. 171,1.22.
4	См новый перевод Мофраса L Architecture de Vitruve, Ch L. Maufras, Pans, Panchkouke, 1847,
2 vol m-8 Tome I, livre I, chap. I p 43 См также этот же пассаж в другом переводе в издании: Les
dix livres d’Architecture de Vitruve avec les notes de Perrault, E. Tardieu, A, Coussin fils. Paris, 1859,
m-4‘ p 12
5	Apollomi Pergaei conicorum libri octo etc edidit Edmundus Hqlleius. Oxoniaie, 1710, in-fol. Cm
Предисловие-p 3,1 33
Cm Les Oeuvres Complètes d 'Archimède, P VerEecke, Paris-Bruxelles, 1921, in-8, переводе древ¬
негреческого на французский введение, примечания.

Введение к первому переводу с древнегреческого на французский язык
Л«
ниям. Наконец, в этих предисловиях упоминаются Коной Самосский, Трасидей и
Никотелес Киренайские, которые до самого Аполлония трактовали некоторые те¬
оремы о пересечении кривых второго порядка неполным и неправильным образом.
Однако у Аполлония были и преследователи. По сведениям Евтокия, био!раф
Гераклид утверждал, что первым изобретателем теорем о конических сечениях был
Архимед, а так как он не опубликовал их, то Аполлоний якобы присвоил эти пруды
себе1. Мнение этого биографа не было признано исторической критикой, посколь¬
ку, несмотря на то что в трудах Архимеда приводится множество превосходных те¬
орем о конических сечениях, которые привели его к квадратуре парабаты2 3), и хотя
они и содержат великолепные теоремы о конусах второго порядка, который он ис¬
пользовал для создания теории метацентра'), легко увидеть, что в его доказатель¬
ствах часто приводятся свойства конических сечений, в связи с которыми он делает
отсылку к элементарным трактатам, написанным его предшественниками, Аристе -
ем Старым и Евклидом. Эти работы, к сожалению, не дошли до наших дней4. При
этом из предисловия к первой книге Конических сечений следует, что Аполлоний и
не претендовал на что-то большее, чем составление компиляции теорем, представ¬
лявших собой обший фонд знаний о кривых второго порядка, к которым он доба¬
вил свои собственные открытия. Эти знания после Платона мало-помалу обогаща¬
лись исследованиями его основных учеников: Аристея, Евдокса Книдского, Менех-
ма, Динострата, а затем Евклида и Архимеда5.
Папп Александрийский6, греческий геометр конца VI в. (о времени его жизни и
сейчас нет единого мнения, но все согласны, что он умер не позднее IV в. — Прим,
ред.}, в работе которого Математическое собрание помимо его собственных геоме-
зга
га
1	См. Commentaire d’Eutocius в вышеуказанном издании Аполлония: Heiberg, Vol. Il, р 69, 1,8.
2	Les Œuvres d'Archimède, ibid., с переводом P. Ver Eecke. Cm De la Quadrature de la parabole,
pp. 377-404.
3	Ibidem, Des Corps flottants, liv. Il, pp 421-463.
4	Резюме основных свойств конических сечений, упоминаемых в работах Архимеда, можно найти
в статье J.L. Heiberg: Die Kenntmsse des Archimedes über die Kegelschnitte (Zeitschrift fur Mathematik
und Physyk, Historisch-lrterarische Abtheilung, 1880, pp. 41-67) (a также 8, c. 28. - Прим ред.).
5	На эту тему см. работы: H.G. Zeuthen Die Lehre von den Kegelschmtten imAlterium (Copenhague,
1886) и G. Loria II penodo aureo délia geometria greca (Modène, 1895).
6	Работы Паппа: Математические собрания (MaQqpaTiKai Xuvaytuyat) на французский язык не пере¬
ведены, хотя и заслуживают того. Греческий тексте 7 книгах был полностью опубликован впервые в
прошлом веке под названием: Pappi Alexandrin/ collectioms quae supersunt edidit, latma mterpretatione
et commentants mstruxit Fred. Hultsch. Berolini, 1875-1878, 3 vol. in-8.
До этого великолепного критического издания существовали лишь частичные и содержащие
ряд ошибок издания греческого текста: 1 ) фрагмент второй книги, опубликованный Жаном Валли¬
сом (Jean Wallis) после Аристарха в Оксфорде в 1668 г. ш-8 и III томе Opéra Mathematica, 2) часть
предисловия к книге VII Euclide David Gregory (Oxford, 1703, in-fol.); 3) все предисловие к книге VII
работы Аполлония De la segmentation proportionnelle, пер. с арабского Ed Halley (Oxford, 1706, in-
8); 4) вторая часть книги V, Eisemann, Paris, 1824, in-fol. При этом с конца XVI в. существовал ла¬
тинский перевод шести книг, с 3-го и до последнего тома, выполненный блестящим итальянским
математиком Коммандино, с комментарием Гвидо Убальдо. Работа называется: Pappi Alexandnnî
Mathematicae Collectiones, a Fed. Commandmo Urbmate in latinum conversae et commentants illustrate.
Pisauri, 1588, in-4. Данный перевод под редакцией Манолезиуса был перепечатан с тем же назва¬
нием в Болонье в 1660 г., in-foi. Поскольку первое издание Коммандино стало редкостью, мы будем
далее ссылаться на второе, а также на греческое издание Hultsch Для справки также приводим не¬
давнее издание греческого текста с немецким переводом для книг VII, VIII: Die Sammlung des Pappus
vonAlexandrien. Grieschisch unddeutsch herausgegeben von C.J. Gerhardt, zweiterBand. Halle, 1871.
35

Введение к первому переводу с древнегреческого на французский язык
трических, астрономических и механических работ содержится масса ценных све¬
дений о потерянных сегодня трудах геометров Античности, представляет нам Апол¬
лония как человека тщеславного, завистливого к соперникам и не пропускающего
случая их очернить1 Папп не указывает нам более или менее современного источ¬
ника, из которого он почерпнул такие сведения о характере геометра, жившего за 5
столетий до него. Однако если он сформировал свое мнение, как мы полагаем, на
•и
основе собственных текстов Аполлония, которыми тот предваряет каждый том свое-
и»
го сочинения, отнюдь не пытаясь систематически очернять других геометров, то мы
видим тут не более чем критику, ни в чем не выходящую за рамки законного права.
\Папп писал, имея в виду предисловие Аполлония к 1-й Книге'. «Вот каково то ме¬
сто к трем или четырем линиям, по поводу которого Аполлоний расточает себе ве¬
ликие похвалы, не обнаруживая никакой благодарности к своему предшественни¬
ку». - Прим. ред.].
Действительно, в предисловии к своей первой книге Аполлоний упрекает Евкли¬
да в недостаточности его работ в том, что касается пространств с тремя и четырьмя
линиями2. Он совершенно справедливо добавляет, что Евклид едва ли продвинул¬
ся бы дальше в этой области, если бы не его собственные новые открытия в области
конических сечений. Не более смелым является и суждение Аполлония в другом ме¬
сте предисловия к его четвертой книге, где, после того как он сообщает, что желает
более подробно, а главное, более ясно по сравнению с предшественниками тракто¬
вать различные вопросы, связанные с пересечениями прямых и конических сече¬
ний, а также пересечениями конических сечений между собой, он упрекает Коно-
на Самосского в том, что тот не привел достаточных доказательств, либо виниг Ни-
котелеса. поставившего под сомнение полезность тех же вопросов для обсуждения
задач, решение которых опосредовано коническими сечениями.
Оценки Паппа показывают нам на практике, что вопросы приоритета, зачастую
сложно разрешимые, вставали уже перед учеными Александрийской школы. Позд¬
нее мы увидим, как в эпоху Ренессанса они выродятся в эпистолярные перебранки
ученых, порой ожесточенные и громкие. Тем не менее обостренное рвение к науке,
следствием которого они являются, в итоге приведет к новым открытиям.
•i»
»I»
Среди многочисленных трудов Аполлония самым значительным является трак¬
тат 0 конических сечениях Эта работа состоит из восьми книг, семь первых из кото¬
рых до нас дошли. При этом в нашем распоряжении лишь 4 первых книги на грече-
' См Pappus, Hultsch, vol II, liv III, p 673; либо латинский перевод Commandin, p. 249
‘ Папп (ки Vil), комментируя этот пассаж предисловия Аполлония, сообщает нам, что это про-
странство с 3 и 4 линиями соответствует точкам как произведению расстояний от них до двух дан¬
ных прямых линий, либо равно квадрату расстояний от них до третьей линии, либо произведению
расстояний от них до двух других данных прямых.
Подробные сведения о способе трактовке пространства с тремя и четырьмя линиями можно
найти в работе H G Zeuthen Die Lehre von den Kegelschnitten im Altertum, Copenhague, 1886
36

Введение к первому переводу с древнегреческого на французский язык
ском, остальные три дошли до нас в арабской версии, датирующейся IX в., обнов¬
ленной и переведенной на латынь в XVIII в.
По заявлению самого Аполлония в письме, которым он сопровождает свой трак¬
тат, отправляя его геометру Евдему, четыре первые книги не открывают нам ново¬
го направления геометрии, представляя собой упорядоченную компиляцию более
ранних знаний о конических сечениях.
Первая книга, содержащая 60 теорем, начинается с 8 определений, связанных с
созданием поверхностей и объема прямых и наклонных конусов, с сопряженными
диаметрами и осями кривых линий. Три первые теоремы, рассматривающие сече¬
ние конуса плоскостью, проходящей через его ось, относятся к осевому или основ¬
ному треугольнику конуса. Две следующие доказывают, что для наклонного конуса
с круговым основанием любое параллельное или противоположное сечение явля¬
ется кругом. Следующие теоремы рассматривают кривые линии, образуемые пло¬
скостью сечения, пересекающей все образующие на одной и той же поверхности ко¬
нуса, затем плоскостью сечения, параллельной одной из образующих, и, наконец,
плоскостью сечения, пересекающей обе поверхности конуса. Эти теоремы подводят
нас к понятию параметра, который Аполлоний называет «прямой стороной»; позд¬
нее геометры Ренессанса долгое время обозначали его словом «latus rectum». Затем
они подводят нас к понятиям абсциссы и ординаты, доказывая постоянство соот¬
ношения квадрата ординаты к абсциссе для кривой, образованной плоскостью се¬
чения, параллельной одной из образующих конуса. Теоремы 11, 12 и 13, довольно
сложные для прочтения, являются самыми важными для первой книги. В них го¬
ворится об основных свойствах параболы, гиперболы и эллипса — свойствах, ко¬
торые Аполлоний выводит из стереотомического рассмотрения кривых. При этом
мы знаем, что предшественники Аполлония, а именно Платон, Аристей, Евклид и
Архимед, рассматривали все три конических сечения исключительно как получае¬
мые плоским сечением, перпендикулярным к образующей, остроугольного, прямо¬
угольного и тупоугольного конусов. Поэтому в трудах Архимеда1 парабола все еше
описывается как сечение прямого прямоугольного конуса, гипербола — как сечение
прямого тупоугольного конуса, а эллипс — как сечение прямого остроугольного ко¬
нуса. Трактат Аподпония, таким образом, впервые говорит об этих трех конических
сечениях как полученных плоскими сечениями какого-либо одного и того же ко¬
нуса с круговым основанием. При этом сама общая идея получения кривых второ¬
го порядка приписывается Аполлонию геометром Гемином, чье свидетельство со¬
хранилось у Евтокия в следующем пассаже его комментария к первой книге Кони¬
ческих сечений’. «Однако позднее Аполлоний Пергский стал вообще считать, что все
сечения получаются из любого конуса, прямого или разностороннего, различны¬
ми способами, при которых плоскость пересекает конус, что Гемин приводит в 6-й
книге Математической науки1. Евтокий далее говорит: «Аполлоний, рассматривав-
• •
’ См вышеуказанное издание перевода Трудов Архимеда П фер Ээке. Введение, с. 35, а так¬
же книгу О коноидах и сфероидах, с 137-236 [На русском языке см. 8].
2 См. Аполлоний, в вышеуказанном издании Heiberg, vol. II: Eutocii commentaria in cónica, p
171,1 18.
37

Введение к первому переводу с древнегреческого на французский язык
шин прямой или разносторонний конус, получил различные сечения посредством
различного наклона плоскости»1.
Эти свидетельства, впрочем, недостаточны, чтобы заключить, что Аполлоний
был первооткрывателем получения конических сечений в каком-либо конусе с кру¬
говым основанием; они, скорее, указывают на то, что он первым применил этот ис¬
ключительный способ получения на основе некоего специального трактата, посвя¬
щенного кривым второго порядка. Действительно, не следует забывать, что Евклид
уже писал в Явлениях, что, если конус или цилиндр разрезается плоскостью, не па¬
раллельной к его основанию, полученная кривая может быть сечением остроуголь¬
ного конуса, то есть эллипсом; в то время как Архимед, между прочим, упоминает в
одном из пассажей своей работы, что плоские сечения, пересекающие все образую¬
щие конуса, являются окружностями либо сечениями остроугольного конуса. Хотя
эти последние намеки на сечение какого-либо конуса некой плоскостью подразуме¬
вают покалишь эллипс, тем не менее они показывают нам соображения более ран¬
ние по отношению к Аполлонию, и они вполне могли быть обобщены до параболы
и гиперболы в каком-нибудь не дошедшем до нас труде.
Однако можно допустить с некой долей вероятности, что именно Аполлонию
мы обязаны самими наименованиями параболы, гиперболы и эллипса, которыми
он заменю вышеуказанные «описания», используемые до него. Хотя эти описания
и соответствовали в действительности совершенно рациональному способу образо¬
вания, который прежде всего рассматривался для трех конических сечений, Апол¬
лоний. очевидно, очень быстро заметил, насколько их повторение затрудняет пони¬
мание текста доказательств Архимеда, его непосредственного предшественника; и
потому разумно, что он создал эти столь образные наименования, которые современ¬
ные геометры сохранили, позаимствованные собственно из характеристик каждой
из трех кривых, свойств, которые как раз обнаруживают их декартовы уравнения2.
Втеореме 14 рассматривается - впервые у геометров Античности - вторая ветвь
гиперболы, полученная расширением секущей плоскости до пересечения со второй
поверхностью конуса, и именно в теореме 14 Аполлоний, в отличие от своих пред¬
шественников, рассматривает обе ветви гипер
воположные сечения*’ как образующие одну-единственную кривую, которая таким
образом становится центрированным коническим сечением, как эллипс.
Далее теоремы прерываются второй серией из трех определений, относящихся к
центру к поперечной оси и к площади прямоугольника, в основании которого нахо¬
дится поперечный диаметр, а высотой которого является параметр; эта характерная
плошать, которая далее часто встречается в доказательствах последующих теорем и
из которой Аполлоний выводит понятие сопряженного диаметра, рассматри
как среднее пропорциональное сторон этой площади прямоугольника.
Втеореме 17 говорится о касательной к коническому сечению как прямой, про¬
везенной по краю диаметра параллельно прямым, приведенным к этому диаметру.
о
»1»
•“а1
MJ
м
СК
м
М
м
ется
м:
' Ibidem, р. 175,1.15
г См Книгу I, теоремы 11,12 и 13, в примечаниях.
3 колею&’хиа de di TOtcrirrat тоцш агпкЕфшщ то есть подобные сечения называются противо¬
положными См Книгу I теорему 14 и примечание.
38

Введение к первому переводу с древнегреческого на французский язык
Следует отметить, что Аполлоний доказывает в теореме 32, что никакая прямая не
может находиться между касательной и кривой, размышляя в той же манере, что и
Евклид, в теореме 16 своих Элементов, относительно касательной к окружности.
Первая книга завершается прекрасными теоремами о свойствах касательных и со¬
пряженных диаметров, а также задачами, имеющими отношение к построению ко¬
нических сечений при определенных заданных элементах.
Краткое предисловие сообщает нам, что Аполлоний через посредством своего
сына отправлял вторую книгу своего труда Евдему в Пергам, предлагая ему ознако¬
мить с ней Филонила, с которым он познакомился в Эфесе. В этой второй книга со¬
держится 53 теоремы. Первые посвящены основным свойствам асимптот. Аполлоний
характеризует асимптоту уже в первой теореме, доказывая, что если прямая линия
проводится между центром гиперболы и точкой, полученной в результате проведе¬
ния касательной по краю диаметра, соприкасаясь с этой касательной, из точки ка¬
сания, то квадрат длины этой линии будет равен четверти «фигуры», то есть четвер¬
ти прямоугольника, в основании которого находится диаметр, а высотой которого
является параметр, соответствующий этому диаметру, и соединительная прямая ли¬
ния не будет пересекаться с гиперболой. Далее ряд теорем относится к касательным
ш
•м
и сопряженным диаметрам, а книга завершается двумя задачами, предлагающими
провести в коническом сечении касательную, образующую заданный острый угол.
при том что диаметра проходит через точку касания.
Книга 3 содержит 56 теорем. 15 первых доказывают отношения между треуголь¬
никами и четырехугольниками, полученными из пересечения касательных с кони-
•ж
ческими сечениями, при диаметрах, проведенных через точки касания, а следую¬
щие 8 теорем касаются прямоугольников, образованных сегментами, полученны¬
ми из пересечений хорд, проведенных в конических сечениях. Большинство теорем
уже в своих формулировках приводятся непосредственно к случаю окружности. Сле¬
дующие 10 теорем относятся к секущим и их гармонической пропорции. В теоре¬
ме 41 доказывается, что. если три касательные к параболе пересекаются, они делят¬
ся в одинаковом соо
число касательных к параболе, уже подразумевала способ построения этой кривой
посредством касательных. В теореме 63 доказывается особое свойство касательной
к гиперболе, секущей по асимптотам сегменты, произведение которых постоянно,
и таким образом доказывается постоянство площади треугольника, образованно¬
го касательной и двумя асимптотами. Последние теоремы открывают нам несколь¬
ко фокальных свойств конусных сечений. Теорема 45. в частности, доказывает, что
в гиперболе и эллипсе сегмент касательной, отсеченный двумя перпендикулярами,
проведенными к крайним точкам оси из фокусов виден под прямым утлом. В тео¬
реме 49 доказывается, что прямые линии, соединяющие основание перпендикуля¬
ра. опушенного из фокуса на касательную.
ками оси. В теореме 50 доказывается дтя гиперболы и эллипса, что если провести
прямую линию из центра до пересечения с касательной, параллельно радиус-векто¬
ру из точки касания этой касательной, то длина этой прямой будет равна половине
длины оси. В теореме 51 доказывается дтя гиперболы, что разность расстояний от
каждой точки до обоих фокусов постоянна и равна поперечной оси. в то время как
в теореме 52 доказывается дтя эллипса, что сумма длин таких радиус-векторов по-
39
1»Ж
•ж
с*
»!•
ЛЖ
тношении. Эта теорема, позволяющая провести сколь угодное
.«с»:
м.

Введение к первому переводу с древнегреческого на французский язык
стоянна и равна длине большой оси. В этих двух последних теоремах подразумева¬
ется возможность провести гиперболу и эллипс одним движением.
Интерес предыдущих теорем состоит в основном в том, как они выделяют понятие
тех замечательных точек, которые геометры эпохи Ренессанса назовут позднее фоку¬
сами из-за их оптических свойств, но которые Аполлоний называет просто точками,
полученными из применения1. Этот перифраз в действительности нам показывает, что
Аполлоний получает фокусы, применяя, следуя поперечной оси гиперболы либо боль¬
шой оси эллипса, от каждого окончания этих осей прямоугольную плошадь, эквива¬
лентную четверти фигуры, то есть четверти прямоугольника, основанием которого яв¬
ляется ось, а высота которого задается соответствующим параметром. Площадь ква¬
драта в случае гиперболы увеличивается, а в случае эллипса уменьшается. Хотя этот
метод применения площадей приводит Аполлония к определению фокусов только для
центрированных конусов, то есть гиперболы и эллипса, из этого нельзя заключить, что
он не знал о фокусе параболы, или образующей в конических сечениях - элементов,
упоминания которых мы не находим в тех трудах Аполлония, которые дошли до нас.
При этом, если в Конических сечениях Аполлония в самом деле являются самым ста¬
рым подлинным документом, в котором фокусы представлены нам явным образом,
можно считать, что Аполлоний не был первооткрывателем этих точек. Прежде всего
если он не встречал фокальных свойств у своего непосредственного предшественника,
Архимеда, то только потому, что этот последний, хотя, безусловно, и знал их как уже
изученные современной ему наукой, не имел в них потребности для своих теорем ка¬
сательно еще одной замечательной точки, независимой от фокусов, центром для ко¬
нических сечений и коноидов. Далее, несмотря на то что координация накопленных
ранее знаний о конических сечениях уже завершена в работе Аполлония, это не под¬
разумевает. что он хотел изложить все теории, рассмотренные в работах, уже ставших
классическими в его время, подобно четырехтомной работе Евклида в Конических се¬
чениях. логически связанной с более ранним пятитомным сочинением Аристея о ге¬
ометрических телах?, то есть о конических сечениях, рассматриваемых с геометриче¬
ской точки зрения, и особенно подобно тому трактату, который уже Евклид написал
о поверхностных местах3, то есть местах, состоящих из поверхностей конуса, цилин¬
дра. сферы и других поверхностей второго порядка. Однако, если все эти работы для
нас потеряны [Аристея и Евклида], можно предположить, что в них уже содержалось
понятие фокусов, или что в них даже была намечена теория, поскольку Папп, кото¬
рый безусловно располагал этими трудами, смог вывести из них или найти в них им¬
плицитно [скрыто) знаменитые леммы, ведущие к описаниям трех конических сече¬
ний с помощью фокуса и биссектрисы. Эти леммы, в частности, устанавливают и до¬
казывают, что места точек, таких как расстояния от каждого из них до неподвижной
точки идо неподвижной прямой, находятся в постоянном соотношении, это эллипс,
парабола или гипербола, в зависимости от того, является соотношение меньшим, рав¬
ным или большим, чем единое целое4 Наконец, можно считать, что Аполлоний при-
м
•I».
•IC
1Ж
1Ш
*1«
НВ
•1«.
ШИ
i»l«
•I»
«1«.
«1«.
ти ек n]v хараро/л^	cTqpcia, букв : точки, полученные из применения, то есть при¬
менения определенных площадей, в условиях, определенных выше в тексте
2	(HEpEOl ТОХО1.
3	тояси ярое Ejnqxn aa
4	См. Pappus, ed. Hulsch, vol II, liv VII, pp. 1006-1015
40

Введение к первому переводу с древнегреческого на французский язык
давал значение собственно открытиям малочисленных теорем, посвященных фоку¬
сам, без сомнения, он упомянул об этом в одном из своих предисловий, — так сказать
в порядке напоминания об известной веши, как он это делает в теореме 45 книги 3.
Напротив, он бы изложил это определение в отдельной серии специальных теорем.
Когда Аполлоний заканчивал свою четвертую книгу, он потерял своего друга Евде-
ма, геометра, которому он уже посвятил на тот момент свои первые книги, в письмах,
полных пожеланий выздоровления, которое, затянувшись, уже предвещало немину¬
емую смерть, и потому он посвятил остальные свои книги Атталу, вероятно первому
царю Пергамы, которого он хвалит за любознательность и желание ознакомиться с
его трудами. В книге 4 содержится 57 теорем. 23 первые, с доказательствами со сведе¬
нием к абсурдному, в действительности являются не более чем повторениями теорем
30—40 книги 3, и мы укажем лишь на 9-ю, в которой говорится о
дения из одной точки двух касательных к коническому сечению. 34 последующие тео¬
ремы лишь рассматривают отношения конических сечений с длиной окружности кру¬
га. Эти последние теоремы не новы; поскольку Аполлоний говорит нам в своем пре¬
дисловии, что некоторые из них уже были изложены Кононом Самосским; что они
были доказаны и эти доказательства подверглись критике со стороны геометра Нико-
телеса и что сам Никотелес ставил вопросы того же плана, хотя и не приводил к ним
доказательств. Хотя Конон Самосский должен считаться предшественником Апол¬
лония в теории пересечения кривых второго порядка, ему в основном не хватало по¬
нятия двух ветвей гиперболы, образующей одну кривую линию, чтобы продвинуть¬
ся в тон области, где старые геометры должны были находить до определенной сте¬
пени те ресурсы, которые нам дает обсуждение полного уравнения второго порядка.
Таки образом эта теория может считаться по большей части оригинальной работой
Аполлония, не только из-за той строгости, с которой он доказывает теоремы, извест¬
ные задолго до него, четкого порядка, в котором он их излагает, или особых случаев,
которые он рассматривает, но прежде всего потому, что он был первым, кто признал
большую пользу этой теории для синтеза и для обсуждения огромного множества ге¬
ометрических задач.
Пятая книга, в которой содержится 73 теоремы, полностью посвящена максималь¬
ной и минимальной линиям, то есть самым длинным и самым коротким прямым,
которые можно провести от точки к периметру конического сечения. Предполагая
в первую очередь, что данная точка находится на оси конического сечения, Аполло¬
ний решает ряд задач замечательно элегантным способом. Затем он расширяет свои
поиски до случая, когда точка находится за пределами оси; это приводит его к более
сложным теоремам, таким, как, например, теорема 42, где, определяя минималь¬
ную прямую, которую можно провести отточки, находящейся внутри параболы, за
пределы оси, он использует остроумную конструкцию, вводя равностороннюю ги¬
перболу, пересечение которой с параболой дает нужную точку. Большинство теорем
этой книги поразительно сходятся с современными теориями о нормалях поднор¬
малях и лучах кривой линии, при этом уже здесь можно наблюдать зачатки эволют1.
•It
•It
•It
•л
•It
Mt
•it
Mt
Mt
lit
зможности прове-
Mt
•It
Mt
1 Теория эволют открыта Гюйгенсом, которую он изложил впервые в своей знаменитой работе
Christ. Нидепн horologius oscillatorium, sive de motu pendulorum ad orologia aplato demonstrationes
geometriaie, Pansus, 1673, in-fol.
41

Введение к первому переводу с древнегреческого на французский язык
Книга 6 в основном касается равенства и подобия конических сечений и их сег¬
ментов. Подобие и гомотетия в кривых второго порядка, однако, не являлись чем-то
совершенно новым, так как Аполлоний в своем предисловии сообщает нам, что он
собирается трактовать ее более развернуто и более ясно, чем его предшественники,
I Г
дополнив ее несколькими теоремами, которых до него никто не касался.
Тридцати трем теоремам этой книги предшествуют 10 определений, соответствен¬
но равенства и подобия конических сечений и их сегментов, оснований и диаметров
этих сегментов, подобия прямых конусов. Десять последних теорем представляют
собой задачи, чье решение поражает своей элегантностью. Три из них предлагают
сечение данного прямого конуса плоскостью, определяющих параболу, гиперболу
или эллипс заданных размеров, а три другие предлагают средство построения пря¬
мых конусов, подобных данному прямому конусу, также соответствующими пара¬
боле. гиперболе или эллипсу заданных размеров соответственно.
Книга 7, содержащая 51 теорему, представляет собой великолепное изложение
теории сопряженных диаметров. Теорема 12 доказывает, в частности, впервые по¬
стоянство разницы квадратов сопряженных диаметров для гиперболы. Аполлоний
при этом заявляет в кратком предисловии к этой книге, что эти теоремы по большей
части новые, и привлекает внимание к их полезности в решении определенных за¬
дач по коническим сечениям, которые явились предметом изучения 8-й и послед¬
ней книги, к сожалению, до наших дней не сохранившейся.
Конические сечения Аполлония подверглись многочисленным комментариям со
стороны греческих и арабских геометров. Первый комментарий, сделанный Паппом* 1
в его труде, который мы упоминали выше, состоит из лемм по коническим сечени¬
»1«
II».
ям. которые для него характерны и которые он почерпнул у предшествующих авто¬
ров. некоторые из которых, в целях пояснения темных или сложных теорем Апол¬
лония. доказывают по методу древних геометров, то есть с точки зрения чистой ге¬
ометрии, определенные промежуточные отношения, о которых текст Аполлония
умалчивает и которые сегодня легко доказываются при помощи алгебраической ге¬
ометрии. Леммы Паппа, посуди, не дают нам существенной помощи в понимании
определенных доказательств Аполлония; но те леммы, которые относятся к Кони¬
ческим сечениям. дают ценные сведения о характере задач, которые ставила эта кни-
га. безвозвратно потерянная и которые послужили ос но
нием для превосходной
О
конъектурной реконструкции, предложенной Галлеем (Halley) в 1710 г.2
До нас не дошло ни слова из комментария геометра Серена из Антиссы, который
говорит, что он сам его составил, упоминая, между прочим, концовку доказатель¬
ства теоремы 16 трактата, озаглавленного О сечениях цилиндра и конуса-.
См . Pappus вышеуказанное издание Hultsch или Commandin. Эти леммы Паппа можно най¬
ти в издании Аполлония Галлеем где они приводятся в начале различных книг, в которых тракту¬
ются, а также в критическом издании Гейберга (vol. II, рр. 143 seqq ), в котором приводится толь¬
ко греческий текст лемм Паппа, относящихся к 4 первым книгам Аполлония.
См вышеуказанное издание Аполлония Halley, р. 137
1	Время жизни Серена из Антиссы неясно Но в любом случае он жил до Марина, геометра V
в н.э, который упоминает его в своем комментарии к Данным Евклида (Марин Неаполитанский
(450-495) - Прим ред.) Прекрасная и значительная работа Серена, перевода которой на фран¬
цузский язык пока нет, была издана на греческом с латинской версией Галлеем после публикации
указанного издания Аполлония См с 16 теорему 16,1,42
42

Введение к первому переводу с древнегреческого на французский язык
•1И
Согласно краткому пассажу в Лексиконе Суида1, дочь геометра Теона Алексан¬
дрийского, знаменитая Гипатия, трагически погибшая в 415 г, написала ученый ком¬
ментарий на Конические сечения Аполлония. Этот комментарий, а также другой, ко¬
торый она написала на Арифметики Диофанта, пропали во время пожара в Алексан¬
дрийской библиотеке в 389 г. | Неужели это был единственный экземпляр? А если и
так, то ведь сгорел он еше при ее жизни и она могла его восстановить, — Прим. ред.].
Четвертый комментарий был составлен Евтокием2, и, поскольку он относит¬
ся только к четырем первым книгам Конических сечений Аполлония, есть основа¬
ние полагать, что Евтокию не были известны следующие книги, текст которых, по
всей видимости, уже на тот момент был потерян еще в VI в. |он не мог быть потерян
совсем, ведь арабы-то сделали перевод этих книг. — Прим. ред.\. Этот комментарий
содержит общие соображения по работе Аполлония, в частности, по новому мето¬
ду, при помощи которого геометр рассматривает образование конических сечений;
он приводит несколько лемм, предназначенных, как и леммы Паппа, для поясне¬
ния определенных неясных мест текста, а на некоторых теоремах он останавлива¬
ется либо чтобы вывести из них следствия, либо чтобы рассмотреть особые случаи,
которые могут для них присутствовать. Более того, пенно то, что Евтокий сохра¬
нил для нас несколько версий доказательств, которые Аполлоний привел в первом
наброске своего трактата; версии, на которые Аполлоний ссылается в сопроводи¬
тельном письме к своему труду геометру Евдему следующим образом: «А поскольку'
случилось так, что некоторые из тех, кто бывал у меня, получили первую или вто¬
рую книги до внесения в них исправлений, то не удивляйся, что они задают вопро¬
сы различным образом».
Вспомним, наконец, арабского комментатора Абдольмелека из Шираза, от ко¬
торого осталось 8 лемм, относящихся к книге 7 Конических сечений3; персидского
геометра Абальфата Испаганского, от которого до нас дошла сжатая версия Кони¬
ческих сечений на арабском, снабженная комментарием, о котором мы поговорим
позднее, а также арабского математика, Ибрагим-ибн-Синам-ибн-Сабита4, которо¬
му приписывается комментарий на первую книгу Конических сечений Аполлония5.
1	См.: Suidas, Lexicon, graece, recognovitl. Bekker, Berolim,1854, gr in-8‘, p. 1059.
2	Комментарий Евтокия был впервые опубликован на греческом с латинской версией в выше¬
указанном издании Аполлония Галлеем, в котором он расположен после соответствующих тео¬
рем Критическое издание греческого текста Евтокия было приведено в вышеуказанном издании
Аполлония Heiberg, vol. II, рр. 168 sqq.
3	Леммы Абдольмелека из Шираза были переведены с арабского на латынь Галлеем и опубли¬
кованы в начале книги 7 его издания Аполлония, с. 97. Эти 8 лемм относятся к равенству сумм или
неравенству квадратов и прямоугольников, построенных на определенных отрезках данных пря¬
мых линий.
4	Ибрагим-ибн-Синам-ибн-Сабит, арабский врач и математик, род. в год эгира 296 (908-909
гг.), ум. в Мухарреме в 335 г (946 г) (внук Сабита ибн Корры. - прим ред ). Его комментарий к пер¬
вой книге Конических сечений Аполлония не был обнаружен, а среди других работ, рукописи кото¬
рых сохранились, был опубликован только небольшой трактат о квадратуре параболы: Abhandlung
über die Ausmessung der Parabel von Ibrahim b Sinam b Thatut, aus dem Arabischen übersetzt und
kommentiert, von H. Suter. Vierteljahrsschrift der naturforschenden Gesellschaft in Zürich. 63, Zurich,
1918, pp. 214-228.
5	Die Mathematiker und Astronomen der Araber und ihre Werke, von H Suter, Abhandlungen zur
Geschichte der mathematischen Wissenschaften, t. X, Leipzig, 1900, pp. 53-54
43

Введение к первому переводу с древнегреческого на французский язык
Аполлоний написал и другие работы, представляющие собой отличный образец
геометрического анализа; однако о них мы знаем лишь через несколько сохранив¬
шихся фрагментов и кратких изложений в работе Паппа1.
Первая из этих работ - работа, которую Папп упоминает под названием О про¬
порциональном делении на отрезки1 *. Она делилась на 2 книги, содержащие 20 лемм и
181 теорему о различных случаях, представленных в решении задачи, формулиров¬
ку которой нам дает Папп: «Изданной точки провести прямую линию, которая от¬
режет на двух данных прямых, до заданных точек на этих прямых, отрезки, соотно¬
шение которых было бы равным заданному»’. Если сопоставить решение этой за¬
дачи и теорему 41 из третьей книги Конических сечений, в которой доказывается, что
три пересекающиеся касательные к одной параболе секутся соответственно в од¬
ном и том же соотношении, то ясно, что Аполлоний с этого момента мог провести
и»
сколь угодно касательных к параболе и что, вследствие этого, он мог разрешить за¬
дачу построения параболы посредством касательных.
Арабская версия этой работы, в большей или меньшей степени сжатая, была от¬
крыта в конце XVII в в Бодлианской библиотеке в Оксфорде Эд. Бернардом, ко¬
торый взялся за ее перевод на латынь, но вскоре оставил эту попытку ввиду край¬
ней поврежденное™ рукописи. Астроном Галлей4 вернулся к этому крайне сложно¬
му тексту, но прежде занялся изучением арабского языка и предоставил перевод на
ele
См Папп в вышеуказанном изд. греческого текста Hultsch, Vol. Il, Irv Vil, p 640, либо выше¬
приведенный латинский перевод Commandin, рр. 242-252.
2	ттр 0'алоатоцт|д тои Хоуои, букв об отсечении отношения или соотношения.
Формулировку мы приводим здесь, с греческого текста Паппа. См Hultsch, Vol. Il, livre Vil, p
640.1,6
* Галлей Эдмунд, знаменитый английский математик и астроном, род в 1656 г, ум в 1742 г Уже
в возрасте 19 лет разработал новый метод определения элементов планетарных орбит. Обнару¬
жение им значительных ошибок в астрономических таблицах, бывших в употреблении в его вре¬
мя , заставило его предпринять более серьезное исследование расположения неподвижных звезд.
Атак как Флемстид и Гевелий уже пытались создать каталог видимых звезд в северных широтах,
он взял на себя задачу наблюдений в другом полушарии С этой целью в 1676 г. он отправился на
остров Св Елены, где составил каталог из 360 южных звезд и где, помимо того, он наблюдал про¬
хождение Меркурия через Солнце Это навело его на мысль определить параллакс Солнца через
прохождение Венеры. По приезде во Францию он наблюдал с Кассини в 1680 г. большую комету,
затем отправился на два года изучат земной магнетизм Эти исследования довели его до 52-го гра¬
дуса южной широты Результаты этих исследований были опубликованы в 1701 г. в работе General
Chart of variation of the compass Он наблюдал комету в 1682 г. Этой комете впоследствии дали его
имя Он рассчитал ее орбиту и предсказал возвращение в 1759 г.; его прогноз оправдался с точ¬
ностью до нескольких дней (см. Synopsisastronomiae cometicae Oxford, 1705). В 1703 г. он препо¬
давал геометрию в Оксфордском университете, а в 1720 г занял место Флемстида в Гринвичской
обсерватории В возрасте 64 лет он замахнулся на систематическое наблюдение Луны и прожил
достаточно долго, чтобы увидеть окончание работы, что должно было составить 18 лет. Помимо
решения многочисленных геометрических задач и открытия свойства локсодромии иметь стере¬
ографической проекцией логарифмическую спираль мы обязаны Галлею великолепными труда¬
ми в области математической археологии Он опубликовал последовательно потерянные работы
Аполлония затем первое издание греческого текста первых трех книг Конических сечений Апол¬
лония: наконец, первое издание греческого текста с переводом на латынь трактата О сфере и ци¬
линдре Серена из Антиссы .
44
• •

Введение к первому переводу с древнегреческого на французский язык
латынь в 1706 г.'Эта работа послужила Лвг. Рихтеру основой для немецкого перево¬
да, изданного в Элбинге в 1836 г. Другая интересная реконструкция этого трактата
была сделана А. Дистервегом в 1824 г.1 2 3
Другая пропавшая работа носила название Об отсечении согласно площади '. Она
состояла из двух книг, соответственно содержащих 48 и 66 теорем. Все эти теоремы
относились к особым случаям, представленным задачей, которую Папп формули¬
рует следующим образом: «Из заданной точки провести прямую линию, секущую
на двух заданных прямых до точек, заданных на этих прямых, отрезки, ограничива¬
ющие эквивалентную заданной площадь»4.
Если сравнить решение этой задачи с теоремами 42 и 43 третьей книги Кониче¬
ских сечений, легко увидеть, что оно уже позволяло построить определенное коли¬
чество касательных к эллипсу и к гиперболе и, следовательно, построить эти два ко¬
ш
нических сечения посредством касательных.
У нас есть несколько попыток реконструкции этого трактата: одна предложена
Галлеем в 1706 г.5 6, другая, более широкая, интересна с точки зрения античного гео¬
метрического анализа, предложенного А. Дистервегом в 1827 г? Наконец, послед¬
няя принадлежит М.Г. Грабову - 1834 г.7 *
Третья работа с названием Две книги о делении на отрезки, выполненном опреде¬
ленным способом* касалась задачи, которую Папп формулирует следующим образом:
«Рассечь неопределенную прямую в некой точке так, чтобы квадрат, построенный на
одной из отсеченных прямых до заданных точек на этой прямой, или прямоуголь¬
ник, ограниченный двумя отсеченными прямыми, находился в заданном соотноше¬
нии либо с квадратом отсеченной линии, либо с прямоугольником, ограниченным
отсеченной линией и прямой линией, заданной в другом месте, либо с прямоуголь¬
•Ж
.о
ником, ограниченным двумя отсеченными линиями одной или другой стороны по
желанию из заданных точек»9. Папп сообщает нам, что две книги этой работы содер¬
жали 83 теоремы, перед которыми следовали в первой книге 27 лемм, во второй — 24.
Реконструкция этой работы, связанной с теорией, роль которой для древних
сравнима с ролью инволюции для современных геометров, интересовала многих
ученых-геометров. Первая реконструкция была предложена В. Снеллиусом в Лей¬
дене в 1609 г., в работе, получившей в свое время признание, и в которой, помимо
1	Apollonii Pergaei de Sectione Rationis libri duo, ex arábico latine versi. Accedunt ejusde de Sectione
Spain hbn duo restituía praemittitur Pappi Alexandnni praefatio (graece édita) ad septimu Collectionis
mathematicae cum lemmatibus ejusdem Pappi in hos Apollonii libros, opera ac studio Edmund» Hellen.
Oxonii, 1706, in-8*.
2	Die Bûcher des Apollonius de Sectione Rationis von W.A. Diesterweg, Berlin. 1824, tn-8‘, fig
3	tt|ç ô‘anoro|ir|ç tou /œpiou ßißZia. букв книги об отсечении площади См.: Pappus, éd. Hultsch.
Vol. Il, livre Vil p 640, либо в латинской версии: Commandin, р. 242.
4	Эту формулировку мы буквально переводим с греческого текста Паппа: Hultsch, Vol. Il, livre
Vil, p. 642,1.2 Commandin 242.
5	См. работу Галлея, указанную выше.
6	Die Bucher des Apollonius von Perga «De sectione Spatii« wiederhergestellt von W.A. Diesterweg,
Elberfeld; 1827, in-8‘.
7	M G. Grabow, De Sectione Spatii, Francort, 1834, in-8*.
ö tt|ç ôtœpiop£\T|ç Topr|ç ßißkici ß, букв, две книги об определенном сечении.
9 Эту формулировку мы приводим по греческому тексту Паппа. Hultsch, Vol. Il, livre VII, p. 642
Commandin p. 243
о
45

Введение к первому переводу с древнегреческого на французский язык
прочего, содержится попытка реконструкции двух первых работ Аполлония, о кото¬
рых мы только что говорили1. Еще одна реконструкция была предпринята в Лондо¬
не в 1772 г. Дж. Лоусоном2 *, который вскоре после этого переиздал работу Снеллиу-
са с некоторыми улучшениями’. Третья реконструкция принадлежит А. Дистервегу,
1822 г.4 Наконец, последняя реконструкция, в которой число теорем увеличилось,
была предложена М Г. Грабовым в 1828 г.5
Аполлонии написал значительную работу, разделенную на две книги, о точках
касания6 В работе были представлены теоремы, в которых между трех каких-ли¬
бо элементов с заданным положением: точек, прямых линий и кругов, необходи¬
мо провести окружность, проходящую через точки в случае с заданными точками
и касающуюся заданных прямых и окружностей. Согласно Паппу, эта работа со¬
стояла из 21 леммы, 60 теорем и 11 задач, из которых самой замечательной и самой
сложной была задача с окружностью, касающейся трех заданных окружностей7 *. И
хотя эта последняя задача считается сейчас элементарной, реконструкция ее реше¬
ния, утраченного уже во времена Паппа, возбуждало любопытство величайших ге¬
ометров прошлых веков, втом числе Виета, Декарта и Ньютона. Именно Виет пер¬
вым занялся этим, предложив в качестве вызова ее решение бельгийскому геометру
Адриану ван Ромену”, только что сообщившему ему о своем знаменитом решении
уравнения 459. В решении, переданном Адрианом ван Роменом, центр окружности
О
•I«
о
О
tja
9
Apollonius Batavus, seu exsuscitata Apollonii Pergaei geometría VJ Snellius, Lugdum Batavorum,
1608, m-4'
The two books of Apollonius Pergaeus concerning determinate sections, etc , by J Lawson, London,
1773
The two books of Apollonius Pergaeus concerning determinate sections as they have been restored
by Willenbroidus Snelhus, by J Lawson, London, 1773
4	WA. Diesterweg, De sectione determínala, Mayence, 1822, in-8‘.
1	Apollonius Pergaeus. Die Bucher De Sectione Derermmata, analyt. bearb u. durch e Anhang v
vielen Aufgaben ähnl vermehrt v Grabow. Frank! ,1828, in-8’
0 E/qç oc toGtoiç T(ov oiatpov coTiv ßißZia ovo, то есть вслед за предыдущими работами идут
две книги о точках касания См Pappus, éd Hultsch, Vol. II, livre Vil p. 644, либо в латинской вер¬
сии. Commandin. р 243
См Pappus, éd Hultsch, Vol. Il, livre Vil p 648, либо в латинской версии Commandin, р. 244
В этом же пассаже Папп приводит нам общую формулировку серии задач, аналогичных задаче
Аполлония, по точкам касания «При заданных элементах: точках, прямых линиях и окружностях,
провести окружность заданного размера, которая проходит через точку или через точки в слу¬
чае с заданными точками, и которая будет касательной либо к заданным прямым, либо к задан¬
ным окружностям» Также см на эту тему следующие исследования С. Hellwig, Das Problem des
Apollonius. Halle 1856.а такжеДО Berkham, Das Problem des Pappus von den Berührungen, Halle, 1857,
Адриан Ван Ромен (Van Roomen) бельгийский врач и математик, род в Лувене (Левене) в 1561
г, ум e Майнце в 1615 г Он преподавал сначала математику в Лувенском университете, затем ме¬
дицину в Вюрцбургском Написал множество работ, номенклатуру и анализ которых можно най¬
ти в статье, посвященной Адриану ван Ромену Н Bosmans, Biographie Nationale, AcadémieRoyale
des Sciences des Lettres et es Beaux-Arts de Belgique tome XIX col 848-889
Уравнение c 45 градусом известное как «Уравнение Адриана ван Ромена», которое часто
путают с общей формулой, определяющей хорду 45-й части дуги с заданной хордой, изложено
в следующей, ставшей довольно редкой работе Ideae mathematicae pars prima, sive mathodus
potygonorum qua laterum perimetrorum et arearum cojuscumque polygom mvestigandorum ration
exactísima et certísima ; una com ciruh quadratura contmentur Autore Adriano Romano Lovaniensi
medico et mathematio. Lovanu apud Joannem Masium, 1593, m-4’. В этой же работе Адриан ван Ро¬
мен дает соотношение окружности с диаметром с 16 знаками после запятой, до настоящего мо¬
мента это самый точный расчет
46

Введение к первому переводу с древнегреческого на французский язык
располагался в точке пересечения двух гипербол1; но оно не удовлетворило Виета,
предложившего другое, более простое и более соответствую шее, по его собственно¬
му мнению, методике античных геометров, которые допускали введение лишь пря¬
мой и окружности в решении того, что они называли «плоскостные задачи». Виет
обнародовал свое решение в работе Apollonius Gaulois [Аполлоний Галльский), заме¬
чательном труде, изданном в Париже в 1600 г.2 3, в котором он частично восстанавли¬
вает трактат Аполлония о точках касания.
Декарт рассмотрел задачу с помощью алгебраического анализа, и из его Пе¬
реписки (Correspondance) следует, что упорная работа завершилась первым выра¬
жением, которое было настолько сложным, что время, которое он предполагал
затратить на геометрическое построение, он оценивал в три месяца. Второе ре¬
шение он не закончил’. Это исследование привело Декарта к рассмотрению за¬
дачи Аполлония в пространстве, а также предложению Ферма по общей форму¬
лировке этой задачи4: «При заданных 4-х элементах между точками, плоскостями
и сферами, описать сферу, проходящую через точки и касательную к плоскостям
или сферам».
После Декарта задача окружности, касающейся трех заданных окружностей стала
предметом множества алгебраических трудов, в частности это касается Елизаветы,
дочери Фридриха, богемского короля, которая передала Декарту аналитическое ре¬
шение, не менее сложное, чем то, которое предложил он сам. Ньютон привел в сво¬
ей Универсальной арифметике5 * * аналитические решения для некоторых случаев задачи
Аполлония, которые ведут к геометрическим построениям, о которых уже говорил
Виет. С другой стороны, в аналитических решениях маркиза Лопиталя* последова¬
тельно рассмотрены задачи в случаях с 3 различными данными окружностями, с 2
равными окружностями из 3 заданных, и с 3 заданными неравными окружностями.
Наконец, можно еше найти интересные аналитические решения для особых случа¬
ев задачи Аполлония у Томаса Симпсона", Роберта Симеона8, Дж. Лоусона9, Вель-
1	Решение Адриана ван Ромена изложено в работе: Problème Apolloniacum quodatis tnbus circulis,
quaeritureos contingens, antica ab illustri viro D Franscisco Vieta consihano Regis Gall ¡arum, ac libellorum
suppheum in Regia Magistro, omnibus mathematicis sed potissimum Belgu ad construendum propositum,
jam vero per belgam Adnanum Romanum constructum Wirceburgi, 1596, in-4* fig. Эта небольшая и
очень редкая работа стала объектом анализа, с воспроизведением рисунка текста г-на Босманса
Н. Bosmans S J , Annales de la Société Scientifique de Bruxelles, tome XXIX, 1er fascicule, janvier 1905
2	Francisa Vieta Apollonius Gallus, seu exsuscitata Apollonu Pergaei Ttcpi
C Adnanum Romanum Belgam Pansus, 1600, in-4*.
3	Descartes, Lettres, édition de Paris, 1727, tome III, Lettres 72-73 Переписка Декарта стала пред¬
метом первых 5 томов недавнего издания Œuvres de Descartes, Charles Adam, Paul Tannery, Paris
1897-1908, Il vol. in-4*.
4	Varia Opera mathematica D Petn de Fermat, Tolosae, 1679, in-fol. Французский перевод работ
Ферма можно найти в работе Oeuvres de Fermat, Р; Tannery, C Henry, Paris, 3 vol., 1891-1896 (ла¬
тинский текст и перевод на французский язык).
Newtoni Arithmetica universalis, cum commentants Joh. Castillionei Amstelodami, 1760,2 vol. in-4*.
Также см. французский перевод этой работы; N Beaudeux, Paris, 2 vol. in-4*. (Problèmes XU I, XLVII).
” Traité analytique des sections coniques, parl'Hospital, Pans, 1776, in-4‘, p. 374.
См. следующие работы Симпсона: Thomas Simpson Eléments de géométrie traduits de l'anglais
de Th. Simpson, Pans, 1771, 2 vol., in-8*; Select exercises for young proficients in the mathematics.
Londmi, 1771 (см задачу 13).
B Rob Simson, Opera quaedam reliqua mathematica, Glasguae, 1776. in-6
9 См вышеуказанную работу Дж. Лоусона, ссылка на которую будет далее в тексте.
47

Введение к первому переводу с древнегреческого на французский язык
дике1, Ламбера де Мюлуза2 3, Холландиуса’, Обберрайта4, Темпельхофа5, Шваба6, Па¬
уля Фризи7, Торелли’, Фусс4 * и Эйлера10 * Что касается решения в чисто геометрическом
смысле для общего случая, то ест ь для случая с окружностью, касающейся трех неравных
окружностей, то оно было предложено Ньютоном вето знаменитом труде Математиче¬
ские начала натуральной философии"), где он ловко сводит пересечение двух гипербол из
решения Адриана фон Ромена к пересечению двух прямых12). Трактат Аполлония о точках
касания я в шея предметом множества более или менее удачных попыток реконструкции.
Первая попытка, попытка Виета, весьма неполная, представлена в его Apollonius Gaulois,
об этом труде мы уже говорили. В1607 году Марино Гетальди предложил решение для не¬
скольких особых случаев задачи сточками касания в работе, к которой мы вернемся на
предмет реконструкции другого трактата Аполлония. Обе предыдущие попытки рекон¬
струкции - Виета и Гетальди - были продолжены Дж. Лоусоном, который опубликовал
их в 1764 году с существенными дополнениями13). В 1795 году Гийом Камерер издал в Готе
небольшую работу; которая впоследствии стала очень редкой. В ней последовательно при¬
водятся. греческий текст фрагментов трактата Аполлония о точках касания в том виде, в
котором ихдонесдонас Папп, греческий текст, впервые опубликованный на основе двух
рукописей, парижской и страсбургской, в сопровождении латинской версии, лемм Пап¬
па. на тему того же трактата, реконструкция при помощи алгебраического анализа задачи
с окружностью, касающейся трех заданных окружностей14). И наконец, реконструкции
к
•II
•Г*»
Woldike, Problema de descnbendo circulo, qui très datos estrinsecus occurrendo tangat
Copenhague, 1793.
2	J H. Lambert, Deutscher Gelehrter Briefwechsel. Berlin, 1781-1787, 5 vol., in-8’ См Vol I, pp
310,325, vol IV, p 425
3	Ibidem, vol. I, p 308
4	Ibidem, vol. IV, p 256
5	Особые случаи, рассмотренные Г Ф Темпельхофом, можно найти во втором издании немец¬
кого перевода Алгебраических элементов Clairault, Berlin, 1778, p. 209 sqq.
Euchdis Data, verbessert und vermehrt von Robert Simson, aus dem Englisch übersetzt, und mit einer
Sammlung geometnscher, nach der analytischer Methoden der Alten aufgelöster Probleme begleitet von
J C. Schwab, Stuttgart, 1780, см задачи 16,18, 22 и 29.
Paul Fnsii Operum tomus pnmus Algebram et Geometriam analyticam complectens, Mediolani, 1782,
p. 64
8	Josephi Torelhgeometrica, Veronae, 1769, in-8‘, pp 1-74; 115.
j New commentant Academiae Scientiarum Petropolitanae. Petropoli, 1747-75. Vol. VI, pp 95 sqq.
11 Ibidem
’ Newtoni Philosophie naturalispnncipia mathematica. Londini, 1725, in-4“ Kh. 1, лемма 1. См
также Les principes mathématiques de la philosophie naturelle de Newton, trad. Mme du Chastelet,
Pans, 1759,2 vol., in-4’
' Можно найти великолепное изложение решения задачи с тремя касательными к окружности в
paôoTeCataian ThéorémesetProblémesdegéométrieélémentaire.i)eéd.,Pans, 1879, in-8‘, p. 206, prob XXVIII
' The two books of Apollonius Pergaeus concernmg tangencies as they hâve been restored by Fr
Vieta and MannusGethaldus.with a Supplement by J Lawson Cambridge, 1764, in-4’ Эта работа была
впервые перепечатана в Лондоне в 1771 г, ш-4’, под тем же заголовком, во второй раз - в Лондо¬
не в 1781 г in-4’, с несколько сокращенным названием.
14 АроНопиde Tachombus quaesupersunt. ас maxime lemmata Pappi in hoslibrosgraece nunc primum
édita e codtcibus manustriptis, cum Vietae librorum Apollon» restitutione, adjectis observatiombus,
computabonibusac probtematts Apolloniani histona, a Joanne Guilielmo Camerer, Gothae, 1795, pet. in-
8*. fig Эта небольшая интересная работа содержит в приложении короткое аналитико-тригоно¬
метрическое решение утраченной задачи Аполлония с окружностью, проходящей через заданную
точку и касательную за пределами двух заданных окружностей. Это решение, которым мы обяза¬
ны Роту, устно передавшему его Камереру, приводит к более элегантному геометрическому по¬
строению, чем то, которое предложил Виет в своем Apollonius Gaulois.
48
О

Введение к первому переводу с древнегреческого на французский язык
К.Г. Хауманна1 1817 г., а также реконструкции В.Л. Христманна2 3 1821 г. В этой по¬
следней, в частности, содержится критическое исследование реконструкции Виета.
Папп сообщает нам, что Аполлоний написал работу О плоских местах- в двух кни¬
гах, в которых содержалось 147 теорем, столько же рисунков и 8 лемм4. Если судить
по более чем ясным формулировкам теорем второй книги, которые также дошли до
нас благодаря Паппу5, должно быть, эта работа представляла собой внушительный
сборник свойств прямой и окружности, которые соответствуют современному по¬
строению уравнений первого и второго порядка.
Утраченный трактат Плоские места явился предметом ряда исследований - ре¬
конструкций. Порой работа Отца Гаспара Шотта, опубликованная в Вюрцбурге в
1658 г.6, неверно рассматривалась как реконструкция данного трактата, поскольку,
хотя эта работа и содержит в действительности ряд теорем, аналогичных тем, ко¬
торые сообщает нам Папп, следует отметить, что доказательства носят чисто ана¬
литический характер, и, следовательно, совершенно иной, нежели доказательства,
приводимые Аполлонием. Напротив, можно рассматривать в качестве интересных
реконструкций средствами чистой геометрии прежде всего реконструкцию англий¬
ского геометра Роберта Симеона, написанную на латыни в 1749 г., сопровожденную
великолепным исследованием методов античных геометров7 *. Эта работа была пере¬
ведена на немецкий язык Камерером в 1796 г.“3атем следует упомянуть реконструк¬
цию, которой стала одна из первых работ знаменитого Ферма9. Наконец, не стоит
забывать более свежую работу М. Гардинера10 11, представляющую собой попытку ре¬
конструкции всех пяти приведенных нами трактатов Аполлония.
Аполлоний написал важную работу под названием О наклонениях". В ней содер¬
жался ряд теорем, в которых прямые наклонные линии, то есть линии, направлен¬
ные в определенную точку, на заданном расстоянии отсекаются двумя заданными
линиями. По тем сведениям, которые мы находим у Паппа, эта работа, состоящая из
двух книг, содержала 38 лемм, 125 теорем12 и 54 задачи13. Некоторые из этих задач да¬
вали почву для дискуссии, а Папп приводит полную формулировку многих из них14.
3KS
■ж
•ж
••ж
•ж
к
ев
’ С G. Haumann, Versuch einer Wiederherstellung der Bucher des Apollonius von Perga von den
Berührungen, Breslau, 1817, in-8’.
2	Apollonius suevus, sive tactionum problema nunc demum restitutum, accedente censura in Vietam
auctore Gu. Lud. Christmann, Tubingue. 1821.
3	totiüiv ejoheöüjv öuo, те. две [книги] о плоских [геометрических] местах. См.: Pappus, ed Hultsch,
t. II, liv. VII, p. 660, либо в лат изд Commandin, р. 247.
4	См Pappus, ibidem, t. II, liv. VII, p. 670, либо в лат изд. Commandin, р. 249
5	См. Pappus, ibidem, t II, liv. VII, p. 666, либо в лат изд. Commandin, р. 248
Magiae Universalis Naturae et Artis, pars III, Mathematica, sive Thaumargus mathematicus, a P.
Gaspre Schotto, Herbipoli, 1658, in-4*.
7 Apollinii Pergaei locoru pianorum libri II restituti a Rob. Simson, Glasguae, 49, in-4*, fig.
11 Apollinius von Pergen ebene Oerter Wiederhergestellt von Robert Simson, Aus dem Lateinnischen
übersetzt von Johann Wilhelm Camerer, Lipsiae, 1796, in-8’
9	Vana opera mathematica D. Petri de Fermat, Tolosae, 1679, in-fol.
10	The three sections, the tangencies and a loci problem of Apollonius and porismatic developments,
by M. Gardiner, Merbourne, 1860, m-8*
11	Ncuoewv био, те. две [книги] о наклонениях. См.: Pappus, ed Hultsch, t. II, liv. VII, p. 670, либо
в лат изд. Commandin, р. 249
12	Pappus, ibidem, p. 672.
13	Pappus, ibidem, p 820
14	Pappus, ibidem, p. 670.
49

Введение к первому переводу с древнегреческого на французский язык
Известно, что задачи с секущими большей частью не решаются в рамках эле¬
ментарной геометрии, поскольку их аналитическое исследование, приводящее к
уравнениям второго порядка, сводится к определению точек пересечения кони¬
ческих сечений. Следовательно, если работы Аполлония по коническим сечени¬
ям должны были естественным образом привести его к рассмотрению задач с се¬
кущими, то из этого, однако, нельзя заключить, что все теоремы его отдельного
трактата О наклонениях принадлежат ему в полном смысле слова. Действитель¬
но, общая задача с секущей, проходящей через заданную точку и пересекающей¬
ся на определенном расстоянии, с двумя прямыми или кривыми линиями, была
известна давно, в частности, благодаря Аристотелю, который, уже упоминая ее,
притом, что конические сечения известны не были, смог получить для нее лишь
механические, то есть эмпирические, решения. С другой стороны, Архимед, жив¬
ший примерно за полвека до Аполлония (Архимед был примерно на 25 лет стар¬
ше Аполлония. - Прим.ред,), приводит дополнительно, с многократными повто¬
рениями. особые случаи для задачи с секущей и доказывает тем самым, что ре¬
шения уже были достоянием науки его времени. В частности, он использует эти
решения в остроумных предварительных теоремах своего трактата: О спиралях1,
внутри одной из теорем своего трактата: О сфере- и, наконец, в 8-й теореме своей
книги Олеммах3. Однако эти особые случаи как раз входят в категорию задач, ко¬
торые Папп называет задачами с объемными телами4, поскольку их решение тре¬
бует введения сечений геометрических тел, то есть конических сечений; понятие,
которое он. с одной стороны, противопоставляет понятию плоскостных задач\
требующих лишь использования линейки и циркуля, то есть речь идет о линиях,
лежащих в одной плоскости и, с другой стороны, ¡инейных задач\ требующих ис¬
пользования других линий, помимо кривых второго порядка, то есть линии, ле¬
жащих на нерегулярных поверхностях, либо в сложных движениях, таких как спи¬
рали, квадратрисы. конхоиды и циссоиды. Таким образом, можно заключить, что
утраченный труп О наклонениях не был полностью оригинальным, а скорее, пред¬
ставлял собой компиляцию, в которой Аполлоний привел задачи о секущих, уже
получивших решение до него, определил число решений, которое они допускают,
обе у дю условия их возможности, а также прибавил свои собственные открытия.
Также можно предположить, что Аполлоний не брезговал в своем трактате меха¬
ническими, то есть эмпирическими, решениями, предложенными некоторыми
из его предшественников, для некоторых задач с секущими. Тем более мы рас¬
полагаем эмпирическим решением, в том виде, как его донесли до нас Евтокий1
Les Œuvres d Archimède, вышеприведенное изд. перевода P. Ver Eecke. Des Spirales, prop. V,
VI, Vil. VW. IX, pp 246-253
2	Ibidem cm :Delà Sphère et du Cylindre, liv II, p 101
J Ibidem cm Le livre des Lemmes, prop. VIII, p 532.
4 rncpca Cm Pappus, éd. Hultsch, vol II, liv VII, p 670 et vol. I, liv III, p. 54,1. 7.
ь Езгахоа, Pappus, vol I, liv III, p. 54
• ypapuirriKu. Pappus, vol I liv III, p 54
См. решение Аполлония в греческом тексте комментария Евтокия к книге 2 трактата О сфере
и цилиндре Архимеда eArchimedisopera omnia cum commentanis Eutocii, iterum edidit J.L. Heiberg,
bpsiae, 1910-1913 2 vol, m-8*. Vol III, p. 64

Введение к первому переводу с древнегреческого на французский язык
•Ж
•ж
•Ж
и Филопон1, которое предложил сам Аполлоний относительно популярной в ангин¬
ную эпоху задачи о двух средних пропорциональных между двух заданных отрезков.
Эта задача, для которой, впрочем, мы располагаем целой серией античных реше¬
ний — одни приблизительные, другие строгие — была уже поставлена, но не полу¬
чила решения, за 400 лет до Рождества Христова Гиппократом Хиосским, который
поставил решение знаменитой делосской задачи об удвоении куба в зависимость от
нахождения двух средних, заявляя, что если бы было возможно вставить две сред¬
ние пропорциональные прямые линии между стороной заданного куба и удвоением
этой стороны, то первая из этих двух линий оказалась бы стороной искомого куба.
Впрочем, Папп еще рассматривал частично эмпирические решения как могущие на
законном основании заменить конические сечения, если построение этих кривых в
плоскости представляет какую-либо трудность2 3.
Согласно одному пассажу в комментарии Ямвлиха на Категории Аристотеля, ко¬
торый он сохранил в комментариях к Симплицию' на Физику Аристотеля, Аполло¬
ний, по-видимому, нашел квадратрису, которую назвал «сестрой кохлоиды». Одна¬
ко Папп говорит нам, что кохлоида — это кривая, изобретенная Никомедом4, кри¬
вая, которую мы называем конхоидой; так же, как и Евтокий, описывающий нам
прибор, построенный Никомедом для ее построения5, и, как и Прокл, который со¬
общает нам, что Никомед привел построение и признаки этой кривой и использо¬
вал ее для трисекции угла6. Таким образом, Аполлоний знал конхоиду7, и потому
вполне возможно, что он решил определенные задачи своего трактата О наклонени¬
ях на манер так называемых линейных задач, вводя эту трансцендентную кривую,
поскольку мы знаем, что все задачи, связанные с секущей, проходящей через задан¬
ную точку и ограниченной определенной длиной между двумя заданными отрезка¬
ми, из которых один является прямой, можно решить через конхоиду, полюсом ко¬
торой является точка, через которую должна пройти секущая*.
Напротив, мы точно знаем, что в работе Аполлония не рассматривались все за¬
дачи с секущими по образу так называемых геометрических задач, то есть посред-
’ Иоанн Филопон, греческий философ-эклектик, одна из работ которого четко дати[
333 г. эпохи Диоклетиана, что с
скольким работам Аристотеля, в частности на обе Аналитики. В своем комментарии к Поздней¬
шим Аналитикам он приводит решение задачи Аполлония. Эта работа, опубликованная Альдом
Старшим в Венеции в 1504 г., была перепечатана в 1534 г. Латинская традиция восходит к Gratiolus,
Венеция, 1542 г. Филопон первым в Античности порвал с ложными представлениями о динамике
школы Платона, согласно которым движение какого-либо тела может продолжаться только если
оно постоянно поддерживается непрерывным усилием, и допустил, что стрела продолжает свое
движение без участия поколебленного воздуха уже за счет кинетической энергии выпустившего
ее лука. Идеи Филопона, долгое время отрицавшиеся, смогли выйти на первый план лишь в XVI
в., когда Буридан взял энергию, сообщенную снаряду (Филопон и Буридан писали об импетусе,
но это не энергия. - Прим ред), за основу новой динамики.
2	См.: Pappus, éd Hultsch, vol III, liv VIII, p. 1070 либо в лат. изд Commandin, р. 463.
3	Simplicii in Ahstotelis physicorum libros VIII commentana, edidit H. Diels Berohni, 1882-1895 2
vol. in-8’ Cm.: vol I, p. 60.
4	Cm.: Pappus, éd. Hultsch, vol. I, liv. Ill, p 58 и liv. IV, p. 242.
5	См. вышеуказ. изд. Архимеда Heiberg, комм Ebtokmb.voI Ill, рр 98-106.
6	Proclus, éd. Fnedlein, p. 272.
7	Конхоида - это кривая, чье уравнение в полярных координатах выглядит р а + h cos <р.
0 В качестве специальной работы по конхоидам см.: Conchoides Nicomedeae aequaUo et indoles,
Car. Witte, Goettinguae, 1813.
¿Ж
•м
51

Введение к первому переводу с древнегреческого на французский язык
ле
ством конических сечений; однако ему удалось рассмотреть некоторые из них как
•плоскостные* задачи, которые можно решить при помощи линейки и циркуля. Это
касается, например, задачи, формулировку которой Папп сохранил следующим об¬
разом: «При заданном ромбе, одну сторону которого мы продолжаем, провести пря¬
мую, равную заданной длине во внешнем угле, наклоненную в сторону противо¬
положного угла»1, то есть проходящую через вершину угла, противоположного до¬
полнительному углу этого внешнего угла. Решение этой прекрасной задачи было
реконструировано позднее в нескольких вариантах Марино Гетальди2 3, Христианом
Гюйгенсом1 и Гюго де Омериком4.
Тот огромный интерес, который геометры последних веков испытывают к зада¬
чам. рассмотренным Аполлонием в его утраченной работе О наклонениях, дал мно¬
жество попыток более или менее масштабных попыток реконструкции со стороны
Марино Гетальди5, Александра Андерсона6, Самуэля Хорсли7 и Реубеном Барроу,
опубликовавшим свое эссе вместе с работой по баллистике8.
Аполлоний, по-видимому, написал работу О винте, содержание которой нам не¬
известно На этот предмет есть лишь несколько отсылок у позднейших геометров.
Прокт нам говорит сначала в первой части своего комментария на Начала Евклида:
«Винт, все части которого подобны и могут совпадать друг с другом, как это дока¬
зывает Аполлоний в своей рукописи «О винте»9. Вновь возвращаясь к этому пред¬
мету; он говорит нам в другом месте: «Этот винт имеет сходные части, как доказал
Аполлоний»10. Наконец, Папп в книге 8 Математического собрания упоминает Апол¬
лония в связи с доказательством механической теоремы, относящейся к построению
винта с простым шагом и входящего в зацепление с барабаном с косыми зубьями11.
Таким образом, становится вероятным, что рукопись Аполлония, которую цитиру¬
ет Прокт, содержала, по крайней мере, геометрическую теорию винта.
В эпоху, когда появился Аполлоний, пифагорейской школой уже давно было
введено пять правильных тел: куб, тетраэдр, октаэдр, икосаэдр и пятиугольный
ЙЙ
Мы приводим формулировку с греческого текста Паппа. См : Hultsch, liv VII, р. 670. либо в лат
изд. Commandin, р. 249
2	Marini Gethaldi de resolutione et compositione mathematica libri V, Romae, 1630, in-fol, fig
3	Christ Hugenn de circuit magnitudme inventa, etc Lugduni Batavorum, 1654, pet in-4*.
J Analysis geometries, sive nova et vera methodus resolvendi dam problemata geometries quam
arittimeticasquaestiones authore Ant HugonedeOmerique. Gadibus, 1698, pet. in-4‘, fig.
' Mar Gethaidi Apollonius redivivus seu restituta Apollonu Pergaei mclinationum geometria, ejusdem
vanorumproblematum collect® Venetiis. 1607, petit in-4* fig.
6	Alexandri Andersom Aberdonensis suppiementum Apollonu redivivi, sive analysis problematis
hactenus desiderati ad Apollonu Pergaei doctnnam nepi vEuacmv, a Marino Gethaldo Patricio Ragusmo
hucusque non tta pridem restitutam, etc. Parisiis, apud Hadnanum Beys, 1612, pet. in-4’. (Небольшая
редкая работа вышедшая у Адриана Бейса, зятя Плантена, сохранившийся экземпляр которой мы
изучали в музее Плантена в Антверпене )
ApollontiPergaeimclinationumhbnduo Restituebat Sam. Horsley, Oxonn, 1770, in-4*.
Реконструкция Хорсли была в свободной форме переведена на немецкий язык под названием:
Apollonius von Perga »De Inclmationibus* wiederhergestellt von Sam. Horsley, nach dem latemischen
fret bearbertet von Dr WA Diesterweg Berlin, 1823, VIII + 158, pp in-8*.
8	A restitution of the geometrical treatise of Apollonius Pergaeus on inclinations, also the theory of
gunnery or the doctrine of proiectiles in non resisting medium, by Reuben Burrow. London, 1779, pet. in-4’
9	sspi tov KoyZiou cm Proclus вышеук изд Friedlein, p. 105
• Ibidem, p. 105
Cm Pappus, ed. Hultsch. vol III liv VIII, p 1110, либо в лат. изд. Commandin, liv. VIII, prop XIV, p 480
52

Введение к первому переводу с древнегреческого на французский язык
додекаэдр. На этой основе - первая попытка натурфилософии, которую мы на¬
ходим в Тимее Платона. Поскольку все эти полиэдры могут быть вписаны в сфе¬
ру, которая считается самой совершенной формой, необходимой для физического
мира, то их изображения были присвоены составным элементам четырех элемен¬
тарных тел, из гармоничного сочетания которых состоит Вселенная: земля, вода,
воздух и огонь. Очевидно, что геометрия, которая в эпоху создания этих представ¬
лений продвинулась далеко вперед, должна была освободиться от большинства
индивидуальных свойств этих полиэдров, мистическая роль которых в космого¬
нии древних превратилась в реальную роль, которая нам известна по кристалло¬
графии современников. Однако знание их сравнительных свойств, безусловно,
оставалось довольно неполным, поскольку, как мы знаем от Гипсикла Алексан¬
дрийского1, что Аполлоний написал о «сравнении додекаэдра и икосаэдра, впи¬
санных в одну и ту же сферу»2. Единственное, что мы знаем об этой работе, — это
сведения, предоставленные в следующем отрывке из работ Гипсикла: «Одна и та
же окружность огибает пятиугольник додекаэдра и треугольник икосаэдра, впи¬
санных в одну и ту же сферу, и, как было написано, с одной стороны, Аристеем в
своей работе о сравнении пяти фигур, а с другой стороны, Аполлонием в его вто¬
рой публикации, связанной со сравнением додекаэдра с икосаэдром, что поверх¬
ность додекаэдра к относится к поверхности икосаэдра точно так же, как сам до¬
декаэдр относится к икосаэдру, так как перпендикуляр, проведенный из центра
сферы к пятиугольнику додекаэдра, является тем же, что и перпендикуляр, про¬
веденный к треугольнику икосаэдра»3.
Также Прокл с
•Ж1
шает нам, что Аполлоний написал об иррациональных неупо¬
рядоченных величинах4. Об этих рукописях, связанных с несоизмеримыми величи¬
нами, нам не было известно ничего, пока в 1853 г. математик и востоковед Ф. Веп-
ке (Е \\bepcke) не переиздал арабскую версию комментария Паппа на 10-ю книгу7
Начал Евклида5. Этот текст начинается, во французском переводе, предложенном
самим Вепке, следующим образом: «Позднее великий Аполлоний, чей гений до¬
стиг своих высот в математике, прибавил к этим открытиям замечательные теории,
явившиеся плодом неустанной работы и т.д.»6. Немного далее приводится следую¬
щий пассаж: «Наконец, Аполлоний выделил классы иррациональных чисел и от¬
крыл науку об иррациональных неупорядоченных числах, которых привел огром¬
ное множество, пользуясь конкретными методами» и т.д.?Этот документ, слишком
©
1	Гипсикл Александрийский, геометр и астроном II в до н.э., которому приписывается книга
14 Элементов Евклида, в то время как 15-я книга датируется уже VI в. н.э.
2	ncpi tt]ç стиукрюсох; тои ошбскасброи кш той EiKooaEôpov ujv aç тгр' auTT|v apaipav eyypaçopEs wv
См этот пассаж Гиксикла в томе 5 (с. 2) работы Euclidis opéra omnia ediderunt L J Heiberg, H. Menge.
Lipsiae, 1883-1895, 8 vol. in-12.
Ibidem, vol. V, p. 6. Пассаж, который мы переводим здесь дословно с греческого текста, за не¬
имением перевода на какой-либо современный язык.
4	Ta ncpi T(BV атактшу алаусоу. См.: Proclus, изд. Friedlem, р 74
5	Woepcke, Essai d une restitution de travaux perdus d'Apollonius sur les grandeurs irrationnelles,
d'après les indications tirées d'un manuscrit arabe. ( Mémoires présentés à l’Académte des Sciences, Pans,
1853, XIV, pp. 658-728) См отчет Michel Chasles о Mémoire de Woepcke, Journal de Mathématiques
pures et appliquées. Paris, 1854, tome XIX.
6	См вышеуказ Mémoire de Woepcke, p 691.
7	Там же, p 693.
53

Введение к первому переводу с древнегреческого на французский язык
длинный для полной цитаты, по сути, довольно пространный, заканчивается следу¬
ющим образом: «Иррациональные числа подразделяются на неупорядоченные, то
есть ге, которые скорее подвержены порче и уходят в бесконечность и, во-вторых,
на упорядоченные, являющиеся темой, ограниченной изучением, и которые к не¬
упорядоченным относятся как рациональные к иррациональным. Однако Евклид
•г»
•А
•I»
занимался только упорядоченными, которые являются однородными по отноше¬
нию к рациональным, не отдаляясь от этих последних в существенной мере; затем
Аполлоний занялся неупорядоченными, разница между которыми по отношению
к рациональным очень велика»1.
Предыдущие открытия в этой области, аллюзию на которые мы находим в пер¬
вом пассаже, который мы процитировали, по всей вероятности, относятся в первую
очередь к Пифагору, который, согласно одному месту из Прокла касательно пер¬
вой книги Евклида, открыл «теорию иррациональностей»2 *, а далее к Феодору Ки¬
ре некому, к тому месту, на которое ссылается между делом Платон в следующем от¬
рывке из своего диалога Теэтет, или О знании: «Феодор объяснял нам что-то о кор¬
нях, таких как корни из трех или пяти, доказывая, что они несоизмеримы подлине
с корнем единицы; и далее он брал подряд каждый корень до корня из 17, и на нем
уже остановился* и т.д/
Еще во времена Аполлония теория чисел, будучи наиболее абстрактной наукой,
так сказать лишенной твердо установленных методов, уже была полностью основа¬
на на пифагорейской школе, оставаясь все еше полностью подчиненной алфавит¬
ной системе счисления, в некотором смысле будучи стерилизованной отсутстви¬
ем какого бы то ни было позиционного веса, связанного с положением знаков. С
другой стороны, пластичный гений греков, мало склонный к слишком глубокому
абстрагированию, довольно долго держал научную арифметику в рамках линей¬
ных чисел4 *, чисел поверхностей1 и чисел тел6, чтобы еше у Евклида величины мож¬
но было лишь с трудом отделить от геометрического представления и наделить их
символами7. Таким образом, вероятно, что потерянные работы, которые мы толь¬
ко что привели у Аполлония, об иррациональных величинах, не слишком осво¬
бодились от геометрического выражения численных свойств с тем, чтобы рассма¬
тривать число в его абсолютной чистоте. Тем не менее нам известно, что Аполло¬
ний занимался логической, то есть практической, арифметикой. Действительно,
важность, которую Папп приписывает трудам Аполлония в этой области, застав¬
»1»
ляет предположить, что эти труды, расширяя систему счисления греков, которая
ограничивалась мириадом в квадрате, имели авторитет, сравнимый с авторите¬
том Начал Евклида в геометрии, установив окончательно систему счисления чи¬
1	Ibidem, р 701.
q Twv о/дупл* храуратсо. см Proclus ed. Fnedlem, р 65.
Œuvres de Platon, новое издание с примечаниями, кратким содержанием и оглавлением, с
очерком о философии Платона, написанном М Schwalbe, в первой части книги, и введением к Ре¬
спублике Armé Martin, Parts 1845,2 vol., gr m-8‘ Cm t. Il, Téétète, p. 424.
4 To есть чисел, имеющих только один множитель, то есть первых, в геометрическом смысле
представляющих длины
- То есть образованных произведением двух множителей.
6	То есть образованных произведением трех множителей или измерений.
1	Евклид, книги 5,7,8 и 9

Введение к первому переводу с древнегреческого на французский язык
сел, возведенных в степень; эта система счисления была введена уже Архимедом
в его известном Псаммите (Исчислении песчинок)'. До нас дошел лишь небольшой
отрывок из трактата Аполлония об умножении; и при этом мы лишь можем вос¬
становить его через анализ, который приводит Папп во фрагменте, уцелевшем из
книги 11 его Математического собрания. В этом анализе находятся 12 теорем из 26,
приведенных в изложении нового метода Аполлония по умножению больших чи¬
сел* 2. Этот метод был основан на двух основных теоремах, которые, с одной сторо¬
•л
ны, устанавливали правила умножения единиц, десятков и сотен между собой, а
с другой — умножения некоего числа на десятки, сотни и тысячи мириад некоего
порядка. Папп воспроизводит вычисления в качестве математического воссозда¬
ния метода Аполлония, который тот приводит, предлагая в качестве примера най¬
ти огромное число, полученное умножением всех 38 букв греческого стиха, взятых
в своем численном значении1 *.
Еше один отголосок арифметических работ Аполлония мы находим у Евтокия,
который заканчивает свой комментарий на трактат Измерение круга Архимеда не¬
которыми соображениями общего порядка о соотношении окружности и диаметра.
Помимо прочего, мы читаем у него следующее: «Следует отметить, что Аполлоний
Пергский также доказал это посредством других чисел, что приводит к еше больше¬
му приближению в Быстром получении результатов^. И он замечает, что если изме¬
рение, приведенное Аполлонием, и является более строгим по сравнению с Архи¬
медовым, то Архимед и не ставил себе иной цели, кроме как найти приближение,
отвечающее практическим целям5. Таким образом, Аполлоний, очевидно, написал
работу под названием Быстрое получение результатов6, в которой он применял свой
новый метод, чтобы вернуться через числа более высокого порядка и путем более
совершенных операций к определению соотношения окружности к диаметру, ко-
’ Œuvres d'Archimède, вышеук. изд. P Ver Eecke, L’Arénaire, рр 353-377.
2	Pappus, éd. Hultsch, vol. I, liv II, p. 6. Латинское издание Commandin не приводит книгу II, гре¬
ческий текст которой в XVI в. еще не был обновлен.
3	Приводим эту строку: АрТЕ,о6лд KÀEiyc кратод céo/ov cvvca Koupai. См : Pappus, éd Hultsch,
vol I, p. 20.
' Мы приводим перевод этого места согласно Евтокию: Ioteov ôe, ou каг АлолАхлуюд о Перуаюд
Ev та) Qkutokud аито ói acpiOpojv стсрои' cm то сил eyyug paÀÀov ayaycov.
См Archimedes opera, etc. Вышеук. изд. Heiberg, vol. III, Eutocn commentqnus in dimensionem
Circuli, p. 258,1. 16, либо изд. Torelli (Oxford 1792), p. 216,1. 1.
5	Ibidem, Heiberg, vol. III, p. 258,1. 20, либо изд. Torelli (Oxford 1792), p. 216,1. 5 При этом в ком¬
ментарии Евтокия приводится этот другой пассаж: алл eoti pcv тоито то ßiß/jov. cnç qnxnv HpaoxEiôrig
ev та) Архщг|0оОд Bia) XpEtaç avayicaiov, т e «но, как говорит Гераклид в своей Жизни Архимеда, эта
книга необходима для практических задач (букв, потребностей жизни)» (см.: Heiberg, vol. III, p. 228,
I 19 или Torelli, p 204,1. 45).
6	Слово íhcuTOKtov («быстрые роды») довольно странно в качестве названия работы о числах.
Возможно, это слово сильно искажено, поскольку разные рукописи дают разные версии в этом от¬
ношении. Текст Евтокия, который мы находим в тексте Архимеда изд Торелли (р 216,1.1 ), содер¬
жит слово nKDToßoü) из парижской рукописи, в то время как издание Гейберга - слово Йкитокко
из другой парижской рукописи
В отношении утраченной работы ÍIkutoktov можно привести следующие работы:
1	)Schmidt, Zeitschrift für das Gymnasialwesen, herausgeg von Mutzell, Berlin, 1855
2)Friedlein, Die Zahlzeichen und das elementare Rechnen der Griechen und Römer, Erlangen, 1869.

Введение к первому переводу с древнегреческого на французский язык
торое Архимед дал первым1, и этот метод по-видимому привел его к более близко¬
му значению по сравнению с его предшественником.
В своем комментарии на Данные Евклида геометр Марин2 ссылается на работу
Аполлония, которая являлась своего рода кратким изложением Начал Евклида, хотя
и была по большей части посвящена задачам обиходной геометрии’. Эта работа к V
в. не должна была еше исчезнуть, поскольку во многих местах комментария Прок-
ла на Начала Евклида приводятся подлинные цитаты. В первом отрывке приводит¬
ся новый подход, при помоши которого Аполлоний приводит понятие линии как
результата прямого постижения чувствами4. В этих трех отрывках приводится спо¬
соб Аполлония определять угол как стяжение в одной точке поверхности или гео¬
метрического тела в виде линии или сломанной поверхности5. В трех других отрыв¬
ках. где он выступает в качестве противника Евклида, приводятся и подвергаются
критике попытки доказательств некоторых аксиом. В частности, это касается до¬
казательства равенства ввиду того, что предметы занимают одно и то же место, то
есть исходя из совпадения, в противовес понятию равенства, принятого в качестве
общего понятия у Евклида6. В обоих пассажах вновь приводятся повседневные ге¬
ометрические построения, как, например, построение, где проводится разделение
данной прямой на две равные части посредством линейки и циркуля’, что мало от¬
личается от Евклида, а также построение, в котором выполняется возведение пер¬
пендикуляра в некоей точке заданной прямой линии8. Наконец, Прокл излагает нам
О
' Les Œuvres d Archimède, вышеуказанное издание Р Ver Eecke, см Измерение круга, рр. 127-
134
Этот знаменитый трактат Архимеда содержит лишь три теоремы, которые, вероятно, были
частью более объемной работы, которую Папп называет Об окружности круга (см. Pappus, éd
Hultsch, vol I, p. 312) Архимед в ней геометрически доказывает, что соотношение окружности к ди¬
аметру находится между 31/7 и 310/71 и что соотношение площади круга к квадрату его диаметра
примерно равно 11/14, однако он не сообщает нам о выборе двух значений V3 1351/780 с прибли¬
жением по избытку и 265/153 с приближением по недостатку, что лежит в основе вычислений (см
Zeuthen Nogle hypotheser от Arkhimedes kvadratrodsberegning. Tidsskriftfor Mathematik. Raekke
VI, Aargang 3, p 150) С другой стороны, отрывок из Метрик Герона Александрийского, новое из¬
дание которого было опубликовано в 1896 г. Н Schone (Herons von Alexandria Vermessunglehre
und Dioptra, griechisch und deutsch, Leipsig, 1903, p 66) упоминает утраченный труд Архимеда О
призмах и Цилиндрах, в котором он, по-видимому, определил соотношение окружности и диа¬
метра в пределах 3,1416016 > i > 3,1415904. что является более жесткими рамками по сравне¬
нию с трактатом Измерение Круга. Paul Tennery заметил, что эти пределы, то есть 195882/62351
> х > 211872/67441. как он предлагает исправить дроби текста, испорченного Героном, дают в
точности соотношение 355/113 Адриана Метиуса в качестве общего приведенного, общего для
разложений этих пределов на непрерывные дроби (см.: Mémoires scientifiques de Р Tannery, J. L.
Heiberg, H G. Zeuthen. Paris, 1912-1920,4 vol. parus, vol III, p. 149)
Марин, греческий геометр и философ V в., оставил нам комментарий на книгу Данные Евкли¬
да, текст которого был впервые опубликован в работе Euclidis Data, Cl. Hardy graece nunc primum
edid’t, latine vertit, scholnsque il lu st ravit; adjectus est Marini commentants graece et latine Lutetiae
Parisiorum 1625, in-4‘ Это довольно редкое издание, его удачно сменило критическое издание
Евклида Heiberg. Menge, уже упомянутое в предыдущей сноске, в томе 6 которого ( 1896) содер¬
жится текст Данных и комментарий Марина.
См. вышеук изд. Hardy, р 2 или Heiberg.
См Produs éd Friedlein p. 100 (рус перевод см 15]
Ibidem, рр 123,124,125
Ibidem, рр 183,194
Ibidem, рр 279,280
to/cfen? p 282
•я®
4
€
а
56

Введение к первому переводу с древнегреческого на французский язык
способ, при помощи которого Аполлоний строит треугольник, равный треугольни¬
ку, три стороны которого нам известны, и ругает это построение, поскольку в нем
используются две теоремы Евклида относительно двух равных прямых, стягиваю¬
щих равные дуги в равных кругах1 2.
По-видимому, из подробного рассмотрения этих цитат следует, что Аполлоний
задумал и выполнил до определенной степени план трактата по практической гео¬
метрии, определения которого более всего соответствовали данным простого опы¬
та и в котором определенные аксиомы Евклида представали в виде простых для до¬
казательств теорем. И хотя цитаты и размышления Прокла не отвечают нам на во¬
прос, собирался ли Аполлоний также рассмотреть знаменитый постулат Евклида3
в качестве теоремы, чье доказательство непросто, трактат Аполлония выступает в
некотором смысле первой попыткой ответа на определенные умонастроения гео¬
метрического мышления его эпохи, а также как попытка пересмотра классического
труда Евклида, часть которого, содержащая определения и аксиомы, является если
не самой неаккуратной, то как минимум самой слабой.
Как и большинство мэтров античной науки, Аполлоний преда
Время не пощадило его трудов в области этой самой прекрасной из всех наук. Одна¬
ко в пространном пассаже А¡ъмагеста Птолемея ему приписывается если не откры¬
тие, то, по крайней мере, доказательство способа представления эпициклами феноме¬
нов стояния и попятного движения планет3 S. Впрочем, это подтверждает Прокл в сво¬
ей работе Очерк астрономических гипотез*, где он упоминает, что Птолемей пользуется
этим доказательством в книге 12 Агьмагеста-. С другой стороны. Птолемей Хенн во
фрагменте своей работы, о которой мы говорили выше6, сообщает, что работы Апол¬
лония по теории Луны стоили ему прозвания «Эпсилон», по форме в виде полумеся¬
ца, которая свойственна этой греческой букве. Наконец, в работе, которую св. Иппо¬
лит написал против еретичества', в последнем пассаже говорится, что Аполлонии оце¬
нил расстояние от поверхности Земли до окружности Луны в пятьсот мириад стадиев^
•ж
•I*
•ж
•ж
лж
•ж
•ж.
•ж
•ж
•ж
•ж
к
лж
•м
та
та
’ Ibidem, рр. 335, 336.
2	Этот постулат Евклида, который некоторые рукописи приводят среди аксиом (аксиома 11),
был изложен следующим образом Приводим его по переводу Peryrard -Paris, 1809. in-8*): « И
если прямая, падающая на две прямые, образует внутренние углы, по одну сторону, меньшие двух
прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы мень¬
ше двух прямых».
3	Математическое сочинение Клавдия Птолемея, впервые переведенное на французский язык
по рукописям Императорской Библиотеки г-ном М. Halma (с греческим текстом), с примечания¬
ми М Delambre. Paris, 1813-1816, 2 vol. in-4* См. vol. Il, Itv. XII, рр. 312, sqq
4	Работа Прокла под названием Улояиликя;; twv aorpovopixtuv шго0е
краткое изложение систем Гиппарха, Аристарха Самосского и Клавдия Птолемея Его греческий
текст был впервые издал в Базеле в 1540 году, ш-4', а на французский язык был переведен абба¬
том Halma в вышеуказанном издании.
Hypothèses et époques des planètes de C. Ptolémée et hypothèses de Proclus Diadochus, traduites
par Halma (grec et français). Paris, 1820, in-4*. Cm : p. 128
• Cm. c. 2 данного предисловия, примечание 1.
S	Hippolyti refutations omnium haeresium hbrorum decern quae supersunt gr et lat. recognovit L
Duncker, F. G. Schneidewin, Gottingue, 1856-1859, in-8*. Cm.: liv. IV, p. 66
8	На тему оценки расстояния, приписываемой Аполлонию, см. статью. Paul Tannery Anstarque
de Samos (Mémoires de la Société des sciences physiques et naturelles de Bordeaux, 2er • séné, 1883,
t.V, pp. 237-258, или Mémoires scientifiques de P. Tannery, pub. Heiberg, Zeuthen, Pans, 1920-1922,
vol I, p. 390).
та
57

Введение к первому переводу с древнегреческого на французский язык
(Если это птолемеевский стадий, равный 185 м, то получается 925 000 км, то есть
м
примерно в 2,4 раза больше расстояния до Луны. - Прим, ред.)
Наконец, необходимо отметить, что Аполлоний написал две работы по оптике,
в которых для исследования природных феноменов он пользовался ресурсами гео¬
метрии. Действительно, сохранился фрагмент на греческом языке и з области мате¬
матики, в котором Аполлонию между делом приписывается трактат по катоптрике
и трактат о зажигательных зеркалах1.
Работы Аполлония частично стали известны на Западе благодаря арабам, унас¬
ледовавшими греческую науку, задолго до того, как были открыты греческие тек¬
сты. Работы Аполлония переводились, компилировались и комментировались
арабами и персами начиная с IX в., одновременно с Началами Евклида, трактатом
Сферика Феодосия Триполийского, О сферических треугольниках Менелая и не¬
сколькими работами Архимеда. Первое арабское проникновение трудов Аполло¬
ния заметно уже в работе по оптике, которую Вителлио2 написал в XI11 в. и кото¬
рая, по сути, является лишь трактатом по оптике, написанным Альхазеном (Ибн
аль-Хайсам), знаменитым арабом, обосновавшимся в XI в. в Испании (он жил не
в Испании, а сначала в Басре, потом в Каире. - Прим, ред.); в этом трактате при¬
водятся некоторые теоремы Аполлония, а также первая попытка теории прелом¬
ления и сумерек1. Другие свидетельства в пользу знакомства с работами Аполло¬
ния арабских ученых мы находим в первой попытке создания латинской версии,
усеянной арабскими словами, датирующейся XIII в., которую довольно правдопо¬
добно приписывают Герарду Кремонскому4, а также в итальянском переводе трак¬
тата Альхазена, датирующемся XIV в.5
' Этот фрагмент греческого текста был опубликован Belger - Hermès, XVI, p 279), за ним после¬
довало критическое исследование со стороны Гейберга (Zeitsch. f. Math. u. Physik, XXVIII, p. 124)
г Vrtellio, или Vrtello, премонстрантский монах и польский математик из семьи Циолеков, ро¬
дился в 1260 г и переехал в Италию, где он, в духе своего времени, латинизировал свою фами¬
лию. которая по-польски означала быка (vitulus). Его работы свидетельствуют о знании им. столь
редком в его эпоху, трудов греческих математиков В частности, он внес свой вклад в возврат из
забвения работ Аполлония Его исследования по оптике увенчались комментариями на работу
арабского физика Альхазена, любопытной работой, состоящей из 10 книг, рукопись которой была
издана лишь в первой половине XVI в под названием Vitellionis Mathematici doctisstmi ncpi олпкцо,
id est de natura, ratione et project tone radiorum visus, luminum, coIorum at que formarum quam vulgo
Perspectivam vocanthbriX. Nonmbergae, 1535, m-fol., fig. Второе издание в Нюремберге датирует¬
ся 1541 г Вителлин посвящает свой труд другу св. Фомы Аквинского Willem van Moerbeke, которо¬
му мы обязаны первым латинским переводом трактата О плавающих телах Архимеда.
Интересный анализ Оптики Вителлио можно найти в работе Histoire de la Perspective ancienne
et moderne. Poudra, Paris, 1864. m-8‘, pp 32-41
1 Трактат по Оптике Альхазена был напечатан во второй половине XVI в вместе с трактатом Ви¬
таллия изд. Risner. Opticae Thesaurus. Alhazenii Arabis Libri septem, nunc primum editi. Ejusdem Liber
de Crepuscuhs etNubium ascensionibus Item Vitelhonts Thunngopoloni LiboX Omnes instaurait, figuris
illustrait et aucti.adjectisetiam en Alhazenum Commentants a Federico Risnero Basileae, 1572, in-fol,
fig (Королевская библиотека Бельгии, v 5057).
4	См. работу Wustenfeld Die Übersetzungen arabischer Werke in das lateinische, p 79
' Cm Intorno ad una traduzione italiani fatta nel secolo décimo quarto del tra tta to d Ottica d 'Alhazen
mathematico d> secolo uno décimo nota di Enr Narducct, Roma, 1871, in-4*.

Введение к первому переводу с древнегреческого на французский язык
•Я
Первый греческий текст Конических сечений Аполлония появился в Италии в соста¬
ве цепных рукописей, привезенных с Востока знаменитым филологом Франциском
Филельфом1, который после преподавания в Венеции отправился в 1420 году в каче¬
стве секретаря венецианской дипломатической миссии в Константинополь, где он
занялся изучением арабского языка и литературы под руководством Иоанна Хризо-
лора. Эта рукопись оставалась в тени на протяжении трех четвертей века, пока Джор¬
джо Валла не перевел несколько фрагментов на латынь. Эти фрагменты были опубли¬
кованы в Венеции в 1501 г. в его посмертном издании De expetendis etfugiendis rebus2.
Полная латинская версия четырех первых книг Конических сечений, единствен¬
ных имевшихся в греческой рукописи, была выполнена венецианским математиком
Джованни Батиста Мемом. Эта версия, многочисленные неточности и пропуски ко¬
торой свидетельствуют о недостаточном знании греческого языка, была издана по¬
сле смерти автора его племянником Джованни-Мария Мемом под названием Opera
ApoUonii Pergaeiphilosophi, trad, per J.В. Метит, patricium Venetium. \fenetiis, 1537, in-43.
Недостаточность этого перевода определила желание Франческо Мавролико4
сделать новый, с учетом ошибок Мема.
1	Франциск Филельф, род. в Толентино в 1398 г. Начал свою деятельность в Венеции в возрас¬
те 20 лет Однако его желание совершенствоваться в изучении греческого и арабского языков за¬
ставило его отправиться в Константинополь в 1420 г в качестве секретаря посла Венецианской
республики. Там он учился под руководством Иоанна Хризолора, зятем которого он стал. Уваже¬
ние, которого он добился в Константинополе, позволило ему удостоиться расположения импера¬
тора Иоанна Палеолога, который отправил его в 1424 г. в качестве посла к султану Ахмету. В 1427
г. он вернулся в Венецию с ценным грузом манускриптов. Его противоречивый нрав заставил его
несколько раз менять место жительства, и умер он во Флоренции в 1481 г., куда явился по при¬
глашению Лоренцо Медичи. Филельф был одним из тех людей, которые способствовали распро¬
странению классической литературы. Ему мы обязаны латинскими переводами Риторики Ари¬
стотеля, Киропедии Ксенофонта, а также нескольких работ Лисия и Плутарха. Он вел широкую
переписку, и его письма, написанные на латыни, впервые изданные Винделином Спирским в Ве¬
неции в 1472 г, являются ценным историческим документом того времени Отличное исследова¬
ние жизни и работ Филельфа было выполнено Lancelot, Mémoires de lAcadémie des Inscnptions et
Belles-Lettres, vol X, p. 69.
2	Джорджо Валла, врач и математик, род. в г. Пьяченца в 1430 г., ум. в Венеции, является ав¬
тором латинских версий книги 14 Начал Евклида, приписываемой Гипсиклу; трактата Астролябия
Никифора Грегораса, трактата Душа Мира Тимея Локрского; трактата О Сфере Прокла, трактата
О Небе Аристотеля, а также трактата по астрономии Аристарха Самосского Эти переводы были
изданы в Венеции в 1498 г. в книге, ставшей редкостью. Его работа De expetendis et fugiendis rebus
представляет собой некую энциклопедию, состоящую из трех книг по арифметике, 5 книг по му¬
зыке, 6 книг по геометрии и 4 книг по астрономии и медицинской астрологии.
3	Эта книга стала настоящим раритетом
4	Франческо Мавролико, знаменитый итальянский геометр, который во Франции больше из¬
вестен под именем Марулль, род. в Мессине в 1494 г., ум. в 1515 г Преподавал математику в Мес¬
сине. Его трактат по коническим сечениям замечателен тем, что представляет впервые несколько
свойств этих кривых, выведенных из тех, которые соответствуют им в круге Он заметил, что тень
края указателя солнечных часов ежедневно описывает дугу конического сечения, и на основе это¬
го наблюдения вывел новые гномические правила Ему мы обязаны введением секущих в триго¬
нометрические расчеты, он создал таблицу, которую опубликовал вслед за латинским переводом
трактата О Сфере Феодосия (Мессина, 1558, tn-fol.) Помимо его работ, опубликованных по боль¬
шей части уже после его смерти, по арифметике, геометрии, перспективе, космографии и по ре¬
конструкции книги 5-й Конических сечений Аполлония он оставил множество неизданных трудов,
сведения о которых приводятся в следующей работе Scritti inediti di Francesco Maurolico pubbhcati
dal prof. Fed Napoli. Roma, 1876, in-4*.
tit
59

Введение к первому переводу с древнегреческого на французский язык
Однако этот перевод издан не был1.
Второй перевод четырех первых книг Конических сечений, выполненный на ос¬
нове нескольких греческих манускриптов, включая перевод лемм Паппа, коммен¬
тария Евтокия и двух книг Серена Антинопольского под названием De la Section du
Cylindre et du Cône был выполнен Федериком Коммандино: Apollonii Pergaei conicorum
libn priores quatuor, una cum Pappi Alexandnni lemmatibus et commentahis Eutocii Ascalonitae;
item Sereni Antissensis philosophi libri de sectione cylindri et coni; quae omnia nuper Fed.
Commandinus Urbinasegraeco convertit. Bononiae, 1566, in-fol., fig.2 *
B 1626 г. в Париже появилось издание с перепечаткой версии Comniandin Archimedis
opera, niechanicorum libri; Apollonii Pergaeiconicorum et Sereni de sectione cylindri. Lutetiae,
in-164
ul»'
¿•ж
В 1655 г. была издана замечательная работа отца Клаудио Рикардо под названи¬
ем Apollonii Pergaei conicorum libn IV, cum commentahis R. P. Claudii Richardi, Antwerpiae,
pet. in-fol4. Эта работа является лишь комментарием на первые четыре книги Апол¬
лония на основе версий Мема и Коммандино, к которым автор добавляет из своей
личной коллекции четыре другие книги по коническим сечениям в качестве конъ¬
ектурной реконструкции четырех последних книг Аполлония, на греческом утра¬
ченных, но в ту эпоху уже появившихся в арабской версии.
В 1675 г. в Лондоне было издано сокращенное издание четырех первых книг Ко¬
нических сечений, написанных на латыни Исааком Барроу, который был учителем
Ньютона в Кембриджском университете. Эта работа, в которой формулировки тео¬
рем переведены довольно приблизительно, а доказательства либо сокращены, либо
изложены алгебраическим методом, носит название Archimedis opera, Apollonii Pergaei
conicorum libn /К Theodosii Spherica, methodo nova il lust rata et succincte demonstrata, per
Is. Barrow. Londini. pet. in-4°.
Заметим, наконец, что последнее издание латинского перевода Коммандино,
пересмотренное и исправленное Nie. Buti, имело место в Пистое. Италия, и носи¬
ло название Apollonii Pergaei conicorum libri quatuor; Sereniphilosophi Antissensis libri duo.
Pistoni Hetruriae, 1696, in-fol., fig.
Книги 5,6 и 7 Конических сечении Аполлония, греческий текст которых, по всей
видимости, исчез во времена Евтокия, поскольку этот комментатор никак не упо¬
минает их и едва ли знает, были переизданы лишь в XVII в. в различных арабских
версиях, резюме или комментариях.
Первые арабские рукописи, в которых содержались работы Аполлония, были
привезены с Леванта в 1629 г. Якобусом Голиусом5, профессором востоковедения в
См Histoire des Sciences mathématiques en Italie ,G. Libri, Paris, 1841,4 vol., in-8‘, Vol III, p 233
1 Раритет.
’ Раритет
4 Раритет, один экземпляр которого хранится в Антверпене в Музее Плантена Мы изучали его
‘ Якоб Голиус, род в Гааге в 1596 г, ум в 1667 г В течение некоторого времени преподавал грече¬
ский язык в Ла Рошели пока в 1622 г не отправился в Марокко в составе посольского корпуса Респу¬
блики Соединенных Провинций, где принялся изучать арабский язык. В 1625 г. он уехал в Левант, где
совершенствовался в восточных языках В1629 г, после нескольких путешествий в Аравию, Месопо¬
тамию, а также проживания некоторое время в Константинополе он вернулся в Голландию с драгоцен¬
ным грузом рукописей, написанных на различных азиатских языках, и стал преподавать в Лейденском
университете Именно ему мы обязаны огромным числом исследований по литературе и науке Азии.

Введение к первому переводу с древнегреческого на французский язык
Лейдене. Мы не знаем, какие обстоятельства помешали этому ученому реализовать
задуманный им проект перевода этих рукописей, которые после его смерти еше дол¬
гое время никак не использовались. Голиус, очевидно, сообщил нескольким эруди¬
там о содержимом своих манускриптов; так, уже Марен Мерсенн упоминает новые
книги Аполлония и даже приводит некоторые из его теорем в своих работах в 1644 г.‘
Тем не менее последние книги Конических сечений продолжали считаться утра¬
ченными, и знаменитый итальянский геометр Винченцо Вивиани даже попытался
реконструировать книгу 5 Аполлония, в которой, по сведениям Паппа, речь шла
о максимальной и минимальной линиях, могущих быть проведенными из точ¬
ки. заданной на окружности или коническом сечении. Однако в 1658 г. итальян¬
ский геометр Борелли открыл в библиотеке Медичи во Флоренции арабский ма¬
нускрипт, в надписи на котором упоминались Конические сечения Аполлония. Этот
манускрипт, очевидно, принадлежавший Голиусу, включал в себя Леммы Архиме¬
да, на тот момент еще неизвестные, и книги 5, 6 и 7 Конических сечений Аполло¬
ния, — сокращенные и переработанные персидским геометром Абальфатом аль-
Исфахани в 994 г., в эпоху халифа Абу Калигьяра. Однако Вивиани, опасаясь, чтобы
это открытие не лишило его плода его собственных трудов, заручился молчанием
Борелли о содержимом рукописи до публикации его собственной работы, кото¬
рая вышла во Флоренции в 1659 г.2 Сравнение, которое можно сделать между ра¬
ботой Вивиани и книгой 5 Аполлония, показывает, что Вивиани не только вос¬
становил большую часть теорем греческого геометра, но и затронул в своей работе
более широкий круг проблем, в некотором роде дополнив познания древних от¬
носительно конических сечений.
Борелли предложил перевести рукопись Ат-Исфахан и на латынь Абрахаму Эк¬
келленсису (Ибрагиму ать-Хакилани)\ преподававшему восточные языки в Риме,
где он занялся работой над многочисленными примечаниями, которые стали необ¬
ходимыми ввиду сжатости и неясности текста. Работа вышла в 1661 г. под названи¬
ем Apollonii Pergaei conicorum libri И, VI, VII. paraphraste Abalphato Asphahanensi, nunc
primum editi; additus in calce Archimedis assumptorum Uber, ex codicibus arabicis manuscr.
Abrahamus Ecchellensis latinos reddidit; Jo. Alfonsus Boreilus curam in geomeiricis versiom
contulit, et notas uberiores in Universum opus adjecit. Florentiae, in-fol.
Другой арабский манускрипт, содержащий краткое изложение и комментарий на
три последние книги Аполлония, написанный в 1250 г. Абдольмелеком из Шира-
’ См.: ЕМ. Mersenni opera. Pansus, 1644, 2 vol in-4\
2	Знаменитая работа Вивиани носит название De maximis et minimus geometnca divinatio tn
quintum conicorum Apollonii Pergaei nunc desideratum, auctore V Viviani. Florentiae. 1659, in-fol
3	Абрахам Эккелленсис, ученый-востоковед, род в конце XVI в. в деревне Эккель в Сирии Сте¬
пень доктора философии и теологии получил в Маронитском колледже в Риме, позднее стал про¬
фессором арабского и сирийского языков 8 Колледже Пропаганды. В 1630 г. он отправился в Па¬
риж, чтобы помочь Ги Леджею в подготовке его многоязычной Библии. Он принял участие в работе,
переведя книгу Руфь на латынь и арабский, а книгу Маккавеев на арабский Умер в 1652 г. в Риме,
куда был вызван для участия в составлении арабской версии Писаний. Эккелленсису мы обяза¬
ны латинским переводом ценных арабских работ, таких как Chromcon Orientate Ibn-Ar-Rahib (Pans,
1653), книги V, VI, VII Конических сечений Аполлония и книги Леммы Архимеда, греческий текст ко¬
торой утрачен. Более подробные сведения о жизни и работе Абрахама Эккелленсиса можно най¬
ти в работе G. Dandini Voyage au Mont Liban, trad. Rich Simon, Paris, 1685.
«
О
LCt
61

Введение к первому переводу с древнегреческого на французский язык
L©
за, был привезен из Леванта в 1641 г. ориенталистом Кристианом Рау1, который пе¬
ревел его на латынь, и опубликовал в Киле в 1669 г. под названием Apollonii Pergaei
conicarum sectionum, a Christ. Ravio, in-8‘.
Полный текст книг 5,6 и 7 Конических сечении был открыт лишь в начале XVII
в. через другой арабский манускрипт, принадлежавший Голиусу, проданный его на¬
следниками Нарциссу Маршу, архиепископу Армахскому в Ирландии2. Этот ману¬
скрипт, копия которого существовала в Бодлианской библиотеке в Оксфорде, содер¬
жала полную версию семи первых книг Конических сечений Аполлония, составленную
в IX в. арабским математиком Абуль-Хасан Сабитом ибн Куррой аль-Харрани3, пе¬
реработанную Бени Мозом и исправленную в 1260 г. персидским геометром и асзро-
номом Насиром-ад-Дином Туси4.
Именно эта арабская версия, имеющая особую ценность, позволила великому
английскому астроному Галлею предложить в 1710 г. свое монументальное изда¬
ние семи книг Конических сечений Аполлония под следующим общим названием:
Apollonii Pergaei conicorum libri octo et Serení Antissensis de sectione Cyhndri et Com libri
duo. Oxomae, in-fol. fig.5
Это издание, в котором вплоть до своей смерти принимал участие Давид Грегори,
в том. что касается греческого текста, и которое Галлей завершил в одиночку, состо¬
ит из трех частей. Первая включает греческий текст из первых четырех книг Кони¬
•Л
Chnstian Rau (Ravius), ученый-востоковед, род в Берлине в 1603 г, ум в 1677 г, изучал древ¬
ние языки в Виттенбергском университете Далее он направился в Амстердам, где учился у Вос-
сиуса, и в Лейден, где изучал арабский язык у Голиуса. Его желание поехать на Восток увенчалось
назначением его на место секретаря посольства Голландии в Константинополе в 1639 г. Он совер¬
шил путешествие в Левант, где совершенствовался в восточных языках и откуда привез в 1641 г. в
Англию более двух тысяч манускриптов, купленных от имени ученого Ашера, ирландского примаса.
С этого времени он преподавал арабский язык соответственно в Грешем-колледже ( 1642), в Утрех¬
те (1646), в Оксфорде (1647), в Упсале (1651), в Киле (1669) и, наконец, во Франкфурте в 1672 г.
Обычно этот манускрипт значится под названием Codex Armachanus.
Абуль-Хасан Сабит ибн Курра аль-Харрани, знаменитый арабский философ и математик,
род. в Харране, Месопотамия, в 835 г, ум в 900 г Проживал в Багдаде в качестве астролога ха¬
лифа Аль-Мутадида Написал примерно 500 работ на арабском и 16 на сирийском языке. Извест¬
ны его арабские переводы Начал Евклида, трактата О сфере Архимеда, Альмагеста Птолемея, Об
истолковании Аристотеля, нескольких работ Галена и, наконец, Конических сечений Аполлония.
4	Этот ценный арабский манускрипт, написанный в городе Марата в Персии, который был подпи¬
сан и датирован переписчиком 10-м днем месяца шаабана персидского 702 г. (30 марта 1302 г. ), за¬
вершается примечанием, указывающим на то, что книга 8 Конических сечений Аполлония не была
переведена на арабский так как не был обнаружен греческий текст.
Работа носит три следующих подзаголовка 1 ) Apollonii Pergaei conicorum libri IV pnores cum
PappiAlexandrmi lemmatis etEutocnAscalonitae commentants, excodd. Mss Graecis edidit Edmundus
HalletuS; 2) Apollonii Pergaet conicorum libri très postenores (sc Vms, Vlms, Vllms) ex arabico sermone
m latmum convenu cum PappiAlexandrmt lemmatis. Subpcitur liber conicorum octavus restitutus. Opéra
et studio Edmundi Helleti, 3 ) Serem philosophi Antissensis de Sectione Cyhndri et Coni libri duo, ex codd
mss edidrt Edmundus Halleius.
Эта работа, ставшая библиографической редкостью, является прекрасным примером типо¬
графского искусства начала XVIII в Напечатанная в две колонки на плотной бумаге и с широкими
полями, она содержит более 500 отличного качества рисунков и украшена великолепным алле¬
горическим фронтисписом, гравированным Боргерсом (Borghers) в 1704 г., а также гравюрой на
заголовке его же авторства В настоящем издании воспроизводится этот же фронтиспис. Грави¬
ровочная доска с небольшими изменениями в аллегорическом плане была вновь использована
примерно сто л₽ г спустя для выпуска фронтисписа, украшающего великолепное первое оксфорд¬
ское издание Архимеда, предпринятое Торелли
62
•Ж
•1Л
•я
•It

Введение к первому переводу с древнегреческого на французский язык
•Ж
ческих сечении, опубликованных впервые вместе с латинской версией Коммандино,
более или менее исправленной, а также греческие тексты лемм Паппа и коммента¬
рий Евтокия вместе с латинскими версиями. Вторая часть включает латинский пе¬
ревод книг 5, 6 и 7, сделанный по арабской версии Сабита ибн Курры; греческий
текст с латинским переводом лемм Паппа относительно этих книг, а также конъ¬
ектурную реконструкцию книги 8, выполненную Галлеем. Наконец, третья часть
включает греческий текст и латинскую версию двух книг Серена Антинопольского
О сечении цилиндра и конуса.
Критическое издание греческого текста первых четырех книг Конических сече¬
ний было предложено в 1893 г. великолепным эллинистом Гейбергом (J.L. Heiberg),
профессором Копенгагенского университета. Оно носит заголовок Apollonii Pergaei
quae exstant, cum commentants antiquis edidit et latine interpretatus est J. L. Heiberg, Lipsiae,
1891-93, 3 vol., in-8°, fig. Это издание, в котором за основу были взяты все известные
в настоящее время греческие рукописи, сопровождается латинской версией, в кото¬
рой некоторые пассажи приведены более кратко и в современных понятиях. Помимо
этого, оно включает все фрагменты утраченных работ Аполлония, которые только воз¬
можно было найти у других авторов Античности: греческий текст лемм Паппа и, на¬
конец, греческий текст вместе с новым латинским переводом комментария Евтокия.
Критическое издание арабского текста трех последних книг Конических сечений
было выполнено Л. Никсом (L. Nix). Однако оно не было завершено, и в печать вы¬
шел лишь один фрагмент, который заканчивался на седьмой теореме пятой книги’.
Геометрический труд Аполлония еще не был полностью переведен ни на один
современный язык. Оба современных исследования, которыми мы располагаем на
настоящий момент, являясь, впрочем, весьма содержательными, никоим образом не
снижают того интереса, который представил бы полный и точный перевод, а также
не компенсируют возможности созерцать этот археологический математический па¬
мятник во всей его изначальной красоте,
пленном в Германии Г. Бальзамом, в свободной форме переложены на современный
математический язык формулировки задач Конических сечении, а их доказательства
либо сильно сокращены, либо приведены в современных понятиях1 2. Второе иссле¬
дование, выполненное в Великобритании, г-ном Т.Л. Хитом (T.L. Heath), с глубо¬
ко ученым предисловием, включает в себя основные теоремы, изложенные совре¬
менным языком, в порядке, соответствующем современным теориям конических
сечений, и полностью перелагает доказательства на современный научный язык3.
Буквальный перевод Конических сечении Аполлония, который мы впервые при¬
водим на французском языке, берет за основу греческий текст критического изда¬
ния Гейберга в первых четырех книгах и латинскую версию Галлея, в которой взята
за основу арабская, трех следующих книг, греческий текст которых утрачен.
Антверпен, октябрь 1921 г.
<»!•
•Ж
1	Das fünfte Buch der Conica des Apollonius von Perga in der arabischen Übersetzung des Thabi—
ibn-Corrah Ludwig Nix Leipzig, 1889.
2	Des Apollonius von Perga sieben Bucher über Kegelschnitte, nebst den durch Hailey wieder
hergestellten achten Buche, deutcsh bearbeitet von H Balsam, Berlin, 1861, in-8’, fig
3	Apollonius of Perga. Treatise on conic sections edited in modern notation, with introductions mclusing
en essay on the earlier history of the subject, by T L. Heath, Cambridge, 1896, in-8‘, fig
63

1.0 ПЕРЕВОДЕ
»1»
Предлагаемая книга представляет собой впервые осуществленный полный пере¬
вод на русский язык первых четырех книг Аполлония «Конические сечения». Пере¬
вод сделан с древнегреческого текста издания Гейберга 1891-1893 гг. [26, 27[.
Условно считается, что было трое великих античных математиков: Евклид, Ар¬
химед и Аполлоний Пергский. Но, в отличие от первых двух, Аполлоний на русский
язык не переводился, за исключением первых двадцати теорем [9[. Отсутствие пере¬
вода на русский язык тем более удивительно, что труд Аполлония начиная с XVI в.
неоднократно переводился сначала на латынь, а со второй половины XIX в. и вплоть
до нашего времени - на современные европейские языки. Переводили, впрочем,
чаше всего только первые четыре книги.
Первые переводы на латынь соответствовали древнегреческому оригиналу и фор¬
мул там не было. Таковы, например, первое полное издание четырех книг в Венеции
И.Б. Мема (1537), перевод Ф. Коммандино (1566) и, считающееся классическим,
издание Э. Галлея (1710). Исключением является весьма вольный перевод И. Бар¬
роу (1675). С середины XIX века, поскольку словесные описания сильно затрудня¬
ли читателей, их стали заменять алгебраическими формулами (Г. Бальзам, И. Гей-
берг,АЧвдтина).ТХизсдаже менял по собственному усмотрению и доказательства
и порядок изложения, вероятно, пытаясь сделать текст более пригодным в качестве
учебника Видимо, все это и дало основание Б.А. Розенфельду сказать, что «боль¬
шинство переводов были по существу пересказами» [ 17, с. 5].
Получается, что если точно следовать источнику; то он будет слишком труден для
понимания, а если осовременить его, то это будет уже не перевод, а пересказ. Какой
же путь избрать, чему следовать?
И.Н Веселовский в предисловии к сочинениям Архимеда писал: «Есть два спо¬
соба переводить древних классиков математики: можно строго держаться характера
изложения подлинника... или желать его в современном изложении... Подготовляя
настоящее издание, переводчик избрал средний путь: сохранив изложение Архиме¬
да постольку, поскольку его чтение не затруднит читателя, он добавил современные
алгебраические формулировки» [ 1, с. 3].
АвотДД. Мордухай-Болтовской переводил «Начала» Евклида, «решительно от¬
казываясь перекладывать что-либо из “Начал” на современную алгебраическую сим¬
волику», обосновывая это тем, что, во-первых, такая символика совершенно чужда
Евклиду. а во-вторых, тем, что перевод предназначен «не только для учителя, который
мог бы удовлетвориться вольным переводом... но и для лиц, ведущих работу по исто¬
рии математики, заинтересованных в получении неискаженного Евклида» [ 11, с. 5].
Соображения Мордухай-Болтовского вполне резонны, но если «неискаженного
Евклида» современный читатель читать еше может, то неискаженного Аполлония
вряд ли По крайней мере, у Аполлония довольно много теорем, малопонятных без
обработки Поэтому мы решили сделать так: дать обработанный перевод с алгебра-
•I»
ла
64

Предисловие
ическими формулами, понятный современному читателю, но, конечно, не переде¬
лывая доказательств подобно Хизсу, и наряду с этим дословный перевод с древне¬
греческого, который к тому же будет более понятным, благодаря наличию осовре¬
мененного текста. Печатать же билингву вряд ли стоит, поскольку в Интернете легко
найти тексты и на древнегреческом, и на латыни.
В латинском переводе Гейберга вставлено много ссылок на Евклида и на преды¬
дущие теоремы Аполлония. Они облегчают понимание доказательств, но, на наш
взгляд, их слишком много. У нас ссылок на Евклида намного меньше, поскольку пред¬
полагается, что читателю известны основные теоремы из школьной геометрии. По¬
ложения Евклида, на которые ссылки все же остались, помешены в книге отдельно.
В отличие от многих других изданий, на чертежах изображены не условные, а ре¬
альные конические сечения, поэтому изображения точно соответствуют размерам
отрезков и доказываемым соотношениям. Обозначения на чертежах повторяют обо¬
значения Галлея и Гейберга, но иногда мы от этого отступаем. Дело в том, что если
имеется ряд связанных между собой теорем, то для удобства читателя обозначения
в них должны быть единообразны. Но в те времена удобство читателя никого не за¬
ботило. В связи с этим мы поменяли обозначения в некоторых рисунках, оставив в
таких случаях прежние в рисунках к дословному переводу.
В тексте Гейберга теоремы никак не называются, а просто нумеруются. В других
изданиях обычно проводится различие между теоремами и задачами на построение,
а обшее их название - Предложения. При этом Предложения, теоремы и задачи ну¬
меруются иногда отдельно. У нас нумерация единая, а задачи на построение просто
выделены в оглавлении полужирным шрифтом.
Аполлоний не нумеровал определения, поэтому у разных авторов получилось раз¬
ное их количество: Мем следует Аполлонию, то есть не нумерует их. у Коммандино и
Галлея их 19, а у Гейберга — 8. Поскольку перевод у нас с Гейберга, то мы, естествен¬
но, используем разбиение Гейберга, но приводим для справки и разбиение Галлея.
В книгах Аполлония, как и в большинстве других древнегреческих текстов, нет
оглавления, что сильно затрудняет нахождение нужного материала. Поэтому мы со¬
ставили к нему оглавление в виде кратких заголовков к Предложениям. По техни¬
ческим причинам эти заголовки попали и в основной текст. В результате случается,
что они повторяют формулировку теоремы, данную ниже Аполлонием, что может
вызвать некоторое недоумение. Кроме того, мы составили распределение теорем по
темам. Очевидно, что одна и та же теорема может относиться к разным темам, да и
набор тем достаточно условен, как и распределение теорем по ним, но, возможно,
эта классификация будет хоть в чем-то полезна читателю.
'НТЕ
•I»
ИЕ
•ГЕ
2. О ТЕРМИНОЛОГИИ АПОЛЛОНИЯ
Терминология Аполлония несколько отличается от современной, а кроме того,
она не всегда однозначна. Так, диаметром он называет иногда отрезок между про¬
тиволежащими ветвями гиперболы, а иногда и всю прямую. Где это не затрудняет
понимания, мы оставляли терминологию Аполлония. В других же случаях исполь¬
зовали современную. Все это оговорено в сносках и примечаниях, но, чтобы не ис-
•Ж

Предисловие
/Л
кать их каждый раз в тексте, мы приводим здесь список некоторых терминов, упо¬
требляемых Аполлонием и пояснения к ним.
Вершина кривой. Вершиной Аполлоний называетточку пересечения кривой с ди¬
аметром. Это не точка пересечения конического сечения с осью, как принято сей¬
час, а вершина или предел любого диаметра, то есть любая точка кривой.
Гипербола. Гипербола у Аполлония - это одна из ветвей, а обе ветви он называ¬
ет противолежащим и сечениями, противолежащими гиперболами или просто проти¬
волежащими.
Ордината. Слово ордината означает упорядоченная. Аполлоний называет улоря-
дочеиными прямыми (ординатами) параллельные секущие, которые делятся попо¬
лам диаметром, а также параллельную им касательную, проходящую через верши¬
ну, поскольку она ведь тоже «упорядочена». В подстрочнике, там, где это удобно,
мы даем дословный перевод, уточняя в скобках, что это ордината, в других же слу¬
чаях пишем просто ордината. В конце концов, слово ордината можно считать уже
переводом на русский.
Отрезок и прямая. Под словом прямая Аполлоний понимает отрезок, который
проводится от одной точки до другой и может быть продолжен далее. Отсюда по¬
стоянно употребляемые им выражения проведем прямую АВ, проведем и продолжим
прямую АВ. Слово же отрезок означает у него только часть, выделенную на уже про¬
веденной прямой, но он нигде не пишет проведем отрезок АВ. Такую же терминоло¬
гию мы встречаем и у Декарта и даже еще позже. Современное словоупотребление
установилось лишь в XIX в.
Равенство фигур. Если в дословном переводе сказано, что. например, треуголь¬
ники равны, то, как правило, это означает только равенство площадей (то же самое
и у Евклида).
Умножение. В соответствии с тогдашними взглядами (см., например, Евклид VII,
Опр 16) Аполлоний не употребляет слова умножение, если речь идет не о целых чис¬
лах, а пишет: составим прямоугольник. Причем если перемножаются, например, сто¬
роны АВ и ВС, то Аполлоний записывает это в виде АВС.
Latus rectum (лат.), dpöia лХсира (древнегр.), сторона отвесная — отрезок, прове¬
денный, как правило, перпендикулярно плоскости кривой через точку ее пересече¬
ния с диаметром (слово сторона здесь употребляется в том смысле, что это сторона
прямоугольника, составленного из latus rectum и latus transversum). Его длина равна
хорде, проходящей через фокус параллельно касательной к этой точке. Если диа¬
метр является осью, то половина этой хорды называется сейчас параметром. В этом
случае latus rectum равен удвоенному параметру. Latus rectum - важнейший эле¬
мент в геометрии Аполлония, поскольку умножая его на абсциссу параболы полу¬
чаем квадрат ординаты. В алгебраической формулировке у2 = 2рх. Для гиперболы и
2 0 Ь2 2
эллипса, у‘ = 2рх ±—х где второе слагаемое - избыток, или недостаток. Отсюда
а
и древнегреческие названия этих кривых. В тех случаях, когда важна только длина
latus rectum, его можно, разумеется, проводить так, как это удобно.
Поскольку в русскоязычной литературе повсеместно используется бессмыслен¬
ный перевод прямая сторона, мы, чтобы не путать читателя, оставили в дословном
66
•ж
»I«

2 О терминологии Аполлония
переводе именно этот термин. М. Шаль писал, что первоначальное название отрез¬
ка было latus erectum, которое потом заменили на latus rectum, а затем на параметр
¡23, с. 18]. Такого же мнения придерживался и Мордухай — Бол говской (оба без ссы¬
лок на источник информации). Между тем уже в первом переводе на латынь (Мем)
и далее (Коммандино, Галлей) написано именно rectum. И только в примечании к
(I, 12) Галлей пишет: «...или, вернее, erectum».
Latus transversum (лат.), rcXayta nXcvpä (древнегр.), сторона поперечная, сторона,
лежащая накрест, или diametrum transversum — диаметр, ограниченный с двух сто¬
рон коническим сечением.
Эйдос (clSog) - обычно прямоугольник, сторонами которого являются latus rectum
и latus transversum. Но это слово наряду с тетрсгушуод может означать у Аполлония и
просто какой-то прямоугольник, или даже, как в (1, 41), параллелограмм. В пере¬
воде мы используем его только для обозначения прямоугольника Lr х Lt. Слово эй¬
дос первоначально означало облик, наружность, но потом приобрело и другие зна¬
чения: форма, красота, идея1 и т.д. В латинских текстах его переводят как фигура,
но, по нашему мнению, в качестве термина эйдос подходит лучше, поскольку сло¬
во фигура давно уже стало русским и имеет много разных значений.
Интересно замечание Б.А. Розенфельда, что Аполлоний, возможно, вкладывал в
это понятие философский смысл, аналогичный понятию идеи у Платона [18, с. 55],
ведь эйдос однозначно определяет гиперболу и эллипс и как бы является идеей со¬
ответствующей кривой. Но как тогда быть с параболой? Эйдоса у нее нет, и получа¬
ется, что сама парабола есть, а ее идеи — нет.
эн
•Tu
<ГС
ЛЖ
Кирбятьев С. В.
и ЭЙДОС.
67

ДРЕВНЕГРЕЧЕСКИЙ АЛФАВИТ
ро
сигма
тау
хи
эта
омикрон
пси
тэта
омега
Оо
Пл
00,3
ипсилон
Буква
| Название
Буква
Название
Буква
|	А а
альфа
Н
йота
рр
вр
бета
Кк
каппа
2а~
гамма
АА
ламбда
(лямбда) 1
'	т7~
Д5
дельта
Мр
мю(ми)
У и
Ее
эпсилон
N V	1
ню (ни)
Фф
I гс
дзета
[I]
КСИ
Хх
Тш
£2 (О
Ни
Название
фи
СВОЙСТВА ПРОПОРЦИИ
Если
а___с
Ь (Г
то, очевидно,
1)^
с
Ь
2>° *
а
с
. 3)
С
э
4)-^_
а±Ь с+(1
5)
а+Ь
а-Ь
а+Ь _с±(]
Ь ~сГ
с+<1
6>
С~(1
а а ±с
Ь Ь±с1 '
68

АПОЛЛОНИИ ПЕРГСКИИ
КОНИЧЕСКИЕ
СЕЧЕНИЯ
КНИГА I
ПИСЬМО К ЕВДЕМУ
«Аполлоний приветствует Евдема.
в и все прочее
рошо. Я так¬
же вполне здравствую.
Когда я посетил тебя в Пергаме, я заметил, что ты хочешь познакомиться с напи¬
санными мной “Коническими сечениями’’. Поэтому посылаю тебе эту первую кни¬
гу в исправленном виде; остальные я отправлю, когда сам буду ими доволен. Ведь
ты, конечно, должен помнить, что я тебе сказал о причине, заставившей меня при¬
няться за сочинение этих книг, а именно о желании, выраженном геометром На-
вкратом, когда он гостил у меня в Александрии, и о том, что, поскольку он торопил¬
ся отплыть, я как можно скорее написал этот труд в восьми книгах так, как мне это
приходило в голову и передал ему без всякой отделки, имея намерение потом улуч¬
шить. Я это сделал после, когда появилось свободное время. А поскольку случилось
так, что некоторые из тех, кто бывал у меня, получили первую и (или) вторую кни¬
ги, до их переделки, то не удивляйся, если эти книги попадутся в друтой редакции.
Четыре первые из этих восьми книг посвяшены изложению начал.
Первая книга содержит способ получения трех сечений и противолежащих сече¬
ний, а также их основные свойства, изложенные более полным и более обшим спо¬
собом, чем у других писавших об этом.
Во второй книге излагаются свойства диаметров, осей сечений, асимптот и не¬
которые другие веши, полезные для диоризмов*. Из этой книги ты узнаешь, что я
•л
»1»
называю диаметрами и осями.
Третья книга содержит много замечательных теорем, полезных для построения
телесных мест и для диоризмов. Большинство этих теорем и притом наилучшие —
* О диоризмах см. ниже Примечание 1
69

Книга I
новые. Открытие их показало, что Евклид не выполнил построение места к 3 и 4 ли¬
ниям, но дал лишь построение части этого места, взятой случайным образом, и что
он даже и с ним не вполне справился, ибо не было возможности выполнить пра¬
вильное и полное построение без того нового, что найдено мною*.
В четвертой книге рассматривается, сколькими способами конические сечения
пересекаются между собой и с окружностью круга. Эта книга содержит также то, что
не было известно ни одному из моих предшественников, а именно: во скольких точ¬
ках две противолежащие гиперболы могут пересекаться одним коническим сечени¬
ем, окружностью круга или двумя противолежащими гиперболами.
Остальные книги посвящены дальнейшему развитию теории. Первая из них [пя¬
тая] более подробно рассматривает минимумы и максимумы, вторая [шестая] - рав¬
ные и подобные конические сечения, третья [седьмая] рассматривает диоризмы, и
четвертая [восьмая! содержит решения задач, определенные диоризмами. Если все
это издать, то читатель сам сможет судить обо всем этом.
Будь здоров!»
L©
»и
к
»г»:
Примечание ред. 1
Диоризмы - это ограничения, накладываемые на параметры, «когда спрашива¬
ют. возможно искомое или невозможно, а если возможно, то при каких условиях и
сколькими способами» [ 15, с. 184]. Далее Прокл пишет: «Всякая совершенная зада¬
ча и теорема должна содержать в себе следующие разделы: предложение, выставле¬
ние, ограничение. построение, доказательство, заключение», а затем он разъясняет
смысл каждого пункта и приводит примеры 115, с. 184-191,226-228,294-298]. Л еонт
- первый, кого упоминают в связи с диоризмами. Согласно Проклу, «Л еонт составил
Начала, более тщательные как по количеству, так и по полезности доказываемого; и
он нашел ограничения, когда искомая задача может быть разрешена и когда не мо¬
жет» [15, с. 84]. О самом же Леонте известно только то, что он был моложе Платона.
о
Л!»
»!•
•1»
•а
Примечание ред. 2
Эта задача была, по-видимому, сформулирована Евклидом и частично им реше¬
на. Но об этом решении кроме нескольких слов в предисловии Аполлония ничего
не известно. Спустя 500 лет об этой задаче рассказывает Папп в «Математическом
собрании» (нит. по: 5, с. 18-20]: «Если даны по положению три прямые, и из одной
и той же точки проведены подданным углом к этим трем прямым другие три пря¬
мые и если дано отношение прямоугольника, заключенного двумя из проведенных
прямых к квадрату третьей, то точка будет находиться на данном по положению те¬
лесном месте, т.е. на одном из трех конических сечений».
Иначе говоря, даны три прямые А, В и С, и надо найти точку Л из которой под
заданными углами проводятся к ним три прямые а, Ьнс так, что выполняется соот¬
ношение a b = к с2, где к - какое-то число. Кроме того, требуется определить кри-
•а
’ Речь идет о знаменитой задаче, в которой требуется построить геометрическое место точек
к 3 или 4 линиям Подробнее см Примечание 2
70

Письмо к Евдему
вую, которую образуют эти точки. Папп
пишет, что искомая линия представляет
собой коническое сечение. Если же ли¬
ний четыре, то соотношение будет: a b
— k-C'dy и точка по-прежнему лежит на
коническом сечении. А вот если
сти таким же образом пять или шесть
прямых, то неизвестно, на какой линии
будет лежать точка Р. А уж если пря¬
мых больше шести, то даже и соотно¬
шение нельзя будет написать, так как
«не существует ничего, что содержало
бы больше, чем три измерения». Ведь
трем сомножителям у греков соответ¬
ствует параллелепипед, а четырем - уже
ничего, поскольку /7-мерные тела, от¬
рицательные длины и прочие абстрак¬
ции они не рассматривали.
Но уже Декарт понимал, что прямых может быть сколько угодно. Папп пишет,
что эта задача полностью так и не была решена: «Однако вопрос о геометрическом
месте к трем или четырем линиям, который, по словам Аполлония по поводу его 111
книги, не был разрешен с достаточной полнотой Евклидом, не смог быть разрешен
до конца ни им самим, ни кем-либо другим. Не было даже ничего добавлено к тому,
что написал об этом Евклид».
Полное аналитическое решение для любого числа прямых было дано Декартом
в 1-й и 2-й Книгах его «Геометрии». Геометрическое решение для четырех прямых
приводит Ньютон в «Математических началах натуральной философии* (Книга I,
лемма XIX), заключая его такими словами: «В этой лемме, как видно, изложено ре¬
шение задачи древних о четырех линиях. Задача эта была предложена Евклидом,
продолжена Аполлонием, и такое решение, как приведенное выше, т.е. исполняе¬
ко
мое геометрическими сопоставлениями, а не аналитическим расчетом, и изыски¬
валось древними». Надо сказать, решение Ньютона настолько простое и короткое,
что непонятно, почему оно так и не было найдено древними греками.
Сейчас эту задачу редко где увидишь, но вот, например, М. Шаль считал ее ос¬
новополагающей в теории конических сечений:
«Эта задача, получившая со времени Декарта название задача Паппа, уже испытала
на себе глубину соображения Евклида и Аполлония. Они решили ее только для трех
и четырех прямых и нашли, что в этом случае искомое геометрическое место есть ко¬
ническое сечение; отсюда проистекает следующее общее свойство этих кривых: если
в коническое сечение вписан какой-нибудь четырехугольник, то произведение рас¬
стояний каждой точки кривой от двух про
тивоположных сторон находится в посто-
янном отношении к произведению расстояний той же точки от двух других сторон.
Ньютон дал чисто геометрическое доказательство этой прекрасной теоремы и с
выгодою употреблял ее в Principia mathematica philosophiae naturalis. Сочинения о ко¬
нических сечениях, появившиеся вскоре после этого знаменитого сочинения Ньюто-
71

Книга!
•I«
•Г»
на. заимствовали из него эту теорему, но не извлекли из нее всех приложений, к ко¬
торым она способна; позднее она как бы совершенно исчезла из теории конических
сечений. А между тем. по нашему мнению, она представляет самое общее и плодо¬
витое свойство этих кривых. Достаточно сказать, что из нее, как прямые следствия,
проистекают следующие теоремы: известный мистический шестиугольник Паскаля,
теорема Дезаргаоб инволюции шести точек; постоянное отношение между произве¬
дением ординат и произведением отрезков главной оси; прекрасная теорема Нью¬
тона об органическом образовании конических сечений; наконец, еше одна теоре¬
ма. основывающаяся на понятии об ангармоническом отношении, из которой про¬
истекает множество свойств конических сечений. Кстати, прибавим здесь, что эта
последняя теорема обладает сама по себе такой общностью и так просто доказыва¬
ется a prion, что мы предполагаем принять ее за основное предложение теории ко¬
нических сечений» [23, с. 41,42].
»1«
ОПРЕДЕЛЕНИЯ I
1.	Если от некой точки к окружности круга, не
лежащего в той же самой плоскости, что и точка,
проведена прямая, причем она проведена в беско¬
нечность в обе стороны. и при неподвижности этой
точки данная прямая, двигаясь по окружности кру¬
га. вернется в свое изначальное положение, то по¬
верхность, описанную этой прямой и составленную
из двух поверхностей, имеющих общую вершину, я
называю конической поверхностью, а неподвижную
точку - ее вершиной, прямую же, проводимую че¬
рез точку и середину круга, - осью (рис. 1).
2.	Конусом я называю фигуру, ограниченную кру¬
гом и находящуюся между вершиной и окружностью
крута конической поверхностью, вершиной конуса
- точку, которая является также вершиной поверх¬
ности, осью конуса - проводимую от вершины к се¬
редине круга прямую, основанием - круг.
3.	Прямыми конусами я называю такие, кото¬
рые имеют оси, перпендикулярные основаниям, а
наклонными - конусы, оси которых не перпенди-
рис. 1
м
кулярны основаниям.
4.	Диаметром любой плоской кривой линии я называю прямую, которая все
хорды данной линии, проведенные как параллельные какой-либо прямой, рас¬
секает пополам (рис. 2)*; а вершиной кривой линии я называю предел диаметра
' Предполагается, хотя это требует доказательства, что середины всех параллельных хорд ле¬
жат на одной прямой Доказано это будет в Предложении 7.
72

Определения I
на кривой линии*; каждая же из этих парал¬
лельных прямых сопряжена с определенным
диаметром**.
5.	Схожим образом и поперечным диаме¬
тром двух кривых линий***, лежаших в одной
плоскости, я называю прямую, которая, рассе¬
кая две эти линии, делит пополам все секущие
каждой из них, проведенные параллельно ка¬
кой-либо прямой (рис. 3).Вершинами же кри¬
вых линий я называю пределы диаметров, рас¬
положенных на данных кривых линиях. А так¬
о
же я называю диаметром прямую, проведенную
междудвух кривых линий, не пересекая их, ко¬
торая рассекает пополам все прямые, параллель¬
ные какой-либо
прямой и отсеченные кривы¬
ми; каждая из этих прямых сопряжена с диа¬
метром (рис. 4).
6.	Сопряженными диаметрами одной или двух кривых линий я называю прямые,
каждая из которых является диаметром и рассекает прямые, параллельные друго¬
му, пополам (рис. 5 и 6).
7.	Осью же одной или двух кривых линий я называю диаметр, который пересе¬
кает ординаты под прямым углом.
*	То есть вершиной Аполлоний считает, в отличие от того, что мы под этим понимаем сейчас,
любую точку кривой, что, собственно, делает излишним этот термин
** Так сказали бы сейчас. У Аполлония же сказано не сопряжена, а тгтггуцЛ'ох; - надлежащим
образом [упорядочена], а по-латыни - огб1па|1гп. Отсюда и нынешняя ордината Аполлоний назы¬
вает также ординатой касательную, проведенную через точку пересечения диаметра и кривой. Аб¬
сциссами же у него служат отрезки диаметров. Абсцисса (лат.) - отделенный (отрезок]
*	* * бшцетрод тгХаугод (древнегреч.), сНап^гит [гапыегаит (лат) Две кривые линии - это, оче¬
видно, противолежащие ветви гиперболы.
73

Книга I
•а
8.	Сопряженными осями одной или двух
кривых линий я называю сопряженн ые ди¬
аметры, которые пересекают прямые, па¬
раллельные другому диаметру под прямым
углом,
ж
И



1
11
1.	Если от некой точки к окружности кру¬
га. не лежащего в той же самой плоскости, 1по
и точка, проведена прямая, причем она про¬
ведена в бесконечность в обе стороны, и при
неподвижности этой точки данная прямая,
двигаясь по окружности круга, вернется в свое
изначальное положение, то поверхность, опи¬
санную этой прямой и составленную из двух
поверхностей, имеющих общую вершину, я
называю конической поверхностью.
2.	А неподвижную точку я называю ее
вершиной.
3.	Прямую же, проводимую через точку
и середину круга, я называю осью.
4.	Конусом я называю фигуру, ограниченную кругом и находящейся между вер¬
шиной и окружностью круга конической поверхностью.
5.	А вершиной конуса я называю точку, которая является также вершиной по¬
верхности.
6.	Осью конуса я называю проводимую от вершины к середине круга прямую.
7.	Основанием я называю крут.
8.	Прямыми конусами я называю такие, которые имеют оси, перпендикуляр¬
ные основаниям.
9.	Наклонными я называю конусы, оси которых не перпендикулярны основаниям.
* Полная картина должна быть как на рис. 7. но о длине сопряженного диаметра будет ска¬
зано только в Определениях II, а о сопряженных гиперболах - в последнем Предложении Книги I

Предложения
10.	Диаметром любой плоской кривой линии я называю прямую, которая все
хорды данной линии, проведенные как параллельные какой-либо прямой, рассе¬
кает пополам.
11.	Вершиной кривой линии я называю предел диаметра на кривой линии.
12.	Каждая же из этих параллельных прямых проведена упорядоченно к диаметру.
13.	Схожим образом и поперечным диаметром двух кривых линий, лежащих в
одной плоскости, я называю прямую, которая, рассекая две эти линии, делит по¬
полам все секущие каждой из них, проведенные параллельно какой-либо прямой.
14.	Вершинами же кривых линий я называю пределы диаметров, расположен¬
ных на данных кривых линиях.
15.	А также я называю диаметром прямую, проведенную между двумя линиями,
которая рассекает пополам все прямые, параллельные какой-либо прямой и отсе¬
ченные кривыми.
16.	Каждая из этих прямых проведена упорядоченно к диамезру.
17.	Сопряженными диаметрами одной или двух кривых линий я называю пря¬
мые, каждая из которых является диаметром и рассекает прямые, параллельные дру¬
гому, пополам.
18.	Осью же одной или двух кривых линий я называю диаметр, который пересе¬
кает ординаты под прямым углом.
19.	Сопряженными осями одной или двух кривых линий я называю сопряженные
диаметры, которые пересекают прямые, параллельные другому под прямым углом.
ПРЕДЛОЖЕНИЯ
Предложение 1. Прямая, соединяющая вершину
конуса с любой точкой конической поверхности, ле¬
жит на ней
Прямые, проведенные от вершины конической по¬
верхности к ее точкам, находятся в поверхности.
Пусть точка А - вершина конической поверхно¬
сти, на которой взята некоторая точка В, и их сое¬
диняет прямая АГВ. Я утверждаю, что АГВ нахо¬
дится в поверхности.
Допустим, что это не так и пусть ДЕ будет пря¬
мой, описывающей поверхность, а ЕЯ - кругом, по
которо
му проходит ДЕ. Если при сохранении точ¬
ки А прямая ДЕ проводится по окружности круга
ЕЯ, то она пройдет и через точку В, и две прямые
будут иметь те же самые пределы.
Итак, невозможно, чтобы прямая, соединяю¬
щая А и В, не находилась в поверхности. Следова¬
тельно, она находится в поверхности.

Книга I
Добавление
Также очевидно, что, если от вершины к некоторой точке из тех, которые нахо
дятся внутри поверхности, проводится прямая, то она будет попадать внутрь кони
ческой поверхности, а если она проведена к некоторой точке из тех, которые нахо
дятся вне поверхности, то она будет находиться вне поверхности.
Предложение 2. Прямая, соединяющая две любые точки конической поверхности
кроме вершины, лежит внутри конической поверхности, а ее продолжения — вне
Если на любой из конических поверхностей, со¬
единяющихся в вершине, взять две точки и прове¬
сти через них прямую, не проходящую через вер¬
шину, то эта прямая окажется внутри поверх¬
ности, а продолженная дальше, окажется вне ее.
Пусть А - вершина конической поверхно¬
сти, а ВГ - круг, через который проводится
описывающая поверхность прямая. На кони¬
ческой поверхности возьмем две точки Л и Е,
и пусть соединяющая их прямая ДЕ не прохо¬
дит через точку А.
В этом случае я утверждаю, что прямая ДЕ
окажется внутри поверхности, а прямая, про¬
веденная дальше, - вне поверхности.
Проведем и продолжим далее прямые АЕ и
АД. пересекающие окружность круга в точках
В и Г. Соединяющий эти точки отрезок ВГ ле-
жит внутри круга и, как следствие, внутри ко¬
нической поверхности. Возьмем на отрезке ДЕ
некоторую точку' X и проведем прямую А2, ко¬
торая пересечет прямую ВГ в точке Н, ибо она
принадлежит той же плоскости. А поскольку
Н лежит внутри конической поверхности, то
и АН будет находиться внутри нее, равно как
и точка ¿(1,1 Добавление). Сходным образом
может быть доказано, что все точки отрезка ДЕ
лежат внутри конической поверхности, ибо вся
прямая ДЕ находится внутри нее.
Пусть отрезок ДЕ будет продолжен до неко¬
торой точки 0. Тогда я утверждаю, что его про¬
должение находится вне конической поверх¬
ности Предположим, что это не так и некото¬
рая его часть Е0 находится внутри конической
А
2. рис. 1а
2. Р“с-
76

Предложения
я»
поверхности. Тогда, если мы проведем прямую
через точки А и 0, то она будет либо касаться
окружности круга, либо проходить через неко¬
торую точку, лежащую внутри него. Однако это
невозможно, ибо она пересечет прямую В Г в
точке К, лежащей вне его. Следовательно, Е0
лежит вне конической поверхности. Таким об¬
разом, ДЕ лежит внутри конической поверхно¬
сти, а ее продолжения — вне ее.
2. рис. 1с
Предложение 3. Сечение конуса плоскостью,
проходящей через вершину, есть треугольник
Если конус рассекается плоскостью. про¬
ходящей через вершину, то сечением являет -
ся треугольник.
Пусть дан конус с вершиной в точке А и
основанием ВГ, который рассекается неко¬
торой плоскостью, проходящей через точ¬
ку А и пересекающейся с поверхностью ко¬
нуса по линиям АВ и АГ, а с основанием по
прямой В Г.
В этом случае я утверждаю, что АВГ есть
треугольник.
Поскольку линии, соединяющие верши¬
ну А с точками В и Г, образуют пересечение
А
3. рис. 1
секущей плоскости и конической по¬
верхности и принадлежат им обеим, то они есть прямые*. Но и ВГ — прямая, а по¬
тому АВГ есть треугольник.
Таким образом, если конус рассекается плоскостью через вершину, сечением бу¬
дет треугольник.
Предложение 4. Сечение конуса плоскостью, параллельной основанию, есть круг
Если любая из двух поверхностей, которые соединяются в вершине, рассекается ка¬
кой-либо плоскостью, параллельной окружности, по которой движется описывающая
поверхность прямая, то плоскость, внутри поверхности, будет кругом, с центром на
оси, а фигура, заключенная между этим кругом и вершиной, есть конус.
‘ Но это как раз и надо доказать.
77

Книга I
Пусть конус с вершиной в точке А и лежа¬
щим в основании кругом ВГ. пересекается не¬
которой плоскостью. параллельной основанию,
по линии АЕ. Я утверждаю, что эта линия есть
круг с центром на оси.
Пусть Т - центр круга ВГ Проведем прямую
К1 Она является осью (Опр I, I) и пересека¬
ется с секущей плоскостью в точке Н Прове¬
дем через Аг плоскость. Тогда ее сечением бу¬
дет треугольник АВГ (1. 3) А поскольку точки
А, Н и Е находятся и в секущей плоскости, и в
плоскости АВГ, то АН Е является прямой. Возь¬
мем на кривой АЕ некоторую точку 0 и прове¬
дем и про
должим дальше прямую АО Она пере¬
сечется с окружностью ВГ в точке К. Проведем
прямые НО и 7К А поскольку две параллель¬
ные плоскости АЕ и ВГ рассекаются плоскостью
АВГ.тоДЕи ВГпараллельны(ЕвклидХЕ 16). По
той же самой причине параллельны Н0 и 7.К.
Тогда ® = 2Г =
АН НД НЕ Н0
А™ как/В гг = /К. топ Нд = НЕ = Н0
Схожим образом мы покажем, что все прямые
■	• “=
4. рис. 1с
78

Предложения
Следовательно, линия ДЕ есть круг, имеющий центр на оси.
И очевидно, что фигура, ограниченная кругом ДЕ и конической поверхностью,
которая лежит при вершине в точке А, будет конусом.
Одновременно этим доказано, что общим сечением, плоскости и треугольника,
проходящего через ось, будет диаметр круга.
Предложение 5. Другое сечение, дающее круг и называемое противоположным
А
5. рис. 1
Если наклонный конус делится плоскостью,
проходящей через ось и перпендикулярной осно¬
ванию, а перпендикулярно ей другой плоскостью,
отделяющей при вершине треугольник, подобный
осевому треугольнику, но расположенный проти¬
воположным образом, то сечением второй пло¬
скости будет круг, а само такое сечение назовем
прот ивоположн ьш.
Пусть наклонный конус с вершиной в точ¬
ке А и основанием ВГ пересечен двумя взаим¬
но перпендикулярными плоскостями, из кото¬
рых первая, перпендикулярная его основанию,
проходит через ось конуса, образуя в пересече¬
нии с ним треугольник А В Г. а вторая отсекает
от него подобный, но расположенный противо¬
положным образом треугольник АКН, так что 7
АКН = 7 АВ Г. И пусть она образует на поверх¬
ности линию Н0К.
В этом случае, я утверждаю, что линия Н0К
•1»
Н
5. Рис. 2. Вид со стороны
сечения НО К
есть окружность.
Проведем от некоторых точек 0 и Л, лежа¬
щих на линиях Н0К и ВАГ, перпендикуляры 07
и ЛЕ к плоскости треугольника АВГ, которые
попадут на
что 70 параллельна МЛ. Проведем через точ¬
ку 7 прямую Л7Е, параллельную В Г. А так как
и 70 параллельна ЛМ. то плоскость, содержа¬
щая прямые 70 и ДЕ. будет параллельна осно¬
ванию конуса (Евклид XI, 15), а посему ее пере¬
сечение с конической поверхностью есть круг с
диаметром ДЕ (I. 4).
Следовательно (Евклид VI, 8), Л7-7Е = 702.
А поскольку ДЕ и В Г параллельны, то угол
АДЕ равен углу АВГ, углы же АКН и АВГ рав¬
ны по построению. Следовательно, угол АКН
•ж
79

Книга I
А
равен углу АДЕ, а углы Д2Н и Е2К равны как
вертикальные. Поэтому треугольник Д7Н по-
7Е zн
добен треугольнику Е7К и 	=	, отку-
ЯК 7А
да Д7 7Е = 7К-7Н.
Однако, поскольку Д7 7Е = 702, то спра¬
ведливо и К7-7Н = 7©2.
Сходным образом мы можем доказать, что
квадрат каждого из перпендикуляров, опушен¬
ных от линии Н0К на прямую НК равен произ¬
ведению отрезков, на которые они ее разбивают.
Следовательно, сечение наклонного конуса
второй плоскостью есть круг с диаметром Н К*.
5. Рис. 3. Сечение плоскостью АВ Г
Предложение 6. Отрезки между точками
конической поверхности, параллельные от¬
резкам, перпендикулярным основанию осе¬
вой плоскости, делятся ею пополам
Если конус делится плоскостью, проходя¬
щей через ось, и от некоторой точки, лежа¬
щей на поверхности конуса, но не принадле¬
жащей стороне треугольника, содержащего
ось, проводится прямая, параллельная отрез¬
ку, перпендикулярному основанию треуголь¬
ника, то она пересечется с этим треуголь¬
ником, а продолженная дальше до конической
поверхности, будет разбиваться им пополам.
Пусть дан конус с вершиной А и осно¬
ванием ВГ, тогда его общее сечение с пло¬
скостью, проходящей через ось есть треу¬
гольник АВЕ Если теперь от произвольной
точки окружности М, лежащей в основа¬
нии, провести отрезок МЧ перпендикуляр¬
ный диаметру ВГ, а от точки Д, лежащей на
6. Рис. 1а
* Таким образом, существует два способа рассечения конуса, дающие подобные ему кониче¬
ские сечения (в нашем случае АНК и АЛЕ)
80

Предложения
поверхности конуса, но не принадлежащем
сторонам треугольника, проведен отрезок
ДЕ параллельно отрезку ММ, то я утверж¬
даю, что этот отрезок ДЕ, будучи продол¬
жен, пересечется с плоскостью треугольника
АВГ, а продолженный далее до второго пе¬
ресечения с поверхностью конуса, разбива¬
ется на две равные части этой плоскостью.
Проведем прямую АД, которая пересе¬
чет окружность круга ВМГ в точке К, от
которой проведем отрезок К0Л перпенди¬
кулярно к ВЕ Тогда, если провести отре¬
зок А0, то поскольку в треугольнике А0К
ДЕ параллельна К0, то ДЕ, проведенная
г
л
Е
6. Рис. 1с
дальше, пересекается с А0. Однако АО на¬
ходится в плоскости треугольника АВЕ Сле¬
довательно, ДЕ пересекается с плоскостью
треугольника АВЕ Поэтому она и пересе¬
кается с А0 в некоторой точке 7 и, будучи
проведена дальше, встретится с поверхно¬
стью конуса в точке Н.
Я утверждаю, что \7 = 7Н.
Точки А, Н и Л расположены на поверх¬
ности конуса и одновременно в плоскости,
проведенной через А0, АК, ДН и КА, кото¬
рая является треугольником (I, 3). Поэто¬
му точки А, Н и Л находятся на общем се¬
чении поверхности конуса и треугольника.
Следовательно, линия, проведенная через А, Н и А, является
треугольнике АДК параллельно основанию КА проведен отрезок АН, то
ОЛ
Но отрезок КА перпендикулярен диаметру круга В Г. значит, К0 = 0А.
Следовательно, дг = 7Н.
О
прямой. А поскольку в
к© дг
гн
81

Книга I
Предложение 7. Диаметр и ординаты конического сечения
Ест конус пересекается с плоскостью,
проходящей через ось и со второй плоскостью,
пересекающей основание конуса по прямой,
перпендикулярной основанию треугольника,
содержащего ось, или его продолжению, то
принадлежащие второй плоскости прямые,
параллельные перпендикулярной прямой, бу¬
дут попадать в общее сечение секущей пло¬
скости и треугольника, расположенного на
оси, а проведенные дальше вплоть до другой
части сечения, будут рассекаться общим се¬
чением на две равные части.
Если конус является прямым, то прямая,
расположенная в основании, будет перпенди¬
кулярной общему сечению секущей плоскости
и треугольника, расположенного на оси, а если
конус наклонный, то она не всегда будет пер¬
пендикулярной, но только в том случае, ест
плоскость, проведенная через ось, перпенди¬
кулярна основанию конуса
Пусть дан конус с вершиной в точке А и
основанием ВГ. пересекающийся с плоско¬
стью АВ Г. проходящей через его ось, и с дру¬
гой плоскостью, пересекающей основание
ВГ по прямой ЛЕ, ему перпендикулярной, и
образующей коническое сечение ХХЕ. Об¬
щим сечением этой плоскости и треугольни¬
ка АВГ является 7.Н И пусть от некоторой
точки 0, принадлежащей сечению Л2Е, про¬
веден параллельно прямой ЛЕ отрезок 0К.
Я утверждаю, что он пересечется с ¿Н. а
проведенный дальше до другой части сече¬
ния AZE. будет рассекаться на две равные
части прямой ZH*.
Поскольку'АН перпендикулярна ВГ, то
•ж
прямая 0К, проведенная параллельно АН,
пересекается с треугольником АВГ, а прове¬
денная дальше до другой части поверхности,
рассекается на две равные части треугольни¬
ком АВГ ( 1,6). А поскольку прямая, 0К пере-
7. Рис. 1
А
7. Рис. 2.
* Следовательно, 2Н-диаметр конического сечения, а 0М-ордината (см сноску 2 к Опр 1Л)-
82

Предложения
секается с треугольником А
и находится
в плоскости сечения А7Е, то, следователь-
но, она попадает в общее сечение секущей
плоскости и треугольника АВГ. Общим се¬
чением плоскостей является 7Н.
Итак, прямая, про
веденная через О па¬
раллельно прямой ДЕ, пересекает 7Н. А
веденная дальше до другой части сече¬
ния А7Е, она рассекается на две равные ча¬
сти прямой 7Н.
Возможны три случая: или конус явля¬
ется прямым, или треугольник АВГ, распо¬
ложенный на оси, перпендикулярен кругу
ВГ, или ни то ни другое. Пусть прежде все¬
го конус будет прямым (рис. 2). Поэтому и
треугольник АВГ будет перпендикулярен
кругу В Г. А поскольку прямая АЕ прово¬
дится перпендикулярно диаметру ВГ — об¬
щему их сечению, то АЕ перпендикулярна
и треугольнику АВГ, а значит, она перпендикулярна всем прямым, расположенным
на треугольнике АВГ. Следовательно, она также перпендикулярна 7Н.
Пусть конус будет не прямым (рис. За и 36). Если треугольник, расположенный
на оси, перпендикулярен кругу ВГ, то мы схожим
разом покажем, что АЕ перпен¬
дикулярна 7Н.
И пусть треугольник АВГ, лежащий на оси, не будет перпендикулярен кругу ВГ
(рис. 1). Я утверждаю, что и АЕ не перпендикулярна 7Н. Допустим, что последнее не-
верно. Но тогда ДЕ перпендику¬
лярна одновременно В Г и 7Н,
А	7. Рис. ЗЬ
а значит, она перпендикуляр¬
на плоскости, содержащей ВГ и
7Н. Однако плоскостью прямых
В Г и Н7 является АВГ. Следова
тельно, АЕ перпендикулярна тре-
угольнику АВГ. Поэтому также
все плоскости
»г*
веденные че¬
рез нее, перпендикулярны треу¬
гольнику АВГ. Но одной из пло-
скостей, проведенных через ДЕ,
является круг В Г. По этой при¬
чине круг ВГ перпендикулярен
треугольнику АВГ. А это проти¬
•Ж
воречит гипотезе.
Следовательно, ДЕ не пер¬
пендикулярна 7Н.
, п
83

Книга I
Добавление
Отсюда ясно, что прямая ¿Н есть диаметр сечения дгЕ, ибо она разбивает на две
равные части отрезки прямых, лежащих внутри сечения и параллельные некоторой
прямой АЕ, причем они могут быть и не перпендикулярны ¿Н.
Предзожение 8. Условие того, что коническое сечение простирается в бесконечность
А
Ес ш конус пересекается с некоторой пло¬
скостью, проходящей через ось, образуя тре-
угольник, и с плоскостью, пересекающей ос¬
нование конуса по прямой, перпендикулярной
основанию этого треугольника, а диаметр
конического сечения или параллелен одной из
сторон треугольника, или пересекается с ней,
вне вершины конуса и если поверхность кону¬
са и секущая плоскость, продолжаются до
бесконечности, то и коническое сечение про¬
должается до бесконечности, тогда как се-
кущие, параиельные основанию конуса, от¬
деляют на диаметре отрезки любой наперед
заданной величины.
Пусть конус с вершиной А и основани¬
ем ВГ пересекается плоскостью, проходя¬
щей через ось, образуя треугольник АВГ,
и другой плоскостью, пересекающей круг
ВГ по прямой АЕ, перпендикулярной В Г,
и образующей такое сечение Л2Е, что его
диаметр ¿Н или параллелен прямой АГ.
8. Рис. I
или пересекается с ней вне точки А.
Тогда, я утверждаю, что если поверхность конуса и секущая плоскость продолжа¬
ются до бесконечности, то и сечение А2Е продолжается до бесконечности.
Продолжим поверхность конуса и секущую его плоскость, в результате чего про¬
должатся и прямые АВ, АГ и 7Н А поскольку гн или параллельна АГ или пере¬
секается с ее продолжением за точкой А, то они никогда не пересекутся. Пусть 7Н
продолжена до некоторой точки© Проведем отрезок КОЛ параллельно ВГ и M0N
- параллельно ЛЕ Тогда плоскость, содержащая отрезки КА и MN, параллельна
плоскости, содержащий отрезки ВГ и ЛЕ. Следовательно, плоскость KAMN, ле¬
жащая внутри конуса, есть круг (1,4). А так как точки Д, Е, М и N лежат в секущей
плоскости, они также лежат на поверхности конуса. Но поверхность конуса продол¬
жена до круга KAMN вместе с секущей плоскостью, значит, и сечение AZE продол¬
жено до точек Ми V Таким же образом мы докажем, что и сечение MAZEN увели¬
чивается до бесконечности, если поверхность конуса и секущая плоскость прово¬
дятся до бесконечности.
84

Предложения
И ясно, что можно отделять на диаметре сечения от точки Ъ отрезки любой на¬
перед заданной величины. Пусть, например, равна данному отрезку. Проведем
через Е прямую параллельную ЛЕ. Она будет встречаться с сечением в точках М и
N так же, как и прямая, проведенная через точку О, будет пересекаться с сечением
в точках М и N. Следовательно, некоторая прямая, пересекающая сечение, прово¬
дится параллельно ЛЕ и отделяет на диаметре любой заданный отрезок от точки И*.
Предложение 9. Если сечение конуса не противоположное и не параллельно осно
ванию, то оно не окружность
•I»
Если конус рассекается плоскостью, пересекающейся с каждой из двух сто¬
рон треугольника, содержащего ось, но не параллельной основанию и не являющейся
противоположной**, то сечение не будет окружностью.
Пусть конус с вершиной А и основанием ВГ пересечен некоторой плоскостью,
ему не параллельной и образующей сечение ЛКЕ. В этом случае я утверждаю, что
ЛКЕ не будет кругом.
Предположим, что это не так. Пусть указанная плоскость пересекается с плоско¬
стью, содержащей основание конуса по линии ZH, из точки 0, являющейся центром
круга ВГ, проведем отрезок 0Н, перпендикулярный ZH, а через него и через ось -
плоскость, пересекающую коническую поверхность по прямым АВ и АГ. Посколь¬
ку точки Л, Е и Н лежат в плоскости, образу¬
ющей сечение ЛКЕЛ, и в плоскости, образу¬
ющей треугольник А В Г, то они находятся на
пересечении плоскостей.
Следовательно, линия НЕД является пря¬
мой. Тогда, если через некоторую точку’ К.
лежащую на сечении ЛКЕ, провести отрезок
КЛ, параллельный ZH, то он будет разделен
на две равные части точкой М (I, 7), из чего
следует, что ДЕ есть диаметр круга ЛКЕЛ (I, 7
Добавление), ведь мы предположили, что это
* Возможно, Аполлоний хотел сказать, что диаметр, как и сечение, продолжается до беско
вечности.
** См (1,5).

Книга I
круг. Проведем параллельно ВГ прямую NME. Тогда плоскость прямых N2 и КА
параллельна плоскости прямых ВГ и гн, т.е. основанию, а сечением ее будет круг
ИКЕА (1,4). А поскольку гн перпендикулярна ВН.то и КА перпендикулярна №.
Следовател ьно, N М • М
Однако и АМ МЕ = КМ2, ибо мы предположили, что сечение АКЕЛ есть окруж-
км2.
:
NM ME
ность с диаметром АЕ. Следовательно, NM-ME = AM М Е и —77 = 77“ .
AM Mr.
Откуда мы заключаем, что треугольники AMN и EME подобны, а углы ANM и
МЕЕ равны Но угол ANM равен углу АВГ, ибо NE параллельна прямой ВГ. Поэто¬
му уголАВГ равен углу МЕЕ, и следовательно, сечение АКЕЛ является противопо¬
ложным (I, 5), что противоречит условию. Следовательно, линия АКЕЛ не являет¬
ся окружностью.
•I»:
Предложение 10. Конические сечения являются выпуклыми кривыми
Если на коническом сечении лежат две точ¬
ки, то отрезок, их соединяющий, лежит вну¬
три сечения, а его продолжения - вне.
А
IJL
Пусть дан конус с вершиной А, основани¬
ем ВГ, пересекаемый плоскостью, проходящей
через ось. по треугольнику АВГ. и другой пло¬
скостью, образующей сечение АЕ2, на кото¬
ром лежат две точки Н и 0. Тогда я утверж¬
даю, что отрезок, соединяющий эти точки,
будет лежать внутри сечения АЕ7. а его про¬
должения - вне.
Если конус с вершиной А и основанием
ВГ пересекается плоскостью, проходящей че¬
рез ось, а также проводится прямая через точ¬
ки Н и 0, лежащие на его поверхности, но не
принадлежащие одной стороне треугольника
АВГ, то отрезок, их соединяющий, не прохо¬
дит через точку А, а потому он лежит внутри
конуса, а проведенный далее - нет (1,2). По¬
этому в первом случае он попадает в сечение
А2Е. а во втором - нет.
10. Рис. 1
•Л
Предложение 11. Определение и уравнение параболы. Latus rectum
Если конус пересекается с плоскостью, содержащей ось, образуя треугольник, и со
второй плоскостью, пересекающей основание конуса по прямой, перпендикулярной ос¬
нованию треугольника, и если диаметр сечения параллелен одной из сторон треуголь-
86

Предложения
ника, то квадрат любой ординаты, параллельной общему сечению секущей плоскости
и основания конуса, равен площади прямоугольника*, ограниченного отрезком, отде¬
ленным ординатой на диаметре сечения и другим некоторым отрезком, который име¬
ет отношение к части стороны треугольника, расположенной между вершиной конуса
и сечением, равное отношению квадрата на основании треугольника, к прямоугольни¬
ку, ограниченному остальными двумя сторонами этого же треугольника.
Назовем такое сечение параболой.
Пусть конус с вершиной А и основа¬
нием В Г пересекается плоскостью, про¬
ходящей через ось, образуя в сечении тре¬
угольник АВ Г, и второй плоскостью, пе¬
ресекающей основание конуса по прямой
ДЕ, перпендикулярной ВГ, образуя на по¬
верхности конуса сечение дгЕ, диаметр
которого ¿Н параллелен АГ, и от точки 7
проведен отрезок ¿0, перпендикулярный
2© ВГ2
диаметру гн, такой, что	=	, а
А/ АВ АГ
на сечении взята некоторая произвольная
точка К, через которую проведена ордина¬
та КА. параллельная ДЕ. Тогда я утверждаю,
что КЛ2 = Z0•ЛZ.
Проведем через точку Л отрезок ММ,
параллельный В Г. А поскольку КА парал¬
лельна ДЕ, то плоскость, содержащая от¬
резки КА и ММ параллельна плоскости, со¬
держащей отрезки ВГ и ДЕ, т.е. основанию
1 1. Рис. 1
конуса. Поэтому плоскость прямых КА и MN есть круг с диаметром MN ( 1,4). А КА
перпендикулярна MN, посколькуДЕ перпендикулярна ВГ. Поэтому КА2 = MA-AN.
Z0 ВГ2 ВГ2 ВГ ВГ
А поскольку	=	и	=

' AZ АВ-АГ AB AT АВ АГ
Z0 ВГ ВГ
то и	=	.
AZ АГ АВ
ВГ MN МЛ
Однако, так как	=	=

АГ AN KL
ВГ _ MN _ МЛ _ AN
АВ ~ AM ~ ZM ~ AZ ’
то,следова-
Z0 МЛ AN
тельно,	=

AZ AZ AZ
, или
Z0 МЛ-AN
AZ AZ-AZ
*
Аполлоний всегда пишет, равен прямоугольнику, треугольники равны, подразумевая равен¬
ство площадей. То же самое и у Евклида. В дальнейшем, мы будем придерживаться современной
терминологии, не оговаривая это специально.
** МЫ МЛ МИ-МЛ
(свойство пропорции № 6).
AM ZM
AM -ZM AZ
87

Книга I
Z0 Z0AZ	МЛ-AN Z0AZ
С другой стороны, — = - -- --, а значит,	_ - _"	.
AZ AZ AZ	AZ • AZ	AZ • AZ
Отсюда MA-AN = Z0 AZ, однако, как нам уже известно, КА2 = MA AN, поэто¬
му КА2 = Z0AZ.
Назовем такое сечение параболой, а отрезок Z0 - отвесной стороной секущих,
упорядоченно проведенных к диаметру ZH, [ ôpôia rcÀEupà (древнегр.), latus rectum
(лат.) - прямостоящая сторона, отвесная сторона]*.
комментарий ред.
Предложения 11-13 являются ключевыми, так как в них даны и определения
трех конических сечений и вывод их уравнений.
Еще в Определениях Аполлоний ввел, по сути, косоугольную систему координат.
При этом за ось абсцисс принимается какой-нибудь диаметр, а за ось ординат - ка¬
сательная к кривой в точке ее пересечения с диаметром. В Предложении 11 Апол¬
лоний дает определение параболы и выводит ее уравнение КА2 = Z0 AZ . Конечно,
Аполлоний никаких уравнений не писал (и в переводах Коммандино или Галлея их
тоже еше нет). Он говорит не об умножении Z0 на AZ, а о прямоугольнике 0ZA,
равновеликом квадрату КА. (Аполлоний, как и другие античные математики того
времени, употреблял слово умножение только по отношению к целым числам)**.
Словом парабола (napaßoXii) - приложение) называлось приведение площадей к
одному основанию для их сравнения. В данном случае площади КА2 приводятся к
latus rectum Это позволяет для любой абсциссы ZA геометрически найти ордина¬
ту; а значит, построить параболу. Построим квадрат, равновеликий прямоугольнику
0ZA Для этого опишем вокруг отрезка ZA
+ Z0 окружность, тогда перпендикуляр ZК
будет равен ординате КА (рис. 2). Так мож¬
но построить параболу, если ординаты пер¬
пендикулярны диаметру, то есть если ди¬
аметр является осью В произвольном же
случае необходимо знать еще и угол меж¬
ду ординатами и диаметром. Однако, как
ни странно, как раз о построении Аполло¬
ний пока ничего не говорит. Он обратит¬
ся к этому вопросу лишь в Предложении
52 и следующих за ним, но и там речь пой¬
дет не о построении параболы, ест и задан
latus rectum, а о построении конуса, сече¬
нием которого будет эта парабола.
•It.
»I«
•I»
»I»
HE
Ж
SUS
* В русскоязычной литературе обычно переводится как двойной параметр, или не имеющим
смысла выражением прямая сторона. В дальнейшем, мы будем употреблять этот термин в латин¬
ском варианте без перевода
** Что понимали греки под умножением см Евклид VII, Опр. 16.
88
О

Предложения
Предшественники и совре¬
менники Аполлония (Менехм,
Аристей, Евклид, Архимед) назы¬
вали это сечение не «парабола», а
^сечение прямоугольного конуса»*.
Дело в том, что до Аполлония рас¬
сматривали частный случай - се¬
чение прямого конуса плоско¬
стью, перпендикулярной обра¬
зующей. Если угол при вершине
конуса был прямым, то, очевид¬
но, получалась парабола (рис. 3).
Поскольку Аполлоний рассма¬
тривал не только прямые, но и на¬
клонные конусы с произвольным
углом при вершине, то прежнее
LÖfi
та
наименование уже не подходило.
А
7 7. Рис. 3
Рассмотрим теперь подробнее множитель Z0 или latus rectum (обозначим его Lr),
являющийся у Аполлония одним из важнейших параметров:
Для сечения прямоугольного конуса Ьг в точке 7 равен 2AZ = 27ГЧ, что легко дока-
г© вг2
зать с помощью рис. 2 и уравнения	=	.
К7 АВ ■ АГ
Архимед называл параметрр. равный половине Ьг ^прямая, проведенная до оси»
|1,с. 25].
Ьг у Аполлония определяется через атрибуты конуса. Но какой он имеет смысл,
если коническое сечение рассматривать само по себе, безотносительно к конусу?
Как известно, каноническое уравнение параболы у2 — 2рх, где р — параметр, рав¬
ный половине хорды, проведенной через точку фокуса перпендикулярно оси. Он
равен двойному фокусному расстоянию. Сравним каноническое уравнение с урав¬
нением КА2 = 70 Л2 . Ясно, что Ьг — это отрезок, равный фокальной хорде, или 4Е
Но уравнение, полученное Аполлонием, справедливо не только для оси, айв об¬
щем случае, когда ординаты образуют с диаметром некоторый угол а. Оказывает¬
ся , что и тогда Ьг равен фокальной хорде, параллельной касательной в точке пере¬
сечения кривой и диаметра.
Для доказательства напишем уравнение параболы в косоугольных координатах
Х'О’У* и тем самым найдем значение параметра р\ а затем покажем, что длина фо¬
кальной хорды равна 2р’.
Пусть диаметр пересекает параболу в точке у^, тогда ось О’У’является ка-
эта
сательной, уравнение которой У
—(х+х0)
Уо
•It
• •
* У Архимеда один раз встречается слово парабола и один раз эллипс, но, скорее всего, они
вставлены переписчиками.
89

Книга I
Подставив в уравнение параболы у =у0 + y’sina ;
х =Ху+х’ + y'cosa получим (у(( + y’sina)2 = 2р(х0 + х’ + У соях). Раскроем скобки и
приведем подобные члены:
y'4m2a+2y'(y0sina-pcosa) = 2px' + (2px0 ~Уо) •
Учитывая, что выражения в
скобках равны нулю, получа¬
ем уравнение параболы в косо¬
угольных координатах:
4—х = 2pY
sur a
Очевидно, что AB = -^-
cosa
где Ах - проекция АВ на ось ОХ’.
Уравнение же фокальной хор¬
ды, поскольку она параллельна
касательной ОУ', будет таким:
J=z(x.f)=4_^
V М 2)'
Найдем Дх. Для этого приравняем выражения для параболы и хорды
\2	: Г '	2
• Л
=2рх и.учитывая,что= 2рх0. получим х2 ~(р + 4хо)х + -^- = 0
yt2=l
-2
.»»I«
%
Т р
- Х~ —
УоА 2 7
Р
..2
Тогда	*i 2-^4х0 + 2Рхо 2
__ sin а _ р
В свою очередь, так как	~, то
LU л La.	Va
1
cosa ~ y0sina ’ а значиг’
/о
АВ=—?—2у
Л sm a
2р
sin a
7 2р
а + 1=-7-Г“
sin а'
№ в " • а.	ч ж I
Итак. АВ-—— ~^Р ,а следовательно, latus rectum равен длине фокальной
sin а
хорды, параллельной ординате.
•2
Предложение 12. Определение и уравнение гиперболы
Если плоскость проходит через ось конуса, образуя треугольник, а другая плоскость
пересекает основание конуса по прямой, перпендикулярной основанию треугольника, и
ёиаметр полученного сечения пересекает одну из сторон указанного треугольника вне
90

Предложения
вершины конуса, то квадрат ординаты,
опущенной на диаметр из любой точки
сечения, равен сумме площади прямоу¬
гольника, ограниченного отрезком, от¬
деленным ординатой от диаметра се¬
чения и другим некоторым отрезком,
и площади прямоугольника, подобного
прямоугольнику, одна сторона которого
есть latus rectum, а другая — часть диа¬
метра сечения, расположенная вне ко¬
нической поверхности.
кт
Назовем такое сечение гиперболой *.1
Пусть конус с вершиной А пересе¬
кается с плоскостью.
В
ходящей че-
рез ось и их пересечением является тре¬
угольник АВГ, а вторая плоскость, пе¬
ресекает основание конуса по прямой
ДЕ, перпендикулярной основанию ВГ
треугольника и образует коническое
сечение Д7Е. Его диаметр 7Н, будучи
продолжен, пересекается с продолже¬
нием стороны АГ вне вершины кону¬
са в точке И. Проведем параллельно
7Н прямую А£, которая пересечется
с В Г, а перпендикулярно 7Н отрезок
70, такой, что справедлива пропорция
zn AS2
Z0 ~ BE-ЯГ
Если теперь из некоторой точки К, лежащей на сечении, опустить на диаметр
ординату КА, параллельную ДЕ, провести отрезок АРЕ, параллельный ¿О, и отре¬
зок О0Е, а также отрезки 0Р и ЕП, параллельные то я утверждаю, что КА2 рав¬
но площади прямоугольника 7Е.
Этот прямоугольник составлен из двух, один из которых получен приложением
70 к 7А, а второй подобен прямоугольнику 70-70.
Пусть через точку Л параллельно В Г проведен отрезок ММ Так как КА парал¬
лелен прямой ДЕ, то плоскость, содержащая отрезки КА и ММ параллельна пло¬
скости, содержащей отрезки ДЕ и ВГ, т.е. основанию конуса. Следовательно, пло¬
скость, содержащая отрезки КА и ММ пересечет конус по кругу с диаметром ММ
(1,4), которому отрезок КА перпендикулярен.
•Ж
* илсрРоХп - избыток. То есть речь, очевидно, пойдет о сечении, квадрат ординаты которого ра¬
вен прямоугольнику 1_г плюс еще что-то Аполлоний называет гиперболой, как это было принято
тогда, одну ветвь, а обе - про
тиволежащими сечениями, или просто противолежащими
91

Книга!
va2 — МЛ * AN.
Поэтому КЛ - мл
*у2 AS AS
АтаккакF° Z0 BS ST
AS ZH ZA AS _OH _ QA
Однако BS _ BH ” MA " Sr НГ AN
ZÖ.ZÄ.ßA
Следовательно, ZQ " MA AN
ПЛ ZA-OA
an~ma-an
ZQÍ1A ZA-Í2A
В силу чего— = 7
Z0 Л
QA ZA QA ZA-НА _ ZA QA
,T0 ZA-ЛЕ _ MA-AN '
MAAN.
ZA
НоЙХ
МЛ-AN
А поскольку — = ——”
ЛЕ ZAA
Отсюда следует, что ZA AS
Следовательно, так как MA AN = КА2, то КА2 = ZAAE.
Однако ZA-AH = S(ZE).
Следовательно, квадрат отрезка КЛ равен площади прямоугольника ZE, состав¬
ленного из прямоугольника, имеющего своими сторонами прямые Z0 и ZA и пря¬
моугольника 0Н, подобного прямоугольнику Q0*.
Назовем такое сечение гиперболой, отрезок Z0 - отвесной стороной секущих
упорядоченно проведенных к диаметру ZH [latus rectum), a ZQ - поперечной сторо¬
ной [шута (древнегр.), latus transversum (лат.), она же diametrum transversum (Опр. 1,5)|.
Комментарий ред.
Предшественники и современ¬
ники Аполлония называли гипер¬
болу »сечение тупоугольного кону¬
са» При этом плоскость, как и в
случае с параболой. пересекала ко-
нус перпендикулярно одной из об¬
разующих (рис .2).
Из уравнения
ZQ AZ2
Z0 ВЕ7Г
дует что в точке Z для сечения ту-
ТоестъК\'=20 \2+0П или в современной записи, если начало координат совладает с
вершиной ’■итерболы / = 2рх+/дхд Второе слагаемое и является «избытком».
92

Предложения
поугольного конуса Lr = 2ZN —
1KL • tga. Это верно также и для
эллипса, а у параболы tga = I.
Приведем еще один спо¬
соб нахождения Lr, по-
видимому. оставшийся не¬
известным древнегреческим
математикам. Отложим на
оси конуса отрезок АТ = AZ
(рис. 3) и рассечем конус пло¬
скостями, проходящими через
точки Т и Z параллельно осно¬
ванию. Проведем в этих плоскостях отрезок ZX и параллельно ему ТУ. Очевидно,
что ТУ = АТ • tga. А так как АТ = AZ, то TY = AZ • tga. Следовательно, Lr = 2TY, то
есть latus rectum равен диаметру круга, проведенного параллельно основанию конуса на
расстоянии от вершины, равном KL. В общем виде, то есть для произвольного кону¬
са и для любого конического сечения, эта теорема была доказана Я. Бернулли (см.
Приложение 3).
•к
Выясним, как и в про
шлый раз, какой смысл имеют Z0 (Lr) и новая величина ZQ
Ш). Пусть сначала диаметр является осью. Возьмем каноническое уравнение гипер¬
болы и, поскольку у Аполлония начало координат лежит при вершине гиперболы,
Ь Г,	3	7	2	2Ь2 Ь2 2
то есть сдвинуто вправо на а, имеем у = — Л\х + а) -а , откуда у =	х + —х.
а	'	а а
Сравним полученное уравнение с уравнением Аполлония КА2 = Z0 • КТ + 0П • А2
1Ъ~
Ясно, что г© или Lг равняется	, а учитывая, что из подобия треугольников
а
Z0Q и Р0—
У У	У -у*
0П =— лz , то есть 0П =	ЛZ, имеем КА2 =ЬгЛ2 + — лг2.
гп	и	ы
Следовательно, Lt = 1а. А так как у гиперболы длина фокальной хорды, прове-
1Ъ2
денной перпендикулярно к оси, равна	, то Lr — это отрезок, равный Фокальной
а
хорде. Очевидно также, что Lt — это расстояние между ветвями гиперболы.
А если взять произвольный диаметр? Как и в случае с параболой, возьмем урав-
2 Ь ( 2	2 \
нение гиперболы у = — (х -а ) и перейдем к косоугольной системе к
а х '
У- Уо+х'sinp + y'sina х = х0 +x'cosp + ycosa(pnc. 4).
Опуская элементарные, но довольно-таки длинные преобразования, получим
93

Найдем теперь длину фокальной хорды. Ее уравнение, поскольку она параллель-
на касательной OY, будет таким: У =
2 (я-с), где с = OF = у/а2 + Ь2. Как
а
шлый раз, найдем Ах и АВ =
Уо
Снова опустим длинные преобразова-
cosa •
ния и напишем конечный результат: АВ = —•
a
< > 2
^222
2~ Х0 + Х0 ~ &
J-
Следовательно,
а ■ АВ , а АВ ,2
~T~X+~2drX ’тоесть’^ =
а • АВ
~d~
Lt = 2d.
В предельном случае, когда ¿ = аих0 = сц имеем. Ьг = АВ =
и Lt = 2а.
94

Предложения
Предложение 13. Определение и уравнение эллипса
Если конус рассекается плоскостью через ось и другой плоскостью, пересекающей
обе стороны осевого треугольника, но ни параллельно основанию конуса, ни противопо¬
ложным образом*, и если плоскость основания конуса и секущая плоскость пересека¬
ются по прямой, перпендикулярной основанию осевого треугольника или его продолже¬
нию, то квадрат прямой, опущенной на диаметр из любой точки конического сечения
параллельно общему сечению плоскостей, равен площади прямоугольника, ограниченно¬
го некоторым отрезком и отрезком диаметра между основанием ординаты и вершиной
сечения, уменьшенной на площадь прямоугольника, подобного прямоугольнику, состав¬
ленному из ука занного отрезка и диаметра сечения.
Такое сечение назовем эллипсом **.
Пусть конус с вершиной
А и основанием ВГ. пересе¬
кается с плоскостью, про¬
ходя шей через ось, обра¬
зуя в пересечении треу¬
гольник А В Г, и со второй
плоскостью, пересекающей
обе стороны осе
гольника, но ни параллель¬
но основанию конуса, ни
противоположным обра¬
зом. На поверхности конуса
она создаст линию с диаме¬
тром 7.С1. А обшим сечени¬
ем секущей плоскости и той
плоскости, в которой нахо¬
дится основание конуса, бу¬
дет прямая ДТ. перпендику¬
лярная В Г.
Проведем от точки А
прямую АЕ, параллель¬
ную диаметру ¿О, а от точки £ отрезок 70, перпендикулярный £Г1, такой, что
13. Рис. 1. Пересечение плоскостей по линии Д Т
•ж
•ж
•ж
•ж
•ж
7.0 _ А£2
г®~В2ЕГ
Возьмем на сечении некоторую точку К и проведем к диаметру прямую КА, па¬
раллельную ДТ. В этом случае, я утверждаю, что квадрат КА равен площади пря-
* см. (1,5)
** еХХец/ц - недостаток, нехватка. То есть сечение, квадрат ординаты которого равен прило¬
жению минус еще что-то
95

Книга I
öS
моугольника, ограниченного £& и /А, уменьшенной на площадь прямоугольника
П0РЕ, подобного прямоугольнику • 70 .
Пусть будут проведены отрезок 00, и отрезок АЕР параллельный ¿0, а также от¬
резки 0Р и НП, параллельные IX, и через точку А - отрезок МЬ1, параллельный ВГ.
Тогда, поскольку МИ параллелен ВГ, а КА параллелен АТ, то плоскость, содержащая
отрезки МЫ и КА, параллельна плоскости, содержащей ВГ и ДТ(Евклид XI, 15), т.е.
основанию конуса, и образует сечение, представляющее собой окружность с диаме¬
тром М1Ч (1,4). Так как КА - перпендикуляр к МЬ1, то КА2 = МА • ЛИ .
АХ2 АХ АХ
Поскольку	=	‘77^ а из подобных треугольников следует
ВЕ-ЕГ ВЕ ЕГ
АХ2 АХ АХ АХ _ ОН _ ПЛ	ZQ ZA ОЛ
ВХ ХГ_ВХ XT , ХГ ~ НГ _ AN ,Т0 Z0 ‘ AM AN
ZA ПЛ ZA QA
Атак как—~, то поскольку треугольники QZ0 и QAE подоб-
ЛМ AN AM "AN
ZQ ZA QA QA
Z0 ЛМ • AN ЛЕ
QA
ZA QA
ZAQA
ZAQA
Но
=	, поэтому
— 	 -----
АЕ
ZAAE
AM-AN
ZAAE
следова¬
тельно, AM • AN = ZA • AE.
А так как KA2 = MA • AN, то KA2 = ZA•AE.
Следовательно, квадрат ординаты, опущенном на ди¬
аметр из любой точки сечения, равен площади прямоу¬
гольника, образованного отрезками Z0 и ZA за вычетом
плошади прямоугольника ПЕР0, подобного прямоуголь¬
нику ZQ • Z0*. Назовем такое сечение эллипсом, Z0
- latus rectum, a ZQ - latus transversum.
13. Рис. 2
’ То есть КЛ2 - И0 • \2 - 0ГI • Х2, или в современной записи, если начало координат совпадает
с вершиной эллипса / = 2рх 0 (цх)х Вычитаемое и является «недостатком».
96

Предложения
13. Рис. 3
Коммензарий ред.
Предшественники и современни¬
ки Аполлония называли эллине се¬
чением остроугольного конуса (рис.
3). Как и в предыдущем случае, Ьг =
27М = 2А7ч$и, а также верна теорема
Я. Бернулли.
Выясним, какой смысл имеют г©
(Бг) и (Ы). Возьмем канониче¬
ское уравнение эллипса и, посколь¬
ку у Аполлония начало координат ле¬
жит у вершины, то есть сдвинуто вле¬
во на а, получим у = —у1а2-(х-а)' ,
2	2Ь2 Ь2 2
откуда у =	х—-х .
а а~
Сравним полученное уравнение с уравнением Аполлония КА2 = =	- 0П«Л7.
Ясно, что, как и в предыдущем случае, Ьг =
, и = 2а, где а — большая полу¬
ось эллипса, а Ь - малая. А так как у эллипса длина
ля
перпендикулярно к оси, равна
1Ь2
	, то Ьг - это отрезок, рав-
ный фокальной хорде.
Если же диаметр произволь¬
ный. то все преобразования ана¬
логичны тем, что имели место
в случае гиперболы, за исклю¬
чением знаков. Уравнение эл¬
липса в косоугольных коорди¬
натах (рис. 4) будет иметь сле¬
дующий вид:
I
кальной хорды, проведенной
I
где г = Лх2 + у2 - радиус эллипса.
97

Книга!
Длина фокальной хорды, параллельной касательной в точке пересечения кривой
и диаметра равна АВ--
а
,2 а АВ , а-АВ
, следовательно, у 		х	г- • х
г	2г
а AB	Lr а-АВ
Итак. Lr =	, а поскольку — = —т-, то Lt = 2r.ü предельном случае, ког-
r	' Lt 2г
2Ь2
да г = а и х° = а, имеем Lr = АВ = — и Lt-2a .
а
Представим полученные результаты в виде двух таблиц
Таблииа / Диаметр является осью конического сечения
Парабола
Гипербола
Эллипс
Уравнение
/ = Lr-x
/ = Lr • x + Lr/Lt
y^Lr-x- (Lr/Lt )-x*
Длина фокальной хорды
4F
2tí/a
2&/a
Laïus rectum
4F
2tí/a
2tr7a
Latus transversum
—
2a
2a
Таблица 2. Произвольный диаметр
Парабола
Гипербола
Эллипс
Уравнение
/ = Lr*x
f=Lfx +Lf/Lt
К = Lr‘X -(Lr/Lt )•)/
Длина фокальной хорды (AB)
4F/sin!a
2(b> , , Л
Latus rectum
4F/sjd'u
d
, a AB
Lr =

r
1 Latus transversum
**
2d
2r
Предложение 14. Определение и основное свойство противолежащих сечений
Если конические поверхности, расположенные при вершине, рассекаются плоско¬
стью, не проходящей через вершину, то на каждой из поверхностей образуются сече¬
ния, называемые гиперболами, у которых будет общий диаметр, общий latus transversum
и равные latus rectum ординат, проведенных к диаметру параллельно прямой, лежащей
в основании конуса.
Г
Назовем такие сечения противолежащими*.
Пусть дана коническая поверхность с вершиной в точке А, пересеченная пло-
скостью, не п
ходящей через вершину и образующей сечения AEZ и H0K. В этом
* Здесь впервые в истории геометрии рассматривается вторая ветвь гиперболы.
98

Предложения
случае я утверждаю, что каждое из
этих сечений является гиперболой.
Пусть дан круг BArZ, через ко- „
торый проведена прямая, описы- “
ваюшая коническую поверхность,
а за вершиной проведена парал¬
лельная ему плоскость, сечение
которой с конической поверхно¬
стью образует круг ЕНО К (I, 4).
Общими сечениями Н0К, ZEA
и кругов являются отрезки ZA и
НК. Они будут параллельны (Ев¬
клид XI, 16). Осью конической по¬
верхности является прямая AAY, а
центры кругов — Л и Y. Проведем
через точку Л диаметр ВГ, перпен¬
дикулярный ZA, и пересечем конус
плоскостью, проходящей через В Г
и ось, которая пересечет круги по
параллельным огрезкам ОЕ и ВГ, а
коническую поверхностью по пря¬
мым BAO и ГАЕ. Тогда по постро¬
ению ЕО будет перпендикулярна
НК, поскольку В Г перпендикуляр¬
на ZA, и они, соответственно, па¬
раллельны, а так как точки М, Е,
0 и N лежат в плоскости, прове¬
денной через ось, и в плоскости,
образовавшей сечение, линия ME0N
ййе
ЙЕ
•1Е
•I».
ЙЕ
Г
А
и
* \
является прямой. И ясно, что четверки точек
Е, 0, А, Г и В, Е, А, О лежат на двух прямых BAO и ГАЕ, ибо они принадлежат ко¬
нической поверхности и плоскости, проведенной через ось.
Проведем отточек© и Еотрезки 0Р и ЕП. перпендикулярные прямой ©Е, а че¬
рез вершину А проведем прямую ЕТ, параллельную прямой ME0N.
0Е	АЕ2 0Е АТ2
Пусть окажется, что	=	,	=	.
ЕП ВЕ ЕГ 0Р ЕТТО
Л поскольку конус с основанием ВГ рассекается плоскостью через ось, образуя
треугольник А В Г, и другой плоскостью, пересекающей основание конуса по прямой
AZ, перпендикулярной ВГ и образующей на поверхности конуса сечение AEZ, а пря¬
мая МЕ пересекается вне вершины конуса со стороной треугольника, содержащего
ось, и так как через точку А была проведена АЕ параллельная диаметру сечения ЕМ,
0Е АЕ2
а от точки Е была проведена ЕП, перпендикулярная ЕМ такая, что		 =	,
ЕП ВЕ • ЕГ
1ЙЕ
»I»
ЙЕ
»I»
99

Книга I
то, следовательно, сечение AEZ есть гипербола, для которой ЕП есть latus rectum
для прямых, проведенных как ординаты к ЕМ. и 0Е есть latus transversum (1, 12). И
схожим образом, Н0К есть гипербола с диаметром 0N, 0Р - latus rectum для пря-
мых, проведенных как ординаты к 0N, а 0Р - latus transversum.
Далее, я утверждаю, что 0Р= ЕП.
Ибо, поскольку ВГ параллельна прямой ЕО, то из подобия треугольников следу-
AI АТ
ет, что —
zr
AS. АТ
ЕВ " ТО '
Однако
АХ2 АХ
ВХХГ ХГ
АХ АТ2 АТ АТ
хв " нт то " TH то
Следовательно,
АХ2 _ АТ2
ВХХГ_ТНТО'
0Е АХ2 0Е АТ2 0Е 0Е
л тлк как ЕП " ВХ • ХГ ' 0Р ’ TH ■ ТО ’ Т° ЕП " 0Р
Следовательно. ЕП = 0П.
Предложение 15. Ордината, проведенная через середину диаметра эллипса, есть со
пряженный диаметр
at
Если через центр диаметра эллипса проведена в обе стороны ордината, то квадрат
прямой, проведенной к ней из любой точки сечения параллельно диаметру, равен площади
прямоугольника, ограниченного некоторым отрезком и отрезком ординаты, отделенным
указанной прямой, уменьшенной на площадь прямоугольника, подобного прямоугольнику,
образованному ординатой и ее laïus rectum, а сама эта прямая, проведенная к ординате
и продолженная до другой части сечения, будет рассекаться ею на две равные части*.
КС
Пусть дан эллипс с диаметром АВ. и через середину диаметра Г проведена ор¬
дината к диаметру. пересекающая эллипс в точках Е и А, а отрезок А/, перпендику-
АВ АЕ
лярный к АЕ, такой что ~~ -	.
А/ АВ
Проведем через некоторую точку Н, лежащую на сечении, прямую Н0Ф, парал¬
лельную 0А. Пусть будет проведена прямая Н0, а от точки 0 проведена и продол¬
жена прямая 0А. параллельная Д2 и также от точек Т и А отрезки ¿К и АМ, парал¬
лельные 0Д.
* То есть ордината, проведенная через середину диаметра, будет сопряженным диаметром,
поскольку все хорды параллельные диаметру, она делит пополам (Опр 1,4 и 6). Соответственно,
у нее будет и свой latus rectum Чертеж во многом повторяет чертеж к Предложению 13, но ни вод¬
ном известном нам издании этого не замечают, и все изображается в одной плоскости.

Предложения
В этом случае я утверждаю, что
квадрат Н0. равен плошади пря¬
моугольника ZA0K, уменьшен¬
ной на пдошадь прямоугольника
AKZM. подобного прямоуголь¬
нику образованному ординатой
ЕД и ее latus rectum AZ.
Пусть AN есть latus rectum ор¬
динат к диаметру АВ.
П1
ведем
отрезок BN, а от точки Н - Н~,
параллельный ДЕ, и пусть через Е
и Г будут проведены ЕОУ и Г ПР,
параллельные, а через N. О и П
- NYP, ЮЕ и ПТ, параллельные
прямой АВ.
Далее, согласно (1, 13), ДР =
8(АП) и НЕ2= 8(АО)‘. А посколь-
ВА _ ВГ _ ПТ
AN ~ ГП TN
ВГ=ГА =
ТП, ГП = АТ, то АТ = TN и, сле¬
довательно, АП = ТР и ЕЕ = ТУ.
Так как 8(ТО) = 8(ОР) (Ев¬
клид I, 43) и 1У является об-
75. Рис. 1 (На чертеже latus rectum \Zуменьшен
приб.1изите.гьно в 1,5
шим. то 8(ТЕ) - Б^Е), или 8(ТУ) = 8^Е), а ТЕ является общим, поэтом) 8(ТР) =
8(АО)+8(ОП), и так как АП = ТР. то 8(АП) = 8(АО)+8(ОП).
Следовательно, 8(АП) - 8(АО) = 8(ОП).
Но, как было сказано, 8(АП) = ДГ2. 8(АО) = НЕ2, поэтому ДР - НЕ2 = 8(ОП)
= ОЕ • ЕП.
Атак как ДЕ в Г рассекается на равные части, а в 0 - на неравные, то (Евклид II,
5) ДГ2 = ©Г2 + Е0 • 0Д** и ДГ2 - НЕ2 = Е0 • 0Д.
Следовательно, Е0 • 0Д = ОЕ • ЕП .
АВ ДЕ	ДЕ ДЕ2 ДГ2
А ПОСКОЛЬКУ 	=	, ТО	=	Т- =	7 .
AZ AB	AZ АВ‘ ГВ2
ДЕ ПГ ГВ
Но ДГ = S(An) = ПГ* ГА= ПГ* ГВ, поэтомх =	,—
' AZ ГВ*
ДЕ Е0
С другой стороны, — = — .
AZ 0А
ПГ Е0 Е0-0Д ОЕ ЕП
следовательно. = =	=	-—
ГВ 0А 0А-0Д ОЕ‘
И так как Е0 • 0Д = ОЕ • ЕП , то 0А • 0Д = ОЕ2 = Н®2.
* Аполлоний, как и Евклид, обычно (но не всегда) обозначает прямоугольники двумя буквами,
значающими противолежащие вершины. Площадь мы традиционно обозначаем как Б. хотя
это и нарушает общий стиль
** ПустьЛГ=а,а *0Г = Ь Тогда данное выражение эквивалентно выражению аг = Ь +(а+Ь)(а-Ь).

Книга I
Таким образом, прямая Н0 в квадрате равна площади прямоугольника М0, которая
меньше площади ¿0 на площадь прямоугольника 7Л, подобного прямоугольнику .
Далее, я утверждаю, что Н0, проведенная дальше в другую часть сечения, рассе¬
кается на две равные части ординатой ДЕ.
Пусть она будет проведена дальше и пересечется с сечением в точке Ф, и пусть
через Ф будет проведена ФХ, параллельная прямой НЕ, а через X - ХЧ\ параллель¬
ная прямой АН А поскольку Н
НЕ2
ФХ, то также и НЕ2 = ФХ2.
ASEO,	АХ НО
, поэтому

ФХ! = АХХТ	АН Х'Р
ЕО ЕВ АХ ЕВ
Но(1,13)|
А поскольку — = —, то—77 = — и, вычитая единицу слева и справа, по-
ХТ ХВ Ал ХВ
ХЕ ХЕ
ЛУЧИМ — = —.
АЕ ХВ
Поэтому АН = XВ.
А так как АГ = ГВ, то ЕГ = ГХ.
Сзедовательно, Н0 = 0Ф.
Таким образом, НФ рассекается на две равные части ординатой ДЕ.
Предложение 16. Прямая, проведенная через середину диаметра противолежащих
параллельно ординатам к нему, есть сопряженный диаметр
Если через центр диаметра противолежащих проведена прямая, пара.иельная ор¬
динате к диаметру, то она есть диаметр противолежащих, сопряженный с первым.
102
¡6. № '

Предложения
•Л
•I»
Пусть даны противолежащие с диаметром АВ и центром Г, через который прове¬
дена прямая ЛЕ, параллельная ординатам к диаметру. Я утверждаю, что есть ди¬
аметр, сопряженный с диаметром АВ.
Пусть latus rectum противолежащих являются отрезки АЕ и BZ, и пусть будут про¬
ведены и продолжены дальше отрезки AZ и ВЕ. В одном из сечений возьмем точ¬
ку Н и проведем прямую Н0, параллельную АВ. От Н и 0 проведем ординаты Н К и
0Л, а через К и А — прямые КМ и AN, параллельные АЕ и BZ.
Тогда поскольку Н К = Л0, то Н К2 = Л02.
Нотаккак(1, 12) НК2= КМ-АН и Л02 = AN • ВЛ, то КМ • КА = AN • ВЛ .
АЕ BZ	АЕ КМ
Атак как (1, 14) АЕ = BZ. то	=	, а из подобия треугольников	=	.
АВ АВ	АВ КВ
BZ AN	KM AN
	=	, откуда	=	.
АВ ЛА ' КВ ЛА
КМ КМ КА AN AN ВЛ	КМ-КА AN-ВЛ
А поскольку	=	,	=	, то	=	и. соответ-
’ КВ	КВ-КА ЛА ЛА ВА	КВ-КА	ЛА-ВЛ
КМ-КА КВ КА
ственно,	=	. ■	. Однако ранее было доказано, что КМ • КА = ЛN • ВЛ ,
ЛN ВЛ ЛА • ВЛ
поэтому К В • КА = ЛА • ВЛ .
Следовательно. КА = ВЛ*. А так как АГ = ГВ, то КГ = ГЛ.
Следовательно, НЕ = Е0.
Таким образом, отрезок Н0 разбивается на две равные части отрезком ЕГЛ и па¬
раллелен прямой АВ. Следовательно (Опр. I, 6), ЕГД есть диаметр, сопряженный с
диаметром АВ.
* Пусть КА-а, В\ = Ь, АВ-с. Тогда (а +с)а =(Ь+с)Ь. Следовательно. а2-£г-с(Ь~а). что возмож¬
но только в случае, если а = Ь
103

Книга I
ОПРЕДЕЛЕНИЯ II
1. Серединная точка диа¬
метра на гиперболе и эллипсе
пусть называется центром се¬
чения, а прямая, проведенная
от центра к сечению, - его ра¬
диусом.
2. Схожим
разом и се¬
рединная точка на противо¬
лежащих пусть называется
центром*.
3. Прямую же, проходя¬
щую через центр параллельно
ординатам к диаметру, имею¬
щую серединное отношение
сторон эйдоса и разбиваемую
центром на две равные части,
Определения II. Рис. 1 (ЬГ—
сопряженный диаметр)
назовем вторым [сопряжен¬
ным! диаметром**.
Предложение 17. Прямая, проведен¬
ная через вершину параллельно ордина¬
те, лежит вне сечения (то есть является
касательной)
Если через вершину конического сечения
проводится прямая, параллельная некото¬
рой ординате, то она лежит вне сечения.
'л
Пусть дано сечение конуса с диаме¬
тром АВ. Я утверждаю, что прямая, про¬
веденная через вершину А, параллельно
ординате, лежит вне сечения.
* Тогда надо доказать, что центры всех диаметров совпадают В (1,47 и 48) будет доказано об¬
ратное положение, что любая прямая, проведенная через центр, есть диаметр.
" Определение сопряженного диаметра уже было дано в (Опр. I, 6), а то, что он параллелен
ординатам доказано в двух предыдущих Предложениях, поэтому здесь на самом деле определя¬
ется только его длина Эйдосом, как выяснится в (I, 38), Аполлоний называет прямоугольник, со¬
ставленный из ¿/и и, который определяет вид и форму конического сечения, а серединное отно¬
шение сторонэйдоса - это — = —, где О - сопряженный диаметр. Определение его длины никак
£> ¿л
не следует из предыдущего текста, и Аполлоний не дает никаких пояснений, почему длина сопря¬
женного диаметра именно такая

Предложения
Допустим, что она лежит внутри сечения как, например, АГ А поскольку в се¬
чении конуса взята некая точка Г, то прямая, проведенная от точки Г как парал¬
лельная ординате, будет пересекаться с диаметром АВ, и он будет рассекать ее на
две равные части (Опр. I, 4). Следовательно, АГ, проведенная дальше за точку А,
будет рассекаться АВ на две равные части. А это невозможно, поскольку АГ, про¬
веденная дальше, окажется вне сечения. Следовательно, прямая, проведенная че¬
рез точку А параллельно ординате, окажется вне кривой, то есть является каса¬
тельной к сечению.
Предложение 18. Прямая, проведенная параллельно касательной или секущей че¬
рез точку, лежащую внутри конического сечения, есть секущая
Прямая, проведенная параллельно касательной или секущей через точку, лежащую
внутри конического сечения, есть секущая.
•Ж
Пусть дано коническое се¬
чение и пересекающаяся с ним
прямая А/В, которая, будучи
продолженной в любую из сто¬
рон, окажется вне сечения. И
пусть через точку Г, лежащую
внутри сечения, проведена пря¬
мая ГД, параллельная АВ.
В этом случае, я утверждаю,
что ГД есть секущая.
Пусть от некоторой точки А
сечения Е проведена прямая
ЕХ. Поскольку ГД параллельна
АВ, а прямая АВ пересекается с
I
ЕХ, то, следовательно, и ГД пе¬
18. Рис. 1 и 2
ресечется с ЕХ. Если это про
зойдет между точками Е и X, то очевидно, что она пересечется с этой прямой рань¬
ше, чем с сечением, поскольку ЕХ лежит внутри сечения (I, 10); если же вне точки
Е, то она пересечется с сечением раньше, чем с ЕХ. Следовательно, ГД пересекается
с сечением в одной точке. Схожим образом мы докажем, что она пересекается с дан¬
ным коническим сечением и во второй точке. Таким образом, ГД является секущей.
Предложение 19. Прямая, проведенная параллельно касательной или секущей че¬
рез точку, лежащую внутри конического сечения, есть секущая
Прямая, проведенная внутри любого сечения параллельно ординате, пересекается с
этим сечением.
105

Книга!
Пусть дано коническое сечение и че-
рез некоторую точку В диаметра АВ
ведена прямая ВГ, параллельная ордина¬
те к диаметру.
В этом случае я утверждаю, что В Г пе¬
ресекается с этим сечением.
Пусть на сечении будет взята некая
точка А. Так как точка А также лежит
на сечении, прямая, проведенная через
\
точку А к А, будет секущей, отрезок ко-
1
й АА лежит внутри сечения (1, 10).
А поскольку прямая, проведенная через
точку А параллельно ординате к диаме¬
тру, лежит вне сечения и АА пересекает¬
ся с ним, а ВГ тоже параллельна ордина¬
те к диаметру, то ВГ пересекается с АД.
Если она пересечется с ней между точ¬
ками А и А, то она сначала пересечется
с прямой АА, а потом с сечением; если
же она пересекается с секущей вне отрез-
ка АА в некоторой точке Е, то она ранее
пересекается с сечением в точке Г. Сле¬
довательно. прямая, параллельная ор¬
динате к диаметру, проведенная от точ¬
ки В, будет пересекаться с сечением*.
Предложение 20. Квадраты ординат параболы относятся как абсциссы
Ес.т из двух точек параболы провести ординаты к диаметру, то квадраты их д шн
будут относиться так же, как расстояния от вершины, отделенные ими на диаметре.
Пусть дана парабола с диаметром АВ. на которой взяты некие точки Г и А, и
пусть от них проведены ординаты ГЕ
и Аг. В этом случае я утверждаю, что
A2?=ZA
ГЕ2 ’ ЕА
Пусть АН есть latus rectum. Тогда
(I.ll) AZ2 = AH*ZA, ГЕ2 = АН-ЕА.
AZ2 AHZA
Следовательно. —г=	.
ГЕ' АН ЕА
’ Можно доказать проще прямая ВГ параллельна ординате, а значит, и касательной. Следова¬
тельно, она пересекается с сечением (1,18)
17

Предложения
АН ZA ZA
анеа’еа'
AZ2 ZA
Таким образом,	у =	.
ГЕ2 ЕА
Предложение 21. Отношения квадратов ординат к абсциссам и другим отрезкам ди¬
аметра у гиперболы и эллипса
Если на гиперболе, эллипсе ши окруж¬
ности круга* проведены прямые как орди¬
наты к диаметру, то квадрат ординаты
так относится к площади прямоугольни¬
ка, образованного отрезками диаметра
от основания ординаты до вершины се¬
чения и от основания ординаты до кон¬
ца диаметра, как latus rectum относит¬
ся к latus transversum, а квадраты орди¬
нат относятся между собой так же, как
площади прямоугольников, стороны кото¬
рых есть указанные отрезки диаметра.
21. Рис. I
* Аполлоний постоянно использует эту формулировку, хотя ясно, что все, доказанное для эл¬
липса, верно в частном случае и для круга Дело в том, что прямые и круги греки относили к пло¬
ским геометрическим местам, а конические сечения - к телесным, поскольку они получались рас¬
сечением тела. То есть круг и коническое сечение относились как бы к разным разрядам [ 18, с. 32.
94]. Подробнее см, отрывок из М Шаля в конце данного Предложения В дальнейшем в подобных
случаях мы не будем упоминать про круг.
Пусть дана гипербола или эллипс с
диаметром AB, latus rectum АГ, и про¬
ведены ординаты к диаметру АЕ и ZH.
В этом случае я утверждаю, что
ZH2 _ АГ ZH2 _ АН НВ
АННВ ~ АВ " ДЕ2 “ АЕ ЕВ '
Проведем и продолжим В Г, а через
точки Е и Н проведем отрезки EG и НК,
параллельные АГ. Тогда (1, 12 и 13) ZH2
= АН • КН, АЕ2 = АЕ • 0Е.
АГ КН АН КН
А поскольку 	=	=	,
АВ НВ АН НВ
ZH2 АГ
107

Книга I
И таким же образом,
ДЕ2 _АГ
ЛЕЕВ АВ
Поэтому
гн2 _ ле2
АН НВ-ЛЕЕВ
Откуда
гн2 _ аннв
ДЕ2 “ ЛЕ ЕВ
О геометрических местах (М. Шаль)
♦ Местом в геометрии называется последовательность точек, из которых каждая
решает предложенную задачу, или каждая обладает известным свойством, не при¬
надлежащим никакой точке, взятой вне этого места. Древние подразделяли геоме¬
трические места на различные роды. Они называли прямую линию и круг плоски¬
ми местами, потому что их прямо чертили на плоскости; телесными местами назы¬
вались конические сечения, потому что они получались на теле (конус); наконец,
линейными местами назывались все кривые высших порядков, как конхоиды, цис¬
соиды, спирали и квадратриксы» [23, с. 4).
Предложение 22. Прямая, соединяющая две точки параболы или гиперболы, пере¬
сечется с диаметром
о
Если прямая, пересекается с параболой ши гиперболой в двух точках и не пересекается
с диаметром внутри сечения, то, будучи продолжена, она пересечется с ним вне сечения.
Пусть даны парабола или гипербола с ди¬
аметром АВ и соединяющий принадлежа¬
щие им точки Г и Д отрезок прямой. В этом
случае я утверждаю, что отрезок ГД, будучи
продолжен, пересекается с диаметром АВ
вне сечения.
Пусть от точек Г и Д, принадлежащих па¬
раболе. проведены две ординаты ГЕ и ДВ.
»1»
»1»
•I»
ГЕ2 АЕ
В этом случае (1.20) —у = —- и АЕ >АВ.
ДВ- АВ
Поэтому ГЕ > ДВ, а
Г
ме того, они яв¬
ляются параллельными, следовательно, от¬
резок ГД, будучи продолжен, пересечется с
диаметром АВ вне сечения.
108

Предложения
22. Рис. 2. Гипербола
Пусть от точек Г и А, принадлежа¬
щих гиперболе, проведены две парад-
дельные ординаты ГЕ и АН. Посколь-
ГЕ2	АЕ • ЕВ
кунагиперболе(1,21)1й? = ^п^,
то ГЕ2 >АН2, и, кроме того, они явля¬
ются параллельными, следовательно,
отрезок ГА, будучи продолжен, пере¬
сечется с диаметром АВ вне сечения.
Предложение 23. Прямая, соединяющая две точки эллипса между сопряженными
диаметрами, пересечется с ними вне сечения
Если прямая пересекает эллипс в
двух точках дуги, заключенной меж¬
ду двумя диаметрами, то она пере¬
секает эти диаметры вне эллипса *.
Пусть дан эллипс с диаметрами
АВ и ГА и прямая Е7, пересекающая
его в точках дуги, заключенной меж¬
ду этими диаметрами. В этом случае
я утверждаю, что Е7, проведенная
дальше, пересекает диаметры АВ и
ГА вне сечения.
Проведем от точек Е и 7 к ди¬
аметру АВ ординаты ЕН и 70, а
к диаметру АГ — ординаты ЕК и
ЕН2 АН НВ
г©2” леев ’
7А, тогда (I. 21)
гл2 _ ДА-АГ
ЕК2 “ ДККГ '
* Очевидно, что теорема верна только для сопряженных диаметров, а иначе, если угол между
ними невелик, можно провести секущую параллельно одному из диаметров (рис. 2). Сопряжен¬
ный же диаметр будет в этом случае с ней пересекаться, следовательно, условие теоремы не вы¬
полняется.
109

Книга I
Но (Евклид II, 5) АН • НВ > А© • ©В, поскольку Н ближе к центру эллипса, чем
0 и аналогично ДА • АГ > АК • КГ.
Поэтому и ЕН2 > г©2, гл2 > ЕК2.
При этом ЕН параллельна прямой г©, а 7Л параллельна прямой ЕК. Следова¬
тельно, Е2 пересечется с диаметрами АВ и ГА вне сечения**.
Предложение 24. Касательная к параболе или гиперболе пересекается с диаметром
Есш прямая имеет с параболой или гиперболой одну общую точку и лежит вне сече-
ния, то она пересекается с диаметром этой кривой.
Пусть даны парабола или гипербола, имеющие с прямой ГЕ, лежащей вне сече¬
ния. одну общую точку Л.
В этом случае я утверждаю, что касательная ГЕ пересекается с диаметр
24. Рис. 2а, 2Ь. Гипербола
“ Имеется в виду, что ордината ЕН параллельна и диаметру АГ, а поскольку 2Е пересекает две
параллельные прямые, то она пересечет и третью, причем вне эллипса, так как продолжение 2Е
за точку Е находится уже вне его
ПО

Предложения
i«.
Пусть на сечении будет взята некая точка 7. и проведена прямая Эта прямая
пересечется с диаметром сечения (I, 22). Предположим, что она пересечется с ним
в точке А, тогда ДЕ лежит между сечением и прямой 7ЛА. Поэтому касательная, бу¬
дучи продолжена, пересечется с диаметром вне сечения*.
Предложение 25. Касательная к эллипсу в точке между сопряженными диаметрами«
пересечется с их продо.тжениями
Если прямая имеет с эллипсом одну общую точку между двумя ¡сопряженными]**
диаметрами, и, будучи проведена дальше в любую из двух сторон, попадает вне сече¬
ния, то она пересечется с продолжениями этих диаметров.
Пусть дан эллипс с ¡сопряженными)
диаметрами АВ и ГД и прямая EZ, касаю¬
щаяся его в точке Н, заключенной между
ними.
этом случае я утверждаю, что EZ
пересечется с продолжениями диаметро
в.
Проведем от точки Н к АВ и ГД ор¬
динаты Н0 и НК. Поскольку НК парал¬
лельна прямой АВ, а прямая HZ пересе¬
кается с Н К, то она пересекается и с АВ.
Сходным
разом заключаем, что EZ пе¬
ресекается ис ГЛ.
/
25. Рис. 1
Предложение 26. Прямая, параллельная диаметру параболы или гиперболы, пере¬
секается с сечением только в одной точке
Прямая, параллельная диаметру параболы или гиперболы, пересекается с сечением
только в одной точке.
Пусть дана парабола с диаметром ВАГ и latus rectum АЛ, и проведена прямая EZ,
параллельная прямой АВ.
В этом случае я утверждаю,
что Ег, проведенная дальше,
пересечется с параболой толь¬
ко в одной точке.
Пусть от некоторой точки Е
параллельно ординате проведен
отрезок ЕН к диаметру. Выбе¬
рем на диаметре такую точку Г,
* Проще было провести секущую параллельно касательной. Поскольку секущая пересечется с
диаметром, то и параллельная ей касательная тоже. Это относится и к следующему Предложению.
** Очевидно, что теорема верна только для сопряженных диаметров.
111

Книга I
•I«
26. Рис. 2. Гипербола
/
что ЛА • АГ > Н Е2.
Проведем к диаметру ординату Г0, тогда (I, II)
Г02 = АЛ*АГ.
Следовательно, Г02 > ЕН2 и Г0 > ЕН, и они являются параллельными. Тогда EZ,
будучи продолжена, пересекает Г0, а потому пересекается и с параболой в некото¬
рой точке К.
Допустим, что она пересекается с параболой не только в точке К, но еще и в точ¬
ке К. Но если прямая EZ пересекает параболу в двух точках, то она пересекается с
диаметром сечения (1,22), а это невозможно, ибо мы предположили, что она парал¬
лельна диаметру. Таким образом,
EZ, будучи продолжена, пересе¬
кается с параболой только в од¬
ной точке.
Пусть теперь сечением будет
гипербола с диаметром AB, latus
rectum - АЛ, и пусть будет про¬
ведена прямая ВЛ и продолжена
дальше, а отточки Г - параллель¬
ная АЛ прямая, пересекающаяся
с ВЛ в точке М. Тогда поскольку
ГМ’АГ> АЛ-АГи (1,12) Г02 =
ГМ • АГ, а точка Г выбрана так,
чтоАЛ*АГ> ЕН2,то Г02> ЕН2.
Поэтому Г0 > ЕН и получим
то же самое, что и в случае с па¬
раболой.
Предложение 27. Если отрезок пересекается внутри параболы с диаметром, то, про¬
долженный в любую сторону, он с ней пересечется
Если отрезок, пересекается с диаметром
внутри параболы, то, будучи продолжен в лю¬
бую из сторон, он пересечется и с ней.
©
©
Пусть дана парабола с диаметром АВ, ко¬
торый пересечен в точке Д отрезком, лежа¬
щим внутри сечения.
В этом случае я утверждаю, что этот отре¬
зок, будучи продолжен в любую из двух сто¬
рон, пересечется с параболой.
Пусть от точки А проведена касательная
АЕ. Тогда отрезок или параллелен прямой
АЕ, или нет.
27. Рис. 1
Е
112

Предложения
Если он ей параллелен, то, будучи продолжен в любую из двух сторон, пересе¬
чется с параболой (I, 19).
Если же он не параллелен АЕ, то, будучи продолжен, пересечется с АЕ в неко¬
торой точке Е, а следовательно, раньше он пересечется с ветвью параболы в какой-
то точке Н.
Далее, я утверждаю, что этот отрезок НД, будучи продолжен в другую строну, так¬
же пересечется с параболой в какой-то точке Г.
Пусть AM - latus rectum, HZ - ордината к диаметру, а отрезок АВ такой, что .
Проведем отрезок ВК параллельный ординате, который пересечет НД в точке Г.
АВ АД
Тогда, поскольку АЛ2 = АВ • AZ , то	=	.
АД AZ
,	ВД АВ	ВД2 АВ2
Вычитая справа и слева единицу, получим	=	, следовательно,	у- =	у-.
AZ АД	AZ АД‘
ВД2 _ ЛВ
AZ2 ” AZ.
Однако поскольку АД- = АВ • AZ , то, подставив, получим
ВД2 ВГ2
С другой стороны, из подобия треугольников —=- =	7
AZ ZH
АВ АВ-AM	ВГ2 АВ AM
И поскольку	=	, то	г =	.
' AZ AZ AM	ZH" AZ AM
„	ВГ2 ZH2
Отсюда 	=	.
АВ AM AZ AM
АВ:АД = AA:AZ.
Однако (I, 11) ZH ’ = AZ • AM, а значит, ВГ2 = АВ • AM.
Но поскольку AM есть latus rectum, а ВГ параллельна ординате, то она тоже яв¬
ляется ординатой. Следовательно, парабола проходит через Г и НА пересекается с
сечением в точке Г.
Предложение 28. Если внутри гиперболы проведен отрезок, параллельный каса¬
тельной к противолежащему сечению, то продолженный в любую сторону, он пересе¬
чется с гиперболой
28. Рис. 1
Если через точку, лежащую
внутри гиперболы, провести пря¬
мую, параллельную касательной к
противолежащему сечению, то
эта прямая, продолженная в лю¬
бую из двух сторон, пересечется
с гиперболой.
нс
Пусть даны противолежащие
с диаметром АВ и прямая ГД, ка-
сающаяся сечения (А), а через
точку Е лежащую внутри сече¬
ния (В), проведена прямая Е£,
параллельная ГД.
113

Книга I
В этом случае я утверждаю, что EZ пересечется с сечением (В) в двух точках N и Н.
Поскольку ГА пересекается с диаметром AB (I, 24), а EZ ей параллельна, то она
тоже пересекается с диаметром в точке Н. Пусть будет выбрана такая точка 0, что
А0 = ВН.
Проведем через 0 прямую 0К, параллельную EZ, и опустим из точки К на диа¬
метр ординату' КЛ. Отложим на диаметре отрезок НМ, равный А© и проведем пря¬
мую MN, параллельную ординате КЛ.
Тогда, поскольку' КЛ параллельна прямой MN, К0 параллельна EN, а прямая ЛМ
- обшая для треугольников, то треугольники К0Л и NMH подобны, а поскольку
Л0 = НМ, то и равны, а значит, КЛ = NM и КЛ2 = NM2.
И так как А0 = ВН, Л0 = НМ и АВ общая, то ВЛ = AM.
Следовательно, ВЛ • ЛА = МА • М В,
ВАЛА АММВ
Поэтому	г- =	z—.
КЛ2 NM2
ВАЛА Lt	АММВ Lt
Атак как (1,21)	z—=—, то и ——z— = — , а значит, точка N при над-
КЛ2	Lr NM2	Lr
лежит сечению, как и точка К.
Следовательно,EZ пересекается с сечением в N. Схожим образом мы можем до¬
казать, что прямая EZ пересекается и со второй противолежащей.
Предложение 29. Если прямая, проходящая через центр противолежащих, Пересе
кает одно из сечении, то она пересекает и другое сечение
Если прямая, проходящая через центр противолежащих, пересекает одно из сече¬
ний, то она пересекает и другое сечение.
о
1Л
Пусть даны противолежащие с диаметром АВ, центром Г, и прямая ГД пересека¬
ет сечение (А).
В этом случае я утверж¬
даю, что она будет пересе¬
кать и сечение (В)*.
Опустим на диаметр ор¬
динату ДЕ, основание кото¬
рой отстоит от вершины А на
расстояние ЛЕ, отложим от
вершины В равный ему от¬
резок Вг и проведем из точ¬
ки 7 ординату ZH. Посколь¬
ку Вг -АЕ и АВ является их
обшей частью, то	и
ВЕ,АЕ = Аг*гВ.
с».
* Но это же прямо следует из (Опр.1,5) и (Опр II, 2)’
114

Предложения
де2 Ьг гн2 и де2 _ гн2
АпоСкольку(1,21)Б^ = -	= и ’10 ^71=
Но так как ВЕ•АЕ = КТ • /В, то АЕ2 = 7Н и ДЕ = ТН.
Тогда поскольку ЕГ=Г7, ЕТ — прямая, а ДЕ параллельна 7Н, то ДГН также пря¬
мая (Евклид VI, 32).
Следовательно, продолжение ДГ пересечет (В).
»ТЕ
Предложение 30. Отрезок, проведенный через центр до пересечения с эллипсом или
противолежащими, делится центром пополам
Если через центр эллип¬
са или противолежащих про¬
водится прямая, то ее отре¬
зок, заключенный между двумя
точками пересечения с эллип¬
сом или гиперболой разбивает¬
ся этим центром на две рав¬
ные части *.
с».
Пусть даны эллипс или
противолежащие с диаме¬
тром АВ и центром Г, а че¬
рез центр проведена неко¬
торая прямая ДГЕ.
В этом случае я утверж¬
даю, что ДГ = ГЕ.
Проведем ординаты Д7
и ЕН. А поскольку (I, 21)
гд2 Ьг
А22В_Ы "
НЕ2 Ьг
	= —, то
АННВ
гд2 _ не2
дг-гв " ан нв нл"
дг • гв гд2
АННВ НЕ2'
гд2 гг2
А так как	г =	г
НЕ2 НГ2
дг гв ан нв
ТО	7	=	Г

гг2 нг2
В (Опр. II, 1) ведь уже сказано, что центр сечения - это точка, разбивающая все диаметры
пополам.
115

Книга I
Отсюда следует, что*
Но так как АГ2 = ВГ2, то 2Г2 = ГН2.
Таким образом, гг = ГН, а ¿Д и НЕ являются параллельными. Следовательно,
ДГ = ГЕ (Евклид VI, 4).
Предложение 31. Если из точки на диаметре, находящейся слева от центра, прове¬
сти прямую, встречающуюся с правой ветвью гиперболы, то ее продолжение попадет
внутрь сечения.
Если через точку, лежащую на диаметре противолежащих и отстоящую от вер¬
шины одного из сечений на расстояние большее, чем половина диаметра, провести пря¬
мую, достигающую этого сечения, то продолжение прямой будет лежать внутри него.
о
Пусть дана гипербола
с диаметром АВ, центром
О, и через точку диаметра
Г, отстоящую от вершины
одного из сечений на рас¬
стояние, большее, чем по¬
ловина АВ. проведена пря¬
мая ГД к этому сечению.
В таком случае, я ут¬
верждаю, что ее продол¬
жение, будет лежать вну¬
три него.
Допустим, что прямая
ГДЕ лежит вся вне сечения,
и от ее точек Е и Д прове¬
дены ординаты ЕН и Д0.
а также предположим сначала, что АГ = ГВ.
Тогда поскольку Жг > Жг, а также, поскольку ЕН и Д0 параллельны
Д02	Д02	'	Д0' ©Г
„ гн2 АННВ НГ2 АН НВ
(1,21)—Г=	,то —Г>	.
де2 АО0В 0Г2 А0 0В
ЕН2 НГ2
* Нижеследующее выражение следует для эллипса из 3-го, а для противолежащих из 4-го свой¬
ства пропорции Докажем его, например, для эллипса Обозначим отрезки, на которые разбитдиа-
а(6 + с + </) с/(а + 6 + с)
метр а Ь с, с! Тогда исходное выражение примет вид.	и	=	;	 Учитывая, что а+б
о	с
а(2Ь+а) с!(2с + с1)	(а + 6)*	+
= с+(1, получим —г,— »	-2—. Прибавив слева и справа единицу, имеем: —-г— =	?—,
ос	Ь	с
что и следовало доказать,
116

Предложения
Отс юда
нг2
АН НВ
ГВ2 ГВ2
АН-НВ А0-0В ’
0Г2
>	 и, вычитая с обеих сторон единицу, получим*
А0-0В
что невозможно.
Следовательно, продолжение ГД лежит не вне сечения, а внутри него.
А прямая, проведенная от некоторой точки на отрезке АГ через Д, тем более по¬
падет внутрь сечения, так как попадает ниже ГД,
1
Предложение 32. Между касательной и сечением не лежит никакая прямая
Если через вершину конического сечения проведена прямая, параллельная ординате
к диаметру, то никакая другая прямая не будет лежать между этой прямой и кони¬
ческим сечением.
Пусть сначала сечением конуса будет парабола с диаметром АВ и через точку А
проведена прямая АГ, параллель¬
ная ординате к диаметру (рис. 1).
Доказано, что она лежит вне се¬
чения (I, 17). В таком случае я ут¬
верждаю, что не существует ника¬
кой другой прямой, лежащей меж¬
ду прямой АГ и сечением.
Допустим, что все-таки суще¬
ствует такая прямая АД. Проведем
от точки Д ординату к диаметру ДЕ,
пересекающую параболу в точке Н,
и пусть latus rectum ординат будет
ГЛ
ДЕ2 НЕ2
AZ. А поскольку	=- >	z
ЕА2 ЕА2
,	ДЕ2 EA-AZ
11) НЕ2 = ЕА-AZ, то	т>

2 ЕА2
32. Рис. 1
т ДЕ
,	. То есть —,
ЕА ЕА	ЕА	ЕА
Проведем теперь ординату 0КЛ от прямой АД, пересекающую диаметр в такой
ДЕ2 AZ
точке 0, что	7 =	.
ЕА2 А0
*
Для левой части равенства
Докажем, что числитель равен ГВ2: НГ - ГВ = НВ, а если АГ = ГВ, то НГ+ГВ = АН.
Перемножив почленно, получим НГ2 - ГВ7 = АН • НВ.
Следовательно, НГ2 - АН • НВ = ГВ7.
Аналогично и с правой частью.
117

Книга!
AZ AZ ■ Aö
Тогда, поскольку	аЕ>"
К0: ©А'
А02 А0‘
Следовательно. К0
0Л, что абсурдно. Таким об¬
разом, никакая другая пря¬
мая не будет лежать между
прямой АГ и сечением
Пусть теперь сечением
будет гипербола или эллипс
(рис 2 и 3) с диаметром АВ.
Ьг = М и пусть проведена
и продолжена прямая В2, а
также прямая АГ параллель¬
ная ординате
Было доказано, что АГ
М1».
лежит вне сечения.
Я утверждаю, что ника¬
кая другая прямая не будет
лежать между этой прямой
и сечением.
Предположим, что су¬
ществует такая прямая АЛ.
Проведем прямую ЛЕ, па¬
раллельную АГ. и прямую
ЕМ, параллельную latus
rectum AZ. Тош U, 12 и 13)
НЕ2 = АЕ*ЕМ.
Продолжим ЕМ до точки
N такой, что ДЕ-=aE-EN
а ,01 точки - пересечения
AN и BN проведем прямую
параллельную AZ. а из
точки 0 - прямую 2К, па¬
раллельную ординате ДЕ.
N
Т2 Рис. 3
Тогда, поскол«удЕ, = ДЕ.Е|ч
Атак
как сп
Аллино, ЧТО
EN
АЕ
илиЕ21 = £Е_ TOEN=^Ei
ЛЕ АЕ ’ ЛЕ АЕ2 '
=0 ДЕ2 К©2	£©	К©2
«А’ ДЕ2 0АГ'Т°0Л~0А2

Предложения
Следовательно, К0 есть среднее пропорциональное между Е0 и 0А и К0? ~
0А•0Е.
Но по свойству сечения (I, 12 и 13) Л02 = 0А*0Е.
Поэтому К02 = Л02, что абсурдно.
Следовательно, никакая другая прямая не будет лежать между прямой АГ и се¬
чением.
Предложение 33. Если прямая, пересекающая параболу, отделяет на диаметре вне
кривой отрезок, равный абсциссе, то эта прямая — касательная
Если через некоторую точку па¬
раболы проведена ордината к диаме¬
тру, и отрезок, отложенный на диа¬
метре вне параболы от ее вершины, ра¬
вен отрезку, отделенному ординатой
на диаметре, то прямая, проведенная
от конца этого отрезка к указанной
точке, касается сечения.
Пусть дана парабола с диаме¬
тром АД и проведена ордината ГД.
Отложим на диаметре отрезок ЕА
такой, что ЕА=ДЕ. В этом случае я
утверждаю, что АГ лежит вне сече¬
ния (рис. 1).
Предположим, что ее часть лежит
внутри сечения и проведем ординату
НВ, параллельную ГД (рис. 2а и 2Ь).
„	нв2 гв2
Поскольку	=- > —. а
’ ГД2 ГД2
гв2 АВ2	НВ2 ВЕ
	Г =	Г и (1, 20) Т- = , то
ГД2 АД2	ГД2 ДЕ
ВЕ АВ2
ДЕ АД2
ВЕ
Далее, так как —
ЛЕ
4ДЕЕА
4ВЕЕА АВ2
ТО	>	г- И
4ДЕЕА АД“
4ВЕ ЕА 4ДЕ ЕА
АВ2 > АД2
что невоз-
119

Книга I
можно, поскольку 2ЕА=2АЕ=АА, а значит, 4АЕ • ЕА = ФА2 . Но, с другой стороны,
4ВЕ * ЕА < АВ\ поскольку Е не я мнется центром отрезка ЛВ. Следовательно, АГ
не оказывается внутри сечения, а касается его.
Предложение 34. Если прямая, пересекающая гипербазу или эллипс делит диаметр
в определенном отношении, то эта прямая - касательная
Если на гиперболе или эл¬
липсе берется точка, от нее
проводится к диаметру орди¬
ната, а latus transversum разде¬
лен так, что его отрезки от¬
носятся друг к другу как от¬
носятся отрезки, заключенные
между основанием ординаты
и его концами, то прямая, со¬
единяющая точку, взятую на
нем, и точку на сечении, каса¬
ется сечения.
Пусть даны гипербола или
эллипс с диаметром АВ и ор¬
динатой ГА.
Тогда, если на прямой, со¬
держащей диаметр, взята точ-
ВА ВЕ
ка Е такая, что	= —, то я
АЛ АЕ
утверждаю, что ЕГ есть каса¬
тельная к сечению (рис. 1 и 3).
Предположим, что она,
напротив, пересекает его в
точке Г (рис. 2 и 4) и через не¬
которую ее точку Z от точки
0 сечения проведена орди¬
ната к диаметру 0ZH, тогда
как через точки А и В прове¬
дены прямые АА и ВК. па¬
раллельные прямой ЕГ, а от
точек диаметра В, А и Н че¬
рез точку Г проведены отрез¬
ки ВЕ, ДК и НМ.
120

Предложения
П ос кол ьку с п ра ведя и -
ВД ВЕ
на пропорция	=

АД АЕ
и также пропорции
ВД ВК
АД ” AN
ВЕ ВГ ВК
АЕ
ГЕ NE
то,сле-
Тогда
ВК ВК
довательно,	=	.
AN NE
Откуда AN = NE, а
поэтому (Евклид II, 5)
AN • NE > АО • ОЕ, в силу
NE АО
>	.
AN
N
Однако —	,
Оп вм
Тогда справедливо не-
КВ АО
равенство	>	, а по-
ВМ AN
этому КВ • AN > ВМ • АО
чего

ОЕ
КВ
, а из подобия треугольников В КД, ЕГД и NAA следу-
KB AN ВДАД ВМАО ВНАН
ет, ЧТО	;— =	;— ,	; =	z—
ГЕ2 ДЕ2 ГЕ2 НЕ2
Следовательно,
ВДАД ВНАН
ДЕ2 > НЕ2
ВДАД ГД2
Однако, поскольку (1,21)	=	j
ВН • АН НО“
ДЕ2 ГД2
В силу чего ОН < 7Н, а это невозможно. Следовательно, ЕГ не пересекает гипер¬
болу или эллипс, а касается их.
Предложение 35. Касательная к параболе отделяет на диаметре отрезок, равный аб¬
сциссе (обратное Предложению 33)
Eaiu прямая касается параболы, то ордината, проведенная от точки касания к диа¬
метру, отделяет от вершины сечения отрезок, равный расстоянию от вершины до точ¬
121

Книга!
ки пересечения касательной и диаметра, и никакая прямая не попадает в простран¬
ство, расположенное между касательной и сечением*.
Пусть дана парабола с
диаметром АВ, и от неко¬
торой ее точки Г проведе¬
ны касательная ГА и орди¬
ната ГВ.
В этом случае я утверж¬
даю, что АН = НВ.
Допустим, что это не так,
а АН=НЕ, где точка Е есть
основание какой-то ордина¬
ты Е£. Но тогда отрезок Аг,
является касательной (1,33)
и, будучи продолжен, пере¬
сечется с АГ, Но это невоз¬
можно, ведь тогда две раз¬
личные прямые будут иметь две общие точки. Следовательно, АН = Н В.
Также я утверждаю, что никакая прямая не будет лежать в пространст ве, распо¬
ложенном между прямой АГ и сечением**.
Допустим, что такой прямой является АГ. Отложим отрезок НЕ, равный отрез¬
ку' НА, и проведем ординату Е1. Тогда отрезок А7 есть отрезок касательной (1, 33)и
лежит вне сечения, а значит, его продолжение пересечется с АГ. Но две рахчичные
прямые не могут иметь две общие точки. Следовательно, никакая прямая не попа¬
дает в пространство, расположенное между сечением и прямой АГ.
Предложение 36. Касательная к гиперболе и эллипсу делит диаметр в том же от¬
ношении, что и ордината, проведенная из точки касания (обратное 11редложению 34)
Если прямая касается гиперболы или эллипса, а из точки касания проведена орди¬
ната, то отношение отрезков, на которые касательная делит диаметр равно отно¬
шению диаметра, сложенного с абсциссой ординаты к этой абсциссе, и никакая другая
прямая не попадает между касательной и данным сечением***.
Пусть даны гипербола, или эллипс с диаметром АВ и от точки Г проведены ка¬
сательная ГЕ и ордината к диаметру ГА.
ВЛ ВЕ
В таком случае я утверждаю, что ~— =	.
АЛ АЕ
* Предложение, обратное (1,33)
“ Это уже было доказано в (I 32).
Предложение, обратное (1,34).
122

Предложен ия
Допустим, что это не
так. Тогда проведем такую
ординату 7Н, для которой
выполняется соотношение
ВН ВЕ
АН" АЕ*
Следовательно, прямая.
ходящая через точки
Е к 7, касается сечения (I,
34), а поэтому она пересе¬
чется с ЕГ. Но тогда оказы¬
вается, что из одной и той
же точки Е можно прове¬
сти две различные прямые,
которые затем пересекут¬
ся, что абсурдно.
Я утверждаю также, что
никакая прямая не лежит
между сечением и прямой
ГЕ*.
Допустим, что это не
так, и между сечением и
прямой ГЕ лежит Г0. Вы¬
берем на диаметре точку7
Н такую, что выполняет-
В0 __ вн
—-—.и прове-
дем ординату Н7. Тогда
прямая, проходящая че¬
рез точки 0 и 7, касается
сечения, а потому она пе¬
ресечется с О Г. Но тогда
окажется, что из одной и
36. Рис. 2
той же точки 0 можно
вести две различные пря¬
мые, которые затем пере¬
секутся, что абсурдно. Следовательно, никакая прямая не лежит между сечением и
прямой ГЕ.
Это уже доказано в (I, 32).
123

Книга!
Предложение 37. С
тношения между квадратом ординаты гиперболы или эллипса
и отрезками, отсекаемыми на диаметре ординатой и касательной
Если прямая, касающаяся гипер¬
болы или эллипса, пересекается с
диаметром* и от точки касания к
нему проведена ордината, то площадь
прямоугольника, ограниченного отрез¬
ками, соединяющими центр сечения с
основанием ординаты и с точкой пе-
ресечения касательной с диаметром,
равна квадрату половины диаметра,
а площадь прямоугольника, ограничен¬
ного отрезками, соединяющими осно-
вание ординаты с точкой пересечения
касательной и диаметра и с центром
сечения, так относится к квадрату
ординаты, как latus transversum от¬
носится к latus rectum.
Пусть даны гипербола или эллипс
с диаметром АВ и центром Н и каса¬
тельная к ней ЕЛ, из точки касания
•а
которой проведена ордината ЕМ к диаметру.
НМ НА = НВ2'
В таком случае я утверждаю, что ду,
ЕМ2
Lt •
Lr ,
Ведь поскольку ЕЛ касается сечения, а ЕМ есть ордината к диаметру, то справед-
' АЛ АМ
лива пропорция (1.36 — =	.
АВ ВМ
Л	АМ + ВМ АЛ + ЛВ
Откуда, прибавляя справа и слева по единице, получим	=	.
ВМ	АВ
Половины первых членов пропорции в случае гиперболы равны
►. Следовательно,
1
2
(ал+лв)=нв
НМ НВ
ВМ ”лв
• Для гиперболы и параболы было доказано (1,24), что касательная всегда пересекается с диа¬
метром, но Аполлоний почему-то постоянно вставляет эти слова в формулировки теорем. В даль¬
нейшем мы будем их опускать, если речь идет не об эллипсе.

Предложения
НМ НВ
Поэтому*
НВ НА ’
НМ
А поскольку

' ВМ
в силу чего Н М • НА = Н В2.
НВ НА НА _ АВ
НА “ АВ ’10НМ ” ВМ ’
АМ МЛ
А прибавив слева и справа единицу, получим	=	.
НМ ВМ
Поэтому АМ • ВМ = АМ • НМ .
. „ АМВМ Ы	ЛМНМ Ы
А так как (1,21)	=— = —, то и	;— = —
ЕМ2	Ьг	ЕМ2	Ьг
на эллипсе выходит следующее:
НА НВ
Следовательно,	=

АВ ВМ
4 НА НВ
и** 	=	.
НВ НМ
Поэтому НА• НМ = НВ2.
Далее, так как
НЛНМ = ЛМНМ + НМ2
НВ2 = АМ-ВМ + НМ2
то, вычитая из двух равенств
бшее слагаемое НМ2, получаем АМ • НМ = АМ • ВМ,
ЛМНМ АМВМ
в силу чего	т— =	;—.
ЕМ2 ЕМ2
АМВМ Ы	ЛМНМ и
А так как	г— = — , то и 	;— = — .
ЕМ2	Ьг	ЕМ2	Ьг
Предложение 38. Те же соотношения для сопряженного диаметра
Если прямая, касающаяся гиперболы или эллипса, пересекается с продолжением
второго диаметра, и от точки касания проведена к нему прямая, параллельная перво¬
му, то квадрат половины второго диаметра равен площади прямоугольника, стороны
которого есть отрезки, заключенные между центром и точками пересечения второго
диаметра с прямой и с касательной, а площадь прямоугольника, ограниченного суммой
/Л
* 6-е свойство пропорции
** 4-е свойство пропорции
• Г
125

Книга I
этих отрезков и отрезком, соеди¬
няющим центр с точкой пересече¬
ния второго диаметра и прямой, па¬
раллельной первому диаметру, так
относится к квадрату прямой, про¬
веденной из точки касания ко вто¬
рому диаметру, как laius rectum к
latus transversum.
Пусть дана гипербола или эл¬
липс с диаметрами АН В и ГН А и
проведены касательная EAZ, Пере¬
се каюшаяся с ГД в точке Z и пря¬
мая 0Е, параллельная АВ, а из точ¬
ки касания опущена ордината к
первому диаметру. В этом случае
н© нг=нг2
я утверждаю, что 0ZH0 _ Lr .
Е02	~ Lt .
МЛ НМ Lt
Так как ЕМ является ординатой, то (I. 37) ———z— = —
ЕМ Lr
„	, Lt	ГД	Lt AB2	НВ2
С другой стороны, (Определения 11,3) — = — , а значит, — =		 =

ГД Lr	Lr	ГД	НГ*
„	НВ2 мл нм
Следовательно, —г=	;—.
НГ2 ЕМ2
.	МЛ НМ МЛ НМ МЛ
А поскольку		— =	=

■ ЕМ2 ЕМ ЕМ ЕМ
НМ НВ2 МЛ
	 	 то 	=
Н0 НГ2 ЕМ
НМ НЛ нм
и© " Hz не,
НВ2 НЛНМ
или —г =	.
нг2 Hz не
HZH0 НМНЛ
Следовательно,		 =

нг2 НВ2 ■
А так гак (1,37) НМ-НЛ= НВ!.,тои H0-HZ= НГ=.
А поскольку (1, 37)
0ZH0 Lr
Ее2 =и
Lr _ ЕМ2 ЕМ ЕМ _ HZ Н0 0Z Н0 0Z ■ Hg
Lt МЛ HM ” МЛ HM ” НЛ ЕО " Е0 Е0 Ев’
126

Предложения
Докажем при тех же самых условиях, что отношение отрезков, на которые каса¬
тельная делит второй диаметр, равно отношению отрезков, заключенных между точ¬
кой пересечения с ним прямой, параллельной первому диаметру, и его концами.
Ведь доказано, что Н0 • Н7 = НГ2, так как НГ=НЛ, то Н0* *Н7=НГ* НД.
Н7 НГ
Следовательно,	=	.
НД Н0
нг нг
Тогда для гиперболы* 	=	.
7д Г0
~Ч1/ 2НГ
Удвоим первые члены пропорции 	=	.
7Д Г0
гг-гд Д0-Г0
А поскольку 2Н7 = Г7 - 7Л и 2Н Г = Д0 - Г0 , то	=	.
гд г©
Следовательно, — =	, что и требовалось доказать.
7Д Г0
Добавление
Следовательно, очевидно из того, что мы сказали, что прямая Е7 касается сече¬
ния. если будет 7Н • Н0 = НГ2, или если 70 • 0Н имеет отношение к 0Е2, о како¬
вом мы сказали, ведь обратное было доказано.
Примечание ред.
Дня эллипса верно отношение, обратное выведенному, что доказывается тем же
' .	/	Н7 НГ
с пос ооо м (рис. 2): =	.
7Д Д0
Удвоим первые члены про-
2Н7 2НГ
порции	=	.
гд д©
А поскольку 2Н7 =
Г7+7Д и 2НГ = Г0^0Л, то
Г7 + 7Д Г0 + Д0
7Д ~ Д0
Г7 Г0
Следовательно, — =	.
та де
Предложение 39. Очевидное следствие из Предложения 37
Если из какой-то точки гиперболы или эллипса проведены касательная и орди-
ната, то отношение длины ординаты к отрезку, заключенному между ее основани¬
ем и точкой пересечения касательной с диаметром, равно отношению отрезка, за¬
ключенного между основанием ординаты и центром к длине ординаты, умножен¬
ному на отношение latus rectum к latus transversum** .
tit
*	4-е свойство пропорции
*	* У Аполлония здесь, как и в Предложениях 40 и 41. сказано не умноженное. а составленное,
поскольку он не применял слова умножение к непрерывным величинам
127

Книга I
Пусть дана гипербола или
эллипс с диаметром АВ и цен¬
тром 2 и проведены касатель¬
ная ГА, а из точки касания -
ордината к диаметру ГЕ. В
этом случае я утверждаю, что
ГЕЕ/ Ьг$
ед’ге и
Пусть выбран такой отрезок
Н, что справедлива пропорция
Е2*ЕД=ГЕ*Н.
А поскольку (1,37)
ЕГЕД Ы
—— = —, то. учитывая,
ГЕ2 Ьг
что Е2* ЕД = ГЕ* Н, получим
ГЕ Н _ Н _ И
ГЕ2 "ге’Ьг
.	ГЕ ГЕ Н
А так как — =

ЕД Н ЕД
ГЕ 1_г Н Ег
и —=— а — = —, то
Н Ы, ЕД ГЕ
ГЕ Е2 и
еа’ге и
pj	39. Рис. 2
I	1
Предложение 40. Очевидное следствие из Предложения 38
Если прямая, касающаяся гиперболы или эллипса, пересекается со вторым диаме¬
тром, а из точки касания к нему проведена прямая, параллельная первому*, то отно¬
шение ее длины к отрезку, заключенному между ее основанием и центром сечения, рав¬
но отношению отрезка, заключенного между ее основанием и точкой пересечения ка¬
сательной со вторым диаметром, к длине вышеозначенной прямой, умноженному на
отношение latus transversum к latus rectum.
EZ ЕЛ Lt
‘ Это равенство - очевидное следствие равенства ~~ = —•
доказанного в (I, 37).
*• Речь идет конечно же о сопряженных диаметрах.
1И

Предложения
0ZH0_Lr
Е02	" Lt
40. Рис. 2
Пусть дана гипербола или
эллипс с центром Н и диаме¬
трами АВ и ГД и проведены ка¬
сательная Е7, а также от точки
касания прямая Е0 ко второму
диаметру, параллельная АВ. В
таком случае я утверждаю, что
Е0 _ 0Z Lt ф
Н0 Е0 Lr ’
Пусть выбран такой отрезок
К, что Е0 • К = 0Z • Н0.
А поскольку (I, 38)
Lr Е0К
Lt ” Е02 Е0
С другой стороны.
Е0 Е0 К	Е0 Lt
	=	где	= —
Н0 К Н0	К Lr
А так как 0Z • Н0 = Е0 • К,
К 0Z Е0 0Z Lt
или	=	.то	=	.
Н0 Е0 Н0 Е0 Lr
Предложение 41. Сумма и разность площадей равноугольных параллелограммов, по¬
строенных на радиусе и ординате гиперболы
Если на ординате к диаметру гиперболы ши эллипса, а также на радиусе строят¬
ся равноугольные параллелограммы и отношение ординаты ко второй стороне первого
параллелограмма равно отношению радиуса к другой стороне второго парсшелограм-
ма. умноженному на отношение latus rectum к latus transversum. то площадь параллело¬
грамма, построенного на отрезке, заключенном между центрам и основанием ординаты,
подобного параллелограмму, построенному на радиусе, для гиперболы
равна сумме tuo-
67
. ~	ez-не и
Это равенство - очевидное следствие равенства	, доказанного в (I, 38).
Е0* Lt
129

Книга I
щадей параллелограммов, по
строенных на радиусе и на ор
динате, а для эллипса разно
сти этих площадей.
Пусть дана гипербола
или эллипс с диаметром АВ
и центром - Е (рис. 1а, 1Ь).
Тогда если построена орди¬
ната ГД, а на отрезках ЕА и
ГЛ построены равноуголь¬
ные параллелограммы AZ* и
такие,что
£А = АЕ Lr
ГН ’ EZ Lt ’
то я утверждаю, что для ги¬
перболы площадь паралле¬
лограмма ЕР, построенно¬
го на ЕД и подобного парал¬
лелограмму AZ, будет равна
сумме площадей параллело¬
граммов AZ и Н Д, а для эл¬
липса — разности.
Пусть latus rectum от¬
носится к latus transversum,
как ГД к некоторому отрез¬
ку Г0: — = — , ясно, что
Г0 Lt
ГД ГД2
Г0 ГД-Г0
С другой стороны, (1.21)
очевидно,	тпАЕ ГД ГД Г0
га г© гн Ег ге'ге гн’
Следовательно =
EZ ГН
——— = —, следовательно.
АД • ДВ Lt
АД • ДВ = ГД • Г0 .
А поскольку
ГД _ АЕ Lr _ АЕ ГА и.
ГН _ EZ Lt EZ Г0
’ Напомним,
130
ЧТО Аполлоний
часто обозначает четырехугольники двумя буквами

Предложения
,	Г0 ГДГ0 АЕ АЕ2 АЕ2 ГДГ0
А так как — =	 и — =	, то	=	.
ГН ГА ГН Ег АЕ Ег АЕ Ег ГД ГН
Но мы уже доказали, что АА • АВ = ГА • Г0 .
Следовательно,
АЕ2 _ АА-АВ АА АВ _ ГА ГН
АЕЕг_ГДГН АЕ2 ~АЕЕг
Однако
ГД ГН
АЕ Ег
5(АН)
БСлг) ’
ведь
они равноугольные паралле¬
лограммы и имеют отношение
площадей, составленное из от-
ч	ГН ГА
ношении сторон — и —.
АЕ Ег
Следовательно,
АД ДВ_5(ДН)
АЕ2 ” 8(А2) ’
В случае ги пер¬
лы скажем, что*
АДДВ + АЕ2 5(ДН)-1-5(А2)
АЕ2 ”	8(Аг)
то есть
ДЕ2 5(ДН) + 5(Аг)„
АЕ2 " БСдг)
т ДЕ2
Так как —- равно отношению
АЕ2
Б(ЕР) и 5(А2), то, следовательно,
8(ЕР) = 8(ЛН) + 8(А7).
А в случае эллип¬
са сделаем так (рис. 2а. 2Ь):
АЕ2-АДДВ 5(Аг)-8(АН)
АЕ2 "	5(Аг)
и, схожим
разом, получим
АЕ2 8(Аг)-8(АН)
АЕ2" 8(Аг) ’тоееть
8(ЕР) = 8(А7) — 8(АН).
7	41, Рис .2Ь
* Здесь и далее для эллипса используется 3-е свойство пропорции
АД* ДВ = АЕ2 = ДЕ2, так как АХ* АВ = (ДЕ - ЕА)• (ВЕ + ДЕ). Перемножая скобки и учитывая,
что ЕА = ВЕ, получим ХЕ2. Для эллипса это не получится, поэтому там берут не сумму, а разность.
131

Книга I
Предложение 42. Равенство площадей треугольника и параллелограмма, составлен¬
ных из прямых, параллельных касательной, ординате и диаметру параболы
Если прямая касается параболы и из точки касания проведена ордината, а из не¬
которой точки параболы проведены к диаметру две прямые параллельно касательной
Ilf
и ординате, проведенным из точки касания, то площадь треугольника, образованного
ими и диаметром, равна площади параллелограмма, ограниченного диаметром, прямой,
проведенной из точки касания параллельно диаметру, а также прямыми, проведенны-
ми из вышеупомянутой некоторой точки и из вершины параболы параллельно ординате.
©В S(H0)
VI, I)
Пусть дана парабола с диаметром АВ, касательная АГ и ордината Г0. Тогда, если
из некоторой точки параболы А будут проведены прямые AZ, параллельно ордина¬
те, ЛЕ, параллельно касательной, а также ГН параллельно диаметру и ВН парал¬
лельно Г0, то я утверждаю, что плошадь треугольника AEZ равна площади парал¬
лелограмма HZ.
Поскольку АГ касается сечения, и Г0 есть ордината к диаметру, то (1, 35) АВ = В0.
Поэтому А0 = 2 В0.
Следовательно, площадь треугольника АГ0 равна площади параллелограмма ВГ
Г©2 0В	Г®2 S(AT0)
А поскольку (1.20)~“7“-~- и (Евклид VI, 19)"Г^2
AZ ZB
S(AT0) _ S(H0)
ZB S(HZ)’,U S(EAZ) " SiHZ)’11'™ S(H®) S(HZ) ’
А поскольку S(Ar0)=S(H0), то и S(EaZ) = S(HZ).
AZ' S(EAZ)’а(Евкл1и
S(AT0) S(EAZ)
.то
132

Предложения
Предложение 43. Соотношение между площадями трех треугольников, составленных
из диаметров и прямых, параллельных ординате и касательной гиперболы или эллипса
<7
Если прямая касается гипербо¬
лы или эллипса и из точки касания
проводится ордината к диаметру,
а из вершины сечения — прямая,
ей параллельная и пересекающая¬
ся с радиусом, проведенным через
точку касания, и через некоторую
точку сечения проводятся две пря¬
мые к диаметру, одна из которых
параллельна касательной, а другая
ника, образованного этими прямы¬
ми и диаметром будет отличать¬
ся от площади треугольника, огра¬
ниченного радиусом, диаметром
и прямой, проходящей через неко¬
торую точку сечения параллель¬
но ординате, на величину площа¬
ди треугольника, ограниченного
этим же радиусом, диаметром и
прямой, проходящей через верши¬
ну сечения параллельно ординате.
133

Пусть дана гипербола или
эллипс с диаметром АВ, цен¬
тром Г и проведены касатель¬
ная АЕ, ордината Е7 и ради¬
ус ГЕ, соединяющий центр Г с
точкой касания. Тогда, если из
точки Н, лежащей на сечении,
проведены прямые Н0, парал¬
лельно касательной и МН К, па¬
раллельно Е2, а из точки В пря¬
мая ВЛ, параллельно Е7, то я
утверждаю, что площадь тре¬
угольника ГМК отличается от
площади треугольника ГАВ на площадь треугольника 0Н К.
ЕЯ ¿Г
Поскольку ЕЛ есть касательная, а - ордината, то (I, 39) — =

хд е%
Г	Г	А	Е2 НК
С другой стороны, из подобия треугольников следует, что — =	и
ХД К0 Е£ ЛВ
„ НК ВГ Ьг
Поэтому —=	.
' К0 ЛВ Ь
Ьг
П'
¿г вг
Тогда из доказанного в (1,41) следует, что площадь треугольника ГКМ отличает¬
ся от площади треугольника ГАВ на площадь треугольника 0Н К, поскольку то же
самое отношение уже было установлено для площадей параллелограммов, плоша¬
ли которых вдвое больше рассматриваемых площадей.
Предложение 44. Продолжение Предложения 43 для противолежащих
£1
Если прямая касается одной
из противолежащих гипербол и
от точки касания проведены ор¬
дината и радиус, продолженный
до пересечения со второй проти¬
волежащей, а через точку' пере¬
сечения проведена прямая, па¬
раллельная ординате, то если из
некоторой точки второго сече¬
ния провести к диаметру пря¬
мые, параллельные касательной
и ординате первого сечения, то
площадь треугольника, образо¬
ванного ими и диаметром, бу¬
дет равна площади треугольни¬
ка, образованного диаметром,
44. Рис. /
134

Предложения
ординатой, проходящей через упомянутую некоторую точку, и радиусом, уменьшенной
на площадь треугольника, ограниченного диаметром, касательной. проведенной через
вершину, и радиусом.
Пусть даны противолежащие (А) и (В) с диаметром АВ, центром Г и ка
дельной
лГЧ, а из точки касания проведена ордината ЕО и радиус ЕГ,
ж
долженный до пе¬
ресечения с (В) в точке Е. Тогда если из точки В провести прямую ВА параллельную
ЕО, до ее пересечения с ЕЕ, а из некоторой точки Н. лежащей на сечении (В), про¬
вести ординату НК и прямую Н0, параллельную Е1Ч, то я утверждаю, что 8(0НК) =
8(ГМК)-5(ГЛВ).
Проведем касательную ЕЛ и ординату Е7. Поскольку (А) и (В) суть противоле¬
жащие с диаметром АВ. прямая ЕГЕ, проходящая через центр, есть также их диа¬
метр, а прямые EN и ЕД касаются противолежащих в точках их пересечения с ди¬
аметром ЕЕ, то ЕЛ параллельна Е1М. А так как Н0 параллельна прямой ЕЫ, то она
параллельна и ЛЕ, а НК, очевидно, параллельна ВА. Тогда ввиду того, что (В) есть
гипербола с диаметром АВ и центром в Г, ЕЛ касается сечения в точке Е, ордина¬
ты НК и ВЛ, параллельны прямой Е£, а Н0 параллельна прямой ЕЛ, то 8(0НК) =
5(ГМК) - 8(ГЛВ), ибо это было доказано в (I, 43)*.
Предложение 45. Аналогичное свой
ство по отношению к сопряженному ди
аметру
Если прямая, касающаяся гиперболы
или эллипса, пересекается с сопряжен¬
ным диаметром, и от точки касания про¬
ведены две прямые, из которых одна па¬
раллельна первому диаметру, а вторая
проходит через центр, и из некоторой
точки, лежащей на сечении, проведены
прямые, первая из которых параллель¬
на касательной, а другая — первому диа¬
метру, то площадь треугольника, обра¬
зованного ими и вторым диаметром, для
гиперболы будет равна площади треуголь¬
ника, одна из сторон которого есть вто¬
рой диаметр, а две другие есть прямые,
одна из которых проведена из упомянутой
* Если в предыдущем Предложении НК и Н0 были параллельны ординате и касательной «сво¬
его» противолежащего сечения, то теперь - «чужого», а значит, дело сводится к доказательству
того, что эти ординаты и касательные параллельны друг другу. Ординаты к общему диаметру па¬
раллельны по определению, а согласно (1,17 и 32) прямая, проведенная через вершину и парал¬
лельная ординате, есть касательная, причем единственная. Следовательно, ЕЫ и ЕЛ параллель¬
ны, так как у диаметра НЕ конечно же есть ординаты.
135

Книга!
а
Ж
некоторой точки параллельно пер¬
вому диаметру, а другая соединяет
точку касания с центром гиперболы,
сложенной с площадью треугольни¬
ка, ограниченного касательной, от¬
резком, соединяющим точку касания
с центром, и вторым диаметром, а
на эллипсе эта площадь равна раз¬
ности этих площадей.
Пусть дана гипербола или эл¬
липс с центром 0, диаметрами АО
и 0Л, а от некоторой точки Г про¬
ведена касательная Г МЛ. И пусть
из точки касания провели прямые
Г0 и ГД, параллельную диаметру
А0. а из некоторой точки сечения
В провели прямые ВЕ параллельно касательной и В/ параллельно ГЛ. В этом слу¬
чае я утверждаю, что на гиперболе 8(В2Е) = 8(Г0Л) + 8(Н20), а на эллипсе 8(ВгЕ)
= 5(Г0Л) - 5(Нг@).
Проведем ординаты ГК и BN параллельно диаметру 0, а прямую АР параллель¬
но касательной ГЛ*.
т , ,п ГК К0 Ьг
Тогда (1,39)

с*
»в
ГК КМ Ьг
, или — 		.
КМ ГК и К0 ГК Ы
КМ ГД	ГК ГД Ьг
Но из подобия треугольников	= —, поэтому —— = —-	.
ГК ДА	К0 ДА Ы
Построим сначала на ординатах ГК и BN и на радиусе параллелограммы ГД0К,
ГЛЛТ, А0РП. ВгЕТ и ВМУ2’, и пусть В/’ = Нг. Они будут равноугольны, а по¬
скольку подобны соответствующие треугольники, то ГДАТ и ВМУ2’ подобны А0РП.
„ ’ ГД А0	ГК А0 Ьг
Кроме того, — = —, следовательно,	=	.
ДА 0Р	К0 ОР Ы
Тогда(1,41) ГАЛТ) = 8(ГД0К) + 8(А0РП), или 8(ГЛА) = 8(ГД0) + 8(А0Р).
Очевидно также, что 8(ГДЛ) = 8(ГД0)+ 8(Г0А) и 8(А0Р) = 8(Г0Л).
„	ГК ¿0	г0 А0 Ьг
С друтой стороны, — = —, а значит, — =	.
"	к© нг	нг ©р ы
Следовательно (1.41), 8(ВгЕЧ')=5(А0РП)+8(г,В^), или 8(В2Е)=8(А0Р)+8(Н20)
А поскольку 8(А0Р) = 8(Г0Л), то 8( В2Е) = ,8(Г0Л) + 8(Н20), что и требова¬
лось доказать
Аналогично доказывается и для эллипса.
•I»
* Доказательство изложено Аполлонием очень кратко, поэтому для облегчения понимания мы
расписали его немного подробнее
136

Предложения
45. Рис. 2с
45. Рис. 2Ь
М
45. Рис. 2(1
Предложение 46. Все диаметры параболы параллельны, а отрезки, параллельные
касательной к вершине (по Аполлонию), есть ординаты
Если прямая касается параболы, то другая прямая, проведенная через точку каса¬
ния параллельно диаметру, будет рассекать на две равные части отрезки прямых, па¬
раллельных касательной и лежащие внутри сечения*.
Пусть дана парабола с диаметром АВА и касательная АГ. Тогда если через точку
Г провести отрезок 0М, параллельный диаметру, а от некоторой точки Л, лежащей
на сечении, провести отрезок Л^Е, параллельный касательной АГ, то я утверж¬
даю, чтoZN = 1МЛ.
* То есть эти отрезки есть ординаты, а сама прямая - это диаметр. Следовательно, все диа¬
метры параболы параллельны.
137

Книга!
Проведем к диаметру ординаты 0В,
К2М и АМА. Тогда если на основании (1,
42) 5(ЕЛА) = Б(ВМ) и 5(Е7.Н) = Б(В К),
то5(НМ) = 8(А2НД).
Поскольку пятиугольник \1AHZN
является общим для них, то отнимая
его от НМ и дгНА, получим 5(К№7) =
8(Л2НА).
А так как К2 параллелен ЛМ, то ZN
= КА* **.
Предложение 47. Отрезки, параллельные касательной к гиперболе или эллипсу, есть
ординаты к диаметру, проходящему через точку касания
Если касательная к гиперболе или эллипсу пересекается с диаметром, то прямая,
проходящая через точку касания и центр, будет рассекать на две равные части отрез¬
ки прямых, проведенных внутри сечения параллельно касательной**.
»1»
•ди
Пусть дана гипербола или эллипс с диаметром АВ, центром Г и касательной АЕ.
Тогда если провести и продолжить прямую ГЕ, а через некоторую точку сечения
N провести прямую 0Н параллельно касательной, то я утверждаю, что N0 = ОН.
* Поскольку подобные треугольники, имеющие равные площади, равны
** То есть всякая прямая, проходящая через центр эллипса или гиперболы, является диаме¬
тром этого конического сечения. У эллипса касательная может и не пересекаться с диаметром
но тогда ГЕ будет ординатой, а значит, тоже будет делить секущие, параллельные касательной и
диаметру пополам П, 15)
138

Предложения
Проведем ординаты AB, ENZ и НМ К. Тогда (1, 43) S(ONZ) = S(ABZE), S(H0K)
= S(ABKM), следовательно S(HKZN) = S(MKZE).
Поскольку пятиугольник MKZNO для них общий, то, вычитая его, получим
S(OHM) = S(ONE).
А так как отрезок Н М параллелен EN, то NO = ОН.
Предложение 48. Продолжение Предложения 47 для противолежащих
Если проведена касательная к од¬
ному из про
тиволежащих сечений, а
через точку касания и центр проведе¬
на и продолжена прямая, то отрезок,
параллельный касательной и лежа¬
щий внутри второго сечения, разби¬
вается ею на два равных отрезка *.
Пусть даны противолежащие (А)
и (В) с центром Г и касательной ЛК
к (А). Тогда если провести и продол¬
жить прямую АГ, а через некоторую
точку N второго сечения провести
отрезок NH, параллельный ЛК, то
я утверждаю, что NO = ОН.
и®
ЙЕ
ЙЕ
П1
о.
ведем касательную ЕЛ к сечению (В). Она будет параллельна ЛК и NH (I,
44). Тогда (I, 47)NO = ОН.
Предложение 49. Доказывается, что отрезок, удовлетворяющий некотором} усло¬
вию, есть latus rectum
Если проведена касательная к параболе и через точку касания проводятся прямая,
параллельная диаметру, и ордината к нему, а от вершины — прямая, параиельная орди¬
нате, и если отрезок касательной, расположенной между' этой прямой и точкой каса¬
ния, так относится к отрезку прямой, параллельной диаметру, расположенному между
точкой касания и прямой, проведенной от вершины, как некоторый отрезок относит¬
ся к удвоенному отрезку касательной, заключенному между точкой касания и точкой
пересечения с диаметром, и если проводится секущая, параиельная касательной, то
квадрат половины секущей будет равен площади прямоугольника, ограниченного ее аб¬
сциссой и некоторым отрезком.
ли
Пусть дана парабола с диаметром ГВ и касательной ГД, а через точку касания Д
проведен и продолжен отрезок гд, параллельный ГВ. Тогда если проведена ордина-
* Продолжение этой темы в (II, 34 и 35).
139

Книга I
та BZ* и отрезок Н такой, что
ЕД Н
— =	, а на сечении взята
AZ 2ГД
некая точка К, через которую
проведена прямая КАП, парал-
лельная касательной, то в таком
случае я утверждаю, что КА2
- Н • ДА , то есть что Н - latus
rectum для диаметра ZД (1,11)
Проведем ординаты ДЕ
и КМ. Поскольку ГД касает¬
ся сечения, а ДЕ есть ордина¬
та, то (1,35) ГВ = BE, а так как
ВЕ= ZA. то ГВ = ZA и, следо¬
вательно, треугольники ЕГВ и
EZA равны
Присоединяя к каждому из
этих треугольников многоугольник Д№ МВЕ, получим, что 5( ГИ) = 8(/М).
Апоскольку (1,42)5(ИМ) = 5(КПМ), то, отнимая от и от КПМ четырехуголь¬
ник АМ, получим, что 5(АКГЧ) = 5(ГА).
Но /ЛАП = ZKAN, поэтому** КЛ-AN = 2ГД-ДЛ.
u	ЕД Н	ЕД КА Н КА
Но, как оыло сказано, — =	и, кроме того, — =	, то	=	.
AZ 2ГА	AZ AN 2ГА AN
Однако
2ГД 2ГДДЛ
КЛ__КЛ^_
а an’ka-an
Таким образом.
Н АЛ
KAAN 2ГДАЛ
Но, так как KA*AN = 2ГД ЛЛ, то, следовательно, КА2 = Н • АА.
Предложение 50. То же для гиперболы и эллипса
Если касательная к гиперболе или эллипсу пересекается с диаметром и через точку
касания проводится другой диаметр, с которым пересекается ордината, проведенная
от вершины, и отрезок касательной, заключенный между точкой касания и ордина¬
той, так относится к отрезку другого диаметра, заключенному между этой точкой и
ординатой, как некоторый отрезок к удвоенному отрезку касательной, заключенному
между диаметром и точкой касания, то квадрат отрезка любой прямой, параллельной
касательной, заключенного между точками ее пересечения с гиперболой и с другим ди¬
аметром, равен площади прямоугольника, образованного ее абсциссой и отрезком, за-
* См. сноску 2, к (Опр 1,4).
** Так как площадь параллелограмма равна аЬ • эта, а треугольника - вдвое меньше
140

Предложения
ключе иным между вышеуказан¬
ной точкой и точкой пересечения
с прямой, проходящей через конец
некоторого отрезка и точку, сим¬
метричную точке касания отно¬
сительно центра.
О
В случае гиперболы эта пло¬
щадь будет превосходить пло¬
щадь прямоугольника, подоб¬
ного прямоугольнику, ограни¬
ченному удвоенной прямой.
расположенной между центром
и точкой касания и некоторым
отрезком, а на эллипсе эта пло¬
щадь будет меньше площади той
же самой фигуры.
Пусть дана гипербола или эл¬
липс с диаметром АВ, центром
— Г, касательной ДЕ, и прове¬
дена прямая ЕГ и продолжена в
обе стороны, причем КГ = ГЕ.
И пусть через точку В проведена
ордината В7Н, а отточки
ведена прямая, перпендикуляр¬
ная ЕГ, на которой
отложен от-
гЕ Е©
резок Е0, такой, что	=	.
ЕН 2ЕД
Тогда если мы проведем и
продолжим К0 и через неко¬
торую точку сечения Л прове¬
дем прямые АМЕ, параллель¬
ную ЕД, и АРЫ, параллельную
ВН, а также МП. параллельную
Е0, то в этом случае я утверж¬
даю, что ЛМ2=ЕМ МР*.
Проведем через точку Г прямую ГХО, параллельную КП. Тогда
ЕГ
ГК
и так как ЕГ = ГК. то ЕЕ = Е0.
гн Е0
А поскольку	=	 и ЕЕ = ‘Л Е0, то
ЕН 2ЕД
гЕ ЕЕ
ЕН ” ЕД
* То есть что Е0 - 1аШ5 гесШт (1,12)
141

Книга I
ZE ЛМ	ЛМ	ЕЕ
Однако в силу подобия треугольников — =	, поэтому	= —.
ЕН MP	МР	ЕД
А поскольку мы уже доказали (1,43), что на гиперболе S(PNT) = S(HBT) + S(ANE),
wwS(PNr) = S(rAE) + S(ANS)*.
A на эллипсе S(PNT) = S(HBT) - S(ANE), т.е. S(PNT) + S(ANE)=S(rAE) и при
исключении на гиперболе треугольника ГАЕ и четырехугольника NPME, а на эл¬
липсе и круге - треугольника МЕГ получается, что S(AMEI) = S(MEAE).
Но гак как ME параллельна прямой АЕ, и ZAMP = ZEME, то** ЛМ-МР =
ЕМ-(ЕА+МЕ).
МГ М
Поскольку же
МГ MO	MO ME
и	=	то	=

ГЕ ЕА ГЕ ЕЕ	ЕЕ ЕД
Тогда, прибавляя единицу справа и слева, получим
МО + ЕХ М2 + ЕД
И, по-
ЕЕ
ЕД
МО + ЕЕ ЕЕ
меняв члены пропорции, получим	= —.
ME + ЕД ЕД
МО+ЕЕ _ (МО+ЕРЕМ IE ZE
°днак° м= + Ед"(МН + Ед)ЕМ "
ЛМ2
—	, поэтому
ЕД ЕН МР ЛМ-МР	7
ЛМ
(МО+ЕРМЕ _ ЛМ2
(МН+ЕД)ЕМ ~ ЛМ-МР
(МО+ЕРМЕ (М= + ЕД)МЕ
И наоборот, —;.	= -- ---- ■
IIÎ
ЛМ2
Однако ЛМ-МР = ЕМ (ЕА+МЕ), поэтому ЛМ2 = ЕМ (МО + ЕЕ) и ЕЕ = Е0, Е0
= ОП.
Следовательно, Л М2 = Е М М Р.
Прелтожение 51. То же для противолежащих
Если прямая касается одного из противолежащих сечений и через точку касания про¬
водится другой диаметр, с которым пересекается ордината, проведенная от вершины, и
отрезок касательной, заключенный между точкой касания и ординатой, так относит¬
ся к отрезку другого диаметра, заключенному между этой точкой и ординатой, как не¬
который отрезок к удвоенному отрезку касательной, заключенному между диаметром
и точкой касания, и в другом сечении параллельно касательной проведена прямая, то
квадрат ее отрезка, заключенного между точками пересечения с гиперболой и с другим
* Это Аполлоний докажет в (III, 1)
” Так как удвоенная площадь треугольника равна ab • sirxz, а трапеции - площади параллело¬
грамма, составленного из двух трапеций
142

Предложения
диаметром, равен площади
прямоугольника, образован¬
ного ее абсциссой и отрезком,
заключенным между выше¬
указанной точкой и точкой
пересечения с прямой, прохо¬
дящей через конец некоторо¬
го отрезка и точку, симме¬
тричную точке касания от¬
носительно центра *.
Пусть даны противо¬
лежащие с диаметром
и центром Г и пусть будет
проведена прямая ДЕ, каса¬
ющаяся сечения (А). Про¬
ведем и продолжим даль¬
ше в обе стороны ГЕ, а так¬
же проведем касательную BZH. Пусть также для некоторого отрезка выполняется
ZE У
ЕН " 2 ЕЛ
Уже доказано (I, 50). что прямая ЛМ будет в квадрате равна плошали прямоуголь¬
ника ЕП. Я утверждаю, что то же самое получается и на сечении (В) для прямой Р1.
Пусть через точки А и К будут проведены касательные АТ№ и КТО. И посколь¬
ку (А) и (В) суть противолежащие, а ЕД и КО касаются их, то ЕД и КО параллельны
и равны (I, 44), а также ГЕ = ГК, следовательно, ГД = ГО.
2Е	Ч7 У	ТК	4х
А так как треугольники подобны, то поскольку — =	=	, то и	=	.
ЕН 2ЕД 2КО	КК 2КО
Поскольку (В) является гиперболой с диаметром АВ, КО - касательная, AN про-
ТК Ч7
ведена как ордината, =	’ а лю^ые прямые проводятся от сечения к продол¬
женной ГК как параллельные прямой КО, то этим доказано, что утверждение вер¬
но и для него (I, 50).
f
убавление (задачи на построение)
Из доказанного очевидно, что: на параболе все прямые, параллельные некое¬
му первоначальному диаметру, являются диаметрами (I. 46); на гиперболе, эллип¬
се и противолежащих все диаметры, проводятся через центр (I, 47 и 48)** . Следо¬
вательно: на параболе прямые, проведенные к любым диаметрам как параллельные
касательным, в квадрате будут равны площадям прямоугольников, составленных из
* То есть утверждение, доказанное в предыдущем Предложении для ординат одного противо¬
лежащего, верно и для ординат другого.
“ Доказано обратное все прямые, проходящие через центр являются диаметрами.
143

Книга I
latus rectum и абсциссы; на гиперболе и противолежащих - тем же площадям, сло¬
женным с площадями подобных им прямоугольников, а на эллипсе — уменьшен¬
ным на эти же площади.
И все, что мы прежде доказали, применимо к сечениям как для изначальных
диаметров, так и дня любых других*.
Предложение 52. Построение конуса, сечение которого есть парабола с заданным
Ег и прямым углом между ординатами и диаметром
Если на плоскости за¬
дана прямая, ограниченная
с одной стороны, необходи¬
мо построить на этой пло¬
скости сечение конуса, назы-
* *
ваемое параболой, так что
ее диаметром будет данная
прямая, вершиной - предел
прямой, и если любая орди¬
ната проводится от сече¬
ния к диаметру под заданным
углом. то ее квадрат будет
равен площади прямоугольни¬
ка, одна из сторон которого
равна абсциссе, а вторая -
заданному отрезку прямой.
/Л
/Л
9Л
М
\
Н
Г
&
Л
52. Рис. 1
Пусть дан отрезок АВ на
плоскости и отрезок ГД, и пусть заданный угол сначала будет прямым. Надо постро¬
ить на плоскости, содержащей отрезок АВ, параболу, так что ее диаметром будет
АВ, ординаты проведены под прямым углом к АВ, то есть диаметр является осью,
а latus rectum - ГЛ.
Продолжим АВ до точки Е, приняв, что ГН = ‘/«ГД и ЕА > ГН. а некоторый отре¬
зок 0 есть среднее пропорциональное между отрезками ГД и ЕА, то есть
ГД 02
Тогда — = —у, но так как ГЛ<4ЕА, то0? < 4ЕА2,0 < 2ЕА, ЕА + ЕА > 0, а зна-
ЕА ЕА2
чит, можно из 0 и двух ЕА построить перпендикулярно заданной плоскости треу¬
гольник EAZ, такой, что ЕА = AZ, a ZE = 0.
с»
0 ЕА
* До сих пор ни о каких «изначальных» диаметрах ничего не говорилось Согласно Добавлению
получается, что все доказательства относились именно к ним, а теперь Аполлоний объясняет, как
проводить другие диаметры и доказал, что у них тоже есть свои 1_г (I,49-51). Возможно, под изна¬
чальными диаметрами он понимал оси сечений. Но зачем это все, если все доказательства были
верны для любых диаметров9

Предложения
Проведем АК параллельно 2Е, 2К параллельно ЕА и построим конус с верши¬
ной в точке 2, основанием которого является круг с диаметром КА. лежащий в пло¬
скости, перпендикулярной плоскости, содержащей прямые А2 и 2К. Конус будет
прямым, ибо А2 - 2К.
Пресечем его плоскостью, параллельной кругу КА, получив в пересечении круг
М№ (I, 4), перпендикулярный плоскости, содержащей отрезки М2 и 214; пере¬
сечение круга М1ЧЕ с треугольником М2\ есть отрезок ДЖ, являющийся диаме¬
тром последнего. Пресечение этого круга с заданной плоскостью есть отрезок ЕЛ.
Поскольку круг ДЖЕ перпендикулярен треугольнику М2ГЧ, а тот, в свою очередь,
перпендикулярен плоскости, в которой лежит АВ. то отрезок ЕЛ, по которому они
пересекаются, перпендикулярен треугольнику М2№ и, соответственно, треуголь¬
нику К2А, в силу чего ЕЛ перпендикулярен всем прямым, лежащим в плоскости
M2N и проходящим через В.
Но тогда он перпендикулярен ДЖ и АВ. А поскольку конус с основанием MNE
и вершиной 2 рассечен плоскостью, перпендикулярной треугольнику М2Н и об¬
разующей круг ДЖЕ, а также другой плоскостью, пересекающей основание кону¬
са по прямой ЕЛ, перпендикулярной отрезку МИ, являющегося пересечением кру¬
га МЕЫ и треугольника М2ГЧ, а отрезок АВ, являющийся пересечением плоскости,
содержащей параболу и треугольника М21Ч, параллелен отрезку образующей кону¬
са 2КМ, то сечение конуса плоскостью, содержащей АВ и параллельной 2КМ, есть
парабола, диаметром которой является АВ, а прямые, проведенные к АВ. проведе¬
ны под прямым углом, ибо они параллельны ЕЛ, перпендикулярному АВ. Тогда по-
Л1».
•Г».
ГД
скольку
ГД _ АК
AK “ AZ
и ЕА = А2 = 2К. а 0 = Е2 = АК, то
ГА _ АК2 _ АК2
AZ AZ2 " AZ ZK
Следовательно, ГД есть latus rectum сечения, ведь это доказано в (I. 11)*.
ЕА
Поэтому также
Комментарий ред.
Вопреки заявленному в формулировке, Аполлоний рассказывает вовсе не о том,
как построить параболу с ординатами, перпендикулярными диаметру и с заданным
latus rectum, а о том, как построить конус, сечением которого будет эта парабола.
Построение начинается с того, что АВ проводят до точки Е, а затем появляется
-	ГД 0
отрезок 0, удовлетворяющий условию
ГД
ЕА
♦I»
0
0
0
Но в чем смысл этого условия и где та точка Е, до которой надо продолжить ди¬
аметр?
* В Предложении 11 доказывается, что если ГД удовлетворяет условию
В£2 = ГЛ АВ А поскольку —-— = —~, то удовлетворяет.
2 2 М А2 * 2К
ГЛ _ МЛ
А2 ~ N2 ZM'
145

Книга I
Предположим, что конус уже построен. По построению отрезки 0 и АК параллель-
ны и равны, а также ЕА = AZ = ZK. Тогда, из
ГА
AZ
АК?
AZ2
получается, что ГА =
АК^
AZ
ГА	АК	ГА	0	_	ГА	0
следовательно, — = —, или — = —. То есть если выполняется условие — = —,
АК	Аг	0	ЕА	0	ЕА
то отрезок 0 параллелен основанию конуса, значит, это дает нам способ постро¬
ить основание. Отрезок жеАЕ может быть любым, так как его удлинение приводит
лишь к тому, что вершина конуса будет «отъезжать» дальше.
О построении же самой параболы см. комментарий к (I, II).
Предложение 53. Построение параболы с произвольным углом между ординатами
и диаметром
Пусть при тех же самых пред¬
посылках заданный угол не будет
теперь прямым. Допустим, он ра¬
вен Z0AE*.
Отложим на стороне заданно¬
го угла отрезок АО = ГА Прове¬
дем отрезок 0Е, перпендикуляр¬
ный АЕ. от точки Е - прямую ЕА,
параллельную ВО. а из точки А опу¬
стим к ЕА перпендикуляр АЛ. при¬
чем ЕА в точке К разделим пополам
и проведем отрезок КМ, перпенди¬
кулярно к ЕА, который продолжим
в противоположную сторону к точ¬
кам Z и Н, причем КМ такой, что
AV=KAKM.
Но если даны две прямые КА и
КМ, составляющие прямой угол,
причем прямая КА определена положением точки К, а КМ - своей величиной, то
можно описать параболу с вершиной в точке К, чьей осью будет КА, а КМ - latus
rectum (1,11 и 52). И эта парабола пройдет через точку А, поскольку АЛ - ордина¬
та, а прямая АЕ будет касательной, поскольку EK = KA (I, 33). Но так как 0АВ еще
нс
КО
* Имеется в виду что заданы отрезок ГЛ и угол (-)АЕ Нужно через точку А провести параболу, у
которой ОА - диаметр, ГА - latus rectum в этой точке, а ординаты, проведены под углом ©АЕ к ди¬
аметру На этот раз, речь идет уже о построении именно параболы, которое сводится к построе¬
нию ее относительно оси Но вот как реально это сделать, опять же ни слова

Предложения
и параллельна ЕЛ, то и 0АВ - диаметр сечения (I, 46), следовательно, ординаты,
проведенные от сечения к нему параллельно касательной АЕ, будут рассекаться им
пополам. Поскольку же ZAE0 = ZAHZ, а угол 0АЕ общий, то треугольники А0Е
и AZH подобны.
m	А0 AZ	2А0 ZA
Поэтому	=	 и	=	.
' АЕ АН	2АЕ АН
ГД
Но так как ГЛ = 2А0, то	=	Следовательно, ГЛ есть latus rectum (I, 49).
2АЕ АН
Предложение 54. Построение № 52 для гиперболы
Если на плоскости за¬
даны два отрезка, образу¬
ющих прямой угол, один из
которых продолжен за вер¬
шину до некоторой точки,
надо построить гиперболу,
лежащую в плоскости угла,
для которой продолженный
отрезок является диаме¬
тром, другой — laïus rectum,
вершиной — вершина пря¬
мого угла, а квадрат лю¬
бой ординаты, проведенной
от сечения к диаметру, ра¬
вен площади прямоугольни¬
ка, одной из сторон кото¬
рого является абсцисса, а
второй — latus rectum, сло¬
женной с площадью прямо¬
угольника подобного пря¬
моугольнику, ограниченно¬
му заданными отрезками*.
о.
Пусть будут даны две прямые АВ и
должена до точки Д. Надо найти гиперболу, лежащую в плоскости угла АВГ с диа¬
метром АВЛ, вершиной В и latus rectum — ВГ, тогда квадрат любой ординаты к ди¬
аметру, проведенной под заданным углом, будет равен площади прямоугольника.
* То есть, эйдосу, ограниченному 1_г и И. Напомним, что площадь подобного прямоугольника
(1,12) Конечно же, как и в (1,52) 1_г вовсе не обязан задавать плоскость вместе с АВ И
ится отнюдь не сама кривая, а ее конус, сечением которого она и будет
равна Lt
как и в (I, 52), стро
•к
147

Книга I
ограниченного latus rectum и абсциссой, сложенной с площадью прямоугольника,
подобного прямоугольнику, построенному на АВ и ВГ.
Пусть сначала ордината составляет с диаметром прямой угол и через АВ проведе¬
на плоскость, перпендикулярная исходной, а в ней через точку К, разбивающую от¬
резок АВ пополам, проведем и продолжим перпендикуляр ЕК и опишем круг AEBZ,
который пересечется с ЕК в точке Л, тогда ЕА является диаметром. И пусть отноше¬
ние ЕК к КА не больше, чем АВ:ВГ.
»I»
»It
»i».
„ EK AB	AB ЕК
Если — = —, воспользуемся точкой Л, если же это не так, то пусть	=	.
КА ВГ	ВГ КМ
Тогда проведем через точку М отрезок MZ, параллельный АВ, и проведем AZ, EZ
и ZB. а через точку В отрезок ВЕ, параллельный EZ. Поэтому, поскольку ZAZE =
ZEZB, а ZAZE = ZAEB и ZEZB = ZEBZ, то также ZEBZ = ZZEB, а значит, ZB = ZE.
Построим конус, с вершиной в Z, имеющий основанием круг ВЕ, перпендику¬
лярный треугольнику BZE Этот конус будет прямым, так KaKZB = ZE.
Поэтому если продолжить ZB, ZE и MZ и конус пересечь с плоскостью, парал¬
лельной кругу' ВЕ, то сечением будет круг НП0Р с диаметром Н0. Пересечением
круга НП0Р и плоскости, содержащей отрезки АВ и ВГ, является отрезок ПАР, пер¬
пендикулярный Н0 и АВ, ибо круги ЕВ и Н0 суть сечения конуса, перпендикуляр¬
ные треугольнику ZH0, содержащему ось, которому перпендикулярна плоскость,
содержащая отрезки АВ и ВГ. Поэтому их общее сечение ПАР перпендикулярно Н0
и АВ. Таким образом, все прямые, пересекающие ПАР и расположенные на плоско¬
сти ZH0, образуют с ПАР прямые углы. А поскольку конус с основанием Н0 и вер¬
шиной Z. пересекается с плоскостью НП0Р, перпендикулярной треугольнику ZH0,
а также плоскостью, содержащей ВА и отрезок ПАР, перпендикулярный НА0 и, так
как пересечение плоскости, в которой лежит сечение ПВР, и плоскости, рассекаю¬
щей конус через ось, есть отрезок АВ, который, будучи продолжен заточку В, пере¬
секается с продолжением отрезка HZ в точке А. то на основании доказанного пре¬
жде (Г 12) сечение ПВР есть гипербола с вершиной в точке В, а ординаты к отрезку
ВД, составляют с ним прямой угол, ибо они параллельны прямой ПАР. А посколь-
АВ_ ЕК ЕК _EN_EN-NZ AB_EN-NZ
ВГ ” КМ " КМ ” NZ ” NZ2 ’Т0 ВГ " NZ2 '
АВ
А так как треугольники AN Ей NBZ подобны, то EN-NZ = AN-NB и —
AN NB AN BN
Очевидно, что	г— =	.
NZ2 NZ NZ
С другой стороны, из подобия треугольников следует
' NZ АН ОН
AB ZO ZO Z02
а значит. —■=	=	.
ВГ ОН 00 НО 00
Итак,
AN NB
NZ2
BN _ ZO
NZ " 00'
AN _ AA _ ZO
•i»
Z02
и Z0 параллельна прямой АА. Следовательно, АВ есть latus
ВГ НО • 00
transversum, а ВГ - latus rectum, ведь это было доказано в (I, 12).
148

Предложения
Предложение 55. Построение № 53 Х1Я гиперболы
Пусть заданный угол ВА0
теперь отличен от прямого.
Требуется описать гиперболу,
так чтобы ее диаметром был от¬
резок AB, latus rectum — АГ, и
•я
прямые, проведенные как ор¬
динаты, были проведены под
углом 0АВ.
Пусть АВ рассекается на два
равных отрезка в Л, а на АА бу¬
дет описан полукруг AZA, к ко¬
торому параллельно прямой АА
проведена прямая ZH, такая,
ZH2 АГ
что	=	*.
НА НА АВ
<В
Проведем прямую Z0A и
отложим АЛ такой, что АЛ2 =
ZAA0,
Г	55. Рис. 1
Затем продолжим ZA и отложим АК - АД. На продолжении AZ выберем точку М
такую, что AZ ZM = AZ1.
Проведем теперь КМ, а через точку Л отрезок SN, перпендикулярный KZ. При
заданных двух прямых КЛ и AN, перпендикулярных друг другу, пусть будет описана
гипербола, latus transversum которой равен КА, latus rectum - AN, а ординаты, про¬
веденные к диаметру, перпендикулярны к нему (1, 54).
Сечение будет проходить через А, поскольку AZ ZM = AZ2 (1, 12), а прямая А0
будет его касаться, поскольку АЛ2 = ZA A0 (1, 37). Наконец, АВ есть диаметр, по¬
скольку проведен к сечению из центра А (Добавление к Предложениям 47—51).
Так как
II«
АГ _ АГ
AB ~ 2А0
ZH2 _ АГ _ АГ АГ _ АГ 2А0	2А0 _ А0 _ ZH
НА НА АВ 2АА 1 2АА ~ 2А0 2АА * 2АА ~ АД ~ НА
ZH
НА '
ZH2 ZH ZH
С другой стороны,	=	.
НА НА АН НА
АГ ZH
Следовательно, 	=	.
2А0 НА
Но из подобия треугольников
ZH _ АО
НА~ АЕ
, то
* Такого равенства не было в предыдущих теоремах. Вероятно. Аполлоний получил его, двига¬
ясь назад от того, что ему надо доказать А доказать надо, что АГ 2А0 = АО АН, так как тогда АГ яв¬
ляется 1_г О том, каким же образом провести эту прямую, см. комментарий после Предложения
149

Книга!
АО
A3
Следовательно, АГ есть latus rectum (I. 50)
Комментарий ред.
Аполлоний ничего не говорит о том, как реально провести ХН, а между тем это не
такая уж простая задача. Поскольку нам не удалось ни найти, ни придумать какого-
то более или менее простого построения, воспользуемся способом, предложенным
Артуром Чвалиной (25, с. 72).
На рис. 2 приведе¬
на часть предыдуще¬
го чертежа с необходи¬
мыми обозначениями
Поскольку угол а рав¬
ный углу 0АВ задан,
то для построения достаточно найти у. Из чертежа видно, что ПА = у etga + х-г,
HA = y c/ga+x + r ZH= . Учитывая, чтог2 “*2 = У2, получим
sma	J
HhHA= ■_? |y(cos2a-sin2a) + 2xsinacosal =	cos 2a+ х sin 2a).
sin aL v	7	J sin a
ZH2 у	_ АГ
Следовательно,	= z • r-r тх.
НАНА ycos2a + x-sin2a АВ
Отсюда АВ • у = АГ(у • cos 2a + х • sin 2a), у (АГ cos 2a - АВ) = - АГ • х • sin 2a.
Возведем в квадрат, учтем, чтох2 + у2 = г2, и извлечем квадратный корень. Тог¬
да получаем у'¡АГ2 - 2 АВ • АГ cos 2a + АВ2 = г • АГ sin 2a.
Теперь построим треугольник со сторонами АВ и АГ и углом между ними, рав¬
ным 2а (рис. 3). Отложим на АГ отрезок АЕ = г и опустим на АВ перпендикуляр ЕП
= rsin2a. От точки В отложим отрезок BI
= ЕП и проведем параллельно АГ прямую
IT. И з подобия треугольников следует, что
1т = в , или IT ВГ = АГ BI. Но BI = ЕП
АГ ВГ
= г sin2a , а отрезок ВГ, согласно теореме
косинусов равен квадратному' корню, сто¬
ящему возле у Следовательно, у = IT
Дальнейшее построение очевидно.
Интересно, а как сам Аполлоний пред¬
полагал проводить ZH?
»!♦.
•1»
не
У
•и
55. Рис. 3
В
150

Предложения
Предложение 56. Построение № 52 для хыинса (диаметр больше. чем Lr)
О
Если на /носкости заданы два отрезка, образующих прямой угол, то надо построить
в /носкости угла сечение, называемое эллипсом, для которого один из отрезков являет¬
ся диаметром, вершиной — вершина прямого угла, а квадрат любой ординаты, проведен¬
ной от сечения к диаметру, равен площади, недостающей до /пощади прямоугольника,
одна из сторон которого — абсцисса, а вторая — latus rectum, на величину прямоуголь¬
ника подобного прямоугольнику, ограниченному заданными отрезками* *.
Пусть даны перпендикулярные друг другу отрезки АВ > АГ. Нужно описать в пло¬
скости. содержащей эти отрезки, эллипс,
диаметр которого АВ, вершина - А. latus
rectum - АГ, а ординаты будут проведены
от сечения к диаметру под заданным углом
и в квадрате будут равны площади прямоу¬
гольника, ограниченного АГ и абсциссой,
за вычетом площади прямоугольника, по¬
добного прямоугольнику .
Пусть сначала заданный угол будет пря¬
мым. Проведем через АВ плоскость, пер¬
пендикулярную плоскости, содержащей
отрезки АВ и АГ, и опишем лежащий в ней
сегмент окружности АЛВ, опирающийся
на АВ. с серединой в точке Л, из которой
проведем хорды АЛ и АВ. Отложим отре¬
зок АЕ = АГ. Тогда, если будут проведе¬
ны: через Е отрезок ЕО, параллельный АВ, через О - OZ, параллельный АВ. а так¬
же AZ, пересекающей продолжение АВ в точке Е, то из подобия треугольников по-
АВ АВ АА ЕА
лучится 	=	=	=	.
АГ АЕ АО EZ
Проведем и продолжим AZ и ZB, а также через некоторую точку О, лежащую на
продолжении ZB, проведем ОН, параллельно АЕ, которая пересечется с продол¬
жением АВ в точке К, и продолжим ZO так, чтобы она пересеклась с НК в точке
Л. Теперь в плоскости, перпендикулярной треугольнику 0HZ. опишем вокруг ОН
круг HNO. являющийся основанием конуса, с вершиной в точке Z. Этот конус бу¬
дет прямым, потому что HZ = Z0. Докажем это. Так как дуга АА равна дуте АВ. то
угол АВА равен углу AZB.
И так как ZEZA = zZAA+ZZAA и ZZ.AA = ZZBA, ZZAA = ZAZB. то ZEZA =
ZABA = ZBZA.
Поскольку АЕ параллельна АН, то ZEZA= ZZHO, ziAZB — Z.ZOH и, значит,
ZZH0 = ZZ0H.
¿Г 2
* То есть ограниченного 1л и Н. Напомним, что площадь подобного прямоугольника равна“' *
(I, 13) Как и в предыдущих случаях, £г вовсе не обязан вместе с АВ задавать плоскость эллипса.
И опять же, строится не эллипс, а его конус.
151

Книга I
Отсюда HZ = Z0.
Так как круг перпендикулярен плоскости 0HZ, а та перпендикулярна плоско¬
сти, содержащей прямые АВ и АГ, то пересечение последней с кругом также будет
перпендикулярно плоскости 0HZ. Пусть КМ будет их общим сечением. Тогда КМ
является перпендикулярной АК и КН. И поскольку конус, чье основание есть круг
HN0, а вершина - точка Z, рассекается плоскостью через ось, образуя в сечении
треугольник H0Z, и другой плоскостью прямых АК и КМ, пересекающей плоскость
основания конуса по прямой КМ, перпендикулярной НК, и данная плоскость пе¬
ресекается со сторонами конуса ZH и Z0, то полученное сечение есть эллипс с ди¬
аметром АВ, а проводимые ординаты проводятся под прямым углом, поскольку они
параллельны прямой KM (1,13).
АВ АЕ AEEZ ВЕ-ЕА
И поскольку — = —
АГ EZ
EA AK ZA	AB ZA ZA
EZ " КН ‘ АН '	АГ ~ Л0 АН
п AB ZA2
Поэтому — =

‘ АГ Л0 ЛН
А раз это так, то АГ есть latus rectum сечения, как доказано в (I, 13).
ez2
EZ2
ZA ZA
■ —— ■ • —■■■ ■■
И
ИЛ0ЛН Л0ЛН
BEEA BE EA BE BK _ ZA
EZ2 _EZ EZ 1 EZ'K0_A0’
ZA2
Предложение 57. То же построение, но диаметр меньше, чем Lr
При тех же самых предпосылках пусть АВ <АГ, и вокруг ди¬
аметра АВ требуется описать эллипс, так что АГ - latus rectum.
Пусть АВ рассекается на два равных отрезка в А и пусть
через А перпендикулярно к АВ будет проведена ZE такая,
4ToZE: = AB Ar nZA = AE.
Проведем отрезок ZH, параллельный прямой АВ, такой,
АГ ZE
что — = —.
AB ZH
Тогда ZE > ZH.
.	,Г.,О,Г АГ ZE2 ZA?
А поскольку ZE- = АВ АГ, то — = —- = —- .
АВ АВ2 АД*
„	ze гд2 ze za-де
Следовательно —=—г, или — =	т—.
ZH АД2 ZH АД*
А если даны две перпендикулярные друг другу прямые,
большая из которых ZE, то можно описать эллипс, у которо-
го диаметр ZE, а latus rectum - ZH (I, 56). Этот эллипс будет
.	ZE ZA ДЕ
проходить через А, потому что — =	z—, а гак как АЛ =
ZH АД2
АВ. он также проходит через В (1,21).
Таким образом, эллипс построен на диаметре АВ.
57. /’wc. /
152

Предложения
АГ ZA2
АГ ZA2
А поскольку 	=	7 и АД* = ДА ЛВ, го
АВ АД-	АВ
Следовательно, АГ есть latus rectum (1, 21).
АД AB
Предложение 58. Построение № 53 для эллипса
Пусть при тех же самых пред¬
посылках заданный угол ВАД не
будет прямы*.
И пусть АВ в точке Е разбивает¬
ся пополам, на отрезке АЕ описан
полукруг, и выбираем на АЕ точку
Н такую, что для отрезка гн, па¬
раллельного АД, выполняется про-
X
гн2 аг
порция**	=	.
НЕНА АВ
Проведем и продолжим Аг и
Е£. Отложим отрезок Е0, опре¬
деленный как среднее пропорци¬
ональное между ЕЛ и Е7: ЕД- Е2
= Е02.
•X«
Продолжим Е0 за точку Е и
пусть Е0 = ЕК. Далее, проведем
КА так, чтобы	а че¬
рез точку 0 к прямой КД перпен¬
дикуляр МЕМ, который паралле¬
лен А7Л, поскольку угол А2Е пря¬
N
мой. И при заданных двух прямых К0 и 0М, перпендикулярных друг другу, опишем
эллипс, так что К0 будет диаметром, а 0М - latus rectum, а ординаты, проведенные
к К0, составляют с ним прямой угол (I, 56 и 57).
Сечение будет проходить через А, потому что (1, 13) Z0-ZA = AZ2.
¡3
А поскольку 0Е = ЕК, АЕ = ЕВ, то сечение пройдет через В, Е будет его центром,
АВ - диаметром (Добавление к 1, 47-51), а ДА будет касаться сечения, так как (I,
38) ЕД EZ = Е02.
ZH2 АГ
Тогда поскольку справедлива пропорция	=	,
НЕ • НА АВ
АГ _ АГ 2ДА АГ ДА н ZH2 _ ZH ZH AT ДА _ ZH ZH
АВ " 2ДА АВ _2ДА АЕ НЕ НА " НЕ НА 2АД АЕ~ НЁ' НА
* То есть если заданы отрезки АВ и АГ и угол ВАЛ, то через точку А нужно провести такой эллипс,
у которого АВ - диаметр, АЛ - касательная к сечению, а АГ - latus rectum в точке А.
** См. примечание к (I, 55)
153

Книга I
ДА ZH	АГ ZH
Однако — =
АЕ
=	, ПОЭТОМУ	-
НЕ	2АА НА
ZH НА
А поскольку	то АГ есть latus rectum (1, 50).
НА AN
Предложение 59. Построение противолежащих, если заданы Ег, диаметр (М) и угол
между ординатами и диаметром
Если даны две прямые, перпен¬
е
дикулярные друг другу, надо по-
строить такие противолежа¬
щие, что их диаметром будет
одна из этих прямых, вершиной
- пределы диаметра, а квадра¬
ты ординат, проведенных в лю¬
бом из сечений, будут равны пло-
шадям прямоугольников,
сторон которых является вто¬
рая прямая, а другой - абсцисса,
сложенная с площадью прямоу¬
гольника, подобного прямоуголь¬
нику, ограниченному заданными
/Л
прямыми.
Пусть заданными двумя прямыми, определенными как перпендикулярные друг
другу, будут BE и ВО, а заданным углом будет Н.
Нужно описать противолежащие вокруг одной из прямых так. что ординаты бу¬
дут проводиться под углом Н к диаметру.
Пусть будет описана гипербола, у которой BE - диаметр, Bö - latus rectum, а пря¬
мые к BE. продолженной дальше, будут проведены к ней как ординаты под углом
Н Ведь как это сделать, показано прежде (I, 55). Поэтому пусть через Е к BE будет
проведен перпендикуляр ЕК, равный ВО, и тем же самым образом будет описана
другая гипе!
Очевидно, что эти сечения суть противолежащие с одинаковыми latus rectum и
общим диаметром
»ж
©
•ж
Предложение 60, Построение сопряженных гипербол
Если даны две прямые, делящие друг друга на две равные части, надо построить две
пары противолежащих так, чтобы эти прямые были сопряженными диаметрами и что-
154

Предложения
бы квадрат одного диаметра был равен пло¬
щади прямоугольника. ограниченного другим
диаметром и latus rectum вторых противоле¬
жащих, и схожим образом, второй диаметр
60. Рис. I
те был равен площади прямоугольни¬
ка, ограниченного первым диаметром и latus
rectum первых противолежащих.
Пусть заданными прямыми, рассекаю¬
щими друг друга на два равных отрезка, бу-
дут АГ и ДЕ. Нужно описать
в
тиволежа-
шие вокруг одного из диаметров так, что
АГ и ДЕ будут сопряженными диаметра¬
ми, а ДЕ2 = АГ-АГ и АГ2 = ДЕД/.
ведем перпендикулярно АГ отре-
зок АГ такой, чтобы АГЛГ = ДЕ2*. Те-
перь можно описать противолежащие (А)
и (В), у которых диаметром будет АГ, latus
rectum — АГ, и прямые, проведенные от
сечения к диаметру как ординаты, будут
параллельны ЛЕ (I, 59). Поэтому ДЕ бу¬
дет другим диаметром противолежащих,
ведь он является средним
Ж
порциональным между АГ и АГ, а в В рассекается на
два равных отрезка (Опр. И, 3).
Пусть теперь Д/ будет такой, что ДЕ Д/ = АГ2, и Д/ перпендикулярен ДЕ. Тогда
при заданных двух прямых ДЕ и Д/, перпендикулярных друг другу, можно описать
противолежащие (Г) и (Д), так что диаметром будет ДЕ, latus rectum — AZ, и пря-
мые, проведенные как ординаты, будут параллельны АГ. Поэтому АГ будет диаме-
м сечений (Г) и (Д).
Следовательно, АГ рассекает на два
равных отрезка прямые, расположен¬
ные параллельно прямой ДЕ в сечени¬
ях (А) и (В), а ДЕ — прямые, параллель¬
ные прямой АГ, а это и нужно было по¬
лучить (Опр. 1, 6).
Такие сечения назовем сопряженны¬
ми.
Комментарий ред.
Прямоугольник, равновеликий за¬
данному прямоугольнику, или в данном
60. Рис. 2
Л
Г
* Чтобы найти отрезок АГ, необходимо построить прямоугольник со стороной АГ равновели¬
кий квадрату со стороной ЛЕ (см. Комментарий ред в конце Предложения).
155

Книга!
случае, квадрату, древнегреческие математики строили следующим образом*. Про¬
должим две стороны квадрата на расстояние, равное АГ (рис. 2). Затем проведем и
продолжим диагональ получившегося прямоугольника до пересечения с продолже¬
нием стороны квадрата. Дальнейшие построения очевидны из чертежа. Тогда АГ-АГ
= ДЕ2 (Евклид 1,43).
Найти сторону АГ можно, и постро¬
ив прямоугольный треугольник с ка¬
тетами ДЕ и АГ (рис. 3). Если теперь
провести перпендикуляр к АД, то его
пересечение с продолжением АГ дает
АГ, поскольку точки А, А и Л лежат на
окружности.
например- [1 с
22,23]

ДОСЛОВНЫЙ ПЕРЕВОД КНИГИ I
<
ОПРЕДЕЛЕНИЯ I
»1«
Если от некой точки к окружности круга, не лежащего в той же самой плоскости,
что и точка, проведена прямая, причем она проведена в бесконечность в обе сто{
ны, и при неподвижности этой точки данная прямая, двигаясь по окружности кру¬
га, вернется в свое изначальное положение, то поверхность, описанную этой прямой
и составленную из двух поверхностей, имеющих общую вершину, каждая из кото¬
рых простирается в бесконечность в том случае, если описывающая прямая беско¬
нечна, я называю конической поверхностью.
А неподвижную точку я называю ее вершиной.
Прямую же, проводимую через точку и середину круга, я назы
ваю осью.
Конусом я называю фигуру, ограниченную кругом и находящейся между верши¬
ной и окружностью круга конической поверхностью.
А вершиной конуса я называю точку, которая является также вершиной поверх¬
ности.
Осью конуса я называю проводимую от вершины к середине крута прямую.
Основанием я называю круг.
Прямыми конусами я называю такие, которые имеют оси, перпендикулярные
основаниям.
Наклонными конусами я называю те, которые не имеют оси. перпендикуляр¬
ные основаниям.
Диаметром любой кривой линии, которая находится водной плоскости, я назы¬
ваю прямую, проведенную от кривой линии, которая все прямые на данной линии,
проведенные как паратлельные какой-либо прямой, рассекает пополам.
Вершиной кривой линии я называю предел диаметра на кривой линии.
Каждая же из этих параллельных прямых проведена упорядоченно к диаметру.
Схожим образом поперечным диаметром двух кривых линий, лежащих в одной
плоскости, я называю прямую, которая, рассекая две данные кривые линии, все пря¬
мые на каждой из них, проведенные параллельно какой-либо прямой, делит пополам.
157

Дословный перевод книги I
Вершинами же кривых линий я называю пределы диаметров, расположенных на
данных кривых линиях.
А также я называю диаметром прямую, расположенную между двумя линиями,
которая рассекает пополам все прямые, параллельные какой-ли
прямой и отсечен¬
ные кривыми, притом каждая из параллельных проведена упорядоченно к диаметру.
Каждая из этих прямых проведена упорядоченно к диаметру.
Сопряженными диаметрами одной или двух кривых линий я называю прямые
линии, каждая из которых является диаметром и рассекает прямые, параллельные
другому, пополам.
Осью же одной или двух кривых линий я называю прямую линию, которая явля¬
ется диаметром для них и рассекает параллельные прямые на прямые углы.
Сопряженными осями кривой линии и двух кривых линии я называю прямые,
которые, будучи сопряженными диаметрами, рассекают параллельные друг другу
прямые на прямые углы.
158

Дословный перевод книги I
1
Прямые, проведенные от вершины конической поверхности к точкам на поверхно¬
сти, находятся в поверхности.
Пусть будет коническая поверхность, чьей вершиной будет точка А, пусть будет
взята некоторая точка В на конической поверхности и пусть их соединяет некая пря¬
мая АГВ. Я утверждаю, что прямая АГВ находится в поверхности.
Допустим, что она не находится в конической поверхности, ДЕ будет прямой, опи¬
сывающей поверхность, а Е7 - кругом, по которому проведена прямая ЕЛ. Если при
сохранении точки А прямая ДЕ проводится по окружности круга Е2, то она пройдет
и через точку В, и две прямые будут иметь те же самые пределы.
Итак, невозможно, чтобы прямая, соединяющая А и В, не находилась в поверх¬
ности. Следовательно, она находится в поверхности.
»!•
1П
Добавление
Также очевидно, что если от вершины к некой точки из тех, которые находятся
внутри поверхности, проводится прямая, то она будет попадать внутрь конической
поверхности, а если она проведена к некоторой точке из тех, которые находятся вне
поверхности, то она будет находиться вне поверхности.
•К
•I*
2
Если на .¡юбой из поверхностей, которые соединяются в вершине, берутся две точки,
и прямая, соединяющая данные точки, не попадает на вершину, то данная прямая ока¬
жется внутри поверхности, а прямая, проведенная дальше, окажется вне поверхности.
Пусть будет коническая поверхность, вершиной которой является точка А, а круг,
через который проводится описывающая поверхность прямая, — ВГ. и пусть будут
взяты на любой из поверхностей, которые соединяются при вершине, две точки Л
и Е, а соединяющая их прямая ДЕ пусть не попадает на точку А. В этом случае я ут¬
верждаю, что прямая ДЕ окажется внутри поверхности, а прямая, проведенная даль¬
ше, - вне поверхности.
Пусть будут проведены прямые АЕ и АЛ, и они также пусть проводятся дальше
Они будут касаться окружности круга, а именно - в точках В и Г. Пусть их соединяет
прямая ВГ. Поэтому ВГ будет внутри круга и как следствие внутри конической по¬
верхности. Пусть на ЛЕ будет взята некоторая точка Z, и пусть будет проведена даль¬
ше прямая AZ. Данная прямая попадет на прямую ВГ. Ведь треугольник ВГА лежит в
одной плоскости. Пусть данная прямая попадет в точке Н. А поскольку Н находит¬
ся внутри конической поверхности, то и АН будет находиться внутри конической
поверхности. Поэтому и точка Z находится внутри конической поверхности. Схо¬
жим образом может быть показано, что все точки на ЛЕ находятся внутри кониче¬
ской поверхности. Так что вся прямая ЛЕ находится внутри конической поверхности.
Пусть прямая ЛЕ будет проведена дальше к некоторой точке 0. Тогда я утверж¬
даю, что она будет находиться вне конической поверхности. Ведь если возможно,
то пусть некоторая ее часть, а именно 0, будет находиться внутри конической по¬
верхности, и пусть будет проведена дальше соединяющая точки прямая А0. Она бу¬
дет касаться или окружности круга, или точки внутри его. Однако это не
159

Дословный перевод книги I
Ведь она касается проведенной дальше прямой ВГ в некоторой точке К. Итак, Е0
находится вне конической поверхности.
Итак, ДЕ находится внутри конической поверхности, а ее продолжение - вне.
Если конус делится плоскостью через вершину, то сечением будет треугольник.
Пусть будет конус, вершиной которого будет точка А, основанием круг ВГ. Пусть
конус будет рассекаться некой плоскостью через точку А, и пусть она сделает сече¬
ниями на поверхности линии АВ и АГ, а в основании - прямую ВГ. В этом случае я
утверждаю, что АВГ есть треугольник.
Ведь поскольку соединяющая А и В линия есть общее сечение для рассекающей
плоскости и дня конической поверхности, то АВ есть прямая. Схожим образом и АГ
есть прямая. В свою очередь, и ВГ есть прямая. Следовательно, АВС есть треугольник.
Следовательно, если конус рассекается плоскостью через вершину, сечением бу¬
дет треугольник.
•А
4
Если любая из двух поверхностей, которые соединяются в вершине, рассекается ка¬
кой-либо плоскостью, параллельной кругу, через который проводится описывающая по¬
верхность прямая, то плоскость, помещенная внутрь поверхности, будет кругом, име¬
ющим центр на оси, а фигура, ограниченная кругом и конической поверхностью, заклю-
ченная между секущей плоскостью и вершиной, будет конусом.
Пусть будет коническая поверхность, вершиной которой является точка А, а кру¬
гом, через который проводится описывающая поверхность прямая, будет ВГ, и она
будет делиться некоторой плоскостью, параллельной кругу В Г, и пусть она сдела¬
ет сечением на поверхности линию ДЕ. Я утверждаю, что линия ДЕ есть круг, име¬
ющий центр на оси.
Пусть будет взят центр / круга ВГ, и пусть будет проведена соединяющая точки пря¬
мая №.. Следовательно, она является осью и пересекается с делящей плоскостью. И
пусть она пересекается в точке Н, и пусть через КЬ будет проведена некая плоскость.
Следовательно, сечением будет треугольник АВГ. А поскольку точки Л, Н, Е находят¬
ся в секущей плоскости, они также находятся в плоскости АВГ, а ДНЕ является пря¬
мой Итак, пусть на линии ДЕ будет взята некоторая точка 0; и пусть будет проведена
и продолжена дальше прямая А0. Она будет касаться окружности В Г. Пусть она ка¬
сается ее в точке К; и пусть будут проведены прямые Н0 и 7К. А поскольку две па¬
раллельные плоскости ДЕ и ВГ рассекаются некоторой плоскостью АВГ, то их общие
сечения будут параллельными. Следовательно, ДЕ параллельна ВГ. По той же самой
причине Н0 параллельна №. Таким образом, /А к АН равно 7 В к ДН равно 7Г к НЕ
равно7КкН0 И поэтому три (прямые) равны между собой: В7, К7, 7Г. Также рав¬
ны между собой следующие (прямые): ДН, Н0, НЕ. Схожим образом мы покажем, что
все прямые, попадающие от точки Н на линию ДЕ. являются равными между собой
Следовательно, линия ДЕ есть круг, имеющий центр на оси.
Также очевидно, что фигура, окруженная кругом ДЕ и конической поверхностью,
которая отведена им к точке А, будет конусом.
160

Дословный перевод книги I
И схожим образом показывается, что общим сечением, рассекающим плоскость
и треугольник, проходящего через ось, будет диаметр круга.
5
Если наклонный конус делится через ось плоскостью, перпендикулярной основанию,
и также рассекается другой плоскостью, перпендикулярной треугольнику, проходяще¬
му через ось, так что она отделяет от вершины треугольник, подобный треугольнику,
проходящему через ось, но расположенный противоположным образом, то сечением бу¬
дет круг, а такое сечение пусть называется противоположным.
Пусть будет наклонный конус, чья вершина будет точка А, основанием — круг ВГ,
и пусть он рассекается через ось плоскостью, перпендикулярной кругу' В Г, и пусть
она сделает сечением треугольник АВГ И пусть он будет рассекаться другой пло¬
скостью, перпендикулярной треугольнику и отделяющей при точке А треугольник
АКН, подобный треугольнику АВГ и расположенный противоположным образом;
и выходит так, что угол АКН равен углу АВГ. И пусть она сделает сечением на по¬
верхности линию Н0К. Я утверждаю, что линия Н0К есть круг.
Пусть будут взяты некоторые точки 0 и Л на линиях Н0К и ВГ; и от точек 0 и А
к плоскости треугольника АВГ проводятся перпендикулярные прямые. Они будут
попадать на общие сечения плоскостей. Они попадают на них как прямые 20 и ЛМ.
Следовательно, 20 параллельна ЛМ. И пусть будет проведена через 2 прямая А2Е,
параллельная В Г. Однако 20 параллельна ЛМ. Следовательно, плоскость прямых
20 и АЕ параллельна основанию конуса. Поэтому это есть круг, чей диаметр есть
прямая АЕ. Следовательно, А2Е равно 20 в квадрате. А поскольку АЕ параллельна
ВГ, то угол ААЕ равен углу АВГ Однако, по нашему' предположению, угол АКН ра¬
вен углу АВГ. Следовательно, угол АКН равен углу ААЕ. И углы, расположенные на
точке 2, равны по расположению. И поэтому треугольник /12Н подобен треугольни¬
ку К2Е. Следовательно, Е2 к 2К равно Н2 к 2А, и, таким образом, Е2А равно 20.
Однако мы показали, что А2Е равно 20 в квадрате. Поэтому К2Н равно 20 в ква¬
драте. Схожим образом мы покажем, что все прямые, проведенные отлинии Н0К к
Н К как перпендикулярные, могут быть равны прямоугольнику отрезков прямой НК.
Следовательно, сечением является круг с диаметром НК.
6
Если конус делится плоскостью через ось и на поверхности конуса берется некая
точка, которая не находится на стороне треугольника, расположенного на оси, и от
нее проводится прямая, параллельная некоторой прямой, [проведенной] от окружности
круга перпендикулярно к основанию треугольника, то она пересечется с треугольником
на оси, и, проведенная дальше вплоть до другой части поверхности, она будет рассе¬
каться на две равные части треугольником.
Пусть будет конус, чьей вершиной будет точка А, основанием - круг В Г, и пусть ко¬
нус будет дел иться плоскостью через ось, и пусть она сделает общим сечением треу¬
гольник АВГ. И пусть от некой точки М, лежащей на окружности ВГ, будет проведена
перпендикулярная к ВГ прямая ММ И пусть будет взята на поверхности конуса неко¬
торая точка А и через точку А пусть будет проведена прямая ЛЕ. параллельная прямой
К£
161

Дословный перевод книги I
НЕ
МЫ. Я утверждаю, что прямая ДЕ, проведенная дальше, встречается с плоскостью треу¬
гольника АВГ, а проведенная к другой стороне конуса, пока она не пересечется с его по¬
верхностью, она будет рассекаться на две равные части плоскостью треугольника АВГ.
Пусть будет проведена АЛ и продолжена дальше. Следовательно, она пересека¬
ется с окружностью круга ВГ. Пусть она пересекается с ним в точке К; и от точки
К к ВГ пусть будет проведена перпендикулярная прямая КОЛ. Следовательно, К0
является параллельной М1Ч, соответственно, ДЕ. Пусть от точки А к точке 0 будет
проведена прямая А0. Поскольку в треугольнике А0К ДЕ параллельна 0К, то по¬
этому ДЕ, проведенная дальше, наталкивается на А0. Однако А0 находится в пло¬
скости треугольника АВГ. Следовательно, ДЕ пересекается с плоскостью треуголь¬
ника АВГ. Поэтому она и пересекается с А0. Пусть она пересекается с ней в точке
7\ и пусть будет проведена дальше прямая Д7, пока она не встретится с поверхно¬
стью конуса. Пусть она пересечется с ней в точке Н. Я утверждаю, что Л7 равно ¿Н
Поскольку точки А, Н и Л расположены на поверхности конуса, однако в пло¬
скости, проведенной через А0, АК, АН и КА, которая является треугольником с вер¬
шиной конуса, то поэтому точки А, Н и Л находятся на общем сечении поверхности
конуса и треугольника. Следовательно, линия, проведенная через А, Н и Л, являет¬
ся прямой. А поскольку в треугольнике АЛК ДН проведена как параллельная осно¬
ванию К0Л, а отточки А проводится дальше некая прямая А70, то К0 к 0Л равно
Л7 к 7Н. Однако К0 равно 0А. поскольку в круге ВГ КЛ перпендикулярна к диа¬
метру. Следовательно, Д2 равно ¿Н.
7
Ест конус рассекается плоскостью через ось и рассекается другой плоскостью, се¬
кущей плоскость, в которой расположено основание конуса, то если она рассекает по
прямой, перпендикулярной основанию треугольника, расположенного на оси, или той
же самой прямой, проведенной дальше, то прямые, проведенные сечением, возникшим
на поверхности конуса, которое сделала секущая плоскость, проведенные как парал¬
лельные прямой, перпендикулярной основанию треугольника, будут попадать в общее
сечение секущей плоскости и треугольника, расположенного на оси; а проведенные даль¬
ше вплоть до другой части сечения, они будут рассекаться им на две равные части. А
если конус является прямым, то прямая, расположенная в основании, будет перпенди¬
кулярной общему сечению секущей плоскости и треугольника, расположенного на оси;
а если конус является наклонным, то она не всегда будет перпендикулярной, но только
в том случае, если плоскость, проведенная через ось перпендикулярна основанию конуса.
Пусть будет конус с вершиной в точке А, основанием будет круг В Г. И пусть он
рассекается плоскостью через ось, и пусть она сделает сечением треугольник АВГ.
И пусть он рассекается другой плоскостью, рассекающей плоскость, в которой рас¬
положен круг ВГ. по прямой ЛЕ или перпендикулярной ВГ, или ей же, проведенной
дальше, и пусть она сделает сечением на поверхности конуса AZE. Общим сечени¬
ем секушей плоскости и треугольника АВГ является ZH. И пусть на сечении AZE
будет взята некая точка 0, и пусть будет проведена через точку 0 ©К, параллельная
прямой ДЕ Я утверждаю, что0К встретится с ZH, а, проведенная дальше до другой
части сечения AZE, будет рассекаться на две равные части прямой ZH.
162

Дословный перевод книги I
•Т€
Поскольку конус с вершиной в точке А и с основанием в круге ВГ рассекается
плоскостью через ось, и она делает сечением треугольник АВГ, и на поверхности бе¬
рется некая точка 0, которая не находится на стороне треугольника АВГ, а АН яв¬
ляется перпендикулярной ВГ, следовательно, прямая, проведенная через 0 как па¬
раллельная АН, т.е. 0К, пересекается с треугольником АВГ, а проведенная дальше
до другой части поверхности, рассекается на две равные части треугольником. А по¬
скольку прямая, проведенная через точку 0 как параллельная прямой АЕ встреча¬
ется с треугольником ABI' и находится в плоскости сечения AZE, то, следователь¬
но, она попадает в общее сечение секущей плоскости и треугольника АВГ А общим
сечением плоскостей является ZH. Поэтому прямая, проведенная через 0 как па¬
раллельная прямой АЕ, попадает на ZH. А проведенная дальше до другой части се¬
чения AZE, она рассекается на две равные части прямой ZH.
Поэтому или конус является прямым, или треугольник АВГ, расположенный на
оси, перпендикулярен кругу ВГ, или ни то ни другое.
Пусть прежде всего конус будет прямым. Поэтому и треугольник АВГ будет пер¬
пендикулярен кругу ВГ. А поскольку плоскость АВГ перпендикулярна плоскости ВГ,
а водной из плоскостей проводится АЕ, перпендикулярная ВГ, т.е. общему их сече¬
нию ВГ, то поэтому АЕ является перпендикулярной треугольнику АВГ. Следователь¬
но, она перпендикулярна всем прямым, которые касаются ее, и расположенных на
треугольнике АВГ. Следовательно, она также перпендикулярна ZH.
Пусть конус будет не прямым. Если треугольник, расположенный на оси, перпен¬
дикулярен кругу ВГ, то мы схожим образом покажем, что АЕ перпендикулярна ZH.
И пусть треугольник АВГ, лежащий на оси, не будет перпендикулярен кругу ВГ. Я
утверждаю, что и АЕ не перпендикулярна ZH. Ведь если это возможно, то пусть бу¬
дет. Однако она перпендикулярна ВГ. Следовательно, АЕ перпендикулярна каждой
из обоих ВГ и ZH. И она поэтому будет перпендикулярна плоскости, проведенной
через ВГ и ZH. Однако плоскостью прямых ВГ и HZ является АВГ. Следовательно,
АЕ перпендикулярна также треугольнику АВГ. Поэтому также все плоскости, про¬
веденные через нее, перпендикулярны треугольнику АВГ. Однако одной из плоско¬
стей, проведенных через АЕ, является круг ВГ. По этой причине круг ВГ перпендику¬
лярен треугольнику АВГ. И треугольник АВГ перпендикулярен кругу ВГ. А это про¬
тиворечит гипотезе. Следовательно, АЕ не перпендикулярна ZH.
Добавление
Отсюда ясно, что гН является диаметром сечения АгЕ, поскольку она рассека¬
ет на две равные части прямые, проведенные как параллельные некоторой прямой
АЕ, и что возможно, чтобы некоторые параллельные рассекались на две равные ча¬
сти диаметром гн и не являются перпендикулярными.
8
Если конус рассекается плоскостью через ось и рассекается другой плоскостью, се¬
кущей основание конуса по прямой, перпендикулярной основанию треугольника, распо¬
ложенного на оси, и если диаметр возникшего на поверхности сечения или параллелен
какой-либо стороне треугольника, или пересекается с ней вне вершины конуса, а по¬
163

Дословный перевод книги I
верхность конуса и секущая плоскость проводятся дальше до бесконечности, то также
сечение увеличивается до бесконечности, а некая прямая, проведенная от сечения ко¬
нуса как параллельная прямой, расположенной на основании конуса, отделяет от вер¬
шины сечения на диаметре любую заданную прямую.
Пусть будет конус с вершиной в точке А, а основанием будет круг В Г. И пусть он
рассекается плоскостью через ось; пусть она сделает сечением треугольник АВГ. И
пусть он рассекается другой плоскостью, секущей круг ВГ по прямой АЕ, перпен¬
дикулярной В Г Пусть она сделает сечением на поверхности конуса линию AZE. А
диаметр ZH сечения AZE пусть будет или параллелен прямой АГ, или, проведенная
дальше, она пусть натолкнется на нее вне точки А. Я утверждаю, что, если поверх¬
ность конуса и секущая плоскость проводятся дальше до бесконечности, сечение
AZE также увеличивается до бесконечности.
Пусть будут проведены дальше поверхность конуса и секущая плоскость. Ясно,
что прямые АВ. АГ и ZH вместе проводятся дальше. А поскольку ZH или параллель¬
на АГ. или, проведенная дальше, пересекается с ней вне точки А, то прямые ZH и
АГ, проведенные дальше к частям Г и Н, никогда вместе не пересекутся. Следова¬
тельно, пусть они проводятся дальше, и пусть на ZH будет взята некая точка 0, и че¬
рез точку© пусть будет проведена К0Л, параллельная ВГ, M0N — как параллельна
ДЕ. Поэтому' плоскость прямых КА и MN является параллельной плоскости пря¬
мых ВГ и ДЕ Следовательно, плоскость K.AMN есть круг. А поскольку точки А, Е,
М и N находятся в секущей плоскости, они также находятся на поверхности конуса
и, соответственно, - в общем сечении. Следовательно, AZE увеличилась до точек М
и N. А поскольку поверхность конуса и секущая плоскость увеличиваются до круга
KAMN, сечение MAZEN увеличивается до точек М и N. Поэтому схожим образом
мы докажем, что и сечение AZE увеличивается до бесконечности, если поверхность
конуса и секущая плоскость проводятся до бесконечности.
И ясно, что некая прямая, проведенная от прямой Z0 к точке Z, будет отделять
любой данной прямой равную прямую. Ведь если установим ZH как равную данной
прямой и проведем через Н параллельную ДЕ, она будет встречаться с сечением так
же, как и прямая, проведенная через точку 0, будет наталкиваться на сечение в точ¬
ках М и N. Следовательно, некоторая прямая, наталкивающаяся на сечение, прово¬
дится как параллельная прямой ДЕ и отделяющая от ZH к точке Z равную прямую
при помощи данной прямой.
9
Если конус рассекается плоскостью, пересекающейся с каждой из двух сторон тре¬
угольника, расположенного на оси, но не проведенной ни параллельно основанию, ни как
противоположная, то сечение не будет кругом.
Пусть будет конус с вершиной в точке А, а основанием будет круг В Г. И пусть он
рассекается некой плоскостью, ни параллельной основанию, ни противоположной;
и пусть она сделает сечением на поверхности линию АКЕ. Я утверждаю, что линия
АКЕ не будет кругом.
Допустим это. если это возможно, и пусть секущая плоскость пересекается с ос¬
нованием, и обшим сечением плоскостей будет ZH, а центром круга ВГ пусть будет
164

Дословный перевод книги I
0; и от нее к ZH пусть будет проведен перпендикуляр 0Н; и пусть через Н0 и че¬
рез ось будет проведена дальше плоскость и пусть она сделает сечениями на кони¬
ческой поверхности прямые ВА и АГ. А поскольку точки Д, Е и Н находятся на пло¬
скости ДКЕ и на плоскости |проведенной через] А. В и Г, то поэтому точки Д, Е и
Н находятся в общем сечении плоскостей. Следовательно, НЕД является прямой.
Пусть на линии ДКЕ будет взята некоторая точка К и через К пусть будет проведе¬
на КА, параллельная ZH. Следовательно, КМ равно ЛМ. Таким образом, ДЕ есть
диаметр круга ДКЛЕ. И пусть через М будет проведена NME, параллельная прямой
ВГ. Однако КА также параллельна ZH. Поэтому плоскость прямых NE и КМ па¬
раллельна плоскости прямых ВГ и ZH, т.е. основанию, а сечением будет круг. Пусть
это будет NKE. А поскольку ZH перпендикулярна ВН, то и КМ перпендикулярна
NE. Следовательно, NME равно КМ в квадрате. Однако ДМЕ равно КМ в квадра¬
те. Ведь мы предположили, что линия ДКАЕ является кругом, а его диаметром яв¬
ляется ДЕ. Следовательно, NME равно ДМЕ. Поэтому MN к МД равно ЕМ к МЕ.
По этой причине треугольник ДМ N подобен треугольнику EME, а угол ANM равен
углу МЕЕ. Однако угол ANM равен углу ABE ведь NE параллельна прямой ВГ. По¬
этому угол АВГ равен углу МЕЕ. Следовательно, сечение является противополож¬
ным. А это противоречит гипотезе. Следовательно, линия ДКЕ не является кругом.
10
Если на сечении конуса берутся две точки, то прямая, проведенная между точка¬
ми, будет попадать в сечение, а если она проводится дальше, то она будет вне сечения.
Пусть будет конус с вершиной в точке А, а основанием будет круг ВГ. И пусть он
рассекается плоскостью через ось и пусть она сделает сечением треугольник АВГ.
И пусть он рассекается другой плоскостью и пусть она сделает сечением на поверх¬
ности конуса линию ДЕг; и пусть буд^т взяты на линии ДЕ2 две точки Н и 0. Я ут¬
верждаю, что прямая, соединяющая точки Н и 0, попадает на линию ДЕ2, а прове¬
денная дальше - находится вне ее.
Поскольку конус с вершиной в точке А и основанием в круге ВГ рассекается пло¬
скостью через ось, и берутся некоторые точки Н и 0 на его поверхности, которые
не находятся на стороне треугольника, расположенного на оси, то прямая, соеди¬
няющая Н и 0, не попадает на точку А и, следовательно, прямая, соединяющая Н и
0, попадает в конус; а проведенная дальше - не попадает. Поэтому в первом случае
она попадает в сечение ДЕг, а во втором — нет.
м
11
Если конус рассекается плоскостью через ось, и при этом рассекается другой пло¬
скостью, рассекающей основание конуса по прямой, перпендикулярной основанию тре¬
угольника, расположенного на оси, и если диаметр сечения является параллельным од¬
ной стороне треугольника, расположенного на оси, то квадрат на любой прямой, ко¬
торая проводится от конического сечения до диаметра сечения параллельно общему
сечению секущей плоскости и основания конуса, будет равной прямоугольнику, огра¬
ниченному прямой, отделенной ею на диаметре до вершины сечения, и другой некото¬
рой прямой, которая имеет отношение к прямой, расположенной между углом конуса
165

Дословный перевод книги I
ЙВ
и вершиной сечения, равное квадрату на основании осевого треугольника к прямоуголь¬
нику, ограниченному остальными двумя сторонами треугольника. Пусть такое сече¬
ние называется параболой.
Пусть будет конус с вершиной в точке А и основанием в круге В Г. И пусть этот
конус рассекается плоскостью через ось, и пусть она сделает сечением треугольник
АВГ. И пусть он рассекается другой плоскостью, секущей основание конуса по пря¬
мой ЛЕ, перпендикулярной ВГ; и пусть она сделает сечением на поверхности конуса
линию лгЕ. А диаметр сечения Ш будет параллельным одной стороне треугольни¬
ка, расположенного на оси АГ; и от точки Т будет проведена 70, перпендикулярная
2Н; и пусть окажется, что квадрат на ВГ к ВАГ равен 70 к 7А, а на сечении пусть
будет взята некоторая произвольная точка К, и через точку К пусть будет проведена
КА, параллельная ЛЕ. Я утверждаю, что квадрат на КА равен 07А.
Пусть будет проведена через Л М14, параллельная ВГ. Однако КА является па¬
раллельной ЛЕ. Следовательно, плоскость прямых КА и параллельна плоско¬
сти прямых ВГ и ЛЕ, т.е. основанию конуса. Поэтому плоскость прямых КА и
является кругом с диаметром МЫ. А КА перпендикулярна МК1, поскольку ЛЕ пер¬
пендикулярна ВГ. Поэтому MAN равно квадрату на КА. А так как квадрат на ВГ к
ВАГ равно©/ к ТА. и ВГ в квадрате к ВАГ равно (ВГ к ГА) на (ВГ к ВА). Следова¬
тельно, &Т к ТА равно (ВГ к ГА) на (ГВ к ВА). Однако ВГ к ГА равно М1М к №А рав¬
но МА к Л7 и ВГ к ВА равно М№ к МА равно ЛМ к М7 равно ЫЛ к 7А. Поэтому
®Т к ТА равно (МА к М) на (М к7Л). Однако (МА к А7) на (4Л к 7) равно MЛN
кХТА Следовательно, &Т к 7А равно МАИ к АТА. А при взятой общей высоте ТХ
квТАравновгд к АТА. Поэтому МАК к АТА равно 07Л к АТА. Следовательно,
МАИ равно ОТА. Однако MЛN равно квадрату на КА. По этой причине также ква¬
драт на КА равен ОТА.
Назовем такое сечение параболой, а прямая 07 пусть называется прямой (отвес¬
ной) стороной для прямых, проведенных упорядоченно к диаметру 7Н.
12
Если конус рассекается плоскостью через ось и рассекается другой плоскостью, се¬
кущей основание конуса по прямой, перпендикулярной основанию треугольника, распо¬
ложенного на оси, а диаметр сечения, проведенный дальше, пересекается с одной сторо¬
ной осевого треугольника вне вершины конуса, то квадрат на любой прямой, проведен¬
ной от сечения к диаметру параллельно общему сечению секущей плоскости и основания
конуса, будет равен площади, смежной с некоторой прямой, к каковой имеет отноше¬
ние проведенная пряная, расположенная в диаметре сечения, однако простирающаяся
под углом треугольника, лежащего вне сечения; это отношение равно квадрату прямой,
проведенной от вершины конуса к основанию треугольника и параллельной диаметру се¬
чения, к прямоугольнику, ограниченному частями основания, которые производит про¬
веденная прямая: данное отношение, имеющее как ширину прямую, отделенную на ди¬
аметре от вершины сечения конуса, и превосходящее на прямоугольник, подобный схо¬
жей фигуре, ограниченной прямой, находящейся под углом треугольника, расположенного
вне, и смежным отрезком. Назовем такое сечение гиперболой.
166

Дословный перевод книги I
•ТС
Пусть будет конус с вершиной в точке А и
с основанием в круге В Г. И пусть этот конус
рассекается плоскостью через ось. и пусть она
сделает сечением треугольник АВГ. Пусть он
рассекается и другой плоскостью, секущей
основание конуса по прямой ДЕ, перпенди¬
кулярной основанию ВГ треугольника АВГ,
и пусть она сделает сечением на поверхно¬
сти конуса линию AZE, а диаметр сечения
ZH, проведенный дальше, пусть будет пере¬
секаться с одной стороной АГ треугольника
/\ВГ вне вершины конуса в точке 0. И пусть
через А будет проведена АК. параллельная ди¬
аметру сечения ZH и пусть она будет рассе¬
кать В Г, а от Z пусть будет проведена ZA, пер¬
пендикулярная ZH; и пусть окажется, что КА
в квадрате к В КГ равно Z0 к ZA, а в сечении
пусть будет взята прои звольная точка М, а че¬
рез М пусть будет проведена MN, параллель¬
ная прямой ДЕ, а через N пусть будет прове¬
дена N0E, параллельная прямой ZA. Пусть
0А будет проведена дальше к точке Е, а че¬
рез точки А и Е пусть будут проведены АО и
ЕП, параллельные прямой ZN. В этом случае я утверждаю, что MN в квадрате рав¬
но ZE, которая лежит при ZA, имеет как ширину ZN и превосходя АЕ, подобную
прямоугольнику 0ZA.
Пусть будет через N проведена PNL, параллельная прямой ВГ. Однако NM па¬
раллельна прямой ДЕ. Поэтому плоскость прямых N1N и PL параллельна плоско¬
сти прямых ВГ и ДЕ. т.е. основанию конуса. Следовательно, если плоскость пря¬
мых MN и PL проводится дальше, то сечением будет круг с диаметром PNL. A MN
ей перпендикулярна. Поэтому PNS равно квадрату на MN. А поскольку квадрат на
АК к ВКГ равно Z0 к ZA и АК к ВКГ равно АК к КГ на АК к КВ, то получается, что
Z0 к ZA равно АК к КГ на АК к КВ. Однако АК к КГ равно 0Н к НГ равно 0N к
NL и АК к КВ равно ZH к НВ равно ZN к NP. Следовательно, OZ к ZA равно 0N к
NL на ZN к NP Однако 0N к NL на ZN к NP равно 0NZ к LNP. По этой причине
0NZ к LPN равно 0Z к ZA равно 0N к NE. А при взятой обшей высотой ZN полу¬
чается 0N к NE равно 0NZ к ZNE. Поэтому также ONZ к LNP равно 0NZ к ENZ.
Следовательно, LNP равно ENZ. Схожим образом мы докажем, что MN в квадрате
равно LNP. Также MN в квадрате равно ENZ. Однако ENZ равно параллелограмму
EZ. Следовательно, квадрат на MN равен прямоугольнику EZ, который находится
при прямой ZA, имея шириной ZN и превосходящий АЕ, подобное прямоугольни¬
ку 0ZA. Назовем подобное сечение гиперболой, AZ назовем прямой стороной для
прямых, проведенных упорядоченно к ZH, a Z0 — поперечной.
• •
167

Дословный перевод книги I
п
•л
я
/Л
Eau конус рассекается
плоскостью через ось и рас¬
секается другой плоскостью,
пересекающейся с каждой из
сторон треугольника, распо¬
ложенного на оси, но не про¬
веденной ни параллельно ос¬
нованию конуса, ни противо¬
положно, и если тоскость, в
которой находится основа¬
ние конуса, и секущая пло¬
скость пересекаются по пря¬
мой, перпендикулярной или
основанию треугольника,
расположенного на оси, или
прямой, проведенной дальше,
то квадрат на любой пря¬
мой, которая проводится от
сечения конуса до диаметра
сечения параллельно общему
сечению плоскостей будет
равна площади, смежной с некоторой прямой, к каковой диаметр сечения имеет отно¬
шение, состоящее в том, что квадрат на прямой, проведенной от вершины конуса па¬
раллельно диаметру сечения вплоть до основания треугольника относится к прямоуголь¬
нику, ограниченному прямыми, отведенными к сторонам треугольника, это отношение
имеет шириной прямую, отведенную на диаметре от вершины сечения и не достающее
до схожей фигуры и до расположенного схожим образом прямоугольника, ограниченно¬
го диаметром и параметром. Пусть такое сечение на зывается эллипсом.
Пусть будет конус с вершиной в точке А и с основанием в круге ВГ. И пусть он
рассекается плоскостью через ось и пусть она сделает сечением треугольник АВГ И
пусть он рассекается другой плоскостью, пересекающейся с каждой из двух сторон
треугольника, расположенного на оси, однако проведенной не как параллельной
основанию конуса, ни наоборот. И пусть она сделает сечением на поверхности ко¬
нуса линию ЛЕ. А обшим сечением секущей плоскости и той плоскости, где нахо¬
дится основание конуса, пусть будет ZH, которая перпендикулярна ВГ; а диаметром
сечения пусть будет ЕД; и пусть от Е будет проведена Е0, перпендикулярная ЕЛ, а
через А пусть будет проведена АК, параллельная ЕД. И пусть окажется, что как ЛЕ
к 0К, так и квадрат на АК к ВКГ, и пусть в сечении будет взята некая точка Л и че¬
рез не пусть будет проведена ЛМ, параллельная ZH. В этом случае я утверждаю, что
ЛМ в квадрате будет равна плошали, находящейся при прямой Е0, которое имеет
шириной ЕМ и не достает до фигуры, схожей с прямоугольником Д Е0 [ДЕхЕ0].
Пусть будет проведена Д0, а через М пусть будет проведена MEN, параллельная
прямой 0Е, а через 0 и Е пусть будут проведены 0N и ЕО как параллельные прямой
Ум
»?
»?
168

Дословный перевод книги I
ЕМ, а через М - ПМР, прямой ВГ. А поскольку ПР параллельна ВГ и ЛМ параллель¬
на ZH, то плоскость прямых ЛМ и ПР параллельна плоскости ZH и ВГ, т.е. основа¬
нию конуса. Следовательно, если плоскость проводится через ЛМ и П Р. то сечени¬
ем будет круг с диаметром ПР. Л ей перпендикулярна ЛМ. Поэтому ЛМ в квадра¬
те равно ПМР А поскольку АК в квадрате к ВКГ равно ЕА к Е0, и АК в квадрате к
ВКГ равно ЛК к КВ на АК к КГ, и АК к КВ равно ЕН к НВ равно ЕМ к МП, и АК к
КГ равно АН к Н Г равно ДМ к М Р. то АЕ к Е0 равно ЕМ к МП на АМ к М Р. Одна¬
ко ЕМ к МП на АМ к МР равно ЕМ А к ПМР. Поэтому ЕМ А к ПМР равно ЕД к ЕО
равно АМ к МЕ. Но при МЕ - общей высотой, АМ к МЕ равно АМЕ к EME. Следо¬
вательно, EME к ПМР равно АМЕ к EME. Поэтому ПМР равно EME. Схожим об¬
разом мы докажем, что ПМР равно ЛМ в квадрате. Следовательно, EME равно ЛМ
в квадрате. По этой причине ЛМ в квадрате равна площади МО, находящейся при
0Е, который имеет шириной ЕМ и не достает до площади OV, схожей с прямоуголь¬
ником AE0. Назовем такое сечение эллипсом, а Е0 назовем прямой стороной для
прямых, проведенных упорядоченно к АЕ, а ЕА — поперечной.
ваюшая
роведе-
14
Если поверхности, расположенные при вершине, рассекаются плоскостью, прове¬
денной не через вершину, пусть на каждой из поверхностей будет сечение, называемое
гиперболой, и у обоих сечений будет один и тот же диаметр, а прямые стороны, прове¬
денные к диаметру как параллельные прямой, расположенной на основании конуса, бу¬
дут равны, а общая поперечная сторона эйдоса будет прямой, расположенной между
вершинами сечений. Назовем такие сечения противолежащими.
Пусть будут поверхности, расположенные при вершине, с вершиной в точке А, и
пусть они рассекаются плоскостью, не проходящей через вершину. И пусть она сде¬
лает сечениями на поверхности AEZ и H0K. В этом случае я утверждаю, что каждое
из сечений AEZ и H0K будет сечением, называемым гиперболой.
Пусть будет круг BAÍZ, через который будет проведена прямая, описы
поверхность; и пусть на поверхности, расположенной при вершине, будет щ
на параллельная ему плоскость ЕНОК. Обшими сечениями сечений НОК и ZEA и
кругов являются ZA и НК. Следовательно, они будут параллельны. А осью кониче¬
ской поверхности пусть будет прямая AAY, а центрами кругов — Л и Y; и пусть от Л к
точкам В и Г будет проведена дальше прямая, перпендикулярная ZA; и пусть через
ВГ и ось будет проведена плоскость. Она сделает сечениями в кругах параллельные
прямые НО и ВГ, а сечениями на поверхности - BAO и ГАЕ. Поэтому ЕО будет пер¬
пендикулярна НК, поскольку В Г перпендикулярна ZA и каждая из них параллельна
другой из них. А так как плоскость, проведенная через ось, пересекается с сечения¬
ми в точках М и N, расположенных вне линий, то очевидно, что данная плоскость
рассекает и линии. Пусть она рассекает их в точках О и Е. Следовательно, точки М,
Е, О и N лежат в плоскости, проведенной через ось, и в плоскости, в которой рас¬
полагаются линии. Поэтому линия ME0N является прямой. И ясно, что Е, 0. А и
Г и В, Е, А и О располагаются на той же самой прямой. Ведь они лежат на кониче¬
ской поверхности и в плоскости, проведенной через ось. Поэтому пусть от 0 и Е бу¬
дут проведены 0Р и ЕП, перпендикулярные прямой ОЕ, а через А пусть будет про¬
169

Дословный перевод книги I
ведена ЕАТ, параллельная прямой М E0N. И пусть окажется, что 0Е к ЕП равно АЕ
в квадрате к ВЕГ и Е0 к 0Р равно АТ в квадрате к ОТЕ. А поскольку конус с вер¬
шиной в точке А и основанием круге ВГ, делится плоскостью через ось, и она сде¬
лана сечением треугольник АВ Г »делится другой плоскостью, секущей основание
конуса по прямой AMZ, перпендикулярной ВГ, и она сделала сечением на поверх¬
ности AEZ, а диаметр МЕ, проведенный дальше, пересекся с одной стороной треу¬
гольника, расположенного на оси, вне вершины конуса; а через точку А была про¬
ведена AZ, параллельная диаметру сечения ЕМ, а от точки Е была проведена ЕП,
перпендикулярная ЕМ, то получается, что Е0 к ЕП равно АЕ в квадрате к ВЕГ; сле¬
довательно, сечение AEZ является гиперболой, ЕП - прямой стороной для прямых,
проведенных упорядоченно к ЕМ, 0Е - поперечной стороной эйдоса. И схожим об¬
разом НОКесть гипербола с диаметром 014,а0Р- прямая сторона ординат, прове¬
денных к 0N 0Е - поперечная сторона эйдоса.
Я утверждаю, что 0Р равно ЕП. Ведь поскольку ВГ параллельна прямой ЕО, то
получается, что АЕ к ЕГ равно АТ к ТЕ и АЕ к ЕВ равно АТ к ТО. Однако (АЕ к ЕГ)
на (АЕ к ЕВ) равно АЕ в квадрате к ВЕГ и (АТ кТ0) на (АТ к ТО) равно АТ в квадра¬
те к ЕТО. Следовательно, АЕ в квадрате к ВЕГ равно АТ в квадрате к ЕТО. Однако
0Е к ЕП равно АЕ в квадрате к ВЕГ и 0Е к 0Р равно АТ в квадрате к ЕТО Поэтому
также 0Е к ЕП равно Е0 к 0Р. Следовательно, ЕП равно 0Р.
«а
15
Если на эллипсе упорядоченная прямая /ордината/, проведенная от центральной точ¬
ки диаметра в обе части, проводится дальше вплоть до сечения, и окажется, что она
проведена дальше к диаметру, а диаметр - к некой прямой, то квадрат на любой пря¬
мой, которая проводится от сечения к проведенной дальше прямой /ординате/ как па¬
раллельная диаметру, будет равен прямоугольнику, лежащему воне соразмерной ему
третьей прямой, который имеет шириной прямую, отведенную к сечению, и не доста¬
ет до эйдоса фигурой, схожей с прямоугольником, ограниченного той прямой, к кото¬
рой они проводятся, и параметром, а проведенная дальше, вплоть до другой части сече¬
ния, она будет рассекаться на две равные части прямой, к которой она была проведена.
Пусть будет эллипс с диаметром АВ; и пусть АВ рассекается на две равные части
в точке Г, а через точку Г пусть будет проведена ордината и продолжена в обе части
вплоть до сечения АГЕ, а от точки А пусть будет проведена АЕ, перпендикулярная
АЕ. И пусть окажется, что АВ к АЕ равно АЕ к АВ, и пусть будет взята на сечении
некая точка Н, и через Н будет проведена Н0, параллельная АВ. Пусть будет прове¬
дена ЕЕ, а через 0 будет проведена 0Л, параллельная АЕ; и пусть через 7. и Л будут
проведены 1К. и ЛМ, параллельные 0А. В этом случае я утверждаю, что квадрат на
Н0 равен АЛ. которая лежит при ЛЕ, имея шириной А0 и не достает на фигуру ЛЕ,
схожую с прямоугольником ЕАЕ [ЕАхАЕ].
Пусть будет прямая сторона AN для ординат, проведенных к АВ; и пусть будет
проведена В14, а через Н - НЕ. параллельная прямой ДЕ; и пусть через Е и Г будут
проведены ЕО и ГП, параллельные прямой АГ, а через 14, О и П - ОЕ и ТП. па¬
раллельные прямой АВ Таким образом, АГ в квадрате равно АП и НЕ в квадрате
равно АО А поскольку ВА к АГч равно ВГ к ГП равно ПТ к Т1М и ВГ равно ГА рав-
170

Дословный перевод книги I
•Г*
ноТП, ГП равно ТА, то АП равно ТР, ЕТ равно ТУ. Атак как ОТ равно ОР и NO яв¬
ляется общей, то ТУ равно N1. Однако ТУ равно ТЕ и ТЕ является обшей. Поэтому
NП равно АО плюс ПО, т.е. ПА равно АО плюс ПО. Следовательно, ПА делить на
АО равно ОГГ Однако АП равно ГЛ в квадрате, АО равно ЕН в квадрате, ОП равно
ОЕП; поэтому ГЛ в квадрате делить на НЕ в квадрате равно ОЕП. А так как ЛЕ в Г
рассекается на равные части, а в 0 — на неравные части, то Е0Л плюс Г0 в квадра¬
те равно ГД в квадрате равно Е0Л плюс ЕН в квадрате. Таким образом, ГЛ в квадра¬
те делить на ЕН в квадрате равно Е0Л. Однако было ГЛ в квадрате делить на НЕ в
квадрате равно ОЕП. По этой причине Е0Л равно ОЕП. А поскольку ЛЕ к АВ равно
АВ к ЛZ, то ДЕ к лг равно ДЕ в квадрате к АВ в квадрате равно ГД в квадрате к ГВ в
квадрате. Однако ГЛ в квадрате равно ПГА равно ПГВ. Поэтому также ДЕ к лг рав¬
но П ГВ к ГВ в квадрате равно Е0 к 0Л равно Е0Л к Л0Л равно ПЕО к ОЕ в квадра¬
те. И следовательно, Е0Д равно ПЕО. Поэтому ЛОЛ равно ОЕ в квадрате равно НО
в квадрате. Следовательно, Н0 в квадрате равна прямоугольнику ЛА, лежащему при
ЛZ, который меньше на фигуру схожую с прямоугольником EДZ.
В этом случае я утверждаю, что 0Н, проведенная дальше в другую часть сечения,
рассекается на две равные части ЛЕ.
Пусть она будет проведена дальше и пересечется с сечением в Ф, и пусть через Ф
будет проведена ФХ, параллельная прямой НЕ, а через X - ХТ, параллельная пря¬
мой АН А поскольку НЕ равно ФХ, то также и НЕ в квадрате равно ФХ в квадрате.
Но НЕ в квадрате равно АЕО, ФХ в квадрате равно АХТ. Поэтому ОЕ к ТХ равно
ХА к АЕ. И АЕ к ТХ равно ЕВ к ВХ. Следовательно, также ХА к АЕ равно ЕВ к ВХ.
и при извлечении ХЕ к ЕА равно ХЕ к ХВ. Поэтому АЕ равно ХВ. Однако также АГ
равно ГВ. Следовательно, ЕГ равно ГХ. Поэтому Н0 равно 0Ф. Таким образом, ОН,
проведенная дальше к другой стороне сечения, рассекается на две равные части Л0.
I
»I*
16
Если через среднюю точку поперечной стороны противолежащих проведена некая
прямая, параллельная прямой, проведенной упорядоченно [ординате], то это будет ди¬
аметр противолежащих, сопряженный с первым диаметром.
Пусть будут противолежащие с диаметром АВ, и пусть АВ рассекается на две рав¬
ные части в Г, а через Г пусть будет проведена ГА, параллельная прямой, проведен¬
ной к нему упорядоченно. Я утверждаю, что диаметр ГА соединен с диаметром АВ.
Пусть прямыми сторонами будут прямые АЕ и BZ, и пусть проведенные AZ и ВЕ
будут проведены дальше; и пусть в другом сечении будет взята некая точка Н, и че¬
рез нее пусть будет проведена НО, параллельная прямой АВ. И пусть от Н и 0 бу¬
дут проведены упорядоченно НК и 0Л, через К и Л - КМ и AN, параллельные пря¬
мым АЕ и BZ. А поскольку НК равно 0Л. то НК в квадрате равно 0Л в квадрате.
Однако НК в квадрате равно АКМ, ОЛ в квадрате равно BAN. Поэтому АКМ рав¬
но BAN. А так как АЕ равно BZ, то АЕ к АВ равно BZ к ВА. Однако АЕ к АВ равно
МК к KB, ZB к ВА равно NA к ЛА. Поэтому также МК к КВ равно NA к ЛА. А при
КА, общей высотой. МК к КВ равно МКА к ВКА, а при ВЛ, обшей высотой, NA к
ЛА равно NAB к АЛВ. Поэтому также МКА к ВКА равно NAB к АЛВ. И поочеред¬
но МКА к NAB равно ВКА к АЛВ. И МКА равно NAB. Следовательно, ВКА равно
171

Дословный перевод книги I
АЛВ. По этой причине АК равно АВ. Но АГ равно ГВ. Поэтому КГ равно ГА. И так¬
же НЕ равно Е0 Итак. Н0 рассекается на две равные части НГ и параллельна пря¬
мой АВ. Следовательно, диаметр ЕГД соединен с диаметром АВ.
Другие определения
Серединная точка диаметра на гиперболе и эллипсе пусть называется центром
сечения, а прямая, проведенная от центра к сечению, - радиусом сечения.
Схожим образом и серединная точка на противолежащих пусть называется цен¬
тром поперечной стороны.
Прямая же, проведенная от центра как параллельная прямой, проведенной упо¬
рядоченно, имеющая серединное отношение сторон эйдоса и рассекаемая от цен¬
тра на две равные части, пусть называется вторым диаметром.
•и
17
Если на сечении конуса от вершины линии проводится прямая, параллельная прямой,
проведенной упорядоченно, то она окажется вне сечения.
Пусть будет сечение конуса с диаметром АВ. Я утверждаю, что прямая, прове¬
денная от вершины, т.е. отточки А, как параллельная прямой, проведенной упоря¬
доченно [ординате), окажется вне сечения.
Если возможно, то пусть она попадает внутрь сечения как АГ. А поскольку в се¬
чении конуса взята некая точка Г, то прямая, проведенная от точки Г как параллель¬
ная прямой, проведенной упорядоченно, будет пересекаться с диаметром АВ и он
будет рассекать ею на две равные части. Следовательно, АГ, проведенная дальше,
будет рассекаться АВ на две равные части. А это невозможно, поскольку АГ. прове¬
денная дальше, окажется вне сечения. Следовательно, прямая, проведенная от точ¬
ки А как параллельная прямой, проведенной упорядоченно, не окажется внутри ли¬
нии. Поэтому она окажется вне и, таким образом, коснется сечения.
•г».
Если прямая, пересекающаяся с коническим сечением, проведенная дальше в любую
из двух сторон, попадает вне сечения, а внутри сечения берется некая точка, и через
нее проводится прямая, пара.цельная пересекающейся прямой, то прямая, проведенная
дальше в любую из двух сторон, пересекается с сечением.
Пусть будет коническое сечение и пересекающаяся с ним прямая AZB, прове¬
денная дальше в любую из двух сторон, пусть она окажется вне сечения; пусть бу¬
дет взята внутри сечения некая точка Г, и пусть через нее будет проведена ГА. парал¬
лельная прямой АВ. Я в этом случае утверждаю, что ГД, проведенная дальше в лю-
издвух сторон
, пересечется с сечением.
Пусть на сечении будет взята некая точка Е, и пусть будет проведена Е%. А по¬
скольку АВ параллельна ГД, а некая прямая ЕЪ пересекается с АВ, то, следователь¬
но, ГД, проведенная дальше, пересекается Е7.. А если она пересекается между Е и ,
то очевидно, что она пересекается с сечением; а если она пересекается вне точки Е,
то она пересекается с сечением раньше. Следовательно, ГД, проведенная дальше к
172

Дословный перевод книги I
частям Д и Е, пересекается с сечением. Схожим образом мы докажем, что она, про¬
веденная дальше к частям 7 и
дальше в любую из двух сторон, пересекается с сечением.
•ж
19
В любом коническом сечении всякая прямая, которая проводится от диаметра как
параллельная прямой, проведенной упорядоченно (ординате], пересекается с сечением.
Пусть будет конус с диаметром АВ, и пусть будет взята на диаметре некая точка В;
и пусть через нее будет проведена В Г, параллельная прямой, проведенной упорядочен¬
но. В этом случае я утверждаю, что ВГ, проведенная дальше, пересекается с сечением.
Пусть на сечении будет взята некая точка Д; однако А также находится на сече¬
нии. Поэтому прямая, проведенная от А к Д, будет попадать в сечение. А поскольку
прямая, проведенная от А как параллельная прямой, проведенной упорядоченно,
окажется вне сечения, а АД пересечется с ним, и ВГ параллельна прямой, проведен¬
ной упорядоченно, то ВГ пересекается АД. А если она пересекается между точками
А и Д, то ясно, что она также пересекается с сечением; а если она пересекается вне
точки Д, как бы в Е, то она пересекается с сечением раньше. Следовательно, пря¬
мая, проведенная от В как параллельная прямой, проведенной упорядоченно, бу¬
дет пересекаться с сечением.
•ж
20
Если на параболе от сечения проводятся упорядоченно к диаметру две прямые, их
квадраты будут относиться между собой как прямые, отделенные ими на диаметре
от вершины сечения.
Пусть будет парабола с диаметром АВ. и пусть будут взяты на ней некие точки Г
и Д, и пусть от них будут проведены к АВ упорядоченно ГЕ и Д2. Я в этом случае ут¬
верждаю, что как квадрат на дг относится к квадрату на ГЕ, так и ¿А к АЕ.
Пусть прямая сторона будет АН. Следовательно, квадрат на Д2 равен ¿АН, ква¬
драт на ГЕ равен ЕАН По этой причине как квадрат на Д2 к квадрату на ГЕ, так и
¿АН к ЕАН. Но ¿АН к ЕАН равно ¿А к АЕ. Таким образом, как квадрат на Д¿ к
квадрату на ГЕ, так и ¿А к АЕ.
21
Если на гиперболе, или на эллипсе, или окружности круга проведены прямые упоря¬
доченно к диаметру, то их квадраты имеют отношение к прямоугольникам, ограничен¬
ным прямыми, отделенными ими от пределов поперечной стороны эйдоса, как отноше¬
ние прямой стороны эйдоса к поперечной, а между собой к прямоугольникам, ограничен¬
ным, как мы сказали, отделенными прямыми.
Пусть будет гипербола, или эллипс, или окружность круга с диаметром АВ, а пря¬
мой стороной будет АГ; и пусть к диаметру упорядоченно будут проведены ДЕ и ¿Н.
В этом случае я утверждаю, что квадрат ¿Н к АН В равно АГ к АВ, квадрат ¿Н к ква¬
драту ДЕ равно АН В к АЕВ.
Пусть будет проведена В Г, разделяющая эйдос, а через Е и Н пусть будут проведе¬
ны Е0 и НК как параллельные АГ. Поэтому квадрат ¿Н равен КНА, квадрат ДЕ равен
•ж
173

Дословный перевод книги I
0ЕА. А поскольку КН к НВ равно ГА к АВ, и при АН, взятой обшей высотой, КН к
НВравноКНАкВНА,тоГАкАВравноКНЛк ВНА равно квадрату ZH к ВНЛ. И та¬
ким же образом квадрат ДЕ к ВЕА равно ГА к АВ Поэтому ZH в квадрате к ВНА рав¬
но ДЕ в квадрате к ВЕА. И поочередно квадрат ZH к квадрату ДЕ равно ВНЛ к ВЕА.
22
прямая, не пересекающаяся с диаметром внутри сечения, пересекает парабо¬
лу или гиперболу в двух точках, то проведенная дальше, она будет пересекаться с диа¬
метром сечения вне сечения.
Пусть будет парабола или гипербола с диаметром АВ, и пусть некая прямая осу¬
ществляет сечение в двух точках- Г и Д. В этом случае я утверждаю, что ГА, прове¬
денная дальше, пересекается с диаметром АВ вне сечения.
Пусть от Г и А будут проведены упорядоченно ГЕ и АВ [ординаты]. Сначала пусть
сечением будет парабола. А поскольку на параболе ГЕ в квадрате к АВ в квадрате
равно ЕА к АВ, и АЕ больше АВ, то ГЕ больше АВ. По этой причине ГЕ в квадрате
больше АВ в квадрате. И они являются параллельными. Следовательно, ГА. прове¬
денная дальше, пересекается с диаметром АВ вне сечения.
Теперь пусть сечением будет гипербола. А поскольку на гиперболе ГЕ в квадрате
к ВД в квадрате равно ZEA к ZBA, то получается, что также и ГЕ в квадрате больше
ДВ в квадрате. И они являются параллельными. Итак, ГД, проведенная дальше, пе¬
ресекается с диаметром сечения вне сечения.
III
23
Если прямая, расположенная между двумя диаметрами, производит сечение эллип¬
са, то, проведенная дальше, пересекается с каждым из двух диаметров вне сечения.
Пусть будет эллипс с диаметрами АВ и ГД; и пусть некая прямая ЕХ производит
сечение, лежащее между диаметрами АВ и ГД. В этом случае я утверждаю, что ЕХ,
проведенная дальше, пересекается с любым из двух диаметром АВ и ГА вне сечения.
Пусть от Е и г будут проведены упорядоченно к АВ НЕ и ХЕ), а к АГ - ЕК и XX.
Сзедовательно. получается квадрат ЕН к квадрату ХЕ) равно ВНА к В0А, квадрат гл
к квадрату' ЕК равно ДЛГ к ДКГ. Однако ВНА больше ВОА, ведь Н находится посе¬
редине; и ДЛГ больше ДКГ. Поэтому также Н Е в квадрате больше ХЕ) в квадрате, XX
в квадрате больше ЕК в квадрате. Поэтому НЕ больше ХЕ), XX больше ЕК. И НЕ па¬
раллельна прямой ZO, а XX параллельна прямой ЕК. Следовательно, ЕХ, проведен¬
ная дальше, пересечется с любым из диаметров АВ и ГД вне сечения.
24
Если прямая, совпадающая с параболой или гиперболой в одной точке и проведенная
дальше в каждую из двух сторон, попадает вне сечения, то она пересечется с диаметром.
Пусть будет парабола или гипербола с диаметром АВ; и пусть прямая ГДЕ со¬
впадает с ней в точке А, и, проведенная дальше в любую из двух сторон, она попа¬
дет вне сечения В эзом случае я утверждаю, что она пересекается с диаметром АВ.
Пусть на сечении будет взята некая точка Z, и пусть будет проведена А/. Следо¬
вательно, XX. проведенная дальше, пересечется с диаметром сечения. Пусть она пе¬
174

Дословный перевод книги I
ресечется с ним в точке А. И ГДЕ расположена между сечением и прямой 2ЛА. По¬
этому ГДЕ, проведенная дальше, пересечется с диаметром вне сечения.
25
Если прямая, совпадающая с эллипсом между двумя диаметрами и, проведенная
дальше в любую из двух сторон, попадает вне сечения, то она пересечется с каждым
из диаметров.
Пусть будет эллипс с диметрами АВ и ГД; и пусть некая прямая встречается с
ним между двумя диаметрами в Н, и, проведенная дальше в любую из двух сторон,
попадает вне сечения. В этом случае я утверждаю, что Е2 пересечется с любым из
диаметров АВ и ГД.
Пусть от Н к АВ и ГД будут проведены упорядоченно Н0 и НК. Поскольку НК
параллельна прямой АВ, а некая прямая Н2 пересекается НК, следовательно, она
пересекается и с АВ. Схожим образом Е2 пересекается и с ГД.
26
Если на параболе или гиперболе будет проведена прямая, параллельная диаметру се¬
чения, то она пересечется с сечением только в одной точке.
Пусть сначала будет парабола с диаметром АВГ и с прямой стороной АД, и пусть
будет проведена Е2, параллельная прямой АВ. В этом случае я утверждаю, что Е2.,
проведенная дальше, пересечется с сечением.
Пусть будет взята некая точка Е на Е2, и от Е пусть будет проведена ЕН, парал¬
лельная прямой, проведенной упорядоченно ¡ординате]; и пусть ЛАГ больше НЕ в
квадрате, а от Г пусть будет проведена упорядоченно вверх Г0. Поэтому 0Г в ква¬
драте равно ДАГ. Однако ДАГ больше ЕН в квадрате. Следовательно, также 0Г в ква¬
драте больше ЕН в квадрате; по этой причине также ОГ больше ЕН. И они являют¬
ся параллельными. Следовательно, Е2, проведенная дальше, рассекает ОГ. Таким
образом, она пересекается с сечением.
Пусть она пересекается с ним в К.
Я же утверждаю, что она пересекается с ним только в точке К. Ведь если возмож¬
но, пусть она пересекается с ним также в Л. А поскольку прямая рассекает парабо¬
лу в двух точках, то, проведенная дальше, она пересечется с диаметром сечения, а
это невозможно. Ведь мы предположили, что они являются параллельными. Таким
образом, Е2, проведенная дальше, пересекается с сечением только в одной точке.
Пусть сечением будет гипербола, АВ - поперечной стороной эйдоса, а АД — пря¬
мой стороной; и пусть будет проведена ДВ и продолжена дальше. И пусть при тех
же самых приготовлениях от Г будет проведена ГМ, параллельная прямой АД. А по¬
скольку МГА больше ДАГ и Г0 в квадрате равно МГА. ДАГ больше НЕ в квадрате;
также получается Г0 в квадрате больше ЕН в квадрате. Поэтому также Г0 больше
ЕН, и выйдет то же самое, что и прежде.
не
веденная дальше в любую из сторон,
Если прямая делит диаметр параболы, то, про
она пересечется с сечением.
175

Дословный перевод книги I
Пусть будет парабола с диаметром АВ, и пусть ее рассекает некая прямая ГД вну¬
три сечения. В этом случае я утверждаю, что ГД, проведенная дальше в любую из
двух частей, пересечется с сечением.
Пусть от А будет проведена АЕ, параллельная прямой, проведенной упорядочен¬
но ¡ординате]. Следовательно, АЕ попадает вне сечения. Таким образом, ГД или па¬
раллельна прямой АЕ, или нет.
Если она ей параллельна, то она проведена упорядоченно; по этой причине, про¬
веденная дальше влюбую из двух сторон, она пересечется с сечением.
Пусть она не будет параллельной АЕ, и, проведенная дальше, пересечется с АЕ
в Е. И ясно, что она пересечется с сечением на сторонах, где расположена Е. Ведь
если она пересекается с АЕ, то она производит сечение гораздо раньше.
Я утверждаю, что она, проведенная дальше в другую строну, пересечется с сечени¬
ем. Пусть МА будет прямой стороной, а HZ - проведенной упорядоченно, и пусть АД
в квадрате равно BAZ; а ВК, параллельная прямой, проведенной упорядоченно, пусть
пересекается ДГ в Г. Поскольку ZAB равно АД в квадрате, то АВ к АД равно ДА к AZ.
Поэтому так же ВА к AZ равно ВА к АД. И по этой причине так же ВД в квадрате к ZA
в квадрате равно ВА в квадрате к АД в квадрате. Однако поскольку АД в квадрате равно
BAZ, то ВА к AZ равно ВА в квадрате к АД квадрате, т.е. BAZ равно ВД в квадрате к AZ
в квадрате. Однако ВД в квадрате к AZ в квадрате равно ВГ в квадрате к ZH в квадрате и
АВ к AZ равно ВАМ к ZAM. Таким образом, ВГ в квадрате к ZH в квадрате равно ВАМ
kZAM И поочередно ВГ в квадрате к ВАМ равно ZH в квадрате к ZAM. Однако из-за
сечения ZH в квадрате равно ZAM. Поэтому также ВГ в квадрате равно ВАМ. Но AM
есть поперечная сторона, а ВГ - параллельна прямой, проведенной упорядоченно. Та¬
ким образом, сечение проходит через Г и ГД пересекается с сечением в Г.
.О
■1C
»I«
•I»
•I«
•I«
»!•
••
НС
•1»
28
Если прямая касается одной из противолежащих и если берется некая точка вну¬
три другого сечения и через нее проводится прямая, параллельная касательной, то про¬
веденная дальше в любую из двух сторон, она пересечется с сечением.
Пусть будут противолежащие с диаметром АВ; и пусть некая прямая ГД касает¬
ся сечения А. И пусть будет взята некая точка Е внутри другого сечения, и через нее
пусть будет проведена EZ, параллельная ГД. В этом случае я утверждаю, что EZ, про¬
веденная дальше влюбую из двух сторон, пересечется с сечением.
Поскольку мы показали, что ГД, проведенная дальше, пересекается с диаметром
АВ и EZ является ей параллельной, то, следовательно, EZ, проведенная дальше, пе¬
ресечется с диаметром. Пусть она пересечется с ним Н, и пусть будет установлено,
что АО равно НВ. И пусть через ©будет проведена© К, параллельная прямой ZE; и
пусть будет проведена упорядоченно КА, и пусть будет установлено, что НМ равно
А©; и пусть будет проведена М1М, параллельная прямой, проведенной упорядочен¬
но, и пусть будет продолжена дальше Н N. А поскольку КА параллельна прямой МИ,
а К© - Н14, и АМ является одной прямой, то К0А эквивалентно ГЖМ. И А© равно
НМ; поэтому КА равно МИ. Таким образом, также КА в квадрате равно MN в ква¬
драте И так как А© равно НМ, А© равно ВН и АВ является обшей, то будет ВАравно
АМ. Следовательно, ВАА равно АМВ. Поэтому ВАА к АК в квадрате равно АМВ к
•I»
•а
■и
176

Дословный перевод книги I
ММ в квадрате. Однако как ВЛА относится к ЛК в квадрате, так и поперечная сто¬
рона относится к прямой стороне. По этой причине, также как АМВ к в ква¬
драте, так и поперечная сторона относится к прямой стороне. Следовательно, N на¬
ходится в сечении. Поэтому Е7, проведенная дальше, пересекается с сечением в N.
Схожим образом мы можем доказать, что она, проведенная дальше в другую сто¬
рону, пересекается с сечением.
fi®
•Ж
•Ж
29
Если на противолежащих прямая через центр попадает на любое из двух сечений,
то, проведенная дальше, она будет рассекать другое сечение.
Пусть будут противолежащие с диаметром АВ, и пусть центром будет Г; и пусть
ГД рассекает сечение АД. В этом случае я утверждаю, что она также будет рассекать
другое сечение.
Пусть будет проведена упорядоченно ЕД, и пусть будет установлено, что BZ равно
АЕ, и пусть будет проведена упорядоченно ZH. А поскольку ЕА равно BZ и АВ явля¬
ется обшей, то ВЕА равно AZB. А поскольку как ВЕА к ДЕ в квадрате, так и попереч¬
ная сторона относится к прямой стороне, однако как AZB к ZH в квадрате, так и по¬
перечная сторона относится к прямой стороне, то ВЕА к ДЕ в квадрате равно AZB к
ZH в квадрате. Но ВЕА равно AZВ. Поэтому так же ЕД в квадрате равно ZH в квадрате.
Следовательно, поскольку ЕГ равно TZ, ДЕ равно ZH и EZ является прямой, ЕД
параллельна ZH, то и ДН является прямой. Таким образом, ГД рассекает также и
другое сечение.
•Ж
30
Если на эллипсе или противолежащих прямая проводится от центра в любую из
двух частей, пересекаясь с сечением, то она рассекается в центре на две равные части.
Пусть будут эллипс или противолежащие с диаметром АВ, и пусть центром бу¬
дет Г. И пусть через Г будет проведена некая прямая ДГЕ. В этом случае я утверж¬
даю, что ГД равно ГЕ.
Пусть будут проведены упорядоченно и ЕН. А поскольку, как В2А к ¿А в ква¬
драте, так и поперечная сторона относится к прямой стороне, и так же как АН В к
НЕ в квадрате, так и поперечная сторона относится к прямой стороне, то будет В2А
к гд в квадрате равно АН В к НЕ в квадрате. И при перестановке ВХА к АНВ рав¬
но Д2 в квадрате к Н Е в квадрате. Но Д7 в квадрате к НЕ в квадрате равно ¿Г в ква¬
драте к ГН в квадрате. Таким образом, при перестановке В2А к 7Г в квадрате равно
АН В к ГН в квадрате. Поэтому как в составленном эллипсе, так и на противолежа¬
щих, наоборот, АГ в квадрате к Г2 в квадрате равно ВГ в квадрате к ГН в квадрате;
и при перестановке. Однако ГВ в квадрате равно АГ в квадрате. Поэтому также ГН
в квадрате равно 2Н в квадрате. Таким образом, 7.Г равно ГН. И дг и НЕ являются
параллельными. Следовательно, ДГ равно ГЕ.
31
Если на гиперболе на поперечной стороне эйдоса берется некая точка, отсекающая
до вершины сечения прямую, не меньшую, чем половина поперечной стороны эйдоса, и
177

Дословный перевод книги I
прямая /проведенная/от нее достигает сечения, то данная прямая, проведенная даль¬
ше, попадет внутрь сечения в следующую его часть.
Пусть будет гипербола с диаметром АВ; и пусть будет взята на ней некая точка
Г, отводящая ГВ, не меньшую, чем половина АВ, И пусть некоторая прямая ГД ка¬
сается сечения. В таком случае я утверждаю, что ГА, проведенная дальше, попадет
ж®
внутрь сечения.
Если это возможно, то она попадает вне сечения как ГДЕ; и пусть от произволь¬
ной точки Е будет проведена упорядоченно ЕН, и пусть также будет проведена Д0;
и пусть сначала АГ равно ГВ. Таким образом, поскольку ЕН в квадрате к Д0 в ква¬
драте больше ¿Н в квадрате к Д0 в квадрате, однако ЕН в квадрате к Д0 в квадрате
равно НГ в квадрате к Г0 в квадрате, так как ЕН и Д0 являются параллельными и
7Н в квадрате к Д0 в квадрате равно АН В к А0В из-за сечения, то будет Н Г в ква¬
драте к Г0 в квадрате больше АН В к А0В. Таким образом, при перестановке ГН в
квадрате к АН В больше Г0 в квадрате к А0В. Таким образом, ГВ в квадрате к АН В
больше ГВ квадрате к А0В, что невозможно. Следовательно, ГДЕ не попадает вне
сечения, а внутрь его. По этой причине прямая, проведенная от некой точки на АГ,
тем более попадает внутрь сечения, поскольку попадает ниже ГД.
ш:
32
Если через вершину конического сечения проводится прямая, параллельная прямой,
проведенной упорядоченно /ординате/, то другая прямая не попадает в места между
сечением конуса и прямой.
Пусть сначала сечением конуса будет парабола с диаметром АВ, и пуст ь от Л бу¬
дет проведена АГ, параллельная прямой, проведенной упорядоченно.
Мы доказали, что она попадает вне сечения. В таком случае я утверждаю, что ни¬
какая другая прямая не попадет в места между прямой АГ и сечением.
Если возможно, то пусть она попадает как АД, и пусть на ней будет взята некая
точка Д. Пусть будет проведена упорядоченно ДЕ, и пусть прямой стороной для упо¬
рядоченно проведенных прямых будет А2. А поскольку ДЕ в квадрате к ЕЛ в квадра¬
те больше НЕ в квадрате к ЕА в квадрате и НЕ в квадрате равно /АЕ, то ДЕ в ква¬
драте к ЕА в квадрате больше 7АЕ к ЕА в квадрате, т.е ДЕ в квадрате к ЕА в квадра¬
те больше ТА к АЕ. И пусть будет ДЕ в квадрате к ЕА в квадрате равно ТА к А0, и
пусть через 0 будет проведена 0ЛК, параллельная прямой ЕД. Таким образом, по¬
скольку ДЕ в квадрате к ЕА в квадрате равно ТА к А0 равно ТА& к А0 в квадрате, а
ДЕ в квадрате к ЕА в квадрате равно К0 в квадрате к 0А в квадрате и 7А0 равно 0Л
в квадрате, то К.0 в квадрате к 0А в квадрате равно Л0 в квадрате к 0А в квадрате.
Поэтому К0 равно 0Д, что абсурдно. Следовательно, никакая другая прямая не по¬
падает в площадь, расположенную между прямой АГ и сечением.
Пусть сечением будет гипербола, или эллипс, или окружность круга, чьим диа¬
метром будет АВ, а прямой стороной - АТ. и проведенная ВТ пусть будет продол¬
жена дальше, а от А пусть будет проведена АГ, параллельная прямой, проведенной
Л1».
•Г*
©
и».
упорядоченно.
Доказано, что она попадает вне сечения. Я утверждаю, что никакая другая пря¬
мая не попадет в места, расположенные между прямой АГ и сечением.
178

Дословный перевод книги I
Ведь если возможно, то пусть она попадает как АД, и пусть на ней будет взята не¬
кая точка Д, и от нее пусть будет проведена упорядоченно ДЕ; пусть через Е будет
проведена ЕМ, параллельная прямой AZ. А поскольку НЕ в квадрате равно АЕМ. то
пусть AEN равно ДЕ в квадрате, и проведенная AN пусть рассекает прямую ZM в Н,
а через Е пусть будет проведена Z0, параллельная прямой ZA, и через 0 — 0ЛК, па¬
раллельная прямой АГ. Поскольку ДЕ в квадрате равно AEN, то будет NE к ЕД равно
ДЕ к ЕА; поэтому также NE к ЕА равно ДЕ в квадрате к ЕА в квадрате. Однако NE
к ЕА равно Е0 к 0А, ДЕ в квадрате к ЕА в квадрате равно К0 в квадрате к 0А в ква¬
драте. Следовательно, Е0 к 0А равно К0 в квадрате к 0А в квадрате. Поэтому ана¬
логичное среднее есть К0 между Е0А. По этой причине 0К в квадрате равно А0Н
Однако также из-за сечения Л0 в квадрате равно А0Е. Поэтому будет К0 в квадра¬
те равно Л0 в квадрате, что абсурдно. Следовательно, никакая другая прямая не по¬
падает в место, расположенное между прямой АГ и сечением.
33
Если на параболе берется некая точка, и от нее проводится упорядоченно к диаме¬
тру прямая [ордината], и прямая, проведенная за его предел, устанавливается как рав¬
ная прямой, отделенной на диаметре от вершины, то прямая, проведенная от такой
возникшей точки к взятой точке, касается сечения.
Пусть будет парабола с диаметром АВ, и пусть будет проведена упорядоченно ГД,
и пусть устанавливается, что АЕ равно ЕД, и пусть будет проведена АГ. В этом случае
я утверждаю, что АГ, проведенная дальше, окажется вне сечения.
Если возможно, то пусть она окажется внутри сечения как ГС, и пусть будет щ
ведена упорядоченно НВ. А поскольку квадрат на ВН к квадрату на ГД больше ква¬
драта на ZB к квадрату на ГД, а ХВ в квадрате к ГД в квадрате равно ВА в квадрате к
АД в квадрате, Н В в квадрате к ГД в квадрате равно ВЕ к ДЕ, то будет ВЕ к ЕД боль¬
ше ВА в квадрате к АД в квадрате. Однако ВЕ к ЕД равно 4ВЕА к 4АЕД. Поэтому так¬
же 4ВЕА к 4АЕД больше ВА в квадрате к АД в квадрате. При перестановке 4ВЕА к
АВ в квадрате больше 4АЕД к АД в квадрате; а это невозможно, ведь поскольку АЕ
равно ЕД, то будет 4АЕД равно АД в квадрате; однако 4ВЕА меньше ВА в квадрате,
ведь Е не является точкой, находящейся посередине. Следовательно, АГ не оказы¬
вается внутри сечения и поэтому не касается его.
•Г”
лтг
т
34
Если на гиперболе, или на эллипсе, или на окружности круга берется некая точка, а
от нее проводится прямая упорядоченно к диаметру [ордината], и то отношение, ко¬
торое имеют между собой прямые, отведенные от проведенной упорядоченно прямой к
пределам поперечной стороны эйдоса, имеют и отрезки поперечной стороны, располо¬
женные при вершине, то прямая, соединяющая точку, взятую на поперечной стороне и
точку на сечении, касается сечения.
Пусть будет гипербола, или эллипс, или окружность круга с диаметром АВ. и
пусть будет взята на сечении некая точка Г, и от точки Г пусть будет проведена упо¬
рядоченно ГД, и пусть окажется, что ВД к ДА равно ВЕ к ЕА; пусть будет проведена
ЕГ. В этом случае я утверждаю, что ГЕ будет касаться сечения.
•а
179

Дословный перевод книги I
Если возможно, то пусть она рассекает как ЕГ2, пусть на ней будет взята некая
точка 2, и пусть будет проведена упорядоченно Н20, а через А и В пусть будут про¬
ведены АЛ и ВК, параллельные прямой ЕГ; и пусть проведенные АГ, ВГ и Н Г будут
проведены дальше к М,Еи К. А поскольку ВЛ к ЛА равно ВЕ к ЕА, и также ВА к ДА
равно ВК к АМ и ВЕкАЕ равно ВГ к ГЕ равно ВК кЕ1Ч, то получается, что ВК к AN
равно ВК к 1ЧЕ. Поэтому AN равно 1МЕ. Таким образом, А№ больше АОЕ. По этой
причине № к ЕО больше ОА к АМ Однако МЕ к ЕО равно КВ к ВМ. Таким обра¬
зом, КВ к ВМ больше ОА к АМ Поэтому КВ на AN больше МВ на АО. Тогда КВ на
AN к ГЕ в квадрате больше МВ на АО к ГЕ в квадрате. А из-за сходства треугольни¬
ков ВКА, ЕГД и МАЛ выходит, что КВ на AN к ГЕ в квадрате равно ВЛА к ДЕв ква¬
драте и МВ на АО к ГЕ в квадрате равно ВНА к Н Е в квадрате. Поэтому получается,
что ВЛА к ДЕ в квадрате больше ВНА к Н Е в квадрате. При перестановке тогда ВЛА
к ВНА больше ДЕ в квадрате к НЕ в квадрате. Однако ВЛА к ВНА равно ГД в ква¬
драте к НО в квадрате. И ЛЕ в квадрате к ЕН в квадрате равно ГЛ к 2Н в квадрате.
Поэтому также ГД в квадрате к ОН в квадрате больше ГА в квадрате к 2Н в квадра¬
те. По этой причине ОН меньше ¿Н; а это невозможно. Следовательно, ЕГ не про¬
изводит сечения и поэтому не касается его.
•II
35
Если прямая касается параболы, пересекаясь с диаметром вне сечения, то прямая,
проведенная от точки касания упорядоченно к диаметру [ордината!, отделяет на ди¬
аметре от вершины сечения прямую, равную прямой, расположенной между вершиной
и касательной, и никакая прямая не попадает в места, расположенные между каса¬
тельной и сечением.
Пусть будет парабола с диаметром АВ, и пусть будет проведена упорядоченно ВГ,
а АГ будет касаться сечения. В этом случае я утверждаю, что АН равна НВ.
Если возможно, то пусть она не будет равна, и пусть будет установлено, что НЕ
равно АН. пусть будет проведена упорядоченно Е2. и пусть будет проведена ХЕ По¬
этому А2. проведенная дальше, будет пересекаться с прямой АГ, а это невозможно,
ведь тогда пределы будут теми же самыми для двух прямых. Таким образом, АН не
будет не равна НВ Следовательно, она равна ей.
Также я утверждаю, что никакая прямая не будет попадать в места, расположен¬
ные между прямой АГ и сечением.
Ведь если возможно, то пусть Г А попадает, и пусть будет установлено, что Н Е рав¬
но НА, и пусть будет проведена упорядоченно ЕЕ. Таким образом, прямая, прове¬
денная от А к 2. касается сечения; поэтому она, проведенная дальше, окажется вне
сечения. По этой причине она пересекается с АГ, и пределы будут теми же самыми
для двух прямых, что абсурдно. Следовательно, никакая прямая не попадает в ме¬
ста, расположенные между сечением и прямой АГ.
36
Если прямая касается гиперболы, или эллипса, или окружности круга, пересекаясь с
поперечной стороной эй доса, и проводится упорядоченно прямая [ордината! от точки
касания к диаметру, то получается, что как прямая отделенная касательной от пре¬
180

Дословный перевод книги I
дела поперечной стороны по отношению к прямой, отделенной касательной от другого
предела поперечной стороны, так и прямая отделенная проведенной упорядоченно пря¬
мой от предела поперечной стороны по отношению к прямой, отделенной проведенной
упорядоченно прямой от другого предела поперечной стороны, так что прямые, соот¬
ветствуя друг другу, являются непрерывными, и никакая другая прямая не будет попа¬
дать в места, расположенные между касательной и сечением конуса.
Пусть будет гипербола, или эллипс, или окружность круга с диаметром АВ, и
пусть их касается ГД; пусть будет проведена упорядоченно ГЕ. В таком случае я ут¬
верждаю, что ВЕ к ЕА равно ВЛ к ДА.
Если это не так, то пусть ВЛ к ДА равно ВН к НА, и пусть будет проведена упоря¬
доченно Нг. Следовательно, прямая, проведенная от Д к 7, касается сечения; поэ¬
тому она, продолженная дальше, пересечется с ГД. Таким образом, пределы для двух
прямых оказываются одинаковыми, что абсурдно.
Я утверждаю, что никакая прямая не окажется между сечением и прямой ГД.
Ведь если возможно, то пусть она окажется там как ГД, и пусть выйдет, что ВО к
0А равно ВН к НА, пусть будет проведена упорядоченно Н7; таким образом, пря¬
мая, проведенная от О к 7, продолженная дальше, пересечется с О Г. Тогда пределы
двух прямых окажутся теми же самыми, что невозможно. Следовательно, никакая
прямая не окажется между сечением и прямой ГД.
•1Г
37
Если прямая, касающаяся гиперболы, или эллипса, или окружности круга, встре¬
чается с диаметром, и от точки касания упорядоченно к диметру проводится прямая
/ордината/, то прямая, отделенная от проведенной упорядоченно прямой до центра се¬
чения, вместе с прямой, отделенной от касательной до центра сечения, составляют
фигуру, равную квадрату радиуса сечения, а вместе с прямой, расположенной между
проведенной упорядоченно прямой и касательной, составляет площадь, которая имеет
отношение к квадрату проведенной упорядоченно прямой, каковое отношение имеется
у поперечной стороны к прямой.
Пусть будет гипербола, или эллипс, или
окружность круга, чьим диаметром будет АВ,
и пусть будет проведена касательная ГД; пусть
будет проведена упорядоченно ГЕ, а центром
пусть будет 7. В таком случае я утверждаю,
что Д7Е равно 7В в квадрате, и как ДЕ7 к ЕГ
в квадрате, так и поперечная сторона отно¬
сится к прямой.
Ведь поскольку ГД касается сечения, и
ГЕ проведена упорядоченно, то получается,
что АД к ДВ равно АЕ к ЕВ. Следовательно, в
процессе складывания АД плюс ДВ к ДВ рав¬
но АЕ пл юсЕВкЕВ.И пусть будут взяты по¬
ловины предшествующих. И тогда получает¬
ся на гиперболе; 7Е равно одной второй АЕ
181

Дословный перевод книги I
плюс ЕВ. гв равно одной второй АВ. Таким об¬
разом, ZE к ЕВ равно ZB к АВ. И при преобра-
зовании Ег к гВ равно 7. В к ZA. Следовательно,
ЕгА равно ZB в квадрате. А поскольку ZB к ЕВ
равно гВ к АВ равно ХЕ к АВ, и при перестанов-
ке ХЕ к ЕЕ равно АВ к ВЕ. И в процессе склады-
вания АЕ к EZ равно АЕ к ЕВ. Поэтому ЛЕВ равно ZEA. А как АЕВ к ГЕ в квадрате,
так и поперечная сторона относится к прямой. Поэтому так же как ZEA к ГЕ в ква¬
драте, так и поперечная сторона относится к прямой.
А на эллипсе и круге выходит следующее: AZ равно одна вторая АА гы юс АВ. Z В
равно одной второй АВ. Поэтому получается, что ZA к АВ равно ZB к ВЕ. Поэтому
при преобразовании ZA к ZB равно BZ к ZE Таким образом, AZE равно BZ в квадра¬
те. Однако AZE равно AEZ плюс ZE в квадрате и BZ в квадрате равно АЕВ плюс ZE в
квадрате. И пусть как общее отбрасывается EZ в квадрате. Таким образом, выходит,
что AZE равно АЕВ. Поэтому будет AEZ к ГЕ в квадрате равно АЕВ к ГЕ в квадрате.
Однако так АЕВ к ГЕ в квадрате, как поперечная сторона относится к прямой. Сле¬
довательно, так AEZ к ЕГ в квадрате, как поперечная сторона относится к прямой.
м бу-
38
Если прямая, касающаяся гиперболы, или эллипса, или окружности круга, встреча¬
ется с диаметром, и от точки касания проводится прямая к тому же самому диаме¬
тру, параллельная другому диаметру, то прямая, отделенная прямой, проведенной та¬
ким образом, от центра сечения, вместе с прямой, отделенной касательной от центра
сечения, составляет площадь, равную квадрату половины другого диаметра, а вместе
с прямой, расположенной между прямой, проведенной к диаметру, и касательной, со¬
ставляет площадь, которая имеет такое отношение к квадрату прямой [проведенной!
к диаметру, какое существует между прямой стороной эйдоса и поперечной.
Пусть будет гипербола, или эллипс, или окружность круга, чьим диамет|
дет АН В, а вторым диаметром - ГН А; и пусть Е.Аг касается сечения, пересекаясь с
ГА в Е. пусть 0Е будет параллельна прямой АВ В этом случае я утверждаю, что гН0
равно НГ в квадрате, и как Н(^ к 0Е в квадрате, так и прямая сторона относится к
поперечной. Пусть будет проведена упорядоченно МЕ. Однако как поперечная сто¬
рона ВА относится к ГА, так ГЛ относится к прямой стороне. Поэтому так же как по¬
перечная сторона относится к прямой, так и АВ в квадрате к ГА в квадрате; и также
четыре отрезка, те НА в квадрате к НГ в квадрате. Поэтому также НМ на МЛ к МЕ
в квадрате равно НА в квадрате к Н Г в квадрате. Однако Н МЛ к М Е в квадрате рав¬
но НМЕ на ЛМЕ равно НМ0на АМЕ Поэтому, наоборот, ГН в квадрате к НА в ква¬
драте равно ЕМ к МН на ЕМ к МЛ равно 0Н к НМ на ЕН к НА. Однако ОН к НМ
на гН к НА равно ZH0 к МНЛ. Таким образом, получается, что ZH0 к МНЛ рав¬
но ГН в квадрате к НА в квадрате. И при перестановке получается, что ¿НО к ГН в
квадрате равно МНЛ к НА в квадрате Однако М НА равно НА в квадрате. Следова¬
тельно, также ZH0 равно Н Г в квадрате.
А поскольку снова как прямая сторона относится к поперечной, так и ЕМ в ква¬
драте к НМЛ, и ЕМ в квадрате к НМЛ равно ЕМ к НМ на ЕМ к МЛ равно ОН к 0Е
182

Дословный перевод книги I
на 7Н к НА равно 0Н к 0Е на к 0Е равно ¿0Н к 0Е в квадрате, то получается,
что как 70Н к 0Е в квадрате, так и прямая сторона относится к поперечной.
Докажем при тех же самых условиях, что отношение отрезков, на которые каса¬
тельная делит второй диаметр равно отношению отрезков, заключенных между точ¬
кой пересечения с ним ординаты и его концами.
Нужно доказать при тех же самых предположениях, что какое отношение имеет
прямая, расположенная между касательной и пределом диаметра, к прямой, распо¬
ложенной между касательной и вторым пределом диаметра, такое отношение име¬
ет прямая, расположенная между вторым пределом и прямой, проведенной упоря¬
доченно, к прямой, находящейся между другим пределом и упорядоченно прове¬
денной прямой.
Ведь поскольку 7Н0 к 0Е равно НГ в квадрате, т.е. 7Н0 равно ГН А ведь ГН рав¬
но НА. то получается, что к НА равно ГН к Н0. И при преобразовании 7Н к 7А
равно НГ к Г0. И пусть будут взяты двойные из предшествующих; с другой сторо¬
ны, Г7 плюс ¿А равно 2Н7, поскольку ГН равно НА, и ГА равно 2НГ. Поэтому Г7
плюс /А к 7А равно АГ к Г0. И при сортировке получается, что Г7. к 7Л равно А0 к
0Г, что и нужно было доказать.
»а
Добавление
Следовательно, из того, что мы сказали, очевидно, что прямая Е2 касается се¬
чения, если будет 7Н0 равно НГ в квадрате, или если 70Н имеет отношение к 0Е
в квадрате, о каковом мы сказали, ведь обратное было доказано.
СК
•тс
39
Если прямая, касающаяся гиперболы, или эллипса, или окружности круга, пересе¬
кается с диаметром, и от точки касания к диаметру проводится упорядоченно пря¬
мая /ордината/, то если будет взята любая из двух прямых, или, с одной стороны, пря¬
мая, которая расположена между прямой /ординатой] и центром сечения, или, с другой
стороны, прямая, расположенная между' прямой /ординатой] и касательной, то пря¬
мая /ордината] будет иметь отношение к ней, составленное из того отношения, ко¬
торое другая из тех прямых к прямой /ординате], и из того отношения, которое име¬
ет прямая сторона зйдоса к поперечной.
Пусть будет гипербола, или эллипс, или окружность круга, чьим диаметром бу¬
дет АВ, а центром пусть будет Z, и пусть будет проведена ГА, касающаяся сечения,
и пусть будет проведена упорядоченно ГЕ. В этом случае я утверждаю, что ГЕ имеет
отношение к любой из двух прямых ZE и ЕА, составленное из того отношения, ко¬
торое имеет прямая сторона к поперечной, и того отношения, kotoi
гая из прямых ZE и ЕА к ЕГ.
Пусть будет ZEA равно ЕГ на Н А поскольку как ZEA к ГЕ в квадрате, так и по¬
перечная сторона относится к прямой, и ZE на ЕА равно ГЕ на Н. то получается, что
как ГЕ на Н к ГЕ в квадрате, т.е. как Н к ЕГ. так и А поскольку ZEA равно ГЕ на Н,
и поперечная сторона относится к прямой, то выходит, что EZ к ЕГ равно Н к ЕА. А
так как ГЕ к ЕА равно ГЕ к Н на Н к ЕА. и как ГЕ к Н, так и прямая сторона отно-
»3
»1».
183

Дословный перевод книги I
сится к поперечной, и Н к ЕЛ равно /Е к ЕГ, ГЕ к ЕД имеет отношение составлен¬
ное из того отношения, которое имеет прямая сторона к поперечной, и из того, ко¬
торое имеет /Е к ЕГ.
О
»1«
40
Если прямая, касающаяся гиперболы, или эллипса, или окружности круга, пересека¬
ется со вторым диаметром, и от точки касания проводится прямая к тому же самому
диаметру, параллельная другому диаметру, и если будет взята любая из двух прямых,
или прямая, которая расположена между прямой, проведенной к диаметру, и центром
сечения, ши прямая, которая расположена между той прямой и касательной, то пря¬
мая, проведенная к диаметру, будет иметь отношение к той прямой, составленное из
того отношения, которое имеет поперечная сторона к прямой [стороне], и то, кото¬
рое имеет другая из данных прямых к прямой, проведенной к диаметру.
Пусть будет гипербола, или эл¬
липс, или окружность круга АВ,
чьим диаметром будет В/Г. а дру¬
гим диаметром Л/Е, и пусть будет
проведена касательная ОЛА. а АН
будет параллельна прямой В Г. В
таком случае я утверждаю, что АН
будет иметь к одной из двух пря¬
мых ОН и /Н отношение, состав¬
ленное из того отношения, которое Е
имеет поперечная сторона к пря¬
мой, и того, которое имеет другая
из них к НА.
Пусть будет НА на К равно
ОН/. А поскольку имеется, что
как прямая сторона относится к
поперечной, так и ОН/ к НА в ква¬
драте, и НА на К равно ОН/, то
получается также, что как НА на
К к НА в квадрате, т.е. как К к АН,
так и прямая сторона относится
к поперечной. А поскольку АН к
Н/ равно АН к К на К к Н/. и как
НА к К, так и поперечная сторо¬
на относится к прямой, и К к Н/
равно ОН к НА, поскольку ОН/
равно АН на К. АН к Н/ имеет
отношение, составленное из того
отношения, которое имеет попе¬
речная сторона к прямой, и того,
которое имеет НО к НА.
ЙЕ
184

Дословный перевод книги I
Если на гиперболе, или эллипсе, или окружности круга проводится упорядоченно к
диаметру прямая [ордината], и на прямой и на радиусе описываются равноугольные па¬
раллелограммы, а сторона [ордината] имеет отношение к оставшейся стороне фигуры,
которое имеет отношение, составленное из отношения радиуса к оставшейся стороне
фигуры, и того, которое имеет прямая сторона сечения к поперечной, то фигура, опи¬
санная прямой, расположенной между центром и упорядоченной прямой [ординатой],
подобная фигуре, описанной радиусом, на гиперболе превышает фигуру, описанную ор¬
динатой, фигурой описанной радиусом, а на эллипсе и окружности круга она при присо¬
единении фигуры, описанная ординатой, равна фигуре, описанной радиусом.
Пусть будет гипербола, или эллипс, или окружность круга, чьим диаметром бу¬
дет АВ, а центром - Е; и пусть будет проведена упорядоченно прямая ГА, и на ЕА
и ГА равноугольной фигуры пусть будут начерчены КТ и АН, и пусть ГА к ГН имеет
отношение, составленное из того отношения, которое имеет АЕ к ЕА, и того, кото¬
рое имеет прямая сторона к поперечной. В этом случае я утверждаю, что для гипер¬
болы фигура на ЕА, подобная фигуре AZ, будет равна фигуре AZ плюс АН, а для эл¬
липса и круга фигура на ЕА, подобная фигуре AZ при присоединении фигуры НА,
равна фигуре AZ.
Пусть будет так, что как относится прямая сторона к поперечной, так АГ к Г0.
И поскольку как АГ к Г0, так и прямая сторона к поперечной, и АГ к Г0 равно АГ
в квадрате к АГ0, и как относится прямая сторона к поперечной, так и АГ в квадра¬
те - к ВАА, то получается, что ВАА равно АГ0. А поскольку АГ к ГН имеет отноше¬
ние, составленное из того отношения, которое имеет АЕ к EZ, и того, которое име¬
ет прямая сторона к поперечной, т.е. АГ к Г0; и, кроме того, АГ к ГН равно АГ к Г0
на 0Г к ГН, и получается, что АЕ к EZ на АГ к Г0 равно АГ к Г0 на 0Г к ГН. И от¬
брасывается отношение, которое естьобшее, АГ к Г0. Поэтому АЕ к EZ равно 0Г к
ГН К тому же 0Г к ГН равно 0ГА к НГА, АЕ к EZ равно АЕ в квадрате к AEZ. Тогда
выходит, что 0ГА к НГА равно ЕА в квадрате к AEZ. Однако мы уже доказали, что
0ГА равно ВАА. Следовательно, ВАА к НГА равно АЕ в квадрате к AEZ. При пере¬
становке ВААк АЕ в квадрате равно НГА к AEZ. Однако НГА к AEZ равно АН kZA.
ведь они суть равноугольные параллелограммы и имеют отношение, составленное
из сторон НГ к АЕ и ГА к EZ. Поэтому также ВАА к ЕА в квадрате равно НА к КТ.
Поэтому нужно сказать, что на гиперболе ВАА плюс АЕ в квадрате к АЕ в ква¬
драте равно НА плюс AZ к AZ, т.е. АЕ в квадрате к ЕА в квадрате равно НА плюс AZ
к КТ. Однако как ЕД в квадрате к ЕА в квадрате, так и фигура, начерченная на ЕА,
схожая с фигурой КТ, относится к КТ. Поэтому как НА плюс КТ к AZ, так и фигу¬
ра на ЕД, схожая с фигурой AZ, относится к КТ. Следовательно, фигура на ЕД, схо¬
жая с фигурой КТ, равна фигуре НА плюс КТ.
К на эллипсе и на окружности круга мы утверждаем, что. поскольку квадрат АЕ
к КТ равно ААВ к АН, получается также, что как относится целое к целому, так и
оставшееся к оставшемуся. А если от квадрата ЕА отбрасывается ВАА, то остается
квадрат АЕ. Поэтому квадрат ДЕ к КТ деленное на АН равно АЕ в квадрате к КТ.
Однако как АЕ в квадрате к КТ, так и ДЕ в квадрате относится к фигуре, описанной
ДЕ, схожей с фигурой КТ. По этой причине как АЕ в квадрате к КТ деленное на АН.
185

Дословный перевод книги I
так и ЛЕ в квадрате относится к фигуре, описанной ЛЕ, схожей с фигурой А7. Поэ¬
тому фигура на ЛЕ, схожая с фигурой А/, равна различию Аг деленное на ЛН. Сле¬
довательно, сопряженная фигура ЛН равна фигуре А/.
Если прямая, касающаяся параболы, пересекается с диаметром, и из точки каса¬
ния к диаметру проводится упорядоченно прямая /ордината/, а от некой точки, взя¬
той на сечении, проводятся к диаметру две прямые, причем одна из них параллельна ка¬
сательной, а другая - ординате, проведенной от точки касания, то треугольник, воз¬
никший из них, равен параллелограмму, ограниченному прямой, проведенной от точки
сечения параллельно касательной к вершине и прямой, отделенной ими /на диаметре/.
Пусть будет парабола, чьим диаметром будет АВ, и пусть будет проведена АГ, ка¬
сающаяся сечения; и пусть будет проведена упорядоченно прямая Г0; и пусть от не¬
кой точки будет проведена Л/, через Л проведем ЛЕ, параллельно прямой АГ, через
Г - ГН, параллельно прямой В/, а через В - ВН, параллельно прямой 0Г.
случае я утверждаю, что ЛЕ/ равно Н7.
Ведь поскольку АГ касается сечения, и Г0 проведена как ордината, то получа¬
ется, что АВ равно В0. Поэтому А0 вдвое больше 0В. По этой причине А0Г равно
ВГ. А поскольку Г0 в квадрате к Л/ в квадрате равно 0В к В/ из-за сечения, и Г0
в квадрате к \7. в квадрате равно АГ0 к ЕЛ/, 0В к В/ равно Н0 к Н7, то получает¬
ся, чтоАГ© к ЕЛ/ равно 0Н к/Н. Поэтому при перестановке А0Г к ВГ равно ЕЛ/
к Н/. Однако АГ0 равно Н0. Следовательно,ЕЛ/ равно Н7.
Если прямая, касающаяся гиперболы, или эллипса, или окружности круга, пересека¬
ется с диаметром, и от точки касания к диаметру проводится упорядоченно прямая
/ордината/, а через вершину проводится прямая, параллельная данной, пересекающа¬
яся с прямой, проведенной через точку касания и центр, и от взятой некой точки про¬
водятся две прямые к диаметру, одна из которых параллельна касательной, а другая
- ординате, проведенной от точки касания, то треугольник, образованный ими на ги¬
перболе, будет на треугольник, отведенный от прямой, проведенной через центр и точ¬
ку касания, меньше, чем треугольник, находящийся на радиусе и подобный тому отве¬
денному треугольнику, а на эллипсе и окружности круга он /при] отведенном к центру
треугольнике будет равен треугольнику, описанному радиусом, схожим с тем отведен¬
'«И
ным треугольником.
Пусть будет гипербола, или эллипс, или окружность круга, чьим диаметром бу¬
дет АВ, центром - Г; и пусть будет проведена ЛЕ, касающаяся сечения, а также ГЕ,
ордината Е/, и пусть на сечении будет взята некая точка Н; пусть будет проведена
Н0, параллельная касательной, и пусть будет проведена упорядоченно прямая Н К,
а через В - ордината ВЛ. В этом случае я утверждаю, что треугольник КМ Г отлича¬
ется от треугольника ГЛВтреугольником НК0.
Ведь поскольку ЕЛ касается сечения, а Е7 проведена как ордината, то к /Л
имеет отношение, составленное отношением Г/ к 7Е и того, которое имеет прямая
сторона к поперечной. Однако Е/ к /Л равно НК к К0 и Г/ к 7Е равно ГВ к ВЛ.
1X6

Дословный перевод книги I
Поэтому НК к К® будет иметь отношение, составленное из отношения ВГ к ВЛ и
того, которое имеет прямая сторона к поперечной. А из-за того, что мы доказали
в Х1П теореме, треугольник ГКМ отличается от треугольника ВГЛ треугольником
Н®К; ведь относительно параллелограммов, которые больше их удвоенных, го же
самое уже доказано.
Если прямая, касающаяся одной из противолежащих, пересекается с диаметром, и
та
от точки соприкосновения проведена упорядоченно к диаметру прямая ¡ордината!, и
проводится через вершину другого сечения прямая, параллельная данной, пересекающа¬
яся с прямой, проведенной через точку касания и центр, и при взятии некоторой точки
на сечении проводятся к диаметру прямые, одна из которых параллельна касательной, а
другая — ординате, проведенной от точки касания, то треугольник, образованный ими,
будет меньше треугольником, который отделяет прямая ¡проведенная! через центр се¬
чения, треугольника, описанного радиусом и подобного отделенному треугольнику.
Пусть будут противолежащие (прямые) АХ и
ВЕ, чьим диаметром будет АВ, а центром — Г; и
пусть от некой точке Ъ на сечении ХА будет про¬
ведена ХН, касающаяся сечения, пусть будет про¬
ведена упорядоченно прямая ХО, и ХГ пусть бу¬
дет продолжена дальше, так что получится ГЕ;
и пусть через В будет проведена ВЛ, параллель¬
ная ХО, а на сечении ВЕ пусть будет взята некая
точка N. и от N пусть будет проведена упорядо¬
ченно прямая N0, и пусть будет проведена N К,
•ГЛ
та
параллельная прямой ХН. В таком случае я ут¬
верждаю, что N®K равно ГМ® деленное на ГМЛ.
Пусть же через Е будет проведена ЕЛ, касающаяся сечения ВЕ, а также пусть бу¬
дет проведена ордината ЕЕ. Поскольку ХА и ВЕ являются противолежащими, ди¬
аметр которых АВ, а прямая ХГЕ проведена через центр и ХН и ЛЕ касаются сече¬
ний, то ЛЕ параллельна ХН. Однако NK параллельна прямой ХН, поэтому NK так¬
же параллельна прямой ЕЛ, а М® - параллельна прямой ВЛ. А так как гиперболой
является ВЕ с диаметром АВ и центров в Г, а ЛЕ касается сечения и проведена орди¬
ната ЕЕ, а ВЛ параллельна прямой ЕЕ, и на сечении взята точка N, от которой про¬
ведена ордината N®, а KN параллельна прямой ДЕ, то получается, что N®K равно
®МГ деленное на ВГЛ, ведь это было доказано в теореме 43.
45
Если прямая, касающаяся гиперболы, или эллипса, или окружности круга, пересека¬
ется со вторым диаметром, а от точки касания к тому же диаметру проводится пря¬
мая, параллельная другому [первому! диаметру, и через точку касания и центр прово¬
дится прямая, и через взятую на сечении некоторую точку проводятся две прямые ко
второму диаметру, одна из которых параллельна касательной, а другая — ординате1,
та
’ Имеется в виду прямая ГЛ.
187

Дословный перевод книги I
©
о
©
то треугольник, образованный ими, будет на гиперболе больше треугольника, который
отсечен ординатой и прямой, проведенной к центру, треугольником, чьим основанием
является касательная, а на эллипсе и на круге он будет равен при прибавлении отде¬
ленного треугольника, треугольнику, чьим основанием является касательная, а верши¬
ной - центр сечения.
Пусть будет гипербола, или эллипс, или окружность круга АВГ, чьим диаметром
будет А0, а другим диаметром - Д0, центром - 0; и пусть ГМА касается в Г, пусть
будет проведена ГД как параллельная прямой А0, а проведенная 0Г пусть будет про¬
должена дальше; пусть на сечении будет взята некая точка В, и от В пусть будут про¬
ведены ВЕ и BZ, параллельные прямым АГ и ГД. В этом случае я утверждаю, что на
гиперболе BEZ равно H0Z плюс ЛГ0, а на эллипсе и на круге BEZ плюс ZH0 рав¬
но ГА0.
Пусть же будут проведены ГК и BN, параллельные прямой ДО. Поскольку ГМ
выступает касательной, и ГК проведена как ордината, то ГК к КО будет иметь отно¬
шение, составленное из отношения, которое имеет МК к КГ, и того, которое имеет
прямая сторона эйдоса к поперечной. Однако МК к КГ равно ГД к КО. Поэтому ГК
к К0 имеет отношение, составленное из отношения ГД к ДА и того, которое име¬
ет прямая сторона к поперечной. И треугольник ГДЛ есть фигура, описанная КО, а
ГКО, как и ГА0 - фигура, описанная ГК и ДО. Таким образом, на гиперболе треу¬
гольник ГДЛ треугольником ГК0 больше треугольника, описанного АО, схожего с
треугольником ГЛА, а на эллипсе и на круге ГА0 вместе с ГДЛ равен тому же самому
|треугольнику!, ведь это доказано в гипотезе 41 на фигурах, которые больше тех же
самых удвоенных. А поскольку треугольник ГДЛ от ГК0 или ГАО отличается треу¬
гольником, описанным А0, схожим с треугольником ГДЛ, а также отличается треу¬
гольником ГДЛ, то треугольник Г0А равен треугольнику, описанному АО, схожему
с треугольником ГДЛ. Поэтому, поскольку треугольник BZE подобен треугольнику
ГДА и треугольник HZ0 подобен треугольнику ГД0, они имеют то же самое отно¬
шение И треугольник BZE описан N0 между ординатой и центром, а треугольник
HZ0 описан ординатой BN,Te.Z0. И на основе доказанного прежде BZE отлича¬
ется от H0Z треугольником, описанным А0, схожим с треугольником ГДЛ. Следо¬
вательно, он также отличается от треугольника ГЛ0.
46
Если прямая, касающаяся параболы, пересекается с диаметром, то прямая, прове¬
денная через точку касания, параллельно диаметру, по направлению к сечению будет рас¬
секать прямые, проведенные в сечении параллельно касательной, на две равные части.
Пусть будет парабола, чьим диаметром будет АВА, пусть АГ касается сечения,
через Г пусть будет проведена 0ГМ, параллельная прямой АД, пусть на сечении бу¬
дет взята некая точка Л и пусть будет проведена Л^Е, параллельная прямой АГ. В
этом случае я утверждаю, что ЛИ равно N7.
Пусть будут проведены упорядоченно прямые В0, KZN и АМА. Поскольку на ос¬
новании доказанного в гипотезе 42 ЕМ равно ВМ и Е7Н равно ВК, то получается,
что НМ равно Л7НЛ. Пусть отбрасывается общее - пятиугольник МЛН/ГЧ; поэто¬
му К7№ равно ЛМ№ А К/ параллельна прямой ЛМ. Следовательно, равно ЛЬЕ
»I«.
188

Дословный перевод книги I
47
Если прямая, касающаяся гиперболы, или эллипса, или окружности круга, пересе¬
кается с диаметром, и через точку соприкосновения и центр проводится прямая к от¬
резкам сечения, то она будет рассекать на два равных отрезка прямые, проведенные на
сечении как параллельные касательной.
Пусть будет гипербола, или эллипс, или окружность круга, чьим диаметром будет
АВ, центром - Г; пусть будет проведена ДЕ, касающаяся сечения, пусть будет прове¬
дена и продолжена дальше ГЕ, пусть на сечении будет взята некая точка N, и через N
будет проведена параллельная 0NOH. В таком случае я утверждаю, что NO равно ОН.
Пусть будут проведены упорядоченно прямые ENZ, ВЛ и НМ К. Таким образом,
на основании доказанного в теореме 43 получается, что 0NZ равно ABZE, H0K рав¬
но ЛВКМ. По этой причине также NHKZ равно MKZE. Пусть отбрасывается как
общее пятиугольник ONZKM. Поэтому получается, что ОМН равно NEO; МН па¬
раллельна прямой NE; следовательно, NO равно ОН.
•’г
.•Л
48
Если прямая, касающаяся одной из противолежащих, пересекается с диаметром,
и через точку соприкосновения и центр проведенная дальше прямая рассекает дру¬
гое сечение, и если любая прямая проводится в другом сечении как параллельная
касательной, то она будет рассекаться на два равных отрезка данной прямой, про¬
долженной дальше.
Пусть буду! противолежащие, чьим диаметром будет АВ, центром — Г; пусть КЛ
касается сечения А, пусть будет проведена и продолжена дальше АГ, пусть на сече¬
нии В будет взята некая точка и пусть через N будет проведена NH, параллель¬
ная прямой ЛК. В этом случае я утверждаю, что NO равно ОН.
Пусть же через Е будет проведена ЕД, касающаяся сечения; тогда ЕД параллельна
прямой ЛК. По этой же причине она параллельна и прямой NN. Поэтому посколь¬
ку BNH является гиперболой с центром Г, ДЕ является касательной, проведена ГЕ,
а на сечении взята точка N и через нее проведена NN как параллельная прямой ДЕ,
то на основании доказанного прежде получается, что NO равно ОН.
та
та.
49
Если прямая, касающаяся параболы, пересекается с диаметром, и через /точку] ка¬
сания проводится прямая, параллельная диаметру, а от вершины проводится прямая,
параллельная проведенной /через точку касания/ ординате, и если выходит, что так
относится отрезок касательной, расположенный между прямой, параллельной орди¬
нате, и точкой касания к части прямой, параллельной диаметру, находящейся между
точкой касания и пересечением с прямой, как некая прямая относится к удвоенной ка¬
сательной, и если через сечение /параллельно касательной] проводится любая прямая
к прямой, проведенной через точку касания параллельно диаметру, то она в квадрате
будет равна прямоугольнику, ограниченному добавленной прямой и прямой, отведенной
к точке соприкосновения.
Пусть будет парабола, чьим диаметром будет МВГ, ГД — касательной; пусть че¬
рез Д будет проведена ZAN, параллельная прямой ВГ, пусть будет проведена упоря¬
та
189

Дословный перевод книги I
доченно прямая ZB, и пусть получится, что ЕД к AZ равно Н к 2ГД, пусть на сече¬
нии будет взята некая точка К, пусть через К будет проведена КАП, параллельная
прямой ГД. В таком случае я утверждаю, что КА в квадрате равно Н на ДА, т.е. если
ДА - диаметр, то прямая сторона есть Н.
Пусть же будут проведены упорядоченно прямые ДЕ и KNM. И поскольку ГД ка¬
сается сечения, а ДЕ проведена как ордината, то получается, что ГВ равно ВЕ. Одна¬
ко ВЕ равно 7Л\ поэтому также ГВ равно ZA. По этой причине также ЕГВ равно EZA.
Пусть будет присоединена общая фигура AEBNM. Тогда выходит, что ArMN равно
ZM равно КПМ. Отбрасывается как общее четырехугольник АП MN. По этой при¬
чине получается, что KAN равно АГ. Но угол ДЛП равен углу KAN. Поэтому KAN
равно 2ЛДГ. И поскольку ЕД к AZ равно Н к 2ГД и также ЕД к AZ равно КА к AN,
то также Н к 2ГД равно КА к AN. Однако КА к AN равно КА в квадрате к KAN, Н
к 2ГД равно Н на ДА к 2ГДА. Таким образом, КА в квадрате к KAN равно Н на ДА к
2ГАЛ. И при перестановке, однако, KAN равно 2ГДЛ. Следовательно, также КА в
квадрате равно Н на ДА.
50
Если прямая, касающаяся гиперболы, или эллипса, ши окружности круга, пересека¬
ется с диаметром, и через точку соприкосновения и центр проводится дальше прямая,
и от вершины проведенная прямая как параллельная проведенной упорядоченно прямой
пересекается с прямой, проведенной через точку соприкосновения и центр, и если полу¬
чается, что как отрезок касательной, расположенный между точкой соприкоснове¬
ния и проведенной упорядоченно прямой, относится к отрезку прямой, проведенной че¬
рез точку соприкосновения и центр, расположенному между точкой соприкосновения
и проведенной упорядоченно прямой, так относится некоторая прямая к удвоенной ка-
сательной, и если проводится любая прямая как параллельная касательной от сечения
к прямой, проведенной через точку соприкосновения и центр, то в квадрате она будет
равна площади прямоугольника, лежащего воне добавленной прямой и имеющего ши¬
риной прямую, отделенную от той при точке соприкосновения, на гиперболе она будет
превосходить прямоугольник, схожий с эйдосом, ограниченный удвоенной прямой, рас¬
положенной между центром и точкой соприкосновения, и добавленной прямой, а на эл¬
липс и на круге ей будет не хватать до той же самой фигуры.
Пусть будет гипербола, или эллипс, или окружность круга, чьим диаметром бу¬
дет АВ, центром - Г, а ДЕ будет касательной; пусть проведенная ГЕ будет продол¬
жена дальше в любую (из двух) частей, пусть будет установлено ГК равно ЕГ, и че¬
рез точку В пусть будет проведена упорядоченно прямая BZN, через Е же пусть бу¬
дет проведена Е0, перпендикулярная ЕГ, и пусть получится, что ZE к ЕН равно Е0
к 2ЕД; пусть будет проведена и продолжена дальше 0К, пусть будет взята на сече¬
нии некая точка А и через нее пусть будет проведена АМЕ, параллельная прямой ЕЛ
и APN, параллельная прямой ВН, и пусть будет проведена МП, параллельная пря¬
мой Е0 В этом случае я утверждаю, что AM в квадрате равно ЕМП.
Пусть через Г будет проведена ГЕО, параллельная прямой КП. И поскольку ЕГ
равно ГКиЕГ кКГ равно ЕЕ к Е0, то получается также ЕЕ равно Е0. А поскольку
ZE к ЕН равно 0Е к 2ЕД, и ЕЕ равно одной второй Е0, то получается ZE к ЕН рав-
»I«:
•I».
•л
•А
II»:
190

Дословный перевод книги I
но ЕЕ к ЕД Однако ¿Е к ЕН равно ЛМ к МР; поэтому ЛМ к МР равно ЕЕ к ЕД. А
поскольку мы уже доказали, что на гиперболе Р1МГ равно НВГ плюс ЛN
•1»Ж
•Ж
, т.е. PN Г
равно ГДЕ плюс АМН, а на эллипсе и круге Р1МГ равно НВГ деленное на Л\Е, т.е.
РГЧГ плюс АМЕ равно ГДЕ и при отбрасывании общего на гиперболе — треугольни¬
ка ЕГД и четырехугольника ^МЕ, а на эллипсе и круге — треугольника МЕГ по¬
лучается, что АМР равно МЕДЕ. Однако МЕ параллельна прямой ДЕ, и угол АМР
равен ЕМЕ; поэтому АМР равно ЕМ на (ЕД плюс МЕ). А поскольку МГ к ГЕ равно
МЕ к ЕД, МГ к ГЕ равно МО к ЕЕ, то МО к ЕЕ равно МЕ к ЕЛ. И в процессе скла¬
дывания МО плюс ЕЕ к ЕЕ равно МЕ плюс ЕД к ЕД; и перестановке МО плюс ЕЕ к
ЕМ плюс ЕД равно ЕЕ к ЕД. Однако МО плюс ЕЕ к МЕ плюс ДЕ равно (МО плюс
ЕЕ) на ЕМ к (МЕ плюс ЕД) на ЕМ, и ЕЕ к ЕД равно £Е к ЕН равно ЛМ к МР равно
ЛМ в квадрате к ЛМ на МР; поэтому (МО плюс ЕЕ) на МЕ к (МЕ плюс ДЕ) на ЕМ
равно ЛМ в квадрате к ЛМ на МР. И при перестановке (МО плюс ЕЕ) на МЕ к МЛ
в квадрате равно (МЕ плюс ЕД) на МЕ к АМР. Однако ЛМР равно МЕ на (МЕ плюс
ЕД); поэтому также ЛМ в квадрате равно ЕМ на (МО плюс ЕЕ). И ЕЕ равно Е0, Е0
равно ОП. Следовательно, ЛМ в квадрате равно ЕМП
/Л
51
Если прямая, касающаяся одного из противолежащих, пересекается с диаметром,
и через точку касания и центр дальше вплоть до другого сечения проводится прямая, и
от вершины проводится прямая, параллельная проведенной упорядоченно прямой и пе¬
ресекается с прямой, проведенной через точку касания и центр, и если получается, что
как отрезок касательной, расположенный между прямой [параллельной] проведенной
упорядоченно и точкой касания, относится к отрезку прямой, проведенной через точ¬
ку касания и центр, расположенному между точкой касания и прямой [параллельной]
проведенной упорядоченно, и так относится некоторая прямая к удвоенной касатель¬
ной, и любая прямая в другом сечении проводится к прямой, проведенной через точ¬
ку соприкосновения и центр параллельно касательной, то [она] в квадрате будет рав¬
на прямоугольнику, лежащему воне полученной добавленной прямой, имеющему шири¬
ной прямую, отведенную к точке соприкосновения, и превосходящему фигурой, схожей
с эйдосом, ограниченным прямой, расположенной между противолежащими, и добав¬
ленной прямой.	&
Пусть будут противолежащие,
•Ж
чьим диаметром будет АВ, цен¬
тром - Е, пусть будет проведена
ГД, касающаяся сечения В; пусть
будет проведена и продолжена
дальше ГЕ, пусть будет проведе¬
на упорядоченно прямая ВАН, и
пусть выйдет, что ЛГ к ГН равно
К к 2ГД. Уже очевидно, что пря¬
мые, проведенные на сечении ВГ
как параллельные прямой ГД к
продолженной дальше прямой
i
<
191

Дословный перевод книги I
ЕГ будут в квадрате равны прямоугольникам, лежащим возле прямой К, имеющими
шириной прямые, отведенные к точке соприкосновения, и превосходящими фигу¬
рой, схожей с эндосом Г2 на К. Ведь 2Г равно 2ГЕ. В этом случае я утверждаю, что
то же самое получается и на сечении ТА
Пусть через Т будет проведена М2, касающаяся сечения А2; пусть будет прове¬
дена упорядоченно прямая А21Ч. И поскольку ВГ и А2 сугь противолежащие, а ГД
и МТ касаются их, то ГД будет параллельна и равна М2. Также и ГЕ равно Е2; по¬
этому ЕД равно ЕМ А поскольку АГ к ГН равно К к 2ГД равно К к 2М2, то также
Н2 к 2N равно К к 2М2. Поскольку А2 является гиперболой с диаметром АВ, М2
- касательная, AN поведена как ордината, а Н2 к 2N равно К к 2М2. любые пря¬
мые проводятся отсечения к продолженной Е2 как параллельные прямой 2М, то
они в квадрате будут равны прямоугольнику, ограниченному прямой К и прямы¬
ми, отведенными к точке К, и превосходящему фигурой, схожей с эйдосом Г2 на К.
Из доказанного также очевидно, что на параболе все прямые, параллельные
первоначальному диаметру, являются диаметрами, а на гиперболе, эллипсе и проти¬
волежащих все диаметры проводятся через центр, вследствие чего на параболе, пря¬
мые, проведенные к любым диаметрам как параллельные касательным, в квадрате
будут равны прямоугольникам, лежащим возле той же самой прямой, на гиперболе
и противолежащих - площадям, лежащим возле той же самой прямой и превосхо¬
дящим ту же самую фигуру, на эллипсе - пространствам, лежащим возле гои же са¬
мой прямой и недостающим до той же самой фигуры, и все, ч го мы прежде доказа¬
ли, применимо к сечениям при применении изначальных диаметров, и то же самое
применимо при остальных д
явленных диаметрах.
Если при прямой, заданной на плоскости, определенной в одной точке, найти на пло¬
скости сечение конуса, называемое параболой, так что ее диаметром будет данная пря¬
мая, вершиной - предел прямой, и если любая прямая проводится от сечения к диаме¬
тру под заданным углом, то она будет равна в квадрате прямоугольнику, ограниченно¬
му прямой, отделенной от вершины сечения, и другой заданной прямой.
Пусть будет задана прямая АВ, имеющая предел в А. и пусть будет задана другая
прямая ГА по величине, и пусть заданный угол сначала будет прямым. Поэтому сле¬
дует найти на подлежащей плоскости параболу, так что ее диаметром будет АВ. вер¬
шиной - А, прямая сторона - ГД, и будут проведены ординаты под прямым углом,
т.е так. чтобы АВ являлась осью.
Пусть АВ будет проведена дальше до Е, и пусть будет принято ГН равно одной
четвертой ГА, пусть ЕА больше ГН, пусть же 0 будет взята как пропорциональ¬
ная середина прямых ГА и ЕА. Таким образом, ГА к ЕА равно 0 в квадрате к ЕА в
квадрате. Однако ГА меньше 4ЕА; поэтому также 0 в квадрате меньше 4ЕА в ква¬
драте; тогда 0 меньше 2ЕА; поэтому ЕА плюс ЕА больше 0. Поэтому может полу¬
читься, что из 0 и двух ЕА образуется треугольник. Пусть он на ЕА образует тре¬
угольник ЕА2, перпендикулярный подлежащей плоскости, так что ЕА равно А2
и 0 равно 2Е, и пусть будет проведена АК, параллельная прямой 2Е, и пусть бу¬
дет проведена 2К параллельная прямой ЕА. и пусть будет образован конус, вер¬
192

Дословный перевод книги I
шиной которого будет точка 7, основанием же — круг, описанный вокруг диаметра
КА, перпендикулярный плоскости А7К Этот конус будет прямым, ведь А7 рав¬
но Пусть же конус рассекается плоскостью, параллельной кругу КА, и пусть
он сделает сечением круг ММЕ. т.е. перпендикулярный плоскости М71Ч, и пусть
общим сечением круга М№ и треугольника MZN будет М1М; тогда оно являет¬
ся диаметром круга. И пусть общим сечением подлежащей плоскости и круга бу¬
дет НА. И поскольку круг М№ перпендикулярен подлежащей плоскости и так¬
же треугольнику М71^*, то их общее сечение ЕЛ перпендикулярно треугольнику
МгЬ!, т.е. КгЛ; поэтому оно также перпендикулярно всем прямым, касающимся
его, и прямым, расположенным на треугольнике. Таким образом, оно перпенди¬
кулярно любой из прямых и АВ. И поскольку конус, чьим основанием являет¬
ся круг М^, вершиной - точка 7, и он рассечен плоскостью, перпендикулярной
треугольнику MZN и которая делает сечением круг М№Е, и к тому же он рассечен
другой плоскостью, а именно подлежащей, секущей основание конуса по прямой
ЕЛ, перпендикулярной МТЧ, которая является общим сечением для круга МК’Е и
треугольника М7К1, общее же сечение АВ подлежащей плоскости и треугольни¬
ка M7N параллельно стороне 7КМ конуса, то возникшее на подлежащей плоско¬
сти сечение конуса есть парабола, диаметром которой является АВ, и ординаты к
АВ будут проводиться под прямым углом; ведь они параллельны прямой ЕЛ, пер¬
пендикулярной АВ. И поскольку ГД к 0 равно 0 к ЕА и ЕА равно Аг равно 7К,
и 0 равно Е7 равно АК, то ГД к АК равно АК к К7. Поэтому также ГД к А7 рав¬
но АК в квадрате к А7 в квадрате равно АК в квадрате к А7К. Следовательно, ГД
есть прямая сторона сечения, ведь это доказано в теореме 11
53
При тех же самых предпосылках пусть заданный угол не будет прямым, и пусть
ему будет равен угол 0АЕ, пусть А0 равно одной второй ГД, и пусть от 0 будет про¬
ведена 0Е, перпендикулярная АЕ, через Е пусть будет проведена ЕЛ, параллельная
прямой В0, а от А к ЕЛ пусть будет проведена перпендикулярно АЛ. и пусть ЕЛ в
К рассекается на два равные отрезка, и от К к ЕЛ пусть будет проведена перпен¬
дикулярно КМ и пусть она будет продолжена дальше к 7 и Н; и пусть будет ЛКМ
равно АЛ в квадрате. Если же даны две прямые ЛК и КМ, из которых КЛ дана по
положению как определенная при К, а КМ — по величине, то пусть под прямым
углом будет описана парабола, чьим диаметром будет КЛ, вершиной - К, а пря¬
мая сторона — КМ, как было доказано выше; и пусть она проходит через А, по¬
скольку ЛКМ равно ЛМ в квадрате, и пусть она касается сечения ЕА, так как ЕК
равно КЛ. И 0А параллельна прямой ЕКЛ; поэтому 0АВ есть диаметр сечения, и
прямые, проведенные от сечения к нему как параллельные прямой АЕ, будут рас¬
секаться АВ на два равных отрезка. А поскольку угол АЕ0 равен углу' АН7, а угол,
расположенный при А, есть общий, то А0Е подобен АН7. Поэтому 0А к ЕА рав¬
но 7А к АН. Таким образом, 2А0 к 2АЕ равно 7А к АН. Однако ГД равно 20А; тог¬
да 7А к АН равно ГД к 2АЕ. Следовательно, на основании доказанного в теореме
49 ГД есть прямая сторона.
* Круг МИ- перпендикулярен треугольнику М2Гх1, а уже тот - подлежащей плоскости.
193

Дословный перевод книги I
•1C
•I»
54
Если даны две ограниченные прямые, перпендикулярные друг другу и при одной из них,
продолженной дальше, найти сечение конуса на продолженной прямой, которое назы¬
вается гиперболой, расположенной на плоскости прямых, так что прямая, проведенная
дальше будет диаметром сечения, вершиной же - точка, расположенная на угле, и если
любая прямая проводится от сечения к диаметру, создавая угол, равный заданному, то
в квадрате она будет равна прямоугольнику, лежащему воне другой прямой, имеющему
шириной прямую, отделенную упорядоченной прямой [ординатой] и превосходящему фи¬
гурой, подобной и подобно расположенной эйдосу, ограниченному изначальными прямыми.
Пусть будут заданы две прямые АВ и ВГ, перпендикулярные между собой; пусть
АВ будет продолжена дальше до А. Поэтому нужно на плоскости АВ Г найти гипер¬
болу, чьим диаметром будет АВА, вершиной - В, а прямая сторона - ВГ; и прямые,
проведенные от сечения к ВА под заданным углом в квадрате будут равны площадям,
лежашим при прямой ВГ, имеющих шириной прямые, отделенные к В, превосходя¬
щих фигурой, схожей и схожим образом расположенной с прямоугольником АВГ.
Поэтому прежде всего пусть заданный угол будет прямым, и пусть от АВ будет
проведена плоскость, перпендикулярная подлежащей плоскости, и пусть на ней во¬
круг АВ будет описан круг AEBZ, так что отрезок диаметра круга, расположенный
на отрезке АЕВ, к отрезку диаметра, расположенного на AZB, не имеет отношения,
большего, чем АВ к ВГ, и пусть АЕВ в точке Е будет рассекаться на два равных от¬
резка. Пусть от Е к АВ будет проведена перпендикулярная ЕК и пусть она будет про¬
должена до Л, тогда ЕЛ является диаметром. Если же АВ к ВГ равно ЕК к КА, мы
пользуемся точкой Л; если же это не так, то пусть АВ к ВГ равно ЕК к КМ меньше
КА, и пусть через М будет проведена MZ, параллельная прямой АВ, и пусть будут
проведены AZ, EZ и ZB; и через В пусть будет проведена ВЕ, параллельная прямой
ZE. Поэтому поскольку угол AZE равен углу EZB, а угол AZE равен углу АЕВ, угол
EZB равен углу EBZ, то также угол EBZ равен углу ZEB; поэтому также ZB равно
ZE. Пусть будет образован конус, вершиной которого пусть будет точка Z, основа¬
нием же - круг, описанный вокруг диаметра ВЕ, перпендикулярный треугольнику
BZE. Этот конус будет прямым, ведь ZB равно ZE. Поэтому пусть будут продолже¬
ны дазьше BZ. EZ и MZ, и пусть конус рассекается плоскостью, параллельной кругу'
ВЕ; тогда сечением будет круг. Пусть (это) будет Н П Р, так что диаметром круга будет
Н0. Обшим же сечением круга НО и подлежащей плоскости пусть будет П АР; тог¬
да ПАР будет перпендикулярна любому из НО и АВ; ведь любой круг ЕВ и ОН пер¬
пендикулярен треугольнику ZHO, и подлежащая плоскость перпендикулярна ZHO;
поэтому их общее сечение ПАР перпендикулярно ZHO, таким образом, также оно
образует при всех прямых, касающихся его и расположенных на той же самой пло¬
скости прямые углы. А поскольку конус, чье основание есть круг НО, вершина - Z,
рассечен плоскостью, перпендикулярной треугольнику^НО, а также рассекается
другой гы ос костью, а именно подлежащей по прямой ПАР, перпендикулярной Н АО,
и общее сечение подлежащей плоскости и треугольника HZO есть АВ, продолжен¬
ное дальше до В, пересекается с HZ в А, на основании доказанного прежде сечение
ПВР будет гиперболой, вершиной которой является точка В, а ординаты к ВЛ, бу¬
дут проводиться под прямым углом; ведь они будут параллельны прямой П АР. И по-
MI».
194

Дословный перевод книги I
скольку АВ к ВГ равно ЕК к КМ, и ЕК к КМ равно EN к NZ равно ENZ к NZ в ква¬
драте, то АВ к ВГ равно ENZ к NZ в квадрате. А ENZ равно AN В. Поэтому АВ к ГВ
равно AN В к NZ в квадрате. Но ANB к NZ в квадрате равно AN к NZ на BN к NZ, и
AN к NZ равно АА к АН равно ZO к ON, и BN к NZ равно ZO к О0 Поэтому АВ к
В Г равно ZO к ОН на ZO к О0 равно ZO в квадрате к НО0. Таким образом, АВ к ВГ
равно ZO в квадрате к НО0. И ZO параллельна прямой АА. Следовательно, АВ есть
поперечная сторона, а ВГ — прямая сторона, ведь это было доказано в теореме 12.
55
Пусть же заданный угол не будет прямым, и пусть заданными прямыми будут
АВ и АГ, и пусть заданный угол будет равен углу ВА0. Нужно описать гиперболу,
так что ее диаметром будет АВ, прямой стороной — АГ, и ординаты будут проводит¬
ся на угле 0АВ.
Пусть АВ рассекается на два равных отрезка в А, и пусть на АА будет описан по¬
лукруг Агд. Пусть к полукругу будет проведена прямая гн, параллельная прямой
А0, образующая ZH в квадрате к АН А равное АГ к АВ, и пусть будет проведена Z0A
и продолжена дальше до А. Пусть АЛ будет серединой для гЛ0, и пусть будет, что АК
равно ЛА, лгм равно Аг в квадрате. Пусть будет проведена КМ, и пусть через Л бу¬
дет проведена Л^ перпендикулярная Кг, и продолжена дальше до Е. При заданных
двух прямых КЛ и Л^ определенных как перпендикулярные друг другу; пусть бу¬
дет описана гипербола, поперечной стороной которой будет КЛ. прямой стороной
— ЛИ, а прямые, проведенные от сечения к диаметру, будут проводиться на прямом
угле, имеющие шириной прямые, отделенные к Л, превосходящей фигурой, схожей
с прямоугольником КЛ№ Сечение же будет проходить через А, поскольку Аг в ква¬
драте равно АгМ. И А0 будет касаться его, ведь гд© равно АЛ в квадрате. Поэтому
АВ есть диаметр сечения. А поскольку ГА к 2АА равно ГА к АВ равно гн в квадрате
к АН А, и ГА к 2АА равно ГА к 2А0 в квадрате на 2А0 к 2АА, и 2А0 к 2АА равно 0А к
АА равно гН к НА, то ГА к АВ равно ГА к 2А0 на гн к НА Однако также гн в ква¬
драте к АНА равно гн к НА на гн к гА. Поэтому ГА к 2А0 на гн к НА равно гн к
НА на гн к НА. Отбрасывается общее отношение гн к НА/ Поэтому ГА к 2А0 рав¬
но гн к НА. Но гн к НА равно ОА к АЕ. Таким образом, ГА к 2А0 равно А к АН.
Если это так, то АГ есть прямая сторона, ведь это доказано в теореме 50.
•Ж
•Ж
•ж
•ж
»ж
•ж
йй
I
/Л
56
Если даны две прямые, перпендикулярные друг другу, и найти описанное вокруг од¬
ной из них, как диаметра, сечение конуса, называемое эллипсом, расположенное на той
же самой плоскости прямых, так что его вершиной будет точка, находящаяся на пря¬
мом угле, то прямые, проведенные от сечения к диаметру на заданном угле, в квадрате
будут равны прямоугольникам, лежащим возле другой прямой, имеющим шириной пря¬
мую, отделенную от вершины сечения, не достающим фигурой, схожей и схожим обра¬
зом расположенной с эйдосом, ограниченным заданными прямыми.
Пусть заданными прямыми будут АВ и АГ, перпендикулярные между собой, из
которых больше АВ. Поэтому нужно на подлежащей плоскости описать эллипс, так
что его диаметром будет АВ, вершиной - А, прямой стороной — АГ, а прямые, про¬
•ж
1Ж
195

Дословный перевод книги I
веденные упорядоченно от сечения к АВ, будут проведены на заданном угле и в ква¬
драте будут равны площадям, лежащим возле прямой АГ, имеющие шириной пря¬
мые, отведенные кА. недостающим до фигуры, схожей и схожим образом распо¬
ложенной с прямоугольником ВАГ [ВАхАГ].
Пусть прежде всего заданный угол будет прямым, и пусть от АВ проводится пло¬
скость, перпендикулярная подлежащей, и пусть на ней и на АВ будет описан отре¬
зок круга AAB. серединой которого будет А; пусть будут проведены АА и АВ. и пусть
будет АЗ равно АГ. пусть через Е будет проведена ЕО, параллельная прямой АВ, а
через О - OZ, параллельная прямой АВ, пусть будет проведена AZ и пусть она пе¬
ресечется с продолженной дальше АВ в Е. Поэтому получается АВ к АГ равно ВА
к АЕ равно АА к АО равно AZ к EZ Пусть будут проведены и продолжены даль¬
ше AZh BZ, пусть на ZB будет взята некая точка Н, пусть через нее будет проведе¬
на НА. параллельная прямой ДЕ, и пусть она пересечется с проведенной дальше АВ
в К; пусть ZO будет проведена дальше и пересечется с N К в Л. А поскольку окруж¬
ность [дуга] АД равна окружности [дуге] АВ, то угол АВА равен углу AZB. И посколь¬
ку угол EZA равен углу ZAA+ZAA, а угол ZAA равен углу ZBA, угол ZAA равен углу
ZBA, то угол EZA равен углу АВА равен углу BZA. Однако АЕ параллельна АН. Поэ¬
тому угол EZA равен углу ZНО. угол AZB равен углу Z0H, поэтому также угол ZH0
равен углу Z0H и ZH равно Z0.
Пусть будет вокруг 0Н описан круг H0N, перпендикулярный треугольнику 0HZ,
и пусть будет образован, чьим основанием будет круг N0H, а вершиной - точка Z;
конус будет прямым, потому что HZ равно Z0. И поскольку круг H0N перпендику¬
лярен плоскости 0HZ, и так как подлежащая плоскость перпендикулярна плоско¬
сти H0Z, то их общее сечение также будет перпендикулярно плоскости H0Z По¬
этому пусть КМ будет их общим сечением. Тогда КМ является перпендикулярной
каждой из АК и КН И поскольку конус, чье основание есть круг H0N, а вершина
- точка Z, рассекается плоскостью через ось и делает сечением треугольник H0Z, а
также рассекается другой плоскостью прямых АК и КМ, которая есть подлежащая
плоскость, по прямой КМ, перпендикулярной НК, и данная плоскость пересека¬
ется со сторонами конуса ZH и Z0, то возникшее сечение есть эллипс, чьим диа¬
метром является АВ. а проводимые ординаты проводятся на прямом угле; ведь они
параллельны прямой КМ. И поскольку АЕ к EZ равно AEZ к EZ в квадрате равно
ВЕ на ЕА к EZ в квадрате, и ВЕ на ЕА к EZ в квадрате равно ВЕ к EZ на АЕ к EZ, а
ВЕ к EZ равно ВК к К0, АЕ к EZ равно АК к КН равно ZA к АН, то ВА к АГ равно
ZA к АН на ZA к Л0 И ZA к АН на ZA к А0 равно ZA в квадрате к НА на Л0. Поэ¬
тому ВА к АГ равно ZA в квадрате к HA0. Если это так, то АГ есть прямая сторона
сечения, как доказано в теореме 13.
•1»
57
При тех же самых предпосылках пусть АВ меньше АГ. и пусть следует, что вокруг
диаметра АВ будет описан эллипс. так что АГ будет прямой стороной.
Пусть АВ рассекается на два равных отрезка в А, и пусть от А к АВ будет прове¬
дена перпендикулярно Е^, и пусть гЕ в квадрате равно ВАГ, так что ТА равно АЕ,
и пусть будет проведена ZH, параллельная прямой АВ, и пусть получится АГ к АВ
196

Дословный перевод книги I
равно ЕХ к ХН; поэтому ЕХ больше ХН. А поскольку ГАВ равно ЕХ в квадрате, то
ГА к АВ равно ХЕ в квадрате к АВ в квадрате равно АХ в квадрате к ДА в квадрате.
Однако ГА к АВ равно ЕХ к ХН, Поэтому также ЕХ к ХН равно АХ в квадрате к ДА
в квадрате. Но ХА в квадрате равно ХА на ДЕ; тогда ЕХ к ХН равно ЕД/ к АД в ква¬
драте. А при двух прямых, определенных как перпендикулярные друг другу, большая
из которых ЕХ, пусть будет описан эллипс, чьим диаметром будет ЕХ, а прямой сто¬
роной — ХН; поэтому сечение будет проходить через А, потому что ХАЕ к ДА в ква¬
драте равно ЕХ к ХН. И АД равно ДВ; поэтому оно также проходит через В. Таким
образом, вокруг АВ описан эллипс. А поскольку ГА к АВ равно ХА в квадрате к ДА
в квадрате, и ДА в квадрате равно АДВ, то ГА к АВ равно ХА в квадрате к АДВ. Сле¬
довательно, АГ есть прямая сторона.
58
Пусть заданный угол не будет прямым, и пусть ему будет равен угол ВАД, и пусть
АВ в Е рассекается на два равных отрезка, и пусть на АЕ будет описан полукруг А/Е,
и пусть на нем будет проведена гн, параллельная прямой АД, ХН, пусть образует
7Н в квадрате к АНЕ равно ГА к АВ, и пусть будут проведены и продолжены даль¬
ше А/ и Е7, и пусть между ДЕ/ серединой будет Е0, и пусть устанавливается, что
ЕК равно Е0, и пусть 0/Л равно АХ в квадрате, и пусть будет проведена КА, а от 0
к прямой &Х пусть будет проведена перпендикулярно 0МЕ, которая будет парал¬
лельна прямой А/Л; ведь угол, находящийся при X является прямым. И при задан¬
ных двух прямых К0 и 0М, определенных как перпендикулярные друг другу, пусть
будет описан эллипс, так что диаметром поперечным будет К0, а прямой стороной
эйдоса будет 0М, и ординаты к 0К, будут проводиться на прямом угле. Таким обра¬
зом, сечение будет проходить через А, потому что ХА в квадрате равно 0/Л. И по¬
скольку 0Е равно ЕК, АЕ равно ЕВ, то сечение также будет проходить через В, Е
будет центром, а диаметром — АВ. И ДА будет касаться сечения, так как ДЕ/ рав¬
но Е0 в квадрате. А поскольку ГА к АВ равно ХН в квадрате к АН Е, а ГА к АВ равно
ГА к 2ДА на 2АД к АВ равно ГА к 2ЛА на ДА к АЕ, и ХН в квадрате к АНЕ равно ХН
к Н Е на ХН к НА, то ГА к 2АД на ДА к АЕ равно /Н к Н Е на /Н к НА. Однако ДА к
АЕ равно ХН к НЕ. Изымая общее отношение, получаем ГА к 2АД равно ХН к НА
равно ЕА к АЬТ Если это так, то АГ есть прямая сторона эйдоса.
ЙЕ
ЙЕ
59
Если для двух данных прямых, перпендикулярных друг другу, найти противолежащие,
такие, что их диаметром будет одна из двух прямых, вершиной — пределы прямой, то и
прямые, проведенные в одном из двух сечений на заданном угле [ординаты], в квадрате
будут равны площадям, лежащим возле другой прямой и превосходящим фигурой, схо¬
жей с прямоугольником, ограниченным заданными прямыми.
Пусть заданными двумя прямыми, определенными как перпендикулярные друг
другу, будут ВЕ и В0, а заданным углом будет Н. Поэтому нужно описать противо¬
лежащие вокруг из одной из прямых ВЕ и В0, так что ординаты будут проводить¬
ся на угле Н.
197

Дословный перевод книги I
И пусть при заданных двух прямых ВЕ и В0 будет описана гипербола, так что
диаметром поперечным будет ВЕ, прямой стороной эйдоса — 0В, и пусть прямые
к ВЕ, продолженной дальше, будут проведены как ординаты на угле Н. Ведь каким
образом это может получиться, было показано прежде. Поэтому пусть через Е к ВЕ
будет проведена перпендикулярная ЕК, которая равна прямой В0, и тем же самым
образом будет описана другая гипербола AEZ, так что диаметром будет ВЕ, прямой
стороной эйдоса - ЕК, и ординаты, проведенные отсечения, будут проводиться на
угле, который расположен на соседнем угле Н. Поэтому очевидно, что сечения В и
Есуть противолежащие и они имеют одинаковый диаметр, и прямые стороны |latus
rectumj у них равны.
»з:
й®
60
Если при двух заданных прямых, рассекающих друг друга на два равных отрезка,
описать вокруг одной из них противолежащие сечения, то их сопряженные диаметры
будут заданными прямыми, а диаметр двух противолежащих в квадрате будет равен
эйдосу других противолежащих и схожим образом диаметр других противолежащих в
квадрате будет равен эйдосу других противолежащих.
Пусть заданными двумя прямыми, рассекающими друг друга на два равных от¬
резка, будутЛГ и ДЕ Нужно поэтому описать противолежащие вокруг одного из ди¬
аметров, так что АГ и ЛЕ будут на них сопряжены, а ЛЕ в квадрате будет равна эй¬
досу противолежащих, описанных
жащих, описанных вокруг ДЕ.
Пусть будет АГА равно ДЕ в квадрате, и ЛГ будет перпендикулярна ГА. И при за¬
данных двух прямых АГ и ГЛ, перпендикулярных между собой, пусть будут описа¬
ны противолежащие ТАН и 0ГК, так что поперечным диаметром будет ГА. прямой
стороной - ГЛ, и ординаты, проведенные от сечения к ГА, будут проводиться на за¬
данном угле. Поэтому ДЕ будет другим диаметром противолежащих; ведь он име¬
ет серединное отношение между сторонами эйдоса и, будучи параллельным упоря¬
доченной прямой, в В рассекается на два равных отрезка. И пусть поэтому будет ДЕ
на М равно АГ в квадрате, и ДТ пусть будет перпендикулярна ДЕ. И при заданных
двух прямых ДЕ и Л/, расположенных как перпендикулярные друг другу, пусть бу¬
дут описаны противолежащие MЛN и ЕЕО, так что поперечным диаметром будет
ДЕпрямой стороной эйдоса - М, и прямые, проведенные как ординаты к ДЕ, будут
проводиться на заданном угле; поэтому также АГ будет другим диаметром сечений
МДЫ и ЕЕО. Следовательно, АГ рассекает на два равных отрезка прямые, распо¬
ложенные как параллельные прямой ДЕ между сечениями ТАН и 0ГК, а ДЕ - пря¬
мые, параллельные прямой АГ; а это и нужно было получить.
Такие сечения пусть называются сопряженными.
•д
•3
•з
»3
/Л
»3
in
198

АПОЛЛОНИИ ПЕРГСКИИ
КОНИЧЕСКИЕ
СЕЧЕНИЯ
КНИГА II
ПИСЬМО К Е
I
ЕМУ
Аполлоний приветствует Евдема.
Если ты здравствуешь, то это весьма хорошо. Я также вполне здравствую. Я ото¬
слал к тебе сына Аполлония, чтобы он передал тебе написанную мной вторую кни¬
гу «Конических сечений*. И посему прочти ее внимательно и поделись ей с теми,
кто достоин подобных предметов. И поделись ей также с Филонидом, которого я
рекомендовал тебе в Эфесе, если он будет поблизости от Пергама. Заботься о сво¬
ем здоровье. Будь здоров.
ПРЕДЛОЖЕНИЯ
Предложение 1. Если прямые, проведенные из центра гиперболы, отсекают отрез¬
ки касательной, квадраты которых равны четверти площади эйдоса, то они не имеют с
кривой общих точек (асимптоты)
Если на прямой, касающейся гиперболы, отложить в обе стороны от точки ка¬
сания отрезки, квадраты которых равны четвертой части площади эйдоса* для дан¬
ной точки, то прямые, проведенные из центра сечения через концы этих отрезков, не
имеют общих точек с сечением.
Пусть дана гипербола с диаметром АВ, центром Г, latus rectum — BZ, и пусть
на касательной отложены от точки касания отрезки BD и BE такие, что**
ВД2 =ВЕ2 =-ABBZ.
4
* Напомним, что эйдос - это прямоугольник, стороны которого есть latus rectum и latus
lb2 ,U
transversum (см. I, Определения II, сноска 2). Его площадь равна	2а = 4Ь .
а
** О том, как построить отрезок, квадрат которого равен площади заданного прямоугольни¬
ка, см комментарий к (I, 11).
199

Книга II
АВ А0 • 0В
В этом случае я утверждаю,
что прямые ГА и ГЕ, будучи про¬
должены, не пересекаются с се¬
чением.
Предположим, что ГА пере¬
секается с сечением в Н, и по¬
строена ордината к диаметру
Н0, которая параллельна пря¬
мой АЕ.
Тогда поскольку
Д«=_Д5^игв’ = ’ав2,
вг АВВ7	4
а согласно условию
ВД2 =^АВ-Вг,то
4
АВ _ ГВ2 _ Г02
вг ~ дв2 ~ ©н2
С другой стороны (I, 21),
— =	, поэтому		 =

вг ен2	эн2 ©н
Следовательно. А0 0В = Г©2, а это абсурдно (Евклид 11,6). Следовательно. ГЛ
не пересекается с сечением. Схожим образом мы докажем, что и ГЕ не пересекает¬
ся. Следовательно. ГД и ГЕ суть асимптоты.
Предложение 2. Нельзя провести другие асимптоты под меньшим углом
ем, что никакая асим-
асимптота существует
При тех же самых
предпосылках утверж-
птота не пересекает
угол, ограниченный пря¬
мыми ГД и ГЕ.
Допустим, что такая
прямую, параллельную
ГД. которая пересечет
указанную асимптоту в
точке 0.
Отложим АН = В0
и проведем и продол¬
жим отрезок Н0 Пусть
К. Л, Nh М. Поскольку
он пройдет через точки
а

Предложения
В0 = ДН, то равны и параллельны ДВ и Н0. Так как диаметр АВ разбивается точкой
Г на два равных отрезка, и он продолжен на отрезок ВЛ, то (Евклид II, 6) АЛ ВЛ +
ГВ = ГЛ2.
Так как отрезок НМ параллелен ДЕ, то НЛ=ЛМ.
А поскольку Н0 = ДВ, то НК > ДВ.
Однако и КМ > ВЕ, поскольку ЛМ > ВЕ. Следовательно НК КМ > ДВ ВЕ, то есть
НК КМ> ДВ2.
2 ’
_	,, ,,.АВ АЛ-ЛВ ... ,, ЛВ ГВ2	ГВ2 ГА2
Тогда поскольку (I, 21)	=	— и <11, 1)	= —г, а также 	- =

вг лк2	в/ дв2	дв2 лн
гл2 ал■лв
ТО	г =	5— .
АН2 ЛК2
А так как ГЛ2 относится к АН2, как и уменьшенное АЛ ВА относится к умень-
ГВ* ГЛ2 р™2
шейному ЛК2, то, следовательно*, ——— =

, , откуда ВД2 = НК КМ ,
НК-КМ АН' ВД2
что абсурдно, ведь мы доказали, что НК КМ > ДВ2.
Следовательно, Г0 не есть асимптота сечения.
Предложение 3. Касательная пересекается с асимптотами и делится точкой касания
пополам, а квадраты отрезков равны четверти площади эйдоса
Если прямая касается гипер¬
болы, то она пересекается с обе¬
ими асимптотами и делится точ¬
кой касания на два равных отрез¬
ка, причем квадрат каждого из
них равен четверти площади эй¬
доса, построенного на диаметре,
проходящем через точку касания.
Пусть дана гипербола с цен¬
тром Е, асимптотами Е/ и ЕН, а
прямая К0 касается ее в точке В.
¿11
* Имеется в виду следующее: из последнего выражения следует, что
ГЛ2-АЛ-ЛВ лн2-лк
Вычтем из девой и правой части единицу:	=	—
АЛ-ЛВ	ЛК
Учитывая,что ЛН2-ЛК2 = (ЛН-ЛК)(ЛН + ЛК) = НК-КМ, подучим
4	АЛ-ЛВ
п	ГВ2 АЛ ЛВ ГЛ2 ГВ2
Отсюда	=	;— =	- = —г
НК КМ ЛК2 ЛН‘ ВД2
201

Книга II
Я утверждаю, что эта прямая, продолженная в обе стороны, пересечется с асимптота¬
ми Е2и ЕН.
Допустим, она не пересечется. Продолжим ЕВ до точки А так, чтобы ЕД = ЕВ,
тогда ВЛ - будет диаметром. Отложим на касательной отрезки В® и ВК, квадраты
которых будут равны четвертой части площади эйдоса при ВЛ, и пусть будут про¬
ведены Е® и ЕК. Они будут асимптотами (И, 1), что абсурдно (11, 2), ведь мы уже
предположили, что Е7 и ЕН являются асимптотами. Следовательно, К®, проведен¬
ная дальше, пересечется с асимптотамиЕ7 и ЕН.
Далее, я утверждаю, что Вг2 и ВН- равны четвертой части площади эйдоса при ВД.
Пусть, они не равны ей, а равны квадраты каких-то отрезков В® и ВК. Тогда Е®
и ЕК суть асимптоты (II, 1), что абсурдно (11, 2). Следовательно, В72 и ВН2 равны
четвертой части площади эйдоса при ВД.
Предложение 4. По¬
строение гиперболы,
проходящей через дан¬
ную точку при заданных
асимптотах
/Л
По двум прямым, обра¬
зующим данный угол, и ле¬
жащей внутри него точ¬
ке построить проходящую
через нее гиперболу, для ко¬
торой эти прямые суть
асимптоты.
Пусть дан угол ВАГ и
внутри него точка Д, че¬
рез которую нужно про¬
вести гиперболу с асим¬
птотами АВ и АГ.
мл
Проведем отрезок ДА
и продолжим его до точки Е так, чтобы ЕА = АД.
Проведем теперь отрезок \Т, параллельно прямой АВ и отложим отрезок ТГ -
ТА, а также проведем ГД и продолжим до пересечения с АВ.
Пусть имеется отрезок Н, определенный равенством (11,1)* ГВ2 = ЕД- Н, и пусть
через точку А проведена гипербола с диаметром ЕА, у которой каждая ордината в
квадрате будет равна плошали прямоугольника, стороны которого — отрезок Н и аб¬
сцисса, сложенной с площадью прямоугольника подобного прямоугольнику, огра¬
ниченному отрезками ЕЛ и Н (I. 54 и 55).
Тогда поскольку А7 параллельна прямой ВА и ГТ = ТА, то ГД = ДВ.
Поэтому ГВ2 = 4ГД2,
♦А
»!•
»А
•ж
не
‘ О том, как его построить см. комментарий к (I, 60)

Предложения
Но также и ГВ2 = ЕД- Н , а потому ГД2 = ДВ2 = 'А ЕД- Н.
Следовательно, АВ и АГ суть асимптоты описанной гиперболы (II, 1).
Предложение 5. Прямая, касающаяся параболы или гиперболы в точке пересечения
кривой и диаметра, параллельна ор¬
динате к этому диаметру
Если диаметр параболы или ги¬
перболы разбивает лежащую вну¬
три кривой секущую на две рав¬
ные части, то прямая, касающа¬
яся сечения в точке, совпадающейд
с концом диаметра, будет ей
параллельна*.
Пусть дана парабола или ги¬
пербола с диаметром ДЕ и отре¬
зок ИВН касается сечения, кото- Ц
рое также пересечено с отрезком
АЕГ, разбитым диаметром сече¬
ния на два равных отрезка так,
что АЕ = ЕГ.
В этом случае я утверждаю, что
АГ и ИН параллельны.
Предположим, что это не так.
и проведем через точку Г прямую Г0, параллельную прямой ИН, и проведем отре¬
зок 0А. Поскольку АВГ есть парабола или гипербола с диаметром ДЕ и касатель¬
ной ИН, параллельной Г0, то (1, 46 и 47) ГК = К0. Однако ГЕ = ГА. Поэтому А0 и
КЕ будут параллельны, что невозможно, ведь А0, продолженная дальше, пересека¬
ется с ВД (1, 22).
Предложение 6. То же для эл¬
липса
Если диаметр эллипса разби¬
вает секущую, не проходящую че¬
рез центр, на два равных отрезка,
то прямая, касающаяся сечения на
пределе диаметра, будет парал¬
лельна секущей.
6. Рис. 1
* В (1.17 и 32) было доказано, что прямая, параллельная ординате, есть касательная и что она
единственная, следовательно касательная параллельна ординате В (1,44) Аполлоний уже исполь¬
зовал это положение как доказанное
203

Книга II
Пусть дан эллипс с диаметром АВ, разбивающим прямую ГД, не проходящую че¬
рез центр, в точке Е на два равных отрезка ЛЕ = ЕГ.
В этом случае я утверждаю, что прямая, касающаяся сечения в точке А, парал¬
лельна прямой ГЛ.
Допустим, что это не так. Проведем прямую Л7, параллельную касательной. Тогда
отрезок лг должен разбиваться диаметром АВ на две равные части (1,47) АН = 7Н.
Однако ЛЕ = ЕГ. следовательно, Гг и НЕ являются параллельными, что абсур¬
дно Ибо если Н есть центр сечения АВ, то Г7 пересечется с АВ (1, 23), а если нет. то
предположим, что центром будет точка К, и проведем отрезок ЛК. продолженный
до точки О, и отрезок ГО Тогда ЛК = К0 и ЛЕ = ЕГ.
Следовательно. ГО параллельна прямой АВ. Но ей также параллельна Г7, что аб¬
сурдно Следовательно, прямая, касающаяся сечения в точке А, параллельна пря¬
мой ГА
Предложение 7. Прямая, проходящая
через точку касания и середину секу шей,
параллельной касательной, есть диаметр
Есзи прямая касается конического се¬
чения. а секущая ей параиеаьна, то пря¬
га
мая. проходящая через точку сопри кос-
новения и центр секущей, есть диаметр.
Пусть дано коническое сечение (АВГ), касательная 7ВН, параллельная ей секу¬
щая АГ. и пусть будет проведена прямая ВЕ. проходящая через точку соприкосно¬
вения и центр отрезка секущей. В этом случае я утверждаю, что отрезок ВЕ есть ди¬
аметр сечения
Допустим, что это не так. и диаметром
сечения является В0
Тогда А0 = 0Г. что абсурдно, ибо АЕ
= АГ.
Следовательно. В0 не есть диаметр се¬
чения. Тем же самым способом мы дока¬
жем, что никакая другая прямая, кроме
ВЕ, не будет диаметром
Предложение 8. Если прямая пересека¬
ется с гиперболой в двух точках, то, отрез¬
ки, отсекаемые асимптотами, будут равны
Если прямая пересекается с гиперболой
в двух точках, то она пересечется и с асим¬
204

Предложения
птотами, а отрезки, заключенные между точками пересечения и асимптотами, бу¬
дут равны.
Пусть дана гипербола (АВГ), с асимптотами ДЕ и Д2, и некоторая прямая АГ
пересекает ее в двух точках. В этом случае я утверждаю, что она пересечется и с ее
асимптотами.
Пусть АГ делится на два равных отрезка точкой Н, тогда ДН есть диаметр сече¬
ния (I, 7). Следовательно, прямая, касающаяся гиперболы в точке В, параллельна
прямой АГ (II, 5).
Поскольку АГ и К0 параллельны, и К.0 пересекается с ДК и Д0 (11, 3), то АГ так¬
же будет пересекаться с ДЕ и Л/ в точ¬
ках Е и 7.
А так как 0
= ВК,тогН = НЕ.
Следовательно, поскольку ГН = НА,
то 7Г - АЕ.
Предложение 9. Если прямая пересе¬
кающаяся с асимптотами, рассекается ги¬
перболой пополам, то она есть касательная
Если прямая, пересекающаяся с асим¬
птотами, рассекается гиперболой на два
равных отрезка, то она имеет с ней толь¬
ко одну общую точку.
Пусть прямая ГД, пересекающаяся с
асимптотами АГ и АЛ, рассекается на два
равных отрезка в точке Е.
В этом случае я утверждаю, что она не
имеет другой обшей точки с сечением. До¬
пустим, что это не так и она совпадает с
гиперболой еще в одной точке В. Тогда (II, 8) ГЕ = ВЛ, что абсурдно, ибо мы пред¬
положили, что ГЕ = ЕД.
Следовательно, ГД не имеет более с сечением ни одной обшей точки.
Предложение 10. Площадь прямоугольника, ограниченного отрезками, на которые
делит гипербола секущую, ограниченную асимптотами, равна четвертой части площа¬
ди эйдоса
Если секущая пересекается с асимптотами, то площадь прямоугольника, ограни¬
ченного отрезками, на которые ее делит гипербола в одной из точек, равна четвертой
части площади соответствующего эйдоса.
Пусть дана гипербола (АВГ) с центром Е, асимптотами ЕЛ и Е7 и прямая Д/,
пересекающая гиперболу в точках А и Г И пусть АГ разбивается в точке Н на два
равных отрезка, и проведена и продолжена прямая НЕ так, что ВЕ = Е0, а из точ¬
ки В восставлен перпендикуляр ВМ к плоскости, содержащей гиперболу. Тогда 0В

Книга II
ЕВ2
ЕН ЕВ
2
есть диаметр, а ВМ пусть равен latus
rectum. В эгом случае я утверждаю,
что ДА AZ = Ar rZ = -0B -BM,
4
Проведем через точку В прямую
KL, касающуюся сечения. Она бу¬
дет параллельна прямой AZ (П, 5).
А поскольку мы доказали ранее
,, 0В ЕВ2 ЕН2
(II. I).что	= —- =—-и.кро-
ВМ ВК2 НА2
,,, 0В 0Н НВ
ме того (1, 21).	=

ВМ НА
eh2 ен нв
НД2” НА2
А так как ЕН относится к НА2
гак же, как ОН НВ , уменьшенное
на некоторую величину, относится
к НА2, уменьшенному на tv же величину, то*	2 v
ДА-AZ НА" ЬК.
Отсюда следует, что ДА А7 = ВК2.
Схожим образом мы докажем, что также ДГГ2 = ВЛ2.
Однако, так как (II, 3)ВК2 = ВЛ2 =-0В ВМ, то АА-А£ = ЛГ-Г2 = —0ВВМ.
4	4
Предложение II. Прямая, пресекающая
стороны утла, дополнительного к углу между
асимптотами, пересечется с гиперболой толь¬
ко в одной точке, а произведение отрезков,
на которые ее делят асимптоты, равно ква¬
драту параллельного ей радиуса
Если прямая пересекает две стороны
угла, дополнительного к углу, образованно¬
му асимптотами, то она пересечется с ги¬
перболой только в одной точке, а площадь
прямоугольника, ограниченного отрезками
ЕН2 НА2
* Это выражение можно получить следующим образом
0Н НВ НА2 ’
Уменьшая правую и левую часть на единицу, получим
Отсюда ЕН2-0Н НВ _ вН НВ _ ЕН2
НД1 - НА2 НА2 НА2
ЕН2 - ОН НВ _ НА2 - НА2
0Н41В	" НА2
Далее,НА2-НА2 = (НД-НА)(НД+ НА) = ДА AZ, а ЕН2-0Н НВ =ЕВ2 (Евклид II, 6).

Предложения
этой прямой между гиперболой и асимптотами, равна одной четверти квадрата диа¬
метра, ей параллельного.
Пусть дана гипербола с асимптотами АГ и АД и пусть через некую точку Е будет
проведена прямая Е7, рассекающая АГ в точке 7.
Она пересечется с гиперболой только в одной точке, так как прямая АВ, парал¬
лельная ей, есть диаметр (I, 26). Пусть она пересечется в точке Н.
В этом случае я утверждаю, что Нг НЕ
= АВ2.
Проведем ординату 0НЛК, тог¬
да касательная ГВД будет ей параллель¬
на (II, 5). А поскольку Г1
ГВ2 ГВ ВД _ ГВ ВД
АВ2 _ АВ2 _ АВ АВ
С другой стороны, из подобия треуголь-
ГВ ОН	ВД ' КН
ников следует, что	=	,		=	,
АВ НИ	АВ НЕ
ГВ2 ОН КН
поэтому	=

ав2 нг НЕ .
„	ОН КН он кн
Но ПОСКОЛЬКУ			 , то
нг не нгнЕ
ГВ2 ОН КН
АВ2 " нг НЕ
И наоборот,
0НКН HZHE
АВ2
. Но так
как м ы дока зал и, что (I Г 10) 0Н КН = ГВ2, то,
следовательно, также HZ HE = AB2.
Предложение 12. Произведение двух про¬
извольных отрезков от любой точки гипербо¬
лы до асимптот не зависит от выбора точки,
если отрезки попарно параллельны
Если от некоторой точки, принадлежащей
гиперболе, провести две прямые, образующие
произвольные углы с асимптотами, и от неко¬
торой другой точки провести прямые, парал¬
лельные первым, то площади прямоугольников,
ограниченных соответственно параллельными
прямыми, будут равны.
Пусть дана гипербола с асимптотами ВА
и ВГ, и от ее точки Д проведены прямые ДЕ
и дг к асимптотам, а от другой точки Н -
прямые Н© и НК, параллельные ДЕ и \7
• ж
X
л

Книга II
В таком случаен утверждаю, что AEAZ = Н0 НК
Г
Проведем прямую ЛН и продолжим дальше к А и
Поскольку(II, 10)АДДГ = АН НГ.то —= —
АД НГ
.	,	АН Н6
А так как из подобия треугольников —
АЛ
ЛЕ и
ЛГ AZ __Н0 AZ
,то
НГ НК
ЛЕ
НК
Следовательно, АЕ AZ = Н0 Н К*.
Предложение 13. Прямая, параллельная
асимптоте, пересекается с кривой только в
одной точке
о.
Если через площадь, ограниченную асим¬
птотами и гиперболой, проходит прямая, па¬
раллельная одной из асимптот, то она пере¬
сечется с гиперболой только в одной точке.
Пусть дана гипербола с асимптотами
АГ и АВ. и через точку Е, принадлежа¬
щую одной из них, проведена Ег, парал¬
лельная АВ. В таком случае я утверждаю,
что эта прямая пересечет гиперболу в од¬
ной точке.
Допустим, что они не пересекутся. Тог¬
да. взяв на сечении некую точку Н, про¬
ведем через нее отрезки НГ и Н0, парал¬
лельные асимптотам АГ и АВ. и пусть для
некоторой точки Z выполняется условие
НГ Н0 = АЕ Ег*\
а также проведем прямую АК, которая
пересечет гиперболу в точке К. Проведем
теперь из точки К отрезки КЛ и КД, па¬
раллельные прямым АГ и АВ, для кото¬
рых будет выполняться равенство (II, 12)
НГ-Н0=КЛКА.
»!•
•1Г
•Ю
•г»:
Однако ранее мы предположили, что
НГ Н0 = AE EZ , а тогда получается ра¬
венство КА КА = АЕ EZ = КЛ ЛА, что не¬
возможно. ибо КЛ > EZ и ЛА > АЕ.
* Теорема верна если параллельные прямые попадают на одни те же асимптоты и ооразуют
подобные треугольники Г \7, ГНК и АНН, АЛЕ В противном случае (рис 2) - нет.
*• Очевидно что если выполняется это условие, то точка 7 (как и далее точки К и М, которые на
самом деле совпадают с ней) находится на гиперболе, но будем пока считать, что она может быть
где угодно (см. реальную картину на рис 2)
20Х

Предложения
Следовательно, EZ пересекается с сечением.
Пусть она пересекается в некоторой точке М.
В таком случае я утверждаю, что она не будет пересекаться с ним ни в какой дру¬
гой точке.
Допустим, что она пересечется с ним еще и в точке N, и проведем через точки М
и N прямые МЕ и NB, параллельные прямой ГА. Поэтому (II, 12) ЕМ -ME = EN NB
что невозможно. Следовательно, она не пересекается с сечением ни в какой дру¬
гой точке.
Предложение 14. Асимптоты неограни
ченно сближаются с кривой
Асимптоты и гипербола, будучи продол¬
жены неограниченно, снижаются друг с дру¬
гом так, что расстояние между ними ста¬
новится меньше любого наперед заданного.
Пусть дана гипербола с асимптотами
АВ и АГ, и пусть заданным между ними
расстоянием будет К. В таком случае я ут¬
верждаю, что прямые АВ и АГ, будучи не¬
ограниченно продолжены вместе с сече¬
нием, постоянно сближаясь с друг другом,
достигнут расстояния меньшего, чем К.
Проведем параллельные секущие E0Z и
ГН А, а также проведем отрезок А0 и про
должим его до г..
Поскольку (II, 10) rH HA=E0 0Z,
НА Е® '
ТО 	=

0Z ГН
•ж
В
Однако АН > ¿О, поэтому’ Е0 > ГН
Схожим образом мы докажем, что следующие расстояния будут еще меньшими.
Допустим, что ЕА < К и через точку А проведена ЛN параллельная асимптоте АГ.
Она пересечет гипербазу в точке N (II, 13). Проведем через N прямую М\В парал¬
лельную прямой
Тогда М N = ЕА < К
Дополнение
Отсюда очевидно, что из всех прямых, не пересекающихся с гиперболой, наи-
лее сближаются с ней асимптоты АВ и АГ, а угол ВАГ наименьший из всех углов.
ограниченных прямыми, не имеющими с гиперболой
ших точек.
Предложение 15. Асимптоты противолежащих совпадают
Асимптоты противолежащих сечений являются общими.
209

Книга II
Пусть даны противолежащие
с диаметром АВ и центром Г. В
этом случае я утверждаю, что
асимптоты противолежащих (А)
и (В) - общие.
Проведем касательные ЛАЕ
и гВН Они параллельны (И, 5).
Пусть квадраты отрезков ЛА.
АЕ. ¿В и ВН равны четвертой
части плошади эидоса. лежа¬
щего возле АВ. Тогда ЛА = АЕ
= гв= вн
И пусть будут проведены ГЛ.
ГЕ, ГХ и ГН. Так как ЛАЕ па¬
раллелен 2ВН то очевидно, что
ЛГ и ГН. а также ГЕ и ГХ лежат
г
на одних и тех же прямых. А по¬
скольку сечение (А) есть гипербола с диаметром АВ и касательной ЛЕ и квадраты
отрезков ЛА и АЕ равны четвертой части плошади эидоса. лежащей возле прямой
АВ. то ЛГ и ГЕ суть асимптоты сечения (А) (П, 1). По той же самой причине ГХ и
ГН суть асимптоты сечения (В). Следовательно, асимптоты
I
тиволежаших сече¬
ний являются общими.
Предложение 16. Отрезки прямой между противолежащими и асимптотами равны,
если она пересекает стороны угла,
дополнительного к образованно¬
му асимптотами
Если прямая пересекает сто¬
роны угла, дополнительного к
углам, содержащим противо¬
лежащие, то она пересечется с
любым из сечений та 1ько в одной
точке, а ее отрезки, зак ¡юченные
между кривыми
и асимптотами.
будут равны.
Пусть даны про
тиво1ежащие
(А> и (В) с центром Г и асимпто¬
тами АН и Е2, и проведена пря¬
мая 0К, пересекающая асим¬
птоты. В этом случае я утверж¬
даю, что она пересечет каждое
из противолежащих только в
одной точке.
210

Предложения
Ведь поскольку АН и - асимптоты сечения (А) и ©К их пересекает, то она
пересечется с каждым про
тиволежащим только в одной точке (II, II). Пусть 0К
пересечется в точках А и М.
Проведем через центр Г диаметр АГВ, параллельный АМ. Тогда (II, 11) КАА0
= АГ2, 0М-МК = ГВ2, а поэтому КА А0 = 0М МК.
Следовательно, А0 = МК*.
Предложение 17. .Асимптоты противолежащих и сопряженных им сечений являют¬
ся общими
Асимптоты противолежащих и со¬
пряженных им сечений являются общими.
Пусть даны противолежащие и со¬
пряженные им сечения с сопряженны¬
ми диаметрами АВ и ГА и центром Е. В
этом случае я утверждаю, что их асим¬
птоты являются общими.
Проведем через точки А, В, Г и А
касательные ¿АН, Н0А, 0ВК и КГ2;
тогда 7Н0К есть параллелограмм (II,
5). ПГ
»г».
ведем 7Е0 и КЕН. Эти отрез¬
ки суть диагонали параллелограмма.
следовательно, они делят друг друга на
две равные части в точке Е А посколь¬
ку площадь эйдоса, лежащего возле АВ,
равна ГА2 (I, 60), и ГЕ = ЕД, то квадраты отрезков ТА. АН, КВ и В0 суть четвертые
части его площади. Поэтому 2Е0 и КЕН суть асимптоты сечений (А) и (В) (II, 1).
Схожим образом мы докажем, что они суть асимптоты сечений (Г) и (А). Следова¬
тельно. асимптоты
тиволежащих и сопряженных им сечений являются
Предюжение 18. Прямая, пересекаю¬
щаяся с одним из сопряженных сечений,
пересекается с каждым из сечений, лежа¬
щих рядом, только в отпой точке
Если прячая, пересекающаяся с одним из
сопряженных сечений, будучи продолжена
в любую из сторон, попадает за его преде¬
лы, то она пересекается с любым из сече¬
ний, лежащих рядом, только в одной точке.
18. Рис. 1
„	КА НМ
’ Поскольку — = —- , то, прибавив справа
МК АН
А так как К \ + М К * НМ + АН = АМ, то АО « Р
шими.
211

Книга II
Пусть противолежащими сопряженными сечениями буду! (А), (В), (Г) и (А), и
пусть некоторая прямая ЕЕ пересекается с сечением (Г) и, продолженная дальше в
любую из двух сторон, попадет вне сечения. В этом случае я утверждаю, что она пе¬
ресечется с (А) и с (В) только в одной точке.
Пусть Н0 и КЛсуть асимптоты сечений. Тогда прямая ЕЕ пересечется с каждой из
них (II, 3). И очевидно, что она пересечется с (А) и (В) только водной точке (II, 16).
Предложение 19. Касательная к сопряженному сечению дели гея точкой касания по¬
полам
Г« Г.'
Если прямая касается одного из
сопряженных сечений, то она пере¬
секается с лежащими рядом сечени¬
ями и рассекается точкой касания
на два равных отрезка.
Пусть (А) и (В), (Г) и (А) суть
■
тиволежашие и сопряженные
им сечения и пусть некоторая пря¬
мая ЕГ7 касается сечения (Г). В та¬
ком случае я утверждаю, что она пе¬
ресечется с сечениями (А) и (В) и в
точке касания Г будет разбиваться
на два равных отрезка.
Очевидно, что она пересечется с
сечениями А и В (II, 18), допустим,
в точках Н и 0.
В этом случае я утверждаю, что ГН = ГО.
Ведь если будут проведены асимптоты сечений КА и МЬ1, то (II, 16) НЕ = го и
(11,3) ГЕ=Гг.
Следовательно, ГН = Г0.
Предложение 20. Две прямые, проведенные из центра так, что каждая параллельна
касательной к конечной точке другой, есть сопряженные диаметры
Если прямая касается одного из противолежащих, и через их центр проводятся две
прямые, первая из которых проходит через точку касания, а вторая, параллельная ка¬
сательной, пересекается с одним из сопряженных сечений, то прямая, касающаяся со¬
пряженного сечения в точке пересечения, будет параллельна прямой, проведенной через
точку касания и центр, а прямые, проведенные через точки касания и центр, будут со¬
пряженными диаметрами противолежащих сечений.
Пусть даны сопряженные противолежащие сечения, сопряженными диаметра¬
ми которых будут АВ и ГЛ, центром - X. Проведем касательную ЕЕ к сечению (А),
»!•
212

Предложения
(Л)
п	ХК
Поэтому
которая пересечется с ГД в точке Т,
прямую ХЕ, которая пересечется с
(В) (В) в точке Е. прямую ХН. парал¬
лельную касательной, а также пря¬
мую 0Н, касающуюся сечения (Г)
в точке Н. В таком случае я утверж¬
даю. что0Н параллельна прямой ХЕ,
а НО и ЕЕ являются сопряженными
диаметрами.
Проведем ординаты ЕК, НА и
ГРП к диаметрам, параметрами |Ьг)
I для которых являются АМ и ГМ. А
поскольку (1,60)	и (1.37)
АМ ГД
АВ _ ХК К/ ГХ = НА2
АМ" ЕК2 ГД~ХЛ-Л0
хккг	нл2
ЕК2 ~ ХЛ Л0
~	хк к2 хк кг
Однако 	-— =	и
ЕК2 ЕК ЕК
НА2 НЛ НЛ
ХА Л0
ХА Л0
, то
кг НА НЛ
ЕК ЕК ~ ХА Л0
■ л /•	К7. НА
Так как ЕК. Кг и ¿Е параллельны соответственно ХА, НА и НХ, то	= ——
ЕК ХА
_ г ХК НА
Таким образом,	=	.
ЕК Л0
Поскольку стороны, стягивающие равные углы с вершинами в точках К и А. яв¬
ляются пропорциональными, то треугольники ЕКХ и Н0Л подобны.
Следовательно, ¿ЕХК = ¿ЛН0.
Кроме того, ¿КХМ = ¿АНХ.
Почленно вычитая, получаем, что ¿ЕХН = ¿0НХ.
Следовательно, ЕХ параллельна прямой Н0.
ПН 0Н
Пусть	=	, поэтому £ есть половина Ьг сечений (Г) и (Д), определенного
НР £
при диаметре НО (I, 55). А поскольку ЕТ пересекается с ГА, который есть один из
диаметров сечений (А) и (В), то ТХ ЕК = ГХ2.
Ведь если от точки Е провести прямую, параллельную КХ. то прямоугольник,
ограниченный отрезком ТХ и отрезком, заключенным между центром и точкой пе¬
ресечения указанной параллельной с диаметром ДГ, который равен ЕК, будет, со¬
гласно (1, 38), равен квадрату ГХ.
•я
»1«.
»!•
•I»
* Согласно (I, 60), АВ АМ = ГД2, АВ'= ГЛ Г\. Поделив почленно, получим нужное выражение.
213

Книга II
2 •
ГХ ТХ2
Отсюда получим* * — = —
ЕК ГХ
ТХ ЛТ
Так как треугольники ТХ2 и ЕК/ подобны, то	= — .
ек кг
, тг з(тхг)	тх тг з(тхг)
А поскольку (Евклид VI, 1 — = —т	т, то = — = —;	г.
Ег в(ЕХ2)	ЕК Е£ в(ЕХ2)
Из построения следует также, что треугольники ТХ/ и ЕК/ подобны, а значит
,п> ТХ 2 8(тхг) 8(ТХ2) „
(Евклид VI, 19),—-г =—,	. = —	г .
ГХ 8(ХГП) 8(Н0Х)
8(тхг) вПхг)
Таким образом, ——- - — 	- »следовательно, 8(Н0Х) = 8(Н Е/).
8(ЕХ/) 8(Н0Х)
Кроме того, /0НХ = /ХЕ/, так как ЕХ и Н0. Е/ и НХ параллельны. А так как
стороны, заключающие равные углы в треугольниках равной площади, обратно про¬
порциональны (Евклид VI, 15), то Н0-НХ = Е/ ЕХ.
д	ПН 0Н	НР ЕХ
А поскольку	=	, а также в силу параллельности отрезков	=	, то
НР I	ПН Е/
I НХ ЕХ ЕХ2
	и	=

ЕХ=^
Е/ ~0Н
Д±'Се 0Н 0Н НХ Е/ ЕХ Е/
п	I НХ ЕХ2	, I НХ 0ННХ
Поэтому 	=	и, наоборот, 	— =	.
0Н НХ ЕХ Е/	ЕХ2 ЕХ Е/
Однако Н0 НХ = Е/ ЕХ.
Следовательно, ЕНХ = ЕХ-.
Очевидно, Е НХ есть четвертая часть площади эйдоса, лежащего возле прямой
НО, поскольку НХ есть ее половина, а Е есть половина Ьг.
Далее, так как ЕХ - ХЕ, то ЕХ2 = ’/♦ ЕЕ2, а следовательно. ЕЕ2 равен площади пря¬
моугольника. приложенном к прямой НО.
Схожим образом мы докажем, что квадрат НО равен площади прямоугольника,
приложенной к прямой ЕЕ. Следовательно. ЕЕ и НО суть сопряженные диаметры
противолежащих сечений (А), (В), (Г) и (А).
•я
Предложение 21. У сопряженных диаметров касательные пересекаются на одной
из асимптот
При тех же самых предпосылках нужно доказать, что точка пересечений касатель¬
ных.¡ежит на одной из асимптот.
*	Умножив обе части на ТХ и разделив на ГК' и ЕК
ХГ XII хг хг
•	* Докажем, что БГХГП) = Б/ННХ) Их отношение равно	=	 А поскольку ХН ХА = ХГ2
хахн хе ха
(I, 37), то площади равны.
214

Предложения
Пусть будут противолежащие и им сопря¬
женные сечения с диаметрами АВ и ГД, и пусть
11
»а
ведены касательные АЕ и ЕГ. В таком случае
я утверждаю, что точка Е лежит на асимптоте.
Поскольку ГХ2 равна четвертой части пло¬
щади эйдоса, лежащего при АВ (I, 60), а ГХ2 =
АЕ2, то АЕ2 равна четвертой части той же площа-
ди. Проведем ЕХ, которая есть асимптота (II, I).
Следовательно, точка Е лежит на асимптоте.
Предложение 22. Произведение отрезков из
(II, 10) равно квадрату параллельного им радиуса
Если на сопряженных противолежащих се¬
чениях через центр проводится прямая к проти -
волежащим сечениям, и параллельная ей прямая,
пересекающаяся с одним из лежащих возле сече¬
нии и с асимптотами, то прямоугольник, ограниченный двумя отрезками, на которые
сечение разбивает расстояние между точками пересечения с асимптотами, будет ра¬
вен квадрату радиуса.
Пусть даны противолежащие и сопряженные и пусть асимптотами будут EXZ и
НХ0. Тогда, если через цен гр X проведена прямая ГД, а также параллельная ей 0Е,
пересекающая подряд одно из противолежащих сечений и асимптоты, то я утверж-
Пусть КА делится точкой М на два
равных отрезка, а отрезок MX будет
продолжен до п рот и вол ежащего сече¬
ния, toi да АВ есть диаметр противоле¬
жащих (1.51 Добавление). А посколь¬
ку касательная, проведенная через точ¬
ку А. параллельна прямой Е0, то Е0
есть ордината к АВ*. Следовательно,
АВ и ГЛ суть сопряженные диаметры
(Опр I, 6). Поэтому ГХ2 равен одной
четвертой части площади эйдоса. ле¬
жащего возле АВ ( 1,60).
Но четвертая часть его площади рав¬
на (II, 10) .
Следовательно, EK К0 = ГХ2.
* Тут перепутаны причина и следствие. Е0 - ордината так как она делится диаметром пополам
а согласно (II, 5), касательная параллельна ординате но здесь это вовсе не нужно.
215

Книга II
Предложение 23. Произведение отрезков секущей, ограниченных соседними сопря¬
женными сечениями, равно удвоенному квадрату параллельного им радиуса
Если на противолежащих и сопря¬
женных сечениях от центра проводится
радиус к любому из них и проводится па¬
раллельная ему прямая, пересекающаяся
с тремя лежащими воне друг друга сече-
ниями, то прямоугольник,
oei
ничейный
двумя отрезками, на которые сечение
разбивает расстояние между точками
пересечения с сопряженными сечениями,
будет вдвое больше квадрата радиуса.
Пусть даны противолежащие и со¬
пряженные им сечения с центром в точ¬
ке X, и пусть от X к любому из сечений
веден радиус ГХ и проведена КА.
параллельная ГХ. рассекающая расположенные возле друг друга три сечения. В та-
ком случае я утверждаю, что КМ МЛ = 2ГХ2.
Пусть будут про
ведены асимптоты сечений EZn Н0; тогда (П. 22) ГХ2 = ЕМ-М0
и (И. 11) ГХ:= КЕ К0.
Но ЕМ-М0 + КЕК0 = КМ МЛ, поскольку концы равны (И. 8 и 16)*.
Следовательно, КМ-МЛ = 2ГХ2.
Предложение 24. Две прямые, пересекающие параболу в двух точках каждая, пере¬
секутся друг с другом
Если две прямые пересекают параболу в двух
точках каждая так, что ни одна точка пересе¬
чения любой из них не лежит на дуге, заключенной
между точками пересечения другой, то эти прямые
пересекаются друг с другом вне сечения.
Пусть дана парабола и две прямые АВ и ГД,
пересекающиеся с ней, так что ни одна точка пе¬
ресечения любой из них не лежит на дуге, заклю¬
ченной между точками пересечения другой. В та¬
ком случае я утверждаю, что они. будучи продол¬
жены, пересекутся между собой.
Пусть через точки пересечения этих прямых с
параболой В и Г будут проведены диаметры сече¬
ния ЕВ/ и НГ0. Они параллельны (I, 51 Добав-
с»
* Так в оригинале Вероятно, имеется в виду, что КБ = 0Л и ЕМ = N0 Тогда КМ = ЫЛ, а значит, К1Ч
= МА. И, раскрывая скобки, получим ЕМ МО + КЕ ЕМ + КЕ М0 +КЕ? = КЕ(КЕ + МЕ) + М0(КЕ + ЕМ) =
= (КЕ + ЕМИКЕ + М0) - КМ КЫ = КМ М

Предложения
ление), и каждый из них пересекает параболу только в одной точке. Проведем ВГ,
тогда /ЕВГ + /НГВ равен двум прямым, а ДГ и АВ образуют с ВГ углы меньшие,
чем два прямых. Следовательно, эти прямые пересекаются между собой вне сече¬
ния (Евклид 1, постулат 5).
Предложение 25. То же для гиперболы
Если каждая из двух прямых пересекается
с гиперболой в двух точках, и точка пересече¬
ния ни одной из них не лежит на дуге, заклю¬
ченной между точками пересечения другой, то
прямые пересекаются вне сечения, но внутри
угла, его содержащего.
Пусть дана гиперболас асимптотами АВ и
АГ и две прямые EZ и Н0, пересекающие ее
так. что точка пересечения ни одной из них
не лежит на дуге, заключенной между точка¬
ми пересечения другой. В этом случае я ут¬
верждаю, что эти прямые будут пересекаться
вне сечения, но внутри угла ГАВ.
Пусть отрезки AZ и А0 будут продол же -
ны и проведена прямая Z0. Поскольку прямые EZ и Н0 лежат внутри углов AZ0 и
A0Z, сумма которых меньше двух прямых, то EZ и Н0 пересекаются между собой
вне сечения, но внутри угла ГАВ. Схожим образом мы докажем это, если даже EZ и
Н0 касаются сечений*.
Предложение 26. Две секущие, не проходящие через центр эллипса, не делят друг
друга пополам
Если две прямые, не проходящие через центр эллипса пересекаются внутри него, то
они не рассекают друг друга на два равных от¬
резка.
Пусть два отрезка прямых ГД и EZ, не
ходящие через центр 0, рассекают друг дру-
га на два равных отрезка в точке Н, а отрезок
Н0 продолжен до точек А и В, лежащих на
эллипсе или круге.
Поскольку АВ есть диаметр, разбиваю¬
щий отрезок EZ на две равные части, то пря¬
мая, касающаяся эллипса в точке А, парал¬
лельна отрезку Е2 (II, 6). Схожим образом
* Почему-то в предыдущем Предложении о касательных ничего не сказано.
217

Книга II
мы докажем, что она также параллельна прямой ГА. Но тогда Е/ и ГД также парал¬
лельны, что невозможно.
Следовательно. ГД и ЕЛ не рассекают друг друга на два равных отрезка.
Предложение 27. Касательные к концам диаметра эллипса параллельны
Если две прямые касаются эллипса,
то они будут параллельны, при условии,
что отрезок, соединяющий точки со¬
прикосновения, проходит через центр,
а если нет, то они пересекаются по ту
же сторону от центра [где находится
соединяющий их отрезок].
Пусть дан эллипс с касательными
ГАД и EBZ, и пусть отрезок АВ, соеди¬
няющий точки касания,
ж
ходит че¬
рез центр. В таком случае я утверждаю,
что ГД и ЕЛ являются параллельными.
Поскольку' ,4В есть диаметр и ГД ка¬
сается сечения в А. то она параллельна
ординатам к диаметру (1.17). По той же
самой причине и BZ им параллельна
Следовательно, ГД и EZ являются па¬
раллельными.
Пусть АВ не про
ходит через центр, как это показано на втором чертеже. Прове -
дем диаметр А0. а через Л - касательную ЛК, тогда ЛК и ГД параллельны.
Следовательно, EZ. проведенная дальше, пересечется с ГД по ту же сторону от
центра, в каковой лежит секущая АВ (Евклид I, постулат 5).
Предложение 28. Прямая, рассекающая две параллельные секущие пополам, есть
диаметр
Если на сечении конуса некая прямая рассекает две параллельные хорды на два рав¬
ных отрезка, то она будет диаметром сечения*.
Пусть на сечении конуса две параллельные прямые АВ и ГД в точках Е и Л рассе¬
каются на два равных отрезка В таком случае я утверждаю, что прямая, проведен¬
ная через Е и Z и продолженная в обе стороны, есть диаметр сечения.
tii
* Ср с Определением 4 в Книге I «Диаметром любой плоской кривой линии я называю пря¬
мую. которая все хорды данной линии, проведенные как параллельные какой-либо прямой рас¬
секает пополам«.
218

Предложения
Допустим, что это не так, и диаметром является Н70.
Тогда Г0 = 0Д, что абсурдно, ибо мы предположили,
что ГЕ = ЕД.
Таким образом, Н0 не есть диаметр. Схожим обра¬
зом можно доказать, что н и какая другая прямая, кроме
Ег, не будет диаметром.
Следовательно, Е7 будет диаметром сечения.
Предложение 29. Прямая, проведенная от точки пере¬
сечения двух касательных к середине отрезка, соединяю¬
щего точки касания, есть диаметр
Если две касательные к коническому сечению пересе¬
каются, то прямая, проведенная от точки их пересече¬
ния к середине секущей соединяющей точки касания, бу¬
дет диаметром сечения.
Пусть дано сечение конуса, проведены касательные
АВ и АГ, и пусть отрезок ВГ рассекается на две равных
части в А. В таком случае я утверждаю, что АД есть диаметр сечения.
Допустим, что диаметр — ДЕ, и проведем
прямую ЕГ, пересекающую сечение в точке
7, а также через эту точку проведем 7КН,
параллельно ГДВ.
Поскольку ГД = ДВ. то 70 = 0Н.
Атак как прямая, касающаяся сечения в
точке Л, параллельна ГВ (И, 5 и 6) и ¿Н па¬
раллельна прямой ГВ, то и 7Н параллельна
этой касательной. Поэтому (I, 49 и 50) 7Н
= 0К, чего не может быть.
Следовательно, ДЕ не есть диаметр.
Схожим образом мы докажем, что ника¬
кая другая прямая, кроме АД, не является
диаметром*.
»1«
Предложение 30. Диаметр, проведенный от точки пересечения двух касательных,
делит пополам отрезок, соединяющий точки касания (Предложение, обратное № 29)
Если две прямые, касающиеся конического сечения, пересекаются, то диаметр, про¬
веденный от точки их пересечения, будет рассекать на два равных отрезка секущую,
соединяющую точки касания.
‘ Совсем не обязательно доказывать, что ИН = ОК с помощью касательной Достаточно было
сослаться на определение диаметра в Книге I (Опр. 1,4)
219

Книга II
Пусть дано коническое сечение, две каса¬
тельные к нему прямые АВ и АГ, и проведен
отрезок ВГ, соединяющий точки соприкос¬
новения, а через точку А - диаметр сечения
АД. В таком случае я утверждаю, что ВД = ДГ.
Предположим, что это не так. Допустим,
что ВЕ = ЕГ, тогда АЕ тоже диаметр сечения
(II, 29), что абсурдно.
Ведь если сечение есть эллипс, то диаме-р^—
тры пересекутся в точке А и центр сечения
окажется лежащим вне его, что невозмож¬
но; если же сечение есть парабола, то диа¬
метры пересекаются между собой, что также
невозможно; если же сечение есть гипербо¬
ла. то точка пересечения касательных к ней
расположена внутри угла, заключающего ги¬
перболу (II, 25). но точка пересечения диаме¬
тров гиперболы есть ценгр сечения.
Следовательно, невозможно, чтобы ВЕ
= ЕГ.
4
А
Ч
ч
%
%
ч
Ч
ч
ч
ч
А
Е
31. Рис. 2
Предложение 31. Касательные к концам ди¬
аметра гиперболы параллельны. Если же это не
диаметр, то они пересекутся в той стороне от
соединяющей их прямой, где находится центр
Касательные к двум противолежащим будут
параллельны. если прямая, соединяющая точки
соприкосновения, проходит через центр (рис. 1),
а если нет, то они пересекутся с той же
стороны от прямой, соединяющей точки ка¬
сания, где находится центр (рис. 2).
30. Рис. 1
31. Рис. 1
Пусть даны противолежащие (А) и (В), со¬
прикасающиеся с ними прямые ГАД и ЕВ/,
и пусть прямая, проведенная от А к В, снача¬
ла проходит через центр. В таком случае я ут¬
верждаю, что ГД и Е/ параллельны.
Ведь поскольку сечения являются щ
волежащими, АВ — диаметр, и одного из них
ГД касается в точке А. то прямая, проведен¬
ная через В параллельно прямой ГД есть ка-
•5НТВ
220

Предложения
сательная ко второму в точке
Следовательно, ГД и Е7 параллельны* **.
Допустим, что отрезок АВ не проходит через центр сечения; тогда проведем диа¬
метр сечения АН, и прямую ©НК, касающуюся сечения (В). В таком случае 0К па¬
раллельна ГД. Прямые Е2 и 0К касаются одной и той же гиперболы, поэтому они
пересекаются (II, 25). А поскольку ©К и ГД параллельны, то Е2 пересечется и с ГД.
И очевидно, что они пересекаются с той стороны от АВ, где находится центр.
Предложение 32. Касательные или секущие к противолежащим пересекаются вну¬
три угла, дополнительного к углам, содержащим сечения
Если прямые пересекаются с каждым из противолежащих, или касаются их, или рас¬
секают их в двух точках, и пересекаются между собой, то точка их пересечения лежит
в одном из углов, дополнительном к углам, заключающим противолежащие.
Пусть даны противолежащие, и прямые
АВ и ГД, которые касаются двух противоле¬
жащих в произвольных точках или пересе¬
кают каждое из них в двух точках. В таком
случае я утверждаю, что точка их пересече¬
ния будет принадлежать углам, дополни¬
тельным к углам, заключающим противо-
лежащие.
Пусть 2.К и 0К суть асимптоты, тогда
прямая АВ пересечется с асимптотами (11,8),
допустим, в точках 0 и Н. А поскольку мы
предположили, что 2К и 0К пересекают¬
ся, то очевидно, точка их пересечения бу¬
дет лежать ли
внутри угла 0AZ, либо вну¬
три угла КАН. Схожим образом мы дока¬
жем это, если они касаются сечения (II, 3).
Предложение 33. Касательная или секу¬
щая к одному противолежащему не имеет общих точек со вторым
КС
Если прямая пересекается с одним из противолежащих или касается его, то она не
будет иметь общих точек со вторым противолежащим, но будет лежать внутри угла,
заключающего первое и внутри углов, дополнительных к углу, заключающему сечение.
Пусть даны противолежащие (А) и (В), и пусть прямая ГД пересекает (А) так. что
продолженная в обе стороны она лежит вне сечения В таком случае я утверждаю,
что прямая ГД не пересекается с (В).
* См примечание к (1,44).
** Поскольку касательная только одна (I, 32).
221

Книга II
Пусть будут проведены асимптоты сече¬
ний Е7 и НО, тогда ГЛ, будучи продолже¬
на, пересечется с ними (II, 8), допустим, в
точках Е и 0. Следовательно, она не пере¬
секается с (В)*.
И очевидно, что она попадет в три про¬
странства. А если прямая пересекается с каж¬
дым из противолежащих сечений, то она не
пересечется в двух точках ни с одним из них;
ест и же она будет пересекаться в двух точках,
то из-за того, что мы доказали выше, она не
пересечется с другим сечением.
33. Рис. 1
Предложение 34. Прямая, проходящая через точку касания одного из противолежа¬
щих и середину секущей другого, параллельную касательной, есть диаметр
Если прямая касается одного из противолежащих сечений и через другое противоле¬
жащее проводится секущая, ей параллельная, то прямая, проходящая через точку со¬
прикосновения и середину секущей, есть диаметр противолежащих.
Пусть (А) и (В) - противолежащие сечения, и пусть прямая ГА касается первого
из них в точке А, а через другое сечение проведена секущая Е7, параллельная ГА и
разбиваемая точкой Н на два равных отрезка.
есть диаметр противолежащих.
Предположим, что это не так и диаме-
1
м является А0К. Тогда прямая, касаю¬
щаяся (В) в точке 0, параллельна ГД (11,
31). Но ГА также параллельна прямой Е7,
поэтому касательная параллельна и Ег.
Тогда (I, 47), ЕК = К2,что невозможно,
ен = нг.
Следовательно, А0К не есть диаметр
противолежащих сечений Таким обра¬
зом, ди а метро
м является
таком случае я утверждаю, что АН
Предложение 35. Если диаметр разбивает секущую пополам, то касательная к дру
гому противолежащему, проходящая через конец диаметра, параллельна секущей
Если диаметр разбивает секущую на одном из противолежащих сечений на два равных
отрезка, то прямая, касающаяся другого в конце диаметра, параллельна этой секущей.
*
одну из асимптот, но прямая не может два раза пересечься с другой прямой
То есть, чтобы ГЛ пересеклась со вторым противолежащим, она должна сначала пересечь

Предложения
Пусть (Л) и (В) суть противолежащие,
а их диаметр АВ разбивает секущую ГЛ се¬
чения (В) в точке Е на два равных отрезка.
В таком случае я утверждаю, что пря¬
мая, касающаяся (А) в точке А, параллель¬
на ГЛ.
Допустим, что это не так, и какая-то
другая прямая лг параллельна касатель¬
ной. Тогда (I, 48) ЛН = Нг.
Однако ЛЕ = ЕГ, поэтому Г7 и ЕН па¬
раллельны (Евклид VI, 2), что невозмож¬
но, ибо Г7, продолженная дальше, пере¬
секается с ЕН (I, 22).
Следовательно, Л7 не параллельна прямой, касающейся сечения в точке А, и ни¬
какая другая прямая не параллельна ей.
к по
Предложение 36. Если секущие проти¬
волежащих параллельны, то прямая, сое¬
диняющая их середины, есть диаметр
Если каждое из противолежащих сече¬
ний пересечено параллельными прямыми, то
прямая, соединяющая их середины, есть ди¬
аметр противолежащих* **.
Пусть (А) и (В) - противолежащие, их
секущие ГД и Е7 параллельны, и каждая
из них разбивается на два равных отрез¬
ка в точках Н и 0.
В таком случае я утверждаю, что Н0 есть диаметр противолежащих.
Допустим, что это не так, и диаметром является НК. Тогда прямая, касающаяся
сечения (А) в точке А. параллельна ГЛ (II, 5). Но она также параллельна и Е2. Та¬
ким образом (I, 48), ЕК = К/, что невозможно, так как Е0 =
Поэтому диаметром противолежащих сечений является не НК, а Н0.
ме ГЛ*.
Предложение 37. Если прямая, проведенная не через центр, рассекает противоле¬
жащие сечения, то отрезки, проведенные из центра параллельно ей и через ее середи¬
ну, есть сопряженные диаметры
Если прямая, проведенная не через центр, рассекает противолежащие сечения, то
отрезки, проведенные через центр паралзельно ей и через ее середину', есть сопряжен¬
ные диаметры.
* Лучше было бы сказать, что, следовательно, лг не делится в точке Н пополам, а значит она
не параллельна касательной
“ Но ведь это говорится в Определении I, 5.
223

Книга II
Пусть (А) и (В) - противолежащие се¬
чения с центром X, и их пересекает пря¬
мая ГА, не проходящая через центр и раз¬
биваемая точкой Е на два равных отрезка.
В таком случае я утверждаю, что ЕХ
и отрезок АВ, проведенный параллель¬
но прямой ГЛ есть сопряженные диаме¬
тры противолежащих*.
»1»
Пусть через центр будет проведен от¬
резок А2, а также отрезок Г/. Тогда (I,
зо) дх = хг.
Однако также ДЕ = ЕГ, поэтому ЕХ и
Г7 параллельны.
Продолжим диаметр АВ до точки Н,
принадлежащей №.
Тогда поскольку ЛХ = X/, то ЕХ = Н7 и ГН = Н7, а значит, № — ордината к ди¬
аметру. Поэтому прямая, касающаяся сечения в точке А, параллельна Г/ (И, 5). а
также прямой ЕХ.
Следовательно, ЕХ и АВ - сопряженные диаметры противолежащих (I, 16).
Предложение 38. Прямая, соединяющая точку пересечения касательных к проти¬
волежащим и середину отрезка между точками касания, и прямая, проходящая через
центр параллельно ему - сопряженные диаметры
Если две касательные к противолежа¬
щим пересекаются, то прямая, проведен¬
/Л
ная через точку их пересечения и середи¬
ну отрезка, соединяющего точки касания
и прямая, проведенная через центр парал¬
лельно этому отрезку, будут сопряженны¬
ми диаметрами.
Пусть ГХ и ЛХ - касательные к про¬
тиволежащим (А) и (В) и
ведены от¬
резок ГД, разбиваемый точкой Е попо¬
лам, и отрезок ЕХ.
В таком случае я утверждаю, что ЕХ и
отрезок, проведенный через центр парал¬
лельно ГД, - сопряженные диаметры**.
Допустим, что это не так, и диаме¬
тром является отрезок №, проведенный
о
• Это следует из (1,51 Добавление) и (Опр. I, 6).
“ Этот отрезок не изображен на чертеже, так как очевидно,
касается лишь отрезка ЕХ
цто он диаметр и доказательство

Предложения
•I».
Й
»I«
от точки Е в некоторую точку 7_. Тогда АХ, будучи продолжена, пересечется с ним в
точке г, а отрезок Г7 пересечется с одним из противолежащих (I, 32) в некотоу
точке А, через которую проведена АВ, параллельная прямой ГД. Поскольку же ЕЛ
есть диаметр, и разбивает прямую ГД на два равных отрезка, то он разбивает на два
равных отрезка и прямые, ей параллельные (Опр. I, 4). Следовательно, АН = НВ, а
поскольку ГЕ = ЕД, то АН - Н К.
Но тогда НК = НВ, что невозможно. Следовательно, Е7 не есть диаметр
проти вол ежаш их*.
Предложение 39. Прямая, проведен¬
ная через точку пересечения касательных к
противолежащим и центр, проходит через
середину отрезка между точками касания
Если две касательные к
тиволежа-
щим сечениям пересекаются, то прямая,
проведенная через центр и точку пересе¬
чения касательных, будет проходить че¬
рез середину отрезка, соединяющего точ¬
ки касания.
Пусть (А) и (В) суть противолежащие
с центром в точке О, которых касаются
две пересекающиеся прямые ГЕ и ЕЛ, и
пусть будет проведены ГД и диаметр ЕХ.
В таком случае я утверждаю, что Г2 = ХЛ.
Допустим, что это не так, и ГД разбивается на два равных отрезка точкой Н. Тог¬
да, ЕН есть диаметр (II, 38). Однако ЕХ есть также диаметр. Следовательно, каса-
тельные пересекаются в центре п
тиволежаших, что абсурдно (II. 32). Следова¬
тельно, TZ = ZA.
Предложение 40. Если через точку пересечения двух касательных к противолежа¬
щим провести прямую, параллельную отрезку, соединяющему точки касания, то прямые
между зочками пересечения ее с кривыми и серединой этого отрезка есть касательные
Если две прямые, касающиеся противолежащих, пересекаются, и прямая, проведен¬
ная через точку их пересечения параллельно прямой, соединяющей точки касания, пе¬
ресекается с каждым сечением, то прямые, проходящие через эти точки пересечения
и середину прямой, соединяющей точки соприкосновения, касаются противолежащих.
Пусть X - центр противолежащих (А) и (В), которых касаются две прямые ГЕ и
ЕД, ГД - прямая, которая разбивается точкой © на два равных отрезка, а ZEH — пря-
* Это доказательство того, что ЕХ - диаметр, а то, что он сопряженный, доказано в предыду¬
щем Предложении.
225

Книга II
мая, параллельная ГД В таком случае я
утверждаю, что прямые 70 и 0Н каса¬
ются сечений.
Проведем параллельно ГЛ прямую
АВ, а также прямую Е0. Тогда они яв¬
ляются сопряженными диаметрами (11,
38), а ГЛ проведена ко второму диаметру
как ордината и ГЕ, касающаяся (А), с
ним пересекается. Поэтому (1, 38) пло¬
щадь прямоугольника ЕХ-Х0 равна ква¬
драту половины второго диаметра, или
четвертой части плошади эйдоса, лежа¬
щего при АВ А поскольку 7Е есть ор¬
дината ко второ
му диаметру; то прямая
70 касается сечения (А) (1.38)*. По той
же причине Н0 касается сечения (В)
Следовательно, 70 и 0Н касают¬
ся сечении (А) и (В)
Предложение 41. Две прямые, проходящие не через центр противолежащих, не мо¬
гут делить друг друта пополам
£сш две прямые, проходящие не через центр противолежащих, пересекаются, то
они разбивают друг друга на два неравных отрезка.
Пусть (А) и (В) суть противолежащие
с центром X, а секущие их прямые ГВ
се
»1»
и АЛ, не проходящие через центр, пе¬
ресекаются в точке Е. В таком случае
я утверждаю, что они разбивают друг
друга точкой пересечения на два не¬
равных отрезка.
Допустим, что это не так и они раз¬
бивают друг друта на два равных отрез¬
ка. Тогда отрезок ЕХ, соединяющий
точку Е с центром X. есть диаметр, а
отрезок НХ7, параллельный прямой
ГВ. есть диаметр, сопряженный с ЕХ
(11, 37). Таким
разом, прямая, каса¬
ющаяся сечения в точке 0, параллель¬
на прямой ЕХ (1.49 и Опр. 1.6) По той
же самой причине поскольку проведен-
• Это уже теорема, обратная 38-й если 2Е - ордината, а ЕХ Х(Э равно квадрату половины вто¬
рого диаметра, то	- касательная
226

Предложения
пая 0ХК параллельна АЛ, то прямая, касающаяся сечения в 0, параллельна прямой
ЕХ. Следовательно, прямая, касающаяся сечения в точке 0, параллельна прямой,
касающейся сечения в точке 2, т.е. две прямые, касающиеся сечения в разных точ¬
ках, параллельны, что абсурдно, ибо мы уже доказали, что они пересекаются (II, 31).
Следовательно, ГВ и АД, не проходящие через центр, разбивают друг друга точ¬
кой пересечения на два неравных отрезка.
Предложение 42. То же для для противолежащих и сопряженных
Если две прямые, проведенные на двух
противолежащих и им сопряженных сече¬
ниях не через центр, рассекают друг дру¬
га, то они не рассекают друг друга на два
равных отрезка.
Пусть даны противолежащие и им
сопряженные (А) и (В), (Г) и (Л) с цен-
м в ючке X, и проведены две прямые
Е2 и Н0, не проходящие через центр
и пересекающиеся в точке К. В таком
Т!
1
•А
•Л
случае я утверждаю, что отрезки Е7 и
Н0 разбивают друг друга на две нерав¬
ные части.
Допустим, что на равные, и пусть бу¬
дут проведены через центр X отрезок АВ,
параллельный Е2, и ГЛ, параллельный
Н0, а также КХ. Тогда КХ и АВ суть со¬
пряженные диаметры (II, 37). По той же
самой причине КХи ГД являются сопряженными диаметрами. Поэтому прямая, ка¬
сающаяся (А) в точке А, параллельна прямой, касающейся сопряженного сечения
(Г) в точке Г (Опр. I, 6 и II, 5)*, что невозможно, ибо они пересекаются, посколь¬
ку прямая, касающаяся сечения в точке Г, пересекает (А) и (В), а прямая, касающа¬
яся сечения (А), пересекает (Д) и (Г) (11, 19), и очевидно, что точка их пересечения
К лежит внутри угла АХГ (II, 21).
Следовательно, ЕЯ и Н0, не проходящие через центр, не разби
на два равных отрезка точкой пересечения.
вают друг друга
Предложение 43. Два диаметра противолежащих, проведенные к середине некото¬
рой секущей и параллельно ей, являются сопряженными
Если прямая пересекает одно из противолежащих сечений в двух точках, и через
центр проводятся две прямые, одна из которых к середине секущей, а вторая — парал-
* Так как каждая из них параллельна КХ
227

Книга II
дельно ей, то эти прямые будут сопря¬
женными диаметрами.
Пусть даны противолежащие и со¬
пряженные (А) и (В), (Г) и (А) с цен-
I
м X, и некоторая прямая пересекает
сечение (А) в точках Е и Т. Тогда, если
из центра провести прямую ХН. разби¬
вающую отрезок Е2 пополам, и прямую
ГХЛ, параллельную ЕТ. то в таком слу¬
чае я утверждаю, что АХ и ГХ есть со¬
пряженные диаметры.
Поскольку АХ есть диаметр, продол¬
жение которого разбивает на два рав¬
ных отрезка, то прямая, касающаяся се¬
чения в точке А, параллельна прямой
АХ (II, 5), а значит, и прямой ГХ. А по¬
43. Рис. 1
скольку сечения являются противоле¬
жащими, и от центра X к точке сопри¬
косновения проведена АХ. а ГХ прове-
дена параллельно касательной, то прямые АХ и ГХ - сопряженные диаметры, как
это было доказано прежде (II, 20).
Предложение 44. Построение диаметра заданного ко
нического сечения
Надо найти диаметр заданного конического сечения.
Пусть он будет найден, и пусть им будет Г0. Тог¬
да для прямых, проведенных как ординаты В7 и А0 и
продолженных дальше, будет ВТ = ТЛ и А0 = 0Е. Та¬
ким образом, если мы провели параллельные прямые
ЕА, то будут найдены точки Т и 0. Следователь¬
но, диаметр Г0 найден построением.
и»:
Этим способом и построим диаметр: проведем па¬
раллельные прямые ВА и АЕ, каждая из которых будет
рассекаться пополам в точках Т и 0. Тогда Г70 будет
диаметром сечения. Тем же самым способом мы най¬
дем и другие любые диаметры.
Предложение 45. Нахождение центра эллипса и гиперболы
Найти центр заданного эллипса и гиперболы.
Это очевидно. Ведь если проводятся два диаметра сечения АВ и ГА (II, 44), то там,
где они пересекаются, и будет центр сечения, как было доказано (I, 47).
228

Предложения
Предложение 46. Построение оси
•ж
ЛЖ
•ж
Найти ось конического сечения.
Пусть сначала заданным сечею
са будет парабола, в которой нахо^
ки г, Г и Е. Следует найти ее ось.
Пусть проведен диаметр АВ (II,
АВ есть ось, то задача решена, если же нет, то предположим, что она проведена, и
пусть осью будет ГД; тогда ГД параллельна прямой АВ (1,51 Добавление) и она рас¬
секает на два равных отрезка прямые, проведенные к ней перпендикулярно (Опр. 1,
7). А прямые, перпендикулярные ГД, также перпендикулярны АВ. поэтому ГД рас¬
секает на два равных отрезка прямые, перпендикулярные АВ. Если мы проведем
Е7 перпендикулярно АВ, то ЕД — дг. Этим мы получим точку Д. Тогда через Дпро-
ведем ГД, параллельно построенному диаметру АВ. Таким образом, получаем ГД.
Построим следующим образом: Дана парабола, на которой находятся точки Z, Е
и А, и пусть будет проведен ее диаметр АВ, перпендикулярно к которому проведем
ВЕ и продолжим дальше до г. Если же ЕВ = Вг, то очевидно, что АВ есть ось; если
же нет, то разделим Е2. на два равных отрезка, пусть это будет Д и проведем ГД. па¬
раллельно прямой АВ. Очевидно, что ГД есть ось сечения. Ведь, будучи проведен¬
ной как параллельная диаметру, т.е. будучи сама диаметром, она рассекает прямую
Е7 на два равных отрезка и перпендикулярна ей. Таким образом, ГД найдена как
ось данной параболы.
И очевидно, что парабола имеет только одну ось. Ведь если это будет, допустим
АВ, то она будет параллельна прямой ГД. И она рассекает прямую Е2; тогда она так¬
же рассекает ее на д
»!•
•I»
•Ж
ва равных отрезка. Поэтому ВЕ = В7, что абсурдно.
229

Книга II
Предложение 47. Построение оси гипер¬
болы и эллипса
Найти ось данной гиперболы или эллипса.
Пусть теперь сечение будет гиперболой
или эллипсом. Надо найти его ось.
Допустим, что она найдена и пусть ею бу¬
дет КД, и пусть центром сечения будет К; тог¬
да КД перпендикулярна проведенным к ней
ординатам (Опр. 1, 7) и рассекает их на два
равных отрезка.
Проведем ГАА, КА и КГ. А поскольку ГД
= ДА, то также КГ - КА.
Если мы возьмем на сечении какую-то
точку Г, то этим определим отрезок ГК. По¬
этому круг, описанный из центра К радиусом
КГ, пройдет и через точку А. Однако сечение
АВГ задано. Поэтому можно найти точку А,
а значит, и отрезок ГА; и ГД = ЛА. С другой
стороны, точка К тоже задана, следователь¬
но, задана и ось ЛК
Построим следующим образом: Пусть бу¬
дут заданы гипербола или эллипс АВГ и най¬
ден центр в точке К (II, 45). Выберем на сече¬
нии некоторую точку Г и опишем из центра
К крут радиусом КГ. Проведем отрезок ГА и
разобьем его на два равных отрезка точкой Д.
Проведем также КГ, КЛ, КА, из которых КД
продолжим до В*.
А поскольку АЛ = ГД, а КД есть обшая сто-
•л


\
X
\
к	 \
1 Е
у
/ /
г
1
I
^к
Л
^к
^к
/
	1
у
г
1
I
\
/
/
\
\
у
/
Л
у
\ ;
/
А
N
47. Рис.2
• г
М
ЙИ
м
/
рона, то стороны ГЛ и ЛК будут равны сторонам АД и ЛК, а значит, основание КА
равно основанию КГ** Следовательно, отрезок КВЛ, проведен перпендикулярно
прямой ГЛА. И он рассекает ее на два равных отрезка. Следовательно, КД есть ось
гиперболы или эллипса.
Пусть через К будет проведена МКМ. параллельная прямой ЕА; тогда М1М есть
ось сечения, сопряженная с КЛ (Опр. 1,8).
Предложение 48. Сечения не могут иметь других осей
Исходя из ранее доказанного, показать, что указанные сечения не могут иметь дру¬
гих осей.
КМ
* Для эллипса
“ Вообще-то, КА и КГ равны поскольку они радиусы, а равенство треугольников не доказано,
так как необходимо еще и равенство углов между сторонами.

Предложения
Допустим, что кроме оси КД существует дру¬
гая ось КН. Тогда при проведенной перпендику¬
лярно оси и продолженной А0 получим (Опр.
1, 4) АО = ОД, поэтому АК = КА.
Однако также АК = КГ.
Следовательно, КА = КГ, что абсурдно.
Очевидно, что в случае гиперболы окруж¬
ность АЕГ не пересекается с сечением между^
точками А и Г; в случае эллипса проведем пер¬
пендикулярно МК отрезки ГР и А£.
Поэтому поскольку КГ= КА (ибо они есть
радиусы окружности)*, то КГ2 = КА2.
А поскольку ГР2 + РК2= КГ2 и АХ2 + £К2 =
КА2, то ГР2 + РК2= Л12 + £К2, а потому ГР2 -
ЛЕ2=£К2- КР2.
Атак как, с другой стороны**. MPPN + РК2
= КМ2 и MS-SN 4- SK2 = КМ2, то МР PN + РК2
= MS-SN + SK2.
Поэтому LK2- РК2 = MPPN — MS-SN.
Но мы уже доказали, что ГР2 - AS2 = SK2
- КР2, следовательно, ГР2 - AS2 = MPPN -
MS-SN.
С другой стороны, ГР и AS проведе¬
ны как ординаты к диаметру, значит (I, 21),
ГР2 AS2
MP PN ~ME SN .
А так как мы доказали, что соответствую¬
щие члены пропорции составляют еще и равные
разности, то ГР2 = MP PN. AS = MS-SN ♦*♦.
Таким образом, линия ГАМ есть круг****, что абсурдно, ведь мы предположи-
ли. что она есть эллипс.
* Имеется в виду, что если окружность пресечется с эллипсом, допустим, в точке А, то равен¬
ство КГ и КД уже не абсурдно, а очевидно. Значит, надо доказать, что они не пересекаются
•* Можно доказать это так еслиМР РМ + РК2 = КМг, тоМР РМ = КМ'-РК = (КМ - РК) (КМ + РК)
= МР РМ Таким же образом доказывается и следующая формула
а21 ъ1
— и а-
(1
<»!•
То есть если
с
вой и правой части пропорции — = —, получим
Ьг d
: ~b: = с- d, то a -c.b-'- d. Доказательство: вычтя единицу из ле-
2	-	a2-b2 c-d п
	:— =	. Поскольку равны числители, то
Ьг d
\
л
•7с
равны и знаменатели.
Полученные равенства выполняются только для окружности а поскольку А-произвольная
точка кривой, то все точки кривой лежат на окружности
231

Книга II
Предложение 49. Построение касательной к коническому сечению из точки, нахо¬
дящейся вне его
49. Рис. 1
Надо провести касательную к коническому
сечению от точки, находящейся не внутри него.
Пусть заданным сечением конуса б\дет сна¬
чала парабола (рис. 1), чьей осью является пря¬
мая ВЛ. Следует провести, как было предполо¬
жено, от заданной точки, находящейся не вну¬
три сечения, касательную.
Эта точка может находиться или на самой ли¬
нии, или вне сечения.
1.	Пусть точка А находится на сечении, и пусть
проведена касательная АЕ. Проведем АД пер¬
пендикулярно оси параболы. Тогда (1,35) ВД =
ВЕ. а ось ВЛ задана, поэтому заданы отрезок ВЕ
и точки В и Е Задана также и точка А; поэтому
теперь можно провести АЕ.
Построим следующим образом: От точки А
проведем перпендикуляр АД к оси параболы, отложим ВЕ = ВД и проведем прямую
АЕ. Очевидно, что она касается сечения.
2.	Пусть заданной точкой на оси будет Е и пусть проведена АЕ, касающаяся сече¬
ния. Проведем перпендикуляр АД, тогда ВД = ВЕ, а ВЕ задан, поэтому задан и отре¬
зок ВЛ и точки В и Л. Так как ДА есть перпендикуляр к оси, то ДА задан по постро¬
ению. По этой причине задана точка А. Однако так как задана также и Е, то, следо¬
вательно. положение АЕ задано.
Построим следующим образом: Отложим ВД = ВЕ, и от Л к ЕД пусть будет прове¬
дена перпендикулярно ДА, пусть будет проведена АЕ. Тогда очевидно, что АЕ каса¬
ется сечения.
А если заданная точка совпадает с В, то было доказано, что прямая, проведенная
перпендикулярно от В, касается сечения (I, 17).
3.	Пусть теперь заданная точка Г не находится на оси. Допустим, что проведена
касательная АГ, и пусть через Г будет проведена прямая, параллельная оси парабо¬
лы. Проведем от точки А к этой прямой ординату А7, тогда (I, 35) ГН = ¿Н.
Таким образом, заданы точки Н и X. а так как А7 проведена как ордината, г.е.
параллельна прямой, касающейся сечения в точке Н, то положение Аг задано. Та¬
ким образом, задана точка А. Однако точка Г также задана. Следовательно, задано
положение касательной АГ.
Построим следующим образом Через точку Г проведем прямую параллельно оси
и отложим на ней отрезок Н7, равный ГН, а затем проведем прямую ХА. парал¬
лельную касательной к точке Н. Теперь можно провести прямую АГ. Задача решена.
•л
•I»
•л
м
»I«.
•I»
»I*.
К
»1C».
Пусть теперь сечением будет гипербола (рис 2), чьей осью будет ГВД, центром
- Ö, асимптотами - 0Е и 0Z, а latus transversum - ВГ. Точка, через которую надо
232

Предложения
провести касательную может быть распо¬
ложена на самом сечении, или на оси, или
внутри угла Е(Э£, или внутри дополнитель-
ного, или внутри вертикального ему, или же
на одной из асимптот, содержащих сечение.
1. Пусть заданная точка А лежит на сече¬
нии, и пусть проведена касательная АН. Про¬
ведем отрезок АД перпендикулярный к оси
_ ГД ГН
•К
93
и
гиперболы. Тогда (1, 34) — =	.
ВД НВ
Однако отношение — задано, ибо зада-
ВД
ны оба отрезка, следовательно, задано и от¬
ношение 	. Но диаметр ГВ известен, зна-
НВ
чит, задана и точка Н*, как и точка А, следо¬
вательно, касательная АН задана.
Построим следующим образом'. Из точки
А опустим на ось гиперболы перпендику¬
49. Рис. 2
ляр АД. Поскольку справедлива
I
порция
ГД ГН
— =	, то точка Н задана, и мы мо-
ВД НВ
жем провести прямую АН. Очевидно, что АН есть решение задачи и очевидно, что
от Н может быть проведена в другую сторо
ну другая прямая, касающаяся сечения.
•I»
2. Пусть заданная точка Н лежит на оси, и пусть проведена касательная АН. Опу¬
стим из точки А на ось гиперболы перпендикуляр АД. Тогда по той же самой причи-
„ ЪП	ГД ГН
не (I, 34) справедлива пропорция — =	.
ВД НВ
Но ГВ задана, следовательно, задана точка Д, а так как отрезок АД проведен
перпендикулярно, то он задан по построению. Однако также и сечение задано, по¬
этому точка А определена. А так как и точка Н задана, то и отрезок АН построен.
Построим следующим образом: Определим точку Д с помощью пропорции
о
ВД НВ
Проведем из нее перпендикуляр ДА и проведем отрезок АН. Очевидно, что это и
есть искомая касательная и что от точки Н таким же образом можно провести пря¬
мую, касающуюся сечения с другой стороны.
•I».
о
Однако как найти отрезок НВ построением9 Покажем, что он равен половине среднего гармо-
ГД ГН
нического отрезков (-)В и ВД. Пусть они равны соответственно а и Ь. Тогда соотношение	=

ДВ НВ
выглядит так.	~~ Н&. Отсюда	. Среднее гармоническое можно найти, напри-
Ь НВ	а + Ь
мер, с помощью трапеции: если а и Ь - основания трапеции, то среднее гармоническое будет от¬
резком, проведенным через пересечение диагоналей параллельно основаниям.
о
233

Книга II
кл мл‘
3. При тех же самых предпосылках пусть заданная точка К находится в простран¬
стве, расположенном внутри угла 70Е, и ог точки К проведена прямая КА, касаю¬
щаяся сечения. Проведем и продолжим К0 так, чтобы 0Л = 0Ь1, тогда все они бу¬
дут заданы. Следовательно, также и отрезок НА будет задан. Продолжим его и про-
NN4
ведем к нему ординату АМ, тогда (1, 34)
КК	Ш ,,
Однако отношение	задано, тогда также задано отношение	. И точка А
КЛ	МЛ
задана, поэтому и точка М определена. Теперь проведем через М ординату, парал¬
лельную прямой, касающейся сечения в Л. Л так как сечение задано, то тем самым
найдена и точка А. Но и точка К задана, следовательно, АК есть искомая касательная
Построим следующим образом: Если при прежних предположениях заданной точ¬
кой будет К и отрезок К0 будет продолжен так, что 0А = 014, то, то с помощью про-
ык	_
порции
— = —- можно определить точку М. Затем проведем МА, параллельную
КЛ МЛ
прямой, касающейся сечения в Л, и прямую КА, которая и является искомой каса¬
тельной. Очевидно, что от точки К таким же образом может быть проведена пря¬
мая, касающаяся сечения с другой стороны.
4. При тех же самых предпосылках пусть заданная точка X лежит на одной из асим¬
птот (рис. 3) и пусть проведена искомая касательная 7АЕ. Проведем через точку А
отрезок АД, параллельный асимптоте Е0. Поскольку АЕ = КХ (II, 3), то Д0 = \Х.
К так как ¿0 задана, то задана и точка А. Через нее проведем прямую ЛА, парал¬
лельную асимптоте Е0, тогда ее положение задано. Поскольку сечение задано, то за¬
дана и точка А, а так как задана точка 7, то, следовательно, касательная ¿АЕ найдена.
Построим следующим образом: Пусть 0Е и 07 - асимптоты, на одной из которых
расположена заданная точка X, а отрезок 07 рассечем в Л на два равных отрезка. Че¬
рез точку Д проведем прямую ЛА, параллельную 0Е, а через точку А - отрезок 7А.
А поскольку 7Д = Д0. то ТА = АЕ.
Следовательно, по доказанному выше (II, 9),
ТАЕ касается сечения.
4. При тех же самых предпосылках пусть за¬
данная точка К лежит внутри утла, дополнитель¬
ного к углу Е07 (рис. 4) и, допустим, проведена
искомая касательная КА. Проведем и продол¬
жим прямую К0. Ее положение задано, поэто¬
му если на сечении берется какая-то точка Г, и
через Г проводится ГД, параллельная К0. то ее
положение также будет задано. Если ГД рассе¬
кается точкой Е на два равных отрезка, то поло¬
жение прямой 0Е будет задано, и она будет диа¬
метром, сопряженным с К0 (Опр 1,6). Поэтому
пусть будет 0Н = 0В. и пусть через А будет про¬
ведена АА. параллельная прямой 0В,
ЙЕ
ЙЕ
234

Предложения
Тогда поскольку КА и ВН суть сопряжен¬
ные диаметры, и ЛК - касательная, а АЛ па¬
раллельна прямой ВН, то К0-0Л равно чет¬
вертой части эйдоса, лежащего у ВН (I, 38;
II, 40 примечание). Поэтому К0-0Л задано.
И задана К0, тогда можно найти 0Л, а сле¬
довательно, и положение Л. И если через Л
провести ЛА, параллельно прямой ВН, то
положение ЛА будет задано. Однако задано
также сечение; поэтому положение точки А
определено. А поскольку задана и К, то КА
есть искомая касательная.
Построим следующим образом: Пусть за¬
данная точка К находится в пространстве.
которое мы обозначали, и пусть проведен¬
ная К0 будет про
должена дальше. Возьмем
на сечении некоторую точку Г и проведем
ГЛ, параллельно прямой К0. Рассечем ГД точкой Е на два равных отрезка, и пусть
проведенная У0 будет продолжена дальше так, что 0Н = 0В. Тогда НВ есть latum
(гапБУегеигп, сопряженный с К0Л, следовательно, К0-0Л равно четвертой части эй¬
доса, построенного на ВН. Поскольку К0 задано, то можно определить положение
точки Л. Проведем прямую, параллельную ВН. Сечение задано, следовательно, за¬
дана и точка А. Тогда очевидно на основе обратимости теоремы, приведенной рань¬
ше (I, 38), что прямая КА касается сечения.
5. Если же точка будет задана в пространстве, расположенном между ¿0 и0П,
то касательную провести невозможно, ибо прямая, касающаяся сечения, будет рас¬
секать прямую Н0, а потому пересечется с каждой из 70 и 0П, что невозможно из-
за доказанного в Предложениях (I, 31) и (II, 3)*.
Пусть сечением будет эллипс, чьей осью будет ВАГ, а центром — 0.
йе
1. Пусть заданной точкой на се¬
чении будет А, и нужно, чтобы от А
была проведена прямая, касающая¬
ся сечения. Допустим, что проведены
касательная АН и ордината АЛ. Тогда
А задана и имеем соотношение (1,36)
ГА ГН
ВД ~ НВ .
Отношение —задано,еледова-
ВД
ГН
тельно, задано и —, значит, можно
НВ
* Достаточно было просто сослаться на (I, 31).
235

Книга II
I
найти положение точки Н. Однако задана также А, следовательно, положение пря¬
мой АН задано.
Построим следующим образом: Проведем перпендикуляр к оси АД. Справедлива
ГД Тн
пропорция, — = —, чем определен отрезок НВ. Проведем АН. Очевидно, что как
ВД НВ
и на гиперболе, прямая АН касается сечения (1, 34).
2. Пусть заданной точкой будет точка К. через которую требуется провести каса¬
тельную КА. Допустим, она проведена и пусть проведенная к центру Л прямая КЛ0
будет продолжена до сечения, тогда она будет задана. И если АМ проводится как
, NM <
ордината к диаметру АТ, то (I, 34)
Ж	ИМ
Однако отношение	задано, поэтому также задано отношение	. Тем са-
КЛ	МЛ
мым найдена точка М, через которую проведем прямую МА, параллельно прямой,
касающейся сечения в точке Л и, таким образом, зададим прямую МА. Поэтому А
задана. Однако задана также К. Следовательно, положение КА задано.
Построение производится согласно вышеприведенному анализу.
МЛ КА
Предложение 50. Построение касательной, образующей заданный угол с осью.
Надо провести прямую, касающуюся заданного конического сечения, которая обра¬
зует с осью угол, равный заданному острому углу.
Пусть сначала сечением конуса будет парабола (рис. 1) с осью АВ. Необходимо
провести прямую, касающуюся сечения, которая образуете АВ угол, равный задан-
Допустим, проведена касательная ГД, тог¬
да ¿ГД В задан. Опустим из точки касания
перпендикуляр ГВ на ось, тогда также задан
угол, находяшийся при В. Поэтому задано
АВ
отношение	. Однако также задано отно-
ВГ
ДВ	АВ
шение —*, следовательно, задано	.
АВ	ВГ
Тогда ¿ВАГ также задан, и он располо¬
жен на оси АВ и на заданной точке А, следо¬
вательно, задано положение второго луча АГ.
Однако и сечение также задано, в силу чего
задана точка Г. Таким образом, положение
ГД задано и ГД касается сечения.
Построим следующим образом: Пусть за¬
данным сечением конуса является парабола
ДВ
• Э'20'35’
236

Предложения
с осью АВ, а заданным острым углом - Е/Н, и на Е/ взята точка Е, а из нее прове¬
ден перпендикуляр ЕН. Из точки 0, рассекающей отрезок 7Н на два равных отрез¬
ка, проведем прямую 0Е. Построим теперь угол ВАГ, равный углуН0Е, и проведем
АГ до пересечения с кривой в точке Г. Проведем к оси перпендикуляр ГВ и отло¬
жим на ней отрезок АА = АВ.
Тогда ГА и есть искомая касательная.
В таком случае я утверждаю, что /ГАВ = Z EZH.
D	ZH АВ 0Н АВ ZH
Ведь поскольку	и	= т—г , то
50. Рис. 3
Н
Л
ОН АВ НЕ ВГ
И также углы, расположенные при Н и В, яв¬
ляются прямыми, следовательно, /ГАВ = / Е7Н.
Пусть теперь сечением будет гипербо¬
ла (рис. 2) с центром X, и пусть она зада¬
на. Допустим, что проведена касательная
ГА. Проведем ГХ и отрезок ГЕ, перпендику¬
лярный оси, тогда задано отношение (I, 37)
EXEA Lt	ЕГ2
	;— =—.а также отношение ——~. посколь-
ЕГ2	Lr	ЕД'
ку заданы углы ГАЕ и АЕГ. Поэтому задано также
EX ЕА	ЕХ
отношение		— и тем самым отношение —.
ЕА2	ЕА
Следовательно, можно построить угол при
вершине X.
Поэтому при заданном положении прямой
ХЕ, и при заданной точке X мы можем провести
под этим углом прямую ГХ. Так как задано по¬
ложение сечения, то задана и точка Г, следова¬
тельно, ГА и есть искомая касательная.
Пусть проведена асимптота сечения, тогда
ГА, будучи продолжена, пересечется с асимпто¬
той в некоторой точке Z. Тогда /ZAE > ZZXE.
Следовательно, чтобы построение было воз¬
можно, заданный острый угол должен быть боль¬
ше половины угла, ограниченного асимптотами.
Построим следующим образом'. Пусть задана
гипербола с осью АВ и асимптотой XZ (рис. 3),
а заданный острый угол ZK0H > ZAXZ и пусть
/К.0А = ZAXZ.
Тогда, если от точки А восставлен к АВ пер¬
пендикуляр AZ, а на отрезке Н0 будет взята не¬
которая точка Н, и от нее проведен перпендикуляр к 0К. то, поскольку утлы при А
и К являются прямыми, справедлива пропорция 	=

AZ КА.
237

Книга II
К®	К®	АХ	К®	АХ2	К®2
А так как > , то и —— > ——, а значит,	, >	. .
КА	КН	AZ	КН	AZ	КН2
АХ2 Lt	Lt К®2
Однако так как (II, 1) у = —, то и — > 77777 •
AZ? Lr	Lr КН
АХ2
Поэтому если отношение квадрата какой-то величины к КН- будет равно		,
А2
то она будет больше, чем К0:.
Допустим, квадрат этой величины будет равен КМ К0, и пусть будет проведена
КМ2 КМ К® КМ2 АХ2
НМ. А поскольку КМ’ЖМК®, то и		5— > т.е.	г >	г •
КН2 КН2 КН2 лг2
2 •
п	лу;	а	г	КМ'
Пусть теперь АХ2 так относится к квадрату какой-то другой величины, как

КН
Тогда она будет меньше, чем А/2 и прямая, проведенная от X к взятой точке, про¬
изведет схожие треугольники*. Поэтому /АХ7 > /КМН и /АХГ = /КМН, тогда ХГ
рассекает сечение (II, 2). Проведем от Г касательную ГА (II, 49)** и опустим пер¬
пендикуляр ГЕ. Очевидно, что треугольник ГЕХ подобен треугольнику КМН. Поэ-
ЕХ2 КМ2
тому	г =	г
ЕГ2 КН2 .
Lt ЕГ2 КН2
— то	=

Lr ’ EX EA KMK0
EX KM
и, соответственно,	=	.
ЕА К0
ЕГ КН
, из которой сле-
„ EXEA Lt KM КО
Однако поскольку (I, 37)  	¿— = — и	у
EI ~ Lr КН‘
ЕГ2 КН2 ЕХ2 КМ2
А поскольку —у =	у, то	=

EX* KM2 EX EA КМ К®
т	ЕГ КН
Тогда, учитывая, что — =	, получим пропорцию — =

ЕХ КМ	ЕА К0
дует, поскольку углы, расположенные при Е и К, прямые, что /ЕАГ = /К0Н.
Z
Пусть сечением будет эллипс (рис.
4) с осью АВ, и пусть он задан
Допустим, что касательная проведе¬
на, тогда задан /ГАА. Проведем пер¬
пендикулярно оси отрезок ГЕ, чем бу-
ЕД2
дет задано отношение —
ЕГ
Пусть X есть центр сечения и про¬
веден радиус ХГ. тогда задано отноше-
ЕГ2 Ьг
ние(1’37)ытги-
а
у
. .... -
В
2 •
•ж
•ж
* То есть если мы отложим на Аг отрезок, равный этой величине, и соединим его конец с X, то
получим треугольник, подобный треугольнику КМН.
*’ На этом построение заканчивается, а далее доказывается, что угол Е0Г равен заданно¬
му углу КОН Построение сводится к нахождению угла КМН (см комментарий в конце теоремы).
238

Предложения
ЕД:
Поэтому также задано отношение l;; -
ЕД ЕХ
ЕД	ЕГ
Но так как задано и отношение —, поэтому также задано отношение ■—.
ЕГ	ЕХ
Атак как угол, расположенный при вершине Е, является прямым, то угол с вер¬
шиной в точке X. задан. Он расположен при заданной прямой, поэтому и точка Г
определена, а от нее проведена касательная Г Л, следовательно, положение Г Л задано.
Построим следующим образом: Пусть ZHK есть заданный острый угол, и на его
стороне HZ взята точка Z. из которой опушен перпендикуляр Z0.
I4	0Z2 Lr
И пусть	= —.
Н0-0К Lt
Проведем KZ и построим угол ZAXr такой, что /ЛХГ = ZXKZ. Теперь проведем
ГД, касающуюся сечения (II, 49).
В таком случае я утверждаю, что ГД решает задачу, т.е. что ZTAE = ZZH0.
„	EX 0К EX2 0К2
Ведь поскольку справедлива пропорция 	=	, то —г =	г • а также
ЕГ 0Z ЕГ' 0Z'
ЕГ2 0Z2
—■	= -••• • - ибо каждая из них есть то же самое отношение latus rectum
ЕД ЕХ Н0 0К
к latus transversum. Тогда из выше приведенных равенств получится пропорция
EX2 0К2	EX 0К
——■— = —	, а значит, и — =

ЕД-ЕХ Н0 0К	ЕД Н0.
EX 0К
С другой стороны, —■ =	, следо
ЕГ 0Z
и, С
il*.
»!•
ЕД НО
вательно, — =	, то есть стороны, содер-
ЕГ 0Z
о
М
жашие прямые углы, являются соразмерными.
Поэтому ZГДE = ZZH0.
Следовательно, ГД есть решение задачи.
»г»
Комментарии ред.
Построение сводится к тому, что необходимо найти точку Г. Если известен угол
КМ Н. то для этого надо только построить равный ему угол с вершиной в X. При этом
не надо находить «другую величину», которая будет нужна, лишь для доказательства
того, что угол КМ Н меньше угла AXZ. Если найти отрезок КМ, то угол КМ Н будет
определен, но Аполлоний не пишет, как это сделать, а вводит величину (обозначим
а АХ
ее а), про которую известно, что	=	и что а2 = КМ-К0. Следовательно, надо
КН AZ
найти сначала а. а потом и КМ. Поскольку осАг = КН АХ , то для этого нужно по¬
строить прямоугольник со стороной AZ, равновеликий прямоугольнику КН АХ , а
затем прямоугольник со стороной К0, равновеликий квадрату а а . Как это сделать,
показано в комментарии к (I, 60). Такая же картина и в случае эллипса: там сначала
надо найти величину а, а затем, учитывая, что а2 = Н0-0К , и 0К. Возможно, эти
построения считались
щеизвестными, и по этой, или по какой-то другой причи¬
не, Аполлоний про них не говорит.
239

Книга II
Предложение 51. Построение касательной к параболе и гиперболе, которая образу¬
ет с диаметром, проведенным через точку касания, угол, равный заданному острому углу
Провести прямую, касающуюся коническо¬
го сечения, которая образует с диаметром,
проведенным через точку касания, угол, рав¬
ный заданному острому углу*.
Пусть сначала сечением конуса будет па¬
рабола (рис. 1) с осью АВ, а заданный угол -
0. Нужно провести прямую, касающуюся па¬
лы, которая
веденным от точки соприкосновения угол,
равный углу©.
Пусть касательная ГД к параболе прове¬
дена так, что она составляет с диаметром ЕГ,
проходящим через точку соприкосновения,
угол ЕГД, равный углу©, и пусть ГД пересе¬
кается с осью параболы в точке Д. Поскольку
АД параллельна прямой ЕГ, то ¿АДГ = ¿ЕГД.
Однако так как ¿ ЕГД задан, то, следо-
вательно, ¿АДГ также задан.
Построим следующим образом: Пусть дана парабола с осью АВ, а заданным углом
та
является ©.
ведем отрезок ГД, касающийся сечения и
разующий с осью угол
АДГ, равный углу © (II, 50). а через точку Г проведем ЕГ, параллельную прямой АВ.
А поскольку ¿АДГ = ¿© и ¿.АДГ = ¿ЕГД, то ¿ЕГД = ¿©.
Пусть теперь сечением будет ги¬
пербола (рис. 2) с осью АВ, центром Е,
асимптотой ЕТ, касательной к ней ГД и
заданным острым углом О. Допустим,
что проведен диаметр ГЕ и проведем
ГН перпендикулярно оси.
Тогда задано отношение 1д к Ьг, а зна-
ЕН НА
чит, задано и отношение (I, 37)	—.
ГН
Пусть будет взят отрезок ¿0, явля¬
ющийся хордой окружности, стягива¬
ющей дугу, равную углу О, а от точки
К окружности, являющейся вершиной
угла, проведем перпендикуляр КА, обра-
¿А • А0
зуя, таким образом, отношение	,—.
кл2
* То есть задан угол и надо найти точку, через которую проведем касательную.
240

Предложения
и
И пусть оно равно —. Проведем также 7 К и К0.
ен-нд глло и
Поскольку 77К0 = /ЕГД и	— =	;; /1— = —, то и треугольники К7Л и
ГН КЛ Ьг
ГЕН, К70 и ГЕД будут подобны*. Следовательно, 7К70 = 7ГЕД.
Построим следующим образом: Пусть задана гипербола, с осью АВ, центром Е, и
задан острый угол О.
И
Пусть заданное отношение — будет равно отношению частей некоторого отрез-
Ьг
ХУ
ка	 и пусть УФ рассекается точкой У на два равных отрезка (рис. 3).
ХФ
Проведем горизонтально отрезок 70, являющийся хордой окружности, стяги¬
вающей дугу меньшую, чем половина круга**. Опустим из центра окружности на
70 перпендикуляр NO, который пусть рассекается точкой П на два отрезка соглас¬
но отношению 	. Проведем через П отрезок ПК, параллельный прямой 70, а от
ХФ
точки К к продолженной 70 проведем перпендикуляр КЛ, а также 7К и К0. Про¬
должим ЛК дальше до М и проведем к ней от точки N перпендикуляр №. Тогда он
параллелен прямой 70.
Очевидно, будет справедлива пропор-
N11 ЕК ' УФ
ция	=	=	.
ПО КЛ ХФ
51. Рис. 3
М
•Ж
1
1
I

X
УФ мк
Если удвоить УФ и -К, то	=	.
ХФ КЛ
Прибавив слева и справа единицу, по-
ХУ МЛ
лучим	=	.
ХФ КЛ
МЛ МЛ КЛ
Но очевидно, что

КЛ
ХУ МЛКЛ
поэтому	=	;	.
ХФ КЛ2
С другой стороны (Евклид III, 36),
МЛ КЛ 7Л Л0
КЛ2 КЛ2
. ху и глл© и
А так как	= —,тои	-— = —.
ХФ Ьг КЛ2 Ьг
* Докажем их подобие Пусть ¿ЛГН = а, а ¿0КЛ = 0. Тогда последнее равенство можно запи-
сать так: /£ (а + Г2) • tga = # (/7 + И) tg/3. Отсюда +	=	• Если а> 0, то правая часть меньше
единицы, а левая - больше, и наоборот. Поэтому равенство возможно только при а = 0 Следова¬
тельно, треугольники К7\ и ГЕН подобны, а значит, и zKZ0 = ¿ГЕД.
” Аполлоний смотрел на это с другой стороны: «.. и на ней отрезок круга, больший, чем по¬
лукруг»
• « •
241

Книга II
, ТО
Пусть от А восставлен к АВ перпендикуляр АТ (рис. 2). Было доказано, что (II, 1)
ЕАг_Ы
АТ2 ” Ег'
гл2 гл л© гл2 еа2
А поскольку	то
Углы, расположенные при А и А, являются прямыми, значит, /ЛУК < ¿АЕТ.
Следовательно, если мы построим угол АЕГ равный /Л2К, то ЕГ пересечется с
сечением в некоторой точке Г (II, 2) Проведем от нее касательную ГА (II, 49) и пер¬
ги п	^ен-нд и гл л© Ён-нд
пендикуляр ГН. Поскольку (I. 37)		— = — , то	;— =	-— и треуголь-
ГН2 Ьг АК2 НГ2
ники К7А и ГЕН, КОЛ и ГАН, К70 и ГЕА будут подобными.
Следовательно, ZEГA = ¿гКО = ¿О.
Ы
Если же отношение — равно единице, то КА касается круга 70К, и прямая,
Ьг
проведенная от центра N к точке К параллельно прямой 70 дает решение задачи.
Предложение 52. В эллипсе угол, образованный касательной и радиусом, проведен¬
ным к точке касания не меньше угла, дополнительного к углу, образованному прямыми,
соединяющими конец малой оси и концы большой оси
Если прямая касается эллипса, то угол,
который она образует с диаметром, прове¬
денным через точку касания, не меньше
угла, дополнительного к углу, образован¬
ному прямыми, соединяющими конец ма¬
лой оси с концами большой оси
Дан эллипс с осями АВ и ГА и центром
Е. Пусть АВ будет большой осью, а прямая
НА касается сечения в точке 7.
Проведем АГ, ГВ, 7Е, и продолжим ГВ
до Л. В таком случае я утверждаю, что не
может быть, чтобы 7А70 < 7АГ0.
Ведь 7В или параллельна прямой АВ,
или нет.
Л
52. Рис. 1
»I«
Пусть сначала она будет параллельна ( рис. 1).
Так как АЕ = ЕВ, то А0 = 0Г А так как ZE - радиус, то касательная парал¬
лельна прямой АГ (II, 6) Однако и 7Е параллельна прямой АВ, следовательно, че¬
тырехугольник 70ГА есть параллелограмм. Тогда ZA70 = 7ЛГ0*.
А поскольку АЕ = ЕВ > ЕГ. то 7АГВ тупой, a 7ЛГО - острый. По этой причине
ZA70 также острый угол. Следовательно, ZHZE есть тупой.
* Далее., сверх заявленного, Аполлоний докажет, что угол Н2Е тупой.
242

Предложения
Пусть 2Е не параллельна прямой АВ (рис, 2).
Проведем перпендикуляр 7К. По¬
скольку 7Е не параллельна АВ, то угол
АВЕ не будет равен углу 7ЕК, а так как
углы, при Е и К прямые, то отношение
ЕВ2	КЕ2
—гне равно
ЕГ2
„	ЕВ2 ЛЕЕВ
С другой стороны, —- =	—
ЕГ2 ЕГ2
согласно (I, 21) и (I, 37),
НККЕ 1Л
ЛЕЕВ и
ЕГ2 ” Ьг
52. Рис. 2
Поэтому не будет верна и
порция
КЕ2
к/2
НККЕ
кг2
К/2 .
л
л
Следовательно, НК не равно КЕ.
Пусть за отрезок круга будет принят КУМ, принимающий угол, равный углу АГВ
(рис. 3). Но /АГВ является тупым; тогда КУМ меньше дуги полукруга.
Возьмем точку Е так, чтобы	, и проведем через нее перпендикуляр УХ,
также отрезки КУ, УМ и перпендикуляр ОТП, разбивающий КМ в точке Т на д
равных отрезка, из чего следует, что он есть диаметр. Пусть точка Р будет центром
круга, и от нее проведен перпендикуляр РЕ, а от точки О отрезки ОК и ОМ. А по¬
скольку /КОМ = /АГВ и каждый из отрезков - АВ (рис. 2) и МК (рис. 3) рассека¬
ется в точках Е и Т пополам, а углы, расположенные при Е и Т, являются прямыми,
НТ2 ЕВ2
то треугольники ОТК и ГЕВ - подобны. Следовательно -	.
X
О
т
52. Рис. 3
Поскольку же ТР = ЕЕ, и РО > ЕУ, то
РО ЕУ
РТ > ЕЕ .
..	„ РО ЕУ
И наоборот, — <	.
ОТ УЕ
Если же взято удвоение предшествующего,
ПО ХУ
то	<	, а если слева и справа вычесть еди-м
ОТ УЕ
ПТ ХЕ
НИНУ, то	<	.
ОТ УЕ
ПТ ЬГТ2 ЕВ2 и НККЕ
Однако	= —г=—г = — =-	:—-
ОТ ОТ2 ЕГ2 Ьг кг2
(Пояснение: Так как ПО - диаметр круга,
ПТ КГ	ПТ ЫТ2
то — = —, или  = —
КТ ОТ	ОТ ОТ
р
2 '
243

Книга II
НК.-К.Е №-аМ
		;—<	*
кг2
V-2	'
К
ЫТ2 ЕВ2
А поскольку углы N01 и ЕГВ равны, то =	•
л	ЕВ2 НККЕ Ы.
Однако было доказано, что —г =	— = — |,
ег2 кг~ Ьг
НККЕ ХЕ	НККЕ ХЕ-УЕ
поэтому кг2 < у= ’т0 есть кг2 < у~2_'или
НККЕ
Поэтому если мы приравняем отношение ———-г— к отношению произведения
! ЕМ к некоторой другой величине, то последняя будет большей, чем УЕ2.
НК КЕ КЕ-ЕМ
Допустим, это будет ЕФ:	т— =	г—.
К2 ЕФ
НК КЕ
Тогда, поскольку —— = —- и К/ и -Ф - перпендикуляры, то /Н7Е = /КФМ**.
КЕ 2.\1
ЕФ2
Поэтому (Евклид I, 21) /КУМ > /Н7Е, атак как /АГВ = /КОМ = /КУМ, то
и /АГВ > /Н/Е, а для дополнительных углов: /Аг© > /АГ0.
Следовательно, неравенство /Лг© < /АГ© не выполняется.
Предложение 53. Построение касательной к эллипсу, которая образует с диаметром,
проведенным через точку касания, заданный острый угол
о
Надо провести прямую, касающуюся заданного эллипса, которая образует с диаме¬
тром, проведенным через точку касания, угол, равный заданному острому углу, при этом
требуется, чтобы этот угол был не меньше угла, дополнительного к углу, обра зованно¬
му прямыми, соединяющими конец малой оси с концами большой оси***.
Пусть дан эллипс с большой осью АВ, малой - ГА, центром Е, и проведены АГ и
ГВ, а заданным будет/У, не меньший, чем /НГ7; поэтому также /АГВ не меньше/Х.
Заданный угол У может быть или боль¬
ше угла Н П или равен ему.
Пусть сначала /У = /.Н Гг (рис. 1).
Проведем через точку Е прямую ЕК.
параллельную В Г, а через точку К пря¬
мую 0Н, касающуюся сечения (II. 49).
АЕ Аг
Поскольку АЕ = ЕВ и — = — , то А/
ев гг
= /Г, а ЕК есть радиус, следовательно,
прямая, касающаяся сечения в точке К,
параллельна прямой АГ (II, 6). Однако
* Это следует из подобия треугольников МЕХ и УЕМ.
•• Перемножив почленно два предыдущих равенства, получим, что гНЖ = /КФЕ, а разделив
- что /кгк = гЕФМ.
То есть надо найти точку, через которую проведем касательную Вопрос о величине угла
осмотрен в предыдущем Предложении.

Предложения
и прямая ЕК параллельна прямой НВ,
поэтому КНГ2 есть параллелограмм, в
силу чего ¿НК/ =/НГ2, а ¿НГ/ =2У,
следовательно, ¿Н1С/ =¿7.
Пусть теперь ¿У > ¿НГ/ (рис. 2)*.
Тогда наоборот, ¿X < ¿АГВ.
Возьмем круг (рис. За и 36), в ко¬
тором будет построен угол М1МП. рав¬
ный углу X, и через точку О, разбиваю¬
щую отрезок МП на два равных, прове¬
дем перпендикуляр а также отрезки
55. Рис. 2Ь
0
Л
МЫиТЧП.
Тогда очевидно, что ¿М1ЧП < ¿АГВ.
Однако ¿МЬЮ = '¿¿ММП и ¿АГЕ = ’¿¿АГВ , поэтому ¿МЬ1П < ¿АГЕ.
N
Р
о а	т
*  	•
р
53. Рис. ЗЬ
53. Рис. За
* Очевидно, возможны два варианта проведения касательной
245

Книга II
_	r _	МО AE	M°2 , AE2
Так как углы при Е и О прямые, то	<	и, соответственно, , < ™2 •
7 и	ON ЕГ	ON2 ЕГ
OP АЕ-ЕВ	, OP Lt
АтаккакАЕ2 = АЕ-ЕВи МО2 = МО-ОП*, то^^- <—.-,а значит(1,21),^у < “•
Поэтому предположим, что latus transversum относится к latus rectum, как части
соа
некоторого отрезка шт. а именно	, который рассекается точкой о на два равных.
ОР соа	ат
Тогда —— < —.
ON аг
NP сот
Прибавив справа и слева единицу, получим	< —.
ON ат
Пусть Ф будет центром круга, тогда, учитывая, что NP = 2ON и шт = 2ат, имеем
0N от
		<—.
ON ат
п	ОФ аа
Вычитая слева и справа единицу, получим	< —.
ON ат
Выберем теперь на прямой NO точку I такую, чтобы выполнялось равенство
ОФ оа
Ясно, что 01 меньше, чем 0N.
Проведем теперь IH и ФТ параллельно МП и НТ параллельно NP.
ОФ ЕЧР
Очевидно, что	= —.
01	22	от ТН
Прибавив слева и справа единицу, получим — =— , а умножив обе части на
сот НТ	ат
два, имеем — =— .
ат ЕН
_	coa ЕТ	соа
Теперь вычтем слева и справа единицу: — - —, а так как —
ат ЕН	ат Lr ЕН Lr
Проведем теперь МЕ и НП и построим угол АЕК, равный углу МПН. Затем про¬
ведем через точку К прямую НО, касающуюся сечения (II, 49), и ординату КА.
А поскольку /НПЕ = ZKEA, и углы при точках Е и А - прямые, то треугольни¬
ки НПЕ и КЕА равноугольны.
_	_	.. п	ЕТ-Е
Далее, так как ЕТЕ— = МЕЕП , то — =

ЕН ЕН2 ЕН2 Lr
А поскольку (I, 37) — =	—, то треугольники КОЕ и НМП подобны**
Lr КА'
и /МНП = ZOKE, a ZMHn = ZMNn = ZX, поэтому также Z0KE = ZX.
Следовательно, угол HKZ, дополнительный к углу ОКЕ равен углу Y.
Lt ET Lt
, то	=	.
MEET! Lt
‘ Это следует из подобия треугольников M0N и РОП.
“ Из подобия треугольников -П1 и КЕ\ следует, что
HS _КЛ
1П “ ЛЕ
если умножить почленно это
выражение на
0Л ЛЕ
то получим, что
МЕ 0Л
SS КЛ
следовательно, ZzlMI = ZK0A, и тре
MS ЕП
SS2
угольники под

ДОСЛОВНЫЙ ПЕРЕВОД КНИГИ II
I
Если прямая касается вершины гиперболы, и на ней отделяются равные отрезки в
обе стороны, равные четвертой части эйдоса, построенного на диаметре, то прямые,
проведенные из центра сечения к концам отрезков, отделенных на касательной, не пе¬
ресекаются с сечением.
Пусть дана гипербола с диаметром АВ, центром - Г, прямой стороной —
пусть ДЕ касается сечения в В. и пусть также будет ВЛ в квадрате равно ВЕ в квадра¬
те равно одной четвертой ABZ ¡ABxBZ], а прямые ГД и ГЕ пусть будут продолжены.
В этом случае я утверждаю, что они не пересекаются с сечением.
Предположим, что ГД пересекается с сечением в Н, и пусть будет построена упо¬
рядоченно прямая к диаметру Н0 ¡ордината], которая в силу перпендикулярности к
нему будет параллельна прямой ДВ. Тогда поскольку АВ к BZ равно АВ в квадрате к
ABZ, и ГВ в квадрате равно одной четвертой АВ в квадрате, ВД в квадрате равно ABZ,
то АВ к BZ равно ГВ в квадрате к ДВ в квадрате равно Г0 в квадрате к0Н в квадрате.
Однако также АВ к BZ равно А0В |А0х0В] к 0Н в квадрате. Поэтому ГО в квадрате
к 0Н в квадрате равно А0В к 0Н в квадрате. Таким образом, А0В равно Г0 в ква¬
драте, что абсурдно. Следовательно, ГД не пересекается с сечением. Схожим обра¬
зом мы докажем, что и ГЕ не пересекается. Следовательно, ГД и ГЕ суть асимптоты.
2
При тех же самых предпосылках нужно доказать, что никакая асимптота не пе¬
ресекает угол, ограниченный прямыми \ГЕ.
Если возможно, пусть будет проведена Г0, и пусть через В будет проведена В0,
параллельная ГД, и пусть она пересечется с Г0 в 0, тогда по построению ДН равно
В0, а Н0 продолжим так. чтобы он проходил через точки К. Л и N. Поскольку В0
равно ДН, то равны и параллельны ДВ и Н0. Так как диаметр АВ разбивается точ¬
кой Г на два равных отрезка и к нему приложена известная ВЛ, то АЛВ плюс ГВ в
квадрате равно ГА в квадрате. Так как НМ параллельна ДЕ, то и НА равно ЛМ. По¬
скольку Н0 равно АВ, то НК больше ДВ. Однако и КМ больше ВЕ, поскольку' АМ
больше ВЕ, следовательно, МКН больше ДВЕ, т.е. больше ДВ в квадрате. Поэтому
поскольку АВ к Вг равно ГВ в квадрате к ВЛ в квадрате, и АВ к Вг равно АЛВ к ЛК
в квадрате и ГВ в квадрате к ВД в квадрате равно ГЛ в квадрате к АН в квадрате, то
ГА в квадрате к АН в квадрате равно АЛВ к ЛК в квадрате.
А поскольку ЛГ в квадрате относится в точности к АН в квадрате, как и отнятое
АЛВ относится к отнятому ЛК в квадрате, то, следовательно, ГВ в квадрате к МКН
равно ГЛ в квадрате к АН в квадрате равно ГВ в квадрате к ДВ в квадрате, откуда ДВ
в квадрате равно МКН, что абсурдно, ведь мы доказали, что МКН больше ДВ в ква¬
драте. Следовательно, Г0 не есть асимптота сечения.
3
Если прямая касается гиперболы, /то] пересекается с асимптотами и точкой ка¬
сания делится на два равных отрезка, а квадрат каждого из этих отрезков будет ра¬
вен одной четверти эйдоса, построенного на диаметре, проведенном через точку со¬
прикосновения.
247

Дословный перевод книги II
Пусть гиперболой будет АВГ, центром же ее - Е, асимптотами - ¿Е и ЕН, и пусть
некая прямая 0К касается ее в В. В этом случае я утверждаю, что 0К, проведенная
дальше, столкнется с 7Е и ЕН.
Если возможно, то пусть она не сталкивается, и пусть проведенная ЕВ будет
проведена дальше, и пусть будет установлено, что ЕД равно ВЕ; поэтому ВД есть
диаметр. Поэтому пусть будет установлено, что 0В в квадрате и ВК в квадрате бу¬
дут равны четвертой части эйдоса при ВД, и пусть будут проведены Е0 и ЕК. Они
суть асимптоты, что абсурдно, ведь мы уже предположили, что ХЕ и ЕН являют¬
ся асимптотами. Следовательно, К0, проведенная дальше, столкнется с асимпто¬
тами ХЕ и ЕН в X и Н.
Я же утверждаю, что В г в квадрате и ВН в квадрате равны четвертой части эй¬
доса при ВД.
Пусть они не будут равны, но, если возможно, то В0 в квадрате и ВК в квадрате
будут равны четвертой части эйдоса. Поэтому Е0 и ЕК суть асимптоты, что абсурдно.
Следовательно. /В в квадрате и ВН в квадрате равны четвертой части эйдоса при ВД.
•I».
4
Если даны две прямые, образующие угол и точка, расположенная внутри угла, надо
через /эту] точку провести коническое сечение, называемое гиперболой, таким обра¬
зом, что данные прямые будут асимптотами.
Пусть АГ и АВ будут двумя прямыми, включающими произвольный угол, распо¬
ложенный при А. и пусть будет задана некая точка Д, и нужно через Д на асимпто¬
тах ГАВ описать гиперболу.
Пусть будет проведена .АД и продолжена дальше к Е, и пусть будет АЕ равно ДА, и
пусть через Д будет проведена Д2, параллельная прямой АВ, и пусть будет XГ равно
\Х. и пусть проведенная ГД будет продолжена до В, пусть получится ДЕ на Н равно
ГВ в квадрате, и при проведенной дальше АД пусть вокруг нее через Д пусть будет
описана гипербола таким образом, что упорядоченные прямые [ординаты], в квадра¬
те будут равны прямоугольникам, лежащим возле прямой Н. превосходящим фигу¬
рой, схожей с эйдосом ДЕ на Н. А поскольку \Х параллельна прямой ВА, и ЕХ рав¬
но ТА, то также ГД равно ДВ. Поэтому ГВ в квадрате равно 4ГД в квадрате Однако
ГЕ в квадрате равно ДЕ на Н. Тогда ГД в квадрате равно ДВ в квадрате равно одной
четвертой ДЕ на Н. Следовательно, АВ и АГ - асимптоты описанной гиперболы.
5
Если диаметр параболы или гиперболы рассекает некую прямую на два равных от¬
резка, то прямая, касающаяся сечения на пределе диаметра, будет параллельна пря¬
мой, рассеченной на два равных отрезка.
Пусть АВГ будет параболой или гиперболой, чьим диаметром будет ДВЕ, пусть
¿ВЫ касается сечения, и пусть же на сечении будет проведена некая прямая АЕГ. даю¬
щая. что АЕ равно ЕГ В этом случае я утверждаю, что АГ и ХИ будут параллельными.
Ведь если это не так, то пусть через Г будет проведена Г0, параллельная прямой
2Н. и пусть будет проведена 0А. И поскольку АВГ есть парабола или гипербола,
чьим диаметром является ДЕ, а касательной - ХИ, и ей параллельна Г0, то ГК рав-
24Х

Дословный перевод книги II
но К.0. Однако ГЕ равно ЕА. Поэтому А0 будет параллельна КЕ, что невозможно,
ведь, продолженная дальше, она сталкивается с ВА.
6
Если диаметр эллипса ши окружности круга рассекает некую прямую, проведенную
не через центр, на два равных отрезка, то прямая на пределе диаметра касающаяся се¬
чения будет параллельна прямой, рассеченной на два равных отрезка.
Пусть будет эллипс или окружность круга, чьим диаметром будет АВ, и пусть
АВ рассекает в Е на два равных отрезка прямую ГА, проведенную не через центр.
В этом случае я утверждаю, что прямая, касающаяся в А сечения, будет параллель¬
на прямой ГА.
Допустим, что это не так, а если возможно, то пусть А7 будет параллельна пря¬
мой на касательной А. Поэтому будет АН равно 7Н. Однако АЕ равно ЕГ. Тогда Г7 и
НЕ являются параллельными, что абсурдно. Ведь если Н есть центр сечения АВ, то
Г7 будет сталкиваться с АВ, а если нет, то пусть будет предположен в качестве цен¬
тра К, и пусть проведенная АК будет продолжена дальше к 0, и пусть будет прове¬
дена Г0. Поэтому АК равно К0 и также АЕ равно ГЕ, а ГО параллельна прямой АВ.
Однако ей также параллельна Г7, что абсурдно. Следовательно, прямая, касающа¬
яся в А, параллельна прямой ГА.
7
Если прямая касается конического сечения или окружности круга, и на сечении про¬
водится прямая, параллельная данной, и рассекается на два равных отрезка, то прямая,
проведенная от точки соприкосновения к серединной (находящейся посередине) точке,
будет диаметром сечения.
Пусть сечением конуса или окружности круга будет АВГ. касательной — 7Н. и
пусть АГ будет параллельна прямой 7Н, АГ, которая в Е будет рассекать на два рав¬
ных отрезка, пусть будет проведена ВЕ. В этом случае я утверждаю, что ВЕ будет ди¬
аметром сечения.
Допустим, что это не так, тогда пусть диаметром сечения будет В0. Таким обра¬
зом, А0 равно 0Г, что абсурдно, ведь АЕ равно АГ. Следовательно, В0 не будет ди¬
аметром сечения. Тем же самым способом мы докажем, что никакая другая прямая,
кроме ВЕ, не будет диаметром.
•ж
8
Если прямая совпадает с гиперболой в двух точках, то, проведенная дальше в лю¬
бую из сторон она пересечется с асимптотами, и прямые, отсеченные асимптотами
и сечением, будут равны.
Пусть АВГ будет гиперболой, ЕА и А7 - асимптотами, и пусть некоторая прямая
АГ пересекается с АВГ. В этом случае я утверждаю, что она, проведенная дальше в
любую из сторон, пересечется с асимптотами.
Пусть АГ в Н рассекается на два равных отрезка, и пусть будет проведена АН; тог¬
да она будет диаметром сечения. Таким образом, прямая, касающаяся в В, являет¬
ся параллельной прямой АГ. Пусть касательной будет 0ВК. Тогда она будет пересе¬
»1«
249

Дословный перевод книги II
каться с ЕД и Д/. А поскольку АГ и К0 параллельны, и К0 сталкивается с ДК и Д0,
то АГ также будет пересекаться с ДЕ и Д/.
Пусть она пересекается в Е и И 0В равно В К; поэтому также /Н равно НЕ.
Следовательно, ГХ равно АЕ.
£с/ш прямая, пересекающаяся с асимптотами, рассекается на два равных отрезка
гиперболой, то с сечением она имеет только одну общую точку.
Пусть же прямая ГА, пересекающаяся с асимптотами ГАД, рассекается на два рав¬
ных отрезка в точке Е. В этом случае я утверждаю, что она не имеет более с сечени¬
ем ни одной
шей точки.
Допустим, что она совпадает и в В. Тогда ГЕ равно ВД, что абсурдно, ведь мы
предположили, что ГЕ равно ЕД. Следовательно, она не имеет с сечением никакой
другой общей точки.
10
Если какая-либо прямая, секущая сечение, сталкивается /пересекается/ с двумя
асимптотами, то прямоугольник, ограниченный прямыми, отсеченными между асим¬
птотами и сечением, будет равен четвертой части эйдоса при диаметре, который рас¬
секает на два равных отрезка прямые, параллельные проведенной прямой.
Пусть АГ будет гиперболой. ДЕ и ЕХ - асимптотами, и пусть будет проведена не¬
кая прямая ¿\Х, рассекающая сечение и асимптоты, и пусть АГ рассекается в Н на
два равных отрезка, и пусть будет проведена НЕ, пусть будет установлено Е0 рав¬
но ВЕ, и пусть от В к 0ЕВ будет проведена перпендикулярно ВМ тогда В0 есть диа¬
метр, ВМ - прямая сторона. В таком случае я утверждаю, что ДА/ равно одной чет¬
вертой 0ВМ равно XГД
Пусть через В будет проведена КА касающаяся сечения; тогда она параллельна
прямой &Х А поскольку мы доказали, что0В к ВМ равно ЕВ в квадрате к ВК в ква¬
драте равно ЕН в квадрате к НА в квадрате, и 0В к ВМ равно 0Н В к НА в квадрате,
то также ЕН в квадрате к НА в квадрате равно 0НВ к НА в квадрате. А поскольку
как ЕН в квадрате целиком относится к АН в квадрате целиком, так и отнятое ©Н В
к отнятому АН в квадрате , то также и оставшееся ЕВ в квадрате к остальному ДА/
равно ЕН в квадрате к НА в квадрате равно ЕВ в квадрате к ВК в квадрате. Поэто¬
му /АД равно ВК в квадрате.
Схожим образом мы докажем, что так же ДГ/ равно ВЛ в квадрате. Однако КВ в
квадрате равно В А в квадрате. Следовательно, также /АД равно /ГД.
Если какая-либо прямая рассекает каждую из двух прямых, которые заключают
угол, расположенный при угле, содержащем гиперболу, то она столкнется с сечением
только в одной точке, и прямоугольник, ограниченный прямыми, отделенными между
асимптотами и сечением, будет равен четвертой части квадрата диаметра, прове¬
денного как параллельного секущей прямой.
250

Дословный перевод книги II
•Ж
Пусть будет гипербола, чьими асимптотами будут ГА и АА, и пусть ДА будет про¬
должена дальше к Е, и пусть через некую точку Е будет проведена Е7, рассекающая
прямые ЕА и АГ.
Очевидно, что она будет сталкиваться с сечением только в одной точке, ведь пря¬
мая, проведенная через А как параллельная прямой Е7, как АВ будет рассекать угол
ГАД и столкнется с сечением и будет его диаметром; таким образом, EZ столкнется
с сечением только в одной точке.
Пусть она столкнется в Н.
В таком случае я утверждаю, что ЕН7 равно АВ в квадрате.
Пусть через Н будет проведена ордината ОН КА; тогда прямая, касающаяся в В,
будет параллельна прямой НО. Пусть это будет ГД. А поскольку ГВ равно ВД, то ГВ в
квадрате к ВА в квадрате равно ГВД к ВА в квадрате равно ГВ к ВА на ДВ к ВА Одна¬
ко ГВ к ВА равно ОН к Н7, ДВ к ВА равно НК к НЕ Поэтому получается ГВ в квадра¬
те к ВА в квадрате равно ОН к на КН к НЕ И также КНО к ЕН7 равно ОН к
наКН к НЕ. Поэтому КНО к ЕН7 равно ГВ в квадрате к ВА в квадрате. И при пере¬
становке КНО равно ГВ в квадрате равно ЕН7 к АВ в квадрате. Однако мы доказа¬
ли, что КНО равно ГВ в квадрате. Следо
тельно, также EHZ равно АВ в квадрате.
12
Если от некоторой точки на сечении проводятся две прямые к асимптотам при про¬
извольных углах, и от некой [другой] точки на сечении проводятся параллельные [им],
то прямоугольник, ограниченный параллельными прямыми, будет равен прямоугольни¬
ку, ограниченному прямыми, к которым проведены параллельные.
Пусть будет гипербола, асимптотами которой будут АВ и ВГ, и пусть на сечении
будет взята некая точка Д; пусть от нее к АВ и ВГ будут проведены ДЕ и дг, пусть на
сечении будет взята другая точка — Н, и пусть через Н будут проведены НО и НК,
параллельные прямым ЕД и Д2. В таком случае я утверждаю, что ЕД7 равно ОН К.
Пусть же будет проведена ДН и продолжена дальше к А и Г. А поскольку АДГ рав¬
но АН Г, то АН к АД равно ДГ к ГН. А АН к АД равно НО к ЕД, ДГ к ГН равно к
НК. Поэтому ОН к ДЕ равно Д7 к НК Следовательно, ЕД7 равно ОН К.
Если на месте, ограниченном асимптотами и сечением, проводится некая прямая,
параллельная другой асимптоте, то она столкнется с сечением только в одной точке.
Пусть будет гипербола, асимптотами которой будут ГА и АВ, пусть будет взята
некоторая точка Е, и пусть через Е будет проведена Е2. параллельная прямой АВ. В
таком случае я утверждаю, что она столкнется с сечением.
Допустим, она не столкнется, тогда на сечении пусть будет взята некая точка Н, и
пусть через Н будут проведены НГ и НО, параллельные прямым ГА и АВ, и пусть ГН©
равно AEZ, и пусть будет проведена и продолжена дальше AZ; в таком случае она бу¬
дет сталки
ны КА и КД, параллельные прямым ГАВ; поэтому ГНО равно ДКА Однако мы пред¬
положили, что ГНО равно AEZ. Поэтому ДКА равно AEZ равно КАА, что невозмож¬
но, ведь КА больше EZ и АА больше АЕ. Следовательно, EZ сталкивается с сечением.
ться с сечением. Пусть она столкнется в К, и пусть через К будут проведе-
•Ж
АЖ
251

Дословный перевод книги II
Пусть она сталкивается в М.
В таком случае я утверждаю, что она не будет сталкиваться ни в какой другой
точке. Допустим, что она будет сталкиваться в N, и пусть через М и N будут прове¬
дены МЕ и NB, параллельные прямой ГА. Поэтому EME равно ENB что невозмож¬
но. Следовательно, она не сталкивается ни в какой другой точке.
14
Асимптоты и сечение, продолженные до бесконечности, все более сближаются друг
с другом и достигают расстояния меньшего, чем любое заданное расстояние.
Пусть будет гипербола, асимптотами которой будут АВ и АГ, и пусть заданным
расстоянием будет К. В таком случае я утверждаю, что прямые АВ и АГ и сечение,
продолженные дальше, всегда более сближаются с друг другом и будут достигать
расстояния меньшего, чем К.
Пусть же будут проведены параллельные касательной Е07 и ГН А, и пусть будет
проведена А0 и продолжена до Е. А поскольку ГНЛ равно 70Е, то АН к ХО равно
0Е кГН. Однако АН больше 70; поэтому также 0Е больше ГН. Схожим образом
мы докажем, что следующие расстояния будут меньшими.
И пусть будет принято, что ЕЛ меньше К. пусть через Л будет проведена ЛN па¬
раллельная прямой АГ; тогда она столкнется с сечением Пусть она столкнется с ним
в N и пусть через N будет проведена ММ3 параллельная прямой Е7. Следователь¬
но, М№ равно ЕЛ меньше К.
Дополнение
Отсюда очевидно, что из всех прямых, не встречающихся с сечением, более близ¬
ки к нему АВ и АГ, и затем угол ВАГ меньше, чем любой угол, ограниченный други¬
ми прямыми, не встречающимися с сечением.
И£
15
Асимптоты противолежащих сечений являются общими.
Пусть будут противолежащие сечения, диаметром которых будет АВ. центром - Г
В этом случае я утверждаю, что асимптоты А и В сечений - общие.
Пусть через точки А и В будут проведены ЛАЕ и 7ВН, касающиеся сечений; в та¬
ком случае они параллельны. Поэтому пусть будет установлено, что АА. АЕ, 7В и ВН
равны в квадрате одной четвертой части эйдоса, лежащего возле АВ; тогда АА рав¬
но АЕ равно 7В равно ВН. И пусть будут проведены ГА, ГЕ, Г7 и ГН. Поэтому оче¬
видно из-за параллельности, что ГА. ГЕ. Г7иГН находятся на одной и той же пря¬
мой. А поскольку есть гипербола, чьим диаметром является АВ, касательной - АЕ,
и каждая из АА и АЕ равна квадрату четвертой части эйдоса, лежащего возле прямой
АВ, то ГА и ГЕ суть асимптоты. По той же самой причине 7Г и ГН суть асимптоты
сечения В. Следовательно, асимптоты противолежащих сечений являются общими.
•1€
»!•
ЙЕ
16
Если на противолежащих сечениях проводится прямая, рассекающая каждую из пря¬
мых, которые заключают в себе угол, расположенный на углах, содержащих сечения, то
252

Дословный перевод книги II
м
»ТС
она будет сталкиваться с любым из противолежащих сечений только в одной точке, и
прямые, отделенные от нее сечениями при асимптотах, будут равны.
Пусть А и В будут противолежащими сечениями, центром которых будет Г, а асим¬
птотами - ДГ/ и ЕГ7; пусть будет проведена некая прямая ©К, рассекающая лю¬
бую из ДГ и Г7. В таком случае я утверждаю, что она, продолженная дальше, стол¬
кнется с любым из этих двух сечений только в одной точке.
Ведь поскольку ДГН и ЕГ7 суть асимптоты сечения А, и проведена некая пря¬
мая ©К, рассекающая любую из прямых, заключающих затем угол ДГ/, то К©, про¬
долженная дальше, сталкивается с сечением. Пусть она сталкивается с ним в Л и М.
Пусть через Г будет проведена АГВ, параллельная прямой ЛМ; тогда КА© рав¬
но АГ в квадрате, ©М К равно ГВ в квадрате. Поэтому также КА© равно 0М К и А©
равно КМ.
•В
Асимптоты сопряженных противолежащих сечений являются общими.
Пусть будут сопряженные противолежащие сечения, сопряженным диаметром
которых будут АВ и ГД, центром — Е. В этом случае я утверждаю, что их асимпто¬
ты являются общими.
Ведь пусть через точки А, В и Г будут проведены касательные /АН, НА©, ©ВК
иКГ/; тогда /Н0К есть параллелограмм. Поэтому пусть будут проведены ¿ЕО и
КЕН; в таком случае эти прямые суть диаметры параллелограмма, и все они рассе¬
каются на два равных отрезка в точке Е. А поскольку эйдос, лежащий возле прямой
АВ, равен ГД в квадрате и ГЕ равно ЕД, то каждая из в квадрате, АН в квадра¬
те, КВ в квадрате и В© в квадрате есть четвертая часть эйдоса, находящегося возле
прямой АВ. Поэтому £Е<Э и КЕН суть асимптоты сечений А и В. Схожим образом
мы докажем, что они же суть асимптоты сечений Г и Д. Следовательно, асимптоты
сопряженных противолежащих сечений являются общими.
Е£
18
Если прямая, встречающаяся с одним из сопряженных противолежащих сечений,
продолженная в любую из двух сторон, попадает вне сечения, то она будет совпадать
с любым из лежащих возле сечений только в одной точке.
Пусть сопряженными противолежащими сечениями будут А, В, Г и Д, и пусть не¬
кая прямая Е/ столкнется с Г и, продолженная дальше в любую из двух сторон, по¬
падет вне сечения. В этом случае я утверждаю, что она столкнется с любым из двух
сечений А и В только в одной точке.
Пусть Н© и КД будут асимптотами сечений. Тогда Е/ сталкивается с каждой изН©
и КА. Поэтому очевидно, что она столкнется с сечениями А и В только в одной точке.
19
Если на сопряженных противолежащих сечениях проводится некая прямая, касаю¬
щаяся какого-либо сечения, то она сталкивается с лежащими возле сечениями и в точ¬
ке соприкосновения рассекается на два равных отрезка.
253

Дословный перевод книги II
Пусть А, В, Г и А будут про
тиволежашими сопряженными сечениями, и пусть не¬
которая прямая ЕГ7 касается сечения Г. В таком случае я утверждаю, что она, про¬
долженная дальше, столкнется с сечениями А и В и в Г будет рассекаться на два рав¬
ных отрезка.
Очевидно, что она столкнется с сечениями А и В. Пусть она столкнется в Н и 0.
В таком случае я утверждаю, что ГН равно Г0.
Ведь пусть будут проведены асимптоты сечений КА и М№ Тогда ЕН равно 70,
ГЕ равно Г7 и ГН равно Г0.
20
Если прямая касается одного из противолежащих сечений, и через их центр прово¬
дятся две прямые, одна из которых через точку касания, другая как параллельная ка¬
сательной, покуда она не столкнется с одним из расположенных сечений, то прямая,
касающаяся сечения в точке пересечения, будет параллельна прямой, проведенной че¬
рез точку касания и центр, а прямые, проведенные через точки касания и центр, будут
сопряженными диаметрами противолежащих сечений.
Пусть будут сопряженные противолежащие, сопряженными диаметрами кото¬
рых будут АВ и ГА, центром - X. и пусть будет проведена, касающаяся сечения А,
Е7, и, продолженная дальше, пусть она столкнется с ХГ в Т, пусть будет проведена
ЕХ, и пусть она будет продолжена дальше до Е, и пусть через X будет проведена ХН,
параллельная прямой Е2, пусть через Н будет проведена, касающаяся сечения, 0Н.
В таком случае я утверждаю, что 0Н параллельна прямой ХЕ, и НО и ЕЕ являются
сопряженными диаметрами.
Пусть будут проведены ординаты КЕ, МА и ГРП, и пусть параметрами будут АМ
и ГМ А поскольку ВАкАМ равно N Г к ГА и ВА к АМ равно ХК7 к КЕ в квадрате ,
N Г к ГА равно НА в квадрате к ХА0. то также ХК7 к ЕК в квадрате равно НА в ква¬
драте к ХА0. Однако ХК2 к КЕ в квадрате равно ХКкКЕна7КкКЕи НА в ква¬
драте к ХА на А0 равно НА к АХ на НА к А0. Поэтому ХКкКЕна7КкКЕ рав¬
но НА к АХ на НА к А0. Из каковых отношений есть 7К к КЕ равно НА к АХ; ведь
каждые ЕК, К7 и 7Е параллельны каждым ХА, АН и НХ. Таким образом, ХК к КЕ
равно НА к А0. И стороны, заключающие равные углы, расположенные при К и А,
являются соразмерными; поэтому подобны и треугольники ЕКХ и Н0А, и они име¬
ют равные углы, под которыми протянуты соответствующие стороны. Поэтому угол
ЕХК равен углу АН0 А также угол КХН равен углу АНХ, поэтому также угол ЕХН
равен углу 0НХ. Следовательно, ЕХ параллельна прямой Н0.
Пусть будет П Н к Н Р равно 0Н к Е. Поэтому Е есть половина параметра диаметра
НО на сечениях Г и А. А поскольку другой диаметр сечений А и В есть ГА, и ЕТ стал¬
кивается с ним, то ТХ на ЕК равно ГХ в квадрате; ведь если мы от Е проведем пря¬
мую, параллельную КХ, то прямоугольник, ограниченный прямой ТХ и прямой, от¬
веденной параллельной, будет равен квадрату ГХ. Поэтому ТХ к ЕК равно ТХв ква¬
драте к ХГ в квадрате. А ТХ к ЕК равно Тг к равно треугольник ТХг к Е7Х и ТХ в
квадрате к ГХ в квадрате равно ХТ7 к ХГП равно ХТ7 к Н0Х. Таким образом, 1X7 к
Е7ХравноТ7ХкХН0. Поэтому Н0Х равно ХЕ7. А они имеют также угол 0НХ равен
ХЕ7; ведь ЕХ, Н0 и Е7, НХ параллельны. Поэтому стороны, заключающие равные
•д«
•М
»!•
•ж
919
»г*
254

Дословный перевод книги II
углы, находятся в противоположной пропорции; тогда Н® к ЕХ равно Е7 к НХ; та¬
ким образом, ®НХ равно ХЕ7. А поскольку £ к ®Н равно PH к НП, и PH к НП равно
ХЕ к Е7 ведь они параллельны, то также £ к ®Н равно ХЕ к Е7. А при взятой общей
высоте ХН£ к®Н равно! на ХН к®Н на НХ, и ХЕ к Е7. равно ХЕ в квадрате кХЕ7.
Поэтому также £ на ХН к ®НХ равно ХЕ в квадрате к ХЕ на Е7. И при переста¬
новке £ на ХН к ЕХ в квадрате равно ®НХ к 7Е на ЕХ. Однако ®НХ равно ХЕ7. По¬
этому также £ на НХ равно ЕХ в квадрате. £ на НХ есть четвертая часть эйдоса, ле¬
жащего возле прямой НО; ведь НХ есть половина прямой НО и £ есть половина па¬
раметра; и ЕХ в квадрате равно одной четвертой ЕЕ в квадрате; ведь ЕХ равно ХН.
Поэтому ЕЕ в квадрате равна эйдосу, лежащему возле прямой НО. Схожим образом
мы докажем, что НО в квадрате равна эйдосу, лежащему возле прямой ЕЕ. Следова¬
тельно, ЕЕ и НО суть сопряженные диаметры противолежащих сечений А, В, Г и А.
21
При тех же самых предпосылках нужно доказать, что пересечение касательных на¬
ходится на одной из асимптот.
Пусть будут сопряженные противолежащие сечения, диаметром которых будет
АВ и ГА, и пусть будут проведены касательные АЕ и ЕГ. В таком случае я утверж¬
даю, что точка Е находится на асимптоте.
Ведь поскольку ГХ в квадрате в квадрате равна четвертой части эйдоса, лежаще¬
го при АВ, ГХ в квадрате равно АЕ в квадрате, то и АЕ в квадрате равна четвертой
части эйдоса, лежащего при АВ. Пусть будет проведена ЕХ; тогда она есть асимпто¬
та. Следовательно, точка Е находится на асимптоте.
22
Если на сопряженных противолежащих сечениях от центра проводится прямая к
любому из сечений, и проводится прямая, парапетная ей, и пересекающаяся с одним
из лежащих возле сечений и с асимптотами, то прямоугольник, ограниченный возник¬
шими отрезками прямой, проведенной между сечением и асимптотами, будет равен
квадрату радиуса.
Пусть А, В, Г и А будут сопряженными противолежащими сечениями, и пусть
асимптотами будут ХЕ7 и ХН®, пусть от центра X будет проведена прямая ХГА, и
пусть будет проведена параллельная ей ®Е, рассекающая подряд сечение и асим¬
птоты .
Пусть КА рассекается в М на два равных отрезка, и пусть проведенная МХ будет
продолжена дальше; тогда АВ есть диаметр сечений А и В. А поскольку прямая, ка¬
сающаяся в А, параллельна прямой Е®, то Е® проведена к АВ как ордината. Центр
есть X; следовательно, АВ и ГА суть сопряженные диаметры. Поэтому ГХ в квадра¬
те равна четвертой части эйдоса, лежащего возле АВ. Однако четвертой части эйдо¬
са, лежащего возле АВ, равно ®КЕ. Следовательно, также ®КЕ равно ГХ в квадрате.
23
Если на сопряженных противолежащих сечениях от центра проводится прямая к
любому из сечений, и проводится парапетная ей прямая, пересекающаяся с тремя ле-
255

Дословный перевод книги II
•I»
жащими возле сечениями, то прямоугольник, ограниченный полученными отрезками
прямой, проведенной между тремя сечениями и асимптотами, будет вдвое больше ква¬
драта радиуса.
Пусть А, В, Г и А будут сопряженными противолежащими сечениями, пусть цен¬
тром сечений будет X, и пусть от X на любое из сечений попадает некая прямая ГХ,
и пусть будет проведена КА, параллельная прямой ГХ, рассекающая расположен¬
ные возле три сечения. В таком случае я утверждаю, что КМЛ равно 2ГХ в квадрате.
Пусть будут проведены асимптоты сечений Е7. и Н0. Тогда ГХ в квадрате равно
ОМЕ равно ОКЕ. А ОМЕ плюс ОКЕ равно ЛМК, поскольку концы равны. Следо¬
вательно, также ЛМК равно ГХ в квадрате.
ап
24
Если две прямые пересекаются с параболой каждая из них в двух точках, и точка
пересечения ни одной из них не заключена в точках пересечения другой, то прямые пе¬
ресекаются друг с другом вне сечения.
Пусть АВ ГА будет параболой, и пусть две прямые АВ и ГА пересекаются с АВ ГА, и
пусть точка пересечения ни одной из них не заключается в точках пересечения другой.
В таком случае я утверждаю, что они, продолженные дальше, пересекутся между собой.
Пусть через В и Г будут проведены диаметры сечений ЕВ/ и Н ГО; тогда они па¬
раллельны и каждая из них рассекает сечение только в одной точке. Пусть же будет
проведена ВГ; тогда угол ЕВГ плюс ВГН равны двум прямым, АГ и ВА, продолжен¬
ные дальше, образуют углы меньшие, чем две прямые. Следовательно, они пересе¬
каются между собой вне сечения.
•I».
»г»
•г»
25
Если каждая из двух прямых пересекается с гиперболой в двух точках, и точка пе¬
ресечения ни одной из них не заключается в точках пересечения другой, то прямые пе¬
ресекаются между собой вне сечения, но внутри угла, содержащего сечение.
Пусть будет гипербола, чьими асимптотами будут АВ и АГ, и пусть две прямые
Е/ и НО рассекают сечение, и точка пересечения ни одной из них не заключена в
точках пересечения другой. В этом случае я утверждаю, что Е/ и НО, продолжен¬
ные дальше, будут пересекаться вне сечения, но внутри угла ГАВ.
Пусть проведенные А/ и АО будут продолжены дальше, и пусть будет проведе¬
на /О И поскольку Е/ и НО, продолженные дальше, рассекают углы А/О и АО/,
а эти углы меньше двух прямых, то Е/ и НО, продолженные дальше, пересекаются
между собой вне сечения, но внутри угла ВАГ.
Схожим образом мы докажем это, если даже Е/ и НО касаются сечений.
•а
•г«
26
Если на эллипсе или на круге две прямые, не проходящие через центр, рассекают друг
друга, то они не рассекают друг друга на два равных отрезка.
Ведь если это возможно, то пусть на эллипсе или на круге две прямые ГА и Е/,
проходящие не через центр, рассекают друг друга на два равных отрезка в Н, центром
же сечения пусть будет О, и пусть проведенная НО будет продолжена дальше к А и В.
256

Дословный перевод книги II
А поскольку АВ есть диаметр, рассекающий прямую Е7 на два равных отрезка, то
прямая, касающаяся в А, параллельна прямой EZ. Схожим образом мы докажем, что
она также параллельна прямой ГД. Поэтому ЕХ также параллельна прямой ГД, что
невозможно. Следовательно, ГД и Е7 не рассекают друг друга на два равных отрезка.
•ж
27
Если две прямые касаются эллипса или круга, то прямые касательные будут парал¬
лельны, если прямая, соединяющая точки соприкосновения, проходит через центр, если
нет, то они пересекаются в той же самой части центра.
Пусть АВ будет эллипсом или кругом, пусть касательной выступает ГАД и ЕВг,
и пусть будет проведена АВ, и пусть она проходит сначала через центр. В таком слу¬
чае я утверждаю, что ГД и EZ являются параллельными.
Ведь поскольку АВ есть диаметр сечения, ГЛ касается в А, то ГД параллельна ор¬
динатам, проведенным к АВ. По той же самой причине также Е7. параллельна тем
же самым прямым. Следовательно, ГД и EZ являются параллельными.
Пусть АВ не проходит через центр, как на втором чертеже, и пусть будет прове¬
ден диаметр А0, а через 0 - касательная К0Л; тогда КА и ГД параллельны. Следо¬
вательно, Е7, проведенная дальше, пересечется с ГД в той же самой части центра,
в каковой находится АВ.
о
•ж
ЙЕ
28
Если на сечении конуса или на круге некая прямая рассекает две параллельные пря¬
мые на два равных отрезка, то она будет диаметром сечения.
Пусть на сечении конуса две параллельные прямые АВ и ГД в Е и Z рассекаются
на два равных отрезка, и пусть проведенная EZ будет продолжена дальше. В таком
случае я утверждаю, что она есть диаметр сечения.
Ведь если это не так. то пусть (это] будет, если возможно, H0Z. Тогда прямая,
касающаяся в Н, параллельна прямой АВ. Поэтому она также параллельна прямой
ГД. И Н0 есть диаметр; тогда Г0 равно 0Д, что абсурдно, ведь мы предположили,
что ГЕ равно ЕД. Таким образом, Н0 не есть диаметр. Схожим образом мы докажем,
что никакая другая прямая, кроме EZ, не будет диаметром. Следовательно. EZoyaeT
диаметром сечения.
ЙЕ
29
Если на сечении конуса или на окружности круга две касательные прямые пересека¬
ются, то прямая, проведенная от точки их пересечения к точке середины прямой, сое¬
диняющей точки касания, будет диаметром сечения.
Пусть будет сечение конуса или окружность круга, и пусть будут проведены, ка¬
сающиеся его, АВ и АГ. пересекающиеся в А. пусть проведенная ВГ рассекается на
два равных отрезка в Д, и пусть будет проведена АД. В таком случае я утверждаю,
что она есть диаметр сечения.
Если возможно, то пусть ДЕ будет диаметром, пусть будет проведена ЕГ; тогда
она будет рассекать сечение. Пусть она рассекает сечение в Z. и пусть через 7- будет
проведена 2КН. параллельная прямой ГДВ. А поскольку ГД равно АВ. то 7& рав¬
257

Дословный перевод книги II
но 0Н. И так как прямая, касающаяся в Л (сечения), параллельна прямой ВГ, и /Н
параллельна прямой ВГ. то и /Н параллельна касательной в А. Поэтому Х& равно
0К, что не может быть. Поэтому ДЕ не есть диаметр. Схожим образом мы докажем,
что никакая другая прямая, кроме АД, не является диаметром.
30
Если две прямые, касающиеся конического сечения или окружности круга, пересека¬
ются, то диаметр, проведенный от точки пересечения, будет рассекать на два равных
отрезка прямую, соединяющую точки соприкосновения.
Пусть ВГ будет сечением конуса или окружностью круга, пусть будут проведе¬
ны, касающиеся его. две прямые ВА и АГ, пересекающиеся в А, пусть будет прове¬
дена ВГ, и пусть через А будет проведен диаметр сечения АД. В таком случае я ут¬
верждаю, что ДВ равно АГ.
Пусть это не так, но если возможно, пусть ВЕ равно ЕГ. пусть будет проведена АЕ;
тогда АЕ есть диаметр сечения. Однако АД также является диаметром сечения, что
абсурдно. Ведь если эллипс есть сечение, А - точка, в которой пересекаются диаме¬
тры, то центр сечения будет находиться вне сечения, что невозможно; если же сече¬
ние есть парабола, то диаметры пересекаются между собой; если же сечение есть ги¬
пербола, и ВА и АГ пересекаются с сечением, не включая в себя точек пересечения,
то точка их пересечения расположена внутри угла, заключающего гиперболу; одна¬
ко в нем она также расположена, ведь мы предположили, что она есть центр, если
диаметры - ЛА и АЕ, что абсурдно. Следовательно, не получается, что ВЕ равно ЕГ.
Л*
»к
31
Ес ¡и каждого из двух противолежащих сечений касаются две прямые, то касатель¬
ные будут параллельны если прямая, соединяющая точки соприкосновения, проходит через
центр, если нет. то они пересекаются друг с другом в той части, где расположен центр
Пусть А и В будут противолежащими сечениями, пусть их касаются ГАЛ и ЕВ/ в
точках А и В. и пусть прямая, проведенная от к В, сначала проходит через центр. В
таком случае я утверждаю, что ГЛ и Е/ параллельны.
Ведь поскольку сечения являются противолежащими, диаметром которых есть
АВ, и одного из них ГД касается в А, то прямая, проведенная через В как параллель¬
ная прямой ГД, касается сечения. Однако его также касается Е/. Следовательно, ГЛ
и ЕХ параллельны.
Пусть же прямая, проведенная от А к В. не проходит через центр сечения, пусть
тогда будет проведен диаметр сечения АН, и пусть будет проведена касающаяся се¬
чения 0К, тогда 0К параллельна ГЛ И поскольку ЕХ и 0К касаются гиперболы,
они пересекаются. И 0К и ГД параллельны. Следовательно, ГД и Е/. продолжен¬
ные дальше, пересекаются. И очевидно, что они пересекаются в той части, где на¬
ходится центр.
»1»
32
Если прямые пересекаются с каждым из противолежащих сечений или касают¬
ся в одной точке, или рассекают в двух точках, и, продолженные дальше, данные пря¬
258

Дословный перевод книги II
•Ж
О
мые пересекаются, то точка их пересечения будет находиться на расположенном ря¬
дом угле, заключающем сечение.
Пусть будут противолежащие сечения, их или касаются в одной точке, или рас¬
секают в двух точках прямые АВ и ГА, и пусть данные прямые будут продолжены
дальше. В таком случае я утверждаю, что точка их пересечения будет находится на
угле, расположенном рядом с углом, включающим в себя сечение.
Пусть ¿Н и ОК будут асимптотами сечения; тогда АВ, продолженная дальше, пе¬
ресечется с асимптотами. Пусть она пересечется в О и Н. А поскольку мы предпо¬
ложили, что ¿К. и ОН пересекаются, то очевидно, они пересекаются или в площа¬
ди под углом 0А7, или в площади под углом КЛН. И схожим образом мы докажем
это, если они касаются сечения.
•Э
нс
»!•
33
Если прямая пересекается с одним из противолежащих сечений и проведенная даль¬
ше в любую из сторон попадает вне сечения, то она не будет пересекаться с другим се¬
чением, но будет попадать в три места, одно из которых есть площадь, расположен¬
ная под углом, заключающим сечение, а две другие площади расположены под углами,
находящимися возле угла, заключающего сечение.
Пусть А и В будут противолежащие сечения, пусть сечение А рассекает некая пря¬
мая ГА и проведенная дальше в любую из сторон пусть попадает вне сечения. В та¬
ком случае я утверждаю, что прямая ГА не пересекается с сечением В.
Пусть же будут проведены асимптоты сечений Е£ и НО; тогда ГА, продолжен¬
ная дальше, пересечется с асимптотами. И пересекается она с ними только в Е и О.
Следовательно, она не пересекается с сечением В.
И очевидно, что она попадет в три площади. Ведь если прямая пересекается с
каждым из противолежащих сечений, то она не пересечется в двух точках ни с од¬
ним из них; если же она будет пересекаться в двух точках, то из-за того, что мы до¬
казали выше, она не пересечется с другим сечением.
34
Если прямая касается одного из противолежащих сечений и проводится в другом се¬
чении параллельная ей другая прямая, то прямая, проведенная от точки соприкоснове¬
ния к середине параллельной, будет диаметром противолежащих сечений.
Пусть А и В будут противолежащие сечения, и пусть некоторая прямая ГД ка¬
сается одного из них А в А, и пусть в другом сечении будет проведена Е7, парал¬
лельная прямой ГД, и пусть в Н она рассекается на два равных отрезка, пусть бу¬
дет проведена АН. В таком случае я утверждаю, что АН есть диаметр противоле¬
жащих сечений.
Если возможно, то пусть [диаметр] — А0К. Тогда прямая, касающаяся сечения в
О, параллельна прямой ГА. Но ГА также параллельна прямой Е7; поэтому прямая,
касающаяся в О, параллельна прямой Е7. Таким образом, ЕК равно К/, что невоз¬
можно, ведь ЕН равно №.. Следовательно, АО не есть диаметр противолежащих се¬
чений. Таким образом, АВ есть диаметр.
259

Дословный перевод книги II
35
Если диаметр на одном из противолежащих сечений рассекает некоторую прямую
на два равных отрезка, то прямая, касающаяся другого сечения в пределе диаметра, бу¬
дет пара.ие.1ьна прямой, рассеченной на два равных отрезка.
Пусть А и В будут противолежащими сечениями, пусть же их диаметр АВ на се¬
чении В прямую ГА в Е рассекает на два равных отрезка. В таком случае я утверж¬
даю, что прямая, касающаяся сечения в А, параллельна прямой ГД.
Если возможно, то пусть М будет параллельна прямой, касающейся сечения в
А; тогда АН равно Н2. Однако также ДЕ равно ЕГ. Поэтому параллельна ЕН па¬
раллельны, что невозможно, она, продолженная дальше, пересекается с ней. Сле¬
довательно, не параллельна прямой, касающейся сечения в А, и ни одна другая
прямая не параллельна ей, кроме ГА.
»!•
36
Если на каждом из противолежащих сечений проводятся параллельные прямые, то
прямая, соединяющая их серединные точки, будет диаметром противолежащих сечений.
Пусть А и В будут противолежащими сечениями, и пусть на каждой из них бу¬
дут проведены параллельные прямые ГА и Е1, и пусть каждая из них рассекается на
два равных отрезка в точках Н и 0, пусть будет проведена Н0. В таком случае я ут¬
верждаю, что Н0 есть диаметр противолежащих сечений.
Если это не так, то пусть диаметром будет НК. Тогда прямая, касаюшаяся сече¬
ния в А, параллельна прямой ГА; поэтому она также параллельна прямой Е2. Таким
образом, ЕК равно К2, что невозможно, так как Е0 равно 02. Поэтому НК не есть
диаметр противолежащих сечений. Следовательно, Н0 есть диаметр.
•л
37
Если прямая, проведенная не через центр, рассекает противолежащие сечения, то
прямая, проведенная от ее точки, находящейся посередине, к центру, есть диаметр про¬
тиволежащих сечений, называемый прямым, диаметр же поперечный, есть соединен¬
ная с ним и проведенная от центра прямая, параллельная прямой, рассеченной на два
равных отрезка.
Пусть А и В будут противолежащими сечениями, и пусть сечения А и В рассекает
прямая ГА. проведенная не через центр, и пусть она рассекается в Е на два равных
отрезка, пусть центром сечений будет X. пусть будет проведена ХЕ, и пусть через X
будет проведена АВ, параллельная прямой ГА. В таком случае я утверждаю, что АВ
и ЕХ суть сопряженные диаметры сечений.
Пусть будет проведена АХ и продолжена дальше до 2, и пусть будет проведена
Г2. Тогда АХ равно Х2 Однако также АЕ равно ЕГ. поэтому ЕХ и 2Г параллельны.
Пусть ВА будет продолжена дальше к Н. И, поскольку АХ равно Х2, то также ЕХ
равно 2Н, поэтому также ГН равно 2Н. Таким образом, прямая, касаюшаяся сече¬
ния в А, параллельна прямой Г2. По этой причине она также параллельна прямой
ЕХ. Следовательно, ЕХ и АВ суть сопряженные диаметры.
260

Дословный перевод книги II
38
Если две пересекающиеся прямые касаются противолежащих сечений, то прямая,
проведенная от точки пересечения к середине прямой, соединяющей точки касания, бу¬
дет диаметром противолежащих прямых, который называется прямым, а диаметр
поперечный есть соединенная с ним прямая, проведенная через центр, как параллельная
прямой, касающейся точек соприкосновения.
Пусть А и В будут противолежащими сечениями, и пусть сечений касаются ГХ
и ХА, пусть будет проведена ГА и рассекается на два равных отрезка в Е. Пусть бу¬
дет проведена ЕХ. В таком случае я утверждаю, что ЕХ есть диаметр, а поперечный
диаметр есть соединенная с ним прямая, проведенная через центр как параллель¬
ная прямой ГА.
Если возможно, то пусть диаметром будет ЕХ, и пусть будет взята некоторая точ¬
ка 7; тогда АХ будет пересекаться с ЕХ. Пусть она пересекается в X, пусть будет про¬
ведена ГХ', тогда ГХ будет пересекаться с сечением. Пусть она пересекается в А, и
через А пусть будет проведена АВ. параллельная прямой ГА. А поскольку ЕХ есть
диаметр и рассекает прямую ГА на два равных отрезка, то он также рассекает на два
равных отрезка прямые, параллельные ей. Таким образом, АН равно Н В. И посколь¬
ку ГЕ равно ЕА, и они находятся на треугольнике Г7Д, то также АН равно НК. Поэ¬
тому также НК равно НВ, что невозможно. Следовательно, Е7 не будет диаметром.
39
Если две пересекающиеся прямые касаются противолежащих сечений, то прямая,
проведенная через центр и точку пересечения касательных, будет рассекать на два рав¬
ных отрезка прямую, соединяющую точки касания.
Пусть А и В будут противолежащими сечениями, и пусть будут проведены каса¬
ющиеся сечений А и В две прямые ГЕ и ЕА, и пусть будет проведена ГА, пусть будет
проведен диаметр ЕХ. В таком случае я утверждаю, что ГХ равно ХЪ.
Если это не так, то пусть ГА рассекается в Н на два равных отрезка, пусть будет
проведена НЕ; в таком случае НЕ есть диаметр. Однако ЕХ есть также диаметр, цен¬
тром же является Е. Следовательно пересечение касательных находится в центре се¬
чений, что абсурдно. Таким образом, ГХ и Х\ не неравны. Следовательно, они равны
40
Если две прямые, касающиеся противолежащих сечений, пересекаются, и через точ¬
ку пересечения проводится прямая, параллельная прямой, соединяющая точки касания
и пересекающаяся с сечениями, то прямые, проведенные от точек пересечения к сере¬
дине прямой, касающейся точек соприкосновения, касаются сечений.
Пусть А и В будут противолежащими сечениями, и пусть будут проведены две
прямые ГЕ и ЕА, касающиеся сечения А и В, пусть будет проведена ГА; пусть через
Е будет проведена ZEH, параллельная прямой ГА, и пусть ГД рассекается в О на два
равных отрезка, и пусть будут проведены Z0 и ОН. В таком случае я утверждаю, что
прямые ZO и ОН касаются сечений.
Пусть будет проведена ЕО; тогда ЕО есть диаметр recta, а поперечный диаметр
есть прямая, соединенная с ним, проведенная через центр как параллельная пря¬
261

Дословный перевод книги II
мой ГЛ. Пусть за центр будет взята [точка) X, и пусть будет проведена АХВ, парал¬
лельная прямой ГЛ. Таким образом, 0Е и АВ суть сопряженные диаметры. И Г0
проведена ко второму диаметру как ордината, ГЕ же, касаясь сечения, пересека¬
ется со вторым диаметром; поэтому прямоугольник ЕХ0 равен квадрату полови¬
ны второго диаметра, т.е. четвертой части эйдоса, лежащего при АВ. И посколь¬
ку 7Е проведена как ордината, и проведена 70, из-за этого 70 касается сечения
А. По этой же причине Н0 касается сечения В. Следовательно, 70 и 0Н касают¬
ся сечений А и В.
41
Если на противолежащих сечениях две прямые, проведенные не через центр, рассе¬
кают друг друга, то они не рассекают друг друга на два равных отрезка.
Пусть А и В будут противолежащими сечениями, и пусть на А и В две прямые ГВ
и АД, проведенные не через центр, рассекают друг друга в Е. В таком случае я ут¬
верждаю, что они не рассекаются на два равных отрезка.
Допустим, что они рассекаются, тогда пусть центром сечения будет X, и пусть
будет проведена ЕХ, тогда ЕХ есть диаметр. Пусть через X будет проведена Х7, па¬
раллельная прямой ВГ; тогда Х7 есть диаметр и он сопряжен с ЕХ. Таким образом,
прямая, касающаяся сечения в 7, параллельна прямой ЕХ. По той же самой причи¬
не поскольку проведенная 0К параллельна АЛ, то прямая, касающаяся сечения в
0, параллельна прямой ЕХ; по этой причине также прямая, касающаяся сечения в
7, параллельна прямой, касающейся сечения в 0, что абсурдно, ведь мы уже дока¬
зали, что они пересекаются. Следовательно, ГВ и АЛ, проведенные не через центр,
не рассекают друг друга на два равных отрезка.
о
42
Если на двух сопряженных противолежащих сечениях две прямые, проведенные
не через центр, рассекают друг друга, то они не рассекают друг друга на два равных
отрезка.
Пусть А, В, Г и Л будут соединенными противолежащими сечениями, и пусть на
сечениях А, В, Г и Л две прямые Е7 и Н0, проведенные не через центр, рассекают
друг друга в К. В таком случае я утверждаю, что они не рассекают друг друга на два
равных отрезка.
Допустим, что они рассекают, тогда пусть центром сечений будет X, и пусть бу¬
дет проведена АВ, параллельная прямой Е7, пусть будет проведена ГЛ, параллель¬
ная прямой 0Н, пусть будет проведена КХ; тогда К.Х и АВ суть сопряженные диаме¬
тры. По той же самой причине также ХК и ГЛ являются сопряженными диаметрами.
Поэтому также прямая, касающаяся сечения в А, параллельна прямой, касающейся
сечения в Г, что не
яся сечения в Г, рассекает сечения А и В, а прямая, касающаяся сечения в А, рассе¬
кает сечения Л и Г; и очевидно, что точка их пересечения находится в площади, рас¬
положенной под углом АХГ. Следовательно, Е7 и Н0, проведенные не через центр,
не рассекают друг друга на два равных отрезка.
О'
262

Дословный перевод книги II
43
Если прямая рассекает одно из сопряженных противолежащих сечений в двух точ¬
ках, и прямая проводится через центр к середине секущей, а другая - параллельно секу¬
щей, то эти диаметры будут сопряженными диаметрами для противолежащих сечений.
Пусть А, В, Г и Л будут соединенными противолежащими сечениями, и пусть не¬
которая прямая рассекает сечение А в двух точках Е и Я, и пусть ЕЯ рассекается в Н
на два равных отрезка, центром же будет X, пусть будет проведена ХН, и пусть бу¬
дет проведена ГХ, параллельная прямой ЕЯ. В таком случае я утверждаю, что пря¬
мые АХ и ХГ — сопряженные диаметры.
Ведь поскольку АХ есть диаметр и он рассекает прямую ЕЯ на д
ка, то прямая, касающаяся сечения в А, параллельна прямой ЕЯ\ по этой причине
она параллельна прямой ГХ. А поскольку сечения являются противолежащими, и
проведена прямая, касающаяся одного из них в А, а от центра X к точке соприкос¬
новения проведена ХА, и ГХ проведена как параллельная касательной, то прямые
ХА и ГХ — сопряженные диаметры; ведь это было доказано прежде.
ва равных отрез-
44
Надо найти диаметр заданного конического сечения.
Пусть будет задано сечение конуса, в котором находятся точки А, В, Г, Д и Е.
Надо найти ее диаметр.
Пусть он будет найден, и пусть им будет Г0. Тогда для прямых проведенных как
ординаты \Я и Е0 и продолженных дальше будет Д7 равно ЯВ и Е0 равно 0А. Та¬
ким образом, если мы установили в положении прямые ВД и ЕА, которые парал¬
лельны, то будут даны точки 0 и Я. Следовательно. 07 Г дан по положению.
Этим способом пусть и получается: пусть будет дано сечение конуса, в котором
находятся точки А, В, Г, Л и Е, и пусть будут проведены прямые ВД и АЕ, и пусть они
рассекаются на два равных отрезка в 7 и 0. И проведенная 70 будет диаметром се¬
чения. Тем же самым способом мы найдем и другие любые диаметры.
45
Надо найти центр заданного эллипса или гиперболы.
Это, однако, очевидно. Ведь если проводятся два диаметра сечения АВ и ГЛ, то
там, где они рассекают друг друга, и будет центр сечения, как было доказано.
46
Надо найти ось конического сечения.
Пусть сначала заданным сечением конуса будет парабола, в которой находятся
точки 7, Г и Е. Следует найти ее ось.
Пусть будет проведен диаметр АВ. Если АВ есть ось, то полученное будет пред¬
положенным; если же нет, то пусть будет получено, и пусть осью будет ГД; тогда ось
ГД параллельна прямой АВ и она рассекает на два равных отрезка прямые, прове¬
денные к ней перпендикулярно. А прямые, перпендикулярные ГД, также перпен¬
дикулярны АВ; поэтому ГД рассекает на два равных отрезка прямые, перпендику¬
лярные АВ. Если же мы установим Е7 как перпендикулярную АВ. то она будет зада-
•Ж
263

Дословный перевод книги II
на по положению, и по причине, которую мы указали, ЕД равно Д7. Поэтому дано
Д. Тогда через данную точку Д проведена ГД, параллельная заданной прямой АВ по
положению; следовательно, ГД задано по положению.
И пусть будет построено следующим образом; пусть будет дана парабола, на ко¬
торой находятся точки 7. Е и А, и пусть будет проведен ее диаметр АВ; пусть к ней
будет проведена перпендикулярно ВЕ и продолжена дальше до 7. Если же ЕВ рав¬
но В/, то очевидно, что АВ есть ось; если же нет, то пусть Е7 рассекается в Д на два
равных отрезка, и пусть будет проведена ГД, параллельная прямой АВ. Поэтому оче¬
видно, что ГД есть ось сечения. Ведь, будучи проведенной, как параллельная диаме¬
тру, т.е. будучи самим диаметром, она рассекает прямую Е7 на два равных отрезка и
на прямые углы. Следовательно, ГД найден как ось данной параболы.
И очевидно, что только одна ось параллельна параболе. Ведь если это будет, до¬
пустим. АВ, то она будет параллельна прямой ГД. И она рассекает прямую Е7; тогда
она также рассекает ее на два равных отрезка. Поэтому ВЕ равно В/, что абсурдно.
•л
•и
»!•
•М
47
Надо найти ось данной гиперболы или эллипса.
Пусть АВ Г будет гиперболой или эллипсом. Надо найти ее ось.
Пусть она будет найдена, и пусть ею будет КД, и пусть центром сечения будет К;
тогда КД рассекает на два равных отрезка и на прямые углы прямые, проведенные
к ней как ординаты.
Пусть будет проведена ГДА, пусть будет проведена КА и КГ. А поскольку ГД рав¬
но ДА, то также ГК равно КА. Если же установим заданную точку Г, то будет дана
ГК Поэтому круг, описанный центром К. а также радиусом КГ, будет проходить че¬
рез А и будет задан по положению. Однако сечение АВГ дано по положению. По¬
этому дана .А Однако задана также Г; тогда ГА задано по положению. И ГД равно
ДА; поэтому задана Д, следовательно, задана К. Поэтому ДК задана по положению.
И пусть будет построено способом; пусть буден задана гипербола или эллипс
АВГ, и пусть будет взят ее центр К; и пусть на сечении будет взята некоторая точка
Г, и пусть центром К и радиусом КГ описывается круг ГЕА. и пусть будет проведе¬
на ГА и пусть она рассекается на два равных отрезка в Д, пусть будут проведены КГ.
КД, КА и продолжены дальше до В.
А поскольку АД равно АГ, ДК есть обшая, то две прямые ГДК будут равны АДК.
и основание КА равно основанию КГ. Поэтому КВД рассекает прямую АДГ на два
равных отрезка и на прямые углы. Следовательно, КД есть ось.
Пусть через К будет проведена МК1Ч. параллельная прямой ГА; тогда есть
ось сечения, сопряженная с ВК.
»и.
48
Нужно исходя из доказанного затем доказать, что другие оси не принадлежат тем
же самым сечениям.
Допустим, что так же будет другая ось КН. Тогда тем же самым способом, что и
прежде, при проведенной перпендикулярно А0. А0 равно 0Л; поэтому также АК
равно КА. Однако также АК равно КГ. Поэтому также КА равно КГ, что абсурдно.
М.
264

Дословный перевод книги II
Очевидно, что на гиперболе кругАЕГ в другой точке между А, В и Г не пересе¬
кается с сечением; а на эллипсе пусть будут проведены перпендикулярно ГР и ЛХ.
Поэтому поскольку КГ равно КА, ведь они радиусы, то также ГК в квадрате рав¬
но КА в квадрате. А ГР в квадрате плюс РК в квадрате равно ГК в квадрате. И КХ
в квадрате плюс ХА в квадрате равно ЛК в квадрате. Поэтому ГР в квадрате плюс
РК в квадрате равно АХ в квадрате плюс ХК в квадрате. Тогда ГР в квадрате дели¬
мое на АХ в квадрате равно ХК в квадрате делимое на КР в квадрате. А поскольку,
наоборот, MPN плюс РК в квадрате равно КМ в квадрате, и также MXN плюс ХК
в квадрате равно КМ в квадрате, то MPN плюс РК в квадрате равно MXN плюс
ХК в квадрате. Поэтому ХК в квадрате делимое на КР в квадрате равно MPN де¬
лимое на MXN. А мы доказали, что ХК в квадрате делимое на КР в квадрате рав¬
но ГР в квадрате делимое на АХ в квадрате; поэтому ГР в квадрате делимое на ХА
в квадрате равно MPN делимое на MXN, и поскольку ГР и АХ проведены как ор¬
динаты, то ГР в квадрате к MPN равно АХ в квадрате к MXN; а мы доказали, что у
те равно MXN. Таким образом, линия ЛГМ есть круг, что абсурдно, ведь мы пред¬
положили, что она есть эллипс.
49
При заданном коническом сечении и точке, расположенной не внутри сечения, надо
провести от этой точки прямую, касающуюся сечения в одной точке.
Пусть заданным сечением конуса будет сначала парабола, чьей осью будет ВА.
Поэтому следует от заданной точки, не находящейся внутри сечения, провести пря¬
мую, как было предположено.
Поэтому заданная точка находится или на самой линии, или на оси, или на осталь¬
ном пространстве, расположенном вне.
Пусть А будет находиться на самой линии, и пусть будет линия, и пусть это будет
АЕ, и пусть будет проведена перпендикулярно АА; она будет задана по положению.
А ВЕ равно ВА; и ВА является заданной; поэтому задана также ВЕ. Задана В; поэто¬
му задана Е. Однако задана также и А; поэтому АЕ задана по положению.
Пусть это получается таким образом; пусть от А будет проведена перпендикуляр¬
но АА. и пусть будет установлено ВЕ равно ВА, и пусть будет проведена АЕ. Поэто¬
ЙЕ
му очевидно, что она касается сечения.
Опять пусть заданной точкой на оси будет Е. И пусть она будет, пусть будет про¬
ведена АЕ, касающаяся (сечения), и пусть будет проведена перпендикулярно АЛ.
Тогда ВЕ равно ВЛ. ИВЕ является заданной; тогда задана также и ВЛ. И В задана;
поэтому задана также Д. И АА есть перпендикулярная; поэтому ЛА задана по поло¬
жению. По этой причине задана А. Однако задана также Е. Следовательно, АЕ за¬
дана по положению.
И пусть получается следующим образом; пусть будет ВЛ равно ВЕ, и от Д к ЕЛпусть
будет проведена перпендикулярно ЛА, пусть будет проведена АЕ. Тогда очевидно,
что АЕ касается сечения.
И очевидно, что также, если заданная точка тождественна В, прямая, проведен¬
ная перпендикулярно от В, касается сечения.
265

Дословный перевод книги II
Пусть же заданной точкой будет Г, и пусть она будет, пусть будет ГА, и пусть че¬
рез Г будет проведена TZ, параллельная оси, т.е. прямой ВД; поэтому TZ задана по
положению. И пусть от А к TZ будет проведена ордината AZ; тогда ГН равно ZH. И
Н задана; тогда задана также Z. И ZA проведена ордината, т.е. параллельна прямой,
касающейся сечения в Н; тогда ZA задана по положению. Таким образом, задана А.
Однако Г также задана. Следовательно, ГА задана по положению.
И пусть получается следующим образом; пусть через Г будет проведена TZ. па¬
раллельная прямой ВД, и пусть будет установлено ZH равно ГН, пусть будет прове¬
дена ZA, параллельная прямой, касающейся сечения в Н, и пусть будет проведена
АГ. Поэтому очевидно, что она решает вопрос.
Снова пусть будет гипербола, чьей осью будет ДВГ, центром же - 0, асимптота¬
ми - 0Е и 0Z. Поэтому заданная точка будет дана или на сечении, или на оси, или
внутри угла E0Z, или в площади, расположенной рядом, или одной из асимптот,
содержащих сечение, или в площади, расположенной между прямых, которые со¬
держат угол, расположенный углом Z0E на вершине.
Сначала пусть на сечении будет А, и пусть это будет, и пусть будет касательная АН,
пусть будет проведена перпендикулярно АД. а поперечной стороной эйдоса пусть
будет ВГ. Поэтому ГД к ДВ равно ГН к НВ. Однако отношение ГД к ДВ задано, ведь
каждая из них задана; тогда также задано отношение ГН к НВ. И ВГ задана; поэ¬
тому Н задана. Однако задана также А; следовательно, АН задана по положению.
Пусть получается следующим образом; пусть от А будет проведена перпендику¬
лярно АД, и пусть будет ГН к НВ равно ГД к ДВ, и пусть будет проведена АН. Поэ¬
тому очевидно, что прямая АН касается сечения.
И снова пусть на оси будет заданной точкой Н, и пусть это будет, пусть будет про¬
ведена касательная АН, пусть будет проведена перпендикулярно АД. Поэтому по той
же самой причине получается ГН к НВ равно ГД к ДВ. И ВГ задана; тогда задана Д.
И ДА проведена перпендикулярно; тогда ДА задана по положению. Однако также
сечение задано; поэтому задана А. Однако также задана Н; следовательно, АН за¬
дана по положению.
Пусть получается следующим образом; пусть будет предположено то же самое, и
пусть будет ГД к ДВ равно ГН к НВ. и пусть будет проведена перпендикулярно ДА,
и пусть будет проведена АН. Поэтому очевидно, что прямая АН решает проблему и
от Н может быть проведена в другую сторону другая прямая, касающаяся сечения.
При тех же самых предпосылках пусть заданная точка К находится на плоша¬
ли, расположенной внутри угла EZ0, и пусть отсюда следует, что от К проводится
прямая, касающаяся сечения. И пусть это будет КА, и пусть проведенная КО будет
продолжена дальше, и пусть будет установлено 0N равно Л0; тогда все (они) будут
заданы. Поэтому также AN будет задана. Пусть же будет проведена ордината к MN
АМ; тогда будет также N К к КА равно МN к МЛ. Однако отношение N К к КЛ зада¬
но; тогда также задано отношение MN к МЛ. И Л задана; поэтому задана также М.
И проведена МА, параллельная прямой, касающейся сечения в Л; тогда МА задана
по положению. Однако также задано по положению сечение АЛ В; поэтому А зада¬
на. Однако задана также К. Следовательно, АК является заданной.
л»
26í

Дословный перевод книги II
т
И пусть получается следующим образом: пусть будет предположено то же самое,
и пусть заданной точкой будет К, пусть проведенная К.0 будет продолжена дальше,
и пусть будет установлено 0N равно Л0, и пусть N К к КЛ равно NN4 к МЛ, и пусть
будет проведена МА, параллельная прямой, касающейся сечения в Л, и пусть будет
проведена КА. Следовательно, КА касается сечения.
И очевидно, что также от К может быть проведена другая прямая, касающаяся
сечения, в другую сторону.
При тех же самых предпосылках пусть заданная точка / будет на одной из асим¬
птот, которые содержат сечение, и пусть нужно будет, чтобы от 7 была проведена
прямая, касающаяся сечения. И пусть это будет сделано, пусть это будет /АЕ, и пусть
через А будет проведена АД, параллельная прямой Е0. Поэтому Д0 равно Л/, по¬
скольку также /А равно АЕ. И /0 задана; тогда Д задана. И через заданную точку Д
проведена /кА, параллельная прямой 0Е, заданной по положению; тогда /А задана
по положению. Однако задано также по положению сечение; поэтому задана А. Од¬
нако также задана 7\ следовательно, /АЕ задана по положению.
Пусть получается следующим образом: пусть АВ будет сечением, Е0 и 0/ - асим¬
птотами, и пусть заданная точка 7 будет расположена на одной из асимптот, содер¬
жащих сечение, и пусть /0 рассекается в Д на два равных отрезка, и пусть через Д
будет проведена ДА, параллельная прямой 0Е, и пусть будет проведена /А. А по¬
скольку /Д равно ДО, то также /А равно АЕ. Следовательно, из-за того, что мы до¬
казали выше /АЕ касается сечения.
При тех же самых предпосылках пусть заданная точка находится в площади, рас¬
положенной под углом, который находится рядом с прямыми, касающимися сечения,
и пусть этой точкой будет К. Поэтому нужно, чтобы от К была проведена прямая, ка¬
сающаяся сечения. И пусть это будет КА, и пусть проведенная К0 будет продолжена
дальше; тогда она будет задана по положению. Поэтому если на сечении берется задан¬
ная точка Г, и через Г проводится ГД, параллельная прямой К0, то она будет задана по
положению. И если ГД рассекается в Е на два равных отрезка, и проведенная 0Е про¬
должена дальше, то она будет задана по положению, и диаметр будет сопряжен с К0.
Поэтому пусть будет установлено 0Н равно В0, и пусть через А будет проведена АЛ,
параллельная прямой В0. Тогда поскольку КЛ и ВН суть сопряженные диаметры, и
АК - касательная, а АЛ параллельна прямой ВН, то она равна четвертой части эйдо-
са, лежащего рядом с ВН. Поэтому К0Л задано. И задана К0; тогда также задана ©Л.
Однако она также задана по положению; и 0 задана; поэтому задана также Л. И через
Л проведена ЛА, параллельная прямой ВН, заданной по положению; поэтому ЛА за¬
дана по положению. Однако по положению задано также сечение; поэтому задана А.
Однако задана также К; следовательно, КА задана по положению.
Пусть получается следующим образом: пусть будет предположено то же самое,
а заданная точка К будет находиться в площади, которую мы обозначали, и пусть
проведенная К0 будет продолжена дальше, и пусть будет взята некоторая точка Г;
пусть будет проведена ГЛ, параллельная прямой К0, и пусть ГД рассекается в Е на
два равных отрезка, и пусть проведенная Е0 будет продолжена дальше, и пусть бу¬
дет установлено 0Н равно В0; тогда НВ есть поперечный диаметр, сопряженный
с К0Л. Поэтому пусть будет установлено К0 на 0Л равна четвертой части эйдоса,
•Ж
•Ж
267

Дословный перевод книги II
лежащего возле ВН, и через Л пусть будет проведена АА, параллельная прямой ВН,
пусть будет проведена КА. Поэтому очевидно на основе преобразования приведен¬
ной [раньше) теоремы, что прямая КА касается сечения.
Если же точка будет задана в площади, расположенной между 7©П, то проблема
неразрешима. Ведь прямая, касающаяся сечения, будет рассекать прямую НО, по¬
этому она пересечется с каждой из 70П, что невозможно из-за доказанного в 31-й
[теореме] первой книги и в третьей [теореме] данной книги.
Пусть при тех же самых предпосылках сечением будет эллипс, и пусть заданной
точкой на сечении будет А, и нужно, чтобы от А была проведена прямая, касающа¬
яся сечения. И пусть так и будет, и пусть это будет АН, и пусть от А к оси ВГ будет
проведена ордината АД; тогда Д задана, и получится ГД к ДВ равно ГН к НВ. И за¬
дано отношение ГД к ДВ; тогда задано также отношение ГН к НВ. Поэтому задан Н.
Однако задана также А. Следовательно, АН задана по положению.
И пусть получается следующим образом: пусть будет проведена перпендикуляр¬
но АД. и пусть будет ГН к НВ равно ГД к ДВ, и пусть будет проведена АН. Поэтому
очевидно, что как и на гиперболе, прямая АН касается сечения.
И пусть же снова заданной точкой будет К, и нужно, чтобы была проведена каса¬
тельная. Пусть это будет, и пусть это будет КА, и пусть проведенная к центру 0 пря¬
мая К0Л будет продолжена до N. тогда она будет задана по положению. И если АМ
проводится как ордината, то NN1 к МЛ равно 1ЧК к КА. Однако задано отношение
КИ к КА; поэтому также задано отношение МЫ к МЛ. Поэтому М задана. И прове¬
дена МА; ведь она параллельна прямой, касающейся сечения в Л. Таким образом,
МА задана по положению. Поэтому А задана. Однако задана также К. Следователь¬
но, КА задана по положению.
То же самое сложение было и в предыдущем [случае].
я®
50
Надо провести прямую, касающуюся заданного конического сечения, которая на оси
в той же части, в которой есть пересечение, будет состав ¡ять угол, равный заданно¬
му острому углу.
Пусть сначала сечением конуса будет парабола, чьей осью будет АВ. Поэтому
надо, чтобы была проведена прямая, касающаяся сечения, которая на оси АВ в той
же самой части, в которой расположено пересечение, составляет угол, равный за¬
данному острому углу.
Пусть так и будет, и пусть прямой будет ГА; тогда угол ВАГ задан. И пусть будет
проведена перпендикулярно В Г; тогда также задан угол, находящийся при В. По
этой причине задано отношение АВ к В Г. Однако также задано отношение ВД к ВА.
Тогда также задано отношение АВ к ВГ. И угол, расположенный при В, задан; тог¬
да угол ВАГ также задан. И он расположен на прямой ВА, заданной по положению
и на заданной точке А; поэтому ГА задана по положению. Однако сечение также за¬
дано по положению; поэтому задана Г И ГА касается сечения; следовательно, ГД
задана по положению.
Пусть получается следующим образом: пусть заданным сечением конуса сначала
будет парабола, осью которой будет АВ, а заданным острым углом — Е7Н, и пусть
268

Дословный перевод книги II
на Е7 будет взята точка Е, пусть будет проведена перпендикулярно ЕН, и пусть 7Н
рассекается в 0 на два равных отрезка, пусть будет проведена 0Е, и пусть образует¬
ся, что угол ВАГ равен НОЕ, и пусть будет проведена перпендикулярно ВГ, и пусть
будет установлено АА равно ВА, и пусть будет проведена ГД. Таким образом, ГД ка¬
сается сечения.
В таком случае я утверждаю, что угол ГДВ равен Е7Н.
Ведь поскольку 7Н к Н0 равно ДВ к ВА, и также 0Н к НЕ равно АВ к ВГ, то из-
за равенства получается 7Н к НЕ равно ДВ к ВГ. И углы, расположенные при Н и
В, являются прямыми; таким образом, угол 2 равен углу Д.
Пусть же заданным сечением будет гипербола, и пусть она будет, и пусть сече¬
ния касается ГД, и пусть за центр сечения будет взята X, пусть будет проведены ГХ
и перпендикулярная ГЕ. Тогда задано отношение ХЕД к ЕГ в квадрате; отношение
поперечной стороны к прямой стороне то же самое. И задано отношение ГЕ в ква¬
драте к ЕД в квадрате, ведь задан каждый из углов ГДЕ и ДЕГ. Поэтому задано также
отношение ХЕД к ЕД в квадрате, поэтому задано также отношение ХЕ к ЕГ. И угол,
расположенный при Е, задан; тогда задан также угол, расположенный при X. Поэ¬
тому при прямой ХЕ, заданной по положению и при заданной точке X проводится
на заданном угле прямая ГХ; тогда ГХ задана по положению. Однако также задано
по положению сечение; поэтому Г задано. И ГД проведена как касательная; следо¬
вательно, ГД задана по положению.
Пусть будет проведена асимптота сечения 7Х; тогда ГД, продолженная дальше,
будет пересекаться с асимптотой. Пусть она пересекается в 2. Тогда получится угол
7АЕ больше 2\\. Поэтому для построения необходимо, чтобы заданный острый
угол был больше половины угла, ограниченного асимптотами.
Пусть задача ставится следующим образом: пусть будет задана гипербола, осью
которой будет АВ, а асимптотой - Х7, и заданный острый угол К0Н больше АХ7,
пусть угол КОЛ равен АХ7, и пусть от А к АВ перпендикулярно будет проведена А7,
и пусть на Н0 будет взята некоторая точка Н, и пусть от нее перпендикулярно к 0К
будет проведена НК. А поскольку угол 7ХА равен Л0К, и также углы, расположен¬
ные при А и К, являются прямыми, то ХА к К2 равно 0К к КА. А 0К к КА больше
0К к КН. Поэтому также ХА к К2 больше ©К к КН. Тогда также ХА в квадрате к \2
в квадрате больше ОК в квадрате к КН в квадрате. Однако как ХА в квадрате к К2 в
квадрате, так и поперечная сторона к прямой стороне; тогда также отношение по¬
перечной стороны к прямой стороне имеет отношение большее, чем 0К в квадра¬
те к КН в квадрате. Поэтому если мы сделаем, чтобы ХА в квадрате к А/ в квадра¬
те, как другая величина к КН в квадрате, то она будет больше, чем 0К в квадрате.
Пусть есть МК0, и пусть будет проведена НМ. А поскольку МК в квадрате больше
МК0, то МК в квадрате к КН в квадрате больше МК0 к КН в квадрате, те. МК в
квадрате к КН в квадрате больше ХА в квадрате к К2 в квадрате. И если мы сдела¬
ем, что как МК в квадрате к КН в квадрате, так ХА в квадрате относится к другой
величине, то она будет по величине меньше, чем А7 в квадрате; и прямая, прове¬
денная от X к взятой точке, произведет схожие треугольники, и поэтому будет угол
2Х\ больше Н М К Тогда пусть будет установлено, что угол АХГ равен Н МК; поэто¬
му X Г будет рассекать сечение. И пусть она рассекает в Г, и пусть от Г будет прове -
ЛГ»
X»
о
269

Дословный перевод книги II
дена ГД, касающаяся сечения, и пусть будет проведена перпендикулярно ГЕ; тогда
треугольник ГХЕ подобен треугольнику НМ К. Поэтому ХЕ в квадрате к ЕГ в ква¬
драте равно МК в квадрате к КН в квадрате. Однако как поперечная сторона отно¬
сится к прямой стороне, так и ХЕД к ЕГ в квадрате и МКО к КН в квадрате. И на¬
против, будет ГЕ в квадрате к ХЕД равно НК в квадрате к МК0. Поэтому равным
образом ХЕ в квадрате к ХЕД равно МК в квадрате к М КО. Поэтому также ХЕ к ЕД
равно МК к КО. А было также ГЕ к ЕХ равно НК к КМ. Поэтому из равенства ГЕ
к ЕД равно НК к КО. И углы, расположенные при Е и К, являются прямыми; тог¬
да угол Д равен НОК.
Пусть же сечением будет эллипс, осью которого будет АВ. Нужно поэтому про¬
вести прямую, касающуюся сечения, которая на оси при тех же самых, частях, в ко¬
торых находится сечение, содержит в себе угол, равный заданному острому углу.
Пусть это будет так, и пусть этой прямой будет ГА; тогда угол ГЛА задан. Пусть
будет проведена перпендикулярно ГЕ; поэтому задано отношение ДЕ в квадрате в
квадрате к ЕГ в квадрате. Пусть X будет центром сечения, и пусть будет проведена
ГХ. Тогда задано отношение ГЕ в квадрате к ДЕХ; ведь то же самое есть отношение
прямой стороны к поперечной стороне. Поэтому также задано отношение ДЕ в ква¬
драте к ДЕХ. Поэтому также задано отношение ДЕ к ЕХ. Однако также задано от¬
ношение ДЕ к ЕГ, поэтому также задано отношение ГЕ к ЕХ. И угол, расположен¬
ный при Е, является прямым; тогда угол, расположенный при X, задан. И он распо¬
ложен при заданной по положению прямой и при заданной точке; поэтому точка Г
задана. И от заданной точки Г проведена касательная ГД; следовательно, ГД зада¬
на по положению.
И пусть задача ставится следующим образом: пусть 7Н0 будет заданным острым
углом, и пусть на 7Н будет взята точка 7, и пусть будет проведена перпендикулярно
70, и пусть выйдет, что как относится прямая сторона к поперечной стороне, так
70 в квадрате относится к НОК, и пусть будет проведена К7, а центром сечения
пусть будет X, и пусть образуется угол АХГ равен углу НК7, и пусть будет проведе¬
на ГД, касающаяся сечения. В таком случае я утверждаю, что ГД решает проблему,
т.е. что угол ГДЕ равен 7Н0.
Ведь поскольку ХЕ к ЕГ равно К0 к 70, то также ХЕ в квадрате к ЕГ в квадрате
равно К0 в квадрате к 70 в квадрате. А также ГЕ в квадрате к ДЕ в квадрате на ЕХ
равно 70 в квадрате к КОН; ведь каждая из них есть то же самое отношение прямой
стороны к поперечной стороне. И равным образом тогда получится ХЕ в квадрате к
ХЕД равно КО в квадрате к НОК. Поэтому также ХЕ к ЕД равно КО к 70. А также
ХЕ к ГЕ равно КО к 70. Поэтому из равенства ЕД к ЕГ равно НО к 70. И стороны,
содержащие прямые углы, являются соразмерными; поэтому угол ДЕ равен 7Н0.
Следовательно, ГД решает проблему.
псе
51
Надо провести прямую, касающуюся конического сечения, которая с диаметром,
проведенным через точку касания, содержит угол, равный заданному острому углу.
Пусть сначала заданным сечением конуса будет парабола с осью АВ, и пусть за¬
данным углом будет О. Поэтому нужно провести прямую, касающуюся параболы,
«г«
270

Дословный перевод книги II
которая вместе с диаметром, проведенным отточки соприкосновения, содержит
угол, равный углу 0.
Пусть так и будет, и пусть будет проведена касательная ГД к ЕГ, диаметру, про¬
веденному через точку соприкосновения, и содержащая угол ЕГЛ, равный углу 0,
и пусть ГД пересекается с осью в Д. А поскольку АД параллельна прямой ЕГ, то угол
АДГ равен ЕГД. Однако угол ЕГД задан; ведь угол ЕГД равен 0; следовательно, угол
АДГ также задан.
Пусть складывается следующим образом: пусть будет парабола, чьей осью будет
AB,	и пусть заданным углом будет©. И пусть будет проведена ГД, касающаяся сече¬
ния, к оси, производя угол АДГ, равный углу 0, и пусть через Г будет проведена ЕГ,
параллельная прямой АВ. А поскольку угол 0 равен АДГ и угол АДГ равен ЕГД, то
также угол О равен ЕГД.
Пусть сечением будет гипербола, чьей осью пусть будет АВ, а центром — Е, асим¬
птотой - ЕТ, заданным острым углом - £1, касательной — ГД, и пусть будет прове¬
дена ГЕ, создающая проблему, и пусть будет проведена перпендикулярно ГН. Тог¬
да задано отношение поперечной стороны к прямой стороне; поэтому также зада¬
но отношение ЕНД к ГН в квадрате. И пусть будет взята как заданная прямая 70,
и на ней отрезок круга пусть будет описан, принимая угол, равный углу О; тогда он
будет больше полукруга и пусть из некой точки на окружности К будет проведена
перпендикулярно КА, производя отношение 7Л0 к ЛК в квадрате, равное отноше¬
нию поперечной стороны к прямой стороне, и пусть будут проведены 7К и К0. А
поскольку угол 07К равен ГЕД, и как поперечная сторона относится к прямой сто¬
роне, так и ЕНД к НГ в квадрате и 7Л0 к ЛК в квадрате, и треугольники К7Л, ЕГН
и 70К, ЕГД будут подобны. Следовательно, угол 07К равен ГЕД.
И пусть получается следующим образом: пусть заданной гиперболой будет АГ. осью
- АВ, центром - Е, а заданным острым углом - и пусть заданное отношение по¬
перечной стороны к прямой стороне будет равно отношению ХТ* к ХФ, и пусть ТФ
рассекается в У на два равных отрезка, и пусть как заданная прямая будет взята 70,
и на ней отрезок круга, больший, чем полукруг, пусть описывается, принимая утол,
равный углу О, пусть будет 7К0, и пусть за центр будет взята N. и пусть от N к 70
будет проведена перпендикулярно NO. и пусть NO согласно отношению УФ к ФК
рассекается на два отрезка в П, и пусть через П будет проведена ПК, параллельная
прямой 70, и пусть от К к продолженной дальше 70 будет проведена перпендику¬
лярно КЛ; пусть будут проведены 7К и К0. и пусть ЛК будет продолжена дальше до
M,	и пусть от N к ней будет проведена перпендикулярно N5; тогда она параллель¬
на прямой 70. И по этой причине NП к ПО равно ЕК к КЛ равно УФ к ФХ. И если
взяты удвоения предшествующих, то Т'Ф к ФХ равно МК к КЛ. И в сочетании ТХ
к ХФ равно МЛ к ЛК. Однако МЛ к ЛК равно МКЛ к ЛК в квадрате; поэтому так¬
же ТФ к ФХ равно МКЛ к ЛК в квадрате равно 7Л0 к ЛК в квадрате. Однако как
ТФ к ФХ, так поперечная сторона относится к прямой стороне; поэтому так же как
7Л0 к ЛК в квадрате, так поперечная сторона относится к прямой стороне. И пусть
от А к АВ будет проведена перпендикулярно АТ. А поскольку имеется, что как ЕА
в квадрате к АТ в квадрате, так поперечная сторона относится к прямой стороне, а
также как поперечная сторона относится к прямой стороне, так и 7Л0 к ЛК в ква¬
»!•
271

Дословный перевод книги II
драте, и гл в квадрате к ЛК в квадрате больше гЛ0 к ЛК в квадрате, то также будет
гл в квадрате к ЛК в квадрате больше ЕА в квадрате к АТ в квадрате. И углы, рас¬
положенные при А и Л, являются прямыми; тогда угол г меньше Е. Поэтому обра¬
зуется угол АЕГ равен лгК; поэтому ЕГ будет пересекаться с сечением. Пусть она
пересекается в Е Поэтому пусть от Г будет проведена касательная ГД; и пусть будет
проведена перпендикулярно ГН; тогда как поперечная сторона относится к прямой
стороне, так и ЕНД к ГН в квадрате. Поэтому также гЛ0 к ЛК в квадрате равно ЕН
на НД к НГ в квадрате. Поэтому будут подобными треугольники Кгл, ЕГН и К0Л,
ГНД и К20, ГЕД. Следовательно, угол ЕГД равен гК0 равен О.
Если же отношение поперечной стороны к прямой стороне равно по отношению
к равному, то КЛ касается круга гК0, и прямая, проведенная от центра к К, будет
параллельна прямой г©, и разрешает проблему.
•Ж
ЛЖ
52
Если прямая касается эллипса, то угол, который она составляет с диаметром, про¬
веденным через точку касания, является не меньшим, чем тот, который находится ря¬
дом с углом, ограниченным прямыми, преломленными при середине сечения.
Пусть будет эллипс, осями которого будут АВ и ГД, центром же - Е, и пусть АВ
будет большой осью, a HZA касается сечения, и пусть будут проведены АГ, ГВ, ZE,
и пусть В Г будет продолжена дальше до Л. В таком случае я утверждаю, что нет та¬
кого, что угол AZE меньше ЛГА.
Ведь ZE или параллельна прямой ЛВ, или нет.
Пусть сначала она будет параллельна; и АЕ равно ЕВ; поэтому также А0 равно
0Г. И ZE есть диаметр; тогда прямая, касающаяся сечения в Z, параллельна пря¬
мой АГ. Однако также ZE параллельна прямой ЛВ; поэтому Z0TA есть параллело¬
грамм; тогда угол ÁZ& равен ЛГ0.
И поскольку АЕ равно ЕВ больше ЕГ, угол АГВ есть тупой; поэтому угол ЛГА
есть острый. По этой причине угол AZE есть острый угол. Следовательно, угол HZE
есть тупой.
Пусть EZ не параллельна прямой ЛВ, и пусть будет проведена перпендикуляр¬
ная ZK; тогда нет такого, что угол ЛВЕ равен ZEA. Однако прямой угол, располо¬
женный при Е, равен прямому углу, расположенному при К; тогда не получается,
что ВЕ в квадрате к ЕГ в квадрате равно ЕК в квадрате к KZ в квадрате. А ВЕ в ква¬
драте к ЕГ в квадрате равно АЕВ к ЕГ в квадрате равно поперечная сторона к пря¬
мой стороне равно НКЕ к KZ в квадрате. Поэтому не получается, что НКЕ к KZ в
квадрате равно КЕ в квадрате к KZ в квадрате. Следовательно, не выйдет, что НК
равно КЕ. Пусть за отрезок круга будет принят MYN, принимающий угол, равный
углу АГВ; а угол АГВ является тупым; тогда отрезок полукруга MYN является мень¬
шим. Поэтому пусть будет № к ЕМ равно НК к КЕ, и пусть от Е будет проведена
перпендикулярно YEX, и пусть будут проведены NY, YM, и пусть MN рассекается в
Т на два равных отрезка, и пусть будет проведена перпендикулярно ОТП ; тогда она
есть диаметр. Пусть Р будет центром, и пусть от него будет проведена перпендику¬
лярно РЕ, и пусть будут проведены ON и ОМ. А поскольку угол MON равен АГВ, и
каждая из АВ и MN рассекается в Е и Т на два равных отрезка, и углы, расположен -
•ж
о
»ж
•ж
272

Дословный перевод книги II
ные при Е и Т, являются прямыми, треугольники же и ВЕГ - подобны. Поэто¬
му будет Т\ в квадрате к ТО в квадрате равно ВЕ в квадрате к ЕГ в квадрате. И по¬
скольку ТР равно ЕЕ, и РО больше ЕУ, то РО к РТ больше ЕУ к ЕЕ. И наоборот, РО
к ОТ меньше ЕУ к ЕЕ. И если взято удвоение предшествующего, то ПО к ТО мень¬
ше ХУ к УЕ. И ПТ к ТО меньше ХЕ к УЕ.
Однако ПТ к ТО равно TN в квадрате к ТО в квадрате равно ВЕ в квадрате к ЕГ
в квадрате равно поперечная сторона к прямой стороне равно НКЕ к К/ в квадра¬
те. Поэтому НКЕ к К/ в квадрате меньше ХЕ к УЕ, т.е. меньше ХЕУ к УЕ в квадра¬
те, т.е. НКЕ к К7 в квадрате меньше к УЕ в квадрате. Поэтому если мы дела¬
ем, как НКЕ к К7 в квадрате, так MEN относится к другой величине, то она отно¬
сится к большей, чем ЕУ в квадрате.
Пусть будет Н КЕ к К7 в квадрате равно MEN к ЕФ в квадрате. Из-за этого полу¬
чается угол Н7Е равен МФН Поэтому угол MYN больше Н7Е, т.е. угол АГВ боль¬
ше Н7Е, и угол, расположенный рядом Л70 больше ЛГ0. Следовательно, не полу¬
чается, что угол Л70 меньше АГ0.
ли
53
Надо провести прямую, касающуюся заданного эллипса, которая при диаметре,
проведенном через точку касания, создает угол, равный заданному острому углу; тогда
нужно, чтобы заданный острый угол был не меньше угла, который расположен рядом с
углом, ограниченным прямыми, преломленными при середине сечения.
Пусть будет заданный эллипс, чьей большей осью пусть будет АВ, меньшей осью
- ГД, центром - Е, пусть будут проведены АГ и АВ, и пусть заданным углом будет У,
не меньший, чем угол АГН; поэтому также угол АГВ не меньше угла X.
Поэтому будет угол У больше АГН или У равен АГН
Пусть сначала У равно АГН; и пусть через Е будет проведена ЕК, параллельная
прямой ВГ, и пусть через К будет К0, касающаяся сечения. Поэтому поскольку АЕ
равно ЕВ, и АЕ к ЕВ равно А7 к 2Г, то также А7 равно Г7. И КЕ есть диаметр; поэ¬
тому прямая касается сечения в К, т.е. прямая 0КН, и она параллельна прямой ГА.
Однако ЕК параллельна также прямой НВ; поэтому К7ГН есть параллелограмм; и
по этой причине угол НК7 равен НГ7. А НГ7 равен У. Следовательно, также угол
НКЕ равен У
Пусть же, однако, будет У больше АГН; поэтому, наоборот, угол X меньше АГВ.
Пусть будет взят круг, на котором пусть будет отделен отрезок, которым пусть бу¬
дет МЬШ, принимая угол, равный углу X, и пусть МП в О рассекается на две рав¬
ные части, и пусть от О к М П будет проведена перпендикулярно К'ОР; и пусть будут
проведены MN и 1МП; поэтому будет угол МК1П меньше АГВ. Однако МТ^О равен
одной второй МГЧП и АГЕ равен одной второй АГВ; поэтому МКЮ меньше АГЕ. И
углы, расположенные при Е и О, являются прямыми; поэтому АЕ к ЕГ больше ОМ
к ОН Поэтому также АЕ в квадрате к ЕГ в квадрате больше МО в квадрате к NO в
квадрате. А АЕ в квадрате равно АЕВ и МО в квадрате равно М ОП равно \'ОР По¬
этому АЕВ к ЕГ в квадрате больше РО к ОН т.е. поперечная сторона к прямой сто¬
роне имеет отношение меньшее, чем РО к ОН Поэтому пусть получится, что как
поперечная сторона относится к прямой стороне, какОА’ к А’С, и пусть рассека-
ли
ли
273

Дословный перевод книги II
, ЕТ, ФТ. Поэтому будет А’я к А'^ равно ФО к 01 равно ‘РЕ к ЕЕ,
ется в я на два равных отрезка. А поскольку поперечная сторона имеет отношение к
прямой стороне, меньшее, чем РО к 014, то также ОА' к А’£ больше РО к 0Г4. И при
составлении	к ^А’ больше PN к N0. Пусть Ф будет центром круга; поэтому также
ЯС к ОХ’ больше ФМ к N0 И сортировке А’я к А'£ больше ФО к 014. Поэтому пусть
получится А’я к А’£ равно ФО к Ю которая меньше, чем 014, и пусть будут проведе¬
ны параллельные 1
и при составлении я? к£А’ равно ТЕ к ЕЕ. И при взятии удвоенных предшествую¬
щих к ^А’ равно ТЕ к ЕЕ. И в вычитании ОА' к А'£ равно ТЕ к ЕЕ равно попереч¬
ная сторона к прямой. Пусть же будут проведены МЕ и ЕП, и пусть при прямой АЕ
и ее точке Е образуется угол АЕК равен МПЕ, и пусть через К будет проведена КО,
касающаяся сечения, и пусть будет проведена ордината КА. А поскольку угол М ПЕ
равен АЕК, и прямой угол, расположенный при Е, равен углу, расположенному при
Л, то треугольники ЕЕП и КЕЛ равноугольны. И как поперечная сторона относится
к прямой стороне, так и ТЕ к ЕЕ равно ТЕЕ к ЕЕ в квадрате равно МЕП к ЕЕ в ква¬
драте. Поэтому треугольники КАЕ, ЕЕП и КОЕ, МЕП являются подобными; поэто¬
му угол МЕП равен 0КЕ. А угол МЕП равен М14П равен X, поэтому также угол 0КЕ
равен X. Следовательно, углы, расположенные рядом с ними, равны НКЕ равно У.
Следовательно, прямая, касающаяся сечения, НО проведена к диаметру КЕ,
проведенному через точку соприкосновения, создавая угол НКЕ, равный заданно¬
му углу У; а это и надо было осуществить.
274

АПОЛЛОНИИ ПЕРГСКИИ
КОНИЧЕСКИЕ
СЕЧЕНИЯ
КНИГА III
Предложение 1. Площади треугольни¬
ков, образованных двумя касательными и
диаметрами, проведенными через точки ка¬
сания, равны
Если прямые, касающиеся конического
сечения, пересекаются, и через точки каса¬
ния проведены диаметры, то площади полу¬
ченных таким образом треугольников, име¬
ющих общей вершиной точку пересечения ка¬
сательных, равны.
Пусть коническое сечение АВ - пара¬
бола, касательные к которой АГ и ВД пе¬
ресекаются в точке Е, а через точки А и В
проведены диаметры ВГ и АД пересекаю¬
щиеся с ними в точках Г и Д. В таком слу¬
чае я утверждаю, что площадь треугольни¬
ка АЕД равна площади треугольника ВЕГ*.
Проведем А/, параллельную прямой
ВД, поэтому она проведена как ордината.
В таком случае если коническое сечение
есть парабола, то площадь параллелограм¬
ма AABZ равна площади треугольника АЕД
(1,35). И при изъятии
щего четырехуголь-
ника АЕВ2 оставшиеся треугольники АЕД
и ВЕГ имеют равные площади.
Пусть теперь сечение есть гипербола
(рис. 2)** или эллипс с центром в точке О.
‘ Для параболы уже было доказано в (1,49), что эти треугольники еще и равны.
** Случай, когда точки касания находятся на противолежащих, Аполлоний рассмотрит в (III, 4).

Книга III
Поскольку Аг есть ордината к диаметру ОВ и АГ касается сечения, то будет вы¬
полняться равенство (I, 37) 20 ОГ = ВО!.
т го во	го2 го
Тогда — = —, поэтому —-= —.
ВО ГО	' ВО2 ГО
д /Г	,П1 го2 Б(Аог) /г.	,, го эСлог)
А так как (Евклид VI, 19)— =	и (Евклид VI, 1)- = ^^ ,то
5(АОг) 5(АОг)
Б(АОГ)” 8(ВОД) ’
Следовательно, 8(АОГ) = 8(ВОД).
И после изъятия общего для них четырехугольника ДОГЕ* остаются два треу¬
гольника АЕД и ВЕГ. площади которых равны.
4/
/. Рис. За	I. Рис. ЗЬ
Предложение 2. Площади треугольника и четырехугольника, образованных диаме¬
трами, касательными и параллельными им прямыми, равны
Ес ¡и при тех же самых предпосылках через точку, лежащую на коническом сечении,
проведены параллельно касательным прямые, пересекающие диаметры, то площадь тре¬
угольника, образованного касательной, секущей и диаметром будет равна площади че¬
тырехугольника, образованного касательной, параллельной ей прямой, секущей и диа¬
метром. проходящим через другую точку касания.
Пусть АЕГ и ВЕД - касательные к коническому сечению, АМ и В/ - диаметры,
и пусть будет взята на сечении некоторая точка О. и проведены ОКА и 0М7, парал-
о
* В случае эллипса изымается (рис За) или, наоборот, добавляется (рис ЗЬ) четырехуголь¬
ник ДОВЕ-

Предложения
точками Ли В)
таком случае я утверждаю, что площадь четырехугольника
дельные касательным.
0Г равна площади треугольника AIM.
Ведь поскольку доказано, что площадь треугольника 0КМ равна площади четы¬
рехугольника КГ (I, 42 и 43)*, то, прибавив к ним (или отняв от них) площадь об-
* В (I, 43) доказывается, что для гиперболы 8(Н0К)=8(ГМК) - 8(ГЛВ). а разность этих площа¬
дей равна площади ЛМВК. Фигуры Н0К и \МВК аналогичны 0КМ и АКЛГ в данном Предложении
277

Книга III
г
г
2. Рис. 3. Эллипс
Если при тех же самых предпосыл¬
ках на сечении взять две точки и через
них провести прямые, параллельные ка-_
сательным, вплоть до диаметров, то Г
площади четырехугольников, возникших
в результате проведения этих прямых и
опирающихся на диаметры, будут рав¬
ны между' собой.
шего четырехугольника А0, получаем, что
площадь треугольника AIM равна площа¬
ди четырехугольника О Г.
Предложение 3. Площади двух четыре¬
хугольников, образованных диаметрами и
прямыми, проведенными из двух точек кри¬
вой параллельно касательным через точ¬
ки пересечения диаметров с кривой, равны
278

Предложения
Пусть дано сечение, к которому проведены касательные в точках А и В, и диаме¬
тры такие же, как в (IN, 1). Тогда если на сечении взять две произвольные точки Z
и Н, и провести через / прямые Z0KA и NZIM, а через Н - NHEO иН0ПР, парал¬
лельные касательным, то я утверждаю, что S(AH) = S(PZ) и S(AN) = S(MH).
А поскольку мы доказали прежде (III, 2), что S(ГН) = S(PnA), S(MIA) = S(EZ) и
так как S(PnA) = S(МIA)+S(PI), то S(iH) = S(iZ)+S(PI), или S(rH) = S(r0)+S(PZ).
Если теперь отнять справа и слева Г0, получим равенство S(AH) = S(PZ), а сле¬
довательно, и S(AN) = S(MH).
Предложение 4. Предложение 1 для противолежащих сечений
Если две прямые, касаются
противолежащих и через точки
касания проведены диаметры, то
площади треугольников, образо¬
ванных касательными и диаме¬
трами, будут равны.
Пусть даны противолежащие
(А) и (В) с центром О, и касаю¬
щиеся их прямые АЕ и ВЕ пе-
ресекаются в точке Е. Проведем
прямые АВ и ОЕ, а также прямые
АО и ВО, пересекающие каса¬
4. Рис. I.
тельные в точках А и Г, а проти-
волежашие в точках 0 и К.
В гаком случае я утверждаю, что площади треугольников АОГ и BOA, а также
АЕА и ВЕГ равны
Проведем через точку 0 касательную 0Z. которая будет параллельна прямой АГ
(11.31). Тогда поскольку АО = 00, то треугольники АОГ и 0OZ равны (Евклид VI,
19). А поскольку (III, 1) S(0OZ) = S(BOA), то S(AOT) = S(OOZ).
Следовательно, и S(AEA) = S(BEr).
Предложение 5. Площадь треугольника равна сумме двух других (гипербола)
Если две прямые, касающиеся
I
тиволежащих, пересекаются и через точку.
принадлежащую одному из сечений, проводятся две прямые, одна - параллельно
касательной, другая - параллельно прямой, соединяющей точки касания, то пло¬
щадь треугольника, образованного отрезками этих двух прямых, и диаметром, про
веденным через точку пересечения касательных, отличается от площади треуголь¬
ника, отделенного от него касательной, на площадь треугольника, образованного
этой касательной, прямой, параллельной соединяющей точки касания и диаметром.
проходящим через точку касания.
279

Книга III
5. Рис. I. Точки касания лежат
на противолежащих
,4
Пусть даны противолежащие сечения
(А) и (В) с центром О, или одно из них, а
также касательные АЕ и ВЕ. И пусть про¬
ведена прямая АВ, а также ВО и ОЕ, про¬
долженные дальше. От некоторой точки
0 на сечении проведем прямую 0ДН Г, параллельную АВ и прямую 0М, параллель¬
ную касательной ВЕ.
В таком случае я утверждаю, что 5(НМ0) = 8(НЕД) = 8(ВГД)*?
Поскольку отрезок ОЕ лежит на диаметре (II, 39 и 38), АВ есть ордината к нему и
0Г ей параллельна, а 0М параллельна касательной ВЕ, то (1,45) 8(НМ0) = 8(ГОН)
= 8(ОВЕ).
Следовательно, 8(НМ0) = 8(НЕД) = 8(ВГА) и очевидно, что 8(ВГД) = 8(ДЕМ0).
ллельнои ей прямой, се-
Предложение 6. Повто
рение Предложения 2
Если при тех же самых
предпосылках на одном из
противолежащих сечений
берется некоторая точка, а
от нее проведены параллель-
но касательным прямые, то
площадь четырехугольника,
образованного касательной,
•1«
тиволежащих, а •-» для одного У Аполлония говорится о противолежащих,
♦ <+» для двух про
но теорема верна, если касательные проведены и только к одной ветви, на что указано еще в ком¬
ментариях Евтокия, приведенных у Коммандино и Галлея

Предложения
кущей и диаметром, будет равна площади треугольника, возникшего в результате пе¬
ресечения той же самой касательной, секущей и другого диаметра*.
Пусть даны противолежащие с диаметрами ДОХ и BOY, и сечения (А) касаются
прямые АГ и ВЛ, пересекающиеся в точке Е. Тогда если от некоторой точки сече¬
ния 0 провести прямые 0КЛ и 0MZ, параллельные касательным АГ и ВЛ, то S(0r)
= S(AIM).
Поскольку (А) и (
жащие, и АГ касается сечения (А), пере¬
секаясь с ВО, а 0Л параллельна прямой
АГ, то площадь четырехугольника 0Г будет
равна площади треугольника АIМ (111,2).
Предложение 7. Предложение 3 для
противолежащих сечений
Еаи при тех же самых предпосыл¬
ках на каждом из сечений берется по не¬
которой точке** и от них проводятся
прямые, параллельные касательным, то
площади четырехугольников, образован¬
ных проведенными таким образом пря¬
мыми и прилегающих к диаметрам, бу¬
дут равны между собой.
Пусть при тех же самых предпосыл-
\N
ках на двух противолежащих сечениях
взяты точки 0 и К. через которые про-
ведены 0Е и К1М, параллельные каса¬
тельной АФ, а также 0N и КТ - парал¬
лельные касательной ВЕ.
В гаком случае я утверждаю, что
справедливо то, что было сказано в
предпосылке***.
Дока*ано(1Н,6), что S(0T) = S(A1M).
Следовательно, прибавив, слева и
справа S(O1), получим S(O0) = S(AOr).
А поскольку (111, 1) S(AOr) = S(BOA)
и S(BOA) = S(OK)****, то S(O0) = S(OK).
7. rue. 2.
•LtM
•I»
* Очевидно, что это Предложение 2, но не для любого сечения, а для гиперболы Вт
противолежащее сечение здесь совершенно не нужно.
Они берутся между точками пересечения диаметров и сечений. Другой случай рассмотрен
в Предложении 10.
3	То есть что Б(ОГ) = S(KM) и S(0H) = S(КЛ).
4	Это можно доказать, если провести касательную¥у (рис 2). Тогда, как только что было дока¬
зано для правого сечения, S(OK) = S(YyO), и поскольку S(YyO) = S(AOT) (III, 4), то S(OK) = Э(АОГ), а
значит, S(OK) = S(BOA).
281

Книга III
Если теперь к обеим площадям прибавить S(ON), то S(0T)
S(On),TO S(0H) = S(KA).
Предложение 8. Если через точки пе¬
ресечения диаметров со второй гипербо¬
лой будут проведены прямые, параллель¬
ные касательным, то площади четыреху¬
гольников, образованных диаметрами,
касательными и параллельными им пря¬
мыми, равны
= S(KM),
а если
Пусть при тех же самых предпосыл¬
ках через точки пересечения диаметров
со второй гиперболой будут проведены
прямые, параллельные касательным.
В таком случае я утверждаю, что пло¬
щади четырехугольников АННЕ и TEZT,
El и ТО равны.
Поскольку мы доказали равенство
площадей треугольников АНО и 0BZ
(111, 1), а прямая АВ параллельна пря-
__ АЕ BE	АЕ
мои HZ*, то— = — и, наоборот,		—,
ЕН EZ	АН BZ
«л ГА АВ
И еще — = —, так как центр делит диаметры пополам (1.30).
АЕ BE
п	ГА АВ
Поэтому	= —.
' АН BZ
И треугольники подобны из-за параллельных**, поэтому (Евклид VI, 19)
S(TTA) S(EAB)
SÜH0)= S(B0Z)и наоборот-
Атак как (III, I) S(AHO) = S(BOZ), то также S(ETA) = S(EAB).
Тогда поскольку S(AH0) = S(BOZ). то S(AEOZ) = S(TH0T).
И, вычитая общую S( Е0), получим S(EAH Е) = S( TEZT), что и гребовалось доказать
Поскольку ГО и AZ параллельны и ГЕ = ЕА, то треугольники ГОЕ и AEZ равны.
В силу тех же причин равны треугольники AEI и ВЕН.
А так как (НЕ 1) S(BEH) = S(AEZ), то Б(ГОЕ) = S(AEI).
Атак как мы доказали, что S(EAHE) = S(TEZT), то, прибавив слева и справа рав¬
ные площади, получим, что SCHI) = S(TO).
• Добавив 5(АВ0), получим, что БСАВН) = БСАВг), а так как основание этих треугольников об¬
щее, то и высоты равны. Следовательно, нг параллельна АВ.
ГАЛВГТ
ан "вг’нв'ег итд
ЕД
** Параллельны Н0 и ГТ, 0Z и Ед, поэтому
282

Предложения
Предложение 9. Еше одно равенство площадей четы¬
рехугольников (гипербола)
Если при тех же самых предпосылках точка К ле¬
жит на гиперболе между двумя диаметрами, а точка
В совпадает с точкой пересечения одного из диаметров
с данным сечением и через них проведены параллельные
прямые*, то в таком случае я утверждаю, что поща¬
ди четырехугольников АД и ХМ равны.
Это очевидно, поскольку мы доказали (111, 7). что
S(BOA) = S(OK).
Следовательно, S(BEM) = S(KA). Тогда, прибавив
S(AE), получим S(AM) = S(AA).
Предложение 10. Вариант Предложения 7
Пусть при тех же самых
предпосылках точки & и К на¬
ходятся вне дуг, заключенных
между точками пересечения ди¬
аметров и сечений. Тогда нуж¬
но доказать, что Я(®МНП) =
S(KnXT)**.
Поскольку АФ и BZ касают¬
ся сечения, АХ и BY суть диа¬
метры. проведенные через точ¬
ки соприкосновения, а КТ, КП,
0П и 0N параллельны каса¬
тельным, то S(OTQ) = S(QHK)
+ S(AOT)***.
И по тем же причинам
S(MOZ) = S(AZ0) + S(BOA),
а так как (III, 1) S(AOT) =
S(BOA), то S(OTQ) - S(QHK)
= S(MOZ) — S(AZ0).
Следовательно, S(OTQ) +
S(AZ0) = S(MOZ) + S(QHK).
Тогда, прибавив слева и справа общую площадь шестиугольника 0ZOQKП. мы
получим, что 8(0МНП) = 8(КПЛТ).
* Так в оригинале Ясно, что через К проводятся прямые, параллельные касательным в точках
А и В, а через В - касательная, а также прямая, параллельная касательной в точке А.
** Для точек, лежащих между точками пересечения с диаметрами, это уже было доказано в (III, 7).
*“ Это можно доказать, если провести через X касательную Тогда площадь отсекаемого ею
треугольника равна S(AOT) (Евклид VI, 19), a S(XT) = S(QHK) (III, 2).
283

Книга III
Предложение 11. Повторение Предложения 5
Если при тех же самых предпосылках на сечении берется некоторая точка, и от нее
проводятся параллельные, одна - касательной, другая - прямой, соединяющей точки
касания, то площадь треугольника, образованного ими при диаметре, проведенном через
точку пересечения касательных, отличается от площади треугольника, образованно¬
го касательной и диаметром, проведенным через точку касания, на площадь треуголь¬
ника, отделенного от него касательной к этому же сечению*.
/\-
К®
I
I
11. Рис. 1.
7
Пусть даны противолежащие (А) и (В) (рис. 1) или гипербола с центром О (рис.
2) и касательные АЕ и ВЕ, а также проведены прямые АВ и ЕОК Тогда если, на¬
пример, на сечении (В) будет взята некоторая точка 0, от которой будут проведены
0ДНГ, параллельная прямой АВ, и 0М - параллельная касательной ВЕ, то в таком
случае я утверждаю, что 5(НМ0) = 5(НЕД) ± Б(ВГД).
Ранее было доказано, что А В рассекается прямой ЕСМ на два равных отрезка (11,
39), а № есть сопряженный диаметр. Поэтому А№ есть ордината к №.
Поскольку № есть диаметр, ВЕ касается сечения, а AN проведена как ордината
к диаметру №, и от взятой на сечении точки 0 проводятся прямые 0Н. параллель¬
ная АВ, и 0М - параллельная ВЕ, то (I, 45) 5(НМ0) = 8(ГОН) ± 5(ВОЕ).
Следовательно, $(НМ0) = $(НЕД) ± 5(ВГД).
Очевидно также, что 5(ВГД) = 5(ДЕМ0).
• Предложение 11 - это, очевидно, Предложение 5

Предложения
Предложение 12. Еще одно равенство площадей четырехугольников (гипербола)
Если при тех же самых предпосылках на одном из противолежащих сечении берут¬
ся две точки и от каждой проводятся прямые, параллельные касательной и прямой, со¬
единяющей точки касания, то площади четырехугольников, образованных отрезками
этих прямых и диаметрами, будут равны.
Пусть на сечении будут взяты произвольные точки В и К. через которые прово¬
дятся прямые ВМ№ и КЕОУП, параллельные прямой АД, а также ВЕР и КЕ, парал¬
лельные касательной АЕ.
В таком случае я утверждаю, что 5(ВП) = 8(КР).
Поскольку было доказано (III, 11), что 8(АОП) = 5(КЕ) и 8(АМЫ) = 8(ВЕ), то
(рис. 1) 8(КР) - 8(ВО) = 8(МП) или (рис. 2) 8(КР) + 8(ВО) = Б(МП).
Следовательно, если прибавить или отнять общую 8(ВО), то 8(ВП) = З(КР).
Предложение 13. Площади треугольников, образованных двумя касательными к смеж¬
ным сопряженным гиперболам и диаметрами, проведенными к точкам касания, равны
Если на сопряженных противолежащих сечениях прямые, касающиеся рядом рас¬
положенных сечений, пересекаются, и через точки касания проводятся диаметры, то
площади двух треугольников, образованных касательными и диаметрами с общей вер¬
шиной в центре противолежащих, будут равны.
Пусть даны противолежащие и сопряженные сечения с центром в точке и пусть
две прямые АЕ и ВЕ касаются сечений в точках А и В
В таком случае я утверждаю, что 8(В®7) = 8(А0Н).
285

Книга III
ведем прямые AK и ЛОМ,
I
параллельные BE. Поскольку BE
- касательная, и через нее про-
веден диаметр ЛОВ, а ДМ ей па¬
раллельна, то ЛМ есть диаметр,
сопряженный с диаметром ВЛ
(II, 20), в силу чего АК есть ор-
дината к ВЛ. Так как АН касает¬
ся сечения, то (I. 38) КО ОН =
КО ВО
ВО-, или — = —.
ВО ОН
Л КО АК АО
Однако — = — = —.
во вг ге
„	АО ВО
Следовательно,— = — ,
ог ОН
или АО ОН = ВО OZ .
А поскольку сумма ZB0Z и ZH0Z равна двум прямым, то S(BOZ) = S(A0H)*.
Предложение 14. Если к двум смежным сопряженным гиперболам проведены ка¬
сательные. а через точки касания диаметры, то плошадь треугольника, образованного
этими диаметрами и прямой, параллельной одной из касательных, равна сумме площа¬
дей двух других треугольников
Если при тех же самых пред¬
посылках на любом из сечений бе¬
рется некоторая точка и от нее
проводятся прямые, параллельные
касательным, то площадь получив¬
шегося треугольника с вершиной в
центре, отличается от площади
треугольника с той же вершиной,
имеющего основанием параллельную
указанной прямой касательную, на
пющадь треугольника, ограничен¬
ного этими двумя прямыми и диа-
мепц
При тех же самых предпосыл¬
•i».
ках пусть будет взята на сечении
(В) некоторая точка Н, через которую будут щ
ведены EL и ЕТО, параллельные пря¬
мым АН и BZ. В таком случае я утверждаю, что S(0OT) = S(0ZB)+ S(TLE).
Пусть от точки А будет проведена АУ, параллельная прямой Вг. Поскольку по той
же самой причине, что и прежде, ЛОМ есть диаметр сечения (А), сопряженный ему
• Площадь треугольника равна, как известно, 0,5ab sina, а синусы смежных углов равны
286

Предложения
есть А0В, АН — касательная, a AY параллельна диаметру А0М, го (1,40)
AY = Lt 0Y
YH “ Lr AY
где Lrсоставляет эйдос с latus transversum AM.
AY ET 0Y 0T 0B
Учитывая, что	= — ,	= — = — и то, что как latus transversum AM от-
YH TZ AY TO BZ
носится к latus rectum при нем, так и latus rectum противолежащих относится к latus
D	ET Lr 0B
transversum ВЛ, получаем — 		.
TZ Lt BZ
Следовательно (1,41), S(0OT) = S(0ZB)+ S(TZE)*, а кроме того (III, 13), S(0OT)
= S(AH0)+ S(TZE).
Предложение 15. Если к гиперболе проведены две касательные, а через точки каса¬
ния диаметры, то площадь треугольника, образованного одним из диаметров и прямы¬
ми, проведенными из некоторой точки на сопряженном сечении параллельно касатель¬
ным равна сумме площадей двух других треугольников
Если прямые, касающиеся одного из противолежащих, пересекаются, и через точ¬
ки касания проведены диаметры, а от одной из точек, взятой на любой из сопряжен¬
ных проводятся прямые, параллельные касательным, то площадь треугольника, обра¬
зованного этими прямыми и одним из диаметров, больше площади треугольника, воз¬
никшего при этом построении и имеющего вершиной центр, на площадь треугольника,
имеющим основанием касательную, а вершиной — центр противолежащих сечений.
Пусть даны противолежащие (А)
и (В) и сопряженные (Г) и (А) с цен¬
тром 0, касательные АЕ и ВТ, а также
диаметры АФ и ВТ, проведенные че¬
рез точки соприкосновения. И пусть
на сечении (А) взята точка Е, через
которую проведены Егл, параллель¬
ная касательной ВТ, и ЕУ, параллель¬
ная АЕ. В таком случае, я утверждаю,
что Б(ЕАУ) = ЬаЫЭ) + 5(0ГВ)* **».
Проведем прямую Е0Н параллель¬
но касательной В Г, прямую Н1К па¬
раллельно касательной АЕ и ЕО па¬
раллельно диаметру ВТ. Тогда ЕН и
ВТ суть сопряженные диаметры (11,
20), а ЕА0О - параллелограмм.
Поскольку ВГ касается сечения и
В0 проведена через точку соприкос¬
новения, а другая касательная есть
В (1,41) говорится о параллелограммах, но ясно, что соотношение верно и для треугольников.
** Возможно и другое расположение треугольников: см рис. 2
Или S(0AE), так как их площади равны (III, 2).
287

Книга III
BA MN
АЕ, то если для некоторого отрезка MN выполняется равенство	=

BE 2ВГ
он яв-
ляется latus rectum для ВТ (1,50)*.
ВА МП
Если же MN рассекается в П на два равных отрезка, то	.
п	п	ЕН ВТ
Пусть теперь для некоторого отрезка Р выполняется	.
ЕН
Тогда Р будет численно равно latus rectum для ЕН (I, 60).
ВД МП	ВД2 МПМПВ0
Ипоскольку—= —,а —= ^^и —= -^r^-,To
ВД2 МПВ0
ВА ВЕ ВГВ0 '
Далее. МП • BO^’A MN • ВТ, а согласно (1,60), MN • ВТ = ЕН2 = 40Н2, посколь¬
ку MN является latus rectum для ВТ.
ВД2 _ 0Н2	ВД2 ВДВЕ
Тогяа вТвЁ=вгв©и-наоборот-^=БГ^-
•I»
Кроме того, поскольку тре¬
угольники АВЕ и Н01 подоб-
ВД2 в(ДВЕ)
ны,т0 ен2~8(н01)’апо'
скольку треугольники АВЕ и
ГВ© имеют общий угол, то
ВД ВЕ _8(ДВЕ)
ВГ В0~8(ГВ0)'
8(ДВЕ) Э(ДВЕ)
ПоэточуИ=И'
а значит. 5(Н©1) = 5(ГВ8).
Таким образом, будет $(Н©К)
= 8(10К) + 5(Н01) = 5(1©К)+
^ГВ6).
В0 В0 МП
Поскольку же —- = —— • ——,
ВГ МП ВГ
В0 ВТ Р
МП ВД В0 Р ВД
ВГ _ВЕ Т0 ВГ ~ ЕН BE
ЕН
* Там доказывается, что если	.
ЕН 2ЕА ’ Т0 верн0 = ЕМ • МП , а значит, согласно (III, 12),
Ев есть latus rectum
288

Предложения
ла
В0 Л0
Так как В Г и ХА параллельны, то треугольники 0ГВ и 0ZA подобны и -gp- =
Л0 _ Р ВД _ Р 0Н	Л0 Lr 0Н
азначит, —- —	или —= —
AZ ~Н BE	01	AZ	Lt 01
Теперь так как (А) есть гипербола, имеющая диаметром ЕН, и ее latus rectum есть
Р, а от некоторой точки S проведена ордината LO, в то время как на отрезках, заклю¬
ченных между центром и точками пересечения диаметра с касательной и прямой,
ей параллельной, а также радиусе 0Н построены треугольник Н01, а на ординате
SO или 0А, ей равной, — треугольник 0AZ и схожим образом на 00, заключенной
между центром и той же ординатой, или на ХА, равной ей, построен треугольник
SAY, подобный треугольнику H0I, и все они связаны вышеуказанными отношени¬
ями, то (I, 41) S(LAY) = S(ZA0) + S(0rB).
Предложение 16. Квадрат отношения отрезков касательных равен отношению про¬
изведения двух отрезков к квадрату третьего
Если две касательные к коническому сечению пересекаются и от некоторой точки се¬
чения проводится прямая, параллельная одной из них и пересекающая сечение и другую ка¬
сательную, то квадраты отрезков касательных, заключенные между точками касания и
точкой их пересечения, относятся между собой так же, как площадь прямоугольника, сто¬
роны которого равны отрезкам указанной прямой, заключенным между точкой ее пересе¬
чения с другой касательной и точками, в которых она пересекается с сечением, к квадрату
отрезка, заключенного между точкой касания и точкой пересечения прямой и касательной.
/Л
Е
А
' 1
16. Рис. 1а. Парабола
(точка А вне дуги А В)
16. Рис. lb. Парабола (точка
А между точками А и В)
289

Книга III
Пусть дано коническое сечение, касательные к которому АГ и ВГ пересекаются
в точке Г, и пусть будет взята на сечении некоторая точка А, через которую прово-
ВГ2 гЕ • ЕД
дится прямая ¿Е, параллельная ВГ В таком случае я утверждаю, что =	-2 .
Пусть от точек А и В будут проведены и продолжены диаметры А® и ВЛ, а через
точку А - АМ1Ч, параллельная прямой АЛ.
Тогда поскольку (1,46-47) КД = Кг и ДЕ приложена, то (Евклид 11, 6)*	• ЕД
+ КД2 = КЕ2.
КЕ2 Б (КЕЛ)
А поскольку треугольники КЕЛ и	подобны, то (Евклид VI, 19) ^^7 = $
КЕ2 _ КД2	_ КЕ2	гЕЕД
11 8(КЕЛ) “ БВСДЫ) ’ поэтому” $(КЕЛ) “ 5(ЛД) '
КЕ2	ВГ2	ВГ2 /ЕЕД
Таким же образом, поскольку	. то	.
Ранее было доказано (III, 2), что 5(АЕН) = Б(ЛД), а также что (III, I) треуголь¬
ники ВГЛ и ГА0 равны.
л
16. Рис. 2. Гипербола (мы далее не приводим рисунков
16. Рис. 3. Эллипс)
для разных положений тонки Л, так как они
аналогичны рисункам к Предложению 2)
* Это можно доказать и так. 2Е = 2КЛ + Е\, следовательно,	• ЕА + КЛ? = (ДЕ + К \)? = КЕ
КЕ2 КЕ2-КД2 гЕ ед
«4
О
5(КЕЛ) 8(КЕЛ)-5(КДМ) Б(М) 6'всвойствопропорции)
2ЭД

Предложения
В Г2 ZE-ЕД
Т0ГДа S(TA0) ‘ S(AEH) НаОбОр°Т’
А так как (Евклид VI, 19)
ВГ2 ZE-ЕД
S(AEH)
S(rA0)
ZE-ЕД S(AEH)
ВГ2 ~ S(rA0)'
АЕ2 ZE ■ ЕД АЕ2
АГ2 ,Т° ВГ2 _ АГ2
и, наоборот,
Предложение 17. Квадрат отношения отрезков касательных равен отношению про¬
изведений отрезков, на которые разбивают друг друга параллельные им секущие
Если две касательные к сечению
пересекаются, а через две произволь¬
ные точки на нем проводятся прямые,
параллельные этим касательным, то
квадраты отрезков касательных меж¬
ду точками касания и точкой их пе¬
ресечения относятся между собой как
площади прямоугольников, ограничен¬
ных отрезками секущих, на которые
они разбиваются точкой их пересече¬
ния и сечением.
Пусть дано коническое сечение
общего вида, касательные АГ и В Г,
©
и пусть на нем взяты произвольные
точки А и Е, через которые прове¬
дены КО и АО, параллельные каса-
тельным.
В таком случае я утверждаю, что
АГ2 KZ-ZE
ВГ2 0Z-ZA'
©
Проведем и продолжим диаметры ААМИ и ВОЕП, а от точек А и Е - АЕ и ЕМ,
параллельные касательным. Поскольку КО и АО параллельны касательным, то (I,
46,47) К1 = 1Е, АН = НО, а так как КЕ в точке I рассекается на равные отрезки, а в
Я - на неравные, то, следовательно (Евклид II, 6)*, К7 • 7,Е +	= ЕР .
И поскольку треугольники Е1М и 21А вследствие параллельности сто{
сяподобными,ТО(ЕвкЛИдУ1,19)^у=^,поэтому**	5(2М)-
еГ аг2 кг-гЕ аг2
В силу тех же свойств треугольников	и ^уу =	.
* Доказательство аналогично доказательству, приведенному в сноске к (III, 16).
1 •
Доказательство аналогично доказательству, приведенному во второй сноске к (III, 16)
291

Книга III
Атак как (111. 1) ГAN = ГПВ и (III. 3) 5(гМ) =
©г гл
Таким же образом доказывается, что $(“ §(гпв)’
_	аг2 кг гЕ
Тогда очевидно, что —г  	■
гв2 ©г • гд
кг гЕ аг2
5(г=),т° 5(2Е) -8(гпв)-
вг2
Предложение 18. Предложение 16 для противолежащих
Если две касательные к одному из противолежащих пересекаются, а на втором бе¬
рется некоторая точка, от которой проводится прямая, пара^иельная одной из них и
пересекающая это сечение и другую касательную, то квадраты отрезков касательных
между их точкой пересечения и точками касания относятся друг к другу как площадь
прямоугольника, ограниченного отрезками, заключенными между точкой пересечения
секущей и касательной и точками пересечения секущей с противолежащим, к квадра¬
ту отрезка касательной, заключенного между точкой касания и точкой ее пересече¬
ния с секущей.
Пусть даны противолежащие и касательные к одному из них АГ и В Г, а через точ¬
ки соприкосновения проведены диаметры АМ и ВМ. Тогда если на сечении (В) бу¬
дет взята некоторая точка А, через которую проведена прямая Ег, параллельная пря¬
мой В Г, то я утверждаю, что ВГ ЕЛ
•I»
.АГ2 ЛЕ/
Поскольку BN - диаметр гиперболы, а прямая А/ параллельна касательной В0,
то (1,48) го = ОА.
а

Предложения
Е
А так как Д7 в точке О рассе¬
кается на равные отрезки, то (Ев¬
клид II,6)* ЕД- Е7 + ДО2 = ЕО2.
Проведем через точку Д от¬
резок ДЕ параллельный пря¬
мой АЕ. Тогда треугольники
ЕОЛ и ДОЕ подобны, а поэтому
ЕО2 ДО2
-7	г = —7	г и поэтому так-
БСЕОА) Б(ДОЕ)
ЕО2	ЕД • Е2
же остальное —	г = г.
Б(ЕОЛ) Б(ДЛ)
А так как соответствующие
треугольники подобны,то
ЕО2 _ В Г2
S(EOA) = S(BTA) И
ЕД-EZ ВГ2
Б(ДЛ) "S(BTA) ’
Учитывая, что (111,6) S(AA) = S(AEH), а также что треугольники В ГЛ и АГО рав-
/п,	ЕД-EZ Bf2
ны (111,1), получим	=
С другой стороны, из подобия треугольников следует, что
„	ЕДЕг ВГ2
Следовательно, справедливо	— =	.
АЕ2 АГ2
S(AEH) S(AT0)
АЕ2 " АГ2
Предложение 19. Предложение 17 для /X	Хм
противолежащих
Если две прямые, касающиеся противо¬
лежащих, пересекаются, и проведены две
прямые, параллельные касательным, пере¬
секающие друг друга и обе ветви каждого
сечения, то квадраты отрезков касатель¬
ных, заключенных между точкой их пересе¬
чения и точками касания, относятся друг
другу как площади прямоугольников, огра-
\\	X /
\ X	s	/
\ X
\ \
р/S/х
\
\
\
ниченных отрезками секущих, расположен¬
ными между точкой их пересечения и точ¬
ками пересечения с ветвями сечений.
Пусть даны противолежащие с диа¬
метрами АГ и ВД и центром Е, и пусть
касательные А7 и Д7 пересекаются в 7.
Z
19. Рис. 1.
* Здесь и далее см. сноски к (III, 16).
293

Книга III
Тогда если от любых произвольных точек противолежащих проведены прямые НА
дг2 нлл1
и МЛ. параллельные касательным, то я утверждаю, что —=- =	.
МЛ • ЛЕ
Пусть через точки 1 и Н проведены 1П и ЕР, параллельные Л7 и Д7. Тогда, по-
лг2 ел2 ©12
скольку (Евклид VI, 19)	= 8(0ЛОР ^0|пГ а в точке 0 отрезок НI рас-
секается на равные отрезки (1,48), следовательно (Евклид II, 6), НА • Л1 = 0Л2 —0Р
t AZ2 HAAI
и* S(AZS) " S(mOA) '
Но, с другой стороны (111,4), S(AZL) = S(AZT) и (III, 10) S(inOA) = S(KPEA),
AZ2 HAAI
BCW4eroS(AZT) = S(KPSA)-
ZA2 _ МЛ • ЛЕ
MT04HOTaK*eito) = S(KrëA)-
AZ2 HA ■ AI
Следовательно, —7 = ———.
ZA’ МЛ-ЛН
Предложение 20. Отношение произведения отрезков, на которые касательная раз¬
I
бивает прямые, проведенные между противолежащими параллельной прямой, соеди-
няюшей точки касания, к квадрату отрезка касательной есть постоянная величина
Если две касательные к противолежа¬
щим сечениям пересекаются и через точку
пересечения проведена прямая, параллель-
ная прямой, соединяющей точки касания,
и проводится другая, параллельная eù пря¬
мая, то площадь прямоугольника, ограни¬
ченного отрезками, проведенными от точки
&
пересечения касательных к сечениям, так
относится к квадрату отрезка касатель¬
ной, как площадь прямоугольника, ограни¬
ченного отрезками второй прямой, на ко¬
торые она разбивается касательной, от¬
носится к квадрату отрезка касательной,
отделенного этой прямой.
Пусть даны противолежащие с цен¬
тром Е и касательными AZ и Г2, прямая
АГ. а также проведены и продолжены Е7
и ЛЕ. И пусть через точку 7 будет прове¬
дена прямая, параллельная АГ, а на одном
СЁ
•Ж
‘ См сноски к (III, 16)
294

Предложения
из противолежащих взята некоторая точка К. через кеглею тоже п
параллельная АГ. В таком случае я утверждаю, что
•I»
прямая,
. ведена
КАЛЕ*
AZ2 АЛ2
Пусть от точек К и П будут проведены КП и ВР. параллельные касательной AZ.
BZ2 К£2 AZ2 КА ЛЕ
Тогда(ЕвклидУ1Н9;П,5)^^ = ^^=^^ = 5^х^».
С другой стороны, поскольку (II, 39, 38) BS2 = BZ • ZA , а также (III, 11) S(BZP)
= S(A0Z) и (III, 5) S(KAZn) = S(ANA), то BZ'
S(A0Z) S(ANA)
a	zc \/i io\ S(A0Z) S(AAN)
А так как (Евклид VI, 19)		— =	-— , следовательно, справедливо
AZ2 АЛ2
BZZA KAAH
ZA2 ” АЛ2
Предложение 21. Предыдущее отношение равно отношению произведений отрез¬
ков двух прямых, параллельных, одна — касательной, а другая — прямой, соединяю¬
щей точки касания
Если при тех же самых предпосылках на одном из сечении берутся две точки, через
каждую из которых проводятся две прямые, одни параллельно касательной, а другие
параллельно прямой, соединяющей точки соприкосновения, то площадь прямоугольника,
ограниченного отрезками, проведенными от точки пересечения касательных к сечени¬
ям параллельно прямой, соединяющей точ¬
ки соприкосновения, так относится к ква¬
драту отрезка касательной, как площадь
прямоугольника, составленного из отрез¬
ков, на которые секущая, проведенная че¬
рез одну из указанных точек параллельно
касательной, делит прямую, проведенную
через другую точку параллельно прямой,
соединяющей точки касания, относится
к площади прямоугольника, составленного
из отрезков этой секущей, заключенными
между точкой ее пересечения с указанной
прямой и точками пересечения с гиперболой.
При тех же самых предпосылках че¬
рез точки Н и К, лежащие на одном из
* Поскольку точка К берется произвольно, то и ВЛ не обязана проходить через точку 2 Важно
лишь, чтобы она была параллельна АГ, то есть была ординатой к диаметру ЕР
“ Как и в предыдущих теоремах, имеется в виду, что поскольку точка I разбивает КН на рав¬
ные, а \ - на неравные части, то (см. примечание к Предложению 16) КЛ* \Н = К1 - и, соглас¬
но 6-му свойству пропорций, получаем данное равенство
295

Книга III
сечений, проведены N Н Р и КТ, параллельные прямой А7, а также НМ и КО, па¬
раллельные прямой АГ.
В таком случае я утверждаю, что
BZZA
AZ2
AZ2
Ведь поскольку (Евклид VI, 19)	;
S(AZ0)
AZ2
то*,
НО2
ЕН2
КОРО
NO-OH
АЛ2
“ S(АДМ) “ SCHOT') " S(EHM) ’
ЕО2-ЕН2	AZ2 _NOOH
SÎAZ0) S(EO'P)-SCEHM) И(1,47иП1, l6)S(AZ©)_ S(H>P) ‘
Атаккак(Ш, 5) S(AZ0) = S(BZY) и (III, 12) S(H'P) = S(KP), то
AZ2 NO-OH
S(BZY)” S(KP) ’
г г	,1И	S(BZY) S(BZY) S(KP)
С другой стороны, мы доказали (III, 20 , что		— =	=	.
BZ“ BZ -ZA КООП
AZ2 NO • ОН
Следовательно, справедлива пропорция •	_ • =	и, очевидно, ей об-
BZ • ZA КО • OQ
BZ ZA КО ОЯ
ратная	— ~.
NL1 N0 ОН
Предложение 22. В случае противолежащих Ы и Ег относятся как произведения
отрезков, на которые ордината и прямая, параллельная диаметру, делят друг друга
Если две параллельные прямые касаются противолежащих сечений и проводятся не¬
которые прямые, рассекающие друг друга и сечение, одна — параллельно касательным,
а другая - параллельно диаметру, соединяющему точки касания, то этот диаметр.
или latus transversum, так относится к
latus rectum, как площадь прямоугольника,
ограниченного отрезками, расположен¬
ными между точкой пересечения прямых
и сечениями, к площади прямоугольника,
ограниченного отрезками, расположен¬
ными между' этой же точкой и сечением.
Пусть даны про
ти вол ежащие и каса¬
тельные к ним АГ и ВД, параллельные
друг другу, и пусть точки соприкосно¬
вения соединяет прямая АВ Тогда если
провести прямые НЕЕ и КЕЛМ парал¬
лельные прямым АВ и АГ, то я утверж-
Ы НЕ • ЕЕ
даю. что — =	.
Ьг КЕ • ЕМ
♦
порции
296

Предложения
Проведем через точки Н и Е прямые Н7 и ЕГ4, параллельные прямой АГ.
Поскольку АГ и ВЛ, касающиеся сечения, параллельны, то АВ есть диаметр
(II, 31) и отрезки КЛ, ЕЙ и Н7 есть ординаты (I, 47 и 48), то, следовательно (1,21),
Ы ВА ЛА ВЫ-ИА ВЫ-ЫА
ЕЛ2
Lr КЛ2
N2
.	х.ж	ВА ЛА ZA-NA
А так как NA = BZ (I, 12), то BN = ZA и	=— =	z—, поэтому точно так же
КЛ2 ЕЛ2
7Л лм	см.	ВАЛА ZA NA ZA-AN
оставшееся ZAxAN относится к остатку КЕхЕМ*. то есть	;— =	z— =

КЛ2 ЕЛ2 КЕЕМ
и, соответственно, как АВ относится к latus rectum.
Атак как ZA*AN = НЕ • ЕЕ, то, следовательно, АВ или latus transversum относит-
,	НЕЕЕ
ся к latus rectum, как	.
КЕЕМ
Предложение 23. Квадрат отношения отрезков касательных к противолежащим ра¬
вен отношению произведений отрезков двух пересекающихся параллельных им прямых,
на которые они делят друг друга
Если даны противолежащие и им со¬
пряженные и точка пересечения каса¬
тельных к противолежащим лежит вну¬
три одного из сопряженных сечений, а
также проведены прямые, параллельные
касательным, пересекающие друг друга
и сопряженные, то квадраты отрезков
касательных, заключенных между точ¬
кой их пересечения и точками касания,
относятся друг к другу, как площади
прямоугольников, ограниченных отрез¬
ками, на которые разбиваются точкой
их пересечения отрезки прямых, распо¬
ложенные между сечениями.
Пусть даны противолежащие (А) и (В) и им сопряженные (Г) и (А) с центром К,
•л
первых из которых касаются АХ и ЕЛ, пересекающиеся в точке Л, и пусть прове¬
дены диаметры и ВЕ. Тогда если от точки Н проведена прямая НО, параллель-
ЕЛ2 0ЕНЕ
ная АЛ и от О - прямая 0£, параллельная ЕЛ, то я утверждаю, что —у = —
О
Поскольку ВЕ - диаметр, ЕЛ касается сечения, а 0£ ей параллельна, то 0П = П^
и по той же причине НМ = МО.
ВА ЛА ZA NA BA AA-ZA NA
Так в тексте. Имеется в виду, что - • , =	,— =	—j—зтп	• Раскладывая знаме-
КЛ ЕЛ	КЛ —ЕЛ‘
натель как разность квадратов и учитывая, что ВЛ = ZA + AN. получим после несложных преобра¬
зований нужное равенство.
297

Книга III
Пусть через I проведена прямая ХТ, параллельная АЛ, а от О - ОУ, параллельная
ЕЛ" ПХ- ПЕ2	ЕЛ2 ®ЕЕЕ
; то также остальное* 5(ЕЛф)~ 8(гт).
ЕЛ.Атаккак5(£лф) s(nrr) S(nsN)
Но, с другой стороны (III, 4), S(EA4>) = S(AAX) и также (выводится из III, 15)
S(TE) = S(EY).
ЕЛ2 _ 0Е • EX
n°3T0MyS(AAX)= SteYi
а также**
АЛ2 _НЕ-ЕО
S(AAX)_ S(SY) ’
Следовательно, —у =	.
АЛ Hr г.0
Предложение 24. Если прямые, параллельные сопряженным диаметрам, пересека¬
ются между четырьмя сечениями, то произведение отрезков одной прямой плюс произ¬
ведение отрезков другой, у множенное на квадрат отношения этих диаметров, равно уд¬
военному квадрату половины диаметра, находящегося в числителе
Если от центра противолежащих и сопряженных проведены сопряженные диаме¬
тры, а napa.i ie.ibHo им проведены прямые, пересекающие друг друга и сечения, и точка
их пересечения лежит между четырьмя сечениями, то площадь прямоугольника, огра¬
ниченного отрезками, на которые разбивается прямая, параллельная диаметру про¬
тиволежащих, сложенная с площадью прямоугольника, ограниченного отрезками, на
которые разбивается прямая, параллельная сопряженному диаметру, умноженной***
на отношение квадратов этих ди-
аметров, равна удвоенному квадра¬
ту половины диаметра противоле¬
жащих.
Пусть даны противолежащие
(А), (Г) и сопряженные (В) и (Л) с
центром в Е, через который прове¬
дены сопряженные диаметры АГ и
ДВ и параллельные им гН01КЛ и
М№ЕОПР, пересекающиеся в точ¬
ке Е, лежащей между четырьмя се¬
чеНиями внутри угла между асим¬
птотами, ли
внутри дополнитель¬
ного угла, или на асимптоте.
• То есть, по 6-му свойству пропорций,
0
X
П12 - ПЕ2
ЕЛ2
S(EAO) S(nXT)-SinZN) S(EXTN)
** Аналогичные выкладки с треугольниками А \Х MOY и МЕР
Напомним, что Аполлоний не употреблял термины «-умножение» и «произведение» по отно
шению к непрерывным величинам Далее мы не будем это особо оговаривать
298

Предложения
В таком случае я утверждаю, что ZS • ЕЛ + ME • ЕР • -у = 2АЕ2*.
АЕ
Пусть будут проведены асимптоты сечений LET и УЕФ, и через точку А каса¬
тельная ЕНАФ.
Пусть точка Е находится внутри угла £ЕФ или YET (рис. 1).
LA • АФ АЕ2
Поскольку (П, 1) LA • АФ = АЕ2, то	j— =	Г »
а ЕА АФ _ ХА АФ	АЕ АЕ
3 АЕ2 “ АЕ АЕ
..	_	LA Nr. АФ П
Из подобия треугольников следует, что	=	и

АЕ Е0 АЕ
АЕ2
Тогда
ЕК
АЕ
№П- ДЕ2+№П
NE П
а© ЕК Е0 ЕК АЕ2+Е© ЕК‘
С другой стороны (II, 11 и 16), ДЕ2 = ПМ • MN = PN • MN и точно так же АЕ: =
KZ • Z0 = Z0 • ОЛ .
ДЕ? NE-nE + PNMN
Поэтому ~з
АЕ
0-EK + Z0-0A '
АЕ2
АЕ2
ME ЕР
E0EK + KZZ0’
I
*
п
АЕ2
(Подставим —у в исходную фор¬
мулу. )
Теперь нужно только доказать, что
¿Е • ЕЛ + Е0 • ЕК + Кг • г© = 2АЕ2
или, так как АЕ2 = Кг • г©, что гн • ЕЛ
+ Е0 • ЕК = АЕ2.
Действительно, это так, ведь г
+ Е0*ЕК = г0«0Л*** = Кг-г0 = АЕ2.
2, Пусть отрезки гл и М Р пересекают¬
ся в точке 0, лежащей на одной из асим¬
птот (рис, 2). (То есть точка Е совпада-
ет с точкой 0.1
АЕ2
* Аполлоний проводит доказательство так: сначала находит отношение . _2 , а затем подстав-
ЛЕ
ляет его в формулу, которую надо доказать.
** Это можно доказать так: поскольку ПЕ = ЕР - РП, а РЫ
РЫ-МЫ - (ЕР + ЫЕ)* МЫ. Сложив почленно эти выражения и раскрыв скобки, получим (учитывая,
что РП = МИ) искомый результат.
***	- Е© + ТЕ, а ©Л - ЕЛ - Е0 Тогда Л© • Т0 = ТЕ•
скобке равно ЕК, поскольку ТЕ + Е© = КЛ.
Р + NE, то Nr.- ПЕ = Nr(EP - РП) и
X + Е0- (_ \ - Е© - Zx), а выражение в
299

Книга III
ДЕ2 М0-0Р
Поскольку (11, 11,16) АЕ2 = 7.® • 0Л и ДЕ2 - М0 • 0Р , то 2 -	.
АЕ‘ ¿0 0А
АЕ2
I Подставим —- в исходную формулу.]
АЕ2
Тогда должно быть 220 • 0Л = 2АЕ2, и это очевидно выполняется.
Пусть теперь точка г., расположе¬
на внутри угла LEY или ФЕТ (рис. 3).
Тогда так же, как и в первом случае,
ДЕ2 № ■ ПЕ
получается	.
АЕ	г.0 • —К
А так как ДЕ2 = ПМ • ММ =
Р№ • и АЕ2 = 20 • 0Л , то
ДЕ2 _ ЫЕ-ПЕ _ Р\М\
АЕ2 Е0ЕК 20-0Л .
ДЕ2 ДЕ2-№-П=
Т0ГДа АЕ2 " АЕ2 - Е0 • ЕК '
ДЕ2 РМ-ММ-КЕ-НЕ
АЕ2" АЕ2-Е0ЕК '
Следовательно,
ДЕ2 М	ф
АЕ2 ~ АЕ2 - Е0 • ЕК *
или
HP
{Подставим
АЕ2
АЕ2
в исходную формулу. ]
Теперь остается доказать, что 2Н • НА + (АЕ2 - Н0 • НК) = 2АЕ2, или, поскольку
АЕ2 = 20 • 0Л , что 2Н • НА - Н0 • НК = 20 • 0Л.
Это выполняется, так как 2Н • НА = (20 + Н0) • (0А - Н0) = 20 • 0Л + Н0 (0А -
20- Н0), и тогда 2Н • НА - Н0 • НК = 20 • 0А + Н0 (0Л - 20 - Н0 - НК).
А поскольку Н0 т НК = 0К, 0А - 0К = КА, а КА = 20, то выражение в скоб¬
ке обращается в нуль.
Предложение 25. Предложение 24 в случае, если точка пересечения лежит внутри
одного из противолежащих
Пусть при тех же самых предпосылках точка пересечения прямых, параллельных
диаметрам АГ и ВА, находится внутри сечения (А) или (В).
В таком случае я утверждаю, что площадь прямоугольника 2Н • НА будет боль-
ше удвоенного квадрата половины диаметра про
тиволежащих на величину плоша-
* Это доказывается аналогично первому случаю так как РЫ = ЫП + РП, ЫЕ = ЕР - РЫ, а
РП - МЫ, то, подставив это, раскрыв скобки и приведя подобные члены, получим, что числи¬
тель равен - ЕР? + РЫ• ЕР + ЕР• РП = ЕР- (-ЕР + РЫ + РП) =ЕР*МЕ.

Предложения
ди прямоугольника М- • ЕР, умножен-
АЕ2
ной на отношение ~	? *.
ДЕ2
По той же причине, что и ранее (III,
ДЕ2 № ■ ПН
24)’ АЕ2 ~Е0 -К '
Атак как (II, 11 и 16)ДЕ2 =
пм • ми, ае2 = кг • г©, то
ДЕ2 ПМ-МИ
ае2_ кгг© ’
С другой стороны (II, 11 и 22),
ЫЕПЕ ПМКШ ПМ-МЫ
е©ек‘ кг г© ” ©I ¿к
учитывая, что** МЕ*ПЕ=ПМ*1'М
+ МЕ-ЕР,Е0-ЕК = 01-1К +
1Е*ЕХ, получим***
N5-Па _ МЕ ЕР ДЕ2
Е0 ЕК ~ 1Е ЕХ ~ АЕ2’
АЕ2
| Подставим полученное выражение для
в исходную
зек
рмулу.]
1
I
Теперь необходимо доказать, что ТЕ • ЕА - 1Е* ЕХ = 2АЕ2.
Поскольку (II, 23) 71 • 1А = 2АЕ2, то остается доказать, что 7Е’ЕА — 1Е*ЕХ =
г! ЧА.
Это выполняется, так как 7Е • ЕА - 1Е • ЕХ = (£\ + 1Е) • (ЕХ • ХА) - 1Е • ЕХ =
71*ЕХ + 1Е • ЕХ + 71 • ХА + 1Е-ХА- 1Е-ЕХ = 71-ЕХ + 71-ХА+ 1Е-ХА.
Учитывая, что ХА = £\ (II, 11), получаем 7Е’ЕА - 1Е* ЕХ = 7 ЦЕХ + ХА + 1Е)
= 71-1А.
Что и требовалось доказать.
Предложение 26. Предложение 24 в случае, если точка пересечения, лежит внутри
одного из сопряженных
Пусть при тех же самых предпосылках точка Е пересечения прямых, параллель¬
ных прямым АГ и ВД, находится внутри сечения (А) или (Г).
В таком случае я утверждаю, что плошадь прямоугольника 7ЕхЕА бу¬
дет меньше плошади прямоугольника МЕхЕР, умноженной на отношение
‘ То есть 73 ЕА + МЕ
жения 24.
АЕ2
• ЕР	г- = 2АЕ2 Доказательство аналогично доказательству Предло-
ДЕ
“ МЕ* ПЕ= (МЕ + МИ)(МЕ + МП) = МЕ? + МЬ1 • МЕ + МЕ* ПМ + М1М • ПМ = ПМ* МЫ + МЕ -(МЕ + МЫ
+ ПМ). Поскольку МИ = ПР (II, 11), то равенство доказано. Аналогично, ЕО-ЕА = (01 + 1Е)*(1К - 1Е) =
©НК +1Е• (1К - 01 - 1Е). Учитывая, что 01 =ХК (II, 11), выражение в скобке равно 1Е • ЕХ
*** 6-е свойство пропорции.
301

Книга III
на величину удвоенного квадрата
половины диаметра противолежащих*.
Поскольку ранее было доказано (III,
24),чю^=*Е^=--М5-5Р
АЕ2 Е0ЕК Е0ЕК + К2-г©
и АЕ: = КИ • Хв , то, следовательно,
ДЕ2 _ МЕ ЕР
АЕ2 Е0ЕК + АЕ2 '
[Подставим полученное выражение
АЕ2
для а_2 в исходную формулу.]
АЕ
Теперь необходимо доказать, что
ТЕ* ЕЛ -I- 2АЕ2 = Е0 *ЕК + АЕ2, или,
ТЕ • ЕЛ + АЕ2 = Е0 • ЕК .
А поскольку (П, 11 и 16) АЕ2 =
¿0 • 0Л, то ТЕ • ЕЛ = Е0 • ЕК — 70 • 0Л.
Это действительно так, поскольку ранее было доказано (III, 24), что Z0 • 0Л +
ZE • ЕЛ = Е0 • ЕК.
О
т
Предложение 27. Предложение 24 для эл¬
липса
Длина .atus weoum уыеныдена вдвое
(ZH<NH)
Если проведены сопряженные диаметры
эллипса и параллельные им секущие, то сумма
квадратов отрезков, лежащих на секущей, па¬
раллельной первому диаметру, прибавленная к
сумме площадей прямоугольников, построенных
на отрезках секущей, параллельной второму
диаметру и подобных прямоугольнику, ограни¬
ченному вторым диаметром и его latus rectum,
равна квадрату первого диаметра.
Пусть в эллипсе с центром Е проведе¬
ны два сопряженных диаметра: ВЛ и АГ, и
параллельные им секущие NO и КМ, пере¬
секающиеся в точке Z. В таком случае я ут¬
верждаю, что сумма NZ2 и Z02 вместе с пло¬
щадями прямоугольников, построенных на
То есть ZE-cA-eMS-£P —— = 2АЕ2 Доказательство аналогично доказательству Предло-
Ас
жения 24.
302

Предложения
KZ и ZM и подобных прямоугольнику, ограниченному АГ и его latus rectum, равна
квадрату диаметра ВД*.
Пусть от N будет проведена NE, параллельная АЕ, тогда она проведена к ВЛ как
ордината.
Пусть ВП есть latus rectum, тогда (1, 13)	=	а следовательно, — = ^£_.
АГ ВД	ВД ВД2
Однако ВЛ2 равно площади эйдоса, построенного на АГ (1, 15), равной АГ ’АО,
ВП АГ2
поэтому	=	.
• ВД АГ-АО
ВП
С другой стороны (I, 21),—

ВД BE - ЕД
Следовательно, площади прямоуголь¬
ников, построенных на NE и КЛ и подоб¬
ных прямоугольнику, построенному на АГ,
равны BE • ЕЛ и ВЛ • АД.
А поскольку прямая N0 в точке Н рас¬
сечена на равные отрезки (Опр. I, 6), а в
точке Z - на неравные, то** NZ2 + Z02 =
2(H02 + ZH2) = 2(NH2 + ZH2).
По той же самой причине также KZ2 +
ZM2 = 2(КЛ2 + ZA2), следовательно, пря¬
моугольники, построенные на KZ и ZM и
подобные прямоугольнику АГ • АО, по пло¬
щади вдвое больше фигур, схожим образом
построенных на КЛ и ZA. Однако площа¬
ди фигур, построенных на КЛ и ZA, рав¬
ны ВЛ • ЛЛ и BE • ЕД, и NН2 + ZH2
+ ЛЕ2, поэтому площадь NZ2 + Z02 с пло¬
щадями фигур, построенных на KZ и ZM
вдвое больше, чем (BE • ЕЛ) + (ВЛ • ЛД) +
ЕЕ2 + ЛЕ2.
А поскольку ВД рассечена в Е на равные
отрезки, а в Е - на неравные, то BE • ЕЛ -ь
+ ЕЕ2= BE2.
И по той же причине ВЛ • ЛД + ЛЕ2 —
ЕЕ2+ ЛЕ2 = 2ВЕ2.
Поэтому площадь NZ2 + Z02 вместе с площадями фигур, построенных на KZ и
ZM, и подобными фигуре, построенной на АГ, равна 4ВЕ2 или ВД2.
NH2
ВП К.Л2
" ВД _ВЛЛД
О
•к
Е2
Длина latus erectum уменьшена вдвое
А
Г
27. Рис. 2.
(ZH>NH)
BE2, следовательно, В- • ЕЛ + ВЛ • ЛД+
,	,	,	АГ KZ ZM
* То есть NZ + Z0 + KZ • х + ZM • у = ВД\ при этом — = — =
у
где х и у - вторые стороны пря¬
моугольников.
*• NZ = NH - ZH = НО - ZH, a Z0 = Н(-) + ZH
303

Книга III
Предложение 28. Отношение сумм квадратов секущих, параллельных сопряженным
диаметрам, равно отношению квадратов этих диаметров
Если проведены сопряженные диа-
метры, противолежащих и им сопря¬
женных и параллельно им проведены
две прямые, пересекающиеся друг с дру¬
гом и сечениями, то суммы квадратов
отрезков этих прямых относятся как
квадраты диаметров.
Пусть даны противолежащие и со¬
пряженные с центром Е, а также диа¬
метры АГ и ВЛ, параллельно которым
проведены прямые и Л1Ч, пересе¬
кающиеся друг с другом в точке Н.
„	ЛН1 2 + Н№ АГ2
Я утверждаю, что —;	- = —
гн2+нк2 ВА
Проведем от точек 7 и Л ординаты
»ж
•ж
28. Рис. 1.
»!•
2 •
ЛЕ и ZO; они параллельны диаметрам (Опр. 1,6), и отточки В отложим latus rectum
ВП. перпендикулярный диаметру ВА. Ранее было доказано (III, 27) и (I, 21), что
ВП АГ2 АЕ2 ZO2 ГЕНА
BE2
ВО ОД
АГ2
Поэтому* —- =
вд2
ГЕ EA + ZO! + AE2 ГЕ ■ =А + ©Е2 + АЕ2
'ле2+воод+ве2 ”ме2+во од+ве2
А так как (Евклид II, 6)** ГЕ • гА + АЕ2 = ЕЕ2 и ВО’ОА + BE2 = ОЕ2,
АГ2 ЕЕ2 + ОЕ2 ЛМ2+НМ2
то —- = — 	- = —-	—.
В А2 ME2 + OE2 Z02 + не2
С другой сторо
ны. было доказано, что (III, 27) ЛН: + HN2 = 2(ЛМ2 + НМ2) и ZH2
+ HK2 = 2(ZO2 + H02).
Следовательно,
АГ2
ВА2
АН2 + HN2
ZH2+HK2
Предложение 29. Аналогичная тео¬
рема для отрезков, отделяемых асим¬
птотами
Ест при тех же самых предпосыл¬
ках прямая, параллельная первому диа¬
метру пересекает асимптоты, то сум¬
ма квадратов отрезков, ограниченных
точкой ее пересечения с прямой, парал-
1	6-е свойство пропорции,
2	Это легко показать алгебраически, если учесть, что ГЕ = 2АЕ + ЕА
304

Предложения
дельной второму диаметру и точками пересечения с асимптотами, сложенная с поло¬
виной квадрата первого диаметра, относится к сумме квадратов отрезков прямой, па¬
раллельной второму диаметру, заключенных между точкой пересечения этих прямых и
сечениями, как квадраты этих диаметров.
Пусть при тех же предпосылках прямая ЛN пересекает асимптоты в точках Е и
ЕН2 + НО2 + - АГ2
2
О. Следует доказать, что	;	—
гн2+нк2
АГ2
ВЛ2 ‘
Поскольку ЛЕ = ON (II, 16), то АН2 + HN2 = ЕН2 + НО2 + 2Nr. • ЕЛ = ЕН2 +НО2
+ 2АЕ;*.
Но(П1, 28)
AH2+HN2
ZH2+HK2
АГ2
ВД2
АН2+НО2+2ЕА2 АГ2
поэтому также	?	z	= —г
ZH2 + HK2 ВД2
Предложение 30. Прямая, проведен¬
ная параллельно одной из асимптот от
пересечения касательных до секущей,
соединяющей точки касания, делится
гиперболой пополам
Если через точку пересечения двух
касательных к гиперболе проведена пря¬
мая, параллельная одной из асимптот,
то ее часть, лежащая между этой точ¬
кой и прямой, соединяющей точки каса¬
ния, будет разбиваться сечением на два
равных отрезка**.
Пусть дана гипербола с асимптота¬
ми EZ и ZH и касательными АД и ДГ,
пересекающимися в точке Д, и пусть проведена секущая АГ, а также прямая ДКЛ па¬
раллельно 2.Е. В таком случае я утверждаю, что ДК = КА.
Проведем и продолжим в обе стороны ¿Д, и пусть г© = ZB. Проведем через точ¬
ки В и К отрезки ВЕ и К>4, параллельные прямой АГ, тогда они проведены какор-
.	„г-,	- Д№ гв2
динаты. А поскольку треугольники ВЕг и N КА подобны, то	.
д№ гв2 ©в
Но(П, 1)	г =—г = .
ЫК2 ВЕ2 Ьг
, м	,, 0В ОЫ-ЫВ	ДМ2 ОКИВ
А с другой стороны (1, 21), — =	7— , поэтому	г =	г— и, следова-
ьг Ж2	' ЫК2 ЫК2
NK2
тельно, Д№ = ON•N В.
Поскольку же АД касается сечения, а AM есть ордината, то (1, 37) ZA* ZM = ZB2.
* Пусть ЛЕ = ОЫ = а, гн = Ь, НО = с Тогда (а+Ь)?+(а+с)' = 1т'+сг+2а(а+Ь+с) Далее, из (II, 11) сле¬
дует, что №*ЕЛ = АЕ2.
** С теоремами 30-37 тесно связаны теоремы, помещенные в (IV, 1-23).
305

Книга III
Поэтому также 7Л • 7М + Д№ - 7 В2 + 0N • N8.
Но так как* 7В2 + 0№ • N6 = 7ЬР, то 7Д • 7М + ДЬ12 = 2№.
Поэтому ввиду того что отрезок ДМ рассечен в точке N на два равных отрезка**,
а К№ и ЛМ параллельны, то ЛК = КА.
Предложение 31. Предложение 30 для противолежащих
Кеш через точку пересечения
двух касательных к противолежа¬
щим проведена прямая, пара, цель¬
ная одной из асимптот, то ее от-
резок, лежащий между этой точ¬
кой и прямой, соединяющей точки
касания, будет разбиваться сече¬
нием на два равных отрезка***.
Пусть даны противолежащие
(А) и (В) с нент|
CS
м в 7, касатель¬
ные к ним - АЛ и ГД, а прямая
АГ. соединяющая точки сопри¬
косновения, будет продолжена
дальше, и 7Е будет асимптотой.
Пусть также будет проведена пря¬
мая ДКА. параллельная асимпто¬
те 7Е. В таком случае я утверж¬
даю, что ДК = КА
•I»
Проведем Л7 и продолжим дальше до точки Р, и пусть через точки 7 и К будут
проведены 07ВМ и КН, параллельные прямой АГ, а через К и В - KN и ВЕ. парал¬
лельные прямой ДР.
MN2 7В2
Поскольку треугольники NKM и ВЕ7 подобны, то =
MN2 0NNB
Ранее было доказано (III, 30), что	г- =	=—, поэтому MN- = 0N • N В.
NK2 NK2
2 '
м
Прибавив к обеим частям 7В:, получим**** М№ + 7В2 = 0№ • N В 4- 7 В2 = 7ЬГ = КН2.
„	'	ке2 мы2 гв2
С другой стороны, из подобия треугольников имеем —у = -	= —у.
,	КЗ2 М№+2В2	КН2	ЗА2
А так как —г=	;	г, то““ 	;	г =	;	г .
ед2 ж2+ве2 мк-Чгв2 ж2+ве2
* Пусть 02 = ТЪ = а, МВ = Ь. Тогда нижеследующее выражение эквивалентно равенству а* +
+(2а+Ь)Ь = (а+Ь)<
** Поскольку 2А• гм = гы-- ЛЬг, то	ИМ = (ИЫ - \Ы)(2М +	ММ) Сократив на г
получим гм = гы + ЛМ Но ведь 2М = 2№ + ЫМ Следовательно, ЛИ = 1ЧМ
**• Ясно, что это Предложение 30 для противолежащих
*•** поскольку гы2 - гв' = (гы + гв) • (гн - гв) = ом • ыв.
6-е свойство пропорции
306

Предложения
Но КЕ2 = МЬ12 + вг2, значит, ЕД2 = N К2 +
Учитывая, что N К2 = Е72, а ВЕ2 есть квадрат половины второго диаметра (II, 1),
получим (I, 38) ВЕ2 = Д7 • 7Р, а следовательно, ЕД2 = Е72 + Л7 • ¿Р.
Поэтому ДР в Е рассекается на два равных отрезка*, а так как РА и КЕ парал¬
лельны, то ДК = КА.
Предложение 32. Если проведена секущая, соединяющая точки касания, а через точ¬
ку пересечения касательных параллельная ей прямая, то отрезок, проведенный из се¬
редины секущей параллельно одной из
асимптот, делится гиперболой пополам
Если через точку пересечения двух
касательных к гиперболе проведена пря¬
мая, параллельная секущей, соединя¬
ющей точки касания, то отрезок, за¬
ключенный между серединой секущей и
этой прямой, проведенный параллельно
одной из асимптот, будет разбиваться
сечением на два равных отрезка.
Пусть дана будет гипербола с цен¬
тром 2, которо
й касаются прямые АД
и ДГ, и пусть проведена секущая АГ, а
прямая Д7 продолжена в обе сторо¬
ны до точек М и 0. При этом (II, 30)
АМ = МГ.
И если параллельно АГ проведена
прямая ДА, а параллельно асимптоте
- прямая МА, то в таком случае я утверждаю, что ЛК = КМ.
Пусть через точки В и К проведены прямые ВЕ и К1Ч, параллельные АГ. Тогда,
гв2 МЬ12 ®Ы-ЫВ
как было доказано ранее (III, 30),—у = ■	=	-—, поэтому ©И *N8= ММ2.
ВЕ МК 1ЧК
Кроме того, поскольку АД является касательной и АМ - ординатой к диаметру,
то(1,37) мг* дг = гв2.
Следовательно, 0М • N В + г В2 = М7 • Т М №.
Но** 0М • МВ + 7В2 = 2№, а значит, иМ7-\7. + ММ2 = 7М2.
Поэтому ДМ в точке N рассечена на два равных отрезка***, а так как ЛА и МК
параллельны, то ЛК = КМ.
• Так как ЕЛ2 - ЕЙ2 = (ЕЛ- Е2) • (НА+Е2) = (^Л - ЕИ) • Аг, то, сократив на дг, получим, что
ЕД - Е2 = 2Р, или ЕД = ЕИ+ИР.
“ Это доказывается так же, как и в предыдущем Предложении: ©N*N8 = гЬР - 7.8' = (ги -
2В)’(2Ы+ гВ) = ЫВ(2М+ гВ), и, сократив на ЫВ, получим верное равенство 0Ы = гы+гв.
*** Так как М7 *Л2 = ИЫ2- М№ = М2-	- МЫ), то, сократив на Мг, получим что дг + МЫ =
С другой стороны, очевидно, что Х2. + ЛИ = ¿Ы. Следовательно, МЫ = \Ы.
•ж
307

Книга III
Предложение 33. Предложение 32
для противолежащих
Если через точку пересечения двух
касательных к противолежащим про¬
ведена прямая, параллельная прямой,
соединяющей точки касания, то от¬
резок, проведенный к этой прямой от
середины прямой между точками ка¬
сания параллельно одной из асимптот,
будет разбиваться сечением на два
равных отрезка.
Пусть даны противолежащие с
центром 7. касательные АД и ДГ, и
пусть будут проведены асимптоты,
прямая АГ, соединяющая точки со¬
прикосновения и отрезок Д7, про¬
долженный до пересечения с АГ в
точке М Очевидно, что АГ рассека¬
ется в М на два равных отрезка (II, 30). Пусть затем через точки Д и 7 проведены и
продолжены прямые НУ и ОВ, параллельные АГ, а через М - отрезок МКЛ, парал¬
лельный одной из асимптот.
В таком случае я утверждаю, что ЛК = КМ.
Пусть будут проведены отрезки ВЕ и КИ, параллельные прямой ДМ, а также от¬
резок КН, параллельная прямой АГ.
7В2	• N8
Как было доказано ранее (III, 30), —? =	=—.
ВЕ2	МК2
л . ИВ2 0№КВ + 2В2
Поэтому* —г =	;	г—.
ВЕ2 МК2 + ВЕ2
/л
•ж
7В2	7Ъ12
Но (III, 31)	• N6 + 7В = 7№, следовательно. —- =			- .
ВЕ МК2 + ВЕ2
Кроме того, поскольку (I. 37) М7* Д7 = ВЕ2 и NK2 = 7Е2, то справедлива про-
гв2 г№	нк2
порция г = т	= —-	.
ВЕ2 г£‘+М7 дг 7Е2+М7Д7
НК
ТВ2 ”К2
А так как из подобия треугольников 7ВЕ и ЕКМ следует, что —г = ——=- , то
ВЕ2 ЕМ
НК2 ЕК2
—т = — 	 а значит, и 7Е2 + М7 • Л7 = ЕМ2.
ЕМ2 7Е2+М7Д7
Поэто%гу ДМ в точке Е рассекается на равные отрезки**, а так как ДА и КЕ па¬
раллельны, то ЛК = КМ.
НК
‘ 6-е свойство пропорции.
Доказывается таким же
азом, как и в предыдущем Предложении.
308

Предложения
Предложение 34. Если от точки на асимптоте проведена касательная, а через точку
касания прямая, параллельная этой асимптоте, то отрезок, проведенный от точки асим¬
птоты, делится гиперболой пополам, если он параллелен второй асимптоте
Если на одной из асимптот гиперболы бе¬
рется некоторая точка, и от нее проводится
касательная, а через точку касания прово¬
дится прямая, параллельная этой асимпто¬
те, то отрезок, проведенный через взятую
точку параллельно другой асимптоте, будет
рассекаться сечением на равные части*.
Пусть дана гипербола, на асимптоте
которой взята произвольная точка Г, че¬
рез которую проведена касательная ГВЕ,
а через точку В — прямая 7Н, параллель¬
ная асимптоте ГД. И пусть параллельно
другой асимптоте проведен отрезок ГАН
В таком случае я ут верждаю, что ГА =
АН.
Пусть же через точку А будет прове¬
дена прямая А0, параллельная асимптоте ГД, а через В - ВК, параллельная другой
асимптоте ЕД. Поскольку (П, 3) ГВ = ВЕ и ВК параллельна ДЕ, а 2Н - ГД то ГК =
КД и - 7Е.
Атак как В/ = ГК = ДК, А0 - ГЛ и (II, 3) КВ • В/ = ГА* А0, то ГН • ГК - ГА* ГД.
Поэтому —= —.
ГК ГА
Но так как ГД = 2ГК, то ГН =
2АГ.
Следовательно, ГА = АН.
Предложение 35. Если от точки
на асимптоте проведена секушая, то
отрезки, образующиеся при этом, от¬
носятся как отрезки, на которые се¬
кушая внутри сечения делится пря¬
мой, параллельной асимптоте и про¬
веденной из точки касания
Если при тех же предпосылках
от некоторой точки на асимптоте
гиперболы проведена прямая, пересе-
• Обратная теорема - см. (IV. 8).

Книга III
•1«
кающая ее дважды, то отрезки прямой, заключенные между этой точкой и точками
пересечения секущей с гиперболой, так относятся друг к другу, как отрезки, на кото¬
рые прямая, проходящая через точку касания параллельно этой же асимптоте, делит
лежащую внутри сечения часть секущей *.
Пусть дана гипербола с асимптотами ГД и ДЕ, касательной ГВЕ, прямой 0В, па¬
раллельной асимптоте ГД, и пусть через Г будет проведена некая прямая EAAZH,
rZ ZA
пересекающая сечение в точках А и Z. В таком случае я утверждаю, что	=	.
ГА ЛА
Пусть через точки Г, А, В и Z будут проведены ГЕ, КМ, ОР и ZY, параллельные
асимптоте ДЕ, а также через точки А и Z - AS и ТЕ, параллельные прямой ГД.
Поскольку (II, 8) ГА = ZH, то КА = ТН.
Но очевидно, что КА = Д£, поэтому AS = ТН.
Кроме того, ГК = ДУ, а значит, ГУ = ДК.
ГУ ЛК
Поэтому	=	.
ГК ГК
ГУ	TZ YZ
С другой стороны, из подооия треугольников следует	=	=	, а так как
ГК	Г А КА
ДК MK Э(МД)
YZ=MK.to —= —= -^*.
ДК 8(ДФ)	S(MA) 8(ДФ)
Ясно, что по той же причине — =	. поэтому	.
Так как (И, 12) S(AA) = S(BA) и (поскольку ОД = ГО) S(BA) = S(BT), то
8(МД)_8(ДФ)
S(BD ”s(®D’
S(MA) S(0M)
а так как фигуры ДФ и 0М, ФГ и ВК равны, получим --у = $ jg j •
Если взять равенство S(KL) = S(O0) (II, 12) и вычесть справа и слева S(AП), то
имеем S(Kil) = S(П0), а если к обеим частям получившегося равенства прибавить
S(AB), то S(BK) = S(A0).
в(МД) в(0М)
Тогда, учитывая, что В Г = АД, получим	~ '¿(АО) ’
8(мд) мк гг
Но, как уже было доказано, -у- -т = —— = зтт и очевидно, что
Ь(АЛ) КА 1А
8(ем) мф гд
8(А0) ~ ФА ~ ЛА
„	гг гл
Следовательно, — =	.
ГА ЛА
* Обратная теорема - см. (IV, 5).
** Площади треугольников, имеющих одинаковые высоты, относятся как их основания (Евклид
1 ). В данном случае ЛК - общая высота а МК и КА - основания

Предложения
Предложение 36. Предложение 35, если вместо секущей проведена прямая, пересе¬
кающая оба противолежащих
Если от некоторой точки на
асимптоте проведена касательная
к гиперболе, а также прямая, пере¬
секающая оба противолежащих, то
отрезки, заключенные между этой
точкой и точками пересечения ука¬
занной прямой с противолежащими,
относятся друг к другу как отрезки,
заключенные между теми же двумя
точками и точкой, в которой эту
прямую пересекает прямая, прохо¬
дящая через точку касания парал¬
лельно асимптоте.
Пусть (А) и (В) - противолежа¬
щие сечения с центром Г, АГ и 7Г
- асимптоты, и пусть на будет
взята точка Н, от которой проведе¬
ны касательная НВЕ и прямая Н0
г
гак, что она не параллельна АГ и не рассекает сечение в двух точках. Было доказано
(II, II), что прямая 0Н, продолженная дальше, пересекается с ГА, и по этой при¬
чине пересекается с сечением, например, в точке А. Проведем теперь через В пря¬
мую ЛК, параллельную £Г.
АН АК
В таком случае я утверждаю, что	.
Проведем от точек А и 0 отрезки AN и 0М, параллельные асимптоте 7Н, а от
точек В, Н и 0 отрезки ВЕ, НП и Р\ параллельно асимптоте АЕ. Тогда, поскольку
АН А0
(Ц,16)АД = Нв,ТО —= —.
АН N1 А0 ГТ	N2 ГЕ
Но(ЕвклидУ1,2) —= — и* ** — = — следовательно,— = —
А поскольку площади прямоугольников, имеющих одинаковую высоту, относят-
N1 8(ИГ) ГЕ _ 8(РГ)
И — -	.
ся как их основания (Евклид VI, 1), то	и “ оГтЛ •
Е0 о(0Г) ЕН Б^РН)
8(ЫГ)	8(РГ) ЗСМГ)_ ¿(МГТ+ЗСРГ) _
Следовательно,	= ^уи« 8(©Г) ~ 8(0Г)+8(РН) " 8(0Г)+8(РН)
Далее, так как ВЕ = ВН (II, 3), а НП и ГЕ параллельны, то ВЛ = ВП. следова¬
тельно,
SUN)
_ . ..Дл	.2Т.Т-
* Поскольку треугольники ГЛН и 1(-)Н подобны
** 6-е свойство пропорции.
311

Книга III
А поскольку (II, 12) 8(ВГ) = 8(0Г), то Б(0Г) = 8(ВН).
5(ЫГ) SUN) SUN)
1°гда 8(0Г) " 8(вн) + 8(рН) _ 8(рЕ) '
Атак как Б(ВГ) = 8(0Г), то 8(МВ) = 8(ЕО), следовательно, 8(0Г) = 8(ВН).
БСМГ) SUN)
Поэтому 8(©г)" 8(Л0)'
8(ЫГ) N2 АН
мы доказали, что
5(0Г) Е0 Н0'
SUN) №
С другой стороны (Евклид VI, 1),			 =	, а из подобия соответ-
5<Л0) р® НР лк
ствуюших треугольников и свойства пропорции следует, что	=	, то есть
8(ЛИ) ИР АК	Р0 К0
8(Л0) Р0 К© ‘
АН АК
Следовательно,	=	.
Н0 К0
Предложение 37. Отношение
между отрезками, на которые се¬
кущая, проведенная из точки пере¬
сечения касательных, разбивает¬
ся кривой и прямой, соединяющей
точки касания
Если две касательные к кониче¬
скому сечению пересекаются, а из
точки пересечения проведена неко¬
торая прямая, рассекающая его в
двух точках, то отрезки, заключен¬
ные между этими точками и точ¬
кой пересечения касательных. отно¬
сятся друг к другу как отрезки ука¬
занной прямой, заключенные между
этими же точками и точкой ее пере¬
сечения с прямой, соединяющей точ¬
ки касания*.
Л
•ж
Пусть дано сечение конуса. АГ	мая АВ и отрезок ГдЕг. В таком
и ВГ - касательные к нему и пусть проведены пря
ГХ ХЕ
случае я утверждаю, чю — = ■—.
ГД ЕД
* Далее эта тема рассматривается в (IV, 1-9)
312

Предложения
, по-
ЕО
37. Рис. 3. Гипербола — противолежащие
Пусть через точки Г и А будут про¬
ведены диаметры сечения Г0 и АК, а
через точки А и 7Г — прямые АП и 7Р.
параллельные касательной АГ, а также
ЛМ и N0, параллельные секущей АВ.
Поскольку ЛМ и N0 параллель-
гг лг гм дм
ны,то —
1 А
гм
этому ——
АО
37. Рис. 2. Гипербола
Однако (Евклид VI, 19)
гм2 5(гмр)
до2" б(доп) и
бСлмг)
БС-ОГ) ’следовательно-
5(дмг) _ §(гмр) = з(лгрг) *
Б(ЕОГ) ~ 5(ДОП) “ 5(НДПГ) *
Но (III, 2) S(AZPD = S(AKA)
и S(EAnT) = S(AEN), поэтому
ЛМ2 _ S(AKA)
2 ~S(AHN)’
rz2 ЛМ2
Однако j—= "~q2"» следователь-
rz2 s (AKA)
н0, ГД2 ~ S(AHN) •
ЕО
Г
Ж
37. Рис. 4. Эллипс
* 6-е свойство пропорции
313

Книга III
а так как (Евклид VI, 2)
АН
Л
Если при тех же самых пред¬
посылках через точку пересече¬
ния касательных проводится
прямая, параллельная секущей,
соединяющей точки касания, а
араоола
38. Рис. 2. Гипербола
rZ ZE
ЕД
314
S(AKA) ЛА2
С другой стороны (Евклид VI, 19),
ЛА2 _ ZE2 ZE2 _ S(AKA)
г“ед2’тоед2 S(AEN)'
TZ2 ZE2
Следовательно, —у = —;
ГД2 ЕД2
Предложение 38. Отноше¬
ние между отрезками, на кото¬
рые прямая, проведенная из про¬
извольной точки сечения через
середину секущей, соединяю¬
щей точки касания, разбивает¬
ся кривой и этой секущей
—
дог
Ж х •
/	JT
/к/ \
/v \
1
*	I г
>	Ч	• г
ж
произвольная прямая, проведенная че¬
рез середину этой секу шеи, рассека¬
ет сечение в двух точках, то отрез¬
ки, на которые секущая разбивает ее
внутри сечения, относятся друг к другу
как отрезки указанной прямой, заклю¬
ченные между точкой ее пересечения с
прямой, параллельной секущей и точ¬
ками ее пересечения с кривой.
Пусть АГ и ВГ - касательные к се¬
чению, АВ - прямая, соединяющая
точки соприкосновения, АК и ГМ -
диаметры; тогда АВ в точке Е рассе¬
кается на два равных отрезка (И, 30
и 39). Пусть от Г будет проведена ГО,
параллельная секущей АВ, а через Е

Предложения
пусть будет проведена произвольная
прямая £0.
В таком случае я утверждаю, что
гЕ_го
ЕА ~ ОА
38. Рис. 3. Гипербола — противолежащие
2 *
АН
38. Рис. 4. Эллипс
Проведем через £ и А прямые ЛМ и
Д1Ч, параллельные АВ, а также прямую
£Р, параллельную АГ. Ранее было дока-
... ЛА2 ЛМ2
зано, что (111, 37) —г =

АН- НО
ла2 гЕ2
Но (Евклид VI, 2)* 	Т = —т.
АН2 ЕД2
а с другой стороны (Евклид VI, 2),
лм2 лг2 го2
2 " ГН2 ~ од2 ’
гЕ2 го2 гЕ го
Поэтому —Г =—Г и — = —.
ЕД2 ОД2 ЕД ОД
Е0
Предложение 39. Предложение 37 для случая, когда прямая пересекает обе проти¬
волежащие
Если две касательные к противолежащим, пересекаются, а через точку пересечения
проведена прямая, пересекающая каждое сечение и прямую, соединяющую точки каса¬
ния, то отрезки, заключенные между этой точкой и точками пересечения с противо¬
лежащими, относятся друг к другу как отрезки указанной прямой, заключенные меж¬
ду этими же точками и точкой ее пересечения с прямой, соединяющей точки касания.
* Поскольку \А - 7Т, АН = 27 и ЛГ = 2Р
315

Книга III
•ж
Пусть Г - центр противоле¬
жащих, АД и АВ - касательные.
Проведем и продолжим АВ и ГД,
а через точку Д проведем некото¬
рую прямую ЕН. В таком случае я
ДЕ НЕ
утверждаю, что — = —.
дг нг
Проведем и продолжим АГ, а
от точек Ей/ проведем прямые
ЕК и ТЕ, параллельные АВ. а так¬
же ЕП и ТР. параллельные АД.
А поскольку ЕК и ¿Е парад-
МН
лельны, то справедлива про-
Е© ¿М
порция	=	и наоборот,
©г ме
Е0 _ 0Е
Вл ~МЕ
Е02	0£2
ПоэтомуБГм?'
А так как соответствующие треугольники подобны, то (Евклид VI, 19)
Е02 _5(Е0П) 0Е2 _ Б(ДЕ0)	Б(Е0П) _ 5(ДЕ0)
гм2 ■ БСгмр)и мн2 " б(нмд) ’ “еловательно- 5(гмр) " б(нмд) •
Но поскольку (111.5) S( Е0П) = S(ALK) + S(A0L) и S(ZM Р) = S(ANE) + S(EMA), то
S(AZ0) S(AZK)+S(A0E)
S(MEA)"s(ANE)+S(HMA)’
S(ASK) SU©I)
Отсюда имеем-
Б(АЕК) АК2 НЕ2
Но так как треугольники подобны, то (Евклид VI, 19)	~ „„2**
д^АЛЫ А™ НТ"
Б(Д0Е) _ 0Д2 _ ДЕ2
и б (нмд) ~ дм2" дг2'
ДЕ НЕ
Следовательно, — = —.
ДТ Ш
Предложение 40. Предложение 38 - частный случай
Если через точку пересечения двух касательных к противолежащим проводится пря¬
мая. параллельная прямой, соединяющей точки касания, а произвольная прямая, прове- •
• 6-е свойство пропорции
ГТ
Поскольку — =
AN
АЕ
АО
НЕ
’"^HZ
АЕ
АО
316

Предложения
40. Рис. 1.
денная через середину прямой,
соединяющей точки касания,
пересекает противолежащие,
то отрезки, на которые пря¬
мая, соединяющая точки каса¬
ния, разбивает ее между проти¬
волежащими, относятся друг к
другу как отрезки между точ¬
кой ее пересечения с параллель¬
ной прямой и точками пересе¬
чения с противолежащими*.
Пусть Г - центр противоле¬
жащих, АД и ДВ - касательные,
АВ - прямая, соединяющая
точки касания, a ZAH - па¬
раллельная ей прямая. Про¬
ведем и продолжим диаметры
ГД и ГА, тогда АВ в точке Е рассекается на два равных отрезка (II, 39). Если теперь
провести из произвольной точки 0 на кривой прямую 0ЕКЛ, то в таком случае я ут-
Л0 0Е
верждаю, что	=	.
ЛК ЕК
Проведем через точки 0 и К прямые EN и КП, параллельные АВ, прямые 0Р и
KL, параллельные АД.
Поскольку МН и ПУ параллельны, то из подобия треугольников МАЕ и АПУ еле-
НА МА
дует, что	=	.
AY АП
►м (Е)Е
Но так как КП, АВ и EN параллельны, то (Евклид VI, 2)-^- = ^-, а из-за подо-
0Е 0N
бия треугольников 0EN и ЕОК имеем	=	.
ЕК ОК
„ 0N МА	0N2 МА2
Итак,	=	, а значит,	т- = -—т.
ОК АП	ОК2 АП2
, ,	„ 0N2 S(0NP) МА2 S(MAS)
Однако (Евклид VI. 19)	, поэтому
S(0NP) S(MAE)
S(OKI) ” S(AnY) ’
С другой стороны (111,11), S(0NP) = S(MAE) + S(MNA), S(OKE) = S(AnY) +
S(MA=) + S(MNA) S(MA£)
8(ПОД), поэтому ¿(Апу)+-8(под) =	■
8(МА=)	8(МЬ!Д)
Отсюда, согласно свойству пропорции, следует, что $дцу)'= §(ПОД)' *
* Очевидно, что Предложение 40 - это просто частный случай Предложения 38, но там доказа¬
тельство намного короче.
317

Книга III
А гак как треугольники подобны, то (Евклид VI, 19)
5(М>1Д) М№
8(МАЕ) _ ЕА2
8(АПУ) ~ АУ2 И
БСПОД) ПО2 ’
„	М№ ЕА2
Следовательно,	г = —;
ПО2 АУ2
и мм2
Но	т- =
по2
ЫД2 Л©2	ЕА2	©Е2
=	7 =	г , а С другой стороны,	7 =	7	.
ОД2 ЛК2	АУ2	ЕК2
„	Л©2	0Е2	Л© ©Е
Следовательно, г = —г и очевидно, что = .
ЛК‘ ЕК.2	ЛК ЕК
Предложение 41. Отношения отрезков, на которые три касательные к параболе де¬
лят друг друга, равны
Если три прямые, касающие¬
ся параболы, пересекаются меж¬
ду собой, то каждая из них будет
разбита точками взаимного пере¬
сечения и точками касания на от¬
резки, находящиеся в одном и том
же отношении.
Пусть дана парабола с каса¬
тельными АЛЕ. Г7Е и АВ/. В
таком случае я утверждаю, что
гг _ ед гв
гЕ “ да ~ вд ’
Пусть секущая АГ в точке Н
рассекается на два равных отрез¬
ка Тогда прямая, проведенная от
Е к Н, является диаметром (И. 29).
И пусть сначала Д2 касается кривой в точке 0*, тогда Д7 будет параллельна АГ (II,
5) и делится в 0 пополам А так как и ЕН делится в 0 пополам (I, 35), то очевидно
(Евклид VI. 2), что АК = КЕ. ГЛ = ЛЕ и утверждение доказано.
Пусть теперь Л2 касается кривой в точке В Проведем и продолжим прямую МВ,
параътельную ЕН, а через точки А и Г - отрезки АО и ГП, паратлельные Д2. А по¬
скольку МВ и Е0 параллельны, то МВ является диаметром, и так как касается
сечения в точке В. то АО и ГП - ординаты к диаметру. Если же МВ- диаметр, ГМ
- касательная, ГП - о^дината^о МВ = ВП (I 35), следовательно, М7 = 7Х А по¬
скольку и ГЛ = ЛЕ. то	= —.
Г1 ГЛ
•А
* То есть совпадает с Кл
318

Предложения
ГЕ
гм гг
И наоборот, — = —.
ГЕ ГЛ
гм ге гг
Однако ТЁ=Ы ’тогда Ы ГН
ГЛ ГН
А — =	, ведь с обеих сторон отношение отрезка к вдвое большему.
ГЕ ГА
ГЯ ГЕ	ГЕ ГА
Перемножив почленно два последних равенства, получим — =	или — = —
ГЕ ГА,	Г2 Г—
ГЕ ГА
И £Е ~ ЕА *’
ГЕ
ГЕ
АЕ АК
’ А1Ч _ ДА .
ГЯ ГЕ	ЕЪ
Умножая почленно на	=	, получим —
ГЕ Г А	7Е ЕА
И опять же, поскольку МВ - диаметр. AN - касательная, АО - ордината, то (1.
35) N8 = ВО и (Евклид VI, 2) ИД = ДА. А также уже доказано, что АК = КЕ.
др	~	—
Следовательно,	=	 и, наоборот,
АК ДА
АЕ АН	АК	АН
— , ПОЭТОМУ	=	.
А	ДА	ЕА
АЕ АГ
, ведь отношение отрезков равно двум.
Но
АК
А
АК АН
АЕ АГ ЕД ГЕ
Перемножив почленно два последних равенства, получим — =	и — = —Е-**
ДА АЕ ДА ЕА
гг ЕД
*	гг ГЕ
А так как мы уже доказали, что — =	, то
¿Е ЕА ИЕ ЛА
Далее, из подобия треугольников следует, что —— =	.
ЕА АО
Атак как МВ = ВП, то ГП = 27В, и так как N8 = ВО, то АО - 2ВД.
¿В
Г
Поэтому
А ВД
гг ед гв
Итак, доказано, что =	= —
£Е ДА ВД
Предложение 42. Произведение отрезков параллельных касательных, отсекаемых
третьей касательной, равно четвертой части площади эйдоса
Если через концы диаметра гиперболы, противолежащих ши эллипса проведены пря¬
мые, парсшельные ординате, а с ними пересекается какая-то третья касательная, то
она будет отделять от них такие отрезки, что площадь прямоугольника, образованно¬
го ими, равна четвертой части /пощади эйдоса***
О
€•«
* 4-е свойство пропорции.
“ 3-е свойство пропорции.
Напомним, что эйдосом Аполлоний называет прямоугольник, образованный 1т и 11.
319

Книга III
й точке К. Прове-
Пусть АВ - диаметр, от концов
которого А и В проведены касатель¬
ные к сечению, а от некоторой точ¬
ки сечения Е проведена касатель¬
ная, пересекающаяся с ними в точ¬
ках Г и Д.
В таком случае я утверждаю, что
АГ • ВД равно четвертой части пло¬
щади эйдоса, лежащего возле АВ.
Пусть центром будет Т. и пусть
через него будет проведена и про¬
должена прямая гн, параллельная
АГ и В А. А поскольку АГ и ВД па- М
раллельны (II, 31), то гн лежит на
сопряженном диаметре (I, 16 и II,
5). Пусть отрезок гн равен его по¬
ловине, тогда квадрат ХН равен чет¬
вертой части площади эйдоса (Опр.
11,3. Кн. I).
Очевидно, что ДГ и АВ пересе¬
кутся в некоторо
дем через Е прямую ЕА, параллель¬
ную АГ, и ЕМ. параллельную АВ А
поскольку о, 37) кг • дг = Аг2, то
кг = Аг	кг ка кг
лг ~ дг	лг ~ ад ~ гв
И наоборот,	.
ка кг
Тогда, вычитая или прибавляя
слраваи слева единицу, получим
КА~кг
А так как соответствующие

ники подобны, то — = -—  = .
ка аг' кг го
и, следовательно, — = —
аг го
Поэтому ДЕ* г© = АГ• ВД =
гм • го.
А так как (I, 38) гм • г© = гн2, то
АГ • ВД — гн* и, значит, АГ • ВД равно
четвертой части площади эйдоса.
)шие тре\то ль-
ЛЕ КЙ ВД
6-е свойство про
порции.

Предложения
В случае если точки Н и Е у эллипса совпадают (рис. 3), то АГ = 7Н = ВД
и ясно, что АГ • ВД = 7Н2, то есть АГ • ВД равно четвертой части площади эйдоса.
Предложение 43. Произведение отрезков, отсекаемых касательной на асимптотах
- постоянная величина
Если прямая касается гиперболы, то она
от асимптот отделяет отрезки, составля¬
ющие прямоугольник, площадь которого рав¬
на площади прямоугольника, ограниченного
отрезками, отделенными касательной, про¬
веденной к точке, расположенной на оси*.
Пусть дана гипербола с осью ДВ и асим¬
птотами ДГ и ДЕ, и пусть через точку В про¬
ведена касательная ZBH и произвольная ка¬
сательная ГА0. В таком случае я утверждаю,
что ГД • Д0 = ZA • Д Н.
Пусть от А и В будут проведены АК и
ВЛ, параллельные асимптоте ДН, и АМ и
BN, параллельные прямой ГД.
Тогда поскольку ГА0 касается сечения,
то (II, 3) ГА = А0, а потому Г0 = 2А0, ГД =
Следовательно, ГД • Д0 = 4АМ • АК.
Тем же самым способом мы докажем, что ZA•ДН = 4BN • ВЛ.
Атак как (II, 12) АМ • АК = В№ • ВЛ. то ГД • Д0 = гдв ДН.
Точно так же можно это доказать, если ДВ. будучи диаметром, не является осью.
Предложение 44. Прямые, проходящие
через точки пересечения касательных с асим¬
птотами, параллельны прямой, соединяющей
точки касания
Прямые, проходящие через точки пересе¬
чения двух касательных с асимптотами, бу¬
дут параллельны прямой, соединяющей точ¬
ки касания.
Пусть дана гипербола или противоле¬
жащие сечения с асимптотами ДГ и ДЕ, и
касательными - ГАг и ЕВН, и проведены
прямые гн, ГЕ и АВ. В таком случае я ут¬
верждаю, что они параллельны.
Г.
44. Рис. 1.
* То есть это произведение - постоянная величина
321

Книга III
Ведь поскольку (111, 43) ГД*AZ =
ГД НА
НА* АЕ, то — = — и, значит, прямые
АЕ AZ
ГЕ и Н7 параллельны (Евклид VI, 2). Сле¬
довательно, треугольники ГЕ0 и Н70
подобны.
Поэтому
Z0 H0
Zr " НЕ
А так как ZГ и НЕ вдвое больше, чем
7 А иО/Н Ъ ¿Г НЕ
ТА и Н В (11, 3), то — = —.
ТА НВ
Перемножив почленно два последних
20 Н0
равенства, получим
ZA НВ
Следовательно, HZ и АВ параллель¬
ны (Евклид VI, 2).
Г
Предложение 45. Углы между прямыми, соединяющими фокус эллипса или гипер¬
болы с точками пересечения произвольной касательной и перпендикуляров, проведен¬
ных от концов оси, будут прямыми
Если через концы оси эллипса, гипербо¬
лы И1 и противолежащих проведены перпен¬
дикуляры к ней, а на оси определены такие
точки, что произведение отрезков, заклю¬
ченных между каждой из них и концами
оси равно четвертой части площади эй-
доса, то углы, возникающие, если любую
из этих точек соединить с точками, об¬
разующимися при пересечении произволь¬
ной касательной с перпендикулярами, бу¬
дут прямыми*.
Пусть дано сечение с осью АВ, и
пусть АГ и ВЛ - перпендикуляры к
ней, а ГЕЛ - касательная. И пусть
А22В = АННВ = -£гЫ.
4
45. Рис. I.
Тогда, если провести ГТ и ГН, АТ и АН, то углы ГТА и ГН А будут прямыми.
Мы ранее доказали, что АГ* ВЛ равно четвертой части площади эйдоса (III, 42),
но и АТ • ZB равно тому же. следовательно, АГ • ВД = КТ •
* В Предложениях 45-52 Аполлоний вводит, по сути, понятие фокуса эллипса и гиперболы и
исследует свойства этих точек, не вводя для них специального наименования.

Предложения
Поэтому
АГ
AZ
ZB
ВА
и углы, располо¬
женные при А и В, являются прямыми,
а поэтому ZAiZ = ZBZA,
ZAZf = ZZAB.
И поскольку ZГAZ прямой, то ZAГZ
+ ZAZГ тоже равны одному прямому. А
так как ZAГZ = ZBZA, то сумма ZBZЛ
+ ZAZГ будет равна одному прямому.
Следовательно, оставшийся угол лгг
является прямым. И мы таким же спо-
м докажем, что также ZTHA явля¬
ется прямым.
Z
Предложение 46. Углы, образованные теми же прямыми с касательными, будут равны
При тех же самых предпосылках прямые, проведенные из тех же точек на оси к точ¬
кам пересечения касательных, образуют с касательными равные углы.
При тех же самых предпосылках я утверждаю, что ZAiZ = ZArH, ZTAZ = ZBAH.
Поскольку мы доказали (III, 45), что углы TZA и ГН А являются прямыми, то круг,
описанный на диаметре ГА, будет проходить через точки Z и Н, поэтому ZArH =
ZAZH, так как они стягиваются одной и той же дугой окружности. А мы доказали,
что (III, 45) ZAZH = ZArZ, следовательно, ZArZ = ZArH.
И тем же самым способом мы докажем, что также ZTAZ = ZBAH.
46. Рис. 2.
323

Книга III
Предложение 47. Прямая, проведенная из точки пересечения тех же прямых к точ
ке касания, будет перпендикулярна касательной
При тех же самых предпо¬
сылках прямая, проведенная из
точки пересечения проведенных
прямых к точке касания, будет
перпендикулярна касательной.
Пусть будет предположено,
что и прежде, ГН и 7Л пересе¬
каются между собой в О, а Л Г
и ВА, продолженные дальше,
пересекаются в К, и пусть бу¬
дет проведена прямая 0Е.
В таком случае я утверж¬
даю, что 0Е перпендикуляр¬
на ГД.
Д
Если это не так, то пусть от точки 0 будет проведена 0Л, перпендикулярно ГЛ.
А поскольку (III, 46) /ГД2 = /ВДН и /ДВН = /ДА0, так как они прямые, то треу¬
гольники ЛВН и ДЛ0 подобны.
ДН ДВ
Следовательно. —■ = —.
Д0 ДА
дн гг
Однако подобны и треугольники ДН0 и Г£0, поэтому	=	, а поскольку
Д0 Г0
г гг аг
подобны треугольники АГ£ и ЛГ0. то — = —
Г0 АГ
• 1-е свойство пропорции.
324
»1«.
~ ДВ ВК
Однако — =	, поэтому
АГ АК
ДА ВК
АГ " АК '
Пусть от Е будет проведена
ЕМ. параллельная прямой АГ.
тогда она проведена к АВ как
ордината, следовательно (1,36),
ВК вм
АК МА *
А так как (Евклид VI, 2)
ВМ ДЕ
^^• = —, то, окончательно,

Предложения
АЛ ДЕ
— = — , что абсурдно. Следовательно, к ДГ не перпендикулярна никакая пря
АГ ЕГ
мая, кроме 0Е.
Предложение 48. Пря¬
мые, проведенные от точ¬
ки касания к фокусам, об¬
разуют равные углы с ка¬
сательной
При тех же самых пред¬
посылках нужно доказать,
что прямые, проведенные
от точки касания к тем же
точкам на оси, образуют
вные углы с касательной.
При тех же предпосыл¬
£

48. Рис. 1.
ках пусть будут проведе¬
ны Е7 и ЕН.
В таком случае я утверждаю, что ZTEZ = ZAEH.
Поскольку углы ДН0 и ДЕ0 являются прямыми (III, 45 и III, 47), круг, описан-
ный вокруг диаметра Д0, про
ходит через точки Е и Н. Поэтому ZДEH = ZД0H. ведь
они опираются на одну и ту же дугу;
Точно так же докажем, что ZГEZ = ZГ0Z.
‘ В случае гиперболы они просто совпадают
А так как утлы ZГ0Z и ZЛOH
равны*, то очевидно, что и ZГEZ
= ZДEH.
Примечание
Свойство, доказанное в данном
Предложении, означает, в случае
эллипса, что лучи света, выходя¬
щие из одного его фокуса, отраз¬
ившись. соберутся в другом фоку¬
се. Фокус -очаг, костер (лат.). Тер¬
мин введен И. Кеплер
В случае гиперболы, лучи све¬
та. выходящие из фокуса, отразят¬
ся от нее таким образом, что про¬
должения отраженных лучей пе¬
ресекутся в другом фокусе.

Книга III
ПО
Предложение 49. Если от одного из фокусов проводится перпендикуляр к касательной,
то прямые, проведенные от точки их пересечения к концам оси, образуют прямой угол
Если при тех же самых
предпосылках от одной из тех
же точек на оси проводится
перпендикуляр к касательной,
то прямые, проведенные от
точки, возникшей таким об¬
разом, к концам оси, образу¬
ют прямой угол.
При тех же предпосылках
пусть, например, отточки Н
будет про
ведена НО, перпен¬
дикулярная ГД, а также от¬
резки АО и ВО.
В таком случае я утверж¬
даю, что угол АОВ является
прямым.
Так как ¿ДВН и ¿Д0Н
являются прямыми, то круг,
описанный на диаметре ДН,
проходит через точки О и В, следовательно ¿В0Н =
¿ВДН, пос кальку они опираются на одну и ту же дугу.
Атак как (III, 45) ¿АНГ = ¿ВАН, то ¿АНГ = ¿ВОН.
Но ¿АНГ = ¿А0Г*.
49. Рис. 2.
Следовательно, ¿ВОН = ¿АОГ
и ¿АОВ = ¿ГОН.
Однако ¿ГОН является пря¬
мым, следовательно, также и
¿АОВ является прямым.
Предложение 50. Прямая, про¬
веденная от центра сечения к каса¬
тельной, равна половине оси, если
она параллельна прямой, соединя¬
ющей фокус и точку касания
Если при тех же предпосылках
от центра сечения к касательной
параллельно прямой, соединяющей
одну из тех же точек на оси и точ-
Если описать круг диаметром ГН, то углы АНГ и АОГ будут опираться на дугу АГ Очевидно, что
точки Аи© лежат на окружности, так как углы ГАН и ГОН - прямые.
326

Предложения
ку касания, проводится пря¬
мая, то она будет равна по¬
ловине оси.
При тех же предпосыл¬
ках, пусть центром будет
0, и пусть проведена пря¬
мая Е7, а АГ и ВА пересе¬
каются в точке К. Прове¬
дем параллельно Е7 пря¬
мую 0Л. В таком случае я
утверждаю, что 0Л = 0В.
Пусть будут проведены
ЕН, АЛ, АН и АВ, и пусть
через точку Н будет про¬
ведена НМ, параллельная
прямой Е2. А поскольку
А/ = Н В, А0 = 0 В, следо¬
вательно 7£) = 0Н, то (Ев¬
клид VI, 2) ЕЛ = ЛМ.
Ранее мы доказали (III,
48), что/ГЕг = ¿МЕН.
Но, так как прямая
Е7 параллельна МН, то
¿ГЕ/= ¿МЕН и ¿ЕМН
= ¿MEH.
Следовательно, ЕН =
НМ.
А так как мы доказали,
что ЕЛ = ЛМ, то НА пер¬
пендикулярна ЕМ. Тогда из
(111,49) следует, что ¿АЛ В
М
50. Рис. 2.
является прямым и круг,
описанный вокруг диаметра АВ, проходит через точку Л, откуда 0Л = 0В
Предложение 51. Разность расстояний от фокусов до произвольной точки на
противолежащих равна длине оси
Если на внешней части оси противолежащих задать две точки, у каждой из которых
произведение расстояний до концов оси равно четвертой части площади эйдоса, то
разность расстояний от них до любой точки гиперболы равна длине оси.
Пусть АВ — ось противолежащих, Г — центр, и заданы такие точки Е и А, что
ЕЛ ЕВ = ДА ДВ = -Ег-и.
4

Книга III
НЕ
И пусть они соединены прямы¬
ми EZ и ZA с некоторой точкой Z на
гиперболе. В таком случае я утверж¬
даю, что EZ - ZA = АВ*.
Проведем через Z касательную
ZK0, а через Г прямую НГ0, парал¬
лельную прямой ZA, тогда ZH0Z =
ZKZA и (111, 48) ZKZA = ZHZ0, а
значит, ZH0Z = ZHZ0, следователь¬
но, Н0 = HZ.
А поскольку АЕ = ВА, АГ= ГВ и
ЕГ = ГД, то ЕН = HZ, поэтому Н0 =
ЕН, следовательно, EZ = 2Н0.
Так как мы доказали ранее (Ill,
5О),чтоГ0= rB,ToEZ = 2(Hr+ГВ). (Д)
Однако ZA = 2НГ и АВ = 2ГВ,
следовательно, EZ = ZA + АВ и EZ
-ZA = AB.
	Д'.
К
\ IA
В\
Предложение 52. Сумма расстояний от фокусов до произвольной точки на эллип¬
се равна длине оси
Если на большой оси элшпса определены две точки, у каждой из которых произве¬
дение расстояний до кониов оси равно четвертой части площади эйдоса, то сумма рас¬
стояний от них до любой точки эллипса равна длине оси.
Пусть большая ось эллипса - АВ, а центр - Н, и пусть на АВ определены точки
Г и А, такие, что АГ ГВ = АД ДВ^-ЬгТд.
4
Тогда, если от точек Г и А
ведены линии ГЕ и АЕ. со¬
ставляющие ломаную ГЕА, то
я утверждаю, что ГЕ + АЕ =
АВ**.
Пусть ZE0 - касательная.
и пусть через центр эллипса
проведена прямая НК0. па¬
раллельная ГЕ. Тогда, посколь¬
ку (III, 48) ZZEГ = ZДE0и.
очевидно, ZZEГ = ZE0K, то
ZE0K = ZДE0.
Поэтому 0 К = КЕ
0
•Ж«
• Сейчас, как известно это одно из определений гиперболы
*' Сейчас это одно из определений эллипса

Предложения
Из того, что АН = НВ и АГ = ДВ, следует, что ГН = НА, а значит, ЕК = КД.
Тогда ЕД = 2ЕК = 20К, а ГЕ = 2КН.
В силу этого ГЕ + ЕД 2(КН +0К) = 20Н.
Но так как (III, 50) АВ = 20Н, то ГЕ + ЕЛ - АВ.
Предложение 53. Если через концы
диаметра провести касательные, то про¬
изведение отрезков, отсекаемых на них
прямыми, проведенными из тех же то¬
чек через какую-нибудь точку на сече¬
нии, равно плошали эйдоса
Если от концов диаметра эллипса или
противолежащих проводятся касатель¬
ные, и из тех же точек проводятся через
некоторую точку на сечении прямые, то
прямоугольник, составленный из отрез¬
ков, отсекаемых на касательных, имеет
площадь, равную площади эйдоса.
Пусть АГ — диаметр сечения, и че¬
рез точки А и Г проведены прямые, па¬
раллельные некоторой ординате В/, пе¬
ресекающейся с сечением в точке В. И
пусть через эту точку проведены прямые
АВ и ГВ. отделяющие на касательных
отрезки АД и ГЕ. В таком случае я ут¬
верждаю, что АД • ГЕ = Ьг • Ы.
Ранее было доказано (1, 21), что
лг гг_ ы
2В2	~ Ьг ’
И очевидно, что это отношение рав-
АГ2
но

АГЬг
AZ Zr AZ Zr
А ПОСКОЛЬКУ —Yq2— =

АГ-Lr ZB ZB
АГ2 ~ AZ ZV
Но в силу подобия
ZB _ ГЕ ZB
ZB ZB’
треугольни-
АД
А7	__	—, поэтому
ков AZ АГ Zr АГ
АГ Lr _ ГЕ АД АД ГЕ
АГ2 "АГ АГ” АГ2 ‘
Следовательно, АГ • Lr = АД • ГЕ . или АД • ГЕ = Lr - Lt.
329

Книга III
Предложение 54. Соотношение, которое словами кратко не
описать: (AZxfH)AP = ЕВ2:ВД2)х(АД*ДГ):‘ЛАР
Если две прямые, касающиеся ко¬
нического сечения, пересекаются и че¬
рез точки касания проводятся пря¬
мые, параллельные касательным, и
от этих же точек через некоторую
точку кривой проводятся прямые,
54. Рис. la. Парабола
(общий вид)
отсекающие отрезки на параллель¬
ных прямых, то отношение площади
прямоугольника, ограниченного эти¬
ми отрезками, к квадрату прямой,
соединяющей точки касания, равно
отношению квадрата внутреннего
отрезка прямой, соединяющей точ-
ку пересечения касательных и сере¬
дину секущей, к квадрату внешней
части, умноженному на отношение
изведения отрезков касательных к
четвертой части квадрата секущей.
Пусть АД и ГД - касательные
к сечению, а секущая АГ делится
отрезком ДЕ на две равные части.
Тогда, если от А будет проведена
прямая А2, параллельная ГД, а от
Г - прямая ГН, параллельная АД,
и через некоторую точку сечения
проведены и продолжены до яю
ресечения с параллельными пря¬
мые АН и TZ, то я утверждаю,
AZ-ГН ЕВ2 АД АТ
АГ2 ~ВД2' 1^:
4
Z
Пусть же через точки 0 и В про
ведены прямые КОЛ и MBN, парал¬
лельные АГ Очевидно, что MBN касается сечения (1, 32). А поскольку АЕ = ЕГ, то
МВ = BN и КО = ОЛ, а также (Г 46,47) 00 - ОЕ и, следовательно, К0 = ЕЛ, а зна¬
чит, и КЕ - 0 Л
Тогда поскольку МВ и МА касаются сечения и КОЛ параллельна прямой MBN,
то(1Н, 16)
АМ2
МВ2
АК2
КНК0
AM2 АК2
или, что то же самое, 	=	.
MB BN 0Л К0
330

Предложения
Атак как (Евклид VI, 2)*
ГО АМ ГО-АМ ГЛ-АК
		= » ТО	г— = ——о—.
ГЛ АК АМ2 АК2
Перемножив почленно
эти два равенства, получим
ГО-АМ _ ГЛ-АК
МВ-ВМ~0Л-К0
Очевидно, что
ГЛ-АК ГЛ АК
0Л-К0 0Л 0К ’а
в силу под
ствующих треугольников
гл ак лг гн лг гн
0Л 0К АГ АГ АГ2
Следовательно,
ГО-АМ _ Аг-ГН
мв в№ АГ2
Но
ГО-АМ _ ГО-АМ МЛ-МД
МВ ВИ “ мд-мд мв-ви ’
значит,
ГО-АМ МД-МД Аг ГН
ИД-МД МВ ВМ АГ2
Л ГО АМ ЕВ
Однако	=	=	,
МД МД ВД
поэтому
ГЫ АМ _ЕВ;
ЫД • МД _ ВД2 "
54. Рис. 2. Гипербола
54. Рис. 3. Эллипс
Аг-ГН ЕВ2 кд-мд
АГ2 “ВД2 ’мв-вк
Л из подобия треугольников
МД • МД	АД ■ ДГ
следует	=	.
МВ ВМ ГЕ-АЕ
Итак,
лг-гн
АГ2
ЕВ2
ВД2
АД-ДГ
* А также 3-е свойство пропорции.
331

Книга III
Предложение 55. Подобное соотношение для противолежащих:
А0хЬ1Д:АД2:= АНхНЛ:ГН1 2
55. Рис. 1.
Если через точку пересечения ка¬
сательных к противо зежащим про¬
ведена прямая, параллельная прямой,
соединяющей точки касания, через
которые проведены прямые, парал¬
лельные касательным и прямые, свя¬
зывающие эти точки с некоторой
точкой сечения, то эти прямые от¬
секают на указанных параллельных
такие отрезки, произведение кото¬
рых так относится к квадрату пря¬
мой, соединяющей точки касания, как
произведение отрезков касательных
относится к квадрату отрезка, па¬
раллельного указанной прямой, огра¬
ниченного кривой и точкой пересече¬
ния касательных.
Пусть проведены касательные к -
противолежащим АН иДН, отрезок АД и прямаяГНЕ, параллельная АЛ, а через точ¬
ки А и Д - прямые АМ и ДМ, параллельные касательным ДН и АН. Тогда если на
сечении А7 будет взята некоторая точка 7. и через нее будут проведены г^ и гД0,
А0-КД АН ДН	ГН’
то я утверждаю, что	ч— =		—, или, что то же самое, А„	~ ~~.
АД2 ГН2	АНДН А0 ЫД
Проведем прямую 7В параллельно АД.
ен2 вл ■ лг
Ранее мы доказали (III, 20), что —у =	.
АН АЛ
•л
гн2 кг-лг
Но (II, 38) ЕН = ГН и ВК = лг* следовательно, имеем —-у =	— •
АН ДА"
п ДН ДА	ДН- ДЛ‘
Однако	=	. а значит,	=	.
АН АК	АН-АН ДЛ-АК
гн2 кклг
Перемножив почленно, получим	=	.
АН АН АЛ-АК
о	кг лг кг лг
В то же время	=	, а поскольку соответствующие треугольники
АЛ АК АК АЛ
.. кг ад лг ад
подобны, то	=	,	=	.
АК	АЛ А0
1 Прямая, соединяющая Н и середину АЛ, - сопряженный диаметр, а значит, он делит ВХ по¬
полам. Но очевидно, что он делит пополам и КА. Следовательно, ВК ~ XX.
332

Предложения
В результате имеем
довательно
АН-АН
ГН2 _ АА АА
AH AH~AN А0
АА2
A0 NA '
АА АА АА2
но так как		=

AN А0 А0 • NA
, то, сле-
Преддожение 56. Предложение 54 для противолежащих
Если проведены две касательные к одному из противолежащих и через точки каса¬
ния проведены прямые им параллельные, а от тех же точек к некоторой точке друго¬
го сечения проведены прямые, их пересекающие, то площадь прямоугольника, ограни¬
ченного отрезками, отсеченными ими от параллельных, будет иметь к квадрату секу¬
щей, соединяющей точки касания отношение, равное отношению квадратов отрезков
между точкой пересечения диаметра со вторым противолежащим, центром и середи¬
ной секущей, умноженному на отношение произведения отрезков касательных, заклю¬
ченных между точками касания и точкой их пересечения к четвертой части квадрата
прямой, соединяющей точки касания.
Пусть даны противолежащие сечения (А) и (В) с центром О, касательными
AEZH и ВЕ0К, и проведены секущая АВ, соединяющая точки соприкосновения,
которая разбивается точкой А на два равных отрезка, прямая АЕОДЕ, а от точек А
К
Г
I
I
56. Рис. /,
I Z
|	У
333
г г

Книга III
и В параллельные касательным прямые АМ и ВГЧ. Если теперь на сечении (А) взять
некоторую точку Г и провести через нее прямые ГМ В и ГАК то я утверждаю, что
ВЫАМ_ЛД2 АЕЕВ_ЛД2 ЛЕ ЕВ
АВ2” " ЛЕ2 1 ХВ2 ~ ДЕ2 АЛЛВ
4
Тогда если Г и А проведены НГК и гД0, параллельные АВ, то 0Д = дг и КЕ — ЕН.
Из равенства же ЕГ = ЕП следует, что ГК = НП. Так как (А) и (В) суть проти¬
волежащие, В0 и 0Д - касательные, а КН параллельна прямой Д0, то (III, 18)
ВО2 ВК2
0Д2 _ПККГ’
вк2
©ЬЕг _ АЕ^ЕВ
11 ©ДДг~ АЛ АВ ’
В02
А так как 0Д2 = ©Д • Аг и ПК* КГ = КГ« ГН,то	.
0Д • Дг КГ • ГН
ц	гл ©в на вк	лг ©в вкан
в тоже самое время ———;;, поэтому из равенства	=

©в- вк2	©д дг кг гн
в результате введения в левую часть пропорции среднего члена 0Е • Ег следует,
лгевАг-вв	©Е-Ег	Аг©в	лд2
что ©д дг ©Е Ег	©д • дг а также ©е • Ег	де~
ВКАН АД"	ЛЕ ЕВ	ВК АН	ВК
поэтому	“ л г 2 ‘ а *	’а также	=

КГГН ДЕ	АЛЛВ	КГГН	КГ
_	ВК АМ АН BN
В то же самое время —- =	, =	, следовательно,
КГ АВ ГН АВ
ВЬГАМ ЛД2 ЛЕ ЕВ АД2 ЛЕ ЕВ
АН
ГН
ЛЕ2 1^2 ДЕ2 АЛ ЛВ
4
334

ДОСЛОВНЫЙ ПЕРЕВОД КНИГИ III
•s
1
Если прямые, касающиеся конического сечения
или поверхности круга, пересекаются, и через точ¬
ки касания проводятся диаметры, пересекающи¬
еся с касательными, то полученные таким обра¬
зом треугольники, которые расположены при вер¬
шине, равны.
Пусть АВ будет сечением конуса или окруж¬
ности круга, и пусть АГ и ВЛ, пересекающиеся в
Е, касаются АВ, и пусть через А и В будут прове¬
дены диаметры сечения ГВ и АД, пересекающи¬
еся с касательными в Г и Д. В гаком случае я ут¬
верждаю, что АДЕ равно ЕВГ.
Пусть же от А будет проведена А2, параллель¬
ная прямой ВЛ; поэтому она проведена как упо¬
рядоченная прямая |ордината]. В таком случае на
параболе АДВ7 равно АГ7, и при отбрасывании
общего АЕВг, оставшийся треугольник АЛЕ ра¬
вен ГВЕ. В остальном же пусть диаметры пересе¬
каются в центре Н.
А поскольку А7 проведена как ордината, и
АГ касается сечения, то 7Н Г равно ВН в квадра¬
те. Тогда 7Н к НВ равно ВН к НГ; поэтому так¬
же 7Н к Н Г равно 7Н в квадрате к Н В в квадра¬
те. А 7Н в квадрате к Н В в квадрате равно А7Н к
АН В, и 7Н к НГ равно А7Н к АН Г. Поэтому так¬
же А7Н к АН Г равно А7Н кДНВ. Поэтому АНГ
равно ДНВ. Пусть будет отнят общий ДНГЕ, по¬
этому оставшийся треугольник АЕД равен ГЕВ.
У
2
При тех же самых предпосылках если на сечении
или окружности круга берется некоторая точка и
через нее проводятся прямые, параллельные каса¬
тельным, вплоть до диаметров, то четырехуголь¬
ник, возникший на одной из касательных и на од¬
ном из диаметров, будет равен треугольнику, воз¬
никшему на той же самой касательной и на другом
диаметре.
Пусть АВ будет сечением конуса или окруж¬
ностью круга, а касательными АЕГ и ВЕД, диа¬
метрами - АД и В Г; и пусть будет взята на сече¬
нии некоторая точка Н, и пусть будут проведены
НКЛ и HMZ, параллельные касательным. В та¬
ком случае я утверждаю, что AIM равно ГАН I.
Е
/
Г
335

Книга III
Ведь поскольку доказано, что НКМ рав¬
но АЛ, то пусть будет прибавлен или отнят
общий четырехугольник А1. Тогда получит¬
ся, что А1М равно ГН.
3
Если при тех же самых предпосылках на се¬
чении или окружности круга взять две точки и
через них провести прямые, параллельные каса¬
тельным, вплоть до диаметров, то четыреху¬
гольники, возникшие из проведенных таким об¬
разом прямых и расположенные на диаметрах,
будут равны между собой.
Пусть будут сечение, касательные и диа¬
метры такими же, как мы сказали прежде; и пусть на сечении будут взяты две про¬
извольные точки 2 и Н, пусть через X будуг проведены 70КА и N71М, параллель¬
ные касательным, а через Н - НЕО и 0ПР. В таком случае я утверждаю, что АН рав¬
но М0 и ЛN равно Р№
А поскольку мы доказали прежде, что треугольник РПА равно четырехугольни¬
ку ГН, AMI равно TZ и АРП равно AMI плюс четырехугольник ПМ,то ГН равно TZ
плюс четырехугольник ПМ. Поэтому ГН равно Г0 плюс PZ. Пусть отбрасывается
общая Г0; тогда оставшаяся AN равно 0М. Следовательно, AN равно PN.
Если две прямые, касающиеся противоле¬
жащих сечений, пересекаются и через точки
касания проводятся диаметры, пересекающи¬
еся с касательными, то треугольники, рас¬
положенные при касательных, будут равны.
Пусть А и В будут противолежащими се¬
чениями, и пусть касающиеся их АГ и В Г
пересекутся в Г; пусть центром сечений бу¬
дет А. пусть будут проведены АВ и ГА, ко¬
торая будет продолжена до Е, и пусть так-
же будут проведены АА и ВА и продолжены
дальше до Z и Н. В таком случае я утверж¬
даю, что АН А равно BAZ и ArZ равно ВГН.
Пусть через 0 будет проведена касающаяся сечения 0А; тогда она параллельна
прямой АН. А поскольку АА равно Д0, то АНА равно 0АА. А А0Л равно BAZ; поэ¬
тому также АНА равно BAZ. Следовательно, также ATZ равно ВГН.
Если две прямые, касающиеся про
тиволежащих сечений, пересекаются, и на одном
из сечений берется некоторая точка и от нее проводятся две прямые, одна параллель-
336

Дословный перевод книги III
но касательной, другая параллельно прямой, со¬
единяющей точки касания, то треугольник, об¬
разованный ими при диаметре, проведенном че¬
рез точку пересечения [касательных! отличается
от треугольника, отделенного при точке пере¬
сечения касательных, треугольником, отделен¬
ным касательной и диаметром, проведенным че¬
рез точку касания.
Пусть А и В будут противолежащими сече¬
ниями, центром которых будет Г, и пусть каса¬
тельные ЕД и Д7 пересекаются в Д, и пусть бу¬
дут проведены Ег и ГД, которая будет продол¬
жена дальше; и пусть проведенные 7Г и ЕГ будут
продолжены дальше, и пусть на сечении будет
взята некоторая точка Н, и пусть через нее бу¬
дет про
ведена0НКЛ, параллельная прямой Е2
и НМ - параллельная прямой Д2. В таком случае
я утверждаю, что Н0М равно К0Л плюс КА/.
А поскольку мы доказали, что ГД есть диа¬
метр противолежащих сечений, и Е7 проведе¬
на к нему как ордината, а Н0 параллельна пря¬
мой Ег и МН параллельна прямой дг, то МН0
равно ГЛ0 плюс ГД2. Следовательно, М Н0 рав¬
но КОЛ плюс К7Л. И очевидно, что К2А рав¬
но МН КА.
6
Если при тех же самых предпосылках на од¬
ном из противолежащих сечений берется неко¬
торая точка, и от нее проводятся прямые, па¬
раллельные касательным, и пересекающиеся с
касательными и диаметрами, то четырехуголь¬
ник, образованный ими при одной из касательной
и при одном диаметре, будет равен треугольни¬
ку, возникшему при той же самой касательной и
другом диаметре.
Пусть будут противолежащие сечения, диа-
в
м которых пусть будет АЕГ и ВЕД, и пусть
сечения АВ касаются А2 и ВН, пересекающиеся в 0, и пусть будет взята на сечении
некоторая точка К, и пусть от нее будут проведены КМЛ и К№. В таком случае я
утверждаю, что четырехугольник К7 равен треугольнику А1М.
Поскольку АВ и ГД являются противолежащими сечениями, и АВ касается се¬
чения А/, пересекаясь с ВД, а КА проведена параллельно прямой А2, то треуголь¬
ник А1М равен четырехугольнику К2.
337

Книга III
7
Если при тех же самых предпосылках на
каждом из сечении берутся некоторые точки, и
от них проводятся прямые, параллельные этим
касательным и пересекающиеся с касательны¬
ми и диаметрами, то четырехугольники, об¬
разованные проведенными таким образом пря¬
мыми, размещенные на диаметрах, будут рав¬
ны между собой.
Пусть будет предположено то, что мы ска¬
зали прежде, и пусть на каждом из сечении бу¬
дут взяты точки К и Л, и пусть через них будут
проведены МКПРХ и МТЛО, параллельные
прямой А7, и МОКЕ и ХФУЛТ, параллель¬
ные прямой ВН. В таком случае я утверждаю,
что выходит то, что было сказано в предпосылке.
Ведь поскольку треугольник А01 равно четырехугольнику РО, то пусть будет при¬
ложено ЕО; поэтому треугольник АЕ2 равно КЕ. А также треугольник ВЕН равно че¬
тырехугольнику ЛЕ, и треугольник АЕ7. равно ВНЕ; поэтому также ЛЕ равно 1КРЕ.
Пусть будет приложено 1ЧЕ; следовательно, ТК равно 1Л; и также КУ равно РЛ.
Пусть при тех же самых предпосылках вместо К и Л будут взяты Г и Л, на кото¬
рых диаметры пересекаются с сечениями, и пусть через них будут проведены пря¬
мые, параллельные касательным
В таком случае я утверждаю, что АН равно ¿Г и Е! равно ОТ
А поскольку мы доказали. что АНО равно 0В7. и прямая от А к В параллельно
прямой, проведенной от Н к/, то АЕ к ЕН равно ВЕ к Е7 и при преобразовании ЕА
к АН равно ЕВ к ВЯ. И также ГА к АЕ равно АВ к ВЕ; ведь каждая из двух больше
удвоенной каждой из двух. Поэтому в равной мере ГА к АН равно АВ к ВЕ. И тре¬
угольники подобны из-за параллельных, поэтому ГТА к А0Н равно ^ВА к 0В7 И
при перестановке АНО равно 0В7, поэтому также ТАГ равно АВЕ.
Из которых АН0 равно В07, как мы доказали; оставшаяся А0 равно Г0. Поэ¬
тому также АН равно Г7.
А поскольку ГО и А7 параллельны, то ГОЕ равно АЕ7. Тем же самым способом
также АЕ! равно ВЕН. И ВЕН равно АЕ7; поэтому также ГОЕ равно ЛЕЕ И также
НА равно 2Г; следовательно, Е! равно ОТ.
9
Если при тех же самых предпосылках одна точка К находится между диаметра¬
ми, а другая точка тождественна с одной из Г и А, как Г, и проводятся параллельные,
то в таком случае я утверждаю, что треугольник ГЕО равно четырехугольнику КЕ и
КО равно АЛ/.

Дословный перевод книги III
И это очевидно. Ведь мы доказали, что
треугольник ГЕО равно АЕ7, и АЕ7 равно
четырехугольнику КЕ, то также ГЕО рав¬
но четырехугольнику КЕ. Следовательно,
ГРМ равно КО, а КГ равно АО.
10
Пусть при тех же самых предпосыл¬
ках точки К и Л будут взяты не ¡между
точками], где пересекаются диаметры с
сечениями.
Поэтому нужно доказать, что четы¬
рехугольник ЛТРХ равен четырехуголь¬
нику ОХК1.
Ведь поскольку А7 и ВН касаются се¬
чения, и АЕ и ВЕ суть диаметры, прове¬
\
денные через точки соприкосновения, а
АТ и К1 параллельны касательным, то ТУЕ
равно УОА плюс Е7А, и тем же самым спо¬
собом также EEI равно iPK плюс ВЕН. И
AEZ равно ВЕН. Поэтому TEY дел и мое на
YQA равно ЕЕ I делимое на SPK. Поэтому
будет TYE плюс ЕР К равно ЕЕ I плюс YQA.
И пусть будет приложен общий KEEYAX,
следовательно, ЛТРХ равно QXK1.
11
Если при тех же самых предпосылках на
каждом сечении берется некоторая точка,
и от нее проводятся параллельные прямые,
одна — касательной, другая — прямой, соеди¬
няющей точки касания, то треугольник, об¬
разованный ими при диаметре, проведенном
через точку пересечения касательных отли¬
чается от треугольника, отделенного при
касательной и диаметре, проведенном через
точку касания, треугольником, отделенным
при точке пересечения касательных.
Пусть АВ и ГД будут противолежащими
сечениями, и пусть касательные АЕ и ДЕ пе¬
ресекаются в точке Е, центром же пусть бу-
м
339

Книга III
дет 0. Пусть будут проведены АД и Е0Н,
и пусть на сечении АВ будет взята неко¬
торая точка В, пусть через нее будет про¬
ведена BZA, параллельная прямой АН,
и ВМ - параллельная прямой АЕ. В та¬
ком случае я утверждаю, что BZM равно
АКА плюс KEZ.
Ведь очевидно, что АД рассекается Е0
на два равных отрезка, и Е0 есть диаметр,
сопряженный с ним, который проводит¬
ся через 0 параллельно прямой АД, по¬
этому АН проведена к НЕ как ордината.
Поскольку НЕ есть диаметр, АЕ ка¬
сается сечения, а АН проведена как ор¬
дината, и при взятой на сечении точке В
к ЕН проводятся BZ, параллельная пря¬
мой АН и ВМ. параллельная прямой АЕ.
то очевидно, что BMZ равно A0Z плюс
0АЕ. Следовательно, также BZM равно
АКА плюс KZE.
И схожим образом доказано, что
ВКЕМ равно АКА.
/Л
•ж
Если при тех же самых предпосылках на одном сечении берутся две точки и от каж¬
дой проводятся параллельные, то тем же самым способом четырехугольники, образо¬
ванные ими, будут равны.
Пусть будет все то же самое, что и прежде, и пусть на сечении будут взяты про¬
извольные точки В и К. и пусть через них проводятся АВМ№ и КЕОУП, параллель¬
ные прямой АД. и ВЕР и ЛКЕ - параллельные прямой АЕ. В таком случае я утверж¬
даю, что ВП равно КР.
Ведь поскольку было доказано, что АОП равно КОЕЕ и AMN равно ВМЕР. то КР
делимое на ВО равно МП или КР плюс ВО равно МП. И если прибавить или отнять
общую ВО, то ВП равно ЕЕ.
13
Если на сопряженных противолежащих сечениях прямые, касающиеся рядом располо¬
женных сечении, пересекаются, и через точки касания проводятся диаметры, то треу¬
гольники, общая вершина которых есть центр противолежащих сечений, будут равны.
Пусть будут сопряженные противолежащие сечения, на которых пусть будут рас¬
положены точки А. В, Г и Д, и пусть ВЕ и АЕ касаются сечений А и В. пересекаясь в
Е, центром же пусть будет 0, и пусть проведенные А0 и В0 будут продолжены даль¬
ше до Д и Г. В таком случае я утверждаю, что BZ0 равно АН0.
340

Дословный перевод книги III
•ж
Пусть же через А и 0 будут проведены АК и ЛОМ, параллельные прямой ВЕ. По¬
скольку В2Е касается сечения В, и через точку соприкосновения проведен диаметр
ЛОВ, и ЛМ параллельна прямой ВЕ, то ЛМ есть диаметр, сопряженный с диаме¬
тром ВЛ, который называется вторым диаметром; по этой причине АК проведена к
ВЛ как ордината. И АН касается сечения; поэтому КОН равно ВО в квадрате. Тог¬
да КО к 0В равно ВО к НО. Однако КО к 0В равно КА к В2 равно АО к 02, поэто¬
му также АО к £($ равно ВО к НО. И угол В©г плюс НОг равен двум прямым; сле¬
довательно, АНО равно ВОг.
•I»
14
Если при тех же самых предпосылках на любом из сечении берется некоторая точка
и от нее проводятся к диаметру прямые, параллельные касательным, то треугольник,
возникший при центре, отличается от треугольника, получившегося на том же самом
угле, треугольником, имеющим в качестве основания касательную, а вершиной — центр.
Пусть все останется тем же самым, пусть будет взята на сечении В некоторая точ¬
ка Е, и пусть через нее будет проведена EPI, параллельная прямой АН, и ЕТО - па¬
раллельная прямой ВЕ. В таком случае я утверждаю, что ООТ равно ELT плюс 0BZ.
Пусть от А будет проведена AY, параллельная прямой BZ. А поскольку по той же
самой причине, что и прежде, ЛОМ есть диаметр сечения АЛ, ЛОВ, сопряженная с
ним, есть второй диаметр, и от А АН касается сечения, a AY проведена как парал¬
лельная прямой ЛМ, то AY к YH будет иметь отношение, составленное из отноше¬
ния OY к YA и отношения, которое имеет поперечная сторона эйдоса, находящего¬
ся возле ЛМ, к прямой стороне. И AY к YH равно ET к TL и OYk YA равно ОТ к ТО
равно 0В к BZ, и как поперечная сторона эйдоса, лежашего возле ЛМ, относится
к прямой стороне, так и прямая сторона эйдоса, лежашего возле ВЛ, относится к
поперечной стороне. Поэтому отношение ET к TZ будет иметь отношение, состав¬
ленное из отношения ОВ к BZ или ОТ к ТО и отношения, которое имеет прямая
сторона эйдоса, лежашего возле ВЛ, к поперечной стороне. И из-за того что мы до¬
казали в первой книге, получается, что ТОО равно ETE плюс BZO. Поэтому также
при прибавлении АНО.
«ж
15
Если прямые, касающиеся одного из противолежащих сопряженных сечений, пере¬
секаются, и через точки касания проводятся диаметры, и на любом из сопряженных
сечений берется некоторая точка, и от нее проводятся прямые к диаметрам, парал¬
лельные касательным, то треугольник, образованный ими на сечении больше треуголь¬
ника, полученного на центре, треугольником, имеющим основанием касательную, вер¬
шиной же — центр противолежащих сечений.
Пусть будут противолежащие АВ, Н2, Т, Е, центром которых пусть будет О, и пусть
ВЛГ и АЛЕ касаются сечения АВ, и пусть через точки соприкосновения А и В будут
проведены диаметры А02Ф и ВОТ. и пусть на сечении Н2 будет взята некоторая
точка I, и пусть через нее будет проведена 12Л, параллельная прямой В Г, и IV па¬
раллельная прямой АЕ. В таком случае я утверждаю, что ЕЛУ равно ОЛ2 плюс ОГВ.
•ж
•ж
341

Книга III
Пусть же через © будет проведена Е©Н, параллельная прямой ВГ, а через Н К1Н,
параллельная прямой АЕ, и 10, параллельная прямой ВТ; поэтому очевидно, что
ЕН и ВТ суть сопряженные диаметры, прямая 10, параллельная прямой ВТ, про¬
ведена к ©НО как упорядоченная прямая | ордината) и ЕЛ0О есть параллелограмм.
Поскольку ВГ касается сечения, и В© проведена через точку соприкосновения,
и другая касательная есть АЕ, то пусть будет АВ к ВЕ равно М N к 2ВГ; поэтому МН
есть прямая сторона эйдоса, лежащего возле ВТ. Пусть МИ рассекается в П на два
равных отрезка; поэтому АВ к ВЕ равно М П к ВГ. Поэтому пусть будет ЕН к ТВ рав¬
но ТВ к Р; поэтому Р будет прямая сторона эйдоса, лежащего возле ЕН. И посколь¬
ку АВ к ВЕ равно МП к ГВ, а АВ к ВЕ равно АВ в квадрате к АВЕ, и МП к ГВ равно
МП на В© к ГВ©, то АВ в квадрате к АВЕ равно П М на В© к ГВ©. А М П на В© рав¬
но ©Н в квадрате, поскольку ЕН в квадрате равно ТВ на МИ, и МП на В© равно од¬
ной четвертой ТВ на МИ, Н© в квадрате равно одной четвертой НЕ в квадрате; поэ¬
тому будет АВ в квадрате к АВЕ равно Н© в квадрате к ГВ©. И при перестановке АВ
в квадрате к Н© в квадрате равно АВЕ к ГВ©. И АВ в квадрате к ©Н в квадрате рав¬
но АВЕ к Н©1; ведь данные треугольники подобны; и АВЕ к ГВ© равно отношению
треугольников АВЕ к ГВ©. Поэтому АВЕ к Н©1 равно АВЕ к ГВ©. Тогда Н©1 рав¬
но ГВ©. Таким образом, будет Н©Кравно©1К плюс 10Н равно ©IК плюсГВ©. По¬
скольку ©В к ВГ равно ©В к МП на МП к ВГ и 0В к МП равно ТВ к МИ равно Р к
ЕН и МП к ВГ равно АВ к ВЕ, то ©В к ВГ равно АВ к ВЕ на Р к ЕН. И поскольку ВГ
и ЕЛ параллельны, и треугольники ©ГВ и ©лг подобны, и ©В к ВГ равно ©Л к
то ©Л к ЛZ равно Р к ЕН на АВ к ВЕ равно Р к ЕН на 0Н к©1. А поскольку Нг есть
гипербола, имеющая диаметром ZH, прямая сто[
проведена упорядоченно прямая [ордината| ЕО, и на радиусе ©Н описан треуголь¬
ник ©1Н, и на ординате ЕО или ©Л ей равной, 0ЛZ, и на ©О, расположенной меж¬
ду центром и ординатой, или на ЕЛ равной ей треугольник ЕЛУ подобный треуголь¬
нику ©1Н. описанному на радиусе и они имеют составные отношения, как мы ска¬
зали, то будет ЕЛУ равно ©^ плюс ©ГВ.
MIIJ
•к
•Ж
•ж
•а
на есть Р, а от некоторой точки I
1
16
Если две прямые, касающиеся сечения конуса или окружности круга, пересекаются,
и от некоторой точки на сечении проводится прямая, параллельная одной из касатель¬
ных и рассекающая сечение и другую касательную, то будет как квадраты касательных
соотносятся между собой, так площадь, ограниченная прямыми, расположенными меж¬
ду сечением и касательной, относится к квадрату прямой, отделенной точкой касания.
Пусть АВ будет сечением конуса или окружностью круга, и пусть ЛГ и ГВ каса¬
ются сечения, пересекаясь в Г, пусть будет взята на сечении АВ некоторая точка Л,
и пусть через нее будет проведена EAZ, параллельная прямой ГВ. В таком случае я
утверждаю, что ВГ в квадрате к АГ в квадрате равно ZEA к ЕА в квадрате.
Пусть же через А и В будут проведены диаметры АН© и КВА, а через А — AMN,
параллельная прямой АЛ; поэтому ясно, что АК равно K.Z и АЕН равно ЛА и ВАГ
равно АГ0.
Поскольку же ZK равно КА, и АЕ приложена, то ZEA плюс АК в квадрате равно
КЕ в квадрате И поскольку треугольники ЕЛК и AN К являются подобными, то ЕК
*11
342

Дословный перевод книги Ш
в квадрате к КД в квадрате равно ЕКЛ к AN К. И при перестановке ЕК в квадрате
к ЕЛК равно ДК в квадрате к AN К. поэтому также остальное ZEA к АЛ равно ЕК в
квадрате к ЕЛК. И ЕК в квадрате к ЕЛК равно ГВ в квадрате к ЛГВ; поэтому также
ZEA к ЛА равно ГВ в квадрате к ЛГВ. И АЛ равно АЕН и ЛГВ равно А0Г; тогда так¬
же ZEA к АЕН равно ГВ в квадрате к А0Г При перестановке ZEA к ГВ в квадрате
равно АЕН к А0Г. И АНЕ к А0Г равно ЕА в квадрате к АГ в квадрате; поэтому так¬
же ZEA к ГВ в квадрате равно ЕА в квадрате к АГ в квадрате. И при перестановке.
Ф1
•V
•г*
•V
17
Если две прямые, касающиеся сечения конуса или окружности круга, пересекают¬
ся, и на сечении берутся две произвольные точки, и от них на сечении проводятся пря¬
мые, параиельные касательным и рассекающие друг друга и линию, то будет, что как
квадраты касательных соотносятся между собой, так и прямоугольники. ограничен¬
ные прямыми, взятых тем же самым способом.
Пусть АВ будет сечением конуса иди окружностью крута. и АГ и ГВ касаются се¬
чения АВ, пересекаясь в Г. и пусть будут взяты на сечении произвольные точки Л
и Е, и пусть через них проводятся EZIK и AZH0. параллельные прямым АГ и ГВ.
В таком случае я утверждаю, что АГ в квадрате к ГВ в квадрате равно KZE к 0ZA.
Пусть же через А и В будут проведены диаметры AAMN и ВОЕП и пусть будут
продолжены дальше касательные и параллельные вплоть до диаметров, и пусть от А
и Е будут проведены АН и ЕМ. параллельные касательным: поэтому очевидно, что
KI равно IЕ, 0Н равно НА.
Поэтому поскольку КЕ в I рассекается на равные отрезки, а в Z - на неравные, то
будет KZE плюс Z1 в квадрате равно El в квадрате. И поскольку из-за параллельных
являются подобными, то EI в квадрате к IME равно IZ в квадрате к ZIA. Поэтому
также остальное KZE к ZM равно EI в квадрате к МЕГ И EI в квадрате к IME рав¬
но ГА в квадрате к ГAN; поэтому KZE к ZM равно АГ в квадрате к ГAN. A ATN рав¬
но ГП В и ZM равно ZH; тогда KZE к ZH равно АГ в квадрате к ГВП. Схожим обра¬
зом мы докажем, что также 0ZA к EZ равно ГВ в квадрате к ГП В. А поскольку KZE
к ZE равно АГ в квадрате к ГП В и напротив ZH к 0ZA равно ГПВ к ГВ в квадрате, в
равной мере будет АГ в квадрате к ВГ в квадрате равно K.ZE к 0ZA.
•Ж
•Ж
•и
•Ж
i-íl
1
Если две прямые, касающиеся противолежащего сечения, пересекаются, и на одном
из сечений берется некоторая точка, от которой проводится прямая, пара.1лельная од¬
ной из касательных, рассекающая сечение и другую касательную, то получается, что
как квадраты касательных относятся друг к другу, так и прямоугольник, ограничен¬
ный прямыми, расположенными между сечением и касательной относится к квадрату
прямой, отделенной точкой касания.
Пусть АВ и MN будут противолежащими сечениями, касательными пусть будут
АГА и ВГ0, и пусть через точки соприкосновения проводятся диаметры АМ и BN,
пусть на сечении MN будет взята некоторая точка А, и через нее пусть будет прове¬
дена EAZ, параллельная прямой В0.
те к ГА в квадрате равно ZEA к АЕ в квадрате.
343

Книга III
Пусть же через А будет проведена АЕ, параллельная прямой АЕ. А поскольку АВ
есть гипербола и ее диаметр есть BN, касательная - В0, AZ параллельна прямой В0,
то ZO равно ОД. И ЕД приложена; поэтому ZEA плюс ДО в квадрате равно ЕО в ква¬
драте. И поскольку ЕЛ и АЕ параллельны, то треугольники ЕОА и АЕО подобны.
Поэтому ЕО в квадрате к ЕОА равно АО в квадрате к ЕЛО, поэтому также остальное
AEZ к ЛА равно ЕО в квадрате к ЕОА. А ОЕ в квадрате к ОЕЛ равно ВГ в квадрате
к ВГА. поэтому также ZEA к АЛ равно ВГ в квадрате к В ГЛ. А ДА равно АЕН, ВАГ
равно АГ0, поэтому ZE на ЕД к АЕН равно ВГ в квадрате к АГО. И также АЕН к ЕА
в квадрате равно АГ0 к АГ в квадрате. Поэтому в равной мере ВГ в квадрате к ГА в
квадрате равно ZEA к ЕА в квадрате.
•lí
•I».
19
Если две прямые, касающиеся противолежащих сечении, пересекаются, и проводятся
прямые, параллельные касательным и рассекающие друг друга и сечение, то получает¬
ся, что как квадраты касательных относятся друг другу, так и прямоугольник, ограни¬
ченный прямыми, расположенными между сечением и точкой пересечения прямых, от¬
носится к прямоугольнику, ограниченному прямыми, взятыми тем же самым способом.
Пусть будут противолежащие сечения с диаметрами АГ и ВЛ, и центром Е, и пусть
касательные AZ и ZA пересекаются в Z, и пусть от любых произвольных точек бу¬
дут проведены Н01КЛ и MNEOA, параллельные прямым AZ и ZA. В таком случае
я утверждаю, что AZ в квадрате к ZA в квадрате равно HAI к МАЕ.
Пусть через Е и I будут проведены 1П и ЕР, параллельные прямым AZ и ZA А
поскольку AZ в квадрате к AZI равно 0Л в квадрате к 0ЛО равно 01 в квадрате к
01П, то также остальное HAI к 1ПОЛ равно AZ в квадрате к AZI. A AZI равно AZT
и ПОЛ1 равно КРЕЛ; поэтому также AZ в квадрате к ATZ равно HAI к РЕАК. A ATZ
к ZA в квадрате равно РЕАК к МАЕ. Следовательно, также в равной мере AZ в ква¬
драте к ZA в квадрате равно HA¡ к МАЕ.
20
Еаи две прямые, касающиеся противолежащих сечений, пересекаются, и через точ¬
ку пересечения проводится прямая, параллельная прямой, соединяющей точки соприкос¬
новения, пересекающаяся с каждым сечением, и проводится другая прямая, параллель¬
ная той же самой прямой и рассекающая сечения и касательные, то получается что
как прямоугольник, ограниченный прямыми, попадающими от точки пересечения на се¬
чения, относится к квадрату касательной, так и прямоугольник, ограниченный пря¬
мыми, расположенными между сечениями и касательной, относится к квадрату пря¬
мой, отделенной в точке касания.
Пусть АВ и ГЛ будут противолежащие сечения, чьим центром будет Е. а касатель¬
ными - AZ и TZ, и пусть будут проведены АГ и EZ, АЕ, которые будут продолжены
дальше; пусть через Z будет проведена BZ0, параллельная прямой АГ, и пусть будет
взяга некая точка К, пусть через нее будет проведен KAIMNE, параллельный прямой
АГ В таком случае я утверждаю, что BZA к ZA в квадрате равно КАЕ к АА в квадрате
Пусть от К и В будут проведены КП и ВР, параллельные прямой AZ А посколь¬
ку BZ в квадрате к BZP равно KI в квадрате к К1П равно AI в квадрате к AIZ рав¬
•де
•i».
•г»
•I».
344

Дословный перевод книги III
но КАЕ к КЛ7П и ВТ в квадрате равно В7Д, ВР7 равно А70, КЛТП равно АЛК!, то
В7Д к А70 равно КАЕ к АЛЫ. А А70 к А7 в квадрате равно AЛN к АЛ в квадрате;
следовательно, В7А к ТА в квадрате равно КАЕ к АЛ в квадрате.
21
Если при тех же самых предпосылках берутся две точки, и через них проводятся пря¬
мые, одна параллельно касательной, а другая параллельно прямой, соединяющей точ¬
ки касания, рассекающие друг друга и сечение, то получается, что как прямоугольник,
ограниченный прямыми, проведенными от точки пересечения к сечениям, относится к
квадрату касательной, так и прямоугольник, ограниченный прямыми, расположенны¬
ми между сечениями и точкой пересечения, относится к прямоугольнику, ограниченно¬
му прямыми, расположенными между сечением и точкой пересечения.
Пусть будет то же самое, что и прежде, и пусть будут взяты точки Н и К, и пусть
через них будут проведены NEHOnP и KZT, параллельные прямой АТ, и НМЛ и
KOOIX^PQ, параллельные прямой АГ. В таком случае я утверждаю, что В7А к ТА в
квадрате равно KOQ к NOH.
Ведь поскольку АТ в квадрате к А70 равно АЛ в квадрате к АЛМ равно ЕО в
квадрате к EOT равно ЕН в квадрате к ЕН М, то как вся ЕО в квадрате относится к
целой EOT, так отделенное ЕН в квадрате относится к отделенному ЕНМ. Поэто¬
му также остальное NOH к НОТМ равно АТ в квадрате к А70. А А70 равно BYT,
НОТМ равно КОПТ; тогда АТ в квадрате к B7Y равно NOH к КОРТ Мы же дока¬
зали, что BYT к ВТ в квадрате равно КОРТ к KOQ равно BYT к В7Д; поэтому в рав¬
ной мере АТ в квадрате к В7Д равно NOH к KOQ. И наоборот, В7Д к ТА в квадра¬
те равно KOQ к NOH.
•и
22
Если две параллельные прямые касаются противолежащих сечений и проводятся не¬
которые прямые, рассекающие друг друга и сечение, одна — параллельная касательной,
другая — параллельная прямой, соединяющей точки касания, то получается, что как
поперечная сторона эйдоса, находящегося возле прямой, соединяющей точки касания,
относится к прямой стороне, так и прямоугольник, ограниченный прямыми, располо¬
женными между сечениями и точкой пересечения, относится к прямоугольнику, огра¬
ниченному прямыми, расположенными между сечением и точкой пересечения.
Пусть А и В будут противолежащими сечениями, а касательными - параллель¬
ные АГ и ВД, и пусть будет проведена АВ. Тогда пусть будет проведена ЕЕН, парал¬
лельная прямой АВ. и КЕЛМ, параллельная прямой АГ. В таком случае я утверж¬
даю, что как АВ относится к прямой стороне эйдоса, так и НЕЕ к КЕМ.
Пусть через Н и Е будут проведены ЕЬ1 и НТ, параллельные прямой АГ.
А поскольку АГ и ВЛ, касающиеся сечения, параллельны, АВ есть диаметр и к
нему проведены ординаты КА, EN и НТ. то АВ к прямой стороне равно ВЛА к ЛК
в квадрате равно В№ к №Е в квадрате равно ВМА к ЛЕ в квадрате. Поэтому как це¬
лое ВЛА относится к целому ЛК в квадрате, так и отделенное В1МА, т.е. 7А1Ч, ведь
ЫА равно ВТ, относится к отделенному ЛЕ в квадрате, поэтому также оставшееся
7ЛN относится к оставшемуся КЕМ, как АВ относится к прямой стороне. А ZЛN
•ж
345

Книга III
равно НЕЕ, следовательно, как АВ поперечная сторона эйдоса относится к прямой,
так и НЕЕ к КЕМ.
•I»:
23
Если на сопряженных противолежащих сечениях две прямые, касающиеся противо¬
лежащих друг другу сечений, пересекаются в любом из сечений, и проводятся прямые,
параллельные касательным и рассекающие друг друга и другие противолежащие сечения,
то получается, что как квадраты касательных относятся друг с другом, так и пря¬
моугольник, ограниченный прямыми, расположенными между сечениями и точкой пере¬
сечения. к прямоугольнику, ограниченному прямыми, взятыми тем же самым образом.
Пусть АВ, ГД, Е7и Н0 будут сопряженными противолежащими сечениями, цен¬
тром же их пусть будет К, и пусть АФГЛ и ЕХАЛ, касающиеся сечений ЛВ и Е7, пе¬
ресекаются в Л, пусть будут проведены АК и ЕК и пусть они будут продолжены даль¬
ше до В и X, и пусть от Н будет проведена Н ММЕО, параллельная прямой АА и от 0
- 0ПРЕХ, параллельная прямой ЕЛ. В таком случае я утверждаю, что ЕЛ в квадра¬
те к ЛА в квадрате равно 0ЕХ к НЕО.
Пусть через X будет проведена ХТ, параллельная прямой АЛ, от О — ОУ. парал¬
лельная прямой ЕЛ. А поскольку диаметром сопряженных противолежащих сече¬
ний АВ, ГА, ЕХ и НО является ВЕ, и ЕЛ касается сечения, ей параллельно проведе¬
на 0Х, то 0П равно ПХ и по той же самой причине Н М равно МО. А поскольку ЕЛ
в квадрате к ЕФЛ равно ПХ в квадрате к ПТХ равно ПЕ в квадрате к П\Е. то так¬
же остальное ©ЕЕ к ТКЕХ равно ЕЛ в квадрате к ФАЕ. И ЕФЛ равно АЛХ и Т^Х
равно ЕРУО: поэтому ЕЛ в квадрате к АЛХ равно ©ЕХ к ЕОУР. А АХЛ к АЛ в ква¬
драте равно ЕРУО к НЕО. Следовательно, в равной мере ЕЛ в квадрате к АЛ в ква¬
драте равно 0ЕХ к НЕО.
•и
•It
24
Если на сопряженных противолежащих сечениях от центра к сечениям проводятся
две прямые, и одна из них есть поперечный диаметр, другой же берется как прямой, и
проводятся некоторые прямые, параллельные этим диаметрам, пересекающие друг дру¬
га и сечения, и имеется точка пересечения на площади, расположенной между четырь¬
мя сечениями, то прямоугольник, ограниченный отрезками прямой, параллельной попе¬
речному диметру вместе с площадью прямоугольника, ограниченного отрезками прямой,
параллельной прямому диаметру, ¡большей] квадратом поперечного диаметра к квадра¬
ту прямого диаметра, будет равен двойному квадрату половины поперечного диаметра.
Пусть А. В. Г и Л будут сопряженными противолежащими сечениями, центром
которых пусть будет Е, и пусть от Е будет проведет поперечный диаметр АЕГ и по¬
перечный диаметр ЛЕВ, и АГ - параллельная Пусть будут проведены 7Н01КЛ и
MNEOnP, параллельные прямой АВ и пересекающиеся в
положена сначала внутри угла ХЕФ или УЕТ В таком случае я утверждаю, что ZEA
вместе площадью, к которой имеет отношение МЕЛ, которое имеет АГ в квадрате к
АВ в квадрате, равен плошади 2АЕ в квадрате.
Пусть же будут проведены асимптоты сечении ХЕТ и УЕФ. и через А касательная
ХНАФ. А поскольку ХАФ равно ЛЕ в квадрате, то ХАФ к ЕА в квадрате равно ЛЕ в
•IU
•л
; пусть же г. будет рас-
о
' ’1
•
»1»:
346

Дословный перевод книги III
квадрате к ЕА в квадрате. А ЕАФ к АЕ в квадрате равно ЕА к АЕ на ФА к АЕ. Но ХА
к АЕ равно NE к Е0, ФА к АЕ равно ПЕ к ЕК; поэтому ДЕ в квадрате к АЕ в квадра¬
те равно NE к Е0 на ПЕ к ЕК равно nEN к KE0 равно ДЕ в квадрате плюс FIEN к
АЕ в квадрате плюс КЕ на Е0.
А ДЕ в квадрате равно F1MN равно PNM, и тем же образом АЕ в квадрате равно
KZ0 равно A0Z; поэтому ДЕ в квадрате к ЕА в квадрате равно FIEN плюс PNM к
KE0 плюс A0Z. A FIEN плюс PNM равно РЕМ; поэтому ДЕ в квадрате к ЕА в ква¬
драте равно РЕМ к KE0 плюс KZ0. Поэтому нужно доказать, что ZEA плюс KE0
плюс KZ0 равно 2ЕА в квадрате. Пусть отбрасывается общее АЕ в квадрате равно
KZ0. Поэтому остальное, подлежащее доказательству, есть KE0 плюс AEZ равно
АЕ в квадрате. И это получается, ведь КЕО плюс AEZ равно A0Z равно KZ0 рав¬
но АЕ в квадрате.
Пусть же ZA и М Р на другой асимптоте пересекаются в 0. Тогда Z0A равно АЕ в
квадрате и M0P равно ДЕ в квадрате; поэтому ДЕ в квадрате к ЕА в квадрате равно
M0P к Z0A. Поэтому мы хотим, чтобы 2Z0A равно 2АЕ в квадрате. И это получается.
Пусть же Е, расположена внутри угла ХЕК или ФЕТ Тогда тем же самым обра¬
зом из-за составного отношения будет ДЕ в квадрате к ЕА в квадрате равно nEN к
KE0. A nMN равно ЛЕ в квадрате равно PNM и A0Z равно АЕ в квадрате. Поэто¬
му PNM к A0Z равно nEN к KE0. Поэтому также остальное РЕМ к АЕ в квадрате
делимое на KE0 равно ДЕ в квадрате к ЕА в квадрате. Поэтому нужно доказать, что
ZEA плюс АЕ в квадрате делимое на KE0 равно 2АЕ в квадрате. Пусть отбрасыва¬
ется общее АЕ в квадрате равно Z0A. Поэтому остальное, подлежащее доказатель¬
ству. - KE0 плюс АЕ в квадрате делимое на KE0 равно АЕ в квадрате. И это полу¬
чается, ведь KE0 плюс АЕ в квадрате делимое на KE0 равно АЕ в квадрате.
25
Пусть при тех же самых предпосылках точка
пересечения прямых, параллельных прямым
АГ и ВД, находится внутри одного из сечений
Д и В, как ниже описали, в Е.
В таком случае я утверждаю, что прямоу¬
гольник, ограниченный отрезками прямой,
параллельной поперечному диаметру, то есть
ОЕ^ площадью прямоугольника, ограничен¬
ного отрезками прямой, параллельной прямо¬
му диаметру, т.е. РЕМ, с отношением квадра-
та прямого диаметра к квадрату поперечному
диаметра, будет больше удвоенного квадрата
половины поперечного диаметра.
По той же самой причине ДЕ в квадрате к
ЕА в квадрате равно Пг.0 к А ДЕ в квадрате равно ПМ0. АЕ в квадрате равно
ЛОХ. Поэтому также ДЕ в квадрате к АЕ в квадрате равно ПМ0 к АОХ. А поскольку
П0Е к ЛЕХ равно ПМ0 к АОХ равно ПМ0 к ХТЛ, то также остальное РЕМ к ТЕК
равно ДЕ в квадрате к АЕ в квадрате. Поэтому следует доказать, что OEN равно ТЕК
347

Книга III
плюс 2АЕ в квадрате. Пусть отбрасывается общее ТЕМ, поэтому остальное, подле¬
жащее доказательству, ОТ№ равно 2АЕ в квадрате. И это получается.
Если точка пересечения 5 параллельных
прямых расположена внутри одного из сече¬
ний А и Г, как было предположено, то прямо¬
угольник, ограниченный отрезками прямой,
параллельной поперечному диаметру АЕ7,
площадью прямоугольника, ограниченного от¬
резками другого диаметра РЕН. с отношени¬
ем, которое имеет квадрат прямого диаметра
к квадрату поперечного диаметра, будет мень¬
ше квадрата половины поперечного диаметра.
Ведь поскольку по той же самой причи¬
не, что и прежде, ДЕ в квадрате к ЕА в квадра¬
те равно ФЕХ к КЕ0, то также целое РЕН к
КЕ0 плюс АЕ в квадрате равно ДЕ в квадрате
к ЕА в квадрате. Поэтому нужно доказать, что
АЕ7 плюс 2АЕ в квадрате равно КЕ0 плюс АЕ в квадрате. Пусть отбрасывается
шее АЕ в квадрате; тогда остальное, подлежащее доказательству, есть Аг.7 плюс АЕ
в квадрате равно К=0, т.е. равно КЕО делимое на АО/. И это получается, ведь
А07 плюс АЕ/ равно КЕ0
27
Если проводятся сопряженные диаметры эллипса или окружности круга, и один из
диаметров берется как прямой, а другой как поперечный, им пара.ыельно проводятся
две прямые, пересекающиеся между собой и с линией, то квадраты прямых, отделен¬
ных между точкой пересечения прямых и линией, на прямой, проведенной параллельно
поперечному диаметру, при взятых фигурах, описанных на прямых, отделенных на пря¬
мом диаметре, проведенном пара.иельно прямой, между точкой пересечения прямых и
линией, фигурах, которые подобны и подобным образом описаны с эйдосом, подлежа¬
щим к прямому диаметру, равны квадрату поперечного диаметра.
Пусть АВГД будет эллипсом или окружностью круга, чьим центром пусть будет
Е, и пусть будут проведены два его сопряженных диаметра, прямой — АЕГ, а попе¬
речный - ВЕД, и пусть будут проведены NZH0 и KZAM, параллельные прямым АГ
и ВД. В таком случае я утверждаю, что NZ в квадрате плюс Z0 в квадрате при взя¬
тых прямоугольниках на KZ и ZM. схожих и схожим образом описанных с эйдосом,
находящимся возле АГ, равно ВД в квадрате.
Пусть от N будет щ
ордината. И прямой стороной пусть будет ВП А поскольку ВП к АГ равно АГ к ВД,
то также ВП к ВД равно АГ в квадрате к ВД в квадрате. Однако ВД в квадрате равен
эйдосу, лежащему возле АГ. Поэтому как ВП к ВД, так и АГ в квадрате относится к
эйдосу, лежащему возле АГ. Однако как АГ в квадрате относится к эйдосу, лежаше-
/Л
ооведена NE, параллельная АЕ, тогда она проведена к ВД как
ж»;
М
•1«
348

Дословный перевод книги III
му возле АГ, так и № в квадрате относится к фигуре, лежащей возле ИЕ, и подоб¬
ной эйдосу, лежащему возле АГ. Поэтому так же как П В к ВЛ, так и ЫЕ в квадрате от¬
носится к фигуре, лежащей возле №, схожей с эйдосом, лежащим возле АГ. Поэто¬
му также ПВ к ВД равно МЕ в квадрате к ВЕД. Поэтому фигура при т.е. при 7Л,
приложенная и подобная эйдосу, лежащему возле АГ, равна прямоугольнику ВЕД.
Схожим же образом мы докажем, что фигура, находящаяся возле КА, подобная эй¬
досу, находящемуся возле АГ. равна прямоугольнику ВЛД. А поскольку прямая N0
в Н рассечена на равные отрезки, а в Ъ - на неравные, то 07 в квадрате плюс ZN
в квадрате равно 20Н в квадрате плюс Н7 в квадрате равно 2ГМН в квадрате плюс в
квадрате Н7 в квадрате. По той же самой причине также М7 в квадрате плюс 7К в
квадрате равно 2КЛ в квадрате плюс Л7 в квадрате, и фигуры, описанные на М7К.
подобные эйдосу, описанному на АГ, вдвое больше фигур, схожим образом описан¬
ных на КА7. Однако фигуры, описанные на КЛ7, равны прямоугольникам ВЕД и
ВЛД, и N4 в квадрате плюс Н7 в квадрате равно ЕЕ в квадрате плюс ЕЛ в квадра¬
те ; поэтому N7 в квадрате плюс 70 в квадрате с фигурами, описанными на К7М и
схожими с эйдосом, лежащим возле АГ, вдвойне больше, чем ВЕД плюс ВЛД плюс
ЕЕ в квадрате плюс ЕЛ в квадрате. А поскольку прямая ВД рассечена в Е на равные
отрезки, а в Е - на неравные, то ВЕД плюс ЕЕ в квадрате равно ВЕ в квадрате. И та¬
ким же образом ВЛД плюс ЛЕ в квадрате равно ВЕ в квадрате. Поэтому также ВЕД
плюс ВЛД плюс ЕЕ в квадрате плюс ЛЕ в квадрате равно 2ВЕ в квадрате. Поэтому
N7 в квадрате плюс 70 в квадрате вместе с фигурами, описанными на К7М и схо¬
жими с эйдосом, лежащим возле ГА, равны 4ВЕ в квадрате. Однако также ВД в ква¬
драте равно 4ВЕ в квадрате. Поэтому N7 в квадрате плюс 70 в квадрате при взятых
фигурах, описанных на К7М и схожих с эйдосом, лежащим возле АГ, равны ква¬
драту ВД в квадрате.
28
Если на противолежащих сопряженных проводятся сопряженные диаметры, один из
этих диаметров берется как прямой, другой — как поперечный, и параллельно им про¬
водятся две прямые, пересекающиеся между собой и сечениями, то квадраты прямых,
взятых между точкой пересечения прямых и сечениями, на прямой, проведенной парал¬
лельно прямому диаметру, по отношению квадратам прямых, отделенных между точ¬
кой пересечения прямых и сечениями, на прямой, проведенной параллельно поперечному1
диаметру, имеют такое отношение, которое имеет квадрат прямого диаметра по от¬
ношению к квадрату поперечного диаметра.
Пусть А. В, Г и Д будут сопряженными противолежащими сечениями, прямым
диаметром пусть будет АЕГ, а поперечным диаметром — ВЕЛ, и пусть параллельно
им будут проведены 7Н0К и ЛНМ1^. пересекающиеся между собой и сечениями.
В таком случае я утверждаю, что АН в квадрате плюс в квадрате к 7Н в квадра¬
те плюс НК в квадрате равно АГ в квадрате к ВД в квадрате.
Пусть же от 7 и Л будут проведены упорядоченно прямые ¡ординаты] ДЕ и 70;
тогда они будут параллельны прямым АГ и ВД. Пусть же от В будет проведена прямая
сторона поперечной стороны ВЛ как ВП. Поэтому очевидно, что ПВ к ВЛ равно АГ
в квадрате к ВД в квадрате равно АЕ в квадрате к ЕВ в квадрате равно 70 в квадрате
•ю
•Ж
•ж
»г*
349

Книга III
к ВОД равно ГЕА к ЛЕ в квадрате. Поэтому как один из предшествующих относит¬
ся к одному из последующих, так и все предшествующие относятся ко всем последу¬
ющим; поэтому также АГ в квадрате к ВЛ в квадрате равно ГЕА плюс АЕ в квадрате
плюс OZ в квадрате к ДО В плюс ВЕ в квадрате плюс ЛЕ в квадрате равно ГЕА плюс А Е
в квадрате плюс Е0 в квадрате к ДО В плюс ВЕ в квадрате плюс М Е в квадрате. А ГЕА
плюс АЕ в квадрате равно ЕЕ в квадрате, ДОВ плюс ВЕ в квадрате равно ОЕ в квадра¬
те; поэтому АГ в квадрате к ВД в квадрате равно ЕЕ в квадрате плюс Е0 в квадрате к
ОЕ в квадрате плюс ЕМ в квадрате равно ДМ в квадрате плюс МН в квадрате к Z0 в
квадрате плюс 0Н в квадрате. И как мы доказали NH в квадрате плюс НА в квадрате
равно 2ЛМ в квадрате плюс МН в квадрате, ZH в квадрате плюс Н К в квадрате равно
2Z0 в квадрате плюс 0Н в квадрате. Следовательно, также АГ в квадрате к ВЛ в ква¬
драте равно АН в квадрате плюс HN в квадрате к ZH в квадрате плюс Н К в квадрате.
Ml
29
Если при тех же самых предпосылках прямая, параллельная прямому диаметру, рас¬
секает асимптоты, то квадраты прямых, выделенных на прямой, проведенной парал¬
лельно прямому диаметру, .между точкой пересечения прямых и асимптотами, при взя¬
той половине квадрата прямого диаметра к квадратам прямых, выделенных на прямой,
проведенной параллельно поперечному диаметру, между точкой пересечения прямых и
сечениями, имеют такое отношение, которое имеет квадрат прямого диаметра по от¬
ношению к квадрату поперечному диаметру.
Пусть будет то же самое, что и в предыдущей предпосылке, и пусть N А рассека¬
ет асимптоты в Е и О. Нужно доказать, что ЕН в квадрате плюс НО в квадрате плюс
одна вторая АГ в квадрате к ZH в квадрате плюс Н К в квадрате равно АГ в квадрате
к ВД в квадрате равно ЕН в квадрате плюс НО в квадрате плюс 2ЕА в квадрате к гн
в квадрате плюс НК в квадрате.
Ведь поскольку АЕ равно ОЬГ то АН в квадрате плюс Н N в квадрате равно ЕН в
квадрате плюс НО в квадрате плюс 2№Е на ЕА равно ЕН в квадрате плюс НО в ква¬
драте плюс 2АЕ в квадрате. Но АН в квадрате плюс Н№ в квадрате к ZH в квадрате
плюс НК в квадрате равно АГ в квадрате к ВД в квадрате; поэтому также АН в ква¬
драте плюс НО в квадрате плюс 2ЕА в квадрате к ZH в квадрате плюс Н К в квадра¬
те равно АГ в квадрате к ВД в квадрате.
«и
30
Если две прямые, касающиеся гиперболы, пересекаются, и через точки касания про¬
водится прямая, и прямая проводится как параллельная одной из асимптот через точ¬
ку пересечения, рассекая сечение и прямую, соединяющую точки соприкосновения, то
прямая, расположенная между' точкой пересечения и прямой, соединяющей точки со¬
прикосновения, сечением будет рассекаться на два равных отрезка.
Пусть АВГ будет гипербола, АДГ - касательные, EZH — асимптоты, пусть будет
проведена АГ, и пусть через Д будет проведен ДКА параллельно ZE. В таком случае
я утверждаю, что ДК равно КА.
Пусть же будет проведена ZABM, и пусть она будет продолжена в каждую сто¬
рону, и пусть будет установлено, что Z0 равно BZ, пусть же через точки В и К будут
ЙК
М.
•It
350

Дословный перевод книги III
проведены ВЕ и КГМ, параллельные прямой АГ; тогда они проведены как ордина¬
ты. А поскольку треугольники ВЕ7 и ЛГМК подобны, то ЛN в квадрате к ГМК в ква¬
драте равно В/ в квадрате к ВЕ в квадрате. Но как в квадрате к 7ГМ в квадрате,
так и 0В в квадрате относится к прямой стороне; поэтому так же как ДN в квадра¬
те к ГМК в квадрате , так и (ЭВ относится к прямой стороне. И как 0В относится к
прямой стороне, так и 0ГМВ к ГМК в квадрате; поэтому также Д1М в квадрате к ГМК в
квадрате равно 0ГМВ к ГМК в квадрате. Поэтому 01МВ равно ДГМ в квадрате. И также
М7Л равно в квадрате, поскольку АД касается сечения, а АМ проведена как ор¬
дината. Поэтому также ©N6 плюс / В в квадрате равно М7Л плюс ДГМ в квадрате.
Но 0ГМВ плюс Я В в квадрате; поэтому также М7Д плюс ДГМ в квадрате равно /N8
квадрате; тогда ДМ в N рассечена на два равные отрезка, имея лежащей возле Л7. И
КГМ и ЛМ параллельны. Следовательно, ДК равно КА.
1ЙС
31
Если две прямые, касающиеся противолежащих сечении, пересекаются, и через точ¬
ки касания проводится прямая, а через точку пересечения проводится прямая парал¬
лельно асимптоте, рассекающая сечение и прямую, соединяющую точки касания, то
прямая, расположенная между' точкой пересечения и прямой, соединяющей точки ка¬
сания, будет рассекаться на два равных отрезка.
Пусть А и В будут противолежащими сече¬
ниями, АГВ - касательными, пусть проведен¬
ная АВ будет продолжена дальше, и пусть 7Е
будет асимптотой, пусть через Г будет проведе¬
на ГН0, параллельная прямой 7Е. В таком слу¬
чае я утверждаю, что ГН равно Н0.
Пусть будет проведена ГЕ и продолжена даль¬
ше к Д, и пусть через Е и Н будут проведены
ГМЕКМ и НЕ, параллельно прямой АВ, а через
Н и К - К/ и НА, параллельные прямой ГД.
Поскольку К7Е и МЛН подобны, то КЕ в
квадрате к К7 в квадрате равно МЛ в квадрате к АН в квадрате. А мы доказали, что
ЕК в квадрате к К7 в квадрате равно ГМЛК к ЛН в квадрате. Поэтому 1МЛК равно МЛ
в квадрате. Пусть будет прибавляется общая КЕ в квадрате; тогда ГМЛК плюс КЕ в
квадрате равно МЛ в квадрате плюс КЕ в квадрате равно ЛЕ в квадрате равно НЕ в
квадрате. А НЕ в квадрате к МЛ в квадрате плюс КЕ в квадрате равно ЕГ в квадрате
к ЛН в квадрате плюс К7 в квадрате; тогда ЕГ в квадрате равно НЛ в квадрате плюс
К7 в квадрате. А ЛН в квадрате равно ЕЕ в квадрате и КТ в квадрате равно квадра¬
ту половины второго диаметра, т.е. К7 в квадрате равно ГЕЛ; поэтому ГЕ в квадрате
равно ЕЕ в квадрате плюс ГЕЛ. Поэтому ГЛ в Е рассекается на два равных отрезка,
а в Е - на неравные отрезки. И Л0 и НЕ параллельны; следовательно, ГН равно Н0.
•г*
32
Если две прямые, касающиеся гиперболы, пересекаются, и через точки касания про¬
водится прямая, и проводится через точку пересечения касательных прямая, парал-
351

Книга III
лельная прямой, соединяющей точки касания, и через находящуюся на середине прямой,
соединяющей точки касания, точку проводится прямая, параллельная одной из асим¬
птот, то прямая, выделенная между средней точкой и параллельной ¡прямой!, будет
рассекаться сечением на два равных отрезка.
Пусть АВГ будет гиперболой, чьим центром будет А, ДЕ — асимптотой, А7 и 7.Г
- касательными, пусть будут проведены ГА и 7А, которые будут продолжены до Н
и 0; поэтому очевидно, что А0 равно 0Г. И пусть через £ будет проведена /К, па¬
раллельная прямой АГ, а через 0 - 0ЛК параллельно прямой АЕ. В таком случае я
утверждаю, что КА равно 0Л.
Пусть через В и Л будут проведены АМ и
ВЕ, параллельные прямой АГ; тогда получа¬
ется, как мы доказали прежде, АВ в квадрате
к ВЕ в квадрате равно 0М в квадрате к МА в
квадрате равно ВМН к МЛ в квадрате. Поэто¬
му НМВ равно М0 в квадрате. Однако также
0Д7 равно АВ в квадрате, поскольку А/ явля¬
ется касательной и А0 проведена как ордина¬
та. Поэтому НМВ плюс АВ в квадрате равно
0А7 плюс М0 в квадрате равно ДМ в квадра¬
те. Поэтому 70 в М рассечена на два равных
отрезка, имея возле А7. И К7 и ЛМ параллель¬
ны; следовательно, КА равно Л0.
33
Если две прямые, касающиеся противолежащих сечений, пересекаются, и через точ¬
ку касания проводится прямая, а через точку пересечения касательных проводится пря¬
мая, параллельная прямой, соединяющей точки касания, и через находящуюся на середи¬
не прямой, соединяющей точки касания, точку проводится прямая параллельно одной из
асимптот, пересекаясь с сечением и прямой, проведенной через точку пересечения, то
прямая, расположенная между средней точкой и паралтельной ¡прямой], рассекается
сечением на два равных отрезка.
Пусть АВГ и АЕ7 будут противолежащими
сечениями, АН и АН - касательными, центром
- 0, асимптотой - К0, пусть же будет прове¬
дена и продолжена дальше 0Н, пусть также
будет проведена АЛА; тогда очевидно, что она
рассекается в Л на два равных отрезка. Пусть
же будут проведены через Ни0В0ЕиГН7,
параллельные прямой АД, а через Л - прямая
ЛММ, параллельная прямой 0К. В таком слу¬
чае я утверждаю, что ЛМ равно МЫ.
Пусть же будут проведены от Е и М ЕК и
М2, параллельные прямой Н0, а через М -
МП, параллельная прямой АД.
»!•
•Ж
/Л
и«
352

Дословный перевод книги III
Поэтому поскольку из-за того, что мы доказали прежде, т.е. 0Е в квадрате к ЕК
в квадрате равно ВНЕ к ЕМ в квадрате, то 0Е в квадрате к ЕК в квадрате равно ВЕЕ
плюс 0Е в квадрате к КЕ в квадрате плюс ЕМ в квадрате равно в квадрате 0г. в ква¬
драте к КЕ в квадрате плюс ЕМ в квадрате. А мы доказали, что Н0Л равно КЕ в ква¬
драте, и ЕМ в квадрате равно 0П в квадрате; поэтому 0Е в квадрате к ЕК в квадрате
равно 0Е в квадрате к Л0Н плюс 0П в квадрате равно МП в квадрате к Л0Н плюс
0П в квадрате. А 0Е в квадрате к КЕ в квадрате равно М П в квадрате к ПЛ в квадра¬
те, поэтому МП в квадрате к ПЛ в квадрате равно МП в квадрате к Н0Л плюс 0П в
квадрате. Поэтому ЛП в квадрате равно Н0 в квадрате на 0Л плюс 0П в квадрате.
Поэтому прямая ЛН в П рассекается на равные отрезки, а в 0 - на неравные отрез¬
ки. И МП и NN параллельны; следовательно, ЛМ в квадрате равно МЫ.
34
Если на гиперболе на одной из асимптот берется некоторая точка, и от нее пря¬
мая, которая касается сечения, и через точку касания проводится прямая, параллель¬
ная асимптоте, то прямая, проведенная через взятую точку как параллельная другой
асимптоте, будет рассекаться сечением на равные отрезки.
Пусть АВ будет гиперболой, ГДЕ — асимптотами, и пусть на ГД будет взята про¬
извольная точка Г, и пусть через нее будет проведена ГВЕ, касающаяся сечения, а
через В - ZBH, параллельная прямой ГД, а через Г - ГАН параллельно прямой ДЕ.
В таком случае я утверждаю, что ГА равно АН.
Пусть же через А будет проведена А0, параллельная прямой ГД, через В - ВК, па¬
раллельная прямой ДЕ. А поскольку ГВ равно ВЕ, то также ГК равно КД и AZ равно
ZE. А поскольку KBZ равно ГА0, и BZ равно ДК равно ГК, и А0 равно ДГ, то ДГА
равно КГН. Поэтому ДГ к ГК равно ГАГ. Но ДГ равно 2ГК; поэтому также ГН рав¬
но 2АГ. Следовательно, ГА равно АН.
•ж
35
Если при тех же самых предпосылках от взятой точки проводится прямая, рассека¬
ющая сечение в двух точках, то получается, что как целая [прямая] относится к сна¬
ружи отделенной части, так и части прямой, отделенной внутри.
Пусть АВ будет гиперболой, ГДЕ - асимптотами, ГВЕ - касательной, 0В - па¬
раллельной, и пусть через Г будет проведена некая прямая ГАЛ2Н, рассекающее се¬
чение в А и Z. В таком случае я утверждаю, что ZГ к ГА равно ТХ к АЛ.
Пусть же через Г, А,
ные прямой ДЕ, а через А и Z — АПЕ и TZPME, параллельные прямой ГД.
Поэтому поскольку АГ равно гн, то также КА равно ТН. Но КА равно ДЕ;поэтому
также ТН равно ДЕ. Таким образом, также ГК равно ДЧЕ И поскольку ГК равно ДЧ*,
то также ДК равно ГУ. Поэтому ДК к КГ равно УГ к ГК. А УГ к ГК равно ZГ к ГА
равно МК к КА равно МД к ДА, и ДК к КГ равно 0К к КМ поэтому также МЛ к ЛА
равно 0К к КМ А АЛ равно ДВ равно ОМ ведь ГВ равно ВЕ и ДО равно ОГ. Поэ¬
тому ДМ к ON равно К0 к К\, и остальное М0 к ВК равно ДМ к ОМ И поскольку
КЕ равно 00, то пусть отбрасывается общее ДП; поэтому остальное КП равно ПО.
Пусть прилагается общее АВ; тогда целое КВ равно А0. Таким образом, МД к ЛА
353

Книга III
равно М0 к0А. Но МЛ к ДА равно МК к КА равно /Г к ГА, и М0 к 0А равно МФ
к ФА равно ¿Л к ЛА. Следовательно, также ¿Г к ГА равно 7.Х к ЛА.
36
Если при тех же самых предпосылках прямая, проведенная от данной точки, не рас¬
секает сечение в двух точках и не параллельна асимптоте, то она будет пересекаться
с противолежащим сечением и как целая /прямая/ относится к части между сечением
и параллельной, проведенной через точку соприкосновения, так и прямая, расположен¬
ная между противолежащим сечением и асимптотой, будет относиться к прямой, рас¬
положенной между асимптотой и другим сечением.
Пусть А и В будут противолежащими сечениями, центром которых пусть будет
Г. ДЕ и 7Н - асимптотами, и пусть на ГН будет взята точка Н. и пусть от нее будет
проведена касательная НВЕ, а Н0так, что она не параллельна прямой ГЕ и не рас¬
секает сечение в двух точках.
Было же доказано, что прямая 0Н. продолженная дальше, пересекается с ГЛ, и
по этой причине пересекается с сечением. Пусть она пересекается в А. и пусть че¬
рез В будет проведена КВЛ, параллельная прямой ГН. В таком случаем я утверж¬
даю, что АК к К0 равно АН к Н0.
Пусть от А и 0 будут проведены 0М и АЬ1, параллельные прямой ГН. а от В. Н
и 0 - ВЕ. НП и Р0^ параллельно прямой ДЕ. Поэтому поскольку АЛ равно Н0,
то АН к Н0 равно Д0 к0Н. Но АН к Н0 равно ЫЕкЕ0и Д0 к0Н равно ГЕ к ЕН;
поэтому также МЕ к Е0 равно ГЕ к ЕН. Но N1 к Е0 равно 1ЧГ к Г0 и ГЕ к ЕН рав¬
но РГ к PH: поэтому также 1ЧГ к Г0 равно ГР к PH И как одно относится к одно¬
му, так и все относится ко всему, поэтому МГ к Г0 равно к Г0 плюс PH. И по¬
скольку ЕВ равно ВН, то также АВ равно ВП и ЛЕ равно ВН. А ЛЕ равно Г0; поэ¬
тому также ВН равно Г0. Поэтому 1ЧГ к Г0 равно ЛN к ВН плюс PH, (Л1Ч) к РЕ. А
РЕ равно Л0, поскольку также Г0 равно ВГ и МВ равно Е0. Поэтому ТЧГ к Г0 рав¬
но 1ЧЛ к Л0 Но ?^Г к Г0 равно кЕ0 равно АН к Н0, и ЫЛ к Л0 равно М2* к Р0
равно АК к К0 Следовательно, также АК к К0 равно АН к Н0.
•Л
•1«
37
Если две прямые, касающиеся сечения конуса, или окружности круга или противо¬
лежащих сечений, пересекаются, и к точкам их касания проводится прямая, а от точ¬
ки пересечения касательных проводится прямая, рассекающая линию в двух точках, то
получается, что как целая [прямая] относится к части, отведенной вовне, так и ча¬
сти, полученные при помощи прямой, соединяющей точки касания.
Пусть АВ будет сечением конуса, АГ и ГВ - касательными, пусть будет проведена АВ,
и пусть будет проведена ГДЕ/. В таком случае я утверждаю, что TZ к ГД равно ZE к ЕД.
Пусть же через Г и А будут проведены диаметры сечения Г0 и АК, а через Z и Л -
ДП, ZP. AZM, NAO, параллельные прямым А0 и АГ. Поскольку же AZM и ЕЛО па¬
раллельны. то Zr к ГД равно AZ к ЕД равно ZM к ДО равно ЛМ к ЕО; поэтому так¬
же ЛМ в квадрате к ЕО в квадрате равно ZM в квадрате к ДО в квадрате. Однако ЛМ
в квадрате к ЕО в квадрате равно ЛМ Г кЕГО,и/Мв квадрате к ОД в квадрате рав¬
но ZPM к ДПО, поэтому также ЛГМ к ЕОГ равно ZPM к ЛПО равно ATPZ к ЕГПД.
354

Дословный перевод книги III
Однако ATPZ равно АЛК и ЕГПЛ равно ANE; поэтому ЛМ в квадрате к ЕО в ква¬
драте равно АЛК к ANE. А ЛМ в квадрате к ЕО в квадрате равно ZT в квадрате к ГД
в квадрате, АЛК к ANE равно ЛА в квадрате к АЕ в квадрате равно ZE в квадрате к
ЕЛ в квадрате; поэтому также ZT в квадрате к ГЛ в квадрате равно ZE в квадрате к
ЕЛ в квадрате. Следовательно, ZT к ГД равно ZE к ДЕ.
/Л
38
Если при тех же самых предпосылках через точку пересечения касательных прово¬
дится прямая, параллельная прямой, соединяющей точки касания, и [произвольная] пря¬
мая, проведенная через середину прямой, соединяющей точки касания, рассекает сече¬
ние в двух точках, то получается, что как целая прямая относится к части, выделен¬
ной вовне между сечением и параллельной, так и части, полученные при помощи прямой,
проведенной к точкам касания.
Пусть АВ будет сечением, АГ и ВГ - касательными, АВ - соединяющей точки
соприкосновения, AN и ГМ — диаметрами; поэтому очевидно, что АВ в Е рассека¬
ется на два равных отрезка.
Пусть от Г будет проведена ГО, параллельная прямой АВ, а от Е пусть будет про¬
ведена 7ЕЛО. В таком случае я утверждаю, что ZO к ОД равно ZE к ЕД.
Пусть же от 7 и Д будут проведены лгКМ и Д0НЕ^ параллельные прямой АВ,
а через 7 и Н — гР и НП, параллельные прямой ЛГ. Тем же самым способом, что и
прежде, мы докажем, что ЛМ в квадрате к ЕО в квадрате равно в квадрате ЛА в ква¬
драте к АЕ в квадрате. А ЛМ в квадрате к ЕО в квадрате равно ЛГ в квадрате к ГЕ в
квадрате равно ZO в квадрате к ОД в квадрате, и ЛА в квадрате к АЕ в квадрате рав¬
но ZE в квадрате к ЕД в квадрате; поэтому ZO в квадрате к ОД в квадрате равно 7Е
в квадрате к ЕД в квадрате и ZO к ОД равно ZE к ЕД.
•Ж
39
Если две прямые, касающиеся противолежащих сечений, пересекаются, и через точ¬
ки касания проводится прямая, а от точки пересечения касательных проведенная пря¬
мая рассекает каждое из сечений и прямую, соединяющую точки касания, то получа¬
ется, что как целая прямая, так проведенная, относится к части, выделенной вовне
между сечением и прямой, соединяющей точки соприкосновения, так и части прямой,
полученные при помощи сечений и точки пересечения касательных.
Пусть А и В будут противолежащими сечениями, чьим центром пусть будет Г,
АД и ДВ - касательными, и пусть проведенные АВ и ГЛ будут продолжены дальше,
пусть через Д будет проведена некоторая прямая EAZH. В таком случае я утверж¬
даю, что ЕН к HZ равно ЕД к AZ.
Пусть будет проведена и продолжена дальше АГ, и пусть от Е и Z будут проведены
Е0Е и ZAMNEO, параллельные прямой АВ, и ЕП и ZP - параллельные прямой АЛ.
А поскольку ZE и ЕЕ параллельны, и на них попадают EZ, ЕЕ и ОМ, то получает¬
ся, что Е0 к 0Е равно ZM к МЕ. И при перестановке Е0 к ZM равно 0Е к ЕМ; поэ¬
тому также 0Е в квадрате к MZ в квадрате равно ОЕ в квадрате к ЕМ в квадрате. А Е0
в квадрате к MZ в квадрате равно Е0П к ZPM, 0Е в квадрате к ЕМ в квадрате равно
Л0Е к ЕМД; поэтому также Е0П к ZPM равно Д0Е к НМЛ. А Е0П равно АЕК плюс
•ж
•ж
•ж
»ж
•ж
• •
355

Книга III
0ДЕ и PMZ равно AEN плюс ДМЕ; поэтому Д0Е к ЕМД равно ALK плюс ОДЕ к AEN
плюс НМЛ и ALK к ANE равно AL0 к ДЕМ. A ALK к ANE равно КА в квадрате к AN в
квадрате равно ЕН в квадрате к ZH в квадрате и A0L к ЕДМ равноОД в квадрате к ДМ в
квадрате равно ЕД в квадрате к AZ в квадрате. Следовательно, ЕН к HZ равно ЕД к AZ.
40
Если при тех же самых предпосылках через точку пересечения касательных прово¬
дится прямая, параллельная прямой, соединяющей точки касания, и прямая, проведен¬
ная от середины прямой, соединяющей точки касания, рассекает каждое сечение и пря¬
мую, параллельную прямой, соединяющей точки касания, то получается, что как це¬
лая прямая, проведенная таким образом, относится к части, выделенной вовне между
параллельной и сечением, так и части прямой, полученные при помощи сечений и пря¬
мой, соединяющей точки касания.
Пусть А и В будут противолежащими сечениями, чьим центром будет Г, каса¬
тельными - АД и ДВ, и пусть будут проведены АВ и ГДЕ; тогда АЕ равно ЕВ. И от Д
пусть будет проведена ZДH, параллельная прямой АВ. от Е таким же образом ЛЕ. В
таком случае я утверждаю, что 0Л к ЛК равно 0Е к ЕК.
Пусть от 0 и К будут проведены NM0E и КОП, параллельные прямой АВ. и 0Р
и КЕ - параллельные прямой АД, и пусть будет проведена ЕАГТ.
А поскольку ЕДУ и МАП попадают на параллельные ЕМ и КП, то ЕА к АУ равно МА
»г«
к АП. Однако ЕА к AY равно 0Е к ЕК; и 0Е к ЕК равно 0N к КО из-за подобия треу¬
гольников 0EN и КЕО; поэтому 0N к КО равно МА к АП. Поэтому также 0N в ква¬
драте к КО в квадрате равно МА в квадрате к АП в квадрате. Однако 0N в квадрате к КО
в квадрате равно 0PN к KLO. МА в квадрате к АП в квадрате равно ЕМ А равно АУП,
поэтому также 0NP к KOL равно ЕМА к АУП. А 0NP равно ЕАМ плюс MNA и LOK
равно АУП плюс ДОП; поэтому также ЕМА плюс MNA к АП плюс ПЛО равно ЕМА к
ПУА. Поэтому также NMA к ДОП. как целое относится к целому. А ЕМА к АУП равно
ЕА в квадрате к АУ в квадрате, MAN к ПДО равно MN в квадрате к ПО в квадрате; поэ¬
тому также MN в квадрате к ПО в квадрате равно ЕА в квадрате к АУ в квадрате. Одна¬
ко MN в квадрате к ПО в квадрате равно NA в квадрате к ОД в квадрате, ЕА в квадрате к
АУ в квадрате равно 0Е в квадрате к ЕК в квадрате, NA в квадрате к ДО в квадрате рав¬
но 0Л в квадрате к ЛК в квадрате; поэтому также 0Е в квадрате к ЕК в квадрате равно
0Л в квадрате к ЛК в квадрате. Следовательно, 0Е к ЕК равно 0Л к ЛК.
Если три прямые, касающиеся параболы, пересекаются между собой, то они будут
рассекаться согласно одному и тому же отношению.
Пусть АВГ будет параболой, АДЕ, EZГ и ДВг - касательными. В таком случае я
утверждаю, что ГТ к ТЕ равно ЕД к ДА равно / В к ВД.
Пусть АГ в Н рассекается на два равные отрезка.
Очевидно, что прямая, проведенная от Е к Н, является диаметром.
Если же она проходит через В. то ДZ будет параллельна прямой АГ и ЕН будет
рассекаться в В на два равные отрезка, и по этой причине получается, что АД равно
ДЕ, ГТ равно ТЕ, и искомое очевидно
356

Дословный перевод книги III
•и
Пусть она не проходит через В, но через 0, и пусть через 0 будет проведена К0Л,
параллельная прямой АГ; тогда она будет касаться сечения в 0, и из-за того, что мы
сказали, получается, что АК равно КЕ и АГ равно ЛЕ. И пусть через В будет прове¬
дена ММЗЕ, параллельная прямой ЕН, а через А и Г - АО и ГП. параллельные пря¬
мой КТ. А поскольку МВ и Е0 параллельны, МВ является диаметром; и Л7 касает¬
ся сечения в В; тогда АО и ГП проведены как ординаты. И поскольку МВ есть диа¬
метр , ГМ - касательная, ГП - проведена как ордината, то получается, что МВ равно
ВП; поэтому также МТ равно 7Г. И поскольку МТ равно ТГ и ЕЛ равно АГ, то МГ
к ГТ равно ЕГ к ГЛ. И при перестановке МГ к ГЕ равно ТГ к ГЛ. Однако МГ к ГЕ
равно ЕГ к ГН; тогда также ТГ к ГЛ равно ЕГ к ГН. А НГ к ГА равно АГ к ГЕ; ведь
каждая вдвое больше; поэтому в равной мере АГ к ГЕ равно ЕГ к Г7, и, при преоб¬
разовании ЕГ к Е7 равно ГА к АЕ; и при разделении ГТ к ТЕ равно ГЕ к ЕА. И об¬
ратно - поскольку М В есть диаметр, AN - касательная, АО - проведена как орди¬
ната, то N6 равно ВО и N А равно ДА. А также ЕК равно КА; поэтому АЕ к АК равно
к АД, и, при перестановке ЕА к AN равно КА к АА. А ЕА к AN равно НА к АЕ;
поэтому также КА к АА равно НА к АЕ. И также ГА к АН равно ЕА к АК; ведь каж¬
дая из них вдвойне больше каждой; поэтому в равной мере ГА к АЕ равно ЕА к АД;
и при разделении ГЕ к ЕА равно ЕА к АА. А мы также доказали, что ГЕ к АЕ равно
ГТ к ТЕ; поэтому Г7 к ТЕ равно ЕА к АД. А поскольку, наоборот, ГЕ к ЕА равно ГП
кАО, и ГП равно 2В7, а так как также ГМ равно 2М2 и АО равно 2ВА, и посколь¬
ку также AN равно 2ЫД, то ГЕ к ЕА равно ТВ к ВА равно ГТ к ТЕ равно ЕД к ДА.
•I»
42
Если на гиперболе, эллипсе, или окружности круга, или противолежащих сечениях
от пределов диаметра проводятся прямые, параллельные проведенной упорядоченно пря¬
мой /ординате], а другая некоторая прямая проводится таким же образом как каса¬
тельная, то она от них будет отделять прямые, заключающие прямоугольник, равный
четвертой части эйдоса, лежащего воне того же самого диаметра.
Пусть же будет некоторое из сечений, о которых мы сказали, чьим диаметром
пусть будет АВ, и пусть от А и В будут проведены АГ и АВ, параллельные прямой,
проведенной как ордината, и пусть другая прямая ГЕА касается сечения в Е. В таком
случае я утверждаю, что АГ на ВА равно четвертой части эйдоса, лежащего при АВ.
Пусть центром будет Т, и пусть через него будет проведена 7Н0, параллельная
прямым АГ и ВА. А поскольку АГ и ВА параллельны, и им также параллельна 7Н,
то диаметр сопряжен с АВ; поэтому 7Н в квадрате равно четвертой части эйдоса,
лежащего при АВ.
А если на эллипсе или круге 7Н проходит через Е, то АГ равно 7Н равно ВА, и
немедленно ясно, что АГ на ВА равно 7Н в квадрате, т.е. равенство четвертой части
эйдоса, лежащего при АВ.
Пусть она не проходит через Е, и АГ и ВА, продолженные дальше, пересекутся в
К, и пусть через Е будет проведена ЕА, параллельная прямой АГ, и ЕМ - параллель¬
ная прямой АВ. А поскольку К7Л равно КТ в квадрате, то К7А равно ТА к ТА и КА
к АЛ равно К7 к ТК равно КТ к ТВ. И напротив, ВТ к ТК равно ЛА к АК. И в соче¬
тании или в разделении ВК к К2 равно ЛК к КА. Поэтому также АВ к Т& равно ЕЛ
357

Книга III
к ГА. Поэтому ДВ на ГА равно 70 на ЕА равно 07М. Однако 07М равно 7Н в ква¬
драте, т.е. равен четвертой части эйдоса, лежащего возле АВ. Следовательно, также
ДВ на ГА равно четвертой части эйдоса, лежащего при АВ.
43
Если прямая касается гиперболы, то она от асимптот к центру сечения отделяет
прямые, заключающие прямоугольник, равный прямоугольнику, ограниченному прямы¬
ми, отделенными касательной к вершине сечения, расположенной при оси.
Пусть АВ будет гиперболой, ГДЕ - асимптотами, ВД - осью, и через В пусть бу¬
дет проведена 7ВН, и произвольная касательная ГА0. В таком случае я утверждаю,
что 7ДН равно ГД0.
И пусть от А и В будут проведены АК. и ВЛ, параллельные прямой ДН, и АМ и
ВТЧ, параллельные прямой ГД. А поскольку ГА0 касается сечения, то ГА равно А0.
Поэтому Г0 равно 20А, ГД равно 2АМ, Д0 равно 2АК. Тогда ГД0 равно 4КА на АМ.
Тем же самым способом мы докажем, что 7ДН равно 4АВ1Ч. А КАМ равно АВЬГ Сле¬
довательно, также ГД0 равно 7ДН.
Тем же самым способом мы докажем это, если некоторая другая ДВ является ди¬
аметром и не является осью.
к?
44
Если две прямые, касающиеся гиперболы или противолежащих сечений, пересекают¬
ся с асимптотами, то прямые, проведенные к точкам пересечения, будут параллельны
прямой, соединяющей точки касания.
Пусть АВ будет гиперболой или противолежащими сечениями, ГДЕ - асимпто¬
тами, ГА07 и ЕВ0Н - касательными, и пусть будут проведены АВ, 7Н и ГЕ. В та¬
ком случае я утверждаю, что они параллельны.
Ведь поскольку ГЛ7 равно НДЕ. ГД к ДЕ равно НА к Д7; поэтому ГЕ и 7Н па¬
раллельны И по этой причине получается 07 к 7Г равно 0НкНЕ. АНЕкНВ рав¬
но Г7. к А7; ведь каждая вдвое больше каждой. Из равенст
но 07 к ТА. Следовательно, 7Н и АВ параллельны.
поэтому 0Н к НВ рав-
45
Если на гиперболе, эллипсе, окружности круга или противолежащих сечениях от
пределов оси проводятся перпендикулярные прямые, и площадь, равная четвертой ча¬
сти эйдоса прикладывается в каждую часть, на гиперболе и противолежащих сечени¬
ях превосходящую эйдос, а на эллипсе не доставая, и проводится прямая, касающаяся
сечения и пересекающаяся с перпендикулярными прямыми, то прямые, проведенные от
точек пересечения к точкам, возникшим в результате приложения, о которых мы ска¬
зали, образуют прямые углы.
Пусть будет некоторое сечение из тех, о которых мы сказали, чьей осью пусть бу¬
дет АВ, и пусть АГ и ВЛ - будут перпендикулярными, ГЕД - касательной, и пусть
будет приложена площадь, равная четвертой части эйдоса, в каждую часть таким об¬
разом, как мы сказали, А7В и АН В, и пусть будут п|
ком случае я утверждаю, что углы Г7Д и ГНД являются прямыми.
л •
ведены Г7, ГН, А7 и ДН. В та-
358

Дословный перевод книги III
Ведь поскольку мы доказали, что АГ на ВД равно четвертой части эйдоса, при¬
ложенной к АВ, однако также А/В равно четвертой части эйдоса, то АДВ равно А/
на /В. Поэтому ГА к А/ равно /В к ВД. И углы, расположенные при А и В, являют¬
ся прямыми; поэтому угол АГ/ равен В/Д, угол Л/Г равен /ДВ. И поскольку угол
ГА/ прямой, угол АГ/ плюс А/Г равны одному прямому. И мы также доказали, что
угол АГ/ равен Д/В; поэтому угол Г/А плюс Д/В будут равны одному прямому. Сле¬
довательно, оставшейся угол Д/Г является прямым. И мы таким же способом дока¬
жем, что также угол ГНД является прямым.
При тех же самых предпосылках прямые, проведенные к касательным,
ют равные углы.
При тех же самых предпосылках я утверждаю, что угол АГ/ равен ДГН, угол ГД/
равен ВДН.
Ведь поскольку мы доказали, что каждый угол Г/Д и ГНД является прямым, круг,
описанный вокруг диаметра ГД, будет проходить через Т и Н; поэтому угол ДГН ра¬
вен Д/Н, ведь они расположены на одном и том же отрезке круга. А мы доказали,
что угол Д/Н равен АГ/, поэтому также угол ДГН равен АГ/. И тем же самым спо¬
собом мы докажем, что также угол ГД/ равен ВДН.
47
При тех же самых предпосылках прямая, проведенная отточки пересечения про¬
веденных прямых к точке касания, будет перпендикулярна касательной.
Пусть будет предположено, что и прежде, и пусть ГН и /Д пересекаются между
собой в 0, а ГД и ВА, продолженные дальше, пусть пересекаются в К, и пусть будет
проведена Е0. В таком случае я утверждаю, что Е0 перпендикулярна ГД.
Если это не так, то пусть от 0 будет проведена 0Л, перпендикулярно ГД. А по¬
скольку угол ГД/ равен НДВ и угол ДВН равен ДА© как прямые, то треугольники
ДНВ и Л0Д подобны. Поэтому НД к Д0 равно ВД к ДА. Однако НД к Д0 равно /Г
к Г0, поскольку углы, расположенные при / и Н, являются прямыми, а углы рас¬
положенные при 0 равными; и Г/ к Г0 равно АГ к ГА из-за сходства треугольни¬
ков А/Г и АГ0, поэтому также ВД к ДА равно АГ к ГА. И при перестановке ДВ к ГА
равно ДА к АГ. Однако ДВ к ГА равно ВК к КА; поэтому также ДА к ГЛ равно ВК к
КА. И пусть от Е будет проведена ЕМ, параллельная прямой АГ. тогда она прове¬
дена к АВ как ордината; и получается ВК к КА равно ВМ к МА. А ВМ к МА равно
ДЕ к ЕГ; поэтому также ДА к АГ равно ДЕ к ЕГ, что абсурдно. Следовательно. 0А не
перпендикулярна, и никакая другая прямая, кроме 0Е.
При тех же самых предпосылках нужно доказать, что прямые, проведенные от
точки касания к точкам, возникшим в результате приложения
разуют с касатель¬
ной равные углы.
Пусть будет предположено то же самое, и пусть будут проведены Е/ и ЕН. В та¬
ком случае я утверждаю, что угол ГЕ/ равен Н ЕД.
359

Книга III
Ведь поскольку углы ДЕ® и ДН® являются прямыми, круг описанный вокруг
диаметра Д0, проходит через точки Е и Н. Поэтому угол ДН® равен ДЕН, ведь они
расположены на одном и том же отрезке. По той же самой причине также угол ГЕ7
равен Г02. А угол Г02 равен Д®Н, ведь они расположены при вершине. Следова¬
тельно, также угол ГЕ2 равен ДЕН.
49
Если при тех же самых предпосылках от одной из тех же точек проводится пер¬
пендикуляр к касательной, то прямые от точки, возникшей таким образом, на преде¬
лах проведенной оси, образуют прямой угол.
Пусть будет предположено то же самое, и пусть от Н будет проведена Н®, как
перпендикулярная, к ГЛ, пусть будут проведены А® и В®. В таком случае я утверж¬
даю, что угол А®В является прямым.
Ведь поскольку угол ЛВН и Д0Н являются прямыми, то круг, описанный во¬
круг диаметра ДН, проходит через ® и В, и угол Н0В равен ВДН. А мы доказали,
что угол АН Г равен ВДН Поэтому также угол В0Н равен АН Г равен А® Г. Поэто¬
му также угол Г®Н равен А®В. Однако угол Г®Н является прямым; следовательно,
также угол А® В является прямым.
»1»
50
Если при тех самых предпосылках от центра сечения к касательной проводится пря¬
мая, параллельная прямой, проведенной через точку касания и одну из тех точек, то
она будет равна половине оси.
Пусть будет то же самое, что и прежде, и пусть центром будет 0, пусть будет про¬
ведена Е2. и пусть ДГ и ВА пересекаются в К. пусть через ® будет проведена ®Л, па¬
раллельная прямой Е2. В таком случае я утверждаю, что ®Л равно ®В.
Пусть будут проведены ЕН, АЛ, АН и АВ, и пусть через Н будет проведена Н М,
параллельная прямой Е7. А поскольку А7В равно АН В. то А7 равно Н В. Однако
также А® равно 0В, поэтому также равно ®Н. Поэтому также ЕЛ равно ЛМ. А
поскольку мы доказали, что угол ГЕ2 равен ДЕН и угол ГЕ2 равен ЕМН, то также
угол ЕМН равен МЕН. Поэтому также ЕН равно НМ. А мы доказали также, что ЕА
равно АМ, поэтому НА перпендикулярна ЕМ. Тогда из-за того, что мы доказали, что
угол АЛ В является прямым, круг, описанный вокруг диаметра АВ. проходит через Л.
И ®А равно ®В, следовательно, также радиус полукруга ®Л равно ®В.
яг
51
Если к оси гиперболы или противолежащих сечений площадь, равная четвертой ча¬
сти эйдоса, прикладывается к каждой части, превосходящей эйдос, и прямые, прове¬
денные от точек, возникших в результате приложения, преломляются в любой точке
сечений, то большая превосходит меньшую осью.
Пусть будет гипербола или противолежащие сечения, чьей осью пусть будет АВ,
Г - центром, пусть равны четвертой части эйдоса прямоугольники АЛВ [АД ДВ[ и
АЕВ [АЕ ЕВ|, и отточек Е и Д при линии Е£ и ТА пусть ломаются. В таком случае я
утверждаю, что Е£ равно £\ плюс АВ.
360

Дословный перевод книги III
Ведь пусть через Т будет проведена касательная 7К0, а через Г - НГ0, парал¬
лельная прямой поэтому угол К0Н равен К2Д; ведь они равны наоборот. Од¬
нако угол К/Л равен Н70; поэтому также угол Н70 равен Н0г. Поэтому Нг рав¬
но Н0. А 7Н равно НЕ, поскольку АЕ равно ВД, АГ равно ГВ и ЕГ равно ГД. По¬
этому также Н0 равно ЕН, поэтому гЕ равно 2Н0. И поскольку мы доказали, что
Г0 равно ГВ, Е7 равно 2НГ плюс ГВ. Однако 7Д равно 2НГ и АВ равно 2ГВ. Сле¬
довательно, Е7 равно 7Д плюс АВ.
НЕ
52
Если на эллипсе к большей оси прикладывается площадь, равная четвертой части
эйдоса, и прямые, проведенные от точек, возникших в результате приложения, прелом¬
ляются в любой точке сечений, то они будут равны оси.
Пусть будет эллипс, чьей большей осью пусть будет АВ, и четвертой части эйдо¬
са пусть будут равны АГВ, АДВ, и от Г и Д на линии пусть ломаются ГЕ и ЕД. В та¬
ком случае я утверждаю, что ГЕД равно АВ.
Пусть ТЕО — будет касательной, Н — центром, и пусть через него будет прове¬
дена НК0, параллельная прямой ГЕ. А поскольку же угол ГЕ7 равен 0ЕК, и угол
7ЕГ равен Е0К, то также угол Е0К равен 0ЕК. Поэтому также 0К равно КЕ. И по¬
скольку АН равно НВ и АГ равно ДВ, также ГН равно НД; поэтому также ЕК равно
КД. Тогда ЕД равно 20К, ЕГ равно 2КН, и ГЕД равно 2Н0. Однако также АВ равно
2Н0. Следовательно, АВ равно ГЕД.
53
Если на гиперболе, эллипсе, окружности круга или противолежащих сечениях от пре¬
делов диаметров проводятся прямые, параллельные прямой, проведенной как упорядо¬
ченная прямая [ордината], и от тех же самых пределов прямые проведенные через одну
и туже точку линии рассекают параллельные, то прямоугольник, ограниченный отде¬
ленными отрезками, равен эйдосу, лежащему при том же самом диаметре.
Пусть АВГ будет одним из сечений, о которых мы сказали, чьим диаметр
будет АГ, и пусть будут проведены АД и ГЕ, параллельные прямой, п|
упорядоченная прямая, пусть будут проведены АВЕ и ГВД. В таком случае я утверж¬
даю. что АД на ЕГ равен эйдосу, лежащему при АГ.
Пусть же от В будет проведена В7, параллельная прямой, проведенной как орди¬
ната. Поэтому как А/Г к 7В в квадрате, так и поперечная сторона относится к пря¬
мой стороне и АГ в квадрате к эйдосу. Однако А7 на гг к ¿В в квадрате равно А/ к
/В на ГТ к ¿В. Поэтому отношение эйдоса к АГ в квадрате равно 7В к ТА на ВТ к
ГТ. А КТ к ТВ равно АГ к ГЕ и ГТ к ¿В равно ГА к АД, поэтому отношение эйдоса к
АГ в квадрате равно ГЕ к ГА на АД к ГА. И также АЛ на ГЕ к АГ в квадрате равно ГЕ
к ГА на АД к ГА, поэтому как эйдос относится к АГ в квадрате, так АД на ГЕ к АГ в
квадрате. Следовательно, АД на ГЕ равно эйдосу, лежащему при АГ.
•ж
•ж
»ж
1Ж
«ж
м пусть
веденной как
•ж
54
Если две прямые, касающиеся сечения конуса, или окружности круга, пересекаются,
и через точки соприкосновения проводятся пара.1лельные касательным, и от точек ка-
361

Книга III
сания к той же самой точке линии проводятся прямые, рассекающие параллельные, то
прямоугольник, ограниченный отделенными частями, имеет такое отношение к ква¬
драту прямой, соединяющей точки касания, составленное из того отношения, кото¬
рое имеет внутренний отрезок прямой, соединяющей точку пересечения касательных
и находящуюся посередине точку прямой, соединяющей точки касания, к остальному,
и того отношения, которое имеет прямоугольник, ограниченный касательными, к од¬
ной четвертой части квадрата прямой, соединяющей точки касания.
Пусть АВГ будет сечением конуса или окружности круга, АД и ГД - касательны¬
ми, пусть будет проведена АГ и пусть она рассекается в Е на два равные отрезка, и
пусть будет проведена ДВЕ, пусть от А будет проведена А7, параллельная прямой
ГД, от Г - ГН, параллельная прямой АД, и пусть на линии будет взята некоторая точ¬
ка 0. а проведенные А0 и Г0 пусть будут продолжены к Н и Ъ. В таком случае я ут¬
верждаю, что на ГН к АГ в квадрате равно ЕВ в квадрате к ВД в квадрате на АДГ
к одну четвертую АГ в квадрате равно ЕВ в квадрате к ВД в квадрате на АДГ к АЕГ.
Пусть же от 0 будет проведена К0ОЕЛ, параллельная прямой АГ, а от В - М В1М;
тогда очевидно, что касается сечения. А поскольку АЕ равно ЕГ, также МВ рав¬
но В1Ч КО равно ОД и 00 равно ОН, К0 равно ЕЛ. Тогда поскольку М В и МА каса¬
ются сечения и К0Л проведена параллельно прямой МВ, то АМ в квадрате к МВ в
квадрате равно АК в квадрате к ЕК0, то есть АМ в квадрате к М В на ВИ равно АК в
квадрате к Л0К. АМГ на МА к МА в квадрате равно АГ на КА к КА в квадрате. Тог¬
да в равной мере N Г на МА к №М равно АГ на КА к Л0К. А АГ на КА к А0К рав¬
но ГАО на АК0 равно ¿АГ на НГА равно НГ на ¿А к ГА в квадрате. Поэтому МГ на
МА к МВМ равно НГ на ¿А к ГА в квадрате. А ГМ на МА к N6 на ВМ равно ГМ на
МА к МДМ на МДМ к МВМ при взятом центральном отношении МДМ. Тогда НГ на
¿А к ГА в квадрате равно ГМ на АМ к МДМ на МДМ к МВМ. Однако МГ на АМ к
МДМ равно ЕВ в квадрате к ВД в квадрате и МДМ к МВМ равно ГДА к ГЕА; следова¬
тельно, НГ наХЕ к АГ в квадрате равно ВЕ в квадрате к ВД в квадрате на ГДА к ГЕА
55
Если две прямые, касающиеся противолежащих сечений, пересекаются, и через точ¬
ку пересечения проводится прямая, параллельная прямой, соединяющей точки касания, и
от точек касания проводятся прямые, параллельные касательным, а от точек касания
к одной и той же точке другого сечения прямые продолжаются, рассекая параллельные,
то прямоугольник, ограниченный отделенными частями, к квадрату прямой, соединя¬
ющей точки касания, будет иметь такое отношение, которое имеет прямоугольник,
ограниченный касательными, к квадрату прямой, проведенной через точку пересечения
и параллельной прямой, соединяющей точки касания, до самого сечения.
Пусть АВГ и AEZ будут противолежащими сечениями, АН и НД - касательны¬
ми. пусть будет проведена АД, и пусть от Н будет проведена ГН Е, параллельная пря¬
мой АД, а от А - АМ, параллельная прямой ДН, от Д - ДМ, параллельная прямой
АН, и пусть на сечении AZ будет взята некоторая точка Z, и пусть будут проведены
AMZ и ZA0. В таком случае я утверждаю, что ГН в квадрате к АНД равно АД в ква¬
драте к А0 на NA.
Пусть же через Z будет проведена ZAKB, параллельная прямой АД.
362

Дословный перевод книги III
А поскольку мы доказали, что ЕН в квадрате к НА в квадрате равно ВЛ/ к АЛ в
квадрате и ГН равно ЕН, ВК равно Л/, то ГН в квадрате к НА в квадрате равно К/Л
к ЛА в квадрате. Однако также АН в квадрате к АНА равно АЛ в квадрате к АЛ на АК;
поэтому в равной мере ГН в квадрате к АНА равно К/Л к АЛ на АК. Однако К/Л к
АК на АЛ равно /К к КА на /Л к ЛА. А ТК к КА равно АА к ДМ /Л к ЛА равно АА к
©А; поэтому ГН в квадрате к АН А равно АА к AN на АА к АО. А АА в квадрате к АО
на МА равно АА к AN на АА к АО. Следовательно, ГН в квадрате к АНА равно АА в
квадрате к 1МЛ на АО.
•Ж
56
Если две прямые, касающиеся одного из противолежащих сечении, пересекаются, и
через точки касания проводятся параллельные касательным, а от точек касания к од¬
ной и той же точке другого сечения проводятся прямые, рассекающие параллельные, то
прямоугольник, ограниченный отделенными частями, будет иметь отношение к квадра¬
ту прямой, соединяющей точки касания, составленное из того, которое имеет часть
прямой, соединяющей точку пересечения и находящуюся посередине точку, расположен¬
ную между находящейся посередине точкой и другим сечением, к прямой, расположен¬
ной между тем же самым сечением и точкой пересечения, и тем, которое имеет пря¬
моугольник, ограниченный касательными, к одной четвертой части квадрата прямой,
соединяющей точки соприкосновения.
Пусть АВ и ГА будут противолежащими сечениями, чьим центром пусть будет О,
АЕ/Н и ВЕОК — касательными, пусть будет проведена АВ и пусть она рассекается
в Л на два равных отрезка, и пусть проведенная ЛЕ будет продолжена до А, и пусть
от А будет проведена АМ, параллельная прямой ВЕ, а от В - ВМ параллельная пря¬
мой АЕ, и пусть на сечении ГА будет взята некоторая точка Г, пусть будут проведе¬
ны ГВМ и ГАМ В таком случае я утверждаю, что BN на АМ к АВ в квадрате равно
ЛА в квадрате к АЕ в квадрате на АЕВ к одной четвертой АВ в квадрате равно ЛА в
квадрате к АЕ в квадрате на АЕВ к АЛ В.
Пусть же от Г и А будут проведены НГК и ОА/, параллельные прямой АВ; тог¬
да очевидно, что ОА равно А/ и КЕ равно ЕН. Однако также ЕГ равно ЕП; поэто¬
му также ГК равно НП. АВ и АГ - противолежащие сечения, ВЕ0 и ОА — касатель¬
ные, КН параллельна прямой АО, то ВО в квадрате к ОА в квадрате равно ВК в ква¬
драте к ПКГ. А ОА в квадрате равно ОА/, ПКГ равно КГН; поэтому ВО в квадрате к
©А/ равно ВК в квадрате к КГН. Однако также ТА на ОВ к ОВ в квадрате равно НА
на КВ к КВ в квадрате; поэтому в равной мере КТ на ОВ к ОА/ равно КВ на АН к
КГН. А при взятом центральном отношении ОЕ/, А/ наОВ кОА/ равно А/ на ОВ
к ОЕ на Е/ на ОЕ/ к ОА/. И А/ на ОВ к ОЕ/ равно ЛА в квадрате к АЕ в квадрате ,
ОЕ/кОА/ равно АЕВ к АЛВ; поэтому АН на ВКкКГН равно ЛА в квадрате к АЕ в
квадрате на АЕВ к АЛВ. А АН на КВ к КГН равно ВН к КГ на АН к НГ. Однако КВ
к КГ равно МА к АВ. АН к НГ равно BN к ВА. Следовательно, МАкАВ на N8 к ВА
равно ЛА в квадрате к АЕ в квадрате на АЕВ к АЛВ равно АМ на BN к АВ в квадрате.
363

АПОЛЛОНИЙ ПЕРГСКИЙ
КОНИЧЕСКИЕ
СЕЧЕНИЯ
КНИГА IV
ПИСЬМО К АТТАЛУ
•а
«Аполлоний приветствует Аттала!
Некоторое время назад я выпустил первые три книги из восьми “Конических се¬
чений'1, которые послал Евдему из Пергама. Однако он скончался, поэтому я решил
послать остальные книги тебе, поскольку ты принимал самое деятельное участие в
моей научной деятельности - и поэтому я посылаю тебе четвертую книгу.
В четвертой книге дается ответ на вопрос, каково наибольшее число точек, в ко¬
торых конические сечения пересекаются между собой и с окружностью круга, если
они не совпадают полностью друг с другом. Далее, в каком наибольшем числе то¬
чек могут пересекаться коническое сечение и круг с парой противолежащих гипер¬
бол, а также два противолежащих сечения двумя другими и, кроме того, еше неко¬
торые похожие проблемы.
О первой из этих проблем писал Конон из Самоса в его труде, посланном Тра-
сидею. однако, его доказательства не безупречны. За это его по праву порицал Ни-
котелес из Кирены. Что касается второй проблемы, то Никотелес, в его направлен¬
ном против Конона сочинении, говорит, что она разрешима. Но этого решения я
ни у него, ни у других не нашел. О третьей же проблеме и упомянутых похожих, на¬
сколько я знаю, вообще ни у кого ничего нет.
Все названные проблемы, решения которых я нигде не нашел, требуют для сво¬
его доказательства в качестве основы много разных и необычных теорем, которые
я уже доказал в первых трех книгах. Те, что еше отсутствуют, я привожу в этой кни¬
ге. Их рассмотрение даст основу для решении задач и диоризмов. Никотелес, кста¬
ти. говорит, конечно же из-за его разногласия с Кононом, что найденные тем тео¬
ремы не имеют вообще никакой ценности для диоризмов, однако в этом он неправ.
Потому что, если даже можно совсем обойтись без них, то все-таки многое легче
понятье их помошью Например, имеет ли задача несколько решений и как мно-
364

Предложения
го, или она неразрешима. Такое предварительное представление является хорошим
исходным пунктом для исследования, а также эти теоремы полезны для анализа ди-
оризмов. Однако, даже оставив в стороне саму полезность, эти задачи имеют цен¬
ность сами по себе. Ведь в математике что-то мы по какой-то причине признаем, а
что-то другое отвергаем.
ПРЕДЛОЖЕНИЯ
Предложение 1. Предложение, обратное (III, 37). Если из точки Д проведены две
касательные и секущая, пересекающаяся с сечением в двух точках, то прямая, прове¬
денная через точку касания, пересечется с кривой в другой точке касания, если она де¬
лит секущую в том же отношении, что и в (III, 37)
Если от точки, лежащей вне кони¬
ческого сечения, проведены касатель¬
ная и секущая, пересекающая кривую в
двух точках, а между этими двумя точ¬
ками берется третья, разбивающая ле¬
жащую внутри сечения часть прямой на
отрезки, отношение которых равно от¬
ношению отрезков, заключенных между
внешней точкой и точками пересечения
секущей и кривой, то прямая, проведен¬
ная от точки касания через точку деле¬
ния, вторично пересечет кривую в точке
касания прямой, проведенной от внеш¬
ней точки*.
Пусть дано коническое сечение и от
некоторой точки Д, лежащей вне его,
проведены две прямые - касательная
ДВ. и прямая ДЕГ, пересекающая се¬
чение в точках Е и Г, а отрезок ЕГ раз-
л	»4-7	Г/ ГД
бит точкой 7 так, что — = —.
¿Е ДЕ
ЙЕ
В таком случае я утверждаю, что прямая, проведенная через В и пересекается
с сечением в точке касания прямой, проведенной из точки Д.
Пусть проведена касательная ДА, и предположим, что ВА рассекает ЕГ в точке Н,
а не 7 Но поскольку ДВ и ДА касаются сечения, а ВА проведена к точкам касания,
•I»
* Предложения 1-23-это продолжение темы, начатой в (III, 30-37) В частности, данное Пред¬
ложение -
ратное (III, 37).
365

Книга IV
и пересекает секущую в Н, то (III, 37) — = -^, что абсурдно, поскольку — = £А
НЕ ДЕ	гЕ де ’
Поэтому ВА не может рассекать прямую ЕГ в другой точке.
Следовательно, она рассекает ее в 7*.
Предложение 2. Предложение 1 для
гиперболы
Предложение 1 доказывается д1я всех
сечений и только в случае гиперболы по¬
лучается следующее.
Если АВ касается сечения. АГ есть
секущая, пересекающая кривую в двух
точках Е и Г, и дуга, заключенная меж¬
ду ними содержит точку соприкосно¬
вения В, а точка А лежит внутри угла,
ограниченного асимптотами, то тогда,
так же как и в первом случае, необхо¬
димо от точки А провести прямую ДА,
касающуюся сечения, и доказательство
проводится тем же самым способом**.
Предложение 3. Предложение 1 для ги¬
перболы (другой вариант)
При тех же самых предпосылках точ¬
ка соприкосновения В лежит вне дуги, за¬
ключенной между точками Е и Г а точка
Л располагается внутри угла, ограничен¬
ного асимптотами.
О
* Надо было доказать что А - точка касания, а доказывали, что ВА пройдет через точку Z Ко¬
нечно же пройдет, раз это доказано в (III. 37). Доказывать же, что нет другой такой точки Н, нет
смысла, так как две прямые пересекаются только в одной точке. Доказательство могло бы бьггь
таким. Допустим, что BZ пересечется с кривой не в точке А, а в какой-то точке К Но, как было до¬
казано (III, 37), ВА тоже проходит через Z Тогда получится, что прямые ВК и ВА имеют две общие
точки: Z и В Следовательно, допущение неверно Либо просто сослаться на (III, 37), а поскольку
положение прямой полностью определяется двумя точками, то теорема доказана Это замеча¬
ние относится и к доказательствам Предложений 4-23.
В этом и в следующем Предложениях ничего не доказывается, а говорится, по сути, о том,
что две касательные провести можно, если точка X находится внутри угла, ограниченного асим¬
птотами. Если же она находится внутри дополнительного угла, то вторая касательная проводится
к другому противолежащему (см Предложение 4)
366

Предложения
Тогда можно провести от точки А другую касательную ЛА и доказать остальное
тем же самым способом.
Предложение 4. Предложение 1 для противолежащих, если точка А расположена
внутри угла, дополнительного к углу, ограниченному асимптотами
при тех же самых предпосылках дуга, заключенная между точками Е и Г со¬
держат точку касания А, а точка Д расположена внутри угла, дополнительного к углу,
ограниченному асимптотами, то прямая, проведенная от точки касания к точке де¬
ления секущей, пересекается с противолежащим сечением в такой точке, что прямая,
проведенная к ней от А, касается противолежащего сечения.
Пусть даны противолежащие (А) и (В),
их асимптоты КА и MN, точка Д лежит
внутри угла AHN, прямая ДА касается се¬
чения (А), а прямая ДГ пересекает его,
причем дуга, заключенная между точка¬
ми Е и Г, содержит точку А. И пусть так-
Г2 ГД
же выполняется соотношение — = —.
гв ДЕ
Нужно доказать, что прямая, прове¬
денная от 7. к А и далее, пересекается с
сечением (В) в такой точке В. что пря¬
мая, проведенная к ней от Д, касается его.
Пусть проведена касательная ДВ, и
предположим, что ВА рассекает ЕГ вточ-
ГН
ке Н, а не Z. Но тогда (III, 37) —
НЕ
ГД
ДЕ’
гг ГД „
что абсурдно, поскольку — = — . Поэтому ВА не может рассекать прямую ГЕ в
¿Е ДЕ
другой точке.
Следовательно, она рассекает ее в точке 7.
Предюжение 5. Если выполняются условия Предложения 1, а точка А лежит на асим¬
птоте, то проведенная прямая параллельна асимптоте. Предложение, обратное (III, 35)
Если при тех же самых предпосылках точка А принадлежит одной из асимптот. то
прямая BZ, будет параллельна той же асимптоте*.
* Предложение, обратное (III, 35),
367

Книга IV
Пусть при тех же самых предпо¬
сылках точка Д принадлежит неко¬
торой асимптоте ММ Требуется до¬
казать, что прямая, проведенная от В
параллельно М№ пройдет через точ¬
ку г*.
Допустим, что это не так и она
пройдет через точку Н.
т /111 ГН ГД
Тогда (III, 35) — = — , что не-
НЕ ДЕ
возможно.
Предложение 6. Если из одной точ¬
ки проведены две касательные и, парал¬
лельно асимптоте, отрезок, разделен¬
ный кривой пополам, то прямая, про¬
веденная через точку касания и конец
отрезка, пересечется с гиперболой в
другой точке касания
Если из некоторой точки вне гипер¬
болы проведены касательная и отрезок,
параллельный одной из асимптот, дли¬
на которого равна удвоенному рассто¬
янию между внешней точкой и точкой
пересечения с кривой, то прямая, со¬
единяющая между собой конец этого
отрезка и точку касания, будучи про¬
должена, пересечет гиперболу в точке
касания прямой, проведенной от внеш¬
ней точки.
Пусть дана некоторая точка Д, на¬
ходящаяся вне гиперболы, но внутри
угла, ограниченного асимптотами, и
от нее проведены касательная ДВ, и
отрезок Д7, параллельный одной из
асимптот, который точкой пересече¬
ния с кривой разбит пополам. В та-
*
Но ведь в формулировке Предложения говорится другое' Доказывать же, что прямая
дет через точку Z, нет смысла, так как это уже было доказано в (III, 35), то есть получается его пол-
ное повторение Должно быть Требуется доказать, что прямая, проведенная от В через точку 2,
параллельна МЫ.

Предложения
ком случае я утверждаю, что прямая BZ, будучи продолжена, пересечется с сечени¬
ем в точке А, которая есть точка касания прямой ДА.
Пусть будет проведена ЛА, касающаяся сечения, и допустим, что отрезок ВА, пе¬
ресекает ДЕ не в Z, но в другой точке Н. Поэтому (III, 30) ДЕ = ЕН, что абсурдно,
ведь мы доказали, что ДЕ = EZ.
Предложение 7. Предложение 6,
если точка Д лежит вне угла между
асимптотами
Пусть при тех же самых предпо¬
сылках точка Д лежит внутри угла,
дополнительного к углу, ограниченному
асимптотами. В таком случае я ут¬
верждаю, что получится то же самое.
Пусть же будет проведена каса¬
тельная Д0. Допустим, что 0В попа¬
дает не на Z, но наточку Н. Поэтому
ДЕ = ЕН, что абсурдно, ведь мы до¬
казали, что ДЕ = EZ.
Предложение 8. Если выполняют¬
ся условия Предложения 6, а точка Л
лежит на асимптоте, то проведенная
прямая параллельна этой асимптоте.
Предложение, обратное (III, 34)
Пусть при тех же самых предпо¬
сылках точка Д принадлежит одной из
асимптот. В таком случае я утверж¬
даю, что прямая, проведенная от точ¬
ки касания к точке Z, лежащей на пря¬
мой, параллельной асимптоте, парал¬
лельна другой асимптоте*.
Пусть при тех же самых предпо¬
сылках ЛЕ = EZ, и от точки В парал¬
лельно асимптоте MN будет прове¬
ден отрезок ВН. Тогда ДЕ = ЕН (III,
34), что абсурдно, ибо мы доказали
(III, 34), что ДЕ = EZ.
* Предложение, обратное (III, 34).
369

Книга IV
Предложение 9. Если из точки Д проведены две секущие, то прямая, делящая их в
том же отношении, что и в (III, 37), пересечет кривую в точках касания прямых, про¬
веденных из Л. Друтое Предложение, обратное (III, 37)
Если от внешней точки проводят¬
ся две прямые, пересекающие кони¬
ческое сечение в двух точках каждая
и внутренние части секущих разде¬
лены на отрезки так, что их отноше¬
ние равно отношению отрезков, за¬
ключенных между внешней точкой
и точками пересечения секущих с
кривой, то прямая, проведенная че¬
рез точки деления, встретится с ко¬
ническим сечением в точках сопри¬
косновения с ним прямых, исходя¬
щих из внешней точки*.
Пусть от некоторой точки Д, лежашей вне сечения, проведены секущие Д0Е и
А I/	ЕЛ ДЕ гк дг
ДН£, так разделенные точками Л и К на отрезки, что	=	, 	=	.
АО Д0 КН ДН
В этом случае я утверждаю, что прямая, соединяющая точки Л и К, продолжен¬
ная в обе стороны, будет пересекаться с сечением в точках соприкосновения его с
прямыми, проведенными из точки Д.
Поскольку ДЕ и Д/ каждые в отдельности пересекают сечение в двух точках, мо¬
жет получиться, что от Д проводится диаметр сечения. Поэтому также и касатель¬
ные проводятся в каждую сторону**.
Проведем секущие ДЕ и Д2, касательные ДВ и ДА и прямую АВ, соединяющую
точки соприкосновения Допустим, что она либо вообще не проходит через точки
Л и К. либо проходит только через одну из них.
Пусть она проходит только через Л, а прямую 2Н пересекает в точке М.
Тогда= что абсурдно, ведьмы доказали (III, 37), что — = — .
МН АН	'	КН АН
Если же АВ не проходит ни через Л, ни через К, то точно так же приходим к абсурду.
о.
•а
•I»:
•к
•а
о
Предложение 10. Предложение 9 для гиперболы
При тех же предпосылках, если коническое сечение представляет собой гиперболу,
а часть кривой, заключенная между точками пересечения с ней одной секущей, содер¬
жит точки пересечения с другой, и точка Д расположена внутри угла, ограниченного
* Предложение, обратное (III, 37)
** Непонятно, что он хотел этим сказать
370

Предложения
асимптотами*, то доказательство проводится как было сказано прежде и ранее го¬
ворилось во втором Предложении.
Предложение 11. Предложение 9 для гиперболы (другой вариант)
Если при тех же самых предпосылках в дуге между точками пересечения кривой с
одной секущей не содержатся точки пересечения с другой, а точка А расположена вну¬
три угла, ограниченного асимптотами, то доказательство проводится так же, как
в Предложении 9
Предложение 12. Предложение 9, если точка А лежит вне угла между асимптотами
Если при тех же предпосылках дуга, ограниченная точками пересечения с одной се¬
кущей, содержит точки пересечения с другой, а внешняя точка, из которой проведе¬
ны секущие, принадлежит углу, дополнительному к углу, ограниченному асимптота¬
ми, то прямая, проведенная через точки деления и, продолженная дальше, пересечется
с противолежащими в таких точках, что прямые, проведенные к ним от внешней точ¬
ки, будут их касаться.
Пусть даны противолежащие (А) и (В) с центром О, асимптотами MN и а
точка А принадлежит углу ПОЬ1, и пусть проведены из точки А две прямые АЕ и А2,
о
* То есть если можно провести обе касательные.
371

Книга IV
каждая из которых пересекает (А) в двух
точках, так что дуга гн содержит дугу'
де ек дг гл
Е6. Пусть далее — =	, — =	.
Д0 К0 ДН АН
Требуется доказать, что прямая, про¬
веденная через точки К и Л, пересечет¬
ся с противолежащими в таких точках,
что прямые, проведенные от них к точ¬
ке Д, будут касательными.
Пусть отточки Д проведены ДВ и ДА,
касающиеся сечений. Предположим, что
прямая ВА либо вообще не проходит че¬
рез точки К и Л, либо проходит только
через одну из них.
Пусть она проходит только через точ¬
ку К и пересекает прямую гн в точке X.
•I».
»!•
Тогда (III, 37)
дг гх
АН "ХН
с	& 7Л
что абсурдно, ведь мы доказали, что	=	.
ДН АН
Если же ВА не проходит через обе точки К и Л, то точно так же приходим к абсурду.
Предложение 13. Если выполняются условия Предложения 9, а точка Д лежит на
асимптоте, то прямая, проведенная через точки деления секущих, параллельна этой
асимптоте и пересечется с кривой в точке касания
Если при тех же предпосылках точка А расположена на одной из асимптот, то пря¬
мая, проведенная через точки деления секущих, будет параллельна асимптоте, содер¬
жащей точку Д и, продолженная дальше, пересечется с кривой в точке касания пря¬
мой, проведенной из точки Д.
Пусть на одной из асимптот взята точка Д, от которой проведены касательная ДВ
де ек дг гл
и секущие, разделенные так, что — =	,	=	.
Д0 К0 АН АН
В таком случае я утверждаю, что прямая, проведенная от В параллельно асим¬
птоте ПО, будет проходить через К и Л*.
Предположим, что это не так, и она проходит либо через одну из них, либо во¬
•I»
обще через них не проходит.
дг гх
Пусть она проходит через точки К и X. Тогда (111,35)	=	, что абсурдно
ДН XII
* Опять, как и в Предложении 5 условие переделано Должно быть: Я утверждаю, что прямая,
проведенная через точки К и параллельна асимптоте ПО и пересекается с кривой в точке каса¬
ния прямой, проведенной из точки Л.
372

Предложения
Следовательно, она прохо¬
дит через обе указанные точ¬
ки. Если же она не проходит
через обе точки Л и К, то точ¬
но так же приходим к абсурду.
Предложение 14. Если из
точки Д, лежашей на асимпто¬
те, проведены касательная и две
секущие, одна из которых удов¬
летворяет условию Предложе¬
ния 1, а другая - Предложения
6, то проведенная прямая парал¬
лельна этой асимптоте и пересе¬
чется с кривой в точке касания
Если при тех же предпосылках из точки Д, расположенной на одной из асимптот,
проведены две прямые — ДЕ, рассекающая гиперболу в двух точках, и_ЛН,_параллелъная
другой асимптоте*, и затем на ЛЕ взята такая точка К, что
долженной далее ЛИ — точка Л, такая,
что АН = НА, то прямая, проведенная
через точки К и Л, будет параллельна
асимптоте и будет пересекаться с се¬
чением в точке касания прямой, про¬
веденной от Д.
Так же как и в предыдущей теоре¬
ме, я утверждаю, что прямая ВЛ, па¬
раллельная асимптоте ДО, пройдет
через точки К и Л**.
Допустим, что она пройдет толь-^z
ко через К, но тогда не выполняется
равенство АН = НА (Ill. 34), что аб¬
сурдно. Если же она пройдет толь¬
ко через точку Л, то не выполняет¬
ся ДЕ ЕО = EK КО (111. 35), что так¬
же абсурдно. Если же она вообще не
проходит через К и Л, то и в этом слу¬
чае мы приходим к абсурду.
/Л
•I»
S
Ч
Ч
ч
ч
Vx
X
X
*
*
О.
ч
ч
*
*
*
*
*
*
г
*
*
X
X
Z
X
✓
✓
*
*
*
*
*
г
Ч
Ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
/4. Рис. 1
*
ч
*
*
ДЕ ЕК
а на про-
*
*
ч
ч
N
ч
ч
ч
ч
ч
ч
* Предпосылки, получается, уже не совсем те, что в Предложении 9
“ Снова доказывается не то, что заявлено. Должно быть. Я утверждаю, что прямая, проведен¬
ная через точки К и Л параллельна асимптоте АО и пересекается с кривой в точке касания пря¬
мой, проведенной из точки Д.
373

Книга IV
Предложение 15. Предложение 4 для случая, когда прямая, удовлетворяющая со¬
отношению, пересекает оба прогиволежащих, а А лежит внутри угла, образованного
асимптотами
Если через некоторую точку, распо¬
ложенную между противолежащими,
проведены касательная к одному из них
и прямая, рассекающая их и продолжен¬
ная так, что отношение отрезков, за¬
ключенных между этой точкой и про¬
тиволежащими равно отношению всей
упродолженной прямой к ее продолже¬
нию, то секущая, проходящая через точ¬
ку касания и конец продолжения, пере¬
сечет кривую в точке соприкосновения
ее с прямой, исходящей из точки, распо¬
ложенной между противолежащими*.
Пусть даны про
тиволежашие (А) и
(В), и через точку А, расположенную
между ними внутри угла, ограничен-
15. Рис. 1
ного асимптотами
■
ведены каса-
тельная А2, и прямая ААВ, пересека¬
ющая противолежащие и продолженная до такой точки Г, что
АД
ДВ
АГ
ГВ
и»:
Нужно доказать, что прямая ZT, продолженная дальше, пересечется с сечением,
а прямая, проведенная от точки пересечения к А. будет касаться сечения.
Поскольку точка А расположена внутри угла, заключающего сечение, можно про¬
вести от нее вторую касательную АЕ. Предположим, что прямая ZE пройдет не че¬
рез точку Г, но через точку Н.
АД АН	АД	АГ
Тогда (¡11.37)	= -—, что абсурдно, ибо мы предположили, что	=	**.
ДВ НВ	ДВ	ГВ
Предложение 16. То же самое, если точка А лежит внутри дополнительного угла
Пусть при тех же предпосылках точка А принадлежит углу, дополнительному к
углу, ограниченному асимптотами. В таком случае я утверждаю, что прямая, прове¬
денная от 2 к Г, пересечется с противолежащим сечением, а прямая, проведенная от
точки пересечения к А, будет касаться противолежащего сечения.
* Очевидно, точка А должна лежать внутри угла, образованного асимптотами. Это и следую¬
щее Предложения можно рассматривать как варианты (IV, 1) в случае, если прямая, удовлетворя¬
ющая соотношению, пересекает оба противолежащих.
*• - См. сноску 2 к Предложению I.

Предложения
16. Рис. 1
/
/
4
ч
ч
к
Ш
Пусть будет то же самое и пусть точ¬
ка Д принадлежит углу, дополнитель¬
ному к углу, ограниченному асимпто¬
тами, и от нее проведена касательная
ДЕ к сечению (А). Проведем и п|
р н жим дальше прямую EZ.
Предположим, что она прошла не
через точку Г, но через точку Н. В та-
'	АД АН
ком случае (III, 39)
— 		, что аб-
ДВ НВ
сурдно, ибо мы предположили, что
АЛ _ АГ
ДВ _ГВ
Предложение 17. Предложение 5
для противолежащих
Пусть при тех же самых предпосыл¬
ках точка Д расположена на одной из
асимптот. В таком случае я утверж¬
даю, что прямая, проведенная от 7к Г,
будет параллельна асимптоте, на ко¬
торой расположена точка Д *.
/ 7. Рис. 1
Пусть при тех же самых предпо¬
сылках точка Д расположена на одной
из асимптот, а через точку Z проведе- 6
на прямая, ей параллельная. Допу¬
стим, что она проходит не через точ¬
ку Г, но через точку Н. Тогда (III, 36)
— =	, что абсурдно. Следовательно, прямая, проходящая через точку Z парал-
ДВ НВ
лельно асимптоте, проходит через Г.
Предложение 18. Предложение 12 если прямая, проведенная из точки А, пересекает
оба противолежащих, а Д лежит внутри угла, образованного асимптотами
Если через некоторую точку, расположенную между противолежащими, проведены
две прямые, рассекающие их и продолженные так, что отношение отрезков, заключен¬
ных между указанной точкой и противолежащими, равно отношению продолженных
прямых к их продолжениям, то секущая, проходящая через концы этих прямых, пересе¬
чет кривую в точках соприкосновения ее с прямыми, исходящими из точки пересечения.
‘ Это Предложение 5 для двух противолежащих и, соответственно, обратное (III, 36).
375

Книга IV
Пусть (А) и (В) - противолежа¬
щие сечения, и пусть точка А распо¬
лагается между ними. Пусть сначала
она располагается внутри угла, огра¬
ниченного асимптотами, и пусть че¬
рез А будут проведены и продолже¬
ны прямые ААВ и ГА®. Тогда АА >
АВ и ГА > А®, поскольку BN = АМ
(II, 16). Пусть они продолжены так.
АА АК ГА ГН
что — = , —• = .
АВ КВ А® Н®
В таком случае я утверждаю, что
не.
секущая, проведенная через точки К
и Н, будет пересекаться с сечением,
а прямые, проведенные от А к точкам пересечения, будут касаться сечения.
Ведь поскольку А расположена внутри угла, ограниченного асимптотами, можно
провести от А две касательные (11,49). Пусть будут проведены АЕ и Е7, и секущая -
Е7. Тогда Е2 будет проходить через точки К и Н.
рез одну из них, другая прямая будет рассекаться в другой точке, которая будет де¬
лить ее в том же самом отношении (111, 37), что невозможно. Если же она не прохо¬
дит через них вообще, то абсурд получается в отношении обеих точек.
•II
Предложение 19. То же самое, если точка А лежит внутри дополнительного угла
Пусть при тех же самых предпо¬
сылках точка А находится внутри
угла, дополнительного к углу, ограни¬
ченному асимптотами В таком слу¬
чае я утверждаю, что прямая, про¬
веденная через К и И и продолженная
дальше, будет пересекаться с обоими
противолежащими сечениями, а пря¬
мые, проведенные от точек пересече¬
ния к точке А, будут касаться сечений.
Пусть же от А будут проведены ка¬
сательные АЕ и к каждому из се¬
чений. Тогда прямая, проведенная
через Е и X, будет проходить через
К и Н. Если же нет, то она проходит
либо через одну из них, либо вообше не проходит ни через одну, и мы снова придем
тем же самым способом к абсурду (111, 39).
же
ни
•ж
•л
м.
376

Предложения
Предложение 20. Предложение 13, если две прямые пересекают оба противолежа¬
щих и удовлетворяют условию Предложения 1
Если при тех же предпосылках выбранная точка лежит на одной из асимптот, то
прямая, проведенная через концы продолжении, параллельна асимптоте, содержащей
эту точку, и пересекает гиперболу в точке касания прямой, проведенной от точки на
асимптоте.
Пусть при тех же предпосылках
точка А находится на одной из асим¬
птот. В таком случае я утверждаю,
что прямая, проходящая через точ¬
ки К и Н, параллельна асимптоте и
пересекает гипероолу в точке сопри¬
косновения прямой, исходящей из
точки на асимптоте.
Пусть от А будет проведена каса¬
тельная Д7, и от X будет проведена
прямая, параллельная асимптоте, на
которой находится А. Тогда она бу¬
дет проходить через К и Н. Ведь если
(Л)	(В)
это не так, то либо она
ходит че¬
рез одну из них, либо не проходит
ни через одну, и получается тот же
самый абсурд, что и прежде (III, 36).
Предложение 21. Предложение 14 для противолежащих
Пусть точка А по-прежнему располагается на одной из асимптот, и пусть пря
мая АВ, параллельная другой асимптоте, будет пересекаться с сечением только в од
ной точке В, а прямая ГА& — с обои¬
ми сечениями. Продолжим АВ и ГА& \ 4
до точек К и П, таких, что КВ = В А, (д\
ГА _ ГН
аА©”Н0
В таком случае я утверждаю, что
прямая, проведенная через точки К и
Н, будет параллельна асимптоте, на
которой находится точка А, а пря¬
мая, проведенная от точки пересе¬
чения с кривой к точке А, будет ка¬
саться сечения.
21. Рис. 1
Пусть же будет проведена каса¬
тельная АХ, и пусть от X будет про¬
377

Книга IV
ведена прямая, параллельная асимптоте, на которой находится точка А; тогда она
будет проходить через К и Н. Если же это не так, то получается, как и раньше, аб¬
сурд (111. 36).
Предложение 22. То же самое, если точка А лежит внутри дополнительного угла
Пусть при тех же предпосылках
точка А находится теперь внутри
угла, дополнительного к углу, ограни¬
ченному асимптотами.
В таком случае я утверждаю, что
прямая, проведенная через К и Ни про¬
долженная дальше, будет пересекать¬
ся с обоими противолежащими сечени¬
ями, а прямые, проведенные от точек
пересечения к точке А, будут касать¬
ся противолежащих сечений.
»г»
•ж
Пусть от А будут проведены ка¬
сательные АЕ и А7 к каждому из се¬
чений. Тогда прямая, проведенная
через Е и 7. будет проходить через
К и Н. Допустим, что она проходит
либо через одну из них, либо вооб¬
ще не проходит ни через одну. Если
она проходит только через Н, то от-
/
резок АВ не будет равен
К (III, 31), что абсурдно. Если только через К, то не полу-
ГА ГН
чается, что — = —
А0 Н0
(111, 39), что тоже абсурдно. Если же она в
ше не проходит
•ю
через К и Н, то тем более.
Предложение 23. Если из точки А проведены две касательные и, параллельно асим
птотам, два отрезка, которые делятся кривыми пополам, то прямая, проведенная через
их концы, пройдет через точки касания
Пусть точка Л находится внутри угла, дополнительного к углу, ограниченному асим¬
птотами, и от нее проведены две прямые \Н и &К, параллельные асимптотам. И пусть
/Л
они рассекаются точками пересечения с противолежащими так, что \В=ВН и \А=АК.
В таком случае я утверждаю, что прямая, проведенная через К и Н. будет пересекать¬
ся с сечениями, а прямые, проведенные от точек пересечения к А. будут их касаться.
с»
Пусть от А будут проведены касательные АЕ и \7 к каждому из сечений. И допу¬
стим, проведенная и продолженная Е7 не будет проходить через К и Н. То есть она
либо проходит через одну из них, либо вообще ни через одну. Тогда или АА не будет
«и
378

Предложения
%
(А)
г
ч.
23. Рис. 1
9
*
равна АК, или АВ не будет равна ВН,
или и то и другое (III, 31). И во всех
этих случаях выходит абсурд. Следо¬
вательно, ЕХ проходит через К и Н.
Предложение 24. Два конических
сечения не могут частично совпадать*.
Два конических сечения не могут
пересекаться так, чтобы часть дуги
у них была общей, а часть — нет.
Допустим, что ААВГ и ЕАВГ - д
сечения конуса, ко¬
торые пересекаются таким образом, что дуга АВГ у них об¬
щая, а дуги АА и АЕ — нет. Пусть через точку В проведе¬
на касательная, а на общей дуге паратлельная ей секущая
АО. Проведем через точку В и середину секущей диаметр
ВН, а через некоторую точку А - прямую АЕГ, паратлель-в
ную АО. В таком случае (Опр 1,4) для одного сечения бу¬
дет АХ = XГ, а для другого Ег = ¿Г.
Следовательно, АХ = ЕХ, что невозможно.
ПН
•М
Г
л
24. Рис. 1
/	Н
X
Предложение 25. Два конических сечения не могут пере¬
сечься более чем в четырех точках
Два конических сечения могут пересекаться не более чем в четырех точках.
Допустим, что сечения пересекают¬
ся в пяти точках А. В. Г, А, Е, следующих
друг за другом и между ними нет никаких
других точек пересечения. Проведем пря¬
мые АВ и ГА. Если речь идет о парабо¬
лах и гиперболах, то прямые пересекут¬
ся вне их (11,24, 25)*. Пусть они пересе¬
кутся в точке А. Выберем на отрезках АВ
и АГ такие точки О и П, чтобы выполня¬
25. Рис. 1
ла АО АЛ АП
лись соотношения	=	и	=	:
АВ ОВ АГ ПГ
*	- Все следующие Предложения до конца IV Книги - теоремы о пересечениях и касаниях ко¬
нических сечений.
*	Это могут быть любые сечения в любых сочетаниях. Но если пересекаются эллипсы с эллип¬
сами, то прямые могут пересечься (рис 5), а могут, и нет (рис 4)..

Книга IV
Тогда отрезок ОП. будучи продолжен в обе стороны, пересечется с сечением в
точках 0 и R*, а прямые Л0 и AR будут касательными (IV, 9). Поскольку между точ¬
ками В и Г не существует точек пересечения, то ЕЛ пересечет обе кривые в точках
ЕЛ EN
М и Н. При этом для Н будет справедлива пропорция (Ш, 37)	=	, а для М
AH NH
ЕЛ EN
—- =	, что невозможно. Следовательно, допущение неверно**.
AM. NM
25. Рис. 4
Ш
Если же АВ и ДГ параллельны, то се¬
чениями будут эллипсы (рис. 4). Пусть
АВ и ГД разбиваются на равные отрезки
точками О и П, и через них проведем и
продолжим прямую ПО, которая пере¬
сечет эллипсы в точках 0 и И. Тогда 0В
будет диаметром круга (II, 28), к которо¬
му проведены ординаты АВ и ГЛ. Если
- Можно, конечно, взять и точки пересечения с другой кривой, это не меняет дела
г - Данное доказательство возможно, только если гиперболы и параболы пересекаются так,
как представлено на рис 1 Такое расположение кривых изображается во всех известных нам из¬
даниях Аполлония Но дело в том, что так они пересекаться не могут даже и в четырех точках, ведь,
например, у гипербол асимптоты пересекаются в этом случае лишь трижды. Реальная картинка
дана на рис. 2. Пересечение гипербол в четырех точках показано на рис. 3 (аналогичная картинка
и для парабол), но в этом случае доказательство Аполлония неприменимо.
380
•ж

Предложения
провести прямую £NN11-1, параллель¬
но АВ и ГА, то она пересечется с пря¬
мой 0И, и с каждой из кривых в точ¬
ках М и Н, поскольку между А и Г нет
других точек их пересечения.
А тогда для М будет выполняться
равенство (Опр. 1,4) NN1 = а для
Н N14 = ЕЫ, то есть N14 = N14, что не¬
возможно.
Предложение 26. Если два кониче¬
ских сечения касаются друг друга в од¬
ной точке, то они могут иметь кроме это¬
го не более двух общих точек
Если два конических сечения каса¬
ются друг друга в одной точке, то они
могут иметь кроме этого не больше
двух общих точек (рис. 1)*.
Пусть два сечения касаются друг друга в точке А.
В таком случае я утверждаю, что они не могут иметь больше двух
ших точек.
Допустим, что есть три общие точки В, Г, А следующие друг за другом и между ними
нет никаких других (рис. 2). Проведем и продолжим отрезок ГВ, а также касатель¬
ную к точке А, которая касается, очевидно, обоих сечений. Пусть они пересекаются
в точке Л. Выберем на ГВ точку П такую, чтобы выполнялось равенство
ГЛ
АВ
ГП
пв
* Такое расположение кривых возможно, но возможно и подобное рис 2 в предыдущем Пред
ложении. А тогда данное доказательство не подходит
381

Книга IV
Тогда если будет проведена прямая
АП, то она пересечется с сечениями в
точках 0 и И, а прямые Л0 и ЛР, прове¬
денные отточек ее пересечения к точ¬
ке Л, будут касательными к ним (IV, 1).
А так как прямая АА рассекает оба се¬
чения, то получается такое же абсурд¬
ное утверждение, о котором мы гово¬
рили прежде (IV, 25). Следовательно,
они не могут пересекаться более, чем
в двух точках.
Если же у эллипсов, ГВ и АЛ па¬
раллельны (рис. 3), то доказательство
1
ится тем же самым способом, что
и прежде (IV, 25). поскольку было до¬
казано. что А0 есть диаметр.
Предложение 27. Два конических сечения, касающиеся друг друга в двух точках, не
имеют других общих точек
Если два конических сечения касаются друг дру¬
га в двух точках, то они не имеют других общих
точек (рис. 1).
Пусть два сечения касаются друг друга в точ¬
ках А и В. В таком случае я утверждаю, что они
не совпадают нив одной другой точке.
27. Рис. /
парабола
\ гипербола
Допустим, что они совпадают в точке
Г (рис. 2), и пусть сначала Г будет распо¬
ложена вне дуги между А и В, и пусть от
А и В будут проведены касательные. В та¬
ком случае они будут касаться обеих ли¬
ний и, как в предыдущем Предложении,
пересекутся в точке Л. Проведем прямую
ГЛ, пересекающуюся с сечениями в точ¬
ках М и Н, и секущую АВ, которая пере-
•3
382

Предложения
сечется с ГЛ в точке N. Тогда для одного сечения получится (III, 37)	=	, а для
ЛН КН
ГЛ ГК
другого	=	, что абсурдно.
ЛМ NN1
Предложение 28. Предложение 27 для
эллипсов
Если ГН параллельна прямым, касающим-
сяв А и В, как в случае эллипсов, то, проведя
АВ, мы заключаем, что это диаметр сече¬
ний (II, 27) и секущая, проведенная из точ¬
ки Гпараллельно касательным, будет раз¬
биваться им в точке N пополам, что аб¬
сурдно, так как получится, что НН = Л/Л.
Следовательно, сечения не будут иметь
щих точек, кроме
28. Рис. 1
Предложение 29. Предложение 27 для случая, когда общая точка находится меж¬
ду точками касания
Допустим теперь, что точка Г расположена между точками соприкосновения двух
конических сечений.
Очевидно, что сечения не касают¬
ся друг друга в точке Г. поскольку по
условию они касаются только в двух
точках. Следовательно, в точке Г они
пересекаются*.
Пусть от точек А и В проведены ка¬
сательные АЛ и ВЛ и пусть отрезок АВ
разбивается точкой 7. пополам. Тогда
Л2 есть диаметр сечения (II, 29). Но
он не проходит через точку Г. ибо если
бы это было так. то прямая, проведен¬
ная через нее параллельно АВ. каса¬
лась бы обоих сечений (II, 5 и 6), что невозможно. Проведем теперь от точки Г от¬
резок ГКНМ параллельно прямой АВ. В таком случае для одного сечения получа¬
ется (Опр. I. 4) ГК = КН, а для другого ГК = КМ.
Следовательно, КМ = КН. что невозможно.
Если же касательные к сечениям параллельны, то мы тем же самым способом,
что и выше, докажем, что это невозможно.
* - То есть если Г - точка касания, то ((V 27) другой точкой касания может быть только еще одна
383

Книга IV
Предложение 30. Парабола не может касаться другой параболы более чем в одной точке
яг
Парабола не может касаться другой параболы более чем в одной точке (рис. 1).
•и
сечений и пересекутся в точке Л (рис.
2). Проведем теперь отрезок АВ, который рассекается точкой 2 пополам, и отрезок
Л2*. Поскольку два сечения АН В и АМВ касаются друг друга в двух точках А и В,
то они не пересекаются ни в какой другой точке (IV, 27—29). Поэтому \2 рассекает
оба сечения. Пусть он рассекает их в точках Н и М. В таком случае для одного сече¬
ния получается (I, 35), что АН = Н7, а для другого ДМ = М/, что невозможно. Сле¬
довательно, парабола не может касаться другой параболы более чем в одной точке.
•и
1«К
Предложение 31. Парабаза не может касаться гиперболы в двух точках, находясь
вне нее
Парабола не может касаться гиперболы в двух
точках, находясь вне нее (рис. 1).
Пусть даны парабола АН В и гипербола АМВ
касающиеся друг друга в точках А и В, от кото¬
рых проведены прямые, касающиеся обоих се¬
чений в этих точках и пересекающиеся в точке А
(рис. 2). Проведем отрезок АВ, разбивающийся
точкой 2 на д
которая является диаметром сечений (II, 29) и
поэтому, продолженная дальше, проходит через
центр гиперболы А.
•и
а
МП]
равных отрезка, и прямую Л7,
•и
* - Который является диаметром (II, 29)
384

Предложения
Поскольку сечения АН В и АМВ ка¬
саются в точках А и В, они не пересека¬
ются ни в какой другой точке (IV, 27—
29), в силу чего Л7 пересекает каждое
из них, например, в точках Н и М, а
тогда по свойству гиперболы (I, 37)
AZ AM MZ
	=	=	* *. HoAZ>AM,no-
АМ ЛА МЛ
этому и MZ > МЛ.
Но пос
= НА, что не
зможно.
Предложение 32. Парабола не может
касаться эллипса с внутренней стороны
в двух точках
Парабола не может касаться эллип¬
са с внутренней стороны в двух точках.
Пусть даны эллипс АН В и парабола
АМВ. соприкасающиеся в двух точках
А и В, от которых проведены прямые,
касающиеся сечений и пересекающие¬
ся в точке Л, а также проведена прямая
АВ, рассекаемая точкой Z на два рав¬
ных отрезка. Пусть также проведена и
продолжена прямая лг. Как уже гово¬
рилось ранее (IV, 31), она пересекает
оба сечения в точках Н и М и проходит
через центр эллипса Л. Тогда по свой-
•1«.
•а
ству эллипса (I. 37)
АЛ
АН
АН
AZ
• •
Но АЛ > ДН. поэтому и НЛ > HZ.
Но по свойству параболы (I, 35) МЛ = MZ, что невозможно.
Предложение 33. Гипербола не может касаться гиперболы в двух точках
Гйпербола не может касаться гиперболы в двух точках, если у них общий центр***.
•м
* - Поскольку по 6-му свойству пропорций и выражения в скобках равны Мг и МЛ.
“См. сноску к предыдущему Предложению.
*** Если гиперболы, касаются друг друга в двух точках, у них всегда общий центр, поскольку
оба центра лежат на одной прямой \7. (II, 29), и каждый из них находится посередине между про¬
тиволежащими, а значит, центры совпадают Следовательно, гиперболы вообще не могут касать¬
ся друг друга в двух точках.
385

Книга IV
Предположим, что две гиперболы АН В
и АМВ, имеющие один и тот же центр А,
касаются друг друга в точках А и В, от ко¬
торых проведены касательные, пересека¬
ющиеся в точке Л. Пусть будет проведена
и продолжена прямая ЛА, пересекающая¬
ся с прямой АВ. В таком случае она рас¬
секает АВ в точке Т на два равных отрез¬
ка (П, 30). Поэтому, как уже говорилось
ранее (IV, 31), XI пересечет оба сечения в
каких-то точках Н и М. Тогда для гипербо¬
лы АН В будет выполняться равенство (1,37)
XX ДА = АН2, а для гиперболы АМВ А/ АЛ
= АМ2.
Следовательно, ДМ2 = АН2, что невозможно.
Предложение 34. Если эллипсы касаются друг друга в двух точках и их центры со¬
впадают, то прямая, соединяющая точки касания, проходит через центр
Если эллипсы касаются друг друга в двух точках и их центры совпадают, то пря¬
мая, соединяющая точки касания, проходит через центр* (рис. 1).
Пусть два эллипса касаются друг друга в точках А и В, и от этих точек проведены
касательные к сечениям, допустим, пересекающиеся в точке Л (рис. 2). И пусть от¬
резок АВ разбивается точкой X пополам. Тогда XX есть общий диаметр эллипсов (II,
из
* Если гиперболы касаются друг друга в двух точках, у них всегда общий центр, поскольку оба
центра лежат на одной прямой \2 (II 29), и каждый из них находится посередине между проти¬
волежащими, а значит, центры совпадают Следовательно, гиперболы вообще не могут касаться
друг друга в двух точках.

Предложения
29). Предположим, что общим центром сечений является точка А, не лежащая на АВ,
тогда для одного эллипса будет верно (I, 37)ЛА 7А НА2, а для другого ЛА-7Л МА?.
Тогда НА2 = МА2, что невозможно. Следовательно, прямые, касающиеся кривых
в точках А и В, не будут пересекаться, но тогда они параллельны и АВ является ди¬
аметром. А значит, он проходит через центр, что и следовало доказать.
Предложение 35. Конические сечения не могут пересекаться более чем в двух точ¬
ках, если выпуклости дуг, заключенные между точками пересечения, являются разно-
направленными.
Коническое сечение не может пересекаться с
коническим сечением более чем в двух точках, если
выпуклости дуг, заключенные между точками пе¬
ресечения, не направлены в одну сторону.
Допустим, сечение конуса АВГ пресекается
с другим сечением ААВЕГ в точках А, В, Г, при¬
чем выпуклости дуг, заключенных между точка-
нс
ми пересечения, направлены в разные стороны.
Если на сечении АВГ провести секущие АВ и ВГ,
то они образуют угол. И те же самые прямые, об¬
разующие тот же самый угол, лежат внутри сече¬
ния ААВЕГ. Но поскольку выпуклости сечений
направлены в разные сто{
ны, то и вершина од¬
©
ного и того же угла должна одновременно быть
ращена тоже в разные стороны, что невозможно.
Предложение 36. Если коническое сече¬
ние имеет с одним из противолежащих две
общие точки и выпуклости дуг между' ними
однонаправлены, то его продолжения не пе¬
ресекутся с другим противолежащим
Если коническое сечение имеет с одним
из противолежащих две общие точки, и обе
дуги, расположенные между ними, будут об¬
ращены выпуклостями в одну и ту же сто¬
рону, то это сечение, продолженное далее,
не пересечется с другим противолежащим.
I
Пусть (А) и ATZ — противолежащие,
ABZ - сечение конуса, имеющее с ArZ
общие точки А и Z так, что дуги ABZ и
ArZ обращены выпуклостями в одну и ту
36. Рис. 1
387

Книга IV
же сторону. В таком случае я утверждаю, что кривая ABZ, будучи продолжена в обе
стороны, не пересечется с противолежащим (А).
Проведем прямую AZ. Тогда, поскольку (А) и ArZ являются противолежащими,
и прямая AZ пересекает AiZ в двух точках, то она, продолженная дальше, не пере¬
секается с противолежащим (А) (II, 33). Следовательно, и сечение ABZ с ним не пе¬
ресечется.
Предложение 37. Если коническое сечение имеет общую точку с одним из противо¬
лежащих, то оно не будет иметь с другим более двух общих точек
Если сечение конуса имеет общую точку с одним из противолежащих, то оно не бу¬
дет совпадать с другим более чем в двух точках (рис. 1).
Пусть даны противолежащие (А) и (В),
и пусть коническое сечение АВГ имеет с
(А) общую точку А, а с (В) - В и Г.
В таком случае я утверждаю, что ука¬
занное сечение не будет иметь с (В) дру¬
гих общих точек.
Допустим, что оно пересекается с ним
в точке А (рис. 2) Тогда сечение ВГА со¬
впадает с (В) более чем в двух точках, при
этом дуги, заключенные между ними, об¬
ращены выпуклостями в противополож¬
ные стороны, что невозможно (IV. 35)*.
як
•в
37. Рис. 3
х
X
Схожим образом это доказывается, если сечение АВГ касается противолежаще¬
го сечения.
Предложение 38. Коническое сечение имеет с противолежащими не более четырех
общих точек
Сечение конуса имеет с противолежащими сечениями не более четырех общих точек.
‘ Это верно и для двух пар противолежащих гипербол.

Предложения
Это с очевидностью следует из того, что, имея с одним противолежащим одну
общую точку, сечение не может иметь с другим более двух (IV, 37).
Предложение 39. Если коническое сечение касается изнутри одного из противоле¬
жащих, то оно не будет иметь общих точек с другим
Если сечение конуса касается одного из противолежащих изнутри, то оно не будет
иметь общих точек с другим противолежащим.
Пусть (А) и (В) будут противоле¬
жащими сечениями, и пусть сечение
ГАД касается указанным образом се¬
чения (А).
В таком случае я утверждаю, что
ГАД не будет иметь общих точек с (В).
Проведем через точку А касатель¬
ную Е7. Она касается обеих кривых,
поэтому не будет пересекаться с (В) (11,
33). Следовательно, сечение ГАД также
не будете ним пересекаться.
Предложение 40. Если коническое сечение касается каждого из противолежащих в
одной точке, то оно не имеет с ними других общих точек
Ест сечение конуса касается каждого из противолежащих в одной точке, то оно
не имеет с ними других общих точек.
Пусть даны противолежащие (А) и
(В), с которыми сечение АВГ соприка¬
сается в точках А и В.
В таком случае я утверждаю, что оно
не имеет других
щих точек с сечени¬
ями (А) и (В).
Поскольку АВГ касается кроме (А),
также и (В), то оно не может касаться
сечения (А) изнутри (IV, 39). Тем же
способом мы докажем, что оно не будет
касаться изнутри и сечения (В).
Проведем теперь прямые ДАН и ВЕ,
касающиеся (А) и (В). Очевидно, они
будут касаться и сечения АВГ. Пред¬
положим, что существует другая пря¬
мая А7, касательная к (А), которая пе¬
ресекает АВГ в точке Z. Тогда прямая
40. Рис. 1
389

Книга IV
АН оказывается лежащей между касательной А/ и самим сечением (А), что невоз¬
можно (1,36).
Следовательно, ни одна из них, кроме АН, не касается сечения АВГ, и поэтому
очевидно, что АВГ не имеет общих точек с проти
лежащими (А) и (В).
Предложение 41. Если гиперболы пере¬
секаются в двух точках, имея между ними
противоположные выпуклости, то их про¬
тиволежащие не имеют общих точек
Если гиперболы пересекаются в двух точ¬
ках, имея между этими точками противо¬
положные выпуклости, то их противолежа¬
щие не имеют общих точек.
Пусть даны две пары противолежащих
(А) и (В), (Г), и (А) и пусть (А) пересека¬
ется с (Г) в точках А и В. имея противопо¬
ложно направленные выпуклости.
В таком случае я утверждаю, что (В) и
(А) не имеют общих точек.
Проведем прямую АВ и продолжим ее
до какой-то точки Н. Поскольку АВН пе¬
»1».
«я
ресекает (А), а продолженная в обе сторо¬
ны, оказывается вне сечения, то она не бу¬
дет пересекаться с сечением (В) (И, 33). Но
точно так же она пересекает и (Г), а зна¬
чит, не пересекается с (А). Следовательно,
(В) и (А) не пересекаются*.
I
Предложение 42. Если гипербола пересекается с обоими противолежащими, то се¬
чение, противолежащее ей, не имеет ни с одним из них двух общих точек
Если гипербола пересекается с обоими противолежащими, то сечение, противоле¬
жащее ей, не имеет ни с одним из них двух общих точек (рис. 1).
Пусть даны противолежащие (А) и (В), и пусть гипербола (Г) пересекается с каж¬
дым из них.
В таком случае я утверждаю, что сечение (А), противолежащее ей, не будет иметь
с (А) или с (В) двух общих точек.
* Очевидно, что таким же образом доказывается, что если две гиперболы касаются друг друга,
имея в точке касания разнонаправленные выпуклости, то их противолежащие не пересекаются
Аполлоний, почему-то этого не заметил, из-за чего ему пришлось придумывать доказательства к
Предложениям 42,43, 47, 51 и выделить в виде отдельной теоремы Предложение 54
390
•X

Предложения
НЕ
Предположим, что оно пересекается с (А) в точках Д и Е (Рис. 2). Проведем и
продолжим до какой-либо точки 0 прямую ДЕ. В таком случае ДЕ0 не пересека¬
ет сечение (Г), поскольку имеет две общие точки с противолежащим (Д) (II, 33), а
также не пересекается с сечением (В), поскольку имеет две общие точки с проти¬
волежащим (А). Следовательно, сечения (В) и (Г) не пересекаются, что противоре¬
чит предположенному.
По той же самой причине (Д) не будет касаться сечения (А) или (В). Ведь прове¬
денная Е0 будет касаться обоих сечений; поэтому из-за касания сечения (Д) она не
будет пересекаться с (Г) (И, 33), а из-за касания (А) не пересекается с (В). Следова¬
тельно, сечения (В) и (Г) не пересекаются, что противоречит предположенному*.
ЯЕ
Предложение 43. Если гипербола рассекает каждое из противолежащих в двух точ¬
ках, а дуги между ними имеют противоположные выпуклости, то сечение, противоле¬
жащее ей не будет иметь общих точек ни с одним из этих противолежащих
Если гипербола рассекает каждое из противолежащих в двух точках, и дуги, заклю¬
ченные между ними, имеют противоположные выпуклости, то сечение, противолежа¬
щее ей не будет иметь общих точек ни с одним из этих противолежащих*.
Пусть гипербола (Г) пересекает каждое из противолежащих (А) и (В) в двух точ¬
ках так, что ее дуги, заключенные между точками пересечения, имеют выпуклости,
‘ Можно доказать это проще, опираясь на Предложение 41. если (А) и (Л) пересекаются в двух
точках или касаются, то (В) и (Г) не пересекаются, а это противоречит предположенному
* Это верно и в случае, если выпуклости направлены в одну сторону (IV. 45).
391

Книга IV
43. Рис. 2
противоположные выпуклостям дуг
этих противолежащих. В таком слу¬
чае я угверждаю, что сечение (А), про¬
тиволежащее ей, не будет пересекать¬
ся с (А) и (В).
Допустим, оно пересекается с (А)
в точке Е, и пусть будут проведены и
продолжены дальше ГА и АВ. Они пе¬
ресекутся друг с другом в какой-то точ¬
ке О, которая будет располагаться вну¬
три угла, ограниченного асимптота¬
ми сечения (Г) (II, 25). В таком случае
прямая, проведенная отточки Е, рас¬
положенной на сечении (А), к О, ока¬
зывается внутри угла АОВ. А посколь¬
ку между точками Г и А не будет точки
Е. расположенной на гиперболе (А), и
ГАО пересекается с Е0, то точка 0 бу¬
дет расположена внутри асимптот сече¬
ния (А)*. Но (В) есть его противолежа¬
щее сечение. Тогда прямая, проведен¬
ная от В к 0, оказывается внутри угла
Г0Е, что абсурдно, ведь та же самая
прямая принадлежит углуА0В. Сле¬
довательно, Е7 не будет пересекаться
ни с одним из сечений А и В.
Комментарий ред.
Предложение можно доказать по-
разному. Можно использовать способ.
примененный Аполлонием в Предло¬
жении 51 (рис. 2).
Предположим, (А) пересекается с
(А) в точке Е, и пусть будут проведены
и продолжены дальше ГА и АВ, пере¬
секающиеся в точке 0. И если прямая,
проведенная от Е к 0, щ
•а
водится от се¬
чения (А), она оказывается внутри угла
А0В. Однако если прямая Е0 прово¬
дится от (А), то она попадет в угол, дополнительный к углу АОВ. что невозможно,
так как мы предположили, что точки Е совпадают, а тогда Е0 не может попасть од¬
новременно в два этих угла.
* Это верно, если Е0 есть касательная или секущая, что вовсе не
зательство, в общем, неверно
язательно, поэтому дока-

Предложения
©
Другой способ. Поскольку (А) и (Г) пересекаются в двух точках, то их противо¬
лежащие (В) и (А) не имеют общих точек (IV, 41). А поскольку пересекаются в двух
точках (В) и (Г), то их противолежащие (А) и (А) тоже не пересекаются. Следова¬
тельно, (А) не пересечется ни с (А), ни с (В).
Очевидно, что, как и в Предложении 41 все вышесказанное верно, если гипер¬
бола касается противолежащих.
Предложение 44. Если две гиперболы пе¬
ресекаются в четырех точках, то их проти¬
волежащие не имеют общих точек
Если две гиперболы пересекаются в че¬
тырех точках, то их противолежащие не
имеют общих точек.
Пусть даны две пары противолежащих:
(А) и (В), (Г) и (А), и пусть (Г) пересекает
(А) в четырех точках А, В, Г и А.
В таком случае я утверждаю, что (В) и
(А) пересекаться не будут.
Предположим, что они пересекаются
в К. Проведем и продолжим прямые АВ
и АГ, которые пересекутся в точке Л (II,
25). Пусть на них взяты такие точки П и Р,
АЛ АП
что выполняются соотношения	=	;
АВ ПВ
(Л)
АЛ АР
— = —. Тогда прямая РП, продолжен
ная далее, пересечется с каждым сечением,
и прямые, проведенные из точки Л к точ¬
кам пересечения, касаются сечений (IV, 9).
Теперь проведем и продолжим прямую
•Ж
КА. Она пересечет (А) и (Г) в точках М и
При этом для Т справедлива про¬
порция (III, 39)*	=	, а для М —
КА 7Л
Ж NN1
	=	, что невозможно. Следователь-
КЛ МЛ
но, сечения (В) и (А) не пересекаются**.
* - Очевидно, что таким же образом доказывается, что если две гиперболы касаются друг дру¬
га, имея в точке касания разнонаправленные выпуклости, то их противолежащие не пересекаются.
Аполлоний, почему-то этого не заметил, из-за чего ему пришлось придумывать доказательства к
Предложениям 42, 43, 47, 51 и выделить в виде отдельной теоремы Предложение 54
“ - Можно доказать это проще, опираясь на Предложение 41. если (А) и (Л) пересекаются в
двух точках или касаются, то (В) и (Г) не пересекаются, а это противоречит предположенному.

Книга IV
Предложение 45. Если гипербола пересекается в двух точках с одним противолежа
щим, имея одинаково направленные выпуклости, а со вторым у нее одна обшая точка
то сечение, противолежащее ей, не будет иметь общих точек ни с одним из этих проги
волежащих
Если гипербола пересекается в двух точках с одним противолежащим, имея одина
ково направленные выпуклости, а со вторым у нее одна общая точка, то сечение, про¬
тиволежащее ей, не будет иметь общих точек ни с одним из этих противолежащих*.
Пусть гипербола (А) пересекается с про¬
тиволежащим (Г) в точках А и В, а с (А)
имеет одну общую точку Г.
В таком случае я утверждаю, что ее про¬
тиволежащее (В) не будет иметь общих то¬
чек ни с (Г) ни с (А).
Проведем и продолжим прямые АГ и
В Г, которые не пересекутся с сечением (В)
(II, 33). Однако они также не будут пере¬
секаться с (А) в другой точке, кроме точки
Г, ведь если они пересекутся в другой точ¬
ке, то они не могут пересечься с противо¬
лежащим ему сечением (Г) (П, 33), тогда
как по условию они с ним пересекаются.
Итак, прямые АГ и ВГ пересекаются с (А)
только в одной точке, а с (В) вообще не
пересекаются. Следовательно, (В) лежит
внутри угла ЕГ7. а значит, оно не имеет
общих точек с (Г) и (А).
Предложение 46. Если гипербола имеет с одним из противолежащих три общие точ
ки, то их противолежащие будут иметь только одну общую точку
Если гипербола имеет с одним из противоле¬
жащих три
точки, то их противолежащие
могут совпадать только в одной точке (рис. 1).
Пусть даны противолежащие (А) и (В), (Г)
и (А), причем (А) имеет с (Г) три общие точки
А, В и Г В гаком случае я утверждаю, что (В) и
/
(А) будут совпадать не более чем в одной точке.
Предположим, что этих точек две: А и Е.
Проведем прямые АВ и АЕ, которые либо па¬
раллельны. либо нет.
46. Рис. 1
* - Это верно и в случае, если выпуклости направлены в одну сторону (IV. 45)
394

Предложения
Пусть они сначала параллельны (рис. 2) и разбиваются пополам точками Н и 0.
Проведем и продолжим прямую Н0. Тогда она есть диаметр всех сечений (II, 36), а
АВ и ЛЕ - ординаты к нему. Проведем теперь параллельно АВ прямую ÍNEO, так¬
же являющейся ординатой к диаметру и пересекающейся с сечениями в точках Е
и О. Если эти точки совпадают, то сечения имеют четыре общие точки, но их три,
следовательно, 5 и О не совпадают. Тогда для (А) будет (Опр. 1, 4) ÍN = NO, а для
(Г) TN = NE.
Следовательно, NO = N5, что невозможно.
Пусть теперь АВ и ЛЕ не параллельны (рис. 3), но, продолженные дальше, пе¬
ресекутся в точке П. И пусть параллельно АП будет проведена ГО, которая пересе¬
чется с прямой ДП в точке R. Пусть также АВ и ЛЕ, разбиваются точками Н и 0 по¬
полам, и через них проведены диаметры HLI и 0А>М, а от точек I, Л, М проведены
касательные IT, АТ и MU, к сечениям. Тогда IT будет параллельна ДП, а АТ и MU
соответственно АП и OR (II, 5).
MY2	АП-ПВ	ЛТ2	АП-ПВ	MY2	ЛТ2
А поскольку (III, 19) '-„т = —и —у = ———, то - - ; = —
YI2	ДППЕ	ТГ	ДППЕ	YI2	TI
MY2 ЕР-РГ ЛТ2	ОР-РГ
По той же самой причине -;" z - =	и —у =	.
YI2	ДРРЕ	Т1*	ДРРЕ
Следовательно, ОР РГ = ЕР РГ, что невозможно.
2 •
Предложение 47. Если гипербола касается одного противолежащего сечения, а дру¬
гое рассекает в двух точках, то сечение, противолежащее ей, не будет иметь с ними об¬
щих точек
Если гипербола касается одного противолежащего сечения, а другое рассекает в
двух точках*, то сечение, противолежащее ей, не будет иметь с ними общих точек.
* Пропущено «имея щ
тивоположно направленные выпуклости между ними», а иначе это по¬
вторение Предложения 45.
395

Книга IV
Пусть (А) и (В) будут противолежащими сечениями, и пусть гипербола (Г) рас¬
секает сечение (А) в А и В, а сечения (В) касается в Л, и пусть (А) противолежит се¬
чению (Г).
В таком случае, я утверждаю, что (Д) не имеет общих точек с (А) и (В)*.
Допустим, пусть она пересекается в АВ в Г (рис. 2), и пусть будет проведена АВ,
и пусть через Д будет проведена касательная прямая, пересекающаяся с АВ в 7; тог¬
да Ъ будет расположена внутри асимптот сечения АВД. И ему противолежит ГЕ; тог¬
да прямая, проведенная от Г к 7, окажется внутри угла В7Д. А поскольку же гипер¬
бола есть АВГ, АВ и Г7 пересекаются, и точки пересечения А и В не содержат точку
пересечения Г, точка Т расположена внутри асимптот сечения АВГ. И ему противо¬
лежит Д; тогда прямая, проведенная от Д к 7, окажется внутри угла А7Г, что абсур¬
дно, ведь она так же попадала на угол В7Д. Следовательно, ГЕ не пересекается ни с
одним сечением из АВГ и Л.
Предложение 48. Если гиперболы пересекаются в двух точках, а в одной касаются,
то их противолежащие не имеют общих точек
Если гипербола пересекается с гиперболой в двух точках, а в одной ее касается, то
их противолежащие не имеют общих точек.
/г/
Пусть даны две пары противолежащих: (А) и (В), (Г) и (Л), расположенные так,
что (А) в точке А касается (Г), а в точках В и Г они пересекаются.
* Далее у Аполлония приводится доказательство, содержащее ту же ошибку, что и доказатель¬
ство (IV, 43). Между тем теорема доказывается просто Проведем через точку \ касательную М к
сечениям (Г) и (В). Она не пересекается с (Л), так как их разделяет асимптота По той же причине
она не пересекается и с (А). Следовательно, (А) и (А) не имеют общих точек, так как между ними
лежит \2 То же в отношении (Д) и (В) (IV, 41)
Вообще же это Предложение - частный случай (IV, 43).
396

Предложения
\ XX
\ у
X \
48. Рис. 2
ЛИ
В таком случае я утверждаю, что (В) и (Д) не имеют общих точек.
Предположим, что Д — общая точка. Проведем и продолжим прямую ВГ, и каса¬
тельную от точки А. Пусть они пересекутся в точке 7. Тем же самым способом, что
и прежде (II, 25), мы докажем, что точка 7 расположена внутри угла, ограниченно¬
го асимптотами противолежащих (А) и (Г).
Проведем и продолжим прямую Д7, которая пересечет (А) и (Г) в точках Н и К
Г7 ГЛ
между точками А и В. Выберем на прямой Х7 такую точку Л, чтобы — =	.
¿В АВ
Проведем и продолжим прямую АЛ, которая пересечет (А) и (Г) в некоторых
точках М и N*, тогда прямые ZN и ZM будут касаться сечений ¿IV, 1), и также, как
ЕЛ ЕК
и прежде, получится (III, 39), что из-за одного сечения — =	, а из-за другого
AZ KZ
ЕД ЕН
— =	, что невозможно.
AZ HZ
Следовательно, противолежащие сечения (В) и (Д) не пересекаются**.
Предложение 49. Если гиперболы касаются друг друга в одной точке и пересекают¬
ся в другой, то их противолежащие не имеют общих точек
Если гипербола, касающаяся одного противолежащего сечения, в другой точке пе¬
ресекается с ним, то сечение, противолежащее ей, совпадает с другим противолежа¬
щим не более чем в одной точке (рис. 1).
•It
•It
* Вообще-то, в (III, 39) сказано, что касательные проведены к противолежащим, а не к одной из
гипербол, как здесь, но пропорция все равно справедлива
** Здесь, как и в Предложении 25, гиперболы так пересекаться не могут. А если гиперболы пе¬
ресекаются так, как на рис 2, то доказательство не подходит Доказать можно, например, так про¬
ведем и продолжим прямую АВГ. Она не пересекается с (В) и (Д) (II, 33) и проходит между асим¬
птотами Следовательно, (В) и (Л) не имеют общих точек.
397

Книга IV
49. Рис. I
Пусть даны две пары противолежащих (А) и (В), (Г) и (А), причем (А) и (Г) каса¬
ются в точке А, а в точке Г они пересекаются.
В таком случае я утверждаю, что их противолежащие совпадают не более чем в
одной точке.
Предположим, что есть две такие точки: Е и 7. Проведем прямую Е/, а через точ¬
ку А касательную А К. Они или параллельны или нет.
Пусть сначала они будут параллельны (рис. 2). Проведем и продолжим прямую
АМ, где М - середина Е7. Тогда АМ является диаметром всех противолежащих (II,
34). Проведем теперь из точки Г прямую, параллельную прямым АК и Е7. Она пе¬
ресечет гиперболы (Г) и (А) в точках А и В. Тогда для одного сечения будет (Опр. 1,
4) ГЛ = ЛА, а для другого ГЛ = ЛВ.
Однако это невозможно.
л».
398

Предложения
Пусть теперь прямые АК и Е7 не параллельны (рис. 3), но пересекаются в точ¬
ке К. Тогда В Г пересекается с Е7 в некоторой точке Ь1, а прямая АМ разбивает по¬
полам секущую Е7 и пересекает сечения в точках Е и О от которых проведены ка-
АП2
сательные НП и ОК, параллельные Ел (II, 5). Тогда получается, что -р^- =
„„	ВЫ-ЫГ ди-ыг
силу чего (111, 19)	=	.
£N•N7	£N-N7
АР2
=	Г. в
РО2
Следовательно, BN NГ = AN КГ, что невозможно*.
Предложение 50. Если гиперболы касаются друг друга в одной точке, то их проти¬
волежащие имеют не больше двух обших точек
Если гипербола касается одного противолежащего сечения в одной точке, то сече¬
ние, противолежащее ей, будет иметь с другим противолежащим не более двух общих
точек (рис. 1).
Пусть даны две пары противолежащих (А) и (В), (Г) и (Л), причем (А) и (Г) каса¬
ются друг друга в точке А.
В таком случае я утверждаю, что (В) и (Л) будут иметь не более двух общих точек.
Допустим, что этих точек три: А, Е и 0. П[
и (Г), а также секущую ЛЕ.
Предположим сначала, что АК и ЛЕ параллельны (рис. 2), и пусть ЛЕ разбива¬
ется точкой Л пополам. Тогда прямая АЛ есть диаметр всех сечений (II, 34). Прове¬
дем теперь от точки 0 параллельно ЛЕ прямую 0Е7Н. Тогда из рассмотрения од¬
ного сечения следует (Опр. 1,4), что 0Е = Е7, а из рассмотрения другого 0Е = ЕН.
Следовательно. Е2=ЕН, что невозможно.
* Доказательство неверно, так как предполагается, что точки О, Е и А лежат на одной прямой,
но это не так, поскольку МЕ и МО - диаметры, и они попадут не в точку А (ведь АК не параллель¬
на ЕП или ОР), а в точки Т и Л Следовательно, точки О, Е и А не лежат на одной прямой (рис. 4)
399

Книга IV
50. Рис. 3
Пусть теперь прямые АК и АЕ не парал¬
лельны, но пересекаются в точке К (рис. 3).
И пусть продолженные АК и 07Н пересе¬
каются в точке Р. Тогда тем же самым спо-
собом, что и прежде, докажем (III, 19), что
из рассмотрения сечения (А) следует, что
АК • КЕ ZP • Р0
чения(В)
ДККЕ
АК2
, а из рассмотрения се-
HP • PO
РА2
Поэтому НР Р0 = 7Р Р0, что невозмож¬
но. Следовательно, (В) и (А) будет пересе¬
каться не более чем в двух точках*.
Предложение 51. Если гипербола касается обоих противолежащих, то ее противо¬
лежащее не имеет с ними общих точек (частный случай № 43)
Если гипербола касается обоих противоле¬
жащих сечений, то сечение, противолежащее
ей, не будет иметь с ними общих точек.
Пусть (А) и (В) будут противолежащими
сечениями, и пусть гипербола (Г) касается их
в точках А и В, и пусть ей противолежит (А).
В таком случае я утверждаю, что (А) не пе¬
ресекается ни с одним из сечений (А) и (В).
Предположим, оно пересекается с (А) в
точке А, и пусть от А и В будут проведены
прямые, касающиеся сечений. В таком случае
они будут пересекаться между собой в точке
Г, расположенной внутри угла, образованно¬
го асимптотами сечения (Г). Тогда ГА, если
ее продолжить, будет находиться внутри угла
АГВ. Однако она также оказывается внутри
угла ВГ7, что абсурдно. Следовательно, (А)
не пересекается с (А) и (В)**.
с»
5/. Рис. 1
\
\
\
\ (В)
Z
Предложение 52. Если одни противолежащие касаются других в одной точке каж¬
дое, имея одинаково направленные выпуклости в точках касания, то они не имеют дру-
гих общих точек
Если одни противолежащие касаются других в одной точке каждое, имея одинако¬
во направленные выпуклости в точках касания, то они не имеют других общих точек.
* Это доказательство неверно по той же причине, что и предыдущее.
** Предложение 51 - это частный случай Предложения 43
4
13.

Предложения
Пусть противолежащие сечения ка¬
саются друг друга в точках А и Д.
В таком случае я утверждаю, что они
не имеют других общих точек.
Допустим, что Е - еще одна общая
точка. Тогда, поскольку гипербола, ка¬
ЯС
сающаяся одного из противолежащих
в точке Д, совпадает с ним и в Е, то (А)
имеет с (Г) не более одной общей точ¬
ки (IV, 49). Проведем касательные А0
и Д0, а также прямую АД. Проведем
также прямую ЕВГ, параллельную АД, а
через точку 0 - сопряженный диаметр
К0Л. Он будет разбивать в точке К на
две равные части отрезок АД (II, 39).
Тогда отрезки ЕВ и ЕГ делятся в точке
Л пополам (Опр. I, 4), а значит, ВЛ =
ГЛ, что невозможно. Следовательно, противолежащие не имеют других общих точек.
Предложение 53. Если две гиперболы касаются друг друга в двух точках, то их про¬
тиволежащие не имеют общих точек
Если гипербола касается одного противолежащего сечения в двух точках, то сече¬
ние, противолежащее ей, не будет иметь общих точек с другим противолежащим*.
Пусть даны две пары противолежащих: (А) и (В), (Г) и (А). И пусть (А) и (Г) ка¬
саются друг друга в двух точках А и В.
В таком случае я утверждаю, что (В) и
(Д) не пересекаются между собой.
Допустим, что они пересекаются в точке
Е. Проведем касательные АН и ВН, а также
отрезок АВ. Проведем и продолжим пря¬
»а
•тс
мую ЕН, которая пересечет сечения (А) и
< В) в точках Г и Д, а отрезок АВ в точке 0.
Тогда, поскольку АН и ВН касаются сече¬
ний, а отрезок АВ соединяет точки сопри¬
косновения, то для сечения (А) получится
0Е 0А	/ОЧ0Е' 0Г
(III, 39), что — =	, а для (В) — = —,
ЕН АН	ЕН ГН
что невозможно.
Таким образом, (В) и (Д) не пересека¬
ются между собой.
•ю
‘ Напомним, что касаться друг друга в двух точках гиперболы, находящиеся в одной плоско-
сти, не могут (IV, 33).
401

Книга IV
Предложение 54. Если две гиперболы касаются друг друга, имея в точке касания про¬
тивоположно направленные выпуклости, то их противолежащие не имеют общих точек
Если две гиперболы касаются друг друга, имея в точке касания противоположно на-
о.
правленные выпуклости, то их противолежащие не имеют общих точек.
Пусть даны две пары противолежа¬
щих (А) и (В), (Г) и (А), расположен¬
ные так, что (А) касается (Г) в точке Е.
В таком случае я утверждаю, что их
противолежащие (В) и (А) не имеют об¬
щих точек.
Проведем через точку Е касатель¬
ную ЕН, тогда, поскольку она касает¬
ся (Г), то не пересекается с (А) (II, 33).
А поскольку она касается (А), то не пе¬
ресекается и с (В). Следовательно, ЕН
оказывается между сечениями (В) и (А),
а значит, они не имеют общих точек*.
54. Рис. 1
Предложение 55. Две пары противо¬
лежащих сечений пересекаются не более
чем в четырех точках*.
Две пары противолежащих сечений пе¬
ресекаются не более чем в четырех точ-
«а
55. Рис. 7
Даны (А) и (В), (Г) и (А) — две пары
противолежащих сечений.
1.	Пусть сначала сечение (Г) рассе¬
кает сечения (А) и (В) в четырех точках
К, Л, М, N. имея противоположно на¬
правленные выпуклости (рис. 1).
Тогда сечение (А), противолежащее
сечению (Г), не будет пересекаться ни
с одним из сечений (А) и (В) (IV, 43).
2.	Пусть теперь (Г) рассекает сече¬
ние (А) в двух точках, а сечение (В) в
одной (рис. 2).
Тогда (А) не будет пересекаться с (В)
(IV. 41). Если же (А) пересекается с (А),
* Очевидно, это частный случай Предложения 41
“ Предложения 55-57 являются обобщением предыдущих Предложений, касающихся вопро¬
сов о пересечениях и касаниях противолежащих
402
М1О

Предложения
I9
то оно может пересечься только в одной точке. Ведь если оно пересекается с (А) в
двух точках, то сечение (Г), противолежащее ей, не пересекается с другим противо¬
лежащим сечением (В) (IV, 43), а мы предположили, что оно пересекается в точке М.
3.	Если (Г) рассекает (А) в двух точках, а (А) пересекается с (А) (рис. 3), то сече¬
ние (А) не будет пересекаться с (В) (IV, 41), и не пересекается с (А) более чем в двух
точках (IV, 37)*.
4.	Если же (Г) рассекает каждое из противолежащих в одной точке (рис. 4), то (А)
не будет пересекаться ни с одним из них в двух точках (IV, 42)**. Таким образом,
‘ Если пересекутся в двух точках, то это будет рис. 1, повернутый на 90'
“ С одним из противолежащих (Л) может вообще не пересечься, рис. 4а.
о
403

Книга IV
из-за того, что мы сказали, и обрат¬
ного сечения (А) и (В) не будут пе¬
ресекаться с (Г) и (Д) более чем в че¬
тырех точках.
5.	Допустим, гиперболы пересе¬
каются в четырех точках, имея меж¬
ду точками пересечения одинаково
направленные выпуклости (рис. 5).
Тогда их противолежащие не будет
пересекаться друге другом (IV). Од¬
нако же (Д) не будет пересекаться и с
(А) (IV, 36), и. таким образом, снова
две пары противолежащих не пере¬
секутся более чем в четырех точках*.
6.	Если же гиперболы пересекают¬
ся в трех точках (рис. 6), то их проти¬
волежащие пересекутся только в од¬
ной точке (IV, 46).
А в остальных случаях мы скажем
то же самое, что и выше**.
Таким образом, во всех случаях,
которые можно помыслить, очевид¬
но, что п
тиволежашие сечения пе¬
Л
ресекаются с противолежащими сече¬
55. Рис. 6
ниями не более чем в четырех точках.
Предложение 56. Если гипербола соприкасается с другой гиперболой в одной точке,
то они пересекаются не более чем в двух других точках
Если противолежащие касаются противолежащих в одной точке, то они пересека¬
ются не более чем в двух других точках.
Даны две пары противолежащих (А) и (В), (Г) и (Д). Пусть сначала (Г) касается
(А) в точке К так, что они имеют в ней противоположно направленные выпуклости,
а с (В) пересекается в двух точках А и М (рис. 1)***.
1.	Поскольку (Г) пересекается с (В) в двух точках так, что дуги, ограниченные
точками пересечения, имеют противоположные выпуклости, то (А) не будет пере¬
секаться с (А) (IV, 41). Атак как (Г) касается (А) в точке К, имея противоположные
выпуклости, то (Д) не будет пересекаться и с (В) (IV, 54). Поэтому (Д) не будет пе¬
ресекаться ни с одним из сечений (А) и (В), следовательно, две пары противолежа¬
щих пересекаются только в двух точках.
* Как уже было сказано в сноске к (IV, 44) так пересекаться гиперболы вообще не могут..
** Аполлоний разобрал вроде бы все случаи 4+0 - рис 1,3 и 5; 3+1 - рис. 2 и 6, 2+2 - рис. 4, о
чем он далее и говорит.
*** Пересечься же в трех точках они не могут (IV, 35), поэтому все сводится к доказательству
того, что (Л) не пересечется с (А) и (В) а это рассмотрено в (IV 47).
404

Предложения
56 Рис. 3
2.	Пусть теперь (Г) пересекается с сечени¬
ем (В) только в одной точке Л (рис. 2). Сле¬
довательно, (А) не пересекается с (В) (IV, 54)
и может иметь с (А) только одну общую точ-
ку, ибо если (А) пересечется с (А) в двух точ¬
ках, то (В) не сможет пересечься с (Г) (IV.
41), а мы предположили, что они пересека-
ются в одной точке.
3.	Если же (Г) не пересекается с (В) (рис.
3), то (А) тоже не будет с ним пересекаться
(IV, 54), но может пересечься с (А) не более
чем в двух точках (IV, 35).
Если же сечения имеют одинаковые вы¬
пуклости, то получаются те же самые дока¬
зательства.
Таким образом, утверждение доказано
для всех случаев.
Комментарий
Рассмотрим случаи, когда сечения имеют одинаковые выпуклости. Возможны.
опять же, три варианта:
4.	Согласно (IV, 48), противолежащие (В) и (А) не пересекутся. А также не пере-
секаются (А) с (А) и (Г) с (В) (IV, 36).
Как уже было сказано в сноске к (IV, 48), такое расположение гипербол невозмож-
но, хотя оно и приводится в различных изданиях Аполлония (Е. Halley, I.L. Heiberg,
A. Czwalina). Если же изобразить что-то на него похожее, имея дело с реальными ги-
405

Книга IV
56. Рис. 5
перболами, то противолежащие непременно
пересекутся между собой. Реальная картина
изображена на рис. 2 к (IV. 48).
5. Согласно (IV, 49) (В) и (А) пересекут¬
ся в одной точке: кроме того, (А) с (А) и (Г) с
(В) не пересекутся, так как если через точку
К провести общую касательную, то она бу¬
US
дет их разделять.
6. (В) и (А) пересекутся в двух точках (IV,
50); (А) с (А) и (Г) с (В) не пересекутся по той
же причине, что и раньше.
Предложение 57. Если противолежащие сечения касаются противолежащих сече¬
ний в двух точках, то они не будут иметь других общих точек
Если противолежащие сечения касаются противолежащих сечений в двух точках,
то они не будут иметь других общих точек.
Даны две пары противолежащих (А) и (В), (Г) и (А); и пусть сначала они касаются в
точках К и А (рис. 1) Тогда (А) не будет пересекаться ни с одним из сечений (IV. 51)*.
Пусть теперь (Г) касается гиперболы (А) в точках К и Л (рис. 2)**. Тогда (А) не
будет пересекаться с (В) (IV. 53).
Пусть же (Г) касается сечения (А) в точке К, а (В) сечения (А) в точке Л. так, что
в точках касания они обладают противоположной выпуклостью (рис. 3)*** Тогда
Oj
•ю.
о.
* А сечение (Г) не может пересечься с (А) и (В) ни в какой другой точке (IV, 40).
« ♦
Как уже было сказано, гиперболы не могут касаться друг друга в двух точках (IV. 33), поэто¬
му этот пункт не имеет смысла.
. Как было доказано, это невозможно (IV, 54), поэтому данный пункт тоже не имеет смысла.
406

Предложения
(А) не будет пересекаться с (А), а посколь¬
ку (В) касается (А), то (Г) не будет пересе¬
каться с (В).
л
57. Рис. 3
5* Рис. 4
Если же (Г) касается (А) в точке К. а (А) касается (В) в точке Л. и они ос
в этих точках одинаково направленными выпуклостями (рис. 4). тосечеям* не
дут пересекаться ни в какой другой точке (IV. 52). II (Л) не будет пересекаться«.
а (Г) с (В> (IV. 39).	’	—«и».
Следовательно. во всех случаях, которые \южно помыслить. утверждение

Книга IV
ДОСЛОВНЫЙ ПЕРЕВОД КНИГИ IV
Если взять вне конического сечения или окружности круга некую точку, и от нее
две прямые попадают на сечение, одна из которых касается сечения, другая рассека¬
ет его в двух точках и вся прямая, рассекающая сечение, имеет такое отношение к ча¬
сти, выделенной между точкой и линией, согласно которому прямая, отделенная вну¬
три, рассекается таким образом, что прямые являются соответствующими той же
самой точке, то прямая, проведенная от точки касания к точке деления, пересекает¬
ся с линией, а прямая, проведенная от точки пересечения к точке, расположенной сна¬
ружи, касается линии.
Пусть АВГ будет сечением конуса или окружности круга, и пусть будет взята не¬
которая точка А внутри сечения, и пусть от нее АВ касается сечения в В, пусть ДЕГ
рассекает сечение в Е и Г. и пусть ГА к ДЕ равно Г7 к 7Е.
В таком случае я утверждаю, что прямая, проведенная от В к X пересекается с се¬
чением, и прямая, проведенная отточки пересечения к А касается сечения
Пусть от А будет проведена касательная АА, а проведенная ВА. если это возмож¬
но. рассекает прямую ЕГ не в X. но в Н. Поэтому поскольку ВД и АА касаются сече¬
ния, ВА проведена к точкам соприкосновения, и проведена ГА, рассекающая сече¬
ние в Г и Е, и проведена АВ, рассекающая сечение в Н, то ГД к АЕ равно ГН к НЕ,
что абсурдно, ведь мы предположили, что ГА к АЕ равно ЕХ к ХЕ. Поэтому ВА не
рассекает прямую ГЕ в другой точке. Следовательно, она рассекает ее в X.
2
Это вообще доказывается в отношении всех сечений, а в отношении только гипер¬
болы имеется следующее.
Если АВ касается сечения, АГ рассекает сечение в двух точках Е и Г, и точки Е и
Г содержат точку соприкосновения В, и точка А расположена внутри угла, ограни¬
ченного асимптотами, то доказательство осуществляется тем же самым способом;
ведь возможно от точки А провести другую прямую ДА, касающуюся сечения, и осу¬
ществить доказательство тем же самым способом.
•Ж
•Ж
3
При тех же самых предпосылках точки Е и Г пусть не содержат точку касания В,
и пусть точка А располагается внутри угла, ограниченного асимптотами.
Тогда возможно провести от Д другую касательную ДА и доказать остальное тем
же самым способом.
4
Если при тех же самых предпосылках точки пересечения Е и Г содержат точку со¬
прикосновения В, а точка А расположена на угле, который расположен на находящем¬
ся рядом углом, ограниченном асимптотами, то прямая, проведенная от точки каса¬
ния к точке деления, пересекается с противолежащим сечением, а прямая, проведен¬
ная от точки пересечения, касается противолежащего сечения.
408

Дословный перевод книги IV
Пусть В и 0 будут противолежащими сечениями, КА и МЕМ - асимптотами, а
точка А пусть находится на угле ЛЕМ, и пусть от нее АВ касается сечения, пусть АГ
рассекает сечение, и пусть точки пересечения Е и Г содержат точку соприкоснове¬
ния В, и пусть будет ГА к АЕ равно Гг к 7Е.
Нужно доказать, что прямая, проведенная от В к г, пересекается с сечением 0,
а прямая, проведенная от точки пересечения к А, касается сечения.
Пусть же от А будет проведена касательная А0, и пусть проведенная 0В, если воз¬
можно, проходит не через 7, а через Н. Тогда ГА к АЕ равно ГН к Н Е, что абсурдно,
ведь мы предположили, что ГА к АЕ равно Г7 к 7Е.
•Ж
|Ц.
5
Если при тех же самых предпосылках А является точкой на какой-либо из асим¬
птот, то прямая, проведенная от В к 7, будет параллельна той же самой асимптоте.
Предположим то же самое, и пусть точка А находится на некоторой асимптоте
ММ. Нужно доказать, что прямая, проведенная от В параллельно прямой ММ по¬
падает на 7.
Пусть она не попадает, и пусть, если это возможно, это будет ВН. Тогда ГА к АЕ
равно ГН к НЕ, что невозможно.
6
Если берется некоторая точка вне гиперболы, и от нее к сечению проводятся две
прямые, одна из которых — касательная, другая — параллельна одной из асимптот, и
прямая, равная прямой, отделенной на параллельной между сечением и точкой, про¬
долженная дальше на ней, полагается находящейся внутри сечения, то прямая, прове¬
денная от точки касания к точке, получившейся таким образом, будет пересекаться
с сечением, и прямая, проведенная от точки пересечения к точке, находящейся вне се¬
чения, будет касаться сечения.
Пусть ЛЕВ будет гиперболой, пусть будет взята некоторая точка А, находящаяся
вне сечения, и пусть сначала А располагается внутри угла, ограниченного асимпто¬
тами, и пусть от него касается сечения ВА, и пусть АЕ7 будет параллельна другой
асимптоте, и пусть будет установлено, что АЕ равно Е7. В таком случае я утверждаю,
что прямая, проведенная от В к 7, пересечется с сечением, а прямая, проведенная
отточки пересечения к А, будет касаться сечения.
Пусть будет проведена АД, касающаяся сечения, и проведенная ВА, допустим,
рассекает АЕ не в но в другой точке Н. Поэтому АЕ равно ЕН, что абсурдно, ведь
мы предположили, что АЕ равно Е7.
7
Пусть при тех же самых предпосылках точка А расположена на угле, который на¬
ходится рядом с углом, ограниченным асимптотами. В таком случае я утверждаю, что
получится то же самое.
Пусть же будет проведена касательная Д0, и проведена 0В, допустим, она попа¬
дает не на 7, но на Н. Поэтому АЕ равно ЕН, что абсурдно, ведь мы предположи¬
ли, что АЕ равно Е7.
409

Книга IV
8
Пусть при тех же самых предпосылках точка А расположена на одной из асимптот,
а остальное пусть будет тем же самым.
В таком случае я утверждаю, что прямая, проведенная от точки касания к краю вы¬
деленной прямой, проведена параллельно асимптоте, в которой расположена точка А.
Пусть же будет то же самое, что мы уже сказали, и пусть будет установлено, что
АЕ равно Е2. и пусть от В параллельно прямой будет проведена, допустим, ВН.
Тогда АЕ равно ЕН, что абсурдно, ведь мы предположили, что АЕ равно ЕТ.
9
Если от той же самой точки проводятся две прямые, рассекающие каждая в двух
точках сечение конуса, или окружность круга, и как целые прямые относятся к выде¬
ленным вовне частям, так и делятся части, выделенные внутри, так что соответству¬
ющие части располагаются воне той же самой точки, то прямая, проведенная через
точки деления. будет пересекаться с сечением в двух точках, а прямые, проведенные от
точек пересечения к точке, расположенной вовне, будут касаться линии.
Пусть АВ будет одной из линий, о которых мы сказали, и пусть от некоторой точ¬
ки А будут проведены АЕ и М, рассекающие линию, одна - в 0 и Е, другая - в 2 и
Н, и пусть будет АЕ к 0А равно ЕА к Л0, А2 к АН равно 2К к КН. В таком случае я
утверждаю, что прямая, проведенная от Л к К к каждой части, будет пересекаться с
сечением, а прямые, проведенные отточек пересечения к Абудут касаться сечений.
Поскольку ЕА и ТА каждые в отдельности рассекают сечение в двух точках, может
получиться, что от А проводится диаметр сечения. Поэтому также и касательные прово¬
дятся к каждой части. Пусть будут проведены касательные АВ и АА, и проведенная ВА.
допустим, пусть проходит не через Л и К, а либо через одну из них, либо никакую и з них.
Пусть сначала она проходит только через Л и рассекает прямую 2Н в М. Тогда
2А к АН равно 2М к МН, что абсурдно, ведь мы предположили, что 2А к АН рав¬
но 2К к КН.
Если же ВА не проходит через точки Л и К, то на АЕ и А2 получается абсурдность.
еж
10
А только на одной гиперболе это однако так: если точки пересечения одной прямой
содержат точки пересечения другой прямой и точка А расположена внутри угла, огра¬
ниченного асимптотами, то получается то же самое, что мы сказали прежде, и как
раньше было сказано во второй теореме.
11
Если при тех же самых предпосылках точки пересечения одной прямой не содержат
точки пересечения другой, то точка А будет расположена внутри угла, ограниченного асим¬
птотами и чертеж и доказательство будут теми же самыми, что и в девятой теореме.
12
Если при тех же самых предпосылках точки пересечения одной прямой содержат
точки пересечения другой, и взятая точка расположена на угле, который расположен
410

Дословный перевод книги IV
рядом с углом, ограниченным асимптотами, то прямая, проведенная через точки деле¬
ния, продолженная дальше, пересечется с противолежащим сечением, а прямые, про¬
веденные от точек пересечения к точке А, будут касаться противолежащих сечений.
Пусть ЕН будет гиперболой, МЕ и ОП - асимптотами, Р - центром, и пусть точ¬
ка Л будет расположена на угле ЕРП, пусть будут проведены АЕ и АТ, каждая по от¬
дельности, рассекая гиперболу в двух точках, и пусть Е и О содержатся Т и Н. и пусть
же будет ЕА к Д0 равно ЕК к К0, ТА к АН равно ТА к АН. Нужно доказать, что пря¬
мая, проведенная через К и Л, пересечется с сечением ЕТ и противолежащим се¬
чением, а прямые, проведенные от точек пересечения к А, будут касаться сечений.
Тогда пусть М будет противолежащим сечением, и пусть от А будут проведены
АМ и АЕ, касающиеся сечения, и пусть проведенная МЕ, допустим, не будет прохо¬
дить через К и Л, но или через одну из них, или ни через одну.
Сначала пусть она проходит через К и рассекает прямую ¿Н в X. Тогда ¿А к АН
равно Х2 к ХН, что абсурдно, ведь мы предположили, что ТА к АН равно ТА к АН.
Если же МЕ не проходит вообще через К и Л, то в случае с ЕЛ и АТ получается
абсурд.
13
Ей и при тех же самых предпосылках точка А расположена на одной из асимптот
при тех же предпосылках, то прямая, проведенная через точки деления, будет парал¬
лельна асимптоте, на которой расположена точка, и продолженная дальше, она бу¬
дет пересекаться с сечением, а прямая, проведенная от точки пересечения к точке, бу¬
дет касаться сечения.
Пусть будет гипербола, асимптоты, и пусть на одной из асимптот будет взята А, и
пусть прямые будут проведены дальше и будут разделены, как было сказано, и пусть
от А будет проведена касательная АВ. В таком случае я утверждаю, что прямая, про¬
веденная от В как параллельная прямой ПО, будет проходить через К и Л.
Ведь если это не так, то она проходит либо через одну из них, либо вообще че¬
рез них не проходит.
Пусть она проходит только через К. Тогда ¿А к АН равно 7Х к ХН, что абсурдно.
Следовательно, прямая, проведенная от В как параллельная ПО, не проходит толь¬
ко через К. Следовательно, она проходит через обе точки.
us
14
Если при тех же самых предпосылках точка А расположена на одной из асимптот,
и АЕ рассекает сечение в двух точках, а параллельная другой асимптоте АН, в одной Н,
и получается, что АЕ к Д0 равно ЕК к KQ, и устанавливается на продолженной даль¬
ше АН, что АН равно НА, то прямая, проведенная через точки К и А, будет параллель¬
на асимптоте и будет пересекаться с сечением, а прямая, проведенная от точки пере¬
сечения к А, будет касаться сечения.
Тем же самым способом, что и в предыдущей гипотезе, я утверждаю, что при
проведенной касательной АВ прямая, проведенная от В как параллельная асимпто¬
те ПО, будет проходить через точки К и Л.
411

Книга IV
Тогда если она проходит только через К, не получается ДН равно НА, что абсур¬
дно. Если она проходит только через Л, то не получается, что ЕД к Д0 равно ЕК к КО.
Если же она вообще не проходит через К и Л, то в обоих случаях получается абсурд.
15
Если на противолежащих сечениях берется некоторая точка между двумя сечения¬
ми, и от нее одна прямая касается одного сечения, а другая — рассекает оба сечения, и
как прямая, расположенная между одним сечением, которого не касается та прямая,
и точкой, относится к прямой, расположенной между точкой и другим сечением, так
и некоторая прямая, большая прямой, расположенной между сечениями, относится к
продолжению, расположенному на данной продолженной прямой и при том же самом
пределе и соответствующей части, то прямая, проведенная от предела большей пря¬
мой к точке касания, будет пересекаться с сечением, а прямая, проведенная от точки
пересечения к взятой точке, будет касаться сечения.
Пусть А и В будут противолежащими сечениями, и пусть между сечениями бу¬
дет взята некоторая точка Д, расположенная внутри угла, ограниченного асимпто¬
тами, и пусть от нее будет продолжена касательная Д7, и АДВ, рассекающая сече¬
ние, и пусть АД к ДВ равно АГ к ГВ. Нужно доказать, что прямая, проведенная от 7
к Г и продолженная дальше, пересечется с сечением, а прямая, проведенная от точ¬
ки пересечения к Д, будет касаться сечения.
Поскольку же точка Д расположена внутри угла, заключающего сечение, можно
провести от Д также и другую касательную. И пусть будет проведена ДЕ, а проведен¬
ная 7Е. допустим, будет проходить не через Г, но через Н. Тогда АД к ДВ равно АН к
НВ, что абсурдно, ведь мы предположили, что АД к ДВ равно АГ к ГВ.
М
•I».
16
Пусть при тех же предпосылках точка Д располагается на угле, который расположен
рядом с углом, ограниченным асимптотами, и пусть остальное будет тем же самым.
В таком случае я утверждаю, что прямая, проведенная от ¿к Г, пересечется с про¬
тиволежащим сечением, а прямая, проведенная отточки пересечения к Д, будет ка¬
саться противолежащего сечения.
Пусть будет то же самое, и пусть точка Д будет расположена на угле, который рас¬
положен рядом с утлом, ограниченным асимптотами, и пусть от Д будет проведе¬
на касательная сечения А ДЕ, и пусть будет проведена и продолжена дальше Е7, и,
допустим, она будет проходить не к Г, но к Н. Поэтому АН к Н В равно АД к ДВ. что
абсурдно ведь мы предположили, что АД к Д В равно АГ к ГВ.
17
Пусть при тех же самых предпосылках точка Д расположена на одной из асимптот.
В таком случае я утверждаю, что прямая, проведенная от Г будет параллель¬
на асимптоте, на которой расположена точка.
При прежних предпосылках пусть точка Д будет расположена на одной из асим¬
птот, и пусть через 7 будет проведена прямая, и они параллельны, и, если можно,
она будет проходить не через Г, но через Н. Тогда АД к ДВ равно АН к Н В, что абсур¬
412

Дословный перевод книги IV
дно. Следовательно, прямая, проведенная от 2. параллельно асимптоте будет про¬
ходить через Г.
л»
18
Если на противолежащих сечениях между двумя сечениями берется некоторая точ¬
ка, и от нее проводятся дальше две прямые, пересекающие оба сечения, и какое отно¬
шение имеют прямые, расположенные между точкой и одним сечением, к прямым, рас¬
положенным между другим сечением и той же самой точкой, такое отношение имеют
прямые, большие, чем те, которые отводятся между противолежащими сечениями, к
их продолжению, то прямая, проведенная через пределы больших прямых будет пересе¬
каться с сечениями, а прямые, проведенные от точек пересечения к взятой точке, бу¬
дут касаться линий.
Пусть А и В будут противолежащими сечениями, и пусть точка Д располагает¬
ся между сечениями. Пусть сначала она располагается на угле, ограниченном асим¬
птотами, и пусть через А будут проведены дальше АДВ и ГА0. Тогда АД больше ДВ,
ГД больше Д0, поскольку BN равно АМ. Пусть же АД к ДВ равно АК к КВ, ГД к Д0
равно ГН к Н0.
В таком случае я утверждаю, что прямая, проведенная через К и Н, будет пересекаться
с сечением, а прямые, проведенные от А к точкам пересечения, будут касаться сечения.
Ведь поскольку Д расположена внутри угла, ограниченного асимптотами, можно
провести от Д две касательных прямых. Пусть будут проведены ДЕ и Е7, и пусть бу¬
дет проведена Е7; тогда она будет проходить через точки К и Н. Ведь если она про¬
ходит только через одну из них, другая прямая будет рассекаться в другой точке на
том же самом основании, что невозможно. Если же она не проходит через них во¬
обще, то в отношении обеих точек получается абсурд.
©
©
©л
©
19
Пусть же точка А находится на угле, который лежит рядом с углом, ограничен¬
ным асимптотами, и пусть прямые, рассекающие сечение, будут продолжены дальше.
В таком случае я утверждаю, что прямая, продолженная дальше через К и Н. бу¬
дет пересекаться с обоими противолежащими сечениями, а прямые, проведенные
отточек пересечения к Д, будут касаться сечений.
Пусть же от А будут проведены касательные обоих сечений ДЕ и Д2; тогда пря¬
мая, проведенная через Е и 2, будет проходить через К и Н. Если же нет, то она про¬
ходит либо через одну из них, либо вообще не проходит ни через одну, и мы снова
придем тем же самым способом к абсурду.
»!♦
20
Если выбранная точка находится на одной из асимптот, и остальное является тем
же самым, то прямая, проведенная через пределы продолжений, будет параллельна асим¬
птоте, на которой находится точка, а прямая, проведенная от точки к пересечению
сечения и прямой, проведенной через пределы, будет касаться сечения.
Пусть А и В будут противолежащими сечениями, и пусть точка Д будет находить¬
ся на одной из асимптот, пусть остальное будет тем же самым В таком случае я ут-
413

Книга IV
верждаю, что прямая, проведенная через К и Н, пересечется с сечением, а прямая,
проведенная отточки пересечения кА, будет касаться сечения.
Пусть от А будет проведена Д7, и пусть от 7 будет проведена прямая, параллель¬
ная асимптоте, на которой находится А; тогда она будет проходить через К и Н. Ведь
если это не так, то либо она проходит через одну из них, либо не проходит ни через
одну, и получается тот же самый абсурд, что и прежде.
21
Пусть снова А и В будут противолежащими сечениями, и пусть точка А располага¬
ется на одной из асимптот, и пусть АВК, параллельная другой асимптоте, будет пе¬
ресекаться с сечением только в одной точке В, ГАЕ) же будет пересекаться с обоими
сечениями, и пусть будет ГА к Д0 равно ГН к НЕ) и АВ равно В К.
В таком случае я утверждаю, что прямая, проведенная через точки К и Н, бу¬
дет пересекаться с сечением и будет параллельна асимптоте, на которой находится
точка А, а прямая, проведенная отточки пересечения к А, будет касаться сечения
Пусть же будет проведена касательная А7, и пусть от 7 будет проведена прямая,
параллельная асимптоте, на которой находится точка А; тогда она будет проходить
через К и Н. Если же это не так, то получается прежний абсурд.
ям
22
Пусть таким же образом будут противолежащие сечения и асимптоты, и пусть
точка А будет взята таким же образом*; ГАЕ) будет рассекать сечение, а АВ — па -
раллельна другой асимптоте, и пусть ГА к АЕ) равно ГН к НЕ) и АВ равно В К.
В таком случае я утверждаю, что прямая, проведенная через К и Н. будет пересе¬
каться с обоим противолежащими сечениями, а прямые, проведенные от точек пе¬
ресечения к А, будут касаться противолежащих сечений.
Пусть же будут проведены касательные ДЕ и А7, и пусть будет проведена Е7, до¬
пустим. что она не проходит через К и Н, но либо проходит через одну, либо — ни
через одну. Если она проходит только через Н, то АВ не будет равна прямой ВК, но
некоторой другой, что абсурдно. Если же она проходит только через К, то не полу¬
чается. что ГА к А0 равно ГН к Н0, а некоторая другая (прямой) относится к дру¬
гой. Если же она вообще не проходит через К и Н, то в обоих случаях выходит абсурд.
•ж
»1».
23
Пусть снова А и В будут противолежащими сечениями, и точка А расположена на
угле, который расположен рядом с углом, ограниченным асимптотами, и пусть будет
проведена В А, рассекающая сечение В только в одной точке В и параллельная другой
асимптоте, и пусть АА будет рассекать сечение А тем же самым образом, и пусть бу¬
дет АВ равно ВН, АА равно АК.
В таком случае я утверждаю, что прямая, проведенная через К\\ Н, будет пере¬
секаться с сечениями, а прямые, проведенные от точек пересечения к А, будут ка¬
саться сечений.
* Это, очевидно, описка, так как точка Л лежит теперь внутри угла.
414

Дословный перевод книги IV
Пусть будут проведены касательные ДЕ и Д7, и пусть проведенная Е2, допустим,
не будет проходить через К и Н, Тогда она либо проходит через одну из них, либо
вообще ни через одну, или она ДА не будет равна прямой АК, но некоторой другой
прямой, что абсурдно; или не будет получаться, что ДВ равно ВН, или ни одна не бу¬
дет равна другой, и снова в обоих случаях выходит абсурд. Следовательно, Е£ про¬
ходит через К и Н.
I1 г
24
Коническое сечение не пересекается с коническим сечением или окружностью круга
таким образом, что частью они одно и то же, а частью не совпадают.
Допустим, сечение конуса ДАВГ пересекается с окружностью круга ЕАВГ, и пусть
их общая часть будет той же частью АВ Г, а АД и АЕ пусть не будут общими, и пусть
на них будет взята точка 0, и пусть будет проведена 0А, и пусть через произволь¬
ную точку Е будет проведена ЛЕГ, параллельная прямой А0; пусть А0 рассекается
на два равные части в Н, и пусть через Н будет проведен диаметр ВН7. В таком слу¬
чае прямая, проведенная через В параллельно прямой А0, будет касаться обоих се¬
чений и будет параллельна прямой ДЕГ, и на одном сечении будет Д7 равно 7Г, а на
другом Е7 равно 7Г. Поэтому также Д7 равно 7Е, что невозможно.
25
Коническое сечение не рассекает конического сечения или окружности круга более,
чем в четырех точках.
Если возможно, то пусть оно рассекает в пяти точках А, В, Г, Д, Е, и пусть точки
пересечения А, В, Г, Д, Е расположены рядом, не допускающие между собой ничего,
и пусть будут проведены и продолжены дальше АВ и ГД; в таком случае они будут на
параболе и гиперболе пересекаться вне сечений. Пусть они пересекаются в Л, и пусть
АЛ к АВ равно АО к ОВ и ДА к АГ равно ДП к ПГ. Тогда прямая, проведенная от П к
О, продолженная в обе стороны, будет пересекаться с сечением, а прямые, проведен¬
ные от точек пересечения к Л, будут касаться сечений. Тогда пусть она будет пере¬
секаться в 0 и Р, и пусть будут проведены 0Л и АР; в таком случае они будут касать¬
ся сечений. Поэтому ЕА рассекает оба сечения, поскольку между В и Г нет никакой
точки пересечения. И пусть она рассекает в М и Н. Таким образом, из-за одного се¬
чения будет ЕА к АН равно Е1Ч к №Н, а из-за другого - ЕЛ к АМ равно ЕХ к NN1. А
это невозможно. Следовательно, не получается то, что мы предположили в начале.
Если же АВ и ДГ параллельны, то сечениями будут эллипсы или окружность кру¬
га. И пусть АВ и ГД рассекаются в О и П на два равные части, и пусть будет проведена
ПО и продолжена в обе стороны; в таком случает она будет пересекаться с сечения¬
ми. Тогда пусть она пересекается в 0 и И Таким образом. ОР будет диаметром круга
и к нему проведены упорядоченные прямые [ординаты] АВ и ГД. Поэтом) пусть от
Е параллельно прямым АВ и ГД будет проведена ЕХМН. В таком случае ЕМН рас¬
секает прямую 0Р и обе линии, поскольку ничто не является точкой пересечения,
кроме А, В, Г и А. Из-за этого на одном сечении получается ХМ равно ЕХ. а на дру¬
гом - ХЕ равно N14; поэтому также NN1 равно ХН А это невозможно.
•м
•Ж
•г»
•г»
.Г.
•а
НЯ
»1»
О
415

Книга IV
Л«
26
Если те линии, о которых мы сказали, касаются друг друга в одной точке, то они
не совпадают более, чем в двух в других точках.
Ведь пусть две некоторые линии, о которых мы сказали, касаются друт друга в точке
А. В таком случае я утверждаю, что они не пересекаются в других точках больше двух.
Допустим пусть они пересекаются в В, Г, А, и пусть точки пересечения будут рас¬
положены рядом, не допуская между собой ничего [то есть между ними нет других
точек пересечения!, и пусть будет проведена и продолжена дальше В Г, пусть от А
будет проведена касательная АА, в таком случае она будет касаться двух сечений и
будет пересекаться с ГВ. Пусть она пересекается в А, и пусть получается, что ГА к
АВ равно ГП к ПВ, пусть будет проведена и продолжена дальше АП. В таком случае
она будет пересекаться с сечениями, а прямые, проведенные от точек пересечения
к А, будут касаться сечений. И пусть она будет продолжена и пересекается в 0 и И,
пусть будут проведены 0А и АК тогда они будут касаться сечений. Таким образом,
прямая, проведенная от А к А, рассекает оба сечения, и получается тот же самый аб¬
сурд, о котором мы говорили прежде. Следовательно, они не рассекают друг друга
более, чем двух точках.
Если же на эллипсе или на окружности круга ГВ и АА параллельны, то мы полу¬
чаем доказательство тем же самым способом, что и прежде, поскольку мы доказа¬
ли, что А0 является диаметром.
27
Если те линии, о которых мы сказали прежде, касаются друг друга в двух точках,
они не совпадают ни в одной другой точке.
Пусть из линий, о которых мы сказали, две касаются друг друга в двух точках А и
В В таком случае я утверждаю, что они не будут совпадать в другой точке.
Допустим, пусть они встречаются в Г, и пусть сначала Г будет расположена вне
точек соприкосновения А и В, и пусть от А и В будут проведены касательные; в та¬
ком случае они будут касаться обеих линий. Пусть они касаются и пересекаются в А,
как на первом чертеже*, и пусть будет проведена ГА, в таком случае она будет рас¬
секать оба сечения. Пусть она рассекает в Н и М, и пусть будет проведена AN В. Та¬
ким образом, на одном сечении получается ГА к АН равно ГГЧ к N14, а на другом -
ГА к АМ равно ГТЧ к NN1. что абсурдно.
•1С
28
Если ГН параллельна прямым, касающимся в А и В, то как на эллипсе на втором чер¬
теже, проведя АВ, мы заключаем, что она есть диаметр сечения. Поэтому как ГН, так
и ГМ будут рассекаться в N на два равных отрезка, что абсурдно. Следовательно, ли¬
нии не будут совпадать кроме только точек А и В.
29
Пусть же Г будет расположена между точками соприкосновения, как на третьем
чертеже.
* У нас на втором.
416

Дословный перевод книги IV
»!•
©
Очевидно, что линии не касаются друг друга в Г, ведь было предположено, что
они касаются только в двух точках. В таком случае пусть они рассекают сечение в Г,
и пусть от А и В будут проведены касательные АЛ и ЛВ, пусть будет проведена АВ и
пусть она рассекается в Т на две равные части; тогда прямая, проведенная от Л к
будет диаметром. Она же не будет проходить через Г, ведь если она будет проходить
через нее, то прямая, проведенная через Г параллельно прямой АВ, будет касаться
обоих сечений; а это невозможно. Поэтому пусть будет проведена от Г параллельно
АВ прямая ГКНМ; в таком случае на одном сечении получается ГК равно КН, на
другом - КМ равно КГ. Поэтому также КМ равно КН. что невозможно.
Если прямые касательные параллельны, то мы тем же самым способом, что и
выше, докажем также, что это невозможно.
»1».
I
30
Парабола не будет касаться параболы в более, чем одной точке.
Допустим, пусть параболы АН В и АМ В будут касаться в точках А и В, и пусть бу¬
дут проведены касательные АЛ и ЛВ, в таком случае они будут касаться обоих сече¬
ний и пересекаться в А.
Пусть будет проведена АВ и пусть она рассекается в 7 на две равные части, и пусть
будет проведена Л2. А поскольку две линии АН В и АМВ касаются друг друга в двух
точках А и В, то они не пересекаются ни в какой другой точке; поэтому Л7 рассе¬
кает оба сечения. Пусть она рассекает их в Н и М. в таком случае из-за одного сече¬
ния ЛН равно Н7, из-за другого — ЛМ равно М7, что невозможно. Следовательно,
парабола не будет касаться (параболы | в более чем одной точке.
©
31
Парабола не будет касаться гиперболы в двух точках, оказываясь вне ее.
Пусть АН В будет параболой, АМВ - гиперболой, и, допустим, пусть они каса¬
ются в А и В. и пусть от А и В прямые, касающиеся обоих сечений А и В. которые
пусть пересекаются в точке Л, и пусть будет проведена АВ и пусть она рассекается в
7 на два равные части, и пусть будет проведена Л2.
Таким образом, поскольку сечения АН В и АМВ касаются в А и В, они не пере¬
секаются ни в какой другой точке; в таком случае Х7 рассекает сечения в одной и
другой точках. Пусть она рассекает в Н и М, и пусть Л7 будет продолжена дальше;
тогда она будет проходить через центр гиперболы. Пусть центром будет Л, поэтому
из-за гиперболы 7Л к ДМ равно ДМ к ДА равно 7.М к МЛ. Однако ¿Д больше ДМ,
поэтому также 7М больше МЛ. Но из-за параболы 7Н равно НЛ, что невозможно.
©
©
I
©
32
Парабола не будет касаться эллипса или окружности в двух точках, оказываясь
внутри них.
Пусть АН В будет эллипсом или окружностью круга, АМВ - параболой, и пусть,
допустим, она касается их в двух точках А и В. и пусть от А и В будут проведены пря¬
мые, касающиеся сечений и пересекающиеся в Л, и пусть будет проведена АВ и пусть
она рассекается в 7 на два равные части, и пусть будет проведена А2; в таком случае
•1*
417

Книга IV
она будет рассекать оба сечения в той и другой точке, как мы говорили. Пусть она
будет рассекать их Н и М, и пусть М будет продолжена дальше до А, А же пусть бу¬
дет центром эллипса или круга. Тогда из-за эллипса или круга будет ЛА к АН равно
АН к М равно АН к Н7. Однако ЛА больше АН; поэтому также АН больше Н7. Но
из-за параболы ЛМ равно Мг, что невозможно.
33
Гипербола не будет касаться гиперболы в двух точках, имея одинаковый центр.
Пусть же гиперболы АН В и ЛМВ. имея одинаковый центр А, допустим, касают¬
ся А и В, и пусть от А и В будут проведены касающиеся их пересекающиеся между
собой АЛ и Л В, и пусть будет проведена и продолжена АЛ.
Однако пусть также будет проведена АВ. В таком случае А7 рассекает прямую
АВ в 2. на два равных отрезка. Поэтому А7 будет рассекать сечения в Н и М. Таким
образом, из-за гиперболы АН В будет 7АЛ равно АН в квадрате, а из-за гиперболы
ЛМВ, однако 7Л\ равно АМ в квадрате. Следовательно, МА в квадрате равно АН в
квадрате, что невозможно.
34
Есш эллипс касается эллипса или окружности круга в двух точках, имея одинако¬
вый центр, прямая, соединяющая точки касания, проходит через центр.
Пусть же линии, о которых мы говорили, касаются друг друга в точках Л и В,
и пусть будет проведена АВ, и пусть через А и В будут проведены прямые, каса¬
ющиеся сечений и. допустим, пусть они пересекаются в Л, и пусть АВ рассекает¬
ся в Z на два равных отрезка, и пусть будет проведена AZ. В таком случае AZ есть
диаметр сечений.
Допустим. А есть центр, тогда из-за одного сечения AAZ равно АН в квадрате, из-
за другого, однако, AAZ равно МЛ в квадрате. Тогда НА в квадрате в квадрате равно
АМ в квадрате, что невозможно. Поэтому прямые, касающиеся от А и В, не будут
пересекаться; тогда они параллельны и АВ является диаметром. Следовательно, он
проходит через центр, что и следовало доказать.
Коническое сечение конуса или окружность круга не будет пересекаться с кониче¬
ским сечением или окружностью круга более чем в двух точках, не имея тех же выпу¬
клостей в этой части.
Допустим, пусть сечение конуса или окружность круга АВГ будет пресекаться с
сечением конуса или окружностью круга ААВЕГ в более чем двух точках А, В, Г, не
имея тех же выпуклостей в этой части.
Поскольку на линии АВГ взяты три точки А, В и Г и проведены линии АВ и ВГ.
они при тех же самых частях, при которых находятся вогнутости линии АВГ, заклю¬
чают утол. По той же самой причине АВГ заключают тот же самый угол при тех же
самых частях, при которых находятся вогнутости линии ААВЕГ. Поэтому линии, о
которых мы говорили, имеют вогнутости при тех же самых частях и поэтому также
имеют выпуклости, что невозможно.
418

Дословный перевод книги IV
Если коническое сечение или окружность круга пересекается с одним из противо¬
лежащих сечений в двух точках, и линии, расположенные между точками пересечения,
имеют при тех же самых частях вогнутости, то линия, продолженная через точки пе¬
ресечения, не будет пересекаться с другим противолежащим сечением.
Пусть Д и АEfZ будут про
тиволежашими сечениями, и пусть ABZ будет сечени¬
ем конуса или окружностью круга, пересекающимся с другим противолежащим се¬
чением в двух точках А и Z, и пусть сечения ABZ и AiZ имеют при тех же самых ча¬
стях вогнутости. В таком случае я утверждаю, что линия ABZ, продолженная даль¬
ше, не будет пересекаться с Д.
Пусть же будет проведена AZ. А поскольку Д и ATZ являются противолежащи¬
ми сечениями, и прямая AZ рассекает гиперболу в двух точках, продолженная даль-
•I»:
ше, она не будет пересекаться с противолежащим сечением Д. Следовательно, ли¬
ния ABZ не будет пересекаться с Д.
/Л
Если коническое сечение или окружность круга пересекается с одним из противоле¬
жащих сечений, оно не будет пересекаться с остальным из них в более чем двух точках.
Пусть А и В будут противолежащие сечения, и пусть пересекается с А сечение
конуса или окружность круга АВГ и рассекает противолежащее сечение В в В и Г.
В таком случае я утверждаю, что оно не будет пересекаться с ВГ в никакой дру-
гой точке.
•г»
Допустим оно пересекается в Д. Тогда ВГД пересекается с сечением ВГ более чем
в двух точках, имея вогнутости при тех же самых частях, что невозможно.
Схожим образом мы докажем это, если линия АВГ касается противолежащего
сечения.
38
Коническое сечение или окружность круга не пересекается с противолежащими се¬
чениями более чем в четырех точках.
Это очевидно из того, что, пересекаясь с одним противолежащим сечением, не
пересекается с остальным более чем в двух точках.
ДВЕ
39
Если коническое сечение или окружность круга касается одного противолежаще¬
го сечения в вогнутой части, то оно не будет пересекаться с другим противолежащим
сечением.
Пусть А и В будут противолежащими сечениями, и пусть ГАД касается сечения А.
В таком случае я утверждаю, что ГАД не будет пересекаться с сечением В.
Пусть от А будет проведена касательная ЕА7. Тогда она касается обеих линий в
А, поэтому она не будет пересекаться с В. Следовательно, ГАД также не будет пе¬
ресекаться с В.
419

Книга IV
Если коническое сечение или окружность круга касается противолежащих сече¬
ний каждого в одной точке, то оно не пересекается с противолежащими сечениями ни
в какой другой точке.
Пусть А и В будут противолежащими сечениями, и пусть коническое сечение или
окружность круга касается А и В в точках А и В. В таком случае я утверждаю, что ли¬
ния АВГ не будет пересекаться с сечениями А и В ни в какой другой точке.
Таким образом, поскольку линия АВГ касается сечения А, пересекаясь также с В
в одной точке, она не будет касаться сечения А в вогнутой части. Тем же самым об¬
разом мы докажем, что также не будет касаться таким образом сечения В. Пусть бу¬
дут проведены касающиеся сечений А и В АА и ВЕ в таком случае они будут касать¬
ся линии АВГ. Допустим, есть еще другая [касательная] А/ и рассекает [АВГ]. Таким
образом, прямая между касательной А7 и сечением А оказывается АН, что невоз¬
можно. Следовательно, они не касаются АВГ, и поэтому очевидно, что АВГ не пе¬
ресекается
А
тиволежащими сечениями А и В ни в какой другой точке.
•Ж
41
Если гипербола пересекается с одним противолежащим сечением в двух точках, имея
противоположные выпуклости, то сечение, противолежащее ей, не будет пересекать¬
ся другим противолежащим сечением.
Пусть АВА и 7 будут противолежащими сечениями, и пусть гипербола АВГ пере¬
секается с АВА в точках А и В, имея выпуклости, противоположные вогнутостям, и
пусть противолежащим сечению АВГ будет Е. В таком случае я утверждаю, что оно
не будет пересекаться с 7.
Пусть будет проведена АВ и продолжена до Н. В таком случае, поскольку прямая
гиперболу АВА рассекает АВН и, продолженная в обе стороны, оказывается вне се¬
чения. она не будет пересекаться с сечением 7. Поэтому схожим образом из-за ги¬
перболы АВГ она не пересекается с противолежащим сечением Е. Следовательно,
Е не будет пересекаться с 7.
О
42
Если гипербола пересекается с обоими противолежащими сечениями, то сечение,
противолежащее ей, не будет пересекаться ни с одним противолежащим сечением в
двух точках.
Пусть А и В будут противолежащими сечениями, и пусть гипербола АГВ пере¬
секается с каждым противолежащим сечением А и В. В таком случае я утверждаю,
что сечение, противолежащее гиперболе АГВ, не будет пересекаться с сечениями А
и В в двух точках.
Допустим, пусть оно пересекается в А и Е, и пусть проведенная АЕ будет продол¬
жена дальше. В таком случае из-за сечения АЕ прямая ДЕ не будет пересекаться с
сечением АВ, а из-за АЕД она не будет пересекаться с В. ведь она будет проходить
через три данные места, что невозможно. Тем же самым способом мы докажем, что
она не пересекается с сечением В в двух точках
420

Дословный перевод книги IV
»!•
По той же самой причине она не будет касаться обоих сечений. Ведь проведен¬
ная 0Е будет касаться обоих сечений, поэтому из-за сечения ДЕ она не будет пере¬
секаться с АГ, а из-за АЕ она не пересекается с В. Следовательно, и АГ не пересека¬
ется с В, что противоречит предположенному.
л:»
43
Если гипербола рассекает оба противолежащих сечения в двух точках, обладая вы¬
пуклостью, противоположной каждому из них, то сечение, противолежащее ей, не бу¬
дет пересекаться ни с одним из противолежащих сечений.
Пусть А и В будут противолежащими сечениями, и пусть гипербола ГАВД рассе¬
кает оба сечения А и В в двух точках, имея выпуклую противоположную часть. В та¬
ком случае я утверждаю, что сечение EZ, противолежащее ей, не будет вообще пе¬
ресекаться с сечениями А и В.
Допустим, пусть оно пересекается с А в Е, и пусть будут проведены и продолже¬
ны дальше ГА и ДВ; тогда они пересекаются между собой. Пусть они пересекаются
в 0; тогда 0 будет располагаться на углу, ограниченном асимптотами сечения ГАВД.
И его противолежащее сечение есть EZ; в таком случае прямая, проведенная от Е к
0, оказывается на углу, ограниченным А0В. И поскольку же ГАЕ есть гипербола, и
ГА0 и 0Е пересекаются, точки пересечения Г и А не будут содержать Е, а точка 0
будет расположена внутри асимптот сечения ГАЕ. И ВД есть его противолежащее
сечение; тогда прямая, проведенная от В к 0, оказывается внутри угла Г0Е, что аб¬
сурдно, ведь та же самая |прямая | оказывалась на углу А0В. Следовательно, EZ не
будет пересекаться с одним из сечений А и В.
44
Если гипербола рассекает одно противолежащее сечение в четырех точках, то сече¬
ние, противолежащее ей, не будет пересекаться с другим противолежащим сечением.
Пусть АВГД и Е будут противолежащими сечениями, и пусть гипербола рассека¬
ет сечение АВГД в четырех точках А, В. Г и Д, и пусть противолежащим ей сечением
будет К.
Допустим, пусть они пересекаются в К, пусть будут проведены и продолжены даль¬
ше АВ и ГД; в таком случае они будут пересекаться между собой. Пусть они пересе¬
каются в Л, и пусть будет АЛ к АВ равно АП к ПВ, ЛА к АГ равно ДИ к КГ. Поэтому'
прямая, продолженная дальше через П и И, будет пересекаться с каждым сечением, и
прямые, проведенные от Л к точкам пересечения, касаются сечения. Тогда пусть будет
проведена и продолжена дальше КА. в таком случае она будет рассекать угол ВАГ и се¬
чения в одной и другой точке. Пусть она рассекает в Т и М. Таким образом, получается
из-за противолежащих сечений A0ZH и К, ТЧК к КА равно к Ъ\, а из-за АВГД и
Е, N К к КА равно N14 к МЛ, что невозможно. Следовательно, Е и К не пересекаются.
•I«.
•I»
•I»
•I«
45
Если гипербола пересекается с одним противолежащим сечением в двух точках,
имея вогнутости при тех же самых частях, с другим же в одной точке, то сечение,
противолежащее ей, не будет пересекаться ни с одним из них.
421

Книга IV
Пусть АВ и Г будут противолежащими сечениями, и пусть гипербола АГВ пере¬
секается с АВ в А и В, а с Г в одной точке Г, и пусть сечению АГВ будет противоле-
жашее А. В таком случае я утверждаю, что А не будет вообще пересекаться с АВ и Г.
Пусть же будут проведены и продолжены дальше АГ и ВГ. Таким образом, АГ и
ВГ не будут пересекаться с сечением А. Однако они также не будут пересекаться с Г
в другой точке, кроме Г. Ведь если они пересекаются в другой точке, то они не пе¬
ресекаются с противолежащим сечением АВ, а мы предположили, что они пересе¬
каются с ним. Поэтому прямые АГ и ВГ пересекаются с сечением Г только в одной
точке Г, а с А вообще не пересекаются. Поэтому А расположено на угле ЕГ7. Следо¬
вательно, сечение А не пересекается с АВ и Г.
46
Если гипербола пересекается с одним противолежащим сечением в трех точках, то
сечение, противолежащее ей, будет пересекаться с другим противолежащим сечени¬
ем только в одной точке.
Пусть АВГ и AEZ будут противолежащими сечениями, и пусть гипербола АМВГ
пересекается с АВ Г в трех точках А, Ви Г, и пусть сечению АМ Г противолежит АЕК.
В таком случае я утверждаю, что ДЕК не будет пересекаться с AEZ более чем в од¬
ной точке.
Допустим, она пересекается в А и Е, и пусть будут проведены АВ и АЕ.
В таком случае они или параллельны, или нет.
Пусть сначала они будут параллельны, и пусть АВ и АЕ в Н и 0 будут рассекаться
на два равных отрезка, и пусть будет проведена Н0; тогда она будет диаметром всех
сечений, и АВ и АЕ проведены к ней как упорядоченные прямые [ординаты]. Пусть
же от Г параллельно прямой АВ будет проведена TNEO; поэтому и она сама будет
проведена к диаметру как ордината и будет пересекаться с сечениями в одной и дру¬
гой точке. Ведь если она пересекается в той же самой точке, то они не пересекаются
в трех точках, но в четырех. Поэтому на сечении АМВ будет TN равно NE, а на се¬
чении ААВ - TN равно NO. Следовательно, также ON равно NE, что невозможно.
Пусть АВ и АЕ не будут параллельны, но продолженные дальше пусть будут пе¬
ресекаться в П. и пусть будет проведена ГО, параллельная прямой АП и пусть она
пересекается с АП, продолженной дальше до Р, и пусть АВ и АЕ в Н и 0 рассекается
на два равных отрезка, и пусть через Н и 0 будут проведены диаметры HLI и 0АМ,
а от I, А, М - касающиеся сечений IUT, MU, АТ; тогда IT будет параллельна прямой
АП, а АТ и MU - прямым ATI и OR. А поскольку МU в квадрате к UI в квадрате рав¬
но АП В к АП Е, АП В к АПЕ равно АТ в квадрате к TI в квадрате, также будет MU в
квадрате к U1 в квадрате равно АТ в квадрате к TI в квадрате, по той же самой при¬
чине М U в квадрате к UI в квадрате равно ЕРГ к АРЕ и АТ в квадрате к TI в квадра¬
те равно ОРГ кАРЕ. Следовательно, ОРГ равно ЕРГ, что невозможно.
же
•Ж
•Ж
Ю.
•э
47
Если гипербола касается одного противолежащего сечения, а другое рассекает в
двух точках, то сечение, противолежащее ей, не будет пересекаться ни с одним из них.

Дословный перевод книги IV
Пусть АВГ и А будут противолежащими сечениями, и пусть гипербола АВА рас¬
секает сечение АВГ в А и В, а сечение А касается в А, и пусть сечению АВЛ противо¬
лежит ГЕ. В таком случае я утверждаю, что ГЕ не пересекается ни с одним сечением
АВГ и А. Допустим, пусть она пересекается в АВ в Г, и пусть будет проведена АВ, и
пусть через А будет проведена касательная прямая, пересекающаяся с АВ в г, тогда
1 будет расположена внутри асимптот сечения АВА. И ему противолежит ГЕ, тог¬
да прямая, проведенная от Г к Ъ окажется внутри угла В7Д. А поскольку же гипер¬
бола есть АВГ, АВ и пересекаются, и точки пересечения А и В не содержат точку
пересечения Г, точка Т расположена внутри асимптот сечения АВГ И ему противо¬
лежит А; тогда прямая, проведенная от А к г, окажется внутри угла Аг Г, что абсур¬
дно, ведь она так же попадала на угол В7А. Следовательно, ГЕ не пересекается ни с
одним сечением из АВГ и А.
48
Если гипербола касается одного противолежащего сечения в одной точке, а в двух
с ним пересекается, то сечение, противолежащей ей, не будет пересекаться с проти¬
волежащим сечением.
Пусть АВГ и А будут противолежащими сечениями, и пусть гипербола АНГ в А
касается, а в В и Г рассекает, и пусть сечению АНГ противолежит Е. В таком случае
я утверждаю, что Е не пересекается с А.
Допустим, оно пересекается в А, и пусть будет проведена ВГ и продолжен а дальше
к Z, и пусть от А будет проведена касательная AZ. Тем же самым образом, что и пре¬
жде, мы докажем, что точка Z расположена внутри угла, ограниченного асимптота¬
ми. И AZ будет касаться обоих сечений, a AZ, продолженная дальше, будет рассекать
сечения между А и В в Н и К. И пусть будет TZ к ZB равно ГА к АВ, и пусть прове¬
денная АА будет продолжена дальше; поэтому она будет рассекать сечения в одной
и другой точках. Пусть она рассекает в N и М; тогда прямые, проведенные от Z к N
и М, будут касаться сечений, и тем же самым образом, что и прежде, из-за одного
сечения получается ЕА к AZ равно ЕК к KZ, а из-за другого, однако, ЕД к AZ равно
НН к HZ, что невозможно. Следовательно, противолежащее сечение не пересекается
49
Еош гипербола, касающаяся одного противолежащего сечения, в другой точке пе¬
ресекается с ним, то сечение, противолежащее ей, имеет с другим противолежащим
сечением не более чем одну общую точку.
Пусть АВГ и Е7Н будут противолежащими сечениями, а гипербола ААГ пусть
касается в А, а в Г рассекает, и пусть сечению ААГ противолежит Е70. В таком слу¬
чае я утверждаю, что оно имеет с другим противолежащим сечением не более од¬
ной общей точки.
Допустим, пусть оно пересекается в двух точках Е и и пусть будет проведена
Е7, и пусть через А будет проведена АК, касающаяся сечений.
Тогда они или параллельны или нет.
Сначала пусть они будут паратлельны, и пусть будет проведен диаметр, делящий
прямую Е7 на два равных отрезка; тогда он будет проходить через А и будет диаме-

Книга IV
тром сопряженных сечений. И пусть через Г будет проведена параллельно прямым
АК и Е7 ГЛАВ; в таком случае она будет рассекать сечения в одной и другой точках.
Поэтому на одном |из сечений] будет ГЛ равно АЛ, а на другом, однако, ГЛ равно
ЛВ. Этого, конечно, не может быть.
Пусть АК и Е/ не будут параллельны, но пусть они пересекаются в К, и пусть
ГД, проведенная как параллельная прямой АК, пересекается с Е/ в !Ч, и пусть АВ,
деля прямую Е/ на два равных отрезка, рассекает сечения в Е и О, и пусть от Е и О
будут проведены касательные сечений ЕП и ОР. Тогда получается, что АП в квадра¬
те к ПЕ в квадрате равно АР в квадрате к ИО в квадрате, поэтому ДК1Г к £N7 равно
ВК'Г к Е^. Следовательно, ДМГ равно ВТЧГ, что невозможно.
50
Если гипербола касается одного противолежащего сечения в одной точке, то сече¬
ние, противолежащее ей, будет пересекаться с другим противолежащим сечением не
более чем в двух точках.
Пусть АВ и ЕДН будут противолежащими сечениями, и пусть гипербола АГ ка¬
сается сечения АВ в А, и пусть сечению АГ противолежит ЕЛ/. В таком случае я ут¬
верждаю. что ЕД/ будет пересекаться с ЕДН не более чем в двух точках.
Допустим оно пересекается в трех точках Д, Е и 0, и пусть будет проведена каса¬
ющаяся сечений АВ и АГ АК, и пусть проведенная ДЕ будет продолжена дальше, и
пусть сначала АК и ДЕ будут параллельны; и пусть ДЕ рассекается в Л на две равные
части, и пусть будет проведена АЛ. Тогда АЛ будет диаметром для сопряженных се¬
чений и рассекает сечения между Д и Е в М и N. И пусть от 0 будет проведена па¬
раллельно прямой ДЕ 0/Н, тогда на одном сечении будет 0Е равно Е/, а на другом,
однако, 0Е равно ЕН. Поэтому также Е/ равно ЕН, что невозможно.
Тогда пусть АК и ДЕ не будут параллельными, но пусть они пересекаются в К. и
остальное пусть останется тем же самым, и пусть продолженная дальше АК пере¬
секается с /0 в И. Тем же самым способом, что и прежде, мы докажем, что на сече¬
нии /ЛЕ ДКЕ к АК в квадрате равно /И0 к ИА в квадрате, а на сечении НЛЕ, одна¬
ко, ЛКЕ к АК в квадрате равно НИ0 к ИА в квадрате. Поэтому Н И0 равно /И0, что
невозможно. Следовательно, ЕЛ/ пересекается с ЕДН не более чем в двух точках.
Если гипербола касается обоих противолежащих сечений, то сечение, противоле¬
жащее ей, не будет вообще пересекаться ни с одним из них.
Пусть А и В будут противолежащими сечениями, и пусть гипербола АВ касает¬
ся обоих сечении в А и В. и пусть ей противолежит Е. В таком я утверждаю, что Е не
пересекается ни с одним из сечений А и В.
Допустим, она пересекается с А в Д, и пусть от А и В будут проведены прямые,
касающиеся сечений; в таком случае они будут пересекаться между собой внутри
асимптот сечений АВ. Пусть они пересекаются в Г, и пусть будет проведена ГЛ; тог¬
да ГЛ будет находиться на месте, расположенном между АГ и ГВ. Однако она также
оказывается между ВГ и Г/, что абсурдно. Следовательно, Е не пересекается с А и В.
424

Дословный перевод книги IV
52
Если противолежащие сечения с двух сторон касаются /других/ противолежащих
сечений в одной точке /каждое/, имея при тех же самых частях вогнутости, то они не
встречаются в другой точке.
Пусть же противолежащие сечения касаются друг друга в точках А и Д. В таком
случае я утверждаю, что они не встречаются ни в какой другой точке.
Допустим же, они встречаются в Е. Поскольку же гипербола, касающаяся одного
противолежащего сечения в Д, пересекается с ним в Е, АВ не имеет с АГ более од¬
ной общей точки. Пусть от А и Д будут проведены А0 и 0Д, касающиеся сечений, и
пусть будет проведена АД, и пусть через Е параллельно прямой АД будет проведена
ЕВГ, и пусть от 0 будет проведен второй диаметр противолежащих сечений 0КЛ;
тогда он будет рассекать прямую АД в К на две равные части. Тогда ЕВ и ЕГ в Л рас¬
сечены на две равные части. Поэтому ВЛ равно АГ, что невозможно. Таким обра¬
зом, они не встречаются ни в какой другой точке.
»!•
ХЛ
•1».
»1»:
53
Если гипербола касается одного из противолежащих в двух точках, то сечение, пг_
тиволежащее ей, не будет встречаться с другим противолежащим.
Пусть АДВ и Е будут противолежащими сечениями, и пусть гипербола АГ каса¬
ется сечения АДВ в двух точках А и В, и пусть сечению АГ противолежит 7. В таком
случае я утверждаю, что 7 не встречается с Е.
Допустим, оно совпадает в Е, и пусть от А и В будут проведены касательные к се¬
чениям АН и Н В, и пусть будут проведены АВ и ЕН, которая пусть будет продолже¬
на дальше; тогда она будет рассекать сечения в одной и другой точках. И пусть она
выступает таким образом как ЕНГД0. Тогда поскольку АН и НВ касаются сечений,
а АВ соединяет точки соприкосновения, на одном сопряженном сечении будет 0Е
к ЕН равно 0Д к ДН, а на другом - 0Е к ЕН равно 0Г к ГН, что невозможно. Таким
образом, 7 не встречается с Е.
о.
с»
/Л
V/
•и
54
Если гипербола касается одного из противолежащих, обладая противоположной вы¬
пуклой частью, то сечение, противолежащее ей, не будет встречаться с другим про¬
тиволежащим.
Пусть А и В будут противолежащими сечениями, и пусть касается сечения А ги¬
пербола АД в А, и пусть сечению АД противолежит 7. В таком случае я утверждаю,
что 7 не встречается с В.
Пусть от А будет проведена касательная сечений АГ, тогда АГ из-за АД не пере¬
секается с 7, а из-за А она не будет пересекаться с В. Следовательно, АГ оказывает¬
ся между сечениями В и 7, и очевидно, что В не пересекается 7.
55
Противолежащие сечения рассекают противолежащие сечения не более чем в че¬
тырех точках.
425

Книга IV
Пусть АВ и ГД будут противолежащими сечениями, а другими противолежащими
сечениями пусть будут АВГД и Е2. Пусть же сначала сечение АВ ГД рассекает каж¬
дое сечение АВ и ГД в четырех точках А, В, Г и Д, имея противоположную выпуклую
часть, как на первом чертеже. Таким образом, сечение, т.е. противолежащее сечению
АВГД Е2, не будет пересекаться ни с одним из сечений АВ и ГД.
Однако пусть АВГД рассекает сечение АВ в А и В, сечение же Г - только в Г, как
на втором чертеже, тогда ЕХ не будет пересекаться с Г. Если же с АВ пересекается
Е2, то оно пересекается только в одной точке. Ведь если оно пересекается с АВ в двух
точках, то сечение, противолежащее ей, АВГ не пересекается с другим противолежа¬
щим сечением Г. А мы предположили, что она пересекается только в одной точке Г.
Если же, как на третьем чертеже, АВГ рассекает сечение АВЕ в двух точках А и
В. а с АВЕ пересекается Е2, то она не будет пересекаться с Д, и не пересекается бо¬
лее чем в двух точках с АВЕ.
Если же, как на четвертом чертеже, АВГД рассекает каждое сечение в одной точ¬
ке. Е2 не будет пересекаться ни с одним в двух точках. Таким образом, из-за того,
что мы сказали, и обратного, сечения АВГД и Г2 не будут пересекаться с ВЕ и Е2,
противолежащими им более чем в четырех точках.
Если же сечения при тех же самых частях имеют вогнутости, одно рассекает дру¬
гое в четырех точках А. В, Г и Д, как на пятом чертеже, Е2 не будет пересекаться с
другим сечением. Однако же Е2 не будет пересекаться с АВ; ведь, таким образом,
снова АВ не будет пересекаться с противолежащими сечениями АВГД и Е2 более
чем в четырех точках.
Если же. как на шестом чертеже, АВГД пересекается с другим сечением в грех
точках, Е2 пересекается с другим сечением только в одной точке.
А в остальных случаях мы скажем то же самое, что и выше.
Поэтому во всех случаях, которые можно помыслить, относительно распределе¬
ний очевидно предположение, что противолежащие сечения пересекаются с про¬
тиволежащими сечениями не более чем в четырех точках.
АЖ
*1»
56
Если противолежащие сечения касаются противолежащих сечений в одной точке,
то они пересекаются не более чем в двух других точках.
Пусть АВ и ВГ - противолежащие сечения, а другие -Ди Е2. и пусть ВГЛ каса¬
ется сечения АВ в В, и пусть они имеют противоположную выпуклую часть, и пусть
сначала ВГД пересекается с ГД в двух точках Г и Д, как на первом чертеже.
Поэтому поскольку ВГД в двух точках рассекает противоположную выпуклую
часть. Е2 не будет пересекаться с АВ. Поскольку снова ВГД касается сечения АВ в
В, имея противоположную выпуклую часть, Е2 не будет пересекаться с ГД. Поэто¬
му Е2 не будет пересекаться ни с одним из сечений АВ и ГД; следовательно, они пе¬
ресекаются только в двух точках Г и Д.
Но пусть сечение ГД рассекает ВГ только в одной точке Г, как на втором чертеже.
Таким образом. Е2 не будет пересекаться с ГЛ, однако она будет пересекаться с АВ
только в одной точке. Ведь если Е2 пересекается с АВ в двух точках, то ВГ не будет
пересекаться с ГД, а мы предположили, что она пересекается с ней в одной точке.
426

Дословный перевод книги IV
Если же В Г не пересекается с сечением Д, как на третьем чертеже, из-за того, что
мы сказали прежде, Е£ не будет пересекаться с Д, и Е7 будет пересекаться с АВ не
лее чем в двух точках.
Если же сечения имеют вогнутости, расположенные при тех же самых частях, то
получаются те же самые доказательства.
Следовательно, во всех случаях, которые можно представить, очевидно доказа¬
но наше предположение относительно распределений.
57
Если противолежащие касаются противолежащих в двух точках, то они не будут
встречаться в другой точке.
Пусть АВ и ГД будут противолежащими сечениями, и пусть другими противоле¬
жащими сечениями будут АГ и Е2, пусть сначала они, как на первом чертеже, ка¬
саются в А и Г.
Таким
их сечений АВ и ГД в точках А и Г, Е1
не будет встречаться ни с одним из сечений АВ и ГД.
Пусть же они касаются, как на втором чертеже. Тогда мы схожим
разом дока¬
жем, что ГД не пересекается с Е7..
Пусть же, как на третьем чертеже, Г А касается сечения АВ в А, а Д - сечения Е1
ьТ. Тогда поскольку АГ касается АВ, обладая выпуклой противоположной частью,
Ег не будет пересекаться с АВ. Поскольку же снова ¿Д касается Е7.. ГА не будет пе¬
ресекаться с дг.
Если же АГ касается сечения АВ в А. а ЕГ - сечения ГД в Г, и они обладают во¬
гнутостями, расположенными при тех же самых частях, как на четвертом чертеже,
они не будут пересекаться нив какой другой точке. И Е7 не будет пересекаться с АВ
Следовательно, во всех случаях, которые можно представить, очевидно доказа¬
но наше предположение относительно распределений.
427

Распределение предложений по темам
РАСПРЕДЕЛЕНИЕ предложений по темам
ТЕМА
№
1
2
Диаметры
3
Касательные
5
Углы и параллельность
10
12
Численные соотношения
между квадратами и про¬
изведениями отрезков
18, 19,22,23,
26-31
30, 33-36,
46-48
7, 37, 39, 46-
48
20,21,37-40,
49-51
7, 28-30, 34-
36
7, 15, 20,21,
49-51
14, 16,28-31,
44, 48,51,59
Ординаты
Фокусы и их свойства
44-49
1-15
5, 8, 13, 14,
17, 20,21
4,7, 12, 15-
23, 36-57
1-4, 6, 7,
9-16, 18,
19, 22,23
53-56
39-41
53-56
23
Пересечение конуса с
прямыми и плоскостями.
Определение параболы,
гиперболы и эллипса
Диаметры сопряженные
КНИГА I
1-14
15, 16,38,40,
45, 60
17,24,25,
32-36
КНИГА II
КНИГА III
КНИГА IV
20,21,37-39,
43,49
5,6, 9, 19,21
27,31-33,40,
49-51,53
20,41,42
Пересечение прямых
и кривых
Численные соотношения
между отрезками
9
13
14
15
16
17
42И
Площади реальных фигур
(соотношения)
Асимптоты и отрезки,
отсекаемые ими
или на них
Пересечение кривых
между собой
Задачи на построение
Сопряженные гиперболы
Предложения, относящи¬
еся к проективной гео¬
метрии
52-60
11, 13, 18
24-26, 32, 33,
41,42
8, 16, 19
3, 10-12, 22-
5,6, 27,31,
35,52
1-3,8-12,
14-17,21,22
4, 44-51,53
15, 16, 31-36
17, 18-23,37,
38,42,43
30-41,50-52
16-29,42,43
29, 34, 35,
43,44
45-48, 50-52
4-8,10-12
18-22,31,
33, 36-40,
42,44-51,53
55,56
13-15, 23-26,
28,29
30-40,41-43,

	Предложения, на которые было больше трех ссылок
предложения, на которые было больше трех ссылок
№ Предложения
1
2______
3
Книга 1
|	Книга II
|	13
|	5
I	13	'
Книга III
8
1	4
| Книга IV
4
| 8
5
6
I	16
|	5
|	4
|	8
|	11
| 6
|	4
|	9
1 12
1 9
| 6
	13

	5

| 16
10
| 20
|	4
1 4
| 21
|	23
| 22
|	д
|	25
1 6~
Г	29
7
30	|
5
4
7
31 ~~
32 -
		 33	|
8
	34	|
5	|
35	|
36	|
11	|
3	|
_	37	|
25	|
9 1
	38
		39
10 |
5
7
5 1
	41
___________46
		47
4	|
5	I
10	|
4	1
_	48	~
	49
6	I
4	|
7

_	50
		51
5	|
4	|
_	60
7	Г
429

ПРИЛОЖЕНИЯ
ТЕОРЕМЫ ЕВКЛИДА, НА КОТОРЫЕ ЕСТЬ ССЫЛКИ
ТЕКСТЕ*1
1.	5-й постулат
И если прямая, падающая на две прямые, образует внутренние и по одну сторо¬
ну углы, меньше двух прямых, то, продолженные, эти две прямые неограниченно
встретятся с той стороны, где углы меньше двух прямых.
1.21
Если в треугольнике на одной из сторон от кон¬
цов восставлены будут внутрь две прямые, то вос¬
ставленные прямые [вместе] будут меньше двух
остальных сторон треугольника, но будут заклю¬
чать больший угол.
Действительно, пусть в треугольнике АВС вос¬
ставлены внутрь из сторон ВС будут от КОННОВ В,
С восставлены внутрь две прямые ВЭ и ЭС; я ут¬
верждаю. что ВЭ и ЭС [вместе] меньше остальных в
двух сторо
н треугольника ВА и АС, но заключают
угол ВЕ>С, больший, чем ВАС.
1.43
Во всяком параллелограмме дополнения распо¬
ложенных по диаметру параллелограммов равны
между собой.
Пусть будет параллелограмм АВСЭ, диаметр
же его АС, по АС же пусть будут параллелограм¬
мы ЕС, PH, так называемые же дополнения - В К,
КО, я утверждаю, что дополнение ВК равно до¬
полнению КО.
II.	5
Если прямая линия рассечена на равные и неравные [отрезки], то прямоуголь¬
ник, заключенный между неравными [отрезками] всей прямой, вместе с квадратом
на отрезке между сечениями равен квадрату на половине.
В самом деле, пусть какая-либо прямая АВ рассечена на равные части в С, на не¬
равные же в О: я утверждаю, что прямоугольник, заключенный между АО и ОВ вме¬
сте с квадратом на СО. равен квадрату на СВ**.
А	а	С Ь й	а-Ь	В
	 I— ■■ ■■ I — —	1 .1 I ■ ■■■■ II I » ■ ■	■ I

Теоремы даны в переводе Д Д Мордухай-Болтовского, но, поскольку мы не приводим дока¬
зательств, лишние детали на чертежах убраны. Также убраны сноски и ссылки.
Если обозначить отрезки как на чертеже, то все сводится к очевидному равенству
(а + Ь) (а - Ь) + Ьг = аг
430

Теоремы Евклида, на которые есть ссылки в тексте*
11.6
Если прямая линия рассечена пополам и к ней по прямой приложена какая-либо дру¬
гая прямая, то прямоугольник, заключенный между всей прямой с приложенной и самой
приложенной, вместе с квадратом на половине равен квадрату на /прямой/, составлен¬
ной из половины и приложенной.
В самом деле, пусть какая-либо прямая АВ рассечена пополам в точке С, к ней
же «по прямой» приложена какая-либо другая ВО; я утверждаю, что прямоугольник,
заключенный между АО и ЭВ вместе с квадратом на СВ, равен квадрату на СО*.
А а С а В Ь й
■	—	— 		-»

III.	36
Если вне круга взята некоторая точка, и из нее на круг па¬
дают две прямые, и одна из них пересекает круг, другая же ка¬
сается, то прямоугольник, /заключенный/ между всей секущей
и внешним отрезком, содержащимся между этой точкой и вы¬
пуклой частью обвода, будет равен квадрату на касательной.
Пусть вне круга АВС взята некоторая точка О, пусть от
О на круг АВС падают две прямые ОС | А], О В; и пусть ОСА
пересекает круг АВС, ОВ же его касается; я утверждаю, что
прямоугольник, заключенный между АО и ОС, равен ква¬
драту на О В.
VI. 1
Треугольник и параллелограмм, находящиеся под одной и той
же высотой, [относятся/ друг к другу как основания.
Пусть треугольники будут АВС, АСО, параллелограммы
же ЕС, С1 под одной и той же высотой АС; я утверждаю, что
будет: как основание ВС к основанию СО, так и треуголь¬
ник АВС к треугольнику АСО и параллелограмм ЕС к па¬
раллелограмму СЕ
VI. 2
Если в треугольнике параллельно одной из сторон проведена
в
некоторая прямая, то она пропорционально рассекает стороны
треугольника; и если стороны треугольника рассечены пропор¬
ционально, то прямая, соединяющая сечения, будет параллель¬
на остающейся стороне треугольника.
Пусть в треугатьнике АВС параллельно одной из сторон ВС
проведена ОЕ; я утверждаю, что будет как ВИ к НА. так и СЕ к ЕА
...Но вот пусть в треугольнике АВС стороны АВ, АС рас¬
секаются пропорционально, как ВО к ОА. так и СЕ к ЕА; со¬
единим ОЕ; я утверждаю, что ОЕ параллельна ВС.
©
* Теорема эквивалентна равенству (2а + Ь) Ь + а2 = (а - Ь)?.
431

Приложения
VI. 8
Если в прямоугольном треугольнике проведен из пря¬
мого угла к основанию перпендикуляр, то треугольники
при перпендикуляре подобны и целому, и между собой.
Пусть будет прямоугольный треугольник АВС,
имеющий прямой угол ВАС, и пусть проведен из А
к ВС перпендикуляр AD; я утверждаю, что каждый
из треугольников ABD и ADC подобен целому АВС
и.
и также между с
VI. 15
В равных треугольниках, имеющих по одному равному углу,
стороны при равных углах обратно пропорциональны; и из тре¬
угольников, имеющих по одному равному углу, равны те, у ко¬
торых стороны при равных углах обратно пропорциональны.
Пусть будут равные треугольники ABC, ADE, имеющие
по одному равному углу - угол ВАС, равный DAE; я утверж¬
даю, что в треугольниках АВС и ADE стороны при равных
углах обратно пропорциональны, [то есть] как СА к AD, так
и ЕА к АВ.
VI. 19
Подобные треугольники находятся друг к
другу в двойном отношении* соответствен¬
ных сторон.
Пусть подобные треугольники будут АВС
и DE1, имеющие угол при В, равный углу при
Е, и как АВ к ВС, так и DE к EI, так что ВС
соответственна с EI; я утверждаю, что треу¬
гольник АВС к треугольнику DE1 имеет двойное отношение ВС к ЕЕ
«а
¥1.32
Если два треугольника, имеющих две стороны,
пропорциональные двум сторонам, приставляются
одним углом так, чтобы соответственные сторо¬
ны были и параллельны, то остальные стороны тре¬
угольников будут по Iодной! прямой.
Пусть будут два треугольника АВС, ИСЕ, имею¬
щих две стороны ВА, АС пропорциональные двум
сторонам ЭС, ЭЕ, как АВ к АС и ОС к РЕ, и АВ
параллельна ОС, АС же ОЕ; я утверждаю, что ВС
будет по (одной] прямой с СЕ.
•г»
* То есть в отношении квадратов
432

Теоремы Евклида, на которые есть ссылки в тексте*
VII. Опр. 16
Говорят, что число умножает число, когда сколько в нем единиц, столько раз со¬
ставляется умножаемое и что-то возникает.
XI. 15
Если две прямые, касающиеся друг друга*, парал¬
лельны двум прямым, касающимся друг друга, не на¬
ходясь в одной и той же плоскости /с ними/, то ¡про¬
ходящие/ через них плоскости параллельны.
В самом деле, пусть две прямые АВ, ВС, каса¬
ющиеся друг друга, будут параллельны двум пря¬
мым ЭЕ, Е1, касающимся друг друга, но находясь
водной и той же плоскости; я утверждаю, что (про¬
ходящие! через АВ, ВС, ЭЕ, Е1 плоскости, будучи
продолжены, не встретятся друг с другом.
XI. 16
Если две параллельные плоскости пересекают¬
ся какой-нибудь плоскостью, то общие их сечения
будут параллельны.
Пусть две параллельные плоскости АВ, CD пе¬
ресекаются плоскостью EIHG,
шие же сечения
пусть будут El, HG; я утверждаю, что EI будет па¬
раллельна HG.
* Имеющие общую точку
433

Приложения
ШКАЛА ВРЕМЕН ЖИЗНИ ГЕОМЕТРО
500
450
550
100
200
250
300
150
350
400
Времена жизни древнегреческих математиков, упоминающихся в книге
434

Теорема Бернулли
ТЕОРЕМА БЕРНУЛЛИ
Теорема Бернулли латинский текст и чертежи.
JACOBI
BERNOULLI,
OPER А
Tomits Primus.
Sumpdbus Hxrcdum ’CRAMER
& Fratrum PHILIBERT.
M. DCC. XL1V.
435

Приложения
$i8 CONSTRUCTIO PROBLEMATUM SOLIDORUM
Xyxvü cxPcdK1U5 dan	quis íecum rite penfitaverit , fa-
’ tebitur ♦ & hoc invento, non levcm Geometría: acccilioncm fa-
itdm eile.
ANNO T А T l 0.
tefl March. HosriTALllJ Trailtrtut
Aiidljtiats de Se.hombuf Canten ,
Lib. IX. Prop. ia. pag.
Ilirtim conPruäjonum funda-
metHum \idcfis N’. LI V. Propp.
29-55. ex qjAl non difficile eil lin¬
gulas dimonllrarc. Videri ctiam po-
№. XXXV HI.
NOVUM THEOREMA
PRO
DOCTRINA
SECTIONUM CONICARUM,
Per Jac. Bernoulli.
An Fr i IV /1 1 *UM ‘ in mau’ria Veteribus ac Rcccntionbus adeo
|\/| frita, reliütm eile aliquid, quod corum indultriam ad-
Ku .pjic X ▼ X huc ertugerit, prricrtim propnetatem adco generalem ,
cojulinodi eil hax> qux lequitur :
Fi in triangulo per axtm cení ACD, demittatnr a vértice in ba-
ß* perpendtcularii AI, er ex ea alfcindaiur AN. atjuahf per»
penda ulart Aß, ex eodtm ver tice a in di ame t rum ex ge ñera-
ticite com -JeAienu HO demi'h > ac per N agaenr FE paral-
lela
436

Теорема Бернулли
NOVUM THEOREMA DE CONI- SECTIONIBUS. 419
le la bafi. fecant entra trianguli per axem in F & E . trit FF
Latttt Reel tern etm-Sedi finir,
DEMO N STRATI O.
Ducantur AQ^& AL parallels diametro HO & bafi CD,
quaruin prior lccct îpl'ani FE 111 G; crunrquc Triangula FAG,
HAL, HCO, ut 5c AGF, MLA, MOD, fimilia: icd &
AL-=AG [ cil cnim angulus LAN — angulo BAG, dempto-
que communi BAN, angulus LAB — N AG ; prætcrca anguh
ABL, ANG, rctli, & latus AB-= laten AN , ac proptcrca
Triangula ABL, ANG fnniha & æqualia J Hinc
1» In Farabcla. F G : AF = AL [AG] : AH; quarc
Rcâanguluna F AG = AH x I G. Sed , ex A p 0 L lün 10 *,
Red. F AG [AHxtG]: F G1 [ = A H : FG ] = AH : R
[Latus rcüum Parabola: J Ergo FG vcl FE = R.	F. D,
Idem ex aha proprietate rarabola HO: CO == AG [AL vcl
OQ J : FG- Hinc H O x F G = C O Q,— O P — [ ex natura
Parabola: J HOxR. Ergo FG vcl F E R. E. D.
1, in Hyperbola dr Elliffi• FG: AG = AL: LH (unde FGx
LH = GAL. ) Irem A G : G E = ML: A L > quarc ex a^uo
per fur bate, FG; GE = ML: LH; &, eomponend» feu dividen¬
de , FE : GE = MH ; LH > permutando^ue F E : M H = G E :
LH —FGE: FGx LH IG AL feu GA]==R: MH, ex
Apollonio f. Frgo FE = R. E. D.
Idem ex alia proprietate h arum Seîlionum:
GEAG = LA : ML , & AG : FG = LH : LA, unde per¬
turb at e Se comporte , vcl divifim, ut antca , pennutando^ue FE:
MH = GE : LH = GE. AG -F AG [ AL ] LH == OD : MO +
Jxr. Bernoulli ORera.	H h b	OC ;
* Conic. L II.
t Conic. I. ix Ôc 13.
В последней строчке текста и далее в подобных случаях, Бернулли, в формуле
GE GEAG
ODOC
=	ставит почему-то знак +.
LH AG • LH
МО НО
437

Приложения
NOVUM Т И Е О R Е М А
Num. ОС: ИО — COD [ О Р1 ] : М О И = R : М Н , ex natura
XXXV III $calonum. Ergo FE = R. E. D.
j. 7n Circule bafj fubcontrarie pofito, r£ cvidcntior eft, quam
et dcmonftrationc indigcat.
Dcmcu'lratio univerfdis pre omnibus jecliombus.
Ducatur H7 bafi parallcla, fecans jplám A Q in X, cntquc
HZ: FE —HX [LA leu AGj : Ю—НО: ОС —НЛ R>
per ca quz habet WaLLiSIUS in TracLttn de Stchoatbus Coni-
cis pag. zg. J7. & 43. i-rgo FE = R. E. D.
Corollarium I. Si ccntro A, radio quocunquc AB , in piano
trianguh per axem , dcicriptus fit circulus, & circa ilium rotc-
tur planum B O , tangens iubmdc cjus penphenam > lecansquc
bafin com fccundum redam OP, qua: bafi tnanguh per axem
perpendiculars eft, omnes hac rotationc gemtx* Coni - Setlioncs,
five Parabolz, Hyperbolz, Flliples, five demque Circuli, idem
habebunt Latus redum, zqualc videlicet redz FE.
Cor ollar i um II. Quia Al CDr=:AN [AB] . FE [R Ji fc-
quitur, in quavis Coni-Sedione, Latus redum cfic quarram pro
portionalcm ad A I, C D & A B. Unde, vcl ex hoc indicio ,
colligo , nihil huculquc conftmlTc Comcorum Scriprortbus de
hoc Theorematc, cum non vcnfimilc fit, illas (fi fcivilTcnt) dc-
fignaturos runic rationcm Parametn ad al am redam , per rario-
ncm Quadra» CD ad Rcdangulum CAD (ut in Parabola aut
Redanguli CQD ad Quadratum AQ ( ut in Hyperbola & Hiip-
fi,) quam ramen per fimpheem rationcm redarum conftannum
CD St Al , & quidem univcrlahtcr in quavis fedionc, charade-
rilare potuilfcnt.
•If
Cum Frarn hzc aperuilTem, mox cadcm fins quoque demon-
ftratKmbus mvnivt; qvas, qu a non inconcuinz rr.ihi vifz font,
Ыс fubjungam; quod m novo Thcorcmatc facile nicrcbitur vc-
niam :
I. in Fardóla FG: HX = AG [HX]: A Xi proinde
HX‘
438

Теорема Бернулли
de coni-sectioni
и s.
421
HX' = FGx АХ; eft autem * НА • r
[FGxAXJ^HA: FG. Ergo FG vel FE
НАхАХ: HX*
R. & Е. AXXXVlll
Num.
Aliter. AH: F G — AH i H X + HX.- FG AF.- FG ■+•
HX [AG].- FG = AFxAG; FG* = AH.-R*. ErgoFG =
R. £-.£• D.
1. In Hjfcrboln & Elliffi. MH- FE=='MH. HZ + H7-
FE ==AG : GF + AX: AG [HX] — AG.-GE + AG.- GF
= AG>: EGF == MH , R f bgo FE = R. о. к Л ’
* Лpoll on. Conic. I. II.
t Apollon. Conic. I. 12. <5c 1 j.
jPwafn* fa.
439

Приложения
*
№ XXXVIII. НОВАЯ ТЕОРЕМА В ОТНОШЕНИИ УЧЕНИЯ О КОНИЧЕСКИХ
СЕЧЕНИЯХ ЯКОБА БЕРНУЛЛИ
Удивительно, что в предмете, который столько раз исследовался древними и но¬
выми учеными, до сих пор осталось что-то, до чего и по сей день не коснулось их
усердие; особенно когда речь идет о столько обшем свойстве, как нижеследующее.
Если в треугольнике ACD, проведенном через ось конуса, опустит ь от вершины на
основание перпендикуляр AI и отсечь на нем отрезок AN, равный перпендикуляру АВ,
опущенному из той же вершины А на диаметр НО, продолженный вне конического се¬
чения, а через N провести прямую FE, параллельную основанию и рассекающую сторо¬
ны осевого треугольника в точках F и Е, то FE, будет Latus Rectum конического сечения.
•г»
•А
•А
ДОКАЗАТЕЛЬСТВО
Проведем прямые AQ и AL, параллельные диаметру НО и осно
торых первая пересечет FE в точке G. При этом образуются подобные треугольники
FAG, HAL, НСО, а также AGE, MLA, MOD. Тогда AL=AG (ведь ZLAN = ZBAG, с
общим углом BAN, следовательно, ZLAB = ZNAG, а кроме того, углы ABL и ANG
прямые и АВ = AN, поэтому треугольники ABL, ANG, подобные и конгруэнтные).
Отсюда:
ванию CD, из ко-
1 .Для параболы
AHFG = AFAG.
Из подобия треугольников FAG и HAL, и равенства AL=AG, следует, что
FG _ AL _ AG
AF”aH~AH
Разделим на FG2
AH FG_ AF AG
FG2 " FG2 '
AFAG АН
Но (Аполлоний 1,11) —. (R - Latus Rectum параболы)
АН • FG АН АН
Тогда ——;— = —- = —-.
FG FG R
То есть FG = R.
Что и требовалось доказать.
То же самое, из другого свойства парабо
лы.
Из подобия треугольников FAG и НСО и равенства AL = AG следует, что
— = —= —= ^=>HOFG = COOQ = OP2
СО FG FG FG	.
Но так как по свойству параболы (Аполлоний 1.11) ОР2 = НО R,
то НО FG = НО R FG = R.
440

№ XXXVIII Новая теорема в отношении учения о конических сечениях Якоба Бернулли
Что и требовалось доказать.
2.	Для гиперболы и эллипса
Из подобия треугольников FAG и HAL и равенства AL=AG следует, что
— = — = — => FGLH = AG2.
AG EH LH
AG ML
Точно так же	=	.
GE AL
ЕС МЕ
Умножим почленно на первую пропорцию:	= 7—7.
СЕ ЕН
ЕЕ МН
Прибавив слева и справа единицу, получим —— =	.
СЕ ЕН
ЕЕ СЕ ЕС СЕ ЕС СЕ
Отсюда следует	=	=	=	—у—.
МН ЬН Рб-ЬН Аб2
ЕС СЕ_ Я
Дтя гиперболы и эллипса, согласно Аполлонию (1,12 и 13),—А ^2""" ~ 7777-
АО" МН
ЕЕ Я
Следовательно,	=	 и ЕЕ = И.
МН МН
Что и требовалось доказать.
Тоже самое из другого свойства этих сечений.
GE LA
Из подобия соответствующих треугольников следует, что —— = ——
AG ML
AG LH
и —~ =

FG LA
СЕ БС
Перемножим почленно и переставим средние члены пропорции:—7 = 777-
ЕН МШ
СЕ СЕ + ЕС БЕ
Согласно свойству пропорции,	=	=	.
ЕН ЕН + МЕ МН
GE GE • AG
Однако —— =	77—77 .
LH AG • LH
СЕ 00
и, учитывая, что из подобия треугольников следует	=	и
АС МО
АС _ ЕА _ БС ОС	ЕЕ СЕ ОЭ ОС
ЬН ” ЬН _ Ав ” НО’ получаем мн ~ ьн " МО НО '
А так как для гиперболы и эллипса, согласно Аподюнию (1,12 и 13),
441

Приложения
R
~МН
R
		и
МН
FE= R.
♦
ч
OD ОС
МО НО
FE
то	=
МН
Что и требовалось доказать.
3.	В круге, расположенном противоположно основанию, дело очевидно и не требу¬
ет доказательства.
Универсальное доказательство для всех типов сечений
Проведем параллельно основанию прямую HZ, рассекающую AQ в точке X.
HZ HX HO
Тогда, поскольку HX = LA = AG,	=	=	.
FE FG ОС
НО HZ
Но (см. Wallisius in Tractatu de Sectionibus Conicis, c. 28, 37 и 43)	=

ОС R
Следовательно, FE - R. Что и требовалось доказать.
Следствие I. Если вокруг центра А описать круг с любым радиусом АВ в плоско¬
сти осевого треугольника, а вокруг него вращать плоскость ВО, которая касается
окружности, рассекая основание конуса по отрезку ОР и которая перпендикулярна
СЭ - основанию осевого треугольника, то все сечения, полученные от этого враще¬
ния, будь то параболы, гиперболы, эллипсы или. наконец, круги, будут иметь одну
и ту же отвесную сторону (В) сечения, равную отрезку РЕ.
AI	AN AB
Следствие II. Поскольку —- = —— = —-, то для любого конического сечения
CD FE	R
Latus Rectum есть четвертый член у пропорции AI, CD и АВ.
Отсюда, из этого доказательства, я заключаю, что об этой теореме до сих пор ни¬
чего не было известно тем авторам, которые писали о конических сечениях; хотя и
это очень странно, но они должны были бы (если бы знали о ней) рассчитать отно¬
шение параметра к другому отрезку, через отношение квадрата CD к прямоуголь¬
нику CAD (как в параболе), или прямоугольника CQD к квадрату AQ (как в гипер¬
боле и эллипсе)*, а не через простое отношение постоянных отрезков CD и AI, ко¬
торые имеются в любом сечении.
*	Непосредственно такой формулы там нет, но она легко выводится из формул в тексте.
и СО2 К _С(?0О
*	То есть	= —	— и 7777 ~ 7	Не совсем понятно, почему они должны были бы
АН СА АЭ МН	Ар
рассчитывать именно так, а не через отношение отрезков А кроме того, у Аполлония эти форму¬
лы как раз есть.
442

№ XXXVIII. Новая теорема в отношении учения о конических сечениях Якоба Бернулли
Когда я показал это брату, он вскоре подтвердил это собственными выкладками;
которые, поскольку казались мне вполне стройными, я присоединил здесь к своему
рассуждению; ибо они, несомненно, заслуживают снисхождения в новой теореме.
1. Для параболы
• /
очередь.
Треугольники АТС и АНХ подобны, было доказано, что АС = АЬ; в свою
БС Аб НХ
гак как А1ЛХ - параллелограмм, то АЬ = НХ. Следовательно,	=	- ——
НХ АХ АХ
поэтому НХ2 = ТС АХ.
АН АН-АХ
С Другой стороны (Аполлон ИЙ 1, 11),	= ——2— .
К НХ
АН АН
Подставив предыдущее выражение, получим	.
Следовательно, ТС или ТЕ = И. Что и требовалось доказать.
Другим способом.
АН _ АН • НХ _ АГ • НХ _ АБ • АС _ АН
ИС _ НХ-БС ~ Ев Бй ~ Бй2 И ’
Следовательно, ТС или ТЕ = И. Что и требовалось доказать.
2. Для гиперболы и эллипса (I, 12 и 13)
МН _MH HZ_ AG АХ
FE ” HZ-FE “ GE AG’
Атак как AG = AL = НХ, то, согласно (I, 12 и 13), получаем
AGAX_AGAG_ AG2 МН
GE-НХ " GE-GF _GE GF _ R ’
Следовательно, FE = R. Что и требовалось доказать.
443

Приложения
СПИСОК ЛИТЕРАТУРЫ
1. Архимед. Сочинения / Пер. и комм. И Н. Веселовского. - М.: Физматгиз, 1962.
2.	Бурбаки //. Очерки по истории математики. — М.: КомКнига, 2007.
3.	Бан дер Варден Б.Л. Пробуждающаяся наука Математика Древнего Египта, Вавилона
и Греции / Пер И.Н. Веселовского - М.: Физматгиз, 1959.
4.	Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики
/ Пер. с франц. - М.: Мир, 1986.
5 Декарт Р. Геометрия. М. -Л Государственное объединенное научно-техническое изд-
НКТП СССР. 1938
6.	История математики с древнейших времен до начала XIX столетия / Под ред. А.П
Юшкевича. - Т. 1. - М.: Наука, 1970
7.	Каган В.Ф. Архимед. - М -Л.: Государственное издательство технико-теоретической
литературы, 1949.
8.	Кольман Эрнест. История математики в древности. - М.: Гос. изд-во физматлитерату-
ры. 1961.
9.	Конические сечения, с комментариями Эвтокия / Пер И. Ягодинского // Известия
Северо-Кавказского гос университета. 1928. № 3(15). С. 130-152.
10.	Лурье С.Я Архимед. М. - Л.; Изд-во Академии наук СССР, 1945.
11.	Начала Евклида / Пер. с греч. и коммент. Д.Д. Мордухай-Болтовского при редакци¬
онном участии И.Н Веселовского и М Я Выгодского. М. - Л.: ГТТИ, 1949-1951.
12.	Нейгебауер О. Точные науки в древности - М.: УРСС, 2003.
13	Прасолов В В. Геометрические задачи Древнего мира. - М.: ФАЗИС, 1997
14	Прасолов В.В. Три классические задачи на построение: удвоение куба, трисекция угла,
квадратура круга. - М.: Наука, 1992.
15.	ПроклДиадох. Комментарий к первой книге «Начал» Евклида (пер А. И Щетникова)
-М.: Русский Фонд Содействия Образованию и Науке, 2013. — (Приложение № И! к журна¬
лу «Аристей Вестник классической филологии и античной истории»).
16.	Птолемей К Альмагест: Математическое сочинение в тринадцати книгах / Пер с древ¬
негреческого. И.Н. Веселовского/ Ин-т истории естествознания и техники РАН, Науч. ред.
Г.Е. Куртик - М . Наука, Физматлит, 1998.
17.	Романский И.Д. История естествознания в эпоху эллинизма и Римской империи. -
М.: Наука, 1988.
18.	Розенфельд Б.А. Аполлоний Пергский - М : МЦНМО, 2004.
19.	Розенфельд Б.А ., Хайретдинова Н Г. Сабит ибн Корра (836-901). — М.: Наука, 1994.
20 Рыбников К.А. История математики. 1 - М.: Изд-во Московского университета, 1963.
21.	Цейтен И Г. История математики в древности и в Средние века. — М.: Книжный дом
«Л ИБ РОКОМ», 2015.
22.	Чистяков В.Д. Три знаменитые задачи древности. — М.: Учпедгиз, 1963.
23.	Шаль М Исторический обзоръ происхождешя и развитая геометрическихъ методовъ.
- М.: 1883. - T. 1 / пер. с франц (М. Chasles. Bruxelles, 1837).

Приложения
24. Шереметевский В. II. Исторический очерк развития анализа и его приложений к гео¬
метрии. В кн.: Лоренц Г. Элементы высшей математики. Т. 1. - М.: Т-во И.Д Сытина. 1910
26. Heiberg I.L. Apollonn Pergaei. Vbl. 1 MDCCCXC1.
27.	Heiberg I.L. Apollonii Pergaei. \bl. II. MDCCCXCIII.
28,	Zeuthen II.G. Die Lehre von den Kegelschnitten im Altertum. - Kopenhagen, 1886.
445

НАУЧНОЕ ИЗДАНИЕ
SCIENTIFIC EDITION
АПОЛЛОНИЙ ПЕРГСКИЙ
КОНИЧЕСКИЕ СЕЧЕНИЯ
Под общей редакцией А.А. Панферова, С В Кирбятьева.
APOLLONIUS FROM PERGE
CONIC SECTIONS
Editors by A. A. Panferov, S V. Kirbyatyev
ИЗДАТЕЛЬСТВО «ЮСТИЦИНФОРМ»
юридическая, экономическая и деловая литература;
журналы «Право и экономика», «Вестник арбитражной практики»,
«Журнал предпринимательского и корпоративного права»
«YUSTITSINFORM» PUBLISHING HOUSE
legal, economic and business literature;
magazines «Law and Economics», «Bulletin of arbitration practice»,
«Journal of Entrepreneurship and Corporate Law»
Главный редактор В А. Вайпан
Chief editor V A Vaypan
Генеральный директор В В Прошин
CEO VV. Proshin
Подписано в печать 24 12 2018
Формат 70x100/16 Бумага офсетная Печ л 36 4 Тираж 500 экз
Signed in pnnt 24 12 2018
Size70x100/16 Off set printing, 36 4 paper off set Cond Pec I The circulation of copies
Юстмцинформ
119607, г Москва, ул Лобачевского, 94,
Yustitsinform
119607, Russia, Moscow, Lobachevsky street, office 7
Phone number Ten (495) 232-12-42
http //wwwjusinf ru E-mail: info@jusinf ru