Jfonг| л яр ные
ПО МАТЕМАТИКЕ
А.Г. ДОРФМАН
ОПТИКА
КОНИЧЕСКИХ
СЕЧЕНИЙ
ФИЗ М АТГИЗ-1959

ПОПУЛЯРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
ВЫПУСК 31
А. Г. ДОРФМАН
ОПТИКА
КОНИЧЕСКИХ
СЕЧЕНИЙ
Государственное издательство
физико-математической литературы
МОСКВА 1959

ii-2-1
АННОТАЦИЯ
В предлагаемой книге рассматриваются
оптические свойства конических сечений
(эллипса, гиперболы, параболы).
Книга рассчитана на учащихся старших
классов и может быть использована для
работы в школьных математических круж-
кружках.
В основу книги положены лекции, про-
прочитанные автором в школьном математи-
математическом кружке при Сталинградском педа-
педагогическом институте.

ПРЕДИСЛОВИЕ
Эта книжка рассчитана на широкий круг читателей,
в особенности на участников и руководителей школьных и
студенческих математических кружков. Содержащийся в ней
материал по геометрической оптике может быть использован
и в кружках физики.
Из четырех разделов книжки два первых посвящаются
общим сведениям о конических сечениях, два последующих —
собственно оптическим свойствам этих кривых. Каждый раз-
раздел заканчивается дополнением (отмеченным звездочкой),
которое предназначено главным образом для более углублен-
углубленных занятий и может быть опущено без ущерба для пони-
понимания остального текста.
В основу книжки положены лекции, прочитанные мною
на школьном математическом кружке при Сталинградском
государственном педагогическом институте.
Считаю своим долгом выразить искреннюю благодарность
В. Г. Болтянскому, прочитавшему рукопись и сделавшему
ряд критических замечаний.
Автор
1*

I. КОНИЧЕСКИЕ СЕЧЕНИЯ
1.	Совокупность всех прямых, проходящих через одну
и ту же точку 5 и касающихся сферы (рис. 1), образует
поверхность, называемую конусом. Каждая из этих
прямых называется образую-
образующей конуса.
Обе поверхности — сфера
и конус — касаются по окруж-
окружности п. Точка 5 называется
вершиной конуса. Прямая,
проходящая через эту точку
и центр сферы, является осью
вращения конуса.
Вершина делит конус на две
симметрично расположенные
части. Каждая из них назы-
называется полбй конуса. Часть
пространства, ограниченная по-
полой, называется полостью
конуса.
Таким образом, конус со-
состоит из двух пол и соответ-
соответственно имеет две полости.
2.	Каждое плоское сечение
конуса называется кониче-
коническим сечением.
Плоскости, проходящие через вершину конуса, дают три
вида сечений: точку, прямую и пару прямых.
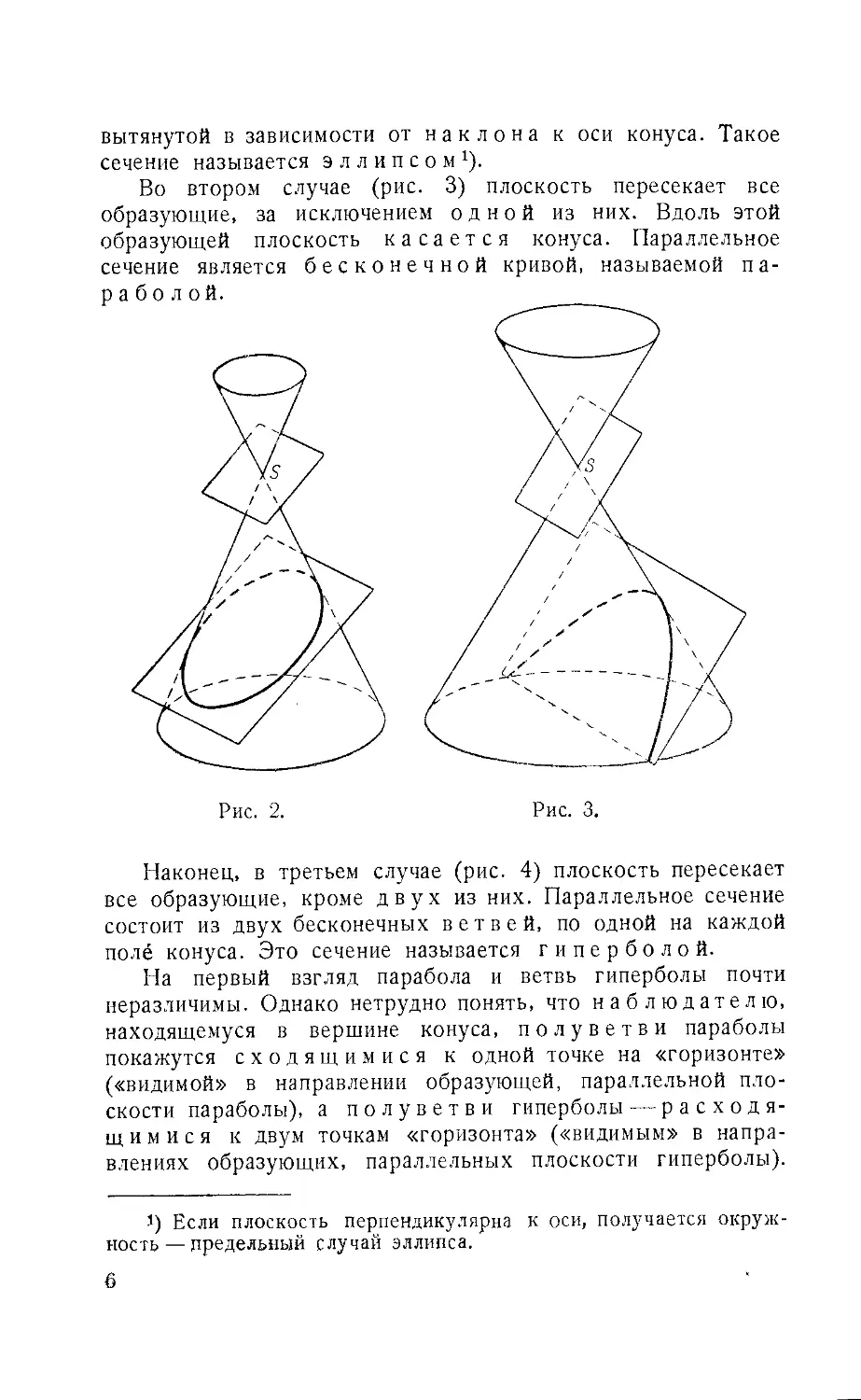
В первом случае (рис. 2) плоскость пересекает все
образующие конуса. Очевидно, параллельное сечение
имеет вид замкнутой овальной кривой, более или менее
Рис. 1.

вытянутой в зависимости от наклона к оси конуса. Такое
сечение называется эллипсом1).
Во втором случае (рис. 3) плоскость пересекает все
образующие, за исключением одной из них. Вдоль этой
образующей плоскость касается конуса. Параллельное
сечение является бесконечной кривой, называемой па-
параболой.
Рис. 2.
Рис. 3.
Наконец, в третьем случае (рис. 4) плоскость пересекает
все образующие, кроме двух из них. Параллельное сечение
состоит из двух бесконечных ветвей, по одной на каждой
поле конуса. Это сечение называется гиперболой.
На первый взгляд парабола и ветвь гиперболы почти
неразличимы. Однако нетрудно понять, что наблюдателю,
находящемуся в вершине конуса, полуветви параболы
покажутся сходящимися к одной точке на «горизонте»
(«видимой» в направлении образующей, параллельной пло-
плоскости параболы), а полуветви гиперболы — расходя-
расходящимися к двум точкам «горизонта» («видимым» в напра-
направлениях образующих, параллельных плоскости гиперболы).
1) Если плоскость перпендикулярна к оси, получается окруж-
окружность— предельный случай эллипса.
6

8. Для более подробного ознакомления с коническими
сечениями требуются некоторые дополнительные построения.
2 В основе большинства из
них лежат две простые тео-
теоремы:
(а)	Если а и Ъ — две каса-
касательные к сфере, проведен-
проведенные •¦ из одной и той же
точки S, то отрезки этих
касательных от общей точ-
точки S до точек касания А
и В равны между собой
(рис. 5).
(б)	Если а и C — две пло-
плоскости, пересекающиеся по
прямой с и касающиеся сферы
в точках А и В, то от-
отрезки касательных, проведен-
проведенных из любой точки прямой с
к точкам А и В, образуют
равные углы с прямой с
(рис. 6).
4*.1) Заставим точку 5	Рис. 4.
перемещаться по продолжению
радиуса ОР сферы (рис. 1). По мере того как эта точка
будет приближаться к концу радиуса, конус все более будет
С
Рис. 5.
Рис. 6.
«выравниваться». В пределе он сольется с касательной пло-
плоскостью к сфере в точке Р; при этом окружность касания п
1) Для понимания основного текста чтение пунктов, отмечен-
отмеченных звездочкой, не требуется.

Рис.7.
обратится в точку касания Р, а образующие перейдут
в касательные к сфере в этой точке (рис. 7).
Если, напротив, точка 5 будет уда-
удаляться по продолжению радиуса ОР,
то конус все более будет «вытяги-
«вытягиваться». В пределе окружность каса-
касания п перейдет в большой круг
сферы — «экватор», а все образующие
конуса окажутся параллельными между
собой. Конус превратится в поверх-
поверхность, называемую цилиндром
(рис. 8).
Рассмотрим наклонное сече-
сечение цилиндра — эллипс1).
1) Приведем в соприкосновение с плоскостью сечения
две сферы, вписанные в цилиндр (рис. 9). Точки прикосно-
прикосновения обозначим через Fl и F2. Произ- 	__^^
вольную точку М сечения соединим
с точками F1 и F2 отрезками F±M и F2M.
Через ту же точку М проведем обра-
образующую, касающуюся сфер в точках
и yV2 (на окружностях пх и п2).
Согласно теоре-
теореме (а)
Но NXM + N2
= NXN2. Значит,
т. е. сумма расстоя-
расстояний от произвольной
точки сечения до
двух неподвижных
точек F1 и F2 по-
постоянна (не зависит	Рис. 8.	Рис. 9.
от выбора точки М).
2) Плоскости окружностей nv n2 и плоскость эллипса
пересекаются по прямым dv d2 (рис. 10). Проведем две
!) То, что это сечение действительно есть эллипс в том
смысле, как он определен в п. 2, ясно из дальнейшего (см. прило-
приложение 7).
8

плоскости перпендикулярно к этим прямым: одну — через
ось цилиндра и точки Fv F2; другую — через какую-нибудь
точку М эллипса. Первая плоскость пересекает цилиндр по
образующим АС и А'С, вторая — по образующим MN
и M'N'.
Рис. 10.
Рис. 11.
Треугольники A\NP и ACD подобны (так как имеют
соответственно параллельные стороны). Поэтому
Ш_
МР
АС
CD '
Но по теореме (a) MN = MFV Следовательно,
A4Fi AC
МР
CD '
т. е. отношение расстояния от произвольной точки
сечения до неподвижной точки Fx к расстоянию до непо-
неподвижной прямой dx постоянно.
3) Плоскость эллиптического сечения и плоскость, касаю-
касающаяся цилиндра, пересекаются по прямой Т{Г2, касаю-
касающейся эллипса (рис. 11).
9

Обе плоскости касаются «верхней» сферы в точках F1
и Ni, поэтому согласно теореме (б)
IF1MT1=IT1MNV	A)
Эти же плоскости касаются «нижней» сферы в точках F2
и N2. Значит, снова по теореме (б)
I F2MT2= I T2MN2.	B)
Но углы в правых частях A) и B) равны как вертикальные.
Следовательно, равны углы и в левых частях:
/ F.MT, = I F2MTZ,
т. е. в произвольной точке М сечения отрезка F-^M и F2M
образуют равные углы с касательной.
Исследуя в дальнейшем конические сечения, мы
часто будем пользоваться теми же идеями, какими только
что пользовались применительно к предельному случаю
конуса — цилиндру.
Приложения
1.	По одну сторону круга (на его оси) помещен точеч-
точечный источник света, а по другую сторону—плоский экран.
Какой вид имеет очертание тени круга в зависимости от
наклона экрана?
Ответ. Окружность, эллипс, парабола, ветвь гиперболы.
2.	Доказать, что расстояние между точками Mt и М2
параболы (гиперболы) неограниченно возрастает при неогра-
неограниченном удалении этих точек по параболе (гиперболе).
Указание. Предварительно выяснить, как изменяется длина
отрезка М1М2 — общей хорды кругового сечеиия конуса и пара-
параболы (гиперболы).
3.	Доказать теоремы (а) и (б) п. 3.
4.	Во что перейдет окружность, начерченная на конусе,
при указанном в п. 4 обращении конуса в плоскость (если
при этом каждая образующая перемещается, как твердое
тело, поворачиваясь вокруг точки 5)?
Ответ. В окружность.
5.	Доказать, что геометрическое место точек, сумма рас-
расстояний которых от двух фиксированных точек постоянна,
есть эллипс — наклонное сечение цилиндра.
10

6. Полагая, что г и 8 — расстояния точки М плоскости
эллипса от Fx и dx соответственно (рис. 10), доказать, что
на касательной отношение у принимает наименьшее значение
в точке касания.
Указание. Выяснить, как изменяется отношение у на пря-
прямой, параллельной dx.
Н. ЭЛЛИПС, ГИПЕРБОЛА, ПАРАБОЛА
5. Рассмотрим эллиптическое сечение конуса (рис. 12).
Приведем в соприкосновение с плоскостью сечения две
сферы, вписанные в конус.
Точки прикосновения Fx и F2,
называемые фокусами эл-
эллипса, соединим с произволь-
произвольной точкой М сечения отрез-
отрезками FXM = rx и F2M — r2;
эти отрезки называются фо-
фокальными радиусами-
векторами точки М. Обра-
Образующая, проходящая через
точку М, касается сфер в точ-
точках Nx и N2. Длина отрезка
NXN2 не зависит от выбора
точки М (и обозначается че-
через 2а). Согласно теореме (а)
FXM = NXM, F2M = N2M.
Но
Значит,
FxM-{-F2M = NXN2. C)
Равенство C) показывает,
что эллипс есть геометри-	рИс. 12.
ческое место точек, сумма
расстояний которых от двух фиксированных точек по-
постоянна1).
!) Обратно, геометрическое место точек, сумма расстояний
которых от двух фиксированных точек постоянна, есть эллипс —
сечение конуса (см. приложение 7).
11

д
о
Пользуясь формулой C), легко установить многие свойства
эллипса (в частности, такие, которые не усматриваются «сразу»
из его определения, при-
принятого в п. 2). Отметим
следующие.
Средняя точка О от-
резка FXF2 = 2с (рис. 13)
_ является центром сим-
симметрии эллипса. Пря-
Прямая, проходящая через
фокусы, является осью
			симметрии и на-
14	зывается фокальной
Рис 13.	осью. Прямая, проходя-
проходящая через центр О пер-
перпендикулярно к фокальной оси, также является осью сим-
симметрии. Эллипс пересекается с осями в точках Av A2
и Вх, В2, называемых вершинами эллипса. Они являются
серединами сторон описанного
прямоугольника. Отрезок АХА2
фокальной оси называется
большим диаметром эл-
эллипса; он равен отрезку NXN2
образующей конуса: АХА2 —
= Л/1Л/2 = 2а. Отрезок ВХВ2 —
= 2Ь называется малым диа-
диаметром эллипса (очевидно,
Эллипс тем более отличается
от окружности, чем больше
отношение отрезка FXF2 — 2с
к отрезку АХА2 = 2а. Это отно-
отношение называется эксцент-
эксцентриситетом эллипса. Эксцен-
Эксцентриситет окружности равен
нулю.
6. Рассмотрим теперь гипер-
гиперболическое сечение (рис. 14).
Так же, как и в случае	РИС- ^-
эллипса, имеются две вписанные
в конус сферы, касающиеся плоскости сечения (с той, однако,
разницей, что они расположены в разных полах конуса).
Точки касания Fx и F2, называемые фокусами гиперболы,
12

соединим с произвольной точкой М сечения, т. ё. прове-
проведем так называемые фокальные радиусы-векторы
F1M = r1 и F-,M = r2 точки М гиперболы. Образующая,
проходящая через точку М, касается сфер в точках Nx и Nz,
определяющих отрезок Л^М>=2а (его длина не зависит
от положения точки М).
По построению
По теореме (а)
= N2M.
Значит,
Рис. 15.
Если выберем точку М
на другой ветви гиперболы,
то аналогичным образом по-
получим:
F2M — F1M = NtN2. E)
Две формулы'—D) и E)—
можно записать в виде одной
г1 — г2\ = 2а. F)
Эта краткая формула показывает, что гипербола есть
геометрическое место точек, разность расстояний кото-
которых от двух фиксированных точек постоянна1).
При помощи формулы F) устанавливается, что гипербола
имеет центр симметрии О (рис. 15), делящий отрезок
FxF2 = 2c пополам, и две взаимно перпендикулярные оси
симметрии. Одна из них называется фокальной или дей-
действительной осью; она проходит через фокусы и пере-
пересекает гиперболу в двух точках Ах, А2 — вершинах ги-
гиперболы; другая из них не пересекает гиперболу и называется
мнимой осью. Отрезок АХА2 действительной оси называется
диаметром гиперболы. Он равен отрезку NXN2 образую-
образующей конуса, т. е. АХА2 = 2а.
Гипербола, аналогично эллипсу, вполне определяется
прямоугольником, симметричным относительно осей и отсекаю-
отсекающим на них отрезки АгА2 = 2а и ВХВ2 = 2Ь (Ь2 = с2 — а2).
Прямые, на которых лежат диагонали этого прямоугольника,
См. приложение 8.
13

называются асимптотами гиперболы. Гипербола заключена
внутри одной пары вертикальных углов между ними и не-
неограниченно приближается к ним по мере удаления
в бесконечность (приложение 15).
7. Наконец, рассмотрим параболическое сечение (рис. 16).
В этом случае существует только одна сфера, вписанная
в конус и касающаяся плоскости сечения. Точка касания F
называется фокусом параболы.
Плоскость окружности п и плоскость параболы пересе-
пересекаются по прямой d, называемой директрисой параболы.
Рис. 16.
Рис. 17.
Покажем, что любая точка М параболы равноудалена
от фокуса F и директрисы d.
Для этого заметим, что образующая, параллельная пло-
плоскости параболы, касается сферы в точке L, диаметрально
противоположной фокусу, а плоскость SLM пересекает
плоскость параболы по прямой МР, перпендикулярной к ди-
директрисе.
В плоскости SLM лежит образующая SM, касающаяся сферы
в точке N. Очевидно, треугольники SLN и MPN подобны
между собой.
По теореме (a) SL = SN и соответственно MN = МР.
По той же теореме MN = MF. Следовательно, MF = МР,
что и утверждалось.
Прямая FD (рис. 17), проходящая через фокус F перпен-
перпендикулярно к директрисе, является осью симметрии
14

паоаболы Точка пересечения оси с параболой называется
веРрш ин0Й парабол'ы. Отрезок FD оси (Расстояние Фокуа
от директрисы) называется параметром параболы. Вер
Г
^То-аинГвГе сзойство параболы -ж,, вы=
таким образом: парабола является геометрическим местом
Рис. 18.
точек отношение расстояний которых от фокуса а
директрисы постоянно {равно единице). Аналогичными
эллипса.

G)
Плоскость, проходящая через прямую SL, параллельную
фокальной оси эллипса, пересекает конус по образующей SM,
а плоскость эллипса—по прямой МР, перпендикулярной ди-
директрисам. Образуются подобные треугольники SLN и MPN.
Из подобия этих треуголь-
треугольников следует, что
MN _SN
МР~~~ SL *
Длины отрезков SN и SL
не зависят от положения
точки N по окружности п
(или точки М на эллипсе).
Кроме того, по теореме (а)
MN = FM; отсюда и из G)
следует, что
FM _SN
МР~~ SL'
Эта формула показывает,
что эллипс есть геометри-
геометрическое место точек, отно-
отношение расстояний кото-
которых от фокуса и дирек-
директрисы постоянно.
Вполне аналогично уста-
устанавливается то же свойство
эллипса по отношению к
другому фокусу и другой
директрисе.
Плоскости круговых сечений пх и пг и плоскость г и-
перболы пересекаются по прямым dx и d2, называемым
директрисами гиперболы (рис. 19).
Плоскость, проходящая через прямую SL, параллельную
фокальной оси гиперболы, пересекает конус по образующим
SN и SN', а плоскость гиперболы — по прямой МР, перпен-
перпендикулярной к директрисам. Образуются подобные треуголь-
треугольники SLN и MPN. Из подобия этих треугольников следует,
что
MN SN	(8)
Рис. 19.
МР
SL '
Правая часть этой пропорции не зависит от выбора
точки М (или точки N). По теореме (а) ММ — F%M. Отсюда

и из (8) получаем:
MP SL •	v '
Для точки М', взятой на другой ветви, из подобия
Д M'PN' со Д 5Z.yV'
следует пропорция
M'N' __ SN'
М'Р ~~ S'L •
Но по теореме (a) M'N' = FXM'; следовательно,
Wp^~sT-	A0)
Формулы (9) и A0) показывают, что гипербола есть
геометрическое место точек, отношение расстояний
которых от фокуса и директрисы постоянно.
Аналогичным свойством обладает гипербола относительно
фокуса и директрисы, соответствующих «нижней» поле конуса.
Приложения
7.	Дан эллипс с фокусами Fx, F2 и диаметром 1а. По-
Построить конус, в сечении которого получается данный эллипс.
Указание. Воспользоваться рисунком 12 и свойством впи-
вписанной и вневписанной окружностей треугольника (эти окружности
касаются стороны треугольника в точках, равноотстоящих от ее
концов).
8.	Дана гипербола с фокусами Fx, F2 и диаметром 1а.
Построить конус, в сечении которого получается данная
гипербола.
Указание. Обобщить способ, указанный в приложении 7.
9.	Две плоскости, касающиеся конуса, пересекаются по
прямой, перпендикулярной к его оси. Третья плоскость перпен-
перпендикулярна к первым двум. Доказать, что в сечении конуса
и его пары касательных плоскостей третьей плоскостью
получается гипербола и ее пара асимптот (в предельном
случае — пара образующих, по которым две плоскости ка-
касаются конуса).
10.	Доказать, что все параболы подобны между собой.
Указание. Использовать свойство параболы, доказанное
в п. 7.
2 Зак. 3622. А. Г. Дорфман	]7

11.	Доказать, что парабола и любой угол с вершиной
внутри параболы пересекаются.
Указание. Предварительно рассмотреть случай, когда вер-
вершина угла совпадает с фокусом параболы.
12.	Для любой точки М эллипса (гиперболы) справедлива
f	С
формула у = —, где г — расстояние точки М от фокуса,
8 — расстояние точки М от директрисы (ближайшей к фокусу).
Доказать.
13.	Для эллипса и гиперболы, имеющих общие вершины
и общую фокальную ось, доказать предложение: если дирек-
директрисы эллипса проходят через фокусы гиперболы, то дирек-
директрисы гиперболы проходят через фокусы эллипса, и на-
наоборот.
14.	Доказать, что геометрическое место точек, равноуда-
равноудаленных от данной точки F и данной окружности С, есть кони-
коническое сечение: эллипс, если F лежит внутри С, гипербола,
если F лежит вне С; наконец, парабола, если С~—прямая
(предельный случай окружности).
15.	Дана гипербола с фокусами Flt F2 и диаметром 2а.
Из фокуса Fx как из центра описана окружность С радиуса 2а,
а из фокуса F2 проведена касательная F2O к окружности С.
Доказать, что: а) прямая, перпендикулярная к отрезку F2G
и делящая его пополам, есть асимптота гиперболы; б) отрезок
перпендикуляра от асимптоты до гиперболы убывает и ста-
становится произвольно малым с удалением его в бесконечность.
Указание. Для доказательства утверждения б) использовать
построение точек гиперболы, которое следует из приложения 14.
III. ОПТИЧЕСКИЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ
9. Коническое сечение, не проходящее через вершину
конуса (рис. 1—4), можно рассматривать как проекцию
окружности на секущую плоскость (проектирующие пря-
прямые совпадают с образующими).
Плоскость эллипса и плоскость, касающаяся конуса вдоль
образующей SAL пересекаются по прямой 7\Г2 (рис. 20).
Эта прямая является проекцией касательной к окружности
и называется касательной эллипса.
Покажем, что фокальные радиусы-векторы образуют
равные углы с касательной 7\Г2 в точке М,

Действительно, с Одной стороны, обе плоскости касаются
«верхней» сферы в точках А^ и Ft; отсюда по теореме (б)
С другой стороны, эти плоскости касаются «нижней»
сферы в точках N2, F2\
снова по теореме (б)
A2)
Но углы в правых
частях A1) и A2) равны
как вертикальные. Следо-
Следовательно, равны углы и
в левых частях, т. е.
A3)
Утверждение доказано.
Этот результат вместе
с известным из оптики
законом зеркального
отражениях) приводит
к следующему выводу.
Лучи, исходящие из
одного фокуса, зеркаль-
зеркально отражаясь от эл-
эллипса, сходятся в дру-
другом фокусе (рис. 21).
10. Пусть далее,
М — точка гиперболы
(рис. 22). Тогда пло-
плоскость, касающаяся ко-	рис .?о
нуса в точке М (по обра-
образующей SM), пересекает плоскость гиперболы по прямой Т{Г2,
касающейся гиперболы. Пользуясь теоремой (б), заклю-
заключаем, что
*) В данной точке данной кривой луч падения и луч отражения
образуют равные углы с касательной. Иначе говоря, отражение
в данной точке кривой происходит по тому же закону, как отра-
отражение от касательной в той же точке.
2*	19

Рис. 21.
Рис. 22.
20

Следовательно,
Таким образом, фокальные радиусы-векторы точки М ги-
гиперболы образуют равные углы с касательной в этой точке.
Отсюда согласно закону зеркального отражения (см. сноску
па стр. 19) следует, что лучи, исходящие из одного фокуса,
Рис. 23.
зеркально отражаясь от гиперболы, расходятся по
направлениям лучей, исходящих из другого фокуса
(рис 23).
11. Переходя к случаю параболы (рис. 24), рассмотрим
две касательные плоскости конуса: одну, содержащую
образующую SL, параллельную оси параболы; другую,
содержащую образующую SM, пересекающую параболу в точ-
точке М. Первая из них параллельна плоскости параболы,
вторая пересекает эту плоскость по касательной Т{Гг
к параболе в точке М. Обе плоскости пересекаются по пря-
прямой ST, параллельной касательной Т{Г2. Плоскость образую-
образующих SL и SM пересекает плоскость параболы по прямой
LXL2, параллельной оси параболы.
Согласно теореме (б)
= /_LST.
A5)
Углы в левых частях A5) равны между собой (как вну-
внутренние накрест лежащие при параллельных ST и 1\Т2);
следовательно,
/_F MT2.
21

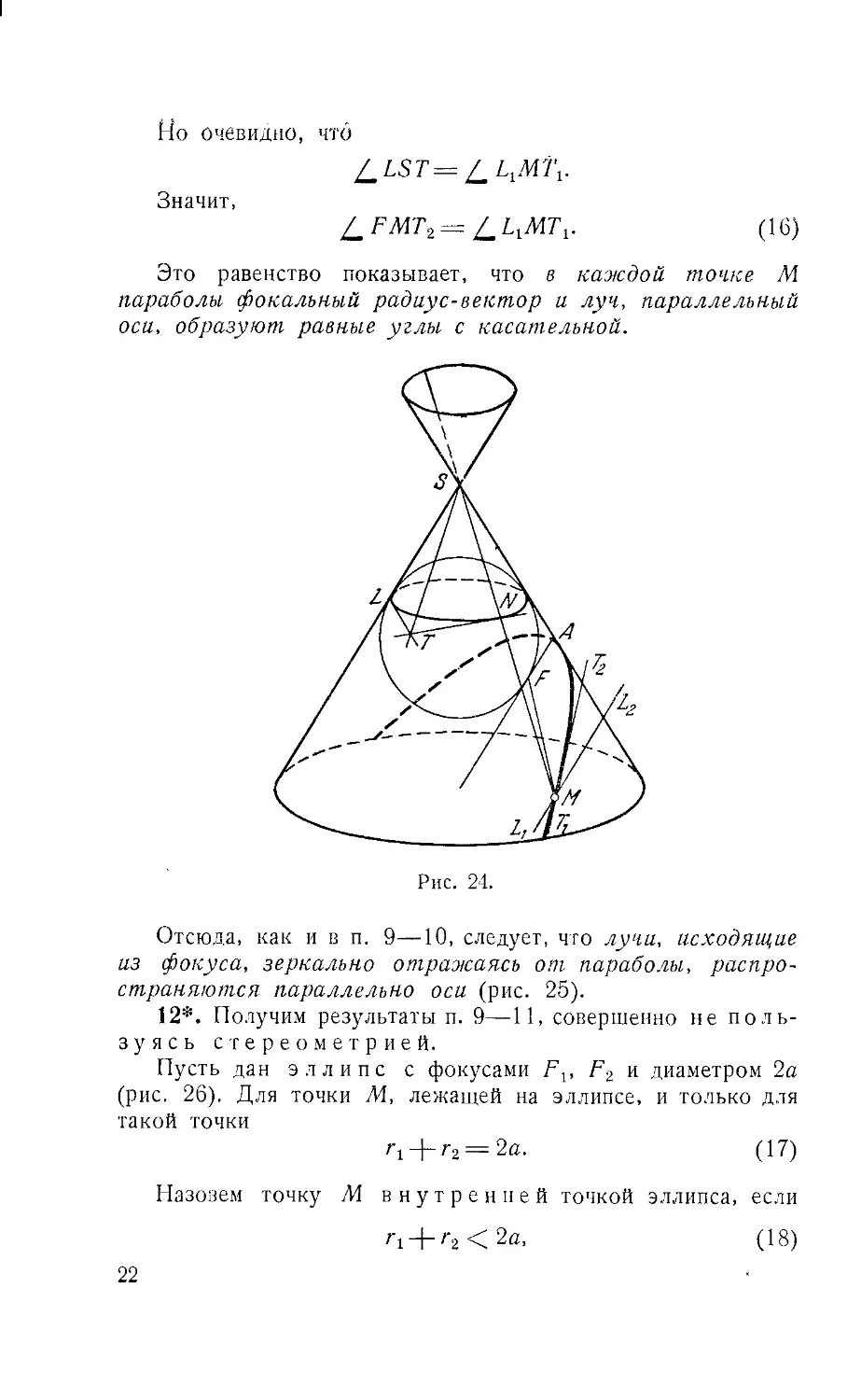
Но очевидно, что
l_LST= l_LxM'l\.
Значит,
/_FMT2= ?_LyMTv	A6)
Это равенство показывает, что в каждой точке М
параболы фокальный радиус-вектор и луч, параллельный
оси, образуют равные углы с касательной.
Рис. 24.
Отсюда, как и в п. 9—10, следует, что лучи, исходящие
из фокуса, зеркально отражаясь от параболы, распро-
распространяются параллельно оси (рис. 25).
12*. Получим результаты п. 9—11, совершенно не поль-
пользуясь стереометрией.
Пусть дан эллипс с фокусами Fv F2 и диаметром 2а
(рис. 26). Для точки М, лежащей на эллипсе, и только для
такой точки
гх + г2=2а.	A7)
Назовем точку М внутренней точкой эллипса, если
гх + г2<2а,	A8)
22

и его внешней точкой, если
гх + г2>2а.	A9)
Среди всех прямых, проходящих через данную точку
эллипса, касательная выделяется тем свойством, что все
ее точки, кроме точки касания,
являются внешними1).
Если М — точка касания, а
NV — любая другая точка каса-
касательной, то вследствие A7) и A9)
Рис. 25.
Рис. 26.
ломаная FlMF2 короче ломаной F1M'F2- Вместе с тем, лома-
ломаная FtMF, где F — точка, симметричная F2 относительно
касательной, короче ломаной
F^M'F. Но тогда ломаная FtMF
совпадает с отрезком FXF.
Отсюда следует, что
B0)
Рассмотрим, далее, гипер-
гиперболу с фокусами
диаметром 2а (рис.
точек М гиперболы
для них
-г,\ =
Flt F2 и
27). Для
и только
B1)
Рис. 27.
!) Существование и единственность касательной в данной
точке кривой (эллипса, гиперболы или параболы) принимаем без
локазательства (см., однако, приложение 21).
23

Точка М называется внутренней точкой гиперболы,
если
B2)
ki — г2|>2«.
и ее внешней точкой, если
ki — г2|<2о.	B3)
Все точки касательной, кроме точки	касания,
язляются внешними. Пусть Ж— точка касания,	а Ж'—¦
любая другая точка касательной. Тогда вследствие B1) и B3)
| FtM' — F2M'
— F2M
а поэтому, аналогично случаю эллипса,
?_м	1	1	Zm	2	1'	\	/
Формула A4) доказана.
Рассмотрим, наконец, параболу с фокусом F и дирек-
директрисой d (рис. 28). Для точек Ж параболы и только для них
расстояние г от фокуса равно
расстоянию 8 от директрисы:
г = 8.	B5)
Точка Ж называется вну-
внутренней точкой параболы,
если
г < 8,	B6)
и ее внешней точкой, если
г > 8.	B7)
Прямая, одна точка кото-
которой лежит на параболе (а все
остальные находятся вне па-
параболы), называется каса-
касательной.
Пусть Ж—точка касания, Ж' — любая другая точка
касательной, Р — внутренняя точка параболы, лежащая на
прямой MQ, параллельной оси, и M'Q'\\MQ. Учитывая B5)
и B7), запишем очевидные неравенства:
РЖ' 4- №F > РЖ' 4- M'Q' > РЖ 4- MQ.
Таким образом, ломаная PMF короче ломаной PM'F.
Поэтому
24
Рис.

Из формул B0), B4) и B8), как и в п. 9—И, сле-
следуют оптические свойства эллипса, гиперболы и параболы.
Приложения
16.	Внутри эллипса с фокусами Ft и F2 дана точка Р.
Построить кратчайшую ломаную FZMP с вершиной М на
эллипсе.
Указание. Провести луч F-J3. Точка встречи этого луча и
эллипса является вершиной М искомой ломаной. Для доказатель-
доказательства сравнить ломаную F%MP с ломаной F^M'P, где М' — точка
эллипса, отличная от точки М.
17.	Внутри гиперболы с фокусами Fv F2 и диаметром 2а
дана точка Р (со стороны Ft). Построить кратчайшую лома-
ломаную FtMP с вершиной М на гиперболе.
Указание. Провести луч F2P- Вершина М искомой лома-
ломаной FXMP лежит на пересечении луча с гиперболой. Для доказа-
доказательства сравнить ломаные F\MP и F\M'P, где М и М! — точки
на одной и той же ветви. Воспользоваться отрезком F-JW и окруж-
окружностью с центром F^ и радиусом 2а.
18.	Внутри параболы с фокусом F и директрисой d дана
точка Р. Построить кратчайшую ломаную FMP с верши-
вершиной М на параболе.
Указание. Из точки Р опустить перпендикуляр PQ на
директрису. Вершина М искомой ломаной FMP получится в пере-
пересечении этого перпендикуляра и параболы. Для доказательства
сравнить ломаные FMP и FM'P, где М' — точка параболы, отлич-
отличная от точки М. Воспользоваться перпендикуляром M'Q', опущен-
опущенным из точки М' параболы на директрису.
19.	Внутри выпуклого четырехугольника ABCD проходит
произвольная кривая линия MXMQM2 с началом Mt на сто-
стороне AD, точкой Мо на стороне CD и концом Мг на сто-
стороне ВС. Пусть М — произвольная точка кривой и известно,
что ломаная АМ0В короче ломаной АМВ. Доказать, что
/_ AM0D = /_ ВМ0С.
20.	Пользуясь результатами приложений 16—19, полу-
получить доказательства теорем п. 9—11 (или п. 12*).
21.	Доказать теорему существования и единственности
касательной в данной точке данной параболы: биссектриса
угла FMQ (рис. 28) и только она является касательной.
Указание. Допущение, что на биссектрисе есть точка Р,
лежащая внутри параболы, приводит к противоречию: оказывается,
что &MPQ = /\MPF; однако PQ=/=PF, по определению внутрен-
25

Йей точки (п. 12), — следовательно, биссектриса — касательная.
Касательная неизбежно будет биссектрисой (п. 12).
22.	Даны две прямые и точка. На одной из данных пря-
прямых определить положение точки, отношение расстояний
которой от данной точки и от другой из данных прямых
достигает наименьшего значения.
Указание. Воспользоваться приложением 6.
23.	Доказать, что касательные плоскости конуса вдоль
пары образующих (рис. 4) пересекают плоскость гиперболы
по ее асимптотам.
Указание. Исходя из определения асимптот в п. 6, устано-
установить предварительно, что асимптота является предельным положе-
положением касательной при неограниченном удалении точки касания.
24.	Эллипс вместе со своими касательными вращается
вокруг фокальной оси. В результате эллипс описывает
поверхность, называемую эллипсоидом вращения,
а каждая касательная к эллипсу—касательный конус
эллипсоида.
Касательная плоскость конуса в точке касания конуса и
эллипсоида называется касательной плоскостью
эллипсоида. Прямая, проходящая через данную точку по-
поверхности перпендикулярно к касательной плоскости в той же
точке, называется нормалью поверхности.
Из геометрической оптики известно, что луч падения
и луч отражения лежат в одной плоскости с нормалью
и составляют с нею равные углы (закон зеркального
отражения).
Показать, что лучи, исходящие из одного фокуса, после
зеркального отражения от эллипсоида, сходятся в другом
фокусе.
IV. ОПТИКА КОНИЧЕСКИХ СЕЧЕНИЙ
13. Существуют ли другие кривые, обладающие такими же
оптическими свойствами, какими обладают конические
сечения? Например, нет ли кривых, отличных от пара-
параболы и отражающих лучи точечного источника по параллель-
параллельным прямым?
Оказывается —нет. Не существует кривых, отличных от
конических сечений и обладающих их оптическими свойст-
свойствами, их оптикой.
26

Прежде чем доказать это, сформулируем следующее
утверждение.
Если в плоскости, покрытой всевозможными пря-
прямыми, параллельными между собой (рис. 29), помещена
произвольная кривая МгМ2 (не содержащая отрезков дан-
пых прямых), то на этой кривой существует хотя бы
одна точка М, в которой
касательная х) не совпадает
с прямой покрытия.	/
Это утверждение предста-
представляется настолько очевидным,
что вряд ли вызывает какие-
либо сомнения. Оно будет при-
применяться в несколько обобщен- М,
ном виде.
14. Сформулируем теперь
следующую теорему.	Рис. 29.
Если пучок лучей, выходя-
выходящих из точки Fu после отражения
рается в точке Fz, то кривая
от кривой С соби-
есть эллипс с фокусами
Fx и F2.
Для доказательства покроем плоскость всевозможными
эллипсами с фокусами /71
и F2 (рис. 30). Назовем
эти эллипсы линиями
покрытия плоскости.
Пусть М — произвольная
точка (не лежащая на от-
отрезке FXF2). Очевидно,
из всех прямых, прохо-
проходящих через точку М,
только та, которая совпа-
совпадает с касательной к н-
нии покрытия, отра-
отражает луч FtM в точку F2.
Допустим, что какой-
либо участок MtM2
Рис. 30.
!) Касательная в точке М кривой определяется как предельное
положение секущей ММ' при неограниченном приближении точки М'
по кривой к точке М. Это понятие вводится в первых главах
любого курса анализа (см. также вып. 13 настоящей серии:
А. И. М а р к у ш е в и ч, Комплексные числа и конформные отобра-
отображения, Гостехиздат, 1954).
27

кривой С не принадлежит линии покрытия. Тогда, по-
подобно тому как в п. 14, замечаем, что на этом участке
существуют точки, в которых касательные к кривой С не
совпадают с касательными к линиям покрытия и, значит,
лучи, отраженные кривой С, не попадают в точку F2, вопреки
условию теоремы. Таким образом, кривая С действительно есть
эллипс с фокусами Fx и F2-
Для других конических
сечений вопрос, поставлен-
поставленный в п. 13, решается вполне
аналогично.
В отношении гиперболы
имеет место следующая
теорема.
Если пучок лучей, выхо-
выходящих из точки Fv после
отражения от кривой С,
расходится по продолже-
продолжениям лучей, исходящих из
точки F2, то эта кри-
кривая— гипербола с фоку-
фокусами Ft и F2 (или пря-
прямая— мнимая ось такой
гиперболы).
Доказательство этой теоремы проводится, как и в случае
эллипса: плоскость покрывается всеми гиперболами
с общими фокусами Fv F2 и их общей мнимой осью (рис. 31);
в каждой точке М покрытия определяется положение пря-
прямой, отражающей луч FtM по направлению луча, исходя-
исходящего из точки F2; допущение, что кривая С не принадлежит
линии покрытия, приводит к противоречию с условием тео-
теоремы (по таким же наглядным соображениям, как в п. 13).
Рекомендуем читателю провести доказательство более по-
подробно.
В отношении параболы справедлива следующая теорема.
Если пучок лучей, идущих от точечного источника F,
отразившись от кривой С, становится пучком парал-
параллельных прямых, то кривая С является параболой
с фокусом F (и осью, принадлежащей пучку отраженных
лучей).
Эта теорема доказывается, как и предыдущие. Отметим
только, что плоскость покрывается параболами с общим
фокусом F и общей осью (рис. 32).
28
Рис. 31.

Выразим коротко содержание приведенных выше теорем.
Отражение пучка лучей также в виде пучка лу-
лучей имеет место для конических и только для кони-
конических сечений, когда источник света помещен в одном
аз фокусов. При этом зеркально отраженные лучи обра-
образуют сходящийся, расходящийся или параллельный пучок,
смотря по тому, является
ли зеркало эллиптическим,
гиперболическим или пара-
параболическим.
15*. В заключение приве-
приведем доказательства теорем
п. 14 средствами дифферен-
дифференциального исчисления 1).
Пусть точка М (х; у) опи-
описывает кривую С, обладающую
оптическим свойством эллипса
относительно точек Fy (с; 0) и
F-i (— с; 0) (рис. 33). Тогда для
каждого момента времени t
у
Рис. 32.
fj	О
Рис. 33.
F,
сумма расстояний г у -)- л2 точки М от Fy и F2 выразится формулой
+ гъ = У\х - су + уз 4- У (х + су + у»,
B9)
где х = х it) и у = у (t). Дифференцируя B9) по времени t, по-
получим:
(х + с)х'
/ , / (-у — с)х'

у/
J) Дифференцирование функций разъясняется в вып. 17 на-
настоящей серии: В. Г. Болтянский, Что такое дифференциро-
дифференцирование? Гостехиздат, 1956.
29

С другой стороны, для точки Мх (Xi, yt), описывающей эллипс
с фокусами F±, F% и диаметром 2а, имеем:
+ cy + yi = 2a,	C1)
где x-i = x-i(t), yi==yi(O- После дифференцирования C1) no t по-
получим:
(Хл—сЛх'. + у.у'. (х.-\-с)х'.-\-у.у'л
\r- Z У+Л 7=- = °- C2)
Согласно условию в точке М касательная к кривой С совпа-
совпадает с касательной к эллипсу с фокусами Fi и /> Поэтому
в точке М выполняются равенства
: уг
x = xv у = у1, х : уг = х[: у[	C3)
(последнее означает совпадение направлений касательных). Из C0),
C2) и C3) следует, что
г[ + г'г = 0.
Отсюда
ri + ri = const,
т. е. точка М описывает эллипс с фокусами Fx и F2.
Для гиперболы или параболы доказательство аналогично.

ОГЛАВЛЕНИЕ
Предисловие 		3
I. Конические сечения		5
П. Эллипс, гипербола, парабола		11
III.	Оптические свойства конических сечений		18
IV.	Оптика конических сечений		26

ДбрфмаН Абрам Григорьевич.
Оптика конических сечений.
Редактор И. А. Угарова.
Технический редактор К. Ф. Брудно.
Корректор К. В. Булатова.
Сдано в набор 27/Х 1958 г. Подписано к пе-
печати 13/1П 1959 г. Бумага 84x108/32. Физ.
печ. л. 1. Условн. печ. л. 1,64. Уч.-изд.
л. 1,29.	Тираж 15 000 экз.	Т-00943.
Цена 40 к. Заказ №. 3622.
Государственное издательство
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Типография № 2 им. Евг. Соколовой
УПП Ленсовнархоза. Ленинград,
Измайловский пр., 29.