Author: Розен Р.
Tags: компьютерные технологии медицинские науки физика математика биология инженерия
Year: 1969
Text
Р Розен
ПРИНЦИП
ОПТИМАЛЬНО СТИ
В БИОЛОГИИ
OPTIMALITY PRINCIPLES
IN BIOLOGY
ROBERT ROSEN
Committee on Mathematical Biology
The University of Chicago
LONDON
BUTTERWORTHS
1967
Р. Розен
ПРИНЦИП
ОПТИМАЛЬНОСТИ
В БИОЛОГИИ
Перевод с английского и предисловие
д-ра физ.-мат. наук
В. М. ВОЛОСОВА
ИЗДАТЕЛЬСТВО «МИР» • МОСКВА 1969
УДК 681,142: 57+61
В книге излагаются простейшие методы математи-
ческой постановки и решении ряда биологических задач
иа основании представлений об оптимальности. Для чте-
ния книги не требуется предварительной биологической
подготовки, а в области математики достаточно зна-
комства с основными понятиями дифференциального и
интегрального исчисления.
Предназначена для биологов, желающих ознакомиться
с математическими методами исследования, для матема-
тиков, физиков и инженеров, занимающихся проблемами
биологии, а также для тех, кто хочет получить общее
представление о роли математики в биологии.
Редакция биологической литературы
2-10-2
127-09
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Книга Р. Розена посвящена применению в биологии неко-
торых математических методов исследования, связанных в ос-
новном с оптимизацией решения ряда задач. Часть вопросов,
затронутых в книге, рассматривается более подробно и глу-
боко, чем это обычно делается в популярных изданиях, и, кроме
того, в ней используются элементы высшей математики. Но
вместе с тем от серьезных научных сочинений эта книга отли-
чается тем, что она не претендует на полное, исчерпывающее
решение проблем; многие рассуждения автора носят поясни-
тельный и наводящий характер, а детальное исследование часто
заменяется качественными, эвристическими соображениями.
Таким образом, книга занимает промежуточное положение
между популярной брошюрой и научным изданием. Основная
цель автора состоит в том, чтобы привлечь внимание читателей
к математическим исследованиям в биологии, подготовить их
к чтению специальной литературы и самостоятельным иссле-
дованиям в' этой области. В книге имеются многочисленные
ссылки на оригинальную научную литературу, относящуюся
к затронутым проблемам.
Для чтения книги требуется совсем небольшая математи-
ческая подготовка. Достаточно, чтобы читатель был знаком
с методами элементарной математики, изучаемыми в средней
школе, и имел общее представление об основных понятиях ана-
литической геометрии, дифференцировании и интегрировании.
Читатель, не обладающий такой подготовкой по высшей мате-
матике, все же сможет ознакомиться с некоторыми разделами
книги, в которых элементы высшей математики не встречаются
и которые можно изучать независимо от других разделов.
В своем предисловии автор приводит схему, иллюстрирующую
основные внутренние связи между отдельными главами, и с ее
помощью читатель сможет выбрать такую последовательность
изучения различных разделов книги, которая будет для него
наиболее удобна. Что касается биологии, то все необходимые
сведения из этой области вводятся и достаточно подробно по-
ясняются в самой книге.
6
Предисловие к русскому изданию
В книге почти совсем не рассматриваются некоторые важ-
нейшие достижения биологии, относящиеся к последним деся-
тилетиям; так, например, в ней нет даже упоминания о молеку-
лярной биологии и биохимической генетике. Большая часть
обсуждаемых вопросов относится к классическим проблемам
биологии (филогенез и онтогенез, аллометрия, гомеостаз, регу-
ляция простейших функций организма и т. п.). Математический
аппарат, используемый автором, опирается в основном на тео-
рию экстремумов функций; кратко рассматриваются понятия
вариационного исчисления, теории устойчивости решений обык-
новенных дифференциальных уравнений и теории управления.
Полные формулировки теорем приводятся не всегда; еще реже
даются строгие доказательства, но при этом интуитивные и
физические представления, связанные с различными математи-
ческими аспектами, обсуждаются достаточно полно и четко.
Математикам, не встречавшимся ранее с задачами матема-
тической биологии, эта книга укажет ряд областей исследова-
ния, в которых могут быть плодотворно применены математи-
ческие методы. Биологам полезно будет узнать, какие серьезные
результаты могут быть получены с помощью сравнительно
скромного математического аппарата, о котором идет речь
в книге. И наконец, эта книга несомненно будет полезна в по-
знавательном отношении всем, кто интересуется применением
математических методов исследования в биологии.
В. М. Волосов.
ПРЕДИСЛОВИЕ АВТОРА
Несмотря на то что в настоящее время имеется много пре-
восходных элементарных руководств по математической биоло-
гии, меня в течение многих лет не покидала мысль о том, что
в учебной литературе все еще не охвачены многие важные
вопросы. Такое положение создает трудности для лиц, инте-
ресующихся этой областью знания, и требует от них затраты
значительных усилий. Настоящая книга написана для того,
чтобы заполнить эти пробелы в литературе или по крайней мере
уменьшить их число. Говоря точнее, имеются в виду следующие
цели: а) представить в доступной форме хотя бы некоторые из
основных связей, существующих между совершенно различ-
ными на первьш взгляд областями науки, относящимися к ма-
тематике, физике и биологии; б) указать на те области, где
относительно просто могут быть найдены важные, не решенные
до настоящего времени проблемы; в) описать достаточно по-
дробно математические методы, с помощью которых можно по-
дойти к решению таких проблем, и, наконец, г) побудить чита-
теля к попытке сформулировать и решить эти задачи. Я сде-
лал попытку написать такую книгу, которую мне самому
хотелось бы иметь в своем распоряжении, когда много лет
назад я впервые решил обратиться к трудной, но увлекательной
области применения математических методов в биологии.
Указанные выше цели делают необходимым и, я полагаю,
желательным стремление скорее к более широкому охвату
материала, нежели к более глубокому проникновению в отдель-
ные вопросы. Мне кажется, что в особенности необходимо от-
метить те аналогии, черты сходства и общие объединяющие
идеи, которые лежат в основе многих внешне существенно отли-
чающихся друг от друга областей науки, и научить читателя
рассматривать их как единое согласованное целое. После этого
он уже сможет обратиться к детальному изучению многих спе-
циальных сочинений. Без такой подготовки масса излишних
8
Предисловие автора
подробностей будет только препятствовать пониманию и со-
здаст для читателя дополнительные трудности.
Мы надеемся, что специалисты согласятся с этой точкой
зрения и не будут слишком сурово критиковать схематичность
и стремление к чрезмерным упрощениям, неизбежно присущие
такой программе. Для восполнения этих недостатков в тексте
приводятся ссылки на оригинальную литературу и объясни-
тельные замечания, в которых указана дополнительная лите-
ратура, относящаяся к материалу, затронутому в основном
тексте. Конечно, многие вопросы остаются тем не менее не-
охваченными, но мы надеемся, что в книге все же содержится
довольно много сведений, позволяющих достаточно точно пред-
ставить себе общую картину развития данной области науки.
Всякий биолог заметит, что приведенные в книге ссылки на
чисто биологическую литературу относятся большей частью
к источникам по крайней мере двадцатилетней давности и свя-
заны с проблемами, которые особенно интересовали биологов
старшего поколения. Поразительные успехи молекулярной био-
логии, характеризующие то направление, в котором биологи-
ческие науки развивались в течение последних двух десятиле-
тий, в книге совсем не затрагиваются; о ДНК, например, вовсе
нигде не упоминается. Следует отметить, однако, что эти более
старые проблемы отнюдь не были разрешены с помощью но-
вейших исследований на молекулярном уровне, а были лишь
попросту заменены другими вопросами. Эти старые проблемы
связаны с самой сутью организации и развития биологических
форм: гомеостазом, онтогенезом, филогенезом. Для биологии
важно не выпускать из виду эти проблемы. Можно надеяться,
что новая формулировка этих задач с помощью* современной
терминологии послужит по крайней мере побудительным моти-
вом для исследования этих задач и позволит приблизиться к их
решению.
Более существенный, по-видимому, момент заключается
в том, что автор решительно придерживался — настолько, на-
сколько это было возможным,— непрерывных и детерминисти-
ческих моделей, не рассматривая дискретные и стохастические
варианты. Это обстоятельство может вызвать возражение со
стороны некоторых читателей, поскольку многие вопросы био-
логии опираются в конечном счете на факты, относящиеся
к популяционной генетике, связанной с дискретными и стоха-
стическими представлениями. Такой подход можно оправдать
теми же соображениями, на основании которых кинетика хими-
ческих систем описывается с помощью дифференциальных
уравнений. Конечно, совсем не говорить о дискретных и сто-
хастических моделях было невозможно, поэтому в книге упо-
Предисловие автора
9
минаются некоторые вопросы, относящиеся к теории перцеп-
трона, стохастической теории обучения и динамическому
программированию. Однако обсуждение таких вопросов носит
чисто эвристический характер, и мы при этом стремимся глав-
ным образом к тому, чтобы отметить связь изучаемых моделей
с реальными исходными объектами изучения и побудить чита-
теля к самостоятельному исследованию таких проблем. О тео-
рии нервных сетей Мак-Каллока и Питтса в книге упоминается
лишь очень кратко, а о теории конечных автоматов и ее много-
численных приложениях к задачам «самоорганизации», игра-
ющим ведущую роль в современных исследованиях в биологии
и смежных с нею областях науки, не говорится совсем. Имеется,
однако, превосходное введение в теорию таких конечных моде-
лей (М. Arbib, Brains, Mashines and Mathematics, McGraw-
Hill, New York, 1964), и мы советуем читателю обратиться
к этой книге и к указанным в ней литературным ис-
точникам.
В математическом отношении материал книги соответствует
примерно уровню знаний студентов, оканчивающих высшее
учебное заведение, или начинающих аспирантов. Некоторые,
быть может, мало знакомые читателю понятия, такие, как «то-
пология» или «компактность», вплетены логически в изложение
отдельных вопросов, и студентам следует обратить на них вни-
мание, хотя мы и не имели возможности разъяснить эти поня-
тия достаточно подробно. В ряде случаев сделаны ссылки на
различные источники по поводу некоторых других результатов,
которые также не рассмотрены в книге детально, так как это
увело бы читателя слишком далеко от основного материала.
10
Предисловие автора
Мы полагаем, что такого рода литературные указания играют
также и определенную воспитательную роль, так как умелое
пользование дополнительной литературой составляет важную
часть самостоятельной работы над материалом, не включенным
в обязательные программы. Этого нельзя достигнуть без прак-
тики, а книги с «замкнутым» изложением не способствуют
приобретению такого опыта.
Выше мы привели схему, на которой изображены основные
логические связи между различными главами книги. Эта схема
поможет читателю уяснить себе взаимоотношения различных
идей, затронутых в книге. В действительности между этими
идеями имеется много других, более тонких связей, которые
здесь не указаны, и разобраться в них можно только после
того, как будет прочитан весь текст. Более того, максималь-
ную пользу из книги можно извлечь, лишь прочитав ее не-
сколько раз.
Буффало, Нью-Йорк Роберт Розен
Гл а в а 1
ОБЩИЕ ПОНЯТИЯ
1.1. Оптимальность в науке и технике
Представление о том, что природа во всех своих проявле-
ниях стремится к экономии, является одним из старейших
принципов теоретической науки. Изучение развития и различ-
ных вариаций этой идеи со времен древних греков до наших
дней весьма увлекательно само по себе. Люди, одушевляющие
природу или видящие в законах природы проявление божест-
венного разума, непосредственно приходят к понятиям «эко-
номии», или оптимальности. При таком подходе нет ничего
более естественного, чем мысль о том, что природа выполняет
свои задачи таким способом, который является в некотором
смысле наилучшим из всех возможных. И действительно, на
этой основе, как известно, были созданы целые метафизиче-
ские системы. ~
В общем случае трудно, однако, сформулировать принцип
оптимальности, или экономии, количественно. Создается впе-
чатление, что при этом каждое отдельное проявление закона
природы требует специального рассмотрения. Тем не менее
существует ряд общих руководящих принципов, которые при-
менимы для изучения оптимальности в различных естествен-
ных науках. Обсудим сейчас, что имеется в виду, когда говорят,
что некоторая форма, или процесс, или конструкция опти-
мальны. Полезно, пожалуй, обратиться вначале к проблемам
техники, которые, разумеется, и послужили первоначальным
источником идей оптимальности. Подумаем, например, о том,
какую конструкцию инженер считает оптимальным решением
некоторой интересующей его задачи.
Инженер обычно имеет дело с проблемой конструирования
некоторого устройства, способного выполнить определенную
задачу при заданных рабочих условиях. Допустим, что инженер
должен спроектировать мост. С каждой конструкцией, которая
может считаться решением этой задачи, непременно связы-
вается определенная цена, измеряемая количественно в каких-
нибудь общепринятых единицах, скажем в долларах или кило-
ватт-часах (выбор определенных единиц измерения необходим
для того, чтобы можно было сравнивать между собой
12
Глава 1
различные конкурирующие решения задачи). За оптимальное
решение принимается такое или такие, которые" удовлетворяют
В’Сём поставленным требованиям, т. е. выполняют предписанную
задачу в заданных рабочих условиях при минимальной цене.
Из приведенного рассуждения вырисовывается первый из упо-
мянутых общих принципов: при изучении оптимальности, ко-
торое всегда носит количественный характер, необходимо выде-
лить некоторый однозначно определенный класс конкурирую-
щих решений рассматриваемой задачи и каждому такому
решению приписать определенную цену таким образом, чтобы
цены, соответствующие различным конкурирующим решениям,
можно было сравнивать друг с другом.
Совершенно ясно, что выбор решения, которое при данных
условиях будет оптимальным, зависит от определения класса
конкурирующих решений и от способа установления цены каж-
дого решения. Некоторая конструкция моста может, например,
оказаться оптимальной при условии, что мост должен быть
сделан из какого-то сорта стали; но если допустить возмож-
ность применения более легкого или более прочного материала
(и тем самым расширить множество конкурирующих конструк-
ций), то может обнаружиться, что прежнее решение уже не
будет больше оптимальным. Имея в виду некоторые соображе-
ния, которые будут развиты далее, нахождение оптимального
решения можно назвать отбором (или искусственным отбором).
Выражаясь математическим языком, мы можем сказать, что
на множестве всех конкурирующих решений данной задачи
задается некоторая оценочная функция (или функционал), ко-
торая каждому элементу этого множества ставит в соответствие
какой-то элемент, принадлежащий некоторому линейно упоря-
доченному множеству цен. Задача определения оптимального
решения сводится, таким образом, к выделению такого реше-
ния, которому соответствует минимальная цена. Иными сло-
вами, при техническом конструировании проблемы оптимиза-
ции могут быть в принципе всегда сформулированы как мате-
матические задачи на минимум *. С математической точки
зрения решения таких задач однозначно характеризуются по-
ставленными условиями, и в следующей главе мы подробно
обсудим математические методы, относящиеся к этому вопросу.
1 Некоторые задачи оптимизации более естественно формулируются как
задачи на максимум, а не на минимум (см. примечание на стр. 194 в гл. 11 и
разд. 12.2). Однако формально задачи этих двух видов эквивалентны: задача
минимизации функции f (х) тождественна задаче максимизации —f (х) и об-
ратно. Большая часть вопросов, рассматриваемых в этой книге, естественным
образом связана с задачами на минимум
Общие понятия
13
1.2. Принцип оптимальности в физике 1
Физика дает ряд превосходных примеров задач такого рода,
и здесь полезно будет кратко провести их сравнительный
анализ (более подробное обсуждение придется отложить до сле-
дующей главы, где будут развиты соответствующие матема-
тические методы). Остановимся на некоторых известных при-
мерах, сыгравших особенно важную роль в развитии теорети-
ческой физики.
В качестве первого из них, соблюдая историческую после-
довательность, следует назвать принцип наименьшего времени
Ферма. Это основной принцип геометрической оптики, и он
гласит, что луч света, распространяющийся в некоторой опти-
ческой среде (у которой, например, показатель преломления
может от точки к точке изменяться), выбирает из всех возмож-
ных траекторий такую, при которой время движения мини-
мально2. Заметим, что принцип Ферма приводит к задаче
именно такого типа, который мы обсуждали выше. Во-первых,
все условия этой задачи вполне однозначно определены,
а именно речь идет- о движении луча света из некоторой на-
чальной точки в некоторую конечную точку через произвольную
оптическую среду. Во-вторых, с этой задачей связано одно-
значно определенное множество допустимых решений — это
множество всех физически возможных траекторий, соединя-
ющих две заданные точки. Наконец, каждой такой траектории
соответствует некоторое число, характеризующее в определен-
ном смысле цену данной траектории, а именно время, затра-
ченное световым лучом на переход по этой траектории. Прин-
цип Ферма говорит, что в этом случае оптимальной траекторией
будет та, которой соответствует наименьшая цена (т. е. наи-
меньшее время перехода), и в природе движение светового
луча происходит именно по такой оптимальной траектории.
Следующий физический принцип этого же типа, о котором
здесь следует сказать, является в точном смысле слова анало-
гом принципа Ферма в механике — это известный принцип, на-
именьшего действия Мопертьюи. Этот принцип относится к дви-
1 В механике и физике такие принципы называются вариационными —
Прим перев
2 В гл 2 будет показано, что при математическом решении задач, свя-
занных с принципом Ферма и другими вариационными принципами, опти-
мальное решение не обеспечивает, вообще говоря, действительного минимума
функционала Фактически гарантируется лишь то, что оптимальное решение
будет стационарным Однако в большинстве реальных физических задач дей-
ствительное оптимальное состоиние оказывается связанным, как правило,
с минимумом (а не с точкой перегиба, максимумом или каким-нибудь другим
типом стационарного решения)
14
Г лава 1
жению механических систем и в наиболее общей своей форму-
лировке утверждает, что при реальном движении произвольная
механическая система выбирает из всех возможных траекторий,
при движении по которым сохраняется энергия, ту траекторию,
которая минимизирует определенную механическую величину,
называемую действием. В применении к системам, у которых,
кроме полной энергии, сохраняется также и кинетическая
энергия и равнодействующая внешних сил равна нулю, этот
принцип сводится к утверждению, что из всех траекторий, со-
гласующихся с требованием сохранения энергии, система вы-
бирает ту траекторию, которая минимизирует время перехода
Аналогия с принципом Ферма здесь’вполне очевидна, и она
имеет важное теоретическое значение* 2. В принципе Мопертьюи
мы опять-таки имеем дело с некоторым множеством допусти-
мых решений механической задачи, которое однозначно харак-
теризуется поставленными условиями (т. е. с множеством воз-
можных траекторий изучаемой системы, согласующихся с усло-
вием сохранения энергии) и каждому элементу которого отве-
чает некоторое число (величина действия), соответствующее
цене, связанной с движением по этой траектории. Принцип Мо-
пертьюи указывает, что оптимальное решение определяется
траекторией, на которой минимизируется действие, и что ре-
альное движение системы происходит именно по этой тра-
ектории.
Очень интересно отличие третьего вариационного принципа,
встречающегося в физике, от приведенного выше принципа
* См. разд. 2.11. Полезно познакомиться со следующим эвристическим
рассуждением, относищимся к этому вопросу: обозначим через Т и V соответ-
ственно кинетическую и потенциальную энергии системы, а действие для этой
системы запишем как (Г — V)t. Сохранение полной энергии означает, что
r+K=const. Если кинетическая энергия тоже сохраняется, то T=const,
а значит, также и V=const. Поэтому (Г—V)= const, и действие оказывается
попросту пропорциональным времени перехода, откуда и следует то, что
утверждалось.
2 Аналогия между этими двумя вариационными принципами была отме-
чена в 1834 г. Гамильтоном, который подчеркнул устанавливаемое этой анало-
гией соответствие между геометрической оптикой и классической механикой.
Ввиду того, что геометрическая оптика является частным случаем волновой *
оптики, высказывалось мнение, что Гамильтон мог бы в принципе построить
на основе этой аналогии механический аналог волновой оптики Этот меха-
нический аналог, который мы теперь называем волновой механикой, был от-
крыт лишь в 1926 г., когда Шрёдингер вывел свое волновое уравнение. Чи-
татель может найти изложение волновой механики, опирающееся на эту точку
зрения, в небольшой монографии Флинта [1].
Многие физические вариационные принципы оказываются родственными
друг другу. Г. Вейл [2] показал, например, что принцип Ферма можно вывести
из формулировки принципа относительности, опирающейся иа понятие геоде-
зической линии.
Общие понятия
15
Мопертьюи. Речь идет об известном принципе Гамильтона —
едва ли не самом важном из вариационных принципов теоре-
тической физики. Этот принцип, как и принцип Мопертьюи,
связан с механическим действием. Он напоминает принцип Мо-
пертьюи тем, что в нем с каждым элементом множества допу-
стимых траекторий рассматриваемой механической системы
связывается значение действия, соответствующее этой траек-
тории, которое и характеризует цену этой траектории. Однако
он существенно отличается от принципа Мопертьюи в опреде-
лении допустимого множества возможных траекторий, которые
могут быть выбраны. В принципе Мопертьюи берутся лишь те
траектории, которые согласуются с требованием сохранения
энергии. А в принципе Гамильтона рассматриваются траекто-
рии, которые возникают при так называемых виртуальных пе-
ремещениях. При этом фиксируется время перехода и варьи-
руются лишь пространственные координаты системы (вариации
координат должны быть при этом подчинены ограничениям
связей, наложенным на систему). Эти два множества допусти-
мых траекторий, соответствующих обоим принципам, вообще
говоря, различны, так как нет оснований предполагать, что
вдоль траекторий, образующихся при виртуальных перемеще-
ниях, энергия должна сохраняться. Поэтому, несмотря на то
что в других отношениях эти принципы весьма сходны, они
имеют совершенно разные области применения. Принцип Га-
мильтона является значительно более общим ((принцип
Мопертьюи можно на самом деле вывести из принципа Га-
мильтона) и, как уже говорилось, служит краеугольным
камнем большинства важнейших разделов теоретической
физики.
Указанное различие между принципами Мопертьюи и Га-
мильтона чрезвычайно ярко иллюстрирует тот факт, что ха-
]эактер оптимального решения задачи существенно зависит от
того, каким именно образом определено множество допусти-
мых решений, даже в том случае, когда используется одна и
fa же оценочная функция. Такого же различия естественно
ожидать и в том случае, когда берется другая оценочная функ-
ция, а множество возможных решений сохраняется.
Укажем здесь, не упоминая о деталях, еще одну область
физики, где возникают такие же задачи. Интересный пример
этого типа дает общая теория относительности, согласно кото-
рой действительная траектория материальной частицы, движу-
щейся между двумя точками в силовом поле, соответствует
геодезической линии, или кривой наименьшей длины (напом-
ним, что, поскольку между силовым полем и кривизной про-
странства существует определенная связь, линия наименьшей
16
Глава 1
длины, по которой движется частица, не совпадает с обычной
прямой линией, как это имеет место в евклидовом простран-
стве) .
С математической точки зрения нахождение геодезической
линии, или кривой наименьшей длины, соединяющей две точки
на заданной поверхности, представляет собой одномерную за-
дачу, и она может быть непосредственно обобщена на случай
многих измерений. Двумерное обобщение этой задачи состоит
в том, что требуется найти и описать поверхность (или поверх-
ности) наименьшей площади, ограниченную некоторой задан-
ной замкнутой кривой в трехмерном пространстве. Это так на- •
зываемая задача Плато. Задача Плато тесно связана с при-
менением принципа минимальности в физике, так как всякая
тонкая оболочка, например пленка жидкости, ограниченная
в пространстве некоторым замкнутым контуром, стремится
принять конфигурацию поверхности наименьшей площади. Это
нетрудно доказать исходя из того, что виртуальное изменение
поверхности такой пленки (рассматриваемой как механическая
система в состоянии равновесия) связано с нулевой виртуаль-
ной работой (см. разд. 2.10). Свойство тонких пленок, связан-
ное с их стремлением принимать конфигурацию поверхностей
наименьшей площади, находит непосредственное применение
в биологии и может быть использовано при исследовании ряда
интересных проблем, относящихся к формам живых организ-
мов (см., например, [3], в особенности гл. VII). Обсуждение
физической стороны явлений, связанных с этим свойством тон-
ких пленок, можно найти в книге Джуса [4].
Упражнение
Сформулируйте явно условия, определяющие множества до-
пустимых решений и оценочные функции в последних двух
оптимальных задачах.
Совершенно очевидно, что подход, основанный на принципе
экономии, или оптимальности (если понимать эти термины
именно в том смысле, о котором говорилось выше), должен
иметь весьма большое значение при изучении самых разнооб-
разных физических проблем. О важных следствиях этого факта
пишет в своей книге Голдстейн [5]: «...почти во всех областях
физики для вывода «уравнений движения» (физических си-
стем), например уравнений Ньютона, Максвелла или Шрёдин-
гера, могут быть использованы (вариационные) принципы.
Поэтому, когда принцип (такого рода) принимается за основу
формулировки физических законов, обнаруживается, что раз-
личные области физики обладают, по крайней мере в некото-
рой степени, структурной аналогией. Когда результаты экспе-
Общие понятия
17
риментов приводят к необходимости изменения физических
представлений, относящихся к какой-то области физики, эта
аналогия часто указывает, каким образом сходные изменения
могут быть проведены и в других областях... (например) при
описании электромагнитного поля с помощью (принципа Га-
мильтона) обнаруживается возможность разработки методов,
позволяющих построить квантовую электродинамику...»
Мы покажем далее, что и в биологии последовательное при-
менение общей формулировки принципа оптимальности также
позволяет рассмотреть широкий круг задач; в этом, собственно,
и заключается главная цель этой книги.
1.3. Принцип оптимальности и отбор в биологии1
Теперь мы обратимся к следующему основному вопросу:
каким образом идеи оптимальности проявляются в биологиче-
ском мире и как можно на их основе разработать удобную и
практически полезную математическую теорию? Сначала сле-
довало бы спросить, почему, собственно, можно рассчитывать
на то, что независимо от теологических или эстетических со-
ображений черты принципа оптимальности должны проявиться
в живой природе. В физике, например, введение вариационных
принципов, таких, скажем, как принципы Ферма или Мо-
пертьюи, оправдывается только тем, что мы в конечном счете
реально убеждаемся в их практической применимости. Что
касается биологии, то и здесь можно привести достаточно по-
следовательные и подчас даже основанные на количественном
анализе рассуждения, которые в определенной степени оправ-
дывают поиски таких принципов и помогают их сформулиро-
вать. Эти рассуждения основываются на явлении естественного
отбора и на давлении отбора, влияние которого сказывается
почти на каждой черте строения, функции и деятельности био-
логических индивидуумов.
Что же представляет собой естественный отбор? В общих
чертах, эвристически, можно рассматривать естественный отбор
как результат конкуренции (или, придерживаясь терминологии
Дарвина, «борьбы») между теми индивидуумами или процес-
сами, которые оказались вместе в одних и тех же общих для них
1 Мы не можем здесь на нескольких страницах уделить достаточно вни-
мания этим сложным и многообразным вопросам, поэтому по поводу даль-
нейших деталей, относящихся к этому краеугольному камню биологии, чита-
тель должен обратиться к другим литературным источникам Укажем две пре-
восходные книги [6, 7], с которыми полезно ознакомиться перед чтением спе-
циальной литературы, а также очень хорошую монографию Рента [8] На эти
книги мы будем постоянно ссылаться в соответствующих местах гл 4—6
1-8 Глава!
условиях среды. Интуиция подсказывает, что те индивидуумы,
которые способны к более эффективной конкуренции, чем дру-
гие, имеют больше шансов победить в этой борьбе, что выра-
жается не только в их выживании как индивидуумов, но, что
еще важнее, и в их успехе в оставлении потомства. Введем
теперь следующие допущения: а) преимущество, обнаружива-
емое определенными индивидуумами в борьбе за существова-
ние в данных условиях среды, может передаваться их по-
томству; б) данные условия среды остаются неизменными
достаточно долго. Тогда в популяции в целом будут накапли-
ваться индивидуумы, обладающие указанными преимущест-
вами, и в конечном счете возникнет тенденция, при которой
формы, обладающие неблагоприятными признаками, начнут
исчезать из популяции; это утверждение в некоторых простых
случаях может быть строго доказано ’. В отношении естест-
венного отбора можно сразу отметить одну весьма важную
черту — то, что все виды преимуществ в борьбе за существова-
ние, независимо от их первоначальной природы, в конечном
счете выражаются в различиях в плодовитости (в предположе-
нии, что наши условия «а» и «б» выполняются), и именно это
различие в плодовитости в конце концов приводит по истечении
достаточно длительного промежутка времени к преобладанию
форм, имеющих эти признаки1 2.
Принимая во внимание процесс естественного отбора,
можно, таким образом, ожидать, что живые организмы, пре-
бывающие совместно в течение достаточно долгого времени
в определенной совокупности окружающих условий, будут по-
степенно приобретать такие признаки, которые являются опти-
мальными для этих условий. Это означает, что организмы, бу-
дут приобретать такие черты, которые в данной определенной
среде наверняка не скажутся отрицательно на их способности
конкурировать с соперниками.
Мы можем теперь выдвинуть основную гипотезу, заключа-
ющуюся в следующем: организмы, обладающие биологической
структурой, оптимальной в отношении естественного отбора,
1 Это утверждение является частным случаем хорошо известного прин-
ципа исключения Гаузе [9], который утверждает, что два вида не могут не-
ограниченно долго сосуществовать в одной и той же экологической нише, т. е.
один нз них в конце концов должен быть полностью вытеснен. По поводу экс-
периментальных исследований, основанных иа этом принципе, см., например,
статью Парка [10]. (Следует отметить, что многие экологи не признают спра-
ведливости принципа Гаузе, указывая, что в природе два вида никогда не за-
нимают в точности одну и ту же экологическую нишу.)
2 «Плодовитость», грубо говоря, соответствует «приспособленности» (тер-
мин, применяемый в популяционной генетике; см. гл. 11, разд. 11.4 и, в част-
ности, примечание па стр. 194).
Общие понятия
19
оптимальны также и в том смысле, что они минимизируют не-
которую оценочную функцию, определяемую исходя из основ-
ных характеристик окружающей среды. Это чрезвычайно естест-
венное предположение называют принципом оптимальной кон-
струкции (principle of optimal desighn) и большую часть на-
шей книги мы посвятим разработке некоторых приложений
этого принципа. В тех случаях, когда принцип оптимальности
1 Представление об оптимальном строении организмов, разумеется, ие
ново; эта идея часто встречается (или по крайней мере подразумевается)
в значительной части старой литературы по количественной биологии (см,
например, обширную литературу о медовых сотах, приведенную на стр. 525 и
далее в цитированной ранее книге д’Арси Томпсона [3]) Изучение формы
медовых сот до сих пор служит источником важных математических исследо-
ваний, относящихся к оптимальности (см., например, [11])*. Однако в явной
форме принцип оптимальной конструкции первым сформулировал Рашевский
([12], в особенности стр. 292 и далее)
Совсем недавно некоторые геометрические соображения, сходные по идее
с теми, которые встречаются в литературе о медовых сотах, были применены
для объяснения симметрии сферических вирусов (см, например, [13—15]).
Здесь уместно будет также отметить, что идеи о возникновении оптимальной
структуры в результате естественного отбора были перенесены некоторыми
исследователями на молекулярный уровень при рассмотрении проблемы проис-
хождения жизни. На основании таких представлений «молекулярной эколо-
гии», возможно, удастся связать современную молекулярную биологию, в осо-
бенности в ее сравнительном аспекте, с «глобальными» идеями оптимальности,
развиваемыми в этой книге. Для того чтобы читатель лучше почувствовал дух
этих идей, приведем несколько цитат из опубликованного недавно обзора
Дж. Уолда [16]:
«Такие молекулы, как хлорофилл, играющий ключевую роль в фотосин-
тезе, гемсодержащие пигменты, участвующие в дыхании, нли каротиноиды
и витамин А, с помощью которых осуществляется фоторецепция, представ-
ляют собой продукт происходивших на нашей планете длительных и строгих
процессов отбора, постоянно направленных к достижению оптимальных ре-
шений. Все эти молекулы обладают свойствами, соответствующими именно
тем функциям, которые они выполняют в организмах; у меня нет сомнения
В том, что чем ближе мы подойдем к пониманию природы того или иного
Процесса, тем яснее будет, почему именно этн молекулы, а не другие возникли
при отборе. Подчас такие молекулы обнаруживают странную смесь благо-
приятных и неблагоприятных свойств; так, например, все молекулы хлоро-
филла имеют одно странное свойство: они хуже всего поглощают свет как раз
на тех длинах волн, интенсивность которых в солнечном свете на поверхности
Земли и под водой максимальна. Очевидно, молекулы хлорофилла должны
обладать другими, благоприятными для фотосинтеза признаками, которые
значительно перевешивают отмеченный недостаток.. »
«Резюмируя, можно сказать, что, сталкиваясь с проблемами, по сути уни-
версальными, организмы повсюду обнаруживают тенденцию решать эти про-
блемы одним и тем же путем; путь этот — выбор тех типов молекул, которые
в данной ситуации — в пределах данной органической структуры—представ-
ляют оптимальное или почти оптимальное решение... Выбор такого рода,
по-видимому, всюду управляется естественным отбором... вследствие (от-
бора) выживают наиболее приспособленные, т. е. проявляется тенденция
к оптимизации, в результате молекулы и приобретают упомянутые выше свой-
ства».
20
Глава 1
удается подвергнуть прямой проверке, обнаруживается очень
хорошее совпадение теоретических результатов с данными
непосредственных биологических наблюдений. В общем случае,
однако, отнюдь не очевидно, каким образом можно установить
подходящую оценочную функцию; в этом, собственно, и за-
ключается основная трудность и искусство применения этого
принципа.
1.4. Качественные аспекты оптимальности в биологии
Ранее было показано, что задачи оптимизации в физике и
технике обладают некоторыми вполне определенными харак-
терными чертами. Они должны быть сформулированы таким
образом, чтобы можно было построить некоторое однозначно
определенное множество потенциально возможных решений и
чтобы с каждым таким потенциально возможным решением
можно было ассоциировать определенное число, представляю-
щее цену, соответствующую этому решению. Тогда задача со-
стоит в том, чтобы найти такое решение, с которым связана
наименьшая цена. Допустим, что мы приняли сделанные выше
допущения относительно связи между отбором (плодовитостью)
и принципом оптимальности в биологии. Каким же образом,
спрашивается, можно выразить законы образования биологи-
ческих форм и функций организмов в рамках этой схемы?
Прежде всего, конечно, следует попытаться определить раз-
личные цены, с_ которыми нам предстоит иметь дело при рас-
смотрении специфических биологических проблем. Во-первых,
известно, ч/б" каждый элемент структуры, такой, скажем, как
глаз, ухо или сосудистая система, имеет определенную мета-
болическую цену, которая должна быть выражена в 'некой
метаболической «валюте», общей для всех организмов. Эта
цена, грубо говоря, соответствует энергии, расходуемой орга-
низмом на образование и поддержание рассматриваемого
элемента структуры. Поскольку любой организм располагает
лишь ограниченным запасом энергии, можно считать, что при
прочих равных условиях ^птимальн.оа_£труктурой (или струк-
турами) будет такая, которая обеспечивает наименьший рас-
ход метаболической энергии (достаточный в то же время для
нужд организма). В ряде случаев, например для популяции
бактерий, это может быть подтверждено экспериментально ’.
1 Мутантный штамм, у которого один из ферментных белков «дерепрессн-
рован» (т е продолжает синтезироваться в условиях, когда для обмена ве-
ществ он не требуется, см разд 9 5), в процессе отбора уступает штамму ди-
кого типа, у которого такой синтез имеет место лишь тогда, когда он метабо-
лически необходим Такие мутанты быстро элиминируются из популяции,
Общие понятия
21
Кроме этой метаболической, или внутренней, цены, опреде-
ляемой неизбежными расходами энергии на образование и под-
держание некоторого органа, нужно ввести также и определен-
ную внешнюю цену, связанную с давлением отбора. Эта
последняя цена находит свое отражение в относительной
плодовитости организмов, обладающих данным органом, по сра-
внению с другими (идеализированными) организмами, отлича-
ющимися от рассматриваемых только строением этого органа.
Как уже было показано, действие отбора сводится в сущности
к тому, что организм, у которого какой-то орган менее эффекти-
вен в борьбе за существование, как бы «наказывается» или
«платит штраф». Полная цена данной определенной структуры
дблжна быть, таким образом, равна алгебраической сумме вне-
шних и внутренних цен (умноженных, если это требуется, на
соответствующим образом подобранные множители для приве-
дения их к одинаковым размерностям)
Здесь следует отметить некоторые типичные качественные
черты описанной выше ситуации, которые позволяют создать
общее представление о сущности принципа оптимальности
в биологии:
1. Интуитивно ясно, что для каждого типа органа сущест-
вует 'числовое значение оо (называемое верхней границей или
порогом), такое, что если полная цена какого-либо органа
этого типа превзойдет сто, то организм становится нежизне-
способным.
2. Обозначим через а полную цену, а через I и Е — соответ-
ственно внутреннюю и внешнюю цены, так что о = 1+Е. Вели-
чины ст, I и Е являются здесь оценочными функциями, опреде-
ленными как раз в том смысле, как об этом ранее говорилось,
т. е. каждая из них приписывает всякому элементу множества
возможных форм строения организмов определенное число,
соответствующее некоторому определенному органу или про-
цессу жизнедеятельности.
3. Если на всем множестве допустимых решений значение Е
мало и относительно постоянно, то полная цена ст конкурирую-
щих структур в основном начинает зависеть лишь от внутрен-
ней метаболической цены. Так, например, если организм жи-
вет в таких условиях, где нет особой необходимости в зрении,
то для него самым лучшим будет такой глаз, цена которого
минимальна. Если в данной среде вообще нельзя ничего ви-
деть, то лучше вовсе не иметь глаз (/ = 0), что в действительности
в которой они образуются, если только эта популяция не находится постоянно
в таких условиях среды, при которых данный белок все время требуется для
поддержания метаболизма
22
Глава 1
и наблюдается у хорошо известных слепых рыб, обитающих
в пещерах, куда не проникает дневной свет.
4. Если же Е является главным слагаемым в полной цене,
тогда в общем случае оптимальным решением (или решениями)
будет такое, которое минимизирует Е, даже если при этом и
не достигается одновременная минимизация I. Если при данных
условиях окружающей среды лишь небольшое число возмож-
ных структур минимизирует Е, то, как и в предыдущем случае,
будет существовать лишь небольшое число оптимальных форм,
и тогда давление отбора на неоптимальные формы будет за-
висеть от того, насколько резко выражено различие в цене
между оптимальными формами и остальными. Можно отме-
тить в связи с этим, что во всех тех случаях, когда давление
отбора велико, все организмы, которым благоприятствуют опре-
деленные среды, постепенно приобретают одни и те же особен-
ности независимо от существующих между ними других разли-
чий. В экологии это положение известно как принцип конвер-
генции или закон конвергентной эволюции. Можно привести
много примеров конвергенции: альбинизм и отсутствие глаз
у пещерных животных (рыб, .млекопитающих и насекомых);
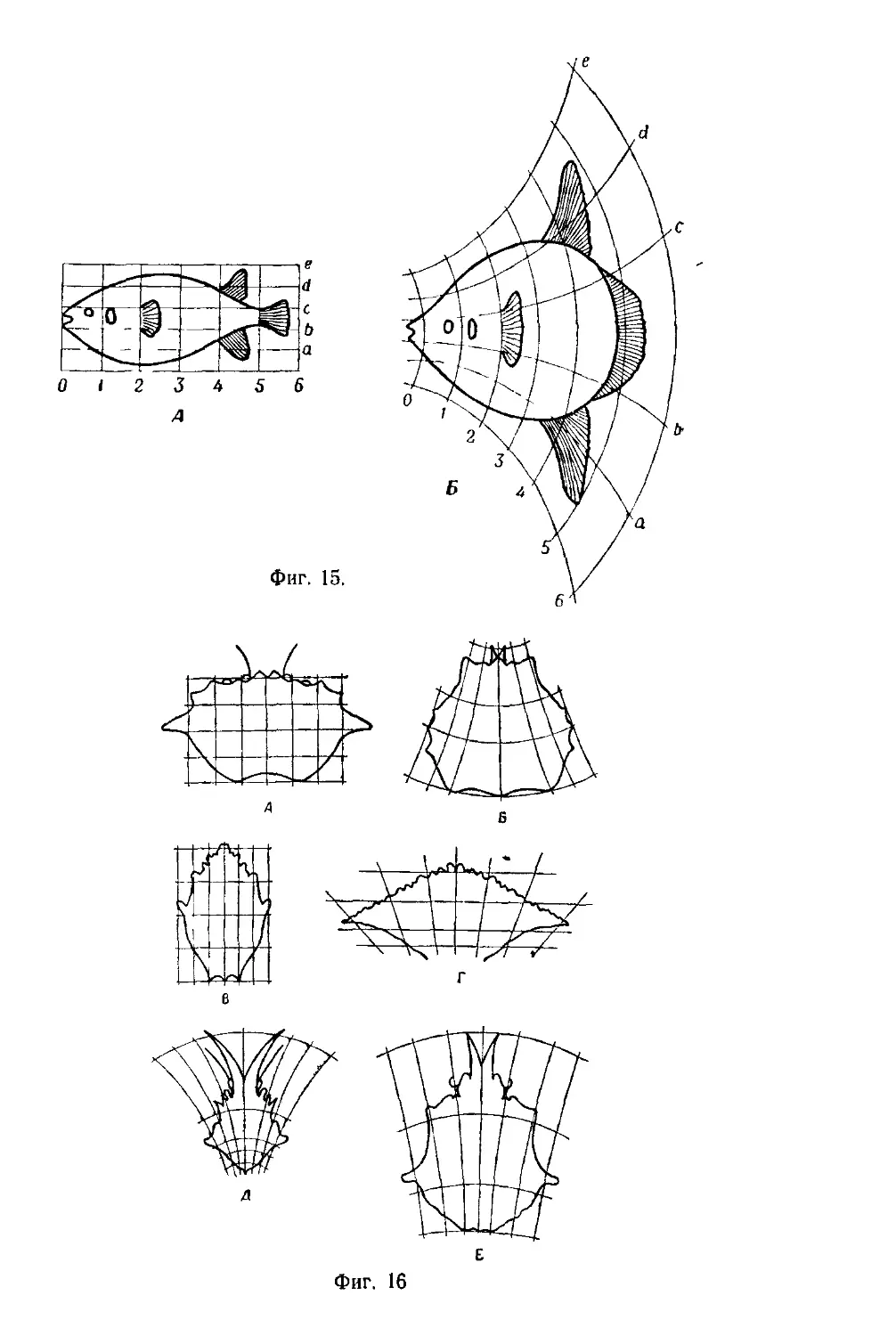
подобие форм у различных хищных морских позвоночных
(акулы, морской щуки, дельфина, ихтиозавра); поразительное
сходство между австралийскими сумчатыми формами и со-
ответствующими формами высших млекопитающих, обитающих
в аналогичных условиях окружающей среды в других частях
света. Можно было бы привести сотни других примеров та-
кого рода.
5. Если обе величины / и Е малы и приблизительно равны
на всем множестве допустимых структур в данных условиях
среды, то давление отбора будет слабым и не найдется основа-
ний для предпочтительного выбора одной структуры из всех
остальных. Это приведет к сильному полиморфизму, т. е. к боль-
шому разнообразию форм и структур организмов, обитающих
в данных условиях. Такие ситуации имеют для эволюции боль-
шое значение, так как они могут породить процесс, который
часто называют адаптивной радиацией.
Итак, проведенный выше анализ, несмотря на свой прибли-
женный характер, указывает на тесную связь между давлением
отбора в некоторых условиях среды и степенью конвергенции,
наблюдаемой среди организмов, обитающих в данной среде.
Это может быть в принципе количественно описано с помощью
введенных выше оценочных функций и в конечном счете выра-
жено в терминах оптимальности. Грубо говоря, сильная кон-
вергенция свидетельствует о том, что эти оценочные функции
минимизируются одной-единственной или небольшим числом
Общие понятия
23
структур, и, следовательно, о сильном давлении отбора; если
минимум достигается на многих структурах, то это указывает
на слабое давление отбора и высокую степень полиморфизма.
Важно заметить, что все эти экологические правила непосред-
ственно устанавливаются как следствия принципа оптималь-
ности и что такие задачи могут быть математически четко
сформулированы и исследованы, причем это дает возможность
получить точную информацию также в отдельных частных
случаях.
Глава 2
ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ
2.1. Введение
В предыдущей главе было показано, что при нахождении
оптимального решения некоторой задачи требуется соблюдение
следующих трех условий: а) должен быть определен класс
всех допустимых решений задачи; б) каждому такому решению
должно быть отнесено определенное число, выражающее соот-
ветствующую цену; в) в множестве всех цен должна быть най-
дена наименьшая. Начиная с гл. 3, мы будем рассматривать
первые два условия, которые в основном связаны с областью
естественных наук, а данную главу посвятим третьему условию,
представляющему собой чисто математическую задачу.
В условии «в» самое сложное понятие связано с термином
«наименьший». Приступить к формулировке любой задачи об
оптимизации можно лишь в том случае, если мы располагаем
способом, позволяющим сравнивать цены, соответствующие
любым двум потенциально возможным решениям, и определять,
какая из этих цен больше и какая меньше. С математической
точки зрения это означает, что множество рассматриваемых
цен должно быть линейно упорядочено. Если цены, как это
•обычно имеет место, выражаются вещественными числами, то
это требование выполняется автоматически; для любой задан-
ной пары различных вещественных чисел а, b всегда либо
а<Ь, либо Ь<а. Последнее представляется настолько очевид-
ным, что на первый взгляд вряд ли стоит об этом говорить так
подробно; тем не менее, как будет показано далее, это положе-
ние создает основу всего математического аппарата решения
задач на отыскание минимума. Итак, изучение условия «в»
следует начать с обсуждения понятия отношения порядка
в множестве вещественных чисел и некоторых модификаций
этого понятия.
2.2. Отношение порядка в множестве вещественных чисел
Пусть R — множество вещественных чисел; условимся обо-
значать обычное отношение порядка для элементов этого мно-
жества известным символом < или более общим символом .
Основные математические методы
25
Если S — некоторое множество вещественных чисел, то
говорят, что оно ограничено сверху, если найдется такое ве-
щественное число М, что для любого х 6 S выполняется нера-
венство х^Л1. Аналогично множество S называется ограничен-
ным снизу, если существует такое вещественное число L, что
L<Jx для всякого x£S. Числа М и L, обладающие указанными
выше свойствами, называются соответственно верхней и ниж-
ней гранями S. Множестве S, обладающее и верхней и нижней
гранями, называется ограниченным.
Пусть S — некоторое ограниченное сверху множество. До-
пустим, что среди всевозможных верхних граней S имеется
некоторая верхняя грань Af0, которая обладает следующим
свойством: для любого сколь угодно малого наперед заданного
положительного числа е>0 всегда найдется такой элемент
x£S, что Мо—е<х. Такая верхняя грань называется точной
верхней гранью S. Точно так же нижняя грань Lo является
точной нижней гранью ограниченного снизу множества S, если
для любого сколь угодно малого положительного числа е>0
найдется такой элемент х С S, что x<L0 + e ’.
Упражнение
Докажите, что ограниченное множество S не может иметь
более одной точной верхней грани и более одной точной ниж-
ней грани.
Теперь возникает такой вопрос: можно ли утверждать, что
всякое ограниченное множество чисел обладает точной верх-
ней и точной нижней гранями? Ответ на этот вопрос для нас
чрезвычайно важен, потому что если данное множество цен
не имеет точной нижней грани, то оптимальное решение рас-
сматриваемой задачи, очевидно, не существует, поскольку,
какое бы решение мы ни взяли, всегда в этом случае найдется
другое решение с меньшей ценой. Этот вопрос интересен и
с чисто математической точки зрения, так как он связан с ря-
дом других важных идей.
Возьмем теперь такой пример. Предположим, что в неко-
торой задаче приходится иметь дело только с множеством R
рациональных чисел (например, пусть в рассматриваемой опти-
мальной задаче встречаются. лишь такие цены, которые выра-
жаются числами вида а/b, где а и b — целые числа). Нетрудно
в этом случае построить ограниченное сверху множество ра-
циональных чисел, у которого нет рациональной точной
1 Отметим, что приведенные здесь определения точной верхней и точной
нижней граней эквивалентны указаниям на то, что точная верхняя грань —
это наименьшая из всех верхних граней, а точная нижняя грань — наиболь-
шая из всех нижних граней —Прим, перев.
26
Глава 2
верхней грани. Так, например, последовательность рациональ-
ных чисел
1; 1,4; 1,41; 1,414; 1,4142; 1,41421...
обладает тем свойством, что квадраты ее элементов все более
и более точно приближаются к числу 2 (члены этой последова-
тельности представляют собой не что иное, как последователь-
ные приближения, образующиеся при разложении числа ]/2
в бесконечную десятичную дробь). Но, как хорошо известно,
не существует рационального числа х, такого, что х1 2 = 2, и
поэтому нетрудно убедиться в том, что какую бы рациональную
верхнюю грань М множества, состоящего из членов приведен-
ной выше последовательности, мы ни взяли, всегда найдется
другая рациональная верхняя грань, меньшая, чем М.
Рассматриваемое в этом примере множество обладает, ра-
зумеется, точной верхней гранью в множестве вещественных
чисел — ею служит число У~2. Оказывается, системе всех ве-
щественных чисел вообще свойственна характерная черта, что
всякое множество вещественных чисел, ограниченное сверху,
обладает точной верхней гранью, и всякое множество вещест-
венных чисел, ограниченное снизу, обладает точной нижней
гранью ’.
Это свойство множества всех вещественных чисел, о кото-
ром мы только что говорили, называется полнотой-, имея в виду
свойство полноты, можно сказать, что в множестве всех ве-
щественных чисел нет «пропусков», или «дырок». Полнота
тесно связана с топологией множества всех вещественных чисел
и его подмножеств и, следовательно, с понятием непрерывности
функций вещественных переменных. Нам будет полезно по-
этому более подробно ознакомиться с этими важными предста-
влениями.
2.3. Замкнутые и открытые множества
Обозначим через S некоторое множество вещественных чи-
сел, не обязательно ограниченное. Говорят, что S— замкнутое
множество (или, просто, что S замкнуто), если точные верхняя
1 Множество всех вещественных чисел с определенными в нем алгебраи-
ческими операциями образует так называемое поле. Отношение порядка ве-
щественных чисел удовлетворяет аксиоме Архимеда, а именно для любого ве-
щественного числа я>0 существует столь большое целое положительное число
N>0, что ~j^~<a. В связи с обсуждаемым здесь свойством полноты отметим,
что вещественные числа образуют единственное, с точностью до изоморфизма,
полное архимедовски упорядоченное поле, т. е. всякое архимедовски упоря-
доченное поле изоморфно некоторому подполю поля вещественных чисел. По
этому поводу см., например, [17].
Основные математические методы
27
и нижняя грани всякого ограниченного подмножества S' мно-
жества S также принадлежат S. Говорят, что множество S
вещественных чисел является открытым множеством (или, ко-
роче, что S открыто), если его дополнение1 является замкну-
тым множеством.
Рассмотрим примеры. Пусть а, b — два различных вещест-
венных числа. Возьмем множество всех вещественных чисел х,
удовлетворяющих неравенствам Это множество, оче-
видно, ограничено, и читатель легко может убедиться в том,
что оно замкнуто. Такое множество называется замкнутым
промежутком или сегментом с концами а, b и обозначается
символом [а, &]. С другой стороны, как нетрудно показать,
множество чисел х, таких, что а<х<&, образует открытое мно-
жество. Это множество называется открытым промежутком
или интервалом и обозначается символом (а, Ь).
Далее, всюду, за исключением тех случаев, когда это будет
особо оговорено, мы будем рассматривать ограниченные про-
межутки, т. е. такие, для которых —оо<а<6<^оо. Мы видим,
что ограниченное множество можно определить как множество,
целиком содержащееся в некотором открытом (ограниченном)
промежутке. Существуют также и такие множества веществен-
ных чисел, которые не являются ни открытыми, ни замкнутыми.
Так, например, множества, определяемые соотношениями
а<х<^6 или а^х<Ь, ни открыты, ни замкнуты.
Понятие открытого множества и свойства, которыми обла-
дают все открытые подмножества вещественных чисел, играют
основную роль при изучении топологии множества веществен-
ных чисел. Это понятие лежит в основе представления о непре-
рывности и образует прототип для построения других более
общих топологических пространств. Открытые промежутки иг-
рают весьма важную роль ввиду простоты их строения,
а также потому, что произвольное открытое множество может
быть всегда построено некоторым каноническим способом из
открытых промежутков. Здесь нет необходимости более глу-
боко затрагивать этот предмет, и мы ограничимся лишь тем,
что приведем две важные теоремы. В дальнейшем мы увидим,
что одно свойство открытых множеств, выражаемое этими
теоремами, часто используется для эквивалентного общего
определения понятия открытого множества. Доказательство этих
теорем даст читателю некоторое представление о том, каким
образом топологическое определение открытого множества
1 Дополнение S множества S определяется следующим образом: число
х(5в том и только в том случае, когда х£ S.
28
Глава 2
естественным образом вытекает из определения, первоначально
основанного на представлении об отношении порядка.
Теорема 2.1
Пусть S — некоторое непустое открытое множество вещест-
венных чисел. Тогда для любого элемента х этого множества
найдется открытый промежуток 1, удовлетворяющий следующим
двум условиям: а) I является подмножеством S и б) х£1.
Иными словами, для каждого элемента открытого множества
5 существует некоторый открытый промежуток, целиком при-
надлежащий этому множеству и содержащий данный элемент.
Доказательство
Обозначим дополнение S через Т. Тогда S и Т исчерпывают,
согласно определению дополнения, все вещественные числа, и
не существует ни одного вещественного числа, одновременно
принадлежащего S и Т. Пусть теперь х £ S. Рассмотрим сле-
дующие два множества:
А: множество всех у £Т, таких, что у<х;
В: множество всех у 6 Т, таких, что х < у.
Ясно, что Л и В не могут быть одновременно пустыми, за ис-
ключением того случая, когда само Т пусто. В последнем слу-
чае множество S содержит все вещественные числа, и утвер-
ждение теоремы становится тривиальным.
Допустим теперь, не ограничивая общности, что А непусто.
Тогда х, согласно определению, есть верхняя грань А. В то же
время, однако, х не может быть точной верхней гранью А.
В самом деле, поскольку множество Т в соответствии со сде-
ланными предположениями замкнуто и А служит подмножест-
вом Т, из допущения, что х — точная верхняя грань А, следо-
вало бы, согласно определению замкнутого множества, что
х£Т, а это противоречит тому, что x^S, так как S и Т не
имеют общих элементов. В то же время у А имеется точная
верхняя грань, скажем уо, и у0<Сх- В таком случае можно ука-
зать вещественное число г, такое, что г/о<2<х, и, очевидно,
zes.
Если множество В пусто, то всякое другое число z', такое,
что x<z', принадлежит S, и тогда открытый промежуток (z, z')
удовлетворяет условиям теоремы. Остается теперь рассмотреть
тот случай, когда В не пусто. Это делается с помощью рассу-
ждения, аналогичного предыдущему: х служит нижней гранью
В, но не может быть его точной нижней гранью. Поэтому, если
Уо' — точная нижняя грань В, то х<уо', и существует такое
Основные математические методы
29
число г', что x<z'<t/o', и, очевидно, z' £ S. Тогда интервал
(z, z') удовлетворяет требуемым условиям, и теорема полностью
доказана.
Легко доказывается также и следующая теорема, обрат-
ная предыдущей.
Теорема 2.2
Пусть S — некоторое непустое множество чисел. Допустим,
что для всякого х0 6 S можно указать такой открытый проме-
жуток I, что х0 61, и I полностью содержится в S. Тогда мно-
жество S открыто.
Доказательство
Допустим, что S не открыто. Тогда по определению допол-
нение S множества S не замкнуто. Если вспомнить определе-
ние замкнутого множества, то последнее означает, что в S су-
ществует такое ограниченное подмножество А, что либо его
точная верхняя грань, либо его точная нижняя грань (либо обе
вместе) не входят в множество S. -Предположим, например,
что а0 есть точная верхняя грань А и ao^S (т. е. a065). Со-
гласно определению точной верхней грани, для любого е>0 в А
существует элемент, превосходящий а0—е. Следовательно, вся-
кий открытый промежуток, содержащий а0, будет содержать
точки, принадлежащие А, и, следовательно, точки из S. Но это
противоречит сделанным предположениям; откуда и вытекает
наша теорема.
Эти две теоремы показывают, что в случае вещественной
прямой утверждение, что открытое множество — это такое мно-
жество, в которое вместе с каждым его элементом входит
также и некоторый открытый промежуток, содержащий этот
элемент, эквивалентно данному ранее определению открытого
множества. Это свойство может быть, таким образом, исполь-
зовано для определения понятия открытого множества. Мы уви-
дим далее, что смысл такого определения может быть сохранен
в некоторых случаях, когда рассматриваемое множество нельзя
естественным образом упорядочить и поэтому первоначальное
определение неприменимо.
Этот прием, состоящий в переопределении математического
понятия, которое было ранее определено способом, неудобным
для обобщения, в новых терминах, относящихся к некоторому
эквивалентному, но более общему свойству, часто встречается
в математике. Мы еще не раз с этим встретимся, в частности
в связи с понятиями компактности множества.
30
Глава 2
2.4. Непрерывность
Этот раздел мы начнем с введения некоторых основных
терминов, относящихся к понятию функции, с которыми чита-
тель, быть может, не вполне знаком. Если f — некоторая функ-
ция, заданная (определенная) на некотором множестве ве-
щественных чисел, то это множество называется областью за-
дания (областью определения) f. Далее, за исключением тех
случаев, когда это будет особо оговорено, мы предполагаем,
что области задания всех рассматриваемых функций являются
промежутками, замкнутыми или открытыми, ограниченными
или неограниченными. Если х есть некоторый элемент области
задания, то значение, которое f принимает в точке х, мы обо-
значим, как обычно, через f(x); совокупность всех значений,
которые функция f принимает, когда х пробегает всю область
задания f, называется множеством значений (областью зна-
чений) функции f. Если S — это некоторое подмножество
области задания f, то f(S) означает совокупность всех значе-
ний, принимаемых f, когда аргумент пробегает S; f(S) назы-
вается образом S, соответствующим функции f. Аналогично,
если Т является некоторым подмножеством множества значе-
ний f, то через f~'(T) обозначают множество всех чисел х из
области задания f, таких, что f(x) б Т. Такое множество
f~}(T) называется прообразом Т, соответствующим функции f.
Наконец, график f — это множество, состоящее из упорядочен-
ных пар (х, f(x)), которое изображается известным образом
в виде линии, отнесенной к некоторой прямоугольной системе
координат на плоскости.
Мы предполагаем, что читатель знаком с понятием непре-
рывного отображения (непрерывной функции); для полноты
изложения мы приведем здесь соответствующее определение.
Говорят, что функция f непрерывна в некоторой точке х0, взя-
той из области ее задания, если для любого вещественного
числа е>0 существует такое вещественное число б>0, что, если
|х —х0|<б, то |f(x) — f (х0) I <е. С интуитивной точки зрения
это означает, что если х лежит близко к х0 в области задания f,
то f(x) лежит близко к f(x0) в множестве значений f (здесь в
и б попросту служат мерами «степени близости»). Функцию f
называют непрерывной, если она непрерывна в каждой точке
своей области задания. Наконец, говорят, что функция f ку-
сочно-непрерывна, если она непрерывна во всех точках своей
области задания, за исключением некоторого конечного мно-
жества точек.
Следующая теорема говорит о важном отношении между
понятием непрерывности и понятием открытого множества.
Основные математические методы
31
Мы предлагаем читателям доказать эту теорему самостоятельно
в качестве упражнения.
Теорема 2.3
Если функция f непрерывна, и Q—произвольное открытое
подмножество множества значений f, то f“’(Q) является откры-
тым подмножеством области задания f. Обратно, если функция
f такова, что для любого открытого подмножества Q множества
значений f подмножество f~’(Q) области задания f открыто, то
f непрерывна.
Упражнение
Останется ли эта /еорема справедливой, если в ее форму-
лировке всюду заменить «открытые множества» на «замкну-
тые множества»?
Прежде чем перейти к конкретным проблемам, введем еще
одно понятие. Множество вещественных чисел, которое одно-
временно и замкнуто и ограничено, называется компактным.
Связь между компактностью и непрерывностью на веществен-
ной прямой выражается следующей теоремой:
Теорема 2.4
Если функция f непрерывна и S — компактное подмножество
области задания f, то множество f(S) компактно (т. е. непре-
рывный образ компактного множества компактен).
Доказательство
Доказательство этого утверждения распадается естествен-
ным образом на две части.
1. Образ f(S) ограничен.
Допустим противное. Тогда в f(S) можно найти последова-
тельность точек i/i, г/г, • • •, Уп. такую, что 1уп1>п для
каждого целого п. При этом должна также существовать по-
следовательность %], Хг, • •., хп,.. . элементов из S, такая, что
Уп = 1(хп) для каждого и. Поскольку S компактно, т. е. огра-
ничено и замкнуто, точная верхняя грань х0 множества чисел
X], Хг,..., хп,... существует и принадлежит S, и из определе-
ния точной верхней грани отсюда сейчас же следует, что най-
дется некоторая подпоследовательность хП1, х„2,..., xnft , . . . ,
такая, что расстояние |xnft—х0| стремится к нулю при &->оо.
Так как х0£3, то f(xo)€f(S). Вследствие непрерывности для
любого произвольно заданного е>0 существует такое 6>0,
что
из | хПк - х01 < 8 следует, что | / (хпJ - / (х0) | < в
32
Г лава 2
Но f(x0) —это некоторое фиксированное число, а из сделанного
предположения следует, что последовательность чисел f(xnft)
неограниченно возрастает, и мы приходим, таким образом,
к противоречию, из которого и следует справедливость первой
части нашего доказательства.
2. Образ f(S) замкнут.
Опять-таки допустим противное. Тогда найдется подмно-
жество /(5), такое, что либо точная верхняя грань Т, либо
точная нижняя грань Т (либо обе вместе) не являются эле-
ментами f(S). Мы можем, не ограничивая общности, допу-
стить, что точная верхняя грань Т, равная, скажем, у0, не при-
надлежит множеству f(S). Определение точной верхней грани
указывает, что для всякого е>0 должен существовать элемент
у£Т, такой, что у>уо—е. Таким образом, всякий открытый
промежуток, симметричный относительно у0, должен содержать
некоторый элемент из Т. В частности, для любого целого числа
п можно указать некоторый элемент уп С Т, такой, что | уп —
—Совокупность всех таких уг образует в Т некоторое
подмножество. Мы видим далее, что должна также существо-
вать последовательность чисел xlt х2, • хп, • ,, из множества
S, такая, что yn = f(xn) при каждом п. Из ограниченности S
вытекает ограниченность множества чисел хп, которое обладает
поэтому точной верхней гранью Хо, и эта точная верхняя грань
ввиду замкнутости S должна принадлежать S. Из последова-
тельности Xi, Х2,..., хп,... можно выбрать некоторую подпо-
следовательность хп, , х„п,..хп. ,..., такую, что limxn=Xo-
1 2 k-*a> *
И так как функция / непрерывна, отсюда следует, что
—f(xo) |-»-0 при k-+oo. Кроме того, по построению lim| f (хп.) —
—z/ol=O. Таким образом, f(x0)—y0. Но тогда из того, что
х0 £ 5, следует, что у о €f(S), что противоречит сделанному пред-
положению, и это полностью завершает доказательство тео-
ремы.
Эта доказанная нами простая теорема играет центральную
роль в математической теории, связанной с решением опти-
мальных задач. Во многих случаях она гарантирует существо-
вание решений таких задач. Встречается также ряд важных
случаев, когда эту теорему применить нельзя, и в этом состоят
основные трудности изучаемой нами теории. Мы увидим
в разд. 2.8, что определение компактности, которое было дано
выше, применимо лишь к тем ситуациям, которые в определен-
ном смысле конечномерны; этот способ определения компакт-
Основные математические методы
33
ности непосредственно не обобщается на более широкий класс
проблем, когда приходится рассматривать бесконечномерные
пространства. Понятие компактности должно быть для подоб-
ных случаев определено другим, более общим способом (|см., на-
пример, [18]). Теорема 2.4 остается справедливой и в этом бо-
лее общем случае, но приведенный ранее способ ее доказа-
тельства уже оказывается неприменимым. В некоторых задачах
приходится рассматривать такие бесконечномерные простран-
ства, которые не являются локально компактными (т. е. в них
могут быть элементы, не имеющие компактной окрестности),
и тогда теорема 2.4 не может быть использована для решения
задачи об оптимизации.
2.5. Максимумы и минимумы непрерывных функций
одной независимой переменной
Пусть функция f непрерывна. Говорят, что в некоторой
точке Хо из своей области задания функция f имеет относитель-
ный максимум, если можно указать открытый промежуток /,
содержащий х0, такой, что f(x0) служит точной верхней гранью
множества f(/). Аналогично f ймеет в точке у0, принадлежащей
ее области задания, относительный минимум \ если найдется
такой открытый промежуток /, содержащий у0, что f(yo) яв-
ляется точной нижней гранью для f(J) 1 2. График, изображен-
ный на фиг. 1, наглядно поясняет эти определения.
- Обратим внимание на то, что, если, скажем, интервал I
взять столь большим, что в него попадет точка х0', то f(x0)
перестанет быть точной верхней гранью f (I) \ этим и объясня-
ется применение термина «относительный» в приведенных выше
определениях. Непрерывная функция может, таким образом,
иметь несколько относительных максимумов и относительных
минимумов. Совершенно очевидно также, что, если для f(x0)
выполняется условие существования экстремума по отношению
к некоторому открытому промежутку /, то это значение функ-
ции сохраняет роль экстремума и в том случае, если взять лю-
бой меньший открытый промежуток I', содержащийся в I, та-
кой, что Хо € I'-
Теперь можно отметить две разные математические проб-
лемы, относящиеся к задаче определения максимумов и мини-
мумов. Первый и наиболее важный вопрос заключается
в следующем: при каких условиях можно гарантировать
1 Относительные максимумы н минимумы объединяются общим названием
«экстремумы». — Прим, перев
2 Подразумевается, что интервалы I н I, о которых здесь говорится, це-
ликом принадлежат области задании функции f. — Прим, перев.
34
I лава 2
существование максимумов и минимумов? И второй вопрос: если
известно, что экстремумы существуют, то как их найти? Ниже
для ряда важных случаев даются ответы на эти вопросы.
Сначала о существовании экстремумов. Последняя теорема
предыдущего раздела говорит, что непрерывный образ замк-
нутого и ограниченного множества тоже замкнут и ограничен.
Далее, ограниченное множество имеет и точную верхнюю и точ-
ную нижнюю грани. Кроме того, замкнутое множество всегда
содержит свои точную верхнюю и точную нижнюю грани. Не-
прерывный образ такого множества точно так же содержит
свои точные грани. Сказанное весьма близко к утверждению,
что непрерывная функция, заданная на компактном множестве,
всегда имеет максимум и минимум. Это и на самом деле так,
если только специально оговорить, что как максимальное, так
и минимальное значения достигаются не на границе области
задания функции f. Так, если, например, область задания f
есть сегмент 1 = [а, &], то ни f(a), ни f(b) не должны совпадать
с точными верхней и нижней гранями множества f(I).
Необходимость такой оговорки заключается в том, что мак-
симумы и минимумы определялись выше в терминах, относя-
щихся к открытым промежуткам. В тех случаях, коЛда точные
грани достигаются функцией f внутри области ее задания,
никакой разницы для открытых и замкнутых промежутков не
возникает. Но, если точная верхняя или нижняя грани f дости-
Основные математические методы
35
гаются на одном из концов /, данные выше определения макси-
мума или минимума уже не соответствуют такой ситуации;
значение функции на указанном конце промежутка I нельзя
при этом считать максимумом или минимумом в смысле при-
веденного ранее определения Фиг. 2 наглядно иллюстрирует
сказанное.
Упражнение
Рассмотрим заданную на сегменте [Л, В] функцию у — ах + Ь
(где а>0), график которой представляет собой отрезок прямой
линии. Имеет ли она на этом сегменте максимум или минимум?
(Этот пример служит прототипом задач линейного программи-
рования; см. разд. 12.2.)
Теперь, когда вопрос о существовании максимумов и мини-
мумов непрерывной функции в известной мере выяснен, обра-
тимся к задаче их нахождения. Путь для определения макси-
мумов и минимумов указывается следующей хорошо известной
теоремой.
Теорема 2.5
Если функция f имеет в точке х0 относительный максимум
или минимум и первая производная f'(x0) в этой точке суще-
ствует, то f'(xo) =0.
Доказательство
Возьмем тот случай, когда в точке х0 имеется относительный
максимум f. Пусть I — некоторый открытый промежуток, такой,
что f(xo) служит точной верхней гранью /(/). Пусть у£1, п
допустим вначале, что у<Уо- Тогда разность у—х0 отрица-
тельна. По предположению выражение f(y)—f(x0) тоже
1 В подобных случаях применяются термины «краевой максимум» или
«краевой минимум» («краевые экстремумы»), — Прим перев
36
Глава 2
отрицательно (или, во всяком случае, не положительно). Тогда
разностное отношение
/(у) — /(-*о)
у — *о
неотрицательно (надо отметить, что это выражение непрерывно
по у во всех точках, где оно определено). С другой стороны,
если у£1 и у>х0, то аналогичные рассуждения показывают, что
это отношение неположительно. Следовательно, это отношение
принимает неположительные значения для всех у, лежащих
справа от х0, и неотрицательные значения для всех у, распо-
ложенных слева от х0- Так как по предположению производная
в точке Хо Существует, отсюда следует, что f'(x0) =0.
В случае, когда в точке х0 достигается относительный мини-
мум, доказательство проводится аналогично, и мы предостав-
ляем его читателю.
Доказанная теорема утверждает, что обращение в нуль
производной в некоторой точке области задания функции яв-
ляется необходимым условием существования максимума или
минимума. Однако по ряду причин эта теорема не дает пол-
ного решения задачи о нахождении экстремумов. Во-первых,
вполне очевидно, что производная вовсе не обязательно вообще
должна существовать в той точке, где достигается максимум
или минимум. Например, на фиг. 3 производная в точке х0 не
существует, а в точке х0' обращается в бесконечность, но
в обеих точках, согласно нашему определению, в действитель-
ности имеются относительные максимумы.
Если даже исключить из рассмотрения случаи такого типа
(что, впрочем, с точки зрения практических приложений, неже-
лательно) и обратиться исключительно к таким функциям f,
которые обладают непрерывными производными во всех точках
Основные математические методы
37
областей своего задания, эта теорема все же указывает всего
лишь необходимое условие существования экстремумов. Дело
в том, что производная f может обратиться в нуль и в такой
точке х0, где нет ни относительного максимума, ни относитель-
ного минимума f. Такую точку называют точкой перегиба
(фиг. 4). В этом случае значение f(x0) не совпадает ни с точ-
ной верхней, ни с точной нижней гранями /(/), какой бы ин-
тервал I, содержащий х0, мы ни взяли.
Хотя условие обращения в нуль первой производной и не
исчерпывает, таким образом, вопроса о нахождении экстрему-
мов непрерывной функции, оно является чрезвычайно полезным.
Всякая точка х0, в которой производная f обращается в нуль,
называется стационарной точкой1 (существуют, разумеется,
методы, позволяющие в определенных случаях решить вопрос
о том, что именно в действительности имеется в данной стацио-
нарной точке — относительный максимум, относительный
1 Этот-термин применяется в связи с тем, что, если функция f имеет ста-
ционарную точку х=х0 и h есть малая первого порядка, то f(x0+h) =/(х0)
с точностью до величин более высокого порядка малости. В этом смысле зна-
чение f(x) в точке х=х0 «стационарно» при бесконечно малых приращениях
независимой переменной
Для достаточно гладких функций справедливость этого утверждения мо-
жет быть, например, непосредственно усмотрена из формулы Тейлора, со-
гласно которой
Л2
/ (хо + h) = f (х0) + hf (xq) + -g- f" (xq) +
+ члены более высокого порядка малости относительно h,
так как по предположению f'(x0) =0. Этот факт следует сравнить со след-
ствием теоремы 2.7, содержащим аналогичное утверждение для случая ва-
риационной задачи Отмеченное обстоятельство оправдывает применение
в вариационных задачах термина «стационарная кривая».
38
Глава 2
минимум или точка перегиба, но здесь нет необходимости оста-
навливаться на этих вопросах).
Прежде чем переходить к более сложным проблемам,
посмотрим, какое отношение указанные выше идеи имеют к тем
вопросам, которые рассматривались в первой главе. Пусть f—
некоторая непрерывная функция с определенной областью за-
дания S. Предположим, что множество S можно рассматри-
вать как совокупность допустимых решений некоторой задачи
об оптимизации, а значения оценочной функции, связанные
с различными индивидуальными решениями, совпадают с чи-
слами f(x). Как было показано выше, в случае, когда мно-
жество S компактно, существует решение с минимальной ценой.
Если это решение лежит внутри S, то’оптимальное решение
следует искать среди стационарных точек f, если f вс^)ду диф-
ференцируема на S, т. е. в тех точках xgS, где f'(x)=O. Мно-
гие оптимальные задачи действительно могут быть решены
в рамках этой схемы. Существуют тем не менее и такие про-
блемы оптимальности, к которым такой метод решения непри-
меним.
2.6. Функции многих независимых переменных
Мы обратимся теперь к изучению таких функций, области
задания которых представляют собой множества, состоящие из
систем п упорядоченных вещественных чисел, которые можно
записать, скажем, в виде (хь х2,..., хп). Совокупность всех
возможных систем п чисел такого вида называется веществен-
ным п-мерным евклидовым пространством, а сами упорядочен-
ные системы (xi, х2,..., хп) называются точками этого про-
странства. Здесь нет необходимости подробно рассматривать
свойства таких пространств. Двумерное евклидово пространство
может быть интерпретировано как множество точек на обыч-
ной плоскости.
Топология евклидовых пространств может быть построена
способом, весьма близким к тому, который применялся для ве-
щественной прямой. Основным здесь является понятие откры-
того п-мерного прямоугольного параллелепипеда, аналогичное
понятию открытого промежутка. Открытым n-мерным прямо-
угольным параллелепипедом называется множество точек
(xi, х2, ..., хп), удовлетворяющих условиям
ai < xi < ^i,
^2 < Х2 < ^2>
Основные математические методы
39
где (a2,b2),..., (ап, bn)—произвольно взятые п от-
крытых промежутков вещественной оси. Точно так же, как и
в случае вещественной прямой, общее понятие открытого мно-
жества «-мерного евклидова пространства можно определить,
исходя из следующего условия: S есть открытое множество,
если для всякой точки из S можно указать некоторый открытый
прямоугольный параллелепипед, содержащий эту точку и це-
ликом лежащий внутри S. Замкнутое множество «-мерного
евклидова пространства определяется, как и раньше, как мно-
жество, дополнение которого открыто. Наконец, множество
считается ограниченным, если оно содержится в некотором
открытом прямоугольном параллелепипеде.
Заданная в «-мерном евклидовом пространстве функция,
принимающая вещественные значения, называется, как и
раньше, непрерывной в том случае, если прообраз всякого от
крытого множества, лежащего в области значений этой функ-
ции, представляет собой открытое подмножество области за-
дания этой функции. Из этого определения, в частности, сле-
дует, что непрерывная функция « переменных непрерывна
также и по каждой из переменных в отдельности во всякой
точке своей области определения. «-Мерное евклидово про-
странство обладает также свойством локальной компакт-
ности, и непрерывные образы компактных множеств (огра-
ниченных и замкнутых) опять-таки замкнуты и огра-
ничены.
Определения максимумов и минимумов функций, заданных
в «-мерном евклидовом пространстве, аналогичны соответст-
вующим определениям для функции одной независимой пере-
менной. Так, например, говорят, что функция f имеет относи-
тельный максимум в точке (ai, а2, .. . , ап), если найдется от-
крытый «-мерный параллелепипед /, содержащий эту точку,
такой, что /(аь а2,..., ап) служит точной верхней гранью f(I).
Аналогично определяется и относительный минимум. Приведен-
ные в предыдущем разделе рассуждения, касающиеся сущест-
вования максимумов и минимумов, переносятся без существен-
ных изменений и на этот случай. Остается лишь обсудить во-
прос о том, каким образом находятся те точки, в которых
функция многих независимых переменных имеет экстре-
мумы.
Как будет показано, эта задача решается с помощью ре-
зультатов, полученных ранее в предыдущем разделе. Предпо-
ложим, что функция f задана в некоторой области S, представ-
ляющей собой открытое множество «-мерного евклидова
пространства; допустим также, что в точке (яц а2, .... ап) £S
имеется, скажем, относительный минимум f и что f обладает
40
Г лав a 2
в S первыми частными производными. Введем новую вещест-
венную переменную t и определим с помощью соотношения
F(Z) = /(a1-|-A1/, Й2 + h2t,..an-\-hnt) (2.1)
функцию F(t), где hi, h2, hn — произвольные, но фиксиро-
ванные числа. Поскольку f имеет в точке (йь й2,..., ап) ми-
нимум, функция F(t) должна иметь минимум при t — Q. Полная
производная F'(t) выражается следующей хорошо известной
формулой:
рг _____ df dx\ । df dx2 . I df dxn
' ' dxi dt ‘ dx2 dt "T" • • • “r gXn at ' \ • f
Но, согласно определению F(t), мы имеем соотношения
Xi = a14~A1/, л2 = й2 + h2t,..., xn = an-\-hnt,
и поэтому при любом I (1 i^n)
4*1 —h.
Таким образом, из (2.2) получается, что
/?'(/)=/?! 4^- + л2-^- + ...+ап4^--
' ' 1 дхх 1 2 дх% 1 1 п дхп
Полагая £ = 0, находим
(23)
где значения частных производных берутся в точке
(йь й2,..., ап).
Вспомним теперь, что числа hi были выбраны совершенно
произвольно, и, следовательно, выражение (2.3) должно обра-
щаться в нуль при всяком выборе /г,. Это может быть только
в том случае, если сами частные производные обращаются,
в нуль, т. е. в точке (й]; а2..ап) непременно выполняются
равенства
Совершенно аналогичные рассуждения справедливы и в том
случае, когда в точке (й], й2, ..., й„) достигается максимум.
Теорема 2.6
Если функция f имеет в точке (йь й2, .. . , йп) относитель-
ный максимум или относительный минимум и обладает в этой
Основные математические методы
41
точке первыми частными производными, то эти производные
обращаются в данной точке в нуль.
Следует заметить, что эта теорема вполне аналогична тео-
реме 2.5, и ее можно по существу рассматривать как след-
ствие этой теоремы. Как и в предыдущем разделе, эта теорема
дает всего лишь необходимые условия существования локаль-
ных экстремумов; существует большое число различных типов
стационарных точек [т. е. точек, в которых выполняется условие
(2.4)], в которых нет ни максимумов, ни минимумов. Точно
так же существует много интересных случаев, когда условия
теоремы не выполняются (например, когда, существуют не все
частные производные), а экстремумы все же имеются. Тем не
менее эти две теоремы играют важную роль в различных при-
ложениях.
2.7. Случай бесконечного числа независимых переменных.
Вариационное исчисление
Как было установлено, существенного различия в методах
отыскания максимумов и минимумов функций одной ’перемен-
ной и функций многих переменных нет. Однако многие важ-
ные и интересные задачи, связанные с нахождением максиму-
мов и минимумов, не могут быть решены с помощью методов,
указанных выше. Задачи такого рода требуют более общей
постановки и развития новых и более тонких аналитических
методов. Постановка таких задач связана с привлечением
бесконечномерных пространств и функций бесконечного числа
независимых переменных, заданных на таких пространствах.
Соответствующие аналитические методы решения подобных за-
дач относятся к той области математики, которая называется
вариационным исчислением.
В истории математики возникновение вариационного исчис-
ления относят обычно к известной задаче о брахистохроне,
предложенной Бернулли !. Эта задача приводит к определению
1 В 1696 г. И. Бернулли поставил следующую задачу: найти кривую, по
которой материальная частица, движущаяся в вертикальной плоскости под
действием сил тяжести, перейдет из заданной точки А в заданную точку В
за минимальное время. Подробности, касающиеся задачи о брахистохроне и
ее решения (этим решением оказывается дуга циклоиды), читатель может
найти в любом стандартном учебнике по вариационному исчислению [19—22]
Интересно отметить, что Бернулли решил задачу о брахистохроне, пользуясь
принципом Ферма; н его решении кривая иаискорейшего спуска идентифици-
ровалась с траекторией светового луча, распространяющегося в оптической
среде с переменным показателем преломления, подобранным соответствую-
щим образом.
42
Г л-а в а 2
кривой линии у = у(х), минимизирующёй некоторый функцио-
нал; по терминологии гл. 1, совокупность допустимых решений
в задаче о брахистохроне представляет собой некоторое мно-
жество функций, а не множество точек, как это было в задачах,
которые мы рассматривали до сих пор.
Надо, однако, сказать, что с математической точки зрения
различие между пространством точек и пространством функций
не так уже велико, как может показаться с первого взгляда.
Возьмем, например, некоторое фиксированное целое положи-
тельное число N и рассмотрим «пространство», отстоящее из
всех многочленов степени не выше N, зависящих от одной пе-
ременной. Элемент такого «пространства» может быть запи-
сан в виде многочлена
р(х)=аохЛГ-|-а1хЛГ_1 .. + <2/v,
где коэффициенты аг — вещественные числа. Известно, однако,
что свойства любого многочлена р(х) степени N полностью
определяются его коэффициентами (а0, ..., aN), которые
можно рассматривать просто как систему (2V+1) упорядочен-
ных вещественных чисел. В этом смысле, таким образом, между
функциональным пространством многочленов Степени не выше
N и обычным (Л^+1)-мерным евклидовым пространством
(о многомерных евклидовых пространствах говорилось в пре-
дыдущем разделе) наблюдается изоморфизм.
Разовьем эту идею дальше. Из курса элементарного мате-
матического анализа известно, что при определенных условиях
всякая достаточно гладкая функция f(x) разлагается в степен-
ной ряд вида
f (%) = 6ZjX • • * “I- О-пХп Ч- • • •
(так называемый ряд Маклорена) и, следовательно, может
быть сколь угодно точно аппроксимирована многочленами. По
известной теореме Вейерштрасса (см., например, [18]) произ-
вольная непрерывная функция, заданная на сегменте .[а, Ь],
может быть равномерно аппроксимирована на этом сегменте
многочленами. Разложения подобного рода указывают, что,
если многочлены n-й степени можно отождествить с системами
(п+1) упорядоченных чисел — коэффициентов этих много-
членов, то многие другие функции можно представить беско-
нечными последовательностями вида («о, alt а2,..., ап,...),
состоящими из коэффициентов таких разложений. Функции,
принадлежащие некоторым другим классам, можно разложить
в тригонометрические ряды (ряды Фурье), и тогда каждая такая
функция характеризуется последовательностью своих коэф-
фициентов Фурье. Мы можем, таким образом, не вдаваясь
Основные математические методы
43
в детали, сказать, что проблемы, связанные с изучением опре-
деленных классов функций, можно рассматривать как про-
блемы, относящиеся к пространствам бесконечного числа из-
мерений. Функции, заданные на таких бесконечномерных про-
странствах, можно отождествить с функциями, определенными
на некотором множестве функций, и в соответствии с обычной
терминологией мы будем называть такие функции функциона-
лами. Следовательно, такие задачи, как задача о брахисто-
хроне, можно сформулировать в виде требования минимизации
функционалов, определенных на бесконечномерных простран-
ствах.
Попытки применения ранее изложенных методов к про-
странствам бесконечного числа измерений приводят к много-
численным затруднениям. Основная причина этих трудностей
заключается в том, что топология таких пространств сущест-
венно отличается от топологии встречавшихся нам ранее конеч-
номерных пространств. Так, например, понятие ограниченности
множества невозможно в общем случае определить в тех терми-
нах, которые применялись в конечномерном случае, и опреде-
ление компактности, данное ранее, не может быть непосред-
ственно перенесено на такие пространства. В этих случаях
компактность определяется с помощью другого свойства 1, ко-
торым обладают также и ограниченные замкнутые множества,
лежащие в конечномерных пространствах. При этом оказы-
вается, что в общем случае все бесконечномерное пространство
может и не быть локально компактным.
Вследствие этого теорема 2.4 о существовании максимумов
и минимумов в таких случаях неприменима. Но главный вопрос,
который прежде всего должен быть решен в связи с задачей
о минимизации, как раз связан с существованием решения; во
многих случаях и в самом деле оказывается, что решение не
существует 2.
1 Это свойство, называемое обычно свойством Гейне—Бореля [в русской
математической литературе его называют бикомпактиостью. •— Перев.}, заклю-
чается в следующем. Пусть имеется подмножество S некоторого пространства
(топологического) и некоторое семейство Q открытых подмножеств этого про-
странства. Если для всякого элементах£S существует некоторое открытое
множество Q£Q, такое, что то говорят, что семейство Q покрывает S
Говорят, что S обладает свойством Гейне—Бореля, если из всякой системы й
открытых множеств, покрывающей S, можно выделить подсистему й' С Q, со-
стоящую из конечного числа множеств, принадлежащих системе Q, и покры-
вающую S. Можно показать, «что множество вещественных чисел компактно
(т. е. ограничено и замкнуто) в том и только в том случае, когда оно обла-
дает свойством Гейне—Бореля. То же самое справедливо и для компактных
подмножеств n-мерного евклидова пространства
2 Будет полезно, по-видимому, указать литературу по затронутым здесь
вопросам. Весьма полное изложение результатов, относящихся к вопросу
44
Глава 2
2.8. Уравнение Эйлера
Основное содержание почти всех задач классического ва-
риационного исчисления можно сформулировать следующим
образом: требуется найти функцию г/(х), которая минимизирует
заданный функционал J(у) вида* 1
Xi
^(V) = J У(х)> y'(x))dx, (2.5)
где F(x, у,у')—некоторая функция, так называемое ядро Цу).
Как уже говорилось в предыдущем разделе, функцию у(х)
можно, вообще говоря, рассматривать как точку (а0, а1( а2,...)
некоторого бесконечномерного пространства. По аналогии со
случаем конечного числа измерений можно попытаться вычи-
слить все частные производные
dJ dJ dJ
дао ’ да1 ’ да2 ’ ’ ’ ’
и приравнять их нулю, для того чтобы определить неизвестную
функцию у(х), минимизирующую функционал J (у). Такая
попытка сталкивается, однако, с серьезными затруднениями, и
требование обращения в нуль частных производных приходится
заменить некоторым другим условием. При переходе от ко-
нечномерного случая к бесконечномерному, как уже говорилось,
понятие компактности приходится определять в новых терми-
нах, и аналогично этому условие минимизации должно быть
выражено с помощью некоторого другого свойства, которое,
в частности, соответствует и тому методу, который был приме-
нен в конечномерном случае, но допускает в то же время
обобщение на более широкий класс задач.
Вместо того чтобы просто привести сейчас обычный стан-
дартный вывод этого общего условия, мы получим его здесь,
о существовании решений применительно к задачам вариационного исчисле-
ния, можно найти в книге Форзита [19] Менее подробное изложение общих
сведений по этому вопросу см. в гл 4 руководства Куранта и Гильберта [18]
Имеется много хороших более старых учебников по вариационному исчисле-
нию (например, книги Блисса, Больца, Адамара и Ганкока), написанных
примерно в одной и той же манере О конечномерных задачах читатель может
прочитать у Ганкока [20] Современный подход к вариационному исчислению
развит в учебнике Гельфанда и Фомина [21] В книге Вайнштока [22], по-
священной этим же проблемам, делается упор на приложения вариационного
исчисления в физике и технике
1 Функционалы такого вида рассматривались еще в самом начале разви-
тия вариационного исчисления при изучении классических задач На первый
взгляд может показаться, что это функционалы весьма частного вида, однако
на самом деле такое интегральное представление возможно при очень общих
условиях для широкого класса функционалов
Основные математические методы
45
обобщив те приемы исследования, которые применялись в ко-
нечномерных задачах, это позволит читателю более четко
представить себе, каким образом это новое условие возникает
и какое оно имеет отношение к ранее изученному материалу.
С этой целью допустим сейчас, что мы имеем дело с функци-
ями у(х), представляющими собой многочлены степени не выше
N, которые могут быть, следовательно, представлены в виде
у (-^)== <*<)* Ч- а^х^’ 1 (2.6)
и отождествлены с точками (Л(+1)-мерного евклидова про-
странства. Надо ясно представить себе, что вариация такой
функции эквивалентна вариации коэффициентов аг, определя-
ющих точку (2V+1) -мерного евклидова пространства. Мы мо-
жем, таким образом, положить
у=у(а0, alt..aN).
Тогда выражение (2.5) записывается в виде
/(у) = J F (х, я0> aN)dx. (2.7)
Теперь мы имеем дело с конечномерным случаем, и, согласно
теореме 2.6, необходимое условие минимизации J многочле-
ном у состоит в том, что
-^- = -^-=...= ^- = 0. (2.8)
дао да-L daN '
В случае когда допустимо дифференцирование под знаком ин-
теграла, мы имеем •
JL- Х( ^-dx= 4- (29)
да0 ~~ J дао J ду да0 + ду' да0 ‘
Xq Xq L j
Частные производные вычисляются дифференциро-
ванием функции (2.6):
_дУ_ _ vn ду' v-i
да0 да0
Таким образом, (2.9) записывается в виде
-^- = [ + ^r\dx. (2.10)
да$ J ду ' ду' ' '
A) L J
46
Глава 2
Замечая теперь, что
дг^ЛГ-1 dF d / N dF\ iy d ( dF \ (C> 1 n
dy' dx ( dy' ) dx dy' j ’ \ )
и подставляя (2.11) в (2.10), получаем
f x + f xN ". (2.12)
дао •' dy dx \dyf I 1 I dyr / ' '
Xq •- ' '-I ' ' XQ
Совершенно аналогично
Теперь используем условие (2.8) и приравняем найденные
частные производные нулю. Можно показать, что обращение
в нуль всех этих частных производных приводит к соотноше-
нию 1
dF____d ( &F \ л
dy dx \dy' j
(2.14)
Уравнение (2.14) называется дифференциальным уравнением
Эйлера, и оказывается, что это и есть условие, обобщающее
ранее изученные результаты, которое применимо также и
к бесконечномерному случаю.
Если провести вывод уравнения (|2.14) вполне математически
строго, то из соответствующих рассуждений будет следовать,
что многочлен у, минимизирующий функционал (2.5) (если та-
кие многочлены вообще существуют), должен удовлетворять
1 Если в действительности ограничиться функционалами, заданными толь-
ко для многочленов, то уравнение (2.14) вытекает из условия обращения
в нуль всех выражений (2.12), (2.13) лишь при весьма жестких ограничения^.
Следует также заметить, что задача о минимизации функционала (2.5) рас-
сматривается обычно при некоторых определенных краевых условиях; напри-
мер, требуется, чтобы концы кривых, среди которых ищется экстремальное
решение, были закреплены или перемещались по некоторым направляющим
кривым и т. п.; можно, разумеется, рассматривать и кривые со свободными
концами. В случае когда концы кривых не закреплены, к уравнению (2.14) до-
бавляются некоторые дополнительные необходимые условия. Подробности,
касающиеся затронутых здесь вопросов, см., например, в книге Гельфанда и
Фомина [21]. — Прим, перев.
Основные математические методы
47
уравнению Эйлера. Ясно также, что всякая другая стационар-
ная кривая функционала J (у) будет тоже удовлетворять этому
уравнению. Следовательно, уравнение Эйлера дает нам необ-
ходимое условие, аналогичное требованию обращения в нуль
первых частных производных, полученному в конечномерном
случае; так-как это условие всего только необходимо, выясне-
ние вопроса о том, соответствует ли данная стационарная кри-
вая минимуму, или максимуму, или стационарному решению
какого-нибудь другого типа, требует дополнительного иссле-'
дования.
2.9. Вывод уравнения Эйлера
Будем теперь считать, что мы имеем дело с функционалом
типа (2.5) совершенно общего вида, определенным на беско-
нечномерном пространстве. Допустим, известно, что Y (х) яв-
ляется стационарной кривой для J(у). Возьмем теперь опре-
деленным образом выбранное семейство функций у(х), которые
образуют в некотором смысле «окрестность» У, а именно по
аналогии с (2.1) положим
у(х) = Г(х)4-ет)(х), (2.15)
где в — произвольный (малый) параметр, а т](х)—произвольно
выбранная, но фиксированная функция, такая, что ц(Х[) =
= т](Хо)=О (это обеспечивает условие у(х) = У(х) на концах
х—х0 и x=xj. На этом семействе J (у) можно рассматривать
как функцию одной вещественной переменной в:
Xi
/(у) = /(е) = J F (л, У, y}dx =
*0
Xi
= J F (х, r-j-ет), Y' + rf)dx. (2.16)
Допустим, что подынтегральное выражение в (2.16) можно
разложить в ряд Тейлора:
F(x, Г + ет), Г' + е>1') = Д(х, Y, Y') + (erj+
+ члены более высокого порядка малости относительно в.
(2.17)
48
Глава 2
Теперь из того факта, что У минимизирует 1(у), вытекает,
что точка е = 0 является стационарной точкой 7 (е), т. е.
=0 при е = 0. (2.18)
Подставим (2.17) в (2.16) и допустим, что (2.16) можно диф-
ференцировать под знаком интеграла; тогда
di С* Г dF । , dF ,
J TfyF + члены более высокого порядка
малости относительно е dx. (2.19)
Учитывая (2.18), получаем
О-ГН-ЗГ-Н’т&К (2.20)
Хо L J
Вывод уравнения Эйлера завершается далее интегрированием
по частям второго слагаемого под знаком интеграла в уравне-
нии (2.20) с учетом того, что ц (xj =ц (х0) =0. Эта процедура
приводит к тождеству
Г dF d { dF\\ , Л
J V ду dx [ду' ) °-
XQ l x /J
Так как функция т](х) выбиралась произвольно, выражение
в квадратных скобках, стоящее в последнем интеграле, должно
обратиться в нуль, а это как раз и приводит к уравнению Эй-
лера (2.14).
Приведенное доказательство позволяет также установить
одно важное следствие, которое нам понадобится в дальнейшем,
в частности в разд. 3.5; оно выражается следующим утвержде-
нием:
Теорема 2.7
Если значения е столь малы, что членами порядка е2 и
более высокого порядка малости можно пренебречь, то тогда
7(e)—/(0) = 0 с точностью до членов высших порядков.
Доказательство
Достаточно рассмотреть соотношение (2.17), из которого
и следует, что
7 (г) - 7 (0) = е J + + е2Г,
Основные математические методы
49
где член в2Г соответствует высшим членам степенного разложе-
ния по в. Согласно (2.20), первое слагаемое обращается здесь
в нуль, откуда и получается нужный нам результат.
Эта теорема допускает важную физическую интерпретацию.
Предположим, что F— это сила, действующая на механическую
систему, а у(х) —траектория движения системы; тогда работа,
произведенная при перемещении системы из положения Хо в Х\
под действием силы F, как раз равна интегралу J. Допустим
теперь, что траектория У(х) минимизирует эту работу, тогда
разность /(в)—/(0) равна разности работ, соответствующих
траекториям У(х) и у(х) = У(х)+ет](х). По доказанной тео-
реме, ввиду того что У(х) —стационарная кривая, эта разность
равна нулю с точностью до малых второго и более высокого
порядка малости. Мы приходим, таким образом, к следующему
важному заключению: бесконечно малые вариации траектории,
соответствующей минимальной работе, связаны с нулевой вир-
туальной работой.
2.10. Пример
Интересно рассмотреть здесь простой пример, показыва-
ющий, как применяется уравнение Эйлера. Предположим, что
нам нужно найти такую дугу у (х), соединяющую на плоскости
точки (Хо, уо) и (xi, у\), которая имеет минимальную длину.
Совершенно очевидно, что решением этой задачи должен слу-
жить отрезок прямой. Из элементарного курса математического
анализа известно, что длина дуги кривой у(х), соединяющей
две такие точки, выражается функционалом вида
х,
/(у)= f Vi+(/)2^-
•*0
Сравнивая этот функционал с выражением (2.5), мы видим,
что его ядром является функция
Г(х, у, у') = /1 +(У')2 •
В этом случае функция F имеет очень простую структуру, так
как она не зависит ни- от х, ни от у, а зависит только от аргу-
мента у'. Вычисляя слагаемые, входящие в уравнение Эйлера,
мы находим, что
dF __р dF ____ у'
~ ’ ду' ~ у! + ‘
50
Глава 2
= 0.
Уравнение Эйлера приобретает, таким образом, вид
d / у’
dx \ /1 +(У')2
Это уравнение имеет очевидный интеграл
V1 + (У')2
(где К— произвольная постоянная), откуда следует, что
у' — const,
т. е. у=ах+Ь. Следовательно, уравнение Эйлера приводит как
раз к такому решению, о котором мы говорили, а именно
к прямой линии.
2.11. Некоторые обобщения. Функция Лагранжа
Материал, изложенный в предыдущих разделах, демонстри-
рует основные черты вариационного исчисления, хотя на самом
деле многие интересные проблемы, с которыми имеет дело ва-
риационное исчисление, и не укладываются в рамки этой
простейшей схемы. Здесь достаточно будет лишь отметить не-
которые важные задачи, не касаясь их детального разбора;
при желании читатель сможет без труда ознакомиться с их
решением более подробно по указанной ранее литературе.
Вопрос о существовании максимумов и минимумов в вариа-
ционных задачах. Как уже было сказано в разд. 2.7, тот факт,
что определение компактности, данное для конечномерного слу-
чая, не переносится непосредственно на бесконечномерное про-
странство, указывает на то, что некоторые вариационные задачи
могут и не иметь решения. Изучение критериев, которые при
определенных условиях гарантируют существование решений,
и методов проверки, позволяющих в ряде случаев выяснить,
осуществляется ли в действительности на данной стационарной
кривой минимум или нет, составляет содержание важного раз-
дела вариационного исчисления, которому посвящена большая
литература. Имеется класс вариационных задач, в которых ре-
шение в общем случае не существует, но которые могут обла-
дать решением, если соответствующим образом сузить семей-
ство допустимых кривых у (х), подчинив их некоторым дополни-
тельным ограничениям. Задачи такого рода наиболее интересны
и трудны, но здесь мы не имеем возможности изложить эту
тему более подробно.
Основные математические методы
51
Задачи с подвижными границами. Многие задачи физики и
математики сводятся к вариационным задачам того типа, ко-
торый мы здесь рассматривали, но при этом часто приходится
рассматривать такие случаи, когда пределы интегрирования
в интеграле (2.5) не являются постоянными заданными чис-
лами. Так, например, задача, рассмотренная в разд. 2.10,
может быть сформулирована в более общем виде, а именно,
вместо того чтобы искать кривую наименьшей длины, соединя-
ющую две фиксированные точки, можно поставить вопрос
о кривой наименьшей длины, соединяющей фиксированную
точку с заданной кривой или точки на двух заданных кривых.
Так, скажем, принцип Мопертьюи, связанный с минимизацией
действия, о котором говорилось в разд. 1.2, приводит в общем
случае как раз к задачам такого типа. Эти задачи с «подвиж-
ными границами» тоже очень важны и интересны, и мы опять
отсылаем читателя по этому поводу к цитированной выше
литературе.
Случай нескольких независимых переменных. Другое естест-
венное обобщение задачи, связанной с минимизацией функци-
онала вида (2.5), состоит в постановке вариационной задачи
для кратного интеграла от функции нескольких независимых
переменных. Вывод уравнения, являющегося аналогом урав-
нения Эйлера для случая кратных интегралов1, не требует
привлечения существенно новых идей, и читатель может и сам
попытаться установить его, не прибегая к литературе.
Случай нескольких неизвестных функций. Задача о миними-
зации интеграла, ядро которого зависит от нескольких неиз-
вестных функций и их производных, представляет собой еще
одно обобщение простейшей задачи, изученной ранее, и мы
должны обсудить этот вопрос здесь более подробно, так как
это важно для нашего дальнейшего исследования. Функцио-
налы такого типа имеют вид
л
J F (/, и, И1, и2, и2, .. ., ип, u'n)dt, (2.21)
«о
где «1, п2, • • , «п — функции, зависящие от одной независимой
переменной t. Чрезвычайная важность такой задачи связана,
в частности, с тем, что гамильтоновский принцип наименьшего
действия приводит как раз к подобным задачам. В этом прин-
ципе в качестве функции F выступает так называемая функция
Лагранжа, роль независимой переменной t играет время,
а неизвестными функциями и их производными являются
1 Так называемое уравнение Остроградского — Прим перев.
52
Глава 2
соответственно координаты и скорости (обобщенные) рассма-
триваемой механической системы
Вывод уравнений Эйлера, соответствующих этой задаче,
сводится к простому повторению тех рассуждений, которые
приводились в разд. 2.9. Как и там, допустим, что функции
U2(t),... ,Un(t) определяют стационарную кривую, и для
каждой из них олределим класс функций, представляющий
собой «окрестность» этой функции, т. е. положим
где, как и раньше, rp(^o) = г]г(^) =0 при каждом i
Подставляя эти выражения в интеграл- (2.21), мы выражаем
его как функцию вида I (ei, е2, , еп). Как известно из разд.
2.6, необходимое условие минимума 7(еь г2,..., еп) состоит
в том, что при ег = 0 все частные производные должны обра-
щаться в нуль:
а/(еь ег,..., £д) Z = 1, 2,../г.
Непосредственные вычисления, аналогичные проведенным
в разд. 2.9, приводят к формулам
д!
(•' / dF . < dF \ ,,
После интегрирования по частям мы, как и раньше, выводим
уравнения Эйлера
dF____d ! dF \ _0>
<4 dt du, ’
i = 1, 2,..., n.
Таким образом, в случае п функций решение задачи характе-
ризуется интегральными кривыми системы п уравнений эйле-
ровского типа, содержащих вторые производные неизвестных
функций.
Обсудим теперь отношение полученного результата к нью-
тоновской механике.
Пусть имеется некоторая произвольная механическая си-
стема. Будем считать, что ее движение может быть описано
как изменение во времени ее так называемых обобщенных
координат, т. е. в каждый момент времени t должны быть
известны значения п функций вида
<71(0, •••> ^(0-
Основные математические методы
53
Предполагается, что число п является инвариантом данной
системы; если при попытке описания движений этой системы
найдено меньше, чем п функций, то движение не определяется
полностью, а большее число функций приводит к переопреде-
ленной математической задаче. Это число п называется числом
степеней свободы изучаемой системы.
Полное описание движения системы сводится, таким обра-
зом, к определению п координатных функций, т. е. в конечном
счете к выводу уравнений, из которых эти функции могут быть
найдены. Совокупность таких уравнений называется системой
уравнений движения данной механической системы.
В разд. 1.2 мы указывали, что реальному движению меха-
нической системы соответствует минимум (или, более точно,
стационарное значение) связанной с данной системой меха-
нической величины, называемой действием. Эта величина вы-
ражается интегралом вида
J L (qx, qn, qn, t}dt, (2.22)
>0
где L — ядро функционала — есть некоторая функция коорди-
нат системы и их производных по времени (т. е. обобщенных
скоростей), которая называется функцией Лагранжа. Для кон-
сервативных систем, т. е. систем, в которых полная энергия
остается постоянной, функция Лагранжа оказывается попросту
равной разности между кинетической и потенциальной энер-
гией системы.
Интеграл (2.22) имеет как раз тот вид, о котором мы гово-
рили выше. Требование минимизации этого интеграла приводит
к системе п уравнений Эйлера, соответствующих п степеням
свободы рассматриваемой системы. Такие уравнения в меха-
нике (их называют уравнениями Лагранжа) образуют систему
уравнений движения данной механической системы. Как -будет
показано далее в разд. 5.2, эти уравнения в общем случае
представляют собой дифференциальные уравнения второго
порядка относительно координат системы, и их общее решение
полностью описывает данную систему. Более подробно об этих
уравнениях говорится в гл. 10.
Глава 3
КРОВЕНОСНАЯ СИСТЕМА
3.1. Введение
Кровеносной системой называют совокупность артерий, ка-
пилляров и вен, по которым кровь переносится от сердца ко
всем частям тела и затем возвращается обратно к сердцу.
Функциональная целостность кровеносной системы есть необ-
ходимое условие существования всех известных высших орга-
низмов. Поэтому как в интересах практики, так и для теории
важно разобраться в принципах организации и структуры этой
системы.
"Морфология кровеносной системы млекопитающего неве-
роятно сложна. Общая длина кровеносных сосудов оценивается
примерно в 100 000 км (большую часть этой длины составляют
мельчайшие сосуды, капилляры). Эти сосуды пронизывают
каждый орган тела; любая клетка тела удалена от ближайшего
капилляра не более чем на расстояние, равное нескольким диа-
метрам клетки. При изучении строения этой системы как на
живом организме (например, на перепонке задней лапы ля-
гушки), так и на коррозионном препарате1 с первого взгляда
возникает впечатление, что невозможно выдвинуть какую-ни-
будь простую гипотезу, которая позволила бы количественно
описать кровеносную систему. Именно в силу такой сложности
кровеносной системы млекопитающего она представляет собой
прекрасную модель, иллюстрирующую эффективность приме-
нения простейших методов, опирающихся на принцип оптималь-
ности в биологии. Как будет далее показано, многие тонкие
детали анатомии и физиологии этой системы, которые на пер-
вый взгляд кажутся безнадежно сложными, можно довольно
просто объяснить и точно количественно описать с помощью
рассуждений, основанных на разумном применении принципа
оптимальности. Более того, кровеносная система обладает тем
1 Для получения коррозионного препарата какого-либо органа (например,
легкого, печени, почки) сосуды этого органа наполняют под давлением через
основной питающий ствол окрашенной жидкой пластмассой После того как
пластик затвердеет, мягкие ткани растворяют разбавленной кислотой В ре-
зультате получается точная копия системы сосудов, пронизывающих этот
орган.
Кровеносная система
55
свойством, что из всех важнейших систем организма она наи-
более легко поддается теоретическому анализу. Физическая
сторона протекающих в ней процессов (например, вопросы,
относящиеся к движению потока жидкости через сосуды и
к диффузии газов и растворенных веществ) изучена достаточно
хорошо, и физиологические функции этой системы также вполне
ясны. Поэтому в данном случае нет необходимости привлекать
какие-нибудь ограничительные предположения или сильные
упрощения, что приходится делать во многих других областях
физиологии. И наконец, что особенно существенно, важное
физиологическое значение кровеносной системы указывает, что
на нее должно сильно влиять давление отбора, и поэтому
(см. разд. 1.3) к ней могут быть непосредственно применены
методы оптимизации.
Одна из характерных черт кровеносной системы, в особен-
ности относящаяся к артериям и капиллярам, заключается
в том, что сосуды многократно ветвятся. Способ ветвления
различен: в одних случаях от главного ствола отходят боковые
ветви (будем для краткости называть это ответвлением), в дру-
гих наблюдается деление на две (или более) ветви (это назы-
вается разветвлением или бифуркацией).
3.2. Ответвление
Исходя из принципа оптимальности, можно легко решить
вопросы, касающиеся угла между основным стволом и боковой
ветвью и отношения диаметров основного ствола и боковой
ветви. В этом разделе мы подсчитаем оптимальный угол
отхождения боковой ветви от основного ствола, исходя из
некоторой подходящим образом подобранной оценочной
функции.
Допустим, что основной ствол, имеющий радиус г0, идет по
направлению от точки А к точке В (фиг. 5). Предположим
также, что отходящая от него боковая ветвь предназначена для
питания некоторой точки С, не лежащей на прямой линии, со-
единяющей точки А и В. Будем считать радиус этой ветви
известным и обозначим его через и.
Теперь ставится такой вопрос: в какой точке сосуда АВ
должно возникнуть это ответвление?
Представим себе движение потока жидкости через систему
трубок постоянного фадиуса и рассмотрим то количество ра-
боты, которое должно быть потрачено на прокачивание дан-
ного количества жидкости через эту систему. Требуемая работа
измеряется сопротивлением, которое система оказывает потоку
жидкости; чем оно больше, тем большая работа должна быть
56
Глава 3
затрачена на прокачивание жидкости через систему. Если го-
ворить о кровеносной системе, в которую кровь нагнетается
сердцем, работающим за счет метаболической энергии, то
представляется очевидным, что чем меньше сопротивление кро-
веносной системы, тем она более эффективна. Применительно
к данной задаче принцип оптимальности говорит, что отходя-
щий от основного ствола сосуд должен начинаться в той точке
D, которая минимизирует сопротивление участка ADC. Одним
словом, при этом первом простейшем подходе к изучению
структуры кровеносной системы соответствующая оценочная
функция попросту должна определяться полным сопротивле-
нием системы потоку крови.
Интуитивно представляется очевидным, что сопротивление
системы трубок должно находиться в прямой зависимости от
полной длины системы, т. е., чем больше расстояние, которое
должен пройти поток, тем больше сопротивление.' Нетрудно
также заметить, что зависимость сопротивления от радиусов
трубок имеет обратный характер: чем меньше радиусы, тем
больше сопротивление. Обращаясь к' фиг. 5, мы видим, что
самое меньшее значение полной длины получится, если ответ-
вление начнется прямо в точке А. Это, однако, уменьшило бы
в целом средний радиус системы. С другой стороны, система
будет обладать наибольшим возможным средним радиусом,
если ответвление DC будет расположено перпендикулярно ос-
новному стволу, но при этом существенно возрастет полная
длина системы.
Для того чтобы решить эту задачу при выбранной оценоч-
ной функции, положим сопротивление, приходящееся на еди-
ницу длины основного ствола АВ, равным Rv, а через Rb обо-
значим сопротивление единицы длины ответвляющегося сосуда.
Кровеносная система
5Т
Полное сопротивление RT участка ADC будет тогда выра-
жаться как
+ (3.1>
где — длина AD и — длина DC. Воспользовавшись эле-
ментарными тригонометрическими формулами, можно следу-
ющим образом выразить эту величину через угол 0:
Ят = ЯЛ (ctg 90 — ctg 9) + ЯЛ cosec 9. (3.2)
По закону Пуазейля которому подчиняется поток жидкости
в жестких трубках, удельные сопротивления Rv и Яъ выра-
жаются через соответствующие радиусы формулами
Я„ = кгё4-, Яь — кгТ\
где k — некоторый коэффициент пропорциональности, завися-
щий от вязкости и плотности жидкости. Подставляя эти соот-
ношения в (3.2), мы находим RT как функцию угла 0:
Ят (е) = const 4- k\ /-4-------]. (3.3)
\ rl r° /
Чтобы найти значение 0, минимизирующее (3.3), нужно лишь
продифференцировать (3.3) и приравнять результат нулю, что
приводит к следующему оптимальному значению угла 0шт:
9mln = arc cos (rf/го). (3.4)
Упражнение
Удостоверьтесь, что приведенное значение Omin действительно,
определяет минимум.
3.3. Решение той же задачи при выборе другой
оценочной функции
Прежде чем сравнивать результат (3.4) с эмпирическими
данными, проведем исследование несколько дальше. При вы-
воде формулы (3.4) предполагалось, что достаточно лишь
минимизировать полное сопротивление течению жидкости.
Известно, однако, что на поддержание любой анатомической
структуры организм должен потратить определенное коли-,
чество энергии, т. е. совершить определенную работу; отсюда
в соответствии с результатами разд. 1.4 следует, что эта работа
1 Закон Пуазейля был первоначально установлен экспериментально, но он
может быть также выведен из элементарных принципов гидродинамики См к
например, [4], стр. 212—213.
58
Глава 3
должна быть включена в оценочную функцию, которую тре-
буется минимизировать. Вполне естественно допустить, что
работа, затраченная на поддержание некоторой части крове-
носной системы, связана прямой зависимостью с объемом
этой части.
Заметим, что объем сосуда ADC при значении угла бтш,
вычисленного по формуле (3.4), не минимизируется.
Упражнение
Найдите значение угла, минимизирующего объем сосуда ADC.
Итак, оценочная функция, включающая полное сопротивле-
ние и учитывающая объем сосуда ADC, не минимизируется
выражением (3.4). Выполняя вычисления и принимая во вни-
мание предыдущие рассуждения, мы находим, что новая оце-
ночная функция выражается как
К Х4тсГ1). (3.5)
Здесь К — некоторый постоянный коэффициент пропорциональ-
ности, а выражение в скобках — не что иное, как объем
участка ADC.
Применяя те же приемы вычислений, что и раньше, мы
приходим теперь к следующему выражению для оптимального
угла ответвления:
г* k + Кг60
9Ш1П = arc cos — • . (3.6)
Гц k + Kr\ v '
Заметим, что в предельном случае при ri->r0 выражение (3 6)
переходит в (3.4). Точно так же и в предельном случае Г1->-0
получается такой же результат, как и по формуле (3.4). При
прочих, непредельных ситуациях формулы (3.4) и (3.6) дают
разные результаты.
Как же эти результаты, полученные с помощью столь не-
сложных рассуждений, согласуются с действительными фак-
тами, наблюдаемыми при изучении кровеносной системы?
В частности, какая из двух формул, (3.1) или (3.6), определяет
оценочную функцию, дающую результат, более близкий к ре-
альности? В литературе имеется ряд экспериментально уста-
новленных правил, относящихся к ветвлению сосудов, которые
приписываются В. Ру. Д’Арси Томпсон [3] формулирует их сле-
дующим образом:
1. Если некоторая артерия разветвляется на две одинако-
вые ветви, то они отходят под одинаковыми углами к основному
стволу.
Кровеносная система
59
2. Если одна из двух ветвей тоньше другой, то более тол-
стая ветвь, или продолжение основной артерии, образует с ос-
новным стволом меньший угол, чем тонкая ветвь.
3. Все ответвления, которые столь малы, что они практи-
чески не уменьшают основной ствол, отходят qt него под боль-
шим углом.
(Читателю, быть может, будет интересно сравнить рас-
суждения Гесса, относящиеся к обоснованию формулы (3.4),
Ответвление
которые цитирует д’Арси Томпсон, с тем выводом, который
был приведен выше.)
Следует подчеркнуть, что из этих правил лишь одно,
а именно третье, вполне согласуется со сделанными нами пред-
положениями и совместимо с обеими формулами (3.4) и (3.6).
Но тут следует принять во внимание, что наша гипотеза отно-
силась исключительно к случаю ответвления сосуда, а первые
два из перечисленных правил относятся к разветвлениям.
Фиг, 6 наглядно поясняет различие этих двух понятий.
Мы видим, таким образом, что оба полученных нами ре-
зультата в известной степени согласуются с данными эмпири-
ческих наблюдений, но мы должны развить эти рассуждения
дальше, чтобы включить также и случай разветвления сосу-
дов; лишь после этого можно будет понять законы, по кото-
рым происходит ветвление сбсудов в кровеносной системе.
Сказанное означает, что следует принять во внимание эффекты,
связанные с участками, аналогичными DB на фиг. 5.
3.4. Замечание об единицах измерения и размерностях
Отвлечемся на время от наших рассуждений, чтобы рассмо-
треть физический смысл введенной нами оценочной функции.
Для этого следует познакомить читателей, которым это неиз-
вестно, с понятием размерности различных физических величин,
встречающихся в тексте.
60
Глава 3
В механике все измерения сводятся в конечном счете к из-
мерению длины, масСы и времени, и, следовательно, результат
измерения любой физической величины, встречающейся в ме-
ханике, можно выразить в виде последовательных измерений,
относящихся лищь к массе, длине и времени. Например, ско-
рость определяется как длина, отнесенная к единице времени,
ускорение измеряется скоростью, отнесенной к единице вре-
мени, или длиной, отнесенной к квадрату времени. Сила по-
лучается умножением массы на ускорение, т. е. измеряется
единицей массы, умноженной на единицу длины, отнесенную
к квадрату времени, и т. п.
Основные величины — масса, длина и время — называются
основными физическими размерностями, а размерность любой
другой механической величины представляется некоторой фор-
мулой вида malbta, где I, т, t — символы единиц длины, массы
и времени, а а, Ь, с — рациональные числа. Надо заметить, что
размерность физической величины не зависит от того, каким
именно способом выбираются единицы измерения основных
величин: например,' скорость определяется единицей длины,
отнесенной к единице времени, независимо от того, будет ли
она измерена сантиметрами в секунду или километрами в час.
При составлении уравнения, связывающего физические ве-
личины, нельзя складывать величины разных размерностей.
Так, скорость можно складывать со скоростью, работу — с ра-
ботой, но нельзя прибавлять скорость к работе. Физическое
уравнение должно быть однородным в отношении размерностей,
т. е. размерности выражений, стоящих слева и справа от знака
равенства, должны быть одинаковы. Анализ размерностей,
в котором подобные понятия изучаются систематически, пред-
ставляет самостоятельный интерес для изучения, но здесь мы
не будем касаться дальнейших деталей этого предмета (см., на-
пример, [23]). С попыткой применить анализ размерностей не-
посредственно к биологическим задачам можно познакомиться
в статьях Сталя [24, 25].
Обратимся теперь к оценочным функциям (3.1) и (3.5).
Функция (3.1) выражает сопротивление потоку жидкости, и
размерность сопротивления (выраженная через т, I, t) есть
т/-4^-1. Но с функцией (3.5) дело обстоит уже не тая просто.
Первое слагаемое здесь опять-таки есть сопротивление, но
второй член пропорционален объему, т. е. величине с размер-
ностью /3. Однако размерность можно приписать также и ко-
эффициенту пропорциональности. Для соблюдения размерност-
ной однородности нужно, чтобы эта постоянная имела размер-
ность ml^t. Если это условие выполнено, то оценочная
функция (3.5) тоже будет иметь характер сопротивления.
Кровеносная система
61
В дальнейшем нам будет, однако, удобно изменить физи-
ческую размерность оценочной функции (3.5) и вместо сопро-
тивления системы рассматривать мощность, рассеиваемую при
движении жидкости, т. е. работу, произведенную жидкостью
в единицу времени. Мощность чшеет размерность ml2t~3. Раз-
мерность сопротивления переходит в размерность мощности
при умножении на множитель с размерностью l6t~2. Надо от-
метить, что эта последняя размерность как раз равна квадрату
размерности потока: размерность потока есть l3t~l. Таким обра-
зом, всегда можно получить мощность, рассеянную в гидравли-
ческой системе, умножая сопротивление этой системы на квад-
рат потока. В частности, первому слагаемому в выражении
(|3.5) можно придать размерность мощности. Размерность вто-
рого члена тоже можно преобразовать к мощности, причем для
этого не нужно даже изменять его форму, а достаточно лишь
изменить размерность постоянной К- В данном случае, как
нетрудно проверить, постоянной К нужно придать размерность
ml~xt~3. Если все это сделано, то вместо (3.5) за оценочную
функцию принимается выражение
Рт = fRr + к ((8.7)
где f — поток. Надо принять также во внимание, что если поток
f задан, то всегда можно так выбрать единицы измерения,
чтобы f2=l. В этом случае (3.7) формально совпадает с (3.5),
хотя физический смысл и размерности этих выражений будут,
разумеется, совершенно разными. Читатель может также легко
проверить, что при вычислении оптимального значения угла,
соответствующего (3.7), получается то же самое, что и в слу-
чае (3.5); различие состоит лишь в том, что в формуле (3.6)
нужно заменить k на f2k.
3.5. Разветвление кровеносных сосудов
Возвращаясь к нашей основной задаче, возьмем теперь для
оценочной функции полученную нами формулу (3.7). Это по-
зволит нам использовать для рассуждений изящный прием,
идея которого в основном принадлежит Муррею [26, 27] и ко-
торый позволяет избежать сложных вычислений, возникающих
при попытке исследовать случай разветвления прямыми ме-
тодами.
Укажем вначале на то, что формула (3.7) позволяет найти
оптимальную величину радиуса отдельного сосуда фиксирован-
ной длины, если задан поток через этот сосуд. Для отдельного
62
Глава 3
неразветвленного сосуда длины L и радиуса г функция (3.7)
имеет вид
PT = fRT + KM. (3.8)
Дифференцируя это выражение по г и приравнивая производ-
ную нулю, мы находим, что Рт принимает минимальное зна-
чение при выполнении соотношения
Подставляя (3.9) в (3.8), мы находим, что при оптимальном
значении f рассеяние мощности, приходящееся на единицу
длины, связано с радиусом сосуда выражением
= (3.10)
где у — некоторая постоянная.
Теперь допустим, что оптимальная конфигурация разветвле-
ния, при которой (3.7) минимизируется, известна и соответст-
вует расположению точек А, В, С, D на фиг. 7—9. На основа-
нии теоремы (2.7) мы знаем, что при смещениях первого по-
рядка малости в оптимальной конфигурации оценочная функ-
ция изменяется на величину, не превосходящую второго порядка
малости. Значит, с точностью до бесконечно малых высших
порядков, величина функционала Рт не изменится, если заме-
нить минимизирующую конфигурацию «близкой» к ней конфи-
гурацией, отличающейся от нее величинами первого порядка
малости. Рассмотрим теперь следующие три частных случая
выбора конфигурации, «близкой» к оптимальной (фиг. 7—9).
Здесь отрезок прямой ВВ' считается бесконечно малой вели-
чиной первого порядка, которая обозначается далее через б.
Радиусы и длины трех элементов АВ, ВС, BD оптимальной кон-
фигурации обозначим соответственно через го, Ео; И, Lj;
г2, 7-2-
Обратимся к фиг. 7. Оптимальный участок АВ здесь пре-
терпевает возмущение, выражающееся в увеличении его длины
на величину б; при этом оптимальные участки ВС и BD с точ-
ностью до малых второго порядка укорачиваются соответ-
ственно на величины б cos 0 и 6cos<p. Если рассматриваемый по-
ток оптимален [в том смысле, что потоки и радиусы на каждом
участке связаны соотношением вида (3.9)], то изменения
«цены», связанные с переходом к возмущенным участкам АВ',
В'С, B'D, пропорциональны соответственно величинам Го2б,
ri26cos0, Г22бсоэ<р. Но, как было сказано, сумма этих
Фиг. 9.
64
Глава 3
приращений (с точностью до малых второго порядка) должна
быть равна нулю, т. е.
/о8 = Г1& cos 9 + г2§ cos <р. (З.П)
Выполняя аналогичные вычисления для случаев, изображенных
на фиг. 8 и 9, мы соответственно получаем
= Го§ cos 9 — rfy cos (9 + <р), (3.12)
= ГоЗ cos cos (9 <р). (3.13)
Решая уравнения (3.11) — (3.13), мы находим для трех углов
6, <р и (<р+0) значения
г о + г? — г i
cose= ,3J4»
eosT=--°+J~r; . (3.15)
2Г0г 2
cos(9 + ?) = <°~rH-l. (3.16)
"1'9
Эти выражения можно упростить с помощью соотношения (3.9).
Мы видим, что в оптимальном случае поток f пропорционален
кубу радиуса сосуда. Обозначим потоки в сосудах АВ, ВС, CD
соответственно через f0, flt fz- Ясно, что fo = fi + f2- Отсюда, учи-
тывая (3.9), мы находим, что
_3___ 3 [ 3
Го — Л “Г Г2 •
(3.17)
Последнее соотношение весьма важно. Подставляя (3.17)
в (3.14), (3.15), (3.16), получаем
cos 9
COS <р =
«•4 „4 / „3 „3\ 3
Г0 ~Г Г2 V О Г2)
^2
cos(9-|- <р) =
4
(3.18)
(3.19)
(3.20)
Кровеносная система
65
Читателю следует самостоятельно убедиться в том, что с по-
мощью полученных выражений можно объяснить количественно
правила Ру, о которых говорилось ранее. Сравнение оптималь-
ных углов разветвления, вычисленных по полученным форму-
лам, с реальными углами, наблюдаемыми на коррозионных
препаратах легкого кошки [26, 27], обнаруживает их хорошее
совпадение. Можно поэтому по меньшей мере считать, что
оценочная функция (3.7) дает хорошее приближение для оце-
ночной функции, соответствующей реальным ситуациям, так
что механизм разветвления артерий действительно может быть'
объяснен с помощью идеи оптимизации выбранной оценочной
функции
Упражнение
Предельный случай, характеризуемый значениями <р = 0,
ro=f2, соответствует ответвлению сосудов, рассмотренному
в разд. 3.3. Сводятся ли формулы (3.14) — (3.16) в этом случае
к выражению (3.6), установленному ранее для угла ответвле-
ния? Если нет, то как вы объясните это расхождение?
Вычислите оптимальный угол разветвления, используя оце-
ночную функцию (3.1). Сравните ваш результат с теми, кото-
рые были получены выше; в предельном случае <р = 0, гй = г2
проведите сравнение с формулой (3.4).
3.6. Оптимальный радиус отходящей ветви
Задача определения оптимального радиуса при выборе
оценочной функции (3.7) решается формулой (3.17). Здесь
имеется, однако, один интересный частный случай, заслужи-
вающий специального упоминания. Допустим, что первичный
сосуд разветвляется на два сосуда одинакового радиуса,
т. е. Г1 = Г2- Тогда из формулы (3.17) следует, что rQ—y2ri, или
^ = 0,794^. (3.21)
Это совпадает с результатом, полученным Коном [28], который
пользовался рассуждениями, на первый взгляд совершенно от-
личными от приведенных здесь. Однако читатель, интересу-
ющийся этим вопросом, может убедиться, что оценочная функ-
ция, фигурирующая в вычислениях Кона, на самом деле
эквивалентна той, которая была выбрана выше.
1 При изучении крупных артерий, отходящих от аорты, которые питают
кровью важнейшие органы, нужно, разумеется, принимать во виимаиие другие
анатомические факты, которые играют в этом случае более важную роль, не-
жели условие минимизации выражения (3 7). Однако в отношении второсте-
пенных артерий и артериол сформулированный здесь результат остается
справедливым.
66
Глава 3
3.7. Радиус аорты [28]
Мы видим, что если радиус г0 некоторого сосуда известен,
то радиусы отходящих от него ветвей можно вычислить, исполь-
зуя условие оптимальности по отношению к оценочной функции
(3.7). Следовательно, если дан радиус начального сосуда кро-
веносной системы, т. е. аорты, то в принципе можно вычислить
радиусы всех других сосудов кровеносной системы. Теперь воз*
никает такой вопрос: можно ли на основании соображений
оптимальности непосредственно вычислить радиус аорты?
Для этого, во-первых, нужно решить вопрос о выборе подхо-
дящей оценочной функции, из условия оптимизации которой
должен быть определен радиус аорты. На первый взгляд,
можно как будто воспользоваться тем же функционалом (3.7),
который был столь успешно применен для вычислений, связан-
ных с разветвлением сосудов. Приходится, однако, признать,
что для вычисления радиуса аорты этот функционал уже не-
применим. Как уже отмечалось, согласно формуле (3.9), усло-
вие оптимальности по отношению к оценочной функции (3.8)
заключается в том, что радиус сосуда пропорционален куби-
ческому корню из потока. Коэффициент пропорциональности
оказывается при этом равным
16*]
(3.22)
где т] — динамический коэффициент вязкости крови, о — ее
плотность. [Размерность отношения о/т] есть Но ее
можно представить в виде (ml2t~2) (Z-3Z_|), т. е. как отношение
размерности энергии к размерности произведения объема на
время.] В обычной системе единиц CGS эта константа была
оценена Мурреем [29] приблизительно как 19 000 эрг]см3сек.
Используя это значение и беря т] равным 0,03 пз (пз — пуаз,
единица вязкости: 1 пз равен 1 дн • сек!см2), мы находим, что
постоянная (3.22) в единицах CGS равна примерно 3,8 • 106.
У человека поток [ оценивается примерно в 100 см? 1сек, так
что, согласно (3.9),
1002 = (3,8 • 106)г6,
откуда следует, что г~0,4 см. В действительности радиус
аорты человека равен примерно 1,5 см, из чего следует, что
радиус аорты не определяется оптимизацией по функцио-
налу (3.8).
С помощью качественных соображений также нетрудно
установить, что выражение (3.8) неприменимо для вычисления
радиуса аорты. В аорту поступает вся порция крови, вытал-
Кровеносная система
67
киваемой сердцем, и скорость тока крови в аорте в этот мо-
мент значительно выше, чем в любой другой точке кровенос-
ной системы. На больших скоростях в потоке возникает извест-
ное в гидродинамике явление турбулентности, и в этом случае
те простые соотношения, которым удовлетворяет давление жид-
кости при небольших скоростях, теряют свою силу. В частности,
на продвижение некоторого количества жидкости в турбулент-
ном потоке требуется затратить значительно больше работы,
чем в простом ламинарном потоке, так как при турбулентности
значительная доля энергии рассеивается.
При каких же условиях возникает турбулентность? Поток
жидкости в жесткой трубке радиуса г, имеющий среднюю ско-
рость v, характеризуется так называемым числом Рейнольдса,
представляющим собой безразмерную величину:
р = -^. (3.23)
Для каждой жидкости существует критическое значение числа
Рейнольдса, при превышении которого образуется турбулент-
ный поток; при значениях р ниже критического поток является
ламинарным. Это критическое значение определяется не на
основании теоретических предпосылок, а экспериментально; для
крови оно равно примерно 1000.
Скорость потока обратно пропорциональна площади попе-
речного сечения сосуда. Следовательно, для цилиндрического
сосуда (а аорту можно приближенно считать длинным цилин-
дром) скорость потока обратно пропорциональна квадрату ра-
диуса; в этом случае число Рейнольдса (3.23) обратно пропор-
ционально радиусу. Таким образом, малые значения радиуса
аорты несовместимы с небольшими значениями числа Рей-
нольдса, т. е. с условиями ламинарности потока в сосуде.
Иными словами, простая минимизация сопротивления и затрат
энергии на поддержание системы недостаточны для объясне-
ния величины радиуса аорты. Значение радиуса аорты чело-
века, полученное выше с помощью такой оценочной функции,
соответствовало бы существенно турбулентному потоку в аорте.
С качественной точки зрения можно представить себе два вы-
хода из положения: следует предположить, что должен быть
больше либо размер сердца, либо радиус аорты. Конечно,
последнее условие, т. е. увеличение радиуса аорты по сравне-
нию с величиной, полученной на основании прямой минимиза-
ции оценочной функции, связанной с затратами энергии, яв-
ляется гораздо менее ограничительным.
На основании приведенных выше данных нетрудно вычи-
слить наименьшее значение радиуса аорты, совместимое с
68
Глава 3
условием ламинарного течения при заданном минутном объеме
сердца *. (Надо заметить, что здесь мы по существу имеем дело
не с минимизацией, а скорее с «пороговой» задачей.) Средняя
скорость потока в аорте выражается формулой
v = С^г2,
где С — минутный объем сердца, а г — радиус аорты. Под-
ставляя это выражение в (3.23) и полагая о/г|==37, р^ЮОО,
Фиг. 10.
мы находим общее соотношение между радиусом аорты и ми-
нутным объемом сердца:
г>0,013С. (3.24)
У человека минутный объем сердца С равен приблизительно
100 см31сек, поэтому из (3.24) находим
1,3 см.
Поскольку радиус аорты человека равен примерно 1,5 см, мы
видим здесь действительно очень хорошее совпадение величин,
если учесть, что при расчетах использовались весьма прибли-
женные данные. Следует также отметить, что точки, соответ-
1 В действительности на некоторых участках сердечного цикла некоторая
турбулентность в аорте, по-видимому, все же возникает (см., например, [30]).
Одиако это ие оказывает значительного влияния иа наши рассуждения, касаю-
щиеся строения аорты.
Кровеносная система
69
ствующие действительным значениям минутного объема сердца
и радиуса аорты у различных организмов (фиг. 10), лежат
очень близко к изображенной на том же графике прямой
/ = 0,013 С.
3.8. Капилляры
Развитые выше методы позволяют непосредственно получить
ряд дальнейших характеристик кровеносной системы; затем их
можно проверить, сравнив’с эмпирическими данными. В ка-
честве первого приближения предположим, что каждый сосуд
кровеносной системы (за исключением, разумеется, аорты)
образуется в результате разветвления более крупного сосуда.
Допустим далее, что эти разветвления удовлетворяют условию
оптимальности в том смысле, что радиусы крупных и мелких
сосудов подчиняются соотношению (3.21). Зная, что у млеко-
питающих капилляры имеют радиус порядка 5 • 10~4 см, мы
можем "теперь поставить вопрос об определении числа п после-
довательных разветвлений, необходимых для того, чтобы можно
было перейти от аорты, имеющей радиус га, к капилляру ра-
диуса 5 • 10~4 см.
Из сделанных предположений непосредственно следует, что
требуемое число разветвлений п должно удовлетворять соотно-
шению
(0,794)"ra = 5 • 10~4. (3.25)
У собаки, например, можно считать го = 0,5 см. Подставляя это
значение в соотношение (3.25) и разрешая это уравнение отноГ
сительно п, мы находим, что п равно примерно 30.
Из предположения .о том, что каждый сосуд образуется
в результате ветвления более крупного сосуда, следует, что
общее число сосудов кровеносной системы можно оценить при-
мерно числом
230 1Q9.
Общее число капилляров, которые в соответствии с выбран-
ной моделью возникают в результате последних разветвлений,
составляет как раз половину числа всех сосудов, т. е. равно
приблизительно 0,5 • 109. Рашевский [31] (см. также [28]) ука-
зывает для собаки число капилляров, равное примерно 1,2 • 109,
и уже этот результат хорошо совпадает с данными наших рас-
четов. В действительности можно предположить, что эти оценки
согласуются еще более точно, если принять во внимание то,
что на самом деле трудно эмпирически различить истинные
капилляры (т. е. сосуды, возникающие при конечных
70
Глава 3
разветвлениях) и сосуды, которые образуются, скажем, на двад-
цать девятом или двадцать восьмом разветвлении.
В приведенных выше рассуждениях предполагалось, что
действительный радиус капилляра известен из эмпирических
наблюдений. Можно, однако, непосредственно вычислить этот
радиус, исходя из соображений оптимальности. Основная идея,
на которой базируются такие расчеты, заключается в том, что
лимитирующим фактором, ограничивающим радиус капилляра,
является скорость диффузии важнейших метаболитов из ка-
пилляра в окружающие ткани. Соответствующие рассуждения
не требуют привлечения новых принципов, и поскольку они
довольно громоздки, мы не будем разбирать их детально и
отошлем по этому поводу читателя к оригинальной литературе
[28, 31].
3.9. Замечание об эритроцитах 1 * *
Изучение эритроцитов млекопитающего дает поучительный
пример применения принципа оптимальности в биологии. Это
сравнительно простой, с качественной точки зрения, вопрос, и,
вероятно, есть смысл обсудить его здесь. Мы ограничимся лишь
качественным подходом, так как детальный математический
анализ этой задачи, основные приемы которого были проиллю-
стрированы в предыдущих разделах, хотя и не очень сложен,
но достаточно громоздок.
Прежде всего заметим, что в форме и строении эритроци-
тов различных млекопитающих имеется много общего. Рассмо-
трим в качестве типичного примера эритроцит человека. Отвле-
каясь от деталей, можно считать, что он представляет собой
круглый диск диаметром примерно 8-10'4 см и толщиной
2 • 10-4 см. Форма двух круговых поверхностей этого диска не
является плоской: в центре они расположены ближе друг
к другу, чем по краям, и это придает ему характерную двояко-
вогнутую форму. Число эритроцитов в крови невероятно ве-
лико: в каждом кубическом миллиметре крови обычно содер-
жится 4 000 000 — 6 000 000 этих клеток.
Как известно, главная функция эритроцитов состоит в том,
что с их помощью осуществляется перенос кислорода и га-
зообмен между кровью и окружающими тканями. Основную
роль в переносе кислорода и газообмене играет белок гемо-
1 Имеется превосходная обзорная статья Лемана и Хантсмана по срав-
нительной биологии эритроцитов, содержащая обширную библиографию; эта
статья составляет гл. 2 книги «Функции крови» [32]. Гл. 1, 4, 8 и 9 этой книги
тоже имеют отношение к нашим рассуждениям.
кровеносная система
71
глобин. 30—35% веса каждого эритроцита составляет гемо-
глобин, 60—65% веса — вода, а остальное приходится на долю
липопротеидов, небольшого числа ферментов и еще некоторых
малых молекул, образующих какую-то пока еще не вполне вы-
ясненную структуру. В отличие от других видов клеток эри-
троциты млекопитающих не имеют ядра.
Для того чтобы лучше представить себе различные харак-
терные черты оптимальности в строении эритроцитов, допу-
стим, что требуется искусственно создать некую циркулиру-
ющую жидкость, которая бы с оптимальной эффективностью
осуществляла перенос и обмен газов. В соответствии с прин-
ципом оптимальной конструкции следует ожидать, что эта
идеальная циркулирующая жидкость будет достаточно близка
к крови млекопитающих.
Первый вопрос, который должен быть решен при создании'
такой жидкости, заключается в следующем: должна ли такая
идеальная жидкость вообще содержать форменные элементы
(клетки)? На первый взгляд кажется нерациональным помещать
весь гемоглобин внутри клеток, создавая таким образом до-
полнительный барьер (клеточную оболочку), препятствующий
свободной диффузии газов в окружающие ткани и обратно.
Не будет ли кровь, в которой гемоглобин свободно растворен
в плазме (как это имеет место у многих беспозвоночных),
более эффективна в переносе кислорода и газообмене? Про-
стейшие соображения показывают, что это вовсе не так. Во-пер-
вых, если бы весь гемоглобин, необходимый для удовлетворения
метаболических потребностей человеческого организма, был
растворен в объеме жидкости, равном обычному объему пла-
змы, то этот раствор оказался бы чрезмерно вязким. Для под-
держания циркуляции такого раствора потребовался бы очень
большой расход энергии и, следовательно, очень большое
сердце. Далее, при течении вязкой жидкости в цилиндрическом
сосуде трение между стенками сосуда и слоями жидкости,
прилегающими к стенкам, замедляет движение этих слоев,
т. е. движется преимущественно лишь та часть жидкости, кото-
рая находится в центре сосуда. В этом случае у стенок сосуда
создавался бы неподвижный слой плазмы, что сводило би на
нет все преимущества, которые мыслимы при осуществлении
газообмена свободным гемоглобином, находящимся в плазме.
Можно, следовательно, заключить, что свободный гемоглобин
в плазме совершенно неэффективен и что он должен быть упа-
кован в особые форменные элементы. Таким образом, рассу-
ждения, опирающиеся на принцип оптимальности, приводят
к выводу о необходимости существования эритроцитов у таких
организмов.
72
Глава 3
о
Определим теперь оптимальную форму таких элементов,
вопрос о существовании которых был сейчас решен положи-
тельно. Коротко говоря, здесь должны быть приняты во вни-
мание следующие факторы:
1. Для оптимальной эффективности газообмена площадь
поверхности, приходящаяся на единицу объема, у таких эле-
ментов должна быть максимальной.
2. Эти элементы должны быть такими, чтобы их движение
было связано с минимальным рассеянием энергии; так, ска-
жем, возмущение линий тока плазмы в кровеносной системе
должно быть минимальным.
3. Элементы не должны оседать и тем самым закупоривать
кровеносные сосуды, т. е. циркулирующая плазма должна
максимально увлекать их.
4. Размер элементов должен соответствовать диаметру мель-
чайших сосудов кровеносной системы.
Первое требование — о том, что у оптимальных элементов
площадь поверхности, приходящаяся на единицу объема, дол-
жна быть максимальной,— имеет внешнее сходство с так назы-
ваемой изопериметрической задачей 1 — одной из классических
задач вариационного исчисления. В данном случае, однако,
видно, что мы имеем дело с задачей, которая вообще не имеет
решения (см. разд. 2.7), так как твердое тело может быть де-
формировано так, что площадь его поверхности будет сколь
угодно велика при условии сохранения его объема неизменным.
Вместе с тем очевидно, и это совсем нетрудно доказать, что
дискоидальное тело будет при том же объеме обладать значи-
тельно большей площадью, чем сферическое. Непосредственные
измерения, проведенные для реальных эритроцитов, показывают,
что выигрыш в площади поверхности оценивается примерно
в 30%. Таким образом ясно, что элементы скорее должны иметь
дискоидальную форму, нежели сферическую (|хотя, очевидно,
для поддержания дискоидальной конфигурации требуется неко-
торая добавочная энергия).
Изучая двояковогнутую форму типичного эритроцита млеко-
питающего, Хартридж [33] еще много лет назад отметил, что
«... наиболее эффективная форма этих частиц, по-видимому,
будет такой, которая допускает насыщение всего содержимого
в течение одного и того же промежутка времени —• так, чтобы
края не насыщались раньше, чем центр, и наоборот». Но края
диска с плоскими круговыми поверхностями подвержены воз-
1 Простейшая изопериметрическая задача состоит в определении плоской
кривой заданной длины, ограничивающей максимальную площадь. Решением
этой задачи служит, разумеется, окружность.
Кровеносная система
73
действию окружающей среды с трех сторон, тогда как централь-
ные части — только с двух; поэтому диффузия газовых молекул
в центральной части диска затруднена по сравнению с диф-
фузией их вблизи краев. Единственная возможность ликвиди-
ровать такое неравенство состоит в том, чтобы диск в центре
был тоньше, чем по краям. Такая форма очень напоминает дво-
яковогнутую форму эритроцита млекопитающего.
На основании гидродинамических соображений нетрудно по-
казать вполне строго, что дискоидальная форма, удовлетворя-
ющая требованию 1, обеспечивает и выполнение условий 2 и 3.
Так, например, известно [34, 35], что рассеяние энергии при тече-
нии суспензии по трубке минимально в том случае, когда сус-
пендированные частицы сконцентрированы вблизи оси трубки
(т. е. в области минимальных относительных сдвигов слоев).
Можно показать, что при дискоидальной форме суспендирован-
ных частиц они как раз и будут концентрироваться вблизи оси;
тем самым минимизируется как энергия, рассеиваемая потоком,
так и тенденция частиц к оседанию. Более того, для суспензии
дискоидальных частиц все эти свойства оказываются выражен-
ными сильнее, чем .для суспензии, содержащей сферические
частицы такого же объема.
Наконец, соотношение (3.25) показывает, что существует
некоторый верхний предел для объема идеальных гипотетических
элементов. Действительно, поскольку в идеальном случае каж-
дая частица должна нести максимально возможное количество
гемоглобина, интуитивно ясно, что размеры частиц должны быть
близки к максимально допустимым: они должны обладать ра-
диусом, близким к величине 10-4 см *.
Сходство идеальной циркулирующей жидкости с той, кото-
рой реально обладают млекопитающие, весьма значительно. Это
соответствие между теоретически предсказанными и реально
наблюдаемыми результатами показывает, насколько полезен
принцип оптимальности для понимания и теоретического пред-
сказания важнейших черт анатомического строения биологиче-
ских форм.
1 В разд. 3.8 было отмечено (см. [28, 31]), что радиусы капилляров можно
определить непосредственно, исходя из соображений оптимальности. Эти со-
ображения не связаны с размерами эритроцитов, так что, определяя радиус
эритроцита на основании радиуса капилляра, мы не впадаем в порочный круг.
Глава 4
ОНТОГЕНЕЗ И ФИЛОГЕНЕЗ
4.1. Введение
В предыдущей главе было проиллюстрировано применение
принципа оптимальной конструкции к изучению биологических
структур. Такие исследования имеют, несомненно, весьма важ-
ное значение, но с точки зрения биолога они не совсем полно-
ценны. Дело в том, что биолога прежде всего интересует взаи-
модействие различных биологических структур, рассматривае-
мых как части единого целого, а в нашем исследовании
сосудистой системы мы рассматривали сосуды изолированно от
организма, частью которого они являются.
Оказывается, однако, что проблема комплексного изучения
различных функций и структур и их взаимодействия в целост-
ном и нормально функционирующем организме также представ-
ляет собой область, к которой можно применить теорию опти-
мальности. Цель настоящей главы состоит в том, чтобы позна-
комить читателя с некоторыми важными биологическими
представлениями (быть может, ему незнакомыми), которые
лежат в основе проблем, рассматриваемых в следующих двух
главах. Мы обсудим эти вопросы не столь последовательно, как
в предыдущих главах, и уделим основное внимание их качест-
венной стороне, но в гл. 5 вновь вернемся к математическим
методам исследования.
4.2. Некоторые основные понятия: онтогенез и филогенез
Биолога чрезвычайно интересует процесс изменения организ-
мов во времени, и особенно те последовательности неизбежных
структурных изменений, которые, по-видимому, детермини-
руются природой организма и которые мы обычно называем
развитием.
Наиболее очевидные процессы развития — это те процессы,
которые протекают в течение жизни отдельного биологического
индивидуума. Жизнь каждого индивидуума начинается с одной
клетки, которая обычно практически не дифференцирована
(если не считать дифференциации на анимальный и вегетативный
полюсы). В процессе дробления яйца и дифференциальной спе-
Онтогенез и филогенез
75
циализации возникающих при этом клеток развивающийся ор-
ганизм претерпевает ряд резких и чрезвычайно сложных изме-
нений формы и функции. Важнейшей чертой заключительной
стадии этого процесса — взрослой формы — у высших организ-
мов является способность ,к половому размножению; в дальней-
шем вплоть до смерти индивидуума никаких существенных
изменений не происходит.
Этот процесс, в результате которого из одной клетки часто
довольно сложными путями возникает взрослая форма, назы-
вают онтогенезом или процессом индивидуального развития.
У многих организмов онтогенез распадается на ряд четко очер-
ченных стадий. У насекомых и лягушек, например, имеются
продолжительные и относительно статические личиночные ста-
дии (соответственно стадии гусеницы и головастика), при кото-
рых развивающийся организм ведет свободный образ жизни и
кажется вполне «взрослым», но не обладает способностью
к размножению *. По истечении определенного промежутка вре-
мени личинка претерпевает полный метаморфоз, 'в результате
которого появляется подлинно взрослая форма, зачастую совер-
шенно отличная от личиночной. В развитии многих других
организмов личиночная стадия отсутствует.
В отношении онтогенеза нам сейчас важно отметить, что
весь этот процесс полностью завершается в течение относи-
тельно короткого промежутка времени. Переход от оплодотво-
ренной яйцеклетки к взрослой форме чаще всего (за исключе-
нием, пожалуй, некоторых растений, в частности древесных
форм) занимает не более 20 лет, а у многих форм он заканчи-
вается в течение нескольких недель или месяцев.
Когда биолог описывает какой-либо биологический вид, он
обычно основывается на признаках взрослой формы. Так, говоря
о виде, имеют в виду бабочку или лягушку, а не гусеницу или
головастика. Взрослая форма какого-либо вида представляет
собой результат ряда онтогенетических превращений, и этот
ряд в известном смысле отражает процесс развития данной
формы. Но теория эволюции показывает, что существуют и дру-
гие вопросы, относящиеся к становлению внешней формы вида,
и поэтому мы сейчас перейдем к совершенно другому аспекту
развития организма.
1 Для этого утверждения, как это всегда случается в биологии при по-
пытке сформулировать какое-либо общее правило, можно указать довольно
интересные исключения Личинки некоторых насекомых и амфибий обладают
способностью к неограниченному размножению. При этом наблюдается два
типа явлений: 1) педогенез — способность размножаться в личиночной стадии;
2) неотения — сохранение личиночных черт во взрослом состоянии
76
Глава 4
Теория эволюции учит, что каждый вид возникает в резуль-
тате морфологических изменений ранее существовавших видов
и действия естественного отбора. Отсюда следует, что проис-
хождение каждого данного организма можно проследить ретро-
спективно в глубь геологических эпох вплоть до момента воз-
никновения жизни на Земле. Поэтому всякий индивидуум,
принадлежащий к данному виду, представляет собой также конеч-
ный этап ряда эволюционных изменений, т. е. изменений формы,
которые происходили в процессе эволюции этого вида. Эта
последовательность называется процессом филогенетического
развития или филогенезом.
Вполне очевидно, конечно, что онтогенез и филогенез дан-
ного организма во многих чертах существенно отличаются друг
от друга. Онтогенез, например, поддается прямому изучению;
его можно наблюдать в лаборатории или в поле. Филогенез,
напротив, не часто поддается лабораторному изучению. Лишь
очень редко, в весьма частных случаях, оказывается возможным
непосредственно наблюдать явления, напоминающие филогене-
тические превращения1. Изучение филогенеза — это поле дея-
тельности эволюциониста и палеонтолога, а изучением онтоге-
неза занимаются эмбриологи и в последнее время биохимики.
. Несмотря на указанные различия, между этими двумя
процессами развития существует много общего. Эти общие черты
онтогенеза и филогенеза и их отношение к принципу оптималь-
ности мы и обсудим в следующих разделах. Более подробно эти
проблемы рассматриваются в гл. 5 и 6.
4.3. Рекапитуляция. Биогенетический закон
Как только биологи поняли, что каждый организм представ-
ляет собой конечный этап двух различных процессов развития,
возникло естественное стремление найти связь между этими
двумя процессами, тем более что даже при самом поверхност-
ном изучении онтогенеза и филогенеза между ними обнаружи-
вается поразительное сходство.
Рассмотрим сначала филогенетические ряды. Согласно тео-
рии эволюции и палеонтологическим данным, жизнь на нашей
планете началась, очевидно (или по крайней мере приобрела
свои характерные отличительные черты), в виде какой-то сво-
бодно живущей одиночной клетки. Далее, по-видимому, произо-
шел переход от отдельных изолированных клеток к многокле-
1 В связи с этим можно упомянуть о таком интересном примере резуль-
татов действия отбора, как индустриальный меланизм См, например, работу
Кеттлуэлла [36]
Онтогенез и филогенез
77
точным организмам, возможно, через промежуточную колони-
альную стадию (примеры колониальных организмов, которые
существуют и в настоящее время, можно найти в начальных
курсах биологии). Затем эти многоклеточные организмы при-
обрели, по всей вероятности, исключительное разнообразие, и
кто-то из них (скорее всего группа, родственная современным
кольчатым червям или кишечнополостным) в конце концов дал
начало ветви, ведущей к позвоночным. Палеонтологические дан-
ные с несомненностью свидетельствуют о том, что первые позво-
ночные были морскими животными и что древнейшие позвоноч-
ные представители филогенетического ряда, ведущего к млеко-
питающим и человеку, имели жабры. У этих древнейших
позвоночных не было настоящего костного скелета, но они
обладали хрящевым скелетом.
Рассмотрим теперь стадии онтогенетического развития ти-
пичного позвоночного. Онтогенез начинается с одной клетки
(оплодотворенной яйцеклетки) —точно так же, как и филоге-
нетический ряд. В результате многократного дробления опло-
дотворенной яйцеклетки возникает колония одинаковых кле-
ток— бластула. При дальнейшей дифференцировке возникает
форма, напоминающая беспозвоночное животное. На несколько
более поздней стадии развивающийся организм, или эмбрион,
приобретает первичный скелет, состоящий из хряща. Он
обладает также рядом жаберных или висцеральных дуг, на:
поминающих жабры типичного морского позвоночного (у
акул и костных рыб эти органы развиваются в настоящие
жабры).
Совершенно очевидно, что параллелизм онтогенеза и фило-
генеза, который обнаруживается уже при самом поверхностном
сравнении этих двух процессов и оказывается гораздо более
глубоким при более детальном исследовании, определенно ука-
зывает на существование некоторого общего биологического
принципа, лежащего в основе этих двух процессов. Вопрос этот
в свое время весьма широко обсуждался, и поэтому здесь целе-
сообразно привести краткий обзор этой дискуссии.
Из гипотез, относящихся к параллелизму онтогенеза и фило-
генеза, пожалуй, наиболее широко распространена гипотеза,
впервые выдвинутая Геккелем [37, 38] и его последователями *.
Эта гипотеза утверждает, что последовательность событий в он-
тогенезе представляет собой повторение, или рекапитуляцию,
соответствующих стадий филогенетического ряда. Эта точка
1 Идеи, напоминающие взгляды Геккеля, высказывались и значительно
раньше. Прекрасный исторический обзор по этому вопросу написан Мейером
[39]
78
Глава 4
зрения, если признать ее правильной, приводит к ряду важней-
ших выводов, которые Геккель и другие не замедлили сделать.
Во-первых, гипотеза рекапитуляции, или биогенетический закон,
как ее стали называть, служит прямым доказательством спра-
ведливости теории эволюции (т. е. представления о том, что
всякому сохранившемуся до нашего времени организму пред-
шествует некоторый филогенетический ряд). Ведь каждый орга-
низм проходит процесс онтогенеза, и если онтогенез повторяет
филогенез, то каждый организм должен обладать также и фи-
логенезом.
Еще более важное следствие теории рекапитуляции состоит,
однако, в том, что эмпирическое исследование процесса онто-
генеза дает возможность непосредственно изучать филогенез.
Иными словами, если бы биогенетический закон был действи-
тельно справедлив, это означало бы, что филогенез можно ис-
следовать с помощью тех же прямых количественных методов,
которые применяются для изучения онтогенеза. Из этого сле-
довало, что если бы мы научились расшифровывать язык река-
питуляции, то стало бы доступным непосредственное проникно-
вение в процесс филогенеза, невозможное сейчас ввиду непол-
ноты палеонтологической летописи.
Надежды эти оказались, однако, необоснованными по при-
чинам, представляющим интерес для нашего дальнейшего ис-
следования. В своей первоначальной формулировке биогенети-
ческий закон утверждал, что если некоторая более развитая
форма В возникла из более простой формы А, то все стадии
онтогенеза, соответствующие промежуточным формам, лежащим
между А и В, попросту последовательно добавляются к онто-
генезу формы А. Такие случаи, однако, если они и встречаются,
чрезвычайно редки. Более того, выяснилось, что при онтогенезе
наблюдается инверсия и нарушение последовательности стадий,
соответствующих этапам известного филогенетического ряда;
некоторые из стадий просто выпадают. И наоборот, онтогенез
может содержать такие стадии, которые вообще никак не
удается истолковать с точки зрения филогенеза. В связи с этим
была специально создана новая терминология и предприняты
попытки видоизменить биогенетический закон, чтобы согласо-
вать имевшиеся факты с основными положениями теории река-
питуляции; постепенно положение все более запутывалось, и
в конце концов от этого теоретического принципа пришлось
отказаться
1 Убедительную критику биогенетического закона см., например, в работах
Гарстанга [40] или Шамуэя [41]
Онтогенез и филогенез
79
Несколько рискуя чрезмерно упростить этот сложный во-
прос, отметим здесь две характерные черты онтогенеза, затруд-
няющие применение биогенетического закона:
1. Довольно часто встречающиеся в онтогенезе выпадения,
а также добавления стадий, которым, по-видимому, нельзя
найти параллелей в филогенезе, и выраженные нарушения по-
рядка следования этих стадий, не оказывающие заметного вли-
яния на окончательный результат процесса онтогенеза.
2. В более общем смысле, вариабельность того, что можно
было бы назвать «временем онтогенеза», по сравнению с фикси-
рованной, точной последовательностью, характерной для «вре-
мени филогенеза».
Эти трудности, возникшие на пути применения биогенети-
ческого закона, побудили других биологов к поискам какого-
нибудь иного объяснения параллелизма онтогенеза и филоге-
неза, само существование которого никем не оспаривалось.
Пытаясь преодолеть отмеченные выше’ трудности, Лилли и
другие авторы 1 выдвинули иную точку зрения. Согласно этому
взгляду, основной недостаток теории рекапитуляции Геккеля
заключался в том, что филогенез рассматривался как после-
довательность взрослых форм, а онтогенез — как «ускоренное
повторение» этой последовательности форм. По новой теории,
филогенез скорее следовало рассматривать как последователь-
ность полных онтогенезов. Иными словами, всякое изменение,
возникшее на некоторой стадии онтогенеза какого-то развива-
ющегося организма А, приводит к изменениям во взрослой
форме А, а также в онтогенезе всех потомков А. Поэтому пра-
вильно, пожалуй, считать эту точку зрения диаметрально про-
тивоположной взгляду Геккеля, и, перифразируя, сказать, что
«филогенез повторяет онтогенез». Гарстанг [40] сформулировал
это следующим образом:
«[Онтогенез] воспроизводит последовательные ступени [пред-
ковой дифференциации] не потому, что в нем отражаются по-
следовательные взрослые формы, а потому, что онтогенез вся-
кого организма представляет собой в известных пределах видо-
изменение онтогенеза его предшественника, и именно этими
предшественниками создается и определяется филетическая ли-
ния взрослых форм».
У этой теории имеются свои собственные трудности. Так,
Геккель, например, мог истолковать наблюдаемый в процессе
эмбрионального развития переход от хрящевого скелета к кост-
ному как рекапитуляцию имевшего место в процессе филогенеза
перехода от акул с хрящевым скелетом к настоящим рыбам
1 Эти идеи очень ясно изложены в книге де Бира [42].
80
Глава 4
с костным скелетом. А сторонники взглядов Лилли вынуждены
в этом случае утверждать, что хрящ является необходимым
предшественником кости и что кости у развивающегося орга-
низма (как в филогенезе, так и в онтогенезе) вообще не могут
образоваться никаким иным путем, кроме как через промежу-
точный этап хряща. Аналогично они должны признать, что он-
тогенез наземных позвоночных непременно должен проходить
через промежуточную стадию пресловутых жаберных дуг и жа-
берных щелей ’. Неизбежность бесчисленного множества такого
рода утверждений вызывает недоверие к этой точке зрения.
Нужно отметить также, что идея Лилли, которая не была свя-
зана ни с каким определенным механизмом, полностью
лишена той силы научного предвидения, которая составляла
одну из наиболее привлекательных черт биогенетического за-
кона.
Мы увидим, однако, что те общие соображения, которые бу-
дут развиты ниже, приводят к теории, весьма сходной с гипоте-
зой Лилли.
4.4. Онтогенез и естественный отбор
Для того чтобы стало ясно, к каким выводам приводят со-
ображения, высказанные в нескольких последних разделах,
надо отметить еще один существенный момент. Важнейшее раз-
личие между онтогенетическим и филогенетическим рядами за-
ключается в следующем: если филогенез управляется исключи-
тельно естественным отбором, то онтогенез задуман так, чтобы
почти на всех стадиях или даже полностью быть свободным от
давления отбора. Как мы увидим, это простое обстоятельство,
если как следует понять его значение, позволяет объяснить мно-
гие черты сходства, а также и различия между этими двумя
процессами. Оно дает нам также возможность использовать ма-
тематические методы исследования для решения ряда важных
1 Очень четкая формулировка такой точки зрения приводится на стр. 277
книги Рассела [43] (эту книгу мы настоятельно рекомендуем тем, кто пола-
гает, что важны лишь те биологические идеи, которые имеют отношение к мо-
дели Уотсона—Крика): «Клайненберг... отмечает ...что многие эмбриональ-
ные органы образуются лишь для того, чтобы стимулировать развитие дефи-
нитивных органов. Так, хорда является необходимым предшественником по-
звоночника, а хрящ — предшественником кости «С этой точки зрения, — пи-
шет он, — многие рудиментарные органы предстают перед нами в новом
свете. Трудно было бы понять их упорное сохранение' в длинных филогенети-
ческих рядах, если бы они были всего лишь остатками давно прошедших и
забытых стадий. Возможно, что на самом деле они имеют гораздо большее
значейие... чем обычно полагают. Если в процессе филогенеза они выполняли
роль промежуточных органов... они несут те же функции и в онтогенезе .. ».
Онтогенез и филогенез
81
проблем, к которым иначе нельзя найти непосредственного под-
хода.
Разъясним сначала смысл утверждения, что в течение всего
или почти всего процесса онтогенетического развития давление
отбора отсутствует. Вспомним, что давление отбора, как это
было показано в гл. 1, можно всегда выразить в терминах диф-
ференциальной способности к размножению у конкурирующих
форм. Если же в какой-либо экологической нише нет конкури-
рующих форм, то в ней, по определению, не может проявиться
давление отбора. Теперь остается только рассмотреть вопрос
о том, действительно ли развивающийся организм в течение
большей части онтогенеза или на всем его протяжении не раз-
деляет свою нишу ни с каким другим организмом.
У высших организмов «ограждение» развивающегося эмбри-
она от прямой конкуренции особенно разительно. У млекопи-
тающих несколько эмбрионов обычно развиваются одновре-
менно в одной матке, но каждый из них имеет, как правило,
свои собственные зародышевые оболочки, свою собственную
плаценту и свою собственную пуповину. У птиц и яйцекладущих
рептилий каждый эмбрион физически изолирован от окружаю-
щей среды и имеет свой собственный запас пищи. То же самое
наблюдается у всех прочих представителей растительного и жи-
вотного царства, хотя у более простых форм механизм, обеспе-
чивающий такую изоляцию, менее совершенен и, вероятно, ме-
нее эффективен.
Справедливость утверждения об отсутствии отбора при он-
тогенезе оспаривалась на том основании, что у многих видов
имеются стадии свободно живущих личинок, которые, разу-
меется, непосредственно конкурируют друг с другом. Небольшая
часть действительно важных онтогенетических изменений про-
исходит до достижения личиночной стадии, а все сказанное
выше относится ко всем тем стадиям онтогенеза, которые пред-
шествуют личиночной стадии.
Упражнение
Рассмотрите вопрос о селективном значении отсутствия
конкуренции в течение онтогенеза. (Указание: как влияет мини-
мизация конкуренции между- развивающейся молодью на пло-
довитость?)
Если, таким образом, мы готовы признать, что во время
онтогенеза прямое давление отбора играет минимальную и ча-
сто пренебрежимо малую роль, то теперь можно свести воедино
результаты всех наших рассуждений.
82
Глава 4
4.5. Онтогенез и принцип оптимальности
В гл. 1 и в предыдущих разделах настоящей главы были
установлены следующие положения:
1. У конкурирующих организмов давление отбора является
главным фактором, определяющим их структуру.
2. Влияние давления отбора может быть математически опи-
сано как оптимизация биологической структуры.
3. Филетические ряды состоят из форм, живущих в условиях
конкуренции, и, следовательно, согласно п. 2, подчинены прин-
ципу оптимальности.
4. При онтогенезе давление отбора играет в лучшем случае
совершенно незначительную роль, и поэтому нет никаких осно-
ваний предполагать, что онтогенез непосредственно подчиняется
каким-либо принципам оптимальности.
5. Тем не менее между онтогенетическим и филогенетиче-
ским рядами имеется значительное сходство.
В отношении п. 4 можно сказать, что приведенные в литера-
туре 1 многочисленные примеры появления в онтогенезе струк-
тур, не играющих существенной роли в развитии, противоречат
представлению о природе как о машине, создающей оптималь-
ные структуры.
Вопрос теперь состоит в том, можно ли применить матема-
тические методы, основанные на принципе оптимальности,
к проблемам онтогенетического развития. Исходя из п. 5, это
было бы возможно, если бы удалось установить соотношение
между филогенезом и онтогенезом. Ведь, согласно п. 3, филоге-
нетические превращения можно исследовать на основе принципа
оптимальности, и поэтому выяснение вопроса о соотношении ме-
жду филогенезом и онтогенезом позволило бы перенести, по
крайней мере в формальном смысле, результаты исследования
филогенеза в область онтогенеза.
Но, с другой стороны, п. 4 утверждает как будто нечто со-
всем противоположное — что нет никаких оснований предпола-
гать оптимальность (в каком бы то ни было смысле) структур,
возникших в онтогенезе. Итак, применение методов оптимизации
к онтогенезу встречается с двумя основными затруднениями:
а) надо объяснить, каким образом могут быть одновременно
справедливыми утверждения 4 и 5 и б) требуется выяснить со-
отношение между онтогенезом и филогенезом.
Оба поставленных вопроса в значительной степени разъяс-
1 См , например, книгу Рента [8] (в особенности стр 257—258) Эта книга
поможет читателю представить себе действительную степень трудности этих
проблем, которые мы здесь рассматривали в высшей степени упрощенно
Онтогенез и филогенез
83
няются, если вспомнить, что в онтогенезе давление отбора от-
сутствует. Это означает, что любое добавочное изменение, воз-
никшее в онтогенезе, сохраняется на всем его протяжении, так
как в это время отбора изменений не происходит. По окончании
онтогенеза некоторые из этих изменений приведут к взрослым
формам, обладающим каким-то селективным преимуществом;
эти формы будут сохраняться отбором. Некоторые изменения
окажутся вполне нейтральными, т. е. не вызовут изменений
у взрослой формы. Другие приведут к возникновению селективно
невыгодных признаков и к элиминации обладающих ими форм.
Одним словом, любые модификации в онтогенезе, которые не
снижают плодовитости взрослой формы, имеют тенденцию
сохраняться неограниченно долго. Это как раз и означает, что
возникшие в процессе филогенеза структуры взрослых организ-
мов, которые в какое-то время оказываются оптимальными, со-
хранят те онтогенетические стадии, от которых они возникли.
Далее эти стадии сохраняются и у всех последующих форм,
поскольку на протяжении самого онтогенеза они не подвер-
гаются отрицательному отбору.
Эта точка зрения в известной степени близка к взглядам
Лилли, о которых говорилось раньше. Однако мы избегаем при
этом ряда трудностей, с которыми сталкивается теория Лилли.
Еще важнее то, что это позволяет применить методы оптимиза-
ции ко многим проблемам онтогенеза, хотя процесс отбора пря-
мой роли в онтогенезе и не играет. Все преимущества такого
подхода мы продемонстрируем в гл. 5 и 6.
Глава 5
ПРИНЦИП ОПТИМАЛЬНОСТИ И АЛЛОМЕТРИЯ
5.1. Определяющая система функционалов
Предположим, что ученый имеет дело с некоторым объектом,
обладающим определенной пространственной структурой, на-
пример с автомобилем. Первое, что он должен сделать при ис-
следовании этого объекта, — это измерить его, т. е. получить
некоторое множество данных — длин, площадей, объемов, масс
и т. п., — которое характеризует этот предмет. Так, например,
за множество данных, характеризующих автомобиль, можно
принять полную его длину, расстояние между осями передних и
задних колес (колесная база), радиус коленчатого вала, объем
цилиндра двигателя и т. д. Если принять во внимание и то, что
автомобиль движется, то можно предпринять также и даль-
нейшие измерения, например определить скорость, силы трения,
возникающие между шинами и различными видами дорожных
покрытий, и т. д. Можно, таким образом, заполнить целые тома
цифрами, каждая из которых получается в результате некото-
рого измерения, произведенного с данным автомобилем, и сово-
купность всех таких данных будет полностью характеризовать
этот автомобиль.
Если мы примем во внимание, что каждый данный автомо*
биль является лишь отдельным представителем широкого класса
различных (но родственных) между собой механических транс-
портных средств, то можно перейти к их сравнительному изу-
чению. Для этого можно повторить для всех прочих автомоби-
лей все те измерения, которые были произведены с первым.
Различные представители этого класса механических транспорт-
ных средств, например седаны, купе, фургоны, кабриолеты и пр.,
могут сильно друг от друга отличаться; мы видим, что их сра-
внительное изучение становится довольно сложным.
Каждый автомобиль обладает своей особой формой, и каж-
дое отдельное измерение характеризует какую-то специфи-
ческую черту этой формы. Каждый вид измерения (длины, ко-
лесной базы и т. и.) ставит в соответствие данной форме неко-
тороечисло, а именно результат определенного процесса изме-
рения, предпринятого для этой формы. Следовательно, всякий
процесс измерения порождает некоторый функционал — "в том
Принцип оптимальности и аллометрия
85
смысле, как этот термин и был определен, — заданный на мно-
жестве всех изучаемых объектов. Полную систему таких функ-
ционалов мы назовем определяющей системой функционалов.
Существует важная аналогия между функционалами, задан-
ными на некотором (определенным образом выбранном) классе
физических или биологических объектов, и теми «наблюдае-
мыми» параметрами, с помощью*которых описываются меха-
нические системы, обсуждавшиеся в разд. 2.11. Будем исходить
из того, что состояние механической системы в каждый момент
времени может быть полностью определено экспериментально
найденными значениями, которые принимают некоторые вели-
чины— полная энергия, пространственные координаты и им-
пульсы (относящиеся либо к реальным частицам, образующим
систему, либо к фиктивным — скажем, к центрам масс). Дей-
ствительно, поскольку предполагается, что поведение системы
полностью характеризуется ее уравнениями движения, любой
наблюдаемый параметр этой системы может быть в принципе
выражен через решение этих уравнений; следовательно, система,
состоящая из N частиц, полностью характеризуется заданием
6N параметров (трех пространственных координат и трех со-
ставляющих импульса каждой частицы). В случае определяю-
щей системы функционалов общего вида ситуация может ока-
заться и не столь простой, но следует уяснить себе, что значения
совокупности функционалов определяющей системы, заданных
для объектов некоторого вида, характеризуют всякий индиви-
дуальный объект точно таким же образом, как совокупность
наблюдаемых параметров характеризует механическую систему.
В общем случае не все функционалы этого типа могут ока-
заться независимыми друг от друга. Остальная часть этой главы
посвящена одному особому роду соотношений, часто встречаю-
щемуся при изучении зависимости между двумя такими функ-
ционалами.
5.2. Зависимости между функционалами. Аллометрия
Ученый обычно не удовлетворяется одними только измере-
ниями объекта или группы объектов, которые он изучает; как
правило, он- пытается найти какие-то зависимости или хотя бы
корреляции между результатами различных видов измерений.
Такие зависимости позволяют, естественно, проникнуть в сущ-
ность природы изучаемых объектов и в конечном счете пока-
зывают ученому, как эти объекты себя ведут и почему это про-
исходит именно так, а не иначе.
Если мы не располагаем априори какой-либо информацией
о таких зависимостях между функционалами, то наиболее
«6
Глава 5
естественный способ выявления характера этой зависимости
состоит в том, что по имеющимся наборам значений двух функ-
ционалов строится график. Если между множествами значений
изучаемых функционалов существуют какие-нибудь простые за-
висимости, то обычно это обнаруживается на графике довольно
просто. Так, например, возвращаясь к автомобилю, возьмем
численные значения, скажем1, полной длины автомобиля и ра-
диуса рулевого колеса и, отложив их на осях координат, отме-
тим соответствующие точки координатной плоскости. При этом
получится множество разбросанных точек, и никакой простои
Фиг/ 11.
зависимости между ними подме-
тить не удастся. Но теперь по-
смотрим на фиг. 11. Здесь на осях
отложены логарифмы полной дли-
ны и логарифмы колесной базы
для автомобилей разных марок.
Мы видим, что точки очень точно
ложатся на прямую линию, что
указывает на простую зависи-
мость между логарифмом полной
длины L и логарифмом колесной
базы W; эта зависимость выра-
жается формулой
log Z == ^ log UZ 4-ЛГ,
где k, К—константы. Полагая A=logC, где С — другая посто-
янная, мы можем переписать эту зависимость в форме
L — CWk.
(5.1)
На фиг. 12 построены точки, соответствующие значениям лога-
рифма полной длины L и логарифма рабочего объема цилиндра
Р для автомобилей разных марок. Здесь зависимость между
логарифмами опять-таки выражается прямой линией и связь
между L и Р выражается в виде
L = CPk'. (5.2)
Соотношения (5.1) и (5.2) имеют, очевидно, одинаковую мате-
матическую природу. Поразительно то, что очень многие функ-
ционалы, относящиеся к форме автомобилей, оказываются свя-
занными соотношениями того же типа, что и соотношения между
L и W или между L и Р. Аналогичные соотношения получаются
и для функционалов, заданных на других классах механических
транспортных средств, например самолетах и локомотивах.
Принцип оптимальности и аллометрия
87
Обращаясь теперь к функционалам, относящимся не к тех-
ническим, а к биологическим объектам, мы обнаруживаем та-
кие же соотношения. Рассмотрим фиг. 13, взятую как и фиг. 11
из книги Гексли [44]', а также фиг. 14, взятую из книги Рашев-
ского [12].
На фиг. 13 графически изображены зависимости длин туло-
вища, головы и хвоста от полной длины для рыбы Orthopristis
chrysopterus, а на фиг. 14 — зависимость между длиной и шири-
ной туловища у взрослых форм различных млекопитающих.
Множество других примеров биологических систем, у которых
функционалы такого типа связаны аналогичными соотношени-
ями, читатель может найти в классической книге Гексли [44] и
Фнг. 12.
в литературе, которая в ней цитируется. (Заметим, кстати,—
это будет иметь значение для нашего дальнейшего исследова-
ния,— что график на фиг. 13 относится к некоторой онтогенети-
ческой ситуации, не имеющей, строго говоря, аналогии в кон-
струкции технических сооружений, таких, как, например, авто-
мобиль, но к графику на фиг. 14 это замечание не относится.
Мы обсудим это замечание более детально в разд. 5.5, но сейчас
читатель, имея в виду соображения, изложенные в предыдущей
главе и особенно в разд. 4.5, должен обратить внимание на фор-
мальную аналогию между этими графиками.)
Существует, таким образом, большое число разнообразных
функционалов, заданных на самых различных множествах
объектов (как органических, так и неорганических), значения
которых связаны уравнением вида
у = а.х$.
1 Эта книга представляет собой классическое сочинение по аллометрии;
читатель найдет в ней полезное обсуждение законов аллометрического роста
н их отношения к другим проблемам биологии, а также ссылки на более ран-
нюю литературу.
Фиг. 14
Принцип оптимальности и аллометрия
89
Выражаемую этим уравнением закономерность, систематическое
изучение которой для организмов было впервые предпринято
Гексли [44], называют законом гетерогонии или, иначе, законом
неравномерного или аллометрического роста. Это единственный
вид явной зависимости между функционалами, относящимися
к биологическим объектам, который был подвергнут система-
тическому изучению. Как мы покажем в разд. 5.4, аллометрия
оказывается тесно связанной с представлениями об оптимально-
сти," й эта”связь“может быть изучена с помощью теории, которая
далее будет развита. В гл. 6 изучаются более общие соотно-
шения между функционалами, и на основании принципа опти-
мальной конструкции делается ряд выводов, относящихся к этим
более сложным ситуациям.
5.3. Обратная задача вариационного исчисления
В гл. 1 мы кратко описали основные вариационные прин-
ципы теоретической физики. Действительный ход рассуждений,
связанных с открытием этих принципов, был обратным по от-
ношению к той формальной последовательности выводов, кото-
рая приводилась в гл 2. Эти рассуждения были индуктивными:
исследователи отправлялись от известного семейства траекто-
рий и предполагали, что эти траектории являются стационар-
ными кривыми для некоторого функционала, тогда как мы в гл. 2
считали, что первоначально задается оценочная функция
(или, что то же самое, задается ядро этого функционала),
а задача состоит в том, чтобы определить соответствующее семей-
ство стационарных кривых. Искусство и проницательность та-
ких ученых, как Ферма и Гамильтон, состояли именно в том,
что они сумели построить соответствующие функционалы.
В чисто математических исследованиях также возникают
подобные задачи. Так, например, если задано какое-то семей-
ство кривых линий, лежащих на некоторой поверхности, то
можно поставить задачу об определении такой «функции рас-
стояния», по отношению к которой эти кривые являются гео-
дезическими. Задачи такого типа вполне аналогичны тем про-
блемам, которые приходилось рассматривать Ферма или Га-
мильтону. В данном разделе как раз и будут развиты общие
методы решения таких задач. Мы будем при этом следовать
тому подходу, который был применен Дарбу [45] при иссле-
довании сформулированной выше задачи о геодезических.
Приступая к исследованию этого вопроса, мы должны
прежде всего четко сформулировать математическую поста-
новку задачи. Как и всегда, лучше всего начать с эвристиче-
ских рассуждений и ограничиться вначале наиболее простыми
90
Глава 5
ситуациями. Предположим, что имеется некоторое семейство
функций у=у(х), и мы хотим найти функционал (оценочную
функцию), выражающийся в виде интеграла
J(У)— (х, У, y')dx, (5.3)
для которого эти кривые служат экстремалями (стационар-
ными кривыми). Задача сводится при этом к определению
ядра F.
Вспомним теперь результаты, которые мы получили раньше
при изучении вариационных задач: если функция F дана, то
стационарные кривые функционала J представляют собой не
что иное, как решения уравнения Эйлера вида
(5.4)
ду dx уду' у ' ’
Второе слагаемое, входящее в это уравнение, можно записать
в развернутом виде, пользуясь известной формулой для вы-
числения полной производной:
й!ф । dy , dty dy’
dx dx ‘ dy dx dy' dx '
где ф — произвольная функция переменных х, у, у', для ко-
торой существуют частные производные, фигурирующие в этой
формуле. Полагая Ф = ^уг , находим, что
d / dF \ d^F . , &F . „ &2F
dx у ду' у дх ду' ‘У дуду' ' У (5 у')2 ’
и уравнение Эйлера приобретает вид
dF д^Р , d2F „ d2F
ду дхду' У дуду’ ^ У (ду')2 •
Уравнение (5.5)-—это обыкновенное дифференциальное урав-
нение второго порядка, содержащее неизвестную функцию
у(х). Поэтому общее решение этого уравнения должно зави-
сеть от двух произвольных постоянных, и соответствующие ин-
тегральные кривые, являющиеся стационарными кривыми
для /, образуют некоторое двухпараметрическое семейство,
уравнение которого можно записать в виде
у = ¥(х, а, £), (5.6)
где а, р — упомянутые произвольные параметры. Следова-
тельно, мы должны предположить, что заданное первона-
чально семейство функций представляет собой некоторое двух-
параметрическое семейство вида (5.6).
Принцип оптимальности и аллометрия
91
Надо отметить, что если задано двухпараметрическое се-
мейство функций, то можно, вообще говоря, найти такое диф-
ференциальное уравнение второго порядка вида
У" = ё(х, у, у’), (5.7)
для которого кривые этого семейства являются интегральными
кривыми. Допустим, например, что семейство (5.6) задано и
что функции, входящие в это семейство, дважды дифферен-
цируемы. Выполняя дифференцирование, мы получим три
уравнения, содержащие х, у, у', у", а и |3. Если эти уравнения
совместны, то можно, вообще говоря, исключить из них а и [3
и получить уравнение вида (5.7), которому будут удовлетво-
рять все функции (5.6).
Упражнение
Покажите, что двухпараметрическое семейство кривых, оп-
ределяемое формулой у=ах$, представляет собой семейство
интегральных кривых дифференциального уравнения второго
порядка вида
луу"-х(у')2 + у'у==0. (5.8)
Итак, задача сводится теперь к определению функции
F (х, у, у'), такой, чтобы уравнение (5.7) (представляющее
собой дифференциальное уравнение второго порядка, кото-
рому удовлетворяют функции заданного семейства (5.6)) слу-
жило уравнением Эйлера для соответствующего функцио-
нала J. Вернемся к уравнению Эйлера (5.5), которое теперь
нужно рассматривать как уравнение для неизвестной функ-
ции F (а не для у, как раньше). Ввиду (5.7) это уравнение
записывается в форме
df _ &F __ , д^П _ d?f
ду дх ду' У ду ду' & (д у' )2 ( • ‘
Для того чтобы привести это уравнение к более удобному
виду, продифференцируем (5.9) по у' и положим
(5.10>
тогда для функции М получается уравнение
дМ , , дЛ4 . дМ dg .. /с 11Y
-з--рУ -з---кЯтт =------тгт М, (5.11)
дх 1 Л ду 1 6 ду' ду' ' '
представляющее собой линейное дифференциальное уравне-
ние первого порядка в частных производных. При опреде-
ленных условиях это уравнение может быть решено (см.,.
92
Глава 5
например, [46]), и в результате дляЛ1 как функции переменных х,
у, у' находится явное выражение.
Полученное выражение можно теперь подставить в (5.10)
и решить получающееся при этом дифференциальное уравне-
ние второго порядка, содержащее F как неизвестную функ-
цию. Таким образом, поставленная задача оказывается пол-
ностью решенной.
Обратим теперь внимание на то, что поскольку (5 10) —
дифференциальное уравнение второго порядка в частных про-
изводных, его общее решение зависит в общем случае от двух
произвольных функций, скажем от Z(x, у) и ц(х, у). Эти
функции должны быть такими, чтобы для F выполнялось
также и уравнение (5.9), а в остальных отношениях они могут
быть выбраны произвольно.
При этих вычислениях мы встречаемся и с другими вели-
чинами, которые могут быть выбраны произвольно. Функция М
не определяется уравнением (5.11) однозначно и в общем слу-
чае выражается как произвольная функция, зависящая от
двух функций: ф(х, у у'), ^(х,.у, у') (интегралов так назы-
ваемой характеристической системы обыкновенных дифферен-
циальных уравнений, соответствующей (5.11)); следовательно,
Л4 = Ф(ф, %). При этом требование, чтобы для F выполнялось
уравнение (5.9), в общем случае не определяет Ф однозначно.
Итак, вообще говоря, существует бесконечное множество раз-
личных функций F, таких, что для соответствующего функ-
ционала J кривые семейства (5.6) служат экстремалями.
Отмеченное обстоятельство можно проиллюстрировать на
простейшем примере, который будет важен для нас в даль-
нейшем. Допустим, что нам дано двухпараметрическое семей-
ство прямых линий вида
y = ax + ? (5.12)
и требуется найти все функции F, при которых для функцио-
нала вида J эти линии являются экстремалями. Уравнение
типа (5.7), для которого функции (5.12) служат решениями,
имеет вид
у" —0, (5.13)
и при этом оказывается (подробности см. у Дарбу [45]), что
М можно записать в форме
М = Ф (у', у — -’ey'), (5.14)
1де Ф — произвольная функция.
Принцип оптимальности и аллометрия
93
Нетрудно проверить (для этого следует использовать из-
вестный факт, который мы здесь не доказываем (см., на-
X
пример, [47]), заключающийся в том, что если Р (х) = J
xi
dP (х) \
то f(x)=—чт0 решением уравнения (5.10) в случае,
когда М имеет вид (5.14), является выражение
(у' — /)Ф(х, у — xt) dt X (х, у)у' + р.(х, у),
о
Точно так же легко убедиться в том, что для того чтобы при
выборе функции F такого вида удовлетворялось уравнение
(5.10), произвольные функции А, ц должны быть выбраны так,
чтобы
д~>. др.
дх ду '
Из этого условия следует, что
. дч _________________________ дч
К~~~ду~> ~дх~ ’
где у=у(х, у) —некоторая функция от х, у, которая должна
обладать соответствующими частными производными, а в осталь-
ных отношениях произвольна.
5.4. Аллометрия и принцип оптимальности
Выше было показано, что в общем случае функционалы,
входящие в определяющую систему функционалов, не явля-
ются независимыми друг от друга и существуют некоторые со-
отношения, связывающие их значения. Предположим, что име-
ются два таких функционала и и v, и пусть они связаны соот-
ношением вида f (и, v) =0 (так, например, если бы для и, v
имела место аллометрия, то это соотношение записывалось бы
в форме f (и, v)=u — аи₽=0). Допустим также для простоты,
что эти два функционала полностью характеризуют рассматри-
ваемый класс форм, на котором они заданы. - В этом случае
каждая конкретная форма F, принадлежащая этому классу,
характеризуется парой чисел u(F), v(F) и может быть поэтому
представлена точкой на (и, у)-плоскости.
Если теперь F пробегает весь класс допустимых форм, то точ-
ка (и (F), v (F)) движется вдоль кривой f (и, v) =0, образующей
94
Глава 5
геометрическое место точек, соответствующих всем рассматри-
ваемым формам. Если уравнение f — О заменить другим
уравнением /4 = 0, то соответственно получится другая кривая
линия на (и, и)-плоскости. Теперь возникает следующий вопрос:
каким образом из множества всех возможных соотношений та-
кого рода можно выделить именно то соотношение вида /=0,
которое действительно справедливо с биологической точки
зрения?
Приведенные ниже рассуждения указывают в известной сте-
пени путь решения этого вопроса. Каждой форме F функцио-
налы и, v относят пару чисел u(F), v(F), которые, как мы пред-
положили, полностью характеризуют рассматриваемую форму.
В гл. 1 говорилось о том, что эти численные значения обычно
можно установить, исходя из некоторых соображений, связан-
ных с принципом оптимальности. В гл. 3 было показано, каким
образом эти вычисления могут быть в действительности выпол-
нены. Однако те методы, которыми мы пользовались в гл. 3,
не вскрывают, вообще говоря, связей между различными функ-
ционалами; они позволяют лишь определить оптимальные для
данных условий значения тех или иных функционалов. Мы ви-
дим все же, что искомое соотношение / = 0 должно быть сов-
местимо с найденными на основании принципа оптимальности
результатами, относящимися к каждому отдельному функцио-
налу; другими словами, если известно, что, согласно принципу
оптимальности, для данной формы u(F)=a и v(F)=b, то функ-
ция f должна быть такой, чтобы выполнялось равенство
f (а, Ь) =0.
Следовательно, сама искомая функция f по существу пол-
ностью определяется условиями оптимальности, которые были
сформулированы в гл. 1 и применены в гл. 3. Однако те ло-
кальные методы, которыми мы пользовались в гл. 3, не позво-
ляют судить о свойствах соотношения /=0 «в целом». Для по-
лучения таких сведений должны быть развиты более общие
методы.
Поскольку искомое соотношение вида f = 0 выделяется из
класса всех таких возможных соотношений некоторыми усло-
виями оптимальности, то естественно предположить, что функ-
ция f сама может быть непосредственно определена в терминах
оптимальности. Это предположение означает, что можно по-
строить соответствующий функционал (оценочную функцию),
заданный на множестве всех допустимых функций g(u, о), ко-
торый оптимизируется (минимизируется) искомой функцией f.
Совершенно ясно, что такие оценочные функции играют в за-
даче об определении соотношений между функционалами та-
кую же роль, какую играли оценочные функции, рассмотренные
Принцип оптимальности и аллометрия
95
в гл. 3, в задаче об оптимизации отдельных функционалов.
Попытаемся теперь кратко описать один метод, который позво-
ляет построить такие оценочные функции.
Пусть и и V — это два функционала, о которых говорилось
выше; допустим, имеются основания предположить, что связь
между ними соответствует закону аллометрии, т. е. и = аор.
Возьмем вместо и, v соответственно логарифмы их значений;
тогда наше допущение о справедливости аллометрического за-
кона означает, что, если F пробегает всю совокупность изучае-
мых форм, то точка (log u(F), logo(F)) при этом движется по
прямой линии на плоскости переменных (logu, logo). При раз-
личных способах выбора начальной и конечной формы полу-
чатся различные прямые линии, и поэтому возникает вопрос:
можно ли найти такой функционал (оценочную функцию), за-
данный на множестве всех допустимых функций g (и, v), опреде-
ляющих соотношения вида' g=0, чтобы все рассматриваемые
прямые линии на плоскости (log и, log v) были его стационар-
ными кривыми?
Теперь можно использовать результаты, полученные в пре-
дыдущем разделе. В соответствии с этими результатами такую
оценочную функцию всегда можно построить, причем бесчислен-
ным множеством различных способов. В данном случае, по-
скольку речь идет о минимизации функционала прямыми ли-
ниями, можно принять за такой функционал длину дуги кри-
вой, лежащей в (log и, log о)-плоскости. Обратно, если такая
оценочная функция будет задана, то аллометрические соотно-
шения между функционалами будут непосредственно вытекать
из условий оптимальности (надо заметить, что эти рассужде-
ния, относящиеся к оптимальности, отличаются от тех ло-
кальных методов, которые разрабатывались в гл. 3, и их
можно было бы вообще рассматривать независимо от этих
методов).
В связи с этим интересно отметить еще один момент. Ранее
мы уже указывали на аналогию между механическими систе-
мами, состояния которых определяются значениями наблюдае-
мых параметров, и биологическими объектами, которые могут
быть охарактеризованы некоторой определяющей системой
функционалов. Эта аналогия может быть усилена путем сле-
дующих рассуждений. Возьмем механическую систему, состоя-
щую из одной материальной точки с одной степенью свободы.
Состояние такой системы полностью определяется, если из-
вестны две функции времени — пространственная координата
x(t) и импульс p(t)=mx(t). Эти две функции связаны соот-
ветствующим уравнением движения, которое можно рассмат-
ривать как уравнение Эйлера некоторой вариационной задачи.
96
Глава 5
Заметим теперь, что независимую переменную t можно исклю-
чить из двух соотношений x=x(t) и p=p(t), и тогда движение
системы будет описываться траекторией на (х, р) -плоскости,
которая определяется некоторым уравнением вида f (х, р)—0.
Таким образом, соотношение вида f=0 определяется здесь
уравнением движения, т. е. некоторыми условиями оптималь-
ности, которые можно непосредственно отнести к траекториям
на (х, р) -плоскости.
Можно сделать еще несколько интересных замечаний, от-
носящихся к приведенным выше рассуждениям. Во-первых,
вполне очевидно, что описание соотношений между функцио-
налами в терминах условий оптимальности аналогично построе-
нию некоторого «лагранжиана» и соответствующего ему урав-
нения движения на (и, и)-плоскости. Во-вторых, эту теорию
можно непосредственно обобщить на случай произвольного
числа переменных. И наконец, в-третьих, исключение времени,
о котором говорилось выше в связи с рассмотрением механи-
ческой системы, и соответствующий выбор одйого из наблю-
даемых параметров х, р в качестве новой независимой пере-
менной наводят на одну интересную мысль, дополняющую
наше представление о характере изменений, происходящих
в состоянии системы. Вместо того чтобы описывать независимо
друг от друга изменения х и р, происходящие в реальном фи-
зическом времени, мы можем теперь следить лишь за измене-
ниями, скажем, переменной х в зависимости от значений р,
рассматривая р как независимую переменную, играющую роль
времени и полностью определяющую состояние изучаемой си-
стемы. С этой точки зрения можно с каждой системой связать
ее «собственное время». Значение этого замечания в свете
аналогии между функционалами, которые мы рассматривали,
и наблюдаемыми параметрами механической системы мы об-
судим в следующем разделе.
5.5. Закон аллометрического роста в онтогенезе:
развивающиеся системы
Большая часть важных примеров, рассмотренных Гексли
и другими в связи с феноменологическим изучением алломет-
рии, относится к развивающимся системам. Помимо того, что
очень удобно иметь дело с последовательностью форм, кото-
рую можно рассматривать в лабораторных условиях, разви-
вающиеся системы обладают еще рядом особенностей, кото-
рых мы не находим в филогенетических рядах или в последо-
вательностях археологических артефактов. Эта особенность
развивающихся систем, в связи с которой нужно сейчас же
Принцип оптимальности и аллометрия
97
вспомнить последнее замечание предыдущего раздела, заклю-
чается в следующем: у развивающихся систем значения, ко-
торые принимает какой-то функционал (скажем, х), являются
явными функциями реального времени t. Это объясняется тем,
что сама форма F такой системы изменяется во времени, т. е.
F=F(t), и поэтому x(F)=x(F(t))=x(t). Можно поэтому ска-
зать, что всякий конкретный функционал, определенный для
развивающейся системы, обладает некоторой определенной
скоростью роста во времени, и эту скорость можно определить,
попросту вычисляя производную х'(t) (в предположении, что
такая производная существует для всех t).
Пусть теперь имеются два функционала x(t) и y(f), опре-
деленные для развивающейся системы; тогда можно исклю-
чить время и найти соотношение, связывающее лишь значения
х и у. Посмотрим теперь на частном примере, какие отсюда
можно сделать выводы. Наиболее часто встречающийся закон
развития, которому подчиняются функционалы вида x(t), свя-
занные с биологическими объектами, заключается в том, что
скорость роста x'(t) оказывается пропорциональной самой ве-
личине х(£) в рассматриваемый момент времени. Т'аким об-
разом,
л'(/) = ** (О, (5.15)
где k (этот коэффициент можно назвать показателем скорости
роста) — постоянная величина *. Решение этого уравнения, ха-
рактеризующего многие биологические системы, имеет вид
= (5.16)
(где %о — значение функционала х в некоторый начальный мо-
мент времени t0). Закон, выражаемый уравнением (5.16), на-
зывается экспоненциальным.
Пусть теперь х и у — два функционала, подчиняющиеся
закону (5.16). Тогда
Х = Х^'«~1°\ у = у^-^ .
Отсюда следует, что
хо
* Уравнением такого типа при k>0 описываются многие процессы с поло-
жительной обратной связью В гл 7—9 рассматриваются процессы с отрица-
тельной обратной связью, которые часто могут быть описаны таким же урав-
нением при k<0
98
Глава 5
Иными словами, для растущих систем любые два функцио-
нала, подчиненные экспоненциальному закону, оказываются
связанными законом аллометрического роста. По-видимому,
первым этот факт отметил Гексли. Разумеется, экспоненциаль-
ный характер роста представляет собой не единственный
случай, который приводит к аллометрии.
Упражнение
Покажите, что необходимое и достаточное условие того,
чтобы функционалы х, у были связаны законом аллометрии,
состоит в том, чтобы они удовлетворяли уравнению вида
Отсюда следует, что если x'=f(t), y'=g(t)—скорости измене-
ния функционалов х, у соответственно, то для выполнения за-
кона аллометрии необходимо и достаточно, чтобы при исклю-
чении t из этих двух соотношений получалось уравнение
вида (5.17).
Предполагая далее, что проявление закона аллометриче-
ского роста для функционалов х и у, заданных для некоторой
растущей системы, является следствием экспоненциального
характера изменения их во времени, мы приходим к опреде-
ленной конкретной интерпретации постоянных а, Р; мы увидим,
что в терминах такой интерпретации аир естественно назвать
«структурными постоянными». Оказывается, что а целиком
определяется начальными значениями, а р является отноше-
нием показателей k, характеризующих скорость изменения
х и у. Как следствие этого перехода от двух уравнений
вида (5.16), характеризующих скорости изменения функциона-
лов, к одному уравнению теория аллометрии не включает
в себя явной зависимости от времени (время, как отметил
Нидхэм, исключается). Как уже было сказано в предыдущем
разделе, теория аллометрии заменяет t некоторым функцио/
налом (мы его обозначили через х), который при этом на-
чинает играть роль «физиологического времени», т. е. быстрота
изменения другого функционала у измеряется уже не по отно-
шению к абсолютному времени t, а по отношению к функцио-
налу х, выступающему в роли «физиологических часов». Неко-
торые биологи считают, что отсутствие в теории аллометрии
явной зависимости от абсолютного времени t является ее
серьезным недостатком, особенно при изучении растущих си-
стем; но на самом деле, хотя теория аллометрии действительно
не позволяет (см., например, приведенное выше упражнение)
Принцип оптимальности и аллометрия
99
установить характер явной зависимости функционалов от вре-
мени, отсутствие зависимости от абсолютного времени является
здесь скорее кажущимся, чем реальным.
Гексли (см. [44], особенно гл. 4, стр. 104—148) попытался
связать теорию аллометрии для растущих систем с так назы-
ваемыми «градиентами роста». Для иллюстрации этой простой
идеи допустим, что некоторый функционал х (скажем, полная
длина тела) принят за параметр, характеризующий время,
и рассмотрим функционалы уь у2, .. уп (например, длины
последовательных сегментов конечности некоторого насекомого
или членистоногого). Соответствующие аллометрические соот-
ношения имеют вид
у1 = а1л₽1, у2 = а2х9г,..., уп=аях₽«. (5.18)
Если предположить, что функционалы х, уь .. ., уп подчиня-
ются экспоненциальному закону роста, то коэффициенты Pi,
р2,.. ., рп представляют собой, очевидно, отношения соответ-
ствующих показателей скорости роста.
В случае когда для последовательности (5.18) выполняются
неравенства
₽г>₽2> . - (5.19)
Гексли говорит, что вдоль конечности имеется градиент роста,
в том смысле, что скорость роста максимальна вблизи туло-
вища и последовательно убывает по мере удаления от туло-
вища., Вопрос о существовании таких градиентов в течение
долгого времени с большим интересом обсуждался эмбриоло-
гами и морфологами; оказывается, что в действительности та-
кие случаи, когда выполняются соотношения вида (5.18) и
(5.19), широко распространены. По мнению Гексли, теория
аллометрии позволяет определить местонахождение специфи-
ческих центров роста, в которых берут начало градиенты
роста (местонахождение центра роста можно определить эм-
пирически, изучая изменение коэффициента р для последова-
тельности функционалов ух, у2,..., уп того типа, которая рас-
сматривалась выше). Наличие таких градиентов всегда связы-
вают с существованием градиента концентрации некоторого
особого вещества, фактора роста, который синтезируется
в центре роста: теоретически это создает возможность морфо-
логического определения той области, где это вещество син-
тезируется, и в конечном счете установления его химической
природы. К настоящему времени в эмбриологии уже имеется
значительное число работ, посвященных химическим факторам
100 Глава 5
роста, но, к сожалению, в большинстве из них не делается
никаких теоретических выводов.
Здесь следует упомянуть о попытке найти закон химиче-
ской аллометрии, принадлежащей Нидхэму [48]. Ему удалось
найти большое количество фактов, свидетельствующих о том,
что в растущих организмах между концентрациями некоторых
специфических веществ и общим весом существуют алломет-
рические соотношения. В разд. 6.7 мы более подробно рас-
смотрим значение результатов Нидхэма с этой точки зрения.
Это можно будет рассматривать как логическое распростра-
нение развитых выше идей на ситуации более общего харак-
тера.
Глава 6
ПРИНЦИП ОПТИМАЛЬНОСТИ И ТЕОРИЯ
ТРАНСФОРМАЦИЙ д’АРСИ ТОМПСОНА
6.1. Теория трансформаций д’Арси Томпсона
В последней главе своего фундаментального труда «О росте
и форме» [3], на который мы уже неоднократно ссылались,
д’Арси Томпсон выдвинул гипотезу, которую он рассматривает
как идею общего аналитического подхода к изучению формы
у близкородственных видов. Эта гипотеза формулируется весьма
просто и в основном сводится к следующему: если принять
форму какого-то данного организма за эталон и отнести эту
форму к некоторой декартовой прямоугольной системе коорди-
нат, то форму всякого организма, достаточно близкого к началь-
ному, можно рассматривать как результат непрерывной дефор-
мации исходной координатной системы.
Для того чтобы получить общее представление о принципе
д’Арси Томпсона, достаточно рассмотреть его приложение
к ряду частных случаев. Следуя Томпсону, мы, не ограничивая
общности, возьмем для простоты лишь двумерные проекции.
На фиг. 15, А схематически изображена рыба Diodon в де-
картовой системе координат. Если деформировать первоначаль-
ную систему координат так, как это сделано на фиг. 15, Б, то
очертания Diodon переходят в контуры рыбы Orthagoriscus,
которая внешне значительно отличается от Diodon (а в дей-
ствительности очень близка к ней). Пожалуй, еще более эффект-
ный пример применения принципа д’Арси Томпсона представлен
на фиг. 16. Здесь спинные щиты нескольких разновидностей
ракообразных сравниваются со спинным щитом ракообразного
Geryon, форма которого принята за начальную (фиг. 16, А).
Остальные пять форм, получающиеся из Geryon с помощью
приведенных на схемах деформаций прямоугольной декартовой
системы координат, к которой отнесен контур Geryon, изобра-
жают соответственно спинные щиты Corystes, Scyramathia, Ра-
ralomis, Lupa и Chorinus. Деформации такого рода можно по-
строить для представителей любого биологического типа, и сам
д’Арси Томпсон приводит большое количество таких примеров.
Д’Арси Томпсон возлагал большие надежды на роль своей
теории трансформаций в сравнительной биологии. Он полагал,
что эта теория, развитая соответственным образом, позволит
Фиг. 16
Теория трансформаций д’Арси Томпсона
103
биологам, исходя из анатомических черт некоторого одного вида,
вычислять все количественные характеристики любых других
видов, достаточно близких к первоначальному. Это дало бы,
например, возможность в точности восстановить строение вы-
мерших форм, известных лишь по скудным ископаемым остат-
кам (Томпсон и сам разработал последовательность трансфор-
маций, относящихся к эволюции лошади от Eohippus до Equus).
Это позволило бы точно так же установить структуру таких
переходных форм, о которых у нас вообще нет никаких данных.
С помощью аналогичных методов можно было бы попытаться
подойти к решению многих тонких проблем таксономии, фило-
генеза и онтогенеза.
Теория д’Арси Томпсона страдает, однако, одним существен-
ным недостатком, который сводит к нулю ее значение для био-
логии — во всяком случае как теоретического метода. Дело
в том, что эта теория трансформаций (в той форме, в какой ее
предложил Томпсон) является полностью эмпирической, фено-
менологической; она ни в малейшей степени не раскрывает
природы механизма', лежащего в основе изменений форм орга-
низмов, и поэтому в научном отношении бесполезна. (Точно так
же обстояло дело и с эволюционной теорией до тех пор, пока
не был понят механизм процесса эволюции, в чем и заключался
великий научный вклад Дарвина.) Сказанное выше справедливо,
несмотря на то что были предприняты многочисленные попытки
применить метод Томпсона к реальным задачам сравнительной
биологии (см., например, [49]) и что, по мнению многих биоло-
гов, теория Томпсона могла бы иметь важное значение, если бы
удалось придать ей форму, пригодную для практического ис-
пользования.
В настоящей главе исследуется связь теории трансформаций
Томпсона с принципом оптимальности и*обсуждается, в какой
мере идея оптимальности позволяет подвести под гипотезу
Томпсона требуемый теоретический фундамент. При изучении
этих вопросов возникает также и ряд серьезных математических
проблем.
6.2. Некоторые эвристические рассуждения
Теперь, не стремясь к большой строгости, мы покажем, каким
образом можно объяснить теорию трансформаций Томпсона,
исходя из принципа оптимальности; мы будем при этом в основ-
ном опираться на те соображения, которые были развиты
в предыдущей главе.
Вспомним, что всякая биологическая форма F может быть
охарактеризована совокупностью числовых параметров, соответ-
ствующих значениям функционалов, образующих некоторую
104
Глава 6
достаточно обширную определяющую систему функционалов
для этой формы. Допустим, как это делалось раньше, что для
этого достаточно взять два функционала и и и, так что всякая
допустимая форма F будет соответствовать единственной точке
(u(F), v(F)) на (и, о)-плоскости. Кроме того, если F непре-
рывно изменяется во множестве всех допустимых форм, то точка
(u(F), v(F)) должна перемещаться вдоль некоторой стационар-
ной траектории соответствующего эйлеровского уравнения. Эта
кривая определяет некоторую зависимость вида f(w, о)=0
между функционалами и, v.
Так как функция f определяет интегральную кривую неко-
торого дифференциального уравнения второго порядка, то
можно предположить, что она всюду, за исключением, быть мо-
жет, отдельных точек, обладает вторыми производными и тем
более кусочно-непрерывна. Пусть форма F такова, что
f(u(F), и(Е))=0. Допустим, что (и', v') —это некоторая другая
точка, которая удовлетворяет следующим требованиям:
a) f(u', v')=Q и б) (и', v') близка к (u(F), v(F)). Условие «б»
означает, что и7 близко к u(F) и v' близко к v(F), и такое
предположение ввиду непрерывности f вполне естественно. Со-
гласно сделанным допущениям, при этом должна существовать
такая форма F', что u' = u(F') и v'=v(F'). Но тогда наше рас-
суждение как раз и показывает, что формы F и F' должны быть
близки друг к другу во множестве всех допустимых форм. От-
сюда следует, что непрерывное перемещение вдоль кривой
f(u, и)=0 соответствует непрерывному изменению формы F во
множестве всех допустимых форм. Если теперь предположить,
что можно одновременно непрерывно изменять значения и и о,
то, обращая эти рассуждения, мы заключаем, что непрерывное
перемещение вдоль кривой f(u,v)' = 0 эквивалентно, за исключе-
нием, быть может, некоторого конечного числа отдельных
случаев, непрерывному изменению самих биологических форм.
Таким образом, из приведенных выше рассуждений непосред-
ственно вытекает, в частности, теория трансформаций Томпсона.
Здесь нужно сделать одно важное замечание. Как было,
показано, непрерывное (в смысле теории д’Арси Томпсона) пз1-
менение органической формы F соответствует тому случаю,
когда и н v одновременно непрерывно изменяются. Если такая
одновременная непрерывность не имеет места, то деформация,
непрерывная по отношению к функционалу и, вполне может вы-
звать разрывное изменение v, и наоборот.
Упражнение
Пусть прямолинейный отрезок L с фиксированными концами
А и В имеет единичную длину. Обозначим через С произволь-
Теория трансформаций д’Арси Томпсона
105
ную спрямляемую дугу, соединяющую те же точки. Определим
на множестве спрямляемых дуг с заданными концами два функ-
ционала и (С) и v (С); за значения и (С) примем длины дуг С,
а значения v (С) положим равными площадям, ограниченным
линиями С и L. Укажите последовательность кривых Сь С2, ...
..., Сп, .... такую, что v (Сп) ->0 при п->оо и в то же время
и (Сп) не стремится к единице.
Приведенный пример показывает, что если кривая С пере-
водится в L посредством деформации, которая непрерывна по
отношению к одному только функционалу v(C). то длина и (С)
может при этом изменяться разрывно, несмотря на то что кри-
вые С определены таким образом, что значения ц(С) прибли-
жаются к нулю. С точки зрения биологии это означает, что если
функционалы, определенные для данной формы F, не непре-
рывны все одновременно, то изменение формы, непрерывное по
отношению к некоторым из них, может оказаться разрывным
по отношению к остальным. Поскольку в действительности эти
функционалы вовсе не обязательно должны быть одновременно
непрерывными, такой случай является наиболее общим. Это
дает, таким образом, возможность включить в теорию Томпсона
также и изменения, не являющиеся непрерывными. Однако мы
подчеркиваем, что для обоснования самой первоначальной тео-
рии Томпсона непременно требуется одновременная непрерыв-
ность всех рассматриваемых функционалов, и в дальнейших
рассуждениях мы будем предполагать, что это условие всюду,
где это необходимо, выполнено.
Итак, мы показали, что при выполнении упомянутого выше
ограничения непрерывную трансформацию близкородственных
видов к1ожно объяснить на основании гипотезы оптимальности.
Более того, это позволяет сделать ряд дополнительных выводов.
С одной стороны, непрерывная трансформация, наблюдаемая
среди близкородственных форм, отнюдь не произвольна; она
однозначно определяется соответствующим уравнением Эйлера
и поэтому самым существенным образом зависит от выбора
используемой оценочной функции (функционала). С другой
стороны, в случае, когда не все точки (и, о)-плоскости, отвечаю-
щие данному классу форм, попадают на единственную кривую,
принцип оптимальности требует, чтобы эти точки определяли
некоторое семейство стационарных кривых того же самого
эйлеровского уравнения. Поскольку уравнение Эйлера есть
уравнение второго порядка, оно обладает общим решением,
зависящим от двух произвольных постоянных (параметров).
Таким образом 1) принцип оптимальности допускает взаимные
переходы только между теми формами, которые принадлежат
106
Глава 6
одной и той же стационарной кривой', 2) разные стационарные
кривые характеризуются различными значениями произвольных
постоянных, т. е. различными начальными условиями. Некото-
рые дополнительные рассуждения, касающиеся связей между
различными решениями, будут приведены в последующих раз-
делах при обсуждении понятия устойчивости.
Так как стационарная кривая полностью определяется зна-
чениями двух произвольных постоянных, то для выделения
некоторой конкретной стационарной кривой достаточно задать
две точки плоскости. Отсюда, как следствие, можно извлечь
несколько методов изучения биологических форм при наличии
относительно скудной информации:
1. Пусть даны две точки плоскости, относительно которых
известно или предполагается, что они лежат на одной и той же
стационарной кривой. Тогда можно восстановить формы всех
промежуточных организмов (разумеется, лишь в той степени,
в какой они определяются выбранной системой функциона-
лов) .
2. Допустим, что задан некоторый отрезок стационарной
кривой; тогда можно единственным образом продолжить эту
кривую в сторону, соответствующую росту времени, т. е. «в бу-
дущее», и тем самым предсказать дальнейшее развитие изучае-
мых биологических форм.
3. Заданный отрезок стационарной кривой можно единствен-
ным способом продолжить в сторону уменьшения времени, т. е.
«в прошлое», и восстановить картину развития рассматриваемых
биологических форм в прошлом.
Значение этих трех способов научного предвидения для
изучения филогенеза очевидно. В отношении первого нужно
отметить, что сам д’Арси Томпсон с замечательным успехом
провел ряд исследований в этом направлении. Он проследил
развитие промежуточных форм черепа в филетической линии
развития лошади от древней Eohippus до современной Equus.
В нашей терминологии это означает, что формы черепа Eohip-
pus и Equus были использованы для нахождения некоторой
единственным- образом определенной стационарной кфивой,
с помощью которой были восстановлены различные промежуточ-
ные формы. Так как ископаемые остатки, относящиеся к филе-
тической линии, ведущей к современной лошади, представлены
исключительно широко, можно сравнить гипотетические проме-
жуточные формы с соответствующими ископаемыми формами.
При этом обнаруживается замечательное совпадение, за исклю-
чением расхождений в случае ископаемого Parahippus. Томпсон
в связи с этим предположил, что Parahippus в действительности
не принадлежит к филетической линии развития от Eohippus
Теория трансформаций д’Арси Томпсона
107
до Equus, и в настоящее время палеонтологи разделяют эту
точку зрения.
Возможности второго и третьего методов в теоретическом
отношении еще более интересны, но, насколько известно автору,
никаких прямых попыток их применения никогда не предпри-
нималось. Изложенную теорию можно было бы испытать
непосредственно на реальных биологических системах, используя
известные аллометрические соотношения, возникающие при
искусственном отборе (скажем, при выведении пород животных
и сортов растений с заранее заданными свойствами).
В разд. 6.3 мы рассмотрим одно важное следствие, непо-
средственно вытекающее из развитой здесь теории. Математи-
ческие методы, которые будут при этом разработаны, найдут
применение и в дальнейшем (разд. 7.1) в связи с изучением
ситуаций совсем другого рода.
6.3. Устойчивость
Сейчас нужно будет ввести одно новое понятие, важное для
изучения принципа оптимальности. Заглавие этого раздела
подсказывает читателю, что это понятие связано с кругом во-
просов, относящихся к устойчивости изучаемых нами систем.
Поскольку эти системы (при том способе их описания, которым
мы до сих пор пользовались) характеризуются дифференциаль-
ными уравнениями эйлеровского типа, изучение их устойчивости
сводится к математическим задачам, связанным с исследованием
поведения решений соответствующих дифференциальных урав-
нений. Эти чисто математические проблемы составляют содер-
жание так называемой теории устойчивости, которая предста-
вляет собой один из наиболее плодотворно и активно развиваю-
щихся разделов теории дифференциальных уравненийМы не
можем, конечно, детально излагать здесь эти вопросы, но при-
водимое ниже краткое обсуждение даст читателю возможность
почувствовать, насколько важное значение имеет теория устой-
чивости, и понять, каким образом соответствующие представле-
ния применяются в этой книге.
Для того чтобы придать нашим рассуждениям конкретность,
рассмотрим в качестве примера механическую систему, дви-
жущуюся по некоторой траектории в пространстве состояний
этой системы (т. е. пространстве, точки которого характери-
зуют состояния данной системы). Эта траектория является
1 Подробное изложение теории устойчивости и ссылки на обширную ма-
тематическую литературу можно найти у Веллмана [50] или у Чезари [51] Бо-
лее общий подход, имеющий прямое отношение к гл. 10 этой книги, развит
в книге Немыцкого и Степанова [52].
108
Глава 6
стационарной кривой уравнения Эйлера, соответствующего
некоторой оценочной функции, или функционалу (связанному
с функцией Лагранжа для данной системы). Что означает
утверждение, что рассматриваемое движение устойчиво? Интуи-
тивно вполне очевидно, что представление об устойчивости свя-
зано с тем, каким образом система отзывается на возмущения
(малые), приложенные к системе извне. Пусть к системе прила-
гается понимаемое в этом смысле возмущение (т. е. в некоторый
момент времени ее положение претерпевает малое смещение,
а затем система предоставляется самой себе). Спрашивается,
что можно сказать о характере движения системы, получившей
такое возмущение?
Интуитивно опять-таки вполне очевидно, что рассматриваемое
движение системы следует считать устойчивым, если выпол-
няются одно (первое) или оба следующих условия: 1) траекто-
рия возмущенного движения все время остается в некотором
определенном смысле близкой к невозмущенной траектории,
2) с течением времени возмущенная траектория сколь угодно
близко приближается к невозмущенной. В математике первое
условие обычно называют условием устойчивости (по Ляпу-
нову), а если выполняются оба требования, то говорят об асимп-
тотической устойчивости (по Ляпунову). Асимптотическая
устойчивость наиболее часто представляет интерес для прило-
жений, например в технике. Грубо говоря, она означает, что,
если к системе приложить малое кратковременное возмущение,
когда она находится в состоянии равновесия, то со временем
система вернется к этому состоянию. В последующих главах
мы увидим, что понятие асимптотической устойчивости играет
центральную роль при изучении гомеостаза биологических си-
стем. Теперь перейдем к четкой формулировке этих понятий.
Мы ограничимся рассмотрением дифференциальных уравне-
ний второго порядка, так как нам здесь приходится иметь дело
именно с такими уравнениями; соответствующие обобщения на
уравнения произвольного порядка проводятся непосредственно,
и мы предлагаем читателю сделать это самостоятельно. Допу-
стим, что нам дано дифференциальное уравнение вида
У" = Л*, У, У')- (О-Ч
Решения этого уравнения можно записать в виде
у(х) = у(х, а, ₽), (6.2)
где а, р — произвольные постоянные. Как правило, нас инте-
ресует, разумеется, некоторое определенное решение. Для того
чтобы выделить такое решение, нужно указать соответствующие
Теория трансформаций д'Арси Томпсона
109
значения параметров а, 0, а для этого обычно задаются так
называемые начальные значения', иными словами, задача со-
стоит в том, чтобы выделить такое решение, для которого у и
у' принимают при некотором начальном значении независимой
переменной х=х0 заданные значения у(хр), у'(х0). Выражение
(6.2) можно, в частности, переписать в виде
У (*)=У(х, у(х0), у'(х0))- (6.3)
Итак, решения (6.1) образуют двухпараметрическое семей-
ство кривых на (х, у)-плоскости.
Пусть zi, z2—две точки на прямой линии или на плоскости
(х, z/); условимся обозначать расстояние между этими точками
через llzi—z2||.
Как мы уже выяснили, понятие устойчивости связано с со-
поставлением близких друг к другу решений дифференциального
уравнения (6.1). Но что именно следует здесь понимать .под
«близкими» решениями? Поскольку каждое решение уравнения
(6.1) определяется заданием значений параметров у(хй), у'(х0),
входящих в (6.3), можно было бы, например, считать в опре-
деленном смысле близким (в начальный момент) два решения
Ух(х), У2(х), для которых при некотором заданном начальном
значении х=хо выполняются соотношения
|| Ух К) - У2 (*0) || < "ll- II X (Хо) - У2 (Хо) II < ^2 > (6.4)
где т)1, т]2 — некоторые предварительно выбранные малые поло-
жительные числа. Допустим теперь, что какое-то определение
«близости» решений (6.1) уже принято; каким образом мы
должны тогда точно определить понятие устойчивости решений
(6.1), интуитивное представление о котором мы выше обсу-
ждали? Здесь прежде всего нужно заметить, что, если рассма-
триваемое решение у\(х) уравнения (6.1) определено для всех
значений х^>х0, то нужно потребовать, чтобы все решения (6.1),
которые считаются близкими к //i(x), тоже были определены для
всех значений x^xq. В самом деле, если бы всегда можно было
найти решение, которое в некоторой точке х, лежащей в проме-
жутке от хо до + оо, обращается, например, в бесконечность, то
независимо от того, насколько близко это решение подходит
в каких-то точках к z/i(x), интуитивно ясно, что об устойчивости
здесь говорить не приходится. Поэтому введем следующее тре-
бование:
1°. Пусть г/1(х)—решение уравнения (6.1), определенное
для всех х£ [х0, оо).Потребуем, чтобы существовала пара поло-
жительных вещественных чисел гц, г]2, таких, что, каково бы ни
было решение z/2(*) уравнения (6.1), удовлетворяющее условию
но
Глава 6
(6.4), это решение тоже было определено для всех хС[х0, °°).
Требование 1° гарантирует, что значения У\(х), у2(х) опре-
делены для всех значений х~^ х0, если решения yit у2 достаточно
близки друг к другу в начальной точке х=х0, и это дает воз-
можность сформулировать следующее важное определение
устойчивости решения уДх):
2°. Пусть для произвольного е > 0 найдется б > 0, такое, что
d<min(i)i, ц2) и при выполнении условия ||yi(x0)—у2(х0)|| < б,
II#/(*о)—У2 (хо) II < б для всех xC[xq, оо) справедливы неравен-
ства ||«/1 (х) — у2 (х) ||<е, II#/ (х) — у2 (х) ||<е. Решение у\ (х),
удовлетворяющее требованиям 1° и 2°, называют устойчивым
(в смысле Ляпунова) *.
Упражнение
Докажите, что всякое решение #i(x), устойчивое по отноше-
нию к начальным значениям z/i(xq), у\(хо), устойчиво также и
по отношению к начальным значениям z/Дхо'), #/(х0') при лю-
бом Xq > х0.
Вполне очевидно, что условие устойчивости 2° говорит о не-
прерывной зависимости значений функции у(х) от начальных
значений у(хо), У'(х0), взятых в достаточно малой окрестности
устойчивого решения, при #(x0)-»-t/i (х0), /(хо)->#/(хо).
Что касается асимптотической устойчивости, то ее опреде-
ление строится следующим образом:
3°. Пусть условия 1°, 2° выполняются и б>0 — величина,
указанная в условии 2°. Решение yi(x) называется асимптота-
чески устойчивым, если существует такое б'> 0, б'^б, что из
неравенств
II К) - У 2 N II < 8'- II VI К) - У~2 (*о) II <8'
вытекают соотношения limllyj (х) — y2(x)ll = lim[|y'1(x)—у'(х)11=0,
А» со д»оо
Часто встречается такой случай, когда решение не является
устойчивым или асимптотически устойчивым по отношению ко
всем близким решениям, но может рассматриваться как устой-
1 Определение устойчивости или асимптотической устойчивости поДяпу-
нову иногда формулируют для нулевого решения у(х) = 0 рассматриваемого
дифференциального уравнения или системы дифференциальных уравнений, от)
носительно которых предполагается, что они обладают таким тривиальным
решением Это связано с тем, что состояние механической системы, находя-
щейся в равновесии, как раз описывается при определенных условиях нулевым
решением составленного соответствующим образом дифференциального урав-
нения или системы таких уравнений (см гл 10), и от устойчивости этого ну-
левого решения зависит, будет ли система возвращаться в положение равно-
весия после достаточно малого возмущения Имеется большое число хороших
математических книг, в которых рассматривается понятие устойчивости по
Ляпунову и различные его модификации (см, например, [53, 54])
Теория трансформаций д’Арси Томпсона
111
чивое или асимптотически устойчивое, если взять для сравнения
не все близкие решения, а лишь определенный их класс. Такого
рода ограниченная устойчивость называется условной устойчи-
востью. Здесь имеется некоторое сходство с ситуацией, имеющей
место в вариационном исчислении (разд. 2.7), о которой мы уже
говорили: может случиться, что изучаемая задача о миними-
зации не имеет решения, если рассматривать вариации самой
общей природы, но если обратиться к ограниченному соответ-
ствующим образом классу вариаций, то при этих дополнитель-
ных условиях задача допускает решение.
Упражнение
Возьмем дифференциальное уравнение второго порядка
у" = 0, общее решение которого имеет вид у = ах+Ь. Устойчивы
ли какие-либо решения этого уравнения? Имеет ли это уравне-
ние асимптотически устойчивые решения? Пусть теперь дано
определенное решение у = аох+Ьо. Ограничимся классом лишь
таких близких решений, у которых а = ай. Будет ли некоторое
заданное решение этого типа условно устойчиво по отношению
к решениям этого класса? Будет ли оно условно асимптотически
устойчивым?
Здесь имеется еще одно обстоятельство, на которое следует
обратить внимание. Рассмотрим случай, соответствующий
фиг. 17, на котором изображены интегральные кривые диффе-
ренциального уравнения (первого порядка) вида у'=1—у2.
Здесь решение у = — 1 ни устойчиво, ни асимптотически устой-
чиво (оно, как говорят, неустойчиво вправо, т. е. при х->+оо),
и все решения, близкие к у =—1, для которых уо—у(^) > 1.
асимптотически приближаются к другому решению у= + 1, ко-
торое асимптотически устойчиво (и сами по себе эти решения
тоже являются асимптотически устойчивыми). Такой вид сходи-
мости к устойчивому (или асимптотически устойчивому) реше-
нию характерен для широкого класса задач теории устойчивости.
112
Глава 6
6.4. Устойчивость по отношению к замене переменных
Мы уже знаем, что уравнения Эйлера, относящиеся к какой-
нибудь вариационной задаче, можно рассматривать как уравне-
ния движения некоторой механической системы. Что касается
уравнений движения, то они должны полностью определять все
черты рассматриваемого движения. Кроме того, уравнения дви-
жения можно записать по отношению к любой системе обобщен-
ных координат, и получающиеся при этом для разных систем
координат уравнения в общем случае отличаются друг от друга.
Но все эти уравнения относятся все-таки к одной и той же меха-
нической системе, а координаты этой системы в любой системе
координат можно записать как непрерывные функции ее коор-
динат в другой координатной системе; поэтому естественно было
бы ожидать, что имеются некоторые инвариантные свойства,
характеризующие все те различные формы уравнений движе-
ния, которые можно составить для описания данной механиче-
ской системы и которые, таким образом, можно найти, применяя
к некоторой исходной системе уравнений движения соответ-
ствующее преобразование координат или замену переменных.
В частности, можно было бы как будто априори допустить, что
траектория движения, оказавшаяся устойчивой по отношению
к какой-то одной системе уравнений движения, останется устой-
чивой и при непрерывной замене переменных, т. е. при преобра-
зовании системы координат самого общего вида.
Эти предположения оказываются в общем случае неверными,
что можно проиллюстрировать на простых примерах. Возьмем,
например, уравнение (5.8), решение которого выражает закон
аллометрического роста вида у = ахь.
Упражнение
Покажите, что решения уравнения (5.8), имеющие вид
у = а.хь, у которых b < 0, устойчивы и асимптотически устойчивы
по отношению к близким решениям, для которых б < | b |,
тогда как при 6^0 все решения неустойчивы.
Если, однако, взять от обеих частей аллометрического соот-
ношения у=ахь натуральные логарифмы и положить м = 1п у,
и = 1п х, то двухпараметрическое семейство аллометрическПХ кри-
вых, рассмотренное выше, преобразуется в двухпараметриче-
ское семейство прямых вида u = bv + c, которое представляет/со-
ери
бой семейство решений уравнения -^-=0. Упражнение, приве-
денное в предыдущем разделе на стр. 111, показывает, что все
решения этого уравнения неустойчивы. Другими словами, при
замене переменных устойчивые решения (5.8) (т. е. такие реше-
Теория трансформаций д’Арси Томпсона
113
ния, для которых &<0) могут перейти в неустойчивые решения
преобразованного дифференциального уравнения.
В том, что устойчивость может не сохраняться при замене
переменных, нет ничего удивительного; например, точно так же
f 11
сходящаяся последовательность 17Г1, «=1. 2, 3 переходит
в расходящуюся последовательность {/г} , п—1, 2, 3 ..., если
й 1
применить преобразование вида У=~ > которое непрерывно
всюду, за исключением начала координат. Мы не можем здесь
подробно обсуждать эти факты, но читателю следует подумать
по поводу сохранения свойств устойчивости при непрерывном
преобразовании координат.
6.5. Некоторые выводы
Принцип оптимальности приводит к выводу, что траектории,
лежащие в пространстве состояний сравнимых биологических
систем и описывающие изменения соответствующих функциона-
лов,’) заданных для этих систем", при определенных условиях
отвечают__непрерывной трансформации самих биологических
форм в реальном физическом*"пространстве. Следовательно, для
биологических форм, подверженных действию естественного от-
бора, теория трансформаций Томпсона должна быть справед-
лива. Выше было также показано, что если начальная и конеч-
ная формы некоторой последовательности форм известны, то это
однЬзначно определяет соответствующую траекторию в про-
странстве состояний.
Какие же выводы относительно родственных форм можно
теперь сделать, используя понятие устойчивости? Если данная^
траектория устойчива, то все траектории, расположенные доста-
точно «близко» к ней в некоторой начальной точке, будут
«близки»'к ней на всем своем протяжении. Если данная траек-
тория асимптотически устойчива, то все траектории, которые
в начальной точке достаточно «близки» к данной, будут в даль-
нейшем становиться сколь угодно «близкими» к ней.
Обратимся опять к случаю, когда имеется всего два опреде-
ляющих функционала х и у. Тогда при такой простой ситуации
всякий возможный организм соответствует определенной точке
на х, у-плоскости. Допустим, что данная форма определенным
образом развивается и этому развитию отвечает перемещение
точки (х, у) вдоль некоторой траектории от точки (х0, уо),
соответствующей какому-то начальному моменту времени, до
точки (Xi, У1). Спрашивается, что произойдет, если развитие
114
Глава 6
начнется с формы, соответствующей некоторой другой точке
(х</, Уо), такой, что разности |х0—х0' |, | у0—у0'\ малы? Ответ
на этот вопрос несомненно зависит от устойчивости исходной
траектории. Если исходная траектория устойчива, то все такие
траектории будут к ней близки и, следовательно, расстояние
между точкой (xb i/i) исходной траектории и соответствующей
ей точкой (xf, у/) близкой траектории будет мало. Значит,
в случае устойчивости никогда не будет наблюдаться возникно-
вения дивергирующих форм из некоторого исходного ансамбля
очень близких индивидуумов. Аналогичное заключение тем более
справедливо и для случая асимптотической устойчивости
исходной траектории.
Если же, с другой стороны, исходная траектория неустой-
чива, то существуют близкие к ней в начальный момент траек-
тории, которые с течением времени начнут сильно от нее отли-
чаться. В этом случае исходный ансамбль очень близких форм
порождает ряд дивергирующих форм, причем дивергенция
с течением времени становится все более заметной.
Рассмотрим, наконец, и такую ситуацию, которая соответ-
ствует фиг. 17. Можно, скажем, начать с ансамбля, состоящего
из различных форм, например таких, которые представлены точ-
ками А, В, С. С течением времени, как можно в этом случае
заметить, эти различные формы сходятся примерно к одной и
той же предельной форме. Следует отметить сходство этой
ситуации с биологической конвергенцией (гл. 1).
В качестве иллюстрации этих идей рассмотрим уравнение
(5.8), из которого вытекают законы аллометрии вида у = ахь.
Эти решения устойчивы при b < 0, и поэтому у последователь-
ности форм, подчиняющейся закону аллометрии с отрицатель-
ным показателем Ь, не может проявиться дивергенция, характер-
ная для процесса эволюции В то же время для последователь-
ностей, происходящих от первоначально близких индивидуумов
и отвечающих траекториям с положительным показателем Ь,
может наблюдаться сильная дивергенция, так как эти решения
неустойчивы. Можно также показать, что тот тип конвергенции,
который соответствует ситуации, изображенной на фиг. 17, для
систем, подчиняющихся закону аллометрии, обычно, за ис-
ключением некоторых особых случаев, не имеет места zb—био-
логии.
Ввиду того что траектории, соответствующие закону алломет-
рии, устойчивы вправо (при х->-+оо), когда b < 0, и устойчивы
влево (при х-э—оо), когда b > 0, закон аллометрии можно
использовать также для того, чтобы выявить первоначальные
формы, от которых произошли известные последовательности,
так как эти траектории можно продолжить влево.
Теория трансформаций д'А реи Томпсона
115
6.6. Онтогенез и теория трансформаций
В двух последних главах было показано, каким образом
на основании соображений, базирующихся на представлении об
оптимальности, можно исследовать общие соотношения между
функционалами, определенными для биологических форм, и не-
которые важные свойства этих функционалов. Если исходить
теперь из тех общих положений, которые мы установили в отно-
шении принципа оптимальности, то естественно ожидать, что
оптимальные закономерности скорее будут непосредственно
проявляться при филогенезе, чем при онтогенезе. В соответствии
с соображениями, высказанными в гл. 4, такие закономерности
могут также косвенным образом обнаружиться и при онтогенезе.
Однако, как было отмечено, механизмы проявления оптималь-
ных закономерностей для этих двух типов развития совершенно
различны, и аналогия между ними носит лишь формальный
характер.
Все эти положения становятся совершенно ясными при изу-
чении соотношений частного вида, соответствующих аллометри-
ческому закону, В случае филетических рядов эти соотношения
выводятся из условий оптимальности, которые являются в ко-
нечном счете следствием естественного отбора. С другой сто-
роны, в предыдущих главах при изучении онтогенеза, т. е.
последовательных стадий индивидуального развития, было по-
казано, что у развивающихся систем, подчиняющихся экспонен-
циальному закону роста, всегда наблюдается аллометрический
рост. Однако с той точки зрения, которую мы здесь приняли,
тот или иной вид закона роста развивающейся системы скорее
есть не причина, а следствие характерных соотношений между
функционалами, определенными для этой системы. Так, если
соотношение между двумя такими функционалами, отвечаю-
щими некоторому филетическому ряду, не соответствует закону
аллометрии и этот филетический ряд отражается в онтогенезе,
то соответствующий онтогенетический ряд должен подчиняться
не экспоненциальному закону, а тем зависимостям, которые
получаются при исключении времени из соотношений между
этими функционалами. Таким образом, эта теория позволяет
в определенном смысле построить законы развития, исходя из
соотношений между функционалами, полученных с помощью
принципа оптимальности; причем эти соотношения" могут вообще
не иметь непосредственной связи с самим законом развития изу-
чаемой системы.
Все эти вопросы очень важны, так как при феноменологи-
ческом подходе создается впечатление, что томпсоновскую тео-
рию трансформаций можно непосредственно применить для
116
Глава 6
изучения как филогенеза, так и онтогенеза. В связи с этим при-
ведем цитату из Медавара ([49], стр. 168), касающуюся теории
Томпсона: «... нет никакого сомнения в том, что действитель-
ная область ее применения относится не к изучению эволюции,
а к исследованию развития, к самим процессам трансформации,
а не к их окончательным результатам. (В трансформациях
д’Арси Томпсона в применении теории к эволюции «реальные»
биологические изменения выступают лишь как вторичные эф-
фекты; реальные изменения, лежащие в основе трансформа-
ций. .. не могут быть изучены с помощью его собственных ме-
тодов. ..)»
Однакр та точка зрения, которая была развита в последних
трех главах, приводит к совершенно противоположному заклю-
чению. И в самом деле, приходится признать, что трудно усмот-
реть какой-либо смысл в применении теории Томпсона к про-
блемам онтогенеза, хотя они и обнаруживают некоторое поверх-
ностное сходство с проблемами филогенеза.
6.7. Теория «биохимических трансформаций» Нидхэма
В своей интересной статье, на которую мы уже раньше ссы-
лались, Нидхэм [48] приводит многочисленные данные, свиде-
тельствующие о том, что некоторые функционалы, связанные
с химической природой живых организмов (т. е. с их химиче-
ским составом, а не с формой), подчиняются аллометрическим
закономерностям при онтогенезе. В том, что такие соотношения
существуют, нет в конечном счете ничего удивительного, так как
изменения формы в процессе онтогенеза обычно связаны с из-
менениями в химическом составе. С современной точки зрения
многие соотношения, установленные Нидхэмом, представляются
весьма грубыми (он, например, строит графики зависимости об-
щего содержания жира, или гликогена, или неорганических ве-
ществ во всем организме от общего сухого веса), но они имеют
все же определенный смысл и заслуживают дальнейшего изуче-
ния. Главное состоит в том, что сравнительное изучение химиче-
ской аллометрии4 приводит Нидхэма к заключению о сущест-
вовании некоторого «общего химического плана», свойственного
всем организмам, и о возможности преобразовать одну, биохи-
мическую систему в другую с помощью определенных простран-
ственно-временных трансформаций. Он рассматривал это обсто-
ятельство как некоторый шаг к развитию теории «биохимичес-
ких трансформаций». В своей работе Нидхэм ([48], стр. 107)
пишет:
«Если, таким образом, у животных действительно сущест-
вует некоторый общий химический план развития, то следует
Теория трансформаций д’Арси Томпсона
117
подойти к этому вопросу с точки зрения пространственно-вре-
менных преобразований. Д’Арси Томпсону удалось с помощью
последовательных деформаций декартовой системы координат
построить трансформацию одной морфологической структуры
в другую... точно так же и общий химический план претерпе-
вает пространственно-временные трансформации... Ламберт и
Тесье [55]... выдвинули в качестве основного биологического
закона утверждение о существовании гомологии между живот-
ными как в пространстве, так и во времени... они предполо-
жили, что «в гомологические моменты жизненного цикла два
гомологичных органа должны иметь одинаковый качественный
и количественный химический состав» ... далее, Ламберт и
Тесье считают, что животные одинаковой формы, имеющие раз-
личные размеры, имеют одинаковую пространственно-времен-
ную форму. Исследование химической гетерогонии приводит
к заключению, что животные различной формы и размеров об-
ладают одним и тем же основным общим химическим планом
развития, который может в широких пределах претерпевать
пространственно-временные трансформации...»
Эти гипотезы Нидхэма представляют очевидный интерес
в связи с соображениями, развитыми в этой главе. Эта теория
интересна также и с исторической точки зрения как ранний
предшественник современных попыток построения так называе-
мой реляционной биологии '. В пояснение этой мысли приведем
лучше еще одну цитату из работы Нидхэма:
«... Когда мы рассматриваем зависимость между содержа-
нием в организме некоторого химического вещества и массой
всего организма, мы поднимаемся до весьма высокого уровня
абстракции: 1) мы пренебрегаем морфологией организма; 2) мы
пренебрегаем факторами питания; 3) мы пренебрегаем абсо-
лютными значениями изучаемых величин, т. е. тем самым де-
лаем допущение, что соотношение между некоей химической
единицей и химическим целым одинаково у организмов самых
разных размеров; 4) мы пренебрегаем фактором времени...
Что же в таком случае остается? Ничего, кроме системы отно-
шений или соотношений, которые, возможно, являются общими
для всех животных и которые на самом деле оказываются оди-
наковыми у многих животных; т. е., иными словами, остается
общий химический план развития животных. Возмущающее
1 Мы здесь ограничимся простым упоминанием о реляционном подходе
к изучению биологической организации Этот подход, интенсивно развиваю-
щийся в последние годы Рашевским, Розеном и другими, позволяет по-иовому
осветить некоторые важные и еще не решенные проблемы биологии Элемен-
тарное изложение этих вопросов и литературные ссылки можно найти в книге
Рашевского [12] и работе Розена [56]
118
Глава 6
влияние времени затрудняет изучение этого плана, если рас-
сматривать ход развития как функцию времени, но при подходе
с точки зрения гетерогонии временной фактор исключается и
контуры общего плана становятся различимыми».
Итак, рассматривая идеи д’Арси Томпсона, Нидхэма, Уод-
дингтона, Гексли и других, относящиеся к биологическим транс-
формациям, мы обнаруживаем контакты между принципом оп-
тимальности и гипотезами реляционной биологии. Эта широкая
область теоретической биологии, богатая важными биологиче-
скими идеями, допускает применение математических методов
исследования. Сделано в ней еще очень мало, и исследователи,
занимающиеся математической биологией, могут найти в ней
широкое поле деятельности.
Глава 7
ВВЕДЕНИЕ В ПРОБЛЕМЫ ГОМЕОСТАЗА
В БИОЛОГИИ
7.1. Общие замечания
Обратимся теперь к рассмотрению физиологических функций
живых организмов и тех анатомических структур, которые осу-
ществляют эти функции. В данной главе мы обсудим с качест-
венной точки зрения механизмы гомеостаза, с тем чтобы в даль-
нейшем, отправляясь от этих результатов, полученных на ос-
новании интуитивных соображений, провести более полное
исследование.
Предположим, что с помощью тех методов, которые обсу-
ждались выше, нам удалось составить представление об опти-
мальной структуре механизма, предназначенного для осущест-
вления определенной физиологической функции при некоторых
заданных условиях среды. Теперь нужно поставить следующий
вопрос: при каких обстоятельствах можно быть уверенным
в том, что этот механизм будет оптимальным и для некоторого
диапазона условий среды? Ведь в реальном мире всегда возни-
кают различные случайные изменения, флуктуации и возмуще-
ния, и каждое из них может вызвать отклонение каких-то усло-
вий среды от тех, при которых та или иная часть системы фун-
кционирует оптимально.
В общем случае у нас нет оснований рассчитывать на то, что
некоторая конструкция, оптимальная при каких-то определенных
внешних условиях, сохранит свои оптимальные свойства при
изменении этих условий. Очевидно, у системы существуют
только две возможности в какой-то мере оградить себя от влия-
ния изменений во внешней среде: 1) примириться с субоцди-
мальной тактикой в каждой данной среде в качестве расплаты
за вполне приемлемую тактику в широком диапазоне возмож-
ных сред; 2) создать специфические буферные механизмы, под-
держивающие условия среды, в которой действует оптимальная
система, на постоянном уровне, несмотря на колебания внеш-
них условий.
Каждый из этих двух возможных способов защиты от флук-
туаций условий среды имеет свои собственные достоинства и не-
достатки, при оценке которых следует учитывать, о какой
именно системе идет речь. Достоинство первого варианта со-
120
Глава 7
стоит в том, что в этом случае требуется лишь одна система,
способная действовать в широком диапазоне условий среды; оче-
видный недостаток заключается здесь в том, что поведение сис-
темы будет в общем случае только субоптимальным. Преиму-
щество второй из указанных выше возможностей заключается
в том, что система все время ведет себя оптимальным образом,
но это происходит за счет того, что создается и поддерживается
некоторая добавочная система регулирования. Если речь идет
о регуляции физиологических функций, то здесь всегда или
почти всегда мы встречаемся со второй возможностью; в то же
время в биологических популяциях, подвергающихся воздейст-
вию изменений во внешней среде, осуществляется обычно первая
возможность.
Упражнение
Рассмотрите относительные преимущества этих двух воз-
можностей, исходя из интенсивности конкуренции.
В связи с обсуждением устойчивости (асимптотической) си-
стем, описываемых дифференциальными уравнениями, мы уже
фактически познакомились с одной из возможностей сопротив-
ления системы изменениям внешних условий. В самом деле,
в принципе асимптотическая устойчивость этих систем и яв-
ляется, вообще говоря, необходимым и достаточным условием
наличия такого сопротивления. Однако для биологических си-
стем обычно важно, чтобы возврат к оптимальному состоянию
после возмущения происходил быстро, а именно «асимптотиче-
ский» характер асимптотической устойчивости становится с этой
точки зрения неудовлетворительным. Мы покажем далее, что
основная черта всякого регуляторного механизма состоит в том,
что он обеспечивает значительно более быстрое и точное воз-
вращение рассматриваемой системы к оптимальному состоянию,
чем если бы она была предоставлена самой себе.
Сохранение постоянства внутренней среды организма при
наличии случайных колебаний во внешней среде называется
гомеостазом *. Многие простые физические и химические системы
обнаруживают некоторые гомеостатические свойства простей-
шего типа, т. е. тенденцию сопротивляться тем или иным изме-
1 Термин «гомеостаз» был введен'в 1932 г. физиологом У. Кенноном. Его
книга [57], представляющая собой общий обзор механизмов гомеостаза в фи-
зиологии, до сих пор читается с большим интересом. Как это обычно бывает,
само представление о гомеостазе в биологических системах возникло значи-
тельно раньше, чем появился термин, применяемый теперь для описания этого
явления; идея постоянства внутренней среды у высших организмов была ши-
роко распространена среди французских физиологов XIX столетия. Позже
Н. Винер [58] указал на существование по существу таких же механизмов го-
меостаза в регуляции нервной и мышечной активности. Более подробно обо
всех этих идеях будет сказано в дальнейших главах.
Введение в проблемы гомеостаза в биологии
121
нениям во внешней среде. Рассмотрим, например, находящуюся
в химическом равновесии систему типа
A + B^C + D.
Пусть теперь на эту систему действует возмущение, а именно
пусть к ней добавляется некоторое количество одного из реаген-
тов, скажем А. Закон действия масс говорит нам, что в этом
случае равновесие будет сдвинуто в сторону прямой реакции,
в результате чего внесенный в систему избыток А в конце кон-
цов будет исчерпан. Действительно, закон действия масс часто
формулируется в следующей форме: изменение концентрации
любого реагента в системе, находящейся в химическом равно-
весии, приводит к сдвигу равновесия в сторону реакции, нейтра-
лизующей это изменение. Аналогичное утверждение справедливо
и по отношению к любым другим изменениям внешних условий,
влияющих на скорость химической реакции (например, изме-
нениям температуры).
Закон действия масс применим ко многим биологическим
системам, из которых наиболее широко известны буферные си-
стемы. Буфер — это раствор, обладающий способностью под-
держивать на постоянном уровне концентрацию ионов водо-
рода, т. е. величину pH. Водный раствор любой слабой кислоты
частично диссоциирует в соответствии с уравнением
НХг±Н+4-Х- (7.1)
до тех пор, пока не устанавливается равновесие. Если к, этому
раствору добавляется щелочь, то концентрация ионов Н+ пони-
жается, и это приводит к сдвигу равновесия вправо; в резуль-
тате освобождается добавочное количество водородных ионов,
что уравновешивает эффект, вызванный введением щелочи.’
Если, напротив, к раствору добавляются ионы водорода, то
равновесие сдвигается влево, и это опять-таки способствует
сохранению концентрации водородных ионов на постоянном
уровне. Таким образом, раствор всякой слабой кислоты дейст-.
вует как буфер, т. е. он сопротивляется изменениям pH. В крови,
например, где величина pH должна поддерживаться на строго
определенном уровне, существует несколько сложных буферных
систем, основанных на реакциях типа (7.1), рассмотренных выше
(где X — бикарбонат), а также на буферных свойствах белков
крови, таких, как гемоглобин и сывороточные альбумины.
Примером гомеостаза в физических системах может служить
известный закон Ленца. Этот закон утверждает, что ток, инду-
цированный в проводнике при изменении пронизывающего его
магнитного потока, направлен так, чтобы его магнитное поле
противодействовало вызвавшему его изменению.
122
Глава 7
Свойство систем, находящихся в равновесии, сопротив-
ляться любому изменению внешних условий, которое было нами
проиллюстрировано на примерах закона действия масс и за-
кона Ленца, было впервые сформулировано как общее свойство
таких систем Лешателье. Рассмотрим теперь подробно третью
систему, для которой выполняется принцип Лешателье.
7.2. Пример: гармонический осциллятор
Идеализированной моделью одномерного гармонического ос-
циллятора может служить частица массы т, прикрепленная
к пружине и способная перемещаться лишь вверх и вниз. Допу-
стим, что в состоянии равновесия частица находится в начале
координат, и ее смещение из положения равновесия опреде-
ляется единственной переменной координатой х.
По закону Гука, при отклонении пружины от положения
равновесия в ней возникает восстанавливающая сила F, направ-
ленная против той силы, которая вызвала отклонение, и по ве-
личине пропорциональная отклонению; этот закон записывается
в виде формулы
F= — kx, (7.2)
где k — положительная постоянная, зависящая только от мате-
риала и формы пружины. Таким образом, простой гармониче-
ский осциллятор обнаруживает сопротивление любой силе, вы-
зывающей отклонение. По второму закону Ньютона
Из (7.3) и (7.2) вытекает дифференциальное уравнение вто-
рого порядка, определяющее отклонение х как функцию вре-
мени. Общее решение этого уравнения записывается в виде
x = Acos<»/-|-5sina)/, (7.4)
где А, В — произвольные постоянные, a to= Vk[tn— частота
возникающего колебательного движения. Если положить для
простоты х= 1 при / = 0, то решение примет вид
x = cos®/. (7.5)
График этого решения изображен на фиг. 18.
Состояние равновесия осциллятора соответствует тривиаль-
ному решению х(/)=0 (т. е. случаю, когда в формуле (7.4)
А = 5 = 0). Мы видим, что это решение не является, очевидно,
Введение в проблемы гомеостаза в биологии
123
асимптотически устойчивым, т. е. система, подчиняющаяся лишь
уравнениям (7.2), (7.3), никогда не вернется к положению рав-
новесия, если ее отклонить от этого положения. Таким образом,
простой гармонический осциллятор непригоден в качестве хо-
рошего регулирующего устройства.
В действительности, однако, никакой реальный гармониче-
ский осциллятор не подчиняется в точности закону (7.2). Дви-
жение его происходит всегда в среде, обладающей большей или
iW
Фиг. 18.
меньшей вязкостью, и поэтому на движущуюся частицу дейст-
вует сила трения. Обычно принимают, что эта сила пропорцио-
нальна скорости х частицы и направлена опять-таки против
движения частицы. Итак, в вязкой среде восстанавливающая
сила может быть записана в виде
F = — kx — [Jx- k, Р>0. (7.6)
Из (7.3) и (7.6) мы получаем уравнение
х+-^-х+—х = 0. (7.7)
1 пг 1 m ' 7
Решение уравнения (7.7) ищется обычно в виде
x = Cev,
и если предположить, что выполняется условие р2<4 km (ус-
ловие «малого затухания»), то это приводит к общему решению
(7.7) вида
* - г- ««' (л соз * + В <)
(7.8)
Вводя опять для простоты условие х=1 при 1=0, находим для
этого случая решение
х = е-»«'соз(/А-^)л (7.9)
124
Глава 7
Упражнение
Убедитесь в справедливости формулы (7.8).
Упражнение
Исследуйте движение в случае р2> 4 km (условие «сильного
затухания»).
_ -(₽/2m) t
Обратим теперь внимание на то, что множитель е ,
представляющий собой амплитуду колебательного движения,
является в данном случае убывающей функцией времени. Та-
кие колебания называются затухающими (точнее, колебаниями
с отрицательным затуханием). Чем больше коэффициент трения
Р, тем скорее амплитуда этих колебаний приближается к нулю.
Фиг. 19.
Заметим также, что затухание влияет и на частоту возникаю-
щих колебаний; при отсутствии затухания угловая частота
1 Л k 1Г k р2
равна у —, а при наличии трения она равна у —--------
Наличие затухания приводит, очевидно, к тому, что триви-
альное решение x(t) =0 уравнения (7.7) становится как устой-
чивым, так и асимптотически устойчивым, причем быстрота,
с которой система приближается к своему положению равно-
весия, определяется величиной затухания. Характерный график
затухающих колебаний изображен на фиг. 19.
Мы предполагали, что сила, вызвавшая отклонение системы,
была приложена в момент £ = 0, а затем действие ее прекрати-
лось. Реакция системы на воздействие такого типа описывается
так называемой переходной характеристикой. Как будет далее
показано, изучение переходных характеристик систем^различ-
ного типа играет важную роль в теории систем управлений. Но
при исследовании системы важно также знать, как она реаги-
рует на постоянно действующее возмущение. Соответствующую
характеристику также удобно рассмотреть на примере гармо-
нического осциллятора.
Введение в проблемы гомеостаза в биологии
125
Предположим сейчас, что, кроме восстанавливающей силы
и силы трения, к осциллятору приложена также внешняя сила
G(t), не зависящая от отклонения х, т. е. являющаяся функцией
одного лишь времени. Допустим, например, что эта сила имеет
колебательный характер: G(/)=G0cosipZ. Тогда уравнение дви-
жения осциллятора принимает вид
х + + (7.10)
Заметим, что (7.10) при Go = O переходит в (7.7). Уравнение
(7.7) линейно и однородно, в то время как (7.10) —это неодно-
родное уравнение, так как оно содержит не зависящее от х сла-
гаемое Go cos ф/.
Для решения (7.10) можно применить известные теоремы
теории линейных дифференциальных уравнений (эти теоремы
подробно излагаются во всех курсах дифференциальных урав-
нений; см., например, [19]), согласно .которым общее решение
уравнения (7.10) можно представить в виде суммы его любого
частного решения и общего решения соответствующего одно-
родного уравнения (7.7).
Здесь нам нет необходимости вдаваться в подробности, свя-
занные с решением уравнения (7.10) (см., например, [4]). Доста-
точно будет отметить, что у него существует такое частное ре-
шение g(t), которое соответствует незатухающим колебаниям
той же частоты, что и частота вынуждающей силы G(i), но
амплитуда и фаза которого в общем случае отличны от ампли-
туды и фазы G(t). Это частное решение уравнения (7.10), та-
ким образом, следует (по частоте) за колебаниями внешней
нагрузки. Если прибавить к этому частному решению общее
решение (7.8) уравнения (7.7), то получится общее решение
уравнения (7.10). Отсюда можно сделать два вывода о поведе-
нии системы': 1) колебания системы содержат составляющую,
соответствующую переходному режиму колебаний, которая це-
ликом определяется параметрами самого осциллятора (т. е.
параметрами р, k, m). Влияние этой составляющей постепенно
становится исчезающе малым ввиду затухания; 2) кроме того,
имеется составляющая, соответствующая стационарному ре-
жиму колебаний, который в основном определяется характером
внешней силы, приложенной к осциллятору. Влияние парамет-
ров осциллятора на эту составляющую сказывается лишь в том,
что они входят в выражения для амплитуды и фазы колебаний,
но частота установившегося режима колебаний от них не зави-
сит. Характерный вид графика решения (7.10) изображен на
фиг. 20.
126
Глава 7
Таким образом, на простом примере гармонического осцил-
лятора мы показали, что свойства линейной системы полностью
определяются, если известно, как она ведет себя в переходном и
в стационарном режимах. При изучении такого рода систем ин-
женеры часто используют прием, заключающийся в том, что си-
стема приводится в такие состояния, в которых независимо друг
от друга выявляются ее свойства в обоих этих режимах. Эти
Переходный <
•s рехил! ।
\ I Стационарный режим
Фиг. 20.
приемы исследования, играющие важную роль в теории, назы-
вают соответственно анализом переходных процессов и анали-
зом стационарных процессов (или частотным, анализом). Более
подробно мы остановимся на этих методах в следующей главе.
Упражнение
1. Предположим, что вынуждающая сила, входящая в урав-
нение (7.10), имеет вид G(/)=const. Исследуйте режимы коле-
баний такой системы.
2. Как изменится стационарный режим системы (7.10), если
коэффициент р не будет строго положительным? Как связана
положительность р с устойчивостью (или асимптотической ус-
тойчивостью) этой системы? Как сформулировать ответы на эти
два вопроса в виде некоторого общего правила?
7.3. Замкнутые системы
В этом разделе мы лишь кратко упомянем о некоторых важ-
ных идеях, которые будут более подробно развиты в следующей
главе.
Рассмотренный в предыдущем разделе простой) гармониче-
ский осциллятор, колеблющийся в условиях вязкого трения,
представляет собой типичный пример так называемой разомк-
нутой системы. Как было показано, эта система обладает спо-
собностью сопротивляться отклонению от положения равнове-
Введение в проблемы гомеостаза в биологии
127
сия. Однако, с точки зрения инженера, такая система далеко не
идеальна. Можно, в частности, отметить, что в этом случае
время, необходимое для уменьшения амплитуды колебаний до
некоторой заданной величины, зависит от амплитуды и коэффи-
циента р (который здесь является постоянным); чем больше ам-
плитуда, тем больше указанный интервал времени.
Представим себе теперь такой осциллятор, 'у которого коэф-
фициент трения р не постоянен, а является некоторой моно-
тонно возрастающей функцией отклонения х. В этом случае при
увеличении отклонения сила сопротивления, вызванная трением,
тоже будет возрастать, и этот эффект проявится тем сильнее,
чем быстрее растет р с ростом х. Интуитивно представляется
очевидным, что такая сила сопротивления будет оказывать на
колебания тормозящее действие, и если подобрать соответст-
вующим образом функцию р(х), то можно добиться того, чтобы
амплитуда колебаний за сколь угодно малый промежуток вре-
мени уменьшилась до любой заданной величины.
Когда функция р(х) выбирается так, что затухание начинает
зависеть описанным выше образом от отклонения, то тем самым
в систему вводится так называемая обратная связь (точнее, от-
рицательная обратная связь). В этом случае простая разомкну-
тая система, рассмотренная выше, переходит в замкнутую си-
стему, и в результате ее эффективность как средства управле-
ния и регулирования значительно увеличивается (надо также
отметить, что при этом уравнение движения (7.7) этой системы
становится нелинейным) *.
Упражнение
Исследуйте свойства решений уравнения (7.7) для случаев,
когда р(х) =х и р(х) =х2.
Система с обратной связью характеризуется тем, что откло-
нение данного состояния системы от требуемого служит источ-
ником сигнала, поступающего на ее вход, в результате чего она
изменяет свое состояние так, чтобы это отклонение стало мини-
мальным. Понятие обратной связи является основой теории
систем управления как в технике, так и в биологии, и в следую-
щей главе будут развиты математические методы исследования
таких систем.
В большинстве случаев технические и биологические системы
управления принадлежат к замкнутым системам и содержат
один или несколько контуров обратной связи. В технике обычно
1 Вид обратной связи, который иллюстрируется этим примером, типичен
для физиологических систем регулирования; такую обратную связь обычно на-
зывают параметрической (более подробные сведения об этом см. в разд. 11.1).
В технике обратная связь часто вводится другим, более простым способом.
128
Глава 7
делят эти устройства на два класса: 1) следящие системы, на-
значение которых состоит в том, чтобы отслеживать, т. е. точно
воспроизводить изменения некоторой величины, определяемой
внешними условиями, и 2) системы регулирования, действие ко-
торых сводится в основном к поддержанию регулируемой вели-
чины на некотором постоянном уровне, несмотря на колебания
внешних условий. Эти классы систем управления различаются
в деталях, но основные принципы их работы по существу оди-
наковы.
Типичным примером технической следящей системы служит
система автоматического управления огнем зенитных орудий,
обеспечивающая упреждающее регулирование прицела орудия.
Другой, более близкий нам пример — это приспособление, пово-
рачивающее антенну телевизора или радиоприемника в направ-
лении источника сигнала. В качестве типичного примера техни-
ческой системы регулирования можно упомянуть обычный тер-
морегулятор, который управляет тягой печки так, чтобы темпера-
тура в комнате оставалась неизменной, несмотря на колебания
температуры воздуха на улице. Во всех этих случаях ра-
зомкнутая система оказалась бы непригодной, так как она не
обладает достаточной быстротой и подвижностью, необходи-
мыми для выполнения поставленных задач; поэтому системы
такого рода обязательно должны содержать цепь обратной
связи, т. е. принадлежат к замкнутым системам.
Упражнение
Сопоставляя величины, играющие аналогичную роль в опи-
сании работы терморегулятора и в описании движения гармони-
ческого осциллятора при наличии контура обратной связи (см.
начало этого раздела), проведите детальное сравнение работы
этих устройств.
7.4. Биологические механизмы гомеостаза и принцип
оптимальности
Представления об управлении, т. е. поддержании гомеостаза,
имеют важнейшее значение для физиологии (см. примечание на
стр. 120). В подавляющем большинстве случаев биологические
механизмы гомеостаза представляют собой замкнутые системы,
действующие с помощью отрицательной обратной свяэи. Много-
численные примеры таких систем приводятся в гл.; 9; подробное
обсуждение этих вопросов мы отложим до тех пор, пока в гл. 8
не будет развит соответствующий математический аппарат.
Каким же образом концепции гомеостаза связаны с идеями
оптимальности, обсуждением которых мы до сих пор занима-
Введение в проблемы гомеостаза в биологии 129
лись? Мы можем уже сейчас указать ряд важных точек сопри-
косновения этих понятий, которые читатель, вероятно, уже за-
метил сам. Первый и наиболее очевидный факт заключается
в том, что работа регуляторной системы, действующей с по-
мощью отрицательной обратной связи, в точном смысле слова
сводится к минимизации одной или нескольких величин, харак-
теризующих отклонение действительного состояния системы от
некоторого желаемого состояния. В предыдущих главах были
развиты общие математические методы, применимые к различ-
ного рода задачам на минимум; естественно поэтому ожидать,
что эти методы должны сыграть важную роль в изучении сис-
тем регулирования.
Существует и более глубокая связь между понятием опти-
мальности и принципами действия биологических систем управ-
ления, так как эти системы в той же мере подвержены непосред-
ственному действию естественного отбора, как и те особенности
формы живых организмов, о которых мы говорили раньше. Та-
ким образом, из принципа оптимальной конструкции непосред-
ственно следует, что точно так же, как мы говорим об оптималь-
ных формах организмов, мы можем говорить об оптимальных ме-
ханизмах регулирования их функций Ч Вполне естественно
поэтому, что идеи оптимальности и математические принципы,
выражающие эти идеи, играют важную роль-в теории биологи-
ческих систем управления на самых разных уровнях исследова-
ния.
1 Как было показано, методы оптимизации могут быть применены" для
сравнительного изучения биологических форм (см гл 4—6) Точно так же
можно попытаться построить аналогичную сравнительную теорию биологиче-
ских механизмов управления. Здесь мы не ставим своей целью разработать
такую теорию, но хотим отметить, что эта область представляет обширнейшее
поле деятельности для дальнейших исследований по теоретической биологии.
Глава 8
связь между входными и выходными
СИГНАЛАМИ СИСТЕМЫ
8. 1. Входные и выходные сигналы
Один из плодотворных методов изучения систем управления
и вообще любых систем заключается в том, что рассматриваются
реакции, или выходные сигналы этих систем, возникающие при
всевозможных допустимых формах входных сигналов, поступаю-
щих извне. До самого последнего времени такой метод изучения
занимал в технике и в литературе, посвященной теории управле-
ния, ведущее место. Здесь мы обсудим вкратце некоторые важ-
ные понятия, относящиеся к этому вопросу, а в следующей главе
продемонстрируем, каким образом эти понятия могут быть непо-
средственно использованы для изучения некоторых биологиче-
ских систем управления.
Входной сигнал, поступающий в данную систему, можно
рассматривать как некоторую функцию времени, скажем F(V),
а выходной сигнал, или реакцию системы, — как какую-то дру-
гую функцию времени, например y(t). Поведение системы, со-
ответствующее входному сигналу F(t), описывается уравнением
(обычно дифференциальным), связывающим входную функцию
F(f) с выходной функцией y(f).
Следует с самого начала отметить, что в имеющейся лите-
ратуре по теории управления большая часть исследований по-
священа линейным системам, т. е. таким системам, которые опи-
сываются линейными дифференциальными уравнениями. Только
в этом случае удается разработать общую аналитическую тео-
рию; аналитическое изучение нелинейных систем ограничивается
по большей части такими случаями, в которых возможна линеа-
ризация. В случае линейной системы ее поведение полностью
определяется некоторым линейным дифференциальным урав-
нением. Это уравнение позволяет определить так называемую
передаточную функцию, с помощью которой при лю^омг-зддан-
ном входном сигнале может быть вычислен выходной сигнал.
Наиболее плодотворным математическим методов, который
может быть использован в этой области, является преобразова-
ние Лапласа. Исторически именно успешное применение этого
преобразования и других так называемых «операционных мето-
дов» к техническим задачам побудило математиков к интенсив-
Связь между входными и выходными сигналами системы
131
ному изучению такого рода методов. В результате был достиг-
нут двойной выигрыш: во-первых, было положено начало раз-
витию важной области чистой математики и развита строгая
теория операционных методов и, во-вторых, применявшиеся
в технике прикладные методы получили, наконец, теоретический
фундамент и были развиты более сильные методы, которые
можно было применить к более широкому и новому классу при-
кладных проблем.
В качестве типичного примера системы, которая может быть
описана с помощью изучения зависимости между входными и
выходными сигналами, рассмотрим вновь гармонический осцил-
лятор. Роль входного сигнала F(t) играет здесь внешняя сила,
вызывающая отклонение системы, а выходным сигналом y(f)
служит отклонение системы от положения равновесия. При изу-
чении свободных колебаний осциллятора можно считать, что
возмущающая сила имеет следующий специальный характер:
она отлична от нуля лишь в некоторый начальный момент t =
= to и равна нулю при всех значениях времени t>t0; в момент
t=t0 система получает под действием силы F(t) (входного сиг-
нала) некоторое смещение из положения равновесия. После
этого момента осциллятор находится лишь под действием вос-
станавливающей силы вида (7.2) или (7.6), и с этого времени
и должен быть определен выходной сигнал у (t). Этот пример
нужно иметь в виду при рассмотрении более строгой теории
в следующих разделах.
8.2. Передаточная функция
Допустим, что рассматривается линейная система, у которой
выходной сигнал y(f) связан с входным сигналом F(t) с по-
мощью линейного дифференциального уравнения n-го порядка
вида 1 * * * * *
а„у<л>+ ап_1у("“1) + ...+ а0 = /7(/) (az = const, п).
(8-1)
Поведение такой системы полностью определяется, если задать
некоторые начальные значения у (0) =Дь у' (0) =Аг, ...
.. „ у(п-1) (0) =Ап.
1 При изучении физической системы, описываемой уравнением такого
вида, можно, не ограничивая общности, положить ао=О. Это просто соответ-
ствует тому, что за положение равновесия системы выбрано значение у=0, и
при отсутствии внешних возмущений (т. е при F(/) =0) такая система дол-
жна обладать частным решением, соответствующим этому положению равно-
весия (т. е. функция y(t) = 0 должна быть решением этого уравнения).
132
Глава 8
Преобразование Лапласа представляет собой совершенно
естественный метод изучения таких уравнений; его применение
к решению дифференциальных уравнений напоминает примене-
ние логарифмов к решению некоторых простейших алгебраиче-
ских уравнений. В случае алгебраических уравнений примене-
ние логарифмов упрощает решение задачи, так как при этом ум-
ножение чисел перех.одит в сложение логарифмов и возведение
в степень сводится к умножению логарифма числа на показа-
тель степени. Аналогично этому преобразование Лапласа сво-
дит дифференцирование к операции умножения. В результате
применения преобразования Лапласа к дифференциальному
уравнению n-го порядка это последнее сводится к некоторому
алгебраическому уравнению степени п. В случае вычислений
с помощью логарифмов можно, используя антилогарифмы, найти
решение интересующей нас задачи; сходная ситуация имеет
место и для преобразования Лапласа: существует обратное пре-
образование, которое позволяет вернуться от решения получен-
ного алгебраического уравнения к решению исходного диффе-
ренциального уравнения.
Пусть теперь f(t)—произвольная непрерывная функция и
для нее существуют все производные и интегралы, которые нам
в дальнейшем потребуются. Обозначим через s новую незави-
симую переменную (в общем случае приходится рассматривать
комплексную переменную s) и определим новую функцию ф(в)
с помощью следующего соотношения:
<ф(«)= J f (t)e~st dt. (8.2)
о
Функция ф($) называется преобразованием Лапласа функции
f(t), и соотношение (8.2), определяющее связь между f(t) и
ф($), обозначают часто с помощью операторной записи
Ф(5) = L [/(/)]. (8.3)
Оператор L обладает, очевидно, свойством линейности в том
смысле, что
L {af^+bgW = aL {f(t)\+bL [g(/)](
где a, b — постоянные числа. Существует также и обратный опе-
ратор L-1, определяющий обратное преобразование Лапласа:
L-'Ltf = • Более подробно читатель может ознакомиться
Связь между входными и выходными сигналами системы
133
с этим вопросом и с явным выражением для L~* l по специальной
литературе *.
Если применить преобразование Лапласа к обеим частям
уравнения (8.1), то ввиду линейности оператора L
anL +an_.L [y(«-D] +.. , + а0£ [у] = £ [F(Z)]. (8.4)
Выражение L[y(f)] мы обозначим через iq(s), и теперь нужно
выразить члены Ь[у№ (/)], k~^ 1, через функцию iq ($).
Прежде всего убедимся в том, что Z.[z/'(/)] = sr] (s)+z/(0).
Действительно, в соответствии с определением
ОО
А [у' (Z)] = J y'e~stdt.
о
Интегрируя теперь по частям, мы находим, что
(* e~st 1
7l(s)= J y(/)e~rf^ =-----— у(/) +4-1 [/(01-
О о
Отсюда непосредственно получается требуемое соотношение
A[yf(/)]=S7](s) + y(0). (8.5)
Используя (8.5), можно по индукции доказать, что в общем слу-
чае получается формула
к
L [y(*)(/)] =sft7i(s)- 2 А = 1,2,.... п, (8.6)
j=i
которую нам и нужно было вывести.
Упражнение
Проверьте правильность формулы (8.6).
Возвращаясь теперь к системе (8.1), мы видим, что с по-
мощью формулы (8 6) уравнение (8.4), эквивалентное (8.1),
может быть записано в следующем виде:
(п. \
2 <M*h(s)= L [/=(/)]+ Г,
й = 0 J
где Г — некоторый многочлен относительна переменной $, коэф-
фициенты которого определяются начальными условиями,
____ль
1 Существует большое число книг, посвященных преобразованию Лапла-
са, одни из них относятся к чисто математическому исследованию этого во-
проса, Другие предназначены для технических приложений (см, например,
[59, 60])
134
Глава 8
выбранными для рассматриваемой системы (т. е. числами ‘Ао,
At, ..Ап). Решая это уравнение относительно г) (s), получаем
= Utm+Г}. (8.7)
2
й=0
Решение исходной системы (8.1) можно теперь получить, при-
меняя к обеим частям выражения (8.7) обратное преобразование
Лапласа.
Выражение (8.7), полученное для г) (s), представляет собой
произведение двух сомножителей. Первый из них — величйна,
обратная многочлену, образующемуся при замене в левой
части исходного уравнения (8.1) на sk, — называется передаточ-
ной функцией рассматриваемой системы. Если, как это часто
бывает в прикладных задачах, начальные значения выбраны
так, что постоянные А{ равны нулю, то многочлен Г тоже равен
нулю и (8.7) принимает вид
= ---L [F(/)]. (8.8)
2 a»s*
ft = 0
При этих условиях передаточная функция, которую мы обо-
значим через G ($), попросту равна отношению преобразования
Лапласа выходного сигнала к преобразованию Лапласа вход-
ной функции. Таким образом, ясно, что передаточная функция
представляет собой выражение, на которое нужно умножить
преобразование Лапласа входной функции F(t), чтобы получить
преобразование Лапласа выходного сигнала.
Важное значение передаточной функции заключается в том,
что в принципе она позволяет получить полную информацию
о соотношении между входным и выходным сигналами системы,
для которой она найдена, и, следовательно, о поведении систе-
мы. С ее помощью можно, например, получить полную инфор-
мацию относительно устойчивости системы (в технических при-
ложениях в вопросах устойчивости обычно интересуются устой-
чивостью тривиального решения у = 0 уравнения (8.1) при F(t) =
= 0). Нетрудно показать, что устойчивость имеет или не имеет
места в зависимости от некоторых простых свойств, которыми
обладают корни (они могут быть комплексными) многочлена
п
эти корни являются полюсами передаточной функции
й=0
1 Как указывалось в разд. 6.3, исследование асимптотической устойчи-
вости в смысле Ляпунова проводится обычно для тривиального решения; для
системы (8.1) это сводится к изучению устойчивости нулевого решения y(t) =
Связь между входными и выходными сигналами системы
135
Что касается стационарных режимов линейной системы, то
при их ^изучении существенны две характерные черты, которые
система обнаруживает при реакции на входной сигнал некото-
рого специфического характера, а именно на гармоническое воз-
действие вида Л со sco/. При этом, с одной стороны, изменяется
амплитуда сигнала и это изменение характеризуется коэффици-
ентом усиления системы. С другой стороны, при формировании
системой выходного сигнала происходит сдвиг фазы колебаний.
И коэффициент усиления, и сдвиг фазы существенно сказы-
ваются на устойчивости системы обе эти величины могут быть
вычислены с помощью передаточной функции. И обратно, если
известны коэффициент усиления и сдвиг фазы линейной системы,
то это полностью определяет передаточную функцию: сущест-
вует целый ряд методов, позволяющих получить явное
=0 при F(t)s0 (в соответствии с ранее сделанным замечанием предпола-
п
гается, что ао=О). Многочлен можно записать в виде ап(з — si)(.s—
k=o п
— s2)... (s — sn), где Si — корни уравнения = Допустим сейчас,
й=0
что все эти корни различны.
В этом случае нетрудно убедиться в том, что общее решение уравнения
(8.1) при F(t)=O определяется выражением
у(/)=Д1^ + ... + AneSnt
(вывод этой формулы см., например, [19], стр. 66), где Аг — произвольные
постоянные. Если в начальный момент на систему подействует мгновен-
ный импульс, вызывающий начальное смещение (последнее выражается, на-
пример, начальным условием у(0)=К^0), то• система всегда возвращается
при t —оо к положению равновесия у=0 в том и только в том случае, если
при t -*оо общее решение стремится к нулю. Это означает, что каждый член,
входящий в общее решение, должен при t -*• оо стремиться к нулю.
Корни Sj в общем случае могут быть комплексными. Пусть Sj=a+bi, где
s.t at ibt ibt
a, b — вещественные числа; тогда e } =e e . Сомножитель e представляет
в комплексной форме гармонические колебания, и в частности | e,bt | С 2 для*
s ,t
всех t. Таким образом, асимптотическое поведение члена е 1 полностью опре-
деляется вещественной частью а корня sj. Если а>0, то eat стремится к бес-
конечности при неограниченном возрастании t, и тогда устойчивость невоз-
j ./
можна. При а = 0 выражение е 7 содержит осциллирующие члены, и поэтому
асимптотическая устойчивость в этом случае, вообще говоря, не имеет места.
Наконец, если а<0, то eat стремится к нулю при t—«оо. Следовательно,
асимптотическая устойчивость в общем случае имеет место лишь при условии,
что вещественные части всех корней Sj отрицательны.
1 Выяснение вопроса о влиянии коэффициента усиления и сдвига фазы
на устойчивость линейной системы ие очень сложно, но, поскольку этот факт
используется далее в разд. 9.2, здесь имеет смысл лишь указать читателю
литературу по этому вопросу. Прекрасное изложение этой темы можно найти
в книге Арендта и Таплина [61].
136
Глава 8
выражение для передаточной функции, если заданы коэффи-
циент усиления и сдвиг фазы.
Передаточные функции позволяют, наконец, легко исследо-
вать также и системы из нескольких звеньев и выяснить, каким
образом изменение передаточных функций отдельных звеньев
влияет на передаточную функцию всей системы в целом.
8.3. Интегральные уравнения для линейных систем
Отметим здесь еще одну интересную интерпретацию переда-
точной функции, имеющую самостоятельный теоретический ин-
терес. Один из важнейших методов исследования систем, свой-
ства которых заранее-не известны, состоит в том, что в систему
вводится определенный стандартный входной сигнал и рас-
сматриваемся выходной сигнал, характеризующий ее реакцию
на это воздействие. Из стандартных входных сигналов такого
типа очень часто используется так называемый единичный им-
пульс (точнее, единичная импульсная функция, или б-функция
Дирака). По формальному определению эта функция прини-
мает нулевые значения при всех значениях t, кроме значения
f=0, где она полагается бесконечной, и вводится также усло-
вие нормировки
f 8 (0^ = 1.
— 00
Можно представить себе б-функцию как предел постоянного им-
пульса величины а, имеющего продолжительность 1/а, при
а—>-оо; так что в действительности б-фуикция может быть
сколько угодно точно аппроксимирована импульсом такого типа.
Допустим теперь, что единичный импульс подается на вход не-
которой линейной системы, находившейся до этого в состоя-
нии покоя. Это означает, что в качестве функции F(t) в фор-
мулу (8.8) нужно подставить б-функцию б (/). Нетрудно убе-
диться в том, что
L [8(0] =J — 1.
о
Поэтому из (8.8) получается равенство
^(s)=a(s); (8.9
другими словами, передаточная функция системы оказывается
как раз равной преобразованию Лапласа выходного сигнала,
соответствующего входному сигналу вида единичной импульс-
ной функции.
Связь между входными и выходными сигналами системы
137
Разовьем наши рассуждения несколько дальше, так как этот
вопрос имеет важное теоретическое значение. Применяя к ра-
венству (8.9) обратное преобразование Лапласа, находим
у(0=Я(^
где H(t) =£-I[G(s)]. Но y(t) представляет выходной сигнал, со-
ответствующий единичному импульсу, поданному на вход си-
стемы в момент t — Q. Единичный импульс, подаваемый в некото-
рый момент времени aj>0, можно, очевидно, записать как
б(/—он). Предположим теперь, что, кроме единичного импульса,
приложенного к системе в момент / = 0, при / = ai подается
также добавочный единичный импульс. Тогда в формулу (8.8)
нужно подставить
F(Z)==8(O + 8(^_ai);
откуда тотчас же следует, что
Если, в общем случае,
N
/=(/)= 2
й=1
ТО
N
Й = 1
а в пределе, если
т
F (/) = J В (/ — a) da,
о
то
т
у (0 = $ H(t~a}da. (8.10)
о
т
Заметим теперь, что F(t)~ д(/—a) da представляет собой не
что иное, как входной сигнал продолжительности Т, величина
которого равна 1, а (8.10) —сигнал на выходе, соответствующий
этому входному сигналу. Таким образом, мы рассматриваем этот
входной сигнал как непрерывную последовательность единичных
импульсов. Аналогичное построение может быть проведено и для
произвольной кусочно-непрерывной функции F(t); всякая такая
138
Глава 8
функция может быть представлена в виде суперпозиции единич-
ных импульсов, помноженных на соответствующие амплитудные
множители, а реакция системы на эту входную функцию пред-
ставляется в виде суммы или интеграла выходных сигналов, со-
ответствующих таким отдельным импульсам Иными словами,
оказывается, что для каждого значения t, 0 t Т,
т
F (/) = J F (а) В (/ — а) da,
о
а соответствующий выходной сигнал записывается в виде так
называемого интеграла свертки
г т
у (Z) = J F (а) Н (t — а) da. = J Н {a)F(t — a) da (8.11)
о о
(в последней формуле переход от первого интеграла ко второму
производится с помощью замены переменной интегрирования t
на t—a). Приведенные рассуждения не дают еще, разумеется,
строгого доказательства, но они имеют важное эвристическое и
теоретическое значение, так как формула (8.11) позволяет непо-
средственно выписать в явной форме выходную функцию линей-
ной системы при произвольном входном сигнале F(t). Инте-
1 Этот результат выражает одно из важнейших свойств линейных диффе-
ренциальных уравнений и систем, описываемых такими уравнениями Основ-
ной факт, на который опирается проведенное выше исследование, состоит
в том, что если y2(t) —два различных решения линейного однородного
дифференциального уравнения, то их линейная комбинация Ay^t) + By2(t)
также является решением этого уравнения, а если эти функции суть решения
соответствующих неоднородных уравнений с правыми частями Fi(t), F2(f), то
линейная комбинация Ayt(t) + By2(t) удовлетворяет неоднородному уравнению
с правой частью, равной AFi(t) +BF2(t). Применяя терминологию, которой
мы пользовались при изучении систем, описываемых таким уравнением, можно
выразить приведенное выше утверждение следующим образом: реакция ли-
нейной системы на последовательные импульсы представляет собой алгебраи-
ческую сумму выходных сигналов, соответствующих каждому импульсу в от-
дельности (с учетом, разумеется, сдвигов фаз сигналов) Это свойство выра-
жает так называемый принцип суперпозиции, и интеграл свертки (8 11) есть
не что иное, как общее математическое выражение этого принципа Именно
в этом смысле интегральное соотношение (8.11) и дифференциальное уравне-
ние (8.1) эквивалентны и описывают одну и ту же систему. Не Всегда, однако,
можно легко перейти от данного интегрального уравнения (8.1ч) к соответ-
ствующему дифференциальному уравнению вида (8.1).
Доказательство того, что всякую непрерывную функцию (а на самом деле
даже всякую интегрируемую функцию) можно рассматривать как предел по-
следовательности ступенчатых функций, можно найти в литературе (см., на-
пример, [62], стр. 30 и далее).
Связь между входными и выходными сигналами системы
139
тральное представление (8.11) можно использовать вместо ис-
ходного дифференциального уравнения (8.1) для эквивалентного
определения рассматриваемой линейной системы (см.разд. 10.4).
8.4. Передаточные функции систем из нескольких звеньев
Допустим, что имеется некоторая линейная система, обла-
дающая передаточной функцией G (s), на вход которой подается
сигнал и при этом получается выходной сигнал у2(0-
Тогда по определению
7)2 (s) = O(s) 7]j (s),
где r]i(s)> T12(s)—преобразования Лапласа сигналов yi(t) и
Уг(О соответственно. Обычно такую систему изображают в виде
структурной схемы, показанной на фиг. 21.
Фнг. 21.
Фиг. 22.
Пусть теперь выходной сигнал такой системы служит вход-
ным сигналом для второй системы этого же типа, т. е. образо-
вана система из двух звеньев, соединенных последовательно
(фиг. 22).
Какой же будет передаточная функция всей этой системы,
если передаточные функции составляющих ее звеньев суть со-
ответственно Gi(s) и G2(s)? Эта искомая передаточная функция
равна по определению отношению преобразования Лапласа вы-
ходной функции к преобразованию Лапласа входного сигнала
рассматриваемой системы. Выполняя вычисления, находим, что
= Д2з<£1_ = q (s) q (s).
’ll (s) ’ll (s) 1)2 (s) '
Итак, передаточная функция системы, состоящей из двух после-
довательно соединенных звеньев, равна произведению переда-
точных функций этих звеньев. Аналогичный результат справед-
лив и для систем, состоящих из любого числа последовательно
соединенных звеньев.
Рассмотрим теперь параллельное соединение, изображенное
на фиг. 23. Легко показать, что в этом случае передаточная
функция всей системы есть сумма
Oj(s)-4-G2(s).
140
Глава 8
Таким образом, два звена, соединенных параллельно,- обра-
зуют систему, передаточная функция которой складывается из
передаточных функций отдельных звеньев. Этот результат
также легко обобщается на произвольное число звеньев, соеди-
ненных параллельно.
Из полученных выше двух простых результатов следует, что,
зная передаточные функции отдельных звеньев, мы можем
Фиг. 23.
вычислить передаточную функцию произвольной системы, по-
строенной из этих звеньев с помощью последовательных и па-
раллельных соединений. Обратно, если дана некоторая система,
передаточная функция которой известна, то ее можно Предста-
вить (обычно многими различными способами) в виде комби-
наций сумм и произведений других передаточных функций. Оба
эти факта играют важную роль при исследовании и конструи-
ровании любых систем регулирования и следящих систем,
в частности при теоретическом изучении биологических систем
регулирования. Однако нужно подчеркнуть еще раз, что рас-
сматриваемая нами теория применима только к линейным си-
стемам, описываемым линейными уравнениями.
8.5. Системы с обратной связью
Мы уже упоминали кратко о системах с обратной связью
в предыдущей главе и теперь рассмотрим этот вопрос более под-
робно, используя развитую выше теорию..
Из замечаний, сделанных ранее по поводу систем с обрат-
ной связью, должно быть уже вполне ясно, что системы управ-
ления,. в которых используется обратная связь, должны со-
стоять по крайней мере из двух звеньев; одно из( них — это
объект управления, а другое — управляющее устройство, или
регулятор.
Объект управления — это та система, которую нужно под-
держивать в определенном режиме работы; в одних случаях
требуется, чтобы, несмотря на флуктуации условий среды, у нее
Связь между входными и выходными сигналами системы
141
сохранился определенный рабочий режим (система регулирова-
ния), в других — система должна следовать изменениям того
или иного параметра, характеризующего внешнюю среду (сле-
дящая система). Эти цели достигаются за счет того, что сигнал
на входе объекта управления изменяется на определенную ве-
личину, зависящую от того, насколько состояние объекта уп-
равления в данный момент времени t отклоняется от требуе-
Задающий
сигнал
Сигнал-
ошибки
Объект
Контур обратной связи
Фиг. 24.
мого состояния. Следовательно, входной сигнал объекта управ-
ления (или некоторая его составляющая) должен
вырабатываться некоторой другой системой —регулятором, ко-
торый определяет, насколько состояние объекта управления
^(5) - ^(S)-Tl0(S)
Фиг. 25.
’fo(S)
отклоняется от требуемого, и затем формирует для него нуж-
ный входной сигнал, под влиянием которого это отклонение
минимизируется. Для работы регулятора необходимо, чтобы он
получал входные сигналы как от внешней среды, так и от са-
мого объекта управления (это и есть то, что принято называть
обратной связью).
Типичная структурная схема системы с обратной связью
изображена на фиг. 24, где приведены общепринятые названия
различных звеньев, или блоков. Для обозначения.того, что сиг-
нал ошибки получается вычитанием выходного сигнала, посту-
пающего по каналу обратной связи, из входного задающего
сигнала, применяется схема, показанная отдельно на фиг. 25.
Из передаточных функций Gi(s), Gz(s), относящихся
соответственно к управляющему устройству и к объекту
142
Глава 8
управления, можно получить ряд других передаточных функций,
характеризующих поведение всей системы с обратной связью
в целом и ее отдельных частей. Во-первых, используя формулу,
полученную ранее для последовательного соединения, мы нахо-
дим, что
-^1=О1(з)С?2(з). (8.12)
Выражение (8.12) называется передаточной 'функцией разомк-
нутой системы, так как здесь не учитывается контур обратной
связи. Из него можно получить две другие передаточные функ-
ции.
Вычисляя отношение т]о (») /т]» (s) ’ т- е- передаточную функцию
замкнутой системы, из (8.12) находим
(s)O.2($)-^тг-
’ll (s) 1 V / / 7[/
Но по определению 7]e(s) =т)< (s)—Л о («). и поэтому
(S)G (S)[1 _
7|( (S) ’ 2V ' [ 7Ц (S) J
Еще раз используя (8.12), получаем
4>(s) _____________________ Qi ($)02($) ,я 1
7iz(s) l + Oi(s)O2(s) •
Наконец, принимая во внимание (8.13), вычисляем передаточ-
ную функцию для сигнала ошибки:
($) __ ($) ($) 1 _ “40 (^)_______1_______ /о 1 л \
ъ(в) —1 7]Z(s) — l+GJslGjU) •
Система, изображенная на фиг. 24, представляет собой клас-
сическую следящую систему. Вполне очевидно, что выходной
сигнал такой системы воспроизводит задающий сигнал, а свой-
ства передаточных функций (8.12) — (8.14) позволяют оценить,
насколько хорошо система выполняет свое назначение. (Заме-
тим, что эти передаточные функции должны зависеть от пара-
метров, характеризующих физические свойства тех деталей, из
которых собрана система, — от коэффициентов затухания, соб-
ственных частот и т. д.).
На фиг. 26 показана структурная схема классической си-
стемы регулирования. При работе этой системы задающий сиг-
нал является постоянным и соответствует заданному значению
регулируемой величины (это так называемая уставка, например
заданное значение температуры в термостате); в этом случае
приходится рассматривать еще один дополнительный входной
Связь между входными и выходными сигналами системы
143
сигнал, преобразование Лапласа которого обозначено на схеме
через r]d(s). Этот сигнал характеризует влияние флуктуаций па-
раметров внешней среды. Как и в предыдущем случае, переда-
точные функции, характеризующие работу системы регулиро-
вания, могут быть выписаны без труда, причем для удобства
Фиг. 26.
МОЖНО ПОЛОЖИТЬ Т]г («) =0 (ТЭК ЧТО при ЭТОМ Т)е («) =—Цо («)):
= (8.15)
To(S) _ °2(S) .
7ld(S) ~ 1 + Oj (s) G2(s) -
^(s)____________G2(S) .
ria(s) l+.Oi(s)O2(s) ’
Выражения (8.15) — (8.17) соответствуют передаточным функ-
циям разомкнутой системы,, выходного сигнала в замкнутой
системе и сигнала ошибки в замкнутой системе.
Упр ажнение
Выведите самостоятельно формулы (8.15) — (8.17).
С теоретической точки зрения между системой регулирова-
ния и следящей системой никакой существенной разницы нет;
все зависит в конечном счете от того, что принимается за вы-
ходной сигнал. Так, например, мы относим терморегулятор
к системам регулирования, так как его задача состоит в под-
держании температуры в комнате на заданном уровне, но этот
результат достигается за счет того, что этот механизм приводит
в движение заслонку печи, следуя определенным образом за
флуктуациями температуры в комнате. Поэтому, если за выход-
ной сигнал принять параметр, характеризующий положение за-
слонки, то тот же самый терморегулятор можно рассматривать
144
Глава 8
как следящую систему. На практике термином «следящая
система» нередко пользуются в широком смысле для обозначе-
ния систем и того и другого типа.
8.6. Некоторые замечания
В двух последних разделах были изложены элементарные
принципы классического инженерного подхода к анализу об-
щих систем управления. Такого же рода методы исследования
преобладали в связи с этим и при изучении механизмов управ-
ления в живых организмах. В определенных границах, прису-
щих этому методу (его применимость ограничена тем, что он
может быть использован лишь для линейных систем), такой
подход к изучению физиологических систем оказался весьма
плодотворным. Теперь, однако, будет целесообразно подчерк-
нуть некоторые теоретические аспекты проведенного выше об-
суждения, что позволит, взглянуть на биологические системы
с более общей точки зрения.
Прежде всего нужно отметить, что при изложении нашей
теории мы нигде не рассматривали те специфические физические
процессы, которые описывались изучаемыми уравнениями.
В действительности оказывается, что одни и те же уравнения
пригодны для описания широкого класса (потенциально неогра-
ниченного) различного рода систем, например разнообразных
механических систем, электрических, гидравлических и т. п.
Единственное условие, которому должна удовлетворять для
этого система, состоит в том, чтобы соотношение между ее вход-
ным и выходным сигналами описывалось линейным дифферен-
циальным уравнением вида (8.1). Иными словами, классиче-
ский метод теории управления соответствует высокому уровню
абстрагирования от конкретных свойств физического мира.
Разумеется, такая теория, обладающая столь большой сте-
пенью общности, во многих случаях оказывается крайне полез-
ной. Именно этим объясняется, например, плодотворность при-
менения аналоговых вычислительных машин при исследовании
сложных систем. Аналоговая вычислительная машина — это
в принципе не что иное, как чисто электрическая система, скон-
струированная таким образом, что происходящие в ней про-
цессы описываются таким же уравнением (8.1), какими описы-
вается механическая или гидравлическая система, кбторую по
тем или иным причинам невозможно исследовать, йепосредст-
венно. Теоретически такого рода электрический аналог всегда
может быть построен, и в той мере, в какой речь идет о внеш-
них характеристиках исследуемой системы, т. е. о зависимости
между ее входными и выходными сигналами, можно быть уве-
Связь между входными и выходными сигналами системы
145
ренным, что результаты, полученные при изучении аналога, бу-
дут применимы и к самой моделируемой системе. Аналоговым
устройствам такого рода посвящена обширная и очень инте-
ресная литература ’.
Та общность, которой обладает теория управления, в свою
очередь поднимает новые и важные вопросы теоретической био-
логии. Ведь метод, опирающийся на изучение зависимости
между входными и выходными сигналами, сам по себе не дает
никаких сведений о тех действительных физических процессах,
которые лежат в основе этой зависимости, наблюдаемой у не-
известной нам, быть может, очень сложной системы. Если по-
ложиться лишь на эти грубые математические аналогии, то ме-
тоды теории управления относятся скорее к классам эквивалент-
ных физических устройств (под эквивалентными устройствами
мы понимаем такие, которые удовлетворяют одним и тем же
соотношениям между входными и выходными сигналами), чем
к самим отдельно рассматриваемым устройствам. Поэтому, для
того чтобы на основании результатов теории управления сде-
лать выводы о механизмах работы отдельных систем, нужно
вернуться от этих широких классов к отдельным представите-
лям этих классов; такого рода обращение является весьма слож-
ной проблемой и требует получения новой информации, кото-
рую нельзя извлечь с помощью самих методов теории управ-
ления1 2.
Из того, что методы теории управления не учитывают специ-
фических механизмов изучаемых систем, следует один факт,
который представляет известный самостоятельный интерес. Все
системы регулирования и следящие системы, к какому бы типу
они ни принадлежали, должны получать энергию от некоторого
внешнего источника, которая обеспечивала бы их работу. Вы-
ходным сигналом регулятора в замкнутой системе служит
обычно некоторая сила, действующая непосредственно на
объект управления, и поэтому регулятор непременно должен по-
лучать энергию извне. Правда, в некоторых редких случаях за-
дающий сигнал может служить также и для непосредственного
снабжения системы энергией, но в общем случае такую схему
осуществить невозможно. Существование такого источника энер-
гии никак явно не отражается на уравнениях, описывающих
систему, и поэтому zoh м<?жет быть выбран совершенно произ-
вольно; это создает дополнительную степень произвола в выборе
того типа физических систем, которые могут быть использованы
1 В частности, можно рекомендовать очень удачную книгу Олсона [63].
2 В связи с обсуждаемым здесь вопросом о том, каким образом может
быть получена (хотя бы частично) требуемая дополнительная информация
в пределах некоторого ограниченного класса систем управления, см. разд. 10.4.
146
Глава 8
для представления, или «реализации», некоторой конкретной
системы, описываемой уравнением типа (8.1).
Какие же выводы из всего этого может сделать биолог? Для
биолога основной интерес представляют те специфические ме-
ханизмы, которые лежат в основе изучаемой им физиологиче-
ской функции, а не весь класс эквивалентных механизмов в це-
лом. И если биолог собирается применить какую-то общую
теорию, такую, скажем, как теория систем управления, для об-
щего исследования биологических систем, в его распоряжении
должны быть определенные методы для выбора соответствую-
щих специфических механизмов из того класса механизмов,
к которому относится применяемая теория А для этого необхо-
дим некоторый общий принцип, или критерий, лежащий вне
этой теории.
Принцип оптимальной конструкции как раз и позволяет вы-
работать такой критерий при решении задач управления и регу-
лирования. В технике дело в этой о’бласти обстоит очень просто,
так как технические справочники, используемые инженерами
при конструировании, представляют собой не что иное, как со-
брания критериев выбора, которые можно рассматривать с той
же самой точки зрения, из которой мы исходили в предыдущей
главе при обсуждении естественного отбора. Главная роль прин-
ципа оптимальности в теоретической биологии заключается
именно в том, что он позволяет переходить от самого общего и
абстрактного рассмотрения биологических функций к одному
или нескольким механизмам частного характера, которые реа-
лизуют эти функции оптимальным образом в реальных биологи-
ческих системах.
Для читателя было бы поучительно сравнить по уровню аб-
страктности теорию управления и, скажем, теорию «химической
гетерогонии» Нидхэма (разд. 6.7). В этом пункте можно вновь
отметить контакт с реляционной биологией, о которой мы
раньше упоминали, так как цель реляционной биологии состоит
в том, чтобы систематически исследовать классы биологических
систем, определенные общими реляционными соотношениями, и
выработать методы, позволяющие перейти от этих общих
свойств таких классов к определенным заключениям относитель-
но специфических структур и механизмов, которые мы находим
в конкретных биологических системах. Однако подробное обсу-
ждение этих вопросов уже выходит за рамки задачэтой книги.
Глава 9
НЕКОТОРЫЕ БИОЛОГИЧЕСКИЕ СИСТЕМЫ
УПРАВЛЕНИЯ
9.1. Введение
В гл. 7 мы уже говорили о том, что многие механизмы го-
меостаза в биологических системах представляют собой по су-
ществу системы управления именно в том смысле, в каком эти
термины применялись и развивались в гл. 8. Это означает, что
они содержат один или несколько контуров обратной связи,
с помощью которых система определяет отклонение действи-
тельного ее состояния от требуемого. Другими словами, меха-
низмы гомеостаза, как и технические системы управления, ко-
торые рассматривались в гл. 8, представляют собой по большей
части устройства, управляемые сигналом ошибки, или, как го-
ворят, рассогласованием.
В этой главе мы вкратце рассмотрим некоторые встречаю-
щиеся в живой природе регуляторные механизмы, которые
были исследованы с позиций теории управления или к иссле-
дованию которых можно подойти с этих позиций. Эти резуль-
таты представляют собой первые шаги в изучении той области,
которая обещает стать одним из важных разделов количест-
венной биологии и медицины. К сожалению, имеется ряд факто-
ров, затрудняющих и замедляющих прогресс в этой области;
укажем на некоторые из них.
Прежде всего следует подчеркнуть, что большая часть мето-
дов, рассмотренных в гл. 8, была развита инженерами, которых
в первую очередь интересовали вопросы синтеза систем управ-
ления, предназначенных для выполнения точно определенного
круга задач В технике свойства тех элементов, из которых
должна быть построена требуемая система, хорошо известны,
'и задача инженера состоит обычно в том, чтобы определить
выходной сигнал системы при заданном сигнале на ее входе
или, реже, восстановить форму входного сигнала по результа-
там наблюдения некоторого выходного сигнала. В биологии же
основная проблема имеет совсем другую природу; здесь тре-
буется путем изучения входных и выходных сигналов системы
установить ее структуру л характеристики. При этом возникают
задачи, для решения которых обычные инженерные методы не-
возможно применить непосредственно без серьезных изменений
148
Глава 9
и модификаций. Такое приспособление старых методов к новым
задачам может осуществить лишь исследователь, хорошо зна-
комый как с математическими и инженерными методами, так и
с биологией, а подобная комбинация встречается пока не так
уж часто.
Даже такие биологические системы, при изучении которых
можно использовать более или менее привычные для инже-
нера методы исследования, создают для исследователя ряд
трудностей, вытекающих из собственной природы этих систем.
Наиболее серьезные из них связаны с тем, что большинство
биологических систем выполняет одновременно несколько раз-
личных функций, и поэтому трудно вычленить, как анатомиче-
ски, так и функционально, те части системы, которые инженер
мог бы рассматривать как отдельные компоненты. Вследствие
этого биолог никогда не может быть вполне уверен, что он
правильно учел все входные сигналы, относящиеся к изучаемой
системе, или сумел измерить все ее выходные сигналы. Все это
создает ряд методологических вопросов первостепенной важ-
ности.
Наконец, отметим, что даже в тех ситуациях, при которых
указанные выше трудности удается в определенной мере устра-
нить, механизмы биологического гомеостаза почти всегда ока-
зываются нелинейными. И поэтому для того, чтобы в биологии
можно было использовать изящный математический аппарат
исследования линейных систем, приходится применять различ-
ные методы линейных приближений или обращаться к методам
аналогового моделирования.
Все же, несмотря на все эти трудности, некоторые процессы
регулирования в биологии в настоящее время довольно хорошо
изучены и, как мы далее увидим, ценность результатов, полу-
ченных при этом количественном анализе, с лихвой окупает
затраченные усилия.
1 Кроме тех биологических регуляторных механизмов, о которых мы здесь
расскажем, имеется ряд других регуляторных систем, которые в настоящее
время начинают изучать количественными методами или теория которых до-
статочно созрела для применения таких методов. Можно, например, упомя-
нуть о различных системах с обратной связью, участвующих в гормональной
регуляции, таких, как система регуляции содержания сахара и инсулина
в крови или гипофизарно-щитовидная система (по поводу последней см., на-
пример, [64]). Многочисленные примеры механизмов гомеостазагдает система
кровообращения (о некоторых из них мы уже упоминали раньше). Превос-
ходный обзор многочисленных биологических регуляторных систем был опу-
бликован в 1964 г. [65].
Очень интересный регуляторный механизм, знакомый всем тем, кто про-
ходил хотя бы начальный курс биологии, имеется у растений. Это механизм,
основанный на открывании и закрывании устьиц. Хотя он довольно сложен,
многие его черты в настоящее время объяснены (см„ например, [66]), и сей-
Некоторые биологические системы управления
149*
9.2. Регуляция величины зрачка
Глаз позвоночного дает нам поучительный пример, иллю-
стрирующий особенности природы биологических систем управ-
ления. Функция глаза состоит в том, что он собирает световые
лучи, идущие из внешней среды, и формирует из них соответ-
ствующее изображение на сетчатке; из этого изображения мозг
затем извлекает информацию об окружающей среде. В глазу
человека существует сложная система взаимосвязанных регу-
ляторных механизмов, обеспечивающих в каждый момент вре-
мени такое состояние глаза, при котором изображение на сет-
чатке является «оптимальным».
Одна из таких систем, например, связана с фокусировкой
изображения на сетчатке, что достигается с помощью так на-
зываемого процесса аккомодации. Когда изображение на сет-
чатке дефокусируется, информация об этом передается охва-
тывающей хрусталик цилиарной мышце, которая играет здесь
роль управляющего устройства. Ее сокращение (или расслаб-
ление) изменяет радиус кривизны хрусталика (и, следова-
тельно, его фокусное расстояние) таким образом, чтобы изобра-
жение на сетчатке вновь сфокусировалось. Благодаря аккомо-
дации изображение движущегося объекта держится все время
в фокусе, так что механизм аккомодации можно рассматривать
как следящую систему.
Другая система, действующая в глазу, регулирует количество
света, попадающего на сетчатку. Как известно, любая опти-
ческая система работает наиболее эффективно при некоторой
оптимальной интенсивности света, которая и должна поддержи-
ваться на строго определенном уровне; этот факт известен
каждому фотографу-любителю. В глазу человека имеется не-
сколько механизмов регуляции интенсивности света, падающего
на сетчатку, в том числе механизмы, действующие на уровне
самой сетчатки (например; адаптация к свету и к темноте).
Однако механизмы адаптации играют лишь вспомогательную
час уже можно, по-видимому, подвергнуть этот вопрос количественному ис-
следованию. (Устьица представляют собой также прекрасный пример опти-
мальной формы, и этот вопрос может быть исследован с помощью методов,
развитых в гл. 3. Так, например, исходя из чисто физических соображений,
можно показать, что диффузия газов через поры происходит быстрее и эф-
фективнее, чем через сплошную поверхность раздела, и что у пор существует
оптимальная апертура. Размеры и форма устьиц очень близки к оптимальным.
Более того, при чисто инженерном подходе к этому вопросу становится ясно,
что диффузия будет наиболее эффективной в том случае, когда поры нахо-
дятся на достаточном расстоянии друг от друга, так, чтобы при этом области
диффузии соседних пор не перекрывались; экспериментально можно подтвер-
дить, что устьица размещаются на поверхности листа как раз в соответствии
с результатами этих рассуждений.)
150
Глава 9
роль, и их мы здесь касаться не будем. Наиболее важный и
прямой способ регуляции освещенности сетчатки — это способ,
используемый в фотокамере или в микроскопе; в этих устрой-
ствах для этой цели имеется диафрагма переменной площади,
которая может открываться шире, когда интенсивность падаю-
щего света становится ниже оптимальной, и частично закры-
ваться, когда эта интенсивность превышает оптимальную. Глаз
млекопитающего снабжен аналогичным устройством, характе-
ристики которого мы здесь и рассмотрим.
Вначале изложим вкратце анатомию глаза. В передней части
глаза, непосредственно за прозрачной защитной оболочкой
(роговицей), расположено маленькое круглое отверстие — зра-
чок, через которое свет попадает внутрь глаза. Это отверстие
проходит через центральную часть радужной оболочки — тон-
кой мышечной ткани, имеющей кольцевидную форму. Радуж-
ная оболочка состоит из двух мышц-антагонистов — кольцевой
мышцы (сфинктера), сужающей зрачок, и радиальной мышцы
(дилататора), расширяющей его. Функция этих двух мышц,
составляющих в анатомическом отношении одно целое, регу-
лируется разными нервными цепями. Функцией сф/инктера ве-
дает цепь, замыкающаяся в головном мозгу, и ее компоненты,
относящиеся к парасимпатической нервной системе, родст-
венны тем, которые управляют цилиарной мышцей (при акко-
модации глаза на близко расположенный объект сфинктер дей-
ствительно всегда сокращается). Дилататор же иннервируется
элементами, относящимися к симпатической нервной системе,
Некоторые биологические системы управления
151
центры которой расположены в спинном мозге. Описываемая
структура изображена на фиг. 27.
Обращаясь теперь к физиологии радужной оболочки, мы,
естественно, обнаруживаем, что при высокой интенсивности
света возбуждается сфинктер и зрачок сужается, а при низкой
интенсивности возбуждается дилататор и зрачок расширяется.
Более того, оказываеЛя, что оба глаза тесно связаны; даже если
яркий свет падает лишь на один глаз, сужаются зрачки обоих
глаз (так называемая содружественная реакция). Этот факт
имеет важное значение, так как при изучении механизма регу-
ляции зрачка наблюдают обычно не тот глаз, который возбу-
ждается непосредственно, а содружественную реакцию другого
глаза.
В качестве исходной гипотезы введем сейчас предположение,
что механизм регуляции величины зрачка представляет собой
систему управления, структурная схема которой была изобра-
жена на фиг. 26. Такое допущение будет оправдано далее срав-
нением тех количественных выводов, которые из него вытекают,
с результатами экспериментального наблюдения работы этой
системы. «Уставкой», т. е. требуемым значением регулируемой
величины, служит здесь оптимальная интенсивность света, па-
дающего на сетчатку, входным сигналом — интенсивность света
во внешней среде и сигналом ошибки — разность между этими
двумя величинами. Система управления состоит из кольцевой
и радиальной мышц радужной оболочки и нервных цепей, регу-
лирующих их функцию. Назначение системы — изменять пло-
щадь зрачка таким образом, чтобы уменьшилась величина сиг-
нала ошибки.
Далее, учтем, что выходным сигналом регулятора является
площадь зрачка, которую можно считать прямо пропорцио-
нальной интенсивности света, падающего на сетчатку. Таким
образом, в норме, т.’ е. при замкнутом контуре обратной связи,
выходные сигналы регулятора и объекта управления могут быть
сделаны здесь численно равными, если выбрать подходящим
образом единицы измерения. Поэтому передаточную функцию
объекта управления в этой системе можно принять равной еди-
нице.
Теперь попробуем написать выражение для передаточной
функции всей системы регулирования в целом. Если полную
передаточную функцию разомкнутой системы обозначить Здесь
через G0(s), то, согласно формуле (8.16), передаточная функ-
ция замкнутой системы, которую мы здесь обозначим через
Gc(s), запишется в виде
<91>
152
Глава 9
(поскольку передаточная функция объекта управления равна
единице). Чрезвычайно удачно здесь то, что передаточную
функцию Go(s) можно непосредственно определить опытным
путем. Численные результаты экспериментов, проведенных Стар-
ком и его сотрудниками, позволили получить прямую количе-
ственную информацию о коэффициенте усиления и о фазовых
соотношениях для системы управления Зрачком в условиях,
когда контур обратной связи был разомкнут. Для этого на глаз
направляли узкий пучок света столь малого диаметра, что со-
кращение зрачка не могло влиять на интенсивность света, по-
падающего в глаз. На основании полученных данных была
вычислена передаточная функция G0(s) [67—69]:
0,1б5~°-Ш
Oo(s)~ (1 +o,ls)3 •
Отсюда, используя формулу (9.1), можно получить выражение
для передаточной функции, характеризующей работу всей
системы в целом.
Имея в своем распоряжении передаточную функцию Gc(s),
можно теоретически предсказать ряд эффектов и проверить ис-
ходную гипотезу с помощью экспериментальных наблюдений.
Таким образом удалось подтвердить, что существенной чертой
этой системы является малая величина коэффициента усиления,
и поэтому ей присуща устойчивость. Были выполнены вычисле-
ния, которые показали, что если коэффициент усиления увели-
чится на некоторую определенную величину, то должна возник-
нуть неустойчивость, выражающаяся в появлении колебаний,
причем частота таких колебаний может быть определена теоре-
тически. Наличие высокого коэффициента усиления означает по
определению, что малое изменение выходного сигнала регуля-
тора вызывает большие изменения выходного сигнала объекта
управления. Ситуация, соответствующая случаю высокого ко-
эффициента усиления, изображена схематически на фиг. 28.
Было действительно обнаружено, что при таких условиях в си-
стеме самопроизвольно возникают колебания и частота их очень
близка к расчетной [70, 71].
Каково значение этих результатов для дальнейших биологи-
ческих и медицинских исследований? Вполне очевидно, что сле-
дующий шаг должен состоять в том, чтобы на основании дан-
ных анатомии и физиологии идентифицировать компоненты
структурной схемы рассмотренного регулятора с\теми реаль-
ными биологическими структурами, которые действительно
участвуют в механизме регуляции величины зрачка. Эта задача
разрешима, ибо передаточная функция системы (в норме) из-
вестна, причем можно представить себе несколько путей ее ре-
Некоторые биологические системы управления 153
шения. Например, известно, что некоторые лекарственные пре-
параты сильно действуют на определенные компоненты этой
системы, что приводит к соответствующим количественным из-
менениям передаточной функции. Такие эффекты можно исполь-
зовать, с одной стороны, для исследования соотношений между
реальной анатомией системы и ее теоретической структурной
схемой и, с другой стороны, для количественного определения
биологических эффектов, вызываемых такими препаратами.
Далее, исследуя модельную систему управления, можно изучить
с количественной стороны различные патологические состояния
глаза. Известно, например [72], что если у человека, страдаю-
щего множественным склерозом, механизм регуляции величины
зрачка приводится в неустойчивое состояние (при помощи опи-
санного выше эксперимента с узким световым пучком), то ча-
стота колебаний зрачка будет отличаться от нормальной. Это
можно интерпретировать как изменение параметров системы,
-вызванное патологическими изменениями в самих нервных пу-
тях. Можно поэтому рассчитывать, что удастся количественно
исследовать такие изменения с помощью количественного ана-
лиза системы управления зрачком, используя как передаточ-
ную функцию, так и действительные данные анатомии и физио-
логии. Можно представить себе множество других способов
использования результатов такого анализа для проникновения
в сущность биологических и медицинских проблем, связанных
с этой регуляторной системой.
Не должно, однако, создаваться впечатление, что механизм
регуляции величины зрачка уже полностью изучен. Обсуждав-
шаяся нами выше модель является довольно грубым линейным
приближением к реальной системе; по поводу конкретной при-
роды и численных характеристик этого приближения мы отсы-
лаем читателя к оригинальным работам Старка и его сотруд-
ников [67—71]. Далее, как уже было ранее отмечено, регуляция
величины зрачка — это лишь один из нескольких способов,
посредством которых глаз регулирует интенсивность света,
154
Глава 9
падающего на сетчатку. И обратно, этот механизм играет также
определенную роль в других регуляторных процессах, происхо-
дящих в глазу, например в аккомодации. Таким образом,
центральная проблема идентификации тех анатомических струк-
тур, которые воплощают компоненты рассматриваемой системы
управления, все еще представляет большие трудности для реше-
ния (если вообще эта задача может быть до конца решена).
Тем не менее важно отметить, что, несмотря на грубость тех
гипотез, которые были привлечены в описанном нами исследо-
вании, оно дало возможность извлечь много ценной информации.
9.3. Терморегуляция
Для выживания любого организма необходимо, чтобы интен-
сивность метаболических процессов поддерживалась на некото-
ром определенном уровне. Но биохимические реакции весьма
чувствительны к температуре, что объясняется двумя основными
причинами. Во-первых, как и у всех химических реакций, их
скорость строго зависит от температуры *, и поэтому даже при
умеренном понижении температуры скорости важных биохими-
ческих процессов могут упасть ниже уровней, необходимых для
жизнедеятельности организма. Во-вторых, для многих биохими-
ческих реакций организма существенное значение имеет целост-
ность некоторых упорядоченных химических структур, сравни-
тельно мало устойчивых к колебаниям температуры. Так,
многие белки даже при умеренном нагревании теряют свою
биологически активную конформацию (т. е. денатурируют);
например, активность важного пищеварительного фермента
трипсина при температуре всего 45° (нормальная температура
тела равна 37°) понижается более чем на 50% в результате
денатурации. Поэтому многие организмы могут существовать
лишь в довольно узком диапазоне температур, в пределах кото-
рого возможно поддержание нужного уровня биологической
активности.
По своей способности регулировать температуру тела позво-
ночные делятся на две группы. У так называемых пойкилотерм-
ных, или холоднокровных, животных (рыб, земноводных и
пресмыкающихся) температура тела следует за температурой
окружающей среды. Поэтому при низкой температуре среды они
1 Некоторое время назад интенсивно разрабатывалась теория, согласно
которой регуляция температуры осуществляется посредством регуляции ско-
ростей реакций в многоступенчатых химических процессах, в основе этой тео-
рии лежало представление Крозье о «главной реакции» (см. [73], гл. 8,
стр. 200—214).
Некоторые биологические системы управления
155
становятся вялыми и малоподвижными, а при повышении тем-
пературы наблюдается обратная картина. Такие животные вы-
нуждены избегать пребывания в среде, где они в течение дли-
тельного времени оказываются подверженными действию очень
высокой или очень низкой температуры, и поэтому они обитают
преимущественно в умеренном и тропическом климатах. В отли-
чие от них птицы и млекопитающие обладают способностью
поддерживать свою внутреннюю температуру на некотором
постоянном уровне в широком диапазоне температур внешней
среды; их называют гомойотермными, или теплокровными,
животными. В этом разделе мы рассмотрим механизмы термо-
регуляции у гомойотермных организмов, опираясь в основном
на работы Бензигера и его сотрудников (74—76].
Вполне бчевидно, что механизм терморегуляции у гомойо-
термных животных должен быть значительно сложнее упоми-
навшихся нами простых терморегуляторов, сконструированных
для регулирования внутренней температуры помещений. Про-
стой терморегулятор, например, реагирует на повышение
внутренней температуры тем, что он уменьшает соответственным
образом интенсивность горения (ограничивая, скажем, доступ
воздуха в топку), и чем выше внутренняя температура, тем
сильнее уменьшается интенсивность горения. Для гомойотерм-
ных организмов такой вид регуляции неприемлем. Для них
источником тепла служит определенная система биохимических
реакций, непрерывное протекание которых жизненно необходимо
для организма, и если они будут подавлены, то само существо-
вание терморегуляторного механизма потеряет смысл. В орга-
низмах скорее следовало бы искать что-то похожее на откры-
вающееся окно, т. е. механизм, непосредственно удаляющий из
системы тепло со скоростью, превосходящей скорость тепло-
образования.
Рассмотрим теперь вкратце различные явления, связанные
с терморегуляцией у млекопитающих. Из того, что было сказано
ранее, следует, что должны существовать два типа таких явле-
ний: для сохранения тепла в условиях холодной среды и для
удаления лишнего тепла в условиях теплой среды. К первому
типу относится хорошо известное явление мышечной дрожи,
которое вызывает локальное повышение метаболической актив-
ности и тем самым приводит к выделению тепла, а также реф-
лекс, известный под названием «гусиная кожа», назначение
которого у животных с шерстным покровом состоит в том, чтобы
приподнять волоски теплоизолирующего слоя (подшерстка).
Наиболее известное из явлений второго типа — это потоотделе-
ние, увеличивающее теплоотдачу посредством испарения; другое
явление того же типа — расширение кровеносных сосудов кожи,
156
Глава 9
способствующее усилению притока крови к поверхности тела и,
следовательно, также увеличивающее теплоотдачу.
Таким образом, в системе терморегуляции у млекопитающих
имеется целый ряд исполнительных устройств. В. настоящее
время наиболее хорошо изучено потоотделение и его зависи-
мость от температуры внешней среды; поэтому в дальнейших
рассуждениях мы для простоты будем считать, что в системе
терморегуляции действует один этот механизм. С точки зрения
теории систем управления можно теперь поставить следующие
вопросы: 1) Что служит входным сигналом для этой системы?
2) Что здесь играет роль управляющего сигнала? 3) Что является
выходным сигналом?
Вначале обсудим природу входного сигнала, который 'соот-
ветствует, конечно, величине т]<г($) на фиг. 26. В течение многих
лет предполагалось, что этот входной сигнал контролируется
миллионами тепловых и холодовых терморецепторов, находя-
щихся в коже, и что тем самым именно температура поверхности
тела определяет интенсивность потоотделения. Но, как заметил
Бензигер, это соответствовало бы тому, что терморегулятор,
предназначенный для регулирования температуры в помещении,
получал бы входные сигналы только от многочисленных термо-
метров, расположенных снаружи. И действительно, эксперимен-
тальные исследования, проведенные недавно с помощью новых
методов, показали, что входной сигнал в этом процессе форми-
руется внутри организма в области гипоталамуса, расположен-
ной в основании головного мозга. Было также установлено, что
гипоталамус осуществляет непосредственную нервную регуля-
цию функции потовых желез, т. е. его выходной сигнал (сигнал
.ошибки) регулирует интенсивность потоотделения. Таким обра-
зом, гипоталамус — это не просто совокупность пассивных про-
водящих путей; он включает в себя целую регуляторную систему,
входящую в механизм терморегуляции, или, во всяком случае,
те его элементы, которые непосредственно относятся к процессу
потоотделения.
Объектом управления служат сами-потовые железы, которые
воспринимают импульсы, исходящие из гипоталамуса, как си-
гналы, определяющие уровень их активности, т. е. скорость
выделения пота. Можно считать, что эта скорость непосред-
ственно- определяет общую степень охлаждения тела за счет
испарения (следует, правда, помнить, что частично интенсив-
ность испарения зависит и от параметров окружающей среды,
например от влажности). В результате охлаждения изменяется
температура и самого гипоталамуса, и цепь обратной связи
оказывается таким образом замкнутой.
Некоторые биологические системы управления
157
Наиболее важная часть этого исследования терморегуляции
еще впереди: нужно построить передаточные функции регуля-
тора и объекта управления и выяснить механизм, с помощью
которого формируется заданное значение регулируемой вели-
чины (уставка). Такие исследования только еще начались, но
они вполне перспективны. Знание этих передаточных функций
позволило бы, например, проникнуть в природу действия некото-
рых бактериальных токсинов, вызывающих повышение темпера-
туры тела, и определить место приложения их действия (одно из
наиболее правдоподобных предположений на этот счет, прини-
маемых в данное время, состоит в том, что эти токсины каким-то
образом сдвигают «уставку» в системе терморегуляции). При
изучении этих передаточных функций могут также проясниться
такие проблемы, как вопросы эволюции механизмов терморегу-
ляции у гомойотермных животных, но это уже задачи будущих
исследований.
Из сказанного выше можно было бы вывести заключение,
что функция потовых желез находится под контролем одного
только гипоталамуса и что кожные терморецепторы никакой
роли здесь не играют. В определенных пределах это, по-види-
мому, верно, но следует указать, что существуют ситуации,
в которых эти рецепторы играют большую роль в терморегуля-
ции, чем гипоталамус. Так, было показано, что при охлаждении
кожи ниже определенного порога потоотделение может быть
заторможено независимо от температуры гипоталамуса. Наблю-
дения такого рода свидетельствуют о том, что у гомойотермных
животных вся система терморегуляции в целом весьма сложна.
И наконец, уместно будет сказать, что, как указывает Бензи-
гер, гипоталамус и сетчатка весьма тесно связаны в морфоге-
нетическом смысле. Не исключено, что этот факт является всего
лишь простым совпадением, но, с другой стороны, он указывает,
возможно, на какую-то существенную взаимосвязь между этими
на первый взгляд совершенно различными системами. Это сооб-
ражение также может., послужить стимулом к дальнейшим
исследованиям в области биологических систем управления и
их математического описания.
9.4. Дыхательный хемостат
Благодаря работам Грея [77], Гродинза [78], Дефара [79] и
других исследователей механизмы гомеостаза, участвующие
в регуляции дыхания у человека, подвергнуты значительно бо-
лее полному математическому анализу, чем все другие биологи-
ческие системы управления. Конечно, нельзя утверждать, что
все проблемы регуляции дыхания в основном уже решены; это,
58
Глава 9
естественно, не так. Но теория регуляции дыхания развита уже
до такой степени, что все ее многочисленные ценные достижения
и некоторые слабые стороны видны вполне отчетливо. Мы рас-
смотрим здесь эти проблемы крайне бегло и за более подроб-
ными сведениями отсылаем читателя к оригинальной литературе.
Известно, что если напряжение углекислого газа в крови
поднимается выше «нормального» уровня (при физической на-
грузке или при вдыхании воздуха с высокой концентрацией СОг),
то частота дыхания (вентиляция) возрастает, и в результате
этой гипервентиляции напряжение СОг в крови вновь понижа-
ется. И обратно, если при намеренной гипервентиляции напря-
жение СОг в крови падает ниже нормального уровня, то это
приводит к замедлению дыхания, вследствие чего напряжение
СОг в крови вновь повышается. Будем считать, что напряжение
СОг в крови представляет собой регулируемую величину в про-
стой системе регулирования, структурная схема которой была
изображена на фиг. 26. Выходным сигналом управляющего
устройства будет тогда степень вентиляции, а возмущающим
воздействием — парциальное давление СО2 во вдыхаемом воз-
духе.
В общих чертах биологическая система, о которой идет речь,
схематически изображена на фиг. 29, частично заимствованной
из книги Гродинза [78].
Эта модель представляет собой типичный прймер идеализа-
ции, к которой часто прибегают при математическом исследова-
нии физиологических систем. Тело здесь попросту разделено на
Некоторые биологические системы управления
159
два «отсека», из которых один представляет легкие, а второй —
всю остальную часть тела. Оба эти отсека рассматриваются
просто как два функционально различных резервуара для газов,
содержащих СОг, и в остальных отношениях лишены какой-либо
внутренней структуры. Надо подчеркнуть, что эта идеализация
проводится только в функциональном, а не в анатомическом
•отношении, так-что, например, сама легочная ткань, в которой,
как и во всех других тканях, происходят метаболические про-
цессы, относится, согласно данной модели, не к легочному,
а к тканевому резервуару. Эти два резервуара связаны между
собой двумя сосудами, один из которых представляет в целом
всю артериальную кровеносную систему (т. е. все те функцио-
нальные элементы, которые участвуют в переносе крови от лег-
ких к другим тканям), а второй —всю венозную систему (кото-
рая переносит кровь обратно из тканей в сердце и легкие). Хотя
рассмотрение организма как системы, состоящей из двух «отсе-
ков», может показаться весьма упрощенным, оно тем не менее
позволяет учесть все существенные детали, относящиеся к про-
блеме регуляции дыхания, и позволяет отвлечься от подробно-
стей, не имеющих к ней прямого отношения.
Легочный и тканевой резервуары вместе с соединяющими их
сосудами представляют собой объект управления и вначале
рассматриваются изолированно от остальной части системы.
Для облегчения математического исследования вводится ряд
упрощающих предположений, но здесь мы отметим лишь не-
которые из них:
1. Легочный и'тканевой резервуары имеют постоянные объ-
емы Ка и Кт соответственно.
2. СОг поступает в легкие с вдыхаемым воздухом со скоро-
стью VaF, где УЛ — скорость вентиляции и F—концентрация
СОг во вдыхаемом воздухе. Кроме того, СОг поступает в легоч-
ный резервуар с венозной кровью со скоростью 73.
3. СО2 удаляется из легких с выдыхаемым воздухом (со
скоростью 71) и с артериальной кровью (со скоростью q2)-
4. СО2 поступает в тканевой резервуар, образуясь в про-
цессе обмена (со скоростью М), а также с артериальной кровью
(со скоростью 72). СОг удаляется из тканевого резервуара ве-
нозной кровью со скоростью 7з.
Пусть теперь 0л, 0т обозначают соответственно концентра-
ции СОг в легочном и тканевом резервуарах. Тогда результи-
рующие скорости изменения,концентрации СОг в легких и в тка-
нях можно записать в следующем виде:
1 (уАК -W3 - 7i - ?2) (9.2)
dt Ка
160
Глава 9
И
(9.3)
Соотношения, выражающие qt, q2 и q2 через 0л, 0т и различные
другие параметры, можно найти из условий равновесия для по-
токов СО2. Например, при равновесии
= (9.4)
и
0rC — q?j, (9.5)
где С — минутный объем сердца (см. разд. 3.7). Наконец, еще
одно условие равновесия выражается уравнением
q2=C&A + CS, (9.6)
где R и S — постоянные, связанные с характеристиками про-
цесса поглощения СО2.
Следуя Гродинзу, будем рассматривать концентрации 0д, 0т
как выходные сигналы объекта управления, а за входной сигнал
(возмущающее воздействие) примем Прочие параметры,
такие, как VA, считаются постоянными. Подставляя выражения
(9.4) — (9.6) в (9.2) и (9.3) и исключая 0Г из первого уравнения,
полученного в результате подстановки, и 0а — из второго, мы
приходим к следующей системе уравнений:
(9.7)
(9.8)
Это и есть система уравнений объекта управления, аналогичных
(8.1). При конкретном выборе формы F (скайсем, в виде сту-
пенчатой функции или единичного импульса) можно решить эти
уравнения и получить передаточную функцию\цдя_ изолирован-
ного объекта управления. Можно отметить, что объект управле-
ния, рассматриваемый изолированно, вполне линеен.
Некоторые биологические системы управления
161
Как уже было отмечено, в приведенном выше выводе ско-
рость вентиляции VA предполагалась постоянной. Если провести
все прежние рассуждения, но предположить, что величина F
постоянна, a VA является функцией t, то уравнение (9.8)-оста-
нется справедливым, а (9.7) нужно заменить значительно более
сложным уравнением. Не выписывая его, укажем, что, хотя
зависимость величины VA от t непосредственно не отражается
на линейном характере объекта управления, коэффициенты
дифференциальных уравнений уже не будут постоянными. По-
этому те методы исследования, которые развивались раньше,
в принципе будут пригодны и для этого случая, но потребуется
несколько модифицировать их применительно к этой более об-
щей ситуации.
Обратимся теперь к фиг. 29 и рассмотрим объект управления
совместно с управляющим устройством, или регулятором. Мы
видим, что VA является выходным сигналом регулятора, а 0т
подается к регулятору по каналу обратной связи и служит,
таким образом, его входным сигналом. Следовательно, в замкну-
той системе V А должно (быть выражено как функция 0Г. При
подстановке полученного выражения для VA в (9.7) это уравне-
ние станет нелинейным. Здесь мы вновь встречаемся с «пара-
метрической обратной связью», о которой уже упоминалось
раньше; это понятие будет более подробно рассмотрено
в разд. 11.1.
Уравнение, описывающее работу самого регулятора, запи-
сывается совсем просто:
vA=k(or — e°} + k',
где k и k' — константы, 6^ — уставка. Таким образом, объект
управления и регулятор, если их рассматривать изолированно
друг от друга, вполне линейны (хотя уравнение для объекта
управления может иметь переменные коэффициенты). Раздель-
ное изучение этих двух систем дает возможность получить очень
ценную информацию о механизме регуляции дыхания; по этому
поводу мы отошлем читателя к цитированной оригинальной
литературе.
В заключение рассмотрим систему, которая построена по
схеме, аналогичной фиг. 29, но регулируется другим способом:
в ответ на возрастание F выходной сигнал регулятора вызывает
не увеличение VA, а уменьшение коэффициента R. Такую си-
стему удается полностью описать в линейных терминах, и это
позволяет избежать всех математических трудностей, относя-
щихся к нелинейным системам и к уравнениям с переменными
коэффициентами. Но реальное осуществление такой системы
162
Глава 9
в живой природе невозможно. Мы сталкиваемся здесь с обстоя-
тельством, аналогичным тому, о котором мы говорили, когда
сравнивали механизм терморегуляции у гомойотермных живот-
ных с действием простого технического терморегулятора: ком-
пенсация сравнительно кратковременных изменений во внешней
среде не может производиться за счет понижения общей интен-
сивности обмена.
Конечно, кратко описанные выше методы могут быть улуч-
шены. Можно также освободиться от ряда упрощающих, но до-
вольно произвольных допущений, которые были неявно сделаны
в приведенном выше исследовании [79]. Следует, кроме того,
указать, что механизм регуляции напряжения СО2 в крови
тесно связан с другими регуляторными механизмами, особенно
с теми, которые регулируют напряжение кислорода и величину
pH; в работе Гродинза эти последние процессы по существу не
учитывались. Тем не менее ясно, что важнейшие основы здесь
заложены и что проведенное математическое исследование дыха-
тельного хемостата может служить моделью для изучения дру-
гих биологических регуляторных механизмов, управляемых
рассогласованием.
9.5. Регулирование химических реакций в клетке
Процесс обмена в организме слагается из многих тысяч
координированных химических реакций, непрерывно протекаю-
щих в клетках. Для выживания организма необходимо, чтобы
все эти реакции были строго согласованы между собой, и по-
этому не удивительно, что в большинстве клеток имеется мно-
жество эффективных механизмов регулирования скоростей
реакций. Назначение этих регуляторных механизмов может быть
двояким: одни из них служат для поддержания гомеостаза
внутри клеток, а другие регулируют определенные изменения
активности клеток (например, в случае дифференцировки клеток
у высших организмов). В этом разделе мы обратимся в основ-
ном к механизмам, осуществляющим первую функцию, а к во-
просу о механизмах, связанных с клеточной дифференцировкой,
вернемся в гл. 11.
Реакции, происходящие в клетках, характеризуются несколь-
кими особыми свойствами. Их первая и наиболее важная отли-
чительная черта состоит в том, что большинство из них проте-
кает лишь в присутствии высокоспецифичных органических
катализаторов, называемых ферментами. Утверждение, что
«фермент Е катализирует превращение вещества А в вещество
В», записывают сокращенно в виде
А—-В.
Некоторые биологические системы управления
163
Выражение «специфичный» означает, что каждый фермент ка-
тализирует лишь те реакции, в которых принимает участие
некоторый строго ограниченный класс вещества А; каждое такое
вещество называется субстратом данного фермента. Для мета-
болической . активности большинства клеток требуются тысячи
различных ферментов; по существу, метаболическая активность
любой клетки определяется природой и концентрацией тех фер-
ментов, которые в ней присутствуют. В настоящее время счи-
тают, что функция генов, или наследственного материала клетки,
сводится именно к синтезу специфических ферментов.
Один из возможных способов регулирования клеточных хи-
мических реакций заключается в регулировании скорости фер-
ментативных реакций. Это приводит нас ко второй особенности
реакций, происходящих в клетках. Очень часто они объединя-
ются в длинные последовательности, или цепи, вида
Ао^-->аЛ-А2-^->...^А„, '
в которых продукт одной реакции становится субстратом для
следующей. Отдельные последовательности взаимосвязанных
химических реакций принято обозначать термином метаболиче-
ский путь. Далее мы будем рассматривать такие метаболические
пути, которые заканчиваются синтезом некоторого важного
«етаболита, например аминокислоты. Что касается количествен-
ых соотношений, то ясно, что скорость образования конечного
продукта какого-либо метаболического пути может регулиро-
ваться за счет изменения активности любого из ферментов Еь
Ег, ... данного пути '. Но поскольку на каждую из этих реакций
затрачивается определенное количество энергии, наиболее эко-
номной с энергетической точки зрения является регуляция, осу-
ществляемая за счет первого фермента Еь
Это приводит нас к первому механизму химической регуля-
ции — так называемому торможению конечным продуктом, или
ретроингибированию. В этом случае конечный продукт Ап обра-
зует с ферментом Ei комплекс (AnEi), неспособный катализи-
ровать реакцию А0->Аь Другими словами, Ап служит ингиби-
тором для Еь
1 Опубликовано много превосходных обзоров, посвященных биологическим
аспектам механизмов индукции, торможения и репрессии; мы укажем лишь
иа статью Уилсона и Парди [80], а также на статью Умбаргера в книге «Ре-
гуляторные механизмы клетки» [81] (в этой книге имеется много важных
статей, посвященных регуляторным механизмам на молекулярном уровне, и
мы настоятельно рекомендуем ее тем, кто желает получить дальнейшую ин-
формацию по этой активно развивающейся отрасли совремеииой молекуляр-
ной биологии)
164
Глава 9
Легко понять значение этого механизма для клетки. Если
Ап — какой-нибудь важный, метаболит (например, одна из
аминокислот), то для непрерывного течения метаболического
процесса количество Ап в клетке должно все время поддержи-
ваться на некотором определенном уровне. Следовательно, син-
тез А„ должен быть отрегулирован таким образом, чтобы коли-
чество Ап было всегда достаточным для удовлетворения мета-
болических потребностей клетки, но при этом не было слишком
большим. А для этого нужно, чтобы скорость синтеза Ап в ка-
ждый момент времени зависела от содержания Ап в клетке
в этот момент, причем эти величины должны быть связаны об-
ратной зависимостью: чем больше содержание Ап (или, что то
же самое, чем медленнее Ап поглощается в процессе метабо-
лизма), тем ниже должна быть скорость синтеза Ап. Таким
образом, механизм регуляции синтеза, основанный на ретро-
ингибировании, представляет собой классическую систему регу-
лирования’с обратной связью, в которой объектом управления
служит скорость образования Аа и уставкой — определенное
оптимальное содержание Ап. Используя известные математиче-
ские методы кинетики ферментов ', можно вывестй дифферен-
циальные уравнения, описывающие процесс торможения конеч-
ным продуктом; для некоторых случаев такой вывод действи-
тельно был проделан. Но даже для сравнительно простых
систем получающиеся уравнения оказываются очень сложными
и, почти неизбежно, нелинейными, так что применение изложен-
ной ранее линейной теории встречается с большими трудностями.
Поэтому здесь нет необходимости более подробно останавли-
ваться на математическом описании процессов торможения
конечным продуктом, и мы отметим лишь, что применение мето-
дов моделирования на вычислительных машинах позволило
сделать ряд интересных выводов относительно этих механизмов.
Обратимся теперь к рассмотрению еще одного механизма
химической регуляции и предположим, что некоторый метабо-
лический путь блокирован вследствие большого избытка мета-
болита Ап (пусть, например, среда, в которой развивается
клетка, содержит большое количество Ап, так что клетка не
нуждается в синтезе этого метаболита). Ясно, что в этих усло-
виях дальнейший синтез ферментов Ei, Е2, ..., Еп также стано-
вится ненужным. Поэтому для клетки было бы энергетически вы-
годно, если бы синтез этих ферментов (скажем, синтез фер-
мента Е]) регулировался концентрацией Ап аналогично тому,
1 Изучение кинетики ферментативных реакций, элементарное в математи-
ческом отношении, представляет собой очень важный метод биологических
исследований. Доступное изложение вопросов кинетики^фермеитов можно
найти в обзоре Рейнера [82].
Некоторые биологические системы управления
165
как регулируется активность фермента Ер Такое явление наблю-
дается во многих клеточных системах — это так называемая
репрессия конечным продуктом. Механизм, с помощью которого
осуществляется эта репрессия, по-видимому, довольно сложен,
и в последнее время он служил предметом многочисленных
дискуссий '. Как уже было указано, в настоящее время считают,
что синтез ферментов находится под прямым генетическим
контролем, и в явлении репрессии участвуют, по-видимому, не-
посредственно сами гены.
Торможение и репрессию ферментов какого-либо метаболи-
ческого пути могут, разумеется, вызывать и продукты других
метаболических путей. Многие бактерии, например, способны
использовать в качестве источников энергии различные виды
сахаров. Для того чтобы ввести тот или иной Сахар в клетку
и осуществить серию обменных превращений, ведущих к глав-
ным этапам, на которых происходит выделение энергии, тре-
буется особый набор ферментов. Если в среде имеется лишь
один вид сахара Sj, то клетка перестает нуждаться в фермен-
тах, катализирующих отдельные этапы обмена других сахаров,
и встречаются случаи, когда продукты обмена Si обладают спо-
собностью подавлять или репрессировать ферменты, катализи-
рующие превращения других видов сахара.
Это приводит нас еще к одному, последнему, но Ьчень
важному регуляторному механизму, который обычно называют
индфщией ферментов (пожалуй, лучше называть его дерепрес-
сией). В некоторых случаях субстрат какого-либо фермента
(или какое-то вещество, специфически связанное с этим субстра-
том) способен «индуцировать» синтез другого фермента, кото-
рый раньше в клетке не синтезировался. Если предположить,
что отсутствие синтеза некоторого фермента в клетке, которая
при других условиях способна осуществлять этот-синтез, вызы-
вается репрессией (при участии конечного продукта или какого-
либо иного механизма), то ясно, что один из способов индуци-
ровать этот фермент состоит в удалении репрессора. Экспери-
мент показывает, что такое явление действительно встречается;
индуктор обладает способностью противодействовать влиянию
репрессора и таким образом осуществляет дерепрессию данного
фермента. Допустим, например, что бактериальная клетка росла
на среде, содержащей лишь глюкозу; тогда ферменты, катали-
зирующие превращения галактозы, будут в ней репрессированы.
Если теперь поместить клетку в среду, содержащую галактозу,
1 Обсуждение различных точек зрения на механизм репрессии можно
найти в книге «Регуляторные механизмы клетки» [81] (особенно интересны
статьи Жакоба и Моно и Магасаиика).
166
Глава 9
то окажется, что галактоза вызывает дерепрессию ферментов
того метаболического пути, на котором она сама подвергается
обменным превращениям; таким образом, галактоза действует
как индуктор ферментов «галактозного пути», ранее в клетке
отсутствовавших. Следовательно, индукция и репрессия — это
две стороны одного и того же регуляторного механизма.
В механизмах репрессии объектом управления является
скорость синтеза фермента, а уставка определяется оптимальной
концентрацией метаболита А„ (случай «репрессии конечным
продуктом»). Проводя те же рассуждения, что и раньше, можно
выписать выражения для передаточных функций этих механиз-
мов; поскольку, однако, детали взаимодействия репрессора
с генетической единицей (называемой обычно опероном), обеспе-
чивающей регуляцию синтеза фермента, в настоящее время еще
не ясны, можно представить себе целый ряд возможных меха-
низмов такого рода. Надо надеяться, что такие исследования
прольют свет на действительную природу взаимодействия
репрессора и оперона; во всяком случае, они, вероятно, помогут
создать некоторые модельные системы, удобные для прямого
изучения В настоящее время уже выполнен ряд исследований 1
по моделированию на аналоговых и цифровых вычислительных
машинах таких систем, в которых регуляция осуществляется на
основе индукции и репрессии.
Жакоб и Моно2, а также ряд других исследователей пола-
гают, что, исходя из репрессии и индукции как средства регуля-
ции различных метаболических путей, вполне можно объяснить
дифференцировку клеток в процессе онтогенеза у многоклеточ-
ных организмов. Биологи долгое время не могли объяснить,
почему клетки одного и того же организма, происходящие от
одной и той же родительской клетки, столь сильно различаются
между собой; действительно, нельзя найти почти ничего общего
между клетками желез, клетками мышечной ткани и нервными
клетками. Жакоб и Моно предположили, что соответствующие
последовательности процессов репрессии и индукции ферментов
в клетках, происходящих от одной оплодотворенной яйцеклетки,
могут1 объяснить эти различия.
1 См , например, [83, 84]. Читатель может обратиться также к серин ста-
тей Чанса и его сотрудников; краткий обзор и дальнейшие ссылки на лите-
ратуру можно найти в статье Чанса [85] Можно заметить, кстати, что модели,
построенные при исследовании регуляции ферментативных реакций, оказались
применимыми и к регуляции размеров популяций в экологических системах
хищник — жертва [86]
2 См, например, [126], стр 397 и далее Надо указать, что результаты
самых последних работ, посвященных процессу дифференцировки, делают из-
ложенную выше простую схему Жакоба и Моно менее привлекательной в ка-
честве модели дифференцировки у высших организмов.
Некоторые биологические системы управления
167
Посмотрим, например, на фиг. 30, где схематически изобра-
жена одна из гипотез, предложенных этими авторами. Здесь Si,
S2 — начальные субстраты ферментов Eiy Е2 соответственно,
а конечными продуктами являются Рь Р2. Пунктиром а.\Ь2 отме-
чено, что продукт Pi тормозит реакцию S2^-P2, а пунктиром
a26i — что продукт Р2 тормозит реакцию S! Рь Контур обрат-
ной связи PiC^E] означает, что Pi служит индуктором для Е\ и
в результате существования связи" а.]Ь2 действует как репрессор
на Е2. Точно так же Р2 является индуктором для Е2 и репрессо-
ром для Еь Нетрудно заметить, что в этой системе сначала
Фиг. 30
будут идти обе реакции, но в конце концов, в зависимости от
каких-то локальных флуктуаций, начнет вырабатываться один,
И ТОЛЬКО ОДИН, ИЗ ВОЗМОЖНЫХ продуктов Р1, Р2. Если взять вто-
рую такую же систему, то она может «сработать» иначе, и эти
две системы представляются нам «дифференцированными» в от-
ношении их выходных реакций на входные сигналы.
В цитированной работе Жакоба и Лоно обсуждаются также
и другие гипотетические системы, в которых могут идти про-
цессы, напоминающие дифференцировку, и все они построены
целиком на тех регуляторных механизмах, о которых мы гово-
рили выше. Схемы, весьма сходные с фиг. 30, мы рассмотрим
в совсем другой связи в разд. 11.3рассмотренные здесь модели
регулирования оказываются вполне эквивалентными моделям
обучения и адаптации, предложенным Ландалем и другими бо-
лее 30 лет назад.
1 См. в особенности примечание на стр. 192 в гл. 11.
Глава 10
ДИНАМИЧЕСКИЕ СИСТЕМЫ И ТЕОРИЯ
ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
10.1. Введение
В гл. 8 и 9 был проведен обзор основных методов теории
управления, относящихся к анализу зависимости между вход-
ными и выходными сигналами, и их приложений к широкому
классу систем, представляющих интерес для физики и биологии.
Было уже отмечено, что математические методы, использован-
ные при развитии этого аппарата, отличны от тех, которые при-
менялись в предыдущих главах; если там мы рассматривали
вариационные принципы и соответствующие им эйлеровские
уравнения, то в гл. 8 мы имели дело с преобразованием Лапласа
и линейными дифференциальными уравнениями n-го порядка.
Дальнейшее развитие этой теории связано с интегральной теоре-
мой Коши и другими результатами теории функций комплекс;
ной переменной.
В этой главе описывается другой подход к задачам теории
управления, и по своему духу он, обладая более высокой общ-
ностью, значительно ближе к методам первых глав, чем к теории
систем управления, связанной с анализом связей между вход-
ными и выходными сигналами. Этот подход позволяет сформу-
лировать общую задачу теории оптимального управления, для
изучения которой сведений, приводившихся ранее, недостаточно.
Практические приложения этой новой теории ограничиваются
в основном кругом линейных задач, по крайней мере в том
плане, который связан с отысканием решений в аналитической
форме; мы здесь сталкиваемся с ситуацией, напоминающей
в этом смысле приложения метода анализа систем с помощью
изучения их реакций на входные сигналы. Эта теория интен-
сивно развивалась в течение последних пяти — десяти лет, и
ее результаты нашли применение в чрезвычайно широком клас-
се важных технических и научных проблем. Мы, естественно,
рассмотрим лишь самые основные положения этой теории, от-
сылая читателя по поводу различных деталей и многочисленных
приложений к обширной оригинальной литературе.
Динамические системы
169
10.2. Абстрактная теория динамических систем
Мы уже рассматривали уравнения Лагранжа, описывающие
движение механической системы, и выяснили, что эти уравнения
представляют собой уравнения эйлеровского типа для опреде-
ленной вариационной задачи, в которой в качестве «оценочной
функции» выступает действие, а ядром соответствующего функ-
ционала служит функция Лагранжа L. Если рассматриваемая
система имеет N степеней свободы, то для описания ее движе-
ния требуется система из N таких уравнений второго порядка;
каждое такое уравнение соответствует одной из обобщенных
координат, а каждая обобщенная координата соответствует
одной из степеней свободы системы. Решение этой системы
уравнений представляет каждую обобщенную координату
Xi=Xi(t) как явную функцию времени, и это полностью опре-
деляет движение системы и все ее динамические характеристики.
Абстрактная теория динамических систем, которая разраба-
тывается в ряде важных разделов чистой и прикладной матема-
тики ’, представляет собой, в определенном смысле, обобщение
и дальнейшее теоретическое развитие лагранжевского подхода
к задачам классической механики. Для иллюстрации этого об-
стоятельства нам придется сначала ввести некоторые новые по-
нятия из механики.
В разд. 5.2 мы видели, что уравнения Эйлера в общем слу-
чае представляют собой дифференциальные уравнения второго
пбрядка относительно координат системы. Общее решение си-
стемы W таких^равнений содержит поэтому 2N произвольных
постоянных. Часто бывает удобно заменить каждое из уравне-
ний второго порядка эйлеровского типа парой уравнений пер-
вого порядка. Такой переход к уравнениям первого порядка
всегда может быть выполнен некоторым каноническим способом,
и мы продемонстрируем это на примере одного уравнения вто-
рого порядка вида y"=f(x, у, д'). Определим новые неизвестные
1 Многие важные разделы современной чистой математики возникли на
основе идей теории динамических систем, рассматривавшихся в физике. Ис-
точником развития этих современных математических идей послужили работы
Пуанкаре [87] и Биркгофа [88] На основе этих исследований возникли совре-
менные «глобальные» методы теории дифференциальных уравнений (по по-
воду литературы см. примечание на стр. 107 в гл. 6), важнейшие представле-
ния дифференциальной геометрии и теории непрерывных групп [89], теория
вариационного исчисления в целом, которую называют теперь теорией Морса
[90], и большая часть представлений эргодической теории и теории отобра-
жений с инвариантной мерой (см, например, [91]). Из всех этих исследований
выросли в настоящее время самостоятельные математические дисциплины.
Теория динамических систем и сейчас продолжает ставить важные проблемы,
решение которых несомненно приведет к развитию в будущем новых разделов
науки.
170
Глава 10
функции и, v, полагая и=уяи=у'. Тогда уравнение y"=f (х, у, у')
переходит в эквивалентную систему двух уравнений первого
порядка вида
«' = V,
v’ = f(x, и, v).
В общей системе W уравнений второго порядка эйлеровского
типа такой переход означает, что в качестве неизвестных функ-
ций системы 2М уравнений первого порядка, эквивалентной
исходной системе, выбираются обобщенные координаты Xt(t)
(Г= N) и их производные х/ (/) (i= 1, N). Конкретный
выбор значений 2N произвольных постоянных определяет неко-
торую начальную точку (xj (t0), xN(t0), х/^о), • , xN'(t0))
в 2Й-мерном пространстве переменных (хь ..,, xN, х/, .. ., xN'),
и это приводит к однозначному выбору определенной интеграль-
ной траектории x{(t), Xi (t); Z= 1, ..., N, соответствующей реше-
нию системы, удовлетворяющему этим начальным условиям.
Пространство, элементами которого служат последователь-
ности 2W переменных вида (хь .... xN, х/, ...» xN'), обычно
называют в механике фазовым пространством данной механи-
ческой системы, а каждый элемент (хь ..., xN, х/, . .., xN')
(точка фазового пространства) называется состоянием этой си-
стемы. Если состояние системы известно в каждый момент вре-
мени, то это, очевидно, полностью определяет ее поведение,
которое и должно быть найдено с помощью уравнений движе-
ния. Такой метод описания механической динамической системы
с помощью траекторий в фазовом пространстве оказывается
очень удобным, и поэтому обычно рассматривают не исходную
систему W эйлеровских уравнений второго порядка, а преобра-
зованную систему 2W дифференциальных уравнений первого
порядка.
Основные черты описанного выше подхода классической
механики к изучению движения механических систем сводятся
к следующему:
1. В каждый момент времени с изучаемой системой можно
связать некоторый математический объект, называемый состоя-
нием системы в данный момент времени; для механических си-
стем состояние представляется точкой 2А/-мерного евклидова
фазового пространства, где N—число степеней свободы си-
стемы.
2. Поведение системы описывается системой уравнений дви-
жения (в случае механических систем — 2М уравнений первого
порядка), в которой каждое уравнение соответствует одной из
координат хь ..., xN, х/, ..., xN' фазового пространства.
Динамические системы.
171
3. Предполагается, что существует совокупность правил, по-
зволяющих (по крайней мере, теоретически) определить по со-
стоянию системы значение любого из ее параметров.
Законы механики действительно непосредственно приводят
к этим трем утверждениям. Можно, однако, поступить иначе
и принять положения 1—3 в качестве аксиом. Это приводит
к определению нового класса математических объектов, удо-
влетворяющих этой системе аксиом. Как это обычно бывает
в таких случаях,** новая теория, полученная с помощью такого
рода обобщения, оказывается значительно богаче, чем началь-
ная частная теория; эта новая теория называется абстрактной
теорией динамических систем. Всякая конкретная механическая
система порождает, очевидно, некоторую динамическую систему,
принадлежащую тому классу, который изучается в абстрактной
теории; но существуют также и самые разнообразные системы
другого типа, которые также охватываются этой общей теорией.
Некоторые из них будут рассмотрены далее.
10.3. Входные и выходные сигналы динамических систем 1
Рассмотрим теперь связь между теорией динамических систем
и тем подходом, который был намечен в нескольких последних
главах, т. е. методом исследования зависимости между входными
и выходными сигналами системы. Если в качестве примера взять
гармонический осциллятор, то эта связь оказывается довольно
тесной; гармонический осциллятор был специально выбран для
этой цели как пример реальной динамической системы, к которой
непосредственно может быть применен метод анализа входных и
выходных си13|рлов. Далее мы более подробно обсудим некото-
рые специфические свойства этой системы.
В случае гармонического осциллятора входным сигналом слу-
жит вынуждающая сила, а выходным — возникающее под влия-
нием этой силы смещение системы из положения равновесия.
Вместо отклонения от положения равновесия выходным сигна-
лом можно было бы считать любой другой наблюдаемый пара-
метр системы; для этого требуется лишь, чтобы этот параметр
был функцией координат (т. е. переменных, описывающих «со-
стояние системы»), которые определяют движение системы.
В общем случае всякая внешняя сила, приложенная к системе,
будет называться входной функцией (сигналом), а любой пара-
метр системы, который может быть выражен в виде непрерывной
1 Изложение базируется в основном на работах Калмана, подробно ис-
следовавшего линейные динамические системы. Читатель, интересующийся
этими вопросами, может обратиться к оригинальным статьям [92—95].
172
Глава 10
функции ее координат, будет называться выходной функцией
(сигналом) L
Заметим, в частности, что тогда можно рассматривать как
выходной сигнал и само состояние системы и таким -образом
формализовать это понятие, которое не было четко определено
ранее. (Дальнейшее обсуждение понятия состояния системы
в терминах входных и выходных сигналов будет приведено
в гл. 11, где изучаются адаптивные системы.)
Центральный вопрос теории динамических систем заклю-
чается в следующем: можно ли, варьируя входные сигналы, вы-
нудить динамическую систему произвести заранее предписанный
выходной сигнал. Или в более частной форме: можно ли так
подобрать входной сигнал, чтобы система пришла в результате
этого в некоторое заданное состояние? Как следствие этого
вопроса появляется еще одна проблема, из которой, собственно,
И возникает теория оптимального управления: каким образом
выбрать входные данные так, чтобы переход системы в задан-
ное состояние происходил «наилучшим» (оптимальным) спо-
собом?
Совокупность входных сигналов (входных функций) динами-
ческих систем называют просто управлением. Интуитивные
представления подсказывают, что под влиянием внешних сил
(управления) система переходит в фазовом пространстве с од-
ной траектории на другую, и тем самым множество состояний,
которые она может принимать, существенно изменяется и рас-
ширяется. Вот типичный пример движения такого рода: допу-
стим, что баллистический снаряд или космический аппарат,
отклонившись от заданного движения, перешел на другую
траекторию. Можно ли, выбирая соответствующим образом
управление (осуществляемое обычно _с помощью тормозных
ракетных двигателей), заставить аппарат вернуться на задан-
ную траекторию?
Очевидно, что при таком высоком уровне абстракции, на
котором ставились все эти проблемы, в общем случае трудно
ожидать конкретного ответа на вопрос о существовании опти-
мального управления в той или иной конкретной задаче.
В частности, при изучении зависимостей между видными и
1 Приведенное определение выходного сигнала имеет несколько более об-
щий смысл, чем то, которое давалось ранее В исследованиях Калмана по тео-
рии линейных динамических систем [92—95] рассматриваются н такие наблю-
даемые параметры системы, которые ие являются управляемыми; последнее
означает, что их значении зависят не только от природы входных и выходных
сигналов, ио и от иных факторов, характеризующих систему. Такая ситуация
возникает, грубо говоря, в случае, когда система обладает некоторой доба-
вочной степенью свободы, недоступной прямому наблюдению извне.
Динамические системы
173
выходными сигналами мы обнаружили, что этот подход при-
годен лишь для линейных систем, и все основные результаты
существенно зависели от этого ограничения. Поэтому можно
ожидать, что для решения вопросов абстрактной теории дина-
мических систем (по крайней мере для получения аналитиче-
ских результатов) придется накладывать на систему такие же
жесткие ограничения. В соответствии с этим нас теперь будут
интересовать линеаризованные задачи теории динамических
систем, которые и обсуждаются ниже
10.4. Линейные динамические системы
Рассмотрим для иллюстрации динамическую систему, состоя-
ние которой определяется одной переменной x=x(t) (заметим,
что для описания реальной механической системы требуется,
как правило, по крайней мере два уравнения для двух фазовых
координат). В общем случае уравнение движения системы вы-
ражает производную х'(I) через значения самой функции х(1)
и управление, или входной сигнал, который мы обозначим через
u(t). Если предположить, что уравнение движения линейно, то
тогда оно должно записываться в виде
x’(t) = Ax(t) + Bu(t), (10.1)
где коэффициенты А, В являются в общем случае функциями
времени t. Допустим, что за выходной сигнал принят некоторый
параметр y(t), и предположим, что x(t) и y(t) связаны соот-
ношением вида
у(/) = Сх(0, (Ю.2)
где С в общем случае также является функцией t. Соотношения
(10.1) и (10.2) вместе полностью определяют рассматриваемую
систему; за входной сигнал здесь принимается u(t), а за выход-
ной — y(t).
В предыдущих главах, где системы рассматривались с точки
зрения зависимости между их входными и выходными сигна-
лами, было введено понятие передаточной функции. Поэтому,
для того чтобы описать поведение рассматриваемой динамиче-
ской системы с помощью зависимости между ее выходным си-
гналом y(t) и входным сигналом u(t), нужно построить соответ-
ствующую передаточную функцию. Формально, как и раньше,
ее можно определить как отношение преобразования Лапласа
y(t) к преобразованию Лапласа u(t). Можно также приложить
к системе единичный импульс u(t)—6(t), и тогда результирую-
щий выходной сигнал y(t) должен в соответствии с (8.9) как
174
Глава 10
раз равняться обратному преобразованию Лапласа H(t) от пе-
редаточной функции системы. Для произвольного входного си-
гнала u(t) соотношение, определяющее соответствующий вы-
ходной сигнал y(t), выражается формулой
т
У (0 — J Н (t — а) и (а) da.
о
Наиболее интересный вопрос состоит здесь в том, чтобы вы-
яснить связь между определенной только что передаточной
функцией и структурой той абстрактной динамической системы,
которая соответствует в указанном выше смысле этой функции.
Как уже отмечалось ранее, общее представление о системах,
характеризуемых сигналами на их входах и выходах, находится
на более высоком уровне абстракции, чем понятие динамической
системы; в общем случае существует множество различных аб-
страктных динамических систем, обладающих одной и той же
передаточной функцией, но существенно отличающихся друг от
друга в их индивидуальном поведении. Однако по поводу дета-
лей, касающихся «реализации» системы с заданной передаточ-
ной функцией в виде конкретной динамической системы, чита-
тель должен обратиться к специальной литературе; наиболее
интересны в этом отношении цитированные выше статьи Кал-
мана и сотрудников (в особенности [94, 95]). При изучении этих
вопросов следует также иметь в виду материал разд. 11.1.
10.5. Оптимальное управление
Заметим, что абстрактную линейную динамическую систему
вида (10.1) можно в определенном смысле считать функциона-
лом, зависящим от управляющей функции u(t). Действительно,
каждая конкретная управляющая функция u(t) выделяет неко-
торую определенную систему типа (10.1), и каждая такая
система порождает свое собственное семейство траекторий (при
этом всякому заданному начальному состоянию отвечает един-
ственная траектория). Будем считать, что все эти семейства
траекторий вложены в одно и то же общее фазовое простран-
ство, так как вариация управляющей функции не вносит новых
степеней свободы.
Что же понимается под оптимальным управлением? Если
вспоминать то, что было сказано ранее относительно задач об
оптимизации, то очевидно, что в данном случае для постановки
такой задачи должны выполняться два условия: 1) должно быть
определено семейство допустимых систем, каждая из которых
обнаруживает заданный тип поведения; 2) должна быть указана
Динамические системы
175
некоторая величина, характеризующая свойства каждой из этих
систем; ее значения принимаются за значения оценочной функ-
ции (функционала), и эта функция должна быть минимизиро-
вана соответствующим выбором оптимальной системы. Примем
за рассматриваемое семейство допустимых систем совокупность
динамических систем вида (10.1); тем самым первое условие
будет выполнено. Для выполнения второго условия остается
лишь задать некоторым образом функционал, определенный на
множестве допустимых управлений w(i).
В конкретных приложениях теории оптимального управле-
ния оценочную функцию выбирают обычно в виде функционала
того частного вида, который мы ранее рассматривали, т. е. в виде
функционала, выражающегося интегралом от некоторого ядра.
В большинстве таких приложений ставится задача о переходе
динамической системы из некоторого заданного начального со-
стояния в некоторое заданное конечное состояние, соответствую-
щее какому-то конечному моменту времени t[. Для осуществле-
ния такого движения класс допустимых управлений u(t) должен
состоять из таких функций u(t), для каждой из которых точки,
соответствующие начальному и конечному состояниям, лежат
на одной и той же траектории (на практике обычно бывает
достаточно, чтобы точка, определяющая конечное состояние,
лежала достаточно близко к рассматриваемой траектории).
Каждое конкретное движение системы, определяемое некоторой
управляющей функцией u(t) из описанного выше класса, можно
теперь оценить с помощью двух критериев, каждый из которых
следует принимать во внимание при постановке задачи о выборе
оптимального управления: первый критерий связан с величиной,
оценивающей отклонение конечного состояния системы от тре-
буемого, а^рторой — с величиной, оценивающей в целом движе-
ние системы от начального до конечного состояния. В этом
смысле оценочная функция должна содержать по крайней мере
два слагаемых, соответствующих критериям 1 и 2.
Для того чтобы записать нужные нам выражения в явном
виде, обозначим через xu(t, х0, t0) то решение уравнения (10.1),
которое удовлетворяет заданному начальному условию
хи(^о)=хо (где х0 — это начальное состояние), а через X] обо-
значим заданное конечное состояние, которое система должна
принять в конечный момент времени t\. Тогда с учетом замеча-
ний, сделанных в разд. 10.4, наиболее общая форма оценочной
функции должна иметь вид
Ldxu(tx, х0, t0), *i) + J L2(xu(t, х0, t0), u(t), t)dt, (10.3)
t0
176
Глава 10
где первое слагаемое — функция L; — характеризует отклонение
того состояния системы, которое она принимает при выбранном
управлении u(t) в момент /р от заданного конечного состояния
Xi, а второе слагаемое есть интеграл, с помощью которого в об-
щем виде оценивается в целом движение системы от начального
до конечного момента времени. Такое представление оценочной
функции в виде двух слагаемых должно напомнить читателю те
двухчленные оценочные функции, с которыми мы встречались
раньше (см. разд. 1.4 и 3.3). Как и в ранее рассмотренных слу-
чаях, может оказаться (и обычно это так и бывает), что опти-
мальное решение не оптимизирует каждое слагаемое в отдель-
ности.
Определенная выше оценочная функция представляет собой
функционал, определенный на множестве допустимых управлений
u(t). Управление u(t), минимизирующее этот функционал, и
будет оптимальным управлением по отношению к этому функ-
ционалу. На практике иногда оказывается, что вклад, вносимый
первым членом, сравнительно мал по отношению к величине
второго, интегрального члена, и тогда проблема минимизации
всего функционала сводится к минимизации одного только
интеграла. Обратим внимание на то, что этот интеграл имеет
вид
6
J L2(t, x(t),
<0
Задача минимизации такого интеграла в высшей степени напо-
минает обычную задачу вариационного исчисления, которая
относится к интегралу вида
J £.(/, x(f), x'{t))dt.
*0
Основное различие между этими двумя интегралами состоит
в том, что в первом из них фигурирует управление н(0, а не
производная Как будет показано в разд. 10.6, с теорети-
ческой точки зрения это различие не так уж велико. Однако
в практическом отношении это (как и ряд других отличий от
классических задач вариационного исчисления) приводит к не-
обходимости развития некоторых новых и более сильных мето-
дов исследования. Эти новые методы, в теоретическом плане
в той или иной степени эквивалентные друг другу, представляют
собой обобщение классического вариационного исчисления на
более широкий круг новых задач.
Динамические системы
177
Наиболее, пожалуй, известными из этих методов являются
принцип максимума Понтрягина [96] и метод динамического
программирования, развитый Веллманом [97, 98]. В этих мето-
дах используется и обобщается тот факт (известный из класси-
ческого вариационного исчисления), что всякий отрезок стацио-
нарной кривой сам по себе тоже является некоторой стацио-
нарной кривой. Однако подробное обсуждение этих вопросов
выходит за рамки данной книги, и по этому поводу мы отсылаем
читателя к цитированной выше литературе и другим обзорам
по этим проблемам, появившимся за последнее время Отме-
тим здесь, однако, что возможность применить методы теории
оптимального управления к широкому классу внешне совер-
шенно различных проблем позволяет взглянуть на эти разно-
образные проблемы с некоторой единой точки зрения (ср. с за-
мечанием Голдстейна на стр. 16). Как будет показано в гл. 11
и 12, эти соображения позволяют связать друг с другом ряд
важных областей теоретической .биологии, на первый взгляд
не имеющих друг к другу прямого отношения1 2.
10.6. Обратная связь
В гл. 8 мы рассматривали понятие обратной связи, изучая
теорию систем, описываемых зависимостью между их входными
и.выходными сигналами. В этом разделе мы покажем, каким
образом обратная связь проявляется в задачах теории опти-
мального управления динамическими системами.
Если дана некоторая динамическая система, которая должна
служить в качестве системы регулирования или следящей си-
стемы, то траектория этой динамической системы в фазовом
пространстве будет, очевидно, зависеть соответственно от задаю-
щего сигнала или сигнала возмущения, поступающих из внеш-
ней среды. В технических задачах нам известно обычно состоя-
ние среды только в данный момент времени и в прошлом, а то,
что может случиться в будущем, как-правило, совершенно
неизвестно. Поэтому в общем случае не всегда возможно
априори определить конкретное управление u(t), которое
1 См, например, интересную статью Дрейфуса [99], полезно сравнить ее
с работой Калмана [93]
2 Рекомендуем читателю недавнюю работу Гудвина [100] По-видимому,
те идеи, о которых говорилось в этой главе, могут быть положены в основу
ряда унифицирующих концепций в теоретической биологии Подход Гудвина
представляет по крайней мере одно из направлений, в которых могли бы раз
рабатываться эти идеи Отправным пунктом в этой работе является описание
разнообразных регуляторных процессов, протекающих в клетке, о которых
мы говорили в разд 9 5, в основном в тех математических терминах, которые
разрабатывались в гл 8
178
Глава 10
сможет оптимизировать поведение системы независимо от того,
как изменятся входные сигналы в будущем. Вместо этого нужно
построить такую управляющую функцию, которая учитывала бы
информацию, получаемую из рассмотрения настоящего и про-
шлых состояний системы. Это означает, что управляющая функ-
ция должна выражаться непосредственно через функцию x(t),
описывающую состояния системы:
«(Z) = /(x(Z)),
где u(t), x(t) подчиняются условию минимизации (10.3). Но по
определению x(t) есть не что иное, как выходной сигнал си-
стемы, a u(t) —сигнал на входе системы. Таким образом, вход-
ной сигнал системы формируется на основании данных, касаю-
щихся выходного сигнала, и, следовательно, мы имеем здесь
дело с явлением, которое как раз и называлось обратной связью
в наших прежних рассуждениях.
Подчеркнем теперь некоторые основные факты, относящиеся
к обратной связи в теории динамических систем. Необходимость
введения обратной связи вызывается тем, что отсутствует пол-
ная информация о том, как изменяются во времени действую-
щие на систему сигналы из внешней среды, под влиянием кото-
рых ее поведение отклоняется от предписанного. Обратная
связь позволяет получить ту необходимую информацию, с по-
мощью которой может быть выбрана нужная форма управле-
ния, приводящая к минимизации выражения (10.3). Следова-
тельно, динамическая система, функционирующая в качестве
системы управления, и вообще всякая система, движение кото-
рой минимизирует выражение типа (10.3), распадается, как и
ранее, минимум на две подсистемы: управляемую подсистему,
вырабатывающую выходные сигналы всей системы в целом, и
управляющую подсистему, или регулятор, который формирует
закон управления на основании данных, доставляемых обратной
связью, и подает нужный сигнал управления на вход управляе-
мой системы. На каждом этапе управления регулятор, можно
сказать, принимает решения, руководствуясь имеющейся в его
распоряжении информацией относительно управляющей функ-
ции u(t) и тем самым о траектории системы в целом (эта тер-
минология заимствована из теории адаптивных систем). Такой
тип поведения, при котором система переходит от «нежелатель-
ного» (по отношению к заданному оптимальному управлению)
поведения к такому, которое в этом смысле «желательно», назы-
вают часто «адаптацией», особенно в тех случаях, когда закон
оптимального управления выражается неявно в виде «поощре-
ний» или «наказаний». Способность к адаптации характерна
для самых разнообразных биологических систем.
Глава 11
АДАПТИВНЫЕ СИСТЕМЫ В БИОЛОГИИ
11.1. Введение
В этой главе мы вкратце рассмотрим системы, способные
к адаптации, т. е. такие системы, которые в случае необходи-
мости могут изменить свое поведение таким образом, чтобы пе-
рейти к более предпочтительному (или оптимальному) типу по-
ведения в зависимости от конкретной ситуации во внешней
среде. Уже из такой поверхностной характеристики адаптивных
систем можно видеть, что к адаптивным системам относятся
как системы управления, о которых шла речь в гл. 8, так и об-
суждавшиеся в гл. 10 динамические системы, оптимизирующие
заданную оценочную функцию.
Ясно, что изучение общей теории адаптивных систем важно
для широкого, круга естественных наук. У живых организмов
наблюдаются самые разнообразные формат адаптивного пове-
дения. Биологи" и психологи хотели бы, естественно, понять
принципы такого поведения, а в разнообразных прикладных
дисциплинах биологические системы адаптивного управления
рассматриваются как прототипы разного рода «мыслящих
машин».
Многочисленные источники интереса к этим проблемам поро-
дили огромную литературу, охватывающую широкий круг проб-
лем, относящихся к адаптивным системам самых различных ти-
пов, и тем, кто’впервые знакомится с этой литературой, часто
кажется, что в ней имеется множество противоречий, небреж-
ностей и неясностей. Такое положение по существу неизбежно,
так как в создании этой литературы принимали более или менее
равное участий инженеры, биологи, психологи, экономисты,
а также представители всевозможных промежуточных и сме-
шанных областей современной науки. В этом разделе мы попы-
таемся разобраться в нескольких возможных источниках этого
смешения идей и методов.
Центральным понятием в теории адаптивных систем любого
типа является понятие состояния системы, имеющее своим ис-
точником абстрактную”теорйю*“дйнамических систем; состояние
системы в каждый момент времени определяется значениями,
которые принимают в данный момент времени некоторые
180
Глава 11
величины, выбранные в качестве «координат состояния». Мы ви-
дели~также, что в случае динамической системы координаты со-
стояния можно рассматривать как выходные сигналы этой си-
стемы. В разд. 10.3 было отмечено, что это обстоятельство позво-
ляет ввести понятие состояния в теорию систем, характеризуемых
зависимостью между их входными и выходными сигналами. Та-
ким образом, понятия состояния системы и ее выходного сиг-
нала сливаются друг с другом, и поэтому мы имеем право
в дальнейшем использовать эти термины как взаимозаменяемые.
При таком подходе видно, что основное уравнение (8.1), с по-
мощью которого мы описывали связи между входными и вы-
ходными сигналами в теории линейных систем управления, иг-
рает роль, аналогичную уравнениям движения в теории дина-
мических систем.
Адаптивная система — это такая система, у которой для
каждого возможного сигнала на ее входе существует множество,
состоящее из одного или более предпочтительных состояний, или
предпочтительных форм выходного сигнала. Адаптивный харак-
тер системы означает, что если первоначально состояние сис-
темы не является предпочтительным, то она будет далее дей-
ствовать таким образом, чтобы в конце концов достигнуть ка-
кого-то предпочтительного состояния.
Теперь нужно более внимательно рассмотреть вопрос о том,
каким образом могут быть выполнены такие изменения состоя-
ния (выходного сигнала). С формальной точки зрения здесь
возникает следующий вопрос: пусть дана некоторая система и
задан также сигнал f(t) на ее входе. Обозначим соответствую-
щую реакцию системы, или ее выходной сигнал, через g(t). До-
пустим, однако, что та реакция системы, которая при входном
сигнале f(t) является предпочтительной, есть h(t)=£g(t). Ка-
ким образом может быть осуществлено такое изменение, в ре-
зультате которого реакция системы станет предпочтительной?
Априори можно представить себе следующие два способа:
I. Желательно получить выходной сигнал вида h(t). Пусть
известно, что система будет вырабатывать такой сигнал в том
случае, если на ее вход поднять сигнал k(t). Но, как было ска-
зано, в действительности входным сигналом является f(t). Сле-
довательно, для получения желаемого результата можно начать
изменять входной сигнал f(t) до тех пор, пока он не совпадет
с нужным сигналом k(t), а затем подать этот преобразованный
сигнал на вход системы
II. Пусть опять требуется получить выходной сигнал вида
h(t). Пусть известно, -что существует такая система, у которой
взаимосвязь между входными и выходными сигналами (или,
что то же самое, передаточная функция) такова, что при задан-
Адаптивные системы в биологии
181
ном входном сигнале f(t) эта новая система дает желаемую
реакцию h(t). В этом случае, следовательно, можно подвергнуть
изменению саму систему, вызывая тем самым такие изменения
передаточной функции, чтобы в результате преобразованная
система вырабатывала выходной сигнал h(t) при подаче на ее
вход сигнала f (t).
В большинстве адаптивных систем, рассмотренных нами ра-
нее, использовался способ I. В этих системах входной сигнал
с помощью контура обратной связи преобразовывался в сигнал
ошибки, и действие этого последнего приводило систему в со-
стояние, при котором вырабатывался требуемый выходной сиг-
нал; это выполнялось с помощью регулятора. Для замкнутых
линейных систем, описываемых линейными дифференциальными
уравнениями с постоянными коэффициентами, этот способ по
существу единственно возможный.
• Способ II связан со значительно более радикальными изме-
нениями самой системы и поэтому осуществляется- в механиче-
ских регулирующих устройствах довольно редко. В самом деле,
в системах, характеризуемых зависимостью между входным и
выходным сигналами, изменение передаточной функции требует
изменения коэффициента типа А{ в уравнении (8.1), что в свою
очередь связано с изменением физических постоянных того
устройства, которое реализует эту систему. Например, в случае
гармонического осциллятора коэффициенты Аг выражаются
через массу m и коэффициент упругости k пружины. Для
изменения передаточной функции осциллятора пришлось бы
рассматривать эти величины как функции времени. Если бы
изменения этих величин регулировались обратной связью, то
они стали бы также и функциями отклонения х вида m — m(x, t),
k = k(x, t). Очевидно, что в этом случае уравнение вида (8.1)
неизбежно будет существенно нелинейным.
В случае динамической системы, описываемой уравнениями
(10.1), (10.2), осуществление способа I также связано лишь
с изменением управления и не требует вариации коэффициен-
тов А, В, С, тогда как способ II приводит к тому, что эти коэф-
фициенты выражаются как функции координаты х, т. е. опять-
таки к существенной нелинейности уравнений системы. Таким
образом, в тех случаях, когда мы ограничиваемся линейными
системами управления, способ II должен быть исключен, и нет
поэтому ничего удивительного в том, что до сих пор мы с ним
не встречались.
Однако во многих биологических системах, а также в ряде
важных технических устройств, процесс адаптации управляется
с помощью способа II; это и есть так называемая параметриче-
ская обратная связь. Именно поэтому при математическом
182
Глава 11
описании биологических процессов так часто приходится рас-
сматривать нелинейные системы. Мы советуем читателю поду-
мать, в свете наших прежних рассуждений об оптимальности и
естественном отборе, над интересным вопросом о том, почему
встречающиеся в природе адаптивные системы так часто выби-
рают возможность II, а не I.
Литература, относящаяся к адаптивным системам, содержит
несколько основных источников многочисленных неточностей и
путаницы. Во-первых, редко с достаточной ясностью учиты-
вается различие между методом описания систем с помощью
передаточных функций и методом, опирающимся на теорию
динамических систем, и еще реже этот вопрос рассматривается.
Во-вторых, не слишком часто в явной форме подчеркивается
различие между обоими способами адаптации; это не делается
даже в тех случаях, когда оба эти механизма сосуществуют
в единой сложной системе. В результате этого термин «состоя-
ние» может (и это часто в действительности бывает) употреб-
ляться в литературе по адаптивным системам по крайней мере
в нескольких различных смыслах, иногда даже в одной и той же
статье. И наконец, во многих источниках рассматриваются раз-
личные частные виды адаптивных устройств, которые описы-
ваются таким образом, что к ним нельзя применить ни один из
описанных выше методов, несмотря на то что применяется тер-
минология, близкая к этим методам. Очень важно и необходимо
установить в этой области определенную стандартизацию как
в отношении основных понятий, так и терминологии, но до тех
пор, пока это не будет сделано, литература по этим вопросам
будет содержать массу трудностей для’неспециалиста. Справед-
ливости ради, однако, следует отметить, что состояние литера-
туры по адаптивным системам вполне типично для такой об-
ширной и новой области науки и свидетельствует о том,
что здесь еще будет получено множество новых важных ре-
зультатов.
11.2. Пример. Распознавание изображений и перцептрон
Очень важной и во многих отношениях типичной проблемой
теории адаптивного управления является проблема распознава-
ния изображений. Одна из форм этой проблемы возникла пер-
воначально в биопсихологии в связи с изучением восприятия
гештальта. Общеизвестно, что человека или животное с по-
мощью специальной тренировки можно научить распознавать
символы — скажем, узнавать букву «А», и после того как этот
опыт приобретен, субъект может распознавать этот символ не-
зависимо (в определенных пределах) от его размеров, ориента-
Адаптивные системы в биологии
183
ции и любого конкретного способа представления. Эта способ-
ность распознавания не зависит, таким образом, от частного
вида пространственного расположения буквы «А» в данном ее
представлении и основана на своего рода абстракции от таких
конкретных представлений. Одна из основных задач теории рас-
познавания изображений состоит в выяснении механизма этой аб-
стракции и описании ее в терминах оптимизации поведения
субъекта. С этим связана другая, техническая цель — суметь
создать такое техническое устройство, которое могло бы «рас-
познавать» изображения. Инженерные задачи конструирования
таких устройств в технике, естественно, связаны с биологиче-
скими аспектами проблемы распознавания изображений, так
как инженеру полезно знать, каким образом решает эту про-
блему природа. Машина, способная к распознаванию изобра-
жений, может быть использована для многих повседневных и
важных целей, например для расшифровки электрокардиограмм
с целью выявления патологии или для обнаружения неприятель-
ских самолетов по изображению на экране радиолокатора.
С другой стороны, биолога интересует конструкция технических
устройств такого рода, так как они могут служить моделями,
помогающими проникнуть в существо биологических проблем
распознавания изображений.
Прежде чем перейти к общему обсуждению проблемы рас-
познавания изображений, упомянем кратко об одном классе
технических устройств, которые действительно можно приме-
нить для распознавания изображений, причем с точки зрения
стороннего наблюдателя подобное устройство (его называют
перцептроном !) распознает изображения во многих отношениях
так же, как это делают животные или люди. Типичная, хотя и
простая схема перцептрона приведена на фиг. 31.
Первый, входной слой перцептрона называют часто сенсор-
ным слоем или «сетчаткой». Он состоит из ряда сенсорных эле-
ментов (фотоэлементов), расположенных определенным обра-
зом—скажем, в виде квадратной решетки пХ«. Когда на этот
слой проецируется изображение, одни фотоэлементы возбуж-
даются, а другие нет. Линии, соединяющие эти фотоэлементы
с элементами слоя II, передают, следовательно, простой бинар-
ный сигнал: 1, если фотоэлемент возбужден, и 0 в противном
случае. Можно поэтому сказать, что каждый фотоэлемент мо-
жет находиться в двух состояниях; набор состояний всех
1 Перцептрон был впервые описан Ф. Розенблаттом в 1958 г. В первона-
чальном изложении имелся ряд противоречий, и с тех пор была проделана
большая работа по усовершенствованию этой схемы. Наиболее близкое, по-
жалуй, к окончательному варианту изложение этого вопроса содержится
в книге Розенблатта [101] «Принципы нейродинамики».
184
Глава 11
фотоэлементов определяет состояние всего сенсорного слоя
в целом.
Таким образом, сенсорный слой превращает непрерывное
вначале изображение в некоторую конечную дискретную сово-
купность двоичных символов; если в решетке имеется п2 фото-
элементов, то существует 2п2 возможных состояний этой сово-
купности. Переход от непрерывной модели к дискретной требует
привлечения совсем других математических методов исследова-
ния; вместо аналитических и топологических проблем здесь вы-
ступают задачи комбинаторики. Такая «дискретизация» типична
Сенсорные Ассоциативные Промежуточный Реагирующие
элементы элементы слои- элементы
II
Фиг. 31.
Ш
для методов теории адаптивных систем, и ротому при анализе
таких систем широкое применение находят* цифровые вычисли-
тельные машины. Для описания таких дискретных систем вво-
дится также дискретное время, т. е. рассматриваются лишь про-
межутки времени, кратные некоторым конечным дискретным
единицам измерения времени.
Слой II состоит из ассоциативных элементов, каждый из ко-
торых получает сигналы от всех фотоэлементов !; на выходе ас-
социативного элемента возникает двоичный сигнал, зависящий
от характера полученного входного сигнала, т. е. от состояния
сетчатки в данный момент времени. Число ассоциативных эле-
1 Вполне очевидно, что основная идея схемы перцептрона может быть
реализована многими способами (см [101]) Так, например, каждый ассоциа-
тивный элемент может получать входные импульсы только от некоторого слу-
чайного подмножества сенсорных элементов, ассоциативные элементы могут
быть разбиты на несколько подгрупп, эти элементы могут быть определен-
ным образом связаны друг с другом и т. п.
Адаптивные системы в биологии
185
ментов меньше числа фотоэлементов в слое I, и поэтому выход-
ной сигнал, или состояние, слоя II описывается более короткой
последовательностью двоичных символов, чем состояние сенсор-
ного слоя.
Между слоями II и III находится промежуточный слой, со-
стоящий из элементов, число которых равно числу ассоциатив-
ных элементов; каждый элемент этого промежуточного слоя
соответствует одному из элементов слоя II. Элемент промежу-
точного слоя, соответствующий i-му ассоциативному элементу,
приписывает выходному сигналу этого элемента некоторый
«вес» Wi.
На выходе перцептрона (слой III) находится один или
несколько реагирующих элементов. Входным сигналом для каж-
дого реагирующего элемента служит некоторая последователь-
ность чисел, определяемая «взвешенными» состояниями ассо-
циативных элементов. Каждый реагирующий элемент Qj фор-
мирует сумму вида
(ИЛ)
где через at обозначен выходной сигнал i-ro ассоциативного
элемента, а — вес этого выходного сигнала. Каждый реаги-
рующий элемент характеризуется некоторым числовым значе-
нием 0 (которое называется порогом). Выходной сигнал реаги-
рующего элемента может принимать значения 1 или 0 в зави-
симости от того, превосходит ли сумма вида (11.1) пороговое
значение 0 или нет соответственно. (В более общем случае
в слое III может быть много таких элементов, но в данном слу-
чае на нашей схеме изображен лишь один.)
Если требуется, чтобы перцептрон, скажем, распознавал изо-
бражение буквы «А», то при предъявлении этой буквы реаги-
рующий элемент должен выдавать сигнал 1, а в противном слу-
чае— сигнал 0. Обычно в начале своей работы перцептрон не
выполняет этой задачи. Каким же образом можно добиться
того, чтобы он изменил свое поведение так, чтобы всегда полу-
чался нужный результат?
Во-первых, должны быть предусмотрены способы, посред-
ством которых машине можно было бы сообщить, была ли ее
реакция на представленное изображение верной или нет. Если
реакция верна, то никаких изменений в устройстве не требуется.
Если же реакция оказывается неверной, то по некоторым фик-
сированным правилам производится изменение весовых коэффи-
циентов Wj. Иными словами, производится изменение переда-
точной функции промежуточного слоя, и правила, по которым
это изменение выполняется, зависят от выходного сигнала си-
стемы, т. е. они формируются с помощью обратной связи.
186
Глава 11
Основная математическая проблема теории перцептрона за-
ключается в следующем: существует ли для некоторого заранее
заданного типа поведения этого устройства такое множество
весовых коэффициентов Wi, при котором поведение системы
всегда будет таким, какое требуется? И далее, если это так, то
существует ли такой алгоритм для изменения величин Wi, ко-
торый независимо от характера последовательности изображе-
ний, предъявляемых сетчатке, приводил бы к требуемым изме-
нениям за конечный промежуток времени. Эта последняя про-
блема называется проблемой сходимости для перцептрона, и
большая часть литературы по теории перцептрона посвящена
разнообразным доказательствам сходимости при различных'
предположениях
Изложенный формализм означает, что при каждом конкрет-
ном выборе коэффициентов Wi перцептрон по существу разде-
ляет множество состояний сенсорного слоя на два непересекаю-
щихся класса, а именно на класс состояний, при которых вы-
ходные элементы возбуждаются, и класс состояний, при
которых они не возбуждаются. Модификация коэффициентов
Wi приводит к изменению этих двух классов. Требуется так из-
менить поведение перцептрона (т. е. множество коэффициентов
w^, чтобы класс состояний сетчатки, соответствующий возбу-
ждению выходных элементов, в точности совпадал с тем клас-
сом, который образуется при проецировании на сетчатку изо-
бражения буквы «А» в некоторой определенной ориентации.
Строение перцептрона весьма тонко приспособлено к таким мо-
дификациям. Слой II играет роль «абстрагирующего» устрой-
ства, ибо он упрощает последовательность, соответствующую со-
стоянию сенсорного слоя, некоторым заранее заданным спосо-
бом, зависящим от начальных связей между слоями I и II.
Можно предположить, что двоичный выходной сигнал каждого
ассоциативного элемента соответствует наличию или отсут-
ствию некоторого абстрактного свойства в символе, который
представлен сетчатке. Элементы промежуточного слоя припи-
сывают каждому такому свойству некоторый вес, т. е. отмечают
его «относительную важность» для характеристики первона-
чального изображения. Способность соответствующим образом
изменять весовые коэффициенты выглядит, таким образом,
в точности так, как будто перцептрон может отбирать наиболее
1 Особенно четко этот вопрос изложен в работе Новикова [102]. См. также
статью Чарнса [103], которая особенно интересна, так как в ней используются
методы линейного программирования (см. разд. 12.2), которые, как оказы-
вается, могут быть переформулированы в понятиях, связанных с проблемой
сходимости.
Адаптивные системы в биологии
187
характерные признаки того конкретного символа, который он
должен узнать.
Увеличивая число реагирующих элементов, можно построить
машину, способную выполнять более общую задачу и распозна-
вать две, три и более букв, т. е. делить множество состояний
сетчатки на два, три и более классов, каждый из которых соот-
ветствует возбуждению одного или более выходных элементов.
Были построены машины такого типа, способные распознавать
буквы латинского алфавита (см. по этому поводу обзорную
статью Хоукинса [104]). Относительно подробностей, касаю-
щихся этих и других более еложных вариантов идей перцепт-
рона, мы отсылаем читателя к цитированной литературе.
На примере перцептрона мы выяснили, что операционально
изображение представляет собой не что иное, как определенный
набор входных сигналов некоторой системы и что эта система
может распознать его в том и только в том случае, если каждый
входной сигнал из этого набора вызывает некоторую однозначно
определенную реакцию, или выходной сигнал системы. Способ-
ность устройств, распознающих изображения, к адаптации опре-
деляется тем, что они могут так изменять зависимость между
их входными и выходными сигналами, чтобы в результате их
реакция на данное изображение совпала с требуемой.
Прежде чем покончить с обсуждением схемы перцептрона,
отметим различие между этой схемой и теми системами управ-
ления или регулирования, с которыми мы имели дело раньше.
В идейном отношении наиболее существенным является отсут-
ствие в схеме перцептрона (фиг. 31) контура обратной связи и
какого-либо управляющего блока, или регулятора. Наличие ре-
гулятора здесь лишь неявно подразумевается. Он представ-
ляется в виде совершенно отдельной системы, которая сравни-
вает выходной сигнал перцептрона с нужной формой выходного
сигнала и затем в соответствии с некоторым фиксированным
правилом или алгоритмом модифицирует коэффициенты иц.
Таким образом, действие регулятора сводится к изменению пе-
редаточной функции перцептрона, а не к изменению его вход-
ного сигнала. В отсутствие такого регулятора и той цепи обрат-
ной связи, которую он неявно осуществляет, перцептрон теряет
свойства адаптивной системы.
Итак, в схеме перцептрона управляющее устройство, или
регулятор, играет роль Deus ex Machina. Ему должна быть из-
вестна «правильная» реакция на каждое конкретное изображе-
ние, представленное перцептрону, и оно должно также обладать
способностью применять алгоритм, с помощью которого изме-
няются коэффициенты Wi. После завершения процесса сходи-
мости (т. е. после того, как весовые коэффициенты примут
188
Глава 11
свои оптимальные значения) регулятор отключается от схемы
действия перцептрона. Поскольку регулятору «неизвестны» зна-
чения w.i (а известно лишь, ведут или не ведут они к правиль-
ной реакции), трудно представить себе, чтобы-алгоритм можно
было воплотить в форме, в той или иной степени напоминаю-
щей передаточную функцию регулятора.
Отмеченное обстоятельство приводит к тому, что исследова-
ние зависимости между входными и выходными сигналами пер-
цептрона по духу своему сильно отличается от методов изучения
систем, которые мы рассматривали в гл. 8. В математиче-
ском отношении здесь основной упор делается на доказательство
сходимости к оптимальному поведению при. заданном конкрет-
ном алгоритме (и, разумеется, на доказательство того, что такое
оптимальное поведение существует). Для построения такого
алгоритма можно применить математические методы вариаци-
онного исчисления и различные стохастические обобщения, опи-
санные в гл. 10, но сама схема перцептрона, описанная выше,
строится независимо от такого алгоритма.
11.3. Обучение
До сравнительно недавнего времени считалось, что способ-
ностью к обучению на основании опыта обладают только живые
организмы. Обучение распознаванию изображений представ-
ляет собой один частный вид обучения, к которому способны
живые организмы, но многие его черты типичны для процесса
обучения вообще. Поэтому в данном разделе нам будет по-
лезно еще раз вернуться к проблеме распознавания изображе-
ний.
Одна из характерных черт адаптивных устройств, способ-
ных распознавать изображение, заключается в том, что описа-
ние оценочной функции, минимизируемой при работе этих
устройств, нигде явно не входит в их схему. Обучение происхо-
дит с помощью подкрепления (положительного или отрица-
тельного) некоторых реакций системы на определенные входные
сигналы. Если реакция системы совпадает с требуемой, то она
получает положительное подкрепление; если же она оказывается
неподходящей, то подкрепление будет отрицательным. Такой
метод, грубо говоря, аналогичен методу поощрений и наказа-
ний, применяемому при тренировке животных, воспитании ма-
леньких детей и т. п. Таким образом, можно сказать, что адап-
тивная система стремится минимизировать получаемое ею отри-
цательное подкрепление.
Функция регулятора в перцептроне состоит как раз в созда-
нии такого подкрепления, т. е. регулятор играет роль инструк-
Адаптивные системы в биологии
189
тора или тренера. Но в отличие от обучения человека или жи-
вотных, при котором применяется как положительное, так и от-
рицательное подкрепление, в перцептроне регулятор создает
только отрицательные подкрепления; это означает, что перцеп-
трон не получает «поощрения» за правильный ответ, но «нака-
зывается» за неправильный ответ.
Как нетрудно себе представить, существует обширная лите-
ратура по вопросам математической теории обучения. В первых
работах (см., например, [105]) делались в основном попытки ус-
тановить характер поведения организмов при обучении, подвер-
гая количественному исследованию нейронные модели. Позже,
однако, специалисты по теории обучения по большей части зани-
мались постановкой и анализом специальных экспериментов по
обучению, и основное внимание уделялось стохастическим ас-
пектам этих процессов, а не нейронным механизмам. Эти сто-
хастические теории во многих отношениях сходны с теорией,
которой мы коснулись в разд. 11.2.
Вначале будет, пожалуй, интересно описать одну простую
нейронную модель обучения, предложенную Ландалем [106]. Ос-
новные контуры этой модели указаны на фиг. 32.
На этой схеме S] и S2 представляют два стимула одинако-
вой интенсивности, поступающие из внешней среды. Действие
лишь одного стимула — Si или S2— вызывает соответственно
реакцию /?1 или R2. Проблема возникает тогда, когда оба
190
Глава 11
стимула — 5i и 52— действуют одновременно. В случае, изобра-
женном на фиг. 32, предполагается, что правильной реакцией
является /?1, т. е. что схема «заучивает» /?ь Контуры обратной
связи С, С' играют роль регуляторов, создающих требуемое
подкрепление. Контур С создает «положительное» подкрепле-
ние; если возникает реакция Ri, то влияние контура сцЬ^С уси-
ливается. Контур С' производит отрицательное подкрепление;
при возникновении реакции Т?2 влияние контура а2Ь2С' ослаб-
ляется. Перекрестные связи <Zi62, a2bi являются тормозными:
стимул 51 тормозит реакцию R2, а стимул 52 — реакцию R\.
Торможение в точке а2, производимое через контур С', ослаб-
ляет, естественно, торможение реакции R\, осуществляемое че-
рез связь a2Z?i.
Какова будет реакция системы на первую стимуляцию — Ri
или /?2 — зависит от случайных обстоятельств, но даже из каче-
ственных соображений ясно, что при повторных стимуляциях эта
система рано или поздно начнет все время давать реакции Ri.
Количественное исследование, например расчет ожидаемого
числа неверных ответов при N пробах, проведенное на основа-
нии теории нейронного возбуждения Рашевского (см. [127],
особенно гл. 32)< дает результаты, очень близкие к ситуациям,
наблюдаемым в ряде опытов по обучению; по поводу подроб-
ностей мы отсылаем читателя к работе Ландаля [107].
Сравнивая фиг. 32 со схемой перцептрона (фиг. 31), легко
заметить большое сходство между ними, особенно если два
выхода на фиг. 32 заменить одним выходом, предположив, что
он может принимать два состояния (приписав, скажем, Ri дво-
ичную цифру 1, a R2— цифру 0), и, кроме того, объединить кон-
туры С, С' в один общий блок. Схема на фиг. 32 должна также
напомнить читателю схему на фиг. 30, так как модель эмбрио-
нальной дифференцировки, основанная на теории химической
регуляции, формально тождественна простым -моделям обуче-
ния Ландаля ’. Этот факт далеко не случаен и имеет большое
значение (см. по этому поводу разд. 11.4).
Обратимся теперь к проблемам и методам, характерным для
стохастической теории обучения [109, ПО], для чего рассмотрим
опыты по обучению крысы .в лабиринте, который состоит из
1 Формальная эквивалентность между нейронными схемами обучения и
моделями дифференцировки Жакоба и Моно в неявном виде учитывается
в статье Сугита [108]. В этой работе по существу показана аналогия между
моделями Жакоба и Моно и теорией дискретных нервных сетей Мак-Калло-
ка—Питтса (см [12], стр. 207—229). Ввиду хорошо известного соответствия
между дискретными сетями и непрерывными нейронными моделями Ландаля
это позволяет непосредственно перейти от модели дифференцировки к моделям
обучения Ландаля и наоборот.
Адаптивные системы в биологии
191
ряда последовательно разветвляющихся проходов. У каждого
разветвления (пусть их число равно, скажем, N) крыса сталки-
вается с двумя альтернативами, а именно с вопросом о том, по-
вернуть ли ей вправо или влево. С самого начала у нее нет ни-
какой внутренней причины для предпочтения одной из этих
возможностей другой, и поэтому вначале она делает выборы по
большей части случайно. После того как крыса выберется из
лабиринта несколько раз и каждый раз получит у выхода по-
ощрение в виде кусочка пищи, вероятности того, что она выбе-
рет поворот налево или направо при каждом конкретном вы-
боре, начинают существенно отличаться от того случайного
распределения, которое наблюдалось вначале; в каждом случае
они оказываются все более близкими к 1 или к 0. В конце кон-
цов эти вероятности стабилизируются, и тогда можно сказать,
что крыса «научилась» выбираться из лабиринта. Такие экспе-
рименты позволяют получить очень ценную информацию отно-
сительно процесса обучения; так, например, это дает возмож-
ность установить, сколько проб требуется для того, чтобы ве-
роятности стабилизировались, как это время стабилизации
зависит от числа N и как оно изменяется в зависимости от сте-
пени подкрепления.
Такого рода эксперименты лежат в основе стохастической
теории обучения. Предполагается, что субъект поставлен перед
некоторым множеством альтернатив, в которых он должен сде-
лать последовательные выборы, или испытания. Предположим
для простоты, что имеются лишь две альтернативы: Ль А2.
Пусть рп-\ — вероятность того, что при (п—1)-м испытании
выбирается возможность Л^ тогда 1—pn-i есть вероятность
того, что при этом испытании выбирается возможность Л2.
Задача состоит теперь в том, чтобы найти вероятность рп вы-
бора Л1 при п-й пробе, зная рп-\ и «правильность» выбора, про-
изведенного при (п—1)-й пробе (оценкой «правильности» слу-
жит характер подкрепления). Обычно полагают, что имеют
место правила, определяемые линейными зависимостями,
а именно
Pn = ai + aiPn-i’ (И.2)
если при (п—1)-й пробе было выбрано Ль и
Рп = а2+%рп-1, (11.3)
если было выбрано Л2. Здесь а\, а2, си, а2— подобранные соот-
ветствующим образом постоянные, характеризующие «правиль-
ность» полученного результата. Таким образом, если задана на-
чальная вероятность ро (равная, скажем, 1/2), то получается ряд
192
Глава 11
последовательных вероятностей, определяющий стохастический
процесс *.
Определенный таким способом стохастический процесс по-
зволяет получить очень ценную информацию. Так, например,
можно выразить «ожидаемое» значение вероятности рп для лю-
бого номера п пробы через константы alt а2, си, а2, ро- Это дает
возможность предсказать, скажем, число проб, требуемое для
достижения определенных уровней обучения, степень подкреп-
ления, требуемую для того, чтобы обучение некоторой задаче
достигалось при заданном числе проб, и т. д. Значения этих по-
стоянных могут быть оценены на основании анализа экспери-
ментальных данных. Детальное обсуждение математических
проблем, связанных со стохастической теорией обучения, и срав-
нительный анализ теоретических и экспериментальных резуль-
татов можно найти в цитированных ранее работах [109, 110].
Как уже было указано, стохастическая теория обучения
чрезвычайно абстрактна. В ней рассматривается лишь некото-
рое множество абстрактных элементов, называемых пробами,
каждому из которых соответствует возможность выбора между
элементами некоторого множества взаимоисключающих «реак-
ций». При каждой пробе вероятности, связанные с выбором
различных реакций, преобразуются с помощью определенных
правил, записываемых в виде линейных соотношений типа
(11.2), (11.3). Ввиду такой степени абстракции существует мно-
жество различных типов физических и биологических систем,
реализующих ситуации, возникающие в абстрактной стохасти-
ческой теории обучения. (Напомним, что в разд. 8.6 аналогич-
ное замечание было сделано по поводу теории систем, описы-
ваемых с помощью передаточных функций.) Укажем еще, что
стохастические модели обучения можно реализовать и не при-
влекая схем, аналогичных описанной выше схеме Ландаля (см.,
например, [111]). Кроме того, их можно также реализовать с по-
мощью таких устройств, как перцептрон; читателю должно уже
быть понятно значительное сходство между перцептроном и
различными стохастическими моделями.
11.4. Еще раз об онтогенезе и филогенезе
В этом разделе мы обсудим вкратце весьма близкую связь
между оптимальным характером структуры живых организмов,
обсуждавшимся в гл. 4—6, и оптимальным характером функций
1 Как указывалось в предисловии, стохастические модели в этой книге ие
рассматриваются Подробное описание таких моделей и обширную литературу
по этому вопросу читатель может найти в книгах Буша и Мостеллера [109]
и Буша и Эстеса [110].
Адаптивные системы в биологии
193
адаптивных систем. Такая связь неоднократно отмечалась и
раньше, однако ее редко использовали в явной форме. Наши
рассуждения неизбежно будут поверхностными и неполными, но
внимательного читателя они подведут к ряду не изученных до
сих пор интересных и важных проблем, относящихся к самым
различным областям математической биологии.
Основное утверждение, которое мы хотим здесь высказать,
состоит в следующем: популяция сходных организмов, претерпе-
вающая эволюцию во времени, представляет собой адаптивную
систему в том точном смысле, в каком этот термин употреб-
лялся’ ранее. Для того чтобы придать этому утверждению опре-
деленный смысл, нужно определить множество входных сигна-
лов, или стимулов, предъявляемых данной системе, множество
возможных выходных сигналов, или ответных реакций, и правила
подкрепления, которые являются функцией ее реакций на опре-
деленные входные сигналы.
Будем теперь считать, что внешняя среда, в которой нахо-
дится данная популяция, предъявляет в каждый момент вре-
мени t каждому организму из данной популяции некоторый
класс ситуаций (Д] (t),A2 (t),...,AN (/))• Для простоты пред-
положим, что всякая такая ситуация, скажем Дг-(0, требует от
организма принятия решения, выражающегося некоторым дво-
ичным сигналом; такое решение может состоять либо в выборе
определенной ответной реакции Ri, либо в отказе от Ri. Итак,
в каждый момент времени 1 каждый организм из данной попу-
ляции должен определить множество, состоящее из N двоичных
сигналов, соответствующих этим решениям. [Слово «решение»
употребляется здесь, конечно, не в антропоморфическом, а, так
сказать, в «метаболическом» смысле; например, организм мо-
жет стоять перед возможностью синтезировать или не синтези-
ровать определенный метаболит при внешних условиях, харак-
теризуемых множеством (Д1 (/), Да (0, • ••, Дх (0-] '
Фактором, посредством которого популяция получает поло-
жительное или отрицательное подкрепление, является естест-
венный отбор. Тот организм, который принимает «неверное» ре-
шение (например, решение Ri, создающее для него неблагопри-
ятную ситуацию по сравнению с теми организмами, которые
приняли противоположное решение), «получает взыскание», и
вполне очевидно, что организм, постоянно принимающий невер-
ные решения, будет в конечном счете элиминирован из популя-
ции. Вследствие этого в популяции будут накапливаться такие
организмы, каждый из которых выбирает «правильные» реше-
ния при стимулах, предъявляемых внешней средой, и, следова-
тельно, вся популяция в целом будет приближаться к состоя-
нию, оптимальному для данной среды. В этом смысле
194
Глава 11
оптимальность означает максимальную жизнеспособность всей
популяции в целом.
Переходя к более подробному обсуждению, можно предполо-
жить, что в некоторый начальный момент времени t0 всякий
(скажем, j-й) организм из данной популяции характеризуется
некоторым множеством «вероятностей ответных реакций», соот-
ветствующих стимулам, предъявляемым внешней средой; пусть
стимулу Дг(^о) соответствует вероятность pi (/о) в том смысле,
что pi. (to) является начальной вероятностью выбора реакции
Ri на стимул At (t0) (ввиду предположения о том, что выборы
реакций характеризуются двоичными сигналами, вероятность
отсутствия реакции R{ при стимуле Дг-(/0) равна 1—pi (to). Эти
вероятности могут, естественно, меняться при переходе от од-
ного организма к другому.
Вся популяция в целом характеризуется поэтому множе-
ством «средних» вероятностей pi(to), определяемых формулами
м
Pi(to) = 7Г 2 (*о); »= 1,..м,
у = 1
где М — размер популяции. Совокупность средних вероятностей
можно принять за «состояние» популяции, рассматриваемой как
адаптивная система. Под влиянием естественного отбора, дей-
ствующего на отдельные особи популяции, ее состояние будет
изменяться во времени, причем характер этого изменения будет
зависеть от начального распределения вероятностей и правил
подкрепления. Если предположить, что для этих правил имеет
место теорема сходимости такого типа, как упомянутая раньше
(интуитивные соображения подсказывают, что в общем случае
так и должно быть), то популяция будет все ближе и ближе
подходить к состоянию, являющемуся оптимальным по отноше-
нию к данной среде *.
Из всего сказанного может создаться впечатление, что аппа-
рат теории адаптивных систем, примерами которых служат та-
1 Этот вопрос рассматривается строго в математической теории популя-
ционной генетики. За основные переменные в этой теории принимаются час-
тоты генов в популяции, и ставится задача отыскать скорость изменения этих
частот в разных условиях Каждому индивидуальному генотипу приписывают
некоторую формально определенную численную величину, называемую «при-
способленностью», которая рассматривается как мера конкурентоспособности
индивидуума, несущего этот генотип. Таким образом, изменение частот генов
в популяции определяет, каким образом приспособленность популяции изме-
няется во времени. Основная идея популяционной генетики состоит в том,
что приспособленность по самому своему определению должна стремиться
к максимуму; в сущности скорость увеличения приспособленности использу-
ется как мера Давления отбора на данную популяцию. Многие из этих идей
принадлежат Фишеру [112], который провел аналогию между возрастанием
Адаптивные системы в биологии
195
кие устройства для распознавания изображений, как перцептрон
или разнообразные модели стохастической теории обучения, мо-
жет быть целиком применен непосредственно к эволюциони-
рующим популяциям. Однако на самом деле здесь приходится
столкнуться с рядом проблем, которые делают эту задачу зна-
чительно более сложной, чем она кажется на первый взгляд.
Некоторые из этих проблем мы сейчас и обсудим.
Главная трудность состоит в том, что вероятности Pi(f) —
основные параметры, используемые при любом способе подхода
к этим вопросам в терминах теории адаптивных систем, — не
выражают те свойства реальных организмов или популяций, ко-
торые до/,гупны прямому наблюдению; их нельзя также (по
крайней мере в настоящее время) выразить через другие непо-
средстг/щно наблюдаемые свойства организмов. Наиболее до-
ступах такому наблюдению те свойства, которые связаны с функ-
ционалами, рассмотренными в разд. 5.1, и поэтому приспосо-
бительные реакции организмов и популяций по отношению
к внешним условиям следовало бы измерять с помощью вариа-
ций таких функционалов. Естественно ожидать, что каждый та-
кой функционал может быть выражен как функция состояния
соответствующего организма, т. е. через вероятности pl (t). Но,
не имея специфической информации о виде этой зависимости
в каждом конкретном случае, невозможно, по-видимому, пе-
рейти от результатов, полученных в теории адаптивных систем,
к феноменологическому описанию процессов филогенеза с по-
'мощью тех типов функционалов, которые рассматривались
в гл. 5 и 6. А в том, что касается филогенеза, биологов интере-
сует, по крайней мере в настоящее время, именно эта феноме-
нологическая теория.
Эти рассуждения можно продолжить. Одна из важнейших
черт феноменологической теории филогенеза заключается в том,
что в ней мы постоянно встречаемся1 с законом аллометрии. Но
аллометрический закон описывает зависимости между функцио-
налами определяющей системы. А соотношения такого типа для
приспособленности популяции под действием естественного отбора и возрас-
танием энтропии, которое утверждается вторым законом термодинамики.
Предположения Фишера относительно скорости возрастания приспособленности
в значительной степени усилил Кимура [113]; он выдвинул в качестве общего
принципа утверждение, что в течение любого заданного промежутка вре-
мени естественный отбор вызывает такие изменения частот генов в популяции,
которые максимизируют приспособленность популяции. Мы, естественно, не
можем обсуждать здесь подробно эти идеи и их различные разветвления,
в частности потому, что по природе своей эти проблемы являются в основ-
ном стохастическими. Но нам хотелось бы привлечь внимание читателя к фор-
мальному и логическому сходству принципа Кимура и принципа оптимально-
сти в биологии в свете идей, рассмотренных в этом разделе.
196
Глава 11
известных адаптивных систем в настоящее время не установ-
лены, главным образом потому, что в теории обучения и тео-
рии распознавания изображений, с одной стороны, и в идеях,
связанных с рассмотрением эволюционирующих популяций,
с другой, упор делается на разных аспектах изучаемых явлений.
Можно надеяться, что существование таких соотношений, как
закон аллометрии, в свое время даст возможность проникнуть
в природу тех правил подкрепления, по которым действует есте-
ственный отбор, и это откроет новые интересные области иссле-
дования для тех, кто занимается также теорией обучения и тео-
рией распознавания изображений.
Онтогенез. Из обсуждения зависимости между филогенезом
и онтогенезом, проведенного в гл. 4, вытекает, что, если фило-
генез можно рассматривать как адаптивный процесс.то про-
цессы онтогенеза должны (по крайней мере, формально), тоже
обнаруживать четко Выраженные черты адаптации. Это в зна-
чительной степени проясняет ту тесную аналогию, которая была
замечена между схемами дифференцировки (например, схемой
Жакоба и Моно, о которой говорилось выше) и схемами обу-
чения и обусловливания, предложенными Ландалем. Такой ана-
логии следует ожидать между любыми двумя различными пред-
ставлениями одной и той же абстрактной теории; именно такого
типа аналогия существует, например, между механическими и
электрическими осцилляторами, описываемыми одним и тем же
уравнением вида (7.10).
Сделаем в заключение еще одно замечание. Подход к изуче-
нию эволюционирующих популяций с позиций теории адаптив-
ных систем, при котором естественный отбор рассматривается
как фактор, осуществляющий подкрепление, по-видимому,
вполне естествен и плодотворен. Конечная цель такого метода
состоит в обосновании феноменологической теории, развитой
в гл. 6 на основании идеи оптимальной структуры индивидуаль-
ных организмов, или, в терминах теории адаптивных систем, на
основании их тенденции к оптимальному поведению (в данном
случае — в стремлении к максимальной плодовитости). Утвер-
ждение, что такое обоснование действительно может быть полу-
чено, представляет собой элегантную новую формулировку при-
веденных в гл. 1 соображений о том, что принцип оптимальной
конструкции можно было бы вывести из действия естественного
отбора. С этой точки зрения цель теории адаптивных систем со-
стоит не в чем ином, как в построении строгого доказательства
принципа оптимальной конструкции. Поиски такого доказатель-
ства, по-видимому, приведут ко многим новым важным идеям,
связанным с математическим подходом к изучению свойств
живых организмов.
Глава 12
МАТЕМАТИЧЕСКИЕ МОДЕЛИ В БИОЛОГИИ
И ЭКОНОМИКЕ
12.1. Введение
В разд. 4.3 уже указывалось, что жизнь на Земле началась,
по-видимому, с образования свободноживущих одноклеточных
организмов из более простого, предбиологического материала.
Термин «свободноживущий» означает здесь, что каждый инди-
видуум, принадлежащий к популяции сходных организмов,
относительно независим от остальных членов популяции.
В частности, каждый индивидуум полностью сохраняет способ-
ность осуществлять все необходимые биологические функции,
в частности наиболее важную из них— функцию размно-
жения.
Эволюция организмов типа клеточных колоний внесла в био-
логию новый элемент в отношении как физиологии отдельных
членов колонии, так и биологии популяций. Организм, входя-
щий в состав колонии, был в известной мере защищен от давле-
ния отбора, действовавшего на свободноживущие организмы,
причем эта защита была тем эффективнее, чем выше был уро-
вень организации этой колонии. Вместе с тем отбор стал дейст-
вовать на самое колонию как независимую единицу, конкури-
рующую с другими колониями. Полная биологическая автоно-
мия каждого индивидуума, входящего в состав колонии,
была бы, очевидно, неблагоприятна для колонии в целом, и
опять-таки тем более неблагоприятна, чем выше уровень орга-
низации колонии. Иными словами, полная биологическая авто-
номия каждого отдельного члена колонии становилась несов-
местимой с высоким уровнем организации колонии, и поэтому
члены таких колоний должны были подвергнуться косвенному
отбору в отношении их ценности в качестве составной части
общей колониальной организации
Эволюционный переход от колониальной организации к на-
стоящим многоклеточным организмам принес с собой новую
характерную черту—разделение функций между отдельными
клетками организма. В частности, в многоклеточных организ-
мах имеется одна линия клеток, предназначенных лишь для по-
лового размножения. Эта специализированная линия клеток на-
зывается зародышевой линией. Все прочие клетки такого
198
Глава 12
организма объединяются под общим названием сома, и с точки
зрения размножения организма как целого клетки сомы сте-
рильны. Это отличие было подчеркнуто Вейсманом [114], и оно
исключительно важно для понимания механизма наследствен-
ности у многоклеточных организмов.
Таким образом, многоклеточный организм состоит уже не из
свободноживущих клеток; каждая его клетка выполняет одну
или несколько функций, которые имеют значение только как со-
ставные элементы жизнедеятельности организма в целом.
В этих условиях давление отбора уже не действует непосред-
ственно на отдельные клетки, а направлено на организм клк
единое целое ’.
Взаимоотношения индивидуальных многоклеточных организ-
мов друг с другом развивались в том же направлении, что и
взаимоотношения предшествовавших им свободноживущих оди-
ночных клеток. Сначала отдельные особи (за исключением об-
лигатных паразитов и некоторых симбионтов) были независимы
от остальных особей этой популяции. Затем некоторые виды
многоклеточных организмов неизбежно сами приобрели своего
рода колониальную форму организации, и тогда на такую орга-
низацию начало непосредственно действовать давление отбора;
как следствие этого, у наиболее высокоразвитых колониальных
форм появляется разделение труда.
Стабильные колониальные агрегаты многоклеточных орга-
низмов, в которых наблюдается некоторая степень разделения
труда, называют обычно сообществами, а организмы, образую-
щие такие сообщества, называют общественными. Наиболее
известные и хорошо изученные сообщества — это сообщества
муравьев, пчел, ос и термитов.
Из высказанных н^ми соображений и принципа сходимости
с очевидностью вытекает, что структура сообществ многокле-
точных организмов должна быть во многом аналогична струк-
туре многоклеточных организмов, состоящих из отдельных кле-
ток. Такие аналогии были подмечены Платоном, их обсуждал
и Фома Аквинский. С течением времени в этой области сложи-
лась обширная литература, охватывающая сочинения самого
разнообразного плана — начиная от чисто философских работ
(например, труды Гоббса, Руссо, Гегеля) и кончая детальными
1 В гл 7 и 9 было рассмотрено несколько физиологических механизмов
гомеостаза у многоклеточных организмов, в частности механизмов, связанных
с обеспечением постоянства внутренней среды Нетрудно понять, что такое
постоянство внутренней среды организма минимизирует конкуренцию между
его клетками, органами и тканями, т. е защищает их от конкуренции друг
с другом и от контакта с внешней средой. По этому поводу мы отметим,
что там, где минимизируется конкуренция, отбор прекращается.
Математические модели в биологии и экономике
199
зоологическими исследованиями. Мы не намереваемся углуб-
ляться здесь в эту литературу, но важно отметить, что аналогия
между структурой многоклеточного организма и структурой со-
общества значительно глубже, чем обычно думают; особенно
это относится к сообществам насекомых. В этих сообществах
разделение труда повлекло за собой соответствующую биологи-
ческую дифференциацию; любой школьник знает, например, что
между рабочей пчелой, трутнем и маткой имеются большие
морфологические различия. В соответствии с этим сообщества
насекомых делят на касты, основываясь непосредственно на
биологических признаках, причем каждая структурная модифи-
кация определяет роль соответствующего индивидуума в сооб-
ществе. Это разделение на касты аналогично дифференцировке
в многоклеточном организме, которая тоже основана на морфо-
логических и вытекающих из них функциональных различиях
индивидуальных клеток, обладающих одними и теми же наслед-
ственными задатками. Более того, такие касты, как рабочие
’особи или солдаты, стерильны; это различие между стерильными
и половыми кастами в таких сообществах очень напоминает
различие между клетками зародышевой линии и соматическими
клетками, о котором говорилось выше. Более того, гнезда, ко-
торые строят общественные насекомые разных видов, обладают
признаками, которые являются такими же надежными видо-
выми признаками, как особенности раковины у моллюсков, на-
ружного скелета у насекомых и внутреннего костного скелета
у высших позвоночных *.
Человеческое общество не основано, разумеется, на биологи-
ческой дифференциации, но разделение труда в нем тем не ме-
нее существует. В наши цели не входит философское обсужде-
ние этих проблем; мы хотим лишь отметить, что ввиду много-
численных аналогий между структурой организмов и структурой
сообществ изучение последних может дать весьма полезную ин-
формацию, позволяющую проникнуть в сущность биологиче-
ских явлений. В определенном смысле организмы и сообщества
можно рассматривать как реализации одних и тех же абстракт-
ных математических моделей [так же как механический и элек-
трический осцилляторы описываются одним и тем же уравне-
нием вида (7.10)], и поэтому физиолог, изучающий свойства
многоклеточных организмов, и, скажем, экономист, изучаю-
щий экономику человеческого общества, с математической
точки зрения могут прийти к одним и тем же математическим
1 Обсуждение параллелей между организмами и сообществами, а также
ссылки на обширную литературу можно найти в работах зоолога А Эмерсона
[115, 116].
200
Глава 12
моделям. В прошлом такой метод рассуждения часто использо-
вался в общественных науках; можно рассчитывать на то, что
с помощью такого ^подхода биологу также удастся узнать нечто
новое.
12.2. Задачи программирования в экономике
Экономика является одной из наиболее развитых общест-
венных наук, и в ней шире всего применяются количественные
методы. Она представляет собой такую область общественных
наук, которая наиболее удобна для построения математических
моделей и формализации. Поэтому в свете отмеченной выше
аналогии между математическими моделями, которые строятся
в биологии и в экономике, полезно попытаться отыскать среди
экономических моделей те черты, которые, возможно, имеют
отношение к биологии и дадут возможность глубже проникнуть
в сущность биологических явлений, и затем сравнить эти мо-
дели с их чисто биологическими аналогами. Такое сравнение
имеет смысл особенно потому, что, как оказывается, большая
часть аппарата математической экономики опирается в явном
виде на соображения оптимальности.
Несмотря на отмеченное выше сходство, большая часть ма-
тематических моделей в экономике была построена независимо
от их биологических аналогов. Тем не менее в свете тех общих
соображений, которые здесь были высказаны, можно ожидать,
что обнаружатся широкие области, в которых экономические
модели (по крайней мере, в основных своих принципах) смы-
каются с теми общими положениями принципа оптимальности
в биологии, которым посвящена данная книга.
Попытаемся теперь продемонстрировать то, что было здесь
сказано, хотя, быть может, и в несколько ином аспекте. Успеш-
ная конкуренция в некоторой экономической ситуации требует
максимизации прибыли (мы будем понимать под прибылью по-
просту разность между затратами, связанными с получением
или изготовлением товаров для продажи, и ценой, по которой
эти товары будут проданы). В общем случае предприниматель
вначале располагает некоторым количеством различных видов
сырья, из которых могут быть изготовлены разнообразные то-
вары. Следовательно, для того чтобы наиболее эффективно
участвовать в конкуренции, предприниматель должен решить
проблему наилучшего распределения принадлежащего ему
сырья с тем, чтобы изготовленные из него товары давали наи-
большую прибыль. Задачи такого типа, возникающие во мно-
гих областях экономики и смежных с ней наук, называют
обычно задачами программирования. Естественно, что такие
Математические модели в биологии и экономике
201
задачи были весьма тщательно исследованы. Для нас пред-
ставляет определенный интерес более подробное изучение этих
проблем; читатель заметит, конечно, много точек соприкоснове-
ния между этими задачами и теми вопросами, которые мы об-
суждали раньше.
Допустим, что имеется фабрика, которая может произво-
дить два вида различных товаров, скажем Si, s2, изготовляемых
из трех видов сырья: rlt г2, г3. Пусть известно, что прибыли, по-
лучаемые от продажи единиц товаров Si, s2, равны соответст-
венно pi, р2 (как было сказано выше, прибыль принимается
равной разности между стоимостью производства товара и про-
дажной ценой). Предположим далее, что для производства од-
ной единицы товара Sj(/=1,2) требуется затратить а^(i= 1,2,3;
/=1, 2) единиц сырья гг(г = 1, 2, 3) и что фабрика располагает
запасом в Яг (i=l, 2, 3) единиц сырья гг (i=l, 2, 3).
Владелец фабрики должен теперь решить, сколько единиц
Xi, х2 товаров Si> s2 соответственно должно быть произведено,
для того Чтобы максимизировать прибыль. В данном случае
прибыль р(Х\, х2) определяется простым линейным выражением
вида
/?(%1, л2)==/,1л1 + р2л2. (12.1)
Теперь следует отметить, что решение (хь х2) этой задачи
должно удовлетворять ряду ограничений. Так, например, нельзя
использовать больше сырья, чем в данный момент имеется на
складе, и поэтому должны выполняться неравенства
#11-^1 ~Ь ®12-^2 ^1">
«21-^1 + «22-^2 < , (12.2)
^31-^1 4“ ®32-^2 R3 •
Далее, мы имеем неравенства
х}^0, х2^0, (12.3)
и, наконец, важное условие заключается в том, что pi, р2 не
равны одновременно нулю.
Сформулированная только что задача принадлежит к зада-
чам линейного программирования, так как неизвестные величины
Xi, х2 в каждое из соотношений этой задачи [а именно, (12.1) —
(12.3)] входят линейно, т. е. в первой степени. Такие линейные
задачи лучше всего изучены и обычно наиболее доступны иссле-
дованию *.
1 Имеется несколько превосходных руководств по теории и приложениям
метода линейного программирования, в частности [117—119]
202
Глава 12
Следует сравнить формулировку этой задачи с общей фор-
мулировкой проблем оптимальности, приведенной в гл. 1 и 2.
Как отмечалось, постановка всякой задачи об оптимизации
включает выбор оценочной функции, заданной на корректно
определенном пространстве допустимых решений, которая дол-
жна быть минимизирована (или, как в данном случае, макси-
мизирована). В нашем случае оценочная функция задается
в явном виде формулой (12.1); обратимся теперь поэтому
к пространству решений.
Неравенство х2^Г) показывает, что всякое возможное реше-
ние (х\, х2) этой задачи представляется точкой на (xi, х2) -плос-
кости, лежащей не ниже оси Xi (т. е. линии х2=0). Аналогично
неравенство xt 0 говорит о том, что каждое допустимое реше-
ние (хь х2) должно лежать не левее оси х2 (линия Х]=0). Сле-
довательно, все допустимые решения расположены в первом
квадранте (хь х2) -плоскости.
Заметим далее, что прямая линия
^11^1 “Ь ^12-^2 ===^?1 (12.4)
(при условии ai2=#0) разбивает (хь х2)-плоскость на две полу-
плоскости так, что для всех точек (хь х2), расположенных выше
этой линии, имеет место неравенство ацХ1 + а12х2>/?1, а для то-
чек, лежащих ниже этой линии или на ней, anXi+ai2x2
Итак, все точки (хь х2), удовлетворяющие первому из нера-
венств (12.2), должны лежать на прямой (12.4) или ниже ее.
Если эта линия лежит вне первого квадранта (хь х2)-плоскости,
то, очевидно, поставленная задача не имеет решения. Мы, на-
против, предположим, что линия (12.4) проходит через первый
квадрант.
Аналогично остальные два неравенства (12.2) ограничивают
пространство (множество) решений теми точками (хь х2), ко-
торые расположены в полуплоскостях, лежащих соответственно
не выше прямых
^-21-^1 ~Ь ^22^2 — ^?2>
^31Х] 4- л32х2 — Ъ-
Множество допустимых решений представляет собой, таким об-
разом, пятиугольник (заштрихован на фиг. 33), ограниченный
осями Xi и *2 и линиями (12.4), (12.5).
Теперь решение задачи сводится просто к тому, чтобы опре-
делить, какие точки (Xi, х2) из пространства решений максими-
зируют оценочную функцию, т. е. прибыль p(xi, х2), выражае-
мую формулой (12.1). Прежде всего вполне очевидно, что точка,
являющаяся решением, должна лежать на границе простран-
(12.5)
Математические модели в биологии и экономике
203
ства решений. В самом деле, если бы решением была какая-то
внутренняя точка (%i*, %2*), то можно было бы тотчас же при-
менить теорему 2.6, и тогда, согласно (12.1),
др
дхх
др
дх2
а это противоречит первоначальному предположи ,ю, что р\,
р2 не обращаются одновременно в нуль. Далее 'нетрудно пока-
| Ось х2
зать, что искомое решение должно в действительности совпа-
дать с одной из вершин пятиугольника, т. е. с одной из точек
0, Р\, Рг, Рз, Рь изображенных на фиг. 33.
Упражнение
Докажите последнее утверждение. (Указание: предполо-
жите, что величины прибыли р различны в двух вершинах, и по-
- кажите, что тогда прибыль монотонно изменяется при переме-
щении в ту или иную сторону вдоль прямой, соединяющей эти
две вершины.)
Приведенные выше рассуждения переносятся без существен-
ных изменений на случай любого числа товаров а,.
Совершенно аналогичная ситуация возникает во многих дру-
гих экономических проблемах, например в транспортных зада-
чах (см. [117], гл. 10), в задачах о распределении и назначении
204
Глава 12
персонала (см. [117], стр. 152—154) и многих других1. Каждая
из этих областей служит источником задач линейного програм-
мирования, т. е задач о минимизации линейной оценочной функ-
ции при наличии линейных ограничений
Существует много важных задач программирования, не от-
носящихся к линейным, и они не могут быть непосредственно
решены с помощью тех методов, которые были здесь намечены.
Более того, многие допущения, которые были неявно сделаны
при формулировке разобранной выше задачи о программиро-
вании, нереальны с точки зрения экономики. Так, например,
предполагалось, что прибыли р\, ръ постоянны, т. е независимы
от времени. Но на самом деле эти величины, так же как и пара-
метры аг], в общем случае зависят от времени и даже подвер-
жены недетерминированным изменениям. Таким образом, пред-
приниматель, встречаясь с задачами программирования, обычно
располагает неполной и изменяющейся во времени информа-
цией. К задачам такого типа может быть применен так назы-
ваемый метод динамического программирования2 Вспомним
также, что сходные проблемы встречались нам в разд. 10.4
в связи с задачами совсем иного рода
Поведение предпринимателя, который в ситуации, связанной
с применением метода динамического программирования, стре-
мится к максимизации своей прибыли и для этого меняет свой
образ действий некоторым оптимальным способом, несомненно
аналогично поведению адаптивных систем общего типа, стремя-
щихся избежать отрицательного подкрепления, поступающего
из внешней среды. Уже одно это замечание говорит о том, что
должны существовать широкие области применения общих ме-
тодов динамического программирования к задачам, возникаю-
щим в теории адаптивных систем. В разработке прямых прило-
жений методов программирования к таким биологическим зада-
чам? как задачи теории обучения, сделаны еще только первые
шаги3; основные трудности, связанные с этими проблемами,
были отмечены в разд. 11 4
Для того чтобы проиллюстрировать, каким образом можно
применить простейшие методы программирования для изучения
интересных биологических ситуаций, рассмотрим следующую
1 В книге Гасса [117] приведен обширный и удобный обзор литературы
по приложениям линейного программирования к широкому классу промыш-
ленных, экономических и военных задач (см стр 205—213)
2 Ряд примеров, иллюстрирующих приложение метода динамического про-
граммирования к таким задачам, можно найти в литературе (см, например,
[120])
3 Применение общих методов динамического программирования для изу-
чения биологических процессов адаптации кратко описано у Веллмана [121]
Математические модели в биологии и экономике
205
гипотетическую проблему. Предположим, что бактериальная
клетка помещена в среду, содержащую некоторое число, ска-
жем п, различных сахаров $ь ..., $п. Пусть при утилизации
каждой единичной порции сахара s, (i=l, ..., п) клетка полу-
чает энергию, равную Ег кал. С другой стороны, для поглоще-
ния этой порции сахара st (i=l, .... п) из среды (активный
перенос), а также для создания и поддержания соответствую-
щего метаболического аппарата клетка должна затратить неко-
торое количество энергии, скажем кал. Сколько же единич-
ных порций каждого сахара нужно ввести в клетку, чтобы число
полученных ею калорий было максимизировано?
Задача такого типа может быть решена с помощью стан-
дартных методов программирования. Исходя из концепции ес-
тественного отбора, следует предполагать, что реальная бакте-
рия, находящаяся в такой ситуации, будет придерживаться той
оптимальной формы поведения, которая выводится с помощью
метода программирования. Было бы интересно проверить, так ли
это в действительности. При физиологических исследованиях
возникает множество других задач программирования, каждая
из которых позволяет проверить возможность использования
методов оптимизации для решения биологических задач.
Было бы полезно на самом деле провести такую проверку
хотя бы для некоторых задач такого рода.
12.3. Экономика и теория игр
Невозможно говорить о математических методах в эконо-
мике, не упомянув хотя бы кратко теорию игр, первоначальное
развитие которой было положено фон Нейманом [122] и которая
была применена к исследованию разнообразных проблем эконо-
мики фон Нейманом и Моргенштерном [123].
Теория игр, грубо говоря, связана с доказательством сущест-
вования оптимальных стратегий для нескольких игроков, дейст-
вия которых подчинены определенным правилам игры, и с раз-
работкой методов непосредственного вычисления таких страте-
гий. Если один из игроков, скажем Р, придерживается
оптимальной стратегии, то это означает, что Р независимо от ме-
тодов игры других игроков выигрывает не меньше (или проиг-
рывает не больше) некоторого фиксированного количества, опре-
деляемого лишь правилами игры. (Последнее вовсе не означает,
что игрок, придерживающийся оптимальной стратегии, всегда
обязательно будет в выигрыше; в общем случае это не означает
даже и того, что он выигрывает больше, чем если бы он принял
какую-нибудь неоптимальную стратегию.)
206 Глава 12
Таким образом, теория игр тесно связана с задачами опти-
мизации. Многие аспекты теории игр действительно могут быть
полностью описаны в терминах тех математических методов, ко-
торые были развиты в других областях. Можно довольно просто
показать, что широкий и важный класс игр сводится к задачам
линейного программирования в той степени, в которой дело сво-
дится к вычислению оптимальных стратегий, и наоборот, все
задачи линейного программирования могут быть интерпретиро-
ваны как задачи, относящиеся к некоторым играм этого класса
(см., например, {124]). Другие типы игр могут оказаться экви-
валентными более общим задачам программирования. Такая
математическая эквивалентность говорит о том, что теория игр
создает еще один метод идейного подхода к тем проблемам оп-
тимальности, которые могут быть сформулированы в терминах
методов программирования {125].
ЛИТЕРАТУРА
1. Flint Н. Т., Wave Mechanics, Methuen, London, 1929.
2. Weyl H, Space, Time, Matter, Dover, New York, p 244, 1950.
3. Thompson D’Arcy W., On Growth and Form (revised edition),
Macmillan, New York, 1945.
4. J о о s G., Theoretical Physics (2nd edn), Hafner, New York, pp. 220—225,
1950.
5. Goldstein H., Classical Mechanics, Addison—Wesley, Reading, Mass.,
pp. 46—47, 1950. (Голдстейн Г., Классическая механика, Гостех- '
издат, М., 1957.)
6. “20th Century Darwinism”, Cold Spring Harbor Symposium on Quan-
titative Biology, Vol. 24, 1959.
7. Evolution After Darwin, Vol. 1, “The Evolution of Life", So! Tax (ed),
University of Chicago, Chicago, 1960.
8. Rensch B., Evolution Above the Species Level, Methuen, London,
1959.
9. Гаузе Г. Ф., The Struggle for Existeince, Williams and Wilkins, Bal-
timore, 1934.
10. Park T., Experimental Studies of Interspecies Competition, Ecol.
Monogr., 18, 265—308 (1948).
11. Toth L. F, What the Bees Know and What They Do Not Know, Bull.
Am. math, Soc., 70, 468—481 (1964).
12. Rashevsky N., Mathematical Biophysics (3rd edn), Dover, New York,
vol. Il, 1960.
13. Caspar D L. D , К1 u g A., Physical Principles in the Construction
of Regular Viruses, Cold Spring Harbor Symposium, Vol. XXVII, 1—24
(1962).
14. “Structure and Assembly of Regular Virus Particles” in Viruses, Nucleic
Acid and Cancer, Williams and Wilkins, Baltimore, pp. 27—29, 1963.
15. Mayor H. D., Icosahedra! Viruses —A Geometric Approach to their Ma-
turation, ibid., 63—67
16. Wald G„ The Origin of Life, PNAS, 52, 595—611 (1964).
17. Van der Waerden B. F., Modern Algebra, Vol. I, Ungar, New York,
p 209, 1950. (Ван дер Варден, Современная алгебра, Гостехиз-
дат, 1947.)
18. С our ant R., Hilbert D., Methods of Mathematical Physics, Vol. I,
Interscience, New York, p. 65, 1953. (Курант P. и Гильберт Д.,
Методы математической физики, Гостехиздат, М.—Л., 1951.)
19. F о г s у t h A. R., Calculus of Variations, reprinted by Dover Publica-
tions, New York, 1950.
20 Hancock H., Theory of Maxima and Minima, reprinted Dover, New
York, 1960.
21. Гельфанд И. M., Фомин С. В., Вариационное исчисление, Физ-
матгиз, М., 1961.
208
Литература
22. W е i n s t о с к R., Calculus of Variations, McGraw-Hill, New York, 1952.
23. Bridgman P. W., Dimensional Analysis (revised edition), Yale Uni-
versity Press, 1956.
24 Stahl W. R., Dimensional Analysis in Mathematical Biology 1, Bull,
math. Biophys., 23, 355—376 (1961).
25. Stahl W. R., Dimensional Analysis in Mathematical Biology II, Bull,
math. Biophys., 24, 81—108 (1962).
26. Murray C. D., The Physiological Principle of Minimum Work I, Proc,
nat. Acad. Sci., 12, 207—214 (1926).
27. Murray C. D., The Physiological Principle of Minimum Work Applied
- to the Angle of Branching of Arteries, J. gen. Physiol., 9, 835—841
(1926).
28. Cohn D., Optimal Systems: I The Vascular System, Bull. math.
Biophy, 16, 59—74 (1954); Optimal System II: The Vascular System,
ibid., 17, 219—227 (1955).
29. Murray C. D., The Physiological Principle of Minimum Work II,
Proc. nat. Acad. Sci, 12, 299—304 (1926).
30. MacDonald J., The Occurrence of Turbulent Flow in the Rabbit
Aorta, J. Physiol., 118, 340—347 (1952).
31. Rashevsky N., Mathematical Biophysics, Dover, New York, Vol. II,
Chap. XXVII, 1960.
32. Lehman H., Huntsman R. G., Why are Red Cells the Shape
They Are? Functions of the Blood, R. G. MacFarlane and A. H. T. Robb
(eds.), Academic Press, New York, 1961.
33. Hartridge H., The Shape of the Red Blood Corpuscle, J. Physiol.,
53, 81—85 (1919).
34. Jefferey A., Proc. roy. Soc. A, 107, 161 (1922).
35. В а у 1 i s s L. E., Rheology of Blood and Lymph, Deformation and Flow
in Biological Systems, A. Frey-Wissling (ed.), Interscience, New York,
1952.
36. Kettlewel 1 H. B. D., Investigations on the Evolution of Melanism
in Lepidoptera, Proc. roy. Soc., B, CXLV, 297 (1956).
37. H a e с к e 1 E , Generelle Morphologie der Organismen, Berlin, 1866.
38. H a e с к e 1 E., The Evolution of Man, transl. J. McCabe, Peter Eckler,
New York, 1906.
39. Meyer A. W., Some Historical Aspects of the Recapitulation Idea.,
Quart. Rev. Biol., 10, 379—396 (1935).
40. Garstang W., The Theory of Recapitulation, A Critical Restatement
of the Biogenetic Law, J. Linn. Soc. (Zoology), 35, 81—101 (1922).
41. Shumway W, The Recapitulation Theory, Quart. Rev. Biol, 7, 93—99
(1932).
42. D e Beer G. R., Embryos and Ancestors, Oxford University Press,
Oxford, 1940
43. R u s s e 11 E. S., Form and Function, Murray, London, 1916.
44. Huxley J., Problems of Relative Growth, Methuen, London, 1932.
45. Darboux G., Le<?ons sur la Theorie Generale des Surfaces, Vol. Ill,
Gauthier-Villars, Paris, pp. 53—58, 1894.
46. Forsyth A. R., Differential Equations, 6th edn, Macmillan, London,
p. 430, 1948.
47. С о u г a n t R., Differentia! and Integral Calculus, Vol. I, Interscience,
New York, 19*59. (Курант P., Курс дифференциального и интеграль-
ного исчисления, изд-во «Наука», 1967.)
48. Needham J., Chemical Heterogony and the Ground-plan of Animal
Growth, Biol. Rev., 9, 79—109 (1934).
49. Clark W. E., Med a war P. B. (eds.), Essays on Growth and Form,
Oxford University Press, Oxford, 1945.
Литература
209
50. Bellman R., Stability Theory of Differential Equations, McGraw-Hill,
New York, 1953. (Веллман P., Теория устойчивости решений диф-
ференциальных уравнений, ИЛ, М., 1954.)
51. Cesari L., Asymptotic Behavior and Stability Problems in Ordinary
Differential Equations, Springer, Berlin, 1959. (Чезари Л., Асимпто-
тическое поведение и устойчивость решений обыкновенных дифферен-
циальных уравнений, изд-во «Мир», М., 1964.)
52. Н ем ыцки й В. В., Степанов В. В., Качественная теория диф-
ференциальных уравнений, Гостехтеоретиздат, М„ 1949.
53. L a Salle J. Р., L е f s с h е t z S., Satbility by Lyapunov’s Direct
Method- with Applications, Academic Press, New York, 1961.
54. 3 у б о в В. И., Методы А. М. Ляпунова и их применение, Изд-во
ЛГУ, 1957.
55. L a m b е г t R-, Teissier G., Theorie de la Similitude Biologique,
Annis Physiol. Physicochim Biol., 2, 212—246 (1927).
56. Rosen R., Relational Biology and Bionics, I. E. E. E. Trans, on Mili-
tary Electronics, MIL 7, 160-162 (1963).
57. Cannon W., Wisdom of the Body, Norton, New York, 1932.
58. Wiener N., Cybernetics, Wiley, New York, 1948. (Винер H., Ки-
бернетика, Сов. радио, 1958.)
59. Widder D. V., The Laplace Transform, Princeton University Press,
Princeton, 1941.
60. Churchill R. V., Operational Mathematics (2nd edn), McGraw-Hill,
New York, 1958.
61. Ahrendt W. R., Taplrn J. F., Automatic Feedback Control,
McGraw-Hill, New York, 1961.
62. Riesz F., Nagy B. v. Sz., Functional Analysis, Ungar, New York,
p. 30, 1956.
63. Olson H. F., Dynamical Analogies (2nd edn), van Nostrand, New
York, 1958.
64. Ciba Foundation Symposium, Regulation and Mode of Action of Thyroid
Hormones, Little, Brown and Co., Boston, 1957.
65. Homeostasis and Feedback Mechanisms, XVIII of the Symposia for the
Society of Experimental Biology, Academic Press, New York, 1964.
66. H e a t h О. V. S., Light and Carbon Dioxide in Stomatai Movements,
Handb. d. Pflanzenphysiologie, vol. XVII, 415—464, Springer, Berlin
(1956).
67. S t a r k L, Stability, Oscillations and Noise in the Human Pupillary
Servomechanism, Proc. IRE, 47, 1925—1939 (1959).
68. S t a r k L., Sherman P. M., A Servoanalytic Study of Consensual
Pupil Reflex to Light, J. Neurophys., 20, 17—26 (1957).
69. S t a r k L., Herman H. T., The Transfer Function of a Photoreceptor
Organ, Kybernetik, I, 124—129 (1961).
70. Stark L., Oscillations of a Neurophysiological Servomechanism Pre-
dicted by Nyquist Stability Criterion, Selected Papers in Biophysics,
- Yale University Press, New Haven, 1959.
71. Stark L., Cornsweet T. N, Testing a Servoanalytic Hypothesis
for Pupil Oscillations, Science, 127, 588 (1958).
72. Wybar К. C., Ocular Manifestations of Disseminated Sclerosis, Proc,
roy. Soc. Med., 34, 180—189 (1950).
73. Johnson F. H, Eyring H., Polissar M. J.,' The Kinetic Basis
of Molecular Biology, Wiley, New York, pp. 200—214, 1954.
74. В e n z i g e r T. H., On Physical Heat Regulation and the Sense of Tem-
perature in Man, Proc. nat. Acad. Sci., 45, 465—659 (1959).
•75. Benziger T. H., Pratt A. W., К i t z i n g e r C., The Thermostatic
Control of Human Metabolic Heat Production, ibid., 47, 730—739 (1961).
210
Литература
76. В е n z i g е г Т. Н., The Diminution of Thermoregulatory Sweating
During Cold Reception at the Skin, ibid., 1683—1688 (1961).
77. G г a у J. S., The Multiple Factor Theory of Respiratory Regulation,
AAF Schoo! of Aviation Medicine Report I, Project No. 386, 1945.
78. G г о d i n s F. S., Control Theory and Biological Systems, Columbia
University Press, New York, 1963. (Гродинз Ф., Теория регулиро-
вания и биологические системы, изд-во «Мир», М., 1966.)
79. D е f а г е s J. G , Cybernetic Analysis of the Respiratory Chemostat,
in Physicomathematica! Aspects of Biology, N. Rashevsky (ed.), Aca-
demic Press, New York, pp. 196—239, 1962.
80. W i 1 s о n A. C., Pardee A. B., Comparative Aspects of Metabolic
Control, Comparative Biochemistry, vol. I (Florkin and Mason, eds),
Academic Press, New York, pp. 73-—118 (1963).
81. Umbarger H. E., Feedback Control by Endproduct Inhibition, Cold
Spring Harbor Symposium, 26 (1961). (Регуляторные механизмы
клетки, стр. 390, изд-во «Мир», М., 1964.)
82. R е i п е г J. М., Behavior of Enzyme Systems, Burgess, Minneapolis,
1959.
83. Heinmets F., Herschman A., Quantitative Analysis of Metabolic
Processes; I. Phys. Med. Biol., 4, 238—253 (1960); II, Bull, math,
Biophys., 23, 277—296 (1961); Ill, ibid., 69—90 (1961).
84. F u k u d a N., Sugita M., Mathematical Analysis of Metabolism I.,
J. Theoret. Biol., I, 440—-459 (1959).
85. C h a n с e B., Control Characteristics of Enzyme Systems, Cold Spring
Harbor Symposium, Vol. XXVI, 289—299 (1961). (Регуляторные меха-
низмы клетки, стр. 371, изд-во «Мир», М., 1964.)
86. G а г f i п k е 1 D., Digital Computer Simulation of Ecological Systems,
Nature, London, 194, 856—857 (1962).
87. P о i n с a r e’s Methodes Nouvelles de Mechanique Celeste (reprinted) Dover,
New York, 1957.
88. В i г к h о f f G. D., Dynamics Systems. Am. math. Soc. Colloquium Publ.,
Vol. 9, (1927).
89. Gottschalk W H., Hedlund G. A., Topological Dynamics, Am.
math. Soc. Colloquium Pub!., Vol. 36, 1955.
90. Morse M., The Calculus of Variations in the Large, Am. math. Soc.
Colloquium Publ., Vol. 18, 1934
91. Halmos P. R., Lectures on Ergodic Theory, Math. Soc. Japan, 1956.
(X а л м о ш П., Лекции по эргодической теории, ИЛ, M., 1959.)
92. К а 1 m a n R. Е., Contributions to the Theory of Optimal Control, Bol.
de la Soc. Mat. Mexicana, 102—119, 1960.
93. К a 1 m a n R. E., The Theory of Optimal Control and the Calculus of
Variations, RIAS Tech. Rep., 61—63.
94. К a 1 m a n R. E., Mathematical Description of Linear Dynamical Sy-
stems, J. SIAM Control Ser. A., I, 152—191 (1963)
95. К a 1 m a n R. E., Ho Y. C., Narendra K. S., Controllability of
Linear Dynamical Systems, Contributions to Differential Equations, I,
189—212 (1964).
96. Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В.,
Мищенко Е. Ф., Математическая теория оптимальных процессов,
Физматгиз, 1961.
97. Bellman R., Dynamic Programming, Princeton, 1957. (Беллман P.,
Динамическое программирование, ИЛ, М., 1961.)
98. В е 11 m a n R., Adaptive Control Processes, Princeton University Press,
Princeton, 1961.
99. Dreyfus S. E., Dynamical Programming and the Calculus qf Varia-
tions, J. Math. Anal. Appl., I, 228—239 (1960).
Литература
211
100. Goodwin С., Temporal Organization in Cells: A Dynamic Theory of
Cellular Control Processes, Academic Press, New York, 1963. (Гуд-
вин Б., Временная организация клетки, изд-во «Мир», М., 1966.)
101. Rosenblatt F., Principles of Neurodynamics: Perceptrons and the
Theory of Brain Mechanisms, Spartan Press, Washington D. C., 1962.
Розенблат Ф., Основы нейродинамики, изд-во «Мир», М., 1965.)
102. Novikoff A., On Convergence Proofs for Perceptrons, Mathematical
Theory of Automata Symposium, Brooklyn Polytech., 1962.
103. Charnes A., The Geometry of Convergence of Simple Perceptrons,
J. Math. Anal. Appl., 7, 475—481 (1963).
104. H a wkins J. K„ Self-Organizing Systems—A Rewiew and Commen-
tary, Proc. IRE, 49, 31—48 (1961).
105. H о u s e h о 1 d e r A. S., La nd ahi H. D., Mathematical Biophysics
of the Central Nervous System, Principia Press, San Antonio, 1945.
106. L a n d h a 1 H. D., Studies in the Mathematical Biophysics of Discri-
mination and Conditioning I, Bull. math. Biophys., 3, 13—26 (1941).
107. L a n d a h 1 H. D., Studies in the Mathematical Biophysics of Discri-
mination and Conditioning II: Errors, Trials and Number of Possible
Responses, Bull. math. Biophys., 3, 71—77 (1941).
108. Sugita M., Functional Analysis of Chemical Systems in vivo Using
a Logical Circuit Equivalent, J. Theoret. Biol., I, 415—430 (1961).
109. Bush R. R., M о s t e 11 e r F., Stochastic Models for Learning, Wiley,.
New York, 1958. (Буш P., Mo стел лер Ф., Стохастические методы
обучаемости, Физматгиз, М., 1962.)
НО. Bush R. R., Estes S., (eds), Studies in Stochastic Learning Theory,
Stanford University Press, Stanford, 1959.
111. Martinez H. M., Studies in Stochastic Learning Theory II, Bull,
math. Biophys., 26, 63—75 (1964).
112. Fisher R. A., Genetical Theory of Natural Selection, 2nd revised edn,
Dover Publications, New York, pp. 39—40, 1958.
113. Kimura M., On the Change of Population Fitness by Natural Selec-
tion, Heredity, 12, 145—167 (1958).
114. W e i s s m a n n A., The Germ Plasm, Scribner, New York, 1893.
115. Emerson A., Social Coordination and the Superorganism, Am. Midi.
Nat., 21, 182—209 (1939).
116. Emerson A., The Superorganismic Aspects of Society, Structure et
Physiologie des Societes Animates, Colloques Internationaux du Centre
National de la Recherche Scientifique, XXXIV, Paris, pp. 333—349,
1952.
117. Gass S., Linear Programming, McGraw-Hill, New York, 1958.
118. Charnes A., Cooper W. W., Management Models and Industrial
Applications of Linear Programming, Wiley, New York, 1961.
119. Bale D., Theory of Linear Economic Models, McGraw-Hill, New York,
1960.
120. Studies in the Mathematical Theory of Inverntory and Production,
K. J- Arrow, S. Karlin, H. Scarf (eds), Stanford University Press, Stan-
„ ford, 1958.
121. Bellman R, Dynamic Programming, Learning and Adaptive Proces-
ses, COINS Symposium, J. Tou and R. H. Wilcox (eds), Spartan Press,
Washington, D. C. pp. 375—380, 1964.
122. Von Neumann J., Zur Theorie der Gesellschaftsspiele, Math. Ann.,
100, 295—320 (1928).
123. VonNeumann J., Morgenstern O., Theory of Games and Economic
Behavior, 3rd edn, Princeton University Press, Princeton, 1953.
124. Karlin S., Mathematical Methods and Theory in Games, Programming
and Economics, 2 vols., Addison—Wesley, Cambridge, Mass., 1959.
212
Литература
125. L е w о n t i n R. J., Evolution and the Theory of Games, J. Theoret.
Biol., 1, 382—403 (1961).
126. Jacob F., Mo nod J., Teleonomic Mechanisms in Cellular Metabo-
lism, Growth and Differentiation, Cold Spring Harbor Symposium, Vol.
XXVI, 389—401 (1961). (Регуляторные механизмы клетки, стр. 477,
изд-во «Мир», М., 1964.)
127. Rashevsky N., Mathematical Biophysics, Dover, New York, Vol. I,
1960.
ОГЛАВЛЕНИЕ
Предисловие к русскому изданию.................................... 5
Предисловие автора ................................................ u 7
Глава 1. Общие понятия............................................. 11
1.1. Оптимальность в науке и технике........................ 11
1.2. Принцип оптимальности в физике........................ 13
1.3. Принцип оптимальности и отбор в биологии'............. 17
1.4. Качественные аспекты оптимальности в биологии ... 20
Глава 2. Основные математические методы....................... 24
2.1. Введение.............................................. 24
2.2. Отношение порядка в множестве вещественных чисел . 24
2.3. Замкнутые и открытые множества........................ 26
2.4. Непрерывность........................................ 30
2.5. Максимумы и минимумы непрерывных функции одной
независимой переменной..................................... 33
2.6. Функции многих независимых переменных................. 38
2.7. Случай бесконечного числа независимых переменных.
Вариационное исчисление................................... 41
2.8. Уравнение Эйлера................................ . 44
2.9. Вывод уравнения Эйлера . . .................. 47
2.10. Пример................................................ 49
2.11. Некоторые обобщения. Функция Лагранжа................. 50
Глава 3. Кровеносная система.................................. 54
3 1. Введение............................................. 54
3.2. Ответвление........................................... 55
3.3. Решение той же задачи при выборе другой оценочной
функции.................................................... 57
3.4. *3амечание об единицах измерения и размерностях ... 59
3 5. Разветвление кровеносных сосудов..................... 61
3 6. Оптимальный радиус отходящей ветви................... 65
3.7. Радиус аорты [28]..................................... 66
3.8. Капилляры............................................. 69
3.9. Замечание об эритроцитах ........................ 70
Глава 4. Онтогенез и филогенез...................................... 74
4.1. Введение................................................ 74
4 2. Некоторые основные понятия: онтогенез и филогенез . . 74
4.3. Рекапитуляция. Биогенетический закон.................... 76
214
Оглавление
4 4. Онтогенез и естественный отбор.......................... 80
4.5. Онтогенез и принцип оптимальности ... .... 82
Глава 5. Принцип оптимальности и аллометрия ... 84
5.1. Определяющая система функционалов....................... 84
5 2. Зависимости между функционалами. Аллометрия ... 85
5.3. Обратная задача вариационного исчисления................ 89
5.4. Аллометрия и принцип оптимальности...................... 93
5.5. Закон аллометрического роста в онтогенезе:
развирающиеся системы....................................... 96
Глава 6 Принцип оптимальности и теория трансформаций д’Арси
Томпсона........................................................ 101
6.1. Теория трансформаций д’Арси Томпсона................... 101
6.2. Некоторые эвристические рассуждения.................... 103
6.3. Устойчивость........................................... 107
6.4. Устойчивость по отношению к замене переменных .... 112
6.5. Некоторые выводы....................................... 113
6.6. Онтогенез и теория трансформаций....................... 115
6.7. Теория «биохимических трансформаций» Нидхэма ... 116
Глава 7. Введение в проблемы гомеостаза в биологии .... 119
7.1. Общие замечания........................................ 119
7.2. Пример: гармонический осциллятор....................... 122
7.3. Замкнутые системы................................ ... 126
7.4. Биологические механизмы гомеостаза и принцип опти-
мальности . . . '.......................................... 128
Глава 8. Связь между входными и выходными сигналами системы 130
8.1. Входные и выходные сигналы.................... 130
8.2. Передаточная функция.......................... 131
8.3. Интегральные уравнения для линейных систем .... 136
8.4. Передаточные функции систем из нескольких звеньев . 139
8 5. Системы с обратной связью................... 140
8 6. Некоторые замечания......................... 144
Глава 9. Некоторые биологические системы управления .... 147
9 1. Введение............................................ 147
9.2. Регуляция величины зрачка....................... ... 149
9.3. Терморегуляция................................. .... 154
9.4. Дыхательный хемостат.................................. 157
9.5. Регулирование химических реакций в клетке ............ 162
Глава 10. Динамические системы и теория оптимального управле
ния.........................................................
Введение..........................................
Абстрактная теория динамических систем............
Входные и выходные сигналы динамических систем .
Линейные динамические системы.....................
Оптимальное управление...................
168
168
169
171
173
174
177
10. f
10.2.
10.3.
10.4.
10.5.
10.6. 'Обратная связь
Оглавление 215
Глава 11. Адаптивные системы в биологии.......................... 179
11.1. Введение............................................. 179
11.2. Пример. Распознавание изображений и перцептрон . . 182
'11.3. Обучение............................................. 188
11.4. Еще раз об онтогенезе и филогенезе................... 192
Глава 12. Математические модели в биологии и экономике . . . 197
12.1. Введение............................................. 197
12.2. Задачи программирования в экономике.................. 200
12.3. Экономика и теория игр............................... 205
Литература....................................................... 207