А. Н. Денисенко
Теоретическая
радиотехника
СПРАВОЧНОЕ ПОСОБИЕ

А. Н. Денисенко
УДК 621.398.97@31)
ББК 32.84
ДЗЗ
СИГНАЛЫ
Теоретическая
радиотехника
СПРАВОЧНОЕ ПОСОБИЕ
Денисенко А. Н.
ДЗЗ Сигналы. Теоретическая радиотехника. Справочное пособие. -
М: Горячая линия-Телеком, 2005. - 704 с: ил.
ISBN 5-93517-214-3.
В сжатой, приемлемой для инженерной и исследовательской практики
форме обобщены и достаточно полно изложены методы анализа детерми-
детерминированных сигналов (часть 1) и случайных сигналов и шумов (часть 2), ис-
используемые в теоретической радиотехнике. В каждом разделе теоретиче-
теоретическая часть заканчивается расчетными выражениями и примерами расчета
по ним.
Для инженеров и исследователей, работающих в области радиотехни-
радиотехники, преподавателей, студентов старших курсов радиотехнических факульте-
факультетов вузов, аспирантов.
ББК 32.84
Адрес издательства в Интернет www.techbook.ru
e-mail: radios_hl@ mtu-net.ru
Справочное издание
Денисенко Александр Николаевич
СИГНАЛЫ
ТЕОРЕТИЧЕСКАЯ РАДИОТЕХНИКА
Справочное пособие
Редактор А. Е. Павлов
Корректор В. П. Петрова
Художник Л. Г. Летинов
Подготовка оригинал-макета Ю. Н. Рысина
Лицензия ЛР № 071825 от 16.03.99 г.
Подписано к печати 02.10.2004. Формат 60x90 1/16
Уел печ л. 44. Изд №214. Тираж 1500 экз.
Москва
Горячая линия - Телеком
2005
ISBN 5-93517-214-3
© А. Н. Денисенко, 2005
© Оформление издательства
«Горячая линия-Телеком», 2005

С глубочайшим уважением и благодарностью
Т.В.Ковыловой и Д.С.Малисову,
моим феноменальным школьным учителям.
ПРЕДИСЛОВИЕ
Настоящее время - время информационных технологий и ком-
коммуникационных систем. Интернет, системы связи (в том числе нахо-
находящиеся в стадии интенсивного развития - мобильные системы),
телевизионные системы, системы мониторинга и другие различного
назначения, менее распространенные, но не менее важные, это все
проявления тенденций развития цивилизации. Основным носителем
информации всех известных и мыслимых систем описанного плана
являются сигналы. (Сигнал и определяется как физический процесс,
предназначенный для переноса информации или содержащий ее).
В этих условиях теория сигналов, методы их исследования пред-
представляют несомненный интерес не только для радистов, как это час-
часто считалось до последнего времени, но и для специалистов самых
различных областей. Особое внимание уделяется цифровой обра-
обработке сигналов. Именно цифровая обработка предоставляет наи-
наибольшие возможности при разработке и совершенствовании различ-
различного рода систем.
Книга «Сигналы», представляющая справочное пособие, по-
посвящена описанию и методам анализа детерминированных и слу-
случайных сигналов и шумов. Методы исследования сигналов находят-
находятся в динамике, обусловленной прежде всего технологическим про-
прогрессом. К настоящему времени накоплен достаточно большой
объем материала по исследованию различных видов сигналов;
список работ, посвященных этой тематике, обширен. Однако явно
ощущается недостаток в литературе, где в достаточно сжатой и
приемлемой для инженерной и исследовательской практики форме
обобщенно излагались бы методы анализа сигналов различного
вида. Тем более есть необходимость проведения анализа как де-
детерминированных, так и случайных сигналов в рамках единого ме-
методического подхода. Автор полагает, что в книге нашли отражение
все известные направления исследований основных видов сигна-
сигналов как детерминированных, так и случайных.
Основу книги, как указывалось, составляют известные методы
анализа детерминированных и случайных сигналов; они обобщены

Предисловие
и дополнены оригинальным материалом, полученным автором. Ка-
Каждый законченный фрагмент книги содержит расчетные выраже-
выражения, которые могут быть использованы для получения алгоритмов и
программ расчета основных характеристик сигналов. Однако рас-
расчетные выражения сами по себе не всегда позволяют оценить
влияние различных параметров на характеристики сигналов. Такую
оценку в определенной степени могут дать многочисленные приме-
примеры и графики, построенные по результатам расчета. Этим объяс-
объясняется то обстоятельство, что книга содержит большое число таб-
таблиц и рисунков (графиков).
В последнее время проявляется повышенный интерес к вейв-
лет-преобразованиям. Вейвлеты представляют семейство функций,
описывающих сигналы и используемых главным образом для пре-
преобразований изображений, в первую очередь их сжатия и переноса.
Содержание вейвлет-преобразований выходит за пределы пред-
представляемой книги, поскольку они находятся уже в области приме-
применения сигналов. Однако материал книги является той теоретиче-
теоретической базой, которая лежит в основе этого сравнительно нового ме-
метода обработки сигналов.
Книга содержит две части: часть 1 «Детерминированные сигна-
сигналы» и часть 2 «Случайные сигналы и шумы».
Первая часть посвящена методам исследования детерминиро-
детерминированных сигналов. В разд. 1 рассматриваются различные формы
представления сигналов, дается геометрическая интерпретация
сигналов. Приводится краткая классификация сигналов, которая
позволяет более четко понять логику построения книги.
В разд. 2 изложены основы обобщенного спектрального анали-
анализа сигналов. Рассматривается разложение сигналов по элементар-
элементарным составляющим (представленных временных функций, описы-
описывающих сигналы,в виде обобщенного ряда Фурье). Приведены
примеры такого разложения с использованием многочленов Ле-
жандра, Чебышева, Лагерра, Эрмита и функций Уолша. При анали-
анализе сигналов и цепей указанные функции могут иметь и другое при-
приложение, в том числе при аппроксимации и интерполяции сигналов
и их характеристик. Поэтому рассмотрение ортогональных систем
функций дает не только примеры обобщенного спектрального ана-
анализа, но имеет и самостоятельное значение.
В разд.З излагаются основы гармонического анализа сигналов:
временная функция, описывающая сигнал, раскладывается в три-
тригонометрический ряд Фурье или используется ее преобразование
Фурье. При анализе сигналов наряду с преобразованием Фурье
может найти применение и его модификация - преобразование

Предисловие
Хартли. Совместное рассмотрение этих двух видов преобразова-
преобразований дает возможность сравнительной оценки их эффективности.
Широкое применение при анализе сигналов находит и преобра-
преобразование Лапласа. Оно используется, прежде всего, при анализе
сигналов в линейных цепях. Особенности преобразования Лапласа
и его применения рассматриваются в разд. 4.
Содержание разд. 5 составляет корреляционный анализ де-
детерминированных сигналов. Определены корреляционные функции
периодических и непериодических сигналов. Даны соотношения,
связывающие корреляционные функции со спектрами сигналов.
Дискретизации и восстановлению непрерывных сигналов посвя-
посвящены разд. 6 и 7. Дискретизация и восстановление сигналов лежат
в основе цифровой обработки. Этим во многом определяется объем
и содержание разделов. Рассматриваются дискретные преобразова-
преобразования (преобразование Фурье, z-преобразование, дискретное преобра-
преобразование Хартли) и их применение при анализе сигналов. Дается об-
общая постановка задачи восстановления непрерывного сигнала по его
дискретным значениям. Как пример рассматривается интерполяция
непрерывного сигнала с помощью многочленов Лагранжа и ряда Ко-
тельникова. Содержание разд. 7 составляет сплайновая интерполя-
интерполяция сигнала. Приводятся расчетные выражения для получения вре-
временных функций непрерывных сигналов по их дискретным значениям
с помощью различных видов сплайнов, которые могут использовать-
использоваться при цифровой обработке сигналов.
Описанию и анализу узкополосных сигналов посвящен разд 8.
В нем рассмотрены характеристики и методы анализа в общей по-
постановке, безотносительно к видам узкополосных сигналов.
В последующих разделах проведен анализ различных видов узко-
узкополосных сигналов: с амплитудной модуляцией - разд. 9; с угловой
модуляцией - разд. 10; импульсных с частотной линейной и нелиней-
нелинейной модуляцией - разд. 11; кодированных сигналов - разд. 12.
Вторая часть книги посвящена описанию случайных сигналов
и шумов, объединенных общим понятием «случайные процессы»,
и методам их анализа. В соответствии с общим замыслом книги
основной целью является обобщение методов исследования слу-
случайных сигналов и шумов, нашедших наиболее широкое примене-
применение в статистической радиотехнике, изложение их в виде, доступ-
доступном для инженерной и исследовательской практики.
В разд. 14 приводится краткая классификация случайных про-
процессов, описание их характеристик. Одномерному распределению
случайных процессов посвящен разд. 15, многомерное распределе-
распределение случайных процессов рассматривается в разд. 16. Совместное

Предисловие
распределение случайных процессов и распределение их функцио-
функциональных преобразований рассмотрено в разд. 17. Спектральный ана-
анализ случайных процессов составляет содержание разд. 18. Методы
анализа узкополосных случайных процессов изложены в разд. 19.
Эти методы используются при анализе модулированных случайных
процессов: с амплитудной и угловой модуляцией. В разд. 20 рас-
рассматриваются выбросы случайных процессов, их характеристики,
методы описания и исследования. Методы анализа прохождения
случайных процессов через линейные цепи изложены в разд. 21.
В разд. 22 приводятся методы анализа нелинейных преобразований
случайных процессов. Как иллюстрация методов анализа линейных и
нелинейных преобразований в разд. 23 проводится анализ случай-
случайных процессов на выходе аналогового коррелятора.
Список литературы по каждой части книги включает книги, из-
изданные на русском языке за последние десятилетия. В него также
включены несколько ранних работ, которые в силу несомненных дос-
достоинств представляют не только исторический, но и практический
интерес. В их числе работы на английском языке, не переведенные
полностью на русский. Более полная, а точнее, просто библиогра-
библиография, в книге по такому широкому направлению, которое определено
ее названием, в условиях развитой информационной системы пред-
представляется нецелесообразной. Тем более, что число работ, связан-
связанных с выбранной темой, увеличивается с нарастающим темпом, и
любая библиография к моменту издания книги будет неполной.
Использованные во 2 части справочного пособия термины, оп-
определения и обозначения по возможности приводились в соответст-
соответствии с общепринятыми и рекомендованными ГОСТ 21878-76 «Слу-
«Случайные процессы и динамические системы», термины и определе-
определения. Однако вследствие неполноты и несовершенства указанного
ГОСТа и отсутствия установившейся терминологии и определений
ряда понятий, используемые в пособии, кому-нибудь могут показать-
показаться не совсем удачными.
Книга рассчитана на широкий круг читателей: студентов стар-
старших курсов вузов радиотехнических специальностей, аспирантов,
преподавателей вузов, радиоинженеров и исследователей. Приня-
Принятая последовательность изложения материала от простого к более
сложному позволяет использовать книгу как справочное, так и учеб-
учебное пособие по дисциплинам радиотехнического профиля, где объ-
объектом изучения являются сигналы.
Автор выражает искреннюю благодарность Р.С.Плотникову
и В.В.Гритченко за помощь при компьютерном построении графи-
графиков, приведенных в книге, и ее оформлении.

ЧАСТЫ.
ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ

Раздел 1.
СИГНАЛЫ И ИХ ПРЕДСТАВЛЕНИЕ
Сигналом будем называть физический процесс, несущий ин-
информацию или предназначенный для ее передачи. В зависимости
от частоты несущего колебания различают сигналы звукового, ра-
радио, оптического и других диапазонов. Объектом изучения радио-
радиотехники являются радиосигналы. Их частоты лежат в интервале от
3 кГц до 3000 ГГц. Этот интервал разбит на девять диапазонов, ка-
каждый из которых занимает полосу от 0,3-10п до 3-1 ОТц D < п < 12)
(табл. 1.1).
Математический аппарат, используемый при анализе сигналов,
позволяет проводить исследования без учета природы сигналов.
Однако для понимания содержания характеристик сигналов удоб-
удобнее обращаться к их физическому наполнению. С учетом этого в
дальнейшем сигнал будем рассматривать как колебание в радио-
радиотехнической цепи.
Математическая модель сигнала, как правило, представляет
функцию времени, задаваемую в виде аналитического выражения,
графика или таблицы. Термин «сигнал» обычно и используется как
эквивалентный временной функции, описывающей колебание. Та-
Такое описание сигнала является наиболее распространенным, но
оно не исключает и другие формы представления сигналов.
Полезным является представление сигнала в виде взвешенной
суммы более простых составляющих - разложение временной
функции, описывающей сигнал, в ряд по системе базисных функ-
функций. Такое разложение позволяет свести анализ сложного сигнала
к анализу его более простых составляющих. С другой стороны,
представление сигнала в виде ряда может использоваться и как
исходное при его описании.
Для временной функции, описывающей сигнал и удовлетворяю-
удовлетворяющей некоторым условиям, возможно интегральное преобразование.
Интегральное преобразование позволяет перейти от временной
области определения сигнала к области выбранного параметра.
8

Сигналы и их представление
Таблица 1.1,
Классификация диапазонов частот
Но-
Номер
диа-
пазо-
пазона
4
5
6
7
8
9
Диапазон
частот
3 ... 30 кГц
30...
300 кГц
300 ...
3000 кГц
3...
30 МГц
30...
300 МГц
0,3...
ЗГГц
Назва-
Название
частот
Очень
низкие
(ОНЧ)
Низкие
(НЧ)
Сред-
Средние
(СЧ)
Высо-
Высокие
(ВЧ)
Очень
высо-
высокие
(ОВЧ)
Ультра-
высо-
высокие
(УВЧ)
Диа-
Диапазон
волн
100...
10 км
10...
1 км
1000...
100 м
100...
Юм
10...
1 м
100...
10 см
Назва-
Название
волн
Мириа-
метро-
вые
(сверх-
длин-
длинные)
Кило-
метро-
метровые
(длин-
(длинные)
Гекто-
метро-
вые
(сред-
(средние)
Дека-
метро-
метровые
(корот-
(короткие)
Метро-
Метровые
Деци-
метро-
метровые
Примеры
использования
Дальняя навигация,
связь с подводными
лодками
Радиовещание, на-
навигационные систе-
системы, маяки
Морские радиостан-
радиостанции, радиоканалы,
сигналы бедствия;
радиовещание
Радиовещание,
связь, телеграфия,
телефония
Радиовещание, те-
телевидение, назем-
наземная подвижная
связь, управление
воздушным движе-
движением, такси, навига-
навигационные средства,
радиолокация, ра-
радиоастрономия
Телевизионные,
навигационные сис-
системы, спутниковая
связь, радиовысо-
радиовысотомеры, радиоре-
радиорелейная связь

Раздел 1
Но-
Номер
диа-
пазо-
пазона
10
11
12
Диапазон
частот
3...
30 ГГц
30...
300 ГГц
300 ГГц ...
ЗТГц
Назва-
Название
частот
Сверх-
высо-
высокие
(СВЧ)
Крайне
высо-
высокие
(КВЧ)
Гипер
высо-
высокие
(ГВЧ)
Диа-
Диапазон
волн
10...
1 см
10...
1 мм
1...
0,1мм
Назва-
Название
волн
Санти-
метро-
метровые
Милли-
метро-
метровые
Деци-
милли-
метро-
вые
Примеры
использования
Радиолокация, ра-
радиоастрономия; ра-
радиорелейная,
спутниковая связь
Космическая связь
В ряде случаев анализ в области выбранного параметра оказы-
оказывается более простым и, следовательно, предпочтительным в ис-
исследовательской практике. Формула обращения интегрального
преобразования позволяет осуществить обратный переход к вре-
временной функции. Интегральное преобразование может быть исход-
исходным при задании сигнала.
Описанию сигналов большую образность придает их геометри-
геометрическая интерпретация. Представление сигналов в виде векторов
позволяет проводить их исследования известными методами мно-
многомерной геометрии.
Указанные формы представления сигналов рассматриваются
ниже, более подробно.
1.1. Описание сигналов временными функциями
1.1.1. Действительные сигналы
Разнообразие возможных видов сигналов отражается прежде
всего при их описании во временной области. Примерами аналити-
аналитического описания сигналов во временной области являются:
гармонический сигнал (рис. 1.1, а)
s(f)= Vcos(a>0t + <p),
импульсные сигналы:
10

Сигналы и их представление
s(t)=Ve~at,t>0 (рис. 1.1,6), s(t)=Ve-Vf2 (рис. 1.1,в),
модулированные сигналы:
с амплитудной модуляцией
s(f)=l4i + McosQf]cosco0f. (Рис- 1-1>г)>
с частотной модуляцией
s(t) = Vcos[(aQt + mslnQt], (рис. 1.1 ,д).
Число примеров описания сигналов временными функциями
увеличивают последующие разделы и табл. 3.1.
При описании сигналов полезными оказываются разрывные
функции, приведенные в табл. 1.2.
Единичная ступенчатая функция.
Определяется как скачок от 0 до 1 в момент t = О (рис. 1.2,а)
[i,f>0 v '
Скачок в момент убудет обозначаться как a(t-10) (рис.1.2,6).
Единичную ступенчатую функцию называют также функцией
включения, так как умножение а@на временную функцию s(t)
(рис. 1.2,в)
s,(t) = a(t)s(t) A.2)
означает начало сигнала в момент t = 0. Для сигнала, начинающе-
начинающегося в момент t0, можем записать (рис. 1.2,г):
St(t) = o(t-t0)s(t). A.3)
Сигнал, ограниченный во времени с двух сторон, может быть
представлен в виде (рис. 1.2,д)
s,(t) = [c(t-t,)-c(t-t2)]s(t). A.4)
Выражение в квадратных скобках в A.4) описывает прямо-
прямоугольный импульс, имеющий амплитуду, равную единице,
s(t) = a(t-t,)-a(t-t2). A.5)
11

Раздел 1
Рис. 1.1
Единичный импульс.
Для функции, описывающей прямоугольный импульс, иногда
вводят специальное обозначение
rect(x) =
1,-1/2 < х< 1/2
О, при остальных зачениях х
A.6)
12

Сигналы и их представление
Таблица 1.2.
Разрывные функции
№
п/п
Функция
График функции
a(t) =
\\t>0
10, / < О
c(t)
О
o(t-t0) =
\Xt>t0
[o,t<to
/
О U
5@ =
°°,t = О
o,?*o
fifth
too
w
b(t-to) =
~J=t0
o,t*to
$H)i
oo
\(t)
0 tr,
sign(t) =
1, f>0
-1, f<0
sip{t)
-1
rect(t/x) =
fi,|f/x|<1/2
[0,|f/i|>1/2
rectl
Л °i'
rect{[t-to]/z) =
1,|f-fo|/T<1/2
0, t-t0 /t>1/2
rect *-ф
1
0 fo-|t f0 fo-|t f
Прямоугольный импульс длительности хи определяется как
(рис. 1.3,а)
Г1,ти/2<Г<т0/2
/SCf(f/Tu) =
О, при остальных значениях t
A.7)
13

Раздел 1
Рис. 1.2
Обозначение запаздывающего на время t0 импульса имеет вид
(рис. 1.3,6)
rect(t~to/xu) =
%to-cu/2<t<to+Tu/2
О, при остальных значениях t
A-8)
Знаковая функция.
Функция знака sign(x) (сигнатура) равна единице, знак которой
изменяется при переходе t через нуль (рис. 1.4)
14

Сигналы и их представление
si9n{t) = {u>o° ¦ A-9)
Очевидно, функция знака связана со ступенчатой функцией со-
соотношением
a{t) = ^[[ + sign(t)]. A.10)
Импульсная функция.
Импульсная или 6-функция представляет импульс бесконечно
малой длительности в точке / = 0, имеющий бесконечно большую
амплитуду и площадь, равную единице:
5(" = teo°' 1ад<*=1- AЛ1)
Импульсную функцию можно рассматривать как предел, к кото-
которому стремится прямоугольный импульс длительностью х и ампли-
амплитудой 1/т при т->°° (рис. 1.5).
Импульсная функция представляет производную ступенчатой
функции
dv{t)/dt = S(t), A.12)
и наоборот, ступенчатая функция может рассматриваться как инте-
интеграл от импульсной функции
^Ф^'^ио- A13)
Из определения импульсной функции следует
со оо
\s(tW-to)dt = s(to)jb(t-to)dt = s(to). A.14)
— оо —оо
Соотношение A.14) отражает фильтрующее свойство импульс-
импульсной функции.
15

Рис. 1.3
•+t
1.1.2. Комплексные сигналы
При описании и анализе некоторых видов сигналов (в первую
очередь узкополосных) используется понятие комплексного сигнала
s@ = |s(f)|e^( A.15)
где s(f)|, (p(f) - модуль и аргумент комплексной величины s(t).
Комплексная величина s(t) может быть также представлена
в виде
s@ = Re[s@]+/lm[s(f)], A.16)
где Re, Im - действительная и мнимая части комплексной
величины.
Из A.15) и A.16) получим:
lm\s(t)
s(t} = jRe2\s(thlm2ls(t)]; фМ^гсГд-™. A.17)
16
Раздел 1

Сигналы и их представление
Рис. 1.6
Комплексный сигнал можно рассматривать как вектор на ком-
комплексной плоскости с действительной осью - осью абсцисс и мни-
мнимой осью - осью ординат (рис.1.6). Такое рассмотрение подключа-
подключает пространственное воображение, расширяет рамки анализа сиг-
сигналов.
Длина вектора равна модулю комплексной величины, угол между
вектором и осью абсцисс равен аргументу cp(f). Проекции вектора на
оси координат равны действительной и мнимой частям комплекс-
комплексной величины.
Комплексная форма описания сигнала позволяет в ряде случа-
случаев упростить математические операции, проводимые с сигналами.
Иллюстрацией удобства, связанного с использованием комплекс-
комплексной формы описания сигналов при их анализе, служат последую-
последующие разделы (начиная с разд. 8).
1.2. Представление сигналов ортогональными рядами
Временная функция, описывающая сигнал s(t), может быть
представлена в виде взвешенной суммы, как правило, более про-
простых базисных функций фп@
A.18)
где сп - постоянные коэффициенты.
Такое представление сигнала означает, что сигнал рассматри-
рассматривается как совокупность элементарных колебаний, взятых с соот-
соответствующими коэффициентами. Разложение функции s(t) по сис-
системе базисных функций {фп@} особенно удобно, если система
функций является ортогональной. Система функций {фп@} называ-
17

где ||фп|| - норма функций (pn(t).
При ||ф„| = 1 система функций {<pn(t)} называется ортонормиро-
ванной.
Коэффициенты ряда A.18) (с учетом A.19) ) определяются вы-
выражением
U
с" = Па \s(t)(pn(t)p(t)dt, л = ОД 2..., A.20)
Ы| I
Разложение s(t) по ортогональной системе функций называется
обобщенным рядом Фурье, а коэффициенты ряда - обобщенными
коэффициентами Фурье. Совокупность коэффициентов разложения
называется спектром сигнала в выбранной системе базисных
функций. В обобщенный ряд Фурье может быть разложена любая
функция, квадратично интегрируемая на интервале [ta, tb].
Некоторые виды ортогональных систем базисных функций, ко-
которые могут быть использованы при описании и анализе сигналов,
приведены в табл. 1.3. Примеры их применения при спектральном
анализе сигналов даны в разд. 2.
В практике анализа периодических сигналов наибольшее при-
применение получил тригонометрический ряд Фурье, в котором в каче-
качестве базисных функций выбраны тригонометрические функции
ею
s(t) = -5- + ^(ал cosrKo^t + bn sinrm^t), A.21)
где со, - частота сигнала.
Коэффициенты тригонометрического ряда Фурье A.21) опреде-
определяются выражениями
2 Гг2 2 7
ап = — j s@cosnoi^tdt; bn = — I s@sinm^tdt, A.22)
-772 -TI2
18
Раздел 1
ется ортогональной с весом p(t) на интервале [ta, tb], если выпол-
выполняется следующее равенство:

Сигналы и их представление
где Т = 2п1щ - период сигнала.
Форма записи тригонометрического ряда может быть несколько
иной
где
A.23)
A.24)
При представлении сигнала в виде A.23) он определяется сово-
совокупностью амплитуд Ап и фаз фл. Совокупность амплитуд Ап на-
называется амплитудным спектром, а совокупность фаз ф„- фазо-
фазовым спектром.
Тригонометрический ряд Фурье описывает разложение сигнала
на гармонические составляющие, позволяет проводить анализ сиг-
сигнала в частотной области. Анализ с его использованием называет-
называется гармоническим.
В качестве примера рассмотрим сигнал, представляющий пе-
периодическое колебание пилообразной формы (рис. 1.7,а). Для него
тригонометрический ряд A.23) имеет вид:
s(t) = 2/n(sin&J-'\/2sin2(xiJ + '\/3sin3(i)J-J\/4sin4(i)J+ ...),
где щ = 2п/Т - частота, Т— период сигнала.
Таблица 1.3.
Ортогональные системы функций
№
п/п
1
2
3
Ф„(х)л = 0Д2
1 cosnx sinnx n ЛП
1 , г- . i— i П - V-,-..
rLenr,n = 0,±1>...
л/2я
Многочлены Лежандра
Pn(x)= n1 d"(x2-ir
"v ' 2nrii dx" v '
[-Л.71]
[-71, Я]
[-1.1]
pW
1
1
1
1
1
2
2n + 1
19

Раздел 1
№
п/п
4
5
6
7
8
9
Фл(х)а7 = 0,1,2
Многочлены Чебышева 1 -го рода
Тп(х) = cos(narccos x)
Мне
у.(
гочлены Чебышева 2-го рода
л sin[(n + i)arccosx]
х) 1 ~
л/1-х2
Многочлены Лагерра
Ln(x) = ^^l(e-^)
л! dx" v ;
Многочлены Эрмита
Функции Радемахера
го(х) = 1, г„(х) = s/flf/7{sin2;I7cx)
п = 1,2,...
Функ
/Со
0 npi
/с=1
.ции Хаара
= 1,
2Л+1 2"+1
V^T2^-1 2/с
V ' 2-1 ^Х^2"+1
л других значениях х
,2,4 2"; л = 0, 1,2, ...
М.1]
[-1.1]
[О.оо)
[0,1]
[0,1]
р(х)
1
е^
1
1
я, л = 0
^,л^0
2
я
~2
1
2"п!л/а7
1
1
20

Сигналы и их представление
№
п/п
10
Фя(х)л = 0,1,2
Функции Уолша
т п"
pal(n,x) = Yllrk(x)}
пк - /с-й разряд представления п
в двоичном коде;
гк(х)- функции Радемахера
м,
hadfr^YlMx)]
(пкI - к-м разряд представления
п в инвертированном двоичном
коде
т • Ы
wal{n,x) = Y\lrk(x)]
(пк) = пк® лк+1,
© - символ поразрядного
суммирования по модулю 2
[0,1]
[0,1]
[0,1]
рМ
1
1
1
1
1
1
Амплитудный спектр сигнала приведен на рис. 1.7,6. Спектр да-
дает представление о распределении амплитуд сигнала по частоте.
а)
Рис. 1.7
21

Раздел 1
1.3. Интегральное представление сигналов
Одним из представлений сигналов, нашедших применение при
их описании и анализе, является интегральное представление сиг-
сигналов.
При некоторых условиях для функции, описывающей сигнал во
временной области s(t), существует интегральное преобразование
S(x)=\y(x,t)s(t)dt, A.25)
г
где \|/(x,f) - заданная функция (ядро интегрального преобразова-
преобразования); Т- область определения функции s(t).
Интегральное преобразование позволяет осуществить переход
от временной области определения функции к области параметра
х. Операциям над сигналом во временной области соответствуют
операции в области параметра х. Операции в области параметра х
могут быть проще, следовательно, расширяются возможности про-
проводимого анализа.
Формула, позволяющая восстановить сигнал s(t) по известной
функции S(x), называется формулой обращения интегрального
преобразования
s{t) = J4>{t,x)S{x)dx, A.26)
х
где (p(f, x) - базисная функция.
Выражения A.25) и A.26) устанавливают взаимно однозначное
соответствие между функцией s(t) и ее интегральным преобразова-
преобразованием S(x). Функция S(x) является интегральным представлением
сигнала, может быть исходной при описании сигнала.
Из известных интегральных преобразований одним из наиболее
часто используемых при анализе сигналов является преобразова-
преобразование Фурье
оо
S(co)= Js@e~fo'cfr, A.27)
где со - параметр преобразования, частота.
Ему соответствует обратное преобразование
22

Сигналы и их представление
s(f) = — f S(tu)e"" dhx A.28)
Интеграл Фурье A.28) дает описание сигнала в виде суммы гар-
гармонических составляющих с непрерывной последовательностью
частот ш. Спектральный анализ сигналов с использованием такого
представления входит в понятие гармонического. Функция S(w) на-
называется спектральной плотностью или спектром сигнала s(t).
С помощью A.28), имея спектральную плотность, можно перейти
к описанию сигнала во временной области.
В общем случае S(a) является комплексной величиной. Как ком-
комплексная величина она записывается в виде
SH^SMle^, A-29)
где |S(o))|, (р(со) - модуль и аргумент комплексной величины,
амплитудный и фазовый спектры сигнала.
Примером служит преобразование Фурье временной функции,
описывающей сигнал, экспоненциального вида
s(t) = Ve~at,t>0.
Преобразование Фурье s(t):
S((B)=-^7- .
а + кй
Амплитудный и фазовый спектры сигнала описываются выраже-
выражениями
V
рИ|= 2+ „ 1/2, Ф(о) = -arctg(co/a).
Графики амплитудного и фазового спектров сигнала представ-
представлены на рис. 1.8. Они дают представление о плотности распреде-
распределения амплитуд и фаз сигнала по частоте.
Другим интегральным преобразованием, широко используемым
при анализе сигналов, является преобразование Лапласа
S(p) = js(t)e-ptdt, A.30)
о
где р = а+ /со - комплексная величина.
23

Раздел 1
Рис. 1.8
Преобразование Лапласа в ряде случаев расширяет возможно-
возможности анализа сигналов по сравнению с преобразованием Фурье, ча-
чаще используется при анализе прохождения сигналов через цепи.
Переход от изображения сигнала S(p) к оригиналу s(t) осуществ-
осуществляется с помощью обратного преобразования Лапласа
A.31)
При а = 0 выражение A.30) переходит в интеграл Фурье для
функции s(t), равной нулю при t < 0.
Возможны и на практике используются другие виды интеграль-
интегральных преобразований. Некоторые из них, наиболее распространен-
распространенные, приведены в табл. 1.4.
Таблица 1.4.
Интегральные преобразования
№
п/п
1
2
S(x)
Преобразование Фурье
js(t)e^{dt
— QO
Преобразование Хартли
Г s(t) casa) tdt,
casa>t - cos о t + sin со t
s(t)
— fs(to)ew'ah)
CO
— fs(a))caso) tdoi
— oo
24

Сигналы и их представление
1.4. Векторное представление сигналов
При анализе сигналов часто обращаются к их геометрической
интерпретации. Такой подход придает описанию сигналов большую
образность, позволяет проводить исследования сигналов извест-
известными методами многомерной геометрии.
Элемент X Л/-мерного пространства представляется как точка
или вектор с координатами хь х2, ..., xN. Само пространство рас-
рассматривается как совокупность таких элементов или пространство
векторов.
Если определено расстояние между двумя точками пространст-
пространства Х(хь х2,..., xN) и Y(yh y2,..., Ул/)> то пространство называется мет-
метрическим. Наиболее часто используется метрика, определяемая
выражением
A.32)
л=1
25

Раздел 1
Пространство с метрикой A.32) называется Л/-мерным евклидо-
евклидовым пространством. Оно обычно и рассматривается при векторном
представлении сигналов.
При геометрической интерпретации множеству сигналов ставит-
ставится в соответствие векторное пространство. Сигналы изображаются
векторами, а операции с сигналами заменяются операциями с век-
векторами.
Сигнал, описываемый выражением
A.33)
может рассматриваться как Л/-мерный вектор (рис. 1.9). Ортонор-
мированная система базисных функций {(pn{t)} образует коорди-
координатную систему в Л/-мерном евклидовом пространстве. Функции
(pn(t) представляют единичные векторы (орты), коэффициенты
сп- проекции вектора s(t) на оси координат.
Координаты вектора определяются скалярным произведением
Длина вектора определяется как
A.34)
A.35)
Рис. 1.9
Рис. 1.10

Сигналы и их представление
Векторы можно рассматривать лишь тогда, когда они имеют ко-
конечную длину. Из A.35) следует, что геометрическую интерпрета-
интерпретацию допускают только сигналы с ограниченной энергией
tb
^s2(t)dt <oo. A.36)
ta
Совокупность сигналов с ограниченной энергией образует про-
пространство сигналов (рис. 1.10). В нем сумме сигналов
s(t)=s,(t)+s2(t) A.37)
соответствует сумма векторов. Если сигналы Si (t) и S2(t) заданы
на интервале времени [ta, tb] в единой системе координат
/V N
т = ^пЧ>п«); 52@ = 2>2ЛФл@. A.38)
Л=1 /7=1
то суммарный вектор s(t) определяется координатами с1п + с2п.
Его длина равна
N
л=1
Скалярное произведение двух векторов Si(t) и S2(t) определя-
определяется выражением
Величина, описываемая A.40), представляет взаимную энергию
сигналов.
Путем поворота системы координат относительно начала коор-
координат можно получить бесчисленное множество координатных сис-
систем. Замена координатной системы означает замену системы ба-
базисных функций, используемых при разложении сигнала, изменяет-
изменяется спектр сигнала. Свойства же векторов, отражающие свойства
сигналов, остаются неизменными, в том числе длины векторов,
расстояния и углы между векторами.
27

Представление сигнала в виде тригонометрического ряда Фурье
позволяет получить следующее выражение для энергии сигнала:
где Ап — коэффициенты ряда Фурье.
Таким образом, можем записать
jVaM=^J|sH2<*o; /s2^M=4+Z4' A-45)
'а Га
Соотношения A.45) представляют различные формы записи ра-
равенства Парсеваля, позволяют определить энергию сигнала, имея
преобразование Фурье временной функции, описывающей сигнал,
или ее представление в виде ряда Фурье.
28
Раздел 1
Все понятия Л/-мерного евклидова пространства при Л/—>°°
обобщаются на бесконечномерное гильбертово пространство.
1.5. Энергия и мощность сигналов
Важнейшими характеристиками сигналов являются энергия и
мощность. Энергия сигнала s(t) за интервал времени [ta, tb] опреде-
определяется выражением
Используя интегральное преобразование сигнала, выражение
для энергии можно записать иначе. Так, вводя преобразование Фу-
Фурье, получим
A.41)
A.42)
A.43)
A.44)

Сигналы и их представление
Энергия суммы двух сигналов за интервал времени [ta, tb] равна
tb tb tb tb
E = j[Si(t)+s2(t)]2dt = js?(t)dt + 2Js,(t)s2(t)dt + jsi(t)dt =
U ta ta tb
= E1+2E12 + E2,
где f ?, E2 - энергии сигналов s2(t) и s2(t); E12 - взаимная энергия
двух сигналов.
Если сигналы ортогональны и выполняется условие
tb
js,(t)s2(t)dt = O, A.47)
t.
то их энергии аддитивны:
Е=Е, + Е2. A.48)
Степень взаимозависимости двух сигналов в общем случае опи-
описывается корреляционной функцией
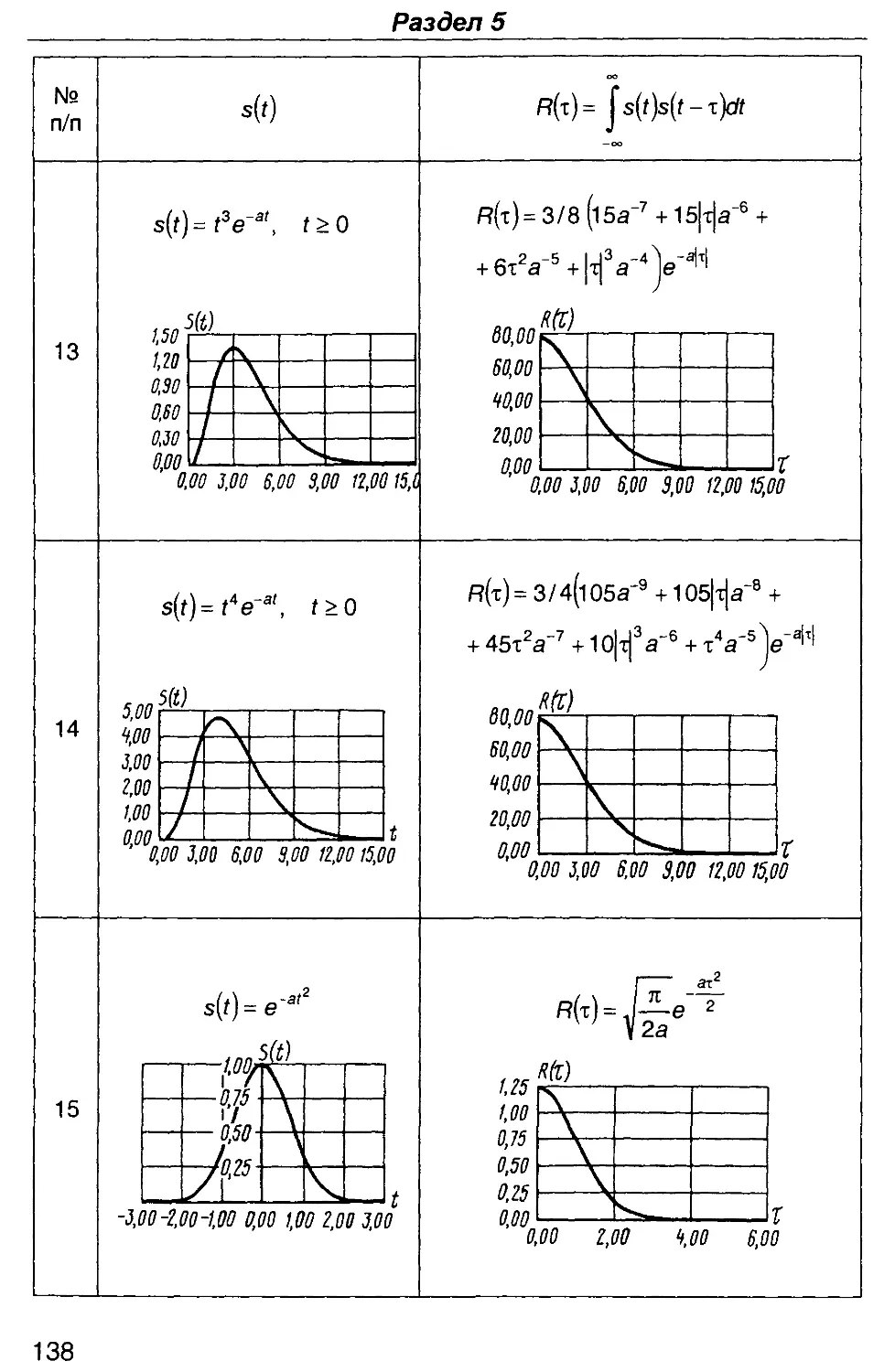
оо
R,2(x)= js,(t)s2(t + T)dt, A.49)
где т - смещение во времени одного сигнала относительно другого.
Выражение A.49) записано для непериодических сигналов с ог-
ограниченной энергией. Подчеркивая то, что рассматриваются два
сигнала, функцию Я12(т) называют взаимной корреляционной
функцией. При т = 0 взаимная корреляционная функция описывает
взаимную энергию сигналов
Я12@)= ]s,(t)s2(t)dt = E12. -A-50)
С учетом A.50) выражение A.46) можем записать в виде
Е= Е, + 2Я12@) + Е2. A.51)
Корреляционная функция может также характеризовать взаим-
взаимную зависимость двух значений одного сигнала s(t), разнесенных во
времени
29

Раздел 1
Ru(t)= js(t)s(t + T)dt. A.52)
В этом случае она называется автокорреляционной функцией.
При т = 0
Ru@)=]s2(t)dt, A.53)
автокорреляционная функция равна энергии сигнала.
Средняя мощность сигнала за интервал времени [ta, fc] опреде-
определяется выражением
Средняя мощность суммы двух сигналов за интервал времени
[ta, tb] равна
A.54)
A.55)
- взаимная мощность.
Для периодического сигнала, имеющего период, равный Т,
средняя мощность определяется выражением
Для двух периодических сигналов srft) и s2(t), имеющих один и
тот же период Т, взаимная корреляционная функция описывается
выражением
30

Сигналы и их представление
772
*12(T) = 7 \s,(t)s2(t + T)dt. A.57)
-7/2
При Si(t)=S2(t)=s(t) из A.57) получим выражение для автокорре-
автокорреляционной функции периодического сигнала
Г/2
Яц(т) = - js(t)s(t + T)dt. A.58)
-772
Прит = Оимеем
Rn@) = P. A.59)
Таким образом, автокорреляционная функция периодического
сигнала при т = 0 описывает среднюю мощность сигнала.
Рассмотренные энергетические характеристики сигналов явля-
являются основными, к ним приходится обращаться в дальнейшем при
анализе различных видов сигналов.
1.6. Основные виды сигналов
Все возможное разнообразие сигналов можно свести к несколь-
нескольким видам, которые составляют основу их классификации.
Одним из основных признаков, по которым различаются сигна-
сигналы, является предсказуемость сигнала (его значений) во времени.
Различают детерминированные и случайные сигналы. К детерми-
детерминированным (регулярным) относят сигналы, которые описываются
функциями времени, или для которых задано правило их получе-
получения. Такими сигналами, например, являются периодические после-
последовательности импульсов определенной формы, высокочастотные
колебания, модулированные по заданному закону, двоичные по-
последовательности символов, формируемые заданным способом, и
т. д. Значения детерминированного сигнала определены в каждый
момент времени. К случайным сигналам относятся сигналы, значе-
значения которых в любой момент времени невозможно предсказать с
вероятностью, равной единице. К ним относятся высокочастотные
колебания, модулированные шумом, колебание на входе приемни-
приемника, источником которого является космическое излучение, и др.
Строго говоря, все сигналы, которые встречаются на практике, яв-
являются случайными. Даже при формировании сигнала определен-
определенного вида всегда имеются случайные изменения во времени его
31

Раздел 1
параметров. Другие сигналы, такие как речевые, имеют случайный
характер вследствие самого содержания передаваемой информа-
информации. С этой точки зрения детерминированные сигналы представ-
представляют только математическую модель реальных сигналов. Однако
принятые модели часто достаточно хорошо описывают реальные
сигналы (в первую очередь, когда флуктуации имеют малые значе-
значения) и удобны при их анализе.
Передача информации с помощью сигналов может произво-
производиться непрерывно во времени или в некоторые фиксированные
моменты. В зависимости от характера передачи информации (не-
(непрерывно или дискретно) различают непрерывные или аналоговые
и дискретные сигналы. Аналоговые сигналы повторяют или зависят
от закона непрерывного изменения физических величин, информа-
информацию о которых они содержат; описываются непрерывными или ку-
кусочно-непрерывными функциями времени. Дискретные сигналы
представляют последовательность коротких импульсов, амплитуды
которых соответствуют мгновенным значениям непрерывного сиг-
сигнала или соответствующей физической величины. Значения сигна-
сигнала в выделенные моменты времени называются выборочными зна-
значениями или отсчетами. Дискретные сигналы (дискретные во вре-
времени), квантованные по уровню и представленные цифровым ко-
кодом, называются цифровыми сигналами. В связи с широким приме-
применением цифровой обработки цифровые сигналы становятся все
более распространенным видом сигналов. При анализе цифровые
сигналы чаще всего заменяются дискретными, а их отличие от
цифровых интерпретируется как шум.
В зависимости от ширины спектра выделяют узкополосные и
широкополосные сигналы. Узкополосным называют сигнал, спектр
которого сосредоточен в относительно узкой (по сравнению со
средней частотой) полосе. Понятие узкополосного сигнала являет-
является довольно условным. Однако с его введением связано удобство
описания и анализа сигналов.
Для передачи информации на расстояние и в ряде других слу-
случаев используются высокочастотные колебания. Непосредствен-
Непосредственным носителем информации, как правило, является низкочастот-
низкочастотный сигнал. Перенос информации на высокочастотное, несущее
колебание производится в процессе модуляции. В качестве несу-
несущего, кроме высокочастотного колебания, может быть использова-
использована также периодическая последовательность импульсов. Таким об-
образом, можно выделить немодулированные и модулированные сиг-
сигналы. Модулированные сигналы представляют несущее колебание
32

Сигналы и их представление
(гармоническое колебание или периодическую импульсную после-
последовательность), параметры которого изменяются под воздействием
модулирующего (управляющего) сигнала. Возможна амплитудная,
угловая и смешанная виды модуляции гармонического колебания.
Понятие угловой модуляции объединяет два вида модуляции: фа-
фазовую и частотную. При модуляции импульсной последовательно-
последовательности выделяют: амплитудную, фазовую, частотную и модуляцию
длительности импульсов (широтно-импульсную модуляцию). Воз-
Возможны смешанные виды модуляции.
В качестве модулирующего сигнала может использоваться кодо-
кодовая последовательность различных символов. Сигнал, получаю-
получающийся в результате модуляции несущего колебания такой последо-
последовательностью, называется кодированным сигналом.
Приведенная краткая классификация сигналов не рассчитана на
полноту охвата всего их разнообразия. Однако, помимо системати-
систематизации сигналов, она позволяет уяснить и принцип выбора структуры
книги.
33

Раздел 2.
ОБОБЩЕННЫЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ
Спектральный анализ сигналов основан на представлении сиг-
сигнала в виде взвешенной суммы элементарных составляющих,
в математическом плане - разложении функции, описывающей сиг-
сигнал во временной области, в ряд по системе базисных функций.
Такое разложение позволяет свести анализ сложного сигнала
к анализу его более простых составляющих.
При разложении сигналов чаще всего используются: система
тригонометрических функций, ортогональные системы многочле-
многочленов, в первую очередь, Лежандра, Чебышева, Лагерра, Эрмита,
функций Уолша и др. При их применении для сигналов с ограни-
ограниченной энергией обеспечивается средняя квадратичная сходимость
ряда, в который раскладывается функция, описывающая сигнал.
Ортогональные системы функций полезны также при аппрокси-
аппроксимации и интерполяции сигналов и их характеристик, находят при-
применение при кодировании передаваемых сообщений, в вейвлетных
преобразованиях и в ряде других случаев. Таким образом, анализ
сигналов с использованием ортогональных систем функций имеет
широкое приложение, является неотъемлемой частью общего ана-
анализа сигналов. Описание ортогональных систем функций использу-
используется в дальнейшем - в других разделах книги, частей 1 и 2.
В этом разделе рассматриваются наиболее распространенные
ортогональные системы функций и их применение при спектраль-
спектральном анализе сигналов.
2.1. Обобщенный ряд Фурье
Функция, описывающая сигнал во временной области s(t), мо-
может быть представлена в виде взвешенной суммы базисных функ-
функций ортогональной системы {фп@}
s(O = f>ncpn(f), B.1)
34

Обобщенный спектральный анализ сигналов
где сп - постоянные коэффициенты.
Такое представление сигнала означает, что сигнал рассматри-
рассматривается как совокупность элементарных колебаний, взятых с соот-
соответствующими коэффициентами.
Для ортогональной на интервале [ta, tb] системы функций {фл@1
выполняется следующее равенство
где р (t) — весовая функция; ||<pn| - норма функций фп(г).
При ||ф„|| = 1 система функций {(pn(f)} называется ортонормиро-
ванной. Коэффициенты ряда B.1) с учетом B.2) могут быть опре-
определены как
сл=щ|5@Фп«р('К " = 0,1,2,... B.3)
Ряд, в который раскладывается функция s(t), сходится в сред-
среднем квадратичном, если выбранная система базисных функций яв-
является полной. Ортогональная система считается полной, если не
существует никакой другой функции, не входящей в систему, кото-
которая была бы ортогональна ко всем функциям данной системы.
В обобщенный ряд Фурье может быть разложена любая функ-
функция, квадратично интегрируемая на интервале [ta, tb]. Это означает,
что анализ с использованием обобщенного ряда Фурье может про-
проводиться для сигналов с ограниченной энергией на рассматривае-
рассматриваемом интервале. Разложение функции s(t) по ортогональной системе
функций B.1) называется обобщенным рядом Фурье. Совокупность
коэффициентов разложения называется спектром сигнала в вы-
выбранной системе базисных функций.
Коэффициенты Фурье обладают следующим свойством. Любая
частичная сумма ряда Фурье
N
*Л,М=1>пфп@ B'4>
/7=0
наилучшим образом аппроксимирует функцию s(t). Это означает,
35
B.2)

Раздел 2
что средняя квадратичная ошибка такой аппроксимации сигнала с
весом p(t)
B.5)
имеет наименьшее значение по сравнению с ошибками, сопровож-
сопровождающими описание сигнала в виде B.4) с коэффициентами, отлич-
отличными от B.3). Учитывая, что g2n >0, из B.5) получаем неравенство
Бесселя
Х|с/Ы|2 <ls2(t)p(t)dt, B.6)
п=0 *
la
которое при N —> °° переходит в равенство Парсеваля
Х1с/1ы2=152^^^- (z7)
Равенство B.7) означает, что ряд B.1) сходится в среднем квад-
квадратичном к функции s(t).
Некоторые ортогональные системы базисных функций, которые
могут быть использованы при описании и анализе сигналов и их
характеристик, приведены в табл. 1.3.
2.2. Спектральный анализ сигналов на основе системы
тригонометрических функций
При анализе сигналов наиболее часто используется разложение
временной функции, описывающей сигнал, в тригонометрический
ряд Фурье (разложение по ортогональной системе тригонометриче-
тригонометрических функций). Сигнал представляется в виде взвешенной суммы
гармонических составляющих. Спектральный анализ, основанный
на таком представлении сигналов, называется гармоническим. Ис-
Используемая система функций {cos nx, sin nx} является ортогональ-
ортогональной и полной на интервале [-я,я]. Эта система периодическая, со-
сохраняет свою ортогональность и полноту на любом интервале дли-
длительностью 2тг.
36

Обобщенный спектральный анализ сигналов
Периодический сигнал s(t), имеющий частоту повторения со^
можно представить в виде
s(t) - — + ^ (an cos no) т t + bn sin rm^ t), B.8)
л=1
где со, = 2к/Т; Г- период сигнала.
Ортогональность базисных функций приводит к следующим ра-
равенствам:
О, п ф m
Т/2, n = m
Предполагается, что функция s(t) является квадратично интег-
интегрируемой на интервале периодичности [-Г/2, Г/2]. Такие функции
описывают сигналы с конечной мощностью.
От B.8) можно перейти к несколько иной форме записи тригоно-
тригонометрического ряда Фурье
Периодический сигнал рассматривается как сумма гармониче-
гармонических составляющих с амплитудами Ап, и начальными фазами фп.
Совокупность амплитуд {Ап} -амплитудный спектр, а совокупность
начальных фаз {фп} -фазовый спектр сигнала. Спектры сигналов
37

Раздел 2
Рис. 2.1
в базисе тригонометрических функций называются частотными
спектрами.
Как следует из B.11), спектры периодических сигналов являются
дискретными или линейчатыми, интервал дискретизации по частоте
определяется частотой сигнала со1 (или его периодом Т,
щ=2п/Т), рис. 2.1.
В качестве примера рассмотрим прямоугольное колебание (ме-
(меандр), рис. 2.2,а. Для него из B.10) получим
Рис. 2.2
38

Обобщенный спектральный анализ сигналов
Таким образом,
_|4/ял, л = 1,3,5,...
п [0,л = 0,2,4,-
s(t) = 4/rc(sinoy +1/3sinScy+ 1/5sin5Gy + ...).
Переходя к форме записи B.11), имеем (рис. 2.2,6)
2.3. Спектральный анализ сигналов на основе
многочленов Лежандра
Система многочленов Лежандра {Pn(t)} ортогональна на интер-
интервале [-1, 1] с весом p(t) = 1. Многочлены Лежандра определяются
выражением
P"(() = rti;rS('2)"''7 = 0'1>2'- <212)
Многочлены первых порядков (рис. 2.3):
PoW=1.
P:(t)=t,
P2(t)=1/2Ct2- 1),
P3(t)= 1/2{5t3-3t), B.13)
P4M=1/8C5f4-3Of2+3),
P5Cf;=1/8F3f5-7Of3+15f).
Условие ортогональности многочленов Лежандра записывается
в виде
1 f 0, т * п
\pm(t)Pn(t)dt = \ 2 • B.14)
J , т = п
-1 [2п + 1
Функция s(t) раскладывается в ряд по многочленам Лежандра
оо
5@ = ?слРп@. B-15)
/7=0
с коэффициентами
39

Раздел 2
Рис. 2.3
B.16)
Совокупность коэффициентов B.16) представляет спектр сигна-
сигнала s(t) в базисе многочленов Лежандра.
В качестве примеров рассмотрим некоторые виды функций, опи-
описывающих сигналы во временной области.
1. Сигнал описывается степенным многочленом
где ап - постоянные коэффициенты.
Переходя к безразмерной величине х = 2t/xu, запишем
л=0
40
Разложим функцию в ряд по многочленам Лежандра

Обобщенный спектральный анализ сигналов
Приравнивая в левой и правой частях равенства коэффициенты
при слагаемых с одинаковыми степенями х, получим систему урав-
уравнений для определения коэффициентов сп.
При Л/ = 2; а0=1; а^ = 0; а2 = -1, находим Со = 2/3; с^ = 0; Сг = -2/3.
2. Косинусоидальный импульс
s(t) = cos—,Щ< — .
Переходя к безразмерной величине х = 2tlxu, запишем
41
Коэффициенты сп определяются выражением
Вычисляя интеграл получаем
сп = 21 я; Ст = 0; с2 = -0,68 ; с3 = 0; с4 = -0,03.
2.4. Спектральный анализ сигналов на основе
многочленов Чебышева
Многочлены Чебышева первого рода определяются выражением
B.18)
B.17)
Многочлены Tn(t) первых порядков (рис. 2.4):
h(t) = t,
T2{t) = 2t2-1,
T3(t) = 4t3-3t,
T^t) = Q^-Qt2 + '[,
T5(f) = 16f5-2Of3 + 5f.

Раздел 2
Рис. 2.4
Многочлены Tn(t) ортогональны на интервале [-1, 1] с весом
B.19)
Многочлены Чебышева второго рода Un(t) определяются через
многочлены первого рода
B.20)
Функция s(t) раскладывается в ряд по многочленам Tn(t)
B.21)
с коэффициентами
Совокупность коэффициентов B.22) представляет спектр сигна-
сигнала s(t) в базисе многочленов Чебышева.
42

Обобщенный спектральный анализ сигналов
Примеры разложения в ряд по многочленам Чебышева.
1. Функция s(t) = eat, \i\ < 1 •
В ряде случаев разложение функции s(t)'no многочленам Чебы-
Чебышева на интервале [-1, 1] сводится к разложению функции s(cost)
на интервале [-п,п] по косинусам. Для рассматриваемой функции
используем известное соотношение
где 1п(а) - функция Бесселя.
Замена f = cos(p дает
Аналогично, из разложений по косинусам можно получить сле-
следующие разложения по многочленам Чебышева.
43

Раздел 2
2.5. Спектральный анализ сигналов на основе
многочленов Лагерра
Многочлены Лагерра Ln(T) ортогональны на полуоси [0,°°) с ве-
весом p(t) = e'. Определяются выражением
Ln(t) = (-1) V -^-('V'), п = 0,1, 2,... B.23)
Многочлены Ln(t) первых порядков имеют вид:
Li(t)=t-1,
L2(t)=t2-4t+2, B.24)
L3(t)=t3-9t2+1Qt-6,
L4(t) = f4- 16f3+ 72f2- 96f + 24,
Ls(t) = t5- 25tA + 200t3~ 600f2+ 600Г- 120.
Условие ортогональности многочленов Лагерра:
7 , [0,гпфп
e\(W)df =
J [(n!J,m=n.
При t -> oo многочлены Ln(t) расходятся. Поэтому при разложе-
разложении сигналов обычно используют функции Лагерра
ln(t) = ±e-t!2Ln(t). B.25)
Графики Функций ln(t) первых порядков показаны на рис. 2.5.
Функции ln(t) ортогональны и нормированы
]^'Н:^п- <2-2б)
о L
Функция s(t) раскладывается в ряд по функциям Лагерра
оо
s(f) = XcnW B.27)
п=0
с коэффициентами
44

Обобщенный спектральный анализ сигналов
Рис. 2.5
B.28)
Совокупность коэффициентов B.28) представляет спектр сигна-
сигнала s(t) в базисе функций Лагерра.
Пример.
Сигнал описывается выражением s(t) = e~at-e~bt, t>0.
Из B.28) находим
2.6. Спектральный анализ сигналов на основе
многочленов Эрмита
Многочлены Эрмита Hn(t) ортогональны на всей оси (-°°,°°)
с весом е ^. определяются выражением
B.29)
Многочлены Hn(t) первых порядков:
45

Раздел 2
H0(t)=l,
H,(t) = 2t,
H2(t) = 4t2-2, B.30)
H4(t)=16t4- 48f2+12,
H5(^ = 32?5-160f3+120f.
Условие ортогональности многочленов Эрмита:
7 2 {0, т*п
\е'! HJt)Hn(t)dt = \ . B.31)
При f-»±<» многочлены Нл^ расходятся. Поэтому при разло-
разложении сигналов удобнее использовать функции Эрмита
hn(t) = е-'г/2"л@ф2лЛ • B-32)
Графики функций hn(t) первых порядков показаны на рис. 2.6.
Функции hn(t) ортогональны и нормированы
—оо ^
Разложение s(t) по функциям Эрмита
оо
s(f) = ]TcA@ B.33)
л=0
имеет коэффициенты
сп= js(t)hn(t)dt. B.34)
Совокупность коэффициентов B.34) представляет спектр сигна-
сигнала s(t) в базисе функций Эрмита
Пример.
Сигнал - гауссов импульс s(t) = е~а{2 •
46

Обобщенный спектральный анализ сигналов
Рис. 2.6
Коэффициенты разложения определяются выражением
2.7. Спектральный анализ сигналов на основе функций
Уолша
Спектральный анализ сигналов на основе функций Уолша нахо-
находит практическое применение прежде всего при исследовании сиг-
сигналов, формируемых в цифровых устройствах.
2.7.1. Системы функций Уолша
Функции Уолша являются кусочно-постоянными знакоперемен-
знакопеременными функциями, принимающими значения 1 или -1. Они опреде-
определяются с помощью функций Радемахера rn(t) (рис. 2.13)
B.35)
где л =1, 2,... - порядок функции; х= t/T, T- интервал времени.
Функции Радемахера имеют вид меандра, ортонормированы.
Все они являются нечетными относительно середины интервала
47
Вычисление интегралов дает

Раздел 2
определения и не образуют полной системы, следовательно, не
могут быть использованы при разложении функций в ряд Фурье.
Ортогональная система кусочно-постоянных функций становится
полной при переходе к функциям Уолша. Функции Уолша опреде-
определяются произведением функций Радемахера. Принцип формирова-
формирования этого произведения задает систему функций Уолша. Наиболь-
Наибольшее применение нашли системы функций Уолша, известные как
системы Пэли, Адамара и Хармута (Уолша).
Система Пэли. Функция Уолша с номером л в системе Пэли за-
задается произведением функций Радемахера с номерами к, равны-
равными разрядам двоичного представления л. При двоичном представ-
представлении число П записывается в виде
B.36)
где т - число разрядов.
Функции Уолша в системе Пэли определяются как
B.37)
где п - порядок функции Уолша.
Двоичное представление л для значений от 0 до 15 приведено
в табл. 2.1.
Таблица 2.1.
Двоичное представление порядка функций Уолша
в системах Хармута (Уолша), Пэли и Адамара
№
п/п
0
1
2
3
4
5
Система Хармута
(Уолша)
0000
0001
0011
0010
0110
0111
Система Пэли
0000
0001
0010
0011
0100
0101
Система Адамара
0000
1000
0100
1100
0010
1010
48

Обобщенный спектральный анализ сигналов
№
п/п
6
7
8
9
10
11
12
13
14
15
Система Хармута
(Уолша)
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000
Система Пэли
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Система Адамара
0110
1110
0001
1001
0101
1101
0011
1011
0111
1111
Система Адамара. Получается из системы Пэли записью раз-
разрядов двоичного представления номера функции Уолша п в обрат-
обратном порядке
B.38)
Комбинации nm.k+h соответствующие первым номерам функции
Уолша, приведены в табл. 2.1.
Система Хармута. Эту систему можно получить из системы Пэ-
Пэли, представляя номер соответствующей функции Уолша в коде
Грея. Код Грея получается последовательным суммированием по
модулю два соседних разрядов двоичного разложения п, начиная с
младшего.
Обозначив /с-ый разряд кода Грея <nk>, запишем
<nk>=nk®nk+,, B.39)
где знак ф означает операцию поразрядного суммирования по мо-
модулю два
@ 00 = 0,0 ©1 = 1,100 = 1,101 = 0).
Выражение для функции Уолша в системе Хармута имеет вид
wal(n,x) = fl[rk(x)]<nk>- B-40)
/с=1
49

Раздел 2
Рис. 2.7
Комбинации <л*>, соответствующие нумерации Функций Уолша,
приведены в табл. 2.1. Определение функций Уолша первых по-
порядков п < 15 в системе Хармута через функции Радемахера в со-
соответствии с B.40) дано в табл. 2.2.
Таблица 2.2.
№
п/п
0
1
2
3
4
5
6
7
8
9
Функции Уолша
(л4 лЗ п2 п1)
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
в системе Хармута (Уолша)
wal(n,rt) = П ШхЛпк
wal @,x) = 1
wal A,х) = п(х)
wal B,x) = г2(х)
wal C,х) = г2(х)
wal D,х) = г2(х) г3(х)
wal E,х) = п(х) г2(х) г3(х)
wal F,х) = п(х) г3(х)
wal G,x) = г3(х)
wal (8,х) = гз(х) г4(х)
wal (9,х) = п(х) г3(х) ц(х)
50

Обобщенный спектральный анализ сигналов
№
п/п
10
11
12
13
14
15
(л4 лЗ л2 л1)
1111
1110
1010
1011
1001
1000
wa\{n,k) = П WxJ\nk
wal A0,x) = п(х) г2(х) г3(х) г4(х)
wal A1,х) = г2(х) г3(х) г4(х)
wal A2,x) = г2(х) г4(х)
wal A3,х) = п(х) Г2(х) г4(х)
wal A4,х) = п(х) и{х)
wal A5,x) = г4(х)
Графики функций Уолша, упорядоченных по Хармуту, изображе-
изображены на рис. 2.8. Соответствующие нумерации функций Уолша в сис-
системах Пэли и Адамара приведены в двух правых столбцах на
рис. 2.8. Из графиков функций Уолша, приведенных на рисунке,
видно, что порядковый номер функции в системе Хармута равен
числу пересечений ее графика с осью абсцисс на интервале [0, 1].
Поэтому нумерация функций Уолша по Хармуту называется также
упорядочением по частоте.
В системе Хармута четные относительно середины интервала
функции чередуются с нечетными. Эти функции имеют соответст-
соответственно четные и нечетные номера. В этом функции Уолша в системе
Хармута подобны тригонометрическим функциям и их по аналогии
иногда обозначают:
четные cal(n,x) = wal(n,x), n = 2k,
нечетные sal(n,x) - wal(n,x), n = 2k+1.
Рассмотренные системы содержат одни и те же функции Уолша,
только расположенные в различной последовательности.
2.7.2. Свойства функций Уолша
Из свойств функций Уолша, определенных на интервале [0, 1],
отметим следующие.
1. Функции Уолша являются периодическими с периодом, рав-
равным единице
\ыа\{п,х±к) = wai(n,x), k= 1,2,... B.41)
2. Модуль функции Уолша равен единице, среднее значение для
л* 0 равно нулю
| wal(n, х)\ = 1; j wal(n, x)dx - 0.
B.42)
51

Раздел 2
Рис. 2.8
52

Обобщенный спектральный анализ сигналов
3. Функции Уолша ортонормированны на интервале [0, 1]
f wal(n, x)wal(k, x)dx = \ ' П ~ . B.43)
J [0,n*k
4. Произведение двух функций Уолша является также функцией
Уолша
wal(n,x)wal(/c,x) = wal(m,x). B.44)
Для систем Пэли и Адамара
m = n®k, B.45)
для системы Хармута
т=<<л>©</с>>, B.46)
где символ < > означает преобразование кода Грея в двоич-
двоичный код.
5. Параметры лих симметричны: любые выводы относительно
п справедливы для х и наоборот.
Такой вывод следует непосредственно из выражений B.37),
B.38) и B.40).
2.7.3. Спектры сигналов в базисе Уолша
Сигнал, описываемый интегрируемой функцией s(t) и опреде-
определенный на интервале [0, Т], можно разложить в обобщенный ряд
Фурье по функциям Уолша
оо
s{t) = ^cnwal{n,t/T),O<t/T<J\, B.47)
л=0
где
Совокупность коэффициентов сп представляет спектр сигнала в
базисе Уолша или спектр Уолша. При вычислении спектров Уолша
выражение для сп целесообразно представить несколько в иной
форме. Разобьем интервал значений t/T на N участков, в пределах
которых функция wal(n,t/T) постоянна. С учетом этого выражение
для сп запишем в виде
53

Раздел 2
ЛМ«с+1
сп=-^ \s(t)wal(n,t/T)dt. B.48)
Из B.48) получим
Л/-1 tfr+1
cn=-Ywal(n,k/N) fs(t)dt. B.49)
/(=0 ft
С учетом того, что функции Уолша равны ±1, выражение B.49)
запишем в виде
Л/-1 *+1
*=0 Г/с
где апG^ = 0 или 1, определяет знак функции Уолша на интервале
Примеры спектров Уолша.
1. Спектр Уолша прямоугольного импульса s(t) = 1, 0 < t < т
(рис. 2.9)
Из B.50) находим
' k=0
Спектр Уолша прямоугольного импульса зависит от соотноше-
соотношения между т и Т. При т/ Т = 2V, где v - целое положительное число,
с учетом значений функций Уолша получим
cn=M2\n = 0X-..,2v -^.
Разложение прямоугольного импульса по функциям Уолша име-
имеет вид
Спектр состоит из 2V составляющих с одинаковыми амплитуда-
амплитудами, равными 1/2V. Спектр содержит конечное число составляющих.
При х1Тф2х' структура спектра изменится.
54

Обобщенный спектральный анализ сигналов
Рис.2.9
2. Спектр Уолша треугольного импульса (рис. 2.10)
При описании треугольного импульса
(t/T,0<t<T/2
' \\-t/T,T/2<t<T
удобно перейти к безразмерному времени x = t/T
, х fx,0<x<1/2
S(X) = 4
[1-х,1/2<Г<1
В соответствии с B.50) находим:
55

Раздел 2
Спектры Уолша при нумерации Хармута и Пэли изображены на
рис.2.10, бив.
3. Спектр Уолша синусоидального импульса (рис. 2.11)
Для синусоидального импульса
s@ = sin—f,O<f<7",
переходя к безразмерному времени x = t/T, запишем
s(x") = sin7ix, 0< х<1.
Из B.50) в системе Хармута находим (рис. 2.11):
Г 2
с0 = sinnxdx = —;
Jo
56

Обобщенный спектральный анализ сигналов
Рис. 2.11
Спектры Уолша рассматриваемого сигнала при нумерации Хар-
мута и Пэли приведены на рис.2.11 ,б и в.
2.7.4. Свойства спектров Уолша
При анализе сигналов с использованием функций Уолша полез-
полезно учитывать свойства разложения сигналов в базисе Уолша -
спектров Уолша.
1. Спектр суммы сигналов равен сумме спектров каждого из сиг-
сигналов.
Спектр сигнала в системе функций Уолша определяется коэф-
коэффициентами разложения B.47). Для суммы сигналов коэффициен-
коэффициенты разложения определяются выражением
57

к=0
где апк- коэффициенты разложения сигнала sk(t).
2. Умножение сигнала на функцию Уолша с номером П изменяет
номера коэффициентов разложения ск по закону двоичного сдвига
по модулю два
s{t)wal(nJ/T) = ^ckwal{k®nJ/T) = Yjck(Bnwal{k,t/T). B.53)
к=0 к=0
3. Спектр Уолша произведения сигналов srft) и s2(t). определен-
определенных на интервале [0, 7) и имеющих спектры c\,cl, равен
4. Свертку сигналов s7^ и s2(^
т
s@ = Js,(f-T)S2(x)cfc B.55)
о
можно представить в виде
s(t) = Tj^clc2k, B.56)
к=0
где с^.с^ - спектры Уолша сигналов s^t) и s2(t).
Рассмотренные разложения по ортогональным системам при-
применимы к любым функциям, удовлетворяющим некоторым услови-
условиям, сформулированным ранее. Они могут использоваться как при
анализе сигналов, так и их характеристик. Ряды с ограниченным
числом членов могут рассматриваться как аппроксимирующие. Ко-
Коэффициенты разложения, определенные как коэффициенты Фурье,
обеспечивают оптимальность такой аппроксимации.
58
Раздел 2

Раздел 3.
ГАРМОНИЧЕСКИЙ АНАЛИЗ СИГНАЛОВ
В основе гармонического анализа детерминированных сигналов
лежит представление временной функции, описывающей сигнал, в
виде тригонометрического ряда Фурье или ее интегральное преоб-
преобразование Фурье - сигнал рассматривается как бесконечная или
конечная совокупность гармонических составляющих. В радиотех-
радиотехнике из всех видов спектрального анализа сигналов гармонический
анализ получил почти исключительное применение. Поэтому поня-
понятия спектральный и гармонический анализ часто имеют одно со-
содержание. Широкое применение гармонического анализа при опи-
описании сигналов объясняется рядом причин, главные из которых
связаны с распространением гармонических колебаний в природе и
простотой аппаратурной реализации методов их анализа.
3.1. Гармонический анализ периодических сигналов
Гармонический анализ периодических сигналов основан на раз-
разложении временной функции s(t), описывающей сигнал с периодом
Г и частотой u>i=2n/T, по ортогональной системе тригонометри-
тригонометрических функций {cos/tco^, sinnwiO- Для периодической функции s(t)
тригонометрический ряд Фурье имеет вид
оо
s@ = — + y?(ancosna}<lt+ bnSinno)^). C.1)
Коэффициенты ряда определяются выражениями
772 п Т/2
ап=— \ s(f)cos лш Jdt; bn = — I s(t)s'\nгко ^tdt. C.2)
-Т/2 -Т/2
Функция s(t) должна быть квадратично интегрируемой на ин-
интервале периодичности {-Т/2, Т/2]. Такие функции описывают пе-
периодические сигналы с ограниченной мощностью.
59

Раздел 3
Для четной функции s(t), как это следует из C.2),
Периодический сигнал представляется в виде суммы гармони-
гармонических составляющих с амплитудами Ап и начальными фазами фл.
Совокупность амплитуд {Ап} определяет амплитудный спектр,
а совокупность начальных фаз {фл} - фазовый спектр сигнала
(рис.3.1,а). Как следует из C.5), спектры периодических сигналов
являются дискретными или линейчатыми, интервал дискретизации
по частоте равен частоте сигнала а^ = 2л/ Г.
Тригонометрический ряд Фурье можно записать в комплексной
форме
где
7/2
-772
Переход от C.1) к C.7)
е'0) = cos oof + /sino)f.
60
C.7)
C.8)
очевиден с учетом формулы Эйлера
C.9)
для нечетной функции s(t):
Обычно при анализе сигналов используется разложение s(t)
в виде

Гармонический анализ сигналов
Рис.3.1
Коэффициенты сп в общем случае являются комплексными ве-
величинами
сп=\с„\еР" =ne[cn]+i\m[cn].
(З.Ю)
При использовании комплексной формы ряда Фурье сигнал оп-
определяется совокупностью комплексных амплитуд {сп}. Модули
комплексных амплитуд |с„| описывают амплитудный спектр, аргу-
аргументы фл - фазовый спектр сигнала (рис. 3.1,6).
Представив C.8) в виде
772 Т/2
cn=— \s(t)cosrm>itdt-i— {s(t)s\nn(i)^dt, C.11)
-Г/2
-Г/2
получим
Как следует из записанных выражений, амплитудный спектр об-
обладает четной, а фазовый - нечетной симметрией
61

Раздел 3
С„\ = \С-п\, ФЛ=Ф_Л- C-13)
Из сопоставления выражений C.2) и C.11) следует
an=2Re[cJ; Ь„ = -2lm[cJ; An=2\cn\. C.14)
В качестве примера рассмотрим периодическую последователь-
последовательность прямоугольных импульсов (рис. 3.2,а). При разложении пе-
периодической последовательности прямоугольных импульсов в три-
тригонометрический ряд Фурье из C.2) получим амплитудный и фазо-
фазовый спектры в виде (рис.3.2,б):
При использовании комплексной формы ряда Фурье
Амплитудный и фазовый спектры сигнала равны
Предельным видом ряда Фурье является интеграл Фурье. Пе-
Периодический сигнал при Г -»оо становится непериодическим. Под-
Подставив C.8) в C.7), запишем
C.16)
из C.8) следует:
62

Гармонический анализ сигналов
Рис. 3.2
Преобразуя C.16), при Т —> оо (в этом случае со у-> с/со и псо у= со),
получаем
C.17)
В квадратных скобках записан интеграл Фурье, он описывает
спектральную плотность сигнала
63

Раздел 3
Выражение C.17) примет вид
2тг
Записанные соотношения представляют прямое и обратное
преобразования Фурье. Они используются при гармоническом ана-
анализе непериодических сигналов.
3.2. Гармонический анализ непериодических сигналов
Прямое и обратное преобразования Фурье устанавливают вза-
взаимно однозначное соответствие между сигналом (временной функ-
функцией, описывающей сигнал s(t) ) и его спектральной плотностью
S(co):
S((o)= \s{t)e-btdt, s{t) = — fsMe^dh). C.18)
J 2я J
Соответствие по Фурье обозначим:
s(f)<-»S(o>). C.19)
Условием существования преобразования Фурье является аб-
абсолютная интегрируемость функции s(t)
оо
j\s(t)\dt <оо. C.20)
—оо
В практических приложениях более удобным является условие
интегрируемости квадрата этой функции
оо
\s2(t)dt<oo. C.21)
— оо
Для реальных сигналов условие C.21) эквивалентно условию
C.20), но имеет более очевидный физический смысл: условие
C.21) означает ограниченную энергию сигнала. Таким образом,
можем считать возможным применение преобразования Фурье к
сигналам с ограниченной энергией. Это непериодические (импульс-
(импульсные) сигналы. Для периодических сигналов разложение на гармо-
64

Гармонический анализ сигналов
нические составляющие производится с помощью ряда Фурье.
Функция S((o) в общем случае является комплексной
S(co) = Re[s(co)] + / lm[s(co)]; S(to) = ^((ф^, C.22)
где Re, Im - действительная и мнимая части комплексной величины;
|S(co)|, ф(о))- модуль и аргумент комплексной величины:
|sH = VRe2[S(m)]+lm2[s(<4 Ф(ш) = агс1д*|.
Модуль спектральной плотности сигнала |S(a)]j описывает рас-
распределение амплитуд гармонических составляющих по частоте, на-
называется амплитудным спектром. Аргумент ф(со) дает распределе-
распределение фазы по частоте, называется фазовым спектром сигнала. Ам-
Амплитудный спектр является четной функцией, а фазовый спектр -
нечетной функцией частоты
|S((o)| = |S(-co)|; ф(ш) = -ф(-ш). C.23)
С учетом формулы Эйлера C.9) выражение для S(to) запишем в
виде
S(co) = f s(f)cos со tdt - / f s(f)sin со tdt. C.24)
Если s(t)четная функция, то из C.24) получим
оо
S(w) = 2 f s(t)cos со tdt. C.25)
о
Функция S(w), как следует из C.25), является действительной
функцией. Фазовый спектр определяется как
ГО, S(w)>0,
[±я, S(o))<O.
Для нечетной функции s(t) из C.24) получим
S(co) = -/2[s(f)sinсо tdt. C.27)
о
65

Раздел 3
Функция S(o)) является чисто мнимой, фазовый спектр
[я/2 1тВД>0
44 y j-rc/2, lm[S(a))]<0
Любой сигнал можно представить как сумму четной ^(t) и нечет-
нечетной sH(t) составляющих
s(t) = s4(t)+sH(t). C.29)
Возможность такого представления становится ясной с учетом
следующих равенств:
«,(»)=*,(- 0={Ш* 4- 01 МО=-sH(-0={WO- s(- 01.
Из C.24) и C.29) получим
S(o) = 2f s^(f)coso) faff - /2fsH(f)sina) fcff. C.30)
о о
Следовательно, для действительной и мнимой частей спек-
спектральной плотности сигнала можно записать:
Re[s(o))]= z\s4(t)cos(D tdt; lm[s(co)]= -2f sH(f)sinco tdt.
о о
Таким образом, действительная часть спектральной плотности
представляет преобразование Фурье от четной составляющей,
мнимая часть - от нечетной составляющей сигнала. Действитель-
Действительная часть комплексной спектральной плотности сигнала является
четной, а мнимая часть - нечетной функцией частоты.
Спектральная плотность сигнала при ш = О
S@)= \s(t)dt C.31)
равна площади под кривой s(t).
В качестве примеров получим спектры некоторых сигналов.
1. Прямоугольный импульс (рис. З.З.а)
66

Гармонический анализ сигналов
где хи - длительность импульса.
Спектральная плотность сигнала
67

Раздел 3
Графики амплитудного и фазового спектров сигнала приведены
на рис. 3.3,б,в.
2. Сигнал, описываемый функцией
5("=(Й)Те'а' '>°-°=*
Спектральная плотность сигнала определяется выражением
Интегрируя по частям л-1 раз, получаем
имеет спектральную плотность
S(o) = -^-.
а + /со
Графики амплитудного и фазового спектров изображены на рис.
3.4Дв.
Сигнал (рис. 3.5,а)
s(t)=te~at, t>0,
имеет спектральную плотность
\а + ко)
Графики амплитудного и фазового спектров - рис. 3.5,6,в.
Число примеров увеличивает табл. 3.1.
Сравнение C.18) и C.8) показывает, что спектральная плотность
одиночного импульса при т«Г отличается от коэффициентов ряда
Фурье периодической последовательности импульсов только мно-
множителем 1/Г.
68

Гармонический анализ сигналов
С учетом указанного соотношения определение спектра периоди-
периодического сигнала в ряде случаев можно упростить, используя преобра-
преобразование Фурье C.18). Коэффициенты ряда Фурье находятся как
C.32)
где S(co) - спектральная плотность одного импульса.
Таким образом, при определении амплитудного и фазового
спектров периодических сигналов полезно иметь в виду следующие
равенства:
C.33)
69

Раздел 3
в)
Рис. 3.5
Коэффициент 1/Т может рассматриваться как интервал частот
между соседними составляющими спектра, а спектральная плот-
плотность как отношение амплитуды составляющей сигнала к интерва-
интервалу частот, которому соответствует амплитуда. С учетом этого ста-
становится более понятным термин «спектральная плотность». Не-
Непрерывные амплитудный и фазовый спектры одиночного импульса
являются огибающими дискретных амплитудного и фазового спек-
спектров периодической последовательности таких импульсов.
С помощью соотношений C.33) результаты, приведенные
в табл. 3.1, можно использовать для определения спектров перио-
периодических последовательностей импульсов. Такой подход иллюст-
иллюстрируют следующие примеры.
70

Гармонический анализ сигналов
Рис.3.6
1. Периодическая последовательность прямоугольных им-
импульсов (табл. 3.1, п. 1), рис. 3.2.
Записанное выражение повторяет результат примера п.3.1.
2. Периодическая последовательность меандровых импульсов
(табл. 3.1, п.2), рис. 3.6, рис. 3.2.
71

Раздел 3
3. Периодическая последовательность экспоненциальных
импульсов (табл. 3.1, п.8), рис. 3.7.
Ап =
Рис. 3.7
72

Гармонический анализ сигналов
Таблица 3.1
Сигналы и их спектры
73

Раздел 3
74

Гармонический анализ сигналов
75

Раздел 3
76

Гармонический анализ сигналов
77

Раздел 3
C.34)
78
3.3. Частотные спектры сигналов, представленных
в виде обобщенного ряда Фурье
При представлении сигнала в виде обобщенного ряда Фурье
полезно иметь преобразование Фурье базисных функций. Это по-
позволит от спектра в базисе различных ортогональных систем пе-
перейти к частотному спектру. Ниже приведены примеры частотных
спектров некоторых видов сигналов, описываемых базисными
функциями ортогональных систем.
1 .Сигналы Лежандра.
Преобразование Фурье многочлена Лежандра (разд. 2) имеет вид
п = 1, 2, ... - многочлен Лежандра; /n+1 (w) - функция Бесселя.
Используя C.34), от сигнала, представленного в виде ряда

Гармонический анализ сигналов
с коэффициентами
можно перейти к спектральной плотности сигнала
Выражение C.35) описывает спектральную плотность сигнала
s(t) в виде ряда.
Графики составляющих спектра с номерами 1-3 приведены на
рис.3.8.
2. Сигналы Лагерра.
Преобразование Фурье функции Лагерра имеет вид
п= 1,2, ... - функции Лагерра.
Используя C.36), от сигнала, представленного в виде ряда раз-
разложения по многочленам Лагерра (разд. 2)
с коэффициентами
можно перейти к спектральной плотности сигнала
C.37)
79

Раздел 3
Рис.3.8
3. Сигналы Эрмита.
Преобразование Фурье функции Эрмита имеет вид
C.38)
где
80

Гармонический анализ сигналов
Из C.38) следует, что функции Эрмита обладают свойством
трансформируемое™, т.е. функции и их преобразования Фурье
равны (с точностью до постоянных коэффициентов). Используя
C.38), от сигнала, представленного в виде ряда разложения по
многочленам Эрмита
можно перейти к спектральной плотности сигнала
4. Сигналы Уолша.
Частотные спектры сигналов Уолша (сигналов, описываемых
функциями Уолша) определяются следующим преобразованием
Фурье:
81
с коэффициентами
C.39)
где wal(n,x) - функция Уолша.
Так как функции Уолша имеют N участков постоянных значений,
то
где хк - значение х на к-ом интервале.

Раздел 3
Из C.41) получим
N—1
Sw» = ?wal(n,x^x,sinc^^e-ft)(x*+x-)/2, C.42)
к=0
где Ахк = хк+^-хк.
Так как функции Уолша принимают значения ±1, то C.42) можем
записать в виде
Л/-1 а "(к)
5т(ш)=?(-1) Ихкъш^е^*^, C.43)
/с=0
где а п(к) - 0 или 1 определяет знак функции wal(n,xk).
На рис. 3.9 приведены графики амплитудных спектров первых
шести сигналов Уолша.
3.4. Спектры сигналов, описываемых
неинтегрируемыми функциями
Преобразование Фурье существует только для сигналов с ко-
конечной энергией (для которых выполняется условие C.21)). Расши-
Расширить класс сигналов, анализируемых с использованием преобразо-
преобразования Фурье, позволяет чисто формальный прием, основанный на
введении понятия спектральной плотности для импульсной функ-
функции. Рассмотрим некоторые из таких сигналов.
1. Импульсная функция.
Импульсная функция (или 5 - функция) определяется как
«-Н:'-!' C44)
Из определения импульсной функции следует ее фильтрующее
свойство
J8(t-to)s(t)dt = s(to). C.45)
Спектральную плотность импульсной функции определим как
S(co)= $8A-10)е-шсН = е-ш°. C.46)
82

Гармонический анализ сигналов
83
Рис.3.9
Амплитудный спектр равен единице, фазовый спектр
ф(со) = -cof0 (рис. 3.10).
Обратное преобразование Фурье дает

Раздел 3
C-48)
Используя полученные выражения, определим спектральные
плотности некоторых видов сигналов, описываемых функциями,
для которых не существует преобразования Фурье.
2. Постоянный сигнал s(t) = s0.
С учетом C.48) получим (рис. 3.11)
C.49)
C.50)
Спектральная плотность сигнала получится с учетом C.48)
в виде
Рис. 3.11
84
Рис. 3.10
По аналогии с C.47) для частотной области запишем
3. Гармонический сигнал.

Гармонический анализ сигналов
C.51)
C.52)
C.53)
C.54)
C.55)
C.56)
C.57)
85
Единичную ступенчатую функцию a(f) будем рассматривать
как предельный вид экспоненциального импульса
Для сигнала
по аналогии с C.52) найдем
4. Единичная ступенчатая функция.
Экспоненциальный импульс представим в виде суммы четной и
нечетной составляющих C.29)
При а-> О
s4(t) =1/2 для всех значений t,

Раздел 3
Действительная часть спектральной плотности соответствует
четной составляющей сигнала, мнимая часть - нечетной состав-
составляющей. Переходя к пределу при а —> 0, получим
C.58)
C.59)
где <->- символ соответствия по Фурье.
Спектральные плотности некоторых сигналов, описываемых
неинтегрируемыми функциями из наиболее часто встречающихся
на практике, приведены в табл. 3.2.
Таблица 3.2.
Спектральные плотности неинтегрируемых функций
№
п/п
1
2
3
4
5
6
s(t)
1
5@
S('±'o)
sign{t)
o(t)
COS@0t
sincoof
S(w)
2я8@
1
2
ко
О,55(ш) + —
/со
7l8((O - (O0 ) + 7l6((O + (O0 )
- ot5((o - co0) + отб(со + co0)
86

Гармонический анализ сигналов
3.5. Свойства преобразования Фурье
и их использование при анализе сигналов
3.5.1. Свойства преобразования Фурье
При анализе сигналов полезно учитывать свойства преобразо-
преобразования Фурье. Основные из них следующие.
1. Аддитивность.
Спектр суммы сигналов равен сумме спектров сигналов, т.е.
k&(t) + k2s2(t) + ... + knsn(t) <-> k,Si(со) + k2S2(to) +...knSn(со), C.60)
где <-» - символ соответствия по Фурье,
s,@<->S,(a>); %(f)«*3>(co);...; sn(t)^Sn{u>). .
2. Смещение во времени.
Сигнал при смещении на время t0 определяется выражением
sz(t) = s,(t-k) = ± }s,M в•*-<•)*> = ± ][sM)e^!' ] е"»сН
где t0- смещение сигнала во времени.
Таким образом,
s(f-*„)<-> S1(cD)e-^^=|S1(co)|e/D)-aj/o). C.61)
Как следует из записанных выражений, спектр сигнала, запаз-
запаздывающего на время t0, равен произведению спектра исходного
сигнала и множителя запаздывания e~*°f°. Амплитудный спектр
такого сигнала равен амплитудному спектру исходного сигнала, фа-
фазовый спектр - сумме фазового спектра исходного сигнала и ли-
линейной функции времени (рис. 3.13).
3. Изменение масштаба времени.
При сжатии (растяжении) сигнала во времени s2(t) = &[(kt)
(рис. 3.15) спектр определяется выражением
оо оо
S2(co)= ^82^)е-шсИ= $ф1)е-шсН.
Переходя к новой переменной, получаем
87

Раздел 3
Рис. 3.13
или
C.62)
Таким образом, сжатие (расширение) сигнала в к раз приводит
к расширению (сжатию) его спектра в к раз (рис. 3.14).
4. Смещение спектра сигнала.
Если спектр сигнала смещен по частоте на величину со, то
Рис. 3.14
88

Гармонический анализ сигналов
Таким образом,
W=Js,@
89
C.63)
т.е. произведению сигнала на множитель фазового сдвига е*°0'
соответствует смещение всех составляющих спектра по частоте на
величину соо.
5. Дифференцирование и интегрирование.
Для первой производной s(t) имеем
т.е. дифференцированию п раз сигнала по t соответствует умно-
умножение спектра на (ко)"
Аналогично для интеграла от s(t)
6. Произведение двух сигналов.
Для сигнала, равного произведению двух сигналов
s{t) = s,(t)s2(t),
C.64)
C.65)
получим
Для п -й производной получим

Раздел 3
запишем
Подставляя в записанное выражение
получаем
В полученном выражении имеем
Спектральная плотность произведения двух сигналов определя-
определяется как
Таким образом,
где ® - символ свертки; спектр произведения двух сигналов равен
свертке их спектров с коэффициентом 1/2л;
Аналогично можно показать, что произведение двух спектров
S^w^ (со) соответствует свертке функций s,(f) и S2(t)
7. Корреляционная функция сигналов.
C.67)
90
C.66)

Гармонический анализ сигналов
Для интеграла
js,(x)s,(t + x)dt,
где т - смещение во времени, по аналогии с C.66) получим
S;(o))S2(co).
Таким образом,
f s,(т) ^ (t + x)dt <-> S;(o)S2(со). C.68)
Для s:(t) = s2(t) = s(t) имеем
J s(x) s(f + t) dt ^ |s(cof = W(co). C.69)
Величина |S(oj]J = W(co) представляет спектральную плотность
энергии сигнала. Таким образом, корреляционной функции сигнала
соответствует спектральная плотность энергии.
При т = 0
{s2(^ = ^-J|s(cofob. C.70)
Выражение C.70) представляет равенство Парсеваля. Каждая
часть равенства описывает энергию сигнала.
Основные свойства преобразования Фурье отражены в табл. 3.3.
Таблица 3.3.
Свойства преобразования Фурье
№
п/п
1
s(t) =1/2тг fs(w)ewtdai
s(t)
-н*>
S(co)= fs(Oe-|U)t<#
|S(o))| = \S (чо)|, argS(o)) = - argS(-co)
91

Раздел 3
№
п/п
2
3
4
5
6
7
8
9
10
11
12
sCO =1/2тс fs(co;eto>t cfco
s^ = sr-0
s^ = -sr-0
ki^(t)±k2s2(t)
s(at), a > 0
s(af)e±All°f, a > 0
dns(t)
dtn
\s(t)dt
Stf)Sz(t)
S(<o)= fs(f)elwt c/f
S(w) = S(-co) = 2 f s(f; ooscof d/
S(cu) = - S(-co) = -/2 fs(^sino)f df
1/a S (a/a)
S(oi)e±Mt°
S(w±oo0)
i/zicoSfco;
1/2nfsi(x)S2((o-x/)dx =
= 1 /2njs,((i)- x) S2(x)dx =
= 1/2nS^(u))®S2(oi)
92

Гармонический анализ сигналов
3.5.2. Примеры использования свойств преобразования Фурье
при определении спектров сигналов
1. Сигнал, изображенный на рис. 3.15.
Спектральная плотность прямоугольного импульса единичной
амплитуды, симметричного относительно начала координат, опи-
описывается выражением
„/ \ . СОТ .
S(to) = xusinc—-,
где хи - длительность импульса.
Сигнал можно рассматривать как совокупность (сумму) двух
прямоугольных импульсов. Используя свойство 1, запишем
93

где
где w1 - частота сигнала.
Преобразование Фурье C.71) дает
Таким образом, спектральная плотность периодического сигнала
представляет бесконечную сумму импульсных функций, умножен-
умноженных на соответствующие коэффициенты и расположенных на час-
частотах, кратных частоте сигнала.
94
С учетом свойства 2 и решения примера 1 п. 3.2 получим
Амплитудный и фазовый спектры определяются выражениями
2. Периодический сигнал.
Используя выражение для спектральной плотности гармониче-
гармонического сигнала, определяем спектральную плотность периодического
сигнала. Периодический сигнал s(t) представим в виде ряда Фурье
C.71)
C.72)
или

Гармонический анализ сигналов
3. Произведение сигнала и гармонического колебания.
C.74)
Преобразование Фурье левой и правой частей C.74) с учетом
п.8 табл. 3.3 дает
C.75)
C.76)
95
из C.75) получим

Раздел 3
Рис.3.17
96
фазовый спектр
На рис. 3.17,6 изображены амплитудные спектры сигнала при
различных значениях со0.
4. Треугольный импульс.
При определении интеграла Фурье некоторых видов сигналов
часто удобнее сначала произвести дифференцирование сигнала,
найти преобразование Фурье производной, а затем перейти к пре-
преобразованию Фурье исходного сигнала. Удобство такого приема
связано с тем, что в результате дифференцирования некоторых
видов сигналов появляется последовательность импульсных функ-
функций, для которых известно преобразование Фурье. Метод приведе-
приведения к импульсным функциям поясним на примере определения
спектра сигнала в виде треугольного импульса (рис. 3.18,а).

Гармонический анализ сигналов
8л/ти ю
Рис. 3.18
Дважды продифференцировав функцию s(t), получим (рис. 3.18 6,в)
^l^[S(t + rj2)-2S(t)+S(t-rj2)].
и* Тц
Преобразование Фурье левой и правой частей записанного вы-
выражения дает
где S((o) - спектральная плотность сигнала s(t).
После преобразования получим
Амплитудный спектр сигнала показан на рис.3.18,г.
97

или после преобразования
S(M) = So(o>fn^aT/2}e-^^. C.78)
sin(cor/2)
При /V—><*>
S(a))=^(a)) 1_ю7.. C.79)
С учетом C.78) результаты, приведенные в табл. 3.1, можно ис-
использовать для определения спектров пачек различных импульсов.
1. Пачка прямоугольных импульсов (табл. 3.1, п.1), рис. 3.19.
S(co) = хи 5тс^1и.М^Т/2) ,(л/-1>оТ/2
W u 2 sin(aO72)
2. Пачка меандровых импульсов (табл. 3.1, п.2), рис. 3.20.
S(to)- /4-sin2 ^^ sin(A/co7/2)c._,(A/,1)o,r/2
со 4 sin((o7/2)
98
5. Пачки импульсов.
Пачки идентичных сигналов (импульсов) составляют достаточно
обширный класс сигналов, встречающихся в инженерной практике.
Поэтому спектральный анализ таких сигналов, помимо иллюстрации
методического подхода, представляет самостоятельный интерес.
Спектральная плотность пачки импульсов определяется как
сумма спектральных плотностей каждого из импульсов. При иден-
идентичной форме импульсов, обозначив спектральную плотность пер-
первого импульса SQ(co), для пачки импульсов запишем
S(w)=50(w)+S0(a))e"")T+... + S0((o)e-'(A/-iVor, C.77)
где 7- период следования импульсов в пачке; N- число импуль-
импульсов в пачке.
В C.77) множитель е"*07 учитывает смещение во времени каждо-
каждого последующего импульса по отношению к предыдущему. Из C.77)
с учетом формулы суммы геометрической прогрессии получим
Раздел 3

Гармонический анализ сигналов
3. Пачка треугольных импульсов (табл. 3.1, п.З), рис. 3.21.
99
4. Пачка косинусоидальных импульсов (табл. 3.1, п.4), рис.3.22.
3.6. Спектральный анализ сигналов на основе
преобразования Хартли
Преобразование Хартли является одним из интегральных пре-
преобразований, которые могут найти применение при анализе сигна-
сигналов, представляет модификацию преобразования Фурье. Отличи-
Отличительная особенность преобразования Хартли состоит в том, что
оно является действительным интегральным преобразованием.
Практически для всех сигналов, для которых существует
преобразование Фурье, существует и преобразование Хартли.
Рис. 3.19

Раздел 3
Рис. 3.21
100
Рис.3. 20

Гармонический анализ сигналов
s(t)
А'А Л Л-
\S((O
2,1-
1.8-
1.5-
1,2-
0,9-
0,6-
0,3-
)\
.
1
0
-ти/2 0 ru/2
Т/ти = 4
л/ = з
л
Л л
Л
л L Л
1 2
3.6.1.
Г 27
|S((O)|
4,2-1
3,6-j |
Н 1 1
Ч i
°НУ У.У
3 4 0 1
Рис. 3.22
Преобразование Хартли
Т/хи
Л/ =
1
2
= 4
6
3 ^
(О
Интегральные преобразования Хартли (прямое и обратное)
имеют вид
Н(о))= Js(f)caso)fc#,
C.80)
ОО
s(t) = — f H((o) casw tdw,
2л J
C.81)
где casx = cos x+sin x.
Прямое C.80) и обратное C.81) преобразования Хартли явля-
являются действительными и обладают взаимной симметрией.
Представляя сигнал как сумму четной и нечетной составляющих,
преобразование Хартли запишем в виде
Н(а))=Нч(со)+Нн(со)
C.82)
Если сигнал описывается четной функцией Sh (t), то из C.80)
101

C.83)
C.84)
Сравнение выражений для преобразований Фурье и Хартли по-
позволяют установить взаимосвязь между ними - между H(w) и S(co) :
Н(со) = Re[S(co)] - lm[s(w)], C.85)
S(o))=H4(o))-/HH(o)).
Из C.85) следует, что для сигнала, описываемого четной функ-
функцией,
H(co)=S((o) C.86)
а для сигнала, описываемого нечетной функцией,
H(o)) = -/S(to). C.87)
Свойства преобразования Хартли отражены в табл. 3.4. Там же
для сравнения приведены соотношения, характеризующие свойст-
свойства преобразования Фурье.
Таблица 3.4.
Свойства преобразования Хартли
№
п/п
Сигнал s(f)
Преобразование
Фурье S(o)
Преобразование
Хартли Н((о)
102
получим
Раздел 3

Гармонический анализ сигналов
№
п/п
Сигнал s(t)
Преобразование
Фурье S(to)
Преобразование
Хартли Н(ш)
3.6.2. Примеры преобразований Хартли некоторых сигналов
Особенности преобразования Хартли иллюстрируют следующие
примеры.
1. Прямоугольный импульс.
Для симметричного прямоугольного импульса из C.83) находим
(рис. 3.23)
При смещении импульса на интервал т/2 его преобразование
Хартли определяется как
Н((о) = icasutdt = (sincoTy -coscoiy +1)/co.
о
2. Меандровый импульс.
Для меандрового импульса из C.84) получим (рис. 3.24)
103

Раздел 3
Рис. 3.24
104

Гармонический анализ сигналов
Рассмотрение преобразования Хартли, его особенностей, по-
позволяет сделать выводы о практике его применения при анализе
сигналов. Действительные величины, получающиеся при использо-
использовании преобразования Хартли, дают определенные удобства при
анализе сигналов и расчете их характеристик на инженерном уров-
уровне. К удобствам преобразования Хартли следует отнести и его
симметричность.
Однако преобразование Фурье является более физичным -
в большей степени отвечает установившимся представлениям
о спектре как о совокупности гармонических колебаний. Преобразо-
Преобразование Хартли дает разложение по сумме двух составляющих, одна
из которых сдвинута по фазе относительно другой на к/2.
Преобразование Хартли приводит к более сложным выражени-
выражениям прежде всего для произведения и свертки функций. Указанные
операции встречаются довольно часто при анализе сигналов, и это
обстоятельство нельзя не учитывать.
105

Раздел 4.
АНАЛИЗ СИГНАЛОВ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
ЛАПЛАСА
При анализе прохождения сигналов через цепи широкое приме-
применение нашло преобразование Лапласа. Это объясняется, в част-
частности, тем, что класс функций, для которых существует преобра-
преобразование Лапласа, шире, чем тот, для которого существует преобра-
преобразование Фурье, а односторонность преобразования Лапласа при
анализе линейных цепей практически не накладывает дополни-
дополнительных ограничений.
Особенности преобразования Лапласа и его применение при
анализе сигналов описываются в настоящем разделе.
4.1. Преобразование Лапласа и его свойства
Преобразование Лапласа функции s(t) имеет вид
S(p) = js(t)e-ptdt, D.1)
о
где р = а + ка - комплексная или действительная величина.
Интеграл Лапласа отображает функцию s(t) в функцию ком-
комплексной переменной р. Функция s(t) называется оригиналом, S(p) -
изображением. Обратное преобразование позволяет вернуться во
временную область, перейти от изображения к оригиналу, описывае-
описываемому временной функцией. Соответствие функций по Лапласу обо-
обозначим тем же знаком, который использовался ранее при рассмот-
рассмотрении преобразования Фурье
s(t) о S(p).
Операциям, проводимым над сигналами во временной области, со-
соответствуют операции в области комплексной переменной р.
В ряде случаев они оказываются проще, и перевод анализа в область
комплексной переменной р позволяет упростить анализ.
106

Анализ сигналов на основе преобразования Лапласа
Функция s(t), описывающая сигнал, является кусочно-
непрерывной, равна нулю при отрицательных значениях t. Условие
существования преобразования Лапласа устанавливается нера-
неравенством
\s(t)\ < Meat, D.2)
где Mv\ а- постоянные.
Неравенство D.2) ограничивает скорость нарастания функции
s(t). При выполнении D.2) интеграл D.1) абсолютно сходится для
всех р, у которых Re[p]>a.
Сравнивая преобразования Лапласа и Фурье, отметим, что если
преобразование Лапласа существует для функций, удовлетворяю-
удовлетворяющих условию D.2), то для существования преобразования Фурье
требуется сходимость интеграла
Условие сходимости интеграла является более жестким. Таким
образом, если для функции s(t) существует преобразование Лапла-
Лапласа, то для нее не обязательно должно существовать преобразова-
преобразование Фурье. Условию D.2) удовлетворяют, в частности, функции
coscof и sinatf (/ > 0). Для них а можно положить равным нулю:
\s(t)\<M. Указанному условию удовлетворяет и степенная функция tn
(п > 0), так как такая функция растет медленнее е* (Mm tn/e' = О при
t~>oo).
При равенстве действительной части р нулю (р = ко) интеграл
Лапласа переходит в интеграл Фурье для сигнала, обращающегося
в нуль при t < 0. Односторонность преобразования Лапласа часто
не ограничивает класс рассматриваемых сигналов, прежде всего
при анализе их прохождения через цепи.
При анализе сигналов с использованием преобразования Лап-
Лапласа полезно учитывать его свойства. Они аналогичны свойствам
преобразования Фурье.
1. Аддитивность.
Если
D.3)
107
то

Раздел 4
k,s,(t) + k2s2(t) <-> k,S,(p) + k2S2(p), D.4)
где kh k2 -постоянные коэффициенты,
т. е. линейной комбинации оригиналов соответствует такая же
комбинация изображений.
2.Запаздывание.
s(t-to)^js(t-tQ)e-ptdt
= e-pt° Js(f- to)e'p{t'to)d{t-10) = S{p)e~pt°.
о
3. Подобие.
s(kt) <-> \s(kt)e~ptdt = 1/ k\s(t)e~ptlkdt = MkS{plk). D.6)
о о
4. Смещение.
eats{t) ^ jeats(t)e-ptdt = js{t)e-{p-a)dt = S(p-a). D.7)
о о
5. Дифференцирование оригинала.
s(t) <-> is(t)e~ptdt=-s(O) + pS(p).
о
Аналогично можно получить
s{n){t) <-> -s(n)@) - ps("-2)@) -... - pn-1s(O) + pnS{p). D.8)
При s@) = s@) = s-@) =... = s(n~1)@)
s{n\t)^pnS(p). D.9)
6. Интегрирование оригинала.
По аналогии с. п. 5 при s/Oj = 0 получим
108

Анализ сигналов на основе преобразования Лапласа
\s{t) dt <r? MpS{p). D.10)
о
7. Свертка функций.
Свертке функций h(t) и s(t) соответствует произведение изобра-
изображений
t t
\h(x)s(t-x)dx = \h{t-x)s(x)dx <-> H(p)S(p). D.12)
о о
Произведению оригиналов соответствует свертка изображений
в комплексной плоскости.
Приведенные основные свойства преобразования Лапласа от-
отражены в табл. 4.1.
В качестве примеров рассмотрим преобразования Лапласа не-
некоторых видов сигналов. При этом будем предполагать, что функ-
функция, описывающая сигнал, при t < 0 равна нулю.
1. Сигнал s(t) = eat.
Преобразование Лапласа
109
При а = 0 получим изображение ступенчатой функции
S(p) = Mp.
Интеграл Лапласа для ступенчатой функции сходится при
Re/pj > 0.
2. Сигнал s{t) = sin со t = M2i(ebt - е~ы).
Преобразование Лапласа получим с учетом результата первого
примера

Раздел 4
найдем
3. Прямоугольный импульс.
Рассматривая s(t) как разность ступенчатой функции и ступенча-
ступенчатой функции, смещенной нат, с учетом результата первого приме-
примера получим
Таблица 4.1.
Свойства преобразования Лапласа
При задержке импульса относительно начала координат на
время to с учетом п.2 табл. 4.1 найдем
110

Анализ сигналов на основе преобразования Лапласа
S(p) = ~O-e'pz)e-pt°.
Р
4. Периодическая последовательность прямоугольных им-
импульсов.
Используя свойства преобразования Лапласа - аддитивности и
запаздывания, получим преобразование Лапласа периодической
последовательности идентичных импульсов прямоугольной формы
в виде
S(p) = 1A - ??-<*) + 1A - e-pt)e-pT+—0 - е-р1)е~2рТ +... =
Р Р Р
= 1A -e~fnW + e-pT + e-2pT + ...)= 1"е^7 ,
Р РA-е-рГ)
где первое слагаемое представляет изображение первого прямо-
прямоугольного импульса, второе - изображение прямоугольного импуль-
импульса, задержанного на время, равное одному периоду Г, и т. д.
5. Периодическая последовательность меандровых импульсов.
Решение получим аналогично решению предыдущего примера.
ад, 1-*~" =lthEL.
рA + е-рт) Р 2
Число примеров преобразований Лапласа увеличивает табл. 4.2.
Таблица 4.2.
Сигналы и их преобразования Лапласа
111

Раздел 4
№
п/п
Оригинал, s (t)
Изображение, S (р)
4.2. Обратное преобразование Лапласа
Переход от изображения S(p) к оригиналу - временной функции,
описывающей сигнал s(t), производится с помощью обратного пре-
преобразования Лапласа
D.13)
112

Анализ сигналов на основе преобразования Лапласа
Интегрирование в D.13) происходит по любой бесконечной пря-
прямой Re[p] = о, лежащей в области абсолютной сходимости интегра-
интеграла Лапласса от s(t).
Вычисление интеграла D.13) производится с использованием
теоремы о вычетах:
s@ = ^7 \S(p)eptdp = Y,Res[S(p)ept;ak], D.14)
где ак - особые точки функции S(p); Res[f(z),a] - вычет функции f(z)
относительно точки а.
Суммирование в D.14) производится по всем особым точкам.
В особой точке а предел функции f(z) либо равен бесконечности,
либо функция вообще не имеет предела. В первом случае эту точку
называют полюсом функции f(z) , во втором - существенно особой
точкой. Если точка z = а является полюсом функции f(z) , то она яв-
является нулем функции \ff{z).
Рассмотрим применение D.14) к достаточно общему случаю
описания сигналов в области параметра р простой рациональной
дробью
где А(р), В(р) - многочлены, степень многочлена А(р) меньше сте-
степени В(р).
Предполагается, что многочлены А(р) и В(р) не имеют общих кор-
корней, и дробь не сократима. Функция S(p) имеет конечное число осо-
особых точек. Эти точки являются нулями знаменателя В(р), следова-
следовательно, полюсами функции S(p). Использование выражения для вы-
вычета в полюсе любого порядка приводит к следующему выражению:
где ак- нули знаменателя В(р); пк- их кратность.
Формула D.15) называется формулой разложения.
Знаменатель В(р) содержит множитель (p-aijnk , и его можно
представить в виде
В(р) = (р-ак)п*В,(р). D.16)
113

Раздел 4
Тогда
Р^ак (p-ak)n* в,(р) В,(р)
В том случае, когда полюсы простые, выражение D.15) упроща-
упрощается
S(p) = ^^s@ = y^^'. D.18)
^ В{р) ^В(ак)
Если корнь знаменателя равен нулю, то В(р) можем представить
в виде
В(р) = рВ:(р), D.19)
где В^О) * 0.
С учетом D.19) запишем
В(р) = В,(р) + рВ\(р). D.20)
При этомБ@) = В^@), а В(ак) = акВ'{ак). При записи последне-
последнего равенства учтено, что В^Эк) = 0, так как все ненулевые корни
многочленов В(р) и B-i(p) совпадают.
Таким образом, получим
Хр^Жв-Ш-^^Ш + У АМ е>*<. D.21)
В(р) рВу{р) fl,@) ^акЩ{ак) }
Сумма в D.21) берется по всем ненулевым корням многочлена
В(р) или по всем корням Bi(p).
В качестве примера рассмотрим изображение
114
В записанном выражении имеем А(р)=~\, В(р)=р(р+а)(р+Ь), В1(р)=
=(р+а)(р+Ь). Производная В11(р)=(р+а)+(р+Ь). Корни знаменателя:
Pi=0, Р2=-а, Рз=-Ь.
В соответствии с D.21), получим

Анализ сигналов на основе преобразования Лапласа
При нахождении оригинала по его изображению возможен
и иной подход, который наиболее часто используется в инженерной
практике. Он заключается в том, что выражение
что совпадает с ранее полученным результатом.
Сигналы (оригиналы), соответствующие наиболее часто встре-
встречающимся преобразованиям Лапласа (изображениям) в виде дроб-
дробно-рациональных выражений, приведены в табл. 4.3. Более полная
таблица дана в [ 28 ].
Таблица 4.3.
Обратные преобразования Лапласа
дробно-рациональных функций
№
п/п
Изображение
Оригинал (сигнал^
115
раскладывается на простые дроби. Оригинал находится с помощью
известных формул однозначного соответствия оригинала и изобра-
изображения, сведенных в таблицу. В частности, рассмотренное выше:
Для условий приведенного выше примера запишем

Раздел 4
№
п/п
Изображение
Оригинал (сигнал^
116

Анализ сигналов на основе преобразования Лапласа
№
п/п
Изображение
Оригинал (сигнал^
117

Раздел 4
№
п/п
Изображение
Оригинал (сигнал,)
118

Анализ сигналов на основе преобразования Лапласа
№
п/п
Изображение
Оригинал (сигнал,)
119

Раздел 4
№
п/п
Изображение
Оригинал (сигнал^
120

Анализ сигналов на основе преобразования Лапласа
121

Раздел 4
№
п/п
Изображение
Оригинал (сигнал^
122

Анализ сигналов на основе преобразования Лапласа
Изображение
Оригинал (сигнал,)
123

Раздел 4
124

Анализ сигналов на основе преобразования Лапласа
125

Раздел 4
126

Раздел 5.
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ СИГНАЛОВ
Понятие корреляции первоначально появилось применительно
к случайным процессам. Позднее корреляционная функция была
использована как характеристика детерминированных сигналов.
Она описывает свойства сигналов во временной области, связана
со спектральными характеристиками сигналов. Для радиолокаци-
радиолокационных сигналов корреляционная функция является важнейшей ха-
характеристикой, определяющей потенциальные возможности раз-
разрешения системы.
5.1. Корреляционные функции периодических сигналов
Корреляционная функция периодического сигнала s(t), имеюще-
имеющего период Т, определяется выражением
772
Д(т) = у js(t)s(t + x)dt. E.1)
-772
Корреляционная функция одного сигнала называется автокор-
автокорреляционной функцией.
При т = 0 автокорреляционная функция
772
Я@) = у js2(t)dt E.2)
-Т/2
равна средней мощности сигнала.
Нормированная величина
г(х) = ^
Я@)
носит название нормированной корреляционной функции.
В качестве примера рассмотрим автокорреляционную функцию
гармонического сигнала
s(f) = Vcos(co0f + (р).
127

где 7 = 27i/coo.
Как следует из полученного результата, автокорреляционная
функция гармонического сигнала представляет косинусоидальную
функцию переменной т с тем же периодом и амплитудой, равной
средней мощности сигнала.
Очевидно такую же автокорреляционную функцию имеют все
гармонические сигналы той же частоты независимо от их началь-
начальной фазы.
Корреляционная функция периодических сигналов srft) и s2(t),
имеющих одну и ту же частоту соо (период Т - 2л/со0), определяется
выражением
772
Я.2(*) = у \s,(t)s2(t + T)dt, E.3)
-772
называется взаимной корреляционной функций. При т = 0 она рав-
равна взаимной мощности сигналов
1 т/2
«|2@) = у \s,(t)s2(t)dt. E.4)
-772
Нормированная взаимная корреляционная функция определяет-
определяется как
/«(т> =-5к&.
Я12@)
В качестве примера рассмотрим взаимную корреляционную
функцию гармонических сигналов
Sj(f) = V^costOgf и s2(f) = V2sinaHf.
Она определяется как
128
Она равна
Раздел 5

Корреляционный анализ сигналов
Т/2
^12(Т) = ~ j ^icosw0f\/2sinaH(f + x)dt = ——sin(o0T,
-772
г12(т) = sinwox.
Если изменить порядок следования рассматриваемых функций
под знаком интеграла, получим
ff2i(T) = —7r-sinco0T = fi12(-T).
5.2. Соотношение между корреляционной функцией
и спектром периодического сигнала
Соотношение между автокорреляционной функцией периодиче-
периодического сигнала и его спектральной плотностью мощности описывается
рядом Фурье. Чтобы получить его, запишем выражение для периоди-
периодического сигнала s(t) с периодом Т = 2я/соо в виде ряда Фурье
оо
s(t)= ?С(А7)е/лш°', E.5)
где
С(п) = - js(t)e-inaotdt. E.6)
-Г/2
Подставляя E.5) в выражение для автокорреляционной функ-
функции, получим
R(x)= fjC(n)\2e^\ E.7)
П = —оо
Выражение E.7) представляет ряд Фурье, в который расклады-
раскладывается автокорреляционная функция сигнала. Коэффициенты ряда
Фурье определяются как
Т/2
|С(п)|2 = Л/(л) = у JR(x)e-im°xck. E.8)
-Г/2
При т = О
129

Переходя к тригонометрическому ряду Фурье, получим
2 4 °° л2 л °°
Я(т) = ^- + -^(а2 + Ьл2)созп(о0т = ^- + -^^со8паHт, E.12)
4 ^ п=1 ^ п=1
где
2 7 2 7
ап = — s( О cos nwo №> bn=— \s{ t) sin noHfaff.
-Г/2 -Г/2
При т = О имеем
Г/2 2 °°
Ж0) = у }82(()Й = ^ + 1ХЛ„2. E.13)
-T/2 n=1
Выражение E.13) представляет равенство Парсеваля для пе-
периодического сигнала.
Как следует из записанных выражений, автокорреляционная
функция периодического сигнала является периодической функ-
функцией т.
130
Величина R@) описывает среднюю мощность сигнала, \С(п)\
характеризует распределение мощности сигнала по частоте, пред-
представляет спектральную плотность мощности. Как следует из запи-
записанных выражений, спектр является дискретным, включает состав-
составляющие, описывающие мощности гармоник на частотах, кратных
частоте сигнала.
С учетом четности автокорреляционной функции выражения
E.7) и E.8) можно записать в виде

Корреляционный анализ сигналов
Соотношения между взаимной корреляционной функций перио-
периодических сигналов, имеющих один и тот же период, и их спектрами
могут быть получены аналогично E.7) и E.8).
Я12(х) = ?с;(л)С2(А7)е/лм°т, E.14)
1 г/2
C;(n)C2(n) = N,2(n) = j JR,2(x)e-im^ck. E.15)
-772
Величина C*i(n)C2(n) = N12(n) представляет взаимный спектр
мощности сигналов Si(t) и s2(t).
5.3. Корреляционные функции
непериодических сигналов
Корреляционная функция непериодического сигнала определя-
определяется выражением
Я(т)= js(t)s(t + T)dt, E.16)
—оо
где х- смещение во времени.
Для действительного сигнала корреляционная функция является
действительной четной функцией
ОО ОО
Я(х) = js(t)s{t + x)dt= js(t-T)s(t)dt = R(~x). E.17)
Максимального значения корреляционная функция достигает
при т = 0. К этому выводу можно придти, рассмотрев выражение
оо оо оо
j[s{t)-s(t + x)fdt = 2J s2{t)dt-2Js(t)s(t + z)dt>0,
из которого следует:
Я@)-Я(х)>0 или Я(О)>Я(х).
Корреляционная функция непериодического сигнала при х = 0
равна энергии сигнала
131

Раздел 5
E.18)
Нормированная корреляционная функция непериодического
сигнала определяется как
В качестве примеров рассмотрим корреляционные функции не-
некоторых сигналов, описанных в табл. 3.1.
1. Прямоугольный импульс (табл. 3.1, п. 1), рис. 5.1.
2. Экспоненциальный импульс (табл. 3.1, п.8), рис. 5.2.
s(t) = e-at,t>0.
При т>0
оо оо
Я(т)= [s(t)s(t-x)dt= \e-ate-a{t-x)dt = — e~at.
j J 2a
132
Рис. 5.1

Корреляционный анализ сигналов
3. Гауссов импульс (табл. 3.1, п.15), рис. 5.3.
Корреляционные функции непериодических сигналов, приведен-
приведенных в табл. 3.1, сведены в табл. 5.1. Так как корреляционная функ-
функция является четной, графики построены только для т > 0.
4. Пачка из двух прямоугольных импульсов (рис. 5.4).
При т>0
133
на интервале

Таблица 5.1.
134
Раздел 5
Корреляционные функции сигналов
на интервале
на интервале

Корреляционный анализ сигналов
135

Раздел 5
136

Корреляционный анализ сигналов
137

Раздел 5
138

Корреляционный анализ сигналов
139

Раздел 5
5. Пачка из N прямоугольных импульсов (рис. 5.5).
При т>0
140
где tr(x) - треугольная функция;

Корреляционный анализ сигналов
Рис. 5.5
Сравнивая выражения для автокорреляционных функций оди-
одиночных и периодических сигналов одного и того же вида, отметим,
что при длительности сигнала значительно меньшей периода авто-
автокорреляционную функцию периодического сигнала можно получить,
взяв автокорреляционную функцию одиночного сигнала с коэффи-
коэффициентом 1/Г- периодическим ее повторением на оси т.
Корреляционная функция двух непериодических сигналов s^t) и
s2(t) определяется выражением
E.19)
где т - смещение одного сигнала относительно другого во времени.
Выражение E.19) имеет смысл только для сигналов, имеющих
ограниченную энергию, для которых выполняются неравенства:
141

Раздел 5
определяет взаимную энергию сигналов.
Нормированная взаимная корреляционная функция определяет-
определяется как
Если изменить порядок следования функций в выражении для
корреляционной функции
142
Как и для периодических сигналов, если корреляционная функ-
функция определена для двух сигналов, она называется взаимной кор-
корреляционной функцией, в отличие от автокорреляционной, опреде-
определяемой для одного сигнала.
Для взаимной корреляционной функции имеет значение порядок
следования функций под знаком интеграла. Для Я12(т) и Я12(т)
получим следующее соотношение:
Примеры взаимных корреляционных функций.
1. Сигналы - экспоненциальный и прямоугольный импульсы
(рис. 5.6,а.)

Корреляционный анализ сигналов
143
равно Я12(т) прит<0.
Графики Я12(т) и R2-\(i) приведены на рис. 5.6,6.
2. Сигналы - треугольный и прямоугольный импульсы (рис.
5.7,а.)
Рис. 5.6

Раздел 5
Изменяя порядок следования функций, получаем.
При т<0
эта функция равна Я12(т) при. т>0.
При т>0
равна Я12(т) при т>0.
Графики Я12(т) и Я21(т) приведены на рис. 5.7,6.
5.4. Соотношение между корреляционной функцией
и спектром непериодического сигнала
Автокорреляционная функция непериодического сигнала s(t)
связана со спектральной плотностью энергии W(w) преобразова-
преобразованием Фурье
E.22)
144

Корреляционный анализ сигналов
E.24)
Соотношение E.23) может быть получено из E.16)
где S*((o )S((o )= I S (to) 12 = W(co).
Учитывая четность функций Я(т) и IV(co), E.22) и E.23) можем
записать в виде:
145
E.23)
Рис. 5.7
E.25)
E.26)

Раздел 5
Выражение E.26) представляет равенство Парсеваля. Каждая
из частей этого равенства определяет энергию сигнала. Как следу-
следует из E.26), энергия сигнала численно равна площади под кривой
W((o). Кривая W(($) характеризует распределение энергии сигнала
по частоте.
Так как преобразование Фурье автокорреляционной функции
равно квадрату модуля спектральной плотности сигнала, то авто-
автокорреляционная функция не содержит информации о фазовом
спектре. Имея автокорреляционную функцию сигнала, можно вос-
восстановить только амплитудный спектр, но нельзя получить фазово-
фазового спектра сигнала.
Примеры определения автокорреляционных функций с исполь-
использованием спектральных плотностей сигналов приведем для некото-
некоторых сигналов, включенных в табл. 3.1.
1. Сигнал s(t) = sech(at), (табл. 3.1, п.6 ).
146
3. Сигнал s(t) = te~a'2 (табл. 3.1. п. 16).
2. Сигнал s(t) = е , t > 0 , (табл. 3.1. п.8).

Корреляционный анализ сигналов
Аналогично E.22) и E.23) можно подучить соотношения, связы-
связывающие взаимную корреляционную функцию непериодических сиг-
сигналов s-\(t) и s2(t) с взаимной спектральной плотностью энергии
W12(CD)
Я|2(т) = тг fWi2(a))e^Tdo = J- ГS1t(a))S2((o)e'a)Tcb , E.27)
2л J 2тг J
— оо —оо
W,2(«) = |я12(т)е^^. E.28)
5.5. Интервал корреляции и эффективная ширина
спектра сигнала
Для каждой корреляционной функции непериодического сигнала
можно определить такое минимальное значение смещения во вре-
времени г/с, при котором абсолютное значение корреляционной функ-
функции будет меньше заданной величины (близко к нулю). Величину т*
называют интервалом корреляции. Интервал корреляции пред-
представляет наибольший интервал задержки (смещения), на котором
корреляционная функция имеет значение, существенное для ре-
решаемой задачи.
Интервал корреляции, как и понятие корреляции, первоначально
был введен в рассмотрение для случайных процессов (разд. 18). Для
детерминированных сигналов он определяется по аналогии. В ряде
практических приложений корреляционного анализа он оказывает-
оказывается полезным понятием.
Наиболее часто используют следующие определения интервала
корреляции.
1. Интервал корреляции, определяемый по заданному значению
нормированной корреляционной функции
\г(тк)\>г, E.29)
где е - заданное значение (например, е = 0,05); тк - максимальный
интервал, на котором выполняется записанное неравенство.
2. Интервал корреляции, определяемый значением интеграла
нормированной корреляционной функции или ее абсолютного зна-
147

Раздел 5
чения
148
E.31)
При таком определении интервал корреляции численно равен
основанию прямоугольника, высота которого равна максимальному
значению нормированной корреляционной функции г@) = 1, а пло-
площадь равна площади под кривой г(т) или г(т)|. Второе определе-
определение интервала корреляции чаще используется при явно выражен-
выраженном колебательном характере корреляционной функции.
3. Интервал корреляции, определяемый значением интеграла от
квадрата нормированной корреляционной функции
Значения хк, определяемые из приведенных выражений, близки
друг другу- Выбор их, как правило, диктуется удобством при реше-
решении конкретной задачи.
Если для определения ширины корреляционной функции ис-
используется понятие интервала корреляции, то для определения
ширины спектра сигнала вводится понятие эффективной ширины
спектра. Эффективную ширину спектра определим как длину наи-
наибольшего интервала на оси частот, на котором спектральная плот-
плотность энергии еще имеет существенное для решаемой задачи зна-
значение.
При определении эффективной ширины спектра сигнала можно
использовать, как и при определении интервала корреляции, не-
несколько подходов.
1. Эффективная ширина спектра А определяется из условия,
аналогичного E.9), - максимальная полоса частот, внутри которой
значение нормированной спектральной плотности энергии сигнала
еще превосходят заданное значение
E.32)

Корреляционный анализ сигналов
2. Эффективная ширина спектра определяется заданным значе-
значением интеграла нормированной спектральной плотности энергии
сигнала
149
E.33)
Величина А, определяемая E.33), представляет ширину равно-
равномерного спектра энергии сигнала, имеющего энергию, равную энер-
энергии рассматриваемого сигнала.

Раздел 6.
ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ
СИГНАЛОВ
Непрерывные сигналы могут задаваться выборочными значения-
значениями, взятыми через определенные интервалы времени. Такое пред-
представление непрерывного сигнала называется дискретизацией. Дис-
Дискретизация сигнала позволяет сократить время работы канала пере-
передачи информации, лежит в основе цифровой обработки сигналов.
Обратная операция - восстановление непрерывного сигнала по
его дискретным значениям. В математическом плане она означает
интерполяцию временной функции, описывающей сигнал, по ее
выборочным значениям.
В разделе изложены методы анализа дискретных сигналов и
восстановления непрерывных сигналов по их выборочным значе-
значениям. Дискретизация и интерполяция, рассматриваемые примени-
применительно к сигналам, могут быть использованы и в отношении раз-
различных характеристик сигналов.
6.1. Дискретные и цифровые сигналы
Передача информации с помощью сигналов может произво-
производиться непрерывно или в некоторые фиксированные моменты вре-
времени. В зависимости от характера передачи информации различа-
различают непрерывные и дискретные сигналы. Непрерывные (аналого-
(аналоговые) сигналы повторяют закон изменения физических величин, ин-
информацию о которых они содержат, описываются непрерывными
или кусочно-непрерывными функциями времени (рис.6.1,а). Дис-
Дискретный сигнал представляет последовательность коротких им-
импульсов, амплитуды которых соответствуют мгновенным значениям
непрерывного сигнала или физической величины (рис. 6.1,6).
Дискретные сигналы чаще всего формируются при цифровой
обработке для использования в ЭВМ: непрерывные сигналы дис-
кретизируются во времени и квантуются по уровню, (рис. 6.1,в). Та-
Такие сигналы, представленные цифровыми кодами, называются
цифровыми.
150

Дискретизация и восстановление непрерывных сигналов
При квантовании по уровню значение сигнала округляется до
ближайшего дискретного значения. Ошибка, сопровождающая
квантование, представляет случайную величину, не превышающую
половину шага квантования. При постоянном шаге квантования
распределение ошибки подчиняется равномерному закону. После-
Последовательность ошибок при каждом шаге дискретизации аналогово-
аналогового сигнала во времени можно рассматривать как случайный дис-
дискретный процесс. Вследствие этого обычно квантованный сигнал
представляют в виде суммы дискретного сигнала и шума квантова-
квантования, а анализ цифровых сигналов сводится к анализу прежде всего
дискретных сигналов, значения которых соответствуют значениям
исходного непрерывного сигнала.
6.2. Спектр дискретного сигнала
При дискретизации непрерывный сигнал заменяется совокупно-
совокупностью его значений, взятых в заданные моменты времени. Как пра-
правило, интервал между выбранными моментами времени интервал
дискретизации - берется постоянным. Это условие предполагается
и в дальнейшем. Выборка осуществляется с помощью стробирую-
щего сигнала, представляющего последовательность импульсов
малой длительности, в пределе - описываемых импульсной функ-
функцией. Примеры дискретных сигналов приведены в табл. 6.1.
Если непрерывный сигнал представлен выборочными значе-
значениями, взятыми через заданный интервал времени, то получаю-
получающийся дискретный сигнал может быть записан в виде
где s(t) - непрерывный сигнал; Г- период дискретизации.
F.1)
151

Раздел 6
Стробирующая последовательность 8-функций
F.2)
называется выборочной функцией (рис. 6.2,а). Ее как периодиче-
периодическую функцию можно представить в виде ряда Фурье
F.3)
Спектральная плотность выборочной функции определяется
преобразованием Фурье F.3)
F.4)
Таблица 6.1
Дискретные сигналы
152

Дискретизация и восстановление непрерывных сигналов
Как следует из F.4), периодической последовательности им-
импульсных функций на временной оси соответствует периодическая
последовательность импульсных функций на оси частот (рис. 6.2,6).
153
Рис. 6.2

Раздел 6
Используя свойства преобразования Фурье, из F.1) получим
спектральную плотность дискретного сигнала sg(t). Она определя-
определяется с учетом F.1) как свертка спектральных плотностей сигналов
s(t) и g(t) под знаком суммы
154
Как показывает F.5), спектр дискретного сигнала - периодиче-
периодический, бесконечный, получается периодическим повторением спек-
спектра исходного сигнала (с коэффициентом 7/7) на оси частот с ин-
интервалом ш, =2п/Т (рис. 6.3,6).
При описании дискретного сигнала стробирующий сигнал в F.1)
рассматривается как последовательность бесконечно узких им-
импульсов, описываемых 5 -функцией. На практике же этот сигнал
представляет последовательность импульсов конечной длительно-
длительности. Периодическая последовательность видеоимпульсов, полу-
получающаяся при формировании выборки из непрерывного сигнала, в
этом случае может быть описана как (рис. 6.4,а)
sg(t) = s(t)u(t), F.6)
где s(t) - непрерывный сигнал; u(t) - периодическая последова-
последовательность прямоугольных импульсов единичной амплитуды, дли-
длительности т, с периодом Т.
Рис. 6.3

Дискретизация и восстановление непрерывных сигналов
Рис. 6.4
Представляя стробирующую последовательность прямоуголь-
прямоугольных импульсов в виде ряда Фурье
F.7)
F.8)
Спектральная плотность сигнала s(t) найдется как преобразова-
преобразование Фурье F.8) (см. разд. 3)
где S((x)) - спектральная плотность сигнала s(t).
155
дискретный сигнал F.6) запишем в виде

^ Раздел 6
Как следует из F.9), спектр дискретного сигнала получается по-
повторением спектра исходного непрерывного сигнала через интер-
интервал, кратный щ=2п/Т. Огибающая спектра дискретного сигнала
определяется спектром стробирующих импульсов (рис. 6.4,6).
Одной из важных задач, решаемых при дискретизации сигналов,
является выбор интервала дискретизации. Увеличение интервала
может привести к безвозвратной потере информации о сигнале. С
другой стороны, при уменьшении интервала дискретизации теряют-
теряются преимущества дискретизации. Представление о максимально
допустимом интервале дискретизации можно получить из анализа
спектра дискретного сигнала (рис. 6.3 и рис. 6.4). Непрерывный сиг-
сигнал можно восстановить, пропуская дискретный сигнал через
фильтр нижних частот. Верхняя частота полосы пропускания
фильтра должна превышать максимальную частоту в низкочастот-
низкочастотной части спектра сигнала. В то же время соседние составляющие
спектра сигнала не должны перекрываться. Таким образом, интер-
интервал дискретизации должен выбираться из условия:
2ыт<щ или T<M2fm=n/am, F.10)
где wm = 2nfm - максимальная частота в спектре сигнала.
Интервал дискретизации сигнала, определяемый F.10), называ-
называется интервалом Найквиста или Котельникова.
Возможна дискретизация и спектра сигнала. По аналогии с F.10)
условие дискретизации на оси частот может быть записано в виде
Q<2n/Tc, F.11)
где Тс - длительность сигнала.
При выполнении условия F.11) восстановление спектра сигнала
по его дискретным значениям производится без потерь.
6.3. Дискретное преобразование Фурье и его свойства
Спектральная плотность непрерывного сигнала определяется его
преобразованием Фурье. Обратное преобразование позволяет найти
временную функцию сигнала по его спектральной плотности. Дискре-
Дискретизация позволяет получить дискретный сигнал и соответствующий
дискретный спектр. Однако для дискретного сигнала переход от вре-
временного описания к спектру и обратно более удобно производить,
используя дискретное преобразование Фурье (прямое и обратное).
Выражение для спектральной плотности дискретного сигнала,
заданного на интервале [0,Гс], при достаточно малом значении ин-
156

Дискретизация и восстановление непрерывных сигналов
тервала дискретизации Г можем записать в виде
где N - число интервалов дискретизации, N = Тс/Т; Тс - длитель-
длительность сигнала; Г- интервал дискретизации.
Если спектральная плотность сигнала S(a)) определяется для
выборочных значений частоты со = nQ., то F.12) примет вид
Выражение F.13) представляет дискретное преобразование Фу-
Фурье (ДПФ). Аналогично для обратного ДПФ можно получить
Дискретное преобразование Фурье связывает дискретный сиг-
сигнал с его дискретным спектром, является удобным алгоритмом для
численного расчета спектра сигнала по его временной функции
157
В F.12) и F.13) N = ТС1Т. С учетом F.11) получим
Формулы ДПФ с учетом F.15) обычно записываются в виде:
Sn является периодической функцией частоты с периодом, равным

Раздел 6
и сигнала (временной функции) по его спектру. При использовании
ДПФ полезно учитывать его свойства. Они аналогичны свойствам
преобразования Фурье - табл. 6.2.
Таблица 6.2
Свойства дискретного преобразования Фурье
В качестве примера рассмотрим ДПФ сигнала в виде симмет-
симметричного треугольного импульса (рис. 6.5). Сигнал может быть пред-
представлен пятью выборочными значениями
158
Подставляя выборочные значения в F.13), запишем
Таким образом,
Рис. 6.5

Дискретизация и восстановление непрерывных сигналов
Спектральная плотность исходного импульса описывается вы-
выражением (разд. 3)
S(w) = 2Tsinc2(oT.
Из него получим
S@) = 27", S(±Q) = 0,8137, S(±2Q) = 0.
Отличие значений спектра, полученных с использованием пре-
преобразования Фурье и ДПФ, определяет ошибку, появляющуюся при
использовании ДПФ в качестве алгоритма расчета спектра сигнала.
6.4. Алгоритмы быстрого преобразования Фурье
Дискретное преобразование Фурье представляет алгоритм расче-
расчета спектральных характеристик сигнала. Однако его использование
часто связано с большим объемом вычислительных операций, что
может приводить к значительной затрате времени. Сократить объем
вычислительных операций при расчете ДПФ позволяет переход
к алгоритмам быстрого преобразования Фурье (БПФ). Предложено
несколько алгоритмов БПФ. В дальнейшем в качестве примера рас-
рассмотрим алгоритм БПФ, обычно используемый при числе отсчетов
Л/ = ZP, где п - целое число.
Исходную последовательность выборочных значений сигнала
разобьем на две части - с четными Swn нечетными номерами SnH
Сомножитель qn = e in2nlN перед суммой второго слагаемого
учитывает задержку skH относительно sk4 на один временной ин-
интервал.
Выражение F.17) представим в виде
159

Раздел 6
N
Выражение F.18) записано только для п< 1. Чтобы опреде-
определить Sn для больших значений п, используем свойство периодично-
периодичности ДПФ
F.20)
Л/
F.21)
Таким образом, записаны выражения для расчета Sn: при
л<Л//2-1 выражение F.18), при Л//2<л<Л/-1 выражение F.21).
В соответствии с записанными выражениями процесс вычисления
ДПФ можно представить схематически как показано на рис. 6.6. Ум-
Умножение на cf" обозначено стрелкой с множителем, сложение - кру-
кружочками.
Рис. 6.6
160
F.19)

Дискретизация и восстановление непрерывных сигналов
Линии вверх от точки соответствуют сумме, вниз - разности вели-
величин на входе. Дальнейшее уменьшение объема вычислений можно
достичь разбиением каждой из последовательностей Sm и SnH и т.д.
до получения простейших двухэлементных последовательностей.
Найдя ДПФ двухэлементных последовательностей, можно опре-
определить ДПФ четырехэлементных, восьмиэлементных и т.д. после-
последовательностей. Очевидно, что N должно быть равным 2П (л - це-
целое число). Программы расчета ДПФ с использованием алгоритмов
БПФ приведены во многих работах.
6.5. Дискретное преобразование Хартли и его свойства
По аналогии с ДПФ может быть введено в рассмотрение и дис-
дискретное преобразование Хартли (ДПХ). Прямое и обратное дис-
дискретные преобразования Хартли записываются в виде
H(n) = 2^s(k)cas——; s(/c) =-?/-/( n)cas——, F.22)
л=0 л=0 N
где casx = cosx + sinx.
ДПФ S(n) и ДПХ Н(п) связаны между собой достаточно очевид-
очевидными соотношениями
S(n) = H4(n)-iHH(n); H(n) = Re[S(n)]-\m[S(n)], F.23)
где Нч(п) и Нн(п) - четная и нечетная составляющие преобразова-
преобразования Хартли:
H4(n) = 7;[H(n) + H(N-n));HH(n) = ±[H(n)-H(N-n)]. F.24)
При использовании ДПХ целесообразно учитывать его свойства.
Основные свойства ДПХ приведены в табл. 6.3.
С целью сокращения времени расчетов при использовании пре-
преобразования Хартли предложены алгоритмы быстрого преобразо-
преобразования Хартли.
Преобразование Хартли для действительных функций s(t) дает
действительные функции, что позволяет говорить об определенных
удобствах ДПХ при использовании преобразования на инженерном
уровне. К удобствам применения ДПХ следует отнести и симмет-
симметричность прямого и обратного преобразований. Усложнение выра-
выражений для ДПХ свертки и произведения функций по сравнению
с ДПФ является отрицательным моментом.
161

Раздел 6
6.6. Z-преобразование и его использование при анализе
дискретных сигналов
6.6.1. Z-преобразование
Преобразование Лапласа, используемое при анализе непрерыв-
непрерывных сигналов, полезно и при анализе дискретных сигналов.
Для непрерывного сигнала преобразование Лапласа имеет вид
F.25)
где р - комплексная величина.
Таблица 6.3
Свойства дискретного преобразования Хартли
162

Дискретизация и восстановление непрерывных сигналов
Для дискретного сигнала
из F.25) получим
Выражение F.27) является дискретным преобразованием Лап-
Лапласа. Обозначив ерТ = z, выражение F.27) запишем в виде
F.26)
F.27)
Записанное выражение представляет z-преобразование дис-
дискретного сигнала s(nT). Исходя из условия существования преобра-
преобразования Лапласа (разд. 4) можно записать условие существования
и z-преобразования. Z-преобразование существует, если величина
\s(nT)\ возрастает медленнее степенной функции
\s(nT)\ < Мгп. F.29)
Область сходимости ряда F.28) включает всю плоскость, за ис-
исключением круга радиуса г. Величина г называется радиусом схо-
сходимости.
Примеры z-преобразований некоторых видов сигналов.
1. Сигнал, описываемый экспоненциальной функцией.
2. Гармонический сигнал.
163

^ Раздел 6
3. Сигнал, описываемый степенной функцией.
Расширяет число примеров табл. 6.4.
Имея z-преобразование дискретного сигнала, можно получить
спектр сигнала. Для этого необходимо сделать подстановку
F.30)
в z-преобразование сигнала.
Определение сигнала s(nT) no S(z) производится с помощью об-
обратного z-преобразования. Обратное z-преобразование получается
подстановкой еР = z в обратное преобразование Лапласа
F.31)
При решении F.31) используются различные методы, чаще все-
всего метод вычетов и метод разложения на простые дроби (разд. 4).
Метод вычетов. Если S(z) является действительной функцией
переменного z, то F.31) можно решить с помощью теоремы о выче-
вычетах (разд. 4)
164
Z-преобразования сигналов
Таблица 6.4

Дискретизация и восстановление непрерывных сигналов
Подставляя выражение для S(z) в F.32), получаем
Метод разложения на простые дроби.
Если S(z) представляет рациональную функцию z или z-1, ее
разложение на простые дроби имеет вид
F.33)
где полюсы рк. различны, т.е. рк ф рт при к * т,
Сигнал s(nT) получается суммированием обратных z-
165

Раздел 6
преобразований каждого члена F.33). Таким образом,
Z-преобразование, являясь одной из форм преобразования Ла-
Лапласа, обладает аналогичными свойствами. Использование
свойств z-преобразования позволяет упростить анализ дискретных
сигналов.
6.6.2. Свойства z-преобразования
Из свойств z-преобразования прежде всего отметим следующие.
1. Аддитивность.
где п-по= т.
Таким образом,
F.34)
F.35)
где кп - постоянные коэффициенты; <-> - знак соответствия вре-
временной и z-функций.
2. Задержка во времени.
Для
имеем
F.38)
F.36)
F.37)
F.39)
При л0 = 1
166

Дискретизация и восстановление непрерывных сигналов
s(nT-T)<r>S(z)z-\ F.40)
Как следует из F.40), задержке сигнала на интервал дискрети-
дискретизации Г соответствует умножение z-преобразования сигнала на z1.
С учетом F.40) можем получить z-преобразование разности
s(nT)-s{nT-T)
s(nT)-s{nT-T)<H>S(z)-S{z)z^ =—S(z). F.41)
3. Свертка дискретных сигналов.
Свертка дискретных сигналов описывается выражением
Y,Si(kT)s2(nT-kT) = ^8,[nT-kT)S2(kT) F.42)
Ас=О k=0
ИЛИ
п п
Ас=О /с=0
Выражение для z-преобразования свертки
S(z) = fj(fjsv<s2n_k)z-n F.44)
л=0 /с=0
запишем в виде
SUHf^S^rVf-". F.45)
n=0 k=0
При к > п, s2n-k = 0, верхний предел второй суммы можно заме-
заменить на ©о. После обозначения п - к= т, выражение для S(z) при-
примет вид
ЗД = YL^~ks2mz-m = XW*f>2mz-m = S,{z)S2(z). F.46)
m=0k=0 k=0 m=0
Таким образом, получим
167

Раздел 6
Рассмотренные свойства z-преобразования и некоторые другие
приведены в табл. 6.5.
Таблица 6.5
Свойства z-преобразования
168

Дискретизация и восстановление непрерывных сигналов
6.7. Восстановление непрерывного сигнала
по дискретным значениям
Задача восстановления сигнала по его дискретным значениям
в математическом плане сводится к отысканию функции, описы-
описывающей сигнал, которая в заданные моменты времени принимает
заданные значения (равные дискретным значениям сигнала), а в
остальные моменты описывает сигнал с какой-то степенью точно-
точности. Указанная операция без конкретизации физического содержа-
содержания рассматриваемой функции составляет содержание общей за-
задачи интерполяции. К интерполяции временной функции сигнала
приходится прибегать и тогда, когда известно аналитическое опи-
описание сигнала, но функция, описывающая сигнал, является слож-
сложной, имеются определенные трудности ее расчета. В этом случае
вычисляют значения сигнала для нескольких моментов времени и
по ним строят более простую (интерполирующую) функцию, с по-
помощью которой определяют значения сигнала в остальных точках.
Так же можно поступать и при задании сигнала с помощью графика
(осциллограммы).
6.7.1 Интерполяционные многочлены
Определение непрерывного сигнала по его дискретным значе-
значениям означает восстановление сигнала. В математическом отно-
отношении эта операция сводится к описанию временной функции
сигнала s(t), заданной своими значениями в заданные моменты
времени, с помощью функции cp(f), принимающей те же значения
169

Раздел 6
Рис. 6.7
в указанные моменты времени (рис. 6.7). Функцию ф@ называют
интерполирующей, точки, в которых заданы значения функции, уз-
узлами интерполяции.
Чаще всего интерполирующую функцию задают в виде много-
многочлена
F.48)
где q>k(t) - базисные функции; ак- постоянные коэффициенты.
При заданной совокупности базисных функций (pk(t) интерполи-
интерполирующая функция cp(f) определяется только коэффициентами ак.
Найти коэффициенты можно, составив систему уравнений, исполь-
используя F.48), записанных для заданных моментов времени (для кото-
которых известны значения сигнала)
к=0
Матрица системы уравнений имеет вид
F.49)
F.50)
170

Дискретизация и восстановление непрерывных сигналов
При написании матрицы учтено, что для однозначного опреде-
определения коэффициентов необходимо, чтобы число строчек матрицы
было равно числу столбцов.
Выражение для ак получится в виде
ак=^> F-51)
где А - определитель матрицы; Ак получается из А путем замены
/с-го столбца столбцом s(tk).
Таким образом, интерполирующая функция будет определяться
выражением
Ф@ = ?%*(')• F.52)
к=0
Раскладывая определитель Д^ по элементам /с-го столбца, вы-
выражение для ак получим в виде
F.53)
л=0
где Акп - соответствующее алгебраическое дополнение.
С учетом F.53) из F.52) получим другую форму записи
интерполяционного многочлена
Ф@ = !>('* W)- F.54)
к=0
Коэффициенты ряда F.54) представляют значения s(t) в узлах
интерполяции. Функции Ok(t) определяются базисными функциями
Фя@ и узлами интерполяции (to,tb...tN). Очевидно равенство
Как следует из F.55), функция <J>k(t) должна удовлетворять
условию
171
F.55)

Раздел 6
ФМ = \ . F.56)
Форма представления интерполирующей функции F.54) являет-
является наиболее удобной для практического использования; в ней в ка-
качестве коэффициентов многочлена фигурируют выборочные значе-
значения сигнала.
Качество интерполяции функции при заданных узлах интерполя-
интерполяции зависит только от выбора интерполяционных многочленов. Ин-
Интерполяционными многочленами могут быть степенные многочлены,
ортогональные многочлены и сплайновые функции. В радиотехнике
чаще используется ряд Котельникова. Одно из основных его досто-
достоинств связано с тем, что в качестве коэффициентов ряда использу-
используются дискретные значения, которыми задается сигнал.
В настоящем разделе рассматриваются интерполирующие
функции на основе степенных многочленов, многочленов Лагранжа
и функций Котельникова. В разд. 7 рассматривается сплайновая
интерполяция.
6.7.2. Степенные многочлены, многочлены Лагранжа
В выражении для интерполирующей функции F.48) в качестве
интерполяционного многочлена может быть использован степенной
многочлен. Степенной многочлен, описывающий сигнал, запишем в
виде
172
F.57)
Графики базисных функций многочлена даны на рис. 6.8. Они
определены на всей оси времени, неограниченно возрастают
с увеличением порядкового номера.
Матрица системы уравнений F.50) в этом случае примет вид

Дискретизация и восстановление непрерывных сигналов
Рис. 6.8
Матрица дает определитель Вандермонда или степенной опре-
определитель. Переходя к форме записи многочлена F.54), выражение
для базисных функций получим в виде
F.58)
F.59)
Многочлен F.59) называется интерполяционным многочленом
Лагранжа. При постоянном шаге по оси t, когда
t1-t0 = t2~t1=... = tN- tN_, = h, обозначив t-to/h = x, запишем
F.60)
173
Таким образом, интерполирующая функция cp(f) будет описы-
описываться выражением

Как следует из F.62), погрешность интерполяции сигнала опре-
определяется значениями (N+1) -производной интерполируемой функ-
функции и многочлена
W(t) = (t-to)(t-t,)...(t-tN). F.63)
Многочлен W(t) обращается в нуль в узлах интерполяции
to,tb...tn. Переходя через нули, меняет знак, принимая в интерва-
интервалах между ними экстремальные значения (рис. 6.9), значения экс-
экстремумов будут различны. В районе больших экстремумов можно
ожидать больших погрешностей. Погрешность будет особенно ве-
велика для значений вне интервала [to,tN], т.е. в том случае, когда
многочлен Лагранжа используется для экстраполяции функции.
Примеры интерполяции функций с использованием многочлена
Лагранжа приведены в конце разд. 7.
174
Раздел 6
Таким образом, выражение для интерполяционного многочлена
Лагранжа примет вид:
Интерполяционный многочлен Лагранжа (p(f) совпадает с ис-
исходной функцией, описывающей сигнал s(t) в узлах интерполяции
to,tb...tn. В остальных точках он будет отличаться от s(t). Исключе-
Исключение составляет тот случай, когда сигнал описывается степенным
многочленом степени не выше N. В этом случае ср(/) и s(t) будут
тождественно равны.
Многочлен Лагранжа обладает хорошими интерполяционными
сойствами при сравнительно небольшом числе узлов интерполя-
интерполяции. При большой степени многочлена (на практике N> 5) возника-
возникают трудности вследствие "раскачки" полинома между узлами ин-
интерполяции.
Отличие фG) от s(t) определяет погрешность интерполяции. По-
Погрешность оценивается неравенством
F.61)
F.62)

Дискретизация и восстановление непрерывных сигналов
N четное Л/ нечетное
Рис. 6.9
6.7.3. Ряд Котельникова
Для восстановления непрерывного сигнала s(t) по его дискрет-
дискретным значениям в радиотехнике чаще всего используется ряд Ко-
Котельникова
оо
s(t)= ^s(nT)s\nmm(t-nT), F.64)
где Г- интервал дискретизации, Г <я/сот; сот - максимальная час-
частота в спектре сигнала;
s\nc(x) = s\n(x)/x.
Записанное выражение может рассматриваться как разложение
непрерывного сигнала в ряд по ортогональной системе функций
(рис.6.10)
<pn(f - nT) = sin aojt - nT) F.65)
с коэффициентами, равными значениям сигнала в выбранные мо-
моменты времени.
Если сигнал определен на интервале [0, Тс], то число интерва-
интервалов разбиения равно
Д/ = 1с. - ТсШт F.66)
Т п
а ряд Котельникова примет вид
Л/-1
s(t) = ^s(nT)s\naom(t - nT). F.67)
л=0
Ряд Котельникова может быть записан и для частотной области
175

Раздел 6
где S(w) - спектральная плотность сигнала s(t); Q = 2n/Tc - интер-
интервал дискретизации по частоте.
Общее число выборочных значений определяется как
F.69)
Примеры восстановления спектров сигналов по их дискретным
значениям с использованием ряда Котельникова приведены в кон-
конце разд. 7.
Взяв выборочные значения сигнала, можно произвести его сту-
ступенчатую аппроксимацию
F.70)
где Г- интервал дискретизации сигнала по времени.
Выражение для спектральной плотности сигнала запишем в виде
176
Рис. 6.10

71
л=0
Выражения F.72) - F.75) аналогичны ряду Котельникова. Они
позволяют восстановить сигнал по дискретным значениям спектра
и спектр по дискретным значениям сигнала.
177
Дискретизация и восстановление непрерывных сигналов
Из F.71) с учетом F.70) получим
Для четной функции s(t) запишем
Аналогично можно подучить выражение, связывающее сигнал с
выборочными значениями спектральной плотности
Для действительной функции S(nQ.) получим

Раздел 7.
ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
С ПОМОЩЬЮ СПЛАЙНОВ
Одним из видов интерполирующей функции является сплайно-
вая функция, или сплайн. Сплайн описывает интерполируемую
функцию на каждом частном интервале дискретизации. Так, если
функция задана на интервале [t0, fo], который выборкой разбит на
частные интервалы [tk, tk+1], то сплайны дают описание функции на
каждом частном интервале [tk, tk+1], а их совокупность описывает
функцию на всем интервале ее задания (рис. 7.1). Обычно сплайн
представляет степенной многочлен. Такого вида сплайны и рас-
рассматриваются в дальнейшем.
Интерполирующая функция qk(t) называется сплайном степени
п дефекта v, если она удовлетворяет следующим условиям:
на каждом интервале [tk, tk+1] функция является многочленом
степени п;
G.1)
/=о
непрерывна и имеет на концах интервала (п - v) непрерывных про-
производных, т.е.
Рис. 7.1
178

Восстановление непрерывных сигналов с помощью сплайнов
Ф/Г)(^-5) = ф1Г)(^ + 5) при 5^ 0, ц = О, 1,...,n-v.
Говорят, сплайн обладает n-v степенью гладкости.
Предельный вариант сплайна - кусочно-линейная функция,
применяемая при линейной интерполяции. Такую функцию можно
рассматривать как сплайн первой степени (п = 1) дефекта 1
(v = 1/ Простейшими сплайнами, пригодными для использования
на практике, являются кубические сплайны третьей степени де-
дефекта 2 или 1. На их примере рассмотрим общий подход к по-
построению сплайнов.
В дальнейшем излагаются методы построения сплайнов более
сложной структуры, приводятся выражения для различных видов
сплайнов, даются примеры их применения при восстановлении не-
непрерывных сигналов - интерполяции временной функции, описы-
описывающей сигнал.
Одним из достоинств сплайновой интерполяции является то,
что не требуется равномерной сетки интерполяции функции. В то
же время на практике чаще всего используется постоянный интер-
интервал дискретизации сигнала. Вследствие этого в дальнейшем рас-
рассматривается вариант с равномерной сеткой интерполяции. Сплай-
Сплайны, построенные на равномерной сетке интерполяции, называются
стационарными. Целесообразность такого рассмотрения подкреп-
подкрепляется еще и тем, что в этом случае выражения, описывающие
сплайны, и приводимые в качестве иллюстрации методы, получа-
получаются проще.
7.1. Кубические сплайны первой степени гладкости
Сплайны третьей степени дефекта 2 называются кубическими
сплайнами первой степени гладкости или эрмитовыми кубическими
сплайнами. Исходными данными для их получения являются зна-
значения сигнала s(tK) и его первых производных в узлах интерполяции
(ds/dt)tk. На каждом частном интервале [tK, tK+1] сплайн описывается
выражением
Ф*@ = а*о + au(t- **) + a*2(f - tkf + ak3(t-tkf. G.2)
В точках дискретизации сплайн и его первая производная равны
значениям сигнала и его производной
4>k(tk) = s(tk);vk(tk) = S'(tk). G.3)
179

Раздел 7
Из G.2) и G.3) для начала и конца каждого частного интервала
[tx, ^к+r] получим четыре уравнения, которые позволяют определить
четыре коэффициента {ако, аК1, аК2, ак3), задающие сплайн. С уче-
учетом значений этих коэффициентов выражение для сплайна G.2)
примет вид
Ф/с@ = 5(^)A-тJA + 2т) + 5(^+1)т2C-2т) +
+ s-(^)/7rA-TJ-s-(^+1)/7r2A-T),
где x = (t-tk)/h,h=tk+,-tk.
Если функция задана только своими значениями (наиболее рас-
распространенный на практике случай), для задания значений на кон-
концах частного интервала [tK, tK+1] можно использовать следующее
выражение:
~(, j = s(tk)-s(tk_i) tk+,-tk + s(tk+,)-s(tk) tk-tk_.
На границах интервала задания функции:
Z(t)_s(t,)-s(t0) - ,_s(tN)-s(tN_i)
s\To)-—;—; > svn)-—,—: • \'-b)
r1 ~ r0 lN ~ r/V-1
В практике интерполяции сигналов и их характеристик наиболее
удобной формой представления интерполирующей функции явля-
является следующая (разд. 6)
N
ф@ = ^5,Ф,@, G.7)
/с=1
где sk = s(tK) - дискретные значения сигнала (значения интерполи-
интерполируемой функции в узлах интерполяции).
Приводя выражения для сплайнов к виду G.7), для случая
tk+1 - tk= h, so=sN= 0 получим:
на первом интервале
Ф^тИтО + т-т2),
Ф2(х) = тA-тJ,
где т = t - tk I h,
на /с-м интервале [tk, tk+1]
180

Восстановление непрерывных сигналов с помощью сплайнов
Ф*_,(т) = -0,5A -хJ,
Фк(х) = 1 -2,5т2 + 1,5т3,
G-9)
Фк+,(т) = х@,5 + Зх-2,5х2),
Ф^+2(т) = 0,5т2A-т).
на последнем интервале
Ф,-1(х) = 1-2т2+тЗ,
Фл/-2(х) = хО-2т + т2)-
7.2. Кубические сплайны второй степени гладкости
Большую гладкость интерполяции обеспечивает кубический
сплайн второй степени гладкости (дефекта 1). Он представляет
многочлен третьей степени G.2), его значения в узлах интерполя-
интерполяции равны значениям сигнала
q>(tk) = sk, G.11)
имеет в узлах интерполяции непрерывные первые две производ-
производные
Ф^-5) = ф^+5),5->0, |х = 1. 2.. G.12)
При описании сплайна на частном интервале [tk, tk+1] использует-
используется его запись в виде G.7).
Чтобы выполнить условие G.12), продифференцируем дважды
G.4) и для tk- левой границы интервала [tk, tk+1] (х = 0) получим
y(tk) = 6(sk+i-sk)/h2-2Bs'k + s)<+i)/h. G.13)
Аналогично для правой границы интервала [tk.h Ц (х = 1) найдем
y(tk) = 6(sk-sk^)lh2+2Bs'k + sk_i)/h. G.14)
Приравнивая G.13) и G.14), получаем
Ms*_i + 4s;t + s^+1) = 3(s^+1 - sfc_1). G.15)
181

Раздел 7
Такие уравнения могут быть получены для узлов интерполяции
при к = 2,..., N - 1. Полученная система уравнений должна быть до-
дополнена соотношениями для производных на границах общего ин-
интервала [t0, tN], позволит однозначно определить все производные
s'k. Таким образом, сплайн на каждом частном интервале опреде-
определяется всей совокупностью значений sk и краевыми условиями. В
этом смысле такой сплайн называется глобальным. Он требует
большого объема вычислений, особенно при большом значении N.
Рассмотренные кубические сплайны дефекта 1 обладают дос-
достаточно хорошими интерполяционными свойствами. Однако син-
синтез таких функций связан с определенными трудностями и для
них характерен большой объем вычислений. Поэтому при интер-
интерполяции функций (восстановлении непрерывных сигналов по их
дискретным значениям) более удобными могут оказаться локаль-
локальные сплайны.
7.3. Подход к построению локальных сплайнов
Одним из достоинств сплайновой интерполяции является воз-
возможность решения задачи при неравномерной сетке интерполяции.
Однако более простыми являются стационарные сплайны - сплай-
сплайны, формируемые на равномерной сетке. На их примере и рас-
рассмотрим принцип построения локальных сплайнов.
Для построения локальных сплайнов могут использоваться раз-
различные подходы. В настоящем разделе дается достаточно простой,
изложенный в [38]. Ограничимся рассмотрением случая, когда
сплайны представляют степенные многочлены.
Рассмотрим функцию s(t), заданную своими значениями stf*) = sK
в точках дискретизации {tk},k = О,1,2,...,Л/, на интервале [t0, tN]. Вы-
Выделим интервал [Ть Т2], границы которого: T^e[tk_vtk]
и 7G [f*if*+i] (Рис- 7-2)- В окрестности точки Т1 возьмем симмет-
симметрично (N^) точек дискретизации tk.1t tk, tk.2, tk+h..., построим много-
многочлен Li(t), проходящий через соответствующие значения функции
Sk-ь sk, sk_2, sk+i,... и содержащий (N^1) членов.
Аналогично построим многочлен L2(t) на точках, выбранных
симметрично Т2, проходящий через значения функции sk, sk+1, sk.u
sk+2>... содержащий (N2+^) членов.
На интервале [Ти Т2] построим многочлен (pk(t), содержащий
Л/,+Л/2+3 членов.
Коэффициенты многочлена найдем из условий:
многочлен проходит через точки L^T-t), sk ,.L2 (T2);
182

Восстановление непрерывных сигналов с помощью сплайнов
Рис. 7.2
производные многочлена на границах интервала совпадают с
производным и Lift) и L2(t):
G.16)
Уравнения, составленные исходя из условий G.16), позволяют
определить коэффициенты многочлена ф/ДО- Преобразовав его к
виду G.7), получим сплайн, описывающий функцию на интервале
[Ть Т2], имеющий требуемый вид.
Аналогично выделим интервал, примыкающий слева к [Ть Т2] и
на нем построим многочлен (p*_i(f) так же, как строился (pk(t). За-
Затем на интервале, примыкающем справа к [Ть Т2], построим много-
многочлен ф*+1@ • Таким образом, получим совокупность многочленов на
всем интервале задания функции, многочлены проходят через за-
заданные точки, имеют определенное число производных на грани-
границах выделяемых интервалов. На первом интервале [to, T^] и по-
последнем [Т2, tN] интерполирующая функция совпадает с многочле-
многочленами ЦA) и L2(t) соответственно.
Используя изложенный подход к синтезу локальных сплайнов
и обеспечивая заданное число непрерывных производных, можно
получить различные виды сплайнов, описывающих заданную
функцию.
183

Раздел 7
7.4. Локальные сплайны нечетной степени гладкости
Ниже рассматривается метод синтеза локальных стационарных
сплайнов, имеющих нечетное число непрерывных производных.
Синтез сплайнов производится с использованием общего подхода,
описанного в п. 7.3.
7.4.1. Локальные сплайны первой степени гладкости
Кусочно-линейная интерполяция не имеет большого практиче-
практического значения. Чаще используются сплайны более высокого по-
порядка. Однако на ее примере проще рассмотреть подход и основ-
основные особенности интерполяции на основе локальных сплайнов.
Функция, описывающая сигнал, задана дискретными значениями
на интервале [t0, tN] с равномерной сеткой и постоянным шагом h
(рис. 7.2).
Выделим интервал [Г,, Т2], где 7} = 0,5(^_-, + tk) и Т2 = 0,5(^ + ^+1).
Определим значения функций Lrft) и L2(t) и их первых производных
на границах интервала [Ть Т2] с использованием линейной интер-
интерполяции
mTi) = 0,5(sk_i+sk),
ЦТ,) = УЦ8к-зк.,),
L^(T2) = 0,5(sk + sk+,),
^(T2) = 1//7(s,+1-sJ."
На интервале [Ть Т2], построим степенной многочлен четвертой
степени
4
<M0=5>m(f-ym G.18)
так, как это описано в п.7.3: на границах интервала значения много-
многочлена и его первых производных совпадают со значениями, опре-
определяемыми G.17), а в точке tk - значением sk
Ч>к(Т,) = ЦТ,),
184

Восстановление непрерывных сигналов с помощью сплайнов
для базисных функций Ok(t) получим следующие выражения.
На первом интервале:
Из G.17) - G.19) получим выражения для коэффициентов мно-
многочлена G.18)
Таким же образом можно построить многочлены <pk(t) на всех
частных интервалах. На первом интервале и последнем функция
восстанавливается линейно.
Преобразуя полученную совокупность многочленов {(pk{t)} к виду
G.19)
G.20)
G.21)
G.22)
185
На последнем интервале:
На /с-м интервале [tk-0,5h,tk + 0,5h], к = 2,...,Л/-1, Л/>3:

Раздел 7
Флм(т) = т,
Фл,(т) = 1 + т, G.23)
Ф,(т) = 0,/ < Л/-2,т = Mh{t- tN).
Графики базисных функций приведены на рис. 7.3 - 7.5 (в конце
раздела). Примеры восстановления непрерывных сигналов по их
дискретным значениям с помощью степенных локальных сплайнов
приведены на рис. 7.6 - 7.8 (интервал дискретизации - единица).
Сплайны с одной непрерывной производной являются наиболее
простыми. Качество интерполяции функций с их использованием
такое же, как и при использовании эрмитовых сплайнов. Оно может
оказаться достаточным при интерполяции относительно простых
зависимостей.
7.4.2. Локальные сплайны третьей степени гладкости
Используя общий подход, проведем построение локальных
сплайнов третьей степени гладкости. Для этого выделим интервал
[Ть Т2], с границами на серединах смежных частных интервалов
разбиения (рис. 7.2):
T,=0,5(tk_, + tk),T2=0,5(tk + tk+,).
Через точки sk.2,...,sk+i проведем многочлен L-i(t) третьей степе-
степени. Выражение для него будет иметь вид:
Ц-с) = sk_, + x/6(-2sk_2 -3sk_, + 6sk - s^+1) +
+ x2/2(s/f_2 -2sk^ + s/f) + x3/6(-s/f_2 +sk_, -3sk + sk+,),
где T = 1/A?(f-f/f_1).
Для левой границы интервала [Th T2], получим:
/^ (т* - 0,5/7) = 1/16(-sk_2 + 9sk_, + 9sk - sk+,),
L,(xk -0,5л) = 1/24n(S/f_2 -27s^ + 27s, - sM),
L\{xk -0,5/7) = M2h2(sk_2 - sk_i -sk+ sk+1),
Ц(тк -0,5/7) = Mhz{-sk_2 +3sk_i -3sk+sk+i)
Через точки sk.-\,...,sk+2 проведем многочлен L2(t) третьей степени
(аналогично многочлену U(t)). Так же, как для Ц($, получим зави-
зависимости для значения L2(t) и трех его производных на правой гра-
186

Восстановление непрерывных сигналов с помощью сплайнов
нице интервала [Гь Т2], в точке tk+ 0,5/7. Эти значения описываются
G.25) при увеличении индекса s на единицу.
В соответствии с общим подходом, изложенным в п.7.3, на интер-
интервале [ТЬТ2], строится многочлен 8-й степени q>k(t), Л/, = Л/2 = 3. Так же
строятся многочлены на всех остальных интервалах. На первом и
последнем интервалах для интерполяции используются многочлены
L-\(t) и L2(t), проведенные через первые и последние четыре точки
соответственно. Полученная таким образом совокупность степенных
сплайнов осуществляет интерполяцию функции на всем заданном
интервале, плавно соединяя исходные дискретные значения. Преоб-
Преобразуя полученную совокупность многочленов к виду G.7), получим
следующие выражения для базисных функций <t>k(t).
На первом интервале:
Ф1(т) = -0,ЗЗЗЗт + 0,5т2 -0,1667т3,
Ф2(т) = 1-0,5т-т2+0,5т3,
Ф3(т) = т + 0,5т2-0,5т3) G.26)
Ф4(т) =-0,1667т+ 0,1667т3,
Ф,(т) = 0,/>5, x = Mh(t-t2).
На /с-ом интервале [tk- 0,5/?, tk+0J5h], /с = 3,...,Л/-2, Л/>5:
Фк.2(х) = 0,0625т - 0,3516т2 + 0,0702т3 + 1,6146т4 -
- 0,3684т5 -3,7083т6+ 0,3509т7+ 3,5т8,
Фк.-,(х) = -0,625т + 1,9062т2 - 0,1404т3 - 6,4583т4
+ 0,7368т5 + 14,8333т6 -0,7018т7 - 14т8
Ф/rftM -3,1094т2+9,6875т4-22,25т6+21 т8, G.27)
Ф*+1=Ф/с-1И),
Ф/с+2=Ф/с-2И),
Ф,(т) = 0 , /< к-3,1> к+ 3, т = Mh{t- fk).
На последнем интервале базисные функции определяются
G.26) с учетом следующих соотношений:
Фл/-*(т) = Ф*A-т),* = 1,...А
Ol{z) = 0,l<N-4,T = Mh{t-tN_2).
187

Раздел 7
Рассматриваемые сплайны могут быть получены только при Л/>4.
Графики базисных функций при некоторых значениях Л/ изобра-
изображены на рис. 7.3 - 7.5. Примеры восстановления непрерывных сиг-
сигналов по их дискретным значениям с помощью степенных локаль-
локальных сплайнов приведены на рис. 7.6 - 7.8.
7.5. Локальные сплайны четной степени гладкости
На основе общего подхода (п. 7.3) получим расчетные выраже-
выражения для стационарных многочленных моделей, имеющих четное
число непрерывных производных. Это наиболее простые локально-
сплайновые модели.
7.5.1. Локальные сплайны второй степени гладкости
Функция, описывающая сигнал (или его характеристику), задана
дискретными значениями на интервале [to, tN] с постоянным шагом
(рис. 7.2). Выделим частный интервал [tk) tk.^] и определим значения
первых двух производных на границах выделенного интервала. Для
этого проведем через точки s^^ и sk+1 степенной многочлен вто-
второй степени
M0=i>,n('-'*)m. . G.29)
m=0
Коэффициенты многочлена определяются из следующей систе-
системы функций:
Ьо = sk,
b,=M2h(-sk^+sk+,), G.30)
b2=Uh2(sk_,-2sk + sk+,).
Из G.29) с учетом G.30) найдем производные на левой границе
выделенного интервала:
Ц1к) = V2h(sk+,-sk_,),
mtk) = Mh2(sk^-2sk + sk+,).
Аналогично построим степенной многочлен второй степени L2(t),
проходящий через точки sk, sk+1, sk+2- Производные L2(t) на правой
границе выделенного интервала найдутся так же, как G.31):,
188

Восстановление непрерывных сигналов с помощью сплайнов
L2(tk+^) = M2h(sk+2-sk),
4('*+i) = 1/'h2(sk -2Sfc+1 + sk+2).
Построим на интервале [tk, tk+1] степенной многочлен (pk(t) пятой
степени
5
т=0
где т = 1 /h(t-tk), te [tk, tk+:], удовлетворяющий граничным условиям
Ф/с(^+1) = s/c+1>
ф(/Г)(^+1) = 4ц)(^+1),ц = 1.2.
С учетом G.34), G.31) и G.32) получим следующие выражения
для коэффициентов многочлена G.33):
3q = Sk,
a,=1/2(-slf_l+s/t+1)l
32=1/2E^-28^+8^), G35)
а3 = 3/2E^! -3s^ +3s^+1 -sk+2),
a4 = -5/2(sk_, -3sk + 3s^+1 - s^+2),
a5 = S/c-1 ~ 3S^ + 3S^+1 - S^+2.
Аналогично получим всю совокупность многочленов {ф/ДО}. На
первом частном интервале и последнем функция описывается мно-
многочленами Lrft) и L^t), проведенными через первые три и последние
три точки. Преобразуя полученную совокупность многочленов к виду
G.7), получим следующие зависимости дли базисных функций Orft).
На первом интервале:
0^1) = 1-1,51 +0,5т2,
Ф2(х) = 2т-х2, G36)
Ф3(х) = -0,5т + 0,5т2,
Ф/(т) = 0,/>4,т = 1/Л('-'2)-
На /с-м интервале [tk,tk+^], k = 2,...,N-2, Л/>4:
189

Раздел 7
фкА (Х) = -0,5т + 0,5т2 + 1,5т3 - 2,5т4 + т5,
фк(х) = 1 - т2 - 4,5т3 + 7,5т4 -Зт5,
фк+1 (Т) = о,5т + 0,5т2 + 4,5т3 - 7,5т4 + Зт5, G.37)
Фк+2(т) = -1,5т3 + 2,5т4 -т5,
0l{T) = O,l<k-2;l>k + 3,T = Mh(t-tk).
На последнем интервале:
Фл/_2(т:) =-0,5т + 0,5т2,
Флм(*) = 1-с2. G.38)
0w(x) = 0,5т + 0,5т2,
Ф/(т) = 0, / < Л/-3, т = Mh(t- tN).
Графики базисных функций при некоторых значениях Л/ изобра-
изображены на рис.7.3 - 7.5. Примеры восстановления непрерывных сиг-
сигналов по их дискретным значениям с помощью степенных локаль-
локальных сплайнов приведены на рис. 7.6 - 7.8.
7.5.2. Локальные сплайны четвертой степени гладкости
При переходе к сплайнам, имеющим непрерывными четыре
первые производные, качество интерполяции (гладкость) улучша-
улучшается. Принцип их построения описан в п. 7.3. Операции построения
сплайна аналогичны описанным в п. 7.5.1.
Выделим интервал [tk, tk+1] (рис. 7.2), и на левой границе интер-
интервала через пять точек sk.2, sk.h..., sk+2степенной многочлен
L,(t)=^bm(t-tk)m. G.39)
Приравнивая значения функции и многочлена G.39) в выбран-
выбранных точках, получаем следующие выражения для коэффициентов:
ьо = $к>
b,=U12h(sk_2-8sk_i+Qsk+i-sk+2),
bг=V24h2(-sk_2+^6sk_,-30sk + ^6sм-sk+2), G.40)
Ь3 =1/12/73(-s^_2 +2s^ -2sk+1 + sk+2),
b4 = 1/24/74(s*_2 -^s^ +6S* -4s*+1 +5^).
Дифференцирование G.39) с учетом G.40) дает выражения для
первых четырех производных на левой границе рассматриваемого
интервала в виде:
190

Восстановление непрерывных сигналов с помощью сплайнов
mtk) = ^/^2h(sl<_2-Qsk_1 + Qsk+1 - sk+2),
L!(tk) = ^/^2h2(-sk„2 + ^6sk_^-зosk + ^6sk+,-sk+2).
L%tk) = M2h3{-sk_2+2sk_i-2sk^+sk+2),
Lf'(tk) = VhA{sk_2-4sk_i+6sk-4sk+i + sk+2).
Аналогично задается степенной многочлен L^t) на правой фанице
выделенного интервала, который проходит через точки sk.1,...,Si(+3 •
Для него получим:
li(tM) = 1/12/Ks^ -8sfc + 8sfc+2 -sfc+3),
LZ(tM) = 1 /12h2 (sk_, +1б8к- 3OS^+1 +16sk+2 - sk+3).
L"(tk+i) = 1/2/73(-s^ +2sk -2sk+2 + sk+3),
?t**+i) = 1 / h4{sk_, - 4sk + 6s^+1 - Ask+2 + sk+3).
На интервале [tk, tk+1] строим степенной многочлен девятой
степени
Ф,(Г)=^аттт( G.43)
где x = Mh(t-tk).
Многочлен проходит через точки sk и sk+h на границах интервала
имеет производные, равные G.41) и G.42). Из этих условий опре-
определяются коэффициенты в G.43):
3q = Sk,
а1 = 1/'\2h(sk_2 -8sk_i + 8sk+i -sk+2),
a2 = M24h2{-sk_2 +16s^_! -30sk + '\6sk+i-sk+2),
аъ=М12&{-8к_2+28к_1 -2sk+i+sk+2),
a4=V24h4(sk_2-Ask_i+6sk-4sM+sk+2), G44)
a5 = -10/3(sfc_2 -5sk_i +Wsk -10sfc+1 +5sk+2 -sk+3),
a6 =-3,4129a5,
a7=4,425a5,
a8 =-2,5875a5,
a9 =0,575a5.
Аналогично строятся многочлены <pk(t) на всех частных интер-
интервалах [tk, tk+i] при к = 3,...,N-2. На первом и последнем интервалах
интерполируемая функция описывается многочленами L-,(t), прохо-
191

Раздел 7
дящим через первые пять ее значений, и L2(t), проходящим через
последние пять значений функции.
Преобразуя полученные многочлены к виду G.7), получаем сле-
следующие выражения для базисных функций.
На первом интервале:
Ф: (т) = 1 - 2,0833т + 1,4583т2 - 0,4167т3 + 0,0417т4,
ф2 (Т) = 4т - 4,3333т2 + 1,5т3 - 0,1667т4,
ф3 (х) = -Зт + 4,75т2 - 2т3 + 0,25т4,
Ф4(т) = 1,3333т-2,ЗЗЗЗт2+1,1667т3 -0,1667т4,
Ф5(т) = -0,25т + 0,4583т2 -0,25т3 +0,0417т4,
0/(T) = O,/>6,T = 1//?(f-f1).
На /с-м интервале [tk,tk+^], к = 3,...,Л/-2,Л/>6:
Фк.2(х) = 0,0833т -0,0417т2 + 0,0833т3 +0,0417т4-
-3,3333т5 +11,375т6 -14,75т7 +8,625т8 - 1,9167т9,
фкш1(т) = - 0,6667т + 0,6667т2 + 0,1667т3 - 0,1667т4 +
+16,6667т5 - 56,875т6 + 73,75т7- 43,125z8 + 9,5833т9,
фк(х)^ - 1,25^+ 0,25т4- 33,3333т5+ 113,75т6- 147,5т7+
+ 86,25т8-19,1667т9,
Ф/м = ФкСМ,
Фк+г = Фк-10-ч),
Фк+з = Фк-А^),
Ф, = 0 , 1 < /е- 3 ,1 > /с + 4, т = Mh(t- tk). G.46)
На последнем интервале базисные функции симметричны функ-
функциям на первом интервале, вычисляются по G.45) с учетом сле-
следующих соотношений:
Ф^5+М = Фк(т),к = Х...,5,
Ф/((т) = 0,/с<Л/-5,т = 1//7(Г-ГЛ/_4). [ ' }
Рассматриваемые сплайны могут быть получены только при Л/ > 5.
Графики базисных функций при некоторых значениях Л/ изобра-
изображены на рис. 7.3 - 7.5. Примеры восстановления непрерывных сиг-
сигналов по их дискретным значениям с помощью степенных локаль-
локальных сплайнов приведены на рис. 7.6 - 7.8.
Анализ приведенных на рис. 7.6 - 7.8 интерполяционных функ-
функций, построенных с использованием ряда Котельникова, многочле-
многочленов Лагранжа и сплайновых функций, дает возможность сравнить
качество интерполяции для различных видов исходных сигналов.
192

Восстановление непрерывных сигналов с помощью сплайнов
Ряд Котельникова
Рис. 7.3
193
Многочлен Лагранжа
Сплайны 1 с. г.
Сплайны 2 с. г.
Сплайны 3 с. г.
Сплайны 4 с. г.

Раздел 7
Многочлен Лагранжа
Сплайны 3 с. г.
Рис. 7.4
194
Ряд Котельникова
Сплайны 1 с. г.
Сплайны 2 с. г.
Сплайны 4 с. г.

Восстановление непрерывных сигналов с помощью сплайнов
Многочлен Лагранжа
Сплайны 2 с. г.
-0,50 у
Рис. 7.5
195
Ряд Котельникова
Сплайны 1 с. г.
Сплайны 3 с. г.
Сплайны 4 с. г.

Раздел 7
Ряд Котельникова
Многочлен Лагранжа
4,0
6.0
Рис. 7.6
196
Сплайны 1 с. г.
Сплайны 2 с. г.
Сплайны 3 с. г.
Сплайны 4 с. г.

Восстановление непрерывных сигналов с помощью сплайнов
Ряд Котельникова
Многочлен Лагранжа
Рис. 7.7
197

Раздел 7
Ряд Котельникова
Многочлен Лагранжа
Рис. 7.8
198

Раздел 8.
УЗКОПОЛОСНЫЕ СИГНАЛЫ
Узкополосные сигналы составляют широкий класс сигналов, ко-
которые формируются и обрабатываются в различных радиотехниче-
радиотехнических системах. Это прежде всего различные виды модулированных
сигналов. Особенности структуры узкополосных сигналов опреде-
определили возможность, а часто и необходимость, особого подхода к их
описанию и анализу, а, следовательно, целесообразность их от-
отдельного рассмотрения.
8.1. Описание узкополосного сигнала
К узкополосным сигналам относятся сигналы, спектры которых
сосредоточены в относительно узкой по сравнению со средней час-
частотой полосе (рис. 8.1,а). Узкополосный сигнал описывается выра-
выражением
и@ = y(f)cos[co0f + ф@] = V(t)cosO(t), (8.1)
где V(t) , O(t) - амплитуда и фаза сигнала; ш0- несущая частота.
Амплитуда V(t) и фаза q(t) содержат передаваемую информа-
информацию, являются функциями времени и представляют модулируемые
параметры сигнала. Это медленно меняющиеся функции времени,
их изменения за период 2к/щ незначительны, таким образом, вы-
выполняется условие узкополосности сигнала.
Для описания узкополосного сигнала используется и комплекс-
комплексная форма записи
i/(f) = Re[\Z@e*°°f], (8.2)
где
V(t) = V(t)em (8.3)
- комплексная огибающая сигнала.
199

Раздел 8
Рис. 8.1
Как следует из (8.2), узкополосный сигнал определяется несу-
несущей частотой соо и комплексной огибающей V(t).
Комплексная огибающая сигнала может быть представлена
в виде
V(t) = Vc(t) + iVs(t) = V(t)cosq>(t) + iV(t)s\ny(t), (8.4)
где Vc(t) = V(t)cos<p(t); Vs(t) = V(t)s\n<p(t) - квадратурные состав-
составляющие сигнала.
С учетом (8.4) получим
200

Узкополосные сигналы
Графически комплексный сигнал V(t) изображается в виде век-
вектора на комплексной плоскости длины V(t) (рис. 8.1,6). Вектор со-
составляет угол cp(Yj с действительной осью. Длина вектора V(t) и угол
между вектором и действительной осью q(t) изменяются во време-
времени. Сама система координат вращается по часовой стрелке с угло-
угловой скоростью (Оо. Узкополосному сигналу соответствует проекция
вектора на действительную ось.
8.2. Сумма и произведение узкополосных сигналов
При анализе узкополосных сигналов, в частности, при анализе
прохождения их через цепи, в ряде случаев приходится рассматри-
рассматривать сумму узкополосных сигналов и их произведение. Запишем
выражения, описывающие их.
Сумма двух узкополосных сигналов с одинаковой несущей час-
частотой (Оо
ц@ = V,@cos[co0f + ФЛ0], (Q 5)
u2(t) = V2(t)cos[a0t + 4>2(t))' K ' }
представляет также узкополосный сигнал с той же частотой (Оо
u(t) = ц@ + u2(t) = V(t)cos[io0t + Ф@] • (8.6)
Выражение для u(t) с использованием комплексной формы мож-
можно записать в виде
17@ = Re[\/@e4'] = Re[Vi(f)efo°f ] + Re[1/2(f)e*°°f], (8.7)
где\Л@, ^г@ - комплексные огибающие сигналов Ui(t), u2(t).
Комплексная огибающая суммарного сигнала равна сумме ком-
комплексных огибающих исходных сигналов
V(t) = V^t) + V2(t). (8.8)
Огибающая суммарного сигнала определяется выражением
Произведение двух узкополосных сигналов с несущими частота-
частотами U>i И @2
201

Раздел 8
ц@ = Ц@сО8[ОI? + ф1@],
U2{t) = V2{ t) COS[C021 + ф2 @]
запишем в виде
^@^@ = Re[l/i@em'f]-Re[^2@efc>2f]- (8.Ю)
Для произвольных комплексных величин zr и z2 имеет место
следующее равенство:
Re[z1]Re[z2] = -iRe[zlz2] + iRe[z1*z2], (8.11)
где z-комплексно-сопряженная величина.
С учетом (8.11) для произведения узкополосных сигналов получим
^@w2@ = Re[-^i@U2@e'(Wi+W2)'] + Re[-l/iX@^2@e/((O2"C)l)/]. (8.12)
Произведение узкополосных сигналов представляет сумму двух
сигналов (8.12), один из которых имеет несущую частоту, равную
сумме частот a»i и сог , а второй имеет несущую частоту, равную
разности частот а^ и аJ.
8.3. Спектр узкополосного сигнала
Спектральная плотность узкополосного сигнала u(t) определяет-
определяется его преобразованием Фурье
оо оо
S(w) = [uWe-^dt = [ReiV^e^le^dt. (8.13)
Действительную часть комплексной величины z можно предста-
представить в виде
Re[z] = -l(z+z*), (8.14)
где z*~ комплексно-сопряженная величина.
С учетом (8.14) из (8.13) получим
S(co) = - J[V^(f)e*°0' + V We-^fc-^dt =
. "" ' • (8.15)
= \ \ [WOe~'(w"COo)f]cyf + -JuV)e-/(@+c)o)fc/f.
202

Узкополосные сигналы
Величина
оо
U(a)= jVWe-^dt (8.16)
представляет спектральную плотность комплексной огибающей
сигнала. Таким образом, спектральная плотность узкополосного
сигнала определяется спектральной плотностью комплексной оги-
огибающей, соотношением, которое следует из (8.15)
S(co) =-l/(to-©о)+ -L/*(a) + (oo). (8.17)
Спектральную плотность комплексной огибающей можно пред-
представить в виде
L/(co) = |t7(a))|e^(CO), (8.18)
где |С/((о)|,фу(о)) - амплитудный и фазовый спектры комплексной
огибающей сигнала (рис. 8.2,а).
Спектр комплексной огибающей сосредоточен в области низких
частот. Спектр узкополосного сигнала S((o) получается путем пере-
переноса спектра комплексной огибающей L/(co) из окрестности нулевой
частоты в окрестность несущей частоты ±ооо (с коэффициентом 1/2),
рис. 8.2,6.
Sw>oN = |^-coo), Sw<o(co) = ^l/(a> + a>o). (8.19)
Спектры в области положительных и отрицательных частот не
должны заходить за начало координат, что и определяет условие
узкополосности.
Примеры.
1 .Спектральной плотности комплексной огибающей сигнала
(рис. 8.3,а)
.... . сот,.
L/(co) = ти sin с—-,
где ти - параметр зависимости (длительность сигнала),
соответствует спектральная плотность сигнала (О) > 0), рис. 8.3,6,
203

Раздел 8
2. Спектральной плотности комплексной огибающей сигнала
(рис. 8.4,а)
U(co) = U0e~4a,
где а - параметр зависимости,
соответствует спектральная плотность сигнала (со >0), рис. 8.4,6,
(со-соо)г
S(w) = 1/2U0e~ 4a .
204

Узкополосные сигналы
(О
205
Рис. 8.3
Рис. 8.4

Раздел 8
8.4. Корреляционные функции узкополосных сигналов
Автокорреляционная функция сигнала определяется выражением
Я(т)= \u(t)u(t + T)dt. (8.20)
Для узкополосного сигнала
u(t) = Re[V{t)eia°t] (8.21)
с учетом (8.11) из (8.20) получим
Я(т) = Refe^ j-V(t)V(t + x)e'2o)°foff +
(8.22)
+ Re[e*°°T \-V*(t)V(t + x)dtl
Функция V(t) является низкочастотной, медленно меняется в
течение периода несущего колебания 2кЛй0. Вследствие этого зна-
значение первого интеграла в (8.22) может быть принято равным нулю.
Таким образом, выражение для автокорреляционной функции узко-
узкополосного сигнала запишется в виде
Я(т) = Re[e"°°T \-V*(t)V(t + x)dt] = Яе[ЯДт)еЧт], (8.23)
где
оо
Rv(z) = V2JV*(t)V(t + T)dt. (8.24)
Величина Rv(i) представляет автокорреляционную функцию
комплексной огибающей сигнала. Так как V(t) является комплекс-
комплексной величиной, то в общем случае Rv(t) представляет комплексную
функцию. Автокорреляционная функция узкополосного сигнала R(x)
является действительной. Соотношение, связывающее ее с авто-
автокорреляционной функцией комплексной огибающей (8.23), анало-
аналогично тому, которое связывает узкополосный сигнал с его ком-
комплексной огибающей. Часто целесообразно сначала определить
206

Узкополосные сигналы
автокорреляционную функцию комплексной огибающей сигнала,
а затем перейти к корреляционной функции узкополосного сигнала.
Примеры.
1. Корреляционной функции комплексной огибающей сигнала
(рис.8.5)
Я„(*) = ЯЛ0)A-т/ти),
где ти - длительность сигнала,
соответствует корреляционная функция узкополосного сигнала (т > 0)
Я(т) = Яи@)A-т/ти)созоHт.
2. Корреляционной функции комплексной огибающей сигнал
(рис.8.6)
Я,(т) = Я„@)е~ 2 ,
где а - параметр зависимости, соответствует корреляционная
функция узкополосного сигнала
Рис. 8.5
207

Раздел 8
Рис.8.6
Взаимная корреляционная функция двух узкополосных сигналов,
имеющих одинаковую несущую частоту шо,
^-iaiJi
(8.25)
(8.26)
Подставляя (8.25) в (8.26), с учетом (8.11) получаем
В (8.27) величина
208
определяется выражением
(8.27)

Узкополосные сигналы
Rv^(T) = ^jV%(t)V2(t + T)dt (8.28)
представляет взаимную корреляционную функцию комплексных
огибающих сигналов. Соотношение, связывающее ее с взаимной
корреляционной функцией рассматриваемых узкополосных сигна-
сигналов, имеет вид, аналогичный (8.23)
fl12(T) = Re[R,12(x)e^]. (8.29)
При использовании свойства преобразования Фурье, можно по-
получить соотношение, связывающее автокорреляционную функцию
комплексной огибающей сигнала Rv(x) со спектральной плотностью
энергии Wv(($)
Wv(a) = -l|U(co)|2 = JRv(T)e-^ck, (8.30)
Rv(t) = ^- \wv{u)e™cku. (8.31)
2тс J
При т- 0 имеем
Rv@) = -±-\wv(a)cb. (8.32)
С учетом (8.24) и (8.32) можем записать
\v(t) dt = — f|L/(co) 2 dfco. (8.33)
J 271 J1
что представляет равенство Парсеваля для комплексных огибаю-
огибающих узкополосных сигналов.
Выражение для спектральной плотности энергии узкополосного
сигнала запишем в виде
И/(ю) = Гя(х)в~юп(Л = JRe[Rv(T)eK[)oZ]e-bzdz. (8.34)
209

Раздел 8
Из (8.34) аналогично (8.17) получим
WM = ^l/^(co-w0) + |w>) + aH), (8.35)
где Wv((u}- спектральная плотность энергии комплексной огибаю-
огибающей
Спектральная плотность энергии комплексной огибающей явля-
является действительной величиной, поэтому в (8.35) отсутствует обо-
обозначение комплексно сопряженной величины второго слагаемого.
Как следует из (8.36), спектральная плотность энергии узкополосно-
узкополосного сигнала имеет две составляющие - в области положительных
частот 1/21/1/^@)-(оо) и отрицательных частот M2Wv({u + (uq) .
Соотношения, аналогичные (8.30) и (8.31), связывают взаимную
корреляционную функцию с взаимной спектральной плотностью
энергии комплексных огибающих узкополосных сигналов
^12(о))Л(У;((о)У2(ш) = |яИ2(т)е-тЛ, (8.37)
ЯИ2(*) = 7Г- Ги^2Hereto. (8.38)
8.5. Аналитичесий сигнал
При анализе узкополосных сигналов в ряде случаев пользуются
понятием аналитического сигнала. Аналитический сигнал опреде-
определяется как
Z(t) = u(t) + iu(t), (8.39)
л л
где u(t) - узкополосный сигнал, описываемый (8.1); u(t)~ сигнал,
сопряженный с u(t) по Гильберту
«) = -!"№*. (8.40)
П J 1-Х
210

Узкополосные сигналы
Аналитический сигнал, как комплексная величина, определяется
модулем \Z(t)\ и аргументом (pz(t)
Z(t) = \Z(t)\e^'\ (8.41)
Для сигнала
u{t) = V(t)cosO(t) (8.42)
сопряженный сигнал, определяемый (8.40), равен
u(t) = V{t)s\n0(t). (8.43)
С учетом (8.42) и (8.43) выражение для аналитического сигнала
(8.39) получим в виде
Z(t) = V{t)cos0(t) + iV{t)s\nO(t). (8.44)
Модуль аналитического сигнала равен огибающей узкополосного
сигнала
\Z(t)\ = iu2(t) + u2(t) = V(t), (8.45)
а аргумент фазе
Л
qz = arctg^ = 0{t). (8.46)
С учетом (8.45) и (8.46) выражение (8.41) можем записать в виде
Z(t) = V(t)e*{t) = V{t)e^ . (8.47)
Таким образом, аналитический сигнал представляет комплекс-
комплексный сигнал, введенный при описании узкополосного сигнала (8.2).
8.6. Обобщенная корреляционная функция сигнала
Для характеристики точности и разрешающей способности ра-
радиолокационных систем используется обобщенная корреляционная
функция. Она определяется как корреляционная функция ком-
комплексных огибающих узкополосных сигналов с различной частотой
(как правило, без коэффициента 1/2).
Комплексные огибающие узкополосных сигналов u-i(t) и u2(t), от-
отличающихся только сдвигом несущей частоты О., при Q «шо, пред-
представим в виде
211

Раздел 8
V,(t) = V(t), 1/2(f) = 1/@eCf. (8-48)
С учетом (8.48) от определения взаимной корреляционной
функции комплексных огибающих узкополосных сигналов перейдем
к выражению для обобщенной корреляционной функции
R(t,Q) = \v{t)Vi'{t-x)esltdt. (8.49)
— оо
Функция R(x,Q) связана со спектральными плотностями огибаю-
огибающих сигналов соотношением
R(x,Q) = — fL/(w-Q)LT(w)emcrto. (8.50)
2п J
Функция R{x, Q) характеризует разрешающую способность сис-
системы, в которой используется рассматриваемый сигнал, поэтому ее
называют также функцией неопределенности.
При Q = 0 имеем
Я(т,0) = j\/(t)V*{t-x)dt, (8.51)
или
Я(т,0) = — j\U(a>f еЬхсЬ. (8.52)
Функция R(x, 0) является функцией неопределенности по даль-
дальности. Она равна удвоенной величине автокорреляционной функ-
функции комплексной огибающей сигнала. Максимальное значение по-
получается при т = 0. Чем больше значение \R(x, 0)/ отличается от
\R@, О)), тем легче могут быть различены две цели, отличающиеся
запаздыванием отраженного сигнала т. Обычно разрешение целей
характеризуется квадратом функции неопределенности \R(x,Q.)t-
Постоянная разрешения по запаздыванию определяется как
212
(8.53)

Узкополосные сигналы
Используя спектральную плотность комплексной огибающей
сигнала и учитывая равенство Парсеваля, (8.53) можем записать в
виде
(8.54)
(8.55)
(8.56)
Постоянная разрешения по частоте определяется аналогично
постоянной разрешения по запаздыванию
(8.57)
Функция неопределенности дает возможность оценить степень
различения сигналов, отличающихся значениями запаздывания т и
частоты Q. Чем ближе |Я(т, Q)\ по значению к |Я@,0)|, тем труднее
различаются сигналы, отличающиеся запаздыванием т и частотой Q.
Мерой совместной разрешающей способности по запаздыванию
и частоте может служить эффективная площадь неопределенности
(8.58)
213
При т = 0 функция неопределенности равна

Раздел 8
В качестве примеров рассмотрим функции неопределенности
некоторых видов сигналов.
1. Сигнал с прямоугольной огибающей и постоянной частотой.
V(t) = V0,\t\<xu/2.
Выражение для функции неопределенности имеет вид:
Модуль функции неопределенности
2. Сигнал с прямоугольной огибающей и линейно изменяющейся
частотой (разд. 11)
V(t) = V0eiat2/2,\i\<Tu/2.
Функция неопределенности описывается выражением
214
Из него получим

Узкополосные сигналы
Из записанного выражения получим
8.7. Дискретизация узкополосного сигнала
Принципы дискретизации непрерывного сигнала могут быть рас-
распространены на узкополосный сигнал
(8.59)
Комплексная огибающая V(t), имеющая спектр, ограниченный
частотой Асо/2 (рис.8.7), может быть представлена рядом Котель-
никова
(8.60)
(8.61)
(8.62)
215
Модуль функции неопределенности
Коэффициенты ряда определяются как
период дискретизации выбирается из соотношения

Раздел 8
Рис. 8.7
С учетом (8.60) и (8.61) выражение для узкополосного сигнала
запишем в виде
(8.63)
Выражение (8.64) представляет ряд Котельникова для узкопо-
узкополосного сигнала. Он описывает сигнал, спектр которого заключен
в ограниченной полосе частот Aw. Ряд Котельникова для узкопо-
узкополосного сигнала включает слагаемые, которые имеют вид моду-
модулированных колебаний с несущей частотой Wo, фазой ц>(пТ) и оги-
огибающей
(8.64)
Если длительность сигнала равна Гс, то число интервалов раз-
разбиения равно N =ТС/ Т. Таким образом, ряд Котельникова для узко-
узкополосного сигнала можем записать в виде
216

Узкополосные сигналы
л/-1 sin — (t-nT)
u(t) = Yv(nT)-—2 cos[co0f + (p(n7-)]. (8.65)
л=о ™(t-nT)
Выборочные значения сигнала задаются двумя параметрами
V(m) и ц>(пТ).
8.8. Модулированные сигналы
Узкополосными сигналами чаще всего являются модулирован-
модулированные колебания. Модулированные колебания представляют высоко-
высокочастотные колебания, на которые накладываются низкочастотные,
несущие информацию. Выбор несущей частоты высокочастотного
колебания производится исходя из условий распространения ра-
радиоволн, приема их антеннами и ряда других факторов. Переда-
Передаваемая информация содержится в сигнале, накладываемом на вы-
высокочастотное колебание. Наибольшая частота спектра сигнала,
содержащего информацию, должна быть значительно меньше не-
несущей частоты. Процесс наложения сигнала, содержащего инфор-
информацию, на высокочастотное колебание называется модуляцией.
Сигнал, содержащий передаваемую информацию, называется мо-
модулирующим. Модулируется несущее колебание путем изменения
одного или нескольких параметров. Наиболее часто несущим коле-
колебанием является гармоническое. Однако могут использоваться и
другие виды колебаний, например, периодическая последователь-
последовательность импульсов или шум. Гармоническое колебание можно моду-
модулировать по амплитуде, фазе или частоте. Модуляция по фазе или
частоте носит название угловой модуляции. В дальнейшем рас-
рассматриваются гармонические колебания с различными видами мо-
модулями.
217

Раздел 9.
АМПЛИТУДНО-МОДУЛИРОВАННЫЕ СИГНАЛЫ
При амплитудной модуляции (AM) под воздействием модули-
модулирующего (управляющего) сигнала, несущего информацию, изменя-
изменяется амплитуда сигнала. Как правило, AM сигнал является узкопо-
узкополосным, относительное изменение амплитуды за один период не-
несущего колебания мало. Такие сигналы, узкополосные амплитудно-
модулированные, и рассматриваются в настоящем разделе.
9.1.Описание AM сигнала
Узкополосный AM сигнал с гармоническим несущим колебанием
описывается выражением (рис. 9.1,а)
u(t) = V(t)cos((*0t + <f>0), (9.1)
где V(t) -амплитуда; соо,(ро -частота и начальная фаза несущего
колебания.
Выражение для AM сигнала может быть записано также в ком-
комплексной форме
u(t) = Re[V(t)eka°t], (9.2)
где V(t) = V(f)e*Po -комплексная огибающая сигнала; при фо=О
комплексная огибающая сигнала V(t) совпадает с амплитудой V(t).
Графически комплексный сигнал можно изобразить в виде век-
вектора на комплексной плоскости. Длина вектора равна V(t), изме-
изменяется во времени (рис. 9.1,6). Угол между вектором и действи-
действительной осью постоянен и равен ф0. Система координат враща-
вращается по часовой стрелке с угловой скоростью щ. Проекция векто-
вектора на действительную ось в каждый момент времени описывает
AM сигнал u(t).
218

Амплитудно-модулированные сигналы
Рис. 9.1
9.2. Тональная амплитудная модуляция
При амплитудной модуляции амплитуда зависит от модулирую-
модулирующего сигнала s(t). Эта зависимость, как правило, линейная
(9.3)
где к- коэффициент пропорциональности.
Вид модулирующего сигнала определяет спектр AM сигнала.
Простейший модулирующий сигнал - гармонический. При гармони-
гармонической или тональной модуляции AM сигнал описывается выраже-
выражением (рис. 9.2,а)
(9.4)
где М = ks01 Vo - коэффициент модуляции, М < 1, О., Эо - частота
и начальная фаза гармонического модулирующего сигнала, Q «соо .
Исходя из (9.4), AM сигнал можно представить в виде суммы
гармонических составляющих и определить спектр тонально AM
сигнала
(9.5)
219

Раздел 9
Рис. 9.2
Из (9.5) следует, что тонально AM сигнал включает три гармониче-
гармонические составляющие: несущее колебание и два боковых с частотами AM
сигнал включает три гармонические составляющие: несущее колеба-
колебание и два боковых с частотами ш0 ± О.. Графики амплитудного и фа-
фазового спектров приведены на рис. 9.2,б,в. Амплитудный спектр
имеет четную симметрию относительно несущей частоты, а фазо-
фазовый - нечетную относительно начальной фазы. Ширина спектра
равна удвоенной частоте модуляции 20..
220

Амплитудно-модулированные сигналы
Средняя мощность тонально AM сигнала может быть определе-
определена из (9.5) как сумма средних мощностей спектральных состав-
составляющих
Р = Р0 + Р8=Р0A + М2/2), (9.6)
где Ро - мощность несущего колебания; Р5 - мощность боковых
составляющих.
Мощность боковых составляющих Р5 равна Л^/2 от мощности
несущего колебания Ро.
9.3. Многотональная амплитудная модуляция
Модулирующий сигнал, как правило, имеет сложный спектраль-
спектральный состав (рис. 9.3). В этом случае AM сигнал можно записать
в виде
N
u(t) = Vo[\ + ^ Мп cos(Qnf + 0n)]cos(coof + фо)
n=1 , (9.7)
где &П,6П -частоты модуляции (Q^<Q2<--<^n <<шо) и началь-
начальные фазы составляющих модулирующего сигнала;
(9.8)
Из (9.7) после преобразования получим представление сигнала
в виде суммы гармонических составляющих
u{t) = V0cos{u>0t + q>0) +
Л г т (9-9)
+ V0/22^Mn{cos[(u0 + Qn)t + (p0+Qn] + cos[((x>0-Qn)t + (p0-Qn]}.
л=1
Анализ (9.9) показывает, что при многотональной модуляции AM
сигнал содержит несущее колебание и полосы верхних и нижних
боковых составляющих. Амплитудный спектр сигнала имеет четную
симметрию относительно оо0 , фазовый - нечетную симметрию, от-
относительно ф0 (рис. 9.4). Ширина спектра AM сигнала равна удво-
удвоенной максимальной частоте модуляции
221

Раздел 9
Рис. 9.3
(9.10)
Выражение (9.9) и график спектра, приведенный на рис.9.4, по-
показывают, что спектр модулирующего сигнала полностью отобра-
отображается в боковой полосе спектра AM сигнала. Боковые полосы яв-
являются зеркальными копиями одна другой. Это свидетельствует об
избыточности передачи информации двумя боковыми полосами.
Средняя мощность AM сигнала при многотональной модуляции
определяется из (9.9) как сумма средних мощностей несущего ко-
колебания и боковых составляющих
(9.11)
Рис. 9.4
222

Амплитудно-модулированные сигналы
На долю всех боковых составляющих приходится
/7=1
от мощности несущего колебания.
9.4. Амплитудная модуляция периодической
последовательностью импульсов
Одним из видов многотональных AM сигналов является перио-
периодическая последовательность радиоимпульсов (рис. 9.5). Такой AM
сигнал удобнее записать в виде
(9.12)
где s(t) - модулирующая периодическая последовательность ви-
видеоимпульсов.
Модулирующий сигнал s(t) описывается рядом Фурье (раздел 3)
где О. - 2п/Т, Т- период последовательности импульсов.
(9.13)
Рис. 9.5
223

Раздел 9
Амплитуды sn и начальные фазы вп определяются следующи-
следующими выражениями:
sn=j\S(nQ)\,Qn = 4>(nQ), (9.14)
где S(oi) - спектральная плотность одного импульса модулирующей
последовательности.
Подставив (9.13) в (9.12), получим
u{t) = [s0 /2 + ^ sn cos{nQt + Qn )]VQ cos(oHf + Фо) = A) cos(co0/ + cp0) +
л=1
N
+ ^An{cos[((d0 + nQ)t + %+Qn] + cos[{(»0-nQ)t + qH-Qn]}, (9.15)
где Aq = V0s0/2, An = V0sn/2, n = 1,2
Как следует из (9.15), спектр сигнала является дискретным, рас-
расположен в окрестности несущей частоты ш0. Огибающая дискрет-
дискретного спектра периодической последовательности радиоимпульсов
по форме совпадает с непрерывным спектром одиночного видео-
видеоимпульса модулирующей последовательности.
Используя табл.3.1, из (9.14) можно найти спектры периодиче-
периодических последовательностей радиоимпульсов различной формы. Та-
Такой подход иллюстрируют следующие примеры.
1. Периодическая последовательность прямоугольных
радиоимпульсов.
Модулирующий сигнал описывается выражением (табл. 3.1, п. 1).
... Т 2Т ^ . Л77ГТ
s(t) = — + —> sine cosлеоЛ,
T Т *-* Т
где х,Г = 2тс/со1 -длительность и период следования периодиче-
периодической последовательности прямоугольных импульсов.
Подставляя выражение для s(t) в (9.12), при ф0 = 0 получим
s(f) = -5-cosco0f+ -^-^sinc [cos(aH - noi^t + cos(w0 + /%>!)*].
n=1 '
Амплитудный спектр описывается выражением
224

Амплитудно-модулированные сигналы
На рис. 9.6 спектр изображен при со > 0.
2. Периодическая последовательность симметричных тре-
треугольных радиоимпульсов.
Амплитудный спектр описывается выражением (табл. 3.1, п.З),
рис. 9.7
3. Периодическая последовательность косинусоидальных ра-
радиоимпульсов.
Рис. 9.7
225

Раздел 9
Амплитудный спектр описывается выражением (табл. 3.1,п.4),
рис. 9.8
9.5. Амплитудная модуляция непериодической
последовательностью импульсов
Одиночный радиоимпульс описывается выражением
u(f) = s(f)V0cos(w0f + (p0), |f|<T,
(9.16)
где s(t) - модулирующий импульс; т - длительность модулирующе-
модулирующего видеоимпульса.
В (9.16) s(t) представляет огибающую модулирующего импульса.
Спектральная плотность сигнала (9.16) определяется преобразова-
преобразованием Фурье (разд. 3)
(9.17)
где S((o) - спектральная плотность модулирующего сигнала s(t).
При ф0 =0 (рис. 9.9, а,б)
(9.18)
Примеры одиночных радиоимпульсов взяты для модулирующих
сигналов, описанных в табл. 3.1, при ф0 = 0.
Рис. 9.8
226

Амплитудно-модулированные сигналы
Рис. 9.9
1 .Прямоугольный радиоимпульс (табл. 3.1, п.1), рис. 9.10 (со > 0)
_ . . VQx. . (со-соо)т . (со + соо)т.
SAM((*) = -^[s\ncK 2o; +sincv 20/ ].
2. Гауссов радиоимпульс (табл. 3.1, п.15), рис. 9.11 (со > 0)
5/Ш(со) = УН &е-(со-Шо)^/4а + е-(со-со0)^/4а]
2 V я
Рис. 9.10
227

Раздел 9
Рис. 9.11
Аналогично могут быть получены спектры пачек радиоимпуль-
радиоимпульсов. Модулирующим сигналом является пачка видеоимпульсов.
Спектральная плотность пачки радиоимпульсов может быть полу-
получена из (9.17) с учетом выражений, приведенных в разд. 3.
(9.19)
где So(co) -спектральная плотность одного видеоимпульса в пачке;
Г- интервал следования импульсов в пачке.
Амплитудный спектр в области положительных частот описыва-
описывается выражением
(9.20)
Используя (9.21) и табл. 3.1, можно найти спектры пачек радио-
радиоимпульсов различной формы. Такой подход иллюстрируется сле-
следующими примерами.
1. Пачка прямоугольных радиоимпульсов (табл. 3.3, п.1), рис. 9.12.
228

Амплитудно-модулированные сигналы
229
2. Пачка треугольных радиоимпульсов (табл. 3.1, п.З), рис. 9.13
3. Пачка гауссовых радиоимпульсов (табл. 3.1, п. 15), рис. 9.14

9.6. Балансная амплитудная модуляция
Балансная модуляция (БМ) является одним из видов амплитудной
модуляции. Ее можно рассматривать как операцию, при которой
производится перемножение модулирующего сигнала и несущего
колебания. При балансной модуляции сигнал не содержит не-
несущего колебания, это положительный момент при формировании
AM сигнала.
Выражение для БМ сигнала записывается в виде
i/@ = s(f)V0cos((o0f + (p0).
Для тонально БМ сигнала
s(f) = Mcos(Qf + 90)
имеем
(9.21)
(9.22)
230

Амплитудно-модулированные сигналы
Рис. 9.14
(9.23)
Как следует из (9.23), при балансной модуляции спектр модули-
модулирующего сигнала переносится в окрестность несущей частоты.
Однако сама несущая отсутствует (подавляется). Вследствие этого
такой вид модуляции называется амплитудной модуляцией без не-
несущей.
Выражение для многотонального БМ сигнала получится из (9.21)
с учетом (9.9)
231

Раздел 9
Амплитудный спектр сигнала (9.24) показан на рис. 9.15.
Спектр включает две симметричные полосы верхних и нижних бо-
боковых составляющих. Ширина спектра БМ сигнала определяется вы-
выражением (9.11). Средняя мощность многотонального БМ сигнала
(9.25)
значительно меньше, чем при обычной амплитудной модуляции
(9.12).
Спектральная плотность БМ сигнала может быть определена
исходя из (9.21). При ф0 = 0 получим (рис. 9.16),
(9.26)
Как указано, при балансной модуляции уменьшается мощность
передатчика по сравнению с обычной амплитудной модуляцией. В то
же время необходимая полоса частот остается такой же. В обоих
случаях получаются две боковые полосы, каждая из которых несет
информацию, содержащуюся в модулирующем сигнале. Сузить не-
необходимую полосу частот можно, если подавить в спектре AM сигна-
сигнала несущую и одну боковую полосу.
Q)
Рис. 9.16
232

Амплитудно-модулированные сигналы
Рис. 9.17
Такой вид амплитудной модуляции называется однополосной ам-
амплитудной модуляцией с подавленной несущей или просто однопо-
однополосной амплитудной модуляцией.
9.7. Однополосная амплитудная модуляция
При однополосной амплитудной модуляции (ОМ) сигнал содер-
содержит только одну боковую полосу частот. Выражение для многото-
многотонального ОМ сигнала получаем из (9.9)
(9.27)
Знак плюс в (9.27) соответствует сигналу с верхней боковой по-
полосой частот (рис. 9.17), а знак минус - с нижней боковой полосой.
При однополосной амплитудной модуляции ширина спектра
(9.28)
где QN - максимальная частота модуляции, что вдвое уже, чем при
обычной амплитудной модуляции, описываемой (9.10).
Средняя мощность многотонального ОМ сигнала равна
Рис. 9.18
233

Раздел 9
Р=Ро^М2п/4. (9.29)
Спектральная плотность ОАМ-сигнала описывается выражением
S0M(<*) = V0M/2{V2[ S(co-co0)+ S((o + @0)]±
± 1 / 2[S(co - co0 )sign{(o - oH) - S(co + coo )sign(w + co0)]}"
Знак плюс в (9.30) соответствует описанию спектра с подавленной
нижней боковой полосой, а минус - с подавленной верхней полосой
(рис. 9.18).
234

Раздел 10.
СИГНАЛЫ С ФАЗОВОЙ И ЧАСТОТНОЙ МОДУЛЯЦИЕЙ
Сигналы с угловой модуляцией, как правило, являются узкопо-
узкополосными. Ширина их спектра значительно меньше несущей часто-
частоты. Такие сигналы и рассматриваются в разделе.
10.1. Описание сигналов с угловой модуляцией
Узкополосный сигнал с угловой модуляцией описывается выра-
выражением (рис. 10.1,а)
u(t) = Vocos[(dot + q>(t)] = Vocos0(t) A0.1)
или в комплексной форме
u(t) = Re[V(t)eK0°t], A0.2)
где V(t) = Voekp{t) - комплексная огибающая сигнала; l/0,aH,(p(f)-
амплитуда, частота и фаза сигнала.
Комплексный сигнал может быть представлен в виде вектора дли-
длины Уона комплексной плоскости (рис. 10.1,6). Вектор составляет с дей-
действительной осью угол ф@, который изменяется во времени. Сама
система координат вращается по часовой стрелке с угловой скоростью
(uq. Проекция вектора на действительную ось описывает сигнал u(t).
Понятие угловой модуляции включает фазовую и частотную мо-
модуляцию. При фазовой модуляции (ФМ) под воздействием модули-
модулирующего сигнала s(t) изменяется непосредственно фаза ф(г).
Обычно обеспечивается линейная зависимость фазы от модули-
модулирующего сигнала:
(p(f) = (po + /cs(f), A0.3)
где ф0 - начальная фаза; к - коэффициент пропорциональности.
Мгновенная частота ФМ сигнала
.,. d0(t) ckp(t) . ds{t) nnA,
со@ = -^ = со0+-^ = аH + /с-^. (Ю.4)
235

Раздел 10
Рис.10.1
При частотной модуляции (ЧМ) модулирующий сигнал воздейст-
воздействует непосредственно на частоту
co(f) = соо + ks(t). A0.5)
Фаза ЧМ сигнала
q>(t) = q>0 + k\s(t)dt. A0.6)
о
Максимальное отклонение фазы от начальной ср0
/т? = тах|ф@-Ф0|
называется индексом модуляции. Максимальное отклонение часто-
частоты (o(t) от несущей соь
соа =max|o)(f)-cDo|
- девиацией частоты, или девиацией.
Отличие ФМ от ЧМ легче просматривается при простейшем -
тональном (гармоническом) законе модуляции:
s@ = s0cosQf, A0.7)
где s0) Q. - амплитуда и частота модулирующего сигнала.
При тональной ФМ (рис. 10.2)
ф@ = Фо + mcos Ш, A0.8)
236

Сигналы с фазовой и частотной модуляцией
сигнал описывается выражением
u(t) = V0cos(oi0t + mcosQt + <p0), A0.9)
частота равна
a)@ = coo-mQsinnf. A0.10)
Девиация определяется произведением индекса модуляции и
частоты модуляции
соа = тО..
При тональной ЧМ частота (рис. 10.3)
co@ = coo +coacos?2f,
фаза
(p(f) = —-sinfltf + ф0 = ms'mQt + ф0.
Сигнал описывается выражением
i/@ = Vq cos((o0f + msin Qt + cp0).
A0.11)
A0.12)
A0.13)
A0.14)
Индекс модуляции определяется отношением девиации к часто-
частоте модуляции. Таким образом, тонально модулированный ФМ сиг-
сигнал с индексом модуляции т описывается аналогичным выражени-
выражением, что и ЧМ сигнал с девиацией, равной mQ. Отличие заключается
в том, что фаза ФМ сигнала изменяется по закону т cosut, а фаза
ЧМ сигнала - по закону wg/Q.s\nQt.
Рис. 10.2
237

Раздел 10
Рис. 10.3
При ЧМ девиация пропорциональна амплитуде модулирующего
сигнала и не зависит от его частоты. При ФМ индекс модуляции
пропорционален амплитуде модулирующего сигнала и не зависит
от частоты этого сигнала.
10.2. Сигнал с тональной угловой модуляцией
Простейший вид модуляции - тональный. Сигнал с тональной
угловой модуляцией запишем в виде
A0.15)
где V(t) = Voem;q)(t) = ms\r\Qt + (po.
Спектр сигнала определяется при разложении в ряд Фурье ком-
комплексной огибающей сигнала. При ф0 = 0
V{t) = Voeim*nat.
Используя соотношение, известное из теории Бесселевых функций
A0.16)
п=-
где ln(z) - функция Бесселя первого рода п-го порядка от аргумента z,
/_n(z) = H)n/n(z),
для комплексной огибающей сигнала получим
A0.17)
238

Сигналы с фазовой и частотной модуляцией
Подставляя A0.17) в A0.15), запишем
оо оо
u(t) = V0Re[e^ ?/,,(m)eyniif] = Vo ?/n(m)cos(co0+лЯ)/. A0.18)
Анализ A0.18) показывает следующее. Спектр сигнала с угловой
тональной модуляцией является дискретным. Гармоники спектра
отличаются друг от друга на частоты, кратные частоте модуляции.
Амплитуды составляющих спектра определяются функциями
Бесселя. Функции Бесселя являются специальными функциями,
описываются выражением
A0.19)
Рис. 10.4
239
Графики функций Бесселя изображены на рис. 10.4.

Раздел 10
Как следует из A0.18), сигнал с угловой тональной модуляцией
включает несущее колебание с амплитудой Volo(m) и бесконечное
множество парных боковых составляющих с частотами озо ± пО. и
амплитудами Voln(m). Причем фазы верхних и нижних составляю-
составляющих сигнала нечетных номеров п отличаются на величину п. Ам-
Амплитудные спектры сигналов для некоторых значений т приведены
на рис. 10.5. Наибольшее значение амплитуды имеет составляю-
составляющая, номер которой определяется эмпирическим выражением [20]
л = m-0,8086m3 -0,0606m 3 -0,0316т
-1
A0.20)
По мере увеличения номера л амплитуды боковых составляю-
составляющих убывают, стремясь к нулю. Ширина спектра определяется эм-
эмпирическим выражением
A0.21)
Рис.10.5
240

Сигналы с фазовой и частотной модуляцией
Как следует из A0.21), при увеличении индекса модуляции ши-
ширина спектра стремится к величине 2тО. (или 2сод). Следовательно,
при больших индексах модуляции ширина спектра сигнала, можно
считать, равна удвоенному значению девиации. При малом индексе
модуляции ширина спектра стремится к удвоенному значению час-
частоты модуляции BQ).
При малом индексе модуляции (т«1) можно принять
10(т) = ХЦт)« т/2; при п>2,1п{т) « 0. A0.22)
С учетом A0.22) выражение A0.18) запишется в виде
u{t) = Vo coswof + -^-cos((o0 + u)t --^-cos((o0 - Sl)t. A0.23)
Спектр такого сигнала подобен спектру AM сигнала и включает:
несущее колебание с амплитудой Vo и две боковые составляющие
с частотами соо ± О. и амплитудами mV(/2. Причем фаза нижней со-
составляющей смещена по отношению к верхней на величину п. Ши-
Ширина спектра равна удвоенной частоте модуляции BQ).
Средняя мощность сигнала с угловой модуляцией может быть
определена из A0.18) как
P = Po[/o(™) + 2/i2() + ...] = Po, A0.24)
V2
где Ро = —— средняя мощность несущего колебания;
/?(т) + 2/12(/т>) + ... = 1. A0.25)
Как следует из A0.24), средняя мощность сигнала с угловой мо-
модуляцией равна средней мощности несущего колебания.
10.3. Сигнал со сложным периодическим
законом модуляции
Любой периодический модулирующий сигнал можно разложить в
ряд Фурье, представить в виде взвешенной суммы гармонических
составляющих. Условия, необходимые для такого разложения, обыч-
обычно выполняются. Однако использование разложения при определе-
определении спектра сигнала с угловой модуляцией (путем подстановки в
A0.1) или A0.2) разложения ф^ в ряд Фурье) приводит к выражению,
неприемлемому для целей анализа и расчета спектра сигнала. Ис-
241

Раздел 10
ключение составляют законы угловой модуляции, которые приводят
только к изменению огибающей сигнала. К таким модулирующим сиг-
сигналам относится меандр. В других случаях более удобным оказыва-
оказывается подход, при котором определяется спектр импульсного ЧМ сиг-
сигнала с длительностью, равной периоду непрерывного сигнала, а за-
затем выполняется переход к спектру периодического сигнала. Ниже
дано определение спектра сигналов с некоторыми достаточно рас-
распространенными законами угловой модуляции.
10.3.1. ФМ сигнал с модуляцией меандром
При модуляции гармонического колебания меандром происходит
скачкообразное изменение модулируемого параметра - манипуля-
манипуляция; при ФМ - скачкообразное изменение фазы (рис. 10.6,а)
A0.26)
где Г- период модуляции.
Комплексная огибающая такого сигнала определяется как
(рис.10.6,6)
A0.27)
Спектр сигнала удобнее определить через спектр огибающей.
Раскладывая в ряд Фурье огибающую сигнала, запишем (разд. 3)
A0.28)
Рис. 10.6
242

Сигналы с фазовой и частотной модуляцией
С учетом A0.28) из A0.2) получим следующее выражение для
ФМ сигнала:
A0.29)
Спектр сигнала A0.29) изображен на рис. 10.7.
Аналогичный подход позволяет получить спектр ФМ сигнала, ог-
ограниченного Л/ периодами огибающей (ФМ пачкой прямоугольных
импульсов), рис. 10.8. Спектральная плотность такого сигнала дли-
длительности NT, где Л/ - число импульсов в пачке, Т - период следо-
следования импульсов в пачке, определяется выражением
S(©) = 1/2L/(©-uH) + 1/2I/(u) + uH), A0.30)
где U((?>) - спектральная плотность огибающей сигнала.
Огибающая сигнала V(t) представляет отрезок меандра (рис.
10.8,6).
Спектр пачки меандровых импульсов описывается выражением
(разд. 3)
со
A0.31)
где хи - длительность импульса; Г - период следования импульсов
в пачке.
Так как Т = 2хи, A0.31) можем переписать в виде
Рис. 10.7
243

Раздел 10
A0.32)
Таким образом, выражение для спектра ФМ сигнала, модулиро-
модулированного пачкой меандровых импульсов, примет вид
A0.33)
Первое слагаемое в A0.33) описывает спектральную плотность
сигнала в области положительных частот, второе в области отри-
отрицательных, частот. Амплитудный спектр сигнала в области положи-
положительных частот определяется как
A0.34)
Он симметричен относительно несущей частоты oH,|S((o0)| = 0
(рис. 10.9).
244
Рис. 10.8

Сигналы с фазовой и частотной модуляцией
10.3.2. ЧМ сигнал с модуляцией меандром
При ЧМ меандром изменяется скачкообразно мгновенное значе-
значение частоты (рис. 10.10)
где Г- период модуляции.
Частотно-модулированный сигнал представим в виде суммы
двух сигналов
u(t) = u,(t + Т/4) + u2(t- Т/4), A0.35)
где urft), u2(t) - периодические последовательности прямоуголь-
прямоугольных радиоимпульсов с несущими частотами со1 и cog , периодом Г
и длительностью Т/2, смещенные относительно начала координат
на ± Т/4.
245

Раздел 10
б)
Рис. 10.10
Спектры ui(t) и u2(t) определяются выражениями (разд. 3)
A0.36)
л=1
Из A0.35) с учетом A0.36) получим выражение для периодиче-
периодического ЧМ сигнала
"@ = yCos(o1(f + r/4) + -^-cosoJ(f-r/4) + ^^sinc—•
/7=1
• [cos^ - nQ)(t + Г/4) + cos(w1 + nu)(t + 774) + cos(w2 - nQ) ¦ A0.37)
•(f-774) + cos(@2 + f7Q)(f-774)].
Графики амплитудного спектра сигнала при различных соотно-
соотношениях O)i и 0J приведены на рис. 10.11. Частоты C0i и 0J, как пра-
правило, выбираются кратными частоте модуляции Q = 2к/Т, что и от-
отражено на графиках. Как следует из A0.37), спектр сигнала включа-
включает два несущих колебания с частотами он и Шг и бесконечное число
боковых составляющих с частотами с^ ± пО. и Шг ±л?1
246

Сигналы с фазовой и частотной модуляцией
Рис. 10.11
Аналогичный подход используем при определении спектра ЧМ
сигнала, модулированного пачкой прямоугольных импульсов
(рис. 10.12).
При ЧМ пачкой прямоугольных импульсов сигнал можно пред-
представить в виде A0.35), где u-i(t) и u2(t) обозначают пачки из N пря-
прямоугольных радиоимпульсов с несущими частотами с^ и (Ог. Спек-
Спектральная плотность такого сигнала описывается выражением
(свойства преобразования Фурье)
A0.38)
где Srfw), S2(a>) - спектральные плотности сигналов Ui(t) и u2(t).
Спектральные плотности Si((u), S2((o) определяются как
A0.39)
A0.40)
где U((x)) - спектральная плотность пачки из N прямоугольных ви-
видеоимпульсов (разд. 3).
С учетом A0.38) - A0.40) выражение для спектра сигнала запи-
запишем в виде
247

Раздел 10
A0.41)
Выражение для U((&) имеет вид
A0.42)
A0.43)
A0.44)
Графики амплитудного спектра |S(tt>)|, построенные при различ-
различных соотношениях частот со^ сог приведены на рис. 10.13. Ампли-
Амплитудный спектр имеет максимумы на несущих частотах он и шг.
248

Сигналы с фазовой и частотной модуляцией
8 10 со
Рис. 10.13
249

Раздел 10
10.3.3. ЧМ сигнал с пилообразным несимметричным
законом модуляции
Чтобы определить спектр непрерывного периодического ЧМ
сигнала с пилообразным несимметричным законом модуляции
(рис. 10.14,а), рассмотрим импульсный сигнал с внутриимпульсной
ЧМ по линейному несимметричному закону (рис. 10.14,6). Длитель-
Длительность импульсного сигнала равна периоду следования непрерывно-
непрерывного сигнала. Частота такого сигнала описывается выражением
(a{t) = (D0 + at,\t\<~, A0.45)
2wd _
где а = —-; шд,Т -девиация и период изменения частоты.
Фаза сигнала
<р@ = ~-,|/|<|. A0.46)
Спектральная плотность комплексной огибающей импульсного
ЧМ сигнала определяется выражением
772
U((o) = V0 f e'W^dt. A0.47)
-772
Определение интеграла A0.47) через интегралы Френеля дано
в разд. 11
.пВ. со 2
U(u) = ^Le'4 M< {C(zl) + C(^)]+/[S(z1) + S(^)Jl A0.48)
где В - —^— = —?- = 2/тт; C(z), S(z) - интегралы Френеля;
71 О.
z 2 z 2
C{z) = f cos—dx; S{z) = f sm—dx; A0.49)
Ъ 2 о 2
250

Сигналы с фазовой и частотной модуляцией
Спектральная плотность импульсного ЧМ сигнала S((a) опреде-
определяется через спектральную плотность его комплексной огибающей
Ufa) соотношением (разд. 8)
A0.51)
Переход от спектра импульсного сигнала к спектру периодиче-
периодической последовательности импульсов описан в разд. 3. Комплексный
коэффициент ряда Фурье Сп связан со спектральной плотностью
одиночного импульса равенством
A0.52)
251
Рис. 10.14

Раздел 10
где п,Т- частота и период модуляции.
Графики спектров периодического ЧМ сигнала с пилообразным
несимметричным законом модуляции при различных значениях ин-
индекса модуляции m приведены на рис. 10.15.
Рис. 10.15
252

Сигналы с фазовой и частотной модуляцией
Спектры дискретные, интервал дискретизации равен частоте
модуляции Q = 2п1Т. Пунктирной линией изображены огибающие
спектров. Спектры симметричны относительно несущей частоты соо.
поэтому графики приведены только для со >щ.
10.3.4.ЧМ сигнал с пилообразным симметричным
законом модуляции
График зависимости частоты сигнала от времени изображен на
рис. 10.16,а. Чтобы получить спектр периодического сигнала с таким
законом ЧМ, рассмотрим импульсный сигнал с внутриимпульсной
ЧМ, длительность которого равна периоду модуляции непрерывного
сигнала (рис. 10.16,6). Частоту такого сигнала определим как
co@ = co01 + a)f|, \t\<T/2, A0.53)
где а = —2-; cod-девиация, со01 = соо - сод.
Фаза сигнала описывается выражением
253
A0.54)
Рис. 10.16

Раздел 10
Спектральная плотность комплексной огибающей сигнала опре-
определяется выражением
Решение интеграла имеет вид (разд. 11)
A0.55)
A0.56)
Рис. 10.17
254

где
Сигналы с фазовой и частотной модуляцией
B = ^uL = 2rrr, z,=VflA——); z2=Ve—. A0.58)
л 2cod coa
Выражение A0.56) запишем в виде (разд. 11)
1/(ш) = 21^@))!coscpv1(o)), A0.59)
где |Ц(со)|, фу^со) - модуль и аргумент Ui((a).
Спектральная плотность импульсного ЧМ сигнала для со > 0 оп-
определяется как
S(to) = -U(co-too1). A0.60)
Комплексные коэффициенты ряда Фурье, описывающие спектр
непрерывного ЧМ сигнала, равны
Cn=-S{nQ) =—S(nQ), A0.61)
7 2тг
где Q, Т- частота и период модуляции.
Графики амплитудных спектров ЧМ сигнала с симметричным
пилообразным законом модуляции приведены на рис. 10.17. Они
получены по результатам расчета спектров импульсных ЧМ сигна-
сигналов (разд. 11). Пунктирной линией изображена огибающая спектра
импульсного сигнала, дискреты показаны условно.
255

Раздел 11.
ИМПУЛЬСНЫЕ СИГНАЛЫ С ЧАСТОТНОЙ МОДУЛЯЦИЕЙ
Импульсные сигналы с внутриимпульсной ЧМ находят широкое
применение в радиолокации, связи, измерительной технике и дру-
других областях. Привлекли они внимание прежде всего в связи с по-
поисками способов сжатия импульсных радиолокационных сигналов,
что позволяет повысить разрешающую способность систем. Им-
Импульсные сигналы с линейной ЧМ (ЛЧМ) были первыми сигналами
такого вида, их сжатие осуществляется с помощью согласованных
фильтров.
Стремление к улучшению вида сигнала на выходе согласован-
согласованного фильтра стимулировало исследования более сложных сигна-
сигналов с нелинейной ЧМ (НЧМ). Указанные виды импульсных ЧМ сиг-
сигналов и рассматриваются в дальнейшем - ЛЧМ и НЧМ сигналы,
даются их описание и характеристики.
11.1. Описание ЛЧМ сигналов
Импульсный ЧМ сигнал в общем случае описывается выражени-
выражением
u(t)=V0cos[(»0t + ((>{t)] = Re[v{t)ek°°t'}i, Щ<?±, A1.1)
где V0,(oQ,(p(t),Tu - амплитуда, несущая частота, фаза и длитель-
длительность сигнала; V(t)= Voe^f'- комплексная огибающая сигнала.
Мгновенная частота сигнала
со@ = (оо + ф'@, И<^, A1.2)
где ф (г)- переменная составляющая частоты.
Функция «(f) описывает закон изменения частоты во времени -
закон модуляции.
256

Импульсные сигналы с частотной модуляцией
1м
2
Рис. 11.1
Обычно формируются ЛЧМ сигналы, имеющие нечетную сим-
симметрию функции co(t) относительно ш0 (рис. 11.1)
где а = 2соа/ти; шд -девиация частоты.
Фаза сигнала (рис. 11.1)
Возможна четная симметрия закона модуляции (рис. 11.2)
ш@ = о>о+^' И^у
A1-3)
A1.4)
A1.5)
При четной симметрии фаза сигнала
Рис. 11.2
257

Раздел 11
<p(f) = ^-signW \t\<^, A1.6)
где
,\ f1- f>0
sign(f)i-i,.<o
Зависимость w(f) (или cp(f)) для нечетного или четного законов
ЛЧМ полностью определяют характеристики сигналов - спектр
и корреляционную функцию.
11.2. Спектр ЛЧМ сигнала с нечетносимметричным
законом модуляции
Спектр ЛЧМ сигнала S(co) удобнее определять через спектр его
комплексной огибающей L/(co) (разд. 8)
S(to) = -L/(a)-(o0) + il/*(a) + (o0)l A1.7)
где
т„/2
и((л)= f V(t)e'btdt. A1.8)
-т„/2
Подставляя в A1.8) l/(f) = Ц)е*р^, выражение для спектральной
плотности комплексной огибающей с учетом A1.4) запишем в виде
ф)=1/0 Je^fbm'rt = vb | e[2 jdt. A1.9)
-т„/2 -т„/2
Используя интегралы Френеля
Z о Z
ЯХ2 , л/ ч Г . 71X2
C(z) = Jcos-^-dx, S(z)= J sin ^Lc/x, A1.10)
о о
из A1.9) получаем
258

Импульсные сигналы с частотной модуляцией
A1.13)
A1.11)
- база сигнала;
Амплитудный спектр комплексной огибающей сигнала описыва-
описывается выражением
A1.12)
Для сигналов с большим значением базы (S»1) при со = 0
С учетом A1.15) из A1.13) получим
При со = соа
из A1.13) найдем
A1.15)
A1.16)
A1.17)
A1.18)
259

^ Раздел 11
Таким образом, можно считать, что при больших значениях ба-
базы ширина спектра равна удвоенному значению девиации частоты.
Выражение для спектра комплексной огибающей сигнала A1.9)
представим в виде
При нечетной симметрии закона модуляции, как следует из
A1.4), фаза является четной функцией времени, т.е.
ф@=фИ)
Учтем также, что произведение двух четных или двух нечетных
функций дает четную функцию, а произведение четной функции и
нечетной - нечетную. Для нечетной функции интеграл в сим- мет-
ричных относительно нуля пределах равен нулю. Таким образом, в
A1.19) второй и третий интегралы равны нулю. Выражение для
U((x)) запишется в виде:
ти/2 т„/2
и((о)= \v(t)cos(p(t)cosoitdt + i jV(f)sin<p(f)cosiofc#. A1.20)
-т„/2 -т„/2
Функция и((я) является четной
и(т)=и(-(л). A1-21)
Четными функциями частоты являются амплитудный и фазовый
спектры
\U(a] = \U(- 4 ф» = <?,(- w). A1.22)
О характере амплитудного спектра сигнала можно судить по гра-
графикам, приведенным на рис. 11.3 для различных значений базы В.
Так как амплитудный спектр является четной функцией частоты,
260
A1.19)

Импульсные сигналы с частотной модуляцией
графики приведены только для шH. Как следует из анализа гра-
графиков, амплитудный спектр при достаточно больших значениях
базы является довольно равномерным в полосе частот, ограни-
ограниченной значениями ша|, быстро спадает за пределами указанной
полосы, амплитуда пульсаций спектра уменьшается при увеличе-
увеличении базы сигнала В.
11.3. Приближенное определение спектра ЛЧМ сигнала
Упрощение расчета и анализа спектра ЧМ сигнала дает метод
стационарной фазы. Он основан на использовании приближенного
решения интеграла вида
A1.23)
Значение интеграла A1.23) в основном определяется интерва-
интервалом, на котором скорость изменения колебаний, описываемых по-
динтегральной функцией, является минимальной. Этот интервал
определяется окрестностью той точки, в которой функция \\f(t) ста-
стационарна или скорость ее изменения у (t) минимальна. Функция
ij/(f) представляет фазу колебания, поэтому описываемый метод
называется методом стационарной фазы.
Минимальное значение у @ будет около точки, которая нахо-
находится из уравнения
v'(fo) = O. A1.24)
Раскладывая \j/(f) в ряд Тейлора в окрестности точки f0 и огра-
ограничиваясь в разложении двумя первыми слагаемыми, запишем
v(t)^(to) + lM(t-tof. A1.25)
Подставляя A1.25) в A1.23), получаем
с 2
/ = e*k)Je dt. A1.26)
-с
261

Раздел 11
262
Рис. 11.3

Импульсные сигналы с частотной модуляцией
Как правило, замена пределов интегрирования в A1.26) на ±°°
не оказывает заметного влияния на результат и в рамках прини-
принимаемых допущений вполне оправдана. С учетом известного равен-
равенства
V
Знак перед 71/4 в показателе степени совпадает со знаком
V'fe)- Если уравнение A1.24) имеет несколько решений, то инте-
интеграл A1.28) равен сумме интегралов, взятых для каждого из реше-
решений.
Используя метод стационарной фазы, описанный выше, опре-
определяем спектральную плотность комплексной огибающей ЛЧМ сиг-
сигнала, описываемую A1.9). Интеграл в A1.9) идентичен A1.23) при
\|/(f) = <p(f)-a)f. A1.29)
Равенство, из которого определяется точка стационарной фазы,
имеет вид
ф'(?0)-о) = 0. A1.30)
С учетом выражения для cp(f) получим
*^-ш = 0. A1.31)
Точка стационарной фазы равна
to=^. A1.32)
2wa
Таким образом, имеем
263
A1.27)
A1.28)

^ Раздел 11
Wo) = -r--J Ф(У =— =Т' A1.33)
спектральная плотность описывается выражением
„г \г
.tiB\ со .я
ф) = Ье"ТИ +/',Н<соа. A1.34)
л/в
Амплитудный спектр
что совпадает с A1.16).
11.4. Спектр пачки импульсов с внутриимпульсной ЛЧМ
Пачка радиоимпульсов с внутриимпульсной ЧМ описывается
выражением
Как следует из A1.38), спектральная плотность комплексной
огибающей пачки импульсов определяется суммой спектральных
плотностей импульсов, входящих в состав пачки. Спектральную
264
где Vn(t) - комплексная огибающая л-го импульса; Vn(t)= VQe^n^'\
\/0,аH,фл(/) - амплитуда, несущая частота и фаза колебания /т-го
импульса.
Как узкополосный сигнал u(t) может быть представлен в виде
u(t) = Re\v{t)ebot\ A1.37)
где V(t)= Voe^f' - комплексная огибающая сигнала; cp(f) - фаза
сигнала.
Из равенства A1.36) и A1.37) получим
A1.38)
A1.36)

Таким образом, спектральная плотность комплексной огибаю-
огибающей пачки из Л/ радиоимпульсов с внутриимпульсной ЧМ получает-
получается умножением спектральной плотности комплексной огибающей
одиночного импульса на множитель
Импульсные сигналы с частотной модуляцией
плотность комплексной огибающей любого из N идентичных им-
импульсов с внутриимпульсной ЧМ определим как спектральную
плотность комплексной огибающей первого импульса, умноженную
на множитель смещения (разд. 3)
Un(o))=UoHe-k»{n^T, A1.39)
где Uo(o)) - спектральная плотность комплексной огибающей пер-
первого импульса; Т - период следования импульсов в пачке.
С учетом A1.39) из A1.38) получим
учитывающий число импульсов и период их следования в пачке.
При нечетносимметричном законе ЛЧМ функция Uo(o)) описыва-
описывается A1.11). На рис. 11.4, 11.5 представлены графики амплитудных
спектров комплексной огибающей пачки импульсов с внутриим-
внутриимпульсной ЛЧМ для базы сигнала В = 100 и различных значений па-
параметров: Л/и q = T/xu, где ти - длительность импульса, Г-пери-
Г-период следования импульсов в пачке. На рис. 11.4,а и 11.5,а спектры
приведены для достаточно широкого диапазона частот. Но структу-
структура спектра такова, что из рис. 11.4,а и 11.5,а можно получить пред-
представление только об огибающей спектра. О структуре спектра можно
судить по его фрагментам, выделенным для довольно узкой полосы
частот - рис. 11.4,6 и 11.5,6.
Переход от спектральной плотности комплексной огибающей
к спектральной плотности сигнала определяется ранее приведен-
приведенным выражением A1.7).
265
A1.40)
A1.41)

Раздел 11
266
Рис. 11.4

Импульсные сигналы с частотной модуляцией
б)
Рис. 11.5
267

Раздел 11
11.5. Корреляционная функция ЛЧМ сигнала при нечет-
нечетной симметрии закона модуляции
Корреляционная функция ЛЧМ сигнала связана с корреляцион-
корреляционной функцией его комплексной огибающей следующей соотноше-
соотношением (разд. 8)
R{x) = Re[Rv(x)eki)°x\, A1.42)
где Rv(x) - корреляционная функция комплексной огибающей сиг-
сигнала V{t)=Voei4>®.
Корреляционная функция комплексной огибающей сигнала оп-
определяется выражением
где т - смещение во времени.
Для ЛЧМ сигнала с учетом A1.4) запишем
Решая интеграл в A1.44), получим
fl,(x) = ^fi-Kline ovji-Kj , (ц.45)
где
sinx
sincx = .
х
При малых значениях т « хи разность фаз в A1.43) может быть
определена как
ф@-ф(*-т) = -ф'(т)г, A1.46)
а нижний предел интегрирования принят равным -хи12. С учетом
этого выражение для Rv(x) запишем в виде
268
A1.43)
A1.44)

Импульсные сигналы с частотной модуляцией
Выражение A1.47) представим как
2 ти/2 2 ти/2
Rv{x) = ^- jcos\t(p (t)]dt-i^- Jsinfrcp'(*)]<#. A1.48)
-tu/2 -tu/2
Подынтегральное выражение первого слагаемого представляет
четную функцию, второго слагаемого - нечетную функцию време-
времени. Учитывая, что интеграл в симметричных пределах от четной
функции равен удвоенному интегралу от нуля до верхнего преде-
предела, а от нечетной функции равен нулю, выражение для Rv{t) мо-
можем записать в виде
С учетом равенства (p(t) = at получим
A1.49)
A1.50)
К такому же результату придем исходя из A1.45), пренебрегая
вторым слагаемым в круглых скобках. Как следует из A1.45)
и A1.50) корреляционная функция имеет главный и боковые мак-
максимумы. Ширина главного максимума определяется из соотноше-
соотношения
A1.51)
A1.52)
269

^ Раздел 11
Таким образом, при больших значениях В » 1 ширина главного
максимума значительно меньше длительности импульса и при-
приближение, принятое при нахождении корреляционной функции
A1.50), выглядит вполне оправданными. Отношение длительности
сигнала к ширине главного максимума (корреляционного пика) на-
называется коэффициентом сжатия. Для рассматриваемого сигнала,
как следует из приведенных соотношений, он равен базе сигнала
В. Графики модуля корреляционной функции комплексной оги-
огибающей ЛЧМ сигнала для некоторых значений В приведены на рис.
11.6.
Рис. 11.6
11.6. Спектр и корреляционная функция ЛЧМ сигнала с
четносимметричным законом модуляции
При четной симметрии закона модуляции выражение для спек-
спектральной плотности комплексной огибающей ЛЧМ сигнала A1.8)
примет вид
A1.53)
270

Импульсные сигналы с частотной модуляцией
где
Ц((о)=Ц, J е[ 2 jdt. A1.54)
о
Представим A1.53) в виде
ф) = \Ui((o)e*"M + ^(оф-^'М = 2\U,((o}cos(pvM A1.55)
где qvi(co) -аргумент Ц(о)).
Как следует из A1.55), спектральная плотность комплексной
огибающей ЛЧМ сигнала является действительной функцией час-
частоты. Чтобы определить ее, найдем Ц(со).
По аналогии с A1.11) получим
.пВ( со )
ц(й))=ё1 8 Wz.K^j+^j+^a A1.56)
где В = 2fdTu = d u - база сигнала; С(х), S(x) - интегралы Френе-
71
ля;
rd\ w ^ 4E со
v 2waJ 2 шд
Модуль и аргумент L/^co) описываются выражениями
|4 И = |^V№)+^2)]2+[5(zi)+5(z2)]2, A1.57)
/ч тсвГо)^2 + S(z1)+S(z2) н.и.
ФиМ = "— — +arctg 1 2 . A1.58)
8 {ыд) C{Zi)+C{z2)
С учетом A1.57) и A1.58) из A1.55) можно определить ампли-
амплитудный и фазовый спектры комплексной огибающей сигнала
ИфгЩИ^.И; ФИ = (аС03ф(")>° . A1.59,
±71,СО8фи1@))<0
271

Раздел 11
Графики амплитудного спектра, рассчитанные по приведенным
выражениям, изображены на рис.11.7-11.9. Амплитудный спектр
описывается осциллирующей функцией (выражение для \и(иЦ со-
содержит косинус), поэтому его изображение не всегда возможно
(особенно при больших значениях В). На рис. 11.8,а и 11.9.а пока-
показаны огибающие спектров. Характер осцилляции спектра иллюст-
иллюстрируется рис. 11.8,6 и 11.9,6, где даны фрагменты графиков спек-
спектров.
Характер спектра отражает и приближенное решение, получае-
получаемое методом стационарной фазы. Асимптотическое выражение
для спектра найдем с учетом равенства
at2
v(f) = ш/. A1.60)
Точку стационарной фазы получим из уравнения
Она равна
«6=7^. О1-62)
4wd
В этом случае
/, ч лВГйИ "/.4 4718 ...
ф(У=-Н— ; ф('о)=—т- A1-63)
Выражение для спектральной плотности Ц(со) получим с уче-
учетом A1.28) и A1.63) в виде
A1.64)
Спектральная плотность комплексной огибающей ЛЧМ сигнала
при четносимметричном законе модуляции будет описываться вы-
выражением
272
A1.61)

Импульсные сигналы с частотной модуляцией
A1.65)
Имея спектральную плотность одиночного импульса с четно-
симметричной ЛЧМ, можно получить спектральную плотность пач-
пачки идентичных импульсов, используя подход, описанный в п.11.3,
умножая A1.55) на A1.41).
Корреляционную функцию комплексной огибающей определим,
исходя из A1.48). Расчеты показывают, что вторым слагаемым в
A1.48) можно пренебречь. Это объясняется тем, что под знаком
интеграла - синус с малым значением аргумента. Выражение для
корреляционной функции будет аналогичным A1.50).
11.7. Влияние искажений закона модуляции
на характеристики сигнала
При формировании ЛЧМ сигнала возможны искажения закона
модуляции, которые, как правило, носят колебательный характер.
При нечетносимметричном законе ЧМ такие искажения могут быть
учтены при описании oj(f) следующим выражением (рис. 11.10):
273
Рис. 11.7

Раздел 11
274
Рис. 11.8

Импульсные сигналы с частотной модуляцией
275
Рис. 11.9

Раздел 11
A1.66)
Or л
где а = —-, соа -девиация частоты; Асо, 0 - параметры зависи-
зависимости; О. - частота искажений.
Обозначим ?1)=2п/ти и примем Q = pQv p = 1,2,...Фаза сиг-
сигнала cp(f) с учетом A1.66) равна
A1.67)
где Дф = Аш/Q.
Спектральная плотность комплексной огибающей сигнала опи-
описывается выражением
A1.68)
276
Рис. 11.10

Импульсные сигналы с частотной модуляцией
Используя известное разложение
e±/zsinx= ^/„(zJb1*1*, A1.69)
П= -оо
где ln(z) - функция Бесселя первого рода л-го порядка,
выражение A1.68) представим в виде
, . иг i iA<pcos(Qt+e)-Kut
U(o))=Vo J e 2 dt =
-tu/2
т„/2 ja^+JA(f)SJnt+Q_n)Kot
= V0 j e 2 l 2) dt= A1.70)
-т„/2
^ / x "(ei) Tur2 -'V^v-^-
= Ц,^/п(лФ)е { 2) j e *dt.
"=— -tu/2
Вводя интегралы Френеля C(z) и S(z), получим
Ф)=^о^|1/п(Аф)е1 2je 2. х
xdcfzO+Cfz^l-H/lstzO+StzJ]}
где
z 2 z 2
C(z) = I cos dx; S(z) = I sin dx;
о о A1.71)
z1n = —7=[a)d + (co-nQ)J z1fJ = —T^tcoa -(со-пи)]
Ыка ^jna
При отсутствии искажений закона модуляции (Aoo = o) выраже-
выражение A1.71) описывает спектральную плотность комплексной оги-
огибающей ЛЧМ сигнала, совпадает с ранее приведенным выраже-
выражением.
При малых искажениях (малое значение Дсо) можно принять
Аф
/О(ДФ) = 1, /0(Дф) = -^, при л>2 /п(Дф) = 0.
277

Раздел 11
В этом случае A1.71) примет вид
А е-- -I е--
C/(a))=G0(w)+L/1(o))el 2) + U_1(o))e v % A1-72)
где L/O((o), Ц(о)) и C^w) определяются из выражения
I— «. i{w-nQ.f
иМ=УоЛ-^1пЫУ 2а х Ш73)
V а П=-о= '
при п = 0, п = 1 и л = -1.
Графики модуля спектральной плотности комплексной огибаю-
огибающей ЛЧМ сигнала с искажениями закона модуляции приведены на
рис. 11.11. Сравнение приведенных графиков и графиков, полу-
полученных для ЛЧМ сигнала без искажения закона модуляции (рис.
11.4), показывает появление при искажении закона дополнитель-
дополнительных пульсаций амплитудного спектра. Амплитуда и частота пуль-
пульсаций зависят от параметров, характеризующих искажение закона
модуляции Доз и Q .
Корреляционная функция комплексной огибающей рассматри-
рассматриваемого сигнала получается подстановкой в исходное выражение
Rv(x) = yt Je'M'bpMlrf A1.74)
-ти/2+т
фазы, описываемой A1.67),
\/2 _j3z2 z»l2 iaxt +2A<psin— sin q| f--]+6
Я„(т) = -^е'2 J e 2 [I 2J Jdf A175)
-ти/2+т
Используя разложение A1.69), запишем
,г «L -_ г „t\ in(e-~
2
"vti = \e->2 j;/я 2Аф slnH e
2 _— V
t.,/2
A1.76)
I
ei(ai+nu)t^
-т„/2+т
278

Импульсные сигналы с частотной модуляцией
Рис. 11.11
279

A1.77)
При Дш = О (искажения отсутствуют) выражение A1.77) совпа-
совпадает с выражением для корреляционной функции комплексной оги-
огибающей ЛЧМ сигнала.
При малых значениях т (т« ты), что при больших значениях ба-
базы сигнала В практически не накладывает ограничений на рас-
рассматриваемый интервал т, можно принять
/0 2A(psin— = 1; /J 2A(psin— = Дсот;
/J2A<psin— =0, при л>2
Выражение для корреляционной функции запишем в виде
A1.78)
или
A1.79)
где Я0(т) - корреляционная функция комплексной огибающей ЛЧМ
сигнала (без искажений).
Графики модуля корреляционной функции комплексной оги-
огибающей сигнала при 9 = 0 и различных значениях Дсо и р приве-
приведены на рис. 11.12. Анализ графиков показывает, что искажение
закона ЧМ приводит к увеличению р-го бокового лепестка корреля-
280
Раздел 11
После интегрирования в A1.76) получим при т > 0

Импульсные сигналы с частотной модуляцией
ционной функции. Этот рост заметен только, начиная с некоторого
(порогового) значения Дш.
Практический интерес представляет взаимная корреляционная
функция комплексных огибающих ЛЧМ сигнала и ЛЧМ сигнала
с искажением закона модуляции. Она позволяет оценить огибаю-
огибающую сигнала на выходе фильтра, согласованного с ЛЧМ сигналом
при искажении закона модуляции. Выражение для взаимной корре-
корреляционной функции комплексных огибающих ЛЧМ сигнала без ис-
искажения закона модуляции и сигнала с искажением может быть
записано в виде
ти/2 хи/2
Дц2(т) = - J V^t)V\(t-x)dt = ^- Je'M'b^-t)]^ A1.80)
-Хц/2+т -т„/2+т
где V,(f)=Vfoe*Pi^; V2(t) = VQe**2^ - комплексные огибающие сиг-
сигналов с искажением и без искажения закона модуляции.
Фазы сигналов с искажением и без искажения закона модуляции
описываются A1.67) и A1.4).
При 0 = 0
ф1(/) = —-ДфСоэШ; Ф2@ = —• A1.81)
Подставляя A1.81) в A1.80), получаем
at2
Ф1(?)-ф2(?-т) = + art-A(pcosQt,
Яуп(х) = ?о_в-1ЁГ j^f-^cosQ^^Vf.g-'^-. A182)
-ти/2+т
Т(//2 /aTf->Aq>sinf ДГ--|
f e [ 2)dt.
-т„/2+т
Используя A1.69), выражение для Яу (т) представляем в виде
ЯЦг(т) = ^-е"'г ^/„(ДФ)е 2 Je<"**Vd». A1-83)
"=-°° -ти/2+т
Из A1.83) для т > 0 найдем
281

Раздел 11
Рис. 11.12
282

Импульсные сигналы с частотной модуляцией
A1.84)
A1.85)
A1.86)
A1.87)
A1.88)
A1.89)
283
Подставив в A1.85)
При малых искажениях (Лф «1) можно принять
В этом случае A1.88) запишется в виде
При т « хи получим

Раздел 11
Рис. 11.13
График модуля взаимной корреляционной функции комплекс-
комплексных огибающих сигналов при Дер = 0,2 (В = 100) приведен на рис.
11.13.
11.8. Влияние ступенчатой аппроксимации закона изме-
изменения фазы на спектр сигнала
Преимущества цифровой техники заставляют обращаться к ней
и при формировании ЧМ сигналов. Обычно модуляция производит-
производится изменением фазы, закон изменения фазы получается ступенча-
ступенчатым. Ступенчатый характер изменения фазы приводит к искажени-
искажениям характеристик ЛЧМ сигнала.
При несимметричном законе ЧМ фаза описывается четной
функцией A1.4)
A1.90)
где хи - длительность сигнала; Ь = (оа/ти; ша - девиация частоты.
284

Импульсные сигналы с частотной модуляцией
При использовании цифровой техники фаза изменяется скачко-
скачкообразно через заданный интервал времени Т, описывается кусоч-
кусочно-постоянной функцией
(p(nT)=b(ntf, л = 0Д...,Л/ = !^. A1.91)
С учетом шага квантования фазы
(p(n7")=A(pentier bn Т , п = 0,1,...,Л/, A1.92)
I Аф )
где епйег(л') - целая часть х.
Точность аппроксимации закона изменения фазы A1.90) зави-
зависимостями A1.91) или A1.92) определяется выбором параметров
Т и Дф. Выражение для спектра комплексной огибающей ЛЧМ сиг-
сигнала при нечетносимметричном законе модуляции, исходя из
A1.9), можем записать как
т„/2 т„/2
U((o) = 2V0 fcos<p(f)coscofc(T + /2V0 Jsin(p(f)cosco tdt. A1.93)
о о
Переходя в A1.93) от непрерывной функции <p(f) к кусочно-
постоянной ф(а7Г), интегралы в A1.93) представим в виде
xu/2 w-1 (п+1)Г
| созф(фо8ш tdt = У"созф(лГ) | cosoiTdt =
о л=о пТ A1.94)
= 7sinc ^созф(п7)соз(а7 + 0.5)со7",
2 л=о
хи/2 w-1 (п+1)Г
Гз!пф(^)соБсо tdt = VsirKp(nr) |cosaTdt =
о n=o nT A1.95)
= Tsinc ^з1пф(/?7)соз(л + 0.5)соГ.
2 л=0
Подстановка A1.94) и A1.95) в A1.93) дает
285

Раздел 11
J-/V-1
и(ш) = 2V0 Tsinc —^cos(n + 0,5)шТе^пТ). A1.96)
л=0
Амплитудный спектр описывается выражением
где
/V-1
д(со) = ^cos(n + 0,5)torcos9(/?r)i A1.98)
л=0
Л/-1
Б((о) = ]Г cos(n + 0,5)o)rsin(p(nr) A1.99)
л=0
Выражение A1.97) позволяет рассчитать амплитудный спектр
ЛЧМ сигнала с учетом дискретизации по времени фазы (при циф-
цифровом методе формирования фазы). Результаты расчета ампли-
амплитудного спектра с различными значениями интервала дискретиза-
дискретизации Г в виде графиков представлены на рис. 11.14. На рис. 11.14,а.
приведен график спектра при значении интервала дискретизации
Го , выбранного из условия Найквиста и практически не влияющего
на спектр формируемого сигнала. На рис. 11.14,6 приведен график
спектра ЛЧМ сигнала, сформированного с интервалом дискретиза-
дискретизации 2,570. Влияние дискретизации во времени на спектр сигнала
при задании закона изменения фазы заметно уже при Т - 1,25 Го и
значительно - при Г = 2,5Г0.
11.9. Прохождение ЛЧМ сигнала через согласованный
фильтр
Передача сигналов сопровождается шумами, которые искажают
передаваемую информацию. Обнаружение сигнала на фоне шума,
определение его параметров является одной из важных задач при
передаче информации при помощи радиосигналов. Уменьшение
влияния шумов достигается различными способами, в том числе
выбором характеристик цепей, через которые проходит смесь сиг-
сигнала и шума. Цепи, обеспечивающие обнаружение сигнала на фо-
286
A1.97)

Импульсные сигналы с частотной модуляцией
не шума наилучшим образом, называются оптимальными цепями
или оптимальными фильтрами. Описываются оптимальные фильт-
фильтры с помощью импульсной или частотной характеристик. Выбор в
качестве критерия оптимальности максимального отношения сиг-
сигнал/шум на выходе цепи определяет импульсную характеристику
оптимального фильтра как (часть 2)
h(t)=ks(to-t\ A1.100)
где s(t) - сигнал на входе фильтра; к , t0 - нормирующий коэффи-
коэффициент и задержка.
Как правило, в A1.100) постоянная задержка опускается
и выражение для h(t) записывается в виде
h(t)=ks(-t). A1.101)
Соответствующая частотная характеристика оптимального
фильтра определяется как
H((o)=kS'((o)e'iato, A1.102)
где S(co) - спектр сигнала на входе цепи.
Как и при записи выражения для h(t) постоянная задержка обычно
опускается, нормирующий коэффициент к приравнивается единице
H(w) = S». A1.103)
Таким образом, характеристики оптимального фильтра опреде-
определяются характеристиками обнаруживаемого сигнала. Поэтому та-
такие фильтры называются согласованными. Фильтры, согласован-
согласованные с ЧМ сигналами, выполняют и операцию сжатия импульсов.
С учетом сказанного рассмотрение характеристик сигнала на вы-
выходе согласованного с ЛЧМ сигналом фильтра представляет осо-
особый практический интерес.
ЛЧМ сигнал при нечетной симметрии закона модуляции описы-
описывается выражением
A1.104)
где V0,(a0,Tu - амплитуда, несущая частота и длительность сигнала;
287

Раздел 11
Рис. 11.14
288

Импульсные сигналы с частотной модуляцией
а - скорость изменения частоты; Ц (t) = Vo eiat '2 - комплексная
огибающая сигнала.
Согласованный фильтр имеет импульсную характеристику, оп-
определяемую A1.101)
A1.105)
где ^/2а/я - нормирующий коэффициент.
Сигнал на выходе согласованного фильтра определяется сверт-
сверткой импульсной характеристики цепи и сигнала
A1.106)
В радиолокационных системах, в которых производится сжатие
импульсов, особый интерес представляет влияние эффекта Доп-
плера, вызываемого движением обнаруженного объекта, на вы-
выходной сигнал. Выражение для сигнала с учетом частоты Допплера
записывается в виде
, \t\<^-, A1.107)
где \Л (t) = Vo eiat^2+ut; Q - частота Допплера.
Подставляя A1.105) и A1.107) в A1.106), для f>0 запишем
A1.108)
Преобразуя A1.108) и опуская члены с удвоенной частотой,
найдем
т„/2
-т„/2
A1.109)
289

Раздел 11
Решая интеграл в A1.109) и преобразуя полученное решение,
запишем
sin
A1.110)
1/п2т
COSGHf. A1.111)
Огибающая u2{t) с точностью до постоянного коэффициента
совпадает с A1.45). Таким образом, корреляционная функция ЛЧМ
сигнала позволяет описывать огибающую сигнала на выходе со-
согласованного фильтра (при подаче на вход ЛЧМ сигнала).
Анализ выражения, определяющего u2{t,Q), и расчетного вы-
выражения, полученного для ЛЧМ сигнала, показывает, что они сов-
совпадают с выражениями для обобщенной корреляционной функции
(разд. 8).
Учитывая следующее равенство
а = и>д/ти,
где сод -девиация частоты,
A1.110) можем переписать в виде
A1.112)
При больших значениях wa (при больших значениях базы сиг-
сигнала В = шдти/п) можно принять
A1.113)
290

Импульсные сигналы с частотной модуляцией
Максимум функции u2(t,Q) достигается при значении t, полу-
получаемом из следующего уравнения:
Qxu/2 + (Mdt = 0,
т.е. при f = -QTu/2(oa, где eod -девиация частоты.
11.10 Импульсные сигналы с нелинейной частотной мо-
модуляцией
Для сигналов с внутриимпульсной ЧМ нелинейный закон модуля-
модуляции - наиболее общий случай. Рассмотрение НЧМ сигналов расши-
расширяет рамки анализа импульсных ЧМ сигналов, позволяет исследовать
влияние закона модуляции на характеристики сигнала.
11.10.1. НЧМ сигналы со степенным законом модуляции
Импульсный ЧМ сигнал описывается выражением
где V(t) - комплексная огибающая сигнала;
Vo,coo,(p(f) - амплитуда, несущая частота и фаза сигнала; хи- дли-
длительность импульса.
Частота сигнала определяется как
to@ = too+-$. A1.115)
at
Достаточно общей нелинейной зависимостью для переменной
составляющей частоты, можно считать, является степенная зави-
зависимость. Поэтому при рассмотрении НЧМ целесообразно рассмот-
рассмотреть ее в первую очередь.
При нечетной симметрии закона модуляции (наиболее распро-
распространенный на практике случай) выражение для частоты запишем
в виде (рис.11.15)
w@ = coo + b|f|Psign@, \t\<~, A1.116)
291
A1.114)

Раздел 11
определяющий характер изменения частоты;
Sign(f) = l-1, t<o.
Фаза сигнала в этом случае
A1.117)
Спектральная плотность комплексной огибающей сигнала опре-
определяется выражением
A1.118)
Рис. 11.15
292
девиация частоты; р - показатель степени,

Импульсные сигналы с частотной модуляцией
Интегрирование в A1.118.) с использованием известных решений
возможно только при р = 1 (линейный закон модуляции). В общем
случае решение может быть получено только численным методом.
Спектральную плотность комплексной огибающей сигнала пред-
представим в виде
т„/2 т„/2
A1.119)
ти/2
+ /2V0 J sirxp(f)cos ш tdt.
о
Разобьем интервал [О, iJ2\ на N участков длительностью
At = xu/2N. Аппроксимируем (p(f) кусочно-постоянной функцией,
значения которой совпадают с cp(f) в точках разбиения. При такой
аппроксимации фаза на n-м участке разбиения описывается выра-
выражением
cp(nAf) = -^-(nAt)p+\ n = 0,1, 2,..., N-1. A1.120)
р + 1
Подставляя A1.120) в подинтегральные выражения A1.119),
получим
xu/2 w-1 (Л+1)ДГ
| coscp(f)coso)fc# = Vcoscp(nAf) jcosoofcft =
о "=о ш A1.121)
= —sin Vcos9(nAf)cos[(n + 0.5)o)Afl
ш 2 ?o
tu /2 ^T (п+1)ЛГ
j sirxp(f)coscofc/f s Vsiri9(nAf) j cos oo faff =
о л=0 nAt /-j-j -j22)
= —sin y""sin(p(nAf)cos[(/? + 0.5)coAf}.
л=0
С учетом A1.121) и A1.122) расчетное выражение для 1/(со)
представим в виде
293

Раздел 11
A1.123)
Графики амплитудного спектра комплексной огибающей сигнала
при различных значениях р, полученные в результате расчета
A1.123), приведены на рис. 11.16. Анализ графиков показывает,
что при р =1 (ЛЧМ) спектр является достаточно равномерным в
полосе частот |со| < соа. При уменьшении р (р<1) максимум спектра
появляется на |со| = соа. При увеличении р (р>1) максимум спектра
появляется на частотах близких к ш = 0 . Чем больше р отличается
от единицы, тем более выражен максимум.
Корреляционная функция комплексной огибающей сигнала мо-
может быть определена с использованием выражения A1.49) с под-
подстановкой в него
y'(t)=btp. A1.124)
После подстановки выражение для #v(x) примет вид
Д,М=Ч? Jcos[x(p'@3 dt =V02 \cos(bztp)dt. A1.125)
о о
Решение A1.125) в конечном виде возможно только при р =1 -
выражение A1.50) и р = 2. Для р = 2 из A1.125) получим
A1.126)
где С(х) - интеграл Френеля; В - база сигнала.
В общем случае (при произвольном значении р) решение инте-
интеграла A1.125) возможно только численно. Используя кусочно-
постоянную аппроксимацию
A1.127)
294

Импульсные сигналы с частотной модуляцией
интеграл в A1.115) представим в виде
V2 Л/-1
jcos[zq>'(t)]dt = ^cos[x(p'(rtAO] • A1.128)
О п=О
С учетом A2.15) выражение A2.12) представим в виде
A1.129)
Графики модуля корреляционной функции |Яу(т)|, полученные
при расчете A1.129) при различных значениях р, приведены на
рис. 11.17. Для сравнения дан и график Яу(т)| для ЛЧМ - сигнала
(р = 1). Анализ графиков показывает, что при р < 1 огибающая
имеет лепестковую структуру. По мере уменьшения р главный
максимум сужается, а уровень боковых лепестков растет. При
р >1 лепестковая структура огибающей пропадает, колебания
огибающей сглаживаются, появляется «пьедестал». Сравнение
корреляционной функции комплексной огибающей сигнала со
степенным законом модуляции и ЛЧМ сигнала показывает, что
при р > 1 уровень боковых лепестков уменьшается. Корреляцион-
Корреляционная функция становится более удобной при использовании ее в
системах, где необходимо повысить разрешающую способность
при сжатии сигнала.
11.10.2. НЧМ сигналы с законом модуляции, описываемым
тригонометрическими функциями
Рассмотрим зависимость w(f), описываемую выражением
(рис.11.18)
w(f) = wo + coa sin Ш, Щ< — , A1.130)
где (О0,(х>д - несущая частота и девиация; ти - длительность им-
импульса; 0, = п/хи.
Фаза сигнала
ф(/)=еA-соБШ) |/|<bL t A1.131)
295

296
Раздел 11

Рис. 11.16
297
Импульсные сигналы с частотной модуляцией

Раздел 11
298

о
Рис. 11.17
299
Импульсные сигналы с частотной модуляцией

Раздел 11
где В - — ~ д " - база сигнала.
Q п
Спектральная плотность комплексной огибающей сигнала опре-
определим, подставив A1.131) в A1.118),
т„/2 хи/2
U(o))=VQ JVM0-»']rt = yo |е'[вA-созш)-со^ A1.132)
-V2 -хи/2
Используя A1.69), из A1.132) получаем
ф)=1/оедаТ] ?/п(в)в
A1.133)
Полученное выражение представляет разложение спектральной
плотности комплексной огибающей сигнала в ряд по базисным
функциям
. (со - nu)iu
2
Коэффициенты слагаемых определяются произведением функ-
. я
ций Бесселя /„(??) и множителя е 2 . Число членов ряда
Рис. 11.18
300

Импульсные сигналы с частотной модуляцией
бесконечно. Однако при расчете, учитывая свойства Бесселевых
функций, можно ограничиться числом слагаемых N, зависящим от
В (разд. 10).
Корреляционная функция комплексной огибающей сигнала оп-
определяется A1.43)
2
-т„/2+т
Воспользовавшись разложением A1.69), выражение для Hv(x)
представим в виде
т„/2
При т « ти ( при больших значениях В , это условие практиче-
практически не накладывает ограничений, о чем указывалось ранее ) можно
принять
2Bsin— = о)ат.
301
Подставляя в A1.134) выражение для (p(f), A1.131), запишем
A1.134)
A1.135)
A1.136)
A1.137)

Имея спектральную плотность импульсного ЧМ сигнала, можно
получить спектр соответствующего периодического сигнала (сигна-
(сигнала, получающегося периодическим повторением импульсного сигна-
сигнала с периодом Г = хи). Проиллюстрируем это положение на приме-
примере тонально модулированного ЧМ сигнала (разд. 10). Для этого рас-
рассмотрим импульсный ЧМ сигнал с законом модуляции, описывае-
описываемым зависимостью
где (О0,соа - несущая частота и девиация; ти - длительность им-
импульса; О. = п/хи.
Фаза сигнала
<p@=msinQf, A1.140)
где
а A1.141)
Спектральная плотность комплексной огибающей такого сигна-
сигнала равна
A1.139)
A1.142)
Раздел 11
Выражение для Яу(т) запишется в виде
302
A1.138)

Импульсные сигналы с частотной модуляцией
Полученное выражение представляет разложение функции
U((?>) в ряд по базисным функциям
. (со - пп}си
sine-1 —,
2
с коэффициентами, определяемыми функциями Бесселя 1п(т).
Перейдем к непрерывному, периодическому сигналу с тональ-
тональной модуляцией, который получается периодическим повторением
рассмотренного импульсного сигнала. Период сигнала Т = ти.
Спектр такого сигнала определяется из соотношения
An=j\S(nn), A1.143)
где S((d) - спектральная плотность исходного импульсного сиг-
сигнала.
Как следует из A1.142), функции Бесселя ln(m) определяют
значения спектральной плотности S((o) и спектра непрерывного
сигнала Ап на частотах соо ± nQ.. С учетом этого получим
An = Voln(m). A1.144)
Следовательно, для непрерывного ЧМ сигнала можем записать
СО
u(t) = Vo ]Г ln (m)cos(co0 - пп) t, A1.145)
л=-°°
что совпадает с ранее полученным выражением (разд. 10). Таким
образом, используя спектральную плотность импульсного ЧМ сиг-
сигнала, перешли к известному разложению тонально модулирован-
модулированного сигнала.
11.10.3. НЧМ сигналы с законом модуляции, описываемым
суммой линейной и тригонометрической функций
Рассмотрим зависимость co(f), описываемую выражением
(рис. 11.19)
co(f) = co0 + at + Дсо sin Qt,
A1.146)
М<;—-
м 2
303

Раздел 11
где а = 2(ад/ти, шд-девиация частоты; Аш - параметр зависи-
зависимости; О. = 2п/ти.
Зависимость A1.146) может рассматриваться как один из видов
нелинейных зависимостей u>(t), встречающихся на практике, может
описывать и линейный закон ЧМ с искажениями. Фаза сигнала, со-
соответствующая A1.146), определяется выражением
at2
q(t) = mcosQt, A1.147)
где
Спектральная плотность комплексной огибающей сигнала
Рис. 11.19
304
- база сигнала.

Импульсные сигналы с частотной модуляцией
-т„/2
Решая интеграл A1.149), получим
305
С учетом A1.69) выражение A1.148) перепишем в виде
A1.148)
A1.149)
A1.150)
где
Графики амплитудного спектра |1/(ш)|, полученные в результате
расчета по A1.150) при различных значениях Аы, приведены на
рис. 11.20 (Да) @) и на рис. 11.21 (дсо > 0). Как следует из анализа
графиков, спектр комплексной огибающей сигнала сосредоточен в
полосе частот jcoj < соа. Вид спектра определяется зависимостью
co(f). На частотах, для которых скорость изменения w(f) увеличи-
увеличивается, величина \U(oi\ уменьшается.
Корреляционная функция комплексной огибающей сигнала оп-
оепеляется вьюажением (т > О)
A1.151)

___ Раздел 11
С учетом A1.151) выражение для Я(т) запишем в виде
2
-т„/2+т
Решая интеграл в A1.154), находим
A1.152)
A1.153)
A1.154)
A1.155)
Для малых значений т«ти выражение для Яу(т) может быть
упрощено
Графики модуля корреляционной функции комплексной оги-
огибающей сигнала, построенные для различных Дсо, приведены на
рис. 11.22 и рис. 11.23 (на рис. 11.22 при Дох 0, на рис. 11.23 при
Дсо > 0). Модуль корреляционной функции имеет характерную ле-
лепестковую структуру, которая изменяется при изменении как знака,
так и абсолютного значения Дм. При достаточно больших значе-
значениях (по абсолюной величине) Дсо > 0 лепестковая структура на-
нарушается.
306
Преобразовав A1.152), получим

Рис. 11.20
307
Импульсные сигналы с частотной модуляцией

Раздел 11
Рис. 11.21
308

Импульсные сигналы с частотной модуляцией
Рис. 11.22
309

Раздел 11
Рис. 11.23
310

Раздел 12.
КОДИРОВАННЫЕ СИГНАЛЫ
Особую группу модулированных сигналов составляют коди-
кодированные сигналы, которые получаются путем модулирования
гармонического колебания упорядоченной последовательностью
импульсов. Такие последовательности называются кодовыми.
Наибольшее применение нашли двоичные кодовые последова-
последовательности, которые описываются символами 0 и 1 или -1 и 1
(рис. 12.1). В зависимости от параметра несущего гармонического
колебания, на который воздействует кодовый сигнал, различают
амплитудно-кодированные, фазо-кодированные и частотно-
кодированные сигналы.
Кодовые последовательности используются в различных радио-
радиотехнических системах. Некоторые виды кодовых последовательно-
последовательностей - при формировании радиолокационных сигналов с требуе-
требуемыми корреляционными свойствами. Такие сигналы называют шу-
моподобными.
В разделе дается описание и анализ основных характеристик
кодированных сигналов.
Рис. 12.1
311

^ Раздел 12
12.1. Описание кодированных сигналов
Кодированные сигналы имеют вид последовательности (пачки)
радиоимпульсов одинаковой формы и длительности, отличающих-
отличающихся друг от друга значениями амплитуд, начальных фаз или частот
гармонического несущего колебания.
Одиночный радиоимпульс последовательности описывается
выражением
"nW = an^Wcos[(oH + a)n> + 9n], A2.1)
где ап, оH + (ол,фл - амплитуда, частота и начальная фаза гармо-
гармонического колебания длительности Г на интервале времени (п-1)Т
< t < пТ; щ - центральная частота последовательности радиоим-
радиоимпульсов; rn(t) - функция, описывающая форму импульса.
Обычно используются прямоугольные импульсы, для которых
гп(()=геС([(-(л-1)т]={1|(")Г5'-ПГ' A2.2)
[О, при других значениях t.
Кодированный сигнал описывается выражением
N
u(f)=^anrn(f)cos[(o)o+o)n> + pn], 0<t<NT. A2.3)
л=1
Последовательности символов амплитуд {ссл}, фаз {фл}
и частот {соп} составляют кодовые последовательности; N - число
символов (длина) кодовой последовательности. Кодовые последо-
последовательности определяют закон изменения амплитуды, фазы и час-
частоты гармонического несущего колебания.
В зависимости от вида модуляции различают:
амплитудно-кодированные сигналы (изменяется an; фл = 0, сол = 0);
фазо-кодированные сигналы (изменяется фл; ап = 1, шл = 0);
частотно-кодированные сигналы (изменяется сол; ап = 1, фл = 0);
сигналы со смешанными видами модуляции (изменяются одновре-
одновременно несколько параметров).
Кодированный сигнал, как правило, узкополосный. Выражение
для него может быть записано в комплексной форме
и@ = РеГ\/@е^1, 0<t<NT, A2.4)
312

Кодированные сигналы
- комплексная огибающая одиночного радиоимпульса A2.1).
Таким образом, кодированный сигнал описывается как последо-
последовательность радиоимпульсов, которые отличаются друг от друга
лишь комплексными амплитудами.
Основными характеристиками кодированных сигналов являются
спектр и корреляционная функция. Их удобнее определять через
соответствующие характеристики комплексной огибающей сигнала.
Для комплексной огибающей A2.5) эти характеристики описывают-
описываются следующими выражениями:
спектральная плотность
A3.5)
A2.6).
A2.7)
A2.8)
С учетом очевидности перехода от U((o) и Rv(t) к спектральной
плотности и корреляционной функции кодированного сигнала, ана-
анализ кодированных сигналов в дальнейшем ограничен рассмотре-
рассмотрением характеристик только комплексной огибающей. Указанные
характеристики определены применительно к различным видам
модуляции несущего колебания кодовой последовательностью.
12.2. Амплитудно-кодированные сигналы
Амплитудно-кодированный (АК) сигнал получается в результате
амплитудной модуляции несущего гармонического колебания ко-
кодовой последовательностью.
313
корреляционная функция
где
- комплексная огибающая кодированного сигнала;

Раздел 12
A2.9)
Кодовая последовательность {ап} определяет закон скачкооб-
скачкообразного изменения амплитуды сигнала. При двоичном коде ал
принимает только два значения: 0 и 1. Таким образом, АК сигнал
A2.9) представляет последовательность радиоимпульсов, которые
отличаются лишь значениями амплитуд.
Комплексная огибающая сигнала
A2.10)
совпадает с его огибающей и представляет последовательность
видеоимпульсов rn(t) с амплитудами ап @ или 1).
На рис. 12.2 и 12.3 приведены примеры АК сигналов.
12.2.1. Спектр комплексной огибающей АК сигнала
Спектральная плотность комплексной огибающей АК сигнала
определится путем подстановки A2.10) в A2.7)
Рис. 12.2
314

Кодированные сигналы
л=1
где
A2.11)
A2.12)
- спектральная плотность первого импульса.
Для прямоугольного импульса имеем (разд. 3)
A2.13)
A2.14)
Выражение A2.11) запишем в виде
Здесь SA(<a) описывает спектральную плотность кодовой по-
последовательности {ал}
315

_____ Раздел 12
A2.16)
A2.17)
A2.18)
A2.19)
л=1
Графики амплитудного спектра \SA((o\ для кодовых последова-
последовательностей {ал} (рис. 12.2 и 12.3) приведены на рис. 12.4,а и
12.5,а. Графики изображены для ш> 0, так как амплитудный спектр
симметричен относительно нулевой частоты. Амплитудный спектр
кодовой последовательности ^(ш)) является периодическим с
периодом 2п/Т, имеет осциллирующий характер. Спектр АК сигна-
сигнала представляет результат наложения на спектр прямоугольного
импульса (штриховая линия) спектра кодовой последовательности
(рис. 12.4,6 и 12.5,6).
316
A2.15)
Как следует из A2.14), спектр сигнала определяется спектром
первого импульса и спектром кодовой последовательности с пе-
периодом 2п/Т.
Амплитудный и фазовый спектры комплексной огибающей АК
сигнала находятся из A2.14) как
где

Кодированные сигналы
317
Рис. 12.4

Раздел 12
б)
Рис. 12.5
318

Кодированные сигналы
Для двоичной кодовой последовательности, имеющей М еди-
единиц,
\SA@] = M,\U{0] = TM.
Ширина спектра АК сигнала может быть определении как
Аа)ЛК=2тс/Г.
База АК сигнала - произведение длительности сигнала NT на
ширину спектра Асолк
B=NT^t = N, A2.20)
равна длине кодовой последовательности.
12.2.2. Корреляционная функция комплексной огибающей
АК сигнала
Корреляционная функция комплексной огибающей АК сигнала
определяется A3.8) с подстановкой в него A3.10)
Rv^) = ^f,CLnaklrn(t)rk(t-T)dt. A2.21)
Интеграл в A2.21) с учетом A2.2) запишется в виде
оо оо
\rn{t)rk(t-T)dt= [rect[t-{n-\)T\ect[t-T-{k-i)T]dt =
A2.22)
= \rect(t)rect(t-Ti)dt,
где
Ti=[f-(n-i)r]-[f-x-(/c-i)r] = T-(n-/f)r. A2.23)
Вводя корреляционную функцию одиночного импульса
Я0(т)= jrect(t)rect(t-x)dt, A2.24)
выражение A2.21) перепишем в виде
319

Раздел 12
^М^ЕЕ^ЛМ"-*O]' A2.25)
где все ап и а^, индексы которых находятся вне диапазона
{,2,...,Л/}, равны нулю.
Замена в A2.25) индекса суммирования на т = п-к приводит к
выражению для Rv(t) в виде
^W = ^Z ^п^п-т^-тТ). A2.26)
Величина
RA(m)= f>nccn_m A2.27)
Л=-оо
представляет корреляционную функцию кодовой последователь-
последовательности. В A2.27) все an,an_m с индексами вне диапазона {1,2,...,Л/}
равны нулю. Подставляя A2.27) в A2.26), получим
^M = -i Х^(т)Я0(т-тГ). A2.28)
Очевидно, что Я„(/??) = О при m>N и m<-N. С учетом этого
выражение для корреляционной функции может быть записано
в виде
1 Л/-1
ЯЛт)— У^лН^-тТ), A2.29)
^ m=-(w-i)
где
N
я>,М= Z"^-^ я^(-т)=я/»Н- A2-3°)
n=m+1
Выражения A2.29) и A2.30) показывают, что корреляционная
функция комплексной огибающей АК сигнала представляет сумму
повторяющихся с интервалом Т корреляционных функций одиночно-
320

Кодированные сигналы
го импульса A2.24), максимальные значения, которых определяются
корреляционной функцией кодовой последовательности RA(m).
Для прямоугольного импульса (разд. 5)
A2.31)
i / i ¦ ¦
При т = 0
для двоичной кодовой последовательности
Яи@)=™- A2.33)
При значениях т = тТ
Rv(mT) = ^RA(m)- A2-34)
На рис. 12.6 приведены графики корреляционных функций
Rv(t) для АК сигналов, изображенных на рис. 12.2 и 12.3 (для
т > 0). Корреляционные функции получены как результат наложе-
наложения треугольных импульсов A2.31), обозначенных на рисунке
штриховыми линиями, с амплитудами A2.34), длительностью 27,
следующих с интервалом Т.
12.3. Фазо-кодированные сигналы
12.3.1. Описание ФК сигнала
Фазо-кодированный сигнал представляет последовательность
прямоугольных радиоимпульсов с одинаковыми амплитудами
и получается в результате модуляции фазы гармонического несу-
несущего колебания кодовым сигналом (последовательностью).
Они описываются выражением
u(t)=V0cos[(d0t + <p(t)],0<t<NT, A2.35)
или в комплексной форме
321

Раздел 12
Рис. 12.6
u(t) = РеГ1/@е~*°°'~| ,0<t<NT, A2.36)
где V(t)= l/oe*p^^ - комплексная огибающая кодированного сигнала;
322

Кодированные сигналы
l/o,coo,(p(f) - амплитуда, несущая частота и фаза сигнала; Г-дли-
Г-длительность одного импульса; Л/ - число радиоимпульсов кодирован-
кодированного сигнала.
За время одного импульса фаза может быть постоянной, меня-
меняясь скачком от импульса к импульсу. Кодированный сигнал в этом
случае представляет гармоническое колебание с фазовой манипу-
манипуляцией (рис.12.7).
Возможны сигналы с фазой, непрерывно изменяющейся в течение
определенного интервала времени - сигналы с непрерывной фазой.
Появление таких сигналов связано прежде всего со стремлением по-
получить лучшие спектральные характеристики сигнала, обеспе- чи-
вающие более высокое качество передачи информации
и помехоустойчивость системы.
В общем случае выражение для фазы кодированного сигнала
на одном интервале записывается в виде
п
<р@ = 2я^ ckhkq(t -kT),nT<t<{n +1) Г, A2.37)
к=0
где {ск} - кодовая последовательность; hk называют индексом
модуляции на к-м интервале.
Различают сигналы с постоянным индексом модуляции и с цик-
циклически изменяющимся индексом модуляции. Функция q(t)
в A2.37) называется фазовым импульсом. На интервале [0,17] она
изменяется от 0 до 1/2 L - длина фазового импульса (часто L = 1).
Фаза при этом изменяется в пределах nckhk .
Выражение для частоты сигнала запишется в виде
d п
^) = —[^ + ф)] = щ+2п?скЬкдA-кТ),
/с=0 ' \ • /
n7<f<(n + iO
Рис.12.7
323

Раздел 12
Функция g(t) описывает частотный импульс. Его длительность
равна LT. На рис. 12.8 изображены графики некоторых видов фа-
фазовых и частотных импульсов. На рис. 12.8,а приведен график сту-
ступенчатой функции, на рис. 12.8,6- линейной функции q(t). Линей-
Линейной зависимости q(t) соответствует ступенчатая функция g(t) -
частотная манипуляция. Более плавное изменение фазы может
быть описано различными функциями. Примером такой зависимо-
зависимости является зависимость, описываемая тригоно- метрической
функцией (рис. 12.8,в)
A2.39)
Изменение фазы сигнала во времени поясняется фазовой диа-
диаграммой (рис. 12.9). График на рис. 12.9 иллюстрирует возможные
изменения функции ф(?), описываемой линейной (более тонкие
линии) и тригонометрической функциями.
в;
Рис. 12.8
324

Кодированные сигналы
Рис. 12.9
Характеристики ФК сигналов удобнее определять через харак-
характеристики их комплексных огибающих:
спектральная плотность
A2.40)
A2.41)
корреляционная функция
Указанные характеристики при различных законах изменения
фазы: скачкообразном и линейном (скачкообразный закон измене-
изменения частоты) и описываемом тригонометрической функцией, опре-
определены в [16]. Ниже рассматриваются характеристики ФК сигнала
только со скачкообразным изменением фазы и частоты.
12.3.2. Спектр ФК сигнала со скачкообразным изменением
фазы
Сигналы со скачкообразным изменением фазы нашли практиче-
практическое применение в радиолокации, связи, системах управления и
других областях техники. Кодированный сигнал представляет по-
325

При использовании бинарного кода фаза принимает значение О
или л. В этом случае:
Спектральная плотность комплексной огибающей ФК сигнала
может быть определена из A2.40) подстановкой A2.43). При
rn(f) = 1 имеем
N пТ
U(u))=^bn je-^dt. A2.44)
n=1 (л-1)Г
Спектральная плотность последовательности импульсов опре-
определяется как сумма спектральных плотностей идентичных по фор-
форме импульсов, смещенных во времени каждый относительно пре-
предыдущего на интервал времени Т. Используя свойства преобра-
преобразования Фурье, A2.44) запишем в виде
^)=S0(w)f>ne-'(n-1K A2.45)
л=1
где
326
^ Раздел 12
следовательность радиоимпульсов, у которых от импульса к им-
импульсу скачком изменяется только фаза фп.
где rn(t) - огибающая одиночного, как правило, прямоугольного
импульса.
Кодовая последовательность {фл} задает закон изменения фа-
фазы. Комплексную огибающую сигнала удобнее представить
в виде
A2.42)
A2.43)

Кодированные сигналы
- спектральная плотность первого импульса.
Для прямоугольного импульса
S0(o))=7sinc—е". A2.46)
Выражение для 1/(а)) перепишем в виде
U{(o)=So(ai)sM A3.47)
<
где
- спектральная плотность кодовой последовательности.
Квадрат модуля кодовой последовательности определим из
A2.48) как
Используя формулу Эйлера и учитывая, что косинус является
четной функцией, а синус - нечетной, из A2.49) получим
327
A2.49)
Выражение для фазового спектра найдется из A2.48) в виде
A2.50)
A2.51)
Амплитудный спектр комплексной огибающей получается из
A2.47) как произведение модулей |S0(co)| и \Sk{(i)\:

Раздел 12
^(a)) = |S0(o)|S^D A2.52)
а фазовый спектр - как сумма аргументов Ф0(и>) и Ф/Доа):
ф(а)) = фо(ш)+фл(са). A2.53)
График амплитудного спектра сигнала, модулированного кодо-
кодовым сигналом, изображенным на рис. 12.1, приведен на рис.
12.10,6.
328
Рис. 12.10

Кодированные сигналы
Спектр комплексной огибающей сигнала представляет резуль-
результат перемножения амплитудного спектра прямоугольного импульса
(штриховая линия) и амплитудного спектра кодовой последова-
последовательности (рис. 12.10,а).
При (о = 0 имеем
\So(o] = fjbm\U(o] = Tfjbn. A2.54)
л=1 л=1
Ширину спектра определим как
Дсо = 2тс/Т. A3.55)
Произведение длительности сигнала и ширины его спектра -
база сигнала, равна
Б = А/Г— = Л/. A2.56)
271
Таким образом, база рассматриваемого ФК сигнала определя-
определяется длиной кодовой последовательности.
12.3.3. Корреляционная функция ФК сигнала
со скачкообразным изменением фазы
Корреляционная функция комплексной огибающей ФК сигнала
определяется A2.41) с учетом A2.43)
^W = ^ZZbAj^(^(f-^- A2.57)
л=1 /с=1
Интеграл в A2.57) запишем в виде
оо оо
jrn(t)rk{t-x)dt= jr[t-{n-^T}[t-T-(k-^T]dt =
A2.58)
оо
= \r{t)r{t-x,)dt,
—оо
где r(t) - огибающая одиночного импульса,
T1 = [f-(n-i)r]-[f-x-(/c-i)r] = x-(n-/c)r.
329

Раздел 12
Обозначим Я0(т) корреляционную функцию одиночного им-
импульса,
Ro(*)= ]r(t)r{t-x)dt, A2.59)
а выражение A3.57) запишем в виде
A2.60)
В A2.60) все Ьп и Ьк, индексы которых находятся вне диапазо-
диапазона {1,2,...,Л/}, равны нулю. Произведя замену индекса суммирова-
суммирования т = п - к, запишем
A2.61)
A2.62)
представляет корреляционную функцию кодовой последо- ватель-
ности. С учетом A2.62) получим
A2.63)
Функция Rk(m) - четная, т.е.
A2.64)
Обычно импульсы кодированного сигнала имеют прямоуголь-
прямоугольную форму
330
A2.65)
В A2.61)

Кодированные сигналы
В этом случае
^W=rfi-Ji| И<Г. A2.66)
Как следует из A2.61) и A2.62), корреляционная функция ком-
комплексной огибающей ФК сигнала представляет сумму корреляци-
корреляционных функций одиночных импульсов, максимальные значения
которых определяются значениями корреляционных функций ко-
кодовой последовательности.
При т = 0
Я0@)=Т;( Rk{o) = J]b2n=N; fy@) = ^. A2-67)
л=1 tL
При т = тТ
Rv(mT) = ^Rk(m). A2.68)
Для бинарных кодов функцию Rk(m) удобно определять сле-
следующим образом [40]. Составляется таблица с верхней строкой,
описывающей кодовую последовательность {bn}, и левым столб-
столбцом, описывающим ту же кодовую последовательность, если, чи-
читать ее сверху вниз {b_n}, рис. 12.11. В средней части таблицы за-
записывается результат перемножения элементов {bn} и {Ь_л}. При
этом, если элемент {b_n} имеет знак плюс, то элемент {bn} запи-
записывается в строку без изменения, если знак минус - то со сменой
знаков всех элементов. Запись производится со смещением на
один элемент вправо по отношению к предыдущей строке. Сумма
элементов каждого вертикального столбца дает значение Rk(m).
На рис. 12.11 составлена таблица, а по результатам расчета по-
построен график корреляционной функции комплексной огибающей
ФК сигнала, промодулированного кодовой последовательностью,
изображенной на рис. 12.1.
12.3.4. Коды Баркера
Кодовые сигналы, используемые при фазовой модуляции, могут
быть самыми разнообразными. Их выбор зависит в первую оче-
очередь от того, в какой радиотехнической системе используется сиг-
331

Раздел 12
нал, какие функции выполняет система. Не проводя анализа воз-
возможных видов кодов, используемых при угловой модуляции, оста-
остановимся на наиболее известных и рассмотрим их как иллюстрацию
общих положений.
В радиолокации хорошо известны коды Баркера и /W-после- до-
вательности. Модуляция ими высокочастотных сигналов обеспечи-
обеспечивает высокую разрешающую способность системы. Корреляцион-
Корреляционная функция кодированных сигналов имеет узкий центральный пик
и напоминает корреляционную функцию шума. Такие сигналы на-
называются шумоподобными.
Коды Баркера {bn} определяются как двоичные последователь-
последовательности, имеющие корреляционную функцию вида
Рис. 12.11
332

Кодированные сигналы
A2.69)
Таблица 12.1
Коды Баркера
Определив корреляционную функцию кода Баркера, найдем со-
соответствующую спектральную плотность энергии
A2.70)
где Rk=±l.
Используя известное соотношение [12]
A2.72)
333
Существует всего девять кодов Баркера (табл. 12.1).
Функция Rk(m) является четной. С учетом этого и A2.69) выра-
выражение A2.70) запишем в виде
A2.71)

^ Раздел 12
выражение для \Sk((o\ представим в виде
A2.73)
A2.74)
A2.75)
Корреляционные функции комплексных огибающих сигналов с
кодами Баркера определяются A2.63), их графики приведены в
[15]; там же приведены графики амплитудных спектров комплекс-
комплексных огибающих сигналов.
12.3.5. /W-последовательности
Из кодовых последовательностей, нашедших практическое
применение, особое место занимают последовательности, полу-
получаемые с помощью генераторов, выполненных на регистрах сдви-
сдвига; из них в первую очередь - линейные последовательности мак-
максимальной длины или /^-последовательности. Стремление улуч-
улучшить корреляционные свойства сигналов привело к созданию на
основе М- последовательностей других последовательностей, сре-
среди которых особое место занимают последовательности Голда,
Кассами и некоторые другие.
Схема генератора, формирующего ^-последовательность, в са-
самом общем виде изображена на рис. 12.12. Основой генератора яв-
является регистр сдвига, выполненный на триггерах (Т). Выходы неко-
некоторых каскадов регистра через сумматоры по модулю 2 подключены
к входу первого каскада. Двоичная последовательность
334

Кодированные сигналы
Рис. 12.12
на выходе генератора зависит от числа каскадов регистра, их
начального состояния и вида обратной связи.
Формируемая двоичная последовательность является периоди-
периодической, подчиняется принципу суперпозиции. Вследствие этого та-
такая последовательность может рассматриваться как линейная, а
генератор называется линейным. Максимальное число символов
последовательности за один период составляет
A2.76)
где т - число каскадов.
Зависимость Л/ от числа каскадов генератора т приведена в
табл. 12.2 (/77 < 13). Число Л/ определяет период кодовой после-
последовательности
T0 = NT, A2.77)
где Т - длительность одного символа.
Таблица 12.2
Число М-последовательностей, формируемых
т -каскадным генератором
335

Раздел 12
Последовательность, имеющая максимально возможный для
выбранного способа генерирования период, называется макси-
максимальной или М-последовательностью. Последовательность,
имеющая меньший период, называется немаксимальной.
Генерируемую двоичную последовательность можно получить,
если записать уравнения каждого из триггеров регистра. Символ на
входе первого триггера в п-ом такте определяется уравнением
х0к = ХМ< + Х2к + ••• + х{т-\)к + хтк ¦ A2.78)
В уравнении A2.78) х^к представляет символ на выходе 1-го
триггера в к-ом такте. Учитываются только те триггеры, которые
входят в состав обратной связи. Символ хОк в следующем /с+1-м
такте переходит на вход триггера Т\
Xj\k+1 ~ х1/с + Х2к "•"••• + x(m-1)k + хтк ¦ A2.79)
На входе остальных триггеров регистра в к + 1 такте будут сим-
символы
A2.80)
В качестве примера приведем шестикаскадный генератор
(рис. 12.13). Он формирует следующую двоичную /l/f-последователь-
ность:
336

Кодированные сигналы
Рис. 12.13
111111000001000011000101001111010001110010010110111101
1001101010
Число ^-последовательностей, формируемых m-каскадным ге-
генератором, определяется выражением
L=*M = *M, A2.81)
/л т
где ф(х) - функция Эйлера.
Если число N раскладывается на простые множители, то ф(/\/)
можем представить в виде
A2.82)
где Рк - простой множитель Л/.
Если N простое число, то
ф(Л/) = Л/-1.
A2.83)
/^-последовательности довольно подробно исследованы, со-
составлены таблицы, позволяющие для заданного периода опреде-
определить структуру генератора.
Спектры и корреляционные функции /^-последовательностей
могут быть получены с использованием вышеприведенных выра-
выражений.
Схема линейного генератора /^-последовательностей не допус-
допускает одновременного появления нулей во всех каскадах, включен-
включенных в обратную связь. При установлении нулей в этих каскадах
337

Раздел 12
сигнал на входе первого каскада отсутствует, происходит срыв в
работе генератора. Указанного ограничения лишены генератора,
формирующие нелинейные последовательности (для которых не
выполняется принцип суперпозиции).
Генерирование нелинейных последовательностей может произ-
производиться различными устройствами, в том числе с помощью гене-
генератора на основе регистра сдвига с нелинейными операциями.
Анализ нелинейных генераторов затруднен вследствие большого
их разнообразия и математических трудностей, возникающих вслед-
вследствие нелинейного характера описывающих их уравнений. При опи-
описании спектральных и корреляционных характеристик нелинейных
двоичных последовательностей, могут быть исполь-зованы соотно-
соотношения, приведенные выше для кодовых сигналов.
12.4. Частотно-кодированные сигналы
Частотно-кодированный сигнал представляет последователь-
последовательность радиоимпульсов, которые отличаются друг от друга только
значениями несущей частоты. Закон изменения частоты определя-
определяется модулирующей кодовой последовательностью.
Частотно-кодированный сигнал описывается выражением
N
u(t) = ^rn (f)cos(q>0 + @„) f, 0 < t < NT, A2.84)
л=1
или в комплексной форме A2.2). Комплексная огибающая ЧК сиг-
сигнала
N
V(t)=Yjrn{t)ek*J, 0<t<NT. A2.85)
/7=1
Изменяющаяся частота о>п может быть представлена в виде
(оп=спАо), A2.86)
где {сп} - модулирующая кодовая последовательность (частотный
код); Дсо - шаг квантования по частоте.
На рис. 12.14 приведен пример бинарной кодовой последова-
последовательности {сп} и соответствующий ЧК сигнал.
Спектральная плотность комплексной огибающей ЧК сигнала
определяется A2.6). С учетом A2.85) выражение для спектральной
плотности запишется в виде
338

Кодированные сигналы
Рис. 12.14
/7=1 _о
Спектральная плотность сигнала определяется как сумма спек-
спектральных плотностей радиоимпульсов кодированного сигнала, от-
отличающихся несущей частотой и положением на временной оси.
Спектральную плотность комплексной огибающей ЧК сигнала пред-
представим в виде
A2.88)
При прямоугольной огибающей радиоимпульса спектральная
плотность первого импульса определяется выражением
Из A2.88) определим амплитудный спектр
A2.89)
A2.90)
= 7\
339
A2.87)
и фазовый спектр комплексной огибающей ЧК сигнала

Раздел 12
A2.91)
где
График амплитудного спектра комплексной огибающей ЧК сигнала
(кодовая последовательность рис. 12.14) приведен на рис. 12.15.
2 4 6 8 соГ/Зтг
Рис. 12.15
Спектр симметричен относительно со = О. Как показывают при-
приведенные выражения, спектр ЧК сигнала определяется кодовой
последовательностью {сп} и шагом квантования.
Минимальный шаг квантования выбирается как
Ао) = 2л/Г. A2.92)
При выборе шага квантования и бинарной модуляции база ЧК
сигнала равна
271
т.е. определяется длиной кодовой последовательности.
340
A2.93)

Раздел 13.
АНАЛИЗ СИГНАЛОВ В ЛИНЕЙНЫХ ЦЕПЯХ
Методы анализа сигналов основаны на использовании различных
преобразований, рассмотренных выше. Однако некоторые преобра-
преобразования, такие, как преобразование Лапласа, z-преобразование, ис-
используются в основном при анализе сигналов в линейных цепях
(цифровых фильтрах).
Вследствие этого целесообразно рассмотреть сигналы в ли-
линейных аналоговых цепях и цифровых фильтрах. Без такого рас-
рассмотрения изложение методов анализа сигналов с использовани-
использованием преобразований Лапласа и z-преобразования носило бы фор-
формальный характер.
В разделе рассматривается прохождение сигналов через анало-
аналоговые линейные цепи и цифровые фильтры только как иллюстра-
иллюстрация методов анализа сигналов, и не затрагиваются задачи, связан-
связанные с анализом и синтезом самих цепей.
13.1. Прохождение сигнала через линейную цепь
Одной из основных характеристик линейной цепи является им-
импульсная характеристика h(t). Она определяется как отклик линей-
линейной цепи на воздействие сигнала в виде импульсной функции.
Представив сигнал на входе цепи srft) в виде последовательности
импульсных функций (с соответствующими коэффициентами) и
используя принцип суперпозиции, для сигнала на выходе цепи по-
получим:
t t
s2(t)=\h(T)s,(t-T)dz=\h(t-T)Si(x)dt = h(t)®Si(t). A3.1)
о о
Интеграл A3.1) представляет свертку импульсной характери-
характеристики и сигнала на входе цепи. Знак © в A3.1) и означает свертку
h(t) и Si(t). Интеграл свертки иногда называют также интегралом
Дюамеля. Выражение A3.1) позволяет проводить анализ прохож-
прохождения сигнала через линейную цепь при известной импульсной ха-
характеристике цепи.
341

Раздел 13
В качестве примеров рассмотрим прохождение экспоненциаль-
экспоненциального и прямоугольного импульсов через ЯС-цепь. Импульсная ха-
характеристика цепи имеет вид
h(t) = VTe-tlT,
где Т- постоянная времени цепи.
1. При подаче на вход цепи экспоненциального импульса (рис.
13.1,а)
s,(t) = Ve'at,t>0,
сигнал на выходе цепи определяется выражением (рис. 13.1,6,)
t
s2{t) = VIT[e-x'Te-a{t-x)dx = —^—{e-at-e-tlT).
J 1-aT
2. При подаче на вход цепи сигнала в виде прямоугольного им-
импульса (рис. 13.2,а)
s,(t) = V,O<t<xu.
Сигнал на выходе цепи (рис. 13.2,6):
при 0</<ти:
при t >xu:
б)
342

Анализ сигналов в линейных цепях
Рис. 13.2
В частотной области линейная цепь описывается комплексной
частотной характеристикой. Комплексная частотная характеристи-
характеристика (частотная характеристика) определяется преобразованием Фу-
Фурье импульсной характеристики
A3.2)
Обратное преобразование Фурье позволяет перейти от Н(ш)
к/7@:
A3.3)
Учитывая, что h(t) - О при t < 0 , условие существования преоб-
преобразования Фурье импульсной характеристики записывается
в виде
A3.4)
Записанное условие является условием устойчивости линейной
цепи.
В общем случае частотная характеристика является комплекс-
комплексной величиной и ее можно представить в виде
A3.5)
343

Раздел 13
или
Модуль |Н(со)| представляет амплитудно-частотную характери-
характеристику, аргумент ф(со) - фазо-частотную характеристику цепи.
Частотная характеристика позволяет проводить анализ прохож-
прохождения сигнала через цепь, используя спектральную плотность сиг-
сигнала. Преобразование Фурье левой и правой частей A3.1) дает
(свойство преобразования Фурье)
^(co)=H(u))S,(©)> A3.7)
где S,(co) и S2(cd) - спектральные плотности сигналов на входе и
выходе цепи.
OtS2(co) можно перейти к сигналу на выходе цепи
s2(t) = 1/27I Js2((o)e*°fato = 1/27i f H(co)S,(co)e*°fdw. A3.8)
— oo —oo
Таким образом, имея частотную характеристику, можно прово-
проводить анализ цепи в частотной области. Простота выражения A3.7)
обуславливает простоту спектрального метода анализа.
Примеры.
1. Прохождение экспоненциального импульса через ЯС-цепь.
Сигналу на входе цепи
5,@= e~at, t>0,
соответствует спектральная плотность
s,(«,)=—¦
а + кл
Частотная характеристика ЯС-цепи имеет вид
344
A3.6)

Анализ сигналов в линейных цепях
Н(со) = _1_ ,
v ; 1 + коГ
где Г = RC- постоянная времени цепи.
Спектральная плотность на выходе цепи описывается выраже-
выражением
S2(a))=H(co)S1(w)= 1
A + ло7~Ха+ло)"
Сигнал на выходе цепи определяется обратным преобразова-
преобразованием Фурье S2(co)
оо ео
2W 2я-!_' 2тш ^A + foTXi + ло/а)
Для вычисления интеграла разложим подынтегральную функ-
функцию на элементарные дроби
е ( \ 1 А В
S2(«) =
(i + /ico7Xi + to)/a) 1 + лоГ 1 + ло/а
Из записанного равенства получим
А = ^= , В- 1
1-аТ Л-а1
С учетом выполненного разложения найдем
%«)~И-е-'/г)[,
что совпадает с ранее полученным результатом.
Практика анализа прохождения сигналов через линейные цепи
показывает, что спектральный метод анализа особенно удобен
в том случае, когда при описании сигнала можно ограничиться его
спектром.
Выражение для спектральной плотности энергии сигнала на вы-
выходе линейной цепи можно получить с учетом A3.7) в виде:
И/2(ш) = |нЦ21^(со), A3.9)
где VV1(co) = |S1(co)B и W2(co) = |S2(o))|2 - спектральные плотности
энергии сигналов на входе и выходе цепи.
345

^^_ Раздел 13
Преобразование Фурье спектральной плотности энергии W(oi)
представляет автокорреляционную функцию сигнала
Я (т) <-> И^ю). A3.10)
Величине |/-/(о))| соответствует по Фурье функция
Rh(T)=]h(t)h(t + x)dt, A3.11)
rroo
которая может рассматриваться как автокорреляционная функция
импульсной характеристики цепи. Таким образом,
Я„(т)<->|Н(а>)|2. A3.12)
С учетом A3.11) и A3.12), переходя к временной области, из
A3.9) получим
оо
Я2(т)= \R,(x)Rh(T-x)dx=Rh(x)®R,(x). A3.13)
Выражение для взаимной корреляционной функции сигналов на
выходе и входе цепи записывается в виде
Я21(т) =js2(t)s,(t + T)dt. A3.14)
—оо
Преобразование Фурье левой и правой частей A3.14) дает
Я21(т) <-> S^co^co) = l/V21(co) = Н^ш^^со)!2 = Н*(со) W,(a>).A3.15)
Переходя к временной области, получим
fl2i(T)= \h(t)Ri{t + z)dt. A3.16)
—оо
В записанных соотношениях важно соблюдать требуемую по-
последовательность функций. При изменении последовательности
имеем
Я12(т) «=> S; (co)S2(co) = W,2(co) = ^(«^((о)!2 = H(cu)W,((o) . A3.17)
346

Анализ сигналов в линейных цепях
Таким образом,
Я12(т) = Я21(-т) = JR,(t)h(t + T)dt. A3.18)
Одной из основных характеристик линейной цепи является пе-
передаточная функция. Она определяется аналогично частотной ха-
характеристике - как преобразование Лапласа импульсной характе-
характеристики цепи
H(p) = jh{t)e-ptdt. A3.19)
о
Свертке во временной области, определяющей сигнал на выхо-
выходе линейной цепи
t t
s2{t) = jh{x)Ui(t-x)dx = jh(t-x)s1(x)dx, A3.20)
о о
соответствует произведение передаточной функции и изображения
сигнала на входе (свойство преобразования Лапласа)
S2(p) = H(p)S,(p), A3.21)
где Srfp), S2(p) - преобразования Лапласа сигналов на входе и вы-
выходе цепи.
Обратное преобразование Лапласа A3.21) позволяет опреде-
определить сигнал на выходе цепи
u2{t) = M2ni \s2{p)eptdp. ^ A3.22)
Подходы к решению интеграла A3.22) описаны в разд. 4.
Метод анализа линейных цепей, основанный на использовании
преобразования Лапласа, называется операторным методом. При-
Приведем примеры его применения.
1. Прохождение прямоугольного импульса через ЯС-цепь.
Передаточная функция цепи
H(D)= R = PJ
КИ* Я + 1/рС 1 + рТ'
где Т = RC- постоянная времени цепи.
347

Раздел 13
Чтобы определить h(t), разложим Н(р) на простые дроби:
1 + рГ
Учитывая, что
получим
л(г) = 6(г)-1/7бГ'/7\
Изображение сигнала (прямоугольного импульса) на входе име-
имеет вид
S,(p) =-1A-в"*).
где г-длительность импульса,
сигнала на выходе:
S2(p) = H(p)S1(p) = -^--0-e-pz ) = -J_--J—e~r"\
1 + рт р ^ + pT ^ + pт
Полученному изображению соответствует оригинал
s2@ = e->/r_e-('-)/r.
2. Прохождение прямоугольного импульса через LCR- цепь.
Передаточная функция цепи
Я + pL + i/pC р2 + 2ар + (о?'
где «о = 1/VIc, a = R/2L, R, C,L~ параметры цепи.
Соответствующая импульсная характеристика имеет вид
Ру + а Р2 + а
где рк - корни знаменателя Н(р).
После преобразования получим
h(t) = 2ae~at (cosco0f - а/соо sincoo/).
348

Анализ сигналов в линейных цепях
При достаточно большой добротности цепи (а«соо), можно при-
принять
-at.
h{t) = 2ae aicos(o0t.
Изображение сигнала на выходе цели с учетом изображения
сигнала на входе (прямоугольный импульс, амплитуда равна еди-
единице) получим в виде
ад-..!!...,^-'"'')-
р + 2ар + щ р + 2ар + щ
Оригинал, соответствующий первому слагаемому, определяет-
определяется как
а eftt+—— eP2t <->2a/a)osincoof.
р,+а р2+а
Оригинал, соответствующий второму слагаемому, отличается
только смещением во времени на интервал т . Таким образом,
получим
s^f) = 2a/(M0[e~at sincoof - e~a(t~x) sinco0(f - x )].
Одним из важных применений преобразования Лапласа являет-
является решение линейных дифференциальных уравнений с постоян-
постоянными коэффициентами, описывающих прохождение сигналов че-
через линейные цепи
апи2 + ап_,с1и21 dt + an_2d2u21 dt2 +... + a^dnu2 Idf' = ц (f). A3.23)
Преобразование Лапласа левой и правой частей A3.23) приво-
приводит к следующему выражению
anU2(p) + an_,[pU2(p)-u2@)) +
an_2[p2U2(p)-pu2@)-u2@)] + ... = U,(p)
Перепишем A3.24) в виде
U2(p)[an + an^p+an_2p2 +...]- u2{0)[an_^ + an_2p+...] - A3
-u2@)[an_2+...)-.. = U,(p)
349

Раздел 13
Из A3.25) получим изображение сигнала на выходе цепи
и (р)_Ц(Р) + ^2@)[ап-1+ап-2Р + -] + ^2@)[ап-2+-] + ••• ^ A3.26)
ап + ап_1р + ап_2р2+... + а0рп
Если все начальные значения равны нулю, то
U2(p) = Ш. A3.27)
an + pan_i+an_2p*+... + a0pn
По изображению A3.27) можно получить оригинал - сигнал на
выходе цепи.
Рассмотрим пример использования преобразования Лапласа
при решении дифференциального уравнения
^-3^ + 2u2=2e3i
dt2 dt z
при нулевых начальных условиях.
Переходя к изображению левой и правой частей уравнения, за-
запишем
p<U2(p)-3pU2(p) + 2U2(p) =
р-6
Для изображения сигнала на выходе имеем
2 2
U2(P) = -
(р-3)(р2-Зр + 2) (р-1)(р-2)(р-3)"
Переходя от изображения к оригиналу - сигналу на выходе, по-
получим
u2(f) = e'-2e2'+e3'.
13.2. Прохождение сигнала через узкополосную цепь
13.2.1 Узкополосные цепи, их низкочастотные эквиваленты
Для передачи узкополосных сигналов, как правило, используются
узкополосные цепи. Радиотехническая цепь называется узкополос-
узкополосной (избирательной), если ее частотная характеристика отлична от
нуля в полосе частот, ширина которой значительно меньше средней
частоты (рис. 13.3,а). Такие цепи находят применение в различных
системах и их анализ занимает важное место в общем анализе сиг-
сигналов, цепей и систем.
350

Анализ сигналов в линейных цепях
фМ б) w
Рис. 13.3
В качестве основных характеристик линейной цепи выше рас-
рассматривались импульсная и частотная характеристики, связанные
парой преобразований Фурье
A3.28)
При описании узкополосной цепи целесообразно ввести поня-
понятие низкочастотного эквивалента. Использование этого понятия
позволяет упростить анализ узкополосных цепей.
Для определения низкочастотного эквивалента рассмотрим
цепь, частотная характеристика которой получается смещением
частотной характеристики узкополосной цепи Н(ы) в область низ-
низких частот на значение средней частоты о)о (рис. 13.3,6). Тогда для
области положительных частот можем записать
A3.29)
Цепь с частотной характеристикой, полученной таким образом,
представляет низкочастотный эквивалент цепи. Частотной харак-
характеристике низкочастотного эквивалента соответствует импульсная
характеристика
A3.30)
351

Раздел 13
Обычно частотная характеристика узкополосной цепи является
симметричной относительно средней частоты шо".
|/-/(со0 + со)| = |/-/(со0 -to)|, ср(соо + со) =-ср(соо - со), A3.31)
где |Н(ш)|, ф(со) - амплитудно-частотная и фазо-частотная характе-
характеристики цепи.
Для симметричной частотной характеристики с учетом того, что
импульсная характеристика является действительной функцией
времени, можно записать
hit) = 2Re[— \н((й)высП]. A3.32)
о
Подставляя A3.29) в A3.32), получаем
/7@ = 2Re[— f Нэ(со-со0)еыс*о] =
о
= 2Re[— е1* \Нэ(ы-щ)- e^-^'diu-aio)].
2я J
2п<
0 A3.33)
С учетом узкополосности цепи нижний предел в A3.33) можем
заменить на -°°
оо
/7@ = 2Re[— eb°f \H3(x)eixtdx] = 2Re[h3(t)eko<>t]. A3.34)
Таким образом, записано соотношение между импульсными ха-
характеристиками узкополосной цепи и ее низкочастотного эквива-
эквивалента. Соотношение между частотными характеристиками узкопо-
узкополосной цепи и низкочастотного эквивалента для всей оси частот
получим из преобразования Фурье
оо оо
/¦/(со) = jh(t)ebtdt = 2JRe[h3(t) ebet]dt. A3.35)
о
Используя соотношение для комплексной величины
Re[z] = 1/2(z+z*), A3.36)
352

Анализ сигналов в линейных цепях
где z*- комплексно сопряженная величина.
Из A3.35) получим
Таким образом,
H(co) = H3(co-(iH) + H*((o+oH).
A3.37)
A3.38)
Низкочастотный эквивалент узкополосной цепи является мате-
математической моделью цепи, описываемой импульсной и частотной
характеристиками. Его использование при анализе узкополосной
цепи является приемом, который часто позволяет упростить про-
проводимый анализ. Соотношения A3.34) и A3.38) описывают пере-
переход от характеристик низкочастотного эквивалента к характеристи-
характеристикам узкополосной цепи.
В качестве примера рассмотрим характеристики LRC - цепи
(рис. 13.4,а). Частотная характеристика цепи имеет вид
Рис. 13.4
353

Раздел 13
При выполнении условия узкополосности 1/л/Тс» RI2L можно
принять
Юо=7Г?'
а выражение для Н(ы) преобразовать к виду
1
где T = 2L/R.
Переходя к эквивалентной низкочастотной цепи (рис. 13.4,6),
получаем
Нэ(ш) = —!—.
1 + /wT
Импульсная характеристика эквивалентной низкочастотной це-
цепи имеет вид
h3(t) = MTe-t/T.
От h3(t) можем перейти к импульсной характеристике узкополос-
узкополосной цепи (рис. 13.4,а)
/7@ = 2Re[-e 7 еы] = 2/Т e~t/Tcos(o0t.
13.2.2 Прохождение узкополосного сигнала
через узкополосную цепь
Анализ прохождения сигнала через узкополосную цепь наибо-
наиболее удобно проводить с использованием комплексного представ-
представления сигналов:
на входе
^@ = Refine4'] A3.39)
на выходе
^(O^RelV^Oe^'l A3.40)
где Ц@ = Ц@екР1@, V2(t) = V2(t)e^{t\
354

Анализ сигналов в линейных цепях
Спектральная плотность сигнала на выходе цепи S2(u))
определяется выражением
Ss>((o) = H(a))S,(co). A3.41)
Спектральная плотность сигнала на входе Si(co) определяется
через спектральную плотность его комплексной огибающей Щш)
S,(a)) = 1/2L/1(a)-uH) + 1/2L/i'(a) + co0). A3.42)
Как правило, несущая частота сигнала совпадает со средней
частотой полосы пропускания цепи. С учетом этого условия выра-
выражение для частотной характеристики цепи можем записать в виде
Н(со) = Нэ(а)-аH) + Нэ((о + оH). A3.43)
Подставляя A3.43) и A3.42) в A3.41), получаем
52((о) = 1/2[Нэ(со-со0) + Нэ(со + (о0)]
A3.44)
[Ц(@-0H) + 1/1*(@ + 0H)].
Для узкополосного сигнала A3.44) перепишется в виде
52(со) = 1/2Нэ(со-{о0)Ц((о-аH) + 1/2Н;(а) + (о0)ЦА(со + со0). A3.45)
Учитывая соотношение между спектральной плотностью сигна-
сигнала и спектральной плотностью комплексной огибающей
52(со) = 1/2Ц>(со-со0) + 1/21/2(со + со0), A3.46)
можем определить спектральную плотность огибающей сигнала на
выходе цепи как
1/2(со) = Нэ((о)Ц((о). A3.47)
Соотношения, аналогичные A3.45), можно получить для спек-
спектральной плотности энергии W2(w) на выходе узкополосной цепи
где 1УиМ — спектральная плотность энергии комплексной оги-
огибающей сигнала на входе цепи.
355
A3.48)

Раздел 13
Переходя к временной области, для комплексной огибающей
сигнала на выходе цепи запишем
V2{t) = jv^x)h3{t - x)dx. A3.49)
о
Сигнал на выходе узкополосной цепи описывается выражением
u2(t) = He[V2 e*°°f] = Re[eK0°tjV^x)h3(t-x)dx]. A3.50)
о
Таким образом, записаны выражения, описывающие сигнал на
выходе узкополосной цепи при подаче на ее вход узкополосного
сигнала.
В качестве примера рассмотрим прохождение экспоненци- аль-
ного радиоимпульса
ц@ = Voe~at cosoH/ = Re[\>i@e*°°'], t > 0,
где Ц@ = Voe~at - огибающая сигнала,
через ^СЯ-цепь (рис. 13.4).
Импульсная характеристика эквивалентной низкочастотной це-
цепи имеет вид
h3(t) = MTe~tlT,
где Т= 2UR.
Для огибающей сигнала на выходе цепи запишем
Рис. 13.5
356

Анализ сигналов в линейных цепях
Сигнал на выходе цепи описывается выражением (рис. 13.5)
u2(t) = V (e~at - e~i/T)coswQt.
1-aT
13.3. Прохождение сигнала через цифровой фильтр
При анализе дискретных сигналов и при описании цифровой обра-
обработки сигналов наиболее широкое применение нашло
z-лреобразование. Линейная цепь в цифровом выполнении (соответ-
(соответствующая программа ЭВМ) называется цифровым фильтром. Одной
из основных характеристик цифрового фильтра (как и аналоговой ли-
линейной цепи) является импульсная характеристика. Она представляет
отклик цифрового фильтра на воздействие единичного импульса. Ис-
Используя импульсную характеристику фильтра, для каждого входного
сигнала можно определить сигнал на выходе. Сигнал на выходе опи-
описывается дискретной сверткой импульсной характеристики h(kT) и
сигнала на входе Si(kT)
п п
s2(nT) = ^Si{kT)h(nT - кТ) = ^s^nT - кТЩкТ). A3.51)
/с=0 /г=0
Записанное выражение представляет алгоритм цифровой
фильтрации во временной области. Графическое отображение ал-
алгоритма дано на рис. 13.6.
Рис.13.6
357

Анализ сигналов в линейных цепях
ход - с использованием z-преобразования позволяет упростить
анализ прохождения сигналов через цифровые фильтры.
Одним из методов анализа прохождения сигналов через анало-
аналоговые цепи является метод составления и решения дифференци-
дифференциальных уравнений.
Примером такого уравнения является уравнение, описывающее
прохождение сигнала через ЯС-цепь
ds2 1 _ 1
I So — — Si ,
dt т 2 т 1
где sh s2- сигналы на входе и выходе цепи;
т=ЯС.
Для дискретных сигналов дифференциальному уравнению 1-го
порядка соответствует разностное уравнение
s2(nT)-bs2(nT-T) = aSi(nT), A3.54)
где Т- интервал дискретизации.
Преобразуя уравнение A3.54), запишем
s2{nT) = aSi(nT) + bs2(nT-T). A3.55)
Как следует из A3.55), в цифровом фильтре значение выходно-
выходного сигнала может использоваться при расчетах последующих зна-
значений. Такие фильтры называются рекурсивными.
В общем случае разностное уравнение Л/-го порядка имеет вид
sz(nT)-b,s2(nT-T)-...-bNs2(nT-NT) =
= aQS^(nT) + a^(nT -Т) +... + aMs^(nT - МТ).
Перепишем его в виде
s2(n7) = aos1(nr) + a1s1(nT-T) + ... + aMs1(flT-M7") +
+ b)S2(nT-T) +... + bNs2(nT- NT).
Схема рекурсивного фильтра, реализующая алгоритм A3.57),
представлена на рис. 13.7.
Системная функция такого фильтра найдется, если в A3.56) пе-
перейти к z-преобразованию левой и правой частей
359

^ Раздел 13
На рис.13. 6 элемент задержки обозначен в терминах z-преобра-
зования как z1 (свойство z-преобразования). Схема показывает по-
последовательность вычислительных операций. При расчете значе-
значений выходного сигнала используются только значения входного
сигнала. Фильтры, в которых для расчета выходного сигнала ис-
используются только значения входного сигнала (отсутствует обрат-
обратная связь), называются простыми или нерекурсивными. Для прак-
практической реализации таких фильтров необходимо, чтобы импульс-
импульсная характеристика содержала конечное число членов (или можно
было бы ограничиться конечным числом членов).
При анализе цифровых фильтров наряду с импульсной харак-
характеристикой используется системная функция. Она играет такую же
роль, как частотная характеристика при анализе аналоговых цепей.
Системная функция определяется как z-преобразование импульс-
импульсной характеристики цифрового фильтра
H(z) = ^h(nT)z-n. A3.52)
л=0
Системная функция описывает свойства цифрового фильтра в
области переменного z.
В качестве примера рассмотрим цифровой фильтр, соответст-
соответствующий аналоговой ЯС-цепи. Импульсная характеристика фильтра
имеет вид
h(nT) = е~пТ1х,
где т - постоянная времени. Ей соответствует системная функция
Z-преобразование дискретной свертки A3.51) дает следующее
равенство (свойство z-преобразования)
S2(z) = H(z)S,(z). A3.53)
Таким образом, z-преобразование сигнала на выходе цифрово-
цифрового фильтра равно произведению системной функции фильтра и z-
преобразования сигнала на входе. Обратное z-преобразование
позволяет перейти к сигналу на выходе фильтра. Часто такой под-
358

Раздел 13
A3.58)
A3.59)
Анализ A3.59) показывает, что коэффициенты слагаемых чис-
числителя определяют нерекурсивную часть фильтра,
а коэффициенты слагаемых знаменателя определяют рекурсивную
часть фильтра.
В качестве примера рассмотрим цифровой фильтр, соответст-
соответствующий аналоговой цепи с импульсной характеристикой (колеба-
(колебательный контур)
/7@ = e~a'cosco0f.
Импульсная характеристика цифрового фильтра имеет вид
h(nT) = e~anT costi>0nT = M2{e~anT+^nT + е-апТ-ь°пТ).
Системная функции, соответствующая h(nT), может быть най-
найдена как.
360
Таким образом, получим

Анализ сигналов в линейных цепях
Рис. 13.8
Системной функции соответствует уравнение
s2{nT) = s^(nT) + a^(nT -T) + b^sz(nT -T) + b2S2(nT - 2Т),
где ао = 1; аА = -e"arcosco0V; Ь, = 2e~a7cosaH7"; /^ = -е~аТ.
Схема цифрового фильтра, отражающая полученный алгоритм,
приведена рис. 13.8.
Фильтр, схема которого приведена на рис. 13.7, может быть реа-
реализован несколько иначе. Запишем A3.59) в виде
A3.60)
A3.61)
Рис. 13.9
361
Представим A3.60) как

Раздел 13
где
W(z)= /1(Z) _N. A3.62)
Преобразование, соответствующее W(z), осуществляется с по-
помощью рекурсивного фильтра Л/-го порядка. Выражению A3.61)
соответствует нерекурсивное преобразование сигнала. Таким об-
образом, может быть изображена общая схема цифрового фильтра,
включающая нерекурсивную и рекурсивную части. Дублирующие
элементы схемы (элементы задержки) объединены (рис. 13.9). Та-
Такая схема фильтра называется канонической.
Приведенные примеры иллюстрируют практику применения
z-преобразования, его полезность при анализе дискретных сигна-
сигналов.
362

СПИСОК ЛИТЕРАТУРЫ К ЧАСТИ 1
1. Араманович И.Г., Лунц ГЛ., Эльсгольц Л.Э. Функции комплексного
переменного. Операционное исчисление. Теория устойчивости. -М.: Нау-
Наука, 1965.
2. Баскаков СИ. Радиотехнические цепи и сигналы. -М.: Высшая шко-
школа, 1988.
3. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. -М. :
Наука, 1966.
4. БендатДж., Пирсол А. Применения корреляционного анализа. - М.:
Мир, 1983.
5. Бокс Дж., Дженкинс Г. Анализ временных рядов. Вып.1 и вып.2. -
М.: Мир, 1974.
6. БрейсуДанилэлл Р. Преобразование Хартли. -М.: Мир, 1990.
7. Варакин Л.Е. Системы связи с шумоподобными сигналами. -М.: Ра-
Радио и связь, 1985
8. Варакин Л.Е. Теория сложных сигналов. -М.: Сов. радио, 1970.
9. Гиллемин Э. А. Синтез пассивных цепей. -М.: Связь, 1970.
10. Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обра-
обработка сигналов. -М.: Радио и связь, 1985.
11. Гоноровский И. С. Радиотехнические цепи и сигналы. -М.: Радио и
связь, 1986.
12. Градштейн И.С, Рыжик И.М. Таблицы интегралов, сумм, рядов и
произведений. -М.: Госиздат физико-математической литературы, 1963.
13. Данилов В.Л. и др. Математический анализ. -М .: Изд. Физ. мат.
литературы, 1961.
14. Денисенко А.Н., Стеценко О.А. Теоретическая радиотехника. Сиг-
Сигналы. -М.: Изд. Стандартов, 1993.
15. Денисенко А.Н. Сигналы с фазовой и частотной модуляцией. -М.:
Изд. Стандартов, -1994.
16. Диксон Р.К. Широкополосные системы. -М.: Связь, 1979.
17. Диткин В.А., Прудников А П. Интегральные преобразования и
операционное исчисление. -М.: Изд. Физ. мат. литературы, 1961.
18. Каганов В.И. Радиотехника, компьютер, mathcad. -M.: Горячая ли-
линия-телеком, 2001.
19. Карташов В.Г. Основы теории дискретных сигналов и цифровых
фильтров. -М.: Высшая школа, 1982.
20. Картьяну Г. Частотная модуляция. -М.: Изд. АРНР, 1961.
21. К.Де.Бор. Практическое руководство по сплайнам. -М.: Радио и
связь, 1985.
363

22. Кузнецов Д.С. Специальные функции. -М.: Высшая школа, 1965.
23. Кук Ч., Бернфельд М. Радиолокационные сигналы. -М.: Сов. ра-
радио,-1974.
24. Лезин Ю.С. Оптимальные фильтры и накопители импульсных сиг-
сигналов. -М.: Сов. Радио, 1963.
25. Лэм Г. Аналоговые и цифровые фильтры. -М.: Мир, 1982.
26. Люк Ю. Специальные математические функции и их аппроксима-
аппроксимации. -М.: Мир, 1980.
27. Люстерник Л.А. и др. Математический анализ. -М.: Изд. Физ. мат.
литературы, 1963.
28. Макаров И.М., Менский Б.М. Линейные автоматические системы. -
М.: Машиностроение, 1982.
29. Пестряков В.Б., Афанасьев В.П. и др. Шумоподобные сигналы в
системах передачи информации. -М.: Сов. радио, 1973.
30. Петрович Н.Т., Размахнин М.К. Системы связи с шумоподобными
сигналами. -М.: Сов. радио, 1989.
31. Пышкин И.М., Дежурный И.И. и др. Системы подвижной радио-
радиосвязи. -М.: Радио и связь, 1986.
32. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки
сигналов. -М.: Мир, 1978.
33. Свистов В.М. Радиолокационные сигналы и их обработка. -М.:
Сов . радио, 1977.
34. СибертУ.М. Цепи, сигналы, системы, ч.1 и ч.2. -М.: Мир, 1982.
35. Современная радиолокация. -М.: Сов. Радио, 1969.
36. Стейн С, Джонс Дж. Принципы современной теории связи и их
применение к передаче дискретных сообщений. -М.: Связь, 1971.
37. Справочник по специальным функциям. Под ред. М. Абрамовица и
И. Стиган. -М.: Наука, 1979.
38. Сухорученков Б.И. Математические модели и методы анализа ха-
характеристик летательных аппаратов. -М.: Изд.МО, 1989.
39. Трахтман A.M. Введение в обобщенную спектральную теорию сиг-
сигналов. -М.: Сов. радио, 1972.
40. Тузов Г.И. Статистическая теория приема сложных сигналов. -М.:
Сов. радио, 1977.
41. Тузов Г.И., Сивов В.А. и др. Помехозащищенность радиосистем со
сложными сигналами. -М.: Радио и связь, 1985.
42. Шумоподобные сигналы в системах передачи информации. Под
ред. Пестрякова В.Б. -М.: Сов. радио, 1973.
43. Френке Л. Теория сигналов. -М.: Сов. радио, 1974.
44. Хармут Х.Ф. Передача информации ортогональными функциями. -
М.: Связь, 1975.
45. Хармут X. Теория секвентного анализа. Основы и применения. -М.:
Мир, 1980.
46. Хеминг Р.В. Цифровые фильтры. -М.: Сов. радио, 1980.
47 Янке Е., Эмде Ф., Леш Ф. Специальные функции. -М.: Наука, 1988.
364

ЧАСТЬ 2.
СЛУЧАЙНЫЕ СИГНАЛЫ И ШУМЫ
365

Раздел 14.
СЛУЧАЙНЫЕ ПРОЦЕССЫ, ИХ ХАРАКТЕРИСТИКИ
И КЛАССИФИКАЦИЯ
Все сигналы, формируемые или выделяемые в цепях радиотех-
радиотехнических систем, являются случайными. Случайный характер сиг-
сигналов обусловлен воздействием на источники сигналов различных
по своей природе и проявлениям таких, факторов, как случайный
характер модуляции, разброс параметров элементов передатчика и
др. Когда влияние случайных факторов является незначительным и
им можно пренебречь, сигнал можно рассматривать как детерми-
детерминированный, как колебание, закон изменения во времени которого
задан. Случайный сигнал описывается случайной функцией време-
времени. Такой же характер имеют и шумы - сторонние колебания не
несущие информации. Анализ случайных сигналов и шумов должен
проводиться с привлечением методов теории случайных процес-
процессов. Примеры случайных процессов приведены на рис. 14.1.
14.1. Детерминированные и случайные сигналы
Детерминированный сигнал задается функцией времени или
правилом его получения. Применительно к детерминированным
термин «сигнал» обычно и используется как эквивалент временной
функции, описывающей колебание. Примерами детерминирован-
детерминированных сигналов являются (см. часть 1):
импульсный сигнал
s(t) = X |/|<т/2, s{t)=e"at, 0<t<z, A4.1)
гармоническое колебание
u(t)=V0cos(uHt + 4>0), A4.2)
где Vo, Щ> Фо ~ амплитуда, частота и начальная фаза;
гармонический модулированный сигнал
u(t)=V(t)cos[a>Qt+ q{t)], A4.3)
366

Случайные процессы
Рис. 14.1
где V(t), ф@ - изменяемые во времени параметры;
кодированный сигнал
N
"(О = ?а"г" W00^ + соп) t + фп],
п=1
A4.4)
где аП| соо +о)п, фл- амплитуда, частота и начальная фаза гармо-
гармонического колебания длительности 7 на интервале (n-1)T<t < nT\
со0 - несущая частота; rn(t) - функция, описывающая форму им-
импульса.
367

Раздел 14
Последовательности символов: амплитуд {ап}, фаз {<рп} и частот
{еоп} составляют кодовые последовательности, которые определяют
закон изменения параметров колебания.
Функция, описывающая сигнал s(t), может быть представлена в
виде взвешенной суммы более простых (базисных) функций (pn(t)
оо
5@=ХспФпМ A4.5)
/7=0
где сп - постоянные коэффициенты.
Разложение s(t) по ортогональной системе функций {фп(?)}назы-
вается обобщенным рядом Фурье. Совокупность коэффициентов
разложения представляет спектр сигнала.
Возможно также интегральное преобразование s(t). Наиболее
часто при анализе сигналов применяется преобразование Фурье
S(w)= Js@e"'wf dt. A4.6)
Ему соответствует обратное преобразование
s(t) = — fs(co)e'wfdw. A4.7)
271 J
— оо
Функция S(to) называется спектральной плотностью, или спек-
спектром сигнала.
Непрерывные сигналы могут задаваться выборочными значе-
значениями - значениями, взятыми в определенные моменты времени
(как правило, через заданный постоянный интервал времени). По-
Получаемый таким образом сигнал называется дискретным. Дискрет-
Дискретные сигналы имеют вид последовательности коротких импульсов,
амплитуды которых соответствуют мгновенным значениям непре-
непрерывного сигнала s(t)
sd(t)=^s(nT)8(t-nT), A4.8)
n=0
где Г- интервал дискретизации; 5@ - импульсная функция.
Случайный сигнал представляет случайное изменение во вре-
времени параметра колебания, случайный процесс. На выходе иден-
368

Случайные процессы
тичных источников случайный сигнал, в отличие от детерминиро-
детерминированного, имеет различный вид. Случайное колебание на выходе
одного источника называется реализацией случайного процесса.
Примером реализации может служить осциллограмма случайного
сигнала при однократной развертке ЭЛО (рис.14.2,а). Совокупность
реализаций, полученных на выходе идентичных по своим характе-
характеристикам источников, представляет множество, или ансамбль реа-
реализаций. Ансамбль реализаций имеет вид осциллограммы случай-
случайного сигнала при периодической развертке ЭЛО (рис. 14.2,6).
Рис. 14.2
Описать случайный сигнал с помощью временной функции не-
невозможно - любая временная функция, описывающая отрезок реа-
реализации на выходе одного источника сигнала, не соответствует
сигналу на выходе другого идентичного источника. Случайные сиг-
сигналы поддаются описанию только статистически - с использовани-
использованием вероятностных характеристик или характеристик, функциональ-
функционально с ними связанных. Такими характеристиками являются функция
распределения, плотность распределения вероятностей или мо-
моменты распределения.
Особенности случайных сигналов не позволяют применить к ним
непосредственно интегральные преобразования. Преобразование
Фурье, как инструмент анализа, используется применительно к кор-
корреляционной функции, определяет спектральную плотность мощ-
мощности случайного сигнала. Такое же положение сохраняется
и в отношении дискретных случайных сигналов - по дискретным
369

Раздел 14
значениям можно восстановить только реализацию (отрезок реали-
реализации) случайного сигнала.
Отразить общие черты и отличия детерминированных и случай-
случайных сигналов позволяет и их геометрическая интерпретация. При
обобщенном спектральном анализе детерминированный сигнал
представляется в виде ряда по ортогональной системе функций
s(f)=Ic^(f), A4.9)
где ск - постоянные коэффициенты; {ф*@}~ ортонормированная
система функций.
Свойство ортогональной системы функций:
)флофя(о<*={5 лл=Л A4-1о)
позволяет получить выражения для коэффициентов разложения в
виде
ck = $s{t)pk(t)dt, A4.11)
tb
где [ta, tb J - интервал ортогональности функций yk{t).
Ортонормированная система базисных функций {<pk(t)}образует
координатную систему в Л/-мерном евклидовом пространстве. Функ-
Функции ф^(t) представляют единичные векторы, коэффициенты ск -
проекции вектора s(t) на оси координат. Сигнал, описываемый
A4.9), рассматривается как Л/-мерный вектор (рис. 14.3,а).
Выбор базисной системы функций определяет систему коорди-
координат. Замена системы базисных функций означает смену системы
координат.
Векторы определены только тогда, когда они имеют конечную
длину
370
A4.12)

Случайные процессы
Из A4.12) следует, что геометрическую трактовку допускают
только сигналы с конечной энергией.
Рассматривая случайный процесс, выделяем отрезок реализа-
реализации ?$\t) (рис. 14.3,6). На выделенном интервале времени Zff\t)
можем рассматривать как заданную функцию времени. При выпол-
выполнении некоторых условий ее можем представить в виде обобщен-
обобщенного ряда Фурье, аналогичного A4.9). Ограничиваясь конечным
числом членов ряда, запишем
^)@ = Z W0, A4.13)
/с=1
где ск - коэффициенты разложения; {ф/ДО} ~ система ортонорми-
рованных функций.
Коэффициенты разложения определяются, как и в A4.11)
ck = j^\t)pk(t)dt, A4.14)
где [ta, tb] - интервал ортогональности функций qk(t).
Для выделенного отрезка реализации коэффициенты разложе-
разложения ^определяются A4.14) однозначно. Они описывают вектор в
евклидовом пространстве (рис. 14.3,6). Для другой реализации ко-
коэффициенты будут уже иными, они описывают другой вектор в том
же пространстве. При рассмотрении множества реализаций коэф-
коэффициенты должны рассматриваться как случайные величины, кото-
которым соответствует случайное множество векторов. Нахождению
конца вектора в заданной области пространства соответствует оп-
определенная вероятность.
14.2. Шумы
Формирование, передача и прием сигналов всегда сопровожда-
сопровождаются сторонними колебаниями (колебаниями, не несущими инфор-
информации) - шумом. Источниками шума являются все типы резисторов,
полупроводниковые приборы (диоды, триоды и др.), электронные
и газоразрядные приборы, фотоэлементы, фотоумножители и т.д.,
т.е. активные и пассивные элементы радиотехнических цепей.
Шум в резисторах представляет флуктуации напряжения (тока),
объясняется случайным характером теплового движения электро-
371

Раздел 14
нов. Поэтому эти флуктуации называются тепловым шумом. Квад-
Квадрат эффективного напряжения теплового шума в полосе частот Af
определяется формулой Найквиста
P^AkTRAf, A4.15)
где к- постоянная Больцмана (к = 1,38-103 Дж/град); Г- темпера-
температура источника шума; Я- сопротивление нагрузки.
Более точно формула Найквиста может быть записана в виде
P = 4kTRp(f)Af, A4.16)
где p(f) - коэффициент Планка:
hf
A4.17)
где л -постоянная Планка (л = 6,62-104 Дж- с).
Источником флуктуации, возникающих в вакуумных приборах,
является случайный характер эмиссии и движения электронов
372
Рис. 14.3

Случайные процессы
в этих элементах. Такой шум называется дробовым. Мощность шу-
шума электровакуумного диода в полосе частот Af на нагрузке Я опре-
определяется формулой
P = 2ql0RAf, A4.18)
где q - заряд электрона (q =1,6-10'19 К); /0 - среднее значение тока,
протекающего через диод; Af~ полоса шума на выходе.
В полупроводниковых приборах различают несколько состав-
составляющих внутреннего шума, основными из которых являются тепло-
тепловой и дробовый шумы. Как и в других элементах, природа появле-
появления теплового шума связана с хаотичностью теплового движения
заряженных частиц. Квадрат эффективного значения напряжения
этой составляющей определяется формулой Найквиста. Причина
появления дробового шума в полупроводниковых приборах во мно-
многом такая же, что и в вакуумных приборах.
Спектральные плотности мощности шумов различных источни-
источников отличаются весьма сильно. Так для проволочного резистора
спектральная плотность мощности при комнатной температуре
имеет порядок 101 Вт/Гц, а для тиратронов 10 -10 Вт/Гц. Полоса
частот, занимаемая спектром шума различных источников, изменя-
изменяется в широких пределах. Спектр теплового шума - сплошной и
достаточно равномерный в полосе до 1013 - 1014 Гц.
В процессе исследования шум должен рассматриваться как слу-
случайный процесс, и к нему применимы методы исследования слу-
случайных процессов. Случайные сигналы и шумы объединяет их слу-
случайный характер и, следовательно, для них характерны свои, спе-
специфические методы исследования. Вследствие этого в дальней-
дальнейшем случайные сигналы и шумы будут объединены терминологиче-
терминологически и называться случайными процессами.
Содержание второй части справочного пособия определяется
интересами исследования случайных колебаний в радиотехниче-
радиотехнических цепях. Поэтому в ней излагаются не просто методы теории
случайных процессов, а только те из них, которые в большей сте-
степени отвечают интересам анализа случайных сигналов и шумов, и в
виде, наиболее удобном для рассмотрения случайных сигналов.
Специфика рассмотрения случайных процессов в справочном по-
пособии заключается прежде всего в выборе их характеристик и
очерченного круга задач исследований. Это сказывается на фор-
формировании разделов второй части книги и методике их изложения.
373

Раздел 14
14.3. Основные характеристики случайных процессов
Случайный процесс представляет случайную функцию времени,
и его рассмотрение во временной области, как и детерминирован-
детерминированного сигнала, является наиболее наглядным. Однако если детер-
детерминированный сигнал однозначно описывается временной функци-
функцией, то такое описание случайного процесса невозможно (рис. 14.4).
Случайный процесс в каждый момент времени представляет слу-
случайную величину, которая может принимать различные значения из
области возможных. Таким образом, во временной области случай-
случайный процесс может быть описан только с использованием вероят-
вероятностных характеристик. Наиболее полными из них являются функ-
функция распределения вероятностей (ФРВ) или плотность распреде-
распределения вероятностей (ПРВ). В зависимости от того, сколько момен-
моментов времени выбирается при описании случайного процесса, раз-
различают ФРВ различной мерности (в общем случае л-мерные)
Fn(xh Х2, •••. хп )¦
Рис. 14.4
374

Случайные процессы
От ФРВ можно перейти к ПРВ
«*¦•* *^d"%X^n)- A419)
При описании случайных процессов используются и менее пол-
полные характеристики - моменты распределения
M^k\t^k2{t2)...^{tn) } =
| j...jxk^xk^..xknfn(xbx2,...xn)dx,dx2...dxn. A420)
Начальный момент первого порядка - математическое ожидание
Mfc{t)}=a=jxf,{t)dx A4.21)
описывает постоянную составляющую случайного сигнала. Второй
центральный момент - дисперсия
оо
M^{t)-af}= \{x-aff,{t)dx A4.22)
- мощность переменной составляющей.
Важное место при анализе случайных процессов занимает второй
смешанный центральный момент распределения вероятностей -
корреляционная функция.
A4.23)
Корреляционная функция описывает степень статистической
связи значений случайного процесса или двух случайных процес-
процессов, взятых в два различных момента времени.
Характеристики распределения для широкого класса случай-
случайных процессов (эргодических случайных процессов) могут быть
получены в результате обработки одной реализации. Так матема-
математическое ожидание и дисперсия случайного процесса могут быть
определены как
375

Раздел 14
a = (^k)(t))=yim — j^k)(t)dtt A4.24)
a2 =(H')-af) = lim^ jfeW(O-af d/, A4.25)
где ?,{k)(t) - реализация случайного процесса; <..> - символ усред-
усреднения по времени.
Корреляционная функция эргодического случайного процесса
описывается выражением
^1^2)=7lirri-Ljfe(f1)-a1b(f2)-a2]cyf. A4.26)
-т
Полезной характеристикой при описании случайного процесса
является характеристическая функция, она определяется как сред-
среднее значение функции е"^, где v- действительная величина, вы-
выражением
е
,(у)= \fA(x)emdx. A4.27)
Выражение A4.27) представляет преобразование Фурье ПРВ.
Следовательно, от характеристической функции можно осущест-
осуществить переход к ПРВ с помощью обратного преобразования
/;(х) = — \%(v)e~ivxdv. A4.28)
2л J
Распространив понятие характеристической функции на сово-
совокупность случайных величин ^(^),^2),...,^п)^ выражение для
/7-мерной характеристической функции запишем в виде
en(vbv2,...,vn) =
] J ... je^+^+----*-Vn(x1,x2,..,xll)dfic&f2...df|l. A4'29)
376

Случайные процессы
Обратный переход от характеристической функции к «-мерной
ПРВ определяется выражением
fn\Xj\>X2>--->Xn)-
~jj-Ie"M2 „„y*™*-".'¦W1rt,!...rtV A4-30)
Удобство использования характеристической функции связано в
первую очередь с ее мультипликативным свойством ех+у = ехеу.
Указанные характеристики могут быть распространены на сово-
совокупность случайных процессов.
Реализация непрерывного случайного процесса может рассмат-
рассматриваться как случайное колебание относительно выбранного уров-
уровня х(рис. 14.5).
Выбросы случайного процесса относительного этого уровня ха-
характеризуют поведение случайного процесса во времени и часто
требуют самостоятельного исследования. К основным характери-
характеристикам выбросов, которые определяются при анализе случайных
процессов, относятся: ФРВ или ПРВ длительности положитель-
положительных (над выбранным уровнем) и отрицательных выбросов, средняя
Положительные выбросы
Отрицательные выбросы
Рис. 14.5
377

Раздел 14
частота следования выбросов, средняя частота экстремумов и др.
Анализ выбросов, определение их характеристик является одной
из составных частей общего анализа случайных процессов.
При анализе детерминированных сигналов исключительно по-
полезным оказалось использование преобразования Фурье времен-
временной функции, описывающей сигнал. Исследование переводится в
частотную область, математические операции часто упрощаются.
Преобразование Фурье непосредственно случайных процессов, как
правило, невозможно, не выполняется условие существования
преобразования Фурье. Используется преобразование Фурье кор-
корреляционной функции случайного процесса. Оно определяет спек-
спектральную плотность мощности случайного процесса. Корреляцион-
Корреляционная функция и спектральная плотность мощности связаны друг с
другом парой преобразований Фурье
Л/(со) = J Я(т) e-imck, Я(т) = — J Л/(со) eimck. A4.31)
—оо —оо
Соотношения A4.31) лежат в основе спектрального анализа
случайных процессов. Спектральный анализ - важная часть общего
анализа случайных процессов.
С учетом изложенного в дальнейшем проводится описание
и анализ основных характеристик случайных процессов во времен-
временной и частотной областях. При их рассмотрении необходимо иметь
в виду, что все характеристики случайных процессов взаимосвяза-
взаимосвязаны, они отражают одни и те же свойства случайного процесса,
только описываются с использованием различных подходов.
14.4. Классификация случайных процессов
В зависимости от природы (источника) колебаний, характеристик
устройства, на выходе которого наблюдается колебание, и ряда
других факторов случайные процессы могут обладать разными
свойствами. Из всего возможного разнообразия случайных процес-
процессов выделим только те, которые наиболее часто встречаются в ин-
инженерной и исследовательской практике, и проведем их классифи-
классификацию по основным признакам. Такая классификация позволяет
определить место каждого вида случайного процесса среди воз-
возможного их разнообразия и ввести терминологию, которая будет
использована в дальнейшем.
Различают непрерывные и дискретные случайные процессы
(рис. 14.6). Непрерывный случайный процесс (его реализация) может
378

Случайные процессы
Рис. 14.6
иметь любое значение из области возможных (рис. 14.6,а). Приме-
Примером непрерывного случайного процесса служит шум в радиотехни-
радиотехнической цепи. Дискретный случайный процесс принимает только оп-
определенные значения. Примером такого процесса является коле-
колебание на выходе идеального ограничителя при подаче на его вход
непрерывного случайного процесса (рис. 14.6,6).
Возможен случайный процесс смешанного типа, например, слу-
случайный процесс на выход ограничителя с заданными порогами огра-
ограничения (рис. 14.6,в). Как сложилось на практике, дискретными будем
также называть случайные процессы, получающиеся при дискрети-
дискретизации непрерывных случайных процессов во времени. Такие случай-
случайные процессы представляют периодическую последовательность
379

Раздел 14
коротких импульсов, амплитуды которых соответствуют мгновенным
значениям исходного непрерывного случайного процесса. Отдельно
выделяются импульсные случайные процессы (рис. 14.6,г).
Одним из важных признаков, по которым проводится классифи-
классификация, является вид распределения вероятностей случайного про-
процесса. Широкий класс случайных процессов составляют гауссов-
ские процессы - случайные процессы с нормальным распределе-
распределением мгновенных значений (рис. 14.7,а). Нормальное распределе-
распределение является тем предельным видом, к которому при определенных
условиях стремятся все другие виды распределения. Указанным
обстоятельством в большой степени объясняется то важное место,
которое занимают гауссовские процессы в практике исследований.
Некоторые виды распределений получаются при преобразовании
нормального закона распределения. Так можно получить релеев-
ский закон распределения (рис. 14.7,6") и другие.
Наиболее полной характеристикой случайного процесса являет-
является его л-мерная ФРВ, или л-мерная ПРВ, описывающие случайный
процесс в различные моменты времени. Из общего класса случай-
случайных процессов выделяют случайные процессы, которые полностью
характеризуются ФРВ (ПРВ) первого и второго порядков (от них
можно перейти к ФРВ (ПРВ) любого порядка). Если случайный про-
процесс полностью описывается одномерной ФРВ (ПРВ), то он назы-
называется совершенно случайным.
Рис.14.7
380

Случайные процессы
381
Рис.14.8
Рис. 14.9
Рис. 14.10

Раздел 14
Случайные процессы
Характер изменения параметра
I i
Непрерывные
Дискретные
I
Смешанного вида
Импульсные
Зависимость характеристик от времени
Стационарные
Нестационарные
Эргодические
Неэргодические
Законы распределения
Гауссовские
Релеевские
Ширина спектра
Узкополосные
Широкополосные
Способ Формирования
Модулированные Смодулированные
Вид модуляции
Амплитудно-
модулированная
Фазо-
модулированная
Частотно-
модулированная
Смешанного
вида
Рис. 14.11
382

Случайные процессы
Одним из признаков классификации случайных процессов явля-
является постоянство их характеристик во времени. Различают стацио-
стационарные (рис. 14.8,а) и нестационарные (рис. 14.8,6) случайные про-
процессы. Случайный процесс называется стационарным, если его
ФРВ любого порядка не зависят от выбора начала отсчета на оси
времени.
В классе стационарных случайных процессов особое место за-
занимают эргодические случайные процессы. Случайный процесс
называется эргодическим, если любая его характеристика, полу-
полученная усреднением по ансамблю реализаций, равна характери-
характеристике, подученной при обработке одной реализаций - усреднением
по времени. Выполнение этого условия означает, что поведение
каждой реализации случайного процесса статистически такое же,
как и всего ансамбля реализаций. Случайные процессы, не обла-
обладающие указанным свойством, называются неэргодическими.
В частотной области случайные процессы описываются спек-
спектральной плотностью мощности, или спектром (рис. 14.9,а). В зави-
зависимости от ширины спектра выделяют (как и среди детерминиро-
детерминированных сигналов) узкополосные и широкополосные случайные про-
процессы. Случайный процесс называется узкополосным, если его
спектр сосредоточен в полосе частот, значение которой значитель-
значительно меньше средней частоты (рис. 14.9,6). Из широкополосных слу-
случайных процессов особо выделяют белый шум. Белым шумом на-
называется случайный процесс, имеющий равномерный на всех час-
частотах спектр (рис. 14.9,в). Белый шум физически не реализуем, яв-
является идеализацией, удобной моделью случайных процессов, с
которыми приходится иметь дело на практике.
Из узкополосных процессов следует выделить модулированные
случайные процессы. Они могут иметь шумоподобную несущую,
модулированную как детерминированным, так и случайным сигна-
сигналами, и случайные процессы с гармоническим несущим колебани-
колебанием, модулированным случайным процессом. Второй вид наиболее
распространен. По виду модуляции различают: случайные процес-
процессы с амплитудной (рис. 14.10,а), фазовой и частотной модуляцией
(рис. 14.10,6).
Краткая классификация случайных процессов, приведенная вы-
выше, в обобщенном виде представлена на рис.14.11. Понятия раз-
различных видов случайных процессов, введенные при классифика-
классификации, раскрываются полнее в дальнейшем.
383

Раздел 15.
ОДНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
СЛУЧАЙНОГО ПРОЦЕССА
Случайный процесс в каждый момент времени представляет
случайную величину и наиболее полно описывается одномерной
ФРВ или ПРВ. Менее полными характеристиками, но в ряде случа-
случаев достаточными для описания и анализа случайного процесса,
являются моменты распределения вероятностей. Моменты позво-
позволяют судить только о некоторых свойствах случайного процесса, но
как характеристики часто бывают более простыми и удобными при
его описании. Преобразование Фурье связывает ПРВ с характери-
характеристической функцией случайного процесса. Использование характе-
характеристической функции в ряде случаев позволяет упростить анализ
случайных процессов.
В разделе рассматриваются характеристики случайного процес-
процесса, описывающие его в выбранный момент времени: одномерные
ФРВ и ПРВ, соответствующие моменты распределения вероятно-
вероятностей и одномерная характеристическая функция.
15.1. Одномерная функция распределения и плотность
распределения вероятностей случайного процесса
Случайный процесс в выбранный момент времени t представля-
представляет случайную величину, принимающую значения, равные значениям
реализаций (рис. 15.1). ФРВ этой величины определяется как
F,(x,t) = Р{$(П< х) ^ A51)
где Р{...} - символ вероятности.
Значения Frfx, t) лежат в диапазоне 0...1 (рис. 15.2), могут быть
определены с учетом следующего предельного равенства
Fi(*.0= lim -^, A5.2)
Л/о->« Л/О
384

Одномерное распределение вероятностей
Рис. 15.1
где Nq - общее число реализаций случайного процесса, наблюдае-
наблюдаемых в момент времени t, N(x) - число реализаций случайного про-
процесса не превышающих уровень х в момент времени t
Выражение A5.2) поясняет содержание ФРВ и является исходным
при ее определении в процессе обработки ансамбля реализации.
385

Раздел 15
A5.3)
если она существует, называется ПРВ случайного процесса
(рис. 15.2). Соответственно, имея ПРВ, можно перейти к ФРВ слу-
случайного процесса
A5.4)
Вероятность нахождения значений случайного процесса между
уровнями х1 и х2 равна
Х2
P{x^<^<xz} = F,(x2,t)-F,(xvt)=jf1(x,t)dx. A5.5)
ФРВ и ПРВ зависят от заданного уровня х и момента времени /,
в который рассматривается случайный процесс. Для стационарных
случайных процессов одномерные характеристики распределения
от выбора момента времени t не зависят. Они зависят только от х.
В дальнейшем рассматриваются стационарные случайные процес-
процессы, характеристики которых зависят только от х.
ФРВ дискретного случайного процесса изменяется скачкообраз-
скачкообразно и определяется как (рис. 15.3)
A5.6)
где рк- вероятность появления значения случайного процесса, рав-
равного хк; п- число заданных значений случайного процесса.
Рис. 15.2
386
Производная от ФРВ

Одномерное распределение вероятностей
¦+х
Рис. 15.3
Очевидно
л/
Ей. =1.
/с=1
где N- число возможных значений случайного процесса.
ПРВ дискретного случайного процесса содержит импульсные
функции
A5.7)
Вероятность нахождения значений дискретного случайного про-
процесса между хп и хт равна
A5.8)
к=т
387

Раздел 15
Менее полную, но в ряде случаев достаточную информацию о
случайном процессе содержат моменты распределения вероятно-
вероятностей. Начальный момент л-го порядка непрерывного случайного
процесса определяется выражением
оо оо
mn = M{t,n(t)}= J xV,(x)= J xnf,(x)dx, A5.9)
где М{...} - символ усреднения по ансамблю реализаций.
Для дискретного случайного процесса, принимающего значения
Xi, x2,..., xNc вероятностями р/, р2,..., pN, имеем
N
тп=Их"крк- <15-1°)
/с=1
Начальный момент первого порядка - математическое ожидание
или среднее значение непрерывного случайного процесса
пц = М{ф)}= [ xffa) dx = a. A5.11)
Математическое ожидание дискретного случайного процесса оп-
определяется выражением
m, = ZxA <1512>
к=-\
Случайный процесс с математическим ожиданием, равным ну-
нулю, называется центрированным, его обозначим ^0 (t). Переход к
центрированному случайному процессу очевиден Ь$ (t) = tj(t) - a.
Моменты распределения вероятностей центрированного слу-
случайного процесса называются центральными
т° = лфол@}= ](x-m/f^x)dx. A5.13)
Для дискретного случайного процесса
/с=1
388

Одномерное распределение вероятностей
Центральный момент первого порядка, очевидно, равен нулю.
Центральный момент второго порядка называется дисперсией. Для
непрерывного случайного процесса она определяется как
т°2= J(x-miJfi(x)afx = a2. A5.15)
Для дискретного случайного процесса
m°2 = f^(xk-m/pk = a2. A5.16)
/(=1
Дисперсия характеризует степень отклонения случайного про-
процесса (его мгновенных значений) от математического ожидания.
Величина а называется средним квадратическим отклонением
случайного процесса. Дисперсия связана с начальными моментами
соотношением, получаемым из A5.15) или A5.16)
а2 = т2 - mf = т2 - а2. A5.17)
В общем случае центральные моменты распределения вероят-
вероятностей связаны с начальными следующими выражениями:
т° = т -т2,
2 2 1
A5.18)
Приведенные равенства, а также продолжение их ряда могут
быть получены из A5.13)
Исходные данные, необходимые для определения характери-
характеристик распределения, приведенных выше, получаются в результате
обработки ансамбля реализаций случайного процесса. Такой под-
подход к определению характеристик не всегда удобен и возможен.
Вследствие этого особый интерес представляют случайные про-
процессы, позволяющие получить те же характеристики при обработке
одной реализации - эргодические случайные процессы .
389

Раздел 15 _^
15.2. Эргодические случайные процессы ,
их характеристики распределения
Среди случайных процессов особое место занимают зргодиче-
ские случайные процессы. Случайный процесс называется эргоди-
ческим, если его характеристики распределения вероятностей, по-
получаемые усреднением по ансамблю реализаций, равны характе-
характеристикам, получаемым усреднением по времени при обработке од-
одной реализации. Необходимым условием эргодичности является
стационарность случайного процесса. Свойством эргодичности об-
обладают практически все стационарные случайные процессы, с ко-
которыми приходится встречаться на практике. В некоторых случаях
эргодичность случайного процесса принимается гипотетически.
Для эргодического случайного процесса одномерная ФРВ может
быть определена как (рис. 15.4)
л/
^ (*) = lim-*2l—, A5.19)
T—>°° T
где Т- интервал времени наблюдения; Тк - интервал времени, на
котором мгновенные значения случайного процесса не превыша-
превышают уровень х (на рис. 15.4 - длительности незаштрихованных уча-
участков).
Моменты распределения вероятностей эргодического случайно-
случайного процесса также могут получаться усреднением по времени. Ма-
Математическое ожидание находится как
Рис. 15.4
390
A5.20)

Одномерное распределение вероятностей
где ZfK\t) - реализация случайного процесса; <..-> - символ усред-
усреднения по времени.
Величина A5.20) представляет постоянную составляющую слу-
случайного процесса (рис. 15.4).
Второй начальный момент
< = (feW(')f) = lim ^ } И')? * • A5.21)
описывает среднюю мощность случайного процесса. Средняя мощ-
мощность переменной составляющей (центрированного случайного
процесса) определяется центральным моментом второго порядка -
дисперсией
2 - r ,, J)=lim^jH')-m,fc*. A5.22)
Рассмотренные характеристики и другие, получаемые усредне-
усреднением по времени для эргодических случайных процессов, идентич-
идентичны получаемым из ансамбля реализации. Однако физическое со-
содержание характеристик эргодического случайного процесса (по
крайней мере моментов распределения вероятностей первых по-
порядков) является более очевидным.
15.3. Некоторые виды случайных процессов
В качестве примеров рассмотрим некоторые виды случайных
процессов, их характеристики распределения вероятностей.
1. Гауссовский процесс
Одним из наиболее важных законов распределения случайных
процессов является нормальный. Случайный процесс, имеющий
нормальное распределение, называется гауссовским. Важное ме-
место, занимаемое гауссовским процессом, объясняется рядом при-
причин, из которых следует отметить:
• гауссовский процесс принимается как математическая модель
для большого числа случайных процессов с достаточно строгим
обоснованием;
• нормальный закон представляет тот предельный вид, к кото-
которому при некоторых условиях, часто выполняемых на практике,
приближаются другие законы распределения. Это связано в первую
391

Раздел 15
очередь с тем, что в соответствии с центральной предельной тео-
теоремой теории вероятностей распределение суммы большого числа
независимых случайных величин стремится к нормальному;
• математический аппарат анализа гауссовских процессов наи-
наиболее (или достаточно) прост; стационарный гауссовский процесс
полностью описывается, если известны его математическое ожи-
ожидание и корреляционная функция.
Нередко анализ удается провести только для гауссовских про-
процессов.
Одномерная ПРВ гауссовского процесса описывается выраже-
выражением
t(x) = —L=e 2o . A5.23)
aV27i
Как следует из A5.23), одномерная ПРВ определяется двумя
параметрами: а и о. Параметр а представляет математическое
ожидание случайного процесса
~ (*-*J
т = \xf^x)dx = —)=\xe 2a* dx = a, A5.24)
1 J стл/2тг J
a 2 является дисперсией
m°= Ux-mtff^x)dx = —~= [(x-afe 2°2dx = o2. A5.25)
2 L Gv2n?
Кривая ПРВ гауссовского процесса приведена на рис. 15.5,а.
Она симметрична относительно математического ожидания, имеет
максимум при х = а
f1max(x) = -^- = 0,39894/a.
Максимальная крутизна кривой (точка перегиба) при х = а±о.
ФРВ гауссовского процесса определяется как (рис. 15.5,6)
392
A5.26)

Одномерное распределение вероятностей
Рис. 15.5
Расчет ПРВ и ФРВ гауссовского процесса может производиться
с использованием табулированных функций:
A5.27)
При расчете ФРВ гауссовского процесса может также использо-
использоваться табулированная функция
1 7 -?-
Q{x) = -?=\e 2du. A5.28)
л/2л J
X
Из сравнения A5.27) и A5.28) следует, что
(ЗД = 1 - Ф(х).
Составлены также таблицы интеграла вероятностей (функции
ошибок)
A5.29)
Функция Ф\(х) часто используется в решениях интегралов.
Для малых значений х функция Ф(х) может быть аппроксимиро-
аппроксимирована рядом
_ . 1 1 ^ (-1)УЛ+1
Ф(х) = — + -==•> -^— .
2 72^ат!2лBл + 1)
393

Раздел 15
При достаточно большом значении аргумента полезна следую-
следующая аппроксимация:
х2п+1
Из A5.13) с учетом A5.23) можно получить центральные момен-
моменты распределения гауссовского процесса
A5.30)
2. Релеевский процесс
Преобразование гауссовского процесса может привести к случай-
случайному процессу, имеющему обобщенное распределение Релея. ПРВ
такого случайного процесса описывается выражением (рис. 15.6,а)
A5.31)
где a,G- параметры распределения; /0(х) - модифицированная
функция Бесселя первого рода:
ФРВ релеевского процесса определяется как
394
Рис. 15.6

Одномерное распределение вероятностей
FM = ±]ue~'°' ЬЩ*. A5.32)
Используя известное соотношение
х п
\unln_,{au)du = — ln(ax), а) О, A5.33)
выражение для ФРВ запишем в виде
х2+а2
F,(x)= e^fU)"^ a>0, x>0. A5.34)
При малых значениях отношения а/а, раскладывая функцию
Бесселя в A5.31) в степенной ряд и ограничиваясь первыми двумя
членами разложения, получим
«i(x)-4e~^"fi + ^4l. 05.35)
о2 [ 4о4 у
При больших значениях а/а можно воспользоваться следую-
следующим разложением:
/0(x)«-iL(i+-L- + —Ц- + ...1. A5.36)
л/2юЛ 8х 128х2 J
Ограничиваясь первыми двумя членами разложения, выражение
для ПРВ запишем в виде
-af
ф) = -1=е~ 2°2 1 + -^-L - • A5.37)
П ; aV2^ I, baxjia
При а/а»1 обобщенный закон распределения Релея перехо-
переходит в нормальный с параметрами а и a.
Моменты распределения вероятностей при обобщенном законе
Релея определяются выражением
Jx"+1/0 -^ e2o2dx. A5.38)
395

^__ Раздел 15
Решение интеграла в A5.38) дает
тя-И^1 + !Ц-?д-^]. A5-39)
где Г(х) - гамма-функция; ^(х,, *2>хз)~ вырожденная гипергео-
гипергеометрическая функция.
Если а = 0, то из A5.31) получим распределение Релея
(рис. 15.6,6)
ф) = 4-е 2°2-^>0, A5.40)
/^(х) = 1-е 2°2,х>0. A5.41)
Моменты распределения вероятностей релеевского случайного
процесса определяются выражением
/пп = Bа2^1 + 0 A5.42)
среднее значение
[я
Шн = .—О ,
i ''о
дисперсия
т2 - mf = B --)а2 = 0,429а2.
Некоторые наиболее известные виды распределений непрерыв-
непрерывных случайных величин приведены в табл. 15.1.
3. Телеграфный сигнал
Примером дискретного случайного процесса может служить слу-
случайный процесс, реализация которого изображена на рис. 15.7,а.
Случайный процесс принимает только два значения Д и А^,
а моменты перемены значений случайны. Такой случайный процесс
получается, например, на выходе идеального ограничителя при по-
подаче на вход непрерывного случайного процесса . Его ФРВ равна
396

Одномерное распределение вероятностей
Таблица 15.1
№
п/п
Характеристики распределения вероятностей
случайных величин
Характеристики распределения
вероятностей случайной величины
Нормальное распределение
397
Обобщенное распределение Релея

Раздел 15
№
п/п
Характеристики распределения
вероятностей случайной величины
Распределение Релея
X2
Логарифмическое нормальное распределение
398

№
п/п
Одномерное распределение вероятностей
Характеристики распределения
вероятностей случайной величины
Показательное распределение
Распределение Лапласа (двустороннее показательное)
399

№
п/п
Раздел 15
Характеристики распределения
вероятностей случайной величины
Распределение крайних значений (Фишера-Типпета 1 типа)
Распределение Пирсона 3 типа
г я
400

Одномерное распределение вероятностей
№
п/п
Характеристики распределения
вероятностей случайной величины
Логистическое распределение
т.
Распределение Вейбулла
10
401

Раздел 15
402
Показательно-степенное распределение
Характеристики распределения
вероятностей случайной величины
Равномерное распределение

Одномерное распределение вероятностей
№
п/п
Характеристики распределения
вероятностей случайной величины
Гамма-распределение
13
Распределение Эрланга
14
403

№
п/п
Раздел 15
Характеристики распределения
вероятностей случайной величины
Распределение Накагами
(т-распределение)
т г(т)
D (?)- функция параболического цилиндра
1-
404
Распределение Стьюдента

№
п/п
Одномерное распределение вероятностей
Характеристики распределения
вероятностей случайной величины
Распределение Снедскора
(F-распределение)
17
Распределение хи-квадрат (х2)
18
405

Раздел 15
A5.43)
ПРВ случайного процесса описывается с помощью импульсных
функций
Начальные моменты получаются из выражения
A5.44)
с подстановкой A5.44). Они равны
Математическое ожидание
406
A5.45)
Рис. 15.7

Одномерное распределение вероятностей
пц = Др+А,A-р). A5.46)
Центральные моменты описываются выражением
m° = j(x-m,)nf](x)dx = (A,-m,)np + (A2-m1)n(i-p). A5.47)
Частным случаем рассматриваемого дискретного случайного
процесса является телеграфный сигнал. Телеграфный сигнал
представляет случайный процесс, принимающий значения: -А и А,
моменты перемены знака подчиняются закону Пуассона
Рп=Щ^е~х\ A5.48)
где Рп - вероятность п перемен знака на интервале времени т;
X х = \i - среднее число переменых знака.
Вероятность числа перемен знака на рассматриваемом интер-
интервале времени не более п определяется как
Р(*<Л)=Р2„ = ?М^. A5.49)
С увеличением значения \х = Хт распределение Пуассона при-
приближается к нормальному со средним и дисперсией, равны-
равными ц .Это означает, что для больших значений ц можем записать
следующее выражение:
A5.50)
Поправка 1/2 в A5.50) не является обязательной, но она улуч-
улучшает аппроксимацию нормальным законом при сравнительно не-
небольших значениях ц.
Для телеграфного случайного сигнала р = 0,5
fi(x) = 0,55(x-A) + QJ58(x+A). A5.51)
407

^ Раздел 15
Моменты распределения вероятностей тп = 0.
Вероятность того, что на интервале т не будет перемены знака
(отсутствует пересечение случайным процессом нулевого уровня)
найдется из A5.48)
Р0 = е~к\ A5.52)
Значение Ро определяет вероятность того, что интервал между
пересечениями случайным процессом нулевого уровня будет не
меньше т. Величина
Ъ(т)^-Р0=1-е-кх(х>0) A5.53)
представляет одномерную ФРВ длительности интервалов между пе-
пересечениями случайным процессом нулевого уровня (рис. 15.7,6).
Полученный результат относится только к случайному процессу с
пуассоновским распределением нулей (точек пересечения с нуле-
нулевым уровнем).
ПРВ интервалов между точками пересечения:
ф) = dFb(x)l ск=Хе~Хт(т > 0). A5.54)
Полученное распределение называется показательным с пара-
параметром Л. Математическое ожидание и дисперсия равны
1 2 1
к . A5.55)
15.4. Представление плотности распределения
вероятностей случайного процесса с помощью
ортогональных многочленов
Плотность распределения вероятностей случайного процесса
представляет функцию, которая, как абсолютно интегрируемая,
может быть разложена в ряд по ортогональной системе многочле-
многочленов. В некоторых случаях такое представление ПРВ бывает удоб-
удобным как при анализе самой функции ПРВ, так и при ее расчете.
Примеры применения разложения ПРВ при анализе случайного
процесса на выходе нелинейного устройства приведены в разд. 17,22.
Ряд, в который раскладывается ПРВ, записывается в виде
408

Одномерное распределение вероятностей
'iM=2<VPnM A5.56)
л=0
где {фл(х)} - система базисных функций; сп - постоянные коэф-
коэффициенты.
В качестве базисных функций Фл(х) обычно берутся ортого-
ортогональные многочлены. Это связано прежде всего с удобством опре-
определения коэффициентов разложения. Система функций {фп(х)}
называется ортогональной с весом р (х) на интервале [а, Ь], если
выполняется равенство
г / ч / ч / ч \0, т*п,
J«pm(xUxbM*=J|W|2>m=n/ <15-57>
где ||фп || - норма базисных функций фп(х).
Из A5.56) с учетом A5.57) можно определить коэффициенты сп
как
ь
с" = гЛг J fi (x>p n(x)p(x)c6f. A5.58)
IWI а
В качестве ортогональных многочленов могут быть выбраны мно-
многочлены Лежандра, Чебышева, Эрмита, Лагерра и др. Их краткое
описание и примеры применения при анализе различных функций
даны в первой части книги. При разложении ПРВ случайных процес-
процессов наиболее часто используются многочлены Эрмита и Лагерра.
15.4.1. Разложение ПРВ в ряд по многочленам Эрмита
(ряд Грама - Шарлье)
Удобство применения многочленов Эрмита при разложении ПРВ
связано с тем, что от них достаточно просто перейти к нормальной
ПРВ и ее производным. Разложение же ПРВ в ряд с использовани-
использованием нормальной ПРВ позволяет оперировать с хорошо известной
функцией и, кроме того, судить о степени приближения рассматри-
рассматриваемой ПРВ к нормальной, установить условия, при которых это
приближение будет более близким.
Многочлены Эрмита, применяемые при разложении ПРВ, обыч-
обычно определяются как
409

Раздел 15
л/2я
и ее производными qf*n\x) соотношением
<P{n\x) = ^Le^Hn{x). A5.61)
Функции Нп(х) и ф(л)(х) являются ортогональными, для них
справедливо равенство
1н-м^*НнгГт-«- <15-62'
Вследствие этого возможно представление Цх)в виде ряда
разложения по функциям ф(п)(х)
410
Многочлены Эрмита связаны с нормальной ПРВ
Они ортогональны на всей оси (-<*>; оо ) с весом е :
Первые шесть многочленов:

Одномерное распределение вероятностей
ф) = ^сп^\х\ A5.63)
л=0
Умножение левой и правой частей A5.63) на Нп(х) и интегриро-
интегрирование от -оо до оо приводят к следующему выражению для коэф-
коэффициентов ряда:
cn=^]Hn{xy,{x)dx = ^M{Hn(x)}, A5.64)
где М{...} - символ усреднения.
Таким образом, коэффициенты ряда определяются математиче-
математическим ожиданием многочленов Эрмита, а с учетом выражений для
них A5.60) - начальными моментами случайной величины (случай-
(случайного процесса в выбранный момент времени)
оо
mn= jxnf<(x)dx. A5.65)
—оо
Функция ф(х) представляет нормальную ПРВ случайной вели-
величины с нулевым математическим ожиданием и единичной диспер-
дисперсией. При переходе к ПРВ с произвольными значениями ма-
математического ожидания и дисперсии выражение A5.63) должно
быть заменено следующим (см. п. 15.5.):
'iM = |>n<P(n)M A5-66)
л=0
а A5.64):
сп =UL]HMiy)*-k? ) "i^),Mf ¦ A5.67)
—оо — оо
где т. а2 - математическое ожидание и дисперсия случайной ве-
величины,
2 _2 Х-Юл
G*=m2-mf; y = -.
о
Первые коэффициенты разложения равны
411

Раздел 15
Таким образом, выражение для ПРВ примет вид
A5.68)
A5.69)
где у =
а
Разложение ПРВ в виде A5.69) представляет ряд Грама-
Шарлье. Последовательность получения такого разложения - сле-
следующая: находятся начальные моменты распределения случайного
процесса; в соответствии с A5.18) определяются центральные мо-
моменты и определяются коэффициенты разложения A5.67); записы-
записывается ряд в виде A5.69).
Функции <р*л)(у) табулированы. Пример разложения ПРВ в ряд
Грама-Шарлье дан в разд. 17.
15.4.2. Разложение ПРВ в ряд по многочленам Лагерра
Многочлены Лагерра при описании ПРВ определяются выраже-
выражением
412

Одномерное распределение вероятностей
e~xxn+a), A5.70)
La(x) = ^ + a-x,
La2(x) = ~[(a + ^a + 2)-2x(a + 2)+ х2} A5.71)
La(x) = -[(a + iXa + 2Xa + 3)-3x(a + 2Xa + 3)+
з б
+ 3x2(a + 3)-x-3j
Многочлены Лагерра ортогональны на полуоси [о, °° )с весом
где Г(х) - гамма-функция.
Разложение ПРВ неотрицательной случайной величины в ряд по
многочленам Лагерра записывается в виде
^(xbf^e-WM, A5.73)
где коэффициенты сп определяются выражением
c--?(^b]{L:(x)f'Wdx- A5-74)
Выражение A5.74) получается из A5.73) с учетом A5.72). При
х
переходе к новой переменной у = — запишем
'i(y)=|>ne-VV(yl A5.75)
л=0
где
413
первых порядков:
A5.72)

Раздел 15
A5.76)
A5.77)
ЗШр / о\ /Т73
Константы а и 0 выбираются таким образом, чтобы коэффици-
коэффициенты Ст и с2 были равны нулю. Это условие выполняется при
A5.78)
ГПо - /77
1
где сг - дисперсия случайной величины.
Таким образом, имеем:
A5.79)
414
Из A5.76) с учетом A5.71) найдем

Одномерное распределение вероятностей
Коэффициенты разложения, начиная с с3, определяются до-
довольно сложными выражениями. Вследствие этого представление
ПРВ в виде ряда Лагерра обычно используется только в том слу-
случае, когда можно ограничиться только одним первым членом.
В этом случае
A5.80)
/77'
Пример использования приведенного представления ПРВ дан
в разд. 17.
15.5. Одномерное распределение вероятностей функции
случайного процесса
В цепях радиотехнических систем происходит преобразование
случайного колебания - случайного процесса. Появляется необхо-
необходимость определения характеристик случайного процесса после
его преобразования.
Если случайные величины Z,{t) и г|@ связаны однозначным со-
соотношением (рис. 15.8,а)
у = ф(х) * = Ф~1(у). A5.81)
где (р~1(у) - функция, обратная (р(х),
то это означает, что каждому значению х, принимаемому случайной
величиной ?@, соответствует единственное значение у, прини-
принимаемое r\(t). Вероятность попадания случайной величины ?,{t) в
интервал [х, х + dx] равна вероятности попадания случайной вели-
величины T|(f) в интервал [у, у+ dy]. Таким образом, (рис. 15.8,6)
f^(x)dx=fr],{y)dy, A5.82)
где /^ (х), /ni (у) - одномерные ПРВ случайных величин ?(f) и r\(t).
От A5.82) можно перейти к следующему соотношению, связы-
связывающему ПРВ случайной величины ?(f) с ПРВ tj(f),
415

Раздел 15
A5.83)
Если обратная функция х = ср \у) неоднозначна, то одному зна-
значению у соответствует несколько значений х. х^у), х2(у),..... хп(у).
В этом случае выражение A5.83) должно быть записано в виде
A5.84)
С учетом A5.83) можно получить моменты функции случайной
величины. Если обратная функция Ф~1(у) однозначная, то с учетом
A5.82) можно записать
A5.85)
В качестве примеров рассмотрим некоторые виды преобразова-
преобразований случайных процессов, с которыми приходится иметь дело на
практике.
Рис.15.8
416

Одномерное распределение вероятностей
1. Линейное преобразование (табл. 15.2, п.1).
При линейном преобразовании случайной величины
У = с + Ьх A5.86)
имеем взаимно однозначное соответствие t,(t) и r\(t). Из A5.83)
получим
'>)=^И' <15-87>
Как следует из A5.87), при линейном преобразовании случайной
величины происходит смещение кривой ПРВ на с и изменение
масштаба по осям координат в b раз.
Для гауссовского процесса
(х-аJ
hM = -j=e 2°2 A5.88)
получим
[y-(c+a)f
ф) = -10 2*°г . A5.89)
>j2n\t\o
Таким образом, линейное преобразование гауссовского процес-
процесса не изменяет закона распределения - случайный процесс остает-
остается гауссовским.
2. Квадратичное преобразование (табл. 15.2, п.4).
При квадратичном преобразовании случайной величины
у = х2 A5.90)
каждому значению у соответствуют два значения х
Из A5.84) с учетом A5.91) найдем
МУ) = -М^л/у) + ^(-л/у) I- У>0- <15'92)
2>/У
417

Раздел 15
Таблица 15.2
Плотность распределения вероятностей функции
случайной величины
№
п/п
Функциональная зависимость. Плотность распределения
вероятностей функции случайной величины
ПРВ функции случайной величины (общее выражение)
ПРВ функции нормально распределенной случайной величины
1
418

Одномерное распределение вероятностей
Функциональная зависимость. Плотность распределения
вероятностей функции случайной величины
419
ПРВ функции случайной величины (общее выражение)
ПРВ функции нормально распределенной случайной величины

Раздел 15
420
Функциональная зависимость. Плотность распределения
вероятностей функции случайной величины
ПРВ функции случайной величины (общее выражение)
Ф)=Ф)+Ь(-у\у*о
ПРВ функции нормально распределенной случайной величины

Одномерное распределение вероятностей
№
п/п
Функциональная зависимость. Плотность распределения
вероятностей функции случайной величины
ПРВ функции случайной величины (общее выражение)
ПРВ функции нормально распределенной случайной величины
421

Раздел 15
№ Функциональная зависимость. Плотность распределения
п/п вероятностей функции случайной величины
У [О, х<о
ПРВ функции случайной величины (общее выражение)
fJy)=FvWy)-
2jty
ПРВ функции нормально распределенной случайной величины
,2
422

Одномерное распределение вероятностей
№
п/п
Функциональная зависимость. Плотность распределения
вероятностей функции случайной величины
ПРВ функции случайной величины (общее выражение)
ПРВ функции равномерно распределенной случайной величины
1
423

Раздел 15
№ Функциональная зависимость. Плотность распределения
п/п вероятностей функции случайной величины
ПРВ функции случайной величины (общее выражение)
ПРВ функции нормально распределенной случайной величины
424

№
п/п
Одномерное распределение вероятностей
Функциональная зависимость. Плотность распределения
вероятностей функции случайной величины
ПРВ функции случайной величины (общее выражение)
ПРВ функции нормально распределенной случайной величины
425

Раздел 15
№ Функциональная зависимость. Плотность распределения
п/п вероятностей функции случайной величины
ПРВ функции случайной величины (общее выражение)
Ф) = ±фу)
ПРВ функции нормально распределенной случайной величины
1
426

Одномерное распределение вероятностей
Для гауссовского процесса из A5.92) получим
1
1
, у>0.
Для релеевского процесса
.A5.93)
A5.94)
A5.95)
A5.96)
Случайный процесс r\(t) в этом случае имеет экспоненциальное
распределение (табл. 15.1).
3. Преобразование (табл. 15.2, п.6)
y = bsinx. A5.97)
Каждому значению у соответствует бесчисленное множество
значений х:
xk=nk + (-^karcs\n—, /c = 0 +1, ±2,...
b
Из A5.84) с учетом A5.98) найдем
1
При а = 0(рис. 15.9,6)
получим (рис. 15.9,в)
A5.98)
A5.99)
427

Раздел 15
Наибольший интерес представляет равномерное распределе-
распределение ?, на интервале |xj < я
^=1/2я. A5.100)
В этом случае в A5.99) необходимо учесть три члена - при к = -1,
к= 0 и к= 1 ПРВ случайной величины ti@ примет вид
Ш=—А=г- М<ь- <15-101>
ФРВ, соответствующая A5.101), равна
F_1(y)=0,5 + -arcsin-^-l \y\<b.. A5.102)
1 я b ' '
Некоторые наиболее простые функции случайных величин и со-
соответствующие ПРВ приведены в табл. 15.2.
15.6. Характеристическая функция случайного процесса
Удобной характеристикой случайных процессов, широко исполь-
используемой при их анализе, является характеристическая функция. Ха-
Характеристическую функцию случайного процесса ?,(t) обычно опре-
определяют как математическое ожидание функции е'^\ где v- про-
произвольная действительная величина
/w{e'^(f)}= jf^x)e'vxdx = Q^v), A5.103)
где ^(х) - ПРВ случайного процесса ^(t).
Как следует из A5.103), характеристическая функция является
обратным преобразованием Фурье ПРВ случайного процесса (без
привычного коэффициента 1/2я). Прямое преобразование Фурье
характеристической функции (с коэффициентом 1/2я) дает ПРВ
случайного процесса.
/с1(х) = — \^(v)e-'vxdv. A5.104)
2я J
428

Одномерное распределение вероятностей
Таким образом, ПРВ и характеристическая функция случайного
процесса связаны преобразованием Фурье (прямым и обратным).
Характеристическую функцию можно также определить как обратное
преобразование ПРВ случайного процесса (случайной величины).
Так как e'^(r) | = 1 при всех действительных v, интеграл A5.103)
существует для всех ПРВ, следовательно, характеристическая
функция может быть определена для каждой случайной величины.
Для характеристической функции справедливы следующие соот-
соотношения:
9^0) = 1, \Q,(v] < 1, (-00 < v < оо) A5.105)
Если ПРВ четная, то соответствующая характеристическая
функция является действительной функцией.
В качестве примера определим характеристическую функцию га-
уссовского процесса. Она получается подстановкой A5.23)
в A5.103)
(x-af oV
e(v) = _J= \eivxe 2°2 dx = eaV~ 2 . A5.106)
ал/2я -^
Для центрированного гауссовского процесса имеем
B,(v) = e 2 . A5.107)
Выражения для характеристических функций при некоторых других
видах распределения случайной величины приведены в табл. 15.1.
Если r] = b? + a, (Ьиа- постоянные), то
^(v) = ^(bv)eiav, A5.108)
где Q^(v) и 6л1(^) - характеристические функции случайных вели-
величин ? И Г).
Действительно,
M{eIW]\= м{е"&+а)\= е1шм{е'^\= eimQ^{bv). A5.109)
Удобство использования характеристической функции при ана-
анализе случайных процессов следует из свойств преобразования Фу-
Фурье. В частности, характеристическая функция суммы независимых
429

Раздел 15
случайных величин равна произведению их характеристических
функций.
Производные характеристической функции по параметру v оп-
определяются выражением
A5.110)
Если существует начальный момент л-го порядка случайного
процесса, то из A5.110) получим
E.111)
Таким образом, начальные моменты случайного процесса мож-
можно определить через производные характеристической функции при
v=0
A5.112)
Раскладывая характеристическую функцию в ряд Тейлора, запи-
запишем
A5.113)
A5.114)
Следовательно, характеристическая функция случайного про-
процесса определяется моментами распределения. Учитывая связь
характеристической функции с ПРВ, можно сказать, что моменты
распределения вероятностей определяют и ПРВ случайного про-
процесса. Чем большее число начальных моментов распределения
случайного процесса известно, тем точнее может быть определена
характеристическая функция и ПРВ случайного процесса.
Математическое ожидание и дисперсия случайного процесса
430

Одномерное распределение вероятностей
достаточно просто определяются через производные логарифма
характеристической функции.
Обозначим
V(v) = ln61(v).
Получим
e-(v)
-гМ-ё^. A5-115)
A5.116)
Учитывая, что 9^0) = 1, и A5.111), находим:
V'@)=e;@)=/Mfe}. A5.117)
Таким образом,
Mfe} = ^, A5.118)
/?•@)
/wfe2}-/W2fe}=a2=-\i/''@). A5.119)
Производная л-го порядка логарифма характеристической функ-
функции при v- 0, умноженная на /л, называется семиинвариантом п-го
порядка случайной величины.
Соотношения, аналогичные полученным выше, позволяют убе-
убедиться в том, что семиинварианты любого порядка л представляют
действительную функцию п первых моментов.
431

Раздел 16.
МНОГОМЕРНОЕ РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
СЛУЧАЙНОГО ПРОЦЕССА
Наиболее полное описание случайного процесса на интервале
времени дает л-мерная ФРВ или ПРВ. Они характеризуют стати-
статистически поведение случайного процесса в выбранные моменты
времени. Используя /7-мерные ФРВ и ПРВ, можно получить мо-
моменты распределения вероятностей и другие характеристики слу-
случайного процесса. Среди них особое место занимает второй сме-
смешанный центральный момент - корреляционная функция. Корре-
Корреляционная функция характеризует статистическую связь между
значениями случайного процесса в два различных момента вре-
времени. Преобразование Фурье связывает ее со спектральной
плотностью мощности случайного процесса. Это соотношение
между корреляционной функцией и спектральной плотностью
мощности лежит в основе корреляционного и спектрального ана-
анализа случайных процессов.
В разделе рассматриваются /7-мерные вероятностные характе-
характеристики случайного процесса.
16.1.Многомерная функция распределения и плотность
распределения вероятностей случайного процесса
Двумерная ФРВ описывает случайный процесс t,(t) в два момен-
момента времени ?, и Х2 (рис. 16.1)
F2(xbx2) = P{x(t,)<xbx(t2)<x2}, A6.1)
где Р{...} -символ вероятности.
Функция F2(xbx2)определяет вероятность того, что случайный
процесс ?(f)B момент времени ^ не превышает уровень хь а в мо-
момент времени t2 - уровень х2.
Рассматривая ансамбль реализаций случайного процесса, для
двумерной ФРВ можно записать следующее предельное соотношение
F2(x1,x2)= Jim Щ*й, A6.2)
/vo->°° /v0
432

Многомерное распределение вероятностей
где Л/о - общее число реализаций случайного процесса; N(xb х2) -
число реализаций, значения которых не превышают х1 в момент
времени U и х2 в момент времени t2.
В общем случае двумерная ФРВ зависит от двух выбранных
значений уровня и двух моментов времени, в которые рассматри-
рассматривается случайный процесс. Для стационарного случайного процес-
процесса ФРВ зависит не от рассматриваемых моментов времени, а от
интервала между ними: т = t2 - tA .
Двумерная ПРВ случайного процесса определяется как
fly у \ - d ^2(X1'X2) Mfi'tt
'2(*1'Х2)- Эх,Эх2 ' ( >3)
если ФРВ имеет вторую производную. Она, как и ФРВ, зависит от
значений х^, х2, t:, t2 (для стационарного случайного процесса - от
интервала т между двумя моментами времени, в которые рассмат-
рассматривается случайный процесс).
Рис. 16.1
433

Раздел 16
ФРВ л-го порядка случайного процесса b{t) определяется как
Fn(x1>x2>...Ixn)=Pfe(f1)<x1f^2)<x2l...l4(fn)<xn} A6.4)
Ей соответствует л-мерная ПРВ
'"(х"*г ""'- дх,дх2...дх„ ¦ A65)
ФРВ и ПРВ л-го порядка в общем случае зависят от л моментов
времени .Для стационарного случайного процесса указанные ха-
характеристики зависят только от интервалов времени между рас-
рассматриваемыми моментами - всего л-1 интервал. В дальнейшем
фигурируют только стационарные случайные процессы.
Чем выше порядок ФРВ (ПРВ), тем более детально она описы-
описывает случайный процесс. Однако в полной мере это справедливо
только тогда, когда случайный процесс рассматривается на задан-
заданном ограниченном интервале времени.
Обозначим длительность выделяемого интервала времени Т
(рис. 16.2). Если ФРВ описывает случайный процесс на заданном ин-
интервале в моменты времени, отстоящие друг от друга на М = 77(л - 1):
U , t2= ?i + Af,...,fn = tn.i + At ,то в этом случае л-мерная ФРВ (ПРВ)
представляет тем более полную характеристику случайного про-
процесса, чем больше л.
При л—> °о
FT[x(t)] = \\mFn[x(ti\x{t2\...,x(tn)i A6.6)
если предел в A6.6) существует. Величина FT[x(t)] представляет
функционал распределения вероятностей случайного процесса на
интервале времени. При x(t) = const функционал описывает вероят-
вероятность непревышения случайным процессом заданного уровня на
выбранном интервале времени.
От л-мерной ФРВ можно перейти к ФРВ более низких порядков
/rn_i(x1,x2,...,xn_1)= I Fn\xbx2,.-.,xn)dxm
Z A6.7)
Fn-2\X-\> x2<-> Xn-2/ ~ J ^л-1(Л1>Х2>--->Лл-1/С^п-1>
И Т. Д.
434

Многомерное распределение вероятностей
Рис. 16.2
ФРВ и ПРВ л-мерные позволяют получить моменты распределе-
распределения вероятностей случайного процесса:
начальные моменты распределения
центральные моменты распределения
A6.8)
A6.9)
где а-\, а2)..., ап - математические ожидания случайного процесса в
моменты времени
U,h tn,
для стационарного случайного процесса
&\ = Й2=... = дп = 3.
Важную роль при анализе случайных процессов играет второй
смешанный центральный момент распределения вероятностей -
корреляционная функция.
435

^ Раздел 16
16.2. Корреляционная функция случайного процесса
16.2.1. Определение корреляционной функции
Второй смешанный начальный момент распределения вероят-
вероятностей случайного процесса называется ковариационной функцией
Mfe(W (t2) }=K(tvt2)= J jx,x2f2(xbx2)dx,dx2. A6.10)
Она получается усреднением произведения значений случайно-
случайного процесса, взятых в моменты времени t^ и t2. Второй централь-
центральный момент распределения называется корреляционной функцией
мЦ т-мШ } 1ш-мШ }}=R(tbt2) =
= J j{xi-a^){x2-a2)f2(xbx2)dx^dx2,
©о —со
где аг=М{^(^) ] а2 =M{?(f2) } - математическое ожидание случай-
случайного процесса в моменты времени Ь и Х2.
Подчеркивая, что характеристики относятся к одному случайно-
случайному процессу, их называют автоковариационной и автокорреляцион-
автокорреляционной функциями.
Исходя из приведенных определений получим следующее соот-
соотношение между корреляционной и ковариационной функциями
H(f1,f2) = K(f1f2)-a1a2. A6.12)
При t! = t2 - f A6.12) описывает дисперсию случайного процесса
в выбранный момент времени R(t, t) = a2 .
Нормированная величина центрального момента второго порядка
riw=MMbh±Mkt3Ln=mM. A6.13)
СГ1С2 СТ1СТ2
где ак,ок- математическое ожидание и дисперсия случайного про-
процесса в /с-й момент времени, называется нормированной корреля-
корреляционной функцией или коэффициентом корреляции случайного
процесса.
436

Многомерное распределение вероятностей
Корреляционная функция в общем случае зависит от двух мо-
моментов времени f, и t2, для стационарного случайного процесса -
только от их разности х = t2- th т. е. R(t, t + x) = R(x). Для стационар-
стационарного случайного процесса R(x) = К(х) - а2.
Нормированная корреляционная функция стационарного про-
процесса равна
A6.14)
Она является четной функцией (рис. 16.3) г(т) = г(-т), имеет
максимальное значение при т = 0, т.е. г(т) < л@) = 1, при т—><*>
имеем г(х) —>0 .
Вследствие четности R(x) или г{х) их графики в дальнейшем
приводятся только для т>0.
Корреляционная функция эргодического случайного процесса
может определяться усреднением по времени произведения значе-
значений одной реализации случайного процесса, взятых в моменты
времени, смещенные .один относительно другого на интервал вре-
времени т
A6.15)
Рис. 16.3
437

Раздел 16
где <...>-символ усреднения по времени.
Корреляционная функция является одной из основных характе-
характеристик случайного процесса, широко используемых при его описа-
описании и анализе. Она определяет степень статической связи между
значениями случайного процесса, взятыми в момент времени ^ и t2;
для стационарных случайных процессов - в моменты времени,
разнесенные на интервал т. Сказанное может быть проиллюстри-
проиллюстрировано примерами реализаций случайных процессов и графиками
их корреляционных функций, выполненными в одном масштабе, на
рис. 16.4. Чем более осциллирующий характер имеет реализация,
тем уже корреляционная функция.
Ширина корреляционной функции может быть оценена интерва-
интервалом корреляции.
Рис. 16.4
438

Многомерное распределение вероятностей
16.2.2. Интервал корреляции
Для каждой корреляционной функции можно определить такое
минимальное значение смещения во времени тк, при котором аб-
абсолютное значение нормированной корреляционной функци будет
меньше заданной величины (близко к нулю). Значения случайного
процесса Z,(t) и ^(t + xk) в этом случае можно считать некоррели-
некоррелированными; величину тк называют интервалом корреляции. Иными
словами, интервал корреляции представляет длину наибольшего
интервала времени, на котором корреляционная функция ещё име-
имеет значение, существенное для решаемой задачи.
Используют различные определения интервала корреляции^,
наиболее часто - следующие.
• Интервал корреляции, определяемый по заданному абсолют-
абсолютному значению нормированной корреляционной функции (рис.
16.5,а)
|r(Tfc)|<e,
где е - заданное значение (например, е = 0,05).
• Интервал корреляции, определяемый интегралом от нормиро-
нормированной корреляционной функции или её абсолютного значения
(рис. 16.5,6)
со со
Tk=jr(x)ck или Tk=j\ г(т) |(Л.
о о
При таком определении интервал корреляции численно равен
основанию прямоугольника, высота которого равна максимальному
значению нормированной корреляционной функции т@) = 1, а пло-
площадь равна площади под кривой г(т) или г(х) | (при х > 0).
• Интервал корреляции, определяемый интегралом от квадрата
нормированной корреляционной функции (рис. 16.5,в)
rk=jr2(z)(h.
о
Значения хк, получаемые из приведенных определений, близки
друг к другу, выбор же определения, как правило, диктуется удобст-
удобством при решении конкретной задачи, где понятие интервала корре-
корреляции используется.
439

Раздел 16
б)
Рис. 16.5
16.2.3. Корреляционная функция телеграфного сигнала
В качестве примера корреляционной функции случайного дис-
дискретного процесса приведем корреляционную функцию телеграф-
телеграфного сигнала (разд. 15). Случайный процесс принимает значения 1
или -1. Переход от одного значения к другому происходит скачком
(рис. 16.6,а). Вероятность того, что в интервале времени т проис-
происходит к скачков, описывается ПРВ Пуассона.
A6.16)
где X - среднее число скачков в единицу времени.
Корреляционная функция телеграфного сигнала в соответствии
с A6.11) определяется выражением
A6.17)
Рис. 16.6
440

Многомерное распределение вероятностей
Произведение t,(t)t,(t + т) может быть равно либо 1, либо -1, в
зависимости от того, будет ли выполняться равенство t,(t) = ^(t + T)
или ?(f) = -^(t + х). Равенство ^(t) = Щ + т) означает, что на интер-
интервале х произошло четное число перемен знаков. Вероятность тако-
такого события
Pfe(f) = $(f + T) b^P^e-^^-^Wx). A6.18)
к=0 *f=i dKl
Равенство t{t) =-?,(t + т) означает, что на интервале г произош-
произошло нечетное число перемен знаков. Вероятность такого события
\2/с-1
/с=1 /с=1 ^Л v-
С учетом A6.18) и A6.19) выражение для корреляционной функ-
функции получим в виде
жх)=м{ш«+т) }= рш=ш+х)}- pfeo=~w+х) }=
= е"Хтс/?(Хх) - e"XTs/7(Xx) = е~2Хт.
Равенство получено для х > 0 . Учитывая четность корреляцион-
корреляционной функции, для всех значений х запишем
Я(х)=е~2Х|т|. A6.20)
График корреляционной функции телеграфного сигнала приве-
приведен на рис. 16.6,6.
16.3. Многомерное распределение вероятностей
гауссовского процесса
В качестве примера л-мерных характеристик распределения
случайного процесса приведем характеристики гауссовского про-
процесса: двумерные и в общем случае n-мерные ПРВ и ФРВ.
16.3.1. Двумерные ПРВ и ФРВ гауссовского процесса
Двумерная ПРВ стационарного гауссовского процесса для мо-
моментов времени U и t2 = U+x описывается выражением
441

Раздел 16
A6.21)
где а, о, г - математическое ожидание, дисперсия и нормирован-
нормированная корреляционная функция случайного процесса.
Как следует из A6.21), двумерная ПРВ определяется двумя ве-
величинами: математическим ожиданием а и корреляционной функ-
функцией R( т) = о2г(т), где т = t2 - ^; для центрированного случайного
процесса - только корреляционной функцией.
При расчете f^xb х2) удобнее перейти к нормированным вели-
величинам и рассматривать функцию
Двумерная ФРВ описывается выражением
A6.22)
}du^du2. A6.23)
Функция A6.23) табулирована.
Для частного случая х, = х2 = 0 из A6.23) получим
Ф2@,0) = 0.5 arccos г, @ < arccos г < п).
2я
При г=0
Ф2(х,х) = Ф2(х).
При г= 1
Ф2(х, х) = Ф(х).
A6.24)
A6.25)
A6.26)
Для расчета Ф2 (хь х2) от A6.23) удобнее перейти к несколько
иному выражению. Производя в A6.23) замену переменных
A6.27)
выражение для Ф2 (х:, х2) получим в виде
442

Многомерное распределение вероятностей
x?-rv
Vi-r2
Ф2(хьх2) = -Г=\е-^/2-Г= \e^/2dv,dv2. A6.28)
>/2л j^ л/2я j^
Из A6.28) найдем
6Ф2 1 f х? - 2гх.х2 + х| I
—7^- = ехр<^—* Ц *-к 16.29
cfr I 2A-г2)
2Wi-r2 l J
что позволяет иметь достаточно простое выражение для расчета
двумерной ФРВ гауссовского процесса
Ф2(х1,х2) = Ф1(х1)Ф1(х2) +
х? - 21/ХчХо + х| 1 . • A6.30)
2A -(/) j
Используя A6.29), можно придти и к другому выражению для
расчета двумерной ФРВ
Г. A6.31)
г=0
Выражения A6.30) и A6.31) позволяют получить достаточно
удобные алгоритмы расчета двумерной ФРВ гауссовского случай-
случайного процесса.
Исходя из двумерной ФРВ, полезно найти выражение для веро-
вероятности совпадения (или несовпадения) знаков (полярностей) слу-
случайного процесса в два выбранных момента времени. Эта вероят-
вероятность функционально связана с корреляционной функцией случай-
случайного процесса и используется при её экспериментальном опреде-
определении (знаковые корреляторы).
Вероятность несовпадения знаков стационарного центрирован-
центрированного случайного процесса определяется выражением
оо 0 0»
Рнс = \\Ы^,хг)с1х^ dx2 + J J72(x1f x2)dxA dx2, A6.32)
где 4(^1, x2) - двумерная ПРВ, описывающая случайный процесс в
моменты времени fn t + t.
443

Раздел 16
Преобразуя A6.32), для гауссовского процесса получаем
о о
С учетом A6.24) запишем
рнс = -arccos г(х), A6.34)
где г(х) - нормированная корреляционная функция гауссовского
процесса.
Вероятность совпадения знаков значений случайного процесса,
разнесенных на интервале т, равна
рс = 1 - рнс = 1 -—arccos г(т). A6.35)
я
Как следует из A6.34) и A6.35), вероятность несовпадения (сов-
(совпадения) знаков функционально связана с нормированной корре-
корреляционной функцией гауссовского процесса. Измеряя эту вероят-
вероятность, можно определить корреляционную функцию гауссовского
процесса. В ряде случаев схемная реализация анализатора совпа-
совпадения полярностей случайного процесса оказывается проще, чем
множительного коррелятора.
16.3.2. л-мерная ПРВ гауссовского процесса
ПРВ л-го порядка стационарного гауссовского процесса описы-
описывается выражением
fn{xvx2,.. .,хп) = i =
JBn)nDGn
, , A6.36)
I 1 п п I
444
A6.33)

Многомерное распределение вероятностей
В A6.36) обозначено: а, а2 -математическое ожидание и дис-
дисперсия случайного процесса; D- определитель л-го порядка
A6.37)
гы - нормированная корреляционная функция случайного процесса
в моменты времени tk и t,; DM - алгебраическое дополнение эле-
элемента гм в определителе.
Как следует из A6.36) с учетом определителя D, п-мерная ПРВ
(ФРВ) гауссовского процесса полностью определяется математиче-
математическим ожиданием а и корреляционной функцией Я(т).
Конкретизируя A6.36) для трехмерной ПРВ, запишем
A6.38)
A6.39)
а, о*2,г(т) - математическое ожидание, дисперсия и нормирован-
нормированная корреляционная функция случайного процесса.
16.4. Разложение двумерной плотности распределения
вероятностей в ряд по ортогональным
системам функций
При использовании двумерной ПРВ случайного процесса бывает
полезным её представление в виде ряда разложения по ортого-
ортогональной системе функций, аналогично тому, как это было сделано
в отношении одномерной ПРВ. Такое представление двумерной
445

Раздел 16
ПРВ используется, например, при определении корреляционной
функции случайного процесса на выходе нелинейного преобразо-
преобразователя (разд. 22).
В качестве базисных функций выбираются многочлены орто-
нормированных систем {ф-|П(х1)} и {ф2п(х2)}> имеющие в качестве
весовой функции одномерную ПРВ случайного процесса U (х)
Двумерная ПРВ стационарного случайного процесса записыва-
записывается в виде ряда
f2(xbx2) = ^(х1)^1(х2J]сГ|ф1п(х1)ф2л(х2). A6.41)
С учетом A6.40) коэффициенты сп в A6.41) определяются вы-
выражением
сл= J jf2(xbX2^n(x^2n(x2)dx^dx2. A6.42)
Выберем ФюСх^ = ф20(х2) = 1, тогда из A6.40) получим
J/j(x)dx = 1, A6.43)
что соответствует определению f1 (x) как ПРВ.
Из A6.42) следует:
cb=1. Ci=-VMfeO-^]fe(f + T)-m,J}=r(T). A6.44)
В соответствии с A6.42) определяются и другие коэффициенты
разложения.
Для гауссовских процессов в качестве базисных функций целе-
446
A6.40)

Многомерное распределение вероятностей
сообразно выбрать нормированные многочлены Эрмита Нп (х)
<Рт(х) = -рНп{х). A6.45)
В этом случае ряд, в который раскладывается ПРВ, примет вид
(т1=0, а = 1)
2 2
f2(xbx2) = ^-e~1^^^-Hn(x,)Hn(x2). A6.46)
Пример использования разложения двумерной ПРВ приведен
в разд. 22.
16.5. Условные характеристики распределения
вероятностей случайного процесса
Выражение для двумерной ФРВ случайного процесса ?(f) может
быть записано в виде
F2(x1Ix2) = Pfe(f1)<x1^(f2)<x2} =
= Pfe(f1)<x1}Pfe(f2)<x2/^(f1)<x1}
где Р(А/В) - условная вероятность.
В правой части A6.47) первый сомножитель представляет од-
одномерную ФРВ - F\(Xi). Второй сомножитель - условную ФРВ
/^(х2/х1). Таким образом, A6.47) можно записать в виде
F2(x1,x2) = F1(x1)F2(x2/x1). A6.48)
Из A6.48) получим выражение для условной ФРВ случайного
процесса
F2(x2/x1) = 5i^). A6.49)
Функция F2(x2/ x^)определяет вероятность того, что случайный
процесс %(t) в момент времени \2 не превышает уровень х2 при ус-
условии, что в момент времени ^ он не превышает уровень х^ .
Аналогично A6.49) определяются ФРВ л-го порядка.
С помощью условных ФРВ выражение для л-мерной ФРВ слу-
447

Раздел 16
чайного процесса можно записать в виде
Fn(x1>x2l...lxn) = F1(x1)F2(x2/x1)...Fn(xn/x1,xn_1), A6.50)
где
F (у /у\ - ^(*1'*2) ¦ Fly I у у \ - ^з(Х1>Х2'Хз)
t-2{x2/x,)- , h{x3/xbx2)- ....
П1Х17 Г2\ХЬХ2> A6 51)
Fly /У У У \ - Fn\XbX2>-~>Xn)
...,гп^хл/х11х2,...|хп_1;- .
гп-ПХ1'Х2'"->хл-1/
Такое представление л-мерной ФРВ может оказаться полезным
при её оценке с использованием ФРВ меньшей мерности.
Исходя из условных ФРВ можно определить и условные ПРВ
случайного процесса. Условная ФРВ величены t,(t2), при условии,
что значение величины ?(^) лежит внутри интервала [х^ + Дх],
определяется выражением
х, +Дх х2
f Г/2(х1х2)с/х1сУх2
Pfe(f2)<x2/x1<^1)<x1-bAx}= X1 -~+Ax . A6.52)
pi(xi)^xi
Дифференцируя A6.52) по х2 и переходя к пределу при Дх-* 0,
получим выражение для условной ПРВ случайного процесса
«V*.)-**^- 06.53)
Аналогично можно определить и другие условные ПРВ.
Если значение случайного процесса в момент времени t2 не за-
зависит от того, какое значение принял случайный процесс в момент
времени U , то говорят о статистической независимости ?(^) и ?(f2).
Для независимых случайных величин ?(^)и ?(^2)выполняется ра-
равенство
Pft(f1)<x1,^2)<x2}=P{^1)<x1}Pfe(f2)<x2} A6.54)
или
448

Многомерное распределение вероятностей
F2{x^x2) = Fy(x^{x2). A6.55)
л-мерная ФРВ независимых значений случайного процесса в мо-
моменты времени U, t2, ..., tn равна произведению подномерных ФРВ
п
Fn(xbx2,...,xn) = Y\F,(xk). A6.56)
/с=1
Переходя к ПРВ такого случайного процесса, запишем
п
Шь*2 хп) = ЦЦхк). A6.57)
/с=1
Если равенства A6.56) или A6.57) выполняются для любых мо-
моментов времени (tk*t/),то случайный процесс полностью описы-
описывается одномерной ФРВ (ПРВ). Такой случайный процесс называ-
называется совершенно случайным.
Условные ФРВ или ПРВ позволяют получить условные моменты
распределения вероятностей. Так условное математическое ожи-
ожидание случайного процесса в момент времени t2 при заданном зна-
значении случайного процесса в момент времени t1 (?>(t^) = x<l) опреде-
определяется выражением
МШЬIШ = Ъ}= ]x2f2(x2/x,)dx2. A6.58)
—оо
В качестве примеров приведем условные характеристики рас-
распределения гауссовского процесса. Для стационарного гауссовско-
го процесса условную двумерную ПРВ получим из A6.49)
f2(x2/x1) =
expi- 2^2 1_^ h -aJ -2r(x, -a)(x2 -aJ +(x2 -aJ]+ A6.59)
+ -L(x,-af\
2<5г J
Преобразовав A6.59), запишем
449

Раздел 16
A6.60)
Таким образом, условная ПРВ гауссовского процесса является
нормальной; математическое ожидание равно ау = гх^ + аA - г),
дисперсия Сту = а2A-г2). График условной ПРВ приведен на
рис. 16.7. (а = 0). При г= 0 условная ПРВ переходит в одномерную
ПРВ.
Условное математическое ожидание гауссовского процесса равно
М{Щ)/иЮ = х,}=а + г(х1-а). A6.61)
Если г=0, то условное математическое ожидание совпадает с
безусловным.
Условная дисперсия определяется из A6.60) с учетом A6.61)
A6.62)
Как следует из A6.62), дисперсия не зависит от значения ?,(^), а
зависит только от корреляционной функции случайного процесса.
При г= 0 условная дисперсия совпадает с дисперсией случайного
процесса
450

Многомерное распределение вероятностей
16.6. Распределение случайного процесса
на интервале времени
Одной из задач, решаемой при анализе случайного процесса, яв-
является получение оценки ФРВ на заданном интервале времени - ве-
вероятности того, что случайный процесс внутри заданного интервала
времени Г не превысит установленного уровня х (рис. 16.2). Такой
оценкой может служить (п + 1 j-мерная ФРВ случайного процесса
Рп+1(х) = Р{ад*х, %)<х,...,^л+1)<х}, A6.63)
где *|,*21—>*л+1 - точки разбиения интервала
МпД tk-tk_i=?- = At,k = \2 л + 1.
ФРВ (п + 1)-го порядка представим с помощью условных ФРВ
^+i(^)=^kMKk^)/MMl-^+ik^+i)/^(M.-^(^)]- A6.64)
Условные ФРВ в A6.64) можем приближенно вычислить с помощью
ФРВ меньших порядков. При этом учтем следующее неравенство:
Pfe(fn+1)<x/^1)<x,%)<xI...,%)<x}<
<P{^n+1)<x/^fn_,)<x,...,^n)<x},/f = 0I,2,...)n-1. v * ;
Ограничиваясь в A6.64) ФРВ мерности не выше второй, полу-
получим оценку ФРВ (n+1j-ro порядка в виде
Fn+M<FUtM[x(t2)^(t,)l-F2[x(tn+,)fx(tn)]. A6.66)
Для стационарного случайного процесса выражение A6.66) мо-
может быть записано как
FnM)iF^2[mAt^t}]" A667)
A6.68)
Неравенство A6.68) дает оценку сверху (п+1 )-мерной ФРВ ста-
стационарного случайного процесса с помощью двумерной ФРВ.
Оценка может быть уточнена при использовании ФРВ третьего,
четвертого и т. д. порядков.
451

Раздел 16
Конкретизируем выражение A6.68) для гауссовского процесса.
С целью упрощения записи будем рассматривать центрированный
случайный процесс с а = 1
A6.69)
где Ф(х), Ф2 (х, х) - табулированные функции, описываемые A5.27)
и A6.23).
При достаточно малом значении А? двумерную ФРВ можно раз-
разложить в ряд Тейлора. Ограничиваясь в ряде Тейлора A6.31) пер-
первыми двумя членами, запишем
Учитывая A6.29), выражение A6.70) получаем в виде
A6.70)
A6.71)
A6.72)
A6.73)
452
Рассмотрим следующее предельное соотношение
Для него получим
Таким образом, имеем
С учетом A6.72) выражение A6.71) запишем в виде

Многомерное распределение вероятностей
Подставив A6.73) в A6.69), получим
A6.74)
A6.75)
Переходя к пределу при п—>оо, уточним оценку распределения
случайного процесса на интервале Т
A6.76)
A6.77)
где
В общем виде выражение для ФРВ гауссовского процесса на ин-
интервале времени Г (её оценки) представим как
A6.78)
где
A6.79)
Здесь а, о, г(т) - математическое ожидание, дисперсия и нормиро-
нормированная корреляционная функция случайного процесса.
При Г = 0 случайный процесс рассматривается для одного мо-
момента времени; из A6.78) следует
A6.80)
453
Из A6.74) получим

Раздел 16
что соответствует ожидаемому результату. Чем больше интервал
времени Г, тем меньше FT(x), что также очевидно. Уменьшение
FT(x) при увеличении 7 описывается экспоненциональной зависи-
зависимостью (с отрицательным показателем степени). Графики FT(x)
в зависимости от Т(ХТ) представлены на рис. 16.8.
16.7. Многомерная характеристическая
функция случайного процесса
Понятие характеристической функции, введенное для одной
случайной величены, может быть распространено на совокупность
случайных величин: 4(f1),^(f2),...,4(fn) - значений случайного про-
процесса в различные моменты времени, /7-мерная характеристиче-
характеристическая функция случайного процесса определяется как среднее зна-
значение функции
где vbv2 vn - действительные величины.
Таким образом, /7-мерная характеристическая функция случай-
случайного процесса определяется выражением
= J J...J ^^+^+"-+^-^(х1,х2,..,хя)Л1Л2...Л|1. A6'81)
—оо —оо —оо
Как следует из A6.81), /7-мерная характеристическая функция
представляет /7-кратное обратное преобразование Фурье /7-мерной
ПРВ случайного процесса (без учета коэффициента). Прямое пре-
преобразование Фурье позволяет перейти от характеристической
функции к ПРВ случайного процесса
fn(xbx2,...,xn) = -^-y
оо с» со A6.82)
J J... JeIJ(v1>v2,...,vll)e-'(l''x'+^+-+v"Jf"W1dV2...dVl,.
Из характеристической функции л-го порядка можно получить
характеристические функции меньших порядков
454

Многомерное распределение вероятностей
A6.83)
Характеристическая л-мерная функция позволяет определить
моменты распределения вероятностей случайного процесса. Про-
Производная л-го порядка характеристической функции определяется
выражением
A6.84)
A6.85)
Таким образом, имея характеристическую функцию, можно оп-
455

Раздел 16
ределить ПРВ и начальные моменты распределения вероятностей
случайного процесса.
Если случайные величины независимы, то математическое ожи-
ожидание их произведения равно произведению математических ожи-
ожиданий каждой из них. Исходя из этого, для независимых случайных
величин ?(f1),?(f2),...,?(fn) можем записать
в„(^1^2 ^) = П^). A6.86)
Справедливо и обратное утверждение: если л-мерная характери-
характеристическая функция равна произведению одномерных характеристи-
характеристических функций, то случайные величины являются независимыми.
Для гауссовского процесса выражение для л-мерной характери-
характеристической функции получим с учетом A6.36) в виде
{П а П П I
где ак, о2к, rkl - математическое ожидание, дисперсия и нормиро-
нормированная корреляционная функция случайного процесса.
При п = 2 получим выражение для двумерной характеристиче-
характеристической функции стационарного гауссовского процесса
Q2{vvv2) = expj /а(^ + v2)--a2[vf + 2r,2v,v2 + vfjl. A6.88)
16.8. Марковские процессы
Одной из полезных для практики исследования моделей случай-
случайных процессов является процесс Маркова или случайный процесс
без последствия. Марковским процессом называют такой случай-
случайный процесс, для которого условную ПРВ можно записать в виде
'n(V*i.*2.-".xn-i) = 4(V*n-i). A6.89)
где хк- значение случайного процесса в момент времени tk.
Равенство A6.89) означает, что значение случайного процесса в
выбранный момент времени tn зависит только от того, какое значе-
значение случайный процесс принял в предыдущий момент времени tn.h
456

Многомерное распределение вероятностей
и не зависит от того, какие значения принимал случайный процесс в
предыдущие моменты времени. Таким образом, вся информация о
марковском процессе содержится в двумерной ПРВ. С учетом
A6.89) и исходя из определения условной ПРВ для марковского
процесса л-мерную ПРВ можно определить как
п
/л(*1>*2 Xn) = fMY[f2(Xk/Xk-J- A6.90)
/с=2
Если ПРВ зависит только от интервала времени между сосед-
соседними моментами tk- tk^, то процесс Маркова является стационар-
стационарным. При х,= х2=...= хп= хдля стационарного марковского процесса
запишем
A6.91)
что соответствует равенству в A6.68).
Запишем выражение для ПРВ марковского процесса при п = 3
в виде
f3(xbx2,x3jbt2,t3) = f^xbt^)f2(x2,t2/xbt^)f2(x3,t3/x2,t2). A6.92)
Интегрируя по х2 левую и правую части равенства, получаем
f2(xbx3,tbt3) = f:(xvt:)jf2(x2,t2/xbt^)f2{x3,t3/x2,t2)dx2. A6.93)
Учитывая определение условной ПРВ
^1^з.Мз)^2(х3,^/х1,М, A6.94)
выражение A6.93) запишем в виде
f2(x3,t3/xbt,)= \f2(x2,t2/ xbt,)f2(x3,t3/ x2,t2)dx2. A6.95)
Уравнение A6.95) называется уравнением Смолуховского, или
обобщенным уравнением Маркова. Для стационарного марковского
процесса уравнение Смолуховского записывается в виде
457

^ Раздел 16
4(^3-f3-^i/xi/i) =
7 A6.96)
= J fzix^h-U/XvU)fz(x3,t3-t2/ x2,t2)dx2.
Из уравнения Смолуховского может быть получено дифферен-
дифференциальное уравнение перехода непрерывного марковского процес-
процесса. С учетом обозначений
t2 = t, fj = t-At, t3=T, x-i= x, x3 = y, x2 = z
дифференциальное уравнение запишется в виде
df2(yJ/x,t) {t4xt)df2(y,T/x,t) {
dt 9 ' Эх , A6.97)
где
ШТ)= lim ~ \(z~y)f2(z,T/y,T-At)dz, A6.98)
д?->о At J
оо
/fe(y,D= lim -I \(z-yJf2(z,T/y,T~At)dz. A6.99)
Уравнение A6.97) называется первым уравнением Колмогорова.
Плотность распределения вероятностей марковского процесса
удовлетворяет и второму уравнению Колмогорова
dfP(y,T/x,t) Э г. . _., . _. лч1
о / оу
1Д2 - A6.100)
^¦^к(у,Шу,т/х,о]
Второе уравнение Колмогорова известно также как уравнение
Фоккера-Планка.
При рассмотрении непрерывных случайных процессов исполь-
использование марковской модели связано с определением шага по вре-
временной оси: At = tn - fn-1. При At -ч> 0 марковский процесс переходит
в пуассоновский.
458

Раздел 17.
РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ НЕСКОЛЬКИХ
СЛУЧАЙНЫХ ПРОЦЕССОВ И ИХ ФУНКЦИОНАЛЬНЫХ
ПРЕОБРАЗОВАНИЙ
Характеристики распределения вероятностей, рассмотренные
для одного случайного процесса, могут быть распространены на
совокупность случайных процессов. В разделе рассматриваются
характеристики распределения вероятностей нескольких случай-
случайных процессов, а также характеристики распределения вероятно-
вероятностей функций случайных процессов.
17.1. Совместное распределение вероятностей
двух случайных процессов
Функция распределения вероятности двух случайных процессов
?i (V и ?,2(V определяется как
Fn+m(XbX2,...,Xmyby2,...,ym) = P{UU) < ХЬ...
где Р{...} - символ вероятности.
Функция распределения вероятностей (л+л^-порядка зависит от
(п+т) значений случайных процессов хь х2,...,хп, уи у2,---,Ут& также
от моментов времени th t2,..., tn, th t2,..., tm, в которые рассматри-
рассматриваются случайные процессы. Для стационарных случайных про-
процессов ФРВ зависит не от моментов времени, а от интервалов ме-
между ними.
Функции распределения вероятностей, определяемой A7.1),
соответствует (п+т)-мерная ПРВ
*л+,п(*1.*2.-,Хп.У1.У2 Ут) =
= d^Fn+m(xbx2,...,xn,yby2 ут) A7.2)
dx^dx2...dxndy^dy2...dym
Если ФРВ (ПРВ) двух случайных процессов может быть пред-
представлена в виде произведения ФРВ (ПРВ) каждой из них
459

Раздел 17
...(хп-ап)к"(у,-^(у2-Ь2)^.. A7-5)
-(ym-bm)l'"fn+m{xbx2,...,xn,yby2,...,ym)dx1dx2...
...dxndy,dy2...dym,
где Эк, bk- математические ожидания случайных процессов ^(t) и
?,2(t) в соответствующие моменты времени.
Для стационарных случайных процессов а1 - а2 =...= ап = а, Ь1 =
Ь2=...= Ьт = Ь.
Начальный момент второго порядка совместного распределе-
распределения вероятностей представляет ковариационную функцию случай-
случайных процессов
K,2(tvt2)= jxyf^2(x,y)dxdy, A7.6)
где ^ц2(х, У)- двумерная ФРВ случайных процессов ^(t)v\ b,2(t).
Подчеркивая, что ковариационная функция определена для
двух случайных процессов, ее называют взаимной ковариационной
функцией.
Центральный момент распределения второго порядка пред-
представляет взаимную корреляционную функцию
460
при любом выборе моментов времени, то такие случайные процес-
процессы называются независимыми.
Моменты распределения вероятностей случайных процессов
определяются выражениями:
начальные (порядка р = Ik, +LI,)
центральные (того же порядка)

Распределение вероятностей случайных процессов
fli2(M2)= j(x-a)(y-b)f^2(x,y)dxdy, A7.7)
где a, b - математические ожидания случайных процессов в мо-
моменты времени U, Х2.
Взаимная корреляционная функция стационарных случайных
процессов (также, как и ковариационная функция) зависит не от
моментов времени th t2, в которые рассматриваются случайные
процессы, а от интервала между ними, т.е.
mex=t2-U.
Нормированная взаимная корреляционная функция стационар-
стационарных случайных процессов определяется как
г12(т) = ^^, A7.8)
а1а2
где аД <з2 - дисперсии случайных процессов.
Если \\(Х), bait) - независимые случайные процессы, то из A7.7)
получим
оо
RM,t2)= \(x-a)(y-b)fU2(x,y)dxdy =
A7.9)
= j(x-a)f^(x)dxj(y-b)f^(y)dy = O.
Как следует из A7.9), корреляционная функция независимых
случайных процессов равна нулю. Однако обратное утверждение
неверно.
Взаимная корреляционная функция эргодических случайных
процессов может быть определена как среднее по времени произ-
произведения их реализаций
Я12(т)=<@^ + т)>= lim J- \^(m°2(t + x)dt, A7.10)
-т
где <...>- символ усреднения по времени.
Если задана (п + /т^-мерная ПРВ случайных процессов t^(t) и
?,2(U то может быть определена условная ПРВ - ПРВ совокупности
461

Раздел 17
случайных величин ^(U), ^(t2), ..., ^(tn), при условии, что случай-
случайные величины tz(U), Z&fe),..., t,2(tm ) принимают заданные значения
Ул.Уг, ---.Ут
W*1.*2.->Vyi ,У2,-,Ут) =
_ Гп+т(ХьХ2,-,Хп>УьУ2,-'Ут) <7-11)
Uyi./2.-.ym)
Для независимых случайных процессов ^(t) и t^(t) из A7.11) по-
получим
fn+m(>(bX2,-,xn/yby2,...,ym) = fn(xbx2,...)xn). A7.12)
Для нескольких случайных процессов могут быть определены
и другие условные характеристики распределения аналогично то-
тому, как это было сделано для одного случайного процесса.
17.2. Распределение вероятностей функций
случайных процессов
Ниже приводятся постановка и решение задачи нахождения ха-
характеристик распределения функций двух и более случайных ве-
величин. Рассматриваемые случайные величины - это совокупность
значений случайных процессов в выбранные моменты времени.
Результаты такого анализа могут быть использованы при рассмот-
рассмотрении преобразований случайных процессов в радиотехнических
цепях различного вида.
17.2.1. Функция двух случайных величин
Рассмотрим случайные величины т^ и г\2, определяемые как
функции случайных величин ^ и \2
Л1 =<Pi(?i, 5г).Л2 =Ф2(^1^2)- A7.13)
Случайные величины \Л и \2 представляют значения двух слу-
случайных процессов ^(t) и t,2(t) в различные моменты времени:
?1 = ?i(V и ?2 = WW- Рассмотрение и выводы могут быть отнесены
и к одному случайному процессу в различные моменты времени -
Зависимости, обратные A7.13), запишем в виде
?i = ФТ1(Л1,Л2). ^2 = Ф21(Л1,Л2)- A7.14)
462

Распределение вероятностей случайных процессов
Выражение для двумерной ПРВ случайных величин r]1 , rj2 име-
имеет вид
A7.15)
где ft,2 (*i, x2), fn2 (Уь Уг) -двумерные ПРВ случайных величин ?1f ?,2
ить.ти?;
A7.16)
- якобиан преобразования.
Выражение A7.15) записано для однозначных обратных зави-
зависимостей A7.14). Для неоднозначных зависимостей необходимо
произвести суммирование по числу обратных соотношений, по
аналогии с тем, как это сделано при рассмотрении одного случай-
случайного процесса в разд. 15.
Часто встречается зависимость одной случайной величины от
двух случайных величин
A7.17)
Чтобы получить характеристики распределения г) в этом случае,
рассмотрим прежде всего частный случай зависимости A7.17)
при однозначных обратных зависимостях
^1=ФГ1(Л1).^2=Ф2(Л1.Л2)-
Якобиан преобразования в этом случае равен
A7.18)
A7.19)
A7.20)
463

Раздел 17
В соответствии с A7.15) выражение для двумерной ПРВ запи-
запишется в виде
Плотность распределения вероятностей одной случайной вели-
величины г\2 определяется как
A7.22)
Подставляя A7.21) в A7.22) и вводя обозначение iv = <p1 (у^,
получим
A7.23)
Применительно к зависимости A7.18): т^ = 4i, <Pi(*) = x, из
A7.23) найдем
A7.24)
Таким образом, записано выражение для плотности распреде-
распределения вероятности случайной величины, являющейся функцией
двух случайных величин.
В общем случае, когда в результате функционального преобра-
преобразования случайных величин 4i. ?2. ,4л получается совокупность слу-
случайных величин rib r\2, ...,г\п, выражение для ее ПРВ записывается
в виде
464
A7.21)

Распределение вероятностей случайных процессов
d(xbx2,...,xn)
A7.25)
где
A7.26)
- якобиан преобразования.
При неоднозначности обратных зависимостей в A7.25) необхо-
необходимо произвести суммирование по их числу.
Если из совокупности п случайных величин ^ ^,. Дп получается
совокупность т случайных величин г\ь r\2,...,r}n, (т < п), то чтобы
воспользоваться A7.25), необходимо дополнить систему п - т
функциональных зависимостей равенствами щ = Е,к, к = т + 1,
/77 + 2,..., п. ПРВ случайных величин т^, Лг.-чЛл. получится из
A7.25) интегрированием по ут+ :,-¦¦, Уп-
Моменты распределения вероятностей функции случайных ве-
величин
определяются выражением
A7.27)
При получении выражений для характеристик функций случай-
случайных величин говорилось о нескольких случайных процессах. Од-
Однако приведенные выражения справедливы и для функций значе-
значений одного случайного процесса, взятых в различные моменты
времени.
465

Раздел 17
17.3. Некоторые виды функциональных преобразований
случайных процессов
В качестве иллюстрации общего подхода к нахождению распре-
распределения случайного процесса, получающегося в результате преоб-
преобразования, рассмотрим некоторые виды функциональных зависи-
зависимостей. Выбранные примеры представляют и самостоятельный
интерес, некоторые результаты используются в дальнейшем.
17.3.1. Сумма случайных величин
Для суммы (разности) двух случайных величин
Л = $1±?2 A7-29)
имеем
ffe2. = 1tx2 = y+x1. A7.30)
dx2
С учетом A7.30) получим
№)= jf2(u,y + u)du, A7.31)
где f2 (хи х2) - двумерная ПРВ случайных величин ?,, Ь%.
Если случайные величины ?,ь ?# являются независимыми,
A7.31) примет вид
fr](y)=jf^(u)f^(y + u)du, A7.32)
где /^ (х), ^2 (х) - ПРВ случайных величин ^ и ^.
Используя свойства преобразования Фурье, для суммы двух не-
независимых случайных величин получаем следующее выражение
для характеристической функции
eT,(v) = e§t(v)e§B(v). A7.33)
Вывод из полученного результата распространим на любую ко-
конечную сумму случайных величин: характеристическая функция
суммы независимых случайных величин
равна произведению характеристических функций каждой из них
466

Распределение вероятностей случайных процессов
п
/с=1
Отмеченное свойство часто используется для получения ПРВ
суммы независимых случайных величин - определяется характе-
характеристическая функция суммы (как произведение характеристических
функций слагаемых), а от нее переходят к ПРВ. Пример такого
подхода к определению ПРВ суммы независимых случайных вели-
величин приведен в п.17.5.
Математическое ожидание г) = ^ ± ?2 определяется выраже-
выражением
М{Т)}= J j(x,±x2)f2(xbx2)dxdx = M{^}±M{^2}, A7.35)
где 4 (хи х2) - двумерная ПРВ ^ и ?2.
Для л слагаемых запишем
М{?^} = ][>{^Ь A7-36)
/с=1 /с=1
Таким образом, математическое ожидание суммы случайных
величин равно сумме математических ожиданий каждой из них.
Дисперсия суммы двух случайных величин определяется выра-
выражением
т°г{у\} = М{(^±^2J)-М2^±^2} =
= m%} + m%2}±2R,2x.
Полученное выражение запишем в виде
т20 {г)} = а2 =с2+о22± 2^02^2, • A7.38)
где oi2 ,о22 , г12 -дисперсии случайных величин ^ и ^ и их норми-
нормированная взаимная корреляционная функция.
При г12 (г) = 0 (? ! и Ьг некоррелированные) из A7.38) получим
о2=а? + о|. A7.39)
Для суммы п некоррелированных случайных величин имеем
467

Раздел 17
ог=^о2к. A7.40)
/c=1
Таким образом, дисперсия суммы некоррелированных случай-
случайных величин равна сумме их дисперсий.
Конкретизируем полученные результаты для некоторых видов
распределений случайных величин.
1. Нормальное распределение
Для случайной величины
когда случайные величины ^ и б,2 имеют нормальное распреде-
распределение
f2{xbx2) =
,v A7.41)
1 20,02A-4) J
где аь а2, с/ ,а22 , г12 - математические ожидания, дисперсии и
нормированная корреляционная функция случайных величин ?1f Ь&,
из A7.31) получим
Ш) = -Х- ехр{- ^-f^i A7.42)
V27ta [ 2a2 J
где
a = a:± а2,о2 = a2 + о2г ± 2а:(у2г12- A7.43)
Таким образом, сумма двух нормально распределенных слу-
случайных величин имеет также нормальное распределение.
С учетом того, что линейное преобразование не изменяет нор-
нормального закона распределения, сделанный вывод можно расши-
расширить: любая линейная комбинация нормальных случайных величин
(гауссовских процессов) представляет собой нормальную случай-
случайную величину (гауссовский процесс).
Плотность распределения вероятностей гауссовского процесса
любого порядка определяется математическим ожиданием и кор-
корреляционной функцией. Следовательно, чтобы определить ПРВ
468

Распределение вероятностей случайных процессов
случайного процесса, являющегося линейной комбинацией гаус-
совских процессов, необходимо только определить математиче-
математическое ожидание и корреляционную функцию. Так для суммы двух
гауссовских процессов
Л@ = $1@ + ?2@ A7.44)
получим
а = а,+а2, A7.45)
Я(т) = Я,(т) + 2Я12(т) + Я2(т), A7.46)
где аь а2, R-\(t), R2(t) - математические ожидания и автокорреля-
автокорреляционные функции случайных процессов ^(t) и ?#(t); fii2 (x) - взаим-
взаимная корреляционная функция ^(t) и Ь,2{\.).
2. Релеевское распределение
Плотность распределения вероятности суммы двух независи-
независимых случайных процессов, имеющих релеевское распределение с
одним и тем же параметром а
UX) = JLe-*2'2a\x>0, A7.47)
s 2o2
определяется как
.2
e-yW A748)
3. Показательное распределение
Плотность распределения вероятностей случайных величин ?i и
^2, имеющих показательное распределение, описываются выраже-
выражениями
k (х) = Х,е^х, Ь2(х) = Х2е~^х, A7.49)
где Х-\ и Х2 - параметры распределения.
Для суммы л = ^1 + ^2 >из A7.32) найдем
/л(у) = ^2_(в-^-в-^У)|У>0. A7.50)
Распространяя результат на сумму п случайных величин с пока-
469

Раздел 17
зательным распределением, можно получить
^(у) = Х,Х2..Хп(д,в-^ + q2e-x'y +... + qne-k"y), A7.51)
где
1
17.3.2. Произведение случайных величин
Для произведения двух случайных величин
Л = ^2 A7-52)
в A7.24) имеем ckp2/dx2 = Хь х2 = у2/*i- Из A7.24) получим
МУ)=Г2Н)я' A753)
где f2 (хь х2) - двумерная ПРВ случайных величин.
Если случайные величины ^ и ?2 являются независимыми,
где \у (х), f^2 (х) - одномерные ПРВ случайных величин ?, и ^
Выражение для ПРВ произведения двух случайных величин
конкретизируем для нормального и релеевского распределений.
1. Нормальное распределение
Двумерная ПРВ нормально распределенных случайных величин
описывается A6.22). Подставляя A6.22) в A7.53), для произведе-
произведения двух центрированных случайных процессов получим
710^2^/1-4 1СТ1а2A-Г12 )
где Ко (х) - функция Бесселя второго рода.
470
A7.55)

Распределение вероятностей случайных процессов
Для некоррелированных случайных величин ?i и ?2 (f\2 = 0)
A7.56)
2. Релеевское распределение
Плотность распределения вероятности произведения двух не-
независимых релеевских процессов с одним и тем же параметром
может быть получена из A7.53) с подстановкой в него A7.47)
17.3.3. Частное случайных величин
Для частного случайных величин
A7.57)
A7.24) запишется в виде
Для независимых ^ и ?2
A7.58)
A7.59)
A7.60)
При нормальном распределении случайных величин, имеющих
математические ожидания, равные нулю, для их частного получим
A7.61
Выражения для ПРВ рассмотренных функций двух случайных
величин и их графики при нормальном распределении случайных
величин сведены в табл. 17.1.
471

Раздел 17
Таблица 17.1.
Распределение функций двух случайных величин
Функциональная зависимость.
ПРВ функции случайных величин
ПРВ функции
(общее выражение)
ПРВ функции
(общее выражение)
472
ПРВ функции нормально
распределенных случайных
величин
ПРВ функции нормально
распределенных случайных
величин

Распределение вероятностей случайных процессов
№
п/п
Функциональная зависимость.
ПРВ функции случайных величин
ПРВ функции
(общее выражение)
ПРВ функции
(общее выражение)
ПРВ функции нормально
распределенных случайных
величин
(а, = а2 = 0)
473
ПРВ функции нормально
распределенных случайных
величин

Раздел 17
17.4. Распределение вероятностей производной
случайного процесса
Характеристики распределения вероятностей производной слу-
случайного процесса могут быть получены, исходя из определения
производной
A7.62)
At
Математическое ожидание производной равно
Д'-° t M • A7.63)
аъ (t + At) -a*. @ ,
= |im -? —111 = ^@,
дг-*о At
где а^ ffj - математическое ожидание случайного процесса t,(t) в
момент времени /.
Таким образом, математическое ожидание производной слу-
случайного процесса равно производной математического ожидания
случайного процесса в рассматриваемый период времени. При
этом предполагается, что случайный процесс в этой точке диффе-
дифференцируем. Если случайный процесс является стационарным, его
математическое ожидание постоянно, не зависит от времени: ма-
математическое ожидание производной случайного процесса равно
нулю.
Корреляционная функция производной центрированного слу-
случайного процесса определяется выражением
Чтобы определить корреляционную функцию производной слу-
случайного процесса, сначала запишем выражение для корреляцион-
корреляционной функции разности ?,(t-At) - t,(t).
Mffctt + ДО-«Ш% +ДО-%)» =
= M{[tjit, + At)l{t2 + ДО} - M{%{ty Ш + АО) - A7.65)
-М{^1+А^(У} + МЩЩ)}.
474
A7.64)

Распределение вероятностей случайных процессов
Представим A7.65) в виде
RA(tbt2) = R^+At,t2 + At)-R^(tbt2 + At)-
-R^+At,t2) + R,(tvt2). °7-66)
Разложим первые три слагаемых в правой части A7.66) в ряд
Тейлора
(dRt dRA
R^+At,t2+At) = R^tbt2) + \—^ + -±\At +
dR, d2RL At2
R^+AtJ2) = R^J2) + -^At + --^-— + 03.
Подставляя A7.67) в A7.66), получим
d2Rh p
RA(tbt2) = —^-At2+0. A7.68)
dt:dt2
Из A7.64) с учетом A7.68) найдем
RAtbt2) = ?-. A7.69)
§и 2 dt,dt2 v
Корреляционная функция стационарного случайного процесса
зависит от разности моментов времени т = t2 - tb Для нее получим
^'(т) = -Я?(т). A7.70)
Таким образом, корреляционная функция производной стацио-
стационарного случайного процесса равна второй производной корреля-
корреляционной функции случайного процесса, взятой со знаком минус.
Корреляционная функция n-ной производной стационарного
случайного процесса равна
475
A7.67)

Раздел 17
^(п,(тЫ-1)пЯBп>(т). A7.71)
Так же можно показать, что взаимная корреляционная функция
л-ой и /с-ой производных стационарного случайного процесса опре-
определяется как
^,V^T) = (-irVn+V A7.72)
Исходное выражение для определения взаимной корреляцион-
корреляционной функции случайного процесса и его производной записывается
в виде
A7.73)
Аналогично тому, как это было сделано раньше, предваритель-
предварительно рассмотрим взаимную корреляционную функцию случайного
процесса ?,(U) и разности ?(/2 + At)-Z,(t2):
^(М2) = МЩШ*2+ДО-%)]} =
= М№№*2 + Л0Ч(Ш'2)} = A7.74)
= R^(tbt2 + M)-R^tbt2).
Раскладывая первое слагаемое правой части A7.74) в ряд Тей-
Тейлора, запишем
dRAtbt2)
0*2
С учетом A7.74) выражение для взаимной корреляционной
функции случайного процесса и его производной получим в виде
dRAU,t2)
%(M2)= ^1 • A7.76)
Для стационарного случайного процесса имеем
Изменив порядок следования случайного процесса и его произ-
производной в A7.73), установим
476

Распределение вероятностей случайных процессов
Я^(т) = -Я~(т). A7.79)
Из выражения для определения взаимной корреляционной
функции получим
%@) = #4@) = 0. A7.80)
Таким образом, взаимная корреляционная функция случайного
процесса и его производной для одного и того же момента времени
равна нулю.
Линейное преобразование не изменяет нормального закона
распределения. Следовательно, если существует производная от
гауссовского процесса, то она имеет нормальное распределение -
представляет также гауссовский процесс. Его одномерная ПРВ
описывается выражением
/Иу) = т=1-ехр --?- , A7.81)
где оц2 - дисперсия производной гауссовского процесса,
on2 = -Ry0).
Используя корреляционную функцию гауссовского процесса,
можно записать выражение и для л-мерной ПРВ производной лю-
любого порядка.
Гауссовский процесс и его производная, рассматриваемые
в один и тот же момент времени, как это следует из A7.80), имеют
взаимную корреляционную функцию, равную нулю, являются неза-
независимыми. Выражение для их совместной ПРВ запишется в виде
1 ™( х2 У2!
2na2yf^r t@) [ 2а
где
г((т) = ^,а2 = Я,@). A7.83)
о
Аналогично можно записать выражение и для совместной
л-мерной ПРВ гауссовского процесса и его производной любого
порядка.
477

Раздел 17
17.5. Распределение вероятностей интеграла
от случайного процесса
Интеграл от случайного процесса запишем в виде
4(t) = jh(t,vnv)dv, A7.84)
о
где h(t,v) -заданная функция.
Такой интеграл обычно встречается при анализе прохождения
случайного процесса через линейную цепь.
Интеграл представляет функцию случайного процесса, к кото-
которой сходится интегральная сумма. Таким образом, интегрирование
представляет линейное преобразование случайного процесса.
Математическое ожидание случайного процесса, описываемого
A7.84), равно
a^{t) = МШ) = M{jh(t,v)Uv)dv} =
°, A7.85)
= \h(t,v)M{l~(v)}dv =J h(t,v)a(v)dv.
о о
Для стационарного случайного процесса получим
где а - математическое ожидание случайного процесса.
Корреляционная функция интеграла от случайного процесса
определяется выражением
RJtbt2) = M{r](tMt2)} =
478
A7.87)
A7.86)

Распределение вероятностей случайных процессов
Интегрирование как линейная операция не изменяет закона
распределения гауссовского процесса. Одномерная ПРВ интеграла
от гауссовского процесса t,(t) имеет вид
^1(у) = 7^Гехр|-^?-1' A7-88)
где ап„ ал2 - математическое ожидание и дисперсия интеграла от
гауссовского процесса
t t t
ar]=jh(t,v)a(v)dv, о* = J J h(t,,v,)h(t2,v2)R(vbv2)dv,dv2. A7.89)
0 0 0
17.6. Характеристическая функция случайных процессов
Понятие характеристической функции может быть распростра-
распространено на любую конечную совокупность случайных процессов. Так
характеристическая функция случайных процессов ^ и ?,2, имею-
имеющая порядок n+т, определяется выражением
bn+m(VbV2,...,Vn+m) =
_ f f f ei{v^x^v2x2+...'rvnxn+vnrSxn..i+vn?2xnir2yz+- -+vmmym) _ A7 90)
¦fn+m(xvx2,...,xn,yby2,...,ym)dx:dx2...dxndy^dy2...dym>
где fn+m(...) - n+m-мерная ПРВ случайных процессов ^(t) и c,2(t)-
Для независимых случайных процессов можем записать
Qn+m={vbv2.-'vn+m) =
] ] ...|е'(^1+^+-+^)^1п(х1)х2,..,хл)сУх1сУх2...сУхл
77 7 A7-91)
] ]..]е^У^*+- ^y"}hm(yby2,.,ym)dy,dy2...dym =
= ^^n(vbV2,...,vn)Q^2Jvn+bvn+2,...,vn+m),
где fan (...) - л-мерная ПРВ случайного процесса ^(t); \2т (¦¦¦) -
т-мерная ПРВ случайного процесса ^2(t)-
479

Раздел 17
Таким образом, характеристическая функция независимых слу-
случайных процессов равна произведению характеристических функ-
функций каждого из них.
Если характеристическая функция случайных величин ^ ?&,...,
Нравна 0n(V,, v2,...,vn), то характеристическая функция случайных
величин
где ок, ак - действительные постоянные, определяется выражением
Характеристическая функция п случайных величин g1f, &,...,?, ,
имеющих нормальное распределение, описывается выражением
Qn(^v2,...,vn) = exjp[ik=^akvk-y2k=^l=^akalrklvkv,[ A7.93)
где ак ,ок - математическое ожидание и дисперсия случайной ве-
величины &; гк1 - нормированная корреляционная функция случай-
случайных величин Е,к<, ?,\.
Использование характеристических функций при анализе слу-
случайных процессов в ряде случаев позволяет упростить операции и
сделать анализ более эффективным.
17.7. Метод характеристических функций
Одной из прикладных задач теории случайных процессов яв-
является определение характеристик распределения суммы не-
нескольких независимых случайных величин - выборочных значе-
значений случайных процессов.
Такая задача решается, например, при оценивании помехо-
помехоустойчивости системы обнаружения сигнала. Решение ее с полу-
получением непосредственно выражения для ПРВ функции случайных
величин связано с большими, часто непреодолимыми, трудно-
трудностями.
Более удобным оказывается подход к определению ПРВ через
характеристическую функцию. Характеристическая функция сум-
суммы независимых величин определяется как произведение харак-
характеристических функций каждой из них. Переход к ПРВ от характе-
характеристической функции представляет преобразование Фурье.
480
A7.92)

Распределение вероятностей случайных процессов
17.7.1. Содержание метода
Характеристическая функция случайной величины rj, представ-
представляющей сумму Л/ независимых случайных величин ?ь ??,...,?w
Л = Si + S2+•••+?*. A7.94)
имеет вид
к=1
где дк1 (v) - характеристическая функция случайной величины ?,к1.
Если случайные величины имеют одинаковое распределение,
например, представляют выборку из одного стационарного случай-
случайного процесса, то
Qu(v) = 921(i0 =... = QM{v) = 6,A0, A7.96)
A7.95) записывается в виде
ew(v) = ef(v), A7.97)
где в1 (v) - одномерная характеристическая функция случайной
величины, определяется выражением
6,A/)= jeivxf^(x)dx. A7.98)
— оо
От Qn(v) можно перейти к соответствующей ПРВ
^(У) = 77- \Q"(v)e~lvxdv. A7.99)
Таким образом, чтобы получить ПРВ суммы N независимых
случайных величин, имеющих одинаковое распределение, необхо-
необходимо получить характеристическую функцию одной случайной ве-
величины, возвести ее в Л/-ную степень и найти соответствующее
преобразование Фурье.
481
A7.95)

Раздел 17
Рассмотрим пример нахождения ПРВ суммы независимых слу-
случайных величин с помощью характеристической функции. Опреде-
Определим ПРВ суммы выборочных значений гауссовского случайного
процесса на выходе квадратичного детектора.
17.7.2. ПРВ суммы независимых выборочных значений слу-
случайного процесса с обобщенным релеевским
распределением
Случайный процесс, представляющий смесь гармонического
сигнала и узкополосного шума с нормальным распределеньем,
имеет огибающую, распределение которой подчиняется обобщен-
обобщенному закону Релея (разд. 19)
где А - амплитуда сигнала; а - эффективное значение шума; 10(х) -
модифицированная функция Бесселя первого рода.
Обозначив и/а = х, А/о = с/, выражение для ПРВ огибающей бу-
будем рассматривать в виде
Случайный процесс подается на квадратичный детектор с ха-
характеристической
у = -|-- <17-102)
Плотность распределения вероятности случайного процесса,
выделяемого на выходе детектора, описывается выражением
(разд. 15)
ЦУ) = е-уЛСфу)> A7.103)
где а = cf/2.
Получим ПРВ суммы N независимых выборочных значений слу-
случайного процесса, ПРВ которого описывается A7.103). Такая зада-
задача возникает при описании процесса накопления при некогерент-
некогерентной обработке принимаемых колебаний.
Характеристическая функция, соответствующая ПРВ A7.103),
482
A7.100)
A7.101)

Распределение вероятностей случайных процессов
определяется выражением
A7.104)
где р = /V.
Решение интеграла A7.104) имеет вид [35]
A7.105)
Характеристическая функция суммы Л/ независимых выбороч-
выборочных значений определяется A7.97)
A7.106)
Преобразование Фурье характеристической функции QN дает
ПРВ суммы Л/независимых случайных величин
A7.107)
A7.108)
Графики fn(z) при значениях а, равных 0, 1 и 2, приведены на
рис. 17.1.
Выражение для fn(z) можно представить в виде ряда Грама -
Шарлье (разд. 15).
Начальные моменты распределения случайной величины,
имеющей характеристическую функцию, описываемую A7.106),
определяются как
A7.109)
483

Раздел 17
Рис.17.1
Из A7.109) получим
(Л/+Л-1)! _л/а
A7.110)
A7.111)
484
или

Распределение вероятностей случайных процессов
где iF^J- гипергеометрическая функция.
Первые начальные моменты распределения вероятностей равны
пц = Л/A + а),
т2 = (Л/аJ+2Л/а(Л/ + 1) + Л/(Л/ + 1),
ш3=(Л/аK+3(Л/аJ(Л/ + 2) + ЗЛ/а(Л/ + 1)(Л/ + 2) +
+ Л/(Л/ + 1)(Л/ + 2),
т4=(Л/аL + 4(Л/аK(Л/ + 3) + 6(Л/аJ(Л/ + 2)(Л/ + 3) +
+ 4Л/а(Л/ + 1)(Л/ + 2)(Л/ + 3) + Л/(Л/ + 1)(Л/ + 2)(Л/ + 3).
Центральные моменты распределения вероятностей находятся
из A5.18) с учетом A7.112)
Л77? = 0 ,
т°2 =Л/Bа + 1) = а2.,
2 v ; N A7.113)
А77§ =2Л/(За + 1),
т2 = 12(Л/аJ +12Л/а(Л/ + 2) + ЗЛ/(Л/ + 2),
т°ъ = 120(Л/аJ + 20Л/аEЛ/ + 6) + 4Л/EЛ/ + 6) ,...
Коэффициенты ряда Грама-Шарлье определяются через цен-
центральные моменты следующими выражениями:
A7.114)
Ряд Грама-Шарлье для /^ (z) запишется в виде
W = — [СоФ(У) + СзФC)(У) + с4фD)(у) + с5ФE)(у)+ ...], A7.115)
485

Раздел 17
где (р(у) = м42пе~у /2 ,y=z- m,/oNi mt = Л/A + a), aw= V^O + 2а).
Записанное выражение позволяет определить степень прибли-
приближения /i/zj к нормальной ПРВ. ВыражениеA7.115) показывает, что
при увеличении числа Л/ вес второго и последующих членов в об-
общей сумме уменьшается: все коэффициенты разложения стремят-
стремятся к нулю, за исключением с0. При достаточно большом значении Л/
распределение случайной величины стремится к нормальному
или
A7.116)
Вывод о приближении распределения суммы случайных вели-
величин к нормальному иллюстрируют и графики на рис. 17.1.
Плотность распределения вероятности суммы Л/ независимых
случайных величин, имеющих ПРВ, описываемую A7.107), можем
представить также в виде ряда Лагерра. С учетом равенств:
т1 = N(\ + a), c2N = NBa + A)
выражение для fn (z) получим в виде
A7.117)
При а = 0 имеем m1 = N, o2N = N.
Подставляя A7.117) в A5.78), получим
A7.118)
При рассмотрении суммы независимых случайных процессов,
имеющих распределение, отличное от нормального, необходимо
иметь в виду центральную предельную теорему теории вероятно-
вероятностей. В соответствии с ней при достаточно общих условиях распре-
486

Распределение вероятностей случайных процессов
деление центрированных и нормированных случайных величин с
увеличением числа слагаемых стремится к нормальному, независи-
независимо от законов распределения исходных случайных величин. Приме-
Применительно к случайным процессам это означает, что распределение
суммы независимых выборочных значений одного или нескольких
случайных процессов при увеличении числа слагаемых стремится к
нормальному. Примером такого приближения служит полученное
выражение A7.115) для рассмотренных в п.17.7.2 условий.
17.7.3. Характеристика помехоустойчивости системы
обнаружения сигналов с накоплением
При обнаружении импульсных сигналов на фоне шума с целью
повышения помехоустойчивости системы используется накопление
импульсов. Накопление может рассматриваться как суммирование
амплитуд принимаемых коротких импульсов, поступающих на вы-
выход устройства обработки в определенные моменты времени.
При наличии на входе системы помехи (случайного процесса -
шума) ПРВ колебания будет описываться функциями (рис. 17.2):
fjc*n\x) - когда принимается сигнал, и fjn\x)- когда сигнал отсут-
отсутствует.
О наличии сигнала судят с помощью порогового устройства -
при превышении значения порога V принимается решение о нали-
наличии сигнала, в другом случае - о его отсутствии (рис. 17.2). При
обнаружении сигнала возможны два вида ошибок: пропуск сигнала
(принимается решение об отсутствии сигнала при его наличии на
входе) и ложная тревога (принимается решение о наличии сигнала
при его отсутствии на входе). При уменьшении порога уменьшает-
уменьшается вероятность пропуска сигнала, но увеличивается вероятность
ложной тревоги.
Рис.17.2
487

Раздел 17
При анализе помехоустойчивости системы обычно рассматри-
рассматриваются вероятность обнаружения сигнала р0 и вероятность ложной
тревоги рл. Увеличивая значение порога решающего устройства V
уменьшаем значения как рл, так и р0. Зависимость вероятности об-
обнаружения сигнала от вероятности ложной тревоги и характеризует
помехоустойчивость рассматриваемой системы. Чем выше распо-
расположен график указанной зависимости при заданном отношении
сигнал/помеха на входе, тем выше помехоустойчивость системы.
Как указывалось, одним из путей повышения помехоустойчивости
системы является метод накопления.
Зависимость ро(рп) для системы с накоплением можно получить,
если известна ПРВ случайного процесса на выходе накопителя при
наличии сигнала на входе и его отсутствии. Определение такой
характеристики помехоустойчивости системы является иллюстра-
иллюстрацией использования описанных методов анализа случайных про-
процессов при решении одной из задач, поставленных практикой.
При аддитивной помехе в виде гауссовского шума b,(t) (коге-
(когерентная обработка) колебание на входе:
r\(t) = s(t) + Z(t),
где s(t) - сигнал.
Выражения для ПРВ случайного процесса на входе накопителя
записывается как:
при наличии сигнала на входе
в отсутствие сигнала
где А - амплитуда сигнала на входе; а2 дисперсия случайного
процесса (квадрат эффективного значения) на входе.
Сумма N независимых выборочных значений (случайный про-
процесс на выходе накопителя) имеет также нормальное распределе-
распределение с математическим ожиданием NA и дисперсией М/. Таким об-
образом, ПРВ случайного процесса на выходе накопителя будет опи-
описываться выражениями:
488
A7.119)
A7.120)

Распределение вероятностей случайных процессов
при наличии сигнала на входе
(У- NAJ
^+")(y) = TJ=-e 2^2 , A7.121)
в отсутствие сигнала
1 -?-
^)(у)=-_1^.е 2Л/а2. A7.122)
>/2лЛ/а
Исходя из A7.121) и A7.122) запишем выражения для
вероятности обнаружения сигнала:
оо / ч
вероятности ложной тревоги:
Рл = j>^(y)dy = 1-ф(т^) A7'124)
где \/ - заданный порог; Ф(х) - табличная функция нормального
распределения.
Из A7.123) и A7.124) получим зависимость ро(рп) в явном виде
ро = 1-Ф[ф-1A-рл.)-— ] = 1-Ф[Ф-1A-Рл')->/л/С7], A7.125)
а
где Ф'7^ - функция обратная Ф(х), q = А/о.
Графики РоСРл) при отношении сигнал/шум q = 1 и некоторых
значений /V приведены на рис. 17.3.
При Л/ = 1
Ро =^-ф[ф-\^-pn)-q) A7.126)
Сравнение A7.125) и A7.126) дает основание рассматривать
когерентное накопление как улучшение отношения сигнал/шум
в V/Vpa3.
При некогерентной обработке принимаемых колебаний, накоп-
накоплении на выходе детектора, ПРВ случайного процесса на выходе
накопителя описывается A7.107) или A7.108)
489

Раздел 17
A7.127)
A7.128)
(Л/-1)!
где a =cf/2, q = A/a - отношение сигнал/шум.
При заданном уровне V на выходе накопителя выражение для
вероятности ложной тревоги запишется в виде
A7.129)
Вводя неполную гамма-функцию
A7.130)
A7.131)
490
выражение для рл запишем в виде
В [35] решение A7.129) получено в виде ряда

Распределение вероятностей случайных процессов
Рис. 17.4
10-2 2 3 4 5 10-1 2 3 4 5 *
Рис.17.5
491

Решение A7.135) получено в виде ряда [35]
- , . чЛ/-1/2
2. \тгЛ
л=Л/+1
Выражение A7.131) и A7.134) определяют зависимость ро(рп)-
Графики указанной зависимости для некоторых значений Л/ приве-
приведены на рис. 17.4.
Как указывалось, накопление эквивалентно улучшению отноше-
отношения сигнал/шум. Однако в отличие от предыдущего случая это
улучшение будет различным в разных точках зависимости Ро(рл).
Его можно оценить, сравнивая зависимости Ро(рп) при заданном
значении Л/ и Л/ = 1 (рис. 17.5). Так при q =1 и рл = 10 накопление
при Л/ = 10 эквивалентно улучшению отношения сигнал/шум, рав-
равному 1,7; при Л/ = 50 - 2,6; при Л/ = 100 - 3,5.
492
Раздел 17
Вероятность обнаружения сигнала определяется с учетом
M7.127J как
A7.132)
A7.133)
A7.134)

Спектр случайного процесса
Раздел 18.
СПЕКТР СЛУЧАЙНОГО ПРОЦЕССА
Спектральный анализ является основой исследования детер-
детерминированных сигналов. Это делает целесообразным обращение к
методам спектрального анализа и при исследовании случайных
процессов. Однако особенности случайных процессов делают не-
невозможным простой перенос методов анализа детерминированных
сигналов на случайные процессы. Спектральный анализ случайных
процессов несет особенности, которые требуют отдельного рас-
рассмотрения.
18.1. Понятие спектральной плотности мощности
случайного процесса
Рассматривая реализацию случайного процесса как функцию
времени, формально для нее можем записать преобразование Фу-
Фурье. Однако чаще всего такое преобразование не существует, по
крайней мере, для непрерывных случайных процессов ?,(f): не вы-
выполняется условие абсолютной интегрируемости
оо
\Щ(Л<оо. A8.1)
Преобразование Фурье применимо только к такой характеристи-
характеристике случайного процесса, для которой условие интегрируемости аб-
абсолютного значения выполняется.
Выделим отрезок реализации случайного процесса
ЪТК; \o,t<o,t>T
Отрезок^T(t) представляет функцию времени на интервале [О, Т].
Если для нее существует преобразование Фурье
493

Раздел 18
т
ST{(o) = feT{t)e-K*tdt, A8.3)
о
то применительно к ^T{t) и Sr(co) можем записать равенство Пар-
севаля
J^^jlSrMfd». A8.4)
О -оо
Поделив левую и правую части равенства A8.4) на длину рас-
рассматриваемого интервала времени Т, запишем
7" оо
IJ5«(»)* = ^}l|Sr(a>f*). A8.5)
О -оо
Каждая часть равенства A8.5) описывает среднюю мощность
случайного процесса на интервале Т. При Г-»*» в правой части
равенства под знаком интеграла будет спектральная плотность
мощности случайного процесса. Обозначим ее Л/(оо). Тогда A8.5)
при 7"-> оо запишется в виде
Г оо
fo*I j$2r(f)tf = .i- Ja/(w)*>. A8.6)
о
Спектральная плотность мощности характеризует распреде-
распределение мощности случайного процесса по частоте, имеет четкое
физическое содержание, определяется как аналитически, так
и аппаратурно. Во временной области спектральной плотности
мощности соответствует по Фурье корреляционная функция слу-
случайного процесса.
18.2. Соотношение между спектральной плотностью
мощности и корреляционной функцией
случайного процесса
Рассмотрим центрированный случайный процесс t,(t). Выраже-
Выражение для его спектральной плотности мощности с учетом A8.3) за-
запишется в виде
494

Спектр случайного процесса
A8.11)
A8.12)
495
A8.7)
A8.8)
Преобразуем A8.7)
где R(tbt2)- корреляционная функция случайного процесса.
Для стационарного случайного процесса
A8.9)
A8.10)
произведем замену переменных U и t2 на t = ^ и T = f2-f1, A8.10)
представим в виде
Переходя к пределу, из A8.9) с учетом A8.11) получим
выражение A8.8) запишется в виде

Раздел 18
Таким образом, спектральная плотность мощности определяет-
определяется как преобразование Фурье корреляционной функции случайного
процесса. Обратное преобразование Фурье позволяет перейти от
спектральной плотности мощности случайного процесса к его кор-
корреляционной функции
Я(т) = — |"л/(ш)е*°тс*о. A8.13)
Выражения A8.12) и A8.13), связывающие спектральную плот-
плотность мощности и корреляционную функцию случайного процесса,
называются соотношениями Хинчина-Винера. При их выводе не
оговаривались ограничения, накладываемые на случайные про-
процессы. Однако следует иметь в виду, что преобразование Фурье
возможно только для абсолютно интегрируемой функции, т. е. ко-
когда выполняется неравенство
Указанное условие выполняется только для центрированного
случайного процесса - математическое ожидание которого равно
нулю. Функция же ЛУ(со) может быть спектральной плотностью
мощности случайного процесса только тогда, когда она является
абсолютно интегрируемой
С учетом четности Я(т) и Л/(со) выражения для них можно запи-
записать в виде
оо оо
Л/(со) = 2 f R(T)cos{(#z)ch;, Я(т) = - f /V(co)cos(wr)do. A8.14)
о п о
При использовании A8.14) полезно учитывать свойства косинус-
преобразования Фурье.
Мощность случайного процесса определяется R@), из A8.14)
получим
496

Спектр случайного процесса
оо
Я(о) = -|л/(ш)ско. A8.15)
о
Она численно равна площади под кривой спектральной плотно-
плотности мощности с коэффициентом 1/2я.
Спектральная плотность мощности случайного процесса при
со = 0 определяется выражением
N{0) = 2JR{x)ch, A8.16)
т.е. равна площади под кривой корреляционной функции.
Соотношения A8.14) позволяют получить спектр случайного
процесса, зная корреляционную функцию, или по спектру опреде-
определить корреляционную функцию случайного процесса. Исходной при
описании случайного процесса может быть как одна, так и другая
характеристика.
Нормированная величина спектральной плотности мощности
л(со) = —^— = —!_л/((о), со>0,
j /V(co)cfa)
о
обладает свойствами ПРВ частоты. Величину
О)
F(co)= fn((o)cfco
о
можно рассматривать как ФРВ частоты, она обладает свойствами
ФРВ
O<F(co)<1, jF(a))cfa) = 1.
о
Величина п(ы)скх) представляет вероятность того, что случайный
процесс обладает средней мощностью — Л/(со)с/сов полосе частот
п
[со,со + do].
497

Раздел 18
Рассматривая спектральную плотность мощности как ПРВ (без
учета коэффициента), корреляционную функцию можно отождест-
отождествить с характеристической функцией
В качестве примеров рассмотрим характеристики случайных
процессов различного вида.
1. Спектральной плотности мощности, равномерной в полосе
частот (рис. 18.1,а)
Л/((о) = 1, с^ < |со| < со2,
соответствует корреляционная функция случайного процесса
0J
Я(т) = — | cos(ajr)afr =
n J
= —sind — cos(gHt),
те \2 )
где А = со2 - co1f соо = —! .
Графики г(х) при различных соотношениях со-, и аз2 приведены
на рис. 18.1,6. Как следует из графиков, чем уже полоса частот,
занимаемая спектром (точнее, чем меньше значение отношения
А/со0), тем более выражен осциллирующий характер корреляци-
корреляционной функции.
2. Спектральной плотности мощности случайного процесса
(рис. 18.2,а)
Л/(о)) = cos ям/2(оь |со| < щ
соответствует корреляционная функция (рис. 18.2,6)
498

Спектр случайного процесса
Рис. 18.1
со,т
Рис.18.2
3. Спектральной плотности мощности случайного процесса
(рис. 18.3,а)
Л/((о) = sin2 тссо/ш15 |со| < о>1
соответствует корреляционная функция (рис. 18.3,6)
499

Раздел 18
Рис. 18.3
4. Корреляционной функции случайного процесса (рис. 18.4,6)
Я(т) = Я@)бГт2/2р2
соответствует спектральная плотность мощности (рис. 18.4,а)
= A/@)e-pV/4.
5. Корреляционная функция телеграфного сигнала описыва-
описывается выражением (рис. 18.5,6)
Я(т) = Я@)е~2Х|т).
Рис. 18.4
500

Спектр случайного процесса
0,5 1
а) 6)
Рис. 18.5
Ей соответствует спектральная плотность мощности (рис. 18.5,а)
Число примеров спектров случайных процессов и соответст-
соответствующих им корреляционных функций увеличивает табл. 18.1.
С учетом четности функций графики Л/(со) и Я(х) изображены только
для положительных значений со и т.
Условие существования преобразования Фурье, как указыва-
указывалось, предполагает определение спектральной плотности мощно-
мощности только для центрированного случайного процесса. Расширить
понятие спектральной плотности мощности позволяет формальный
прием, основанный на определении спектральной плотности мощ-
мощности импульсной функции (часть 1). Преобразование Фурье им-
импульсной функции определяется соотношением
A8.17)
A8.18)
A8.19)
501
Обратное преобразование Фурье даёт
По аналогии с A8.18) можем записать

Раздел 18
Таблица 18.1
Спектральные плотности мощности и корреляционные
функции случайных процессов
№
п/п
Спектральная плотность
мощности случайного про-
процесса
Нормированная корреляционная
функция случайного процесса
502

Спектр случайного процесса
Продолжение таблицы 18.1
503

Раздел 18
Продолжение таблицы 18.1
504

Спектр случайного процесса
Продолжение таблицы 18.1
505

Раздел 18
Продолжение таблицы 18.1
506

Спектр случайного процесса
Продолжение таблицы 18.1
507

Раздел 18
Окончание таблицы 18.1
508

Спектр случайного процесса
Исходя из A8.19) получим выражения для преобразований Фу-
Фурье некоторых неинтегрируемых функций.
1. Постоянная составляющая а (разд. 3).
|ае-*отЛ = 2яа5(й>I A8.20)
2. Гармоническая составляющая cosсоот (разд. 3).
f cosco0t e'bxck = 1/2 f (erao° + е^ш°) е'^ск =
= 7i5(co — ш0)+7г5(со + cd0 ).
3. Произведение Я(т) и cosaHx.
Л/л (ш) = J R(x)cos щте'^ск =
— оо
= 1/2 JR(x){ek(]i0 +е-™°)е-шск= A8.22)
= 1 / 2Л/(а) - о)о) +1 / 2Л/(со + соо),
где Л/(о)) = 2\ H(t)cosояс/г.
о
4. Одним из видов случайных процессов, с которыми приходит-
приходится иметь дело в практике исследований, является стационарный
случайный процесс, представляющий сумму квазидетерминиро-
ванных случайных процессов
л
Л^ЬХ^скф^ A8.23)
/г=1
где ^-случайная величина; соя -постоянная величина.
Каждая составляющая h,k cos(o)/cf) представляет гармоническое
колебание со случайной амплитудой, распределение вероятностей
которой не зависит от времени
509

Раздел 18
мУ=О, М&}=о2к,М{Ш = 0. A8.24)
Из A8.23) с учетом A8.24) получим корреляционную функцию
случайного процесса r\(t) в виде
/yT) = ?^cos(avc). A8.25)
Спектральная плотность мощности случайного процесса опре-
определяется преобразованием Фурье Ял(т)
п
Л/л(о)) = 1/2^ по2к[Ь{ы + щ) + 6(ы-щ)}, A8.26)
/с=1
представляет совокупность импульсных функций на частотах ±ык.
Рассмотренный случайный процесс называется случайным про-
процессом с дискретным спектром.
Приведенные соотношения, иллюстрирующие возможности
расширения области преобразования Фурье, использованы в
дальнейшем.
18.3.Эффективная ширина спектра случайного процесса
Если для определения ширины корреляционной функции ис-
используется понятие интервала корреляции, то для спектра случай-
случайного процесса - эффективной ширины спектра. Эффективная ши-
ширина спектра определяется как наибольший интервал на оси час-
частот, на котором спектральная плотность мощности еще имеет су-
существенное для решаемой задачи значение. По аналогии с интер-
интервалом корреляции эффективную ширину спектра случайного про-
процесса можно определить на основе различных подходов.
1. Эффективная ширина спектра А определяется заданным зна-
значением нормированной спектральной плотности мощности случай-
случайного процесса (рис. 18.6)
-^ Л/((о-аH)<е. A8.27)
Л/(соо)
Значение частоты coq принимают равной средней частоте спек-
спектра, при низкочастотном спектре - равной нулю.
2. Эффективная ширина спектра определяется заданным зна-
значением интеграла от нормированной спектральной плотности
мощности (рис. 18.7).
510

Спектр случайного процесса
A8.28)
Величина 2 А представляет ширину равномерного спектра
мощности случайного процесса, имеющего мощность, равную
мощности рассматриваемого случайного процесса.
Аналогично соотношениям Хинчина - Винера, записанным для
одного случайного процесса - A8.12) и A8.13), можно записать
соотношения, связывающие взаимную корреляционную функцию
и взаимную плотность мощности двух случайных процессов ?i@
Рис. 18.7
511
A8.29)

Раздел 18
18.4. Спектр производной и интеграла
от случайного процесса
Используя свойства преобразования Фурье, установим соотно-
соотношения между спектральной плотностью мощности и корреляцион-
корреляционной функцией производной и интеграла от стационарного случай-
случайного процесса.
Корреляционная функция производной стационарного случай-
случайного процесса равна второй производной от корреляционной функ-
функции, взятой со знаком минус (разд. 17)
Я4,(т) = -^(т).
Из A8.14) получим
Я"(т) = -- [со2Л/г((o)cos(ccn)dto, A8.30)
о
где Л/^(со) - спектральная мощность случайного процесса t,(t).
С учетом A8.30) можем записать соотношение, связывающее
спектральные плотности мощности случайного процесса и его про-
производной
Л/^((о) = ш2Л/^(соI A8.31)
где Л/^'(о))- спектральная плотность мощности производной слу-
случайного процесса.
Средняя мощность производной случайного процесса равна
Я^@) = -Я"@) = -|@2Л/^(а))сЬ. A8.32)
о
Нормированная корреляционная функция производной случай-
случайного процесса определяется выражением
512
A8.33)

Спектр случайного процесса
? со,т
б)
Рис. 18.8
Аналогично для л-й производной случайного процесса ^@ за-
запишем
A8.34)
В качестве примеров рассмотрим некоторые виды спектров слу-
случайных процессов и характеристики их производных.
1. Спектральная плотность мощности и корреляционная функ-
функция случайного процесса (рис. 18.8,а)
Л/(ш) = е-м2/@\ Я(т) = Я@)е-ы?т2/4.
Спектральная плотность мощности и корреляционная функция
производной случайного процесса (рис. 18.8,6)
513

Раздел 18
r,(t) = i fco2e-aJ/aJ1 coswrcfo = Ш0)A -со?т2l2)e~^IA .
2. Спектральная плотность мощности и корреляционная функ-
функция случайного процесса (рис. 18.9,а)
Л/(со) = У / ще~^'^, Я(т) = R^9cosBarctgo^T).
1 + cofx
Спектральная плотность мощности и корреляционная функция
производной случайного процесса (рис. 18.9,6)
N. (со) = У3 /со?е"Н/Ш1, Я.(т) = L^cosDarcffif(o1T).
q ? A + cofx )
514

Спектр случайного процесса
Используя полученные соотношения, можно получить и выра-
выражение для спектральной плотности мощности интеграла от слу-
случайного процесса rj(f)
A8.35)
Так, если спектральная плотность мощности и корреляционная
функция случайного процесса описывается выражениями (рис.
18.10,а)
Л/(ш) = со2 /со2е~Н/Ю1, Я(т) = ' *°l ,/2 casCarctswz),
A + cofx )
то спектральная плотность мощности и корреляционная функция
интеграла от случайного процесса равны (рис. 18.10,6)
515

Раздел 18
Анализ графиков рис. 18.8-18.10 позволяет оценить влияние
дифференцирования и интегрирования на характеристики случай-
случайного процесса.
18.5. Дискретизация случайного процесса
и его характеристик
Исходные данные о случайном процессе получаются в резуль-
результате измерений его характеристик, в первую очередь, корреляци-
корреляционной функции и спектральной плотности мощности. Указанные
характеристики используются для определения других, необходи-
необходимых при анализе случайного процесса. Как правило, эти характе-
характеристики определяются как дискретные функции времени (задерж-
(задержки) и частоты. Дискретные характеристики случайного процесса
получаются и при цифровой обработке колебаний. В связи с этим
возникнет ряд важных для практики задач:
выбор интервала дискретизации характеристик случайного про-
процесса;
установление соотношений между дискретными характеристи-
характеристиками случайных процессов;
восстановление непрерывных характеристик случайных процес-
процессов по дискретным и др.
В дальнейшем рассматриваются первые две из названных за-
задач, переход от дискретных к непрерывным характеристикам (ин-
(интерполяция характеристик случайных процессов) описан в первой
части.
18.5.1. Выбор интервала дискретизации
случайного процесса
Преобразование Фурье, используемое при анализе детермини-
детерминированных сигналов, связывает временную функцию, описывающую
сигнал, и спектральную плотность сигнала. При анализе случайных
процессов преобразование Фурье устанавливает связь между кор-
корреляционной функцией и спектральной плотностью мощности слу-
случайного процесса. Эта аналогия позволяет перенести некоторые
выводы в отношении детерминированных сигналов на характери-
характеристики случайных процессов.
Возможность представления непрерывной корреляционной
функции случайного процесса ее дискретными значениями опре-
определяется так же, как и детерминированных сигналов. Корреляци-
Корреляционная функция полностью определяется дискретными отсчетами,
516

Спектр случайного процесса
выполняемыми через интервал времени, выбираемый из условия:
т-, <я/шт, где сот - максимальная частота в спектре случайного
процесса.
Восстановление непрерывной корреляционной функции по дис-
дискретным значениям возможно, например, с помощью ряда Котель-
никова (рис. 18.11)
A8.36)
Дискретная корреляционная функция получается при обработке
выборочных значений случайного процесса. Для центрированного
случайного процесса
A8.37)
где Z>n,?,n+k ~ выборочные значения случайного процесса ^(атг^и
?[(/7 + /OtJ; ti - интервал дискретизации; kzA - смешение во вре-
времени; Л/- общее число выборочных значений.
Ограничение, накладываемое на выбор интервала дискретиза-
дискретизации корреляционной функции, определяет интервал дискретизации
и самого случайного процесса.
.Аналогичный вывод можно сделать относительно интервала дис-
дискретизации по частоте при описании спектральной плотности мощно-
мощности случайного процесса ее дискретными значениями (рис. 18.12).
Рис. 18.11
517

Раздел 18
Интервал дискретизации по частоте выбирается из условия
и>1<п/тк, где хк- минимальное значение задержки, при котором
корреляционная функция может быть принята равной нулю. Ряд
Котельникова, определяющий спектральную плотность мощности
случайного процесса через ее дискретные значения, имеет вид
A8.38)
В качестве предельных значений сот и т^ могут быть выбраны;
эффективная ширина спектра и интервал корреляции. Более стро-
строгий подход к их определению лишен смысла, интервалы дискрети-
дискретизации - по времени и частоте устанавливаются неравенствами.
Общее число выборочных значений равно
2хк 2о)т
—- + 1 или ——+ 1.
Используя дискретные значения корреляционной функции, про-
проведем ее ступенчатую аппроксимацию. Выражение для спектраль-
спектральной плотности случайного процесса запишем в виде
Л/(оо) = 2 f R(x)cosonck = 2^ f R(z)cos ~п>тск =
A8.39)
п=0
518

Спектр случайного процесса
Выражение A8.39) позволяет получить непрерывную функцию
Л/(со) с использованием дискретных значений корреляционной
функции.
Аналогично запишем выражение для корреляционной функции
случайного процесса
д(т) = ^1 sin с^- У Л/(л(о1 )cos[(n + О.бЦт]. A8.40)
я 2 ?о
Выражения A8.39), A8.40) могут быть применены для получения
алгоритмов расчета спектральной плотности мощности по дискрет-
дискретным значениям корреляционной функции и корреляционной функ-
функции - по дискретным значениям спектральной плотности мощности.
18.5.2. Дискретное преобразование Фурье (ДПФ)
Как и при расчете характеристик детерминированных сигналов,
можно записать ДПФ, связывающее дискретную корреляционную
функцию с дискретной спектральной плотностью случайного процесса.
Соотношения, связывающие корреляционную функцию и спек-
спектральную плотность мощности случайного процесса
при достаточно малых значениях т^ и щ могут быть преобразованы
к виду
Выражения A8.41) представляют дискретное преобразование
Фурье (прямое и обратное), связывают дискретные характеристики
случайного процесса: корреляционную функцию и спектральную
плотность мощности. Они позволяют получить удобные алгоритмы
расчета указанных характеристик.
При расчете по A8.41) можно перейти к алгоритмам, значитель-
значительно сокращающим объем вычислительных операций - алгоритмам
быстрого преобразования Фурье (БПФ).
519

Раздел 19.
УЗКОПОЛОСНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Узкополосные случайные процессы составляют широкий класс
случайных процессов. К ним в первую очередь относится колеба-
колебание, модулированное сигналом. В качестве несущего колебания
может быть гармоническое или узкополосное случайное колеба-
колебание, в качестве модулирующего - детерминированный сигнал или
случайный сигнал. Особенности узкополосных процессов, как и
узкополосных детерминированных сигналов, делают целесообраз-
целесообразным их отдельное рассмотрение.
В разделе дается описание и методы анализа узкополосных
случайных процессов. Рассматривается наиболее распространен-
распространенный вид узкополосного случайного процесса - гармоническое ко-
колебание, модулированное случайным процессом.
19.1. Описание и характеристики узкополосных
процессов
19.1.1. Описание узкополосного случайного процесса
Как и детерминированный сигнал, случайный процесс называ-
называется узкополосным, если его спектр сосредоточится в узкой полосе
частот около средней частоты (рис. 19.1).
Узкополосный случайный процесс описывается выражением
ф)= V(t)cos[oHt + ф@]= Vc(t)cosoi0t-Vs{t)s\nM0t, A9.1)
где со0- несущая частота; V(t),(p(t)- огибающая и фаза случайного
процесса;
Vc(t) = V(t)cos <p(f) Vs(t) = V{t)s\n <p(f) A9.2)
Представление случайного процесса в виде A9.1) не ограниче-
ограничено классом узкополосных процессов, однако для узкополосных
процессов оно оказалось наиболее удобным, V(t) и q(t) имеют на-
наглядное физическое содержание. Реализация узкополосного слу-
случайного процесса представляет гармоническое колебание с мед-
медленно меняющейся амплитудой и частотой (фазой) (рис. 19.2).
520

Узкополосные случайные процессы
В отличие от детерминированного сигнала V(t) и q(t) случайного
процесса являются случайными функциями.
Выражение для узкополосного случайного процесса часто удоб-
удобнее записывать в комплексной форме
A9.3)
где V(t) - комплексная огибающая случайного процесса:
V{t)=V{t)e^ = Vc(t)+iVs(t).
Из A9.4) с учетом A9.2) получим
A9.4)
Корреляционная функция узкополосного случайного процесса
?,(t) определяется как
A9.6)
Рис. 19.2
521
символ усреднения.

Раздел 19
Учитывая следующее соотношение для действительной части
комплексной величины z
Re[z] = -l(z+z*), A9.7)
где z* - комплексно сопряженная величина,
из A9.6) с учетом A9.3) получим
A9.8)
= Ре[я„(т)еН,
гдеЯу(т) - корреляционная функция комплексной огибающей узко-
узкополосного случайного процесса:
Яу(т) = 1/2 M\v*{t)V(t + A A9.9)
Как следует из A9.8), при заданном значении несущей частоты
корреляционная функция комплексной огибающей полностью оп-
определяет корреляционную функцию узкополосного случайного
процесса. Это позволяет при нахождении корреляционной функции
узкополосного случайного процесса ограничиться определением
В качестве примеров приведем несколько видов функций Rv(t) .
1. Корреляционной функции комплексной огибающей (рис.
19.3,а)
Rv(T) = Rv@)s\nc{Ax/2)
соответствует корреляционная функция узкополосного случайного
процесса (рис. 19.3,6)
Я(т) = Relflv(T)e*0TJ= ^@)sinc(AT/2)cosoHx.
2. Корреляционной функции комплексной огибающей (рис. 19.4а)
Rv(T) = Rv@)e~"M
522

Узкополосные случайные процессы
Рис. 19.3
соответствует корреляционная функция узкополосного случайного
процесса (рис.19.4, б)
R(T) = Rv,@)e"a)l|T|cos(o0x.
3. Корреляционной функции комплексной огибающей (рис.
19.5,а)
соответствует корреляционная функция узкополосного случайного
процесса (рис. 19.5 б)
Я(т) = Rv@)e~^xZ/4 cosoHt.
Спектральная плотность мощности случайного процесса опре-
определяется как преобразование Фурье корреляционной функции.
Выражение для корреляционной функции узкополосного случайно-
случайного процесса A9.8) с учетом A9.7) запишем в виде
Рис.19.4
523

Раздел 19
а)
Рис. 19.5
ЯМ = У2 КЛФ^ + ^У°Л A9-1°)
Преобразование Фурье левой и правой частей A9,10) дает
A9.11)
где Л/у (со) - спектральная плотность мощности комплексной оги-
огибающей
A9.12)
Как следует из A9.11), спектр узкополосного процесса состоит
из двух зеркально-симметричных по форме составляющих, распо-
расположенных в области частот ±ш0 (рис.19.6). Спектр случайного про-
процесса в области положительных значений частоты описывается
первым слагаемым в A9.11), в области отрицательных значений -
вторым слагаемым. При заданном значении несущей частоты
ш0 спектр случайного процесса полностью определяется спек-
спектральной плотностью мощности комплексной огибающей. Переход
от спектра комплексной огибающей к спектру случайного процесса
предполагает перенос низкочастотного спектра, описываемого
Nv(u>), в область частот ±соо(с коэффициентом 1/2). Таким обра-
образом, при спектральном анализе узкополосного случайного процес-
процесса достаточно исследовать только спектральную плотность мощ-
мощности его комплексной огибающей.
524

Узкополосные случайные процессы
Рассмотрим несколько видов спектров комплексной огибающей
случайного процесса.
1. Спектральной плотности мощности комплексной огибающей
(рис. 19.7,а)
Л/у(со) = 1, |со|<А
соответствует спектральная плотность мощности случайного про-
процесса (рис. 19.7,6") при а) > О
Л/(со ; = 1/2, | ш-ш0 |< Д.
2. Спектральной плотности мощности комплексной огибающей
(рис. 19.8,а)
525

Рис.19.8
соответствует спектральная плотность мощности случайного про-
процесса (рис. 19.8,6)
при w>0
3. Спектральной плотности мощности комплексной огибающей
(рис.19.9,а)
-ffl2/-
Л/„(о))=е /ш'
соответствует спектральная плотность мощности случайного про-
процесса (рис.19.9,6)
при со > О
(ю-ЮрJ
Л/(со) = 1/2е м* .
Л/Дсо),
526
Рис.19.9
Раздел 19

Узкополосные случайные процессы
19.1.2. Белый шум
Идеализацией широкополосного случайного процесса является
белый шум - случайный процесс с постоянной спектральной плот-
плотностью мощности на всех частотах (рис. 19.10,а)
Л/(со) = Л/о = const.
Корреляционная функция белого шума
A9.13)
A9.14)
представляет импульсную функцию в начале координат
(рис. 19.10,6). Нормированная корреляционная функция белого
шума равна
г(т)=Я(т)/Я@)=1, т = 0. A9.15)
Белый шум является только моделью реальных широкополос-
широкополосных случайных процессов: мощность реального случайного про-
процесса ограничена, мощность белого шума бесконечна. Однако
введение понятия белого шума является полезным, в частности,
при анализе прохождения случайных процессов через радиотехни-
радиотехнические цепи, и может не оказывать существенного влияния на ре-
результаты, полученные при его использовании как модели реально-
реального процесса.
19.2. Распределение вероятностей огибающей и фазы
узкополосного гауссовского процесса
Обратимся к записи узкополосного случайного процесса t,(t)
в виде
527
Рис. 19.10

Раздел 19
^)=V(t)cos[^t + y(t)]=Vc(t)cosa0t-Vs(t)s\n(u0t, A9.16)
где
Vc(t)=V{t)cos4>(t), Vs(t) = V{t)s\rup(t). A9.17)
Как следует из A9.16), V^t) и Vs(t) линейно связаны с Щ. Если t,(t)
представляет центрированный гауссовский процесс, то и Vc(t) и Vs(t)
являются также гауссовскими процессами с математическими ожида-
ожиданиями, равными нулю. Вторые моменты распределения равны:
Rc@) = M{\f(t)cos2tp(t)} = с?,
Rs@) = M{\f(t)sin2(p(t)} = d2,
R^O) = M{V(t)cos(p (t)V(t)sin<p(t)} = 0.
Для гауссовских процессов равенство нулю корреляционной
функции означает независимость. Таким образом, совместная ПРВ
Vc(t) и Vs(t) равна произведению их одномерных ПРВ:
Ф>У) = —Ц-e 2°2 • A9.18)
Квадратурные составляющие Vc(t) и Vs(t) связаны с огибающей
и фазой случайного процесса выражениями A9.17). Переход от
Vc(t) и Vs(t) к огибающей и фазе устанавливается соотношением
(раздел 17)
f2(x,y) dx dy = f2(pcos9,psine)p ф dQ = ^(p.0) Ф °^ - A9.19)
где fV(f2(p, Q) - двумерная ПРВ огибающей и фазы.
Такой переход аналогичен преобразованию прямоугольных ко-
координат в полярные. Из A9.19) с учетом A9.18) получим
^2(p.e) = -PT = e2°2. A9.20)
27ГСГ
Плотность распределения вероятностей огибающей найдется
из A9.20) как (рис. 19.11)
A9.21)
528

Узкополосные случайные процессы
Таким образом, распределение огибающей узкополосного слу-
случайного процесса подчиняется закону Релея (разд. 15).
Плотность распределения вероятностей фазы
A9.22)
Как следует из A9.22), ПРВ фазы является равномерной на ин-
интервале [0, 2п]. Огибающая и фаза узкополосного гауссовского
процесса в каждый момент времени являются независимыми.
19.3. Распределение огибающей и фазы смеси
сигнала и шума
Рассмотрим смесь узкополосного гауссовского процесса (шума)
t,(t) и гармонического колебания (сигнала) s(t); частота сигнала
совпадает со средней частотой случайного процесса
T](t) = Zs(t) + s(t)=?s(t)+V0cosu0t. A9.23)
С учетом A9.1) запишем
^@=MO+l/o]coswo'-MOsinwo'- A9.24)
Как узкополосный случайный процесс r\(t) представим в виде
Tj(f) = Ц (t )cos[co0/ + Фт (t)] = Vc1 (r)cos coo t - Vs1 (t )sin coof. A9.25)
В A9.25)
529

Раздел 19
vAt) = J[v2Jt)+V*M ф1(О = а/й&^|.
rneVM=VM+V0, VM=Vs(t).
Совместная ПРВ составляющих Vc^(t) и Vs^(t) равна
A9.26)
A9.27)
Переход к огибающей и фазе выполняется, как показано в
§19.2,
A9.28)
Из A9.28) следует, что огибающая и фаза в рассматриваемом
случае являются зависимыми величинами. Наличие в показателе
степени члена, содержащего pcos8 не позволяет представить
fv<p2(P,Q)как произведение fw(p ) и fa (В).
Плотность распределения вероятностей огибающей определим
как и раньше, интегрированием A9.28) по 6
. 2 , „2
530
A9.29)
Из A9.29) получим (рис. 19.12)

Узкополосные случайные процессы
A9.30)
где 10(х) - модифицированная функция Бесселя первого рода ну-
нулевого порядка.
Таким образом, распределение огибающей смеси узкополосно-
узкополосного гауссовского процесса и гармонического сигнала подчиняется
обобщенному закону Релея (разд. 15).
Плотность распределения вероятностей фазы описывается вы-
выражением (получено с учетом A9.28)) [26].
'Ф1
A9.31)
При
^0 = 0 /^ @) = -L. A9.32)
19.4. Модулированные случайные процессы
Узкополосными случайными процессами часто являются моду-
модулированные колебания. Модулированное колебание представляет
высокочастотное колебание (несущее), на которое наложено низ-
низкочастотное - модулирующее (содержащее передаваемую инфор-
информацию). Наибольшая частота спектра модулирующего колебания
значительно меньше частоты несущего колебания. Это условие и
определяет узкополосность модулированного колебания.
Случайные процессы могут служить в качестве несущего или
модулирующего колебания. Случайный процесс как несущее коле-
колебание является узкополосным, на него накладывается низкочас-
низкочастотный сигнал (детерминированный или случайный). В качестве
модулирующего случайный процесс, как правило, используется при
модуляции гармонического колебания. Этот случай наиболее рас-
распространенный, он и рассматривается в разделе - модуляции слу-
случайным процессом гармонического колебания.
531

Раздел 19
Модулируется несущее колебание путем изменения одного или
нескольких его параметров. В зависимости от изменяемого пара-
параметра различают и вид модуляции. Ниже рассматриваются коле-
колебания с амплитудой и угловой (фазовой и частотой) модуляцией.
19.5. Случайный процесс с амплитудной модуляцией
Случайный процесс с амплитудной модуляцией (AM), как пра-
правило, является узкополосным и при обычной AM может быть пред-
представлен в виде (рис. 19.13)
A9.34)
где Vo, ооо, ф0 - амплитуда, частота и начальная фаза несущего ко-
колебания; t,(t) - модулирующий случайный процесс; М - коэффици-
коэффициент модуляции.
Обращение r\(t) в нуль при M^(t) <-1 означает перемодуляцию.
При AM детерминированным сигналом перемодуляция возникает
только при соответствующем выборе коэффициента модуляции.
Когда модулирующее колебание представляет случайный процесс
с неограниченным распределением его значений, всегда будет
иметь место перемодуляция. Если модулирующий случайный про-
процесс ^(t) имеет ПРВ f^(x) , то вероятность превышения уровня -
1/М(что соответствует перемодуляции) будет равна
A9.35)
Значение Рпм определяет ту относительную часть времени, ко-
когда происходит перемодуляция несущего колебания.
Рис. 19.13
532

Узкополосные случайные процессы
При нормальном распределении модулирующего случайного
процесса из A9.35) получим
Рпм=ф(- 1
где х и2 A9.36)
V27t_
Основными характеристиками модулированного случайного
процесса r\(t) являются корреляционная функция и спектральная
плотность мощности. Корреляционная функция случайного про-
процесса определяется как
ял(т)=л41@п('+'0}. <19-37)
Если перемодуляцией можно пренебречь, то с учетом A9.34) из
A9.37) получим
, х V2 M2V2 , ч
Ht1(t) = -2-cosoHt + ^RfxjcoscooT, A9.38)
где R(t) - корреляционная функция модулирующего случайного
процесса.
Спектральная плотность мощности AM случайного процесса
определяется как преобразование Фурье A9.38)
Л/»= |я,(ф-^(Л=^-5((о-аH) + ^-5(а) +со0)+
A9.39)
M2V2 , . . , .,
+ __^.[Л/(со-а)о)+Л/(а) + а)оI
где N(oi) - спектральная плотность мощности модулирующего слу-
случайного процесса.
В A9.39) первые два слагаемых представляют импульсные
функции на частотах ±шо площадью n\fo/2; вторые два описывают
непрерывную часть спектра в области положительных и отрица-
отрицательных частот - около частот ±азо (рис. 19.14). Таким образом,
спектр AM случайного процесса получается наложением на дис-
дискретную составляющую с частотой ±ыо спектра модулирующего
случайного процесса (с соответствующим коэффициентом). Однако
533

Раздел 19
Рис. 19.14
преобразование спектра случайного процесса при AM как линейное
можно рассматривать только тогда, когда перемодуляцией можно
пренебречь.
Средняя мощность AM случайного процесса равна Яп @)
Мощность несущего колебания -
A9.40)
A9.41)
В качестве примеров рассмотрим различные виды модулирую-
модулирующих случайных процессов.
1 .Спектральная плотность мощности и корреляционная функция
модулирующего случайного процесса (табл. 18.1, п.1)
Л/(ш) = 1, | со | < А, Я(т) = R@)s\nc(AT /2).
Корреляционная функция модулированного случайного процесса
Я(т) = Ио /2 coscooT + М2 V20 /2 F?@)sinc( At/2)coscooT.
Спектральная плотность мощности модулированного случайно-
случайного процесса в области положительных частот (рис. 19.15)
534

Узкополосные случайные процессы
* со
Рис. 19.15
2. Спектральная плотность мощности и корреляционная функ-
функция модулирующего случайного процесса (табл.18.1, п.З)
Щ +0)
Корреляционная функция модулированного случайного процесса
2|/ 2/
-w,t
Спектральная плотность мощности модулированного случайно-
случайного процесса в области положительных частот (рис. 19.16)
3. Спектральная плотность мощности и корреляционная функ-
функция модулирующего случайного процесса (табл. 18.1, п.13)
Рис. 19.16
535

О °-
Рис. 19.17
Корреляционная функция модулированного случайного процесса
Я(т) =л V02 /2 coswqt + M2V02/2 Я@) e'^^costflbx.
Спектральная плотность мощности модулированного случайно-
случайного процесса в области положительных частот (рис. 19.17)
Л/Л(а)) = nV02/2 5((o- coo) + М2 V02 /4 е-(а)-ш°J/ю\
Когда перемодуляцией нельзя пренебречь, характеристики мо-
модулированного случайного процесса можно найти, используя мето-
методы анализа случайных процессов при нелинейных преобразовани-
преобразованиях (разд. 22).
Если модулирующий случайный процесс выходит за пределы
линейного участка модуляционной характеристики (результатом
этого нельзя пренебречь), выражение для AM случайного процесса
принимает вид
A9.42)
где д(х) - функция, описывающая искажения модулирующего слу-
случайного процесса.
Обычно модуляционную характеристику можно аппроксимиро-
аппроксимировать линейно-ломанной кривой. Для нее преобразование Лапласа
имеет вид 1//V (разд. 22). Выражение для AM случайного процесса
в этом случае можно записать в виде
Tf){t)=V0cos((D0t + (p0)+MV0cos((u0t + (p0)\—Q^(v)dv, A9.43)
где С - контур интегрирования.
Корреляционная функция r\(t) определяется выражением
536
Раздел 19

Узкополосные случайные процессы
где 0?2 (vi,v2) - характеристическая функция t,(t).
Решение A9.44) получено в виде ряда [19]:
/ N V2 M2V2 ^ rfn 9п п
Ht1(t) = ^cosoHt + ^cosoHx2^—-о г (т), A9.45)
^ 2 л=1
где о2, /Т/с) - дисперсия и нормированная корреляционная функция
модулирующего случайного процесса.
Коэффициенты hn определяются выражением
hn = -A.^vn-2e-a^l2dv A9 46)
Как указывалось, перемодуляцию можно не учитывать при
а «1/М В этом случае выражение Иц(т) примет вид
ГЦх) = VQ2 /2coso)oT + M2 V02 /2 Я(т )coswoT, A9.47)
что совпадает с A9.38)
Спектр модулированного случайного процесса определяется
преобразованием Фурье
Для Са»О можем записать
Л/П((о) = nV02/2 5(со- (йо) + /4^@)), A9.49)
где N^((xi) описывает непрерывную часть спектра, соответствую-
соответствующую второму слагаемому в A9.45) или A9.47).
Графики спектра модулированного случайного процесса при
спектральной плотности мощности модулирующего случайного
процесса
2 /,.,2
A9.48)
A9.50)
537

Раздел 19
приведены на рис. 19.18 [19]. Там же изображен спектр модулиро-
модулированного случайного процесса, полученный без учета перемодуля-
перемодуляции (кривая, выполненная пунктиром). Сравнение приведенных
кривых показывает определенное расширение спектра модулиро-
модулированного колебания при перемодуляции.
Амплитудно-модулированный случайный процесс при баланс-
балансной модуляции описывается выражением (часть 1)
A9.51)
где tj[t) - модулирующий случайный процесс.
Корреляционная функция модулированного случайного процес-
процесса равна
A9.52)
Преобразование Фурье A9.52) дает спектральную плотность
мощности (при со > 0)
A9.53)
Рис. 19.18
538

Узкополосные случайные процессы
О
Рис. 19.19
где Л/((о) - спектральная плотность мощности модулирующего слу-
случайного процесса Z,(t).
Спектр случайного процесса с балансной AM (рис. 19.19) со-
содержит две симметричные полосы верхних и нижних боковых со-
составляющих. Дискретная составляющая на частоте несущего коле-
колебания отсутствует.
19.6. Случайный процесс с угловой модуляцией
19.6.1. Описание случайного процесса с угловой модуляцией
Случайный процесс с угловой модуляцией, как правило, являет-
является узкополосным, описывается выражением A9.1), рис. 19.19,
A9.54)
где Vo ,соо , \|/(f) - амплитуда, частота и фаза; V(t) = Vo е^A) - ком-
комплексная огибающая случайного процесса.
При угловой модуляции происходит изменение фазы несущего
колебания \\t(t) под воздействием модулирующего случайного про-
процесса Z,(t). Различают два вида угловой модуляции - фазовую (ФМ)
и частотную (ЧМ).
539

Раздел 19
Рис. 19.19
При ФМ модулирующий случайный процесс воздействует на
фазу непосредственно. Фаза определяется как
A9.55)
где ф0 - начальная фаза; l,(t) - модулирующее колебание - стацио-
стационарный центрированный случайный процесс; к - коэффициент
пропорциональности.
Выражение A9.55) описывает линейную зависимость xy(t) от ?,(t) -
это наиболее часто встречающийся случай.
Частота ФМ случайного процесса определяется выражением
v(,)=<oo+^Uo+*i§). A9.56)
При ЧМ модулирующее колебание воздействует непосредст-
непосредственно на частоту
Фаза ЧМ случайного процесса
A9.57)
A9.58)
Выражение для комплексной огибающей модулированного слу-
случайного процесса записывается в виде (ф0 = 0):
при ФМ
A9.59)
A9.60)
540
при ЧМ

Узкополосные случайные процессы
Таким образом, если известно распределение модулирующего
случайного процесса, можно найти распределение фазы и частоты
модулированного случайного процесса (по крайней мере такая
возможность имеется). Используя A9.59) и A9.60), получим корре-
корреляционную функцию и спектральную плотность мощности ком-
комплексной огибающей, а, следовательно, и модулированного слу-
случайного процесса.
19.6.2. Распределение фазы и частоты модулированного
случайного процесса
Определим ПРВ фазы и частоты модулированного случайного
процесса сначала при ФМ. Обозначив f^(x) одномерную ПРВ мо-
модулирующего стационарного случайного процесса %(t), выражение
для ПРВ фазы с учетом A9.55) запишем в виде (разд. 15)
№к{4*)- A9-б1)
Плотность распределения вероятностей частоты с учетом
A9.56) будет равна
где fo(x) - ПРВ производной модулирующего случайного процесса
Для центрированного гауссовского процесса ?>(t)
х2
f (x) = -^e2a\ A9.63)
Л/27Ш
где о2 - дисперсия Z,(t),
из A9.61) получим
(ф-ФоJ (Ф-ФрJ
,,(„) =-_Ue 2< =-Л-е ^ , A9.64)
V27iov V27tfey
(ca-oipJ (со-ШрJ
^(со) = __L_e 2o' = ^_ / ..е2*""®, A9.65)
л/2тгау yl2nky]- Я" @)
где Я^г,) - корреляционная функция модулирующего процесса t,(t);
541

Раздел 19
av2 = l^o2 , av2 = - Л*Я" @) -дисперсии фазы и частоты.
При определении fv((a) учтено, что производная гауссовского
процесса имеет нормальное распределение.
Плотность распределения вероятностей частоты Цы) дает
представление о спектре, выражение A9.65) позволяет судить о
спектре ФМ случайного процесса при модуляции гауссовским про-
процессом.
При ЧМ выражения для ПРВ частоты и фазы модулированного
случайного процесса с учетом A9.57) и A9.58) получим в виде
где f^(y)- ПРВ интеграла от ?,(t).
Плотность распределения вероятностей частоты, описываемая
A9.66), позволяет получить представление о спектре модулиро-
модулированного случайного процесса..
Для модулирующего гауссовского процесса ?,(t) имеем
(to-topJ (co-topf
f» = -^-e 2o* = -L-e2^, A9.67)
V27xctv л/2я/са
(ф-ФоJ (ф-ФоJ
Ф) = ^е 2°* ="-е2к2<, A9.68)
V2Trav л/271/са^
где ov2 = /с^а2; а/ = /Лт/ - дисперсия частоты и фазы; сгп2 - дис-
дисперсия интеграла от Z>(t).
Используя спектральную плотность мощности случайного про-
процесса L,(t), выражения для о/ и а/запишем в виде
Сравнение характеристик распределения фазы и частоты при
ФМ и ЧМ показывает, что отличие ФМ от ЧМ при модуляции слу-
случайными процессами такое же, как при модуляции детерминиро-
детерминированными сигналами.
При описании угловой модуляции детерминированными сигна-
сигналами пользуются такими характеристиками, как индекс модуляции
542

Узкополосные случайные процессы
и девиация частоты. При рассмотрении угловой модуляции слу-
случайных процессов их определения требуют уточнения.
При ФМ случайным процессом целесообразно рассматривать
эффективный индекс модуляции, определив его как
A9.69)
A9.70)
где R(x), a = R@) - корреляционная функция и дисперсия модули-
модулирующего случайного процесса t,(t).
При ЧМ эффективную девиацию частоты определим как
а эффективный индекс модуляции
A9.71)
A9.72)
где
Здесь N(w) - спектральная плотность мощности случайного про-
процесса ^(t).
При модуляции случайным процессом пределы изменения час-
частоты не ограничены. В то же время при соответствующем соотно-
соотношении эффективной девиации и несущей частоты вероятностью
того, что случайная величина - частота примет отрицательные
значения, можно пренебречь. Это условие и означает узкополос-
ность модулированного случайного процесса. В рамках этого усло-
условия и проводится рассмотрение модулированных случайных про-
процессов.
543

Раздел 19
19.6.3. Корреляционная функция и спектральная плотность
мощности комплексной огибающей ФМ случайного процесса
Корреляционная функция комплексной огибающей модулиро-
модулированного случайного процесса определяется выражением A9.9)
Rvix) = M2M{V*(t)V*(t-T)},
где М{...} - символ усреднения.
При ФМ с учетом A9.55) запишем
д.И^^ИМ]}, A9.73)
где ^(t) - модулирующий случайный процесс.
Среднее значение в A9.73) представляет характеристическую
функцию случайного процесса (разд. 15)
Х^) = Ф)-ф-т). A9.74)
Она определяется выражением
ех(*)= )fx(y)etk>dy,
—оо
где fx (у) - одномерная ПРВ случайного процесса %(t).
Плотность распределения вероятности %(t) получим с учетом
A9.74), зная ПРВ модулирующего случайного процесса t,(t) (разд. 15)
оо
Ф)= \f^y + u)du, A9.75)
—оо
где fipfa ,x2) - двумерная ПРВ случайного процесса ^(t).
При модуляции гауссовским процессом распределение %(t) яв-
является нормальным. Характеристическая функция %(t) равна
6х(/с)=е 2 , A9.76)
где сх2 - дисперсия %(t).
При нормальном распределении t,(t) получим
а* = 2[Я@) - Я(т)] = 2а 2[i - r{x)\ A9.77)
544

Узкополосные случайные процессы
где R(x), a = R@), r(x) = R(x)/R(O) - корреляционная функция, дис-
дисперсия и нормированная корреляционная функция модулирующего
случайного процесса ?,(t).
При модуляции гауссовским процессом из A9.73) с учетом
A9.76) и A9.77) получим
яЛтЬ-^е-^'Мт)]. A9.78)
Используя спектральную плотность мощности модулирующего
случайного процесса N((u), выражение для Rv(t) представим в виде
A9.79)
Полученные выражения описывают зависимость корреляцион-
корреляционной функций комплексной огибающей ФМ сигнала от спектра мо-
модулирующего случайного процесса.
Корреляционная функция ФМ случайного процесса определяет-
определяется A9.8). С учетом A9.79) запишем
A9.80)
В качестве примеров рассмотрим некоторые виды модулирую-
модулирующих случайных процессов.
1. Спектр модулирующего случайного процесса - равномерный
в полосе частот (табл. 18.1, п.1), рис. 19.20.
Л/(со) = Л/о, 0 < | со | < А ,
корреляционная функция
а{т) = sincAx /2.
Корреляционная функция комплексной огибающей равна
Я^т) = V02/2 expHcV A - sine At/2],
где а2- дисперсия модулирующего случайного процесса.
График корреляционной функции комплексной огибающей при-
приведен на том же рис. 19.20,а.
545

Раздел 19
Рис. 19.20
2. Спектр модулирующего случайного процесса вида (табл. 18.1,
п.З), рис. 19.21.
нормированная корреляционная функция
г{т)=е~^.
Корреляционная функция комплексной огибающей
RV(T; = V0212 exp[-/cV A - e"w1 ы)].
График корреляционной функции комплексной огибающей при-
приведен на рис. 19.21,а.
3. Спектр модулирующего случайного процесса - гауссовского
вида (табл. 18.1, п. 13), рис. 19.22.
N(u)= е'^1^
нормированная корреляционная функция
Кт)=е-(^х2/4)
546

Узкополосные случайные процессы
б)
Рис. 19.21
Корреляционная функция комплексной огибающей равна
Я^ = Vo2/2expHcV 0 - е-{^2/4))].
График корреляционной функции комплексной огибающей при-
приведен на рис. 19.22,а.
Средняя мощность модулированного случайного процесса рав-
равна Rn@)
При т —> °° имеем
Непрерывной части спектра соответствует
к2
A9.81)
A9.82)
A9.83)
Спектральная плотность мощности комплексной огибающей ФМ
случайного процесса определяется как
547

Рис. 19.22
где
2 со
-»yo
A9.84)
A9.85)
В качестве примеров рассмотрим некоторые виды модулирую-
модулирующих случайных процессов.
1. Спектр и корреляционная функция модулирующего процесса,
описываемого в табл. 18.1, п.1.
Спектральная плотность комплексной огибающей модулирован-
модулированного случайного процесса (рис. 19.20,6)
где а -дисперсия модулирующего случайного процесса.
2. Спектр и корреляционная функция модулирующего процесса,
описываемого в табл. 18.1, п.З.
548
Раздел 19

Узкополосные случайные процессы
Спектральная плотность комплексной огибающей модулирован-
модулированного случайного процесса (рис. 19.21,6)
3. Спектр и корреляционная функция модулирующего случайно-
случайного процесса, описываемого в табл. 18.1, п. 13.
Спектральная плотность комплексной огибающей модулирован-
модулированного случайного процесса (рис. 19.22,6).
о
Графики корреляционных функций и спектров комплексной оги-
огибающей ФМ случайных процессов, модулированных случайными
процессами, характеристики которых приведены в табл. 18.1, даны
в табл. 19.1.
Переход от спектральной плотности мощности комплексной
огибающей к спектральной плотности мощности узкополосного
случайного процесса описывается A9.11)
/V>) = ^AV(w-Wo) + ^AV(co + wo). A9.86)
В A9.84), раскладывая г(т) в ряд Тейлора и ограничиваясь
первыми двумя слагаемыми, получим
G(t) = -/с2/2Я"@)г2 = /с2т2, A9.87)
где ^ =kJ-Fr@)/2.
Подставляя A9.87) в A9.84), запишем
оо
/V^((o)=^02|e-/f'T2cosayrc^ = V^l/o2/2^e"w2/4'<l2. A9.88)
о
Спектральная плотность мощности модулированного случайно-
случайного процесса описывается выражением A9.11). С учетом A9.88) для
нее получим при со > О
2 (со-ш0J
Л/т1((О) = ^0-в <*? . A9.89)
549

Таблица 19.1
Корреляционная функция и спектральная плотность мощности
комплексной огибающей ФМ случайного процесса
Характеристики
№ модулирующего
пп случайного процесса,
л/И; г(х)
Корреляционная функция ком-
комплексной огибающей ФМ
случайного процесса rv(x)
Спектральная плотность мощности
комплексной огибающей ФМ слу-
случайного процесса Л/,, (со)

Продолжение таблицы 19.1

Продолжение таблицы 19.1

Продолжение таблицы 19.1

Продолжение таблицы 19.1

Продолжение таблицы 19.1

Окончание таблицы 19.1

Узкополосные случайные процессы
Как следует из полученных выражений, при принятой аппрокси-
аппроксимации корреляционной функции модулирующего случайного про-
процесса спектральная плотность мощности описывается гауссовской
функцией.
При малом индексе модуляции, ka« 1, в A9.78) может принять
e-*v[i-r(T)Ui-/cV[i-r(T)]. A9.90)
Спектральная плотность мощности комплексной огибающей по-
получается с учетом A.83) и A9.90) в виде
/V^(w) = 7il/025(w)+/c2V02/2A/(w)- A9.91)
Как следует из A9.91), при малом индексе модуляции непре-
непрерывная часть спектра повторяет (по форме) спектр модулирующего
случайного процесса.
19.6.4. Корреляционная функция и спектральная плотность
мощности комплексной огибающей ЧМ случайного процесса
Частотно-модулированный случайный процесс описывается вы-
выражением
Л@ = Vo cos[aHf +v@l = Re^Oe**],
где V(t) - V0(t)e^f)- комплексная огибающая.
Корреляционная функция комплексной огибающей ЧМ случай-
случайного процесса определяется A9.9); с учетом A9.58) выражение
для нее имеет вид
A9.92)
Усредненная величина в A9.92) представляет характеристиче-
характеристическую функцию x(t). Она определяется как
557
фаза случайного процесса;

Раздел 19
6х(/с)= \fx(x)elkxdx, A9.93)
где fx(x) - одномерная ПРВ случайной величины %(f).
При нормальном распределении модулирующего случайного
процесса ЦХ) случайные процессы
t-x
Ф) = \ф)сП и x(t) = \l{t)dt-j^t)dt A9.94)
О 0 0
имеют также нормальное распределение. С учетом определения
характеристической функции гауссовского процесса выражение
для Rv(t) по аналогии с A9.75) получим в виде
Я^^е-^КЦ A9.95)
Я (т)
где Я^т), о^ = Я^@), г^(т) = —-— - корреляционная функция,
Я^@)
дисперсия и нормированная корреляционная функция случайного
процесса t,(t).
Определяя корреляционную функцию С,(t) через спектральную
плотность мощности модулирующего процесса Л/(со), запишем
Я (T) = lfiecosa)T.cfa). A9.96)
71J ш
С учетом A9.96) выражение для Rv(x) представим в виде
VA
A9.97)
Спектральная плотность мощности комплексной огибающей ЧМ
случайного процесса описывается выражением
оо оо
ЛУ1/(ш) = 2|я1/(т)со8акс/т = \/02[е~е(т)со5(отс/г, A9.98)
о о
558

Узкополосные случайные процессы
где
A9.99)
Выражение A9.98) аналогично выражению, описывающему
спектральную плотность мощности комплексной огибающей ФМ
случайного процесса. Отличие заключается в определении G(x).
ЧМ случайный процесс можно представить как ФМ случайный про-
процесс, имеющий иную спектральную плотность мощности. Если
спектральная плотность мощности модулирующего случайного
процесса при ФМ Л/(о)),то при соответствующей ЧМ - Л/(а))/со2.
Корреляционная функция ЧМ случайного процесса определяет-
определяется как
A9.100)
Средняя мощность модулированного случайного процесса равна
При т-^оо имеем
VA
A9.101)
A9.102)
A9.103)
В качестве примеров рассмотрим некоторые виды модулирую-
модулирующих случайных процессов.
1. Спектральная плотность мощности и корреляционная функция
модулирующего случайного процесса описаны в табл. 18.1, п.10.
559
Непрерывной части спектра соответствует

Раздел 19
Корреляционная функция комплексной огибающей модулиро-
модулированного случайного процесса (рис. 19.23,а)
График спектральной плотности мощности огибающей модули-
модулированного случайного процесса A9.98) изображен на рис. 19.23,6.
2. Спектральная плотность мощности и корреляционная функ-
функция модулирующего процесса описаны в табл. 18.1, п. 11.
Л/И = |ш|3/ш?е-Н/в\
г(т) = 1/A + ш2т2J cosDarcfpca1T).
Корреляционная функция комплексной огибающей модулиро-
модулированного случайного процесса (рис. 19.24,а)
560
Рис. 19.23

Узкополосные случайные процессы
График спектральной плотности мощности комплексной оги-
огибающей модулированного случайного процесса A9.98) изображен
на рис. 19.24,6.
3. Спектральная плотность мощности и корреляционная функция
модулирующего случайного процесса описаны в табл. 18.1, п. 12.
Л/(со) = ш4/о)?е>|/ш\
г(т) = 1/A + со2т2M/2 cosEarctguix).
Корреляционная функция комплексной огибающей модулиро-
модулированного случайного процесса (рис. 19.25,а)
Рис. 19.24
561

Раздел 19
Рис. 19.25
График спектральной плотности мощности комплексной оги-
огибающей модулированного процесса A9.98) изображен на рис.
19.25,6.
В A9.95) раскладывая ^(т)в ряд Тейлора и ограничиваясь пер-
первыми двумя слагаемыми, получим
A9.104)
A9.105)
NM =
4/с,
A9.106)
562
Спектральная плотность модулированного случайного процесса
При таком представлении Rv(t) из A9.98) найдем

Узкополосные случайные процессы
Таким образом, спектральная плотность мощности случайного
процесса, модулированного гауссовским процессом, описывается
гауссовской функцией.
При малом индексе модуляции /са^«1 в A9.95) можем при-
принять
A9.107)
Спектральную плотность мощности огибающей определим с ис-
использованием A9.107) и A9.103) в виде
Таким образом, при малом индексе модуляции спектральная
плотность мощности комплексной огибающей ЧМ случайного про-
процесса определяется спектральной плотностью мощности интегра-
интеграла от модулирующего случайного процесса.
563
A9.108)

Раздел 20.
ВЫБРОСЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
Реализация непрерывного случайного процесса представляет
изменение случайной величины во времени - переходы от локаль-
локального минимума к локальному максимуму и наоборот (рис. 20.1).
Если установить уровень х, то можно выделить точки пересечения
реализации случайного процесса с выбранным уровнем - нули и
отрезки реализации над уровнем и под ним - положительные и от-
отрицательные выбросы случайного процесса. Анализ выбросов, их
характеристик позволяет судить о поведении случайного процесса
во времени.
Наиболее полной характеристикой выбросов непрерывного
случайного процесса является ПРВ (ФРВ) длительности выбро-
выбросов. Она дает возможность определить и другие, менее полные,
характеристики, в частности, среднюю длительность и частоту
следования выбросов, дисперсию и др. Однако несмотря на то,
что подход к нахождению ПРВ длительности выбросов был пред-
предложен в одной из ранних работ по теории случайных процессов
[36], строгое решение задачи определения ПРВ (ФРВ) длительно-
длительности выбросов в общей постановке наталкивается на трудности, не
всегда преодолимые на практике. Указанное обстоятельство яв-
является причиной того, что в разделе рассматриваются несколько
Отрицательные выбросы
Рис.20.1
564

Выбросы случайных процессов
подходов к определению характеристик выбросов. Изложены наи-
наиболее простые, дающие результаты с достаточной для инженерной
практики точностью.
20.1. Определение характеристик распределения
длительности выбросов с использованием ФРВ случай-
случайного процесса
Рассмотрим стационарный случайный процесс t,(t) на интервале
времени [t, t + z\. Зададим уровень х и определим вероятность того,
что при условии не превышения случайным процессом уровня х в
точке t в остальных точках выделенного интервала времени он
также не превышает этот уровень. Чтобы определить эту вероят-
вероятность, разобьем интервал времени т на л участков длительностью
At = т/л.
Тогда указанная вероятность будет оцениваться как
Fz(x)=Fn+,(x)/F,(x), B0.1)
где Fn+1(x)-(л+ 1)-мерная ФРВ случайного процесса ?,(t) в моменты
времени t, t + At, t + 2<\t,..., t + т.
Уменьшая длительность интервалов разбиения выбранного ин-
интервала, для Fx(x) получим следующее предельное выражение
Ft(x) = 1/^(x)limFII+1(x). B0.2)
Если значение случайного процесса \(\) внутри выделенного ин-
интервала времени не превышает заданный уровень х, то, следова-
следовательно, пересечение этого уровня снизу вверх происходит только
в точке вне этого интервала. Вероятность того, что случайный про-
процесс не превышает уровень х на интервале т, определяет также
вероятность того, что длительность отрицательных выбросов бу-
будет не меньше т. Если обозначить F_5(t) ФРВ длительности отри-
отрицательных выбросов относительно уровня х, то для нее с учетом
сказанного можно записать
^-бМ = 1-^(х), B0.3)
где FT(x) определяется B0.2).
При невозможности получить предельное значение в B0.2) оце-
оценить F_5(t) можно с помощью (л + 1)-мерной ФРВ случайного про-
565

Раздел 20
цесса B0.1). Используя определение (п + 1)-мерной ФРВ через
двумерную ФРВ (разд. 16), для FT(x) запишем следующее выра-
выражение;
^(хН-^М/^х)]", B0.4)
где F2(x,x) - двумерная ФРВ, описывающая случайный процесс
в моменты времени t и t + At.
Таким образом, оценку ФРВ длительности выбросов получим
в виде
/U(T) = 1-FT(x)-1-[F2(x.xVF,(xr.
Для гауссовского процесса выражение для Fx(x) было уточнено
при л->°о .С учетом ранее полученного результата запишем
B0.5)
B0.6)
где
a, g2, г(т) - математическое ожидание, дисперсия и нормированная
корреляционная функция случайного процесса %(t).
Аналогично получим выражение для ФРВ длительности поло-
положительных выбросов
где
B0.7)
B0.8)
На рис. 20.2 приведены графики ФРВ длительности выбросов:
20.2,а - отрицательных, 20.2,6 - положительных как функции
обобщенного параметра у-г (о)т при различных нормированных
значениях уровня (х - а)/о.
566

Выбросы случайных процессов
B0.9)
где Л/(со) - спектральная плотность мощности случайного процесса.
При х = а
1/
Функция распределения вероятностей длительности положи-
положительных и отрицательных выбросов имеют вид:
B0.10)
567
Рис. 20.2
Как следует из B0.5) - B0.8), оценка ФРВ длительности выбро-
выбросов гауссовского процесса для нормированных значений уровня
определяется второй производной нормированной корреляцион-
корреляционной функции случайного процесса при т = 0.
При определении г (о) полезно учитывать следующее соотно-
соотношение, связывающее г "(о) со спектральной плотностью случайно-
случайного процесса (разд. 18)

Раздел 20
Результат, аналогичный B0.10), получен для случайного про-
процесса, имеющего распределение точек пересечения с нулевым
уровнем, подчиняющееся закону Пуассона, в разд. 15. Совпадение
результатов объясняется тем, что при выводе B0.2) и был сделан
переход к пуассоновскому распределению нулей.
Таким образом, записано выражение для ФРВ длительности
выбросов гауссовского процесса, полученное с некоторыми допу-
допущениями. Ошибка при расчете по нему зависит от т, ошибка
уменьшается с ростом значений т.
Плотность распределения вероятностей длительности выбро-
выбросов найдется из B0.5) и B0.7):
отрицательных выбросов
f.5(T) = a1e^T, B0.11)
положительных выбросов
^W = a2e"a2t. B0.12)
График fs(x) приведен на рис. 20.3, где a = a1 для отрицатель-
отрицательных и a = a2 для положительных выбросов случайного процесса.
Как следует из B0.11) и B0.12), распределение длительности
выбросов, полученное при принятых допущениях, подчиняется по-
показательному закону.
С учетом записанных выражений найдем математическое ожи-
ожидание длительности выбросов, ее среднее значение
B0.13)
568

Выбросы случайных процессов
где а = о^ для отрицательных выбросов, ос = а2 для положительных.
Таким образом, для отрицательных выбросов:
x-a
cpi V-ПО) V а ; ¦[ 2о-
для положительных выбросов
B0.14)
B0.15)
При х = а как для отрицательных, так и для положительных вы-
выбросов имеем
B0.16)
Графики зависимости тср от значений уровня приведены на рис.
20.4. При увеличении значений уровня среднее значение длитель-
длительности отрицательных выбросов увеличивается (рис. 20.4,а), поло-
положительных выбросов - уменьшается (рис. 20.4,6). Поясняют ука-
указанную зависимость отрезки реализаций случайного процесса,
приведенные на рисунках: на рис. 20.4,а заштрихованы отрица-
отрицательные выбросы, на рис. 20.4,6 - положительные, для различных
значений уровня.
С учетом B0.14) - B0.16) выражения для ФРВ и ПРВ длитель-
длительности выбросов можно записать в виде
B0.17)
где тср=тср1 для отрицательных выбросов B0.14), тср=тср2 для
положительных выбросов B0.15).
Сумма средних значений длительности отрицательных и поло-
положительных выбросов представляет средний период их следования
B0.18)
569

Раздел 20
570
Рис. 20.4

Выбросы случайных процессов
B0.19)
B0.20)
Графики среднего значения периода и средней частоты следо-
следования выбросов в зависимости от нормированного значения уров-
уровня приведены на рис. 20.5 и рис. 20.6.
571
Рис. 20.5
Средняя частота следования выбросов равна
Рис. 20.6

Раздел 20
Как следует из анализа графиков, при увеличении абсолютного
значения уровня среднее значение частоты следования выбросов
уменьшается, соответственно, средний период увеличивается.
Результаты B0.13) - B0.20) получены исходя из приближенных
зависимостей ПРВ длительности выбросов. Однако они совпадают
с полученными при строгом подхода (п. 20.3).
Выражения для средней частоты выбросов относительно мате-
математического ожидания гауссовских процессов, характеристики ко-
которых приведены в табл. 18.1, сведены в табл. 20.1.
Дисперсия длительности выбросов с учетом B0.10) - B0.13)
B0.21)
Для отрицательных выбросов гауссовского процесса получим
-#Ч, B°-22)
для положительных выбросов:
i2
B0.23)
Рассмотрим примеры характеристик распределения длительно-
длительности выбросов гауссовского процесса.
1. Гауссовский процесс, имеющий спектр и корреляционную
функцию вида (табл. 18.1, п. 1)
Для него получим
572

Выбросы случайных процессов
2.Гауссовский процесс, имеющий спектр и корреляционную
функцию вида (табл. 18.1, п. 13)
Л/(со)=е-ы2/а)?, г(т)=е-^2/4.
Для него получим
-г"@) = 0J/2,
<-af
3. Гауссовский процесс, имеющий спектр и корреляционную
функцию вида (табл. 18.1, п.4)
Плотность распределения вероятностей длительности выбро-
выбросов при х = а, полученная в соответствии с B0.11) или B0.12), име-
имеет вид
/5(х) = а)/е-(°1т/л.
04 ' /71
График f&(x) изображен на рис. 20.7. На рисунке точками нанесе-
нанесены результаты экспериментальных исследований для случайного
процесса с теми же характеристиками, приведенные в [20].
573
Рис. 20.7

Раздел 20
Таблица 20.1.
Средняя частота следования выбросов
гауссовского процесса
574
Характеристики случайного
процесса
Средняя частота выбросов

Выбросы случайных процессов
575
Характеристики случайного
процесса
Средняя частота выбросов

Раздел 20
20.2. Определение характеристик распределения дли-
длительности выбросов с использованием частотных ха-
характеристик случайного процесса
Прежде чем дать общую постановку задачи, рассмотрим част-
частный случай распределение длительности выбросов случайного
процесса с угловой модуляцией. Такое рассмотрение позволяет
лучше понять и решение задачи в общем виде.
20.2.1. Распределение длительности выбросов случайного
процесса с угловой модуляцией
Случайный процесс с угловой модуляцией описывается сле-
следующим выражением (разд. 19)
576
Характеристики случайного
процесса
Средняя частота выбросов

Выбросы случайных процессов
л@ = Vo cos[(o0f + \|/(f)], B0.24)
где V0,(u0,\\i(t) - амплитуда, несущая частота и фаза сигнала.
При фазовой модуляции (ФМ)
V(f) = <po+ *&(').
где %(t) - модулирующий стационарный случайный процесс; ф0 -
начальная фаза; к- коэффициент пропорциональности.
Частота ФМ сигнала
где f * B0.25)
При частотной модуляции (ЧМ) модулирующий случайный про-
процесс t,(t) воздействует непосредственно на частоту
v(f) = <oo+ *?(*). B0.26)
Зная ПРВ (ФРВ) модулирующего случайного процесса %(t), мож-
можно получить ПРВ частоты модулированного процесса (разд. 19):
при ФМ
Ф) = \'(^) B0-27)
где fr(y) - ПРВ производной ф) = -^-;
dt
при ЧМ
f,M=f{nr) B0-28»
где f^(y) - ПРВ модулирующего случайного процесса \(t).
Мощность модулированного случайного процесса в полосе час-
частот [со,со+сЬ] равна l/02/2 fv((o)du>. Интеграл от этой величины в
пределах возможного изменения частоты дает
1/02/2риМсЬ = ЦJ/2 = а2, B0.29)
о
что соответствует мощности модулированного случайного процесса.
577

Раздел 20
Имея ПРВ частоты модулирующего случайного процесса, можно
получить ПРВ периода следования выбросов
Т = 2n/v B0.30)
и длительности выбросов 8
5 = T/2 = 7t/v. B0.31)
С учетом B0.31) выражение для ПРВ длительности выбросов
случайного процесса r\(t) запишется в виде
4(т) = я/т2^(я/т). B0.32)
Подставляя в B0.32) выражение для ^(со), найдем ПРВ дли-
длительности выбросов случайного процесса при ФМ или ЧМ.
Для гауссовского процесса t,(t)
fl(x) = -jL-e 2a\ B0.33)
л/2тш
где с? - дисперсия t,(t),
из B0.32) при ФМ получим
fM=veie ' Bаз4)
где о^=-/с2Я'(о) - дисперсия частоты; R(x) - корреляционная
функция случайного процесса t,(t),
XQ =7C/C00.
Используя спектральную плотность мощности модулирующего
случайного процесса t,(t), выражение для а2 запишем в виде
р со
o2r=— 7tfco2A/(co)cfco. B0.35)
0
Для ЧМ из B0.32) с учетом B0.28) получим
где а2-дисперсия случайного процесса ?,(t).
578
B0.36)

Выбросы случайных процессов
Определенный интерес представляет рассмотрение распреде-
распределения длительности выбросов на выходе смесителя ЧМ системы.
На вход смесителя подается ЧМ случайный процесс - непо-
непосредственно и после задержки t3. Случайный процесс на выходе
смесителя описывается выражением
Л@ = Vc oosMO -W-t3)], B0.37)
где
t
v|/(f) = (po + /cj4(Oc(f,
о
t,(t)- модулирующий случайный процесс; t3 - задержка.
Частота на выходе смесителя определяется как производная
фазы в B0.37)
vc(t)=k^(t)-^t-t3]. B0.38)
Как следует из B0.38). несущая частота случайного процесса на
выходе смесителя отсутствует. Тем не менее случайный процесс
описывается выраженим, аналогичным выражению для узкополос-
узкополосного случайного процесса B0.24).
ПРВ разности ?(f)-?(f-f3) определяется выражением (разд. 17)
Ку) = |Ч г(".У + u)du' B0.39)
где ^ г[хьхг) ~ двумерная ПРВ Щ) и \(\-13).
При нормальном распределении случайного процесса ?,(t) раз-
разность %(t) - Щ - t3). имеет также нормальное распределение с дис-
дисперсией
а| = 2а2[1-г(У, B0.40)
гдеЯ(т) а2 = Я(о) г(т) = Я(т)/ Я(о) - корреляционная функция, дис-
дисперсия и нормированная корреляционная функция ?(f).
Таким образом, для случайной величины B0.38) при нормаль-
нормальном распределении Z,(t) получим
B0.41)
579

Раздел 20
Средняя частота случайного процесса на выходе смесителя
wcp = f tafu(wjcfco = 2/л/тг коф-г^з). B0.42)
о
Как следует из B0.42), для заданного значения времени за-
задержки средняя частота на выходе смесителя зависит от значения
корреляционной функции модулирующего случайного процесса.
Длительность положительных и отрицательных выбросов слу-
случайного процесса на выходе смесителя связана с частотой соот-
соотношением 5 = 7i/v. Из B0.33) и B0.41) получим (рис. 20.8,а)
(ФТ 1
B0.43)
B0.44)
где
20.2.2. Распределение длительности выбросов случайного
процесса, общая постановка задачи
Центрированный случайный процесс представим в виде
B0.45)
ФРВ длительности выбросов равна (рис. 20.8,6)
Рис.20.8
580

Выбросы случайных процессов
не накладывая на него условия узкополосности. Записанное выра-
выражение аналогично тому, какое описывает случайный процесс с уг-
угловой модуляцией на выходе смесителя (п. 20.2.1). Функции V(t) и
0(t) являются случайными функциями времени. Каждой реализа-
реализации t,(t) соответствуют реализации амплитуды V(t) и частоты v(t).
Двумерную ПРВ случайных величин V(t) и v(t) обозначим f2w (u,a>).
Дисперсия
<?ш2 =ju2fvv2(u,(o)du B0.46)
о
характеризует распределение мощности случайного процесса по
частоте. Такое же распределение дает и спектральная плотность
мощности случайного процесса 1/яЛ/(оо). Однако определить /^(со),
используя B0.46), в общем случае не удается вследствие неопре-
неопределенности задания V(t) и v>(t). Задача упрощается для случайно-
случайного процесса r\(t) с независимыми V(t) и u(f). Для него
ju2fvu2(u,iu)du = fv(a)]u%2Mdu.
о о
Таким образом, для случайного процесса r\(t) имеем
fv(w)= ж п , (о>0. B0.47)
|лУл(со)сЛо
о
Такая зависимость справедлива для клиппированного случайно-
случайного процесса - случайного процесса на выходе идеального ограни-
ограничителя
л@ = sign^f), B0.48)
где ?(f) - случайный процесс на входе.
Спектральную плотность мощности случайного процесса r|(f)
удобнее определить через корреляционную функцию R^a)
Л/л(со) = 2Гят1(т)созаяс/г. B0.49)
581

Раздел 20
Методы определения Я^т) гауссовского процесса изложены
в разд. 22. Для гауссовского процесса имеем
ф)= Ял(т)/Ял@) = 2/7rarcsinr(i)l B0.50)
где г(т) - нормированная корреляционная функция исходного слу-
случайного процесса b[t).
Таким образом, зная корреляционную функцию гауссовского
процесса Я(т) или соответствующий спектр Л/(ш), можно получить
ПРВ или ФРВ частоты.
Функция распределения вероятностей частоты случайного про-
процесса определяется выражением
(О
Fv(co) = j7»c*D. B0.51)
о
В качестве примера рассмотрим гауссовский процесс, имеющий
характеристики:
корреляционная функция (рис. 20.9,а)
г(т) = Ы^Ь2+т2 ,
спектральная плотность мощности (рис. 20.9,з)
Ь
где Ко(х) - модифицированная функция Бесселя.
Плотность распределения вероятностей частоты случайного
процесса описывается выражением
где Е(х) - интегральная показательная функция.
График ПРВ частоты изображен на рис. 20.9,6.
На рис. 20.10 - 20.12 изображены графики ПРВ частоты гауссовских
процессов, характеристики которых приведены в табл. 18.1.
На рис. 20.10 для характеристик - табл. 18.1, п.4
582

Выбросы случайных процессов
0,5
Рис. 20.11
583
Рис. 20.9
Рис. 20.10

Раздел 20
Рис. 20.12
на рис. 20.11 - для характеристик - табл. 18.1, п.5
на рис. 20.12 - для характеристик - табл. 18.1, п.6
В табл. 20.2 изображены графики ПРВ и ФРВ частоты гауссов-
ских процессов, характеристики которых приведены в табл. 18.1.
Период следования выбросов центрированного случайного
процесса относительно нулевого уровня Т связан с частотой v со-
соотношением
B0.52)
Для гауссовского процесса длительности положительных и от-
отрицательных выбросов в среднем равны и связаны с частотой со-
соотношением
B0.53)
С учетом B0.52) и B0.53) выражения для ПРВ периода и дли-
длительности выбросов случайного процесса определим через ПРВ
частоты в виде
B0.54)
584

Выбросы случайных процессов
Исходя из B0.54) запишем выражения для fT(x) и fs(z) с исполь-
использованием гл(т)
B0.55)
Таблица 20.2.
Плотность и функция распределения вероятностей
частоты гауссовского процесса
585
ПРВ частоты fv((a)
ФРВ частоты ^(со)

Раздел 20
586
ПРВ частоты ft)((o)
ФРВ частоты FX) (со)

Выбросы случайных процессов
587
ПРВ частоты /и((о)
ФРВ частоты Fu(oo)

Раздел 20
588
ПРВ частоты ^(ш)
ФРВ частоты Fv (со)

Выбросы случайных процессов
589
ПРВ частоты /и (со)
ФРВ частоты Fu(w)

Раздел 20
590
ПРВ частоты fD((o)
ФРВ частоты Fu((o)

Выбросы случайных процессов
№
ПРВ частоты ^(ш)
ФРВ частоты R
(о
18
О 1
591

Раздел 20
Для гауссовского процесса получим
к
B0.56)
B0.57)
В качестве примера рассмотрим гауссовский процесс, имеющий
корреляционную функцию вида (рис. 20.9,а)
г(т) = -==г.
/о о
Vb2+x2
Исходя из B0.56) и учитывая результат ранее решенного при-
примера, получим
п2т
где Е,(х) - интегральная показательная функция.
При расчете ПРВ (ФРВ) длительности выбросов гауссовского
процесса можно воспользоваться разложением arcsin г(т) в ряд
B0.58)
^й22п(л!JBл + 1)
После подстановки B0.58) в B0.57) получим
4 (х) = 4/тсх2 J r(x)cos( - x)dx +1/6? г3 (x)cosf- xicfx +
+ 3/40 J г5 (x)cos( - х Jdx + 5/112 Jr7 (x)cosj - x ]dx +.. .
B0.59)
где
592
или

Выбросы случайных процессов
B0.60)
или
где т1 =тщ In.
Графики ПРВ и ФРЕЗ длительности выбросов гауссовского про-
процесса с рассматриваемой характеристикой приведены на
рис. 20.13,а,б. На рис. 20.13, пунктирной линией проведены графи-
графики ПРВ и ФРВ длительности выбросов, полученный с использова-
использованием методики, изложенной в п. 20.1. Сравнение графиков позво-
позволяет оценить ошибку, появляющуюся при использовании прибли-
приближенного метода.
Графики ПРВ и ФРВ длительности выбросов центрированных
гауссовских процессов для нулевого уровня и некоторых характе-
характеристик (спектра или корреляционной функции) изображены на
рис. 20.14-20.16.
Для характеристик - табл. 18.1, п.4
на рис. 20.14.
Для характеристик - табл. 18.1, п.5
593
B0.60) примет вид

Раздел 20
10 15 20 <л,х
б)
Рис. 20.13
594
Рис. 20.14
Рис. 20.15

Выбросы случайных процессов
Рис.20.16
Для характеристик - табл. 18.1, п.6
на рис.20.16.
Вид графиков ПРВ длительности выбросов (рис.20.14 - 20.16),
соответствует результатам экспериментального определения ПРВ
случайных процессов, имеющих те же характеристики [20].
Графики ПРВ и ФРВ длительности выбросов гауссовских про-
процессов с различными характеристиками (табл. 18.1), полученные с
использованием описанного подхода, включены в табл. 20.3.
Все изложенное касалось распределения длительности выбро-
выбросов центрированного гауссовского процесса относительно нулевого
уровня. При уровне, отличном от нулевого, необходимо учитывать
различие в длительности отрицательных и положительных выбро-
выбросов. Можно считать, что в среднем длительность отрицательных
выбросов относительно уровня х определяется как
B0.61)
где Т - период следования выбросов, определяемый как 2тг/и,
к = F^(x), F)(x) - одномерная ФРВ случайного процесса ф).
Для положительных выбросов запишем
1-^ = 2яМ B062)
Т v
Таким образом, зная распределение частоты случайного про-
процесса, можно получить и распределение длительности отрица-
отрицательных и положительных выбросов
595

Раздел 20
8-
B0.63)
Имея ПРВ длительности выбросов, можно определить и сред-
среднее значение длительности выбросов
"ср
B0.64)
Однако сложность выражений для ПРВ длительности выбросов
заставляет выбрать несколько иной путь. Используя его, получим
выражения для средней частоты следования в ыбросов и средней
Таблица 20.3.
Плотность и функция распределения вероятностей
длительности выбросов гауссовского процесса
№ ПРВ длительности выбросов f6(x) ФРВ длительности выбросов Fs (т)
596

Выбросы случайных процессов
597
ПРВ длительности выбросов
ФРВ длительности выбросов F6 (т)

Раздел 20
598
ПРВ длительности выбросов /^(т) ФРВ длительности выбросов Г6(т)

Выбросы случайных процессов
№
ПРВ длительности выбросов f6(x)
ФРВ длительности выбросов F6 (т)
599

Раздел 20
600
ПРВ длительности выбросов fb(x) ФРВ длительности выбросов F5(x)

Выбросы случайных процессов
601
ПРВ длительности выбросов f6 (т) ФРВ длительности выбросов F6 (т)

Раздел 20
602
ПРВ длительности выбросов fs(x) ФРВ длительности выбросов F6(т)

Выбросы случайных процессов
длительности выбросов гауссовского процесса относительно нуле-
нулевого уровня.
20.2.3. Среднее значение длительности выбросов
Рассмотрим случайный процесс r|(f) - центрированный гаус-
совский процесс на выходе идеального ограничителя в моменты
времени ^ и t2{t2 ~U = At). Случайный процесс в моменты време-
времени Ц и t2 принимает значения ±1. Полная группа событий описы-
описывается вероятностями:
Р++ - вероятность превышения нулевого уровня в моменты
времени t^ и t2;
Р вероятность непревышения нулевого уровня в моменты
времени f, и t2;
Рн вероятность превышения нулевого уровня в момент вре-
времени tx и непревышения в момент времени t2;
Р- + - вероятность непревышения нулевого уровня в момент
времени ^ и превышения в момент времени t2.
Очевидно,
Р++ + Р__ + Р+_ + Р_+ = 1. B0.65)
Корреляционная функция случайного процесса r((f) определя-
определяется выражением
М{ф2Ш}= /-л(*2 - 0= Ф)=Р++ + Р__ - Р+_ - Р_+. B0.66)
Учитывая для гауссовского процесса равенство
Р+_ = Р_+ = Р, B0.67)
из B0.65) и B0.66) получим выражение для вероятности несовпа-
несовпадения знаков случайного процесса в моменты времени ?, и t2 :
Р = 1/4 [1 - гл(Af)J = 1/4 lrn@)- гл(AOJ• B0.68)
Величина
Mm — = X B0.69)
Af-»O At
представляет среднюю частоту следования выбросов случайного
603

Раздел 20
процесса (подробнее см. п. 20.3). С учетом B0.68) запишем
B0.71)
B0.72)
B0.73)
что совпадает с результатом, полученным ранее.
Среднее значение длительности выбросов относительно нуле-
нулевого уровня равно
B0.74)
что совпадает с B0.16).
Приведенные соотношения, связывающие ПРВ длительности
выбросов и частотные характеристики случайного процесса, могут
быть использованы и при решении обратной задачи - определении
спектра случайного процесса по ПРВ длительности выбросов. Та-
Такая задача возникает, например, при экспериментальной обработ-
обработке реализации случайного процесса, когда в качестве исходной
характеристики наиболее просто получить ПРВ длительности вы-
выбросов.
20.2.4. Решение обратной задачи
ПРВ частоты случайного процесса связана с ПРВ периода вы-
выбросов соотношением
604
С учетом B0.50) получим
где г(т) - нормированная корреляционная функция исходного слу-
случайного процесса Z,(t).
Предел в B0.71) при т -> 0 найдем, применяя правило Лопиталя
Подставляя B0.72) в B0.70), запишем

Выбросы случайных процессов
fv(to) = 2tt/w2 fTBn/(o\ B0.75)
где fT (т) - ПРВ периода выбросов, которая может быть получена
аналогично B0.54).
Плотность распределения вероятностей частоты описывает
нормированную спектральную плотность мощности случайного
процесса на выходе идеального ограничителя
характеризует спектр исходного случайного процесса.
Для гауссовского процесса от Л/^ш) перейдем к корреляцион-
корреляционной функции случайного процесса
Я (со) = — f A/v (w)cos wr crto. B0.77)
тс J
о
Используя соотношение, связывающее гц(х) с нормированной
корреляционной функцией исходного случайного процесса г(т):
rT1(x) = -arcsinr(T), B0.78)
можно получить корреляционную функцию и спектр исходного
случайного процесса
оо
Л/(ш) = 2 [ Я@) r(x)cos ют ск
0 B0.79)
В качестве примера рассмотрим случайный процесс, для кото-
которого ПРВ периода выбросов имеет вид
605
B0.76)
где ti = const, л = 1,2,...
Из B0.75) получим

Раздел 20
Рис.20.17
С учетом B0.76) найдем (рис. 20.17)
^ ; 2л! {^(м)
Величина Л/Л(ш) дает представление о спектре случайного про-
процесса, от нее можно перейти к спектру исходного случайного про-
процесса.
606

Выбросы случайных процессов
20.3. Средняя частота следования и средняя длитель-
длительность выбросов случайного процесса
Имея ФРВ или ПРВ длительности выбросов, можно определить
математическое ожидание - среднюю длительность выбросов
и другие моменты распределения. С учетом того, что ранее было по-
получено приближенное решение для ПРВ длительности выбросов
(п. 20.1) и решение для ограниченных условий (п. 20.2), целесообраз-
целесообразно задачу по определению моментных характеристик выбросов рас-
рассмотреть отдельно, не связывая ее с нахождением ПРВ длительности
выбросов. Рассмотрение проводится для двух случаев: когда извест-
известно совместное распределение случайного процесса и его производ-
производной, и когда известна только двумерная ФРВ случайного процесса.
20.3.1. Определение характеристик выбросов
с использованием совместного распределения случайного
процесса и его производной
Рассмотрим стационарный случайный процесс ф) на интерва-
интервале времени [t, t + 7]. Разобьем интервал Т на л участков длитель-
длительностью At = Т/п. Обозначим вероятность пересечения случайным
процессом уровня х снизу вверх (с положительным значением про-
производной) каждого участка р . Среднее значение числа пересече-
пересечений случайным процессом уровня хна всем интервале Г равно пр.
Средняя частота пересечений уровня х случайным процессом сни-
снизу вверх оценивается выражением
Х^^=Р-. B0.80)
ТЫ
Чем меньше значение Ы, тем точнее записанное выражение.
Точное значение X получим при ДГ—>0
Х= lim -?-. B0.81)
дг-»о At
Величина р определяется вероятностью одновременного вы-
выполнения следующих неравенств:
х - Ах < ф) < х, dt,(t)/dt > 0. B0.82)
Если f^(x,y) ~ двумерная ПРВ случайного процесса ф) и его
производной i)(t)=cfc)(t)/dt в момент времени t, то вероятность вы-
607

Раздел 20
полнения неравенств B0.82) определяется как
Р = ) ]f^(x,y)dxdy. B0.83)
0 Х-Ах
При достаточно малом значении Ал внутренний интеграл
в B0.83) можно представить в виде
f^{x,y)Ax = yf^{x,y)At,
где Ах B0.84)
y=Tf
С учетом B0.84) выражение B0.83) примет вид
P = Atjyf^(x,y)dy. B0.85)
о
Из B0.81) с учетом B0.85) получим
оо
X = jyf^(x,y)dy. B0.86)
о
Таким образом, зная совместную ПРВ случайного процесса
и его производной для одного и того же момента времени, можно оп-
определить среднюю частоту следования нулей случайного процесса
(при пересечении уровня снизу вверх). Эта частота совпадает со
средней частотой положительных выбросов случайного процесса.
Аналогично получается выражение для средней частоты нулей
случайного процесса при пересечении им уровня х сверху вниз.
Оно совпадает с B0.86). Этим же выражением определяется
и средняя частота следования отрицательных выбросов.
Используя X, можно определить среднюю длительность выбро-
выбросов относительно заданного уровня.
Для эргодических случайных процессов среднее время непре-
непревышения уровня х на интервале времени Г может быть определе-
определено как 77^(х), где F^(x) - ФРВ случайного процесса. Среднее число
выбросов на интервале времени Г равно XT.
Таким образом, средняя длительность отрицательных выбросов
равна
^ = TF,(x)/7X=F,(x)/X. B0.87)
608

Выбросы случайных процессов
Средняя длительность положительных импульсов определяется
аналогично
*ч*=Ь-ФШ- B0.88)
Конкретизируем полученные результаты для гауссовского про-
процесса. Совместная ПРВ центрированного гауссовского процесса и
его производной в один и тот же момент времени описывается вы-
выражением (разд. 16)
B0.89)
где а, о2, а(т) - математическое ожидание, дисперсия и нормиро-
нормированная корреляционная функция случайного процесса.
Подставляя B0.89) в B0.86), для средней частоты следования
выбросов гауссовского процесса получим следующее выражение
B0.90)
B0.91)
Используя спектральную плотность мощности случайного про-
процесса Л/(со), запишем
B0.92)
При х = а
B0.93)
609

Раздел 20
Средняя длительность отрицательных выбросов гауссовского
процесса с учетом B0.90) определяется выражением
Средняя длительность положительных выбросов
Таким образом, определены средняя частота следования вы-
выбросов и средняя длительность выбросов с использованием со-
совместной ПРВ случайного процесса и его производной. Получен-
Полученные выражения совпадают с соответствующими выражениями,
приведенными в п. 20.1 и п. 20.2.2.
Средняя частота следования выбросов и средняя длительность
выбросов могут быть также определены с использованием только
двумерной ПРВ случайного процесса.
20.3.2. Определение характеристик выбросов
с использованием двумерной ПРВ случайного процесса
Как было установлено, средняя частота пересечений случай-
случайным процессом заданного уровня снизу вверх определяется сле-
следующим предельным соотношением
X = lim A B0.97)
д^о At
где р - вероятность пересечения случайным процессом уровня х
снизу вверх интервала длительностью At.
610
B0.94)
B0.95)
B0.96)

Выбросы случайных процессов
Вероятность хотя бы одного пересечения случайным процессом
уровня х снизу вверх на интервале времени |/,f + Af] можем опре-
определить как
р=Р{ф)<х, Z,(t + At)>x}. B0.98)
Используя двумерную ПРВ случайного процесса ?(f) для мо-
моментов времени t и t + At, выражение для р запишем в виде
X оо
р= I jf2{xbx2)dx^dx2 =
х'Г х х B0-99)
= J j?(*1.*2>M»f2- J J4(^1.^2^1^2 =F1(X)-F2(X,X)I
где /r2(xi,x2)Fj(x1)iF2(x1)x2) - ПРВ и ФРВ случайного процесса.
С учетом B0.97) выражение для средней частоты следования
выбросов случайного процесса примет вид
X = lim Fi(xbF2(*i.*2) B0 !од)
дг-»о At
Таким образом, имея двумерную ФРВ случайного процесса,
можно определить среднюю частоту следования его выбросов.
Для гауссовского процесса, воспользовавшись соотношениями,
полученными в разд. 16, найдем
Х = — J-r"@)exp|-^|? B0.101)
2л: * [ 2а J
что совпадает с B0.90).
Аналогично можно получить выражения для других средних ха-
характеристик случайного процесса: средней частоты пересечений
случайным процессом заданного уровня сверху вниз, средней час-
частоты следования выбросов, средней длительности отрицательных
и положительных выбросов.
Как следует из сопоставления результатов, оба подхода (с ис-
использованием совместной ПРВ случайного процесса и его произ-
производной и с использованием двумерной ПРВ случайного процесса)
дают идентичные выражения. Они совпадают и с результатами,
полученными на основе решения для ПРВ длительности выбросов,
приведенными в п. 20 1.
611

Раздел 20
20.4. Средняя частота следования экстремумов
случайного процесса
Подходы к определению характеристик выбросов, изложенные
в § 20.3, позволяют найти и среднюю частоту следования макси-
максимумов случайного процесса. Определим ее, используя двумерную
ПРВ случайного процесса.
Рассмотрим стационарный случайный процесс t,(t) на интерва-
интервале времени [t, t + 7]. Интервал Г разобьем на л участков длитель-
длительностью At - Т/п. Средняя частота следования максимумов слу-
случайного процесса определяется выражением, аналогичным B0.97)
X = |im ?&-, B0.102)
m д^о At
где рт - вероятность появления максимума случайного процесса
на интервале времени At.
Вероятность того, что случайный процесс имеет хотя бы один
максимум на интервале At, определяется выражением
Рш = р?@>0, ?(' + Д0<о}, B0.103)
если существует производная случайного процесса ф). Зная дву-
двумерную ПРВ производной случайного процесса, для вероятности
B0.103) запишем
P^(t)>0^{t + At)<0}
7 Г / х , \ /х B0.104)
0-о=
где. ^2(у,у] F^(y] F^2(y,y) - ПРВ и ФРВ производной случайного
процесса r\(t) = ?,'(t).
Таким образом, для средней частоты следования максимумов слу-
случайного процесса получим следующее предельное соотношение
Хт= lim-J-[Fn1@)-Fn2@,0)]. B0.105)
Дг—>0 Д(
Уточним B0.105) для гауссовского процесса ф). Производная
стационарного гауссовского процесса представляет гауссовский
612

Выбросы случайных процессов
процесс с математическим ожиданием, равным нулю, и корреляци-
корреляционной функцией, равной второй производной корреляционной
функции случайного процесса со знаком минус (разд. 16). Для дву-
двумерной ФРВ гауссовского процесса ri(f) при х = 0 по аналогии
с B0.91) получим
где г4^(т) - четвертая производная от нормированной корреляци-
корреляционной функции гауссовского процесса ?,(t).
Таким образом, средняя частота следования максимумов гаус-
гауссовского процесса, определяется его корреляционной функцией
(значениями ее второй и четвертой производных при т = 0). Средняя
частота следования минимумов случайного процесса равна средней
частоте максимумов гауссовского процесса, определяется B0.108).
Вывод выражения для нее аналогичен выводу выражения для Хт.
Определяя среднюю частоту следования максимумов (миниму-
(минимумов) через среднюю частоту выбросов случайного процесса
B0.81), запишем
B0.106)
где гп(т) - нормированная корреляционная функция случайного
процесса r)(f).
С учетом того, что
где Я(т), Ял(т) Ял'(т) - корреляционные функции случайных про-
процессов ф\ r\(t) = ^'(t\ r\(t) соответственно,
из B0.106) найдем
B0.108)
Таким образом, средняя частота максимумов больше средней
частоты выбросов в ^г^4\о)/- г"(о) раз.
613
B0.109)

Раздел 20
В качестве примеров рассмотрим некоторые характеристики
случайных процессов.
1. Гауссовский процесс с характеристиками (табл. 18.1, п.1):
спектральная плотность мощности. Л/(ш) = 1, со1 < |w| < о2, корреляци-
корреляционная функция
где X - средняя частота следования выбросов.
2. Гауссовский процесс с характеристиками (табл. 18.1, п.2):
спектральная плотность мощности
Л/(а))=1-М)|@|<аI(
корреляционная функция
r(t) = sinc2—.
v ) 2
Для него имеем
, 1 V2 , 2л/з,
К^7Е или Хт=~Ж
3. Гаусовский провес с характеристиками (табл. 18.1, п.5):
спектральная плотность мощности
((i)f + 0) /
корреляционная функция
614
Для него имеем
Из B0.103) получим

Выбросы случайных процессов
Для него имеем
Хт-п1= или Хт=-Х.
4. Гаусовский процесс с характеристиками (табл. 18.1, п.6):
спектральная плотность мощности
Для него имеем
Средняя частота следования экстремумов гауссовского процес-
процесса равна
B0.110)
Средний интервал между максимумами или минимумами опре-
определяется как
B0.111)
B0.112)
X
а между экстремумами
615
корреляционная функция

Раздел 21.
ПРОХОЖДЕНИЕ СЛУЧАЙНОГО ПРОЦЕССА ЧЕРЕЗ
ЛИНЕЙНУЮ ЦЕПЬ
Анализ прохождения случайного процесса через линейную цепь
предполагает прежде всего определение характеристик случайного
процесса на выходе цепи при известных характеристиках цепи и
случайного процесса на входе. Методы определения основных ха-
характеристик случайного процесса на выходе линейной цепи со-
составляют содержание раздела.
21.1. Характеристики линейной цепи
Радиотехническая цепь называется линейной, если в отноше-
отношении нее выполняется принцип суперпозиции. Принцип суперпози-
суперпозиции означает, что прохождение сигнала (колебания) через цепь не
зависит от воздействия на цепь других сигналов. Результат воз-
воздействия на цепь суммы сигналов эквивалентен сумме результатов
воздействия на цепь каждого из сигналов. Цепи, для которых ука-
указанное условие не выполняется, называются нелинейными. Ли-
Линейные цепи, параметры которых изменяются, называются линей-
линейными параметрическими. В дальнейшем рассматриваются только
линейные цепи с постоянными параметрами.
Различают временные и частотные характеристики линейных
цепей, в зависимости от того, в какой области (временной или час-
частотной) описываются свойства цепей. Из временных прежде всего
следует отметить импульсную характеристику h(t). Она представ-
представляет отклик цепи на воздействие в виде импульсной функции
5(т^.При подаче на вход цепи сигнала s1 @, сигнал на выходе опи-
описывается выражением
/ t
s2(t)=\h{u)s^(t-u)du={h(t-u)s^{u)du. B1.1)
о о
Интеграл B1.1) называется сверткой, позволяет проводить ана-
анализ прохождения сигнала через линейную цепь при известной им-
импульсной характеристике цепи. Реализация случайного процесса
616

Прохождение случайного процесса через линейную цепь
на входе линейной цепи ^(t) может рассматриваться как заданная
функция времени. Воздействию t,(t) соответствует отклик , реали-
реализация случайного процесса на выходе цепи y\(t)
t t
Л(О = J Ф) Ф -u)du = j h(t - и) *{и) du. B1.2)
о о
В частотной области линейная цепь описывается комплексной
частотной характеристикой. Частотная характеристика представ-
представляет преобразование Фурье импульсной характеристики
оо
Н((о)= J/7(f)e-*°'df. B1.3)
—оо
Обратное преобразование Фурье позволяет перейти от Н(си) к h(t)
h{t) = —\ H^e*» 'dto. B1.4)
Частотную характеристику цепи Н((й), как комплексную величи-
величину, можно представить в виде
H(co) = Re[H(o))]+/lm[H(co)] или Н(со) = |н(со)| е^н^\
Ще\н{,} = ^[н(ф^[Н^)\ ф»,а^2Щ. B1>5)
Модуль I H(u))i называется амплитудно-частотной, а аргумент
Фн(о) - фазо-частотной характеристикой цепи.
Частотная характеристика цепи позволяет получить спектральную
плотность мощности случайного процесса на выходе, зная спектраль-
спектральную плотность мощности случайного процесса на входе Л/((о)
Л/п(о) = |Н(ш)|2Л/й B1.6)
Аналогично понятию частотной характеристики вводится поня-
понятие передаточной функции. Она определяется как преобразование
Лапласа импульсной характеристики цепи
H{p) = ]h{t)e-ptdt, B1.7)
о
где р - р + ло- параметр преобразования.
617

Раздел 21
Ограничения, связанные с применением преобразования Лап-
Лапласа, являются менее жесткими, чем накладываемые условиями
существования преобразования Фурье. Поэтому использование
преобразования Лапласа расширяет рамки анализа прохождения
сигналов через линейные цепи.
Приведенные характеристики линейной цепи позволяют прово-
проводить анализ прохождения сигналов через линейные цепи во вре-
временной и частотной областях. Выражения B1.2) и B1.6) связывают
случайные процессы и их спектры на входе и выходе линейной це-
цепи. Они чаще всего и используются при определении характери-
характеристик случайного процесса на выходе цепи при известных характе-
характеристиках случайного процесса на входе.
21.2. Распределение вероятностей случайного процесса
на выходе линейной цепи
Наиболее полной характеристикой случайного процесса является
ФРВ или ПРВ. Задача определения ФРВ или ПРВ случайного про-
процесса на выходе линейной цепи при известных характеристиках слу-
случайного процесса на входе должна рассматриваться одной из ос-
основных при анализе прохождения случайного процесса через цепь.
Если случайный процесс на входе является гауссовским, то
процесс на выходе будет также гауссовским. Этот вывод следует
из того положения, что любые линейные преобразования нормаль-
нормально распределенной случайной величины не меняют ее закона рас-
распределения вероятностей. ФРВ или ПРВ стационарного гауссов-
ского процесса описываются математическим ожиданием и корре-
корреляционной функцией. Поэтому для описания прохождения гауссов-
ского процесса через линейную цепь достаточно определить мате-
математическое ожидание и корреляционную функцию случайного про-
процесса на выходе цепи.
Если линейная цепь является узкополосной, то при подаче на
ее вход широкополосного случайного процесса с любым законом
распределения, на выходе цепи происходит нормализация случай-
случайного процесса - его распределение приближается к нормальному.
Явление нормализации случайного процесса на выходе узкополос-
узкополосной цепи является следствием центральной предельной теоремы
теории вероятностей. Пояснить это положение помогает анализ
выражения B1.2). Оно может рассматриваться как предельное
дискретной свертки h(t) и \(t)
ц(пТ) = ? h{kT\{nT -кТ)=? h(nT - кТ%(кТ), B1.8)
к=0 к=0
618

Прохождение случайного процесса через линейную цепь
где Т - интервал дискретизации, T<n/u>m; wm - предельная
частота спектра случайного процесса ?,(t).
Чем более узкополосной является линейная цепь, тем большее
число слагаемых в B1.9) имеет достаточно большой вес и должно
учитываться при расчете. Число учитываемых слагаемых при за-
заданной характеристике цепи h(t) будет и тем больше, чем меньше
интервал Г, следовательно, чем более широкую полосу занимает
спектр случайного процесса (сот). При увеличении же числа сла-
слагаемых распределение их суммы стремится к нормальному (цен-
(центральная предельная теорема теории вероятностей).
В общем случае задача нахождения распределения случайного
процесса на выходе линейной цепи при произвольном законе рас-
распределения вероятностей случайного процесса на входе является
довольно сложной. Из возможных подходов к ее решению остано-
остановимся на подходе, основанном на определении моментов распре-
распределения вероятностей случайного процесса на выходе цепи. От
моментов распределения вероятностей можно перейти к характе-
характеристической функции и ПРВ случайного процесса (разд. 15).
Начальный момент n-го порядка случайного процесса на выходе
линейной цепи г\{\) определяется с учетом B1.4) выражением
B1.9)
...Utn-un)du^du2...dun
Меняя порядок усреднения и интегрирования, запишем
тц „ = J{.. jhMhM-hMMUt, - иЖ ' и2У- B1 10)
00 0 \ ¦ )
...Utn-un))du}du2...dun.
Таким образом, для определения момента тА п необходимо
знать момент распределения вероятностей /т-го порядка случайно-
случайного процесса на входе цепи. Ограничиваясь знанием одномерной
ФРВ (ПРВ) случайного процесса на входе цепи и получением с ее
помощью начальных моментов порядка до л включительно, выра-
выражение для л-мерного начального момента случайного процесса на
выходе цепи запишем в виде
619

Раздел 21
00 О B1-11)
duAdu2...dun
Используя моменты распределения, определяемые B1.11), мо-
можем записать выражение для одномерной характеристической
функции случайного процесса на выходе y\(t)
Чем больше известно моментов распределения, тем точнее по-
получим характеристическую функцию и ПРВ случайного процесса на
выходе цепи r\(t). Анализ приведенных выражений в рамках ре-
решаемой задачи, а также выражений для моментов наиболее часто
встречающихся распределений вероятностей (табл. 2.2) показыва-
показывает, что описанный подход к нахождение распределения случайного
процесса на выходе линейной цепи является сложным, часто не-
неприемлемым на практике. Отмеченное обстоятельство является
причиной того, что при анализе случайного процесса на выходе
линейной цепи часто ограничиваются определением математиче-
математического ожидания и корреляционной функции (или спектральной
плотности мощности). При этом берется во внимание, что указан-
указанные характеристики гауссовского процесса полностью его описы-
описывают, а нормальное распределение случайного процесса на выхо-
выходе линейной цепи - довольно распространенный случай.
21.3. Математическое ожидание и корреляционная функ-
функция случайного процесса на выходе линейной цепи
Математическое ожидание случайного процесса на выходе ли-
линейной цепи при подаче на вход стационарного случайного про-
процесса определяется выражением
620
B1.12)
От характеристической функции перейдем к ПРВ случайного
процесса
B1.13)

где а - математическое ожидание случайного процесса на входе
цепи Щ)\ h(t) - импульсная характеристика линейной цепи;
со
k = ^h(t)dt. B1.15)
о
Как следует из B1.14), математическое ожидание случайного
процесса на выходе линейной цепи пропорционально математиче-
математическому ожиданию случайного процесса на входе.
Выражение для ковариационной функции случайного процесса
на выходе линейной цепи запишем в виде
Kn{tbt2)=M{4{tMt2)}=
= J jh{u,)h(u2)MUU ~ u№2 - u2)}du,du2,
где h(t) определено для t >0.
Если случайный процесс на входе t,(t) является стационарным,
то B1.16) примет вид
Кл(т)= } \h(u,)h{u2)K(u,-u2+T)du,du2, B1.17)
где К(т) - ковариационная функция случайного процесса на входе
m,x=t2-u.
Переходя в B1.27) от переменных щ и и2 к и = ц и v = u2-u,
запишем
со
КГ](т)= jp{v)K(T-v)dv, B1.18)
где
621
Прохождение случайного процесса через линейную цепь
B1.14)

Раздел 21
p(i/) = J h(uXu + v)du. B1.19)
Таким образом, ковариационная функция случайного процесса
на выходе линейной цепи определяется сверткой К(х) ир(т). Ино-
Иногда р(т) рассматривают как автокорреляционную функцию им-
импульсной характеристики цепи.
Для центрированного случайного процесса на входе К(т) = Я(т)
со
Яп(т)= jp(v)R(x-v)dv, B1.20)
где Я(т) - корреляционная функция случайного процесса на входе.
Дисперсия случайного процесса на выходе цепи равна
а2=Яп@)= jp(v)R(v)dv, B1.21)
Нормированная корреляционная функция
г(т) = Ял(т)/а2. B1.22)
При воздействии на линейную цепь белого шума, имеющего
корреляционную функцию в виде импульсной функции (разд. 18)
Я(т) = Л/05(х), B1.23)
корреляционная функция случайного процесса на выходе цепи
описывается выражением
Ял(т) = Л/Ор(т) = No jh(u)h(u + T)du, B1.24)
определяется автокорреляционной функцией импульсной характе-
характеристики цепи р(т).
Так автокорреляционная функция импульсной характеристики
ЯС-цепи (табл.18.1, п.1) h(t) = be~bt имеет вид (т > 0)
622

Прохождение случайного процесса через линейную цепь
При подаче на вход такой цепи белого шума корреляционная
функция случайного процесса на выходе определяется из B1.24)
как
Ял(т) = Л/0(Ь/2)ей\
При решении B1.20) наибольшую сложность, пожалуй, пред-
представляет определение пределов интегрирования.
Взаимная корреляционная функция центрированного случайно-
случайного процесса на входе Z,(t) и выходе r\(t) линейной цепи определяет-
определяется выражением
где Я(т) - корреляционная функция случайного процесса на входе.
Как следует из B1.25), взаимная корреляционная функция оп-
определяется сверткой корреляционной функции случайного процес-
процесса на входе и импульсной характеристики цепи.
Изменяя порядок следования функций \(t) и r\(t), получим
Я^(т) = Mft(OS(f+ т)} = MU^t-u)h(u)dul(t + т =
'° -* B1.26)
оо
= JR(x + u)h(u)du,
о
Как следует из сравнения B1.25) и B1.26), Я^(т) * Я^т).
При воздействии на линейную цепь белого шума t,{t), имеющего
корреляционную функцию Я(т) = Я@M(т), из B1.30) получим
Я^(т) = |я@M(т- u)h{u)du = Я@)Л(т), т > 0. B1.27)
о
Таким образом, взаимная корреляционная функция в этом слу-
случае пропорциональна импульсной характеристике цепи.
623
B1.25)

Раздел 21
21.4. Спектр случайного процесса
на выходе линейной цепи
Имея корреляционную функцию случайного процесса на выходе
цепи, можно получить его спектральную плотность мощности. Од-
Однако часто для ее получения удобнее проводить анализ полностью
в частотной области.
Выделим отрезок реализации центрированного случайного про-
процесса t,(t) на входе линейной цепи, имеющей импульсную h(t) и
частотную Н(ш) характеристики. Спектральные плотности сигнала
на выходе и входе цепи связаны соотношением
SX]T{(o)=H((d)St(u). B1.28)
От B1.28) можем перейти к следующему равенству
M{|S,r(»f} = |"H2M{|ST(»f}. B1.29)
Из B1.29) непосредственно следует
Л/л((о) = |Н(о))|2Л/(а)) B1.30)
Таким образом, спектральная плотность мощности случайного
процесса на выходе линейной цепи равна произведению квадрата
модуля частотной характеристики цепи и случайной плотности
мощности случайного процесса на входе.
Во временной области произведению B1.30) соответствует
свертка временных функций. Учитывая, что во временной области
/HfwJ/2 соответствует корреляционная функция импульсной харак-
характеристики р(т), a N(u>) - корреляционная функция случайного про-
процесса на входе я (х), можем записать
/Vn(co) = |H(o))|2Mw)^^(T) =
- - B1.31)
}R{T-v)p{v)dv= jp(z-v"fl{v)dv,
где символ <—>означает соответствие по Фурье,
что совпадает с B1.20).
В качестве примеров в табл. 21.1 и 21.2 приведены наиболее
простые, часто используемые в различных системах, цепи первого
и второго порядков.
624

Прохождение случайного процесса через линейную цепь
Таблица 21.1
Квадраты амплитудно-частотных характеристик цепей
первого порядка
№
п/п
Схема цепи
N
со
625

Раздел 21
№
п/п
Схема цепи
626

Прохождение случайного процесса через линейную цепь
№
п/п
Схема цепи
627

Раздел 21
№
п/п
Схема цепи
10
628

Прохождение случайного процесса через линейную цепь
Таблица 21.2
Квадраты амплитудно-частотных характеристик
цепей второго порядка
№
п/п
Схема цепи
629

Раздел 21
630

Прохождение случайного процесса через линейную цепь
631

Раздел 21
632

Прохождение случайного процесса через линейную цепь
11
1. Для цепи, изображенной в табл. 21.1, п. 1,
633
где Т - постоянная величина.
При

Раздел 21
2. Для цепи второго порядка, изображенной в табл. 21.2, п.З,
Рис.21.2
634
Рис. 21.1
на выходе цепи имеем (рис. 21.1)
При

Прохождение случайного процесса через линейную цепь
/v»=/v(o),2"?2F,^i+2m:7^v
щ + ш J \\- a0o) J + а^
Преобразование Фурье позволяет перейти от спектра случайно-
случайного процесса на выходе цепи к его корреляционной функции
Определение корреляционной функции случайного процесса на
выхода линейной цепи по его спектру часто бывает удобнее, чем
непосредственное определение корреляционной функции во вре-
временной области (в соответствии с выражениями, приведенными в
предыдущем подразделе), даже в том случае, когда приходится
прибегать к численным методам расчета. Иллюстрацией этого по-
положения служат и следующие примеры, связанные с анализом
прохождения случайного процесса через ЯС-цепь с характеристи-
характеристиками:
h(t)=be~bt, \н((о] = Ь/Ь+кй.
1. Корреляционная функция случайного процесса на входе цепи
Я(т)=Я@)е-^,
спектральная плотность мощности случайного процесса на входе
Спектральная плотность мощности случайного процесса на вы-
выходе цепи
635
корреляционная функция случайного процесса на выходе (рис. 21.3)

Спектральная плотность мощности случайного процесса на вы-
выходе цепи
NM-H4 "(<»)=f^^!<°'< ¦
Корреляционная функция случайного процесса на выходе
к2 /,..2
636
Раздел 21
Рис.21.3
2. Корреляционная функция случайного процесса на входе цепи
-ю?тг/
Я(т)=Я@)е Л .
Спектральная плотность мощности случайного процесса на
входе

Прохождение случайного процесса через линейную цепь
Если случайный процесс на входе представляет белый шум, то
спектральная плотность мощности случайного процесса на выходе
цепи определяется только частотной характеристикой цепи
Л/л(ш) = Л/0|Н(со)|2, B1.32)
где Л/о - спектральная плотность мощности белого шума.
При подаче на вход цепи белого шума корреляционная функция
случайного процесса на выхода определяется выражением
Ял(со) = -^ [ |Н(со)|2 cos wrdo, B1.33)
о
т.е. определяется косинус-преобразованием Фурье квадрата моду-
модуля частотной характеристики цепи (с коэффициентом Л/о). Ранее
эта корреляционная функция была определена с использованием
импульсной характеристики.
При описании линейных цепей используется понятие полосы
пропускания, или эквивалентной шумовой полосы. Эквивалентная
шумовая полоса определяется как полоса пропускания цепи с иде-
идеальной (прямоугольной) амплитудно-частотной характеристикой,
соответствующей реальной цепи. Соответствие устанавливается
по равенству среднего квадрата (дисперсии) случайного процесса
на выходе цепи при подаче на вход белого шума. Для низкочастот-
низкочастотной цепи эквивалентная шумовая полоса А может быть определе-
определена из равенства (рис. 21.4,а)
Л/, ~
о
Таким образом, для А получим следующее выражение
А = —ЦЛ|Н(а))|2с*о. B1-34)
В общем случае эквивалентная шумовая полоса определяется
как (рис. 21.4,6)
Д = —ЦЛ|Н(«)|2с*о. B1.35)
ИМ о
637

Раздел 21
Рис.21.4
где о)о - характерная точка внутри полосы пропускания цепи, на-
например, получаемая из равенства:
|Н(шо)| = |ННтах-
Из теоремы Парсеваля следует:
B1.36)
для эквивалентной шумовой полосы получим
B1.37)
638

Прохождение случайного процесса через линейную цепь
Таким образом, B1.37) определяет эквивалентную шумовую
полосу через импульсную характеристику цепи. Так для ЯС-цепи
(табл. 21.1, п.1) с использованием частотной характеристики (вы-
(выражение B1.35)) получим
или с использованием импульсной характеристики (выражение
B1.37))
21.5. Оптимальные линейные цепи
Передача сигналов сопровождается шумами. Поэтому при
приеме сигнала важно выбирать такие характеристики цепи, при
которых влияние сопутствующих шумов будет минимальным. Цепь
с такими характеристиками называют оптимальной цепью или оп-
оптимальным фильтром. Критерии оптимальности могут быть раз-
различными, зависят в первую очередь от задач, решаемых при прие-
приеме сигнала. Если решается задача обнаружения сигнала на фоне
шума, то в качестве критерия оптимальности целесообразно
принять максимум отношения сигнал/шум на выходе цепи. При из-
измерении параметров принимаемого сигнала в качестве критерия
оптимальности принимается минимум среднего квадрата разности
между сигналом на выходе цепи и его истинным значением. Воз-
Возможны и другие критерии оптимальности. Ниже будут рассмотрены
оптимальные линейные цепи, максимизирующие отношение сиг-
сигнал/ шум.
Если на вход цепи поступает аддитивная смесь сигнал s^(t) и
шум ф):
u,(t)=s,(t) + ^(t), B1.38)
то на выхода линейной цепи имеем
u2(t)=L[s,{t)]+ *-Ш= *2 @+ Ш B1.39)
где L - оператор линейной цепи.
639

Раздел 21
В B1.57) s2(f)=L[s1(^)] представляет сигнал, a ^2(t) = L.[^(t)] -
шум на выходе цепи. Требуется определить характеристики ли-
линейной цепи, при которых отношение сигнал/шум на выходе цепи в
заданный момент времени
я = -Щт B1-4°)
M{?{t)}
было бы максимальным.
Сигнал на выходе цепи определяется выражением
s2{t)=\h(u)si(t-u)du, B1.41)
о
где h(t) - импульсная характеристика цепи.
Шум на входе цепи чаще всего можно рассматривать как белый.
На практике это означает, что ширина полосы частот, занимаемая
шумом, значительно больше ширины полосы пропускания цепи.
Дисперсия шума на выходе цепи при подаче на вход белого шума
описывается выражением B1.21). Учитывая, что корреляционная
функция белого шума равна Я(т) = Л/05(т), получим
Mfei@}= °2 = No\h2(u)du, B1.42)
о
где Л/о- спектральная плотность мощности белого шума на входе
цепи.
Отношение сигнал/шум на выходе цепи в момент времени
t0 определим с учетом B1.41) и B1.42)
Найдем такую импульсную характеристику цепи, которая обес-
обеспечивала бы максимальное отношение сигнал/шум B1.43). Для
этого обратимся к неравенству Буняковского-Шварца
640
B1.43)

B1.45)
Анализ B1.45) показывает, что максимум отношения сиг-
сигнал/шум получается когда выполняется равенство
Щ^ = ±]з?Aо-и)с1и. B1.46)
° Wo {
Равенство выполняется при условии
h(t)=ks,(to-t). B1.47)
Постоянная величина к не влияет на вид импульсной характе-
характеристики и ее можно не рассматривать, т.е. полагать
h{t) = s,{to-t). B1.48)
Таким образом, максимум отношения сигнал/шум обеспечива-
обеспечивается линейной цепью, имеющей импульсную характеристику, опре-
определяемую видом сигнала. Цепь, имеющая импульсную характери-
характеристику, описываемую B1.48) называется согласованной цепью или
согласованным фильтром. Как следует из B1.48), импульсная ха-
характеристика такой цепи с точностью до постоянной величины яв-
является зеркальным отражением сигнала, сдвинутым на t0 по оси
времени.
Если сигнал s^(t) имеет спектральную плотность S^co), то сме-
смещению во времени на t0 соответствует умножение на множитель
задержки е~ш°
641
Прохождение случайного процесса через линейную цепь
B1.44)
Равенство в B1.44) имеет место при х(и) = ку(и), где к- посто-
постоянная величина. С учетом B1.44) выражение B1.43) запишем в
виде неравенства

Раздел 21
Si^-O^^Me-*0'0, B1.49)
где знак <-» означает соответствие по Фурье.
Величине s^(to-t) соответствует комплексно-сопряженная ве-
величина S) (со)еки f°. Следовательно, частотная характеристика со-
согласованного фильтра, обеспечивающего максимум отношения
сигнал/шум, описывается выражением
H(o)) = S1*(w) eK0t°. B1.50)
В качестве примера приведем характеристики фильтра, согла-
согласованного с прямоугольным импульсом. Импульсная характеристи-
характеристика цепи, максимизирующей отношение сигнал/шум в момент вре-
времени t0 = ти имеет вид
других значениях t
Такую импульсную характеристику имеет интегрирующая цепь с
постоянной времени хи.
Другой пример согласованного фильтра приведен в разд. 11 -
рассматривается фильтр, согласованный с ЛЧМ сигналом.
Максимальное отношение сигнал/шум на выходе согласованно-
согласованного фильтра определяется с учетом следующего:
js*(to-u)du= jsf{t)dt. B1.51)
о
Выражение B1.51) определяет энергию сигнала за интервал
времени до момента t0. Таким образом, максимальное отношение
сигнал/шум на выходе согласованного фильтра равно 2\0'.
а
Рассмотрение проводилось для случая воздействия на цепь бе-
белого шума. Однако тот же подход может быть использован и в об-
общем случае - при воздействии на цепь шума, имеющего произ-
произвольную спектральную плотность мощности.
В ряде случаев целесообразно несколько изменить постановку за-
задачи оптимизации: задана структура линейной цепи, необходимо вы-
выбрать параметры цепи таким образом, чтобы обеспечивалось макси-
642

Прохождение случайного процесса через линейную цепь
мальное отношение сигнал/шум на выходе. В качестве примера тако-
такого подхода рассмотрим ЯС-цепь с импульсной характеристикой
h{t)=be'bt,
где Mb = RC- постоянная времени цепи.
При воздействии на цепь сигнала в виде прямоугольного им-
импульса сигнал на выходе цепи описывается выражением (рис. 21.5)
Сигнал на выходе цепи достигает максимального значения в
момент времени t = ти . Таким образом, имеем
%(rB)=v(i-e-»'«).
Дисперсия шума на выходе цепи равна
а2 = ЬЛ/0/2.
Следовательно, отношение сигнал/шум определяется выраже-
выражением
Это отношение зависит от выбора постоянной времени цепи
1/Ь (рис. 21.6). Значение Ь, при котором отношение сигнал/шум
достигает максимального значения, определяется из условия
Рис. 21.5
643

Раздел 21
Рис. 21.6
С учетом выражения для отношения сигнал/шум условие, по-
позволяющее находить значение Ь, соответствующее максимуму,
запишется в виде
djsj) = 2V2 2b(i - в Ьт" \иеЬт« - (i - ebT» f
dba2 ~ bN0 b2
От записанного выражения можно перейти к следующему
1 + 2Ьги = еЬг».
Решение последнего уравнения дает следующее значение по-
постоянной времени цепи
Приведенное значение постоянной цепи соответствует макси-
максимальному отношению сигнал/шум в момент времени хи. Макси-
Максимальное отношение получим при подстановке Ьти = 1,256 в выра-
выражение для отношения сигнал/шум
644

Раздел 22.
НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ
ПРОЦЕССОВ
В разделе описываются основные методы анализа случайных
процессов на выходе нелинейных устройств. Рассмотрение про-
проводится для безынерционных преобразователей, отклик которых
в выбранный момент времени является функцией воздействия в
тот же момент времени. Описание методов иллюстрировано при-
примерами, полезными для практики исследования случайных про-
процессов.
В разд. 15 и 17 приведены выражения для ПРФ или ФРВ слу-
случайного процесса после его преобразования. Однако анализ на их
основе часто сопряжен с трудностями, не всегда преодолимыми на
практике. По этой причине при рассмотрении нелинейных преобра-
преобразований часто ограничиваются менее полными характеристиками
случайного процесса, в первую очередь, корреляционной функцией
и спектром. Описания случайного процесса на выходе преобразо-
преобразователя с использованием только указанных характеристик расши-
расширяет число возможных подходов к анализу, которые требуют от-
отдельного рассмотрения.
22.1. Прямой метод определения характеристик
случайного процесса на выходе нелинейного устройства
Прямой метод анализа основан на использовании соотношений,
связывающих характеристики распределения случайного процесса
на входе Z,(t) и выходе устройства r\(t). Если на вход нелинейного
устройства, имеющего характеристику
у = Ф(х), B2.1)
которая задает взаимно однозначное соответствие хиу, воздейст-
воздействует случайный процесс ^(f), имеющий ПРВ ^(х), то ПРВ случай-
случайного процесса на выходе r\(t) определяется соотношениями, при-
приведенными в разд. 15.
645

-1,
B2.2)
где ф 1 (у)-функция, обратная ф(х).
Математическое ожидание случайного процесса на выходе не-
нелинейного устройства может быть найдено как
"Ч = MMf)}= \v(x)k, (х) dx • B2-3)
Момент л-го порядка:
тЦп = M{y]n(t)} = JV (х)^(х)<йг. B2.4)
Второй начальный момент (ковариационная функция) случайно-
случайного процесса на выходе определяется с использованием двумерной
ПРВ случайного процесса на входе ^2(хьх2) выражением
Кл(т) = М{л@п(*+ т)}= J |ф(х1)ф(х2)^(х1)х2)с(х1с(х2, B2.5)
где хь х2- значения случайного процесса Щ) в моменты времени
t и t + т.
Корреляционная функция случайного процесса на выходе нели-
нелинейного преобразователя равна
Ял(т) = М{ф)ф + т)} - M2{r](t)} = Кл{х)- т\ . B2.6)
При определении корреляционной функции может оказаться
полезным разложение двумерной ПРВ случайного процесса ?,(t) в
ряд по ортонормированной системе многочленов (разд. 16)
\2{^х2) = ^{х,)^{х2)^апОп{х,)Оп{х2), B2.7)
л=0
где {Qn(x)} -ортогональная система функций;
an = J \\2{xbx2)Qn{x^)Qn{x2)dx^dx2.
646
Раздел 22

Нелинейные преобразования случайных процессов
Подставив B2.7) в B2.5), получим
Кл(т) = ]Гс2ап, B2.8)
cn= j<p(x)Qn(x)f^(x)dx. B2.9)
Конкретизируем полученное выражение для случая стационар-
стационарного гауссовского процесса на входе
1
где а, а2, г- математическое ожидание, дисперсия и нормирован-
нормированная корреляционная функция случайного процесса ?,(t).
Ковариационная функция случайного процесса на выходе нелиней-
нелинейного устройства y\(t) определяется B2.5) с подстановкой в него B2.10)
B2.10)
Переходя к нормированным величинам и обозначая a/o = q,
выражение B2.11) запишем в виде
B2.11)
B2.12)
647

Раздел 22
Используя разложение двумерной ПРВ гауссовского процесса
?(t) в ряд по многочленам Эрмита (разд. 6)
1 г (X1-qfJ-2r(x1-qf)(x2-q) + (x2-qfJ1 =
-•• ,2'
= ±еМ^-я) ^,-я) }^нм_q)Hn{X2_q)t
271 2 тАп-
где Нп{х) - многочлен Эрмита, выражение для Кц{т) получим
в виде
Кл(т)= у- ] I Ф(ах1)Ф{ох2)|]^Нп(х1 - с?)Нп(х2 - q)
-—~ л=о ^ B2.14)
Разделив переменные интегрирования в B2.14), запишем
Обозначим
Выражение для Кп(т) примет вид
ч^&п^г- B2-16)
л=0 П<
Таким образом, записано выражение для ковариационной
функции на выходе нелинейного устройства в виде ряда, члены
которого содержат степени г(т) и коэффициенты сп, определяе-
определяемые характеристикой нелинейного устройства.
Спектральную плотность мощности случайного процесса на вы-
выходе нелинейного устройства ^(со) определим исходя из B2.16)
B2.15)
B2.17)
648

Нелинейные преобразования случайных процессов
При расчёте B2.17) можно воспользоваться следующим при-
приближенным решением [16]
f rn(x)cos(aick = f [1 + г"@)т2 /2]" cosonck =
= \enr"^2l2coscmck= , V* e2""<°>.
J ^-2Г@)п
С учетом приведенного приближенного решения выражение для
спектра на выходе нелинейного устройства запишется в виде
Как следует из B2.19), спектральная плотность мощности слу-
случайного процесса на выходе нелинейного устройства описывается
выражением в виде ряда, члены которого определяются корреля-
корреляционной функцией случайного процесса на входе (ее второй про-
производной при т = 0) и характеристикой нелинейного устройства.
В качестве примеров рассмотрим характеристики случайных
процессов на выходе некоторых видов нелинейных устройств, на-
находящих достаточно широкое применение в радиотехнике. Помимо
иллюстрации возможностей изложенного подхода, рассматривае-
рассматриваемые примеры представляют и самостоятельный интерес.
22.2. Случайный процесс на выходе нелинейного
устройства со степенной характеристикой
Одним из узлов радиотехнических систем различного назначе-
назначения является детектор. Он представляет последовательно вклю-
включенные нелинейный элемент и фильтр. Нелинейный элемент
обычно имеет степенную характеристику, одностороннюю или дву-
двустороннюю. Ниже рассматриваются нелинейные элементы с ли-
линейной и квадратичной характеристиками.
22.2.1. Односторонняя линейная характеристика
Характеристика нелинейного устройства имеет вид (рис. 22.1)
у = Ьх, х > 0, Ь > 0. B2.20)
649
B2.19)

Раздел 22
Функция распределения вероятностей случайного процесса на
выходе такого устройства r\{t) определяется как
где F^{x) - ФРВ случайного процесса на входе.
Переходя к ПРВ случайного процесса r\(t), получим
^(У) = Гъ@Щу) + и({), у>0,
B2.21)
B2.22)
b^'b'
где f^(x) - ПРВ случайного процесса на входе ?,(t); &(t) - им-
импульсная функция.
Моменты распределения вероятностей /7-го порядка случайного
процесса на выходе устройства определяются выражением
B2.23)
Если f^(x) является четной функцией, то моменты распреде-
распределения четных порядков случайного процесса на выходе устройства
B2.23) можем получить в виде
B2.24)
т. е. выразить через моменты распределения четных порядков
случайного процесса на входе.
ФУ
Рис. 22.1
650

Нелинейные преобразования случайных процессов
Ковариационная функция случайного процесса на выходе уст-
устройства определяется как
Кц(т) = M{i}(t)r)(t + T)} = b2fjx,x2f^(xbx2)dx,dx2, B2.25)
о о
где ^ (хьх2) -двумерная ПРВ случайного процесса на входе ?(f);
хьх2 -значения ?(f) в моменты времени fn t+т.
Конкретизируем полученные результаты применительно к нор-
нормальному и релеевскому распределению случайного процесса на
входе нелинейного устройства.
Нормальное распределение. Для центрированного гауссов-
ского процесса на входе, имеющего ПРВ
1 х2
^ *j2no 2g2
из B2.22) получим
B2.26)
График f^(x) изображен на рис. 22.2.
Учитывая четность функции ПРВ гауссовского процесса, момен-
моменты распределения вероятностей r](f) четных порядков найдем из
B2.24)
-з
651
Рис. 22.2

Раздел 22
"V =^о2лП.З,...Bл-1)], л = 1,2,... B2.27)
Моменты нечетных порядков находятся непосредственно из
B2.23)
D С 9п+1 о„г ., 2/7!
/77П
1B
о
В частности, математическое ожидание r\(t) равно
дисперсия
Ковариационная функция случайного процесса на выходе нели-
нелинейного устройства определяется из B2.11) с учетом выражения
для двумерной ПРВ гауссовского процесса (а = 0)
^(т)= fl р ]]^2exp{-^-22^X^4)dx,dx2. B2.29)
27ia2V1-r2 у0 2а A-г )
Решение двойного интеграла в B2.29) дает
Кл(т) = ~ (г(т) arccos[-r(x)] + д/ГТ2^}- B2.30)
Аналогичный результат получается при использовании разло-
разложения Кц(т) в ряд B2.16). Коэффициенты ряда описываются
B2.15)
-х2
сл = -?= \bxHn{x)e~^dx, B2.31)
где Нл(х) - многочлен Эрмита.
Из B2.31) находятся следующие выражения для сп
652
B2.28)

Нелинейные преобразования случайных процессов
сь=-т=, q=^, cn=-^LHn_2@), л>2. B2.32)
V27I 2 V2n
Подставляя B2.31) в B2.16), выражение для Кп(т) запишем в
виде
к«(т)="I?11+1г(т)+? н"-2@) ^ B2-33)
С учетом следующих равенств для многочленов Эрмита
Н2л@) = (-1)пBл-1)!!, Н2п_,@) = 0
выражение для Кц(т) получается из B2.33) в виде
"V ' 2n X 2 2 ?^ Bл)! "
От него перейдем к следующему
/Сл (т) = -^-{r(x)arccos[-r(T)] + ^-Лт)},
что совпадает с B2.30).
С учетом полученного результата запишем выражения для кор-
корреляционной функция и дисперсии случайного процесса на выходе
Ял(х) = ^- {г(х)arccos[-r(x)] + ^-г2(т) -1},
Zn 2 2 B2.34)
ст2 = я' @) = -^-(тс -1) = 0,341Ь2а2.
2тг
Спектральная плотность мощности случайного процесса на вы-
выходе нелинейного устройства определяется преобразованием Фу-
Фурье B2.34)
Л/Л(ш)= \йц{т)е-™ск. B2.35)
— оо
Для удобства вычисления B2.35) целесообразно Яп(х) пред-
представить в виде ряда. С этой целью используем разложения
653

Раздел 22
, ч я г3 Зг5 3-5-7л7
arccos(-r) = — + г + + + + ...,
2 2-3 2-4-5 2-4-6-7
- г2 г4 Зг6
2 2-4 2-4-6
Ограничиваясь членами, содержащими г в степени не выше
второй, выражение для Ял(т) получим в виде
Подставляя B2.36) в B2.35), находим
Л/_(а>) = — Л/(со) + —Vt \N(o)-x)N(x)dx, B2.37)
4 8тГа «^
где Л/(ш) - спектральная плотность мощности случайного процесса
на входе.
В качестве примера рассмотрим случайный процесс, имеющий
спектральную плотность мощности
Л/(со) = Л/@)е w'.
Ей соответствует корреляционная функция
Я(т) = Я@)е 4 .
Спектральная плотность мощности случайного процесса на вы-
выходе нелинейного устройства описывается выражением
,2
Релеевское распределение. Практический интерес представ-
представляет нелинейное преобразование B2.20) случайного процесса
^(f), имеющего релеевское распределение. Такое распределение
имеет огибающая узкополосного гауссовского процесса (разд. 20).
Одномерная и двумерная ПРВ ВД описываются выражениями
654
B2.36)

Нелинейные преобразования случайных процессов
l(x) = -^e 2°\ х>0, B2.38)
о
i(^i^2) = ^^/o[-1^]exp{--4f4r}. B2.39)
2 ст4A-г) сгA-г) 2сгA-Г)
Плотность распределения вероятностей случайного процесса
на выходе устройства находится из B2.22) с учетом B2.38)
М*) = "^2-е 2bV' У*0- B2.40)
Моменты распределения вероятностей r](t) определяются как
у2
п =_2_|ул+1е 2ь2°гсУу. B2.41)
Моменты распределения нечетных порядков:
,2
Математическое ожидание и дисперсия равны
Выражение для ковариационной функции r\(t) запишем, под-
подставляя B2.39) в B2.25)
655
четных порядков:
B2.42)

Раздел 22
Решение B2.43) с использованием соотношения
а2
f х^10{ах)е-*г*2 dx = Г(^)е^ iFiAxX~), B2.44)
J 2 2 4p
где Г(х) - гамма-функция; 1 F ,(xr, xh x >) - гипергеометрическая
функция,
в виде
B2.45)
Преобразование гипергеометрической функции приводит B2.45)
к следующему виду
Кл(т) = Ь2а2{2Е[г(т)]-[1 - Г2(т)/С[г(т)]]}, B2.46)
где К{х) - полный эллиптический интеграл первого рода; Е ( х) -
полный эллиптический интеграл второго рода.
22.2.2. Односторонняя квадратичная характеристика
Характеристика нелинейного устройства имеет вид (рис. 22.3)
у = Ьх2, х>0. B2.47)
Функция распределения вероятности случайного процесса на
выходе определяется выражением
B2.48)
Плотность распределения вероятности случайного процесса на
выходе равна
Рис. 22.3
656

Нелинейные преобразования случайных процессов
/л1(у) = ^1@M(у) + -1=^1(^)> у>0. B2.49)
Начальные моменты r\(t) определяются выражением
тлл = M{r]n(t)} = bTJ^\{x)dx. B2.50)
Ковариационная функция случайного процесса на выходе уст-
устройства
Кц(т) = M{r\(t)r\{t + x)} = b2\x$?\2{xbx2)dx^dx2 . B2.51)
о
Конкретизируем полученные выражения для нормального и ре-
леевского распределения случайного процесса на входе ^(f).
1. Нормальное распределение.
Для гауссовского процесса на входе
„2
B2.52)
657
из B2.49) получим (рис. 22.4)
Рис. 22.4

Раздел 22
Начальные моменты п-ю порядка определяются выражением
mnn =—а2п[1,3...B/7-1)], п = 1, 2, ... B2.53)
2. Релеевское распределение.
Плотность распределения вероятности случайного процесса на
входе определяется B2.38). Из B2.49) получим
1 -^т
Момент п-го порядка:
mX]n=~-Ijyne^2dy = Bbo2)nrf.. B2.55)
Ковариационная функция r|(f) определяется B2.5). С учетом
B2.39) и B2.47) запишем
B2.56)
Произведя замену переменных z, = xf, z2 = xf, B2.56) перепи-
перепишем в виде
I B2.57)
]b'°[^]exp{-i^№dZ2-
Разложение функции Бесселя в ряд
и почленное интегрирование в B2.57) дает
658

Нелинейные преобразования случайных процессов
С учетом равенства
из B2.57) получим
Кц(т) = 4bV[1 + Л2(т)]. B2.59)
Корреляционная функция r\(t)
Ял(т) = 4Ь2а4г2(т), гп(т) = г2(т). B2.60)
Ковариационную функцию случайного процесса на выходе рас-
рассматриваемого нелинейного устройства можно также определить,
используя разложение двумерной ПРВ по ортогональным много-
многочленам. В качестве ортогональной системы многочленов для ПРВ
целесообразно выбрать систему многочленов Лагерра, а в качест-
качестве весовой функции - одномерную ПРВ.
Двумерную ПРВ случайного процесса на выходе устройства
найдем, используя подход, изложенный в разд. 17. Двумерная ПРВ
случайного процесса на входе описывается B2.39). Переходя от
переменных х, и х2 к переменным
y^=bxf, y2 =bx%, B2.61)
получим якобиан преобразования
Двумерная ПРВ T|(f) будет иметь вид
f-(y^2)=^T7yw^)lexp{-i^&yb BZ63)
где 10 (х) - модифицированная функция Бесселя первого рода.
При г- 0 (т—> °° ) имеем
659
B2.62)
B2.58)

Раздел 22
где одномерные ПРВ f^{y) описываются B2.38).
Разложение двумерной ПРВ B2.63) в ряд по многочленам Ла-
герра имеет вид
У1+У2 со
«"¦*>¦ W - Z^jfcjU^). B2.64)
Используя разложение B2.64), выражение для ковариационной
функции случайного процесса на выходе устройства r\(t) запишем
в виде
Кп<х)= \\У:УгЫУьУ2)с1У&2 =
о о
~<~ У\+Уг
- 1:2п^1{у^ф^ф°2to2 ** - ^-б5)
= 4Ь2а4]Г72лс*,
где
cn = JyLn(y)e^fly.
о
С учетом определения многочленов Jlareppa (разд. 15) найдем
co=Jye~ydy = 1, c1=JyA-y)e"ydy = -1, cn=0
о о
при л > 2 . B2.66)
Подставив значения коэффициентов сп в B2.65), получим
Кп(т) = 4b2q4[1 + г2(т)]. B2.67)
Корреляционная функция случайного процесса на выходе
660

Нелинейные преобразования случайных процессов
Ял(т) = 4Ь2а4г2(т), гп(х) = г2(т). . B2.68)
22.2.3. Двусторонняя квадратичная характеристика
Характеристика нелинейного устройства имеет вид (рис. 22.5)
у = Ьх2 . B2.69)
Плотность распределения вероятности случайного процесса на
выходе устройства описывается выражением (разд. 15)
Момент п-го порядка:
B2.70)
B2.71)
где т^2п - момент распределения 2л-порядка случайного процес-
процесса на входе нелинейного устройства.
Ковариационная функция случайного процесса на выходе уст-
устройства определяется выражением
B2.72)
1. Нормальное распределение t,(t).
Для гауссовского процесса на входе из B2.70) получим (рис. 22.6)
Рис. 22.5
661

Раздел 22
В частности, математическое ожидание и дисперсия:
т^=Ьо2, а2=262а4.
B2.73)
B2.74)
B2.75)
Выражение для ковариационной функции случайного процесса
на выходе запишем в виде
Кл(т) = Ь2М{?2@^ + т)}.
Для гауссовского процесса из B2.76) получим
КМ = Ь2М2&2«)} + 2Ь2М2{Цх)Ы + т)} =
B2.76)
B2.77)
где л(т) - нормированная корреляционная функция случайного
процесса на входе.
Корреляционная функция r\(t)
B2.78)
Спектральная плотность мощности переменной составляющей
случайного процесса на выходе устройства определяется выраже-
выражением
662
Момент п-го порядка равен

Нелинейные преобразования случайных процессов
A/T1(o)) = 4b2fH2(x)cos(car)c/r = — [ Л/(со- x)N(x)dx, B2.79)
о
где Я(т), Л/(со) - корреляционная функция и спектральная
плотность мощности случайного процесса на входе.
Так для гауссовского процесса на входе, имеющего спектраль-
спектральную плотность и корреляционную функцию
22.3. Метод преобразований
При определении корреляционной функции случайного процес-
процесса на выходе нелинейного устройства может оказаться полезным
метод, основанный на использовании преобразования Лапласа
характеристики нелинейного устройства. Этот метод анализа не-
нелинейных преобразований гауссовских процессов в некоторых слу-
случаях позволяет обойти трудности, с которыми приходится сталки-
сталкиваться при применении прямого метода.
22.3.1. Содержание метода
Второй начальный момент случайного процесса на выходе не-
нелинейного устройства r\(t) описывается выражением B2.5)
оо оо
Кл(т) = /ад0л(* + т)}= { |ф(х1)ф(х2)^1(х1,х2)сУх1сУх2, B2.80)
где ф(х) - характеристика нелинейного устройства.
Если характеристика нелинейного устройства допускает преоб-
преобразование Лапласа:
прямое
ф{у) = ^(x)e~ivxdx,
о
663
получим

Раздел 22
обратное
Ф(х) = — [o(v)eivxdv, B2.81)
2tc/J
с
где с - контур интегрирования, то, используя преобразование Лап-
Лапласа характеристики нелинейного устройства, B2.80) можем пред-
представить в виде
К^) =
= ^\0{^)\0{v2)[]]elv^iv^
С, С2 -°о -°°
Внутренний интеграл в B2.82) представляет двумерную харак-
характеристическую функцию случайного процесса на входе
М^2) = J \elv^+lv^\2{x,,x2)dx,dx2. B2.83)
Таким образом, выражение для /Сл(т) запишется в виде
4x) = ^\\°(v№v2)h2(vbv2)dv,dv2. B2.84)
{2п) с,с2
Контуры интегрирования для некоторых распространенных ви-
видов нелинейных устройств приведены в [20].
Основные трудности при использовании B2.84) связаны с опре-
определением двумерной характеристической функции случайного
процесса на входе. Для гауссовского процесса характеристическая
функция описывается достаточно просто и метод преобразований
для ряда характеристик нелинейных устройств оказывается эф-
эффективным.
Характеристическая функция центрированного гауссовского
процесса ?(f) равна (разд. 16)
М^г) = exp{--y(^2 +2rv,v2 + vf)}, B2.85)
где а2, г(т) - дисперсия и нормированная корреляционная
функция случайного процесса на входе t,(t).
664

Таким образом, записано выражение для ковариационной
функции случайного процесса на выходе нелинейного устройства в
виде ряда по степеням нормированной корреляционной функции
гауссовского процесса на входе, коэффициенты ряда определяют-
определяются характеристикой нелинейного устройства.
Преобразование Лапласа некоторых видов характеристик нели-
нелинейных устройств приведены в табл. 22.1. Там же даны выражения
для соответствующих коэффициентов разложения /7П. Расширени-
Расширением табл. 22.1 является таблица в [20}.
Спектральная плотность мощности случайного процесса на вы-
выходе устройства определяется преобразованием Фурье его корре-
корреляционной функции.
#(т) - корреляционная функция случайного процесса на входе.
Рассмотрим примеры использования метода преобразований
при получении характеристик случайного процесса на выходе не-
нелинейного устройства со степенной характеристикой и идеального
ограничителя.
665
Нелинейные преобразования случайных процессов
Подставив B2.85) в B2.84) и используя разложение экспонен-
экспоненциального сомножителя в ряд
B2.86)
B2.87)
B2.88)
B2.89)

Раздел 22
22.3.2. Нелинейные устройства
с односторонней степенной характеристикой
Характеристика нелинейного преобразователя имеет вид
ф(х) = Ьхъ, х>0. B2.90)
Преобразование Лапласа B2.90):
B2.91)
Таблица 22.1
Характеристики нелинейных устройств.
Характеристика
нелинейного
преобразователя
Ф(х)
Преобразо-
Преобразование Лапла-
Лапласа характе-
характеристики
L{xyvxdx
Коэффиценты
Степенная
y = bxv,x>0
Степенная со
смещением
у = b(x-af, х>Ь.
+У
666

Нелинейные преобразования случайных процессов
№
п/п
Характеристика
нелинейного
преобразователя
ф(х)
Преобразо-
Преобразование Лапла-
Лапласа характе-
характеристики
Коэффиценты
onhn
Идеальный ограни-
ограничитель
л -нечетное
У =
667
Идеальный
ограничитель
со смещением
Линейная

Раздел 22
Примечание: г(х) - гамма-функция; D(x) - функция Вебера,
Dn(x)= ё~* '4Нп(х); Н(х) - многочлен Эрмита.
B2.92)
B2.93)
Выражение B2.93) совпадает с полученным ранее прямым ме-
методом B2.32).
22.3.3. Идеальный ограничитель
Характеристика ограничителя имеет вид
1,х>0
B2.94)
668
Характеристика
нелинейного
преобразователя
ф(х)
Преобразо-
Преобразование Лапла-
Лапласа характе-
характеристики
Коэффиценты
С учетом B2.91) из B2.88) найдем
При d = 1 из B2.87) с учетом B2.92) получим

Нелинейные преобразования случайных процессов
Преобразование Лапласа характеристики
0{v) = -. B2.95)
Для центрированного гауссовского процесса на входе выраже-
выражение B2.87) принимает вид
оо 2n n I -ct2v2
to n[ 2nl{
Из B2.96) после ряда преобразований можно получить сле-
следующее выражение для ковариационной функции случайного про-
процесса на выходе
К (х) = 1 + -arcsinг(х), B2.97)
7Е
где г(х) - нормированная корреляционная функция случайного
процесса на входе идеального ограничителя.
Корреляционная функция случайного процесса на выходе иде-
идеального ограничителя описывается выражением
Яп(т) = ^arcsin r(x), B2.98)
к
соответствующая спектральная плотность мощности:
22.4. Метод производных
Если случайный процесс на входе нелинейного устройства яв-
является гауссовским, в ряде случаев появляется возможность упро-
упростить операции получения корреляционной функции случайного
сигнала на выходе.
Упрощения связаны с использованием выражений для произ-
производных ковариационной функции случайного процесса на выходе
устройства исходя из нормированной корреляционной функции
случайного процесса на входе.
669

Раздел 22
22.4.1. Производные корреляционной функции случайного
процесса на выходе нелинейного элемента
При подаче на вход нелинейного устройства гауссовского про-
процесса t,(t) выражение для ковариационной функции случайного
процесса на выходе r\(t) B2.84) имеет вид
2 B2.99)
• Г Гф(^)(р(иг2)ехр{-—(vf + 2rv,v2 + v2)}dv^dv2,
где а2, г(т) - дисперсия и нормированная корреляционная
функция случайного процесса на входе.
Дифференцирование B2.99) по г(т) дает следующее выраже-
выражение
дпКц = (-1) V"
dr° = BЛJ ' а2 B2.100)
• ||<^Ф(\/1)Ф( \/2)ехр{-у(\/12 +2л/^2 + vl)}dv^dv2.
с^сг
Подставляя вместо двумерной характеристической функции га-
гауссовского процесса в B2.100) ее определение через ПРВ
exp{~(vt+2rv,v2 + v22)}= J jeiv^+iv^f,2(xbx2)dx,dx2,
запишем
В B2.101) переменные интегрирования v, и v2 разделяются.
Для каждого интеграла имеет место следующее равенство
670
B2.101)

Нелинейные преобразования случайных процессов
—jvn0(v)e'vxdv = ^^ = (p{n)(x), B2.102)
с
где ф(х) - характеристика нелинейного устройства.
Это равенство получается при дифференцировании B2.81).
С учетом B2.102) из B2.101) получим
-—J- = a2n j ^n\x^{n\x2)fl2{xbx2)dx,dx2, B2.103)
где ^2(xi-x2) -двумерная ПРВ гауссовского процесса на входе.
Записанное соотношение позволяет получить производную кор-
корреляционной функции на выходе нелинейного устройства, удобно
в том случае, когда имеется достаточно простое решение двойного
интеграла B2.103). Такое решение получается, в частности, в том
случае, когда характеристика нелинейного элемента представляет
многочлен и решение интеграла в B2.103) становится очевидным.
Нелинейные устройства с такой характеристикой и рассматрива-
рассматриваются в качестве примеров.
22.4.2. Односторонняя линейная характеристика
Характеристика нелинейного устройства имеет вид
у = ф(х) = Ьх, х>0. B2.104)
Вторая производная B2.104) представляет импульсную функцию
ФB)(х) = Ь5(х). B2.105)
Подставляя B2.105) в B2.103), получим
B2.106)
B2.107)
671
Решение B2.106) с учетом начальных условий при г = 0

672
Раздел 22
B2.108)
B2.109)
B2.110)
B2.111)
B2.112)
B2.113)
что совпадает с B2.30).
22.4.3. Односторонняя квадратичная характеристика
Характеристика нелинейного устройства имеет вид
Для такой характеристики
из B2.103) получим
Начальные условия при г = 0
Из B2.111) с учетом B2.112) получим

Нелинейные преобразования случайных процессов
22.4.4. Идеальный ограничитель
Характеристика идеального ограничителя имеет вид
у = Ч>(х) = V\X^Q- B2.114)
Для такой характеристики получим
Ф'(х) = 26(х), ^- = ,2 ¦ B2.115)
^ W1 - г2
Начальные условия при
г = 0Кц=0. B2.116)
Из B2.115) с учетом B2.116) находим
/CT1(x) = -arcsinr(T), B2.117)
что совпадает с B2.98) результатом, полученным методом преобразо-
преобразований.
673

Раздел 23.
АНАЛИЗ ХАРАКТЕРИСТИК СЛУЧАЙНОГО ПРОЦЕССА
НА ВЫХОДЕ МНОЖИТЕЛЬНОГО КОРРЕЛЯТОРА
Широкое применение корреляторов, в первую очередь при об-
обнаружении сигналов и измерении характеристик сигналов и шумов,
обуславливает практический интерес к их анализу. С другой сторо-
стороны, рассмотрение случайного процесса на выходе коррелятора
является хорошей иллюстрацией применения методов анализа
случайных процессов и прежде всего их линейных и нелинейных
преобразований в практике исследований.
В разделе проводится анализ случайного процесса на выходе
множительного коррелятора, представляющего последовательно
соединенные перемножитель и фильтр, на одном из входов пере-
перемножителя включена линия задержки (рис. 23.1).
23.1. Распределение случайного процесса на выходе
перемножителя
Случайный процесс на выходе перемножителя r\(t) представля-
представляет результат перемножения случайного процесса ?(f) с его копией
после задержки на интервал времени Г (рис. 23.1)
л(гНШ'-т). B31)
Зная двумерную ПРВ случайных величин ?,{t) и
Z,{t-T)-ft (хьх2), можно определить ПРВ их произведения r|(f).
Рис. 23.1
674

Анализ характеристик случайного процесса
Используя результаты, полученные в разд. 17, для ПРВ случай-
случайного процесса r|(f) запишем следующее выражение
00 s ч 0 / ч
*, ,М = \\k{x^fx- \{k\хЛух. B3.2)
о — °°
В дальнейшем будем рассматривать ?(f) как центрированный га-
уссовский процесс. Это наиболее часто встречающийся на практике
случай. Для гауссовского процесса t,(t), имеющего двумерную ПРВ
42(x,x) = . ехр^—* of Л х1 Г» 23-3
где а2, г(х) - дисперсия и нормированная корреляционная функ-
функция §(f),
выражение B3.2) примет вид
г , B3.4)
где Г- задержка на входе коррелятора.
Решая B3.4), получаем
где КЬ(х) - модифицированная функция Бесселя.
Графики ПРВ случайного процесса на выходе перемножителя
приведены на рис. 23.2.
23.2. Корреляционная функция и спектр случайного
процесса на выходе перемножителя
Математическое ожидание случайного процесса на выходе пе-
перемножителя r\(t) равно
mn 1 = M{i\(t)} = M{t{t%(t - Т)} = R(T\ B3.6)
675

Рис. 23.2
где R(T) - корреляционная функция случайного процесса на входе
?,{t); Г - задержка случайного процесса на одном из входов пере-
перемножителя.
Как следует из B3.6), постоянная составляющая на выходе пе-
перемножителя является несмещенной оценкой корреляционной
функции случайного процесса Z,(t).
На постоянную составляющую накладываются флуктуации, ко-
которые представляют источник ошибок измерения корреляционной
функции (рис. 23.3).
Второй начальный момент случайного процесса на выходе пе-
перемножителя (ковариационная функция) определяется моментом
четвертого порядка случайного процесса на входе
Кц (т) = Mfo(f)n(f" х)}= МШ(! - T%(t - x%{t- т - Г)}. B3 7)
Для гауссовского процесса ?(f) имеет место следующее равен-
равенство
мШЬ-№-т№-т-т)}=
= MUt%(t-T)}MUt-x%(t-T-T)}+
+ м&№ - ФШ - m - x - r)}+ (^-b)
+ MUt%(t-x-T)}MUt-T%(t-T)}.
Таким образом, выражение для ковариационной функции слу-
случайного процесса на выходе перемножителя запишется в виде
Кц (т)= Я2G> Я2(х)+ Я(т + Г)я(т- Г) B3 д)
где Я(т) - корреляционная функция случайного процесса на вхо-
Де W) •
676
Раздел 23

Рис. 23.3
Корреляционная функция случайного процесса r\(t)
Rn (т)=Я2(т)+Я(т + Г)я(т-Т). B3.10)
Дисперсия r\(t), характеризующая «размах» флуктуации на вы-
выходе перемножителя, определяется как
о^ = Я2@)+Я2(Г). B3.11)
Нормированная корреляционная функция r)(t):
^(т)=—WWW) ^Щ '
где г(т) - нормированная корреляционная функция случайного
процесса на входе ?@ .
При 7 = 0
Ял(т) = 2Я2М /,М=г2(т). B3.13)
Спектральная плотность мощности случайного процесса на вы-
выходе перемножителя определяется преобразованием Фурье кор-
корреляционной функции ЯТ1(т)
B3.14)
При Г=0 выражение для Л/Л((о) с учетом B3.13) можем записать
в виде свертки спектра случайного процесса на входе (свойства
преобразования Фурье, разд. 3)
677
Анализ характеристик случайного процесса

Раздел 23
B3.15)
где Л/(со) - спектральная плотность мощности случайного процесса
на входе ?(f).
В качестве примера рассмотрим случайный процесс ?(f),
имеющий корреляционную функцию и спектр:
Рис. 23.4
678

Анализ характеристик случайного процесса
При 7 = 0
-рУ
Л/Т1(ы) = 2л/т1(ЗЯ2@)е 4 .
Как и следовало ожидать, корреляционная функция случайного
процесса на выходе перемножителя сужается, спектр - расширя-
расширяется.
На выходе перемножителя включен фильтр. Используя подход,
описанный выше, и результаты, полученные в разд. 21, можно оп-
определить характеристики случайного процесса на выходе фильтра
коррелятора.
23.3. Характеристики случайного процесса на выходе
множительного коррелятора
Случайный процесс на выходе коррелятора (рис. 23.1) описы-
описывается выражением
оо
г,@ = | h{t%(t - uftt -T- u)du, B3.16)
о
где ?(f) - случайный процесс на входе перемножителя; Т - за-
задержка на одном из входов перемножителя; h(t) - импульсная ха-
характеристика фильтра.
Как правило, ширина полосы пропускания фильтра значительно
меньше ширины спектра на выходе перемножителя. Происходит
нормализация случайного процесса на выходе фильтра (разд. 21).
Таким образом, достаточно общим случаем, можно считать, явля-
является нормальное распределение случайного процесса на выходе
коррелятора r((f); его ФРВ или ПРВ определяются математиче-
математическим ожиданием и корреляционной функцией случайного процесса
на выходе фильтра.
Математическое ожидание случайного процесса на выходе кор-
коррелятора равно
где
679
B3.17)

Раздел 23
k = jh(u)du.
о
Как следует из B3.17), математическое ожидание случайного
процесса на выходе коррелятора пропорционально корреляцион-
корреляционной функции случайного процесса на входе. Оно оценивается по-
постоянной составляющей колебания на выходе коррелятора.
Начальный момент второго порядка случайного процесса на
выходе коррелятора f]{t) определяется выражением
Цл@п('-т)}= J ]h(uMu2) B3 18)
M{^-u№t-T-u№-T-u2k{t-T-T-u2)}du,du2,
где h(t) - определена для t > О.
Для момента четвертого порядка гауссовского процесса в
B3.18) запишем
MUt-u,%(t-T-u^(t-x-u2%(t-x-T-u2)} =
= М{ф-и№-Т-и1)}М{ф-т-и2)&-т-Т-и2)} +
+ М{ф-и№-т-и2)}М{ф-Т-и№-т-и2)}+ B3.19)
+ Mfe(f-u1fe(f-x-r-u2))Mfe('-7--ii1fe(f-x-u2)} =
= R2(т) + R2(т + и2 - иА) + Я(т + Т + и2 + и^)r(i-T + u2-u-[)
где Я(х) - корреляционная функция случайного процесса на входе
Корреляционная функция случайного процесса на выходе кор-
коррелятора определяется через начальные моменты распределения
соотношением
Яп(т)= Цл@п('-т)}-М2{л@}- B3.20)
С учетом B3.18) - B3.20) выражение для ЯТ1(т) запишется
в виде
680
B3.21)

Анализ характеристик случайного процесса
Область интегрирования в B3.21) разобьем диагональю и1=и2.
Перейдем от переменных и1 и и2 к и = uh v = и2- и1 для одной по-
половины области и к и = и2, v = и-,- и2 для другой. Тогда выражение
для корреляционной функции случайного процесса на выходе кор-
коррелятора получим в виде
Rjx)= [p(vIr2(t + v)+R{v + T + t)R{v + T + x)+
L {2322)
+ R2{v-t)+R(v + T-x)R(v~t-T)\jv,
где
p(v)= \ h(u)h(u + v)du или р(т) = — [|H(co)|2coscoTflfeD;
-oo 0
H(co) - частотная характеристика фильтра коррелятора.
Дисперсия случайного процесса на выходе коррелятора равна
<
Постоянная составляющая на выходе фильтра, как это следует
из B3.17), является оценкой измеряемой корреляционной функции
случайного процесса на входе ?(f). Флуктуации, накладываемые
на нее, обуславливают ошибку коррелятора. Относительная вели-
величина этой ошибки может быть определена как отношение среднего
квадратического отклонения случайного процесса к его математи-
математическому ожиданию
681
B3.23)
B3.24)

Раздел 23
B3.25)
B3.26)
где Я(т) - корреляционная функция случайного процесса на входе;
г(т) = Я(т)/Я@).
Как следует из B3.26), ошибка определяется: видом и парамет-
параметрами фильтра коррелятора, p(v); корреляционной функцией слу-
случайного процесса на входе, Я(т); задержкой на входе коррелятора, Т.
В качестве примера рассмотрим коррелятор, содержащий
фильтр, имеющий импульсную характеристику вида (например,
RC- цепь)
где Ь- постоянная величина.
Корреляционная функция случайного процесса на входе ?(f)
имеет вид
Для приведенных исходных данных из B3.22) получим
С учетом B3.17) и B3.23) выражение для 8 запишется в виде
682

Анализ характеристик случайного процесса
где
Дисперсия равна
Нормированная корреляционная функция случайного процесса
на выходе коррелятора
,Ьг
Относительная величина ошибки определяется выражением
B3.26)
зависит от постоянной времени фильтра 1/Ь и параметра корре-
корреляционной функции случайного процесса C, от их произведения
683

Раздел 23
Рис. 23.5
Ь = Ьр. На рис. 23.5 приведены графики зависимости 8 от обоб-
обобщенного параметра Ь в интервале значений b от 0,001 до 0,01.
При b < 0,001 можно принять 5 = 1,88л/Ь .
Принимая интервал корреляции случайного процесса на входе
равным хк = 2,4р (Я(тк) = 0,05Я@)), можно считать, что при значе-
значении постоянной времени фильтра Т = (М Ь)>500тк значения отно-
относительной ошибки 5 не превосходят 5%.
Спектральная плотность мощности случайного процесса на вы-
выходе коррелятора r|(f) может быть определена как преобразова-
преобразование Фурье корреляционной функции B3.22)
Она может быть также получена как произведение спектральной
плотности мощности процесса на выходе перемножителя Л/П(со) и
квадрата модуля частотной характеристики фильтра Н(со):
w1,H=|H(mf/v4i(<oi B327)
где Л/п1(со) - спектральная плотность мощности случайного про-
процесса на выходе перемножителя, определяется B3.14).
Для низкочастотного фильтра коррелятора с учетом того, что
полоса пропускания фильтра значительно уже ширины спектра
случайного процесса на выходе перемножителя, можно принять
684

Анализ характеристик случайного процесса
Л/л(@) = |н(а))|2Л/т,1@) B328)
Выражение для Л/ ^о) получим из B3.14) с учетом B3.10) в виде
Для условий рассмотренного выше примера получим
B3.29)
Как следует из выражения для Л/л((о), спектр случайного про-
процесса на выходе коррелятора, имеющего узкополосный фильтр,
определяется частотной характеристикой фильтра.
Подход к анализу случайного процесса на выходе множительно-
множительного коррелятора может быть использован и при анализе с учетом
ограниченного времени наблюдения (кратковременный анализ).
23.4. Кратковременный анализ случайного процесса на
выходе множительного коррелятора
Наблюдение случайного процесса на выходе коррелятора в те-
течение ограниченного интервала времени приводит к дополнитель-
дополнительным ошибкам измерения. Подход к определению этого вида оши-
ошибок аналогичен рассмотренному в п. 23.3, что делает целесооб-
целесообразным связать материал предыдущего подраздела с оценкой ха-
характеристик случайного сигнала на выходе перемножителя и кор-
коррелятора при кратковременном наблюдении случайного процесса.
23.4.1. Оценка корреляционной функции случайного про-
процесса при ограниченном времени наблюдения
При наблюдении случайного процесса на выходе перемножите-
перемножителя в течение времени tk оценкой корреляционной функции центри-
центрированного процесса ?,(t) будет величина
685

Раздел 23
Rk(T,tk) = f\^(t%(t-T)dt,
к о B3.30)
где Г- смещение во времени на одном из входов перемножителя.
Математическое ожидание Rk(T,tk) равно
M{Rk(T, tk)}= МШ{* ~ Т)}= R(T\ B3.31)
где Я(т) - корреляционная функция случайного процесса ?(f).
Результат усреднения B3.31) показывает, что Rk{T,tk) являет-
является несмещенной оценкой корреляционной функции ?(f). Поэтому
ошибку определения корреляционной функции по B3.30) можно
оценивать, оперируя только средним квадратическим отклонением
Rk{T,tk)
о2к{Т, tk)=M{R2k{T, tk)}- M{Rk{T, tk)f. B3.32)
Первое слагаемое в B3.32) определяется выражением
*к*к
M{Rl(TJk)}=y\JM{^Mh-T%(t2Ut2-T)}dt,dt2- B3.33)
tk оо
Подставляя B3.31) и B3.33) в B3.32), запишем
<*l{T.tk) =
Для гауссовского процесса ?(f) подынтегральное выражение в
B3.34) можем записать в виде
мЩ1ь -т)Шк -т)}-м%Ш-т)}= B3 35)
= tf{t2 - 0+ R(t2 - U + T)R(t2 -t,-T\
где Я(т) - корреляционная функция Z,(t).
Подставив B3.35) в B3.34), получим
686

Анализ характеристик случайного процесса
Производя замену переменных, как это было сделано в § 23.3,
получим
o2k{T,tk) = ^\{tk-viR2(v)+R{v + T)R(v-T)\jv. B3.37)
tk о
Выражение B3.37) дает зависимость дисперсии от времени на-
наблюдения tk при заданной корреляционной функции случайного
процесса.
Относительная ошибка определения корреляционной функции
равна
5= aAttk\V B3.38)
M{Rk{T,tk)\
Подставив в B3.38) выражение для ok(T,tk) и Rk(T,tk), запи-
запишем
B3.36)
B3.39)
В качестве примера рассмотрим случайный процесс, имеющий
корреляционную функцию вида
R(T) = R@)e~alA
где a - постоянная величина.
Подставив выражение для корреляционной функции в B3.39),
получим
или
687

Раздел 23
где tk = atk, T -aT.
Как следует из записанных выражений, ошибка зависит от: кор-
корреляционной функции случайного процесса, Я(т); задержки слу-
случайного процесса на входе, Т; времени наблюдения, tk.
Для условий примера - ошибка определяется параметрами а,
7и tk.
При 7= 0 (рис. 23.6)
При достаточно большом значении tk можно пользоваться сле-
следующим приближенным равенством
А
Принимая интервал корреляции тЛ=3/а, (R(Tk)<0,05R@)),
последнее выражение для 5 можем записать в виде
688
Рис. 23.6

Анализ характеристик случайного процесса
Время наблюдения практически не влияет на определение кор-
корреляционной функции случайного процесса при значении
tk > ЗООт^. При выполнении этого неравенства ошибка определе-
определения корреляционной функции составит менее 5%.
23.4.2. Аппаратурное определение корреляционной функции
случайного процесса за ограниченное время
При определении корреляционной функции случайного процес-
процесса за ограниченное время tk случайный процесс на выходе корре-
коррелятора описывается выражением
Л*G"Л)= \h{u)^(t-u%(t-T-u)du. B3.40)
о
Моменты первого и второго порядков r\k{T,tk) равны
где Я(т) - корреляционная функция случайного процесса ?(f).
Дисперсия случайного процесса r\k(T,tk) определяется как
ol(T, tk)= М^ЦТ, tk)}- М2{цк(Т, tk)\ B3.42)
Подставляя B3.41) в B3.42) и используя представление момен-
момента четвертого порядка гауссовского процесса с помощью моментов
второго порядка, получим
tk h B3 43)
= Г f A7(u, )А](^ J/?2 (t/2 ~ ui)+ R(U2 - Ц + T)R(u2 -щ- T)du^dU2-
о о
Произведя замену переменных в B3.43), выражение для
o2k(T,tk) запишем в виде
689
B3.41)

Раздел 23
где
Относительная ошибка оценки корреляционной функции опре-
определяется выражением
B3.44)
B3.46)
Ошибка зависит от времени измерения корреляционной функ-
функции, вида корреляционной функции, вида и параметров фильтра
коррелятора.
При Т = 0
Для RC - фильтра с импульсной характеристикой h{t) = be bt,
и корреляционной функцией экспоненциального вида
690
B3.47)

Анализ характеристик случайного процесса
B3.48)
то, не учитывая возможные ошибки, сигнал на выходе коррелятора
при некоторых условиях (определенных в дальнейшем) можно
представить в виде (постоянный коэффициент принят равным еди-
единице)
691
из B3.47) получим
При tk -» °o имеем
Сравнение выражений для относительной ошибки при ограни-
ограниченном времени измерения и неограниченно большом показывает,
что для условий примера при tk>T = A / b) влиянием времени из-
измерения на ошибку можно пренебречь, ошибка составляет доли
процента.
23.5. Характеристики сигнала на выходе
корреляционного транспонатора
Оценкой корреляционной функции случайного процесса являет-
является постоянная составляющая на выходе коррелятора при фиксиро-
фиксированном значении задержки на входе. Изменение во времени за-
задержки на входе позволяет наблюдать корреляционную функцию в
заданном интервале значений задержки (рис. 23.7). Если задержка
т изменяется во времени с постоянной скоростью

Раздел 23
Рис.23.7
4t)=R(Kt).
B3.49)
Спектральную плотность этого сигнала определим преобразо-
преобразованием Фурье
С учетом B3.48) можно записать
B3.50)
B3.51)
где Л/(со) - спектральная плотность мощности случайного процесса
на входе
B3.52)
Сравнение B3.51) и B3.52) показывает, что спектр сигнала на
выходе коррелятора при изменении задержки во времени повторя-
повторяет по форме спектральную плотность мощности случайного про-
процесса на входе; происходит изменение масштаба по оси частот:
изменяется положение спектра на оси частот и его ширина
(рис. 23.8). Этот результат вытекает непосредственно из свойств
преобразования Фурье.
Однако сделанные выводы справедливы при условии, что сиг-
сигнал на выходе коррелятора соответствует корреляционной функ-
функции. При аппаратурной реализации условия, выполняемые на
практике, отличаются от принятых.
692

Анализ характеристик случайного процесса
Рис. 23.8
Сигнал оценки корреляционной функции при постоянном значе-
значении задержки на входе представляет постоянную составляющую
на выходе перемножителя. При изменении задержки во времени
этот сигнал на выходе безинерционного перемножителя изменяет-
изменяется в соответствии с изменением корреляционной функции R{Kt).
При прохождении сигнала через фильтр коррелятора возникают
искажения, которые приводят к изменению сигнала на выходе. Ес-
Если изменение задержки во времени происходит после того, как сиг-
сигнал на выходе фильтра принял установившееся значение R@), то
в момент времени t (соответствующий задержке т = Kt) сигнал бу-
будет описываться выражением
B3.53)
где h(t) - импульсная характеристика фильтра.
Сигнал, описываемый B3.53), только приближенно соответству-
соответствует корреляционной функции (рис. 23.9). Степень соответствия оп-
определяется соотношением параметров корреляционной функции,
фильтра и скорости изменения задержки во времени. Степень со-
соответствия B3.53) и B3.49) можно оценить относительным значе-
значением разности
Так для RC -фильтра
B3.54)
693

Рис. 23.9
h{t) = be~bt
и корреляционной функции экспоненциального вида
Ошибка определения корреляционной функции найдется из
B3.54), рис. 23.10.
Как следует из записанного выражения и приведенных графи-
графиков, ошибка зависит от:
Кос - крутизны корреляционной функции и скорости изменения
задержки во времени;
b/Ка - соотношения между крутизной корреляционной функ-
функции, скоростью изменения задержки и постоянной фильтра;
т - значения задержки, для которого ведется рассмотрение.
Ошибка, сопровождающая транспонирование спектра, может
быть определена как
694
Раздел 23
из B3.53) получим
Переходя к т, запишем

Анализ характеристик случайного процесса
Для условий рассмотренного примера получим
B3.55)
где д = Ь/К = 1/ТК; Т- постоянная времени фильтра.
Ошибка зависит от тех же параметров, которые влияют на точ-
точность определения корреляционной функции. При заданном виде
корреляционной функции ошибка определяется соотношением
695
Рис. 23.10

Раздел 23
между скоростью изменения задержки и постоянной времени
фильтра. Для каждой корреляционной функции можно установить
такую скорость изменения задержки и выбрать параметры фильтра
таким образом, что ошибка, возникающая при транспонировании
спектра не будет превышать допустимого значения.
Если на вход перемножителя подается гармоническое колеба-
колебание
s(t)= VcosaHf, B3.56)
то при постоянной задержке т на выходе выделяется постоянная
составляющая, соответствующая корреляционной функции
Я(т) = —cos(o0x . B3.57)
При изменении задержки во времени с постоянной скоростью на
выходе фильтра выделяется сигнал (по аналогии с B3.49))
/ х V2 V2
z(t) = —cos(?HKt = —cosQf, B3.58)
где К- скорость изменения задержки во времени, Q = Ксоо.
Таким образом, коррелятор с переменной задержкой на одном из
входов выполняет функции преобразователя частоты. При К = 1CF3
на выходе выделяется также гармоническое колебание с частотой
на три порядка меньше частоты колебания на входе (рис. 23.11). На
рисунке изображены спектральная плотность сигнала на входе
S^w) и выходе 52(со) преобразователя.
Наряду со схемной простотой корреляционный преобразова-
преобразователь частоты обеспечивает помехоустойчивость системы. Если на
коррелятор помимо гармонического колебания воздействует шум,
корреляционная функция которого Яп(т) = Яп@)гл(т), то при изме-
изменении во времени задержки (т = Kt) на выходе преобразователя
Рис. 23.11
696

Анализ характеристик случайного процесса
выделяется непериодическое колебание zn(t) = Rn@)rn(Kt). При
достаточно большом значении т (или t) значение zn(t) может быть
получено достаточно малым (рис. 23.12).
Помимо постоянной составляющей (при переменной задержке
т - медленно меняющаяся во времени составляющая) на выходе
коррелятора присутствуют флуктуации (рис. 23.12). При нормаль-
нормальном распределении шума корреляционная функция флуктуации на
выходе перемножителя определяется выражением B3.10)
где Ял(т) - корреляционная функция шума на входе.
При достаточно большом значении Т имеем
B3.59)
B3.60)
Спектральная плотность мощности флуктуации на выходе пе-
перемножителя определится выражением
B3.61)
где Л/(со) - спектральная плотность шума на входе.
Спектральная плотность мощности колебания на выходе
фильтра
ЧыхМ = |Н(а)|2Л/(ш) B3.62)
Дисперсия колебания на выходе фильтра описывается выраже-
выражением
Рис. 23.12
697

Раздел 23
оо оо
ст2 =- f Л/вых(ш)А)=1 f|H(cof Л/(©)око. B3.63)
о о
Для узкополосного фильтра
1 ' [0, остальные знач. со
из B3.63) получим
а2 = — A/(fi) = — Л/(Ксо0) • B3.65)
Как следует из B3.65), а2 зависит от спектральной плотности
мощности шума (на выходе перемножителя) в полосе пропускания
фильтра и ширины полосы пропускания фильтра. Сужая полосу
пропускания фильтра, можно добиться снижения уровня флуктуа-
флуктуации шума на выходе. Ограничения, накладываемые на выбор по-
полосы пропускания, обусловлены ее влиянием на передачу гармо-
гармонического колебания.
698

СПИСОК ЛИТЕРАТУРЫ К ЧАСТИ 2
1. Амиантов И.Н. Избранные вопросы статистической теории связи. -
М.: Сов. радио, 1971.
2. Бакут П.А. и др. Вопросы статистической теории радиолокации. -М.:
Сов. радио, 1963.
3. Бендат Дж. Основы теории случайных шумов и ее применение. -М.:
Наука, 1965.
4. Бендат Дж., Пирсол А. Применения корреляционного и спектраль-
спектрального анализа. -М.: Мир, 1983.
5. Бендат Дж., Пирсол А. Измерение и анализ случайных процессов. -
М.:Мир, 1974.
6. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и управ-
управление. Вып.1 и вып.2. -М.: Мир, 1974.
7. Вайнштейн Л.А., Зубаков В.Д. Выделение сигналов на фоне слу-
случайных помех. -М.: Сов. радио, 1960.
8. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и
произведений. -М.: Госиздат физико-математической литературы, 1963.
9. Давенпорт В.Б., Рут В.Л. Введение в теорию случайных сигналов и
шумов. -М.: Изд-во.иностр. лит, 1960.
10. Денисенко А.Н. Сигналы с фазовой и частотной модуляцией. -М.:
Изд.Стандартов, 1994.
11. Деч Р. Нелинейные преобразования случайных процессов. -М.:
Сов. радио, 1965.
12. Дженкинс Г., Ватте Д. Спектральный анализ и его приложения. -
М.:Мир, 1971.
13. Засовин Э.А. и др. Радиотехнические и радиооптические системы.
-М.: Изд. Круглый год, 2001.
14. Кокс Д., Льюис П. Статистический анализ последовательностей
событий. -М.: Мир, 1969.
15. Купер Дж., Макгиллем Вероятностные методы анализа сигналов и
систем. -М.: Мир, 1989.
16. Левин Б.Р. Теоретические основы статистической радиотехники. -
М.: Радио и связь, 1989.
17. Лезин Ю.С. Оптимальные фильтры и накопители импульсных сиг-
сигналов. -М.: Сов. радио
18. Липкин И.А. Основы статистической радиотехники, теории инфор-
информации и кодирования. -М.: Сов. радио 1978.
19. Миддлтон. Введение в статистическую теорию связи. -М.: Сов. ра-
радио, т. 1 1961, т.2 1962.
699

20. Некоторые проблемы обнаружения сигнала, маскируемого флюк-
туационной помехой. Сборник статей под ред. И.И. Шнер. -М.: Сов. Радио,
1965.
21. Оуэн. Сборник статистических таблиц. -М.: Изд. ВЦ АН СССР,
1966.
22. Прием импульсных сигналов в присутствии шумов. Сборник пере-
переводных статей. -М.: Гос. Энергетич. Изд., 1960.
23. Романенко А.Ф., Сергеев ГА. Вопросы прикладного анализа слу-
случайных процессов. -М.: Сов. Радио, 1968.
24. Рытов СМ. Введение в статистическую радиофизику. -М.: Наука,
1976.
25. Свешников А.А. Прикладные методы теории случайных функций. -
Л.: Судпромгиз, 1961.
26. Стейн С, Джонс Дж. Принципы современной теории связи и их
применение к передаче дискретных сообщений. -М.: Связь, 1971.
27. Стратанович Р.Л. Избранные вопросы теории флюктуации в ра-
радиотехнике. -М.: Сов. радио, 1961.
28. Тихонов В.И. Статистическая радиотехника. -М.: Радио и связь,
1982.
29. Тихонов В.И. Выбросы случайных процессов, -М.: Наука, 1970.
30. Фалькович. Прием радиолокационных сигналов на фоне флюктуа-
ционных помех. -М.: Сов. радио, 1961.
31. Феллер. Введение в теорию вероятностей и ее приложения т.1 и
т.2.-М.:Мир, 1984.
32. Худсон Д. Статистика для физиков. -М.: Мир, 1967.
33. Шахтарин Б.И. Случайные процессы в радиотехнике. -М.: Радио и
связь, 2000.
34. Янке Е., Эмде Ф., Леш Ф. Специальные функции. -М.: Наука, 1988.
35. Marcum J,l, Swerling P. Studies of target detection by pulsed radar,
IRE Trunsections on information theory, v. IT-6, april 1960.
36. Rice S.O. Mathematical analysis of random noise. BSTJ, 1944, v 23,
N3; 1945,v24,N1.
700

ОГЛАВЛЕНИЕ
Предисловие 3
Часть 1. ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 7
Раздел 1. Сигналы и их представление 8
1.1. Описание сигналов временными функциями 10
1.2. Представление сигналов ортогональными рядами 17
1.3. Интегральное представление сигналов 22
1.4. Векторное представление сигналов 25
1.5. Энергия и мощность сигналов 28
1.6. Основные виды сигналов 31
Раздел 2. Обобщенный спектральный анализ сигналов 34
2.1. Обобщенный ряд Фурье 34
2.2. Спектральный анализ сигналов на основе системы
тригонометрических функций 36
2.3. Спектральный анализ сигналов на основе многочленов
Лежандра 39
2.4. Спектральный анализ сигналов на основе многочленов
Чебышева 41
2.5. Спектральный анализ сигналов на основе многочленов
Лагерра 44
2.6. Спектральный анализ сигналов на основе многочленов
Эрмита 45
2.7. Спектральный анализ сигналов на основе функций Уолша 47
Раздел 3. Гармонический анализ сигналов 59
3.1. Гармонический анализ периодических сигналов 59
3.2. Гармонический анализ непериодических сигналов 64
3.3. Частотные спектры сигналов, представленных
в виде обобщенного ряда Фурье 78
3.4. Спектры сигналов, описываемых
неинтегрируемыми функциями 82
3.5. Свойства преобразования Фурье и их использование
при анализе сигналов 87
3.6. Спектральный анализ сигналов на основе использования
преобразования Хартли
Раздел 4. Анализ сигналов на основе преобразования Лапласа 106
4.1. Преобразование Лапласа и его свойства 106
4.2. Обратное преобразование Лапласа 112
Раздел 5. Корреляционный анализ сигналов 127
5.1. Корреляционные функции периодических сигналов 127
5.2. Соотношение между корреляционной функцией
и спектром периодического сигнала 129
5.3. Корреляционные функции непериодических сигналов 131
5.4. Соотношение между корреляционной функцией
и спектром непериодического сигнала 144
5.5. Интервал корреляции и эффективная ширина спектра сигнала 147
Раздел 6. Дискретизация и восстановление
непрерывных сигналов 150
6.1. Дискретные и цифровые сигналы 150
6.2. Спектр дискретного сигнала 151
6.3. Дискретное преобразование Фурье и его свойства 156
6.4. Алгоритмы быстрого преобразования Фурье 159
701

6.5. Дискретное преобразование Хартли и его свойства 161
6.6. Z-преобразование и его использование при анализе
дискретных сигналов 162
6.7. Восстановление непрерывного сигнала
по дискретным значениям 169
Раздел 7. Восстановление непрерывных сигналов
с помощью сплайнов 178
7.1. Кубические сплайны первой степени гладкости 179
7.2. Кубические сплайны второй степени гладкости 181
7.3. Подход к построению локальных сплайнов 182
7.4. Локальные сплайны нечетной степени гладкости 184
7.5. Локальные сплайны четной степени гладкости 188
Раздел 8. Узкополосные сигналы 199
8.1. Описание узкополосного сигнала 199
8.2. Сумма и произведение узкополосных сигналов 201
8.3. Спектр узкополосного сигнала 202
8.4. Корреляционные функции узкополосных сигналов 206
8.5. Аналитический сигнал 210
8.6. Обобщенная корреляционная функция сигнала 211
8.7. Дискретизация узкополосного сигнала 215
8.8. Модулированные сигналы 217
Раздел 9. Амплитудно-модулированные сигналы 218
9.1. Описание AM сигнала 218
9.2. Тональная амплитудная модуляция 219
9.3. Многотональная амплитудная модуляция 221
9.4. Амплитудная модуляция периодической последовательностью
импульсов 223
9.5. Амплитудная модуляция непериодической последовательностью
импульсов 226
9.6. Балансная амплитудная модуляция 230
9.7. Однополосная амплитудная модуляция 233
Раздел 10. Сигналы с фазовой и частотной модуляцией 235
10.1. Описание сигналов с угловой модуляцией 235
10.2. Сигнал с тональной угловой модуляцией 238
10.3. Сигнал со сложным периодическим законом модуляции 241
Раздел 11. Импульсные сигналы с частотной модуляцией 256
11.1. Описание ЛЧМ сигналов 256
11.2. Спектр ЛЧМ сигнала с нечетносимметричным
законом модуляции 258
11.3. Приближенное определение спектра ЛЧМ сигнала 261
11.4. Спектр пачки импульсов с внутриимпульсной ЛЧМ 264
11.5. Корреляционная функция ЛЧМ сигнала при
нечетной симметрии закона модуляции 268
11.6. Спектр и корреляционная функция ЛЧМ сигнала
с четносимметричным законом модуляции 270
11.7. Влияние искажений закона модуляции
на характеристики сигнала 273
11.8. Влияние ступенчатой аппроксимации закона
изменения фазы на спектр сигнала 284
11.9. Прохождение ЛЧМ сигнала через согласованный фильтр 286
11.10. Импульсные сигналы с нелинейной частотной модуляцией 291
Раздел 12 311
12.1. Описание кодированных сигналов 312
12.2. Ампдитудно-кодированные сигналы 313
12.3. Фазо-кодированные сигналы 321
12.4. Частотно-кодированные сигналы 338
Раздел 13. Анализ сигналов в линейных цепях 341
13.1. Прохождение сигнала через линейную цепь 341
702

13.2 Прохождение сигнала через узкополосную цепь 350
13.3. Прохождение сигнала через цифровой фильтр 357
Список литературы к части 1 363
Часть 2. СЛУЧАЙНЫЕ СИГНАЛЫ И ШУМЫ 365
Раздел 14. Случайные процессы, их характеристики и классификация 366
14.1. Детерминированные и случайные сигналы 366
14.2. Шумы 371
14.3. Основные характеристики случайных процессов 374
14.4. Классификация случайных процессов 378
Раздел 15. Одномерное распределение вероятностей
случайного процесса 384
15.1. Одномерная функция распределения и плотность
распределения вероятностей случайного процесса 384
15.2. Эргодические случайные процессы,
их характеристики распределения 390
15.3. Некоторые виды случайных процессов 391
15.4. Представление плотности распределения вероятностей
случайного процесса с помощью ортогональных многочленов 408
15.5. Одномерное распределение вероятностей
функции случайного процесса 415
15.6. Характеристическая функция случайного процесса 428
Раздел. 16. Многомерное распределение вероятностей
случайного процесса 432
16.1. Многомерная функция распределения и плотность
распределения вероятностей случайного процесса 432
16.2. Корреляционная функция случайного процесса 436
16.3. Многомерное распределение вероятностей
гауссовского процесса 441
16.4. Разложение двумерной плотности распределения
вероятностей в ряд по ортогональным системам функций 445
16.5. Условные характеристики распределения вероятностей
случайного процесса 447
16.6. Распределение случайного процесса на интервале времени 451
16.7. Многомерная характеристическая функция
случайного процесса 454
16.8. Марковские процессы 456
Раздел 17. Распределение вероятностей нескольких случайных
процессов и их функциональных преобразований 459
17.1. Совместное распределение вероятностей
двух случайных процессов 459
17.2. Распределение вероятностей функций случайных процессов 462
17.3. Некоторые виды функциональных преобразований
случайных процессов 466
17.4. Распределение вероятностей производной случайного процесса 474
17.5. Распределение вероятностей интеграла от случайного процесса 478
17.6. Характеристическая функция случайных процессов 479
17.7. Метод характеристических функций 480
Раздел. 18. Спектр случайного процесса 493
18.1. Понятие спектральной плотности мощности случайного процесса 493
18.2. Соотношение между спектральной плотностью мощности
и корреляционной функцией случайного процесса 494
18.3.Эффективная ширина спектра случайного процесса 510
18.4. Спектр производной и интеграла от случайного процесса 512
18.5. Дискретизация случайного процесса и его характеристик 516
Раздел 19. Узкополосные случайные процессы 520
19.1 Описание и характеристики узкополосных случайных процессов 520
19.2. Распределение вероятностей огибающей и фазы узкополосного
703

гауссовского процесса 527
19.3. Распределение огибающей и фазы смеси сигнала и шума 529
19.4. Модулированные случайные процессы 531
19.5. Случайный процесс с амплитудной модуляцией 532
19.6. Случайный процесс с угловой модуляцией 539
Раздел 20. Выбросы случайных процессов 564
20.1. Определение характеристик распределения длительности
выбросов с использованием ФРВ случайного процесса 564
20.2. Определение характеристик распределения длительности выбросов
с использованием частотных характеристик случайного процесса 576
20.3. Средняя частота следования и средняя длительность
выбросов случайного процесса 607
20.4. Средняя частота следования экстремумов случайного процесса 612
Раздел 21. Прохождение случайного процесса через линейную цепь 616
21.1. Характеристики линейной цепи 616
21.2. Распределение вероятностей случайного процесса
на выходе линейной цепи 618
21.3. Математическое ожидание и корреляционная функция
случайного процесса на выходе линейной цепи 620
21.4. Спектр случайного процесса на выходе линейной цепи 624
21.5. Оптимальные линейные цепи 639
Раздел 22. Нелинейные преобразования случайных процессов 645
22.1. Прямой метод определения характеристик случайного
процесса на выходе нелинейного устройства 645
22.2. Характеристики случайного процесса на выходе
нелинейного устройства со степенной характеристикой 649
22.3. Метод преобразований 663
22.4. Метод производных 669
Раздел 23. Анализ характеристик случайного процесса
на выходе множительного коррелятора 674
23.1. Распределение случайного процесса на выходе
перемножителя 674
23.2. Корреляционная функция и спектр случайного процесса
на выходе перемножителя 675
23.3. Характеристики случайного процесса
на выходе множительного коррелятора 679
23.4. Кратковременный анализ случайного процесса на выходе
множительного коррелятора 685
23.5. Характеристики сигнала на выходе корреляционного
транспонатора 691
Список литературы к части 2 699
704