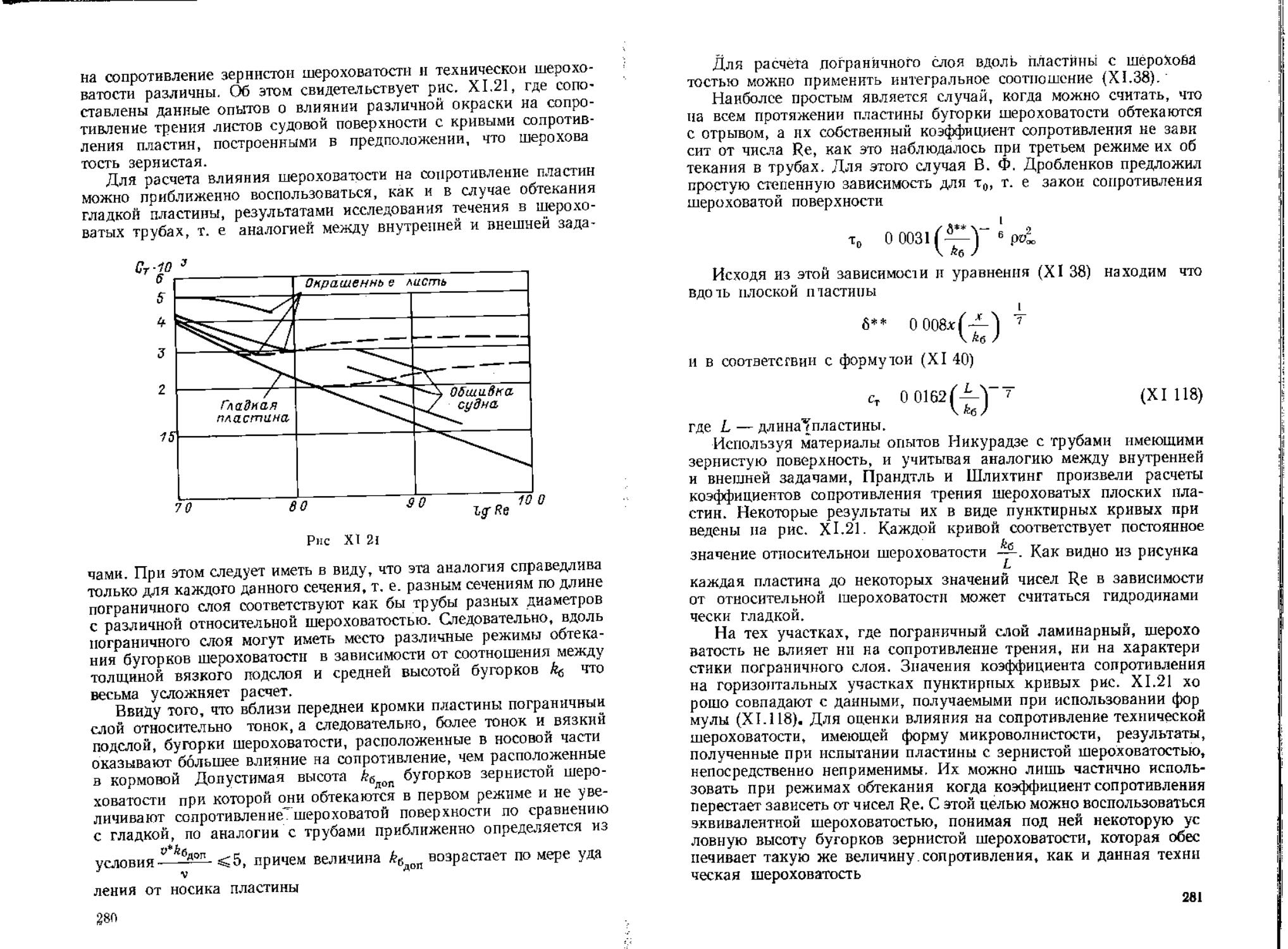
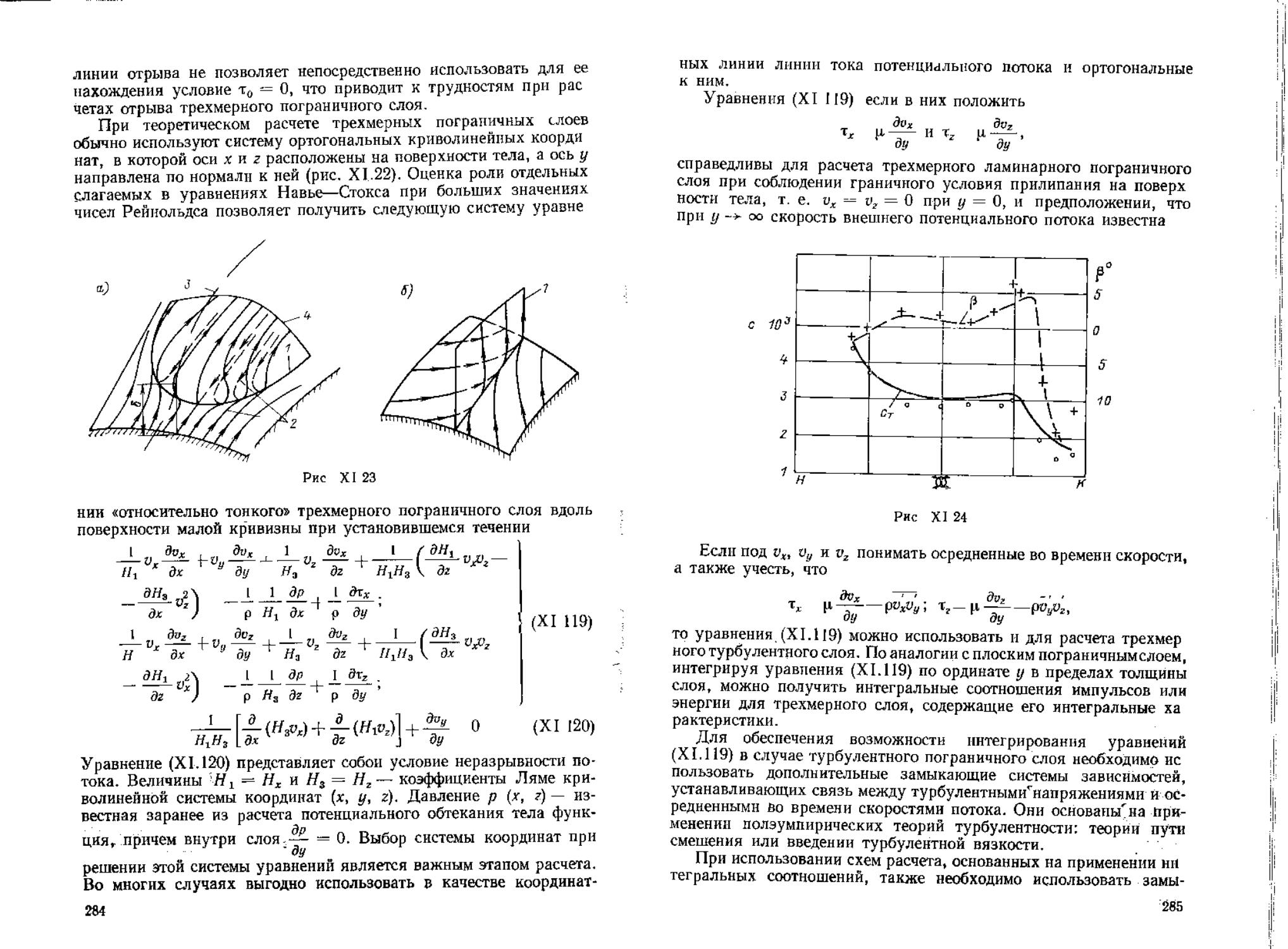
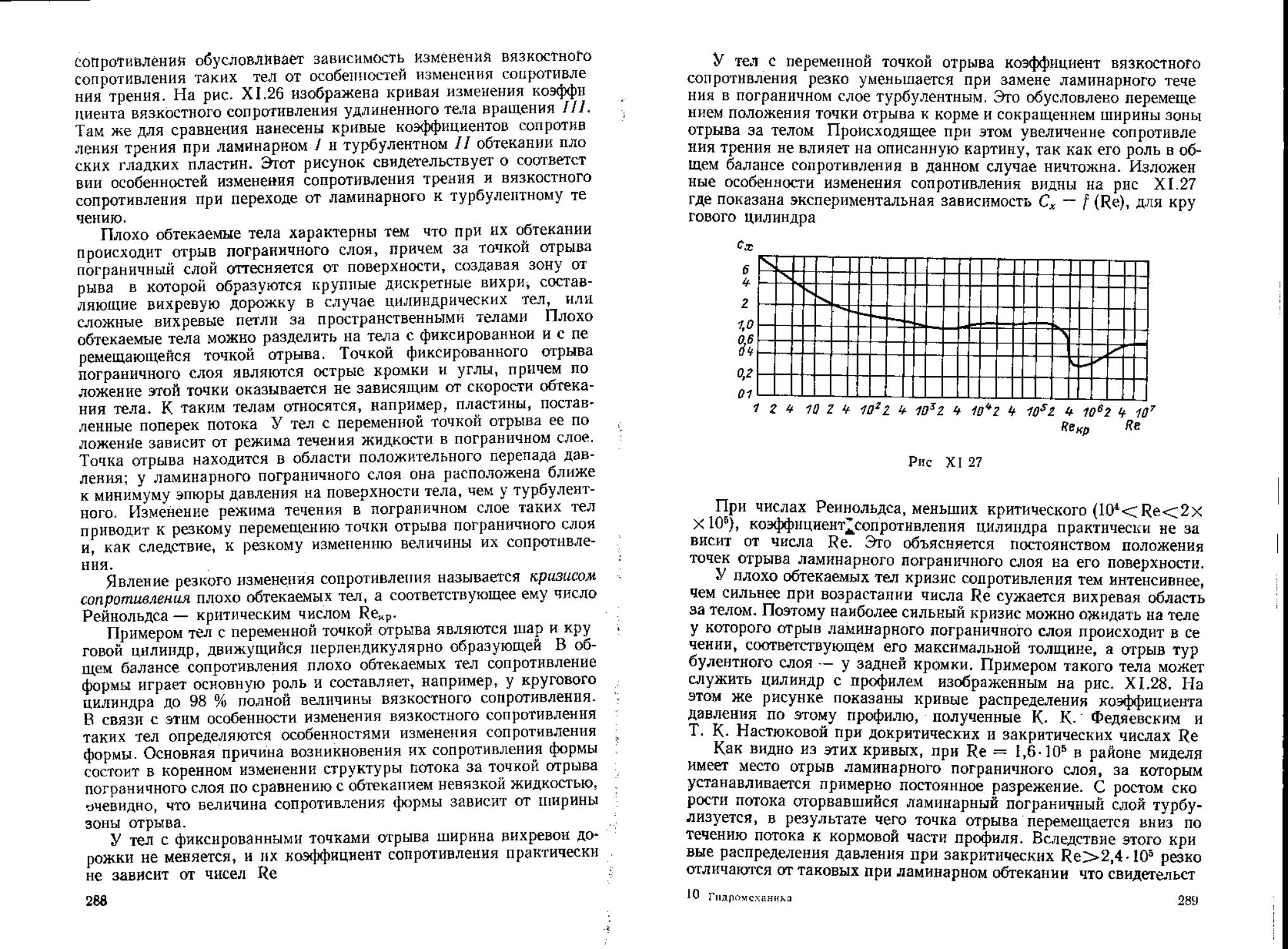
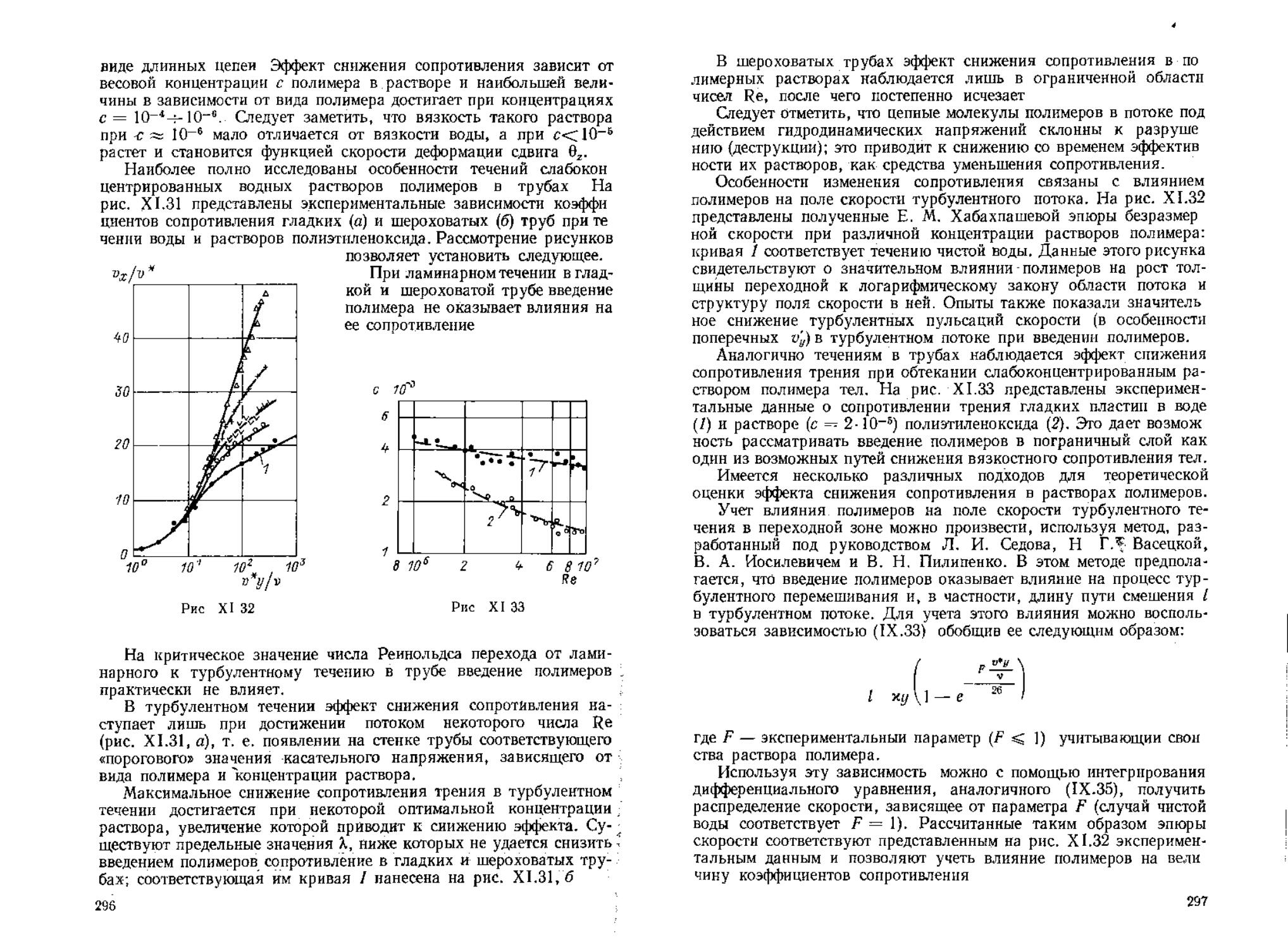
Author: Воиткунский Я.И. Фаддеев Ю.И. Федяевский К.К.
Tags: гидромеханика механика жидкостей и газа механика
Year: 1982
Text
Я И ВОИТКУНСКИИ,
Ю И ФАДДЕЕВ,
К К ФЕДЯЕВСКИЙ
ГИДРОМЕХАНИКА
$
СВОЙСТВА ЖИДКОСТИ
И УРАВНЕНИЯ ЕЕ ДВИЖЕНИЯ
§ 2, Классификация сип.
внешние нормали^ этим площадкам направлены противоположно
(1 11) на AS и используем" (1.12)
Устремим объем тетраэдра к нулю стягивая его в точку к на
pn = ptcos(n х)pycos(n, у)-гр^со&(п, z). (I.I3)
(1 14)
ния, а р*о, /„. — — касательные напр
КОВЫХ^ нХ" С₽аВИ"ВаЯ ” " “0Э<М™™ ”Р"
(I 23)
R vjzndS (1113)
Между скоростями абсолютного v0 и обращенного ообр течения
легко установить связь в виде векторного равенства (рис. III.4).
ляющей в форме произвольной кривой АВ и образующей единич
Прибавим и вычтем в левой части члены
grad — V + j dr
(IV 25)
g.
I
I
I
I
(V Ю)
vx (V 12)
d(iy)
Следовательно, tp и i|> в плоском потоке являются гармониче
сними функциями.
характеристическую функцию
чески этот случай, согласно теореме Стокса, соответствует наличию
в особой точке вихревой нити с циркуляцией Г. Поэтому иногда
это течение называют плоским вихрем- Вне вихревой нити течение
ординатой гх то характеристическая функция потока
(V 26)
течение называемое вихреисточником.У Характеристическая функ
(V 27)
точкой в начале координат, откуда происхо’
4. Плоский диполь Рассмотрим
числа в полярных координатах, легко от
(созб—i sin б)
с центром в начале координат. Величина Л1 — момент диполя
Линия, касательная вектору скорости в начале координат, назы
отрицательной оси х. Точка г - 0 является особой точкой этого
потока: в ней скорость стремится к бесконечности.
Характеристическая функция диполя с осью, образующей угол 0
называются течениями с гидродинамическими особенностями; их
используют в методе наложения для исследования обтекания ци
§ 22 Обтекание кругового цилиндра
В качестве иллюстрации применения метода наложения^рас
ций поступательного потока, текущего параллельно оси х [полагая
в (V.20) а = 0], диполя с осью, направленной вдоль отрицательной
оси х (V.28) и циркуляционного потока (V.24) с центром в начале
а,-у“г+1ГТ+‘^1пг
Величины о», М и Г считаются заданными постоянными Пе-
(V29)
переходя к декартовым координатам в которых
Вычислим радиальную составляющую скоростей рассматри
' дг
Видно, что радиальные с
На основании изложенного получим характеристическую функцию
и потенциал обтекания кругового цилиндра с циркуляцией Г в виде:
(V 31)
Проекции скоростей в потоке вокруг цилиндра
(V 32)
Из этих формул следует что всюду в области течения (при
г > ги) вне цилиндра скорости конечны т е особые точки в потоке
В точках поверхности цилиндра проекции скоростей представ
у -О Ч — 2оа,зше + ^--!-
ф. у}
где А >0 — постоянная. Эта функция представляет собой фунда
<V63)
(OSA) f
потенциальным бесциркуляционным потоком можно выполнить
используя метод интегральных уравнений.
странстве, включая поверхность S тела, распределим на этой по
верхности источники с интенсивностью q (хх, ylt ?1), образующие
потенциал простого слоя (рис. V.13). Потенциал обтекания тела
согласно (V 67) и (V.72) представим в виде
тл vJbtr’^vJlS*
1Ш
ОПРЕДЕЛЕНИЕ ГИДРОДИНАМИЧЕСКИХ
РЕАКЦИЙ ПРИ ДВИЖЕНИИ ТЕЛА
В НЕВЯЗКОЙ ЖИДКОСТИ
(V.7).
Cndl-0
X ф-^-cosO! x)dl JL^smpdZ
Y = ф cos (n y)dl =-------|-фо2со5Рс1/
тает вид ? Р Р Р
Тж--^ f x) + <P-^-cos(n, (,) +
—------^-cos^ x)-r-^-cos^ y)±^-cos^ Z)
Х11
p4rfTi^_‘is—t4',«cos<" ^ds <vi63>
(VII 25)
ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ
’ + 0-^ <vinil>
dl дх \ dy ) dy \ dx )
(VIIT 23)
%”« p Ptp
(VIII 34)
“ - kg-£- (grad A + -^ <Л»'б
-k (gradp),) — (Ла),. (VIIt 35)
"S P"c V
pn o(j- (VIII 46)
где наедены безразмерные радиусы гб - r/L Сила инерции рав-
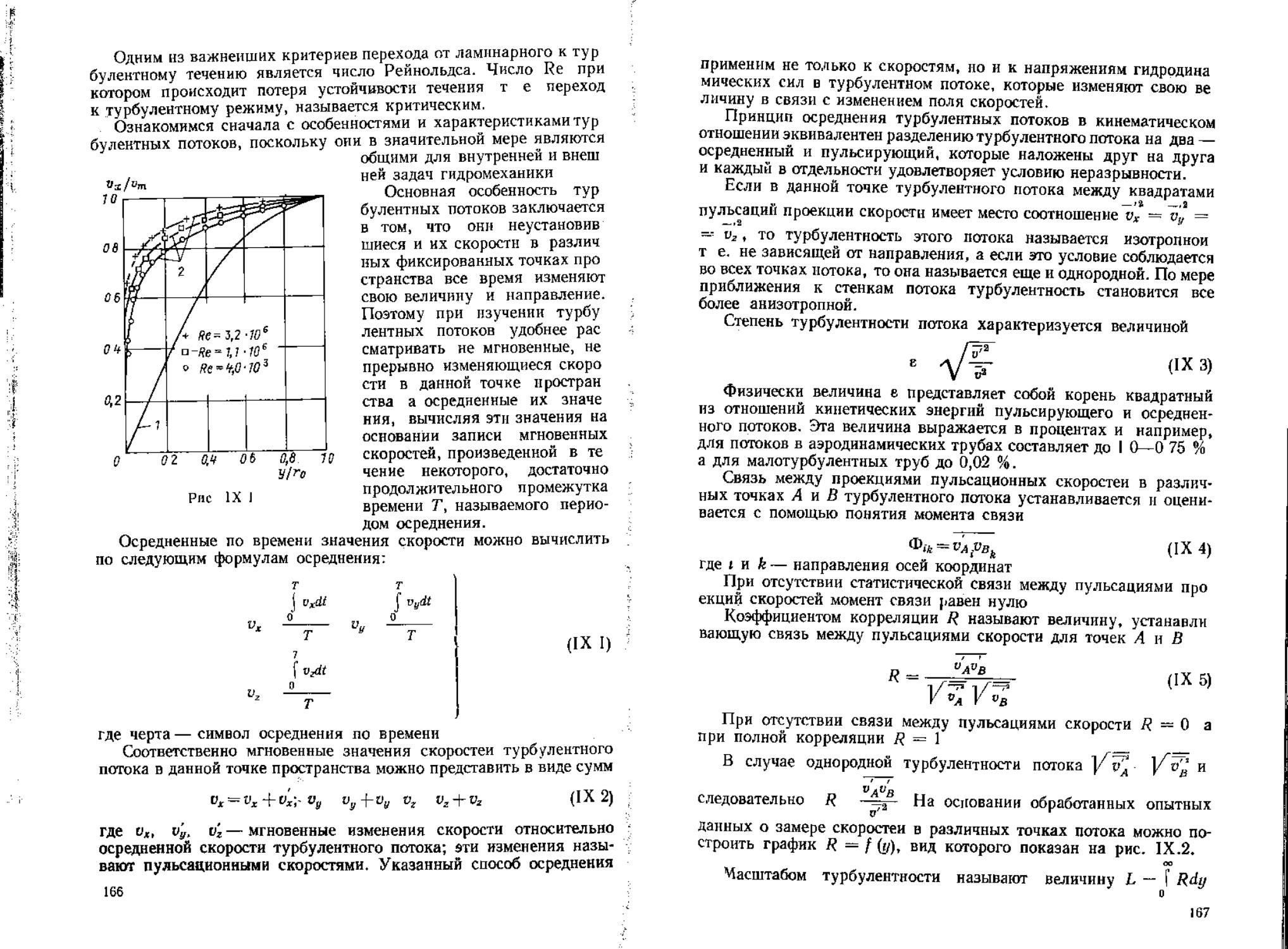
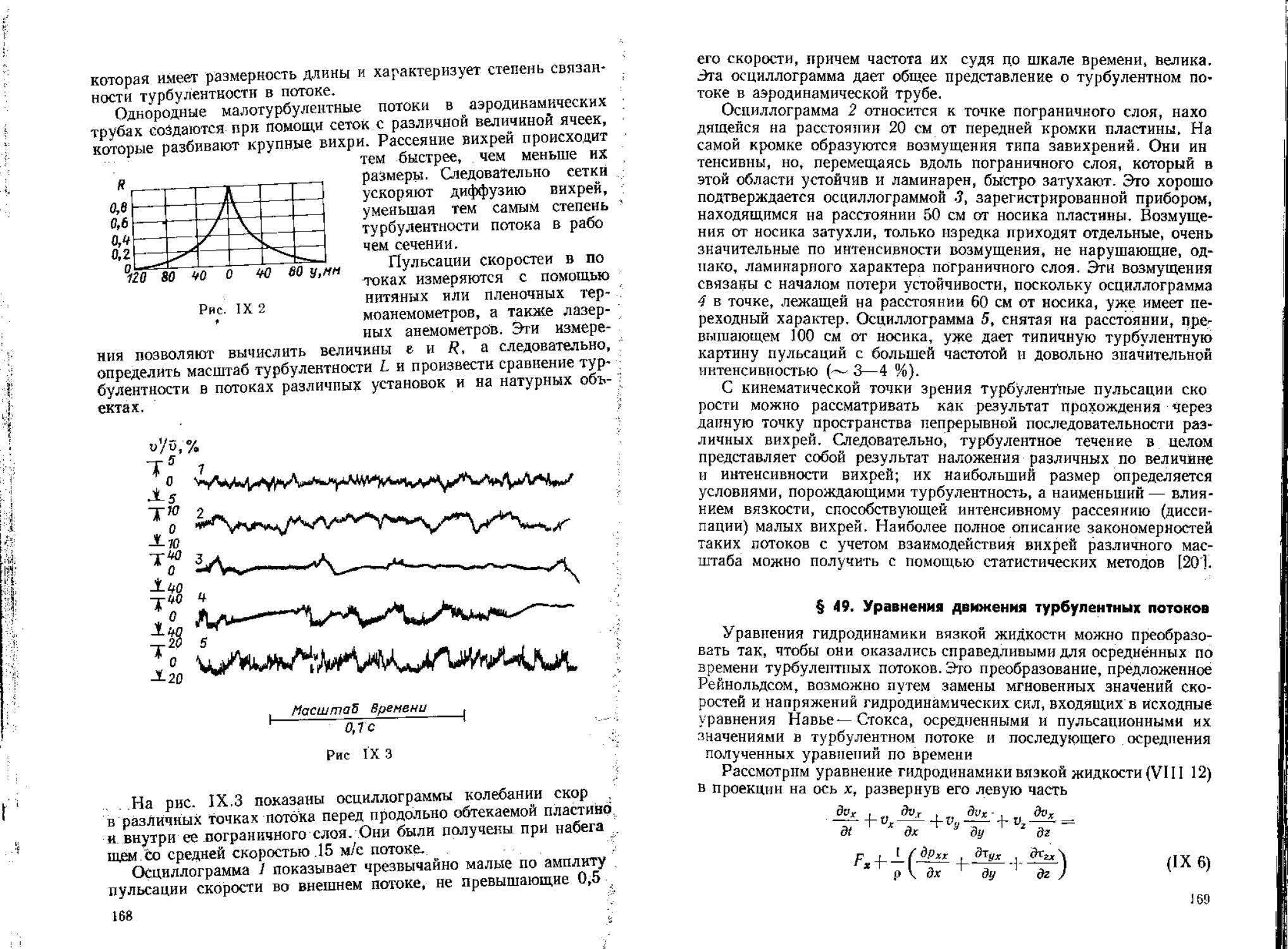
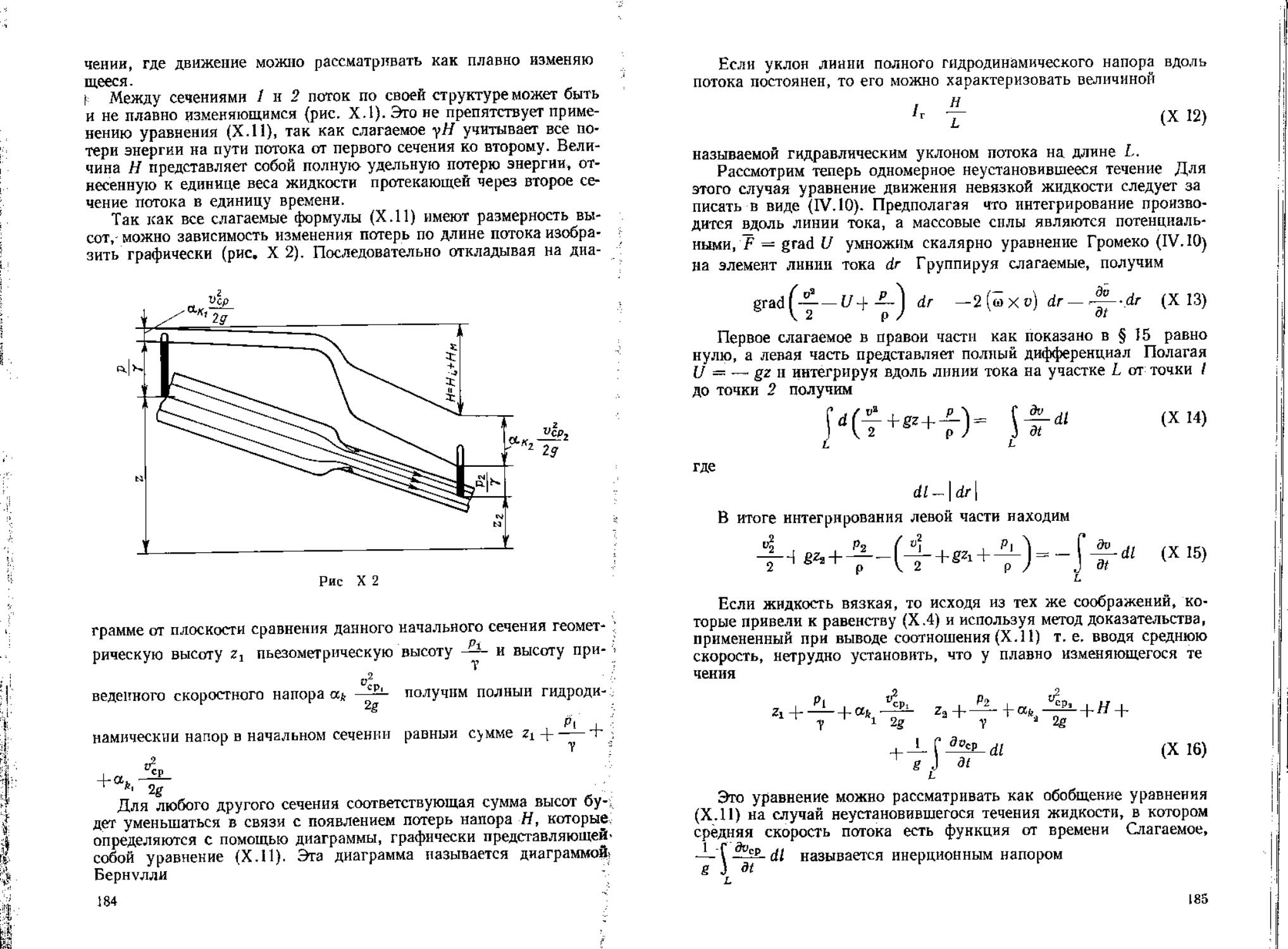
вают пульсационными скоростями. Указанный способ осреднения
(IX II)
(IX 12)
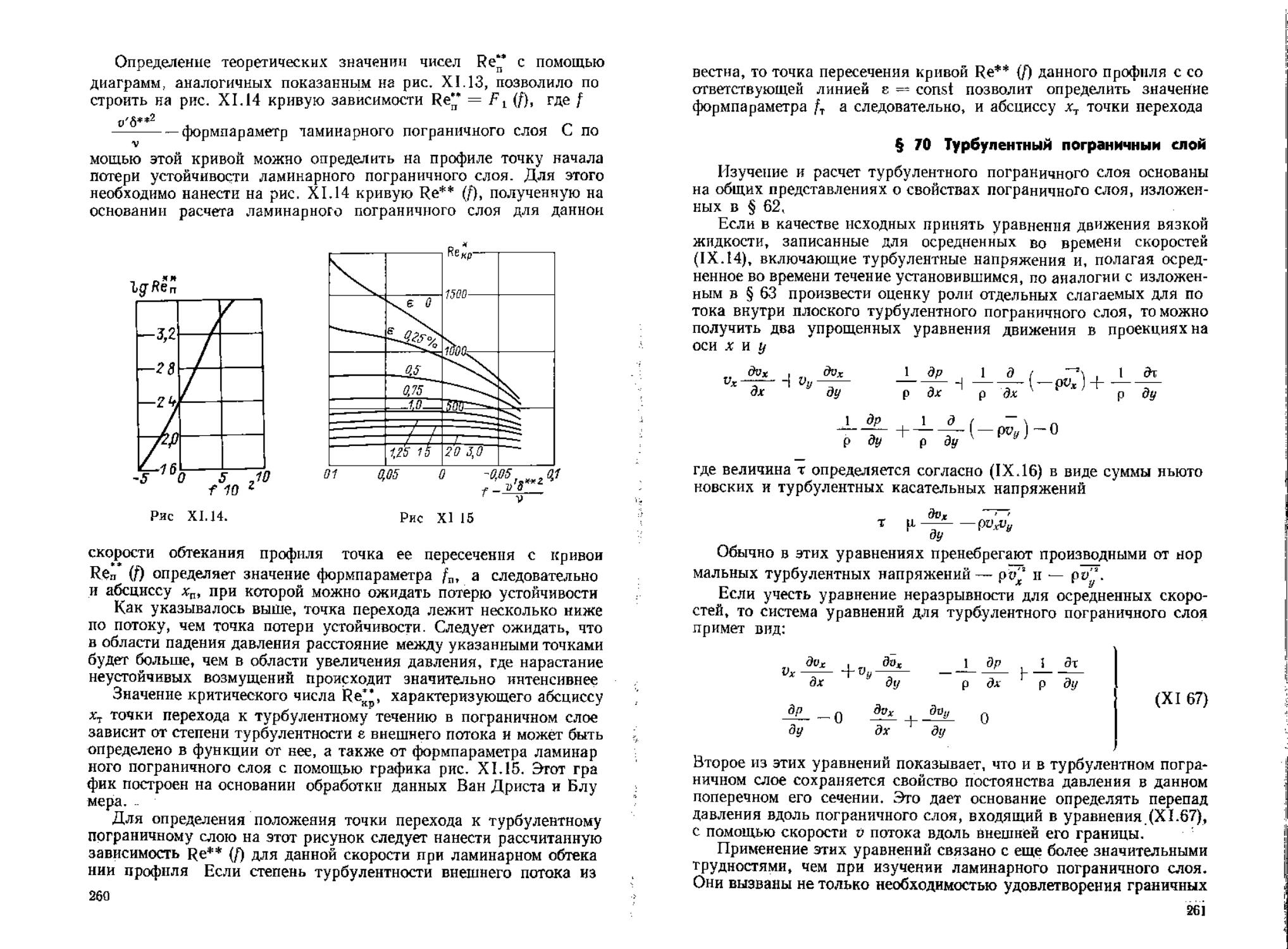
(XI 13)
17^+
т — -г — А А - ----А
ду dz р V дх ду dz )
-Р»л)] (XI 14)
I
I
I
(IX 19)
N pp(^)’ (1Х2°)
ВНУТРЕННЯЯ ЗАДАЧА ГИДРОМЕХАНИКИ
ВЯЗКОЙ ЖИДКОСТИ
(1X34)
Уравнение (X.I6) применяется при решении внутренних задач, когда необходимо учесть влияние нестационарное™ потока на его Н (X 18)
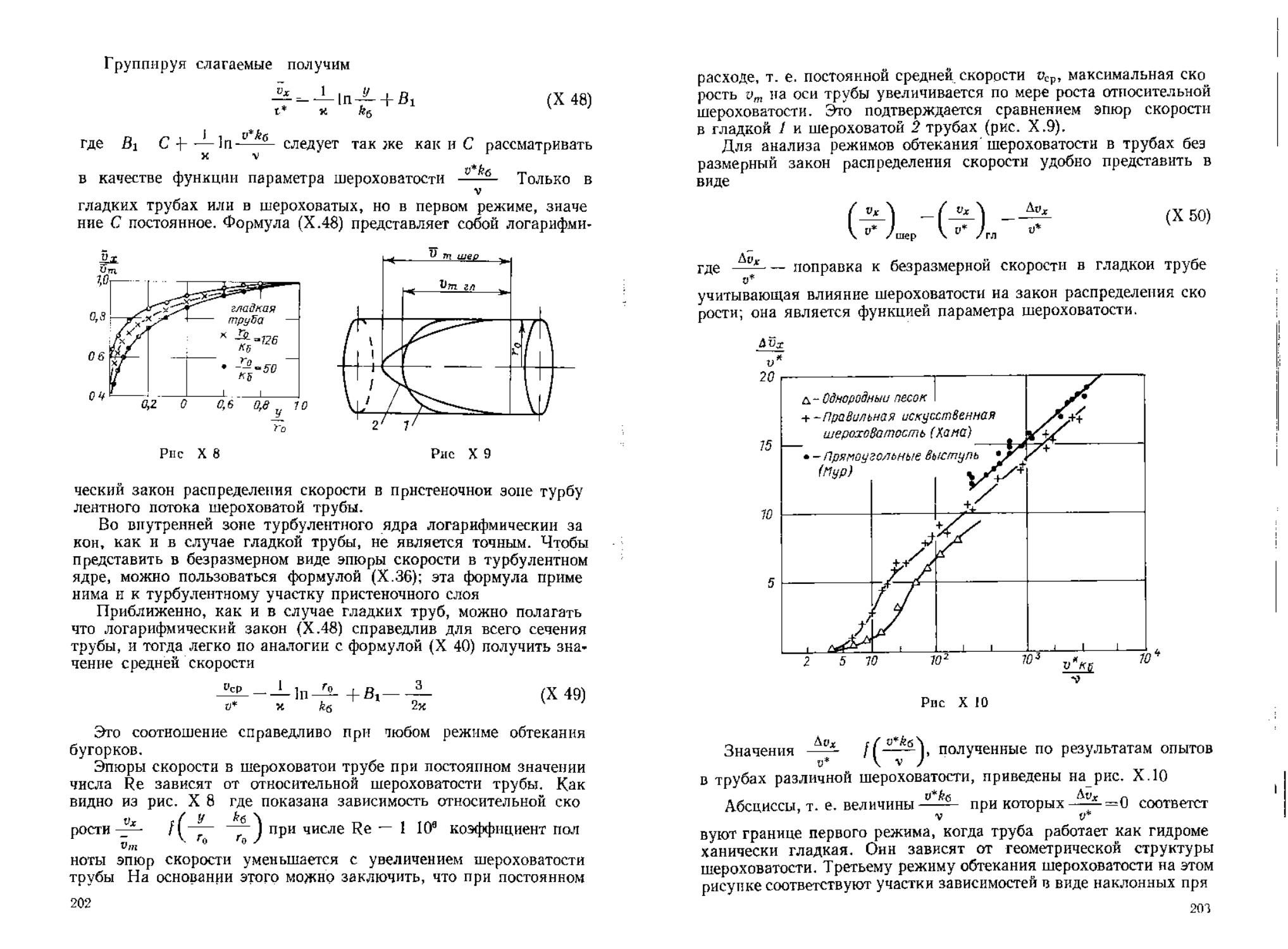
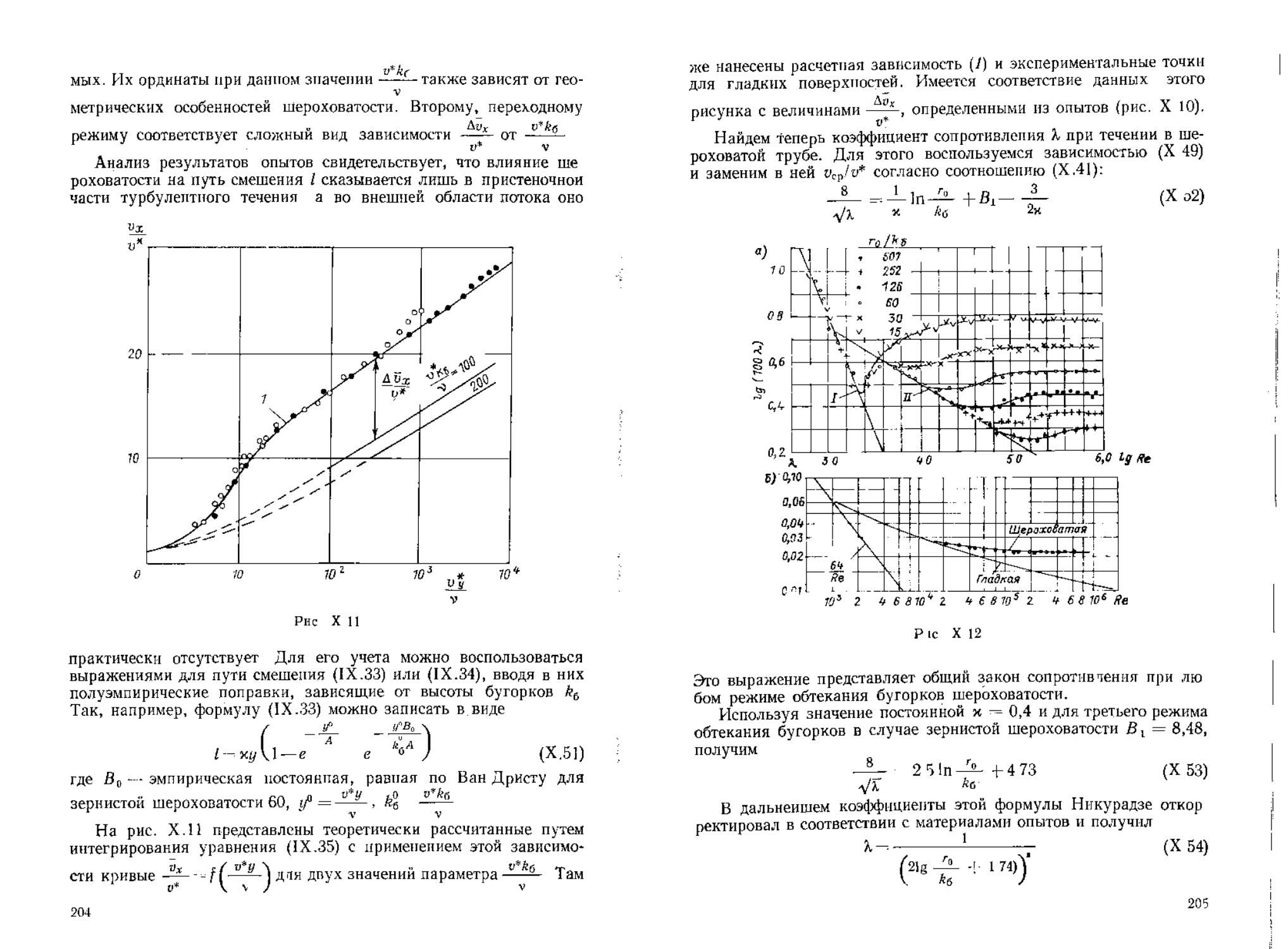
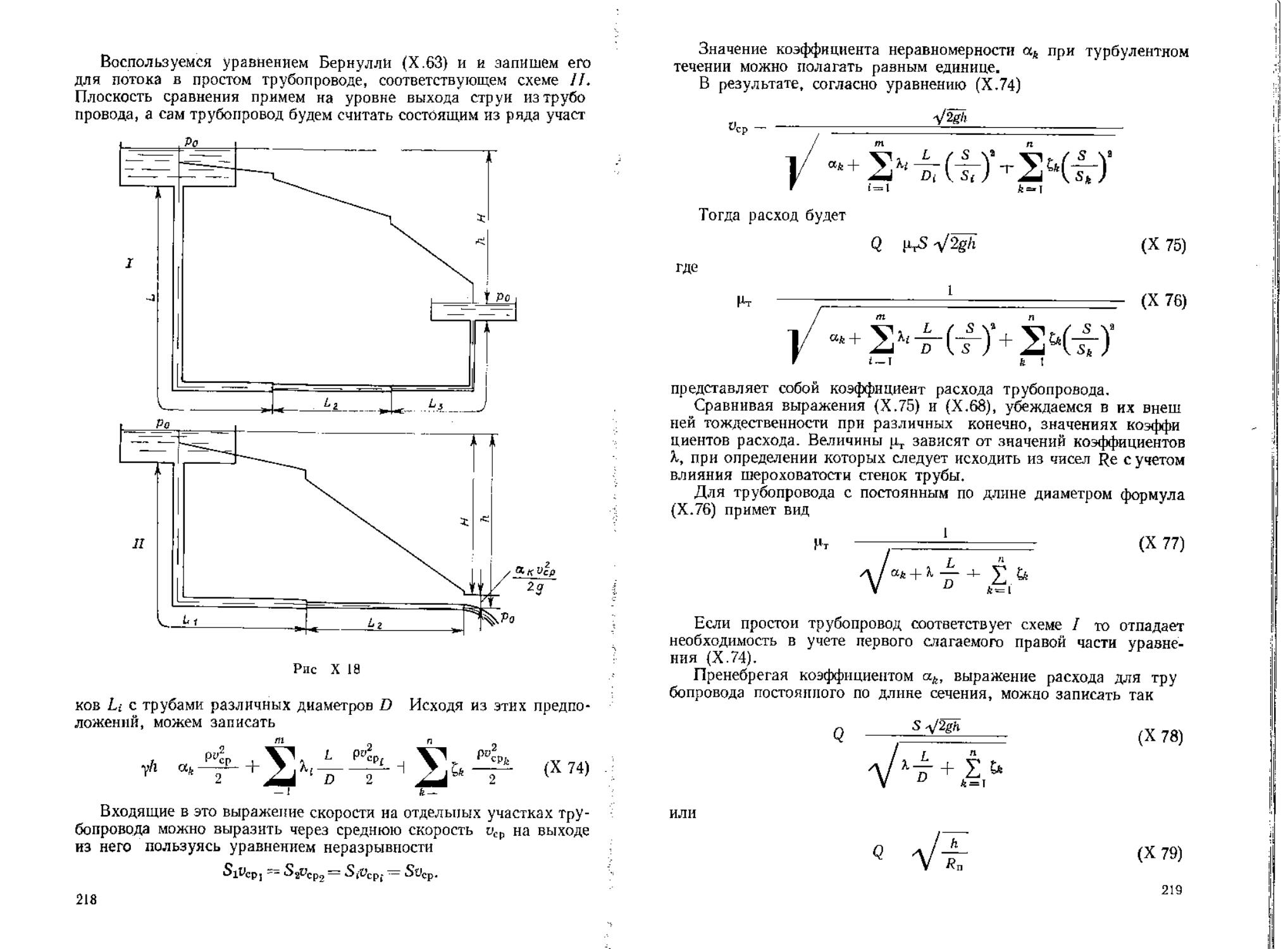
§ 53 Общие формулы для потерь напора критерии3динамиче,ск(И'о^подобияХпотоковХ^'аэтюй адлью^мот11
шения одномерных задач гидромеханики вязкой жидкости воз- можно только при условии создания формул для расчета потерь , напора Н, связывающих величину этих потерь с основными харак- ‘ ловлеяо появлением ссйрйивдения на пути данжеия потока ме жду-раеематрпваемыми...сечениями. Это-севротивление иногда на- . зывают- гидравлическим. С точки зрения расчета гидравлические сопротивления удобно разделить на два вида: сопротивления и свя- занные с ними потери энергии, распределенные по всей длине по- тока, и сопротивления местные. В связи с этим и удельную потерю напора Н можно представить в виде Н = HL + Ни. Она зависит от протяженности участков, в которых условия тече ння различны, например, вследствие разных диаметров или неоди- структуры потока, величины или направления его скорости. ' При расчете потерь напора широко используется принцип на- Й чТотдальнТ' В соответствин с ЭТИМ пРинЦипом предполагается, . ; ’ ристиками потока. Применяя этот принцип ₽можно величину1# для всего потока определить как сумму потерь по длине на отдель- • участке трубы с переменным сечением и местным сопротивлением р С OT„dS — | pndS г J TosdS
(X 17) : — р р f v22dS PlSl—p2S2—
1 Как показывают результаты опытов, это выражение можно рас- У Значения П, и Нк могут быть определены экспериментально. ? t| разность высот zT и ze, разность показаний пьезометров -Р1~Рг- , | установленных в начале и конце участка, где расположено исследу- ' | емое сопротивление, и разность скоростных напоров а*”сР»~* % в потоке При исследованиях, производимых в горизонтальной ? — [t0cos(s x)d5— ] pcos(« x)dS номерности распределения^скорости' по сечению трубы на квадрат
то полученная формула позволит выразить перепад давления в еле-
4- J т0 cos (s х) dS± J p cos (n x) dS
co смоченным периметромWТогда в формуле (Х.19) будет cos (s.
(X 19)
yHL (X 20)
стенке т0 можно согласно (VIII.50) выразить через безразмерный
честве которой в данном случае принимается средняя скорость
Подставив это выражение в (X 20)
(Х21) ;
(X 22)
(X 25)
Постоянную интегрирования С определяем используя граничное
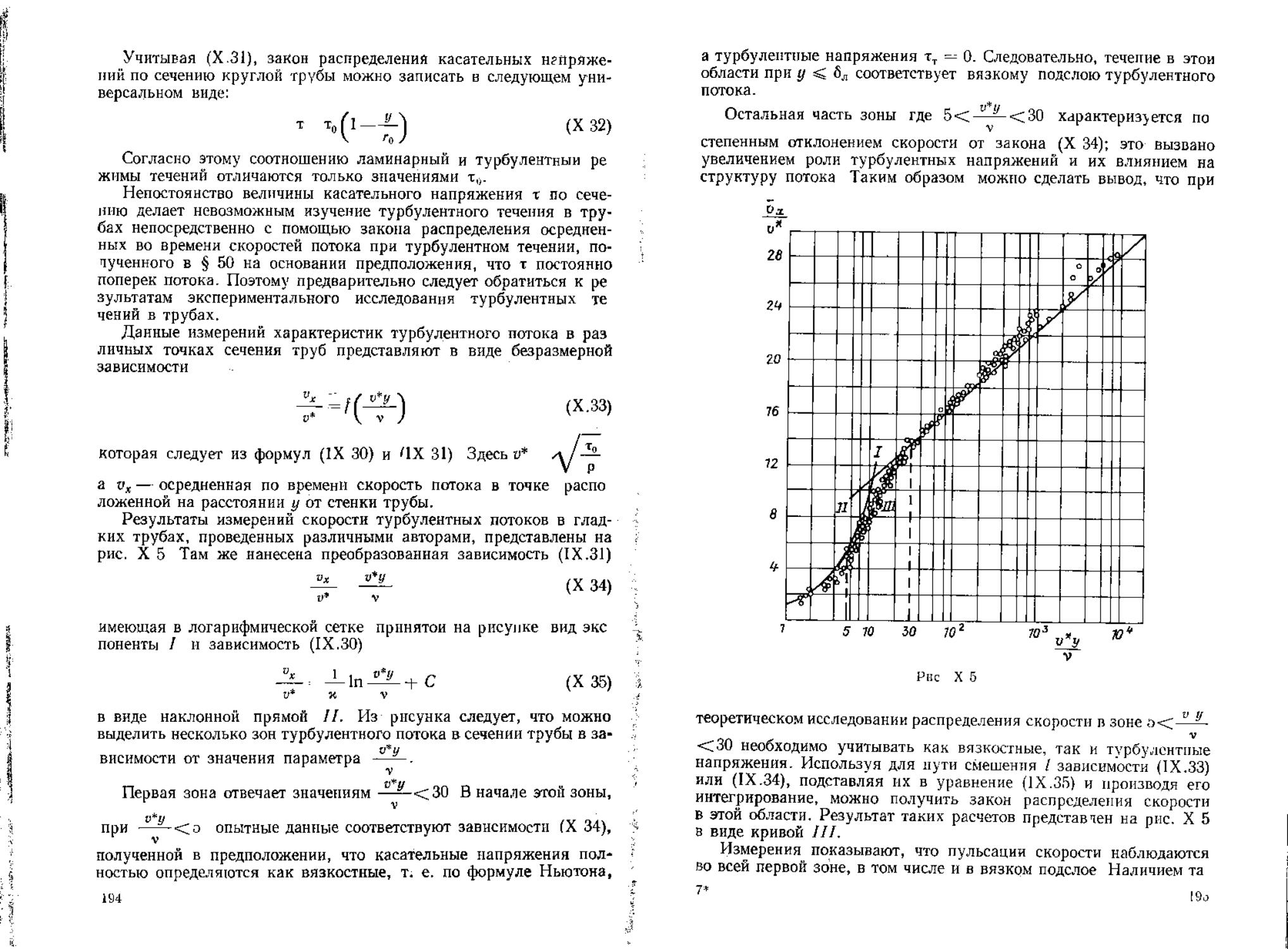
напряжения. Используя для пути смешения I зависимости (IX.33)
или (IX.34), подставляя их в уравнение (IX.35) и производя его
в виде кривой 7//ЗУЛЬТаТ ТЗКИХ расчетов пРеДставчен на рис. X 5
(X 38)
. степени \1п в этой фор
Re = 4-10’ч-3- 10е
т Ve до VI0. Прини
только при l-105’>Re>2,4-J03. Формула (Х.44) позволяет уста
где оно формируется после
2 lg (Re-\А ) —0 8
(X 43)
(X 63)
I
f
i‘s д/2г(л +
Si^cp; SafCp2 = SjOCp. — SvCp.
(X 80)
согласно формуле (X.83) У ''
Q S^f^- K-JTr
Здесь /н, HL । г
It —It R^tiQ^. (X 84)
В-8 “ I
s S S S
(XI 6)
Так как ускорения и силы вязкости
(XI 7)
6** - 0 664 ,
’° 11 (4г).,.» (Х1'2о>
Рассмотрим плоский пограничный слой конечной толщины
вдоль криволинейном поверхности. Применим закон количества
движения к объему жидкости ABCD (рис. X 1.8). заключенному ме
жду двумя бесконечно близкими сечениями пограничного слоя 4й
ницеи счояВС^О&Г + ТВерЛ°}' стснкой AD и внешней гра
с-кцию на ось л количества движения жидкости, переносимых сквозь
слоя можно с ошиокои высшего порядка малости принять скорость
1^6** - | у (a — vt)dt/ [
а “ (XI 34)
об* Ци-lA |
(XI 32)
-М(рЛ") + -^-рЛ*-т. (XI35)
Подставляя сюда из (XI 31) значения величин т и /, находим
<Х136>
RT = pvlf>'i't
Определив по форму те (XI.53) величину f можем вычислить
для любой абсциссы х вдоль поверхности тела толщину потерн
импульса по формуле
(XI 54)
висимостью (IX.16) ₽ Р < ) Р А
области потока внутри пограничного слоя можно получить интег
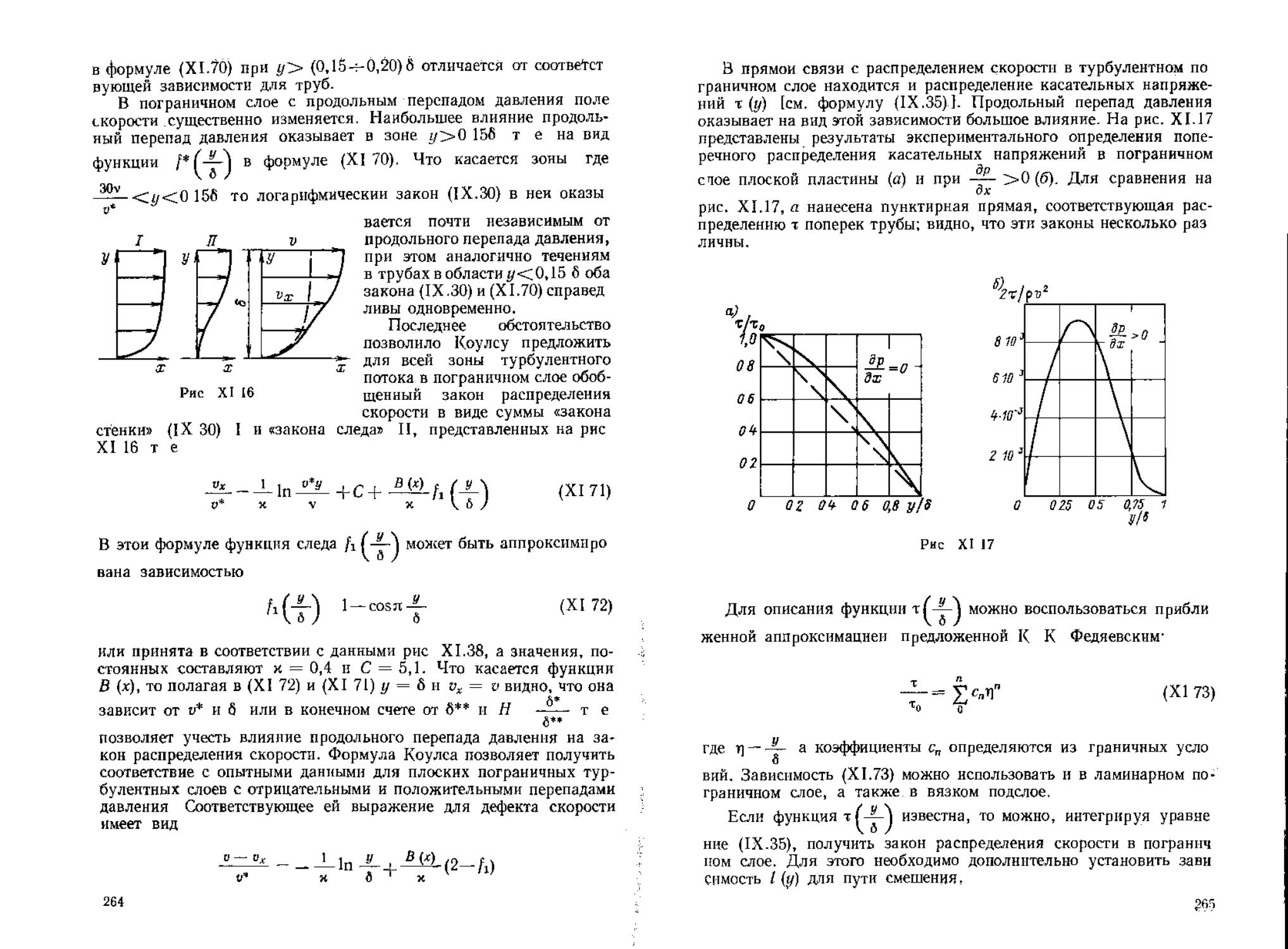
-1-^- [»(6-б*)1
<х,70>
^„2^-0 030б(^-3)“И
профиль скорости определяется единственным параметром р*2.
В непосредственной близости от твердой поверхности ^турбу
" (Х.94)
as 0,585 —0,125g 420,4^
а4 = 0 28 —0 034£-j-(0 1£)9
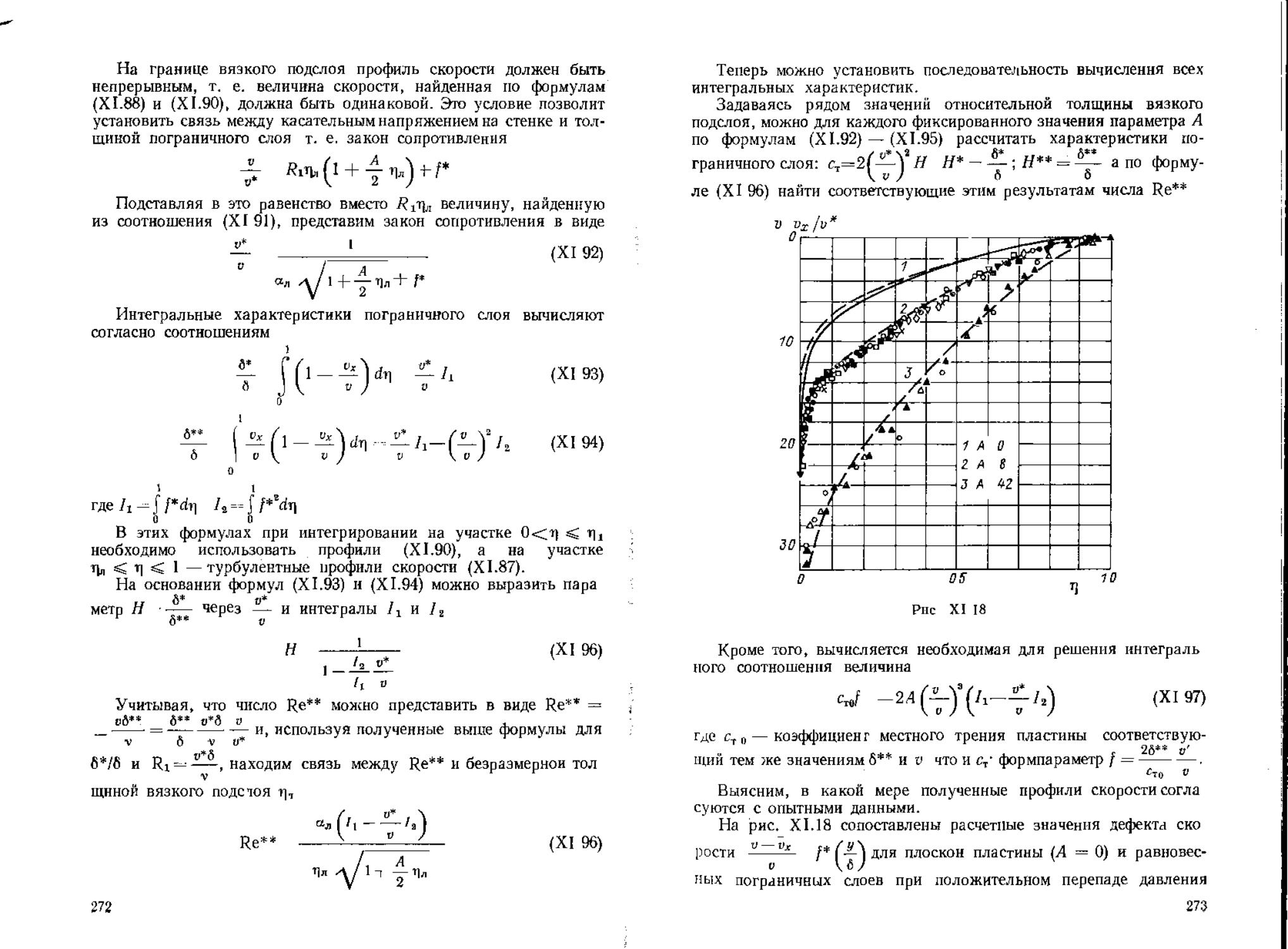
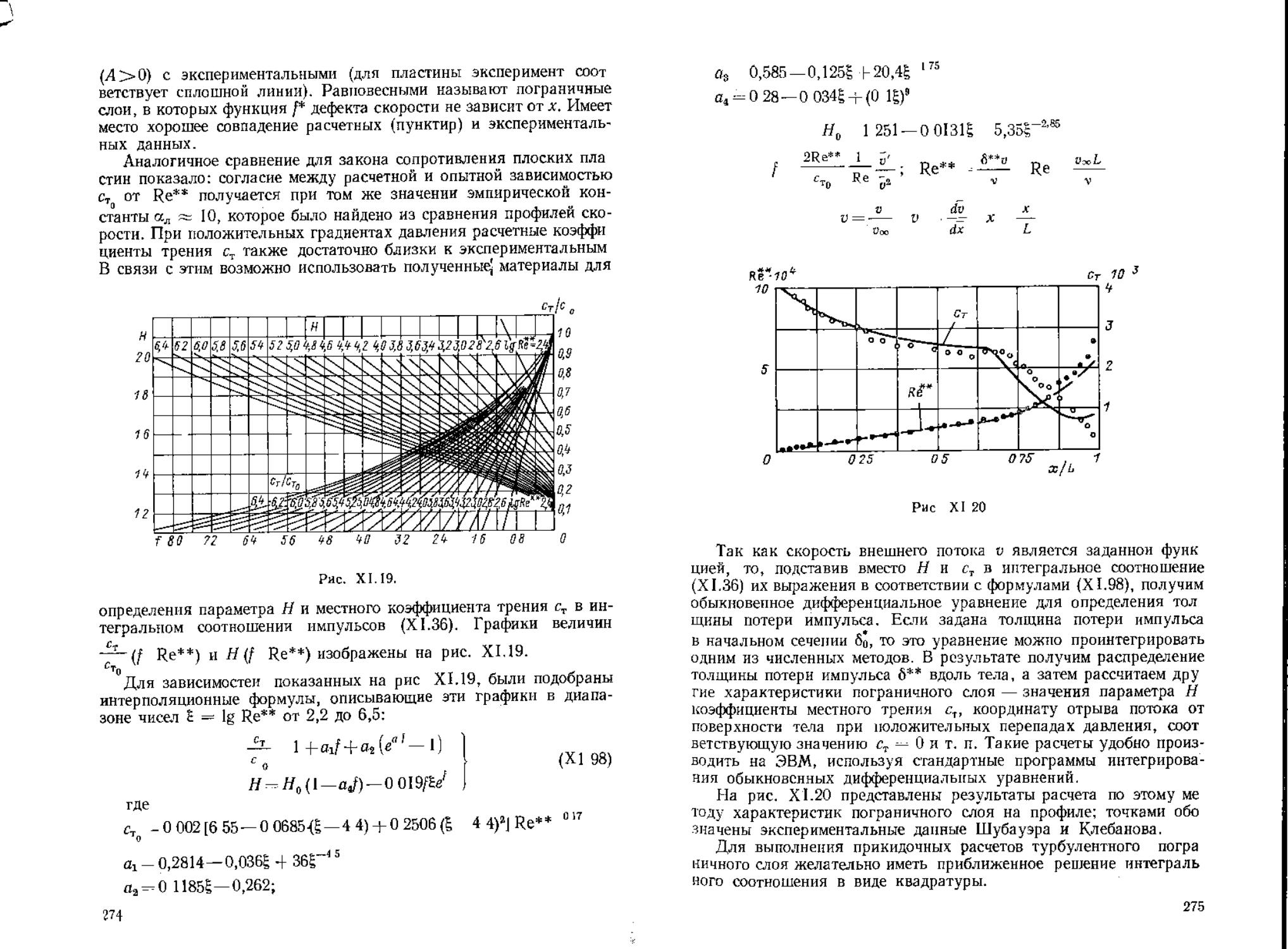
определения параметра Н и местного коэффициента трения ст в ин-
тегральном соотношении импульсов (XI.36). Графики величин
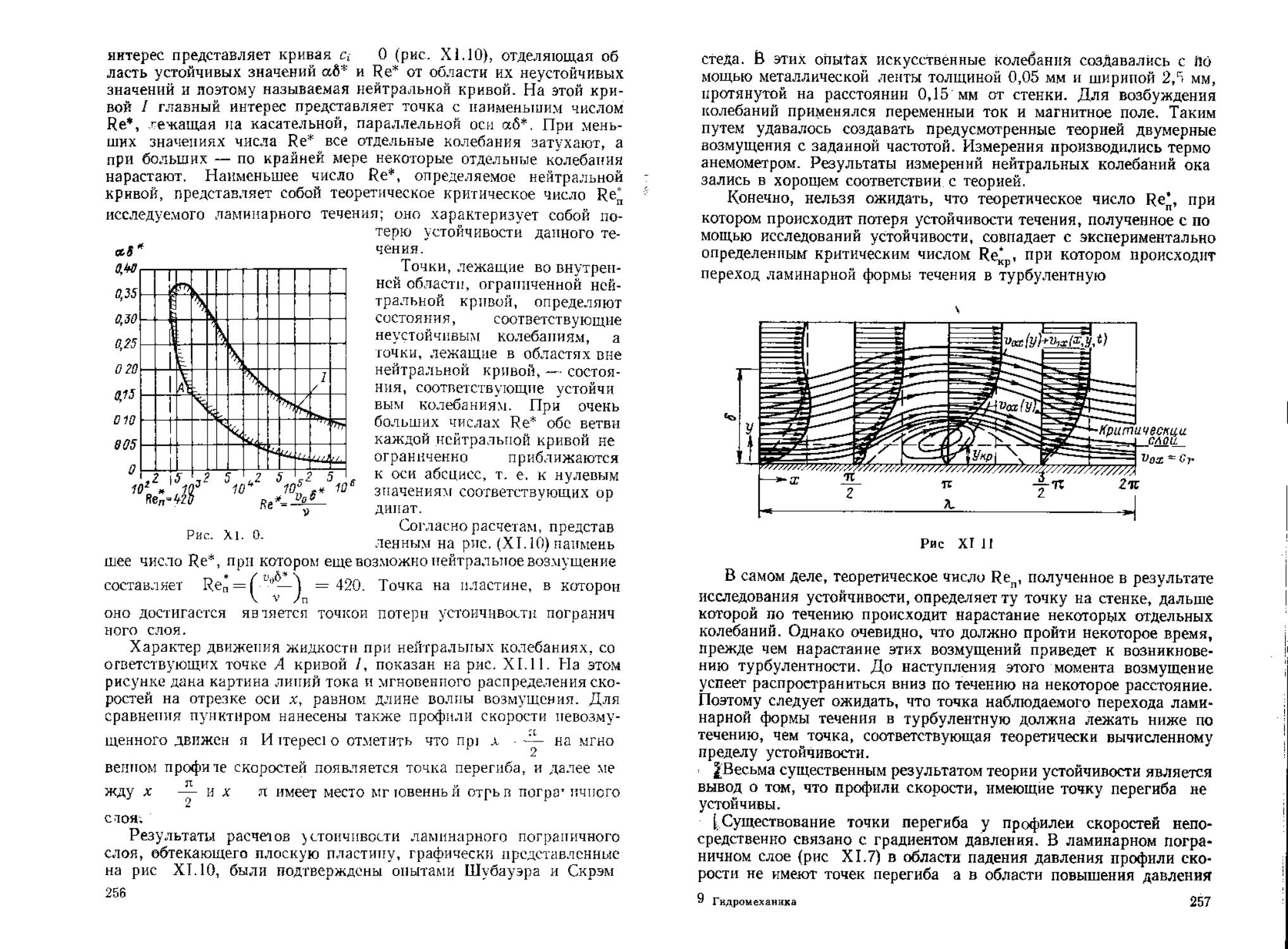
Re**) и Н (f Re**) изображены на рис. XI.19.
° Для зависимостей показанных на рис XI.19, были подобраны
Яо (1—aj) —0 0I9/£^
ст - 0 002 [6 55 — О 0685{£ — 4 4) + 0 2506 4 4)г] Re*
di — 0,2814—0,036£ 4 36Г~4 5
аа-0 1185^—0,262;
Во втором диапазоне lg Re** 3 — 5 5 полагая Fo - 1 179
Re" -(f)2”Re"
” f = - 137Re"LmQ (XI.114)
Для третьего диапазона lg Re“ - 4-6 5 аналогичные фор
при]/|<2
Re" = [?s,Re;’u“ +0 005 98Re f (XI 115)
”об"
V* p°j %
у/1 )
(XI 123)
(Xi 126)
f °§
f
I
I
5
i
I
I?
Из сравнения соотношении (XI 131) и (XI 132) следует что
const
(XI 133)
После замены 6 его значением согласно (XI 33) получим
(XI 134)
Для следа за телом среднее значение величины на поло
вине ширины следа пропорционально т. е. глубине впадины
формула (XI.131) примет вид
а формула (XI 132)
0ч,
6~ (рСд^)2 х2 (XI 138)
(XI 139)
(XI 135)
(XI. 121) и запишем ₽ У Р I fp»* ff» — о*) <iS (y=o —Pk) Pu) vlx Ъ I - R, ® pa.f (XI 136) Ширина a
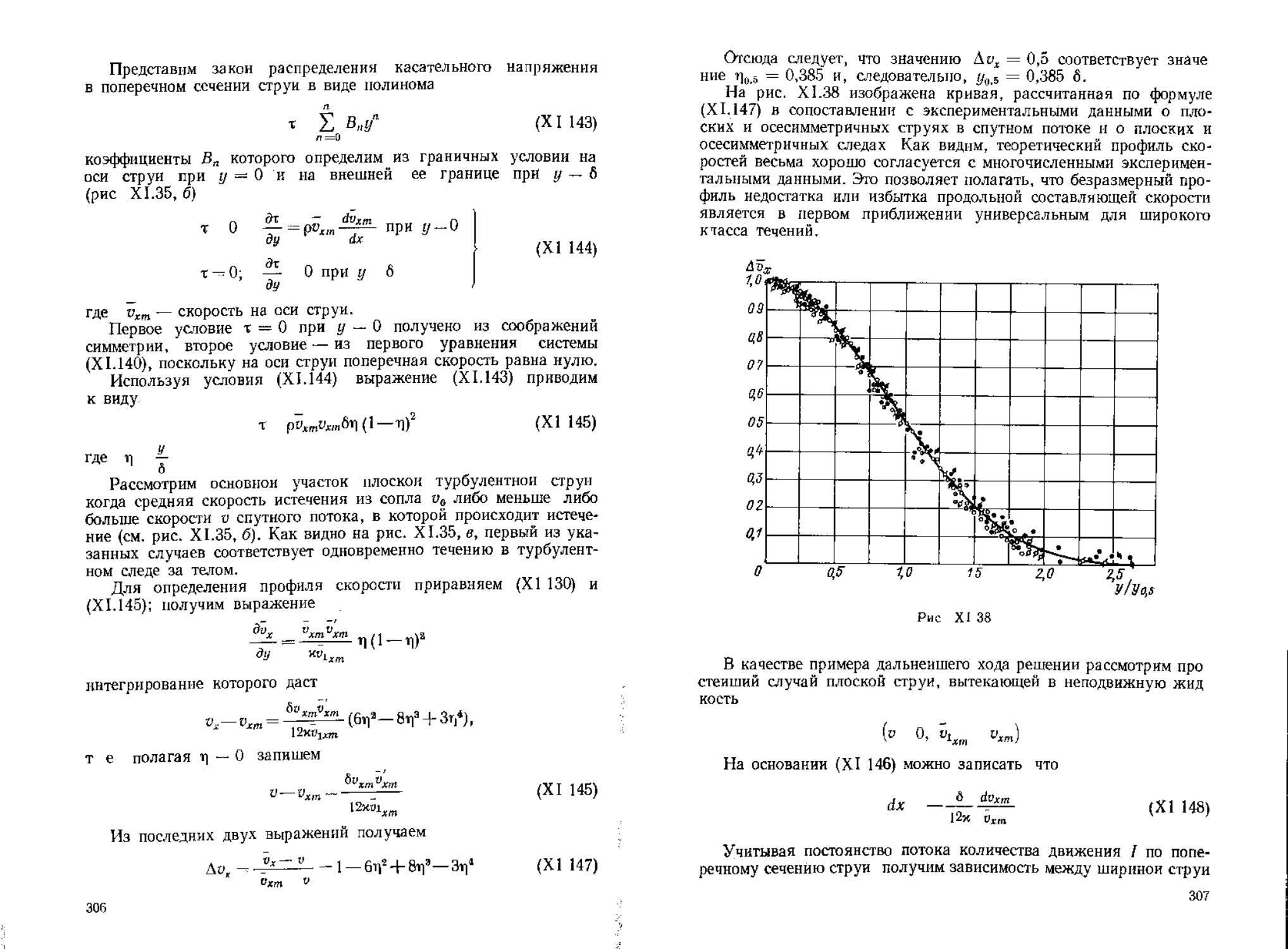
СТРУЯ 4
произведения б ихт или б«,т, входящие в формулу (XI.130),
VT=XCX(yi—Уа)
Рис XI 36
6 (У1—Уа) 0 256л-
в виде полинома, коэффициенты которого определяются на основе
I 2р.Г*^2Рй,.б((^)"Ч-
2p3m6 ,f (1 — 6г,’ + Sr,3 — Зц*) *) ™ у pi£„6
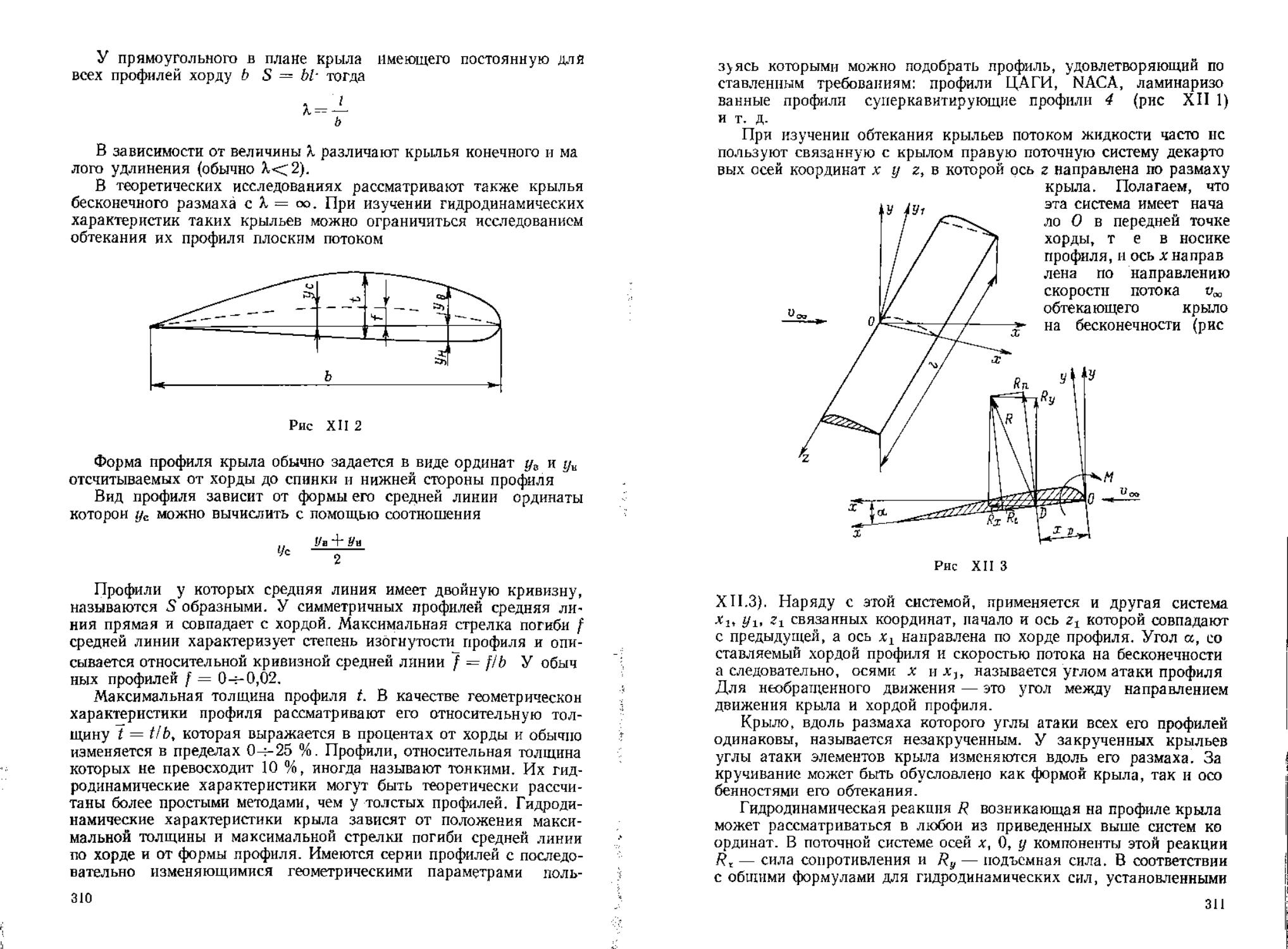
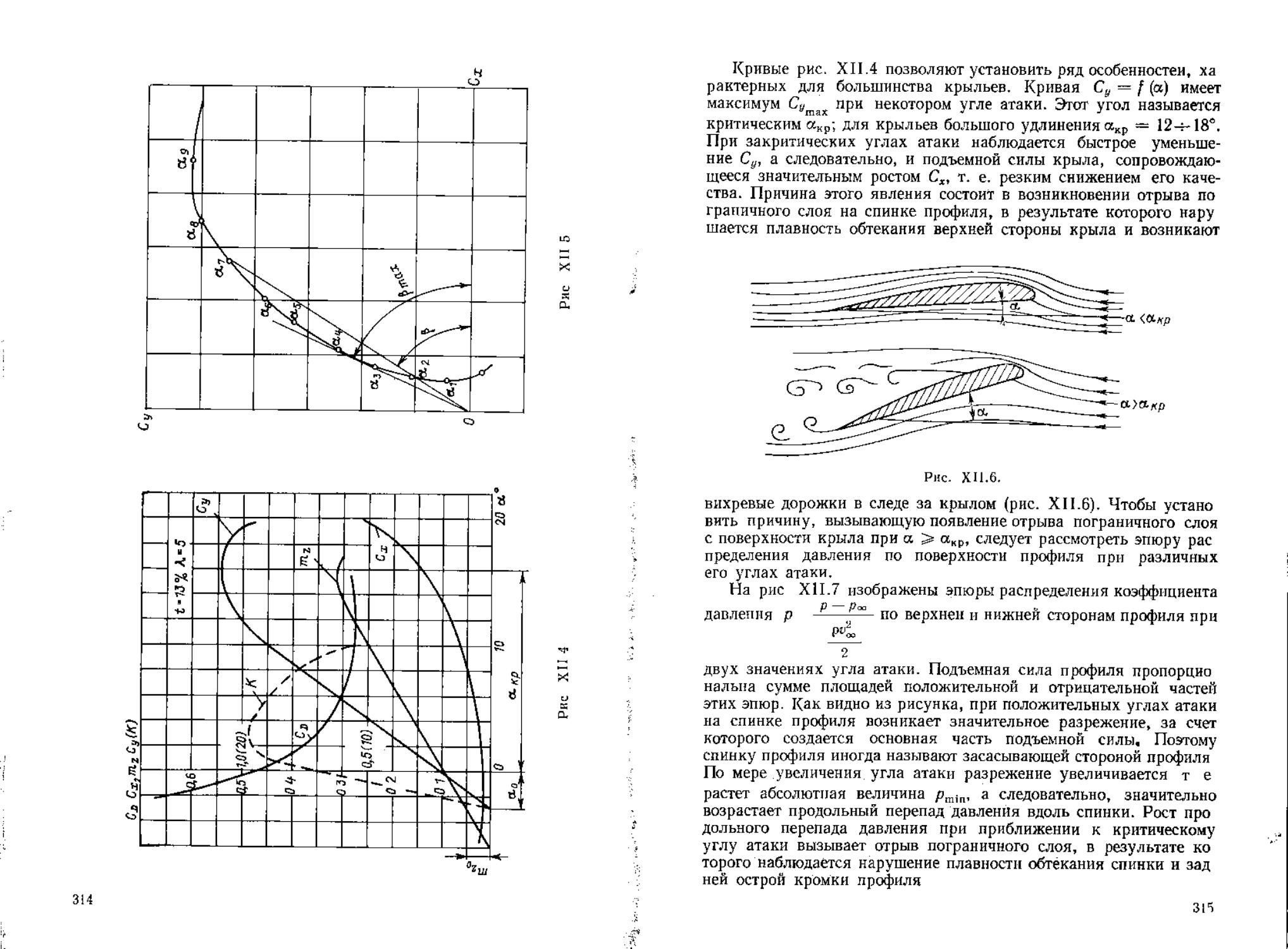
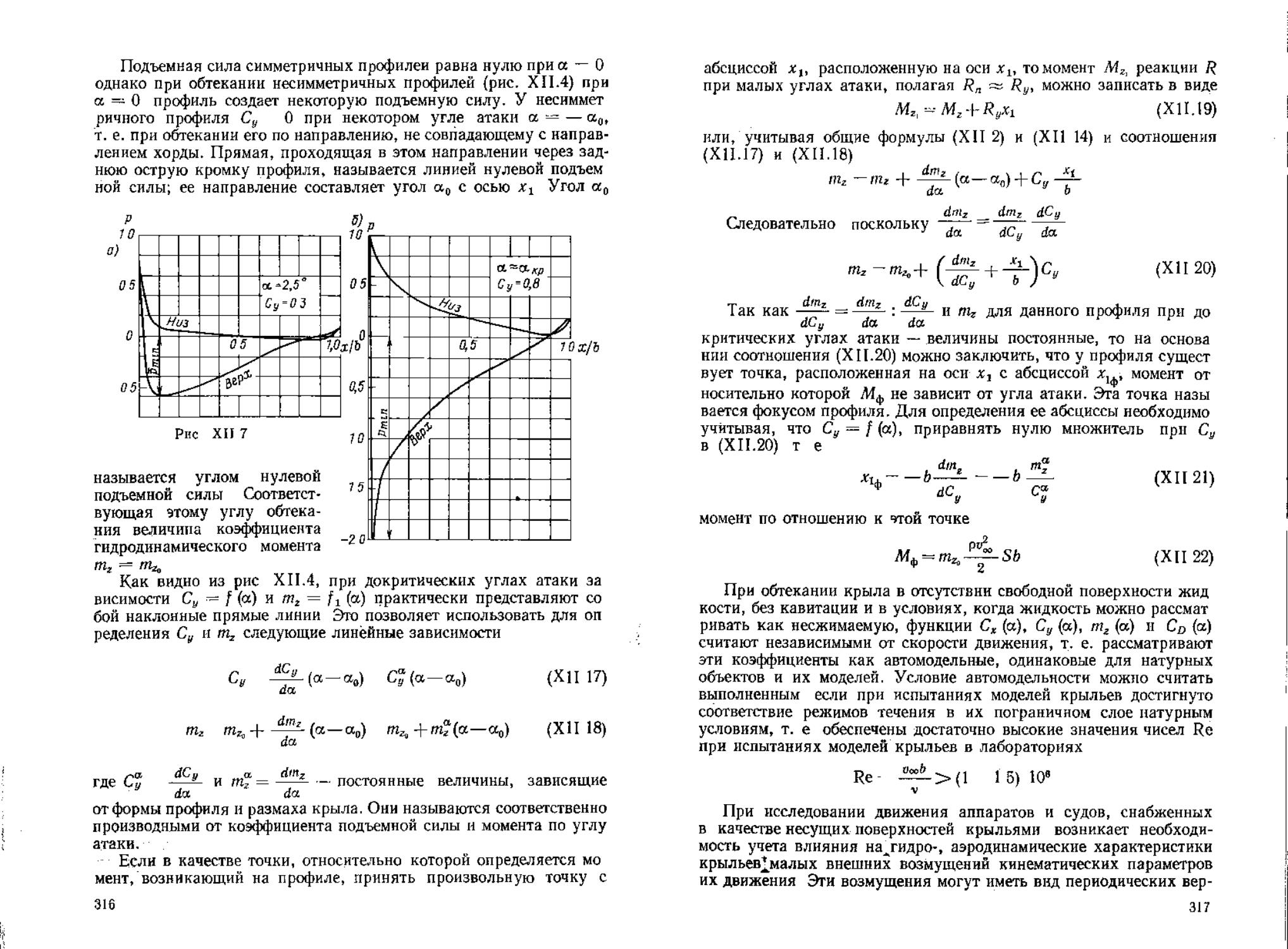
Глава XII
ТЕОРИЯ КРЫЛА
/
л
v
Hi
Рис XII 12
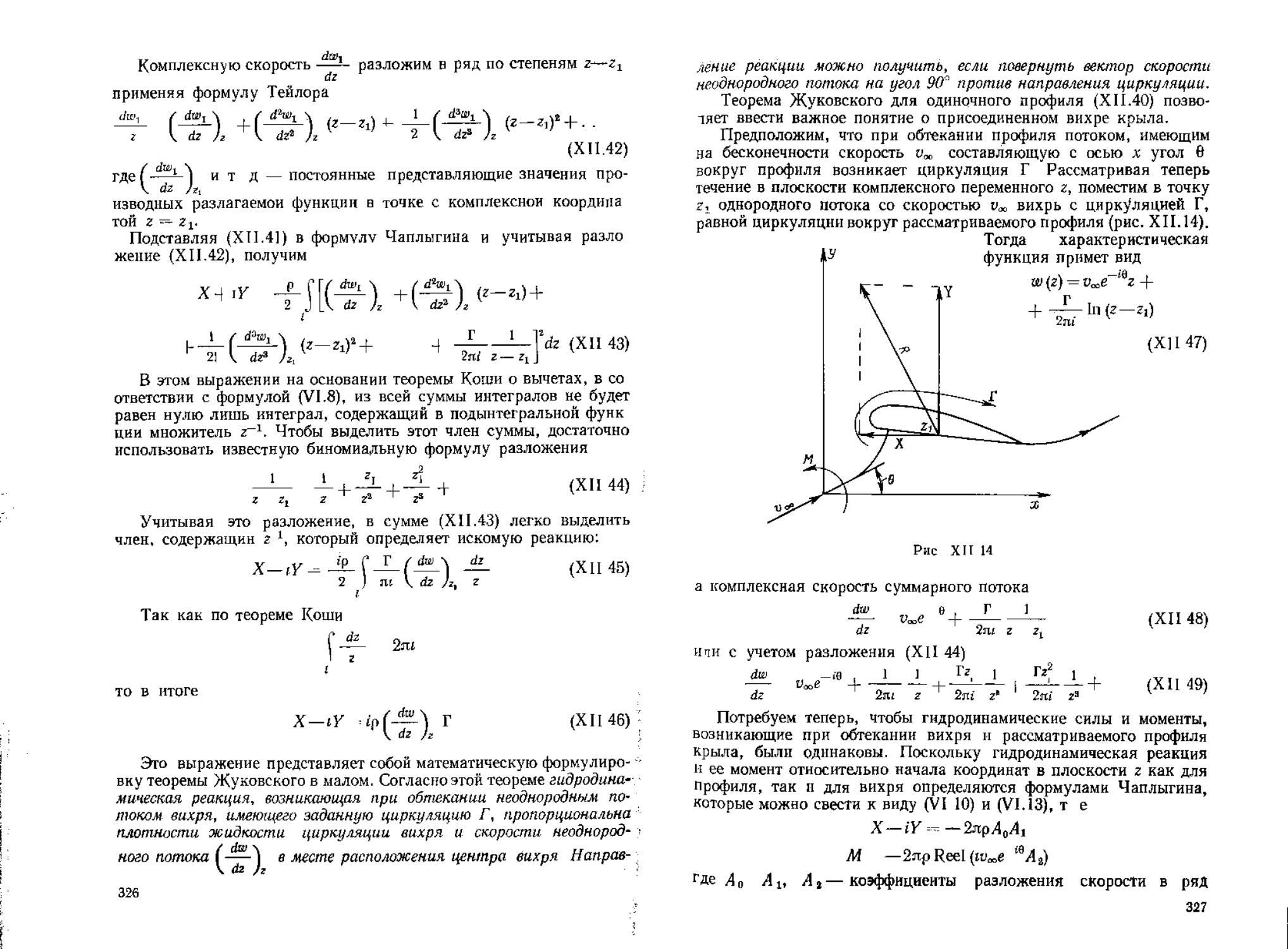
§ ВО Теорема Н. Е
Используя формулы _(XII.3O), (X1I.31) и (ХН.ЗЗ) можно про екции X и У реакции 7? определить из (XII.29): 1 (ХЧ34) Теперь вычислим циркуляцию скорости Г по контуру ABCDA обходя его так, чтобы внутренняя область располагалась слева Эта циркуляция будет равна циркуляции вокруг профиля в решетке При вычислении циркуляции вдоль участков линии тока AD и СВ следует учесть, что контурные интегралы по ним равны, но имеют Г (XII35) й «в iii й5И ?Л Й№!| ii hrtiWBl =1 is = }I? sHiM ; § “ - =S 8 g » й I ФБО: I- 1 iiM !h ! * Hf! Iii й i 5
случае решетка не отклоняет поток. Р ЛГ-(,ЧГ (XII.36) обтекания те/или гидродинамических особенностей. Примером ского для профиля в решетке. П Специальным случаем является теорема Жуковского «в малом»
Y -р%Г (XII 37) при этом гидродинамическую реакцию, когда циркуляция вихря,
В результате вычисляя модуль реакции, находим |К|-рг/?« +<4 ~Р».Г '(XII 38)' Направление линии действия реакции можно установить, если равенства (XII.36) н (XII.37) соответственно умножить на о0л Х^ + У% 0 (XI1.39) Эго условие означает что вектор реакции перпендикулярен вектору и0. Выражение (XII.38) позволяет сформулировать теорему Н. Е Жуковского для профиля в решетке: при обтекании профиля ; кости впереди и позади решетки направление этой реакции можно - определить, если вектор средней скорости о, повернуть на 90° в Так как при выводе формулы (XII.38) рассматривались только расположенного в произвольной точке плоскости комплексного переменного г, составляет величину Г. Если характеристическая “'(г) + !"(—) <хп4!> формулой 4„.(VI.3)^^ риваемый вихрь
324 325
жение (XII.42)^, получим^
4 |r^W‘I43>
х-,г.АШЛ .il. (X1145)
(XII 46)
(XII.50), на-
„рофи^
(XII 51)
Эго — особые точки, где конформность отображения нарушается.
Они являются точками разветвления преобразующей функции.
Чтобы в результате конформного отображения из контура окруж-
ности был получен контур профиля с одной задней острой кромкой,
в соответствующей ей точке с координатой £0 на окружности
комплексная скорость в этой
da> (U)
(XII 83)
(XII 85)
(ХИ 86)
cosi-A^0
(XII 89)
Учитывая (XI 1.85) получаем
•»«sln<x д/•7^(д/_l) (X1I87)
ч,« ’/-з :.„,^ = Чг + г
т7—Э
Cv 2я Vl + а? (а | а0)
(XII 107)
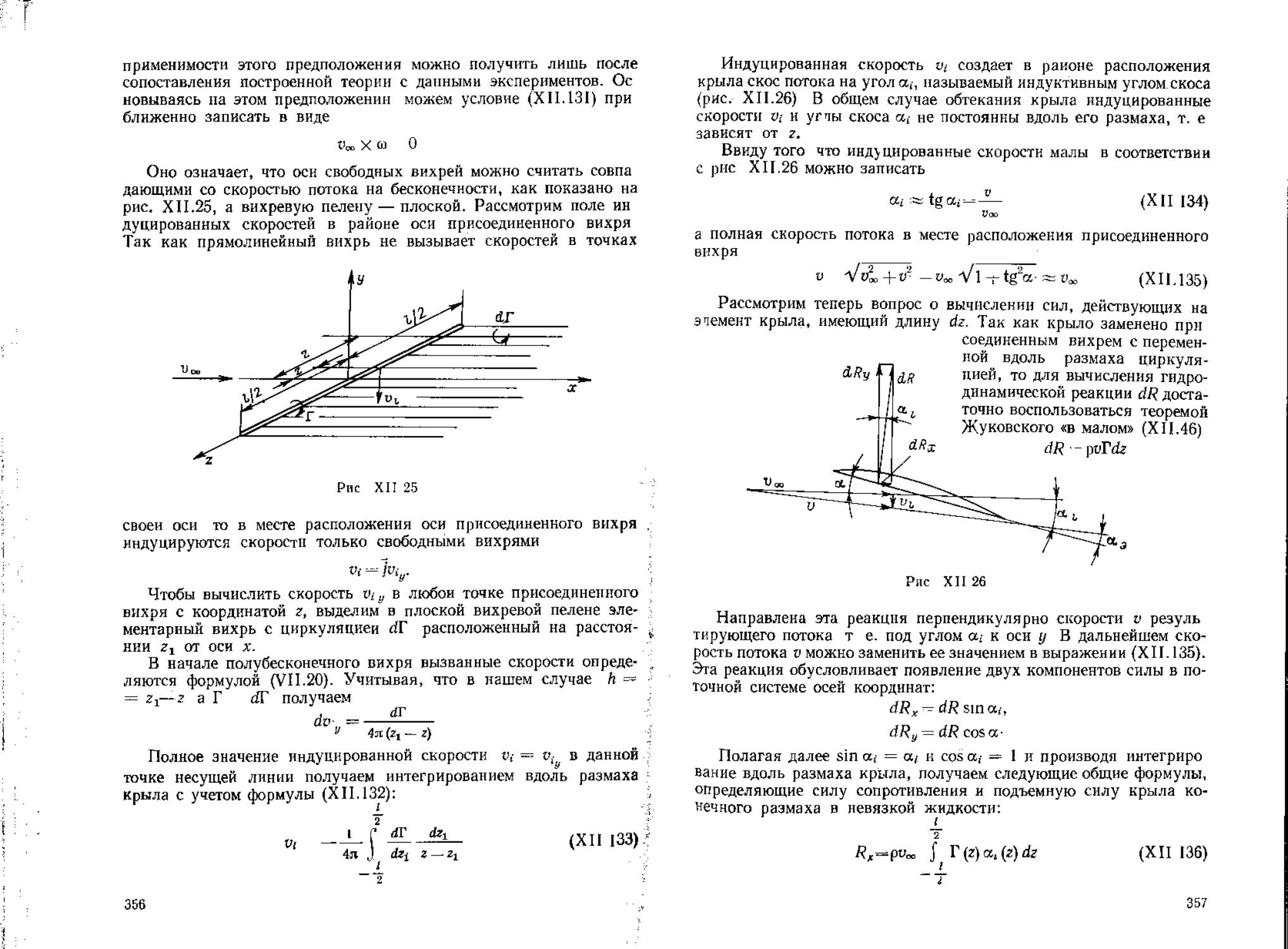
рис. XII.25, а вихревую пелену — плоской. Рассмотрим поле ин
(XII 134)
(XII.135)
= ?!— z а Г dr получаем
dv-y = dr~
Полное значение индуцированной скорости ty = viy в данной
(XII 133)?
2 "
(XII 150)
(XII 151)
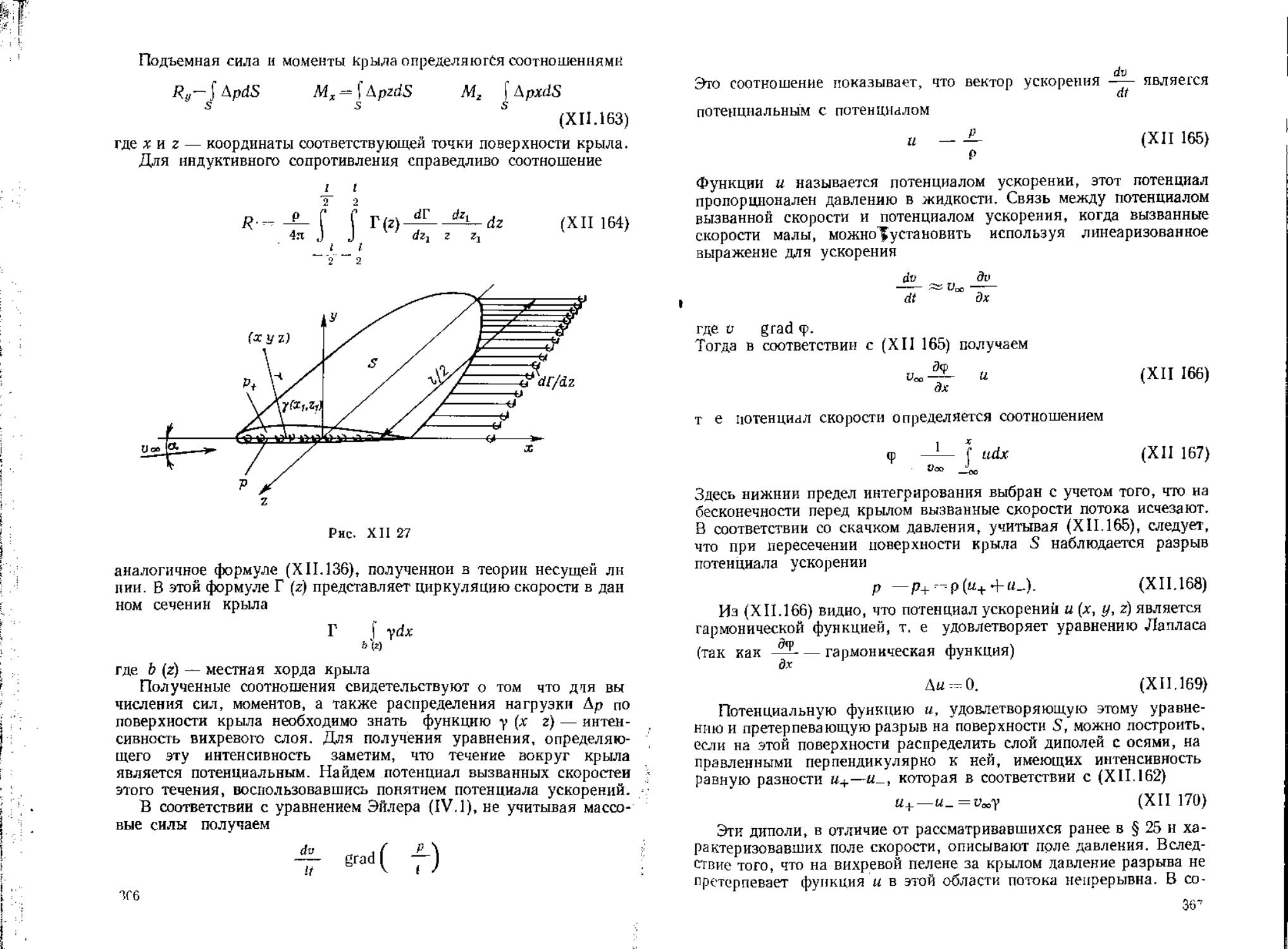
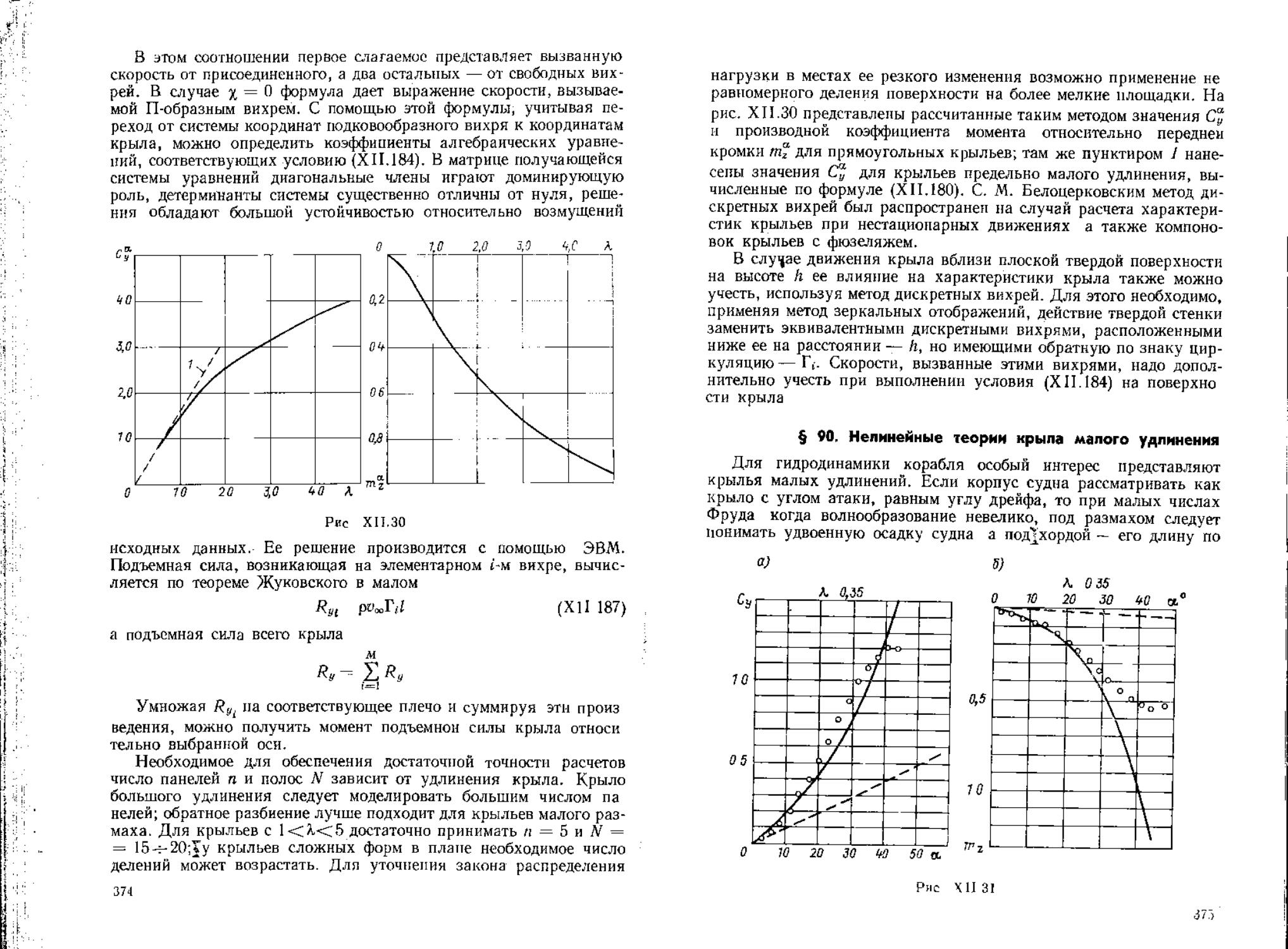
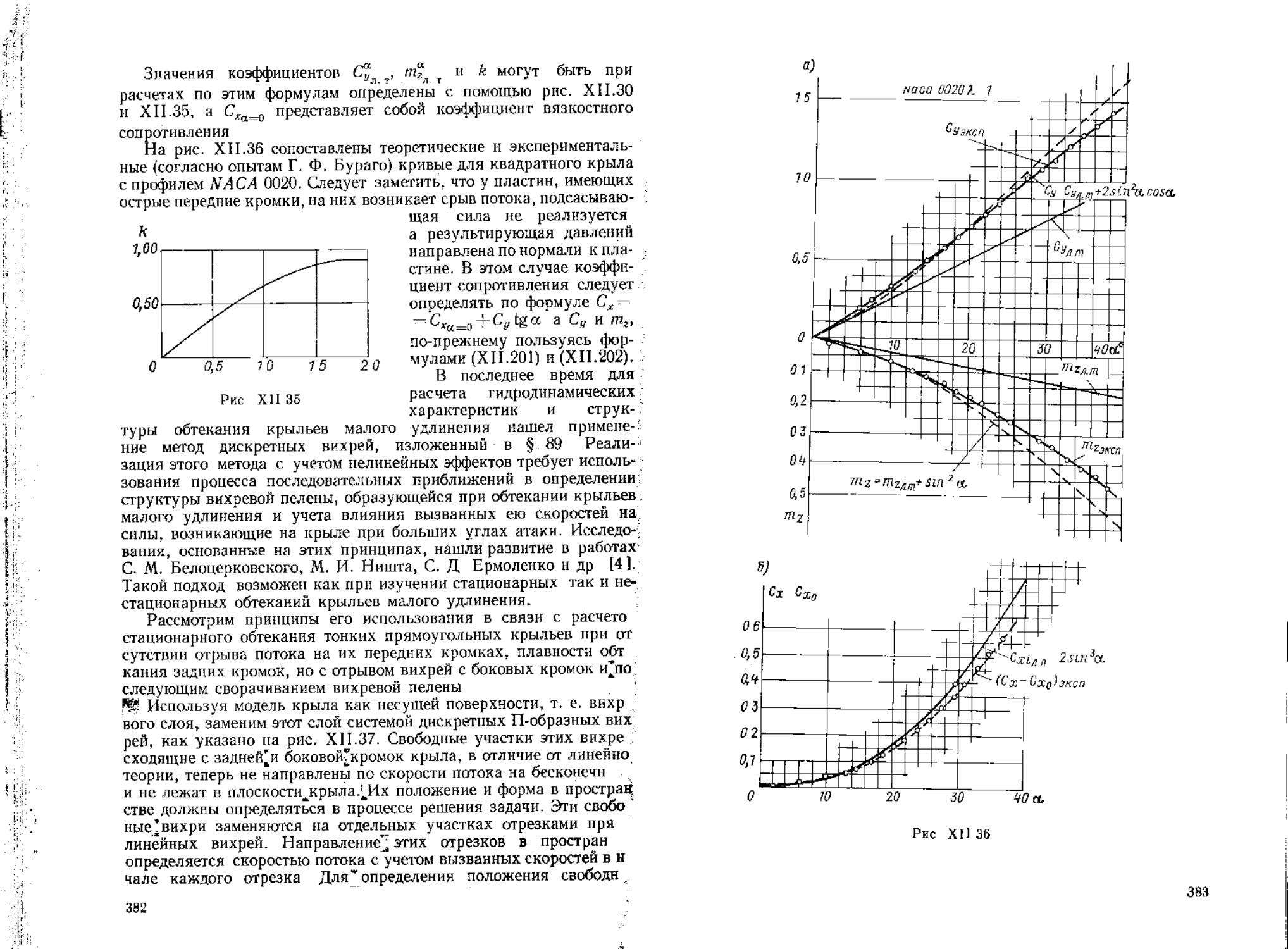
(ХП.8146) В108ч^им°ЭФФИЦИеНТ 1,ОДЪемНОЯ СИЛЫ КрЫЛа ПОЛЬЗУЯСЬ
(XII 152)
ренциальным уравнением (XII.140).
* п |- sin б) Ап sm пб — а -у «j sm 0
(S91 ПХ)
,(w) ~ IД «
(191 ПХ)
(091 ПХ)
Ш-’Д°д '
zpTr^-(z)j J J 4“^
(wi их)
u(x ij z)------------------ST J “>’f*1 <xn 171)
формулу
Ф--^ f Jt(*, (XII 172)
к(т)- -b-
r(«-z,) l(z z,)- S-|(z z,)_[
(z-zj= + s> C T r )
fj, =— «Woo при у О (XII 174)
Рис XII 29
(XII 192)
tg₽ 8^7-
(XII 193)
p [и» cos a -f-f/cpsin (a—₽)] Г02г
(XII 194)
Рис XU 36
_________________Глава XIII
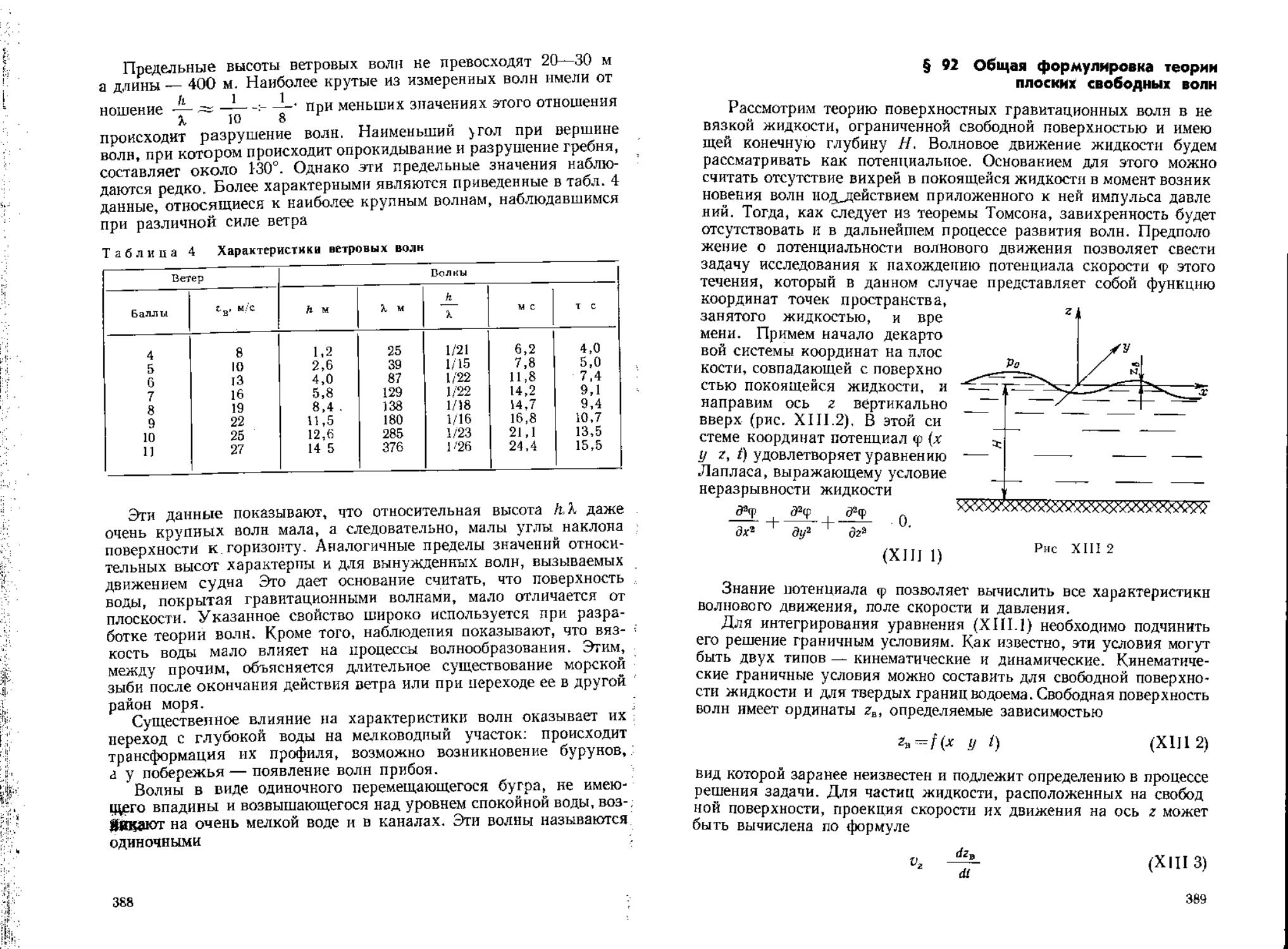
ТЕОРИЯ ВОЛН И ВОЛНОВЫХ
ГИДРОДИНАМИЧЕСКИХ СИЛ
Имея одно уравнение, можем две неизвестные постоянные
Dchk(z^H) (XIII 23)
Учитывая (XIII.15) (XIII.21) и (XIII.23), получаем следующее
~kx)]Dchk(2 + H) (XIII.25)
<p = Ccos(crf—fex)chfe(z
(XI11.26)
— cchkH sin(of —йх) —
a sin (of—kx) (XIII 27)
(XIII 36)
-cos2(at — Ax)Ash kHdx
(XIII 44)
П -ГрМх
Используя для гв его выражение (XIII 27) получим
dS-dx a ПРИ г 0
П^-^-1 (XIII 45)
Как следует из формул (ХШ.44) и (XIII.45), кинетическая и по
Е Т4-П (XIII 46)
ИШШП1
ставляющих^ гидродинамической реакции R В случае тела проиэ
l Г oV.JL
oJ I К cos2 0 / I cos\0
(XIII 80)
R, f k}H{k 0)Г“+
в][-Чгл^- <ХШ8')
н(_а_ в) - f,c^r<+"'“ =+«-«ds
I? I?
Р - Pmln а ? =
получим
/ 2 (ря — Роо)
которая обеспечивает конформно отображение плоскости ш на
Чд — j J .ids
При этом величина кинетической энергии жидкости будет
рассматриваемом случае составляет
(XIV 42)
(XIV 43)
рости погружения клина.
В случае погружения тела с переменной во времени^ вертикаль--
времени, т. е. в конечном счете функцией глубины погружения
°К°Широкий Тцруг вопросов гидродинамики удара и погружения
тел в жидкость рассмотрен Г В.Логвивовичем [17]
ЛИТЕРАТУРА
ОГЛАВЛЕНИЕ
=
ГИДРОМЕХАНИКА