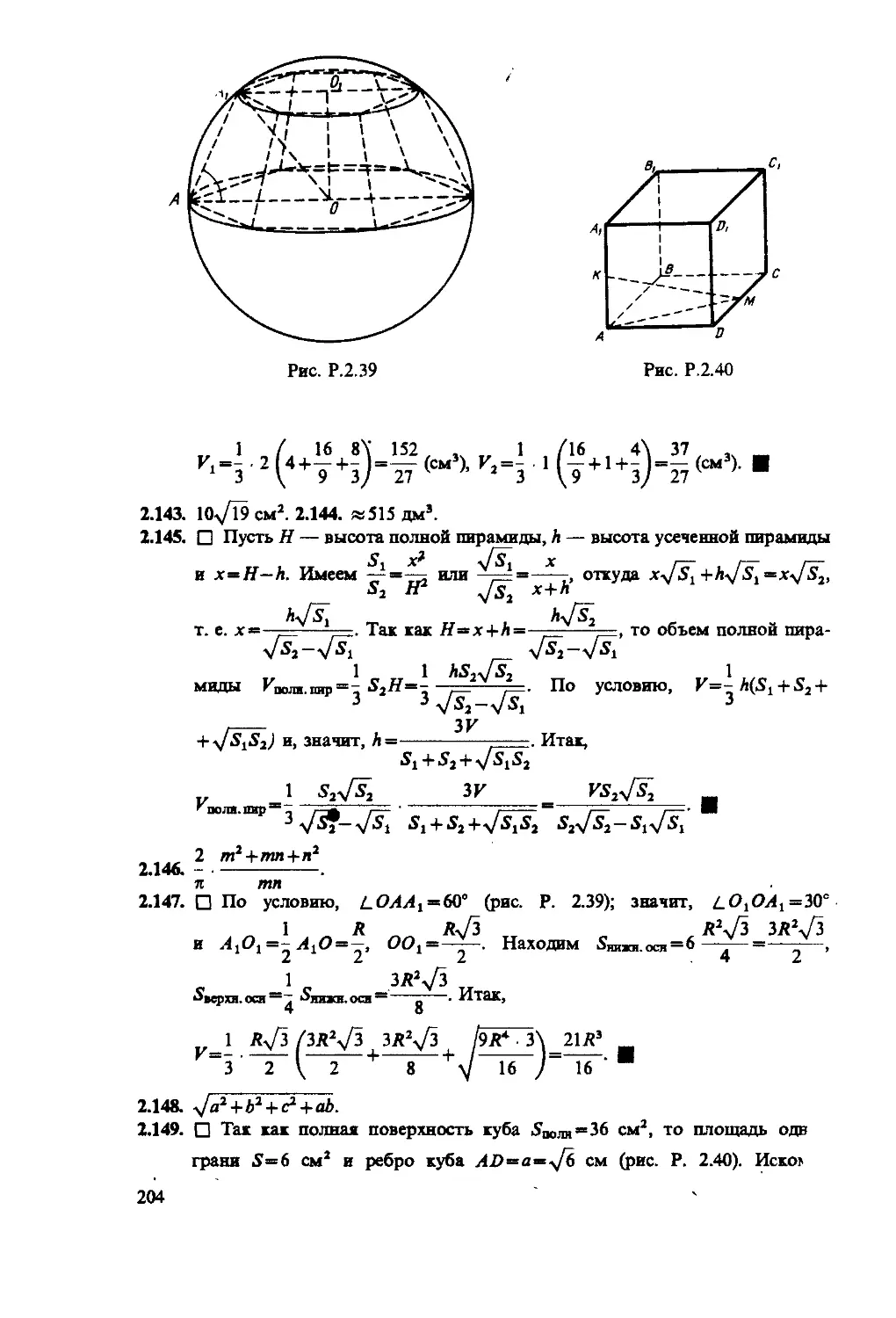
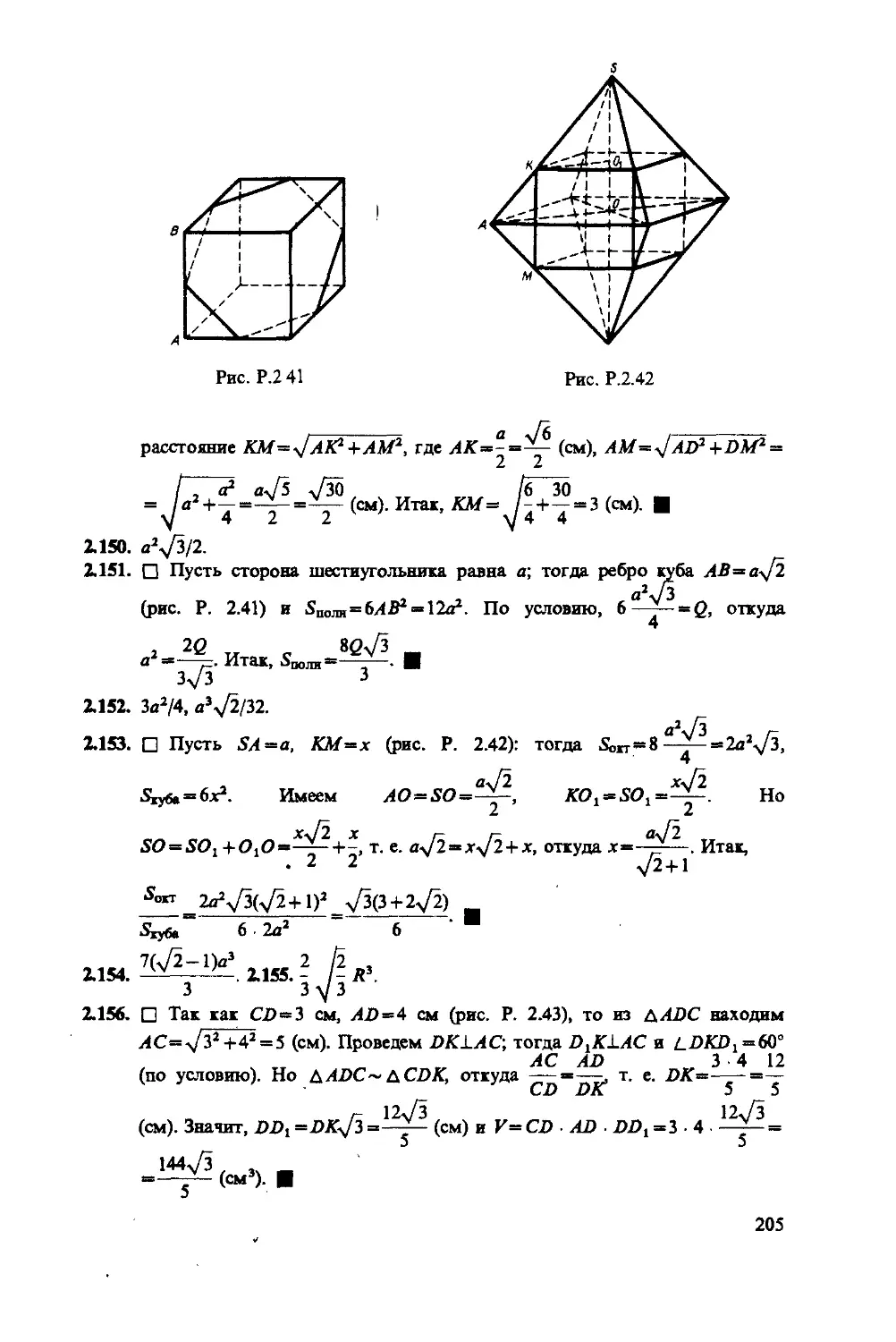
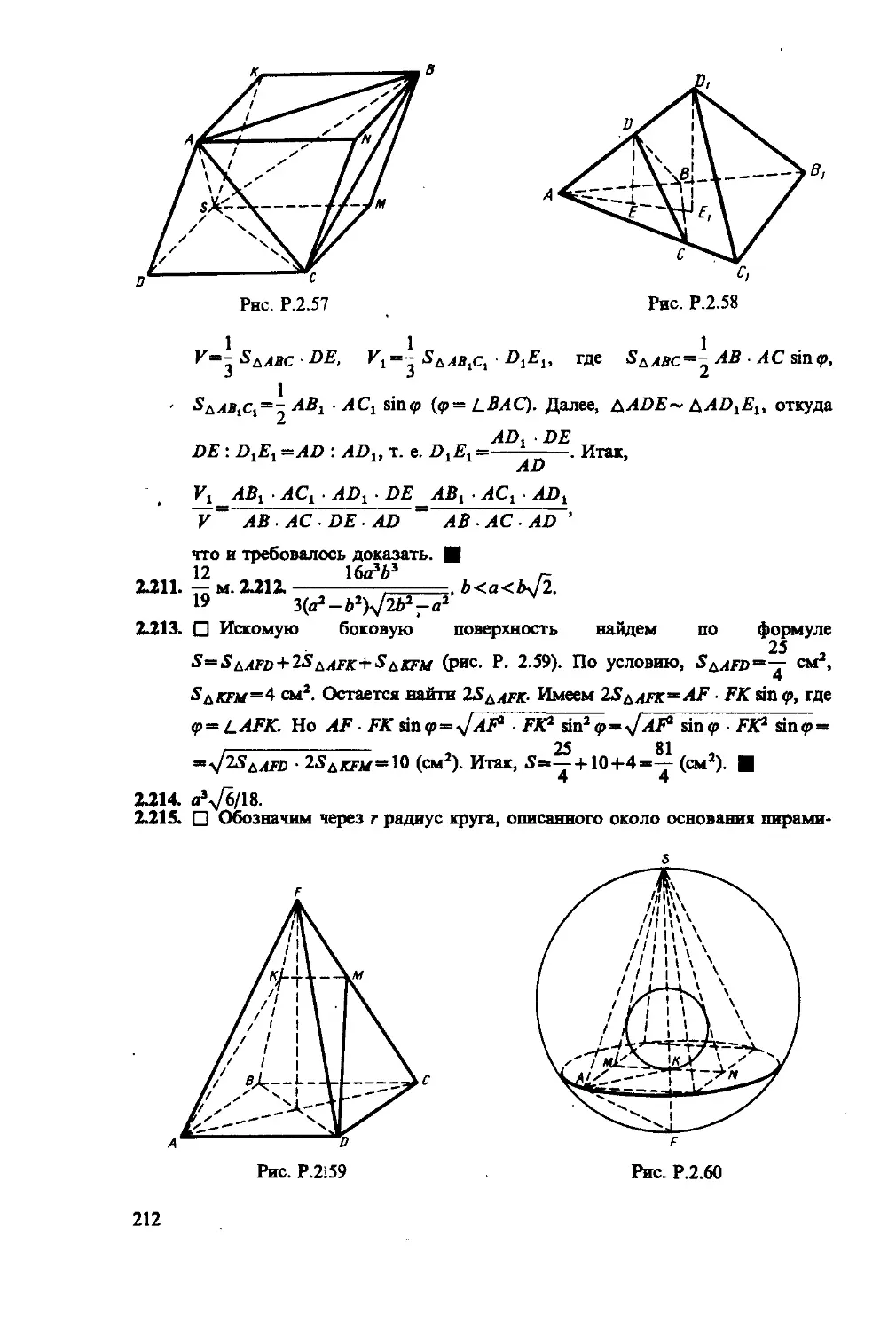
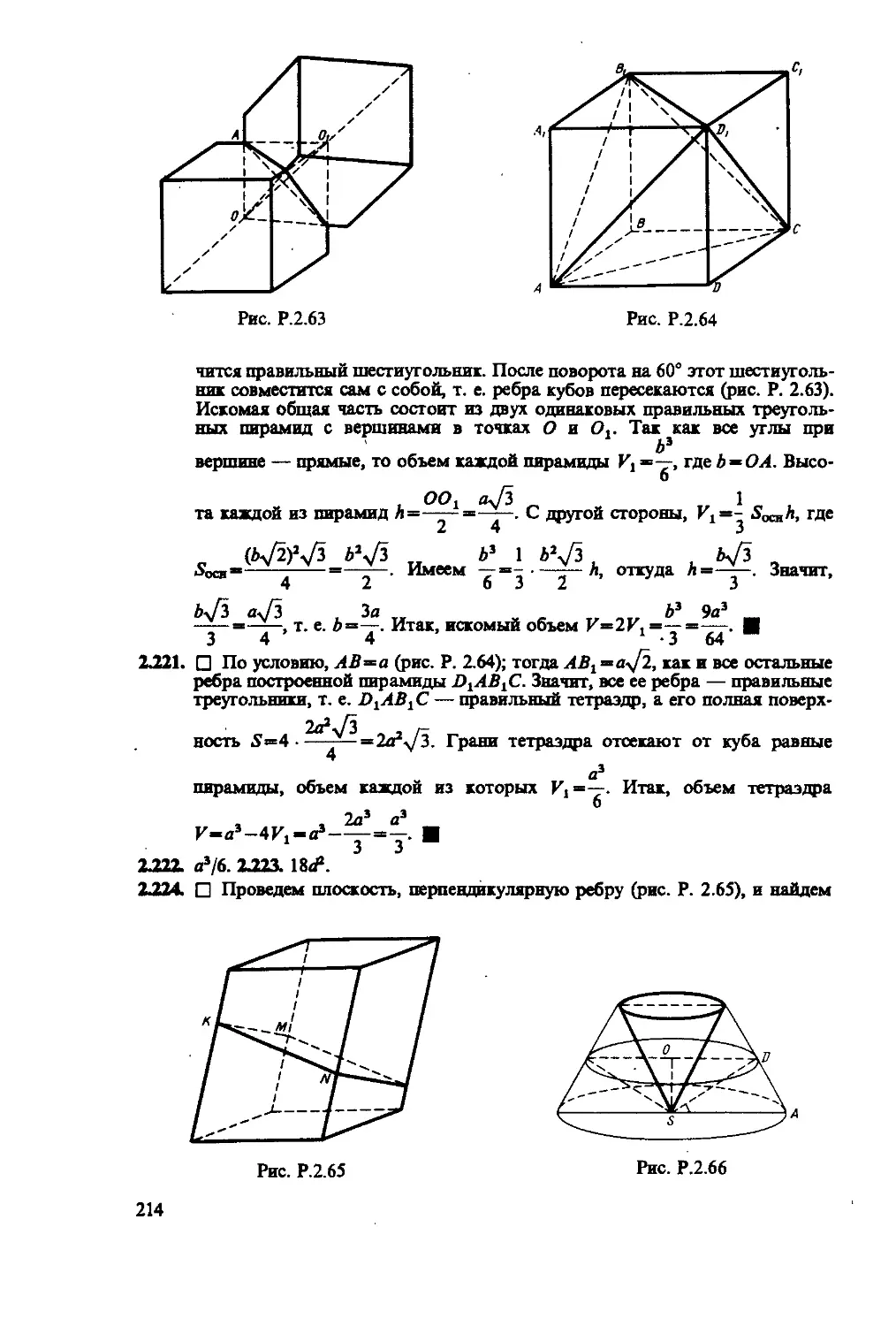
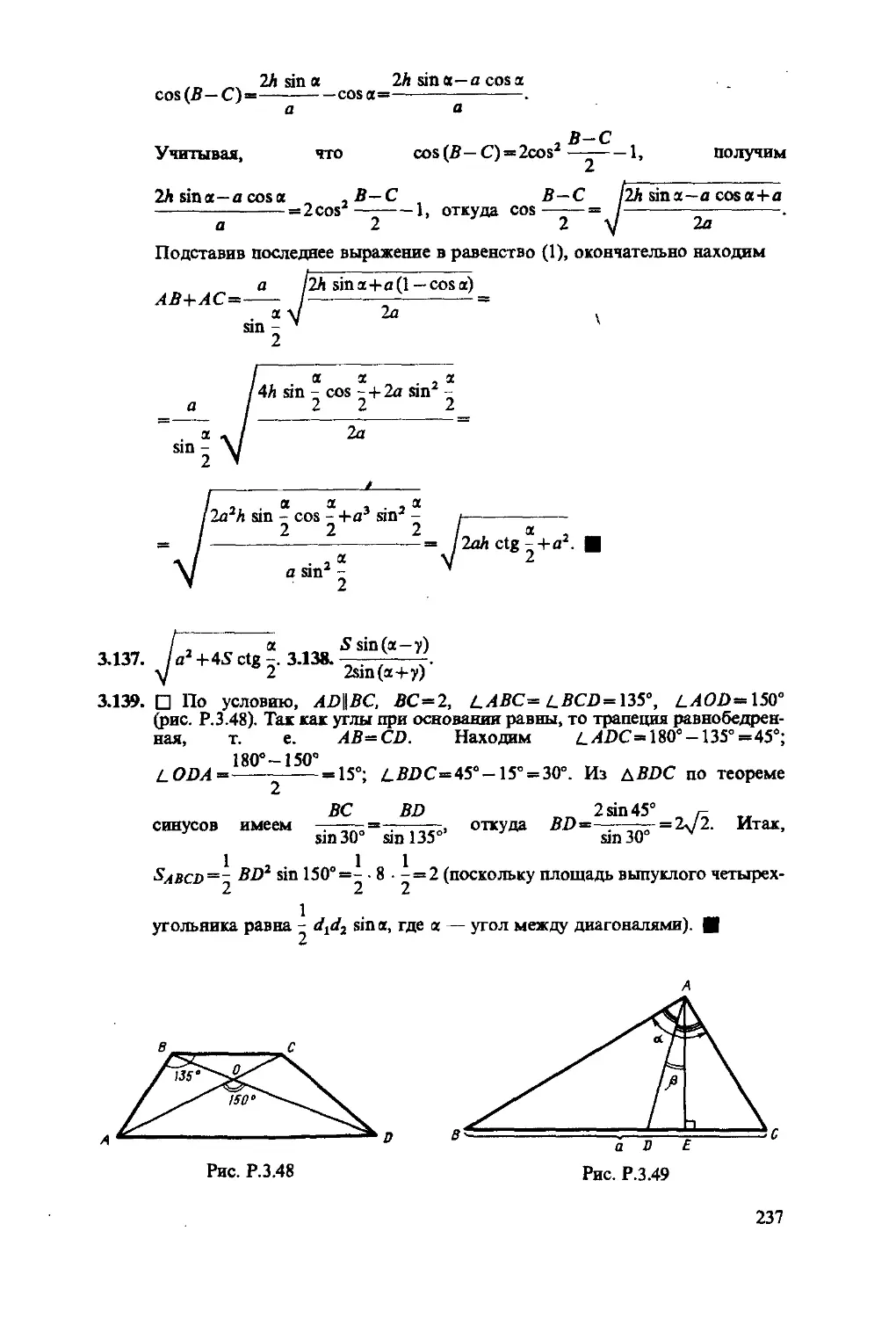
Author: Сканави М.И.
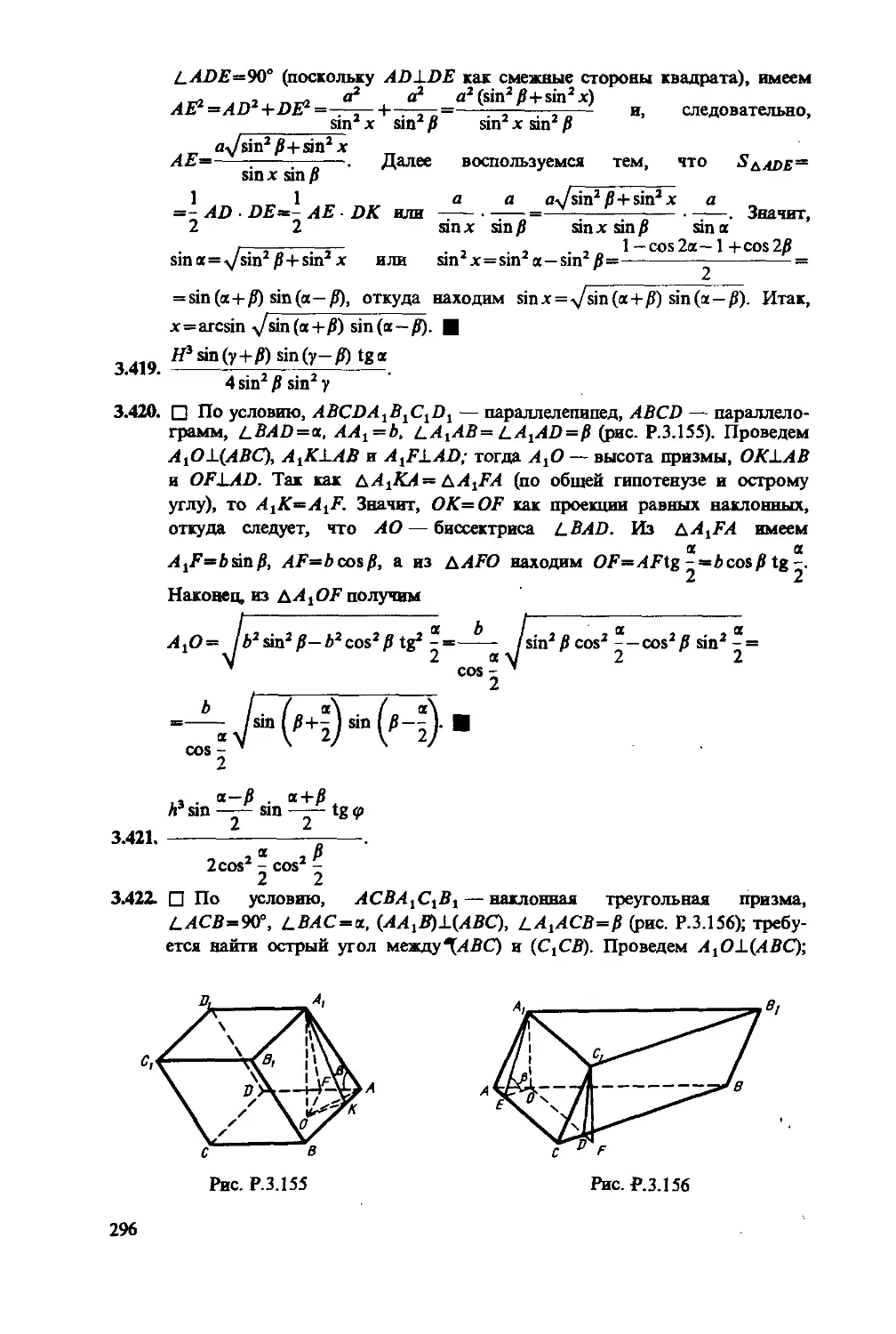
Text
под ред. М.И. Сканави
СБОРНИК ЗАДАЧ ПО МАТЕМАТИКЕ ДЛЯ ПОСТУПАЮЩИХ ВО ВТУЗЫ
(С РЕШЕНИЯМИ). Кн. 2. Геометрия
Книга написана в соответствии с программой по геометрии для поступающих
в вузы. Настоящее издание (6-е — 1992 г.) существенно переработано и
дополнено. Задачи объединены по принципу однородности тем, типов, методов
решения и разбиты на три группы по уровню их сложности. Ко многим задачам
даны подробные решения. В каждой главе приведены сведения справочного
характера и примеры решения задач.
Для поступающих в вузы.
ОГЛАВЛЕНИЕ
Элементы Условия Решения,
теории, задач указания,
Глава 1. Задачи по планиметрии примеры 3 10 ответы 149
Глава 2. Задачи по стереометрии 36 41 189
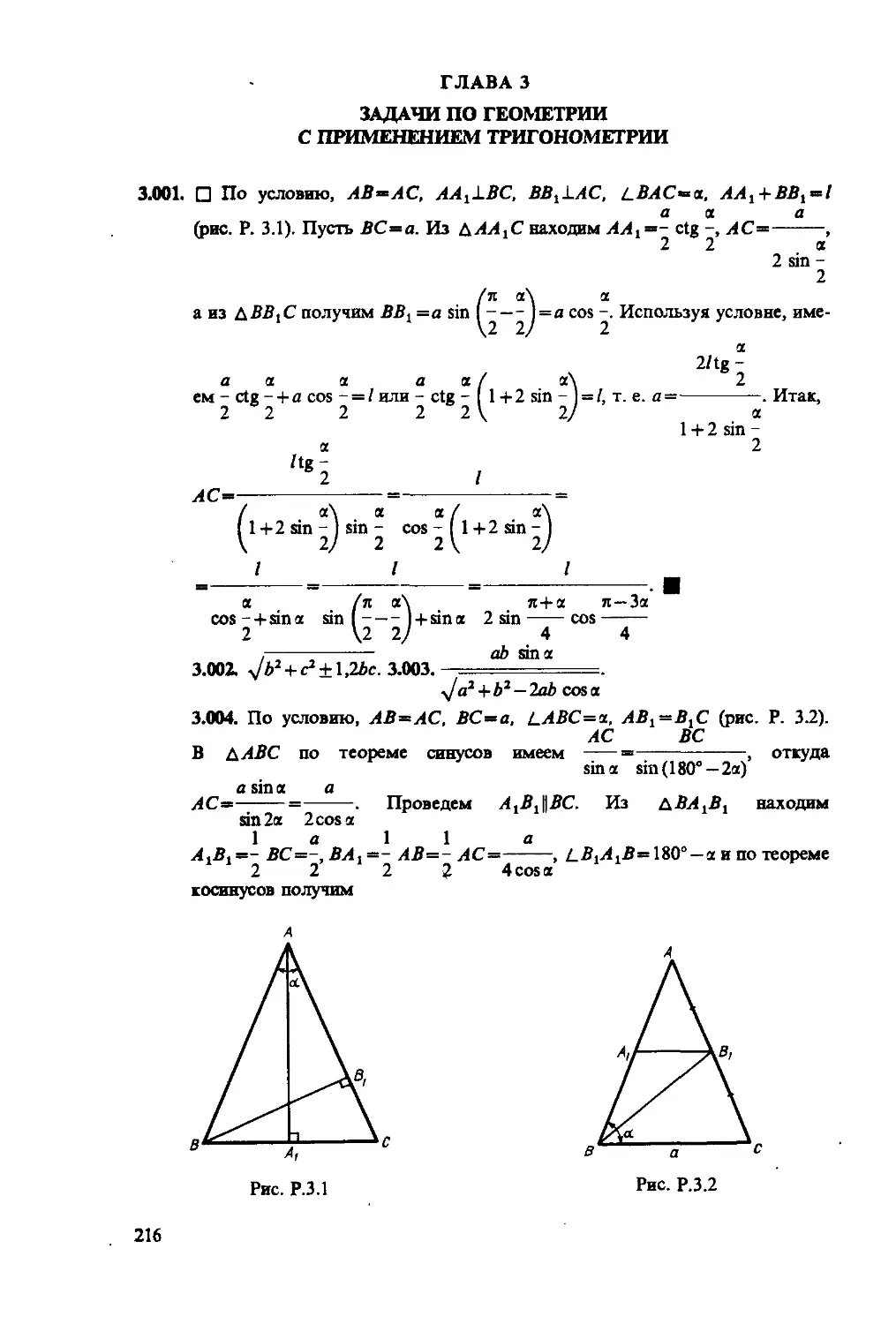
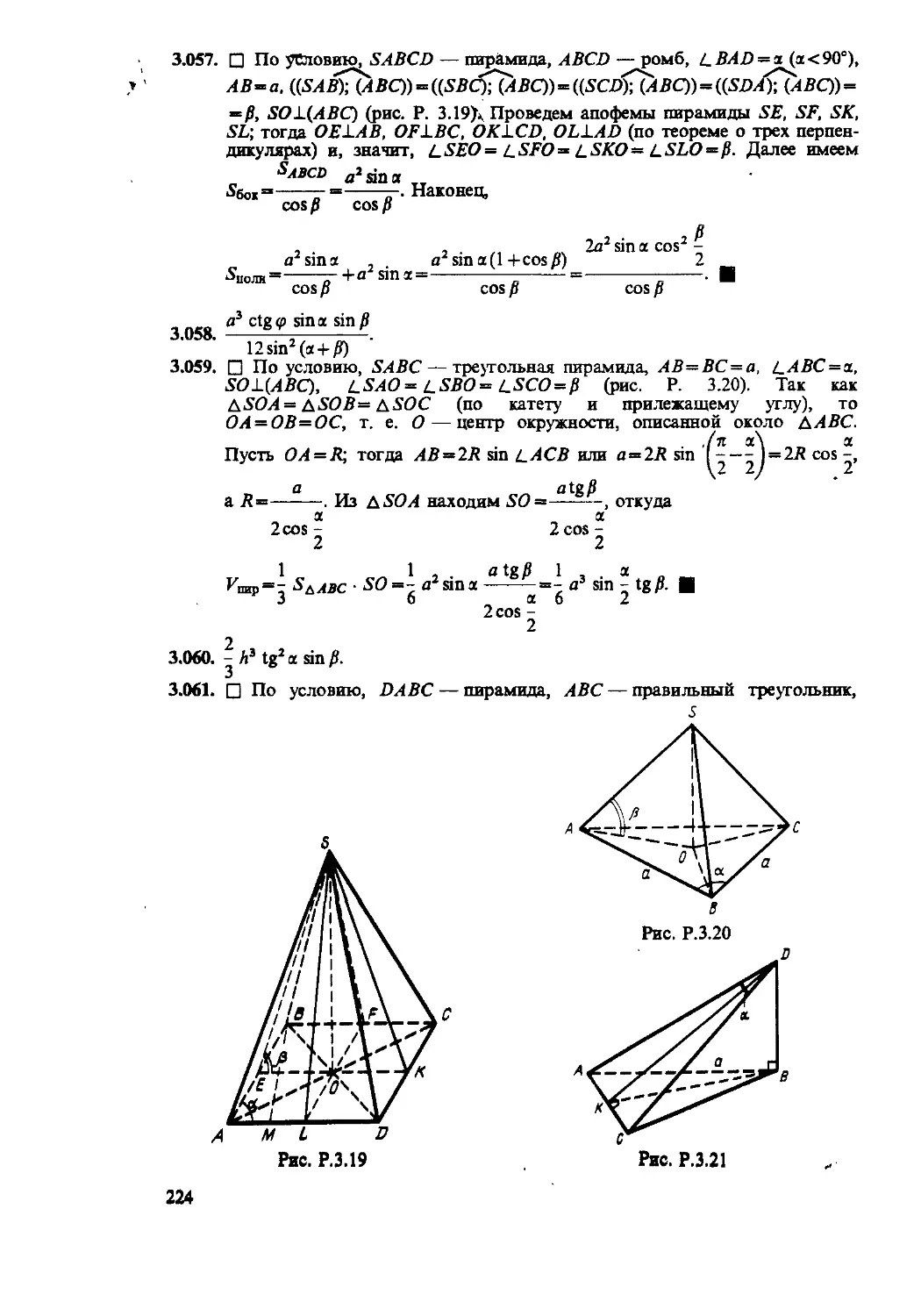
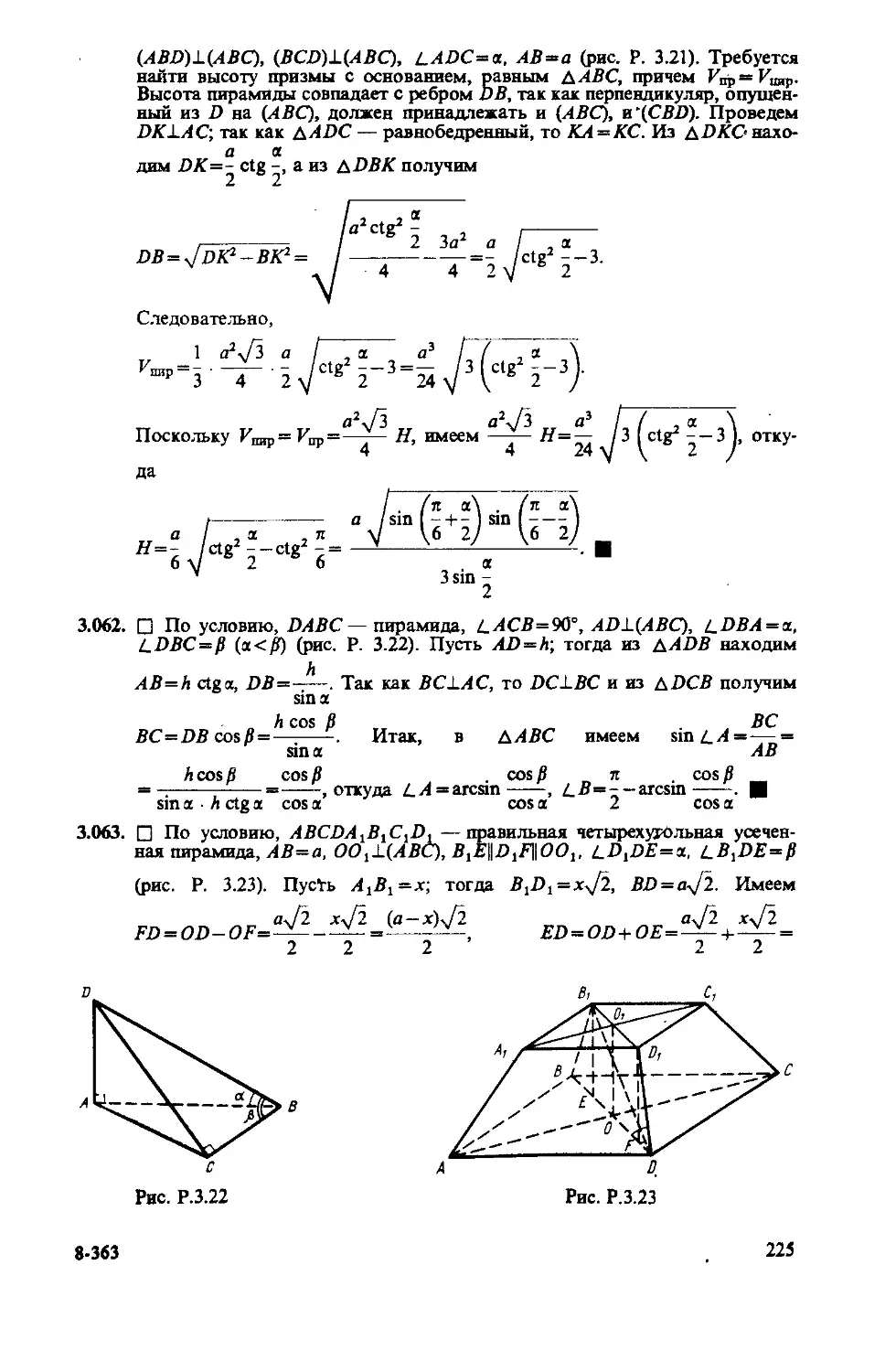
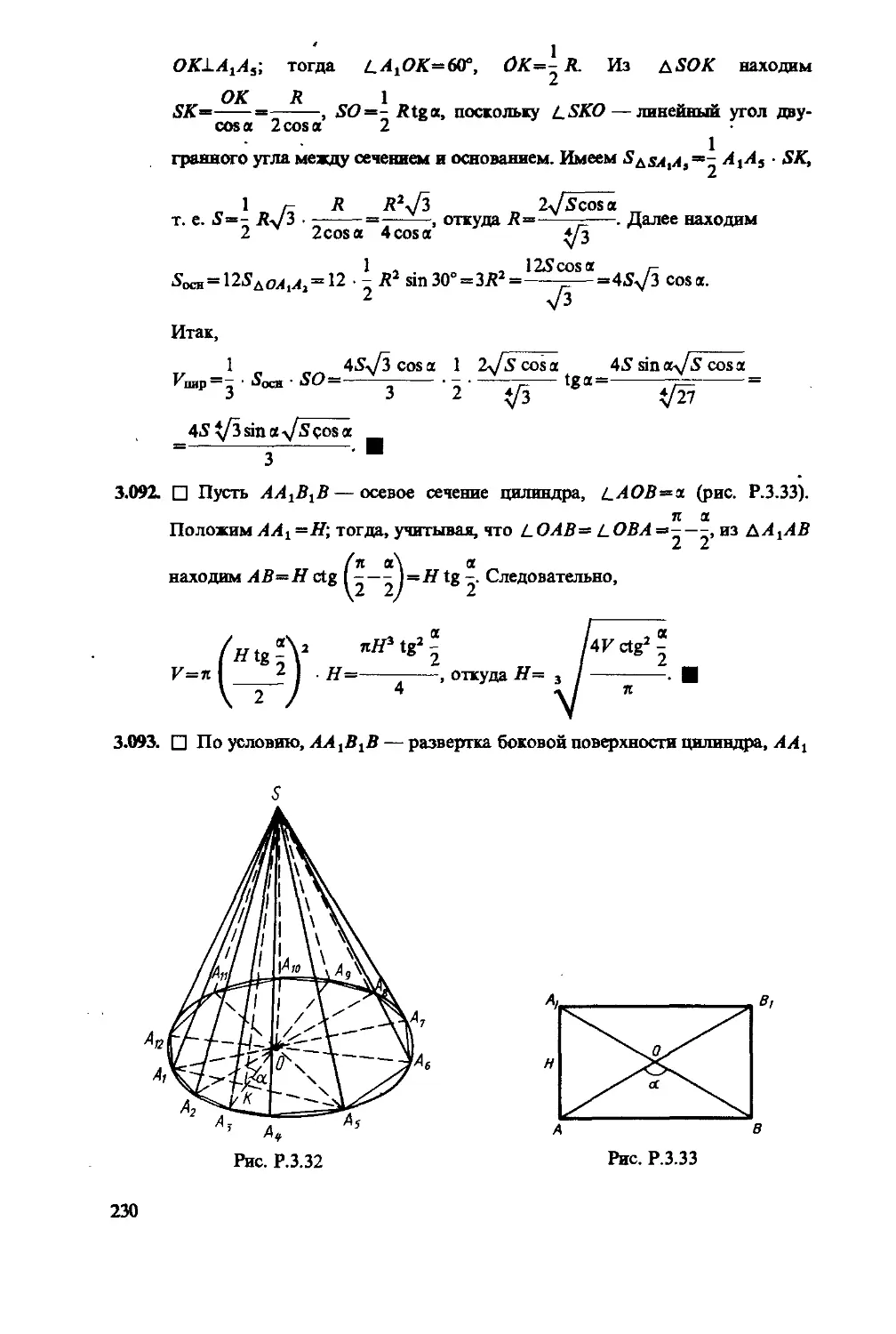
Глава 3. Задачи по геометрии с применением 56 61 216
тригонометрии
Глава 4. Дополнительные задачи DO геометрии 93 98 310
Глава 5. Применение координат и векторов к 106 112 322
решению задач
Приложения. Варианты заданий для самопроверки 119 346
Варианты билетов для вступительных письменных 134 354
экзаменов
ГЛАВА 1
ЗАДАЧИ ПО ПЛАНИМЕТРИИ
ОСНОВНЫЕ ФОРМУЛЫ
1°. Произвольный треугольник (а, Ь, с — стороны; а, 0, у — проти-
волежащие им углы; р — полупериметр; R — радиус описанной окружности;
г — радиус вписанной окружности; 5 — площадь; ha — высота, проведенная
к стороне а):
1 5= aha; 2 (1-1)
1 5=- be sin а; 2 (1.2)
S=^/p(p- а)(р - Ь)(р - с); (1-3)
5 г=~; Р (1-4)
abc я=—, 45 (1.5)
a1 sin В sin С 5= ; 2 sin Л (1.6)
a2=b2 + c2 — 2bc cos а (теорема косинусов); (1.7)
а b с — = = 27? (теорема синусов). sin a sin/7 sin у (1-8)
2°. Прямоугольный треугольник (а, b— катеты; с Ьс — проекции катетов на гипотенузу): — гипотенуза; ас,
1 5= ab; 2 (1-9)
1 5= chc; 2 (1.10)
a + b — c (1.11)
2 ’
3
Я=;; (1-12)
2
а1 + Ъ2 = с2 (теорема Пифагора); (113)
ас hc
Ш <114>
a c (1.15)
bc b (1.16)
b c
а = с sina = c cos fl = b tga = A ctg/J. (1-17)
3°. Равносторонний треугольник:
5=^; (118)
4
а^/з r=—; 6 (1-19)
adi R=^~. 3 (1-20)
4°. Произвольный выпуклый четырехугольник (d1 и d2 —диагонали;
<р — угол между ними; 5 — площадь):
•5=- d,d2 sin<p. (1-21)
2
5°. Параллелограмм (а и b — смежные стороны; а — угол между ними;
йа — высота, проведенная к стороне а):
S=aha = ab sin а = -simp. (1-22)
6°. Ромб:
S=ahtt — a2 sina=~ d±d2. (1-23)
7°. Прямоугольник:
S=ab=- d,d2 simp. (1-24)
2
8°. Квадрат (d — диагональ):
5=а2=^/2. (1.25)
4
9°. Трапеция (а я b — основания; h — расстояние между ними; I — средняя
линия): а + Ь 1 ; (1-26) 2 а + Ь S= h = lh. (1.27) 2
10°. Описанный многоугольник (р — полупериметр; г — радиус вписан-
ной окружности):
S=pr. (1.28)
11°. Правильный многоугольник (а„— сторона правильного п-уголь-
ника; R — радиус описанной окружности; г — радиус вписанной окружности):
а3 = Ву/з;а^ = Яу/2;а6 = В; (1.29)
ла„г 5 (1.30) 2
12°. Окружность, круг (г — радиус; С — длина окружности; S — площадь
круга): С=2пг: (1.31) S=nr1 2. (1.32)
13°. Сектор (/ — длина дуги, ограничивающей сектор; л° — градусная мера
центрального угла; а — радианная мера центрального угла):
/ = га; (1-33) 180° (1-34) 360° 2
ДОПОЛНИТЕЛЬНЫЕ СООТНОШЕНИЯ
МЕЖДУ ЭЛЕМЕНТАМИ ФИГУР
1°. Три медианы треугольника пересекаются в одной точке, которая делит
каждую медиану в отношении 2:1, считая от вершины треугольника.
□ Пусть медианы AD и BE пересекаются в точке О (рис. 1.1). Построим
четырехугольник MNDE, где М и N—середины отрезков АО и ВО. Тогда
1
MN'iAB и Л/А'=- АВ как средняя линия треугольника
1
АОВ; ED\\AB и ED--- АВ как средняя линия тре-
2
угольника АВС. Поэтому MN\\ED и MN=ED, т. е.
фигура MNDE — параллелограмм с диагоналями
MD и NE. Значит, MO = OD и так как МО=АМ, то
AM=MO = OD. Следовательно, точка О делит меди-
ану AD в отношении AO:OD=2:1 и в таком же
отношении эта точка делит медиану BE.
Очевидно, что в том же отношении должна де-
5
лить и третью медиану точка ее пересечения как с первой, так и со второй
медианами. При этом третья медиана не может пересечь их в точках, отличных от
О, поскольку тогда на каждой медиане имелись бы две различные точки, делящие
ее в отношении 2:1, считая от вершины, что невозможно.
2°. Длина медианы треугольника выражается формулой
ща=- \/2{Ь2+ с2) — а2,
где а, Ь, с — длины сторон треугольника.
□ Продолжим медиану AD (рис. 1.2) на расстояние DE=AD и построим
отрезки BE и ЕС. В полученном четырехугольнике АВЕС точка D пересечения
диагоналей АЕ=2та и ВС=а делит каждую из них пополам; следовательно,
АВЕС — параллелограмм. Теперь используем теорему о том, что сумма квад-
ратов длин диагоналей параллелограмма равна сумме квадратов длин его сто-
рон. Составив уравнение и решив его относительно та, получим искомое соот-
ношение.
3°. Длина стороны треугольника выражается формулой
2________________
а=- sjl(m2k+m2k-m2,
где та, ть, тс — длины медиан треугольника.
□ Отметим на медиане AD точку О пересечения медиан треугольника (рис.
1.3); согласно свойству 1°, она делит AD в отношении AO:OD = 2'. 1. Продолжим
1
OD на расстояние DF= OD = - та и соединим точку F с В и С.
3
2 2
Теперь составим уравнение, связывающее длины сторон ВО—- mj, СО = - тс
3 3
2
и диагоналей OF= та, ВС=а параллелограмма OBFC. Решив это уравнение
3
относительно а, получим искомое соотношение.
4°. Биссектриса делит сторону треугольника на отрезки, пропорциональные
двум другим его сторонам.
□ I способ. Пусть CD — биссектриса треугольника АВС (рис. 1.4). Тре-
угольники BDC и ADC с основаниями а, и Ьг имеют общую высоту. Пусть их
площади равны соответственно 5, и тогда S2 :S2 = a1: Ь2. С другой стороны,
1 С 1 С
в силу формулы (1.2) имеем 5Х=- a CD sin —, S2 =- b CD sin —, откуда
S2:S2=a:b. Сравнивая полученные пропорции, заключаем, что а2:Ь2 = а:Ь.
II способ. Пусть LBDC=P (рис. 1.4); тогда CADC=n—p. Согласно те-
С
ореме синусов (1.8), имеем а2 :a=sin — : sin Д (из Д BCD)
6
с с
и />i :2> = sin — : sin(a-/i)=sin — : sin/J (из ДЛС7>). Сравнивая эти пропорции,
заключаем, что ai:a = b1-.b, откуда a1:bl=a:b.
Ill способ. Продолжим биссектрису CD до пересечения в точке Е с прямой
АЕ\\СВ (рис. 1.5). Имеем Да = Д Д (по условию) и Да= Ду (углы при параллель-
ных СВ и ЛЕ и секущей СЕ). Сопоставив эти равенства, получим /_$= L'f-
Следовательно, /\АСЕ — равнобедренный и AE=AC=b; t\AED~ t\BCD (вслед-
ствие равенства углов), откуда al:b1 = a;b.
5 . Длина биссектрисы треугольника выражается формулой
1С=\/ab-a^!,
где а и Ь — длины двух сторон треугольника ABC; at и bt — отрезки третьей
стороны (рис. 1.4).
□ Применив теорему косинусов (1.7) к треугольникам с равными углами
BCD и ACD, составим уравнение
Р+а1-^ Р + Ь2-Ь*
1а1с ~ 2ЫС
откуда Ь(Р + а2 — а21)=а(Р+Ь1 — Ь2) или Pc(b — а) — ab(b—а) = (aib)al - (abl)b1.
Используя равенство abx =ахЬ (вытекающее из свойства 4°), получаем
(b — a)(P—abJ=ab1ai — aibhi или (b — a)(l^ — ab)==—albi(b—a).
Полагая Ъ^а, разделим обе части последнего равенства на Ь—а, откуда
^аЬ-а.Ь,.
6°. Длина биссектрисы треугольника выражается через длины его сторон а,
b и с по формуле
ab{a + b + c\a + b — с)
h = -- ------— .
a+b
□ Запишем соотношение из п. 5° в виде P=ab —at(c—at). Далее, используя
свойство 4°, получаем - =---------, т. е. at —-------. Отсюда находим
Ь с—а1 а+Ь
ас I ас \
Рс~аЬ —---- с—------I и требуемое значение 1С.
а + Ь \ а + Ь/
7°. Для всякого треугольника зависимость между его высотами ha, h/,, hc и ра-
диусом г вписанной окружности выражается формулой
1111
— +
ha hb hc г
7
□ Используя формулы (1.4) и (1.1), записываем: S—rp, 2S=aha = bhf, = chc.
Отсюда находим
I 1 1 а b с a+b+c 1 1 1
4* 4* s 4* 4* — =—. В
ha hb hc 2S 2S 25 2 5 Sr
8°. Площадь 5 равнобедренной трапеции, диагонали которой взаимно пер-
пендикулярны, равна квадрату ее высоты, т. е. S=h2.
□ В равнобедренной трапеции осью симметрии является перпендикуляр MN
к ее основаниям, проходящий .через точку О пересечения диагоналей (рис. 1.6). Так
как LAOD—90°, то AD—2ON и ВС—2ОМ. Следовательно,
SABCD----' MN“(PN+O1^MN“MN^‘‘^-
9°. Высота равнобедренной трапеции, в которую можно вписать окружность,
является средним геометрическим ее оснований.
□ Так как в четырехугольнике, описанном около окружности, суммы длин
а+Л
противоположных сторон равны, то а+Ъ — 2с (рис. 1.7), откуда АВ—-. Далее
2
а — Ъ
имеем АЕ—---- и из прямоугольного треугольника АВЕ находим
2
_ , . , (а+Ь\2 (а—ЬХ1
ВЕ2-АВг~АЕ2,т.е.Е2-1------ ------ -ab.
\ 2 J \2 J
Пример 1. Площадь треугольника АВС равна 30 см3. На стороне АС взята
точка D так, что ADt.DC— 2:3. Длина перпендикуляра DE, проведенного на
сторону ВС, равна 9 см. Найти ВС.
□ Проведем BD (рис. 1.8); треугольники ABD и BDC имеют общую
В
Рис. 1.8
8
высоту BF, следовательно, их площади относятся как длины оснований, т. е.
3
S^abd-S^bdc=AD:DC=2:3, откуда S^bdc=~ Ядлвс=18 см2. С другой сто-
1 1
роны, согласно формуле (1.1), S&Bdc='^BCDE или 18=-ВС-9, откуда
ВС—4 см.
Пример 2. В равнобедренном треугольнике высоты, проведенные к основа-
нию и к боковой стороне, равны соответственно 10 и 12 см. Найти длину
основания.
□ В Д.АВС имеем АВ—ВС, BDLAC, AELBC, BD = 10 см и АЕ= 12 см (рис.
1.9). Пусть АС=х, АВ=ВС=у. Прямоугольные треугольники АЕС и BDC подо-
бны (угол С—общий); следовательно, BC:AC=BD:AE или у:х=10:12=5:б.
Применяя теорему Пифагора (1.13) к &BDC, имеем BC2=BD2+DC2, т. е.
, х2
у^ = 100+—. Решив систему уравнении
У=5
х б’
X2
/ = 100+—,
4
получим х=15. Итак, ЛС=15 см.
Пример 3. Две окружности касаются внешним образом. К первой из них
проведена касательная, проходящая через центр второй окружности. Расстояние
от точки касания до центра второй окружности равно утроенному радиусу этой
окружности. Во сколько раз длина первой окру-
жности больше длины второй окружности?
□ Пусть Oj и О2 — центры окружностей,
А—точка касания (рис. 1.10). Тогда О1Л = Я1,
О1О2 = Я1+ R2, O2A = 3R2 (по условию). Требуется
найти отношение 2nR2:2nR2=R1:R2. В прямо-
угольном треугольнике OtAO2 (2_Л=9О°) имеем
OtO2 = О2А2 + О2А2 или (Я1 + А,)2=Я? + (ЗЯ2)2.
Упростив это равенство, получим =4Я2, откуда
«!:Aj=4.
Пример 4. Точка касания окружности, вписан-
ной в прямоугольный треугольник, делит гипо-
тенузу на отрезки длиной тип. Доказать, что
площадь треугольника S=mn. Найти площадь прямоугольника, вписанного
в данный треугольник так, что одна его вершина совпадает с вершиной прямого
угла, а противоположная вершина — с точкой касания окружности и гипотенузы.
□ Пусть D, Е, F — точки касания (рис. 1.11); тогда AD=AF=m, BD=BE=n,
CE—CF=r — радиус вписанной окружности, р=г+т+п— полупериметр. Да-
9
(г+т)(г+л)
лее, используя формулу (1.9), находим 5=------------------- или
2
2S=r2 +r(m+n)+mn—r(r+m + n) + mn = rp+mn. Так как в силу равенства (1.4)
rp = S, то 2S=S+mn, откуда S=mn.
Пусть CMDK — вписанный прямоугольник. Поскольку DK\\BC, используя
т
гомотетию с центром в Л и коэффициентом к—----, найдем площадь 5,
т+п
треугольника ADK:
т2 т3п
si = 5 д авс ~ ~г=—
(т + п)2 (т+п)2
Аналогично для площади S2 треугольника BDM имеем
„2 М,И3
П ТПП
S2 = S&ABC~------------.
(m+л)2 (т+п)1
Искомая площадь
ли3п + »!Л3 2/и2л2
ScMDK=mn—----------------5-
(л1+л)2 (т + л)2
Пример 5. В прямоугольном треугольнике проведена биссектриса острого
угла; отрезок, соединяющий ее основание с точкой пересечения медиан, перпен-
дикулярен катету. Найти углы треугольника.
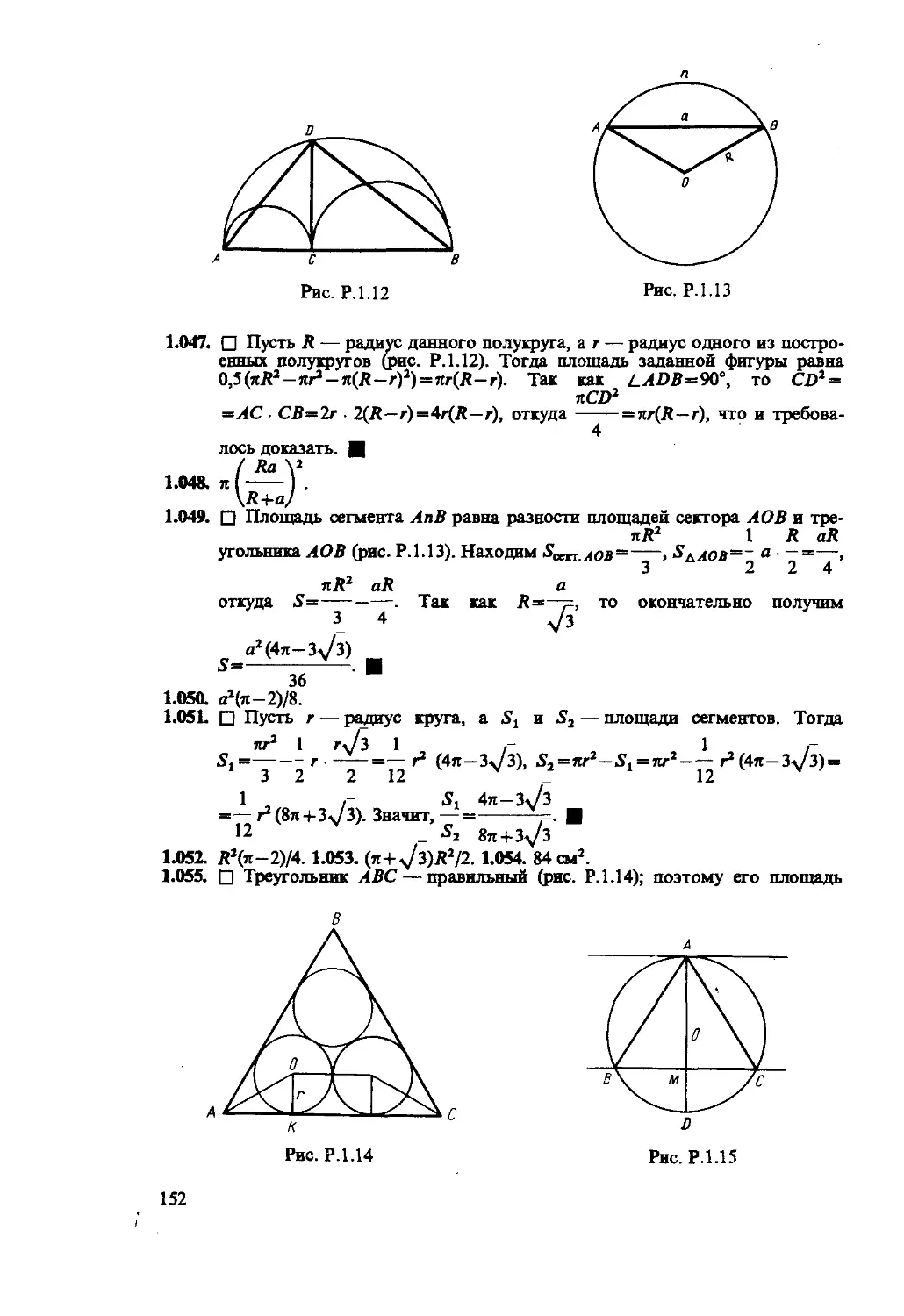
□ Пусть BE — медиана, О — точка пересечения медиан, AD — биссектриса
и ODLBC (рис. 1.12). Согласно свойству точки пересечения медиан, ЕО: ОВ= 1:2.
Так как ООЦЕС, то по теореме Фалеса CD:DB=EO: OB— 1:2. Используя свойст-
во биссектрисы треугольника, получаем CD\DB=AC:AB, т. е. АС:АВ=1:2.
Следовательно, sinВ= 1/2, откуда Z_B=30°, /_Л=60°.
Группа А
1.001. Точка на гипотенузе, равноудаленная от обоих катетов, делит
гипотенузу на отрезки длиной 30 и 40 см. Найти катеты треугольника.
1.002. Медиана, проведенная к гипотенузе прямоугольного тре-
угольника, равна т и делит прямой угол в отношении 1:2. Найти
стороны треугольника.
1.003. Длины сторон прямоугольного треугольника образуют ариф-
метическую прогрессию с разностью 1 см. Найти длину гипотенузы.
1.004. Определить острые углы прямоугольного треугольника,
если медиана, проведенная к его гипотенузе, делит прямой угол
в отношении 1:2.
1.005. Катеты прямоугольного треугольника равны 9 и 12 см. Найти
расстояние между точкой пересечения его биссектрис и точкой пересече-
ния медиан.
1.006. Найти биссектрисы острых углов прямоугольного треуголь-
ника с катетами 24 и 18 см.
1.007. В прямоугольном треугольнике биссектриса острого угла де-
лит противоположный катет на отрезки длиной 4 и 5 см. Определить
площадь треугольника.
1.008. Через вершину прямого угла прямоугольного треугольника
с катетами 6 и 8 м проведен перпендикуляр к гипотенузе. Вычислить
площади образовавшихся треугольников.
1.009. Площадь прямоугольного треугольника равна 2л/3 см2. Опре-
10
делить его высоту, проведенную к гипотенузе, если она делит прямой
угол в отношении 1:2.
1.010. В равнобедренном треугольнике с боковой стороной, равной
4 см, проведена медиана боковой стороны. Найти основание треуголь-
ника, если медиана равна 3 см.
1.011. Основание равнобедренного треугольника равно 4^/2 см,
а медиана боковой стороны 5 см. Найти длины боковых сторон.
1.012. Найти длины сторон равнобедренного треугольника АВС
с основанием АС, если известно, что длины его высот AN и ВМ равны
соответственно п и т.
1.013. В равнобедренном треугольнике основание и боковая сторона
равны соответственно 5 и 20 см. Найти биссектрису угла при основании
треугольника.
1.014. Вычислить площадь равнобедренного треугольника, если дли-
на высоты, проведенной к боковой стороне, равна 12 см, а длина
основания равна 15 см.
1.015. Найти площадь равнобедренного треугольника, если основа-
ние его равно а, а длина высоты, проведенной к основанию, равна длине
отрезка, соединяющего середины основания и боковой стороны.
1.016. Высота, проведенная к основанию равнобедренного треуголь-
ника, равна Н и вдвое больше своей проекции на боковую сторону.
Найти площадь треугольника.
1.017. Найти длины сторон АВ и АС треугольника АВС, если BC=i
см, а длины высот, проведенных к АС и ВС, равны соответственно 6,4
и 4 см.
1.018. В треугольнике длины двух сторон составляют 6 и 3 см.
Найти длину третьей стороны, если полусумма высот, проведенных
к данным сторонам, равна третьей высоте.
1.019. Длина основания треугольника равна 36 см. Прямая, парал-
лельная основанию, делит площадь треугольника пополам. Найти длину
отрезка этой прямой, заключенного между сторонами треугольника.
1.020. На каждой медиане треугольника взята точка, делящая меди-
ану в отношении 3:1, считая от вершины. Во сколько раз площадь
треугольника с вершинами в этих трех точках меньше площади исход-
ного треугольника?
1.021. Прямая, параллельная основанию треугольника, делит его на
части, площади которых относятся как 2:1. В каком отношении, считая
от вершины, она делит боковые стороны?
1.022. Основание треугольника равно 30 см, а боковые стороны 26
и 28 см. Высота разделена в отношении 2:3 (считая от вершины), и через
точку деления проведена прямая, параллельная основанию. Определить
площадь полученной при этом трапеции.
1.023. Из точки А, не лежащей на окружности, проведены к ней
касательная и секущая. Расстояние от точки А до точки касания равно 16
см, а до одной из точек пересечения секущей с окружностью равно 32 см.
Найти радиус окружности, если секущая удалена от ее центра на 5 см.
1.024. Из внешней точки проведены к окружности секущая длиной 12
см и касательная, длина которой составляет 2/3 внутреннего отрезка
секущей. Определить длину касательной.
1.025. Хорда окружности равна 10 см. Через один конец хорды
проведена касательная к окружности, а через другой — секущая, парал-
лельная касательной. Определить радиус окружности, если внутренний
отрезок секущей равен 12 см.
1.026. Две окружности радиусов А=3 см и r= 1 см касаются внеш-
11
ним образом. Найти расстояния от точки касания окружностей до их
общих касательных.
1.027. Из одной точки проведены к окружности две касательные.
Длина каждой касательной 12 см, а расстояние между точками касания
14,4 см. Определить радиус окружности.
1.028. В острый угол, равный 60°, вписаны две окружности, извне
касающиеся друг друга. Радиус меньшей окружности равен г. Найти
радиус большей окружности.
1.029. Через концы дуги окружности, содержащей 120°, проведены
касательные, и в фигуру, ограниченную этими касательными и данной
дугой, вписана окружность. Доказать, что ее длина равна длине исход-
ной дуги.
1.030. В окружности проведены две хорды АВ=а и АС=Ь. Длина
дуги АС вдвое больше длины дуги АВ. Найти радиус окружности.
1.031. Общая хорда двух пересекающихся окружностей видна из их
центров под углами 90 и 60°. Найти радиусы окружностей, если расстоя-
ние между их центрами равно у/з +1.
1.032. В сектор АОВ с радиусом R и углом 90° вписана окружность,
касающаяся отрезков О А, ОВ и дуги АВ. Найти радиус окружности.
1.033. Дана точка Р, удаленная на 7 см от центра окружности
радиуса 11 см. Через эту точку проведена хорда длиной 18 см. Каковы
длины отрезков, на которые делится хорда точкой Р?
1.034. В окружности радиуса г проведена хорда, равная rfl. Через
один конец хорды проведена касательная к окружности, а через дру-
гой — секущая, параллельная касательной. Найти расстояние между
касательной и секущей.
1.035. В большем из двух концентрических кругов проведена хорда,
равная 32 см и касающаяся меньшего круга. Определить длину радиуса
каждого из кругов, если ширина образовавшегося кольца равна 8 см.
1.036. Круг радиуса R разделен двумя концентрическими с ним
окружностями на три равновеликие фигуры. Найти радиусы этих окру-
жностей.
1.037. Площадь кругового кольца равна S. Радиус большей окру-
жности равен длине меньшей окружности. Определить радиус по-
следней.
1.038. Определить площадь кругового кольца, заключенного между
двумя концентрическими окружностями, длины которых равны Сг и С2
(Ct>C2).
1.039. Хорда АВ постоянной длины скользит своими концами по
окружности радиуса R. Точка О этой хорды, находящаяся на расстояни-
ях а и b от концов А и В хорды, описывает при полном обороте
окружность. Вычислить площадь кольца, заключенного между данной
окружностью и окружностью, описанной точкой С.
1.040. Внутри круга радиуса 15 см взята точка М на расстоянии 13
см от центра. Через точку М проведена хорда длиной 18 см. Найти
длины отрезков, на которые точка М делит хорду.
1.041. В круговой сектор с центральным углом в 120° вписан круг.
Найти радиус описанного круга, если радиус данного круга равен R.
1.042. В круговой сектор, дуга которого содержит 60°, вписан круг.
Найти отношение площади этого круга к площади сектора.
1.043. Круг радиуса R обложен четырьмя равными кругами, каса-
ющимися данного так, что каждые два соседних из этих четырех кругов
касаются друг друга. Вычислить площадь одного из этих кругов.
1.044. Три окружности разных радиусов попарно касаются друг
12
друга. Прямые, соединяющие их центры, образуют прямоугольный
^треугольник. Найти радиус меньшей окружности, если радиусы большей
?и средней окружностей равны 6 и 4 см.
1.045. Три равные окружности радиуса г попарно касаются одна
другой. Вычислить площадь фигуры, расположенной вне окружностей
и ограниченной их дугами, заключенными между точками касания.
1.046. Общей хордой двух кругов стягиваются дуги в 60 и 120°.
Найти отношение площадей этих кругов.
1.047. Доказать, что если диаметр полукруга разделить на две про-
извольные части и на каждой из них построить как на диаметре полуок-
ружность (внутри данного полукруга), то площадь, заключенная между
тремя полуокружностями, равна площади круга, диаметр которого ра-
вен длине перпендикуляра к диаметру полукруга, проведенного в точке
деления до пересечения с окружностью.
1.048. Определить площадь круга, вписанного в сектор круга ради-
уса R с хордой 2а.
1.049. Сторона равностороннего треугольника, вписанного в окру-
жность, равна а. Вычислить площадь отсекаемого ею сегмента.
1.050. Сторона квадрата, вписанного в окружность, равна а. Вычис-
лить площадь отсекаемого ею сегмента.
1.051. Круг разделен на два сегмента хордой, равной стороне пра-
вильного вписанного треугольника. Определить отношение площадей
этих сегментов.
1.052. Круг, радиус которого равен R, разделен на два сегмента
хордой, равной стороне вписанного квадрата. Определить площадь
меньшего из этих сегментов.
1.053. В круге радиуса R по разные стороны от центра проведены
две параллельные хорды, одна из которых равна стороне правильного
вписанного треугольника, а другая — стороне правильного вписанного
шестиугольника. Определить площадь части круга, содержащейся между
хордами.
1.054. Три окружности радиусов Rr = 6 см, А2 = 7 см, А3 = 8 см
попарно касаются друг друга. Определить площадь треугольника, вер-
шины которого совпадают с центрами этих окружностей.
1.055. Каждая из трех равных окружностей радиуса г касается двух
других. Найти площадь треугольника, образованного общими внеш-
ними касательными к этим окружностям.
1.056. В круг радиуса R вписаны два правильных треугольника так,
что при их взаимном пересечении каждая из сторон разделилась на три
равных отрезка. Найти площадь пересечения этих треугольников.
1.057. Общая хорда двух окружностей служит для одной из них
стороной вписанного квадрата, а для другой — стороной правильного
вписанного шестиугольника. Найти расстояние между центрами окру-
жностей, если радиус меньшей из них равен г (рассмотреть два возмож-
ных случая расположения окружностей).
1.058. Общая хорда двух пересекающихся окружностей рг.ла
а и служит для одной окружности стороной правильного вписанного
треугольника, а для другой — стороной вписанного квадрата. Опреде-
лить расстояние между центрами окружностей (рассмотреть два воз-
можных случая).
1.059. Одна из двух параллельных прямых касается окружности
радиуса R в точке А, а другая пересекает эту окружность в точках В а С.
Выразить площадь треугольника АВС как функцию расстояния х между
прямыми.
13
1.060. В прямоугольном треугольнике точка касания вписанной
окружности делит гипотенузу на отрезки длиной 5 и 12 см. Найти катеты
треугольника.
1.061. Радиусы вписанной и описанной окружностей прямоуголь-
ного треугольника равны соответственно 3 и 5 см. Найти катеты тре-
угольника.
1.062. Радиус окружности, описанной около прямоугольного тре-
угольника, равен 15 см, а радиус вписанной в него окружности равен
6 см. Найти стороны треугольника.
1.063. Один из катетов прямоугольного треугольника равен 15 см,
а радиус окружности, вписанной в треугольник, равен 3 см. Найти
площадь треугольника.
1.064. Радиус окружности, описанной около прямоугольного тре-
угольника, относится к радиусу вписанной в него окружности как 5:2.
Найти площадь треугольника, если один из его катетов равен а.
1.065. В прямоугольный треугольник вписана полуокружность так,
что диаметр лежит на гипотенузе, а центр делит гипотенузу на отрезки
длиной 15 и 20 см. Найти площадь треугольника и длину вписанной
полуокружности.
1.066. На большем катете треугольника как на диаметре построена
полуокружность. Найти ее длину, если длина меньшего катета 30 см,
а хорда, соединяющая вершину прямого угла с точкой пересечения
гипотенузы и полуокружности, равна 24 см.
1.067. Окружность касается большего катета прямоугольного тре-
угольника, проходит через вершину противолежащего острого угла
и имеет центр на гипотенузе треугольника. Каков радиус окружности,
если длины катетов равны 5 и 12?
1.068. Найти радиус окружности, описанной около прямоугольного
треугольника, если радиус окружности, вписанной в этот треугольник,
равен 3 см, а один из катетов равен 10 см.
1.069. Один из катетов прямоугольного треугольника равен 15 см,
а проекция другого катета на гипотенузу равна 16 см. Найти радиус
окружности, вписанной в треугольник.
1.070. Периметр прямоугольного треугольника равен 2р, а гипо-
тенуза равна с. Определить площадь круга, вписанного в треугольник.
1.071. Найти площадь круга, вписанного в прямоугольный треуголь-
ник, если проекции катетов на гипотенузу равны 9 и 16 м.
1.072. Найти площадь круга, вписанного в прямоугольный треуголь-
ник, если высота, проведенная к гипотенузе, делит последнюю на отрез-
ки длиной 25,6 и 14,4 см.
1.073 Периметр прямоугольного треугольника равен 24 см, площадь
его равна 24 см2. Найти площадь описанного круга.
1.074. Катеты прямоугольного треугольника равны 6 и 8 см. Найти
расстояние от центра вписанной в треугольник окружности до центра
описанной около него окружности.
1.075. Окружность касается одного из катетов равнобедренного пря-
моугольного треугольника и проходит через вершину противополож-
ного острого угла. Найти радиус окружности, если ее центр лежит на
гипотенузе треугольника, а катет треугольника равен а.
1.076. Найти отношение радиуса окружности, вписанной в равнобед-
ренный прямоугольный треугольник, к высоте, проведенной к гипо-
тенузе.
1.077. Боковая сторона равно бедренного треугольника равна 10 см,
основание 12 см. К окружности, вписанной в треугольник, проведены
14
касательные, параллельные высоте треугольника и отсекающие от дан-
ного треугольника два прямоугольных треугольника. Найти длины сто-
рон этих треугольников.
1.07 8. Длина высоты, проведенной к основанию равнобедренного
треугольника, равна 25 см, а радиус вписаннной окружности равен 8 см.
Найти длину основания треугольника.
1.07 9. В равнобедренный треугольник с углом 120° при вершине
и боковой стороной а вписана окружность. Найти радиус этой окру-
жности.
1.08 0. В равнобедренном треугольнике основание равно 30 см, а бо-
ковая сторона равна 39 см. Определить радиус вписанного круга.
1.08 1. Найти площадь равнобедренного треугольника с углом 120°,
если радиус вписанного круга равен ^/12 см.
1.08 2. В равнобедренном треугольнике основание равно 16 см, а бо-
ковая сторона равна 10 см. Найти радиусы вписанной и описанной
окружностей и расстояние между их центрами.
1.08 3. Найти площадь круга, описанного около равнобедренного
треугольника, если основание этого треугольника равно 24 см, а боковая
сторона 13 см.
1.08 4. К окружности, вписанной в равнобедренный треугольник с ос-
нованием 12 см и высотой 8 см, проведена касательная, параллельная
основанию. Найти длину отрезка этой касательной, заключенного меж-
ду сторонами треугольника.
1.08 5. На основании равнобедренного треугольника, равном 8 см,
как на хорде построена окружность, касающаяся боковых сторон тре-
угольника. Найти радиус окружности, если длина высоты, проведенной
к основанию треугольника, равна 3 см.
1.08 6. Из точки А проведены две прямые, касающиеся окружности
радиуса R в точках В и С так, что треугольник АВС — равносторонний.
Найти его площадь.
1.087 . Площадь равностороннего треугольника, вписанного_в окру-
жность, равна Q2. Доказать, что радиус окружности равен
1.088 . В окружность, диаметр которой равен ^/12, вписан правиль-
ный треугольник. На его высоте как на стороне построен другой пра-
вильный треугольник, в который вписана новая окружность. Найти
радиус этой окружности.
1.089 . В правильный треугольник вписана окружность и около него
описана окружность. Найти площадь образовавшегося кольца, если
сторона треугольника равна а.
1.090 . Каждая сторона правильного треугольника разделена на три
равные части, и соответственные точки деления, считая в одном направ-
лении, соединены между собой. В полученный правильный треугольник
вписана окружность радиуса г=6 см. Определить стороны треуголь-
ников.
1.091 . Дан правильный треугольник АВС. Точка К делит сторону АС
в отношении 2:1, а точка М— сторону А В в отношении 1:2 (считая
в обоих случаях от вершины А). Показать, что длина отрезка КМ равна
радиусу окружности, описанной около треугольника АВС.
1.092 . S равносторонний треугольник вписана окружность. Этой
окружности и сторон треугольника касаются три малые окружности.
Найти сторону треугольника, если радиус малой окружности равен г.
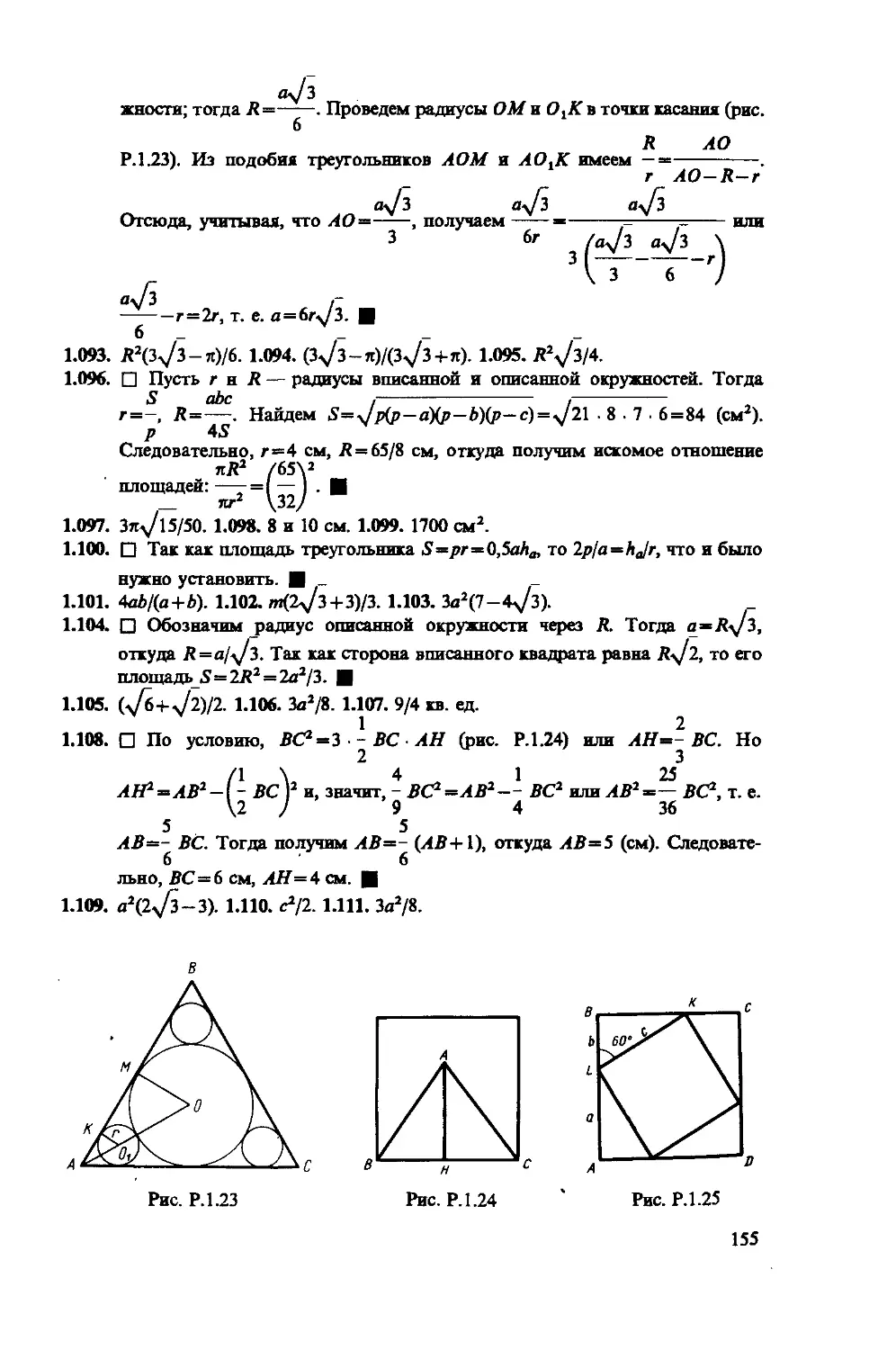
1.093 . На диаметре 2R полуокружности построен правильный тре-
угольник, сторона которого равна диаметру. Треугольник расположен
15
по ту же сторону от диаметра, что и полуокружность. Вычислить
площадь той части треугольника, которая лежит вне круга.
1.094 . На диаметре 2R полукруга построен правильный треугольник,
стороны которого равны диаметру. Как относятся площади частей
треугольника, лежащих вне и внутри круга?
1.095 . В окружность радиуса R вписан треугольник с углами 15°
и 60°. Найти площадь треугольника.
1.096 . Стороны треугольника равны 13,14 и 15 см. Найти отношение
площадей описанного и вписанного в треугольник кругов.
1.097 . В треугольнике длины сторон относятся как 2:3:4. В него
вписан полукруг с диаметром, лежащим на большей стороне. Найти
отношение площади полукруга к площади треугольника.
1.098 . Дан треугольник со сторонами 12, 15 и 18 см. Проведена
окружность, касающаяся обеих меньших сторон и имеющая центр на
большей стороне. Найти отрезки, на которые центр окружности делит
большую сторону треугольника.
1.099 . Расстояние от центра круга до хорды длиной 16 см равно 15
см. Найти площадь треугольника, описанного около круга, если пери-
метр треугольника равен 200 см.
1.100. Доказать, что отношение периметра треугольника к одной из
его сторон равно отношению высоты, проведенной на эту сторону,
к радиусу вписанной окружности.
1.101. В прямоугольный треугольник с катетами а и b вписан квад-
рат, имеющий с треугольником общий прямой угол. Найти периметр
квадрата.
1.102. В правильный треугольник вписан квадрат, сторона которого
равна т. Найти сторону треугольника.
1.103. Найти площадь квадрата, вписанного в правильный треуголь-
ник со стороной а.
1.104. Сторона правильного треугольника, вписанного в окру-
жность, равна а. Вычислить площадь квадрата, вписанного в ту же
окружность.
1.105. На сторонах квадрата вне его построены правильные тре-
угольники, и их вершины последовательно соединены. Определить от-
ношение периметра полученного четырехугольника к периметру данного
квадрата.
1.106. В квадрате, сторона которого а, середины двух смежных
сторон соединены между собой и с противоположной вершиной квад-
рата. Найти площадь полученного треугольника.
1.107. В равнобедренный треугольник вписан квадрат единичной
площади, одна сторона которого лежит на основании треугольника.
Найти площадь треугольника, если известно, что центры масс треуголь-
ника и квадрата совпадают (центр масс треугольника лежит на пересече-
нии его медиан).
1.108. Площадь равнобедренного треугольника равна 1/3 площади
квадрата, построенного на основании данного треугольника. Длины
боковых сторон треугольника короче длины его основания на 1 см.
Найти длины сторон и высоты треугольника, проведенной к основанию.
1.109. Найти площадь правильного треугольника, вписанного в ква-
драт со стороной а при условии, что одна из вершин треугольника
совпадает с вершиной квадрата.
1.110. На сторонах равнобедренного прямоугольного треугольника
с гипотенузой с вне этого треугольника построены квадраты. Центры
16
этих квадратов соединены между собой. Найти площадь полученного
треугольника.
1.111. В квадрате со стороной а середины двух смежных сторон
соединены между собой и с противоположной вершиной квадрата. Опре-
делить площадь внутреннего треугольника.
1.112. В квадрат вписан другой квадрат, вершины которого лежат на
сторонах первого, а стороны составляют со сторонами первого квадрата
углы в 60°. Какую часть площади данного квадрата составляет площадь
вписанного?
1.113. Дан квадрат, две вершины которого лежат на окружности
радиуса R, две другие — на касательной к этой окружности. Найти
длину диагонали квадрата.
1.114. Около квадрата со стороной а описана окружность. В один из
образовавшихся сегментов вписан квадрат. Определить площадь этого
квадрата.
1.115. В сегмент, дуга которого равна 60°, вписан квадрат. Вычис-
лить площадь квадрата, если радиус круга равен 2>/з + ^/17.
1.116. Сторона квадрата, вписанного в окружность, отсекает сег-
мент, площадь которого равна (2п—4) см2. Найти площадь квадрата.
1.117. Площадь прямоугольника равна 9 см2, а величина одного из
углов, образованного диагоналями, равна 120°. Найти стороны прямо-
угольника.
1.118. В круг радиуса R вписан прямоугольник, площадь которого
вдвое меньше площади круга. Определить стороны прямоугольника.
1.119. В прямоугольнике проведены биссектрисы двух углов, приле-
жащих к большей стороне. Определить, на какие части делится площадь
прямоугольника этими биссектрисами, если стороны прямоугольника
равны 2 и 4 м.
1.120. В прямоугольный треугольник с углом 60° вписан ромб со
стороной, равной 6 см, так, что угол в 60° у них общий и все вершины
ромба лежат на сторонах треугольника. Найти стороны треугольника.
1.121. В треугольник вписан ромб так, что один угол у них общий,
а противоположная вершина делит сторону треугольника в отношении
2:3. Диагонали ромба равны тип. Найти стороны треугольника,
содержащие стороны ромба.
1.122. Сумма длин диагоналей ромба равна т, а его площадь равна
S. Найти сторону ромба.
1.123. В ромб с острым углом 30° вписан круг, площадь которого
равна Q. Найти площадь ромба.
1.124. Периметр ромба равен 2 м, длины его диагоналей относятся
как 3:4. Найти площадь ромба.
1.125. Определить сторону ромба, зная, что площадь его равна S,
а длины диагоналей относятся как т: п.
1.126. Периметр ромба равен 2р; длины диагоналей относятся как
т: п. Вычислить площадь ромба.
1.127. Высота ромба равна 12 см, а одна из его диагоналей равна 15
см. Найти площадь ромба.
1.128. Высота ромба, проведенная из вершины тупого угла, делит
его сторону на отрезки длиной т и п (т считать от вершины острого
угла). Определить диагонали ромба.
1.129. Ромб, у которого сторона равна меньшей диагонали, равнове-
лик кругу радиуса R. Определить сторону ромба. ,*#-
1.130. В ромб с острым углом 30° вписан круг, а в круг — квадрат?*
Найти отношение площади ромба к площади квадрата.
17 ♦'
1.131. В пересечение двух равных кругов вписан ромб с диагоналями
12 и 6 см. Найти радиус окружностей.
1.132. В ромб, который делится своей диагональю на два равносто-
ронних треугольника, вписана окружность радиуса 2. Найти сторону
ромба.
1.133. Доказать, что если в четырехугольнике диагонали лежат на
биссектрисах его углов, то такой четырехугольник есть ромб.
1.134. На сторонах ромба как на диаметрах описаны полуокруж-
ности, обращенные внутрь ромба. Определить площадь полученной
розетки, если диагонали ромба равны а и 4.
1.135. Периметр параллелограмма равен 90 см, а острый угол содер-
жит 60°. Диагональ параллелограмма делит его тупой угол на части
в отношении 1:3. Найти стороны параллелограмма.
1.136. Величина одного из углов параллелограмма равна 60°,
а меньшая диагональ 2л/з 1 см. Длина перпендикуляра, проведенного из
точки пересечения диагоналей к большей стороне, равна >/75/2 см.
Найти длины сторон и большей диагонали параллелограмма.
1.137. Перпендикуляр, проведенный из вершины параллелограмма
к его диагонали, делит эту диагональ на отрезки длиной 6 и 15 см.
Разность длин сторон параллелограмма равна 7 см. Найти длины сто-
рон параллелограмма и его диагоналей.
1.138. В параллелограмме с периметром 32 см проведены диагона-
ли. Разность между периметрами двух смежных треугольников равна
8 см. Найти длины сторон параллелограмма.
1.139. В параллелограмме ABCD высота, проведенная из вершины
В тупого угла на сторону DA, делит ее в отношении 5:3, считая от
вершины D. Найти отношение AC .BD, если AD:AB = 2.
1.140. Через точки Л и Е, принадлежащие сторонам АВ и AD
2 1
параллелограмма ABCD и такие, что AR= АВ, АЕ= - AD, проведена
3 3
прямая. Найти отношение площади параллелограмма к площади полу-
ченного треугольника.
1.141. Доказать, что в параллелограмме ABCD расстояния от любой
точки диагонали АС до прямых ВС и CD обратно пропорциональны
дайнам этих сторон.
1.142. Доказать, что если через вершины четырехугольника провести
прямые, параллельные его диагоналям, то площадь параллелограмма,
определяемою этими прямыми, в 2 раза больше площади данного
четырехугольника.
1.143. Две окружности радиуса R с центрами Ох и Ог касаются друг
друга. Их пересекает прямая в точках А, В, С я D так, что АВ= ВС — CD.
Найти площадь четырехугольника ОхАООг.
1.144. В точках пересечения двух окружностей с радиусами 4 и 8 см
касательные к ним взаимно перпендикулярны. Вычислить площадь фи-
гуры ОхАВОг, где АВ — общая касательная к окружностям, а Ох
и О2 — их центры.
1.145. Большее основание трапеции имеет длину 24 см. Найти длину
ее меньшего основания, если известно, что расстояние между серединами
диагоналей трапеции равно 4 см.
1.146. Один из углов трапеции равен 30°, а прямые, содержащие
боковые стороны трапеции, пересекаются под прямым углом. Найти
длину меньшей боковой стороны трапеции, если ее средняя линия равна
10 см, а одно из оснований 8 см.
...1.147. Вычислить площадь трапеции, параллельные стороны кото-
рой содержат 16 и 44 см, а непараллельные — 17 и 25 см.
1.148. Длины параллельных сторон трапеции равны 25 и 4 см,
а длины непараллельных сторон — 20 и 13 см. Найти высоту трапеции.
1.149. Основания трапеции равны а и Ь, углы при большем основа-
нии равны я/6 и я/4. Найти площадь трапеции.
1.150. Вычислить площадь трапеции ABCD (AD]\BC), если длины ее
оснований относятся как 5:3 и площадь треугольника ADM равна 50
см1, где М — точка пересечения прямых АВ и CD.
1.151. Вычислить площадь трапеции по разности оснований, равной
14 см, и двум непараллельным сторонам, равным 13 и 15 см, если
известно, что в трапецию можно вписать окружность.
1.152. В трапеции, площадь которой равна 594 м2, высота 22 м,
а разность параллельных сторон равна 6 м, найти длину каждой из
параллельных сторон.
1.153. Доказать, что площадь трапеции равна произведению длины
одной из непараллельных сторон и длины перпендикуляра, проведен-
ного через середину другой боковой стороны к первой.
1.154. Трапеция разбита диагоналями на четыре треугольника. Най-
ти отношение площадей треугольников, прилегающих к боковым сторо-
нам трапеции.
1.155. Диагональ прямоугольной трапеции и ее боковая сторона
равны. Найти длину средней линии, если высота трапеции равна 2 см,
а боковая сторона 4 см.
1.156. Вычислить площадь прямоугольной трапеции, если ее острый
угол равен 60°, меньшее основание равно а, а большая боковая сторона
равна Ь.
1.157. Прямые, содержащие боковые стороны равнобедренной тра-
пеции, пересекаются под прямым углом. Найти длины сторон трапеции,
если ее площадь равна 12 см2, а длина высоты равна 2 см.
1.158. Определить боковые стороны равнобедренной трапеции, если
ее основания и площадь равны соответственно 8 см, 14 см и 44 см2.
1.159. Диагональ равнобедренной трапеции делит ее тупой угол
пополам. Меньшее основание трапеции равно 3 см, периметр равен 42
см. Найти площадь трапеции.
1.160. В равнобедренной трапеции одно основание равно 40 см,
а другое 24 см. Диагонали трапеции взаимно перпендикулярны. Найти ее
площадь.
1.161. В равнобедренной трапеции длина средней линии равна 5,
а диагонали взаимно перпендикулярны. Найти площадь трапеции.
1.162. Большее основание трапеции в 2 раза больше ее меньшего
основания. Через точку пересечения диагоналей проведена прямая, па-
раллельная основаниям. Найти отношение высоты каждой из двух полу-
ченных трапеций к высоте трапеции.
1.163. Основания равнобедренной трапеции а и Ь, боковая сторона ее
равна с, а диагональ равна d. Доказать, что t/2 = ah + с1.
1.164. Найти диагональ и боковую сторону равнобедренной трапе-
ции с основаниями 20 и 12 см, если известно, что центр описанной
окружности лежит на большем основании трапеции.
1.165. В равнобедренной трапеции даны основания а=21 см, Ь = 9 см
и высота h = 9 см. Найти радиус описанного круга.
1.166. В окружность радиуса R вписана трапеция, у которой нижнее
основание вдвое больше каждой из остальных сторон. Найти площадь
трапеции.
<
19;
1.167. Длины оснований равнобедренной трапеции относятся как
5:12, а длина ее высоты равна 17 см. Вычислить радиус окружности,
описанной около трапеции, если известно, что ее средняя линия равна
высоте.
1.168. Найти площадь равнобедренной трапеции, если ее высота
равна й, а боковая сторона видна из центра описанной окружности под
углом 60°.
1.169. Около окружности с диаметром 15 см описана равнобедрен-
ная трапеция с боковой стороной, равной 17 см. Найти основания
трапеции.
1.170. Площадь равнобедренной трапеции, описанной около круга,
равна S, а высота трапеции в 2 раза меньше ее боковой стороны.
Определить радиус вписанного круга.
1.171. Площадь равнобедренной трапеции, описанной около круга,
равна 32л/3 см2. Определить боковую сторону трапеции, если известно,
что острый угол при основании равен л/3.
1.172. Площадь равнобедренной трапеции, описанной около круга,
равна 8 см2. Определить стороны трапеции, если угол при основании
содержит 30°.
1.173. Площадь равнобедренной трапеции, описанной около круга,
равна S. Определить боковую сторону трапеции, если известно, что
острый угол при основании равен я/6.
1.174. Площадь равнобедренной трапеции, описанной около круга,
равна 5. Определить радиус круга, если угол при основании трапеции
равен 30°.
1.175. В равнобедренную трапецию вписана окружность радиуса Л.
Верхнее основание трапеции в 2 раза меньше ее высоты. Найти площадь
трапеции.
1.176. Найти площадь круга, вписанного в равнобедренную трапе-
цию, если ее большее основание равно а, а угол при меньшем основании
равен 120°.
1.177. В равнобедренную трапецию вписан круг. Одна из боковых
сторон делится точкой касания на отрезки длиной т и п. Определить
площадь трапеции.
1.178. В равнобедренную трапецию вписан круг. Доказать, что от-
ношение площади круга к площади трапеции равно отношению длины
окружности к периметру трапеции.
1.179. Равносторонний шестиугольник ABCDEF состоит из двух тра-
пеций, имеющих общее основание CF. Известно, что АС= 13 см, АЕ= 10
см. Найти площадь шестиугольника.
1.180. Найти сторону правильного шестиугольника, равновеликого
равнобедренной трапеции с основаниями 20 и 12 см, если известно, что
центр описанной окружности лежит на большем основании трапеции.
1.181. Вычислить отношение площадей квадрата, правильного тре-
угольника и правильного шестиугольника, вписанных в одну и ту же
окружность.
1.182. Найти отношение площадей равностороннего треугольника,
квадрата и правильного шестиугольника, длины сторон которых равны.
1.183. В правильный треугольник со стороной, равной а, вписана
окружность, в которую вписан правильный шестиугольник. Найти пло-
щадь шестиугольника.
1.184. Около квадрата, сторона которого равна а, описана окру-
жность, а около окружности — правильный шестиугольник. Определить
площадь шестиугольника.
20
, 1.185. Из точки М, находящейся на расстоянии а от окружности,
приведена к этой окружности касательная длиной 2а. Найти площадь
правильного шестиугольника, вписанного в окружность.
1.186. В правильный треугольник вписана окружность, а в нее —
правильный шестиугольник. Найти отношение площадей треугольника
и шестиугольника.
1.187. На сторонах равностороннего треугольника вне его постро-
ены квадраты. Их вершины, лежащие вне треугольника, последователь-
но соединены. Определить площадь полученного шестиугольника, если
сторона данного треугольника равна а.
1.188. В правильный шестиугольник, сторона которого равна а,
вписана окружность, и около него же описана окружность. Определить
площадь кругового кольца, заключенного между этими окружностями.
1.189. Данный квадрат со стороной а срезан по углам так, что
образовался правильный восьмиугольник. Определить площадь этого
восьмиугольника.
1.190. Доказать, что сумма расстояний от любой точки, взятой
внутри правильного шестиугольника, до всех прямых, содержащих его
стороны, есть величина постоянная.
Группа Б
1.191. Внутри прямого угла дана точка М, расстояния от которой до
сторон угла равны 4 и 8 см. Прямая, проходящая через точку М,
отсекает от прямого угла треугольник площадью 100 см2. Найти катеты
треугольника.
1.192. Высота, проведенная к гипотенузе прямоугольного треуголь-
ника, делит его на два треугольника с площадями Q и q. Найти катеты.
1.193. Периметр прямоугольного треугольника ABC (Z_C=90°) ра-
вен 72 см, а разность между длинами медианы СМ и высоты СК равна
7 см. Найти длину гипотенузы. _
L194. В прямоугольном треугольнике медианы катетов равны у/52
и л/73. Найти гипотенузу треугольника.
1.195. Периметр прямоугольного треугольника равен 60 см. Найти
его стороны, если высота, проведенная к гипотенузе, равна 12 см.
1.196. Найти биссектрису прямого угла треугольника, у которого
катеты равны а и Ь.
1.197. В прямоугольном треугольнике расстояние от середины гипо-
тенузы до одного из катетов равно 5 см, а расстояние от середины этого
катета до гипотенузы равно 4 см. Вычислить площадь треугольника.
1.198. Гипотенуза прямоугольного треугольника равна с. Проекция
вершины прямого угла на гипотенузу делит ее на два отрезка, из
которых меньший относится к большему как больший ко всей гипо-
тенузе. Определить площадь треугольника.
1.199. Определить стороны прямоугольного треугольника, у которо-
го периметр равен 2р, а площадь равна т1.
1.200. Стороны треугольника равны 3, 4 и 5 см. Определить площа-
ди треугольников, на которые разбивается данный треугольник высотой
и медианой, проведенными к большей по величине стороне.
1.201. Высоты треугольника равны 12, 15 и 20 см. Доказать, что
треугольник прямоугольны^
1.202. Числа h2, h2 и й3 выражают длины высот некоторого тре-
угольника. Показать, что если выполняется равенство (hl/h1)1 +
+ (Л1/Л3)2= 1, то треугольник является прямоугольным.
1.203. Медианы треугольника равны 5, ^/52 и -J13 см. Доказать, что
треугольник прямоугольный.
1.204. Числа т2, т2 и т3 выражают длины медиан некоторого
треугольника. Показать, что если выполняется равенство т$+т2 = 5т3,
то треугольник является прямоугольным.
1.205. Площадь равностороннего треугольника, построенного на ги-
потенузе, вдвое больше площади прямоугольного треугольника с ука-
занной гипотенузой. Найти отношение катетов.
1.206. Внутри равностороннего треугольника взята точка М, отсто-
ящая от его сторон на расстояния b, с, d. Найти высоту треугольника.
1.207. Точка М лежит внутри равностороннего треугольника АВС.
Вычислить площадь этого треугольника, если известно, что AM — ВМ=2
см, а СМ = 1 см.
1.208. Показать, что сумма расстояний от любой точки, взятой на
стороне правильного треугольника, до двух других его сторон есть
величина постоянная.
1.209. Основания двух правильных треугольников со сторонами
а и 2а лежат на одной и той же прямой. Треугольники расположены по
разные стороны от прямой и не имеют общих точек, а расстояние между
ближайшими концами их оснований равно 2а. Найти расстояние между
вершинами треугольников, не принадлежащими данной прямой.
1.210. Точка С перемещается по отрезку АВ длиной I. На отрезках
АС и СВ как на основаниях построены правильные треугольники по
одну сторону от АВ. Где нужно взять точку С, чтобы расстояние между
вершинами треугольников было наименьшим?
1^211. В равнобедренном треугольнике угол при основании содер-
жит 72°, а биссектриса этого угла имеет длину, равную т. Найти длины
сторон треугольника.
1.212. В равнобедренном треугольнике угол при вершине содержит
36°, а биссектриса угла при основании равна -^20. Найти длины сторон
треугольника.
1^213. В равнобедренном треугольнике с боковой стороной, равной
Ь, проведены биссектрисы углов при основании. Отрезок прямой между
точками пересечения биссектрис с боковыми сторонами равен т. Опре-
делить основание треугольника.
1.214. Длина основания равнобедренного треугольника равна 12 см,
а боковой стороны — 18 см. К боковым сторонам треугольника прове-
дены высоты. Вычислить длину отрезка, концы которого совпадают
с основаниями высот.
1.215. Основание равнобедренного треугольника равно 8, а боковая
сторона — 12. Найти длину отрезка, соединяющего точки пересечения
биссектрис углов при основании с боковыми сторонами треугольника.
1.216. В равнобедренном треугольнике АВС (АВ=ВС) на стороне
ВС взята точка D так, что BD: DC = 1:4. В каком отношении прямая AD
делит высоту BE треугольника АВС, считая от вершины В1
1.217. Равнобедренный треугольник со сторонами 8, 5 и 5 разделен
на три равновеликие части перпендикулярами, проведенными из некото-
рой точки к его сторонам. Найти расстояние от этой точки до каждой
стороны треугольника.
1.218. Определить углы равнобедренного треугольника, если его
площадь относится к площади квадрата, построенного на его основании,
как ^/з: 12.
1.219. Найти третью сторону остроугольного треугольника, если две
его стороны равны а и Ь, а медианы этих сторон пересекаются под
прямым углом.
1.220. Две стороны треугольника равны 6 и 8 см. Медианы, прове-
денные к этим сторонам, взаимно перпендикулярны. Найти третью
сторону треугольника.
1.221. Высота, основание и сумма боковых сторон треугольника
равны соответственно 24, 20 и 56 см. Найти боковые стороны.
1.222. Дан треугольник АВС, в котором 2hc=AB и LA = 15°. Найти
величину угла С.
1.223. Внутри угла в 60° расположена точка, отстоящая на расстоя-
ния 7? и 2^/7 см от сторон угла. Найти расстояние от этой точки до
сторон угла. __
1.224. Длины двух сторон остроугольного треугольника равны >/13
и 710 см. Найти длину третьей стороны, зная, что эта сторона равна
проведенной к ней высоте.
1.225. Расстояния от точки М, лежащей внутри треугольника АВС,
до его сторон АС и ВС равны соответственно 2 и 4 см. Вычислить
расстояние от точки М до прямой АВ, если АВ= 10 см, ВС= 17 см,
АС=21 см.
1.226. Найти отношение суммы квадратов всех медиан треугольника
к сумме квадратов всех его сторон.
1.227. Найти площадь треугольника, если его высоты равны 12, 15
и 20 см.
1.228. В треугольнике АВС проведена прямая DE, параллельная
основанию А С. Площадь треугольника АВС равна 8 кв. ед., а площадь
треугольника DEC равна 2 кв. ед. Найти отношение отрезка DE к длине
основания треугольника АВС.
1.229. Длины сторон треугольника относятся как т:п:т. Найти
отношение площади этого треугольника к площади треугольника, вер-
шины которого находятся в точках пересечения биссектрис данного
треугольника с его сторонами.
1.230. В треугольнике АВС проведены медианы BD и СЕ; М — точ-
ка их пересечения. Доказать, что треугольник ВСМ равновелик четырех-
угольнику ADME.
1.231. Отношение величин двух углов треугольника равно 2, а раз-
ность длин противоположных им сторон равна 2 см; длина третьей
стороны треугольника равна 5 см. Вычислить площадь треугольника.
1.232. В треугольнике АВС известны: ВС= 15 см, АС= 14 см, АВ—13
см. Вычислить площадь треугольника, заключенного между высотой
и биссектрисой, проведенными из вершины В.
1.233. Стороны треугольника равны 13, 14 и 15 см. Определить
площади треугольников, на которые разбивается данный треугольник
его медианами.
1.234. Медианы одного треугольника равны сторонам другого тре-
угольника. Найти отношение площадей этих треугольников.
1.235. Медианы треугольника равны 3, 4 и 5 см. Найти площадь
треугольника.
1.236. Основание треугольника равно 20 см, медианы боковых сто-
рон равны 18 и 24 см. Найти площадь треугольника.
1.237. Медианы треугольника равны 5, 6 и 5 м. Найти площадь
треугольника.
1.238. Определить площадь треугольника, если две его стороны
равны 1 и V15 см, а медиана третьей стороны равна 2 см.
23
1.239. Определить площадь треугольника, если две его стороны
равны 35 и 14 см, а биссектриса угла между ними содержит 12 см.
1.240. Биссектрисы углов А и В треугольника АВС одинаково накло-
нены к сторонам ВС и АС. Найти зависимость между углами А и В.
1.241. На медиане BD треугольника АВС, площадь которого равна
S, построена точка Е так, что DE=- BD. Через точку Е проведена
4
прямая АЕ, пересекающая сторону ВС в точке F. Найти площадь тре-
угольника AFC.
1.242. На каждой медиане треугольника взята точка, делящая меди-
ану в отношении 1:3, считая от вершины. Во сколько раз площадь
треугольника с вершинами в этих точках меньше площади исходного
треугольника?
1.243. Две окружности касаются внешним образом. Их радиусы
относятся как 3:1, а длина их общей внешней касательной равна 6л/з.
Определить периметр фигуры, образованной внешними касательными
и внешними частями окружностей.
1.244. Две окружности, радиусы которых 4 н 8, пересекаются под
прямым углом. Определить длину их общей касательной.
1.245. Две окружности разных радиусов касаются друг друга внеш-
ним образом. Найти угол, определяемый хордами, соединяющими точку
касания окружностей с точками касания их общей внешней касательной.
1.246. К двум внешне касающимся окружностям радиусов Лиг по-
строена секущая так, что окружности отсекают на ней три равных
отрезка. Найти длины этих отрезков.
1.247. Две окружности радиусов г и Зг внешне касаются. Найти
площадь фигуры, заключенной между окружностями и их общей вне-
шней касательной.
1.248. Две окружности радиусов Лиг касаются друг друга внешним
образом. К этим окружностям проведена общая внешняя касательная,
и в образовавшийся при этом треугольник вписан круг. Найти его
площадь.
1.249. В окружности с центром О проведена хорда АВ, пересека-
ющая диаметр в точке М и составляющая с диаметром угол, равный 60°.
Найти ОМ, если АМ= 10 см, а ВМ=4 см.
1.250. Из одной точки окружности проведены две хорды длиной
9 и 17 см. Найти радиус окружности, если расстояние между серединами
данных хорд равно 5 см.
1.251. Из одной точки окружности проведены две хорды длиной 10
и 12 см. Найти радиус окружности, если расстояние от середины мень-
шей хорды до большей хорды равно 4 см.
1.252. В окружности радиуса R проведены две пересекающиеся пер-
пендикулярные хорды АВ и CD. Доказать, что AC2+BD2=4R.
1.253. Через точку А окружности радиуса 10 см проведены две
взаимно перпендикулярные хорды АВ и АС. Вычислить радиус окру-
жности, касающейся данной окружности и построенных хорд, если
АВ=16 см.
1.254. Через точку Р диаметра данной окружности проведена хорда
АВ, образующая с диаметром угол 60°. Вычислить радиус окружности,
если АР=а и ВР=Ь.
1.255. В круге радиуса R проведены по разные стороны от центра
две параллельные хорды, одна из которых стягивает дугу в £0°, дру-
гая — 120°. Найти площадь части круга, заключенной между хордами.
24
1.256. Периметр сектора равен 28 см, а его площадь равна 49 см2.
Определить длину дуги сектора.
1.257. Найти радиус круга, в сегмент которого, соответствующий
хорде длиной 6 см, вписан квадрат со стороной 2 см.
1.258. Определить площадь сегмента, если его периметр равен р,
а дуга содержит 120°.
1.259. Два круга концентричны, причем окружность меньшего круга
делит большой круг на равновеликие части. Доказать, что часть кольца,
заключенная между параллельными касательными к окружности мень-
шего радиуса, равновелика квадрату, вписанному в меньший круг.
1.260. В угол вписаны три окружности — малая, средняя и большая.
Большая окружность проходит через центр средней, а средняя — через
центр малой. Определить радиусы средней и большой окружностей, если
радиус меньшей равен г и расстояние от ее центра до вершины угла
равно а.
1.261. В угол, содержащий 60°, вписаны пять окружностей так, что
каждая последующая окружность (начиная со второй) касается пред-
ыдущей. Во сколько раз сумма площадей всех пяти кругов больше
площади меньшего круга?
1.262. На отрезке АС длиной 12 см построена точка В так, что АВ=4
см. На отрезках АВ и АС как на диаметрах в одной полуплоскости
с границей А С построены полуокружности. Вычислить радиус окружно-
сти, касающейся построенных окружностей и АС.
1.263. На отрезке АВ и на каждой его половине построены как на
диаметрах полукруги (по одну сторону от АВ). Считая радиус большого
полукруга равным R, найти сумму площадей криволинейных треуголь-
ников, образовавшихся при построении круга, касательного ко всем
трем данным кругам.
1.264. На отрезке АВ взята точка С и на частях АС и СВ отрезка АВ
как на диаметрах построены полуокружности. Доказать, что сумма длин
этих полуокружностей на зависит от положения точки С на отрезке АВ.
1.265. Криволинейный треугольник составлен тремя равными попа-
рно касающимися дугами окружностей радиуса R. Найти площадь этого
треугольника.
1.266. Круг с центром О разделен диаметром АВ на два полукруга.
В одном из них построены два новых полукруга, опирающиеся на О А
и ОВ как на диаметры. В криволинейную фигуру, ограниченную кон-
турами этих трех полукругов, вписан круг. Во сколько раз его площадь
меньше площади данного круга?
1.267. Две окружности радиуса R пересекаются так, что каждая
проходит через центр другой. Две другие окружности того же радиуса
имеют центры в точках пересечения первых двух окружностей. Найти
площадь, общую всем четырем кругам.
1.268. Окружность радиуса R разделена на шесть равных дуг, и внут-
ри круга, ограниченного этой окружностью, через каждые две соседние
точки деления проведены равные дуги такого радиуса, что на дайной
окружности они взаимно касаются. Вычислить площадь внутренней
части данного круга, заключенной между проведенными дугами.
1.269. В прямоугольном треугольнике высота, проведенная к гипо-
тенузе, равна А; радиус вписанной окружности равен г. Найти гипо-
тенузу.
1.270. В прямоугольный треугольник вписана окружность. Точка
касания делит гипотенузу в отношении 2:3. Найти стороны треуголь-
25
ника, если центр вписанной окружности удален от вершины прямого
угла на расстояние >/8 см.
1.271. Площадь прямоугольного треугольника равна 24 см2, а гипо-
тенуза равна 10 см. Найти радиус вписанной окружности.
1.272. Найти площадь прямоугольного треугольника, если даны ра-
диусы Лиг описанного и вписанного в него кругов.
1.273. Найти площадь круга, описанного около прямоугольного тре-
угольника, длины катетов которого являются корнями уравнения
ах1+Ьх+с=0.
1.274. Длины катетов некоторого прямоугольного треугольника яв-
ляются корнями уравнения «х2 + й.г + с=0. '->?>'•< радиус окружности,
вписанной в этот треугольник
1.275. На большом катете прямоугольного треугольника как на
диаметре построена окружность. Определить радиус этой окружности,
если меныпий катет треугольника равен 7,5 см, а длина хорды, соединя-
ющей вершину прямого угла с точкой пересечения гипотенузы и окру-
жности, равна 5 см. ;
1.276. Центр полуокружности, вписанной в прямоугольный 'тре-
угольник так, что ее диаметр лежит на гипотенузе, делит гипотенузу на
отрезки 30 и 40. Найти длину дуги полуокружности, заключенной между
точками ее касания с катетами.
1.277. Прямоугольный треугольник АВС разделен высотой CD, про-
веденной к гипотенузе, на два треугольника BCD и ACD. Радиусы
окружностей, вписанных в треугольники BCD и ACD, равны соответст-
венно 4 и 3 см. Найти расстояние между их центрами.
1.278. Катеты прямоугольного треугольника равны 6 и 8 см. Через
середину меньшего катета и середину гипотенузы проведена окружность,
касающаяся гипотенузы. Найти площадь круга, ограниченного этой
окружностью.
1.279. В прямоугольный треугольник со сторонами 6, 8 и 10 см
вписана окружность. Через центр окружности проведены прямые, парал-
лельные сторонам треугольника. Вычислить длины средних отрезков
сторон треугольника, отсекаемых построенными прямыми.
1.280. Показать, что во всяком прямоугольном треугольнике сумма
полупериметра и радиуса вписанной окружности равна сумме катетов.
1.281. Показать, что во всяком прямоугольном треугольнике сумма
диаметров описанной и вписанной окружностей равна сумме его ка-
тетов.
1.282. Сторона правильного треугольника равна а. Определить пло-
щадь части треугольника, лежащей вне круга радиуса а/3, центр которо-
го совпадает с центром треугольника.
1.283. В круг радиуса R вписан правильный треугольник, высоты
которого продолжены до пересечения с окружностью. Эти точки пересе-
чения соединены между собой, в результате чего получается новый
треугольник. Вычислить ту часть площади круга, которая находится вне
этих треугольников.
1.284. В равносторонний треугольник АВС со стороной а=2 см
вписан круг; точка А является центром второго круга с радиусом 1 см.
Найти площадь пересечения этих кругов.
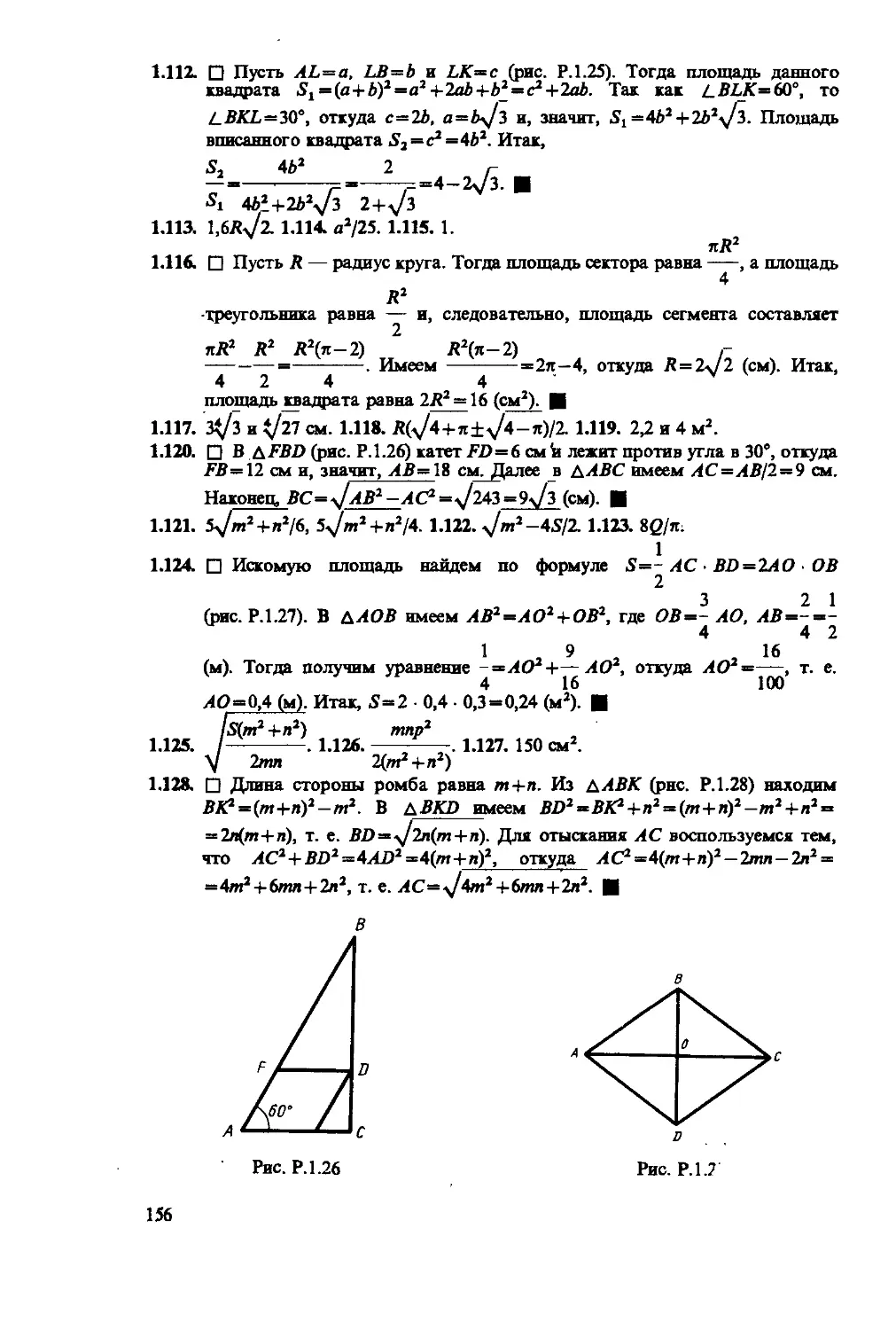
1.285. Внутри правильного треугольника со стороной а расположе-
ны три равные окружности, каждая из которых касается двух сторон
треугольника и двух других окружностей. Найти площадь части тре-
угольника, расположенной вне этих окружностей.
1.286. Центр равностороннего треугольника со стороной, равной
26
6 см, совпадает с центром окружности радиуса 2 см. Определить пло-
щадь части треугольника, лежащей вне этой окружности.
1.287. Около круга радиуса R описаны квадрат и равносторонний
треугольник, причем одна из сторон квадрата лежит на стороне тре-
угольника. Вычислить площадь общей части треугольника и квадрата.
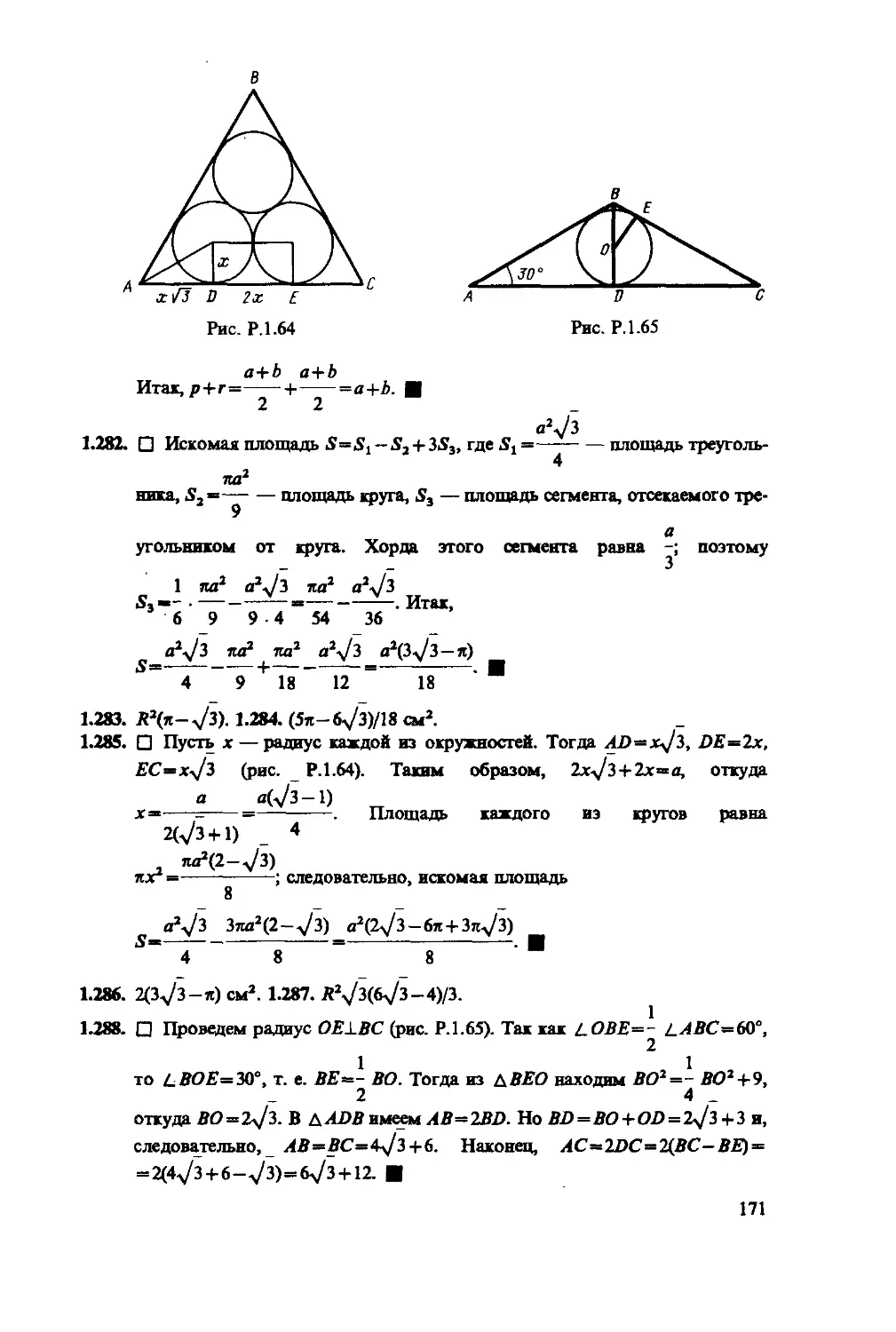
1.288. Около круга радиуса 3 описан равнобедренный треугольник
с острым углом 30° при основании. Определить стороны треугольника.
1.289. Окружности радиусов Л и г касаются друг друга внешним
образом. Боковые стороны равнобедренного треугольника являются их
общими касательными, а основание касается большей из окружностей.
Найти основание треугольника.
1.290. Какими целыми числами выражаются стороны равнобедрен-
ного треугольника, если радиус вписанной окружности равен 3/2 см,
а описанной 25/8 см?
1.291. Один конец диаметра полуокружности совпадает с вершиной
угла при основании равнобедренного треугольника, а другой принад-
лежит этому основанию. Найти радиус полуокружности, если она каса-
ется одной боковой стороны и делит другую на отрезки длиной 5 и 4 см,
считая от основания.
1.292. Дан равнобедренный треугольник с основанием, равным а,
и боковой стороной, равной Ь. Доказать, что центр вписанной окружно-
сти делит биссектрису угла при основании в отношении (а+Ь): Ь, считая
от вершины угла.
1.293. В треугольник вписана окружность радиуса 3 см. Вычислить
дайны сторон треугольника, если одна из них разделена точкой касания
на отрезки длиной 4 и 3 см.
1.294. Дан треугольник АВС такой, что АВ= 15 см, ВС=12 см
и АС =18 см. В каком отношении центр вписанной в треугольник
окружности делит биссектрису угла С?
1.295. Стороны треугольника относятся как 5:4:3. Найти отноше-
ние отрезков сторон, на которые они делятся точкой касания вписанной
окружности.
1.296. Сторона треугольника равна 48 см, а высота, проведенная
к этой стороне, равна 8,5 см. Найти расстояние от центра окружности,
вписанной в треугольник, до вершины, противолежащей данной стороне,
если радиус вписанной окружности равен 4 см.
1.297. В треугольник вписан круг. Прямые, соединяющие центр кру-
га с вершинами, делят площадь треугольника на части с площадями 4,
13 и 15 см2. Найти стороны треугольника.
1.298. Радиус окружности, вписанной в треугольник, равен 2 см.
Точка касания этой окружности делит одну из сторон на отрезки длиной
4 и 6 см. Определить вид треугольника и вычислить его площадь.
1.299. Для треугольника со сторонами 26, 28 и 30 См найти произ-
ведение радиусов вписанной и описанной окружностей.
1.300. Найти площадь треугольника, вписанного в круг радиуса
2 см, если два угла треугольника равны я/3 и я/4.
1.301. Пусть BD — высота треугольника АВС, точка Е — середина
ВС. Вычислить радиус круга, описанного около треугольника BDE, если
АВ=30 см, BC=2f> см и АС=28 см.
1.302. Точка Сг — середина стороны АВ треугольника АВС; угол
СОС1г где О — центр окружности, описанной около треугольника, явля-
ется прямым. Доказать, что |Z_B— LA\ = 90°.
1303. Доказать, что расстояние от ортоцентра (точки пересечения
27
высот) до вершины треугольника больше расстояния от центра описан-
, ной окружности до стороны, противоположной этой вершине.
1304. В треугольнике АВС проведены медианы AL и ВМ, пересека-
ющиеся в точке К. Вершина С лежит на окружности, проходящей через
точки К, L, М. Длина стороны АВ равна а. Найти длину медианы CN.
1305. Дан треугольник со сторонами 10, 24 и 26. Две меньшие
стороны являются касательными к окружности, центр которой лежит на
большей стороне. Найти радиус окружности.
1.306. На отрезке АВ взята точка М, а на отрезках AM и МВ
по одну сторону от прямой АВ построены квадраты, описанные окру-
жности которых пересекаются в точке N. Доказать, что прямая AN
проходит через вершину второго квадрата и что треугольник ANB
прямоугольный.
1.307. Дан квадрат, ст орона которого равна а. Определить стороны
равновеликого ему равнобедренного треугольника, у которого сумма
длин основания и высоты, опущенной на основание, равна сумме длин
двух боковых сторон.
1.308. Окружность касается двух смежных сторон квадрата и делит
каждую из двух других его сторон на отрезки, равные 2 и 23 см. Найти
радиус окружности.
1.309. Окружность радиуса 13 см касается двух смежных сторон
квадрата со стороной 18 см. На какие два отрезка делит окружность
каждую из двух других сторон квадрата?
1310. Найти отношение площади квадрата, вписанного в сегмент
с дугой 180°, к площади квадрата, вписанного в сегмент того же самого
круга с дугой 90°.
1. 311. Через две смежные вершины квадрата проведена окружность
так, что длина касательной к ней, проведенной из третьей вершины,
в 3 раза больше стороны квадрата. Найти площадь круга, если сторона
квадрата равна а.
1312. Внутри квадрата со стороной а на каждой его стороне как на
диаметре построена полуокружность. Найтн площадь розетки, ограни-
ченной дугами полуокружностей.
1.313 . Доказать, что из всех прямоугольников, вписанных в одну
и ту же окружность, наибольшую площадь имеет квадрат.
1.314 . В треугольник со сторонами 10, 17 и 21 см вписан прямо-
угольник с периметром 24 см так, что одна из его сторон лежит на
большей стороне треугольника. Найти стороны прямоугольника.
1315. Вершина прямоугольника, вписанного в окружность, делит ее
на четыре дуги. Найти расстояние от середины одной из больших дуг до
вершин прямоугольника, если стороны его равны 24 и 7 см.
1.316 . В прямоугольнике со сторонами а и b проведены биссектрисы
всех углов до взаимного пересечения. Найти площадь четырехугольника,
образованного биссектрисами.
1.317 . В треугольник вписан ромб со стороной т так, что один угол
у них общий, а противоположная вершина ромба лежит на стороне
треугольника и делит эту сторону на отрезки длиной р и q. Найти
стороны треугольника.
1318. Из вершины острого угла ромба проведены перпендикуляры
к прямым, содержащим стороны ромба, которым не принадлежит эта
вершина. Длина каждого перпендикуляра равна 3 см, а расстояние
между их основаниями 3>/з см. Вычислить длины диагоналей ромба.
1319. Точки М, N, Р, Q являются серединами сторон АВ, ВС, CD
и DA ромба ABCD. Вычислить площадь фигуры, являющейся пересече-
28
наем четырехугольников ABCD, ANCQ и BPDM, если площадь ромба
равна 100 см2.
1320. В ромб со стороной а и> острым углом 60° вписана окру-
жность. Определить площадь четырехугольника, вершинами которого
являются точки касания окружности со сторонами ромба.
1321. Дан ромб ABCD, диагонали которого равны 3 и 4 см. Из
вершины тупого угла В проведены высоты BE и BF. Вычислить площадь
четырехугольника BFDE.
1322. Длины диагоналей ромба относятся как 3:4. Во сколько раз
площадь ромба больше площади вписанного в него круга?
1323. В ромб вписана окружность радиуса R. Найти площадь ром-
ба, если его большая диагональ в 4 раза больше радиуса вписанной
окружности.
1324. Вычислить площадь общей части двух ромбов, длины диаго-
налей первого из которых равны 4 и б см, а второй лолучен поворотом
первого на 90° вокруг его центра.
1325. В треугольник вписан параллелограмм со сторонами 3 и 5 см
и диагональю, равной 6 см. Найти стороны треугольника, если известно,
что диагонали параллелограмма параллельны боковым сторонам тре-
угольника, а меньшая из его сторон лежит на основании треугольника.
1326. В треугольник с боковыми сторонами 9 и 15 см вписан
параллелограмм так, что одна из его сторон длиной 6 см лежит на
основании треугольника, а диагонали параллелограмма параллельны
боковым сторонам треугольника. Найти другую сторону параллелог-
рамма и основание треугольника.
1327. Площадь четырехугольника равна S. Найти площадь парал-
лелограмма, стороны которого равны и параллельны диагоналям четы-
рехугольника.
1328. Параллелограмм ABCD, у которого АВ= 153 см, AD = 180 см,
В£=135 см (BE— высота) разделен на три равновеликие фигуры пря-
мыми, перпендикулярными AD. На каком расстоянии от точки А нахо-
дятся точки пересечения этих перпендикуляров с AD1
1329. Длины сторон и диагоналей параллелограмма равны соответ-
ственно а, Ь, с и f Найти углы параллелограмма, если a4+h4 = c2/2.
1330. Диагонали четырехугольника равны, а дайны его средних
линий равны р и q. Найти площадь четырехугольника.
1331. В окружность вписан четырехугольник с углами 120, 90, 60
и 90°. Площадь четырехугольника равна 9л/3 см2. Найти радиус окру-
жности, если диагонали четырехугольника взаимно перпендикулярны.
1332. Выпуклый четырехугольник разделен диагоналями на четыре
треугольника; площади трех из них равны 10, 20 и 30 см2, и каждая
меньше площади четвертого треугольника. Найти площадь данного
четырехугольника.
1333. Вся дуга окружности радиуса R разделена на четыре большие
и четыре малые части, которые чередуются одна за другой. Большая
часть в 2 раза длиннее малой. Определить площадь восьмиугольника,
вершинами которого являются точки деления дуги окружности.
1334. Диагонали равнобедренной трапеции взаимно перпендикуляр-
ны, а ее площадь равна а2. Определить высоту трапеции.
1335. Диагональ равнобедренной трапеции равна 10 см, а площадь
равна 48 см2. Найти высоту трапеции.
1336. Найти радиус окружности, описанной около равнобедренной
трапеции с основаниями 2 и 14 и боковой стороной 10.
1337. Дан равнобедренный треугольник с основанием 12 см и боко-
29
вой стороной 18 см. Отрезки какой длины нужно отложить от вершины
треугольника на его боковых сторонах, чтобы, соединив их концы,
получить трапецию с периметром, «равным 40 см?
1. 338. Найти среднюю линию равнобедренной трапеции с высотой h,
если боковая сторона видна из центра описанной окружности под углом
120°.
1339. Центр окружности, описанной около равнобедренной трапе-
ции, делит ее высоту в отношении 3:4 (считая от большего основания).
Найти основания трапеции, если ее средняя линия равна высоте, а радиус
окружности равен 10.
1.340 . Каким необходимым и достаточным условиям должна удов-
летворять трапеция, чтобы в нее можно было вписать и около нее можно
было описать окружность?
1.341 . Основания трапеции равны 4 и 16 см. Найти радиусы окру-
жностей, вписанной в трапецию и описанной около нее, если известно,
что эти окружности существуют.
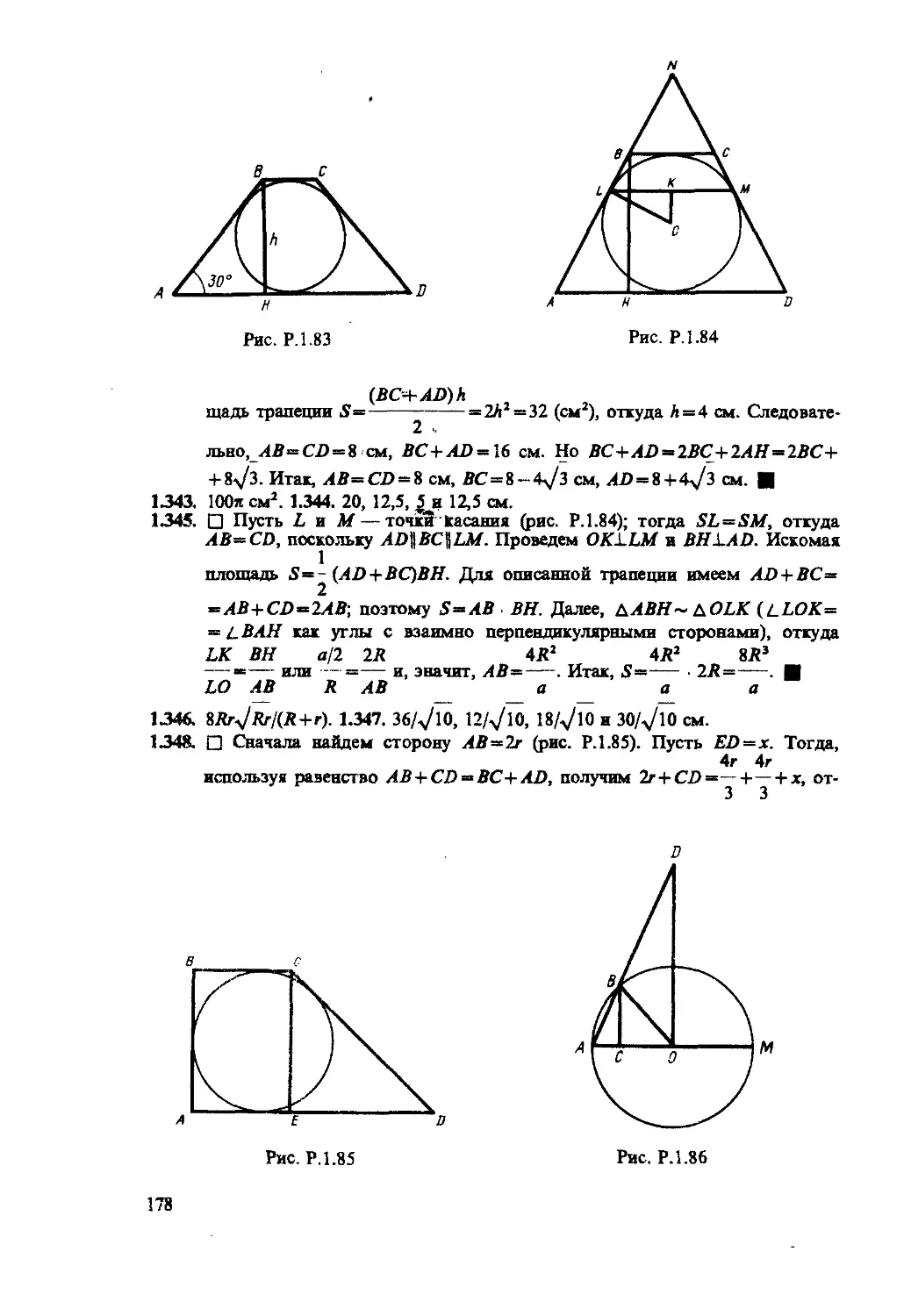
1.342 . Площадь равнобедренной трапеции, описанной около круга,
равна 32 см2. Острый угол трапеции равен 30°. Определить стороны
трапеции.
1343. Высота равнобедренной трапеции равна 14 см, а основания
равны 16 и 12 см. Определить площадь описанного круга.
1.344 . В некоторый угол вписана окружность радиуса 8 см. Длина
хорды, соединяющей точки касания, равна 8 см. К окружности проведе-
ны две касательные, параллельные хорде. Найти стороны полученной
трапеции.
1.345 . В некоторый угол вписана окружность радиуса R, а длина
хорды, соединяющей точки касания, равна а. Параллельно этой хорде
проведены две касательные, в результате чего получилась трапеция.
Найти площадь этой трапеции.
1.346 . Две окружности радиусов R и г касаются внешним образом.
Найти площадь трапеции, ограниченной двумя общими касательными
к этим окружностям и прямыми, соединяющими точки касания.
1.347 . Центр окружности, вписанной в прямоугольную трапецию,
удален от концов ее боковой стороны на расстояния 3 и 9 см. Найти
стороны трапеции.
1348. В прямоугольную трапецию вписана окружность радиуса г.
Найти стороны трапеции, если ее меньшее основание равно 4г/3.
1349. Центр окружности, вписанной в прямоугольную трапецию,
удален от концов боковой стороны на расстояния 8 и 4 см. Найти
среднюю линию трапеции.
1350. Центр круга, вписанного в прямоугольную трапецию, отстоит
от концов боковой стороны на 1 и 2 см. Найти площадь трапеции.
1351. Прямая пересекает окружность радиуса R в точках А и В та-
ких, что иЛ^=45°, а прямую, перпендикулярную диаметру AM окру-
жности и проходящую через ее центр,— в точке D. Прямая, проходящая
через точку В перпендикулярно диаметру AM, пересекает его в точке С.
Найти площадь трапеции OCBD.
1352. Биссектрисы тупых углов при основании трапеции пересека-
ются на другом ее основании. Найти все стороны трапеции, если ее
высота равна 12 см, а длины биссектрис 15 и 13 см.
1.353 . Прямая, параллельная основаниям трапеции, проходит через
точку пересечения ее диагоналей. Найти длину отрезка этой прямой,
заключенного между боковыми сторонами трапеции, если основания
трапеции равны 4 и 12 см.
30
1.354 . Через точку пересечения диагоналей трапеции параллельно
основаниям проведена прямая, пересекающая боковые стороны в точках
М и N. Доказать, что MN=2ab/(a+b), где а и Ъ — длины оснований.
1355. Найти площадь трапеции, диагонали которой равны 7 и 8 см,
а основания — 3 и 6 см.
1356. Основания трапеции равны а и Ъ. Определить длину отрезка,
параллельного основаниям и делящего трапецию на равновеликие части.
1357. В трапеции ABCD известны длины оснований Л£>=24 см
и ВС =8 см и диагоналей АС= 13 см, BD= 5>/17 см. Вычислить площадь
трапеции.
1358. В трапеции ABCD даны основания AD = a, ВС~Ь. На продол-
жении ВС выбрана такая точка М, что прямая AM отсекает от площади
трапеции 1 /4 ее часть. Найти длину отрезка СМ.
1359. В трапеции ABCD с длинами оснований AD —12 см, ВС — 8 см
на луче ВС взята такая точка М, что А М делит трапецию на две
равновеликие фигуры. Найти СМ.
1.360 . Дан квадрат со стороной а. На каждой стороне квадрата вне
его построена трапеция так, что верхние основания этих трапеций и их
боковые стороны образуют правильный двенадцатиугольник. Вычис-
лить его площадь.
Группа В
1361. В треугольнике АВС величина угла А вдвое больше величины
угла В, а длины сторон, противолежащих этим углам, равны соответст-
венно 12 и 8 см. Найти длину третьей стороны треугольника.
1362. Вычислить длину биссектрисы угла А треугольника АВС
с длинами сторон а= 18 см, Ъ= 15 см, с— 12 см.
1363. Точка Cj — основание высоты СС\ треугольника АВС. Найти
зависимость между углами А и В, если CCj=C,A • CtB.
1.364 . Биссектриса угла треугольника делит противолежащую сто-
рону на отрезки длиной 4 и 2 см, а высота, проведенная к той же стороне,
равна л/15 см. Каковы длины сторон треугольника, если известно, что
они выражаются целыми числами?
1365. Через точку D, взятую на стороне АВ треугольника АВС,
проведена прямая, параллельная АС и пересекающая сторону ВС в точке
Е. Доказать, что АЕ, CD и медиана, проведенная через вершину В,
пересекаются в одной точке.
1366. Высота треугольника, равная 2 см, делит угол треугольника
в отношении 2:1, а основания треугольника — на части, меньшая из
которых равна 1 см. Определить площадь этого треугольника.
1.367 . Сторона ВС треугольника АВС равна а; каждая из двух высот,
опущенных на стороны АВ и АС, не меньше стороны, на которую она
опущена. Найти длины сторон АВ и АС.
1.368 . В треугольнике АВС каждая высота hc и /ц не меньше сторо-
ны, на которую она опущена. Найти углы треугольника.
1.369 . В треугольнике АВС со сторонами а—14 см, Ь— 15 см, с—13
см найти расстояние от точки пересечения высот до вершины А.
1.370 . Внутри треугольника АВС взята произвольная точка, и через
нее проведены три прямые, параллельные сторонам треугольника. Эти
прямые делят треугольник АВС на шесть частей, из которых три части
являются треугольниками. Площади этих треугольников равны S\, S2
31
и S3. ^Доказать, *чТО площадь треугольника АВС равна
(«^г+^^а+'У^з)2-
'* 1.371. Вычислить площадь треугольника по двум сторонам
а и b и биссектрисе I угла между ними.
1372. Площадь треугольника АВС равна площадь треугольника
АОВ, где О — точка пересечения высот, равна S2. На прямой СО взята
такая точка К, что треугольник АВК — прямоугольный. Доказать, что
площадь треугольника АВК есть среднее геометрическое между и S2.
1373. Стороны треугольника АВС разделены точками М, N и Р так,
что AM:MB=BN:NC—CP:РА= 1:4. Найти отношение площади тре-
угольника, ограниченного прямыми AN, ВР и СМ, к площади треуголь-
ника АВС.
1374. Треугольник со сторонами 13, 14 и 15 разделен на три равно-
великие части прямыми, перпендикулярными большей стороне. Найти
расстояния до этих прямых от ближайших к ним вершин треугольника,
находящихся на большей стороне.
1375. Основания высот некоторого остроугольного треугольника
соединены прямыми. Доказать, что биссектрисами углов нового тре-
угольника являются высоты исходного.
1376. Даны два правильных треугольника площадью S, из которых
второй получен поворотом первого треугольника вокруг его центра на
угол 30°. Вычислить площадь пересечения этих треугольников.
1377. Биссектриса угла при основании равнобедренного треуголь-
ника делит противоположную сторону так, что отрезок, прилежащий
к вершине треугольника, равен основанию. Доказать, что и биссектриса
равна основанию.
1378. Площадь прямоугольного треугольника равна 2г2/3, где
г — радиус окружности, касающейся одного катета и продолжений дру-
гого катета и гипотенузы. Найти стороны треугольника.
1379. Гипотенуза прямоугольного треугольника равна т, радиус
вписанной окружности равен г. Определить катеты. При каком соот-
ношении между гит задача имеет решение?
1380. Определить острые углы прямоугольного треугольника, если
отношение радиусов вписанной и описанной окружностей равно ^/3 +1.
1381. Расстояние от центра окружности, вписанной в прямоуголь-
ный треугольник, до вершин его острых углов равны -У5 и л/П). Найти
катеты.
1382. В прямоугольном треугольнике ABC (LC=9Q°) проведена
высота CD. Радиусы окружностей, вписанных в треугольники ACD
и BCD, равны 0,6 и 0,8 см. Найти радиус окружности, вписанной
в треугольник АВС.
1383. В прямоугольный треугольник ABC (Z_C=90°) вписана окру-
жность, касающаяся его сторон в точках Alt В2. Сг. Найти отношение
площади треугольника АВС к площади треугольника А^С^ если
ЛС=4 см, ВС=3 см.
1384. В равнобедренный треугольник с основанием 12 см вписана
окружность, и к ней проведены три касательные так, что они отсекают
от данного треугольника три малых треугольника. Сумма периметров
малых треугольников равна 48 см. Найти боковую сторону данного
треугольника. ,
1385. В равнобедренный треугольник вписана окружность. Точки
касания деляг каждую боковую сторону на отрезки длиной т и п, считая
от вершины. К окружности проведены трн касательные, параллельны?
32
каждой из сторон треугольника. Найти длины отрезков касательных,
заключенных между сторонами треугольника.
1.386. В равнобедренном треугольнике АВС дано: АВ=ВС=25 см
и АС= 14 см. Вычислить радиус круга, касающегося ВС в точке D — ос-
новании высоты AD и проходящего через середину АС.
1.387. Сторона правильного треугольника равна а. Из его центра
описана окружность радиуса а/3. Определить площадь части треуголь-
ника, лежащей вне окружности.
1.388. В равносторонний треугольник со стороной а вписана окру-
жность. К окружности проведена касательная так, что отрезок ее внутри
треугольника равен Ь. Найти площадь треугольника, отсеченного этой
касательной от данного.
1.389. В треугольник со сторонами 6, 10 и 12 см вписана окружность.
К окружности проведена касательная так, что она пересекает две боль-
шие стороны. Найти периметр отсеченного треугольника.
1.390. В треугольник с периметром, равным 20 см, вписана окру-
жность. Отрезок касательной, проведенной к окружности параллельно
основанию, заключенный между сторонами треугольника, содержит 2,4
см. Найти основание треугольника.
1.391. Биссектриса угла А треугольника АВС пересекает описанную
около него окружность в точке D. Найти длину хорды DC, если центр
окружности, вписанной в данный треугольник, удален от точки D на
расстояние а.
1.392. Высота и медиана треугольника, проведенные внутри него из
одной его вершины, различны и образуют равные углы со сторонами,
выходящими из той же вершины. Определить радиус описанной окру-
жности, если медиана равна т.
1.393. В треугольнике АВС биссектрисы AD и СЕ пересекаются
в точке F. Точки В, D, Е, F лежат на одной окружности. Показать, что
угол В равен 60°.
1.394. В треугольнике АВС проведены медианы AL и ВМ, пересека-
ющиеся в точке К. Вершина С лежит на окружности, проходящей через
точки К, L, М. Показать, что медиана CN образует со сторонами АС
и ВС такие же углы, что и медианы AL и ВМ со стороной АВ.
1.395. Основания высот остроугольного треугольника АВС служат
вершинами другого треугольника, периметр которого равен 2р. Найти
площадь треугольника АВС, если радиус описанной около него окру-
жности равен R.
1.396. Круг с центром на стороне АВ треугольника АВС касается
двух других его сторон. Найти площадь круга, если а — 13 см, Ь= 14 см,
с— 15 см, где а, b и с — длины сторон треугольника.
1.397. Через точку М, расположенную на диаметре окружности ра-
диуса 4 см, проведена хорда АВ, образующая с диаметром угол 30°.
Через точку В проведена хорда ВС, перпендикулярная данному диамет-
ру. Найти площадь треугольника АВС, если AM: МВ —2 :3.
1.398. Две окружности касаются внешним образом в точке А. Найти
радиусы окружностей, если хорды, соединяющие точку А с точками
касания одной из общих внешних касательных, равны 6 и 8 см.
1.399. Даны две концентрические окружности. Доказать, что сумма
квадратов расстояний от точки одной окружности до конца диаметра
друРЪй окружности не зависит ни от выбранной точки, ни от выбранного
диаметра.
1.400. На отрезке АС дана точка В, причем АВ**4 см, ВС=28 см. На
отрезках АВ, ВС и АС как на диаметрах построены полуокружности
2-363
33
в одной полуплоскости относительно границы АС. Найти радиус окру-
жности, касающейся всех трех полуокружностей.
1.401. В окружность радиуса R вписаны три равные окружности,
касающиеся внешней окружности и попарно друг друга. Вычислить
площадь фигуры, ограниченной этими тремя окружностями.
1.402. В окружность радиуса R вписаны четыре равные окружности,
каждая из которых касается данной и двух соседних. Вычислить пло-
щадь фигуры, ограниченной этими четырьмя окружностями.
1.403. В окружность радиуса R вписаны шесть равных окружностей,
каждая из которых касается данной окружности и двух соседних. Вычис-
лить площадь фигуры, ограниченной этими шестью окружностями.
1.404. Большая из параллельных сторон трапеции равна а, меньшая
равна Ь, непараллельные стороны равны cad. Найти площадь трапеции.
1.405. Длины оснований АВ и ВС трапеции ABCD равны а и Ъ.
Прямая, параллельная АВ, пересекает стороны ВС и AD в точках М и N.
Вычислить MN, если трапеции ABMN и NMCD равновелики.
1.406. В трапецию, у которой меньшее основание равно а, вписана
окружность. Одна из боковых сторон трапеции делится точкой касания
на отрезки т и л, считая от большего основания. Определить площадь
трапеции.
1.407. Диагонали трапеции разбивают ее на четыре треугольника.
Доказать, что если площади двух из них, прилежащих к основаниям
трапеции, равны р2 и q2, то площадь трапеции равна (p + q)2.
1.408. Прямая, параллельная основаниям данной прямоугольной
трапеции, рассекает ее на две трапеции, в каждую из которых можно
вписать окружность. Найти основания исходной трапеции, если ее боко-
вые стороны равны с и d, причем c<d.
1.409. Основания равнобедренной трапеции равны 4 и 8 см, ее
площадь равна 21 см2. Какую сторону пересекает биссектриса угла при
большем основании: меньшее основание или боковую сторону трапеции?
1.410. Около окружности радиуса А=1 см описана равнобедренная
трапеция, площадь которой равна 5 см2. Найти площадь четырех-
угольника, вершинами которого служат точки касания окружности
и трапеции.
1.411. Около окружности радиуса 5 см описана равнобедренная
трапеция. Расстояние между точками касания ее боковых сторон равно
8 см. Найти площадь трапеции.
1.412. Через смежные вершины квадрата проведена окружность так,
что касательная к ней, проведенная из третьей вершины, равна удвоен-
ной стороне квадрата. Найти площадь этого квадрата, если радиус
окружности равен R.
1.413. Окружность радиуса R с центром в точке О разделена точ-
ками А, В, С, D, Е, F на шесть равных частей. Определить площадь
фигуры СОЕ, ограниченной дугой ОС с центром в точке В, дугой ОЕ
с центром в точке F и дугой СЕ с центром в точке А.
1.414. Центры четырех кругов расположены в вершинах квадрата со
стороной а. Радиусы этих кругов равны а. Определить площадь их
общей части.
1.415. В круг радиуса R вписаны равносторонний треугольник и ква-
драт, имеющие общую вершину. Вычислить площадь общей части тре-
угольника и квадрата.
1.416. В прямоугольном треугольнике биссектриса прямого угла
отсекает на гипотенузе отрезки длиной а и Ь. Найти площадь квадрата,
стороной которого является эта биссектриса.
34
1.417. В треугольник с основанием, равным а, вписан квадрат, одна
из сторон которого лежит на основании треугольника. Определить
высоту треугольника и сторону квадрата.
1.418. Две окружности касаются друг друга внешним образом. Че-
тыре точки касания их внешних общих касательных А, В, С, D последо-
вательно соединены. Показать, что в четырехугольник ABCD можно
вписать окружность, и найти ее радиус, если радиусы данных окружно-
стей равны Лиг.
1.419. В четырехугольнике ABCD через середину диагонали BD про-
ведена прямая, параллельная другой диагонали А С. Эта прямая пересе-
кает сторону AD в точке Е. Доказать, что отрезок СЕ делит четырех-
угольник ABCD на равновеликие части.
1.420. В окружность вписан четырехугольник, длины сторон которо-
го равны а, Ъ, с и d. Вычислить отношение длин диагоналей этого
четырехугольника.
1.421. Из каждой вершины, принадлежащей основанию равносто-
роннего треугольника со стороной а, проведены во внутреннюю область
треугольника по два луча, образующих с основанием треугольника углы
15 и 30°. Найти площадь четырехугольника, вершинами которого явля-
ются точки пересечения построенных лучей.
1.422. Правильный треугольник АВС, вписанный в окружность ра-
диуса R, повернут вокруг центра окружности на 90° в положение A tB1Cl.
Вычислить площадь шестиугольника AAtBBiCCA.
1.423. Площадь треугольника равна S. Каждая сторона треуголь-
ника разделена на три части в отношении т: п: т. Определить площадь
шестиугольника, вершинами которого служат точки деления.
1.424. Сторону правильного десятиугольника выразить через радиус
R описанной окружности.
1.425. Найти радиус круга, если площадь круга на Q кв. ед. больше
площади вписанного в него правильного двенадцатиугольника.
ГЛАВА 2
задачи по стереометрии
ОСНОВНЫЕ ФОРМУЛЫ
1°. Произвольная призма (/—боковое ребро; Р — периметр основания;
5 — площадь основания; Н — высота; Рт — периметр перпендикулярного сече-
ния; — площадь перпендикулярного сечения; 5&ж — площадь боковой повер-
хности; V — объем):
*^бож —РсечА (2-1)
V=SH; (2.2)
V=Sml. (2.3)
2°. Прямая призма:
5бож=«- (2.4)
3°. Прямоугольный параллелепипед (а, Ь,с — наль): его измерения; d — диаго-
5бож=РЯ; (2.5)
V—abc; (2.6)
rf2=a2 + Z>2+c2. (2.7)
4°. Куб (а — ребро):
К=а3; (2.8)
(2-9)
V- 5°. Произвольная пирамида (S — площадь основания; Н—высота; - объем):
1 V=~ SH. 3 (2-10)
5бо» 6°. Правильная пирамида (Р — периметр — площадь боковой поверхности): основания; / — апофема;
$бож=5 Pi; 2 (2.11)
1 V=- SH. (2-12)
3
36
7°. Произвольная усеченная пирамида (5t и 52 ’ Л — высота; V — объем): — площади оснований;
Г=^Л(51+52+5/5152). (2.13)
8°. Правильная усеченная пирамида (Рг и Р2 — 1 — апофема; 5бож — площадь боковой поверхности): периметры оснований;
s6oi=~2(p1+p1')1. (2-14)
9°. Цилиндр (R — радиус основания; Н — высота; ;ож — площадь боковой
поверхности; V — объем):
Seo^lnRH; (2.15)
V=nR2H. (2.16)
10°. Конус (Л— радиус основания; Н—высота; / — образующая; 5бож — площадь боковой поверхности; V — объем):
5бож=лЯ/; (2.17)
1 Г= nR2H. 3 (2.18)
11°. Шар, сфера (R — радиус шара; 5 — площадь сферической поверхности; V — объем):
5=4л Л2; (2.19)
4 V=- nR3. 3 (2.20)
12°. Шаровой сегмент (R — радиус шара; Л — высота сегмента; 5 — пло- щадь сферической поверхности сегмента; V — объем):
S=2nRh; (2.21)
X II я h> 1 Ы 1 •— (2.22)
13°. Шаровой сектор (R — радиус шара; Л — высота сегмента; V— объ- ем):
2 V=- itR2h. 3 ‘ (2.23)
ДОПОЛНИТЕЛЬНЫЕ СООТНОШЕНИЯ МЕЖДУ
ЭЛЕМЕНТАМИ ПРИЗМЫ И ПИРАМИДЫ
1°. Пусть в пирамиде выполняется одно из следующих двух условий: а) все
боковые ребра образуют с плоскостью основания равные углы; б) длины всех
боковых ребер равны. Тогда вершина пирамиды проецируется в центр окружно-
37
ста, описанной около основания пирамиды (эта же
точка служит точкой пересечения серединных перпен-
дикуляров к сторонам основания пирамиды).
□ Пусть О — основание высоты л-угольной пи-
рамиды SA,A2...An (рис. 2.1); SA,. SA2, .... SA„— ее
боковые ребра; ОЛ2, ОА2, .... ОА„ — их проекции на
плоскость основания; SA,O, SA2O, .... SA „О — углы,
образуемые ребрами пирамиды с плоскостью основа-
ния. Согласно условию а), эти углы равны; поэтому
равны и прямоугольные треугольники SOA,. SOA2,
.... SOA„, имеющие общий катет SO. Отсюда следует,
что ОА , = ОА2 = ... = ОА„, т. е. точка О равноудалена
от вершин A j, Аг,А„ основания и, значит, является
центром описанной около него окружности.
Если условие а) заменить условием б), то равен-
ство треугольников SOA,, SOA2, .... SOA„ вытекает из того, что, кроме общего-
катета, они имеют равные гипотенузы SA,=SA2 = ... = SA„. Таким образом,
ОА, = ОА2=...ОАп, т. е. О — центр окружности, описанной около основания
пирамиды.
2°. Пусть в пирамиде выполняется одно из следующих двух условий: а) все
боковые грани образуют с основанием равные углы; б) длины всех апофем
боковых граней равны. Тогда вершина пирамиды проецируется в центр окружно-
сти, вписанной в основание пирамиды (эта же точка служит точкой пересечения
биссектрис углов в основании пирамиды).
□ Пусть О — основание высоты и-угольной пирамиды ВА,А2...А„ (рис. 2.2);
SB,, SB2, .... SB„ — апофемы (высоты боковых граней). Проекции апофем ОВ,,
ОВ2, .... ОВ„ на плоскость основания перпендикулярны сторонам основания (по
теореме о трех перпендикулярах) и, следовательно, выражают расстояния от О до
этих сторон, а углы SB, О, SB2O,.... SB „О являются линейными углами соответст-
вующих двугранных углов. Согласно условию а), эти углы равны, поэтому равны
и прямоугольные треугольники SOB,, SOB2, .... SOB„, имеющие общий катет SO.
Отсюда следует, что ОВ,=ОВ2 = ... = ОВ„, т. е. точка О равноудалена от сторон
основания и, значит, является центром вписанной в него окружности.
Если условие а) заменить условием б), то равенство треугольников SOB,,
SOB2, .... SOB„ вытекает из того, что они, кроме общего катета SO, имеют
и равные гипотенузы SB, =SB2 = ... = SB„. Таким образом, ОВ, = ОВ2 = ... = ОВ„,
т. е. О — центр окружности, вписанной в основание пирамиды.
3°. Если в наклонной призме боковое ребро А,В, составляет равные углы со
сторонами основания, образующими вершину А, (рис. 2.3), то основание О высо-
ты В,О лежит на биссектрисе угла А,.
38
□ Построим OC±AtA3, OBLA,An и отрезки BtC, BtB. Согласно теореме
о трех перпендикулярах, имеем и BlBLAlA„. Прямоугольные тре-
угольники A^CBi и AtDBt равны, так как имеют общую гипотенузу А^
и равные углы (LB1AlC= l_BtAxB по условию). Следовательно, B^C^B^D
и &.B,OC= t^BiOD, откуда ОС= ОВ. Итак, точка О равноудалена от сторон угла
At и, значит, лежит на биссектрисе АгО угла А^
Это же утверждение можно сформулировать так: если в трехгранном угле два
острых плоских угла равны, то проекция их общего ребра на плоскость третьего
плоского угла является его биссектрисой.
4°. Если высота треугольной пирамиды проходит через точку пересечения
высот треугольника, лежащего в основании, то противоположные ребра пирами-
ды перпендикулярны. Справедливо я обратное утверждение.
□ Пусть АВ — высота треугольника АВС (рис. 2.4); тогда ВС .LAB и, зна-
чит, BCLAO. Но АО является проекцией ребра AS на плоскость АВС и, следова-
тельно, по теореме о трех перпендикулярах BCLAS.
Аналогично доказывается, что перпендикулярны и две другие пары проти-
воположных ребер пирамиды, т. е. AB1SC и ACLSB.
Докажем теперь обратное утверждение, т. е. что если BCLAS, то основанием
О высоты пирамиды является точка пересечения высот треугольника АВС (рис.
2.4). Так как SO Lili. АВС (по условию), то АО является проекцией SA на
плоскость АВС. Но прямая ВС, принадлежащая плоскости АВС, перпендикулярна
ребру AS (по условию), поэтому BCLAO (согласно теореме о трех перпен-
дикулярах). Следовательно, точка О лежит на высоте АВ треугольника АВС.
Аналогично доказывается, что О принадлежит и другой высоте треугольника
АВС и, значит, является точкой пересечения высот основания пирамиды.
5°. Если SO — высота пирамиды SABC и SALBC, то пл. SAOLBC (рис . 2.4).
□ Имеем SALBC (по условию) и SOLBC (поскольку 5О1пл. АВС). Так как
прямая ВС перпендикулярна каждой из двух прямых SA и SO, лежащих в плоско-
сти SAO, то пл. SAOLBC (согласно признаку перпендикулярности прямой и плос-
кости).
Пример 1. Через медиану BE основания АВС пирамиды АВСВ и середину
F ребра ВС проведена плоскость. Найти объем фигуры ABBFE, если объем
пирамиды АВСВ равен 40 см3.
□ Объем фигуры ABBFE равен разности объемов пирамид АВСВ и ECBF
(рис. 2.5). Чтобы найти объем пирамиды ECBF, сравним его с объемом пирамиды
АВСВ. Для этого достаточно найти отношения площадей их оснований и соот-
ветствующих высот. Так как медиана треугольника делит его площадь на две
равные части, то SaBEC=-^ S^abc- Далее, так как F — середина ребра ВС, то
высота пирамиды ECBF равна половине высоты пирамиды АВСВ. Следователь-
но, = - Клвсо=10 (см3). Искомый объем равен 30 см3.
Рис. 2.4
Рис. 2.5
Рис. 2.6
39
Рис. 2.7
Пример 1. Высота цилиндра равна Н, радиус его основания равен R. В ци-
линдр помещена пирамида, высота которой совпадает с образующей AAt цилин-
дра, а основанием служит равнобедренный треугольник АВС (АВ = АС), вписан-
ный в основание цилиндра. Найти площадь боковой поверхности пирамиды, если
Д.Л = 120°.
□ Проведем ADLBC и соединим точки At и D отрезком AXD (рис. 2.6).
Согласно теореме о трех перпендикулярах, имеем ArDLBC. Так как дуга САВ
содержит 120°, а дуги АС и АВ — по 60°, то ВС=В\]з, AB = R. Из &ABD
находим AD=R/2. Применив теорему Пифагора к треугольнику AAtD, получим
/ „ R2 1 ------ 1 1
A,D= Н2!------= Х/Л2~-4Я^. Следовательно, Е>,л,лв=~ АВ АА<=- RH;
\ 4 2 2 2
Sлл,вс—" ВС А,Р= - R\j3 \JR2+ 4Н2 = ~J3R2+ 12Н2. Окончательно по-
2 2 2 4
лучим
S6ot=2StltAiAB + S^AlBc=RH+- R^3R2 + 12H2^- (4H+j3R2 + 12H2').
4 4
Пример 3. Основанием пирамиды служит правильный треугольник со сторо-
ной, равной а. Одно из боковых ребер перпендикулярно плоскости основания
и равно Ь. Найти радиус шара, описанного около пирамиды.
□ Пусть О — центр шара, описанного около пирамиды ABCD (рис. 2.7).
Тогда OA = OB=OC=OD. Проведем О/С1пл. АВС и OELDB. Поскольку точка
О равноудалена от вершин треугольника АВС, точка К является центром тре-
угольника и ВК—а^З. Далее, так как OB=OD, то EB^ED^bp. По теореме
Пифагора из Д.ОКВ находим
/—-----1b2 1,2 J12a2 + 9b*
ов^оеР+вк2^ у1-+~я‘-— -----------
Пример 4. Дан куб АВСРА^С^ц длина ребра которого равна а. На ребре
AAt взята точка Е так, что Л£=а/4. Найти объем пирамиды, вершиной которой
является точка Ait а основанием — сечение куба, Цроходащее через точки D,
Е и произвольную внутреннюю точку ребра ВВ1.
□ Построив сечение (рис. 2.8), получим на ребре CCj точку 5, служащую
общей вершиной двух треугольных пирамид SEAjK и SEAP&, сумма объемов
которых равна объему четырехугольной пирамиды AiEKSD.
1 1 За За2
Имеем . Расстояние of точки S до плоско-
2 2 4 8
40
1 За3 а3
сти AjED равно а, поэтому VsEAtD’*" ~ а=— Аналогично находим
1 /1 За \ а3 а3 а3 а3
Vsea.K“~ I ”—-а I п“—• Итак, искомый объем есть ——=—.
* 3 \2 4 J 8 884
Группа А
2.001. В основании пирамиды лежит прямоугольный треугольник
с гипотенузой, равной с, и острым углом 30°. Боковые ребра пирамиды
наклонены к плоскости основания под углом 45°. Найти объем пи-
рамиды.
2.002. Каждое из боковых ребер пирамиды равно Ь. Ее основанием
служит прямоугольный треугольник, катеты которого относятся как
т: п, а гипотенуза равна с. Вычислить объем пирамиды.
2.003. Основанием пирамиды служит треугольник со сторонами 6,
5 и 5 см. Боковые грани пирамиды образуют с ее основанием равные
двугранные углы, содержащие по 45°. Определить объем пирамиды.
2.004. Основание пирамиды — равнобедренный треугольник с осно-
ванием 6- см и высотой 9 см. Каждое боковое ребро равно 13 см.
Вычислить объем пирамиды.
2.005. Основанием пирамиды служит треугольник со сторонами а,
а и Ь. Все боковые ребра наклонены к плоскости основания под углом
60°. Определить объем пирамиды.
2.006. Боковое ребро правильной треугольной пирамиды равно I,
а высота равна Л. Определить объем пирамиды.
2.007. Определить объем правильной треугольной пирамиды, если
высота треугольника, служащего ее основанием, равна Л, а апофема
пирамиды равна т.
2.008. Найти объем правильной треугольной пирамиды, у которой
плоский угол при вершине равен 90°, а сторона основания равна 3 см.
2.009. Найти объем правильной треугольной пирамиды, высота ко-
торой равна h, а плоские углы при вершине — прямые.
2.010. Найти объем правильного тетраэдра с ребром, равным а.
2.011. Вычислить объем правильного тетраэдра, если радиус окру-
жности, описанной около его грани, равен R.
2.012. Найтн отношение объема куба к объему правильного тетраэд-
ра, ребро которого равно диагонали грани куба.
2.013. В правильном тетраэдре SABC построено сечение его плоско-
стью, проходящей через ребро АС и точку К, принадлежащую ребру SB,
причем BK:KS=2 :1. Найти объем отсеченной пирамиды КАВС, если
ребро тетраэдра равно а.
2.014. Каждое нз боковых ребер пирамиды равно 269/32 см. Основа-
ние пирамиды — треугольник со сторонами 13, 14 и 15 см. Найти объем
пирамиды.
2.015. Определить объем правильной четырехугольной пирамиды,
если ее боковое ребро составляет с плоскостью основания угол 45°,
а площадь диагонального сечения равна S.
2.016. Боковое ребро правильной четырехугольной пирамиды равно
I н наклонено к плоскости основания под углом 60°. Найти объем
пирамиды.
2.017. Основание четырехугольной пирамиды — прямоугольник
с диагональю, равной Ь, и углом 60° между диагоналями. Каждое из
41
боковых ребер образует с плоскостью основания угол 45°. Найти объем
пирамиды.
2.018. Высота пирамиды равна 8 м. На расстоянии 3 м от вершины
проведена плоскость, параллельная основанию. Площадь полученного
сечения равна 4 м2. Найти объем пирамиды.
2.019. Основанием правильной пирамиды служит многоугольник,
сумма внутренних углов которого равна 720°. Определить объем пира-
миды, если ее боковое ребро, равное /, составляет с высотой пирамиды
угол 30°.
2.020. Найти отношение объема правильной шестиугольной пира-
миды к объему правильной треугольной пирамиды при условии, что
стороны оснований этих пирамид равны, а их апофемы в 2 раза больше
сторон основания.
2.021. Высота правильного тетраэдра равна h. Вычислить его пол-
ную поверхность.
2.022. Найти боковую поверхность правильной треугольной пира-
миды, если плоский угол при ее вершине равен 90°, а площадь основания
равна S.
2.023. Плоский угол при вершине правильной треугольной пирами-
ды равен 90°. Найти отношение боковой поверхности пирамиды к пло-
щади ее основания.
2.024. Сторона основания правильной треугольной пирамиды равна
1 см, а ее боковая поверхность составляет 3 см1. Найти объем пирамиды.
2.025. Найти полную поверхность правильной треугольной пирами-
ды, сторона основания которой равна а, а двугранный угол при основа-
нии равен 60°.
2.026. Центр верхнего основания куба соединен с серединами сторон
нижнего основания. Определить боковую поверхность полученной пира-
миды, если ребро куба равно а.
2.027. Центр верхнего основания куба с ребром, равным а, соединен
с серединами сторон нижнего основания, которые также соединены
в последовательном порядке. Вычислить полную поверхность получен-
ной пирамиды.
2.028. В кубе, ребро которого равно а, центр верхней грани соединен
с вершинами основания. Найти полную поверхность полученной пира-
миды.
2.029. Диагональ квадрата, лежащего в основании правильной четы-
рехугольной пирамиды, равна ее боковому ребру и равна а. Найти
полную поверхность пирамиды и ее объем.
2.030. Найти боковую поверхность правильной шестиугольной пи-
рамиды, высота которой равна Ь, а боковое ребро равно /.
2.031. Апофема правильной шестиугольной пирамиды равна h,
а двугранный угол при основании равен 60°. Найти полную поверхность
пирамиды.
2.032. В треугольной пирамиде боковые ребра взаимно перпендику-
лярны и имеют длины ^/70, ^/99 и ^/126 см. Найти объем и площадь
основания пирамиды.
2.033. Сторона основания правильной треугольной пирамиды равна
а, а двугранный угол при основании равен 45°. Определить объем
и полную поверхность пирамиды.
2.034. Объем правильной треугольной пирамиды, боковая грань
которой наклонена к плоскости основания под углом 45°, равен 9 см3.
Найти полную поверхность пирамиды.
2.035. Центр куба, ребро которого равно а, соединен со всеми его
42
вершинами. Определить объем и полную поверхность каждой из полу-
ченных пирамид.
2.036. Найти полную поверхность и объем правильной четыреху-
гольной пирамиды, сторона основания которой равна а, а угол наклона
боковой грани к плоскости основания равен 60°.
2.037. По стороне основания, равной а, определить боковую поверх-
ность и объем правильной четырехугольной пирамиды, у которой диаго-
нальное сечение равновелико основанию.
2.038. В основании пирамиды лежит квадрат. Две боковые грани
перпендикулярны плоскости основания, а две другие наклонены к нему
под углом 45°. Среднее по величине боковое ребро равно /. Найти объем
и полную поверхность пирамиды.
2.039. Основанием пирамиды служит ромб с острым углом 30°.
Боковые грани наклонены к плоскости основания под углом 60°. Опреде-
лить объем и полную поверхность пирамиды, если радиус вписанного
в ромб круга равен г.
2.040. Боковые ребра правильной треугольной усеченной пирамиды
наклонены к плоскости основания под углом 60°. Стороны нижнего
и верхнего оснований равны соответственно а и b (а>Ь). Найти объем
усеченной пирамиды.
2.041. Основаниями правильной усеченной пирамиды служат квад-
раты со сторонами ей b (а>Ь). Боковые ребра наклонены к плоскости
основания под углом 45°. Определить объем усеченной пирамиды.
2.042. Определить объем правильной четырехугольной усеченной
пирамиды, если ее диагональ равна 18 см, а длины сторон оснований 14
и 10 см.
2.043. В правильной четырехугольной пирамиде сторона основания
равна 6 дм, а высота 4 дм. Найти боковую поверхность усеченной
пирамиды, отсекаемой от данной плоскостью, параллельной ее основа-
нию и отстоящей от него на 1 дм.
2.044. Определить объем октаэдра (правильного восьмигранника),
ребро которого равно а.
2.045. В кубе центры оснований соединены с центрами боковых
граней. Вычислить поверхность полученного октаэдра, если ребро куба
равно а.
2.046. Найти объем куба, если расстояние от его диагонали до
непересекающегося с ней ребра равно d.
2.047. Диагональ прямоугольного параллелепипеда равна 13 см,
а диагонали его боковых граней равны 4>/10 и 3^/17 см. Определить
объем параллелепипеда.
2.048. Стороны основания прямоугольного параллелепипеда равны
аиЬ. Диагональ параллелепипеда наклонена к плоскости основания под
углом 60°. Определить боковую поверхность параллелепипеда.
2.049. Стороны основания прямоугольного параллелепипеда равны
а и Ь. Диагональ параллелепипеда наклонена к боковой грани, содер-
жащей сторону основания, равную Ь, под углом 30°. Найти объем
параллелепипеда.
2.050. Стороны основания прямоугольного параллелепипеда отно-
сятся как т.п, а диагональное сечение представляет собой квадрат
с площадью, равной Q. Определить объем параллелепипеда.
2.051. Определить объем прямоугольного параллелепипеда, если его
диагональ равна d, а длины ребер относятся как т: л: р.
2.052. Определить объем прямоугольного параллелепипеда, диаго-
43
наль которого равна I и составляет с одной гранью угол 30°, а с дру-
гой — 45°.
2.05 3. Измерения прямоугольного параллелепипеда равны 2,
3 и 6 см. Найти длину ребра такого куба, чтобы объемы этих тел
относились как их поверхности.
2.05 4. Из медной болванки, имеющей форму прямоугольного парал-
лелепипеда размерами 80x20x5 см, прокатывается лист толщиной
в 1 мм. Определить площадь этого листа.
2.05 5. В прямом параллелепипеде стороны основания равны а и Ь,
острый угол между ними содержит 60°. Большая диагональ основания
равна меньшей диагонали параллелепипеда. Найти объем параллелепи-
педа.
2.05 6. В прямом параллелепипеде стороны основания равны
а и b и образуют угол 30°. Боковая поверхность равна S. Определить
объем параллелепипеда.
2.05 7. В основании прямого параллелепипеда лежит параллелог-
рамм со сторонами 1 и 4 см и острым углом 60°. Большая диагональ
параллелепипеда равна 5 см. Определить его объем.
2.05 8. Основанием прямого параллелепипеда служит ромб, площадь
которого равна Q. Площади диагональных сечений равны 5, и S2.
Определить объем параллелепипеда.
2.05 9. Основанием прямого параллелепипеда служит ромб. Плос-
кость, проведенная через одну из сторон нижнего основания и проти-
воположную сторону верхнего основания, образует с плоскостью ос-
нования угол 45°. Полученное сечение имеет площадь, равную Q. Опре-
делить боковую поверхность параллелепипеда.
2.06 0. Основанием параллелепипеда служит квадрат. Одна из вер-
шин верхнего основания одинаково отстоит от всех вершин нижнего
основания и удалена от плоскости этого основания на расстояние,
равное Ь. Сторона основания равна а. Определить полную поверхность
параллелепипеда.
2.06 1. Найти объем правильной треугольной призмы, если сторона
ее основания равна а и боковая поверхность равновелика сумме площа-
дей оснований.
2.062 . Найти боковую поверхность правильной треугольной призмы
с высотой h, если прямая, проходящая через центр верхнего основания
и середину стороны нижнего основания, наклонена к плоскости основа-
ния под углом 60°.
2.063 . Боковое ребро правильной треугольной призмы равно высоте
основания, а площадь сечения, проведенного через это боковое ребро
и высоту основания, равна Q. Определить объем призмы.
2.064 . В правильной треугольной призме площадь сечения, проходя-
щего через боковое ребро перпендикулярно противолежащей боковой
грани, равна Q. Сторона основания призмы равна а. Найти полную
поверхность призмы.
2.065 . Найти объем наклонной треугольной призмы, основанием
которой служит равносторонний треугольник со стороной, равной а,
если боковое ребро призмы равно стороне основания и наклонено
к плоскости основания под углом 60°.
2.066 . Площади боковых граней прямой треугольной призмы равны
M,N и Р. Боковое ребро ее равно I. Определить объем призмы.
2.067 . Определить объем наклонной треугольной призму, у которой
площадь одной из боковых граней равна S, а расстояние 4т плоскости
этой грани до противолежащего ребра равно d.
44
2.068 . Определить объем правильной четырехугольной призмы, если
ее диагональ образует с плоскостью боковой грани угол 30°, а сторона
основания равна а.
2.069 . Центр верхнего основания правильной четырехугольной при-
змы и середины сторон нижнего основания служат вершинами вписан-
ной в призму пирамиды, объем которой равен V. Найти объем призмы.
2.070 . Известны площадь основания Р и объем V правильной четы-
рехугольной призмы. Вычислить ее полную поверхность.
2.071 . В основании наклонной призмы лежит параллелограмм со
сторонами 3 и 6 дм и острым углом 45°. Боковое ребро призмы равно
4 дм и наклонено к плоскости основания под углом 30°. Найти объем
призмы.
2.072 . Основание призмы — квадрат со стороной, равной а. Одна из
боковых граней — также квадрат, другая — ромб с углом 60°. Опреде-
лить полную поверхность призмы.
2.073 . Основанием прямой призмы служит ромб. Площади диаго-
нальных сечений этой призмы равны Р и Q. Найти боковую поверхность
призмы.
2.074 . Определить объем правильной шестиугольной призмы, у ко-
торой наибольшая диагональ равна </, а боковые грани — квадраты.
2.075 . Наибольшая диагональ правильной шестиугольной призмы
равна d и составляет с боковым ребром призмы угол 30°. Найти объем
призмы.
2.076 . Правильная шестиугольная призма, боковые ребра которой
равны 3 см, рассечена диагональной плоскостью на две равные четырех-
угольные призмы. Определить объем шестиугольной призмы, если боко-
вая поверхность четырехугольной призмы равна 30 см2.
2.077 . Цилиндр образован вращением прямоугольника вокруг одной
из его сторон. Выразить объем V цилиндра через площадь S этого
прямоугольника и длину С окружности, описанной точкой пересечения
его диагоналей.
2.078 . В цилиндре площадь сечения, перпендикулярного образу-
ющей, равна М, а площадь осевого сечения равна N. Определить объем
и поверхность цилиндра.
2.079 . Радиус основания конуса равен R, а угол при вершине в раз-
вертке его боковой поверхности равен 90°. Определить объем конуса.
2.080 . Боковая поверхность конуса развернута на плоскости в сек-
тор, центральный угол которого содержит 120°, а площадь равна S.
Найти объем конуса.
2.081 . Боковая поверхность конуса вдвое больше площади основа-
ния. Площадь его осевого сечения равна Q. Найти объем конуса.
2.082 . Выразить объем конуса через его боковую поверхность
S и расстояние г от центра основания до образующей.
2.083 . Доказать, что объем конуса равен 1/3 произведения боковой
поверхности на расстояние от центра основания до образующей.
2.084 . Доказать, что объем конуса равен объему цилиндра с тем же
основанием и той же высотой минус произведение боковой поверхности
этого цилиндра на 1/3 радиуса его основания.
2.085 . Высота конуса разделена на три равных отрезка и через точки
деления параллельно основанию проведены плоскости, разбивающие
конус на три части. Найти объем среднего усеченного конуса, если объем
данного конуса равен V.
2.086 . Высота конуса равна диаметру его основания. Найти отноше-
ние площади его основания к боковой поверхности.
45
2.087 . Доказать, что если два равных конуса имеют общую высоту
и параллельные основания, то объем их общей части составляет 1/4
объема каждого из них.
2.088 . Треугольник со сторонами 10, 17 и 21 см вращается вокруг
большей стороны. Вычислить объем и поверхность полученной фигуры
вращения.
2.089 . На основаниях цилиндра с квадратным осевым сечением по-
строены два конуса с вершинами в середине оси (цилиндра). Найти
сумму полных поверхностей и сумму объемов конусов, если высота
цилиндра равна 2а.
2.090 . Около конуса с радиусом основания R описана произвольная
пирамида, у которой периметр основания равен 2р. Определить отноше-
ние объемов и отношение боковых поверхностей конуса и пирамиды.
2.091 . В конус, осевое сечение которого — равносторонний тре-
угольник, вписан шар. Найти объем конуса, если объем шара равен
32тг/3 см3.
2.092 . Определить поверхность шара, описанного около конуса,
у которого радиус основания равен R, а высота равна й.
2.093 . В шар вписан конус, образующая которого равна диаметру
основания. Найти отношение полной поверхности конуса к поверхности
шара.
2.094 . Найти отношение поверхности и объема шара соответственно
к полной поверхности и объему описанного вокруг него конуса с равно-
сторонним осевым сечением.
2.095 . Металлический шар радиуса R переплавлен в конус, боковая
поверхность которого в 3 раза больше площади основания. Вычислить
высоту конуса.
2.096 . Даны шар, цилиндр с квадратным осевым сечением и конус.
Цилиндр и конус имеют одинаковые основания, а их высоты равны
диаметру шара. Как относятся объемы цилиндра, шара и конуса?
2.097 . Высота конуса и его образующая равны соответственно
4 и 5 см. Найти объем вписанного в конус полушара, основание которого
лежит на основании конуса.
2.098 . Конус и полушар имеют общее основание, радиус которого
равен R. Найти боковую поверхность конуса, если его объем равен
объему полушара.
2.099 . Определить объем шара, вписанного в правильную пирамиду,
у которой высота равна й, а двугранный угол при основании равен 60°.
2.100. Найти отношение поверхности и объема шара соответственно
к поверхности и объему вписанного куба.
2.101. Около правильной треугольной призмы, высота которой
вдвое больше стороны основания, описан шар. Как относится его объем
к объему призмы?
2.102. На отрезке АВ как на диаметре построена полуокружность
с центром в точке О, а на отрезках О А и ОВ построены две полуокруж-
ности, расположенные в той же полуплоскости с границей АВ, что
и первая. Найти поверхность и объем фигуры, которая образована
вращением вокруг АВ фигуры, ограниченной этими тремя полуокруж-
ностями, если ЛВ=20 см.
2.103. Равнобедренная трапеция с основаниями 2 и 3 см и острым
углом 60° вращается вокруг меньшего основания. Вычислить поверх-
ность и объем полученной фигуры вращения.
2.104. Вычислить поверхность тела, полученного от вращения ромба
площадью Q вокруг одной из его сторон.
46 . '
2.105. Ромб вращается вокруг своей большей диагонали, а затем
вокруг меньшей диагонали. Доказать, что отношение объемов получен-
ных фигур вращения равно отношению площадей их поверхностей.
Группа Б
2.106. Сторона основания правильной треугольной пирамиды равна
а, а высота, опущенная из вершины основания на противоположную ей
боковую грайь, равна Ь. Определить объем пирамиды. '
2.107. Боковая поверхность правильной треугольной пирамиды
в 3 раза больше площади основания. Площадь круга, вписанного в ос-
нование, численно равна радиусу этого круга. Найти объем пирамиды.
2.108. Площадь того сечения правильного тетраэдра, которое имеет
форму квадрата, равна тг. Найти поверхность тетраэдра.
2.109. Основанием пирамиды служит- равносторонний треугольник
со стороной, равной а. Одна из боковых граней — также равносторон-
ний треугольник и перпендикулярна плоскости основания. Определить
полную поверхность пирамиды.
2.110. Найти объем правильной треугольной пирамиды, у которой
плоский угол при вершине равен 90°, а расстояние между боковым
ребром и противоположной стороной основания равно d.
2.111. Правильная треугольная пирамида рассечена плоскостью,
перпендикулярной основанию и делящей две стороны основания попо-
лам. Определить объем отсеченной пирамиды, если сторона основания
первоначальной пирамиды равна а, а двугранный угол при основании
содержит 45°.
2.112. Правильная треугольная пирамида пересечена плоскостью,
проходящей через вершину основания и середины двух боковых ребер.
Найти отношение боковой поверхности пирамиды к площади основания,
если известно, что секущая плоскость перпендикулярна одной из боко-
вых граней (указать, какой именно).
2.113. Сторона основания правильной треугольной пирамиды равна
а. Через одну из сторон основания проведена плоскость, перпендикуляр-
ная противоположному боковому ребру и делящая эго ребро в отноше-
нии т: п, считая от вершины основания. Определить полную поверх-
ность пирамиды.
2.114. Через вершину основания и середины двух боковых ребер
правильной треугольной пирамиды проведена плоскость. Найти отно-
шение боковой поверхности пирамиды к площади ее основания, если
известно, что секущая плоскость перпендикулярна боковой грани.
2.115. Из середины высоты правильной треугольной пирамиды опу-
щены перпендикуляры на боковое ребро и боковую грань. Длины этих
перпендикуляров равны соответственно а и Ь. Найти объем пирамиды.
При всяких ли а и b задача имеет решение?
2.116. Центры граней правильного тетраэдра служат вершинами
нового тетраэдра. Найти отношение их поверхностей и отношение их
объемов.
2.117. В треугольной пирамиде, каждое из боковых ребер которой
равно а, один плоский угол при вершине — прямой, а каждый из оста-
льных равен 60°. Вычислить объем пирамиды.
2.118. В треугольной пирамиде две боковые грани взаимно перпен-
дикулярны. Площади этих граней равны Р и Q, а длина их общего ребра
равна а. Определить объем пирамиды.
2.119. Боковые грани треугольной пирамиды взаимно перпендику-
лярны, а площади их равны а1, Ь2 и с2. Определить объем пирамиды.
2.120. В треугольной пирамиде все четыре грани — равные равнобе-
дренные треугольники с основанием а и боковой стороной Ь. Вычислить
объем пирамиды. При всяких ли а и b задача имеет решение?
2.121. Найти отношение объемов правильных тетраэдра и октаэдра,
у которых полные поверхности равны.
2.122. Вычислить поверхность шара, вписанного в треугольную пи-
рамиду, все ребра которой равны а.
2.123. Найти площадь поверхности шара, вписанного в пирамиду,
в основании которой лежит треугольник со сторонами 13, 14 и 15 см,
если вершина пирамиды удалена от каждой стороны основания на 5 см.
2.124. Найти объем правильной четырехугольной пирамиды со сто-
роной основания, равной а, и плоскими углами при вершине, равными
углам наклона боковых ребер к основанию.
2.125. В правильной четырехугольной пирамиде двугранный угол
при боковом ребре равен 120°. Найти боковую поверхность пирамиды,
если площадь ее диагонального сечения равна 5.
2.126. В основании четырехугольной пирамиды лежит прямоуголь-
ник, площадь которого равна S, боковые ребра пирамиды равны и об-
разуют с плоскостью основания угол 45°. Угол между диагоналями
основания равен 60°. Найти объем пирамиды.
2.127. Основанием пирамиды служит прямоугольник, площадь ко-
торого равна 5’. Две боковые грани перпендикулярны плоскости основа-
ния, а две другие наклонены к ней под углами 30 и 60°. Найти объем
пирамиды.
2.128. Основанием пирамиды служит ромб с диагоналями d1 и d2.
Высота пирамиды проходит через вершину острого угла ромба. Пло-
щадь диагонального сечения, проведенного через меньшую диагональ,
равна Q. Вычислить объем пирамиды при условии, что ~>d2.
2.129. Основанием пирамиды служит параллелограмм, смежные
стороны которого 9 и 10 см, а одна из диагоналей 11 см. Противополож-
ные боковые ребра равны, а длина каждого из больших ребер составляет
10,5 см. Вычислить объем пирамиды.
2.130. Основанием пирамиды служит параллелограмм, у которого
стороны равны 10 и 8 м, а одна из диагоналей равна 6 м. Высота
пирамиды проходит через точку пересечения диагоналей основания и ра-
вна 4 м. Определить полную поверхность пирамиды.
2.131. Основанием пирамиды служит параллелограмм, у которого
стороны равны 10 и 18 см, а площадь равна 90 см2. Высота пирамиды
проходит через точку пересечения диагоналей основания и равна 6 см.
Определить боковую поверхность пирамиды.
2.132. Основанием пирамиды служит параллелограмм ABCD, име-
ющий площадь т2 и такой, что BDj-AD; двугранные углы при ребрах
AD и ВС равны 45°, а при ребрах АВ и CD равны 60°. Найти боковую
поверхность и объем пирамиды.
2.133. В шар радиуса R вписана правильная четырехугольная пира-
мида. Определить объем этой пирамиды, если радиус окружности, опи-
санной около ее основания, равен г.
2.134. Сторона основания правильной шестиугольной пирамиды ра-
вна а. Вычислить объем пирамиды, если известно, что ее боковая
поверхность в 10 раз больше площади основания.
2.135. Основанием пирамиды служит правильный шестиугольник со ,<
стороной, равной а. Одно из боковых ребер перпендикулярно плоскости
48
основания и равно стороне основания. Определить полную поверхность
пирамиды.
2.136. Сторона основания правильной шестиугольной пирамиды ра-
вна а. Все ее диагональные сечения равновелики. Найти объем и боко-
вую поверхность пирамиды.
2.137. В треугольной усеченной пирамиде высота равна 10 м, сторо-
ны одного основания — 27, 29 и 52 м, а периметр другого основания
равен 72 м. Определить объем усеченной пирамиды.
2.138. Определить объем правильной треугольной усеченной пира-
миды, у которой стороны оснований равны 3 и 2 м, а боковая поверх-
ность равновелика сумме площадей оснований.
2.139. В треугольной усеченной пирамиде через сторону верхнего
основания проведена плоскость параллельно противоположному боко-
вому ребру. В каком отношении разделился объем усеченной пирамиды,
если соответственные стороны оснований относятся как 1:2?
2.140. Определить объем правильной четырехугольной усеченной
пирамиды, если сторона большего основания равна а, сторона меньшего
основания равна Ь, а острый угол боковой грани равен 60°.
2.141. В правильной четырехугольной усеченной пирамиде стороны
оснований равны а и Ь, а боковая поверхность равна половине полной
поверхности. Найти объем пирамиды.
2.142. Стороны оснований правильной четырехугольной усеченной
пирамиды равны 2 и 1 см, а высота 3 см. Через точку пересечения
диагоналей пирамиды параллельно основаниям пирамиды проведена
плоскость, делящая пирамиду на две части. Найти объем каждой из них.
2.143. Высота правильной четырехугольной усеченной пирамиды ра-
вна 3 см, объем ее 38 см3, а площади оснований относятся как 4:9.
Определить боковую поверхность пирамиды.
2.144. Основаниями усеченной пирамиды служат два правильных
восьмиугольника. Сторона нижнего основания равна 0,4 м, а верхнего
0,3 м; высота усеченной пирамиды равна 0,5 м. Усеченная пирамида
достроена до полной. Определить объем полной пирамиды.
2.145. Площади оснований усеченной пирамиды равны 5’j и S2
(S1<S2), а ее объем равен V. Определить объем полной пирамиды.
2.146. Около шара описана правильная четырехугольная усеченная
пирамида, у которой стороны оснований относятся как т: п. Определить
отношение объемов пирамиды и шара.
2.147. В шар радиуса R вписана правильная шестиугольная усечен-
ная пирамида, у которой плоскость нижнего основания проходит через
центр шара, а боковое ребро составляет с плоскостью основания угол
60°. Определить объем пирамиды.
2.148. На ребре двугранного угла 120° взят отрезок длиной с и из его
концов проведены перпендикуляры к нему, лежащие в различных гранях
данного двугранного угла и имеющие длины а и Ь. Найти длину отрезка
прямой, соединяющего концы этих перпендикуляров.
2.149. Найти расстояние между серединами двух скрещивающихся
ребер куба, полная поверхность которого равна 36 см2.
2.150. Дан куб ABCDA^B^C^D^, ребро которого равно а. Через
диагональ АС его грани ABCD проведена плоскость, параллельная
прямой BOt, где О, — центр грани AiB1C1Di. Найти площадь получен-
ного сечения.
2.151. Площадь сечения куба, представляющего собой правильный
шестиугольник, равна Q. Найти полную поверхность куба.
2.152. В правильную четырехугольную пирамиду вписан куб так, что
49
четыре его вершины находятся на апофемах пирамиды и четыре — в
плоскости основания. Все ребра пирамиды равны, каждое из них имеет
длину а. Вычислить полную поверхность и объем куба.
2.153. В правильный октаэдр вписан куб так, что его вершины
находятся на ребрах октаэдра. Во сколько раз поверхность октаэдра
больше поверхности куба?
2.154. Куб, ребро которого равно а, срезан по углам плоскостями
так, что от каждой грани остался правильный шестиугольник. Опреде-
лить объем полученного многогранника.
2.155. В полушар радиуса R вписан куб так, что четыре его вершины
лежат на основании полушара, а другие четыре вершины расположены
на его сферической поверхности. Вычислить объем куба.
2.156. Через вершины А, С и прямоугольного параллелепипеда
ABCDA1B}ClD1 проведена плоскость, образующая с плоскостью ос-
нования двугранный угол 60°. Стороны основания равны 4 и 3 см. Найти
объем параллелепипеда.
2.157. Диагонали граней прямоугольного параллелепипеда равны а,
b яс. Определить его полную поверхность.
2.158. Основанием прямого параллелепипеда служит параллелог-
рамм. один из углов которого равен 30°. Площадь основания равна
4 дм . Площади боковых граней параллелепипеда равны 6 и 12 дм2.
Найти объем параллелепипеда.
2.159. Основанием прямого параллелепипеда служит параллелог-
рамм с углом 120° и сторонами 3 и 4 см. Меньшая диагональ парал-
лелепипеда равна большей диагонали основания. Найти объем парал-
лелепипеда.
2.160. Длины ребер параллелепипеда равны а, b и с. Ребра, длины
которых равны а я Ь, взаимно перпендикулярны, а ребро длиной с об-
разует с каждым из них угол 60°. Определить объем параллелепипеда.
2.161. В наклонном параллелепипеде проекция бокового ребра на
плоскость основания равна 5 дм, а высота равна 12 дм. Сечение,
перпендикулярное боковому ребру, есть ромб с площадью 24 дм2 и диа-
гональю, равной 8 дм. Найти боковую поверхность и объем парал-
лелепипеда.
2.162. Основанием наклонного параллелепипеда служит ромб ABCD
со стороной, равной а, и острым углом 60°. Ребро AAt также равно
я и образует с ребрами АВ и AD углы 45°. Определить объем парал-
лелепипеда.
2.163. Основанием наклонного параллелепипеда служит ромб со
стороной а и острым углом 30°. Диагональ одной боковой грани перпен-
дикулярна плоскости основания, а боковое ребро составляет с плоско-
стью основания угол 60°. Найти полную поверхность и объем парал-
лелепипеда.
2.164. Около шара описан прямой параллелепипед, у которого диа-
гонали основания равны а и Ь. Определить полную поверхность парал-
лелепипеда.
2.165. В правильной треугольной призме через сторону нижнего
основания и противоположную вершину верхнего основания проведена
плоскость, составляющая с плоскостью нижнего основания угол 45°.
Площадь сечения равна S. Найти объем призмы.
2.166. В правильный тетраэдр помещена правильная треугольная
призма так, что вершины одного ее основания находятся на боковых
ребрах тетраэдра, а другого — в плоскости его основания. Ребро тетра-
эдра равно а. Определить объем призмы, если все ее ребра равны.
50
2.167. Основанием призмы АВСА^С} служит правильный тре-
угольник АВС со стороной а. Вершина At проецируется в центр нижнего
основания, а ребро АА2 наклонено к плоскости основания под углом 60°.
Определить боковую поверхность призмы.
2.168. Сторона основания правильной треугольной призмы меньше
бокового ребра и равна а- Через сторону верхнего основания проведена
плоскость, которая составляет с плоскостью основания угол 45° и делит
призму на две части. Определить объем и полную поверхность верхней
части призмы.
2.169. Основанием прямой призмы служит равнобедренный тре-
угольник, основание которого равно а, а угол при нем равен 45°.
Определить объем призмы, если ее боковая поверхность равна сумме
площадей оснований.
2.170. Основанием прямой призмы служит прямоугольный тре-
угольник с гипотенузой, равной с, и острым углом 30°. Через гипотенузу
нижнего основания и вершину прямого угла верхнего основания прове-
дена плоскость, образующая с плоскостью основания угол 45°. Опреде-
лить объем треугольной пирамиды, отсеченной от призмы плоскостью.
2.171. Основанием прямой призмы служит равнобедренная трапеция
ABCD; AB=CD = 13 см, ВС- И см, ЛЛ = 21 см. Площадь ее диагональ-
ного сечения равна 180 см2. Вычислить полную поверхность призмы.
2.172. Доказать, что объем прямой призмы, основанием которой
служит трапеция, равен произведению среднего арифметического пло-
щадей параллельных боковых граней на расстояние между ними.
2.173. Площадь основания прямой треугольной призмы равна 4 см2,
площади боковых граней равны 9, 10 и 17 см2. Определить объем
призмы.
2.174. В основании наклонной призмы лежит правильный треуголь-
ник со стороной, равной а. Одна из боковых граней призмы перпен-
дикулярна плоскости основания и представляет собой ромб, диагональ
которого равна Ь. Найти объем призмы.
2.175. Основанием наклонной призмы служит правильный треуголь-
ник со стороной, равной а. Длина бокового ребра равна Ь, а одно из
боковых ребер образует с прилежащими сторонами оснований углы 45°.
Определить боковую поверхность призмы.
2.176. В наклонной треугольной призме расстояния боковых ребер
друг от друга равны а, b и с. Боковое ребро равно /, высота призмы h.
Определить полную поверхность призмы.
2.177. Расстояние между любыми двумя боковыми ребрами наклон-
ной треугольной призмы равно а. Боковое ребро равно / и наклонено
к плоскости основания под углом 60°. Определить полную поверхность
призмы.
2.178. В основании призмы лежит трапеция. Выразить объем при-
змы через площади 5, и S2 параллельных боковых граней и расстояние
h между ними.
2.179. Объем правильной восьмиугольной призмы равен 8 м3, а ее
высота равна 2,2 м. Найти боковую поверхность призмы.
2.180. Около шара описана правильная треугольная призма, а около
нее описан шар. Найти отношение поверхностей этих шаров.
2.181. Около шара радиуса R описана правильная шестиугольная
призма. Определить ее полную поверхность.
2.182. Конус образован вращением прямоугольного треугольника
площадью S вокруг одного из катетов. Найти объем конуса, если длина
51
окружности, описанной при вращении этого треугольника точкой пересе-
чения его медиан, равна L.
2.183. Треугольник со сторонами, равными а, b и с, вращается
поочередно вокруг каждой из своих сторон. Найти отношение объемов
полученных при этом фигур.
2.184. Радиус основания конуса равен R, а боковая поверхность
равна сумме площадей основания и осевого сечения. Определить объем
конуса.
2.185. Радиус основания конуса равен R. Две взаимно перпендику-
лярные образующие делят площадь боковой поверхности конуса в от-
ношении 1:2. Найти объем конуса.
2.186. Плоскость, проведенная через вершину конуса, пересекает
основание по хорде, длина которой равна радиусу этого основания.
Определить отношение объемов полученных частей конуса.
2.187. Полная поверхность конуса равна nS кв. ед. Развернутая на
плоскость боковая поверхность конуса представляет собой сектор с уг-
лом 60°. Определить объем конуса.
2.188. Высота конуса равна й. Разверткой боковой поверхности это-
го конуса является сектор с центральным углом 120°. Вычислить объем
конуса.
2.189. Радиус основания конуса равен R, а угол развертки его боко-
вой поверхности равен 90°. Определить объем конуса.
2.190. Основание пирамиды есть прямоугольный треугольник. Боко-
вые ребра пирамиды равны, а боковые грани, проходящие через катеты,
составляют с плоскостью основания углы 30 и 60°. Найти объем описан-
ного около пирамиды конуса, если высота пирамиды равна h.
2.191. Угол между образующей конуса и плоскостью основания
равен 30°. Боковая поверхность конуса равна Зтц/з кв. ед. Определить
объем правильной шестиугольной пирамиды, вписанной в конус.
2.192. Определить боковую поверхность и объем усеченного конуса
с образующей, равной I, описанного около шара радиуса г.
2.193. Даны цилиндр и шар. Радиусы основания цилиндра и боль-
шого круга шара равны. Полная поверхность цилиндра относится к по-
верхности шара как т: п. Найти отношение их объемов.
2.194. В цилиндрический сосуд, радиус основания которого А=4 см,
помещен шар радиуса г=3 см. В сосуд налита вода так, что ее свободная
поверхность касается поверхности шара (шар при этом не всплывает).
Определить толщину того слоя воды, который получится, если вынуть
шар из сосуда.
2.195. Параллелограмм, периметр которого равен 2р, вращается
вокруг оси, перпендикулярной диагонали длиной d и проходящей через
ее конец. Найти поверхность фигуры вращения.
Группа В
2.196. Сторона основания правильной треугольной пирамиды равна
а, площадь ее сечения, имеющего форму квадрата, равна т1. Найти
отношение боковой поверхности пирамиды к площади основания.
2.197. Высота правильной треугольной пирамиды равна Н. Найти ее
полную поверхность, если плоскость, проведенная через вершину ос-
нования пирамиды перпендикулярно апофеме противоположной боко-
вой грани, составляет с плоскостью основания угол 30°.
2.198. Через точку, делящую ребро правильного тетраэдра в от-
52
ношении 1:4, проведена плоскость, перпендикулярная этому ребру. Най-
ти отношение объемов полученных частей тетраэдра.
2.199. Доказать, что если тетраэдр ортоцентрический, т. е. такой,
что прямые, содержащие его высоты, пересекаются в одной точке, то:
а) каждые два его противоположных ребра взаимно перпендику-
лярны;
б) если один из плоских углов при какой-либо вершине тетраэд-
ра — прямой, то и другие два плоских угла — прямые;
в) любая его вершина проецируется в ортоцентр противоположной
грани (точку пересечения прямых, содержащих высоты грани);
г) суммы квадратов длин его противоположных ребер равны.
2.200. а) Длины ребер АВ, AC, AD и ВС ортоцентрического тетраэд-
ра равны соответственно 5, 7, 8 и 6 см. Найти длины остальных двух
ребер.
б) Является ли тетраэдр ABCD ортоцентрическим, если АВ=8 см,
ВС= 12 см, DC=6 см?
2.201. В ортоцентрическом тетраэдре ABCD угол ADC — прямой.
1111
Доказать, что — = — + —+—, где п — длина высоты тетраэдра, прове-
й2 а2 Ь2 с2
денной из вершины D, a=DA, b=DB, c=DC.
2.202. В ортоцентрическом тетраэдре ABCD угол АВС — прямой;
St, S2, S3 — площади граней ВАС, BAD, BCD соответственно. Доказать,
что объем тетраэдра равен
2.203. Основанием пирамиды SABC является равнобедренный пря-
моугольный треугольник АВС, длина гипотенузы которого АВ=4,^/1.
Боковое ребро SC пирамиды перпендикулярно плоскости основания,
а его длина равна 2. Найти величину угла и расстояние между прямыми,
одна из которых проходит через точку S и середину ребра АС, а дру-
гая — через точку С и середину ребра АВ.
2.204. Вычислить объем треугольной пирамиды, у которой два про-
тивоположных ребра 4 и 12 м, а каждое из остальных ребер равно 7 м.
2.205. Найти объем треугольной пирамиды, стороны основания ко-
торой равны а, b и с, если каждая из этих сторон равна боковому ребру,
не пересекающемуся с ней.
2.206. Боковые ребра треугольной пирамиды имеют одинаковую
длину и равны а. Из трех плоских углов, образованных этими ребрами
при вершине пирамиды, два содержат по 45°, а третий — 60°. Опреде-
лить объем пирамиды.
2.207. Длины боковых ребер треугольной пирамиды равны а, b и с,
плоские углы, образованные этими ребрами,— прямые. Найти длину
высоты, проведенной к основанию пирамиды.
2.208. Через ребро правильного тетраэдра проведена плоскость, па-
раллельная противоположному ребру. Найти отношение объема полу-
ченного параллелепипеда к объему тетраэдра.
2.209. Два правильных тетраэдра соединены двумя гранями так, что
образуют двойную пирамиду. Центры шести боковых граней этой двой-
ной пирамиды приняты за вершины прямой треугольной призмы. Вычи-
слить объем этой призмы, если ребро тетраэдра равно а.
2.210. Доказать, что объемы двух треугольных пирамид, имеющих
по равному трехгранному углу, относятся как произведения длин трех
ребер равных трехгранных углов.
2.211. Основанием пирамиды SABC служит треугольник АВС такой,
53
что АВ=АС= 10 м и ВС= 12 м. Грань SBC перпендикулярна основанию
и SB=SC. Вычислить радиус шара, вписанного в пирамиду, если высота
пирамиды равна 1,4 м.
2.212. Из середины высоты правильной четырехугольной пирамиды
проведены перпендикуляр длиной а к боковому ребру и перпендикуляр
длиной b к боковой грани. Найти объем пирамиды.
2.213. Через сторону основания правильной четырехугольной пира-
миды проведена плоскость, которая отсекает от противоположной грани
треугольник площадью 4 см2. Найти боковую поверхность пирамиды,
которая отсечена этой плоскостью от данной пирамиды, если боковая
поверхность данной пирамиды равна 25 см2.
2.214. Сторона основания правильной четырехугольной пирамиды
равна а, боковое ребро составляет со стороной угол 30°. Через вершину
основания пирамиды проведена плоскость, перпендикулярная противо-
лежащему боковому ребру. Эта плоскость разбивает пирамиду на две
части. Определить объем части пирамиды, прилегающей к вершине.
2.215. В шар радиуса R вписана правильная четырехугольная пира-
мида, основание которой делит перпендикулярный ему радиус пополам.
Определить поверхность шара, вписанного в пирамиду.
2.216. Найти объем правильной пирамиды, в основании которой
лежит правильный пятиугольник, а боковыми гранями являются пра-
вильные треугольники со стороной а.
2.217. Два равных куба с ребром а имеют общий отрезок АВ,
концами которого являются середины двух противоположных ребер, не
принадлежащих одной грани. Один из кубов получен поворотом другого
вокруг прямой АВ на 90°. Найти объем общей части этих кубов.
2.218. Найти объем общей части двух кубов, если один из них
получен поворотом на 90° другого куба вокруг оси, проходящей через
среднюю линию одной из его граней. Ребро куба равно а.
2.219. Два куба с ребром, равным а, имеют общий отрезок, соединя-
ющий центры двух противоположных граней, но один куб повернут на
45° по отношению к другому. Найти объем общей части этих кубов.
2.220. Диагонали двух одинаковых кубов с ребром, равным а, лежат
на одной и той же прямой. Вершина второго куба совпадает с центром
первого и второй куб повернут вокруг диагонали на 60° по отношению
к первому. Найти объем общей части этих кубов.
2.221. Через концы трех ребер, выходящих из вершин В, D, Аг и Сг
куба ABCDAiBfC^i, ребро которого равно а, проведены плоскости.
Доказать, что полученная фигура есть правильный тетраэдр, и вычис-
лить его полную поверхность и объем.
2.222. Через каждые три вершины куба, расположенные на концах
каждой тройки ребер, сходящихся в одной вершине, проведена плос-
кость. Найти объем тела, ограниченного этими плоскостями, если ребро
куба равно а.
2.223. Расстояние между непересекающимися диагоналями двух
смежных боковых граней куба равно d. Определить полную поверхность
куба.
2.224. Ребро наклонного параллелепипеда равно I. К нему примы-
кают две смежные грани, у которых площади равны т1 и л2, а их
плоскости образуют угол 30°. Вычислить объем параллелепипеда.
2.225. Гранями параллелепипеда служат ромбы, диагонали которых
равны 3 и 4 см. В параллелепипеде имеются трехгранные углы, состав-
ленные тремя острыми углами ромбов. Найти объем параллелепипеда.
2.226. В основании прямой призмы лежит треугольник со сторонами
54
6, 8 и 10 см. Некоторое плоское сечение этой призмы отсекает от
боковых ребер, проходящих через вершины большего и среднего углов
основания, отрезки, равные 12 см каждый, а от ребра, проходящего через
вершину меньшего угла основания,— отрезок в 18 см. Найти объем
и площадь полной поверхности фигуры, ограниченной плоскостью ос-
нования призмы, плоскостями боковых граней и плоскостью сечения.
2.227. Высота цилиндра равна радиусу его основания и имеет длину
а. Через ось цилиндра проведена другая цилиндрическая поверхность,
делящая окружность основания на две дуги, длины которых относятся
как 2:1. Эта цилиндрическая поверхность делит данный цилиндр на две
части. Найти боковую поверхность и объем большей части цилиндра.
2.228. В конус вписан шар. Доказать, что отношение полной поверх-
ности конуса к поверхности шара равно отношению их объемов.
2.229. Отношение высоты конуса к радиусу описанного около него
шара равно q. Найти отношение объемов этих тел. При каких значениях
q задача не имеет решения?
2.230. Конус лежит на плоскости и катится по ней, вращаясь вокруг
своей неподвижной вершины. Высота конуса и его образующая равны
hut. Вычислить площадь поверхности, описываемой высотой коцуса.
2.231. Около шара описан усеченный конус, площадь нижнего ос-
нования которого в а раз больше площади его верхнего основания. Во
сколько раз объем усеченного конуса больше объема шара?
2.232. Доказать, что если в многогранник можно вписать сферу, то
его объем равен 1/3 произведения полной поверхности многогранника на
радиус вписанной сферы.
2.233. Основание пирамиды SABCD есть трапеция с параллельными
сторонами АВ и CD. Доказать, что объем пирамиды равен 4/3 произ-
ведения площади треугольника MSN, где MN — средняя линия трапе-
ции, на расстояние ребра АВ от плоскости MSN.
2.234. Многогранник имеет следующее строение: две его грани (ос-
нования) представляют собой многоугольники, расположенные в парал-
лельных плоскостях; остальные грани (боковые) — трапеции, паралле-
лограммы или треугольники, у которых каждая вершина является одно-
временно вершиной одного из оснований. Доказать, что объем такого
1
многогранника равен - H(S1+S2 + 4S3), где Н—расстояние между
6
плоскостями оснований, S1hS2 — площади оснований, a S3 — площадь
сечения, равноотстоящего от обоих оснований.
2.235. Фигура ограничена сверху и снизу двумя прямоугольниками
со сторонами, равными а, b и аг, Ь2, а сбоку — трапециями. Стороны
прямоугольников параллельны, расстояние между параллельными плос-
костями прямоугольных оснований равно h. Найти объем фигуры.
ГЛАВА 3
ЗАДАЧИ ПО ГЕОМЕТРИИ
С ПРИМЕНЕНИЕМ ТРИГОНОМЕТРИИ
НЕКОТОРЫЕ СООТНОШЕНИЯ
МЕЖДУ ЭЛЕМЕНТАМИ ФИГУР
1°. Площадь параллелограмма ABCD (рис. 3.1) можно вычислить по следу'
ющим формулам:
AC2-BDz
----".-
4
АВ1-AD1
S**--------tgt-AOD,
(б)
где О — точка пересечения диагоналей АС и BD.
□ Используя теорему косинусов (1.7), выразим АС1 из треугольника АС В
и BD1 из треугольника ABD, а затем вычтем из первого равенства второе. Тогда
, ACZ-BDZ
получим AC1-BD2=4AB AD cosA, откуда AB AD=-------------. Наконец, при-
4 cos Л
меняя формулу (1.22), находим
ACZ—BDZ
Sabcd = АВ AD sin Л =-------tgA.
4
Проведя аналогичные рассуждения по отношению к треугольникам AOD
и АОВ, можно установить справедливость формулы (б).
2°. Пусть известны длины b и с двух сторон треугольника АВС и угол А,
образуемый ими (рис. 3.2). Тогда длина биссектрисы AD треугольника, проведен-
ной из вершины этого угла, выражается формулой
2bc cos (Л/2)
□ Имеем ВлАВС=В&АВС+В&А1)д. Используя формулу (1.2), получаем
56
или
1 1 1
- be sin A =~ lab sin (Л/2) 3— lac sin (Л/2)
2 2 2
1
be sin (Л/2) cos(/l/2)=- la(b + c) sm(Ai'i).
2
A 2bc cos (Л/2)
Так как sin — #0, то /„=---------.
2 b + c
3°. Справедливы следующие соотношения между элементами шара и вписан-
ного в него конуса:
шар пирамиды,
в
Рис. 3.3
Z=2J?sina; (а)
P~2RH, (б)
где R — радиус шара, I — длина образующей конуса, Н — его высота, а — угол
между образующей и плоскостью основания.
Такие же соотношения справедливы и для вписанной
боковые ребра которой имеют длину / и составляют
с плоскостью основания угол а.
□ а) Построив осевое сечение конуса, вписанного
в шар (рис. 3.3), получим равнобедренный треугольник
SAB, вписанный в окружность радиуса R. Центром окру-
жности является точка О пересечения высоты SK и сере-
динного перпендикуляра DO к стороне SB, причем SK= Н,
l_SOD= LSBK=a. Из &SDO находим SD=SO sin а, т. е.
Z=2Asina.
б) Продолжим SK до пересечения с окружностью
в точке Е и построим отрезок BE. Тогда получим прямо-
угольный треугольник SBE, в котором катет SB=l есть
среднее геометрическое между гипотенузой SE=2R и про-
екцией SK=H катета SB на гипотенузу SE, т. е.
P=1RH.
4°. Пусть А2В2 — боковое ребро пирамиды или призмы, А2О — его проек-
ция на плоскость основания, сВ^А^О^а., ЕОА1А2=Р, LBiA^—y (рис. 3.4).
Тогда справедливо равенство cos у=cos a cos/f.
□ Проведем высоту боковой грани — отрезок ВгС, тогда ОС1А1А1 (по
57
AtC
теореме о трех перпендикулярах) и из ДЛ1СЛ1 получим cosy =----------. Так как
Aisi
ОAi cosfi OAi
А^^ОА^ cosfi (из ДОСЛ2), to cosy =-------------. Ho-----=cosa (из AXjOBJ;
Ai#i Aisi
значит, cos у=cos a cos fi.U
5°. Пусть a — угол наклона бокового ребра правильной л-угольной пирами-
ды к плоскости основания, 3 — угол наклона ее боковой грани к плоскости
основания, <р — плоский угол при вершине пирамиды, <о — двугранный угол
между смежными боковыми гранями (рис. 3.5). Тогда справедливы следующие
соотношения:
sin(<p/2)
cos a®--------; w
sin (n/n)
. a) cos (я/л)
sin — --------; (o)
2 cos(<p/2)
tg(<p/2) . <D
cosd=-------=cosa sin —. W
tg(n/w) 2
□ а) Пусть О — центр правильного n-угольника, служащего основанием
я(л—2)
пирамиды; At — угол при вершине этого n-угольника. Тогда LAt=--------------=
л
2я я я /я я\ я
=я-----, {_ОА1С=------. Далее имеем OA1=AiC:cosl------------)=Л1С: sin - (из
л 2 л \2 л/ л
Ф
^ОСЛ,У. SA.-A.C-^ - (.. Д5СЛ,). Теперь „ Д50Л, naw».
ОЛ1 АХС А2С sin(<p/2)
cosa=------=-------:--------=--------.
SJj sin (я/л) sin (<p/2) sin (я/л)
б) Пусть E — середина основания A2A„ равнобедренного треугольника
A2DA„. Она принадлежит также биссектрисе АгО угла при вершине А, основания
пирамиды и биссектрисе DE угла А2Е)А„. Из прямоугольных треугольников A2ED
ai /я я\ я
и А1ЕА2 находим A2-D=A2E:sm — и A^^A^'.sin I - )=J1E:cos -. Раз-
2 \2 л/ л
делив первое равенство на второе, получим ^2Z>:^i^2=cos(n/H):sin(<u/2). Так
как АА2А2Е~ AAlSC, то A2D:AiA2=SC:AiS=cos(<p/2'), откуда
(р COS (я/л) 01 cos (я/л)
cos— =--------или sin =------------.
2 sin (<u/2) 2 cos (<p/2)
(я я\ я
-— I = Л 2С ctg - (из
2 л/ л
Ф
дОСЛД 5С=Л,С ctg- (из Д5СЛ2). Поэтому
Л 2С ctg (я/л) tg(<p/2)
cos о =----------=---------,
XtCctg(<p/2) tg(n/n)
откуда, перемножив соотношения (а) и (б), получим
. tg(?>/2) . 01
cos о =-------=cos a sin —.
tg(n/n) 2
58
в
Пример 1. Угол при основании остроугольного равнобедренного треуголь-
ника АВС (АВ=ВС) равен а. В каком отношении, считая от вершины А, высота
BD делит высоту АЕ!
□ Согласно условию, дАВС — остроугольный; значит, точка К пересечения
высот лежит внутри треугольника (рис. 3.6). Пусть AD—a. Из ДАЕС находим
а
АЕ=2а sin а; из t\AKD находим АК=----(l_AKD= 1_С, так как оба угла допол-
sina
а
няют угол KAD до 90°). Далее имеем КЕ=АЕ—АК=2а sin а—---------------=
sin а
a(2sin2a—1) a cos 2а
=-----------=---------. Окончательно получим
sin a sin а
АК a a cos 2а 1
KE sin a sin a cos 2а
Пример 2. Из вершины С ромба ABCD, сторона которого равна а, проведены
два отрезка СЕ и CF (рис. 3.7), делящие ромб на три равновеликие фигуры.
Известно, что cos С = 1/4. Найти сумму CE+CF.
□ Высоты треугольников CED и CFB, проведенные из вершины С, имеют
равные длины и SaCED=Sacfb (по условию); поэтому DE=FB, а значит,
CE=CF и АЕ=АЕ Проведем диагональ АС, которая делит AECF на два
1
равных треугольника. Следовательно, S^xcf—~ $aecf- Так как S/IEcf=S&cfb
1
(по условию), то Eacfb, причем треугольники AFC и FCB имеют
2
1
общую высоту, проведенную из вершины С. Отсюда вытекает, что AF=- FB,
2
2 1
т. е. FB=- а; кроме того, coscos(180° — С)= — cosC=—. Из &FCB по
3 4
теореме косинусов получим
I 4 а2 ~( 1\ 2а 4а
CF= а2+——2а .
V 9 \ 4/ 3 3
8a
Итак, СЕ+ CF=—.
3
Пример 3. Основание пирамиды — прямоугольный треугольник, гипотенуза
которого равна с, а один из острых углов равен а. Каждое боковое ребро
составляет с плоскостью основания угол р. Найти объем пирамиды.
59
в
□ Так как все боковые ребра пирамиды ABCD (рис. 3.8) одинаково наклоне-
ны к плоскости основания, то вершина D проецируется в центр окружности,
описанной около треугольника АВС; для прямоугольного треугольника — в сере-
дину Е гипотенузы АВ. Высота DE треугольника ADB является высотой пирами-
1 1 , 1,
ды. Далее имеем S^abc—^ АС ВС=-^ с2 sina cosa=- с1 sin2<x, DE=BEtgj}=
с
= -tg Окончательно по лучим
2
11, с с3
К=-- с1 sin 2а- tgB=— sin2atgfi.
3 4 2 24
Пример 4. В конус, образующая которого наклонена к основанию под углом
а, вписан шар. Радиус окружности касания сферической и конической поверх-
ностей равен г. Найти длину образующей конуса.
□ В осевом сечении конуса (рис. 3.9) получим равнобедренный треугольник
АВС, в который вписана окружность с центром О — точкой пересечения высоты
BD треугольника и биссектрисы СО угла С. Из точки Б касания окружности
с образующей ВС проведем KE1BD. Очевидно, что КЕ=г, КО Е= я (см. пример
a
ctg-
r а 2
1), OE=OD=------. Из t^ODC находим DC=OD ctg-=r--------, а из &BDC нахо-
sina 2 sin a
a
ctg-
DC 2
дим BC=-----= 2r-----.
cos a sin 2a
Пример 5. Найти площадь боковой поверхности правильной четырехуголь-
ной пирамиды, высота которой равна Я, а величина плоского угла при вершине
равна <р (рис. 3.10).
□ Введем вспомогательный угол
Я
a= LSA2O. Тогда SA2=-----и площадь боковой
sina
поверхности пирамиды выразится следующим
образом:
1 Я2 2Я2 sin <р
^бО1=45д5ЛЛ=4; ~— sm<p=———-.
2 яп2 а яп2 а
Используя связь между введенным углом
а и известными углами <р и /_ОА2А3=п/4 (см.
sin (</>/2)
формулу (a) n. 5), получим cosa=-------=->/2sin(<j?/2). Следовательно,
sin (я /4)
sin2a=l—2sin2(<p/2)=cos<p. Подставляя это выражение в фор-
мулу для 5вож> окончательно находим tg<p.
Группа А
3.001. Сумма двух неравных высот равнобедренного треугольника
равна /, угол при вершине равен а. Найти боковую сторону.
3.002. Даны две стороны b и с треугольника и его площадь, равная
0,4 Ьс. Найти третью сторону.
3.003. В треугольнике даны длины двух сторон а и Ь и угол а между
ними. Найти длину высоты, проведенной к третьей стороне.
3.004. В равнобедренном треугольнике даны основание а и угол
а при основании. Найти длину медианы, проведенной к боковой стороне.
3.005. Около круга радиуса R описана равнобедренная трапеция
с острым углом а при основании. Найти периметр трапеции.
3.006. Основание равнобедренного треугольника равно а, угол при
вершине равен а. Найти длину биссектрисы, проведенной к боковой
стороне.
3.007. Площадь прямоугольной трапеции равна S, острый угол ра-
вен а. Найти высоту трапеции, если ее меньшая диагональ равна боль-
шему основанию.
3.008. В равнобедренный треугольник с углом а при основании
вписана окружность радиуса г. Найти радиус окружности, описанной
около треугольника.
3.009. В равнобедренном треугольнике угол между боковыми сторо-
нами равен а, радиус вписанной окружности равен г. Найти площадь
треугольника.
3.010. Около круга радиуса R описана трапеция с углами а и /? при
большем основании. Найти площадь трапеции.
3.011. Высота BD правильного треугольника АВС продолжена за
вершину В и на продолжении взят отрезок BF, равный стороне треуголь-
ника. Точка F соединена отрезком прямой с вершиной С. С помощью
этого построения показать, что tgl5° = 2 — л/з.
3.012. В прямоугольном треугольнике даны его площадь S и острый
угол а. Найти расстояние от точки пересечения медиан треугольника до
гипотенузы.
3.013. Высота равнобедренной трапеции равна Л, а угол между ее
диагоналями, противолежащий боковой стороне, равен а. Найти сред-
нюю линию трапеции.
3.014. Площадь равнобедренного треугольника равна S, угол между
высотой, проведенной к боковой стороне, и основанием равен а. Найти
радиус круга, вписанного в треугольник.
3.015. Около круга описана прямоугольная трапеция с острым уг-
лом а. Найти высоту трапеции, если ее периметр равен Р.
3.016. Через вершину А равнобедренного остроугольного треуголь-
ника АВС и центр описанной около этого треугольника окружности
проведена прямая, пересекающая сторону ВС в точке D. Найти длину
АО, если АВ—ВС=Ь и LABC=a.
3.017. Площадь равнобедренного треугольника равна S, а проти-
волежащий основанию угол между медианами, проведенными к его
боковым сторонам, равен а. Найти основание.
61
3.018. В равнобедренном треугольнике угол при основании равен а,
радиус вписанного круга равен г. Через вершину угла при основании
и центр вписанного круга проведена прямая. Найти отрезок этой пря-
мой, заключенный внутри треугольника.
3.019. В квадрате ABCD через середину М стороны АВ проведена
прямая, пересекающая противоположную сторону CD в точке N. В ка-
ком отношении прямая MN делит площадь квадрата, если острый угол
AMN равен а? Указать возможные значения а.
3.020. Равносторонний треугольник пересечен прямой, проходящей
через середину одной из его сторон и составляющей с этой стороной
острый угол а. В каком отношении эта прямая делит площадь треуголь-
ника?
3.021. В равнобедренном треугольнике угол при основании равен а.
Найти отношение площади треугольника к площади описанного около
него круга.
3.022. Общая внешняя касательная двух внешне касающихся окру-
жностей составляет с линией центров угол а. Найти отношение радиусов
этих окружностей.
3.023. Угол при основании равнобедренного треугольника равен а.
Найти отношение радиусов вписанной и описанной окружностей.
3.024. Найти отношение периметра трапеции, описанной около
окружности, к длине этой окружности, если углы при большем основа-
нии трапеции равны а. и fi.
3.025. В ромб ABCD и в треугольник АВС, содержащий его боль-
шую диагональ, вписаны окружности. Найти отношение радиусов этих
окружностей, если острый угол ромба равен а.
3.026. Диагональ прямоугольника равна d и делит угол прямоуголь-
ника в отношении т:п. Найти периметр прямоугольника.
3.027. В ромбе через вершину острого угла, равного а, проведена
прямая, делящая этот угол в отношении 1:2. В каком отношении эта
прямая делит сторону ромба, которую она пересекает?
3.028. В равнобедренной трапеции, описанной около круга, отноше-
ние боковой стороны к меньшему основанию равно к. Найти углы
трапеции и допустимые значения к.
3.029. Отношение площади прямоугольного треугольника к площа-
ди квадрата, построенного на его гипотенузе, равно к. Найти сумму
тангенсов острых углов треугольника.
3.030. В параллелограмме со сторонами а и b и острым углом
а найти тангенсы углов, образуемых большей диагональю параллелог-
рамма с его сторонами.
3.031. Найти угол треугольника, если известно, что стороны, заклю-
чающие этот угол, равны а и Ь, а биссектриса угла равна I.
3.032. В квадрат ABCD вписан равнобедренный треугольник AEF-,
точка Е лежит на стороне ВС, точка F— на стороне CD и AE=AF.
Тангенс угла AEF равен 3. Найти косинус угла FAD.
3.033. На меньшем основании равнобедренной трапеции построен
правильный треугольник. Его высота равна высоте трапеции, а площадь
в 5 раз меньше площади трапеции. Найти угол при большем основании
трапеции.
3.034. В прямоугольник ABCD(AB\]CD) вписан треугольник AEF.
Точка Е лежит на стороне ВС, точка F — на стороне CD. Найти тангенс
угла EAF, если AB:BC=BE:EC=CF:FD=k.
3.035. В параллелограмм со сторонами а и Ъ (а<Ь) и острым углом
а вписан ромб; две его вершины совпадают с серединами больших
62
сторон параллелограмма, две другие лежат на меньших сторонах (или
на их продолжениях). Найти углы ромба.
3.036. Даны стороны а, Ь, с и d четырехугольника, вписанного
в окружность. Найти угол, заключенный между сторонами а и Ь.
3.037. Показать, что если в треугольнике отношение тангенсов двух
углов равно отношению квадратов синусов этих же углов, то треуголь-
ник равнобедренный или прямоугольный.
3.038. Доказать, что во всяком треугольнике разность между сум-
мой квадратов любых двух его сторон и произведением этих сторон,
умноженным на косинус угла между ними, есть для данного треуголь-
ника величина постоянная.
3.039. Две высоты параллелограмма, проведенные из вершины тупо-
го угла, равны и h2, а угол между ними равен а. Найти большую
диагональ параллелограмма.
3.040. Высота равнобедренной трапеции равна h. Верхнее основание
трапеции из середины нижнего основания видно под углом 2а, а нижнее
основание из середины верхнего -% под углом 2Д. Найти площадь трапе-
ции в этом общем случае и вычислить ее без таблиц, если й=2, а=15°,
Д=75°.
3.041. Из точки, взятой на окружности радиуса R, проведены две
равные хорды, составляющие вписанный угол, равный а радианам.
Найти часть площади круга, заключенную внутри этого вписанного
угла.
3.042. В сегмент, дуга которого содержит а°, вписан правильный
треугольник так, что одна его вершина совпадает с серединой дуги, а две
другие лежат на хорде. Площадь треугольника равна S'. Найти радиус
дуги сегмента.
3.043. В прямоугольном треугольнике АВС острый угол А равен
а радианам. Дуга окружности с центром в вершине прямого угла С каса-
ется гипотенузы в точке D и пересекает катеты АС и ВС соответственно
в точках Е и F. Найти отношение площадей криволинейных треуголь-
ников ADE и BDF.
3.044. Диагональ прямоугольного параллелепипеда равна I и состав-
ляет с боковым ребром угол а. Найти объем параллелепипеда, если
периметр его основания равен Р.
3.045. В основании прямой призмы лежит прямоугольный треуголь-
ник с острым углом а. Диагональ большей боковой грани равна d и об-
разует с боковым ребром угол р. Найти объем призмы.
3.046. Угол между диагоналями основания прямоугольного парал-
лелепипеда равен а. Диагональ параллелепипеда составляет с плоско-
стью основания угол р. Найти высоту параллелепипеда, если его объем
равен V.
3.047. Основанием прямой призмы служит равнобедренный тре-
угольник с углом а при вершине. Диагональ грани, противоположной
данному углу, равна I и составляет с плоскостью основания угол р.
Найти объем призмы.
3.048. Найти полную поверхность прямого параллелепипеда, если
в основании его лежит ромб с острым углом а и меньшей диагональю d,
а высота параллелепипеда в 2 раза меньше стороны основания.
3.049. В основании прямой призмы лежит равнобедренная трапеция,
у которой диагональ равна а, а угол между диагональю и большим
основанием равен а. Диагональ призмы наклонена к основанию под
углом р. Найти объем призмы.
3.050. Сторона основания правильной четырехугольной призмы рав-
63
на а. Угол между пересекающимися диагоналями двух смежных боковых
граней равен а. Найти объем призмы.
3.051. Основанием прямой призмы служит равнобедренный тре-
угольник, у которого боковая сторона равна а, а угол между боковыми
сторонами равен а. Найти объем призмы, если ее боковая поверхность
равна 5.
3.052. Боковое ребро правильной треугольной пирамиды равно
I и составляет с плоскостью основания угол а. Найти объем пирамиды.
3.053. Высота правильной треугольной пирамиды равна Н, двугран-
ный угол при основании равен а. Найти полную поверхность пирамиды.
3.054. Боковое ребро правильной четырехугольной пирамиды равно
т и наклонено к плоскости основания под углом а. Найти объем
пирамиды.
3.055. Найти объем правильной четырехугольной пирамиды, если
сторона ее основания равна а, а двугранный угол при основании равен а.
3.056. Основанием пирамиды служит прямоугольный треугольник
с острым углом а. Высота пирамиды равна Н. Все боковые ребра
составляют с плоскостью основания один и тот же угол, равный /?.
Найти объем пирамиды.
3.057. Основанием четырехугольной пирамиды служит ромб со сто-
роной а и острым углом а. Все боковые грани наклонены к плоскости
основания под одним и тем же углом /?. Найти полную поверхность
пирамиды.
3.058. Сторона основания треугольной пирамиды равна а, прилежа-
щие к ней углы основания равны а и /?. Все боковые ребра составляют
с высотой пирамиды один и тот же угол <р. Найти объем пирамиды.
3.059. Основанием пирамиды служит равнобедренный треугольник,
у которого боковая сторона равна а, а угол при вершине равен а. Все
боковые ребра наклонены к плоскости основания под углом /?. Найти
объем пирамиды.
3.060. Каждое из боковых ребер четырехугольной пирамиды образу-
ет с высотой угол а. Основанием пирамиды служит прямоугольник
с углом Р между диагоналями. Найти объем пирамида/, если ее высота
равна h. z
3.061. Основанием пирамиды служит правильный треугольник со
стороной а. Две боковые грани пирамиды перпендикулярны плоскости
основания, а равные боковые ребра образуют между собой угол а.
Найти высоту прямой треугольной призмы, равновеликой данной пира-
миде и имеющей с ней общее основание.
3.062. Основанием пирамиды ABCD служит прямоугольный тре-
угольник ABC (Z_C= 90°). Боковое ребро AD перпендикулярно основа-
нию. Найти острые углы треугольника АВС, если L DBA = а и L DBC=Р
3.063. Сторона большего основания правильной четырехугольной
усеченной пирамиды равна а. Боковое ребро и диагональ пирамиды
составляют с плоскостью основания углы, равные соответственно а и р.
Найти площадь меньшего основания пирамиды.
3.064. Стороны оснований правильной л-угольной усеченной .пира-
миды равны а и Ь. Боковая грань составляет с плоскостью основания
угол а. Найти боковую поверхность пирамиды.
3.065. Боковая поверхность правильной треугольной пирамиды
в 5 раз больше площади ее основания. Найти плоский угол при вершине
пирамиды.
3.066. Диагонали боковых граней прямоугольного параллелепипеда
64
составляют с плоскостью основания углы а и Д. Найти угол между
диагональю параллелепипеда и плоскостью основания.
3.067. Найти угол между апофемами двух смежных боковых граней
правильной л-угольной пирамиды, если плоский угол при ее вершине
равен а.
3.068. Боковое ребро правильной треугольной пирамиды образует
со стороной основания угол а. Найти угол между боковым ребром
и высотой пирамиды и допустимые значения а.
3.069. Все боковые ребра треугольной пирамиды составляют с плос-
костью основания один и тот же угол, равный одному из острых углов
прямоугольного треугольника, лежащего в основании пирамиды. Найти
этот угол, если гипотенуза треугольника равна с, а объем пирамиды
равен V.
3.070. Плоскость квадрата составляет угол а с плоскостью, прове-
денной через одну из его сторон. Какой угол составляет с той же
плоскостью диагональ квадрата?
3.071. В грани двугранного угла, равного а, проведена прямая,
составляющая угол fi с ребром двугранного угла. Найти угол между
згой прямой и другой гранью.
3.072. Боковые ребра правильной треугольной пирамиды попарно
взаимно перпендикулярны. Найти угол между боковой гранью и плоско-
стью основания.
3.073. Стороны основания прямого параллелепипеда относятся как
1:2, острый угол в основании равен а. Найти угол между меньшей
диагональю параллелепипеда и плоскостью основания, если высота
параллелепипеда равна большей диагонали основания.
3.074. Найти угол между пересекающимися диагоналями двух смеж-
ных боковых граней правильной четырехугольной призмы, если плос-
кость, в которой они лежат, составляет с плоскостью основания угол а.
3.075. Найти косинус угла между апофемой и диагональю основания
правильной четырехугольной пирамиды, у которой боковое ребро равно
стороне основания.
3.076. Боковая грань правильной треугольной усеченной пирамиды
составляет с плоскостью основания острый угол а. Найти угол между
высотой и боковым ребром пирамиды.
3.077. Отношение боковой поверхности правильной треугольной пи-
рамиды к площади ее основания равно к. Найти угол между боковым
ребром и высотой пирамиды.
3.078. Найти косцнус угла между смежными боковыми гранями
правильной четырехугольной пирамиды, у которой боковое ребро равно
стороне основания.
3.079. Боковое ребро правильной треугольной призмы равно сторо-
не основания. Найти угол между стороной основания и непересекающей
ее диагональю боковой грани.
3.080. Плоский угол при вершине правильной шестиугольной пира-
миды равен углу между боковым ребром и плоскостью основания.
Найти этот угол.
3.081. Отношение одной из сторон основания треугольной пирами-
ды к каждому из остальных пяти ее ребер равно к. Найти двугранный
угол между двумя равными боковыми гранями пирамиды и допустимые
значения к.
3.082. Высота правильной треугольной призмы равна Я. Плоскость,
проведенная через среднюю линию нижнего основания и параллельную
ей сторону верхнего основания, составляет с плоскостью нижнего ос-
3-363 65
нования острый двугранный угол а. Найти площадь сечения, образован-
ного этой плоскостью.
3.083. В основании прямой призмы лежит ромб с острым углом а.
Отношение высоты призмы к стороне основания равно к. Через сторону
основания и середину противоположного бокового ребра проведена
плоскость. Найти угол между этой плоскостью и плоскостью основания.
3.084. В правильной шестиугольной призме плоскость, проведенная
через сторону основания и середину отрезка, соединяющего центры
оснований, составляет с плоскостью основания острый угол а. Найти
площадь сечения, образованного этой плоскостью, если сторона основа-
ния призмы равна а.
3.085. В прямоугольном параллелепипеде диагональ основания рав-
на d и составляет со стороной основания угол а. Через эту сторону
и противоположную ей сторону верхнего основания проведена плос-
кость, образующая с плоскостью основания угол р. Найти боковую
поверхность параллелепипеда.
3.086. Основанием прямой призмы служит равнобедренная трапе-
ция, у которой основания равны а и Ь (а> Ь), а острый угол равен а.
Плоскость, проходящая через большее основание верхней трапеции
и меньшее основание нижней трапеции, составляет с плоскостью нижне-
го основания угол р. Найти объем призмы.
3.087. Через сторону нижнего основания куба проведена плоскость,
делящая объем куба в отношении т.п, считая от нижнего основания.
Найти угол между этой плоскостью и плоскостью основания, если л.
3.088. Через диагональ нижнего основания правильной четыреху-
гольной призмы и противоположную вершину ее верхнего основания
проведена плоскость. Угол между равными сторонами сечения равен а.
Найти отношение высоты призмы к стороне основания.
3.089. Через вершину С основания правильной треугольной пирами-
ды SABC проведена плоскость перпендикулярно боковому ребру SA.
Эта плоскость составляет с плоскостью основания угол, косинус которо-
го равен 2/3. Найти косинус угла между двумя боковыми гранями.
3.090. В основании прямой треугольной призмы лежит равнобедрен-
ный треугольник АВС, у которого АВ=ВС=а и £_ВАС=а. Через сторо-
ну АС проведена плоскость под углом <р(<р<п12) к основанию. Найти
площадь сечения, если известно, что в сечении получился треугольник.
3.091. В правильной двенадцатиугольной пирамиде, ребра которой
пронумерованы подряд, проведено сечение через первое и пятое ребра.
Плоскость сечения образует с плоскостью основания пирамиды угол а,
а площадь этого сечения равна S'. Найти объем пирамиды.
3.092. Диагонали осевого сечения цилиндра пересекаются под уг-
лом, равным а, обращенным к основанию. Объем цилиндра равен V.
Найти высоту цилиндра.
3.093. Разверткой боковой поверхности цилиндра является прямо-
угольник, диагонали которого пересекаются под углом а. Длина диаго-
нали равна d. Найти боковую поверхность цилиндра.
3.094. Развертка боковой поверхности цилиндра представляет собой
прямоугольник, в котором диагональ равна а и составляет с основанием
угол а. Найти объем цилиндра.
3.095. Плоскость, проведенная параллельно оси цилиндра, делит
окружность основания в отношении т.п. Площадь сечения равна S'.
Найти боковую поверхность цилиндра.
3.096. Площадь основания цилиндра относится к площади его осе-
66
вого сечения как т: п. Найти острый угол между диагоналями осевого
сечения.
3.09 7. Плоскость, проведенная через образующую цилиндра, состав-
ляет с плоскостью осевого сечения, содержащего ту же образующую,
острый угол а. Диагональ прямоугольника, полученного в сечении цили-
ндра этой плоскостью, равна I и образует с плоскостью основания угол
р. Найти объем цилиндра.
3.09 8. Разность между образующей и высотой конуса равна d, а угол
между ними равен а. Найти объем конуса.
3.09 9. Расстояние от центра основания конуса до его образующей
равно d. Угол между образующей и высотой равен а. Найти полную
поверхность конуса.
3.100. Найти угол при вершине осевого сечения конуса, если цент-
ральный угол в развертке его боковой поверхности равен а радианам.
3.101. В основание конуса вписан квадрат, сторона которого равна
а. Плоскость, проходящая через одну из сторон этого квадрата и через
вершину конуса, при пересечении с поверхностью конуса образует равно-
бедренный треугольник, у которого угол при вершине равен а. Найти
объем конуса.
3.102. Через две образующие конуса, угол между которыми равен а,
проведена плоскость. Найти отношение площади сечения к полной
поверхности конуса, если образующая конуса составляет с плоскостью
основания угол р.
3.103. Через две образующие конуса, угол между которыми равен а,
проведена плоскость, составляющая с основанием угол р. Найти объем
конуса, если его высота равна h.
3.104. Найти угол между образующей и высотой конуса, у которого
боковая поверхность есть среднее пропорциональное между площадью
основания и полной поверхностью.
3.105. Найти объем конуса, если в его основании хорда, равная а,
стягивает дугу в а°, а высота конуса составляет с образующей угол р.
3.106. Угол при вершине осевого сечения конуса равен 2а, а сумма
длин его высоты и образующей равна а. Найти объем конуса.
3.107. Диагонали осевого сечения усеченного конуса точкой пересе-
чения делятся в отношении 2:1. Угол между диагоналями, обращенный
к основанию конуса, равен а. Длина диагонали равна /. Найти объем
усеченного конуса.
3.108. Сторона ромба равна а, его острый угол равен а. Ромб
вращается вокруг прямой, проходящей через его вершину параллельно
большей диагонали. Найти объем тела вращения.
3.109. Треугольник АВС вращается вокруг прямой, лежащей в плос-
кости этого треугольника, проходящей вне его через вершину А и одина-
ково наклоненной к сторонам АВ и АС. Найти объем тела вращения,
если АВ=а, АС=Ь и /_ВАС=а.
3.110. Радиус круга, вписанного в прямоугольную трапецию, равен
г, острый угол трапеции равен а. Эта трапеция вращается вокруг мень-
шей боковой стороны. Найти боковую поверхность тела вращения.
3.111. Найти острый угол ромба, зная, что объемы тел, полученных
от вращения ромба вокруг его большей диагонали и вокруг его стороны,
относятся как 1: 2^/5.
3.112. Основанием пирамиды служит правильный треугольник. Од-
но боковое ребро перпендикулярно плоскости основания и равно /, два
других образуют с плоскостью основания угол а. В пирамиду вписана
прямая призма; три ее вершины лежат на боковых ребрах пирамиды, три
67
другие — иа основании пирамиды. Диагональ боковой грани призмы
составляет с плоскостью основания угол fi. Найти высоту призмы.
3.113. В конус, образующая которого равна /, вписана правильная
шестиугольная призма с равными ребрами. Найти боковую поверхность
призмы, если угол между образующей и высотой конуса равен а.
3.114. Объем конуса равен V. В конус вписана пирамида, в основа-
нии которой лежит равнобедренный треугольник с углом а между боко-
выми сторонами. Найти объем пирамиды.
3.115. Основанием пирамиды, вписанной в конус, служит четыреху-
гольник, у которого смежные стороны попарно равны, а угол между
одной парой смежных сторон равен а. Найти отношение объема пирами-
ды к объему конуса.
3.116. В конур вписана треугольная пирамида, у которой боковые
ребра попарно взаимно перпендикулярны. Найти угол между образу-
ющей конуса и его высотой.
3.117. Найти боковую поверхность усеченного конуса, описанного
около правильной треугольной усеченной пирамиды, зная, что острый
угол трапеции, служащей боковой гранью пирамиды, равен а и что в эту
трапецию можно вписать окружность радиуса г.
3.118. Основания двух конусов, имеющих общую вершину, лежат
в одной плоскости. Разность их объемов равна V. Найти объем мень-
шего конуса, если касательные, проведенные к окружности его основания
из произвольной точки окружности основания большего конуса, образу-
ют угол а.
3.119. Высота конуса равна Н, угол между образующей и высотой
равен а. В этот конус вписан другой конус так, что вершина второго
конуса совпадает с центром основания первого конуса, а соответст-
вующие образующие обоих конусов взаимно перпендикулярны. Найти
объем вписанного конуса.
3.120. В конус вписан полушар: большой круг полушара лежит
в плоскости основания конуса, а шаровая поверхность касается поверх-
ности конуса. Найти объем полушара, если образующая конуса равна
I и составляет с плоскостью основания угол а.
3.121. Образующая конуса равна а, расстояние от вершины конуса
до центра вписанного шара равно Ь. Найти угол между образующей
и плоскостью основания.'
3.122. Угол между высотой правильной треугольной пирамиды
и боковым ребром равен а(а<я/4). В каком отношении делит высоту
пирамиды центр описанного шара?
3.123. В шар вписан конус. Площадь осевого сечения конуса равна S,
а угол между высотой и образующей равен а. Найти объем шара.
3.124. В конус вписан шар. Отношение радиуса окружности касания
шаровой и конической поверхностей к радиусу основания конуса равно
к. Найти косинус угла между образующей конуса и плоскостью ос-
нования.
3.125. В конус вписан шар, поверхность которого равна площади
основания конуса. Найти косинус угла при вершине в осевом сечении
конуса.
3.126. В полушар вписан конус, вершина которого совпадает с цент-
ром окружности, являющейся основанием полушара; плоскости основа-
ний конуса и полушара параллельны. Прямая, проходящая через центр
основания конуса и произвольную точку окружности большого круга
полушара, составляет с плоскостью основания конуса угол а. Найти
отношение объемов полушара и конуса.
68
3.127. В конус вписан шар. Радиус окружности, по которой касаются
конус и шар, равен г. Найти объем конуса, если угол между высотой
и образующей конуса равен а.
3.128. Найти угол в осевом сечении конуса, если сфера с центром
в вершине конуса, касающаяся его основания, делит объем конуса
пополам.
3.129. Около шара описан усеченный конус, у которого площадь
одного основания в 4 раза больше площади другого основания. Найти
угол между образующей конуса и плоскостью его основания.
3.130. Объем шара равен V. Найти объем его сектора, у которого
центральный угол в осевом сечении равен а.
Группа Б
3.131. В остроугольном треугольнике АВС высота AD — a, высота
СЕ=Ь, острый угол между AD и СЕ равен а. Найти АС.
3.132. Тангенс угла при основании равнобедренного треугольника
равен 3/4. Найти тангенс угла между медианой и биссектрисой, прове-
денными к боковой стороне.
3.133. Площадь равнобедренной трапеции равна S, угол между ее
диагоналями, противолежащий боковой стороне, равен а. Найти высоту
трапеции.
3.134. Найти синус угла при вершине равнобедренного треуголь-
ника, если известно, что медиана, проведенная к боковой стороне,
составляет с основанием угол, синус которого равен 3/5.
3.135. В равносторонний треугольник АВС вписан равносторонний
треугольник A^B^f, точка А, лежит на стороне ВС, точка Вг —на
стороне АС и точка Сг — на стороне АВ. Угол А1В1С1 равен а. Найти
отношение АВ к AiBl.
3.136. В треугольнике даны сторона а, противолежащий ей угол
а и высота h, проведенная к данной стороне. Найти сумму двух других
сторон.
3.137. В треугольнике известны площадь S, сторона а и проти-
волежащий ей угол а. Найти сумму двух других сторон.
3.138. В треугольнике АВС даны острые углы а и у (а>у) при
основании АС. Из вершины В проведены высота BD и медиана BE.
Найти площадь треугольника BDE, если площадь треугольника АВС
равна 5.
3.139. В трапеции меньшее основание равно 2, прилежащие уг-
лы — по 135°. Угол между диагоналями, обращенный к основанию,
равен 150°. Найти площадь трапеции.
3.140. Основания равнобедренной трапеции равны а и Ь (а>Ь), угол
при большем основании равен а. Найти радиус окружности .описанной
около трапеции.
3.141. Большее основание вписанной в круг трапеции равно диамет-
ру круга, а угол при этом основании равен а. В каком отношении точка
пересечения диагоналей трапеции делит ее высоту?
3.142. Боковые стороны трапеции равны р и q (p<q), большее ос-
нование равно а. Углы при большем основании относятся как 2:1.
Найти меньшее основание.
3.143. Внутри данного угла а расположена точка на расстоянии а от
вершины и на расстоянии b от одной из сторон. Найти расстояние этой
точки от другой стороны.
69
3.144. В треугольнике АВС угол А равен а и сторона ВС=а. Найти
длину биссектрисы AD, если угол между биссектрисой AD и высотой АЕ
равен fl.
3.145. Основание треугольника равно а, а прилежащие к нему углы
содержат 45 и 15°. Из вершины, противоположной основанию, проведе-
на окружность радиусом, равным высоте, опущенной на это основание.
Найти площадь части соответствующего круга, заключенную внутри
треугольника.
3.146. Острый угол прямоугольного треугольника равен а. Найти
отношение радиуса вписанной в треугольник окружности к радиусу
описанной окружности. При каком значении а это отношение является
наибольшим?
3.147. Через вершину угла а при основании равнобедренного тре-
угольника проведена прямая, пересекающая противоположную боковую
сторону и составляющая с основанием угол fl. В каком отношении эта
прямая делит площадь треугольника?
3.148. В треугольнике АВС даны острые углы а и у (а>у), прилежа-
щие к стороне АС. Из вершины В проведены медиана BD и биссектриса
BE. Найти отношение площади треугольника BDE к площади треуголь-
ника АВС.
3.149. В треугольнике АВС проведена высота ВМ и на ней как на
диаметре построена окружность, пересекающая сторону АВ в точке К,
а сторону ВС — в точке L. Найти отношение площади треугольника
KLM к площади треугольника АВС, если ДЛ = а и LC=fl.
3.150. В прямоугольном треугольнике АВС проведена биссектриса
AD острого угла А, равного а. Найти отношение радиусов окружностей,
вписанных в треугольники ABD и ADC.
3.151. В прямоугольном треугольнике АВС острый угол при вер-
шине А равен а. Через середину D гипотенузы АВ проведена прямая,
пересекающая катет АС в точке Е. В каком отношении эта прямая делит
площадь треугольника АВС, если £_DEA = fl, АЕ>0,5АС?
3.152. Равнобедренный треугольник с углом а при вершине пересе-
чен прямой, проходящей через вершину угла при основании и состав-
ляющей с основанием угол fl. В каком отношении эта прямая делит
площадь треугольника?
3.153. В каком отношении делит высоту равнобедренного треуголь-
ника АВС точка О, из которой все три стороны видны под одним и тем
же углом (LAOB= L.BOC= L.COA), если угол при основании треуголь-
ника равен а (а>я/6)?
3.154. В окружность радиуса R вписан треугольник, вершины кото-
рого делят окружность на три части в отношении 2: 5:17. Найти пло-
щадь треугольника.
3.155. Через вершины равностороннего треугольника АВС проведе-
ны параллельные прямые AD, BE и CF. Прямая BE лежит между
прямыми AD и CF и делит расстояние между ними в отношении т : п,
считая от прямой AD. Найти угол BCF.
3.156. Медиана BD треугольника АВС пересекается с биссектрисой
СЕ в точке К. Найти СК.КЕ, если LA = a. и LB=fl.
3.157. Стороны параллелограмма относятся как p:q, а диагона-
ли — как т: п. Найти углы параллелограмма.
3.158. Отношение периметра ромба к сумме его диагоналей равно к.
Найти углы ромба и допустимые значения к.
3.159. Высота треугольника делит угол треугольника в отношении
2:1, а основание — на отрезки, отношение которых (большего к мень-
70
шему) равно к. Найти синус меньшего угла при основании и допустимые
значения к.
3.160. Гипотенуза прямоугольного треугольника делится точкой ка-
сания вписанного круга на отрезки, отношение которых равно к. Найти
углы треугольника.
3.161. Найти косинус острого угла ромба, если прямая, проведенная
через его вершину, делит угол в отношении 1:3, а противолежащую
сторону — в отношении 3:5.
3.162. В остроугольном равнобедренном треугольнике радиус впи-
санной окружности в 4 раза меньше радиуса описанной окружности.
Найти углы треугольника.
3.163. Площадь равнобедренного тупоугольного треугольника рав-
на 8, а медиана, проведенная к его боковой стороне, равна >/з7. Найти
косинус угла при вершине.
3.164. Луч, проведенный из вершины равностороннего треугольни-
ка, делит его основание в отношении т.п. Найти тупой угол между
лучом и основанием.
3.165. Через вершину равностороннего треугольника проведена пря-
мая, делящая основание в отношении 2:1. Под какими углами она
наклонена к боковым сторонам треугольника?
3.166. Найти косинусы углов равнобедренного треугольника, у кото-
рого точка пересечения высот делит пополам высоту, проведенную
к основанию.
3.167. Найти косинусы острых углов прямоугольного треугольника,
зная, что произведение тангенсов половин этих углов равно 1/6.
3.168. Показать, что если в треугольнике отношение суммы синусов
двух углов к сумме их косинусов равно синусу третьего угла, то тре-
угольник прямоугольный.
3.169. Сторона треугольника равна 15, сумма двух других сторон
равна 27. Найти косинус угла, противолежащего данной стороне, если
радиус вписанной в треугольник окружности равен 4.
3.170. Основание треугольника равно 4, а его медиана равна
s/b — yjl. Один из углов при основании равен 15°. Показать, что острый
угол между основанием треугольника и его медианой равен 45°.
3.171. Угол при вершине А трапеции ABCD равен а. Боковая сторо-
на АВ вдвое больше меньшего основания ВС. Найти угол ВАС.
3.172. В квадрат ABCD вписан равнобедренный треугольник AEF;
точка Е лежит на стороне ВС, точка F— на стороне CD и AE—EF.
Тангенс ут ла AEF равен 2. Найти тангенс угла FEC.
3.173. Отношение площади прямоугольника ABCD (BC\\AD) к квад-
рату его диагонали равно к. Найти угол EAF, где EuF — соответствен-
но середины сторон ВС и CD.
3.174. Отношение боковых сторон трапеции равно отношению ее
периметра к дайне вписанной окружности и равно к. Найти углы трапе-
ции и допустимые значения к.
3.175. В прямоугольном треугольнике найти угол между медианой
и биссектрисой, проведенными из вершины острого угла, равного а.
3.176. Тангенс острого угла между медианами прямоугольного тре-
угольника, проведенными к его катетам, равен к. Найти углы треуголь-
ника и допустимые значения к.
3.177. Найти синус угла ромба, если из середины его стороны проти-
воположная сторона видна под углом а.
3.178. Сторона треугольника равна а, разность углов, прилежащих
71
к данной стороне, равна я/2. Найти углы треугольника, если его пло-
щадь равна S.
3.179. Найти синус угла при вершине равнобедренного треуголь-
ника, зная, что периметр любого вписанного в него прямоугольника, две
вершины которого лежат на основании, имеет постоянную величину.
3.180. Даны две стороны а и b треугольника и биссектриса I угла
между ними. Найти этот угол.
3.181. Доказать, что если биссектриса одного из углов треугольника
равна произведению заключающих его сторон, деленному на их сумму,
то этот угол равен 120°.
3.182. В сектор радиуса R вписана окружность радиуса г. Найти
периметр сектора.
3.183. Основание треугольника равно а, а углы при основании равны
а и fi радианам. Из противоположной вершины треугольника радиусом,
равным его высоте, проведена окружность. Найти длину дуги этой
окружности, заключенной внутри треугольника.
3.184. Найти отношение площади сектора с данным центральным
углом а радианов к площади вписанного в него круга.
3.185. Меньшая дуга окружности, стягиваемая хордой АВ, содержит
а0. Через середину С хорды АВ проведена хорда DE так, что
DC: СЕ= 1:3. Найти острый угол ACD и допустимые значения а.
3.186. Периметр сектора равен /. Найти расстояние от вершины
центрального угла сектора до центра окружности, вписанной в этот
сектор, если радиус дуги сектора равен R.
3.187. Дуга АВ сектора АОВ содержит а радианов. Через точку
В и середину С радиуса О А проведена прямая. В каком отношении она
делит площадь сектора?
3.188. Радиус дуги сектора равен R, центральный угол АОВ равен
а. Через середину С радиуса ОА проведена прямая, параллельная
радиусу ОВ и пересекающая дугу АВ в точке D. Найти площадь
треугольника OCD.
3.189. Радиус дуги сектора АОВ равен R, центральный угол АОВ
равен а. В этот сектор вписан правильный треугольник так, что одна его
вершина совпадает с серединой дуги АВ, а две другие вершины лежат
соответственно на радиусах О А и ОВ. Найти стороны треугольника.
3.190. В ромб вписана окружность. В образовавшийся криволиней-
ный треугольник (с острым углом) снова вписана окружность. Найти ее
радиус, если высота ромба равна h, а острый угол равен а.
3.191. Высота равнобедренного треугольника равна h и составляет
с боковой стороной угол а(а<л/6). Найти расстояние между центрами
вписанной в треугольник и описанной около него окружностей.
3.192. В равнобедренном треугольнике угол при основании равен а.
Высота, опущенная на основание, больше радиуса вписанного круга на
т. Найти радиус описаннного круга.
3.193. Около круга радиуса г описана равнобедренная трапеция.
Боковая сторона трапеции составляет с меньшим основанием угол а.
Найти радиус круга, описанного около трапеции.
3.194. В круг вписана трапеция. Большее основание трапеции-состав-
ляет с боковой стороной угол а, а с диагональю — угол 0. Найти
отношение площади круга к площади трапеции.
3.195. В равнобедренный треугольник с основанием а и углом а при
основании вписана окружность. Найти радиус окружности, касающейся
вписанной окружности и боковых сторон треугольника.
3.196. В равнобедренном остроугольном треугольнике угол при ос-
72
новаиии равен а, а площадь равна S. Найти площадь треугольника,
вершинами которого служат основания высот данного треугольника.
3.197. Пусть а, Ь, с — длины сторон остроугольного треугольника;
А, В, С — углы, противолежащие сторонам; Ра, Ръ, Ре — расстояния
от центра описанной окружности до соответствующих сторон. В пред-
положении, что А<В<С, расположить Ра, Рь, Ре в возрастающем
порядке.
3.198. Известно, что в треугольнике АВС АВ “а, LC—ct. Найти
радиус окружности, проведенной через вершины А, В и центр окружно-
сти, вписанной в треугольник АВС.
3.199. Пусть ОА — неподвижный радиус окружности с центром
в точке О; В — середина радиуса О А; М — произвольная точка окру-
жности. Найти наибольшее значение угла ОМВ.
3.200. Найти боковую поверхность и объем прямого параллелепипе-
да, если его высота равна h, диагонали составляют с основанием углы
а и /?, а основанием служит ромб.
3.201. Найти объем правильной четырехугольной призмы, если угол
между диагональю призмы и боковой гранью равен а, а сторона основа-
ния равна а.
3.202. Одна из сторон основания прямой треугольной призмы равна
а, а прилежащие к ней углы равны а и fi. Найти боковую поверхность
призмы, если ее объем равен V.
3.203. Основанием прямой призмы служит равнобедренный тре-
угольник, основание которого равно а, а угол при основании равен а.
Найти объем призмы, если ее боковая поверхность равна сумме площа-
дей оснований.
3.204. В основании прямой призмы лежит равнобедренный тре-
угольник с боковой стороной а и углом а между боковыми сторонами.
Диагональ боковой грани, противолежащей данному углу, составляет со
смежной боковой гранью угол <р. Найти объем призмы.
3.205. Диагональ прямоугольного параллелепипеда равна I и состав-
ляет с двумя смежными гранями углы а и fi. Найти объем парал-
лелепипеда.
3.206. Основанием призмы служит правильный треугольник со сто-
роной а. Боковое ребро равно Ъ и составляет с пересекающими его
сторонами основания углы, каждый из которых равен а. Найти объем
призмы и допустимые значения а.
3.207. В правильной треугольной призме сторона основания равна а,
угол между непересекающимися диагоналями двух боковых граней ра-
вен а. Найти высоту призмы.
3.208. В основании прямой призмы лежит треугольник. Два его угла
равны а и Д, а площадь равна S. Прямая, проходящая через вершину
верхнего основания и центр круга, описанного около нижнего основания,
составляет с плоскостью основания угол <р. Найти объем призмы.
3.209. В основании прямой призмы ABCA1BlC1 ле-
жит равнобедренный треугольник АВС с углом а между равными сторо-
нами АВ и АС. Отрезок прямой, соединяющий вершину А1 верхнего
основания с центром круга, описанного около нижнего основания, равен
I и составляет с плоскостью основания угол fi. Найти объем призмы.
3.210. В основании прямой призмы ABCAlBlC1 (АА1 ЦЛВ1ЦСС1) ле-
жит равнобедренный треугольник, у которого АВ—ВС = а и САВС=а.
Высота призмы равна Н. Найти расстояние от точки А до плоскости,
проведенной через точки В, С и А1.
3.211. Основанием прямой призмы АВСА1В1С1 (ААг ЦОС]) слу-
73
жит равнобедренный треугольник АВС (АВ=АС), у которого периметр
равен 2р, а угол при вершине А равен а. Через сторону ВС и вершину А.
проведена плоскость, составляющая с плоскостью основания угол р.
Найти объем призмы. , . .
3.212. Основанием наклонной призмы служит равнобедренная тра-
пеция, у которой боковая сторона и меньшее основание равны а, а ост-
рый угол равен Д. Одна из вершин верхнего основания призмы равноуда-
лена от всех вершин нижнего основания. Найти объем призмы, если
боковое ребро составляет с плоскостью основания угол а.
3.213. Основанием наклонной призмы ABCA^^i (AdJl-BBJICQ)
служит равнобедренный треугольник, у которого АВ=АС=аи L. САВ—
= а. Вершина Вг верхнего основания равноудалена от всех сторон ниж-
него основания, а ребро BtB составляет с плоскостью основания угол р.
Найти объем призмы.
3.214. Основанием наклонной призмы служит прямоугольник со
сторонами а и Ъ. Две смежные боковые грани составляют с плоскостью
основания углы а и р. Найти объем призмы, если боковое ребро равно с.
3.215. Основанием прямой призмы служит треугольник со стороной
а и прилежащими к ней углами а и р. Через эту сторону основания под
углом <р к нему проведена плоскость, пересекающая противоположное
боковое ребро. Найти объем полученной треугольной пирамиды.
3.216. Площадь боковой грани правильной двенадцатиугольной пи-
рамиды равна S. Плоский угол при вершине равен а. Найти объем
пирамиды.
3.217. Основанием пирамиды служит равнобедренная трапеция,
у которой боковая сторона равна а, а острый угол равен а. Все боковые
грани образуют с основанием пирамиды один и тот же угол fl. Найти
полную поверхность пирамиды.
3.218. Основанием пирамиды служит равнобедренная трапеция,
у которой острый угол равен а, а площадь равна 5. Все боковые грани
составляют с плоскостью основания один и тот же угол fl. Найти объем
пирамиды.
3.219. Основанием пирамиды служит прямоугольник. Каждое из
боковых ребер равно / и составляет с прилежащими сторонами основа-
ния углы а и р. Найти объем пирамиды.
3.220. В основании треугольной пирамиды лежит равнобедренный
треугольник, у которого площадь равна S и угол при вершине равен а.
Найти объем пирамиды, если угол между каждым боковым ребром
и высотой пирамиды равен fl.
3.221. Сторона основания правильной четырехугольной пирамиды
равна а. Угол между смежными боковыми гранями равен а. Найти
боковую поверхность пирамиды.
3.222. Основанием пирамиды служит прямоугольный треугольник,
у которого радиус вписанной окружности равен г, а острый угол равен а.
Все боковые ребра пирамиды составляют с плоскостью основания один
и тот же угол fl. Найти объем пирамиды.
3.223. Основанием пирамиды служит прямоугольный треугольник,
у которого гипотенуза равна с, а меньший из острых углов равен а.
Наибольшее боковое ребро составляет с плоскостью основания угол р.
Найти объем пирамиды, если ее высота проходит через точку пересече-
ния медиан основания.
3.224. Из основания высоты правильной треугольной пирамиды на
боковое ребро опущен перпендикуляр, равный р. Найти объем пирами-
ды, если двугранный угол между ее боковыми гранями равен а.
3.225. Из основания высоты правильной треугольной пирамиды на
74
боковое ребро опущен перпендикуляр, равный р. Найти объем пирами-
ды, если двугранный угол между боковой гранью и основанием пирами-
ды равен а.
3.226. Из основания высоты правильной треугольной пирамиды на
боковую грань опущен перпендикуляр, равный d. Найти объем пирами-
ды, если угол наклона бокового ребра к плоскости основания равен а.
3.227. В правильной треугольной пирамиде двугранный угол при
основании равен а, а боковая поверхность равна 5. Найти расстояние от
центра основания до боковой грани.
3.228. Двугранный угол при основании правильной треугольной пи-
рамиды равен а, боковая поверхность пирамиды равна S. Найти рассто-
яние от центра основания до середины апофемы боковой грани.
3.229. Сторона основания правильной четырехугольной пирамиды
равна а, плоский угол при вершине пирамиды равен а. Найти расстояние
от центра основания пирамиды до ее бокового ребра.
3.230. Основанием пирамиды служит ромб со стороной а и острым
углом а. Две боковые грани перпендикулярны основанию, а две другие
наклонены к нему под углом <р. Найги объем и боковую поверхность
пирамиды.
3.231. Основанием пирамиды служит прямоугольник. Две боковые
грани перпендикулярны плоскости основания, две другие составляют
с ней углы а и р. Найти боковую поверхность пирамиды, если высота
пирамиды равна Н.
3.232. Одно боковое ребро треугольной пирамиды перпендикулярно
плоскости основания и равно /, два других образуют между собой угол а,
а с плоскостью основания — один и тот же угол Д. Найти объем
пирамиды.
3.233. Основанием пирамиды служит ромб со стороной а. Две боко-
вые грани пирамиды перпендикулярны плоскости основания и образуют
между собой угол р. Две другие боковые грани составляют с плоскостью
основания угол а. Найти боковую поверхность пирамиды.
3.234. Плоский угол при вершине правильной и-угольной пирамиды
равен а. Отрезок прямой, соединяющий центр основания пирамиды с се-
рединой бокового ребра, равен а. Найти полную поверхность пирамиды.
3.235. Основанием пирамиды служит равнобедренный остроуголь-
ный треугольник, у которого основание равно а, а противолежащий угол
равен а. Боковое ребро пирамиды, проходящее через вершину данного
угла, составляет с плоскостью основания угол Д. Найти объем пирами-
ды, если высота пирамиды проходит через точку пересечения высот
основания.
3.236. В прямоугольном треугольнике с острым углом а через на-
именьшую медиану проведена плоскость, составляющая с плоскостью
треугольника угол р. Найти углы между этой плоскостью и катетами
треугольника.
3.237. Через сторону ромба проведена плоскость, образующая с диа-
гоналями углы а и 2а. Найти острый угол ромба.
3.238. В прямоугольном треугольнике через его гипотенузу проведе-
на плоскость, составляющая с плоскостью треугольника угол а, а с од-
ним из катетов — угол Р- Найти угол между этой плоскостью и вторым
катетом.
3.239. Основанием прямой призмы служит прямоугольный тре-
угольник, у которого один из острых углов равен а. Наибольшая по
площади боковая грань призмы — квадрат. Найти угол между пересека-
ющимися диагоналями двух других боковых граней.
75
3.240. Найти плоский угол при вершине правильной четырехуголь-
ной пирамиды, если он равен углу между боковым ребром и плоскостью
основания пирамиды.
3.241. Сторона основания правильной четырехугольной призмы рав-
на а, ее объем равен V. Найти косинус угла между диагоналями двух
смежных боковых граней.
3.242. Основанием пирамиды служит равнобедренный треугольник,
у которого острый угол между равными сторонами равен а. Все боковые
ребра составляют с плоскостью основания один и тот же угол fi. Через
сторону основания, противолежащую данному углу а, и середину высо-
ты пирамиды проведена плоскость. Найти угол между этой плоскостью
и плоскостью основания.
3.243. Ребра прямоугольного параллелепипеда относятся как
3:4:12. Через большее ребро проведено диагональное сечение. Найти
синус угла между плоскостью этого сечения и не лежащей в ней диагона-
лью параллелепипеда.
3.244. Отношение площади диагонального сечения правильной че-
тырехугольной пирамиды к площади ее основания равно к. Найти
косинус плоского угла при вершине пирамиды.
3.245. Боковая грань правильной треугольной пирамиды составляет
с плоскостью основания угол, тангенс которого равен к. Найти тангенс
угла между боковым ребром и апофемой противолежащей грани.
3.246. Основанием пирамиды служит равнобедренный треугольник,
у которого площадь равна S, а угол между боковыми сторонами равен а.
Все боковые ребра пирамиды составляют с плоскостью основания один
и тот же угол. Найти этот угол, если объем пирамиды равен V.
3.247. Основанием призмы служит прямоугольник. Боковое ребро
составляет равные углы со сторонами основания и наклонено к плоско-
сти основания под углом а. Найти угол между боковым ребром и сторо-
ной основания.
3.248. Диагонали АВ1 и СВ1 двух смежных боковых граней прямо-
угольного параллелепипеда ABCDA1BtClDi составляют с диагональю
АС основания ABCD углы, равные соответственно а и fi. Найти угол
между плоскостью треугольника АВ1С и плоскостью основания.
3.249. В правильной треугольной пирамиде сумма углов, образован-
ных апофемой пирамиды с плоскостью основания и боковым ребром
с той же плоскостью, равна я/4. Найти эти углы.
3.250. Все боковые грани пирамиды образуют с плоскостью основа-
ния один и тот же угол. Найти этот угол, если отношение полной
поверхности пирамиды к площади основания равен к. При каких значе-
ниях к задача имеет решение?
3.251. Косинус угла между боковыми ребрами правильной четырех-
угольной пирамиды, не лежащими в одной грани, равен к. Найти
косинус плоского угла при вершине пирамиды.
3.252. Отношение полной поверхности правильной n-угольной пира-
миды к площади основания равно I. Найти угол между боковым ребром
и плоскостью основания.
3.253. Найти угол между апофемой правильной треугольной пира-
миды и плоскостью ее основания, если разность между этим углом
и углом, который составляет боковое ребро пирамиды с плоскостью
основания, равна а.
3.254. Боковая поверхность треугольной пирамиды равна S, а каж-
дое из боковых ребер равно I. Найти плоские углы при вершине, зная,
что они образуют арифметическую прогрессию с разностью я/3.
76
3.255. Основанием пирамиды служит прямоугольный треугольник,
у которого один из острых углов равен а. Все боковые ребра одинаково
наклонены к плоскости основания. Найти двугранные углы при основа-
нии, если высота пирамиды равна гипотенузе треугольника, лежащего
в ее основании.
3.256. Основанием пирамиды SABC служит равносторонний тре-
угольник АВС. Ребро SA перпендикулярно плоскости основания. Найти
угол между боковой гранью SBC и плоскостью основания, если боковая
поверхность пирамиды относится к площади основания как 11:4.
3.257. Величина угла между боковым ребром правильной четыреху-
гольной пирамиды и плоскостью основания равна величине плоского
угла при вершине пирамиды. Найти угол между боковой гранью и плос-
костью основания.
3.258. Расстояние от стороны основания правильной треугольной
пирамиды до непересекающего ее ребра в 2 раза меньше стороны
основания. Найти угол между боковой гранью и плоскостью основания
пирамиды.
3.259. Боковые грани правильной треугольной призмы — квадраты.
Найти угол между диагональю боковой грани и не пересекающей ее
стороной основания призмы.
3.260. Боковая грань правильной треугольной пирамиды SABC со-
ставляет с плоскостью основания угол а. Через сторону ВС основания
и точку D на боковом ребре AS проведена плоскость. Найти угол между
этой плоскостью и плоскостью основания, если AD:DS=k.
3.261. Сторона основания правильной четырехугольной пирамиды
равна а, ее боковая поверхность равна 5. Найти угол между смежными
боковыми гранями.
3.262. Отрезок прямой, соединяющий центр основания правильной
треугольной пирамиды с серединой бокового ребра, равен стороне ос-
нования. Найти косинус угла между смежными боковыми гранями.
3.263. Линейный угол двугранного угла, составленного двумя смеж-
ными боковыми гранями правильной четырехугольной пирамиды,
в 2 раза больше плоского угла при вершине пирамиды. Найти плоский
угол при вершине пирамиды.
3.264. Основанием пирамиды является прямоугольник ABCD
(ЛВЦСР). Боковое ребро О А перпендикулярно основанию. Ребра ОВ
и ОС составляют с основанием углы, соответственно равные а и
Найти угол между ребром OD и основанием.
3.265. Основанием пирамиды служит правильный треугольник. Две
боковые грани перпендикулярны плоскости основания. Сумма двух не-
равных между собой плоских углов при вершине равна я/2. Найти эти
углы.
3.266. Через диагональ основания и высоту правильной четыреху-
гольной пирамиды проведена плоскость. Отношение площади сечения
к боковой поверхности пирамиды равно к. Найти косинус угла между
апофемами противоположных боковых граней и допустимые значения к.
3.267. В правильной треугольной пирамиде через боковое ребро
и высоту проведена плоскость. Отношение площади сечения к полной
поверхности пирамиды равно к. Найти двугранный угол при основании
и допустимые значения к.
3.268. Косинус угла между двумя смежными боковыми гранями
правильной четырехугольной пирамиды равен к. Найти косинус
угла между боковой гранью н плоскостью основания и допустимые
значения к.
77
3.269. Острый угол ромба, лежащего в основании четырехугольной
пирамиды, равен а. Отношение полной поверхности пирамиды к квад-
рату стороны основания равно к. Найти синус угла между апофемой
и высотой пирамиды, если все ее боковые грани одинаково наклонены
к плоскости основания. Каковы допустимые значения А?
3.270. Найти косинус угла между иепересекающимися диагоналями
двух смежных боковых граней правильной треугольной призмы, у кото-
рой боковое ребро равно стороне основания.
3.271. Боковое ребро правильной треугольной пирамиды в 2 раза
больше стороны основания. Найти угол между апофемой пирамиды
и не пересекающей ее высотой треугольника, лежащего в основании
пирамиды.
3.272. Через вершину квадрата, лежащего в основании правильной
призмы, проведена плоскость параллельно противолежащей диагонали
квадрата под углом а к плоскости основания. Найти углы многоуголь-
ника в сечении призмы этой плоскостью (предполагается, что высота
призмы достаточно велика для того, чтобы этим сечением оказался
четырехугольник).
3.273. Основанием прямой призмы служит равносторонний тре-
угольник. Через одну из его сторон проведена плоскость, отсекающая от
призмы пирамиду, объем которой равен V. Найти площадь сечения, если
угол между секущей плоскостью и плоскостью основания равен а.
3.274. Через вершину правильной треугольной пирамиды и середи-
ны двух сторон основания проведено сечение. Найти площадь сечения
и объем пирамиды, если известны сторона а основания и угол а. между
сечением и основанием.
3.275. В основании пирамиды лежит ромб, один из углов которого
равен а. Боковые грани одинаково наклонены к плоскости основания.
Через середины двух смежных сторон основания и вершину пирамиды
проведена плоскость, составляющая с плоскостью основания угол Д.
Площадь полученного сечения равна S. Найти сторону ромба.
3.276. Основанием пирамиды служит ромб с острым углом а. Все
боковые грани составляют с плоскостью основания один и тот же угол fi.
Площадь сечения, проведенного через большую диагональ основания
и вершину пирамиды, равна S. Найти объем пирамиды.
3.277. Основанием пирамиды служит равнобедренный остроуголь-
ный треугольник, у которого боковая сторона равна Ь, а угол при
основании равен а. Все боковые ребра пирамиды составляют с плоско-
стью основания один и тот же угол р. Найти площадь сечения пирамиды
плоскостью, проходящей через вершину данного угла а, и высоту пира-
миды.
3.278. Сторона основания правильной треугольной пирамиды равна
а, двугранный угол при основании равен а. Пирамида пересечена плоско-
стью, параллельной основанию. Площадь сечения равна боковой повер-
хности образовавшейся усеченной пирамиды. Найти расстояние от секу-
щей плоскости до основания пирамиды.
3.279. В правильной четырехугольной пирамиде проведено сечение,
параллельное основанию. Прямая, проходящая через вершину основа-
ния и противолежащую (т. е. не принадлежащую той же грани) вершину
сечения составляет с плоскостью основания угол а. Найти площадь
сечения, если боковое ребро пирамиды равно диагонали основания
и равно а.
3.280. Высота правильной треугольной пирамиды равна Я. Боковая
грань составляет с плоскостью основания угол а. Через сторону основа-
78
ния и середину противолежащего бокового ребра проведена плоскость.
Найти площадь полученного сечения.
3.281. Найти объем и боковую поверхность правильной треугольной
пирамиды, если плоскость, проходящая через Чггорону основания а и се-
редину ее высоты, наклонена к основанию под углом <р.
3.282. Боковое ребро правильной четырехугольной пирамиды со-
ставляет с плоскостью основания угол а. Через вершину основания
и середину противолежащего бокового ребра проведена плоскость па-
раллельно одной из диагоналей основания. Найти угол между этой
плоскостью и плоскостью основания пирамиды.
3.283. Сторона основания правильной четырехугольной пирамиды
равна а, угол между боковым ребром и плоскостью основания равен
а (а>я/4). Найти площадь сечения пирамиды плоскостью, проходящей
через вершину основания перпендикулярно противоположному боково-
му ребру (т. е. ребру, не лежащему с этой вершиной в одной боковой
грани).
3.284. Высота правильной четырехугольной пирамиды образует
с боковым ребром угол а. Через вершину пирамиды параллельно диаго-
нали основания проведена плоскость, составляющая угол Д со второй
диагональю. Площадь полученного сечения равна S. Найти высоту
пирамиды.
3.285. Высота правильной треугольной пирамиды равна Н и состав-
ляет с боковым ребром угол а. Через сторону основания проведена
плоскость, пересекающая противоположное боковое ребро под углом
fi (/?<л/2—а). Найти объем той части пирамиды, которая заключена
между этой плоскостью и плоскостью основания.
3.286. В правильной треугольной призме плоскость, проведенная
через центр основания и центры симметрии двух боковых граней, состав-
ляет с плоскостью основания острый угол а. Найти площадь сечения,
образованного этой плоскостью, если сторона основания равна а.
3.287. В прямой призме ABCA^B^i (АА, ||ВВ1 ||CCj) стороны ос-
нования АВ и ВС равны соответственно а и Ь, а угол между ними равен
а. Через биссектрису данного угла и вершину А^ проведена плоскость,
составляющая с плоскостью основания острый угол Д. Найти площадь
сечения.
3.288. В правильной треугольной пирамиде с углом а между боко-
вым ребром и стороной основания проведено сечение через середину
бокового ребра параллельно боковой грани. Зная площадь 5 этого
сечения, найти объем пирамиды. Каковы возможные значения а?
3.289. Отрезок прямой, соединяющий точку окружности верхнего
основания цилиндра с точкой окружности нижнего основания, равен
/ и составляет с плоскостью основания угол а. Найти расстояние от этой
прямой до оси цилиндра, если осевое сечение цилиндра есть квадрат.
Каковы возможные значения а?
3.290. Две вершины равностороннего треугольника со стороной
а лежат на окружности верхнего основания цилиндра, а третья вер-
шина — на окружное™ нижнего основания. Плоскость треугольника
составляет с образующей цилиндра угол а. Найти боковую поверхность
цилиндра.
3.291. Точка А лежит на окружности верхнего основания цилиндра,
точка В — на окружности нижнего основания. Прямая АВ составляет
с плоскостью основания угол а, а с плоскостью осевого сечения, прове-
денного через точку В,— угол Д. Найти объем цилиндра, если длина
отрезка АВ равна I.
79
3.292. Два конуса имеют концентрические основания и один и тот же
угол, равный а, между высотой и образующей. Радиус основания вне-
шнего конуса равен А. Боковая поверхность внутреннего конуса в 2 раза
меньше полной поверхности внешнего конуса. Найти объем внутреннего
конуса.
3.293. В основании прямой призмы Я Л СЛ, 5; С, ЦСС,) ле-
жит прямоугольный треугольник ЛВС, у которого больший катет АС
равен а, а противолежащий ему угол В равен а. Гипотенуза АВ является
диаметром основания конуса, вершина которого лежит на ребре Л,С,.
Найти высоту конуса, если ЛЛ, = а/2.
3.294. Угол между высотой и образующей конуса равен а. Через
вершину конуса проведена плоскость, составляющая угол Д с высотой
(/?<а). В каком отношении эта плоскость делит окружность основания?
3.295. Высота конуса равна Н, угол между образующей и плоско-
стью основания равен а. Полная поверхность этого конуса делится
пополам плоскостью, перпендикулярной его высоте. Найти расстояние
от этой плоскости до основания конуса.
3.296. Два конуса имеют общую высоту; их вершины лежат на
противоположных концах этой высоты. Образующая одного конуса
равна I и составляет с высотой угол а. Образующая другого конуса
составляет с высотой угол Д. Найти объем общей части обоих конусов.
3.297. Найти угол между образующей конуса и плоскостью основа-
ния, если боковая поверхность конуса равна сумме площадей основания
и осевого сечения.
3.298. В усеченном конусе диагонали осевого сечения взаимно пер-
пендикулярны и длина каждой из них равна а. Угол между образующей
и плоскостью основания равен а. Найти полную поверхность усеченного
конуса.
3.299. Через две образующие конуса, угол между которыми равен а,
проведена плоскость. Площадь сечения относится к полной поверхности
конуса как 2: я. Найти угол между образующей и высотой конуса.
3300. Высота конуса составляет с образующей угол а. Через вер-
шину конуса проведена плоскость под углом Д (/?>я/2—а) к плоскости
основания. Найти площадь сечения, если высота конуса равна h.
3301. Через вершину конуса проведена плоскость, делящая окру-
жность основания в отношении р: q. Эта плоскость отстоит от центра
основания конуса на расстояние а и составляет с высотой конуса угол а.
Найти объем конуса.
3302. Отношение полной поверхности конуса к площади его осевого
сечения равно к. Найти угол между высотой и образующей конуса
и допустимые значения к.
3303. Катет прямоугольного треугольника равен а, противолежа-
щий ему угол равен а. Этот треугольник вращается вокруг прямой,
лежащей в плоскости треугольника, проходящей через вершину данного
угла и перпендикулярной его биссектрисе. Найти объем тела вращения.
3304. Тупоугольный равнобедренный треугольник вращается вок-
руг прямой, проходящей через точку пересечения его высот параллельно
большей стороне. Найти объем тела вращения, если тупой угол равен а,
а противолежащая ему сторона треугольника равна а.
3305. Найти углы прямоугольного треугольника, если объем тела,
полученного от вращения треугольника вокруг меньшего катета, равен
сумме объемов тел, полученных от вращения треугольника вокруг его
гипотенузы и вокруг большего катета.
3306. Гипотенуза прямоугольного треугольника равна с, его острый
80
угол равен а. Треугольник вращается вокруг биссектрисы внешнего
прямого угла. Найти объем тела вращения.
3307. На отрезке АВ, равном 2R, построена как на диаметре полуок-
ружность и проведена хорда CD параллельно АВ. Найти объем тела,
образованного вращением треугольника ACD вокруг диаметра АВ, если
вписанный угол, опирающийся на дугу АС, равен a (AC<AD).
3308. Большее основание равнобедренной трапеции равно а, острый
угол равен а. Диагональ трапеции перпендикулярна ее боковой стороне.
Трапеция вращается вокруг ее большего основания. Найти объем тела
вращения.
3.309. Сторона правильного треугольника равна а. Треугольник вра-
щается вокруг прямой, лежащей в плоскости «треугольника вне его,
проходящей через вершину треугольника и составляющей со стороной
угол а. Найти объем тела вращения и выяснить, при каком значении
а этот объем является наибольшим.
3310. Плоская ломаная линия состоит из п равных отрезков, соеди-
ненных в виде зигзага под углом а друг к другу. Длина каждого отрезка
ломаной равна а. Эта линия вращается вокруг прямой, проходящей
через один из ее концов параллельно биссектрисе угла а. Найти площадь
поверхности вращения.
3.311. В треугольнике АВС угол А равен а, угол С равен fi и биссект-
риса BD равна I. Треугольник ABD вращается вокруг прямой BD. Найти
объем тела вращения.
3312. Боковая сторона равнобедренного треугольника равна а, угол
при основании равен а. Этот треугольник вращается вокруг прямой,
проходящей через вершину, противолежащую основанию, параллельно
биссектрисе угла а. Найти поверхность тела вращения.
3313. Перпендикуляр, опущенный из центра основания конуса на
образующую, вращается около оси конуса. Найти угол между его об-
разующей и осью, если поверхность вращения делит объем конуса
пополам.
3314. Площадь сегмента равна S, а дуга сегмента равна а радианам.
Этот сегмент вращается вокруг своей оси симметрии. Найти поверх-
ность тела вращения.
3315. При вращении кругового сектора около одного из крайних
радиусов получилось тело, площадь сферической поверхности которого
равна площади конической поверхности. Найти синус центрального угла
кругового сектора.
3316. Высота правильной треугольной усеченной пирамиды равна
Н и является средним пропорциональным между сторонами оснований.
Боковое ребро составляет с основанием угол а. Найти объем пирамиды.
3317. Боковая грань правильной четырехугольной усеченной пира-
миды составляет с плоскостью основания угол а. Плоскость, проведен-
ная через сторону нижнего основания и параллельную ей сторону верх-
него основания, образует с плоскостью основания угол р. Боковая
поверхность пирамиды равна 5. Найти стороны верхнего и нижнего
оснований.
3.318. Боковое ребро правильной четырехугольной усеченной пира-
миды равно стороне меньшего основания и равно а. Угол между боко-
вым ребром и стороной большего основания равен а. Найти площадь
диагонального сечения усеченной пирамиды.
3319. Сторона нижнего основания правильной четырехугольной
усеченной пирамиды равна а, сторона верхнего основания равна Ь.
Боковая грань составляет с плоскостью основания угол а. Через сторону
81
нижнего основания и середину отрезка, соединяющего центры основа-
ний, проведена плоскость, пересекающая противоположную боковую
грань по некоторой прямой. Найти расстояние от этой прямой до
нижнего основания.
3320. Стороны оснований правильной четырехугольной усеченной
пирамиды относятся как т:п (т>п). Высота пирамиды равна Н. Боко-
вое ребро составляет с плоскостью основания угол а. Найти боковую
поверхность пирамиды.
3321. Основаниями усеченной пирамиды служат правильные тре-
угольники. Прямая, проходящая через середину одной стороны верхнего
основания и середину параллельной ей стороны нижнего основания,
перпендикулярна плоскостям оснований. Большее боковое ребро равно
I и составляет с плоскостью основания угол а. Найти длину отрезка,
соединяющего центры верхнего и нижнего оснований.
3322. Две боковые грани усеченной треугольной пирамиды — рав-
ные прямоугольные трапеции с острым углом а и общей меньшей
боковой стороной. Двугранный угол между этими гранями равен Д
Найти угол между третьей боковой гранью и плоскостью основания.
3323. В правильную четырехугольную пирамиду вписан куб; вер-
шины его верхнего основания лежат на боковых ребрах, вершины нижне-
го основания — в плоскости основания пирамиды. Найти отношение
объема куба к объему пирамиды, если боковое ребро пирамиды состав-
ляет с плоскостью основания угол а.
3324. Сторона квадрата, лежащего в основании правильной четы-
рехугольной пирамиды, равна а. В пирамиду вписана правильная четы-
рехугольная призма; вершины верхнего основания лежат на боковых
ребрах, вершины нижнего основания — в плоскости основания пирами-
ды. Диагональ призмы составляет с плоскостью основания угол <р.
Найти объем призмы, если боковое ребро пирамиды составляет с плос-
костью основания угол а.
3325. Сторона основания правильной четырехугольной пирамиды
равна а, а боковое ребро составляет с плоскостью основания угол а.
В эту пирамиду вписан куб так, что четыре его вершины лежат на
апофемах пирамиды, четыре — на основании пирамиды. Найти ребро
куба.
3326. Основанием пирамиды служит квадрат со стороной а; две
боковые грани пирамиды перпендикулярны основанию, а большее боко-
вое ребро наклонено к плоскости основания под углом Д В пирамиду
вписан прямоугольный параллелепипед; одно его основание лежит
в плоскости основания пирамиды, а вершины другого основания — на
боковых ребрах пирамиды. Найти объем параллелепипеда, если его
диагональ составляет с плоскостью основания угол а.
3.327. Боковое ребро правильной четырехугольной усеченной пира-
миды составляет с плоскостью основания угол а. В пирамиду вписан
прямоугольный параллелепипед так, что его верхнее основание совпада-
ет с верхним основанием пирамиды, а нижнее основание лежит в плоско-
сти нижнего основания пирамиды. Найти отношение боковых поверх-
ностей пирамиды и параллелепипеда, если диагональ параллелепипеда
составляет с его основанием угол а.
3328. Основанием пирамиды служит равнобедренный треугольник
с углом а между боковыми сторонами. Пирамида помещена в некото-
рый цилиндр так, что ее основание оказалось вписанным в основание
этого цилиндра, а вершина совпала с серединой одной из образующих
цилиндра. Объем цилиндра равен V. Найти объем пирамиды.
я? ____;
3.329. Боковое ребро правильной треугольной пирамиды равно
а и составляет с плоскостью основания угол а. В эту пирамиду вписан
цилиндр с квадратным осевым сечением (основание цилиндра лежит
в плоскости основания пирамиды). Найти объем цилиндра.
3.330. В цилиндр вписан прямоугольный параллелепипед, диагональ
которого составляет с прилежащими к ней сторонами основания углы
а и fi. Найти отношение объема параллелепипеда к объему цилиндра.
3.331. Одна из граней треугольной призмы, вписанной в цилиндр,
проходит через ось цилиндра. Диагональ этой грани составляет с приле-
жащими к ней сторонами основания призмы углы а и fi. Найти объем
призмы, если высота цилиндра равна Н.
3.332. В конус вписан куб (одна из граней куба лежит в плоскости
основания конуса). Отношение высоты конуса к ребру куба равно к.
Найти угол между образующей и высотой конуса.
3.333. Угол между высотой и образующей конуса равен а. В конус
вписана правильная треугольная призма; нижнее основание призмы
лежит в плоскости основания конуса. Боковые грани призмы — квад-
раты. Найти отношение боковых поверхностей призмы и конуса.
3.334. В конус вписан цилиндр; нижнее основание цилиндра лежит
в плоскости основания конуса. Прямая, проходящая через центр верх-
него основания цилиндра и точку на окружности основания конуса,
составляет с плоскостью основания угол а. Найти отношение объемов
конуса и цилиндра, если угол между образующей и высотой конуса
равен Д.
3335. В конус вписан цилиндр, высота которого равна диаметру
основания конуса. Полная поверхность цилиндра равна площади ос-
нования конуса. Найти угол между образующей конуса и плоскостью его
основания.
3.336. В конус помещена пирамида; основание пирамиды вписано
в основание конуса, а вершина пирамиды лежит на одной из образу-
ющих конуса. Все боковые грани пирамиды одинаково наклонены
к плоскости основания. Основанием пирамиды служит равнобедренный
треугольник с углом а(а>я/3) при вершине. Найти отношение объемов
конуса и пирамиды.
3.337. Основанием пирамиды служит прямоугольный треугольник
с острым углом а. Этот треугольник вписан в основание конуса. Вер-
шина пирамиды совпадает с серединой одной из образующих конуса.
Найти отношение объема конуса к объему пирамиды.
3.338. Основанием пирамиды служит прямоугольный треугольник,
вписанный в основание конуса. Вершина пирамиды совпадает с верши-
ной конуса. Боковые грани пирамиды, содержащие катеты основания,
составляют с плоскостью основания углы а и Д. Найти отношение
объемов пирамиды и конуса.
3.339. Расстояние от середины высоты правильной четырехугольной
пирамиды до ее боковой грани равно d. Найти полную поверхность
вписанного в пирамиду конуса, если его образующая составляет с плос-
костью основания угол а.
3.340. Расстояние от вершины основания правильной треугольной
пирамиды до противоположной боковой грани равно /. Угол между
боковой гранью и плоскостью основания пирамиды равен а. Найти
полную поверхность конуса, вписанного в пирамиду.
3.341. Основанием пирамиды служит равнобедренный остроуголь-
ный треугольник, у которого боковая сторона равна а, а угол между
боковыми сторонами равен а. Боковая грань пирамиды, проходящая
83
через сторону основания, противолежащую данному углу а, составляет
с плоскостью основания угол fl. Найти объем конуса, описанного около
пирамиды, если все ее боковые ребра равны между собой.
3342. Отношение объема прямого параллелепипеда к объему впи-
санного в него шара равно к. Найти углы в основании параллелепипеда
и допустимые значения к.
3.343. Около шара описана прямая призма, основанием которой
служит ромб. Большая диагональ призмы составляет с плоскостью
основания угол а. Найти острый угол ромба.
3.344. Около шара описана прямая призма, основанием которой
служит ромб с острым углом а. Найти угол между большей диагональю
призмы и плоскостью основания.
3345. Основанием прямой призмы, описанной около шара радиуса
г, служит прямоугольный треугольник с острым углом а. Найти объем
призмы.
3.346. Центр шара, вписанного в правильную четырехугольную пи-
рамиду, делит высоту пирамиды в отношении т: п, считая от вершины
пирамиды. Найти угол между двумя смежными боковыми гранями.
3.347. Сторона основания правильной четырехугольной пирамиды
равна а; боковая грань составляет с плоскостью основания угол а. Найти
радиус описанного шара.
3.348. В правильную четырехугольную пирамиду вписан шар. Рас-
стояние от центра шара до вершины пирамиды равно а, а угол между
боковой гранью и плоскостью основания равен а. Найти полную поверх-
ность пирамиды.
3349. Плоский угол при вершине правильной четырехугольной пи-
рамиды равен а. Найти боковую поверхность пирамиды, если радиус
шара, вписанного в эту пирамиду, равен R.
3.350. Радиус шара, описанного около правильной треугольной пи-
рамиды, равен апофеме пирамиды. Найти угол между апофемой и плос-
костью основания пирамиды.
3351. Сторона основания правильной треугольной пирамиды равна
а, плоский угол при вершине пирамиды равен а. Найти радиус вписан-
ного в пирамиду шара.
3352. Радиус шара, вписанного в правильную треугольную пирами-
ду, в 4 раза меньше стороны основания пирамиды. Найти косинус
плоского угла при вершине пирамиды.
3353. В пирамиде, у которой все боковые грани одинаково наклоне-
ны к плоскости основания, через центр вписанного шара параллельно
основанию проведена плоскость. Отношение площади сечения пирами-
ды этой плоскостью к площади основания равно к. Найти двугранный
угол при основании пирамиды.
3354. Основанием пирамиды служит равнобедренный треугольник,
равные стороны которого имеют длину Ь; соответствующие им боковые
грани перпендикулярны плоскости основания и образуют между собой
угол а. Угол между третьей боковой гранью и плоскостью основания
также равен а. Найти радиус шара, вписанного в пирамиду.
3355. Основанием пирамиды служит ромб с острым углом а.. Найти
объем пирамиды, если ее боковые грани образуют с основанием один
и тот же двугранный угол fl и радиус вписанного в нее шара равен г.
3356. Основанием пирамиды служит ромб с острым углом а. Все
боковые грани составляют с плоскостью основания один и тот же угол fl.
Найти радиус шара, вписанного в пирамиду, если объем пирамиды
равен V.
84
3357. Отношение стороны основания правильной n-угольной пира-
миды к радиусу описанного шара равно к. Найти угол между боковым
ребром и плоскостью основания и допустимые значения к.
3.358. Около шара радиуса R описана правильная п-угольная пира-
мида, боковая грань которой составляет с плоскостью основания угол а.
Найти боковую поверхность пирамиды.
3359. Основанием пирамиды служит прямоугольник, у которого
угол между диагоналями равен а. Около этой пирамиды описан шар
радиуса R. Найти объем пирамиды, если все ее боковые ребра образуют
с основанием угол fi.
3.360. Основанием пирамиды служит прямоугольник, у которого
угол между диагоналями равен а. Одно из боковых ребер перпендикуля-
рно плоскости основания, а наибольшее боковое ребро составляет
с плоскостью основания угол Д Радиус шара, описанного около пирами-
ды, равен R. Найти объем пирамиды.
3.361. Боковые ребра и две стороны основания треугольной пирами-
ды имеют одну и ту же длину а, а угол между равными сторонами
основания равен а. Найти радиус описанного шара.
3.362. Две грани треугольной пирамиды — равные между собой
прямоугольные треугольники с общим катетом, равным I. Угол между
этими гранями равен а. Две другие грани пирамиды образуют двугран-
ный угол /?. Найти радиус шара, описанного около пирамиды.
3363. Боковая грань правильной треугольной усеченной пирамиды
составляет с плоскостью основания угол а. Найти отношение полной
поверхности пирамиды к поверхности вписанного в нее шара.
3364. Сторона основания правильной четырехугольной пирамиды
равна а, двугранный угол при основании равен а. В эту пирамиду вписан
шар. Найти объем пирамиды, вершинами которой служат точки касания
шаровой поверхности с боковыми гранями данной пирамиды и произ-
вольная точка, лежащая в плоскости основания данной пирамиды.
3.365. Объем правильной пирамиды равен V. Через центр вписан-
ного в пирамиду шара проведена плоскость, параллельная ее основа-
нию. Найти объем пирамиды, отсекаемой от данной пирамиды этой
плоскостью, если двугранный угол при основании равен а.
3.366. В шар радиуса R вписана правильная четырехугольная усечен-
ная пирамида, у которой большее основание проходит через центр шара,
а боковое ребро составляет с плоскостью основания угол а. Найти объем
усеченной пирамиды.
3367. Найти отношение объема правильной n-угольной пирамиды
к объему описанного шара, если угол между боковым ребром и плоско-
стью основания пирамиды равен а.
3.368. В конус помещен шар так, что их поверхности касаются.
Радиус шара равен R, а угол при вершине осевого сечения конуса равен
2а. Найти объем тела, ограниченного поверхностями шара и конуса.
3369. Отношение поверхности шара, вписанного в конус, к площади
основания конуса равно к. Найти косинус угла между образующей
конуса и плоскостью его основания и допустимые значения к.
3370. Отношение объема шара, вписанного в конус, к объему опи-
санного шара равно к. Найти угол между образующей конуса и плоско-
стью его основания и допустимые значения к.
3371. В шар, радиус которого равен R, вписан конус; в этот конус
вписан цилиндр с квадратным осевым сечением. Найти полную поверх-
ность цилиндра, если угол между образующей конуса и плоскостью его
основания равен а.
85
3372. В полушар вписано тело, состоящее из цилиндра и поставлен-
ного на него конуса. Нижнее основание цилиндра лежит в плоскости
большого круга полушара; верхнее основание цилиндра совпадает с ос-
нованием конуса и касается поверхности шара. Вершина конуса лежит на
поверхности шара. Образующая конуса составляет с плоскостью его
основания угол а. Найти отношение объема тела к объему полушара.
3373. В конус вписан шар. Радиус круга касания поверхности шара
и боковой поверхности конуса равен г. Прямая, проходящая через центр
шара и произвольную точку окружности основания конуса, составляет
с высотой конуса угол а.. Найти объем конуса.
3374. Отношение объема конуса к объему вписанного в него шара
равно к. Найти угол между образующей и плоскостью основания конуса
и допустимые значения к.
3.375. Высота конуса равна Н, угол между образующей и плоско-
стью основания равен а. В этот конус вписан шар. К окружности касания
шаровой и конической поверхностей проведена касательная прямая,
а через эту прямую проведена плоскость параллельно высоте конуса.
Найти площадь сечения шара этой плоскостью.
3376. В шар радиуса R вписаны два конуса с общим основанием;
вершины конусов совпадают с противоположными концами диаметра
шара. Шаровой сегмент, вмещающий меньший конус, имеет в осевом
сечении дугу, равную а0. Найти расстояние между центрами шаров,
вписанных в эти конусы.
3377. В конус вписан шар и к шару проведена касательная плос-
кость параллельно плоскости основания конуса. В каком отношении эта
плоскость делит боковую поверхность конуса, если угол между об-
разующей и плоскостью основания равен а?
3378. Образующая конуса равна I и составляет с высотой угол а.
Через две образующие конуса, угол между которыми равен fi, проведена
плоскость. Найти расстояние от этой плоскости до центра шара, вписан-
ного в конус.
3379. В конус вписан шар. Окружность касания шаровой и коничес-
кой поверхностей делит поверхность шара в отношении 1:4. Найти угол
между образующей конуса и плоскостью основания.
3.380. Образующая конуса равна I и составляет с плоскостью ос-
нования угол а. В этот конус вписан шар, а в шар вписана правильная
треугольная призма, у которой все ребра равны между собой. Найти
объем призмы.
3381. Радиус основания конуса равен R, угол между образующей
и плоскостью основания равен а. В этот конус вписан шар. Через точку
Р, лежащую на окружности касания шаровой и конической поверх-
ностей, проведена касательная прямая к этой окружности, а через эту
прямую проведена плоскость параллельно образующей конуса, проходя-
щей через точку, диаметрально противоположную точке Р. Найти пло-
щадь сечения шара этой плоскостью.
3382. Вершина конуса находится в центре шара, а основание конуса
касается поверхности шара. Полная поверхность конуса равна поверх-
ности шара. Найти угол между образующей и высотой конуса. .
3.383. Найти угол между образующей и основанием усеченного ко-
нуса, полная поверхность которого вдвое больше поверхности вписан-
ного в него шара.
3384. Образующая усеченного конуса, описанного около шара, рав-
на а, угол между образующей и плоскостью основания равен а. Найти
объем конуса, основанием которого служит круг касания шаровой пове-
86
рхности с боковой поверхностью усеченного конуса, а вершина совпада-
ет с центром большего основания усеченного конуса.
3385. В усеченный конус вписан шар. Сумма длин диаметров верх-
него и нижнего оснований конуса в 5 раз больше длины радиуса шара.
Найти угол между образующей конуса и плоскостью основания.
3386. В усеченный конус вписан шар, объем которого в 2 раза
меньше объема конуса. Найти угол между образующей конуса и плоско-
стью его основания. '
3.387. На шаровой поверхности радиуса R лежат все вершины рав-
нобедренной трапеции, у которой меньшее основание равно боковой
стороне, а острый угол равен а. Найти расстояние от центра шара до
плоскости трапеции, если большее основание трапеции равно радиусу
шара.
3388. Найти отношение объема шарового сегмента к объему всего
шара, если дуга в осевом сечении сегмента соответствует центральному
углу, равному а.
3389. В основание шарового сегмента вписан прямоугольный тре-
угольник, у которого площадь равна S, а острый угол равен а. Найти
высоту сегмента, если его дуге в осевом сечении соответствует централь-
ный угол, равный р.
3.390. В шаровой сектор радиуса R вписан шар. Найти радиус
окружности касания поверхностей шара и сектора, если центральный
угол в осевом сечении шарового сектора равен а.
Группа В
3391. Отношение радиуса окружности, вписанной в равнобедрен-
ный треугольник, к радиусу окружности, описанной около него, равно т.
Найти углы треугольника и допустимые значения т.
3.392. Углы треугольника равны А, В и С. Высота треугольника,
проходящая через вершину угла В, равна Н. На этой высоте как на
диаметре построена окружность. Точки пересечения окружности со сто-
ронами АВ и ВС треугольника соединены с концами высоты. Найти
площадь построенного четырехугольника.
3393. В остроугольном треугольнике ABC СА = а радианов
и LB=p радианов, АС=Ь. Через ортоцентр (точку пересечения высот)
и основания высот, опущенных на стороны АВ и ВС, проведена окру-
жность. Найти площадь общей части треугольника и круга.
3394. В остроугольном треугольнике АВС известны углы. Найти
отношение, в котором ортоцентр делит высоту, проведенную из верши-
ны угла А.
3.395. В треугольнике даны две стороны а и b (а>Ь) и площадь
5. Найти угол между высотой и медианой, проведенными к третьей
стороне.
3396. В равносторонний треугольник АВС вписан равносторонний
треугольник DEF', точка D лежит на стороне ВС, точка Е — на стороне
АС и точка F — на стороне АВ. Сторона АВ относится к стороне DF как
8:5. Найти синус угла DEC.
3397. В треугольнике АВС даны острые углы а и у (а>у) при
основании АС. Из вершины В проведены высота BD и биссектриса BE.
Найти площадь треугольника BDE, если площадь треугольника АВС
равна S.
3398. Расстояние между центрами двух внешне касающихся окру- >
87
жностей равно d. Угол между их общими внешними касательными равен
я радианам. Найти площадь криволинейного треугольника, ограничен-
ного отрезком одной касательной и двумя соответствующими дугами
окружностей.
3399. Тангенс угла между медианой и высотой, проведенными к бо-
ковой стороне равнобедренного треугольника, равен 1/2. Найти синус
угла при вершине,
3.400. В остроугольном треугольнике АВС проведены высоты AL
и CN. Найти радиус окружности, проходящей через точки В, Ln N, если
АС-а и LABC~b.
3.401. Стороны параллелограмма равны а и b (а<Ь). Меньшая
диагональ составляет с меньшей стороной тупой угол, а с большей
стороной — угол а. Найти большую диагональ параллелограмма.
3.402. В параллелограмме даны две стороны а и Ъ (а>Ь) и острый
угол я между диагоналями. Найти углы параллелограмма.
3.403. В параллелограмме даны две стороны а и b (а>Ь) и высота h,
проведенная к большей стороне. Найти острый угол между диагоналями
параллелограмма.
3.404. Стороны параллелограмма равны а и Ъ (а<Ь). Из середины
большей стороны параллельная сторона видна под углом я. Найти
площадь параллелограмма.
3.405. Отношение периметра параллелограмма к его большей диаго-
нали равно к. Найти углы параллелограмма, если известно, что большая
диагональ делит угол параллелограмма в отношении 1:2.
3.406. Длины четырех дуг, на которые разбита вся окружность ради-
уса R, составляют геометрическую прогрессию со знаменателем, рав-
ным 3. Точки деления служат вершинами четырехугольника, вписанного
в эту окружность. Найти его площадь.
3.407. Отношение радиуса круга, описанного около трапеции, к ра-
диусу круга, вписанного в нее, равно к. Найти углы трапеции и до-
пустимые значения к.
3.408. Показать, что отношение площади любого треугольника
к площади описанного около него круга меньше 2/3.
3.409. Для остроугольного треугольника образованы три числа, вы-
ражающие отношения длин его сторон к соответствующим расстояниям
от них центра описанной окружности. Доказать, что сумма этих чисел
в 4 раза меньше их произведения.
3.410. В сегмент с центральным углом а вписан правильный тре-
угольник так, что одна его вершина совпадает с серединой хорды
сегмента, а две другие лежат на дуге сегмента. Высота треугольника
равна й. Найти радиус дуги сегмента.
3.411. Прямая, перпендикулярная хорде сегмента, делит хорду в от-
ношении 1:4, а дугу — в отношении 1:2. Найти косинус центрального
угла, опирающегося на эту дугу.
3.412. В сектор POQ радиуса R с центральным углом а вписан
прямоугольник; две его вершины лежат на дуге сектора, две другие — на
радиусах ОР и OQ. Найти площадь прямоугольника, если острый угол
между его диагоналями равен fi.
3.413. В сегмент окружности радиуса R вписаны две равные окру-
жности, касающиеся друг друга, дуги сегмента и его хорды. Найти
радиусы этих окружностей, если центральный угол, опирающийся на
дугу сегмента, равен я(а<п).
3.414. Угол между плоскостями двух равных прямоугольных тре-
угольников АВС и ADC с общей гипотенузой АС равен я. Угол между
88
' равными катетами АВ и AD равен fl. Найти угол между катетами
ВС и CD.
3.415. Один из плоских углов трехгранного угла равен а. Двугран-
ные углы, прилежащие к этому плоскому углу, равны fl и у. Найти два
других плоских угла.
3.416. Даны три попарно взаимно перпендикулярных луча ОМ, ON
и ОР. На луче ОМ взята точка А на расстоянии О А, равном а; на лучах
ON и ОР взяты соответственно точки В и С так, что угол АВС равен а,
а угол АСВ равен Д. Найти ОВ и ОС.
3.417. Отношение двух отрезков, заключенных между параллель-
ными плоскостями, равно к, а углы, которые каждый из этих отрезков
составляет с одной из плоскостей, относятся как 2:3. Найти эти углы
и допустимые значения к.
3.418. Угол между плоскостью квадрата ABCD (Л-ВЦСЛ) и некото-
рой плоскостью Р равен а, а угол между стороной АВ и той же
плоскостью равен fl. Найти угол между стороной AD и плоскостью Р.
3.419. В основании прямой призмы лежит параллелограмм с острым
углом а. Диагонали призмы составляют с плоскостью основания углы
fl и у (fl<y). Найтн объем призмы, если ее высота равна Н.
3.420. Основанием призмы служит параллелограмм с острым углом
а. Боковое ребро, проходящее через вершину данного угла а, равно
b и составляет с прилежащими сторонами основания углы, каждый из
которых равен fl. Найти высоту призмы.
3.421. В основании прямой призмы лежит параллелограмм с острым
углом <р между диагоналями. Диагонали каждой из смежных боковых
граней пересекаются под углами а и fl (а> fl), обращенными к соответст-
вующим сторонам основания. Найти объем призмы, если ее высота
равна h.
3.422. Основанием наклонной призмы служит прямоугольный тре-
угольник с острым углом а. Боковая грань, содержащая гипотенузу,
перпендикулярна основанию, а боковая грань, содержащая катет, приле-
жащий к данному углу, составляет с основанием острый угол fl. Найти
острый угол между третьей боковой гранью и основанием .
3.423. В основании прямой призмы лежит равнобедренная трапеция,
диагонали которой перпендикулярны соответствующим боковым сторо-
нам. Угол между диагоналями трапеции, противолежащий ее боковой
стороне, равен а. Отрезок прямой, соединяющий вершину верхнего
основания с центром окружности, описанной около нижнего основания,
равен / и образует с плоскостью основания угол fl. Найти объем призмы.
3.424. Основанием призмы служит правильный треугольник со сто-
роной а. Боковое ребро равно о и составляет с пересекающими его
сторонами основания углы а н fl. Найтн объем призмы.
3.425. В основании прямого параллелепипеда лежит параллелог-
рамм с диагоналями а и Ь (а>Ь) и острым углом а между ними.
Меньшая диагональ параллелепипеда образует с большей диагональю
основания острый угол fl. Найти объем параллелепипеда.
3.426. Основание прямой призмы — ромб. Одна из диагоналей при-
змы равна а и составляет с плоскостью основания угол а, а с одной из
боковых граней — угол fl. Найти объем призмы.
3.427. В правильной четырехугольной призме ABCDA^B^CiDi
(ААt ||CCS через середины двух смежных сторон основания
DC и AD н вершину Вх верхнего основания проведена плоскость. Найти
угол между этой плоскостью и плоскостью основания, если периметр
сечения в 3 раза больше диагонали основания.
89
3.428. Сторона ВС треугольника АВС, лежащего в основании на-
клонной призмы ABCAtB^i (A At||CCj), равна а, прилежащие
к ней углы равны Д и у. Найти угол между боковым ребром и плоско-
стью основания, если объем призмы равен V и АА^А^В—А^С.
3.429. В кубе ABCDAlB1CiD1 (ЛЛ1||2?2?1||СС1||.О.О1) проведена плос-
кость через середины ребер DDX и DXCX и вершину А. Найти угол между
этой плоскостью и гранью ABCD.
3.430. В основании пирамиды лежит квадрат. Углы, которые образу-
ют боковые грани с основанием, относятся как 1:2:4:2. Найти эти углы.
3.431. Через вершину основания правильной треугольной пирамиды
проведена плоскость перпендикулярно противоположной боковой грани
и параллельно противоположной стороне основания. Эта плоскость
составляет с плоскостью основания пирамиды угол а. Найти плоский
угол при вершине пирамиды.
3.432. Расстояние от центра основания правильной четырехугольной
пирамиды до боковой грани и до бокового ребра равны соответственно
а и А. Найти двугранный угол при основании пирамиды.
3.433. Сторона основания правильной треугольной пирамиды равна
а. Боковая грань составляет с плоскостью основания угол а. Найти
расстояние между боковым ребром и непересекающей его стороной
основания.
3.434. Сторона основания правильной четырехугольной пирамиды
равна а. Угол между высотой пирамиды и боковым ребром равен
a [a^arctg(4/2/2)]. Найти площадь сечения пирамиды плоскостью, про-
веденной через середину высоты перпендикулярно одному из ее боковых
ребер.
3.435. Высота правильной треугольной пирамиды SABC равна Н.
Через вершину А основания АВС проведена плоскость перпендикулярно
противоположному боковому ребру SC. Эта плоскость составляет
с плоскостью основания угол а. Найти объем части пирамиды, заклю-
ченной между плоскостью основания и плоскостью сечения.
3.436. В правильную треугольную усеченную пирамиду вписаны два
шара; один касается всех ее граней, другой — всех ребер. Найти синус
угла между боковым ребром и плоскостью основания.
3.437. Основанием пирамиды FABC служит равнобедренный тре-
угольник АВС, у которого угол между равными сторонами АВ и АС
равен а (а<л/2). В пирамиду вписана треугольная призма AEDA^E^^,
точки Аи Ег hD. лежат соответственно на боковых ребрах AF, CF и BF
пирамиды, а сторона ED основания AED проходит через центр окружно-
сти, описанной около треугольника АВС. Найти отношение объема
призмы к объему пирамиды.
3.438. Правильная треугольная пирамида пересечена плоскостью,
проходящей через ее боковое ребро и высоту. В сечении образовался
треугольник с углом л/4 при вершине пирамиды. Найти угол между
боковой гранью и плоскостью основания пирамиды.
3.439. Через вершину основания правильной четырехугольной пира-
миды проведена плоскость, пересекающая противоположное боковое
ребро под прямым углом. Площадь сечения в 2 раза меньше площади
основания пирамиды. Найти угол между боковым ребром и плоскостью
основания.
3.440. Сторона нижнего основания правильной усеченной четыреху-
гольной пирамиды в 5 раз больше стороны верхнего основания. Боковая
поверхность пирамиды равна квадрату ее высоты. Найти угол между
боковым ребром пирамиды и плоскостью основания.
90
3.441. Основанием пирамиды служит правильный треугольник. Од-
на из боковых граней пирамиды перпендикулярна плоскости основания.
Найти косинус угла между двумя другими боковыми гранями, если они
составляют с плоскостью основания угол а.
3.442. В основании четырехугольной пирамиды лежит равнобедрен-
ная трапеция с основаниями а и Ъ (а>2Ь) и углом <р между неравными
отрезками ее диагоналей. Вершина пирамиды проецируется в точку
пересечения диагоналей основания. Углы, которые составляют с плоско-
стью основания боковые грани, проходящие через основания трапеции,
относятся как 1:2. Найти объем пирамиды.
3.443. В треугольной пирамиде все грани — правильные треуголь-
ники. Через сторону основания проведена плоскость, делящая объем
пирамиды в отношении 1:3, считая от основания. Найти угол между
этой плоскостью и плоскостью основания.
3.444. В правильной четырехугольной пирамиде через два боковых
ребра, не принадлежащих данной грани, проведена плоскость. Отно-
шение площади сечения к боковой поверхности пирамиды равно к.
Найти угол между двумя смежными боковыми гранями и допустимые
значения к.
3.445. Основанием пирамиды ABCDE служит ромб ABCD (ЛВЦС2)).
Высота пирамиды проходит через середину стороны АВ. Боковые ребра
ЕС и ED составляют с плоскостью основания углы а. и fi. Найти косинус
острого угла ромба, если со8а=1Д/з и cos
3.446. Высота правильной четырехугольной усеченной пирамиды ра-
вна Н. Боковое ребро составляет с основанием угол а, а диагональ
пирамиды с основанием — угол fi. Найти площадь сечения пирамиды
плоскостью, проходящей через диагональ пирамиды параллельно не
пересекающей ее диагонали основания.
3.447. Стороны нижнего и верхнего оснований правильной треуголь-
ной усеченной пирамиды равны соответственно а и b (а>Ь). Боковая
грань составляет с плоскостью основания угол а. Найти площадь сече-
ния пирамиды плоскостью, проходящей через среднюю линию боковой
грани и центр нижнего основания.
3.448. В конус, осевое сечение которого — прямоугольный треуголь-
ник, вписан цилиндр; его нижнее основание лежит в плоскости основания
конуса. Отношение боковых поверхностей конуса и цилиндра равно 4д/2.
Найти угол между плоскостью основания конуса и прямой, проходящей
через центр верхнего основания цилиндра и произвольную точку окру-
жности основания конуса.
3.449. Осевое сечение цилиндра — квадрат. Отрезок АВ, соединя-
ющий точку А окружности верхнего основания с точкой В окружности
нижнего основания, равен а и отстоит от оси цилиндра на расстояние Ь.
Найти угол между прямой АВ и плоскостью основания цилиндра.
3.450. Прямоугольник с площадью S и углом а между диагоналями
вращается вокруг оси,* проходящей через его вершину параллельно
диагонали. Найти поверхность тела вращения.
3.451. Пусть АВ — диаметр нижнего основания цилиндра, АХВХ —
хорда верхнего основания, параллельная АВ. Плоскость, проведенная
через прямые АВ и А^В^, составляет с плоскостью нижнего основания
цилиндра острый угол а, а прямая ABt составляет с той же плоскостью
угол Д. Найти высоту цилиндра, если радиус основания цилиндра равен
R (точки А и At лежат по одну сторону от прямой, проходящей через
середины отрезков АВ и АХВХ).
91
3.452. Основанием пирамиды, вписанной в конус, служит четыреху-
гольник, у которого одна сторона равна а, а каждая из остальных трех
сторон равна Ь. Вершина пирамиды лежит на середине одной из образу-
ющих. Найти объем пирамиды, если угол между образующей и высотой
конуса равен а.
3.453. Основанием пирамиды служит равнобедренная трапеция
с острым углом а. Эта трапеция описана около окружности основания
конуса. Вершина пирамиды лежит на одной из образующих конуса, а ее
проекция на плоскость основания совпадает с точкой пересечения диаго-
налей трапеции. Найти объем пирамиды, если образующая конуса равна
I и составляет с высотой угол /?.
3.454. Найти радиус шара, касающегося основания и боковых ребер
правильной треугольной пирамиды, у которой сторона основания равна
а, а двугранный угол при основании равен а.
3.455. Сторона основания правильной треугольной пирамиды равна
а, плоский угол при вершине равен а. В пирамиду вписан шар. Найти
площадь сечения этого шара плоскостью, проходящей через центр ос-
нования пирамиды и перпендикулярной ее боковому ребру.
3.456. Найти радиус шара, вписанного в правильную треугольную
пирамиду, высота которой равна Н, а угол между боковым ребром
и плоскостью основания равен а.
3.457. Сторона основания правильной треугольной пирамиды равна
а, двугранный угол при основании равен а,. В эту пирамиду вписана
прямая треугольная призма; три ее вершины лежат на апофемах пирами-
ды, а три другие — в плоскости основания пирамиды. Найти объем
призмы, если центр вписанного в пирамиду шара лежит в плоскости
верхнего основания призмы.
3.458. В правильную четырехугольную пирамиду вписан шар. К ша-
ру проведена параллельно основанию пирамиды касательная плоскость,
которая делит объем пирамиды в отношении т: п, считая от вершины.
Найти угол между высотой пирамиды и ее боковой гранью.
3.459. Сторона основания правильной четырехугольной пирамиды
равна а, двугранный угол при основании равен а. Найти расстояние от
центра шара, вписанного в эту пирамиду, до бокового ребра.
3.460. Поверхность шара, вписанного в правильную усеченную тре-
угольную пирамиду, относится к полной поверхности пирамиды как
я:6х/з. Найти угол между боковой гранью и плоскостью основания
пирамиды.
3.461. Радиус шара, описанного около правильной четырехугольной
пирамиды, относится к стороне основания как 3:4. Найти угол между
боковой гранью и плоскостью основания.
3.462. Отношение объема правильной треугольной усеченной пира-
миды к объему вписанного в нее шара равно к. Найти угол между
боковой гранью пирамиды и плоскостью основания и допустимые значе-
ния к.
3.463. Отношение объема усеченного конуса к объему вписанного
в него шара равно к. Найти угол между образующей конуса и плоско-
стью его основания и допустимые значения к.
3.464. В конус вложен шар так, что их поверхности касаются. Объем
тела, заключенного между ними, в 8 раз меньше объема шара. Найти
угол при вершине осевого сечения конуса.
3.465. В конус вписан шар. Плоскость, содержащая окружность ка-
сания шаровой и конической поверхностей, делит объем шара в отноше-
нии 5:27. Найти угол между образующей и плоскостью основания.
92
ГЛАВА 4
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ ПО ГЕОМЕТРИИ
Пример 1. Доказать, что в прямоугольном треугольнике величина угла между
медианой и высотой, проведенными к гипотенузе, равна модулю разности вели-
чин острых углов треугольника (рис. 4.1).
□ Пусть ЕС=п/2, CD — высота, СЕ — медиана. Требуется доказать, что
LDCE=\lB— £.А|. Положим LDCE= Lx; тогда LDCA = ЕВ (так как оба угла
дополняют угол А до я/2). В прямоугольном треугольнике длина медианы,
проведенной к гипотенузе, равна половине длины гипотенузы; следовательно,
ЕАСЕ — равнобедренный и ЕЕСА= Lx+ ЕВ= ЕА, откуда Lx= LA- ЕВ. Ес-
ли вершины А и В треугольника поменять местами (см. рис. 4.1), то получим
Ех= LB— LA. Оба результата можно объединить в один: Lx=\LB— LAj.
Пример 2. Доказать, что для любой точки М, принадлежащей произвольному
треугольнику АВС со сторонами а, b и с и высотами ha, Л* и hc (рис. 4.2),
х у z
справедливо равенство —+—I— = 1, где х, у и z — соответственно расстояния от
hb hc
точки М до сторон ВС, АС и АВ. Сформулировать соответствующее свойство для
произвольной точки, принадлежащей равностороннему треугольнику.
□ Соединив точку М с вершинами А, Ви С, получим три треугольника
ВМС, АМС и АМВ, высоты которых соответственно равны х, у и z. Пусть
1
S — площадь треугольника АВС; тогда S=- (ax+by+cz). С другой стороны,
1 1 1
S=- ah„, S= bhb, S=- chc. Комбинируя эти равенства, находим
2 2 2
X у Z
—I----1—= 1.
Лд Ьь hc
В равностороннем треугольнике ha=hb=hc = h, а потому x+y+z=h, т. е.
Рис. 4.2
93
сумма расстояний от произвольной точки, принадлежащей равностороннему
треугольнику, до его сторон постоянна и равна высоте треугольника.
Пример 3. Длина гипотенузы равнобедренного прямоугольного треугольника
равна 40. Окружность с радиусом, равным 9, касается гипотенузы в ее середине.
\ Найти длину отрезка, отсекаемого этой окружностью на одном из катетов.
□ Сначала выясним, имеет ли задача решение при заданных значениях
длины гипотенузы и радиуса окружности. Из геометрических соображений (рис.
4.3) ясно, что для того чтобы окружность с центром О на высоте ВК треугольника
ЛВС пересекала катет ВС в двух точках D и Е, необходимо и достаточно, чтобы ее
радиус ОК был не больше половины высоты В К, но больше радиуса вписанной
в треугольник окружности. Первое соотношение очевидно (9 < 10), второе также
нетрудно проверить^ Радиус г вписанной окружности найдем по формуле r=S/p,
loji-loJi 20 г г
т. е. г=--------т==—-=—=205/2—20. Покажем, что 9>20^J2—20, т. е. что
40+405/2 л/2*1
2
29>2(ц/2. Возведя в квадрат обе части неравенства, получим верное неравенство
841 > 800; следовательно, справедливо и исходное неравенство.
Для отыскания длины отрезка DE проведем OFLDE и радиус ОЕ за-
данной окружности. Вычислим последовательно длины отрезков ВО, OF,
11J 2
FE и, наконец, DE. Имеем ВО=ВК— ОК=11, OF=BO sin45°=------------------,
FE-yJoF1-OF1-^81—— = DE=2FE=^J«2.
Пример 4. В треугольнике АВС точка К, взятая на стороне ВС, делит ее
в отношении 1:3, считая от вершины В, а точка L делит сторону АС в отношении
2:5, считая от вершины А. В каком отношении точка О пересечения прямых ЛК
и BL делит отрезки АК и BL, считая от соответствующих вершин?
□ I способ. Пусть ВК=х, AL=2y (рис. 4.4), тогда по условию КС=Зх,
LC=5y. Пусть, далее, KF=m, OF=n. Из подобия треугольников OKF и А КС
п 1у
имеем — =—, откуда
т Зх ,
"=—. (*)
у Зх
п х+т
Из подобия треугольников BOF и BLC находим —=----, откуда
5у 4х
п 5(х+т)
у 4х
Приравнивая правые части пропорций (*) и (**), после упрощений получаем
94
15х ''ч. 28х
28m=15(x+m), откуда т=—. Следовательно, BF=BK+KF=“— и CF=BC—
28х 24х
—BF=4x——=—. Согласно теореме Фалеса, имеем
13 13
ВО BF 28х/13_7 АО 24х/13 8
ОД=гс“24х/13-б’ ОХ=15х/13=5‘
II способ. Введем следующие обозначения: "ВС—а, (TA-Ъ, АО=х, Т&=у
(рис. 4.5). Тогда векторы 75К и ОВ, коллинеарные соответственно векторам Лб
и Тб, можно записать в виде бХ=аЛб и б7?=/?Тб, где числа а и/) подлежат
определению.
Рассмотрим три замкнутых контура: ОВКО fl), О LAO (II), OKCLO (III). Из
(I) имеем 6Т+ВТ+Т6=О, т. е. [Гул—а—ах=0; из (II) бТ+ТЛ+Лб=б, т. е.
4
2 _ 3 _ 5 _
—у+- 7> + х=0; из (III) 6T+TT+CZ+Z6=5, т. е. ах+- а+~ 5+у=5. В резуль-
тате получим систему уравнений
{— scx+fiy-i— а=б,
4
- - 2т -
х—у+- 5=0,
7
- - 3_ 5
ах+у-1— ан— о = 0.
4 7
_ _Из первого и второго уравнений выразим векторы а и Ъ через векторы
х и у и полученные выражения подставим в третье уравнение. После несложных
преобразований получим
5\_ /7 \_ _
4а— )х+ --ЗД1у=0.
2/ \2 /
Так как векторы х и у не коллинеарны, то это равенство возможно тогда и только
_ _ 5 7
тогда, когда коэффициенты при х и у равны нулю, т. е. 4а— =0, -—3/1=0.
Рис. 4.5
95
I э / э __ __ / _
Отсюда а»-, в—-, т. е. ОК**- АО, оИ—-Ъб. Итак, ЛО:ОК—8:5, BO-.OL^
8 6 8 6
-7:6.
Ш способ. Пусть стороны треугольника АВС представляют собой невесо-
мые стержни, а в вершинах треугольника приложены параллельные силы (рис.
4.6). Предположим, что в вершине С приложена сила, равная 2 Н; тогда в точке
В согласно условиям равновесия (равенство моментов сил относительно точки К)
должна быть приложена сила 6 Н, а в точке К согласно правилу сложения
параллельных сил должна быть приложена сила 8 Н. Рассуждая аналогично
относительно точек А и L, находим, что в точке А должна быть приложена сила
5 Н, а в точке L — сила 7 Н. Наконец, согласно условиям равновесия относитель-
но точки О получаем АО: OK=i: 5 и ВО: OL=1:6.
Пример 5. Боковые ребра треугольной пирамиды попарно перпендикулярны
и имеют длины а, b и с. Найти объем пирамиды.
□ Будем считать основанием пирамиды прямоугольный треугольник ADB
(рис. 4.7), а вершиной — точку С. Так как CD LAD и CDLBD, то в силу теоремы
о перпендикулярности прямой и плоскости СРХпл. ADB и, следовательно, ребро
CD — высота пирамиды. По формуле (2.10) находим объем пирамиды:
1 1 abc abc
V-- StMD.CD--.---.*
Пример 6. Основанием пирамиды ABCD служит остроугольный равнобедрен-
ный треугольник ЛЯС, у которого АВ—ВС— а я АС—b (рис. 4.8). Каждое боковое
ребро равно с. Через центр окружности, описанной около основания, проведена
плоскость, параллельная прямым DB и АС. Найти площадь сечения.
□ Так как треугольник АВС — остроугольный, то центр О описанной около
него окружности лежит внутри треугольника и заданная плоскость пересекает все
грани пирамиды. Далее, из равенства всех боковых ребер пирамиды следует, что
ее вершина D проецируется в точку О (см. гл 2, «Дополнительные соотношения»,
п. 1°) и проекцией DB на плоскость основания служит отрезок ВО, перпендикуляр-
ный стороне АС основания пирамиды. Согласно теореме о трех перпендикулярах,
BDLAC.
Для построения заданной плоскости через точку О проведем прямую МЩАС
(в плоскости АВС), а через точку W — прямую NP\[DB (в плоскости BDC).
Плоскость MNP параллельна прямым АС и BD (в силу признака параллель-
ности прямой и плоскости) и пересекает боковую грань ADC по прямой PQ\\AC,
а боковую грань ABD — по прямой MQIBD. Сечение MNPQ — прямоугольник.,
так как выше было показано, что BDLA С, a MN и NP параллельны соответствен-
но АС я AD.
Найдем длины сторон прямоугольника MNPQ. Заметим, что ВО — радиус
описанной окружности, &ВР — высота треугольника АВС. Пусть BO—R и BF—h.
96
R MN BN bR
Из подобия треугольников MBN и АВС находим ——------—, откуда MN-=—
h b a h
aR a(h-R)
и BNДалее, CN^BC—BN=-------.
PN CN PN h—R
. Из подобия треугольников CNP и CBD
c(h-R)
находим —=— или —=-----------, откуда PN=--------. Следовательно, площадь
BD ВС ch h
сечения
h ’
bcR(h — R)
Smnpq^MN PN--------.
h2
Остается выразить Л и R через известные величины. Из треугольника BFC
— b2, а зависимость между R, ha аз равнобедрен-
a2
ном треугольнике выражается формулой А2=— (см. гл. 3, п. 3°). Подставив эти
2Л
выражения в равенство (*), после упрощений получим
2а1Ьс(2а1 — Ь2)
SMNPQ**
находим h=
(4а2 — Ь2)2
Покажем, что полученная для площади формула имеет смысл, т. е. что
2а2— Ь2 >0. Здесь снова существенно, что равнобедренный треугольник
АВС — остроугольный. Из этого следует, что угол А при основании больше 45°.
bf2 ^2 —
Поэтому совЛ <cos45°, т. е. —<—, откуда Ь<а^2, Ъ2<2а2 и 2а2— Ь2>0.
а 2
Пример 7. Дан куб ABCDA1B1C1D1, длина ребра которого равна а. Найти
объем конуса, вершина которого совпадает с вершиной Blt а окружность основа-
ния проходит через середины трех ребер, выходящих из вершины D.
□ Пусть точки М, N и Р (рис. 4.9) — соответственно середины ребер AD, CD
и DDit т. е. MD*ND^PD^afr. Из равенства
равнобедренных прямоугольных треугольников
DPN, DPM и DMN следует, что MN=MP^
—NP^a^fyl. Далее, из равенства прямоуголь-
ных треугольников ВгМА, BXNC и B^PDX (у ко-
торых один из катетов есть диагональ соответст-
вующей грани куба, а другой — половина ребра
куба) следует, что В{М = B^N ~ BtP —
----------- I а2 Зд
/2д2+~«-у. Значит, точки
М, N и Р равноудалены как от точки D, так и от
точки Поэтому прямая B,D перпендикулярна
плоскости треугольника MNP и пересекает эту
плоскость в точке О — центре окружности, опи-
санной около треугольника MNP. Итак,
ON — радиус основания конуса, ВгО — высота
конуса.
Так как сторона а3 правильного треугольника, вписанного в окружность
радиуса R, выражается формулой аЭ"/ц/з, то Я-Пз/^/з. Следовательно,
4-363
97
ayj i. a - ,---------
ON=—-==—=. Затем из треугольника BtNO находим 1^0=^— ON2 =
1aJ3 у/6
Iva* a1 5a
«, I-----=—- Окончательно получим
V 4 6 2^3
1 a2 5a Sr.a^-J3
V^-n.~ -----------
3 6 2^3 108
4.001. Найти гипотенузу прямоугольного треугольника, если точка
касания вписанной в него окружности делит один из катетов на отрезки
длиной т и п (т < л).
4.002. Сумма длин катетов прямоугольного треугольника равна
8 см. Может ли длина гипотенузы быть равной 5 см?
4.003. Доказать, что в любом треугольнике отношение суммы всех
попарных произведений, составленных из длин сторон треугольника,
к сумме длин его трех высот равно диаметру описанной окружности.
4.004. Длины сторон остроугольного треугольника составляют ари-
фметическую прогрессию с разностью 5 см. Найти наибольшее число,
обладающее следующим свойством: длина большей стороны любого
треугольника указанного типа больше этого числа.
4.005. Медиана некоторого треугольника совпадает с его биссект-
рисой. Доказать, что такой треугольник —равнобедренный.
4.006. Длины сторон треугольника относятся как 2:3:4. В нем
проведена биссектриса наименьшего угла. В каком отношении (считая
от вершины) она делится центром окружности, вписанной в этот
треугольник?
4.007. Биссектриса угла треугольника делит противолежащую сто-
рону на отрезки длиной 8 и 10 см. Найти длины сторон треугольника,
если центр вписанной окружности делит эту биссектрису в отношении
3:2, считая от вершины угла.
4.008. Сторона, биссектриса и высота треугольника, выходящие из
одной и той же вершины, равны соответственно 5, 5 и 2^/б см. Найти две
другие стороны треугольника.
4.009. Две стороны треугольника и биссектриса угла между ними
равны соответственно 60, 40 и 24 см. Найти площадь треугольника.
4.010. В прямоугольном треугольнике найти биссектрису прямого
угла, если гипотенуза треугольника равна с, а один из острых углов
равен а.
4.011. Найти угол при вершине равнобедренного треугольника, если
медианы, проведенные к боковым сторонам, взаимно перпендикулярны.
4.012. Доказать, что сумма квадратов медиан любого треугольника
составляет 75% от суммы квадратов его сторон.
4.013. Тангенс тупого внешнего угла прямоугольного треугольника
равен к. Найти тангенс острого угла треугольника, не смежного с дан-
ным внешним углом.
4.014. Треугольник разбит медианами на шесть частей, не имеющих
попарно общих внутренних точек. Сравнить площади этих частей.
4.015. Доказать, что прямая, проходящая через основания двух вы-
сот остроугольного треугольника, отсекает от него подобный ему тре-
угольник.
98
4.016. Даны отрезок АВ и прямая, не перпендикулярная отрезку
и пересекающая его в точке, не являющейся серединой этого отрезка.
Ученик построил точку Blt симметричную точке В относительно данной
прямой, и заметил, что теперь легко построить треугольник АВС, для
которого биссектриса угла АСВ лежит на данной прямой. Как это
можно сделать?
4.017. Доказать, что длина медианы треугольника меньше полусум-
мы длин заключающих ее сторон.
4.018. Доказать, что если две стороны и медиана одного треуголь-
ника соответственно равны двум сторонам и медиане другого треуголь-
ника, то такие треугольники равны (рассмотреть два случая).
4.019. Доказать, что в прямоугольном треугольнике биссектриса
прямого угла делит пополам угол между медианой и высотой, проведен-
ными к гипотенузе.
4.020. Доказать, что сумма длин высот треугольника меньше его
периметра.
4.021. Три средние линии треугольника разбивают его на четыре
части. Если площадь одной из них равна S, то чему равна площадь
данного треугольника?
4.022. Дан треугольник с площадью 1 и длинами сторон а, b и с.
Известно, что а^Ь^с. Доказать, что
4.023. Какую фигуру образует множество всех вершин равнобедрен-
ных треугольников, имеющих общее основание?
4.024. Сумма длин катетов прямоугольного треугольника равна з.
Найти границы возможных значений длины его гипотенузы с.
4.025. Доказать, что из трех медиан прямоугольного треугольника
наименьшую длину имеет та, которая проведена к гипотенузе.
4.026. Через точку, принадлежащую меньшей стороне треугольника,
провести прямую, отсекающую от него треугольник, подобный дан-
ному. Показать, что существуют четыре такие прямые.
4.027. Дан треугольник АВС. На основании ВС построить треуголь-
ник с той же площадью, но с углом при вершине В, равным половине
угла В данного треугольника.
4.028. Найти длины наименьших сторон всех
тупоугольных треугольников, у которых длины
сторон выражаются целыми числами и со-
ставляют арифметическую прогрессию с раз-
ностью 3 см.
4.029. Пусть ВО — биссектриса угла В пря-
моугольного треугольника ABC, D — середина
катета AC, DO1AC, OELAB, OF1BC, АВ — ги-
потенуза (рис. 4.10). Легко доказать, что
&ВОЕ= &BOF, откуда ВЕ=ВЕ (*) Далее, так
как О А = ОС, то Д ОЕА = Д OFC, откуда АЕ= FC.
(♦*). Складывая равенства (*) и (**), получаем,
что АВ=ВС, т. е. что длина гипотенузы равна
длине катета. Найти ошибку в проведенном до-
казательстве.
4.030. Определить вид треугольника по дли-
нам трех сторон (если такой треугольник воз-
можен): а) 2, 2 и 3; б) 6, 8 и 10; в) 3, 1 и 4;
г) 3, 5 и 7.
4.031. В равнобедренном треугольнике бис-
сектриса угла при основании делит боковую сто-
Рис. 4.10
99
рону на отрезки 4 и 1 см, считая от вершины. Найти длину биссект-
рисы.
4.032. Биссектриса угла при основании равнобедренного треуголь-
ника делит противоположную сторону так, что отрезок, прилежащий
к вершине треугольника, равен его основанию. Доказать, что биссект-
риса также равна основанию треугольника.
4.033. Найти наибольшую площадь прямоугольного треугольника
с данной гипотенузой с.
4.034. Доказать, что если медианы ААХ и ВВХ треугольника АВС
равны, то треугольник равнобедренный: СА = СВ.
4.035. Длины сторон треугольника составляют арифметическую
прогрессию. Высота, проведенная к средней по величине стороне, равна
h. Найти радиус круга, вписанного в треугольник.
4.036. Доказать, что во всяком прямоугольном треугольнике сумма
квадратов длин медиан составляет 150% от квадрата длины его гипо-
тенузы.
4.037. Углы треугольника относятся как 2:3:7. Наименьшая сторо-
на треугольника равна а. Найти радиус окружности, описанной около
треугольника.
4.038. Показать, что если длины сторон некоторого треугольника
составляют геометрическую прогрессию, то и длины высот треуголь-
ника также составляют геометрическую прогрессию.
4.039. Доказать, что угол С треугольника АВС является прямым
в том и только том случае, если длины сторон этого треугольника
связаны равенством АВ1 = АС1 + ВС* (прямая и обратная теоремы Пи-
фагора).
4.040. Из каких точек плоскости данный отрезок виден под данным
углом?
4.041. Какую фигуру образует множество ортоцентров (точек пере-
сечения высот) всех треугольников, имеющих общую сторону, при усло-
вии, что углы, противолежащие этой стороне, равны?
4.042. Какую фигуру образует множество точек пересечения биссект-
рис всех треугольников, имеющих общую сторону, при условии, что
углы, противолежащие этой стороне, равны?
4.043. Окружность каждого из двух равных кругов радиуса R прохо-
дит через центр другого. Найти площадь общей части этих кругов.
4.044. Из точки А проведены два луча, пересекающие данную окру-
жность: один — в точках В и С, другой — в точках D и Е. Известно, что
АВ=1, ВС=1, AD= 10. Определить DE.
4.045. Доказать, что если через точку касания двух окружностей
провести две прямые, пересекающие обе окружности, и точки пересече-
ния прямых с окружностями соединить хордами, то эти хорды парал-
лельны.
4.046. Показать, что 3 <я<4, не пользуясь приближенными значени-
ями числа п.
4.047. Радиус круга с центром в точке О равен 6 см, а его хорда
АВ=3 см. Найти радиус круга, вписанного в сектор АОВ.
4.048. На отрезке АВ произвольно взята точка М. На AM и МВ по
одну сторону от АВ построены квадраты. Около квадратов описаны
окружности, пересекающиеся в точке С. Показать, что луч МС есть
биссектриса угла АСВ.
4.049. Около окружности с центром О описан четырехугольник
ABCD. Найти сумму углов АОВ и COD.
4.050. Центры описанной около треугольника и вписанной в него
100
окружностец^расположены симметрично относительно одной из сторон
треугольника. Найти углы треугольника.
4.0 51. Две окружности имеют только одну общую точку. Через нее
проведена произвольная секущая. Доказать, что касательные в точках
пересечения этой секущей с каждой из окружностей параллельны.
4.0 52. Пары точек А и Аи В и Вг расположены симметрично от-
носительно одной прямой. Доказать, что эти че-
тыре точки лежат на одной окружности или же на
одной прямой.
4.0 53. Доказать, что площадь полукруга, по-
строенного на гипотенузе прямоугольного тре-
угольника, равна сумме площадей полукругов,
построенных на его катетах.
4.0 54. В окружность радиуса R— 1 см вписан
квадрат, а в квадрат — второй квадрат, вершины
которого деляг пополам стороны первого квад-
рата (рис. 4.11). Не вычисляя длины стороны
первого квадрата, доказать, что площадь второ-
го квадрата равна 1 см2.
4.0 55. В прямоугольный круговой сектор радиуса R вписан квадрат
так, что две его вершины лежат на крайних радиусах, две — на дуге
сектора. Найти сторону квадрата.
4.056. В круге радиуса 4 м найти длину хорды, которая видна из
любой точки меньшей дуги окружности под углом 135°.
4.057. В круге радиуса а найти длину хорды, которая из любой точки
большей дуги окружности видна под углом 30°.
4.058. Сторона АВ треугольника видна из вершины С под углом а.
Под каким углом она видна из центра окружности, описанной около
треугольника? Рассмотреть три случая: С — вершина острого, прямого
или тупого угла.
4.0 59. Две точки А и В расположены по разные стороны от прямой
MN. На прямой MN найти точку С такую, что L ACN- LBCN.
4.0 60. В квадрате ABCD точки М и N — середины сторон DC и ВС.
Найти l_MAN.
4.0 61. Каждая сторона выпуклого четырехугольника меньше а. До-
казать, что его площадь меньше а2.
4.0 62. Доказать, что в любой трапеции ABCD (ВС||Л2>) треуголь-
ники АОВ и COD равновелики (О — точка пересечения диагоналей).
4.06 3. В равнобедренной трапеции ABCD дано: AB\\DC, AB=3DC,
cos l_ABC= Доказать, что диагонали трапеции взаимно перпен-
дикулярны.
4.06 4. Одна из сторон пятиугольника имеет длину 30 см. Длины
остальных сторон выражаются целыми числами и составляют ариф-
метическую прогрессию с разностью 2 см, причем длина меныпей из
сторон не превышает 7 см. Найти длины сторон всех пятиугольников,
для которых выполняются эти условия.
4.06 5. Из каких одноименных равных правильных многоугольников
можно сложить паркет?
4.06 6. В окружность радиуса R вписан правильный л-угольник, пло-
щадь которого равна ЗЯ2. Найти л.
4.06 7. Доказать, что сумма расстояний от любой точки, лежащей
внутри правильного многоугольника, до прямых, содержащих его сторо-
ны, равна произведению апофемы многоугольника на число его сторон.
4.06 8. Две диагонали, исходящие из одной и той же вершины пра-
' 101
вильного пятиугольника, разбивают его на три треугольника. Найти
отношение площади треугольника, ограниченного этими двумя диагона-
лями, к сумме площадей двух других треугольников.
4.06 9. Пусть л — число сторон выпуклого многоугольника, a d —
число его диагоналей. Указать все значения л, для которых n>d.
4.07 0. Сколько диагоналей можно провести в выпуклом восьми-
угольнике?
4.07 1. Найти площадь правильного двенадцатиугольника, вписан-
ного в окружность радиуса R.
4ЛП1. В каком выпуклом многоугольнике число диагоналей равно
числу сторон?
4.07 3. Непараллельные стороны трапеции продолжены до пересече-
ния. Доказать, что прямая, проходящая через полученную точку и точку
пересечения диагоналей, делит каждую из параллельных сторон трапе-
ции на две равные части.
4.07 4. Каково наибольшее возможное число острых углов в произ-
вольном выпуклом многоугольнике?
4.07 5. Меньшее основание трапеции равно 6 см. Найти ее большее
основание, если расстояние между серединами диагоналей равно 5 см.
4.07 6. Биссектриса острого угла параллелограмма делит его диаго-
наль на отрезки длиной 3,2 и 8,8 см. Найти стороны параллелограмма,
если его периметр равен 30 см.
4.07 7. Длины параллельных сторон трапеции равны 25 и 4 см,
а длины непараллельных сторон 20 и 13 см. Найти высоту трапеции.
4.07 8. В четырехугольник, три последовательные стороны которого
равны 2, 3 и 4 см, вписана окружность радиуса 1,2 см. Найти площадь
четырехугольника.
4.07 9. Через произвольно выбранную точку на одной стороне парал-
лелограмма и концы противоположной стороны сделаны два разреза.
Определить площадь данного параллелограмма, если площади отрезан-
ных треугольников равны и S2.
4.08 0. Доказать, что точка пересечения биссектрис углов, прилега-
ющих к одной из непараллельных сторон произвольной трапеции, при-
надлежит средней линии трапеции.
4.08 1. Периметр равнобедренной трапеции, описанной около круга,
равен Р. Найти длину средней пинии трапеции.
4.08 2. Доказать, что в четырехугольнике с непараллельными сторо-
нами середины диагоналей и середины двух противоположных сторон
являются вершинами некоторого параллелограмма.
4.08 3. Сформулировать какое-либо утверждение, верное вместе
с ему обратным. Сформулировать какое-либо верное утверждение, но
такое, для которого обратное утверждение является неверным.
4.08 4. Даны две скрещивающиеся прямые. Можно ли провести две
пересекающиеся прямые так, чтобы каждая из них пересекала обе дан-
ные прямые?
4.08 5. На сколько дальше центр верхнего основания куба с ребром
1 удален от вершины нижнего основания, чем от его стороны?
4.08 6. Найти угол между скрещивающимися диагоналями смежных
граней куба.
4.08 7. Куб ABCDA1B1ClDl (ААг||СС,UDDj) пересечен плоско-
стью, проходящей нерез вершины А, С и середину Е ребра DD1. Пока-
зать, что объем пирамиды ACDE равен 1/12 объема куба.
4.08 8. Построить сечение куба ABCDAiB1CiD1, проходящее через
середины ребер AD, AiB1 и СС2.
102
4.08 9. Найти наименьшее целое число градусов, которое может соде-
ржать плоский угол трехгранного угла, обладающего следующим свой-
ством: каждый из плоских углов содержит целое число градусов, причем
эти три числа составляют арифметическую прогрессию с разностью 50°.
4.09 0. Какую фигуру образует множество всех точек, отстоящих от
данной плоскости на расстояние а и от фиксированной точки данной
плоскости на расстояние b (а<Ь)1
4.09 1. Сколько боковых граней содержит призма, у которой 60
ребер?
4.09 2. Доказать, что если все диагонали параллелепипеда имеют
равные длины, то он прямоугольный.
4.09 3. Доказать, что если наклонная образует равные углы с тремя
попарно непараллельными прямыми, лежащими в одной плоскости, то
она перпендикулярна этой плоскости.
4.09 4. Дан куб ABCDA^B^C^Dy с ребром а. Найти расстояние от
прямой, проходящей через ребро ААи до прямой, проходящей через
диагональ BYD.
4.09 5. Существует ли в пространстве точка, равноудаленная от всех
вершин параллелограмма? От всех прямых, содер-
жащих его стороны? Каким свойством должен об-
ладать параллелограмм, чтобы точка, равноудален-
ная от его вершин, была бы равноудалена и от
прямых, содержащих его стороны?
4.09 6. Каким свойством должна обладать тра-
пеция, чтобы в пространстве существовала точка, Л
равноудаленная от ее вершин? Если данная трапе-
ция таким свойством обладает, то какую фигуру
представляет собой множество всех таких точек?
4.09 7. Построить сечение куба плоскостью, про-
ходящей через точки А, В а С (рис. 4.12).
4.09 8. Одно из боковых ребер наклонного па-
раллелепипеда составляет равные острые углы с прилежащими к нему
сторонами нижнего основания. Что представляет собой проекция пря-
мой, содержащей это ребро, на плоскость нижнего основания? При
каком условии эта проекция и диагональ основания лежат на одной
прямой?
4.09 9. Через диагональ нижнего основания произвольного парал-
лелепипеда и середину не пересекающего ее бокового ребра проведена
плоскость. Как относятся объемы полученных при этом частей парал-
лелепипеда?
4.100 . Дан правильный тетраэдр SABC. Под каким углом ребро АВ
видно из середины ребра SCI
4.101 . Пирамида пересечена плоскостью, параллельной основанию.
Построить график функции, выражающей зависимость площади сечения
от расстояния между вершиной пирамиды и секущей плоскостью.
4.102 . В правильном тетраэдре с ребром >/2 см определить расстоя-
ние между двумя скрещивающимися ребрами.
4.103 . Через середину высоты пирамиды проведена плоскость парал-
лельно плоскости основания пирамиды. В каком отношении находятся
объемы полученных многогранников?
4.104 . В основании пирамиды лежит треугольник, длины сторон
которого 30, 40 и 50 см. Вершина большего острого угла основания
принадлежит боковому ребру, имеющему длину 72 см и перпендикуляр-
ному плоскости основания. Найти полную поверхность пирамиды.
103
4.105 . Двугранный угол между двумя смежными боковыми гранями
правильной четырехугольной пирамиды равен а, а высота пирамиды
равна Н. Найти радиус описанного шара.
4.106 . Около правильной пирамиды с высотой 27 см описана сфера
радиуса 18 см. Найти угол наклона бокового ребра пирамиды к плоско-
сти ее основания.
4.107 . Все ребра (в том числе и стороны основания) треугольной
пирамиды равны. Найти отношение радиуса вписанного в пирамиду
шара к ее высоте.
4.108 . Показать, что если пирамида имеет равные боковые ребра, то
около нее можно описать сферу и что радиус этой сферы равен квадрату
длины ребра, деленному на удвоенную длину высоты пирамиды.
4.109 . В треугольной пирамиде скрещивающиеся ребра попарно рав-
ны. Доказать, что полная поверхность пирамиды равна учетверенной
площади одной из ее граней.
4.110 . Высоты всех боковых граней некоторой пирамиды равны.
Под каким углом они наклонены к плоскости основания, если площадь
полной поверхности пирамиды в 1,5 раза больше площади ее боковой
поверхности?
4.111 . В куб помещена четырехугольная пирамида так, что ее ос-
нование совпадает с одной из граней куба, а вершина — с серединой
одного из ребер противоположной грани. Под какими углами боковые
грани пирамиды наклонены к плоскости ее основания?
4.112 . В правильном тетраэдре SABC через ребро АС проведена
плоскость, пересекающая ребро SB в точке л. Доказать, что проекция
вершины В на плоскость сечения лежит на высоте сечения, проведенной
к стороне АС. При каком условии эта проекция совпадает с точкой А?
4.113 . Какому условию должен удовлетворять четырехугольник,
чтобы на нем, как на основании, можно было построить пирамиду
с равным наклоном всех боковых граней?
4.114 . Пирамида, основанием которой служит прямоугольный тре-
угольник с катетами 9 и 8 см, вписана в конус, образующая которого
наклонена к плоскости основания под углом 60°. Найти объем пи-
рамиды.
4.115 . Через среднюю линию основания треугольной пирамиды и ее
вершину проведена плоскость. В каком отношении находятся объемы
полученных пирамид?
4.116 . В правильной четырехугольной пирамиде SABCD (S — ее
вершина) провести сечение через середину ребра SB и прямую MDN,
расположенную в плоскости основания ABCD и параллельную его диа-
гонали АС.
4.117 . Боковые ребра треугольной пирамиды попарно перпендику-
лярны. Найти объем пирамиды, если площади ее боковых граней равны
iSj, Sj и S3.
4.118 . Показать, что если в основании пирамиды, имеющей равные
боковые ребра, лежит прямоугольный треугольник, то одна из боковых
граней пирамиды перпендикулярна плоскости основания.
4.119 . Всякая ли пирамида обладает тем свойством, что около нее
можно описать сферу? Если около пирамиды можно описать сферу, то
где лежит центр этой сферы?
4.120 . Показать, что если около основания пирамиды можно опи-
сать окружность, то все плоскости, перпендикулярные боковым ребрам
пирамиды и делящие их пополам, пересекаются в одной точке.
4.121 . Найти площадь полной поверхности конуса, если его боковую
104
поверхность можно развернуть в круговой сектор с радиусом 1 и с пря-
мым центральным углом.
4.122 . Два конуса имеют общую вершину, а их высоты пересекают-
ся. Показать, что прямая, по которой пересекаются плоскости оснований
конусов, перпендикулярна плоскости, содержащей высоты конусов.
4.123 . В конус, осевое сечение которого — правильный треугольник,
вписан шар, затем вписан второй шар, касающийся первого шара и бо-
ковой поверхности конуса, и т. д. (n-й шар касается (п— 1)-го шара
и боковой поверхности конуса). Найти отношение предела суммы объ-
емов шаров при n-юо к объему конуса.
4.124 . Образующая усеченного конуса составляет с плоскостью ос-
нования угол а. Внутри конуса расположены два шара, касающиеся друг
друга и боковой поверхности конуса, причем первый шар касается
нижнего основания конуса, а второй — верхнего основания. Расстояние
между центрами шаров равно /. Найти радиусы оснований конуса.
4.125 . В усеченном конусе АВ и CD — взаимно перпендикулярные
диаметры нижнего основания, EF — диаметр верхнего основания, па-
раллельный прямой CD. Найти косинус острого угла между прямыми
АЕ и BF, если образующая конуса есть среднее пропорциональное между
диаметрами оснований и составляет с плоскостью основания угол
а (а> л/3).
4.126 . Отношение полной поверхности конуса к поверхности вписан-
ного в него шара равно к. Найти угол между высотой и образующей
конуса и допустимые значения к.
4.127 . Отношение боковой поверхности усеченного конуса, описан-
ного около шара, к сумме площадей его оснований равно к. Найти угол
между образующей и плоскостью основания и допустимые значения к.
4.128 . Найти отношение объема шара к объему вписанного в него
куба.
4.129 . Доказать, что проекция диагонали осевого сечения усеченно-
го конуса на основание равна сумме радиусов окружностей оснований
конуса.
4.130 . Радиус полукруга, лежащего в основании полуцилиндра, ра-
вен 1. Через диаметр полукруга проведена плоскость под углом 45°
к плоскости полукруга. Показать, что в развертке полуцилиндра линия
пересечения проведенной плоскости с цилиндрической поверхностью
полуцилиндра образует дугу синусоиды.
ГЛАВА 5
ПРИМЕНЕНИЕ КООРДИНАТ
И ВЕКТОРОВ К РЕШЕНИЮ ЗАДАЧ
ОСНОВНЫЕ ФОРМУЛЫ
Прямоугольная декартова система координат
на плоскости
1°. Расстояние между точками А1(х1; yj и Л2(х2; у2) находится по формуле
AiA2=J(x2-xl)1 + (y2 -yj)2. (5.1)
С помощью этой же формулы выражается длина отрезка А2А2 или модуль
вектора А2А2 (х2-х2; у2-у2).
2°. Координаты (х; у) середины отрезка с концами А2(х2; yt) и А2(х2; у2)
находятся по формулам
3°. Уравнение прямой с угловым коэффициентом и начальной ординатой
имеет вид
y=kx + q. (5.3)
Угловой коэффициент к представляет собой значение тангенса угла, образуемого
прямой с положительным направлением оси Ох, а начальная ордината q — значе-
ние ординаты точки пересечения прямой с осью Оу.
4°. Уравнение прямой с угловым коэффициентом к, проходящей через точку
А (х0; у0), имеет вид
У-Уо=Кх-хо). (5.4)
5°. Общее уравнение прямой имеет вид
ax+by + c=Q. (5.5)
6°. Уравнения прямых, параллельных соответственно осям Оу и Ох,
имеют вид
х=а, (5.6)
У = Ь. (5.7)
7°. Условия параллельности и перпендикулярности прямых yi=klx+q1
и у2=£2х+<72 соответственно имеют вид
*i=*:2, (5.8)
к2к2 = -1. (5.9)
106
8°. Уравнения окружностей с радиусом Я и с центром соответственно в точ-
ках О (0; 0) и С(х0; у0) имеют вид
х2+у2 = Я2, (5.10)
(х-х0)2 + (у-у0)2 = Я2. (5.11)
9°. Уравнение
у=ах2 + Ьх + с (5.12)
представляет собой уравнение параболы с вершиной в точке, абсцисса которой
х0 = —6/(2я).
Прямоугольная декартова система координат
в пространстве
1°. Расстояние между точками Al(x1; yt; zt) и А2(х2; у2; z2) находится по
формуле
Л1Л2=>/(*2-^1)2 + 0'2-Л)2+(22-21)2. (5.13)
С помощью этой же формулы выражается длина отрезка А,А2 или модуль
вектора А,А2 (х2-х,; у2-у,; z2-zt).
2 . Координаты (х; у; z) середины отрезка с концами А2(х2; у2;zj и А2(х2;у2;
z2) находятся по формулам
3°. Модуль вектора а (ар- а2; а}), заданного своими координатами, находится
по формуле
lal-^/af+nJ+ej. (5.15)
4°. При сложении векторов их соответствующие координаты складываются,
а при умножении вектора на число все его координаты умножаются на это число,
т. е. справедливы формулы
(а,; а2; а3)+(Ь2: Ь2; Ь3)->(а2+Ь2; а2+Ь2; а3 + Ь3), (5.16)
Ца2; а2; а3) = (1л2; 1а2; 2а3). (5.17)
5°. Единичный вектор а0, сонаправленный с вектором а, находится по фор-
муле
5о=4- (5Л8)
И
6°. Скалярным произведением аЪ векторов а и Ъ называется число
а5 = |а| |J| cos<p, (5.19)
где ф — угол между векторами а и Ъ.
7°. Скалярное произведение векторов af.at; а2; а3) и Ъ(Ь2; Ь2; Ь3) выражается
формулой
аЪ=а1Ь1 + а2Ь2 + а3Ь3. (5.20)
В частности, п2=аа = |п|2, откуда \ct\ = y/ai.
8°. Косинус угла между векторами <^at; а2; а3) и Ъ(Ь2; Ь2; Ь3) находится по
формуле
107
оЪ +Дз/>з
008Г "" / — -• (5.21)
’ lal Pl yj a1. + ai+д? <Jb2+bi+bl
9°. Необходимое и достаточное условие перпендикулярности векторов
a(at; а2; а3) и Ъ(Ь1; Ь2; Ь2) имеет вид
аЪ*-0 или fljAi + fljij+ajftj—O, (5-22)
а условие их коллинеарности (параллельности) — вид
д=2Б, где |2|=y< (5.23)
1*1
или
Z>i Ь2 Ь3
10°. Общее уравнение плоскости, перпендикулярной вектору п(а; Ь; с),
имеет вид
ax+by+cz+d—0. (5.25)
11°. Уравнение плоскости, перпендикулярной вектору п(а; Ь; с) и проходящей
через точку (х0; уа; z0), имеет вид
e(x-xo) + Z>(y-y0) + c(z-zo) = 0. (5.26)
12°. Уравнение сферы с центром 0(0; 0; 0) записывается в виде
x2+y2+z1 = R2. (5.27)
Пример 1. В параллелограмме ОАВС даны вершины О (0; 0;), А (3; 6) и
В (8; 6). Найти отношение длин диагоналей ОВ и АС, а также составить уравнения
сторон параллелограмма и диагонали АС.
□ Так как ординаты вершин А и В равны, то АВЦОх (рис. 5.1). Из трех
отрезков ОА, АВ и ОВ сторонами параллелограмма могут быть только О А и АВ,
так как по условию ОВ — диагональ; поэтому ВС ДОЛ и С (5; 0). По формуле (5.1)
находим ОВ-^+б2»^100- ЯС=Л/(5-3)2+(0-б)2=>/40; значит, ОВ:АС=
=>/100:-J— искомое отношение диагоналей.
Согласно формуле (5.3), уравнение стороны ОА имеет вид y^kx+q, где
£=6:3=2 и 7=0; следовательно, у=2х. Используя равенство (5.7), запишем
уравнение стороны АВ: у=6. Далее, так как ВС^ОА, то угловой коэффициент
прямой ВС в силу формулы (5.8) есть к=2, а соответствующее значение q найдем
108
из уравнения y^lx+q, подставив в него вместо х и у координаты точки С (5; 0);
тогда получим 0«= 10+<?, т. е. q— —10; значит, уравнение ВС имеет виду~2х—10.
Наконец, уравнение ОС есть у=0.
Чтобы найти уравнение диагонали АС, воспользуемся тем, что точки А (3; 6)
и С (5; 0) принадлежат прямой АС я, следовательно, их координаты удовлетворя-
ют искомому уравнению. Подставив эти координаты в уравнение kx+q,
получим 6=3fc+^, 0=5fc+?, откуда А:= —3, ?«= 15. Итак, у= — Зх+15 есть уравне-
ние диагонали АС. Н
Пример 2. Составить уравнение окружности, описанной около треугольника,
образованного прямыми у=0,2х— 0,4, у=х+2, у=3~х.
□ Угловые коэффициенты прямых у=х+2иу=8—х равны соответственно
= 1 и к2 = — 1. Так как kJc,^ — 1, то выполняется условие (5.9) перпендикуляр-
ности прямых; значит, Д ЛВС — прямоугольный (рис. 5.2) и центром окружности
является середина его гипотенузы АВ. Найдем точки пересечения прямой
у=0,2х—0,4 с прямыми у=х+2 и у—3—х; решив системы уравнений
(у = 0,2х—0,4, (у = 0,2х—0,4,
(у = х+2 (у = 8-х,
получим точки Л(—3; —1) и В(7; 1) —концы гипотенузы. Используя формулы
(5.2), найдем координаты центра окружности: Oi(2; 0). В силу формулы (5.1)
радиус окружности есть R=O,A=-J(—3—2)2 + (0—l)2=^/26. Наконец, согласно
формуле (5.11), получим искомое уравнение окружности: (х— 2)2+у2 = 26.
Пример 3. Найти единичный вектор, коллинеарный вектору, направленному
по биссектрисе угла ВАС треугольника АВС, если заданы его вершины: Л(1; 1; 1),
В(3; 0; 1), С(0; 3; 1).
□ Найдем координаты и модули векторов ~АЁ и ~аС\ имеем АЙ(2; — 1; 0),
ЙГ(-1; 2; 0), |a5| = vZ22 + (-I)2 -+02 = л/5, |лЕ|=а/(-1)2 + 22 + 02 = лД
Так как |АВ| = |ЛС|, то АВ=АБ+АС является диагональю ромба ABDC (рис.
5.3), а следовательно — биссектрисой угла ВАС. Имеем AD=AB+AC=(2; — 1;
0)+(—1; 2; 0)=(1; 1; 0) и \AD\^-j2. Пусть ё — единичный вектор, сонаправлен-
_________________ _ AD
ный с вектором AD, т. е. Тогда, используя формулу (5.18), окончательно
_/ ! 1 \
получаем е I —-=; —^=; 0 ).
Xyj2 s/2 /
Пример 4. Прямая, параллельная медиане СМ треугольника АВС, пересекает
прямые ВС, СА и АВ соответственно в точках А2, Bt и Сг Доказать, что
Afc+ST7+С5.
Рис. 5.3 Рис. 5.4
109
□ Пусть А^Е^СМ (рис . 5.4). Построим ТБ=2СЛ/=^?+СВ. Очевидно, что
A1CDE — параллелограмм; следовательно, А1ё=ТБ, причем AiE=AlCi+ClE.
Так как AM — медиана треугольника ACD и B^CD, то АС\ — медиана
треугольника ABtE и Л1С1 = <?1£. Теперь имеем ТА+ТВ=ТБ=А1Ё^
Пример 5. Даша два ненулевых вектора а и Ъ таких, что |п+5|=|а—5|.
Доказать, что аА.Ъ.
□ I способ. Если на векторах а иЪ как на сторонах построить параллелог-
рамм, то векторы а+Ъ и а—Ъ совпадут с его диагоналями, длины которых
составляют |п+Б| и |п—2>|. Так как по условию длины диагоналей равны, то
полученный параллелограмм является прямоугольником, откуда д±2>.
II способ. Пусть х=п+Б, у=а—Ъ; тогда х2=(а+1)2=а2+й5+Б2,
у2=а2 —2аЬ+Т>2. Квадрат вектора равен квадрату его модуля; значит,
а2 + 2аЬ+Ъ2={а+Ъ\2 и а2— 2дБ+Р = |о— Ъ\2.
Правые части последних соотношений равны по условию; следовательно,
а2+2аБ+1>2=а2—2аЪ+Ъ2, откуда п5=0; в силу формулы (5.22) это означает, что
а±5.
Пример 6. Даны два отрезка АВ и CD. Доказать, что если
AC2+BD1=AD2+BC2, то ABJ-CD. Верно ли обратное утверждение?
□ Рассмотрим векторы АВ, ТБ, "АС, АБ, ВБ и ВС. В зависимости от их
взаимного расположения может получиться плоская или пространственная фигу-
ра (рис. 5.5). Учитывая, что ВВ2 —(BBl^AB2, преобразуем данное равенство
следующим образом:
ВБ2 -ВС2 = AD2-A&./^-BCjfBD+ВС)=(%Р-Л£)(ЛД+ЛС);
CD CD
T5(B5—AD+BC-AC)=O; -IAS ТБ~0;аВ ТБ=0,
-лв -лв
а это и означает, что ЛВ1.ТБ.
Выполняя преобразования «от конца к началу» (АВ ТБ=0 или
—2ЛВ ТБ=0 или ТБ(ВБ+~ОА+ВС+Та)=0 и т. д.), убеждаемся в том, что
верно и обратное утверждение.
Пример 7. В пирамиде SABC все грани — правильные треугольники; точка
М — центр треугольника АВС, а точка Р делит ребро SC пополам (рис. 5.6).
Найти разложение вектора iiP по векторам АВ, ВС и BS.
ПО
□ Имеем A/.P=A/C—Тс, где "PC=- 33=- (лС—ЛЗ); следовательно,
2 2
MP~MC- (лС—ЛЗ). Теперь найдем МС. В равностороннем треугольнике АВС
2 2
имеем MC—-CN, где CN — высота треугольника; поэтому МС=- NC. Но
1 2 / 1 \ 2 1
ЯС=ЛС-ЛЯ=лг— AS и, значит, J7C=- ( AC— aS )=- A?— AS.
2 3\ 2 J 3 3
Таким образом, окончательно получим
AC-- AS-- АС+- лЗ=- A?-- AS+-AS.U
3 3 2 2 6 3 2
-aS
Пример 8. Доказать, что для всякого треугольника АВС справедливо неравен-
ство cos А+cos В+ cos 3/2.
□ На сторонах треугольника построим единичные векторы е3, ё2, ё3 (рис.
5.7). Суммой этих векторов является некоторый вектор 2, т. е. ё1+ё2+ё3=Э.
Возведем обе части равенства в квадрат:
ё^ +ё^ +ё3 + 2ё3ё3 + 2e^3 + 2ёаё3 =?
или
1 + 1 + 1 +2 cos (л—В)+2 cos (л—Л)+2 cos (я—С)=|2|2-
Так как [2|2>0, то 3—2 cos В—2 cos Л — 2 cosC>0, откуда cos А+cos В+
+ cos С <3/2.
Пример 9. Дан куб ABCDAJiC^i, плавя, ребра которого равна а. Найти
радиус сферы, проведенной через точки А, В, Е и F, где Е и F — точки на ребре
СС1г причем CE=‘EF=FC1.
□ Введем систему осей координат (рис. 5.8), началом которой является
точка ДО; 0; 0). В этой системе точки А, Bv Е и F имеют следующие координаты:
А(а; 0; 0), ВДО; 0; а), ДО’ а; а/3), ДО; а; 2а/3). Пусть О(х; у; z) — центр искомой
сферы. Тогда OA2—OB2 = OE2 = OF2=R2, где R— радиус сферы. Используя
формулу (5.13), выражающую расстояние между двумя точками, получим систе-
му уравнений
(x-a)2+y2+z2=R2, (*)
x2+y2+(z-a)2=A2, (**)
111
х1 + (у—a)2+(z~- 1 -A2,
(...)
x1 + (y—a)2+( z—-) —A2.
(....)
/ aV / 2a\2
Вычитая уравнение (****) из (***), имеем I z—) — I z——j =0, откуда
2z—a=0, т. e. z=aft.. Подставим это значение z в уравнения (*) и (**) и вычтем
(**) из (*); тогда получим х=а/2. Вычитая уравнение (***) из (**), находим
у=7а/18. После_подстановки значений х; у и z в уравнение (**) окончательно
найдем R=a-Jl\ 1/18.
5.001. Дана окружность х2+у2 = 4. Составить уравнение прямой /,
параллельной оси абсцисс и пересекающей окружность в таких точках
М и N, что MN= 1.
5.002. Даны три точки А(2; 1), В(3; —1), С(—4; 0), являющиеся
вершинами равнобедренной трапеции ABDC. Найти координаты точки
D, если AB=kCD.
5.003. Даны вершины треугольника: А(—2; —3), В(— 1; 2), С(4; 1).
Доказать, что ДЛВС — равнобедренный, и составить уравнение пря-
мой, содержащей высоту, проведенную из вершины А.
5.004. В прямоугольной системе координат изображена равнобед-
ренная трапеция с основаниями 6 и 10
и углом <р = 60° при основании (рис. 5.9).
У ‘ Составить уравнения сторон трапеции.
С в 5.005. Составить уравнение окру-
/< жности, проходящей через точки А(2; 0),
\ В(5; 0) и касающейся оси Оу.
\ 5.006. Составить уравнение прямой,
-----------—проходящей через точку (2; 3) и образу-
0 А * ющей с осью Ох угол 120°. Найти пло-
рис 5 9 щадь треугольника, образованного этой
прямой и осями координат.
5.007. На прямой 5х — 2у+9 = 0 най-
ти точку А, равноудаленную от точек В(—2; —3) и С(4; 1), и вычислить
площадь треугольника АВС.
5.008. Длины диагоналей ромба равны 15 и 8 см. Первая диагональ
принята за ось Ох, вторая — за ось Оу. Составить уравнения сторон
ромба и найти расстояние от начала координат до стороны ромба.
5.009. Пусть А—точка пересечения прямых 2х+5у—8 = 0
и х — Зу+4=0; О — начало координат. Найти расстояние О А и со-
ставить уравнение прямой О А.
5.010. Найти координаты вершин С и D квадрата ABCD, если
А(2; 1), В(4; 0).
5.011. Вычислить длины диагоналей АС и BD параллелограмма
ABCD, если Л(1; -3; 0), Д(-2; 4; 1), С(-3; 1; 1).
5.012. Даны две вершины равностороннего треугольника: А(—2; 2),
В(—2; —4). Найти координаты третьей вершины треугольника и его
площадь.
5.013. Известны координаты середин сторон треугольника:
Af/—1; 2), А/2(2; -3), М3(—3; —1). Найти координаты точки пересече-
ния медиан треугольника.
112
5.014. Даны координаты двух вершин треугольника: Л (2; — 1),
В(—3; 5) и координаты точки пересечения медиан этого треугольника:
М(1; 1). Найти координаты вершины С.
5.015. Даны координаты вершин четырехугольника: А(2; —2),
В( — 3; 1), С(7; 7), D{1; 1). Доказать, что ABCD — трапеция, и найти
длину ее средней линии.
5.016. Убедиться в том, что существует только одна точка с коор-
динатами х, у, z, сумма квадратов расстояний от которой до данных
двух точек Л(2; 3; —1), Д1; —1; 3) постоянна и равна 16,5. Найти
координаты этой точки.
5.017. В окружность х2+у2 = /?2 вписан квадрат ABCD. Найти
R и координаты вершин В. С и D, если (5; —12) — координаты
вершины А.
5.018. Дана окружность х2+у2 = 9. Составить уравнение окружно-
сти, проходящей через начало координат и точку Л(1; 0) и касающейся
данной окружности.
5.019. Составить уравнение окружности, проходящей через точку
А(2; 1) и касающейся осей координат.
5.020. Составить уравнение окружности, вписанной в треугольник,
стороны которого лежат на прямых х = 0, у=0 и Зх+4у —12=0.
5.021. Найти длину хорды, образующейся при пересечении прямой
х+у—5 = 0 и окружности (х+1)2 + (у+2)2 = 40.
5.022. Составить уравнения касательных, проведенных к окружности
х2+},2 = 9 из точки ЛГ(5; 0).
5.023. Составить уравнение окружности, описанной около треуголь-
ника, образованного прямой Зх—у+6 = 0 и осями координат.
5.024. Составить уравнение сферы, проходящей через точку
Л(1; —1; 4) и касающейся координатных плоскостей.
5.025. При повороте вокруг начала координат точка Л(6; 8) перехо-
дит в точку j4j(8; 6). Найти косинус угла поворота.
5.026. Даны точки Л(1; 1), В(6; 6), С(5; 4), Z>(2; 1). Доказать, что
ABCD — трапеция, и найти угол а между ее диагоналями.
5.027. Доказать, что треугольник с вершинами А (2; 1), В(3; 0), С(1; 5)
тупоугольный, и найти косинус тупого угла.
5.028. Найти угол между векторами а и Ъ, если (а—Ъ)1 + (23 — З)2 = 56,
|3| = 2 и |3| = 3.
5.029. Даны векторы 3(2; —3; 5), 3(—1; 1; —3) и с(3; 7; 1). Найти
координаты вектора р(х; у; z), если рЗ= 12, рЪ= —би pic.
5.030. Найти косинус угла между диагоналями параллелограмма
ABCD, если ЛБ=3—З + Зс, ЯД = 43—Ъ—с, где а,Ъ,с — единичные попа-
рно перпендикулярные векторы.
5.031. Пусть 7, j и Тс — единичные векторы, направленные вдоль
координатных осей, и 3=6г—2/—3£. Найти косинусы углов, образуемых
вектором 3 с векторами Т, j и Тс.
5.032. Вектор ТТЛ составляет с осями Ох, Оу и Oz углы, соответст-
венно равные а=я/3, /?=я/3, у = я/4; точка В имеет координаты
(—2; —2; —2^2). Найти угол между векторами 7Д? и 7ТВ.
5.033. Медианы боковых сторон равнобедренного треугольника пе-
ресекаются под углом 60°. Найти угол при вершине треугольника.
5.034. В окружности проведены радиусы ОА, ОВ, ОС. Найти вели-
чину угла АОВ, если ТГА+TJB= ОС.
113
5.035. Дан треугольник ABC; BD— медиана, LDBC=9Q°, BD=
= (>/з/4)ЛВ. Найти LABD. __
5.036. В треугольнике АВС угол при вершине А равен 60°, АВ (4; 2; 4),
АС— 1. Найти косинус угла между медианой AAt и стороной АВ.
5.037. В трапеции ABCD дано: вершина Л(3; 0), середина основания
АВ — точка Е(6; — 1), середина основания CD — точка /(7; 2). Боковая
сторона ВС параллельна оси Оу. Доказать, что трапеция равнобедрен-
ная, и найти угол при ее основании.
5.038. Доказать, что луч СМ, где С — вершина прямого угла тре-
угольника АВС, а М — центр квадрата, построенного на гипотенузе
и лежащего вне его, есть биссектриса угла С.
5.039. В правильной четырехугольной пирамиде SABCD длина каж-
дого ребра равна а. Точка MeSC и SM:MC=2: 1. Найти угол между
векторами 7JC и AM.
5.040. В прямоугольном параллелепипеде ABCDA^B^C^Di дано:
A4j = 10, AD = 6, АВ=8. Найти косинус угла между векторами DBr
и AD}.
5.041. Дан куб ABCDAyB^jD,. Найти косинус угла между век-
торами ТЕ?! и DM, где М — середина ребра ССГ
5.042. Известны длины ребер тетраэдра ABCD. Найти косинус угла
между противолежащими ребрами АВ и CD.
5.043. Даны векторы д(6; —8; 5^/2) и 5(2; —4; ^2). Найти угол,
образуемый вектором а—Ъ с осью Oz.
5.044. Даны вершины треугольника: А(—2; 1; —3), В(4; — 7; 1) и
С(1; 2; —1). Найти угол между стороной СА и медианой, проведенной из
вершины С.
5.045. При каких значениях х векторы (х3 — 1)а и 2ха сонаправлены,
если д#0?
5.046. При каких значениях т векторы (т2-гт—2)Ъ и т3Ъ проти-
воположно направлены, если 5^0?
5.047. При каких значениях х векторы (5х— х2)а и а сонаправлены
и |(х — 5)о|<|3а|, если 3^0?
5.048. При каких значениях у_векторы (Зу2 — 11у+6)р и (у2 + 1)р
противоположно направлены, если
5.049. При каких значениях х и у векторы (х; —2; 5) и (1; у; —4)
коллинеарны? _ _
5.050. При каких х верно неравенство |(х—2)а|>3[д|, если
5.051. Даны координаты вершин четырехугольника: А(— 1; 2; 3),
.В(—1; 3; 1), С(—1; 7; 3), Z>(—1; 6; 5). Доказать, что ABCD—пря-
моугольник.
5.052. Найти вектор Ъ, коллинеарный вектору ^(2^/2; —1; 4), если
!5|=10.
5.053. Пусть О — точка пересечения медиан_ треугольника АВС
и Я(2 = й, АС—Б. Разложить АЕ и ЕС по векторам а и Ъ.
5.054. Медианы граней SAB и SAC тетраэдра SABC пересекаются
соответственно в точках MnN. Доказать, что MN\\EC, и найти отноше-
ние |A/jV| : |БС|.
5.055. Пусть К и М — середины сторон ВС и CD параллелограмма
ABCD и ЛХ=а, АМ=Ъ. Выразить векторы ED и ED через а и Ъ.
5.056. В параллелограмме ABCD дано: МеВС и ВМ.МС=Л :2;
NeDC, ZW:JVC= 1:2; Ам=а; AN—Ъ. Выразить векторы ЛВ, AD, MN
и ЕВ через а и Ъ.
114
5.057. В треугольнике АВС дано: ЛВ=а, ZC=5, |Б| = |Б| = 2,
L ВАС—60°. Выразить через аяЪ единичный вектор, направленный по
высоте треугольника, проведенной из вершины А.
5.058. Векторы а, Ъ, с лежат в одной плоскости и образуют попарно
друг с другом углы 2я/3. Разложить вектор а по векторам Бис, если
|д| = 3, |Б|=2, |с)=1.
5.059. Дан прямоугольный треугольник АВС; Z.C=90°, D— осно-
вание высоты, проведенной из вершины прямого угла. Выразить вектор
UZ5 через векторы О и ТВ.
5.060. Дан правильный пятиугольник A1A1A3A4AS. Разложить век-
тор А^А3 по векторам AtA2 и
5.061. К окружности с центром О проведены из точки М две каса-
тельные; А я В — точки касания. Разложить вектор МО по векторам МА
и МВ, если [_ АМВ=а.
5.062. На стороне АВ параллелограмма ABCD взята точка К так,
что АК:КВ=1. Сторона АВ в 3 раза длиннее стороны ВС. Разложить
ТУК по ZB и АТУ и найти отношение DK: АВ, если [_ BAD=60°.
5.063. В ромбе ABCD точки М и N — середины сторон ВС и CD.
Найти LMAN, если i_BAD=6D°.
5.064. Найти угол между медианами катетов равнобедренного пря-
моугольного треугольника, обращенный к гипотенузе.
5.065. Дан правильный пятиугольник ABCDE. Разложить векторы
АВ и АЕ по векторам АС и АТУ.
5.066. Найти длину биссектрисы AM треугольника АВС, если АВ= с,
АС=Ь и LA = a.
5.067. Точки М и N— середины отрезков АВ и CD. Доказать, что
MN^ (AC+BD), MN^ (BC+AD).
5.068. Дан треугольник АВС; М — точка пересечения его медиан.
Доказать, что ОМ<- (ОЛ + ОВ+ ОС), где О — произвольная точка про-
странства.
5.069. В тетраэдре ABCD медиана DD3 грани ADB делится точкой
М в отношении DM: MDt = 3:7. Разложить вектор СМ по векторам СА,
~СВ и ТПУ. _____ _
5.070. Дано: прямая треугольная призма АВСА^В^С^ ВВ^а,
ВС=Ъ и ВА==с; О — точка_пересечения медиан треугольника АВС.
Разложить А,О по векторам а,Ъяс.
5.У1У. Ребро куба ABCDA^B^C^D^ равно 1. Найти угол между век-
торами MN и DC, если MeAAj я АМ:МА1 = 1:2; УеСС2
nCN.NC^l-A.
5.072. Дан прямоугольный параллелепипед ABCDA^iC^D^; AD=a,
DC=b, DD,=c. Найти острый угол между прямыми BDt я A3D.
5.073. Дан тетраэдр ABCD я точка М в плоскости его грани АВС.
Доказать, что для разложения DM = аТУА+роВ+уТУС выполняется раве-
нство a+fl+y= 1.
5.074. В тетраэдре О АВС плоские углы трехгранного угла при вер-
шине О — прямые. Точка Н — основание перпендикуляра, проведен-
ного из вершины О к плоскости грани АВС. Разложить вектор ОН по
векторам ОА, ТУВ я ОС, если ОА=а, ОВ=Ь, ОС—с.
5.075. При каких значениях а и fl вектор а(3; — 1; а) перпендикулярен
вектору Б(2; fl; 1), если |Б| = 3?
115
5.076. Даны три вектора а, Ъ, с. Доказать, что вектор (Бс)д—(ас)Б
перпендикулярен вектору с.
5.077. Доказать, что треугольник с вершинами А(6; —4; 2), В(3; 2; 3),
С(3; — 5; — 1) прямоугольный. __________ _
5.07& Даны единичные векторы т, п и р такие, что т±л, nip и угол
между т_я_р равен _60*\ Найти скалярное произведение векторов
а=3т—2л+р ио= —2т+п—р.
5.079. В треугольнике ЛВС дано: /ЕВ=4? 4-2/, 7С=3?4-4/, где
i и) — единичные взаимно перпендикулярные векторы. Доказать, что
треугольник АВС прямоугольный, и вычислить его площадь.
5.080. Стороны треугольника АВС связаны соотношением
а24-62 = 5с2. Доказать, что две медианы треугольника перпендикулярны.
Верно ли обратное утверждение?
5.081. На сторонах ВС, СА и АВ равнобедренного прямоугольного
треугольника АВС (ДС=90°) даны соответственно точки Я1( Вг, Сг.
Доказать, что отрезки СС, и А1В1 перпендикулярны и равны, если точки
Аг, Bt, С, делят стороны треугольника по обходу в равных отношениях.
5.082. В треугольнике АВС дано: АВ=ВС; D — середина стороны
AC; DK перпендикулярна ВС; точка М — середина отрезка DK. До-
казать, что прямые АК и ВМ перпендикулярны.
5.083. Даны вершины треугольника: ЛГ(1; 1; 4), ЛГ(1; 4; 4) и Х(3; 3; 2).
Доказать, что TFN1.MK, где О — середина стороны МК. Определить вид
треугольника.
5.084. Даны два вектора сЕ?( — 1; 2) и 77В(—4; —2), где О — начало
координат. Найти длину отрезка АВ, площадь треугольника О АВ и дли-
ну медианы ОМ. _
5.085. Дан вектор д(1; —2; 5). Найти координаты вектора Ъ, лежаще-
го в плоскости хОу и перпендикулярного вектору а, если |15|=2\/5.
5.086. Найтн _ единичный вектор, перпендикулярный векторам
a=i+/+2l и i=2i+J+H.
5.087. Доказать, что если биссектрисы двух плоских углов трехгран-
ного угла перпендикулярны, то биссектриса третьего плоского угла
перпендикулярна каждой из них.
5.088. Дано: куб ABCDAIB1C1D1 (вершины основания ABCD рас-
положены по ходу часовой стрелки); К — середина ребра AAl; Н— се-
редина ребра AD; М — центр грани CCiDtD. Доказать, что прямая КМ
перпендикулярна прямой В JI.
5.089. Найти объем треугольной пирамиды, построенной на век-
торах ШГ, ТТВ и ОС, если |ОЛ| = 5, |(ТВ|=2, [UC| = 6, ОЛ • ТТВ=0,
О А • ОС~0, Ов ОС=8.
5.090. Пусть l.j.Ti — единичные векторы, направленные вдоль коор-
динатных осещ и a=2i+y+3afc, "B=a2i+4J— ЗТс. Прн каких значениях
а векторы а и Ъ перпендикулярны?
5.091. В треугольнике АВС точка N лежит на стороне АВ
и AN=3NB\ медиана AM пересекается с CN в точке О. Найти АВ, если
AM=CN=~! см и LNOM=60°.
5.092. В ромбе ABCD длина стороны равна 6, а величина угла BAD
равна я/3. На стороне ВС взята точка Е такая, что ЕС=2. Найти
расстояние от £ до центра симметрии ромба.
5.093. В параллелограмме ABCD точка К — середина стороны ВС,
а точка М — середина стороны CD. Найти AD, если АК=6 см, АМ=3
сми LKAM=60°.
5.094. Найти длину медианы AM треугольника АВС, если АВ= 10
см, АС=6 см и /_ ВАС =60°.
116
5.095. Даны два вектора: а(х; 1; — 1) и 3(1; 0; 1). При каком значении
х справедливо равенство (а+ЗЗ)2 = (а—23)2?
5.096. Дан треугольник АВС; АВ=4 см, ЛС=8 см, L ВАС-60°.
Найти длину вектора TN, где NeBC и BN: NC=3:1.
5.097. В куб вписана сфера. Доказать, что сумма квадратов расстоя-
ний каждой точки сферы до вершин куба не зависит от выбора этой
точки. Найти эту сумму.
5.098. В квадрат вписана окружность. Доказать, что сумма квад-
ратов расстояний точки окружности до вершин квадрата не зависит от
выбора этой точки. Найти эту сумму.
5.099. Около квадрата описана окружность. Доказать, что сумма
квадратов расстояний точек окружности до вершин квадрата не зависит
от выбора этих точек. Найти эту сумму.
5.100. Дан прямоугольник ABCD. Доказать, что сумма квадратов
расстояний любой точки пространства до вершин А и С равна сумме
квадратов ее расстояний до вершин Ви D.
5.101. Доказать, что в прямоугольном параллелепипеде
ABCDA^iC^^ сумма квадратов расстояний любой точки пространст-
ва до вершин A, Bit CeDt равна сумме квадратов ее расстояний до
вершин At, В, С1 и D.
5.102. В окружность вписан треугольник АВС. Прямая, содержащая
медиану СС, треугольника, пересекает окружность вторично в точке D.
Доказать, что СЛ2 + СВ2 = 2СС1 CD.
5.103. Даны векторы д(2; —1; 3), 3(1; —3; 2), с(3; 2; —4). Найти
вектор х, если ха— —5, хЗ= —11, хс = 20.
5.104. Даны векторы д=(3; 2; 2)_и З=(18; —22; — 5). Найти вектор х,
если он перпендикулярен векторам а и 3, образует с осью Оу тупой угол,
а его длина равна 14.. ___ ____
5.105. Найти скалярное произведение векторов АК и BL, если АК
и BL — медианы равнобедренного треугольника АВС, площадь которо-
го равна S, а 4 Л = 120°.
5.106. В равнобедренном треугольнике АВС с площадью S проведе-
ны высоты AM и BN. Найти скалярное произведение AM BN при
условии, что точки М и N лежат на боковых сторонах треугольника,
а длина его основания равна с.
_ 2/и 1 — т2
5.107. Пусть вектор а имеет координаты ----- и -----, а вектор
1 +т 1 +т2
l—k2 2k
3 — координаты —— и ——. Доказать, что оба вектора единичные:
1 + кг 1 + кг
|а| = |7>|= 1. Используя свойство скалярного произведения |а -3|<|а| |3|,
1 (т+к)(1— тк) 1
доказать справедливость неравенства — ---———
5.108. Найти модуль проекции вектора а(7; —4) на ось, параллель-
ную вектору 3(—8; 6).
5.109. Доказать, что для любых четырех данных точек А, В, С,
D имеет место равенство АВ CD + AC ~DB+AD ВС=0.
5.110. Доказать, что если суммы квадратов противоположных ребер
тетраэдра равны, то эти ребра попарно перпендикулярны.
5.111. Доказать, что если в тетраэдре ABCD противоположные реб-
ра попарно перпендикулярны, то АВ2 + CD1 = АС1 + BD2 = AD2 + ВС2.
5.112. Дан пятиугольник ABCDE; точки М, N, Ра Q — середины его
117
сторон АВ, ВС, СР и DE. Доказать, что если U и V — середины МР
и NQ, то вектор 7JV коллинеарен вектору ТЕ. Найти отношение АЕ: UV.
5.113. В окружность с центром О вписан четырехугольник ABCD,
диагонали которого, пересекающиеся в точке Р, взаимно перпендикуляр-
ны. Доказать, что середины сторон АВ и CD, центр О и точка Р являют-
ся вершинами параллелограмма.
5.114. Доказать, что сумма квадратов длин всех ребер параллелепи-
педа равна сумме квадратов длин всех его диагоналей.
5.115. Даны точки А 2(0; 1; 2), Л2(1; 2; 4), Bt(—1; -1; 3), Я2(1; 0; 0); М3
и Мг — середины отрезков АгВ1 и АгВг. Найти вектор Л/1Л/2 и его
модуль.
5.116. Даны вершины треугольника: А(— 1; 1); В(—5; 4) и С(7; 2).
Найти скалярное произведение ТБ ТС и площадь треугольника.
5.117. Даны три ненулевых вектора а, Ъ, с, каждые два из которых
неколлинеарны. Найти их сумму, если (д+5)||с и (5+с)||а.
5.118. Дан параллелограмм ABCD; ТБ\\ЕС, К — середина ВС,
Р — середина DC. Выразить сумму векторов ТБ и ТУБ через векторы
АК=а и ТР=Ъ.
5.119. Единичные_ векторы ё1д ё2, ё3 удовлетворяют условию
ё2 +ё2+е3 =0. Найти ёгё2 +ё2е3 Ч- <ё3ё2.
5.120. Дана неплоская замкнутая линия ABCD. Доказать, что если
LABC= LDAB=90° и DA = CB, то LADC= LBCD.
5.121. Найти отношения, на которые точка Р пересечения биссектрис
треугольника АВС делит каждую биссектрису, если ВС=а, СА — Ь,
АВ=с. ''
5.122. Объем треугольной пирамиды, построенной на векторах ТУТ
ТУБ и 7JC, равен 5. Определить длину вектора 7JU, если ТУТ ТУВ= 1,
ОТ (7С=0,ОТ UC=0, |ОТ| = |ОТ|=2.
5.123. Объем треугольной пирамиды, построенной на векторах ТУТ,
ТУБ и ТУС, равен л/з/3. Определить ТУТ ТУС, если |77В| = 2, |(м|= 1,
|UC|=3, ТУБ ОТ=0, ТУБ ТУС=*Ъ.
5.124. Найти объем треугольной пирамиды, построенной на век-
торах ОТ, ОТ и UC, если |ОТ| = |ОТ| = |ОС| = 5, ОТ • ОТ=0,ОТ • ОС=0,
ТУБ UC—20.
5.125. На плоскости заданы точки А(~6; —1), В{—4; —4),
С(—1; —6), D(—3; —3). Доказать, что ABCD — ромб, и вычислить его
5.126. Дан треугольник АВС; ТВ БС=8, \АВ\ = 10, |ДС] = 6. Найти
длину высоты, опущенной из вершины В. Является ли угол АВС острым
или тупым?
5.127. Даны вершины тэтраэдра: Л(3; —2; 1), В(3; 1; 5), С(4; 0; 3), D(0;
0; 0). Медианы граней ADB и BDC пересекаются в точках Mi и М2.
Найти отношение АС: МхМг.
5.128. Даны координаты вершин пирамиды: 5(0; 0; 2), А(0; 0; 0),
5(1; 0; 0), С(0; 1; 0). Найти координаты точки М, лежащей на оси Oz,
и координаты точки N, лежащей в плоскости SBC, если известно, что
1017(1/3; 1/3; 0).
5.129. Доказать, что для всякого треугольника АВС выполняется
неравенство cos 2А+cos 2В+ cos 20 — 3/2.
5.130. Дан треугольник АВС. Прямая / пересекает прямые ВС, СА,
АВ в точках At, Bt, Cf. Доказать, что векторы ТВ+А1В1, БС+В^,
СТ+С1А1 коллинеарны.
118
ПРИЛОЖЕНИЯ
ВАРИАНТЫ ЗАДАНИЙ
ДЛЯ САМОПРОВЕРКИ
Требуемые вычисления следует производить, не пользуясь техническими
средствами: калькулятором, счетной линейкой, таблицами и т. п.
Вариант I
1. Упростить выражение
и найти его значение при х=7.
( п
2. Найти tga, если tg I a—
\ 4
3. Решить уравнение 4'~‘—3 • 2*"2=1.
4. Найти /(я/4), если Дх)=2у/2 sin3 х.
5. Основание равнобедренного треугольника равно 30, а высота, проведенная
к боковой стороне, равна 24. Найти длину боковой стороны. _________
6. Найти сумму корней уравнения Дх)+4/’(х)=0, еслиДх)=д/х2—6х+10.
пх
7. Найти произведение корней уравнения cos2 — = 1, принадлежащих отрезку
2
[я, Зя].
8. Найти целое число, удовлетворяющее системе неравенств
log1/2(2x-3)> —3,
х2—4х>0.
9. Из точки, отстоящей от плоскости на расстояние 5у2, проведены две
наклонные, образующие с плоскостью углы в 45°, а между собой угол 60°. Найти
расстояние между основаниями наклонных.
10. Вектор а(х; —1; 2) перпендикулярен вектору У(1; 2;0). Найти модуль
вектора а.
Вариант II
1. Вычислить (4-025-2|,'4 5Х4_аи + (25/2)1'э)-
2. Вычислить значение выражения х—y+2z, если х+у=4, y+z=S, x+z=6.
' 1
3. Решить уравнение — lg2=lg(21/x—2).
4. Сколько корней уравнения sinx+cos2x=0 находится на отрезке [—я, Зя]?
5. Дано: tga=3/4; 0<а<л/2. Вычислить значение выражения 25 sin2 a cos a.
119
6. Найти длину отрезка, на котором выполняется неравенство у х+у/х£ 6.
7. Сколько раз пересекает ось абсцисс график функции Дх)—х’+3х2 + 5х?
8. Сумма седьмого и одиннадцатого членов арифметической щюгрессии
равна 10, а сумма пятого и десятого членов равна 1. Найти сумму 20 первых
членов.
х Г
9. Вычислить/(1), еслиДк)-—-----Jx.
зг + 1
10. Боковая сторона равнобедренной трапеции в 3 раза длиннее меньшего
основания. Биссектрисы тупых углов этой трапеции пересекаются в точке, лежа-
щей на основании. Найти отношение площади трапеции к площади треугольника,
образованного меньшим основанием и биссектрисами.
Вариант III
1. Решить уравнение ^/Зх+1 — \J х— 1 =2.
2. В треугольнике с основанием 15 см проведен отрезок, параллельный
основанию. Площадь полученной трапеции составляет 75% площади треуголь-
ника. Найти длину этого отрезка.
3. Упростить выражение
sin(60° + а)
(а\ / а\
15°+- I sin [ 75° — )
4/ \ 4/
/ а\
а затем найти его значение, если sin 30°-I— 1=0,8, 0°<а<90°.
\ 2/
4. Решить уравнение lg2(100x)—lg2(10x)+lgx=9.
5. Найти наименьшее из отрицательных решений неравенства
6. Сколько корней, не превосходящих по абсолютной величине л, имеет
, /Зя \
уравнение 1+ctg2 —|-х |=cos x-sin*x?
\ 2 /
/7V*~3
—1-1 =0.
8. Отношение среднего арифметического двух положительных чисел к сред-
нему геометрическому этих чисел равно 13/12. Найти отношение большего из
заданных чисел к меньшему.
/ Зя\
9. Дано: cos За=2/3. Вычислить значение выражения 81 cos2 ( ба—— 1.
10. Доказать, что функция Дх)=sin2 2х+0,5 cos4x+2sin2x + cos2x принима-
ет одно и то же постоянное значение при любом значении х, и найти это значение.
Вариант IV
1. Вычислить значение А=2®— 10е, где В=1/1о^2, C=2/log210.
2. Найти значение х, удовлетворяющее уравнению
10х:$/2)2=2113 • 4-2/3 :^/б4.
3. Решить уравнение 2у/х—2—\5=у/х—2.
120
4. Найти наибольшее значение х, при котором верно неравенство
2х-5у/х + 2*£0.
S. Найти площадь равнобедренной трапеции, если ее высота равна 16, а диа-
гональ равна 20. 4^,, ,
6. Найти х в градусах, если 0°<х<270° и sin(90o+2x)+sinx—0.'
/ 5я\ а 1
7. Вычислить значение выражения 49:tg2 I а+— )> если “п
8. На двух станках требовалось обработать по 150 деталей, причем на
первом из них обрабатывали в час на 5 деталей больше, чем на втором. На
первом станке работа была начата на 1 ч позже, чем на втором, и, кроме того, она
была прервана на 30 мин. Однако на обоих станках работу выполнили к одному
и тому же сроку. Сколько деталей в час обрабатывали на каждом станке?
9. Решить уравнение
х2 5'/зх-2+,5?+"-5^3х”2+2 + х2 • 5х
6 — х х+3 х + 5
10. Решить уравнение--------------------.
1-х2 х(1—х) х(1+х)
Вариант V
1. В уравнении x2 + bx—12-0 один из корней равен 3. Найти значение
коэффициента Ь.
2. Упростить выражение (2xlil-y~ll*)(2xtt2+y~11*') и вычислить его значе-
ние при х~ 1,2 и у—4. 2
3. Найти сумму корней уравнения 2х ~3 4 5 6 7 5^~3 = 0,01 • (10х-1)1.
4. Решить уравнение 5/2,1х+1 «х-1.
5. Найти сумму целых значений х, удовлетворяющих неравенству х2-3х<4.
6. Используя формулы тождественных преобразований, вычислить
cos 50° сое 40°—2 sin 50° sin 20° cos 20°.
7. Найти наименьший корень уравнения 2 cos2x— 3 sinx—0, лежащий в ин-
тервале (0°, 90°). Ответ записать в градусах.
8. Площадь равнобедренной трапеции 180 см2. Длина средней линии равна
45 см; длина боковой стороны 5 см. Найти длину меньшего основания трапеции.
9. Высота конуса равна 3; угол между высотой и образующей равен 45°.
В этот конус вписан другой конус так, что его вершина совпадает с центром
основания первого конуса, а соответствующие образующие конусов перпендику-
лярны. Найти объем вписанного конуса (положить я»3,14 и округлить ответ до
сотых).
10. Вычислить/(я/2), если Дх)-0,5 sinx tg2x+2,5 cosx.
Вариант VI
4.J5-2J6
1. Вычислить —~
(Уз+У2)(УЗ-У2)
2. Решить уравнение 2х+ч/3х-2“3.
17 2
3. Найти число целых решений неравенства 5-1-<-.
х—2 х+3
4. Решить уравнение logsx+log5(x-4)-1.
5. В равнобедренной трапеции основания равны 24 и 10, а радиус описанной
около нее окружности равен 13. Найти высоту трапеции при условии, что центр
описанной окружности лежит вне трапеции.
6. Найти сумму квадратов наибольшего н наименьшего значений функции
Дх)—х’-Зх+Зх+2 на отрезке [-1, 2].
7. Найти число решений уравнения sin Зх-cos Зх-0 на отрезке [0, я].
121
8. Сумма четвертого и пятого членов геометрической прогрессии равна
20, а сумма третьего и четвертого членов равна 5. Найти шестой член этой
прогрессии.
9. Металлический шар радиуса переплавлен в конус, площадь боко-
вой поверхности которого в 3 раза больше площади основания. Найти высоту
конуса.
10. Решить уравнение 2(arcsinx)2+n2=3n arcsinx.
Вариант VII
1. Вычислить 7'
4—х 4
2. Найти все целые значения х, удовлетворяющие неравенству->1 —.
______ _____ х—5 х
3. Решить уравнение yjx3 4- 8 4-^/х3+8 = 6.
4. Найти корни уравнения 21+log»*4-4t+log2*=110.
5. Равнобедренная трапеция с основаниями 2 и 3 см н углом 60° вращается
вокруг меньшего основания. Найти объем тела вращения и записать ответ,
округлив его до ближайшего целого числа.
6. Сколько корней уравнения cos2 2x+cos2 6х=1 находится в промежутке
[-я/8, я/2]?
7. Найти координату середины отрезка, на котором справедливо неравенство
logo,i(x2-x+8)>-l.
8. Найти два числа, если их среднее арифметическое на 16 меньше большего
из этих чисел, а среднее геометрическое на 8 больше меньшего из них.
/5/2 cos а—2 sin(45°—а)\в
9. Упростить выражение I-------------т=----> .
\2 sm(60° + a)—л/з cos а/
10. Найти наименьшее и наибольшее значения функции у=\/х(1(>~х) в об-
ласти ее определения.
Вариант VIII
1. Решить уравнение ^х—4+7x4-24 = 14.
2. Упростить
а+у/^—Ь^ 4-Jа*—а2Ь2
—^7=----------~== ) : ’ “>Ь>0.
\a+-Ja2 —Ь1 (ЭД
3. Найти больший корень уравнения
lg2(100x)+lg2(10x)= 14+lg
х
4. Найти наименьшее положительное целое х, удовлетворяющее неравенству
yjofix<x-3>>0fi4.
5. Вычислить cos 2а, если tga=0,75.
6. Найти корень уравнения sinх—1=0,5 sin 2х—cosx, лежащий в интервале
0°<х<180°. Ответ записать в градусах.
7. В равнобедренном треугольнике высота относится к основанию как 3:4,
а боковая сторона равна 2>/39 см. Найти площадь треугольника.
8. Металлический цилиндр с диаметром основания rf=4 см и высотой Л=4
см переплавлен в шар. Вычислить радиус этого шара (считать 712 а: 2,3).
122
9. Число 26 разбить на такие два слагаемых, чтобы сумма их квадратов была
наименьшей.
10. Решить уравнение 0,125 4й 3
ОУ
Вариант IX
, _ (72-х/з)Ч27б
1. ВЫЧИСЛИТЬ-------------•
(V6 + 1)(V6-1)
2. Вычислить Зх+y+z, если x4-y4-2z=14, 2x4-y4-z=10, x4-2y4-z=12.
3. Решить уравнение log2(17—2Х)=4—х.
4. Вычислить значение 10х при x=lg 124-(log410)" *.
5. Дано: ctg2a = 3/4, 0<а<я/2. Найти cos2 а.
6. Сколько корней уравнения sinx4-cosx= 1,4 находится на отрезке [—я, Зя]?
7. Найти координату середины отрезка, на котором выполняется неравенст-
во 3 f/x+1 —Ух 4-1 >2.
8. Восьмой член арифметической прогрессии равен 2, одиннадцатый член
равен 11. Сколько членов прогрессии, начиная с первого, надо взять, чтобы их
сумма была равна 30?
9. Найти квадрат наибольшего значения функции Дх)=sin х 4- cos х.
10. Через вершину конуса проведена плоскость, составляющая с плоскостью
основания угол, косинус которого равен 1/3, и отсекающая на окружности основа-
ния дугу в 90°. Расстояние от центра основания до этой плоскости равно 2/Уя.
Найти объем конуса.
Вариант X
х-1 Зх 5
1. Решить уравнение---—------= —.
х 2х—2 2
2. Найти х в градусах, если 180°<х<360° и cos2(180°4-x)4-3 cos2(90°4-x) = 2.
3. Найти наибольшее значение х, при котором справедливо неравенство
х2 +4(7» - х)2 - 21« 0. _______ _________
4. Решить уравнение 2Узх+0,1 = зУзх+0,1 —1.
5. Разность длин оснований трапеции равна 14 см; длины боковых сторон
равны 13 и 15 см. Вычислить площадь трапеции при условии, что в эту трапецию
можно вписать окружность.
6. Моторная лодка прошла 60 км против течения реки и 60 км по течению,
затратив на путь против течения на 50 мин больше, чем на путь по течению.
Найти скорость течения реки, если скорость лодки в стоячей воде равна 21 км/ч.
7. Найти число х, если
</92 • (1/3)6 _ х
(Уз)"1 27-2/3 3(УЗ)4
8. Вычислить значение выражения 27 cos4 2a, если С05(Зя—4a) = 2/3.
9. Найти сумму и произведение корней уравнения
х2 • б-^+б^^х2 6^+62~x.
10. Вычислить значение А, если А =4’, где B=log25 +logl(<10.
123
Вариант XI
1. Найти число х, если
(х-1)(У9)3 92
%/27 • (1/3)3 (^9)3’
2. Решить уравнение 2*~1+2*_24-2*~3=448.
3. Решить уравнение lg(lgx)+lg(lgx3—2)=0.
4. Площадь равнобедренной трапеции, описанной около окружности, равна
32 см2. Найти длину боковой стороны, если угол при основании трапеции
равен я/6.
5. Найти синус большего острого угла прямоугольного треугольника, если
радиус окружности, описанной около треугольника, в 2,5 раза больше радиуса
вписанной окружности.
6. Упростить выражение
/Зя \ /Зя \
tg(n —a) tg I-1-а ] + яп(2я — а) cos (-На — соз2(я — а).
\2 / \2 /
7. Вычислить (O.OOl'83"1+O,01lg0'3+0'5) 2,7.
8. Ha ребре двугранного угла в 120° взят отрезок АВ=3 см; из его концов
в различных гранях к нему восставлены перпендикуляры АС=1 см и BD<=2 см.
Вычислить расстояние между точками С и D.
X
9. Дано: Дх)=----+2. Найти сумму корней уравнения Дх)=/"(*)-
2—х
10. Найти площадь треугольника, образованного отрезками осей Ох и Оу
и прямой, проходящей через точки (0; 4) и (4; 2).
Вариант ХП
1. Найти число 2х, если
*+5,5 /л Гъ (^3-л/2)(379 + Э7б + 374)
__(4+v2)--------------___------------.
2. Найти значение выражения х2+у2, если 2х+у=2, х+3у=3.
3. Решить уравнение log1/2(x— IJ+log^x+D-log^ (7 —х)= 1.
4. Сколько целых значений х удовлетворяет неравенству х2 + 8х<20?
5. Решить уравнение 2х+3.2*+2 = 6,5.
6. Найти значение выражения tg215°+4 tg60°.
7. Сколько корней уравнения sinx—sin 2x+sin Зх=0 находится в промежут-
ке [0, яр
8. Шестой член арифметической прогрессии в 4 раза меньше девятого члена,
а их сумма равна 20. Найти сумму девяти первых членов прогрессии.
9. Найти тачки экстремума функции Дх)=х In х.
10. Через вершины произвольного четырехугольника проведены прямые,
параллельные его диагоналям. Найти отношение площади параллелограмма,
образованного этими прямыми, к плошади данного четырехугольника.
Вариант XIII
1. Найти число Зх, если
’ 2. Найти значение выражения х2— у, если 2х—5у=0, х+ 10у=2.
124
1 Вычислить значение 5х при x=log* 16 + l,51og1/33—lg^5-lg^2.
4. Вычислить длину отрезка, на котором выполняется неравенство х2—х<6.
5. Решить уравнение 4 • 5х—5~x+lglOO=5.
6. Упростив выражение, вычислить cos 20°—sin 20° ctglO”.
7. Сколько корней имеет уравнение cosx— cos3x— sin2x=0 на промежутке
[0, л]?
8. Исследовать функцию Дх)=х34-Зх2 — 5. Сколько раз ее график пересекает
ось Ох?
9. Сумма шестого и девятого членов арифметической прогрессии равна 20,
а их произведение равно 64. Найти десятый член этой прогрессии, если ее первый
член отрицателен.
10. Осевое сечение конуса — равносторонний треугольник. Найти отношение
объема конуса к объему вписанного в него шара.
Вариант XIV
1. Упростить выражение
х-6—64 1 4х2(2х-+-1)
1б4-4х~2 — х-4 4—4х*14-х"2 1— 2х
2. Упростить выражение
1 \ 7 1
1 +-----4-tg2a I ( 1 --------
cos 2a / \ cos 2a
4-tg2a
3. Решить уравнение 1,5 4x+0,5=6x4-2 • 9х-0,5.
4. Сумма первого, третьего и пятого членов арифметической прогрессии
равна — 12, а их произведение равно 80. Найти первый член и разность
d прогрессии, выбрав наименьшее значение at.
х—1
5. Найти сумму всех целых решений неравенства log,/2----
6. Найти число решений уравнения /'(х) = 0 на отрезке [0, 2л], где Дх) =
=4sin2x—3cos2x— 10х. __
7. В равнобедренном треугольнике длина боковой стороны равна 4>/10,
а длина медианы, проведенной к боковой стороне, равна 3^/10. Найти длину
основания треугольника.
8. При каком значении параметра а уравнение lx2—2х—3|=а имеет ровно
три решения?
9. В треугольной пирамиде ABCD грани ЛВС и BCD — правильные тре-
угольники с заданной высотой. Угол между этими гранями равен ср. При каком
значении }/cos ср площадь полной поверхности пирамиды явлется наибольшей?
10. Найти угловой коэффициент касательной, проведенной к параболе
у=х2 —Зх+4 из начала координат, при условии, что абсцисса точки каса-
ния — число положительное.
Вариант XV
1. Решить уравнение
2 1 х—4
-------------4-----—0.
х2—4 х2 —2х х2+2х
2. Вычислить А = 5’, где B=21og25 8 + log1;5 5.
3. Найти наименьшее х, при котором справедливо неравенство
х—3 (л/х-5)2
2 " х—6
125
4. В бассейн проведены три трубы. Первая наполняет его на 4 я дольше, чем
вторая, а вторая — за 1/3 времени, необходимого для наполнения бассейна
третьей трубой. Если все трубы будут действовать одновременно, то бассейн
наполнится за 4 ч. За сколько часов первая и третья трубы, действуя раздельно,
могут наполнить бассейн?
5. Решить уравнение __ _________________________
(х2 —3x)9^2-*+4 • 9х=(х2-Зх)9х+4 •
(5/4)’ • 16»'2
6. Найти число х, если v —----=(16)1/6 • 4 1/2.
</б4х
7. В равнобедренной трапеции боковая сторона равна средней линии, а пери-
метр равен 48. Найти длину боковой стороны.
/л \ а 1
8. Вычислить значение выражения 4tg2 I - + а ), если sin -=—=.
V / 2 7з
9. Решить уравнение х-ух+16=8^х2, х>0.
10. Найти х в градусах, если 0°<х<360° и 2 sin2 (х+270°)—7 sin (х+90°)=4.
Вариант XVI
1. Решить уравнение ___ _______________
х2 • 22>/6 *+42-* = 16 • 4^6 Х + х2 -2~2х.
2. Найти число х, если
^25 -5"1/2 /1\2 / 1 \2
CjlS)1 ^5х W \^2s)
3. Найти значение А, если Л=2В+6С, где B=2/log2 и C=l/log26.
4. Решить уравнение л/42—х=2+^/б—х.
6 3 2
5. Решить уравнение —-——--=-----— 1.
х2 —1 х+1 х-1
/Пл \ /Зя \ 1
6. Вычислить значение выражения 16 sin4-2а I, если sin I-4а )=-.
\ 2 / \2 / 4
7. Две окружности равного радиуса касаются в точке С внешним образом.
Кроме того, каждая из них касается извне третьей окружности радиуса 6,5
в точках Ая В соответственно. Найти площадь треугольника АВС, если АВ=5.
8. Найти наибольшее значение х, при котором верно неравенство
х2+х—45 Зх+1
х-6 2
9. Найти х в градусах, если 90°<х<270° и 3cos2(x+270°)+sin2(x+180°)=1.
10. В первую поездку автомобиль израсходовал 10% бензина, имеющегося
в баке, затем во вторую поездку — 25% остатка. После этого в баке осталось
бензина на 13 л меньше, чем было первоначально. Сколько литров бензина
находилось в баке первоначально?
Вариант XVII
1. Решить уравнение
=6.
126
2. В квадрате ABCD точка Е — середина стороны ВС, а точка F— середина
стороны CD. Найти тангенс угла EAF.
3. Найти сумму всех значений параметра а, при каждом из которых уравне-
ние (а—2)х2—2yJ6 х+а — 1 = 0 имеет ровно один корень.
4. Высота и диагональ равнобедренной трапеции равны соответственно
5 и 13. Найти площадь трапеции.
(я а\
-----1=3.
4 2J
6. Найти сумму всех целых решений неравенства log1/3(2x—1)> —2.
7. Найти длину отрезка, отсекаемого на оси ординат касательной, проведен-
ной к линииy^tyx1 в точке ее пересечения с биссектрисой первого координатного
угла.
8. Точка Л/(2; 5) принадлежит параболе у= — x^+nx+S. Найти ординату
вершины параболы.
9. Боковые грани правильной треугольной призмы — квадраты. Площадь
боковой поверхности призмы равна 144. Найти объем многогранника, вершина-
ми которого служат центры всех граней призмы.
10. Найти значение числа к, при котором равенство
2 sin 4х (cos4 2х — sin4 2х) = sin кх
верно при любом значении х.
Вариант XVIII
1. Найти сумму квадратов корней уравнения х(х—л/з)=1.
2. Решить уравнение log1;2(log2 х— 1) = — 1.
3. Три целых положительных числа образуют геометрическую прогрессию.
Найти третий член прогрессии, если ее второй член на 1 больше первого члена.
4. Найти наименьшее значение функции j[x) = |tgx+ctg х|.
5. В параллелограмме ABCD (ЛВЦ СР) биссектриса тупого угла В пересекает
сторону AD в точке К Найти периметр параллелограмма, если длина АВ равна 12
иЛВ:ВР = 4: 3.
6. Решить систему неравенств
{1
---->1>
2-х
2 ^^зг*.
7. Высота конуса равна 6. Образующая конуса составляет с плоскостью
основания угол 60 . В конус помешена пирамида, основанием которой служит
равнобедренный прямоугольный треугольник, вписанный в основание конуса,
а вершиной — середина одной из образующих конуса. Найти объем пирамиды.
8. Параметр к квадратного уравнения х2—2Ах+3(2А— 3)=0 принимает сле-
дующие значения: 1, 2, 3, 4, 5, 6 и 7. Каждому из указанных значений к соответ-
ствует то или иное число корней заданного уравнения. Найти число всех корней.
Зх—1
9. Решить уравнение 4arctg--= я.
х+3
Дх) 1 ------
10. Найти целый корень уравнения еслиДх)=5/х-Зх + 1.
Вариант XIX
1. Найти наибольшее значение функции Дх) = ^/х2 — 6х +16 на отрезке [1, 6].
х2(х—2)2
2. Решить неравенство------->0. .
iogo.s(x2 +1)
127
3. Найти |х|, если |х—4|+5х- — 8.
4. В параллелограмме ABCD длина диагонали BD, перпендикулярной сторо-
не АВ, равна 6; длина диагонали АС равна 2^/22. Найти длину стороны AD.
s/x^+x+t
5. РАпить уравнение----------2.
х— 1
1+COSX
6. Найти число корней уравнения----0 на отрезке [0, 9л].
tg(x/3)
7. Куб с ребром, длина которого 4^/3, пересечен плоскостью, проходящей
через середины трех его ребер, выходящих из одной вершины. Найти площадь
сечения. _______________________
8. Найти A/5cos(arctgO,75).
9. Найти lim —-==—.
*-»з у*+1 —2
1 1
„ I 1 \ 3 9 27 3"
10. Вычислить I — ]
Х81/
Вариант XX
1. Найти значение числа а, при котором система
2х—у х+Зу
-----1----«2,
3 5
х+2у х—5у
--------“ 3,
2 3
5х—у х—10у
-----------ша
3 2
имеет решение.
2. Найти площаДь фигуры, ограниченной графиками функций у-4—х,
у-4+х, у-|х|.
/яп80 +яп40 \2
3. Найти I--------- .
\ ип70° )
4. Решить уравнение logj(2x)—log2 х4.
5. В прямоугольном треугольнике отношение катетов равно 0,5. Найти тан-
генс острого угла между медианами, проведенными к катетам.
6. Сумма членов бесконечно убывающей геометрической прогрессии равна 9,
а сумма квадратов ее членов равна 40,5. Найти второй член прогрессии.
7. В результате измерений некоторой величины получены следующие пять
значений: 51; 51,2; 51,4; 52,1; 52,3. Найти такое число х, для которого сумма
квадратов разностей между полученными значениями и числом х была бы
наименьшей.
log1(9-x‘ofa2 ) >
8. Решить уравнение--------------1.
х
9. Длина гипотенузы АВ прямоугольного треугольника АВС равна 4. Найти
сумму А% • ЙС+ГО • И + С2 ТВ.
10. Найти наименьший положительный угол (в градусах), удовлетворяющий
уравнению 2со»а(270°+а)+7ип(270°-а)-5.
128
Вариант XXI
1. Решить уравнение >/2x+l+^/х—5.
2. Длина основания равнобедренного треугольника равна 12. Радаус вписан-
ного в треугольник круга равен 3. Найти площадь треугольника.
3. Найти сумму всех целых положительных решений неравенства
4*-1_2*<1,25.
2 sina—cos a
4. Найти tga, если--------= 3.
sina—2cosa
5. Решить уравнение log2log1;2log,x=0.
{COS7tX= —1,
х2-5х2-14х = 0.
7. Найти максимум функции fix)=20х/(х2 +1).
8. Основанием пирамиды ABCF служит правильный треугольник АВС со
стороной, длина которой равна 20. Ребро FB перпендикулярно плоскости основа-
ния и имеет длину, равную 5. Пирамида пересечена плоскостью, параллельной
скрещивающимся ребрам АС и FB так, что в сечении получился квадрат. Найти
длину стороны квадрата.
9. Найти расстояние между точками пересечения параболы у=- х2—- х—3
и прямой 4х+Зу+9 — 0.
10. Решить уравнение |х-4|=х.
Вариант ХХП
1. Выражение (21og225+lg2)log210 преобразовать к виду (A log2 5+В)2.
2. Известно, что точка пересечения прямых 2х+у—9 и fcx+5y—18 принад-
лежит биссектрисе первого координатного угла. Найти число к.
3. Величина угла между боковыми сторонами равнобедренного треуголь-
ника меньше 60°. К боковой стороне проведены медиана и высота, длины
которых соответственно равны 3>/ 5 и 6. Найти длину боковой стороны.
4. Касательная, проведенная к параболе у—зг —5х+10, образует с осью
абсцисс угол 45°. Найта расстояние от точки касания до начала координат.
25 10
— 3.
5. Решить уравнение-----к
2х+1 v„,.
б. Найти cos22a, если sina—cosa-l/^/s.
7. Пятый член арифметической прогрессии равен 4. Какова должна быть
разность прогрессии, чтобы сумма квадратов второго и шестого членов была
наименьшей?
8. В пирамиде ABCF через медиану ВК основания АВС и середину L боково-
го ребра AF проведена плоскость. Найти отношение объема многогранника
BCKLF к объему пирамиды ABKL.
9. Найти сумму всех целых решений неравенства 2х +9 2 <10.
я 1 / 1\ <2
10. Решить уравнение — (6х+1)—- arctgl+arccos I —I—arcin—.
Вариант XXIII
1. Сумма модулей корней квадратного уравнения 4x2+fcx— 3—0 равна 2,
причем модуль отрицательного корня больше положительного корня. Найти
число к.
пх 1
2. Найти наименьший положительный корень уравнения log, ctg — +- — 0.
3. Разность между площадью круга и площадью вписанного в него квадрата
5-363 129
равна 2-^3 (л—2). Найти площадь правильного шестиугольника, вписанного
в этот круг. _____'
4. Решить уравнение 2х+у/х+11 =14.
5. Решить уравнение 2х/9=(sin 15° +tg 30° cos 15°)2.
6. Все четыре грани пирамиды — правильные треугольники. Найти расстоя-
ние между центрами ее двух граней, если площадь полной поверхности пирамиды
равна 81л/3-
Jx1-x-n (г*-1’5-^)
7. Решить уравнение-----------------------=0.
Х4-3
8. Найти длину отрезка, отсекаемого на оси абсцисс касательной, проведен-
ной к графику функции у=у/х2 4-2x4-4 в точке с абсциссой, равной —2.
х2+х+1
9. Найти целое решение неравенства----------<0.
х2 — 12x4-35
10. Найти число корней уравнения sinx4-cos2x=0, принадлежащих отрезку
[0, Зя].
Вариант XXIV
1. Найти сумму всех корней уравнения (х2—7x4-2)1— 13(х2—7х)—26=0.
л
2. Найти sin2 За, если a=2arctgl — arcsin ———.
2 12
3. В прямоугольном треугольнике АВС длины катетов АС я ВС соответст-
венно равны 12 и 8; точка К — середина медианы BD. Найти длину отрезка СК.
4. Решить уравнение log^Ix4 4-х3—6х2—7х)= 4.
5. Найти наименьшее значение'функции Дх)=2*4-22~х на отрезке [0, 2].
& Основанием прямоугольного параллелепипеда ABCDAiBiCiDi
служит квадрат АВСВ, площадь которого равна 50. Точка
О — центр квадрата ABCD 'точки F и К — соответственно середины ребер СС2
и АгВх. Вектор ЪРперпендикулярен вектору ЗХ. Найти объем параллелепипеда.
7. Если некоторое двузйакйое число разделить на произведение его цифр, то
в частном получится 3, а в остатке 9. Если же к сумме квадратов цифр этого числа
прибавить произведение его цифр, то получится искомое число. Найти это число.
/ л\ л
8. Найти sin2x, если tg I Х4— 1—2 tgx=2 и 0<х<~.
\ 4/ 2
9. Точка пересечения прямых 2х—у= 10 и Зх4-2у= 1 принадлежит окружно-
сти с центром в начале координат. Найти радиус этой окружности.
10. Найти произведение всех целых решений системы неравенств
(х2 —5х—6<0,
(х2 —Зх>0.
Вариант XXV
, 1 / 1\
1. Найти положительные корни уравнения х24—-4-3 Х4— 1=8.
г х2 \ х/
2. Решить уравнение logo,5(x—12)= —log2>/x.
3. В треугольнике АВС величина угла С равна 60°, длина стороны АВ равна
л/з1. На стороне АС отложен отрезок AD, длина которого равна 3. Найти длину
стороны ВС, если длина отрезка BD равна 2^/1. ;
4. Биссектриса AD равнобедренного треугольника АВС составляет с основ/
нием АС угол, тангенс которого равен 0,5. Найти косинус угля А ВС.
130
5^Ца координатной плоскости хОу даны прямая х4-5у=4 и два вектора
а(2; -—-3) и'Б(— 1; 5). На данной прямой найти такую точку М, чтобы вектор ОМ
был перпендикулярен вектору 2а4-ЗБ.
6. Основанием четырехугольной пирамиды служит квадрат. Одно из боко-
вых ребер перпендикулярно плоскости основания. Какую длину должна иметь
высота пирамиды, чтобы радиус шара, описанного около пирамиды, был на-
именьшим, если объем пирамиды равен 72?
7. Найти наибольшее значение функции /(x)=2sinx—cos 2х на отрезке
[я/4, Зя/4].
8. Найти/'(2), еслиДх)=х 1п(х2+2х—7).
9. Найти сумму всех рациональных (в том числе и сократимых) дробей со
знаменателем 2, являющимися решениями неравенства 2х4-3 22-х < 13.
10. Найти площадь фигуры, ограниченной графиком уравнения х-|-|у|=2
и осью ординат.
Вариант XXVI
1. Решить уравнение х=2—7 — 10х—х2.
2. Пассажир проехал на поезде 120 км и, пробыв на станции 40 мин, вернулся
с обратным поездом, проходящим в час на 6 км больше, чем первый. Общая
продолжительность поездки составила 8 ч. Сколько километров в минуту проез-
жает каждый поезд?
3. Найти середину промежутка, на котором выполняется неравенство
4Х2 4-4x4- 2(72x4-1)2 < 34.
4. Две окружности равного радиуса касаются в точке С внешним образом.
Кроме того, каждая из них касается извне третьей окружности радиуса 5 в точках
Ая В соответственно. Определить площадь треугольника АВС, если АВ=6.
5. Найти х, если
4-1/3 1б2/3 7J43/4 j
</б4х W $/з2
6. Найти сумму и произведение корней уравнения ___
, 7х+2 -.। , */х+2+1
2х2 -2 +х • 2*+1 =2х2 • 2х4-х . 2^
7. Вычислить А =9 I tg2 |-4а ) I , если cos 2а=—=.
к кг )) ^5
2x4-1 Зх 5
8. Решить уравнение-----(--------=-.
х 2(2x4-1) 2
9. Найти х в градусах, если 0°<х<360° и 2 cos2(х4-270°)=3 sin(х4-270°).
r 1 1
10. Вычислить А, если А =4*4-5 , где В—-----, С=-----.
2 logs 2 log? 5
Вариант XXVII
1. Найти х в градусах, если 90°<х<270° и sin2 (180°4-х)4-3 cos2 (180°4-х)=2.
2. Высота правильной четырехугольной пирамиды равна 2 см, тангенс дву-
гранного угла при основании равен 4/3. Найта площадь полной поверхности
пирамиды.
3. Найти наибольший общий делитель и наименьшее общее кратное чисел А,
ВяС.тдрА =62, В=102 и С=42.
4. В арифметической прогрессии содержится 10 членов. Сумма членов, сто-
ящих на четных местах, равна 50, а членов, стоящих на нечетных местах, равна 35.
Определить первый член и разность прогрессии.
131
5. Найти корень уравнения log* (№+Зх—4)—log*---.
х+4
6. Вычислить А, если А“ 10*4-3е, где В—2/Iogs 10 и С— 1/Iog6 3.
sinx4-2x
7. Найти значение производной функции Дх)—-----в точке х«0.
cosx— 3
8. Найти середину промежутка, на котором выполняется неравенство
х24-7<6х4-у2, гдеу=(7—2х)1/2.
9. Найти квадрат расстояния между точками, координаты которых удовлет-
[х_14-у-1-0,
воряют системе уравнений <
1х-24-у"2=8.
10. Найти х из уравнения 82/3 • 23 * * * (0,5)'2 . х~1 =27 • 2~2.
Вариант XXVIII
1. Для перевозки 60 т груза из одного места в другое требуется некоторое
количество машин. Так как на каждую машину грузили на 0,5 т меньше, то
дополнительно потребовалось 4 машины. Сколько машин было затребовано
первоначально?
2. Найти середину промежутка, на котором выполняется неравенство
1—2х
1O&U5------<0Д
Х4-1
3. Решить уравнение х—(16—х2—6х)1/2—2.
4. Решить уравнение (2x4-1) : х4-2,5х : (2х4-1)=3,5.
5. На отрезке [0°, 360й] найти число различных корней уравнения
1 3
74-4 sinx :---1-----------=0.
cosx cos(90°—2х)
6. Найти сумму и произведение чисел х, у, z, удовлетворяющих системе
”5х—2у—z—2,
4 Зх4-4у—5z—4,
,х4-3у—2z= —1.
7. Вычислить Л—sin(90°—2х), если sin(180°—х) : cos(180°—х)= — 2.
8. Найти коэффициенты к и q уравнения прямой у—кх 4- q, которая пересека-
ет гиперболу у—2,4/х в точках с абсциссами х—2 и х— — 3.
9. Дано уравнение относительно х:
х У—х • Зх-У+1-Зх+1, где у-(х4-2)1'2.
Найти сумму и произведение корней этого уравнения.
(Зх24-2у-*>
10. При каком значении параметра к система уравнений < , „ имеет
(х24-у2 = 117
единственное решение?
Вариант XXIX
7 4 3\
0,5: 1,25 4-- : 1-)
5 7 И/
3
1. Найти число, 3,2% которого равно Л=-
( 1,54-]: 18-
\ 4/ 3
132
2. Упростить выражение
2ayja+byfb — (b—a)\\Jа+^/ъу1 (~Jab—a)\g(A
o3/2 +b*2 (b—a) lg4
3a 3a 3a 3a
3. Упростить выражение sin4 ——6 sin2 — cos2 —I-cos4 ——cos 6a+4.
2 2 2 2
4. Даны три вектора а, Ъ и с, удовлетворяющие условию а— Ъ—с=0. Зная,
что |а| = 3, |5|=4 и |с| = 5, вычислить Ъс — аЪ—са.
5. Известно, что при любом л сумма $„ членов некоторой арифметической
прогрессии выражается формулой 5„=5л2—4л. Найти три первых члена про-
грессии. _____ ______- ____
6. Решить уравнение у]х+Ь—^/Зх—26=\]х—6.
7. Найти корни уравнения log2 (9Х+ 2+7)=2+log2 (Зх+ 2 +1).
8. Около круга радиуса ^/з см описана равнобедренная трапеция с острым
углом 60°. Найти длину средней линии трапеции.
9. Найти х в градусах, если —90°<х<90° и sin(180°—х) cos(90°—1х)=
=cos (270° + Зх) sin (360°+5х).
10. Образующая конуса равна 2 см и составляет с плоскостью основания
угол 30°. Найти объем описанной около конуса пирамиды, основанием которой
служит ромб с тупым углом 150°.
Вариант XXX
1. Найти два первых члена бесконечной геометрической прогрессии
(0<9< 1), сумма которой равна 9, а сумма ее трех первых членов равна 26/3.
2.
Решить систему уравнений '
/9V Z8V-' 1g 64
3. Решить уравнение [ - | • | — 1 =-.
\4/ \27/ 1g 16
и 4(sin2x cos5 6 7 8 9 102x +
2 8
х—12 *9
4. Найти х в градусах, если —80°<х<80°
+cos2x sins2x)+sin34x=l.
5. Найти целые числа х, удовлетворяющие неравенству
6. В правильной четырехугольной пирамиде длины ее бокового ребра и диа-
гонали основания равны л/з см. Найти объем пирамиды.
7. Расстояние между городами А нВ равно 195 км. ИзАвВиизВвА одно-
временно выезжают два поезда и встречаются через 3 ч. Затем они продолжают
свой путь. Поезд из А прибыл в В на 13/14 ч раньше, чем фугой прибыл в А.
Определить скорости поездов.
/ 1\
8. Найти значение производной функции y=3cos [ хн— | фи х=1.
\ х)
9. В прямоугольном параллелепипеде АВСРЛ1В1С1П1 диагонали основания
АС и DB пересекаются в точке М и LABD = 6D°. Определить скалярное произ-
ведение ~АС AD, если =3 и LBMBi=30°.
10. Какое число больше: (log328)2 или log, 20412?
133
ВАРИАНТЫ БИЛЕТОВ
ДЛЯ ВСТУПИТЕЛЬНЫХ ПИСЬМЕННЫХ ЭКЗАМЕНОВ*
Вариант I
1. Упростив выражение дляДх), найти/(х), если
Y 41о^х-°’51^17.
\ у/П-^х )
2. Решить систему уравнений
{2-4х+1 у
4х=-; ,
4х+2-------------2х+>+4
4 23х+у2=4.
3. Число 10 представить в виде суммы двух слагаемых так, чтобы сумма
удвоенного квадрата первого слагаемого и утроенного квадрата второго слага-
емого была наименьшей.
/5л \
4. Найти все корни уравнения 0,5(l+cos2x) cos I——xl—sin x=
\2 /
X X
=4sin - cos - , удовлетворяющие неравенству logH(x+l)>l.
2 2
5. Около круга площади 5 описан ромб с острым углом а. Найти длины
диагоналей ромба.
Вариант II
1. Упростить выражение
3. Найти наименьшее и наибольшее значения функции Ях)=- х3—18х2+28х
3
на отрезке [0; 1,5] и построить ее график на указанном отрезке.
4. Найти все корни уравнения (sinx+cosx)2+cps2x+t£2x=0, лежащие на
отрезке [—л/2, л].
5. Диагонали прямоугольника ABCD пересекаются в точке О, радиус окру-
*
Варианты I—XX предлагались на экзаменах в Московском энергетичес-
ком институте, а варианты XXI—XXXV — в Московском государственном ин-
ституте радиотехники^элекгроники и автоматики.
134
жности, вписанной в треугольник ЛОВ?-равен 2, !~ВОА—а. Найти
произведение TiA ИВ. *
Вариант III
1. Упростить выражение
2а+(я2-1)1/2
((a-1)1'2+(а+1)1'*) ((а-1)3'2 -(а+I)3'2)'
2*+14-х— 1
2. Решить неравенство--------<2.
2х+1
3. Одна бригада может убрать все поле за 8 дней. Другой бригаде для
выполнения той же работы нужно 75% этого времени. Первая бригада прорабо-
тала один день, после чего к ней присоединилась другая бригада, и обе вместе
закончили работу. Сколько дней бригады работали вместе?
/ 15л\
cos I х4----1
\ 2 /
( 9л\
= 2 sin I х4— ) —sin(x4-17n),
\ 2/
4. Найти корни уравнения
принадлежащие области определения функции у=cos - ——.
5. Радиус вписанной в трапецию окружности равен R. Найти площадь трапе-
ции, если ее углы равны 90 и 20°.
Вариант IV
1. Упростить выражение
8л3 8х3 \/ 1 1
1-^/1+4х2 14-^/1 +4х2/ \8х3-2х Sx3+2xj)
2. Найти область определения функции
\ 5/21gx4-1,125 /
х2 х3
3. Найти промежутки монотонности и экстремумы функции fix)=Зх----
3 27
и построить ее график,
л /Зл \ л
4. Найти все корни уравнения tg - sin х sin I —t-x )+sm2 2x=2 cos -, ле-
3 \ 2 / 4
жащие в интервале (—л/12, л).
5. Найти площадь полной поверхности правильной четырехугольной пира-
миды, длина диагонали основания которой равна а, а боковое ребро образует со
стороной основания угол а.
Вариант V
1. Упростить выражение
135
2. Найти область определения функции
Rx)=\Jlg(3^6x+1 + 19)2’5-5.
3. Найти промежутки монотонности и экстремумы функции Дх)=3х—— х3 4
49
и построить ее график.
4. Найти все корни уравнения 0,5(sin3x— sinx)=sin2xcosx—4sin3x, лежа-
щие на отрезке [—я/3, Зя/2].
5. В правильной треугольной призме ABCAlB1Ci биссектрисы основания
АВС пересекаются в точке М. Найти скалярное произведение МА, если
длина стороны основания призмы равна а.
Вариант VI
/9-х6 * * 27-х9 х6 \>
1. Упростить выражение ------------Ч------- ) .
\3—х3 9-х6 ЗЧ-х3/
2. Найти область определения функции
3. Найти промежутки монотонности и экстремумы функции Длу—бх-8х3
и построить ее график.
(я \ я .
х 1—tg - Ч-cos 2х, лежащие на отрез-
ке [—7я/6, 5я/6].
S'. В равнобедренном треугольнике угол при вершине равен а. Найти отноше-
ние площади треугольника к площади круга, описанного около треугольника.
Вариант VII
1. Упростить выражение
Xjl-s/x ^2+y/xJ
(О,!)1»**'1-0-5*'1).
2. Найти область определения функции
л/хч-l Ч- 7 - ^/x+l - (О,5)1о,’0’3)~1/2.
3. Найти промежутки монотонности и экстремумы функции Дх)—О,3х2—
—0,02k3 и построить ее график.
, я /я \ я
4. Найти все корни уравнения 4sin2 - sin I -ч-2х )4-5cos2x4-tg2 -- —5, ле-
3 \2 / 3
жащие в интервале (- Зя, я/2).
S. Боковое ребро правильной четырехугольной пирамиды равно I и образует
с основанием пирамиды угол а. Определить объем пирамиды.
Вариант VIII
1. Упростить выражение
136
(Jx-5lot”2).
2. Найти область определения функции/x)-^/log3 (4 З2х+3 — 1)—2х—3.
3. Найти наименьшее и наибольшее значения функции Дх)—1+5х+х2—х3
на отрезке [—2, 0] и построить ее график на указанном отрезке.
1 2cos2x—1 2>/з tg3x
4. Найти все корни уравнения----4-------------=-------—, лежащие
1—tg2x cos2x+sin2x 1—tg22x
в интервале (—2л/3, 7я/18).
5. Периметр основания правильной четырехугольной призмы равен Р, диаго-
наль призмы образует с высотой призмы угол а. Найти объем призмы.
Вариант IX
/ / 1 1\1/2 / 4 \'1/2\2
1. Упростить выражение I (х6+2х2) I----- ) —I —-----— 1 )
\ \4х‘ 2/ \х8 —2х12/ J
2. Найти область определения функции Дх)=* ——
У 2>/l+log2x+3
3. Найти наименьшее и наибольшее значения функции Дх)=0,5х3+5,25х2 +
+0,25 на отрезке [—1, 1] и построить ее график на указанном отрезке.
/7я \
sin I —f-x ]
/я \ \ 3 /
4. Найти все корни уравнения sin | +х 1=--------, лежащие в интер-
\3 / я
cos - COS X
3
вале (—я, 2л).
5. В конус вписан цилиндр, высота которого равна радиусу основания цилин-
дра. Найти площадь боковой поверхности цилиндра, если образующая конуса
равна I и угол между образующей и высотой конуса равен а.
Вариант X
1. Упростить выражение
/(2+$/4а)2-2х/а 1 \ ia-bja
\ 8^0-4 Ъ^а-фа) (l+t/4a)2
{у 4-х2 «4,
у—х^2
у-2х>2.
3. Найти три положительных числа, составляющих геометрическую прогрес-
сию, если сумма первого и третьего членов прогрессии равна наименьшему
значению функции Дх)=4х2 — 4х+53 на отрезке [0, 1], а квадрат второго равен
0,5/(25,5).
4. Найти вое корни уравнения cos 2x=l+sin2x яп4х, лежащие на отрезке
[—Зл/2, я/2].
5. Диагональ основания прямоугольного параллелепипеда образует со сто-
роной основания угол а, а с диагональю параллелепипеда угол /?. Определить
объем параллелепипеда, если длина его диагонали равна I.
137
Вариант XI
1. Упростить выражение
/ + 1 + l. ., ..
(—-----v У-----JO—L. ] _ iQlog1M («Р+1)
V^+i+l (а*+1)* 2-Ь2 J
(y-tx2*!,
J у+2x^2,
2. Решить графически систему неравенств \ 2.х>
1х>0.
3. Разность между двумя положительными числами равна 4, а разность
между произведением этих чисел и удвоенным кубом меньшего числа принимает
наибольшеегзназение. Найти данные числа.
4. Найта.вее корни уравнения cos2х+(sinх+cosx)2 tgx=tgx(tgx+l), лежа-
щие на отрезкё[—7я/4, я/4].
5. Высота правильной треугольной пирамиды образует с боковым ребром
пирамиды угол а. Найти объем пирамиды, если площадь ее основания равна 5.
Вариант XII
1. Упростить выражение
(л+-\/4а+1)1'2 (^/а3 * * * + ^8А2) .
---==——_ -----==—-Л=-----—----------0,5 • IO10»»*”.
{(^2Ь-уа)2->г^2Ь+^а)2){а-у/2хЛ+2Ь)
{у>4х2 — 4,
—у+2х>0,
у—х>0.
3. Среди всех равнобедренных треугольников, у которых сумма двух равных
сторон и высоты, опущенной на одну из этих сторон, равна 4 см, найти треуголь-
ник наибольшей площади.
, /л У 3
4. Найти все корни уравнения tg2x—2tgx—4 I sin - sinx) (1+cos2x), ле-
жащие в интервале (—я/2, я/2).
5. В конус вписан шар. Найти объем шара, если высота конуса равна h и угол
между высотой и образующей конуса равен а.
Вариант XIII
1. Упростив выражение дляДх), найти/(х), если
/х2+1+^9 + 2(,у/х3-^3-)(у/х-фу1+2у/^Зх(у/^Зх-1-)\
\ (х2+2х—</9 + 1) (х+</з + 1) /
[22х+52> = 5,
2. Решить систему уравнений
3. Производительность труда на заводе трижды увеличивалась на одно и то
же число процентов. В результате число производимых за сутки станков увеличи-
лось с 64 до 125 штук. На сколько процентов каждый раз увеличивалась произ-
водительность труда?
138
г / 7я\ 7л
4. Найти корни уравнения sin2x4-sinx4->/2 sin I х4— )=cos —, удовлегво-
\ 2 / 4
v/я1—X2 3
ряющие неравенству 2 — 1 > 0.
5. Площадь основания правильной четырехугольной пирамиды равна 64 см2,
высота пирамиды равна 4-^2 см. Найти угол между боковым ребром и высотой
пирамиды.
Вариант XIV
1. Упростив выражение дляДх), найти/'(х), если
Дх)
(^/о, 2x4-1)"
*4-1
71овэ«5 * *
2. Решить уравнение 2>/х—lg(25 *+25>/х— \25)=>/х lg4.
3. Сумма бесконечно убывающей геометрической прогрессии равна наиболь-
х4
шему значению функции Дх)=-----16x4-5 на отрезке [2, 6], первый член прогрес-
16
сии равен — 6. Найти знаменатель прогрессии.
4. Найти все корни уравнения
(/х л\ /х л\\ 4я
1 4 2 sin I —|— 1 cos I -— 114-sin2 —=0,
\2 4/ \2 4// 3
2
удовлетворяющие неравенству х4-2я>- x.
5. Основанием пирамиды является прямоугольник с большей стороной, рав-
ной а, и тупым углом между диагоналями, равным а. Длина высоты пирамиды
равна длине окружности, описанной около ее основания. Найти объем пирамиды.
Вариант XV
1. Упростив выражение дляДх), найти/(х), если
2. Решить уравнение (10—3^х+1)(14-3 ''х+1)—10-3 ^'х+1=0.
3. Число 18 представить в виде суммы трех положительных слагаемых так,
чтобы первое слагаемое было равно третьему, а сумма квадратов всех трех
слагаемых была наименьшей.
4. Найти все корни уравнения •
sin
я\
Х4-- 14-cos
6/
=0,5(14-2 sin2 х),
удовлетворяющие неравенству х2—2ях<0.
5. Тупой угол ромба равен а, расстояние от точки пересечения диагоналей до
стороны ромба равно /5. -Найти объем параллелепипеда, высота которого равна
h и основанием является данный ромб.
139
Вариант XVI
1. Упростив выражение дляДх), найти/(х), если
f\+\lx f/16x+t/x2\-2 Jtogo^Z+logo^
Дх)- —-25
X ijx 2+х )
lg(41+x2+2x)
Ъ. Решить уравнение-------------logx+i (х2+2х+1)=0.
1g (9-*)
X Найти число, которое в сумме со своим удвоенным квадратом дает этой
сумме наименьшее значение.
1
4. Найти все корни уравнения —--4tgx= —2, удовлетворяющие неравен-
> COS2X
ству 42х~2*>0.
5. Основанием прямой призмы АВСАХВХС^ является прямоугольный тре-
угольник АВС, длина гипотенузы АВ которого равна а и ВАС = а. Найти скаляр-
ное произведение С^А СГС, если САСХ =fl.
Вариант XVII
1. Упростив выражение дляДх), найти/(х), если
/ \/х 1 'Jх 1 V^X 0,5 log, 2 + log,х
Л*)-|-----т= +------7= “Г-----------Г-2 •
Х1- у2х-1 H-V2X-1/ V*~V2
2. Решить уравнение 1g (9х+27)—xlg3=21g2+lg3.
3. Число 9 представить в виде суммы двух положительных слагаемых так,
чтобы произведение квадрата первого слагаемого на второе слагаемое было
наибольшим.
/5л \ л
4. Найти все корни уравнения cos I ——х )+sin x+cos2 - cos 2х=0, удовлет-
воряющие неравенству ^Jx+it>2*Jit.
5. Основанием пирамиды является правильный треугольник со стороной а.
Одно из боковых ребер перпендикулярно основанию, а каждое из двух других
ребер образует с основанием угол а. Найти площадь боковой поверхности
пирамиды.
Вариант XVIII
1. Упростив выражение для Дх), найти/(х), если
/ l/^A-xlfx </х -21о«»^
Xxt/l+yjzljx 7 </x~V2
[21og3y+logJ(x2-4) = l-21og52,
X Решить систему уравнений |2(2>)->_4-о,1-о,2х=о 3 4
3. Основанием четырехугольной пирамиды является прямоугольник с пери-
метром 24 см; высота пирамиды равна 9 см. Найти длины сторон основания
пирамиды, при которых ее объем является наибольшим.
л
4. Найти все корни уравнения sin - (cos2x—2snr x+l)wl —(sin2x—cos2x) ,
3
удовлетворяющие неравенству ях—x2>0.
140
5. Площадь осевого сечения конуса равна S, а угол между образующей
и высотой конуса равен а. Определить площадь боковой поверхности конуса.
Вариант XIX
1. Упростив выражение дляДх), найти/(х), если
Дх)-^ • 1/(2-2^2х+х2) (2-х2)(Vz+x) • (0,25)log2^^
л/2-х
2. Решить систему уравнений
(1g (Дх2 +у2)=1g 15 +1,
tig (2x4-у) +lg (2х—у) =1g 0,5 4-2.
3. Первый член геометрической прогрессии равен наибольшему значению
функции Дх)=8^3 х—х2, третий член прогрессии равен/'(4^3—6). Найти зна-
менатель прогрессии.
sin2x
4. Найти все корни уравнения---------------tg5x=0, удовлетворяющие
2cos2x—2sin2 -
4
неравенству (х24-1)(3х—8)>0.
5. Радиус круга, вписанного в ромб, равен г, угол между высотой ромба и его
большей диагональю равен а. Найти объем параллелепипеда, высота которого
равна Л, а основанием служит данный ромб.
Вариант XX
1. Упростив выражение дляДх), найти/(х), если
logjX
//х-2'э-х-1'2+1\-‘ х-8'3+2х-2'2+1\ lofcJj
Лх)=\\ v**-V*+i' х'2/3 /
2. Решить систему уравнений
гг^-г’-^-сУз)108’5-^.
(Igx+lg3»lg(7+y).
3. Отношение двух положительных чисел равно 3, а разность между боль-
шим из них и удвоенным квадратом меньшего числа принимает наибольшее
значение. Найти эти числа.
2л
4. Найти все корни уравнения cos4xcosx—3cos3x=tg-sinx sin4x, удов-
летворяющие неравенству lg (9х—Зя 4-1) > 0.
5. В ромб с острым углом а вписан круг. Найти отношение площадей ромба
и круга.
Вариант XXI
1. Решить неравенство х2—(1 —х2)2 > 1.
/----- 2
2. Решить уравнение 7^х—14— —15—0.
>/х-1
141
5
3. Решить иеравеиство 1 +log/3x+|u25 • log,(11 — Зх)>---.
log2(3x + l)
1
4. Найти все решения уравнения tgx—ctg2x=--------, удовлетворяющие
1 +cos2x
неравенству —0,5<х<1.
5. В треугольнике АВС сторона ВС =30 см, медиана ЛХ=15 см, а отрезок,
соединяющий точку пересечения медиан и точку пересечения биссектрис, парал-
лелен АС. Найти две другие стороны треугольника АВС.
6. При каких значениях параметра а уравнение
у* 1) +2(а 1) + _ 42х2 + 84а2+84дх-168а— 84х+91
имеет единственное решение? Найти все такие значения а и соответствующие им
решения.
Вариант XXII
6 1
1. Решить неравенство--------------->2.
(х+2)(х-3) х+2
{yjх+у+2=2,
х2+у2=4.
3. Решить неравенство 27(8 lx2) <х7.
4. Решить уравнение /2яп2 cosx=smx+cosx.
5. В прямоугольном треугольнике АВС из вершины прямого угла А на
гипотенузу ВС опущен перпендикуляр AD. Пусть О1 и О2 — центры кругов,
вписанных соответственно в треугольники ADB и ADC. Известно, что
0,02=2^2 см, а периметр треугольника АВС равен 24 см. Найти катеты
треугольника АВС.
6. Решить неравенство
(х2+х)(1 +\Jx1 — х+3 + ^2х? + \.)>2+Зу]х?-х+3+\12х2 + \.
Вариант XXIII
3—х
1. Решить неравенство j< 1.
90+2х—2х2 .----------
2. Решить уравнение . - ==5/93+2х—2х2.
>/46 + х—х2
cos2x
3. Решить уравнение-----=tg 6х.
l+sin2x
4. Решить неравенство logx+J (3—2х—x2)>logx+1 (1 —Зх).
5. В треугольник АВС вписан ромб, один из углов которого совпадает
с углом А, а противоположная вершина лежит на стороне ВС. Известно,
142
что сторона ромба равна 15 см, его высота--см, а площадь треугольника
2
АВС равна 240>/з см2. Найти стороны треугольника, если известно, что угол
А — тупой.
6. При каких значениях параметра а существует единственная пара чисел
(х; У)> удовлетворяющая соотношению
х2 + (1 + a)y2+(2+2zj)xy + (4 + 6a)x+(4+4a)y+3a+4=0?
Вариант XXIV
{ху=6,
х+у = 5.
х+70 х+10 2х+13
2. Решить неравенство----1-----<-------.
х-2 х+5 х + 3
3. Решить уравнение sin2х+^/бcosх=3cos2х+5/2sinx.
4. Решить неравенство
х— у/х—1 х— у/х — 1
256 3 * -18-16 ’ +32<0.
5. В круге проведены две взаимно перпендикулярные хорды АС и BD,
которые пересекаются в точке Р. Через точку Р и середину ВС проведена прямая,
пересекающая AD в точке N. Доказать, что PN и лЪ перпендикулярны.
6. При каких значениях параметра а система уравнений
Лу|—у—2| |х| —1|,
(2у—х=2а
имеет нечетное число решений?
Вариант XXV
1. Решить систему уравнений
х2+3ху—/ + 3-0.
2. Решить неравенство (1+sinx)(sinx— 5/3cosx+l)>0.
3. Решить уравнение
log/x+1V-----+log5*+‘ ---
Д J х-2 „ х-2
'х-2/ х-2
3
2
4. В треугольнике АВС на стороне АС взята точка К, а на стороне ВС — точ-
ка М. Отрезки AM и ВК пересекаются в точке О. Найти площадь четырехуголь-
ника ОМСК, если площади треугольников АОК, АО В и ОВМ равны соответствен-
но 1, 2 и 3 см2.
5. При каких положительных значениях параметров а и Ь системы уравнений
143
(x2+y2 = a2, (a2x2—y2=0,
< и <
[1 +4sin(x+y) = cos(2x+2y) (Jx|+A|j>—4| = А
имеют одинаковое число решений?
1 8
б. Решить уравнение--— —----------0.
х+2 х2 + 5х+б
Вариант XXVI
1. Решить уравнение №+2(1 + sina)x+4—cos2a=0 (а — действительный па-
раметр). ,
)х-х/ху=28,
2. Решить систему уравнений < —
Л/ху=—12.
3. Решить уравнение
4(sin2x sin2x—->/з sin3x)+- cos2x sin4x=3,/3 sinx cos22x.
/х 23\ 4
4. Решить неравенство logos --i— ) 1ой8х»-юх+з4+2>----------.
\2 4/ log2 (8x2 —10x + 3)
5. В равнобедренном треугольнике ABC (AB=BC) О — точка пересечения
высот. Найти величину угла АВС, если ОВ=АС.
6. Найти все значения параметра а на отрезке [1, 11], для которых больший
из корней уравнения х2 — 6х+2ох+а—13=0 принимает наибольшее значение.
Вариант XXVII
1. Решить уравнение (х—2)(х+2)(х2+3)+5х2=0.
2. Решить неравенство х—5yJ—х+24>0.
3. Решить уравнение
(л\ / л\ / п \
5х+- I cos I 4х+- ) cos I х—— ) =
б/ \ 5/ \ 30/
(п \ / 2л\ / л\
х----+cos I 8х+— +cos 10х+- cos2x.
30/ \ 5 / \ 3/
Зх-4
4. Решить неравенство (-1 2 . >1.
5. В прямоугольном треугольнике АВС на гипотенузу АВ опущена высота
СЕ. На СЕ как на диаметре построена окружность, пересекающая катеты ВС и АС
соответственно в точках К и D. Найти площадь треугольника ЕКВ, если длина
отрезка СК равна 9 см, а длина отрезка AD равна 27/4 см.
6. При всех значениях параметра а решить систему
(Зх2 + 2zj2 +4xy+2zjy + 5ax=4y2.
1(х+а)2 + (х - а)2+8ах+ба2 = 8/.
При каких значениях а система имеет бесконечное множество решений?
144 >
Вариант XXVIII
lJx-l Jx-2
1. Решить уравнение—-----i-------— 1.
Vx-4 Цх-\3
2. Решить неравенство 1—х2<2|х—1|.
3. Решить уравнение sinx+sin2x+sin3x=cosx+coe2x+coe3x.
4. Решить систему уравнений
. 2/ + + Эху
(У =У >
Uogy-2x(y+2x)=-log2y-2x-1 (4Х2+ху +_>>)•
5. Биссектрисы AM н BN треугольника АВС пересекаются в точке О. Извест-
но, что АО=-^3 МО, NO=(^3-V) ВО. Найти углы треугольника АВС.
6. При каких значениях параметра а уравнение
ах4+2х3у+(4а +1) х2у 2 +4ху 3 + 4а_у4 +16а2 — 24а + 5 = 0
имеет единственное решение? *
Вариант XXIX
/2х+х2\а
1. Решить уравнение (--) =1.
\1+2х/
2. Решить неравенство |х—1| >/х2—2х+1>4.
cos4x+l 1
3. Решить уравнение-------= - cos4 2х— 8 sin4 х cos4 х.
ctgx-tgx 2
1
* -Э+logj^-
4. Решить неравенство (1,25)' 1оя‘',7>(0,64)
5. В трапеции ABCD с основаниями ВС и AD диагональ АС, равная \/3 см,
является биссектрисой угла BAD и пересекается с диагональю BD в точке О.
Площади треугольников АВО и AOD относятся как 1 : 3. Найти длины всех
сторон трапеции ABCD, если угол BAD равен 60°.
6. Найти все значения параметра а, при которых уравнение
sin [-sjnx]+i/2\/3 |а|+2 —За2 • cos 1- sinx) = 2
\6 / \6 /
разрешимо. Решить это уравнение при найденных а.
Вариант XXX
4
1. Решить уравнение 3-1--= |х+1|.
|х+1|
2. Решить неравенство (х—2)2sinx>0. Выписать целые решения, принад-
лежащие отрезку [—1, 10].
145
(/л \ /л \\ 1
sin х 4-2 cos Iх \ cos (-4-х )1 sin2x=- cosx.
4. Решить неравенство x2ioe’*4-27<28 31°g‘n*.
5. В прямоугольной трапеции ABCD основание АВ в 1,5 раза больше диаго-
нали АС. Утлы BAD и ADC — прямые, боковая сторона AD равна 4 см. Найти
площадь трапеции ABCD, если диагональ АС является биссектрисой угла DCB.
6. Для каждого значения параметра а решить уравнение
Цх2—4х + а\ + х2—4х+а)у/5х—х1 — 6 = 0.
Вариант XXXI
4 1
1. Решить неравенство----------<2.
(х—2)(х4-1) х+1
к/*У+1=2,
2. Решить систему уравнений <
[у—х=2.
3. Решить неравенство 161-—) <х.
\х2/
4. Решить уравнение 4-sin 3x4- sin х=2 sin
5. В прямоугольном треугольнике АВС из вершины прямого угла А на
гипотенузу ВС опущен перпендикуляр AD. Пусть О, и Ог — центры кругов,
вписанных соответственно в треугольники ABD и ADC. Известно, что
60^/2
Oj О2 -- 2-v' 2, а биссектриса прямого угла равна см. Найти катеты треуголь-
ника АВС.
6. Решить неравенство
(х5+2х)(1 4- х1 - х+4+ -Jlx2 + х+ 1)<3+4>/х5-х+4 + 25/2х2+х+1.
Вариант XXXII
1. Решить неравенство х2 4-(х2—4)2<4.
-------------------------- 13
2. Решить уравнение 2sj 2х — 1-4-11=0.
\/2х-1
log, (9-х) 2~1оМ2
3. Решать неравенство 14---------->--------.
log49(4+x)2 log5 (4 4-х)
4. Найти все решения уравнения
г (1 — Jl) cos3x
tgx4-tg2x-25/2----------------,
cosx—smx sin2x
1
удовлетворяющие неравенствам <х<2.
146
5. В треугольнике АВС высота AD — ^sJ'l см, а радиус окружности, каса-
ющейся ВС и продолжений сторон АВ и АС, также равен Зу/i см. Найти стороны
треугольника АВС, если радиус описанной около него окружности равен
16/5/7 см.
6. При каких значениях параметра а уравнение
g(x О +2(я О +2ax = 3Qx2^.6oa2^.goax_ 120а—60х+66
имеет единственное решение? Найти все такие значения а и соответствующие им
решения.
Вариант XXXIII
1. Решить уравнение 1о&-х2 (sin х+cos х) = 1о& _ х2 sin х.
2. Решить уравнение \/1 — х+,/4 + х=,/Зх2+9х+9.
sin 2х 1 5
3. Решить уравнение--------1--—-=9—ctg2x +------t-tg2x.
l+cos2x cos2x sin2x
4. Решить неравенство log2 llog^-j4|<0,5-J-log*(3log|x|_12— 1).
5. В равнобедренную трапецию ABCD вписана окружность, касающаяся ее
сторон в точках Аи Bt, Су Dt. Известно, что площадь А^С,^ равна 1/8
площади ABCD. Доказать, что угол при большем основании трапеции равен 30°.
6. При каких значениях параметра а уравнение
,21 Vх
x2+-+-=log2a+ad-------
х 2 1+х
имеет единственное решение?
Вариант XXXIV
х+2
1. Решить неравенство - ... == >0.
5/З—2х—х2
х+3 1
2. Решить уравнение----=------.
|х2-9| |3 —|х|1
3. Решить уравнение sin3x cos3x+cos3x sin3x = sin3x sin3x+cos3x cos3x.
4.
Решить неравенство logos ( 3+log г? -— log2-----
5. В треугольник ABC с углом А = 120° вписана окружность, которая касается
стороны ВС в точке Р. На ВС как на диаметре построена окружность и проведен
перпендикуляр к ВС в точке Р до пересечения с этой окружностью в точке К,
причем РК= 15 см. Найти площадь треугольника АВС.
6. При каких значениях параметра к уравнение
|x2-2x-8|x-l| + 13|=jt
имеет шесть решений?
147
Вариант XXXV
1. Решить уравнение х=у/х+2.
1 5 27
X Решить неравенство------н-------<------.
х+3 х2—Зх+9 х2+27
2tgx
3. Решить уравнение tg3x—tgx=----.
cos2x
. г. zjX+kX+3 /лХ+\Х+1 ,, ,<х + 2)’-2
4. Решить неравенство (4 ) +(9 ) >13-6
5. Четырехугольник ABCD вписан в окружность и в него в свою очередь
вписана другая окружность, касающаяся сторон АВ, ВС, CDhAD в точках А р В},
Q, Dv Доказать, что А1С1 и B1D1 перпендикулярны.
6. Найти все значения параметра а, при которых уравнение
log, (у/ах1+ Зх-1 + 2) +logn (ах1+3х+1) = 2
имеет решение. При каких значениях параметра а решение единственно?
РЕШЕНИЯ, УКАЗАНИЯ, ОТВЕТЫ
ГЛАВА 1
ЗАДАЧИ ПО ПЛАНИМЕТРИИ
1.001.
1.002.
1.003.
1.004.
1.007.
1.008.
1.011;
□ По условию, LC—90°, Л2)=30 см, .02?=40 см (рис. Р.1.1). Положим
АС=х, ВС—у. Так как точка, равноудаленная от сторон угла, лежит на его
х 30 4х 16х2
биссектрисе, то , т. е. у——. Но x-t-y—AB или х2+-----------= 70 ,
у 40 3 9
откуда jc2 = 1764. Итак, х = 42 (см), у = 56 (см).
т, m\J3, 2т.
□ Пусть с — длина гипотенузы. Тогда длины катетов равны с — 1
нс — 2. Имеем (с—1)2 + (с —2)2 = с2 или с2 — 6с+5 = 0, откуда с = 5 (см)
(второй корень уравнения не удовлетворяет условию).
60 и 30°. 1.005. 1 см. 1.006. 9^5 и 8^/10 см. ______
I------ х ч/81+х2
□ Пусть ВС=х (рис. Р.1.2). Тогда АВ=^/&1 + х2 и =-----(поскольку
4 5
BD —биссектриса). Отсюда имеем 25х2 = 16(81 +х2), т. е. х—12 (см). Сле-
1 1
довательно, Зллвс—~ ВС АС=- 12 -9 = 54 (см2).
2 _ 2 _
8,64 и 15,36 м2. 1.009. s/з см. 1.010. -710 см.
□ Так как ААВС — равнобедренный, то высота BD является медианой
(рис. Р.1.3); далее, точка пересечения медиан делит каждую из них в от-
10
ношении 2:1, откуда ЛО=— (см). Из ДЛО2> находим
OD=^AO2-AD2 = -(2v/2)2=^ (см), т. е. BD^yJlX (см). На-
конец, из ДВЛС получим ВС=^У(728)2+(2>/2)2 = 6 (см).
149
8
1.012. n1, 2т2!^4т2 — n1.1.013. 6 см. 1.014. 75 см2.
1.015. □ По условию, DK—средняя линия А ЛВС (рис. Р.1.4). Так как
1
BD=DK= ВС, то ДС=30° и BC=2BD. В LBCD имеем CD2 = BC2-BD2
2
а2 а
или ——4BD2 —BD2, откуда BD=—Следовательно,
4 W3
1 ^л/з
S=- AC BD = CD BD =——.
2 12
1.016. Я2 л/3- 1.017. л/41 и 5 см. 1.018. 4 см.
1.019. □ Обозначим искомую длину через х. Тогда из подобия треугольников
ЛВС и LBM (рис. Р.1.5) имеем Л С2 : № = 5 : (S/2), где S' — площадь А АВС.
Отсюда Л С2 =2х2 и х= 18>/2 (см).
1.020. В 64 раза. 1.021. (^/б -i-2) : 1 ИЛИ (>/з + 1):2.
1.022. □ По условию, ЛВ=с = 30 см, АС=Ь—26 см, ВС=а = 28 см (рис Р.1.6).
Тогда р=0,5(а+6+с)=42, р—а—14, р—Ь=16, р—с=12 и по формуле
Герона находим S^abc^'J42 • 14 16 12=336 (см2). Так как
&MNC~&АВС, то Здммс • : СД2=4/25=0,16. Отсюда
определяем площадь трапеции:
•$'д.мхс=336—0,16 • 336 = 282,24 (см2).
1.023. 13 см. 1.024. 6 см.
1.025. □ Проведем радиус в точку Л; так как OAJ.AM, то ОЛ2.ВС и BZ> = 6 см.
(рис. Р.1.7). Пусть ОЛ=г, OD=x. Тогда AD=y/AB2—BD2 = i, т. е. г+х=8
(1). Но OI>2 = OBi2 — BD1 или г2—х2 = 36; так как г2 — х2 = (/Ч-х)(г—х), то
с
Рис. Р.1.6
Рнс. Р.1.7
Рис. Р.1.8
150
г—х = 36/8 = 9/2 (2). Решив систему уравнений (1) и (2), найдем г=6,25
(см). -
1.026. 0 и 1,5 см. 1.027. 9 см. 1.028. Зг.
1.029. □ Пусть R — радиус дуги, г — радиус окружности (рис. Р.1.8). Так как
я 1 1
ДС=—, то Я=- ОС, г=- О,С. Тогда ОС=2А; с другой стороны,
3 2 2
ОС=ОО1 + О1С=Л+г+2г=Л+Зг, откуда R=3r. Следовательно,
1 Зг
/ила=2яЯ - = 2я • — = 2яг.
3 3
1.030. аЧу/^-Ь1.1.031. 2 и ^2. 1.032. R(^2-l).
1.033. □ Проведем диаметр CD через точку Р (рис. Р.1.9), которая разделит его
на отрезки PD и СР длиной 11 —7=4 и 11+7 = 18 (см). Пусть ЛР=х; тогда
РР=18-х. Так как АР РВ=СР PD=4 • 18, то х(18-х)=72 или
х2—18х+72=0, откуда Xj = 12, х2=6, т. е. хорда АВ делится точкой Р на
отрезки длиной 12 и 6 см.
1.034. г/8. 1.035. 12 и 20 см.
1.036. □ Обозначим радиусы внутренних окружностей через R2 и R2. Пусть
5 — площадь самого малого круга; тогда яЛ2=25, я Л2 =35.
, яЯ2 2яЛ2 R [2
Следовательно, яЯ2= — н яЛ2=——, откуда /?]=—= и Л2 = Л
/ 5 С2 —С2
1.037. /-------. 1.038. —----1.039. nab.
у я(4я2 —1) 4я
1.040. □ Проведем ОС .LAB (рис. Р.1.10). Тогда СВ=- АВ=9 см. Из ДОРС
_____________________________ 2
находим OC=:yJoB1-BC1^\2 (см), а из ДОЛ/С получим МС=
= у]оМ1—ОС1=^5 (см). Следовательно, ЛЛ/=9 + 5=14 (см), МВ=9 — 5 =
= 4 (см).
1.041. Ryj3(2->j3). 1.042. 2 : 3. 1.043. пВ.г{3+2^2).
1.044. □ Пусть г — радиус меньшей окружности. Тогда О,О2=г+4, 020,<^г+6
(рис. Р.1.11). Так как О2О2 = О1О^ + О1О1, то 102=(г+4)2+(г+6)2 или
Р +Юг—24=0, откуда г=2 (см) (корень г= —12 не удовлетворяет усло-
вию).
^(2^/3-я)
1.045. ----. 1.046. 3:1.
2
Рис. Р.1.11
151
1.047. □ Пусть R — радиус данного полукруга, аг — радиус одного из постро-
енных полукругов (рис. Р.1.12). Тогда площадь заданной фигуры равна
0,5(яЛ2—яг2—я(Л—г)2)=яг(Л—г). Так как ДЛРВ=90°, то СО2 =
nCD2
=АС СВ=2г . 2(Л—r)=4r(R —г), откуда---=яг(Я—г), что и требова-
4
лось доказать.
I Ra \2
1.0 48. я - .
1.0 49. □ Площадь сегмента АпВ равна разности площадей сектора АО В и тре-
яЛ2 1 R aR
угольника АОВ (рис. Р.1.13). Находим 5^^ лов—-> Saaob—~ а • ~=—>
3 2 2 4
яЛ2 aR а
откуда S=———Так как R^—^, то окончательно получим
Д_а2(4я-35/3)
36 ’ "
1.050. оЧя-гув.
1.051. □ Пусть г — радиус круга, a S1 и S2 — площади сегментов. Тогда
яг2 1 г»/3 1,- 1,-
5!=—--г—=—г2 (4я—З^/З), 52=яг2-5! = яг2-—г2(4я-35/3) =
1 Sj 4я—3\/з
=— НСвя+Зч/З). Значит, —=---------=.
12 V _ St вя+З^/з
1.052. Л2(я—2)/4.1.053. (я+7з)Л2/2. 1.054. 84 см2.
1.055. □ Треугольник АВС — правильный (рис. Р.1.14); поэтому его площадь
152
Рис. Р.1.17
а2>/з
равна------, где а — сторона треугольника. Проведем OKS.AC. Так как
4
LOAK=30°, то АО = 2г, АК*г^З, откуда а = 2тЛ/з + 2т = 2т(х/з + 1)- Сле-
довательно,
5
1.056. R1 Тз/2. 1.057. г(5/б+л/2)/2, г^/б-<У2)/2. 1.058. а(3 + у/з)/6, а(3->/з)/6.
1.059. □ Пусть расстояние между параллельными прямыми равно х (рис. Р.1.15);
тогда площадь 5 треугольника АВС равна 0,5 ВС х. Так как OALBC, то
ВМ-МС и ВМ МС-АМ MD*x(2R-x). Значит, B&H-xQR-x), от-
куда S*0,5x • 2^/2Ях—х2—х^2Хх—х2.
1.060. 8 и 15 см. 1.061. 6 и 8 см. 1.062. 18, 24 и 30 см. 1.063. 60 см2.
1.064. □ Пусть R и г — радиусы вписанной и описанной окружностей, ВС* а
(рис. 1.16). Положим BD “ х-, тогда BL—х (как касательные, проведенные из
одной точки), LA—AK—2R-х (так как ЬАВС — прямоугольный, то
AB-2R). Имеем АС2+ВС2-АВ1 или (г+2Я-х)2+а2-4Л2. Но В-5г/2,
х—а—г и последнее уравнение примет вид (7г—а)2 + а2—25г2 или
12г2—7аг+а2—0, откуда ri—a/З, r2*al^. Этим корням соответствуют зна-
чения (ЛС),-4а/3, (АС^—ЗаЦ. В результате получаем два решения:
1 4а 2а2 1 За За2
1.065. 294 см2; 12л см. 1.066. 20л см. 1.067. 65/18.
1.068. □ Проведем радиусы OD, ОМ и ON в точки касания (рис. Р.1.17). Имеем
OD — OM—CM—CD и, следовательно, ВЛ —10—3—7 (см). Но BD—BN
и AN—AM (касательные, проведенные из одной точки). Положим AN*х;
тогда (х+7)2—(х+3)2 + 102, откуда 8х—60, т. е. х—7.5 (см). Следователь-
но, АВ* 14,5 (см) и получаем ответ: R*0,5АВ*7,25 (см).
1.069. 5 см. 1.070. я/р-с/. 1.071. 25я м2.
1.072. □ Так как Л АВС— прямоугольный и CDS. АВ (рис. Р.1.18), то
АС1* АВ АО-40 • 25,6 и ВС2*АВ BD-40 14,4, откуда ЛС-32 (см),
1
ВС-24 (см) и Вдлвс”" -32 - 24 - 384 (см2). С другой стороны,
ВдлдС-рг-48г. Следовательно, г-8 и 5^,»—лг2-64я (см2).
1.073. 25я см2. 1.074. >/5 см- L075- ^2-^2).
1.076. □ Так как &.АВС— равнобедренный и прямоугольный, то высота CD
является биссектрисой, т. е. ДРСЛ-ДЛ-45° (рис. Р.1.19); поэтому
AD—DC и AC—yj2DC. Но ЛС-ЛХ+ХС-РС+г (AK-AD как касатель-
153
ные, проведенные нз одной точки), откуда r=s]2DC—DC, т. е.
r/PC=V2-l.
1.077. 3, 4 и 5 см. 1.078. 80/3 см. 1.079. о^/з (2-у/3)/2.
1.080. □ Проведем BDJ.AC (рис. Р.120); так как ДАВС — равнобедренный, то
является и медианой. Имеем BD2=AB2—AD, откуда
ВЛ=Л/392—152=36 (см) и, значит, 5=- 30 36 = 540 (см2). Но 5 =/>/=54 т,
откуда г=10 см.
1.081. 2(7 +47з) см2. 1.082. 8/3, 25/3 и 5 см. 1.083. 285,61я см2.
1.084. □ Найдем длину боковой стороны ВС (рис. Р.1.21):
2?С=-ч/2?М2+Л/С2=>/б2 + 82 = 10 (см). Учитывая, что АО — биссектриса
&.АВМ, имеем МО1ОВ=АМ[АВ или г/(8—т)=6/10, откуда г=3 (см). Так
как2>Е||ЛС, то &DBE~ &АВС, т. е. DEjAC^BNIBM или 2>Е/12 = (8 —2г)/8,
откуда DE=3 см.
1.085. 20/3 см. 1.086. ЗЛ27з/4.
1.088. □ По условию, Л=0,5у12. Сторона АВ правильного вписанного тре-
угольника (рис. Р.1.22) равна Я5/3, т. е. 0,5,/12 5/3=3. Найдем сторону
CD нового треугольника: a=\j32 — \,52^\,5^/з. Так как радиус г вписан-
ной в него окружности равен 05/3/6, то окончательно получим
г = 1,5^3 • -5/3/6 = 3/4. |
1.089. яо2/4. 1.090. I25/3 и 36 см.
1.092 □ Пусть о — сторона треугольника, R — радиус вписанной в него окру-
154
ai/з
жности; тогда R=---. Проведем радиусы ОМ и О^К в точки касания (рис.
6
R АО
Р.1.23). Из подобия треугольников ЛОМ и АО. К имеем — =----------.
г AO—R—r
ayj 3 ау/з ау/з
Отсюда, учитывая, что АО=----, получаем----—-------=-----=---или
3 6г /д^/з д^/з \
41 Г’7
flV3
———r = 2r, т. е. a = 6ryJ3.
1.093. Я2(3Л/3 —я)/6. 1.094. (3,/з-я)/(3,/з+я). 1.095. Я2л/з/4.
1.096. □ Пусть г и R — радиусы вписанной и описанной окружностей. Тогда
r=~, R=—. Найдем S=Jp(p — а}(р—Ь)(р— с) = у!1\ 8 7 6 = 84 (см2).
р 4S
Следовательно, г=4 см, Я=65/8 см, откуда получим искомое отношение
яЯ2 /65V
площадей: —- = ( — I .
_ яг2 \32/
1.097. 31ц/15/50. 1.098. 8 и 10 см. 1.099. 1700 см2.
1.100. □ Так как площадь треугольника S=pr=0,5aha. то 1pla=halr^ что и было
1.101.
1.104.
1.105.
1.108.
1.109.
нужно установить. _
4ab/(a+b). 1.102. т(2у/з+3)/3. 1.103. 3a2(7-4yj3).
□ Обозначим радиус описанной окружности через Я. Тогда а—Я^/з,
откуда Я=0/5/3. Так как сторона вписанного квадрата равна Ryjl, то его
площадь_Я=2Я2=2о2/3.
(лА+х/2)/2. 1.106. За2/8. 1.107. 9/4 кв. ед.
_ 1 2
□ По условию, ВС*=3 - ВС • АН (рис. Р.1.24) или АН= ВС. Но
2 3
/1 \ 4 1 25
АН1** АВ1 — (-ВС г и, значит, - ЯС2 “ЛЯ2—- ЯС2 или ЛЯ2 =— ЯС2, т. е.
\2 ) 9 4 36
5 5
ЛЯ=- ЯС. Тогда получим ЛЯ= (ЛЯ+1), откуда ЛЯ=5 (см). Следовате-
6 6
льно, ЯС=6 см, ЛЯ=4 см.
о2(25/з-3). 1.110. с1/2. 1.111. Зо2/8.
155
1.112. □ Пусть AL=a, LB=b и LK=c (рис. P.1.25). Тогда площадь данного
квадрата 51=(а+6)2=а2+2а6+62=с2+2а6. Так как LBLK=60°, то
£_BKL=30°, откуда с=2Л, а=Ь^З и, значит, Sj =4Ь2 + 2Ь2у/з. Площадь
вписанного квадрата 5J=c2=462. Итак,
S2 4Ь2 2 4 2>/з И
Si 4*2+22>27з З+^/з
1.113. 1,6RJ2. 1.114. а2/25. 1.115. 1.
яЯ2
1.116. □ Пусть R — радиус круга. Тогда площадь сектора равна-, а площадь
4
R2
-Треугольника равна — и, следовательно, площадь сегмента составляет
2
яЯ2 R2 Я2(я—2) Я2(я—2)
. Имеем =2я—4, откуда R=2>J2 (см). Итак,
4 2-4-------4
площадь квадрата равна 2R2 = 16 (см2).
1.117. 3$/з и ^27 см. 1.118. Я(^4+я±у^4—я)/2. 1.119. 2,2 и 4 м2.
1.120. □ В &.FBD (рис. Р.1.26) катет FD—fi cmW лежит против угла в 30°, откуда
FB=12 см и, значит, АВ—18 см. Далее в &АВС имеем АС=АВ/2=9 см.
Наконец, BC=-JАВ1-AC1 =yj243 = 9^3 (см).
1.121. 5^т2+п2/6, 5^т2+п2/4. 1.122. Jm2-4S/2. 1.123. 8£/я.
1.124.
1
□ Искомую площадь найдем по формуле S=- АС • BD=2AO ОВ
3 2 1
(рис. Р.1.27). В ДАОВ имеем АВ2=АО2 + ОВ2, где ОВ=- АО, АВ= =-
'42
16
100*
1.125.
1.128.
__ . __ 3
С - . . .. 4
1 9
(м). Тогда получим уравнение -=АО24—АО2, откуда АО2
АО = 0,4 (м). Итак, 5=2 0,4 0,3 = 0,24 (м2).
S(m2+n2) тпр2
—-------. 1.126.--—1.127. 150 см2.
У 2тп 2/т1 +л2)
□ Длина стороны ромба равна m+л. Из &АВК (рис. Р.1.28) находим
ВХ2=(т+п)2—т2. В &BKD имеем BD2=BK2-i-n2 = (m+ri)2— т2+л2 =
= 2п(т+п), т. е. BD=>j2n(m+ri). Для отыскания АС воспользуемся тем,
что АС2 + ВР2=4АР2=4(т+п)2, откуда ЛС2=4(т+л)2—2тп — 2л2 =
=4т2 + 6тп + 2п2, т. е. АС=^4т2 +6»и+2л2.
т. е.
156
Рис. Р.1.28
1.129. Ял/гяД/з. 1.130. 4.1.131. 7,5 см.
1.132. □ Пусть а — сторона ромба, a dl и «/2 — его диагонали (рис. Р.1.29). Так
как высота ромба равна диаметру окружности, то его площадь 5—4а.
1
С другой стороны, d,d2, откуда, учитывая, что di—a, находим d2 — 3.
2
/dA2 (d2\2 , с? 8^/3
Но а2—I— I +1 — I или а2 «— + 16, т. е. а—--.
\2/ \2/ 4 3
1.134. («(а1 +62)—4аЛ)/8. 1.135. 15 и 30 см.
1.136. □ Проведем BNJ.AD (рис. Р.1.30); так как BN—2OM, то BN—^jTS см.
Учитывая, что в is. AN В LABN—VF, имеем AB—2AN и, значит,
4Л№—75+ЛЛ/2, откуда AN—5 см и АВ—10 см. Далее из tsBND получим
ND2—BD2-BN2 —124 - 75 — 49; следовательно, ND—1 см и AD—12 см.
Наконец, из равенства AC2+BDI—2AB2+2AD2 находим
ЛС2 -200 + 288—124 — 364, т. е. ЛС—2^/91 см.
1.137. 10, 17, 21 и ^337 см. 1.138. 12 и 4 см. 1.139. 2 : 1.
1.140. □ Пусть Л — высота параллелограмма ABCD, h2 — высота треугольника
1 h АВ 3
АЛЕ (рис. Р.1.31). Тогда Sabcd-AD Л, 5дЛЛЯ-- АЕ h2. Но
2 AR 2
Следовательно,
Sabcd AD Л
StiAKE - АЕ h
Ле, • Л«
2
AD h
9.
1 1 2
- AD -h
2 3 3
1.143. 5R2 7з/4.
1.144. □ Так как О2А1.АВ и О2В1.АВ, то О2А1О2В и, значит, фигура
О2АВО2 — трапеция (рис. Р.1.32). Касательные в точке С взаимно перпен-
дикулярны, а потому каждая из них проходит через центр другой окружно-
сти, т. е. OjC-4 см, О2С— 8 см, откуда OiO2—\/olC2+OiC2—4y/5 (см).
Рис. Р.1.30
Рис. Р.1.31
157
Проведем OtD^AB и из AOjPOj найдем 0^=^ O1O21 — O1D2 =
= 80 —16 = 8 (см). Следовательно, >$о1лдо2=0,5(8+4) 8 = 48 см2.
1.145. 16 см. 1.146. 2 см. 1.147. 450 см2.
1.148. □ По условию, ВС=4 см, Л2)=25 см, ЛВ=20 см, CD = 13 см (рис. Р.1.33).
Проведем BE .LAD и CFLAD. Пусть BE=CF=h, АЕ=х, FD=y. Тогда из
ААВЕ и &CFD находим Л2 =202 —х2 = 132 — у2. Учитывая, что
у = 25—4—х=21 —х, имеем 202 — х2 = 132 — (21— х)2 или 42х = 672, откуда
х = 16 (см). Итак, Л=>/202-162 = 12 (см).
1.149. (а2 —62)(7з —1)/4. 1.150. 32 см2. 1.151. 168 см2.
1 1
1.152. □ Так как S=- (а+Ь) Л, то - (а+Ь) 22=594, откуда а+Ь=54. Из систе-
2 2
(а+Ь=54,
мы уравнений < находим а=30 (м), 6=24 (м).
_ (а—6 = 6
1.154. 1. 1.155. З^/З СМ.
bJy 6
1.156. □ Высота трапеции равна--, а большее основание равно а+-. Следова-
2 К 2
тельно, ее площадь «
2 8
1 /
Л>= । а+а+~ )
2\ 2/
1.157. 4, 8 и 2^2 см. 1.158. 5 см.
1.159. □ По условию, l_BCA= L.ACD (рис. Р.1.34). Но LBCA= LCAD, а зна-
чит, JLACD — равнобедренный и Л2>= CD. Имеем 3AD +ВС=42; так как
1
ВС=3 см, то AD=13 см. Проведем BKLAD; тогда ЛК=- (13—3)=5 (см)
и из /\АКВ находим ВК=-J\32 — 52 = 12 (см). Итак, S=- (3 + 13) 12=96
(см2).
1.160. 1024 см2.1.161. 25. 1.162. 1 : 3, 2 : 3.
1.164. □ Так как AD — диаметр окружности (рис. Р.1.35), то OD = ОС—10 см.
Проведем CLLAD; тогда OL=6 см н из hCLO находим
CL=-JoC2 — OL2=8 (см). Теперь из hALC и A CLD получаем
ЛС=уС£2 + ЛА2 = х/б4+256=8.у/5 (см) и CD = yJCL2 +LD2 =
=764 + 16=4^/5 (см).;и
1.165. 10,625 см. 1.166. ЗЯ27з/4. 1.167. 13 см.
158
Рис. Р.1.34
1.168. □ Так как центральный угол COD равен 60° (рис. Р.1.36), то вписанный
1
угол CAD равен 30°. Следовательно, А=- АС и из ААКС получим
АК=\]AC1 — CK1=h\j'i. Находим площадь трапеции: 5=- (BC+AD) Л =
= (Л£+КК)Л=ЛК^Л=л7з Л=Л2л/3-И
1.169. 9 и 25 см. 1.170. 1.171. 8 см. 1.172. 4+2у/з, 4-2^/э и 4 см.
1.173. □ Пусть х — длина боковой стороны; тогда высота трапеции равна - х.
Так как трапеция описана около круга, то сумма ее оснований равна сумме
1 1
боковых сторон. Следовательно, площадь трапеции S=- • 2х - х, откуда
_ 2 2
x=s/lS.
1.174. J2SI4. 1.175. 5Л11.176.
1.177. □ ПустьЛХ^т, Д»=л(рис. Р.1.37). Тогда КВ=ВМ~МС~ъАК~АЫ~
= ND=m. Найдем высоту трапеции: h=BH=sjAB1—AH1^
= sj(т+п)1—(т—п)1=2\Jтп. Итак, 5=- (BC+AD) h=(m+n) Л —
(т+п).
1.179. 120 см1. 1.180. 4^5 и 8^5 см.
1.181. □ Пусть В — радиус окружности. Тогда сторона правильного вписанного
а^/з ЗВ^З
треугольника а^В^З и 5Э=------—------. Далее, сторона квадрата
Рис. Р.1.37
a^Ryjl и S^^a^=2R2 и, наконец, сторона правильного вписанного ше-
6Я\/з ЗЛ2л/3
стиугольника ae=>R и 56 =----------—--------. Следовательно,
Г Г 4 2
: S3 : Se-8 : 3^3 : 65/З.
1.182. 73 : 4 : 6>/з. 1.183. сАД8-1-184. fl2V3-
1.185. □ Проведем радиус О А в точку касания (рис. Р.1.38) и обозначим радиус
окружности через г. Тогда в Е.ОАМ имеем (Зл^+Н—(в+гу или
, , , , За 6г2 J3 27а27з
4а2+г2=а2+2аг+г , откуда г=—. Таким образом, S=---=—:---.
2 4 8
1.186. 2 : 1. 1.187. а2 (3 +V3)- 1-188- яв*/4.
1.189. □ Пусть АЕ=х (рис. Р.1.39). Тогда AB=2AEJrEE или 2х+х\/2=а, от-
fl а (2—72)
куда х=--------------. Следовательно, искомая площадь
2 + Т2 2
, 4k2 , 4а2 (4—45/2+2) , г
S^Sabcd-ISдле№=“~~“------------------®2а2 (V2-1).
1.190. □ Соединим произвольную внутреннюю точку Р со всеми вершинами
многоугольника и опустим перпендикуляры на все стороны (или их продо-
лжения). Пусть длины этих перпендикуляров равны dl, d2, */„• Нужно
доказать, что сумма +d2+...+d„ не зависит от Р. Площадь многоуголь-
ника S—0,5a(di + d1+...+dn'), где а — сторона многоугольника. Значит,
4/j+d2+—+</я—25/а, т. е. эта сумма не зависит от выбора точки Р.
1.191. □ По условию, LC—90°, МР~4 см, Mg-8 см, 5длвс“100 см2 (рис.
Р.1.40): требуется найти ВС и АС. Пусть ВС—х, Л С—у, тогда 0,5ху-100,
MP ВР 4 х-8
т. е. ху—200. Так как ^ВРМ~ ДМОА, то —-------- или -----—---.
AQ MQ у—4 8
Следовательно, имеем систему уравнений
' 4 х-8
<у-4- 8 ’ (х+2у-50,
или <
<ху-200 (ху-200,
которая сводится к квадратному уравнению у2—25у +100—0, откуда нахо-
дим У] —5 см, у2—20 см. В результате получаем два решения: Хд — 40 см,
у3—5 см; ха—10 см, у2—20 см.
Рис. Р.1.41
160
i.i92.
1.193. □ По условию, Z_C=90°, АВ+ВС+АС=72 ал, СМ — медиана,
СК—высота, СМ—СК=7 см (рис. Р.1.41); требуется найти АВ. Так как
1
М — центр описанной окружности, то АМ=МВ=МС=- АВ. Воспользу-
2
емся равенством АВ1=ВС1+АС1. Заметим , что ВС?+АС2 =
= (ВС+АС)2—2 ВС АС, откуда АВ2 = (72—АВ)1—2 АВ СК, поскольку
ВС АС=АВ CK—2S, где 5 — площадь треугольника. Таким образом,
приходим к уравнению АВ1 = (72—АВ)2 —2АВ I- АВ— 7 ) или АВ2 +
____ \2 /
+ 130 АВ— 5184=0, откуда АВ— — 65+-У9409 = 32 см (второй корень урав-
нения не удовлетворяет условию).
1.194. 10.
1.195. □ Пусть а V. b — катеты, ас — гипотенуза треугольника. Так как
а+6+с=60, то а+6=60—с, откуда (а+Ь)1 2 = (60—с)1 или a2+2ab+b2 =
= 3600—UOc+c2 (1). Но а1+Ь1=с2, а 6с=0,5аЬ (площадь треугольника).
Подставляя эти выражения в равенство (1), получим с2+24с=
= 3600— UOc+c2 или 144с=3600, т. е. с=25 см. Для определения а и Ь име-
(а+Ь=35,
ем систему уравнений < т. е. а и Ь — корни уравнения
(об=300,
. х?-35х+300-0. Значит, ai=20, aj = 15; Z^ — 15, 62«20. Итак, стороны
треугольника равны 15, 20 и 25 см.
abj~2 200 ,
1.196. ——. 1.197. — см2.
а+Ь 3
1.198. □ Пусть х — больший отрезок гипотенузы. Тогда по условию
с—х х с(>/5-1)
---=~ или х2+сх—с2 «0, откуда х=
х с 2
не удовлетворяет условию). Далее находим
(второй корень уравнения
, c2(3-Js)
г =---------. Обозначив
2
с—х А
имеем -----и, значит,
Л х
через h высоту, проведенную к гипотенузе,
Д/5-l 3-л/5\ , г Гг~~
h1 = cx—x2=c2 (-------------|«с2(>/5-2), т. е. Л-сх/л/5-2. Следова-
\ 2 2 /
1 с2^у] 5-2
тельно, S=- ch =---------.
2 2
1.199.
1.201.
1.204.
р2-п? pi2+m1±J(pl+m2)2— Ът2р2
-----. -------—------------—. 1.200. 2,16, 3 и 0,84 см2.
р 2р
□ Пусть площадь треугольника равна 5. Тогда его стороны таковы:
2S 2S 2S , , _ / 1 1 \ , / 1 1 \
а =—, Ь =—, с=—. Найдем <P+b2=4S2 I—- +—)=452 I-------1--) =
15 20 12 \152 202/ \225 400/
4$2 /1 1 \ 4S2
=—|--|—1=—, откуда а2+Ь2 = с1, т. е. треугольник
25 \9 16/ 144
ный.
□ Обозначим стороны треугольника через а, Ъ, с. Тогда
4/nJ=2(h2+c2)-o2, 4mj=2(a1+c2)—Ь2 (см. дополнительные соотношения
прямоуголь-
6-363
161
Рис. Р.1.42
2° в начале главы). Сложив эти равенства, получим
4(mJ+m^)=4c2+a2+62. По условию, /и2+/и. = 5/и2. Но4/и2=2(а2+62)—с1
^c2+<^+b2 ЗЩа2+&)-<?)
и, значит,--------=--------------, откуда 4с2+«г+62 = 10(а2+62)—
4 4
— 5с2 или с1=а2+Ь1, т. е. треугольник прямоугольный. В
1205. лД 1.206. b+c+d.
1207. □ Обозначим сторону треугольника через а и проведем MDLAB (рис.
Р.1.42). Поскольку АМ=ВМ, точки С, М и D лежат на одной пря-
в2
мой — высоте CD. В ДЛСТ) и 6.AMD имеем (\+MD)2=<?—
а2
MD2=4------. Тогда а2 =4(4—MD2) и получаем квадратное уравнение
4
, , , 3^5-1
(1 + МО)2 = 3(4 - МО2) или 4МО2+2МО -11=0, откуда МО=—----(вто-
4
рой корень не удовлетворяет условию). Далее находим
, , 46-6^5 9+Зл/5
а2 =4(4—МО2) «16-----------------и, следовательно,
4 2
a\j3 (9+3V5X/3 9^3 + 3715
5=-----=----------=-----------«3,4 (см).
4 8 8
1209.
1210. □ Пусть АС^х; тогда CB^l—x (рис. Р.1.43). Проведем DL{AB и опустим
перпендикуляры на АВ из точек О и Е. Так как треугольники ADC
X 1—х I
и СЕВ—правильные, то OZ,=£M=/iC+CM«-4---------------------=-,
2 2 2
(1-х)^3 Ху/3 (/—2х)л/3 . Р 3(Z—2х)2
EL*=----------------------. Следовательно, О£2=—н---------. Рас-
2 2 2 4 4
стояние DE является наименьшим при Z—2х=0, откуда x=Z/2, т. е. точку
С следует взять в середине отрезка АВ.
1211. и(/5+1)/2ит. 12122V5 и 5+Д
1213. □ Так как 6.АВС — равнобедренный, то С£=ЛО и DE^AC (рис. Р.1.44).
т BD
Из подобия треугольников АВС и DBE следует, что —=—-. Учитывая,
AC Ь
BD ВС
что CD — биссектриса, имеем —=—. Положим ЛС=х, BD=y и полу-
DA АС
162
1.214.
1.216.
Рис. Р.1.44
(ту
J х~ь
ним систему уравнений \
I у b
Ьт
откуда у=—
bm b
и далее---------
/ bm\ х
xib-----I
bm
Проведем DK$AC. Так
1 1
откуда ВК—~ BE, KD=- ЕС.
5 5
Ь—т
28/3 см. 1.215. 4,8.
□ Пусть AD пересекает BE в точке F (рис. Р.1.45).
ВК KD BD 1
как Ь.ВСЕ~ &.BDK, то —=—=—=-.
BE ЕС ВС 5
KD KF 1
Далее, так как &KFD~ &AFE, то ———= • Пусть KF=x; тогда FE=5x
ЛЕ ЕЕ 5
Зх
и ВК+х+5х=ВЕ, откуда ВК+6х=5ВК или 6х=4ВХ; т. е. ВК=—. Выра-
2
Зх 5х
зим BF через х: BF=BK+x=—Нх=—. Но FE=5x и, значит,
2 2
BF:FE=12.
1.217. 4^3/3, 4^3/3 и (9-5л/3)/3. 1.218. 30, 30 и 120°.
1.219. □ По условию, ВС—a, AC=b, АЕ и BF— медианы, 4>4MF=90°
(рис. Р.1.46). Положим АЕ—та, BF=mi,. Тогда в tJiME и дЛМ-Есоответ-
т\ 4т* а1 4т1 т* Ь1
ственно имеем —i+-=—, —' 4 —. Складывая эти равенства, полу-
9 9 4 9 9 4
163
5(m2+m2) a2+b2 9(a2+Z>2)
чаем-------=-------- или m2+mf=-----. Наконец, из Е.АМВ нахо-
9 4 * ‘ 20 ______
4(m2+m2) <?+b2 1а2+Ь2
дим АВ2—-------=------, откуда АВ— /——.
9 5 V 5
1.220. 2^5 см. 1221. 26 и 30 см.
1222. □ Обозначим высоту CD через Л, а отрезок AD — через х (рис. Р.1.47).
Имеем LACD—90" — 75°=15°. Проведем AF так, чтобы
l_CAF= LACD = 15°. Тогда Z.ZED = 30° ииэ &ADFполучим AF=FC=2x,
Г Л
DF-x^S. Но DF—h—FC=h—2хи, значит, х=-----==Л(2—^/З). По усло-
2+>/з _
вию, АВ=2Ь; следовательно, BD—AB-AD—lh-x—hJ'S. Наконец, из
&BDC находим BC=s/BD2 + CD2-2h, т. е. 45=30°
и 4С=180° —75° —30° = 75°.
1.223. 14V3/3 см. 1.224. 3 см.
1225. □ Пусть искомое расстояние равно х (рис. Р.1.48). Тогда
5дллгв=0>5 10х=5х. Но Ваамв“^^лвс—8&лмс—8&вмс- Найдем эти
площади: S^abc=-J'2A 14 3 • 7 = 84 см2, 5длл/с=0,5 • 21 2=21 см2,
5двлгс“0>5 • 17 4=34 см2. Следовательно, 5длмв=84 — 55 = 29 (см)2, от-
куда х=5,8 см. В
3 : 4.1227. 150 см2.
1 4
□ Так как Sadec^~ BE НК=2 (рис. Р.1.49), то НК=—аналогично,
2 DE
1 16
$ллвс“~ АС • ВН=8, откуда ВН——. Учитывая, что Ь.АВС~ &.DBE,
2 АС
1.226.
1.228.
DE ВК
находим —=—. Но ВК—ВН—НК и, значит,
АС ВН
ВК ВН-НК НК 4 16 AC DE
—=--------= 1—— = 1——= 1——-. Положим —=х. Тогда
ВН ВН ВН DE AC 4DE АС
1 1 DE 1
х=1 или 4х —4х+1 =0, т. е. х= . Итак, —-=-.
4х 2 АС 2
1229. (т+п)2/(тп).
1231 . □ По условию, ДЛ»2дЛ, ВС—ЛС=2 см, АВ=*5 см (рис. Р.1.50); требу-
ется найти 5длвс- Проведем биссектрису AD-, тогда LABC~ LADC
AC CD
164
в
Рис. Р.1.50
АС 5 АС 5
Далее, так как AD— биссектриса, то —=— или —=------ или
CD BD CD ВС-CD
AC • ВС
AC ВС—AC CD=5CD, откуда CD=---- (2). Из равенств (1) и (2)
АС+5
АС ВС2
следует, что ЛС2=------ или АС2+5АС^ВС2. Учитывая, что
ЛС+5
ЛС=ЛС+2, имеем АС2+5АС=АС2+4АС+4, откуда АС=4 см, ВС=6 см.
Итак,
SAASC~^,5 1,5 2,5 • 3,5-(см2).
4
1.232. 9 см2.
1.233. □ Сначала докажем, что все указанные в условии треугольники равнове-
лики. Имеем $ьаом=&ьсом (рис. Р.1.51), поскольку эти треугольники
имеют одинаковые высоты и одинаковые основания, равные АС 12. Анало-
гично, SbAON=S&BON и SbBOK=SbCOK- Но 5ддол:“>5длоу> так как
‘5длол:=‘5дрол:+‘5длк». ‘5дд5дрох+‘5дляр> я Sadok^Sadon и
S&bkd=S&bnd (у этих треугольников равны основания KD и ND, а также
опущенные из них высоты). Итак, площадь каждого треугольника равна
$ьлвс1(>- Теперь по формуле Герона находим 5длвс=з/21 8 • 7 • 6=84
см2, откуда 5дло№ И см2. В
1.234. □ Каждую медиану исходного треугольника АВС продолжим на 1/3 ее
длины (рис. Р.1.52). Площадь образовавшейся фигуры AMBNCP составит
25дЛЛС (Д5ОС=Д5УС, ь.АОВ= &.АМВ, Ь.АОС= ДЛРС). Длины сто-
165
Рис. Р.1.54
Рис. Р.1.55
рои каждого из треугольников ЛОМ, BOM, BON, CON, СОР, ЛОР равны
2mJ3, 2т2/3, 2т3/3; поэтому ВАмвпср=6$ь.лом- Пусть Sm — площадь
треугольника, построенного на медианах ДЛВС. Тогда 5ьАом=4ВтР
и Влмвнср=2$ьлвс=6 45т/9=85„/3, откуда SaAbc : Sm=4 : 3.
1.235. 8 см2. 1.236. 288 см2.
1.237. □ Площадь &АВСв 3 раза больше площади ДЛОС (О — точка пересече-
1
ния медиан; рис. Р.1.53). Имеем SAAoc—~ АС ОК=КС ОК Но
ОК=ВК=2 (м), KC=JOC1-OB?, где ОС= МС=— (м); отсюда
3 _____________ 3 3
//10V ,8 16 ,
кс= I — I — 22=- (м). Итак, SAAOc=— м2, т. е. SAASC=16 м2.
_ у\з/ з з
1J38. V15/2 см2. 1.239. 235,2 см2.
1.240. □ Рассмотрим два случая (рис. Р.1.54): 1) LAKB= LALB\
2) LAKB= LALC.
1 1
1) LAKB+ LA-\— LB= LALB+ LB-\— LA (суммыуглов треугольника),
2 2
т. е. LA= LB.
1
2) Так как LALC — внешний угол L.ABL, то LALC= LB+- LA. Далее,
2
1 1
LAKB+ LA+- LB—n. Но LAKB= LALC и, значит, LB+- LA**
2 2
1 2я
= я— LA—- LB, arvjBB- LA+ LB=~.
1.241. 25/5.1.242. В 2,56 раза.
1.243. □ Пусть О2В=г; тогда О1А=К=Зг (рис. Р.1.55).. Проведем О2СЦАВ;
имеем AC=r, OlC=2r, О1О2=4г, т._ е. О1О2=2О1С и, значит,
ДСО1О1=30°. Так как ОгС=АВ=6у]з, то из LO2CO2 находим
О1О2=О2С: cos30°=6>/3 : (^3/2)=12, откуда г=3, А=9. Дуги, входящие
в указанную фигуру, содержат соответственно 120 и 240°, поэтому их
2яг 4лА
длины равны — и----. Искомый периметр составляет
3 3
г 2кг 4яЯ
Р=2 • 6V3+—+— = 1273 + 14я.
1Л44. 8. 1.245. я/2.
166
1.246. □ Обозначим искомую длину через 2х. Тогда ЛЯ=4х, AO^yJp^—x1,
BO^yJP—x1 (рис. Р.1.56). Проведем О2С||ЛЯ. В AOjOjC имеем
olc=yJolo12 *-o2C2 ИЛЯ
у]Лг— х2 —у/г1 — x2—yJ(R+r)2 — 16Х2. (1)
Умножив обе части уравнения (1) на ^/я2—х2+л/г2-х2, получим
Я2-г2=л/(Я+г)2-16х2 (j(R1-x1+ Jii-x2\ откуда
______________ Я2 — г2
\jR2-xl+^Jr1~xl=‘-----------— (2)
y/(R+r)2 — 16Х2
Складывая равенства (1) и (2), находим
_____ ___________ Я2—г2
2^ ^^^y/^R+ry-lbx2+-=========. (3)
5/(Я + г)2 — 1б№
Преобразуем правую часть равенства (3):
(Я+г)2 —16х2+Я2-г2 2(Я2+Яг-8х2) 2(Я(Я+г)—8х2)
J(R+r)2-l6^ ^(R+r^-lbx2 >/(Я+г)2—16Х2
Тогда оно примет вид ,/я2—х2 -^/(Я+г)2 —16х2-Я(Я+г)~8Х2 или
(Я2-х2)((Я+г)2-16х2)-(Я(Я+г)-8х2)2 или
Я2(Я+г)2-16Я2х2-х2(Я+г)2 + 16х4«Я2(Я+г)2-16Я(Я+г)х2+64х4.
Учитывая, что х#0, приходим к уравнению 48х2«14Яг~-Я2—г2, откуда
1 /14Яг-я2-г
х=- /----------- (второй корень уравнения не удовлетворяет усло-
1 /14Яг—Я1—г2
вию). Итак, искомая длина составляет 2х=- /---------.
2\ 3
г2(2473-Ня)/6. 1.248. яЯ2г2/(7л +л/г)*-
□ Проведем OPLAB (рис. Р.1.57). Тогда АР=ВР=1 см и МР=*3 см. Так
как Д РМО=60°, то Z. МОР=30° и ОМ-2МР-6 см.
85/8 см. 1.251. 6,25 см.
□ Проведем диаметр CF (рис. Р.1.58). Докажем, что AF=BD как хорды,
стягивающие равные дуги. Действительно, иЛС+иЯ2>=180° (так как
АВ LCD), иЛС+^ЛЯ=180° (поскольку CF — диаметр). Следовательно,
\jAF=<jBD и AF=BD. В прямоугольном треугольнике ACF имеем
ЛС2+ЛЯ2-4Я2, откуда и ЛС2+ЯД/-4Я2.
167
1.253. 8 см. 1.254. Ja'-ab+b2.
яЯ2 Л2л/3
1.255. □ Площадь сегмента с дугой 60° равна Sx --—, а площадь сег-
яЯ2 R2^3
мента с дугой 120° равна Я2 ------. Искомая площадь
1.256.
1.257.
1.258.
1.260.
1.261.
, яг(Я+7з)
S-nR2-S1-S2-—.
14 см. ____
□ Пусть г — искомый радиус. В &АОК (рис. Р.1.59) имеем OK—yJr2—^,
а в &OBN имеем 0№+я№ —ОВ2 или (OK+lf+X—r1. Следовательно,
г2—Ъ+Ьу/г2—9+4 + 1 —г\ ступ» г2—9 — 1, т. е. r—^JXO ал.
□ Обозначим радиус круга через R. Так как дуга сегмента содержит 120°,
2яЯ
то ее длина равна —у, а хорда, стягивающая эту дугу (сторона правиль-
ного вписанного треугольника), равна Ry/з. Тогда периметр сегмента сос-
2яЯ Зр
тавляет р—--ЬЯд/З, откуда Я—-----=. Находим площадь сегмента:
3 _ 2я+373_
яЯ2 Я273 Я2(4я-3^3) Зр1(4я—3^3)
S --------------------w---------s—.
з 4 12 4(2я+3л/3)2
ar a2r
a-r {fl-rf
□ Пусть A — вершина угла, O( и n — соответственно центр и радиус /-й
1
окружности (1-1, .... 5). Так как - ДЛ—30°, то AOt—2r{, AOi-i^2r^i,
2
откуда ЛО/-ЛО/_1 +т;_1 +Т/ или 2г/-2т/_1 +г<_| +г* т. е. г/-Зт/_1. Следо-
вательно, радиусы окружностей образуют геометрическую прогрессию со
знаменателем 3, а сумма площадей пяти кругов составит
S-ят}(1+9+91+9,+9‘)- -7381яг}.
Итак, Я: яг?-7381.
168
Рис. Р.1.60
в
Рис. Р.1.61
1.262. 3 см. 1.263. 5яг2/36.
1.264. □ Пусть длина отрезка АВ равна 21. Обозначим радиус одной из окружно-
стей через х; тогда радиус второй окружности равен I—х. Сумма длин
полуокружностей составляет L=nx+n(l-x)—id, т. е. не зависит от х.
1.265. Я2(273-л)/2. 1.266. В 9 раз.
1.267. □ Каждая из двух последних окружностей проходит через центры первых
двух (рис. Р.1.60), поэтому длина их общей хорды OiO2=R. Искомая
площадь равна удвоенной площади сегмента с центральным углом 60°, т. е.
/яЛ2' Л27з\ Л2(2я—Зд/З) '
\ 6 ~ 4 / 6 И
1.268. 2Я2(3>/3—я)/3. )Ub92rLl(h-2r).
1.270. □ Обозначим радиус окружности через г, а длину гипотенузы через 5х.
Тогда (рис. Р.1.61) ВС=Зх + г, АС=2х+г, поскольку BK=BL, АК=АМ.
Так как Z.OCAf=45°, то r=OC: : ^/2=2 (см). Для площади
треугольника АВС имеем выражение 5=0,5 АС ВС; с другой стороны,
S—pr, где р=0,5 (АВ+ВС+АС). Следовательно, 0,5(2х+2)(Зх+2) =
= 2(5х+2) или Зх2 —5х—2 =0, откуда х=2 см (второй корень уравнения не
удовлетворяет условию). Итак, Л5=10 см, АС=6 см, BC=i см.
1.271. □ Пусть а и b — катеты треугольника. Тогда имеем систему
(ab =48,
< „ откуда a2 + 2ab+b2 = \9f>, <r — 2ab+b2 = 4, т. е. а+6 = 14,
(а2+62 = 100,
а—Ь=2 и, следовательно, а=8 (см), Ь=6 (см). Так как S=pr, то 24= 12г,
т. е. г=2 (см).
1.272. г2 + 2Ял
1.273. □ Радиус окружности, описанной около прямоугольного треугольника,
равен половине гипотенузы. Пусть и, v — длины катетов, ан» — длина
ян*2
гипотенузы; тогда 6=--. Так как и и v — корни уравнения ахг + Ьх+с=0,
4
с b
то uv=~, u+v =—. Учитывая, что h>2=u2+v2, имеем
а а
Ь2 с Ь2 — 2ас
h»2=(u+v)2—2mv=——2-=--------— и окончательно находим
а2 а а2
я(62 —2ос)
5=-----
4а2
169
1.274. -(Л+7л2-2ас)/(2а). 1.275. 5 см.
1.276. □ Проведем радиусы OD и ОЕ в точки касания (рис. Р.1.62). Имеем
О2>=О£=С£=С2), т. е. ECDO — квадрат. Пусть R — радиус окружности;
яЛ
тогда длина дуги- ED равна —. Так как LAEO~ &ODB, то
АЕ АО 30 3 _ , _ , , J302-R2 3
— ш— ~—=-. Но АЕ1=АО1 — ОЕ2=302—R2, откуда----------= или
OD ОВ 40 4 R 4
16(302—Л2)=9Л2 и, значит, R=24. Итак, длина дуги ED равна 12я.
1171. 5^2 см. 1.278. 100я/9 см2.
1.279. □ Сначала найдем радиус вписанной окружности. Имеем
£ 0,5 • 6 • 8 24
г«-=-------------=——2 (см). Далее, так как &АВС~&МРО (рис.
р 0,5(6+8 + 10) 12 .
АВ АС АВ МО 6 2 3
Р.1.63), то -=---, откуда МР—-----------=-- (см). Аналогично,
МР МО АС 8 2
EQ ОЕ ОЕ МО 2-2 8
L.EOQ~ Е.МРО :---=—откуда £2=-----------=----=- (см). Для вы-
МО PM РМ 3/2 3
числения длины DN проведем OLLBC- тогда DN=*DL+LN. Но
8
LEOQ— LLON (по катету и острому углу); значит, ZJV=£2=~ см. Точно
3
так же из равенства треугольников МРО и DLO находим DL=МР=- см и,
3 8 25
следовательно, ZW=-+-=— (см).
2 3 6
1.280. □ Пусть а, Ь, с, р — соответственно катеты, гипотенуза и полупериметр
треугольника, г — радиус вписанной окружности. Тогда
a+b+с а+Ь с с
р+г=*—-—+г=—— +-+г. Рассмотрим сумму -+г. Так как площадь
ab ab
треугольника 5=—=рг, то г=—, откуда
2 2р
с с ab pc+ab ас+Ьс+с2+2дЬ ас+Ьс+а*+Ь2+2аЬ
” + Г в " + ----в-----------»-----------------
2 2 2р 2р 4р 4р
c(a+b)+(a+Ef (a+b)(a+b + c) a+b a+b+c a+b
ИК - - - SK .. —- ЩК , — . .... ад.
4p 4p 2 2p 2
170
a+b a+b
Итак, p+r=------н----=a+b.
2 2
1.282. □ Искомая площадь 5=S1—52+353, где 5t =-----площадь треуголь-
4
па2
ника, 52=------площадь круга, S3 — площадь сегмента, отсекаемого тре-
а
угольником от круга. Хорда этого сегмента равна поэтому
_ _ 3
1 ла2 а2у/з tta2 а2у/з
iS3«- • ——-----«—---------. Итак,
6 9 9 4 54 36
а2у]3 па2 па2 а2ч/з_а2(3л/3-я)
4 9 + 18 ” 12 18 ' И
1.283. R2(n-у/З). 1.284. (5я-б7з)/18 см2.
1.285. □ Пусть х — радиус каждой из окружностей. Тогда AD—Xy/з, DE=2x,
ЕС=Ху/з (рис. _ Р.1.64). Таким образом, 2ху/з+2х=а, откуда
а а(л/3 —1)
х=----=--=--------. Площадь каждого из кругов равна
2(73 + 1) _ 4
, ^(2-73)
. следовательно, искомая площадь
8
а^З Зтш\2-у]з) а^З-Ек+Зп^З)
S ------------------. И
4 8 8
1.286. 2(373-я) см2. 1.287. Я27з(б7з-4)/3.
1.288. □ Проведем радиус OELBC (рис. Р.1.65). Так как LOBE=- LA ВС=60°,
2
1 1
то LBOE=30°, т. е. ВЕ=- ВО. Тогда из LBEO находим ВО2=- ВО2+9,
_ 2 4 _
откуда ВО=2у]з. В ДЯОВ имеем ЛВ=2В2). Но BD=BO+OD=2y/3+3 и,
следовательно,_ AB=BC=4yj3+6. Наконец, АС=ЮС=ЦВС— ВЕ) =
= 2(47з + 6-л/3)=65/з + 12.
171
Рис. Р.1.66
1.289. 2Я2/л/Л-- 1-290. 5, 5 и 6 см.
1.291. □ Согласно теореме о касательной и секущей, имеем (рис. Р.1.66)
ВК?=АВ DB=9 4=36, откуда ВК=6 см, КС=3 см. Проведем радиус
5
ОК в точку касания и ON .LAB. Тогда AN=ND=- см. Так как b.ANO~
~&ОКС (прямоугольные треугольники, у которых LA= LQ, то
КС ОС 3 6
— =—=—=-. Пусть искомый радиус равен г. Тогда ЛО=г, ОС=
AN АО 5/2 5
.------- .------------------ 15
=v/9+r2 и, значит, 6г=5у9+г2 или 36г2=225 + 25г2, откуда г=—=см.
V11
1.293. 7, 24 и 25 см.
AD АС 18 3
1.294. □ Так как CD — биссектриса (рис. Р.1.67>, то —=—=—=-, откуда
DB вс 12 2
AD=9 см, DB=6 см. Далее, длина биссектрисы CD=yJt2 18—9 • 6=9>/2
см (см. дополнительное соотношение 5° в начале главы). Проведем ради-
усы в точки касания и положим CF=x. Тогда, используя равенство каса-
тельных, Шроведенных из одной точки, получим 18—х + 12—х—15, откуда
15 /45 21 15 9 135^7
х=— (см). По формуле Герона находим 5= /— • — • — • - =-----(см2).
2 у 2 2 2 2 4
135^7 45 Зл/7
Но В<=рг, откуда г=----------------:—=------ (см). Значит,
______ 4 2 2
----- /225 63
OC—yJjr+rt* /------1—=65/2 (см). Поскольку CZ>=9>/2 см, точка О де-
у 4 4
лит биссектрису в отношении 2 : 1.
1.295. 3 : 2, 3 : 1, 2 : 1. 1.296. 5 см.
1.297. □ Обозначим стороны треугольника через а, Ь, с. Тогда площади частей
111 8
треугольника равны - аг, - Ьг, - сг, т. е. от =8, Ьг= 26, сг=30, откуда а=-,
2 2 2 г
26 30 /32 24 6 2 96
Ь=—, с=—. По формуле Герона находим 5= /— — • - . Но
г г у г г г г ,
, 96 8
5=4+13 + 15=32 (см2); следовательно, —=32, т. г..«- - /3 сы. Итак, а ~ - -—
г л/з
26 30
см, 6=—= см, с=—= СМ.
V3 ф
в
в
Рис. Р.1.69
1.298. Прямоугольный; 24 см2. 1.299. 130 см2.
1.300. □ Так как САСВ=- (рис. Р.1.68), то АВ=2>/2 см (сторона вписанного
4
я
квадрата). Проведем BDLAC. Тогда, учитывая, что LABD=~, находим
6
1 .-
AD=- АВ=у/2 (см); далее, поскольку t\BDC — равнобедренный,
2 г3 г3 _ _ _
DC=BD=~ АВ=—— -2^2=J6 (см). Значит, AC~AD+DC=^2 + у/б
2 2
(см). Итак, S=-^AC (V2+V^6“0+V3)V3“V3+3 (см2).
1.301. 16,9 см.
1.303. □ Пусть О — центр окружности, описанной около &АВС, и Ot — его
ортоцентр (рис. Р.1.69). Построим &LMN, сторонами которого служат
средние линии заданного треугольника. Высоты &LMN пересекаются
в точке О, поскольку эти высоты перпендикулярны сторонам &. АВС и про-
МО LN 1
ходят через их середины. Но &LMN~А АВС и потому-=—=-, т. е.
AOt ВС 2
АО^2МО.
2
1.304. □ Так как CN— медиана, то СК=- CN (рис. Р.1.70). Соединив точки
3
LM CF 1 1
L и М, получим среднюю линию LM; поэтому-=—=-, т. е. CF=- CN,
АВ CN 2 2
Рис. Р.1.70
Рис. Р.1.71
173
a lai
LM=~, LF=FM=- AN=-, FK=- CN. Имеем LF FM=FK CF.lppota-
2 2 4 6
ведение отрезков хорд, проходящих через точку F). Следовательно,
a2 1 1 aJ3
-=CN- CN. откуда CN=- .
16 6 2 2
1305. 120/17.
1306. □ Соединим вершины квадратов А и С, В и D (рис. Р.1.71). Продолжим
BD до пересечения с АС. Обозначим точку пересечения через N и покажем,
что она совпадает с точкой пересечения окружностей, описанных около
квадратов. Действительно, так как &АСМ— &.BDM, то LACM— LDBM
и потому BNLAC. Но прямые углы BNC и AND опираются на соответст-
вующие диаметры, а значит, точка N принадлежит обеим описанным
окружностям, откуда и следует доказываемое утверждение.
1307. а^Д За^З/Ь и 5ayj3lb. 1308. 17 см. __________
1309. □ Проведем радиус ОК (рис. Р.1.72); тогда KL=^KO2—LO2. Но LO=
- ВЕ= 18-13-5 (см), откуда АХ=>/132 — 52 = 12 (см), ВАГ—13 —12-1 (см).
Итак, сторона квадрата разделена на отрезки 1 и 17 см.
1310. 10 :1. 1311. 65яа2/4.
1312. □ Хорда ОА стягивает дугу 90° (рис. Р.1.73); поэтому пг'щадь половины
яо2 о2 адя—2)
лепестка равна-----—-------. Следовательно, искомая площадь S=8 х
16 8 16
а2(я—2) а2(я—2)
х -------=-------.
16 2
1313. □ Пусть х — сторона прямоугольника, вписанного в окружность радиуса
Я. Тогда его площадь равна х^4Я2—х2. Площадь вписанного квадрата
равна 2Я2. Покажем, что 2Я2>х,/4Я2—х2. В самом деле, из очевидного
неравенства (2Я2—х2)2>0 получаем 4Я*>х2(4Я2 — х2), откуда и следует,
что 2Я2>х>/4Я2—х2 (знак неравенства сохранится, поскольку 2Я2>0
и х -у/4Я2—х2 > 0).
1314. 84/13 и 72/13 см. ------
1315. □ Так как Л С — диаметр окружности (рис. Р.1.74), то Я=0,5л/242+72 =
= 12,5 (см). В ДВОЯ имеем 0Я=л/0Я2-ЯЯ2=л/12,52-122 = 3,5 (см); зна-
чит, MF-12,5-3,5=9 (см), МАГ=12,5 + 3,5 = 16 (см). Из дМЯЯ и ДМЛАГ
находим искомые расстояния: А/Я=-Уа£Я2+ЯЯ2=-У92 + 122=15 (см),
MA^MK^+KA1=^\(>1 + \21='2!3(<m).
174
Рис. Р.1.75
1.316. (Л—а)2/2. 1317. m(p+q)/q, mip + q/lp, p + q.
1318. □ Так как IxAEF—равнобедренный (рис. Р.1.75), то биссектриса AM
перпендикулярна EF и лежит на диагонали ромба. Находим
_ 27 9 3
АМ1=АЕ1-МЕ1=9-----=-, т. е. ЛМ=- (см). В &ACF имеем Z.F-9O0
4 4 2
3
и FMLAC-, следовательно, АР-АС • AM или 9=ЛС~, откуда АС—6
2
(см). Далее, t\ACD~ EAEF (углы при основании равны как углы со
AM EF
взаимно перпендикулярными сторонами) и, значит, --------=— или
OD АС
3/2 Зл/З г
— =-----, откуда OD—J3 см. Итак, BD—2J3 см, АС— 6 см. В
OD 6
1319. 20 см2.
а^З
1320. □ Радиус вписанной в ромб ABCD окружности (рис. Р.1.76) Л=-,
4
поскольку ДЛ=6О°. Четырехугольник KLMN является прямоугольником,
так как его углы опираются на диаметр окружности. Его площадь
S—MN LM, где MN—R (катет, лежащий против угла 30°), LM—R-J3.
, З^л/З
Итак, Я-Я^/З-—
1321. □ Площадь ромба 5=0,5 3 • 4=6=Л2) • BE (рис. Р.1.77). Из &AOD на-
ходим ЛД=^,22 + 1,52 = 2,5 (см) и, следовательно, BE=6 :2,5=2,4 (см).
Далее из &BDE получим DE=>JBD1-B&~j31-2,41~\:& (см). Итак,
Sbedf“2Sьвев** 1>8 2,4=4,32 (см2), н
175
1322. 25/(6я). 1.323. 8Я\/3/3.
1324. □ Искомая площадь 5 равна 4(5дЛОд—SaAfk) (рис. Р.1.78). Находим
5длол=0,5 • 3.2=3 (см1 2 * 4). Сторона ромба равна Л/22 + 32=Л/13 (см).
В Л.АОВ отрезок ОК — биссектриса; тогда, используя формулу
y/ab(a+Ь+с)(д+Ь—с)
1С=----------------- (см. дополнительное соотношение 6° в начале
а+Ь
V6(5+V13)(5-V13) 6^2
главы), получим ОК=------------------=—— (см). Теперь найдем
1 ОК 6
Slafk—~ AF• КН, где КН=—= =- (см), AF=3—2=1 (см); значит,
2 V2 5 6
5длгк=0,6 см2. Итак, 5=4(3—0,6)=9,6 см2.
1325. 9, 9 и 6^2 см. 1.326. +J1 и 18 см.
1327. □ Покажем, что искомая площадь Slump—28 (рис. Р.1.79). Действитель-
но, так как АЦВО и LB\\AO, то ALBO — параллелограмм и, значит,
>5дЛ£Л=>5длол- Аналогично получаем S t,DCN— 8 a doc,
Si,APD=SAAOD, откуда и следует, что SLmnp=2S.
1328. 96 и 156 см. 1329. 45 и 135°.
1330. □ Так как KL, LM, NM, KN — средние линии соответствующих треуголь-
1 1
ников (рис. Р.1.80), то KL=NM=-^AC, KN=LM=-^BD. По условию,
1
AC=BD и, следовательно, KLMN — ромб, площадь которого равна - pq.
2
Пусть искомая площадь равна 5. Тогда 5=5дли)+5ддсо- Но S^akn=
1 1 1
““ 8&abd, аналогично, Sacml-~ S^bcd и, значит, Saakn+S^cml=~ 8.
4 4 4
1
Точно так же получим, что S^kbl+S^mbn^ 8. Итак, площадь вне ромба
4
1 1
равна - 5. Поэтому и площадь ромба равна - S, откуда S=pq.
2 2
1331. 3 см. 1.332. 120 см2.
я
1333. □ Пусть малая дуга содержит х градусов. Тогда 4х+8х=2я, откуда х=-.
6
Значит, восьмиугольник содержит четыре треугольника с центральным
176
ставляет 5= Я2(д/з + 1).
1.334. а. 1.335. 8 или 6 см.
1.336. □ Заметим, что окружность, описанная около трапеции ABCD, описана
и около &ACD (рис. Р.1.81), причем такая окружность единственна. Ее
abc 1
радиус будем искать по формуле Я=—. Имеем S=- AD BE, где
BE=J АВ?-АЕ?=Jотсюда 5*ла>=- 14 8 = 56. Из ДЛСМ
2
находим AC—yjAM2 +МС2 =>/82H-82= 8^/2. Итак,
14 • 10 • 8а/2
*---—_х_ш55/г н
4 • 56
1.337. 6 см. 1.338. й7з/3.
Зх 1х
1.339. □ Пусть ОК=х, AL=y, BK=z (рис. Р.1.82). Тогда MN=z+y^x-i—=—.
4 4
В ДОЛЯ и ДОДЛ имеем ОВ2 = ОК2+ВК2, OA2~OL2+AL2. Таким об-
разом, приходим к системе уравнений
x2+z2 = 100,
9л2
или
10
7х
-_z=y
x2 + z2 = 100, Г x2 + z2 = 100,
Эх2 fix \2 или < 29k2 Ixz „
— +----------z] =100 I----------------+z2 = 100.
. 16 \4 ) l8 2
21X2 Ixz
Вычитая первое уравнение из второго, получаем-——=0, откуда (так
8 2
4z 16т2
как х#0) х=—. Значит, z2H---=100, т. е. z=6. Отсюда находим х=8,
3 9
у=8. Итак, ZD=2y=16, BC=2z=12.
1.340. Трапеция равнобедренная, боковая сторона равна средней линии. 1341.
4 и 5^41/4 см.
1.342. □ Обозначим высоту ВНтрапеции через h (рис. Р.1.83). Тогда AB“2h (так
как ДЛ = 30°), BC+AD=4h (поскольку BC+AD=AB+CD — 2AB). Пло-
Рис. Р.1.83
(BC+AD)h
щадь трапеции S=---------=2Л2=32 (см2), откуда Л=4 см. Следовате-
2 .
льно,Л5=С2)=8 см, BC+AD —16 см. Но BC+AD = 2BC+2AH—2BC+
+ 8>/з. Итак, AB=CD = 8 см, ВС=8 — 4^/з см, Я2) = 8 + 4л/з см.
1343. 100я см2. 1.344. 20, 12,5, 5 и 12,5 см.
1345. □ Пусть L и М — точи касания (рис. Р.1.84); тогда SL=SM, откуда
AB=CD, поскольку AD^BC^LM. Проведем OKLLM и BHX.AD. Искомая
1
площадь S= - (AD+BC)BH. Для описанной трапеции имеем AD+BC=*
2
*=AB+CD=2AB; поэтому S=*AB ВН. Далее, &АВН~ t^OLK (l_LOK=
= LBAH как углы с взаимно перпендикулярными сторонами), откуда
LK ВН а/2 2R 4R2 4R2 8R3
—“— или —=— и, значит, АВ=--------. Итак, 5=-- 2R=----. и
LO АВ R АВ а а а
1346. 8Rry]Rr!{R+r). 1.347. 36Д/Ю, 12/710, 18/л/Ю и ЗОД/10 см.
1348. □ Сначала найдем сторону АВ=2х (рис. Р.1.85). Пусть ED=x. Тогда,
4г 4г
используя равенство AB+CD=BC+AD, получим 2г+С2>=—I----------1-х, от-
3 3
178
куда CD=— + x. В l\CED имеем CD1 = СЕ2 + ED2 или ^y+xj = 4r2+x2,
8г Юг 12г
откуда х=-~. Итак, CD=—, AD——=4r.
3 3 3
1.349. 18V5/5 см. 1.350. 3,6 см2.
1.351. □ В силу условия, ДВОС=45° и, значит, ВС—ОС=—=, ЯС=А—
V2
R R(J2-1') DO АО
— =-----=— (рис. Р.1.86). Так как ДЛВС~ДЛ1>О, то —=—-, от-
V2 V2 ВС Ad
АО ВС R
куда DO=-------=—=—=Я(л/2+1). Находим площадь трапеции:
лс ^2-1
1 1 ( R\ R Л2(3+л/2)
S=- (PO + BQOC=-(AG/2+l)+—=J-;==-------
1.352. 14, 12,5, 29,4 и 16,9 см. 1.353. 6 см.
1.354. □ Пусть AD=a, BC—b (рис. Р.1.87). Так как &МВО~ txABD, то
МО ВО ВО
----=—, т. е. МО=а .—. Аналогично, t\OND~ E.BCD, откуда
a---BD BD
ON OD OD a- BO+b OD
—=—, т. е. ON^b-—. Тогда MN=M0+0N=---------------------=
b BD BD BD
2а ВО a OD
=------, поскольку &AOD~ &ВОС и, значит, -=—, т. е. а-ВО =
BD b ВО
—Ь OD. Учитывая, что BD=BO + OD, окончательно находим
2а ВО 2а 2а 2аЬ
MN=-------=-------=---=---.
BO+OD OD а a+b
1 + 1+_
ВО ь
1.355. 1275 см2. 1.356. Л/(в2+*2)/2-
1.357. □ Проведем BHLAD и CFLAD (рис. Р.1.88). Пусть АН=х; тогда
AF=S + x, DH=24—x. Учитывая, что BH=CF, в ДЛРС и &BHD имеем
Ad-AF2 = BD1-DH1 или 132 - (8 + х)2 = (5^17)2 - (24 - х)2, откуда
64х=256, т. е. х = 4 (см). Тогда CF=s/AC2-AFl=y/l32-l22 = 5 (см).
Следовательно, 5= (24+8) • 5 = 80 (см2).
Рис. Р.1.88
179
За—b a a—3b
1.358, a --при b<3a; - •----при a>3b. 1359. 2,4 cm.
a+h 3
1.360. □ Искомая площадь 5 = 125длос, где О А и ОС — радиусы (рис. Р.1.89).
а
Так как сторона квадрата равна а, то ОА = ОС=~Имеем
V2
1 1 2я л
9длос=_ ОА CD, где CD1OA. Но CD=- ОС, поскольку LAOC=—
2 2 12 6
1 а 1 а а2 За2
Таким образом, 9длос=~ • ~~= ~ • — =~> т. е. 5=—. В
2 J2 2 /2 8 2
1361. 10 см.
1.362. □ Около ДЛ9С опишем окружность и продолжим биссектрису AD до
пересечения с этой окружностью в точке Е (рис. Р.1.90). Так как
BD : DC=c : b=4 : 5, то BD=S см и PC-10 см. Но BD DC=AD DE,
откуда AD Р£=80. Поскольку &ABD~&AEC, имеем АС: АЕ=
=AD : АВ, откуда AD АЕ=1И0. Учитывая, что AE=AD+DE и DE=
=80 : AD, находим AD=10 см.
1363. LA + LB^W или IДЛ-Z..В| = 90°.
1364. □ Положим АВ=х, ВС—у, CE=z (рис. Р.1.91). Так как х :y—AD : DC
(BD — биссектриса угла АВС), то х=2у (1). Кроме того, иэ Е.АВЕд &.СВЕ
имеем: x2 = (6+z)2 + 15 (2), y2=z2+15 (3). Система уравнений (1) — (3)
приводит к квадратному уравнению z2—4z+3=0, откуда z, =1, z2=3. При
z=l получаем ответ: AB=x=S см, ВС=у=4 см, АС=6 см (при z=3 длины
сторон не являются целыми числами). В
1365. □ Пусть прямые АЕ и CD пересекаются в точке L (рис. Р.1.92). Проведем
прямую BL до пересечения со стороной АС в точке М. Так как
ДЛ£М~ Д£Л£, a &CML~ &DKL, то AM : KE=ML : KL, a. CM : DK=
= ML : KL, откуда AM : CM=KE: DK Далее, из подобия l\ABM
Рис. P.1.94
180
и L.DBK, а также &МВС и &КВЕ заключаем, что AM: CM=DK: KE,
т. е. KE : DK=DK : КЕ=Л. Итак BL — медиана и, следовательно, L — об-
щая точка для указанных в условии-трех прямых.
1.366. 11/3 см2.
1.367. □ Пусть hc^hb^AC (рис. Р.1.93). Но АС — наклонная и, значит, AC = hc,
т. е. ДЛВС— прямоугольный, откуда следует, что hb=AB. Так как
hb=AB^AC и hc=AC^AB, то АВ—АС. Итак, гипотенуза ВС=а, катеты
AB=AC=aJ2/2.
1(а+Ь) .--------------
1.368. 45, 45 и 90°. 1369. 33/4 см. 1.371.-^4а2Ь2-Р(а + Ь)2.
4ab
1.372. □ Рассмотрим случай, когда точка О лежит внутри треугольника (рис.
Р.1.94; в случае, когда она лежит вне треугольника, решение аналогично).
По условию, ЕАКВ=90° и KL4.AB, значит, KL?=AL LB. Так как
ДЛДО~ ДСДВ, то AL : LO = CL : LB, откуда AL LB = LO CL, т. е.
KL2=LO CL. Итак,
5длга = 0,5Л5 • KL = 0,5AB^LO CL =
= ^jo,5AB LO 0,5 AB • CL = *jS ьлов S&ACB- В
1.373. 3 : 7. 1.374. -^43 и -J33.
1.375. □ Очевидно, что около четырехугольников AEDC и ABDF можно описать
окружности (рис. Р.1.95), поскольку соответствующие прямые углы можно
рассматривать как опирающиеся на диаметры. В четырехугольнике AEDC
имеем LA = LBDE (каждый из них дополняет LEDC до л). Аналогично,
в четырехугольнике ABDF имеем LA — LCDF (как дополнения LBDF до
я), откуда LBDE= LCDF. Так как LBDE+ LEDA*= LCDF+ LADF=n/2,
то lEDA = LADF. Значит, высота DA является биссектрисой &.EDF.
Точно так же проводится доказательство для остальных высот.
1.376. (,/3-1)5.
1.377. □ По условию, АВ=ВС, AD — биссектриса, BD—AC (рис. Р.1.96); требу-
ется доказать, что AD=AC. Отложим на стороне АВ отрезок АК=АС.
Тогда ДЛХ2)= LADC (сторона AD — общая, АК= AC, LDAK= LDAC),
откуда DK=DC. Так как AK+KB=BD+DC, то KB=DC и, значит,
LBKD — равнобедренный. Поэтому LKBD = LDBK, откуда следует, что
LADC=LC ( LB+ LADK+ LADC= LB+ LA + LC=n, но
LADK=LADCh LA= LCJ. Итак, AC=AD.
1.378. r, 4r/3 и 5r/3.
1.379. □ Пусть F, D, E — точки касания вписанной окружности со сторонами
LABC (рис. Р.1.97). Положим BD=x; тогда DA=m—x. Таг как AD—AE
181
и BF=BD (касательные, проведенные к окружности из одной точки), то
АЕ=т—х, BF=x. Учитывая, что АВ2=ВС2+АС1, получаем уравнение
т2=(х+г)2+(т—х+г)2 или х2—тх+(тг+г2)=0, откуда х=
m+y/m2—4r(r+m) 2r+m±Jm2-4r(r+m)
=----------------, ВС=х+г=---------------'---АС=т+г—х=
2________ 2
2г+тТУ/т2—4г(г+т)
=-----------. Задача имеет решение, если m2— 4г(г+т)^0,
m(V2-l)
т. е. если .
2
1380. 30 и 60°. 1.381. 3 и 4.
1382. □ Так как &DCA~ &DCB (рис. Р.1.98), то АС : ВС=г : Я=3 : 4 (г
3
и R — данные радиусы вписанных окружностей). Отсюда АС=~ ВС и,
следовательно, АВ2=АС2+ВС2=—^ВС2. Пусть х — радиус окружности,
вписанной в ДЛ5С. Тогда, учитывая, что &DBC~&АВС, имеем
5
ВС :АВ=Л : х=4 : 5, откуда х=- 0,8= 1 (см).
1383. 5. 1384. 18 см.
АС АВ
1385. □ Поскольку &АВС~ &DBE (рис. Р.1.99), имеем —=—. Полагая
DE DB
DE=x и учитывая, что DB в У \ г> \в к к А Л С Рис. Р.1.99 182 х 2л л1+л =т—, получим —= и, следовательно, 2 хх т 2 В А в к а Рис. Р.1.100
х —-----. Далее, &АВС~ &KLC, откуда — =—. Пусть KL=y и FL=z
-т+2п KL КС
т + п 2п
(F—точка касания). Тогда--------=-------; так как y+z=n, то
у n—y+z
т + п п п(т+п)
----=-----и, значит, у=----.
у п—у т+2п
1.386. 175/48 см. 1.387. а2(3,/3-л)/18. 1.388. ajl (а-2Л)/12.
1.389. □ Пусть Р — периметр &ADE (рис. Р.1.100); тогда P=AD+DE+AE, где
DE=DL + LE=DS + KE. Значит, P=AS+AK=AB+AC-BS-CK По-
скольку BS = BR, CK=CR, окончательно получим Р—АВ+АС—ВС=16
(см).
1.390. 6 или 4 см. 1391. п.
1.392. □ Так как !_ВНС=90° (рис. Р.1.101), то иЛХС+иВС=180°; в силу усло-
вия, \jAK—<jLC, т. е. иЛС+о5С=180°, и, значит, BL — диаметр окру-
жности. Поскольку диаметр BL не перпендикулярен хорде, но делит ее
пополам, заключаем, что АС — также диаметр. Итак, радиус окружности
равен т.
1.394. • Провести отрезок LM и рассмотреть вписанные углы LMK, LCK,
MLK, МСК
1.395. □ I способ. Соединим центр О описанной окружности с точками А2, В,,
С, (рис. Р.1.102). Имеем ShABC=Sl + S1+S„ где Si = ShABtct-ShBloc.,
S2 = S^A,BC, + SeiAioct. S3 = S^AlBlc+S^AioB,- Проведем радиусы ОА, ОВ,
ОС и установим, что они перпендикулярны соответствующим сторонам
E.AiBlCl. Для этого проведем касательную через точку С; тогда OCECF.
Покажем, что LBFC= 1_ВАА2. Действительно, \jB1C='uA1C (так как
иА2С + иАВ= иВ2С+ мАВ—180°), откуда <иВС— иВ2С=иА2В. Но
ЕВАА2 = ЕВВ2А2 (см. решение задачи 1.375), а, следовательно,
l_BFC= ЕВВ2А2, т. е. и ОСЕА1В1. Аналогично доказываем, что
ОАЕВ2С2 и ОВ1А1С1. Теперь находим
^=2 -®i^i ' r + 2 ' R+z ' R=PR-
II способ. Воспользуемся теоремой косинусов:
BlCi1=AC1l + ASi-2AC1 АВ2 cos А = (AC cos А)2 + (АВ cos^)J-
— 2(А С cos А)(АВ cos A) cos А = (ВС cos А)2,
т. е. В,С2=ВС cosA. Аналогично получим A,CI=ACcosB, А1В1 —
=АВ cos С. Далее имеем
183
2p=AIB1+BlCI + AlCl”AB cosC+BC cosA+ACcosB=
= K(sin24 + sin2B+sin2C),
так как a^lRsinA, A=2KsinB, c=2KsinC. Преобразуем выражение
в скобках:
sin24 +sin2B+sin2C=2sin(H +B) cos(/4—B)+sin2C=
- 2 sin C cos (Л—В)+2 sin C cos С « 2 sin C (cos (Л—В)+cos С)-
=2sinC(cos(/4 — В)—cos (Л + B))=4sin^ sinB sin C,
p
откуда 2p=4B sin A sinB sin С, t. e. — = sin^ sinB sinC. Итак,
2,R
abc 8Я3 sin A sinB sin C , p
-------------------2Л1 ^-=Rp.
4Я 4Я 2Я
4Я
1.396. 313бл/81 см2.
1.397. □ Искомая площадь выражается следующим образом (рис. Р.103):
1 л/З
Яьлвс=2 ВС h, где Л=^- АВ. Но ВС=2ВК=
1 3 1
= 2 • - МВ=МВ=-$ АВ. Отсюда ShABC=-^ х
з -Уз зТз
х - АВ — АВ=—— АВ2. Таким образом, за-
5 2 20 f ,
дача сводится к нахождению АВ2. Опустим на
АВ перпендикуляр ОР и проведем радиус О В;
тогда в &РОВ имеем РВ2 + РО2 = \6. Но
1 AM 2
АР=РВ—- АВ; учитывая, что-----=-, получаем
2 МВ 3
л/з >/з
&МРО находим РО—МР tg30 =— МР—--~ АВ.
АВ2 АВ2 1200 „
Наконец, из уравнения —-—='° получим АВ=—^~. Итак, искомая
180J3 , _
площадь равна —см .
□ Пусть Я = О]В и г=О2С — искомые радиусы (рис. Р.1.104). Проведем
(AC\i (АВ\г , ,
касательную AM. Тогда АМ2=1 — I +( 1 =3 +4 =25, откуда АМ=
= ВМ=МС=5 см, MN=?> см. В &О.ВМ и LOrBN имеем О1ЛГ2=Я2+25,
, , 25
R =16+(O1M—3) ; из этих равенств находим О2М=— см и, значит,
1
AfP=— AB. Далее из
1.398.
184
Я—у см. Наконец, проведем О2В^ВС-, в t^,OxDO2 имеем (Я+г)2 —
= (Я—г)2 + 102, откуда г=— см.
4
1.400. 6 см.
1.401. □ Искомая площадь S~S^abc~3St где S2 — площадь сектора, ограни-
ченного дугой окружности и половинами сторон треугольника (рис.
Qx)\/3
Р. 1.105). Пусть х— радиус малой окружности. Тогда 5=----------
4
Учитывая, что АВ^х-ОВф
о 2 2
и OB=R—х, получаем х=-^^- = В(2\/з — 3). Итак,
2+yft
„ Я2(2>/3-3)2(2л/3-л) ЗЯ2(7-47з)(273-л) _
2 2
1.402. Я2(3 - 2^/2) (4-я). 1.403. 2Я2(3 ^3 - я)/9.
1.404. □ Искомая площадь S^a+^, где Л — высота трапеции (рис. Р. 1.106).
Очевидно, что
а—b “ +yjp—h1, откуда (а— b^cP-h1 - JtP-h1) -чр-с2.
Перепишем эти уравнения так:
yjcp—h1+y/cP—h2 ••‘a-b,
a—b
Следовательно, y/tP—h2—- ( a—b-i——— ), t. e.
2 \ a—b )
,, 4</2(a—6)2 —((a—6)2+</2 —c2)2
A------------4^-------------'
Преобразуем числитель полученной дроби:
4</2(a - b)1 - ((a—bp +<P -c2)2 -
-(W(a-6)+(a-6)2+</2-?)(Ma-6)-(a-6)2-</2 + c2)»
- (W-22></+a2 - 2a/>+1>2+rf2 - c’XW-2Z></-e2 + 2a/> -1>2 - i/2 + c2)-
Рис. P.1.107
185
- ((в,- b+d)2 - <?)(<? - (a— b - d)2)=
= (a— i + c+d)(a—b — c+d)(a—b + c —d)(c—a+b+d).
t "" ...' 1 ---------------1 " , ..
Итак, S=— >j(a—b + c+d)(a-b-c+d)(a—b+c-d)(c—a+b+d).
_____4fa-Z>)
. b^+b2 )—m+a-n
1.405. 7----. 1.406. admn-----.
v 2 a—л
AF BF c
1.408. □ Так как ZD||FHfyBC (рис. P.1.107), to—-=—Используя свойство
HD CH d
CH,
описанных четырехугольников, имеем BC-^i'H-BF+CH
AD+FH=AF+HD=(C- + \\ HD, откуда AD-BC^-f (HD-СН). Заме-
\d J a _______
нив в последнем равенстве HD на d—CH и AD—ВС на у[сР — с2, получим
------ с+d
yjcP—c^c+d—l —— • СН. Следовательно,
d
c + d-jcP-c2 c+d—^jcP — c2
CH=---—Y-------d, BF=*----------- c,
2(c+rf) 2(c+d)
c+d-^<P-c2
---- --- ^Jdi-P=BC+
Цс+d)
FH=BC+
-yjd-c
------Cd—с.
2 v
Находим
BC = CH+BF—FH, to
(. //_. /A_
основания; так как
2ЯС=———(c+d—.J cP— с2), откуда BC =
(-Jc+d+Jd-c)1
AD--------i’
1.409. Боковую сторону. 1.410. 1,6 см2.
1.411. □ Проведем ОКЦ7О (рис. Р.1.108). Тогда искомая площадь
OK OF
S=2OK • 10=20 ОК. Так как &OLF~ &OFK, то —=—, откуда
OF OL
OF2 25
OK=^£-=— (см). Итак, 5=125 см2.
1.411 2Л2/5.
1.413. □ Искомая площадь S=Si—2S1 + 2S3 + 2Si—2Ss, где 5, —площадь сек-
тора Л СЕ, S2 — площадь сектора ВСОА, S3 — площадь Д ABC, St — пло-
— площадь &ВОА
4
щадь сектора BOA, Ss
следовательно,
(рис. P.1.109). Ho S3 = S5 и,
Рис. P. 1.108
186
1 , л 1 . 2л 1 , я nR2
ЗЯ2 2 • - R1 —+2 - R2
1 2 * 2 3 2 3 2 36
1.414. а2(3 — 3у/з+л)/3.1.415. Я2(8х/3-9)/4.
АС ВС
1.416. □ Так как CD — биссектриса (рис. Р.1.110), то —=—. Но
а Ь
АС1+ВС1=(о+Ь)2 или ВС2 + ВС2 = (а+Ь)2, откуда 5С=-^===. Про-
* у]^ + Ь2
DE a a ab
ведем DELAC-, тогда —=-----откуда DE=---------- ВС=—— Далее,
ВС a+b a+b yja2 + b2
? 2^3
cd=deJi и окончательно находим S—CD2 = а И
a adb !- a aJb г- IRr
1.417. -Н—— и 5a + 2ov6 или----и 5a—2aJb. 1.418. -—.
26 26 Я+т
1.419. □ Очевидно, что площади треугольников ЛОЛ и ЛОР равны (рис. Р.1.111);
то же верно и для треугольников ВОС и COD. Следовательно,
5длой+5'дйос=0,5 Sabcd, т. е. 5^дсо=0,5 Sabcd- Так как Sabco=S^abc+
+ $ЬАОС И S hAoc=s lace, to Sabco = sabce=®,5 $abcd-
1.420. (ad+bc) : (ab + cd).
1.421. □ I способ. Очевидно, что искомая площадь Л=- ME KL (рис. Р.1.112).
Найдем ME и - KL. Так как BD — медиана, то MD BD=^~. Заметим,
2 3 6
что ED — радиус вписанной в &АМС окружности, поскольку AL
и MD — биссектрисы углов этого треугольника. Следовательно,
Slamc=^ (AM+MC+AQED=(AM+AD)ED =
(ad3 d\ 0(2,73+3)
Ч 3 +2)£D=fLT- ED-
С другой стороны,
1 1 a2 J3 O2V3
Slahc=- AM MC sinl20°=- . - ^—75-.
£ if J L> iL
a2y/3 o(2J3 + 3) ay/3 a(2-y/3)
Отсюда находим ED=—— :----------------=----—---=--------
12 6 2(2л/3+3) 2
187
„ aJi a(2-j3)' aJ3(2-V3) „ - --
ME=MD—ED=~--------------=—-——-—. Далее, учитывая,
6 2 3
ML AM ML Ji
AL — биссектриса, имеем -----=-- или ----------==—
LC AC MC—ML 3
ML V3 a a(>/3-l) „
——-----=-^> откуда ML—-———------=----——. Наконец, так
<ц/з 3 л/з(7з + 1) 2^3
-----MLi
3
1 7з а(х/3-1)
LMLK^3tf, то - KL=~- ML = -^----\ Итак,
2 2 4
что
или
как
„ 1 Г7 *7з(2-7з) a(V3-l) д2(9-5,/3)
t>KMLE=ME - KL=-------------------=-----------.
2 3 4 12
II способ. Искомая площадь выражается так: S=S ^kmc-S^elc- Заме-
тим, что S&AKC ' S&кмс=АК : КМ, поскольку эти треугольники имеют
равные высоты, проведенные из точки С. Учитывая, что СК — биссект-
риса, имеем ЛК : КМ=АС . СМ=Ji, т. е. S^AKC=Ji $дкмс- Но
1 c^Ji a2 Ji а3(3-7з)
$ьакс+$лкмс=-.$лавс=——, откуда S^kmc=----------р----=---------
3 12 12(73+1) 24
Далее, LAKC~ LELC (l_AKC= lELC, LACK= lECL) и, следователь-
S^akc (AC\2
но,-----= I — I . Отсюда находим
S&ELC \ECJ
(EC\2 / EC \2 S&akc S^akc
Jy-t) S&AKC I — ТЧ/-Т ) S ДАКС """ . 2 1 co W 0/1 l СЛ, ine1
ACJ \2DCJ 4cos 15 2(1 + cos30 )
=----p = (.2-y/i)ShAEC = y/^(^-y/i)ShKMC = (2y/i — 3)ShKMC-
2 + J3
Итак, окончательно получим
S = S д kmc - S д elc=S д kmc—(2-^3 - 3) S' д kmc=
-c -
1.421 9R2/4.
1.423. □ Пусть St, S2, S3 — площади треугольников, отсекаемых сторонами
шестиугольника от ДАВС (рис. Р. 1.113). Покажем, что S,=S2 = S3. Так как
каждый из отсеченных треугольников подобен L.ABC (пропорциональны
две стороны, содержащие общий угол), то
в S, S2 Ss т1
/\ 5 = 5 = 5=(2л,+Л)1' СлеА°вательно>
/ х шестиугольника равна
/ X 3™2 ( 3>”2 \
/\ /\ s~qJJJJ2 5~5\(Ъп+п)2}
Рис. Р.1.113 1-«4. 1.425.
188
1001.
1002.
1005.
1006.
1009.
Глава х
ЗАДАЧИ ПО СТЕРЕОМЕТРИИ
САСВ—90°, (_ВАС=30° (рис. Р.2.1); следовательно,
1 /3
откуда 5<хи=- АС ВС-~—. Проведем SO так, чтобы
2 8
О — центр описанной около &АВС окружности,
□ По условию,
с еч/з
ВС—-, АС=^~,
2 2
АО — ОВ. Тогда
SO — высота пирамиды (см. «Дополнительные соотношения между элеме-
нтами призмы и пирамиды», п. 1°). В &ASO имеем LSАО—45° и, значит,
с 1
SO-AO-? Итак, V=- SOCH
mnc2J 4b2 — с1 , ,
,---J—. 2.003. б см3. 2.004. 108 см3.
12(т2 + п2) 2
□ Согласно условию, АВ—ВС—а (рис. Р. 2.2); поэтому ВН—а2—- —
=- \/4а2—Ь2. Отсюда 5ося=~ АС ВН—^- bd4a2—b2. Проведем высоту
2 2 4
SO. Поскольку все ребра пирамиды одинаково наклонены к плоскости
основания, точка О — центр описанной около JSABC окружности. Пусть
а2Ь а2
радиус этой окружности равен R. Тогда ОВ—R=~-— = .. .. = В &SOB
4о<хя у] 4а2—Ь2
SO - JSB2-OB2 - ^4ОВ2-ОВ2 - овф> -
SB
имеем ОВ——;
2
— ,.... Итак,
Jia^b2
^=- 5<хи 5О=- •
48
значит,
bsj4a2 — b2
4
о*ч/з a2b*j3
у]4а2—Ъ2 f 12
_________________---------. 1008. см3.
4___________27------------8
□ Проведем BD±AC (рис. Р. 2.3). Обозначим сторбиу основания через о.
(P-h2)hJ3
-----2.007.
189
a*J3 а сг\]з
Так как пирамида правильная, то OD—----, AD—DC=~, SOCJi =—-—.
о 2 4
Выразим а через Л. В ДSAC имеем SA = SC, £_CSA = 90°, откуда
а !—z------z А? За* а
LASD = 45° и SD=AD=~. Тогда h = SO~JSD2-OD2 = /------—=-= и,
2 v V 4 36 /6
следовательно, а=Л>/б. Итак,
3 3 4 3 4 2
2.010. a\f2/l2. 2.011. Л\/б/4. 2.012. 3.
2.013. □ Искомый объем найдем по формуле V/c4BC=- Здлвс KN (рис. Р. 2.4),
где SLABC=^~- Так как SOfKN, то BN : NO=BK: KS=2 : 1, откуда
4
BN=- ВО. Но ВО=^^, т. е. BN=^^- и, значит, =
3______ 3 9
Йо* 4<? 2a*Jf> 1 a1 Ji a3Jl
= /--------=——. Итак, V=- ——-------— =——.
х/9 27 9 34 9 18
2.014. 60,375 см’. 2.015. 2Sjs/3. 1016. Ру/з/12.
2.017. □ По условию, BD=b, L АОВ=60° (рис. Р. 15); отсюда легко найти, что
b bj3 b2J3
АВ=-, AD=-^—. Значит, 5ая=АВ • AD=—-—. Так как
2 2 4
LSAO= L_SBO= LSCO= lSDO=№, to SO — высота пирамиды
b 1 6’х/з
и SO=~. Итак, И=- S,™ SO^ y .
2 3 24
4(8/3)’ м’. 2.019. 3/’/16. 2.020. 6>/1833/47. 2.021. ЗЛ2л/з/2.
a2J3 2JS
□ Пусть a — сторона основания; тогда S=----------, откуда а———. Ис-
4 */3
1018.
1021
2y/s
уз
комая боковая поверхность выражается так: 5бОг=3 • - а SD (рис. Р.2.6).
а За1 3 4S г
Но SD—DC=- и, следовательно, 5бот=—• ~^=‘W3.
2 44 _/з
2.023. 73. 1024. ^47/24 см’. 1025. 3а2^3^- 2.JX2A. За2/2.
190
s
Рис. P.2.5
1027. □ Так как ребро куба равно а, то сторона основания пирамиды SABCD
adl 1 adz
равна —— (рис. Р. Z.T). Учитывая, что ОК=- AD=~~, найдем апофему
2 2 4
пирамиды: SK=yj SO2+O&
“ 3ayfz
ar Н—=------. Значит,
8 4
„ л 1 ay/Z Зау/1 За2 „ (ayji\2 е _
5бож = 4 - —— • —-—=—-, 31юли=!( ) +5бож = 2д .
2 2 4 2 \ 2 J
1028. а2(у[$ +1). 1029. ° (1 * —2.030. | yJ(?~h2)Q? + h2).
1 Л
1031. □ Так как l_SKO = GO° (рис. Р. 2.8), то ОК=- SAT»-. Основание пирами-
ды — правильный шестиугольник, поэтому L KOD = 30° и OD. Тог-
да O№ = OD2-KDJ=4A7)2-KDa-3KD2, т. е. Ю=^, DE=ZKD=h^.
6 3
5бож=32>£ • Л=Л2л/з. Итак,
Таким образом, «--------------
4
ЗЛ2д/з
2 ‘ И
ЬОРу/з
SS------XS---
2
•$ПОЛЯ — ^ося + $601
Рис. Р.2.8
191
2.031
1035.
1036.
2.038.
21^/55 см3, 84 см2.1033. ° + 2.034. 1) см2.
□ Так как при указанном построении образовалось 6 одинаковых пира-
д3
мид (рис. Р.2.9), то каждая из них имеет объем И=— и полную поверхность
6
sm„ -а2+4 Л а ОК. Но ОК~ ^ОРг+Р^^^, откуда
$IKOT-a2+a\/2-a2(l + V2).
За2, а'у/уь. 1037. За2,
□ По условию, SC=l, LSBC=*90°, LSCB=45° (рис. Р. 2.10), откуда
I 1 Р\П
SB-BC-*—^. Находим V=- ВС1 SB= v . Полная поверхность выра-
^2 3 12
зится так: Saola=Soal + 2S^sAB+2SiisAD, поскольку S дЛ12>= S' hSBC,
1 1 ( I V Z2 1
S^sad-Sascd- Ho Sasab“^. AB • SB^- I — I =-, S^sad=z AD • SA =
2 2 \л/2/ 4 2
* 7= * Ze ~ • Итак, О|1оля“ —+ ~H-т — z . H
2 Jr 4 2 2 2 2
8г3ч/з , (a3-63)x/3 (a3-Z>3k/2
2.039. 24г2. 2.040. i--12~’ 2<M1, --6~'
2.041 □ Искомый объем выражается формулой v~- (S1+S2+Vs^), где
Sj —196 см2, S2 —100 см2. Найдем h-B^K (рис. Р. 2.11). Имеем
В^К^у]B^—KDi1. Так как BB1D1D — равнобедренная трапеция, то
ЛК-|(5Р-51Л1)-^(14>/2-105/2)-2>/2 (см) и KD-BD~BK-\2y/2
(см), т. е. Л-7182-(12>/2)2-6 (см). Итак, (196+100+140)-872
(см3).
1043. 26Д5 дм2. 2.044. 2.045. a2^.
2.046. □ Расстояние от ребра АА. до диагонали BtD равно расстоянию от этого
ребра до плоскости BB^DxD, т. е. длине отрезка AtE (рис. Р. 2.12). Пусть
ребро куба равно а; тогда из bA^EDi находим If2-а2, откуда a—dy/l.
Итак, Г-a3-2^V2.
192
' 1Л4П. 144 см3. 1048. 2(а+Ь)у/3(а2+Ь2). 2.049. aby]3a2-b2.
1050. □ Искомый объем V^S^h, где Saa = АВ AD (рис. Р. 2.13), Л — высота
параллелепипеда. По условию, BB^D^ — квадрат и, значит, h=yfQ. Най-
дем АВ и AD. Так как АВ : AD—m : п, то AD=— АВ. В &ABD имеем
m
AB2 + AD2=BD2, т. е. АВ2-]—=AB2 = Q; следовательно, АВ=*-^^@ ,
т
АР = Итак, У=АВ AD h = mn<^®.
yjm2 + n2 m2 + n2
1051. 2 2.3I2- 2J0S2‘ 2053. 3 CM’
(m2 + n2+p2)312 8
1054. □ Искомую площадь найдем по формуле S = Vjh, где V — объем листа,
h — его толщина (при этом форма листа значения не имеет). Так как
объемы обоих тел равны, то Г=80 • 20 • 5 = 8000 (см3). Итак,
S=8000/0,1 = 80000 см2 =8 м2.
abjf>ab abS г
1055. —<—. 1056. ----------. 1057. 4v/3 см3.
2 4(а+/>) v
1058. □ Имеем V^S^h, где Soa = Q (по условию); таким образом, следует
найти Л. Так как ABCD — ромб, то З'оа1=^ АС BD (рис. Р. 2.14); учиты-
iS S'
вая, что АС h=S1, BD h=S2, находим АС=-±, BD=^. Отсюда получа-
h h
si s2 , SiSiQ
ем 26=-/ • -/, т. e. Л= Итак, V=
h h \ 2Q у 2
265/2. 1060. 2a(a+j4b2 + a2). 1061. a3/8.
1059.
1062. □ Обозначим сторону основания через а. Тогда 5бох"ЗдА. Проведем
высоту OjO (рис. Р. 2.15). В ^ЛОО2 имеем t_OO1D = 3(F, поэтому
C^D — IOD и 4OD2 — OD2 = h2, откуда ОЛ«Лл/з/3. С другой стороны,
О2>=д>/з/6 и, следовательно, а=2Л. Итак, 5бож=3 • 2Л Л=6Л2.
1063. q /у. 1064. у/з Гге+у\
7-363
193
Рис. Р.2 Л 5
Рис. Р.2.16
2.065. □ Проведем AtK перпендикулярно плоскости АВС (рис. Р. 2.16); тогда
2.066.
1069.
2.070.
2.073.
V—S^abc AtK, где S^abc=—— Учитывая, что L А уАК= 60°, находим
. г, «h/з „ .. *>2л/з Ол/з За3
А,К——. Итак, И=-----•----=—.
1 2 4 2 8
\j(M+N+P){M+N—P)(M+P—N)(N+P—M). 2.067. —. 1068. а3у/2.
2
□ Пусть сторона основания призмы равна а (рис. Р. 2.17). Тогда сторона
Д>/2 а1
основания пирамиды равна —, а площадь этого основания равна —. Обо-
значим объем призмы через имеем Vt =a1h, где Л — высота призмы.
Так как по условию объем пирамиды равен V, то И=- у Л. Но а2Л= У,,
откуда У1—6У.
4jz г- г-
2Р+-. 2.071. 18V2 дм3. 1071 a2(4+V3).
VP
□ Пусть высота призмы равна Л. Так как АВСВ — ромб, то 5бог“4Л5 • Л
(рис. Р. 2.18). Далее, AC1BD (как диагонали ромба) и, следовательно,
„„ Ibd2 AC2 ^Jbd2+ac2 _ „ г—5——j L
АВ— —4~=--------2-----’ Тогда BD2 + АС2 • Л =
- 2-jBD1 h2+AC2 h2. Но BD h — P, AC h—Q (по условию). Итак,
«бож-гл/Р’ + е1.
194
1074.
1076.
1077.
1080.
1081.
1084.
1085.
ЗЛ/з
—1075. —.
10^/5 64
. д2-\/з
□ Пусть АВ=а (рис. Р. 2.19); тогда искомый объем У=6 ---• Л, где
4
Л=3 см — высота призмы. Остается найти а. По условию, боковая поверх-
ность призмы ABCDAiBiCiDi равна 30 см2. Но Sgot — (3AB+A£>) Л; здесь
AD=2a (как диаметр окружности, описанной около правильного шести-
угольника). Следовательно, 5а- 3 = 30, откуда а=2 (см). Итак,
У=6 3 = 18^3 (см3).
И=С$. 1078. Ny/itMi2, nN+2M. 1079. r.R^yfxS^.
□ Пусть радиус основания конуса равен г, а его образующая равна I.
1 2л л/2
Тогда площадь развертки 5=- г • откуда /=
S=Ttrl=itr /—и, следовательно, г=
ле И=- лг2Л, где h=-JP —
3
1 nS
V=------2
' 3 Зл
*е%/ё
• Sr
. 1081 —.
3^3 3
□ Пусть Иццл — объем
нования, Л — высота;
5бо1.цил = 2лгЛ, откуда
Кщл- 2 $>ОЖ. ЦИЛ Г = 2 Кхил = Кгоя • Н
7И/27.1086. V5/5.
Но
найдем по форму-
'2S и
—. Итак,
цилиндра, И„,и — объем конуса, г — радиус ос-
тогда Кил=лг2Л, Ижон=^ яг2Л=^ Ищд. Но
1 2 2
- З'бот.1ил'’=- №Л=- Кщл. Таким образом,
195
2.087.
2.088.
2.090.
□ Пусть радиус основания каждого из данных конусов равен R, а высота
равна Н (рис. Р. 2.20). Тогда объем каждого конуса Kj—- nR2H. Общая
2
часть состоит из двух конусов; ее объем V2=- лг2А, где г — радиус основа-
ния, h — высота. Рассмотрим осевое сечение фигуры. Так как
АО2ОА~ t±O2CB, то АО : ВС^О2О : О2С или R : г—Н : Л. Но Л»у, от-
R 2 R2 Н 1 ,1
куда следует, что г——. Итак, И, =- л — • — =— r.RH= к,.
2 342 12 4
216 п см2, 448 л см3. 2.089. 2л(^/2+ IJo2. 2ла3/3.
□ Пусть общая высота конуса и пирамиды равна Н (рис. Р. 2.21). Обозна-
чим объемы конуса и пирамиды через К, и Г2, а их боковые поверх-
ности — через $! и $2; тогда К, =- nR2H, =r.RI, где / — образующая
конуса. Найдем У2 и S2. Так как периметр основания пирамиды равен 2р,
а основание конуса — вписанная в основание пирамиды окружность, то
площадь основания пирамиды равнаpR, откуда V2 =~ pRH, S2=pl (высота
любой грани равна 7). Итак, — =- itR2H : - pRH^—.—^nRl: pl=—.
К, 3 3 p S2 p
2.091. 24 л см3. 2.092. * ** ** )
2.093. □ Изобразим осевое сечение конуса, которое пройдет через центр шара.
Так как диаметр основания конуса равен образующей, то в сечении полу-
чим правильный треугольник, вписанный в окружность (рис. Р. 2.22). Пусть
/з
радиус шара равен R; тогда AB=R-jb, AD=—~~. Обозначим полную
поверхность конуса через а поверхность шара — через S2. Имеем
52=л —. R'Ji+n лЯ2, 52=4л/?2, откуда S2 : S2=9 : 16.
2.094. Sj : S2=V2 : F2»4 : 9.
4
2.095. □ Так как радиус шара равен R, то объемы обоих тел равны - лЯ3. Пусть
г — радиус основания конуса; тогда, по условию, ^вох^Злт2. С другой
стороны, S&a=nrl, где /—образующая конуса. Поэтому /=3г, откуда
196
1096.
1098.
1099.
1100.
Лв^//2—r2=2r^, т. е. г=^Л. Находим nr2h=^ я h1 • h =
4 3 3 16
1 4 1 г
=— яЛ3. Наконец, из равенства - яй3=— яЛ3 получим А=2Я ^/4.
3 : 2:1.1097. 1152я/125 см3.
2
□ Так как объемы конуса и полушара равны, то К=- лЯ3; с другой
стороны, яЯ2Л, где Л — высота конуса, т. е. Л=2Л. Имеем S^oX=nRl,
где /=>/я2 + Л2 = Я>/5. Итак, S^o^nR1^.
4лЛ3/81.
/а\2 fl2
□ Пусть радиус шара равен R, ребро куба равно а; тогда R —I - 1 =—,
2Я
откуда а=—. Обозначим объемы и поверхности шара и куба соответст-
<3
4 . , 8Л3 ,
венно через У2, V2 и Sj, S2. Имеем K==j nR , P2=<r=—Sl=^nR2,
е.
S^ba^ZR1, откуда V2 : V2=n^/3 : 2, S2 : S2-n : 2.
1101. 64л : 27. 1102. 600л см2, 1000я см3.
1103. □ Искомый объем Р=1цил—2РЖОи. а поверхность 5,= ^шл+25иш> где
Кил» Коя и Зцил, Sum — объемы и боковые поверхности цилиндра и конуса
соответственно (рис. Р. 2.23). Имеем Т'пал=пг2Л, где г—СК, h=AD = 3 см.
Так как DK=^(AD—BC)=^ (см), a CD=2DK=1 (см), то СК=
^1—(СМ)’ С'ледовательно> Кил=Л
(см3), Кон=- я • - -=- (см3), откуда у=~—- = 2л (см3). Наконец, нахо-
3 4 2 8 4 4
л/з г л
дим 51Ил=2лгЛ=2л . -у 3=Зл-»/3 (см2), 5Жоя = лг/=л . — • 1 =~^~ (см2),
откуда 5,= Зял/з+л>/з=4я-»/з (см2).
1104. 4лб.
1105. □ Пусть сторона ромба равна а, а его диагонали равны ЗД и 2d2 (рис.
= ^CD2-DK? =
3 з_9л
4 “Т
Рис. Р.2.23
Рис. Р.2.24
197
s
Р. 2.24). При вращении получается тело, состоящее из двух конусов. Обо-
значим объем и поверхность тела вращения вокруг диагонали АС через
2
и SAC, а вокруг диагонали BD — через VBD и SBD. Тогда Глс=- я4</2,
Ипх.
3 Vbd (2/3) naidj^ а2 Sbd
что и требовалось установить.
а3Ь
2.106. --f_____d.
Х^ЗсР-Ь1 2 3
2.107. □ Объем пирамиды Г=- 5осн SO (рис. Р. 2.25). Пусть сторона основания
равна а, тогда 5,^=——, OD—^^-. По условию, лОЛ2 = ОЛ или OD=~,
4 6 л
aJ3 1 6 „ Зу/З „ 5бож
откуда —т. е. а=—— и Учитывая, что----=3, получим
6 л тц/з л2 5ося
9у/з Л 1 95D
5боЖ=35ост«—т-. С другой стороны, 5бот=3 • - а • SD=—- и, следовате-
л 2 те^/3
9x/3 9SD 3
льно, —Vя—SD=~. Из ASOD находим
л
1 зТз 2J2 2л/б
.Итак,
3 л* л л
SO=y]Sti1-OD1=
4m\/3. 2.109. a2у/з (2+y/5).
□ По условию, BS1SA и BS1SC (рис. P. 2.26), т. e. BS — перпендикуляр
к грани SAC и SD=d. Следовательно, искомый объем Г=- S^acs BS.
В &SAD имеем LSDA =90°, l_ASD=45°, откуда AD=SD=dи ShAcs=<?-
/3
Наконец, в &BSD имеем LBSD—90", BD=2d — =dy[3, откуда
BS=y/BD1-SD2=yl3d2-dl=d42. Итак, с? dyfi=~
2.108.
2.110.
198
5
1111.
1113.
1114.
а3/128. 1111 л/б-
□ Полную поверхность пирамиды найдем по формуле 5ПОЛЖ =
/з 1
=—-----За SD (рис. Р. 2.27). Так как ABOS~ ЛВКВ (прямоугольные
4 2
г , BD ВК <ь/з nc, DI. О\/3
треугольники, имеющие общий угол), то — =— или —— : В$**ВК: —
BS ВО 2 3
ВК т п
т. е. а1 = 2ВК BS. По условию, —=—, откуда KS-— ВК, BS=BK+KS**
KS п т
т+п т , 2m . , (т+п)а2
=----ВК, ВК~-------BS. Значит, а2=----BS2, т. е. BS2=—------.
т т + п т + п 2т
В &SOD имеем SD2 = SO2 + OD2; отсюда, учитывая, что SO2—BS2—ВО2,
, (т+п)а2 а1 а2 Зта2 + 6па2 (т + 2п)а2 „
находим SD2=^-—^~—----------------------------- Итак>
2т 3 12 12m 4m
42 2ym 4 \ у m /
18a3l>3
1116.
1117.
1119.
Тб. 1115.---------7==-
(а2 — — а2
□ Обозначим объемы и поверхности данного и нового тетраэдров соот-
ветственно Vt, S, и V2, S2. Пусть АВ=а (рис. Р. 2.28); тогда DK=aj2. Так
как ADSK~&MSN, то DK: MN=SD : SM=3!2, откуда MN^aj3. Итак,
V2 : И2=а3 : (а/3)3=27 : 1, S, : S2 = a2 : (a/3)2=9 : 1.
a3V2/12 1118. 2PQK3a).
□ Пусть SA=x, SB=y, SC=z (рис. P. 2.29). Из взаимной перпендикуляр-
ности боковых граней следует взаимная перпендикулярность этих ребер,
откуда искомый объем F=- ShJiSB SC<=- xyz. По условию, - ху=а2,
3 6 2
- xz=b2, -yz=c2. Перемножив эти равенства, получим -//г^Л2?.
2 2 о
Итак, К—- abcyfi^- abc^/2. (
о 3
199
s
2.121
□ Для отыскания радиуса шара проведем плоскость через высоту пирами-
ды и апофему (рис. Р. 2.30). Радиус круга в полученном сечении равен
Os/з
радиусу шара. Так как все ребра пирамиды равны а, то SO=——,
OD=-^. Из LSOD находим SO=^JSD1—OD1=a^^. Обозначим радиус
6 3
шара через г, тогда SO,«SO—г. В &.SKOX имеем O^^SO* —SK? или
2 М а* _2 2аГу/1 л Л
r2=(SO—r)2---, откуда г=—-------hr-------, т. е. г=——. Итак,
3 3 3 3 2у/6
1 яд2
*$шарвв4яг в~—В
о
e.
2.123. б4я/9 см2. 2.124. а\/1+у/5/6.
2.125. □ Искомая боковая поверхность выражается так: Sb^lAB SM (рис.
Р. 2.31). Пусть АВг=а, SO—h; найдем соотношение между а и Л. Проведем
AK1SB, CKLSB; так как, по условию, ДЛКС—120°, то ДЛКО=60° и из
а 1 а
&АКО получим ОК~АО ctg60°-— • — •*—Далее, в прямоугольном
у]2 <3 V6
треугольнике SOB имеем OKX.SB, поэтому SB : SO~SO : SK, т. e. Л2 —
200
1126.
2.128.
= SB. SK. Из &SKO следует что SA? = 5O2 —О№=А2—откуда
О
SB2——j—т. С другой стороны, из &SOB находим SB2—Л2+^~. Таким
6л — и 2
образом, Л2+—=———. или 12Л*—2д2Л2+6а2Л2—а*=12Л*, откуда Л=^
2 6Л —о2 2
а 1 adl a2Jl
и SM=—~. По условию, - АС SO=—~ h=S, т. е. 5= . Учитывая,
-/2 2 2 4
что 5бо1 = 2Л5 • SM-2a -^-=a2dZ, окончательно получим S6oi=4S.
>/2
sds^/21. 2.127 Д Sy/S.
□ Искомый объем уД SOCH • SA, где Soo,—- (Рис- 2.32). В LSAO
________ d, 20
имеем SA=y/SO2-AO2, причем АО=^, a SO=-—, так как по условию
2 а2__________________________________________
1 /422 rf? JUQ2-^ „
- d2 SO=Q. Следовательно, SA= ---=-----—----. Итак,
2 у U2 4 2«2
1129.
ИЗО.
r-1.
j L 1
200 cm3.
□ По условию, AB=8 м, AD— 10 m, BD=6 m (рис. P. 2.33). Из равенства
62 + 82 = 102 следует, что t^ABD — прямоугольный и 5оси = 8 6=48 (м2).
Так как ВО1.АВ, то и SB1.AB, а значит,
АВ BS=^ ABy/S02 + 0B1 = [- 8,/42 + 32 = 20 (м2). Проведем
SKX.AD', тогда 5дЛ5'Д=“ AD 5,К=| AD-JSO2 + OK2. Для нахождения ОК
201
воспользуемся тем, что £±OKD~ t±ABD\ имеем ОК : AB^OD : AD, откуда
8-312 ' / 144 4>/34 1
ОК=в—— —— (м). Следовательно, SK=* 116+—- ——-— (м) и S^asd х
10 S 25 5 2
х 10.^^-4734 (м2). Итак, 5ПОЛЯ-48+2 • 20+2 • 4^/34=8(11 +Т34)
(м2). |
2.131. 192 см2.
2.132. □ Обозначим AD через х, a BD — через у (рис. Р. 2.34). Тогда
Зоси-ху—т2. Так как BDLAD, то и SDLAD, т. е. LSDB — плоский угол
двугранного угла и, по условию, LSDB=45°. Через точку О проведем
MKLA В; имеем L SMK = L SKM—60°. Из д SOD следует, что SO = OD —
SO у y-J х2 + у2
а из &SOM — что ОМ=~=—поэтому Sx^MK АВ=———— =
<3 2^/3 <3
_ л „ т1 Гл т2 2 4 4 14
«яг. Но — и, значит, /лг+—т------=лг или х+ти=3х, откуда
* - V Х./3
т кП.
x^—f у^ту/2. Теперь находим
V2
• SO=I т2 ^т ^2=^ т3 i/1.
Остается найти S^^AD SD+AB SM, где AD=x,
SD = OD'f2 = y~,
AB-J^+f, SM^2OM=^=. Итак,
<3
xy-Jl ix2y2+^i m2y/2 Im* 2m* 1 r
2.133. ^(я+у/я1-^) илаUM
2.135. □ Имеем 5Поля“‘5оа1+25д^5/-+25д/-5Е+25д£зд (рис. P. 2.35), где
о2^ Зд2^ а2
5оа,“° ~S~=—ч—> S£ASF=~,
4 2 2
как AELED, то и SE2.ED,
поскольку SA 2. АВ и SA=a. Далее, так
202
SE—^J SA2 +АЕ2 = а2 + 3а2 ^2а, откуда £дея>=- а 2а=а2. Для вычис-
aJ3
ления S^rsE проведем SKLFE} тогда и AKLFE. Учитывая, что АК=—^-
.—5----------------------я / , За2 adj a2jl
{LKAF=30°), SK=dSA2+AK? = la2+-~=-~-, находим S^fse=—-f-.
м 4 4 4
Итак,
„ *2(6+3V3+7b и
1136. 3a3/4, За2л/б/2.
1137. □ Искомый объем F=- H(St + S2 + ^/5i52), где найдем по формуле
Герона. Имеем 2/^ = 27+29+52=108 (м), откуда 52=>/54 27 • 25 • 2=270
, 5. (2р,)2 1082 9
(м2). Так как £^АВС~ £2А1В1С1 (рис. Р. 2.36), то — =——-j=—у=-, т- е-
*з2 (2р2) '2 4
45. 4-270
52 =—1 =-----= 120 (м2). Итак,
9 9
У=^ 10 (270 + 120+^270 • 120) = 1900 (м3).
1138. 1,9 м3.
1139. □ Так как стороны оснований относятся как 1 : 2, то площади оснований
относятся как 1 : 4 (рис. Р. 2.37). Тогда объем усеченной пирамиды У=
1 /---- 1 7
=- Л (5i + 52 + V>si‘S2)=j Л (4-Sj + 52 + 2S2)=- S2h, где S2 — площадь вер-
хнего основания, Л— высота. Но объем призмы ADEA1BiCl составляет
V2 — S2h и, значит, объем оставшейся части пирамиды есть
7 4
У2 = V- У2=- S2h~S2h=- S2h. Итак, V2 : P2 = 3 : 4.
11» 2-141-
3(a+о)
1142. □ Пусть О2О2=х (рис. Р. 2.38); тогда ОО2=3-х. Так как
Л,В1О1В1~&ВО21>, то В^ : ВВ=О2О2 : ОО2 или 1 : 2=х : (3—х), от-
куда х=1 (см). Далее, £2BlD1B~ t\LO2B и, следовательно, В2В2 : ZZ>2 =
2 4
= OOj : ОО2 = 3 : 2, т. е. LO2=-^B2D2, LN=-B1D1. Тогда Sklmn=
=у =у (см2). Итак,
203
„ 1 , Л 16 8\ 152 , „ 1 , /16 , 4\ 37 z Зч _
Kj=- 2 I 4+— +- =—- (см3), Vt=- 1 ( —+ 1+- =— (см3).
1 3 V 9 3/ 27 2 3 \9 3/27
2.143.
2.145.
10^/19 см2. 2.144. « 515 дм3.
□ Пусть Н — высота полной пирамиды, h — высота усеченной пирамиды
• У 1 Х^ yj St X г~ . г— г^г
— z или откуда XyJ S^+hyJ S^xyj S2i
* $2 H yjS2 Х + "
Я»х+л=-—------------—t то объем полной пира-
и х=Н— Л. Имеем
т. е. х«—-=~—у—.
МИДЫ Кюли.пир = з
Так как
hS-t-JS, 1
._v 1 ._.. По условию, К=-Л(51 + 52 +
3
1
3
и, значит, Л —---------,..- Итак,
•Sj + 5, 4* "\j ^1^2
v _1 ЗК VS^i
* ПОЛИ, пир= - I—! !-= г— ! •
Sj 4-S2\/S2 —
_ , 2 т2+тл+л2
2.146. - -----,
я mn
2.147.
По условию, LOj4j4t = 60°
1 Я
^ioi=2Ai°=2’
(рис. Р. 2.39); значит, LOtOJ41=30c
Я>/з < Я2Тз ЗЯ27з
ОО1— . Находим £нижя.осн — о 2 »
•$верхл.ося— ~ *$hi£kh.och
ЗЯ27з
=——• Итак,
8
□
1 Яа/з /ЗЯ27з ЗЯ27з /9Я4 • 3\ 21Я3 _
к-з — (.—+—+/-1б-)-й-
2.148. •Уа2+62 + с2+а6.
2.149. □ Так как полиак поверхность куба ^поли^Зб см2, то площадь ода
грани 5—6 см2 и ребро куба AD^a^yffs см (рис. Р. 2.40). Искоь
204
5
расстояние KM=^jАК1 +АМ1, где (см), AM=~j AD2 +DM1 -
I , a2 aJi J30 1б 30 , „
= /а2+—(см). Итак, Л2Л/= /-+— = 3 (см).
у 4 2 2 у 4 4
1150. а2Тз/2.
1151. □ Пусть сторона шестиугольника равна а; тогда ребро куба АВ=а^/2
(рис. Р. 2.41) и Хполн = 6ЛВ2 = 12о2. По условию, 6 ° —Q, откуда
2 20 8e>/3
а = Итак, Хполн= . |
з^з з
1152. За2/4, a3V2/32.
1153. □ Пусть SA=a, КМ=х (рис. Р. 2.42): тогда Хогг = 8 —-^ = 2д2-Уз,
, a-s/2 ху/1
Хгубв = 6х2. Имеем АО=ХО=—, ЛГО1 = ХО)=-~. Но
ХО = ХО2+О1О=^^+-, т. е. adl^xJl+x, откуда х= . Итак,
. 2 2 ^2 + 1
5<жт^2д25/3(72+1)а_>/3(3 + 272)
Х^&~ 6 • 2д2 6 ‘ "
мяЛУЬ.У.хю.? Ал.,
з з у 3
1156. □ Так как CD=3 см, AD=4 см (рис. Р. 2.43), то из ДЛОС находим
ЛС=>7з2+42 = 5 (см). Проведем DKLAC; тогда D.KLAC и LDKD1=60°
AC AD 3 4 12
(по условию). Но &ADC~t^CDK, откуда —=—т. е. DK=—— =—
CD DK 5 5
(см). Значит, DDt ^DK^/l (см) и V= CD AD • DDt =3 -4 =
144V3, 3. _
=—j— (cm3).
205
2.157. + J &-(<?-J)2+J?-(a2-b2)2.
2.158. □ Объем параллелепипеда У^осн Л, где h — высота параллелепипеда.
Тах как параллелепипед прямой, то высоты боковых граней также равны
Л (рис. Р. 2.44). По условию, LBAD = 30°, АВ h = 6 дм2, AD h = 12 дм2,
т. е. AD=2AB. Пусть BKLAD; тогда ВК=^ Учитывая, что AD ВК—4
дм2, имеем 2АВ ЛВ=4, т. е. АВ=2 (дм); следовательно, Л = 3 дм. Итак,
Р=43 = 12 дм3.
2.159. 36^2 см3. 1160. abcyfift.
1161. □ По условию, 74^=12 дм, АК=5 дм, AtKLAK (рис. Р. 2.45); следовате-
льно, ЛЛ)=.уЛ^ + ЛК2 = 13 (дм). Так как 5л,ии№24 дм2 и АА^ — пер-
пендикуляр к сечению, то искомый объем V=SAilmn • ЛЛ, =24 • 13=312
(дм3). Далее, учитывая, что AtLMN — ромб, имеем 5gox=4ЛЛj • ЛtN. Для
нахождения стороны ромба воспользуемся равенством
SaiLUN=2 ' LN или ^=2 ' & ' откуда 2JV=6 (дм); тогда
Л^=л/з2+42 = 5 (дм). Итак, <5бох:=4 • 13 • 5 = 260 дм2. В
2.161 а3/2. 1163. ^(И-гТз+л/ВЛ а1 ^3/2.
1164. □ Пусть радиус шара равен R. В сечении шара плоскостью, проходящей
через его центр и параллельной основанию параллелепипеда, получим
параллелограмм, описанный около окружности радиуса R. Поскольку
суммы противоположных сторон такого описанного параллелограмма ра-
вны, он представляет собой ромб. Пусть сторона ромба равна т; тогда
искомая полная поверхность 5=25(ХЯ+<5бох=2т - 2Я+4т 2R=6m 2R=
— бЗоо,. Но Socs=-ab и окончательно получим S=3ab. В
Рис. Р.2.46
206
2 2
1167. □ Проведем через ВС сечение, перш.^.^.лрное ААХ (рис. Р. 2.46); тогда
S^-fBC+MC+MBjAAi-fBC+lMCiAA^ Так как 4Лр4О-60° (по
ч 2aJ3
условию), то АА1=2АО~——. Далее в &AMD имеем ДЛ2Ш—300 и,
следовательно, АМ=^^-. Тогда из &АМС находим MC^yjACP—AM1^
,______ 4
-JAS-** и», а
8 4 8
1170. □ Искомый объем Soo, CCt (рис. Р. 2.47). Учитывая, что
с сА^>
LABC=3<3°, находим АС=~, ВС=*~-- и, значит, 5о<я=——. С другой
2 2 8
1 1 cj3
стороны, Soch=- АВ CD, где CD LAB и CD=- ВС=—^—. Так как CD LAB,
2 2 4
то и C^DLAB, т. е. ДС12)С=45° (по условию); поэтому в ^C^DC имеем
Сх/з 1 с2л/з С\]3 с3
CC.—CD^^—.Итлк, К=----------------.
1 4 3 8 4 32
1171. 906 см2. 1173. 12 см3. 1174. Ц75. ab(-/2+l).
8
1176. □ Полная поверхность призмы 5Полн=25осн + '5'бо1- Так как а, Ь, с —рас-
стояния между боковыми ребрами призмы, то а+Ь + с — периметр сече-
ния, перпендикулярного ребру. Следовательно, <9бох"(п+b + c)l—2pl, где
Р’=(а+Ь+с)/2. По формуле Герона находим 5ая=>/р(р—а)(р—2>)(р—с).
Далее, учитывая, что Р“50ет/=5ОснЛ, имеем So^^S^l/h. Итак,
2/ ,--------------
•Suojm=T 'Jp(p-a')(p-b)(p-c) + 2pl.
п
207
1177. 3al+a2. 2.178. 0,5^ + 52)A.
1179. □ По условию, даны объем V и высота h правильной восьмиугольной
призмы. Так как V—SoaJi, то Явя-И/Л; с другой стороны,
S’oc.-le’a+Vi), где а — длина стороны правильного восьмиугольника.
/ Sock | ----------
Отсюда находим а- /------—- J2(J1 -IJSoch- Итак,
V2(l+>/2) 2
Ябож=8лА=472(>/2-1)ИЛ=45/16(72-1)2,2 = 16^/2,2(72-1) (м2).
2.180.
2.181.
2.181
1183.
□ Пусть г и Я — радиусы вписанного и описанного шаров (рис. Р. 2.48);
тогда ЯХ)=Зг, AD2 + BD2=AB2=4AD2 или BD2 = 3AD2, т. е. AD2=3r2. Из
&AKD находим, что ЯЛ2 = КО2+Л2)2=г2+Зг2=4г2, а из &ОКА — что
ОЛ2 = О№+АЛ2=г2+4г2 = 5г2 = Я2. Обозначив поверхности вписанного
и описанного шаров через s и S, имеем s=4nr2, 5=4пЯ2. Итак,
5: л=Я2 : ^ = 5 : 1.
12Л2у/з.
□ Искомый объем И=- лг2Л. Пусть конус образован вращением ДЛЯС
вокруг катета ВС (рис. Р. 2.49); тогда AC=r, BC=h. По условию, rh=S;
2
тогда И=- nrS. Кроме того, по условию, 2л DN=L, где D — точка
пересечения медиан, DNLBC. Но DN : AC=DM : АМ= 1 : 3, откуда
г 2 3L 2 3L
DN=~; значит, - nr=L, т. е. г=—. Итак, V=- nS — = SL.
3 3 2я 3 2п
□ Пусть объемы тел вращения вокруг сторон а, Ь, с равны Уа, Уь. Ус,
1 2 1
тогда Уа=- лЛ2а, Pj=- nh2b, Vc=- лЛ2с, где ha, Aj, hc — соответствующие
. .. 2 .. 2
- ' - з •-“’ з
4 1 4 1
Vb=- nS2 Ус=~ nS1 - Итак,
3 b 3 c
высоты. Учитывая, что aha=bhi)=chc=2S, имеем Уа=- nSha, Уь~- nSht,
2
Ис=- nShc или
Уа : Уь : Кс=-
2.184.
1
6
’’•-Р ?
; лЯ’^Д
В
Рис. Р.2.49
Рис. Р.2.50
208
1187.
1189.
1190.
1192.
1186. □ Пусть ЛО=г, SO—h (рис.„Р. 2.50), V — объем конуса, Г, н — объ-
емы его частей. Найдем как разность между объемами части конуса,
'основанием которой является сектор АОВ, и пирамиды, в основании
которой лежит ЬАОВ. Согласно условию, АВ—т, т. е. АВ — сторона
правильного вписанного шестиугольника и, значит,
Fj— - • nr2h —J Л«- где Sj — площадь сегмента АтВ. Тогда
6 3 3 4 3
V2 = V— Fj =- S2h, где S2=itr2 — Таким образом, : V2 = S2 : S2. Да-
лее находим
„ 1 , А/з г(2л-з7з) „ , г(2л-з7з) АЮл+З^/з)
51пг ___=—_—, s2=„г-------------------------------------—.
Итак, = — .
10л Ч-Зл/З
— nSJiS. 2.188. — nh2.
21 ' 24
□ Пусть I — образующая конуса. Так как длина дуги развертки боковой
2л/
поверхности конуса равна длине окружности основания, то 2лЯ=— (по
4
условию, развертка представляет собой четверть круга), откуда /=4Я.
Найдем высоту конуса: Р — R2 = y/l6R2—R2=Ryfl5. Итак,
10лЛ3/9. 2.191. 27 >/2/8 куб. ед.
□ Для нахождения боковой поверхности усеченного конуса воспользуемся
формулой 5бож=я(г1 +г2)1, где г2 и г2 — радиусы оснований усеченного
конуса. Проведем плоскость через высоту конуса. В сечении получим
равнобедренную трапецию, описанную около круга радиуса г, причем
AD=2r2, ВС=2г1 (рис. Р. 2.51). Для описанного четырехугольника имеем
BC+AD—AB+CD, т. е. 2л1+2г2=2/, откуда 5бож=7Г/2- Объем усеченного
конуса лН((Г1 +r2')2—rtr2), где H=2r, r2+r2=l, r1r2=ri. Последнее
соотношение получается из прямоугольного треугольника ОСО, в котором
ОК2 = СК- KD {LCOD=9G°, поскольку ОС и OD— биссектрисы углов
2
трапеции и, значит,* LOCD+ l_CDO = 90°). Итак, F=- nrfP—r2).
с
Рис. Р.2.51
Рис. Р.2.52
209
5
2.195. - □ Поверхность S тела вращения состоит из боковых поверхностей двух
усеченных конусов, полученных при вращении отрезков ВС и CD (рис. Р.
2.52), и двух конусов, полученных при вращении отрезков АВ и AD. Таким
образом, S=it{KB+AC)BC+n(MD+AC)CD+nKB • AB+nMD • AD. Пре-
образуем это выражение, учитывая, 4TcAD=BC, CD=ABnKB+MD=AC.
Имеем
п(КВ ВС+АС BC + MD АВ+АС АВ+КВ AB+MD ВС) =
~n{{KB+MD)BC+(KB+MD)AB+ACBC+ACAB)=n(2BC+2AB)AC.
Так как, по условию, AC=d, 2ВС+2АВ=2р, то окончательно получим
S=2ndp.
J9n?— За1 + бат
2.196. ----------.
а—т
2.197. □ По условию, плоскость AKL перпендикулярна FD и угол между нею
и плоскостью АВС равен 30° (рис. Р. 2.53). Проведем высоту FO; тогда
L OFD=30° и Д OFD = Д ODC, откуда CD=FO=H, ВС=2Н. Следователь-
4Н2л/з , r FD , „ FD1
но, —-—^H2J3. Далее, в 6.OFD имеем OD =—, FD2 = IF4-,
4 2 4
2Н _ Н г
т. е. FD~-p. Итак, 5ВОЛЯ - + 3 . 2Н -^-З/ЛД
Д
2.198. 4 : 121.
2.199. □ а) I способ. Проведем плоскость через пересекающиеся высоты SO
и AOS (рис. Р. 2.54). Докажем, что ВС — перпендикуляр к этой плоскости
(тогда ЯС1Л5). Действительно, SO — перпендикуляр к плоскости АВС и,
значит, SO.LBC; AOt — перпендикуляр к плоскости BCS и, следовательно,
АО.1ВС. Итак, ВС — перпендикуляр к построенной плоскости и прямая
ВС перпендикулярна любой прямой этой плоскости, в том числе и AS.
Аналогично получим, что BS1.AC, CSLAB.
II способ. Рассмотрим векторы ЛЗ, ~АЙ, US, "ВС. По условию, ~aRlBC,
TTSkBC, т. е. {АН, 2К*)=(773, 7Й?)=0. Учитывая, что 'а5=АЙ+ТТ5, нахо-
дим (aS, ВС)’=((ВП+"nS), ~В(У)=(АН, ВС)+(ВЗ, 7?С)=0, откуда лЗ±ЗС.
6) Пусть LBSC=90°; так как BSLAC (это доказано в п. а)), то BS — пер-
пендикуляр к плоскости ASC, т. е. LBSA-9O0. Далее, ASLBC, ASLBS и,
значит, AS — перпендикуляр к плоскости BCS, т. е. /_Л5С=90°.
в) Пусть О — проекция вершины 5 на плоскость АВС. Плоскость ASOj
проходит через SO (точки S и Н этой прямой принадлежат плоскости
ASOj; так как A SLBC, то и ADLBC, т. е. высота AD проходит через точку
О. Теперь проведем плоскость BSO; она пройдет через О2, поскольку точки
В и Н высоты ВО2 принадлежат это* и Но BS3.AC, а знадит
210
и ВКЗ.АС. Итак, ВК также проходит через точку О, т. е. О — ортоцентр
ААВС. Аналогично докажем, что и другие вершины проецируются в соот-
ветствующие ортоцентры.
г) Для доказательства достроим тетраэдр до параллелепипеда (рис. Р.
2.55). Согласно доказанному в п. a), SALBC, SBJ.AC, SC1AB. Имеем
SA2+BC2=SA2+AN2=SN2, SB2+AC2=SB2+BN2=SN2i SC2+AB2 =
= SC2 + SM2 = CM2. Ho CM=AL, a AL=SN (как диагонали прямоуголь-
ника). Итак, SA2 + ВС2 =S^ +АС2 =>SC2+АВ2.
1200. a) 5^/3 и ,/51; б) нет. 2.203. л/3, 2>/з/3.
2.204. □ По условию, 5Л = 12 м, 2JC=4 м, SB=SC=AB—AC=1 м, т. е. A.BSC
и дАВС — равнобедренные и равные (рис. Р. 2.56). Пусть SDLBC; тогда
BD—CD и SD = AD=\/SB2—BD2=,/49—4=3-^5 (см). Используя формулу
Герона, найдем 6) • 6 • 6=^/(45—36) • 6 •6=18
(м2). Плоскость ASD проходит через высоту SO, поэтому
36 12 1 r г .
SO =——— =—= =-= (м). Далее находим • 4 • Зу/5=6у/5 (м2).
М Зу/s yfi 2
Итак, И=^ • 6->/5 J^=24 (м3).
_ 1 /а’-^ + с2 la2+b2-c2 lb2+c2-a2 а2
1205.- /---------• /----------/----------.1206.—.
3 у 2 V2 V2 12
abc
2.2т. - :
,/ d*b2 + Ь2с2 + с2 о2
2.208. □ По условию, ребра правильного тетраэдра SABC являются диагоналя-
ми граней параллелепипеда DSMCAKBN (рис. Р. 2.57). При этом парал-
лелепипед состоит из следующих частей: 1) тетраэдра SAВС; 2) пирамиды
DACS; 3) пирамиды KABS; 4) пирамиды MBCS; 5) пирамиды NABC.
Объемы пирамид 2) — 5) равны. Пусть V — объем параллелепипеда,
1 2
а Кпир — объем пирамиды; тогда Ипир=- V. Имеем У, т. е.
6 3
V. Итак, V -. И^р-3.
1209. а3Т2/54.
1210. □ Пусть DABC и 2>1ЛЛ1С1 — заданные пирамиды (рис. Р. 2.58); тогда
211
DE, ^“-^длд.с, где $ьлвс=2 АВ • AC sin <р,
' АВг • ACt sin<p (<р= LBAC). Далее, &ADE~ t^AD^E^, откуда
AD, DE
DE : D^Ei =AD : ADlt t. e. D^ =--—. Итак,
Au
V1_AB1AC1AD1DE_ABiAC1ADl
~V AB AC DE AD ABACAD ’
что и требовалось доказать. В
12 16а3*3 г-
2.211. — м. 2.212.---—-----, b<a<bJl.
19 З^-Ь^^-а1
2.213. □ Искомую боковую поверхность найдем по формуле
25
5=5д^/-д+25д^/к+5длтм (рис. Р. 2.59). По условию, 5для>=-г см2,
4
•5дхтм=4 см2. Остается найти ZS^afk- Имеем 2S&afk=*AF FK sin <р, где
<р= L.AFK. Но AF FK АР FK? tin1 <p^yjА^ sin^> • ЛК2 sinp=
^\/2ShJiFD 25дли/=Ю (см2). Итак, S=— + 10+4=— (см2). В
4 4
Z214. <P,j6l\b.
2.215. □ Обозначим через г радиус круга, описанного около основания пирами-
212
_SAF=4t.
: KF, так как,
зЯ Я R-Ji
шю, KF- ... i~=— J’ T- e- r~'~2~ • Проведем апофему SM;
ла KM=^: и SM^KKP+SK1^ 1—+.—=^^. Пусть
2V2 V 8 4 2V2
Гшара — радиус вписанного шара; тогда для площади &SMN получим
следующие два выражения: 5дя/№Гшара(5Л/+КМ)=^ MN SK. Отсюда
имеем
/Я^й я7з\ я^/з-зя „
Лпйря I--—+—zr I —•-----р— или 2Л1пяря(-у 7 + 1)—-37?,
\ 2V2 2г/2/ 4^2
ЗЯ Я(>/7-1)
т. е. гШара=—;=---=—’-------• Итак, искомая поверхность
2G/7 + 1) <
, Я2 г- , яЯ2 г itR1 г
5=4я^=4я — (>/7-1)2=— (8-2^7)=— (4-^7).
1216.
1217.
a3(5 + V5)
24
□ Пусть один из кубов стоит на горизонтальной плоскости, а общий
отрезок соединяет середины его противоположных вертикальных ребер.
Рассмотрим вид сверху (рис. Р. 2.61). Общую часть двух кубов составляет
фигура ACDBEF, при этом CDEF—грань параллелепипеда,
a BED — проекция грани пирамиды (рис. Р. 2.62). Основание пирами-
ды — вертикальная грань параллелепипеда, площадь которой равна
а
DE а. Так как DE=a, ВК=~, то суммарный объем двух пирамид
Ki-2 . в*-^=у. Объем параллелепипеда И2=а2 • CD, где
CD=AB~a = a-jl—a = d(b[2 — 1), т. e. V1=a3{y[2— 1). Итак, объем общей
части Vi+V2=a3 ^+V2-1^ = (3^~2- .
1218. аэ/4. 1219. 2(^2-1>3.
1220. □ Пусть первоначально угол поворота равен 0°. Если провести сечение
через центр общей части двух кубов перпендикулярно диагонали, то полу-
213
читая правильный шестиугольник. После поворота на 60° этот шестиуголь-
ник совместится сам с собой, т. е. ребра кубов пересекаются (рис. Р. 2.63).
Искомая общая часть состоит из двух одинаковых правильных треуголь-
ных пирамид с вершинами в точках О и О,. Так как все углы при
вершине — прямые, то объем каждой пирамиды где О А. Высо-
6
2.221.
2222.
2224.
00. aJ3 1
та каждой из пирамид Л=--«——. С другой стороны, S^h, где
2 4 3
„ (ZV2)2V3 b2^3 „ b3 1 Ь2у/з L t by/3 ,
<%си“— ------=——* Имеем ——- л, откуда л«—. Значит,
by/З <ъ/з За Ь3 9а3
——=——, т. е. о=—. Итак, искомый объем V=2V.=—=—. В
3 4 4 • 3 64
□ По условию, АВ=а (рис. Р. 2.64); тогда АВг как и все остальные
ребра построенной пирамиды DiAByC. Значит, все ее ребра — правильные
треугольники, т. е. DjABjC — правильный тетраэдр, а его полная поверх-
/з
ность 5=4----=2о2л/з. Грани тетраэдра отсекают от куба равные
а3
пирамиды, объем каждой из которых Vt=—. Итак, объем тетраэдра
6
И-а3-4И1-а3-^=у.
o’/б. 2223. 18Л
□ Проведем плоскость, перпендикулярную ребру (рис. Р. 2.65), и найдем
214
т1
I ’
стороны параллелограмма, полученного в сечении. Имеем КМ=
я* 1 2 " т1 п1 . т2пг т'п1
KN~—, откуда 5от-у у яп30°—Итак, V=-Sml=-^~. В
2.225. 9^39/4 см3 *. 2.226. 336 см3, 396 см2.
«и. w.
6
• Доказать, что первый цилиндр проходит через ось
второго.
?2(2-?).
4 ’
2.229.
1230.
1231.
1233.
задача не имеет решения при ?>2.
□ Высота данного конуса также описывает конус (рис. Р. 2.66), образу-
02) SD OD h
ющая которого равна Л. Так как &SOD~ 5.SDA, то — =— или -г-—,,
SD SA h I
откуда OD=—. Итак, искомая поверхность
а + у/а +1
2\[а
□ Проведем отрезки AN и DN (рис. Р.
2.67) и рассмотрим объемы пирамид
SABN, SAMN, SMND и SDNC. Пусть
Vsamn=V\ тогда Vsmnd = V (&ANM и
5.MND равновелики). Имеем Vsabn
: Vsamn=AB : MN, a Vsdnc : Vsmnd =
AB
= CD : MN, откуда Vsabn^ .... У.
MN
CD
УвОИС=-Г/гУ И Vsabn+Vsi>nc =
MN
AB+CD
«—- F=2K Таким образом,
Vsabcd=4V=4Vsamn- ysAMN^yAMSN^yS^sMN^, где Л — указан-
' 4
ное в условии расстояние. Итак, Vsabcd=- S&SMNh- В
1234. □ По условию, площади оснований равны и S2. Разобьем многогран-
ник на пирамиды с вершиной 5, взятой произвольно внутри многогранника
в плоскости сечения, равноотстоящего от обоих данных оснований. Ос-
нованиями пирамид служат боковые грани и основания данного много-
гранника. Тогда искомый объем
1 Я 1 Н „4„ Н
F=3 ‘S12+3S22+^3 S 6*s‘M‘Ni 2 ’
где SbSjMjNj — площади треугольников, аналогичных рассмотренному вы-
ше &SMN (см. решение задачи 2.233). Но где S3 — пло-
н
щадь сечения. Итак, У=— (S1 + S2+4S3), что и требовалось доказать.
6
Л
1235. ~ (2ab + 2albl+ab1+alb).
О
215
ГЛАВА 3
ЗАДАЧИ ПО ГЕОМЕТРИИ
С ПРИМЕНЕНИЕМ ТРИГОНОМЕТРИИ
3.001. □ По условию, АВ** AC, AA^LBC, BB^LAC, LBAC**a, AAi + BBl**l
a a. a
(рис. P. 3.1). Пусть BC=a. Из ДАА^ находим AAi=~ ctg AC=----------,
2 2 a
2 sin -
2
(я a\ a
-J=a cos -. Используя условие, име-
a
/ x 2/tg;
a a a a a / a\ 2
ем - ctg~ + a cos - = Z или - ctg - I 1 +2 sin - ] = /, t. e. a=-. Итак,
2 2 2 2 2\ 2/ a
1 + 2 sin -
a 2
a\ a a ( a\
1 +2 sin - I sin - cos - 1 +2 sin - I
2/2 2 \ 2/
I I I
a /я a\ я + a я —За
cos-+sina sin I- )+sina 2 sin-------cos-------
2 \2 2/ 44
----------- ab sin a
3.001 yjb2 + c2 +1,2bc. 3.003. ...z=.
<Ja2+b2—2ab cosa
3.004. По условию, AB** AC, ВС—a, LABC=a, AB1=B1C (рис. P. 3.2).
AC BC
В biABC по теореме синусов имеем -----------=--------------, откуда
sin a sin(180° —2а)
a sin а а
АС**------=------. Проведем А,ВЛВС. Из ДВА.В, находим
sin2a 2cosa
1 а 1 1 а
А.В.=- ВС=-, ВА.—~ АВ=- АС=------------, /_В,Л1В=180°—а и по теореме
2 2 2 2 4 cos а
косинусов получим
216
a1 a2 a2 a2 a2 a2
21212 =— H----------2---------cos (180° — a) = —I-----— H— =
4 16cos2a 8cosa 4 16cos2a 4
a2 (8 cos2 a +1)
16 cos2 a
a / la ,---------—
2?2?1=- /8+—-=-V9 + tg2a.
4 \ cos'1 a 4
3.005. □ По условию, ABCD — трапеция, AB= CD, О — центр вписанного
в трапецию круга, OELAD, OE—R, i_BAD—a, a< л/2 (рис. Р. 3.3); требует-
ся найти Pabcd=AD + 2AB+BC. Согласно свойству описанного четыреху-
гольника, имеем AD+BC=2AB\ значит, Рлвсв^АВ. Проведем ВК^ОЕ\
22?
тогда BK=2OE=2R. Наконец, из дВКА находим АВ~------------
sina
82?
и Рлвсо =7 •
sina
3.006. □ По условию, АВ^АС, ВС=а, l_BAC=a, LABBt = LB^C (рис. Р. 3.4).
ла ла
Имеем LABC~LACB------------, LB,BC=>-------, l_BB.C~n-
2 2 1 4 4
(л а л а\ л За
----+----)=--,—• Из &ВВ.С по теореме синусов находим
2 2 4 4/ 4 4
а
• a cos -
ВВ1 а 2
-------5— --------, т. е. BBi ------.
/я а\ /я За\ /л За\
sin I--I sin - -I— I sin - -I—
\2 2/ \4 4/ \4 4/
----- rctg(a/2) , , я-a a
3.0 07. J2S ctg a. 3.008. .—3.009. r2 ctg2-----------ctg -.
sin 2a 4 2
. «+Р *~P
4Л sin---cos -—
2 2
3.010.--------------,
sina sin P
3.0 12. □ По условию, в прямоугольном треугольнике АСВ имеем: Z.<4C2?=90V
£.САВшя, ABi^BiC и АС^^С^В, ВВ^СС^шО (рис. Р. 3.5|;
требуется найти расстояние от О до АВ. Проведем CD1AB и положим
217
л
С А, Е в
Рис. Р.3.5
Рис. Р.3.6
3.013.
h h h
CD=h. Из дЛ2)С и д CDB находим AC—--, СВ=---------=----. Так
sina /п । \ cosa
sin — a I
\2 /
1 Л3 /-----
как 5=- АС ВС=-----, то h = -jS sin2a. Проведем OF\\AB, OFf\AC=F,
2' sin 2a
СК ОС 2
OFC\CB=E и OFC\CD=K. Так как LCKO~LCDC., то —=---------=-,
11 11 ______ CD CCj 3
2 1 у/S sin 2a
откуда СЙГ=- С2>,аЛ2)=- CD=---------это и есть расстояние от О до
АВ, поскольку OsFE^AB.
равнобедренной трапеции ABCD имееем: АВ** CD,
ACQBD**O, LCOD=a (рис. Р. 3.6). Так как
угол равнобедренного треугольника AOD, то
1 1
Далее находим B,D=ED+BlE— AD+- ВС**
2 2
□ По условию, в
BB^AD, BB1 = h,
L COD — внешний
a
l_OAD= LODA--.
2
1
=- (AD+BC) **MN, где MN — средняя линия трапеции. Из ДДЛ^ полу-
2
a a
чим B,D=BB, ctg - =h ctg -.
2 2
/---- /я a\ P sin a b sin a
3.014. dS tga tg I -— . 3.015. -3.016.-—.
\4 2} ,fna\ 3a
4 cos I--- sin —
\4 2/ 2
3.017. □ По условию, AB=AC, S^bc—S. AB1=BiC, AC1 — CiB, BB^CCi^O,
LBOC**i (рис. P. 3.7). Имеем Хдвос=“ 5, так как высота
£а.ВОС, проведенная из О, равна высоты ДЛ5С, проведенной из А. Для
нахождения площади t^BOC воспользуемся формулой (1.6):
218
A
*\d N 5
Рис. P.3.9 ЛС2 \2 2/_ C A E Ри< cos2 BC2 cos2
219
a
&MEN найдем ME=a ctga. Отсюда ND=MA—ME=^—a ctga=
a—2actga _ _
=-------. Подставив вместо ND найденное значение, получим
я
Samnd д+д—2actga 1—ctga tga—I ^4
-----—•-----------ss-----=:-----s---------— tg
Sbmnc 3a-a + 2actga 1+ctga tga + 1 it
1+tgatg-
4
2-J3 cos a + sin a 2
3.020.---------------. 3.021. - sin 2 a sm2a. 3.022. ctg2
sin a it
. ti+P a-p
4 sin----cos------
2 2
3.024.------;----—-----.
it sm a sin p
□ По условию, ABCD — ромб (рис. P. 3.10), LBAC=a (a<90°), rt — ра-
диус окружности, вписанной в ромб, г2 — радиус окружности, вписанной
в кА ВС. Пусть АВ=*а. Проведем BE.LAD. В &ВЕА имеем
a sin a
BE=2rl = ashia, откуда rt=—-—. Из &АВС по теореме косинусов нахо-
--------------------------------------- a
ИС=л/2л2—2a2 cos(180°—a)=2a cos -. Следовательно,
a a 1 1
2’длвс=2а+2а cos-=4a cos2 -, S^abc=- a1 sin (180° — a)=- a2 sin а, отку-
2 4 2 2
, a
, a sin a 4 cos'1 -
a2 sin a a sin a r. 4 „ , a _
-----. Итак, -=----------------=2 cos2 -.
, a r, 2a sm a 4
4 cos2 -
4
а
|. 3.023. sin 2а tg -.
3.025.
дим
25дллс
даг3=------
гьавс . г а
4а cosл -
4
3.026.
1_АСВ т
□ По условию, ABCD — прямоугольник, AC=d,----——(рис. Р. 3.11).
LACD п
л я я тя
Так как LBCD=~. то mx+лх»-, х=----------; значит, LACB-—-----
2 2 2(т+л) 2(т + л)
пя /ля
ДЛС2>=—------Из &АВС и ДЛОС находим ВС—d cos —---------------
Цт + ri) 2(/л + л)
„ , пя
DC=я cos-------. Следовательно,
2(т + л)
(тя пя \
dcos 47~T~^ + dc0S ^~Т~\ =
2(?и + л) 2(л? + л)/
я я(т — п) г я(т — п)
=4</cos - cos —--—2\]2dcos--------
4 4(/л + л) 4(лт + л)
220
£К л ‘I** '—к ~~' 1 1
3.027. cos - : cos 3.028. arccos —— и л—arccos — 1. 3.029. —7.
2 6 к к 2k
3.030. j,sina ,_asifla .
a+Acosa A + acosa
3.031.
□ По условию, в L.ABCимеем: AC=b, ВС=а, LACCt = LBCCU ССХ=1\
требуется найти LAC В (рис. Р. 3.12). Пусть АВ=с; согласно свойству
биссектрисы внутреннего угла
АС^ + С^ а + Ь с а + Ь
------—=------или-----=-----, откуда с,д=---- и лс, =с----=----
CJ а СгВ а 3 1 а + Ь 1 а + Ъ а + Ь
Обозначим LACB через а. В LACCX и LBCCi имеем
AC2=b2 + P — 2bl cos BC2=a2 + P—2al cos -. Подставив в эти равенства
Ь2 с2 я
ВС., получим -----------Ъ2 + Р-2Ы cos -
(а + Ъ)1 2
с? +P—2al cos-^, вычитая из второго равенства первое, нахо-
ACt b
CtB a
ac
, откуда CjB=---- и ACj = c----
треугольника,
или
ac
be
3.032.
a + b
LACCx
a _
2
значения АС{ и
а2с2
И (а+Ь)
c2(a2-b2') 2 2 a
— 2/(a—A)cos-
c2=a2 + b2 — 2ab cos а,
= аР + 2ab + b2 — 2l(a + b) cos
=4aAcos -. Так как cos -#0, то
2 2
, 1(°+Ь) _
т. е. a=2arccos —--.
2ab
□ По условию, имеем: ABCD — квадрат, AEF— равнобедренный тре-
угольник, AE=AF, ЕеВС, FeCD, tgLAEF=3 (рис. Р. 3.13); требуется найти
cos LFAD. Для удобства положим LAEF=a, LFAD = 0; тогда
/_£Л£=180° — 2a. Так как LABE— lADF (по катету и гипотенузе), то
0=1 (90° — 180°+2a) = a-45°. Следовательно,
V2
=-у- (cos a + sin а). Учитывая, что tga = 3, находим
1 . 3 т „ J2 4 2J5
cosa«——1, sin a=tga cosa==—Итак, cosp==— • ,
Vio 5/10 2 vio 5
дим
Ho
= a2 + 2ab + b2 — 2l(a + b) cos -
или
a
cos -=•
2
или c2 = (a + b)2 — 2l(a + b) cos
откуда a2 +b2-2aAcosa=
a
21 (a + b) cos - =2ab(1 +cos a) =
l(a + b) a l(a+b)
□ . . откуда -= arccos
2ab 2 2ab
cos p=cos (a—45°)
1+9=—^5-, откуда
cos2 a
iP+k+l a a
3.033.30°. 3.034. —---Л-. 3.035. 2arctg——, n-2arctg—7—. 3.036.
(fc+1)2 />sma Asma
а2+Ь2-с2-<?
arccos------------.
2(ab + cd)
tg A sin2 A
3.037. □ По условию, в lABC имеем ------= —требуется доказать, что
tgB sin2 В
треугольник либо равнобедренный, либо прямоугольный. Из данного раве-
нства получим sin A sin2 В cos В—cos A sin В sin2 А = 0 или sin A sin В х
х (sinB cos В—cos Л sinH)=0. Но sinJ#0, sinB#0, так как А и В — углы
треугольника; ' следовательно, sin2B— sinZd =0 или
Гсо5(Л+В)=0, Г А+В=п/2,
2 cos (Л +B)sm(B-J)=0, откуда . „ => „ . „ Итак, ли-
|_sin(B—Л)=0 £В-Л = 0.
221
Рис. Р.3.15
бо C=n/2, t. e. треугольник прямоугольный, либо A=B, т. e. треугольник
равнобедренный.
- n-ft у/+ cos a
3.039. ------——----------.
sin а
3.040. □ По условию, в трапеции ABCD имеем: AB=CD, BC\\AD, MeAD,
AM=MD, NeBC, BN=NC, BE LAD, BE=h, i_BMC = 2a, i_AND = 2fi (рис.
P. 3.14). Так как &ABM= & CMD и txABN= &NCD (по двум сторонам -
и углу между ними), то BM=MCvtAN=ND. Из &AMNи &BMNнаходим
AM=htgfi. BN=htga. Следовательно,
Sabcd=(AM+BN)h=h1 (tga+tg/J)-——-—
cos a cos p
При Л = 2, a=15° и /1=75° получим
„ 4sin90°_________4 _______8_
ABCD cos 15° cos 75° cos 15° sin 15° sm30°= "
3.041. A2(a + sina). 3.042. -У-У—. 3.043. —--.
2sin2(a/4) я
ctga + a—-
3.044. □ По условию, АВСОА^С^—прямоугольный параллелепипед,
BiD = l, LBiDDi—a, Pabcd=P (рис. P. 3.15). Из ^B^tD находим
PP] = /cosa, a DiBl = DB = l sin a. Положим AB=x, AD=y; тогда
(2x+2y=P, (x+y = P/2, (x2 + 2xy+y2 = P2/4,
\x2+y2 = l2 sin2a, [x2+y2=/2sin2a [x2 +y2 = Z2sin2a.
P2 —4/2sin2a
Вычитая из первого уравнения второе, получим ху=----. Итак,
О
„ P2-4Psin2a l(P2-4P sin2 a) cos a
^пар= у Zcosa= - . И
3.045. - тР ctg3 - ctg a. 3.046. 3/—-.
3 2 yctg2^sina
3.047. □ По условию, ABCA^ByCi—прямая призма, АС=СВ, L.ACB=a,
AiB=l, LAiBA—P (рис. Р. 3.16), требуется найти Vnp=Si,ABC AtA. Из
AAiAB находим ЛЛ^/sin/J, AB=l cosfi, а из ДЛОС получим
ala
DC=AD ctg - =- I cos В ctg -. Следовательно, "
2 2 2
222
Рис. Р.3.16
Рис. Р.3.17
11 ft 1 ft
Рпр=~ /cos р • - I cos/? ctg - / sin/?=~ Рcos2 fi ctg - sin/? =
1 , a
=- P sm2p cosp ctg -.
8 2
„ , [it a \
<P cos2 I-----) , .
3 4 2/ a3 sin 2a tg /?
3.048. ----------2-----3.049.----------------
2 “ 2
sin -
2
3.050. □ По условию, ABCDA1B1C1D1 —правильная четырехугольная призма,
АВ—a, LAiDC1=x (рис. Р. 3.17). Имеем ^jC, =a>/2. Пусть AtD = x; тогда
DC;=x. Из ^A1DC1 по теореме косинусов находим
ft (7 /2
2а1 = 2х2 — 2л2 cos a=4х2 sin2 -, откуда х =—-—. Из Д/ХО,/!, получим
2 a
2 sin -
2
a3 \/2 cosa
Итак, Гпр =-------.
a
2sm -
э
aS a л — a
3.051. — sin - tg-.
2 2 4
3.052. □ По условию, SABC—правильная треугольная пирамида. SA = l,
SO1.(ABC), £_SAO = x (рис. P. 3.18). Из AS АО находим 50 =/sin a,
^O = /cosa, откуда АВ=АОх/3 = 1^]з cosa.
AB1 J'S sjs P cos2 a
ShABC= -----=---------- Итак,
4 4
Следовательно,
1 1 Зч/з Z2 cos2 a , . Z3 ч/з sin 2a cos a
S^abc • SO—- - Zsma = .
3 3 4 о
, ЗЛ^^/Зсова , m3 sin 2a cos a a3 tga fp ctg2 P sin 2a
3.053. ---ct-------. 3.054.------------. 3.055.--3.056.....................
2sin2(a/2) 3 6 3
2?"
3.057. □ По условию, SABCD — пирамида, ABCD — ромб, 2. BAD = a (а <90°),
АВ=a. ((SAB^ABQ) = ((SBQJABC)) ~ ((SCDJAABC)) = ((Sd/^АВС)) -
=Д, SOL(ABC) (рис. Р. 3.19). Проведем апофемы пирамиды SE, SF, SK,
SL; тогда OEJ.AB, OFJ.BC, OKLCD, OLLAD (по теореме о трех перпен-
дикулярах) и, значит, LSEO= LSFO= LSKO= LSLO=p. Далее имеем
Sabcd а^йа
5б«=------=-----Наконец,
cos р cos р
^ПОЛН —
a2 sin а
cos/?
, a2sma(l+cos/()
+a sin a—---------------
cos/?
2a2 sin a cos2
cos p
P
2
_ „ a3 deep sina sinfi
3.058. ---
12sm2(a+P)
3.059. □ По условию, SABC — треугольная пирамида, AB—BC=a, 2_АВС=а,
SOJ.(ABC), £_SAO = l_SBO= L_SCO = p (рис. P. 3.20). Так как
t^SOA = &SOB= &SOC (по катету и прилежащему углу), то
ОА = ОВ=ОС, т. е. О — центр окружности, описанной около ДАВС.
(п а\ а
- ) = 2Я cos -,
a otgP
а R=------. Из A SO А находим SO=--------, откуда
a a
2cos- 2cos-
2 2
Ршч>-| ShABC *50=^ a2 sin а ° t8 a3 sin tgP.
3 о a 6 2
2 cos -
2
2
3.060. - h3 tg2 a sin p.
3.061. □ По условию, DABC — пирамида, ABC — правильный треугольник
224
(ABD)L(ABC), (BCD)L(ABC), LADC=a, AB = a (рис. P. 3.21). Требуется
найти высоту призмы с основанием, равным А АВС, причем Ипр=1/Ш1Г.
Высота пирамиды совпадает с ребром DB, так как перпендикуляр, опушен-
ный из D на (АВС), должен принадлежать и (АВС), и '(CBD). Проведем
DKLAC; так как &ADC — равнобедренный, то КА = КС. Из &DKC нахо-
а а
дим 2)Х'=- ct8 2’ а из получим
3.062. □ По условию, DABC—пирамида, ДЛСВ=90°, ADJ.(ABC), LDBA = x,
t_DBC=fl (а<Р) (рис. Р. 3.22). Пусть AD=h; тогда из &ADB находим
AB=h ctga, DB=-------. Так как BCLAC, то DCLBC и из ADCB получим
sina
„ Л cos /? _ , ВС
BC=DB cos/?=----. Итак, в ДЛВС имеем sinZ_J=— =
sina АВ
h cos fl cos fl . cos fl п it . cos fl _
=---------=-----.откуда Z_J=arcsin-, l_B=—arcsm-.
sin a h ctg a cos a cos a 2 cos a
3.063. □ По условию, ABCDAiBiCiP.—правильная четырехугольная усечен-
ная пирамида, АВ=a, OOi)-(ABC), B1E^DiF\\OO1, l_DiDE=a, l_B1DE=fl
(рис. P. 3.23). Пус’гь AiBj^x; тогда BiDi^Xy/l, BD = a^/2. Имеем
a Ji xJl (a — x)^/l ajl Xy/l
FD = OD-OF=—----ED = OD+OE———- =
2 2 2 2 2
8-363
225
(a+xk/2 (a-x)Jl
---. Из bD^FD находим DtF=FD tga=-----------tga, а из kB^ED
получим BrE— ---------------- - tg/J. Так как D1F=B1E=OO1, то
a sin (а—в)
(а-х) tga=(a+x) tg/? или x(tg/?+tga)=a (tga-tg/1). т. е. х=——-—.
sin(a+/l)
„ ^sin^a-fi)
Итак, SA B CiDt- .2, ,
1111 sin2(a+^)
л(а2-*2) ctg (л/л)
3.064.---------------.
4 cos a
3.06S. □ По условию,
5бох=55длвс (рис.
SABC — правильная треугольная пирамида,
Р.3.24); требуется найти LASB. Пусть SA = l
3 .
и l_ASB=a:, тогда 5бОх=- г sin а. Из ДЛ£2?по теореме косинусов находим
3.066.
3.067.
4/2 sin2 - Ji
( а 2у г- а
АВ2 =2Р—211 cosa=4l2 sin2 тогда 5длвс=-----------=/аЛ/3 sin2 -. Ис-
3 . „ г , х а а г 1а
пользуя условие, имеем: - rsma=5r>/3 sin2 -; 3sin - cos - = 5л/3 sin -;
a Ji a Ji „ x/3 _
tg 2=3": 2=arctg ‘У’ T- e- a=2arctS
arctg^/ctg2 a+ctg2 fl.
□ По условию, 5лвс..л—правильная л-угольная пирамида, ДЛ55=а,
SM и SN — апофемы смежных боковых граней; требуется найти LMSN
(рис. Р.3.25). Проведем SOL(ABC) и соединим О с точками А, В, М и N.
Имеем ДЛО2?=~, £_АВС=^~—Пусть АВ=а. Из &MSB найдем
л л
а а
SM=“ ctg -. Далее из &MNB по теореме косинусов находим
a2 а2
MN2=-------cos
2 2 л
, 2л \
1 +cos — l=acos
л /
д2
2
а из
п(п —2) а1 ( ( 2л'
------=— 1—cos л--------
2 \ \ л
A MSN получим
It
n
226
Or Ct
3/№=253/2-2SM2 cos LMSN=2 — ctg2 - (1 -cos LMSN) =
, . 2 LMSNa
= (T sin2 - ctg2 - .
2 2
Следовательно, a1 cos2 -=a2 sin:
n
LMSN , a
------ ctg2
2 6 2
LMSN n a
sin----=cos - tg -.
2 n 2
{ n a \
Итак, Д 3/^=2 arcsin | cos - tg - |.
\ n 2/
. 2 cos a я я • '/^CV sin a
3.068. arcsin —-<ct<-. 3.069. arcsin-5—. 3.070. arcsin —
V362 г 72
3.071. □ По условию, У1Пу2=/, двугранный угол / равен a, ABeylt (I; AB)t=fl;
требуется найти (рис. Р.3.26). Проведем АО 1у2, АСИ; тогда
1_АСО = а. (как линейный угол двугранного угла АВСО), LABC=[I. Так
как О В — проекция АВ на у2, то L.ABO — искомый угол. Пусть АО = а;
а АС а
тогда АС=----(из ДЛОС), а в &АСВ имеем АВ=—-= .--------—. Нако-
sina sinp sma sinp
АО
нец, из ДЛОЛ находим sin 1_АВО=-^=япа sin/?. Итак,
L ABO = arcsin (sin a sin /О-
3.072. arccos 3.073. arctg /-+^С0---. 3.074. 2 arctg (cos а). 3.075. у/б/6. 3.076.
3 у 5—4cosa
arctg (2 ctg а).
3.077. □ По условию, SABC — правильная треугольная пирамида,
5б„к : S^ABC=k, SO_L(ABC); требуется найти CASO (рис. Р.327). Пусть
SO = h и LASO = a.; тогда в CSOA имеем AO = htga, откуда
AB=AO\fi = h tga 7з> OD=^OA=^htga. Проведем SDLAC и из
CSOD найдем SD=JsO2 + OD2= /л2+-Л2 tg2a=^74+tg2a. Следова-
у 4 2
тельно,
<$бок=| АВ SD=^ h tga-y/з ^/4+182«=^ A2 tga73(4 + tg2a),
ЗЛ2 tg2 a • 73
8ьлвс=-----------•
227
Итак, получаем уравнение
3A2tga^3(4+tg2a) 4 >/4+tg2a /——5--7 , . 4 ,
---- ----^—£—=к; — =к; J4ctg2a+1 =к; 4ctg2a=fc2-l;
4.3A2tg2a -V3 t««
ctga=—, откуда a=arctg —~.
3.078. -1/3. 3.079. arccos (72/4).
3.080. □ По условию, OABCDEF — правильная шестиугольная пирамида,
ОО^ЦАВС), l_FOE= LOFOj (рис. P.3.28). Положим OF=l и Z_£O£=a;
тогда РЕ=у/2Р — '212 cos a=2/ sin Учитывая, что OlF=FE, в COO{F
a
21 sin -
2
имеем cosa=—-—;
a a a a
— 2sin2- + l=2sin2sin -+2sin—1=0;
2 2 2 2
. a -1 + J3 a J3-1
sin -=---; - =arcsin-;
2 2 2 2
3.081. □ По условию,
AC AC AC AC AC ,
—=—=———=—=k
AB BC SA SB SC
„ • s/3-1 _
a = 2arcsin———.
SABC — треугольная
(рис. P.3.29).
пирамида,
Так как
AC
AB=BC=SA=SB = SC =—, то
к
&ASB= A BSC (по трем сторонам). Про-
ведем ADLSB и соединим точки D и С. Тогда ДЛ51> = Д SDC (поскольку
SA = SC, сторона SD— общая и L_ASD= LDSC), откуда следует, что
4 SDC= CSDA =90°. Поэтому С ADC — линейный угол двугранного угла
ASDC, т. е. искомый угол. Из ДЛРС по теореме косинусов находим
А С2 = 2AD2 - 2AD2 cos 4 ADC, где
saJi acJi
AD=—-—=———, так как
2 2к
&ASB— равносторонний. Значит, АС2=2—-z- (1— cos 2.ADC);
4к^
, • 1 LADC 2k2 . L.ADC Ik2 kdi
\-соз l_ADC=—; 2sin2---=—; sin----=
3 2 3 2Л/33
4?4I>C=2arcsin где Oc^y^cl, т. e. 0<£<л/з.
3.082. □ По условию, ABCA^C^ — правильная треугольная призма, AAi=H,
228
AN=NB, BM=MC, ((A1ClM); (ABC)) = a (рис. P.3.30). Проведем BE1AC
и EFWAA^’ LFEB=a как линейный угол двугранного угла. Пусть
BEr\MN=O; тогда FOLMN (по теореме о трех перпендикулярах). Сечение
FE Н
A^NMCi — трапеция, таккакЛ7У||ЛС. Из &FEO находим FO=~—=-—,
sin a sin a
EO = Hctga, откуда BE=2H ctga. Из &BEC получим
</з 2Z7\/3ctga
EC=MN=BE ctg 60° = 277ctga -^- =---\ ; значит, АС=АхСг =
4/7 >/з ctga
=----------. Итак,
3
3
AC+MN г Н T7\/3ctga
Sa^nmc,------------FO=Hji ctg a — --------Л---—
1 2 sin a an a
3.083. □ По условию, ЛВСРЛ1В1С1В1— прямая призма, ABCD — ромб,
L_BAD=a (а<90°), AAt : АВ=к, ClE=EC, ADEF— сечение призмы (рис.
Р.3.31); требуется найти ((ЛВС); (FAD)). Пусть АВ=а; тогда ААх=ка.
Проведем BKLAD; тогда FKLAD (по теореме о трех перпендикулярах)
и L FKB — линейный угол между сечением и основанием ABCD. Из Д Л КВ
найдем BX’=asina; так как EF\\AD, то ВВ=- BBt =- ка. Наконец, из
FB ка к
tg LFKB=—=--------=-----,
В К 2а sin a 2 sin a
AFBK
откуда
получим
k
l_FKB=aictg_-.—. |
2 sin a
3.084. 3.085. 2i?J2 sin (a + ") sina tg/?. 3.086. - (J-b2)(a-b) tg2a tg/?.
2 cos a \ 4/ 8
2m J 2 cos ala2 sin 2a
3.087. arctg-. 3.088. \ 3.089. -. 3.090.-.
m+n 2sm(a/2) 7 2cos<p
3.091. □ По условию, 5Л1Л2Л3...Л12— правильная двенадцатиугольная пира-
мида, SA^a — сечение пирамиды плоскостью, ((5Л1Л^)?^Л1Л2Л3))=а,
(Рис. Р. 3.32). Проведем ВО±(Л1Л2Л3). Пусть ОА{ = В; так как
360°
ДЛ1ОЛ2=-^ = 30°, ДЛ1ОЛ5 = 30° 4 = 120°, то Л2Л5 —сторона правиль-
ного вписанного в окружность треугольника и Л1Л3=Я>/з. Проведем
229
OK1AiA5; тогда /_Л1ОЯ=60°, 0K=^ R. Из &SOK находим
OK R 1
SK=-----=----, SO=- Ktga, поскольку L SKO — линейный угол дву-
cos a zcosa 2
гранного угла между сечением и основанием. Имеем S^sAtAs
1 /— R R?\[з Scos ос
т. е. 5=- Ях/З • -=—откуда Я=------------—. Далее находим
2 2cos a 4 cos a */3
1 . , 125 cos a r
5och = 125aoj1j =12 - Я2 sin 30 °=ЗЯ2=--—=45j3 cos a.
2 V3
Итак,
1 45.73 cos a 1 2-Js cos a 45 sin ads cos a
^пяр=т ^осн • SO — - - • tga = ,— =
3 324/3 4/27
45 5/3 sin a a/5 cos a
;---------------.
3.092. □ Пусть AA1B1B — осевое сечение цилиндра, 1_АОВ—ч. (рис. P.3.33),
n a
Положим AAt-H\ тогда, учитывая, что LOAB= LOBA=^—-, из &АхАВ
/я a\ a
находим АВ—Н ctg-----tg Следовательно,
\2 2/ 2
t . ct / л
/fftg-V ^tg2^ Wctg*!
V=k I 2 ) . j{—------------, откуда H= 3 I--------.
\ т / 4 » I n
3.093. □ По условию, AA1B1B — развертка боковой поверхности цилиндра, AAt
230
Рис. Р.3.35
и ВХВ— его образующие, АВ и А,В, —длины окружностей его основа-
ний, ABi=d, LAOA^a. (рис. Р.3.34). Так как LAOAx—внешний угол
а
равнобедренного треугольника АОВ, то 1_ОВА=^. Из &АХАВ находим
а 2
A jA —d sin AB—d cos Итак,
1 2 2
. a al
5бож=2яЛЯ=ЛВ AA. —d2 sin - cos -=-
2 2 2
c/2 sina.
a3 cos a sm a itS , 4m m n _ ял
3.094.-----------. 3.095.------. 3.096. 2arctg— при — <-; 2arctg— при
4я ял ял л 4 4m
sin---
т + п
m я _____ я/3 sin 2В cos В
->-.3.097.-- —--------
л 4 a cos а
3.098. □ Изобразим осевое сечение конуса; SO — высота конуса, SA и SB — его
образующие (рис. Р.3.35). По условию, SA — SO—d, i_ASO = a. Пусть
R
OA**R. Из &SOA находим SO=R ctga, SA=-—. Используя условие,
sina
R A(l-cosa) а , а „
имеем------R ctga=----------= R tg-=d, откуда R=dctg -. Итак,
sin a sm a 2 2
1
1 1 la
=- kR2 . 50=- яЛ3 ctga=- ctg3 ~ ctga.
V -1
V КОИ — 2
3
nd2
3.099.--------------r------
„ . , (r. a \ .
2 sin ------ sin a
\4 У
sina . _
3.100.
a
2arcsin —. 3.101.
2n
яа3д/со5а
12sin(a/2)’
3.102.
____ яЛ3 / , a\
------------3.103. — ~v-„ cos2 /(+tg - ). 3.104. arcsin
4я cos Д cos2 (Д/2) 3 sin2 /? \ 2}
х/5-l
2
3.105. □ По условию, SAK ~ конус, SO —его высота, BK—хорда, ВК—а,
\jBnK=n, i_OSK=B (рис. Р.3.36). Так как \jBnK=tf, то LBOK—n0. Пусть
R — радиус основания конуса; тогда в Д ОВК имеем
a a а
a2=2R2- 2R2 cosa=4A2 sin2 г. е. <г=2Л sin -, откуда Л=———• Из
2 2 2sin(a/2)
a ctg В
&SOK находим SO = OK ctg —7-с.т. Итак,
2sm (a/2)
231
Рис. Р.3.38
1 Я2 .с0=1 о2 о ctg/? = яд3 ctg/?
3 Л 3^4 sin2 (а/2) 2 sin (а/2) 24 sin3 (а/2)’
3.107. □ Пусть АА1В1В — осевое сечение усеченного конуса, где AAt
и BBY — его образующие, АВ и AtBt — диаметры его оснований,
F и К — центры этих оснований, AB^AiB—O (рис. Р.3.37). Согласно
2 1
условию, АО : OBj=2 : 1, 1_АОВ=а, ABt=l. Имеем АО=- I, OBt=- I,
я а
1_ОАВ= 1_ОВА =---.
2 2
Проведем BiELAB и из f\ABYE находим
2 . . a
2’
fit a
B.E=l sin I -—
\2 2
а _ . а -
=Zcos -. Затем из Д OFA найдем AF=AO sm I sm
al a
и, наконец, из Д OKBt получим KBt = OBX sin - I sin -. Итак,
т, * , a a г a 2 a 2 a 1 л ia\
Ртс им = - / COS - I - Г Sin2 Г Sin2 -+- Г Sin2 - =
3 2 \9 2 9 2 9 2j
lit „ a . , a 7л/3 a
=— r cos - sin2 - w—— sm a sm -.
27 2 2 54 2
3.108. □ По условию, ABCD — ромб, AB—a, LBAD — a (a <90°), MN—ось
вращения, MNflAC, BeMN (рис. P.3.38); требуется найти
Pt.»p=2(Pb£ci>— Vbec)- Трапеция BECD при вращении образует усечен-
ный конус, а треугольник ВЕС — конус. Имеем
(1 \ 2
- я BE(BD2+BD ЕС+ЕС2-ЕС2)\~- it BE BD (BD+EC).
Но BD—2ВО••2ЕС; поэтому Р1.»р—4яЛ£ • ЕС2. Учитывая, что
a a
из Д ВЕС находим ЕС’•a sin -, BE—а сое -. Итак,
2 2
Р; ю—4яа cos- а2 яп1 ^—2тг3 йпа тп -.
^22 2
232
8nr2 cos2
n a
3.109. - ab(a+b) sin a cos -. 3.110.
/cos a sin/?.. 3/2 sin2 2a
------3.113.-------------
sm(a+0) . , (n
4sin2 - + a
\4
3.115. □ По условию, SAE— конус, SABCD—вписанная в конус пирамида,
АВ=ВС, CD=AD, 1_АВС=а (рис. Р.3.39). Проведем SOL (АВС) и обозна-
чим OA=R, SO = H. Отрезок SO является высотой конуса и пирамиды;
1 , a
тогда К10Н=- itR2H. Так как L_ABC=a., то LBAC= L.BCA =90°— -,
l_ADC = 180° —а (согласно свойству четырехугольника, вписанного в окру-
180° —(180°—а) а
жиость) и L_CAD= l_ACD=------------------=-. Таким образом,
£_BAD = LBAC+ A CAD=40°, т. е. ABAD— прямоугольный и BD = 2R.
Аналогично, ABCD — прямоугольный и, значит,
1 ( а\ а
5ллсв = 25ддлв = 2 - АВ AD = 2R sin ( 90°-- 1 2R sin - =
= 4J?2 sin - cos -=2R2 sin a.
2 2
—P—-A 3.111. arccos(l/9). 3.112.
sin2 a
з П4. KcosI(a/2) sina
1 ' л
1 . 2R2H япа Л
Тогда Кпир=- 2R sma Н=---------. Окончательно получим
FlfflP_2A2nsina nR2H_2 sin a
3 :~3 ” д
3.116. □ По условию, DAB — конус, DABC — вписанная в этот конус пирамида,
ADLBD, ADLCD, DB1DC, DOL(ABC) (рис. Р.3.40). Так как DB = DC=DA,
то AADB= AADC= ADBC как прямоугольные треугольники, имеющие
по два равных катета; следовательно, А АВС — правильный. Положим
йк/2 . „„ ОА ау/3 aJ2
АВ=а; тогда DA =——. Из AAOD находим sin LADO=-— =—— : =
2 DA 3 3
х/б х/б
=-^-, т. е. AADO=ncstn —.
6
3 ’
3.117.
3.120.
8>/з яг2 а ,
—. 3.118. V tg2 3.119. —— sitn2 а яп22а.
Зяп2а 2 12
□ Осевое сечение фигуры изображается треугольником SAB, в который
вписан полукруг МпК; SA и SB — образующие конуса, SOI. А В — высота
конуса; АВ — диаметр основания конуса и МК — диаметр полукруга;
О — центр основания конуса и полукруга (рис. Р.3.41). По условию, SA=l,
L_SAO=a. Из ASOA находим О А = 1 cos а. Пусть С — точка касания полу-
шара с боковой поверхностью конуса; тогда OCLSA. Из ДОСЛ получим
ОС= О A sin а=/ cos а sin а=- / sin 2а. Следовательно,
2
2 2 1 1
V=- яОС3=- я • - Р sin3 2а =— яР sin3 2а.
3 3 8 12
3.121.
b r.sJ2S sin 2а
2arctg 3.122. cos 2а, считая от основания. 3.123. —--------=—. 3.124. 1 — к.
а 3 sin2 2а cos а
2 cos2 а
3.125. 7/25. 3.126.-------.
cos 2а tg а
3.127. □ Изобразим осевое сечение фигуры. В сечении получим &SDE, где SD
и SE — образующие конуса, ED — диаметр его основания, SB — высота
конуса, О — центр большого круга вписанного в конус шара, С — точка
касания круга с SD, А — центр окружности, по которой шар касается
боковой поверхности конуса (рис. Р.3.42). По условию, AC=r, l_BSD=a..
Соединим точки О и С; тогда OCLSD, ACLSB-, следовательно,
l_OCA= l_BSD = a. Из ДОЛС имеем ОС=——, а из &OCS находим
cos а
ОС г
SO=------:-----. Но
яп а яп а cos а
SB=SO + OB=SO + ОС =--------I-----
sin а cos а cos а
г „ . , 2^1+sina)
=s-------(1+япа)=----------.
яп a cos а яп 2а
г, __ _____________2r(l+sma)tga г(1+япа) „
Далее из &SBD получим BD=SB tga=------—-----—------5---. Итак,
sm2a cos2 a
яАО2 • SB=- я
Н(1 -I-sin a)2
cos* a
r(l -I-sin a)
an a cos a
234
_ nr3(l+sina)3 w3
3 sin a cos’ a 3 sin a cos2 a
з . . [it a\
7 tgVv
3 sin a cos2 a
3.128.
3.129.
2arccos —-
□ Осевое сечение фигуры представляет собой равнобедренную трапецию
LMMlLi, в которую вписана окружность с центром О (рис. Р.3.43). По
условию, LLi и ММГ — диаметры нижнего и верхнего оснований конуса,
А и В — центры этих оснований. Обозначим радиусы оснований усечен-
ного конуса через Лиг; тогда ttR1 -.nr1 = 4 или Л=2г. Проведем МКЦАВ;
имеем ML=R+r—3r (в силу свойства отрезков касательных, проведенных
из одной точки к окружности), KL=BL—BK—BL—AM=2r—r=r. Из
KL г 1 1
L.MKL находим cos l_MLB=-т. е. i_MLB=zi<xos -.
ML 3r 3 3
3.130. V sin2 -.
4
3.131. □ По условию, ABC — остроугольный треугольник, ADLBC, CEL АВ,
AD = a, CE=b, 1_АОЕ=а (рис. P.3.44). Заметим, что l_ABD= LAOE=a
как острые углы с взаимно перпендикулярными сторонами (О EL АВ,
а Ь
ODLBC). Из &ABD и &ВЕС находим АВ=-—, ВС=-—. В ДЛВС имеем
sin a sin a
a1 b1 lab
AC2=AB2+BC2-2AB BC cosa— . +-r~;---г-j- cosa. Итак,
sin2 a sin2 a sin2 a
J +b2—lab cosa _
AC=~-------;-------.
sin a
3.132. □ По условию, l_DCE= LDEC, tg LDCE=3^, AD=AE
и l_DCL= L_LCE\ требуется найти l_LCA (рис. P.3.45). Так как
tg Д2)С£=3/4<1, то ДДС£<45° и LCDE>90°, t. e. &CDE — тупоуголь-
ный. Проведем DFLCE, AB\\DF. Пусть CE=a; тогда CF=~, FB=~,
2 4
3a 1 1 a 3a „ AB За За 1
CB=—, AB=- DF=- • - • tg LDCE=—. Значит, tg LACB=— =— : —
4 2 2 2 16 CB 16 4 4
1 3 1
и далее LLCA — LLCF— l_ACB=- arctg —arctg -. Теперь находим
2 4 4
/1 3\ 1
/1 3 1\
tg LLCA =tg I - arctg --arctg - =-
V 4 4/ 1/1 3\
1 +- tg - arctg - )
4 \ 2 4 /
235
Рис. Р.3.47
3.133.
3
Пусть arctg - = а; тогда
4
/1 3
tg = arctg -
\2 4
,1 1 16
cos а =--—=-----=—;
l+tg2a 9 25
1+16
11
l-cosa 1 3 4 1
----
1+i2
□ По условию, AB\\DC; AJ)=BC; LBOC=a; Sabcd=$ (рис. P.3.46). Так
4
cosa=~;
5
как LBOC — внешний угол ДРОС, то Д 2?ОС=2ДОРС, т. е. Д ОРС=а/2.
Проведем BNLCD, EF\\BN; из &OFD и ДОЕВ находим OF=DFtg^,
a a
OE= BE tg-. Пусть BN=h; тогда h = OF+OE=(DF+BE) tg -. Ho
, a /a
Sabcd=(DF+BE)h, t. e. S=h2 ctg -, откуда A= Is tg -.
3.134.
3.136.
72/97. 3.135. 2 sin (a+^).
\ 6/
□ По условию, ВС—a, ADLBC, AD=h, LBAC=a. (рис. P.3.47); требуется
найти AB+AC. Пусть R — радиус окружности, описанной около ДЛВС;
тогда a=2R sinJ=2J? sin a,
AB+AC=2A(sin В+sin С)=4Я sin —-— cos ——=
„ . 180° —а B-C „ a B-C
—4R sin-----cos---=4A cos - cos----.
2 2 2 2
Ho R=—.— и, значит,
2 sin a
, „ _ 4a a B-C
AB+AC=-----cos - cos-
2 sin a 2 2
a B-C
=----cos------.
. a 2
sin -
2
„ _Asin(B+C) Asina
Далее вмеем ,a=BD + DC=h ctgB+h ctgC=---------=--------так
sin В sin C sin В sin C
как sinB sinC=-(cos(P—Q—cos(B+Q)=-(cos(B—C)+cosa), to
2A sin a
a=---————-------. Следовательно,
cos (B— C)+cos a
236
2Л sin a 2h sin a— a cos a
cos (B—C)=--------cos a=------------.
a a
Учитывая,
, B-C
cos(B—C) — 2cos2 —--1,
получим
2Л sina—a cosa -В— С B—C 2h sina—a cosa+a
--------------=2 cos-------1, откуда cos-----= /-----------------.
a 2 2 у 2a
Подставив последнее выражение в равенство (1), окончательно находим
а /2Л sin a+a (1 — cos a)
AB+AC=------ /----------------
. a м 2a
яп - ’
2
a a , a
4Л sin - cos ~ + 2a sin2 ,
2 2 2
2a
, ,, . a a , . , a
2a h sin - cos - +<r sin2 - i---------------
2 2 2 / a
----------------------------= / 2ah ctg - + a2.
. 2a у 2
a sin2 - ’
2
Г, a 5 sin (a —y)
3.137. a2 +45 ctg 3.138. —-7----
yj 2 2sin(a+y)
3.139. □ По условию, AD\\BC, ВС=2, LABC= Z_BC7J= 135°, LAOD=150°
(рис. P.3.48). Так как углы при основании равны, то трапеция равнобедрен-
ная, т. е. АВ-CD. Находим L.ADC= 180°-135° =45°;
180°-150°
LODA=-----------= 15°; L.BDC=45°-15° = 30°. Из &BDC по теореме
ВС BD 2яп45° г- „
синусов имеем . — =т откуда BD=~^——- = 2J2. Итак,
sin 30° яп 135° яп 30°
Sabcd—^
BD2 sin 150°=- 8 • -=2 (поскольку площадь выпуклого четырех-
1
угольника равна - rfjrfj яп а, где а — угол между диагоналями).
237
a1+b1 + '^ab cosa
2 sin 2a
3.141.
3.142.^=Д
P
3.143. -jai-b1 sin a—b cosa.
3.144. □ По условию, l_BAC=a, BC=a, l_DAB= L.DAC, AELBC, LDAE=P
a a
(рис. P.3.49). Имеем t_BAD=~, l_ADE=9Q° - ft тогда ДЛВР=9О°-^--
(согласно свойству внешнего угла треугольника),
a a
Z_JCD= 180°--—(90°—ft = 90°+/?—. Пусть AD=l; тотрц по теореме си-
( 2 2
нусов из &ADB и ЛАОС получим:
Следовательно,
I sin -
2
I
----7—г; BD =
/ „ a \ [ a
cos p+- cos [ В+~
\ 2/ \ 2.
a
I /Sin2
---7---DC=------7--;
( n a \ /a
cos p— ) cos B--
V 2/ V 2
, . a / {n a\ { a
I sin - I cos В— 1+cos B+-
2 \ \ 2/ \ 2
a = BD + DC=---->- /' \ 7 / \ ‘
cos \P~2) cos p+-J
/ a\ ( a\
a cos I P— cos I fi+-
, \ 2/ \ 2j
откуда 1=------------------
sm a cos P
I sin a cos p
( a\ ( «
cos I/?--j cos lp+-
3.145. □ По условию, L.ACB=45°, i_ABC=\5°, BC=a, AMLBC, AM — радиус
окружности, E и F — точки пересечения окружности со сторонами АВ
и АС; требуется найти S^fme (рис. Р.3.50). Из &АМС и ЛАМВ находим
МС=AM ctg45°=AM, МВ=АМ ctgi5°. Тогда а=СМ+МВ=
= АМ (1+ctg 15°), т. е. АМ=ц^ Заметим, что ДЛ1В = 18О° —
238
3.146.
3.147.
- (45 ‘ +15°) = 120°. Следовательно,
c 1 яа* 2 * 4 S
^АЕМЕ = ~ * (1 +ctg 15°)1 =3 (ctg45° +ctg 15»)2 =
яа2 sin2 45° sin2 13° яд2(1—cos 30°) яа2(2—>/3)
3sin2 60° = 9 18 ’ "
□ По условию, l_ACB=90°, L СВА = а (рис. P.3.51). Пусть Лиг — соот-
ветственно радиусы описанной и вписанной окружностей; тогда
AC=2Rsina; ВС=2R cos tx. Следовательно, • 4Л2 sina cosa =
S 2Л2 sin a cos a • 2
= 2Л2 sin a cos a. По формуле (2.4) находим r=-=----------------- =
p 2Л(1+sma + cosa)
2X sin a cos a
=----:------, откуда
1 +sma + cosa
a a a / , a , a
4sin - cos - cosa 2sin - cos —sin2 -
2 2 2 \ 2 2
R а а а а. а
2cos2 -+2 sin - cos - cos- + sin-
2 2 2 2 2
a. ( a a\ . , a
= 2sin - cos —sm - ) = sma—2sin -=sma
2\ 2 21 2
1.
(я \
-+в 1 = 1, откуда
4 /
я я я
7+a=-, т. e. a=-.
4 2 4
□ По условию, AB=BC, LACB<=a, t_CAM=P (рис. P.3.52). Пусть AB=a;
тогда
SttAMB 0.5ЛХ AM sin(a—fi) asin(a —fl) sin(a — fl)
SbAMC 0,5ACAManfl 2acosasin^ 2 cos a sin fl’
так как AC=2a cosa.
3.148. □ По условию, 1_ВАС=а, l_BCA=y (a>y), AD=DC, BE — биссектриса
(рис. P.3.53); требуется найти S&bde S&abc- Проведем BF1.AC; тогда
BF BF 11
AB=-—, BC= .—..Имеем S^bde=S^abd—Едаве-. S^abc-- AE BF;
sm a sin у 2 2
£ди>£ j (1/2)Л£ ДЛ 1 АЕ АЕ АВ BF BF siny
-----=--------------=------. Но —=—=--------:---=-----; составим
S&ABC 2 (1/2) АС BF 2 АС ЕС ВС sina siny sina
Рис. Р.3.53
239
sin у
AE sin у AE sin у
теперь производную пропорцию —-—— =----------:— или —;=--------;—.
н АЕ+ЕС sina+smy AC sina+siny
Итак, окончательно находим
S&bde 1 яду sin a—sin у
Seabc 2 sina+siny 2(sina + siny)
а+у . a-у a-у
cos ЯП — tg —
•
„ a-у . а+у а+у
2cos —- sm----- 2 tg —--
2 2 2
3.149. □ По условию, BMLAC, ВМ — диаметр окружности, LBAC=a,
LBCA = р, К и L — точки пересечения окружности со сторонами АВ и ВС
(рис. Р.3.54); ' “ " ~
AM = h ctga,
= - AM ВМ
2
= “ A2 (vis«-rviBpy—- « --;—
2 2 sin a sin P
LMBC=90°~P и так как l_BKM= l_BLM=9G° (как вписанные углы,
опирающиеся на диаметр ВМ), то 1_ВМК=я., i_BML=p. Тогда из LBKM
и &BLM находим KM=h cosa, ML=h cos р. Значит,
КМ ML sin (a+/?)=- h2 cosa co&p sin(a+/?). Окончательно по-
лучим
S^klm (1/2) h2 cos a cos P sin (a+P) sin a sin p 1 . .
------= z----------------------=- sin 2a an 2p.
SbABC (l/2)A2sin(a + /0------4
требуется найти S&klm : $ьлвс- Пусть BM=h-, тогда
MC=h ctg р. Имеем $ьлвс=$ьлмв+$&вмс=
+ ^МС ВМ = ^ВМ (AM+МС)h (h ctg a+ h ctg 0) =
, 1 , sin(a + /?)
(ctga+ctg£)=- h2
Далее,
Z_ Л 2? А/=90° —а,
4
3.150. ---------.
. n + 2a
2 sin —-—
4 1
3.151. □ По условию, Z_C=90°, LCAB=a, AD=DB, LDEA=P, AE>-AC
(рис. P.3.55); требуется найти Sbdec : S(,ade- Проведем DKLAC и поло-
жим DK=h~, тогда EK=h ctg fl, AK=h ctg a, BC=2h (так как BD = AD),
1 ,
AC=2h ctga, ?4K=A(ctga+ctg/i). Далее находим SlAde=-^ h2
(ctg а + ctg Д,
Рис. P.3.54
Рис. P.3.55
^ллдс=2й2 ctga; Sbdec^S^abc—S&ade^ZJi2 ctga—- h2 (ctga+ctg/?)
1 h2
-- h2 (4ctga-ctga—ctg/7)=y (3 ctg a-ctg/7). Итак,
Ssdec 3 ctga—ctg/? 3 tg/?—tga
S&ADE ctga+ctg/? tga+tg/? ’
I a \
cos!-+/?)
3.152. ---5-----4
2 sin - sin/?
2
3.153.
/ n 1
2 sin a— ,
I 61 R2
------------, считая от вершины. 3.154. —.
4
cosa
. a+p а-p
2 sm----cos----- z, . z , ,4
...... 2 2 (p2+ q2)(n2—m2)
3.155. arctg —-—. 3.156. --------;--------. 3.157. arccos
2m+n sina
(p2+q2)(n2— m2) 4 — k2 4 — k2 r
и n—arccos-------z----—. 3.158. arcsin ., и я—arcsin —; J2^k^2.
2pq(n2+m2) k2 k2
3.159. □ По условию, BDLAC, DC: AD = k, DC>AD, l_DBC> l_DBA,
L.DBC: t_DBA=2: \ (рис. P.3.56). Пусть ДРВЛ = а; тогда l_DBC = 2a
и Z_C=90° —2а< Z_J = 90° —а. Имеем sin C=sin(90°—2a)=cos2a. Из
&BDC и &BDA находим DC=DB tg2a, AD-DB tga. Значит,
L DC tg2a 2,2, k-2 u ,
k=—=-------=------1— tg a=-; tg2a=--------, откуда следует, что k>2.
AD tga 1— tg2a к к
Итак,
Пу[3
sin a
2pq(n2+m2)
l-^-2
sinC=cos2a=b<a k
l+tg2a
1
k— 2>-l
1+4T
3.160. - + arcsn^—----
4~ 2(к+1)
3
3.163. —.
5
3.164. □ По условию,
2__ /2 2_ /2
3.161.—. 3.162. 2arcsin—— и arccos-----.
18 4 4
_ , в равностороннем треугольнике ABC имеем
AL:LC=n:m (рис. P.3.57); требуется найти тупой угол ALB. Пусть
т _ b nb
AC=b, AL = nx, LC=mx; тогда пх + тх = о, откуда х=-, AL=-,
т + п т + п
в
Рис. P.3.57
241
mb
LC------
i
Проведем
L
mb—nb
b b_________
Hi 2 2(т+л)
п + п.) (m+nyfi'
. bJ3 b
ВВ1а1Я<?, отсюда BBj=—, BjC=-,
ВВ,
Из LBByL находим tg£BLB1=y-—=
(т+п)у/з
значит, LBLB, =arctg--------,
m — n
e.
Zi'm — n)b m — n
(т+п)у/3
L .|1В = л —arctg-—
_ m—n
3.165. arcsin (5/21/7) и arcsin (>/21/14).
3.166. □ По условию, ЯВ=ЯС, AA,1BC, BB^AC; AA1(^BBI=O, OA = OAt
(рис. P.3.58). Пусть AA^H и £Я=2а. Тогда из £^ААХС находим
А1С=Н tga; с другой стороны, из hAtOC
Н Н (п \ Н
AIC=OA1 tg LA^OC=~ tg l_AOCt=~ tg I --a 1=- ctga.
„ H ,1
Htga=—ctga или tg a=-;
получим
{ л
cos В=cos С = cos I —а
\2
3.167. 3/5 и 4/5.
Значит,
1—tg2a 1
отсюда cos А = cos 2a=---г—
l+tg2a 3
£3
3 '
sin Л + sin В _ ,
3.168. □ По условию,-----------= sm С; требуется доказать, что LABC — пря-
совЛ +cosB
моугольный. Имеем
Я + В А —В
sin-----cos-----
sm^ + sinB 2 2 А + В
----------=---------=tg---------------.
cos^ + cosB А+В А —В 2
cos-----------------cos------
2 2
Тах как sin С=sin (А + В), то
А+В . А+В А+В А+В
tg-----2sm----cos---=0 или sm---
2 2 2 2
l-2cos2^
------—=0;
А+В
cos--
2
Л Л
но sin —-- /0 и, значит, cos (Л + В)=cos С=О, т. е. С=п12.
5
3.169. —. 3.171.
13
sina
arrtg--------. 3.172. 3
2 + cos а
-V5-
Рис. Р.3.59
242
3.173. □ По условию, в прямоугольнике ABCD имеем: ВЕ=ЕС, DF=FC,
S^ibcD ^С2=к (рис. Р.3.59); требуется найти LEAF. Пусть LBAE=x,
LDAF-P; тогда
АВ AD _ 1 _ 1 _ 1
~AB2+AD2~ АВ AD~2BE 2DF~2tga + 2tg^
AD + AB ~AB+~AD
откуда tga+tg/?=—. Далее имеем tg LEAF=tg (^-(a+fl) ) =
2fc \2 j
1 — tga tg/?
=ctg (a+/?)=----—так как
. tga+tg^
1 1
-AD - AB
BE DF 2 2 1
tgatg/?=— •—=------------=-,
6 AB AD AB AD 4
to tg LEAF=— =—, t. e. Z.£4F=arctg —.
2k
2(1 + k) . 2(1 +Jt) . 2(1 +*) . 2(1 +k) , 2
3.174. arcsin —-z—, я-arcsin —-z—, arcsin---—я—arcsin------—; £>—
я*2 я*2 nk nk я-2
tga a
3.175. arctg --.
2 2 . '
3.176. □ По условию, ДЛСВ=90°, ЛЛ1 = Л1С; CA^AJt, tg LAOBt=k (рис.
P.3.60); требуется найти LA и LB. Пусть ЕСВхВ=<р.
2a а
САОВ1 —а; тогда a=<p—tg<p=—, tgi^==—, где ВС=а, АС=Ь. Следова-
b 2d
тельно} д
tg<p—tg«A b 2b 3ab 3
l+tg^tg^ a2 2(b2+a2) /b a\
b2 \a Ъ)
3 3 tg/l 3
------------—-----------gm 2Л.
2(ctg/l+tg/l) 2(1+tg2^) 4
3 4Jt
Отсюда k=- яп2Л; sin2H=—;
4 3
243
„ я 1 . 4fc
arcsin-у
______3 _____1 45 1 45 я я 45
3.177. - tga. 3.178. - arctg - arctg -j +-, - - arctg -j.
4 2 a 2 и 2 2 a
3.179. □ По условию, AB** AC, DEFL — вписанный в &АВС прямоугольник,
периметр которого не зависит от выбора точки Е на АВ (рис. Р.3.61);
требуется найти sin Л. Проведем АА\1_ВС и полохим AAv=h, ВС=а.
Построим еще один прямоугольник, вписанный таким же образом, одна из
сторон которого проходит через точку Н, где АН^НА^ при этом
KR АН
Pknqr-Pdefl (согласно условию). Так как LAKR~ txABC, то —=—>
ВС
ah a fha\
т. е. KR=~=-. Далее, Pknqr=2 (NK+KR) = 2 I-+- 1=а+Л. Пусть
2л 2 \ 2 2 у
DE=x; учитывая, что b.AEF~ L.ABC, получим — =------------, т. е.
ВС АА1
a(h — x) i ah—ax\ 2(xh + ah — ax)
EF= , ..Тогда Pdefl=2(DE+EF)=2\x +—— =—----------т---.
h \ л у л
2(xh + ah — ах)
Поскольку Prnqr~Pdefl> имеем ---------------------=а+л или
2xh+ah—2ах—h2=0, откуда (2х—h)(a—Л)=0. Это равенство должно быть
справедливым при любом значении х; значит, a—h = 0, т. е. h=a. Наконец,
А А.С а а 1
из ДЯЛ.С находим tg -=—у-откуда
2 АА, 2л 2а 2
А
л 2te^ 1 4
Я.и-—-5.
3.180. 2arox>s
2ab
3.18Х □ По условию, ОА^АВ! — сектор, О.— центр вписанной в него окружно-
сти, OA=R, OtA—r (рис. Р.3.62); требуется иайти Рол1лв1‘=2.ОА1 +1ил,в,-
О.В г
В AOjBO имеем OiB—г, OOi = R—r< откуда sm LOOiB**—— =——;
ОО« R — г
244
IuA,b,“2Rarcsin ——; Poa,ab,=*2R I 1 +arcsin —— I.
1 1 R—r * 1 \ R—r)
3.183. □ По условию, в &ABC имеем: BC=a, LC=n радианов, L-B=$ ради-,
анов, AD2.BC, AD — радиус окружности, пересекающей АС и АВ в точках
К и L (рис. Р.3.63); требуется найти /идх. Из &ADC и LADB находим
CD=AD ctga, BD = AD ctg р. Тогда a=CD+DB=AD (ctga+ctg/J), т. e.
a a sin a sin 8
AD=-----------=——-----—• Значит, ДК>1Д=л-(а+/Г), откуда /иИ,=
ctga + ctg/J sin(a+/J)
, m а (л — a-8) sin a sin 8 _
= AD(n-a-P)=----------- -------.
sm(a+/?)
3.184. □ По условию, OAnB — сектор, САОВ=а радианов, О, —центр окру-
жности, вписанной в сектор ОАпВ (рис. Р.3.64). Пусть R — радиус сектора,
г — радиус вписанной окружности; тогда 5(эл„д=-/?2а,
a
г-—-"'--'-- - • --
5О1 = лА
a
В AOj^jO (OlA1J.OA) имеем r= OtAt = OOi sin- = (Я—r) sin - или
a
R sin -
. a . a 2
r+r sin - = R sin откуда r=
2 2
SoAnB *2“(1+Siny
°' 2 л R2 sin2 -
2
. Итак,
a
1 +sin -
2
2а cos2 I---I
\4 4/ _
л sin2
a.
2
3.185. □ По условию, АВ — хорда, uANB=a°; АС=ВС, DE — хорда,
DC : СЕ=1 : 3 ( рис. Р.3.65). Пусть CD=x; тогда EC=3x, ED—4x. Прове-
дем OF±ED и соединим точки О в С, О и А. Так как ОС2.АВ (диаметр MN
перпендикулярен АВ), то LFOC= CACD (острые углы с взаимно перпен-
дикулярными сторонами). Заметим, что FD=~ ED=2x, FC=x. Далее име-
ем ВС AC=DC ЕС или АС2 = х Зх, т. е. AC=x*j3. Из Д ОСА получим
а г" a FС
ОС=АС ctg-=Хх/3 ctg ~, а из &FOC находим sin i_FOC=— =
2 v 2 ОС
245
a a
X ‘4 tg 2
=-------=——. Значит, LACD<= l_FOC=aicsm так как
^>-2
9, f- a
sin ДЛС2><1, то tg откуда T- e- «<120°.
R sin a R1 sin a i-n-
3.186. ------—3.187.------:—. 3.188. —-— (V4-яп2 a-cos a). 3.189.
, (я+2)Я-Г 2a—ana 8
2 cos2 ----
4Л
а
Я яп -
2
. 3.190. *tg2^.
2 6 4
(а я
2 + 6,
3.191. □ По условию, AB=BC, BB^IAC, BBi = h, LABB^a (a 0/6),
О — центр окружности, описанной около A ABC, Ot — центр вписанной
в А АВС окружности (рис. Р.З.бб). Из ДЛ^Л находим ABt=h tga; тогда
AC=2h tga=2A sin2a, где R— радиус описанной окружности, откуда
h tga h
R =----=----г-. Из ДЛЯ,О. получим O,B,=r =
sin 2a 2cos2 a
/я a\ / я a\
=AB< tg (---] = Л tga tg ( - ). Следовательно,
\4 2/ \4 2/
Л . /я a'
OO^h-OB-OiB^h--------------Atgatg ---
2cos a \4 2,
/ /я
япа 1—cos ( —a
2
получим
--Д--A
\ 2 cos[n
cos а яп I -—a
\2
1 sin а (1—sina)
2 cos2 a cos2 a
(2cos2a—1—2sina+2sm2a\ 1—2sina
-----------5 )=Л -z---5— =
2cos a / 2 cos a
. я . /я a\ / я a\
sm —sm а 2Л яп I---I cos — +-
6 \12 2J \12 2J
™ Л 2 s 2 •
cos2 a cos2 a
3.192. □ По условию, AB=BC, LBAC—a, BF1AC, BF=r+m, где r — радиус
246
вписанной окружности (рис. Р.3.67). Пусть R — радиус описанной около
А АВС окружности; тогда AC = 2R sin(180° —2a) = 27?sin2a,
а а
BF^AF tga = 7? sin2а tga, r=OF= AF tg~ = R sin2a tg -. Таким образом,
2 a
R sin 2a tga = m+7? sin 2a tg -
получаем
уравнение
или
(a \
tg a—tg - j =m, откуда
a a
m cos a cos - m cos -
R =--------------=---------—— m
a a a a
2 sin a cos a sm - 4 sin - cos - 4 sin -
2 2 2 2
rd 1 + sin2 a я a , a 1
3.193. —---=---. 3.194.--z------. 3.195. - tg3 -. 3.196. — 5 ctga sin4a. 3.197.
sin2a 2 sin2 a sin 2/i 2 6 2 2
a
Pa>Pb>Pc. 3.198.------.
a
2 cos -
2
3.199. □ По условию, О — центр окружности, О А — неподвижный радиус,
ОВ=ВА, М—произвольная точка окружности (рис. Р.3.68); требуется
найти наибольшее значение [_ОМВ. Пусть LOMB=a, OA = R; тогда
ОВ=—. По теореме косинусов имеем ОВ1 = ОМ2 + МВ2—2ОМ A/Bcosa.
Л2
Полагая МВ=х, получим — = Я2 + х2 — 2Rx cos а или
4
4Х2 — 8Ях cos a + ЗЯ2 =0. Это квадратное уравнение имеет корни, если
Р/4 = 16Я2со52а— 12Я2=4Я2(4со52а— 3)>0, откуда 4cos2a —3>0;
2 cos 2а >1; cos 2а >1/2. Наименьшее значение cos 2a, равное 1/2, соответ-
ствует наибольшему значению 2a, равному я/3. Значит, аяаиб = л/6.
3.200. □ По условию, ABCDAiB1ClDi — прямой параллелепипед,
ABCD — ромб, AAt=h, LACAl = a, £_DBD1=P (рис. Р.3.69). Из ДЛ^С
и (ьВ^ВВ находим AC=h ctga, BD=h ctg/?; тогда
Sabcd = 2 AC BD=- h2 ctga ctg/? и, значит, F=- Л3 ctga ctg/?. Наконец,
из ДABC получим AB = /- h2(ctg2 a + ctg2 /?) = - A-Jctg2a + ctg2/?; поэтому
у 4 2
^бох = 2Л2 Vctg2 a + ctg2
Рис. P.3.68
a3 J cos 2а
3.201. —*----.
sin а
ЗЛОХ □ По условию, ЛЗСА,В,С, - ..-..мая
LABC-P, Ущ,= У Р.3.70).
a2 sin a sin Д a2 sin а яп Д
a “2sin(Jво»_(а+Д))" 2sm(a+P) ’
ВС АС
теореме синусов имеем =----------=---------,
яп а япД яп (а+Д)
. „ asinP „
АС=---------. Поэтому
sin(a + /?)
a (sin (а+Д)+вта+5тД)
Ралвс= ~
призма, АВ = а, С ВАС = а,
Так как V^S^bc Н,
2Уяп(а+Р)
то Согласно
a2 яп а яп Д
а sin а
откуда ВС=~—------,
яп(а+Д)
a
sin (а+Д)
. а+Д / а + Д а-Д\ ,
2а sin--- cos------hcos---- 2а
2 \ 2________2 /
а + Д а + Д
2 sin---cos-----
2 2
а Р
cos - cos -
2 2
а+Д
cos----
2
Итак,
a + B
2 Г sin —-
2
а р
2а cos - cos - „ . , „
с _р тг- 2 ’ 2 2^ш(а+А__________________________
бох длвс д’япаяпД а . Д
cos---- a sin - яп -
2 2 2
з • “
, a sin а sin -
а3 а 2
3.203. — tga tg -. 3.204.--------
8 2 яп<р
3.205. Р sin a sin Д ./cos (а+Д) cos(a—Д).
а2Ь я 5л
ЗЛ06.— ;-<а<—.
2 6 6
3.207. □ По^словию, ABCA^^t —правильная треугольная призма, АВ=а,
(iAtB); (СВ,У)<=а (рис. Р.3.71). Проведем ЛЛГЦСЛ]; тогда В^ВС, ВХК=ВС
и LAxBK=a.. Так как СА^К^ТХР, то из ЬА^К находим
А1К2=2а2 —2a3cosl20°=3a2; Л1ЛГ=а>/з. Пусть А1В=х; тогда в hAtBK
248
имеем х. - 2-v — 2л2 cos а или 2х2(1 —cos а) = 3а2; х2 =-. Наконец,
, а
4sm2 -
2
из получим
, / . , аХ
За2 а2 I 3— 4sm2 - 1
BB2i=A1B2-AlBj =----------а2=— ----------=
4sin2 - 4sin2 -
2 2
/л а\ /л а\
. , а2 cos I - Н— 1 cos I-1
а2 (3 — 2 + 2cos а) a2(l+2cosa) \б 2/ \6 2у
. , а , а . , а
4siir - 4sin2 - sin2 -
2 2 2
3.208.
□ По условию, АВСА^В^С^— прямая призма, LACB=i, LBAC=P,
$&лвс=$, О — центр окружности, описанной около А АВС, сАхОА=<р
(рис. Р.3.72). Имеем ЛС=2ОЛ sin(180° — (a+/?)) = 2CMsin(a+/?). Тогда
.4C2smasin/? 2Ssin(a+/?) „ t
S—----—--------, откуда ЛС2=---------------. Из ДЛ.ЛО находим
2sin(a + /?) sin a sin/?
ACtgp
AA, = OAtgip =--------. Окончательно получим
2sin (a+fl)
.. „ .. „ ACtgV Sy/2Ssn(a+P)tg<i>
V—S • AAl=S —— ------— =----------- ' — =
2sin(ii+/>) 2sin (a+fi) -Jan a sin /?
I S
= S tg<p /-----------------------.
y 2sin (a + /7) sin a sin /?
3.209. P sin 2P cos p sin a cos2
3.210. □ По условию, ABCAiB.Ct — прямая призма, AB=BC=a, LABC—a,
АА,=Н, AlBC — сечение (рис. Р.3.73); требуется найти расстояние от А до
(А1ВС). Проведем ‘АЕА.ВС и соединим А, и Е; тогда Л]£±ЛС (по теореме
249
о трех перпендикулярах). Имеем ВС1(А tAE) и,
следовательно, (А,АЕ)1(А,ВС). Проведем
AD.LAtE; значит, ADj.(AtBC), т. е. AD — ис-
комое расстояние. Из &АЕВ найдем
Л£=аяпа, откуда .Уд^ле®'- Яаяпа, а из
AAjAE получим AE=-J И2 + a1 sm2 а, откуда
5ди1ле=- AD yjrf'+a1 sin2 а. Решив уравне-
ние- Hasina=- АВ J Н2 + a2 sin2 а, окончате-
2 2 v
aHsin a
льно находим AD-—------------
+ a2 sin2 a
условию, ABCA1BiCl—прямая призма, АВ=АС,
АВ+АС+ВС = 2р, £_ВАС=а, АХВС — сечение призмы, LAtBCA = fl (рис.
Р.3.74). Проведем A^-LBC и
3.211. □ I способ. По
а.
положим АВ=х; тогда 5л=ляп -,
2
a a р
ВС=2хяп-, 2p=2jc+2xsm-, откуда х—-------------
1+sin -
далее имеем
a
pcos-
. Поскольку
, . a
1 +яп -
2
LAlKA—fl как линейный угол
между
pcos-tg^
плоскостями (АВС) и (А ,ВС), из А А КА! находим А А, =--------.
a
1 +sm -
вательно, 2
Следо-
1 , . p2 sin a
V=Saabc AA<=- AB2 sina AA, =—7-r—
2 1 eV
2 I 1 +яп -
\ 2/
, a - , a
р sin a cos-tg/? /г яп a cos - tg/?
(aV / a\3 a
1+sin-) 21 1+sin- cos2-
2/ \ 2/2
_ , /n~a} a a
P sin ( -y I sin - cos - tg/?
'—7---7-—\\7-------=P3 ‘8
л —a а
~~tg-tgfl.
(л —a\\3 x
----cos2 -
2 JJ 2
II способ. Пусть AAi^h; тогда из ЬАуАК находим AK=h ctg/?, а из
АК hctgfi а
t^AKB получим АВ=-----------=-------, BK=h ctg fl tg -. Значит,
a a 2
a
BC=2hctgfltg-,
2h ctg fl „ a
откуда 2p=-------------1-2л ctg fl tg - или
a 2
cos -
2
250
a / a\
pcos = h ctg/J I 1 +sin -I, t. e.
a „ . /я —
^cos-tg/f p sin (-^) tgp
Л =---------
a
1 +ЯП 2
. /я—a\
\ 2 / я—a
------7--r- =P tg -7- tg p.
(n—a\ 4
1 +cos --]
\ 2 /
Итак,
V=S&ABC AAX =| ВС АК AA, 2Л3 ctg2 P tg ?=
, ,я — a . a , , я—a a
=P tg3 tg3 p ctg2 P tg - =p3 tg3 tg p tg -.
3.212. □ По условию, АВСОА^С^—наклонная призма, ABCD — трапе-
ция, ADiBC (AD<BC), AD=AB=CD=a, l_BAD = P, 8^ = 8^=
=BlC=B1D, BBl образует с (ABC) угол a (рис. P.3.75). Проведем
B1OX(ABC); так как B1A=BlB=BlC=BiD, то OA = OB=OC=*OD, т. e.
О — центр окружности, описанной около трапеции ABCD. Из LBAD по
О
теореме косинусов находим BD1=2a2—2a2 cos (180°— Д)=4а2со52 -, т. e.
P
BD=2a cos -. Поскольку &.BCD вписан в окружность с центром О, имеем
Р
2а cos -
2 а
BD = 2OBwaP, откуда ОВ=-----------— =-----. Из LB^OB получим
2sitnp _ . Р
2sm -
2
OBi =ОВ tg 1_В1ВО=------. Чтобы определить площадь основания, про-
Р
2sin -
2
ведем DE1BC й из &CED найдем DE=a япр, EC=acosP; тогда
AD+BC
ВС=AD + 2ЕС = а + 2а cos Д. Следовательно, SAbcd=--------- Е>Е=
=a(l +cos Р) a sinр=а* sin /7(1 +cos Д). Итак,
V=a2 sinP(l +СО8Д) a t^“ =2а3 cos3 tga.
2sin -
2
S
Рис. P.3.75
Рис. P.3.76
251
3.213.
a
a3 sin a sin - tg/?
------------------. 3.214.
abc
л —a
2 cos---
4
S
a’sin2 0sin2atg<p
-• Л-41Э» z—: ----zz •
I 6 sm2 (a+P)
I a\
sin I 15 — ).
V 2/
3.216.---------
cos - sin315'
2
3.217. □ По условию, SABCD—пирамида, AB]\DC, AD —ВС, AD=a,
LADC=a, LSABC= LSBCD= LSDCA= LSADB=P (рис. P.3.76). По-
строим линейные углы двугранных углов при основании. Проведем
SO.L(ABC) и ОЕ, OF, OG, ОН — перпендикуляры к сторонам основания.
Так как &SOE= ASOF= £,SOG = &SOH, то OE~OF—OG=OH, т. е.
О — центр окружности, вписанной в основание ABCD\ тогда
АВ +DC=2AD = 2a. Проведем AMLDC и из &AMD найдем АМ=а sina.
„ _ AB+DC ,,, , . „ a2 sin a
Далее имеем SABCD —------ АМ=а sina; ОбоЖ=-----;
2 cos/?
, . 1 „ m 2д2 sm a cos2 -
a sina , . йг sma(14-cosp) 2
*5цоля — ~ bo sina— - — - . В
cos /? cos p cos p
StgB ,----- 4/3 ' ,----------------
3.218. —-— -^/5sina. 3.219. —- cosa cosfiy/ — cos (a 4-/?) cos (a—Д).
6 3
^sV^ctgA a2^
x • a -J — cos a
6sin a cos - ’
2
3.222. □ По условию, DABC — пирамида, LACB=90°, l_BAC=a., r — радиус
вписанной в &ABC окружности, DOL(ABC), LDAO= l_DBO= l_DCO = p
(рис. P.3.77). Так как &DOA = LDOB= &.D0C (по катету DO и равным
противолежащим ему углам), то ОА = ОВ=ОС, т. е. О — середина АВ.
Пусть 01 — центр окружности, вписанной в &АВС. Проведем О2Е±АС;
тогда Oj£=r, АС=АЕ+ЕС=АС+г. Но О,А — биссектриса LBAC\ по-
a
этому AE=r ctg - .откуда
cos/?
(a a
sin -4-cos -
2 2,
ЛС = г ctg- + r=r I ctg-4-1 | =
2 \ 2 '
л a
4~ 2
a
sin -
2
a
sin -
2
г / л a\
rJ2 cos I --- I sina
\4 2/
BC—AC tga=-------------------=
a
sin - cos a
2
r /л a\ a a r- a
2tx/2 cos----sin - cos - rJ2 cos -
v U 2J 2 2 v 2
а /л a\ l л a\ /ла
2sin - sin--] cos (-- sin-----
2 \4 2/ \4 2 \4 2
252
Теперь из &AOD находим OD=AO tg/?=----------г-----и, значит,
[ л а\ а
4sm----sin -
\4 2/ 2
И=- -АС ВС OD=-
3 2 6
Гу/1 cos л/2 cos r^tgp
а /я а\ /я а\ а
sin - sin |---- 4sin---sin -
2 \4 2/ \4 2/ 2
, г- /я а\ а
r V2 ctg I--- I ctg - tg Д
а . /л а\
12sm - sm (--]
2 \4 2/
3.223. □ По условию, SABC — пирамида, BC<AC, AB=c, LACB=90°,
LBAC=a, SO±(ABC), О — точка пересечения медиан, AAt—наиболь-
шая медиана, LSAO=p (рис. Р.3.78). Так как АС=с cos a, ВС=с sina, то из
ДАСА! находим
AAt —Iе2 cos2
c2 sin2 a=- c ^/4 cos2a+sin2 a=- c s/3cos2a + l;
2 2
1 /----5---
- c>/3cos2a+1. Далее из &SOA получим
2
AO = -AA
3
тогда
c^/jcos^a+l tg/}. Итак,
F=- - c sina c cosa - сл/3со52а+1 tg^=— c3 sin2a tg^V2cos2«+l.
3 2 3 36
3.224. □ По условию, SABC — правильная треугольная пирамида, О — центр
основания, OK1SB, ОК=р, LASBC=a (рис. Р.3.79). Построим линейный
угол двугранного угла ASBC. Имеем ACLSB, поскольку SB — наклонная
к (АВС), ОВ — ее проекция на эту плоскость, АС1ОВ. Проведем через АС
плоскость APCLSB; тогда LAPC=a. Так как MP и OK принадлежат
MP MB 3p
(SMB) и MP3.SB. OKLSB, то MP\\OKh, значит, т- e- MP=-^. Из
а Зр а а
&МРС вахошм МС=МР tg-=-ytg-, ^C=3ptg-, откуда
9р2 у[з tg2 ?
В^лвс—------------ Далее, &SOK~ &SOB (прямоугольные треугольни-
4
ОК ОВ л
ки с общим углом OSB)\ поэтому —=—. Отсюда, учитывая, что
OS SB
г а ОВ OS tB 2 °S г a
OB=pyj3 tg -, получим SB=——=-------------= OS~j3 tg -.B A SOB
P'fi tg
р
имеем SB2=OS2 + OB2; 3OS2 tg2- — OS2=3p2 tg2 OS=
Итак,
а.
Г’
2
3.225.
1 У *
V=--------
3
4
а _ _ а
2 9'tg2
tg^-1
8tgia 3-ZZ6’ 4tg2a
3.227. .JT/Г^;. 3.2M.
3 6 cos a
, , . , (л a'
, . , 2rsna cos2 I -
a ,---- aJsm2atg<» \4 2
3.229. - J2cost. 3.230.---и
2 v 3
cos<p
254
“+Д . /я а\ . /л Д\ „ . «
2№ cos------sin I - +- ) яп I - -I— I г яп -
2 \4 2/ \4 2j 2
3.231.--------------:\----------------- 3.232.
яп a sin p 3 яп p
_ , . „ ,/л а\ а . [а п\
2ersinflcos-----] 4п<гsin - яп - Н—) ,
\4 2/ 2 \2 nJ а3 а
3.233.-----------i< 3.234.--------------i3.235. — ctga ctg - tg£.
cosa я 12 2
sm -
1 л
3.236. □ По условию, 2-ЛСВ=90°, LB AC—a., CD, BB2, AAt —медианы тре-
угольника (рис. P.3.80); через меньшую из них проведена'-плоскость у,
(у; (ЛВС))=Д; требуется найти ((ЯС)?у) и ((BQ^y). Докажем, что CD<AAt
CD = [ АВ=- Ja C^TbC1;
2 2
и
CD<BB1;
действительно,
AAt~^AC2+B^-=^4ACr+BC2; BB^JaC2+4BC2. Следователь-
но, CDey. Проведем ЛЛ2±у и AOLCD; тогда LAOA2=/1 как линейный
угол между у и (ABC), LACA2 — угол между катетом АС и у. Пусть
а
АА2 тогда АО=-—Далее, AD —DC как радиусы окружности, описан-
sm р
ной около ДЛЛС; поэтому CDCA^ сВАС~а. Из ДАОС находим
AD а АА
АС=----=--------, а из ДЛЯ,С получим sin LACA2 =—^ = sinasin/J,
яп а яп а яп р АС
т. е. L АСА, =arcsin(sina sin/?). Аналогично найдем угол между катетом
ВС и у. Проведем BB2Ly; тогда LBCB,—искомый угол. Имеем
ВВ2=АА2 = а (поскольку LAA2D = LBB2D) и из &ВВ2С находим
ВВ, а
sin L ВСВ, =—-=----=cosa sin/?, т. е. lBCB2 =arcsin(cosa sin fl).
1 ВС AC tga
3.237. □ По условию, ABCD — ромб, ADefi, LA — острый; диагонали ромба
образуют с Д углы а и 2a (рис. Р.3.81). Пусть О — точка пересечения
диагоналей. Проведем
00.
и sin 2.0.00.=---. Так как
1 0D
00.
значит, stn L ОАО, =-------
1 ОА
LA — острый, то
AC>BD,
255
sin L.OAOV <sin LODOX, т. e. LOAO1 = ci, a LODOi=2a. Пусть OOt=a;
a a A О A sin 2a
тогда OA=——, a OZ)=---. В ЛАОО имеем ctg—=—=—-— = 2 cos a,
sina sin 2a 2 OD sina
откуда —=arcctg (2 cos a), t. e. A=2 arcctg (2 cos a).
I-------:----- 2 >/5-1
arcsin >/sin (a+/?) sin(a—fl). 3.239. arccos - —. 3.240. arccos л——.
V8+sin22a 2
□ По условию, ABCDEFGH — правильная призма, AB=a, Vup=V (рис.
Р.3.82); требуется найти угол между АН и НС. Так как V=a2 DH, то
DH=Vji?. В Л АНС имеем AC2=AH2+HC2-UH HCcos ЛАНС, т. е.
2Л№-ЛС2 2(в2+^)-2д2 V2
cos LAHC=-^------------
2 в 2+~т
tgfl X г)
arctg---.
2 cos а
□ По условию, ABCDA^ByC^Di — прямоугольный параллелепипед,
АВ : ВС : СС, =3:4: 12, AAt^C — диагональное сечение параллелепипе-
да (рис. Р.3.83); требуется найти синус угла между BD1 и (AA^i). Прове-
дем BKJLAC; тогда ВКЦАА^), поскольку BK.LCC,. Пусть О — точка
пересечения диагоналей параллелепипеда; так как ОК — проекция ОВ на
(AAiCi), то LKOB — искомый угол. Положим ЛВ=Зх; тогда ВС=4х,
CCj = 12x, ЛС=5х, ВР1=5/9х2 + 16х2 + 144х2 = 13х. Далее имеем
1 1 Зх • 4х 12х
S&abc=~ АВ • ВС— АС • ВК, откуда ВК=—-—=-—. Наконец, из
2 2 5х 5
ВК 12x2 24
ЛОКВ находим sm Z_KO.ff=—=-—= 65'
3.244. □ По условию, РА BCD — правильная четырехугольная пирамида,
Sapbd : Sabcd “к (рис. Р.3.84); требуется найти cos LDPC. Пусть 2)С=а
0,5 asfih г-
и ОР=Л; тогда -—-5----=it или h=akyj2. Из ЛРОО находим
<г
DP= liable2 +y“^''/2(4it2 + l), а в ЛОРС по теореме косинусов имеем
’ 4k2
а2 =а2(^с2 A-V)—a2(4k2 + \) cos LDPC, откуда cos LDPC=—-=—.
4kr +1
3.238.
3.241.
3.242.
3.243.
2(а2+—т
256
a
_ z3 V COS ~ f~—; 4 f~
( 2 /2sina\ V^cosa
3-245. -J—. 3.246. arctg -------— —— ). 3.247. arccos —-------.
—2. у a v и / 2
3.248. arccos 5/ ctg a ctg /!. 3.249. arctg — и arctg —.
4 2
3.250. □ Согласно условию, в пирамиде SABC... двугранные углы Л С, СВ, BD,...
равны между собой, 5ПОЛИ : Sfct=k; требуется найти двугранные углы при
основании. Воспользуемся формулой 5gor=^ося : cosa, где a — угол между
основанием пирамиды и ее боковыми гранями. Тогда получим
Збо. + Яося -Seox ! 1+cosa 1
к =----------=—---hl =-------hl;------= к, cosa#0; cosa=-—-,
<^ося *^осн COS Cl COS Cl 1
1 1
t. e. a=arccos -—-. Решив неравенство 0<-—-<1, найдем k>2.
3.251. 3.252. arctg cos Д 3.253. arctg
2 \ nJ 2
. S it . S___________ it 2 2
3.254. arcsin arcsm 75. 3.255. -, arctg-----и arctg-----.
13 r 2 sin a cos a
3.256. □ По условию, SABC — пирамида, SAL(ABC), AB^BC=CA,
Sfm ’• £длвс=И : 4 (рис. P.3.85); требуется найти LSABC. Пусть BC=a,
a1 J3
SA=h; тогда >5дллс=—:—; S6oz=2Sasac+S&sbc- Проведем ADLBC;
4
имеем SDLBC (по теореме о трех перпендикулярах), т. е. L SDA=0 — ис-
комый угол. Следовательно,
*5бох™аА+- а SD’*ah+-^
а*^/з а (4й cos/?-ha-Уз)
2 cos/? 4 cos/?
„ a(4hcosp+aJ3) • 4 И 4й 1 11
Согласно условию, имеем---------— —— или —— + - ——. Так
4cos/?a25/3 4 a~J3 cos/? 4
как —--tg/? (из ДЛ5Р), то 2tg^-h>/tg27+4или >/tg2/?-hl -~-
ау/3 4 4
— 2tg/?, откуда следует, что tg/?<—. Решив уравнение, получим tg/?—-,
3
т. е. /?»arctg-.
4
3.257. □ По условию, PABCD — правильная пирамида, SOL(ABC~),
LPDO^ lDPC (рис. Р.3.86); требуется найти LPDCO. Положим
l_PDO~ LDPC^a, PD^a; из LPOD найдем РО—asina, ОД—a cos a.
Пусть M— середина CD; тогда ОМ LCD и PM LCD, т. e. LPMO^tp
является линейным углом двугранного угла PDCO. Находим
OD^]2 a>J2 cosa
DM^OM**—— - ------. Далее, в &PDC имеем
PC-^/^a2 -ha1 — 2д2 cos a-0^2-2 cos a; с другой стороны,
2JC«2DAf—a>/2cosa. Значит, ai/2 (1 — cos a)—a^2 cos a; 1—cos a «cos2 a;
a , « л/*"1
cos2a-hcosa-l—0; cosa—-2-——
2
. Теперь из ДРОМ получим
9-363
257
OP 2asina
r- 2 1 , 4 Vs + l
= V2tga; tg2a=— 1=------y=-l =—~—
cos “ 6-2V5 2
tg<p=V2
3.258. arctg >/2.
+ 1; <p=arctg ^/Vs + l-
3.259. □ По условию, АВСА^С, — правильная треугольная призма, боковые
грани — квадраты (рис. Р.3.87); требуется найти угол между А(\ и ВС. Эти
прямые — скрещивающиеся. Проведем через С, прямую, параллельную
СВ\ этой прямой является СгВи т. е. LACXBX — искомый угол. Пусть
ЛВ=а; тогда из ДЛС1Л1 находим 2а2 = 2о2+а2 — 2аг\/2со& LACJ^, от-
А J1
куда cos £ Л С,/?!=—. Итак, LAC^ = arccos —. И
4 4
/ к \ / а4\
3.260. arctg --tga ]. 3.261. arccos I ——5 ).
\fc-t-3 J \ S1}
3.262. □ По условию, SABC — правильная треугольная пирамида, SO1(ABC),
SK~KB, OK** ВС (рис. P.3.88); требуется найти косинус двугранного угла
ASBC. Пусть АВ-*а. Проведем ОВ1АС; значит, SB1A С (по теореме о трех
перпендикулярах). Затем проведем (ADC)1SB; тогда L.ADC — искомый. •
Так как в прямоугольном треугольнике SOB имеем ОК=ВС=а — меди-
I a* aJ\5
ана, то гипотенуза SB**2a. Из LSMB найдем SM— 14а — -р=—-—.
1 1 V
Далее, используя равенства 5ддус=2 • С2>=- &с ' пол^м
3.263.
3.265.
CD—----------—-------
SB 2 • la
, 15а2 . 15а2
16 16
7
LADC=arccos —.
у/5—1 sin а sin Д
arccos -. 3.264. arctg - -.
2 >/sin(a+^) sin(a—Д)
□ По условию, SABC — пирамида, AB=AC*=BC, (SAB).L(ABC),
(SAC)±(ABC), j_ASB+ L BSC^n/1 (рис. P.3.89). Докажем, что SA — высо-
та пирамиды. Действительно, перпендикуляр, проведенный из точки
---. Наконец, из LADC по теореме косинусов
4
находим а2=-"^-+^*—2 cos LADC, откуда cos LADC—~-. Итак,
16 16 16 15
258
S к (ABC), должен принадлежать и (SAB), и (SAC), т. е. должен принад-
лежать их линии пересечения и, значит, он совпадает с SA. Тогда
ts.SAB= &SAC (по двум катетам); следовательно, CASB= l_ASC, а углы
ASB и BSC не равны. Пусть £_ASB=a, CBSC=0 h 'SB=1. Из условия
следует, что а и Д— острые углы. Из &SAB находим ЛВ=/япа, а из
A SBC по теореме косинусов имеем ^0=5/2?—2/2со5Д=/5/2^1—cos^.
Так как АВ=ВС, то sina=5/2(l—совД) или sin ^—^=5/2(1—cosД);
тогда cos2 Д=2—2совД; со82Д+2со5Д—2=0. Учитывая, что Д — острый
угол, получим cos Д=^/З — !. Итак, Д=arccos (5/3 —1),
а=^-arccos (5/3-1).
3.266. □ По условию, SABCD — правильная пирамида, SOL(ABC),
S&SAC : S^oT = k, SF и SE — апофемы пирамиды (рис. Р.3.90). Пусть АВ=а,
а
LESF=a; имеем SF=--------
„ . а
2 sin -
2
а2 5/2 ctg |
а 2
“g2------—’
а а
(из &SOF), >SO=-ctg-. Следовательно,
лучим уравнение
11 а
> *$бох== П '
2 а
2sin -
2
a2-Ji ctg - sin - 5/2 cos -
k=-------т----- или k=--------
4a2 4
о2
----. Тогда по-
а
sm -
2
ИЛИ COS- = 2^5/2.
2
2
ЭС 1
Итак, cosa=2cos2—l = 16fc2— 1. При этом 16fc2 — 1 < 1; lt2<-,
0<* Л
4
3.267. □ По условию, SABC — правильная пирамида, SBK — сечение, прохо-
дящее через высоту SO и боковое ребро SB, S^sbk' SnOnn=k (рис.
Р.3.91); требуется найти величину LSACB. Так как ОВ — проекция SB
на (АВС) и ОВ1АС, то LSKO — линейный угол двугранного угла SACB.
а\П a-Jl tg а>
Пусть АС = а, LSKO = <{>', тогда из Д SO К имеем SK=—-—,SO=— -.
6со$ф 6
259
3.268.
3.269.
3.270.
Значит,
1 1 aJ
S&SBK=z BKSO*- —
6
_а2>/з 1 ajl _aS/3(cos<p+l)
*^полн~ . +„ • io • —
4 2 6cos<p
Далее находим
S&sbk a2 tg<p 2cos<p
k=-------—----------------
*5поли о 2 2 Ф
8a2V3 cos2 -
4cos<p
8 ’
2 /Ч 2 V
'x/Jcos —
v 2
2cos<p
. ф
tg-
sin<p 2
2
tg ^ = 2*>/3; <p=2arctg(2^v/3),
, , 1 J3
При этом 1 — 12Л2>0; к2<—; 0<к<—.
12 6
□ По условию SABCD— правильная пирамида, cos L (SAD; SDC)*=k
(рис. Р.3.92); требуется найти cos C(SDC; ADC). Учитывая, что AC1SD,
проведем (AKC).LSD; значит, САКС — линейный угол двугранного угла
SD. Затем через SO проведем (SO М) LCD; тогда LSMO — линейный угол
двугранного угла DC. Пусть AD=a, LAKC^a. и LSMO=<p. Имеем
AC^Oyfi и по теореме косинусов из САКС получим
2а2 = 2КС2 — 2КС2 cos а, откуда
косинусов из САКС
а
KC=—j=z. Далее из CCKD находим
KD =
DM СК
----. Но
1-jt
SM СК „„„
---=-— =igLKDM и, следовательно,
DM KD
а ОМ а 2-J—к
-==. Итак, cos<p=---=----'---=
-k SM 2а
sina
к— sin a'
□ I способ. По условию, ABCAlBlCi — правильная треугольная призма,
AAi=AB, АВХ и BCi —непересекающиеся.диагонали (рис. Р.3.93); требу-
260
Рис. Р.3.93
ется найти ((ABj); (BCJ). Пусть АВ=АА1=а. Проведем De (ВС);
тогда LABxD=<p — искомый угол. Из AABD находим ло2=а2 + а2 —
— 2a2cos 120° = За2. В AABiD имеем AD2 = 2АВ, — 2ЛВ2cos<р; так как
АВ2=2а2, то За2 = 4а2—4а2 cos <р, откуда cos ф= 1/4.
II способ. Пусть АБ=т, ВС=п, ААг=р; тогда ABI =р+т, BCi = п+р.
Используя формулу Для нахождения косинуса угла между векторами,
получим
АВ, ЬС, (р+т)(п+р) pn+p2+'inn+mp
cos а> = — ; —====--------=--------2-----=
ИА1 l-®Cil a-Jl a-Jl 2а
0 + a2 + a2cos 120° + 0 1
=--------U2--------4 "
3.271. arccos (->/5/30). 3.272. 2arctg(cosa), я—2arctg(cosa).
3.273. □ По условию, АВСА^С^—правильная треугольная призма,
SABC—пирамида, Vsabc=V- ((SAB); (АВС)) а (рис. Р.3.94). Пусть
3.274.
3.275.
и Л=—tga. Значит,
sin a cos2 а
1 а2^ , а2л/з
АВ = а, SC=h; тогда —— Л, S^SAB=---------
3 4 4 cos a ___________
a’tga 2</F ТзУР5 К/з^ЗУ2
V=—-—, откуда a = —Итак, S&sab=--------------------------
° 5/tga cosa
а2л/з a3 tg a
48 cos a 48
□ По условию, SABCD — пирамида, ABCD — ромб, LBAD=a; двугран-
ные углы АВ, ВС, CD, DA равны, АМ=МВ, AK—KD, МК—сечение,
((SMK)-(ABC)) = fi, Sьзмк= S (рис. Р. 3.95). Проведем SNIMKh соединим
точки О и N; согласно теореме о трех перпендикулярах, ONLMK. Так как
SNe(SMK) и ON е (АВС), то LSNO — линейный угол двугранного угла
a
между (SMK) и (АВС), т. е. LSNO^fi. Пусть AD = a; тогда OD = a sin -,
a 1 . a 1 a
OC=a cos-, МГ=-а51п-, cW=-acos-. Следовательно, S&smk=
2S ON
= NKSN, откуда SN*=~---------. Из ASON находим cosfi=——- =
a SN
asm -
2
261
a . a
acos - aяп - , /-----
2 2 a2 яп a , 8Seos В IScosfi
----или a =-----, T. e. a=2 /—;.
85 яп a xl яп a
2 • 2S
3.276.
3.277.
2S I o . a
------ S ctg Д sin-.
„ “V 2
3 cos - *
2
□ По условию, PABC — пирамида, AB=AC=b, LABC=a, a, LA — ост-
рые углы, РОЦАВС), LPAO= LPBO— LPCO = P, POe(PCM) (рис.
P.3.96); требуется найти S^pmc- Так как ДРОА = ДРОВ= дРОС (по обще-
му катету и противолежащему острому углу), то ОА = ОВ=ОС, т. е.
О — центр окружности, описанной около ДАВС. Значит, HB=25sina, где
b
R— радиус этой окружности, откуда R=—.—. Из ДРОА находим
2 sin a
bteB
PO=AOteB=-------. Далее имеем LBAO= ДОВА=90° — а; ДОВС=
2 яп а
= Z_OCB=a—(90°—а)=2а—90°; ДВМС= 180о-а-(2а-90о)=270о-За.
Проведем AA^LBC и из ДААХВ найдем H1B=6cosa; тогда BC=2Z>cosa.
МС ВС
В ДМВС имеем -—=-------------. Отсюда
sina яп(270 — За)
ВС sin а 26 sin a cos a b sin 2а
МС=----------=------------=--------.
cos За cos За cos За
Окончательно получим
с -1 РП иг-1 ( Asin2g\_ ^cosatg^
ьрмс 2 2 2sina\ cos3a/ 2cos3a
3.278.
a-Ji [п а
------яп I -+-
, “ к8
3 cos -
2
/л a\
sm I-----I tg a. 3.279.
\8 4/
3.280. □ По условию, SABC — правильная треугольная пирамида, SOLfABC),
SO=H, LSACB=a, SM=MB, AMC — сечение (рис. P.3.97). Проведем
SKA.AC; тогда OKLAC и LSKO—а. как линейный угол двугранного угла
262
5
АС. Из i^SOKнаходим OK=H<Ag,a, АС=2л/з OK=2H~J?> ctgа. Проведем
AfA/illSO; тогда MMt=~, KMl=2ffctga. Из 2\МКМГ находим
MK= — +4fF ctg2 a=— Vl + lectg2 a. Итак, S^mac**- AC MK~
4 2 2
= ctga j <T+16ctg2a=^^yj\ + 16ctg2a.
3.281.
3.282.
a3tg<p a2->/3(4tg2p + l)
12 И 4
□ По условию, SABCD — правильная четырехугольная пирамида,
SO —‘ее BMCOja^Z_&4O=a, SM^MC, (AML)IBD (рис. P.3.98); требуется
найти ({АМЕ^АВС}). Так как (AMLftBD, то (AML)f\(SBD)~KL, KL\BD
и (AML)(~\(ABC)=AF, AF^BD. Ho OA2.BD; поэтому RAJ.BD, откуда сле-
дует, что RA1.AF и MA2.AF. Учитывая, что ACLBD и AF^BD, имеем
AC2.AF, т. е. LMAC=<f — искомый угол. Проведем МЕ1.АС. Пусть
SO 1 За
АО=а; тогда 50=atga, ЛГЕ>=—=-atga, АЕ—~; из &МЕА находим
3.283.
ME atga 3a tga tga
tg?=—Итак, <p=arctg-~.
Л£а 2 2. J J
a2 cos 2a
sina
3.284. □ По условию, SABCD — правильная четырехугольная пирамида,
SOJ.(ABC), LASO = a, SEIBD, (SEK) образует с AC угол Д,
(SEK)[}(ABC)=KL, Shsa.=S (рис. P.3.99). Так как (Ж,)||ЯО, то KL^BD;
следовательно, OK^OL и SK=SL. Проведем OF2.(SKL), FeSM, где
A
M — середина КЦ значит, LSMO—^. Пусть SO—h', тогда SM**-.—
sinp
OM=hct%fi (из &SMO). Из &SOA находим OA=htga; поэтому
A (sin a sin в—cosa cos в) Acos(a+8)
AM^OA-OM~hisa-hct&0~—---------;--------=------ i-
cosasin^ cosa snip
263
Так как i^AML — прямоугольный и равнобедренный, то ML=AM. Теперь
найдем
3.285.
с >/7 С1/ Лсоа(«+Д Л й2сов(а+Д) / -Scosa
SbSKL^ML • SM=----------. 2—=---------'^Td’ l,=staP /-, , g,-
cos a an2/? cos a sin2/? ycos(a-h^)
З^/з H3 cos (a—P) sin a tg2 a
8япД
3.286. □ По условию, АБСАНС! —правильная призма, О — центр нижнего
основания, Ог и О2 — центры симметрии боковых граней, АВ—а,
В2В3С3С^— сечение, проходящее через точки О, О2, О2,
((АВС); (В2С2С3))—а (рис. Р.3.100). Так как Ot и О2 равноудалены от
(АВС), то сечение пересекает основания по параллельным прямым, т. е.
В2С2ЦВ3С3, и, следовательно, оно является трапецией. В Д.АВ, С, отрезок
О2О2 — средняя линия, т. е. O2Oil|B1C1; значит, В,С,||В2С2||ВС. Проекция
сечения В2В3С3С2 на (АВС) есть трапеция В2В^С^2, площадь которой
1/2 1 \ 1 ау/3 „ в\/з
— I — а + л I — -——;-—. Итак, ——.
2\3 3/32 12 12cosa
3.287.
a2Z>sin a
2(e+/>)cos/J
3.288. □ По условию, РАВ С — правильная треугольная пирамида, LPBC—л,
РМ^МС, (КМХ)ЦАРВ), ShlMN-S (рис. Р.3.101). Так как РС-2МС, то
5длра=45дкм№45. Имеем 5длрлж- s'n (180°—2a)=- АР2 sin 2л,
8S
т. е. ЛР2- ... Из &.APF находим ЛР»ЛРсо8а, откуда АВ—2АРсо%а
sm 2a
и ОС-
ЗАР cos а
. Теперь из &РОС получим
PO-s]PC2-OC2
'85 165 ctg a /85 (3-4 cos2 a)
sin 2a 3 V 3 sin 2a
264
Рис. Р.3.102
I _
272S(l-2cos2a) ^cosj-cos2gj
Уз sin 2a У 3 sin 2a
У 3 sin 2a
Окончательно находим
165 ctg a
n n
где -<a<~.
6 2
3.289. □ По условию, AKLM — цилиндр, 00, — его ось, А принадлежит окру-
жности верхнего основания, В— окружности нижнего основания, АВ—1,
LABK=a, осевое сечение AMLK — квадрат (рис. Р.3.102); требуется найти
расстояние от 00^ до АВ, Проведем BS^AK и получим сечение BSAK
цилиндра, содержащее АВ; через OOt проведем (EFT)l(SBK). Расстояние
между <7Oj и ^В равно расстоянию между (EFT) и (SBK). Проведем
OPLBK; тогда OPT(SBK), так как OPTS В, а SBf\BK, т. е. ОР — искомое
расстояние. Из t^AKB найдем ВАГ =/cos a, JAT=/sina; отсюда РВ=| /cos a,
ОВ=- EN=- TN=- AK=- /sina. Наконец, из TOP В получим
2 2 2 2
/2sin2a—- /2cos2a=
4
где cos2a<0, откуда
3.290. □ По условию, CDEF—цилиндр, Л С=ЛВ=ВС=а, ЛВ принадлежит вер-
хнему основанию цилиндра, С — окружности нижнего основания цилинд-
ра, (АВС) составляет с CD угол а (рис. Р.3.103). Проведем CQTAB; тогда
DC TAB (по теореме о трех перпендикулярах), (ABC)T(CDQ), так как
ABT(CDQ). Проведем DKT(ABC); DKe(CDQ) и Ke(CQ), т. е.
LDCK=a. В ACDg имеем DC=CQcosa, QD=CQwia, откуда
265
adb cos a. adb sin a
DC=---------; QD =--------. Обозначим радиус основания цилиндра че-
/
рез Я, т. е. OD = OA = OB^R. Из &AOQ находим OQ= /Я2--------или
I______ г V 4
„ °2 „„ aV3sina
Я+ [R—~ = QD—-------------. Решив это уравнение, найдем
у 4 2
„ a(3sin2a+l) Л
Я =-----——•—. Окончательно получим
4л/3 sin a
„ „ e(3sin2a + l) adlcosa 1 . . , „ _
Ябох=2л-----—-----• -----=- no2 (3 sin2 a+1) ctg a.
4V3sina 2 4
nP sin 2a cos3 a
3.291. .
8cos(a+/J) cos(a—/J)
3.292. □ По условию, SCD и — конусы, основания которых имеют
общий центр О. I.CSO-LC^tO^a, OC~R, S&jx. Siwm.scD (рис.
д
P.3.104); требуется найти Vs.c.d,- Из &.SOC находим SC=-----, SO=
sma
= Я ctg a. Пусть OQ =r; тогда S1Cl StO=rctgx. Далее имеем
sin ct
, nR1 nX2(l+sina) w2
Ополи.SCO “ЛЛ !—;— =-----:----; ^6oi.S.C.D. —
sina sma sma
„ 2w2 n^2(l+sma)
Решив уравнение -—=------------------, получим
sm a sm a
i fn x\ /я „
= k cos ----I, t. e. r=Acos----j. Итак,
\4 27 \4 2/
1 1 /it oc\
VslctD,’“i nr’ctga»- nA’cos3 I - -- I ctga.
3 3 \4 2/
(1 +sina)
= _ =
3.293. □ По условию, —прямая призма, LACB=90°, AC^a,
l_ABC^a, AC>BC, AB — диаметр основания конуса SAB, SeA1CI,
266
Рис. Р.3.105
А О С В
Рис. Р.3.106
SO
АА1=а/2 (рис. Р.3.105). Заметим, что окружность основания конуса не
является окружностью, описанной около ДЛЛС; в противном случае конус
не был бы прямым и его высотой было бы боковое ребро, равное а/2.
Проведем SO перпендикулярно основанию конуса и «УКИЛЛ, и соединим
точки К и О. Так как SKL(ABC), SO LAB, SO — наклонная к (ABC),
OK — ее проекция на эту плоскость, то OKI А С. Из ДАВС находим
а а ОК (к. \
АВ=-----, т. е. ОВ=-----. Далее в LAOK имеем — = tg I —a =ctga,
япа 2sina ОА \2 )
а ctg а
откуда ОК=ОА<Ала-=~.—. Наконец, из LSKO находим
2 япа
т? a1 2ctg2 а _а ./sin2 а+ctg2 а
4 4 sin2 а 2 sin а
л/3 sin2 2а cos а sin2 Д
12 sin2 (аЛ-Д)
3.295. 2Я sin2 “. 3.296.
4
3 294 arccos (tgfl/tg а)
п — arccos (tg Д/tg а)’
3.297. 2 arcctg я «39,2°.
3.298. □ Изобразим осевое сечение усеченного конуса. По условию, АВ^А^В,
OOt — ось усеченного конуса, ВВ, — образующая усеченного конуса,
ABi=a, LBiBO = at (рис. Р.3.106). Пусть OB=R2, О^В^Вц тогда
MO=OB=R2, MOl = O1B1 = R2, OO^R^Rz. Проведем BjCHO^; при
этом B1C=O1O=R1 +R2. В LB2CA имеем lB2AC=45°; поэтому
aJl _ В,С ау/2
B,C=AC=R, +Я,=------. Далее из LB,CB находим В,В=~——,
1 1 2 2 ЯПа 2япа
ак/2 ла2
BC=R< — A,=B,Cctga=-— ctgа. Значит, SeOI = n(Rl +R2) ВХВ=--.—.
2 2 sin а
ci\l 2 flv/2 w
Решив систему уравнении л1 + Я2=-—, — /с2 = ^ , найдем Ях =
(п \ (п \
- + а ) /~ a sm I - - a I
=-T- ti-rcigaj =--—-----R2=~t- (l-ctga) =-------—------. Итак,
4 2sma 4 2sina
1 • Ч | I Ч • Ч /
, па3 sin ( - + а па3 sin ( - — а
яд2 \4 / \4
*^полн=т ". "Ь "1 • ч 4* т ; 2
2 sin а 4 sin2 а 4 sin2 а
267
/ /я 1 , /я ,
, / 1— cos(- + 2a 1+1— cos - — 2a
яд2 / „ . \2 / \2
—r-т— I 2 sin a +
4sm a I
2
яд2 , . ,, яд2 ,/a я \ /а я \
г- (2sma + l)=-r-j— sin -+— cos .
4sin2a sin2a \2 12/ \2 12/
3.299. □ По условию, SAB — конус, SAC — сечение его плоскостью, LASC=rt,
SO — высота конуса, S^asc •' >5поля=2 : я (рис. Р.3.107); требуется найти
L.ASO. Пусть SA = l, ОА = Л; тогда 5ш,ля = яЛ/+яЛ2 = яЛ(Л + /)>
1 . . /’sin a 2 Z2 sin a sin a
Имеем ^=4; 7^Г<- Учитывая,
v7+z
Л .
что - = sin<p, где <p—LA SO, получим 4sin2 <p + 4sin<p — sina = 0, откуда
sin =
. Так как <р — острый угол, то
4
л; (n ,
/---;-- •JI COS I------|—1
Jl +sina-1 \4 2/
sin (p =---------=-----------------
2 2
. я—a . a
sin--sm
4 4
/ г- я—a a\
Итак, <p=arcsin у/2 sin-sin - I.
\ 4 4/
3.300. □ По условию, SAB — конус, SO — его высота, SO = h, LASO = z,
SKM— сечение конуса плоскостью, l_SKMB=p (рис. Р.3.108). Проведем
L
SNLKM', тогда 0NLKM и, значит, LSNO=p. В LSON имеем SN =---------,
smp
ON=hctg,p. Далее из LS0M находим ОМ=Лtga и, наконец, из LONM
получим
^^^1В^а-Л2^9-Л^а-с^=А7~СО5(а+ДСО5(а~Д)
sin/? cosa
№д/ — cos(a+/J) cos(a—Д)
Итак, S^skm
sin2 р cos a
Рис. Р.3.108
268
3.301. □ По условию, SCD — конус, SO — его высота, SAB — сечение конуса
LESO=a (рис.
то SELA В (по
плоскостью,
Р.3.109). Из
ОЕ=а.
SO1.AB,
&FEO
\jAnB : uAmB=p : q, OEL(SAB),
a
A SEO найдем SO=------. Так как
sina
трех перпендикулярах) и из
а 2яр пр
Далее имеем <иАпВ=—-, откуда t_AOF=--------.
p+q
а
теореме о
ОЕ
OF=----------------.
sin (90° — a) cos а
OF
Тогда из &AFO получим АО=---------—------------. Итак,
пр пр
cos---- cos a cos---
p+q p+q
следует, что
___ пр
P+q
а2
P=- nAO1 SO = - n
3 3 2 2 *P
cos a cos --
p+q
2па3
а
sin a , пр
3 cos a sin 2a cos -
p+q
п п
3.302. —2arctg к>п.
2 к
3.303. □ По условию, l_ACB=9(F, ВС = а,
LBAC=a., АК—биссектриса угла
ВАС, MNLAK(pac. Р.3.110). Проведем
BB^LMN и CC.LMN и отложим
BJ^BD, С1Е=СЕ. Искомый объем
будем искать по формуле
V т.»р = V DECB — V DAB — V ЛЕС —
= Х-п DE(DB2 + DB ЕС + ЕС2) -
nAD DB2-1- ПАЕ ЕС2.
а
В А Л ВС имеем АВ=-, AC=actg а. Очевидно, что LDBA = 1_ВАК= а/2,
sma
а, а а
LACE= LKAC=a/2. Из &ADB найдем AD=ABwa-=--------------- sin- =
2 sma 2
а
= ---, DB*=AB cos-
„ а 2
2 cos -
2
а
АЕ=АС sin -=а ctga sin - =
2 2
a a a
=----- cos - =
2 sma 2
а
-----. Далее из &АЕС
2sin -
2
находим
. a a cos а
2 а’
2cos -
2
a cos а
a a cosa
EC^AC cos -=-----.
2 a
2 sin -
2
Значит,
_____ a Л
DE=DA+AE=------------1-----=a cos -. Окончательно получим
„ a „ a 2
2cos - 2cos -
2
_ 1 “
FT.,p.=- nacos-
1 a3 1
— я--------------------
3 о • 2 а “ 3
8 sin2 - cos -
2 2
a2 cos a a2 cos2 a
—I---------1---------
a a a
4 sin2 - 4 sin2 - 4 sin2 -
2 2 2,
a3 cos3 a
я--------------=
8 sin2 - cos -
2 2
а2
а
- +
a
2
269
«
I 2cos2 - (14-cos a4-cos2 a) — 1— cos3 a 1 =
a я \ 2 /
24sin2 - cos -
2 2
------------((1 4-cos a) (1 4-cos a4-cos2 ac)— 1 —cos3 a)=
. a
12sma sin -
2
, а а
, ла ctg а ctg - cos -
ла3 , 22
=---------(2 cos а+2 cos2 а)=------.
а 3
12sina sin -
2
3.304. □ По условию, 1_ВАС = ас— тупой угол, АВ=АС, BM.LAC, CNXAB,
ADX.BC. О — ортоцентр (т. е. точка пересечения высот) &АВС, О2О21ВС,
OeOtO2, ВС=а (рис. Р.3.111). Объем тела вращения ixABC вокруг прямой
О2О2 найдем по формуле Ит.вр= VOio2cB-2VOioAB, где
* а а
Уо1огсв=Утл = л ОгВ2 ВС. Имеем LOAM=l_CAD=~, LMOA = 90°-~,
а а ас а ас
a t_OBD=~. Из &0DB и &ADB находим OD=- tg AD=- ctg тогда
2 2 2 2 2
а ос a ( a ac\
O2B=*OD=2 tg-, О A — OD—AD=-^ I tg-—ctg -I. Окончательно получим
„ a2,a 2 afd2,aa2acfac ac\
V2 ,0 = я — tg2 - a— л - I — tg2 -4— tg - I tg —ctg - +
₽ 4 2 3 2\4 2 4 2\B2 2J
a2 ( a a\2\ ла3 ( , ас 1 , ас
+7V8rrt82))=^VB 2~3tS 2-
1 , a 1 1 , a 2 1 , a\ ла3 / , a\ _
— tg2 -4--tg2 -4---ctg2 - 1=— I 3—ctg2 - I.
3 6 2 3 3 8 2 3 3 8 2/ 12 I 2j
3305.
3307.
~ arcsin (2(^2-1)) и arcsin (2(^2-1)).
□ По условию, AB—2R, CDjjAB, О — центр полуокружности, LADC=oc,
AC<AD (рис. Р.3.112). Объем тела вращения ДЛСО вокруг АВ будем
искать по формуле
Pr.Bp=Kto2c+Pojcoo, — ^0,^=- я OjC2 АО2+лО2С2 О2О2 —
1
11 2
-- я OjZ)2 ЛО1=- я OiC1 (ЛО2 + ЗО1О2-ЛО1)=- л О2С2 OtO2,
3
Рис. Р.3.112
270
так как 01/) = 02Си AOt— AOi<~OlOJ. Учитывая, что LABC- ^aDC=i
как вписанные углы, опирающиеся на иАС, из ЕАСВ, где LACB^9d°
(вписанный угол, опирающийся на диаметр АВ), находим BC=-2Rcosa,
ЛС==2Ляпа. В ЕАО2С имеем £о2ЛС=90°—a, ЕО2СА = а,
О2С=AC cos a=2Rsina cosa=Asin2a, О2А=AC sin a=2R sin2 а; тогда
Oj O2=2R—2AO2=2R (1 — 2 sin2 a)=2Rcos 2a. Итак,
2 2
Pj.»p=- лЯ2яп22а 2R cos2a=- nA3sin2a sin 4a.
3.308. □ По условию, ABsDC, AD = BC, AB=a, LDAB=a., BD.LAD (рис.
P.3.113). Объем тела вращения трапеции ABCD вокруг АВ будем искать по
формуле Ут.вр =2Pjed + Vdefc, где DE1.AB, CFLAB. Имеем
2 1 1
Ит.вр=- r.DE1 AE+nDE2 EF=- nDE2 (2AE+3EF)=- nDE1 (a + 2EF) =
1 /12 \ / 4 \
=- nDE2 - a+- (a—2AE) ] = uDE1 I a — - AE I.
3 \3 3 I \ 3 J
Из EADB находим AD=a cost, а из EADE получим
DE=AD sina=a cosa sina=- sin 2a, AE=ADcosa=a cos2 a. Следовате-
льно,
К,
a2 . 2. ( 4 , \ na3 . 2_
=n — snr2a ( a—a cos a =— sm 2a
4 \ 3 J 3
3
—cos a
4
na3 . , 1—2cos2a тш3 , / я\ / я\
=— snr2a----------=— яп22a sin a— яп ad— ).
3 4 3 \ 67 \ 6J
1
3.309. -
2
з P 1
na cos I — a J;
\3 Г
при
n
a=-.
3.310.
2 2 . a
nrra яп
2
3311
a
nr cos ------cos -------
2 2
3 sin2 a
3.312.
8na2 sin a
a I n a \ In a.
cos - cos - +- ) cos ( - — -
2 \6 2} \6 2
8nS sin2 - (1 +cos2- j
3.313. arccos Д=. 3.314.----3315.
*J2 a—sina 5
3316. □ По условию, ABCAiBlCi — правильная треугольная усеченная пира-
мида, 00j = H, ООг=-^ВС ВХСХ, EAtAO = a (рис. Р.3.114). Пусть ВС=а,
Рис. Р.3.114
271
=- н
aJ3 bd3
BlC1^b; тогда OA=~—, 0^=——. Проведем А^ЦОО^, иэ ^AlKA
находим АК^Н ctga и так как АК=АО-КО—АО-А1О1 =
аЛз ЬуГз у/з у/З
---— ——(д—Ь), то — (a—b)=Hctga. Кроме того, из условия
следует, что аЛ—Я3. В результате полупим
„ 1 «abyfi Ь2у/3\ Ну/3L l24
Иус.ш>р=- я^П4-+~4— +—♦“/И (fl +аЛ+й)“
= ~ ((a-b}2 + 3ab}=^(3H1 ctg3 а + ЗЯ2) =
ЯЛ/З, . ,ч Н3у/з _
—Г- ctg3a+l =—V-
4 4 sm2 а
/ 5 а ,------
3.317. sin (а ±в) /—:3318. 2a3cos3 - J — 2 cos 2а.
у 2 sin a sin 2fi 2 v
a(a—b) tga Ibn+ntH2 ,--=—
3319. -i-3320. -----— ctg а 5/2+ctg2 a.
3a—b m—n
3321. □ По условию, ABCA-fi^C^—усеченная пирамида, ABC
и AxBxCt—правильные треугольники, DB=DA, DiB1=DiAi
и DiDlXABC), большее ребро пирамиды равно / и образует с (АВС} угол а,
О и Oj —центры оснований (рис. Р.3.115). Пусть ЛС=а, AiC^—b-, тогда
Оу[з Ьу[з
DC=—^~, DtCi =—-. Проведем C^D^D, A1KJID1D и положим PDj =Л.
Из дСрЕС находим, что С1С=Л/С1Е2 + £С3 =
/ , /аЛз Ач/3\2 / , З(а—Ь)2
= -jh2 + l-~-— ) = Л^2^-д > а ш AAtKA— что
А1А = у/А1К2 + АК2= Знатег> CiOAiA, т. е. 6^6'=/
и LCiCE=a; в ьС^ЕСимеем C^E^lsma, СЕ— /cosa. Проведем 0^0,0;
тогда
ау/3 Ьу/3 (а-Ь)у[з пч
OF^OD-DF^OD-OJ)^-!-------. 0)
6 6 6
ОуГз ЬуГз (а-Ь)уГз
Так как C£=/cosa и CE=DC-DE=DC-DiC^^-----, то
2 2 2
(а—Ь}у/3 2/cos a
----— =/cosa или a—b =-. (2)
2 J3
/cos a
Из (1) и (2) находим OF——-—. Наконец, из ДО^О получим
OO^OiP + OF^ylc^ + OF2^ ^Ряп2а+^^=
I >—------г- / /9(1—cos 2a) l+cos2a / г-— -— _
=-V9sin a+cos a=- /-------1------=-<5—4cos2a.
3^ 3l/ 2 2 3
272
Рис. Р.3.115
Рис. Р.3.116
tea
3.322. arctg —.
cos (fill)
3.323. □ По условию, PABCD — правильная четырехугольная пирамида,
A,BlC1DiA2B2C2D2 — вписанный в нее куб, точки A,, В,, С,, D, принад-
лежат боковым ребрам, а А2, В2, С2, D2 — основанию пирамиды,
РОЦАВС), 1_РАО=а (рис. Р.3.116); требуется найти Ггуба У ияр- Поло-
X4/2
жим D,D2 = x-, тогда Ргуба=-т3. OD2=——. Из t±DxD2D находим
xJl
2)2)2=xctgq; далее имеем OD=-— +х ctg q, PO—ODtga=
х (5/2+2 ctg q)
---------------. tg а. Значит,
2
.. 1 1 вл 2 x2(y/2 + 2ctga)2 x(y/2 + 2ctga)tga_
Кшч,"Г2 Р°~3 4-2
_V2x3(l+V2ctgq)3 т е х3 6ctgq = 3V2ctgq
6 ctg а ' Ищф ^/2 x3(l+>/2ctgq)3 (1 + V2ctgq)3
3.324. □ По условию, SABCD—правильная пирамида, SO—ее высота,
LSAO=a, MQPNM,QiP1Ni — правильная вписанная в нее призма, точки
Q,. Р„ N, лежат на боковых ребрах пирамиды, AD=a, 1_Р,МР=<р
(рис. Р.3.117). Пусть РР,=пг, тогда из &.МРР, имеем MP=mctg</> и,
следовательно,
Hnp=^m2ctg2<p • ти = * m3ctg2<p.
ММ, AM
то -------£=----. Из Д SOА находим
SO АО
ММ. АО ma-Jl 2
=-----------------=znctga. Но
layjl tgq
i\M,MA~ Л SO А,
0^/1
SO=AOtga=——tga, откуда АМ=
2 ЛС/
АМ^АО-МО^-1- МР^-^.
2 2 2 2
adl mctg<p a^/l
6 2 2 1 2ctgq+ctg<p
Решив
. Итак,
Так
как
уравнение
Рис. Р.3.118
' у _? ( “'fi У ct Д tpjZtttfq»
я₽ 2 \2ctga+ctg<pj с ® (2ctga+ctg<p)r
_ e sin a
3.325, -----.
I я \
2sin ~+a I
\4 j
3.326. □ По условию, SABCD — пирамида, ABCD — квадрат, (SBA)A.(ABC),
(SBC)E(ABC), AB—а, большее боковое ребро образует с (АСВ) угол /?;
в пирамиду вписан прямоугольный параллелепипед BEFKB^E^F^Ky, где В,
Е, F, Ке(АВС), точки Blt Et, Ft, Кх принадлежат боковым ребрам пирами-
ды. B}F образует с (АВС) угол я (рис. Р.3.118). Так как боковые ребра
параллелепипеда перпендикулярны (АВС), то ЕеАВ, КеВС, FeBD. Посколь-
ку ABCD — квадрат, BEFK — также квадрат как фигура, гомотетичная
ABCD относительно точки В. Пусть ВЕ=х\ тогда BF^xs/1. Из &BXBF,
в котором LB^FB^z, находим BXB=BF tga. Так как
BA=BC<BD, то SD — наибольшее боковое ребро пирамиды, т. е.
!_SDB-f). Далее имеем FD~BD- BF=(a—x)~Jz. Из ^F1FD находим
F1F*‘FDtgP^(a—хХ/itg^; поэтому (a—x)^f2tg8=x4/2tga, откуда
atgS asinficosa _
х—------ =-----—Окончательно получим
tga+tg)? sin(a+0)
, , г- a5x/isin38 cos3 a sin a azJl sin3 8 cos2 a sin a _
vj «—.
3 527 V2<1+sin2^ sin(a + fl
2 sin2 a cos /1
3328. □ По условию, SABC -- пирамида, CA = CB, LACB=a, ЬАВС вписан
в основание цилиндра, S&KM, ЛЭ/— образующая цилиндра, KS^SM,
(рис. Р.3.119). Обозначим радиус основания цилиндра через Л,
у
а его высоту — через Н; тогда К—яЛ2Я, откуда Л2Я~—. Имеем
п
274
ЛВ=2Л5та и, значит,
, . 1 (я а\
4Л sin2 a sin2 I--
\2 2J , . , а
£длас=------г-;-------------=2Л2 sin a cos2
2 sin а 2
Итак,
1 , , а Я 1 , > & V , a
Кпир =- • 2Л sm a cos2 - . — =- R2Hsin a cos2 - =— sin a cos2 -.
w 3 223 2 Зя 2
, ’ >/2 °3 sin3 2a _ „„ 4 cos a cos В
3.329. ,-----г-. 3.330.---X---—
. J* I n(cos2a+cos2fi)
128 sin3 -+a ' F
\4 /
3.331. □ По условию, А А,В,В — цилиндр, OO, — его ось, ACDA,C,D, — приз-
ма, вписанная в цилиндр, OO,e(AA1DI), CA,DA=a, LA^DC=fl, ОО,=Н
(рис. Р.3.120). Из ДЛ.Л2) найдем AD = ffctga, A,D=-.—. Соединим А,
sma
и С; так как CACD — вписанный и опирается на диаметр AD, то CD А. АС
Ясов в
и, значит, A,C.LCD. Из ДЛ1С2) находим CD=A,Dcosfl =—;---------, а из
sina
ДЛСО получим
АС=
' - , Я2 cos2 Я
Я2 ctg2 а------ = -—
sin a sin а
Я /cos2^—cos 2а_ Ял/sin(а+Д) sin (а—Д)
sin а х/ 2 sin а
a—cos2 /?=
Итак,
1 Я3 cos ву/sin (а + В) sin (а —в)
Ущ, = ShABc ОО,=-CD АС. Н---------^lsin2g
3.332. □ По условию, SABC — конус, SO — его высота, CD£7:'C1.D1£1.F1 — впи-
санный в конус куб, Ср D,, Е., F, — точки, лежащие на боковой повер-
хности конуса, SO . СС,=к (рис. Р.3.121). В ^SO,C, имеем
SO, 2(S0—x)
ctg LASO=—~- =------——, где x=CCj. Отсюда находим ctg2_ASO =
°ic Хл/2
= у/2\-—l)=s/2(fc-l), т. e. Z_^SO=arcctg(V2(Jt-l)).
275
3.333.
9 sin 2a cosa
8 л sin2
3.334. □ Пусть PMN — осевое сечение конуса, KLNlMl — осевое сечение впи-
санного цилиндра, Z_O1AfK=a, РО— высота конуса, 1_МР0=& (рис.
Р.3.122); требуется найти Икоя.: Рди.,. Обозначим радиус основания конуса
через Л; тогда OP=R<AgP (из &РОМ) и nR3ctgfl. Из AOjOAf
находим OOj= Rtga. Так как М1К=ОО1, то из £^MtMK, в котором
1_МРО=$, получим MK=R\gi tg/?. Значит,
0K=0M— MK—R—Atga tg Д»—C°S--+^, откуда
cosa cosp
cos1a cos /?
J*™ nR3ctg Д cos2 Д cos2 a cos3 a cos3 fi
Риал 3 лЛ3 cos2 (a 4- Д) tg a
3335.
2(44-5/6)
arctg-----.
2ctg*Ctgl
я (ctg2 a 4-ctg2/?)
3 sin a sin cos1 (a+Д)
л4-а
4
. . j a’
4 sin a cos -
2
2л/2 ctg “
. 3.340.---;-----.
. , a 9 sin 2a
cos a sin -
2
3336.
3337.
2п
sin 2a'
3338.
2nd1
1 , ла3 cos a tg/?
. 3341.------------.
24 cos3 -
2
3342. □ Изобразим осевое сечение фигуры плоскостью, проходящей через центр
вписанного шара и параллельной основанию. В сечении получим парал-
лелограмм ABCD, равный основанию прямого параллелепипеда, и вписан-
ный в него большой круг вписанного шара с центром в точке О (рис.
Р.3.123). Из этого следует, что основанием параллелепипеда служит ромб.
Требуется найти углы основания параллелепипеда, если : Ишара=£.
276
Обозначим радиус шара через г, тогда высота ромба равна 2г. Проведем
2г
BEA.AD и положим LBAD = a. Из LBEA находим АВ=---------. Тогда
sina
4 Sr3 Sr3 4пг3
Ишара=- nr3, • 2г = -—. По условию, -— = к или
3 sm a sm a 3
6 6 6
sina=—-. Итак, a=arcsin —, l_ADC=n — arcsin —так как 0<sina<l, то
пк ПК ПК
6 6 6
— <1, откуда £>-. При к= основанием параллелепипеда служит квад-
пк п п
рат, т. е. параллелепипед является правильной призмой.
3.343. □ По условию, К— центр шара, ABCDA^B^jD^ — прямая призма, опи-
санная около шара, ABCD — ромб, АС — большая диагональ ромба,
LC1AC=a (рис. Р.3.124). Пусть КО = г; тогда СС, = 2r, АС=2r ctga. Через
точку К проведем (А2В2С2)Ц(АВС); эта плоскость пересечет шар по боль-
шому кругу, вписанному в сечение A2B2C2D2, равное основанию ABCD;
следовательно, высота ромба A2B2C2D2 равна 2г. Проведем OLLAD.
1 OL г
В АЛЛО имеем OL=r, l_OAL=LBAD, sin L О AL=—=-------------— tga.
2 OA rctga
Отсюда AAOL=arcsin(tga); ABH2) = 2arcsin(tga).
(a\ , a (n a\
sm - J. 3.345. 2r3 ctg - ctg -.
2/ 2 \4 2/
3.346. □ По условию, О, — центр шара, вписанного в правильную пирамиду
PABCD, РО — высота пирамиды, РО1 : О1О=т : л (рис. Р.3.125); требует-
ся найти угол между (PDCj и (ВРС). Очевидно, что BDLPC (по теореме
о трех перпендикулярах). Проведем через BD плоскость (BLDYLPC; тогда
BLLPC и DLLPC, т. е. LBLD — линейный угол двугранного угла BPCD.
Пусть DC=a, К — точка касания шара с боковой поверхностью пирамиды
O.K OF па
и PFLDC. Так как LO,KP~ LPOF, то —--=— или — =——: тогда
О2Р PF т 2PF
am а2т2a2 a-Jm2 + n2
PF——. Из LPFC находим РС= /—х--|—=--------------. Теперь восполь-
2л 4л2 4 2л
277
Рис. Р.3.125
зуемся тем, что S^pdc=- DC рр=^ рС' откуда
DC FP а ат 2л ат
DL=------=----- = -----.
рс 2л • ayjm1 + n1 у/пР + п1
Наконец, в &BLD имеем BD1—2DL1—2DL1 cos l_BLD, т. е.
IDLt-BD1 пР+п1 2л?пг п1
cos l_BLD=———j— =— , ,—. =------------2;
2DL1 2егпг 2лРпг nr
п1
1_ВЕО=п—а1ссоь—х.
лг
a(3+cos2e) , , a „ a „ /я a\ a
3.347. -i-------3.348. 8a2 cos a cos2 - ctg2 3349. 4A2tg -+- • ctg 3.350.
4sin2a ,________2 2 \4 2/ 2
/, . /"
/|3_1 a /3яп1з-2/ 23 1
arcsin-----. 3351. - / — ------3.352. —. 3353. 2arccos ——
1 6\J anM 26
V \3 2/
3354. □ I способ. По условию, DABC — пирамида, AB=AC—b, (DAB)V(ABC),
(РАС)ЦАВС), LBDAC=a, LDBCA=a, О — центр вписанного шара (рис.
Р.3.126). Высота пирамиды совпадает с боковым ребром AD, поскольку
перпендикуляр, опущенный из точки D на (АВС), должен принадлежать
и (DAB), и. (DAC), т. е. он совпадает с линией их пересечения. Так как
AB.LAD и ACJ.AD, то С ВАС = а. Проведем DEJ.BC и соединим точки
А и Е; тогда LAED — a. как линейный угол двугранного угла DBCA.
Докажем, что Oe(ADE). Соединим О с точками касания Ор О2, О3,
и проведем О2ЛГ2Х(ЛВС), О3М31.(АВС)-, так как (ADB)1.(ABC)
и (ADC)1.(ABC), то М2е(АС), М3е(АВ); при этом L О2ОО3 = L О3ОО3 =90°
как углы между перпендикулярами к перпендикулярным плоскостям. Но
ОО2 = ОО3 = ОО1=г, где г — радиус вписанного шара, и,
значит,О1ЛГ2=О1М3=г, т. е. О3е(Л£), и так как OOjl(XBC), то Oe{ADE).
г а
Из Ь,О3М2А находим АО3=---------, а из ЬАЕС получим AE^bcos тогда
ос 2
sin -
2
278
а г а
Oi£=£cos-------; наконец, в L.OO^E имеем O^E—rdg-, Составим
2 а 2
яп -
2
, а г а
icos------=rctg-
2 . а 2
ЯП -
2
Asina
уравнение
или
1 , . Л
- Аяпа=г( 1+cos- 1, откуда
Ляпа
/ а\ а
2 I 1 +cos - I 4cos2 -
\ 2/ 4
II способ. Если воспользоваться формулой Ипир=-5тля Л то можно
обойтись без выяснения, где расположен центр вписанного шара. Из
а
&DAE находим H2)=HEtga=Acos - tga. Тогда
1 11, al, a
Ипир=- S^abc AD—- • - A2 sin a Acos - tga=- A3sina tga cos-,
3 3 2 2 6 2
i Яллас ]
.'/Jr.- ;----1-2 • - A • AD=
2 cos a 2
1 ( a\
- A2tga | cosa+1 +2cos - I.
2 \ 2/
ХПоля = s дЛBC + sД BCD + 2X длдс=~ A2 sin a+
11 a
=- A2sina-I— A2tga+A2cos -tg
2 2 2
Окончательно получим
, 1 ,3 . , ®
3 • - A sm a tg a cos -
6 2
- A2tga | cosa+l+2cos-) 2fcos- + l^ 4cos2-
2 \ 2) \ 2 J 4
a=
Asina
Asina
3.355. □ По условию, SABCD — пирамида, SOJ-(ABC), ABCD — ромб,
LDAB=a (а<я/2), LSABC= LSBCD = LSCDA= LSDAB=p, L — центр
вписанного в пирамиду шара, г — радиус этого шара (рис. Р.3.127). Прове-
дем SELAB, SFLBC, SKX.CD, SNLAD и соединим О с Е, F, К и N. Имеем
ОЕ2.АВ, OFXJ3C, OKA.CD, ON±AD (по теореме о трех перпендикулярах);
тогда LSEO= lSFO— LSKO= ESNO=P как линейные углы равных дву-
гранных углов и &SOE= &SOF= &SOK= &SON (прямоугольные тре-
угольники, имеющие общий катет SO и равные противолежащие углы /О-
Из равенства треугольников заключаем, что OE=OF=OK=ON, т. е.
О — точка пересечения диагоналей ромба. Отсюда следует, что в данную
пирамиду можно вписать конус с осью SO. Шар, вписанный в этот конус,
вписан и в пирамиду; следовательно, LeSO и LO=г. Из &LOF находим
Р
OF=г ctg отрезки OF я ON лежат на одной прямой NF, так как OF1.BC
в
и 0N1.AD, а AD^BC; поэтому NF=2rctg -. Проведем BQ^FN. Из t±AQB
2т ctg -
BQ NF 6 2
находим АВ*=-—=-—=—--------, а
sin а яп а яп a
из &SOF получим
В
SO =« OFtg Р=г ctg - tg р. Итак,
279
S
Ишф=^ Sabcd HB2sina • rctg ^tgfi=
^ctg^rinatg^ 4r3tg/?
3 sin1 a , P' "
3smatg’|
3356.
j о 1 jt
- tg - 6 Г sin a ctg/J. 3357. - arcsin
3358.
- я
0<fc^2sin -.
_ . я n
2sm -
n
□ По условию, К — центр шара, SABC...— описанная около него пра-
вильная n-угольная пирамида, SO — высота пирамиды, LSBCO^a,
a
KO<=R (рис. Р.3.128). Из &KOD, где ODX.BC и LODK=~, найдем
a 360° 180°
OZ)=Bctg-. Так как t_BOC=>------, то l_BOD=------,
2 пл
180° _ « 180° „ 180°
BD= OD tg —- Rctg - tg ——, BC=*2Rctg - tg-. Теперь находим
„ a , a 180°
• Actg--n«2ctg2 - tg-,
z z Л
1 a 180°
и • 2Actg - tg---
Z z Л
“ 180°
"tfctg’-tg —
откуда 5бож =--=
cosa
3359. □ По условию,
cosa
SABCD — пирамида, ABCD — прямоугольник,
SES-(ABC), LSAE= LSBE— LSCE= LSDE=p, LAEB—a, О —центр ша-
ра, описанного около пирамиды, R — радиус этого шара (рис. Р.3.129).
Около данной пирамиды можно описать конус, причем высота пирамиды
совпадает с высотой конуса; центр шара, описанного около пирамиды,
совпадает с центром шара, описанного около конуса; поэтому О принад-
лежит SE. Поскольку LESD=9QP—fi, имеем LEOD=2LESD=\9ff"—2/J
(как центральный угол). Из &.OED, где OD=R, находим
EZ>=/?sin(180°—2/?)=.Rsin2/?, откуда BD=2Rnn2p. Из &SED получим
280
5Е—ED tgfl—R sin 2 fl tg fl = 2R sin2 fl. Итак,
F=- Sabcd 8D23ina, 2Xsin2 Д-
1 4
=- • 8Я3 sin2 2fl sin2 fl sin a=- R3 sin2 2fl sin2 fl sin a.
6 3
2R3
3.360. sin 2/? cos/J sin a. 3.361.
a
a COS -
2
4 “
COS* -.
2
3.362. -—
2 cos2 -
2
3.363. □ По условию, ABCAXBXCX —правильная треугольная усеченная пира-
мида, LBxBCA^a, L — центр вписанного шара (рис. Р.3.130); требуется
найти Soojm.yc.imp ; бщара- Пусть АК и АХКХ — высоты оснований; тогда
КХК — высота боковой грани, L АККХ= а как линейный угол двугранного
угла ВХВСА. Далее, пусть О и О, — центры оснований усеченной пи-
рамиды; тогда 00 х — диаметр вписанного шара. Положим LO~R я про-
2R
ведем КхМ\\0х0\ имеем К<М^2г, — (из &К<МК). Обозначив
sina
aj3 bJ3 (а—ЬЪ/з
АВяо, А\В\^Ьу найдем OK.^—~~----------------------------------w2Xctgoc.
6 6 6
Согласно свойству отрезков касательных, проведенных из одной точки
2R
к окружности, КХК^КХОХ + КО—--------. Теперь решив систему уравнений
sin a
Г(а-*Х/3 „„
1--------2Actga,
J 6 г- a t- a
\ _ найдем a"f2J3 Actg 6—2\/3Atg-. Следовате-
| (д+^х/з,,, 2Л 2^2
x 6 sina’
льно,
3(a+b) 2R a\[3
5Я0ЛИ.уе.шп>—j” ' ^+~+— "
281
3 12Я
12Л27
sin2a
1+cosa 1— cos a
------+~------
1 —cosa 1+cosa
(2 + 2cos2a+4) =
^полн.ус.пир 3*/з
Итак,----------=-^~ (3 + 4 ctg2 a).
*^шара 2я
3.364. □ По условию, PABCD — правильная четырехугольная пирамида,
РО.ЦАВС), АВ=а, LPDCO — 'i, Ot — центр вписанного шара, Я2, В2, С*,
D2 — точки касания шара с боковой поверхностью пирамиды, Ме(АВС)
а а
(рис. Р.3.131); требуется найти Vmaj^CjD,- В ^О1ОС1 имеем OjO=- tg-.
Так как LOPC^MP-a, то ДР01С2 = 90°-(90°-а) = а. Из Л.О2О2С2
а а а
находим О2С2 = О2С2 sina=- tg - sina=a sin2 -, O1O2 = O1C2 cosa=
a a a a a a
--tg-cosa. Тогда OO2 = OOj+OtO2=-tg-+-tg - cosa=
it L it
a a a , a a a
tg- (1 +cosa)=a tg - cos2 sina, X2C2=2O2C2 = 2zzsin2 Следова-
2 2 2 2 2 2
1 , a , a
тельно, ‘S^1b2c2oj=~ • 4a sin -=2a sin - и окончательно получим
Тогда
Vma2b2c2d2=j 2a2
ЯП* -
2
a . 1 3 . 4 a . _
- sina=- a sin - sma.
V
3365. ------.
. a
8 cos6 -
2
282
' 366. □ Осевое сечение фигуры представляет соЬои круг с центром К, в который
вписана трапеция ABCD, KeAD, KD = R, £CDK=p, CD — боковое ребро
усеченной пирамиды (рис. Р.3.132). Из LCKD по теореме косинусов нахо-
дим CD=y/2R2—2R2 cos(180°— 2/?)=2Ясоз/?. Проведем CC^IAD и из
ДСС1В получим CC1 = CDsin/l=2Rsin/? cos/1=Я sin 2/1, CtD=CDcosp=
=2Rcos2p. Тогда KC1=EC=KD-ClD=R—2Rcos2P=-Rcos2p. Иско-
мый объем выражается формулой
V—~ CCj (52 4-S2), где
CC1=Rsin2p, St = 2R2, S2 = 2R2cos22p, •JS1S2 = ~2R2cos2p. Следовате-
льно,
V=R sin 2p (2R2 - 2R2 cos 2Д+2R2 cos2 2Д) =
2
=- Я3 sin 2/1 (1-cos 2/1+cos2 2Д).
n sin2 2a sin2 a sin — 4лЯ3 sin* [ - — I , ,
n 14 2/ 4-fc
3.367. . 3.368.---------------------3369.------------, 0 < k <4.
4л 3sina 4 + fc
3.370. □ Изобразим осевое сечение фигуры; SA, SB — образующие конуса,
SO — высота конуса, О2 и О, — соответственно центры описанного и впи-
санного шаров (рис. Р.3.133), отношение их объемов равно к; требуется
найти LSAO. Пусть R и г — радиусы шаров, /_SAO=a, АО=х; тогда
a
ЕОО2В= ДЛ56=180°-2а, ДО2ЯО=-. Из Ь.О2ОВ и ДО2ОЯ находим
х х а
R—------------—-------, r=xtz -. Значит,
sin(180° — 2a) sin2a’ 8 2
a .
xtg-sin2a 4 .
r 2 (1—cosa) 2sin a cosa ,
— =-----------=------------------= 2 (cos a—cos a);
R x sin a
так как — то —=lfk. Решив уравнение 2cosa—2cos2a=V^,
(4/3) лЯ3 Я
получим cosa= 1-^/* 1—откуда Итак,
2____ о
\±J\-23Tk , 1
LSAO=a=arccos---------,
2 8
283
6itA2sin22a , / л\ / л\ nr3 tg2a
3.371. —-------5. 3372. 2 an2 2a cos ( a+- I cos I a—- I. 3373. — —-j—.
(l+2ctga)2 \ 6/ \ 6/ 24cos6a
3374. □ Изобразим осевое сечение фигуры: SB=SC— образующие конуса,
SP— его высота, О — центр вписанного шара (рис. Р.3.134),
Ртои : Ршарж=Р; требуется найти LSBP. Обозначим через А точку касания
шара с боковой поверхностью конуса. Пусть ОЯ=г, PB—R, SP=H\ тогда
R?H
---- , =3 или —г=^- Полагая LSBP=a, из &.SPB и &.ОРВ имеем
(4/3) № 4г3
Н Л a R2H 1 R3 Н ,
- = tga, ~ = ctg—. Но —-5-=- • -=к и, значит,
R г 2 4г3 4 г3 R
1 ,a 1
- ctg3 - tga = K или-----
4 2
а
1 2‘82
—-------- = К ИЛИ---у-----г- = к.
t&3-2 2tg4(1_tg4)
СЕ 1
Пусть tg2 -=х; тогда 2х—2л2—-=0; 2кх2 — 2ix+l =0. Отсюда
3.375.
к±у1к?—2к . а к±^/кг—2к а 1к±у/к2—2к
*=-----; tg2 - «--------—-----; tg - = /----—----;
2к 2 2к 2 у 2к
так как к2— 2Л>0 и к>0, то fc>2. Итак, a=2arctg
3.376.
a
4 cos* -
2
/-a .а
Rd 2 sin - sin* -
N 2 2
---------3377. ------------. 3378.
a fn a\ cosa
2cos - cos---
8 \4 8/
. /« я \
/ctgb+v
--------- X
p
COS -
2
/ ( 8\ ( 8\
x /sin I a+ - | sin I a-I. 3379.
у \ 2/ \ 2/
nR2tg2 sin2 2a. 3382. arctg
arccos 3.380. ^b/Zpcos’atg3-. 3.381.
5 49 2
3383. □ По условию, ABCD — усеченный конус, 5 — центр вписанного шара
(рис. Р.3.135), ^цоли-ус-гон : 5щара=2; требуется найти 1_АВО. Рассмотрим
осевое сечение ABEF усеченного конуса, ООг — ось усеченного конуса.
Введем обозначения: SO=r, OB=Rlt O1A=R2. Проведем AMWOO^, тогда
АМ=ОО1. Согласно свойству сторон описанного четырехугольника,
2AB=BE+AF; имеем AB=R1+RI, BM=R1—R1. Из ЬАМВ находим
2г
Л.+Л,==------, A,-J?, = 2rctga, где а.= LABO. Решив систему уравнений
sina
2r a a
А. +А,=------, А. —A,=2rctga, получим A. =rctg A2=rtg -. Тогда
sina 2 2
АДОЛИ.УР.ХОИ_n(A2 +Ri + (A! + R2)AB)_П\ Ctg 2
*$7пяра 4№
2, 2 “ 4г2
Pr tg2 -+-7-J-
2 sin2 a,
4яг2
/ flf n (g
Аят2 I 1 +cos4 -4-sin* - I 1 +cos* - +sin* -
\ 2 2) 2 2
sin2 a
4яг2 sin2 a
284
Рис. Р.3.135
[ a . , a\* 2 1 . , 1 . ,
1+ cos - + sin- —sin2a 2—sin2a ,
\ 2 2/ 2 2 4 —sin2a
----------------— 2;
sin2 a 2 sin2 a
sura
, • 2 л . 2 2^/5 . 2л/5
5 sin a =4; sma=—= =---; a=arcsm----.
>/5 5 5
3.384. □ По условию, ABCD — усеченный конус, ЛС=а, Q — центр вписанного
шара, LABO=a, О и Ох—центры основании усеченного конуса.
— центр окружности касания шара и боковой поверхности усеченного
конуса (рис. Р.3.136); требуется найти объем конуса OLK. Проведем
АМ^ООс, из ixAMB находим ООХ = АМ=а sin а. Рассмотрим t^LBO- так
как BL=BO (отрезки касательных, проведенных из точки В к шару), то
a a
LBOL= LBLO=90°—-% тогда LLOOv=-. Далее, дОДО1=90° как впи-
санный, опирающийся на диаметр ООХ', поэтому
a a a
OL=‘OO1 cos-=asina cos -. Из &.ONL получим O.V=OLcos- =
a a a a
=asina cos2 LN =OL sin -=asina cos - sin -. Итак,
2 2 2 2
1 1 tx (x 1 a
Volk=- Я LN2 ON=- na3 *sin3 a sin2 - cos* -=— ла3 sin5 a cos2 -.
3 3 2 2 12 2
3.385.
3.386.
3.387.
□ Изобразим осевое сечение усеченного конуса и вписанного в него шара
(рис. Р.3.137). По условию, BC+AD = 5OE. Проведай BM1AD; тогда
BM BC+AD
sin a=sin i_BAM=—Но BM=1OE, AB=---------------- (согласно свойству
AB 2
сторон описанного около окружности четырехугольника). Значит,
5ОЕ 4 . 4 _
sma=2O£ :-----=-, т. е. a=arcsin -.
2 5 5
arctg yfl.
□ По условию, О — центр шара, А, В, С, D — точки, лежащие на ша-
ровой поверхности, OA = R, AD\\BC, BC=AB = CD, AD = R, LBAD = n,
OOiHABC) (рис. P.3.138). Положим AB=a и из Д.АВС найдем
ЛС2 =2д2 —2a2 cos (180° —а)=2д2 (1-t-cos a)=4a2 cos2т. e. ЛС= 2д cos |.
Точка Ot является центром окружности, описанной около ДЛСО; поэтому
a
i4C=2O1Dsina и получаем равенство 2O1Z)sina=2zicos -, откуда
285
Рис. Р.3.138
R-a
OXD=------. Проведем CEA.AD-, тогда DE=—в ECED имеем
2 sin -
2
R-a R
cosa=----, откуда a=------. Таким образом,
2а l+2cosa
R R
О D=------------=-------------------------.
а а { За а\ За
2sin - (l+2cosa) 2sin-+2 sin-sin- 2яп—-
2 2 \ 2 2/ 2
Наконец, из ДООполучим
I--j— R /4 sin2 — -1
OO.= R2--------
4 / л • J 3a n • 3a
V 4 яп2 — 2 яп —
'22
_ R4/2-2cos За— 1 _
. За
2яп —
2
. За
2 sm —
2
3388. □ По условию, АпВ— шаровой
сегмент, О — центр шара,
\jAnB= LAOB=*a (рис. Р.3.139). Пусть R — радиус шара, ОС — перпен-
дикуляр к основанию сегмента, Ot — центр основания сегмента, О^—Н-,
a
тогда H=R—OOi. Из ЬОО^А находим OO^R cos-, откуда
а а
H=R—Rcos =2Rsin2 -. Значит,
2 4
Ршар. сегм — нН?
. ,а/ 2R
яп - ( R--
4 к 3
1 “
яп2 -
4
, . . а
4лЛ3яп* -
4
3
. , a\ 4?tR3 . a
3 —2яп2 - |=-яп* -
4/3 4
a\ 4nR3
2+COS- 1, Рщара=
R
а
R
Рщар.игм . а / а\
Итак,---------=sin* - ( 2+cos - ).
Ршара 4 у 2у
286
3.389. □ По условию, О — центр шара, Oj — центр основания шарового сег-
мента ADB, <uADB в осевом сечении равна fl, АСВ — прямоугольный
треугольник, вписанный в основание шарового сегмента, LBAC—x,
ODL(ABC); S£,ABC=S (рис. Р.3.140). Имеем ВС АС=
1 1 , 4S 2JS
= Л2?sina ABcosa = - J5sin2a или А& = ~.-, откуда АВ= — ----.
2 4 sm2a ,/sin 2 a
Из
AOOiB
находим
О,В АВ
ОВ=^—=------
. fl п . fl
sm - 2 sm -
2 2
— f
12a sin -
„ VSctg-f
р
O1O=O15ctg-=— --------. Следовательно,
DO^OD-OO^OB-OOi
VScos^
? Г
ап - х/я
2
2
sin^n2a
^L-2»j 1 ± -ч/1 —2т
------ и arccos
2
1
2
2
7? sin a
• 3.390. ------. 3.391. 2arcsin
Л 1 П~а
4 cos ---
4
3392. □ По условию, в LABC известны LA, LB, LC, ВВ^Н, О — центр
окружности, OB=OB1 = H!2, D и E— точки пересечения окружности со
сторонами АВ и ВС (рис. Р.3.141); требуется найти Sbdb,e- Имеем
В bdb,ex В&bde+ В ы>в1Е= BD BE sin B + ^BtD В iE sin (180° — /?) =
=^sinB(&D • BE+B^D BtE). Учитывая, что LABBt «90°— LA.
287
LBXBC=W — LC, из t\BDBr находим BD=Hcos(90° — X) = 77sinH,
BjD=HcosA, а из ixB^BE получим BE <=H sin C, BtE= ffcos С. Итак,
1 №
SgDB,E=2 nnB(H2smAsmC+H2cosAcosC)=*— sinB cos(X —C).
3393. □ По условию, ДЛВС— остроугольный, £_Л=а радианов, ДВ=/? ради-
анов, AC=*b, AAjJ.BC, CCjlAB, О — ортоцентр, через точки О, Aj, Q
проведена окружность (рис. Р.3.142); требуется найти площадь общей части
я
&.АВС и построенного круга. Так как EOAjB** LOCtB=-, то
LAjOCjA- LAjBCj^n, т. е. построенная окружность проходит через В,
а ОВ — ее диаметр. Пусть М — ее центр; тогда, обозначив площадь общей
части Е.АВС и окружности через S, получим
У“5дл1мл+‘5дс,мл+‘5<ххт.лл<,ос1“2 MBPwl EAjMB+- A/B2sin EBAfCj +
+^ МВ3 • LAjMCj MB3 (sin LAjMB+wi L.BMCj + LAjMC^J.
я я
В t^ABjB имеем LBtBA-~—а; значит, EMBCj—--а,
a LBMCj-я—2 Q—а^—2а. Далее, в t^BjBC имеем
ДС-^ —(я—(а+Д))-а+//—поэтому LMBAj -а+/)-|,
а Д^ЛДВ^я—2 f й+Д——^"2(я—а—Р). Но ДЛ|ЛДС1*2ДЛ/ВЛ1 +
+2lMBCj, так как Д AjMCj - LAtMO+ EOMCU а последние углы явля-
ются внешними в треугольниках AjMB и CjMB; следовательно,
(д\ /я \
а+Р—- 1+2 I - — а 1-2Д. Тогда искомая площадь выразит-
ся следующим образом:
5-^ MBi (2^+sin (2я—2х—2^)+sin2a)-
MB3 (2^-sin(2a+2^) + sin2a)—МВ3 (2Д+2сов(2а+Д)(—sin^))—
-Л/Я1 (/J-sinр сов(2«+Д)).
Проведем через вершины ДЛВС прямые, параллельные противополож-
288
ним сторонам, и получим ДЯ2В2С2, стороны которого в 2 раза больше
сторон Д.АВС (например, из рассмотрения параллелограммов АВ2СВ
и АВА2С следует, что В2С=АВ=СА2, т. е. А2В2=2АВ. Поэтому точка
О пересечения высот является точкой пересечения серединных перпендику-
ляров ВВ2 и СС2 в &А2В2С2, т. е. центром окружности, описанной около
Д,А2В2С2. Пусть R — радиус окружности, описанной около ДЛВС; тогда
OA2 — OB2 = OC2 = 2R. В ДЯВС имеем />=2BsinB=27?sin^, откуда
b
R——;—- Так как ДЯ2ОС,=2ДВ2 = 2Д, то LA2OB = fi и, значит,
2sinp
OB=OA2cosfi=2Rcos/?=/>ctg/?. Отсюда МВ=^ ОВ=-^ bctgfi и окончате-
льно получим
5=^ 2>2 ctg2 Д (/J—sin Д cos (2я+ /?)).
3.394. . • Воспользоваться тем, что в А А ВС ортоцентр является цен-
cos В cos С
тром окружности, описанной около ДЯ2В2С2, стороны которого проходят
через точки А, В, С и параллельны противолежащим сторонам Д.АВС (см.
задачу 3.393).
3.395. □ По условию, ВС=а, AC=b (a>b), CD1AB, АЕ=ВЕ, Sabc = S (рис.
1 25
Р.3.143); требуется найти LDCE. Так как S—~ absinC, то sinC=—-, т. е.
2 ab
I 452 J a2 b2—4 В2 _
cos С= /1 —; = -----------. Согласно теореме косинусов,
у a2b2 ab
АВ2 =а2 + b2 — 2аЬ — = а2+ b2 — 2<J a2b2—4S2.
ab
Продолжив медиану СЕ на расстояние EF= СЕ и соединив F с точками
А я В, получим параллелограмм CAFB, в котором 4СЕ2 +АВ2=2(а2 +Ь2)
--------------------------5 в2+/>2+25/Л>2—4S2
или 4СЁ2 =а2 +b2 +2\] (Fb2 —4S1, откуда CF?= -------------. Да-
1 25
лее, учитывая, что 5=- АВ CD, имеем CD=—~. Тогда из &CDE находим
2 АВ
DE- l^+b^+^aV^S2 4S2
D 4 a2 + b2-2^a2b2-4S2~
Рис: P.3.143
Рис. p.3.144
10-363
289
J(a2 + b2)2 — 4a2b2 J-b2
ly/J+^-lJaW-AS2 bJ<?+b2-lja2b2-4S2
Окончательно получим
DE (a2-b2)Ja2+b2-2Ja2b2-4S2 a2-b2
tg LDCE=—=- ..........- - ----=——,
CD a2 + b2 — 2-Ja2b2-4S2 2S 4S
a2 — b2
t. e. LDCE=arctg—.
45
3.396. □ По условию, AB=BC=CA, FeAB, DeBC. EeAC. DE=EF=FD,
AB: DF=8 : 5 (рис. P.3.144); требуется найти sin lDEC. Пусть l_DEC=n.
Докажем равенство треугольников DEC и AEF. Имеем DF=EF (по усло-
вию), Д£ПС= 180° —(а + 60°)= 120° —a, C^£F=180°-(a-F60°) = 120°-a,
LAFE-180° — (60°+ 120°—а) = а, т. е. эти треугольники равны по стороне
и прилежащим к ней углам; следовательно, AE=DC. Пусть АС—8х; тогда
DE=5x; пусть, далее, DC—у, тогда ЕС—8х-АЕ=8х—у. Из LDEC по
теореме косинусов имеем DBl—DC2+EC2 — 2ЕС • DC cos 60° или
25х2=уг+(8х-у)2-у(8х-у); 25г2 =3у2-24ху+64х2; у2-8ху+ 13х=0. Ре-
шив это уравнение относительно у, найдем у1=4х+х^/3; у2=4х—х\/з.
r DC DE
Полагая DC=4x+xJ3, из txECD по теореме синусов имеем -—=-—
v sin a sin 60
DCy/3 k(4+V3X/3 4a/3-f3
t. e. sin a=-_ =----'—— —---------; полагая DC=4x—xJ3, получим
2DE Юх 10 v
V3-3
sraa=^o-
a—у .
Stg— sinasmy
2 tr / a /. a\ a\ 3
3397. ----;;---------. 3398. — I 4 cos —л 1 + sm2 - ) +2a sin - ). 3399. - или
sin(a-Fy) 8 \ 2 \ 2) 2J 5
1. 3.400. a ctg a.
3.401. □ По условию, ABCD — параллелограмм, AB=a, BC=b (a<b),
LADB=h, LABD — тупой (рис. P.3.145). Пусть l_A = (?; тогда из LABD
a b . , . . •
по теореме синусов имеем -—= . -------- или asm(a-F^>)=Asina,
sina sin (180 —-a — (p)
. Asina Asina
откуда a-F<p=arcsin----- и ^>=arcsin----а. Значит,
a a
A sin a
LADC= 180°— arcsin-----Fa. Теперь из ДADC по теореме косинусов
а
находим
, , ( A sm a
AC2=a1+b2 — 2oAcos I 180 —arcsin-Fa
\ a
. . ( . A sm a \
=a2-FAi-F2oAcos I arcsin-----a =
\ a /
, ., ( ( . A sin a\
=л2+А'1+2аА I cos I arcsin---] cosa+sin
\ \ a )
, Лапа
arcsin-------
a
, . / / A1 sin2 a A sin2 a'
= л2 + А2 + 2аА I /1-z—cos a-I-
W a a .
290
Рис. Р.3.145
Рис. Р.3.146
= а2 + b2 + 2b (cos а>/а2 —Z>2sin2a + b sin2 а).
Итак, AC=-J a1 +b2 + 2b (cos Ол/а2 — A2 sin2 а + b sin2 а), где а > b sin а.
_ . /а2 —Ь2 \ (а2 — Ъ2 \ 2аЛ
3.402. arcsin - tga ) и я—arcsin -----tga . 3.403. arctg -5—-5.
\ lab ) \ lab } а —о
3.404. □ По условию, ABCD — параллелограмм, АВ=а, AD = b (a<b), АЕ—
= ED, i_ ВЕС=а (рис. Р.3.146). Используя теорему косинусов, в А АВЕ
и txEDC имеем ВЕ2=а2+- Ь2—abcosA, СЕ2=-Ь2+а2—
4 4
— o/>cos(180° —А) = а2-<—b2 + abcosA. Сложив эти равенства, получим
4
ВЕ2 + СЕ2 = 2а2+-Ь2. Теперь применим теорему косинусов к txBEC:
2а2—Л2 2
Ь2=ВЕ2+ЕС2 — 2ВЕ ЕСсо&а или BE ЁС=--------=--------. Следова-
2cos а 4 cos а
тельно,
4а2 — Ь2 4а2—Ь2
Sabcd —2Sьвес = 2ВЕ • £Csina = 2 —---sina=-------tga.
4 cos а 2
3.405. 3 arccos—— и я—3 arccos——.
21t 21t
3.406. 3.407.
4
. /1 /i+Vi+^x . /1 /i+Ji+^x r
arcsin ( - /----- ия-arcsin ( 7 /----- ; k>J2.
\kN 2 ) \ty 2 J
3.410. □ По условию, AFB— сегмент, AK=KB, l_AOB = a, KF—-FE=KE,
KLA.EF, KL=h (рис. P.3.147). Пусть OB=R. Тогда из t^KOB находим
a a
OK^Rcos откуда OL=OX'+AL=J?cos-+Л. Далее, в t\OLE имеем
OLt+Ltf^R.2 или (J?cos-+A
\ 2
. . , a , a 4Л2 _
R sm2 2J?Acos -—“ешив это уравнение, получим
L “ /Z 2Я 4Л* • 2 “
h cos - + h2 cos - H-sin -
д 2 V 2 3 2
2
= R2
или
2 “
sm2 -
2
• 2 “
sm2 -
2
1 2 “
1 +- sin2 -
3 2
h
3.411. □ По условию, ABD — сегмент, BFLAD, AF:FD=<1 :4
иЛВ : uBD = 1 : 2, О — центр окружности сегмента (рис. Р.3.148); требует-
ся найти cos LAOD. Проведем BCftAD и СВЦВВ. Пусть AF=x; тогда
DF=4x, DE=AF=x, BC=EF=3x. Пусть, далее, LAOB=a; тогда
291
о
Рис. Р.3.147
LDOC= LBOC=a (так как <jAB=^jDC=<jCB). Обозначив радиус сегмен-
та через R, по теореме косинусов в &ВОС и &.AOD имеем
9д2 = 2R2 — 2R2 cos а=2R2 (1 — cos а), 25л2 = 2R2 (1 — cos За). Разделим первое
9 1—cosa
равенство на второе и получим —=-----или 9—9 cos За=25—25 cos а.
25 1—cos За
Далее, используя формулу cos За =4 cos3 а—3 cos а, придем к уравнению
36cos3a+27cosa—16+25 cosa=0 или 9cos3a— 13cosa+4 = 0, откуда
9 cos a (cos2 а— 1)—4 (cos а— 1) = 0, (cos а— 1) (9 cos2 а+9 cos а—4) = О,
cosa#l, так как а#0.
, 1
Решив уравнение 9cosa+9cosa—4=0, получим cosa=-; тогда
3.412.
1 1 23
cos Z.XOD=cos3a=4-----3 . - =-.
27 3 27
□ По условию, POQ— сектор, OP=OQ=R, ABCD — вписанный в сек-
тор прямоугольник, АеОР, B&jPQ, CeuPQ, DeOQ, LPOQ = a, LCMD = B
(рис. P.3.149). Проведем OMQBC=£; OM(~\AD=N. Пусть ME=x; тогда
В В
в t\MBE имеем LMBE=~, BE=х ctgИз EANO находим
2 2
ON=AN ctg |=x ctg ctg Далее, в ЕОЕС имеем OE2 + EC2=R2 или
(a B\2
2x+xctg-ctg-J +X2ctg2B=R2, откуда
R2
*2tg2^
,в ( в «\2 ( в “V’
ctg 2 + \2 + Ct82Ct82/ 1+(2tS 2+Ctg2/
Теперь можно найти искомую площадь:
В , В
Sabcd=BC CD=2x ctg - • 2x=4x2ctg | =
47?2tg^
(B a\2'
2tg- + ctg-J
a a
3.413. 42?cos - sin2 -.
4 8
292
3.414. □ По условию, LABC=LAJ)C, LB=LD=90°, ((ABC);(ADC)) = a,
LBAD=P(pm. Р.3.150). Проведем BFLAC; тогда DFLAC, DF=BF (высо-
ты в равных прямоугольных треугольниках, проведенные к гипотенузе),
т. е. LBFD = a. Пусть AB=AD=a, BC=CD = b, BF=h. Из LABD и LDBF
Р р
находим DB2=2a2— 2а2 cos 4а2 sin2 -, откуда DB=2asin-;
DB2=1h2—2k1 cosa=4Л2sin2 откуда /)5=2Asin|. Далее, полагая
LBCD=<f>, из L.BCD получим DB2 = 2b2—2/>2cos^=4/>2sin2 p
. . a
е.
ф р а ф
2>B=2Asin -. Теперь из равенств 2аsin -=2Asin - и 2/>sin -=2Asin - нахо-
Ч>
дим
2
A sin (/?/2)
a sin (a/2)’
2
й — Sin (ф/2)
Ъ sin (a/2) ’
Но
2
- = sin LBAC,
a
Р
h
-=sin Z_BC4=sin(9O°- L ВАС)=cos LBAC. Имеем
О
яп (Д/2) sin (в/2)
sin LBAC= . т. е. L ВАС=arcsin .
яп (а/2) яп (а/2)
. sin (ф/2) / . sin (Д/2)\ sin (ф/2)
cos LBAC-———— или cos arcsin -——— =——
яп (а/2) \ яп (а/2) / яп (а/2)
После преобразований получим
. А ~ °S‘n sin (а/2)-sin2 (Д/2)=
у sin2 (а/2) sin (а/2)
1—cosa—1+cos/l / а+р- а—Р
— 1 sin---sin-----.
2 2
2
/ а+Р a—f}
Итак, <р = 2 arcsin /sin —sm ——.
3.415. □ По условию, О — трехгранный угол, l_MON=a, двугранный угол
ОМ—р, а двугранный угол ON=y (рис. Р.3.151); требуется найти LPOM
и LPON. Возьмем на ОР произвольную точку А и проведем AA^^MON),
ACLOM и АВLON; тогда LACA^P, a LABA! —у. Пусть АА^а) тогда
а а
в L.ACA, и LABA. имеем A<C=actgP, АС=-—A<B=actgy, АВ=——.
япр япу
293
Обозначим LAjOC через <р; отсюда /_А1ОВ=а—д>. В Д^ОС и t^A^OB
А.С . , ч А. В sin (а — а>) А,В actgy
имеем sm<p=-----, sm(a—<р)=---, откуда —:-----=----=------- и далее
AtO AtO sin <р AtC л ctg/?
sina ctg cosa=
cosy sin/?
sin у cos /?’
cosysm/? cosa cosy sm/?+cos a cos P sin у
Ctg <a = - —;----- + ----=-------;---------;-------.
sin a sin у cos p sin a sin a cos p sin у
Из ДОСА1 найдем
OC=AiCctgg>=actgP
a (cos у sin/?+cosa cos/? siny)
cosy sin/? + cosa cosP siny
sin a cos p sin у
sina sin/? siny
Наконец, из ДЯСО получим
ОС a (cos у sinfl+cos a cos в siny) sin в
Ctg £XOA/ = Ctg l_AOC =--=---------;---; —--------------
AC sin a sin p sin у • a
=ctgy sinP sin~‘a+ctga cos/?= sinp ctga(ctgу cos"1 a+ctg/?).
Итак, 1_AOM= 4PO3/=arcctg(sin/? ctga(ctgy cos"1 a + ctg/?)).
Аналогично находим
£.PCW=arctg(siny ctg a (ctg/? cos"1 a+ctgy)).
3.416. □ По условию, OMLON, ОМ LOP, ONLOP, AeOM, OA=a, BeON, CeOP,
l_ABC=a., LACB=P (рис. P.3.152). Проведем ADLBC. Пусть AD=H',
H H
тогда из aADB и A.ADC находим AB= -—, BD=Hdga, AC—-.—
sina sin/?
DC=Hctgp. Так как ODLBC (по теореме о трех перпендикулярах), то
OD2 — BD DC или OD=HyJ<Aga ctgp. Далее, в A.AOD имеем
Н2 —Н2 ctga ctgР—а2, откуда Н-- —; тогда
>/1—ctga ctg/?
а
АВ=------ —. Наконец, из ДЯО2? получим
sinоц/!-ctga ctg/?
.а2 , a2(l — sin1 a+sin a cosa ctg fi) sina sin/?
OB2 =—5-----------------a2 =—-——=--------------—----------- =
sin1 a(l —ctg a ctg Д) sin1 a (sin a sin p—cos a cos P)
294
a2 cos a (cos a sin fi + sin a cos fl)
— sina cos(a + /f)
= -a2ctga tg(a + A),
t. e. OB=a-j—ctga tg(a+/?). Аналогично из
OC=<h/~ctgA tg(a+0).
ДЛОС находим
3.417. □ По условию, a||/J, Леа, Cea, Be fl, De fl, AB : CD=k, AAlJ.fl, CCt±fl,
/.ABA, : LCDCj=2 : 3 (рис. P.3.153). Пусть АА^СС^аи /_АВА1=2^>;
тогда CCDC, =3<р. Так
sin3® AB ,
------=— = k.
sin2<p CD
Далее
имеем
a a
как sin2® =—, sin3®=—~, to
AB CD
3sin<p—4sin3<p
-------------=k;
2 sin <p cos <p
к+>Jk2+4
cos 99 =-------, поскольку cos<p>0. Значит,
3 — 4 sin2 <p = 2k cos q>;
4cos2<p — 2£cosp — 1 =0;
k + \ft2 +4
---------------------. Ho cCDCt — острый или прямой угол (по опреде-
Ф= arccos
лению угла
л
между прямой и плоскостью); поэтому 0<«р<~, откуда
о
<СОБф<1
ИЛИ
<1, т. е. 2у/з^к+у/к2 + 4<4. Решив
V5
2
7з jt+7^+4
2 " 4
(fc+VF+4>2V3, 273^,_ 3 „
систему неравенств < .____ , получим ----<к<-. Итак,
[к+у/к2 +4<4 3 2
k+Jk2+4 „ k+Jk2 + 4 2л/з 3 _
CABAt =2arccos---------, Д CPCj = 3 arccos-
3.418. □ По условию, ABCD — квадрат, Р—плоскость, ((ЛВС); Р)=а,
(Р; (ЛВ))=/? (рис. Р.3.154); требуется найти (Р; (AD)). Проведем через
Л плоскость Pji|P, а затем BBjlP,, CCjXPj, DD^LPi, тогда
(ЛВСЭРР^ЛР, BCQP,=P, CD{\Pi=E, LBAB^=p. Теперь проведем
DK3.AE; очевидно, что D^Jl-AE; тогда LDKDi = a,
-******* а
LD1AD—(P; (AD)) = x. Пусть DDi=at откуда AD==-—. Так как С2)||ЯЛ,
а а
то l_DED< = 1_ВАВ, = 8 и DE=-—-t a DK—------. Учитывая, что
яп р яп а
295
(поскольку ADLDE как смежные стороны квадрата), имеем
яп2 х яп2 р яп2 х яп2 0
и,
следовательно,
sinx япР
____1
=- AD DE=: АЕ DK или
2
sina
2
P+sitfx
Далее воспользуемся тем, 1
a a a-jsm10+ып2 х а
sinx Wi0 sinx sinД япа
. , . , . , 1 — cos2a—1+со$2Д
яп х=sm а—яп В=----------------------=
__________2
находим sin х=л/sin (a+Д) sin(a—Д). Итак,
что •Удло£=
или
= sin (a+Д) sin (a — Д), откуда
х=arcsin -Jsm(a+P) sin(a—Д).
ijio Я’япб’+Д) Йп(у-Д) tga
4 яп Д sin у
3.420. □ По условию, ABCDAlB1CiDl — параллелепипед, ABCD — параллело-
грамм, LBAD=a, AAt=b, LAtAB= LA1AD=0 (рис. P.3.155). Проведем
А^ЦАВС), AiKA-AB и A^LAD; тогда AtO — высота призмы, OKLAB
и OF .LAD. Так как ДЯ1ЛИ=ДЛ1Л4 (по общей гипотенузе и острому
углу), то Я1Х’=Л1/’. Значит, OK=OF как проекции равных наклонных,
откуда следует, что АО — биссектриса LBAD. Из AAtFA имеем
a a
i41f=fcsinft AF=b cos Д, а из ДЛ-FO находим OF=AFtg -=Лсо5Д tg -.
Наконец, из kA^OF получим
— b2co&2 P tg2 -=—/sin2 Д cos2 cos2 Д sin2 - =
2 ax/ 2 2
cos - ’
2
А.О
cos -
2
, . а—Д . а+Д
Л3 яп----яп-----tg <а
2 2
3421.----------*-----в---•
о 2 ® 2 Д
2 COS - COS -
2 2
3.422. □ По условию, АСВА^В! — наклонная треугольная призма,
ДЯСВ=90°, LBAC = a, (АА^ЦАВС), LAiACB=P (рис. Р.3.156); требу-
ется найти острый угол между^ЯВС) и (CjCB). Проведем AiO.L(ABC);
296
OetAAtBJ. Проведем Xt£±XC и соединим О с Е, тогда OELAC
и LAiEO=p. Пусть АВ=с, AiO—a; тогда AC=ccosa (из Л.АВС),
OE=actgP (из кА^О), AE=OEctga=actgP ctga (из ДЛ£О),
£С=ЯС—X£=ccosa—actg/? ctga. Проведем OD^AC, тогда ODLBC. Че-
рез AtO и OD проведем плоскость XjOD; (А^ОУ^СС^/^С^
и BC-HAtOD), поскольку ВС перпендикулярна прямым OD я AtO, лежа-
щим в этой плоскости. Следовательно, LODC^ является тупым углом
между (АВС) и (QCB), так как OD меньше на величину АЕ. Теперь
проведем С^И/ЦО; тогда LC^DF— острый угол между (АВС) и (С, СВ).
С F
В &C1FD имеем tg Д С1В/’=~^;; учитывая, что C1/’=a, DF=
= OF—OD=AC—OD = AC—EC=ccosa. — (ccosa.—a ctga ctg/f)=actga ctg/J,
a
—------—- = tga tgp.
a ctga ctgP
находим tg EC,DF=
Д CjtJB»arctg(tga tg^).
3.423. I3 sin 20 cos p sin a cos2 3.424.
a2b
T
>/3—4(cos2a—cosa cos^+cos2 Д).
„ — ab1 sin« / . --- a3 sin 2a cos a sin 8 3
3.425.------\/sin(/? + a) sin (Ji —a). 3.426. — — 3.427. arccos -.
2 е08 P 4y/cos (a+/?) cos (a—/?) 4
3.428. □ По условию, ABCA1B1C1—наклонная треугольная призма, ВС=а,
LABC=p, LACB=y, AAl=AlB=AiC и Рпр=К(рис. Р.3.157). Проведем
А^ЦАВС). Так как AAi=A1B=A1C, то ОА = ОВ=ОС, т. е. О — центр
окружности, описанной около Д АВС. Пусть R — радиус этой окружности;
a- a2 sin у sin в
тогда a=2J?sin (/?4-у), откуда В=-. ——-, S^ABC= . Обозиа-
2sm(/J+y) 2sin(p+y)
чим угол наклона бокового ребра к плоскости основания через д>; отсюда
ЕА1АО = <р и
a3 sin)? sin у tg <р
V 4sin2(/?+y)
atg^i
X,O=Atgfi>=————-. Следовательно,
2 sin (Д 4-у)
4Ksin2(^-t-y)
tg m=—s--------.
a3 sin P sin у
откуда
Итак,
<p=arctg
4Fsin2(/J+y)
a3sinP siny '
3.429. □ По условию, ABCDA1BlC1D1 — куб, DF=FDi, Djf^KC}, через точки
A, F и К проведено сечение (AFK) (рис. Р.3.158); требуется найти
((ABCWAFK)). Обозначим (AFK) через a; aQ(DD1C1)=P’^, где FK^DC^ как
средняя линия ДТЗ^С],' aPjf^Jj^j) по прямой, параллельной Z>Ct, т. е. по
297
ABi, а/^(Л1Л1С1)=Л1Х'; аР(Д2?1Л1)=Л/’. Таким образом, сечением явля-
ется четырехугольник AB^KF. Далее, а(’')(ЛВС)=Л£||В1ЛС. Проведем
FMS.AE', значит, DMS.AE и LFMD—tp— искомый угол. Пусть AD=a;
а
тогда ВТ’=-. Проведем KL\DDi, имеем DF—средняя линия LELK
а I , a2
и DE=DL=~. Из L.EDA находим АЕ= tri—=——. Учитывая, что
2 у 4 2
1 1 a aJs
E^ade=2 AD ’ АЕ' получим - а=—^- DM, откуда
aJs FD л/5
DM=~—. Наконец, из &FDM найдем tg^=—,
5 DM 2
V5
<p=arctg —.
3.430. □ По условию, SABCD — пирамида, ABCD — квадрат, SOSAABC),
SKLAD, SES.BC, SLS.DC, SFS.AB, LSEO : LSFO :
: LSKO : LSLO=\ : 2 : 4 : 2 (рис. P.3.159). Пусть l_SEO=n-, тогда
l_SFO= LSLO=2a, LSKO=4a. Обозначив SO через H, найдем
O£=tfctga, OK=Hctg4a, OF=OL = Hctg2a. Так как OE+OK=OF+OL
(длины сторон квадрата), то
е.
sm a sin 2a
ctga+ctg4a=2ctg2a; ctga—ctg 2a=ctg2a— ctg4a;---------=-----------;
sin a sin 2a sm 2a sm 4a
sin 4a —sin 2a=0; 2 cos 3a sina=0.
я я
Ho sma#0; тогда cos3a-=0 и так как a — острый угол, то За=-, т. е. а=~.
2 6
я я 2я
Итак, LSEO=~, LSFO = LSLO=-, LSKO=—.
6 3 3
3.431. □ По условию, SABC —^правильная треугольная пирамида,
(BMN)S.(SAC), (BMN)\\AC, ({BMN)^ABC))=a (рис. Р.3.160); требуется най-
ти LASC. Проведем SFS.(ABCy, тогда BFS.AC, BF(~}AC = D, SDS.AC. Так
как MN\AC, то SDS.MN. Далее, (ВМЛ1)П(ЯВС)=В£||М^|ЛС;
LSMB=> LSMB (SB— общая сторона, SN=SM, поскольку Л/У||ЛС,
Z. BSM = L BSN); следовательно, BM^BN и BOLMN, а так как BE^MN, то
BOS.BE и LOBD=a. Пусть FD=a-, тогда AD=aJs. Учитывая, что
LOBD=4, имеем Z.P2>0=90°—а, а l_FSD=a. Из LSFD получим
298
„„a _, AD aJ3 sma /- .
SD=-—, а из &.SDA найдем tg l_ASD=—=—--------=-J3 sina, откуда
sin a SD a
LASD = arctg (^/з sina). Итак, LASC=2LASD=2arctg(yf3 sina).
3.432. □ По условию, SABCD — правильная четырехугольная пирамида,
ЯОЦАВС), OK-L(SAB), О LISA, ОК=а. OL = b (рис. Р.3.161); требуется
найти LSABO. Проведем SES.AB-, тогда (SOE)L(SAB), так как ABLfSOE)
и ABe(SAB); следовательно, LSEO — линейный угол двугранного угла
SABO, OKe(SOE) и KeSE. Пусть LSEO=а. Так как Д SKO ~ LOKE
(LSKO= L ОКЕ=90°, LSOK= L.KEO как углы с взаимно перпендикуляр-
ОК. КЕ
ными сторонами), то —=—. Введем обозначения АВ=х, SO=h; тогда
- =----, т. е. КЕ=—. В Д ОКЕ имеем КЕ= /-а2 и получаем уравнение
Л х 2h у 4
^Х2 X1 2 J2 ,1.2 л 1U _2 4а2Л2
4
OL AL b 2AL , Ьх^2
Аналогично, LSLO~ LOLA и —=— или -=—-, т. е. AL=-——-.
SO АО h 2Л
А?
Далее, в LOLA имеем AL= /---Ъ2 и получаем уравнение
, 4л2Л2 2Л2Л2
Сравнивая значения для хг, приходим к равенству -5=7^—тогда
h —a h —г
a?b* ab
2a2h* — 2a2b2 = b2h2—а2Ь2 или Л2=—,—откуда h= ~ Значит,
2а2-b2' Jtf^b2
4a2 ali>1
, 2а2 — b2 2а2 b2 aby/2
x ~---------=75-----5> T- e- x= ,.-
a b „2 b ^b2-a2
2a2 —b2
299
SO labdb1-^ y/2(b2-a2) „
Теперь из &SOE находим tga=—= , —-----— =—, .-- Воспо-
ОЕ ф^Ь2аЬ42 у/2д2-Ь2
1 yj2a2-b2
льзовавшись формулой l+tg2a=——, получим cosa=---------, т. е.
cos2 a b
a=arccos —-------.
b
3.433. □ По условию, SABC — правильная треугольная пирамида, АВ=а,
LSCBA—x. (рис. Р.3.162); требуется найти расстояние между AS и ВС.
Пусть SO1.(ABC) и SDXBC. Через SO и SD проведем плоскость ASD, а из
точки D проведем DEA.SA. Так как BCZAASD), то DELBC, т. е. DE — ис-
комое расстояние. Учитывая, что l_SDO=a. как линейный угол двугран-
него угла SCBA, из &SOD находим SO = ODtga=—tga. Так как
6
aJ3 1 Зе2 tga a2 tga
AD=-^~, то S&sad=- AD SO=------=-----. С другой стороны,
2 2 24 8
>Sa&u>=- SA DE, где SA найдем из &SOA:
Ic^tgia a2 5/3e2(tg2a+4) aA/3(tg2a+4)
SA=J~1T+J----------6-------------6-----•
a2 tga a73(tg2*+4) ПР
В результате получаем уравнение —-—=— ---—----- DE, откуда
о 12
J£,^tga и
2Vtg2a+4
3.434. □ По условию, SABCD — правильная четырехугольная пирамида, АВ=а,
SQUABCj, LASQ = a
, (EKN)A.SA, SO = OQ, Oe(EKN)
(рис. P.3.163). Имеем i±SEL= &SEK (SE—общий катет, LESL= LESK
как плоские углы в правильной пирамиде); следовательно, SL=SK, т. е.
1 aJl
LK^BD, причем LK=-^ BD=~-. Так как SEL(EKN), то SO — наклонная
к этой плоскости, ЕО — ее проекция на эту плоскость; вследствие того, что
SOLBD, a BD^LK, получаем SOLLKи EOLLK', значит, Skjovl=- LK EN.
aJl 1 aJl
Теперь найдем S6=gi4ctga=--ctga, откуда SO= SQ =—— ctga. Да-
2 2 4
a-yjl,
лее из AOES находим 5£=SOcosa=— ctga cosa и, наконец, из ASEN
4
a-Jl
получим EN=SEtg2a=—— ctga cosa tg2a. Итак,
4
1 a-Jl a-Jl a1
Seknl=t, ------у ctga cosa tg2a=— ctga cosa tg2a.
2 2 4 о
J2
Заметим, что ограничение a < arctg -у- существенно, так как в противном
300
случае нельзя провести сечение EKNL, удовлетворяющее условиям задачи.
В этом случае точка N окажется за пределами ребра SC, что можно
показать, сравнив длины SN и SC. -
3.435. □ По условию, SABC — правильная треугольная пирамида, SO1AABC),
SO = H, Р— сечение, проходящее через A, PLSC, (Р;(АВС))=а (рис.
Р.3.164); требуется найти объем пирамиды, заключенной между Р и (АВС).
Сечение PQ(ASC)=AD, где ADJ.SD; так как BDA.SC, то (ADB)<=P, т. е.
ADB— искомое сечение. Пусть SE— апофема. Имеем &ASD= &BSD
(SA=SB, SD — общая сторона, l_ASD= LBSD); следовательно, AD=BD,
ED А. АВ и CEJ-AB; тогда LCED = a, i_ECD = 90°—a. Из t^SOC находим
3 г
2 - Htga л/3
3 3 2 v г
ОС=Н tga; значит, £С=-ОС=-Htga, АВ=-----------------=,/3 .Htga.
3
Далее из &EDC найдем DC=£Csina=- Htga sina. Проведем DF1.(ABC);
3 3
в &FDC имеем /_Н)С=а и DF=DCcosa=- Htga sinacosa = - И sin2а.
2 2
Итак,
1 3H2tg2a J3 3 . , Зл/З Н3 tg2 a sin2 а
Рдлдс=т----------— - Hsm2a=——:— -----------.
j 4 Z о
3.436. □ По условию, ЯВСЯ1В1С1—правильная треугольная усеченная пира-
мида, К — центр вписанного в нее шара, М — центр шара, касающегося
всех ребер пирамиды, О и — центры оснований пирамиды (рис. Р.3.165);
требуется найти LByBO. Прежде всего отметим, что ХеОО, и КО^КО^
MeOOlt так как точка М равноудалена от всех ребер. Основания пирамиды
пересекают шар с центром М по окружностям с центрами О и Olt вписан-
ным в основания. Положим ОЕ=г, где Е и Ех—середины
сторон ВС и ВjCj. Боковая грань BBiClC пересекает шар с центром М по
окружности, вписанной в трапецию BBiC1C. Согласно свойству сторон
„„ BC+BiCi „
описанного около окружности четырехугольника, ВВХ =---. Пусть
а+Ь
ВС=а, В1С1=Ь; тогда BBt=——. Отрезок ЕЕГ —апофема усеченной пи-
рамиды; в силу свойства касательных, проведенных из одной точки к шару,
301
„„ ay/З by/З (а+Ь)у/з
имеем EE1—r+rl=—— Н—— =——-----.
6 6 6
Проведем fjNUOOj,
и положим OOt=H; тогда из LE^NE находим
№^EEi — EN1 ~а \2^ = ~^ '^алее пР°ведеми в ЬВ^ЬВ
имеем BB2l=B1L2 + BL2. Так как BBi=^-^-, B^L = EEt = ^ +
2 6
а—Ь
BL=—^~, то, подставив эта выражения в предыдущее равенство, получим
a2+2ab+b2 a2 + 2ab+b2 a2 — 2ab + b2
4 ” Ц + 4
или 10аЬ — а2+Ь2 или 12аЬ = (а + Ь)2, т. е. ab = ^ + .
12
. ab (а + Ь)2 а + Ь
Значит, /г=—=———, откуда Я=^. Теперь из &B,FB находим
2Н a+b 1 1
sin Д5,50=sin l_B.BF=---=—----—=-. Итак, sin EBiBO=~.
а + Ь 3(a+b) 3 3
3.437. □ По условию, FA ВС — треугольная пирамида, АВ=АС, L ВАС=а
(а<я/2), AEDA1ElDl — призма, вписанная в пирамиду, A^FA, E^FC,
DxeFB, О — центр окружности, описанной около t^ABC, OeED (рис.
Р.3.166); требуется найти Ущ, : Проведем FL-L(ABC) и положим
FL = H; FL(y(AtD1E1) = L1; пусть LL, =Л. Так как (Л1Р1£1)|(Л5С) (плоско-
сти, в которых лежат основания призмы), то 51Р1||5С (две параллельные
плоскости, пересеченные плоскостью FBC)', значит, DE^BC. Пусть ВС=а;
а
тогда a=2OAsma, откуда ОА=----------. Из &AOD находим
2 sin а
а
atg-
а 2 а а
OD=OA tg-=—;—=---------, т. е. DE=-----. Далее, &ADE~ ^АВС;
2 2sma , а ~ , а
4cos - 2 cos -
2 2
поэтому
302
S^ADE a2 1
S&ASC Be1 a 2
4 cos - • a 4 cos -
2 2
Полагая S^abc—S, находим Skade=---------- Согласно свойству парал-
. a
4 cos* -
2
лельных сечений пирамиды, имеем
S^A.D^yii s (H—h)2 H—h
S^abc ~ ta W~: 7Г
4cos - 5
2
{ , a '
HI 2cos2 - —1
, a , a \ 2
2Hcos2 —Zf=2Acos2 Л=—-----------
2 2 , а
1
, a
2 cos2 -
2
Ясов a
- 2 x
2 cos -
2
Следовательно.
Ипр=--------
. а
4 cos* -
2
Ясов а
, а
2 cos2 -
2
SH cos а
--------, откуда
, а
8 сов6 -
2
S
Sffcosa SH Зсова
^ПИр - в “ 3 о « “
8 cos6 - 8 cos6 -
2 2
2 IJ *7 / 2 2 । | ______
3.438. arctg—. 3.439. arcsin^—-—. 3.440. arctg 1/9+З^/То.
2. о
1+3 cos2а 1 , ,-----— , а> yfi
-----------. 3.442. —(a+b)2yjа(а—2Ь) tg2 —. 3.443. arctg—.
4 24 2 5
3.441.
3.444.
,, d2 5 Я2 sin (а+Р) sin (а—Д)
arccos (81?-1); 0<jt<^-. 3.445. —. 3.446. -------------у— -----------—3.447.
4 12 sin2 a sin 2Д sin Д
7а + ЗЬ .---=---=-------------
——-----V 3 (а1 + b2 + 2ab cos 2л).
144 cos а
3.448. □ Изобразим осевое сечение фигуры: пусть SDC — осевое сечение конуса,
SD и SC— образующие конуса, LDSC=90°, SO2 — высота конуса, О2
и О2 — центры оснований вписанного в конус цилиндра,
^бох.хои : ^бог.пил=4^/2 (рис. Р.3.167); требуется найти угол между DOt
и основанием конуса. Положим O2D = R; тогда SD=R-j2, SO2 = R,
•5'бох.к>н = яА2л/2. Обозначим радиус основания цилиндра через г, а высоту
О2О2 —через Л; тогда 5бох.цял=2лгЛ. По условию, ———=4^/2, откуда
2лгл
R2
— = 8. Но SO2 — h + r=Ry т. е. r=R~h. Подставим это выражение в послед
rh
R2
нее равенство: -----или Л2 = 8ЯЛ — 8Л2. Теперь разделим обе части
(R—h)h
303
уравнения на h2 и получим
Рис. Р.3.168
1 R
| —8 —+ 8 = 0. Учитывая, что
А ,
— =ctg Z_O1Z)O2=ctga (где а —искомый угол), имеем ctg a—8ctga+8=0,
п
откуда ctga=4±2>/2. Итак, a=arcctg(4+25/2).
3.449. □ По условию, — равносторонний цилиндр, А — точка окружно-
сти верхнего основания цилиндра, В — точка окружности его нижнего ос-
нования, АВ=а, АВ отстоит от OOt на расстояние b (рис. Р.3.168); требуется
найти угол между АВ и плоскостью основания цилиндра. Проведем через
AAt и АВ плоскость AAiB; при этом (АА^^ОО^ так как OOi\\AA1.
Проведем O^Dl-AtB; тогда OlDl.(AAiB) и, значит, OlD=b. Пусть ААг=х,
тогда А1С1=х. В ЛАА^ имеем J1A2=a2—х2, т. е. J1B=A/a2—х2,
1 а2—х2
AiD^^AiB^----------. Теперь из ^OlDA1 находим О^А^А^О2 + OtD2
х2 cP-х2 <?+4Ь2 _
или—=----------l-о ; отсюда 2jr=a +4o , х* =---. Следовательно,
4 4 2
В результате получим
J2(a2-4Z>2)
<р=arccos-— --------.
cos z.JBJj=cos<p=
J1B_>/2(a2-4b2)
~АВ~ 2а J
откуда
mi 2B>/sin(«+0)sin(«-0)tgA
3.450. 4я5к/2 sm I -+- I. 3.451.------------------.
\2 4/ sm a cos р
3.452. □ По условию, SAB — конус, SO — его высота, SB — образующая,
LOSB=a., MBCDE — пирамида, вписанная в конус, MS=MB, BCDE — че-
тырехугольник, вписанный в основание конуса, BE=BC=CD=b, DE=a
(рис. Р.3.169). Обозначим радиус основания конуса через R и проведем
Л/Х]|5О. Из &SOB находим 50=A ctg а, откуда МЮ=| 50=^ Actgа. Так
как равные хорды одной окружности стягивают равные дуги, то
\jBE=\jBC=\jCD. Обозначив величину этих дуг че-
рез р, имеем vBE=vBC=vCD=p, а vDAE=360°—3/J. Но впи-
санный угол измеряется половиной дуги, на которую он опирается;
304
1 38
поэтому LDBE=- (360°-ЗД) = 180°—р
LBDE=^ р, LDEB=p, a LDCB=\W°-p. Тогда
$ВСВЕ~ S ьвсв+ s ABED= 2 b2 sin (180° — /J) +
+ - ab sin p = - b(a + b) sin Д,
1 1.1
^пир=^ Sbcde MK=- b(a + b) sin p - Яctg a =
3 6 2
=— b(a+b)Rctga sinp.
Так как C\DBE вписан в основание конуса,
Z>£=2Asin l_DBE=2Rsin\ 180°-—] = 2Asin —
k 2/ 2
TO
3/?
или a = 2/?sin—; значит,
2
P P
R=------—; аналогично, 5£=2Asin LBDE=2Rsin - или b=2R sin -, откуда
„ . 3p 22
2 sin —
a
2
b
R=-------. Таким
P
2 sin -
2
образом, получаем равенство
. ЗД
sin —
ba 2 a
-------=---------или-------=—j
0 . P э . ЗА . А ь
2 яп - 2 яп — яп -
2 2 2
а
ь’3
, Р а ( . р\ а а+Ь
—4sin2 4 ( 1— sin2 - )=- + 1=——;
2 b \ 2) b b
далее имеем
Р ,Р
3sm —4 sin3 -
2 2
71
sin -
2
2 A a+b ,
C°S 2= 4* ’ C0S 2 2VT
Окончательно находим
1 b 1 b p p
Vnxf=^b(a+b)------- ctgasinA=— b(a+b)--------ctga 2sin-cos- =
12 . . P 12 , . P 2 2
2sin- 2sin-
2 ____ 2
i ,2z n A , 1 t2z l\ \[7l+b
=— b2(a+b)cos- ctga=— b2(a + b) ctga =
12 2 12 2y/b
b3/2(a+b)3/2 ctga=^- (ab+b2)3/2 ctga.
24 24
3.453. □ По условию, SMN — конус, SO — высота конуса, LOSN=p,
PABCD — пирамида, ABCD — равнобедренная трапеция, описанная около
основания конуса, LADC^a, SN—1—образующая конуса, PeSN,
РК1(АВС), K—ACC^BD (рис. Р.3.170). Из &SON находим ON—lsmp,
11-363
3.454.
решив которую
a
AC=22 sin p tg -. Значит,
KN , a KN
---=tr - или--------
KM 2 KN+KM , . a
i+tg2^
, a „ , a
‘^2 KN ^2
a
l+tg2^
Наконец, &PKN~ ASON, откуда
SO=lcosp. Так как M и N — точки касания
оснований трапеции с окружностью основа-
ния конуса, то MV=2tW=22sin/J. Проведем
CE’iMN; тогда CE=MN=21sinр. Из ACAD
СЕ 21 sin р
находим CD=-_—=—;------ и, значит,
sma sina
AD+BC 4Psn2p
Sabcd**--~---• MN=CD :.
2 sma
KN BC
Далее, &BKC~ &.AKD, откуда -^77=—-
KM AD
Для нахождения AD и ВС составим систему
уравнений
получим
4/ sm р
AD+BC=2CD=-—
sma
AD—AC=2D£=2ECctga=4/sin/? ctga,
2/sin/?
JD=---
sma
a
(1 + cos a)=2/sin/? ctg -,
, a
*2
KN
2ON , a
i+tg2-
а
=smatg-.
PK_KN
SO~ON
или
РК a
-----=sma tg -,
IcosP 2
т.
e.
a
PK=lcasp sina tg -. Окончательно находим
1 1 4P sin2 P a 2 a
^шгр=- Sabcd PK=~----;----Icosp sma tg-=- Psm^sin2A tg -.
3 3 яп a 23 2
□ По условию, SABC — правильная треугольная пирамида, SO — ее высо-
та, АВ=а, двугранный угол ВС равен ос, К—центр шара, касающегося
основания и боковых ребер (рис. Р.3.171). Так как точка К равноудалена от
боковых ребер, то KeSO. Проведем SD1.BC, тогда OD1.BC и L SDO=x. Из
£к/3
&SOD находим 5O=ODtga=- tgoc, а из &SOA получим
fe2 а2 а /-----------------------s---
у +— tg2a=- V3(tg^a+4). Пусть Е— точка каса-
ния шара с ребром SA; тогда КЕ^КО. Положим KO=R. Так как
£lSEK~&SOA, то
SA
EKSK
~OA~~SA
или
ЗА (SO—R) 6
—= =—, — или
/гц/З \
(—- tga—A ) 6
3A=------ - '—.
>/tg2a+4
Выполним дальнейшие преобразования:
306
3.455.
3.456.
3.457.
5
Рис. Р.3.171
3AA/tg2a+4 = Пд/з tg a—6 А; ЗА f5/tg2a+4+2)=ац/з tg a;
К _ tg a _ а-/з _
3 (-s/tg2 a 4-4 + 2) 3 (5/14-4 ctg2 а 4-2 ctg a)
Пл/з(5/I +4ctg2 a—2ctgа) о^/з
a—2ctga). В
, . , a . (it a\
я<г sir - sn-----
2 \3 2/
/я а\
9sin I -+- ]
\3 2/
□ По условию, SABC — правильная треугольная пирамида, SOS-(ABC),
SO=H, LSAO=a (рис. P.3.172); требуется найти радиус вписанного шара.
Пусть К — центр вписанного шара; соединив К и точку D касания шара
с боковой гранью, получим &SKD~ ASOAj (так как LSDK= lSOA1=<#)° ,
KD SK
LDSQ — общий угол), откуда------=----. Пусть KD=r\ тогда Я— г. Из
OAi SA}
A SO А находим AO = Hctga,
— 5/4 4-ctg2 а. Следовательно,
2г _ 2(77—г) г _ Н-г
Hctga 77^/4 4-ctg2 а ct8a 5/44-ctg2 а ct8a 5/4 + ctg2 а+ctg а
Итак,
Hdga Helga (^44-ctg2a —ctga)
г=—-— —-------=------------------------=
V44-ctg2 а 4-ctg а 4
_ /7ctg2 a (^/itg^a+T -1)
а из получим
SAt
Н
□ По условию, SABC — правильная треугольная пирамида, АВ=а,
(_АВ=а, MNKMiNxKi — прямая призма, вписанная в пирамиду, Mlt Nlt
307
5
Кх лежат на апофемах, М, N, К лежат в (АВС), О — центр вписанного
в пирамиду шара и О&М^К^ (рис. Р.3.173). Проведем SO.L(ABC); тогда
&SOD~ &N1ND, поскольку NNt ||SO, LSDO— LSFO= LSEO^a. Из подо-
NN. ND оф „ „
бия треугольников следует SO = ODtga =
г.
aJ3 а 2 a-J3
=—tga, = ; ND=OD-ON=-~------x, где
6 2 6 6
x=ON. Подставив эти значения в пропорцию, получим
г- а Лк/з \
aV3tg- -6 —------х) -6
2 \6 / г- а г-
---- ------------—L—; а>уз tg -=0^/3 tga— 6xtga, откуда
ба^/З tga ayj3 2
r- I a
3 I tga-tg-
6 tga
а а
6 cos a cos-sin a 12 cos2 -
Далее имеем l\OMN~t\OED (равнобедренные треугольники с равными
„ MN ON
углами при вершине); значит, =—, 0ТКУДа
ED ON
MN=-—---
OD
Окончательно находим
, г- г- а - a
a2^/3 a^3tg- a3 sm -
V^S^unk- NNt=------------=-------.
64cos4--6 128cos’-
2 2
308
. т + п п 2
3.458. 2arctg6/---.3.459.—= .
V т 2 2>/l+ cos2 а
3.460. □ Изобразим сечение фигуры плоскостью, проходящей через центр К впи-
санного шара и апофему DD2 усеченной пирамиды. В сечении получим
трапецию ADD2A,, в которую вписан круг с центром К, касающийся
апофемы DD2 и оснований трапеции в точках О и О2 — центрах окружно-
стей, вписанных в основания усеченной пирамиды (рис. Р.3.174). По усло-
вию, 5Шара: 5уС.пИр=п : 6>/3; требуется найти угол между боковой гранью
и плоскостью основания. Введем следующие обозначения: /_Л11)Л = а,
КО —Г, OD = Rt, ТОГДа *^шара = 4лт2, *^ус.пир =
=рЛ + Л> DDi + S1+S2, где Л = 6ЯгА Р2 = 6А2л/з, S, =ЗЯ?,Д
S2 = 3R2-j3, DD1=Rl+R2 Таким образом,
•Syc. пир = 3^3 (Я1+Я2)(Я]+Я2) + ЗЯ?5/з+3/&/з =
= 3^3 (2А2 + 2Л1Л2+2А2) = 6^/з (A?+A2A2 + Af).
2г
Проведем 02Е\\002 и из ^D2ED найдем DD2=-—, £D=2rctga. Решив
sin ос
{2г
Л2+ R2 ; , г
sm а получим = —— (1 + cos а),
Rt —A2=2rctga, sma
R2=-'- (1 —cosa). Тогда
sma
*5тс (О +cosa)2+(l - cos2 a)+(l - cosa)2)=^|^- (3+cos2 a).
F sm2a sura
я 4w2sin2a я , . ,
Так как------=—то ——---------------=—откуда 3+cos a=4sm a;
•5ус.пир 6y/3 6y3 r2(3+cos2a) 6уЗ
3sin2a+4cos2a=4sm2a; tg2a=4; tga=2, a=arctg2.
3.461. - и arctg2. 3.462. arctg 3463. arctg—~=; k>-.
4 6 2я .Jlk-3 2
я я
3.464. -. 3.465. -.
3 3
ГЛАВА 4
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ ПО ГЕОМЕТРИИ
4.001.'□ Пусть Р, N и К — точки касания вписанной окружности со сторонами
Д.АВС (рис. Р.4.1). По условию, КВ=п, СК**т, где п>т. Положим АВ=х;
тогда AN**AB—NB=x—n. Согласно теореме Пифагора, имеем
х2 = (х—л+т)1 + (т + п)2=>х? = х2 + п2 +т2 — 2хл + 2хт—2тп+т2 + 2тп +
„ , > т2+п2
+л2 =» 2(л-т) = 2(т2 +п2). Итак, АВ=х=-.
л—т
4.002. □ Пусть а и b — катеты, с — гипотенуза прямоугольного треугольника.
Согласно условию, а+Ь —8, т. е. Z>=8—а. Предположим, что с=5; тогда
получим уравнение а2 + (8 —а)2=52 или а2+64 —16а + а2 —25 = 0 или
2а2— 16а+39=0. Но 21/4=64—2 • 39<0 и, значит, это уравнение не имеет
корней. Итак, длина гипотенузы не может быть равной 5 см. В
ab + bc+ac
4.003. □ Докажем, что ----------= 22? (рис. Р.42). Воспользуемся теоремой
а b с
синусов:-----=-----=------=2R, откуда
sin Л sinB sin С
ас ab be
---------------------2R. (1)
с sin J a sin В bsmC
1 1
Ho Вдлвс=_ aisin C=- aha, откуда ha=b sin С (это также непосредственно
2 2
видно из рис. Р.4.2); аналогично, hi,=csm A, 2ie=asinB. Тогда из соотноше-
ний (1) находим ab = 2Rhc, bc=2Rha, ac=2Rht. Сложив эти равенства,
получим
ab+bc+ac
ab+bc+ac=2R (ha+ht, + hc) или-----= 2Я.
ha+h^+hc
4.004. □ Пусть в А А ВС (рис. Р.4.3) АВ=х, ВС=х+5 и ЛС=х + 10, где х>5.
Согласно теореме косинусов, имеем (х+10)2=х2+(х+5)2—2x(x+5)cosB,
х2- 10х+75 (х+5)(х—15) х—15
откуда cosB=---------=------------=-----. Так как 0<cosB<l, то
2х(х + 5) 2х(х+5) 2х
Рис. Р.4.3
310
х—15
0<-----<1. Наименьшим значением х, при котором выполняется это
2х
неравенство, является х=15. Поэтому наибольшее число, обладающее
указанным в условии свойством, есть х + 10=25.
4.005. □ По условию, BD^DC^a, i_BAD=* l_CAD=a (рис. Р.4.4); требуется
доказать, что ДЛВС — равнобедренный. В &.ABD и &ACD по теореме
косинусов имеем a2=c2+m2—2mccosa, o2=62+m2 — Imbcosa. Вычитая
одно выражение из другого, получим (с2—Ь2)—2т(с—6)cosa=0 или
(с—b)(c+b— 2mcosa)=0. Так как c+b—2?ncosa#0, то с=Л>, т. е. ААВС —
равнобедренный.
4.006. □ Согласно условию, в ДЛВС (рис. Р.4.5) АВ=2а, ВС=За, АС=4а.
AD АС 4а 4
Используя свойство биссектрисы треугольника, находим — =—=-=-.
4 8а 3 6а
Так как AD + DB=2a, то AD=- 2а =—, BD=~ 2а=—. Но ВО — биссек-
7 7 7 7-
ОС ВС За 7
триса в &DBC и, значит, —=—=--------=-.
OD BD 6а/7 2
4.007 12, 15 и 18 см.
4.008. □ Находим (рис. Р.4.6) AH=HD = J15-24=1 (см), т. е. /LD =2 см. Далее
ВС АВ 5
имеем —=—=-. Известно, что квадрат длины биссектрисы выражается
DC AD 2
формулой BD2=AB • ВС—AD • DC (см. «Дополнительные соотношения
между элементами фигур», гл. 1, п. 5°). Таким образом, 25=5 • 5х-2 2х
25 50 8 5-25 20
или 25=21х, откуда х=—. Итак, ЛС=2Н—=4 — (см), ВС=---------=5 —
21 21 21 21 21
(см).
4.009 бООл/3 см2.
4.010. □ В &АВС (рис. Р.4.7) имеем АС=с sin а, ВС=с cos а, BD=x, AD—c—x,
х ccosa
I — биссектриса угла С. Так как--=-----=ctga, то x=cctga—xctga,
с—х csina
с с tga ccosa csina
откуда x=-------=---------, c—x=----------. Теперь воспользуемся
1 +ctga sina+cosa sina+cosa
формулой l=yjAC BC—AD DB и получим
/ <?sinacosa / (sina+cosa)2—1
Z= / c2 sin a cos a-------- =c / sin a cos a---------—~ =
\ (sina+cosa)2 \ (sina+cosa)2
311
Рис. Р.4.6 Рис. Р.4.7 Рис. Р.4.8
'sin 2а sin 2а
с sin 2а
с sin 2а
= с
с sin 2а
2 cos (45° — а)
2 l+sin2a
+ COS
• 2 cos2
4.011. □ Пусть АС=х (рис. Р.4.8); поскольку l_OAF= LAOF=45a, имеем
х Зх
OF^AF=~. Но BO=2OF=x, откуда 5F-—. Полагая LABF=P, находим
2 2
AF х/2 1
tg£=—=—=-
BF Зх/2 3
4.012. • Воспользоваться формулами та=- •J2(b1 + cl)—a2, ть=
=- Л/2(а2+с2)-62, тг=-Л/2(а2+А2)—с2 (см. «Дополнительные соотно-
шения между элементами фигур», гл. 1, п. 2°).
4.013. — 1/к. 4.014. Части равновелики. 4.021. 45. 4.023. Прямую, перпендикуляр-
ную основанию и проходящую через его середину. 4.024. [5/5/2, 5]. 4.028. 4, 5, 6,
7 и 8 см. 4.029. Точка пересечения биссектрисы угла В и перпендикуляра DO
должна лежать вне ДЛВС. 4.(130. а) Тупоугольный; 6) прямоугольный; в) невоз-
можен; г) тупоугольный. 4.031. 1,5 см. 4.033. <^/4. 4.035. Л/3. 4.037. а. 4.040. Из
точек дуги окружности, опирающейся на этот отрезок, для которой данный угол
является вписанным.
4.041. □ Предположим сначала, что a — острый угол, противолежащий обшей
стороне всех треугольников (рис. Р.4.9). Рассмотрим одни из таких тре-
угольников и проведем его высоты из концов этой стороны. Тогда, если
ортоцентр лежит внутри треугольника, то угол между Высотами равен
180°—а. Отсюда следует, что множество ортоцентров представляет собой
дугу окружности, хордой которой является общая сторона всех треуголь-
ников. Так как угол между высотами опирается на дугу, равную 360°—2a,
то множество ортоцентров — это дуга, равная 2a. Если же ортоцентр
находится вне треугольника, то угол между высотами равен а. Этот угол
опирается на дугу 2a, т. е. множество ортоцентров лежит на продолжении
той же дуги окружности. Итак, искомое множество точек — это дуга
окружности, равная 360°—2a.
В случае прямого или тупого угла треугольника рассуждения анало-
гичны.
312
Рис. Р.4.9
4.042. * Воспользоваться тем, что если а — данный угол, то угол между биссек-
а
трисами, проведенными к боковым сторонам, равен 90°-I—.
4.043.
□ Так как в ДОЛО, все стороны равны R, то ДЛ 0.5=120° (рис. Р.4.10).
1 1 R1 /з J
Находим A2sin 120°=- R1 sin60°=—-—, ScxrT^oB=- яА2, отку-
1 Л2 /з
да 5<етм=- яА2----—. Итак, площадь общей части двух кругов составля-
3 4
4.044.
А2УЗ_А2(4Я-ЗУЗ)
3 2 6
АЕ АС
□ Поскольку ДЛ2>С~ i^ABE (рис. Р.4.11), имеем —- =—, где АВ=ВС =
АВ AD
10 + х 14
= 7, АО = 10. Пусть В>Е=х; тогда ----=—, откуда 100 + 10х=98, т. е.
х = — 0,2. Такое значение х свидетельствует о том, что точка Е расположена
AD АС 10 14
между А и D, т. е. —=— и, значит, —=——. Отсюда находим
АВ АЕ 7 10-х
х=0,2.
4.046. □ Построим окружность радиуса 1, опишем около нее квадрат и впишем
в нее правильный шестиугольник (рис. Р.4.12). Имеем А*=4(1 + 1)=8,
А6 = 1 6=6, С=2я. Так как Р6<С<РМ то 6<2я<8, откуда 3<я<4.
4.047. □ Пусть С} —середина дуги АВ (рис. Р.4.13). Проведем через точку С,
касательную А1В1 к окружности и рассмотрим подобные треугольники
Рис. Р.4.12
313
4.049.
4.050.
4.055.
4.060.
АОС и A^OCi. Имеем 1г, где ОС=^ОА2-АС1 = у/б1-\,52 =
ОС\
=л/4.5-7,5-1,5>/15 (см), ОС, = 6 см, АС =>1,5 см. Следовательно,
6. 1,5 6 г— г—
AlC^----—==-== = 0,45/15 (см), AiBi«=0,8vl5 (см). Теперь найдем
' 36 6•4 г—
З64—=—= = 1,65/15 (см). Таким образом, полу-
15 5/15
периметр треугольника составляет р=-(3,2^15+0,85/15) = 2-5/15
(см), а его площадь S=^ OCt AtBt=^ 6 • 0,85/15 = 2,45/15 (см2). Нако-
х 5 2,45/И , „ , ч _
нец, используя формулу г=-, получим г—-—-=1,2 (см).
Р 2/15
□ Проведем радиусы ОМ, ON, OP и OQ в точки касания окружности со
сторонами четырехугольника (рис. Р.4.14). Из равенства треугольников
АОМ и AON, BON и ВОР, СОР и COQ, DOQ и DOM заключаем, что АО,
ВО, СО и DO являются биссектрисами углов А, В, С и D. Значит, /_АОВ=
= 180°—а—/1, LCOD= 18О°-у-<5, LAOD = 18О°-а-<5, LBOC= 180°-/?-
— у, откуда 1.АОВ+ L COD = 360° — a—ft—у—6. Но а+Д+у+5=
=^(LA+ LB+ LC+ LD)= 180°. Итак, LAOB+ LCOD = 180°.
Пусть LBDC=x\ тогда LBOC=2x (рис. Р.4.15). Следовательно,
1_ОВС=ЧО° —х, т.-е. LOiBC=40°—х (в силу симметрии точек О и Ot
относительно стороны ВС). Найдем сумму углов &АВС:
180°—х+180°—2х+180°—2х=540°—5х; тогда 540°-5х=180°, откуда
х=72°. Окончательно получим Z. ВЛ С= 180°—72° = 108°, ССВА = /_ВСА =
=|(180°-108°) = 36°.
0,2В 5/1O. 4.056. 45/2 м. 4.057. а. 4.058. 2а; п; 2я-2а.
□ Введем систему координат с началом в точке А(0; 0) и осями координат,
направленными вдоль сторон AD и АВ квадрата (рис. Р.4.16). В этой
системе вектор AM имеет координаты (0,5; 1), а вектор "aR — координаты
оа,=
(i;
0,5). Воспользуемся формулой cos а
Рис. Р.4.15
314
4.061.
= 0,5 • 1 + 1 0,5=1, MjH| = V0,52 + 12 = 0,5vf5, ^=т'12 + 0,52=0,5л/5-
1 4
Итак, cos а =---р----— = -.
0,575-0,575 5
□ Пусть х<а, у<а, z<a, ка— стороны выпуклого четырехугольника
ABCD (рис. Р.4.17). Диагональ АС делит четырехугольник на два треуголь-
ху . 2/ .
ника АВС и ACD, имеющих площади S^ABc=— sin В и S&Adc=~ яп2л
Следовательно,
ху . zt . ху zt а1 а1 „ , _
Sabcd=— sm5+j япП<у+- или SABCd<~^ +у> т. е. SABCD<a2.
4.0 62. □ Найдем площади /хАВС и ixBCD (рис. Р.4.18): S^ABC=^ ВС • Л,
•5ддс»=- ВС Л, где h=BK, т. е. •5дядс=5ддсд- Но
>5длов“5длвс—5ддос, 5дсов=>5длсл—$ьвос и, следовательно,
SbAOB^SbCOD-
4.0 63. □ Проведем СК1АВ и DL1AB (рис. Р.4.19). Пусть 2>С=а, КВ=х; тогда
AB=2x+DC или За=2х+а, откуда х=а. Теперь воспользуемся условием
cos ДЛ5С=-Д=, откуда следует, что CB=a-j5, СК=^]с£1 — КВ1 = 2а. Да-
75
лее из txAKC находим ЛС=->/лХ2+СХ2=->/(2гг)2+(2гг)2=2ггТ/2. Так как
АО ЛВ 3 1
&AOB~ &DOC, то и> значит> ОС=- АС=—Наконец,
а2 а2
в t^DOC имеем РО2+ОС2=—I—=а2=РС2, т. е. DOLOC. В
2 2
Рис. Р.4.18
315
е x^ 4.064. □ Пусть сторона AB пяти-
л • угольника ABODE равна 30 см
(рис. Р-4.20). Далее, пусть ВС=
<у =х" тогда CD=x+2, DE=x+4,
yr ______________________ЕА = х+6, где xeZ, х < 7. Для то-
' д го чтобы получился пятиуголь-
А ник, необходимо выполнение не-
Рис. Р.4.20 равенства х+х+2+х+4+х+
+6>30 или 4х>18, откуда
х>4,5. Таким образом, из усло-
вия 4,5 <х<7 находим целочисленные значения сторон: 5, 7, 9, 11, 30; 6, 8,
10, 12, 30; 7,9, 11, 13, 30. И
4.065. □ Для того чтобы сложить паркет из правильных равных многоуголь-
ников, нужно, чтобы их углы примыкали друг к другу и в точках соприкос-
новения составляли бы в сумме 360° (рис. Р.4.21, а—в). Угол правильного
х (л-2) 180°
л-угольника определяется по формуле а=-------. Так как к каждой
л
360°
точке соприкосновения должны прилегать к многоугольников, то а=-.
к
„ (л-2) 180° 360° L L 2л
Следовательно,--------=—-— или пк— 2к=2п, т. е. к=
л к л —2
1) Если л = 3, то jt=6; в этом случае а=60°, т. е. паркет составлен из
правильных треугольников.
2) Если л=4, то к=4; тогда а=90°, т. е. паркет составлен из квадратов.
3) Если л=5, то соответствующее значение к не является целым; значит, из
правильных пятиугольников паркет составить нельзя.
4) Если л=6, то jt=3; тогда а = 120°, т. е. паркет составлен из правильных
шестиугольников.
Очевидно, что значениями л = 3, л=4 и л=6 исчерпываются все подходя-
щие случаи.
_ 360° Я2 360°
4.066. □ Имеем 1_АОВ=----и, значит, 5длов=— sin---(рис. Р.4.22). Таким
л 2 л
Я2 . 360° ЗА2
образом, получаем равенство — яп---=---, которое выполняется при
2 п п
л = 12.
4.067. □ Возьмем произвольную точку М внутри правильного многоугольника
(рис. Р.4.23). Соединим ее с вершинами многоугольника и опустим перпен-
дикуляры из М на стороны многоугольника. Тогда для площади много-
угольника получим выражение
111а
s=2 вЛ1+2 ЯЛ2 + -+2 ^я = 2 (А1+Л2 + — +л»)-
Рис. Р.4.21
316
С другой стороны, площадь многоугольника равна произведению его
полупериметра на апофему: S=ph. Следовательно,
(Л1+Л2 + ...+Лл) или у А = | (Л! + h2 +... +Л„).
Итак, Л] +Л2 + ... + Л„ = ла.
4.068. □ Пусть ABCDE — правильный пятиугольник (рис. Р.4.24). В нем углы
(5—2) 180°
при вершине составляют ---------= 108°. В ДЛ5С проведем BFLAC; так
как Z.С = Z.BCJ=^ (180°—108°) = 36°, то 1_АСЕ= 108°-2 • 36° = 36°,
CF=acos36° и . ЛС=2дсо8 36°. Далее находим S^abc—-^ n^sin 108° =
=|a2sin72°, £длсе=^ AC2 sin LACE=^ (2а cos 36°)2 sin 36°=о2 cos 36° sin 72°.
Итак,
S&ace д2 cos36° sin 72°
25ьлвс я2 sin 72°
=cos36°®0,81.
, (л — 3)л
4.069. □ Число диагоналей л-угольника определяется по формуле а=—-—.
Нам нужно выбрать только те значения d, которые удовлетворяют усло-
(л—3)л , ,
вию d<n. Тогда л>—-— => 2л>л —Зл => п — 5л<0, т. е. число л при-
надлежит промежутку (0, 5). Так как л — это число сторон многоуголь-
ника, то л>3 и окончательно получаем, что требованию задачи удовлет-
воряют только значения л=3 и л=4.
4.070. 20. 4.071. ЗА2. 4.072. В пятиугольнике. 4.074. 3. 4.075. 16 см. 4.076. 4 и 11 см.
4.077. 12 см. 4.078. 7,2 см2. 4.079. 2(S' + S2). 4.081. Р/4.
4.084. □ Возьмем на прямой р какую-либо точку А и соединим эту точку
с любыми двумя точками Bt и В2 на прямой q. Таким образом, ABt
и АВ2 — две пересекающиеся прямые, которые пересекают обе данные
скрещивающиеся прямые.
4.085. □ Имеем ОХА = jQY+QY + 12=2у> °i£= + (рис.
л/б-л/5
Р.4.25), откуда О'А — ОХЕ=---------.
317
Рис. Р.4.26
4.086. □ Пусть ребро куба равно а; требуется найти угол между диагоналями
А,В и В,С (рис. Р.4.26). Этот угол равен углу между прямыми 2),С и BtС,
поскольку 2>]С||AtB. В &B1D1C имеем В^ =D1C=B1C=ay/2 и, следова-
тельно, LBiCD1=60°.
4.087. □ Имеем (рис. Р.4.27) DE=^a (а— ребро куба), а1,
11 1 1 Vacde ]
Vacde=- т ° • т °’- ^ба=а3- Значит, —------.
j 2. 2. 12. V губя * ~
4.089. □ Для построения данного трехгранного угла с плоскими углами а, Д,
у (рис. Р.4.28) необходимо, чтобы были выполнены следующие условия:
Р~а=у— Д=50°, а+Д+у<360°, а+Д>у. Так как числа ос, Д и у составляют
геометрическую прогрессию, то а+ос+50° + ос+100°<360° или За<210°,
т. е. ос<7О°. Но ос+ос+50°>а+100°, откуда ос>50°. Учитывая, что ос — це-
лое число, получаем ответ: 5 Г.
4.090. Окружность^вляющуЮся основанием конуса с высотой а и образующей 6;
высота конуса перпендикулярна данной плоскости, а вершина находится в фик-
сированной точке этой плоскости. 4.091. 20. 4.094. а^/2/2. 4.095. Да, если парал-
лелограмм является прямоугольником; да, если параллелограмм является ром-
бом. В том случае, когда точка равноудалена и от вершин, и от сторон парал-
лелограмма, он должен представлять собой квадрат. 4.096. Около нее можно
описать окружность, т. е. трапеция является равнобедренной. Для такой трапеции
искомое можество представляет собой перпендикуляр к плоскости ее основания,
проходящий через центр описанной около трапеции окружности. 4.098. Проекци-
ей ребра является биссектриса соответствующего угла основания. Эта проекция
совпадает с диагональю основания, если основание представляет собой ромб.
Рис. Р.4.27
318
4.099.
4.100.
1 :
□
11.
По условию, SM=MC (рис. Р.4.29); требуется найти LAMB. Пусть
ау/з
а — ребро правильного тетраэдра; тогда в LAMB имеем АМ=МВ=——,
откуда по теореме косинусов получим АВ2=AM2+МВ2 —
За2 За2 За2
— 2 AM MB cos LAMB или сг=----1----2 — cos LAMB. Следовате-
4 4 4
(За2 За2 1 1
льно, cos LAMB=i-----а : —=-, т. е. LAMB-arccos -.
\ 2 ) 2 3 3
□ По условию, высота SOl =h (рис. Р.4.30) является переменной. Извест-
/ h\l S&ABC
но, «гто —---==( - , т. е. 5дл1я1с1 , где S&ASc иН — вели-
S&ABC п
чины постоянные в данной задаче. Таким образом, зависимость между
площадью сечения и расстоянием от вершины до секущей плоскости
S&ABC
выражается квадратичной функцией видаfix^kx2, где к=—- >0 — па-
Л
раметр, a x=h — переменная, причем 0<х<оо.
4.102. 1. 4.103. 1 : 7. 4.104. 5040 см2.
4.105. □ По условию, в правильной четырехугольной пирамиде SABCD (рис.
Р.4.31) SO=H, LDFB=a. Пусть ОВ=х; в LDFB имеем LDFO=
a OF SO
и OJ7=xctg-. Так как lOFC~ LSOC, то откуда
2 С/С «эС
ОС SO хН а г
SC=———=-----------=7/tg-. Искомый радиус найдем как радиус окру-
4.101.
OF а
xctg-
жности, описанной около
. abc
LSAC. Используя формулу R=—, получим
45
Л_ SC2 AC SC2
~4 0,550 AC=2SO
4.106. 60°.
1
----------=- Н tg?
2Н 2 2
319
A
Рис. P.4.31
4.107. □ Пусть a — ребро пирамиды SABC, 0M=r — радиус вписанного шара,
Ол/З
SH=h — высота пирамиды (рис. Р.4.32). В &SAF имеем SF=—
^Зо* За* а^/б
4 Тб =ПГ’
ffF=^AF—^~; следовательно, h = SH=
2 aj3
Так как FM=FH, то SM=AH=- AF=—~. Тогда из &SM0 находим
3 3
а1 . 2а2 2агл/б ,
или--НГ=----------1-г, от-
3 3 3
SM2+OM2=SO2 или — +г* = ( ------
3 \ 3
Ох/6 „ г ау/б aJ6 1
куда г=——. Итак, -=—— :-----=-.
12 А 12 3 4
4.110. 60°. 4.111. я/4; я/2; arctg 2; arctg 2. 4.113. В данный четырехугольник можно
вписать окружность. 4.114. бд/435 см*. 4.115. 1 : 3. 4.117. А/2^15'25\/3. 4.119. Нет;
на перпендикуляре к плоскости основания пирамиды, проходящем через центр
описанной около этого основания окружности.
4.121. □ Сектор развертки конуса имеет угол 90° и радиус А = 1; следовательно,
его площадь S1 = nR Площадь боковой поверхности конуса 5,=
4 4
=ttrl=nr (так как /=Л = 1). Но S1=S2 и, значит, -=яг, откуда г=~. Теперь*
4 4
я я 5я
находим площадь полной поверхности конуса: S=S2+5осн=- Н— =—.
4 16 16
4.123. □ Пусть а2 — сторона правильного треугольника АВС, представляющего
собой осевое сечение конуса (рис. Р.4.33); тогда =-^-----радиус вписан-
6
ной в &АВС окружности. Проведем касательную A^WAC и получим
C,D
другой правильный треугольник A iBC^ Так как СС2=—=
_ <3 а1Ч/3 J3 2а2 2а, а. ~
= 2г. : -у--=—— : =—,то а2=ВС,=а,----------=—. Это значит, что сто-
1 2 3 2 3 2 1 1 3 3
рона каждого следующего правильного треугольника в 3 раза меньше
320
стороны предыдущего и поэтому радиусы вписанных в них окружностей
1 1 1
находятся в том же отношении: ri—~ г3=- г2’ —* r"=j гя-1..Соот-
4
ветственно объемы вписанных в конус шаров составляют Р\=-пг3,
4 4 /г \з 1 1
F,=- яг?=- я (— ) =— К, Vn—— К»-1 Итак, объемы вписанных
3 3 \3/ 27 1 27
шаров образуют бесконечно убывающую геометрическую прогрессию со
РУ ' ' . V. 27^
знаменателем I - I , сумма которой равна-7р\з~ 26 ’ Т' е*
1-W
_ т, тл 27Г, 27 4 , 27 4 3^3 al italjj
Y=V1 + V2 + ... + V„+...=-—*=- • - nrl = - • - я . -
26 26 3 26 3 6 32
tt T, 1 яа’х/З
Поскольку ихон=- n [ у 1 2~—24 ’ окончательно нах°Дим
У nalyft _ 6
V^n~ 52 24 ~13’ И
4.124. □ Пусть OA = R и О1В=г — радиусы оснований усеченного конуса,
а МО=х и NOx=y (у<х) — радиусы вписанных шаров (рис. Р.4.34). По
а
условию, х+у=/, Z_J = a. В &.АОМ и ixBO2N имеем A = xctg-,
{ а\ а
r=yctg I 90°—-j=y tg - (1). Далее, в трапеции FHNM проведем NK^HF-,
так как NM=l, КМ=х—у, l_NMK= LBAO — x,
то из &NKM получим х—y=/cosa. Таким об-
fx+y=f,
разом, приходим к системе < , откуда
|х—y=/cos a,
/+/cosa l—lcosa
x =-------, y=-------. Подставив найденные
2 2
значения в равенства (1), окончательно находим
а
/(1+cosa) ctg—
a 2 , , а a
R=X Ctg -=--------------= /cos2 - ctg -,
a
/(l-cosa)tg-
a 2 , . , a a _
r=y tg -=------------=/sm - tg -.
4 /я \ (it \ я
4.125. —cos I-+а) cos I — a I. 4.126. - —2arctg /--------—----, k^2. 4.127.
3 \ 6 / \6 ) 2 4 * 6 V 2k
2arctg
,0<£<2.4.128. яТЗ:2.
ГЛАВА 5
ПРИМЕНЕНИЕ КООРДИНАТ И ВЕКТОРОВ
К РЕШЕНИЮ ЗАДАЧ
5.001. >>±0,5715=0.
5.002. □ По условию, АЁ—кТВ => АВцТВ (1). Находим координаты векторов
АВ и ТВ (рис. Р.5.1): ~ЛВ (1; —2), ТВ (х+4; у), где х и у — координаты
1 — 2
точки D. Из (1) следует, что-=— илиу= —2х—8 (2). Так как трапеция
х+4 у
ABDC — равнобедренная, то |ЛС| = |Ш)| и ЛС^ВВ. Найдем векторы
АС (—6; —1), ИВ (х—3; у + 1) и воспользуемся тем, что ЛС2=~ВВ2; имеем
36 + 1 = (х—3)2+(у + 1)2 или х2+у2 —6х+2у=27 (3). Решив систему уравне-
ний (2) и (3), получим Xj = —1,4, yj = — 5,2 или х2=—3, У2= — 2. Этим
значениям соответствуют два вектора: ИВ (—4,4; —4,2) и ~ВВ (—6; — 1).
Последний вектор коллинеарен АС и, значит, не удовлетворяет условию.
Итак, получаем ответ: D (—1,4; —5,2).
5.003. 5х-у + 7 = 0. 5.004. у=0, у = 2л/з, У=х^3, у=-<Уз(х-10). 5.005.
(x-3,5)2 + (y±V10)2= 12,25. 5.006. у= -х^3 +{3 + 2^3); 6 + 3,5^3 кв. ед. 5.007.
(-1;2); 13 кв. ед.
5.008. □ По условию, АС=15 см, ДО=8 см, откуда находим координаты вер-
шин ромба: А (—7,5; 0), В (0; 4), С (7,5; 0), D (0; —4) (рис. Р.5.2). Угловой
4
коэффициент прямой ВС есть ki =tg (_BCN= — tg l_BCO= —— =
8
= ——. Тогда, зная координаты точки В, составим уравнение стороны ВС:
8
у—4= (х—0) или 8х+15у—60=0. Уравнение стороны AD найдем по
8
известному ее угловому коэффициенту к2 = —— (так как AD\\BC) и коор-
8
динатам точки D: у+4= — — (х—0) или 8х+15у+60=0. Далее, угловой
4 8
коэффициент прямой АВ есть jt2=tg 1_ВАО=— =— и уравнение стороны
А В записывается в виде 8х — 15у+60=0, а уравнение стороны DC — в виде
8х—15у—60=0. Теперь проведем ОКЗ-ВСя для нахождения ОКвоспользу-
Рис. Р.5.1
322
11 ОС ОВ
емся тем, что 5лояг= ОС ОВ=- ОК ВС, откуда ОК=------. По-
д 2 2 ВС
.------ 7,5-4 60
скольку ЛС=5/7,52+41=8,5, находим ОК=—~—=— (см).
5.009. 4л/17/11; у=4х.
5.010. □ Согласно условию, А (2; 1), 5(4; 0) — известные, а С (х,; у2),
2> (х2; у2) — неизвестные вершины квадрата (рис. Р.5.3). Так как длина
стороны квадрата АВ=^21 + \1=у]5 и ВС=АВ, то ВС2=(х1— 4)2+yJ = 5
(1). Найдем угловой коэффициент стороны АВ. Для этого воспользуемся
формулой (5.4), записав ее в виде к=----, где (х; у) — координаты точки
х—х0
0-1 1
В, а (х0; у0) — координаты точки А; тогда получим к=-= —. Но
4 — 2 2
ВС А.АВ и, следовательно, уравнение ВС имеет вид у—0=2 (х—4), т. е.
у=2х—8. Далее, точка С (х2; у2) лежит на ВС и, значит, yi=2xl — 8 (2).
Решив систему уравнений (1) и (2), найдем две точки С (5; 2) и С (3; —2),
которые, как легко убедиться, симметричны относительно точки В.
Для точки С (5; 2) имеем Л? (3; 1), ~ВВ (х2 — 4; у2), откуда, учитывая, что
ACXBD, получаем лС • AD=0 или Зх2—12+у2=0 => у2 = 12—Зх2 (3). Кро-
ме того, ЯО2=(х2—4)2+у2=(Л/5)2+(Л/5)2 или (х2—4)2+у2 = 10 (4). Решив
теперь систему уравнений (3) и (4), найдем две точки D (5; — 3) и D (3; 3).
Чтобы отобрать нужную точку, воспользуемся коллинеарностью векторов
АВ и ТВ. Если D (5; — 3), то ТВ (0; — 5), АВ (2; — 1), т. е. TB^fAB и, значит,
точка D (5; —3) не является вершиной квадрата. Если же D (3; 3), то
CD (—2; 1), т. е. ТВЦАВ. Итак, точки С (5; 2) и D (3; 3) являются вершинами
квадрата.
Рассуждая аналогично, для точки С (3; —2) находим вершину D (1; — 1).
5.011. V33; V105- 5.012. (—24-Зл/3; -В ида (-2-3^3; -1); 9<Уз кв. ед. 5.013.
(-2/3; -2/3). 5.014. С (4; -1). 5.015. 1,5734. 5.016. (1,5; 1; 1). 5.017. 13; В (12; 5),
С (—5; 12), 2) (—12; —5).
5.018. □ Так как уравнение данной окружности имеет вид х2+у2=9, то ее радиус
равен 3. Точка касания В данной и искомой окружностей лежит на линии их
центров ОВ (рис. Р.5.4); поэтому радиус искомой окружности равен 1,5.
Наконец, центр М искомой окружности лежит на перпендикуляре к середи-
Рис. Р.5.3
323
не отрезка О А, т. е. абсцисса центра есть хм=0,5, а его ординату находим
т&ОМК (МКА.ОА) : yu=yj\,52—Q,52=y/2. Однако возможно иное рас-
положение искомой окружности, симметричное с изображенным на рис.
Р.5.4 относительно оси Ох; в этом случае точка М имеет ординату
Ум~ ~у/^--
Заметим, что ординату точки М можно найти другим способом. А именно,
воспользуемся тем, что точка касания В имеет координаты (1; ув) и что эти
координаты удовлетворяют уравнению данной окружности: l2+yj=9 или
ув=±2л/2; так как 3/ПОх, то МК^АВ, т. е. МК — средняя линия
в t^AOB и, значит, уи = + 5/2.
Итак, зная координаты центра М (0,5; ±>/2) и радиус г = 1,5 искомой
окружности, получим ее уравнение: (х—0,5)2+(у^^/2)2=2,25.
5.019. (х—1)2 + (у—1)2 = 1; (х—5)2 + (у —5)2 = 25. 5.020. (х-1)2+(у-1)2 = 1.
5.021. 4^2. 5.022. Зх+4у-15 = 0; Зх-4у-15 = 0. 5.023. (х+1)2 + (у-3)2 = 10.
5.024. □ Уравнение сферы с центром С (х,; yt; zt) и радиусом R записывается
в виде (х—хх)2+(у— yi)2 + (z—Zj)2=J?2 (1). Так как эта сфера касается
координатных плоскостей, то должны выполняться равенства
lxil=b’il = lzil=2? (2). Далее, координаты точки А (1; — 1; 4) удовлетворяют
уравнению (1), т. е. (1— xJ2+(— 1— yj)2+(4—zf)2=R2 или
1 —2х1+х] + 1+2у1 +у2 + 16 — 8Zj +z2—R2 = 0. (3)
Согласно условию (2), имеем х2 +y2+zJ=3J?2 и равенство (3) примет вид
18 — 2х1+2у1 — Sz1 + 2R2 — 0 или 9 — Xj+yj —4z1+J?2 = 0. (4)
Рассмотрим различные случаи расположения центра. Пусть хг>0, У!>0,
Zj > 0 (I октант), т. е. Xj =yi =Zj = J?. Тогда, подставив эти значения в равен-
ство (4), получим уравнение R2—4Л+9=0, которое не имеет решений
(/>/4=4—9<0).
Пусть теперь Х]<0, yj>0, zt>0 (П октант), т. е. |Х11=У! =Zj = R. Тогда
в результате подстановки этих значений в равенство (4) получим уравнение
R —2Л+9=0, которое также не имеет решений.
Последовательно рассматривая остальные координатные октанты, устана-
вливаем, что центр искомой сферы расположен в IV октанте, где Xj > 0,
у.<0, Zj>0 и х1=|у1|=г1=Я. В этом случае получаем уравнение
Я -6Я+9=0, откуда Rt =Я2 = 3,т. е. х. =3, у1= —3, Zj = 3. Итак, искомое
уравнение имеет вид (х—З)2 + (у+З)2+(z— З)5 =9.
5.025. □ Используя формулу (5.21), находим
<5л75й7 6-8+86 24
cos/.ЛОЛ. = - ---- =—.
1^11^1 ^ЗЬ + Ы- л/б4 + 36 25
31 5
5.026. а=arccos—=. 5.027. cosH=- — 5.028. 120°. 5.029. р (2; -1; 1).
5^41 V34
7
5.030. —=.
5^33
6 2 3
5.0 31. —; —. • Воспользоваться тем, что если х, у, z — координаты век-
7 7 7
тора а и a, fl, у — углы вектора соответственно с осями Ох, Оу и Oz, то
х у z
cosa=—, cosfi=—, cosy =—.
14 14 14
324
5.0 32. □ Пусть л — единичный вектор, сонаправленный с SB; тогда
_/ я п п\ _ /1 1 у/1\ __ г
п cos cos cos - 1 или — , а ОВ ( — 2; — 2; —2J2). Обозначив
\ 3 3 4/ \2 2 2 )
угол между SB и SB через а, находим
1 1 V2 Г
- S3 2(-2)+-2(~2)+ 2 (-272)
cos а = _ -- — 1,
|п| |ОВ| 1 4
откуда получаем ответ: а=180°.
5.033. □ По условию, |ВЙ|=|ВС|=а, (ЛЛ/];СЛ/2)=Д=60^гдеЛЛ/1 и CAf2 — ме-
дианы ДЛВС (рис. Р. 5.5); требуется найти (ВВ;ВС)=а. Воспользуемся
формулой
cos fi = ' (1)
ИМ,| |СЛ/2|
С помощью рис. Р.5.5 находим АМ-^ВМ^—Ла, СМг = ЁМг —ЛС. Следо-
вательно,
АЛГ1 СЬГ1='Ш1 ЛМ^-Лл В^-В1?7 ВС+ВВ ВС=
11 11 , /5 \
=- а • - a cosa—а • - a cosO— а a cosO + a . a cosa = tr I - cosa—1 I. (2)
2 2 2 2 ____ \4 J
Так как ДЛВС — равнобедренный, то АМХ = СМ1У откуда
1АЛГ}! '^ЛГ1\='А^21 = (Л^-Ла)2=ВМ\-2Л!Л[Ла + ВА1 =
а2 а \
-----2 - a cosa+a2=a2 (—cosa). (3)
4 2 \4 7
Подставив выражения (2) и (3) в (1), имеем
, /5 \ 5
a2 - cosa—1 I -cosa—1
\4 7 14
cos 60° =---------или - =-----,
№ \ 25
I—cosa) —cosa
\4 7 4
откуда cosa=—, т. е. a=arccos —.
14 14
Рис. Р.5.5
Рис. Р.5.6
325
5.034. 120°.
5.035. □ По условию, LBBC=9d°, ВО={\]31$) АВ, АВ=ВС (рис. Р.5.6); требу-
ется найти LABD=a. Для нахождения угла а будем использовать формулу
ИА ИВ 1
cosa=— Так как ВВ — медиана ДЛЛС, то ВВ=- (ВА+ВС), от-
|Е?| |5б| 2
куда ~ВА=2 "ВВ—ВС. Следовательно,
(25В-ГО)55 2ВВ2-ИС Ив
COSa = 12^—=; =----------- ------. (*)
IBAI |Е5| IBAI |ЛД|
Но BCJ.BB, т. е. ВС ВВ=0, а из равенства ВВ = (у/з!4)АВ следует, что
АВ=(4)^У)ВВ. Тогда равенство (1) примет вид
2ВВ2 V3
cosa=----=-----=—, откуда а=л/6. Н
(4^3)ВВ2 1
13
5.036. ——
2^43
5.037. □ Пусть В (Хр- уД С (х2; у2), В (х3; у3) — неизвестные вершины трапеции
(рис. Р.5.7). Поскольку точка Е (6; — 1) — середина основания АВ, имеем
3+Xj 0+у2
систему-----“6,-------=—1, откуда х2=9, у1=—2, т. е. В (9; —2). Но
2 2
ВС$Оу и, значит, х2=9, а уравнение ВС есть х=9. Далее, точка F (7; 2)
х3+9
— середина основания ВС, откуда ——=7, т. е. х3 = 5. Уравнение пря-
мой АВ имеет вид y+l=fc(x—6); так как Ае^АВ), то 0 + 1 =
=fc(3—6) => fc= —1/3. Поэтому ^= — 1/3 и получаем уравнение ВС:
1 1 13
у—2=—- (х—7) или у= — - х+—. Реш™ систему уравнений прямых ВС
1 13 4 / 4\
и ВС, т. е. х=9 и у=— - х-|—, находим у=-, т. е. С 9; - ]. Наконец,
3 3 3 \ 3/
ординату точки В найдем из равенства -------=2, откуда у3=~, т. е.
326
/ 8\ 4 10 / /8\2 10
D ( 5; -I. Таким образом, ВС»у2—у1=~ + 2^—, AD=/22+(-1 =“>
т. е. BC=AD и, значит, трапеция ABCD — равнобедренная. Положим
ADAS _____________________________________________________( 8\
l_DAB*=u. и воспользуемся формулой cosa=^^-p^. Имеем AD ^2;
8
2 • 6+- (-2)
_ ____ 3 1
АВ. (6; —2), |ЛВ|=2д/10 и, следовательно, cosa =-----=—=, т. е.
1
а=arcos —=. Н
л/10 ___
~СМ СВ
5.038. □ Пусть LMCB=a., l MCA = В (рис. Р.5.8); тогда cosa=^^~_^,
\СМ\ |СВ|
ГлГтЙ
cos 8=— Положим СВ—а, СА=Ь и найдем отношение
|СЛ| jCM]
cosa СЛ/• U5 • |ГЛ| А Г37 • U5
со8Д~ГЙ ГЭЙ |С5|~аГЛ TJ7’
В Д АВС проведем медиану CF и точку F соединим с М. Далее имеем
1 >/а2+А2 1
CF= - АВ—------, FM-- АВ (апофема квадрата), t_FCB= (_FBC= LB,
2 2 2
CM=TTF+FM (рис. P.5.8). Теперь находим скалярные произведения
ГтйГВиГЙГй.-
^^^(ст+^гв^.иг+ж^гг-
Jct+b1 1 aJa2+b2 aJa2 + b2
=----- . a cos В— BB, BC=-cos В—-
2 2 2 2
thja2 + b2
=-----(cos В+sin В)
cos (90° + В) =
(2)
и аналогично
__ __ b-ja2+b2
Гй ГЛ/=--------(cos Л + sin Л). (3)
Подставив выражения (2) и (3) в (1) и заметив, что cos В + sin В=
cosa
= cosH+sinH (так как Л + В=90°), получим---= 1, т. е. а=Д и, значит,
cos/J
СМ — биссектриса угла С.
5.039. □ По условию, SABCD — правильная четырехугольная пирамида,
SA=AB=a, MeSC, SM : МС=2 : 1 (рис. Р.5.9). Положим AD=m, ~AS=h,
AS=p и (DC; АМ)=<р. Искомый угол ф будем искать по формуле
dCaM _____ _______
cosg>=---: (1). Разложим векторы DC и AM по векторам т, п и р.
|5Г| 1Щ
Имеем DC=AB=n, AM=AD+DC+CM. Из
условия SM:MC=2:l следует, что СМ=
=- "U3, где "US=<a3—аС=р~(т+п). Таким об-
разом, лМ=т+~п+~ р—(т + п)=- т+~п+
3 3 3 3
1 _ _ __ -/2_ 2_ 1 \
-I- - р и DC AM = л|-т + -л-|--/>) =
3 \3 3 3 )
1_________ __ ______ _ _
=- (2пт+2п2 + пр). Но пт=0 (так как nlm),
п2=а2 и пр = а2 cos 60°=—; значит, DC АМ=
1 / а2\ 5
- I 2zr-l— )=- а2. Далее
3 \ 2/6
находим |Д?| = а,
/4418__________4____4 __ /8,1 Оу/13
1АМ\= - а2+~ а2+~ а2+~ тп+~ тр+~ пр = а2+-а2- =-.
\ 9 9 9 9 9 9 V 9 2 3
5^/13
Подставляя найденные выражения в равенство (1), получим cos<? =-,
__ 26
5^13
откуда <р=arccos-. Н
5.043.
8 1 а2 + (Р—е2 — Ь2
5.040. —=. 5.041. -=. 5.042. cosx=--------------, где ВС=а, АС=Ь. АВ=с,
5^/17 71° 2cf
DA—d, DB=e, DC=f.
□ Вектор а—Ъ имеет координаты (4; — 4; +J1). Пусть к (0; 0; 1) — единич-
ный вектор, направленный вдоль оси Oz. Полагая (а—Ъ; к)=у, находим
(a-3)JE 4^2 V2 _
cosy=_ - =—3.._r , т. е. у=45°.
5.044. arccos (1/V14).
5.045. □ Данные векторы сонаправлены, если х3 —1 и 2х имеют одинаковые
знаки. Для определения искомых значений х решаем неравенство
2х(х3 —1)>0 и получаем ответ: хе(—со, O)(J(1, оо).
5.046. дге(—оо, — l)(J(0, 2).
5.047. □ Данные векторы сонаправлены, если 5х—х2>0, откуда 0<х<5 (1).
Далее решаем неравенство |х—5| |а| <3 |а|. Учитывая условие (1) и то, что
Й>0, получаем 5—х<3, т. е. х>2 (2). Из (1) и (2) следует, что хе[2, 5).
5.048. уе(2/3, 3). 5.049. х= -5/4, у=8/5. 5.050. хе(-со, - 1)|J(5, со). 5.052.
(4^2; —2; 8) или (-4^/2; 2; -8).
5.053. □ Так как О — точка пересечения медиан ДЛВС (рис. Р.5.10), то
328
Рис. Р.5.10
Рис. Р.5.11
А0 = - АМ1, тогда АМ.=-а, М<С=АС—АМ,=Ъ—а. ВС=2М.С=
3 2 2
= 25 —За, Й5=АЩ + Л775=а- Ъ — а } = За-Ъ.
2 \ 2 J
5.054. □ Пусть AF и АК — медианы граней SAB и SAC, М и N — точки пересе-
чения медиан указанных граней (рис. Р.5.11). Тогда АР=-(аБ+~А$),
аИ=- (aC+AS). Используя свойство точки пересечения медиан треуголь-
ника, находим ZJF=- (Z5+L?3), а7?=- (A^+AS). Значит,
7^N=AN~AM=^ (7T+Z5-7E-ZS)=~ (аС-АБ) = ~ Ж. Итак,
MN=- БС; следовательно, МЩБС и |A/jV| : |5С] =-.
_ __ 4 2_
5.055. ББ = 2(Ь-а), AD=- Ъ— а.
3 3
5.056. □ По условию, АМ=а, АН=Ъ (рис. Р.5.12) и, значит,
__ _____ BM 1 DN 1 МС 2 NC 2
MN=AN—AM=Ъ—а. Так как-----=-, —=-, то----=-, —=- и угол
МС 2 NC 2 ВС 3 CD 3
С — общий у треугольников NCM и DCB. Следовательно,
2 3 т _
LNCM~ &DCB, откуда---=- н ББ=- MN, т. е. BD=~ (Ь—а). Пусть
BD 3 2 2
__ __ _ ___ _____ __ _ _ 3 _
AD—x, АВ=у. Имеем AD—AB=BD или х—у=- (b—a) (1). Далее,
АБ+ВМ~АМ или уч— SC=a, т. е. у!— х=а (2). Остается решить систему
уравнений (1) и (2); в результате получим AD=- Ъ— а, аБ~- а— Ъ.
8 8 8 8
а+Ъ _3 _
5.057. —=. 5.058. а=- Ъ - Зс.
2ч/з 2
329
Рис. Р.5.13
Рис. Р.5.14
5.059. □ Проведем ВКЦАС и DNHCB (рис. Р.5.13). Тогда
________ ___ _ Д __ |ГХ|
CD = CK+CN=mCB + nCA (1). Для решения задачи следует найти т = —-
ICSI
|ЕЁ| ND NA СК NA
и п=^=г. Так как &NAD~&CAB, то — =— или —=— или
|ГЙ| СВ С А СВ С А
СК CA — CN СК CN _______
—=----------или — = 1 ——, т. е. т = 1 — п (2). Но CD LAB => CD 75=0
СВ СА СВ С А
и, значит,
(л1С55+пСЛ)75=0; л»Г5 . А~В + пСА 75=0;
тИС ~ЕА — пАС 75=0; т |5С| |5Л| cos В—п \АС\ |75j cos А =0.
Сокращая на |75| и используя равенство (2), получим
(1 —л) |5С| cos В—п |7С| cosj = 0. (3)
ВС АС
С помощью рис. Р.5.13 устанавливаем, что cos£=—, cosH=-^; тогда
ВС2 пВС1 пАС2 ВС1
равенство (3) примет вид-------------=0. Отсюда находим л=—-
АВ АВ АВ АВ1
ВС1 АС1
и, значит, л1=1—--=---. Подставляя значения т и п в разложение (1),
АВ2 АВ2
ас^+вс2^
окончательно получим CD=-------.
5.060. □ По условию, A1A2A3A4Ai — правильный пятиугольник (рис. Р.5.14);
требуется разложить А2А3 по векторам АгА2 и А^А~5. Запишем очевидное
разложение А3А3=А2А3 +А3А3. Легко установить, что в правильном пяти-
угольнике Л5Л3|М1Л2, т. е. 7777=m7J77, и, следовательно,
___________ _____ ______
Л1Л3=л»Л1Л2 + Л1Л5 (1), где л: =-. (2)
Л2Л2
Пусть Л,Л2=а. Проведем Л4ХЛЛ3Л5 и в ДЛ3Л4Х имеем
180° (5-2)
А3К=А3А4 cos lKA3A4. Так как ДЛ3Л4Л5»-----------= 108°, то
330
Рис. Р.5.15
с
Рис. Р.5.16
180°-108°
/_ХЛ3Л4=----------=36°, откуда
AsA3 = 2A3K=2a cos36°.
(3)
Для нахождения cos 36° воспользуемся равенством sin (2 18°) =cos (3 • 18°).
Тогда, используя формулу cos3a=4cos’a—3cosa, получим уравнение
2 sin 18° cos 18°=4 cos’ 18°—3cos 18°. После сокращения на cos 18°#0 имеем
2sin 18°=4cos2 18°—3 или 2sin 18°=4—4sin2 18°—3. Положим sinl8°=z
и решим квадратное уравнение 4z2 +2z— 1 =0, откуда z=-; так как
4
л/5-1
z>0, то sin 18°=-. Далее находим cos 3 6°=cos (2.18°) = 1—2 sin2 18° =
_4
>/5+1 х/5 + 1
=—-—. Подставив это значение в (3), получим А3А3=а—-—, затем
>/5-|-1
из (2) найдем т=---- и тогда соотношение (1) примет вид
2
____ V5+1________ __
HjHj— A1A1+AlAs. И
5.061. □ Из центра О окружности проведем ON\\BM и OKf'iAM (рис. Р.5.15);
тогда M0=MK+MN, где \Afkj = (фигура MNOK — параллелограмм,
в котором диагональ МО является биссектрисой угла М, т. е.
MNOK— ромб). Следовательно, МО—п(МА + МВ) (1), где и= Так
|Л/Л|
MF МО
как NKLMO, то &MFN — прямоугольный и MN=----------=-----. Затем нз
а а
cos- 2cos-
2 2
a МО 1
А МАО находим МА=МО cos - и, значит, п=----------=------.
2 a a a
2cos - MO cos - 2cos2 -
2 2 2
Подставив это значение в (1), окончательно получим
МО=—-— (МЛ + Л7Я).
a
2 cos2 -
2
331
_L 7 _____ DK J331
5.062. dR=- aS—ad, —=-—.
8 AB 24
13 ____ ____ _ _ __________________ _
5.063. arccos —. * Разложить векторы AM и AN по векторам AB=a и AD = i>.
/ 4\
5.064. arccos I — I.
\ 5/
5.065. □ Через точку В проведем прямую ВКЦСА (рис. Р.5.16). Так как в пра-
вильном пятиугольнике ADflBC, то ~АК и ~AD коллинеарны и противополо-
жно направлены. Имеем АВ=АК+АС, причем AK=kAD, где к<0
|ЛХ] CN
и JA-) =--. Проведем BN1AC и из &BNC найдем АК=СВ=--------------.
\AD\ cos LBCN
1 1 AD 2AD
Так как CN=- AC, AD = AC, то CN=- AD. Поэтому AK=----------=—=---
2 2 2cos36° ^/5-f-i
2AD 2 2(V5-1)
(см. задачу 5.060). Отсюда находим |i|=—=-----=—=—=-------------=
(V5 + 1)AD Vs + 1 4
V5-1 I -V5 _____
=—-—. Учитывая, что k<0, получим k=—-— и, значит, AB=
=—-—AD+aC. Аналогично устанавливаем, что АЁ=—-—АС+
+ AD.
2bc а
5.066. --cos -.
6 + с 2 _
5.067. □ Проведем AKIBD и DK\\AB (рис. Р.5.17). Тогда DK=BA.
Воспользуемся очевидными равенствами AB+BD=AD, АС—АВ=ВС', сло-
жив их почленно, получим AC+BD=AD+BC (1). Далее, с помощью
______________________ ______ ___ ___ 1___ ___ 1_______________
рис. Р.5.17 запишем MN=MB+BC + CN=~ АВ + ВС4— CD, MN=MA +
2 2
+AD+Dft=- SA+AD+- DC. Сложим эти равенства: 2MN=~B€+a6 или
2 2
MN=- (E£+~AD), откуда в силу (1) имеем MN=- (АС+ТП)). Теперь ис-
332
пользуем неравенство |а+5К|а| + |5| и окончательно получим
1 1
MN^ (BC+AD), (AC+BD).
5.069. □ С помощью рис.Р.5.18 запишем равенства
___ ____ _______ 3 ___ ______ ___ _____
ОТ=Г0+Ш7 (1), 7Ш=—D-Dj (2), DD^ADi-AD, (3)
__ ____ __ 1__________ 1 ___ _______
AD = CD—CA (4), Л2>1=- ЛЛ=- (СВ-СА). (5)
Переходя последовательно от (5) к (1), находим
__ 1_ _ „_____________1_ 1__________ _
-D-D1=2 (СЙ-СЛ)-(^-СЛ)=- СЛ+- CA — CD,
„ — 3 /1 1 _\ 3 _ 3 _ 7 _
см=сб+— -ГЗ+- ГА-CD =— ГЙ + — CS+— CD.
10 \2 2 J 20 20 10
_ 1 2_ 3 |<я2 —с2|
5.070. Л[О= —а4— Ъ— с. 5.071. arccos —=. 5.072. arccos —=====—-.
3 3 ^10 ^а2 + Ь2 + <? ^]а2 + <?
5ЛШ. □ По условию, D\f=aDA + PDiS+yDC, где Ме(АВС) (рис. Р. 5.19).
Следовательно,
^A=DA-DSl=(l-a)DA-PDS-yDr, (1)
JIB=DS-D^=-aDA + (l-P)DB-yDC:, (2)
J^=DT-D^l=-aDA-PDS + (l-y)Dr. (3)
Так как Ме(АВС), то векторы МА, МВ и МС компланарны; поэтому
существуют такие числа р, q и г, что phfA+qMB+rMC=t). Используя
разложения (1) — (3), преобразуем последнее соотношение-.
p(l—a)DA—pPDB—pyDi—qxDA + q(l — Р) DB — qy DC—
-raDA-rPDS+r(l -у)5?=5;
0(1 -a)-qa — ra)DA+(-pP+q(l-P)-P')'DB +
+ (-py-qy + r(1-y))DC=^. (4)
Рис. Р.5.19 Рис. Р.5.20
333
Векторы DA, DB и DC не компланарны и, значит, равенство (4) возможно
лишь тогда, когда коэффициенты при DA, ~DB и DC равны нулю:
р — ра—да—га=0,
-рР+д-дР-гР=О,
.-ру—ду+г—гу=О.
Из первого уравнения следует, что
Р
а=-------; аналогично из второго
д
и третьего находим Р =----
р+д+г
•а + Д+у^-И
у—------ Таким образом,
р+д+г
и
5.074. □ Проведем НРЮА, HN+OB
и
НК+ОС (рис. Р.5.20). Тогда
~ОН=~ОР+T)N+7)И=тОА +пбВ+рбС (1), где т, п и р определим из
|О?| |ОХ] ОР ОН
равенств Так как &ОРН~ АОНА, то —=—,
\ОА\ \ОВ\ \ОС\ ОН ОА
ОН2 он2
откуда ОР= и, значит, т=-(2). Для нахождения ОН воспользуем-
ся---------------------------------ОА2
1 1
ся тем, что Ршф=- ShABC ОН=- ЗлА03 ОС (поскольку
3 3
1
с л - abc
&лов •с 2
LAOB— lAOC— lBOC=9V). Отсюда имеем ОН—-----------=------, где
>5длвс ^длвс
ShABC вычислим с помощью формулы Герона:
$ллвс
х
2
2
х
2
2
=- J^+ly/^+^+^yl^+^+C1)-^
4
=-^l(t?+fy&+^—<P=-^j<№+<?<?+№<?.
abc
Следовательно, OH=-^===. Подставив эго значение в (2),
у/а2И2 + а2с1+Ь2с1
а2Ь2с2 Ь2^2
найдем т=——-----— ------=——--------гт- Аналогично находим
(tPb2+tPc2+b2c2)a2 a2b2+a2c2+b2c2
334
в
Рис. Р.5.21
ОН2 а2с2 ОН2 а2Ь2
п=--------------—----и р=-----г=“г^----—-----— Наконец, подстав-
ОВ2 а2Ь2+а2г + Ь2с2 ОС2 fb1+ а2с2+Ь2<*
ляем эти выражения в (1) и получаем ответ:
, Ь2с27УА+а2с27ТВ+а‘Ь1'иС
ОП=--------------------------Я
a2b2+a2c2 + b2cl
5.075. а- —4, Д=2 или а= -8, Д= -2. 5.078. - 11,5. 5.079. 5 кв. ед.
5.080. □ Введем следующие обозначения: j5C=a, ^А=Ъ, АВ=с, A\i^
ВМ2 -т], где АМХ и ВМ2— мелявны &.АВС (рис. Р.5.21). Так как
_ _ 1___________1т
т. =с+~ а, тг=а+~ Ь, то
2 2
------ /_ 1 _\/_ 1 _\ __ 1 , 1 _т 1 _т
m.m,™ сЧ— а И а + ~ b ]=саЧ— <г Ч— сАч— ab.
\ 2 J\ 2 J 2 2 4
(1)
Для нахождения са, сЪ и аЬ воспользуемся тем, что аЧ-Бч-с=П. Имеем
<?Ч-а = —Б => с2+а2 + 2са = Ь2 => са=- (А2 —с2 —а2)
2
(2)
и аналогично
сЪ=- (а2 — с2 — Ь2) (3), д5=-(с2 —д2 —А2). (4)
2 2
Теперь подставим выражения (2), (3) и (4) в равенство (1):
/и1'”г=" (А2 —с2—а2)Ч-- а2+~ (а2 — с2 — Ь2)-1— (с2 — <^ — Ь2) —
2 2 4 8
поскольку, согласно условию, а2 + Ь2 = 5с2. Итак, nii2jn2.
Докажем, что справедливо и обратное утверждение. Действительно, пусть
известно, что т1Л.т2, т. е. Тогда, проведя .чычисленне mt»i2
335
способом, указанным в первой части доказательства, получим
«1^2= - (а2 + Ь2 — 5с2) = 0, откуда а2 + Ь2 = 5с2.
5.081. □ Введем следующие обозначения: СВ=СА=а (рис. Р.5.22),
BAi CBt ACi т (1)
AtC BtA СХВ п
Найдем разложения векторов Aib1 и CCt по векторам "US и (ТА. Имеем
A161 = CB1 — CAi. Но из равенств (1) следует, что САХ =-"US,
т+п
т
a CBi =--СА. Поэтому
т+п
a^-Va-^-^. (2)
т+п т+п
Далее находим CCl=^S+BC1, BCy =*-11А =-(Сл — СВ). Значит,
т+п т+п
(п \ п —— т ---- ” (3)
1----) СВ+----<TZ =---ГВ+-----ГЛ.
т+п/ т + п т+п т+п
Теперь, используя разложения (2) и (3), получим
0 0
в----fa2 — о*7=0 =*
т-Ьп
i7^-1i2=iw1i2=(—) <?+— о2=>ет-|ггТ|.
\m + nj \m+nj
5.082. □ Так как в &АВС (рис. Р.5.23) АВ=ВС, D — середина АС, то BDLAC.
Запишем разложения ЪМ=>~Во+оМ, '%R*‘AD+DR=‘AD + 2DM. Следова-
тельно,
336
лЛ=ТПЯ аБ+ТЯй аБ+ББ 2Бм+2Бм2 =
о
= DM АБ + 2ВБ DM+2DM2. (1)
Пусть LKDC=ai тогда l_DBK= 1_KDC = t (углы с взаимно перпендику-
лярными сторонами) и равенство (1) примет вид
ВЛ? . AK=\DM\ IADI cos а-2 |ВР| |Ш7| cos(90°-a) + 2m72 =
= |W|(|AD| cosa —2 |В5| sina + 2 \DM\).
Ho |7d| cosa = |5C| cosa = |5X|, [B5| sin a = \DK\ (рис. P.5.23), 2 \DM] =\DK\.
Подставив найденные значения в (2), получим
Ш7ЙК=|ш7] ([0*1-2 |5Х]+|5*])=0, т. е. BM.LAK.
5.083. Равнобедренный остроугольный. 5.084. АВ = 5; 5долл=5 кв. ед.; \ОМ\ =2,5.
5.085. □ Так как вектор ЪехОу, то он имеет координаты (х; у; 0). Используя
Гт- (х2+у2 = 20,
условия |о| = 2-75, о Ха, составим систему уравнений < Решив ее,
|х-2у=0.
получим два вектора (4; 2; 0) и (—4; —2; 0).
5.086. (1/л/и; -зд/и; 1/7и)или (-i/Vh;.3/Vh; -i/V11)-
5.087. □ Выберем единичные векторы а0, Ьо и с0, направленные вдоль ребер
трехгранного угла. Тогда направляющие векторы т, п и р биссектрис трех
плоских углов трехгранного угла запишутся в виде т=а0+Ъ0, п = с0 + а0
ир=50 + с0. По условию, mln, откуда
("о+^оХ^о+ао)=°; аосо+Ъос0+а^+Ъ,Ао = 0-, аосо+Ъосо+Ъоао = -1. (1)
Теперь найдем 7пр = аоЪа + Т>2 + аосо+Ъосо = —1 + 1=0 (см. (1)) и, значит,
тГр. Аналогично получим лр=0, т. е. лХр. Н
5.088. □ Пусть AD = a, AAi =ё (рис. Р.5.24). Найдем разложения
и КМ по векторам а, Ъ и с. Имеем В./?=В.А.+А,А+АЯ= —Б — с+- а,
2
^M=K4S +AiD1+DiM; так как 7>1Л7=* О1С=- (3—с), то
1 _ _ 1 _ _ _ 1 т
КМ=- c-f-a+- (5—е)=а+~ Ъ. Следовательно, ВХН КМ=
а—3 —( а+~ 5^=- (а2—За) = 0, поскольку cla, с1Б, аХЗ|, |а| = |3|.
\2 1 \ 2 / 2
Итак, TsJILKM.
12-363
337
й Й £ Й
5.089. Q Так как 32 35=0 и Эл • ОС=0, то OA.LOB и ОА-1.0С, а значит,
Зл±(О.ЙС), т. е. ОА — высота пирамиды АОВС (рис. Р.5.25). Пусть
Z.ВОС=<р; тогда SLOBC=- ОВ OCsatp. Из условия35 • 3?=8 следует,
2
______• __ 2
что |ОД |ОС| собф=8 или 2 • 6cos^>=8, откуда cosq>=~. Учитывая, что
/ 4 VS
0<ф<180°, находим япф=/1—-=—. Таким образом,
1 л/5 Г
S ^овс=^- 2 -6 • — =2V5 (кв. ед.) и окончательно получим
1 1 10^5
Улояс=~ S&OBC АО=- 2у/5 5«—— (куб. ед.).
5.090. 1/2; 4.
5.091. □ По условию, AM—медиана &АВС (рис. Р.5.26) и, значит,
_ 1 . _ _ _ 3_
AM— (аБ+АС) (1). Далее, 23=2^+NC=- Л5—3W (2). Подставив (2)
2 4
____ 7 1 _____ ___ 8 4
в (1), имеем АМ= АВ—- CN, откуда АВ=- АМ+ CN. Следовательно,
8 2 7 7
. 64 . 64__ _ 16 „
АВ*=— АМ2-^— AM CNЧ— С№ =
49 49 49
64 64 16
=— 49+ 7 7 cos 60° + — 49=112,
49 49 49
т. е. 1251=7112=477 (см).
7в.
4 см.'®-.Разложить ЛЛ по векторам 25и AM.
7 см. 5lO95. При х=0. 5.096. 743 см.
□ На рис. Р.5.27 изображены куб ABCDA^C^i и большой круг жписаж-
338
ного в него шара. Введем систему координат с началом в центре шара О.
(а а а\
)>
2 2 2/
а
радиус вписанного шара равен - и уравнение сферы имеет вид
2
л2
x2+y2+z2=—. Для произвольной точки N (Хр- Z]), лежащей на сфере,
4
(а а а \
— х,;-—у,;—z, I. Следовательно,
2 2 2 /
3
NA2=- a2 + (x]+yJ+z?)-a(Xi+y1+z1) = 4iJ-a(x1+y1+z1).
4
(а
а а\ / а а а \
~2’ 2J ~2~У1‘ ~2 ^ / И NCi=a +а^х'+У'+2^-
Теперь находим NA1+NC1l=2a1. Но NA2+NC2 = NB2 + ND21=NC1 +
+NA2 = ND1 + =2а2, т. е. сумма квадратов расстояний от любой точки
N сферы до двух симметричных относительно О вершин куба постоянна
и равна 2а2. Значит, сумма квадратов расстояний от до всех вершин куба
постоянна и равна 2а2 - 4 = 8а2. Н
5.09 8. За2, где а — длина стороны квадрата. 5.099. 4а2, где а — длина стороны
квадрата.
5.101. • Воспользоваться тем, что диагонали прямоугольного параллелепипеда
равны и пересекаются в одной точке.
5.102. □ Имеем ’^A = CC1 + CiA, СВ= CCt + (рис. P.5.28). Тогда
CH2=CCf+2C^-C7 + C72, CB2 = CCt + 2€U; C^B+CjB2. Сложив
эти равенства, получим
339
A
Рис. P.5.29
С A2 + СЙ1 =2CC2 + 2CT^ (Cji +Г^) + Q A2 + Ct B2 =
= 2CC2 + 2C1A2 = 2(CC2 + CiA2), (1)
так как |Cj^| = |C75| и векторы CjA и CtB противоположно направлены.
Далее, согласно свойству пересекающихся хорд, СС, • С1В = С1А С\В=
=» CtA2. Заменив в равенстве (1) СГА2 на CCt CtD, находим С А2 + СВ2 =
= 2СС1(СС1 + С12>) = 2СС1 • СВ.
5.103. х (2; 3; -2). 5.104. х (-4; -6; 12).
5.105. □ По условию, L ВАС—120°, АВ=АС; следовательно, медиана AKJ-BC
и LKAC=60° (рис. Р.5.29). Искомое скалярное произведение будем искать
по формуле
"аК Л = |АХ| |5L| cosa (1), где (AR, HL) = z.
1
В LABK имеем LABK=30°, откуда АК-- АВ (2). Используя разложение
2
~EL=Ha+~aL, находим BL2=BA2 + 2Ea • 'aL+AL2-, так как
1 1
AL= АС= АВ, то
2 2
5 5 1 7 Ji
BL2=- АВ1-^ AL=- АВ2-2ЛЙ - АЙ cos 120°=- ЛВ2; BL=— АВ.
4 4 2 4 2
(3)
_ 1
Далее, KL-OL—OK, где KL=- АВ (KL — средняя линия в ДЛВС),
2
1 Ji 11
OL=- BL=— АВ (см. (3)), ОК=- АК=- АВ (см. (2)). Следовательно,
3 6 3 6
KL2 = OL2-2Ш, ЪК+ ОК2 или
1 , 7 , Ji 1 1 1
- ABr*t— АВ2—2 — АВ • - HBcosaH— АВ2, откуда cosa=--=. (4)
4 36 6 6 36 2^1
Теперь подставим результаты (2), (3) и (4) в (1) и полу- i
340
-w 1 V7 / 1 \ 1 ,
= - AB — AB I-----= =—AB2. (5)
2 2 к 2^7/ 8
Остается выразить AB? _ через данное значение 5. Имеем
1 , V3 , , 4S
S=SAABC= АВ2 sin 120°=— АВ2, откуда А1г=—=. Подставив это вы-
24 73
__ —
ражение в (5), окончательно находим АК BL= —-.
6
5.106. Пусть LMON=a, где О — точка пересечения высот AM и BN (рис. Р.5.30);
тогда
AM BN=\AM\ |7?TV| cosa. (1)
Так как LMON+ LАСВ= 180°, то a =180°— l_C= l_A+ l_B=2l_B и,
значит,
cosa=cos2£=2cos2 Л— 1. (2)
1 2S
Согласно условию, S=Saabc—~ АВ СК, откуда СК=—. Из &СКВ
2 с
находим
_______ 1С2 4^2 j _____:__
BC=jKB? + CK? = l-+—=-^/t? + l6S2 (3)
и, следовательно,
КВ с • 2с с2
cos 5=——— =— ....-. (л\
ВС zj^+ieS2 yJc* + \6S2 1 ’
Теперь выражение (4) подставим в (2):
с* с'-ХЬК2
cosa=2 • —---—-1=------;• (5)
c*+16S4 с4 + 1б№
1
Далее, используя равенство В=Ваавс—~ ВС • AM и соотношение (3),
найдем
ЯМ=— =
ВС ^C*+16S2
(6)
Наконец, учитывая, что AM=BNfa подставляя выражения (6) и (5) в (1),
получим ответ:
_______/ 4cS Vc4- 1б№ 16с2У(с4-1бУ)
ZX71?7?= ------------------——.
\7с4+16У/ с4+1б№ (гпбя2)2
341
5.108. Имеем O/C=npja = |a| cos^ (рис. P.5.31). Отсюда, используя равенство
-т - т - ~аЪ
ао=|а| |о| cos <р, находим npja=—. Так как Ъ — направляющий вектор
оси, на которую проецируется вектор а, то
._ 7(—8) + (—4)6 -56-24
прта=------- —=-----—---= -8, т. е. |npja|=8.
л/64 + 36 Ю
5.109. □ Из произвольной точки О проведем радиусы-векторы ОА=г2, oS=r2,
0(5=г3 и (рис. Р.5.32). Теперь выразим через них нужные нам
векторы: AS=r2—rl, ОБ=г^—73, A^=r3—r2, DS=r2—rt, AD=rt—rlt
SC=r3—r2. Далее находим скалярные произведения
AS ^б=(г2-Г1)(г*-Гз)=Г2Г*-Г1Г*-Г2Гэ-|-Г1Гэ,
АС 'DS=Cr3-'ri)Cr2~ri)='r3r2-r1r2-r3ri+'r1ri,
AD . ГО=(г4-г1)(г3-г2) = гЛ-О?з-':Л + ПО
и, наконец, их сумму AS TD+AS DB+AD • ~Б?5=0.
5.110. □ В тетраэдре SABC проведем SOA_(ABC) (рис. Р.5.33) и выразим векторы
ребер пирамиды через радиусы-векторы OA=rt. OS=r2, ()С=г3 и ~OS=rt.
Имеем ЗА=г2 — rit ~B(5=r3 —r2, SS=r2 — rt, A^=r3 — rt, SC=r3 — r^,
54S=r2 — ri. По условию, SA2 + BC2=SB2 +AC2=SC2 + AB2, откуда, пере-
ходя к радиусам-векторам, получим
r2~2r1rt + ij+r3-2r3r1 + r2 = ij-2r2rt+rl + r2-2r3r1+r2 =
= r2-2r3r4 + r2 + r2-2r2ri+r2. (1)
Но rtrt=r2rt=r3rt=0 (2) (согласно условию перпендикулярности векто-
ров), а потому из равенств (1) следует, что г3г2=г3Г1=г2г1 (3). Тогда
SA •5С=(г1-г*)(г3-г2)=Г1Г3-г*г3-Г1Г1+гЛ=0 (в силу (2) и (3)), т. е.
ВАА.ВС. Аналогично устанавливаем, что SCA.AB, SB А. АС.
5.11X 4 : 1. 5.115. ТГ^Г2 (1,5; 1; -0,5), |^^|=7з,5. 5.116. -29: 14 кв. ед.
342
5.117. □ Имеем
(a+J)|jc =» с=т(а+Ъ)=та + тИ; (5 + c)Ja => Ъ + с = па => ~c=na—Ъ. .
В силу единственности разложения с по векторам а и Ъ заключаем, что
т=п и т= — 1. Значит, т = п= — 1, т. е. с=— а—Ъ. Теперь находим
а+Ъ+'с — а+Ъ —а—5 = 0.
5.118. 2(5-5).
5.119. —1,5.® Из условия +ё2+ё3=б следует, что эти векторы образуют
правильный треугольник и (ё1; ё2)=(ё2; е3)=(е^'е1) = 180°—60°=120°.
5.121. (а+Ь) : с. (Ь + с) : а. (с+а): Ь. 5.122. 6. 5.123. +у/б. 5.124.12,5 куб. ед. 5.125.
5 кв. ед. 5.126. у/ыЦГ)-, 1_АВС — хуыА. 5.127. 3 : 1.
5.128. □ По условию, вершина А (0; 0; 0) совпадает с началом координат,
а вершины В (1; 0; 0), С (0; 1; 0) и 5 (0; 0; 2) лежат соответственно на осях
Ох, Оу и Oz (рис. Р.5.34). Так как искомая точка М должна лежать на оси
Oz, то она имеет координаты (0; 0; z2). Далее, пусть N (х2; у2; z^ — вторая
искомая точка; тогда вектор MN имеет координаты (х2; у2; z2—zj, а,
™/1 1 \ 11
с другой стороны, MN I0) \. Следовательно, х2=~, У2=“,
/1 1 \
т. е. z,=z, и N \ z, ). Остается найти значение z2, что мы и сделаем
\3 3 /
двумя различными способами.
I способ. Общее уравнение плоскости имеет вид ax+by+cz+d—О. По-
скольку Be(SBC), координаты точки В удовлетворяют этому уравнению,
откуда a+d=0 (1). Аналогично, Ce(SBC) => b+d=O (2) и SefSBC) =>
=» 2c+d=0 (3). Из системы (1), (2) и (3) находим а=Ь =2с= -</иуравнение
плоскости SBC примет вид
d 1
— dx—dy— z+d=0 или x+y-i— z—1 =0.
2 2
Наконец, Ne(SBC) и для нахождения zt получаем уравнение
111 2 / 2\ /1 1 2\
-+-+;г1-1=0»откудаа1=-. Нтак,
3 3 2 3 \ 3/ \3 3 3/
343
II способ. Пусть п — нормальный вектор плоскости SBC, т. е. п (а; Ь; с).
Найдем ВС (—1; 1; 0). Так как ~BCe(SBC) и п1ВС, то п ~ВС=0 или
— а+Ь+0 = 0 => а — Ь-, аналогично, TiLSB, где ~SB (1; 0; —2), и, значит,
п SS=0 или а + 0 —2с=0 => а = 2с. Таким образом, a=b = 2c (1). Составим
теперь уравнение плоскости SBC как уравнение плоскости, имеющей нор-
мальный вектор п (а; Ь; с) и проходящей через данную точку 5 (0; 0; 2):
ах+Ьу+с(г~2) = 0. Далее, используя равенства (1), получим
2cx + 2cy+cz— 2с = 0 или 2x + 2y+z— 2=0.
/1 1 \ 22
Наконец, учитывая, что N I Z; 1е(5ВС), имеем ~+~^ + zl — 2=0, откуда
2
Z] = - и получаем тот же ответ.
3
5.129. □ Пусть О — центр окружности, описанной около Д ЛВС (рис. Р.5.35).
Тогда в силу свойства центральных и вписанных углов имеем
ДЛОВ=2ДС, LBOC=2LA, LAOC=2LB. Построим единичные векторы
et, ё2 и ё3, направленные вдоль векторов (5л, SB и SS; их сумма дает
вектор 2, т. е. ё1+ё2+ё3=2. Возведем обе части последнего равенства
в квадрат:
е? + е2 + ^ + 2ё1ё2 + 2ё1ё3+2ё2ёз = </2
или
3 + 2 (cos 2А +cos2B+cos 2С)=22.
Так как <Р^0, то 3 + 2(cos24 + cosB+cos2C)>0, откуда cos2A + cos2B+
+cos 20-3/2.
5.130. □ Введем следующие обозначения (рис. Р.5.36):
АС2 ВА3 СВх
---=т,-----=*п,---=р
С2В А2С BtA
ав-с2в вс-а2с са-в2а
или--------=т,---------= п,-------= р, откуда
в2а
А.С
(1)
с2в
АВ ВС
---«т+1,----— л+1,--—р+1.
с2в а2с в2а
CA
’ В3А
(2)
344
Найдем разложение вектора Л5+Л]/?! по векторам ~АВ и ВС. Имеем
__________________________________________ 1 _____
А,В, = А,С+СВ,. Но из (2) следует, что А,С—---ВС, а из (1) — что
п 4-1
СВ, =рВ,А=р(В,С+&А); поэтому СВ,—рВ,С=р(СВ+'5А') или
(р4-1)СЯ,= — p(ZB+HZ), откуда
СВ, — —---(ЛЯ 4- ЕС?). (3)
р4-1
Тогда получим
___ ______ _______ 1 р 1 __---------------------1— пр
АВ4- А ,В, =» АВА-------------------------------------ВС— —— (АВА- ВС) — — А В а- - ВС.
Л4-1 p-t-l Р + \ (л4-1)(р4-1)
(4)
Аналогично, используя равенства (1), (2), (3), находим
Жа-Т^,=Т^А-ТЦАа-^,=Жа-~ Т^,А-т(^В=
Р
1 р _ 1 ____ тр— 1 _____ р __
— ВС— ----(Л2?4-Е<?)-|-« •--АВ—--------------АВ А----ВС. (5)
р р4-1 «4-1 («4-1)(р4-1) р4-1
Чтобы доказать коллинеарность векторов ^Ва-А,В, и "SCa-B,С,, нужно
установить равенство отношений коэффициентов при AS и ЕГ в разложе-
ниях (4) и (5). Для этого проведем прямую МЩАВ, которая пересечет С,В,
в точке D. Тогда t±A,CD, а t±.AC,B, ~ &.CDB,, откуда
С,В С,А, ВА, АС, АВ, С,В, 1
-J-.-L-l. 1 = „ (6)--------(7)
СВ A,D А,С CD СВ, DB, р
АВ, СВ, 1
поскольку из (1) следует, что-=—1 :-------= —. Находим отношение
СВ, В,А р
АС, С,В АС, АС, С,В 1
: =-=«, откуда =т--=тп = — - ( см. (7)) и, значит,
CD----------------------------------CD-С,В CD-CD-р
тпр = — 1. (8)
Теперь найдем отношения коэффициентов при Л1? и ~БС в разложениях (4)
и (5):
1 тр— 1 «4-1 1—лв р 1 — пр
---.------С-------=-----1 (9)---------------------(Ю)
р4-1 (mA- 1)(р4-1) тр—1 (л4-1)(р4-1) Р4-1 (л4-1)р
1
Из равенства (8.) следует, что л= ——; подставив это значение в отношение
тр
«4-1
(10), получим, что указанное отношение равно--, т. е. оно совпадает
тр— 1
с (9). Тем самым доказано, 'по~АВ+А,В,^ВС+В,С,.
Аналогично доказывается, что ^А + С,А1ЦАВ+А,В1.
345
- ВАРИАНТЫ ЗАДАНИЙ
ДЛЯ САМОПРОВЕРКИ
Вариант I. □ 1. Имеем
х—1 =(л/х+1)(^/х—1), Ху]х— 1 =л/х3—1 =(л/х— 1)(х + -Ух + 1).
Следовательно,
(y/x + iyfy/x-l) (у/х-1)(х+у/х+Г)
А=--------=-----•------=---------+2у/х=
Х + у/х+\ у/х + \
=(у/х— \)2 +2*jx=x + \.
Полагая х=7, найдем Л = 8.
л
2. Используя формулу тангенса разности двух углов и то, что tg - = 1, получим
4
/ л\ 3 tga—1 3
tg a— =- =>--------= => tga=7.
\ 4/ 4 1+tga 4
X—1 I lx
3. Так как 4 = 2 , то уравнение преобразуется следующим образом:
4
- (2Х) -- 2Х-1=0 => (2Х + 1)(2Х—4) = 0 =► 2Х=4 =► к=2.
4 4
4. Имеем
5. По условию, АВ=ВС, AD2.BC, АС=30, AD=24 (рис. Р.П.1). Пусть l_BCA=а;
AD 24 4
тогда в ixADC имеем sina=—=—=-, откуда cosa= АС 30 5 ЕС 15 (где ВЕ2.АС) находим ВС— =— = 25. cos a 3/5 6. Сначала найдем 2х—6 х—3 f'(x) = = - = 2^дг2—6х+Ю — 6x4-10 В X. А л l\. 4 ЕС Рис. Р.П.1 =-. Наконец, из &ВЕС \ с Рис. Р.П.2
346
Тогда данное уравнение запишется в
------- 4(х-3)
-Jx2 — £>„ 10+—--- =—0 или х2 —2х —2=0,
7х2-6х+10
да следует, что xt+x2=2 (второй коэффициент в приведенном квадрат-
t.u>i уравнении).
7. Имеем
пх пх пх
cos2 — = 1 => cos — =+1 -> —=пк => х=2к.
2 2 2
Теперь найдем корни, принадлежащие отрезку [п, Зя]; неравенство л<2Л^Зл
выполняется для значений к = 2, fc = 3 и fc = 4, которым соответствуют корни
х=4, х=6 и х=8. Итак, искомое произведение равно 192.
8. Перейдем от данной системы неравенств к равносильной ей:
pogi/z (2х—3) > — 3, ("0<2х—З<23, [1,5<х<5,5,
< = =>4<х<5,5.
(х2—4х>0 (xfx—4)>0 (х<0 или х>4
Искомым целым числом, удовлетворяющим этому неравенству, является 5.
9. По условию, ADJ.AB, ADLAC, AD=5-j2, LDCA= CDBA=45°, CCDB=6O°
(рис. Р.П.2). Прямоугольные треугольники DAC и DAB — равнобедренные
(один из острых углов равен 45°). Тогда CD=BD=^2 (5л/2)2 = Ю. Теперь,
применяя теорему косинусов к равнобедренному треугольнику CDB, находим
ВС1 = CD2 + BD2 - 2CD BD cos L CDB=
=2 • 100-2 • 100cos60° = 100, т. e. BC=10.
10. Воспользуемся тем, что скалярное произведение перпендикулярных векторов
равно нулю:
а5 = 0 => х 1-1 2+2 • 0=0 => х=2.
Значит, вектор а имеет координаты (2; —1; 2), а его модуль
Й = 722 + (-1)2 + 22 = 3.
Вариант II.□ 1. Находим
(4-0,25-2(,’5)(4’<,’25 + (2V2)1'3) = ^-L-V2^~=+V2V2) =
=--1+6/—-^8-42=--+1-2=--.
2 V 8 2 2
2. Сложив уравнения х+у=4, y+z = 8, x+z = 6, получим 2(x+y+z) = 18 или
x+y + z = 9. Отсюда находим х=9 —(y + z) = l, у=9 — (x+z) = 3, z=9 —
—(х+з»)=5. Искомое выражение есть х—y + 2z= 1 — 3 +10 = 8.
3. Найдем область допустимых значений:
Преобразуя данное уравнение, получим
347
11 11 11
2х / х \ 2х х / 2х\а 2х
lg2 =lgl2-21=>2 = 2-2=><2 1.-2 -2 = 0 =>
1 1 1
(2х \ / 2х \ 2х |
2 +1)12 -2) = 0=>2 = 2 => — =1
/ \ / 2х
4. Имеем
sinx + cos2x=0 => sinx + 1 — 2sin2x=0 => 2(sinx—1) fsinx+- ] = 0.
\ 2/
Далее находим:
л л
1) sin х=1, х = - + 2лл; из условия —л<~ + 2лл<3л следует, что
2 2
Зл 5я 35
—— <2пл<—, т. е. — последнее неравенство выполняется при л=0
и л = 1.
1 I 1\* л
2) sinx= —, х=( — - ) - + пк; отбираем корни, удовлетворяющие условию
2 \ 2/ 6
5л л 7я 11л
—л<х<3л: х=-----, х= —, х——, х =—.
6 6 6 6
Итак, отрезку [—л, Зл] принадлежат шесть корней данного уравнения.
5. Находим
, tg2 а 1 9 1
25 sin2 a cos а=25----• —------=25 ----------• — =7,2.
’** v.+t^. 16Л / »
\ 16/ 7 +1б
6. Здесь х>0. Решаем данное неравенство:
ijх+у/х^б =» (tjх)2 + tjх—6<0 => (^/х + 3)(^/х—2)<0 =>
=> -3<^/х<2 => 0<^/х<2 => 0<х<16.
Итак, искомая длина равна 16.
7. График функции Дх)=х3 +Зх2+5х=х (х2 + 3х+5) пересекает ось Ох только
один раз, поскольку квадратный трехчлен х2+Зх+5 не имеет действитель-
ных корней.
8. Пусть а1 — первый член прогрессии, a d—ее разность. Тогда получим
систему
(a, +6d+a, + 1(М=10, f2a,+16rf=10,
1 => rf=3, а, = —19.
(a1+4d+a1+9d=l (,2a1 + 13rf=l
Следовательно,
(aj+a20)20
S20=^2 2^L------io (2flj + 19d) =190.
2
9. Находим
x2 +1 — 2X2 1 1—x2 1 1
. 2 ,.2----г = , , ,.2-----7=./'(l)=
(jr +1) 2y/x (^ + 1) 2^/x 2
348
Рис. Р.П.З
Рис. Р.П.4
10. По условию, в трапеции ABCD имеем АВ= CD, АВ=ЗВС, BE и СЕ — биссек-
трисы углов АВС и BCD, Ее AD (рис. Р.П.З); требуется найти Sabcd S^bce-
Пусть l_ABE=- LABC=i, ВС=Ь; тогда CD=AB = 3b. Заметим, что
2
1_СВЕ= /_ВЕА=а. и i_BCE=* LCED=a как накрест лежащие углы; значит,
треугольники АВЕ и CDE — равнобедренные и равные. Отсюда следует, что
b d
CD=DE=AB=AE=3b, BE=CE—d. Так как t±BCE~&CED, то -=—, от-
d 3b
куда сЕ^ЗЬ1. Теперь найдем площади £\ВСЕ и &.CED:
1 13,
Sabce=~ BE СЕ sin (180°—2а)=- i/2 sin2a=- A3sin2a,
2 2 2
1 9 ,
£дсгв=~ ED CD sin (180°—2a)=- b2 sin 2a.
Учитывая, что Sabcd^ES&ced+S&все, находим искомое отношение:
Sabcd ZS^ced 9bi йп2а
-----=------+ 1=-------+ 1 = 7.
S&BCE S&BCE 3
- b2 sm 2a
2
Вариант Ш.П 1. Здесь Зх+1>0, x—1>0, откуда х>1. Пусть y/3x+\=u,
1 — v, где и>0, v>0. Тогда данное уравнение равносильно системе
из которой получим 4е—2i?=0, т. е. с.=0, v2=2. Итак, х, = 1,
(u—3v=4,
х2 =5.
2. По условию, АС =15 см, EF^AC, Saefc=0,15S^abc (Рис- Р-П.4). Тогда
S&EBF /FF\2
^дЕВЕ /£р\2
8^еве=025Е&авс- Так как &EBF ~&АВС, то -----------=1 —) или
S&ABC \ACJ
0,25=^—^ , т. е. EF—G,5AC. Итак, £/"=7,5 см.
3. Имеем
449
sin (60° + a)
A =
(a\ f a
30°+- cos I 30° 3—
2/ \ 2,
(a\ ( a
15°+- sin 75° —
4/ \ 4,
(a\ ( a\
30° +- ) cos I 30° 3— )
2/ \ 2/ / a\
---------------= cos I 30° + - ).
2/
(a
60°—-
2
( a
sin I 30° 3—
\ 2.
30°+- 1 = 0,8 и 0°<a<90°, to A=J\ —0,82 = 0,6.
2/
4. Учитывая, что x>0, получим
lg2 (1 OOx) - 1g2 (1 Ox) + 1g x = 9 =>
=> QglOO+lgx)2 — (lg 10 + lgx)2+lgx=9 =►
=> (2+lgx)2 —(l+lgx)2+lgx=9 = lgx=2 =► x = 100.
5. Данное неравенство равносильно следующему:
3+2х 2(х + 1,5)
-----<0=> -1,5«х<4.
х—4
4 —x
Итак, наименьшим отрицательным решением является х= —1,5.
/Зя \ Зя Зя я
6. Здесь sin —|-х ^0, т. е. -л- + х^пп, откуда х# ——\-m=- + nl. Преобразуем
\2 / 2 22
данное уравнение:
, /Зя \
1+ctg2 —hx = cos*x—sin*x =»
\2 J
=> 1 + tg2 x=(cos2 x—sin2 x) (cos2 x + sin2 x) =>
= ——=2cos2x— 1 => 2(cos2x)2 — cos2x— 1 =0 =>
cos2x
=» 2 (cos2 x— 1) | cos2x+-^=0 => cosx= + 1 => х=лк.
\ 2/
Условию |x|<я удовлетворяют три корня.
7. Имеем
/3\Зх-7 /7\7х-3 /ЗЧ3*-7 /3\3-7х
ы -у =04J =у ~
=> 3х-7 = 7х-3 ==• х=1.
8. Пусть хи у (х>у) — искомые числа. Тогда, по условию, —==—. Следова-
2^ху 12
тельно, __ _
1х 1у 13 / 1х\2 13 lx / 1х 3\/ 1х 2\
67у+1-0=>\7>' 2д7у з/°’
/х 2 /х 3 х 9
Тогда /-=-, что не удовлетворяет требованию х>у; /-=-, откуда-=-.
УУ 3 Чу 2 у 4
9. Находим
350
, ( Зт\ . , ,
Л=81 cos | 6а--1-81 sin26a=8l • 4sin2 За cos2 Зз—
\ 2/
«81 • 4(1—cos2 За) cos2 За,
2 5 4
откуда при cos За—- получим А —81 • 4 • - -—80.
3 9 9
10. Данная функция преобразуется следующим образом:
f(x)=sin2 2x+0,5cos4x+2sin2x+cos2x—
— sin22x+(0,5—sin22x)+(l — cos 2x) +cos 2л = 1,5=const.
Вариант IV. □ 1. Преобразуем выражения В и С:
1 2
В —------=log, 6; С—------
log62 log210
21g2—lg4.
Тогда получим
Л = 2|'-10с=21оь6-101И=6-4 = 2.
2. Имеем
— jOj 23/э 2~4,j
10х : (^2)2 = 25'3 4 “2/3 : </б4 =>-=-----=> 10х = 1 =» х-0,1.
vv ' v 23/э 2
3. Здесь х>2. Имеем
2,/х—2—IS—^/x-2 => 2(V*—2)2—V*—2~ 15=0 =>
=> 2(Vx-2-3)(Vjc-2+2,5)=0 => ^/х-2-3 => х-2-81 => х = 83.
4. Учитывая, что х>0, получим
2х-57х + 2«0 => 2(7х)2-5л/х + 2«0 =» 2(7*-2)(,Д-0,5)«0 =>
=► 0,54=7х«:2^ 0,25<х<4.
Искомым наибольшим значением х является х—4.
5. По условию, в трапеции ABCD имеем AB**CD, CE.LAD, СЕ** 16, ЛС=20 (рис.
16 4
Р.П.5). Пусть LCAD=Р; тогда из дЛ£С находим sinp*=——
20 5
--------з
cos/?—>/1 -яп2 Д—Далее, txAOD — равнобед- /:
ренный, причем Z.ЛОР =180°—2Д. Следовательно, / \
1 1 Zz;
AC BD sin LAOD= 20 20 sin2£= А „
2 2 A £ D
-400sin^ сояД-192 (кв. ед.). рИс Р.П.5
6. Имеем
sm(90°+-2x) + sinx=0 => cos2x + sinx = 0 =» 1 — 2sin2x + sinx—0 =»
(
=» 2(япх—1) I япх+- )—0.
V 2/
1
Решив уравнения smx— 1, sinx—— и учитывая, что 0°<х<270°, получим
2
ответ: х,— 90*, х2—210*.
351
7. Преобразуем данное выражение следующим образом:
а а
4 sin* 2 - cos -
49 49 49 sin2 а 2 2
--------=—— =--------—.
( 5я\ ctg2 а cos2 а ( а\2
tg2 а+— 1- 2sin2-
\ 2/ \ 2/
a 1 а 8 48 /9\2
Подставив значения sin2 -=-, cos2 получим Л =49 - - - ) =32.
2 9'2 9 9 9 \7/
8. Пусть I — время работы второго станка (в часах), а х и х—5 — количество
деталей, которые обрабатывали в час соответственно на первом и втором
станках. Тогда, согласно условию, получим систему уравнений
1(7—1,5)х= 150, (7=0,Зх,
ЬГх-5; = 150 (0,Зх2-1,5х-150 = 0
=» х2 —5х—500=0 =» Х; = —20 (не годится), х3=25.
Итак, на первом станке в час обрабатывали 25 деталей, а на втором — 20
деталей.
9. Уравнение имеет смысл, если ,/Зх—2>0, т. е. х>2/3. Выполним преобразова-
ния:
х2 • + + < =>
(х2-25) = 5Х(х2-25) => (5v/3x-2-5X)(x2-25) = 0.
Далее имеем:
1) 5^ЗХ 2=5Х =» л/Зх—2=х =» х2 —Зх + 2 = 0 => X; = 1, х2 = 2;
2) х2 —25=0; х3 = —5 (не годится), х<=5.
Ответ: х=1, х=2, х=5.
10. Здесь х^0, х^ — 1, х^1. Имеем
6—х х + 3 х + 5 6 —х х + 3 х + 5
1—х2 х(1 — х) х(1 + х) (1— х)(1+х) х(1—х) x(l-t-x)
6х—х2—х-3 —х2 —Зх—х —5 + х2-5х
=>----------------------------------=0=>
х(1 - х) (1 + х)
Вариант V. 1. 1. 2. 4,3. 3. 3. 4. 4,1. 5. 6. 6. 0. 7. 30°. 8. 42 см. 9. 3,53. 10. -1,5.
Вариант VI. 1. 4. 2. 1. 3. 4. 4. 5. 5. 7. 6. 41. 7. 3. 8. 64. 9. 4. 10. 1. Вариант VII. 1. 2.
2.1, 2 и 4. 3.2. 4. 5. 5. 6 см3. 6. 8. 7. 0,5. 8. 4 и 36. 9. 8.10.0 и 5. Вариант VIII. 1.40.
2. -25.3. 10.4.1. 5.0,28. 6. 90°. 7. 72 см2. 8. 2,3 см. 9.13 и 13.10. 6. Вариант IX. 1.
1. 2. 11. 3. 0; 4. 4. 48. 5. 0,8. 6. 4. 7. 31,5. 8. 15. 9. 2. 10. 18. Вариант X. 1. 2; 0,25. 2.
225°; 315°. 3. 4. 4. 0,3. 5. 168 см2. 6. 3 км/ч. 7.1. 8.0,75. 9. 6 и 0.10. 2,5. Вариант XI.
1.2. 2. 9. 3. 10. 4. 8 см. 5. 0,8. 6. 0. 7.103. 8. 4 см. 9. 6.10. 16 кв. ед. Вариант XII. 1.
— 9. 2. 1. 3. 3. 4. 11. 5. —1. 6. 7. 7. 4. 8. 0. 9. ут;п= —1/епри х = 1/е. 10. 2. Вариант
352
XIII 1. 6. 2. 0. 3. 1. 4. 5. 5. 0. 6. -1. 7. 5. 8. Один раз. 9. 20.10. 2,25. Вариант XIV.
1. (2х+1)2. 2. 2tg2a.'3. 1. 4. -10; 3. 5. 9. 6. 2. 7. 10.8. 4. 9. -3. 10. 1. Вариант XV.
1. 3. 2. 1,6. 3. 5. 4. 12 и 24. 5. -1; 1. 6. 4. 7. 12. 8. 0,5. 9. 8. 10. 120°; 240°. Вариант
XVI. 1. — 4; -3; 4. 2. 25. 3. 5. 4. -58. 5. 2; 3. 6. 2,25. 7. 9,375 кв. ед. 8. 12. 9. 150°;
210°. 10.40 л. Вариант XVII. 1.4.2. 3/4. 3. 5. 4. 60 кв. ед. 5. 0,8. 6. 10. 7. 6. 8. 6.9. 12
куб. ед. 10. 8. Вариант XVIII. 1. 5. 2. 8. 3. 4. 4. 2. 5. 66. 6.1. 7. 12 куб. ед. 8. 13. 9. 2.
10. 3. Вариант XIX. 1. 4. 2. 2. 3. 3. 4. 7. 5. 3. 6. 3. 7. 6 кв. ед. 8. 2. 9. 4. 10. 3.
Вариант XX. 1. 7. 2. 8 кв. ед. 3. 3. 4. 2. 5. 0,6. 6. 2. 7. 51,6. 8. 3. 9. 16. 10. 120°.
Вариант XXI. 1. 4. 2. 48 кв. ед. 3. 3. 4. 5. 5. 3. 6 7. 7. 10. 8. 4. 9. 5. 10. 2. Вариант
XXII. 1. (2 l'og2 5 +1)2. 2. 1. 3. 10. 4. 5. 5. 12. 6. 0,36. 7. 0,8. 8. 3. 9. 6. 10. 2. Вариант
XXIII. 1. 4. 2. 5. 3. 9 кв. ед. 4. 5.5. 3. 6. 3. 7. 4. 8. 2. 9. 6. 10. 4. Вариант XXIV. 1. 14.
2. 0,5.3. 5. 4. 7. 5. 4. 6. 250 куб. ед. 7. 63. 8. 0,2. 9. 5.10. 20. Вариант XXV. 1.1. 2.16.
3.6. 4. 0,28. 5. (9; -1). 6.6. 7. 3.8. 12.9. 14.10. 4 кв. ед. Вариант XXVI. 1. -2, -1.
2. 0,5; 0,6. 3. 0,75. 4. 18 кв. ед. 5. 4. 6. 3 и 0. 7. 16. 8. -2; -1. 9. 120°; 240°. 10. 12.
Вариант XXVII. 1. 135°; 225°. 2. 24 см2. 3. 2 и 22 134. 4. -5 и 3. 5. -5. 6. 15. 7.
-1,5. 8. 1,75. 9. 2. 10. 4. Вариант XXVIII. 1. 20. 2. -0,4. 3. 1. 4. - 1, 2. 5. 4. 6. -6
и -6. 7. -0,6. 8. 0,4 и 0,4. 9. 5 и 6. 10. 39 и -39. Вариант XXIX. 1. 1000. 2. 0. 3. 4.
4.25.5.1; 11; 21. 6.10.7. -2; -1.8.4 см. 9. -45°; 0°; 45°. 10. 8 см3. ВариантXXX.
1. 6; 2. 2. (2; 3; -3). 3. 2. 4. -52,5°; 7,5°; 37,5°. 5. 10; 11; 13; 14. 6. 6 см3. 7. 30 и 35
км/ч. 8. 0. 9. 20,25. 10. Первое.
ВАРИАНТЫБИЛЕТОВ
ДЛЯ ВСТУПИТЕЛЬНЫХ ПИСЬМЕННЫХ ЭКЗАМЕНОВ
Вариант I. G 1 Так как
fogjx-&,51cg317 21ogj.r-log217 tog, (x*/l7) X3
4 =2 =2 =—,
17
> „4(1 -Л
у*=4(1—23*)
то выражение для f(x) упростится следующим образом:
/ .— (^П—^хЦП + у/Пх+х)^1 х2 .— х2
f(x)-l 17+2^17х+х——------/--------------- - = (V17x)2 -=Л3.
V yj\7-yjx j 17 17
Значит, f‘(x) — Зх2.
2. Исходная система равносильна следующей:
2 • 4 +1—2 —24 у
2+2 2(2*+ 2)
/=4(1-2Ь)
Зх
Уравнение 1—2 =0 имеет решение х=0, а уравнение 1—2 =1 не имеет
решений. Итак, х=0, у=0.
3. Пусть х я у— искомые числа; тогда х+у= 10, а выражение 2х2 + 3 у2 должно
принимать наименьшее значение. Имеем /(х)=2х2 + 3(10—х)2^2х2 +
+3(100—20х+х2)=5(х2—12х+60), /'(х)“5(2х— 12)=10(х—6). Очевидно,
что/'(х)=0 при х = б; если 0<х<6, то/’(х)<0, а если 6<х<10, то/'(х)>0.
Итак, при х=6 функция /(х) имеет минимум. Отсюда следует, что искомыми
двумя слагаемыми являются числа 6 и 4.
(5я \ /я \
——х =cos I —х l=sinx,
2 / \2 /
х х
4 sin - cos • =»2sinx, преобразуем данное уравнение:
2 2
0,5 2см2 х япх—sm*x«2smx => anx(cos3x—sin2x—2)=0 =»
=» stnx(cos2x—2)=0 =» sinx»0 => х«яЕ, Е—0, ±1, ±2, ...
Теперь отберем корни, удовлетворяющие неравенству 1о^(х+1)>1. Так
1
как я>1, то х+1>я, т. е. >я—1. Следовательно, яЕ>я—1 или й>1—.
я
Этому условию удовлетворяют значения к-\, 2, 3, ... . Итак, получаем
ответ: х=яЕ, к&.
S. По условию, ABCD — ромб, ^руга=5, 2_&42>=а
Рис. Р.П.6
(рис. Р.П.6). Проведем CEJ.AD. Введем обозначе-
ния: А С=<Z1M BD=sfL, г — радиус вписаннло кру-
га, CJ?=2r, АВ=ВС=С2>=А27=о. Из равенства
S
S—w1 находим г3 =-. В ДС£2> имеем lCDE^x,
2r , 4Н 4S
в—----, откуда <г=——»---—•. Истсомж зна-
sma sin2x яяп2х
354
чения и d2 найдем с помощью теоремы косинусов, примененной соответст-
венно к &DAC и Д BAD:
= А С2 = 2а2 - 2а1 cos (180° - а) = 2а2 (1 + cos а) =
45 ,а 45
= 2 •-------------. 2cos2 -=-----;
а а 2 а
4 л sin2 - cos2 - л sin2 -
2 2 2
„ , , , , 45 а 45
d^=BD2 = 2a2 — 2a2cosa=2a2(l —cosa) = 2 •-----------. 2sin2 -=-------.
, a , a 2 , a
4я sin2-cos - л cos -
2 2 2
2 IS 2 IS
Итак, di=----d2 =---------
a \ n a \ л
sin - cos -
2 2
Вариант II. □ 1. Заметим, что
x + 7а = (1/x+yja)(yjх2x2a+ljа),
x — yja = ^jx—y]a)(ljx2+yjx2a+yja),
у]ха2—yjx*у]а=у]х yja (yja—x).
Тогда заданное выражение преобразуется так:
</в)’-(-3 ^/Л)э-— 21xyfa.
1 1
2. Используя свойства логарифмов, находим lg Xs =5 lg х, lg— = - - Igx. Об-
у/х 4
ласть определения функции f(x) задается системой неравенств
Гх>0,
] (х>0, (х>0,
< 5 1 => < , => <
] - lgx + - lg2x —3>0 Ug2x + 51gx—6>0 ((lgx + 6)(lgx-l)>0.
Последняя система равносильна совокупности двух систем
(х>0, (х>0,
(lgx>l; Ugx< -6.
Решение первой из них есть х> 10; решением второй является промежуток
0<х^10-6. Итак, получаем ответ: xe(0, 10~6]|J[10, оо).
3. Сначала найдем значения данной функции на концах отрезка [0; 1,5] : Д0)=0,
8
Д1,5)=- 1,53 —18 1,52+28 • 1,5 = 10,5. Теперь найдем критические точки,
принадлежащие этому отрезку. Имеем /'(х) = 8х2 —36х+28; уравнение
/'(х) = 0 имеет корни Xjssl, х2 = 3,5 (последний не принадлежит данному
отрезку). Сравнивая между собой значения Д0)=0, Д1,5)='10,5, Д1) = 38/3,
заключаем, что/яаим=Л0)=0. а-/яалб=Л1) = 38/3. График функции на указан-
ном отрезке схематически изображен на рис. Р.П.7.
п т
4. Здесь cos 2x5*0, т. е. х#--1—. Преобразуем данное уравнение:
355
sin 2л
l+sin2x+cos2x +—'— = 0=>
cos2x
1 4-cos2x
=» (1 -t-cos2x)-t-sin2x-----=> (1+cos2x)(l+tg2x) = 0.
cos2x
п
Из уравнения l+cos2x=0 находим, что х=~+пк, а из уравнения
2
я nl
l+tg2x=0 — что х=--и—. Отрезку [— л/2, л] принадлежат: из первой
8 2
ЯЛ. п
серии значения х3 =— и х3=~, а m второй серии—значения х3=—-,
Зл 7л
> 8 8
5. По условию, ABCD — прямоугольник, OlE=r, LBOA = a (рис. Р.П.8).
a
В АЛОВ имеем Z_OB/1 = Z_OAB=90°—-; так как А О t — биссектриса L.OAB,
1 I я\
то 1_ЕАО^ =45°—. Далее, из t\AEOx находим ^£=rctg 45°— ), откуда
4 \ 4/
(а\
45° — ). Теперь найдем искомое скалярное произведение:
4/
На прт-7Гй=|2л| |2л|=|2л|* 2»4г2 ctg2 [45°--
\ 4
Вариант III. □ 1. Здесь а>1. Имеем
2а + у/ а1 — 1
(V“-1+ V“+1)(V“-1 - Va+ 1)((V“-!)* + О (a + l) + (V“+1)2)
la+Jct-l Ъа+у/а1—}. 1
(a—1 —a—l)(a—1+-</a2 —1+a+1) -2(2a + y/a2-l) 2
2. Так как 2* +1 >0, то
_x+l
2 +x—1 x+l x+1
--------<2 => 2 +x-1^2 +2 => x- i <2^> x^3.
2X + 1
356
3. Первая бригада за один день убирает 1/8 часть поля, а вторая — 1/6 часть.
Пусть х — число дней, которое обе бригады проработали вместе. Тогда
1 Z1 Л
получим уравнение - + (-+- )х=1, откуда х = 3 (дня).
8 \8 6/
4. После применения формул приведения придем к уравнению
|sin х| = sin х+2 cos х. Далее рассмотрим два случая:
1) sinx>0 => sin x = sinx+2cosx => cosx = 0 =>
л
=» x. = + 2лл (с учетом того, что sin x> 0);
2
2) sinx<0=> —sinx=sinx+2cosx => sinx+cosx=0 =>
(л\ л л
x— 1=0 => x—-= — -+2itm . (с учетом того, что
4/ 4 2
л
sinx<0) =» x2 = —- + 2nm.
Теперь найдем область определения функции у = / cos - ——:
cos—>0 => — -+2пк^-<- + 2пк => — п+Мс^х^п+Япк. (1)
4 2 4 4 4
Остается выяснить, при каких значениях лит корни Xj и х2 удовлетворяют
неравенству (1). Находим
п 3 1
— п + 8пк^-+2пп^п + Ыс => — +4к^п^~ + 4к => п=4к;
2 4 4
п 3 5
— п + Зпк^ — + 2пт<п + 3пк =>-+4к => т=4к.
4 8 8
Подставляя эти значения п и т в выражения для xt и х2, получаем ответ:
л л
х, =- + 8лЛ, х,=-|-8л&, кеЪ.
2 4
5. По условию, в трапеции ABCD имеем L BAD = 90°, L ADC=30°, OF=OM=R
(рис. Р.П.9). Так как трапеция описана около окружности, то
ВС+AD = АВ + CD. Но АВ+ CD = 2R+--------= 2R+----= 2R+4R = 6R.
sin L CDE sin 30°
1 1
Итак, SABcd=- (BC+AD)AB=- 6R 2R = 6R2.
„ 2 2
357
Вариант IV. 1. 0,25—4х*. 2. х>л/2. 3. Возрастает на (—9, 3), убывает на
л
(—□о, —9) и на (3, оо); Утш = — 27 при х = — 9, уши=5 при х=3 (рис. Р.П.10). 4. —;
12
5л 7л 11л o^l+tga) х
—; —; —. 5. --------. Вариант V. 1. ----. 2. х>2,5. 3. Возрастает на
12 12 12 2 2-х
(—7, 7), убывает на (—оо, —7) и на (7J оо); Утш = — 14 при х= — 7, ушах = 14 при
л л 5л 7л а2
х=7. 4. —; 0; -; —; л; —. 5. —. Вариант VI. 1. х’. 2. (—оо, 0)(J(l/3, оо). 3.
6 6 6 6 3
Возрастает на (—0,5; 0,5), убывает на (—оо; —0,5) и на (0,5; оо); Ут;п= —2 при
7л 5л л л 5л 2 а
х= —0,5, Утях=2 при х=0,5. 4.-;---; —; —. 5. - sina cos2 -. Вариант
6 6666л 2
VII. 1. —2. — 1 <х<2. 3. Возрастает на (0, 10), убывает на (— оо, 0) и на (10, оо);
V2
5л Зл л 2
уm,n—0 при х=0, утах =Ю при х=10. 4.----------;---; —-. 5. - Р sin a cos2 а.
Вариант VIII. 1. л/2—у/х. 2. х> —2.3.fWBt= —2 при х= — 1,/тиб=3 при х= —2.
Пл 5л л P\/2ctga
4.---;-------; —. 5.-------. Вариант IX. 1. 1 —2х*. 2. х>8. 3./иим = 0,25 при
18 1818 64
л 2л 5л 1 sin2 2а .—
х=0,у^ал6 = 1 при х=1. 4. —; —; —. 5. - лг----. Вариант X. 1. t/4a. 2. См.
3 3 3 2 l+sin2a
Зл 4л 2л л 'л л л
рис. Р.П.11. 3. 2; 10; 50 или 50; 10; 2. 4.-;-; — л;-; —; —; 0; -; -. 5.
2 3 3 2 3 - 3 2
1 7л 5л
- Рsin 2а sin2/? cos/?. Вариант XI. 1. y/b. 2. См. рис. Р.П.12. 3. 5 и 1. 4.-;-;
4 4 4
Зя л 2
-----; -. 5.-= Sy/S ctga. Вариант XII. 1. 0,5. 2. См. рис. Р.П.13. 3. Равнобед-
44 з */27
ренный прямоугольный треугольник, катеты которого равны 4/3 см. • Принять
358
за независимую переменную угол а при основании треугольника, выразить пло-
щадь треугольника как функцию а и исследовать эту функцию на экстремум. 4.
я 4 яЛ3 tg3 а (1 —sin а)3
—; arctg3. 5.----------------. Вариант XIII. 1. f (х)=х+1 —у 3; f (х) = 1. 2.
4 3 cos3 а
2я я 2я Зя
(1; ОХ (0; logs2). X На 25%. 4--р 5. 45°. Вариант XIV. 1.
1 .г 1 5я я
/(х)=- Qjx+TjS)', f(x)=---=. 2. х=16. 3.0,4. 4. xt = —--t-2xk, х2 =-\-2nl;
2 б^Д2 6 6
а
ял3 ctg- _ -
М=-2, -1,0,1,... .5.---------. Вариант XV. I.f(x)=,j3x;f’(x)=^.2.x=1.
я 5я 7я Пя 4Л?и2
X 6; 6; 6. 4. ; —. 5.------. Вариант XVI. 1./(х)=0,25;/’(х)=0. 2. х=2. X
6 6 6 6 sin а
—0,25. 4. X] =-+яАг, x2=arctg3+a/; fc, 1=0,1, 2,.... 5. а2cosa tg/?. ВариантXVII.
4
1 я 5я
1./(х)=Л/х,/’(х) =—=. 2. Xj = 1,x2=2. 3. би 3. 4. х2 = — + 2лЛ, х2 = —-|-2я/; к,
2у/х 6 6
1—2, 3, 4, ... . 5. а2 [ tga+--l/3+4tg2a ). Вариант XVIII. 1./(х)= —х2—1;
\ 4 )
я я я Зя 5
/’(х)= —2х. 2. (-3; 0,5). X 6 и 6 см.. 4. —. 5. ---. Вариант XIX. 1.
6 4 3 4 sin a
/(х)=2л/х + 5;/'(х) =-L. 2. (5; 2^5), (5; -2л/5). 3. ±0,5. 4. x=—, л = 3,4, 5,... 5.
V* 3
4r2A
----. Вариант XX. 1. /(x)=-2x-l; /"(x)=-2. 2. (2; -1). X 0,75; 2,25. 4.
sin 2a
я 2ял 4
x= ±---1----; л = 1, 2, 3, ... . 5.-.
18 3 я sin a
Вариант XXI. □ 1. Полагая y=l—x2, получаем квадратное неравенство
y2+y<0 => X/+1)<0 =» — 1 <у<0. Возвращаемся к исходной переменной:
— 1 <1 —х2<0 => —2< —х2< —1 => 1 <х2<2 =>
=> l<|xf<2=>xe(-V2, -1)U(1, V2).
2. Пусть л/х—1=у, где у>0. Тогда приходим к квадратному уравнению
Ту2—15у+2=0, имеющему корни у2=2, у2 = 1/7. Вернемся к исходной пере-
менной. Имеем i/x— 1 =2, откуда х2 = 5; у/х— 1 = 1/7, откуда х2=50/49. Про-
верка показывает, что оба значения являются корнями данного уравнения.
X Найдем ОДЗ неравенства:
(Зх+1)2>0,
(Зх + 1)2^1, (Х<П/3,
11 —3x>0, =>S*>-V3,
Зх+1>0,
Зх+1^0
359
Используя свойства логарифмов, преобразуем данное неравенство:
log3x+1(ll-3x)
1 +log3x+1 5 •---------— > 51og3x+12;
Iog3x+15
32
1 +log3x+1 (11 —3x) >log3x+1 32; log3x+1 ——— < 1.
11 — 3x
Последнее неравенство распадается на две системы:
Зх+1> 1,
32
Зх+1>—---;
11 —Зх
0<Зх + 1 <1,
32
Зх+1 <-----.
11—Зх
С учетом ОДЗ решаем систему (1), используя то, что 11 — Зх>0:
(х>0, (х>0,
l(3x+l)(ll-3x)>32 Т* (9х2 —30х + 21 <0 ”
{х>0, ]х>0, г
/ 7\ =>\ 7 =» -хе 1,_ .
з(х—1)(х—- ко 1<х«- L 3J
\ 3/ < 3
С учетом ОДЗ решаем систему (2), используя то, что ее второе неравенство
противоположно второму неравенству системы (1):
Ответ: хе(-1/3, 0) |J [1, 7/3].
sinx cos2x
4. TaKKaatgx=---,ctg2x=----------, 1 + cos 2x=2 cos2 x, то данное уравнение
cosx 2sinxcosx
имеет смысл при
{sinx# 0, ял
=> x#—, neZ.
cosx#0 2
После приведения к общему знаменателю получим следующее уравнение:
2cosx sin2x—2cos3x+cosx—sinx=0 =»
=> 2cosx(sin2x—cos2 х)+cosx—sinx =>
=> (cosx—sinx)(1 — 2cos2x—2sinx cosx)=0 =»
=» (cosx—sinx)(cos2x+sin2x)=0.
Оно распадается на два уравнения:
п
1) cosx=sinx => х=— +пк, keZ;
2) cos2x= — sin2x => х=-1— I, IeZ.
8 2
360
Из двух полученных серий корней исходного уравнения выделяем корни,
удовлетворяющие условию — 0,5<х<1. В первой серии это значение
jc1=Tt/4> соответствующее к=0, во второй — значение х2= — я/8, соот-
ветствующее /=0.
Ответ: xt=n/4, х2 — — л/8.
1
5. Введем обозначения: ВС=а, АС=Ь, АВ—с, р = -(а+Ь + с)— полупериметр;
2
г — радиус вписанной в &АВС окружности; Ot — точка пересечения биссек-
трис, центр вписанной окружности; О — точка пересечения медиан (рис.
Р.П.14). Так как ВК=КС и ВС=30 см, то ВК=КС=АК—15 см. Тогда точка
К— центр описанной окружности и, значит, /.Л=90°. Опустим из точек К,
1
ОиО] перпендикуляры из АС; при этом XZ>||O£||O.F\\AB. Имеем KD= с
2
как средняя линия &АВС. По условию, О2О\\АС; следовательно,
OE=O2F=r. Из подобия прямоугольных треугольников АЕО и ADKи свой-
ства точки пересечения медиан треугольника следует
KD АК с 3
— =—=>—=-=> с=3г.
ОЕ АО 2г 2
Далее, согласно свойству касательных, проведенных к окружности из одной
точки, имеем ВС=(АС—г) + (АВ—г) => а = Ь + с — 2г => /> = 30 — г, р = 30 + л
Найдем радиус вписанной окружности, приравнивая различные выражения
для площади Л. АВС:
1 1
•5длдс=2 Ьс=гр => — (30—г) Зг=г(ЗО + г) => г=6 (см).
Итак, 6 = ЛС=30-г=24 (см), с=ЛВ=Зг=18 (см).
6. Преобразуем исходное уравнение к следующему виду:
7^х-1)2+2*‘,_1)2 + 2ах=42(х—1)2 + 84(а—1)2 + 84ах —35 => 7^=42у—35,
где у=(х— 1)2 + 2(а— 1)2+2дх новая переменная. Уравнение относительно
у решаем графически. Из вида графиков z=42y—35 иг»/ (рис. Р.П. 15) ясно,
что может быть не более двух точек пересечения. Подбором находим, что
У1 = 1, У2 =2. Следовательно,
(х_1)2+2(а-1)2+2дх-1. либо (х-1)2+2(в-1)а +2ах-2.
361
Пре<36разуем левую часть этих уравнений:
UA Й2+2(а-1)2 4-2лх=х24-2х (л- 1)4-(а-1)1 + (а— I)1 4-1 =
=(х4-а-1)24-(а-1)24-1.
(а=1,
Если У1 = 1, то (х4-а—1) 4-(а—1)^=0. Тогда •( Исследуем этот случай.
(х=0.
При а=1 получим уравнения (х— 1)24-2х=1, либо (х—1)24-2х=2. Эти урав-
нения имеют решения х=0, х=1, х= — 1, т. е. исходное уравнение не имеет
единственного решения. Значит' а= 1 не удовлетворяет заданному условию.
Пусть а^1. Тогда выражение (х—1)2+2(а—1)2+?:;з яе принимает значение
1; остается исследовать уравнение
(х—1)24-2(а — 1У + 2ах — 2 =» х24-2х(а —1)4-2а2—4а + 1 =0.
Оно имеет единственное решение при условии D = (a-1)2—(2л2— 4а + 1)=0,
откуда 01=0, а2=2. Если а=0, то х= 1, а если а=2, то х= — 1.
Ответ: уравнение имеет единственное решение при а—0 и при а=2 (соответ-
ственно х= 1 и х= — 1).
Г(х)
Вариант XXII. □ 1. Приведем данное неравенство к виду---->0:
Л*)
6 1 6—(х—3)—2(х4-2)(х—3)
----------------->2 => >0 =>
(х4-2)(х—3) Х4-2 (х4-2)(х—3)
—2х24-х4-21 2(х—7/2) (х4-3)
=»----------->0 =*----------------<0.
(х4-2)(х4-3) (х4-2)(х—3)
Применим метод интервалов; отметим на числовой оси нули числите-
ля и знаменателя (—3, — 2, 3, 7/2) и определим знак левой части получен-
ного неравенства на каждом из интервалов. В результате получаем ответ:
хе(—3, -2)U(3, 7/2). _______
2. Возведя обе части первого уравнения в квадрат, получим -Jx+y+2^
=2 => х4-у4-2=4 => у=2—х. Подставив это выражение во второе уравне-
ние, имеем х24-(2—х)2=4 =а-2х2—4х=0 =а-Х]=0, х2=2, соответственно
У1=2, у2=0. Проверка показывает, что обе пары Х]=0, yt=2 и х2=2, у2»0
удовлетворяют заданной системе.
3. Найдем ОДЗ неравенства:
'81эс2>0,
81x^1, fX>°’ Jx>0’
х>0, (х#±-, 1х#~.
х3/9>0 9
Логарифмируем по основанию 9 обе части исходного неравенства (так хак
основание 9 больше 1, то знак неравенства сохраняется):
tog, (27 (81 х2)
<tog,x7.
Используя свойства логарифмов, имеем
362
I x \
21og,l—) log,(81 x2)+log,27<71og,x =>
3
=> 2 (3 log, x— 1) (2+ 2 log, x) +- < 7 log, x.
Положим y=log, x и придем к квадратному неравенству
3
2(Зу-1)(2 + 2у)+-<7у=>
2
, / 1\/ 5\ 1 5
=* 12у2+у —2,5^0 => 12 у+~ ) I у—— )<0 => —.
\ 2/ \ 12/ 2 12
Наконец, подставив log,x вместо у и учитывая, что основание логарифма
больше единицы, получим
1 5 1
—-<log,x<— =» 9 1/2<х<95/12 => -<х<35/6.
2 12 3
Найденное решение принадлежит ОДЗ. Ответ: х6(1/3, 35/6].
4. Возведем левую и правую части уравнения в квадрат и преобразуем получен-
, х
ное выражение, учитывая, что 1 —cosx=2sin -:
2sin2 cosx=sin2x+2sinx cosx+cos2x =sr
2
1 —2cosx = l + 2sinx cosx => sinx cosx+cosx=0 => cosx(l+sinx)=0.
Это уравнение распадается на два: cosx=0 и 1 +sinx=0. Решаем их, учиты-
вая ОДЗ:
{cosx=0,
. , „ fcosx=0, я
1—2cosx>0, =» 2 => х = “ + 2лл, лeZ.
. (sinx>0 2
smx+cosx>0
Г sinx= — 1,
sinx= —1, I
J 1 «
1-2cosx>0, => < cosx^-, => 0-
1 2
sinx+cosx>0 I
^_cosx>l
я
Ответ: x=- +2ял, «eZ.
2
1
5. Введем обозначения: BC=a, AC=b, АВ=с, p=-^a+b+c) — полупериметр
t^ABC; г, г,, г, — радиусы окружностей, вписанных соответственно в ДЛЯС,
ДЛРВ и ДЛРС (рис. Р.П.16). Проведем OjKIBC, O2LLBC, O2MLO1K.
Тогда OiK^ri, O2L=r2, OiM=r1-r1, О2М=г^+г2 и в имеем
O1O2 = O1Af2 + O2M2=>8=(r1-rJ)2 + (»'1+»'J)2=»rJ+^=4. (1)
Так как AD1.BC, то прямоугольные треугольники ABC, ABD, ACD подобны,
откуда
363
A
а с b
-=—=*— = t,
Г rt Г2
b' + c^a1
a = rt,
Ь=г21,
c=rtt,
b2 + c2 = a2
__________________'_________________ I I I \ => r2z2 + r2l2 = r2/2 => r? + H=A (2)
в_____________________________________________________________к n L С
ря PTT1fi Из (1) и (2) находим г2=4, т. е. г=2.
гас. г.11.10 Далее, используя свойство касатель-
ных, проведенных из одной и той же
точки к окружности, в А АВС имеем
ВС = (АС—г) + (АВ—г) =* а=Ь + с—2г =>
=* 2р = 2Ь + 2с—2г =» b+c=p+r => b + с= 12 + 2=14 (см).
Другое соотношение между катетами b и с выводится из сравнения различ-
ных формул для площади ДЛВС;
5кавс~гР=~ Ьс => Ьс=2 • 2 • 12=48 (см2).
2
(Ь+с = 14,
Решив систему ( находим b = 6, с=8 или b=8, с—6. Итак, искомые
катеты равны 6 и 8 см.
6. Найдем О ДЗ данного неравенства. Выражения ^/х2 — х+3 и 7 2х2 +1 определе-
ны на всей числовой оси. Правая часть неравенства положительна, второй
множитель левой части также положителен; поэтому неравенство имеет
смысл при х(х+1)>0, т. е. при х< — 1 или х>0.
Пусть yJx2—xA-3=u, л/2х2+1=«, где м>0, »>0. Тогда х2+х=»2 —и2+2
и исходное неравенство преобразуется следующим образом:
(»2 — м2+2)(1+м+»)—2—Зм—»>0 =>
=» (ю2—u2+2)(1+m+»)— 1 — и—«— 1— 2м>0=*
=> (1+ м+») (»2—м2+2—1)—1 —2м>0 =>
=> (1 +м+»)(»2 — м2 + 1) — 1 — 2м >0 =>
=» (»2—u2)(l+u+»)+l+u+»—1 —2м>0 =>
=» (»2—u2)(l+u+»)+»—и>0=»
=» (»-м)((1+м+»)(м+») + 1)>0.
Так как u>0, »>0, то полученное неравенство эквивалентно неравенству
»—м>0. Возвращаясь к аргументу х, имеем
V2x2 + 1 >>/х2-х+3 => 2х2 + 1>х2-х+3 =>
=> х2+х—2>0 =» (х+2)(х—1)>0.
Ответ: хе(—оо, —2)(J(1, оо).
Вариант ХХШ. □ 1. Перенеся 1 в правую часть неравенства, получим
3—х 2—2х 2(1—х)
-----К0 =*--------<0 =»------<0 =» хе(— оо, — 1)Н[1, оо).
х+1 х+1 х+1
2. Пусть у=45+х—х2; тогда исходное уравнение примет вид ---=у/з+2у.
Возведя обе части уравнения в квадрат и преобразуя, получим
364
4у3 = 3 + 2у + 3у+2у2 => 2у2 — 5у—3=0 =>
=> 2(у— 3)(у+0,5) = 0 =» >>i = 3, у2- — 0,5.
Уравнение относительно у имеет смысл при выполнении следующих условий:
{у>0, р>>о,
1 +у>0, =» м —1, =»у>0.
3+2у>0 (>>-1,5
Так как уг не удовлетворяет условию у > 0, то рассматриваем только значение
>i = 3. Имеем 45+х—х2=3 => х2—х—42=0, откуда х1=7, х2 = —6. Провер-
кой убеждаемся, что оба корня обращают исходное уравнение в тождество.
3. Преобразуем левую часть уравнения, используя формулы приведения и фор-
мулу тангенса половинного угла:
cos2x
1 + яп2х
Теперь исходное уравнение запишется в виде
л, /eZ.
п пп п nl
Ответ: х=—+—, х#—+—: л, /eZ.
28 7 12 6
4. Сначала найдем ОДЗ неравенства:
Лх + 1 >0, Г х> — 1,
J х + 1 #1, J х#0,
) 3 —2х —х2>0, °* ) (х + 3)(х —1)<0,
(.1 — Зх>0 (_х<1/3
=»X6(-1,O)U(0,1/3).
Далее рассмотрим два случая: 1) основание логарифма больше 1; 2) основа-
ние логарифма меньше 1. Имеем:
Сх+1>1, (х>0,
[3 —2х—х2 > 1 — Зх |_(х+1)(х-2)<0=>
fx>0,
=» < =» 0<х<1/3 (с учетом ОДЗ):
1-1«х«2
fO<x+l<l, f-l<x<0,
21 < ' =» 5 =>0-
(3-2х-х2<1-*Зх х>2
Ответ: хе(0, 1/3).
365
5. Введем обозначения: АВ=с, AC = b, h —
высота ромба, а — сторона ромба,
а — тупой угол ромба (рис. Р.П. 17). Из
вершины D ромба проведем высоты
DES.AB и DFLAC (DF=DE= А), которые
являются также высотами в &ABD
и ДЛРС. В &.DFK имеем sinz_Z)AL4 =
DF h Ji
= sin(180° —а)=— ==— => a = 120°.
DK а 2
Из условия СМ2 И Ра‘
венств
1 15^3
S^ABC = S^ADC^-ShjiBD=~ h(b + c) — - (b + c),
2 4
1 7з
8длвс= АС АВ sin 120°=— be
2 4
получаем систему для определения бис:
(6+с=64, (6=24, (6=40,
< => < или <
(6с=960, (с=40 (с=24.
По теореме косинусов находим третью сторону ВС:
ВС2 = 242 +402 —2 24 • 40cos 120° = 3136; ВС=56 (см).
Ответ: 24, 40 и 56 см.
6. Преобразуем левую .часть уравнения, используя формулы сокращенного ум-
ножения:
х2+(1 + а)у2+(2+2а)ху + (4 + 6а)х + (4+4а)у+За+4 =
=а(х2+у2+4+2ху+4х+4у) + 2ах—ах2 — а+(х2+у2 + 2ху+4х+4у+4) =
=а(х+у+2)2 + (х+у+2)2 —а(х—I)2.
Исходное уравнение примет вид (а+1)(х+у+2)2—а(х—1)2=0. Это уравне-
ние имеет единственное решение, если знаки слагаемых одинаковы, т. е. либо
(а+1<0, (а+1>0,
< либо < . Первая система не имеет решений, а решением
(а>0, (а<0
второй служит интервал — 1<а<0. При найденных значениях параметра
а решением исходного уравнения является пара чисел х=1, у= —3.
л
Вариант XXIV. 1. (3; 2), (2; 3). 2. хе(-оо, — 5)(J{—4}(J(—3, 2). 3. х^-4-ял.
* я я
х2 = ( -1) - —+пк; п, k е Z. 4. х е [1; 1,25)И(1,25; 5). 6. а, = -1, а2 = -1 /2, а, = 1 /2.
4 3
I я
Вариант XXV. 1. (1; -1), (-1; 1), (1/3; -4/3), (-1/3; 4/3). 2. хе 2яЛ+-,
I 6
Зя~|
2яА-|— , keZ. 3. Xj = —1/3, х2= —1/4, х3=3. 4. 24 скг. 5. Обе системы имеют по
Ях/2
а=----
2 . 6. х=5.
а6>4
366
Я jr
Вариант XXVI. 1. х— -2 пряо=+2л4, 4 eZ. 2.(49; 9). 3. х, =лл, х,= +-+2як;
2 6
п. кеЪ. 4. хе( —11,5; -10^5; O,5)U(O,75; 1)JJ2,5; оо). 5. 45°. 6. х^-6 при
,- я лк
а= 1. Вариант XXVII. 1. xt г=+>]2. 2. —9<х<0. 3. х, — яя, х2——
4. хе (2,25; 5). 5. 96 см2. 6. (0; а), (-а; — 0,5а), (—1,5а; 0,25а); при л-0 система
имеет бесконечное множество решений вида х—— 2у. Вариант XXVIII. 1.
я
х= 38,6. 2. хе( —да, 1)(J(1, да). 3. х=- + пи, neZ. 4. (1/4; 1). 5.90°, 60°, 30°. 6. х = 0,
4
>=0 при а—1,25. Вариант XXIX. 1. Х]>2= + 1, *з,4= —2±>/з. 2. хе(—оо, — 1)(J
. . Л ЯП , —0.2 Г
(J(3, оо). 3. х——I—, neZ. 4. хе(7~|, 7 ). 5. АВ=ВС=\ см, СО — у/З см,
16 4 _
я -ч/з
Л4> —3 см. 6. х—-+2ял, neZ при а — ±“- Вариант XXX. 1. Xj — —5, х2 —3. 2.
0<х<2, 2<х<л, ял<х<я+лл, nsZ, л#0. Целые решения: 1, 3, 7, 8, 9. 3.
л я 2л4 ' -75 , , х/5 г ,
х,—- + 2ял,х,=—Ч----; л, JteZ. 4. хе(3 , 1XJ(1, 3V ). 5. Пч/2 см2. 6. 2^х<3
2 14 7_
при а^З; 2^х^2+ч/4—а при 3<а<4; х—2, х—3 при а>4. Вариант XXXI. 1.
хе(— оо, -2)(J(-1, 2)(J(2,5; оо). 2. (-3; -1), (1; 3). 3. хе(0, 1/4НЛ »)• 4-
Я
Х1=2яд, х3=~+2я£; л, fceZ. 5. 5 и 12 см. 6. хе(—3, 1). Вариант XXXII. 1.
хе(—2, -73OV3. 2). X х=1. X хе(—4; -3,5)(J(-3; 8,5). 4. Зя/16; Зл/8. X 8, 10
я 12 см. 6. х—1 при а—0, х— —1 при а=2. Вариант XXXIII. 1.х—я/2. 2. Xj = — 3,
5я л
Xj—О. 3. Х] = — -—l-ял, х2=——+ nfc; л, fceZ. 4. хе( —5, —3)|J(3, 5). 6. а—2.
я ял я
Вариант XXXIV- 1. хе(—2, 1). 2. xe[0, 3)(J(3» °0)- 3. х, =^+-у> х2=-+хк; л,
JteZ. 4. хе(-оо, -5^)|J(-5/2, -125/62MJ(l/2, оо). 5. 7х/3 см2- 6. к~4. Вари-
ант XXXV. 1L х=2. 2. хе(— оо, —3){j(3, 1). 3, х—ял, heZ. 4. хе
€(-оо, -2-ч/Зи{~2О-2+ч/2. «э). 6. а>-9/40; единственное решение при
д«-9/40, а=0.
ОГЛАВЛЕНИЕ
Элементы Условия Решения,
теории, задач указания,
примеры ответы
Глава 1. Задача по планиметрии.................... 3 10 149
Глава 2. Задачи по стереометрии.................. 36 41 189
Глава 3. Задачи по геометрии с применением три-
гонометрии ...................................... 56 61 216
Глава 4. Дополнительные задачи по геометрии . . 93 98 310
Глава 5. Применение координат и векторов к ре-
шению задач .................................... 106 112 322
Приложения. Варианты заданий для самопроверка 119 346
Варианты билетов для вступительных
письменных экзаменов ........................... 134 354
Учебное издание
Егерев Виктор Константинович, Зайцев Владимир Валентинович, Кордемский
Борис Анасгасьевич, Маслова Тамара Николаевна, Орловская Ираида Федоров-
на, Позойсюй Роман Исаевич, Ряховская Галина Сергеевна, Суходский Андрей
Матвеевич, Федорова Нина Михайловна
Сборник задач по математике
для поступающих во втузы
(с решениями)
Книга 2. Геометрия