В. И. АЛЕКСАНДРОВ ПОСОБИЕ
ПО МАТЕМАТИКЕ
ДЛЯ ПОСТУПАЮЩИХ
в МГУ
ИЦ1[ ИЗДАТЕЛЬСТВО московского
МГУУ УНИВЕРСИТЕТА
МОСКОВСКИЙ ОРДЕНА ЛЕНИНА
И ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. М. В. ЛОМОНОСОВА
Подготовительные курсы естественных факультетов
Б. И. Александров, М. В. Лурье
ПОСОБИЕ
ПО МАТЕМАТИКЕ
ДЛЯ
ПОСТУПАЮЩИХ
В МГУ
ИЗДАТЕЛЬСТВО МОСКОВСКОГО УНИВЕРСИТЕТА
1977
Борис Иванович Александров,
Михаил Владимирович Лурье
ПОСОБИЕ ПО МАТЕМАТИКЕ
ДЛЯ ПОСТУПАЮЩИХ В МГУ
Редактор Р. Д. Солод
Художественный редактор Н. Ю. Калмыкова
Технический редактор 3. С. Кондрашова
Корректор Г. В. Зотова
Заказная. Сдано в набор 6/IV 1976 г. Подписано к Формат 6Ю X 9Э>/1в Бумага тип. №3 Физ. печ. л. 19,0 Зак. 619	Тираж 16 000 экз.			печати 11/XI 1976 г. Уч.-изд. л. 17,85 Цена 65 коп.
Издательство Д. 5/7.	Московского университета,	Москва,	К-9, ул. Герцена,
Московская типография ’№ 10 С о юз по лигр эфир ом а при Государствен-
ном Комитенте Совета Министров СССР по делам издательств, поли-
графии и книжной торговли. Москва, Mil 14, Шлюзовая наб., 10.
© Издательство Московского университета, 1977 г.
ПРЕДИСЛОВИЕ
Настоящее пособие представляет собой методическое
руководство по математике для учащихся подготови-
тельных курсов МГУ, готовящихся к поступлению на
естественные факультеты.
Подготовка к экзаменам рассчитана на один учеб-
ный год. Учащиеся должны систематически работать
над школьными учебниками, по которым необходимо
повторить программу курса по математике. Никаких
дополнительных знаний сверх школьной программы для
поступления в Московский университет не требуется.
Однако приобрести навыки решения экзаменационных
задач, и особенно задач повышенной трудности, необхо-
димых в первую очередь поступающим на факультеты
с математическим уклоном; можно только в результате
систематической напряженной работы.
В этой книге сформулированы основные темы для
проработки, дан перечень необходимых параграфов
в учебнике и список задач для решения. В конце первой
части помещены контрольные задания для учащихся
заочных подготовительных курсов.
Во второй части пособия приведено большое коли-
чество задач, предлагавшихся на письменных экзаменах
по математике абитуриентам естественных факультетов
МГУ в 1972—1975 гг. Для первого варианта каждого
факультета выполнен подробный разбор, ознакомление
с которым может служить ключом для решения осталь-
ных задач этого факультета. Эта часть книги должна
послужить пособием для приобретения практических
навыков решения задач.
Курсы рекомендуют учащимся ориентироваться на
следующие учебные пособия:
1.	Дорофеев Г. В., Потапов М. К.» Ро-
зов Н. X. Пособие по математике для поступающих
в вузы. М., «Наука», 1971—1976.
2.	Моденов П. С., Новоселов С. И. Пособие
по математике для поступающих в вузы. Изд-во МГУ,
1966.
3.	Л ид с кий В. Б., О вс ян ников Л. В., Ту-
ла йк о в А. Н., Шабунин М. И. Задачи по элемен-
тарной математике. М.» Физматгиз, 1963.
4.	Александров Б. И., Максимов 'В. М.,
Лурье М. В., Колесниченко Д, В. Пособие по
математике для поступающих в вузы. Изд-во МГУ, 1972.
5.	Л у рье М. В., Александров Б. И. Задачи
на составление уравнений. М., «Наука*, 1976.
Подготовительные курсы не располагают этими по-
собиями и не высылают их учащимся.
Авторы
Часть I
МЕТОДИЧЕСКОЕ РУКОВОДСТВО
И КОНТРОЛЬНЫЕ ЗАДАНИЯ
§ 1.	МЕТОДИКА ИЗУЧЕНИЯ
ПРОГРАММНОГО МАТЕРИАЛА
ПО МАТЕМАТИКЕ
УЧАЩИМИСЯ ЗАОЧНЫХ
ПОДГОТОВИТЕЛЬНЫХ КУРСОВ МГУ
Изучение программного материала по математике учащимися
заочных подготовительных курсов МГУ проводится по трем основ-
ным разделам: алгебра, геометрия и тригонометрия.
Работа учащегося-заочника складывается из следующих основ-
ных элементов: чтение учебников, решение задач, выполнение кон-
трольных заданий. Основной формой обучения учащегося-заочни-
ка является самостоятельная работа над учебным материалом.
Подготовка к вступительным экзаменам на любой из факуль-
тетов МГУ является трудоемким делом; его можно успешно вы-
полнить только при систематической и напряженной самостоятель-
ной работе. Готовиться к экзаменам следует систематически в те-
чение всего учебного года. Изучение курса математики в сжатые
сроки перед экзаменами не даст глубоких и прочных знаний и не
приведет к положительному завершению работы.
Самостоятельная работа
над учебными пособиями
Самостоятельная работа над учебными пособиями является
главным видом работы учащегося-заочника, и поэтому от ее орга-
низации зависит многое. Учащимся рекомендуется руководство-
ваться следующими положениями:
1)	избрав какое-нибудь учебное пособие в качестве основного
по определенной части курса математики, учащийся должен при-
держиваться данного пособия при изучении всей части курса
или по крайней мере целого раздела. Замена одного пособия дру-
5
гимч процессе изучения может привести к утрате логической свя-
зи между отдельными вопросами. Для решения задач, однако,
можно использовать различные источники и прежде всего те по-
собия, которые высылаются курсами;
2)	читая учебник по математике, следует переходить к новому
материалу лишь после усвоения предыдущего. Все выкладки и вы-
числения, так же как и соответствующие чертежи учебника, сле-
дует выполнит^ самому после ознакомления с данным материалом
по учебнику или пособию.
Чтение учебника или учебного пособия необходимо сопровож-
дать составлением конспекта, в котором записываются основные
теоремы, их доказательства и выполняется решение типовых задач
и упражнений, имеющихся после соответствующих разделов в учеб-
нике.
Опыт показывает, что основные формулы полезно выписывать
на отдельном листке, который не только поможет запомнить их,
но и будет служить справочным материалом.
Решение задач
Решение задач можно начинать с разбора задач, решенных
в учебнике и разобранных в пособиях, а затем переходить к само-
стоятельному решению задач, рекомендованных по этому разделу.
Решение задач определенного типа должно продолжаться до при-
обретения прочных навыков в их решении. Очень полезно, если
для решения всех задач отведена одна тетрадь. Это дает возмож-
ность впоследствии легко повторить пройденный материал.
Чертежи можно выполнять от руки, но аккуратно. В промежу-
точных вычислениях не следует вводить приближенные значения
корней или каких-либо других выражений. Помните, что большое
количество решенных задач позволит, с одной стороны, глубже
понять изучаемый материал, с другой стороны, определит успех
при решении подобных задач на экзамене.
Умение решать задачи приобретается длительными системати-
ческими упражнениями. Примите за правило каждый день решать
по нескольку задач на тот или иной раздел программы. Опыт
решения задач необходим и для выполнения контрольных работ.
Выполнение
контрольных работ
Выполнение контрольных работ учащимися подготовительных
курсов и рецензирование их преподавателями преследует две цели:
во-первых, осуществление курсами контроля за работой учаще-
гося; во-вторых, оказание ему помощи в вопросах, которые ока-
6
зались для него непонятными. По каждой контрольной работе
учащимся заочных подготовительных курсов будет выслана мето-
дическая записка, в которой дано подробное решение всех задач
этой контрольной работы и приведен анализ типичных ошибок,
встречавшихся при ее выполнении.
К выполнению контрольных работ по каждому разделу курса
или по частям этого раздела учащийся приступает только после
изучения материала, соответствующего данной части программы,
ознакомившись *с примерами решения задач подобного рода, при-
веденных в пособии.
При выполнении контрольных работ требуется, чтобы решения
были записаны в тетради со всеми вычислениями и краткими
объяснениями. В алгебраических примерах нужно объяснять, что
из чего получается, если это необходимо, проводить проверку ре-
шений, указывать возникающие ограничения. Если по характеру
задачи требуется построение чертежа, то он должен быть обосно-
ван, аккуратно .выполнен, все обозначения должны быть четкими
и соответствовать условию задачи. Кроме того, требуется, чтобы
чертеж был крупным. При построении графиков функций следует
использовать общие методы: перенос, сдвиг и т. д.
Если в процессе решения задачи используется какая-нибудь
теорема, то она должна быть названа. ^Очевидным» считается то
утверждение, которое входило в программу курса по математике и
содержится в учебнике. Все геометрические утверждения должны
быть строго доказаны. Не допускайте арифметических ошибок
и строго контролируйте свои вычисления. Контрольные работы,
выполненные без соблюдения изложенных выше правил, не. за-
считываются.
§ 2.	ЛИТЕРАТУРА, РАБОЧИЙ ПЛАН,
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО РАЗДЕЛАМ ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ
ДЛЯ УЧАЩИХСЯ ЗАОЧНЫХ
ПОДГОТОВИТЕЛЬНЫХ КУРСОВ МГУ
Для подготовки к вступительным экзаменам по математике
учащимся рекомендуется использовать следующую литературу,
применительно к которой составлено это пособие.
Основная литература
1.	Кочетков Е. С., Кочеткова Е. С. Алгебра и элемен-
тарные функции, чч. I и II. М., «Просвещение», 1971 —1974.
2.	Киселев А. Н. Геометрия, ч. II. М., «Просвещение», 1971;
а также ч. I любого года издания.
3.	Барыбин К. С. Геометрия. М., «Просвещение», 1972.
7
Дополнительная литература
Александров Б. И., Лурье М. В. Пособие по математике
для поступающих в МГУ. Изд-во МГУ, 1976.
В дальнейшем все перечисленные книги обозначаются сокра-
щенным образом. Например, под обозначением «Кочетковы, ч. I»
следует понимать: Кочетков Е. С., Кочеткова Е. С. Алгебра
и элементарные функции, ч. I; под обозначением «Пособие, § 15,
3(1)» нужно понимать: Александров Б. И., Лурье М. В.
Пособие по математике для поступающих в МГУ, часть 2-я, § 15,
вариант № 3, задача 1.
В каждой теме перечисляются в рекомендуемом порядке номе-
ра параграфов из учебников, который учащийся должен прочесть,
и нолт ер а задач й вариантов, которые он должен решить.
Раздел I. АЛГЕБРА «
Тема 1.
Действительные числа
Основные определения. Изображение действительных чисел
точками на числовой оси. Запись с помощью неравенств множеств
на числовой оси: отрезка, интервала, полуинтервала, полуоси.
Абсолютная величина действительного числа и ее основные свой-
ства. Геометрическая интерпретация абсолютной величины. Реше-
ние уравнений и неравенств, содержащих неизвестное в виде ли-
нейного выражения под знаком абсолютной величины.
Учебник — Кочетковы, ч. I, § 35—48, упражнения № 289—293,
296—299, 305—307, 316—322, 347—353; § 7, 8, упражнения №60—
74, 75—78; § 18, 25, упражнения № 207—219.
Пособие — §4, 1 (1), 2 (1), 3 (1), 4 (1).
Указание. Рассмотрим решение уравнения, содержащего неиз-
вестное под знаком абсолютной величины.
Решить уравнение:
|х—3| —|2х+4|=2.	(1)
Решение. Определение абсолютной величины гласит:
{а, если а>0;
—а, если а<0.
* Общий объем требований по математике, предъявляемых к поступающим
в МГУ, определяется ежегодно издаваемой общей для всех высших учебных за-
ведений «Программой вступительных экзаменов для поступающих в высщие учеб-
ные заведения СССР».
В предлагаемой учащимся курсов рабочей программе отмечены лишь наибо-
лее трудоемкие и имеющие первостепенное значение для решения задач вопросы
из этой программы.
8
Поэтому определим точки, в которых хотя бы одно из выраже-
ний, стоящих под знаком модуля, равно нулю. Это будут числа 3
и —2. Точки —2 и 3 делят все числа на три области, в каждой из
которых уравнение (1) можно записать без знака модуля. Рассмо-
трим возможные случаи.
Г. Будем искать те решения уравнения (1), которые удовле-
творяют системе
х>3,
(х - 3) - (2х + 4) = 2.
Уравнение в этом случае имеет решение х=—9. Однако это зна-
чение не удовлетворяет ограничению х^З, при котором были опу-
щены знаки-модуля. Поэтому х=—9 не является решением урав-
нения (1).
2. Будем искать те решения уравнения (1), которые удовлетво-
ряют системе
1 —2<х<3,
( — (х — 3) — (2х-|-4) = 2.
Решение уравнения имеет вид х=—1. Оно удовлетворяет неравен-
ству— 2^х<3, при условии которого последнее уравнение полу-
чается из исходного. Поэтому х=—1 есть решение уравнения (1).
3. Рассмотрим, наконец, область х<—2. Имеем систему
1 х< —2,
1-(х-3) + (2х + 4) = 2.
Решение уравнения этой системы х=—5 удовлетворяет неравенст-
ву х<—2 и потому является решением и уравнения (1).
Ответ: xi=—1, Хг=—5.
Тема 2.
Линейные уравнения и неравенства
Тождества и уравнения. Неравенства, их основные сврйства.
Строгие и нестрогие неравенства. Двойные неравенства. Линейные
уравнения и неравенства.
Учебник — Кочетковы, ч. I, §1,2, упражнения № 1—5, 13;
§ 9—15, упражнения № 79—116; § 3, упражнения 15—25; § 4,
упражнения № 26—39, 50—56; § 17, упражнения № 133—139; §20
(обратить особое внимание), упражнение № 152; § 21, упражнения
№ 154—164, 179—183.
9
Тема 3.
Системы линейных уравнений
Исследование системы двух линейных уравнений с двумя неиз-
вестными. Определители системы, правило Крамера. Графическая
интерпретация решения системы. Равносильность систем урав-
нений.
Учебник — Кочетковы, ч. I, § 26—34, упражнения № 220—222,
223, 229—232, 234, 236—240, 241, 247—252, 257, 283—286.
Указания. Приведём основные результаты исследования вопро-
са о существовании и числе решений системы двух линейных
уравнений с двумя неизвестными:
ДгХ —|- Ь2у =z С2,
тд,е Oi, Оъ b%, Ci и C2— коэффициенты, действительные числа.
Классификация решений системы линейных уравнений связана
с численными значениями трех определителей:
главного:
Д =
flibi
Д2&2
— Clibz — Ь\С12
и двух частных:
" Дх—
С\Ъ\
С2&2
— Cib2 — Ь\С2*, Ду —
0-1С 1
а2с2
"== OiC2 —-
Возможны следующие случаи:
{. Решение единственное: Л=#0.
x = -z£-, у =
А *
Ду -
А *
Эти формулы называются формулами Крамера.
2.	Решение неединственное или решений нет (система несовме-
стна): Д = 0.
Здесь возможны такие подслучаи:
а)	Д = 0, но один из частных определителей Лх или отличен
от нуля: Дх#=0 или ^=#0. Система несовместна;
б)	Л = 0 и ДХ = ДУ=О и по крайней мере один из коэффициен-
тов при неизвестных х или у отличен от нуля. Система уравнений
имеет бесчисленное множество решений;
в)	Д=0, Дх = Л1/ = 0 и все коэффициенты системы равны нулю.
Система имеет бесчисленное множество решений;
г)	Д=0, ДХ = Л2/ = О, все коэффициенты при неизвестных х и у
равны нулю, но хотя бы одно из чисел С\ или Сг отлично от нуля.
Система не имеет решений.
Рассмотренные случаи допускают следующую геометрическую
интерпретацию: каждое уравнение системы линейных уравнений
10
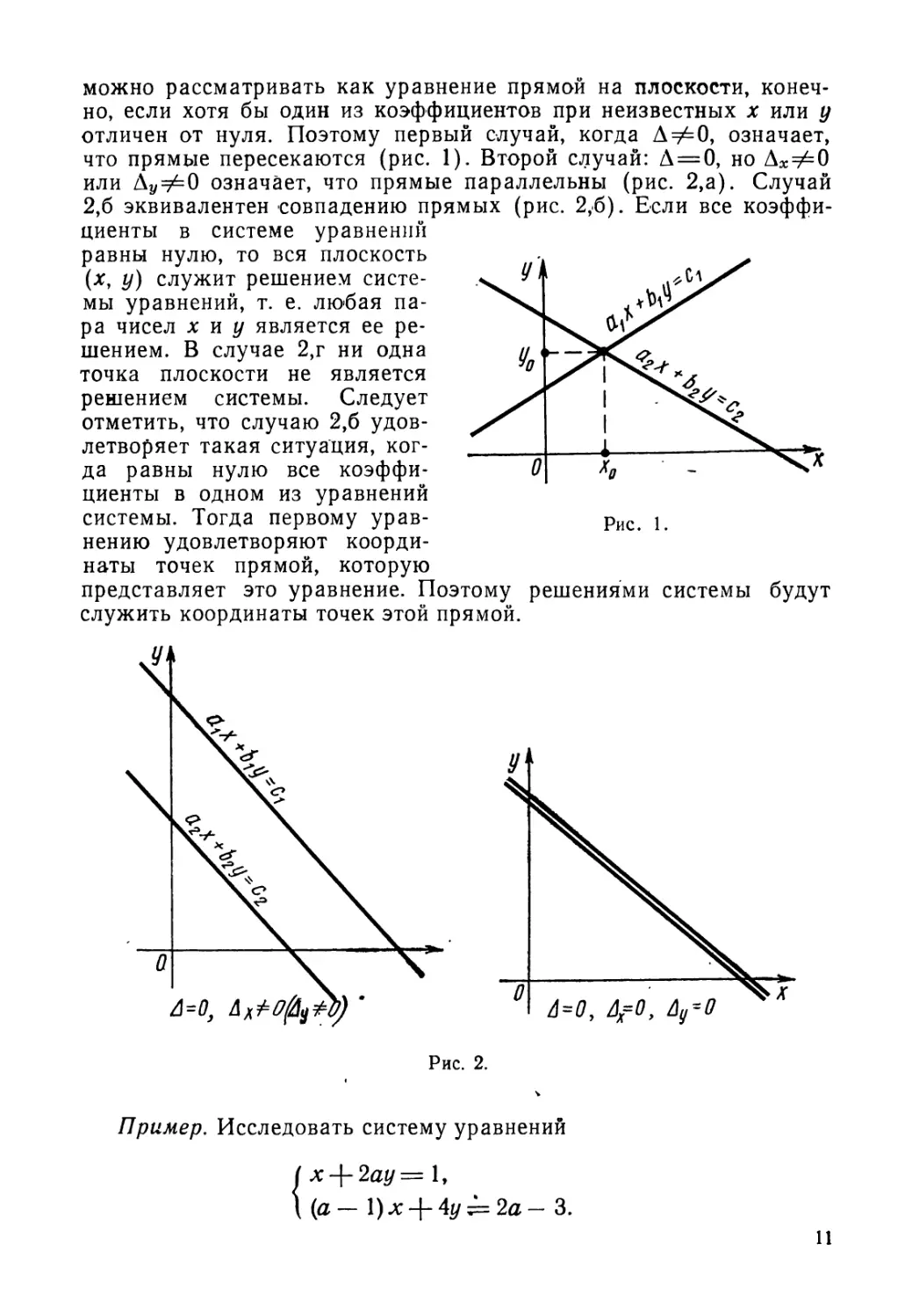
можно рассматривать как уравнение прямой на плоскости, конеч-
но, если хотя бы один из коэффициентов при неизвестных х или у
отличен от нуля. Поэтому первый случай, когда А#=0, означает,
что прямые пересекаются (рис. 1). Второй случай: А = 0, но Аху=0
или Ау#=0 означает, что прямые параллельны (рис. 2,а). Случай
2,6 эквивалентен совпадению прямых (рис. 2,6). Если все коэффи-
циенты в системе уравнений
равны нулю, то вся плоскость
(х, у) служит решением систе-
мы уравнений, т. е. любая па-
ра чисел хну является ее ре-
шением. В случае 2,г ни одна
точка плоскости не является
решением системы. Следует
отметить, что случаю 2,6 удов-
летворяет такая ситуация, ког-
да равны нулю все коэффи-
циенты в одном из уравнений
системы. Тогда первому урав-
Рис. 1.
нению удовлетворяют коорди-
наты точек прямой, которую
представляет это уравнение. Поэтому решениями системы будут
служить координаты точек этой прямой.
Пример. Исследовать систему уравнений
х-\-2ау = 1,
(а — 1) х + 4г/ —= 2а — 3.
11
Решение. Вычислим главный определитель этой системы
1
а— 1
4
= 2(2-]-а —а1).
Если этот определитель отличен от нуля, то решение системы
единственное. Таким образом, если а2—а—2^0, т. е. а=/=2 и
а=/=—1, находим
Дх   4 + 6а — 4а*	__ Д^	а — 2
Д 2(24-а —а«) ’	2(2 +а — а«) ’
Здесь Дх и Лу — частные определители:
Дх —
=4-|-6а —4а1,
а — 1 2а — 3
=а — 2.
1 1
Если а = 2 или а=—1, то главный определитель системы урав-
нений равен нулю и единственного решения нет.
Если а=2, то легко видеть, что равны нулю и оба частных
определителя: Дж=0 и Ди=0. Поскольку в этом случае среди
коэффициентов системы, стоящих при х или у, есть коэффициен-
ты, отличные от нуля, то система имеет бесчисленное множество
решений, связанных соотношением
х+4у=1.
Если а=—1, то частные определители отличны от нуля и си-
стема не имеет решений.
В качестве задач для самостоятельного решения предлагаем
решить следующие задачи, взятые из экзаменационных вариан-
тов МГУ.
Задачи.
 1. При каких значениях параметра а система
12x-l~ay=a-j-2,
I (а-{- 1)х-^-2ау = 2a-j-4
имеет бесконечно много решений?
Ответ: при а=3.
2.	Найти все значения а, при которых система
| 2х-}-а*у = а*-\-а — 2,
1 х-|-2^ = 2
не имеет решений.
Ответ: при а——2.
3.	При каких значениях а система
(а*х-[-(2 — а)у = 4-]-а*,
I ах-]-(2а — 1)у = а±— 2
12
не имеет решений?
Ответ: при а=1.
4.	Числа а, b и с таковы, что система	**
| ах — by = 2а — Ь,
I (<?+ 1)х4-п/= 10-О4-3&
имеет бесконечно много решений, причем х=1, у—3— одно из
этих решений. Найти числа а, Ь и с.
Ответ: а=0, 6 = 0, с=9/4; а=2, Ь=—1, с= 1.
5.	При каких значениях а и b система
{ах у = Ь,
х — у = 2
имеет единственное решение, не имеет решений, имеет бесконечно
много решений?
Ответ: при а#=—1 единственное решение; при а=—1,
—2 система не имеет решений; при а——1, Ь=—2 система
имеет бесконечно много решений.
Тема 4.
Квадратный трехчлен
Основное преобразование. Квадратные уравнения. Теорема
Виета. Исследование знаков корней квадратного трехчлена по его
коэффициентам. График квадратной функции. Различные случаи
расположения параболы по отношению к оси ОХ. Квадратные
неравенства. Решение квадратных уравнений и неравенств, содер-
жащих неизвестное под знаком абсолютной величины.
Учебник — Кочетковы, ч. I, § 49—51, 52—54, 57—62, упражне-
ния № 354—356, 386—390, 391—406, 413—427, 428—430, 434—449;
на упражнения № 451—455 обратить особое внимание.
Указания. К вопросам, связанным с исследованием квадратно-
го трехчлена, приводит большинство экзаменационных задач.
В некоторых из таких задач возникает необходимость провести
анализ корней квадратного уравнения по его коэффициентам. Рас-
смотрим пример такого анализа.
Пример. Найти все значения параметра а, при которых корни
уравнения
(а—2)№—2ах+2а—3=0
действительны, и определить знаки корней.
Решение. Если а=2, то данное уравнение является линейным,
имеет один корень, равный 1/4.
13
При а=/=2 данное уравнение имеет действительные корни, если
дискриминант квадратного трехчлена неотрицателен:
или
откуда находим
Г^а^б; (а=/=2).	(1)
Для определения знаков корней воспользуемся теоремой
Виета:
।	2а
'	2а — 3
** = 7=2*
Корни имеют одинаковые знаки, если их произведение положи-
тельно. Если при этом положительна и сумма корней, то они оба
положительны:
2а — 3
О,
О» х«>0,
2а
а — 2
откуда с учетом (1) находим: 2<а^6. Если при этом сумма кор-
ней отрицательна, то оба корня тоже отрицательны:
2а — 3 п
2а
а — 2
=>Xi<0, Xi<0,
0,
откуда с учетом (1) находим: 1^а<3/2.
Если корни имеют разные знаки, то произведение корней отри-
цательно и выполняется неравенство
<°Xi >°’ °’
откуда находим: 3/2<а<2.
Наконец, если хотя бы один из корней уравнения равен нулю,
то имеет место условие
2а — 3
0,
из которого находим: а = 3/2. Поскольку при а = 3/2 сумма корней
отрицательна, то другой корень уравнения отрицателен.
14
Ответ: корни уравнения действительны при 1^а^6. а. При
2<а^6, оба корня положительны; б. При а=2, один положи-
тельный корень; в. При 3/2<а<2, корни разных знаков; г. При
а = 3/2, один из корней равен нулю, а другой отрицателен; д. При
1 ^а<3/2, оба корня отрицательны.
Решить задачи. Пособие, § 7, 1(5), 3(5); § 8, 1(4), 2(4), 3(4),
4(4); § 11, 4(2), 2(2), 3(2), 4(2); § 26, 1(2), 2(2), 3(2), 4(2).
Тема 5.
Рациональные уравнения и неравенства
Целая рациональная функция (многочлен). Корни многочле-
нов. Разложение многочленов на множители. Дробно-рацио-
нальная функция. Решение рациональных неравенств методом
интервалов.
Пособие, § 12, 1(4), 2(4),'3(4), 4(4); § 17, 1(1), 2(1), 3(1),
4(1).
Пример 1. Решить неравенство
(х-3)(х-2)»(х + 4)
(х-6)«(х + 2)	’
Знак этой дроби зависит от сочетания знаков составляющих ее
сомножителей. Изобразим на числовой прямой точки —4, —2, 2,
3 и 6, в которых обращается
в нуль хотя бы один из сомножи-	__ __	__
телей, стоящих в числителе или
знаменателе этой дроби (рис. 3).	-4-2	2 5	6 X
Тогда числовая прямая разобь-
ется на 6 областей, в каждой из	Рис. 3.
которых все сомножители и, зна-
чит, вся дробь сохраняют определенный знак. Рассмотрим каждую
из этих областей.
При х>6 все сомножители положительны (ставим в этой обла-
сти знак « + »). При переходе в соседнюю область через точку 6 все
сомножители сохраняют знаки потому, что скобка (х—6) входит
в эту дробь в четной степени (поэтому в области 3<х<6 тоже
нужно поставить знак « + »). При дальнейшем движении влево по
числовой оси, при переходе от одной области к другой, знаки « + »
и «—» будут чередоваться, так как каждый раз будет менять свой
знак ровно один из сомножителей. Поэтому имеем
Ответ: х^—4, —2<х^2; 3^х<6; х>6.
Пример 2. Решить неравенство
1 1
х1 2 — Зх + 2 х* — 7х+12
15
Запишем это неравенство в следующем виде:
1
(х—1)(х —2)
1
(х-3) (х -4)
(х« —7х + 12) —(х« —Зх +2)
(х — 1) (х —2) (х — 3) (х — 4)
ИЛИ
2(х — 2.5)
(х- 1)(х —2)(х—3) (х —4)
Решая это.неравенство «методом интервалов» (см. пример 1), по-
лучаем
Ответ:
х<1; 2<х<2,5; 3<х<4.
Тема 6.
Иррациональные уравнения и неравенства
Понятие об арифметическом корне. График функции 'у=
Формулы
/** = 1-4 /р(х) = |/ (х)|.
Область определения иррациональных выражений. Равносиль-
ность уравнений и неравенств. Преобразования, сохраняющие рав-
носильность. Основные особенности решения иррациональных
уравнений и неравенств. О необходимости проверки. Решение
иррациональных уравнений и неравенств и систем уравнений и не-
равенств.
Учебник — Кочетковы, ч. I, § 65, 66, упражнения , Ns 471—482,
503—505.
Пособие, § 13, 1(3), 2(3), 3(3), 4(3); § 16, 1(1),2(1), 3(1),4(1);
§ 18, 1(5), 2(5), 3(5), 4(5); §31, 1 (1), 3(1), 4(1).
Указания. При решении иррациональных уравнений и не-
равенств имеются два основных вопроса, на которые следует обра-
тить особое внимание. Один из них связан с необходимостью
соблюдать ограничения, налагаемые на неизвестные областью опре-
деления иррациональных функций. Следует помнить, что под зна-
ком радикала четной степени могут стоять только неотрицатель-
ные выражения. Например, выражение
16
y = Vf(x)
определено только при тех значениях х, которые удовлетворяют
неравенству
Если в задаче встречается несколько выражений подобного типа,
то областью допустимых значений неизвестного, ОДЗ, будут те
значения х, при которых определены все функции, входящие в за-
дачу.
Другой вопрос, который возникает при решении иррациональ-
ных уравнений или неравенств, связан с равносильностью пре-
образования «возвышение в квадрат» обеих.частей уравнения или
неравенства. Например, совершенно очевидно, что возвышение
в квадрат обеих частей верного числового неравенства 3>—5 при-
ведет к неверному результату, если сохранить знак неравенства
в одном случае, и даст правильный результат в другом слу-
чае: 5>3.
Таким образом, для того чтобы правильно решить задачу, не-
обходимо выделить несколько случаев. Нужно помнить, что если
обе части неравенства или уравнения неотрицательны, то возвы-
шение в квадрат обеих частей этого уравнения или неравенства
с сохранением данного знака между ними приводит к равно-
сильной задаче.
В общем случае решение неравенства

связанное с возвышением в квадрат обеих его частей, распадается
на следующие случаи:
а)
g(x)^0,
(2)
4-0ДЗ функций' f (х) и g (х).
б)
f(x)>0,
g(x)<0.
(3)
Очевидно, что случай, когда /(х)<0, а £(х)^0, не даст решений.
Таким образом, все решения неравенства (1) получаются из ре-
шений систем (2) и (3).
Пример. Решить неравенство
J/x4-3 >х — 9.
2—619
17
Решение. Область допустимых значений в этой задаче опреде-
ляется неравенством —3.
Возвести в квадрат обе части исходного неравенства было бы
ошибкой, так как неизвестно, какой знак имеет его правая часть.
Для х^9 получилось бы неравенство, равносильное исходному,
но при —3^х<9 результат мог бы быть неверным.
Рассмотрим два случая.
' 1). х>9.
Имеем систему неравенств
х>9,
х + 3>(х-9)\
решения которой имеют вид 9^х<13.
2) —ЗСх<9.
Здесь нельзя возводить обе части неравенства в квадрат, посколь-
ку его правая часть отрицательна. Но очевидно, что для тех х,
для которых правая часть отрицательна, а левая часть больше
или равна нулю, неравенство выполнено. Таким образом, в этом
случае неравенство имеет следующие решения: —3^х<9.
Решениями исходного неравенства являются решения обоих
случаев. Объединяя эти множества, получим
Ответ: — 3^х< 13.
Тема 7.
Показательная и логарифмическая функции
Степени с рациональными показателями; степени с иррацио-
нальными показателями. Основные действия со степенями. Пока-
зательная функция и ее график. Свойства показательной функции.
Различия в свойствах показательной функции с основанием, боль-
шим единицы, и показательной функции с основанием, меньшим
единицы; монотонность показательных функций. Решение показа-
тельных уравнений.
Логарифмическая функция и ее график. Свойства логарифми-
ческой функции. Различия в свойствах логарифмической функции
с основанием, большим единицы, и логарифмической функции
с основанием, меньшим единицы; мон^онность логарифмических
функций. Основные формулы теории логарифмов. Переход к ново-
му основанию. Решение логарифмических уравнений.
Решение показательных и логарифмических уравнений и не-
равенств. Необходимость учета ограничений, связанных с областью
определения логарифмической функции, и условий, гарантирую-
18
щих равносильность совершаемых преобразований. Решение сме-
шанных задач, содержащих логарифмическую, показательную, ра-
циональную и иррациональную функции.
Учебник — Кочетковы, ч. I, § 68—86; ч. II, § 174—177, упраж-
нения № 1358—1362, § 178, 179, упражнения № 1365—1374; §180—
182, упражнения № 1375—1390 (на последнее упражнение надо
обратить особое внимание), 1394—1399; § 183—186, упражнения
№ 1449—1454; § 197, упражнения № 1473—1475.
После этого нужно решить задачи: Кочетковы — ч. II,
№ 1479—1507, 1510—4514, 2194—2207, 2213.
Пособие, § 1—35 в порядке возрастания трудности.
Указания. Задачи, в которых встречается показательная и ло-
гарифмическая функции, — традиционный элемент экзаменацион-
ных вариантов по математике, предлагающихся в.МГУ. Проработ-
ку этой темы нужно начать с чтения и конспектирования учебни-
ка. Вслед за этим, а частично и параллельно этому, необходимо
решать задачи из рекомендованных упражнений. Только после
этого нужно переходить к систематическому решению задач из
настоящего пособия. На них можно проверить свои знания и при-
обрести опыт решения экзаменационных задач.
Независимо от того, вызвали эти задачи трудности или нет,
необходимо ознакомиться с приведенными в пособии решениями
и принять во внимание сделанные там мётодические замечания.
Как правило, порядок расположения параграфов в пособии опре-
деляет порядок возрастания трудности задач.
Тема 8.
Последовательности и прогрессии
Общее определение последовательности. Арифметическая и
геометрическая прогрессии. Формула для общего члена последо-
вательности. Сумма п членов арифметической прогрессии. Сум-
ма п членов геометрической прогрессии.
Предел последовательности. Основные свойства пределов. Не-
которые теоремы о существовании пределов последовательности
(без доказательства). Сумма членов бесконечно убывающей гео-
метрической прогрессии.
Учебник — Кочетковы, ч. I, § 127—137, упражнения № 932—
938, 951, 960; упражнения № 964, 969, 971—980,985—988,989—996,
1001 — 1020.
Решить следующие задачи.
1. Биофак, 1970. Даны две геометрические прогрессии аь а2, Дз
и 61, 62, 6з. Известно, что числа fli + fci, а2Ч-^2, аз + 6з снова обра-
зуют геометрическую прогрессию.
Доказать, что aib3=a3bi.
2»
19
'2. Биофак, 1970. Даны две арифметические прогрессии ai, аг,
ази&ь&г, &з> причем &i#=62, и а1+'а2+а3=61-|-624-0з. Известно, что
числа aj&i, а262, agb3 также образуют арифметическую прогрессию.
Доказать, что ai = 62.
3.	Биофак, 1970. Даны'две геометрические прогрессии ai, a2,
а3 и 61, 62, Ь3. Известно, что числа a^bi, a^bt, а3Ь3 образуют ариф-
метическую прогрессию и а1+аг+аз=61+6е+6з.
Доказать, что 01 + 61 = 03+63.
4.	Геофак, 1971. Положительные числа ai, a2, a3, at,, a3 состав-
ляют геометрическую прогрессию. Сумма логарифмов этих чисел
по основанию 2 равна 5. Определить эти числа, если отношение
log2ai к log2a5 равно — 5/3.
Ответ: 32; 8; 2; 1/2; 1/8.
5.	Геофак, 1071. Положительные числа ai, a2, а3, ait а3 состав-
ляют геометрическую прогрессию. Сумма логарифмов чисел ai, аз,
а5 по основанию 3 равна 9. Определить числа ai, a2, а3, а^ а3, если
log3O4 вдвое больше log3a2.
Ответ: 3, 9, 27, 81, 243.
6.	Физфак, 1973. Сумма первых тринадцати членов арифмети-
ческой прогрессии равна 130. Известно, что четвертый, десятый и
седьмой члены этой прогрессии, взятые в указанном порядке,
представляют собой три последовательных члена геометрической
прогрессии. Найти первый член арифметической прогрессии.
Ответ: 10; 70.
Тема 9.
Задачи на составление уравнений
Рассмотреть "следующие основные типы задач на составление
уравнений:
задачи, связанные с понятиями «концентрация и процентное
содержание»;
задачи «на движение»;
задачи, решаемые с помощью неравенств;
задачи, в которых уравнений меньше, чем неизвестных;
задачи с целочисленными неизвестными;
задачи с «альтернативными» условиями. ч
Подробно о каждом из этих типов задач можно прочитать
в книге М. В. Лурье и Б. И. Александрова «Задачи на составле-
ние уравнений», выпущенной издательством «Наука» в 1976 г.,
а также в «Пособии по математике для поступающих в вузы»
Г. В. Дорофеева, М. К. Потапова и Н. X. Розова.
В качестве упражнений рекомендуется прорешать задачи на
составление уравнений, имеющиеся в каждом варианте всех пара-
графов настоящего пособия.
20
Раздел II. ТРИГОНОМЕТРИЯ
Тема 10.
Тригонометрические функции
Градусная и радианная мера углов и дуг. Определение основ-
ных тригонометрических функций числового аргумента. Значения
тригонометрических функций от некоторых аргументов:
~ 7С к к к 2п Зп 5п о
°’ т- — ’ ~’ —’ —’	2*и т< п-
Основные тригонометрические тождества. Область определения
тригонометрических функций и их свойства: четность, периодич-
ность, монотонность и т. п. Графики основных тригонометрических
функций: y=sinx, y=cosx, y=tgx, y=ctgx.
Учебник — Кочетковы, ч. I, § 95—104, 107—111, 113—115; ч. II,
§ 161—164; упражнения: ч. I, стр. 217, X® 645—647, 649, 650, 663,
674, 710—716, 717, 720—727, 732—740; ч. И, № 1'174—1182, 1187,
1194, 1200—1202.
Тема 11. Основные тригонометрические
формулы
Теоремы сложения для основных тригонометрических функций.
Формулы «приведения». Формулы удвоения аргумента. Формулы
деления аргумента пополам. Формулы преобразования произведе-
ния тригонометрических функций в сумму. Формулы преобразо-
вания суммы или разности тригонометрических функций в произ-
ведение.
Тригонометрические преобразования. Доказательство тригоно-
метрических тождеств.
Учебник — Кочетковы, ч. I, § 116; ч. II, § 149—160, 169. Упраж-
нения: ч. I, № 754—763, 770, 771; ч. И, № 1028, 1029, 1031, 1040—
1042, 1056, 1066, 1070, 1099, 1100. Упражнения: № 1126, 1127, 1148,
1167—1169, 1172,.1240,1241, 1244:
Тема 12.
Простейшие тригонометрические
уравнения
Определение обратных тригонометрических функций. Общие
решения элементарных тригонометрических уравнений: sinx=a;
cosx=a; tgx=a; ctgx=a.
21
Учебник — Кочетковы, ч. I, § 117—122, упражнения № 787—
795, 798—801, 803—808, 812—822, 823—826, 829, 831, 834, 835, 845,
1037—1039, 1051, 1052, 1059, 1060, 1107—1110.
Тема 13.
Решение тригонометрических уравнений
Некоторые методы решения тригонометрических уравнений:
применение основных тригонометрических формул; введение новой
неизвестной; однородные уравнения; универсальная подстановка
(выражение основных тригонометрических функций через тангенс
половинного угла), введение вспомогательного аргумента (пре-
образование выражения asinx+fecosx) и т. п.
Учебник — Кочетковы, ч. I, § 123, 124; ч. II, § Г56, 157, 167,
169, 171. Упражнения: № 846—865, 866—878, 1222, 1227, 1230,
1232, 1254—1257, 1260—1264, 1268, 1'271, 1274, 1279, 1282, 1284,
1294, 1298.
Тема 14.
Тригонометрические неравенства
Решение простейших тригонометрических неравенств типа
sinx>a, cosx^a, tgx<a, ctgx^a и т. п.
Графическая интерпретация. Сведение тригонометрических не-
равенств к простейшим.
Учебник — Кочетковы, ч. I, 126, упражнения: ч. I, № 883—887.
Указания. Для решения тригонометрических неравенств удобно
использовать графическое представление тригонометрических
функций или единичный круг. Как это делается, понятно из ука-
занных выше параграфов учебника.
Предлагаем проверить справедливость записи решений следую-
щих простейших тригонометрических неравенств.
Во всех вышеперечисленных неравенствах и = 0, ±1, ±2, ....
В качестве дополнительных упражнений следует решить те
тригонометрические неравенства, которые содержат варианты
данного пособия (часть 2-я).
22
Неравенство
Решения
I. a) sin х 4;-у
1
б) sin х >--у
1
в) sin х <~у
1
г) sinx<—у
д)-гу <sin х<у
II. a) cosx^y
1
6) cos X > — -y
1
в) cos X -y
1
r) COS X < — —	'
1 1
Д) y<cosx< -y
arcsin -у + 2ял x к — arcsin -у + 2тел
/те	те
---у + 2тел < x < -у 4- 2тел
f 1 \
— те — arcsin I-------у I + 2ял < x <
f	1 \
< arcsin I-----у j -{- 2ял
1	я
1) arcsin -у + 2ял x -у + 2ял,
5те	1
2) -у + 2ял < x it — arcsin -y + 2nn
— arccos -у + 2ял < x arccos -у + 2ял —
— arccos -----y^ + 2яп < x < arccos ------у^+2тсл
те	5те
-у + 2тел < х <, -у + 2лл
arccos ----у^ + 2теп<х<2те—arccos --------у^ + 2тел
те	I
I. у + 2лл < х arccos у + 2тел,
I	те
2. —arccos -у + 2тгл «С х < — -у + 2тел.
III. a) tg x >- 3
6) tg X > — 1
в) tg x < 2
Г) |tg x| < 4
Д) tg X < — 1
arctg 3 + теп «С х < -у + ял
-у4-яп<х<-у + ял
те
---у + ял < х < arctg 2 + ял
— arctg 4 + ял < х < arctg 4 + тел
те	те
~ -у 4- ЯП < Х^ — -у + ЯП
23
Неравенство
Решевдя
Продолжение
IV. a) ctg х 3
б) ctg х > — 1
в) ctgx<2
. г) ctg X < — 1
лл < х < arcctg 3 + пп
Зге
гел < х < — + гел
arcctg 2 + х < ге + гел
Зге
-j- + гел < х < ге + гел.
Тема 15.
Смешанные задачи
Следует приобрести практику решения задач, в которых неиз-
вестное содержится в аргументах сложных функций, составленных
из рациональных, иррациональных, показательных, логарифми-
ческих и тригонометрических функций.
Пособие, ч. II, § 2, 1(5), 2(5), 3(5), 4(5); § 5, 1(4), 2(4), 3(4),
4(4); § 9, 4(2, 5), 2(2, 5), 3(2, 5), 4(2, 5); § 21, 1(3), 2(3), 3(3),
4(3); §22, 1(1), 2(1), 3(1),4(1) и другие.
Раздел III. ГЕОМЕТРИЯ
Тема 16.
Треугольники, параллелограммы,
трапеции
Признаки равенства (конгруэнтности) треугольников. Аксиомы
и теоремы о параллельности прямых на плоскости. Основные зада-
чи на построение. Свойства сторон и углов параллелограмма.
Свойства диагоналей параллелограмма, прямоугольника, ромба,
квадрата. Теоремы о средней линии в треугольнике и трапеции.
Геометрическое место точек. Основные виды геометрических мест
точек.
Учебник — Киселев, ч. I, § 33—59, 60—69, упражнения № 1—14,
стр. 40; № 15—38, стр. 41; § 70—83, 87—101, упражнения № 1—20,
21—23, 24—75, стр. 59—62.
Барыбин, глава III, стр. 38—59, упражнения: стр. 61; глава IV.
24
Тема 17.
Подобие треугольников
и многоугольников
Соизмеримость отрезков. Свойство параллельных прямых, пе-
ресекающих стороны угла. Теоремы о подобии треугольников;
признаки подобия треугольников. Теорема о свойстве биссектрисы
внутреннего угла треугольника. Подобие многоугольников. Основ-
ные задачи на построение, использующие теоремы о подобии.
Метрические соотношения в треугольниках. Теорема Пифаго-
ра. Теорема косинусов.
Учебник — Киселев, ч. I, § 144—155, 156^165, 168—176, 181—
185, 186, 187, 188—198, упражнения № 1—,14, 15—20, 21—42, 43—
47, стр. 137—140.
Барыбин, глава 4.
Тема 18.
Измерение площадей
Понятие о площади. Основные допущения о площадях. Пло-
щадь прямоугольника, параллелограмма, треугольника, трапеции,
многоугольника.
Учебник — Киселев, ч. I, § 242—261, упражнения № 1—7,9—12,
15—23, 25—28, 33, стр. 179—180.
Тема 19.
Окружность, круг, их части
Взаимное расположение прямой и окружности, двух окружно-
стей. Вписанные углы. Вписанные и описанные треугольники и
многоугольники. Четыре замечательные точки в треугольнике.
Основные задачи на построение. Пропорциональные линии в круге.
Длина окружности. Площадь круга.
Учебник — Киселев, ч. L, § 103—133, упражнения № 1—6, 7—
19, 20—*54, стр. 80—82, § 136—143, упражнения № 1—13, 14—48,
стр. 87—89; § 199—202, 226—241, '262—268, упражнения № 8, 13,
24, 29, 32, стр. 179—180.
Тема 20.
Основные теоремы стереометрии
Взаимное расположение плоскостей в пространстве. Угол меж-
ду прямой и плоскостью, угол между двумя плоскостями. Призна-
ки параллельности плоскостей прямых и плоскостей, перпенди-
кулярность прямой и плоскости, перпендикулярность плоскостей.
25
Теорема о трех перпендикулярах. Скрещивающиеся прямые. Угол
и расстояние между скрещивающимися прямыми.
Учебник — Киселев, ч. II, § 2—48, упражнения № 5—10,
стр. 25; № 12—20, стр-. 26.
Барыбин, главы V и VI, упражнения к главам V и VI.
Тема 21. ,
Пирамиды, призмы
Свойства граней и диагоналей параллелепипеда. Объем приз-
мы. Пирамиды. Свойства сечений, параллельных основанию.
Объем пирамиды. Правильная четырехугольная пирамида.' Пра-
вильная треугольная пирамида. Куб. * Подобие' многогранников.
Отношение линейных элементов в подобных многогранниках.
Отношение площадей сходственных фигур в подобных многогран-
никах, отношение сходственных объемов.
Учебник — Киселев, ч. II, § 67—93, упражнения № 5—8,‘
стр. 44; № 2—7, 12—15, стр. 67, 68.
Барыбин, глава VII, упражнения к главе VII.
Тема 22.
Круглые тела
Поверхность цилиндра и конуса. Объем цилиндра и конуса.
Поверхность шара и его частей. Объем шара и его частей.
Учебник — Киселев, ч. II, § 105—145, упражнения 1—12, стр. 89.
Барыбин, главы VIII, X, упражнения к главам VIII и X.
Методические замечания
к решению геометрических задач
Для приобретения навыков решения геометрических задач тре-
буется особенно много времени. Поэтому подготовку по геометрии
следует начинать как можно раньше и осуществлять равномерно,
параллельно с повторением других разделов программы.
Содержание программы вступительных экзаменов по геоме-
трии и важные методические указания можно найти в «Пособии
по математике для поступающих в вузы» Г. В. Дорофеева,
М. К. Потапова, Н. X. Розова. М., Физматгиз, 1970—1976 гг.
Там же содержится определенное количество разобранных задач,
иллюстрирующих те или иные особенности экзаменационных за-
дач, предлагавшихся в МГУ.
26
Опыт приемных экзаменов показывает, что наибольшие труд-
ности при решении геометрических задач вызывают стереометри-
ческие задачи, где требуется пространственное воображение и
умение «ориентироваться» в соотношениях между пространствен-
ными фигурами. Не претендуя ни в какой степени на полноту
охвата всех составных частей стереометрии, рассмотрим лишь не-
которые из них, которые, на наш взгляд, представляют собой важ-
ные элементы, часто встречающиеся при решении разнообразных
задач. К каждому из нижеследующих пунктов приведено по не-
сколько методических задач. Они решаются очень просто, способ-
ствуя отработке приемов, необходимых для решения других, более
сложных задач. Поэтому мы советуем решить эти задачи перед
тем как переходить к систематической работе над экзаменацион-
ными стереометрическими задачами.
1. Правильная треугольная пирамида
На рис. 4 приведена правильная треугольная пирамида
SABC. На этом же рисунке показаны основные элементы пра-
вильной треугольной пирамиды:
а — сторона основания пира-
миды;
b — боковое ребро пирамиды;
Н—высота пирамиды;
h — апофема боковой грани;
а — угол между боковым реб-
ром и плоскостью основания»
определяемый как угол между
боковым ребром и его проекцией
на плоскость основания;
Р — угол между плоскостью
боковой грани и основанием. По-
скольку SEJLBC, АЕ1.ВС (Е —
середина СВ), угол AES есть ли-
нейный угол двугранного угла
между рассматриваемыми пло-
скостями;
у — угол между боковым реб-
ром пирамиды и ее высотой.
Длина отрезка АО определя-
ется как 2/3 высоты основания
пирамиды, а ОЕ — как 1/3 этой
высоты. Поэтому ясны следую-
щие соотношения:
ЛО=^р-; ОЕ=^-
3	о
। 71 •
«+т=—’
27
=	+ A« = /7« + £L;
&cosy = //j &sinx = ^y^;	_ (D
Плоскости ASE и BSD, проходящие через высоту пирамиды и,
следовательно, перпендикулярные основанию, играют важную
роль при решении многих задач, связанных с правильной тре-
угольной пирамидой. Каждая из этих плоскостей делит' соответ-
ствующий двугранный угол между боковыми гранями пирамиды
пополам, т. е. служит бисекторной плоскостью такого угла.
Двугранный угол ф между боковыми гранями пирамиды опреде-
ляется из равнобедренного треугольника CFB(FCA_AS и ГВ±ЛЗ,
ДА5С=ДЛ5В, FC=FB). Используя «теорему косинусов», из
этого треугольника получаем
а1 = 2 • FC* — 2 • FC* • cos <р,
(2)
Можно также рассмотреть прямоугольный треугольник CEF-.
5;п ? — __ а	wx
sin 2 FC — 2 FC.	)
Высота боковой грани FC определяется весьма просто, если
заметить, что
b-FC — a-h,
FC^~.	(3)
Полезно отметить, что в правильной треугольной пирамиде
скрещивающиеся ребр.а взаимно перпендикулярны (Л5±ВС,
В5±ЛС, С5±ЛВ, а отрезок FE есть кратчайшее расстояние
между этими ребрами (FE1.BC, FE1.AS):
f£=^I.sina.	(4)
Вокруг всякой треугольной пирамиды можно описать сферу.
Центр сферы, описанной вокруг правильной треугольной пирами-
ды, точка К, лежит на ее высоте или на ее продолжении за точку
О (это становится ясным, если учесть, что прямая OS есть геоме-
трическое место точек, равноудаленных от вершин основания пи-
рамиды).
28
Радиус описанной сферы 7? удобно найти из равнобедренного
треугольника Л/CS:
7?cosy=-y-; # =  2с^	(5>
а)	Если R<H, т. е. а
миды;
б)	если R = H, т. е. а —
пирамиды;
в)	если R>H, т. е.
центр сферы лежит внутри пира-
центр сферы лежит на основании
центр сферы лежит вне пира-
миды.
Во всякую треугольную пирамиду можно вписать шар. Центр
шара, точка К', вписанного в правильную треугольную пирамиду,
лежит на высоте пирамиды в точке ее пересечения с биссектри-
сой угла AES.
Радиус вписанного шара г удобно находить из прямоугольного
треугольника ОК'Е-.
о, К"3 . I • f • q Н л___ ci 3 \	tax
r =—(ksm₽=-r. cosp^-g^-J- s (6)
Задача 1. Правильная треугольная пирамида SABC, рис. 4,
задана двумя элементами: а — сторона основания, Н — высота.
Найти все остальные элементы: а, !0/у, <р, ft, 6, JR, г и V — объем
пирамиды, а также расстояние между скрещивающимися реб-
рами.
Задача 2. Правильная треугольная пирамида ВДВС, рис. 4, за-
дана двумя элементами: b — боковое ребро, ф — угол между боко-
выми гранями. Найти все остальные элементы: а, 0, у, й, Н, a, R9
г и V — объем пирамиды, EF.
Задача 3. Правильная треугольная пирамида, рис. 4, задана
двумя элементами: R— радиус описанного шара, а — угол между
боковым ребром и плоскостью основания. Найти все остальные
элементы пирамиды: 0, у, ф, г, ft, a, ft, Н, EF.
2. Правильный тетраэдр
Если в правильной треугольной пирамиде боковое ребро рав-
но стороне основания а, то такая пирамида называется правиль-
ным тетраэдром.
На рис. 5 изображен правильный тетраэдр. Эта фигура обла-
дает всеми свойствами правильной треугольной пирамиды. Кроме
того, полезно знать* дополнительные свойства правильного
тетраэдра.
29
а)	правильный тетраэдр
имеет центр, точку Д. В этом
центре пересекаются все высо-
ты тетраэдра,отрезки, соединя-
ющие середины скрещиваю-
щихся сторон (бимедианы тет-
раэдра), а также в ней нахо-
дятся центры вписанного и
описанного шаров;
б)	центр правильного тетраэдра делит его высоту в отношении
3 : 1, считая от вершины (SK : ДО=3 : 1);
в)	радиус описанного шара составляет 3/4 высоты пирамиды,
а радиус вписанного шара — 1/4 высоты пирамиды:
r=4-h>
4	4
г)	сечения тетраэдра, параллельные скрещивающимся ребрам,
представляют собой прямоугольники, а то из них, которое прове-
дено через середину ребра — квадрат.
Задача. Пусть сторона правильного тетраэдра равна а.
Проверить справедливость следующих формул:
ГТ 1/~ п 3	1	1/“Т
// = а|/ т; R=-ay —г = ~Га V — •
/2 Q . 2/2	1
-г; р = arcsin —о—; <р = arccos -3-
3. Правильная четырехугольная пирамида
На рис. 6 изображена правильная четырехугольная пирамида
и ее основные элементы:
а—сторона квадрата, лежащего в основании пирамиды;
30
b — боковое ребро пирамиды;
h — апофема;
а — угол между боковым ребром и плоскостью основания;
Р — угол между боковой гранью и плоскостью основания;
у — угол между боковым’ребром пирамиды и ее высотой;
Ф— угол между боковыми гранями пирамиды;
R — радиус описанной сферы;
г — радиус вписанной сферы.
Нахождение большинства элементов правильной четырехуголь-
ной пирамиды похоже на нахождение соответствующих элементов
правильной треугольной пирамиды. При вычислении этих элемен-
тов основную роль играют треугольники, расположенные в пло-
скостях симметрии пирамиды ЛХС, BSD, ESM, проходящих черев
высоту пирамиды и перпендикулярных плоскости основания. Если
известны высота пирамиды Н и сторона основания а, то осталь-
ные элементы пирамиды определяются формулами:
”	т=«/2—;
2)
3)	Л = /30- + 0£-=/я-+4 ши Л=^ =
=s£ А юо>'
4)	b = /а*/4 + /гг (из Д£Е$);
5)	sin(из ДЛГО), ЛО = ^.
Z ЛГ	Л
»п ah п	. bV2
AF = — \ 2<р = arcsm ;
D	Zrl
6)	^cosT = 4;	(из ДЛВК);
7)	r = OE-tg-^-±--tg^- (из &ЕОК').
Задача 1. Правильная четырехугольная пирамида задана дву-
мя элементами: а — сторона основания и ф—угол между боковы-
ми гранями. Найти остальные элементы пирамиды.
Задача 2. Правильная четырехугольная пирамида задана двумя
элементами: R—радиус описанной сферы, а — сторона основания.
Найти все остальные элементы пирамиды.
Задача 3. Правильная четырехугольная пирамида задана двумя
элементами: г — радиус вписанного шара, R — радиус описанного
шара. Найти объем пирамиды. ,
Задача 4. Изучить сечения правильной четырехугольной пира-
миды плоскостями, параллельными диагонали АС и скрещиваю-
31
щемуся с ней ребру SD. В какие из этих сечений можно вписать
окружность?
Замечание. Приведем одно простое утверждение, которое
полезно иметь в виду при решении многих стереометрических задач.
Если в треугольной пирамиде SABC с вершиной S ребро S4
изменить в т раз, ребро SB— в п раз, а ребро SC — в k раз, то
объем пирамиды с той же вершиной S, но с измененными длинами
ребер, исходящих из этой вершины, изменится в mnk раз по
сравнению с объемом первоначальной пирамиды.
Доказательство этого утверждения приведено на стр. 235 на-
стоящего пособия. Там же приведен пример использования этого
утверждения.
4. Куб
с ней диагонали граней куба;
•Рис. 7.
Куб, рис. 7, обладает рядом свойств, которые полезно знать
при решении стереометрических задач. Предлагаем самостоя-
тельно доказать следующие из них:
а)	диагональ куба перпендикулярна любой скрещивающейся
б)	диагонали непараллельных
граней куба образуют между со-
бой угол 60°;
в)	сечение куба плоскостью
(Д'С'В или AD'C), проходящей
через концы ребер куба, исходя- .
щих из одной вершины (В' или D)
является правильным треуголь-
ником;
г)	плоскости треугольников
А'С'В и AD'C параллельны друг
другу, перпендикулярны диаго-
нали куба B'D и делят эту диа-
гональ на три равные части;
д) сечение куба, перпендику-
лярное диагонали куба и прохо-
дящее через ее центр, представ-
ляет собой правильный шести-
угольник.
Большое количество задач связано с плоскостями сечений куба.
Для решения таких задач необходимо уметь построить сечение
куба плоскостью, задаваемой теми или иными условиями (напри-
мер^ по трем точкам, или по двум точкам при условии параллель-
ности данной прямой и т. п.). Предлагаем следующие задачи.
Задача 1. Дан куб ABCDA'B'C'D', где АА', ВВ'9 СС\ DD' —
боковые ребра куба. Найти площадь сечения этого куба плос-
32
костью, проходящей через вершину А и середины ребер В'С' и
C'D'. Ребро куба равно 1.
Построение: рис. 8.
Ответ: 5=7]/ 17/24.
Задача 2. Дан куб ABCDA'B'C'D', где АА', ВВ', СС', DD'—
боковые ребра. В каком отношении делит объем куба плоскость,
проходящая через вершину А, середину ребра ВС и центр грани
DCC'D'?
Построение: рис. 9.
Ответ: 7:29.
Задача 3. Дан куб ABCDA'B’C'D', где АА', ВВ', СС', DD' —
боковые ребра. В каком отношении делит ребро В'С' точка Е, ко-
торая принадлежит плоскости, проходящей через вершину А и
центры граней A'B'C'D' и В'С'СВ?
Построение: рис. 10.
Ответ: 2:1.
3-619
33
5. О чертеже в геометрических задачах
При решении задач по стереометрии первостепенное значение
имеет хорошо составленный чертеж. Чертеж к задаче должен быть
аккуратным, обязательно крупным. На нем должны быть видны
все линии, фигуры, углы и т. п., которые используются при реше-
нии. Необходимо сохранять все начерченные тонкими линиями
вспомогательные построения; они очень часто нужны при решении
задачи. Необходимо прикинуть на черновике (один или несколько
раз), в каком ракурсе удобнее изобразить рассматриваемое тело,
как нагляднее провести сечение.
Надо помнить, что на рисунке изображается параллельная про-
екция заданного тела на плоскость чертежа. При этом искажаются
размеры отрезков и углы, но сохраняются параллельность прямых
и пропорциональность отдельных отрезков, лежащих на прямой.
Обычно стереометричёская задача сводится к решению несколь-
ких плоских задач. Поэтому найдя способ «расчленить» задачу
в пространстве на ряд плоских задач, бывает полезно нарисовать
отдельно сечение или ту плоскую фигуру, которая рассматривает-
ся, При этом нужно сохранить те обозначения, которые были на
общем чертеже.
Излагая решение задачи, надо делать ссылки на применяемые
теоремы, но стараться употреблять поменьше слов, применяя обще-
принятую символику. В чистовике следует делать только основные
выкладки с таким расчетом, чтобы проверяющий решение препода-
ватель или экзаменатор легко в них разобрался.
Об одном свойстве четырехугольника,
вписанного в окружность
В заключение этого раздела приведем одну теорему, которую
полезно знать (см. контрольную работу № 5, мех.-мат. ф-т и др.).
Теорема. Произведение расстояний от любой точки окружно-
сти, описанной около выпуклого четырехугольника, до его противо-
положных сторон или их продолжений равны между собой.
Доказательство. Пусть S — произвольная точка окруж-
ности, описанной около выпуклого четырехугольника ABCD, рис. 11.
Точки Р, Q, М и N являются основаниями перпендикуляров, опу-
щенных из S соответственно на стороны AD, ВС, АВ и CD (или на
продолжений этих сторон). Длины этих перпендикуляров обозна-
чим через а, Ь, с и d соответственно. Нужно доказать, что ab = cd.
Доказательство этого факта следует из подобия пар треуголь-
ников: AAPS~ &CNS и zL4MS~ACQS. Эти треугольники — пря-
моугольные и имеют по равному вписанному углу, опирающемуся
на дугу SD (при этом следует учесть, что угол MAD равен, углу
NCB).
34
§ 3. О ПОДГОТОВКЕ
К ПИСЬМЕННОМУ ЭКЗАМЕНУ
ПО МАТЕМАТИКЕ
Наиболее ответственным при поступлении.в университет явля-
ется письменный экзамен по математике.
В каждом из вариантов письменной работы содержится не-
сколько задач (как правило, пять), на решение и запись которых
отводится четыре часа. Ниже приводятся некоторые варианты экза-
менационных работ, предлагавшихся в МГУ в последние годы.
Как правило, главная беда даже хорошо подготовленных уча-
щихся— неумение распределить время на самом экзамене, быстро
и правильно оформить решение на чистовике. Чтобы избавиться от
этого недостатка, мало одних упражнений в черновом решении
задач. Поэтому необходимо несколько раз устроить репетицию
письменного экзамена. Это означает, что в течение ровно четырех
часов, не вставая с места и не отвлекаясь, нужно решить задачи
какого-либо варианта и записать их на чистовик с необходимыми
объяснениями.
Если вариант оказался слишком простым, в другой раз нужно
взять более трудный. Если же тем не менее за четыре часа все
задание не выполнено, нужно довести его до конца, чтобы узнать,
.сколько времени фактически уходит на всю работу. Необходимо
продумать причину неудачи. Это может быть недостаточная трени-
ровка в решении задач по отдельным темам, или слишком .медлен-
ная запись решений в чистовике, или неудачный порядок решения
задачи и т. д.
Нужно иметь в виду, что среди задач письменного экзамена
всегда одна или две выделяются большей трудностью и необыч-
ностью. Поэтому надо распределить время, отведенное на экзамен
так, чтобы эти задачи не отняли слишком много времени в ущерб
другим, более простым. Прочитав внимательно условия этих задач,
разумно начинать работу с решения более простых для поступаю-
щего задач. Если какая-либо задача не получается, следует взять-
ся за другую, и только тогда, когда сделан максимум возможного
в остальных задачах, можно вернуться к самой трудной. Очень
часто новый подход к задаче оказывается успешным.
Если на экзамене не хватило времени переписать какое-либо
решение в чистовик, надо выделить в черновике те места, где со-
держится решение этой задачи или хотя бы часть его, и оно будет
засчитано полностью или частично. Поэтому важно, чтобы и в чер-
новике был порядок. *
Для самостоятельной работы рекомендуется использовать зада-
чи, приведенные во второй части настоящего пособия.
3*
35
§ 4. КОНТРОЛЬНЫЕ ЗАДАНИЯ
ДЛЯ УЧАЩИХСЯ ЗАОЧНЫХ КУРСОВ
КОНТРОЛЬНЫЕ РАБОТЫ ДЛЯ ПОСТУПАЮЩИХ
НА МЕХАНИКО-МАТЕМАТИЧЕСКИЙ,
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТЫ
И ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ
МАТЕМАТИКИ И КИБЕРНЕТИКИ
Контрольная работа № 1
1.	Произведение четырех целых положительных чисел меньше,
чем их сумма, а сумма трех из этих чисел равна 28. Найти все та-
кие числа.
2.	Решить неравенство
||6х — 1|-|4х+1||<1.
3.	Даны два квадратных уравнения
1)	х2+:(2а+!1)х—а2=0,
2)	х2+ах—1=0.
При каких действительных значениях параметра а эти уравнения
имеют по крайней мере один общий корень?
4.	Указать все действительные а, при которых не существует
ни одного действительного х, удовлетворяющего неравенствам
{(1—д)Х —Д
х — 2(1— а)	’
х — 8 > ах.
5.	а) Решить неравенство
]/ 12 — ЗхЭ3 5л — 2.
б) Для каждого значения а найти все действительные реше-
ния неравенства
— х< 1 -}-х.
6. Найти косинус угла при основании равнобедренного тре-
угольника, зная, что точка пересечения его высот лежит на вписан-
ной в треугольник окружности.
Контрольная работа № 2
1.	а) Имеются три куска различных сплавов золота с серебром.
Известно, что количество золота в 2 г сплава из третьего куска то
же, что во взятых вместе 1 г из первого и 1 г из второго кусков.
Вес третьего куска равен суммарному весу части первого куска,
содержащей 10 г золота, и части второго куска, содержащей 80 г
36
золота. Третий кусок в четыре раза тяжелее первого и содержит
75 г золота.
Сколько граммов золота содержится в первом куске?
б) Две трубы, действуя вместе в течение одного часа, напол-
няют водой 3/4 бассейна. Если сначала первая труба наполнит
одну четвертую часть бассейна, а затем вторая при выключенной
первой доведет объем воды до 3/4 бассейна, то на это понадобится
2,5 ч. Если первую трубу включить на один час, а вторую — на
полчаса, то они наполнят бассейн более чем наполовину.
За какое время наполняет бассейн каждая труба?
2.	а) Решить уравнение
16 sin х—sin 2х= 1—cos 2х.
б) Решить уравнение
cosx-cos 2x + 2sin3x= (cosx + cos Зх) (tg2x + tg2x).
3.	Три последовательных члена геометрической прогрессии ai,
а2 и а3 являются соответственно первым, четвертым и двадцать
пятым членами арифметической прогрессии. Сумма чисел а2, а*
равна 114. Найти знаменатель геометрической прогрессии.
4.	Найти все действительные решения системы
«/*-1^14-2=0,
8 — х2 = (х-}-2у)г.
5.	Центры трех окружностей различных радиусов расположены
на одной прямой, а центр четвертой находится на расстоянии d
от этой прямой. Найти радиус четвертой окружности, если изве-
стно, что каждая из этих окружностей касается трех других.
Контрольная работа № 3
1.	Решить уравнение	-	* !
j/*log* УЗх-log, х = — 1.
2.	Решить неравенство	; J
logs (1 + cos 4х) < 1 4“ l°S/2“ s*n х'
3.	Решить неравенство	/
cos2(x+l) -1g (9—2х—х2)^1.
4.	Из пункта А в пункт В выехал велосипедист, который снача-
ла двигался равноускоренно с ускорением 4 км[ч\ а после того
как его скорость возросла от 0 до v, продолжал двигаться равно-
мерно со скоростью v. Расстояние между пунктами А и В равно
32 км. На первую половину пути велосипедист затратил в полтора
раза больше времени, чем на вторую. Определить скорость и.
37
5.	В основании треугольной пирамиды SABC лежит прямо-
угольный треугольник АВС (угол С прямой). Ребро SA перпенди-
кулярно плоскости основания. В пирамиду вписан шар, радиус ко-
торого равен 1/3 SA. Через вершину S и точку касания шара
с основанием пирамиды проходит плоскость, параллельная ребру
ВС. Эта плоскость делит поверхность шара в отношении 1:4. Най-
ти угол ВАС.
Контрольная работа № 4
1.	а) Правильная четырехугольная пирамида SABCD вращает-
ся вокруг прямой, проходящей через ее вершину S параллельно
стороне основания АВ. Найти объем тела вращения, если известно,
что высота пирамиды равна h, а сторона основания — а. (При вра-
щении указанная прямая остается параллельной стороне АВ.)
б) В треугольной пирамиде SABCc вершиной S боковые гра-
ни образуют одинаковые двугранные углы с плоскостью основания
АВС пирамиды. Окружность, вписанная в основание, касается реб-
ра АВ в точке D, а ребра ВС — в точке Е. Известно, что ZASB=
= 7л/12, ZBSC=5n/12, ZASC=«/2. Найти отношение площади
треугольника DBE к площади треугольника АВС.
2.	Найти все х, удовлетворяющие одновременно следующим
условиям:
(cos 13x = cosx,
cos2x-|-sin5x = 1,
M<3.
3.	Решить систему уравнений
{sin t/-cosx-|-sinx = О,
2 cos2 у 4~sin */-sinx= cos2t/cosx.
4.	Автомобиль выезжает из пункта А и едет с постоянной ско-
ростью v км/ч до пункта В, отстоящего от А на расстоянии 24,5 км.
В пункте В он переходит на равнозамедленное движение, причем
за каждый час его скорость уменьшается на 54 км/ч, и движется
та'к до полной остановки. Затем он сразу же поворачивает обратно
и возвращается в А с постоянной скоростью v км/ч.
Какова должна быть скорость v, чтобы автомобиль быстрее
всего проехал путь от А до остановки и обратно до пункта А ука-
занным выше способом?
5.	Построить графики функций:
a)	t/ = logj_(x» — 7x4-6);
з
б)	t/ = xsinx;
в)	у = *« + х —12 •
38
Контрольная работа № 5
1.	На строительстве дороги в одной смене работало несколько
машин 1-го типа и несколько машин 2-го типа. Одну машину 1-го
типа обслуживают 6 человек, ее производительность в дождь равна
140 Л42 за смену, а в хорошую погоду — 260 м2 за смену. Общая
выработка всех машин 1-го типа за эту смену равна 900 м2. Одну
машину 2-го типа обслуживает 7 человек. Ее максимальная произ-
водительность— 400 м2 За смену. Сколько было машин 1-го и 2-го
типов, если известно, что все машины обслуживало не больше
40 человек и, кроме того, 700 м2 из проделанной работы можно
было выполнить лишь машинами 2-го типа?
2.	Решить уравнение
cos* -у- (1 — У sin х) = ]/2 cos х — У sin 2х.
3.	Пятиугольник ABCDE вписан в окружность. Расстояние от
вершины Е до сторон АВ, ВС и CD (или их продолжений) соот-
ветственно равны а, b и с. Найти расстояние от вершины Е до диа-
гонали AD.
4.	Най^и все значения х, при которых справедливо неравенство
1О8*4	1П- 5 —4х -о
l-logx3 10£*	2-
5.	Даны три уравнения с действительными коэффициентами:
ах2+6х+г=0,
сх2+Ьх+а=0,
х2+а2х+с2=О.
из них имеет по крайней мере один действительный ко-
2)
3)
Каждое
рень. Известно, что любой корень третьего уравнения удовлетво-
ряет первому уравнению и хотя бы один корень второго уравнения
является корнем третьего уравнения. Найти числа а, Ъ, с, если а>\
КОНТРОЛЬНЫЕ РАБОТЫ .
ДЛЯ ПОСТУПАЮЩИХ НА ХИМИЧЕСКИЙ,
БИОЛОГИЧЕСКИЙ, ПОЧВЕННЫЙ,
ГЕОЛОГИЧЕСКИЙ И ГЕОГРАФИЧЕСКИЙ ФАКУЛЬТЕТЫ
Контрольная работа № 1
1.	Имеются два'раствора одной и той же соли в воде. Для по-
лучения смеси, содержащей 10 г соли и 90 г воды, берут первого
раствора вдвое больше по весу, чем второго. Через неделю из каж-
дого килограмма первого и второго растворов испарилось по 200а
воды, и для получения такой же смеси, как и раньше, требует-
39
ся первого раствора уже вчетверо больше по весу, чем второго
Сколько граммов соли содержалось первоначально в 100 г каж-
дого раствора?
2.	Нацти все действительные значения параметра а, при кото-
рых системы уравнений
(ax-j-2y = 2b-j-1,	( 2х Ц- у = аг4-2,
I х -|- у = 3	I х -|- Зу = 3
равносильны.
3.	Найти все значения х, при которых справедливо неравен-
ство
1 1_________________
ж* — Зх + 2	2х* + 9х -|- 4
4.'Решить неравенство
/х2 3х + 2	,	,
х + 4
5. В треугольнике АВС из вершины В к стороне АС проведена
медиана BD. Из вершины А проведен отрезок прямой, который
пересекает медиану BD в точке L, а сторону ВС — в точке М.
В каком отношении точка М делит сторону ВС, если известно, что
В£=1/6-В£>?
Контрольная работа N® 2
1.	В соревнованиях по бегу на дистанции 120 м участвуют три
бегуна. Скорость первого из них больше скорости второго на
Г м/с, а скорость второго равна полусумме скоростей первого и
третьего. Определить скорость третьего бегуна, если известно, что
первый бегун пробежал дистанцию на 3 сек быстрее третьего.
2.	Решить уравнение
3 tgx(7+cos 2х) =2(cos 2х—1):
3.	Решить неравенство
cos 6х--< 2 |/"3 sin Зх.
4.	Найти все решения системы
sin х • cos у -|- sin*	• sin у = cos* -^--sin^
2х-у = ^-.
5.	В треугольнике АВС угол С равен 60°; радиус круга, опи-
санного вокруг этого треугольника, равен 2 1^3. На стороне АВ
взята точка D так, что AD=2-DB и при этом CD=2 У^2. Найти
площадь треугольника АВС.
40
Контрольная работа № 3
1.	Из пункта А в пункт В выехал автомобиль и одновременно
из пункта В в пункт А выехал велосипедист. После встречи они
продолжали свой путь. Автомобиль, доехав до пункта В, тотчас
повернул обратно и догнал велосипедиста через два часа после
момента их первой встречи. Сколько времени после первой встре-
чи ехал велосипедист до пункта А, если известно, что к моменту
второй встречи он проехал 2/5 всего пути от В до А?
2.	Решить уравнение
jZl — cos2x==]/2sinx (cosX-—.
3.	а) Решить уравнение	;
I2+logj, XI+3 = 11 - logj_ X-
5	5
б)	Решить неравенство
log2 (5 — 4х) + log^ (2х — х8) > 2.
Т
в)	Решить систему уравнений
/4.5х-‘4-0, Ь2*+г = 4,2,
1 25х + = 25,5.
4.	Три последовательных члена геометрической прогрессии Я1,
а,2, &з являются соответственно первым, четвертым и двадцать пя-
тым членами арифметической прогрессии. Сумма чисел аг, аз
равна 114. Найти знаменатель геометрической прогрессии.
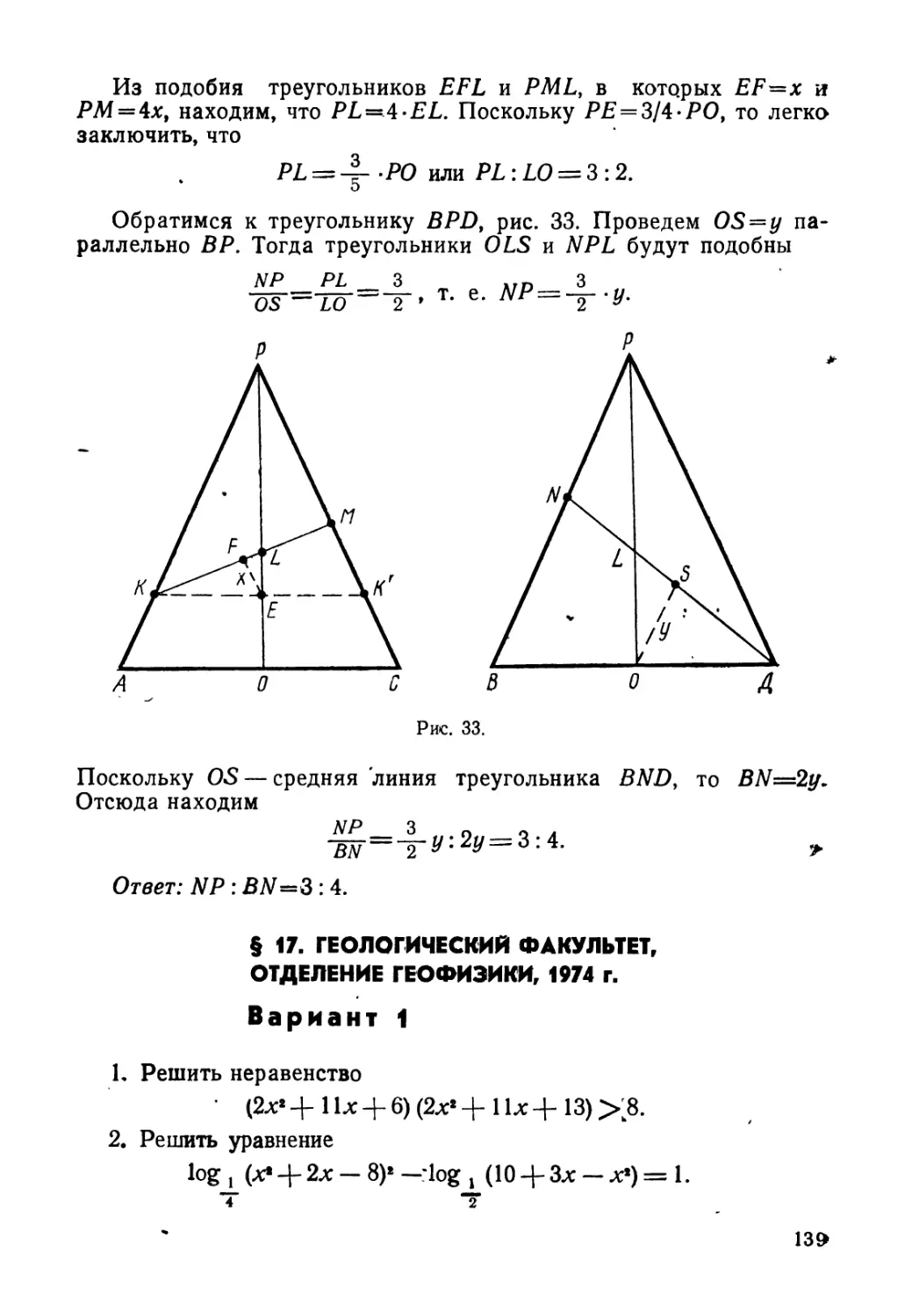
5.	Плоскость проходит через вершину основания А треуголь-
ной пирамиды SABC, делит пополам медиану треугольника SAB,
а медиану SL треугольника iSAC пересекает в точке D такой,
что
SD _ 1
DL 2 *
В каком отношении делит эта плоскость объем пирамиды?
Контрольная работа № 4
1.	К бассейну объемом в 300 м3 подведены три трубы: через
первую и вторую вода поступает, через третью выливается. Если
все три трубы включены одновременно, то количество воды в бас-
сейне увеличивается ежеминутно на 20 м3. Бассейн начали напол-
41
нять водой, включив первую и третью трубы. Более нем через 12
минут после начала работы в бассейне оказалось 100 м3 воды.
В этот момент первую и третью трубы закрыли и включили вто-
рую трубу, завершившую наполнение бассейна. Всего на наполне-
ние бассейна было затрачено 30 мин.
Определить, за какое время наполнился бы бассейн, если бы
его с начала до конца наполняла только вторая труба?
2.	Решить уравнение
3.	Решить уравнение
4. Решить уравнение
2 sin х 4- sin Зх=2 cos х—cos Зх.
5. Три одинаковых прямых круговых конуса, радиусы основа-
ний которых равны г и составляют 3/4 их высоты, расположены
по одну сторону от плоскости Р, а их основания лежат в этой
плоскости. Окружности оснований каждых двух из этих конусов
касаются. Найти радиус шара, лежащего между этими конусами
и касающегося как плоскости Р, так и трех конусов.
Контрольная работа № 5
1.	В магазине спортивных товаров туристы покупали снаря-
жение. Первый купил топорик и спальный мешок, заплатив
18 рублей. Второй купил два спальных мешка и рюкзак, заплатив
35 рублей. Третий купил топорик, спальный мешок и палатку, за-
платив 68 рублей. Четверный купил рюкзак, два спальных мешка
и две палатки. Сколько заплатил четвертый турист?
2.	Решить неравенство
- Iogw(18-2*)log4^
2 *
3.	Найти все пары значений (х, у), являющиеся решениями
системы
;з->.
удовлетворяющие условиям
17С	7Z
те	те
2 <У< 2 *
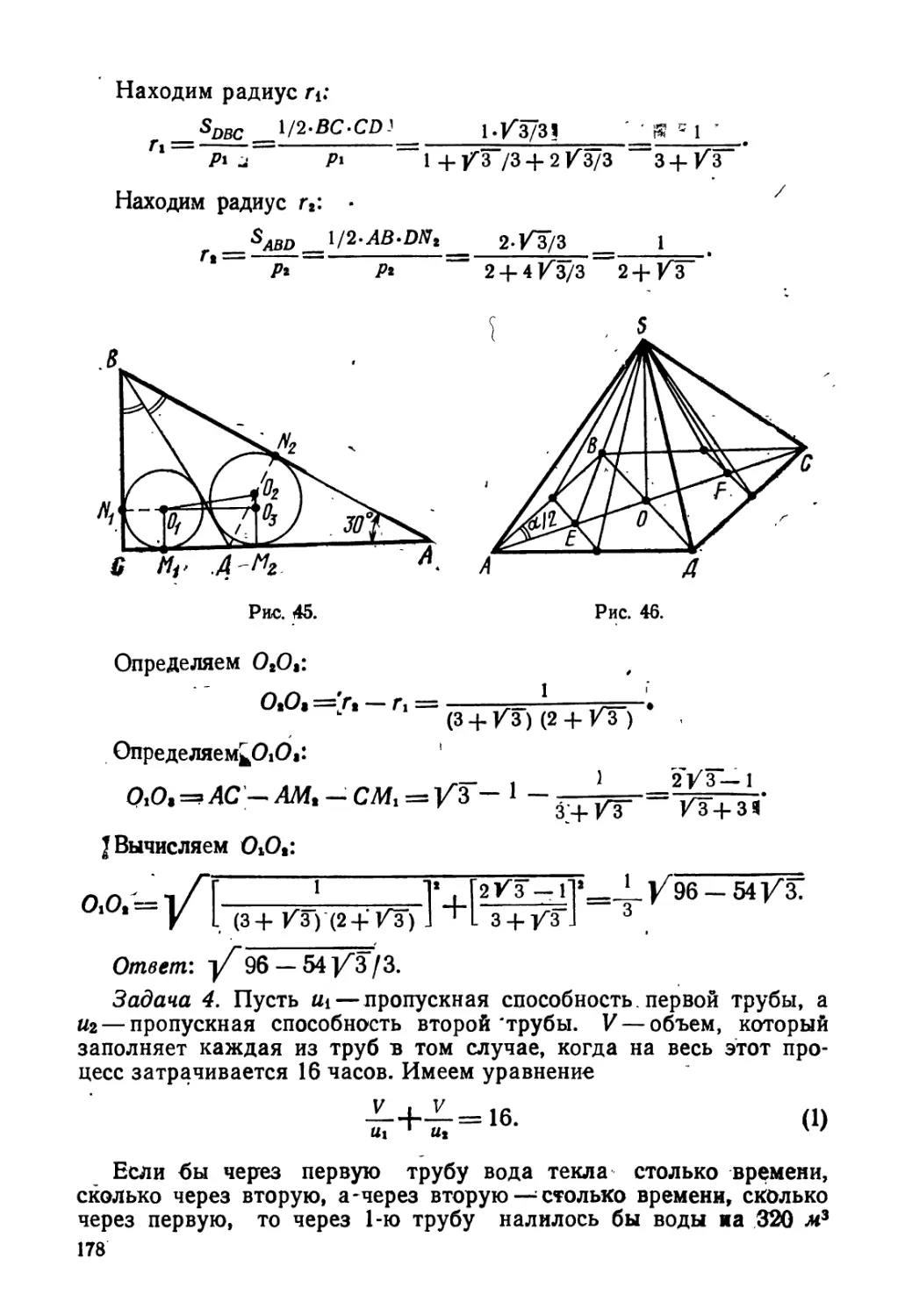
4.	Гипотенуза АВ прямоугольного треугольника АВС равна 2
и является хордой некоторой окружности. Катет АС равен 1 и
лежит внутри окружности, а его продолжение пересекает окруж-
ность в точке D, причем CD — 3. Чему равен радиус окружности?
5.	В правильной треугольной пирамиде SABC с вершиной S
сторона основание ’равна 2 см. Через сторону основания ВС про-
ведено сечение, которое пересекает ребро SA в точке М. Извест-
но, что SM: МА = 1:3, а площадь сечения равна 3 см2.
Найти объем пирамиды SABC.
§ 5.	ЛИТЕРАТУРА, РАБОЧИЙ ПЛАН
И КОНТРОЛЬНЫЕ РАБОТЫ
ПО МАТЕРИАЛУ, ВКЛЮЧЕННОМУ
В НОВУЮ ШКОЛЬНУЮ ПРОГРАММУ
ПО МАТЕМАТИКЕ
В настоящее время в средней школе осуществляется переход
иа изучение математики по новой учебной программе. Этот пере-
ход вызовет, соответствующие изменения и в «Программе для по-
ступающих в ВУЗы СССР», а также будет учитываться при про-
ведении конкурсных экзаменов в течение ближайших нескольких
лет.
В этой части пособия приводится литература, план повторения
и контрольные работы для изучения материала, который включен
в новую школьную программу по математике.
Основная литература
1.	Макарычев Ю. Н., Миндюк Н. Г., Монахов В. М.,
Мур а в ин К. С., Суворова С. Б. (под редакцией А. И. Мар-
кушевича) Алгебра, 8-й класс. М. «Просвещение», 1974 (в даль-
нейшем сокращенно обозначается «Макарычев»).
2.	Колмогоров А. Н., Вейц Б. Е., Демидов И. Т.,
Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и на-
чала анализа (учебное пособие для 9-го класса). М., «Просвеще-
ние», 1975 (в дальнейшем «Колмогоров, 9»).
3.	Колмогоров А. Н., Ивашев-Мусатов О. С., Ив-
лев Б. М., Шварцбурд С. И. Алгебра и начала анализа
(учебное пособие для 10-го класса). М. «Просвещение», 1976,
(в дальнейшем «Колмогоров, 10»).
43
Дополнительная литература
Ивлев Б. М., Крысин А. Я., Мур а вин Кг С., Руден-
ко В. Н., Соколова А. В. Дидактический материал. Алгебра и
начала анализа для 9-го класса. М. «Просвещение», 1975.
ТЕМА 1
Приближенные вычисления
Относительная погрешность. Запись приближенных значений
чисел. Оценка погрешности результатов действий.
Макарычев, §§ 3, 4, стр. 25—42. Упражнения №№ 98—108,
109—113, 114—119, 125—138.
ТЕМА 2
Принцип математической индукции
Формулировка и содержание принципа математической индук-
ции. Применение принципа математической индукции к доказа-
тельству математических предложений.
Колмогоров, 9. § 1, стр. 7—1. Упражнения №№ 12—31.
ТЕМА 3
Комбинаторика. Бином Ньютона
Соединения: перестановки, размещения и сочетания. Форму-
лы для вычисления числа перестановок, размещений и сочета-
ний. Формула Ньютона. Основные следствия.
Колмогоров, 9. § 2, стр. 17—39. Упражнения №№ 32—42, 43—
48, 49—62, 63—69, 70, 71—73, 80—112.
ТЕМА 4
Предел и непрерывность функций
Функции. Основные определения. Возрастание и убывание
функций. Приращение функции. Предел и непрерывность функций
в точке. Теоремы о пределах. Непрерывность основных функций.
44
Колмогоров, 9. § 8, стр. 93—114. Упражнения №№ 265—281,
282—297, 298—306, 309—313, 321—324, 327—336.
ТЕМА 5
Производная функция
Определение производной, ее геометрическая и физическая ин-
терпретация. Примеры вычисления производных. Производная
суммы функций, их произведения и частного. Производная слож-
ной функции. Производные от основных элементарных функций.
Применение производной к исследованию функций.
Колмогоров, 9. §§ 9, 10, 11, стр. 118—162. Упражнения
№№ 349—361, 363—365, 375—377, 378—385, 388—395, 401—447,
465—469, 473—479, 494—496, 497—503, 504—545.
Колмогоров, 10. § 15, стр. 7—>13, §§ 21—23, стр. 103—130.
Упражнения №№ 1—14, 15—28, 32—41, 572—581, 663—669, 711 —
713, 740—773.
ТЕМА 6
Первообразная функции и интеграл
Первообразная функции и ее основное свойство. Три правила
нахождения первообразных. Площадь криволинейной трапеции.
Формула Ньютона — Лейбница. Интеграл. Геометрическая и фи-
зическая интерпретация. Некоторые приемы вычисления инте-
гралов.
Колмогоров, 10. §§ 19—20, стр. 75—100. Упражнения №№ 392—
401, 402-407, 409—418, 419—424, 434—439, 446—450, 458—471,
472—507, 619—622, 784—799, 804—810.
Контрольная работа Ms 6
1.	В прямоугольном треугольнике АВС с прямым углом С,
углом В, равным 30°, и катетом С4 = 1 проведена медиана CD.
Кроме того, из точки D под углом 15° к гипотенузе проведена пря-
мая, пересекающая отрезок ВС в точке F. Найти площадь тре-
угольника CDF. Указать ее приближенное значение в виде деся-
тичной дроби с точностью до 0,01.
2.	Сколькими способами можно расставить на шахматной дос-
ке, имеющей, как обычно, 8X8 клеток, восемь разноцветных фи-
шек так, чтобы на каждой горизонтали и вертикали стояла ровно
одна фишка?
45
3.	Вычислить площадь фигуры, определяемой неравенствами
2х<у<3—х2,
если известно, что координаты всех точек этой фигуры удовлетво-
ряют неравенству х^О.
4.	Между двумя портами, удаленными друг от друга на рас-
стояние 1200 км, с постоянной скоростью курсирует теплоход. За-
траты на рейс в одном направлении слагаются из двух частей.
Первая часть, связанная с обслуживанием пассажиров, пропор-
циональна времени нахождения теплохода в пути, а другая, обу-
словленная стоимостью топлива, пропорциональна кубу скорости
движения. Найти скорость, с которой должен идти теплоход, что-
бы стоимость рейса была минимальной,' если Известно, что при
скорости 30 км/ч затраты равны 4,5 тыс. рублям, причем стои-
мость обслуживания пассажиров составляет 2/3 стоимости топ-
лива.
5.	Построить графики функций и выполнить их исследование
а- У= 4х»+1 ’
б.	y=x«sinx.
Контрольная работа Ms 7
1.	Имеется пять элементов а\, а2, а3, at, а&. Найти число пере-
становок этих элементов, в которых aj не стоит на первом месте,
и а2 не стоит на втором месте.
2.	Ребра прямоугольного параллелепипеда, вычисленные с точ-
ностью до 0,01 см, равны соответственно 4,25 см, 5,12 см и 6,15 см.
С какой наибольшей точностью можно вычислить объем этого па-
раллелепипеда? Найти этот объем.
3.	Если начало системы координат выбрать в точке стояния
корабля, то линию берега можно описать уравнением y=log2x.
Определить под каким углом видят берег с этого корабля.
4.	Доказать, что
1,1.	,_1___13
л + 2 ** л + 2'*" * * "*" 2л ' 24
при любом натуральном п, большем единицы.
5.	Найти член разложения (3x4-5)12 с наибольшим коэффи-
циентом.
Контрольная работа № 8
1.	Оля, студентка второго курса биологического факультета,
проводила эксперименты по выращиванию бактерий в питательной
среде. При этом она заметила, что скорость увеличения числа бак-
терий в любой момент времени пропорциональна числу бактерий
46
которое имеемся в этот момент времени, причем коэффи-
циент пропорциональности равен 0,5 (время измеряется в часах).
По заданию необходимо вырастить колонию бактерий числен-
ностью более 20 000 единиц. Каково наименьшее время, выращива-
ния колонии бактерий указанной численности, если известно, что
Оля первоначально поместила в среду 200 бактерий?
Указание. Составить дифференциальное уравнение для фуйк*
ции N(t) и использовать при его решении начальное условие
N (о) =200.	-	_
2.	Даны треугольник со сторонами, равными У 22 и и
углом 60° между ними и прямоугольник со сторонами, равными 29
и 1/25. Определить, что больше: площадь треугольника или пло-
щадь прямоугольника.
3.	Доказать, что уравнение
|/7=—х2+8х—15
не. имеет решений.
4.	Сколько существует способов разделить группу школьников
из 42 человек на три подгруппы, состоящих из равного числа
людей?
5.	Построить график функции
Зх*4-48_
и выполнить его исследование.
Ч а с т ь II	/х
/
ЗАДАЧИ	/
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
С РАЗБОРОМ ОТДЕЛЬНЫХ ВАРИАНТОВ
§ 1. ГЕОГРАФИЧЕСКИЙ ФАКУЛЬТЕТ, 1972 г.
Вариант 1
1.	Фрукты в магазин были доставлены двумя машинами, по
60 ящиков в каждой; при этом в 21 ящике были груши, а в осталь-
ных— яблоки. Сколько ящиков с грушами было в каждой ма-
шине, если известно, что в первой машине на один ящик с груша-
ми приходилось в три раза больше ящиков с яблоками, чем во
второй?
2.	Найти все решения уравнения
sin2x—cosx+2 sinx=+l,
удовлетворяющие условию
0<х<5.
3.	Найти все значения х, при которых справедливо неравен-
ство
2 log7x—logx49<3.
4.	Найти все числа х и у, для которых
| 2*+'= 4у* 4-1,
( 2*<2у.
5.	Окружность радиуса R проходит через вершины А и В тре-
угольника АВС и касается прямой АС в точке А. Найти площадь
Треугольника АВС, зная, что ЛАВС=[Ь и ZCAB=a.
Вариант 2
1.	Брат и сестра собрали каждый по 40 грибов, из них 52 бе-
лых гриба. Сколько белых грибов собрал каждый, если известно,
что отношение числа белых к числу остальных грибов у брата
в четыре раза больше, чем у сестры?
48
2.	Найти все рёщения уравнения
sin* х — /3 sin 2х — cos* х = — 2,
удовлетворяющие условию
0<х<4.
3.	Найти все значения х, для которых справедливо неравен-
ство
2 logs*—logx27<5.
4.	Найти все числа х и у, для которых
| 4 log1, х1 = 2 log,
I log, Х1^ log, у.
5.	Окружность радиуса с центром в точке О проходит через
вершины А и В треугольника АВС, пересекает отрезок ВС в точ-
ке М и касается прямой АС в точке А. Найти длину отрезка СМ,
зная, что ZACO = a и ЛМАВ=р.
Вариант 3
1.	В двух автоколоннах, по 28 автомобилей в каждой, было 11
«Жигулей», остальные — «Москвичи». Сколько «Москвичей» было
в каждой автоколонне, если известно, что в первой автоколонне
на каждую машину «Жигули» приходилось в два раза больше
«Москвичей», чем во второй?
2.	Найти все решения уравнения
)^3 sinx + 2 cos х =	-f- sin 2х,
удовлетворяющие условию
0<х<2.
3.	Найти все значения х, для которых справедливо неравен-
ство
log2x—logx32<4.
4.	Найти все числа х и у, для которых
г 2*+* = у‘-]-4,
5.	Через вершины В и С треугольника АВС проведена окруж-
ность, которая пересекает сторону АВ в точке К и сторону АС
в точке Е. Найти АЕ, зная, что Л/С=ЛВ=а, ZBCX=a, 2.СВЕ=
= ₽•
4—619	49
Вариант 4	/
1. Два стрелка сделали по 30 выстрелов каждый; при этом
было 44 попадания, остальные — промахи. Сколько раз попал
каждый, если известно, что у первого стрелка на каждый промах,
приходилось в два раза больше попаданий, чем у второго?
. 2. Найти все реШения уравнения
5 cos* х — J/3 sin 2х3 sin* х » 2,
удовлетворяющие условию’
0<х<5.
3.	Найти все значения х, для- которых справедливо неравен-
ство
21ogsX—logx!25<l.
4.	Найти все числа х и у, для которых
| log*, х 4-1 =log.t/*,
UogsXSMog,^.
5.	Дан треугольник АВС. Окружность радиуса /? касается сто-
роны АС в точке М и стороны ВС в точке Р. Сторона АВ пересе-
кает эту окружность в точках К. и Е. Точка Е лежит на- сторо-
не ВК. Найти BE, зная, что ВС=а, CM=b<a, Z.KME=a.
Разбор варианта 1
Задача 1. Обозначим количество ящиков, с грушами в пер-
вой машине через х, а во второй машине — через у. Тогда ящиков
с яблоками в первой машине было (60—х), а во второй — (60—у).
Условия задачи приводят к системе уравнений
гх4-0==21,
I х ____ 1 У
~	I 60 — х	3 60 — у'
которая после исключения величины у дает уравнение
х2+99х—630=^0.
Отсюда находим, что х=6. Здесь, конечно, принято во внима-
ние, что х>0. После этого находим, что ^=15.
Ответ: в первой машине было 6 ящиков с грушами, а во вто-
рой—15.
Задача 2. Представляя sin2x как 2sinx-cpsx, получим
cosx(2 sinx—1) + (2 sinx—1)=0,
или
(2 sinx—1) (cosx+l)=0.
50
Отсюда находим:\
а)	мпх=—1/2, х — (— 1)" -^-4-itn;
б)	cqsx=—1, x=w4-2it/£
> Отберем из полученных решений те, которые удовлетворяют
условию 0<х<5, т. е. определим п из неравенства:
а)	0<(-1)«-у+«л<5.
Легко видеть, что это неравенство может выполняться только
при л=0, п=<1;
б)	0<л+2лп<5.
Здесь подходит только одно значение п: п=0.
Ответ: Xi=-|-, Xi = 5n/6, х» = т.
Задача 3. Допустимыми в этой задаче являются те значениях,
которые больше нуля и не равны единице.
Если воспользоваться формулой перехода к новому основанию,
в данном случае 7:
10&,л=!ан,
® log* а
то получим неравенство
21og, х — j—-— < 3.
6 log, х
При х>1, т. е. когда log7x>0, имеем
2 logM—3 log7x—2<0,
— 4-<1°£'х<2-
Так как основание логарифма больше единицы, то
• -^<х<49.
Учитывая, что сейчас рассматривается случай, когда х>1,’полу,
чаем
1<х<49.
Если 0<х<1, то log7x<0 и тогда
2 log^x—3 log7x—2>0:
a)	log7x>2; х>49,
б)	log7x<~ 1/2; 0<х<1/К7.
Очевидно, что подходят значения х, соответствующие только вто-
рому случаю.
О/иягт: 1<х<49, 0<х< 1/^7.
4е	51
Задача 4. Первое уравнение системы можно записать так:
2х = 2^4-1-.
Тогда неравенство приобретает вид
или
(2у— 1)а<0.
Ясно, что квадрат любого действительного числа отрицательным
быть не может. Значит, 2у—1=0, т. е. #=0,5. Далее находим:
2Я=1,	х=0.
Ответ: х=0; #=0,5.
Задача 5. Чертеж к этой за-
даче представлен на рис. 12.
Пусть точка О — центр указан-
ной окружности. Рассмотрим
ДОЛЯ. В этом треугольнике
угол АО В равен 2to, поскдльку
он измеряется дугой, стягиваю-
щей хорду АВ. В то же время
угол ВАС, равный по условию а,
измеряется половиной этой дуги.
Из ДЛОВ находим хорду
АВ: AB=2R sina. Затем нетруд-
но найти искомую площадь тре-
угольника АВС, в котором из-
вестны все углы и сторона АВ. Используем теорему синусов:
АС	АВ	лг, пг> . sin В
жт ~ Sin (к —a —Р) ’ ЛС — 2/? sin a sln (о +
АВ
Площадь треугольника АВС определяется равенством
. S = 4-'45,?lC-sina =
2/?2-sin’aslnP
sin (a + ₽)
при (а+Р)<л.
§ 2. ГЕОГРАФИЧЕСКИЙ ФАКУЛЬТЕТ, 1973 г.
Вариант 1
1.	На прокладке двух' параллельных трубопроводов работали
два экскаватора. Первый из них начал работать на 30 мин рань-
ше второго. Когда второй экскаватор прокопал 27 м, оказалось,
что он отстает от первого на 1 ле. С какой скоростью копали
экскаваторы, если 'известно, что второй выкапывает в час на
4 м больше, чем первый?
52
2.	Упростить выражение
. 1
i°ej_ —
5	10 + 2/21*
3.	Сторона АВ квадрата ABCD равна 1 и является хордой не-
которой окружности, причем остальные стороны квадрата лежат
вне этой окружности. Длина касательной СК, проведенной из вер-
шины С к той же окружности, равна 2. Чему равен диаметр
окружности?	*
4.	Найти решения уравнения
пХ>+4х__ 1
удовлетворяющие неравенству х>— 3.
5.	Решить уравнение
]/~3 sin2х — 2cos’ х = 2 j/2-j-2cos2x.
Вариант 2
1.	Две машинистки вместе напечатали 65 страниц, причем пер-
вая работала на один час больше второй. Однако вторая машини-
стка печатает в час на две страницы больше первой, и потому она
напечатала на 5 страниц больше. Сколько страниц в час печатает
каждая машинистка?
2.	Упростить выражение
415 iog4 у- (3 - Vej - 6 log, (VT- V2))
3.	Гипотенуза АВ прямоугольного треугольника АВС равна 2
и является хордой некоторой окружности. Катет ЛС=1 и лежит
внутри окружности, а его продолжение пересекает окружность
в точке D, причем CD=3. Чему равен радиус окружности?
4.	Найти решения уравнения
*____х_______	5
х — 4 log, 2 х+ 11 ’
удовлетворяющие неравенству х<—2.
5.	Решить уравнение , 2
2 tg х - 4 ctg х =	tg»-|-— 2-j-ctg1•
53
Вариант 3
1.	Трактор выехал от станции к деревне на -30 мин раньше гру-
зовика. Когда грузовик, обогнав трактор, прибыл в деревню, трак-
тору осталось ехать до деревни еще 3 км. Найти скорости трак-
тора и грузовика, если известно, что скорость грузовика на
20 км/ч больше скорости трактора, а расстояние от станции до
деревни равно 12 км.
2.	Упростить выражение
6]<«vr8 । J е _____3_____1_______________
-t-iog^. Kg-+K2	7+ 2/10
3.	Сторона АВ правильного шестиугольника ABCDEF равна
У 3 и является хордой некоторой окружности, причем остальные
стороны шестиугольника лежат вне этой окружности. Длина каса-
тельной СМ, проведенной к той же окружности из вершины С
(соседней с вершиной В), равна 3. Чему равен диаметр окруж-
ности?
4.	Найти решения уравнения
б**-2* =128,
удовлетворяющие неравенству х>3.
5.	Решить уравнение
— sin* х — У1 — cos 2х.
Вариант 4
1.	Из пункта А в пункт В, расстояние между которйми равно
84 км, выехал велосипедист, а через 2 ч навстречу ему из В в А
выехал. мотоциклист, скорость которого на 48 км)ч больше ско-
рости велосипедиста. Найти их скорости, если известно, что к мо-
менту встречи велосипедист проехал на 16 км меньше, чем мото-
циклист.
2.	Упростить выражение
l610«2 VT(5_/i®) + 81°ei
2	Т
3.	Сторона АВ треугольника АВС является хордой некоторой
окружности. Стороны АС и ВС лежат внутри окружности, продол-
жеййе стороны АС пересекает окружность в точке D, а продол-
жение стороны ВС — в точке Е, причем AB=AC=CD=2, ЕС=
=У 2. Чему равен радиус окружности?
64	'
4.	Найти решения уравнения
х _ 3
х — logs3	х — 3’
удовлетворяющие неравенству х<5.
5.	Решить уравнение
З]/ tg«-|- + 2 + ctg«-f-=16sinx-
Разбор варианта 1
Задача 1. Обозначим скорость, с которой копал землю первый
экскаватор, буквой о м/ч. Тогда скорость второго будет соответст-
венно (о+4) м/ч. Пусть t — время, за которое второй•экскаватор
выкапывает 27 м. Условие задачи приводит' к следующей системе
уравнений:
| =>(*+4-)=2з,
I (o-f-4)f = 27.
Подставляя t из второго уравнения в первое, получим квадрат-
ное уравнение /
и2+2п—’224=0,
положительный корень которого о = 14 дает решение задачи.
Ответ: \4~м/ч, 18 м/ч.
Задача 2. Легко проверить справедливость нижеследующих- ра-
венств:
1
*°ei т
1) 5 5 = 51эд,2 = 2;
2>
3) log. ----^=log1/-i/' 104-2/21 =
= logyr/(/7+/3)« = log^_ (/7 +/3).-
Тогда
2+logy- (/7 - /3) + logy— (/7 4-/5) = 2 + log^ 4 = 6.
Ответ: 6.
Задача 3. Продолжим сторону квадрата ВС до пересечения
с окружностью в точке М; длину хорды ВМ обозначим через х
(рис. 13J.
'55'
По теореме о секущей и касательной, ироведенных к окружно-
сти из одной точки, имеем
(х+1)-1=4,
т. е.
ВМ=х=3.
Проведем OF.LBM и OEJ.AB и соединим точки О и В. Из
прямоугольного треугольника ОЕВ находим
ОВ* = ВЕ*-}-ЕОг,'
Ответ: V10.
Задача 4. Логарифмируя обе части уравнения
.	ох*+4х_ 1
d — 25
по основанию 3, получим равносильное уравнение
х24-4х+2 log35=0.
Поскольку 21og35<4, дискриминант этого квадратного уравнения
положителен и корни уравнения
действительны:
•х = — 2	]/4 — 21og,5.
Корень со знаком «плюс» удовле-
творяет условию задачи х>—3.
Другой корень можно предста-
вить в виде
х = — 2— ]/4 — 2 log, 5 =
= -2-/1ок.зА.
откуда легко увидеть, что он йеньше —3 и поэтому не является
решением задачи.
Ответ: х = — 2 -|- ]/4 — 2 log. 5.
Задача 5. Используя свойство арифметического корня
и формулу
1+cos 2x=2cos2x,
56
запишем данное уравнение в следующем виде:
/3 sin X-cos х — cos’ х — 2 [cos x| = 0.
Теперь необходимо рассмотреть два случая:
a) cosxz^O.	<
cosx(|/3sinx — cosx — 2)==0
1. cos_x = 0, Xt = it/2-[-*«.
2. }^3sinx — cos л — 2 = 0.
Вводя вспомогательный угол, получим
Уз” .	1	.	. ( я \	,
—s— sinx—*-^-cosx = 1, sinlx—s-1 el;
&	Л	у О J
X----?- = ——F	=
v Z	О
— । 
Однако cos%2<0, что не удовлетворяет условию рассматривае-
мого случая.
б)	cosx<0.
Аналогично предыдущему находим
КТ .	1	-	-	. ( те \	«
—£— Sinx £-COSJC=— 1, Sin ( X----g-J = —1;
x — -^-=—^-4-2itn, x,=—J-+2M.
Эти корни также не удовлетворяют условию рассматриваемого
случая, так как cosx3>0. Поэтому новых решений также не по-
лучаем.
Ответ: х = -^—|-п/г.
§ 3. ГЕОГРАФИЧЕСКИЙ ФАКУЛЬТЕТ, 1974 г. £
Вариант 1
1.	Из пункта А в пункт В", расположенный в 24 км от А, одно-
временно отправились велосипедист и пешеход. Велосипедист при-
был в пункт В на 4 ч раньше пешехода. Известно, что если бы
велосипедист ехал с меньшей на 4 км/ч скоростью, то на путь из
А в В он затратил бы вдвое меньше времени, чем пешеход. Найти
скорость пешехода.
2.	Найти все решения уравнения
cos3x-)-sin (х-\-^Л=УЗ cos (х—
57
3.	Решить систему уравнений
4 <_Ly-x=_^,
•	2 J. 2«+» ’
/2х + 14- j/4*+2y + 5 =^V2x + 2t/ + 4.
4.	Дан квадрат'ABCD, сторона которого равна а, й построены
две окружности. Первая окружность целиком расположена внутри
квадрата ABCD, касается стороны АВ в точке Е, а также касает-
ся стороны ВС и диагонали АС. Вторая окружность с центром
в точке А проходит через точку Е. Найти площадь общей части
двух кругов, ограниченных этими окружностями.
5.	Найти все значения х, удовлетворяющие неравенству
4х» + 12х + 5
log. fx*4-2x +
>о.
Вариант 2
1.	Две автоколонны перевозят груз. Машины имеют одинако-
вую грузоподъемность и в каждый рейс загружаются полностью.
Первая автоколонна за один рейс перевозит на 5 т груза больше,
чем вторая автоколонна. Известно, что если число машин в первой
автоколонне удвоить, то для перевозки 120 т груза ей потребуется
сделать на 5 рейсов меньше, чем второй автоколонне. Сколько
тонн груза перевозит за один рейс вторая автоколонна?
2.	Найти все решения уравнения
sin6x — cos (4х 4--y-^=]/r2^sin (fix
3.	Решить систему уравнений
log. (7—2x)4-log, (5х — 7у) = 0,
з
k Vx-j-y-j-3 - /8^2х = УЗх + у-9.
4.	В равнобочную трапецию ABCD вписана окружность, ка-
сающаяся нижнего основания AD в точке Е. Верхнее основание
ВС равно а, угол BAD = 60°. "Вторая окружность, целиком распо-
ложенная внутри трапеции, касается внешним .образом первой
(вписанной) окружности в точке К, касается основания AD в точ-
ке М и боковой стороны DC. Найти площадь фигуры КЕМ, огра-
ниченной меньшей из дуг КЕ, меньшей из дуг МК и отрезком ЕМ.
58
5.	Найти все значения х, удовлетворяющие неравенству
>0.
Вариант 3
1.	Из пункта А в пункт В, расположенный на противополож-
ном берегу озера, одновременно вышли моторная лодка и катер.
К моменту, когда катер прибыл в пункт В, моторная лодка про-
шла половину пути и была в 30 км от В. Известно, что если бы
катер шел из А в Б с большей Скоростью, увеличив ее на 3 км/ч,
то лодка пришла бы в пункт В на 6 ч позже катера. Найти ско-
рость моторной лодки.
2.	Найти все решения уравнения
sin х -|- cos f 5х	=]/"3 sin (Зх -|- it).
3.	Решить систему уравнений
/	\ № J 5
I /ЯГ2 +/2х + «/+14 = /х + г/ + 12.
4.	В треугольнике АВС боковые стороны АВ и ВС равны а,
угол АВС= 120°. В треугольник АВС вписана окружность, касаю-
щаяся стороны АВ в точке D. Вторая окружность с центром в точ-
ке В проходит через точку D. Найти площадь той части вписан-
ного круга, которая находится внутри второго круга.
5.	Найти все значения х, удовлетворяющие неравенству
log.
—< • -4v<°-
log, ( х* — 2х +-jg I
Вариант 4
1.	Два насоса, работая одновременно, наполняют водой бас-
сейн емкостью 60. м3 за полтора часа. Известно, что-если бы ра-
ботал только один второй насос и его производительность была бы
увеличена в полтора раза, то для наполнения бассейна потребова-
лось бы на 2 ч больше времени, чем для наполнения бассейна
59
с помощью только одного первого насоса. Сколько кубометров во-
ды в час подает первый насос?
2.	Найти все решения уравнения	,
cos5х — sin (Зх —j=Y2 cos(4х-|-Зя).
3.	Решить систему уравнений
Г log, (10 — Зл) 4- log, (2х — 5t/) = 0,
J	т
I 4-1/4- 1 - J/11 -3x=V4x4-2i/-12.
4.	В равносторонний треугольник АВС, сторона которого рав-
на а, вписана окружность, касающаяся стороны АВ в точке D.
Вторая окружность, расположенная внутри треугольника АВС,
касается внешним образом первой (вписанной) окружности в точ-
ке К, касается стороны АВ в точке М и стороны ВС. Найти пло-
щадь фигуры DKM, ограниченной меньшей из дуг DK, меньшей из
дуг КМ и отрезком MD.
5.	Найти все значения х, удовлетворяющие неравенству
49х1 — 63х 4-20 р
log __|5х-3|-2
У 5
Разбор варианта 1
Задача 1. Обзоначим скорости велосипедиста и пешехода бук-
вами и и v соответственно. Понятно, что и>4. Уравнения задачи
имеют вид
24 24 .
---------=4,
V	и	’
О 24  24
и — 4	v
Исключая из этих уравнений и, получим квадратное уравнение
для скорости пешехода о:
v2—v—12=0.
Его положительное решение: v=4. Нетрудно подсчитать, что
в этом случае и равно 12 км)ч, т. е. и>4.
Ответ: 4 км/ч.
Задача 2. Воспользуемся известными формулами:
/ 7к .	\	/ те \	.
Sin I -2"'4" х)= — cos Л; COSfX-2"l = smx.
60
Тогда имеем
cos Зх — cos х = /3 sin х
и далее
,	—2sin 2 х sin х = УЗ sin х.
Возможны два случая:	
1) sinx = 0; х = ‘кп.
2) sin2x=—2х = (— 1)п+*
Ответ: х — ъп\ х = (—l)n+l-^—где « = 0, rtl, ±2...»
Задача 3. Из первого уравнения системы,имеем:
4_____1
2у-х	2х+г *
1	_ 1
2и~х~ 2	2*+2 *
у — х — 2 = x-f-2,
у = 2x4-4.
Исключая с помощью этого соотношения у из второго уравнения
системы, получаем иррациональное уравнение
/2х+”14- /8х-рЗ = /6x4-15.
Очевидно, что допустимыми являются те х, которые удовлетворя-
ют неравенству х^—V2. Поскольку обе части уравнения неотри-
цательны, то после их возведения в квадрат получится уравнение,
равносильное исходному:
/(2x4-1) (8x4-13) = - (2х4-1).	(1)
Заметим, что для существования действительных решений у это-
го уравнения необходимо, чтобы выполнялось условие
2х -|- 1 < 0 или х <—.
Сравнивая это условие с условием, ограничивающим ОДЗ, полу-
чаем, что х может равняться только —‘/г. Непосредственной про-
веркой убеждаемся, что х=—‘/г есть решение уравнения (1). Та-
ким образом, х=—‘/г, а у=3.
Ответ: х——‘/г, «/=3.
Задача 4. .На рис. 14 представлен чертеж к этой задаче. Оче-
видно, что первая окружность вписана в равнобедренный прямо-
.	61
угольный треугольник АВС и ее центр О лежит на пересечении
биссектрис этого треугольника. Поэтому радиус OF, проведенный
из центра окружности к точке касания F со стороной АС, является
частью высоты BF -равнобедренного треугольника АВС. Понятно
также, что AE=AF; поэтому нетрудно рассчитать значения ра-
диусов обеих окружностей г и R, первой и второй соответственноз
г — а —
aV 2
2~
= а
2 — V2
2
Для вычисления площади общей части кругов воспользуемся
формулой для площади сегмента в окружности радиуса R, имею-
щего дугу а, рис. 15:
= &OMKN ~	2" S*n а*
$MNK 2	S*n
Для сегмента EPF второй окружности дуга равна л/4; для сегмен-
та EQF первой окружности —Зл/4. Поэтому имеем
S1 и» f	• Я \
bpf=~% %	81Пт) ’
$BQF—~2~Г ^"4“	8Ю-4у • z
Складывая эти выражения, получим величину искомой пло-
щади:
5	_1 р» f	I_1 <-* ( 311 Кг \
^BQFPB— 2 Л \ 4	2 /Т 2 г \ 4	2 ) ‘
62
После подстановки выражений для радиусов обеих окружностей
имеем :-
- П 1(2/2- 1)1.-4].
Ответ-, а* (/2 - 1) [(2 /2 - 1) it - 4]/8.
Задача 5. В области допустимых значений неизвестного дан-
ное неравенство равносильно следующим системам неравенств:
f 4л1 —|— 12х —J— 5	О,
L (log. [\‘4-2x + ^-J >0;
|4x« + 12x4-5<0,
2* (log. (х«4-2х + -^-)< 0.
Решим поочередно, каждую из этих систем.
Объединяя найденные множества, получим:
х<~— и х>-г.
' 4х‘4-12х+6<0,	—Ь
2«	7	9	7
0<х‘ + 2х + 4<1,	9-<х<-4-,
Объединяя найденные множества, получим:
Ответ: х< —5/2; — 9/4 <х< — 7/4; х>1/4.
§ 4. ГЕОГРАФИЧЕСКИЙ ФАКУЛЬТЕТ, 1975 г.
Вариант 1
1.	Бассейн может наполняться водой с помощью двух насосов
разной производительности. Если половину бассейна наполнить,
включив лишь первый насос, а затем, выключив его, продолжить
наполнение с помощью второго насоса, то весь бассейн наполнит-
63
ся за 2 ч 30 мин. При одновременной работе обоих насосов бас-
сейн наполняется за 1 ч 12 мин. Какую часть бассейна наполняет
за 20 мин работы насос меньшей производительности?
2.	Решить уравнение
sin1 х — cos х  cos Зх==-j-.
3.	Решить уравнение
iosv-г log’ v (' “ 4"У
4g21og<(x—2) у '2	=49	'	'	/ y4 10SiX
4.	В треугольнике АВС биссектриса АК перпендикулярна ме-
диане ВМ, а угол АВС равен 120°. Найти отношение площади
треугольника АВС к площади описанного около этого треугольни-
ка круга.
5.	Решить систему уравнений
tg3x = tg
2x+31og /
Вариант 2
1.	Моторная лодка, пройдя 20 км по спокойной воде озера, во-
шла в вытекающую из озера реку и, сразу выключив мотор, про-
плыла по течению реки еще 5 км. Весь описанный путь занял 2 ч.
Затем лодка развернулась и, двигаясь относительно воды с той же
скоростью, как и в начале пути, когда она шла первые 20 км,
вернулась к озеру через 20 мин после разворота. Какова скорость
течения?
2.	Решить уравнение
12 cos* -^-=9—4 coscos
3.	Решить уравнение
,	1 \	.	2х—1
g \ 2х / _ g	,e gglogie (34-х) '
4.	В треугольнике АВС биссектриса АН делит медиану BE
в отношении ВК: КЕ = 2, а угол АС В равен 30°. Найти отношение
площади треугольника ВСЕ к площади описанного около этого
треугольника круга.
64
5.	Решить систему уравнений
ctg4x = tg^-^»
Вариант 3
1. Две артели с разным числом мастеров одинаковой квали-
фикации начали изготовлять шапки, причем каждый мастер делал
по две шапки в день. Сперва работала только первая артель, вы-
пустившая 32 шапки. Затем ее сменила вторая артель, выпустив-
шая еще 48 шапок. Вся эта работа заняла 4 дня. После этого
артели стали работать вместе и за следующие 6 дней изготовили
еще 240 шапок. Сколько мастеров в каждой артели?
2. Решить уравнение
2 sin* х=+sin х • sin Зх.
3; Решить уравнение
(3 х ) ^logu х1 __ gIog’ Y4—х .gloe, (Эх—2) .
4. В треугольнике АВС высота ВН делит сторону АС в отно-
шении АН :НС=4, а угол НВС вдвое меньше угла ВАС. Биссек-
триса АЕ угла В'АС пересекается с ВН в точке К. Найти отно-
шение площади треугольника АВК к площади описанного около
этого треугольника круга.
5. Решить систему уравнений
ctgx = ctg(£ —5),
Вариант 4
' 1. Человек в лодке начал грести против течения быстрой реки.
Однако через 4 мин лодка оказалась на 80 м ниже по течению.
Развернув ее, он перестал грести, и, пока он отдыхал, лодку снес-
ло на 40 м. Затем он принялся грести по течению, причем лодка
двигалась относительно воды с той же скоростью, как и в первые
4 мин, и прошла относительно берега еще 40 м. В целом после
разворота лодки прошло 100 сек. Какова скорость течения?
5—619	65
2.	Решить уравнение
sin -~ sin ^г-=4— cos*
3.	Репшть уравнение
 logy's- (*—О	,,___ log.. х>~|
5	=251ое’Гл*-1 -25 4л*-7 •
4.	В треугольнике АВС биссектриса АН пересекает высоты ВР
и СТ в точках К и М соответственно, причем эти точки лежат
внутри треугольника. Известно, что ВК.‘.КР—2 и МТ: KP=3h-
Найти отношение площади треугольника РВС к площади описан-
ного около этого треугольника круга.
5.	Решить систему уравнений
ctg4x = ctg^=A
4 -__ у .	-4-lOgj_^
3x + 41og^У >=21og	(¥) -36	6 .
’	F я
Разбор варианта 1
Задача 1. Обозначим производительности насосов t>i и о2 со-
ответственно, а объем бассейна примем за единицу. Тогда усло-
вия задачи приводят к системе уравнений
1__।__
2t>i 2о«	2 ’
,	-	' 4 (щ + о,) = 1.
Эти систему нетрудно преобразовать к следующему виду:
.	5
Oi4-Vi=-g-»
Отсюда определяем, что производительность каждого из насосов
может равняться либо */г либо */з. Поскольку требуется опреде-
лить, какую часть бассейна наполняет за 20 мин насос меньшей
производительности, то берем решение У1 = 1/з, т. е. насос меньшей
производительности наполняет за час 7з часть бассейна. Тогда за
20 мин он наполняет V» часть бассейна.
Ответ-. 1/в. -
66
Задача 2. Преобразуя произведение косинусов в условии зада-
чи в сумму
cos х • cos Зх=Ц- [cos'4x -|- cos 2х],
запишем уравнение в следующем виде:
sin* х-g- [cos 4х -|- cos 2х[=-i-
и далее
1	*----g- [2 cos8 2х — 1 -f-’cos 2х] =-|-,
4 cos8 2х 4 cos 2х — 3 = 0.
Это уравнение относительно cos2x имеет единственное решение:
cos2x=-i-.
Второе значение cos2x=—3/2 не годится, поскольку |cos2x|^l.
Таким образом,
о 1'
cos2x=—,
2х = ±4-+2^.
х =	-4—Htfe.
О
Ответ: x=zt-4-it&, где k = 0, ztl, zh2....
О
Задача 3. Область допустимых значений неизвестного опреде-
ляется из системы неравенств:
х — 2>0,
12 —х>0,
х > 0, /
1	- — >0.
X '
Решение этой системы показывает, что 2<х< 12.
Уравнение можно записать следующим образом:
logyjr* ^12—X	2 log» "З/" fl —Д
74 1og<(x-2) у у2	_7	x/ey41ogtx
откуда следует другое уравнение:
2	log, (х - 2) + log2 (12х) = 3 log,	log, х.
5*
67
После приведения подобных членов и'потенцирования получим
log2 (12—х) =logjx (х—2) ],
12—х=х2—2х,
х2— х—12=0.
Корни последнего уравнения равны
*1=4, х2=—3.
Из этих значений только одно удовлетворяет условию 2<х<12.
Ответ: х=4.
Задача 4. Обозначим К' точку пересечения биссектрисы АК
треугольника АВС с его медианой ВМ,
рис. 16. Очевидно, что прямоугольные
треугольники АВ К' и AM К' равны между
собой (по острому углу и общей сторо-
не), откуда следует, что АВ = АМ и, зна-
чит, АС—2 АВ.
Обозначим радиус окружности, опи-
санной вокруг треугольника АВС, через
R. По теореме синусов:
откуда
АС___пр
АС = 2/? sin 120° = Я/3.
Обозначим сторону ВС треугольника АВС через х и применим тео-
рему косинусов:
АС* = АВ«ч-|-ВС* - 2АВ ВС cos 120°,
3₽»=-^-/?»+х* - 2cos 120°.
После упрощений получим квадратное уравнение

положительный корень которого равен
Я/Т(/Тз-1)
4
68
Искомое отношение площадей определяется следующим об-
разом:
1 я/з.я/з(Лз-1) ,	_
SABC ~2	2	4	Г-81П120 __зКз(К13—1).
SKP ~	32л
„ зИГ(/1з —1)
Ответ: ——------
32к
Задача 5. Область допустимых значений неизвестных опреде-
ляется в этой задаче из следующей системы условий:
I	1^=£-^-+*т;
1*>°; *>*•
откуда следует, что
( х>0; |/>0; х^-~-
Преобразуем отдельно члены второго уравнения системы.
__ j "•Х
I о 1_~ I/ «** °gt 16 21ogtit+ log, х —4 .
'	г 16	4x log, x 4-2— log,«t ’
lo —
9 ino-	f4x*\ —	°g> *______2 + 2 log, x — log, re
10g4 7Г k « J	4/4^- — 1	1	Г" »
Y — '	' log, у —	—+— log, x — —logjn
3. 43•”«» Vv == 83	= 8loe*v = y.
Подставляя полученные выражения во второе уравнение, по-
лучим
2х — 5 = — у,
Используя этот результат, запишем первое уравнение системы
в более простом виде:
tg3x=tg(—х)
или
tg3x+tgx=0,
sin 4х -
cos3x«cosx ’
69
Решения этого уравнения имеют вид
4х = «л,
х = ^~, где п = 0, z±zl, ±2 ....
Соответствующие у определяются формулой
Найдем, какие ограничения накладываются областью допусти-
мых значений. Прежде всего, из условий х>0 и х=/= следует,
что п=2, 3, 4 ..., а условие у>0 показывает, что годятся только
п=2 и л=3. Таким образом, возможна только пара решений:
х = «/2,
у = 5 — It;
х = Зя/4,
г- Зк
^ = 5—
Однако первая из этих пар также не годится, поскольку в этом
случае не определены тангенсы, входящие в условие задачи. Един-
ственно возможное решение определяется второй системой.
Ответ-. х—Зп/4, у=5—Зл/2. ’
§ 5. БИОЛОГО-ПОЧВЕННЫЙ ФАКУЛЬТЕТ, 1972 г.
Вариант 1
1.	Два пешехода одновременйо выходят навстречу друг другу
из пунктов А и В и встречаются через три часа. Если бы они оба
вышли из пункта А и пошли в пункт В, причем второй вышел бы
на три часа позднее первого, то второй пешеход догнал бы перво-
го, пройдя две трети расстояния от пункта А до пункта В. Сколько
времени потребуется первому пешеходу на путь из пункта А
в пункт В?
2.	Упростить выражение
tg 2х ctg (70°—х) +tg 2х ctg (20°—х) —
—ctg (20°—х) ctg (70°—х).
3.	Решить уравнение
V log, 4 X—0,75
70
4.	Найти все решения уравнения
sin (logK_ х*х) sin тех+cos тех	cos (log* х2хЛ) = 0.
5.	В треугольнике АВС, площадь которого равна S, проведены
биссектриса СЕ и медиана BD, пересекающиеся в точке О. Найти
Площадь четырехугольника ADOE, зная, что ВС=а и АС—Ь.
Вариант 2
1.	Из города А в город В выезжает автомобиль, и одновремен-
но из города В в город А выезжает автобус. Через четыре часа
они встречаются. Автомобиль приходит в город В на 3 ч 20 мин
раньше, чем автобус приходит в город А.
Сколько времени затрачивает автомобиль на путь из города А
в город В?
2.	Упростить выражение
1 — sin (180е + Зх) cos (270° + 5х) + cos (546* — Зж)-sin (450* + 5х)
[4 + (tg 2х — ctg 2х)2] ~* 1
3. Решить уравнение
1
(/х)1ов"(9х, = (/3)1ов’/Г.
4. Найти все решения уравнения
cos (logx< xKX) — sin (logx [Ух]ех)Ч- 1 
cos ”у- + sin -у-— 1
5. В трапеции ABCD биссектриса угла А пересекает боковую
сторону ВС в точке Е. Найти площадь треугольника АВЕ, если
известно, что площадь трапеции равна S, ее основание АВ=а,
AD=b, CD=c, с<а.
Вариант 3
1. Из пункта А отправляется машина, а через час мотоцикл,
который догоняет машину в пункте В. В этот момент из А отправ-
ляется второй мотоцикл, идущий с той же скоростью, что и пер-
вый. Второй мотоцикл догоняет машину через шесть часов после
своего отправления.
За какое время мотоцикл проходит путь из пункта А в пункт В?
2. Упростить выражение
tg 4х tg (40°—2х) +tg 4х tg(50°—2х) +
+tg (50°—2х) tg (40°—2х).
71
3.	Решить уравнение
g*' (log,x+loe,9) 10g? _ gFlOg, 1.8
4.	Найти все решения уравнения
sin пх -f- sin (logx х3") = cos их — cos (log3 Xм).
5.	В треугольнике АВС биссектрисы AD и BE пересекаются
в точке О. Найти отношение площади треугольника АВС к пло-
щади четырехугольника ODCE, зная, что ВС=а, АС=Ь, АВ = с.
Вариант 4
1.	Три поезда выехали одновременно: пассажирский из горо-
да А в город В, а скорый и товарный из города В в город А. Пас-
сажирский и скорый поезда встретились через 4 ч. Скорый поезд
пришел в город А на 7 ч раньше товарного. Скорость пассажир-
ского поезда в полтора раза больше скорости товарного.
За какое время товарный поезд прошел путь от города В до
города А?
2.	Упростить выражение
sin (2х—540*) sin (4* — 180*) — sin (2х — 270*) sin (450* — 4*) — 1
[4 + 16 (tg 1,5х — ctg 1,5ж)~«]" *
3.	Решить уравнение
ylog*M (5х) — 1  ^.log, 7 q
4.	Найти все решения уравнения
(1 + /3) cos (logy- Xх) 4- (J/3 - 1) (sin 2x - 1) = 0.
5.	В параллелограмме ABCD точка E делит пополам сторону
CD, биссектриса угла АВС пересекает в точке О отрезок АЕ. Най-
ти площадь четырехугольника ОВСЕ, зная, что AD=a, DE—b,
ZABO=a.
Разбор варианта 1
Задача 1. Анализируя условие задачи, замечаем, что величи-
ны с размерностью длины в условие задачи не входят. Поэтому
можно ввести единицу длины, приняв за нее расстояние между
пунктами А и В. Введем далее в качестве неизвестных скорости
пешеходов t>i и ог ед. дл{ч. Тогда искомое время	при-
чем />3.
72
Условия задачи можно записать теперь в виде системы урав-
нений
3 (th -J" Pi) = 1»
2/3 = 2/3_Ь3
01 Яг '
Учитывая, что о = 1/з—th согласно первому уравнению этой си-
стемы, из второго уравнения находим
3 Д 01	01 J 9
2
3
=3,
9о‘, - 7о.+-|-=0-
О
Корни последнего квадратного уравнения — О1=2/з и t>i=1/e, следо-
вательно, ti=3/2 и fe=9. Поскольку£>3, лишь второе значение да-
ет решение задачи.
Ответ: t—Эч.
Задача 2. Заметим, что данное тригонометрическое выражение
определено при условиях:
cos2x=£0, sin(70°—х)#=0, sin(20°—х)^0,
т. е.
х^=45°+90°п, х=#20°+180°п, хУ=70°+ 180°п.
Используя представление тангенса и котангенса через синус и
косинус, а также формулы для синуса и косинуса разности аргу-
ментов, получаем
tg 2х ctg (70° — tg 2х ctg (20° — х) —
- ctg (20° - ctg (7о» - л)=tg 2л	-
— tg (20° + х) ctg (20° — х)=
sin 2х — sin (20* + х) cos (20* — х)
cos (20* + х) sin (20е — х)
sin 2х — -у- (sin 40* + sin 2х)
(sin 40* — sin 2x)
sin 2x — sin 40е
sin 40* —sin2x
1.
Ответ:—1, при x, удовлетворяющих указанным выше ограни-
чениям.
Задача 3. Логарифмируя обе части уравнения по основанию 3,
получаем равносильное уравнение
/log, 3-logj 2 = loge4x
з
73
Возводя в квадрат обе части этого уравнения, получаем
log, 2 = log, 4 + log, х—	(2)
Следует отметить, что последнее уравнение также равносильно
исходному. Поскольку очевидно, что число logs2 положительно,
при возведении в квадрат обеих частей уравнения (1) посторон-
них корней получиться не может. Кроме того, здесь нет необходи-
мости проверять, выполняется ли ограничение, налагаемое на не-
известное х неотрицательностью подкоренного выражения. Для
тех значений х, которые удовлетворяют уравнению (2) это, оче-
видно, выполняется: после возведения в квадрат подкоренное вы-
ражение равно квадрату некоторого числа и, значит, неотрица-
тельно.
Далее находим
log, х=-|- и х=93/4 = 3}/3.
Ответ: х = зКз.
Задача 4. Выполним вычисления:
logv_ х'х = 2«х и log, х2кх = 2itx.
Ух	х
Эти преобразования являются равносильными на множестве до-
пустимых значений
х>0, х#=1.
Обозначая далее у=лх, получаем уравнение
sin 2у+cos 2у+sin у+cos у=0.
Используя преобразование, известное под названием «.введение
вспомогательного аргумента», запишем это уравнение в виде:
У2 cos ^2у —+1^ cos [у----=0,
или
fa 4 \	/	\
cos [2у -	— cos - у V
Последнее равенство приводит к соотношениям	;
2у-^- = ±(^--у^2^.
Отсюда находим:
а)	2itx —^-=— itx -|- 2-xk,
Зх=-|-+2£,
74
Условие х>0 показывает, что k=0, + 1, +2, ... .
б)	2ях--^-= —+
Отсюда
х=—1+2&.
Условия х>0 и х=/=1 показывают, что k—+2, +3....
Ответ: х=*/2+2М при k=0, 1, 2,...; х=—1+2&, при k=2,
3,4, ... .
Задача 5. Для решения данной задачи используем утвержде-
ние,. подробно рассмотренное в этом пособии. Оно заключается
в том, что при изменении сторон
треугольника в т и п раз соот-
ветственно его площадь изменит-
ся в тп. раз.
Площадь четырехугольника
ADOE может быть найдена как
разность площадей /XABD и
и ЛЕВО, рис. 17. Площадь пер-
вого из них равна, очевидно S/2,
поскольку медиана BD делит
площадь треугольника АВС попо-
лам; площадь второго может
быть определена путем подсчета
двух отношений
ЕВ
т=~лв И
п=
ов
DB’
Е
в
которые показывают, во сколько
раз стороны треугольника ЕВО
уменьшены по сравнению со сторонами треугольника ABD.
Величина т находится на основе теоремы о биссектрисе вну-
треннего угла треугольника:
ЕВ а	ЕВ а
~ЁА~~~Ь' Т‘ е’ т~~АВ~~а + ~ь‘
Аналогичным образом находится и другое соотношение. Из
треугольника BDC имеем
ОВ__ а	_ а
~0О~~Ь[2’ Т‘ е‘ П а+Ы2 •
Поэтому отношение площадей ДЕВО и &ABD равно
$&Ево__________________а_____а___________2а3____
S&ABD а 4" b а + Ь/2 (а + Ь) (2а + Ь)
Но площадь £±ABD равна S/2. Значит,
о _______________________	5 • а1
—(а + ь) (2а +ЬУ
75
Окончательно находим,
е _ S	Sa» _ Sb (За + к)
ADOB 2 (а + Ь) (2а + Ь) 2(а-Ь Ь) (2а+ Ь).'
Ответ:
„	VSb(3a + b)
^adob— 2 (а + Ь) (2а + Ь) ‘
$ 6. ФАКУЛЬТЕТ ПОЧВОВЕДЕНИЯ, 1973 г.
Вариант 1
1.	Два экскаватора разной конструкции должны проложить
две траншеи одинакового поперечного сечения длиной в 960 м и
180 м. Вся работа продолжалась 22 дня, в течение который пер-
вый экскаватор прокладывал большую траншею. Второй же экс-
каватор начал работать на 6 дней позднее первого, отрыл мень-
шую траншею, 3 дня ремонтировался и затем помогал первому.
Если бы не нужно было тратить времени на ремонт, то работа
была бы кончена за 21 день.
Сколько метров траншеи может отрыть в день каждый экска-
ватор?
2.	Что больше
(1% Г5-4)	3 ^3)’ или 2 Ып -J- cos’	tg ~ ?
3.	Решить уравнение
(cos х — sin х) ( 1 +	sin 2х^ -f- sin х = 2 cos’ х.
4.	В окружность радиуса (3+ У 3) вписан правильный шести-
угольник ABCDEK. Найти радиус круга, вписанного в треуголь-
ник ACD.	-
5.	Найти все действительные решения уравнения
43х1+х —8 = 2-8	3.
Вариант 2
/
1.	Общий вес снаряжения туристской группы 202 кг. Если рас-
пределить его так, чтобы каждому юноше пришлось нести по
16 кг, а каждой девушке —по 9 кг, то 4 кг останутся нераспреде-
ленными. Поэтому юноши берут себе еще по 2 кг, в результате
чего удается облегчить вес рюкзака каждой девушки на 1 кг,
а одну из них освободить вовсе, причем все снаряжение оказы-
вается распределенным.
76
Сколько юношей и сколько девушеу в туристской группе?
2.	Что больше
arccos (-^-log..^)
ИЛИ
«»— -tg« (—-J.ctg-g-?
3.	Решить уравнение
cos х (КЗ + cos х) — 1 =	-s*n х 0^4" sin хУ
4.	Две окружности радиуса 32 с центрами Oi и Ог, пересе-
каясь, делят отрезок О.Ог на три равные части.
Найти радиус окружности, которая касается изнутри обеих
данных окружностей и касается отрезка О.Ог. -
5.	Найти все действительные решения уравнения
log. (х* + 7) = 5 + log, х-у----?у-.
loU*+v) —
Вариант 3
1.	В 9 часов утра из некоторого пункта выехал мотоциклист.
Спустя 40 мин вдогонку по той же дороге выехал автомобиль.
Через некоторое время из-за неисправности в моторе автомобиль
остановился. На устранение неисправности ушло 10 мин, после че-
го автомобиль возобновил погоню и в 11 часов утра отставал от
мотоциклиста на 40 км.
Если бы поломки не было, а мотоциклист ехал бы со скоро-
стью, на 18 км/ч меньшей, чем была у него на самом деле, то
автомобиль нагнал бы мотоциклиста в 10 часов 40 минут утра.
Найти скорости автомобиля и мотоциклиста.
2.	Что больше
- (log.. 32) (logj_ 2 V2)«
8
ИЛИ
„ . 19» f	17» > ЗЫ
COS* — ctg (----g- \ • Ctg— ?
3.	Решить уравнение
(sin 2х — 1) (sin х+3 sin* х.
77
•4. В окружность радиуса (3+2 ]/Ц) вписан правильный ше-
стиугольник ABCDEK.. Найти радиус круга, вписанного в тре-
угольник BCD.
5. Найти все действительные решенйя уравнения
2* («+*)’__1__|_2.4ж
Вариант 4
1.	Профсоюзный комитет выделил на покупку 7 путевок в дом
отдыха и 20 путевок на турбазу 812 рублей. Однако оказалось,
что путевки в дом отдыха стоят на 1 рубль дешевле, а на турба-
зу — на 4 рубля дешевле, чем планировалось. Поэтому, удалось
купить дополнительно еще одну путевку в дом отдыха и 2 на тур-
базу, причем из выделенных денег осталось еще 4 рубля. Сколько
стоит путевка в дом отдыха и сколько на турбазу?
2.	Что больше
или
cos‘-g- tgL—.tg—.?
3.	Решить уравнение
tg х+sin 2x+ ,	= 1 + 2 sin* (x + -J-J.
4.	Окружность радиуса (1+ 1^2) описана около равнобедрен-
ного прямоугольного треугольника. Найти радиус окружности, ко-
торая касается катетов этого треугольника и внутренним образом
касается описанной вокруг него окружности.
5.	Найти все действительные решения уравнения
5 + log- t , +=log'	, +•
Х + -Б-	х + -у-
о	о
Разбор варианта 1
Задача 1. Пусть Vi и о2 производительности первого и второго
экскаваторов. Поскольку обе траншеи, которые прокладывают
экскаваторы, имеют одинаковое поперечное сечение, условия зада-
чи равносильны следующей системе уравнений:
|22o,-|-13ot=1140,
I 21о, 4-15о,= 1140,
78 ’
решение которой легко находится: 40 м/день и 20 м!день.
Ответ. 40 м!день, 20 м!день.
Задача 2. Произведем вычисление каждого выражения в от-
дельности
1) (log, у_ 4) (log, 3 /3)‘.= (log ± 2*) (loga, 3 2 )• - -1. (А)’=4-;
22	4	7
- п •	. 23гс , 37гс
2)	2SIH-т--COS* “Т“*tg—г-=
/	4	404
= 2.J^C0S.4,tg4.=2.^.(_!^y.1=^.
Надо сравнить числа 3/4 и У2/2. Очевидно, что первое из них,
больше, чем второе. •
. Ответ, первое число больше второго.
Задача 3. Используя формулу синуса двойного угла, раскрывая
скобки и приводя подобные члены, получим
cos x+sin х cos2x—sin2x cos x—2 cos2x=0,
cos x (14- sin x cos x—sin2x—2 cos x) ?= 0,
1)	cosx=0, откуда х=п/2+лп;
2)	1+sinxcosx—sin2x—2cosx=0,
или
cos2x+sin x cos x—2 cos x=0,
cos x (cos x+sin x—2) =0,
a)	cosx=0, x=:r/2-t-nn;
6)	cos x+sin x=2.
Так как
cos x + sin x =
= /2sin (x + 4)^/2,
то последнее уравнение не имеет
решений.
Ответ: х = -^—\-кп.
Задача 4. Пусть R— радиус
круга (рис. 18). Так как DC—R,
AC=R У~3, a AD = 2R и ZACD =
=90°, то для определения радиу-
са вписанного в треугольник ACJD
круга г можно воспользоваться
79
формулами для площади прямоугольного треугольника, записан-
ной двумя различными способами:
S = pr=±-ab.
Здедь р — полупериметр треугольника, а и Ь — его катеты. В на-
шем случае
р=3(2 + /3), а = 3-|-/3 и 7? =^3(3 4-/3).
Имеем:
3 (/3 4-2) г = -L/3 (3 + /3).
Отсюда находим г = /3.
Ответ-. УЗ.
Задйча 5. Сделав подстановку
23х’+* = />0,	t
получим относительно t квадратное уравнение
t2—2t—8=0,
корни которого /1=—2 й /г=4. Первый в силу положительности
t не подходит; второй корень дает
23х*+* = 4, Зл‘4-х = 2, _
т. е. Зха+х—2=0; xt=—1, х2=2/з.
Ответ-. Xi=—1, х2=8/з.
$ 7. БИОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ, 1973 г.
Вариант 1
1.	Три каменщика (разной квалификации) выложили кирпич-
ную стенку, причем первый каменщик проработал 6 ч, второй —
4 ,ч и третий — 7 ч. Если бы первый каменщик работал 4 ч, вто-
рой — 2, третий — 5 ч, то было бы выполнено лишь 2/з всей работы.
''За сколько часов каменщики закончили бы кладку, если бы
они работали все вместе одно и то же время?
2.	Решить уравнение
\	2cos2x—l = (2cos2x+l)tgx.
3.	Решить уравнение
logsin 2Х (tg х + ctg х) = 1 - log’sln и 2.
4.	Через середину М стороны ВС параллелограмма ABCD, пло-
щадь которого равна 1, и вершину А проведена прямая, пересе-
кающая диагональ BD в точке О.~
80
Найти площадь четырехугольника OMCD.
5.	Найти все значения действительного параметра а, для кото-
рых неравенство	<
4х—а-2х—а+3<0
имеет хотя бы одно решение.
Вариант!
1., Из пункта А в пункт В вышел пешеход; одновременно с ним
в ту же сторону выехали велосипедист и автомобиль. Через час,,
когда автомобиль проехал 4 5/е расстояния до В, расстояние между
ним и велосипедистом было в четыре раза больше, чем расстоя-
ние между велосипедистом и пешеходом. В этот момент велосипед
сломался. Когда пешеход прошел еще 760 м, автомобилю
осталось проехать до В еще 4,8 км и в этот момент расстояние
между автомобилем и велосипедистом (оставшимся на месте по-
ломки) оказалось в пять раз больше, чем расстояние между вело-
сипедистом и пешеходом.
Чему равна скорость пешехода?
2. Решить уравнение
ОТ-ctg 2л = 1 +	(ctgx - 1>.
3. Решить уравнение
3—cos2x
дЗ+COS %Х
4. Центры вписанной и описанной окружностей треугольника
АВС лежат по разные стороны от прямой АВ. Длина-стороны АВ
радна радиусу описанной окружности. О—центр вписанной окруж-
ности.
Чему равен угол АО В?
5. Найти все значения действительного параметра с, для кото-
рых неравенство
l+log5(x2+'l) >ldg5(cx2+4x+c)
справедливо при всех х?
2-3tB‘* +
Вариант 3
1. Три бригады вспахали два поля общей площадью в 120 га.
Первое поле было вспахЬно за три дня, причем все три бригады
работали вместе. Второе поле было вспахано за шесть дней пер-
вой и второй бригадами.
6—619	81
Если бы все три бригады проработали на втором поле один
день, то оставшуюся часть второго поля первая бригада могла бы
©спахать за 8 дней.
Сколько гектаров в день вспахивает вторая бригада?
2.	Регйить уравнение
4-tg.J;.sin2l=tgx--ra|s-.
3.	Решить уравнение
logsin х (1 - COS 2*) =	2х 2.
I
4.	Четырехугольник ABCD обладает тем1 свойством, что около
него можно описать и в него можно вписать окружности. Диагона-
ли‘этого четырехугольника перпендикулярны, АВ —CD и радиус
вписанной окружности равен 1.
Чему равна площддь четырехугольника ABCD?
5.	Найти все значения действительного параметра а при кото-
рых неравенство
а-9х + 4(а—1) -Зх+а>1
справедливо при всех х.
Вариант 4
1.	В одном из отсеков судна возникла течь, и отсек оказался
целиком заполненным водой. Для откачки воды включили два на-
соса разной производительности. Течь была устранена через 18 ч,
после этого второй насос выключили и еще ^ерез 12 ч воды в от-
секе не осталось.
Если бы течь устранить не удалось, то два насоса осушили
бы отсек наполовину через 10 ч совместной работы.
За какое время второй насос осушил бы отсек наполовину, ес-
ли бы не удалось устранить течь?
2.	Решить уравнение
X	X
sin*-n- + cos*-K-	. , .
----- ,-----------tg2 х-sin х =-~Цп*+tg« X.
3.	Решить уравнение
1____ 3 + cos 2х
21/+ctB’x _рз.2 3	=8.
4.	В круге проведены два диаметра АВ и CD, М — некоторая
точка. Известно, что АМ=15, 2Ш=20, СМ = 24. Чему равно DM?
5.	Найти все значения действительного параметра с, для кото-
рых неравенство
82
1 + log. ((2x’ + 2x 4I—> log.fcx8 + c)
имеет хотя бы одно решение?
Разбор варианта 1
Задача 1. Обозначим объем всей работы4 через Q единиц, а про-
изводительность работы каждого каменщика — Vi, v2, v3 соответ-
ственно. Тогда условия задачи дают два уравнения:
f 6th 4~ 4о, 4- 7v, = Q,
| 4th -{	-J- бо. = -д- Q.
Получаются два уравнения с четырьмя неизвестными, из которых
сами неизвестные, разумеется, не могут быть, найдены однозначно.
Условие задачи требует найти не каждую неизвестную в от-
дельности, а лишь отношение
Q
V1 + О. + V, *
Это можно сделать, заметив, что из составленной выше систе-
мы уравнений легко находится сумма производительностей рабо-
ты каменщиков*. Вычитая из первого уравнения системы второе,
получим
2 (th4~ V» -|- о.)—-д- Q,
или
»1 + + о«
Ответ: $ ч.
Задача 2. Прежде всего отметим, что
Воспользуемся формулами
cos 2x=cos2x—sin2x;
1 = cos2x +sin2x.
* Подробнее об этом n других типах задач на составление уравнений.можно
прочитать в ~книге М. В. Лурье и Б. И. Александрова «Задачи на составление
уравнений». М.—Л., «Наука», 1976. 
6»	83
Тогда очевидны следующие преобразования:
2 cos 2х - 1 = (2 cos 2х 4-1)
cos’ х — 3 sin1 х = (3 cos1 х — sin* x) sin * ,
cos* x +’sin* x=3 sin x cos x (sin x cos x),
(cos x sin x) (1 — sin x cos x) = (cos x	sin x) • 3 sin x cos x,
v	(cosx-|-sinx)(l — 4sinxcosx) = 0,
(cos x+sin x) (1 — 2 sin 2x) = 0.
Далее находим'
1) cosx+sinx=0,
tgx=—1,
x------------------------------J—
2) 1— 2sin2x = 0,
sin2x=-i-,
x=(-1)^+^.
Ответ'.
х=-^, x=(-ty-k+^-.
Задача 3. Отметим прежде всего область допустимых значе-
ний неизвестного. Она определяется ограничениями
sin2x>0; sin 2x=/=l; sinx#=0; cosx=/=0;
tgx+ctg x>0.
Из первого неравенства следует, что sin х и cos х должны иметь
одинаковые знаки. Тогда остальные неравенства показывают, что
число х должно определять угол, который лежит строго внутри
первой или третьей четверти.
В области допустимых значений имеем
loo- <sinx I cosx>i = 1—100*	2
lu&sln2x ( COSX ' sinx J	lo&sln2xz«
10gsIn 2x sin X COS X	1	10®>*etn 2x
10Ssin2xH^Tel -^Sln 2X 2’
10g%in 2x 2 -I" 10£sIn 2x 2 - 2 = °-
84
«Отсюда находим:
1) 10geln2x2=,—2j
2) logein2x2=1.
Второе уравнение не имеет решений. Первое уравнение приво-
дит к равенству
1 — 2
sin’ 2х
или
sin1 2х«=-^-,
i/T
sin2bc=±z—g—.
Поскольку sin2x>0, то надо взять только положительное зна-
чение синуса.
sin2x=—»—•
&
Ответ-.
' *= (-О’-Не-
задача 4. Четырехугольник OMCD (рис. 19) получается отсе-
чением треугольника ОМВ от треугольника BCD. Площадь тре-
угольника BCD равна, очевидно, */г. Площадь треугольника ОМВ
может быть легко найдена.
Определим отношение
ВО к BD. Поскольку отрез-
ки AM и BE являются ме-
дианами треугольника АВС,
то
W=4’ BO=±BD.
Таким образом, ДОЛ1В
получается из ABCD умень-
шением его сторон соответственно в 2 и 3 раза. Значит, его пло-
щадь составит 11в часть площади треугольника BCD. Действи-
тельно,
пл diz	* Т BD-~s~ ВС
Зьомв -=	sin Z ОВМ =--------2-----Sin Z ОВМ =
1 с
85
Так как SABCD= 1/2, то
о _ 1 . с _ 1	1 _Г5
г>домв 12* °OMCD— 2	12	12’
Ответ: Ча-
Задача 5. Сделаем подстановку
4*=/>0.
Тогда у нас получится квадратное неравенство, содержащее
числовой параметр а:
t2—q/+3—а^О.
Для того чтобы исходное неравенство имело хотя бы одно ре-
шение, нужно, чтобы у полученного квадратичного трехчлена был
хотя бы один положительный корень. В противном случае, т. е.
в случае, когда у него нет действительных корней или оба корня
отрицательны, мы не найдем действительных решений х. В случае
отрицательных корней решения квадратного неравенства, лежащие
между корнями квадратного трехчлена, будут отрицательными.
Величина же t должна быть положительна. В случае отсутствия
действительных корней у квадратного трехчлена мы вообще не
найдем действительных значений L
Действительность корней квадратного трехчлена обеспечивает-
ся неотрицательностью его дискриминанта
£> = а2—4(3—а)>0,
а2+4а—12^0
или
а^2 и	—6.
Для того чтобы узнать, когда хотя бы один из корней будет
положителен, используем теорему Виета,
4 -|~/» = а,
44=3 —а.
При —6 имеем /14=3—а>0, произведение корней поло-
жительно, т. е. корни имеют одинаковые знаки, а поскольку сум-
ма корней /1+/г=а1<0, мы видим, что они оба отрицательны.
Этот случай нам не подходит.
При а>2 имеем: 4+4=«>0, т. е. сумма корней положитель-
на. Значит, хотя бы один из корней квадратичного трехчлена боль-
ше нуля. Итак, а^2.
Ответ: а >2.
86
$ 8. ФАКУЛЬТЕТ ПОЧВОВЕДЕНИЯ, 1974 г.
Вариант 1
1.	Бригада из трех тракторов (два трактора марки А и один
трактор марки Б) вспахивает доле 400 га за 10 суток при одно-
временной работе всех трех тракторов. Один трактор марки Б
вспахивает все это поле на 8-усуток быстрее, чем то же поле
вспахивает один трактор марки А.
Сколько гектаров в сутки вспахивает трактор марки А и трак-
тор марки Б каждый в отдельности?
2.	Решить уравнение
-у 1оК«х* + 1о&* 7ТГ= 2 log* (“Г + 3) •
3.	Найти все решения уравнения
/з-ь 3 cos х + sin 2х
1 + 2sinx
—/3-|- COS X.
4.	Найти все значения а, при которых неравенство *	О
выполняется для всех х таких, что 2<х<4.
5.	В прямоугольном треугольнике АВС угол С = 90°, а сторона
СА=4. На катете СВ взята-точка D так, что CD = l. Окружность
радиуса У"5/2 проходит через точки С и D и касается в точке С
«окружности, описанной около треугольника АВС. Найти площадь
треугольника АВС.
Вариант 2
1.	Из пункта А в пункт В движется с постоянной скоростью
автомобиль. Навстречу автомобилю из пункта В в пункт А дви-
жется с постоянной скоростью мотоцикл, который выехал из пунк-
та Б одновременно с отправлением автомобиля из пункта А. Ско-
рость автомобиля на 20 км/ч больше скорости мотоцикла. Через
1 ч 30 мин автомобиль и мотоцикл встречаются. Найти расстоя-
ние между пунктами А и В, если это расстояние автомобиль про-
езжает на 1 ч 15 мин быстрее мотоцикла.
2.	Решить уравнение
[ (log. х)‘ + 2 log^	(3 log, х — 1) = 2 (log, -у) log, x*.
3.	Найти все решения уравнения
2 (cos х + sin х) + 1 — cos 2х_.хт . • „
2(l+sinx)	—уЗ-l-sinx.
87
4.	Найти все значения а, при которых неравенство * х_'а— <
< 0 выполняется для всех х таких, что 1 < х < 2.
5.	На стороне АС остроугольного треугольника АВС взята точ-
ка D так, что А£)=»1, DC=2 и BD является высотой треугольника
АВС. Окружность радиуса, равного 2, проходящая через точки А
и D, касается в точке D окружности, описанной около треугольни-
ка BDC. Найти-площадь треугольника АВС.
Вариант 3
1.	Три трубы, работая одновременно, наполняют, бассейн водой
за 13 ч 20 мин. Если одновременно работают только первая и вто-
рая трубк, то они вместе наполняют тот же бассейн на 6 ч доль-
ше, чем его наполняет одна третья труба. За один час через вто-
рую трубу протекает воды столько же, сколько через первую тру-
бу. Через третью трубу за один час протекает воды на 3 м3
большем, чем через, первую трубу. Какова емкрсть бассейна?
2.	Решить уравнение
(log, х)г (1 -|- 2 log, х) = (log, 9х) logj_
T
3.	Найти все решения уравнения
1—sin х + Кз sin 2х	1 . .
2 Из cos х — 3	3 г
4.	Найти все значения а, при которых неравенство
(х—За) (х—а—3) <0
выполняется для всех х таких, что 1^х^3.
Вариант 4
1.	Два экскаватора разных марок (один экскаватор марки А
и один экскаватор марки Б), работая одновременно, выкапывают
котлован емкостью 20 000 м3 за 10 суток. Если бы работал только
экскаватор марки Б, то он выкопал бы этот котлован на 8-д-су-
ток скорее, чем тот же котлован выкопал один экскаватор мар-
ки А. Сколько кубических метров в сутки выкапывает каждый из
экскаваторов?
2.	Решить уравнение
log, х* 4- log,	3 log,, (x 4- 4) — 3 log, у42.
88
3.	Найти все решения уравнения
(Уз +2) sin х — sin 2х о I 9<-;пг
f^Tosx------------=<3 + 2 Sin X.
4.	Найти все значения а, при которых неравенство
(х+3—2а) (ж+За—2) < О
выполняется для всех х таких, что 2^х^3.
5.	Дан треугольник АВС, у которого стороны АВ= ]/Т7, ВС=
= 5, АС—4. На стороне АС взята точка D так, что BD является
высотой треугольника АВС. Найти радиус окружности, проходив-
шей через точки А и D и касающейся в точке D окружности, опи-
санной около треугольника BCD.
• Разбор варианта 1
Задача 1. Обозначим производительность одного трактора мар-
ки А через и, а одного трактора марки Б -— через о. Очевидно, что
и<40 и v<40. Система уравнений имеет вид:
( 2и + v = 40,
I 48о — 48и = ио.
Ее решение легко, находится: «=12 га!сутки, о =16 га!сутки.
Ответ: 12 и 16.
Задача 2. Легко заметить, что допустимыми значениями х
являются все числа, удовлетворяющие неравенству х>0. При этом
условии данное уравнение равносильно следующему:
log, х+log,	= log, +P
или -	', .
*(x-M) _x + 6
.x+1	2 •
Далее имеем
x2+x—6=0,
Xt=—3; x2=2.
Очевидно, что подходит только второе решение этого уравнения.
Ответ: х=2.
Задача 3. Исключив из рассмотрения те х, для которых
l+2sinx=0, т. е. sinx=—V2, можно записать
+3 + 3cosx + sin2x = —‘КЗ + cosx —2)/3 sinx + sin2x
или
1 Кз
-2-COSx+-2~sinx=------2~.
89
Последнее уравнение легко преобразуется к следующему виду:
(	я \ Кз“
COS ( X-Г = “"-о--
Отсюда находим
1. х — -^-=^-+2^,
О О 1
х=-^4-2кй.
О 1
2. х—
О	о 1
x=-^- + 2«fe.
Первое множество решений нельзя считать решениями задачи, по-
скольку sin(7n/6)=—Vz. Таким образом, только второе множест-
во х дает решения.
Ответ: х=—л/2+2лк, где k=0, ±1, ±2, ....
Задача 4. В этой задаче требуется подобрать а так, чтббы все
множество чисел от 2 до 4 принадлежало множеству решений
данного неравенства. Найдем сначала решения этого неравенства.
Рассмотрим два случая:
1. а>0. Тогда 2а>а/4>0. Поэтому решения неравенства мож-
нЗ записать так:
-4-	< х < 2а.
2.	а^О. Тогда 2а<а/4^0. Решения неравенства имеют вид:
2а<х<-%~.
Очевидно, что второй случай можно не рассматривать, поскольку
решения в этом случае вообще не содержат положительных х и,
значит, чисел 2^х^4.
Для того чтобы все числа 2^х^4 входили в множество ре-
шений неравенства а/4<х<2а, необходимо выполнение двух не-
равенств а/4<2 и 2а>4. Их совместное решение приводит к усло-
вию •
2<а<8.
Ответ: 2<а<8.
Задача 5. Поскольку окружность радиуса- У^/2 проходит че-
рез вершину С и касается в этой точке окружности, описанной
около прямоугольного треугольника АВС, то ее центр О' находит-
ся на радиусе ОС, рис. 20.
Пусть точка Е является точкой, в которой окружность радиуса
У^5/2 пересекает радиус описанной окружности. Соединим точку
D с точкой Е отрезком прямой. Очевидно, что получившийся тре-
угольник CDE бужт прямоугольным, поскольку вписанный угол
90
CDE опирается на диаметр окружности. Подсчитаем длину отрез-
ка DE:
DE2 = CE2—CD2,
DE=V5 -1=2.
Теперь становится ясным, что длина DE составляет половину дли-
ны катета СА Если бы мы опу-
стили перпендикуляр из точки О
на катет СВ, то его длина также
была бы равна 2, поскольку он
являлся бы средней линией тре-
угольника АВС, проведенной па-
раллельно катету СА. А так как
точки Е if О лежат на одной пря-
мой СО, то из равенства DE—2
следует, что точки Е и О совпа-
дают.
Из проведенного доказатель-
ства следует, что точка D являет-
ся серединой катета СВ и, зна-
чит, длина последнего равна 2.
Отсюда легко следует, что площадь прямоугольного треугольника
АВС равна 4.
Ответ: 4.
§ 9.	БИОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ, 1974 г.
Вариант 1
1.	Пароход плывет от пристани А к пристани В и после деся-
тиминутной стоянки в В возвращается в А, двигаясь в обоих на-
правлениях с одной и той же постоянной скоростью. На пути из
А в В в 8 часов пароход догоняет лодку, которая движется из А
в В с постоянной скоростью 3 км/ч. В 8 часов 10 минут лодка на-
ходится на расстоянии 1,5 км от А. Пароход, направляясь из В
в А после стоянки в В встречается в 8 часов 20 мин с лодкой
и затем прибывает в А в то же время, когда лодка приходит в В.
Определить время прибытия лодки в В.
2.	Решить уравнение
2	1 ^sin2* । 2cos2*_2sin 2jt
3.	В ромбе ABCD со стороной а угол при вершине А равен
2л/3. Точки Е и F лежат на сторонах ВС и АО соответственно, от-
резок EF и диагональ ромба АС пересекаются в точке М. Площади
четырехугольников BEFA и ECDF относятся как 1 :2. Найти длину
отрезка ЕМ, если AM :МС—1 :3.
91
4.	Решить неравенство
logi/4 *+1 <L
' 102i/4(x— 1)
5.	Найти все значения х, для которых величина
/2
у = — «(sinх — cos х)
удовлетворяет'уравнению
2log,(6ctg2у5tgy) = 2 + log ] (6ctgt/ — tgy).
Вариант 2
1.	Автобус отправляется из пункта А в пункт В и после ше-
стиминутной стоянки в В возвращается в А, двигаясь в обоих на-
правлениях с одной н той же постоянной скоростью. На пути из А
в В автобус догоняет в 8 часов 50 минут велосипедиста, который
движется из А в В с постоянной скоростью 15 км!ч. В 9 часов
02 минуты велосипедист находится на - расстоянии 21 км от А.
Автобус, возвращаясь из В в А после остановки в В, встречается
в 9 часов 14 минут с велосипедистом и затем прибывает в А в то
же время, когда велосипедист приезжает в В. Определить время
отправления автобуса из А.
2.	Решить уравнение
дсоз» х _|_ Зсоз 2х — 12- 9«in *-СО8 X'
3.	В ромбе ABCD со стороной а угол при вершине Л равен
л/3. Точки Е и F являются серединами сторон АВ и CD соответ-
ственно. Точка К. лежит на стороне ВС, отрезки АК и EF пересе-
каются в точке М. Найти длину отрезка МК, если известно, что
площадь четырехугольника MKCF составляет 3/в площади ромба
ABCD.
4.	Решить неравенство
loSo„5 Vx + 4
1о2о,5(* + 2) <l
5.	Найти все значения х, для которых величина
у = -g-sinx-cosx
удовлетворяет уравнению
log*(ctg2y+tgi/) = 1 +4-log (9ctgy-tgr/).
~2
92
Вариант 3
1.	Мотоциклист отправляется из пункта А в пункт В и после
десятиминутной стоянки в В возвращается в А, двигаясь в обоих
направлениях с одной и той же постоянной скоростью 48 км!ч.
В момент отправления мотоциклиста из А навстречу ему из В в А
выходит турист, идущий с постоянной скоростью. Турист встре-
чается с мотоциклистом в Г7 часов 15 минут. В 17 часов "25 минут
турист находится на расстоянии 23 км от А. Направляясь из В
в А после стоянки в В, мотоциклист догоняет туриста в 17 .ча-
сов 35 минут. Определить время прибытия туриста в пункт С, на-
ходящийся на полпути между А и В (АС=СВ).
2.	Решить уравнение
__б	— 3t+aln 2х.
3.	В правильном треугольнике АВС со стороной а точки D и Е
являются серединами сторон АВ и ВС соответственно. Точка F
лежит на отрезке DB, точка К лежит на стороне АС. Отрезки FK
и DE пересекаются в точке М. Найти длину отрезка FM, если из-
вестно, что DM-.ME=2 :3, а площадь четырехугольника МЕСЕ
составляет 2Д площади треугольника АВС.
4.	Решить неравенство
16go,i VX -f- 10 <
logo., (х — 2)	•
5.	Найти все значения х, для которых величина
К2л,	। ч
у = -у- (cos х 4- sm х)
удовлетворяет уравнению
log, (tg 2у + ctg у) = 1 + log t (9 ctg у — 5 tg у).
т
Вариант 4
1. Пристани А и В находятся на противоположных берегах
озера. Пароход плывет из А в В и после десятиминутной стоянки
в В возвращается в А, двигаясь в обоих направлениях с одной и
той же постоянной скоростью 18 км/ч. В момент выхода парохода
из А навстречу ему из В в А отправляется движущаяся с посто-
янной скоростью лодка, которая встречается с пароходом в 11 ча-
сов 10 минут. В 11 часов 25 минут лодка находится на расстоянии
3 км от А. Направляясь из В в А после стоянки, пароход догоняет
лодку в 11 часов 40 минут. Определить время прибытия лод-
ки в А.
93
2. Решить уравнение
eln»x
4»ln2x
3. В правильном треугольнике АВС со стороной а точки Е и
D являются серединами сторон ВС и АС соответственно. ‘Точка F
лежит на отрезке DC, отрезки BF и DE пересекаются в точке М.
Найти длину отрезка MF, если известно, что площадь четырех-
угольника ABMD составляет 5/в площади треугольника АВС.
4. Решить неравенство
log1/3 /*+"3
log1/3 (х + 1) < Ь
х 5. Найти все значения х, для которых величина
у = 4" (sin х +	cos х)
удовлетворяет уравнению
log* (tg 2у - 3 ctg у) = 1 + log (ctg у - tg у).
~2
Разбор варианта 1
Задача 1. На рис. 21 изображено расстояние АВ с отмеченными
точками: С — точка, в которой пароход догоняет лодку в 8 часов;
Д — точка, в которой находилась лодка в 8 часов 10 минут; Е —
точка, в которой пароход встретил лодку на обратном пути в А
в 8 часов 20 минут. Все расстояние АВ равно S км. Обозначим
скорость парохода буквой и. Имеем
АД = 1,5 км; СД = 3- -i- = 0,5 км;
CB — S — AC=S — (Ц-------^ = (S — 1) км.
Таким образом, в 8 часов лодка была на расстоянии (3—1) км
от пристани В.
За 10 минут пароход прошел расстояние
CB-\-BE = S — 14-S- 2 = 23 — 3
(ВЕ = 8 — 1 -3- 4-=5 — 21
Поэтому его скорость можно представить так:
и =	= 6(23 -3) км]ч.
94
Кроме того, BE=S—2; АЕ=2.
Так как пароход и лодка шли одно и то же время; то
S —2	2
3 — 6(25 — 3) ’
откуда находим, что S=5/2 км, S—2 = 5/2—2=0,5 км.
От точки Б лодка шла
*	1/2	1
-^-==-g- часа, т. е.. 10 минут.
Ответ: лодка пришла к пристани В в 8 часов 30 минут.
Задача 2. Преобразуем это уравнение следующим образом:
Возможны два случая: .
«
1. cosx = 0; x = -^-\-nk.
2. cosх = sinx, tgx=l; x = —|-ttk.
Ответ: x—nft+itk; x=tt/4+nk; k=0, ±11, ±2 ... .
Задача 3. Четырехугольники ABEF и ECDF представляют со-
бой трапеции с общей высотой, рис. 22. Поэтому отношение их
площадей можно записать следующим образом:
BE+AF_ 1	m
EC + FD 2 •	1 '
Обозначим ЕС через х. Тогда ВЕ=а—х, AF=x)3, DF=a—х/3. Под-
ставляя эти выражения в соотношение (1), определим х:
а — х + х/3  1	__ а
х + а — х/3~~ 2	Г"
95
По условию задачи AM :Л1С=1 :3, т. е.
АС — МС • 1
МС “ 3 ’
где АС=а. Тогда
За—3-МС=МС,
4-МС = За, МС = ^-.
4
Из треугольника МЕС по теореме косинусов находим длину от-
резка ЕМ:
ЕМ* = Л4С» + ЕС* — 2-МС-ЕС -cos-|-,
РД4»— 9д1 _|_ Д1_о- —а- —а- 1  7а*
~ 16'4	2 4 а 2 а 2 ~ 16
ЕМ = ^-
4
Ответ: аУ~7/4.
Задача 4. Область допустимых значений этого неравенства-
определяется условиями х>1 и х#=2.
Знак выражения, стоящего в знаменателе дроби, положителен,
если 0<х—1<1, и отрицателен, если х—1>1. Рассмотрим оба слу-
чая.	__
1. 1<х<"2. Тогда logj_(х — 1) > 0. Имеем:
log! /х+Klogi (•*—!)•
4	4
Так как основание логарифмов меньше единицы, то
1 >х — 1.
Поскольку обе части этого неравенства положительны, то оно
равносильно неравенству
х+1>(х-1)2
или
.	Xе—Зх<0,
решениями'которого будут числа О^х^З. Учитывая, что рассма-
триваются числа 1<х<2, заключаем, что множество 1<х<2 есть
решение исходного неравенства.
2. х > 2. Тогда log j (х — 1) <С 0. Имеем
Т
log1 Ух-Н 1 > logj_ (х — О
4	4
или
/х-Н 1 <х— 1.
96
Так как обе части этого неравенства положительны, то оно равно-
сильно неравенству
х+1<(х— I)2
или	»
х2—Зх^>0,
решениями которого будут числа х^З и х^О. Учитывая, что
в рассматриваемом случае х>2, получим х^З.
Ответ: 1). х>3 2). 1<х<2.
Задача 5. Сначала найдем все решения второго уравнения.
Для этого, отметив, что siny=/=0 и cost/#=0, запишем его в сле-
дующем, более простом виде:
или
1n£r 3 + 2tg*y _ ]n0. 9tgy
10g’ tgi/ —10£» 6—tg^y •
Это уравнение равносильно системе
(3 + 2 tg* у) __ 9 tg у q
tg У	, 6 —tg*y	\
или
((3 + 2 tg!-#)(6 — tg* у) = 9 tg1 у,
I tg У >0.
Отсюда находим
tgf/ = V’3,
или
у =	+ T.k, где k = 0, zt 1, dr 2... .
Найдем теперь все значения х, для которых равенство
(sin х — cosx) = -|—}-я6
выполняется хотя бы при одном целом k. Имеем
У 2 (sin х — cos х) = 1 4- 36,
2 sin (х -	= 1 4- 36,
ЯП
7—619
97
Поскольку, однако, |sin(x—л/4) |^1, то из всех целых k следует
оставить только два: £1=0 и kz=—1.. Рассмотрим оба случая.
1.	k — Q; sin(x — it/4) = 1/2.
а)	х--2кп, х = -^-Ц-2ад;
б)	х—х = ^-\-2кп.
В этих формулах п=0, ±1, ±2 ....
2.	k=—1; sin(x—л/4) =—1.
х — —т-== — 4- + 2*rt, х = --^-4-2ш.
4	2 - 1	4	1
4
Таким образом, все искомые значения' х найдены.
Ответ: х=5л/1-2+2лп; х= 13л/12+2лп; х=—л/4+2лп, п=0,
±1, ±2 ... .•
§ 10. ФАКУЛЬТЕТ ПОЧВОВЕДЕНИЯ, 1975 г.
Вариант 1
1.	Два экскаватора должны вырыть три одинаковых котлована.
Если они будут работать вместе, то выроют их за два дня. Пер-
вый экскаватор может вырыть один такой котлован на день бы-
стрее второго. В один из дней первый экскаватор работал полдня,
а второй работал весь день. Какая часть всей работы была вы-
полнена за* этот день?
2.	Найти все значения переменной величины х, при которых
выражение
3 + sin22x—2sin2x
достигает своего максимального значения.
3.	Решить уравнение
4 "“л-’/''	,0
х+27	=4.
4.	В параллелограмме лежат две окружности, касающиеся
друг друга и трех сторон параллелограмма каждая. Радиус одной
из окружностей равен 1. Известно также,’ что один из отрезков
стороны параллелограмма от вершины до точки касания равен |/3.
Найти площадь параллелограмма.
5.	Доказать без помощи таблиц, что
log» 7 4- (3 + cos -уЛ • log» 2 < 4.
98
Вариант 2
1.	Теплоход от А до В по течению реки идет 3 дня. Путешест-
венник из А и В спустился на плоту, а обратно добирался на
теплоходе. Плоты движутся со скоростью течения реки, причем
известно, что эта скорость строго меньше половины скорости теп-
лохода в стоячей воде. Вся дорога заняла у путешественника 18
дней. Сколько времени занял бы тот же путь, если бы" скорость
течения была в полтора раза больше?
2.	Найти все значения переменной величины х, при которых
выражение
2sin4x+cos2x+2
достигает своего минимального значения.
3.	Решить уравнение
91 1о£2/гVx~ 11 = 41о£«(4"~х) •
4.	В равнобочной трапеции лежат две окружности. Одна из них,
радиуса 1, вписана в трапецию, а вторая касается двух сторон тра-
пеции и первой окружности. Расстояние от вершины угла, образо-
ванного двумя сторонами трапеции, касающимися второй окруж-
ности, до точки касания окружностей вдвое больше диаметра вто-
рой окружности. Найти площадь трапеции.
5.	Доказать без помощи таблиц, что,
tg50° + 2ctg50° + ^<4.
Вариант 3
1.	Два насоса разной производительности, работая одновремен-
но могут наполнить резервуар за 2 дня. Вначале два таких одина-
ковых резервуара были заполнены наполовину. Первым насосом
перекачали содержимое одного из них в другой, после чего с по-
мощью второго насоса заполнили освободившийся резервуар. Вся
работа заняла 6 дней. Сколько времени потребует та же работа,
если насосы поменять местами, т. е. сначала использовать второй
насос, а потом первый?
2.	Найти .все значения переменной величины х, при которых
выражение
2sin2 2х—4cos2 х— 1
достигает своего максимального значения.
3.	Решить уравнение
41'°«4Г2-(х+1>,1	5 з
4	=~~-гА‘-
7*	99
4.	В параллелограмме лежат две окружности. Одна из них,
радиуса 3, вписана в параллелограмм, а вторая касается двух сто-
рон параллелограмма и первой окружности. Расстояние между точ-
ками касания, лежащими на одной стороне параллелограмма, рав-
но 3. Найти площадь параллелограмма.
5.	Доказать без помощи таблиц, что
• log. 31 +(14-|-sin91o)log,I2<8.
Вариант 4
।
1.	Если идти шагом вверх по поднимающемуся эскалатору, то
можно подняться на 10 с раньше, чем стоя на нем. Если же не
идти, а бежать вверх, то можно выиграть еще 5 с. Пассажир,
стоя на эскалаторе, поднялся на половину высоты эскалатора, после
чего последний остановился. Вторую половину подъема пассажир
прошел шагом. Сколько времени занял у него весь подъем, если
известно, что человек бегает в два раза быстрее, чем ходит?
2.	Найти все значения переменной величины х, при которых вы-
ражение
4 cos4 х—3 cos 2х+1
достигает своего минимального значения.
3.	Решить уравнение
10&Гз- (j.-Гх) = 511°^V^х~21-
4.	В прямоугольной трапеции лежат две окружности. Одна из
них, радиуса 4, вписана в трапецию, а другая, радиуса 1, касается
двух сторон трапеции и первой окружности. Найти площадь трапе-
ции.
5.	Доказать без помощи таблиц, что
4 sin163° 4- (15 - cos 89°) cosec4°-63*- < 8.
Разбор варианта 1
Задача 1. Обозначим производительности экскаваторов и и v
соответственно, а всю работу примем за единицу. Система уравне-
ний задачи очевидна:
2(и-Н)=1,
 ’__и
Зо За
Исключая и из второго уравнения с помощью первого, находим:
6v2—7а +1=0,
100
откуда t4=?l, ©2=1/6. Следует учесть, что по условию задачи ы<1
и ©<1. Поэтбму остается значение v, равное 1/6. Тогда ы = 1/3.
Требуется определить часть работы, выполненную экскавато-
рами за тот день, когда первый работал полдня, а второй — пол-
ный день, т. е. найти величину (0,5«+'о). Она равна:
0’5-“+°=-Н"-г=-т-
Ответ: 1/3.
Задача 2. Заметим, что формулы
sin2 2х = 1 — cos* 2х и sin* х =--------—
позволяют записать рассматриваемое выражение только через
cos 2х.
Л =34- (1—cos22x)— (1—cos2x) =—cos2 2x4-'cos 2х+3.
Здесь А — рассматриваемое выражение. После очевидных преоб-
разований («выделение полного квадрата») имеем
А = — jcos* 2х — 2 • cos 2х 4"3<^-=
13	/ о 1
=-^—(cos2x------2") .
Таким образом, рассматриваемое выражение равно числу 13/4 ми-
нус некоторое неотрицательное выражение. Если cos 2х#=0,5, то
Л< 13/4 и только при cos2x=0,5 значение А равно 13/4. Итак, А
достигает максимального значения при cos2x=0,5:
2x = =t-^-4-2^,
6 1
Ответ: х = ±-^-4-чсй, где k = 0,zh l,zt2... .
Задача 3. Заметим, что х>0. Имеем:
274|'«эгг^ |=з=1‘|41«а.,'|
3 414 ,ов3"//|=34-44 |,og’x|,
g|log»x|
х, если log,x>0, т. е. х> 1;
-i-, если,logtх < 0, т. е. 0<х<1.
101
Рассмотрим первый случай: х^\.
Х+Л з • х— з •
Поскольку 5/3> 1, заключаем, что х=5/3 есть решение.
Во втором случае 0<х<1. Имеем
x-4--L=-^
Зх‘ — 10x4-3 = 0,
Хх = 3, х2=4-.
Г	о
•
Неравенству 0<х<1 удовлетворяет только второе решение. Таким
образом, задача имеет два решения: х = 5/3 и х=1/3.
Ответ: х=5/3, х=1/3.
Задача 4. Нетрудно заметить, что обе окружности должны ка-
саться одних и тех же параллельных’ сторон параллелограмма
ABCD, рис. 23, например, сторон AD и ВС. Поэтому радиусы этих
окружностей должны быть равны между собой. Очевидно, что
равняется больший из отрезков стороны параллелограмма от вер-
шины до точки касания, на чертеже АЕ. Поэтому для данного
чертежа угол параллелограмма А будет острым.
Рис. 23.
Из прямоугольного треугольника AEOi (О±— центр первой
окружности) вычисляется AOi:
АО, = |ГЛЕ‘4-Е0‘, = /(/3)«4-1‘ = 2.
Таким образом, угол ЕА01=30°, а угол А равен 60° (ЛО1— бис-
сектриса угла Л).
Рассмотрим прямоугольный треугольник FEOi, в котором угол
EFO, равен 60°, а катет EOi равен 1. Из него легко определяется
’102
отрезок FOi:
Fo	_ 1 _2/з
sin 60*	/3/2	3 •
Зная длину отрезка FOt, можно определить весь отрезок FK:
FK = FOt + О.О. + KOt = 2(F0. Ц- OJW) = 2 (Цр- 4- 1) .
Очевидно, что Г01=К0г (Ог — центр второй окружности).
Площадь параллелограмма находится по формуле
S ab‘cd=AD • BN,
в которой ВЫ— высота параллелограмма. Так как AD — FK, а
ВЫ= 2, то
O/neem;4(2|/3 + 3)/3.
Задача 5. Обозначим log2? буквой t и заметим, что
2</<3.
Данное в задаче неравенство можно записать следующим обра-
зом:
*+ (з + cos 4у4- <4.
Учитывая, что t положительно, получаем:
/* —4£-|- (3 + cos	< 0. ч
Таким образом, необходимо показать, что значение /= k)ga7 удов-
летворяет этому квадратному неравенству.
Поскольку дискриминант квадратного трехчлена в левой части
последнего неравенства неотрицателен
то решения неравенства заключены в области
2 —	1 -cos^</<2 + |/ri-cos^.	(*)
Покажем, что t= iog2? лежит в этой области.
Очевидно, что
2 —	l-cos-^-<2.
103
Докажем,, что
2+уЛ -cqs-£>3.
Заметим, что число 15/7 заключено в интервале
к ~ 15
Т
а косинус для этих значений отрицателен. Поэтому
cos -у- < О
И ' ______________________ _
2 + 1/1 —cos-у->3.
Поскольку значение /=log2 7 удовлетворяет неравенству 2</<3,
то оно лежит в области (*), и утверждение доказано.
ж.
§ 11.	БИОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ, 1975 г.
Вариант 1
1.	Два насоса, работая одновременно, наполнили водой бас-
сейн емкостью 80 Л£3. Если увеличить производительность первого
насоса в 4/3 раза, то он один сможет наполнить бассейн, работая
на два часа дольше, чем работали оба насоса вместе. Если умень-
шить производительность второго насоса на 1 л/3/ч, то он один
сможет наполнить бассейн, если будет работать в 10/3 раза доль-
ше, чем работали оба насоса вместе. Сколько кубометров воды
в час перекачивает второй насос?
2.	Найти все значения действительного параметра р, при ко-
торых квадратное уравнение
7+3
(3x)‘+(3F — 15)х + 4)=0
имеет ровно одно решение. '
3.	Отрезок АВ есть диаметр круга, а точка С лежит вне этого
круга. Отрезки АС и ВС пересекаются с окружностью в точках D
и М соответственно. Найти угол CBD, если площади треугольни-
ков DCM и АСВ относятся как 1 : 4.
4.	Решить уравнение
sinx—2sin2x+sin Зх= 11—2 cosx+cos2x|.
Найти все целые п, удовлетворяющие неравенству
1	/ПГ+5—1
^2cos^--л+8)\.	— П )
104
Вариант 2
1.	Из пункта А в пункт В, расстояние между которыми 100 км,
выехал мотоциклист, и одновременно с ним из В в А выехал ве-
лосипедист. Через некоторое время они встретились в пункте- С и,
продолжив свой путь, прибыли в пункты назначения. На следую-
щий день мотоциклист вернулся в А, а велосипедист — в В. При
этом мотоциклист двигался в 3/2 раза быстрее, чем накануне, и
поэтому на весь путь из В в А затратил на 10 мин меньше, чем на
путь от А до С.в первый день. Скорость велосипедиста во второй
день была на 10 км/ч выше, чем в первый день, и на весь путь из
А в В он затратил в 5/2 раза больше времени, чем на путь от В
до С в первый день. С какой скоростью двигался мотоциклист в
первый день на пути из Ав В?
2.	Найти все действительные значения параметра р, при кото-
рых квадратное уравнение
—+2
(4х)’ + (4Р	-40)х 4-9 = 0
имеет ровно одно решение.
3.	В круге проведены две хорды АВ и CD, пересекающиеся в
точке М. К — точка пересечения биссектрисы угла BMD с хордой
BD. Найти отрезки ВК и KD, если BD = 3, а площади треугольни-
ков СМВ и AMD относятся как 1 : 4.
4.	Решить уравнение
| cosx+2sin2x—cos3x| = 1+2sinх—cos2x.
5.	Найти все целые числа и, удовлетворяющие неравенству
* \
Вариант 3
1.	Две автоколонны, состоящие из одинакового числа машин,
перевозят груз. В каждой из автоколонн машины имеют одинако-
вую грузоподъемность и во время рейса загружаются полностью.
Грузоподъемность автомашин в разных колоннах различна, и за
один рейс первая автоколонна, перевозит на 40 т груза больше,
чем вторая автоколонна. Если уменьшить число машин в первой
автоколонне на 2, а во второй автоколонне — на 10, то первая
автоколонна перевезет 90 т груза за один рейс, а вторая автоко-
лонна перевезет 9Q т груза за 3 рейса. Какова грузоподъемность
одной машины второй автоколонны?
105
2.	Найти все значения действительного параметра р, при кото-
рых квадратное уравнение
— +7
(8х)‘ + (2р	-80)х 4-9 = 0
имеет ровно одно решение.
3.	В треугольнике АВС проведены биссектриса BD угла АВС
и отрезок AM. Точки D и М лежат соответственно на АС и ВС,
К — точка пересечения BD и AM. Площади треугольников AKD и
АМС относятся как 1:6. Найти Сторону АВ, если АВ+ВС=3 и
АВ+ВМ = 2.
4.	Решить уравнение
'cosx—2 sin2x—cos3x=|l—2 sinx—cos2x|.
5.	Найти все целые числа п, удовлетворяющие неравенству
1ое ' х,>0
. IOg(2ctB^_„+7^ V^-~n J U-
Вариант 4
1.	Двое рабочих в первый день работали одно и то же время,
обрабатывая одинаковые детали. При этом первый рабочий обра-
ботал на 30 деталей больше, чем второй. На следующий день пер-
вой рабочий увеличил производительность труда в 1,2 раза и за-
кончил работу на один час раньше, чем в первый день. Второй ра-
бочий во второй день обрабатывал на 5 деталей в час меньше и
проработал в 7/6 раза дольше, чем в первый день. Известно^ что
во второй день каждый из рабочих обработав по 420 деталей.
Сколько деталей в час обрабатывал z второй рабочий в первый
день?
2.	Найти все значения действительного параметра р, при кото-
рых квадратное уравнение
— 4-4
(4х)*4-(2-'Р	-24)х4-1=0
имеет ровно одно решение.
3.	В окружность вписан выпуклый .четырехугольник ABCD,
причем АВ является диаметром окружности. Диагонали АС и BD
пересекаются в точке М. Извёстно, что ВС —3, СМ = 3/4, а пло-
щадь треугольника АВС Ътрое больше площади треугольника
ACD. Найти длину отрезка AM.
4.	Решить уравнение
|sinx+2sin 2х+ sin Зх| = l+2cosx+ cos 2х.
106
5.	Найти все целые числа п, удовлетворяющие неравенству
log .
2tg ------л+ 13
Kte-n \<0
Кп + п + 1/
Разбор варианта'1
Задача 1. Обозначим производительности первого и второго на-
сосов через Vi и v2 соответственно. Тогда условие задачи позво-^
ляет составить следующую систему уравнений:
80 _	80	, о
4 th +	“I А
80	JO'	80
Va — 1	3 v i -f-th
Второе уравнение этой системы позволяет установить линейную
связь между величинами Vi и v2:
7v2—3vi = 10.
Исключая из первого уравнения, получаем уравнение для опре-
деления v2:
90	— 12 J-1
7 th —10 “th —1 "Г 1
или
7u»t — 23t>, — 20 = 0.
Положительный корень этого уравнения равен 4.
Ответ: второй насос перекачивает 4 м3/ч.
Задача 2. Квадратное уравнение имеет единственное решение
только в том случае, если его дискриминант равен нулю. Поэтому
параметр р должен удовлетворять уравнению:
— +з
D = &	—15)*—144 = 0
ИЛИ
— +3
(3 - - 15)* =144,
Т+3
|3₽	— 15|=12.
Возможны два варианта:
—+3	—+3
1) 3Р -15=12; 2) 3Р -15=-12.
1«7
f on-a Первый из этих случаев невоз-
можен, так как
.zOtk	—+з
3* = 27,
м	—-—1-3 = 3, но —#г0.
/ ✓ хтз*7 р	р
/ у<	Х\ Во ВТОРОМ случае имеем
— +3
---------------- 5	3 4'	=3,
Рис. 24.	~р + 3 — I’ Р = — 72 ‘
Ответ: р ——1/2.
Задача 3. Соединим между собой точки В и D, рис. 24, а также
точки А и М. Получившиеся треугольники ABD и АВМ — прямо-
угольные, поскольку соответствующие углы ADB и АМВ опирают-
ся на диаметр окружности. Обозначим угол CBD через а; тогда
угол АСВ' равен (90°—а), так как треугольник CBD — прямо-
угольный.
Составим отношение площадей треугольников DCM и АСВ,
равное по условию 1/4.
о	-4- DC-MC-sin (90* — а)
^DCM	2
5— = П-------------------
АСС	-у АС  ВС - sin (90* — а)
DC-MC _ 1
АС-ВС 4 "
Заметим, что
= cos (90° — а) = sin а; ^|г = cos (90° — а) = sin а.
Тогда
. , 1 . 1
Sinsa = -7- ИЛИ Sina = -5".
4	2
Поскольку а — острый угол, то а=30°.
Ответ: а=30р.
Задача 4. Используем формулы:
a) cos2x=2cos2x—1;
б) sinx+sin3x=2sin2xcosx.
Тогда запись уравнения можно упростить
2sin2xcosx — 2sin2x = |2 cos2x — 2cosx|,
sin2x(cosx — 1) = jcosx(cosx — 1)|, .
2 sin x cos x (cos x— 1) = |cosx(cosx— 1)|.
108
Данное уравнение распадается на две системы
I (cosх(cosx—1)> О,
|2 sin х cos х (cos х — 1) = cosx (cos x— 1).
Уравнение в этой системе имеет следующие решения:.
a)	cosx = 0; х = -^-Ц-топ;
б)	cosx=l; х = 2я/п;
B)sinx=-^-; x = -^--\-2tm, x = ^--]~2vm.
Из найденных решений неравенству удовлетворяют следующие:
x = -^--[-im, x = 2icm, x = -^--j-2im (m = 0,=t 1,±2...).
ц (cosx (cosx — J) < 0,
(2 sinx cos x (cos X — 1) = — cos x (cos X — 1).
Уравнение с учетом неравенства имеет следующие решения:
х =-----------------(т =0,zt 1,zt2...).
Ответ: 1. x = 2wn; 2. х = -^--\-чт\
3. x = -y--]-2itm; 4. х = —у—|~2wn, где т = 0, z±: h rt 2,... .
Задача 5. Анализ выражения, стоящего под знаком логарифма,
показывает, что значения п нужно искать лишь в интервале
—Зг^л<;9.
Тогда возможны два случая.
1. Основание логарифма больше единицы:
2 cos-у — zt-i-8> 1
ИЛИ
п < 7 + 2 cos	.
Очевидно, что 2 cos -у- < 2. Покажем, что 2 cos > 1.
Для этой цели сравним числом 2л/7 с числом л/3, косинус которого
известен и равен 1/2:
2п к
Известно, что в области от 0 до л/2 косинус является монотонно
убывающей функцией. Поэтому косинус большего угла меньше,
'	_	109
чем косинус меньшего угла.
2п	п	1
COS -7->C0S-o-=-7r,
/	О	z
о	... -
2 cos-у-> I.
Таким образом, в первом случае рассматриваются все целые числа
п, удовлетворяющие неравенствам
—3<п^8.
Имеем
Г^+5-i	.
K10 —п	’
/« + 5 - 1 -
Поскольку при рассматриваемых п разность Уп 4- 5 — 1 положи-
тельна, то можно возвести обе части неравенства в квадрат
п + 5 - 2/п+5 + 1 > 10 - п,'
п — 2>/« + 5 .
Отсюда видно, что п—2^0, п^2. Далее:
п2—5п—1^0.
Этому неравенству (с учетом 2^п^8) удовлетворяют три целых
значения и:
п=6, 7, 8.
2.0<2cos-l^-—/г + 8 <+ Здесь нужно рассмотреть единствен-
ное значение п:п = 9. Непосредственной подстановкой этого числа
в неравенство убеждаемся, что
(/Г4-1Х0
и, значит, оно не является решением.
Ответ: п=6, 7, 8.
§ 12. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ОБЩЕЙ ГЕОЛОГИИ, 1972 г.
Вариант 1
_ 1. Решить уравнение
2cos2x+3sinx=0.
2.	Решить систему уравнений
(log,x + log.£‘==0,
 log.x1 — log^i/ = 5.
T
lit
3.	Из пунктов А и В, Неположенных на расстоянии 100 км,
навстречу друг другу одновременно выехали 2 велосипедиста. Че-
рез четыре часа они встретились. После встречи скорость первого
велосипедиста, едущего из А в В, возросла на 5 км/ч, а скорость
второго велосипедиста, едущего из В-в А, возросла на 10 км/ч.
Известно, что первый велосипедист прибыл в пункт В на один
час раньше, чем второй прибыл в пункт А. Определить йервона-
чальную скорость первого велосипедиста.	\
4.	Найти все значения х, при которых справедливо неравенство
5.	Дан треугольник АВС, в котором угол В равен 30°, АВ =
=4 см, ВС=6 см. Биссектриса угла В пересекает сторону АС в
точке D. Определить площадь треугольника ABD.
Вариант 2
1. Решить уравнение
2 sin2 х+5 cos х-Н =0.
2. Решить систему уравнений
logtx Д-log, t/ = 4,
log4(x + y)=-f-.
3«.Два экскаватора, работая совместно, вырывают котлован за
12 ч. Производительность первого экскаватора равна 8 м3[ч. Если
производительность второго экскаватора увеличить на 4 м3/ч, то
второй экскаватор будет вырывать котлован на 15 ч быстрее, чем
первый. Определить производительность второго экскаватора.
4. Найти все значения х, при которых справедливо неравенство
5. В прямоугольном треугольнике АВС с прямым углом В бис-
сектриса угла А пересекает сторону ВС в точке D. Известно, что
BD=4 см, DC=6 см. Определить площадь треугольника ADC.
Вариант 3
1.	Решить уравнение
2 cos2x—5 sin х—4=0.
2.	Решить систему уравнений
’2 log4 х log^ у = — 1,
5
log4x« — log±«/ = 5.
т
111
3.	Из пунктов А и В, расположенных на расстоянии 50 км, на-
встречу друг другу одновременно вышли 2 пешехода. Через 5 ч
они встретились. После встречи • скорость первого пешехода, иду-
щего из А в В, уменьшилась на 1 км/ч, а скорость второго пеше-
хода, идущего из В в А, возросла на 1 км)ч. Известно, что первый
пешеход прибыл в пункт В на 2 ч раньше, чем второй прибыл в
пункт А. Определить первоначальную скорость первого пешехода.
4.	Найти все значения х, при которых справедливо неравенство
, 5. Дан треугольник АВС, в котором АВ=6 см, ВС=7 см, АС=
= 5 см. Биссектриса угла С пересекает сторону АВ в точке D.
Определить площадь треугольника ADC.
Вариант 4
1.	Решить уравнение
2 sin2x—7 cosx—5=0.
2.	Решить систему уравнений
log4x+log*i/;=3,
' log«(x + t/j = 4-..
3.	Два насоса, работая совместно, наполняют бассейн за 8 ч.
Известно, что производительность второго насоса равна 10 м3/ч.
Если производительность первого насоса увеличить на 5 м3/ч, то
бассейн будет наполняться с помощью первого насоса на 10 ч бы-
стрее, чем с помощью второго насоса. Определить производитель-
ность первого насоса.
4.	Найти все значения х, при которых справедливо неравенство
5.	В прямоугольном треугольнике АВС с прямым углом А бис-
сектриса угла В пересекает сторону АС в точке D. Известно, что
АВ = 6 см, ВС=Ю см. Определить площадь треугольника DBC.
Разбор варианта 1
Задача 1. Воспользуемся формулой cos2x=l—sin2jc и перепи-
шем исходное уравнение в виде
2 sin2 х—3 sin х—2=0.
112
Решая это квадратное уравнение, получим
sinx = 2, sinx =----2".	,
Учитывая, что |sinx|s^l, находим решение
1
sinx =----2",
х = —(,-	+
Ответ: х = — (— l)n -g- +
Задача 2. В этой задаче допустимы х и у, удовлетворяющие
ограничениям х>0 и t/>0. Учитывая, что
log3y2=21og3y, log)/3i/=— logs у,
перепишем эту систему в виде
f log» х2 log, у = О,
12 log, х + log, у = 5
и будем рассматривать ее как линейную систему двух уравнений
с двумя неизвестными logsX и log3y. Тогда можно определить
1	Ю ' .	5
log,x = —, log,y = — -g-.
Отсюда находим
х = 81/2; у = 1 / З^/^Э".
Ответ: х = 8уЛ2; у= 1/31Л9.
Задача 3. Пусть скорости первого и второго велосипедистов —
viKm/ч и агкм!ч соответственно. Тогда условие задачи приводит
к системе уравнений
14(о, 4-и.) = 100,
/ 4th________4уг_____.
'	I и» “f“ Ю Vi 5
Исключая t>2 из второго уравнения при помощи первого, полу-
чим квадратное уравнение
o2i+230oi—3675=0,
откуда находим
o'i=—145, o"i=15.
Ответ: 01 = 15 км/ч.
8—619	ИЗ
Задача 4. При всех х, отличных от 1, это неравенство равно-
сильно следующему:
..? + *-+2 >о.
1 —X
Выражение (х+2) перенесено в левую часть неравенства и
приведено к общему знаменателю со стоящей там дробью. Квад-
ратный трехчлен, стоящий в ди-
А	слителе последнего отношения,
положителен при всех х, посколь-
\ ку его дискриминант отрицателен
и nePBbI« коэффициент положите-
.Zo	\ лен. Следовательно, неравенство
\ будет выполнено, если
5	. 1—х>0, т. е. х<1.
Ответ: х<1.
рис 26.	Задача 5. Для нахождения
биссектрисы BD воспользуемся
формулой
а
2ab cos -у-
а + b •’
в которой I — биссектриса, а и b — стороны треугольника, ее за-
ключающие, а — угол между этими сторонами.
- В нашей задаче (рис. 25):
Dn 2.4«6 cos 15*	24 cos 15° ,
BD== io~-=—— •
Площадь треугольника ABD определяется по формуле
S = -^-o/sina/2
или
о 1 л 24 cos 15е	. . со 24 sin 30° о .
SABD = --4------5— • s,n 15 =---5---= 2’4-
Ответ: 2,4 см2.
§ 13.	ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ГЕОФИЗИКИ, 1972 г.
Вариант 1
1.	Поезд метро состоит из нескольких вагонов, причем в каж-
дом вагоне находится одинаковое число пассажиров. Количество
пассажиров в одном вагоне превосходит число вагонов на 9. Когда
на станции во второй 'вагон вошли 10 человек, а из остальных
114’
вышли по 10 человек, то число пассажиров во втором вагоне ока-
залось равным числу пассажиров, оставшихся во всех остальных
вагонах. Сколько пассажиров было первоначально в каждом ва-
гоне?
2.	Решить уравнение
3 tg* х —J- 7 =
2
sin2x ’
3.	Найти все значения х, при которых справедливо неравенство
1 1
-* + 1'
4.	Трапеция KLMN с основаниями KN и LM вписана в окруж-
ность, центр которой лежит на основании KN. Диагональ КМ тра-
пеции равна 4 см, а боковая сторона KL равна 3 см. Определить
длину основания LM.
5.	Три шара попарно касаются друг друга и некоторой плоско-
сти: Точки касания шаров с плоскостью образуют прямоугольный
треугольник с катетом, равным З.см, и* противолежащим углом в
30°.
Определить радиусы данных шаров.
Вариант 2
каждом
Извест-
1. Колхозный сад разбит на несколько участков. На
участке урожай собирает одинаковое число колхозников,
но, что число колхозников, находящихся на одном участке, пре-
вышает число участков на 14. Когда еще 15 колхозников пришли'
на первый участок, а с остальных участков ушли по 15 человек,
то число колхозников на первом участке стало равным числу кол-
хозников, оставшихся на всех остальных участках. Сколько кол-
хозников было первоначально на каждом участке?
2. Решить уравнение
2 sin* х -4-;— = 3.
1 cos* х
3.	Найти все значения х, при которых справедливо неравенство
1^1
^х-2' ,
4.	Около трапеции ABCD с основаниями AD и ВС описана
окружность радиуса 6 см. Центр описанной окружности лежит на
основании AD. Основание ВС равно 4 см. Определить площадь
трапеции.
5.	В треугольнике АВС АС=12 см, АВ—ВС=3 У~Ц) см. Два
шара касаются плоскости треугольника АВС в точках А и С рас-
8*	115
положены по разные стороны от этой плоскости. Расстояние меж-
ду центрами этих шаров равно 15 см. Центр третьего шара нахо-
дится в точке В, и этот шар касается двух данных шаров. Опре-
делить радиус третьего шара.
Вариант 3
В книжном шкафу имеется несколько полок. На каждой полке
лежит одинаковое число книг. Известно, что число книг на полке
превосходит число полок на 5. Когда на первую полку добавили
6 книг, а с каждой из остальных полок сняли по 6 книг, то число
книг на первой полке оказалось равным числу книг на всех
остальных полках вместе. Сколько книг первоначально лежало на
одной полке?
2.	Решить уравнение
3 tg2 х — 4 cos2 х = 8.
3.	Найти все значения х, при которых справедливо неравенство
4.	Около трапеции ABCD с основаниями AD и ВС описана
окружность радиуса 5 ~см. Центр описанной окружности лежит на
основании AD. Основание ВС равно 6 см. Определить диагональ
АС данной трапеции.
5.	Два шара касаются плоскости Р в точках Л и В и располо-
жены по разные стороны от этой плоскости. Расстояние между
‘центрами этих шаров равно 10 см. Третий шар касается двух дан-
ных шаров, . а его центр О лежит в плоскости Р. Известно, что
АО = ОВ=2 10 см, ЛВ = 8 см.
Определить радиус третьего шара.
Вариант '4
1.	На столе стоят коробки с карандашами. В каждой коробке
находится одинаковое число карандашей. Число карандашей, лежа-
щих в одной коробке, превышает число коробок на 8. После того
как во вторую коробку положили 9 карандашей, а из остальных
коробок взяли по 9 карандашей, число карандашей во второй
коробке оказалось на 2 меньше, чем число карандашей, лежащих
во всех остальных коробках. Сколько карандашей лежало перво-
начально в каждой коробке?
2.	Решить уравнение
4sin2x+9tg2x=4.
116
3.	Найти все значения х, при которых справедливо неравенство
К1 + х ^2 — *'
4.	Трапеция KLMN с основаниями LM в KN вписана в окруж-
ность, центр которой лежит на основании КМ. Диагональ LN тра-
пеции равна 4 см, а угол mNK равен 60°. Определить длину осно-
вания LM трапеции.
5.	В треугольнике АВС сторона АВ равна 2 см, сторона ВС
р^вна 4 см, а угол В равен 60°. Три шара касаются плоскости
треугольника АВС в точках А, В и С и попарно касаются между
собой. Определить радиусы этих шаров.
Разбор варианта 1
Задача 1. Пусть п — первоначальной количество пассажиров в
каждом вагоне. Тогда (п—9)—число вагонов (причем п>9, п —
натуральное число). Согласно условию задачи имеем уравнение
п+'10=(п—10) (и—10),
или -
л2—21 и+90=0.
Корни этого квадратного уравнения суть' 15 и 6. Второй корень
является здесь пос,торонним, поскольку л>9.
Ответ: 15 пассажиров.
Задача 2. Используя формулу
-т-1.	= 1 -4-ctg2x
sin2 х 1	°
и вводя подстановку у= tg2x>0, запишем исходное уравнение в
виде
Зу + 7 = 2 4-
ИЛИ
' Зу2.+5у—2=0.
Это квадратное уравнение имеет единственный положительный
корень у=1/3. Возвращаясь к неизвестному х, получаем
tg’x=4-« itgxi= pb.
Общее решение последнего уравнения имеет вид
к I
о 1
117
Легко видеть, что все найденные решения допустимы для ис-
ходного уравнения.
Ответ: х =
о ’
Задача 3. Данное неравенство равносильно совокупности сле-
дующих двух систем:
1)
х+ 1 <0;
2 — х>0;
2)
х+1>0,
Решая первую систему, находим х<—1. Решим вторую си-
стему.
Поскольку обе части второго неравенства системы положитель-
ны, то, возводя неравенство почленно во вторую степень, получим
равносильное неравенство
(х+1)2>2—х>0,
или
х2+3х—1>0 при х<2.
Решая это квадратное неравенство и объединяя его решения
с решением первого неравенства системы, получаем
-3 + /13
2
~	1 —3+К13
Ответ: х < — 1;--—=-
<х<2.
11S
Задача 4. Несложнр показать,
что в окружность может быть
вписана только равнобочная тра-
пеция (рис. 26). Поэтому
Так как угол KMN опирается
на диаметр, то этот угол — пря-
мой. Следовательно, из прямо-
угольного треугольника KMN
можно найти КМ:
КМ=5.
Проведем MPJ-KM и для оп-
ределения высоты МР восполь-
зуемся двумя формами записи
площади треугольника:
-±- КМ • MN = Ц- МР • KN,
т. е.
Л1Р = ^ = 2,4.
ъ	О
Из прямоугольного треугольника MPN получим
РУ = т/9 —1,8.
f	Zo
Тогда
LM=b—2Ptf=l,4
Ответ: 1,4.
Задача 5. Чертеж к задаче представлен на рис. 27. Обоз-
начим радиусы шаров через и, г2 и г3. Расстояние между точками
касания двух шаров на плоскости равно величине соответствую-
щей стороны прямоугольного треугольника. Центры шаров проек-
тируются на плоскость в вершины треугольника ЛВС, а каждая
из сторон этого прямоугольного треугольника является проекцией
на плоскость отрезков, равных сумме пар соответствующих радиу-
сов. На основе этого имеем
АВ — с = KOt = K(ri + г,)2 — (п — г2)2 = 2
Аналогично этому можно получить выражения для двух дру-
гих сторон треугольника:	\
ВС = а = 2 Vrtrt9 AC — b = 2\fглгг.
Отсюда находим
ГхГ2 = ^с\ rtrt= -±-а*, г,Г1 = -±-Ь*.	(1)
119
Из треугольника АВС найдем
а = 3/3, 6 = 3, с = 6.
Перемножая почленно соотношения (1), получим
(г1г2г3)г = -^(аЬс)г или rtrtrt = -^-abc.
Из этого соотношения определяются радиусы всех шаров.
Исключая произведение радиусов каких-либо двух шаров с по-
мощью (1), получаем
__ Ьс ____ ас ____ ab
Подставляя .сюда значения а, b и с, находим:
Г1==/3, г2 = 3/3, г, = А/з.
Ответ: УЗ; 3/3; 0,75 УЗ.
§ 14. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ОБЩЕЙ ГЕОЛОГИИ, 1973 г.
Вариант 1
1. Решить систему
(Ig3-lg(3x) = lg2 1g(2z/),
(lgx-lg2 = lg«/-lg3.
2. Решить уравнение
1	—X
—х+ -Г
4	2-7-2 —4 = 0.
3. Два велосипедиста выехали из пункта А одновременно и
в одном направлении. Первый велосипедист ехал со скоростью
7 км!ч, а второй — со скоростью 10 км/ч. Через 30 мин из пункта
А в jom же направлении выехал третий велосипедист, который
догнал первого велосипедиста, а через полтора часа после этого
догнал и второго велосипедиста.
Определить скорость третьего велосипедиста.
4. В правильной четырехугольной пирамиде SABCD с верши-
ной S сторона основания равна 1 см. Объем пирамиды равен
У~2/3 см3 4. Через сторону основания CD проведено сечение, кото-
рое делит пополам двугранный угол, образованный боковой
гранью SCD и основанием.
Найти площадь сечения.
120
5. Найти все пары значений (х, у), являющиеся решениями си-
стемы
sinx-l-----— = 21X14,
1 cosy '	’
1 з ,______
sinx-------= у 196 — 2
cos у	’
и удовлетворяющие условиям
Вариант 2
1.	Решить систему
1g 5 - lg 00 = 1g 7 • 1g (-0,
Igx-lg7 = lgi/-lg5.
2.	Решить уравнение
9x+i+3x+2_i8=o.
3.	На дороге, представляющей собой окружность длиной 36 км,
пункты А и В являются диаметрально противоположными точка-
ми этой окружности. Велосипедист выехал из пункта А и сделал
два круга. Первый круг он прошел с некоторой постоянной ско-
ростью, после чего уменьшил скорость на 3 км!ч. Известно, что
время между двумя его прохождениями через пункт В равно 5 ч.
Определить скорость, с которой велосипедист прошел первый круг.
4.	В правильной треугольной пирамиде SABC с вершиной S
сторона основания равна 2 см. Через' сторону основания ВС про-
ведено сечение, которое пересекает ребро SA в точке М. Известно,
что : МА = 1 ; 3, а площадь сечения равна 3 смг.
Найти объем пирамиды SABC.
5.	Найти все пары значений (х, у), являющиеся решениями си-
стемы
«*•+J, = 4
L
121
и удовлетворяющие условиям

Вариант 3
1.	Решить систему
1g2- lg(2x) = lg31g(3|/),
Igxlg3 = lg#lg2.
2.	Решить уравнение .	_
16*+	15-4х-|-4.
3.	Три работницы делают игрушки. Первая работница изготав-
ливает 5 игрушек в час, вторая — 8 игрушек в час. Первые две
работницы начали работу одновременно, а третья — на полчаса
позже. Через некоторое время третья работница догнала по коли-
честву изготовленных игрушек первую работницу, а через полтора
часа после этого догнала и вторую работницу.
Определить производительность труда третьей работницы.
4.	В правильной четырехугольной пирамиде SABCD с верши-
ной S сторона основания равна 4 см. Через сторону CD основания
.проведено сечение, которое пересекает грань SAB по средней ли-
нии треугольника SAB. Площадь сечения равна 18 см2.
Найти объем пирамиды SABCD.
5.	Найти все пары значений (х, у), являющиеся решениями си-
стемы
cosx + shb- = T^
cosx-iib-=^“3'-
и удовлетворяющие условиям
Л -	, п.
2'<^Х<'~2
о< tf< «.
122
Вариант 4
1.	Решить систему
f lg71g(6x) — lg6-lg(7y),
1lg у = log, 6 • lg x.
2.	Решить уравнение
3.	Экскаватор роет котлованы емкостью по 20 м3. После того
как был вырыт первый котлован, производительность экскаватора
уменьшилась на 1 м3/ч. Известно, что через шесть с половиной ча-
сов после начала работы было вырыто полтора котлована.
Определить первоначальную производительность экскаватора.
4.	В правильной треугольной пирамиде SABC с вершиной S че-
рез сторону ВС основания проведено сечение перпендикулярно реб-
ру Плоский угол_при вершине пирамиды равен 60°. Высота
пирамиды равна 2)Л2 см.
Найти площадь сечения.
5.	Найти все пары значений (х, у), являющиеся решениями си-
стемы
‘8-' + lK7 = 23/41’
и удовлетворяющие условиям
Разбор варианта 1
Задача 1. Выразим из второго уравнения 1g через 1g х
ь у 1g з
Выполнив логарифмирование в первом уравнении, подставим в
него найденное значение 1gу. Тогда получим
(1g2 3— 1g2 2) lg х=— 1g 3 (1g2 3- lg2 2).
Отсюда находим x=l/3 и затем i/=l/2.
Ответ: х= 1/3, i/= 1/2.
123
Задача 2. Обозначим 2~ж через t. Заметим, что />0. Тогда по-
лучим квадратное уравнение
2/2—7/—4=0.
Если корни 4=—1/2 и /2=4. Первый корень — посторонний.
Поэтому нужно решить уравнение
'	2-х=4
Находим: х=—2.
Ответ: х=—2.
Задача 3. Пусть /ч— время, прошедшее от начала движения
первого велосипедиста до точки, в которой его догнал третий ве-
лосипедист, а акм)ч — скорость третьего велосипедиста. Следует
заметить, что о>10.
~Из условия задачи вытекает уравнение
('~4)» = 7'-
Аналогично этому можно записать уравнение движения относи-
тельно второго и третьего велосипедистов
(,-4-+т),'=10('+т)-
Решая систему уравнений
(/ ^« = 7/,
(/4-1)0=10 (*+4)
путем исключения времени /, получим квадратное уравнение отно-
сительно скорости и:
и2— 18о.+70=0,
корни которого о=9.± )/11. Меньший корень этого уравнения не
удовлетворяет условию о> 10. Поэтому решение задачи дает дру-
гой корень.
Ответ: о = 94-У11.
Задача 4. Представляем читателю самостоятельно показать,
что искомое сечение пирамиды DCMN представляет собой трапе-
цию (рис. 28).
По формуле объема пирамиды можно вычислить высоту Н:
О
Апофему боковой грани SQ определим из треугольника SOQ по
теореме Пифагора
^=/2+4=4.
124
Воспользовавшись теоремой о биссектрисе внутреннего угла
треугольника, находим из SQK:
РК_ РК _ 1
sp w
Следовательно, SP=0,9.
Для определения меньшего основания MN трапеции DCMN
рассмотрим подобные треугольники SMN и SAB.
MN_SP,	SP.AB
АВ SK ’	~~ SK ’
MN =
n 3/2	5
Высота PQ трапеции CDMN является биссектрисой треугольни-
ка SKQ. Используя формулу для определения длины I биссектри-
сы по двум сторонам о и 6 и углу
у между -ними
f___2flbcosy
Z — a+b
(эта формула получается путем
приравнивания площади треу-
гольника, вычисленной по двум
сторонам и углу между ними,
сумме -площадей, на которые бис-
сектриса делит этот треугольник),
найдем высоту PQ:
3 а
' 2*1* Т" *cos~2“
pQ=——з—
1+ 2
где а — угол SQK Далее вычисляем
П/'л 6	л
f^-5-cos-^.
Воспользуемся формулами
S = 4-SQ.KQsina = ^-SO^Q.
Тогда
-1-• 1 •-sina = -|-• 1-J/2, т. e.Sina = ^X^-.
Z Z	Z	о
125
Следовательно,
cos а = /1-8/9 = 4-.
О
Используя формулу косинуса двойного угла, находим
2cos’4—1=4-’ c®sv=/2/3
и, наконец, площадь сечения
с_ AW4-CD Dn 8 Кб
2	— 25 •
Ответ: 8J/6/25.
Задача 5. Обозначим sinx буквой т, 1/cos у — п. Тогда и» усло-
вия задачи следует, что	п>4.
Запишем систему уравнений следующим образом:
т-\- п = 2^К14,
т/г=|л196 — 2.
Вспоминая теорему Виета, заметим, что решения этой системы
являются корнями квадратного уравнения
t* — 2J/14-/ + y496 — 2 = 0.
Находим	v
Здесь возможны два случая:
Первый из них рассматривать не нужно, так как 0^/п^1, п>1.
Второй случай даеТ
sinx = 3/T4 - /2, cosx= 3^4^.
Учитывая условие 0<х<л, находим решения первого уравнения
Xi = arcsin14 — ]/2); х2 = it — arcsin(у!4 — ]^2).
Решениями второго уравнения, удовлетворяющими у словию
---у < у < 4" являются числа
1 1
«1 = arccos	—77=- и у, = — arc cos v=—т=-.
9	^/14+ К2	9	^14+ /2
126
Поэтому рассматриваемая, система имеет четыре решения:
(х„ У1); (Xi, У«); (х», у,)', (х„ yt).
Ответ: х=arcsin (ул14 — V2), у = arccos	;
о — 		1
х — arcsin(у714 — }/2), у = — arccos 3	;
х= « — arcsin (у М — /2), у= arccos	>
х=it — arcsin (у/14 — 1^2), у = — arccos 3 —	.
§ 15. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ГЕОФИЗИКИ, 1973 г.
Вариант 1
1.	Решить систему
х-|-sin (х +1/) =
Зх — sin (х 4*•
2.	Решить неравенство
1
/	— Х+ -г
4	•—7-2”* —4<0.
3.	Два велосипедиста выехали из пункта А одновременно и
в одном направлении. Первый велосипедист ехал со скоростью
7 км)ч. а второй — со скоростью 10 км)ч. Через 30 мин из пункта
А в том же направлении выехал третей велосипедист, который
догнал первого велосипедиста, а через полтора часа после этого
догнал и второго велосипедиста.
Определить скорость третьего велосипедиста.
4.	Решить неравенство
*	'	10£2х-х»(Х----Г)4>0-	'
5.	На плоскости дан прямой угол. Окружность с центром, рас-
положенным внутри этого угла, касается одной стороны угла, пе-
ресекает другую сторону в точках Л и В и пересекает биссектрису
угла в точках С и £>. Длина хорды АВ равна 6 см, длина хор-
ды CD равна 7 см. Найти радиус окружности.
127
Вариант 2
1.	Решить систему
tg(x + i/) — 5х=—9,
,5tg(x4-t/)4-x = 7.
2.	Решить неравенство
х+ Т
16	2 3 <15-4*4-4.
3.	На дороге, представляющей собой окружность длиной
в 36 км, пункты А и В являются диаметрально противоположны-
ми точками этой окружности. Велосипедист выехал из пункта А
и сделал два круга. Первый круг он прошел с некоторой постоян-
ной скоростью, после чего уменьшил скорость на 3 км)ч. Известно,
что время между двумя его прохождениями через пункт В равно
пяти часам.
Определить скорость, с которой велосипедист прошел первый
круг.
4.	Решить неравенство
l°g_4X2+i2x-«14х~ 51 >0.
5.	На плоскости дан прямой угол. Окружность с центром, рас-
положенным вне этого угла, касается биссектрисы прямого угла,
пересекает одну из его сторон в точках А и В и пересекает про-
должение другой стороны в точках С и D. Длина хорды АВ равна
]/*7 см, длина хорды CD равна 1 см.
Найти радиус окружности.
Вариант 3
1. Решить систему
cos (х — у) — 2у = — -|-,
5
3 cos (х — у) 4- У = "2* •
2. Решить неравенство
9*+'+3*+2—18>0.
3. Три работницы делают игрушки. Первая работница изготов-
ляет 5 игрушек в час, вторая — 8 игрушек в час. Первые две ра-
ботницы начали работу одновременно, а третья на полчаса позже.
Через некоторое время третья работница догнала по количеству
изготовленных игрушек первую работницу, а через полтора часа
после этого догнала и вторую работницу.
128
Определить производительность труда третьей, работницы.
4. Решить неравенство
log4" 4 (х —2)* >0.
5. На плоскости дан угол величины л/3. Окружность касается
одной стороны этого угла, пересекает другую сторону в точках А
и В и пересекает биссектрису угла в точках_С и D. Длина хорды
АВ равна V 6 см, длина хорды CD равна 1^6 см.
Найти площадь круга, ограниченного этой окружностью.
Вариант 4
1.	Решить систему
(2у — ctg(x — у) = 3,
(3i/ + 2ctg(x — у) = 8.
2.	Решить неравенство
25-*—5-*+‘>50.
3.	Экскаватор роет котлованы емкостью по 20 м3.' После того
как был вырыт первый котлован, производительность экскаватора
уменьшилась на 1 м3/ч. Известно, что через шесть с половиной ча-
сов после начала работы было вырыто полтора котлована.
Определить первоначальную производительность экскаватора.
4.	Решить неравенство
log t Ч16х-3|<0.
-J'2*—*+Т
5.	На плоскости дан прямой угол. Окружность с центром, рас-
положенным вне этого угла, касается продолжения одной из его
сторон, пересекает другую сторону в точках А и В и пересекает
биссектрису этого угла в точках С и D. Длина хорды АВ равна
см, длина хорды CD равна 2 см.
- Найти радиус окружности.
Разбор варианта 1
Задача 1. Складывая друг с другом уравнения системы, полу-
чим
4х=4, х—1.
После этого имеем одно уравнение
1) =-g-.
9—619
129
Из этого уравнения находим:
//+! = (- 1)"-^- + ™,
У=(-	+	'
Ответ:
х= 1, {/=(—	— 1.
Задача 2. Обозначая 2-х буквой t, получим квадратное нера-
венство
2t2—7t—4 <0.
Решения этого неравенства имеют вид
-4-<*<4-
Учитывая, что показательная функция всегда положительна,
находим
2-*<4, -
—х<2,
х>— 2.
Ответ: х>—2.
Задача 3. Обозначим скорость третьего велосипедиста v км/ч.
Очевидно, что о>10. В тот момент, когда этот велосипедист вые-
хал из пункта А, первый велосипедист находился уже в 3,5 км от
пункта А, а второй велосипедист — в 5 км от А. Третий велосипе-
дист догоняет первого велосипедиста через h ч, а второго вело-
сипедиста — через h ч:
.  3,5	. _	5
Условие задачи равносильно уравнению
^70-^7 = 1.5(о> 10).
Это уравнение легко приводится к квадратному уравнению
V2— 18о+70=О,
которое имеет только один корень, удовлетворяющий условию
t»>10:
о=9 + /ТЕ
Ответ: (9 -(- УТ1) км]ч.
130
Задача 4. Область допустимых значений неизвестных в нера-
венстве
х»	2~) > О
находится из следующих ограничений:
1) 2х —х2>0, 2) 2х — хг^1, 3) хУ=-|-
0 < х< 2; х^= 1.
Объединяя полученные ограничения, находим ОДЗ:
1) 0<л<1; 2) 1<х<-|-.; 3)-|-<-х<2.
Заметим, что выражение	может быть как положитель*-
ным, так и отрицательным. Это связано с четностью показателя
степени, в которую возводится стоящее под знаком логарифма
выражение. Следует также отметить, что формула
logoff (х) ]2ft=2k logoff (х) ],
где k— целое число, не может быть здесь применена, поскольку
она нарушает ОДЗ. В правой части последнего равенства функция
f(x) должна быть обязательно положительной, в то время как в
левой части этого равенства допустимы и отрицательные ее значе-
ния. Поэтому нужно использовать другую формулу, всегда приво-
дящую к равносильному выражению:
loga[f(x)F = 2^10ga|f(x)|.	•
Вернемся к нашему неравенству. Нужно рассмотреть два слу-
чая:
1) 2х—х2>1, (х—1)2<0.
Здесь решений нет;
2) 2х—х2<1, (х—1)2>0.
Это выполняется для всех х из ОДЗ. Поэтому основание у ло-
гарифма в рассматриваемом неравенстве всегда больше единицы.
Имеем
1	.	> 5
2	2 •
Учитывая ограничения ОДЗ, находим
1	.	. < 1	. з	з
2	<CX<CU	2 ’ 2
9*
131
Ответ:
1) -?<х<1; 2) 1<х<4: 3)J-y<x<2.
Задача Пусть точка К —вершина прямого угла (рис. 29).
Легко сообразить, что центр окружности, точка О, лежит выше
биссектрисы прямого угла КД т. е. внутри угла BKD. Действи-
тельно, радиус окружности ON, проведенный в точку касания со
стороной угла, больше, чем рас-
стояние. от центра окружности до
другой стороны угла
ON>KN~OM.
Проведем OEA.CD. Тогда точ-
ка Е будет серединой хорды CD.
По теореме Пифагора имеем
ОС*=ОЕ* + СЕ*(сЕ = ^р) • (1)
Обозначим ОС буквой R. Тогда
из прямоугольного треугольника
А ОМ находим
Рис. 29.
Поскольку FN=KN=OM, то
OF = ON — FN = R-Y’
Из Прямоугольного равнобедренного треугольника OEF имеем
ОЕ=OF =	(я-|/ R* 1-).
Подставляя ОЕ в равенстве, (1), получим уравнение
«=4(«-/л,-4)‘+/
ИЛИ
«/«-4=1.
2R* — 3R* -2 = 0,
Ответ: R = }^2 см.
132
§ 16. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ОБЩЕЙ ГЕОЛОГИИ, 1974 г.
Вариант 1
1.	Решить уравнение
/Т-Р?-л + 3 = 0.
2.	Решить систему неравенств
_52/_6-5'>0,
12.5«' + 5'+>- 12 >0.
3.	Найти все решения уравнения
log4 (1 -р tg1 х) + loga cos 2х — log^ jZcos х = — 2,
удовлетворяющие условию 0^х<2л.
4.	Дан треугольник АВС. Известно, что АВ=4 см, АС=2 см,
ВС=3 см. Биссектриса угла BA С пересекает сторону ВС в точке
К. Прямая, проходящая через точку В параллельно АС, пересека-
ет продолжение биссектрисы АК в точке М. Найти длину отрез-
ка км.
5.	Дана правильная четырехугольная пирамида PABCD с вер-
шиной Р. Сторона основания равна 1 см, высота пирамиды равна
Y2 см. На ребрах РА и, PC взяты точки К и М соответственно,
причем АК: КР=1:3, СМ=РМ. Найти отношение, в котором де-
лится ребрбРВ плоскостью, проведенной через точки D, К и М.
Вариант 2
1.	Решить уравнение
'	Кх + 8-х4-2 = 0.
2.	Решить систему^неравенств
(32*+ » — Зх+г + 6 > 0,
<	ft
(3*х+« _ 2 • 3*+* —[27 < 0.
3.	Найти все решения уравнения
log, (sin х  cos х) — log4 tg2 x + log । cos 2x — 2,
Tj...
удовлетворяющие условию 0^х<2л.
4.	Дан прямоугольный треугольник АВС с прямым углом при
вершине С. Угол САВ равен а. Биссектриса угла АВС пересекает
катет АС в точке К. На стороне ВС как на диаметре построена
окружность, которая пересекает гипотенузу АВ в точке М. Найти
угол AM К.
133
5.	Дана правильная четырехугольная пирамида SABCD с вер-
щиной S. На продолжении ребра CD взята точка К так, что
KD : КС—3 : 4. На ребре SC взята точка L так, что SL : LC=2 : 1.
В каком отношении делит объем пирамиды плоскость, проведен-
ная через точки К, В и L?
Вариант 3
1.	Решить уравнение
j/^+9-]-x + 8 = 0.
2.	Решись систему неравенств
| 6-2*» 4- 2ч — 12>0,
(22»4-20+* — 8< 0.
3.	Найти все решения уравнения
logrr /ctg* + log, iT-tg*£ = 2-
удовлетворяющие условию 0^х<2л.
4.	Дана равнобочная трапеция ABCD. Известно, что AD —10 см,
ВС=2 см, AB = CD=5 см. Биссектриса утла BAD пересекает про-
должение основания ВС к точке К. Найти длину биссектрисы угла
АВК. в треугольнике АВК-
5.	Дан куб ABCDAiBtCiDi, длина ребра которого равна 1 см.
На ребрах AAi, BBi, DDi взяты соответственно точки К, Р и М —
так, что ЛК:Л1К=1 :3, BP :BiP=3:1, DM : DiM=3:1.
Найти объем пирамиды, у которой основанием служит сечение
куба плоскостью, проходящей через точки К, Р и М, а вершина
расположена в точке Ль
Вариант 4
1.	Решить уравнение
J/10 — х — х-|-9 = 0.
2.	Решить систему неравенств
|б-7«-7*+« + 2>0,
( _7«(ж+1)_]_ Ц.7*+* — 30>0.
3.	Найти все решения уравнения
l°g« 1 — tg/Г log 1 sin2х ~ 1°S /Г /1 4-tg‘x = 1,
з
удовлетворяющие условию 0^х<2л.
4.	Дана трапеция ABCD, у которой угол BAD — прямой. На
стороне АВ как на диаметре построена окружность, которая пере-
134
секает диагональ BD в точке М. Известно, что АВ — 3 см, AD =
=4 см, ВС= 1 см. Найти синус угла САМ.
5.	Дан куб ABCDAiBiCiDt, длина ребра которого равна 1 см.
На ребрах BBi и DDt взяты точки К и Р соответственно, причем
ВК:В1К=1:3, DP = PDt. Плоскость, проведенная через точки
А, К и Р, пересекает диагонали A±D и В^С в точках М и Т соот-
ветственно.
Найти длину отрезка МТ.
Разбор варианта 1
Задача 1. Отметим, что х~^—7, и запишем , это уравнение
в следующем виде:
\А х 4~~ 7	х — 3.
. Поскольку левая часть уравнения неотрицательна, то можно
заключить, что всякое его решение должно удовлетворять усло-
вию х^З. При этом данное уравнение равносильно уравнению
х+7=(х—З)2
или
х2—7х+2=0,
которое имеет только одно решение, удовлетворяющее условию
х>3:
7 + /4Т
_ х=—in- •
Ответ: х=(7 + у41/2)|.
Задача 2. Данная система равносильна системе неравенств‘
| 5'(52' — 5' — 6) > О,
j 2-52<-|-5-5z — 12>0.
Пусть 5{ — т, где /п>0. Тогда имеем
| т* — т — 6 > О,
(2тг -|- 5т — 12 > О
или	‘
| (т 4- 2) (т — 3) > 0,	(т < — 2; т > 3,.
I 2(т + 4) (т— 3/2) >0	\т < - 4; т > 3/2.
Учитывая, что тп>0, найдем общее решение системы: т>3.
После этого имеем:
5*>3, />logs3.
Ответ: f>log53.
135
Задача 3. Рассмотрим сначала .условия
cosx>0, cos2x>0, cosx
которые в совокупности с условием 0^х-<2л определяют область
допустимых значений в этой задаче. Условие cosx>0 показывает,
что следует рассматривать только те области х, для которых
0^х<л/2 и Зл/2<х<2л, ,а условие cos2x>0 еще более ограни-
чивает множество рассматриваемых х, оставляя две области:
0<х<4 и ^-<х<2л.	(1)
4	4
В этих областях исходное уравнение преобразуется к следую-
щему виду:
logs	+tg*x-|-log, cos 2х — logs cos х = — 2,
или
Ino- H+tg*X-C0? 2x _ 2
102‘-----cosx
и далее
--—;-------------------------- Л COS X
j/1 -}-tg1x-cos2x = —j— >
cos2x__cosx.
cosx 4 ’
4
4 (2 cos1 x — 1) = cos* x; cos1 x = — •
Учитывая, что cosx>0, имеем окончательно cosx= 1^4/7.
Запишем решения последнего уравнения, которые удовлетво-
ряют условиям (1). Для этого сравним числа и 4/7 и у 2/2. По-,
следнее представляет собой косинус л/4. Имеем
К? .1/4
2' < V 7
Заметим, что косинус в первой четверти монотонно убывает; поэ-
тому большее значение косинуса у меньших чисел. Значит,
Z П	'лГ 4
-т-> arccos V .
4	г (
Поэтому х = arccos 1^4/7 — есть одно из решений уравнения, удов-
летворяющее условию 0^х<л/4. Других решений в первой чет-
верти нет. Однако в области 7л/4<х<2л имеется еще одно реше-
ние:
•	x = 2it — arccos ]/4/7.	/
Механизм нахождения этих решений можно легко понять из
рис. 30.
Ответ: arccos |/ 4/7, 2it — arccos 1^4/7.
136
Задача 4. Чертеж к этой задаче представлен на рис. 31. Преж-
де всего следует заметить, что треугольник АВМ— равнобедрен-
ный. Поскольку ВЛГЦЛС, то Z.BAM=Z_BMA как накрест лежащие.
А так как Z.BAM-Z-MAC, то углы при основании треугольника
АВМ равны и он — равнобедренный. Следовательно, ВМ=4.
Треугольники ВКМ и АКС подобны с коэффициентом подобия,'
равным'2. Поэтому искомый отрезок КМ вдвое больше биссектри-
сы АК. Вычислим поэтому длину биссектрисы АК.
По теореме косинусов, примененной в треугольнике АВС, нахо-
дим косинус угла А, который обозначим 2а:
ВС2=АВ24-АС2—2• АВ • AC-cos 2а,
cos2a— 16+4-9 _ 11
cosza— 2 4 2	16 .
Далее легко найти косинус угла а:
Л 1 -J- cos 2а 27	, / 27
COS’а =---§-----^32 ’ CGSa= У 32 •
137
Обозначим АК буквой I и запишем площадь треугольника
АВС двумя различными способами:
Sляг = -4- АВ • АС • sin 2а = -4~ АВ' I • sin a -J- -4- АС • I • si п «•
Отсюда находим
.__ 2-AB-AC'COsa
1~~ АВ + АС
и после вычислений:
Ответ: 2]/6.
/ = /6, 2/ = 2/6?
Задача 5. Прежде всего п
костью, о которой идет речь- в
Р
Рис. 32.
>строим сечение пирамиды плос-
задаче, рис. 32. Соединим точки К
и D, М и D. Поскольку точки К и
М лежат в плоскости сечения,
то в этой плоскости лежит и весь
отрезок прямой КМ, и, значит,
точка L, в которой он пересекает
высоту пирамиды РО. Таким об-
разом, в плоскости треугольника
PBD имеются уже две точки L и
D, принадлежащие искомому се-
чению. Следовательно, этому се-
чению принадлежит вся прямая
LD, которая пересекается с реб-
ром пирамиды РВ в точке К. Со-
единив точку N с точками К и М,
получим все сечение DKNM.
Метод построения сечения в
этой задаче определяет и метод
вычислений. Он состоит из двух
этапов. На первом этапе рассма-
тривается плоскость треугольника АР С и определяется, в каком
отношении отрезок КМ делит высоту РО, рис. 33. На первом этапе
рассматривается плоскость треугольника BPD и определяется,
в каком отношении отрезок LD делит своим продолжением сто-
рону РВ. При этом оказывается, что размеры пирамиды не имеют
значения для окончательного результата
Рассмотрим сначала ДЛРС. Проведем КК'\\АС и £F||PC. От-
резок EF обозначим через х. Имеем:
РЕ = ±-.РО- РК' = -%--РС; РМ = 2МК' = -^--рС‘,
EF = х; МК' — 2х; РМ = 4х.
При написании этих равенств было учтено, что EF есть средняя
линия треугольника КМК', а М — середина стороны PC.
138
Из подобия треугольников EFL и PML, в которых EF—x и
РМ = 4х, находим, что PL=A-EL. Поскольку РЕ=3!4-РО, то легко
заключить, что
PL^^-PO или PL:LO = 3:2.
О
Обратимся к треугольнику BPD, рис. 33. Проведем OS=y па-
раллельно ВР. Тогда треугольники OLS и NPL будут подобны
Рис. 33.
Поскольку 05 — средняя линия треугольника BND, то BN=2y.
Отсюда находим
NP з о о .
BN 2 У '2у — 3 • 4.
Ответ: NP: J3W=3: 4.
§ 17. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ГЕОФИЗИКИ, 1974 г.
Вариант 1
1.	Решить неравенство
• (2х‘ 4-11x4-6) (2х‘ 4- 11х 4- 13) >8.
2.	Решить уравнение
log 1 (х* 4- 2х — 8)1 — log , (10 4- Зх — х*) = 1.
Т	“
13»
3.	Определить, при каких целых значениях k система
{(arcsin х)8 + (arccos у)8 = n3(k 4-1)»
arcsin х 4- arccos у = z
имеет решения, и найти все эти решения.
4.	В прямой круговой цилиндр с радиусом основания, равным
1 см, вписаны четыре одинаковых шара так, что они лежат на
нижнем основании цилиндра, касаются его боковой поверхности,
и каждый шар касается двух из трех других шаров. Площадь бо-
ковой поверхности цилиндра равна
10п
-----77= СМ‘
(1 + К2)
Найти объем прямого кругового конуса, основание которого
совпадает с верхним основанием цилиндра и который касается
всех четырех шаров.
5.	Дан треугольник АВС. На стороне ВС взята точка Р, а на
стороне АС взята точка М так, что Z_APB = ЛВМА—л/4. Отрезки
АР и ВМ пер.есекаются в точке О. Известно, что площади треу-
гольников ВОР и АОМ равны между собой, ВС=1 см, ВО=
Y2/2 см.
Найти площадь треугольника АВС.
г>
Вариант 2
1.	Решить неравенство
(№+Зх+1) (х2+3х—3) >5.
2.	Решить уравнение
logu (х* — 2х — 3)? — 2 logi, (х‘ 4- х — 2) = Ц-.
3.	Определить, при каких целых значениях система
1(arctg х)г -j- (arccos у)* — it’A,
arctg х 4- arccos у =
имеет решения, и найти все эти решения.
4.	В прямой круговой цилиндр с радиусом основания г=4 см
и высотой /7=12/(3+2 1^3) см вписаны три одинаковых шара
так, что шары касаются верхнего основания цилиндра, его боковой
поверхности и попарно друг друга.
Найти объем прямого кругового конуса, основание которого
совпадает с нижним основанием цилиндра и который касается
всех трех шаров.
140
5.	Дан треугольник АВС. Из вершины А проведена медиана
AM, а из вершины В — медиана ВР. Известно, что угол АРВ ра-
вен углу ВМА, косинус угла АСВ равен 0,8 и ВР=1 см.
Найти площадь треугольника АВС.
Вариант 3
1.	Решить неравенство
. (2x2—Зх—8) (2х2—Зх—6) <3. ’
2.	Решить уравнение
log , (х‘ — х — 6)2 — log^ (4 — Зх — х*) = log.	.
~3
3.	Определить, при каких целых значениях k система
arccos х + (arcsin у)2 — k •
(arcsin у)2 • arccos х —
имеет решения, и найти все эти решения.
4.	В прямой круговой цилиндр с радиусом основания, равным
3/2 см, и высотой, равной 6 (j^2—1) см, вписаны четыре одинако-
вых шара так, что они касаются верхнего основания цилиндра.и
его боковой поверхности, и каждый из шаров касается двух из
трех других шаров.
Найти площадь боковой поверхности прямого кругового конуг
са, основание которого совпадает с нижним основанием цилиндра
и который касается всех четырех шаров.
5.	В треугольнике АВС биссектриса угла при вершине А пере-
секает сторону ВС в точке М, а биссектриса угла при вершине В
пересекает сторону АС в точке Р. Биссектрисы AM и ВР пересе-
каются в точке О. Известно, что треугольник ВОМ подобен треу-
гольнику А ОР, В О = (1 + / 3) • ОР, ВС=1 см.
Найти площадь треугольника АВС.
Вариант 4
1.	Решить неравенство	<
(х2+ 10x4-12) (х24-'Юх4- 13) < 12.
2.	Решить уравнение
log9(x24-5x4-4)2—logs(x2-|-x—6) = 1.
141
3.	Определить, при каких целых значениях k система
’	(arccos x)*+(arctg z/)2-j-(arccos х) (arctg y)=^k,
arccos x — arctg У —
b	t
имеет решения, и найти все эти решения.
4.	_В прямой круговой цилиндр с радиусом основания, равным
(2 )/3+3) см, вписану три одинаковых шара так, что они лежат
на нижнем основании цилиндра, касаются его боковой поверхнос-
ти и попарно друг друга. Объем прямого кругового конуса, осно-
вание которого совпадает с верхним основанием цилиндра, а бо-
ковая поверхность касается всех трех шаров, относится к объему
цилиндра, как у 3 :9.
Найти высоту цилиндра.
5.	В треугольнике АВС на стороне ВС взята точка Р, а на сто-
роне АС взята точка М. Отрезки АР и ВМ пересекаются в точке
О. Известно, что треугольники ВОР, А ОМ и АО В подобны, ВМ=
= 1 см, косинус угла АВС равен 0,6.
Найти площадь треугольника АВС.
Разбор варианта 1
Задача 1. Введем новую неизвестную t посредством равенства
/=2х2+11x4-6.
Тогда неравенство примет следующий вид:
/(/4-7) >8
или
?+7t—8>0.
Его решения: t<—8 и t>\- После этого имеем
1. 2х«+11x4-6<-8, I
2х»4-11х-|- 14 <0,
— 3,5<х< —2.
2. 2л*-р- 11х + 6> 1,
2х*+11х+5>0,
а) х> —0,5; б) х< —5.
Ответ: х<—5; — 3,5<*<—2> х>—0,5.
Задача 2. Область допустимых значений определяется нера-
венствами
Х2+2х—8#=0 и 10+Зх—х2>0,
из которых следует, что —-2<х<2 и 2<х<5.
142
/ Следует специально подчеркнуть, что выражение
ха+2х—8
может быть как положительным, так и отрицательным, поскольку
под знаком логарифма стоит не само выражение, а его квадрат.
Кроме того, в подобном случае следует применить формулу
log ] (х* 4' 2х ~ 8)’ = log J | х* + 2х — 81,
_Т	~ ,
/	ч
которая, очевидно, сохраняет без изменения область определения
этой функции.
|х« + 2х-8|	'
Имеем log^ 104.3х_х2-" = 1.
2
I х* 4- 2х - 81 = Ц- (10 + Зх - х‘).
Для решения 'этого уравнения нужно рассмотреть два случая.
1)	2<х-<5. Тогда х44“2х~8>0 и
х* 4-2х — 8 = Ц-(10 4-Зх - х‘).
Отсюда находим-
— 1 — /зТз _____— 1 + /зТз
Xi —	6	, х, 6
Неравенству 2<х<5 удовлетворяет только второе значение х;
2)	—2<х<2. Тогда -х2+2х—8<0 и
- (х* 4- 2х - 8) = 4“ (10 4“ Зх - •»*)•
Отсюда находим
ч —7 4-/73	— 7 —/73
Х> —-----f’ Х1 =--------2----•
Неравенству —2<х<2 удовлетворяет только первое значение х.
Ответ:
-1+/313	-7 +/73
,	л— 6	’	2
Задача 3. Сделаем замену неизвестных по формулам
t—arcsin х и m=arccos у,
где —л/2^£=^л/2 и 0^/п^л. Тогда исходная система уравнений
примет вид:
р‘4-/п‘ = и‘(&4- 1),
,	|<4-/п = «.
143
Раскладывая сумму кубов в произведение, имеем
0+ «) (f’-J-m* — tm) = «» (Zj+ 1)
или
(i4-m)	- 3/m] = «• (*+ 1)
и с учетом второго уравнения системы
«’ — 3tm — it* (k 4~ 1),
Таким образом, имеем систему двух уравнений
m-\-t —ъ,
содержащую целочисленный параметр k. Оценим, какие значения
может принимать этот параметр.
Поскольку —л/2^/^и/2 и О^т^л, то —л2/2^т/^л2/2.
Поэтому для k возможны три значения k\ — \, k2=—1, £3=0.
Если k=\, то для определения каждой из переменных Ш или t,
получаем квадратное уравнение
-	К1 Л
в .котором р заменяет т или t. Решения этого уравнения имеют
вид
Однако они не дают решений задачи, поскольку одно из них боль-
ше, чем л.
Если k=—1, то аналогичное уравнение имеет вид
/Я —it/? 4--^- = °.
Однако оно не имеет действительных решений.
Таким образом, k—Q. В этом случае получаем
/=0, т—п.
Здесь учтено, конечно, что —n/2=Ctsgw/2. Возвращаясь к перемен-
ным х и у, получаем
arcsin х=0;	х=0;
arccos £/=*л; у=—1.
Ответ: k=Q; х=0, 1/=—1.
144
Задача 4. На рис. 34 представлены «вид сверху» и «вид спере-
ди» геометрических тел, о которых идет речь в задаче. Для того,,
чтобы найти объем конуса, нужно найти его высоту КЕ^Н, или
угол ЕВК= (90°—2а), так как
Н = EB-tg (90° - 2а) = ЕВ -ctg 2а = 1 ~	,
где 2а — угол NBM, a EB=R=1
-радиус основания цилиндра.
Найдем сначала радиусы*
г четырех одинаковых шаров,,
лежащих на основании цилин-
дра. Очевидно, что R=r+OOi„
где 001—расстояние от центра
каждого шара до оси .цилинд-
ра. Имеем
r-}-rV2 = R,
r=, R .
• 1 + ИГ 1 + V 2
Поскольку площадь боковой
поверхности цилиндра извест-
на, то его образующая ВС оп-
ределяется из следующих ра-
венств:
2<RBC=—
Рис. 34.	Рис. 35,
Затем определяется отрезок ВЛ4:
BM=BC-, = -rTV=
Поскольку шар О4 касается как образующей ВС цилиндра, так
и образующей ВК конуса, то ВО\—биссектриса угла NBM. Из пря-
10—619	145.
моугольного треугольника BOiM находим
.	_О,М_ г _ 1
ВМ ВМ 4 *
Таким образом, определяется высота конуса Н:
_ 1 —1/16_ 15
П 2tga 2-1/4	8
и его объем V:
V =	-Н = 4-" • 1 • -£=4г •
О	ООО
- Ответ: 5it/8 см*.
Задача 5. Покажем, что ДЛВС, рис. 35, равнобедренный. По-
скольку площадь АВОР равна площади треугольника А ОМ, то
равны площади треугольников АВМ и АВР. Действительно, каж-
дый из них составлен из ДЛВО и одного из треугольников АОМ
или ВОР. Отсюда следует, что равны высоты треугольников АВР
и АВМ, поскольку они имеют общее основание АВ. Значит, отре-
зок МР, соединяющий точки М и Р, параллелен основанию АВ.
Известно также, что /АРВ = /.ВМА. Поэтому вершины М и Р
треугольников АРВ и АВМ лежат на одной и той же окружности,
проходящей через точки А и В. Отсюда следует, что трапеция
АВРМ вписана в эту окружность и, следовательно, является рав-
нобочной; АМ — ВР, /МАВ — /РВА. Значит, ДЛВС-^равнобед-
ренный.	-	,
Обозначим угол С через 2а. Тогда площадь Д АВС опреде-
ляется формулой
SABC=Ц- • ВС*  sin 2а =	sin 2а = sin a cos а.
Из прямоугольного треугольника BCD находим BD:
BD^BC -sin a=sin a.
Из четырехугольника ОРСМ найдем угол РОМ:
£Р0М = 2ъ - 2а -	- 2а.
Так как /АОВ=/_РОМ, то угол BOD определится равенством:
/BOD = -^^POM = -^--a. '
Из прямоугольного треугольника BOD находим:
• у Dr\r\ BD sin a
s*njBOD = -go=T=->.
. f те	\	sin a
\ 4	J	VT/2
K2* .	.	4 sin a
-^-(cosa-sina^-^,
cos a = 3 sin a
146
или tga=l/3. После этого можно вычислить sin а и cos a
1	3	-----г 1
cos a = - - l -=^-=77=, sin a = l/l — cos2 a =
/l+tg*a /10	Г	/10
а затем и площадь треугольника АВС:
с . /	3
о ,Rr = sin a cos a = -гут.
ЛоС	10
Ответ: 0,3 см2.
/	V
§ 18.	ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ОБЩЕЙ ГЕОЛОГИИ, 1975 г.
Вариант 1
1.	Решить уравнение
4cos 4х+6s in22x + 5cos 2х=0.
2.	Из пункта А в пункт В, расстояние между которыми равно
100 км, одновременно выехали два автобуса. Пройдя половину
пути, первый автобус остановился, постоял 45 мин и поехал даль-
ше со скоростью, на 10 км/ч меньшей, чем первоначальная. Второй
автобус весь путь от А до В прошел с постоянной скоростью
за 4 ч.
Найти первоначальную скорость первого автобуса, если он при-
был в пункт В на час раньше второго.
3.	Решить неравенство
logic 12х + 3|» + 2 log(M3), Ю < 3.
4.	В треугольнике АВС известны стороны: АВ = 6 см, ВС= 4 см,
АС=8 см. Биссектриса угла С пересекает сторону АВ в точк'е D.
Через точки A, D, С проведена окружность, пересекающая сторо-
ну ВС в точке Е. Найти площадь треугольника ADE.
5.	Решить неравенство
/х + 5 < 14-V-x-8 + /(х + 5) (-х-3) •
Вариант 2
1.	Решить уравнение	х
1 2cos‘ х -f- 2 ]Л2 sinx-|-cos2x = 0.
2.	В бассейн проведены две трубы: через первую трубу вода
поступает, через вторую — вытекает Д13 бассейна. Сначала, когда
бассейн был пустым, были открыты обе трубы. Когда треть бас-
сейна была заполнена водой, вторую трубу закрыли. Через пять
часов после открытия труб бассейн был наполнен. Найти про-
10*	147
пускную способность первой трубы, если объем бассейна равен
15000 л«э, а пропускная способность второй трубы равна 2 000 л3/ч.
3.	Решить неравенство
21о£(Зх+1).10 - 3 <Hi 1'3х+1|‘.
ю
4.	В правильном треугольнике АВС проведена окружность, про-
ходящая через центр треугольника и касающаяся стороны ВС
в ее середине D. Из точки А проведена прямая, касающаяся
окружности в точке Е так, что Z.BAE<.^- Найти площадь тре-
угольника АВЕ, если площадь треугольника АВС равна
10/(4—]/2) см3.
5.	Решить неравенство
V (х — 3) ( —х-}-5) > -	14- /-Х4-5.
Вариант 3
1.	Решить уравнение .
—2sin2x+l+isin4x=4cos2x.
2.	Из пункта А в пункт В, расстояние между которыми равно'
40 км, одновременно отправились два туриста, первый пешком,
л второй — на велосипеде. Когда второй турист обогнал первого
на 5 км, первый сел на попутную машину, вследствие чего ско-
рость его движения возросла в 4 раза. Через 2 ч после отправле-
ния из цункта А первый турист догнал второго и прибыл в пункт
В раньше его. НайТи скорость туриста, ехавшего на велосипеде,
-если первый турист шел пешком со скоростью 6 км/ч.
3.	Решить неравенство
3 - 2 bg(x+4),10 > log,о | x-h 41».
4.	В ромбе ABCD со стороной (1+ ]/5) см и острым углом
•BAD=60° расположена на окружность, вписанная в треугольник
ABD. Из точки С к окружности проведена касательная, пересека-
ющая сторону АВ в точке Е. Найти длину отрезка АЕ.
5.	Решить неравенство
J/x 4-“7 — 1 J/"— х — 5 4~ J/ (х 4- ”0 (— х — 5) •
Вариант 4
1.	Решить уравнение
cos 4x+6=7cos 2х.
2.	Экскаватор роет котлован. После того, как было вынуто
20 м3 грунта, производительность экскаватора снизилась на 5м3/ч.
148
Найти первоначальную производительность экскаватора, если че-
рез 8 ч после начала работы было вынуто 50 м3 грунта.
3.	Решить Неравенство
2 1о£(2х-1).10 + log»» 12х - 1|» < log,8.
4.	В равнобедренном треугольнике АВС известны стороны:
АС=4 см, АВ=ВС=В см. Биссектриса угла С пересекает сторону
АВ в точке D. Через точку D проведена окружность, касающаяся
стороны АС в ее середине и пересекающая отрезок AD в точке Е.
Найти площадь треугольника DEC.
5.	Решить неравенство
' • /(х-5)(-х + 7)-Н>-Г^=Г5+К-х + 7.
Разбор варианта 1
Задача 1, Данное уравнение можно представить в следующее
виде:
4 (2cos22x— 1) + 6 (1 —cos22x) + 5cos 2х=0
и далее
2cos22x+5cos 2х+2=0.
Решая это квадратное относительно cos2x уравнение, находим:
1. cos2x=—2, действительных решений нет.
2. cos 2х = — Ц-, отсюда находим: х = ±-	-f-
Ответ: х = -±:+ *k, где k — 0, zt 1, zt2....
Задача 2. Поскольку второй автобус весь путь от А до В про-
шел с постоянной скоростью за 4 ч, то его скорость равна 25 км/ч.
Обозначим первоначальную скорость первого автобуса v. Из
условия задачи следует, что v>25 км/ч. Первый автобуе первую
половину пути прошел за 5Q/u ч, а вторую — за 50/ (v—10) ч. Тог-
да:	,
50 I 3 I 50	_q'
‘V’* “Г
Отсюда следует, что v удовлетворяет квадратному уравнению
9и2—490и +2000=0,
которое имеет два корня vi = 50 и и2=40/9. Учитывая, что и>25,
заключаем, что скорость автобуса радна 50 км!ч.
Ответ: 50 kmJh.
Задача 3. Допустимые значения Неизвестного в этой задаче
определяются неравенствами
Г(2л + 3)’>0,
12х + 3=^1,
откуда находим, что —3/2<х<—1 и х>—1.
149
Поскольку 2х+3>0, то |2х+3|=2х+3. Заметив, что в области
допустимых значений имеет место тождество
10^+3>-=таг. '
запишем данное неравество в следующем виде:
log,.(^ + 3)-+ ,ot..i2U3).-<3-
Обозначив logw(2x+3)3 буквой t, получаем неравенство
или	,
<2-3/+2
Решения этого неравенства имеют вид
/<0;	1<7<2.
Определим теперь решения задачи. Рассмотрим два случая.
1. «0; Iogi0(2x+3)3<0,	X
(2х+3)3<1,
2х+3<1,	х<—1.
Учитывая область допустимых значений, имеем: —3/2<х<—1.
2. 1</<2; l_<log10(2x+3)’<2,
10<(2х + 3)«< 100,
3/Т0,<2х + 3<VW
у 10 - 3 < 2х< ^ГбО - 3,
'4- [3/io - 3] < х < 4- [3/Тоо - 3].
Очевидно, что полученные решения входят в число допустимых.
Ответ:---— 1,
У io — з	^Тбо— з
2	< •« <	2	•
Задача 4. Треугольник АВС, о котором идет речь в задаче,
изображен на рис. 36. Легко показать, что треугольник ADE—
равнобедренный, AD=DE. Действительно, угол ACD равен углу
AED, поскольку они являются вписанными углами, опирающими-
150
ся на одну и ту же дугу окружно-.
сти. По этой же причине равны
между собой углы ПАЕ и DCE.
Если учесть' теперь, что CD — это
биссектриса угла АСВ, то становит-
ся ясным, что угол DAE равен
углу DEA и треугольник ADE—рав-
нобедренный.
Сторона AD этого равнобедрен-
ного треугольника вычисляется из
пропорции
х AD___АС.	.
DB~~ ВС'
вытекающей из известно'го свойства
биссектрисы внутреннего угла тре-
угольника делить противоположную
сторону на части, пропорциональ-
ные прилежащим сторонам.
Обозначим угол при основании равнобедренного треугольника
буквой а. Тогда угол АСВ равен 2а. Его косинус легко находится
по теореме косинусов из треугольника ABQ:
АВ* = А С* + ВС* — 2 • АС • ВС • cos 2а,
о 644-16 — 36
cos 2а =	-----
64
11
16 ’
Пусть DF — высота треугольника ADE. Тогда
Z)f=4-sinа; ДЕ=^-соза,
а площадь треугольника ADE равна
SADB = 16 sin а • cos а = 8sin 2а.
Зная, что cos 2а= 11/16, нетрудно определить sin 2а:
sin 2а = р^1 — cos* 2а = ^13Ё.
16
После этого находим площадь искомего треугольника:
„	_8К35_зКТ5
^ADE —	16	2
Ответ: 3]/Т5/2 см*.
Задача 5. Область допустимых значений в этом примере опре-
деляется системой неравенств:
4	1 х4-5>0,
I — х~ 3>'О,
откуда находим, что ——3.
151
Запишем исходное неравенство в следующем виде:
/х + 5- /—х —3< 1 + К(х-|-5)(-х-3).
Однако, прежде чем возвести обе части ^ого неравенства в квад-
рат, необходимо принять во внимание, что при этом не всегда по-
лучается неравенство, равносильное исходному. Возможны два
варианта.
Рассмотрим первый случай, при котором левая часть этого не-
равенства меньше или равна нулю:
Ух-}-5 - У—х—3 < 0.	(1)
Поскольку правая часть рассматриваемого неравенства представ-
ляет собой сумму единицы и неотрицательного радикала, то оче-
видно, что она положительна. Поэтому все значения х, которые
удовлетворяют неравенству (1), должны являться решениями за-
дачи.
Имеем:	.
Ух	5 < У—х— 3.
Обе части этого неравенства неотрицательны; поэтому оно равно-
сильно следующему неравенству:
х+5<^—х—3
или
х«^—4.
Таким образом, найдена часть решений: —5^х^—4.
Рассмотрим второй случай, т. е. такие значения х, при которых
Ух+5-У-х-3>0	_	(2)
или
—4<х<—3.
Имеем систему неравенств
J	-4<х<-*3,
(/7+5 - У-X - 3< 1 + /(хЦ-5) (-х-3).
Теперь при возведении обеих частей неравенства в квадрат прихо-
дим к равносильной системе неравенств
— 4<х< —3,
2 - 2/(х + 5) (- л: - 3) < 14-
+ (х + 5) (-х-3)+2/(л+ 5)(-х-3).	;
Решим второе неравенство системы. Обозначим
/(х,+ 5)(-х-3) = i > 0.
152
Тогда имеем квадратное неравенство
2—2/<1+/2+2/,
/2+4Л—1>0,
решения которого имеют вид
<> — 2-|-j/5.
Дальнейшее решение очевидно:
Г(х^5)(-х-3)>/5" — 2,
(х+5) (-х-3)>9-4/5,
хг 4- 8х 24 - 4 ]/5" <О,
- 4 -	4/Д-8 < < - 4 + /4 ]/5“- 8.
Нетрудно проверить, что
-4-/4/5'-8<-4, а - 4	4 /5"-8 < - 3.
Поэтому решения системы неравенств второго случая имеют вид:
_	- 4<х<— 4+ \/ 4 /Г- 8.
Объединяя эти значения х с теми, которые были найдены ранее,
получаем
— 5<х< — 4 + |/Л41^5 — 8.
Ответ: — 5<х< — 4-f- ]/ 4 5 — 8.
§ 19. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ГЕОФИЗИКИ, 1975 г.
•Вариант 1
1. Решить уравнение
(х—1)2+|х—1|—2=0.
2..	Решить неравенство
1о&9х^бх+1 9x2 — 18х + 8 < —
3.	Найти все решения системы
{ylnx-Цеу___ ।
ysln4 X+tg4 у_7
удовлетворяющие условиям: 0<х<л, 0<у<л.
4.	На отрезке АВ длины Л см Как на диаметре построена
окружность. Вторая окружность такого же радиуса, как и первая,
153
имеет центр в точке А. Третья окружность касается первой окруж-
ности внутренним образом, второй окружности — внешним об-
разом, а также касается отрезка ЛВ.' Найти радиус третьей окруж-
ности.
5.	Дан правильный тетраэдр РАВС, длина ребра которого
равна а см. Через точки С, Е, М и Р, где Е — середина ребра АВ.
а М— середина ребра АС, проведена сфера.'Найти радиус сферы.
Вариант 2
1.	Решить уравнение
(х—2)2—6= |х—2|.
2.	Решить неравенство
log4xi_4x+1 (4хг - 12х + 8) > ~ log2 4. -
3.	Найти все решения системы
gsin X + COS у _ |
;	25sln# x+cosa и 5
удовлетворяющие условиям: 0<х<л, 0-<1/<л.
4.	Дан правильный треугольник АВС, сторона которого равна
а см. Окружность проходит через центр треугольника и касается
стороны ВС в ее середине М. Прямая, проведенная из вершины
А, касается окружности в точке Е так, что ZZL4E<30°. Найти
площадь треугольника АЕМ.
5.	Дан куб ABCDA'B'C'D' с нижним основанием ABCD и боб-
ковыми ребрами АА', ВВ', СС' и DD'. Длина ребра куба равна
(4—2 V 2)/(]/г23— V 2—3) см. Первая сфера касается нижнего
основания ABCD, боковой грани ВВ'С'С и плоскости АА'С'С. Вто-
рая сфера с центром в точке Л', имеет радиус, вдвое больший, чем
радиус первой сферы, и касается первой сферы внешним образом.
Найти радиус первой сферы.
Вариант 3
1.	Решить уравнение
(х+ 1)2+2|х+11 =3.
2.	Решить неравенство
log 1	(9х* — 6х)<—1.
9х9Ч-6х+1
154
3.	Найти все решенЛ^системы
{ 'gsln х + ctg и	|
gsin4+ctga у _ 3
удовлетворяющие условиям: 0<х<л, 0<г/<л.
4.	На отрезке АВ длины I см как на диаметре построена
окружность. Вторая окружность, радиус которой равен половине
радиуса "первой окружности, касается ее внутренним образом
в точке А. Третья окружность касается первой окружности вну-
тренним образом, второй окружности — внешним образом, а так-
же касается отрезка АВ. Найти радиус третьей окружности.
5.	Дана правильная четырехугольная пирамида PABCD со сто-
роной основания; равной а см. Высота пирамиды, опущенная из
ее вершины Р, также равна а см. Найти радиус сферы, проходя-
щей через точки В, Е, К и Р, где Е — середина ребра AD, а К- -
середина ребра ВС.
Вариант 4
Решить уравнение
(х+2)2=2|х+2|+3.
Решить неравенство
—Г lo& ТГ < lo^+4x+i (4х* - М-
3.	Найти все решения системы
{gtg х + ctg у_ |
2tg*x+ctg«y = 64>
удовлетворяющие условиям: 0<х<л, 0<у<л.
4.	Дан равнобедренный треугольник АВС с основанием АС—
= 6 см и боковой стороной ЛВ=5 см. В треугольник ABD, где
BD — высота треугольника АВС, вписана окружность. Прямая,
проведенная через вершину С, касается окружности в точке Е, при-
чем ЛАСЕ^О. Найти площадь треугольника ОЕС, где О — центр
окружности.
5.	В прямой призме АВСА'В'С'. с боковыми ребрами АА', ВВ'
и СС' нижнее основание АВС является равнобедренным прямо-
угольным треугольником с гипотенузой ВС. Сфера Si с радиусом
( 23— р42—3) еле, касается боковых граней АА'В'В, ВВ'С'С и
нижнего основания АВС. Сфера 5г с центром в точке О' касается
155
сферы Si внешним образом. Известно, что^В=ЛД', и что радиус
сферы Si в два раза меньше радиуса яферы S2. Найти объем
призмы.
Разбор варианта 1
Задача 1. Заметим, что
(х-1)2=|?-1|2- '
Тогда данное уравнение можно рассматривать как квадратное от-
носительно/=|х—1|2:
tz+4—2=0,
fi=l,	f2=—2.
Имеем: 1. lx—11 = Г; Xi=2, Хг=0.
2. |x—1|=—2; решений нет, поскольку |х—1|^0 при
всех значениях х.
Ответ: Xi=2, Хг=0.
Задача 2. Вспомним, что при решении логарифмических нера-
венств важно учитывать, больше или меньше, чем 1, основания
у входящих, в задачу логарифмов. В евязи" с этим данное нера-
венство распадается на две системы неравенств:
	1. 9х2 — 6x-f- 1 > 1, 0	:	 9х2 — 18х 4~ 8	9х2— 6х 4-1 ’
ИЛИ	| 9х2 — 6х -|- 1 > 1, 1 9х2 — 18х-|-8>9х2 — 6х-{- 1.
Здесь учтено, что выражение (9х2—18х+8) положительно в силу
одз.	2. 0< 9х2 — 6х+1 < 1, • ~ 1	~ 1 9x2 — 18x4-8	—6х+1’
или	| 0,<рх2 — 6х+ 1 < 1, t 9х«-6х-Н >9х2- 18х4-8>0.
Здесь так же как и в предыдущем случае учтено, что выражения
(9х2—18x4-8) и (9х2—6х+1) положительны.
156
Рассмотрим первую систему неравенств. Из первого неравенст-
ва системы имеем:
2
X < 0 ' ИЛИ X
и ,
Из второго неравенства: х<С7/12. Объединяя решения этих нера-
венств, получим: х<0 (7/12 < 2/3).
Рассмотрим вторую систему неравенств. Из первого неравенст-
ва системы имеем:
0<^<— или — <xz<—•
2
Из второго неравенства: 7/12<x<-gj, х>4/3. Объединяя реше-
ния этих неравенств, получим: 7/12<х<2/3.
~ Ответ: х<0, 7/12<х<2/3.
Задача 3. Обозначим sinx—ы, tg у=и. При этом заметим, что
в силу условий задачи «>0. Имеем
«4-0 = 0,
1.,
Отсюда находим
1. U1 = -yi = LL.
1/^2”
2. «1 = —о2 = —~2—
Второе решение не удовлетворяет условию и>0; поэтому оно не
рассматривается. Таким образом, остается система
. КГ	КГ.
sinx = —> tgy = , — ’
Условию 0<х<л удовлетворяют только два решения уравнения
sinx=yr2/2 (рис. 37):
к	Згс
И X, = -т-,
4	4
а условию 0 < у < « — только одно [решение
= -У2/2:
( К2~\
f/ = «4-arctg!—5-1-
уравнения tgy =
Заметим, что арктангенс отрицательного числа определяет угол,
заключенный в четвертой четверти, т. е.
я - -	/ КГ\
arctg 2")<0.
157
Поэтому нужно правильно записать то решение уравнения tgi/ =
«=—j/2/2, которое удовлетворяет условию 0<у<л.
Таким образом, задача имеет два решения.
Ответ'. 1) х==4’ arctg( “'V"')’ 2) х = ^-, y=it +
Рис. 37.
Задача 4. Чертеж к этой задаче представлен на рис. 38. Точки
Си D являются центрами второй и третьей окружности соответст-
венно; точка Е служит ос-
нованием перпендикуляра,
опущенного из центра треть-
ей окружности на отрезок
АВ. Легко понять, что мож-
но построить не одну, а две
одинаковые окружности,
удовлетворяющие всем ус-
ловиям задачи, центры ко-
торых лежат внутри обла-
сти MCKBF^ Очевидно так-
же, что точки С, D и F ле-
жат на одной прямой. Аналогично, точки A, G и D лежат на од-
ной прямой.
Обозначим радиус третьей окружности через х. Тогда GD =
=DF=DE^x\ АС=
лл=4+-«; CD = -^-x.
Угол DAE назовем а.
Из прямоугольного треугольника ADE находим
sina = -^----------------------.	(1)
— + *
По теореме косинусов, примененной к треугольнику ADC, имеем
CD8 = AD* 4- AC* — 2 • AD • AC • cos a,
или
cosa =
AD* + AC* — CD*
2-AD-AC
(2)
158
Складывая квадраты выражений (1) и (2), получим уравнение
для определения х:
Рис. 38.
Рис. 39.
Ответ: радиус третьей окружности равен Яр^З/в.
Задача 5. Рассмотрим рис. 39. Построим центр искомой сферы,
точку О. Поскольку эта точка должна быть равноудалена от точек
С, Е и М, то она лежит на перпендикуляре DDi, восставленном
к плоскости основания пирамиды АВС в точке D, центре окруж-
ности, проходящей через точки С,ЕиМ, то есть окружности, опи-
санной вокруг равнобочной трапеции ВЕМС. Легко понять, что
ВС является диаметром этой окружности, а ВЕ=ЕМ=МС=а)2 —
три последовательные стороны правильного шестиугольника, впи-
санного в нее.
Найдем теперь на перпендикуляре DD^ центр сферы О. Для
этого обозначим неизвестное расстояние OD через х, соединим точ-
ки О и Р, проведем отрезок прямой OK\\AD. Радиус сферы обозна-
чим
Из прямоугольного треугольника OBD имеем
^=х2+’(а/2)2.	(1)
х	159
Из прямоугольного треугольника ОКР имеем
R?=OK?+KP2.
Если учесть, wo
OK = DF	FP = al/’4-> КР = а lAj--х,
О	• F О	У О
то получим
Отсюда находим
Сравнивая между собой выражения (1) и (2), получим уравнение
для определения х:
и далее по формуле (1) —радиус сферы R:
Ответ: радиус сферы равен а\^22/8 см.
§ 20.	ХИМИЧЕСКИЙ ФАКУЛЬТЕТ, 1972 г.
Вариант 1
1.	Пристань А расположена в 27 км от пристани В ниже по
течению реки. От пристани А по направлению к пристани В отхо-
дит первая лодка, а через час после ее отхода навстречу ей от
пристани В отходит вторая лодка. Лодки встречаются в 18 км от
пристани В.
Если бы лодки отошли от пристаней А и В навстречу друг дру-
гу одновременно, то они встретились бы через два с четвертью
часа. Найти скорость первой лодки в стоячей воде, если известно,
что она вдвое больше скорости течения реки.
2.	Решить уравнение
1°£х>+6х+8 П°&2хЧ-2х+3 (х*	2х)] = 0.
3.	В трапеции ABCD углы А и D при основании AD соответст-
венно равны 60° и 30°. Точка N лежит на основании ВС, причем
BN: NC = 2. Точка М лежит на основании AD, прямая MN перпен-
дикулярна основаниям трапеции и делит ее площадь пополам.
Найти отношение AM : MD.
160
4.	Основанием треугольной пирамиды SABC служит прямо-
угольный треугольник АВС с прямым углом в вершине В. Ребро
5Д перпендикулярно плоскости треугольника АВС. Через середины
D и Е соответственно ребер АС и ВС проведена плоскость, парал-
лельная ребру SC и образующая в сечении четырехугольник
DEFH (точка F лежит на ребре SB).
Найти площадь четырехугольника DEFH, если известно, что
ВС=а, AC—b, SA = h.
5.	Найти все значения х, для которых выражение
(sin 4x+sin 2х) (3cos2x+2sin 2х—6cos х)
положительно.
Вариант 2
1.	От пристани А одновременно отходят вниз по течению реки
к пристани В две лодки. Первая лодка подходит к пристани В на
два час^ раньше второй.
Если- бы лодки отошли от этих пристаней одновременно, дви-
гаясь навстречу друг другу (первая лодка отходит от пристани А),
то они встретились бы через три часа. Расстояние между пристаня-
ми равно 24 км. Скорость второй лодки в стоячей воде в три ра-
за больше скорости течения реки.
Найти скорость течения реки.
2.	Решить уравнение
6х+8 П°&2х*-tx+з С** + 2^)1 = О*
3.	В треугольнике АВС угол А равен 45°, а угол С — острый.
Из середины стороны ВС опущен перпендикуляр NM на сторону
АС. Площади треугольников NMC и АВС относятся соответствен-
но как 1: 8. Найти углы треугольника АВС.
4.	В прямую призму ABCDA'B'C'D', нижним основанием кото-
рой является ромб ABCD, а АА', ВВ',_ СС', DD' — боковые ребра,
вписан шар радиуса R. Найти площадь сечения призмы плос-
костью, проходящей через вершины А, В, С', если известно, что
Z BAD = а.
5.	Найти все значения'х, для которых-выражение
•	(cosx—cos5x) (2sinx+3cosx+4)
положительно.
Вариант 3
1.	Из двух расположенных на'реке пунктов А и В (В по тече-
нию ниже А), расстояние между которыми равно 36 км, одновре-
менно выходят навстречу друг другу две лодки (первая лодка вы-
ходит из пункта А) и встречаются через три часа после выхода.
11—619	161
Скорость второй лодки в стоячей воде в четыре раза больше ско-
рости течения реки. Расстояние от пункта А до пункта В и обрат-
но первая лодка проходит за 24 ч.
Найти скорость течения реки.
2.	Решить уравнение	,
fiog2x’-i2Х+16 (** + Ml = О-
3.	В трапеции ABCD углы А и D при основании соответственно
равны 60° и 90°. Точка N лежит на основании ВС, причем
BN: ВС=2.3. Точка М лежит на основании AD, прямая MN па-
раллельна боковой стороне АВ и делит площадь трапеции попо-
лам. Найти отношение АВ : ВС.
4.	В треугольной пирамиде SABC (S — вершина, АВС — осно-
вание пирамиды) на стороне АС взята точка Е так, что ВС=3-СЕ.
Найти площадь сечения пирамиды плоскостью, проходящей через
точки D и Е параллельно ребру SC, если известно, что SA=SB,
SC=a, AC=BC=b, ZACB = a.
5.	Найти все значения х, при которых выражение
(cosxsin2x—sinx) (4sinx + 2cosx+5)
отрицательно.
Вариант 4
1.	От расположенного на реке пункта А вверх по течению от-
ходит первая лодка, а через два с половиной часа из пункта А
выходит вторая лодка и догоняет первую в тридцати километрах
от пункта А. После этого обе лодки поворачивают и идут обратно,
причем первая лодка приходит в пункт А через 3 ч, а вторая —
через 2,5 ч, считая с того момента, когда вторая лодка догнала
первую. Найти скорость течения реки.
Примечание: время, необходимое на поворот лодок, считается
равным нулю.
2.	Решить уравнение
log^-2x+2	(*2 + 4Л)1 = °-
3.	В треугольнике АВС угол С равен 30°, а угол А — острый.
Перпендикулярно стороне ВС проведена прямая, отсекающая от
треугольника АВС треугольник CNM (точка'N лежит между вер-
шинами В и С). Площади треугольников CNM и АВС относятся
соответственно как 3: 16. Длина отрезка NM равна половине дли-
ны высоты ВН треугольника АВС. Найти отношение АН: НС.
4.	Найти площадь сечения куба ABCDA'B'C'D' (ABCD — ниж-
нее основание, АА', ВВ', СС', DD' — боковые ребра куба) плос-
костью, проходящей через вершину А и середины ребер. В'С' и
D'C. Ребро куба равно а.
162
5.	Найти все значения х, для которых выражение
(cos х—sin xsin 2х) (3sinx—cos x—4)
отрицательно.
Разбор варианта 1
Задача 1. Обозначим через Vi, — скорости лодок, а через
и — скорость течения реки. Тогда
,	vfc=2u.
Из второго условия задачи следует уравнение
27 _ 9
«1+ 1»2	4
Первое условие задачи можно записать в виде уравнения
П-Со.-и)	=
Vi + Vs '	'	'
Здесь отношение [27—(щ—и)]l(vi+v£...определяет время до
встречу лодок друг с другом, отсчитываемое от момента выхода
второй лодки.
Исключая величины Vi и Уг из третьего уравнения с помощью
двух первых, находим:
ыа—39«+108=0,
1) «1=36 км/ч.
2) «2=3 км!ч.
Первое решение не подходит, так как тогда У1=2ы = 72, а из
второго уравнения следует, что yi+V2=12 (Уа>0). Итак, и=
= 3 км/ч.
Ответ: vi= 6. км/ч..
Задача 2. Это уравнение можно было бы решать путем обыч-
ной процедуры, начиная с исследования области допустимых зна-
чений. Однако, в данном случае проще найти значения х, среди
которых заключены решения уравнения, а затем посредством про-
верки отбросить те из найденных значений х, которые не удовлет-
воряют ограничениям ОДЗ.
Действительно, если
10^+6х+8 11о&х.+2х+3 (*2 - 2*)] = °’
ТО
I°g2x«+2x+3(X2-2^)=1’
и далее
,	хг—2х=±2х2+2х+3.
Отсюда находим: 1) х=—1, 2) х = —3.
11*	163
Непосредственной подстановкой найденных значений неизвест-.
ного в исходное уравнение убеждаемся, что решением задачи слу-
жит только одне.из них: х=—1.
Ответ: х——1.
Задача 3. Чертеж к этой задаче представлен на рис. 40. Обоз-
начим BN=2x, NC=x и MN=h. Тогда
ЛЛ4 = -Д=4-2х; Л1Р = Л/3'+х.
V з 1	г '
Из равенства площадей трапеций ABNM и DMNC находим:
/ л \
2х + \УТ+2х)	ж-НА/Г+х)
2	2
и далее
К~Г .
х о— Л.
»	о
После этого получаем:
h
ла* _ Кз~ +2х з
MD ~~ h КТ + х = 4 ‘
Ответ: AM : MD=3: 4.
Задача 4. На рис. 41 изобра-
жен чертеж к этой задаче. Сече-
ние, о котором .идет речь, строит-
ся следующим образом: в плоско-
сти Л5С проводится средняя ли-
ния DH, а в плоскости треуголь-
ника BCS — средняя линия EF.
Четырехугольник DEFH пред-
ставляет собой параллелограмм.
Рис. 41.
Рис. 40.
Он и является искомым сечением. Поскольку DH\\SC\\EF — так
как плоскость DEFH[\SC-, HF\\DE\\AB — как средние линии соот-
ветствующих треугольников ABS и АВС. Находим
164
Определим высоту параллелограмма DEFH. Для этой цели из
точки Н опустим перпендикуляр НК на линию DE и соединим
точку К с точкой А. По теореме о трех перпендикулярах AK-LKE
и, значит, Л/СЦВС, так как по условию задачи угол В — прямой,
DEWAB hKEIBC.
Тогда площадь сечения находится в виде произведения DE
и НК:'
Ответ:	— а2) (Л*-|- а’), Ь^>а.
Задача 5. Решим неравенство
(sin 4x+sin 2х) (3cos2x + 2sin 2х—6cos х) >0.
Представим его в виде:
(sin 4x+sin 2x)cos x(3cos x+4sin x—6) >0.
Легко заметить, что выражение (3cosx+4sinx—6) всегда от-
рицательно. Действительно, вспоминая преобразование, называе-
мое «введением вспомогательного аргумента»
A cos х -|- В sin х = У А2 -|- В2 sin (<р -|- х),
где
sin<р == А1У'А2-\-В2, eosf = B/|/А2 -|- В*, -
можно заметить, что при всех значениях х
— |/Л2-}- В* < Л cosxsinx< jA4‘4* В2.
В частности,
—5<: 3cos х+4sin х^ 5.
Поэтому	х
3cosx+4sinx—6<0.
Итак, решим неравенство
(sin4x + sin2x)cosx<0,
или
2sin 3xcos2x<0.
Это неравенство эквивалентно системе
sin3x< 0,
COSX^sO.
Решения первого неравенства имеют вид
— *2к& <Зх<2«£, где £ = 0, zt 1, ±2, ...
165
или
- те
“а
k-
На рис. 42 углы, соответствую-
щие полученному неравенству,
заштрихованы. Из заштрихован-
ных областей необходимо отбро-
сить углы, соответствующие огра-
ничению cosx=#0, т. е. углы
x — -^--\-wn, -
где т=0, ± 1, ±2 ,.. .
Ответ:
гс i 2гс < . 2те /	, те .
q-Ч—о"«'<•«< "5"
О О	О	Z I'
Замечание. Те же области можно записать и так:
1)	* +2nfe<x<4-+2«fe,
2)	+ 2^;< х< 4- 2itfc,
3)	n4-2«ft<x<^-4-2^,
4)^- + 2яА<х<2« + 2^, A = 0,±rl, ±2, ... .
$ 21. ХИМИЧЕСКИЙ ФАКУЛЬТЕТ, 1973 г.
Вариант 1
1.	Алик, Боря и Вася покупали трехкопеечные карандаши и
блокноты. Алик купил 4 карандаша и 2 блокнота, Боря — 6 ка-
рандашей и блокнот, Вася-,-3 карандаша и блокнот. Оказалось,
что суммы, которые уплатили Алик, Боря и Вася образуют гео-
метрическую прогрессию.
Сколько стоит блокнот?
2.	Решить неравенство
log4 (5 — 3’) log2	— 1-
166
3.	Найти все действительные х, удовлетворяющие уравнению
sin* х
1	— zi _ гЦ sin x+1.
“1 '
4.	В правильной четырехугольной пирамиде расположен шар
радиуса 2. Этот шар касается боковых граней пирамиды и внеш-
ним образом касается полушара, опирающегося на круг, вписан-
ный в основание пирамиды. Точка касания шара и полушара от-
стоит от основания пирамиды на расстояние, равное одной трети
высоты пирамиды.
Найти объем пирамиды и величину двугранного угла при бо-
ковом ребре пирамиды.
5.	В прямоугольный треугольник АВС вписан квадрат АЕКМ
так, что К лежит на гицотенузе, а Е и М — на катетах. Сторона
этого квадрата относится к радиусу круга, вписанного в треуголь-
ник ЛВС, как (2+]/12) :2.
Найти углы треугольника.
Вариант 2
1.	Объем воды, находящейся во втором из трех баков, равен
среднему геометрическому объемов воды в первом и третьем баках.
Из третьего бака перелили один ковш воды в первый бак и два
ковша — во второй, после чего в первом баке стало 11 л, во вто-
ром — 16 л и в третьем — 10 л воды.
Найти объем ковша.
2.	Решить неравенство
W.. (18 - 2») log,	> - 4-
3.	Найти все действительные х, удовлетворяющие уравнению
i /3sin 2х — 2cos х \	< г>
°?3—х* sin2x-sinx J	°&3—х»
4.	В правильной треугольной пирамиде расположены два шара
Qi и Qz. Шар Qi вписан в пирамиду; шар Q2 касается внешним
образом шара Qi и боковых граней пирамиды. Радиус шара Qi
равен 3, радиус шара Q2 равен 2.
Найти объем пирамиды и величину двугранного угла, образо-
ванного боковыми гранями пирамиды.
5.	В прямоугольный треугольник АВС вписан квадрат так, что
две вершины его лежат на гипотенузе, а две другие на катетах.
Радиус круга, описанного около треугольника АВС, относится
к стороне квадрата как 13:6.
Найти углы треугольника.
167
Вариант 3
1.	Трое рабочих обрабатывали одинаковые детали. К концу
месяца оказалось, что количество деталей, обработанных первым,
вторым и третьим рабочими, образует* геометрическую прогрес-
сию.
Месячный заработок каждого рабочего складывается из части,
пропорциональной количеству обработанных деталей, и премии.
У первого рабочего он составил 150 рублей, у второго —180 руб-
лей, а у третьего —.250 рублей.
Найти, размеры премий, если известно^ что у первого и второго
рабочих они одинаковы, а у третьего — в полтора раза больше.
2.	Решить неравенство
/og* (3* - 1) l«gI/4
3.	Найти все действительные х, удовлетворяющие уравнению
COS9 X	,
4.	В правильной треугольной ..пирамиде расположен шар ра-
диуса 1. В точке, делящей пополам высоту пирамиды, он касается
внешним образом полушара. Полушар опирается на круг, вписан-
ный в основание пирамиды; шдр касается боковых граней пира-
миды.
Найти площадь боковой поверхности пирамиды и величину
двугранного угла, образованного боковыми гранями пирамиды.
5.	В равнобедренный треугольник АВС вписан квадрат так,
что две его вершины лежат на основании ВС, а две другие — на
боковых сторонах треугольника. Сторона квадрата относится
к радиусу круга, вписанного-в треугольник, как 8 : 5.
Найти углы треугольника.
Вариант 4
1.	Три автомобиля едут nq шоссе. Первый и третий удаляются
от пункта А, второй едет навстречу им. В полдень расстояния пер-
вого, второго и третьего автомобилей до А были равны соответст-
венно 60 км, 270 км, 210 км, а через час второй автомобиль ока-
зался между первым и третьим и при этом расстояние от него де
А стало средним геометрическим из расстояний первого и третьего
автомобилей до того же пункта.
Чему равна скорость автомобилей, если известно, что у первого
и третьего автомобилей она одинакова, а у второго — в полтора
раза больше?
168
2.	Решить неравенство
log.^log1/3(2«-5)<2.
3.	Найти все действительные х, удовлетворяющие уравнению
.togs-* sin2xcosx J
4.	В правильной четырехугольной пирамиде расположены два
шара Qi и Qz- Шар Qi вписан в пирамиду и имеет радиус 2, шар
Q2 касается внешним образом шара Qi и боковых граней пирами-
ды. Радиус шара Q2 равен 1.
Найти площадь боковой поверхности пирамиды и величину дву-
гранного угла при боковом ребре пирамиды.
5.	В прямоугольный треугольник АВС вписан прямоугольник
DEK.M вдвое меньшей площади. Вершины. D и Е лежат на гипо-
тенузе ВС, вершины К и М — на катетах.
Найти углы треугольника АВС, если сторона DE прямоуголь-
ника относится к стороне DM каю 5:2.
Разбор варианта 1
Задача 1. Обозначим стоимость блокнота — х коп. Тогда Алик
уплатил (2х+12) коп, Боря—(х4-18). коп, Вася—. (х+9) коп.
Поскольку .числа (2x4-12), (х4-18), (х4-9) образуют геометриче-
скую прогрессию, то
(х+18)2=. (2x4-12) (х4-9). .
Отсюда получаем уравнение
х2—6х—216=0. '
Положительный корень этого уравнения дает ответ задачи:
х=18;
Ответ: х= 18.
Задача 2. Решим неравенство
log* (5 - 3«) log, (Ц^^-1.
Обозначим log2(5—3х) буквой t. Тогда получаем
или
t2—ЗН2>0.
169
Решение неравенства /^>2 и 1. В первом случае
log, (5-3я) >2,
'	(5-3я) -4,
3я <1,
х<0.
Во втором случае
log, (5—3я) < 1,
-	0<5 —Зя<2,
3<3Я<5,
'	l<x<log, 5.
Ответ: 1) х^О; 2) ls^x<logs5.
Задача 3. Решим уравнение
Г з1п> х
(1 _ x»)_,/2J = (i - **) ,inx+I.
Его ОДЗ: — 1<х<1. Если 1— х*^!, т. е. х=£0, то
_____________________ 1	* sin2 х	/
~2 sin х + 1 ’
2sin*x — sinx — 1=0.
1) sinx=l, x=
2) sin x = —i-, x = —~^2itn, xj= —	4- 2жл.
Легко проверить, что из всех найденных решений условию
—1<х<1 удовлетворяет только одно х=—л/6. Отметим, что за-
быть об ОДЗ — значит совершить грубую ошибку.
Рассмотрим оставшийся случай х=0. (Этот случай часто
упускался поступающими.) Легко видеть, что при этом х уравне-
ние удовлетворяется. Значит, число 0 есть решение уравнения.
Ответ: Х1=О, х2=—л/6.
Задача 4. Обратимся к рис. 43, на котором представлен чертеж
рассматриваемой задачи. Поскольку шар касается всех боковых
граней пирамиды, то его центр, точка О, лежит на высоте SF.
Проведем в плоскости боковой грани ASB пирамиды4 SABCD апо-
фему SL и соединим точку L с центром основания, точкой Е. Рас-
смотрим отдельно плоскость &ESL, перпендикулярную боковой
грани ASB. Если из точки О опустить перпендикуляр ОМ на SL,
то это будет радиус шара, равный 2.
Очевидно, что AOAfS-vALES. Обозначая радиус полушария
через х/2 (х— сторона основания пирамиды), составим пропор-
цию
2 _SO
х/2 ~~SL ’	_
170
Обозначим высоту пирамиды буквой Л. Из условия задачи следует»
что.
Л	х .	з
3	2 ’ А	2Х'
Кроме того ясно, что
SO = 4-A-2 = x-2,
О
*
SL = /£.Е«-|-ЗЕ«=. V4- А» х. 
г 4	Z
Рис. 43.
Получаем уравнение
2	ж —2
*/2 = /Тбх/2 ’
решение которого определяет сторону основания
х = 2 (1 + /10).
Высота пирамиды равна соответственно
/1 = 3(14-/10),
а объем пирамиды	~
У = -|~х‘А = 4<1 + ^Тб)*-
Найдем теперь двугранный угол <р между боковыми гранями
пирамиды. Из точек В. и D опустим перпендикуляры на ребро пи-
171
рамиды SC, которые пересекутся, очевидно, в одной точке F. Угол
BFD — искомый. Этот угол проще всего определить из рассмотре-
ния прямоугольного треугольника BEF (EF— биссектриса угла
BFD). В этом треугольнике
BE = -LBD = -i-xV2' = V2 (I+/T0).
Гипотенуза треугольника BF представляет собой высоту боковой
грани пирамиды и, значит, равна удвоенной площади этой грани,
деленной на длину бокового ребра.
Площадь боковой грани вычисляется так:
Боковое ребро SC равно
л* + (Ц^-), = КП(1+|/’То).
Таким образом,
BF ==
КП(1 4- КТО)
= 2]/1°(1+Г10)
и далее
sin 4=1г=V35 ’  * = 2arcsin V 35’
Ответ: V = 4 (КТО -р 1)’; ? = 2 arcsin |/
Задача 5. Пусть АВС — прямоугольный треугольник (рис. 44),
ВС — гипотенуза, АС и АВ — катеты. Обозначим угол В треуголь-
ника х, а гипотенузу — а. Тогда
AC=asinx,	АВ=а cos х(0<х<л/2).
Вычислим радиус окружности,
вписанной в треугольник ’АВС.
Для этого воспользуемся форму-
лой площади треугольника
2 ’
где г — радиус вписанной окруж-
ности, р—периметр треугольника.
Приравнивая это выражение пло-
щаДи треугольника, записанной
.172
через катеты, получим
a’sin х • cos к=а (14- sin х4-cos х) г,
откуда
г__ sin х cos х
и 1+ sin х 4- coo х’
Рассмотрим теперь подобные треугольники ВЕК и ВАС. Составляя
пропорцию из соответствующих сторон треугольников
KE	a cosx — КЕ
a sinx a cosx
найдем сторону квадрата КЕ:
„Р  sin х cos х
а cos х 4- sin x'
Составляя отношение стороны квадрата, вписанного в треу-
гольник, и данной окружности, получим тригонометрическое урав-
нение для нахождения угла треугольника:
ЕЕ _ 1 ।	' 1 4-sinx4-cosx /	« X
~ — 14“ 2 sin х 4- cos х ’ х2 / *
sinxcosX — У2 ,
f . re X i
sin 1x4—7-1=1,
\	4 J
Отсюда следует, что треугольник АВС равнобедренный.
Ответ: 45° и 45е.
§ 22? ХИМИЧЕСКИЙ ФАКУЛЬТЕТ, 1974 г.
Вариант 1
1.	Решить уравнение
j/" 1 4- |/"cos 2x4-1^ 1 — j/^cos 2х —	1 4- V^sin х 4~ V1 — Vein х.
2.	Верно ли, что всякое решение неравенства logs(5x2—21x4-
4-7) >1 будет решением неравенства
logs(x*—4X4-2) >0?
3.	В прямоугольном треугольнике АВС с острым углом А, рав-
ным 3(У*, проведена биссектриса BD другого острого угла В. Найти
расстояние между центрами двух окружностей, вписанных в тре-
угольники ABD и DBC, если длина меньшего катета равна 1.
4.	К двум бассейнам подведены две трубы разного диаметра
(к каждому бассейну своя труба). Через первую трубу налили
173
в 1-й бассейн определенный объем воды и сразу посде этого во
2-й бассейн через 2-ю трубу налили такой же объем вбйы, причем
на все это вместе ушло 16 ч. Если бы через 1-ю трубу вода текла
столько времени, сколько через 2-ю, а через 2-ю —столько време-
ни, сколько через 1-ю, то через 1-ю трубу налилось бы воды на
320 м3 меньше, чем через 2-ю. Если бы через 1-ю трубу проходило
бы на 10 м3]ч, меньше, а через 2-ю — на 10 м3!ч больше воды, то,
чтобы налить в бассейны (сначалав первый, а потом во второй)
первоначальные объемы воды, ушло бы 20 ч. .
Сколько времени лилась вода через каждую из труб?
5.	В основании четырехугольной пирамиды лежит ромб со сто-
роной а и острым углом а. Высота пирамиды проходит через точку
пересечения диагоналей ромба и равна четверти его меньшей диа-
гонали. Найти радиус шара, который лежит на основании пирами-
ды, касаясь основания в точке пересечения диагоналей ромба и
плоскости, проведенной через вершину пирамиды и середины
смежных сторон основания, составляющих угол а. .
Вариант 2
.1. Решить уравнение
jZ 1 + ]/sin 2х -f- ]/" 1 — p^sin 2х = V1 -}- J/cos х -j-1/ 1 — p^cosx.
2.	Верно ли, что всякое решение неравенства log2(8+8x—5х2)>
>2 будет решением неравенства log2(2+2x—х2)>0?
3.	В прямоугольном треугольнике АВС с катетами 3 и 4 верши-
на С прямого угла соединена с серединой D гипотенузы АВ. Най-
ти расстояние между центрами, окружностей, вписанных в тре-
угольники ACD и BCD.
4.	24 школьника разбились на две группы. Первая из них по-
шла в цирк а вторая — в кино. При этом оказалось, что на цирк
и кино было затрачено одинаковое количество денег. Если бы би-
лет в цирк стоил на 20 копеек дешевле, а билет в кино — на 20 ко-
пеек дороже, то, истратив на билеты в цирк и на билеты в кино
те же суммы денег, в цирк и в кино смогли бы пойти вместе 15
школьников. Если бы при прежней стоимости билетов вторая груп-
па школьников пошла в цирк, а первая группа — в кино, то на
билеты в цирк ушло бы на 19 руб 20 коп больше, чем на билеты
в кино.
Сколько стоили билеты в цирк и в кино?
5.	На основании правильной треугольной пирамиды с высотой
Ни радиусом круга, вписанного в основание, равным г, лежит
шар, касающийся основания в его центре. Найти радиус шара,
если плоскость, проведенная через вершину пирамиды' и середины
двух сторон основания, касается этого шара.
174
Вариант 3
1.	Решить уравнение
1 + j/ctg2x У1 —]/"—ctgx=y 1 —1 + V—ctg х.
2.	Верно ли, что всякое решение неравенства
log, (х* — 4х -|- 6) <С — 2 будет решением неравенства
Г
log] (Зх‘ — 14x-f-9)<0?
2—
3.	В прямоугольном треугольнике АВС с острым углом 80° про-
ведена высота CD из вершины прямого угла С. Найти расстояние
между центрами окружностей, вписанных в треугольники ACD и
BCD, если меньший катет треугольника АВС равен 1.
4.	Две хозяйки затратили одинаковое количество денег на
покупки. Первая купила картошку, а вторая—яблоки, причем кар-
тошки было куплено на 8 кг больше, чем яблок. Если бы яблоки
и картошка стоили дороже на 10 коп за килограмм, то в этом
случае первая- хозяйка купила бы картошки на 3 кг больше, чем
вторая — яблок. Если бы при первоначальной стоимости первая
хозяйка купила столько килограмм яблок, сколько у нее оказа-
лось картошки, а вторая купила бы столько картошки, сколько
у нее оказалось яблок, то первой пришлось бы истратить на
3 руб 20 коп больше, чем второй. Сколько стоили килограмм яб-
лок и килограмм картошки?
5.	На основании правильной четырехугольной пирамиды со сто-
роной основания а и, двугранным углом при основании а лежит
шар, касающийся основания в его центре. Плоскость, проходящая
через вершину пирамиды и середины двух смежных сторон осно-
вания, касается этого шара. Найти его радиус.
Вариант 4
1.	Решить уравнение	...
V l.+ /tg2x-|-j/' 1 —/3tgx’=/l — j/tg^x-f-K1
2.	Верно ли, что в сякое решение неравенства log] (5 — 2х — х*)<
 г
<? — 1 будет решением неравенства
log] (8 — Зх — 2х*) < - 1 ?
3.	В прямоугольном треугольнике АВС с катетами 3 и 4 прове-
дена высота CD из вершины С прямого угла. Найти расстояние
между центрами окружностей, вписанных в треугольники ACD
и BCD.
175
4.	Школьник купил в магазине несколько тетрадей и каранда-
шей, причем все тетради стоили столько же, сколько все каранда-
ши, а тетрадей было на три штуки больше, чем карандашей. Если
бы при этом один карандаш стоил на 10 коп дороже, а одна тет-
радь тоже стоила на 10 коп. дороже, то, истратив те же
деньги как на тетради, так и на карандаши, что и раньше,
можно было бы купить тетрадей на одну больше, чем карандашей.
Если бы школьник купил по первоначальной стоимости тетрадей
столько, сколько было куплено карандашей, а карайдашей столь-
ко, сколько было куплено тетрадей, то за карандаши пришлось бы
уплатить на 90 коп. больше, чем за тетради. Сколько стоит один
карандаш и одна тетрадь?
5.	Шар лежит на основании прямого кругового конуса, касаясь
основания в его центре. Плоскость, образующая угол 0 с высотой
конуса, касается шара и отсекает на окружности основания дугу
с острым центральным углом а. Найти радиус шара, если радиус
окружности основания равен /?.
Разбор варианта 1
Задача 1. Необходимо потребовать, чтобы sinx^O и cos2x>0.
Тогда возведение обеих частей этого уравнения в квадрат приво-
дит к равносильному уравнению
1^1 — cos2x = yi—sinx.
Поскольку обе части этого уравнения неотрицательны, то повтор-
ная операция «возведения в квадрат» дает еще одну форму рав-
носильного уравнения
cos 2х= sin х
или	1—2sin2x=sinx,
2sin2x+ sinx—1=0,
решения которого имеют вид
1. sinx=—1; х =—y-|-2ic«.
2. sinx=-^-; х =	+ 2кп, х = —|-2пп.
Однако условиям sinx^O, cos 2х>0 удовлетворяют не все из этих
решений. Легко проверить, что ответами в задаче могут служить
только числа
•	х = -|~-|~2«л и х =	4- 2ип.
Ответ: х=л/6+2лп, х=5л/6+2лп, л=0, ±11, ±2 ....
176
Задача 2: Решим каждое из данных неравенств.	}
1.	Iog,(5x»-21x4-7)>l,
5л» - 21х4-7>3,
5х» — 21х-}-4>0,
 * л >4.
э	-
2.	log, (х» — 4х 4- 2) > О,
х1 — 4х-|--2> 1,
х» —4х-|-1>0,
х<2-УЗ- х>2+/3-.
Теперь становится очевидным, что всякое решение первого нера-
венства будет решением и второго неравенства. Если рассматри-
вать х>4, то ясно, что все такие числа будут больше, чем 2+ УЗ,
т. е. будут служить решениями второго неравенства. То же самое
можно сказать и о числах х<1/5. Очевидно, что все они удовлет-
воряют второму неравенству, поскольку будут меньше, чем
2—У3. Ведь ясно, что 1/5<2—УЗ.
Ответ: верно.
Задача 3. Пусть Ох и О2 — центры окружностей, вписанных
в ADBC и AABD соответственно, рис. 45. Расстояние OiO2 между
этими точками найдем из прямоугольного треугольника O1O2O3,
где Оз — проекция точки Oi на радиус ОгМ2 окружности О2, про-
веденный из ее центра в точку М2 касания со стороной АС тре-
угольника:
О.О, = /0,0», 4-0x0’,.
Найдем стороны О2О2 и O1O3.
Вычислим сначала радиусы окружностей и т2. Для этого ис-
пользуем формулу
где S — площадь треугольника, ар — его полупериметр.
Известно, Что ВС=\, угол А равен 30°. Тогда АВ = 2, .а АС=
= УЗ. Поскольку биссектриса BD делит сторону Л С на части,
пропорциональные сторонам ВС и АВ, то
ГГ)__	1 _. АГ)______о — 2
1 + 2 1 — 3 ’	1 + 2 2 “ 3
Далее из ADBC легко находится гипотенуза BD: .
BD ==УВС*-\-СО* =
Отсюда, в частности, следует, что BD=AD и &ABD— равнобедг
ренный. Поэтому AM2^AN2=*l. Здесь N2 — точка касания окруж-
ности 02 со стороной АВ.
12—619	177
Находим радиус г<;
_ sdbc _ 1/2-BC-CD1______ьКз/з; а ;г
г'~~ и	~~ 1 +/з7з + 2Кз/з — з+ИГ’
Находим радиус г,: •
__^ЛДР	2-Уз/З _	1
* — Pt Pt ~~ 24-4/3/3 “2+ИГ
Рис. 45.	Рис. 46.
Определяем 0,0,:
0,0, — г, — г, = ——г_ (2 + утГ) • ,
Определяемого,:	1
__	]	2*1/3" 1
0,0. = АС - ЛИ. - СМ, = КЗ - 1 - 5-pjzr-=-
I Вычисляем 010,:
л п -1 Г г 1____________Г , [2/3 -1Г-^± /96 - 54 Уз.
V L (з+/з) (г+’/з") J * L з + т^з J 3
Ответ:	96 — 54J/3/3.
Задача 4. Пусть ui—пропускная способность, первой трубы, а
«2 — пропускная способность второй "трубы. V — объем, который
заполняет каждая из труб в том случае, когда на весь этот про-
цесс затрачивается 16 часов. Имеем уравнение
—+—=16.	(1)
а» 1 и,	' '
Если бы через первую трубу вода текла столько времени,
сколько через вторую, а-через вторую — столько времени, сколько
через первую, то через 1-ю трубу налилось бы воды на 320 м3
178
меньше, чем через 2-ю. Этому условию задачи соответствует урав,-
нение
Последнее условие задачи приводит к уравнению
Имеем систему трех уравнений:
(V(Ui + u,)= 16-UiUa,
-• V («!-)-«») (tit— Ui) = 320utUt,
V (и, +	= 20 («?- 10) (ut + 10),
решения которой таковы:
-	«1=30; «а=50, У=300.
Отсюда находим искомые продолжительности:
, зоо 1П . зоо
Л==ЗО-=10 И	/>==5б- = 6
Ответ: 10 часов, 6 часов.
Задача 5. Рисунок к задаче изображен на чертеже 46. Очевид-
но, что радиус R' шара равен радиусу вписанной в треугольник
ESF окружности, где Е и F— середины отрезков АО и ОС соот-
ветственно. Тогда
~ Eaesf/ PkESF'
где SAESP и pABSP — площадь и полупериметр треугольника ESF.
Имеем:
. Saesf==-T EF OS==-y'cos-T 4“’asin4'=T’sina-
Plesf = 4“ (EF + 2'SF) = 4" ° cos T+
+ /£Lcos«4+^sin‘^-=4 (1+cos Г).
Ответ: /? = a sin a/4 (1 -f- cos a/2).
§ 23. ХИМИЧЕСКИЙ ФАКУЛЬТЕТ, 1975 г.
Вариант 1
1. Решить неравенство
g2j—10—з Vx—2	s 51+3
2. На второй остановке в автобус вошло на двенадцать человек
больше, чем вышло на третьей остановке, а на третьей вошло на
три человека меньше, чем вышло на четвертой. Вошло на четвер-
12*	179
той вдвое больше, чем на второй. На четвертую остановку приеха-
ло на тринадцать человек больше, чем уехало с первой. Что боль-
ше и на сколько, число человек, вошедших на второй остановке,
или число человек, вышедших на второй остановке?
Известно, что если бы ’на второй остановке вышло- вдвое боль-
ше человек, чем вошло на третьей, то с четвертой остановки
уехало бы на девять человек больше, чем с (первой.
3.	В треугольнике АВС сторона ВС=5. Окружность проходит
через вершины В и С и пересекает сторону АС в точке К так, что
СЛ=3, лД = 1. Известно, что косинус угла АСВ равен 4/5. Найти
отношение радиуса данной окружности к радиусу окружности,
вписанной в треугольник АВК.
4.	В треугольной пирамиде SABC (S — вершина, треугольник
АВС — основание пирамиды) грань SAC перпендикулярна грани
АВС. Кроме того, SA =SC= 1, а угол при вершине В треугольни-
ка АВС—прямой. Шар касается плоскости основания пирамиды
в точке В, а грани SAC — в точке S. Найти радиус шара.
5.	Найти все значения параметра Ь, при которых система
{cos (у — b) — 2cos х = О,
log. (by - у*) = 21og* (- х) - log] (30
Г
имеет нечетное число решений.
Вариант 2
1.	Решить неравенство
.	—2	1 у 3^	18- Зх+2	1
2.	В хоккейном матче, состоящем из трех периодов, команда
А победила команду В с перевесом в две шайбы, причем ни одна
из команд не забила шайб в свои ворота. В первом периоде ко-
манда А забила столько же шайб, сколько пропустила она в свои
ворота во втором периоде, а в третьем периоде эта же команда
забила на одну шайбу меньше, чем в первом. В первом периоде
команда А пропустила вдвое больше шайб, чем в третьем. Что
больше и на сколько, число шайб, забитых командой А во втором
периоде, или число шайб, забитых командой В в третьем периоде?
Известно, что если бы команда А забила во втором периоде
столько же шайб, сколько она забила в первом, то она выиграла
бы первые два периода с перевесом в пять шайб.
3.	В треугольнике АВС косинус угла ВАС равен 1/2, АВ=2,
АС=3. Точка D ‘лежит на продолжении стороны АС так, что С
находится между А и D, CD—3. Найти отношение радиуса окруж-
ности, описанной около треугольника АВС, к радиусу окружности,
вписанной в треугольник ABD.
180
4.	В треугольной пирамиде SABC (S — вершина, треугольник
АВС — основание пирамиды) углы SAB и SAC прямые. Шар ка-
сается плоскости треугольника АВС в точке А и боковых ребер
SB и SC в их серединах. Найти радиус шара, если -ВС=а и угол
ВАС равен 0.
5.	Найти все значения параметра а, при которых система
sin (а — у) + 2sin х'= О,
21ogu'(a — У) + 41og, у = log, + 31о£“х
имеет четное число решений.
Вариант 3
1. Решить неравенство
Зх	_
42 _|_ 2Х~	< 3 • 21-*-2 **.
2/ В понедельник в библиотеке было выдано на сорок книг
больше, чем во вторник, а во вторник было сдано книг вдвое мень-
ше, чем в среду. В среду было выдано на двенадцать книг мень-
ше, чем во вторник. За эти три дня было выдано столько же книг,
сколько сдано. Что больше и на сколько, число книг, выданных
в среду, или число книг, сданных в понедельник?
Известно, что если бы в понедельник было сдано столько же
книг, сколько сдано во вторник, то за понедельник и среду было
бы выдано на двадцать семь книг больше, чем сдано (за понедель-
ник и среду).
3.	В треугольнике BCD косинус угла BCD равен 3/4, ВС=4,
CD =8. Точка А лежит на стороне CD данного треугольника так,
что СА — 2. Найти отношение площади круга, описанного около
треугольника BCD к площади круга, вписанного в треугольник
ABD.
4.	Дана пирамида SABC (S — вершина, треугольник АВС —
основание пирамиды), в которой ребро АС перпендикулярно гра-
ни 5ЛВ. Шар касается грани ASC в точке S, а грани АВС — в точ-
ке В. Найти радиус шара, если ДС=1, ZACB=Z_BCS=60°.
5.	Найти все значения параметра Ь, при которых система
cos (b — у) — 3cos х = О,
21og, (by — у2) = log, (Зх) - log^y.
Г
имеет нечетное число решений.
181
Вариант 4
1.	Решить неравенство
Зх . уг_“
92	* ,<8-32ж+зГ*
2.	Две шахты соревновались в течение первого квартала. Мар-
товская добыча второй шахты была на четыреста тонн меньше
февральской .добычц первой шахты. Январская добыча первой
шахты равнялась ее'же мартовской добыче и равнялась февраль-
ской добыче второй Шахты. По итогам первых двух месяцев добы-
ча первой шахты оказалась меньше, чем добыча второй шахты на
ддну тысячу тонн. Что больше и на сколько, январская добыча
первой шахты или январская добыча второй шахты?
Известно, что если бы январская добыча второй шахты равня-
лась ее же мартовской добыче, то добыча второй шахты за ян-
варь, февраль, март месяцы оказалась бы больше добычи первой
шахты за эти же месяцы на одну тысячу триста тонн.
3.	В треугольнике АВС косинус угла АСВ равен 2/3, АС=3,
ВС=9. Точка D лежит на стороне ВС так, что CD=3. Найти отно-
шение площади круга, описанного около треугольника ACD, к
площади круга, вписанного в. треугольник ABD.
4.	Шар радиуса R касается всех боковых граней треугольной
пирамиды в серединах сторон ее основания. Отрезок, соединяю-
щий вершину пирамиды с центром шара, делится пополам точкой
пересечения с основанием пирамиды. Найти объем пирамиды.
5.	Найти все значения параметра а, при которых система
|	sin (За — Зу) -|-3 sinx = О,
121og« (а — у) 4- 21og4 (2 У у) .== log, У у -f- 31og, (2х)
имеет четное число решений.
Разбор варианта 1 *
Задача 1. Заметим,, что обозначив
=	53 У-= q>О,
данное неравенство можно записать весьма просто:
Учитывая, что q^>9, получаем квадратное неравенство
182
откуда находим
	-l<f<5.
Поскольку отношение -pfq положительно, имеем
0< —<5,
я
или
у-5_3 Vx-2 <
х _ 5 - 3 Vx^2 < 1,
х —6<3 Vx=2.
Согласно общим правилам решения иррациональных нера-
венств рассмотрим два случая:
а)	2<х<6; в этом случае х — 6<0, 3)/х — 2 =а0.
Поэтому неравенство в.ыполнено и все х от 2 до 6 служат его ре-
шениями.	,
б)	х^б; в этом случае обе части неравенства неотрицательны
и при возведении их в квадрат получается неравенство, равносиль-
ное исходному:
Jx>6	, .Jx>6,
Iх - 6<3 ]Гх^2	((х - 6)‘<9 (х- 2)
или
| х^б
I х* —21x-f-54 <0.
Решения этой системы имеют вид: б^х<18.
Объединяя решения обоих случаев, получаем решение задачи.
Ответ: 2<:х<18.
Задача 2. Обозначим количество человек вошедших и вышед-
ших на 2-, 3- и 4-й остановках соответственно через т\ и /Иг, «1 и
«е, pi и р2. Тогда условие задачи приводит к следующим уравне-
ниям:	-	
mi=n2+12,
П1 = Р2—3,	(1)
pl=2mi.
Кроме того, условие о том, что на четвертую остановку приехало
на 13 человек больше; чем уехало с первой, можно записать сле-
дующим образом:
.	(mrHh)—13. -	(2)
183
Понятно, что это число определяется разностью между числом
пассажиров, вошедших на второй и третьей остановках, и числом
пассажиров, вышедших на этих остановках.
Наконец, последнее уравнение задачи определяется из условия,
что при 7П2=2П1 разность между числом пассажиров, вошедших на
трех остановках и вышедших на них, равна 9:
(mi+ni+pi) —(2/11+П2+Р2) =9.	(3)
Своеобразие настоящей задачи заключается в том, что из по-
лученной системы нельзя определить все шесть неизвестных ве-
личин /Til, tnz, fit, П2, pi и рг, но можно найти искомую разность
(mi—/п2). Для этой цели сложим два первых уравнения системы
(1) и вычтем их сумму из уравнения (2). Получим выражение для
Рг.'
р2=/П2+4.
Поэтому на основании равенств (1) можно написать
П1 = р2-3 = 7772-1- 1,
772 = 7771—12,
/71 = 2/771,
/72=7772 + 4,	. ,
т. е. неизвестные /7Й п2, pi и р2 выразить чер^з mi и т2. Подстав-
ляя последние выражения в.уравнение (3), находим:	а
(/771+ (т2 + 1) +2/771}—[2(7772+ 1) + ( 7771—12) + (??72 + 4)j = 9,
7771—7772= 1,
т. е. определяем искомую разность. Конечно, найти такую разность
удалось только благодаря специальному заданию чисел в условии
задачи.
Ответ: на второй остановке число вошедших пассажиров пре-
восходит число вышедших на 1.
Задача 3. Чертеж к этой задаче представлен на рис. 47. Сое-
диним точки В и К отрезком прямой. Тогда окружность, проходя-
щая через точки В, С и К, будет описанной во круг, треугольника
ВСК. Обозначим радиус этой окружности через /?, угол ВСК —
через а, радиус окружности, вписанной в треугольник АВК — г,
полупериметр треугольника АВК — р. Для нахождения радиусов
R и г используем’известные формулы:
5да = р г=+-ЛС-ВС .1па-4-ЛС ВС.>1п.; 2R = jg-.
Вычисления производим в следующем порядке.
184
1.	Найдем сторону АВ треугольника АВС по теореме косину-
сов:
АВ2=АС2+ВС2—2-АС-ВС- cos а,
АВ2= 16+25—2-4-5-4/5=9,’
ЛВ=3.
(Так как ВС=5, АС=4 и АВ=3, то ДЛВС— прямоугольный.)
2.	Из треугольника АВК находим:
Л'В’ = АК* 4- ЛВ«; КВ = 1*4-3’,
кв=/1о.
О
Рис. 47.	Рис. 48.
3.	Вычислим площадь треугольника АВК:
4.	Найдем радиус окружности, вписанной в треугольник АВК:
г —	________1,5__________3
“ Р ~' (3 + 1 + КТб)/2 — 4+КТо’
5.	Вычислим радиус окружности, описанной вокруг треуголь-
ника ВСК, используя для этого теорему синусов:
№=£. К = ф°-
sin а	о/э	о
185
Тогда искомое отношение радиусов окружностей равно:
R 5/16.	3	5 (5+2 /Тб)
г “ 6	4 +/Тб ~	9
Ответ: [5 (5 + 2
Задача 4. Чертеж к этой задаче представлен на рис. 48. Центр
шара, о котором идет речь в задаче, находится на пересечении
двух перпендикуляров. Один из них восставлен к плоскости
основания в точке В, а другой — к плоскости треугольника ASC
в точке S. Обозначим центр шара через О. Если из точки S опу-
стить перпендикуляр SD на плоскость основания пирамиды АВС,
то точка D будет лежать на ребре АС, поскольку плоскость ASC
перпендикулярна плоскости АВС. Соединив точки D и В отрезком
прямой, получим четырехугольник BOSD, который является квад-
ратом. Действительно, OB||SZ) и OS||BD, т. е. рассматриваемая
фигура — параллелограмм. Учитывая, что угол OBD — прямой и
что OS = OB=\R, получим, что эта фигура — квадрат.
Поскольку SD — высота равнобедренного треугольника 4SC,
то точка D — середина ребра АС. Отсюда следует, что прямоуголь-
ный треугольник ЛВС —равнобедренный. Тогда BD = CD. Таким
образом, имеем \
SD=>BD = CD=R.
Из прямоугольного треугольника SDC, в котором гипотенуза SC
равна 1, находим, что R—У 2/2. •
Ответ: -у-	\
Задача 5. Прежде всего отметим, что допустимые х и у должны
удовлетворять следующим условиям
л
х<0, у>0.
Второе уравнение системы можно преобразовать в этом случае
к виду
log2(&f/—у2) = log2(—Зху),
или
Ьу—у2 = —3ху.
Очевидно, что все допустимые значения х и у, удовлетворяющие
этому уравнению, удовлетворяют также и условию:
by—y2>Q.
Далее это уравнение можно упростить, разделив обе его части на
У (^>0):
Ь—у----Зх.	(1)
Подставим этот результат в первое уравнение системы:
cos Зх=2 cosx.
186
Используя формулу косинуса утроенного аргумента, получим:
4 cos* х — 3 cos х *= 2 cos х, •
5
cos8 X = -7- COS X.
4
1. cosx = 0, x = -^--l~itn, где n = 0, =tl,rt2....
5
2. cos1 x = -^-, решений нет.
Учитывая, что х<0, получим, что п<0, т. е. п=1, —2, —3, ....
Подставим найденные значения х в выражение (1) для у
у = Ь+^ + Ъкп	'
/
и учтем, что i/>0. Очевидно, что	[-*-	р*.
при целых п<0 это возможно	---rf'&r*—«——
только в том случае, если &>0.О
Подберем теперь значения b таким 2	2 i 2	2
образом, чтобы система уравне-	р 49
ний имела .нечетное число реше-
ний.
На рис. 49 изображены числа	—|—Зтсп, где «= — 1, —2,....
Если положительные значения параметра b выбирать согласно
одному из условий
Згс 1 Эл:
—<Ь<^-,
или
2 < D<* 2 ’
и;и
27гс ЗЗтс
— <6<Т
вообще
^-4-6wn<6<^ + 6x/n, где т = 6, 1,2, 3 ...,
то в каждом случае найдется только нечетное количество це-
лых отрицательных чисел п, при которых у>0, т. е. система будет
иметь нечетное количество решений.
Ответ: ^-+ 6wi<b-<где m = 0, 1, 2, 3,... .
187
$ 24. ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ, 1972 г.
Вариант 1
1.	Решить уравнение •
sin3x—sinx-l- cos2x=l.
2.	Решить неравенство
log.,. х* -J- log*.. х < 2.
3.	В двух сосудах имеется вода разной температуры. Из этой
воды составляют смеси. Если отношение объемов воды, взятой из
первого и второго сосудов, равно 1 :3, то температура смеси 49°,
а если 2:5, то температура смеси 48°. Найти температуру воды
в каждом сосуде, считая, что плотность и удельная теплоемкость
воды не зависят от температуры.
4.	На сфере, радиус которой равен 2 м, расположены три
окружности радиуса 1 м, каждая из которых касается двух дру-
гих. Найти радиус окружности» меньшей, чем данные, которая
также расположена на данной сфере и касается каждой из дан-
ных окружностей.
5.	В треугольнике АВС угол В равен л/4, угол С равен л/3. На
медианах ВМ и CN как на диаметрах построены окружности, пе-
ресекающиеся в точках Р и Q. Хорда PQ пересекает среднюю ли-
нию MN в точке F. Найти отношение длины отрезка NF к длине
отрезка FM.
Вариант 2
1.	Решить уравнение
tg Зх—tg х=4 si n х.
2.	Решить неравенство
log3(34x—3^+* + 3) <2 log» 7.
3.	Два автомобиля выезжают одновременно навстречу друг
другу. Первый — из пункта А, второй — из пункта В. К моменту
встречи первЖй автомобиль проехал расстояние в 1,4 раза большее,
чем второй. Если скорость первого автомобиля увеличить на
21. км/ч, то они встретятся в пункте С таком, что АС=2СВ. Найти
скорости автомобилей.
4.	Дан куб ABCDA'B'C'D'; при этом АА'||ВВ'||СС'||Ш)'. Ребро
куба равно а, Е — середина ребра A'D', точка F — середина ребра
АА'. Найти радиус меньшей из двух сфер, проходящих через точки
Е и F и касающихся граней двугранного угла, образованного плос-
костями ВВ'С'С и DD'C'C-
188
5.	В трапеции ABCD основание AD вдвое больше основания
ВС, угол А равен л/4, угол D равен л/3. На диагоналях трапеции
как на диаметрах построены окружности, пересекающиеся в точ-
ках М и N. Хорда MN пересекает основание AD в точке Е. Найти
отношение длины отрезка АЕ к длине отрезка ED.
Вариант 3
1.	Решить уравнение
cos Зх sin х 4~ 2cos*	— х^ — 1.
2.	Решить неравенство
log^-j/x* • log,. (100х) < 3 logit x.
3.	Имеются два слитка сплавов золота и меди. В первом слит-
ке отношение золота к меди 1 :2, а во втором — 2:3. Если спла-
вить 1/3 первого слитка с 5/6 второго, то в получившемся слитке
окажется столько золота, сколько было в первом меди, .а если £/3
первого слитка сплавить с' половиной второго, то в получившемся
слитке окажется меди на 1 кг больше, чем было золота во втором
слитке. Сколько золота в каждом слитке?
4.	На сфере, радиус которой равен 4 м, расположены три
окружности радиуса 2 м, каждая из которых касается двух дру-
гих. Найти радиус окружности, большей, чём данные, которая так-
же расположена на данной сфере и касается каждой из данных
окружностей.
5.	В треугольнике АВС угол В равен л/4, угол С равен л/6. На
медианах ВМ и CN как на диаметрах построены окружности, пе-
ресекающиеся в точках Р и Q. Хорда PQ пересекает сторону ВС
в точке D. Найти отношение длины отрезка BD к длине отрезка
DC.
Вариант 4
1.	Решить уравнение
cos — cos -у = 3 (1 -|- cos х).
2.	Решить неравенство
log, (24Х 4- 2*х) < 21og. 12.
3.	Из пункта А вниз по течению реки отправляется катер, ко-
торый движется относительно берегов со скоростью 10 км/ч. На-
встречу ему из пункта В в тот же момент отправляется лодка. Ка-
189
тер и лодка встречаются между пунктами А й В в такой точке С,
что АС=5-СВ. Если бы катер отправился из-пункта В, а лЬдка —
из пункта А, то они встретились бы в такой точке D, что AD = DB.
Найти скорости катера и лодки в стоячей воде.
4.	Дан куб ABCDA'B'C'D'; при этом AA'\\BB'\\CC'\\DD'. Ребро
куба равно а. Точка Е — середина ребра АА'. На продолжении
ребра DA взята точка F. Точка А лежит между F. и D\ 2FA=AD.
Найти радиус меньшей из двух сфер, касающихся граней двугран-
ного угла, образованного плоскостями ВВ'С'С и DD'C'C и прохо-
дящих через точки Е и F.
5.	В трапеции ABCD основание AD вдвое больше основания
ВС, угол А равен л/4, угол D равен я/б. На диагоналях трапеции
как на диаметрах построены окружности,- пересекающиеся в точ-
ках М и N. Хорда MN пересекает основание В.С в точке F. Найти
отношение длины отрезка BF к длине отрезка FC.
Вариант 5
1.	Решить уравнение
sin Зх— sin x=2cos2 2х.
2.	Решить неравенство
'	У 2 logt0.x >* logic Vх.
3.	В двух сосудах налита вода, в первом сосуде находился 1 л
воды. Температура воды во втором сосуде равна 10°. Если сме-
шать половину воды из второго сосуда со всей водой первого со-
суда, то температура смеси будет 40°. Если же Смешать всю воду
второгр сосуда ссгвсей водой первого, то температура смеси будет.
30°. Сколько воды во втором сосуде и какова температура воды
в первом сосуде? Считать, что плотность и удельная теплоемкость
воды не зависят от температуры.
4.	В трехгранный угол, все плоские углы которого равны а,
помещена сфера так, что она касается всех ребер трехгранного
угла. Грани трехгранного угла пересекают сферу по окружностям
радиуса R. Найти радиус сферы.
• 5. В остроугольном Треугольнике.'АВС угол С равен я/3. На
медианах ВМ и CN как на диаметрах построены окружности, пе-
ресекающиеся в точках Р и Q. Хорда PQ пересекает сторону ВС
в точке D такой, что BD : ОС=~Уз. Найти угол В.
Вариант 6
1.	Решить уравнение
. Зх 5х -	.
COSX-f-COS-g--COS -у — 1.
190
2.	Решить неравенство
logio(lOx) • log2*<2 log210.
3.	Расстояние между городами А и В равно 625 км. Два авто-
мобиля, выехавшие одновременно настречу друг другу, первый —
из А, второй — из В, встретились через 5 ч. Если бы первый авто-
мобиль выехал на 4 ч 10 мин раньше второго, то- встреча прои-
зошла бы через 3 ч после отправления второго автомобиля. Найти
скорости автомобилей.
4.	Дан куб ABCDA'B'C'D'; при этом AA'\\BB'\\CC'\\DD'. Ребро
куба равно а. Точка Е— центр грани A'D'DA. Найти радиус мень-
шей из двух сфер, проходящих через точки А и Е и касающихся
граней двугранного угла, образованного плоскостями ВВ'С'С и
DD'C'C.
5.	В трапеции ABCD основание AD вдвое больше основания
ВС, угол А равен л/6, угол D равен л/3. На диагоналях трапеции
как на диаметрах построены окружности, пересекающиеся в точ-
ках К и. L. Найти отношение площадей четырехугольников, на ко-
торые хорда KL разбивает трапецию ABCD.
Разбор варианта 1
Задача 1. Решим уравнение
•	sin3x—sinx+ cos2x=l.
Выполним тождественные преобразования:
2sinxcos2x+ cos2x=l,
2 s in х cos 2х=2 sin2 х,
sin x (cos 2x— sjn x) =0.
Отсюда находим
1)	sinx = 0; x = itn.
2)	cos2x — sinx — 0,
2 sin* x-<|-sinx — 1 = 0,
«
a)	sinx=—1, x =-----—|-2itn;
6)	si’nx=l/2, x=(— l)n
Ответ: 1) x =	2) x = —2ъп;
3)	x = (- l)"-^- + «n.
191
Задача 2. В этой задаче допустимы х>0. Переходя к основа-
нию 10, получаем
lg2 х+ 1g х—2<0.
Отсюда
—2< 1g х<1,
1/100<х<10.
Ответ: 0,01<х<10.
Задача 3. Обозначим температуру воды из первого и второго
сосудов через 7\ и Т’а соответственно. Очевидно, 7,2>7’1. Это сле-
дует из того факта, что повышение в смеси относительной доли
воды из первого, сосуда приводит к понижению температуры смеси
с 49° при соотношении объемов 1 :3 до 48° при соотношении объе-
мов 2:5. Конечно, здесь принимается, что плотность и теплоем-
кость воды не зависят от температуры.
В силу этого же условия уравнение баланса количества тепла
можно записать так:
49 - Л = 3 (Л - 49),
2(48 —Л) = 5 (Г,—48).
Первое из этих уравнений отражает гот факт, что сколько теп-
ла необходимо для повышения температуры одной единицы объе-
ма воды из первого сосуда от Т\
до 49°, столько же тепла отдают
при охлаждении от температуры
7% до 49° три единицы объема
воды из второго сосуда. Второе
уравнение имеет аналогичный
смысл. Здесь теплоемкости и
плотности сокращаются, ^посколь-
ку в силу условия задачи они счи-
таются независящими от темпера-
туры.
Решая эту систему, находим
7'1=28°, 7’2=56°.
Ответ: 7'1 = 28°, 7’2=56°.
Задача 4. Чертеж к этой зада-
че представлен на рис. 50. ’ Обо-
значим центр сферы посредством
буквы О, а через Oi, О2, О3—
положение на сфере центров окружностей, в которых идет речь
в условии задачи. Точка О4— центр искомой окружности.
Легко усмотреть, что точки О, О], О2, Оз являются вершинами
правильного тетраэдра с ребром, равным 2 м. Действительно, диа-
метр любой из данных окружностей равен 2 м. Поэтому если его
концы соединить с центром сферы, точкой О, получится правиль-
192
ный треугольник. Таким образом, каждую из данных окружностей
можно рассматривать как окружность основания прямого круго-
вого конуса с углом при вершине 60°. Значит, мы имеем три оди-
наковых попарно касающихся прямых круговых конуса с общей
вершиной в точке О. Поэтому ясно, что углы ОгОО2, O1OO3, O2OO4
равны 60° каждый.
В силу симметрии ясно, что центр искомой окружное^, точка
О4 лежит на высоте правильного тетраэдра OOiO2O3. Углы O1OO4,
О2ОО4 и O3OO4 равны между собой и, как легко подсчитать, равны
. КГ
arcsin -5—
о
В то же время углы KiOOi, КгОО2 и КзОО3 между радиусами
сферы, проведенными в центры окружностей Oi, О2 и О3 и точки ка-.
сания Ki, Къ и Кз искрмой окружности с данными окружностями,
равны по 30°. Таким образом, углы KiOO4, КъООь и Д3ОО4 равны
и определяются разностью:
. /Г	*
arcsin -=--f—
3	о
Тогда радиус искомой окружности равен:
о о • Г • КГ 1	, КГ
R = 2 sin arcsin -----= 1-------5—
о о	3
Задача 5. Чертеж к этой задаче представлен на рис. 51 и
рис. 52. Обозначим через О точку пересечения медиан CN' и ВЛГ,
через Oi и О2 — середины медиан, центры построенных окружно-
стей.
Опустим из точек М и N перпендикуляры на основание тре-
угольника ВС. Эти перпендикуляры попадут в точки К и L, л ежа-
13-619	1QQ
щие на окружностях с центром в точках О2 и Oi соответственно.
Данное утверждение следует'из того, что углы МКВ и NLC опи-
раются на диаметры соответствующих окружностей.
Линия центров OiO2 параллельна отрезкам MN и ВС, а общая
хорда окружностей PQ перпендикулярна этим отрезкам. Отсюда
следует, что FM—ST. Поэтому отношение отрезков NF:FM мож-
но найти следующим образом:
NF _ MN — FM _MN — ST ~
FM FM . -JST ‘
Точка S является пересечением OiO2 и МК, а точка Т — хорды
PQ и отревка О\О2. Таким образом, надо найти длины отрезков
•MN, SOt и OiT. .
Обозначим длину основания ВС треугольника через 1. Тогда
длина средней линии MN равна Vz- По теореме синусов находим
стороны треугольника АС и АВ:
АС _ АВ _	1
it	те	( те те \
sin-5-	sin-5- sin( —Ь— \
Отсюда:
АС = /3~- 1, АВ = 2 /Г/(/б’+ ]Г2).
Учитывая, что BAf=2Ki и CN=2R2, где Ki и Л2 — радиусы
окружностей, по теореме косинусов вычисляем радиусы окружно-
стей:
nt _ ю-4/з~	.4-/3"
Pi 1б И Pl 16
В треугольнике СМК угол СМК равен 30°. Значит,
СК = 4- СМ= -^-АС —	1
Поэтому
n„ 1	/з"-1	5-Кз"
ВК= 1------4-=-----4--’
и, наконец,
^О1 = 4-вк=5~Гг-
Z	о
Вычислим теперь длину отрезка ST. Для этого рассмотрим
рис. 52. Расстояние О\О2 очевидно, равно 'А- Составим уравнения
P’l-i/^P*. -X*.
(у — х) = P»i — К’..
194
Легко проверить, что точка Р проектируется на отрезок O1O2.
Здесь х=ОгТ и у=О\Т. Имеем
у — х = 4 (К‘1 — /?•,)
. 1
У+*=— -
^=4- + 2(/?S-№).
Подставляя значения R*t и R*t находим
у=7~3я--=о1т.
О
Тогда
ST= VT~1 •
Подставляя полученные значения отрезков MN и ST в выраже-
ние для отношения NF: FM, получаем ответ:
NF:FM = VW.
*
§ 25. ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ, 1973 г.
Вариант 1
1.	Решить уравнение
]/3 (sin x]4~rsin 2х = 0.
2.	Решить уравнение
/ _£\
3««-‘ = 2 \27* 3J + 1.
3.	Сумма первых тринадцати членов арифметической прогрес-
сии равна 130. Известно, что четвертый, десятый и седьмой члены
этой прогрессии, взятые в указанном порядке, представляют собой
три последовательных члена геометрической прогрессии. Найти
первый член арифметической прогрессии.
4.	Боковые грани треугольной пирамиды SABC с вершиной
S образуют одинаковые двугранные углы с плоскостью основания
АВС пирамиды, SO — высота пирамиды. Известно, что ZASB =
=7л/12, Z.BSC=n/2, Z.SCA=a/3. '
Найти отношение площади треугольника АОВ к площади тре-
угольника АВС.
5.	Дана окружность с центром О. В ней проведены диаметр IL,
хорды IK и KN. Хорда KN пересекает диаметр IL. Из точки N
13*	•	195
опушён перпендикуляр NF на IK (F между / и К), а из тонки F
опущен перпендикуляр FH на IL. Точка S — середина отрезка 10,
точка М — середина хорды KN. Известно, что радиус окружности
равен R, a LH=SRjb.
Найти длину отрезка SM.
Вариант!
1.	Решить уравнение
2sinx+tgx=0.
2.	Решить уравнение
2««4-8 3 ^5 = 0.
3.	Три последовательных члена геометрической прогрессии Oi,
аг и а3 являются соответственно первым, четвертым и двадцать
пятым членами арифметической прогрессии. Сумма чисел alt аг,
а3 равна 114.
Найти знаменатель геометрической прогрессии.
4.	В треугольной пирамиде SABC с вершиной S боковое грани,
образуют одинаковые двугранные углы с плоскостью основания
АВС пирамиды. Окружность, вписанная в основание, касается
ребра АВ в точке D, а ребра ВС — в точке Е.
Известно, что Z_ASB=7nJl2, ZBSC=5л/12, Z.ASC=л/2.
Найти отношение площади треугольника DBE к площади тре-
угольника АВС.
5.	Дана окружность с центром О. В ней проведены хорда CD
и пересекающий эту хорду диаметр АВ. Из точки.!) опущен пер-
пендикуляр DF на AC (F между А и С), а из точки F опущен
перпендикуляр FH- на АВ. Известно, что радиус окружности R,
a AH=R!±.
Найти расстояние от середины отрезка АО до середины отрез-
ка CD.
Вариант 3
1.	Решить уравнение
2sin2x-|-]/3 созх = 0.
2.	Решить уравнение
Ю1+**— 10I_x, = 99.
3.	Сумма первых десяти членов арифметической прогрессии
равна 30. Четвертый, седьмой и пятый члены этой прогрессии, взя-
тые в указанном порядке, представляют собой три последователь-
ных члена геометрической прогрессии.
Найти разность арифметической прогрессии.
196
- 4. В треугольной пирамиде SABC высота SO проходит через
точку О — центр круга, вписанного в основание АВС пирамиды.
Известно, .что Z.SAC=n/3, Z-SCA=n/4, а отношение площади_тре-
угольника АВС к площади треугольника АОВ равна 2—]/3.
Найти угол BSC.
5. В окружность с центром О вписана трапеция ABCD
(5С||ЛД). В этой же окружности проведены диаметр СЕ и хорда
BE, пересекающая AD в точке F-. Точка Н — основание перпенди-
куляра, опущенного из точки F на СЕ, S — середина отрезка ЕО,
М — середина отрезка BD. Известно, что радиус окружности ра-
вен R, a CH=9R/8.
Найти длину отрезка SM.
Вариант 4
1.	Решить уравнение
2 sin x+cos 2х= 1.
2.	Решить уравнение
(4Г-(тГ'-128=0-
3.	Сумма первых пяти членов геометрической прогрессии рав-
на 62. Известно, что пятый, восьмой, одиннадцатый члены этой
прогрессии являются соответственно первым, вторым, десятым
членами арифметической прогрессии.
Найти первый член геометрической прогрессии.
4.	Прямой круговой конус с вершиной S вписан в треугольную
пирамиду SPQR так, что окружность основания конуса вписана
в основание PQR пирамиды. Известно, что Z.PSR = af2, Z_SQR =
= л/4, ZPSQ=7n/12.
Найти отношение площади боковой поверхности конуса к пло-
щади основания PQR пирамиды.
5.	Дан круг с центром О. Через точку внутри круга проведены
диаметр АВ и хорда CD. Из точки D опущен перпендикуляр DF
на хорду AC (F между Л и С), а из точки F опущен перпендику-
ляр FH на АВ. Точка М — середина хорды CD. Известно, что
АМ=2МО,8АН=ЪАВ:
Найти угол АМО.
Вариант 5
. 1. Решить уравнение 
2cosx—ctgx=0.
2.	Решить уравнение
-	з+1
64х - 2 *4-12 = 0.
197
3.	Три различных числа а, Ь, с, сумма которых равна 124,
являются тремя последовательными членами геометрической про-
грессии. Одновременно эти три числа а, b и с являются соответ-
ственно третьим, тринадцатым и пятнадцатым членами арифме-
тической прогрессии. Найти числа а, Ъ, с.
4.	В треугольной пирамиде SKLM высота SO проходит через
точку О — центр окружности, вписанной в основание KLM пира-
миды. Эта окружность касается ребра RL в точке D, а ребра
LM — в точке Е. Известно, что Z.SK.L—a[3, Z.SLK=nll, а отно-
шение площади треугольника DLE к площади треугольника K.LM
равно (3—V 3)/4.
Найти угол LSM.
5.	В окружности с центром О проведены параллельные хорды
PQ и RS, диаметр SE и хорда RE. Хорда RE пересекает хорду
PQ в точке F, из точки F опущен перпендикуляр FH на SE. Из-
вестно, что радиус окружности равен г, a EH=3rl%.
Найти расстояние от середины отрезка ЕО до середины хор-
ды RQ.
Вариант 6
1.	Решить уравнение	'
]/3” cosx — cos 2х = 1.	w
2.	Решить уравнение
5»-‘4-5»-’ = 26.
3.	Известно, что первый, четвертый и тридцать первый члены
арифметической прогрессии являются соответственно четвертым,
седьмым и десятым членами геометрической прогрессии. Сумма
первых четырех членов этой геометрической прогрессии равна 40.
Найти первые два члена геометрической прогрессии.
4.	В треугольную пирамиду SPQR вписан прямой круговой ко-
нус с вершиной S, окружность основания которого вписана в осно-
вание PQR пирамиды. Известно, что ZSQR = n/4, ZSRQ=n/3,
£.PSR=5л/12.
Найти отношение площади боковой поверхности конуса к пло-
щади основания PQR пирамиды.
Разбор варианта 1
Задача 1. Представляя исходное уравнение в виде
sin х-|-2 Sinx cos х = 0,
получим
sinx (]/3^ + 2 cosx) = 0.
198
Отсюда находим:	. ч
a)	sinx = 0, х =	/
б)	-|~2cosx = 0,
COS X =---2~ ’
х = =t	4- 2it/z.
Ответ: х — кп, х = 2кп.
Задача 2. Введем новое обозначение
.	3« = />0.
Тогда получим квадратное уравнение	,
27 1	9
или
t2— Ы—27=0.
Отсюда находим t±=—3, /2=9. Первый корень не дает реше-
ний, так как />0. Поэтому остается /=9
3‘« = 9, х = 4~-
□
Ответ: 2/3.
Задача 3. Пусть аи а2, а3 и т. д. члены арифметической про-
грессии, разность которой обозначим через d. Тогда условие зада-
чи позволяет записать два уравнения:
Su=_£i+^!L. 13 = 130
О*ю —= О* "О».
Здесь Sis—сумма первых тринадцати членов прогрессии.
Поскольку
ai=ai+3d,
. a7=ai+6d,
aio=ai 4-9d,'
a13=ai+12d,
•то из первого уравнения получаем
Oi+6d= 10,
а из второго
(oi+9d)2= (ai+3d) (oi+6rf)
199
или с учетом первого уравнения:
(10+3d)2= (10—3d) • 10.
Отсюда находим два значения разности прогрессии .
di = 0, d2=—10.
Рис. 53.
Соответственно находим ai=10, ai = 70. Очевидно, что оба значе-
ния первого члена прогрессии удовлетворяют всем условиям за-
дачи.
Ответ: 10, 70.
Задача 4. Обозначим ребра пирамиды ЕЛ, SB и SC через а, Ь
и с соответственно (рис. 53), угол
ЛЕС—посредством а.
Проведем высоты боковых граней
пирамиды SD, SE и SF и сое-
диним точки jD, £, F с точкой О.
Очевидно, что прямоугольные
треугольники SDO, SEO и SFO
равны. Это следует из того, что
они обладают одинаковым острым
углом при основании, который яв-
ляется в то же время линейным
.углом двугранного угла между
боковыми гранями и основанием
пирамиды. Отсюда следует, что
g точка О—центр окружности, впи-
санной в основание, а апофемы
боковых граней пирамид равны.
Поскольку площадь каждого
из треугольников АО В, А ОС и
ВОС равна площади проекции со-
ответствующей боковой грани
пирамиды на основание, а угол
проектирования для всех боковых
граней один и тот же, тог отноше-
ние , площади треугольника АОВ к площади треугольника ABG равно
$АОВ___________________________SASB
$АВС $ASB +	+ $BSC
или
7тс
о	cib sin «Q
^АОВ
Л ь ab sin -pg" + ас sin « + Ьс
7 тс
с	sin . п
°АОВ_______________12	_______
7 тс , с	с
slnl2'+'Tslna + ~
200
Таким образом, чтобы найти искомое отношение площадей, нуж-
но найти угол а и отношения ребер с/b и с/а.
Для этой цели используем следующие равенства, которые сле-
дуют из записи площадей боковых граней пирамиды:
1)	be = h
2)	с sin = h,
О
3)	aftsin^ = ft j/a‘4-62—2a/>cosj“
Здесь h — высота боковых граней пирамиды SABC.
Комбинируя первое и второе уравнения, получим
Комбинируя второе и третье равенства, получаем уравнение
для определения отношения а/с:
7л 1^2 — Уз
C0STT =-------2---
7л
. ,7.	‘-“’ТГ	2 + /3-
sm-	j---=----—
sin
7л V2 + V 3
12 —	2
Тогда ^рассматриваемое уравнение приобретает вид
(1 + /3) (-f-Y-2/З	--3 = 0.
201
Отсюда находится положительный корень
а К"6"
с — 2
Определим теперь угол а. Из треугольника ASC с помощью теоре-
мы синусов находим
а _____£__________________________________
к	/ тс \ *
sin -g- sin I а + — I
f тс \	тс
Sin I «4- — 1= sin-g-.
c
~a
Учитывая, что a — положительная величина, получаем
. тс Зтс
1
и окончательно
5тс
® — ТГ'
Теперь можно вычислить искомое отношение площадей тре-
угольников. Оно равно
$АОв_____________L_________________
Sabc Ц-У2+Г—
V о г о
После несложных упрощений получается
$лов 9 + Кз~
§АВС 2®
Ответ: (9+/3)/26.
Задача 5. Чертеж к этой задаче изображен на рис. 54. Обозна-
д ;	чим через Q проекцию точки М
_________ на хорду IK, а через Т — проек-
S
Рис. 54.
цию точки S на эту же хорду.
Проведем через точку S прямую,
параллельную хорде IK, до пере-
сечения с MQ в точке Р. Длину
искомого отрезка SM будем
определять из прямоугольного
треугольника SPM:
SM2=SP2+PM2.
Осуществим этот процесс не-
посредственными вычислениями.
Для этого обозначим угол K7L
через а.
202
1.	Определим сначала длины отрезков IK, IT, IF и IQ. Из
АПЛ:
IK = 2R cos a.
Из A/ST:
IT = 4* cos a.
Из Д/Z/F:
= _L_.
4 cos a
Поскольку MQ — средняя линия треугольника FKN, имеем
/Q = 4[ZF + «l=4EAr + Scosa.
2.	Определим катет SP треугольника SPM:
3.	Вычислим длину отрезка FN:
FN=FC+CN.
.здесь точка С — проекция центра окружности на FN:
FC = OD = R sin a; CN = VR* -.ОС*.
ОС = IF — ID; ID = R cos a.
Здесь точка D проекция центра окружности на IK:	х
ОС = 4— ------Я cos а.
4 cos a
Итак,
FN = R sin a 4-1 / R* — (~r	---R cos а V .
1 I/	14 COS a	J
4. Определим теперь катет PM треугольника SPM:
PM = QM—QP,
QP = ST =4-sina; 0M = 4~TN.
Отсюда
™=4-1/«-(4 тйт-•
203
5. Теперь по теореме Пифагора вычислим длину искомого от-
резка SM:
-4- -к- 1 [R2 3 4 — (Л---------------R cos а У
1	2 I/ д 4 cos а	)
Ответ- SM = R\/'6 /2.
Замечание. Длина найденного отрезка SM не зависит от ве-
.личины угла а. Тем самым показано, что середины гипотенуз пря-
моугольных треугольников FRN, построенных указанным в усло-
вии задачи способом, образуют геометрическое место точек, пред-
ставляющее_собой дугу окружности с центром в точке S и ра-
диусом /?|/6/2.
Отсюда открывается другая возможность решения задачи. До-
казав каким-либо способом (найдите геометрическое доказательст-
во), что рассматриваемое геометрическое место точек М есть дуга
окружности, проходящей,'очевидно, через точку А и середину хор-
ды BL, можно вычислить радиус этой окружности как расстояние
между точкой S и серединой хорды BL.
§ 26. ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ, 1974 г.
Вариант 1
1. Решить уравнение
ctg х
cos 2*
= 24-tg2x.’
2. Решить неравенство
3|х—11 > (х—1)2+1.
3. Решить уравнение
log*»» х — 3 ]/logj х — 4 — 0.
4. В круг радиуса R с центром в точке О вписана трапеция
ABCD (BC<AD и точка О лежит внутри трапеции). Непараллель-
ные стороны трапеции АВ и CD равны R. Точка К — середина ра-
диуса ОА, точка L—середина радиуса OD, точка М'—середина
стороны ВС. Отношение площади трапеции к площади треугольни-
ка KLM равно 4. Найти длину отрезка МС.
204
5. Дана пирамида SABC, все ребра которой равны a, SO —
высота.* Точка Т — середина ребра ВС. На перпендикуляре к плос-
кости АВС в точке Т отложен отрезок ТМ, равный SO. Через точ-
ки S и М проведена плоскость параллельно плоскости АВС, и
в этой плоскости построен правильный треугольник PQR с цен-
тром в точке М и стороной а, так, что точка S — середина отрез-
ка QM. Найти объем общей части пирамид SABC и TPQR.
Вариант 2
1.	Решить уравнение
УЗ— tgx=tg (-у-~ х
2.	Решить неравенство
х2—2|х+1|<0.
3.	Решить уравнение
2 у/ 2 log’u х — у/ log» х — 6 = 0.
4.	Два одинаковых правильных треугольника АВС и CDE со
стороной 1 расположены на плоскости так, что имеют только одну
общую точку С, и угол BCD меньше, чем л/3. Точка К — середина
АС, точка L — середина СЕ, точка М — середина отрезка прямой
BD. Площадь треугольника KLM равна ]/3/5. Найти длину от-
резка BD.
5.	Даны две треугольные пирамиды SABC и NRLM, все ребра
которых равны а. Эти пирамиды имеют общую высоту SW (S —
центр грани KLM и N — центр грани ЛВС). Кроме того, KLIIBC и
пирамиды расположены так, что плоскость, проходящая через K.L
и ВС, пересекает отрезок SN. Найти объем общей части пирамиды
SABC и NKLM.
Вариант 3
1.	Решить уравнение
sin х -|- cos-x — 1 = ctg -у- (cos.x — 1).
2.	Решить неравенство
А |Х|-1)2>2.
3.	Решить уравнение
4- log’y-r - 30	+ 36 = 0.
205
4.	Из точки К, расположенной вне окружности с' центром О,
проведены к этой окружности две касательные МК и NK (М и
N — точки касания). На хорде MN взята точка С (MC<CN). Че-/
рез точку С перпендикулярно к отрезку ОС проведена прямая, пе/
ресекающая отрезок NK в точке В. Известно, что радиус окруж-
ности равен R, Z.MKN=<х, МС=Ь. Найти длину отрезка СВ.
5.	В основании треугольника пирамиды SABC лежит прямо-
угольный равнобедренный треугольник АВС. Точка D — середина
гипотенузы АВ, SD— высота пирамиды, SD=DC = a. Через точку
S проведена плоскость, перпендикулярная к SD, и в этой плоско-
сти построен прямоугольный -треугольник SEF так, что точка S —
вершина прямого угла, SE=SF=a 1^2, а ££||ЛВ. Кроме того,
треугольник SEF расположен так, что плоскость, проходящая че-
рез EF и АВ, пересекает ребро SC. Найти объем общей части пи-
рамид SABC и SDEF.
Вариант 4
1.	Решить уравнение
(в	\	.
Х-]--4-J=CtgX— 1.
2.	Решить неравенство
|х|— 2>(х—2)2.
3.	Решить уравнение
64 log’, V~x — 4 j/log*, х 4- 3 = 0.
4.	На биссектрисе угла с вершиной L взята точка А. Точки К
и М — основания перпендикуляров, опущенных из А на стороны
угла. На отрезке КМ взята точка Р (КР<РМ), и через точку Р
перпендикулярно к отрезку АР проведена прямая, пересекающая
прямую KL в точке Q (К между Q и L), а прямую ML—в точке S.
Известно, что ZJ<LA4=a, КМ=а, QS=b. Найти длину отрез-
ка KQ.
5.	Дана треугольная пирамида SABC, SA=AB=BC—AC=a.
Ребро ВЛ перпендикулярно основанию ЛВС. Точка Н — середина
ВС. Через точку Н проведен отрезок KL, параллельный ВЛ й рав-
ный а, так что точка Н — середина KL. В плоскости АВС проведен
отрезок МА, параллельный ВС и равный а. Найти объем общей
части пирамид SABC и MAKL.
Разбор варианта 1
Задача 1. Воспользуемся формулами
tg2x=	cos2x = 1 + t|,x ,
заметив при этом, что те х, для которых tgx не существует, т. е.
206
п/2+яп не являются решениями исходного уравнения. Обозначим
tgx=t Тогда ,
Имеем:
•	\+t2=2t—2t3+2ta,
2t3—2/+1—/2=0,
2i(t3— 1) — (?—1)=0,
(f2—1) (2f—1) =0.
Поскольку f#'±l, то / = ‘/г.
tgx = -£-, x = arctg-|-4-wn.
Ответ: x=arctg ’/г+ляг, m=0, ± 1, ±2, ... .
Задача 2. Заметим, что верно тождество
‘	(Х_1)2=|Х_1|2
Обозначив t= |х—11 >>0, получим
_ 3^_|_ 1 <^0,
з —/5
2
-з + Кб
2	’
Решения этого неравенства имеют вид:
1.
з—УгГ
2
з + Кб
2	’
Ответ'. (5- /5 )/2<х<(5 + /5’)/2, — (1 + /5)/2<х<
<(/У-1)/2.
Задача 3. Введем обозначение
t = log»x = у^2 log,, х.
Тогда уравнение принимает вид:
Р—3t—4=0
247
и его решениями являются числа /1=4 и /2=—1. Рассмотрим оба
варианта:	/
з,----	/
1. у log»x = 4,	/
log» х = 64, х = 5м.	/
2. у log»x= — 1,	/
log»x —— 1, х = -^~.	/
Ответ: xi = 5,«, xt = -|-.
О
Задача 4. Чертеж к этой задаче представлен не рис. 55.
Обозначим Х.ОВС — а. Тогда /_ВОМ =? — а. Поскольку ДЛВО—
равносторонний, то ^АОВ=л/3 и, следовательно,
£AON = *	а ) = а+ Д_.
Имеем
ВС = 2R  cos а, AD = 2R • sin ( а 4-	\
\ ь J
OM = Rs\na, ON — R cos 6x4- 4г Y
ОТ = 4--cos/а 4-
z \ о У
Имея эти соотношения, находим площади равнобочной трапеции
ABCD и треугольника RLM:
Составляя отношение площадей трапеции и треугольника, по-
лучим уравнение, из которого определяется cos а:	ч
{Yosa-j-siH уа+	|sina + cos	=
= sin (а -|-	[2 sin а -f- cos (а-|- 4г)]
208
или
i	/	j \/	v" з
\ (cos а2-sina-|—^-cosa 1 ( sin a -|--g— cosa —
x-—• sin a) =	sin a -]—i- cos a) (2 sin a 4- cos a —
-4sina)-
Это — однородное уравнение относительно sin а и cosa. Разделив
его части на cos2 а и обозначив tga через /, приходим к урав-
нению
/Т (t 4- ГЗ>=/з- (tyr 4- D*
или
/'=1.
Отсюда имеем: ti =—1, 4=1. Очевидно, что подходит только вто-
рое решение. Итак, tga= l, а=л/4. После этого легко находим, чт.о
МС=/?/2/2.
Ответ-. RV~2I2:
Задача 5. Чертеж к этой задаче представлен на рис. 56. Из
условия равенства отрезков jQS и SM следует, что QM = AO и, зна-
чит, равны высоты оснований пирамид. Поэтому можно заклю-
чить, что равны и ребра пирамид. Общая часть этих пирамид
представляется многогранником SEFNT, который состоит из двух
пирамид: SEFN и TEFN, у которых A.EFN — общее основание,-
а сумма высот равна высоте пирамиды SO. Для того чтобы найти
точки N и F, которые определяют прямые EN и EF, по которым
пересекаются грани AS С и QRT, а также AS В и QPT пирамид,
достаточно провести EN\\AC и EF\\AB. Это легко следует из изве-
14—619	.209
стной теоремы о том, что если плоскость (например, QRT), про-
ходящая через прямую (QR), параллельна другой плоскости
(в данном случае плоскости ASC), то линия пересечения этих
плоскостей (EN) параллельна данной прямой: ЕЛГ||QR||АС. /
Перейдем к вычислениям. Из условия задачи и построения сле-
дует также, что пл. ДЕЕЛ^Нпл. ДАВС. Отсюда имеем:
$efn (ЕК у f\SE \«
$авс	\ А® )	\	)
или
С __________________________ (	Q
^EFN — \SA J ' ABC'
Вычислим сомножители, входящие в последнее соотношение.
Имеем
«j _а? Уз
♦ ° лес	4 
Отрезок SE находится из AEQS. Обозначим /_OAS_ через а.
Поскольку QS || АО, то и угол QS4 равен a. QS = -^^~ /3. Далее
находим: QS = 2SEmcos a; SE = а/(4]/3 cos а), где
а	1
cos а = —: а = —-=г.
Уз	уз
Итак SE = af4. Тогда
«,	__ 1 а* У~3 __а' Уз
^EFN— 16 *	4	— 64 •
Пусть SK = hi,KO=hi. Тогда
гг _____р । тг ________ 1 Л1 У 3	,	।	1 Л1 V~3 . __
V SEFNT—VSEFN~r~V TEFN	3----64~ ’ Й1 “Г T ’ 64 *rt‘—
Ответ: a*V~2/192.
§ 27. ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ, 1975 г.
Вариант 1
'. Решить уравнение
cos (Зх+5)—cos (x+l)=2sin (х+2).
2. Решить уравнение
log J (х+2) log ] (2х^-Зх+2)
9 ~	=7 ~	.
210
' 3. Решить неравенство
2*2 —Их 4-15 п
2* — 6
4. В треугольнике АВС АВ=АС и угол ВАС — тупой. Пусть
D — точка пересечения биссектрисы угла АВС со ртороной АС,
М — основание перпендикуляра, опущенного из А на сторону ВС,
Е — основание перпендикуляра, опущенного из D на сторону ВС.
Через точку D проведен также перпендикуляр к BD до пересече-
ния со стороной ВС в точке F. Известно, что ME=FC = a. Найти
площадь треугольника АВС.
5. В треугольнике АВС угол АСВ -* прямой, АС=а, ВС=За.
Через точку В проведена в пространстве прямая, перпендикуляр-
ная отрезку ВС и на этой прямой взята точка D так, что BD^a.
Двугранный угол между плоскостями, которым принадлежат тре-
угольники BCD и АВС, равен я/3. Шар касается отрезка АВ в та-
кой точке Р, что АВ=3-АР, и касается отрезка CD в такой точ-
ке Q, что CD—3-QD. Найти радиус шара.
Вариант 2
1.	Решить уравнение
2 sin (х+3) cos (4х—1) +sin (Зх—4) =0.
2.	Решить уравнение
log . (х+3)
-т-	/ 1 xlog,(x’+5x+12)
6 “(*)
3.	Решить неравенство
(2—5») (7х2—10х+3) <0.
4.	В прямоугольном треугольнике АВС угол АСВ — прямой.
Пусть Е — точка пересечения биссектрисы угла АВС со стороной
АС, точка D — середина стороны АВ, О — точка пересечения от-
резков BE и CD. Через точку О проведен перпендикуляр к ВО до
пересечения со стороной ВС в точке F. Известно, что FC=b, ОС=
=ЗЬ/2. Найти площадь треугольника АВС.
5.	Два равных треугольника KLM и KLN имеют общую сто-
рону KL, 2j(LM= Z.LKN=nl3, K.L—a, LM=KN=&a. Плоскости
KLM и KLN взаимно перпендикулярны. Шар касается отрезков
LM и KN в их серединах. Найти радиус шара.
,4*	211
Вариант 3	£
1.	Решить уравнение
-sin (х+7) +sin (Зх—1) =cos (х—4).
2.	Решить уравнение
log +9x4-13)
f 1 \log»(x+5) _ 3
3.	Решить неравенство
Зх-2
Ъх* + 22х — 15	"
4.	На биссектрисе острого угла АОС взята точка В. Через точ-
ку'/? проведена прямая, перпендикулярная к ОВ и пересекающая
сторону АО в точке К, а сторону ОС — в точке L. Через точку В
проведена еще одна прямая, пересекающая сторону АО в точке М
(М между О и К), а сторону ОС — в-точке N так, что Z-MON—
= Z.MNO. Известно, что МК=а, LN=3a/2. Найти площадь тре-
угольника MON.
5.	В треугольнике АВС угол АСВ — прямой, ^ВЛС = -^-,
ВС=т. На перпендикуляре к отрезку АС, проходящем в простран-
стве через точку А, взята точка D так, что AD=m. Полуплоскости,
которым принадлежат треугольники АВС и ACD, образуют дву-
гранный угол, равный л/3.
Шар касается АВ в такой точке К, что АК = -^-АВ и касается
5
отрезка CD в такой точке L, что CL = -^ -CD. Найти радиус
шара.
Вариант 4
1.	Решить уравнение
2 sin (2х — 3) cos (XjJ- 1) — sin (Зх — 2) = 0.
2.	Решить уравнение
108 ] (х4-2)
/ 1 \10g,(X»4-2x-H)	—
W =6
3.	Решить неравенство
3x2 —х—14
5 — 2*
212
4.	В треугольнике АВС АВ—ВС. Пусть D — основание перпен-
дикуляра, опущенного из. точки В на сторону АС, Е — точка пере-
сечения биссектрисы угла ВАС со стороной ВС. Через точку Е
проведен перпендикуляр к АЕ до пересечения с продолжением
стороны АС в точке F (С между D и F). Известно, что AD=m,
FC=m/4. -Найти площадь треугольника АВС.
5.	Два равных треугольника KLN и LMN имеют общую сторону
LN,Z_LNK~ Z_NLM = k!§, LN = 2/36, KN = LM=\2 b. Плос-
кость KLN перпендикулярна плоскости LMN. На отрезке KN взята
такая точка Р, что КР = -^-KN, а на стороне LM взята такая
точка Q, что QAf = -|- LM. Шар касается отрезка KN в точке Р
и касается отрезка LM в точке Q. Найти радиус шара.
Вариант 5
1.	Решить уравнение
sin (х—7)—sin (Зх—3) =2 cos (2х—5).
2.	Решить уравненйе
	-	108 . (х«+2х+9)
( П108.(2х^+3)=(1/5) -j-
3.	Решить неравенство
(5х2—12x4-4) (6Ж—2) <0.
♦
4.	В прямоугольном треугольнике АВС угол АСВ — прямой.
Пусть D— точка пересечения биссектрисы угла ВАС со стороной
ВС, точка Е — середина стороны АВ, О — точка пересечения от-
резка AD с отрезком СЕ. Через точку О проведена прямая, пер-
пендикулярная к AD до пересечения со стороной АВ в точке К,
а со стороной АС — в точке М. Известно, что МС=а, ЕК=<2а1^.
Найти площадь треугольника АВС.
5.	В треугольнике АВС угол ВС А — прямой, АС=Ь, ВС=2Ь.
На прямой, проходящей в пространстве через точку В перпенди-
кулярно к отрезку ВС, взята точка D так, что BD=b. Двугранный
угол между полуплоскостями, которым принадлежат треугольники1
АВС и BCD, равен 2л/3.
Шар касается отрезка АВ в такой точке М, что ВМ = АВ и
з
касается отрезка CD в такой точке N, что CN = -^-CD. Найти
радиус шара.
213
Вариант 6
1.	Решить уравнение
2cos (х4-4) cos (2x4-1)—cos (3x4-5) =0.
2.	Решить уравнение
П 4	__ qloge(6-х)
3.	Решить неравенство
2*—3
Зх8— 8x4-5
>0.
4.	В прямоугольнике ABCD (BC>'CD) диагонали АС и BD пе-
ресекаются в точке О. Биссектриса угла CAD пересекает BD
в точке Е. Пусть F— основание перпендикуляра, опущенного из
точки Е на сторону AD, точка К— середина AD. Через точку Е
проведен также перпендикуляр к АЕ до пересечения с диагональю
АС в точке И. Известно, что OH=b, KF=4bf3. Найти площадь
прямоугольника ABCD.
5.	Отрезок LM служит общей стороной двух равных треуголь-
ников KLM и LMN, в которых Z.K.ML=Z_MLN=nl4, LM=2m,
LN=KM=4m ]/~2. Плоскости KLM и LMN взаимно перпендику-
лярны. Шар касается отрезка КМ в такой точке А, что АК=т]/1Г
и касается отрезка LN в такой точке В, что BN=m ]^2. Найти
радиус шара.
Разбор варианта 1
Задача 1. Преобразуем данное уравнение к следующему виду:
-—2 sin (2x4-3) sin (x4-2)=2sin (х4-2)
и далее имеем
1. sin(x-]-2) = 0, x-j-2 = wn, х= — 2-|-wn;
2. sin(2x4-3) = - 1, 2x-{-3 = —J--|-2wn,
2x=--^--3-|-2wn,-
x = —	-I- itm.
4	1
Ответ: x=—2 + ллп, x=—(п + 6)/4 + лт, где m=0, ±1, ±2	-
214
Задача 2. Область допустимых значений неизвестного опреде-
ляется неравенствами
х4-2>0,
2х24-Зх4-2>0,
из которых следует, что х>—2.
Запишем исходное уравнение в следующем виде:
gioe,(x+2)-*______________jioe>(2'«43*+2)'*
или
1 _ 1
(х4-2)«	2х* + 3x4-2 ’
Далее имеем
х2—х—2=0,
Xi=2, Хг=—1.
Поскольку оба значения удовлетворяют условию х>—2, то они
оба служат решениями уравнения.
Ответ: х=2, п=—1.
Задача 3. Возможны два случая.
1.
|2х«- 11лг-4-15>0,	.
(2* —6<0;
{х<2,5 или х>3,
х log, 6.
2.	•
(2х* — llx-f-15<0,
(2х — 6>0;
|2,5<х<3,
|x>log,6.
Рассмотрим первый вариант. Очевидно, что log26<3. Сравним
между собой числа log26 и 2,5.
log.6\/4--
(V —«знак сравнения, заменяющий неизвестный заранее^ знак >
или <.)
5
6 V 2 2 ,
6V/32.
6>/32.
Таким образом, log26>2,5. Тогда решения первого варианта име-
ют вид: х<2,5.
215
Во втором варианте решения имеют вид: log26<x<3.
Ответ: х<2,5; log26<x<3.
Задача 4. Чертеж к этой задаче изображен на рис. 57. Все по-
строения очевидны; заметим только, что точка F лежит на’сторо-
не ВС, а не на ее продолжении,
благодаря тому, что угол ВАС —
тупой.
Введем две неизвестные вели-
чины: х — длину основания и
2а — угол АВС. Биссектрису BD
будем обозначать /, а высоту
AM —Л. Составим два уравнения
для нахождения величин а и х.
Вычислим сначала длину бис-
сектрисы I. Для этого' запишем
двумя различными способами
площадь треугольника АВС:
^АВС— 2 Х' -2 t8-2a_' 2 ^xsin<xH jH’ 2cos2a - sina’
h
Отсюда находим, что
/__ „	2 cos я
t	л 2cos2a+ 1 ’
Из прямоугольного треугольника BDE находим BE:
nr? 1	_ * 2 COS* a
BE = I cos a = x -и-о—гт •
s	2 COS 2a + 1
С другой стороны, BE равен (x/2 +a). Поэтому получаем первое
уравнение
2 COS* a _ x ।
2 cos 2a+1 — 2	.
ИЛИ
____* _ =2a
l + 2cos2a
(1)
Из прямоугольного треугольника BDF можно найти длину от-
резка BF:
BF =_____-_=______—---
- cos a 2 cos 2a + 1
С другой стороны, BF равен (х—а). Поэтому второе уравнение,
которое можно , составить, имеет вид
2 cos 2a + 1
ИЛИ
216
2 cos 2a — 1	/оч
•y-2bos2a+l'=a-	(2)
Систему уравнений (1—2) легко разрешить относительно х и
cos 2а:
х = 5а, cos2a = -j-.
4 д
Теперь легко находится площадь треугольника АВС:
с	1 Q	25/7" ,
$авс “ 4 х tg 2а — а .
Ответ: 25. У7 а2/12.
Задача 5: Чертеж к этой задаче дан на рис. 58. Пусть О —
центр искомого шара, а ОР и OQ его радиусы, проведенные в точ-
ки касания Р и Q соответственно; радиус шара—R.
Рис. 58.	.
Прежде всего заметим, что центр шара, точка О, равноудалена
от точек В и С, т. е. треугольник ОВС — равнобедренный. Дейст-
вительно, рассмотрев два прямоугольных треугольника ОРВ и
OQC, замечаем, что они равны по двум катетам: OP=OQ=R и
ВР =; CQ = 2 • ДВ/3 (очевидно, что AB = CD). Отсюда и следует ра-
венство ОВ = ОС.
Покажем теперь, что плоскость треугольника ОВС является
биссекторной плоскостью двугранного угла между плоскостями
исходных треугольников АВС и BCD. Для этого соединим верши-
ну .треугольника ОВС, точку О, с серединой ребра Е этого дву-
гранного угла. Поскольку треугольник ОВС равнобедренный, то
OE-LBC. Далее, восставим перпендикуляры ЕК и EF в плоскостях
треугольников АВС и BCD соответственно. Очевидно, что точки К.
и F будут серединами гипотенуз АВ и CD, поскольку отрезки ЕК.
и EF будут средними линиями, проведенными в прямоугольных
треугольниках АВС и BCD параллельно катетам. Треугольники
ОРК и OQF равны по двум катетам. Отсюда следует, что ОК=
217
= 0F. Треугольники OEF и OEK так же равны между собой:
OK=OF, ОЕ — общая сторона, EK=EF—a/2. Следовательно, угол
OER равен углу OEF. Кроме того, очевидно, что угол REF являет-
ся плоским углом двугранного угла между плоскостями треуголь-
ников АВС и BCD. Таким образом, доказано, что плоскость тре-
угольника ОВС делит этот двугранный угол пополам; угол OEF
равен л/6.
Перейдем к вычислениям. Обозначим отрезок ОЕ через х, а от-
резок OF — через у. Из прямоугольных треугольников OCQ и ОСЕ
выразим и приравняем друг другу выражения для ОС:
Здесь учтено, что CD =аУг10,.а CD = 2а)/ 10/3.
С помощью теоремы косинусов выразим у из треугольника
OEF, в котором угол OEF равен л/6:
У* = ("£*)*+** “ 2’ “Г 'x cos “Г '	&
Из прямоугольного треугольника OQF имеем
у* = Я1+QF’ = Я* +
Исключая из полученных уравнений (1—3) Я и у, находим зна-
чение неизвестной величины х:
Я* = х — 2- -g- • х • cos-g j-g-,
xs — 2- -x-cos
'5а2 ; /2а ИО У _ , । f За У
18	3 7 — Х "г \. 2 / ’
х =
13а /З
После этого весьма просто вычисляется радиус шара Я:
в ./439
Я — л у 108 •
Ответ: R = a'Vr439[lO8.
218
$ 28. ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ
МАТЕМАТИКИ И КИБЕРНЕТИКИ, 1972 г.
Вариант 1
Г. Решить уравнение
91_(X_1). _ 12 3-(х-1)._^ j _0
2.	Решить неравенство
1____j > |tgx-K3| + K3
COS2 X	ctg X
3.	В прямоугольном секторе АОВ из точки В, как из центра,
проведена дуга ОС (С — точка пересечения этой дуги с дугой АВ)
радиуса ВО. Окружность Si касается дуги АВ, дуги ОС и прямой
ОА, а окружность S2 касается дуги АВ, прямой О А и окружности
Si. Найти отношение радиуса окружности Si к радиусу окружно-
сти S2.
4.	Боковые грани правильной треугольной пирамиды SABC
наклонены к плоскости основания под углом 45°. Шар касается
плоскости основания АВС в точке А и, кроме того, касается впи-
санного в пирамиду шара. Через центр первого шара и высоту
BD основания проведена плоскость. Найти угол наклона этой
плоскости к плоскости основания.
5.	Найти все действительные значения параметра а, при кото-
рых неравенство
tg4 (sin — х’) — 2аtg(sin— хг)-f- a2<0
имеет и притом конечное число решений. Для каждого такого а
указать все решения неравенства;
Вариант 2
1.	Решить уравнение
4f_(x+l)> _3 22-(х+1)«
2.	Решить неравенство
-j^(l — cos2x) > sinx-(l + 11 — 1^2sinx|).
3.	В прямоугольном секторе АОВ проведена хорда АВ и в об-
разовавшийся сегмент вписан квадрат. Найти отношение стороны
квадрата к радиусу окружности, которая касается хорды АВ, ду-
ги АВ и стороны квадрата, перпендикулярной к хорде АВ.
219
4.	Шар касается плоскости основания ABCD правильной четы-
рехугольной пирамиды SABCD в точке А и, кроме того, касается
вписанного в пирамиду шара. Через центр первого шара и сторо-
ну основания ВС проведена секущая плоскость. Найти угол накло-
на этой плоскости к плоскости основания, если (известно, что диа-
гонали сечения перпендикулярны ребрам 5Л и SD.
5.	Найти все действительные значения параметра а, при кото-
рых неравенство
l/3it — 21 х | • £ctg“ (cos х) a ctg (cos х) 4’-	< О
имеет и притом конечное число решений. Для. каждого такого а
указать все решения неравенства.
Варйант 3
1.	Решить уравнение
91-(х+2)« _ 2.32-(х + 2)«	7 __ 0.
2.	Решить неравенство
1____1 |ctgx-l 1+1
sin* х	tg х
3.	В прямоугольном секторе АОВ из точки В как из центра
проведена дуга ОС (С — точка пересечения этой дуги с дугой АВ)
радиуса ВО. Окружность Si касается дуги АВ, дуги ОС и прямой
ОА, а окружность Зг касается дуги ОС, прямой О А и окружности
Si. Найти отношение радиуса окружности Si к радиусу окружно-
сти Зг.
4.	Боковые ребра правильной треугольной пирамиды SABC на-
клонены к плоскости основания под углом 45°. Шар касается плос-
кости основания АВС в точке А и, кроме того, касается продолже-
ния ребра BS за вершину. S. Через центр шара и высоту BD осно-
вания проведена плоскость. Найти угол наклона этой плоскости
к плоскости основания.
5.	Наи?и все действительные значения параметра а, при кото-
рых неравенство
tg2 (cos j/4n2 — л2) — 4atg(cos |/ 4к2 — х2)	22а < 0
имеет и притом конечное число решений. Для каждого такого а
указать все решения неравенства.
220
Вариант 4
1.	Решить уравнение
41_(х_2). _ 23-(Х-2). j _ Q
2.	Решить неравенство
1 -|-cos2x> cosx(l +11 — 2cosx|). -
3.	В прямоугольном секторе АОВ проведена хорда АВ. Окруж-
ность Si с центром на биссектрисе сектора касается хорды АВ я
дуги АВ. Окружность Зг касается хорды АВ, дуги АВ и окружно-
сти Si. Окружность З3, отличная от Si, касается хорды АВ, дуги
АВ и окружности Зг- Найти отношение радиуса окружности Зг
к радиусу окружности З3.
4.	Шар касается плоскости основания ABCD правильной че-
тырехугольной, пирамиды SABCD в точке А и, кроме того, касает-
ся ребра SC. Через центр этого шара и сторону основания ВС
проведена секущая плоскость. Найти угол наклона этой плоскости
к плоскости основания, если плоскость сечения перпендикулярна
грани ЛЗД.
5.	Найти все действительные значения параметра а, при кото-
рых неравенство
]/ 2я — | х | • [ctg1 (sin х) — 2а ctg (sin х) — а] < О
имеет и притом конечное число решений., Для каждого такого а
указать все решения неравенства.
Разбор варианта 1
Задача 1. Введем новую неизвестную посредством равенства
Очевидно, что эта неизвестная может принимать только положи-
тельные значения. Уравнение примет вид
9/2—12/+И=0.
Его решения: / = (2zt|Z3 )/3. Возвращаясь к прежней перемен-
ной, получим:
о—(х—1)’	2 + V 3
d----------3
или	_
/ п. ,2+^3
(X — 1)« = — log, —3-.
Очевидно, что правая часть этого уравнения должна быть не-
отрицательной. Поэтому нужно взять лишь то значение логариф-
221
ма, стоящего в правой части последнего равенства, которое отри-
цательно. Имеем
(х-1)«=-1о&^Д-
и далее
I х - 1| =	1- log, (2-/3*),
- x=l=t/l-logt(2-/T).
Заметим, что решению можно придать и другую форму записи:
х = 1 =t	l+log,(2 + /3*).
Ответ: 1 ±	1 — log, (2 — /3). •
Задача 2. Очевидно, что в данном неравенстве допустимы все
значения неизвестного, для которых sinx#=0 и cosx=/=0, т. е. х=£
=Н=лп/2.
Обозначим tgx буквой t и запишем неравенство в следующем
виде:
(^0)
ИЛИ
7де_/3)-|г-/з"|]>о.
Рассмотрим .три случая.
1.	/>/3*.
Тогда неравенство тождественно выполняется (]/ — /3 | = t — /З").
Поэтому все f>/3 являются его решениями.
2.	0</</3*.
В этом случае неравенство принимает вид
2i(t — /3“)>0.
Поскольку сомножители имеют разные знаки, неравенство при рас-
сматриваемых значениях t не выполняется.
3.	/<0
В этом случае имеем
2/(f-/3*)>0.
Очевидно, что при всех /<0 неравенство выполнено.
Ита!?, подводя итог, получаем
а)	б)/<0.
222
Возвращаясь к прежней переменной, находим
a)	tgx^}/3?	x<-y + wi;
б)	tgx<0, —|- + TOn-<x<wn.
Ответ: -^--рк/п<С х<-^--\-чт; —у 4-itm<x<wn.
Задача 3. Чертеж к этой задаче дан на рис. 59. Центр первой
окружности обозначен буквой Si, а центр второй, окружности —
буквой 5г. Кроме того, введены обозначения D и Ё — точки каса-
ния первой и второй окружности с прямой О А соответственно,
а Н и F — точки касания тех же окружностей с дугой АВ. Радиус
сектора АОВ обозначим R, радиус первой окружности — г, радиус
второй окружности — р.
Можно заметить, что задача имеет не одно решение. Окруж-
ность с центром в точке S4, вписанная в криволинейный треуголь-
ник АЕН, также удовлетворяет всем условиям задачи. Поэтому,
не предполагая единственности решения запишем условия, опре-
деляющие положение центра каждой из окружностей.
Окружность Si касается дуги АВ; пбэтому точки О, Si и Н ле-
жат на одной прямой и
OSi=l?—г.
Эта же окружность касается прямой АО; поэтому расстояние от
ее центра до этой прямой равно г. Отсюда находим длину отрез-
ка ОЕ:
OE = V(R — r)* — r\
Окружность Si касается также дуги ОС; поэтому отрезок SiB
равен сумме радиусов г и R. Из рассмотрения прямоугольного тре-
угольника BRSi можно составить уравнение:
(г = (R - r)« + (R - г)»- г« ]«,
которое после простых преобразований приводит к соотношению
Я = 6г,
дающему связь между радиусами т и R.
Рассмотрим теперь положение второй окружности. Эта окруж-
ность касается окружности Si; поэтому расстояние между их цен-
трами S1S2 равно (г+р).. Та же окружность касается отрезка О А;
поэтому расстояние DSz равно р. Из прямоугольного треугольника
DOS2 находим:
0D = /(1? — р)2 - р’.
223
Теперь можно определить расстояние между точками касания
окружностей Si и S2 прямой О А. В общем случае оно равно "
DE = |	- г)« -г» - V (R-p)‘-p«|.
Знак модуля показывает, что возможны случаи OD<OE и
OD>OE.
Из рассмотрения прямоугольного треугольника MS^Sz, где точг
ка М определяется пересечением отрезков RSi и DSz, можно со-
ставить уравнение
(г +»* = (р - г). +	_ /(R - р). - р«]«,
которое в более простом виде записывается так:
4rр -= {VR(R-2r) - /R(R-2p)l‘.
Разделим обе части последнего уравнения на г2 и заменим всю-
ду отношение R/r на 6. Получаем уравнение
4х = [/6 (6 - 2) - )/6(6-2х) 1‘,
в котором через х обозначено отношение радиусов р/r. После не-
сложных преобразований это уравнение сводится к квадратному
уравнению
16х*-48х-|-9 = О,
224
решения которога
_ б±Кз
Xi,» —--4--.
Таким образом, задача имеет два решения. Отношение радиусов
окружностей равно величине, обратной по отношению к х:
-^-=4(2±/3-).
4(2dt/3)/3.
Ответ:
Задача 4. На рис. 60 изображена пирамида SABC, О2— центр
вписанного в нее шара, а Oi— центр шара, о котором идет речь
в задаче. Поскольку шар Oi касается основания пирамиды в точ-
ке Л, то его центр лежит на пер-
пендикуляре к плоскости основа-
ния, восстановленном из этой точ-
ки. Центр шара, вписанного
в правильную пирамиду, лежит,
очевидно, на ее высоте SM.
Соединим точки Oi и D отрез-
ком прямой. Прямые OiD и BD
определяют плоскость, угол кото-
рой с плоскостью основания надо
найти. Этот угол, обозначаемый
а, равен, очевидно, углу AJDOi.
Поскольку ADX.BD и ЛО1±пл.
АВС, по теореме о трех перпенди-
кулярах O1DA.BD; следовательно, угол ADOi есть линейный угол
двугранного угла между плоскостью сечения и плоскостью осно-
вания. Чтобы найти угол а, определим его тангенс:
^а-=^Г>
где а — ребро основания пирамиды, a R— радиус шара Ор
Для того чтобы, найти радиус шара R, обратимся к рис. 61, на
котором представлен разрез пирамиды по плоскости AES. Радиус
вписанного в пирамиду шара г находится из треугольника ЕМО2.
Линия ЕОг — биссектриса угла MES.
г — —6“ g 8 •
Из прямоугольного треугольника OtOiF, в котором OtOt = R -|-г»
OiF=R — г и FOt = аУз J3, находим:
(/?+г)« = (Я-г)»+_
а1
или
4г/?=4
15—619
225
Подставляя сюда выражение для радиуса вписанного шара г, по-
лучаем
n a^3	"
R = —e-ctg-g-.
После этого определяем тангеит искомого угла
. КГ
tga = —
Котангенс угла л/8 можно найти
ваний:
1 ТС
ctg-g-.
путем следующих преобразо-
Ctg*-8
те
C0S*T
тс
sin«-g-
те
1 +COS-J-
------= 3-21/7.
..	2 —К2
1 —cos-
Отсюда
, тс
ctg-8"
Ответ:
Задача 5.
arctg(j/3 +Г6 )/3.
Введем новую переменную согласно равенству
tg (sin У 9я* — х2) = t.
что х изменяется в пределах: — Зи < х < Зи; величи-
Очевидно,	_______
на синуса при этом не превышает единицы: |sin]/9it‘ — х2|< 1, а
значения тангенса и, значит, переменной t удовлетворяют ограни-
чениям
(0
Для новой переменной имеем квадратное неравенство
" 2at+а 4“ 2^^ О,
для существования решения которого необходимо условие неотри-
цательности его дискриминанта
D = az—а—2>0.
Рассмотрим случай, когда дискриминант равен нулю. Это име-
ет место при а=2 и а——1. В этом случае рассматриваемое нера-
венство имеет только одно решение:
a)	t=2 при а—2:
б)	t=—1 при а = — 1,
В случае а = 2 мы не получаем решений. Имеем
tg sin j/Sht2 — х* = 2,
sin У 9it2 — x1 = arctg 2 -|- tik.
226
Поскольку arctg2— возрастающая функция, то верна цепочка не-
равенств
arctg2>arctg }^3 =-^-> 1, при k = Q;
arctg2 —	—« =------—• 1 при k = — 1,
что показывает отсутствие действительности решений у этого урав
нения. Остальные значения k, очевидно, не годятся.
В случае а=—1 получаем
tg sin ]Л9и* — х’ = — 1,
sin |/’9и‘ — хг = —(k = 0).
Поскольку |it/4|< 1, находим:
1) |^9it‘ — х* = it -|- arcsin	,
2) У 9it‘ — x* = 2it — arcsin	.
Как были найдены эти значения, легко понять из рис. 62.
Решая далее полученные уравнения, определяем х-
Рассмотрим теперь случай, когда D>0. Это имеет место при
а>2 и а<—1. В этом случае решения исходного неравенства за-
писываются в следующем виде:
а — У а* — а — 2 < t < а -|- ]/ а‘ — а —• 2.	(2)
Сравнивая решения неравенства и ограничения (1), можно
сделать вывод: для того, чтобы не-
равенство относительно х имело
решение, необходимо, чтобы у не-
равенств (1) и (2) существовало
хотя бы одно общее значение t.
При этом если у обоих неравенств
существует бесконечно много об-
щих решений, то существует бес-
15*
Рис. 62.
227
конечно много значений х, удовлетворяющих исходному нера-
венству.
Для того чтобы у неравенств (1) и (2) было конечное число
общих решений, необходимо выполнение одного из двух равенств:
1) а — Уа* — а—2= tg 1;
2) а-\-Уа* — а — 2 = — tgl.
Первое уравнение выполняется, очевидно, только при а>2>
>tg 1.
Его решение имеет вид
tgH+£
а ~~ 2tg 1 — 1 •
Легко проверить, что это значение а действительно больше 2:
tga 1 + 2 . „
2tg 1 — 1 ' ’
(tgl—2)г>0.
Здесь было использовано неравенство
tga>a,
выполняющееся для
.	0<а<-^.
Второе уравнение может выполняться только при а<—tg 1 <
<—1. Однако после возведения в квадрат обеих его частей по-
лучаем
tg2 1 + 2
2tg 1 +1 ’
Покажем, что это посторонний корень уравнения. Действительно,
_tg4 + 2_
2tg 1 + 1	s ’
tg* 1 + tg 1 — 2<0.
Последнее неравенство в силу неравенства tg 1 > 1 противоречиво.
Итак, получаем
/ = tgl при a = 2tgi-^ •
Отсюда находим (рис. 62):
1) /9^-л2=-^-;
2)	-
228
Окончательно
~	2 ’
,/|1тс
-	2
Ответ: а = — 1, а =	.
§ 29.	ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ
МАТЕМАТИКИ И КИБЕРНЕТИКИ, 1973 г.
Вариант 1
1.	Решить систему уравнений
(2 sin л sin у cos х = О
11 + sin у cos х = 2 cos2 у sin лг.
2.	Решить неравенство
18Х+91	— Jjj-0.
90	'	'
3.	В прямоугольном треугольнике АВС из вершины прямого
угла С проведена биссектриса CL и медиана СМ. Найти площадь
треугольника АВС, если LM = a, СМ=Ь.
4.	Вершина S пирамиды SABC находится на расстоянии 4 от
центра сферы радиуса 1, которая проходит через точки Л, В, С и
пересекает ребра ВЛ, SB, SC соответственно в точках А', В', С'.
Отношение длин отрезков В'С' и ВС равно У132/15, отношение
площадей треугольников SA'B' и SAB равно а отношение
объемов пирамид SA'B'C' и SABC равно ^/т-
Найти длины отрезков SA', SB', SC'.
5.	Из пункта А одновременно выходят три пешехода и одновре-
менно возвращаются в тот же пункт, обойдя маршрут, состоящий
из прямолинейных отрезков АВ, ВС, CD, DA, которые образуют
разнобочную трапецию (АВ, CD — боковые стороны). На указан-
ных отрезках скорости всех пешеходов постоянны и равны у пер-
вого 6, 8, 5 и 8 км/ч соответственно, у второго — 7, 7, 6 и 8 км/ч
соответственно. Скорость третьего пешехода на каждом из отрез-
ков равна либо 7 км/ч, либо 8 км/ч, причем на всем пути он ме-
няет скорость один раз.
Определить отношение меньшего основания трапеции к боковой
стороне.
229
Вариант 2
1.	Решить систему уравнений
| sin у cos х -f- sin х = О
12 cos* у + sin У sin х = cos 2у cos х.
2.	Решить неравенство
3.	В прямоугольном треугольнике АВС из вершины прямого
угла С проведены биссектриса CL = a и медиана СМ = Ь. Найти
площадь треугольника АВС.	_
4.	Точки А, В, С, D, Е, Г лежат на сфере радиуса ’|/‘2. От-
резки AD, BE и CF пересекаются в точке S, находящейся на рас-
стоянии 1 от центра сферы. Объемы пирамид SABC и SDEF отно-
сятся, как 1 :9, пирамид SABF и SDEC — как 4:9, пйрамид SAEC
и SDBF — как 9 :4. Найти отрезки SA, SB, SC.
5.	Из пункта А одновременно стартуют три бегуна и одновре-
менно финишируют в том же пункте, пробежав по маршруту, со-
стоящему из прямолинейных отрезков АВ, ВС, СА, образующих
треугольник АВС. На каждом из указанных отрезков скорости бе-
гунов постоянны и равны у первого 10,16 и 14 км/ч соответствен-
но, у второго—12, 10 и 16 км/ч соответственно. Третий бегун
в пунктах В и С оказывается не один и меняет скорость на мар-
шруте один раз.
Установить, является ли треугольник АВС остроугольным или
тупоугольным.
Вариант 3
1.	Решить систему уравнений
2 cos х sin у+sin х = 0
' —sin2z/cosx = sinxcosi/4-cosx.
2.	Решить неравенство
юх+31 (5х go"0.
3.	В прямоугольном треугольнике АВС высота, опущенная на
гипотенузу, равна а, а биссектриса прямого угла равна Ь. Найти
площадь треугольника АВС.
230
4.	Сфера проходит через точки А, В, С, D и пересекает отрезки
SA, SB, SC, SD в точках Ai, Bi, Ci, Di соответственно. Известно,
что SDi=9li; DDi^1^, отношение площадей треугольников SAiBi
и S АВ равно 15/з2, отношение объемов пирамид SBiCiDx и SBCD
равно 17О1/4оэв, а отношение объемов пирамид SAiB^ и SABC рав-
но 105/256-
Найти отрезки ВЛ|, SBi и SCi.
5.	Три пешехода одновременно выходят из пункта А и одно-
временно прибывают в пункт D, пройдя по маршруту, состоящему
из прямолинейных отрезков АВ, ВС, СА, AD (ABCD — паралле-
лограмм). На каждом из этих отрезков скорости всех пешеходов
постоянны и равны у первого 3, 6, 5 и 8 км/ч соответственно,
у второго — 4, 5, 6 и 7 км/ч соответственно. Скорость третьего^
пешехода на отрезке AD равна 8 км/ч, а на остальных отрезках*
совпадает либо со скоростью первого, либо со скоростью второго
на соответствующем отрезке, однако,-ни с тем, ни с другим он не
проходит весь маршрут целиком.
Установить, является ли угол АВС острым или тупым.
Вариант 4
1. Решить систему уравнений
sin х cos у + cos х = О
2 sin* у — cos у cos х = cos 2у sin х.
2. Решить неравенство
25
х‘ — 16x4-65
-	64
3. В прямоугольном треугольнике АВС проведена биссектриса
прямого угла CL. Из вершины A (Z.A>45°) на CL опущен пер-
пендикуляр AD. Найти площадь треугольника АВС, если AD = a,
CL=b.
4. Точки А, В, С, D, Ai, Bi, Ci, Di лежат на сфере. Отрезки AAi,
BBi, CCi, DDi пересекаются в точке В, которая делит отрезок DDi
пополам. Известно, что DDi = 2 V6, отношение радиусов вписан-
ных окружностей треугольников SBiC и SBCi равно 3 4 5 * * 8/?, отношение
объемов пирамид SABC и BAiBiCi равно 2450/2i87, а отношение
объемов пирамид SAiBD и SABiDi равно 19в/г25-
Найти отрезки ВЛ, SB, SC.
5. Три бегуна одновременно стартуют в пункте А и одновре-
менно финишируют в том же пункте, пробежав по маршруту, со-
стоящему из прямолинейных отрезков АВ, ВС, СМ, МА (АВС —
треугольник, М — середина отрезка АВ).
231
На каждом из указанных отрезков скорости всех бегунов посто-
янны и равны у первого 13-^-, 10,10,16 км)ч соответственно, у
12
второго — 12-^-, 14, 12, 14 км/ч, соответственно. Третий бегун на
участке ВС бежит рядом с одним из других бегунов, на участ-
ке МА его скорость та же, что на участке АВ, причем на всем пу-
ти меняет скорость не более, чем дважды. Определить, является
ли угол АВС острым или тупым.
Разбор варианта 1
Задача 1. Перепишем даннукь систему в следующем виде:
{2 sin у sin х 4- cos х = 0
2cos2#sinx —sin#cosx = 1.
Будем рассматривать эту систему как -систему двух линейных
уравнений относительно функций sinx и cosx. Ее определитель
2 sin# 1
2 cos2# —sin#
= — 2 (sin2 г/ -4— cos* у) = — 2
всегда отличен от нуля, и поэтому система имеет единственное
относительно функций sinx и cosx решение.
Умножая первое уравнение системы на sin# и складывая ре-
зультат со вторым уравнением, получим
sinx = -£-.
Для нахождения решения можно было бы выразить из системы
cosx и потребовать, чтобы выполнялось тождество
cos2x+sin2x= 1.
Это дало бы уравнение для нахождения величины if. Поступим,
однако, по-другому. Подставляя в систему уравнений найденное
значение sinx, получим
(sin у -|- cos х = 0
Icos2# — sin# cos х= 1.
Второе уравнение системы выполняется в силу первого уравнения.
Поэтому имеем
sin#=—cos х.
Возможны два случая:
1) х = -|—1-2^.
232
Тогда
Кз
cos х = —2~ >
У=-(- i),n4r+wn;
2) х=-^-4-2^.
Тогда
Кз
COS X =-----------------------2~ •
У = (— I)"1- -у 4-wn.
Поэтому исходная система уравнений имеет следующие ре-
шения:
х=-у+2А */ = (-i)'n+*4r+wn: ^+-у-+2^,
у = (— l^-^ + wn.
Здесь k к т принимают независимо друг от друга все целочислен-
ные значения.
Задача: 2. Определим сначала область допустимых значений.
Она получается путем совместного решения системы неравенств
5*--ЙГ>0'
х«- 18x4-91 > О,
х* — 18x4-91^90,	у
откуда находим
х>94-4/5 и 9-4/5’<-^-<х<94-4уб’.
Рассмотрим два случая. Если в основании логарифма стоит
число, большее единицы,
х1 — 18x4-91 >90,
х>94-4/5",
то неравенство равносильно системе
[х>94-4/Г,
|5л-4<1.	
Эта система не,имеет решений.
233
Во втором случае, когда основание логарифма меньше едини-
цы, получается система
^г<х<9 + 4/5-,
решение которой
^-<л<9 + 4/5.
Ответ*. 0,26<х< 9-|-4/5.
Задача 3. Пусть АВС — рассматриваемый прямоугольный тре-
угольник (рис. 63). Точка М, се-
редина гипотенузы АВ, является
центром описанной вокруг треу-
гольника АВС окружности. Поэ-
тому медиана СМ есть радиус
этой окружности. Отрезок ML
всегда меньше половины гипоте-
нузы, откуда следует требование
о том, что а<&.
Отрезок AL равен Ь + а, отре-
Рис. 64.
зок BL равен b—а. Обозначим катет АС буквой х, а катет ВС—у.
Составим систему уравнений
х  Ь + а
у Ь — а
Первое из этих уравнений выражает теорему Пифагора, а вто-
рое — свойство биссектрисы делить противоположную сторону
в отношении, пропорциональном сторонам треугольника.
234
Опуская подробности решения этой системы, которые легко вы-
полнить самостоятельно, приведем окончательный результат
x_K2b(a+b) ' VTbjb-a)
Vat + b* ’ У Va* + b*
Отсюда находим площадь треугольника АВС:
Вавс а* + ьг ’ Ь>а-
Задача 4. Замечание. Прежде чем приступить к решению этой
задачи, рассмотрим некоторые вспомогательные утверждения, ко-
торые будут полезны для решения этой, а также многих других
задач.
1.	Рассмотрим треугольник АВС (рис. 64). Если сторону тре-
угольника АВ изменить в т раз, а сторону АС — в п, раз, т. е. пе-
рейти к треугольнику АВ'С' такому, что
АВ' = т- АВ, АС=П‘АС,
то площадь треугольника изменится в тп раз:
^ДАВ'С' — тП$ЬАВС
Здесь числа т и п произвольны; они могут быть меньше или боль-
ше 1.
Справедливость этого утверждения легко следует из следую-
щих равенств:
SAАВ'С = 4" ^В''АС' •Sin « = 4" (тАВ> {ПАС>* 8’П а = mnS^ABC-
В частности, при т=п получается известное для подобных тре-
угольников утверждение: площади подобных треугольников отно-
сятся как квадраты сходственных сторон.
2.	Рассмотрим теперь произвольную треугольную пирамиду
SABC (рис. 65). Если ребро пирамиды 5Л изменить в т раз, реб-
ро SB —в п раз, а ребро SC — в k раз, т. е. перейти к пирамиде
SA'B'C такой, что
SA'=m-SA, SB'=n-SB, SC'=k-SC,
то объем пирамиды изменится в tnnk раз:
V
v SA'B'C'
— tnnkVSABC
Числа, т, п, k как и раньше, могут быть меньше или больше 1.
Действительно, представим объем каждой из пирамид по фор-
мулам
VSA'B'C' ~ ~3~SbSB'C’ ‘h ’ ^SABC = ~3~BASBC
где h' и h — высоты каждой из пирамид, опущенные на боковые
грани из вершин А' и А соответственно. Составляя отношение
235
объемов пирамид, находим
Vsa'b'c	$д$в'с	h'   h'
VSABC~	$ASBC	h	A
Отношение высот h': h равно m. Это следует из рассмотрения по-
добных треугольников A'D'S и ADS. Таким образом,
VSA'B>C' _
V SABC
mnk,
и утверждение доказано.
Перейдем теперь к решению задачи из варианта, рис. 66.
Обозначим отношение сторон Л'Х : AS через т, B'S :JiS — через k,
C'S : CS — через n. Тогда согласно сказанному выше получим
.88	.	22
mtlk— 225 ’ mk-45“-
Отсюда, в частности, следует, что п=Ч$.
Заметим, что ребра пирамиды SABC представляют собой се-
кущие, проведенные к шару из одной внешней точки, а ребра пи-
рамиды SA'B'C' представляют собой внешние части этих секущих.
Если учесть, что расстояние от вершины S до центра шара рав-
236
но 4, расстояние до максимально удаленной точки шара — 5, а до
минимально удаленной точки шара равно 3, то по теореме о секу-
щих получим:
5Л'-5Л=15, SB'-55=15, SC'SC= 15
ИЛИ	/
т-5Л®=115, k -SB2= 15, n-SC2=15.
Поскольку л = 4/5, то SC = У 75/4. Отсюда находим
SC'=SC =/12.
Рассмотрим-треугольники SB'С' и SBC, общий угол при вер-
шине которых обозначим а. По теореме косинусов находим
(В'С')2= (SB')2+ (SC')2—2(SB') (SC') cos a,
BC2=SB2+SC2-2SB-SC-cos<i.
Эти соотношения можно переписать так:
(B'C')2=k2SB2+n2SC2—2knSB SC cos a,
BC2=SB2+SC2—2SB SC cos a.
Представляя в первое неравенство SB и SC, получим
(B'C')* = 15&4- 15/г-ЗО //in cos a,
Отсюда находим
По условию В'С':ВС = /132/15. Значит,- kn= 132/225. Посколь-
ку д=_4/5, Tojfe= 11/15. Далее находим SB:
ЗВ1=-т-=^гг> SB=-^
к и	Кп
и, наконец, находим SB':
SB' = k-SB = yn.
Поскольку mnk — 88/225, п = 4/5, k= 11/15, то m = 2/3. Да-
лее находим ВЛ:
ВЛ« = — ВЛ =	/10
т 2 ’	2 к
и отрезок 5Л':
5Л' = /п.5Л = |7‘10.
Ответ: ]/10,	J/T2.
237
Задача 5. Обозначим стороны трапеции ABCD (рис. 67) через
х, у, х и z соответственно. Тогда условие о том, что первый и вто-
рой пешеходы пройдут весь путь за одно и то же время, запишет-
ся в виде уравнения:
*	i	# _г *1	2 — * У	2
6	’	8 ~ 5 ’	8	‘ 7 ‘ 7	' 6 ~ 8	’
из которого находим
72	_ 1
1260 Х — 56 'У
или
г/ 16
х “ 5 *
Второе условие сразу нельзя записать в виде одного уравне-
ния: неизвестно, на каких участках какие были скорости. Поэтому
рассмотрим все возможные случаи. Их шесть:
П	х 4-	у	4-	х	।	z	х л_х + У + 2
6’8	’	8	“	7 1“ 8 *
х I	У	I	х	i	2	—	х +у _l~x+z
6 ’	8	’	5	'	8	7’8’
Q\	х ±	У	±	х	±	2	—	Х + Н*_1_ г
6’8*^5’"8 —	7	’ 8 ’
лч х I У t х 4- z_X I #+*+* .
б”г8‘5’8 — в”1”	7
сч х \ У Л_х \ z — x + y_x_x + z
°’	б“*8^5*8 — 8	7
хД_У\х±г^_х + У + х _L 2
;	6 ’ 8 “ 5 ~ 8	8	* 7 ‘
Здесь использовано условие, что скорость менялась только один
раз.
Первое уравнение противоречиво. Из второго уравнения нахо-
дим у/х=83/15, что противоречит выше полученному соотношению.
Рис. 67.
Из третьего уравнения находим
у1х=^1к^ что также противоречит
этому соотношению. Из четверто-
го уравнения получаем z/x = 7/3, из
_ пятого — zlx=^l^ из шестого —
г/х=98/15.
Рассмотрим три последних вы-
вода. Они не противоречат усло-
вию у/х=1в/5. Однако проверим,
238
может ли при таком соотношении сторон существовать трапеция.
Для существования трапеции необходимо
x+y+x^z, 2x+y^z
и
x+z+x^y, 2x+z^y,
т. е.
Решения пятого и шестого уравнений не удовлетворяют этим
условиям; решение четвертого уравнения дает ответ задачи. По-
скольку 7/з<1в/з, то меньшее основание трапеции — г.
Ответ: отношение меньшего основания к боковой стороне рав-
но 7:3.
§ 30.	ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ
МАТЕМАТИКИ И КИБЕРНЕТИКИ, 1974 г.
Вариант 1
1.	Найти все решения уравнения
l^sin (1 — х) = Kcos х ,
удовлетворяющие условию 0^х^2л.
2.	Найти все действительные значения а, при которых каждое
решение неравенства	>
log0>5X2>logo)5(x+2)
является решением неравенства 49х2—4а4<:0.
3.	Найти все значения х, удовлетворяющие одновременно сле-
дующим условиям:
||х-2| + |х-3|=1,
1813х — 974 < 163х‘.
4.	Имеются три несообщающихся между собой резервуара, при-
чем объем третьего не меньше объема второго. Первый резервуар
имеет объем V и может быть заполнен первым шлангом за 3 ч,
вторым шлангом — за 4 ч, третьим шлангом — за 5 ч. К каждому
из резервуаров может быть подключен любой из этих трех шлан-
гов. После того, как к каждому из резервуаров подключают по
одному шлангу каким-либо способом, все шланги одновременно
включаются. Как только какой-то резервуар наполнится, соответ-
ствующий шланг отключается и не может быть подключен в даль-
нейшем к другому резервуару. Заполнение считается оконченным,
если наполнены все три резервуара. При самом быстром способе
подключения заполнение окончится через 6 ч. Если бы все резер-
239
вуары сообщались, то заполнение окончилось бы через 4 ч. Най-
ти объемы второго и третьего резервуаров.
5.	В треугольной пирамиде ЗДВС сумма трех плоских углов
при каждой вершине В и С равна 180° и SA=BC. Найти объем
пирамиды, если площадь грани SBC равна 100 см2, расстояние
от центра описанного шара до плоскости основания АВС равно
3 см.
Вариант 2
1.	Найти все решения уравнения
]/sinx = Уcos (х -{- 2),
удовлетворяющие условию 0^х^2л.
2.	Найти все действительные значения а, при которых каждое
решение неравенства
1 1 >
0,52(х-1)1 <(0,25)(3-х)’
является решением неравенства Юа4 5*2—9^0.
3.	Найти все значения х, удовлетворяющие одновременно сле-
дующим условиям:
(1 х "Ь 51 = |	21 -|- 3,
U114 + 279.x < 139х*.
4. В порту для загрузки танкеров имеются три трубопровода.
По первому из них закачивается в час 300 т нефти, во второму —
400 т, по третьему — 500 т. Нужно загрузить два танкера. Если
загрузку производить первыми двумя трубопроводами, подключив
к одному из танкеров первый трубопровод, а к другому танкеру —
второй, то загрузка обоих танкеров при наиболее быстром из двух
возможных способов подключения займет 12 ч. При этом какой-то
из танкеров, может быть, окажется заполненным раньше, и тогда
подключенный к нему трубопровод отключается и в дальнейшей
загрузке не используется. Если бы' вместимость меньшего по
объему танкера была вдвое больше, чем на самом деле, и загрузка
производилась бы вторым и третьим трубопроводами, то при бы-
стрейшем способе подключения загрузка заняла бы 14 ч. Опреде-
лить, сколько тонн нефти вмещает каждый из танкеров.
5. В треугольной пирамиде SABC суммы трех плоских углов
при каждой вершине А, В и С равны 180°. Найти расстояние меж-
ду скрещивающимися ребрами ЗД и ВС, если известно, что ВС=
= 4 см, АС=5 см, АВ=6 см.
240
Вариант 3
1. Найти все решения уравнения
Kcos х = У sin (х +.2),
удовлетворяющие условию 0^х^2л.
3.	Найти все действительные значения а, при которых каждое
решение неравенства
logj_ (21 — х) < log_i_ 2х‘
з	з
является решением неравенства 9а4—64х2>0.
3.	Найти все значения х, удовлетворяющие одновременно сле-
дующим условиям:
(|х4-3| + |х-2|=5,
(818 — 135х< 137х2.
4.	Три самосвала, грузоподъемность первого из которых 12 т,
второго — не меньше 2 т, а третьего — не меньше чем второго,
должны быть загружены песком с помощью двух транспортеров.
Первый транспортер загружает '/з т песка в минуту, второй — 2/3 г
в минуту. Самосвалы могут подъезжать к транспортерам в любом
порядке, причем загрузка одного самосвала может производиться
только одним транспортером. Кроме того, начав загрузку при по-
мощи одного из транспортеров, самосвал не может уже переехать
на догрузку к другому. Время погрузки считается от начала за-
грузки первого самосвала до окончания загрузки последнего. При
соблюдении этих условий минимальное время загрузки составляет
22,5 мин. Предполагается, что на смену у транспортера загружен-
ного самосвала другим порожним самосвалом время не теряется.
Если же все самосвалы загружаются с помощью лишь одного вто-
рого транспортера, то погрузка занимает 36 мин. Определить гру-
зоподъемности второго и третьего самосвалов.
5.	В треугольной пирамиде SABC суммы трех плоских углов
при каждой вершине5, А и В равны 180°, £С=15ли и /Л СВ = 60°.
Найти радиус описанного шара, если радиус вписанного шара ра-
вен 3 см.
Вариант 4
1.	Найти,все решения уравнения
]/cos (х + 1) = j/cos х,
удовлетворяющие условию 0^х^2л.
16—619	241
2.	Найти все действительные значения а, при которых каждое
решение неравенства
1	2
0,36(3*+2)“ <(0,6)(*+8)>
является решением неравенства 25а4х2—4^0.
3.	Найти все значения х, удовлетворяющие одновременно сле-
дующим условиям:
11 х — 51 = 3 +1 х — 2|,
(1186- 199х<197х‘.
4.	Во дворце водного спорта есть два бассейна и две водопро-
водные линии для их заполнения. Первая линия заполняет в час
объем 5V, вторая линия — объем 6V. К каждому бассейну можно
подключить, любую из линий. После того как подключение одним
из двух возможных способов произведено, линии одновременно
включаются. После заполнения какого-то бассейна соответствую-
щая линия отключается и в дальнейшем для заполнения другого
бассейна не используется. Заполнение считается оконченным, как
только заполнятся два бассейна. Существует самый быстрый спо-
соб подключения линий, позволяющий заполнить оба бассейна за
8 ч. Если бы объем первого бассейна был увеличен вдвое, то за-
полнение можно было бы окончить самое быстрое за 10 ч. Опреде-
лить объемы бассейнов, если известно, что объем первого бассей-
на не больше объема второго бассейна.
5.	В треугольной пирамиде SABC суммы трех плоских углов
при каждой вершине А И В равны 180° и SC=AB. Внутри пирами-
ды взята некоторая точка D, сумма расстояний от которой до трех
фоковых граней SAB, SAC и SBC равна 7 см. Найти расстояние
от центра описанного шара до грани SAB, если объемы пирамид
SABC и DABC относятся как 8: 1.
Разбор варианта 1
Задача 1. Данное уравнение равносильно следующей системе:
{sin (1 — х) = cos х,
cosx > 0, 0<х<2«.
Решим уравнение. Запишем его в следующей форме:
sin (1 — х) = sin — х
Тогда возможны два варианта:
1) 1—х = —x-|-2wn.
242
В этом, случае, очевидно, решений нет;
2)	1— х — п— ---------х)-|-2я/п,
2х = 1 —— 2и/п
или
х --------— 2кт.
Поскольку 0^х^2л, то в последней формуле параметр т мо-
жет принимать только два значения т=—1 и т=—2. Им соот-
ветствуют, значения х, равные 3jt/4+V2 и TnM+Vz. Теперь осталось
проверить, выполняется ли условие cosx^O, гарантирующее, что
найденные значения х удовлетворяют области допустимых значе-
ний. Имеем
Таким образом, исходное уравнение имеет только одно решение:
х=7л/4+1/2.
Ответ: х=7л/4+1/г.
Задача 2. Найдем решения первого неравенства. Учитывая, что
основание обоих логарифмов меньше единицы и, кроме того, х#=0,
имеем
х2^х+2
или
— 1<х<2, х#=0.
Решения второго неравенства имеют вид
или
• (1)
Легко понять, что все значения х, составляющие решения пер-
вого неравенства, удовлетворяют неравенству (1) только в том
случае, если выполняется условие
Последнее имеет место, если —]/7~ и
Ответ: а< —j/V,
16*
243
Задача 3. Решения первого уравнения легко найти, если вспом-
нить, что модуль разности двух чисел есть расстояние между точ-
ками числовой прямой, координатами которых служат эти числа.
Тогда решением уравнения будет любое число х, изображение ко-
торого на числовой прямой удалено от/точек 2 и 3 на расстояния,
сумма которых равна 1. Очевидно, что таких чисел существует бес-
конечно много, а именно, это будет любое число, удовлетворяющее
неравенству 2^х^3.
Квадратное неравенство
163*2—81 Зх+974 >0
имеет следующие решения:
Таким образом, условиям задачи удовлетворяют х=2 и ш/1бз^
<х<3.
Ответ: х —2;	3.
Задача 4. Обозначим объем второго резервуара буквой х,
а третьего — у (у^х). Пропускная способность первого шланга
равна VJ3, второго—V/4, третьего — V/5. Тогда последнее усло-
вие задачи позволяет составить следующее уравнение:
V+x+У _л
V/3 + V/4 + V/5
ИЛИ
I	32 w
x + y=-^V.
Второе уравнение задачи заключено в условии, что время само-
го быстрого наполнения системы резервуаров равно 6 ч. При этом,
однако, неизвестно, к каким резервуарам был подсоединен тот или
иной шланг. Для того чтобы сократить число случаев подлежащих
рассмотрению, заметим, что время наполнения системы резервуа-
ров определяется временем наполнения самого последнего резер-
вуара.
Поскольку при самом быстром способе наполнения резервуа-
ров первый резервуар будет наполнен за 3, 4 или 5 ч, то ясно, что
время. 6 ч относится не к этому, а ко второму или третьему резер-
вуару. Легко понять, что при таком способе к первому резервуару
следует подключить шланг с самой маленькой пропускной способ-
ностью, оставив два шланга с большей производительностью для
второго и третьего резервуаров.
Поскольку объем второго резервуара не превосходит объема
третьего резервуара, то ко второму резервуару следует подключить
2-й шланг, а к третьему резервуару—Ьй шланг.
244
Возможны два случая:
1.	w=6’	2.	V/4<6«
	v/з <6-		~V/3~6,
	•* + !/=		x+l/=4'V,
у-^х.	У^х.
Первая система противоречива. Из второй системы находим: х =
= 2V/15, y=2V.
Ответ: x=2V/15, y=2V.
Задача 5. Пусть фигура SiCSsBSzA представляет собой раз-
вертку боковой поверхности пирамиды SABC на плоскость осно-
вания АВС (рис. 68). Из условия
задачи о том, что суммы всех
плоских углов пирамиды .при вер-
шинах В и С равны 18(Г, следу-
ет, что точки Si, С и S3 лежат на
одной прямой. То же самое мож-
но сказать и о точках S3, В и S2.
Так как SiC=CS3 и SzB = BS3,
то ВС—средняя линия треуголь-
ника 51525з..3начит, S]S2 = 2 • ВС.
С другой стороны, ломаная
Si4S2 также равна 2-ВС. Следо- _____________ .
вательно, точки Sb А и S2 лежат	$з
на одной прямой и фигура	Рис. 68.
SiS2S3 — треугольник.
Площадь треугольника BCS3 равна 100 см2, а следовательно,
площадь всего треугольника 515г53 равна 400 см2, а поскольку АВ
и АС — средние линии треугольника SiSzS3, то площади всех гра-
ней пирамиды SABC равны между собой и равны по 100 cjw2 каж-
дая. Больше того, треугольники Si^C, SzAB, S3BC и АВС равны
между собой. Следовательно, равны и площади кругов, описанных
вокруг каждого из них. Значит, каждая из граней пирамиды
SABC находится на одном и том же расстоянии от центра опи-
санного вокруг пирамиды шара, т.’ е. на расстоянии 3 см.
Соединив центр описанного вокруг пирамиды шара с каждой
вершиной пирамиды SABC, получим, что объем всей пирамиды
составлен из объемов четырех пирамид, у каждой из которых одна
и та же высота, равная 3 см, и одна и та же площадь основания,
равная 100 см2. Объем каждой из таких пирамид равен
4--3-100= 100,
<5
а объем всей пирамиды SABC равен 400 cjw3.
Ответ: 400 см3.
245
§ 31.	ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ
МАТЕМАТИКИ И КИБЕРНЕТИКИ, 1975 г.
Вариант 1
1.	Решить неравенство
Y— х2 — 4х -|- х + 1 >0.
2.	Решить систему уравнений
(ctg (2у — cos2 х) = 1,
бу — 15cos2x^= -у— 1.
3.	На бо'ковых сторонах KL и MN равнобочной трапеции
KLMN выбраны соответственно точки Р и Q так, что отрезок PQ
параллелен основаниям трапеции. Известно, что в каждую из тра-
пеций KPQN и PLMQ можно вписать окружность, и радиусы этих
окружностей равны R и г соответственно. Определить основания
LM и КМ.
4.	На дороге, ведущей из пункта А в пункт В, находится пункт С.
Из пункта А в пункт В по этой дороге с постоянными скоростями
вышли два пешехода. Второй пешеход вышел из пункта А на
12 мин позже первого, но прибыл в пункт В на 18 мин раньше
него. При этом через пункт С пешеходы прошли с интервалом не
более 6 мин. Если бы второй пешеход вышел из пункта А через
15 мин позже первого, увеличив свою скорость на 20%, а скорость
первого пешехода не изменилась, то второй пешеход прибыл бы
в пункт В на 35 мин раньше первого, а через пункт С пешеходы
прошли с интервалом не менее 5 мин. Если бы первый пешеход
уменьшил свою скорость на 1 км/ч, а скорость второго пешехода
осталась первоначальной, то первый пешеход потратил бы на путь
от А до С в 3 раза меньше времени, чем второй пешеход на весь
путь от А до В. Найти длину пути от А до С.
5.	Все ребра треугольной пирамиды ABCD касаются некоторого
шара. Три отрезка, соединяющие середины скрещивающихся ребер
АВ и CD, АС и BD, AD и ВС, равны. Угол АВС равен 100°. Най-
ти отношение высот пирамиды, опущенных из вершин А и В.
Вариант 2
1.	Решить неравенство
]/х24-л-2х4-1 >0.
2.	решить систему уравнений
(cos (2х 4- 6 sin2 у) = 1,
1 Зх — 3 sin* у = — 10.
246
3.	Дана прямоугольная трапеция, основания которой равны а
и b (а<Ь). Известно, что некоторая прямая, параллельная осно-
ваниям, рассекает ее на две трапеции, в каждую из которых мож-
но вписать окружность. Определить радиусы этих окружностей.
4.	В обувном цехе работают две бригады. Каждая из них полу-
чила заказ на пошив одного и того же количества женской и од-
ного и того же количества мужской обуви, причем сначала требо-
валось изготовить женскую обувь. На пошив одной пары обуви
(как мужской, так и женской) бригада затрачивает одно и то же
количество времени. Первая бригада начала работать над заказом
на 7 дней раньше, а закончила выполнение всего заказа на
11 дней позже второй. При этом интервал времени между оконча-
нием пошива бригадами женской обуви был не более 5 дней. Если
бы первая бригада начала работу над заказом на 8 дней раньше
второй, увеличив свою (Производительность на 5%', а производи-
тельность второй бригады не изменилась, то весь’ заказ первая
бригада выполняла бы на 1 дней позже второй, а интервал вре-
мени между окончаниями пошива бригадами женской обуви был
бы не менее двух дней.
Если бы производительность второй бригады увеличилась на
20 пар обуви в день, а производительность первой бригады оста-
валась бы первоначальной, то вторая бригада потратила бы на
пошив женской обуви в 2,4 раза меньше времени, чем первая
бригада на выполнение всего заказа. Определить число пар жен-
ской обуви в заказе.
5.	Дана треугольная пирамида ABCD. Скрещивающиеся ребра
АВ и CD этой пирамиды перпендикулярны, а скрещивающиеся
ребра АС и BD перпендикулярны и равны между собой. Все ребра
этой пирамиды касаются некоторого шара. Найти его радиус, если
длина ребра ВС равна а.
Вариант 3
1.	Решить неравенство
У— х* -f- х + 2 4- 2х — 1 > 0.
2.	Решить систему уравнений
(tg (Зу — 5 cos2 х) = 1,
| Зу — 10cos‘x = -^-1.
3.	На боковых сторонах PQ и ST равнобочной трапеции PQST
выбраны соответственно точки М и N так, что отрезок MN парал-
лелен основаниям трапеции. Известно, что в каждую из трапеций
PMNT и MQSN можно вписать окружность. Найти основания тра-
пеции PQST, если сторона PQ равна с, а отрезок MN равен I
(021).
247
4.	Два самолета, следующие с постоянными скоростями из го-
рода А в город С, пролетают над некоторым пунктом В. Извест-
но, что второй самолет вылетел из города А на 14 мин позже пер-
вого, а в город С прилетел на 16 мин раньше него. При этом над
пунктом В самолеты пролетели с интервалом не более 4'мин.
Если бы второй самолет вылетел из города А через 10 мин по-
сле вылета первого, уменьшив свою скорость на 10%, а скорость
первого самолета не изменилась, то над пунктом В самолеты про-
летели бы с интервалом не менее 2 мин, а в город С второй са-
молет прилетел бы на 10 мин раньше первого. Если бы скорость
второго самолета увеличилась на 40 км/ч, а скорость первого са-
молета не изменилась,- то второй самолет потратил бы на путь от
А до В в 7/з раза меньше времени, чем первый самолет на весь
путь от А до С. Определить скорость первого самолета.
5.	Все ребра треугольной пирамиды ABCD касаются некоторо-
го шара. Три отрезка, соединяющие середины скрещивающихся
ребер АВ и CD, АС и BD, AD и ВС, равны. Угол DBC равен 50°,
а угол BCD больше угла BDC. Найти отношение площадей гра-
ней ABD и АВС.
Вариант 4
1.	Решить неравенство
Vх’ + 4х-5 -2х + 3>0.
2.	Решить, систему уравнений
1 sin (2х + sin1 у) = 0,
— 3sin’y= — 2.
3.	Дана прямоугольная трапеция. Известно, что некоторая пря-
мая, параллельная основаниям трапеции, рассекает ее на две тра-
пеции, в каждую из которых можно вписать окружность. Опреде-
лить основания исходной трапеции, если ее боковые стороны рав-
ны с и d (Od).
4.	Два грузовика доставили со склада на стройку одно и то же
количество кирпича и одно и то же количество цемента, причем
каждый из них доставлял сначала кирпич, а потом цемент, пере-
возя за каждую поездку груз одного и того же веса. Первый гру-
зовик начал работу на 40 мин раньше, а закончил на 40 мин поз-
же второго. При этом интервал времени между окончаниями до-
ставки кирпича грузовиками был не более 20 мин.
Если бы первый грузовик начал работу на ’1 ч 5 мин раньше
второго, уменьшив свою производительность на 10%, а произво-
дительность второго грузовика не изменилась, то второй грузовик
закончил бы работу на 55 мин раньше первого, а интервал вре-
248'
меня между окончаниями доставки кирпича грузовиками был бы
не менее 25 мин. Если бы производительность первого грузовика
уменьшилась на 2 т в час, а производительность второго грузови-
ка не изменилась, то первый грузовик затратил бы на выполнение
всей работы в два раза больше' времени, чем второй грузовик на
доставку кирпича. Сколько всего цемента было доставлено на
стройку?
5.	Дана треугольная пирамида ABCD. Скрещивающиеся ребра
АС и BD этой пирамиды перпендикулярны. Так же перпендику-
лярны скрещивающиеся ребра AD и ВС. Ребра АВ и CD равны.
Все ребра этой пирамиды касаются шара радиуса г. Найти пло-
щадь грани АВС.
Разбор варианта 1
Задача 1. Допустимыми являются те значения х, для которых
—х2—4х ^>0,
х(х+4)^0,
—4^х^0.
Исходное неравенство можно записать следующим образом:
У— х2 — 4х> — х— 1.
Необходимо различать два случая
1. —х—1^0, т. е. х^—1, а с учетом указанных выше ограни-
чений:
—4<^х^ — 1.
В этом случае обе части неравенства неотрицательны и, после воз-
вышения их в квадрат, получится неравенство, равносильное ис-
ходному. Таким образом, имеем
/_4<х<— 1,
| — х* — 4х >(— х — 1)’
или
| — 4<х< — 1,
|2х‘4-6х4- 1 <0.
Отсюда находим:
2. —х—1<0, т. е. х>—1, и далее: —Кх^О. Очевидно, что
все рассматриваемые х удовлетворяют исходному неравенству, по-
скольку при этих х его левая часть неотрицательна, а правая —
меньше нуля.
249
Объединяя множества значений х из обоих случаев, находим
все решения неравенства.
Ответ-.
Задача 2. Из данной системы уравнений следует, что
бу — 15^os’x = -^— 1,
2у — cos‘x = -^-|-^it, ^ = 0,ztrl,zt2... .
Отсюда нетрудно найти у и cos’x.
*	те I 15&те + 1
^=-8-+~2Г^-’
Поскольку 0<Zcos2xsg: 1, то целочисленный параметр k может при-
нимать только два значения: Ai=0 и fe=l.
В первом случае (&=0) имеем.
Зтс + 1
У=^~>
COS‘X = -±..
Отсюда находим
х=rt arccos jZ —[-/nit,
Зге 1	п » 1	। п
У=—/п=0,± 1,±2....
Во втором случае (k = 1) имеем
18д+1
У~~	24	’
cos‘x=^L+J.
или
,	1 /"Зте + 1 I
х = arccos у —-f-mu,
18л + 1
У=—2Г—'
250
Ответ:
х — arccos у	-f- ««;
Зя + r
y~~2A~>
x = zt arccos
18* + 1
У=—24-


где m=0, ±1, ±2, ... .
Задача 3. Чертеж к этой задаче представлен на рис. 69. До-
строим равнобочную трапецию K.LMN до равнобедренного тре-
угольника KSN и опустим из центров данных окружностей Oi и
О2 перпендикулярны в точки их каса-
ния со стороной KL. Проведем
OiC\\KL, угол О1О2С назовем а.
Тогда из треугольника OiO2C, в
котором
О1О2='Г+Л; О2С—г,
находим косинус угла а:
R — r
cos а = yr-,— .
Очевидно, что центры рассматри-,
ваемых окружностей Oi и О2
лежат на высоте равнобедренного
треугольника ASM. Поэтому от-
резок SD равен
SD = —------г = ^—.
COS a	R — Г
Из прямоугольного треугольника
LSD легко определяется LD и за-
тем все основание LM трапеции:
LD = SDctga = -^-,
LAf = 2-LD= +=-.
/Яг
Рис. 69.
Аналогичным образом находится основание KN трапеции.
В треугольнике KSE катет SE равен
—-----1_г д-27?.
COS а 1 I
Поэтому
KN = 2-KE = 2-SEctga,
tfW=2ctgaf-^-+r + 2R\	КУ = -^-.
& COSa	/	*
Ответ: 2г*!УЕг и 2R’/|Z/?r.
251
Задача 4. Обозначим скорости пешеходов через v, и t>2 соответ-
ственно, расстояние АС=х, расстояние СВ=у. Схема составления
уравнений понятна из следующей таблицы:
Условие задачи
1
Уравнение или неравенство
второй пешеход вышел из пункта А
на 1/5 ч позже и пришел в пункт В
на 3/10 ч раньше, чем первый пеше-
ход;
при этом интервал времени между про-
хождением пешеходами пункта С не
превосходит 1/10 ч\
если второй пешеход увеличит свою
/	6
скорость на 20 % ( т. е. и'2 = и2
то, выйдя из А на 1/4 ч позже, он
придет на 7/12 ч раньше, чем первый
пешеход;
если первый пешеход уменьшит
свою скорость на 1 км/ч, то время,
за которое он пройдет АС, в 3 раза
/ меньше времени, за которое
второй пешеход пройдет АВ;
при этом интервал времени между
прохождением пешеходами пункта С
не менее 1/12 ч.
Поясним неравенства, в которые входит абсолютная величи-
на. Дело в том, что заранее не ясно, кто из пешеходов проходит
пункт С первым. Поэтому интервал времени между моментами,
в которые они проходят этот пункт, записывается с помощью абсо-
лютной величины разности соответствующих времен.
Таким образом, имеется система трех уравнений, содержащая
четыре неизвестные величины, и два неравенства. Особенность этой
задачи состоит в том, что именно эти неравенства в совокупности
с уравнениями задачи позволяют получить еще одно недостающее
для решения уравнение. Покажем, как это делается. Из уравнений
(1) и (3) легко определяются величины (х+*/)М и (х+у)1ис
=	£±А = 2,5
V2	Vi
и далее их отношение:
х + # х + к  Vi   4	.
v2 * Vi	v2’	5
Благодаря тому что отношение скоростей пешеходов найдено, мож-
но упростить неравенства задачи. Имеем
252
и далее
и, наконец
1 х
5 th
1
5 .
1
< 10
Аналогично второе неравенство преобразуется к виду
th 4^4*
На рис. 70 изображена картина совмещения решений этих двух
неравенств относительно величин x/vi. Имеются следующие ре-
шения
Покажем, что второе множество решений не соответствует усло-
вию задачи. Для этого обратимся к уравнению (4). Учитывая, что
(х+у)М=2, получаем:
или
_х_=_2___________2_
, th 3 3th
Поскольку ui>0, отношение
2/ (3^1) представляет собой
положительную величину,
то отсюда следует, что x!v.\<A. Таким образом, второе множество
значений отношения x/v\ не является решением задачи. Получив
еще одно дополнительное уравнение, связывающее х и (в чем
и заключалось центральное место решения), имеем систему урав-
нений
х _____ 2
th — 1— 3 ’
х _ 1
th 2 ’
откуда легко определяются х и Vi:
х=2; Vi=4.
Поскольку, в условии задачи не требуется определять остальные
неизвестные, то решение задачи закончено.
Ответ: 2 км.
253
Задача 5. Покажем, что из условия о равенстве отрезков,
соединяющих середины скрещивающихся ребер пирамиды ABCD,
рис. 71, следует, что эти ребра попарно перпендикулярны друг
ДРУГУ- Возьмем, например, отрезки MiNi и M2N2, соединяющие
середины пар ребер AD, ВС и АВ, CD соответственно. Соединим
точки Л41, ЛГ2, ЛГ1, N2 отрезками прямых. Очевидно, что
MiMzWBDWNtNz и МгЛМ!ЛСЦЛ^Л^, как средние линии соответствую-
щих треугольников. Поэтому фигура	— параллелограмм.
Поскольку AfiTVi = 2-^2» то диагонали этого параллелограмма рав-
Д
ны между собой и, следовательно, этот параллелограмм — прямо-
угольник. Значит BD.LAC. Действительно, AliAlallBD; Af2A/rillАС и
AfiA42J_A42A^i. Аналогично доказывается, что ABJlCD и ADLBC.
Таким образом, в условии задачи речь идет о пирамиде, у ко-
торой скрещивающиеся ребра взаимно перпендикулярны и, кроме
того, касаются 'некоторого шара. Покажем, что такая пирамида бу-
дет обязательно правильной.
Для доказательства этого утверждения отметим два следую-
щих факта:
в пирамиде с попарно перпендикулярными скрещивающимися
ребрами каждая вершина проектируется в точку пересечения высот
противоположной ей грани;
в треугольной пирамиде, все ребра которой касаются некоторо-
го шара, суммы противоположных скрещивающихся ребер равны
друг другу.
Действительно, поскольку каждое ребро основания перпендику-
лярно скрещивающемуся с ним боковому ребру пирамиды, являю-
щемуся наклонной плоскостью к плоскости основания, то по теоре-
ме о трех перпендикулярах оно перпендикулярно и его проекции
на эту плоскость. Поэтому каждая из проекций бокового ребра
на плоскость основания будет высотой треугольника, лежащего
254
в основании, и, следовательно, вершина пирамиды проектируется
в точку Пересечения высот основания (точка О на рис. 71 справа;
треугольник АВС по условию — тупоугольный. Поэтому точка О
лежит вне треугольника).
Второе утверждение о равенстве сумм скрещивающихся ребер
AD+ВС = CD+АВ = А С+BD
доказывается точно таким же образом, как и для плоского четы-
рехугольника, описанного около окружности. Нужно только ис-
пользовать теорему о равенстве касательных, проведенных к шару
из одной точки вне этого шара.
Перейдем к доказательству основного утверждения. Обозначим
АВ=с, АО = с', ВС=а, ОС=а', OD = x. и АС=Ь. Высоту BE осно-
вания АВС обозначим hb. Имеем следующее равенство:
AD 4* й = CD+с
или
Ухг + с' * + а=Ух*-\-аГ*+с.	(1)
Найдем связь между отрезками а, а', с и'’с'. Из прямоугольных
треугольников АОЕ и ВСЕ, в которых углы АОЕ и ВСЕ равны как
углы с одинаково направленными и перпендикулярными сторона-
ми, находим
hb АЕ . ht	V сг — h2t
---=—т , т. е.----------=---------.
ас’	а-с’
ИЛИ
Аналогично этому из треугольников ВАЕ и ЕОС с равными угла-
ми ВАЕ и ЕОС находим
	hb с у	ЕС	hb	V а* — h*b “ а' * Т* С‘ с	а’
ИЛИ		
		=	(3)
Сравнивая между собой равенства (2) и (3), получаем
а2+с'2=с2+а'2.	(4)
Объединяя (1) и (4), получим систему равенств
|а-|- Ух*~1~с' 2 = с-|-'|/хг+а7*, '
(а* 4-с' ‘ = е’-|-а' *.
Возводя в квадрат обе части первого уравнения и учитывая вто-
рое уравнение системы, получим
а У х*-{-с'* = с У х*-\-а' *,
255
после чего имеем
(a-j- prл,4-c', = c+K•rt+p,*»
(а 0xl4-c' 2 = с J/’x’-t-®'’.
Рассматривая эти равенства как систему уравнений отно-
сительно выражений а и У х2-^-с'2, приходим к заключению,
что возможны два случая:
1) а = с; Ух2 -j-c' г = Ух2 -\-а' * или
AD = CD, АВ = ВС.
i_.„ 2) ^_а=Ух\-\-а'2; с = Ух* -[-с'2 или
AD=AB, CD = CB.
I. Первый случай-. AD = CD; АВ=ВС.
Если все вышеприведенные рассуждения и вычисления проделать
для той же пирамиды ABCD, приняв А за вершину, а треугольник
BDC — за основание, то получим две возможности: либо AD = AC,
BD=BC и тогда пирамида ABCD — правильная (AADC — равно-
сторонний, BA=BC=BD); либо AD=BD и АС=ВС и опять-таки
пирамида ABCD — правильная (ДЛВС— равносторонний, DA =
=DB = DC). Однако этот случай невозможен, поскольку угол АВС
равен 100°, а не 60°.
II. Второй случай: AD = AB, CD=CB.
Применяя предыдущие рассуждения к пирамиде.ABCD, считая ее
вершиной точку А и основанием — треугольник BDC, приходим
к двум вариантам: либо AD = AC, BD=BC и тогда пирамида
ABCD — правильная (&BDC — равносторонний, AD = AB = AC),
что Невозможно, так как боковая грань АВС такой пирамиды
должна быть остроугольным, а не тупоугольным треугольником;
либо AD—BD и АС=ВС и опять-таки пирамида ABCD — правиль-
ная (ДЛВД— равносторонний, AC=BC=DC), что невозможно,
поскольку боковая грань АВС не является остроугольным тре-
угольником.
Итак, остается единственно возможный случай: пирамида
ABCD — правильная и в ней A.ACD — равносторонний, а точка
В — вершина (BA=BC=BD).	. >
После этого легко вычислить отношение высот пирамиды, опу-
щенных из вершин А и В. Имеем: •
'	У вся = “з" НА'$ьвсо	‘Ив’$&аос‘
Отсюда находим
»А	SbADC
Нв	S&BCD
256
Но отношение площадей треугольников ACD и BCD, имеющих об-
щую сторону CD, равно отношению высот этих треугольников,
опущенных из вершин Л и В на сторону CD. Первая из них равна
3/2, вторая — 6’ctg 50°/2. Таким образом,
^-=1/3. «50».
Ответ: У"3 tg 50°.
§ 32.	МЕХАНИКО-МАТЕМАТИЧЕСКИЙ
ФАКУЛЬТЕТ, 1972 г.
Вариант 1
1.	Найти все значения 'х, при которых справедливо неравенство
log8 х logt|/’14-2x
log2(l+2x)^ log2X
2.	Пункты А и В соединены двумя дорогами, одна из которых
на 3 км короче другой. Из В и А по более короткой дороге вышел
пешеход; и одновременно из А по той же дороге выехал велосипе-
дист. Пешеход и велосипедист одновременно прибыли в А через
два часа после начала движения. За это время пешеход прошел
один раз путь от В до А, а велосипедист проехал два раза в одном
направлении по кольцевому маршруту, образованному двумя на-
званными дорогами.
Найти скорость пешехода и велосипедиста, если известно, что
их вторая встреча произошла на расстоянии 3,5 км от пункта В.
3.	В треугольнике АВС АВ = 20 м, АС=24 м. Известно, что
вершина С, центр вписанного в треугольник АВС круга и точка
пересечения биссектрисы угла А со стороной ВС лежат на окруж-
ности, центр которой лежит на стороне АС.
Найти радиус окружности, описанной около треугольника АВС.
4.	В треугольной пирамида SABC боковое ребро SC равно ребру
АВ и наклонено к плоскости основания АВС под углом 60°. Изве-
стно, что вершины А, В, С и середины боковых ребер пирамиды
расположены на сфере радиуса 1 м.
Доказать, что центр указанной сферы лежит на ребре АВ и
найти высоту пирамиды.
5.	Даны три уравнения с действительными коэффициентами:
1)' х2—(а+Й)х+8=0,
2) х2—й(й + 1)х+с=0,
3) х4—й(й+1)х2+с=0.
17—619
257
Каждое из них имеет по крайней мере один действительный ко-
рень. Известно, что корни первого уравнения больше единицы.
Известно также, что все корни первого уравнения являются кор-
нями третьего уравнения и хотя бы один корень первого уравнения
удовлетворяет второму уравнению.
Найти числа а, Ь, с, если Ь>3.
Вариант 2	'*
/
1.	Найти все значения х, при которых справедливо неравен-
ство
(10g, 4) log. 4=^-» 2.
2.	От пристани А вниз по течению реки одновременно отошли
плот и катер. Катер доплыл до пристани В, вернулся к приста-
ни А и снова от А поплыл до пристани В (без остановок). К при-
стани В плот и катер причалили одновременно, а встретились они
на расстоянии 3 км от пристани А.
Определить скорость течения реки, если известно, что на
путь от А дЬ В катер тратил на полчаса меньше времени, чем на
путь от В до А.
3.	В треугольнике KLM угол L>—тупой, а длина стороны KAf
равна 6 м. Найти радиус описанной около треугольника KLM
окружности, если известно, что на этой окружности лежит центр
окружности, проходящей через вершины К, М и точку пересечения
высот треугольника K.LM.
4.	В треугольной пирамиде SABC АС—АВ, а ребро SA накло-
нено к плоскостям граней АВС и SBC под углом 45°. Известно,
что вершина А и середины всех ребер пирамиды, кроме SA, лежат
на сфере радиуса 1 м.
Доказать, что центр указанной сферы расположен на ребре SA
И найти площадь грани ASC.
5.	Даны три уравнения с действительными коэффициентами:
1)	ах2+Ьх+с=0,
2)	cx2+bx+a=Q,
3)	x2+a2x+c2—0.
Каждое из них имеет по крайней мере один действительный ко-
рень. Известно, что любой корень третьего уравнения удовлетво-
ряет первому уравнению и хотя бы один корень второго уравнения
является корнем третьего уравнения.
Найти числа а, Ь, с, если а>2| с|.
25»
Вариант 3
1.	Найти все значения х, при которых справедливо неравенство
(log, х)г > (log,1 —
2.	Из пункта А кольцевого шоссе одновременно в одном на-
правлении выехали автомобиль и мотоцикл, каждый с постоянной
скоростью. Автомобиль без остановок дважды проехал по всему
шоссе в одном направлении. В момент, когда автомобиль догнал
мотоциклиста, мотоциклист повернул обратно, увеличил скорость
на 16 км/ч и через 22,5 мин после разворота одновременно с авто-
мобилем прибыл в пункт А.
Найти длину всего пути мотоцикла, если этот путь на 5,25 км
короче длины всего шоссе.
3.	В треугольнике АВС угол С — тупой; биссектриса BE угла В
делит сторону АС на отрезки АЕ = 3 м и ЕС=2 м. Известно, что
точка К, лежащая на продолжении стороны ВС за вершину С,
является центром окружности, проходящей через точки С, Е и точ-
ку пересечения биссектрисы угла В с биссектрисой угла АСК-
Определить расстояние от точки Е до стороны АВ.
4.	В треугольной пирамиде SABC известны плоские углы при
вершине S: ZBSC = 90, ZASC=Z-ASB = 60°. Вершины A, S и
середины ребер SB, SC, АВ, АС лежат на поверхности шара ра-
радиуса 3 м.
Доказать, что ребро SA является диаметров этого шара и най-
ти объем пирамиды.
5.	Даны три уравнения с действительными коэффициентами:
1)	х2+ах+ас=0,
2)	х2—bx+c3=0,
3)	х4—Ьх2+сэ=0.
Каждое из них имеет по крайней мере один действительный ко-
рень. Известно, что абсолютные величины корней первого уравне-
ния больше единицы. Известно также, что каждый из корней пер-
вого уравнения является корнем третьего уравнения и по крайней
мере один из корней первого уравнения удовлетворяет втррому
уравнению.
Найти числа а, Ь, с.
Вариант 4
1. Найти все значения х, при которых справедливо неравен-
ство
(log?) log,4.
17*
259
- 2. От пристани А к пристани В против течения реки отошел ка-
тер, собственная скорость которого в стоячей воде в 7 раз больше
скорости течения реки. Одновременно навстречу ему от пристани В,
расстояние которой до А по реке равно 20 км, отошла лодка. На
каком расстоянии от В произошла встреча катера с лодкой, если
известно, что через полчаса после начала движения лодке остава-
лось проплыть 4 км до встречи и что катер затратил на путь до
встречи с лодкой на 20 мин больше, чем на путь от места встречи
до пункта В?
3.	Радиус окружности, описанной около остроугольного тре:
угольника АВС, равен 1 м. Известно, что на. этой окружности ле-
жит центр окружности, проходящей через вершины А, С а точку
пересечения высот треугольника АВС.
Найти длину стороны АС..
4.	В треугольной пирамиде SABC середины всех ребер лежат
на поверхности шара радиуса 2 м; АВ — 3 м, АС=А м. Ребро SA
перпендикулярно плоскости основания АВС.
Доказать, что отрезки, соединяющие середины противополож-
ных ребер пирамиды, являются диаметрами указанного шара, и
найти объем пирамиды.
5.	Даны три уравнения-с действительными коэффициентами:
1)	x2+px+q = 0,
2)	<7х2+рх+1=0,
3)	х2+гх+г(р—1)=0.
Каждое из них имеет по крайней мере один действительный ко-
рень. Известно, что любой корень третьего уравнения удовлетво-
ряет первому уравнению и хотя бы один корень второго уравнения
является корнем третьего уравнения. Найти числа р, q, г, если
q=£\, 0<г<2.
Разбор варианта 1
Задача 1. В этой задаче нужно рассматривать только положи-
тельные значения х. Кроме того, х=#1. При этом очевидно, что ве-
личина 1+2х будет больше, чем единица. Поэтому
log2(l + 2х) >0.
Рассмотрим два случая: 0<х<1 и х>1. -В первом случае
имеем
log, х < 0,
log, (х) log, х > (log, 1 + 2х) log, (1 +'2л).
После упрощений получается
log’, х jS3 log2, (12х)
260
или
|log2x|>|log2(l+2x)|,
—log2x >logz (1 + 2x),
4->1 + 2x.
Поскольку x>0, имеем систему неравенств
|2x‘ + x- КО
I 0<х<1,
решение которой записывается неравенствами
Во втором случае log2x>0, поэтому имеем
(log,х)"Tog,х<(log,уТ+2х)log, (1 + 2х)
и далее
log»,x<log‘,(l+2x),
|log2x|< |log2(l+2x) |,
logzx<log2(l+2x),
xs^l+2x,
x>—1.
Учитывая, что х>1, получаем х>1.
Ответ: 0<х<-^-, х>1.
Задача 2. Обозначим через 3 расстояние между пунктами А и
В, равное длине короткой дороги. Тогда протяженность длинной
дороги равна 3+3.
Пусть ов и »п — скорости велосипедиста и пешехода соответст-
венно. Тогда условия задачи приводят к системе трех уравнений:
' S —2=- 2(^ + 3)
Vb	Vb
 3,5 2S + 3 + S —3,5
ип	vB
ИЛИ
3 = 2оа
23 + 3 = 9,
7 _as—1
t»n Ув
261
Исключая неизвестные уп и vb получаем из последней системы
уравнение для определения расстояния S:
2S + з 1 6S — 1
S ~ 2	7	9
65*-295-42 = 0.
Полученное квадратное уравнение имеет единственный положи-
тельный корень S = 6. Затем находим скорости:
Un==3, Ув==15.
Ответ: 3 км)ч, 15 км!ч.
Задача 3. Пусть центр окружности, вписанной в треугольник
АВС (рис. 72), представляется
3	точкой Oi, центр окружности, про-
/Ч	ходящей через точки Оь D и
/	С, представляется точкой 02.
/	Тогда D—пересечение биссектри-
/	сы Угла со стороной ВС, точ-
ка Е — конец диаметра окруж-
/	у. \ ности 02. Обозначим угол А бук-
вой а» а Угол —буквой р. Ясно,
L/ _	что угол EDC — прямой, посколь-
А Е\ 02 г КУ он опиРается на диаметр
\	/ окружности. Кроме того, понят-
\	/ но, что угол ADE равен углу
Oi СЕ, поскольку они; вписаны
------в одну окружность и опираются
Рис. 72.	«а ОДНУ и ту же дугу.
Радиус окружности, описан-
ной около треугольника АВС, определяется по теореме синусов и
выражается формулой
/? = ^.
(	2 sin а
Так как в условии задачи даны стороны АВ и АС, то сторона ВС
может быть найдена по теореме косинусов, если будет найден
угол а. Таким образом, важно определить угол а.
Рассмотрим треугольник ADC. В нем угол ADE равен р/2, угол
EDC*— прямой. Поэтому
откуда	о_ тс____
р— з 3 '
Запишем теорему синусов для треугольника АВС:
АВ _ АС . 20 _	24
slnp	sin(a + (!) ’ sin₽ sin(a + ₽)
262
или
5	6
Заметив, что
тс	а тс	/ тс । а
"з	з~=-2	(ПГ''Т
получаем уравнение
5	6
Так как л < к, то
Поэтому находим
cos
и далее
3. О	Тъ
arcsin-=--х-	.
О	2
по теореме косинусов сторону
Определим теперь
В С2=202+242—2 • 20 • 24 cos а.
Так как
/о -3	«А . /о 3 \
cos ( 3-arcsin-g-ft ) =sm(3arcsin -=- ),
V	о z J у	□ J
и используя формулу синуса утроенного аргумента
sin 3<р=3 sin ф—4 sin3 ф,
находим
117	.	44
cosa = i25 и SIna = T25 •
Далее вычисляем сторону ВС и радиус описанной окружности R-.
ВС=^,Ь- ^=12,5.
Ответ-. 12,5 м.
Задача 4. Пусть Mi, Мг и Мз — середины ребер ВЛ, SB и SC
соответственно, D — основание перпендикуляра, опущенного из
вершины пирамиды на основание АВС (рис. 73). Справа на рисун-
ке изображен треугольник SCD, являющийся элементом этой
пирамиды.
Четырехугольники ЛМ1М2В, ВМ2М3С и СМ3М1Л представляют
собой трапеции, поскольку М1М2, М2М3 и МзМ1 — средние линии
соответствующих треугольников. Больше того, поскольку каждая
263
из этих трапеций вписана в окружность, возникающую при пере-
сечении плоскостей боковых граней пирамиды с шаром, то все эти
трапеции являются равнобочными (это легко показать отдельно).
Отсюда следует равенство всех боковых ребер пирамиды друг дру-
гу. Действительно, каждая из точек Mi, М2 и М3 делит боковое
ребро пополам, а эти половины равны между собой.
Из равенства боковых ребер пирамиды, представляющих собой
наклонные к плоскости основания, следует равенство проекций
Рис. 73.
этих отрезков: AD = BD = CD, т. е. точка D является центром
окружности, описанной около основания пирамиды. Поэтому центр
шара, о котором идет речь в задаче, расположен на высоте пира-
миды SD.
Рассмотрим теперь треугольник SCD с одним из острых углов,
равным 60°. Шар пересекается с этим треугольником по окружно-
сти, центр которой расположен на SD и проходящей через точки
С и М3. Значит, он лежит на пересечении SD с перпендикуляром,
восстановленным из середины отрезка СМ3. Для прямоугольного
треугольника с углом SCD, равным 60°, такой точкой будет точ-
ка D. Следовательно, центр шара лежит в точке £); CZ) = 1, a SD =
=Л=]/3.
Рассмотрим треугольники SAD и SBD. Поскольку D есть центр
шара, проходящего через точки Л и В, то AD=BD=\. Поэтому
треугольники SAD, SBD и SCD равны между собой. В треугольни-
ке ADB-. AD—BD=1. Сторона АВ этого треугольника, равная по
условию ребру SC пирамиды, равна 2. Поскольку должно выпол-
264
няться «неравенство треугольника»
AB^AD+BD,
которое превращается в равенство только тогда, когда точка D
лежит на стороне АВ, то очевидно, что этот случай и имеет здесь
место.
Ответ: h = y 3 м.
Задача 5. 1-й способ. Поскольку все корни первого уравнения
являются корнями третьего уравнения и хотя бы один корень пер-
вого уравнения удовлетворяет второму уравнению, то это означает,
что все три уравнения имеют по меньшей мере один общий корень.
Обозначим его Хо. Имеем
2) х2о—b(b + l)xo+c=O
и
3) х4о—6(& +1)х2о+с=О.
Обозначая х2о через Xi, видим, что Xi удовлетворяет второму урав-
нению
х2!—Ь(Ь+4)х1+с=0.
Таким образом, наряду с корнем х0 второе уравнение имеет корень
х2о. Покажем, что это различные корни второго уравнения.
Если бы
Х2о=Хо,
то хо=О или х0= 1. Корень хо=0 не удовлетворяет первому уравне-
нию, а корень Хо=1 не подходит в силу условия, что все корни
первого уравнения больше единицы.
Поскольку биквадратная функция, стоящая в левой части
третьего уравнения, — четная функция, то наряду с корнем х0#=Ю
третье уравнение должно иметь корень —х0. Кроме того, решая
это уравнение относительно х2, получим действительное решение
Хо, которое, как уже отмечалось, положительно и больше единицы.
Поэтому третье уравнение имеет еще два действительных корня
rt.y^xo- Отсюда получаем, что первое уравнение имеет два корня
х0 и V Хо.
По теореме Виета наводим:
Г Хо Хо 8,	.(	-£*• ==о,
I Хо + Ухо = (а + Ь)	I x. + x% = b(6'+ 1).
Из двух этих систем, учитывая условие Ь>3, находим параметры
а, b и'с: а=2, Ь—4, с—64.
2-й способ. Введем для удобства вычислений новые обозначе-
ния параметров
а+Ь = т и &(&+!) =k.
265
Рассмотрим условие задачи о том, что все корни первого уравне-
ния являются корнями третьего уравнения. Это означает, что мно-
гочлен четвертой степени, стоящий в левой части третьего уравне-
ния, может быть разложен на квадратичные множители, одним из
которых является квадратный трехчлен, стоящий в левой части
первого уравнения, т. е. должно выполняться тождество:
х4 — kx*-\-c = [х2 — /их-|-8]-[х2-}-** + $•
В этом равенстве а и 0 — коэффициенты второго множителя. Рас-
крывая скобки, получаем
х4 — &х2-|-£ = х* + (а ~ /п)%8 + (8 — am-j-P) х2-|-(8а — pm) хЦ- 8р
Поскольку это равенство есть тождество, то должны быть равны
коэффициенты при одинаковых степенях х в его правой и левой
частях. Это ^приводит к следующим условиям:
а = т,
а —т = 0,
8 — ат 4- Р = — kt
8а — рт — О
€ = 8р.
k — tn* — 8--------
О
Из третьего равенства видно, что возможны два случая: либо
/п=0, либо с=64.
Первый случай невозможен. Если т=0, то первое из данных
в задаче уравнений не имеет действительных решений. Поэтому
с=64. Таким образом, имеем два квадратных уравнения
1) х2—/пх+8=0,
2) х2—Ах+64 = 0,
относительно которых известно, что они имеют по меньшей мере
один общий действительный корень.
. Заметим, что если два уравнения
Л(х) =0 и Е2(х) =0
имеют общий корень Хо, то этот корень удовлетворяет также и та-
кому уравнению:
Е1(х)-Е2(х)=0
(обратное, конечно, не всегда верно). Поэтому если рассматривае-
мые уравнения имеют общий корень, то этот корень находится
266
так:
(х2—тх+8) — (х2—Ах+64) =0,
(А—т)х—56.
Поскольку, однако, А—т#=0, то корень выражается формулой
х = , 56 ; A = ml—16.
k — т ’
Для того чтобы найденное значение общего корня действитель-
но являлось таковым, нужно, чтобы оно удовлетворяло хотя бы
одному из уравнений, например первому (тогда второму оно будет
удовлетворять автоматически). Имеем
Упрощая это выражение и заменяя А на т2—16, получим уравне-
ние четвертой степени для определения т:
mi—9m3—24т2+ 144m+ 648 = 0.
Это уравнение можно преобразовать так:
т3 (т—9) —24 (т2—6т—27) = 0,
т3(т—9)—24(т+3) (т—9) =0,
(т—9) (т3—24т-^7-2) =0.
Заметим, что число 6 является корнем второго сомножителя, по-
следний можно разложить на множители
т3—24m—72= (m—6) (m2+6m + 12),
посДе чего имеем
(m—9) (m—6) (m2+6m + 12) =0.
Квадратичный множитель, стоящий в левой части уравнения,
не имеет корней. Поэтому все решения уравнения таковы:
mi=9, m2=6.
Первое из этих решений не удовлетворяет условиям задачи.
В этом случае первое из данных уравнений, которое при т = 9_при-
обретает вид
х2—9х+8 = 0
имеет своими корнями числа 8 и 1, т. е. не все его корни строго
больше единицы.
При т=6 такое условие выполняется. Имеем
m = a+6 = 6;A=m2—16=20; 6(6+1) =20.
Поскольку известно, что 6>3, то 6 = 4. Окончательно находим, что
а=2.
Ответ: а=2, 6=4, с=64.
267
$ 33. МЕХАНИКО-МАТЕМАТИЧЕСКИЙ
ФАКУЛЬТЕТ, 1973 г.
Вариант 1
1.	-Решить уравнение
cos 2х -|- log* f-|-sin х\ -(- 2 cos х log j sin x =
= 2 cos x + sin2 x log, sin2 x.
2.	В трапеции диагонали равны 3 и 5, а отрезок, соединяющий
середины оснований, равен 2. Найти площадь трапеции.
3.	Решить неравенство
4х + 8 /^Г^х2 > 4 + (х* - х) 2х + 2х+'  х- /2^лЛ
4.	В треугольной пирамиде ABCD грани АВС и ABD имеют-
площади р и q и образуют между собой угол а. Найти площадь
сечения пирамиды, проходящего через ребро АВ и центр вписанно-
го в пирамиду шара.
5.	Найти все пары чисел (х, у), удовлетворяющие условиям
р/ -^-(х — уУ-(х — у)*=^д3 — 2х\
i/>4x* + 4t/x2 + -i- .
Вариант 2
1.	Решить уравнение
-4-cos2-4- (1 — ]/sinx) =}^2cosx — ]/sin2x.
О	Л
2.	В трапеции ABCD точки К и М являются соответственно се-
рединами оснований АВ=5 и С£>=3. Найти площадь трапеции,
если треугольник. АМВ — прямоугольный, a DK. есть высота тра-
пеции.
3.	Решить неравенство
12х-|- У3х* 4-4х* — 4х* loga х2> 3 j/3 4~4x — 4х2 -|-4x2log*x*.
4.	В треугольной пирамиде ABCD ребро CD = a, а перпендику-
ляр, опущенный из середины ребра АВ на CD, равен b и образует
равные углы а е гранями ACD и BCD. Найти объем пирамиды.
5.	Найти все пары чисел (х, у), удовлетворяющие условиям
«/• + у’+ 2х* =Уху — хгу*,
4ху> + у3 4- 4- > 2х2 +]/1 + (2х —у)*.
268
Вариант 3
1.	Решить уравнение
~1 cos 2х	cos2 3 х logj/— tg* х 4- 3 sin x = 2 sin x • log, tg* x.
T
2.	В трапеции ABCD точки К и М являются соответственно
серединами оснований АВ и CD. Известно, что AMJlDK и
CK.LBM, а угол CKD равен 60°. Найти площадь трапеции, если
ее высота равна 1.
3.	Решить неравенство
/2 - 5х — Зх2 + 2х > 2х • 3* • /2-5х —Зх* 4~4х* • 3*.
4.	В треугольной пирамиде ABCD через ребро AD=a и точку
Е — середину ребра ВС — проведено сечение, образующее с граня-
ми ACD и ADB соответственно углы аир. Найти объем пирами-
ды, если площадь сечения ADE равна S.
5.	Найти все пары чисел (х, у), удовлетворяющие условиям
( 4t/2 — 2х2 = ]/2 (х + 2у)г — (х + 2i/)4 5,
I x«4-2<4i/(x2 - 1).
Вариант 4
1. Решить уравнение
5
2 cos2 х — cos 2х= 1	(1 — Kcos х).
2. В трапеции ABCD точка К. — середина основания АВ, М —
середина основания CD. Найти площадь трапеции, если известно,
что D/С есть биссектриса угла D, ВМ есть биссектриса угла В, наи-
больший из углов при нижнем основании равен 60°, а периметр
равен 30.
3. Решить неравенство
5х 4* / 6х2 + х* — х* log, х > (х2 — х) logt х 4-
4~ 5 —|— 5 6 —|- х — х2.
4. Точки К и М являются серединами ребер АВ ir АС треуголь-
ной пирамиды ABCD с площадью основания р. Найти площадь
грани BCD, если сечение DKM имеет площадь q, а основание вы-
соты пирамцды попадает в точку пересечения медиан основа-
ния АСВ.
5. Найти все пары чисел (х, у), удовлетворяющие условиям
( У 2хгу* — Х*у* = у* 4* Хг (1 — х),
I/1-Н*4-1/)2 +•« (2у’ 4- х2) < 0.
269
Разбор варианта 1
Задача 1. Допустимыми в этом уравнении являются те значе-
ния х, для которых выполняется неравенство
sinx>0.
Используя формулы теории логарифмов, запишем это уравнение
в более простом виде:
cos 2х 4—log» sin х---— 2 cos х log» sin x =
= 2 cos x 4- 2 sin2 x log» sin x .
или
log»sinx £------2cosx-|-cos 2x ^4"|cos2x---g—2cosxj =0.
Разлагая последнее уравнение на множители, получим
(log,sinx4-1) (cos2х--—2cosx) = 0.
Если
log» sinx 4-1 = 0,
то это означает, что
1	те
[sinx = -g-, х=(— l)"-g-4-itn.
Если
cos 2х---— 2 cos x — 0,
то
4 cos2 х — 4 cos x — 3 = 0:
a) cos x =	, решений нет;
. 6) cosx =-----y .
Учитывая, что sinx>0, получаем:
x = 4"
Ответ:
1) x=(-;i)n4-+x«’ 2) x=^4-2«n.
270
Задача 2. Пусть АС=3 и BZ) = 5 диагонали трапеции ABCD>
пересекающиеся в точке О (рис. 74). Покажем, что в трапеции
отрезок, соединяющий середины оснований, всегда проходит черев
точку пересечения диагоналей. Это можно сделать многими спо-
собами. Приведем один из них.
Соединим середины оснований, точки Е и F, с точкой О и пока-
жем, что линия EOF — прямая. Рассмотрим £±ОЕС h ^OFA. Лег-
ко видеть, что они подобны. Действительно, Z0i4F = Z_0C£‘>
АО : СО = AF : СЕ. Последнее равенство следует из подобия тре-
угольников ОВС и OAD. а также равенств ЕС={1гВС и AF^^AD.
Из подобия треугольников ОЕС и OF А вытекает равенство углов
EOQ и FOA, которые являются, таким образом, вертикальными.
Отсюда следует, что линия EOF — прямая.
Площадь трапеции ABCD можно вычислить по ее диагоналям
и углу между ними:
S= -^-BD-AC- sin а = 7,5 sin а.
Поэтому постараемся найти синус угла между диагоналями. Обо-
значим угол AOD в &AOD посредством а. Тогда по теореме ко-
синусов будем иметь:
AD2=AO2+OD2—2AO • OD - cos а
или
а’ = (‘ (34 — 30 cos а).
\a+bj '	’
Достроив ДЛОО до параллелограмма AODO', в котором точка F
служит точкой пересечения диагоналей, воспользуемся теоремой
о соотношении между сторонами и диагоналями параллелограмма
AD* 4- О'О’ = 2 • АОг + 20D*
27 1
или
al + (4. * У = 2 (з._£_Л2 + 2	.
* \ Д + Ьу у_ a+bj \ л+Ь/
Подставляя сюда найденное значение для а2, получим
3
cos а =----.
о
Отсюда следует, в частности, что угол а — тупой. Синус этого угла
вычисляется следующим образом: _
sina =]/1 — 9/25 = -|- .
Затем находится площадь tj апеции:
5 = 7,5- 4-= 6.
Ответ: 6.
2-й способ. Проведем через вершину трапеции С линию СК,
параллельную диагонали BD, до пересечения с основанием AD.
Обозначим точку пересечения буквой К- Проведем также CM\\EF
(рис. 75). Достроим треугольник АСК до параллелограмма ACKN,
продолжив СМ за точку М на величину MN=CM. Угол CAD обо-
значим р.
Отрезок АК равен, очевидно, сумме оснований трапеции, а точ-
ка М делит этот отрезок пополам. Действительно, имеем
AM = AF + FM = -^-AD+4"ВС-
Поскольку ~АМ=МК, CM=MN—2, по построению, то ACKN — па-
раллелограмм. Используя формулу, связывающую сумму квадра-
тов диагоналей параллелограмма и сумму, квадратов его сторон,
получаем
АК* + CN* = 2 • AC* -J- 2 • СК*,
АК* — 184-50- 16 = 52,
АК = 2/13.
Итак, полусумма оснований трапеции равна V13.
Определим теперь высоту трапеции. Для этого вычислим сна-
чала угол р. Используя теорему косинусов в треугольнике АСК,
находим
С к* — АС* 4- АК* - 2 • АС • АК • cos ₽,
25 = 94-52 —2-3-2 j/jaFcos р.
Отсюда определяем
3	2
cos 8 = —— и ski В = —=-.
r Ki3 r К13
272
Высота трапеции Л определяется формулой
h = АС  sin fl,
откуда
h____________________________6_
h~ /Тз ’
Площадь трапеции равна
S = -^-AK h, S = 6.
Задача 3. Неравенство
4х + 8|/2 —х2 > 4 4- (х* — х) 2х + 2x+t • х /2 —х2
будем решать следующим образом: сначала сгруппируем члены
4х— (х2 — х) 2х — 4> 2)/ 2 — х* (х-2х — 4),
(х- 2х - 4) - х (х2* — 4) > 2 /2^х^ (х2х - 4);
затем разложим на множители
2 /2^х'2 (х2х - 4) < (х2х - 4) (1 — х)
и, наконец, решим неравенство
(х2х - 4) (2 /2^3? + х - 1) < 0.
Возможны два случая:
1)1x2* — 4>0	2) 1x2* —4<0
\ 2/2^^4-х—1 <0	( 2 /2-х’4-х- 1<0.
Рассмотрим первый случай. Здесь легко решить второе неравенство
системы. Для — ]/Л2<х<]/Л2, составляющих область определения
радикала в левой части неравенства
2 |/2 — х’< 1 — х,
имеем х<1. Тогда это неравенство равносильно следующему не-
равенству:
4(2—х2) <1—2x4-х2
или
5х2 — 2х — 7 > 0,
х>-ё-, х< — 1;
о
_/2<Х<- 1.
18—619
273
Легко заметить, что найденные значения х не удовлетворяют
первой системе неравенств. Если подставлять отрицательны^ зна-
чения х в неравенство
х-2«>4,
то получится противоречие. Поэтому рассмотрим второй случай.
Второе неравенство системы (2) нужно решать при том же
ограничении: —У2<х<У~2, Имеем
2 У2 — хг > 1 — х.
Здесь требуется рассматривать два варианта:
a)	б)-/2<х<1.
Все значения х из первого варианта удовлетворяют рассматри-
ваемому неравенству, так как правая часть этого неравенства по-
ложительная, а левая часть — меньше или равна нулю. Поэтому
осталось проверить, выполняется ли первое неравенство систе-
мы (2). Перепишем это неравенство в следующем виде:
х2*<4.
Заметим, что левая часть неравенства представляет собой про-
изведение двух монотонно возрастающих сомножителей и, значит,
сама растет с ростом х. Поэтому если мы возьмем наибольшее
значение х из отрезка	2 и покажем, что оно удовлетворяет
этому неравенству, то этим самым мы покажем, что и все, значе-
ния х, составляющие первый вариант, удовлетворяют этому нера-
венству. Имеем
j/2-2V~<4,
2УГ< 21'5,
так как |/2< 1,5,"то неравенство доказано. Итак, 1 < х<У 2 являются
решениями задачи.
Рассмотрим второй вариант. В этом случае можно возвести обе
части исходного неравенства в квадрат, получив лри этом равно-
сильное неравенство
5х2—2х—7<0.
Отсюда находим, учитывая ограничение —У 2^.х< 1, что
— 1<?х<1.
Поскольку все найденные значения х меньше, чем число У2, то
в силу причины, указанной выше, они служат решениями задачи.
Объединяя все решения задачи, получим ответ.
Ответ-. — 1 < х < У 2.
Задача 4. Пусть ABCD — произвольная треугольная пирамида
(рис. 76). Обозначив высоту DE грани ABD, опущенную из вер-
шины D на основание АВ, через hlt соответственно высоту CF гра-
ни АВС обозначим hz.
274
Плоскость ABM, проходя-
щая через центр вписанного в
пирамиду шара, является, оче-
видно, бисекторной йлоскостью
для угла между гранями АВС
и ABD. Обозначим высоту МК
треугольника АВМ, проведен-
ную из вершины М к основа-
нию- АВ, через /.
Поскольку все три отрезка
DE, МК и CF перпендикуляр-
ны ребру АВ, можно записать
p = -±-ABhi
q = ±-AB ht, S=±-ABl.
Л
Здесь S — площадь искомого сечения.
Величину отрезка МК легко найти. Этот отрезок служит бис-
сектрисой угла а в треугольнике D'A'C', получающемся проекти-
рованием пирамиды ABCD на плоскость, перпендикулярную ребру
АВ (рис. 76). При этом точки А, В, Е, F, К проектируются в одну
точку; длины отрезков DE, CF и КМ сохраняются, а угол D'A'C'
является двугранным углом пирамиды при ребре АВ.
Запишем площадь треугольника D'A'C' двумя способами:
d'a'c —‘ 2 sin ft	-
и
Sd'a'c := ~2~ sin 2 I sin ~2~ •
Сравнивая эти два выражения между собой, получим
а
. 2hihi cos-q-
l=—L-,—;
Й1 + «I
Подставляя сюда выражения Для hi и ht находим ответ:
а
2pq cos -9“
S =-----г---.
р + я
Задача 5. При решении этой задачи необходимо проявить опре-
деленную находчивость и наблюдательность. Заметим, что выра-
жение, стоящее под знаком радикала в уравнении, представляет
18*	275
собой квадратный трехчлен относительно квадрата разности х и у.
Нетрудно установить, что выполняются неравенства
° < ^ (^ - уг -	4
так, что
Ц- (X - </)’- (х - у)*< 4“ •
Таким образом, находим, что
уг — 2х‘<~
.	3	4
ИЛИ
(1)
Это неравенство во всяком случае необходимо для того, чтобы па-
ра чисел (х, у) удовлетворяла исходной системе.
-Обратимся теперь к неравенству, входящему в эту систему.
Рассматривая его как квадратное неравенство относительно х2,
т. е.
4х« + 4t/x‘ -]—— у< О,
найдем, что при условии неотрицательности дискриминанта
D=4y2+4y—2
выполняются ограничения
-2у- ^4У2+4у^2	-2у+ ^4у2+4у — 2
---------?< Х« <-----------------.
Сравнивая неравенства (1) и (2), исследуем вопрос об
противоречивости. Эти неравенства несовместимы, если
(2)
их не-
или
4у1 - 1 >-4у + 2 /4y»+4«/-2,
(4r/* + 4у - 2) - 2 У4у*-\-4у-2 +1 > О,
(/4//‘ + 4i/-2- 1)‘>0.
Последнее неравенство выполняется при всех допустимых
ниях у, кроме случая, когда
/4«/г4-4«/ — 2= 1
ИЛИ
4у‘-|-4у — 3 = 0; У>=4"’ = _ “Г •
значе-
276
Таким образом, почти при всех значениях у неравенства (1)\ (2)
несовместны. Исследуем два случая.
1) У1 = 1/ъ-
Неравенства (1) и (2) дают
Г	хг > О
| — 1/2<х’<0.
Отсюда находим х=0. Непосредственной проверкой (достаточ-
ность)' убеждаемся, что пара чисел (0, */г) составляет решение за-
дачи.
2) ^ = -3/2.
Неравенства (1) и (2) дают:
| хг> 1
| 1/2<х8<1.
Отсюда находим х2=1 или Xi=l, хг=—1. Непосредственной про-
веркой убёждаемся, что только одна пара чисел составляет реше-
ние задачи: (—1, —3/г).
Ответ-. (О, ‘/г); (—1, —3/г).
§ 34.	МЕХАНИКО-МАТЕМАТИЧЕСКИЙ
ФАКУЛЬТЕТ, 1974 г.
Вариант 1
1.	Решить уравнение
J/-!	sinх-f-cosх = 0.
2.	Решить неравенство
/1 — log,(xs - 2хЦ-2) <log, (5х« - 10х4-10)•
3.	Вокруг треугольника ЛВС описана окружность. Медиана AD
продолжена до пересечения с этой окружностью в точке Е. Изве-
стно, что AB + AD=DE, угол ВЛ£> = 60° и ЛВ = 6. Найти площадь
треугольника ЛВС.
4.	В треугольной пирамиде ABCD ребро DC=9, ребро DB=*
=^AD, а ребро АС перпендикулярно к грани ABD. Сфера радиуса 2
касается грани ЛВС, ребра DC, а также грани DAB в точке пере-
сечения ее медиан. Найти объем пирамиды.
5.	Найти все действительные значения а, для каждого из кото-
рых существуют четыре целых числа (х, у, и, о), удовлетворяю-
щие равенствам	,
x*4-i/I = (lll -а) (а-89),
50 (и* — v2) = а (15а 4- би — а).
277
Вариант 2
1.	Решить уравнение
У 2 sin 2х -|- 2 sin х = 0.
2.	Решить неравенство
У 1 + log, (7л? + 14х + 8) < 1 + log, (7л? + 14х + 8).
3.	Вокруг треугольника АВС описана окружность. Через точ-
ку В проведена касательная к этой окружности до пересечения
с продолжением сФороны С А в точке D. Известно, что AB + AD=
= АС, отрезок CD = 3, угол В АС=60°. Найти периметр треуголь-
ника АВС.
4.	В основании треугольной пирамиды ABCD лежит треуголь-
ник АВС, в котором угол В ЛС=60°, а угол АСВ прямой. Грань
BCD образует угол в 60° с гранью АВС. Ребро BD=2. Сфера ка-
сается ребер АВ, АС и грани BCD. Центр сферы — точка О лежит
на основании пирамиды, и отрезок OD перпендикулярен плоскости
основания пирамиды ABCD. Найти длину ребра АС.
5.	Найти все действительные значения а, для каждого из ко-
торых существуют четыре натуральных числа (х, у, и, v), удовле-
творяющие равенством
•	(* + У) (х + у + 20) = (140 - а) (а - 80),
а (8а*	2п* — а) = (4и* — v*)‘.
Вариант 3
1.	Решить уравнение
У1 +cosx = sin х.
2.	Решить неравенство
Kbg, (2-f-4x —х‘)> log, (1 + 2х — х2).
3.	Окружность радиуса 1 вписана в треугольник АВС, в кото-
ром cos ZABC = 0,8. Эта окружность касается средней линии тре-
угольника АВС, параллельной стороне АС. Найти длину сторо-
ны АС.
4.	В основании треугольной пирамиды ABCD лежит прямо-
угольный треугольник АВС с катетами АС—15 и ВС=20. Боковое
ребро DC перпендикулярно к плоскости основания. Сфера касает-
ся основания АВС, ребра CD и боковой грани ABD в точке Р, ко-
торая лежит на высоте треугольника ABD, опущенной из точки D.
Известно, что DP = 8. Найти объем пирамиды.
5.	Найти все действительные значения а, для каждого из ко-
торых существуют четыре целых числа (х, у, и, v), удовлетворяю-
278
щие равенствам
х‘ + ^ = (107 - а) (а - 91),
54 (а* — о2) = а (15ы —|— За — а).
Вариант 4
I.	Решить уравнение
j/cos ху" 2sinx= 0.
2.	Решить неравенство
/log ] (4х — 3 — х2) > log, (4х — 3 — х2).
Т
3.	Окружность радиуса 3 проходит через вершину В, середины
сторон АВ и ВС, а также касается стороны АС треугольника АВС.
Угол ВАС острый, и sin ZB АС=1/3. Найти площадь треугольника
АВС.
4.	В основании треугольной пирамиды ABCD лежит правиль-
ный треугольник АВС. Грань BCD образует с плоскостью основа-
ния угрл 60°. На прямой, проходящей через точку D перпендику-
лярно основанию, лежит центр сферы единичного радиуса, которая
касается ребер АВ, АС и грани BCD. Высота пирамиды DH в два
раза меньше стороны основания. Найти объем пирамиды.
5.	Найти все действительные значения а, для каждого из кото-
рых существуют четыре натуральных числа (х, у, и, v), удовлетво-
ряющие равенствам
' ху (40 + ху) = (150 - а) (а - 90),
а (8ы* —|— 18t»2 — а) = (4и2 — 9у2)2.
Разбор варианта 2
Задача 1. При решении этого уравнения необходимо принять в®
внимание ограничения, связанные с ОДЗ, и условия, позволяю-
щие после возвышения в квадрат получить уравнение, равносиль-
ное исходному. Поэтому исходное уравнение равносильно системе
' sin 2х > 0,	।
< sinx<0,
t 2 sin 2х =(— 2 sin х)*.
Анализируя эту систему, можно заметить, что структура уравне-
ния такова, что для его решений выражение sin 2х равно квадрату
некоторого действительного числа и, следовательно, автоматически
279
будет неотрицательным. Поэтому систему можно упростить:
J sinx<0,
I sin 2х = 2 sin1 х.
Из уравнения находим
1) sinx = 0, х = тсп,
2) tgx=l, х = -~
В последнем случае, естественно, берутся только те значения не-
известного, для которых sinx^O.
Ответ: х—лп; х = 5л/44-2лп, где п=0, ±1, ±2 ....
Задача 2. Обозначим log2(7x24- 14x4-8) буквой t. Тогда данное
неравенство примет вид
/T+F<l+4-t .
Его решения находятся из системы неравенств
1-Н>0,
1 + 4^0,
или
Отсюда находим —	f>3. После этого имеем:
1) - l<log,(7x«4-14x + 8)<0,
4<7х»+14x4-8 <1
или
x’4-2x-f- 1 < 0.
Первое неравенство может выполняться лишь при одном значении
переменной, х——1, второе неравенство выполняется тождествен-
но. Следовательно, х=—1;
2) log2(7x24-14x4-8) >3,
7х2 4- 14х4-8>8,
х^О и х<—2.
Ответ: х^—2, х=—1, х^О.
280
Задача 3. Пусть АВ—х, AD = y, рис. 77. По теореме о «каса-
тельной и секущей, проведенными к окружности из одной точки»
имеем: DB2=AD-DC. Применяя теорему косинусов к треугольнику
ABD, а также, учитывая, что AB+AD = AC и, следовательно, DC='
= AD + AC=x+2y, получим:
л* + Уг — %ху cos	= у (х 2у)
или
х2+у2+ху=ху+2у2, х=у.
Значит, в ДЛВС ЛС=2х, и этот треугольник — прямоугольный.
Далее находим:
ВС = ЛС • sin-^- = 2х- ~=хУЗ,
о	Z
?АЕС ~ Х + %Х + Х ИЗ = * (3 4“ }^3),
где Равс — периметр треугольника АВС. Так как DC=3x=3, то
х= 1.
Ответ: 3+1/3.
Задача 4. На рис. 78 дан чертеж к этой задаче. О/С, ОР и ОМ—
радиусы данной сферы, проведенные в точки касания /С, Р и М
с ребрами АВ, АС и гранью BCD
соответственно. DN — прямая,
проведенная через вершину пи-
рамиды D и точку М. Очевидно,
что BCLDN. Это следует из тео-
Рис. 78.
ремы «о трех перпендикулярах», поскольку СЮ±пл. АВС по усло-
вию. Очевидно также, что прямая АО — биссектриса угла А осно-
вания пирамиды.
Поскольку BC-LDN и ВС±О7И, то ВС-LON. Поэтому угол
OND = 60° является линейным углом двугранного угла между бо-
ковой гранью BCD и плоскостью основания пирамиды.
281
Из прямоугольного треугольника OND находим DN:
o-v=aJZ6™=T?'OD-
Из прямоугольного треугольника OMD находим OD:
OD — . 0%П1и = 2-0М.
sin £ODM
Поскольку OM = OP = OK. = R, то OD=2P, где R— радиус сфе-
ры. Тогда
Очевидно, что CN—OP=R и CP=ON, так как угол С — прямой
по условию. В треугольнике' OMN :OM±.'MN, a ON=OAf:siny,
т. е. CP=ON=2R/	Из прямоугольного треугольника АОР на-
ходим:
АР = OP- ctg Z А0Р = R К?
и
ле=лр 4-рс=/? /з+2/?//з=5р//з,
Из прямоугольного треугольника АВС имеем:
ВС = AC-tg-^- = 5P
и
NB=BC— CN=4R.
Наконец, используя теорему Пифагора, примененную к треуголь-
нику BDN, составляем уравнение для определения радиуса сфе-
ры R:
Из этого уравнения получаем, что Р = ]/3/4. Тогда
лс=-^_=4--
/3	4
Ответ: 5/4.
Задача 5. Преобразуем второе равенство следующим образом:
2а (4u2 -|- V1) — а* = (4и2 — о2)2,
— а2 -|- 2а (4u2 о2) — (4и2 о2)2 = (4и2 — о2)2 — (4и2	о1)1,
— [а — (4и2	о2)]2 = (4а2 — о2 — 4и* — о2) (4и2 — о2 4«2 +°’)»
— (а — 4и2 — о2)2 = — 2d2‘8u2,
| а — 4и2 — о21 = 4ио,
а = (2и	о)2.
Поскольку и и v натуральные числа, то число а должно быть точ-
ным квадратом некоторого натурального числа (или 0).
282
Левая часть первого равенства положительна. Поэтому
(140—а) (а—80) > 0,
т. е. а должно удовлетворять условиям 80<а<140. В этом интер-
вале существуют три числа, являющиеся точными квадратами це-
лых чисел: 81, 100, 121.
Из первого равенства для суммы (х+у) получается квадрат-
ное уравнение, которое, очевидна, должно иметь целые решения.
Однако только при а=100 это условие выполняется. Таким обра-
зом, решением данной задачи служит число 100.
Ответ: а = 100.
's 35. МЕХАНИКО-МАТЕМАТИЧЕСКИЙ
ФАКУЛЬТЕТ, 1975 г.
*
Вариант 1
1.	Решить неравенство
gg   у х* + 5х-М8-^ ^дх’+бх—49
2.	Найти все пары действительных чисел (х, у), удовлетворяю-
щих условию х>0 и системе уравнений
sin [(х —	у*] = 0,
logy_ jZx’-j-y2 +	2 1о£2< Ух*-]-у* = 2.
3.	Два равных равнобедренных треугольника АВС и DBE
(AB=BC=BD = BE) имеют общую вершину В и лежат в одной
плоскости так, что точки А и С находятся по разные стороны от
прямой BD, а отрезки АС и ОЕ пересекаются в точке К. Известно,
что ZABC= Z.DBE=<i<-^-, Z.MD»0<a. В каком отношении
прямая ВК делит угол АВС?
4.	Сфера радиуса 3/в вписана в четырехугольную пирамиду
SABCD, у которой основанием служит ромб ABCD такой, что
Z BAD = 60°: высота пирамиды, равная 1, проходит через точку К
пересечения диагоналей ромба. Доказать, что существует единст-
венная плоскость, пересекающая ребра основания АВ и' AD в не-
которых точках М, N таких, что MN—4 УЗ/5, касающаяся сферы
в точке, удаленной на равные расстояния от точек М и N, и пере-
секающая продолжение отрезка SK за точку К. в некоторой точ-
ке Е. Найти длину отрезка SE.
5.	Без помощи таблиц найти все значения х в промежутке
—0,5<х<1,5, удовлетворяющие равенству
log» f sin Зх — cos 2х —jo") —(sin 7х — cos 6х —jg- j.
283
Вариант 2
1. Решить неравенство
logr_ (х‘ + 4х + 6) + 6 ]/ log, (х« 4-4х + 6) > 8.
2; Найти все пары действительных чисел (х, у), удовлетворяю-
щие условию и системе уравнений
{4**+ (^+1)’_32_31.2Х*+
COS [it (х‘ + у1)] = 1.
3.	Два равных ромба ABCD (ЛВЦСО, AD IIВ С) и APQR.
(AP||Q/?, A/?||PQ) имеют общую вершину А и лежат в одной плос-
кости. Известно, что ZBAD=Z.PAR=a<n/2, точка R лежит вну-
три ромба ABCD и угол RAD равен р. Стороны ВС и Q-R пересе-
каются в точке К- Найти величину угла ВАК.
4.	В правильную треугольную пирамиду SABC с вершиной S
и основанием АВС вписан шар единичного радиуса; двугранный
угол между основанием пирамиды и боковой гранью равен 60°.
Доказать, что существует единственная плоскость, пересекающая
ребра основания АВ и ВС в некоторых точках М и N таких, что
MN—5, касающаяся шара в точке, удаленной на равные расстоя-
ния от точек М и N, и пересекающая продолжение высоты пира-
миды SK за точку К в некоторой точке D. Найти длину отрез-
ка SD.
5.	Без помощи таблиц найти все значения х в промежутке
—4<х<—2,5, удовлетворяющие равенству
(2 \	2 \
sin х — cos 6х -[—3-) = log, (sin Зх — cos 8х -|- -у ь
о	'	'
Вариант 3
1. Решить неравенство
75  25х>+6х~15	5х4^х-14.
2. Найти все пары действительных чисел (х, «/), удовлетворяю-
щие условию х>0 и системе уравнений
/ Sin [(х + )<2«)« + у»] = 0,
[ |<21ogr_(x«-|-y«) -f- 2 log, Vx* + y* = 3.
3. Два равных равнобедренных треугольника АВС и DBF
(АС=ВС=BD—DF) имеют общую вершину В и лежат в плоско-,
сти так, что точки С и D находятся по разные стороны от прямой
АВ, отрезки АС и DF пересекаются в точке К- В каком отноше-
нии прямая ВК делит угол АВС, если ZDBF=<i, ZCBF=р<а?
4. Сфера радиуса 2 3 4/в вписана в четырехугольную пирамиду
SABCD, у которой основанием служит ромб ABCD такой, что
284
ZBAD = 120°; высота пирамиды проходит через точку К пересече-
ния диагоналей ромба, а ребро SB наклонено к основанию под
углом arctg2 У3. Доказать, что существует единственная плос-
кость, пересекающая ребра основания АВ и AD в некоторых точ-
ках М и N таких, что MN=2 ]/3/7, касающаяся сферы в точке,
удаленной на равные расстояния от точек М и N, и пересекающая
продолжение отрезка SK за точку К в некоторой точке Е. Найти
длину отрезка SE.
5. Без помощи таблиц найти все значения х в промежутке .
—3<х<—1,5, удовлетворяющие равенству
log* (sin 2х + cos Зх —	= log» (sin 6х -|- cos 7х —	•
Вариант 4
1.	Решить неравенство
logrr (х* - 2х + 8) + 2 /log, (х’-2х + 8)> 12.
2.	Найти все пары действительных чисел (х, у), удовлетворяю-
щие условию у^.0 и системе уравнений
। 9**+ (s-i)1 _27 = 26*Зж’+
(cos [2>n-(x*4-l/*)] = 1*
3.	Два равных ромба ABCD (ЛВЦСД, Л£>||ВС) и APQR
(APHQR, AR1IPQ) имеют общую вершину А и лежат в одной плос-
кости. Известно, что Z.BAD = Z.PAR=*a<n/2, Z_QAC=fi. Продол-
жения сторон ВС и QR пересекаются в точке К- Ромбы располо-
жены в разных полуплоскостях относительно прямой АК и в од-
ной полуплоскости относительно прямой AD. Найти угол KAD.
4.	В правильную треугольную пирамиду SABC с вершиной S
и основанием АВС вписан шар радиуса 2; высота пирамиды SK
равна 6. Доказать, что существует единственная плоскость, пере-
секающая ребра основания АВ и ВС в некоторых точках М и N
таких, что MN=7, касающаяся шара в точке, удаленной на рав-
ные расстояния от точек М и N, и пересекающая продолжение вы-
соты пирамиды SK за точку К в некоторой точке D. Найти длину
отрезка SD.
5.	Без помощи таблиц найти все значения х в промежутке
—->к<х<—llz, удовлетворяющие равенству
log ( (cosx4-sin6x-|--^^ = log( (cos3x-|-sin8x-|--^n .
’ T	T
Разбор варианта 1
Задача 1. Введем обозначение
f	49 q
285
Тогда имеем квадратное относительно I неравенство
F+7/—98<0,
I
откуда находим, что —14^t-^.7. Далее имеем:
49 у
х2+'5х—49=0; х2 + 5х—50^0.
Отсюда получаем решения: —
Ответ: —10^х^5.
Задача 2. Упростим сначала второе уравнение системы. Для
этого обозначим буквой t выражение
Тогда получим квадратное уравнение
' (/оч-УГ-2=о,
из которого находим, что t=\. Значит, хг+у2=2п.
Из первого уравнения системы следует, что
(х — У1 == Tin,
где целый параметр п принимает значения: О, 1, 2, 3 ... . Если по-
следнее соотношение упростить с учетом равенства х2+#2=2л, то
получим:
,	2х]/гИ—3'п — кп.
Поскольку х>0, то возможны только три значения п: О, 1, 2. Два
из них дают решения задачи:
1) «=1: х =	2) п = 2: х = /^/2; у = уЪ/2.
y = ^V-tt. _
Ответ: х = Уп, у=:±Уп; х= }At/2, у = ±У7п/2.
Задача 3. Легко понять, что равнобедренный треугольник DBE
получается из равного ему равнобедренного треугольника АВС по-
воротом на угол <р вокруг вершины В, рис. 79. Поскольку угол
AKD измеряется полусуммой дуг AD и СЕ окружности с центром
в точке В и, кроме того, эти дуги равны между собой, то <р=р.
Точка пересечения К отрезков АС и DE может рассматривать-
ся как точка пересечения диагоналей равнобочной трапеции
ADCE, вписанной в окружность с центром в точке В. Поэтому угол
АВК равен половине угла АВЕ, т. е.
£АВК = ^-.
После этого легко вычисляется угол КВС:
^квс=а-^=а-^-
и отношение углов АВК и КВС, равное (а+Р)/(а—р).
886
Заметим, что условие <0<а,
есть условие, гарантирующее, что
отрезки АС и DE пересекаются.
Ответ: (а+Р)/>(а—0).
Задача 4. Чертежи к задаче
представлены на рисунках 80 и 81.
Сначала найдем размеры пи-
рамиды SABCD. Обозначим сто-
рону ее основания AD буквой а.
Тогда высота ромба ABCD равна
a У 3/2, а длина отрезка КЕ, рав-
ного половине этой высоты,—
S
Рис. 79.
и SOT
а У3/4. Из подобия прямоугольных треугольников SKF
(дополнительное построение очевидно) следует
ОТ KF
SK — OK~~ SF
или
3/8
1—3/8
аУТ/4
Отсюда находим, что a = j/3.
Поскольку треугольник ABD — равносторонний, то BD— У 3. Если
на отрезке АК взять точку L такую, что AL=4sAK, и провести че-
рез нее_ отрезок MN\\BD, то длина этого отрезка будет рав-
на 4 J/3/5. Совершенно очевидно, что если через получившиеся
точки М и N провести плоскость, касательную к шару, то эта
плоскость будет удовлетворять всем условиям задачи. Покажем,
что такая плоскость единственная.
Пусть точки М' и N', лежащие на сторонах ромба АВ и AD
соответственно, таковы, что отрезок M'N' равен 4 ]/13/5. Проведем
через точки М' и N' плоскость, касающуюся шара в некоторой точ-
ке Q (на рис. 80 не обозначена), которая равноудалена от точек
М' и N'.. Тогда M'Q=M'K и NrQ=N'K как касательные к шару,
проведенные из одной точки. Поскольку M'Q=N'Q, то M'K=N'K-
Следовательно, и точка 'К должна быть равноудалена от точек М'
и N', что, конечно, невозможно, если отрезок M'N' непараллелен
BD. Если же M'N'WBD и его длина равна 4 У 3/5, то он должен
совпадать с отрезком MN, и т. д.
Для нахождения длины, отрезка SE обратимся к рис. 81, на ко-
тором вынесена плоскость треугольника AS С. Прямая РЕ пред-
ставляет след искомой касательной плоскости на плоскости тре-
угольника ASC. Имеем: АК=а УЗ/2=3/2; LK=l/5AK=0,3. Обозна-
чим КЕ=х. Тогда ОР=3/в, ОЕ=3/&+х., Из подобия треугольников
LKE и О РЕ получаем:
LK ОР	0,3	3/8
-Z7c-=dc: ИЛИ --= г	  ____
РЬ X	/[3/8+х)2—(3/8)2
287
5
Из этого уравнения определяем величину х: х=4/з- После этого
легко находится весь отрезок SE, который равен 7/з.
Ответ: 7/3.
Задача 5. Данное уравнение равйосйльно системе
'	3	3
sin Зх — cos 2х —= sin — cos	—[o’ •
з
sin Зх — cos 2х —[o’ > О,
— 0,5<	1,5.
Решим сначала уравнение этой системы. Имеем
sin 7х—sin 3x=cos 6х—cos 2х,
2 sin 2х cos 5х=—2 sin 4х sin 2х.
Отсюда находим
’1) sin2x=0; x = itn/2;
2) cos 5х + sin 4х = О,
cos 5х 4- cos — 4х^ = О,
2 cos	cos (т—= °-
а)	-т"+"т=_г+1ОТг: ^=-j-4-27c^:
6)	-2~—=-г+^; x=-g-+-g-^
Поскольку значения множества (а) входят в множество (1) имеем:
х = ^~; x = -r4-^-fe,
где п=0, ±1, ±2..;	Л=0, ±1, ±2 ....
288
Отберем из этих значений сначала те, которые удовлетворяют
неравенству —0,5<х<1,5. Имеем
_,0,5< ^-<1,5,
— 1 т.п < 3,
Отсюда ясно, что п = 0. Далее находим
-о,5<4-+-^< 1,5,
------------------------<3 + 4&<—,
ТС	1	тс
 З+Зтс	.	27 — Зтс
4тс	. 4тс
Отсюда ясно, что k=—1, 0, 1. Таким образом, имеются четыре
значения х: xt=0, х2=—л/18, х3=л/6, х4=7л/18. Осталось прове-
рить выполнение неравенства sin3x—cos2x—0,3>0. Делается это
непосредственной подстановкой найденных значений х в неравен-
ство.
1)	х=0; sin 0—cos 0—0,3<0.
Следовательно, х=0 не является решением.
2)	х = «/6; sin 4- - cos.4- — 0,3=1— 0,5 - 0,3 > 0.
Следовательно, х = чг/6 есть решение задачи.
3)	x=-it/18; sinf—~ cos 4-- 0,3 = - 0,5 - 0,3 -
'	\ о у	У
тс । п
— COS -д- < 0.
Следовательно, х=—л/18 не является решением.
О 4) х= 7л/18; sin (7л/6) - cos (7л/9) - 0,3 = - 0,5 - 0,3 - '
7л	2л л о
— cos — = cos -g— 0,8.
Таким образом, необходимо без помощи таблиц сравнить числа
cos (2л/9) и 0,8.
Число 2л/9 соответствует углу 40*. Поэтому для оценки cos 40е
естественно рассмотреть углы 45е и 30*, заключающие угол 40"
между собой. Имеем
30°<40°<45*,
а поскольку в первой четверти косинус монотонно убывает, то
cos 30° > cos 40° > cos 45°,
>	„ лло ^2"
-g- > cos 40° > -у- .
19—619
289
Однако такая оценка cos 40° оказывается слишком «грубой». Дей-
ствительно, ]/3/2sn0,86, а )/2/2~0,75 и полученные оценки не
дают возможности сравнить cos 40° с числом 0,8.
Найдем более близкие к 40° углы, ориентируясь на те из них,
для которых без таблиц можно найти тригонометрические функ-
ции. Таким углом может быть угол 37,5°, который равен разности
60° и 22,5°. Имеем:
Покажем, что правая часть этого неравенства отрицательная.
Тогда нужно сравнить числа
-~K2+/2~+УЗ~К2 —/У
Используя знак сравнения V» заменяющий знак> или <, получим
]<2+К2+ КТ /2—К2 . , 4
4	* 5 ’
Возводя обе части этого неравенства в квадрат, имеем
4 — У^+уб . 16
8 V 25 ’
Так как обе части последнего неравенства неотрицательны, то по-
сле их возведения в квадрат имеем:
8-2ri2Vg.
3§УИ2.
Очевидно, что ]/12 > 3,4. Поэтому
3g</12.
Таким образом, cos(n/3—л/8)<0,8 и, значит, cos(2n/9)—0,8<0.
Следовательно, х=7л/18 не является решением уравнения.
Ответ: x=at/6.
290
ОТВЕТЫ*
$ 1. ГЕОГРАФИЧЕСКИЙ ФАКУЛЬТЕТ, 1972 г.
II.	1. Брат нашел 32 гриба, сестра —20 грибов.
2.	Xi = it/6, х, = 7я/6. 3. 1<х<27; 0< ж'Д/Т/З.
4.	х — j/2, у = 2.
5.	См. = R (V sin’ 0 4" ctg2 а — sin р).
III.	1. 24; 21. 2. xt~ti/2, xt = */6.
3.	1<х<32; 0<х<1/2. 4. х = 2, у = 2.
5.	АЕ = (а/2) • jZsin’P/sin’a-j-S — siпр/sin а).
IV.	1. 24;. 20. 2. Xi = it/3, xt = 4z/3.
3.	1-<х<5р^; 0<х.<1/5. 4. х=,2, у = 2.
5.	BE = ]/’/?’ sin’ а 4~ (а — by — Rsin а.
$ 2. ГЕОГРАФИЧЕСКИЙ ФАКУЛЬТЕТ, 1973 г.
II.	1. 5 cmpfi, 7 стр/ч. 2. 9.
4.	х=-3- /9-20log,2.
5.	х=== и/3 4“	4~
III.	1. 10 км]ч, 30 км]ч. 2. 11. 3. D = 2]/3.
4.	х= 1 4*У 1 4-7log’2. 5. х = ш.
IV.	1. 12 км]ч, 60 км)ч. 2. 25. 3. /? = ]/5.
4.	х = 3 - /9 - 31og23.
5.	х = 4~ 2ш, х=(— l)"+l -g-4"1lZL
* Там, где это не оговаривается особо, буквами т, п и k обозначаются цело
численные параметры, принимающие значения 0, ±1, ±2, ±3, ....
19 •	291
$ 3. ГЕОГРАФИЧЕСКИЙ ФАКУЛЬТЕТ, 1974 г.
II.	1. 15 т. 2.	= х, = (-
3.	х — 3, у = 2.
4.	3 = а* (24 КЗ — 1 lit)/72.
5.	х>1,1; 3/5<х<27/35; 4/7<х<3/5.
III.	1. Ъкм1ч. 2. Х1 = £и/3; x, = rt 5и/12 -j-itn.
3.	х = — 2, у — — 1.
4.	3 = а* (7 - 4 КЗ) (5it/6 - КЗ)/4.
5.	0,2 <х< 0,25; 1,75<х<2,25; - 0,8<х< — 0,25.
IV. 1. 30 м^ч. 2. X! = it(l + 2^)/8; x1 = =t3it/4-|-2itra.
3.	х = 3, у= 1.
4.	3 = а* (24 КЗ - 11®)/б48.
5.	х< —2/5; х>8/5; 4/7<х<3/5; 3/5<х<5/7.
$ 4. ГЕОГРАФИЧЕСКИЙ ФАКУЛЬТЕТ, 1975 г.
„	I
II.	1. 5. 2. x = ±zit/3-|-2it/n. 3. х=1.
4.	КЗ/(14«). 5. х = 5л/6, у = 8 — 5к/2.
III.	1. 8; 12. 2. x = ±it/3-]-wn.
3.	х = 4/3. 4.- 12/(25к).
5.	х = «/2, i/ = 5 —3it/2.
IV.	1. 40. 2. x = ±2i:/3 + 2itm. 3. x = 2.
4.	4K3/(7it). 5. x = 2it/3, z/ = 7-2it.
$ 5. БИОЛОГО-ПОЧВЕННЫЙ ФАКУЛЬТЕТ, 1972 г.
П. 1. 6 ч 40 мин. 2. 8. 3. Xi = 9, х»=1/81.
4.	x = 6Jfe+l. k=l, 2, 3....
5-	$ьаве = а‘5/ (а+с) (а+6 - с).
III. 1. 2 ч. 2. 1. 3. х=1/3.
4.	x = k/2, k=\. 3, 4...;
х =m-|-l/4, m = 0, 1, 2....
5.	(а4-с)(й+г)(а+6+с)/а6(а+6+2с).
IV> 1. 14 ч. 2. -8. 3. Xi=125, x,= l/5.
4.	x = 5it/6-|-bt, x=>/44-b, k = 0, 1,*2....
5.	ab(3a — 0 sin 2а/2 (a-J-6).
292
$ 6. ФАКУЛЬТЕТ ПОЧВОВЕДЕНИЯ, 1973 г.
II.	1. 9 и 6. 2. Второе выражение больше, чем первое.
3.	х= —х = (— 1)п arcsin (——j-itn.
4.	К = 7. 5. Xi = 7, х, = 1.
III.	1. 90 И 120 км.!ч. 2. Первое выражение больше, чем второе.
3.	х = кп. 4. й = 3,2. 5. х= —1.
IV.	1. 35 и 24 рубля. 2. J Первое выражение больше, чем второе.
3. x=±it/3 + 2it«. 4. R = 2. 5. х= 1/8.
$ 7. БИОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ, 1973 г.
II.	1. 5 км)ч. 2. х = я/4-]-«га» х= — я/6-|-«п.
3.	Х = ъп. 4. 11л/12. 5. 2<с<3.
III.	1. 5 га. 2. х=г±я/3-|-’'Л.
3.	х=(-1)«-£-+«п. 4. S = 4. 5. а>1.
IV.	1. 12 ч. 2. x = it/4-]-itn/2. 3. x = it/2-f-«tt.
4.	DM=7. 5. 0<с<8.	-
$ 8. ФАКУЛЬТЕТ ПОЧВОВЕДЕНИЯ, 1974 г.
II.	1. 150 км. 2. хг=2, xt = 8. 3. х= — it/6-f-2it&.
4.	0,5<а<1. 5. 5=ЗУ15.
III.	1. 120 м*. 2. Xi = 9; х,= 1/3.
3.	х= — «/22’ге/г. 4. 0<а<1/3.
IV.	1. Экскаватор марки А—800 мг, экскаватор марки Б—1200 м*»
2.	х = 2. 3. х = it/З2Дж.
4. а< —1/3; а>3. 5. R = 5/6.
$ 9. БИОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ, 1974 г.
II. 1. 8 ч 32 мин. 2. x=fat; x = it/4-|-it(2£+1)/2.
3. MK = aVl3/6. 4. —2<х< - 1, х>0.
5. х=(- 1)‘-^-+4’ х=-4- + ^.
III. 1. 19 ч 00 мин. 2. x = fat; х=
293
3. FAf = a/l9/15. 4. 2<x<3; x>6.
5. x=(- l)‘+*-^~^- + kv x = -=- + 2^.
IV. 1. 11 ч 55 мин. 2. x = it(2£-f-l)/2; x = it/4-|-fot.
3. MF = a/17/12. 4. x> 1; 0>x>- 1. '
5. x=(- l)*+>-^---------y + Ar, x = -J-H-2^.
§ 10. ФАКУЛЬТЕТ ПОЧВОВЕДЕНИЯ, 1975 г.
II.	1. 16 дней. 2. x = ztw/4-{-it/i. 3. xI = 3/2, x, = 9/4.
4.	3 = 9/8/4.
III.	1. 7,5 дней. 2. x = z^it/34-itn 3. Xi =-xt = 1/7.
4.	3 = 37,5.	x ’
IV.	1. 45 сек. 2. x = ±it/6-\-itn. 3. Xi = 8/3, x,= 22/7.
4.	3=65-1-.
□
$ 11. БИОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ, 1975 г.
II.	1. 50 км. 2. р = 1. 3. ВК= 1, KD=2.
4.	х=--^-4-2Ь, л = -|—{-2&с, л = ^-4-2Ьс,
X = k-л.
5.	п=- — 2, — 1, 0, 1, 2,... 11.
III.	1. 3 т. 2. р= —0,5. 3. АВ= 1.
4.	х =	+ 2kn, х = -у- + 2kti, х—---у-|-2£я, x = kn.
5.	« = 5, 6, 7.
IV.	1. 65 деталей в час. 2. р= 1. 3. АМ = ^-.
4.	x = it-f-2feit, х = rtit/2 -|- 2kK, x = -«-it/6 4-2£ic.
5.	л=- 1, 0, 1, 2, 3,... 13.
$ 12. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ОБЩЕЙ ГЕОЛОГИИ, 1972 г.
II. 1. x = zt2«/3 + 2^. 2. х = 4, у=4. 3. 12 м*/ч.
4. х< —3. 5. 12/5 см*.
294
ill. 1. x— (— l)'n+,-^-4~wn- 2* * = 4, y='5. 3. 6 км]ч.
4. x<2. 5. 5 /6/2 cm*.
VI. 1. x =	2я/3-|-2ят. 2. x=8, {/ = 8. 3; 15 м*{ч.
4. x< —4. 5. 15 cm*.
§ 13. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ГЕОФИЗИКИ, 1972 г.
II.	1. 21 колхозник. 2. х = zt я/4	т-к.
3.	х<2, (3-j-/5)/2<x<3.'3. 32/2 см*.
III.	1. 10 книг. 2. x = =tit/3-J-x/n.
3.	х<1, (1/5)/2<х< 2. 4. 4/5 см.
IV.	1. 14 карандашей. 2. х = ?± я/6-|-wn.
3.	х>2, - 1<х<(5 -/ТЗ)/2.
4.	4/3/3 см. 5. 2/3 см, 2/3/3 см, /3/2 см.
$ 14, ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ОБЩЕЙ ГЕОЛОГИИ, 1973 г..
II. 1. х=5, у = 7. 2. х=0. 3. 9 км/ч.
III. 1. х=1/2, у=1/3. 2. х= 1. 3. 10 игр/ч.
4. V=32/3 см*. 5. (xi, у,), (— х„ у,), (xt, я — у,),
(— Xi, я — у,), где Xi = arccos (у420-}-/3),
yt = arcsin 1/(у' 20-}-/3).
VI. 1. х= 1, у— 1. 2. х= — 1. 3. 5 м*/ч.
4.	3 = 3/2 см*. 5. (Xi, у,), (Xi, я — yi), (я-j-Xi, yi),
(я-|-Х1, я — z/i), где Xi = arctg(у 41— у 6),
t/i= arcsinl/(y^ 41-{-/6).
$ 15. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ГЕОФИЗИКИ, 1973 г.
II.	1. х=2, у = я/4 —2-}-£я. 2. х<1. 3. 9 км]ч.
4.	1 <х< 1,5; х^=1,25. 5. £=3/2.
III.	1. у—\, х = г±я/3-[- 1 -|-2£я. 2. х>0. 3. 10 игр)ч.
295
4. 1<х<3, х^З/2, х=/=2. 5. S=it/3 см.1.
IV.	1. t/ = 2, x=it/44-2-|-Jht. 2. х<- 1. 3. 5 м‘/ч.
4. - 1/2<х< 1/8; 1/4<х< 1. 5. 7? = 3 см.
$ 16. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ОБЩЕЙ ГЕОЛОГИИ, 1974 г.
II. 1. х=(5 + /41)/2. 2. х<0, log,2<x<l.
3. x = arccos/4/74-^t; 6 = 0, 1, 2.... 4. ? = arctg(l/cos а).
5. о,/о,= 169/792.
III. 1. x=-(15 + Z5j/2. 2. Iog,2//3<0<1.	_
3. x = arccos (3//l7)-f-b; £ = 0, 1, 2... .4. I = /10/2 cm.
5. o = 7/32 смг.
IV. 1. x=(17+/5)/2. 2. log, 5/7 <x< log, 6/7.
3. к = arccos/3/5k = G, I, 2... .4.'sin? = 1//10.
5. / = /19/18 cm.
§ 17. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ГЕОФИЗИКИ, 1974 г.
11.	1. х< — 4; — 2<х< — 1; х - 1.
2.	х,= —2 —/5; х, = /7/3:
3.	/=Д: x = tgh(l —/7)/4], fz = cos[it(l +/7)/4].
4.	о = 4п/9 см1. 5. 8 = 2/3 см1.
III.	1. —3/2<х<—1; 5/2<х<3.
2.	х, = (- 5 - /Т93)/6; х, = (- 7 + /57)/2.
3.	k = 2: х= cos(и2/4), y = ztl.
4.	8б= 15it/4 см1. 5. 8 = /3/4 см1.
IV.	1. —9<х<-8; —2<х<-1.
2.	х. = (1+3/5)/2, х,= -(2 + 3/2)/2.
3.	jfe=l: x=cos[(/5-|-l)it/4], t/ = tg[(/5— 1) к/4].
4.	/7 = 2(/3 4-3)слг.
5.	8 = 8/15 см.1.
296
$ 18. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ОБЩЕЙ ГЕОЛОГИИ, 1975 г.
II.' 1.. л=и/г+(- 1)п+14- •
2. 4000	3.--! <л<0;	<х<	
4. 1 см*. 5. 4 — j/" 4 /5 — 8 < х < 5.
III. 1. x = rtit/4-(-«га. 2. 9 км/ч.
3. — 4<х< —3,	— 4< х <^100 — 4.
4. 2 см. 5. — 7 < х < — 6 -|- /Ч /5 — 8.
IV. 1. х=яга. 2. 10 м*/ч.
3. 0,5<х< 1, (j/iO-f- 1)/2<х< (/100 + 1)/2.
4. 44/2/45 см*. 5. 6 -	4/5-8 < х < 7.
§ 19. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ,
ОТДЕЛЕНИЕ ГЕОФИЗИКИ, 1975 г.
II.	1. х,= - 1, х2=5. 2. х<0, 7/8<х< 1.
3.	x = it/6, i/=2it/3; х = 5и/6, у = 2it/3.
4.	а‘/6/40 см*. 5. 1 см.
III.	1. х, = —2, х2 = 0. 2. х<-2/3, - 1/12<х<0.
3.	x = it/6, у = it — arcctg0,5; x = 5ir/6, z/ = it— arcctg0,5.
4.	2Z/9 cm. 5. a/29/8 cm.
IV 1. x.= -5, x,= l. 2. x<-l, — l/8<x<0.
3.	X=it/3, y=5it/6; x = 2it/3, у — ц/о.
4.	2 cm*. 5. 8(10-7/2) cm*.
$ 20. ХИМИЧЕСКИЙ ФАКУЛЬТЕТ, 1972 г.
II.	1, 1 км/ч. 2. х= 1. 3. 45°, 45°, 90°.
4.	S = 4R‘/2/ sin a.
5.	2wn<x< it/34-2wn, it/24-2wn<^x<^2it/3-|-2wn,
4r/3 4~ 2wn < x < 3it/2 2wn,
5it/3-|-2itm< x< 2it (1 -Pm)-
III.	1. 2 км/ч. 2. x= 16. 3. 4/3.
297
4.	(4afesina/2)/9.
5.	it/4 "j-*2ittu	x 3it/4 —2*nm,
n (I -f- 2m) < x < 5u/4-J- 2itm,
7it/4 -f- 2«m < x •< 2it (1 -|-m).
IV.	1. 3 км/ч. 2. x = 2. 3. 1/3-. 4. 7a«/T7/24.
5.	2itm<x<?it/44-2itmr it/24-2itm<x<3it/44-2itm,
5it/4 4- 2«m < x < 3w/2 4- 2itm,
7it/4 4-2zmx^x<2it(l -|-m).
$ 21. ХИМИЧЕСКИЙ ФАКУЛЬТЕТ, 1973 г.
II. 1. 2 л. 3. х = »/6. 4. У = 243/3, a = 2 arcsin/7/5.
5. a = arctg 3, p = arctg (1/3).
III. 1. 60 руб., 90 руб. 2. x>2. 0<х<1.
, 3. x = 0, x = zt /3. 4. 5 = 3 /15 (/54-1/ a=2 arcsin /2р.
5. <x = 2 arcsin (3/5), p = it/2 —a/2.
I/ 1. 60 км/ч, 90 км/ч. 2. x>log, 14, log25<x<3.
3. x = z±it/3. 4. 5 = 96, a = 2arcsin(/5/3).
5. a = arctg 2, 0= arctg (l/2).
$ 22. ХИМИЧЕСКИЙ ФАКУЛЬТЕТ, 1974 г.
II. 1. x = it/64-2^. 2. Верно. 3. <x=5 /13/12.
4. Билет в цирк стоит 1 руб, билет в кино — 20 коп.
5. ^ = Яг/(г4-]/г»4-4№).
Hi. 1. х= — it/34-^1t- 2. Неверно. 3. а='у/ 2 — /3.
4. 30 коп., 10 коп. 5. r = atga/(2-j-2 ]/ i 4-2tg2a).
IV. 1. x=nk. 2. Неверно. 3. r = /2.
4. 20 коп., 10 коп. 5. г = Rcos(a/2) cosfi/(l 4-sinp).
§ 23. ХИМИЧЕСКИЙ ФАКУЛЬТЕТ, 1975 г.
II.	1. — 1<х<8. 2. Команда В забила в третьем периоде на две
шайбы больше, чем команда А во втором периоде.
3.	(7 4-4/7)/9. 4.а/(2/3-sinр/2).
5.	3(2m4~ 1)®» m = 0, 1, 2... .
298
III.	1. 0<х<1/4. 2. Число книг, сданных в понедельник на
39 больше, чем число книг, выданных в среду.
3.	128 (3 + 2 /2)/49. 4. г = /3/21
5.	Зл/2+6/ти:<Ь<Зж/2 + 3(2т+ 1)«, m = 0, 1, 2... .
IV.	1.'0<х<4. 2. Январская добыча второй шахты больше
январской добычи первой шахты на 3100 т.
3. 9(11 + 4/6)/50. 4. /?’/3/2/2.
5.	2/пж<а<(2т+1) it, m = 0,l, 2....	z
$ 24. ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ, 1972 г.
II.	1. x = itn, x = zhw/9 + 2it/i/3. 2. х < (log. 4)/2.
3.	49 км]ч, 35 км)*. 4. (5-/7) а/4. 5. /3.
111.	1. х = ж/д/2, х== rtit/З + ж/д. 2. 0, 1<х<1.
3.	1, 2 кг\ 2,4 кг. 4. 2 (1+/2/3). 5. 1:/3.
IV.	1. х = л + 2жл, х = 1±4ж/3 + 4ж/д. 2. x<(log.3)/2.
3.	8 kmJh, Ькм!ч. 4. (7 —/15)а/4. 5. 1:/3.
V.	1. x = it/4+itn/2, х = — ж/2-j-2ж/д, х — (—1)я-^-+ тл.
2.	1<х< 10000. 3. 70°, 2 л. 4. 2Rcos(а/2)//3-4sin*(а/2).
5.	ж/4.
VI. 1. х=4ж/д/3, х = 2«/5 + 4жя/5. 2. 1,/100<х< 10.
3.	60 'км{ч, 65 км]ч. 4. (5-/7) а/4. 5. 3.
$ 25. ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ, 1973 г.
II.	1. x = itfe, x = 7t2x/3 + 2itA:. 2. х=0.
’ 3. <7=1, <7 = 7. 4. (2/3-3)/2. 5. R//2.
/	14з"\
III.	1. х = ж/2 + ж/д, х= (—1)"arcsinI--4—)+’'#.
- 2. х = ~<- 1. 3. — 10 (возможно и d=0).
4.	5ж/12. 5. ЗЯ/2/2.
IV. 1. лг = ха, х = «/2 + 2жга. 2. -4/3.
3.	2(возможно и 62/5 при d=-0). 4. л(4/3 — 3)/13.
5.	arccos (25/28).
V. 1. х = ж/2 + ж«, х = (— 1)п-^-+«/г. 2. log«8; 3.
3. 100, 20, 4 (возможно и 124/3, 124/3, 124/3).
299
4. ж/2.5. г/10/4.
VI. 1. х = it/2ип, х = ±тг/6-|-2-кп. 2. х=1, х=3.
з  	з  	з  
3. ”/»-), «</»-'>/9 , 101 10.
/5-1	’/5-1
$ 26. ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ, 1974 г.
II.	1. x = it/3+^n, х = -т. 2.' 1 -/3<х<1+/£
3.	X! = 2-’, х,= 2« 4. (2-/3)/ У5. 5. а* /2/54.
III.	1. x = 2arcctg(l/2)4-2it/i. 2. х< - 1 -/2, х> 1 +/2.
3.	х,=Зз3, х, = 323
4.	ctg(a/2)/R‘+d«-2^cos(a/2). 5. a»/18.
IV.	1. x—it/4-j-nn, х = к/2•кп. 2. 2<‘х<3.
3.	Xi — 3 , Ха — 3.
4.	]/6* — a‘/2cos(a/2). 5. а* /3/54.
$ 27. ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ, 1975 г.
II.	1. х=-2/5;+Ч«п/5. 2. х = 3.
3.	3/7<x<log»2, х>1. 4. 8/Г16»/5.
5.	а /137/12.
III. 1, x=4-j-it/2 + «n, х=-3/2 + (-l/it/12+«m/2.
2. Xi = —3, Ха = 4. 3. — 5<х<0,6; x>log,2.
4. 75/7a*/16. 5. /п]/265/108.
IV. 1. x = 4/.m. 2. х=0.
3. - 2<x<log,5, х>7/3. 4. 5/TT/n«/7.
5. 6/277.
$ 2». ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
И КИБЕРНЕТИКИ, 1972 г.
II. 1. X=-l±/l -10ga(3-/2).
2. и(2л — 1)<х<2«/г; it/44-2itra<x<3it/4-|-2it/i.
3. a)r = (/5 + /2)(3 + /5)/6/2. 4. arctg(l/2/3).
300
5. a= — 2 ctg* 1 (1 4-2 ctg 1), x = 0;
a = 2, x = ± arccos (—it/4), x= 2it — arccos(—it/4),
x = arccos (— it/4) — 2n.
III.	1. x = - 2 ± •/"log, [3(3-]-/2)/5].
2.	icf 2 —|— тс/z-	x	it (zz —|— 1), it/z	n[ 4 —it/z.
3.	ri/rt = (7 + 2VQ)/6. 4. arctg (2/2-/3).
5.	a = (tg* I -|-2)/2 (2 tg I — I), x = 0, x = rt2it;
a = — 0,5, x= zt/4it2 — arccos2(— it/4),
x = zt V 4it* — [2ir — arccos (— it/4)]’.
IV.	1. x= 2 ±/log, (4 4-2/3).
2,	2it« —|— it/ 2 x 2itft —3it/ 2,
2-Ktt — it/3<x<it/3-|“2it/i.
3.	r,/r, = (50 — 31/2)/4. 4. arctg/2/5.
5.	a= ctg2 1/(4 4-2ctg 1), x = it/2, x= — 3u/2;
a= — 1, x= — arcsin(it/4),x = ±it4-arcsin(it/4),
x = 2it — arcsin (it/ 4).
$ 29. ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
И КИБЕРНЕТИКИ, 1973 г.
П. 1. Х= — it/4'4~it/n, у= it/24~2it£;
X = it/44~ 1t^> У= — it/24-2it&.
2. 0,58 <x<74-4/3. 3. S= (a24- a/a24-862)/4.
4. 1,/2/3, 1//2. 5. Треугольник ABC — тупоугольный.
III. 2. 0,31 <x< 54-2 |/6. 3. S = a262/(2a2-b2).
4. /5, /6, /7. 5. У гол ABC — острый.
IV. 1. x= — it/44-itm, t/=2it&; x = it/44-wn,
у = it4-2-Kk. 2. 0, 32<x<84-3 /7.
3. S = a«&/(2a-b). 4. 5/2, 7/3, 8/3.
5.	Угол ABC — острый.
$ 30. ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
И КИБЕРНЕТИКИ, 1974 г.
II.	1. x=5it/4-l. 2. -3/2/5<а<3/2/5.
3.	х= —2, x>4f/. 4. 3500 т, 4800 г.
301
5.	3/5/2.
III.	1. x = 9x/4-1. 2. a< - 21/7/3, a>2/7/3.
3.	x = 2, -3<x<-2-J||. 4. 3 t, 9 r.
5.	2/21 cm.
IV.	l.x=2it—1/2. 2. -/Щ5<а</2/15.
•3. x=2, x<-3-^. 4. 30V, 48V. 5. 2 cm.
§ 31. ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
И КИБЕРНЕТИКИ, 1973 г.
4
II.	1.	1, 0<х<(54-уТЗ)/6.
2.	х= — 5/2, y = ±zarcsinУ 5/Q-{-т.п;
х= — 5/2, у = :±:arcsinJ/5/6— 'rc/4-|-it/l.
3.	a/d/(/a+/F), ьу^/(УЗ-}-УЬ).
4.	4200 пар. 5. а/2/2.
III.	1. (5- /45)/10 < л <2.
2.	х = arccos/1/5-f-itn, у — 1/3-|-1С/24;
х = rt arccos ]/ 1/5-|-я/б + ^га» У= 1/3-|-Зж/4.
3.	с-1±Ус*-2d. 4. 600 км]ч. 5. /3tg40°.
IV.	I. х<-5, 1 <х<(8+1/22)/3.
2.	х = — 2/7, . t/ = =+z arcsin 2//7 -]~кп,
х— — 2/7 — Зя/7, у = ±arcsin}/ (4 — я)/ 7 -|-т-п.
3.	(dzt/d2 —с2)2. 4. 42 т. 5. 2/Зг2.
§ 32. МЕХАНИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ, 1972 г.
II. 1. 5/121/2. 2. о=3 км!ч.
3. 7? = 2/3 м. 4. ]/3 м*.
III. 1. 0<х<4/5, х = 2.‘ 2. 21 км.^3. 41/2/3 м.
4. 181/2 л». 5. а=-2, 6=20, с = 4.
IV. 1. 1/3<х<2/3. 2. х=8 км. 3. 1/3 м.
4. 21/39 м\ 5. r= 1, р= 1, <7 = 0.
302
$ 33. МЕХАНИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ, 1973 г.
II.	2. 8 = 8. 3.р/2<х<3/2.
4.	V=aI>,sinacpsa/3. 5. х= — 0,5, у= — 1.
III.	1. x = it/6-4-itfe. 2. 8 = 4/3/3.
4.	V = 882 sin a sin р/За sin (a -|- Р).
5.	х= — 2, у = 3/2; х=0, у=— 0,5.
IV.	1. л=2гт, х= — гс/З2wn. 2. 8=15/3.
3.	5/2<х<3. 4. 8 = /4y2-j-p2/2. 5. х= 1, у=-\.
$ 34. МЕХАНИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ, 1974 г.
I.	1. х = 2ш — it/2; х= (2Л: —|— l)it. 2. — 1 <х<3, х^=-1.
3. 8^ = 9/3/4. 4. VAECD = 36. 5. a =100.
111. 1. х = 2пп -|- it/2; x = 2it/z 4-it.
2. 1 -]/3/2<x^ 1 + /3/2; x=H= 1.
3. ЛС=3. 4. VABCD = 450. 5. a = 99.
IV. 1. x=-Tt/44-2itfe. 2. l<x<3, x^=2.
3. 5^= 16/2. 4. /^ = 9/3/8. 5. a=100.
§ 35. МЕХАНИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ, 1975 г.
4
II. 1. x < — 3, x> — 1. 2. x = zt 1, y=l; x = -^-2, у = 0.
3. */2(a —p). 4. 8D = 9. 5. x, = —9it/10, x, = —7it/6.
III. 1. -8<x<2. 2. x=-/2^/2, у = ±=/2^/2;
X=-/2^/4, y = ±/14^/4. 3.’ (a-p)/(a + p).
4. 10#. 5. x=- 11W18.
41	1
IV.' 1. x< —2, x>4. 2. x=zt/3/2. y=-0,5;
x = ^V2, y=0. 3. (a + P)/2. 4. 6#.
5. Xi= — тс/2/	— x/6,	— 7тс/18.
СОДЕРЖАНИЕ
Предисловие .....	........................................................ «	3
Часть I
МЕТОДИЧЕСКОЕ РУКОВОДСТВО
И КОНТРОЛЬНЫЕ ЗАДАНИЯ
§ 1. Методика изучения программного материала по математике уча-
щимися заочных подготовительных курсов МГУ....................... 5
§ 2. Литература, рабочий план, методические указания по разделам
элементарной математики для учащихся заочных подготовительных
курсов МГУ ..................................................... 7
О подготовке к письменному экзамену по математике	....	35
Контрольные задания для учащихся заочных курсов	....	36
Литература, рабочий цлан и контрольные работы по материалу,
включенному в новую школьную. программу по математике .	.	43
Часть II
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
С РАЗБОРОМ ОТДЕЛЬНЫХ ВАРИАНТОВ
Географический факультет,	1972	г.....................................................................48
Географический факультет,	1973	г.....................................................................52
Географический факультет,	1974	г.	 57
Географический факультет,	1975	г.....................................................................63
Биолого-почвенный факультет, 1972 г...................................................................70
Факультет почвоведения, 11973 г.......................................................................76
Биологический факультет, 11973 г............	80
Факультет почвоведения, 1974 г. .	..................................................................87
Биологический факультет, ,1974 г.......................................................'..............91
Факультет почвоведения, 1975 г........................................................................98
Биологический факультет, 1975 г......................................................................10'
Геологический факультет, отделение общей геологии, 11972 г.	. .	И’
Геологический факультет, отделение геофизики, 1972 г..................................................11
Геологический факультет, отделение общей геологии, 1973 г.	. .	12
Геологический	факультет,	отделение	геофизики, 1973	г.	.	.	12
Геологический	факультет,	отделение	общей геологии,	1974 г.	.	.	13
Геологический	факультет, отделение геофизики, 1974 г.	'.	.	.	.	13£
Геологический	факультет,	отделение	общей геологии, ,1975 г.	.	.	147
Геологический факультет, отделение геофизики, 1975 г.................................................15С
Химический факультет, 1972 г................................ *	16С
Химический	факультет,	1973	г.....................................................................  16С
Химический	факультет,	1974	г.......................................................................173
Химический	факультет,	1975	г.......................................................................179
Физический факультет, 1972 г.................................:	188
.Физический	факультет,	1973	г. .	.	. , .	.	.	.	.	. • .	19t
Физический	факультет,	1974	г.....................................................................  20'
Физический	факультет, **1975	г;...................................................................  21С
Факультет вычислительной математики и кибернетики, 1972 г. .	. 219
Факультет вычислительной математик и кибернетики, 1973 г. .	,
Факультет вычислительной математики и кибернетики, 1974 г. 23‘
Факультет вычислительной математики и кибернетики, 1975 г. .	.	24-
Механико-математический факультет, 1972 г..........................................................
Механико-математический, факультет, 1973 г.........................................................2с
Механико-математический факультет, 1974 г..................  .	27S
Механико-математический факультет, 1975 г............................................................28?
еты........................................................  9	29!
* ^^""Sg8S538^^SS^8<EpS?p5XSS^.©ppo^o?n^«Pr	Р*Р