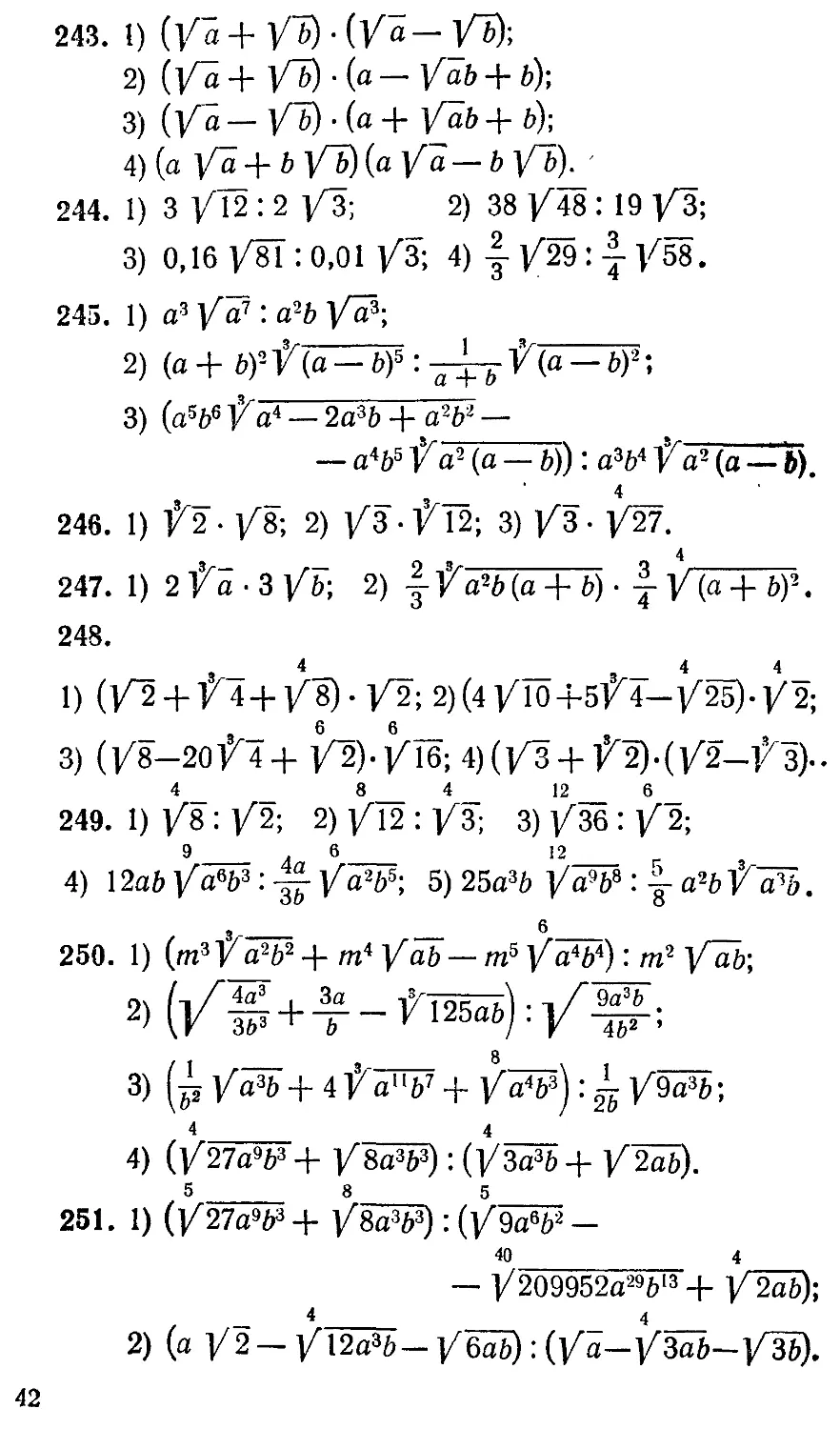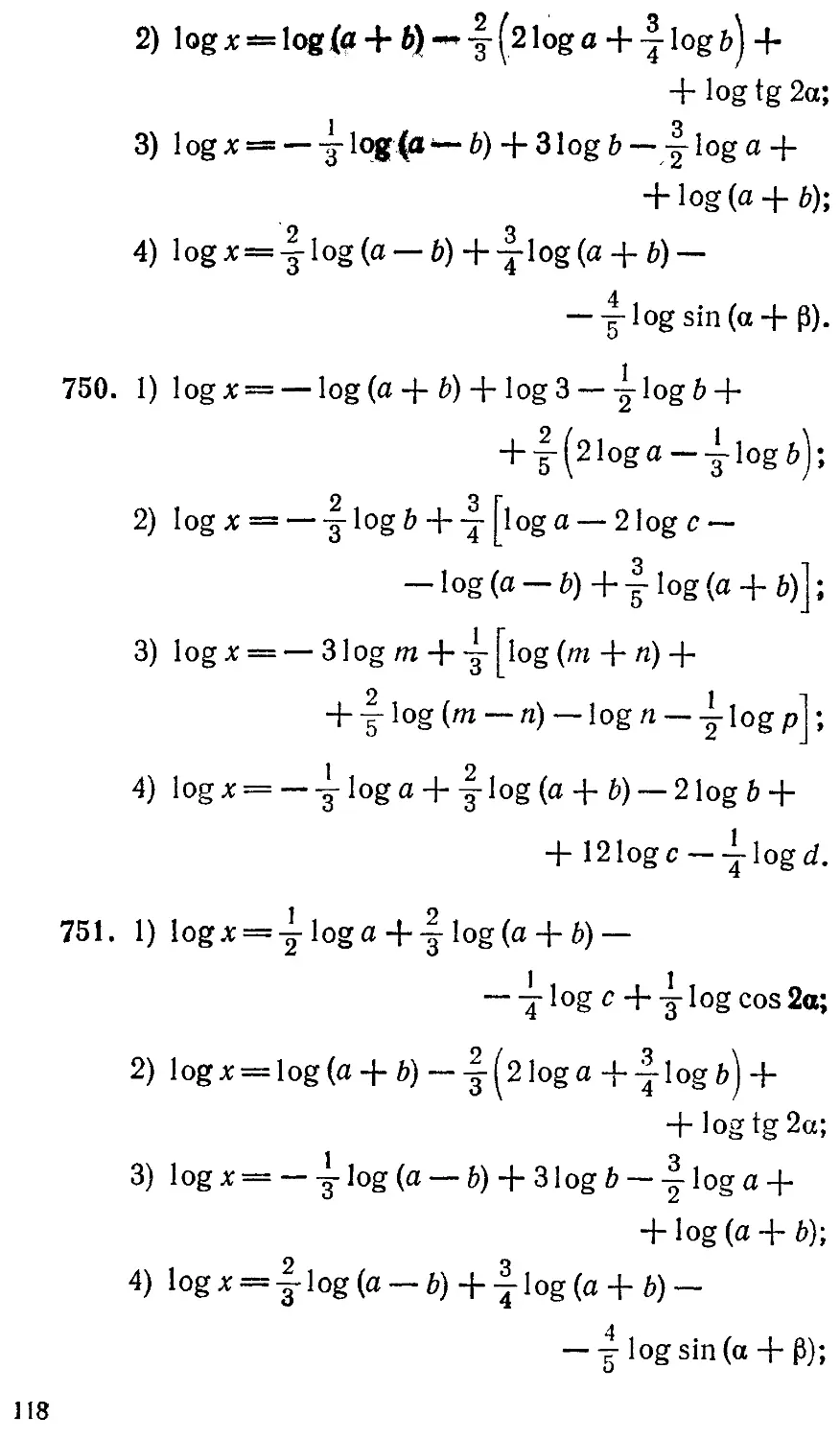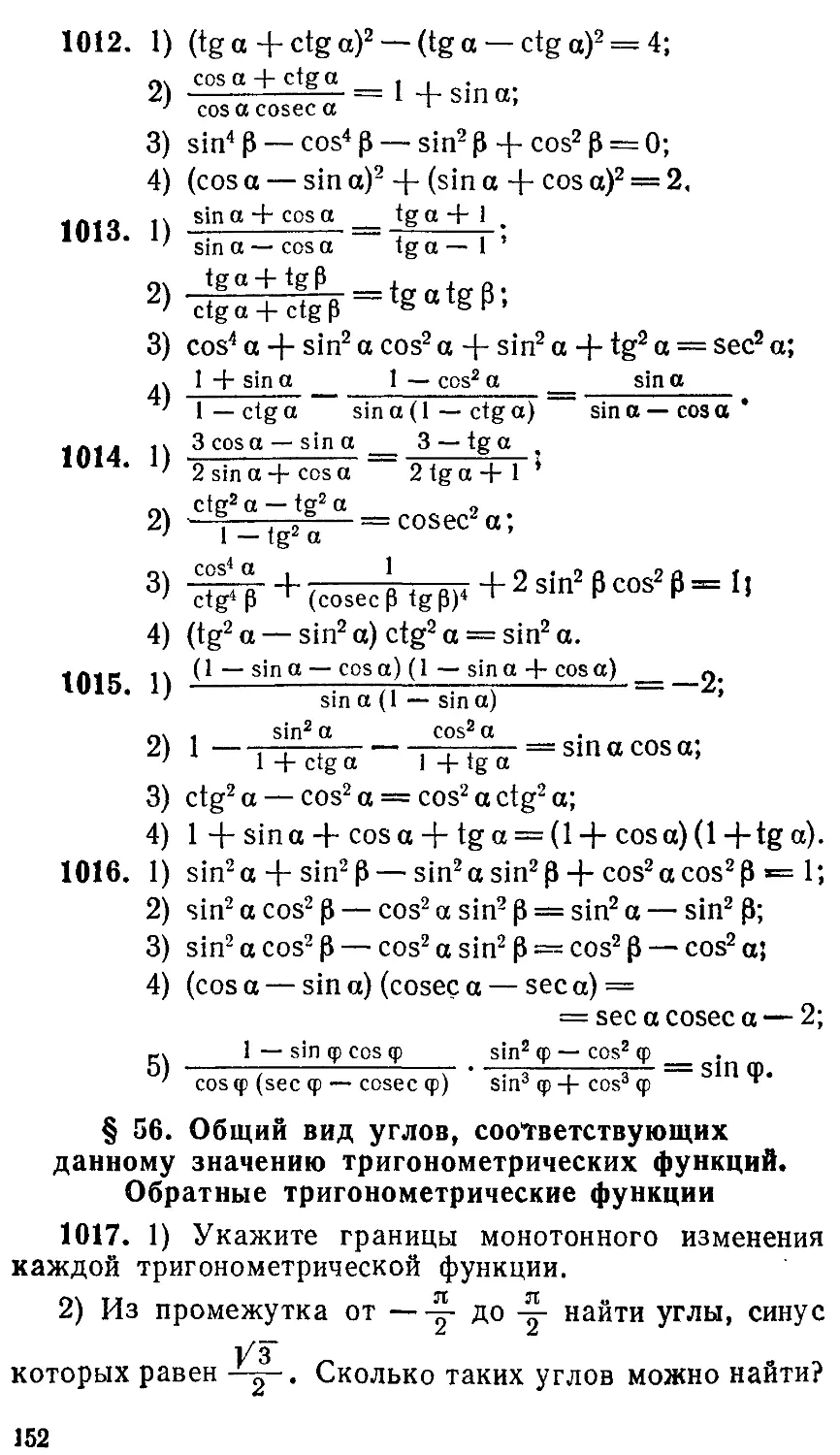Author: Рудник А.Е. Клюева Л.А. Мосолова М.С.
Tags: алгебра математика задачи по математике
Year: 1974
Text
А.Е.РУДНИК, Л.А.КЛЮЕВА, М. С. МОСОЛОВА
СБОРНИК ЗАДАЧ
по
ЭЛЕМЕНТАРНОЙ
МАТЕМАТИКЕ
ДЛЯ ТЕХНИКУМОВ
A. E. РУДНИК, Л. А. КЛЮЕВА, M. С. МОСОЛОВА
СБОРНИК ЗАДАЧ
ПО ЭЛЕМЕНТАРНОЙ
МАТЕМАТИКЕ
для техникумов
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для средних специальных учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1974
512
Р 83
УДК 512
Р
20202-145
053 (02)-74
32-74
© Главная редакция физико-
математической литературы
издательства «Наука», 1974 г.
ОГЛАВЛЕНИЕ
Предисловие ............................................................................................... 7
Глава 1. Арифметика и алгебра...............................................................................9
§ 1. Обыкновенные и десятичные дроби....................................... 9
§ 2. Деление многочленов.............................................................И
§ 3. Разложение многочленов па множители...............................12
§ 4. Действия с дробями.............................................................12
§ 5. Вычисления на логарифмической линейке .... 13
§ 6. Приближенные вычисления. Абсолютная и относи-
тельная погрешность 17
§ 7. Действительные числа.............................................................19
§ 8. Прямая пропорциональная зависимость .................... 22
§ 9. Линейная функция у — kx 4- b и ее график . . 23
§ 10. Обратно пропорциональная зависимость ...................... 25
§ 11. Уравнения первой степени с одним неизвестным . . 2S
§ 12. Системы уравнений первой степени с двумя и более
неизвестными . .............................28
§ 13. Неравенства и системы неравенств первой степени
с одним неизвестным............................... ... 30
§ 14. Степень с рациональным показателем..............................................................34
§ 15. Сложение и вычитание корней.....................................................................40
§ 16. Умножение и деление корней......................................................................41
§ 17. Уничтожение иррациональности в знаменателе и чис-
лителе дроби . . . .* ....................43
§ 18. Степени с нулевым, отрицательными и дробными по-
казателями ...........................................45
Глава 2. Векторы..........................................50
§ 19. Понятие вектора. Равенство векторов. Сложение и
вычитание векторов. Умножение вектора на число.
Разложение векторов.................................. 50
§ 20. Умножение вектора на скаляр. Проекция вектора на
ось. Координаты вектора на плоскости...................53
§ 21. Зависимость между проекцией суммы векторов на
ось и проекциями слагаемых на эту ось. Скалярное
произведение двух векторов...................... . . . 5э
§ 22. Комплексные числа................ ............59
3
§ 23. Сложение и вычитание комплексных чисел .... 61
§ 24. Умножение, деление и возведение в степень ком-
плексных чисел........................................61
Глава 3. Квадратные уравнения и уравнения, приводимые
к квадратным. Квадратные функции и их графики .... 67
§ 25. Функция у = ах2 и ее график..........................67
§ 26. Функция у = ах2 + с и ее график......................68
§ 27. Функция у = ах2 + Ьх + с и ее график.................70
§ 28. Неполные квадратные уравнения......................................................71
§ 29. Полные квадратные уравнения................. . 73
§ 30. Разложение квадратного трехчлена на линейные
множители ..............................................76
§ 31. Исследование квадратного трехчлена . 77
' § 32. Квадратные неравенства.........................................................................................77
§ 33. Исследование корней квадратного уравнения по его
дискриминанту ..........................................79
§ 34. Задачи на составление квадратных уравнений ... 80
§ 35. Иррациональные уравнения............82
§ 36. Биквадратные уравнения............84
§ 37. Двучленные и трехчленные уравнения..86
§ 38. Возвратные уравнения............87
§ 39. Системы уравнений второй степени с двумя и более
неизвестными .......................................... 87
§ 40. Задачи на составление систем уравнений второй
, степени.................................................................................................................91
Глава 4. Прогрессии . ....................................................................................................95
§ 41. Числовые последовательности....................................................................................95
§ 42. Предел последовательности .................................................................................... 96
§ 43. Арифметическая прогрессия.........................................99
§ 44. Геометрическая прогрессия.........................................ЮЗ
Глава 5. Показательная функция и логарифмы................................................................................ПО
§ 45. Показательная и логарифмическая функции . . .ИО
§ 46. Логарифмирование и потенцирование.ИЗ
§ 47. Десятичные логарифмы.............................................119
§ 48. Показательные и логарифмические уравнения . . . 124
§ 49. Соединения....................... ..............130
§ 50. Бином Ньютона....................................................134
§ 51. Сложные проценты.................................................137
Глава 6. Тригонометрические функции любого угла .... 139
•§ 52. Измерение дуг и углов ........................................................................................139
§ 53. Изменение тригонометрических функций с измене-
нием угла. Знаки тригонометрических функций . . 144
§ 54. Построение углов. Графики тригонометрических
функций ...............................................147
§ 55. Зависимость между тригонометрическими функциями
одного и того же угла..................................148
4
§ 56. Общий вид углов, соответствующих данному значе-
нию тригонометрических функций. Обратные тригоно-
метрические функции......................................................................................152
§ 57. Тригонометрические уравнения.............................................157
Глава 7. Теоремы сложения и их следствия...........................................................................159
§ 58. Формулы сложения.159
§ 59. Формулы приведения.......................164
§ 60. Тригонометрические функции Двойного и половинного
углов ...................................................................................................168
§ 61. Преобразование произведения тригонометрических
функций в сумму.....................................................................................174
§ 62. Преобразование суммы тригонометрических функций
в произведение ......................................................................................... 1/4
§ 63. Тригонометрические уравнения ............................179
§ 64. Неравенства...............................................................................181
§ 65. Системы тригонометрических уравнений.........................182
Глава 8. Обзор свойств и графиков элементарных функций . 183
§ 66. Общие свойства функций.........................183
§ 67. Некоторые степенные функции.......................190
§ 68. Дробно-рациональные функции. Асимптоты .... 190
§ 69. Показательная функция, логарифмическая функция
и функции, связанные с ними.........................................................................191
§ 70. Тригонометрические функции. Обратные.тригоно-
метрические функции ............................... 192
§ 71. Разные задачи...........................................................................................197
§ 72. Дополнения к разделу комплексных чисел . . . .199
Глава 9. Предел функции и производная..............................................................................203
§ 73. Предел функции..........................................................................................203
§ 74. Приращение функции......................................................................................205
§ 75. Непрерывность функции...................................................................................206
§ 76. Производная функции, ее геометрический и физиче-
ский смысл............................................. . 206
§ 77. Понятие о второй производной. Ускорение .... 208
§ 78. Возрастание и убывание функции..........................................................................209
§ 79. Экстремумы функции......................................................................................299
Глава 10. Планиметрия......................................
Зависимость между элементами треугольников, четырех-
угольников и некоторых других фигур.............................................................................211
§ 80. Прямоугольный треугольник..............................211
§ 81. Равнобедренный треугольник..............................211
§ 82. Косоугольные треугольники........................................................212
§ 83. Площадь параллелограмма, треугольника, трапеции
и круга. Вписанные и описанные фигуры....................................................................214
Глава 11. Стереометрия...............................: . . 217
§ 84. Перпендикуляр и наклонные к плоскости...................................................................217
§ 85. Угол прямой с плоскостью................................................................................219
§ 86. Параллельные прямые и плоскости.........................................................................220
5
§ 87. Двугранные углы и перпендикулярные плоскости . 223
§ 88. Многогранные углы.225
§ 89. Параллелепипеды и призмы.227
§ 90. Поверхность параллелепипеда и призмы...............................229
§ 91. Пирамида............................................................. 231
§ 92. Усеченная пирамида ...............z...................................................................234
§ 93. Поверхность пирамиды...............................................................235
§ 94. Цилиндр и его поверхность.....................................237
§ 95. Конус и его поверхность.....................................238
§ 96. Усеченный конус и его поверхность.....................................239
§ 97. Объем параллелепипеда, призмы и цилиндра . . . 240
§ 98. Объем пирамиды и конуса.............................................................................243
§ 99. Объем усеченной пирамиды и усеченного конуса . 245
§ 100. Шар и его части......................................................................................246
§ 101. Тела вращения.........................................................................................248
Ответы...........................................................................................................252
Таблица значений тригонометрических функций....................................................................318
ПРЕДИСЛОВИЕ
Настоящий сборник задач составлен в соответствии
с утвержденной программой курса математики для
средних специальных учебных заведений. При составлен
нии задачника было учтено, что в 1975 году техникумы
переходят на новые программы по математике, что сбор-
ник задач предназначается для учащихся дневных, ве-
черних и заочных отделений техникумов всех специаль-
ностей.
В сборнике содержится свыше 6000 задач и приме-
ров, что дает возможность максимально обеспечить уча-
щихся работой в классе и дома. В сборнике предусмот-
рен раздел повторения, который необходим для работы
всем преподавателям и особенно работающим на вечер-
нем и заочном отделениях техникумов.
В разделе повторения основное внимание уделено
арифметике, алгебраическим преобразованиям, уравне-
ниям и неравенствам. Работа по разделу повторения
даст возможность преподавателю выяснить степень под-
готовленности учащихся к прохождению программы
и наметить план ликвидации пробелов по отдельным
темам.
В сборник включены примеры и задачи по темам
программы, вступающей в силу в 1975 году: векторы, со-
единения, бином Ньютона, сложные проценты, обзор
свойств и графиков элементарных функций, обобщение
понятия числа, производные и т. д.
Особое внимание авторы уделили понятию функцио-
нальной зависимости, подбору примеров и задач, спо-
собствующих сознательному усвоению программы.
Задачи по геометрии состоят из двух частей: плани-
метрия и стереометрия. Имеются задачи на вычисление,
доказательство, построение, отыскание геометрических
7
мест точек и взаимное расположение геометрических
элементов в пространстве. При решении ряда задач
можно использовать логарифмическую линейку и таб-
лицы. Приведенное количество задач вполне охватыва-
ет все изучаемые разделы геометрии.
Сборник задач обеспечивает полностью специально-
сти, работающие по программе 200—300 часов. Ограни-
ченный объем книги не позволил отразить ряд тем по
программе, рассчитанной на 380—400 часов, например,
дифференцирование и интегрирование.
Преподавателям, работающим по программе, рас-
считанной на 380—400 часов, рекомендуется пользо-
ваться учебниками по высшей математике для технику-
мов: И. Л. Зайцев «Элементы высшей математики»,
Н. П. Тарасов «Курс высшей математики для технику-
мов», И. Ф. Суворов «Курс высшей математики»,
П. М. Савчук «Сборник задач по высшей математике
для техникумов», Р. А. Калнин «Алгебра и элементар-
ные функции».
По геометрии: П. П. Андреев, Э. 3. Шувалова «Гео-
метрия».
Авторы выражают искреннюю благодарность всем ли-
цам, прочитавшим рукопись, сделавшим критические
замечания и давшим полезные советы, направленные на
улучшение рукописи.
Мы будем признательны всем, кто-найдет время, что-
бы высказать нам свои критические замечания.
Все замечания и пожелания с целью улучшения за-
дачника просим направлять по адресу: 119034, Москва,
Г-34, Кропоткинская набережная, 11, Московский
энергетический техникум.
Авторы
ГЛАВА 1
АРИФМЕТИКА И АЛГЕБРА
§ 1. Обыкновенные и десятичные дроби
1. Найти все делители следующих чисел: 7; 11; 13;
37; 2457; 17331; 24570; 24572; 2300?
2. Приведите примеры чисел, которые делятся на 2;
3; 4; 5; 8; 9; 6; 12 и 15.
3. Найти:
(а) Наибольший общий делитель следующих чисел:
1) 980; 1176; 1225; 2) 250; 320; 810; 490;
3) 660; 1080; 1200; 1500.
(б) Наименьшее общее кратное следующих чисел:
1) 30; 75; 45; 18; 27; 2) 24; 108; 135; 216;
3) 770; 70; 231; 210; НО; 462; 4) 750; 600; 450.
4. (а) Как изменится дробь от прибавления к ее
членам одного и того же числа, если эта дробь: 1) пра-
вильная, 2) неправильная? Приведите примеры.
(б) Назовите два способа сокращения дробей. Какая
дробь называется несократимой?
(в) Назовите условия равенства двух несократимых
дробей.
5. Выполнить действия:
1) 1|+ 1|-0,125;
2) (64~ 1 • (2,8 + °.2);
3) 12} 4'(т-0’125)’’
4) (0,5 4-4 — 4)' (3 + 5,32 -0,12).
9
6. Вычислить:
1)
2)
3)
4)
5)
6)
7)
8)
23, 16
50 + 1 75 .15
55,1 :5 '17
0,03
— 9
9 ^--6,52
40 у • 2 : 9
1
9
0,45 - 0,225
• 62 —— *
* 02 200 ’
Uj^-O.OOOOs)- 1250 ,
— + 15,2:-^;
!^>-°'000,87гФз5ю
1774 + 11,375) — (9 + 3,11б¥1 • (20,001 - 9,986)
| \ О / \ 1 2.0 / J
°-3675-'1й--,-П)+4-0'15
б|+ 0,(5)-0,45(3) ю
О, (7) + 0,54 (6) + 0,02 : 3 ТГ ’
5-5__з А з А
9^4 4
15,8(3): 10 5’ 158 (3) ’
4 + 0,(2) + 0,333 ... + 0,(4)
0,0 (1) + 0,0 (2) + 0,0 (3) + 0,0 (4) ’
[S34 +9.1 (0)] ' 1-2 з4?--5,8(3)
I 4 J оэ
(10^_8>8). 0,(55) ““МЧ-З.К6Т•
7. Найти х:
1) 2х: 12 = 4:6;
2) 4х:(2у • 4) = 80: 50;
3) 2, (3): 0, (3) = 0, (7): х;
4) х : 0, (3) = 0, (12) : 0,1 (6);
5) 0, (4) :х = 3,(3): 2,25;
6) -|-:0,(41) = х:0,8(3);
7) 2,5 : 0,125 = 0,5х : 0,75;
8) 10 : 0,01 =-^-: 0,4х.
10
8. Найти:
1) 8% от 20,4 т; 2) ~ % от 600 т;
3) 62,5% от 248га; 4) 3 | % от 1980.
9. Магазин продал в первый день 15% поступившего
с базы товара, во второй день — 40% остатка. Опре-
делить, сколько процентов поступившего в магазин
товара осталось непроданным.
10. Сколько килограммов воды нужно выпарить
из 0,5 т целлюлозной массы, содержащей 85% воды,
чтобы получить массу с содержанием 75% воды?
11. Найти число, если 1,(4)% его составляют 30,8.
12. Какой процент от числа 800,4 составляют числа
18,2; 20,4; 30,8; 42,5?
13. Сколько процентов составят
1) 0,(2) от 0,(8); 2) 0,(3) от 0,(6);
3) 3,0(5) от 8,0(3); 4) 1, (1) от 7,(7)?
§ 2. Деление многочленов
14. Выполнить деление многочленов:
1) (а2 4- 6а3 4- 21 — 29а): (- 3 + 2а);
2) (Зх3 — 5х2 + 9х — 15): (Зх — 5);
3) (2,4х2у2 4- l,4x3z/ — 0,4х4 + 5,4г/4): (-0,Зху + 0,1х2—
— 0,9/);
4) (4,1а-7-0,1а2—0,1а3+1,5а4): (-0,2а + 0,За24-0,7).
15. Выполнить деление:
1) 1(х + у)2 - (х - z/)2]: [(х + у) + (X - у)]-
2) 1(х + у)4 — (х — г/)4]: [(х + у)2 4- (х — г/)2];
3) [(х 4- у)3 + (х — г/)3]: [(х 4- у) + (х — /];
4) [2 (а — Ь)3 4- 7 (а — Ь)2 4- 7 {а — Ь) 4- 2]: [2 (а — Ь)2 4-
4-3 (а — Ь)+ 1].
16. Упростить выражение
[(60а2 4- 50а — 60): (2а 4- 3) (а 4- 12а2 — 20): (4а 4- 5)]: 30а
и найти его числовое значение при а = — 0,2,
Решить уравнения (17—18):
17. (15х — 10): 5 — (8x4- 12): 4 = 7.
18. x(x —3) —(6х3—12х2):6х = Зх4-4.
11
§ 3. Разложение многочленов на множители
Разложить на множители многочлены (19—23):
19. 1) 7а3д3 4- 49а2д2; 2) 16х#3 — 8#4;
3) 15xm+l — 60хт; 4) Ь2т — с2т;
5) (2п+262/га ^п+2^2т. gj ^m+rt+3 cim~:г~4.
20. 1) 5x(a-b)--3x2(a — b)-4-6x3(b — a);
2) 3m(x2+1) — 2т2 (х2 + 1) 4~ 4т3(х2 4~ 1);
3) 4х(а + b 4- с) 4- 8х2(а 4- b 4- с) 4- 4х3(а 4- b 4- с}\
4) 16х4 (р — q) — 32х3 (q — р~) — 16х2 (q — р).
21. 1) ах2 4- ах — а — Ьх — Ьх2 4" Ь;
2) а — ах 4- ах2 4- Ь — Ьх 4- Ьх2;
3) Ьх — сх 4- ах — сх2 4- Ьх2 4~ ах2;
4) сх2 — ах — сх — Ьх 4- ах2 4- Ьх2.
22. 1) а2 4- 2аЬ 4- Ь2—1; 2) т2—4 — 2тп-\-п2;
3) 2тп— /п24-9 — п2; 4) 25n2—2Qtnn—36 4~ 4т2;
5) 2pq — q2 4~ а2 — р2 4~ 2тп 4- т2.
23. 1) х8 4- х4 4-1; 2) х4 4- х2у2 4- #4;
3) а3 4- 6а2 4- 11а 4- 6; 4) 2а3 4- а2 — 4а — 12;
5) а3 4~ 8а24-17а 4-Ю; 6) а4 4-а3 4-ба2 4-5а 4-5;
7) 432х4# 4- 250х#4; 8) х3 4- х 4- х24-1-(х4-1)2'
§ 4. Действия с дробями
24. Выполнить действия:
25. Упростить выражение:
Ь2 + с2 — 2Ьс
(а - Ь)2 + (Ь - с)2 - (с - а)2 *
26. Упростить выражение, а затем найти его число-
з
вое значение при а = 2у и Ь = — 1:
а — Ь _ а2 + 1>2+ ^ — 2 \ . 4а4 + 4а2Ь + Ь2 — 4
2Ь — а а2 — ab — 2Ь2 ) ’ а2 4- Ъ 4- яЬ 4- а '
12
27. Проверить справедливость равенства:
2а262 + 2Ь2с2 + 2а2с2 — а4 — Ь4 — с4 =
= (Ь-\- с — а) (а 4- b + с) (а — b + с) (а + b — с).
§ 5. Вычисления на логарифмической линейке
28. Составить множества чисел (по пять чисел в
каждом множестве):
1) с порядком, равным нулю;
2) с порядком, равным —1; —2; —3; —4;
3) с порядком, равным 1; 2; 3; 4.
29. Проверить следующие результаты:
№№ п/п Условие Ответ №№ п/п Условие Ответ
1 25,3 • 28,7 728 14 0,182-0,238 0,0433
2 11,13-22,2 247 15 0,42- 1,52 0,638
3 135 • 0,644 86,9 16 3,51 • 14,6 51,3
4 0,238 • 3,82 0,909 17 2,42 • 6,54 15,83
5 6,75 • 3,45 23,3 18 4,83 • 1,47 7,10
6 2,9 - 24,5 71,1 19 0,0145-0,0724 0,001049
7 5,71-3,22 18,38 20 26,8-3,18 85,2
8 0,52 - 4,63 2,41 21 9,73 - 0,00905 0,088
9 0,748 • 0,856 0,641 22 0,0292-0,0126 0,00037
10 34,5 • 2,5 86,3 23 0,39 • 0,0235 0,0092
11 43,6- 11,2 488 24 31,5-67,8 2340
12 0,34-0,113 0,0384 25 0,125-0,148 0,0185
13 42,3 - 2,64 112 26 0,438 • 0,836 0,366
30. Выполнить умножение чисел и сравнить резуль-
таты:
п/л Условие Ответ
1 54,2-65,7-0,00125 4,45
2 0,0056-8,24-24,8-0,921 1,05
3 0,628-4,32-0,824-56,1 125,4
4 1,68-3,24-8,18-0,572 25,5
5 43,2 - 9,24 - 0,018 - 0,822 5,90
6 5,24 • 0,342 - 6,78 • 2,48 • 3,2 96,5
7 542-0,0621 -3,22-0,128 13,87
8 10,4-0,86-0,724- 1,32-3,84 32,8
9 0,093-6,81 -9,37-7,82 46,4
10 0,368-4,21 -8,63-0,48-3,3 21,2
13
31. Выполнить деление чисел и сравнить результаты:
№№ п/п Условие Ответ №№ п/п Условие Ответ
1 27: 1270 0,0213 9 9,59 :243 0,0394
2 404:806 0,501 10 295 : 151 1,952
3 756: 330 2,29 11 7,96:0,384 20,7
4 7,69:3,16 2,43 12 6,46 : 0,0246 262
5 932:87,6 10,63 13 872:44,6 19,55
6 889:50,4 17,63 14 642 :325 1,975
7 911 :357 2,55 15 578 :24,8 23,3
8 448:362 1,235 16 195 :986 0,198
32. Выполнить действия и сравнить результаты:
п = 3.53:
2)
3)
4)
5)
6)
625-4,76- 14,8 _ 9о 1.
124-15,4 ~2с5’1’
732-0,168-7,24-0,542 _
728 • 0,424 • 0,0524 ~
842- 15,6-7,24-0,667 __ ~
672 • 4,25 • 7,65 ~ 2
6,84 • 9,75 • 5,42 • 178 ,
137 - 0,642 - 7,25 - 8,84 1
6,18-712-3;42-0,842 _
0,614- 13,5 • 12,5-8,81 ~
7у 3,16-24,5-6,35-3,26
8,25-3,14-8,42-4,58 “
9,41-5,82-63,7-32,6 = __ .
°' 28,5-5,12-0,244-42,4 '°’4'
33. Вычислить при помощи логарифмической линейки
квадраты данных чисел:
№.Ns п/п Условие Ответ №№ п/п Условие Ответ
1 42 16 11 0,01522 0,000231
2 72 49 12 82,12 6740
3 252 625 13 29,62 876
4 7,022 49,3 14 73,42 5390
5 4,722 22,3 15 95,62 9140
6 38,32 1470 16 67,52 4560
7 75,42 5690 17 6712 450 000
8 0,0532 0,00281 18 9312 867 000
9 0.0842 0,00706 19 23452 5 500 000
10 0,123 2 0,0151 20 18542 3 430 000
14
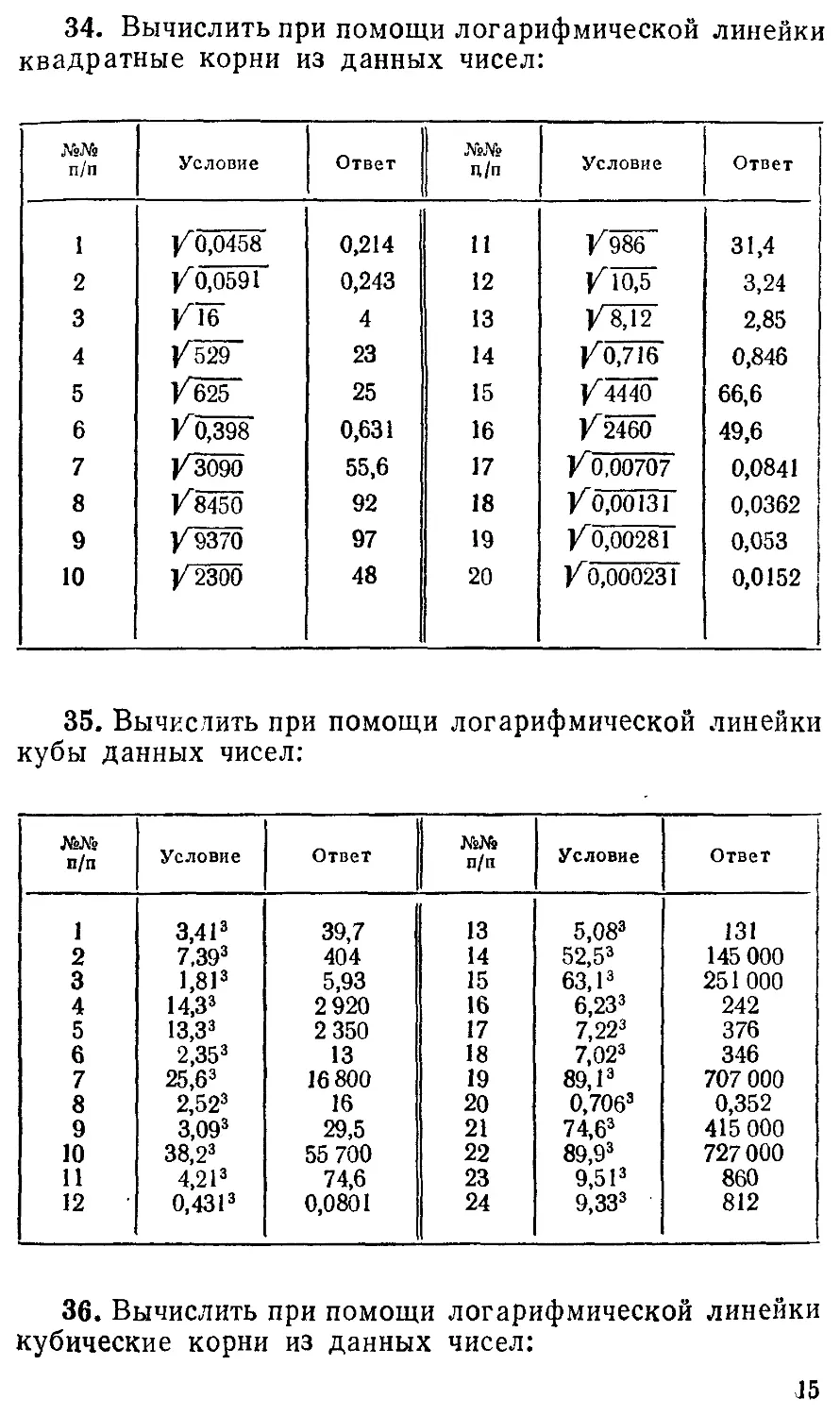
34. Вычислить при помощи логарифмической линейки
квадратные корни из данных чисел:
№№ п/п Условие Ответ №№ ц/п Условие Ответ
1 /0,0458 0,214 11 /986“ 31,4
2 У 0,0591 0,243 12 /ТЩГ 3,24
3 /Тб 4 13 /8jF 2,85
4 У 529 23 14 /бЖ 0,846
5 /б25 25 15 /4440 66,6
6 КО,398 0,631 16 /2460 49,6
7 У 3090 55,6 17 V 0,00707 0,0841
8 /8450 92 18 У 0,00131 0,0362
9 /9370 97 19 У 0,00281 0,053
10 /2300 48 20 У 0,000231 0,0152
35. Вычислить при помощи логарифмической линейки
кубы данных чисел:
№№ п/п Условие Ответ №№ п/п Условие Ответ
1 3,413 39,7 13 5,083 131
2 7.393 404 14 52,53 145 000
3 1,813 5,93 15 63,13 251 000
4 14,33 2 920 16 6,233 242
5 13,33 2 350 17 7,223 376
6 2,353 13 18 7,023 346
7 25,63 16 800 19 89,13 707 000
8 2,523 16 20 0,7063 0,352
9 3,093 29,5 21 74,63 415 000
10 38,23 55 700 22 89,93 727000
11 4,213 74,6 23 9,513 860
12 0.4313 0,0801 24 9,333 812
36. Вычислить при помощи логарифмической линейки
кубические корни из данных чисел:
45
№№ п/п Условие Ответ №№ п/п Условие Ответ
1 jZhT 4,81 10 1^530“ 8,09
2 16 800 25,6 11 3,91
3 5,31 12 1^5^бГ 1,77
4 у 2 350 13,3 13 4,06
5 1^252 6,32 14 У 69 900 41,2
6 ]Х34Т 3,25 15 1^759" 9,12
7 ]^зйГ 6,78 16 У 77 300 42,6
8 У 3 440 15,1 17 ЙХб 4,21
9 1^425" 7,52 18 |^888~ 9,61
37. Выполнить при помощи логарифмической линейки
следующие действия:
№№ п/п Примеры Ответы №№ п/п Примеры Ответы
1 21,6 • У5ЛЗ" 13,46 10 0,626 ,3/“ 14,8 0,11
3,74 3,14 V 88,6
2 6,42 - 5,32 7,8 23,12 11 469,3 /”34б" 0,596
319 V 2111
13,2 ♦ 6,42 /9J 0,?33
3 173,6 12 V 0,0563 • V7,25
°/ 0,07625 0,267 13 6,08 • У 0,0495 10,3
4 V 14,372 15,8-0,00835
-.4/ 1,533 • /0Д4
,У 716,5 205,8 14 1,1
5 V 2,22 -30 V 0,894
6 13,6-/32Д 18,92 0,217 15 91,3-0,162 /Хб 0,503
7 0,685 • /0^8 О,9652 0,690 16 3,34 • /8ДГ 0,96 31,4
8 0,21 • 12,42 20,3 17 26,3 • 11,52 730
/^54 /22,7
9 2,32 • 56,22 8,25 888 18 9,95 - 3,422 /4^5" 54,6
16
§ 6. Приближенные вычисления.
Абсолютная и относительная погрешность
38. Округлить число 20,7853 до пяти значащих цифр
и найти абсолютную и относительную погрешность
получившегося приближенного числа.
39. При взвешивании получен результат 15 кг
(±0,6%). Определить абсолютную погрешность.
40. Длина отрезка, равная 98,8 см, округлена до
1 м. Определить относительную погрешность изме-
рения.
41. Масса тела принята за 60 кг. Определить пределы
допустимых значений массы тела, если относительная
погрешность при определении массы равна 2%.
42. Точное значение величины заключается между
54,98 см и 54,90 см. Определить относительную погреш-
ность измерения.
43. Точное значение величины заключается между
302,35 см и 302,33 см. Определить относительную погреш-
ность.
44. Вычислить площадь прямоугольника, стороны
которого 7,2 см и 34,8 см. Определить относительную
погрешность вычисления.
45. Выразить 4у приближенно десятичной дробью
с тремя десятичными знаками. Определить относитель-
ную погрешность.
46. При двукратном измерении диаметра подшипника
рабочий получил результаты 159,3 мм и 159,28 мм.
Вычислить относительную погрешность.
47. Найти относительную погрешность приближен-
ного значения числа л, если считать л = 3,14 и
л = 3,141592.
48. При прокате прутка диаметром в 30 мм допу-
скается отклонение от -нормы в 3%. На сколько мил-
лиметров можно ошибиться при прокате этого прутка,
не делая брака?
49. Длина участка 25 м (±0,3 м), ширина 20 м
(±0,2 м). Какое из измерений выполнено точнее?
50. Произведено измерение длины детали в 1,82 см
(±0,3%). Определить, какие цифры числа 1,82 см
являются верными.
51. Найти относительную погрешность числа 22,7,
если все его цифры верные.
17
52. Найти относительную погрешность числа 12,48
(±0,02).
53. При взвешивании получен результат 25 кг
(±0,6%). Определить абсолютную погрешность.
Погрешность суммы и разности приближенных чисел
54. Вычислить сумму приближенных чисел 2,7 +
+ 8,35 + 9,124 и ее относительную погрешность.
55. Вычислить сумму приближенных чисел, получен-
ных при замене каждого слагаемого суммы y + y +
+ у+]j +]^ десятичной дробью с двумя десятичными
знаками, и ее относительную погрешность.
3 1 1
56. Вычислить величину суммы 2 — + -уу + 4-у,
заменяя каждое слагаемое десятичной дробью с тремя
верными десятичными знаками, и ее относительную
погрешность.
57. Вычислить сумму длин трех отрезков: 15,42 см;
20,2 см и 23,35 см и ее относительную погрешность.
58. При определении массы пяти предметов полу-
чили: 8,3 кг; 6,28 кг; 2,4 кг; 10,52 кг; 11,0 кг. Вычи-
слить общую массу предметов и относительную погреш-
ность вычисления.
59. Определить разность приближенных чисел 65
и 41 и ее абсолютную погрешность, если погрешность
первого числа равна 0,3, а погрешность второго
равна 0,65.
60. Измерение внешнего и внутреннего диаметра
трубы дало для первого 28,7 см, а для второго 28,3 см.
Вычислить толщину стенки трубы и абсолютную погреш-
ность измерения.
61. Числа 29,6575 и 21,7342 округлить до второго
десятичного знака, определить их разность и относи-
тельную погрешность.
Погрешность произведения и частного
62. Относительные погрешности чисел 80 и 30
соответственно равны 0,3% и 0,2%. Какова относитель-
ная погрешность их произведения?
63. Перемножить числа 53,2 и 25,0 и найти относи-
тельную погрешность их произведения.
18
64. Выполнить действия над приближенными числами:
2,243 + 9,2 • 0,64.
65. Сторона правильной восьмиугольной пластинки
равна 9,6 см (±0,05). Найти периметр пластинки.
66. Определить плошадь круга, если его диаметр
8,7 см. Произвести вычисление с помощью логарифми-
ческой линейки и без линейки, определить относитель-
ную погрешность.
67. Длина рельса 10,65 м. Какова длина десяти
таких рельсов, уложенных друг за другом с зазором
в 1 см? Какова относительная погрешность результата?
68. Ребро куба имеет длину 4,6 (±0,05) см. Найти
его объем.
3 5
69. Вычислить произведение 7ц- 1 ^-, обратив дроби
в десятичные и округлив их до четырех десятичных
знаков. Найти точное значение произведения, абсолют-
ную и относительную погрешность.
70. Вычислить произведение 4,892 • 5,83 с точностью
до 0,1 и определить относительную погрешность произ-
ведения.
71. Вычислить с точностью до 0,1 и определить отно-
сительную погрешность произведения 2,893 • 7,82.
72. Длина окружности равна 68 см (±0,1 см). Найти
ее диаметр.
73. Диаметр ведущего шкива, делающего 240 оборо-
тов в минуту, равен 85 см. Каков диаметр ведомого
шкива, если последний делает 360 оборотов в минуту?
74. Абсолютные погрешности делимого 60,0 и дели-
теля 30,0 соответственно равны 0,05 и 0,03. Какова
относительная погрешность частного?
75. Найти абсолютную погрешность частного
12,81 :4,52.
§ 7. Действительные числа
76. Изобразите на числовой оси 1; /2; /3; 2; 4;
5; 5у*, 6, а также и противоположные им числа.
77. 1) Изобразите на числовой оси все натуральные
числа отрезка [8; 15].
2) Пусть рациональное число г представлено в виде
отношения — (р и q— целые числа, <у^=0). Каким
Q
19
способом можно образовать бесконечное множество чи-
сел, равных г?
78. Докажите, что У2 не является рациональным
числом (т. е. не может быть представлено в виде
где р и q — целые числа/
79. Докажите, что ]/3 есть число иррациональное.
80. Изобразите на числовой оси числа /5; /б;
]/7; /10.
81. Докажите, что:
1) число /5—/2 иррациональное;
2) любое рациональное число может быть предста-
влено бесконечной периодической десятичной дробью;
3) число 0,101001000100001 ... является иррацио-
нальным.
82. С какой степенью точности можно выразить
иррациональное число с помощью рациональных чисел?
Выразить число /2 с помощью рациональных чисел
с точностью до: 0,1; 0,01; 0,001; 0,0001.
83. Пусть W— множество целых чисел х таких, что
— 11 — 5. Выписать его элементы.
84. Опишите множество точек Л4.на плоскости таких,
что ОМ ^R.
2 10 37
85. Исследовать, принадлежат ли числа у-; у/, у/,
5 л f «2 + I | (
— -Q- множеству А = \п—люоое натураль-
ное число)?
86. Даны: 1) А — множество квадратов; 2) В — мно-
жество четырехугольников; 3) С — множество прямо-
угольников; 4) D — множество параллелограммов. Вы-
писать буквы, обозначающие эти множества, в таком
порядке, чтобы каждая следующая обозначала подмно-
жество предыдущего.
87. Найти пересечение числового отрезка [0; 8]
с числовым отрезком [2; 10].
88. Найти пересечение множества чисел вида (я + 1}
с множеством чисел вида [2п].
89. Найти пересечение множеств натуральных дели-
телей чисел 36 и 54.
90. Найти сумму множества четных чисел и мно-
жества нечетных чисел.
20
91. Пусть множество А есть отрезок [1; 5], мно-
жество В — отрезок [2; 7]. Найти: 1) Л f) В, 2) A (J В.
92. Изобразите на числовой оси множество всех
целых чисел на сегменте [ — 10; 10].
93. Из данного множества действительных чисел:
2, (535); 4,123456789 ...; 7, (21); 5, (3);
/4= /I'- /I’- 0.14257...;
0,034057 ...; -1,731843 ; -2,41325 ...;
15,34257891...; /3; /5; /7; /9; /16; /8; /13;
/27; /17; /49; /81; /64; /125; /625
составить множество рациональных чисел и множество
иррациональных чисел.
94. Выполнить действия над действительными
числами:
1) 5,37485... + 4,23143...; 2) 8,1831... —7,2381;
3) 0,11235... + 1,27415...; 4) 12,6321... — 10,0314...;
5) 231 +0,32157...; 6) 4 — 0,41235.
95. Вычислить:
1) 18, (3)+ 19, (4); 2) 16,1(5)+14,21(7);
. 3) 30,2(15) —2,3(4); 4) 0,777 ...—0,444 ...;
5) 1,222... +3,333...; 6) 7,2121 ... —3,1313...;
7) 0,1222... +2,3444...; 8) 0,2(5) + 0,1 (3).
96. Вычислить значения выражений с точностью
до четвертого знака с недостатком:
1) /2 + /3; 2) /3 + /5; 3) /15 + /4;
4) /19+/7; 5) /18 — /3; 6) /23— /ТЬ.
97. Вычислить значения выражений с точностью до
четвертого знака с избытком:
.1) /12 + /3; 2) /13 + /5; 3) /Тб + //_
, 4) /19 + /7; 5) /18 — /3; 6) /23 — /10.
98. Вычислить произведения действительных чисел
С точностью до 0,01:
1) 2,3 и 2; 2) 3 и 2; 3) 5 и 3;
4) 125 и 5; 5) 8 и 2; 6) 7 и 7.
21
Вычислить частное действительных чисел с точностью
до 0,1 (99—100):
99. 1) fa 2) 3)
10°- 2)^; 3)-!|S.
Выполнить действия над действительными числами
(101-102):
101 8,333333333.... _ 8,333333...
+ 3,123456789 ...; 3,123456 ...
109 n v 8,3333333 ... 3,123456789...
* Х 3,1234567,./ 2) 4,333333333 ... *
§ 8. Прямая пропорциональная зависимость
103. В прямоугольной системе координат построить
точки:
1) А (2; 3), В (4; 6), С (5; 7), £> (2,5; 3,5), Е (3,3; 4,2);
2) Л (-2; 3), В (-4; 6), С (-5; 7), D (-2,5; 3,5),
£(-3,3; 4,2);
3) Л(2; —3), £(4; -6), С (5; -7), D (2,5; -3,5),
£(3,3; -4,2); ’
4) А (-2; -3), В (-4; —6), С (-5; -7), D (-2,5; -3,5),
£(-3,3; -4,2).
Каждую группу точек построить на отдельном
чертеже.
104. Выбрав прямоугольную систему координат,
построить точки:
Л (8; 4), £(—8; 4), С (-8; -4), D(8; -4).
Какая геометрическая фигура образуется, если эти
точки соединить между собой?
105. Построить графики функций:
(а) на отдельных чертежах:
1) У = х\ 2) у = ~ х\ 3) У = ^х\ 4) г/ = —ух;
5) у = 2х; 6) у = — 2х; 7) у = Зх; 8) у = — Зх;
(б) на одном чертеже:
1) f/ = 0,2x; 2) z/ = 0,4x; 3) z/ = 0,8x;
4) # = — 0,8х; 5) у = — 0,4х; 6) у = — 0,2х.
22
Проследить за изменением угла, образуемого графиком
функции y=kx с осью Ох.
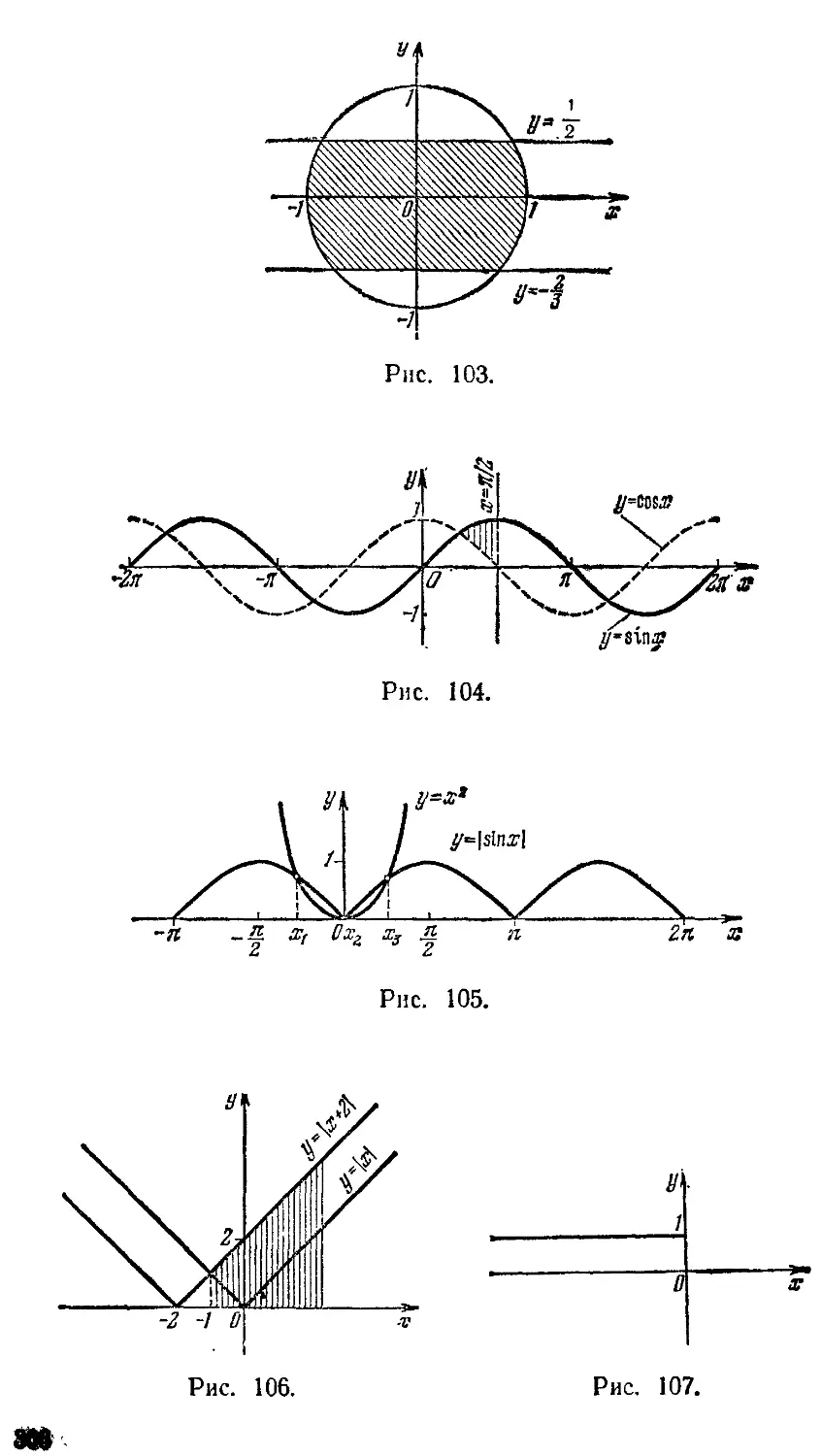
106. Построить графики функций:
1) У = ^х; 2) y = Q- 3) х = 8
О
на одном чертеже и вычислить площадь фигуры, огра-
ниченной этими графиками.
107. Найти координаты точки пересечения графиков
функций у = 2х и у = 5х.
2
108. Построить графики функций у = —х на сег-
ментах:
— 4<х^—1 и [2; 4].
3
109. Построить график функции у = -^х:
1) на сегментах [—5; —2] и [3; 8];
2) в интервалах (—5; —2) и (3; 8);
3) на всей оси — оо < х < оо.
ПО. Пусть /?(х) = |х. Вычислить:
1) Г(—2); 2) F(—1); 3) F (0);
4)F(2); 5)F(6); 6) F (8)
и изобразить найденные значения функции на одном
чертеже.
111. Как называются прямые z/=±x?
112. Построить ординаты графика функции у — — Зх
в точках: (—2; 0); (0; 0); (2; 0).
§ 9. Линейная функция y = kx-\-b и ее график
ИЗ. Построить графики функций:
1) */ = х4~3; 2) у = х — 3; 3) #= —х+3;
4) у = — х — 3
на одном чертеже и вычислить площадь фигуры, огра-
ниченной этими линиями.
114. Построить графики функций: г/= Зх + 2;
у = 0 и х — 2 на одном чертеже и вычислить площадь
фигуры, полученной при пересечении этих графиков.
115. Прямая у = kx + b проходит через точки А (3; 2)
и В (2; 5). Найти k и Ь.
116. Построить графики функций: у —2; у = 4; х = 2;
х — 4 на одном чертеже и найти площадь фигуры,
полученной при пересечении этих графиков.
23
117. Найти точку пересечения прямых
5х -|- Зу = 11 и 2х + р = 4.
118. Велосипедист едет в гору по инерции со ско-
ростью v = (— 1,5/+ 12) м/с. Сколько времени он про-
едет до остановки. (Дать геометрическую иллюстрацию
решения.)
119. На одном чертеже построить графики функций:
!) 1/ = ух + 3; 2) у = -х — 3;
3) ^ = — ух + 3; 4)// = ~уХ — 3
и найти координаты всех точек пересечения этих
графиков.
120. Вагон движется в гору (по инерции) со ско-
ростью v = (— 2t + 40) м/с. Сколько времени он проедет
до остановки? (Дать геометрическую иллюстрацию
решения.)
121. Построить график функции у= — 2х + 5 на
сегменте
122. Найти абсциссы точек пересечения с осью Ох
графиков функций:
1) р = Зх + 5; 2) у — 4х— 2; 3) z/ = 2x + 3.
123. Найти ординаты точек пересечения с осью Оу
графиков функций:
1) у = Зх — 4; 2) у = — Зх + 2; ...
3) у = — 5х + 1; 4) у = — х + 3.
124. Найти наклон прямой y—-kx^3 в точке (2; 8).
125. Найти, при каком значении х функции
у = 3х— 2 и р = 4х+3 принимают одно и то же чи-
словое значение.
126. Выяснить, пересекаются ли прямые р = 3х— 2
и р = Зх + 4, и если не пересекаются, то почему?
127. Решить графически системы уравнений:
Зх— 2у = 4,
2х + у = 5,
I х — у = 1; I х + у = 3; [ 2х + Зу = 7;
| x + z/=5, J х—#=1, ( 4х—Зу = 6,
[2х — у=4; 5Цх+2# = 7; ( Зх + 2у = 13.
24
128. Даны линейные функции f (х) = kxx + b{ и
ф(х) = k2x + b2. Написать зависимость между параме-
трами k{, k2, by, b2 этих функций, если:
1) прямые f(x) и ф(х) пересекаются;
2) прямые f(x) и ф(х) параллельны;
3) прямые f(x) и ф(х) сливаются в одну прямую.
129. Построить графики функций:
1) # = |х |; 2) у=-1 х + 3 |;
3) д/ = | х — 3 |; 4) у = а\ х|;
5) У = х ф-1 х |; 6) у = х — | х |;
7) у = х • | х|; 8) у = -~.
2__2г
9) Известно, что прямые у = —и #=2(1—сх)
параллельны. Найти значение с и построить эти прямые
на одном чертеже.
§ 10. Обратно пропорциональная зависимость
130. Выразить зависимость между длиной окруж-
ности с колеса автомобиля и числом п его оборотов,
если автомобиль прошел путь, равный 100 м. Постро-
ить график этой зависимости.
131. Площадь прямоугольника 24 м2. Выразить за-
висимость между его сторонами хи# формулой и
графически.
132. Построить графики функций:
(а) на отдельных чертежах:
1) </ = ф 2) (/ = -!; 3) =
4) </ = 7’. 5) У—— 4’ 6) » = 4;
(б) на одном чертеже
1) y = 2) у = 3) У =
Сравнить построенные графики в зависимости от коэф-
фициента k.
133. Тело, движущееся равномерно со скоро-
стью v м/с, проходит за t секунд 50 м. Построить гра-
фик зависимости между v и t.
12
134. Построить графики функций # = — и х# -ф 12 = 0
па одном чертеже для х > 0.
25
135. На расстоянии 12 км поезд шел равномерно-
Найти, в какой зависимости находится время t и ско-
рость поезда v на этом расстоянии и построить график.
136. Периметр прямоугольника 8 см. Выразить пло-
щадь прямоугольника как функцию от длины его сто-
роны и построить график.
137. Площадь треугольника равна 9 см2. Выразить
зависимость между его основанием и высотой и постро-
ить график.
138. Указать область определения и область измене-
ния функций: 1) ху = k при k > 0; 2) xy — k при k < 0.
139. Построить графики функций:
1 \ 2 4
у~~ | х + 1| ’
3)|х«/| = 7; 4) у= |л.^7| .
§ И. Уравнения первой степени с одним неизвестным
140. При каком значении х будет у = у'.
1) у — 5х — 8, а # = 12x4-3;
2) у = 3х — 7, а у = — х+1?
141. Решить уравнения аналитически и графичесяй:
1) 2 — | х | = Д,5; 2) |4 — х | = 5;
3) | х — 4 | = 5; 4) | 3 + х | = 2х + 3;
5) 1-1 + 7х| =-9*4-21; 6) | 5 — х | = | х 4- 4 |.
142. Решить уравнения методом интервалов:
1) 1x4-214-1x4-1 1 = 3;
2) | Зх — 4 | 4-1 х 4- 3 | = 4 — Зх;
3)|х|4-|х4-2|4-|2 — х| = х4- 1;
4) | х 4-2 |4-| х 4-3 | = | 1 —х |.
143. Решить уравнения аналитически:
О 7-^=i4h+5; 2)4Ef=7^3+2;
n\ I __ x 2 x 4 I । p-,
'x^T ~ 2x - 8 ’ x - 5 ~ x - 5 + °’
r4 10 — x 15+2x . . 3x — 19 . 4x — 6 Л
5> = + 6> -5T=T+5^7=9-
144. 1) При каком значении x произведение дробей
8х — 3 Зх — 4
----------------------- rj ------
6х - 3 4х - 5
равно 1?
26
2)При.жакеШ.значении х отношение дробей
12х — 7 6х — з
------- и --------
10х+1 5х 4- 1
равно 1?
145. При каком значении у разность дробей
18г/+ 2 15у + 1
У — 4 И Z/ + 5
равна 3?
146. При каком значении а сумма дробей
1 4
а — 3 И а 4-1
равна их произведению?
147. Решить уравнение:
2 1 1
64х3-16х2 —4х+1 “ 1 — 8x4-16х2 14-8х4-16х2*
148. 1) Найти х из т = j . ;
2) найти у из k — -b-y Ту-;
у у + 1 ’
„ч 2 + V
3) наити z из м = —--г;
4) найти т из d2 = 2mn(l + );
7 \ 2ttl /
» 1 „ 4 tn(a +1)
5) наити I из / =--;.
' а — I
149. Решить уравнения (относительно х, у и г):
’ b а * f tn tn
3) a-JH + y- = m^l+±. 4) £±£-2=^i.
’ tn a 1 a c
150. При каком- значении а уравнение
2a + x 8a2 — Зх x 4- a
2a —- x x2 — 4a2 2a 4- x
не имеет решений?
151. При каком значении т уравнение
х 4- m — 2/п2 _ х + /п , х
т2 — х2 т — х /п + х
имеет бесчисленное множество решений?
27
§ 12. Системы уравнений первой степени
с двумя и более неизвестными
Решить системы (152— 160):
152.
1)
X + у = 5,
х — у=\\
2)
( х 4- 2у = 3,
( 5х — у = 4;
J Зх-|-4у = —3,4, [4х — 2у = 2,8,
3) I 6х — 4у = 5,2; 4) I 7х4~4у= —2,6;
Г 0,Зх—0,5у=— 0,9, (2,4х —5,1у=— 10,5,
5Ц 2,1x4- у = 7,2; 6Ц 3x4-2//= 12.
153. ( I/-4 у_____________// (5 - 2у)
х — 2у + 3 х — 3 (х — 3) (х + 3 — 2у)
( 11 — 7х = Зу;
( //(5 — 4//) 5 __ 1—2//
2) ’ (2у - О (Зх - 2у + 1) "Г 2у - 1 1 + Зх - 2у ’
( 304-4у = 7х;
Г х I У __ 2 (ХУ + 2)
3) ] х 4- б ' у 4- 2 (у + 2) (х 4- 5) *
( Зх 4- 1 = 4у;
154.
3)
5){
х + у _ 1
х + 4 4 — х
16 —X2
2х2 — 5
0,7х — 0,3 = у.
5х — Ъу — 6г = 1,
Зг — 13х 4- 4у = 1,
z 4- У 4- 7х = 0;
Зх 4- 4у — Зг = 2,
4у — Зх 4- Зг= 14,
7У 4- 5г = 29;
х — у — г = 0,
х + у — Зг = 2,
2х 4- Зу — 5г = 7;
2) { Зх — 2у — г = 0,
[’5х 4- 2// — 4г = 6;
1 7х — 4//4-г= 12,
4) { 7х4-3//4-2г = 21,
[ 2х — Зу — г = — 1;
2х 4- Зу — г = 7,
Зх —Зу 4- 2г = 2,
4х 4~ 5у — 4г = 3.
6)
D
28
155.
2)
158.
0,4* + 0,5#— 0,3г = 0,6,
0,Зх —0,2#+0,1г = 0,2,
* + # — 2=1;
2 3 _ 5
х + У г/ + 3г 6 ’
4) 3 4 = 2 — 12
х + у х — 2г
1 2 _ 7
У + Зг х — 2г 9 *
1,2х— 0,4# — 0,6г = 5,
0,6# + 0,2г —0,4и = 4,
1) j 0,4х — 0,3# — 0,2/= 1,3,
0,1х — 0,2у -|- 0,1/ = 0,4,
0,2# + 0,1у == 1,7;
( 7х+5#+г—и = а,
2){
7# + 5г + и—х = Ь,
7 z + 5 и + х—у == с,
7и-т~5х +#—z =d‘,
* + # + 2 + / — 4,
2х + 3# —2г —/ = 2,
3Ч 2х — 3# + 2г + t = 2,
( Зх + 4# — 2г — t = 4;
4)!
5х—3#+4г—2/ = 4,
10*+3#-4г4-2/ = 11,
7х—5#+8г—10/ = 0,
4х+5#—8г+Ю/ = 11.
157.
1)
ах + by = с,
ах — by = d',
(
2)i
l
х — т i у — п
—2~+ -S~=m’
х — п . у — tn
-з~ + -Ч—п-
158.
( х ____ у _____ 4аЬ ( d — х__c-j-d-x
id а~6 а + Ь а2 — Ь2 ' . | I/— с У ~ с + d *
' j х . у ________ 4а2 + Ь2 . ) | х — с _ У + d .
[ а - 6 ' а + 6 а2 — bs * I d с ’
у -Ь b а + с
х + с а + b ’
3) | ' 14)
[ с (с — а + х) = b [Ь — а-\-уУ, 7
тх + пу {
5 ~/г’
•^х —0,25#==/.
29
159. 2у (а — 2) -f- а (а — 2) (х + у) = 2 (а — 1),
1) 1 . 2а । , . 2а — 4 а3 — 4а
1 .----ь 1 •-----= 1. —г—г-;
х у а + 1
аху — х + у, ( ау Ьх = сху,
= у — х; 3Ч у + х = ха;
2){
Г 2а (х — ау) — (х + ау) = (х + ау) (х — ау),
1 (х + ау) (х — ау) — 3 (х + ау) = 10а (х — ау).
160.
J Л (* + У) • (а + b) = (х — у): (а — Ь),
7 I ах-\-Ьу = а — с при а У= ± Ь\
j ab2 {у + Ь2) — (а + Ь) (х — а2) (у + Ь2) = а2Ь (а2 — х),
2) j 1 . х~а2 । 1 • У + Ь2 _ „
[ * Ь2 1 ’ а2
161. Определить все значения а и Ь, при которых
система уравнений
( (1 -|- а) х + (а Ь) у = b — а;
I (5 + а)х + 2(а + 6)г/ = д—1
имеет бесчисленное множество решений и при которых
она не совместна.
§ 13. Неравенства и системы неравенств первой
степени с одним неизвестным
162. Сравнить следующие числа и записать связь
(зависимость) между ними с помощью знака неравенства:
1) 23 и 25; 2) —23 и —25; 3) —4,8 и — 17.
163. Переменная величина х изменяется от 3 до 8.
Запишите с помощью знаков неравенства, что х изме-
няется:
1) в закрытом интервале от 3 до 8;
2) в открытом интервале от 3 до 8;
3) в полуоткрытых интервалах от 3 до 8.
164. Перечислить и записать с помощью букв а, Ь,
с и d свойства числовых неравенств.
165. Пусть а > Ь. Следует ли отсюда, что ап > Ьп?
Приведите примеры.
166. Если а>6 и c — d, то всегда ли ac>bd и
у>-|-? Приведите примеры.
30
167. Если а > b и с > d, то всегда ли ас > bd и
у > -^ ? Приведите примеры.
168. Какие знаки имеют числа а и Ь, если:
1) ab > 0; 2) ab< 0?
169. При перемножении следующих неравенств вы-
яснить, любые ли два неравенства одинакового смысла
можно почленно умножать:
| 10 > 5, (— 4> — 8, ( — 15 > — 30.
!Ч12>8; — 6> — 12; 3 4Ч — 10 > — 20;
f 17 > 14, ( 6 > — 20, f — 9 < 5,
I 3 > 2; 5Ц — 2 > - 7; 11 < 14.
170. Всегда ли из а > b вытекает, что ап > Ьп? Ответ
пояснить примерами.
171. Обязательно ли из ап < Ьп следует, что а < Ь?
Ответ пояснить примерами.
172. При каком условии можно делить почленно два
неравенства противоположного смысла? Ответ пояснить
примерами.
173. Пусть а > 0, b > 0 и ап > Ьп (п — натуральное
число); тогда а > Ь. Пользуясь этим правилом, сравните
числа:
1) /5 4-/2 и /10;
3) /з" 4- /Г и /зо';
2) /6 4-/3 и /5 4- /2;
4) /б" 4- /8 и /б- 4- /17.
Используя формулы
£ м
а?, а+1>2,
доказать справедливость следующих неравенств
(174-177):
1741 1)|+4>2 (а>0);
2)«±2 + » + 2>4 (а>0).
3)£+^>4 + у (а>0И&>0);
4) а24- 62 + с24- 3>2(а 4- д4- с);
31
. 5)-y- + -j->a + ^л (а>0, Ь>0, а^= Ь);
6) n3+ 1 < rf + n rH («< - 1);
7)^Т->^ - («>0, д>0);
8) V^b <а>Ъ,Ь> 0).
1?5. (а>0, *>0);
2) (а+1)2+(д+у)2>12,5 (а + д=1,а>0,6>0);
4 176, П —1—>------------- < (а>0, 6>0, с > 0);
у abc а + b + с
2) 1 • 2 • 3 ... п 1).
177‘ 0/3-6 ^9 • 12 ... Зт<3 + 6 + 9 + ^2+ ♦•• + 3/п;
2) f+| + -^>3 (« > 0, 6 > О, ^>0).
178. Решить неравенства аналитически:
.к 2х + 2 4х — 3 2 + 13х . ф
7 — 2 < 14 Р’
2) 25(х—-Шх +4-) + Зх— 1 >(5х — 2)2 + -43х9—1
8х 2 2Эх-з|
3) 9(х+1)=--^^->(Зх+2)(Зх-2)Н-------д—
Решить неравенства аналитически и графически
(179-181):
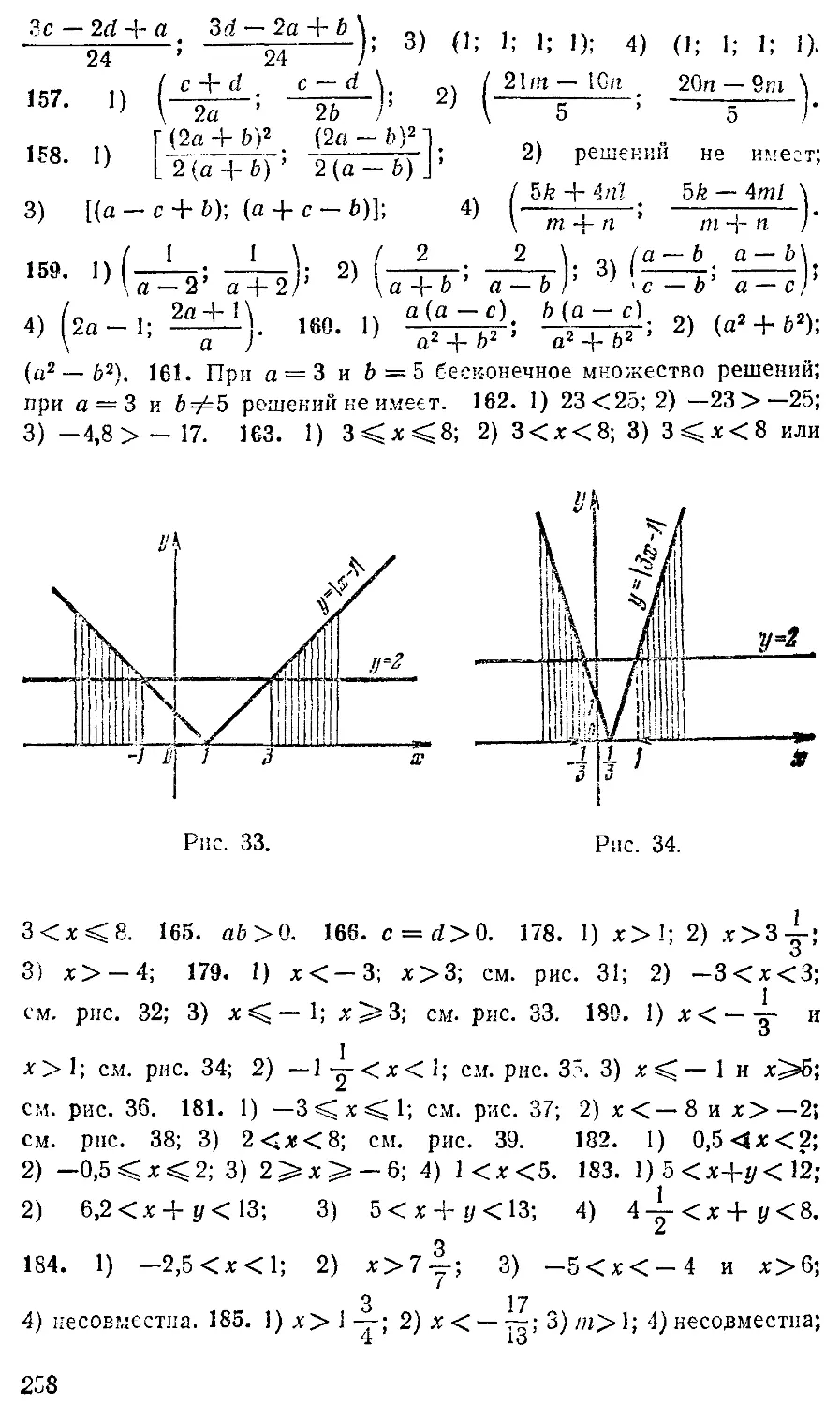
179. 1)|х|>3; 2)|х|<3; 3)|х—1|>2.
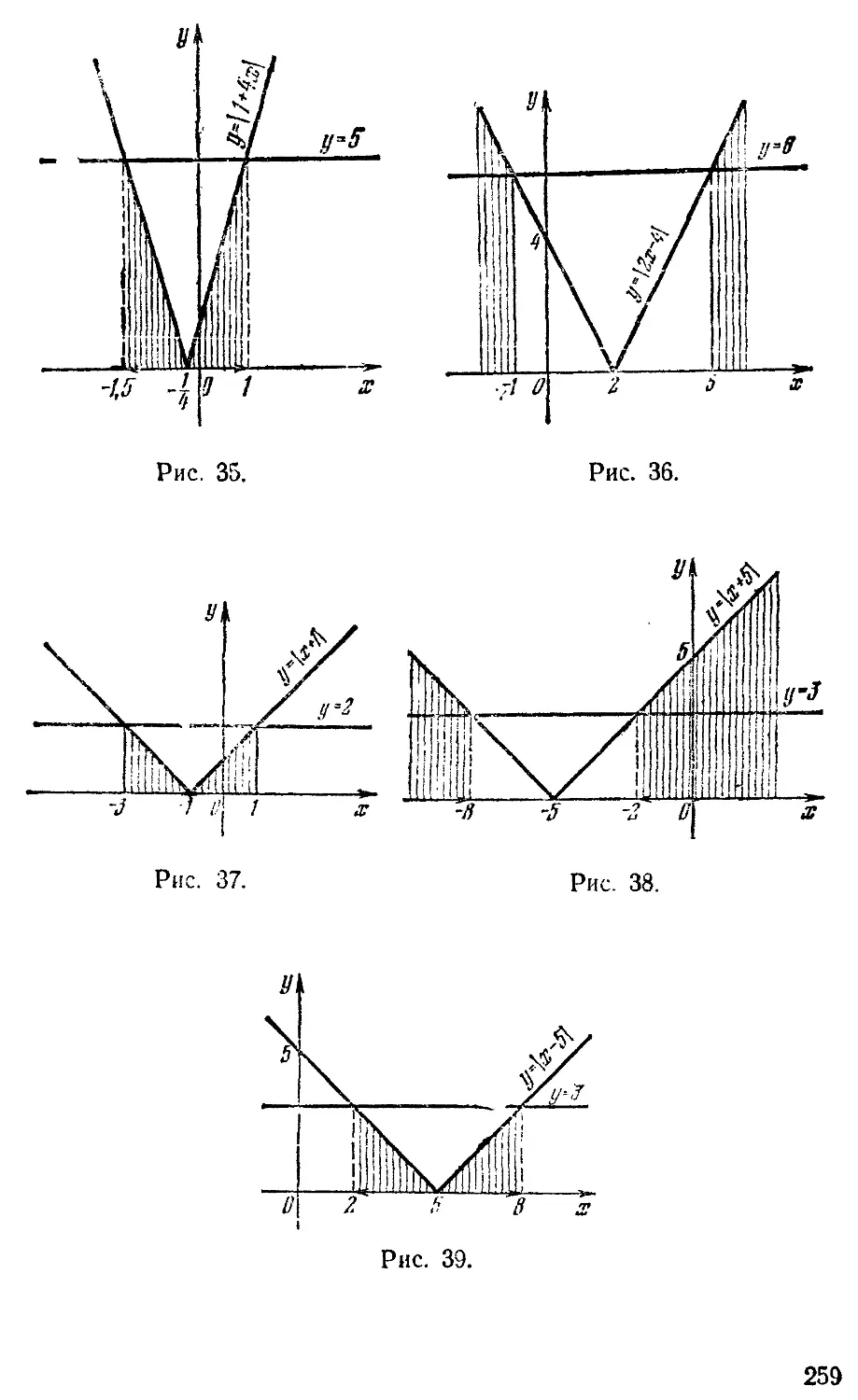
180. 1) | Зх— 1 |> 2; 2) |1 +4х |< 5; 3) | 2х-4 |>6.
181. 1) |х + 1 К2; 2) |х + 5 |> 3; 3) |х— 5 |< 3.
182. В каких интервалах изменяется х, если;
1) 5 < 10х < 20; 2) — 8 < 16х < 32;
3) —14< —7х<42; 4) — 45 < - 9х < - 9.
32
183. В каких пределах заключена сумма х + у, если:
1) 3 < х < 5 и 2 < у < 7;
2) 4,2 < х < 8 и 2 < у < 5;
8)8<4х<16 и 9 < Зг/< 27;
4) 20 < 5х < 25 и 7^ 14г/42.
Решить системы неравенств (184—186):
184.
1)
2)
3)
4)
6х —8<3(4х —3)4- 16,
4(х+П < 3 .р
5 5 Х ’
2 2х- 13
Х > 3 33 ’
+4(^-7) <т-2{;
(х-6) (Зх+ 15) о-
( 5(х—1) 4-5,5 > 2х 4-2,5(х 4~ 1),
| 51х —85 < 34 (х — 1).
185.
186.
1)
2)
3)
4)
5)
1)
( Зх + 5 2х — 1 . х — 6 । -
—-------— > —+5>
X - 3 5х - 1 6х + 1
5^2 3 ’
5 — х х— 1 х + 1 ।
—4 — > 4 1,
4 । 2х — 1 15х + 7 ,
у X — i g > ’
2т +2 4m — 3 2+ 13m .
у 2 14 1 ’
о 1 5 — 4m m — 2 3m + 1
d 3" 6 > 2 3 ’
: л . 2x — 3 . 7x-5
4* + —5—<—2~,
Zi3-2_2.v>5-^.;
| 5x——21,
f 6~x _ Л 2 + 3x 1
j 2 1 5
( |x + 2(2x— 1)< 3x4-1;
I °
33
х
2)
5х
2x — 3 п I 2x — 3
5 2 *+ 3 ’
7x - 1 , 2x - 5 7
2 ‘ 5 10
187. Определить, при каком целом
стема уравнений
значении
k се-
ky __ 1
3 — 3 ’
2Z/= — -g
йм еет отрицательные решения (х < 0 и у < 0).
18S. Определить, при каком целом значении а си-
стема уравнений
8 1
х 5 # — 5 ’
I 2 1
ах-|_
имеет положительные решения (х>0, у > 0); найти
эти решения. При найденном значении а решить си-
стему уравнений графически.
189. Определить, при каких значениях а система
уравнений
( Зх 4- 8ау = — 78,
I 2х — Зу — 5
имеет отрицательные решения (х < 0, у < 0).
Из множества всех найденных значений а выбрать
только целые числа.
§ 14. Степень с рациональным показателем
190. Возвести в степень:
1) (- О2;
4) (-I)2"’3;
7) (—1)2п“1;
10) (—1)4"“3;
13) — (—1)2л±|;
16) — (—З)3.
2) (-2)2;
5) (—2)2";
8) (—1)2л+3;
11) (—1)2"+2;
14) -(-3)4
3) (—1)4
6) (—1)2"+!;
9) (-1)4'1"2;
12) — (-1)2";
15) - (+3)2;
34
Вычислить (191 —193):
191. 1) (22)3; 2) (—2)3; 3) — (—22)3;
4) (42 — З2)3; 5) (З2 —42)3; 6) (42 — 52)2.
192. 1)
2) (-0,2)2 — (—0,02)3 — (—5)2 — (— 1 )2"+
193. 1) х2 + х3— х4 — х при х==— 1;
2) Зх — 2х24-4х3— х4 при х==—3;
3) а2Ьс3 при а = — 1, Ь— — 2, с — — 2;
4) а(Ь2с)3 при а — — 2, b=— 1, с —3.
Возвести в степень (194— 195):
194. 1) (2а)2; 2) (-За)2; 3) -(2а)2; 4) (-2,4)2;
5) (-2аЬ)3; 6) (2 • 3 • 4)3; 7) - (abc)2;
8) I- (~ а) • (- д)Р; 9) -[(- а) • (- Ь) • (-с)р;
/ /7^ / /у2 \3 / \4
ю) (-4г ; н) -4г); 12) \-^ .
’ \ Ь2) ' \ о4) ' \ тп3 /
10- /ааЬсу. „ Г - 4(-2а’). 6* 1=,
195’ ’ 2) “ I н® 1 ’
Г—4 (—2а) • 6 l3, г/ а2Ьс2 р . а2Ь3с* ]3
1 -За J ’ Ц pq J ' p3cs J ’
-ч Г 5ап(Ь + с)/г -]2т+1
5) L ?>bm (р + q}n J ’ 6)(а + ^ + с)^>
7) (а + b 4- с + d)2; 8) (а — b — с — d)2.
196. Извлечь квадратные корни из чисел:
1) 841; 2) 784; 3) 1225;
4) 1849; 5) 7921; 6) 5329;
7) 4624; 8) 2401; 9) 3136;
10) 7225; 11) 57 600; 12) 32 400;
13) 14 400; 14) 28 900; 15) 54 756;
16) 725 904; 17) 488 601; 18) 501 264;
19) 700 569; 20) 632 025; 21) 613089;
22) 22 562500; 23) 5616900; 24) 3 587 236;
25) 2105401; 26) 3426 201; 27) 2 934 369.
197. Извлечь квадратные корни из дробей:
2) 36 . ov 25 , 49 ’ 49 ’ ' 4) J5-; ' 1 81 '
225 625 . 7. 169 289
5) -я-; 6) 529 * 196 •' 8) 676 :
85
9) 0,25; 10) 0,49; 11) 0,81; 12) 2,25;
13) 6,25; 14) 1,69; 15) 2,89; 16) 0,0529.
Вычислить (198—200):
198. 1) М; 2) /27; 3) /=ТГ; ' 4) /^27;
5) /б4.
199. 1) /Тб; 2) /б25“; 3) /=32; 4) /64;
5) /^Й28".
200. 1) V256-; 2)/^; 3) /2395-^;
4) 4497—-; 5) /0,6103515625;
6) /0,1220703125; 7) /6,244140625.
201. Из выражений
1) /=Т; 2) / — 16; 3) /=25; 4) /=8";
5) /=27; 6) /—64*; 7) /=49; 8) /—125;
9) У=32; 10) /о75"
составить множество, которое имеет смысл, и множе-
ство, которое смысла не имеет.
202. Найти области определения радикалов:
1) Ух — 4; 2) /Зх —6; 3) /бх — 4;
4) /7х + 42; 5) /8х 4- 5; 6) /З —2х;
7) /—х4-4; 8) /—Зх —5 .
В следующих выражениях (203—208) найти ариф-
метические значения корней, используя формулу
х, если х > 0,
/х2 = | х | =
— х, если х < 0,
0, если х = 0.
203. 1) /а2; 2) /(—1)2; 3) у(-15)2;
4) /(=Ж 5) /(2-х/.
204. 1) /(5 — х)2; 2) /(х —7)2;
3) /(х24-*4- О2; 4) /х24-2х4- 1 .
36
205. 1) /625"; 2) /576"; 3) /729"; 4) ^27;
5) ]/Тб.
206. 1) /(2 — /3)2; 2) У(1 —/З)2;
3) /(1 — /2)2.
207. 1) У(2 — /б)4; 2) /(2 —/5)3;
3) /(З—/То)6.
208.
1) /(7 — х¥ при х<7; 2) /(7 — х)г при х>7;
3) 1/(12 — х)4 при х^12; 4) 1/(12 — х)4 при 12.
209. Преобразовать корни так, чтобы подкоренные
выражения были положительными:
2/1—1___
1) У —а при а > 0;
3) /=45;
5)
7) У1 — Зх при х > 2,9;
2) /—10;
5 __
4) /-3;
6) Ух — 3 при х < 3;
8) 1/10 — 4х при х>3.
Используя основное свойство арифметического корня,
сократить показатели корня и подкоренного выраже-
ния (210-212):
210. 1) 1/2»; 2) 1/28"; 3) УТ; 4) /25.
211. 1) Уа2; 2) /а3; 3) /а17; 4) Уа*.
212. 1) j/да; 2) /(а-М)3с3; 3) /(а — с5.
Привести арифметические корни к общему показа-
телю (213-215):
213. 1) /2 и /3; 2) /5 и /3; 3) /7 и /12.
214. 1) У а и У~Ь\ 2) У~аЬ и ]/ тп; 3) /а2Ь3 и УаЬ4.
215. 1) Уа+Т и Уа-j-b; 2) У а (b-с) и / а (Ь-с);
3) У (2а— 1) а и / ab2; 4) У а2 — 2ab-\-b2 и
tn___________________
у а2 + ‘2аЬ 4- ь2.
37
Извлечь корни (216—219):
216. 1) V 16а8; 2) j/81a,2Z>4; 3) ]/27«963.
217. 1) 1/ 4.9.16.25 ™ ,7 125-8-64 , V 49-64.81.I00 ’ Г 216-512 ’
3) 1V 8й663с6 , 41 1/ 25‘49‘ 121 V т3п6 ’ ' г 4а4Ь2с3 *
218. 1) / 98(а+ б)4 , V (а + ьу (а - Ь)1й ’ К (а - Ь)2 ’
3) ь/ 64а12613с7 дх / 128а36рс6 V (а+ьу ’ 17 Р 169 (а + 6)4 ‘
219. 1) d / 81а564с3 . 2' а2Ь3х , / (а - 6)2 (”+1>+1 . V (a-b)6’ a- b V (а.6)2п+,х2п+2 ’
3) abx2 т / x2zt+1 (6 + с)п+2 b + с ' апЬп (а — Ь)п
Привести подкоренные выражения к целому виду
путем внесения рационального множителя под ради-
кал (220-222):
220. 1) 2/42_2) 3/| 4/тГ •’ 4) Ж
221. 1) 2) -£ 3) га’]/.
222. I) (a — b)l/+ ,^- ; 2)
' ' ’ г (а — ЬУ Ь~ г т — п
(а-92 ч5/ fr6c7d10 .
' b г {а — Ь)3 ’
Д' а + Ь *Г (а — ьу (с + d)
а — b V а2 + 2аЬ + Ь2
Привести подкоренные выражения к целому вид]^
(223-227):
223. 1) /£; 2) /1; 3) ; 4) ]/£;
5)/|; 6)/|; 7)/£; 8) /X.
224. 1) /1 ; 2) /{; 3) /£;
4) /4 •• б) /X. 6) /X.
38
225. 1) У 2 4 ; 2) ]/ 5 1;
4) /4; 5)/Ц;
3)/4£.
6)/‘4-
226. 1) ; 2) f 4, 3) /А;
4) б)/~6) уГ
227. 1) л-’ 2) а3у/^+4’•
5 /"Z2 ZF"
3)
228. Извлечь ]0,6 с точностью до 0,001 и с той же
точностью вычислить выражение 15 . Сравнить ре-
зультаты. __
229. Пользуясь тем, что У0,8 =1/ 4- — т~У5, из-
F О О
влечь )Л),8 с точностью до 0,001 и вычислить выра-
жение -~-у5. Выяснить, какой результат точнее и на
сколько.
230. ]/0,95 =уТЙГ— сделать аналогично за-
даче 229.
231. Используя равенства
У 8 Д =1/—=42g-, 1/8 — = ]/8^Г,
V 5 '5 /5 V 5 г
т/в-j- =1/2Тб,
г 5 5 ’
вычислить j/ 8 каждым способом отдельно, с точ-
ностью до 0,0001, и результаты сравнить. Какой из
этих трех способов дает более точный результат?
Привести корни к простейшему виду (232—233):
232. 1) 4 /8, j- /50 , у /27 , у /^Тб , /-64;
-Jil/li. 41 (а+Ь)2 ,¥~3 (c3-3c2d + 3cd2— d3).
' 4 г ху ’ ’ c—d? abia+by ’
4) У (144а2 — 288а6 + 144&2) {а —ЬУ с.
39
233.
1 \ 1 + а 1% 8- 126 Ч-6&2 — fe3 (a3b-4a2b2 + 4ab3)(a—2bj,
' -2 — b I с 4- Зас 4- За2с 4- а3с а2 ’
За — 1 I.2 Л(2а + I)14 (а2 4- 2аЬ 4- 62)2 .
2 — b V (За- 1)2‘ (а2- Ь2)2
____________ , . п _______________
3) -£ /ап+2^+Зсп+1. 4) //И«+1^+2С«+3;
гч (а - &)3 1 /(а 4- 6)3п+2 (Ь 4- с)6п+‘ (а 4- c)3n+1
°' (а + &)4 У (а - b)2n binc™ (а - с)п~1
Доказать подобие корней (234—235):
234. 1) /32 и /64; 2) /64, /188, — /2 и /256;
3) /1ба, /25а и /49а; 4) /(а + 6)3 и /(а + д)7.
235. 1) 5]Х(а + 6)4, 4 /- (а + Ь)7 и 1^-(а + 6)4;
2) /++<•
3) /<++ -Юх/^>и
п /-j-- П ___ п __________
4) у ~п~2 , /а2Ь2п и /а2 (а + ^)3п-
§15. Сложение и вычитание корней
Выполнить действия (236—239):
236. 1)/54 4-4/6-3 /216 + 41/4 — 3/98;
ОУ £>
2) /125 + 3/45 + 4]/4~ 0,7 /5 — 0,2/ ОД;
3) (0,6/200 — 5/0Д2) + (4,5]/ 4 + 5у/8Оо);
4> (4/4+1 /4) - (4 у 21 -4 ^2о) •
237. 1)(8/аз+2а/а—За/25а)-(—4/аЗ-За/10ба);
2) /а4 + з/а5 — (2а / а4 — 4а / а2);
3) [/(« + Ь/ - (а + ЬГ /Г+6] +
+ (/(Я=^-5/М^).
40
238.
+ 21/6(a-i)-(|)/ |(a-i)-l);
- 1/^ 2a n24- f~a4--a6 — 1/”n-T1^;
V (a2 — I)2 1 r (I + a)2 ’
1 , Z(a — b) {a2 — b2}_f___2g______
2 V 2a3 V (a + b) (a — b)2
-/2й36 + 2^ + ]/'^±^.
j 1 \ a (a + fe) -| Л(g — b)3 3b {a 4- b) -.Г(a — b}2
' ' a — b V a 4~ b a — b V a2 — b2
3 (a-bb)1/‘(a+ b) (a —b) , /И a2 — b21
4 V (a + b)2 1 V 16 ’
2)a]/b 4&2 (a — b)-V— №b — b3) +
§ 16. Умножение и деление корней
Выполнить действия и упростить (240—252):
240. 1) 3 /5-4y45;2)-2y7-3/T4;3)/3-/6-/2;
4) 51^3 • 0,2^18 • 31^4; 5) | ]/Т25 • /5 ~ 1/3.
О 1 /
241.
1) ihfi + 6)! • (а + b) fa + b;
<у. а — b f/~(a 4~ b)3 ab 4/~а2 — 2аЬ 4- Ь2 5 4/~ 1
> а 4- b г (a — b)2 а — b V a + b ab г а~Ьу
q2 + tab 4- b2 у ab . c-d ^/~ a2b2{c3^3c2d^-3cd2^d3'},
' ab2 V a-{-b c 4- d V a2 4- 2ab 4- b2 *
/ 2-a^a + у . ( 2±a^
\ 2a — / \ 2a 4~ ]^a /
242. 1) (7 /3 — 8 yT2 + 5 ^48) • 0,5 ]/3;
2) (14 ]/5 + 4 У20 —6 /45 + 0,2 /125) • 101/5;
.у /V & + c — V^b — c _ Yb 4- c 4- l^b — c\ с]^Ь2 — c2
+ ~ fFTc - ]rb^c) 4
41
243. 1) (У a + У~Ь)- (/fl-/ft);
2) (Va+ V~b)-(a — Vab + b);
3) (/fl — V~b) • (fl 4" У ab ft);
4) (a Va + b /ft) (a У a — b У~Ь\ '
244. 1) 3 /12 : 2 /3; 2) 38 /48 : 19 /3;
3) 0,16 /81 : 0,01 /3; 4) 4 /29 : | /58.
245. 1) a3 /fl7: a?b /fl5;
2) (a + by-V(a=W : V
3) (fl5z>6 /fl4 — 2fl36 4- a2b2 —
— fl465 /fl2 (fl — ft)): fl3ft4 /fl2 (a —ft).
_ _ _ 3 _ 4 ' ’
246. 1) /2 • /8; 2) /3 • /12; 3) /3 • /27.
247. 1) 2 /fl 3 /ft; 2) |/fl2ft (fl 4-ft) • | /(fl 4-ft)2.
248.
3 _ 4 __ 3 _ 4 4 _
1) (/2 4-/44-/8). /2; 2)(4/104-5/4-/25)./2;
_ 3 _ 6 6 __ _
3) (/8-20И 4+ /2)-/16;4)(/3 + У2)-(/2-/з)-.
4 _ _ 8____ 4 _ 12__ 6 _
249. 1) /8:/2; 2)/12:/3; 3)/36:/2;
9_____________ 6_______ 12____________
4) 12flft /fl6ft3: ~ /fl2ft5; 5) 25a3ft /fl968: 4- fl2ft /Ж
OU о
3 ___ _________ 6________
250. 1) (m3/a2ft2 4- m4 /aft — m5 /a4ft4): m2 /^ft;
f 4a3 1 За 17Т6Ё/.Л • т /" 9a3ft
2> Vr »+ — -VI25ab).y
3) (p/а^б + 4]/'a"&7 + ]«): 1 УМ>Ь;
4 ______ _________ 4 ____ ________
4) (/27fl9ft3 4- /SflSft3): (]/3fl36 4- /2flft).
5 ______ 8 5
251. 1) (/27fl9ft3 4- /^ft3): (/^ft2 -
40 4
— ]/209952fl29ftI34- /2flft);
2) (a /2 — /i2fl3ft— /6flft);(/fl—/3flft—/3ft).
42
4 ___ ______ 4 _______ _
252. 1) (m — Уm3n 4- Уmti — Уmn3) : (Ут 4- Уп);
2) +
§ 17. Уничтожение иррациональности в знаменателе
и числителе дроби
Уничтожить иррациональность в числителе дроби
(253—254):
253. 1) ^2; 2) 3) 4) 5)
'5 '6’ ' 7 ' b ' Ь
__ 4___ 4__________
254. 1) а~^Ь + Ь-, 2) КЦА-1.; 3)
’ 5b ’ ' b ’ а
Уничтожить иррациональность в знаменателе дроби
(255-260):
255. 1) 2) 4-; 3) -Ц?-; 4) -%-
V 9 5|Гз зйоо ьУа)
256. 1) “ ; 2) - -6.+-а= т;
b У а — b а У а -У b
3) -Га-~Ь-—; 4) —.
V(a + b)2 аУ(а-УЬ)5
У (а-У b)n~l V U’ Ка “У
258. 1) -2) ---------; 3) ------
' 3-У 3 З + Кз 5 — У 2
259. 1) Я ; 2) ^-+-' ; 3) 44^.
5У 3 — 4^2 зУт + 2Уп ' 2Ут — ЗУ п
1 \ У т -У п -У У т — п е п\ а + b — У а2 — Ь2 ,
У т -у п — Ут — п ’ а 4- b + У а2 — Ь2
3) + 5 4к 2п
Ут2 + 5 — Ут2 — 5 ’ У т + п + Ут — п
Выполнить указанные действия (261—269):
261. 1) - V~y) •• (х-!/) + -4^=;
\ У х-у У ) У X-У У У
2) (Ут + : (пУт 4- п У тгУ 4- /).
43
262.
44
268. 1) Yu -Vy и v — V~u -Yy и 4- Yu-\-v,
w > О и v > 0;
2)
269. 1)
2)
—4=----------!1±< + ^o.
/ + / 2 t3 + 2 / 2 / \ 2 t)
. 1 + ab
1 + У ab
1 + }^ab
§ 18. Степени с нулевым, отрицательными
и дробными показателями
Вычислить устно (270—272):
270. 1) а0; 2) (а ± 1)°; 3) 2"1; 4) З”2; 5) 10-2.
271. 1) — (—2)-1; 2)-(4-2)“1; 3)-(~2)"2; 4)-(+2)"2.
272. 1) х—1 при х= — 5; 2) — х~3 при х — — 3;
3) — х-4 при х = —2; 4) х-6 при х = — у.
273. Вычислить
1) [(0,2)~13 • 125-3’ • (0,2)4]"2;
2) 15- 10"4 • (2 + 5"3)0 • 23 • 10"2;
3) ~4+3‘(з~) . 2~3 + (0,75)~4 * (—0,5)2 .
' (0,5)-1 +5 + (0,2)0 - 12-З-3
с . ( 1 \о ,
5"5-(0,1)-4 + -4 —5-1
4) ----- + 4» 25.
+(-т)
274. Упростить выражения:
45
о\ Г( ’ Г1 I fa-M-’l ка + Н-1 }.a2 + b2
3НЫ +(—) ]-Ц—) -“]-^Z77r-
275. Вычислить:
1) (4’V + (81 ' Ю4Й - (7 ^Г+ (4,5)';
2) Ш”3 + Ш • 3 + (3^° • 5;
3) (15°Г + (81 • 1О~4)0 25 — (з~0,8 • 50,5 • 8Р) +(4)~2;
4) (5} • IO'4)0’25 4- (4-)'1 “ (53 + 3“2)° + (5"М ’ 50,5 • 25ТГ .
Упростить выражения (276—289):
276. J) +
V а + b + (а — Ь)2
_2
277 1) Уа3 + , а3 (а V~^ —bVb) ,
V4 (а (а - »)Р (а _
2) [а2(а2 + Ь)~2 + Vа2 +J• 2“1:_1+£?+1_.
а (а2 + Ъ) 2 + 1
1
2 । . / з \
278. 1) ----7- (а2 — 1)4-1;
а + а2 4- 1
1
2) 2а + /а2=Т(^Дг+ 1)-1; а +
1 + а {а2 — 1) 2
46
с + /с2-4 + 2 . с-Ус2 -4 + 2 _
с — VW- 4 + 2 "Г с + 2+У с2 -4 °'
279. 1)
2)
280. 1)
2)
Г — -I"1
Цх+ff) 2+(x—t/) 2J . х~Ух2 — у*
Г _ 1 --Г* у
[(х+у) 2 — (х — у) 2]
1 О^-УТ)2.
[(/7-Г»)-1+(/?+Г»)”Т 4/а
1(х + у) — (X — j/) 2 ] . Ух + у
281.
2
—(1 +1^ X2—У2)-^У~2-}-у"',
2)
I ]/ а + у b I
282.
а3 4- 6.
283. ___ ________________
[(х-у)У+*-!/]•[(*-»)/7±f -* + »]•
Г _1 / „ —0,5 ( 1 _1\]6
284. а 3 • Дь3 - а 2 .
\ Ь2 /
1_______1_ 4_ 1 _+ ____1_
285. —а 3 *Ь 12 • а3 • 3 • а 4 • (b *) 12
286.
(х • т)0,5 — т
2 • (4,9)0,5 • 10
х + т
— (тх) 2 : w0,5
14
т~эл.
287
9,5
а2 — 1
£
-(О-1)5
а — 3
а 2 + 1 ' (а - 3)
_2
5
47
288.
9л-0,5 „ < /a0’5 A “°’5 4-
V-2(a’-5+^
289.
— a0,5 — b0,5
-------------frO.5^2 _ b2
2a"9’5
(1 -2a1 2)2 - 1
a
a3 — 2a3
(1 - 2a2) 2 - 1 + 2a2
290.
/1 _ /Д4\"
Xa-l,6+vHM
\ I — a /
При a>0, 6>0 и a2— 6 > 0, показать, что
:2 — b
2
a + Va2 - b
2
b
Упростить выражения (291 — 292):
291. }/ x 4- 40 / 2 4- 56 • /з — 2 / 2 • /х — 1 +
+ 1^x —1^40/2 4-56- /з —2/2 • Ух- 1 .
Указание. Использовать формулу:
/х + Ух2-4х +4 = /х + |х-2|.
292 ( а~2Ь 4- У^б+У^2 А .
1/^2-/’4&2 4-/ 4Й2 + У"16а& /
. а / а Ь}^2Ь -}- b\^a а]^2Ь
а 4- b •
293. Доказать, что ах2 4~ Ьх 4- с = 0, если
— b ± YЬ2 — 4ас
Х =------75-----.
2а
294. Вычислить 5х2 4- Зх 4- 4 при х = — (2 4- /2/
295. Показать, что —. .. ?— = a— b при
X - / х2 - 1 .
1 / а , 1 т / b , _
*= 2-у т +ту - . где a>6>0.
48
Проверить следующие равенства (296 — 301):
296. (8 4-2 /1б) (107 — /б) • (4 — /Тб)7 = 4.
297. 2 /З —/5 .(6 4- 2/5)(/10— /2) = 32.
298. -5.!--2>-2--5Т 5 К
4 4- \ 5 /2 1 У
5-102 +5/8
299. = 2 (61 4- 24 /б)7.
\ 4 } \6 —5/6/ г '
300. - = 4- ------ = /74-/6.
/6 - /3 ~ /7 +/3 V F
301. -7^3 г- 4- 5 _ =/7 4-/5.
/5 -/2 /7 +/2 F
ГЛАВА 2
ВЕКТОРЫ
§ 19. Понятие вектора. Равенство векторов.
Сложение и вычитание векторов. Умножение
вектора на число. Разложение векторов
302. Распределите величины: длина отрезка, угол,
площадь, объем, время, сила, скорость, ускорение, на-
пряженность электрического поля, температура, масса,
плотность, работа, теплоемкость, отвлеченное число —
по графам следующей таблицы.
п/п Могут быть только скалярами Могут быть
скалярами векторами
1 2 3
30?. Как расположить вектор а, чтобы его проекция
на ось Ох была равна: 1) 0; 2) а\ 3)уа; 4) — — а?
304. Как изменится проекция вектора на ось, если
длину вектора увеличить вдвое, втрое?
305. Даны векторы а и Ъ. Как следует направить
эти векторы, чтобы их сумма а + Ь была: 1) наибольшей,
2) наименьшей?
306. Векторы а, Ь, с образуют треугольник АВС.
С помощью этих векторов выразить вектор медианы AD.
50
307. Доказать, что для любых двух векторов а и Ь
Справедливы неравенства
и — b j а Ь | a -j~ b.
308. На рис. 1 изображено пять векторов одинако-
вой длины. Какие из них равны между собой, если
ОВ\\О{А, OB OXD, OCtfOfl,
OC\\O^D, OBtfOC, О^А^(\Ь.
309. Построить следующие векторы на отдельных
чертежах в одном и том же масштабе, считая точку
*2?
Рис. 1.
А (х/, t/j) началом вектора, а точку В(х2; у2) концом,
и определить их длину по формуле АВ = 1АВ[ =
= У(х2 — х2)2 + (у2 — гл)2:
1) А (3; 0), В(8; 0); 2) А (2,5; 0), В(1; 1);
3) А (—4; 0), В (-8; 0); 4) А (2; 3), В (1; 2);
5) А (4; 5), В (7; 8); 6) А(-3; 2), В (4; 3).
310. Построить следующие векторы на одном чертеже
и определить периметр образовавшейся фигуры:
1) А(3; 3), В (6; 6); 2) А, (6; 6), ВДН; 3);
3) А2(3; 3), В2(11; 3).
311. В задаче 310 выразить формулой зависимость
между векторами АВ, А{В{ и А2В2 (по правилу сложе-
ния векторов).
312. Считая векторы АВ и AiBj составляющими си-
лами: | АВ |=Л и [ аЭ| |=В2, где А (4; 2); В [10; (/39+2)]
51
и Ai (4; 2); ВД17; 2), определить их равнодействующую
силу R.
313. Даны векторы АВ и AiBl} где 1) Л(3; 2),
В(5; 21/3) и Л] (3; 2), Bi ^8; у + у 1^6 j. Найти по-
строением третий вектор, равный разности данных двух
векторов, и записать формулой (по правилу сложения
векторов) зависимость между найденным вектором и
двумя данными, а затем вычислить значения всех трех
векторов.
314. Вектор, началом которого является точка
A(xi\ уА, а концом точка В(х2; у2), образует с осью х
угол ф, где tgф= • Найти Угол Ф в следующих
случаях:
1) А (5; 3), В (6; 4); 2) Л (8; 6), В (9; 7);
3) Л (4; -3), В (5; -4); 4) А (-3; 3), В (—2; 2).
315. Дать геометрическую иллюстрацию (рис. 2) ком-
мутативного закона сложения векторов а и Ь.
316. С помощью рис. 3 дать геометрическую иллю-
страцию ассоциативного закона сложения трех векторов.
317. Построить в одной и той же системе координат
векторы, соединяющие пары точек:
1) Л(—2; 5), В (5; 7); 2) ЛД5; 7), В, (10; 8);
3) Л2(10; 8), В2(7; 6); 4) Л3(7; 6), В3(3; 1);
5) Л4(3; 1), В4 (—2; 5).
(а) Как называется образовавшийся многоугольник?
(б) Чему равна сумма всех этих векторов?
(в) Какой вектор называется нулевым?
318. Три вектора расположены в одной плоскости
так, что при | а |= 18 и |&|=16 имеем |а + &| = 26.
Определить |а — &| и изобразить чертеж, где указать
векторы а, Ь, а~\~Ь и а — Ь.
52
319. Три вектора д, Ь и а — Ь расположены в одной
плоскости так, что при |а| = 29 и |&| = 25 имеем
|а— &|==6. Найти | а + Ь | и построить чертеж.
320. Четыре вектора: | АВ |=| с |= 11; | ВС |=| b |=13;
| CD | = [ d | — 15; [ AD | = | а [ = 25 расположены в одной
плоскости и образуют трапецию ABCD с основаниями
AD и ВС. Построить чертеж и найти | с + Ь | и | Ь + d |.
321. Два вектора а и Ь взаимно перпендикулярны,
| а | = 8, | Ь | = 6. Найти | а + Ь | и [а — b |.
322. Покажите на чертеже, что + +
323. Дать геометрическую иллюстрацию:
1) | а + Ъ | = | а — Ь |; 2) | а + Ь | > | а — b
3) | а 4- b | < | а — &|; 4) [ а + & 1 = 1« | — | & |;
5) | а — &|=|д| + |&1; 6)|д + &| = 0.
324. На тело действуют две силы, F[ и F2, под пря-
мым углом друг к другу (Fj ± F2); | Fi | = 40 Н, | F1 — F21=
= 50 Н. Определить | F2 [.
325. Какой угол образуют между собой две силы,
F, и Рг. если |F,| = |F2|=y|F,-F2|-|F,+F2|?
326. Две силы, Fi и F2, такие, что [FI|=15H и
। р21 = 20 Н, действуют на тело, образуя между собой
угол в 30°. Определить | F; + F21, |Fj—F21 и углы,
которые образует равнодействующая F с F{ и F2.
327. При сложении сил Fi и F2, где | Fj | = ЗЗН,
|F21 = 39H, получилось, что |Fi + F2| = 60H. Опреде-
лить угол между силами (векторы расположены в одной
плоскости).
§ 20. Умножение вектора на скаляр. Проекция вектора
на ось. Координаты вектора на плоскости
328. Дан вектор АВ, где Л(0; 0), В(3; 4). Найти и
построить на отдельных чертежах, но в одном масштабе
произведение вектора АВ на число k, равное 2; —2; 4- .
329. Найти длину вектора АВ, если /1(3; 4),
В(-3; -4).
330. Покажите на примерах, что для любых век-
торов а и Ь и произвольных чисел I и k справедливы
следующие равенства:
1) k-(la) = (kl)-a;
2) (k -j-1) а = ka 4- la;
53
ними 120°.
3) k (а + 6) — ka + kb;
4) 0 • а = 0, k -0 = 0, 1а = а, (—1)-а =— а,
(— k) • а = — (k • а).
331. Даны векторы а и Ь, угол между
Построить вектор с = 4а — 36 и определить его длину,
если а — 3, 6 = 4.
332. i и / — единичные векторы сторон АВ и AD
прямоугольника ABCD. Выразить через i и / векторы
АВ, AD, АС, ВС, DA, DB, если ЛВ = 9, Л£>=12.
333. В треугольнике АВС точка О есть точка пере-
сечения трех медиан. Показать, что О А + О В + ОС = 0.
334. В трапеции ABCD дано Z Л = 60° и Z D = 30°;
АВ = 3 /3, ВС —7, CD = 9; точки М и W—середины
сторон ВС и CD. Выразить
векторы АВ, ВС, CD, AD, BD,
AC, AM, MN, AN через еди-
ничные векторы i и j напра-
влений AD и AB.
335. На плоскости распо-
ложен вектор АВ = а (рис. 4).
Выразить этот вектор через
его проекции на оси коорди-
нат ах и ау.
336. Вектор АВ —а обра-
зует с осью Ох угол <р. Найти
проекции этого вектора на оси
координат.
Л (—4; 3), В (0; 6), спроектиро-
337. Вектор АВ, где
вать на оси прямоугольной системы координат и найти
длину проекций и вектора.
338. Вектор АВ, где Л(1; —2), В (—2; —1), спроек-
тировать на оси прямоугольной системы координат и
найти длину проекций и вектора.
339. Ломаную векторную линию АВС спроектировать
на оси координат прямоугольной системы и найти длину
проекций, если А (0; 0), В (4; 3) и С (8; 4).
340. Вычислить проекцию вектора
динат Ох и Оу; <р — угол между осью
нием вектора:
а на оси коор-
Ох и направле-
1)| а [=10, <р = 60°; 2)| а |=12, <р = 30°;
54
3)|а| = 7, ф = 45°; 4)|a|=18, ф=180°;
5) |a [ = 6, ф = 90°; 6) | a [ = 4,8, ср =120°.
341. (а) Вычислить длину вектора а, если его проекции
на оси Ох и Оу соответственно равны ах и ау, а угол
между вектором и осью Ох равен ср:
1) ах = 4, ф = 30°; 2) а^ = 5, <р = 30°;
3) ях = 8,2, ф = 45°; 4)а^=12, ф = 90°;
5)ах = —12, ф=180°; 6)^= + ?, ср = 60°;
7)ах= —4, ф=180°.
(б) 1) Вычислить координаты конца вектора и его
длину, если координаты начала (2; 1) и ах = 3, ау = 7.
2) Вычислить координаты начала вектора и его дли-
ну, если координаты конца (7; 8) и ах — — 4, ау = 5.
3) Вычислить длины векторов а и Ь и углы, которые
они образуют с положительными направлениями осей
Ох и Оу, если ах=12, ау=16 и &х=13, ^=20.
§21. Зависимость между проекцией суммы векторов
на ось и проекциями слагаемых на эту ось. Скалярное
произведение двух векторов
342. (а) Даны векторы а{ах, ау\, Ь {Ьх; Ьу] (в фигур-
ных скобках указаны проекции векторов на оси коорди-
динат). Доказать, что:
1) а + & имеет координаты {ах -J- Ьх\ ау-{-Ьу]-,
2) а — Ь имеет координаты {ах — Ьх; ау — Ьу};
3) ka имеет координаты [kax't kay];
4) -у имеет координаты ; -yj.
(б) Даны векторы а {5; 4} и b {—4; 3}. Найти проек-
ции на координатные оси следующих векторов:
1)а + &; 2) а-b-, 3)-^; 4)
5) 5а; 6) 46; 7) — За; 8) — 46;
9) 1а; 10) —1а; Ц) 4а 4-56.
343. Если а(ах;а^, то | а | = Yа2х 4- а2, ( а | — длина
вектора а. Пользуясь этой формулой, найти длины
следующих векторов:
55
1) a [7; 3}; 2) Ь [/12; /37};
3) Ь {/Й; /47}; 4) Ь [-6; —2).
344. Пусть векторы а и Ь заданы своими проекциями
на оси координат а{3; 2} и & {4; 5}. Определить длины
следующих векторов:
1)|а + &|; 2)| а — 6 |; 3) | 2а + Ь |;
4) | а + 36 |; 5) |у 6) 11 б|.
345. Вектор а через свои проекции на оси координат
может быть выражен в виде a = axi + ayj, где i и
j— единичные векторы координатных осей (или орты
координатных осей). Выразить через хи/ вектор АВ,
если даны координаты концов вектора:
1) Л (5; 2), В(3; 1); 2) Л(-5; -2), В(-3; -1);
3) Л(3; 3), В (2; 2); 4) А (-3; -3), В (-2; -2);
5) Л (4; 0), В(3; 0); 6) Л(0; 0), В (6; -5).
346. Дан вектор а = axi ayj. Найти орт вектора а
в каждом из следующих случаев:
1) а = 21 А- 3]', 2) а = — 2i + 3j;
3) а = 2i — 3/; 4) а = — 2i — 3/; 5) а = 5х + 4/.
Указание. Вектор, который при выбранном масштабе имеет
длину, равную единице, называется единичным вектором или ортом.
Если дан какой-нибудь вектор а = axi + ayj, то единичный вектор а°
того же направления получим, разделив вектор а на его модуль | а |;
a axi + ayj ах ау
(Г = г = —,...... -- = г------ i 4-7-—.. . • j.
‘“I Val + a^ Val + a^ +
Например, если a = 4i -f- 3/, то орт этого вектора равен
ао = j + ../ = 1i 4-2 / = 0,82 + 0,6/.
К42 + 32 /42 + З2 5 5
347. Найти проекции векторов:
1)а + &; 2) а — 6; 3)-а + 6; 4) -а — Ь;
5) 2а + 6; 6) а + 26; 7) - 4а + 56; 8) 5а — 46;
9)4<i + 4z; 10) 5«-
1 3 1
если а = 2 у i + 3/ и 6 = у i — 4 у /.
56
Указание. Если а — axi + ayj, а b — bxi + byj, то
1) пр (а + Ь) = {(ах + Ьх); (ау + ^));
2) пр (та 4- nb) — {(тах + nbx); (тау + nby)},
где ах, Ьх, ау, Ьу — проекции векторов на оси координат, а т и
п — числа.
348. Единичный вектор а составляет с осью I угол
Ф = 60°. Найти проекцию вектора а на I.
349. Единичный вектор а составляет с осью Ох угол
ф = 30°; найти проекции вектора а на оси координат.
350. Единичные векторы а, 6, с составляют с осью I
соответственно углы 60°, 120°, 180°. Найти проекцию
на ось I векторов:
a-J-6-J-c, За+ 26 +с, а + 26 + Зе, 2а+ 36— 4с.
351. Найти проекцию суммы векторов а, 6, с и d
на ось Z, если а = 5, 6 = 6, с = 8, d= 12, а углы, соста-
вляемые этими векторами с осью Z, соответственно
равны 0э, 120°, 180°, 360°. Сделать чертеж и объяснить
геометрический смысл полученного ответа.
352. Вычислить угол между векторами а ~ {1; —2}
и 6 = [—3; 1}.
353. Что называется скалярным квадратом вектора
и чему он равен, если вектор равен а?
354. Объясните на примере и чертеже условие пер-
пендикулярности двух векторов.
3551 Доказать, что г •? + /•/ = 2, если i и j— еди-
ничные векторы.
356. Если а={ах; ау] и 6={6Х; Ьу}, то скалярное
произведение векторов а • 6 = ахЬх + ауЬу. Зная это
свойство, найти произведения векторов:
1) а = 5г + 8/ и 6 = 4г + 3/;
2) а = 41 — 3j и 6 = 4f + 3/;
3) а = i + j и 6 = — i + /;
4) а — — 2i + 3/ и 6 = 5i — 2/.
357. Вычислить, какую работу производит сила
F {Fx; Fy], где Fx и Fy— проекции силы F на оси коор-
динат, когда ее точка приложения, движущаяся прямо-
линейно, перемещается из положения А(ху в поло-
жение В(х2; y-i), если известно, что:
1)F[7;8J, Л (5; 9) и В (3; 5);
57
2) F {4; 2], A (-7; -3) и В (-2; 4);
3)F{5;-3}, 4(1; 1) и В (7; 8);
4) F(—6; 4), А (-2; -2) и В(-3; -3).
358. Две силы F [Fx; Fy] и f[fx; fy] приложены
к одной точке. Вычислить работу, которую производит
равнодействующая этих сил, когда ее точка приложе-
ния, движущаяся прямолинейно, перемещается из по-
ложения А(х1; у{) в положение В(х2', у^. Решить ана-
логичные задачи:
1)F{2;4), f{3;4}, 4(3; 3) и В (2; 2);
2)F{—2; -4}, Л-3; -4}, 4(-3; -3) и В (—2; -2);
3)F(3;-4], f{5;—8}, 4(5;0) иВ(0;3);
4)F{ —2; 5}, f(6;4}, 4(-4;3) и В(2;-3).
359. Угол между двумя векторами вычисляется по
формуле:
axbx + ayby
COS ф = —7=-----г----,
где векторы а{ах, ау\ и Ь [Ьх; Ьу} заданы своими проек-
циями на оси координат. Определить угол между век-
торами а и b для следующих случаев:
1) а (3; 4} и &{1; 2}; 2) а{1; 2} и b {— 3; —2};
3) а (7; 9} и Ь (4; 3}; 4) а [-3; 4} и Ь j-З; —3};
5) а (0; 4} и Ь [0; 4}; 6) —1; —4} и Ь (4; —4).
360. Определить внутренние углы четырехуголь-
ника ABCD, если 4(-2; 1), В(—1; 4,5), С(1; 5,5), £>(3; 3).
361. Определить внутренние углы треугольника АВС,
если 4(3; 4), В (5; 6), С (4; 1).
362. Если векторы а и Ь заданы своими проекциями
на оси координат а \ах; ау\ и Ь{ЬХ\ Ьу\, то условие пер-
пендикулярности векторов имеет вид ахЬх-\~ ауЬу = Ъ,
а условие параллельности
ах _ аУ
(а) Проиллюстрируйте эти условия на чертежах.
(б) Используя условие перпендикулярности векторов,
доказать, что диагонали ромба взаимно перпендику-
лярны.
5$
§ 22. Комплексные числа
363. Показать, что квадратное уравнение х2+1 = 0
не имеет решений в множестве действительных чисел.
364. Построить векторы, соответствующие следующим
числам:
1) 3, —2, /2, —4, 5, /, —/;
2) —1 4-Z, 2 — 3/, -4 + 3/, —3 — 4/.
365. Произвести указанные действия:
1) / /49 + 7/ /64 — 6 /12 + 4 /48;
2) а/ / а + / /а3 — / 4а3 + 5а / а (а > 0).
366. Написать комплексные числа, сопряженные дан-
ным:
1 + Z, 2 —Z, 8 + 5/, /2 + 3/, +
367. 1) Найти а и Ь, если « + />/ = 4 + 5/.
2) Найти а и Ь, если a-\-bi = 0.
3) Составить два комплексных числа, равных друг
другу.
368. 1) Найти модуль каждого из следующих чисел:
1 + 3/, —2 + /, 4 — 2/, 0 + Z, 2 + 3/.
2) Изобразить в одной и той же системе координат
и в одном и том же масштабе следующие комплексные
числа:
3 — 2/, -3—3/, 5 + 0-/, 0 + 2/.
3) Проверить равенства:
а) (2 + 3/)(2 — 3/)=13;
б) (4 + t]/5)(4 — i/5) = 21;
в) (1/7 + //з)-(/7 —г/3)=10.
369. 1) По формуле f = iik+r упростить следующие
выражения:
(a) Z5, /7, (-/)29, (-/)8, /3, /4, /,0, (-/)15, /25> (-/)50,
.80 .—5 .—15 г .х—19 Лп+15.
I , I , I , (— I) , I ,
(б) Г28+А г125 —(—027+<м—(—'Л /,6-/46+г”+Л
О'" + (- О85; (-i)'7 + «”-(- О'4; <'"22 +
+ (_ о26 + (- О18; <гл+3 + «,'1_3.
2) Дать геометрическое представление комплексного
числа г = (2 + 3/)3 и найти его модуль.
<9
3) Дать геометрическое представление комплексного
числа z = (3— 2/)2 и найти его модуль.
4) Упростить следующее выражение и найти его
модуль:
z = (1 + /)3 + (2 - Z)2 + (5 + 3Z)2 - (3 - 2Z)3.
370. Выполнить указанные действия и результаты
изобразить геометрически:
1) г1 = (3 + 2/) + (-3-4/) + (1+/);
2) z2 == (- 5 + 3/) + (4 + 3Z) + (10 + 50;
3) z3 = (4 + 5Z) + (2 + 3/) - (7 - 40.
371. Напишите два таких комплексных числа, сумма
которых была бы равна чисто мнимому числу.
372. Изобразите геометрически комплексное число
z = х 4- *+ если | z j = 1.
373. Показать на примерах, что для комплексных
чисел справедливы переместительный и сочетательный
законы сложения.
374. Построить векторы в прямоугольной системе
координат, соответствующие следующим комплексным
числам:
1) z = 4 + 6r, 2)г= — 1+3/; 3)г = 4 — 3/.
375. Какое число надо прибавить к 2 — Z 5, чтобы
их сумма была равна 0?
376. Какое число надо вычесть из числа 14 + 3Z,
чтобы их разность была равна 9?
377. Напишите два таких комплексных числа zx и г2,
чтобы их сумма была: (а) чисто мнимым числом;
(б) действительным числом.
Найти действительные числа х и у из уравнений
(378-381):
378. 1) 2 + 3Z = 4х + 9уг,
2) -3 —5/ = 2(х—l) + 3(z/—2)/;
3) 7—15Z = 7(3x —4) —5(z/ + 7)Z;
4) 18 + 25Z = 5 (5x — 2) + 100(z/—10)Z.
379. 1) 4 + 8/x + 1 Oiy = 6/ + 3x + 5 г/;
2) 4x + 5y — 9 + 7 (3x — y)i = lOx + \4yi\
3) 3 + 4/x + Ыу = 12/ + 5x — 2y;
4) (4 + 3Z)x + (4 — 3/) r/= 15 — 4Z.
60
380. 1) (2 + г)х — (1 — i)y — 1 4-3Z;
2) х 4- 2/ + 2 4- 4y 4- xi = 5x4-3/ — 3y 4~ yi — 4:
3) (1 4-0x4-(2 + 0i/= 1 +3i;
4) 0,2x 4- 0,5г/ — 2,4/x = 3, Uy 4- 4,2 — 2/.
381. 1) (a 4- 2/) x 4~ (6 4- 50 У — a + 36/;
2) 2ax— 3(6— 4i)y = 2a— 4bi;
3) 3jx 4~ by 4“ axi 4“ byi = 2a — 7bi;
4) 5x 4- ^bi 4- 4zz/ 4- 6г/ = (a 4- b) x — (a — b) i.
§ 23. Сложение и вычитание комплексных чисел
Выполнить действия (382—384):
382. 1) (0,3 4-0,20 4-(0,8 4-0,50 — (0,2 — 0,3/);
2) (2|- 1 1/) + (1-| + з4‘')-(з-2-р);
з) Н-21‘'Н74+4У-2г-
383. 1) (а 4- Ы) 4- (5a 4- 860 + (— 4a — 7bi)',
2) (- 8а 4- 460 4- (— 7a — 56/) — (3a 4- 760;
3) (5a — 8ci) — [(3a 4- 5c/) — (2a 4- 3c/)].
384. 1) [(x 4-#/) + (3x— 2y/)] — [(—x — yi) — (5x~4yi)];
2) [(4x — 5yi) — (7x 4- 6г//)] 4- [(2x 4~ 8г//) + 7yi].
§ 24. Умножение, деление и возведение в степень
комплексных чисел
385. Показать на чертеже, что:
1) умножению числа 2 на 3 соответствует растяжение
вектора, изображающего множимое 2, в три раза без
изменения его направления;
2) умножению числа 2 на (—3) соответствует растя-
жение вектора, изображающего множимое 2, в три
раза и поворот вектора на 180°;
3) умножению числа 2 на 3/ соответствует растяже-
ние вектора, изображающего множимое 2, в три раза
и поворот вектора на 90°.
386. Выполнить умножение (устно):
1.) 5/ • (-2/); 2) 3/ • 2/ /2; 3) 7/ • (-4/);
4) 0,3 • 10/; 5) — аг • 6Z; 6) а/ • bi;
7) (5 4- 3/) • 2/; • 8) (- 3 — 4/) • 2i; 9) (- 7 — 80 • (-3/).
61
387. Выполнить действия:
I) (1—20 (5 — 0; 2) (К2-<)(/3 + </2);
3) (0,5 + 0,21) (2 + 3i); 4) (6 + 0 • (6 — 70-
388. Проверить равенства:
1) (2 +30 • (2 —30 = 13; 2) (4 + г/5)(4-г/5)=21;
3) (/7 + i V3)-(/7—>/з)=10;
4) (-0,5 4-20 (-0,5 — 20 = 4,25.
Выполнить действия (389—392):
389. 1) (2 —Z/5)(1+ 1/5); 2) (5 — 30(5 + 30;
3) (3-i/3)(2 + i/3); 4) (l-Z/2).(l + i/2).
(/2-i)- (3 + 1 /2);
(1 + 1 /3) • (2 /3 + 2Z).
12 — 5i ,
7 3 + 21 ’
6>++-
5-1/2
390. 1) (2 — i)(l — 31); 2)
3) (-3 + 40-(-30; 4)
2 + 3/ .
' 1 - 21 ’
5)
-/2 + 1/б . .
’ • 1 + 1/2 ’
“ -(2 + 0.
I — I
произведения
391. 1) -—
7 1+1/2
3-i ,
51 *
/б-i .
4)
392. 1)
2)
5) 6)
’ 2 /3 - 31 7
393. Найти модули суммы, разности,
и частного следующих двух чисел:
Zj — 2 — 3t; z2 = 4 + 51.
4)
/б" — 2i
2i - 1 .
Выполнить действия и найти модули результатов
(394-395):
394. 1) 2) .(4>+-+2;.
3 — 2/ 3/5 + i /3
395. 1) (4 /3 — 31)2 + 3; 2) (2 — 3 /2 i)3 — 21;
3) (1 — 203 — (1 — 203; 4) (3 + 402 — (4 — 51)2.
Выполнить действия (396—398):
396. 1) (3—//2)’; 2) (-Ц/3 )2;
3)(1 + 1/5)2; 4) (-'-/3 У .
62
397. 1) (37 / 5 + 21)2; 2) (2 — 3i / 2)2;
3) (2i У 5 — 3z)2; 4) (3 + 21 У 3)2.
398. 1) (~l+-2‘ ; 2) (2 — i/3)3;
3) (a — ЫУ, 4) (a + bi)2.
399. По формуле
извлечь следующие корни:
1) /З+^Й; 2) /5^12i; 3) /2 —Зг /5;
4) V20 —4i|Gt; 5) /7 —3/ 6) /-5—12/.
400. Упростить и изобразить геометрически следую-
щие комплексные числа zlf z2, z3:
1) Z{ = (2 + 3z)2; 2) z2 = (3 — 2f)2;
3) z3 = (1 + О3 + (2 - О2 + (5 + 3z)2 - (3 - 2Z)3.
401. Разложить следующие выражения на множители:
1) а2+1; 2) 3 4-а2; 3) 9 + а2; 4) х2 + у2 (а, х, у-
действительные числа). ~
402. Изобразить геометрически, а затем записать
в тригонометрической форме следующие комплексные
числа:
4
Z = 1 + i /8 ’
2) 2=2 — 5г,
1)
3)
z =
' -i + i/з \2 . / - 1 - //з V
< 2 / "Ц 2 /
Произвести указанные действия над числами и изо-
бразить результаты геометрически (403—404):
лпч п . (» + /)3
41М. Zi cqs 18()0 _j_ . sin 180о ,
.. л . . . л \
4l COS -5- + 1 sin —
_ 2+,-
3) г, = у 2 (cos 225° + i sin 225°);
n/ Зл . . . Зл \
2 I cos -g- + i sin
л\ \ " " /
4) г4 =
i24 - i2
€3
404.
1) zx = У~2 (cos 120° + i sin 120°)*^(cos 60°-f-Zsln60°)$
2) z2 = 2 (cos 40° + i sin 40°): Y 3 (cos 10° + i sin 10°);
3) z3 = (1 — i)2: V~2 (cos -^ + i sin
405. Показать, что
1) z] = 1; 2) z] = 1; 3) zj = z2; 4) z% = zp
если _
- 1 - i /3 — 1 +1 /T
=-------r2— и z'2== —— •
406. Как расположены на плоскости комплексные
числа z = 3 +6Z, где b — любое действительное число?
Записать в алгебраической форме следующие ком-
плексные числа (407—409):
407. 1) (cos 225°+ z sin 225°);
2) cos 300° + i sin 300°;
3) 2 (cos 60° + i sin 60°);
4) cos 240° + i sin 240°.
408. 1) Y2 (cos^ + Zsin-^J;
2) 2(cos-y-+ z sin ;
3) cos 2л + Z sin 2л;
4) y2'[cos(-^)+Zsin(-^)].
n . ( ft ... л \
2z cos-77 + 1 sin-x- . .
ллл \ 3 3/ 4л 1 . . 4л
409. 1) -----’ 2) cos T +1 sln Г
3) Qosn+zsinn; 4) Y2 (cos— + Zsin —j.
Выполнить действия (410—412):
410. 1) 0,4 (cos 82° + Zsin82°) • 0,25 (cos 8° + Z sin 8°);
2) у (cos 30° + i sin 30°) • 2 (cos 45° + Z sin 45°);
3) 0,03 (cos 25° + Z sin 25°) • 5 (cos 20° + i sin 20°);
4) 6 (cos 45° + Z sin 45°) • у (cos 15° + Z sin 15°).
64
411. 1) 2 (cos 120° + Z sin 120°): 0,8 (cos 30° + i sin 30°);
2) (cos 135° 4- i sin 135°): ~ (cos 90° + i sin 90°);
3) 0,6 (cos 75° + i sin 75°): 4 (cos 30° + i sin 30°);
О
a\ a a ( 4 ( • • 4 \ , гт ( л I • • л \
4) 4,2 cos -v л 4- i sin -о- л : 7 cos +1 sin .
\ о о / \ z
412. 1) 0,18 (cos л 4~ Z sin л) • 0,6 (cos 4 "H sin4b
\ 0 О /
2) 0,8 (cos 4" Z sin 4 : 4 (cos л 4" Z sin л);
o> 2 / 3л ... 3л \ 6 / 1 . . . 1 \
3) v cos 4-1 sin -77- • T cos v л + г sin v л ;
/ \ Z Z / / \ О О /
л \ ( Л f • • Л \ e /\ л / Л 1 • • «Ft \
4) cos v 4-1 sin -5- . 0,3 cos -5- 4-1 sin .
\ Z Z / \ 0 0 /
Пользуясь формулой Муавра, вычислить следующие
выражения (413—415):
413. 1) [2 (cos 4- Z sin2) (cos 72° 4-Z sin 72°)10;
3) (cos 15° 4“ Zsin 15°)10; 4) ~ (cos 4 4- Z sin 4/
" \ 0 0 /
414. 1) [3(cosl2°4-Zsinl20)]5; 2) [4 (cos 4 4- isin-jVT i
L \ 0 0 /J
3) [-^-(cos 18°4-Z sin 18°)]5; 4) ^2 (cos 4"H s’n7')]6*
415.
1) (cosу 4-Zsin4) '» 2) (cos 30° — Zsin30°)~J;
3) (cos4“ Z sin-4) J 4) (cos 15° — Z sin 150)”10.
Вычислить все значения корней (416—417):
416. 1) 2 = 1^64 (cos 135° 4- Zsin 135°);
2) 2 = /cos72° —Zsin72°;
3) 2 = /cos 22330' 4- Z sin 22°30';
.\ ®Г л . . л
4) 2=1/ COS -7- — iSin-F-.
' r 6 6
417. 1) 2=/^T; 2)
3) 2 =/8; 4)z=V'T.
65
418. Подкоренные выражения преобразовать в три-
гонометрическую форму, затем найти все значения кор-
ней и изобразить их точками на плоскости:
1) z = + 2) 2 = ^ЗД-(1 + <).
419. Указать на плоскости множества точек, изо-
бражающих комплексные числа, модули г и аргументы <р
которых удовлетворяют условиям:
1)г=1, <р = -|; 4) г < 3; 7)0<Ф<-~;
2) г — 2; 5) 2 < г < 3; 8) 0 < <р < л;
3) г<3; 6) <р = V’ 9) 1 <г<2,
О
0<Ф< у.
420. Докажите, что для любых сопряженных ком-
плексных чисел и 22 выполняются соотношения:
1) | 2j • 22 4" 1 P=(J Р+ 1)(| £2|2+ 1);
|2—1) о г212—1).
421. Доказать справедливость равенства
I + 22 I2 + I 2, — Z2 I2 = 2| 2j 2 4- 2 |?2 I2,
где 2! и 22 — два любых комплексных числа.
Сравните с теоремой из геометрии о сумме квад-
ратов диагоналей параллелограмма.
422. Один из корней уравнения
х4 —4х34-7х2 — 16х+ 12 = 0
равен 21. Найти остальные корни уравнения.
423. Составить уравнение наименьшей степени с дей-
ствительными коэффициентами, корнями которого слу-
жат 1 и 1 —i.
ГЛАВА 3
КВАДРАТНЫЕ УРАВНЕНИЯ И УРАВНЕНИЯ,
ПРИВОДИМЫЕ К КВАДРАТНЫМ.
КВАДРАТНЫЕ ФУНКЦИИ И ИХ ГРАФИКИ
425. Построить графики функций задачи 424 на од-
ном чертеже в одном и том же масштабе и отметить
на графиках:
1) область определения и область изменения каждой
из данных функций;
2) точки наименьшего и наибольшего значения каждой
функции;
3) как влияет коэффициент при х2 на форму графика;
4) как влияет знак коэффициента при х2 на напра-
вление ветвей параболы;
5) как изменяется величина у при изменении х от
— оо до 4-оо для каждой из данных функций;
6) пропорциональные зависимости между х и у\
67
7) общую точку графиков всех четырех данных
функций;
8) какие из данных функций являются четными.
426. Парабола у = ах2 проходит через точку (2;8).
Найти коэффициент а и построить иараболу.
427. Парабола у = ах1 проходит через точку (—3;
—12). Найти коэффициент а и построить параболу.
428. Велосипедист движется с ускорением а=0,2 см/с2.
Изобразить график движения велосипедиста, если путь
вычисляется по формуле S = —^~ и от начала его дви-
жения прошло две минуты.
2) Построить графики всех данных функций на од-
ном чертеже и в одном и том же масштабе.
3) Проследите на графиках за областью определе-
ния и областью изменения каждой из данных функций.
4) Отметить на графиках функций те значения х,
при которых указанные выше функции имеют наимень-
шее значение, и найти эти наименьшие значения.
5) Существует ли такое значение х, при котором
какая-либо из данных функций: (а) обращается в нуль,
(б) имеет отрицательное значение?
6) Парабола г/==ах2-|-4 проходит через точку (2; 3).
Найти коэффициент а и построить график функции.
7) Является ли функция у — ах2-\-с четной?
68
430. 1) Вычислить значения у, если:
X —5 -4 -3 — 2 -1 0 1 2 3 4 5
1 , У = "2 х у = — y*2 + 1 у = —у*2 + 2 У = —|-х2 + 3
2) Построить графики на одном чертеже и в одном
и том же масштабе.
3) Проиллюстрировать на графиках область опреде-
ления и изменения каждой из данных функций.
4) Отметить на графиках то значение х, при кото-
ром каждая из данных функций имеет наибольшее или
наименьшее значение.
5) Найти по графику каждой функции те значения х,
которые обращают ее в нуль.
6) Записать интервалы оси Ох для каждой из дан-
ных функций, в которых функция положительна и
в которых отрицательна.
7) Парабола t/ = ax2-{-8 проходит через точку (2; —4).
Найти коэффициент а и построить параболу.
431. Построить графики данных функций на отдель-
ных чертежах:
l)j/ = |x2-3; 2) =
3)У=4*2 + 3; 4) г/ = -±х2 + 3.
Каждую функцию интерпретировать по пп. 3)—6) пре-
дыдущей задачи.
432. Построить графики данных функций на отдель-
ных чертежах:
1) ^ = — 2х2-|-4; 2) t/ = 0,5x2 —2;
3) г/=1 — х2 + 3 1; 4) г/=| Зх2 —-2
69
§ 27. Функция у ~ ах1Ьхс и ее график
433. С крыши дома высотой 15 м брошен верти-
кально вверх мяч с начальной скоростью и0= 10 м/с.
1) Найти зависимость между высотой подъема h и
временем полета мяча t (g = 9,8 м/с ).
2) Составить таблицу изменения высоты полета мяча
в зависимости от изменения времени от начала его
движения до падения на землю.
3) Построить график изменения высоты полета мяча,
откладывая по горизонтальной оси значения t, а по
вертикальной оси значения h.
4) Найти по графику и вычислением:
(а ) Через сколько секунд мяч достигнет наибольшей
высоты?
(б ) На сколько метров от земли поднялся мяч в наи-
высшей точке подъема?
(в ) Через сколько секунд от начала движения мяч
упадет на землю?
Указание. Учитывая высоту дома 15 м и считая hi рас-
стоянием от крыши дома до конечной точки подъема мяча, со-
ставляем уравнение зависимости между высотой подъема h и вре-
менем полета мяча t:
h =15 + ^1, где hi = == 10/ — 4,9/2,
отсюда h — 15 + 10/ — 4,9/2, а затем выполняются остальные пункты
задачи.
434. Периметр прямоугольника 8 см. Выразить пло-
щадь прямоугольника как функцию его стороны и по-
строить график.
435. Построить графики функций:
1) ^ = 1x2 — 4x4-31; 2) // = | х2—2 |х| —8 |;
3) | f/| = x2 — 6х + 5; 4) у = \ -х2 + 3х — 2].
436. Построить графики данных функций в общем
виде:
1) у —ах2: (а) при а >0, (б) при а < СО;
2) у = ах2 4- с; (а) при а: >0, с > Q,
(б) при а >0, с < 0,
(в) при а < СО и с <0;
3) У = а (•< 4~ /п)2: (а) при а>0 и т > 0,
(б) при а < 0 и т < 0;
70
4) у = а (х + т)2 + п: (а) при а > О, m > 0 и п> О,
(б) при а > О, т < О и п < О.
437. Найти экстремальные значения данных функ-
ций и указать, при каких значениях аргумента они
достигаются:
1) у — 2х2 + 4х + 7; 2) у = -^ х2 — 4х + 5;
3) у=-Зх2-|-6х4- 1; 4) у = | 8х2 —8х —6 |;
5) ,7 = 1 х2 —2x4-1; 6) // = 0,4х’4-Зх —4;
7) г/ = | 6х2 —х-1 |; 8) у~\4х~ — 4x4-31.
438. Даны функции:
(a) f (х) = х + у (к > 0); (б) ф (х) = :
(в) ^)=-Дт
1) Найти область определения и область изменения
каждой из этих функций.
2) Определить их точки разрыва.
3) Построить график каждой функции на отдельном
чертеже.
439. Даны функции:
1) у — х3— Зх; 2) у = — х3 4- х2;
3) у = х4 — 4х2; 4) у = х3 — Зх2 4- 2;
5) у = 4 (х4 - Юх2 + 9); 6) у = - 2 (х4 — 2х2 + 1).
(а) Построить графики этих функций.
(б) Какие из этих функций четные?
§ 28. Неполные квадратные уравнения
Решить уравнения (440—442):
440. 1) х2 = 25; 2) х2 = 49; 3) х2 = 36.
441. 1) 5х2—125 = 0; 2) 4х2 — 64 = 0;
3) 0,8х2 —0,2 = 0.
442. 1) 0,04х-— 0,64 = 0; 2) 31 х2 — 303,75 = 0;
3) 2х2 —0,8 = 0; 4) Юх2—100 = 0;
5) х2 —0,16 = 0; 6) 4х2 —0,81 =0.
443. Решить уравнения с буквенными коэффициен-
тами и в каждом уравнении указать, при каких
71
значениях букв данное уравнение имеет действительные
решения:
1) а2х2 = Ь2;
3) La^x2 — 2b = 0;
5) 0,8х2 —-^-=0;
7) 0,05а2х2—1,2562 = 0;
2) 4а2х2— 8с2 = 0;
4) 4х’~=
6) (а — ЬУх2—1;
оч х__2,7а
°' 03а ~~х~‘
444. Решить уравнения в области комплексных чисел:
1)
3)
5)
х2 + 1 = 0; 2) 25х2 + 625 = 0;
0,1х2+-2,5 = 0; 4) 0,04х2 + 0,01=0
5х2 + 14 , Зх2 + 1 . Зх2 + 4 2
—з-----+ ~TZ- = 4; 6) —— = х2;
7x2 + Л2±21 в _ 4х2 _ б
1 4
7)
Решить уравнения (445—448):
445. 1) х (х — 3) = 4х — 6х2; 2) Зх2 + 4х = 2 (х2—Зх);
3) (х —2)2 —4(х+1)2 = 5х4-х2;
4) 5х2 — 8х = — (Зх -f- 2) х.
ЛЛа П 2х + 3 — 5 • 4,5х2 “ 2’8 — 3’4 •
446, 4х “ х ’ 2' 5х 2х ’
3,4х + 2,7 __ х — 2,7 . .к 7,2х + 8,3 _ 59,76
х —3,4 ~ х + 3,4 * 7,2 “51,84 —х*
447. 1) ах2 + Z>x = O;
«к ах + 6 __х — b
* х — а х + а ’
j-x ах — b __ х + Ь
* х + а х — а ’
448.
1) ----2х = -^-;
’ х + а х — а
(а + 6) х___ ах — х2 ф
а — b а-\-Ь *
(а — х)2 + (х — Ь)2 __а'
°' (а - х)2 - (х - Ь}2 “
2) ах2 + (а — Ь}х — ах;
4) ах + 6 _ а ах — b . а& а2 — х ’ аб Л
6) а ' 2“i— = 0- а2 + х
а (Зх + 2а) х — а _х + а е
х2 — а2 х + а х — а*
1 __ а — х t
сх + пх 2ах2 ’
у, a=£b, а-уЬ^Ъ.
72
§ 29. Полные квадратные уравнения
Решить уравнения:
449. 1) х2 — 4х 4-4 = 0; 2) х2 — 10х — 24 = 0;
3) х2 —4х + 3 = 0; 4) х2 — 2х— 3 = 0;
5) х2—2х —8 = 0; 6) х2 + 5х + 6 = 0;
7) х2 —Зх— 10 = 0; 8) х2+ 12х = —35;
9)х24-8х —9 = 0; 10) х2—14х—15 = 0.
450. 1) х2 —6х + 8 = 0; 2) х2 —4х —96 = 0;
3) х24-х=30; 4) х2—х= 12;
5) х2—11х = —30; 6) х2 — 60=11х;
7) х2-|х+| = 0; 8) л-2-51х + ?1 = 0.
451. 1) х2- 11х+| = 0; 2) х2-5|х + 71 = 0;
3) х2 —0,5х + 0,06 = 0; 4) х2 + 0,Эх — 6,3 = 0;
*2- 1 (х-3)2 (х + 3)2 .
о) 3 бх 4 8
(х-6)2 (х + 4)2 (х + 6)(х + 2)
452. Не решая уравнения х2 — 5x4-6 = 0, вычислить:
(a) Xj 4- х2, Х| • х2; (б) х2х2 4- XjX2;
(в) (х, + х2)3 - (х2 + х2); (г) Л + Л;
Х1 х2
U) Л + Л ’ (е) —Z------Ь / 2 ’ <ж) Х1 + 4
Xj Х2 Xj + Х2 Х| +
2) В уравнении (k— 2)х24-(& — 5)х — 5 = 0 опреде-
лить k так, чтобы: (а) х{ = 2; (б) х{ 4- х2 = 3; (в) х{ • х2 =
= —3.
Решить данные уравнения (453—456) по формулам:
(а)х=-|±/4^; (6) х=-6±/^-,
, к — k ±Уk2 — ас
(в) Х =------а-----’
применяя каждую формулу там, где она упрощает на-
хождение корней уравнения.
73
x . 5 Зх2—Юх, х2 — 7х Их « х —4
1) 64“б“ 15 ’ 2> з ю з
1 2х2 - Зх __ (Зх - 1 )2 (х + З)2 .
1 2 “ 5 5 ’
4) 2 + = 1(5х- 1)-1 (Зх — 1).
454.
1\1. х — I _. . Зх + 5 „к . . 4х — 3 _ . . 7 — х ,
1 ’ 2х — 5 “ 1 ’ 5х — 3 ’ 1 ’ 5 + 2х " ’ Зх + З ’
х _____ 8 _________4х_____.
х — 10 х — 6 х2 — 16х + 60 ’
х + 2 . 4 (х + 1) __ х (х — 4) . х — 2
х -2 + 4 — х2 — 4 —х2 Г х + 2 •
455. 1) —1--1 =1—
х — 4 х -р 2 3 — х
QK 3 — 2х . х + 3 3 ,
3-х 1 “ х+ 1 3-х ’
ох 5х — 1 х + 1 __ х — 5 8 — х ,
' 2х — 4 4х х — 2 Зх2 — 6х ’
.v 9х2 + х + 2 20 + х _ 2 (5 — 2х) _ 5 — Зх
, 6х2 — 6 2х — 2 3 (х + I) х + 1
4-г п 5 , 13 _ 17x4-10 .
4£>ь* И "Г хз+! 5(х2-х+1) ’
П\ х2 — X + 16 . 36 + X _ X + 6
х3 + х+т + X3- 1 ” _ К=Т-
Решить данные уравнения графически (первым спо-
собом) (457—459):
457. 1) х2 — 1 == 0; 2) х2 —4 = 0; 3) х2 — 9 = 0.
458. 1) х2 — 2х = 0; 2) х2-ф2х = 0; 3) х2— 4х = 0.
459. 1) 1г2-5^-- = (); 2) х24-х —6 = 0;
3) х2—Зх — 10 = 0; 4) 4х2 + Х = °-
460. Решить данные уравнения графически (вторым
способом):
1) 1х2-^-х —6 = 0; 2) х2 —0,5х — 7,5 = 0;
о о
3) 2х24- ^Х— 1,5 = 0; 4) ^х2— 1,25х — 0,5 = 0.
74
Решить уравнения (461—465):
461. 1) х2 — Зах + 2а2 — ab — Ь2 = 0;
2) хг-^(1 + 2Ь)х +-^ = 0;
3) 4х2 — 4а2х + а4 — Ь4 = 0;
4) х2 — Qbx — (4а2 — 962) = 0.
.л п п х 4~ & _ х2 4~ Q2 — fr2 — ах х 4~ Q ,
* х — а х2 — ах — Ьх ab Ь — х ’
2) cd2 — сх (с — х) = d(x2 — d2), с ф d',
х _|______________2д2______________zax_____.
' х + За * (х + а) (х + За) х2 + 4ах 4- За2 ’
463.
1)
(с 4~ ^) х2 — 4с х 4с2 — 1 _______р
с 4- d * (с 4- d)2 ’
d2z2 । z2 4- k ______________ ck
(c 4- d) (c2 - d2) c.+ d c2 — d2
c ~~~ df
I______cz2
* (c 4- d)2
3) (m 4“n) t2-------т— — dt — mt.
7 ' 1 ’ m + n
464.
465.
1) a (x 4- 6)“J 4- (x — b) (2x 4- a)"1 = 0;
n\ __________z — 1________, 1 __ Z
' c2 — cdz — cd 4- d2z c — d c — dz ’
3) гЦсЧ^ + ?)- + (с-<)^-<3-с2)"-
= (c + 0(c2 + c/ + /T'.
I ч a2x2 — 2a2x 2ax _ a + x _ 2a (3x — a) .
' x2 — a2 * a 4- x a — x x2 — a2 ’
2) (1 4- bx) (a — x) 4- x2 = a2.
466. 1) Найти значение k, при котором один из кор-
ней второго уравнения был бы вдвое больше одного
из корней первого уравнения:
(а) х2 — 5х 4-^ = 0; (б) х2 — 7x4“ 26 = 0.
2) При каких значениях коэффициентов, или при
каком соотношении между ними в уравнении ах2 4- Ьх-\-
4-с = 0:
(а) сумма корней его равна их произведению;
(б) корни обратны друг другу;
(в) корни равны по абсолютной величине, но разных
знаков;
75
(г) один корень равен нулю;
(д) оба корня равны нулю;
(е) один корень вдвое больше другого?
Составить квадратные уравнения по их данным кор-
ням (467-472):
467. 1) —2 и 2; 2) 4" и -т? 3) 0 и 2; 4) 3,2 и 0.
Л £
468. 1) 0 и 3; 2) 2| и з^-; з) о и — 6.
469. 1) •4 и 51; 2) 1 2 о 3 . 1 3- и 2Т: 3) 0,2 и 0,5.
470. 1) а и а; 2) 1 1 и —, а а 3) и О о
471. 1) 0 и а; 2) 0 и —2а; 3) 0 и f.
472. 1) а и Ь; 2) — а и Ь\ 3) а и 2Ь.
§ 30. Разложение квадратного трехчлена
на линейные множители
473. Разложить на множители многочлены:
1) 15х2 —2х—1; 2) 8х2 —2х —3;
3) 4х2 — Зах +1 (2а2 — ab — 62);
4) 8х2-^-(1 —26)х —
5) х2 — а2х + у (а4 ““ &4);
474. Сократить дроби:
.ч 15х2 — 8&х + &2 , пч
12х2 - — &2 ’
а2 + 6а — 91 е дх
а2 + 8а-105’
2х2 — 18хг/ + 28г/2 в
' 4х2 — 4ху — 8уг * '
а2 ,
b ’
6) 4х2 — 12&Х —4а2 +
12а2 — а — 1
За2 + 5а — 2 ’
8х2 + 32х — 360 ,
6х2—72х —210 *
6х2 — Зху — 9г/2
12хг —ЗОхг/ + 18г/2 ’
Разложить на множители выражения (475—476):
475. 1) х2-^х + 1; 2) х2-f-——х1 *,
3) х2 — (14-а)х + а; 4) 4х2 — 2(1 + а)х + а.
476. 1) 2ах2 — (2 + а) х-J-1; 2) ах2 — (2 — За)х — 6;
3) abx2— (Ь — 2а) х — 2; 4) abx2 — (а + Ь2) х + Ь»
76
§ 31. Исследование квадратного трехчлена
Определить, при каких значениях х следующие трех-
члены будут иметь положительные и при каких отри-
цательные значения (477—483):
477.
1) г/= 2х2 — 16х 4-24; 2) ^ = 0,5х2 — х — 7,5;
3) у=- 1,5х24-4х4- 1,5; 4) у= - х2 4- 9х — 14.
478. 1) у — х2— 4x4-3; 2) у = х2 — х —
3) /у = х24-0,5х — 7,5; 4) z/ = 6x2 —7х —3.
479. 1) у=-х24-2х— 1; 2) у = х2 — 2х 4- 1;
3) у==— х2 — 6х — 9; 4) у — х2 4- 6х 4- 9.
480. 1) у = - 16х2 — 8х — 1; 2) у = 9х2— 12х 4- 4;
3) г/ = 4х2— 12х 4-9;
4) у = - Зх2 4- 4х 4- (3 — 2х)2 4- 7.
481. 1) у = х2 — 6x4- 13; 2) —х2 4-6х—13;
3) у = х2 — 4x4-13; 4) у= - х2 — 4х — 13.
482. 1) г/ = 3х24-2х4-1; 2) у = — 2х2 4- 4х — 7;
3) у = 9х2 — 6x4-37; 4) у = - 9х2 4- 6х — 37.
483.
1) i/ = — 0,5х2 4-1>5х 4-5; 2) г/ = -5х24~ 20х-20;
3) г/ = Зх2 4-2х 4-2; 4) у = Зх2 4- 4х — 7;
5) У = — к1 4“ Зх — 4; 6) у = Зх2 4~ 5х — 50.
§ 32. Квадратные неравенства
Решить неравенства аналитически (484—487):
484. 1)х2>1; 2)х2<1; 3) х2 — 4 > 0;
4) х2 — 4 <0; 5) 3(х2— 16) > 0; 6) х2-а2<0.
485. 1) х2—15х> 3(108 — 5х);
2х2-з х2 + з Q
2 4 >
3) ах2 —- > 0, а > 0;
4) х2 — 4а2 — 12аЬ — 962 < 0, а > 0, b>0, a>b.
486. 1) х (х — 2) > 0; 2) 5х (х 4- 3) < 0;
3) 4х(2 — х) < 0; 4) Зх24-х>0.
77
487. 1) 7х2 — Зх < 0; 2) 15х2 > 4х;
3) (х 4- а) (х — Ь) + (х + Ь) (х — а)>
>2а2 — 2Ь2, &>0, а>0, а > Ь\
4) {а + х) (2х + а) + (х — а) (а — 2х) >
> (а 4- 2х)2'— а2, а > 0.
Решить неравенства методом интервалов (488—489):
488. 1) (х~3)-Ц-±..4) > 0; 2) 5) (у.+ 5) < 0;
7 х — 2 7 х — 4
3) Зх2 —- 5х —- 2 < 0; 4) 5х2 — 7х 4- 2 > 0;
5) (6х2 — 2х — 20) (х 4- 3) > 0;
6) (а-х)(х-6) < 0 а о b > о, а > Ь.
’ ах — b ’
х2 + 4х + 3
х2+ 2х + 8
(8 — х) (х — 5)
х2 — 5х + 6
489. 1)
2х — 17 . х — 5 ,
х — 5 х + 2 *
3)
4) (Зх — 1) (4 — х) (2х — З)2 > 0;
х2 + 2х —3 . п (х — 3) (х — 5) (8 — х)3
5) -^-gx+g >о; 6) (х_2)(5ж_7)а
7\ 0>х-5)(4х-7)2”
° (4 _ Зх) (8 — x)2rt± 1
490. Решить неравенства графически:
1) х2 —5x4-6 >0; 2) х2 —2x4- 1>0;
3) х2 — 2х — 3 > 0; 4) х2 4- 2х 4- 3 > 0;
5) 6х — 15 < х2 4- 2х; 6) х2 — 12х 4- 30 > 0.
491. Решить неравенства аналитически:
1) abx2 — b2x-}-a2x — ab>0, а > О, b > 0, а> &;
2) 12х2—-^ах —— < 0, а > 0;
о I и
3) 6а2х2 — + 3/г>о, а > О, b > 0, а > Ъ.
Найти области определения следующих функций
(492-493):
492. О »=^-; 2) «/=^4+^;
3)z/ = V.7^T; 4) у = 2/7^1 -^==.
78
493. 1) у = Ух- + 2х 4- 4;
3) у = /х2 —4х — 12;
2) у=у++уЧ-х;
4) z/ = V( 1 — х) (1 4- 5х);
6) у=]/ -<+•
§ 33. Исследование корней квадратного уравнения
по его дискриминанту
494. При каких целых положительных значениях k
уравнение Зх2— 12х + 3k = 0 имеет два действительных
различных корня?
495. При каких целых отрицательных значениях k
уравнение Зх2 — 8х + k + 6 = 0 имеет два действитель-
ных различных корня?
496. При каком значении tn каждое из данных
уравнений имеет двукратный корень:
1) (2 + т) х2 + 6mx 4- 4m 4- 1=0;
2) х2 4- 2 (tn — 4) x 4“ tn2 — 4m + 3 = 0;
3) (m — 2) x2 + (tn — 5) x — 5 = 0.
497. При каких действительных значениях а корни
уравнения Зх2 — 5ях+12 = 0 будут мнимыми?
498. Найти коэффициент b в каждом из следующих
уравнений, если:
1) 4x2 + Z>x+4 = 0 имеет равные корни (действи-
тельные);
2) 9х2 — 36х+1=0 имеет разные действительные
корни;
3) 16х2 — Ьх + 9 = 0 не имеет действительных корней.
499. 1) В уравнении х2 — ях + 20 = 0 определить
такие целые значения а, при которых его корни будут
лежать в бесконечном интервале х > 3.
2) В уравнении ах- — Зх — 20 = 0 определить те
целые значения а, при которых его корни находятся
по разные стороны отрезка [—2; 3].
3) В уравнении 2х2 —Зх — а — 3 определить те целые
значения а, при которых оба его корня находятся
внутри отрезка [3; 5].
500. Даны уравнения:
1) х2 + 2 (а — 4) х + а2 + За = 0;
2) (а + 3) х2 + 3 (а — 6) х — (8а — 5) = 0;
3) (2 — а) х2 + 3 (2 + а) х — 3а = 0;
4) 4х2 +(7а—- 1)х —За(1 + 5а) = 0.
79
Определить для каждого из них действительные
значения а, при которых корни:
(а ) действительные равные —
(б ) действительные различные (х{ =£ х2);
(в ) мнимые различные.
При каких значениях k решение следующих нера-
венств не зависит от х (501—503):
501. 1) 6х2+12х —5<0;
2) (3 + &)х2 — 5х — 4 < 0;
3) х2 + (£ + 2)х + (86+ О > 0;
4) х2 4-(26 + 2)х-]-9(& — у)>0.
502. 1) 4(1 —-|)х2—з(х—1у) + ^>0;
2) k(k — -|-+-4)х2 — (26 + 2) х + 3 > 0.
503. 1) (1 + &) х2 + 2(& — 1) х—2 (& — 1) < 0;
2) (& — 2) х2 — 4 (у — б)х-б(1 — |б)>0;
3) k(k — -|+ б)х2 + 2(1 — 6)х + 2<0.
504. При каких значениях а следующие выражения
представляют полные квадраты:
1) п(4— -)х2 — 3af 1 +-Ь+ 2а( 1 +-V,
2) а(б —-|)х2 + 5а(-^—1)х —2(3 —а);
3) (а — 1)х2 + 2ах + а(з — у);
4) За(1 +4h3-9(4+ 1)х + 2(а- 11).
§ 34. Задачи на составление квадратных уравнений
505. Знаменатель дроби на 4 больше ее числителя;
если сложить эту дробь с обратной ей дробью, то
сумма будет равна 2-^|-. Найти эту дробь.
506. Числитель дроби на 6 меньше ее знаменателя:
если сложить эту дробь с обратной ей дробью, то
в сумме получится 4-^-. Найти эту дробь.
80
507. Сумма квадратов двух последовательных целых
чисел на 51 больше удвоенного меньшего из этих чисел.
Найти эти числа.
508. На какое число надо разделить 180, чтобы
частное было на 5 больше делителя, а остаток на 7
меньше делителя?
509. В двузначном числе цифра десятков на 2 больше
цифры единиц; если это число умножить на сумму его
цифр, то получится 124. Найти это число.
510. Сумма цифр двузначного числа равна 7. Про-
изведение этого числа на число, полученное из него
путем перестановки цифр, равно 976. Найти это число.
511. В прямоугольнике одна сторона на 8 см больше
другой, а его площадь равна 9 см2. Найти периметр
этого прямоугольника.
512. В треугольнике основание на 4 см меньше
высоты, а площадь равна 96 см2. Найти основание и
высоту этого треугольника.
513. От листа жести, имеющего форму квадрата,
отрезали полосу шириной в 30 мм, после чего площадь
оставшейся части листа стала равна 1000 мм2. Опре-
делить первоначальные размеры листа жести.
514. Двое рабочих, выполняя определенное задание
вместе, могли бы закончить его в 22/5 дня. Если сна-
чала будет работать только один из них, а когда он
выполнит 3/4 всей работы, его сменит второй рабочий,
то все задание будет закончено в 9 дней. За сколько
дней каждый рабочий в отдельности может выполнить
все задание?
515. Двое рабочих, из которых второй начинает
работу на 3 часа позже первого, могут выполнить
работу за 84/? часа. За сколько часов каждый из них
отдельно мог бы выполнить эту работу, если известно,
что второй рабочий может выполнить эту работу на
2 часа быстрее, чем первый?
516. После встречи двух пароходов один из них
пошел на юг, а другой на запад. Через 2 часа после
встречи расстояние между ними было 60 км. Найти
скорость каждого парохода, если скорость одного была
на 6 км/ч больше скорости другого.
517. Расстояние между двумя станциями 96 км.
Один поезд проходит это расстояние на 40 минут бы-
стрее другого. Скорость первого поезда больше скоро-
сти второго на 12 км/ч. Найти скорости обоих поездов.
81
518. Из двух населенных пунктов, А и В, вышли
одновременно два пешехода навстречу друг другу.
При встрече оказалось, что первый прошел на а км
больше, чем второй. Если они будут продолжать путь
с прежней скоростью, то первый придет в В через т
часов, а второй придет в А через п часов после встречи.
Найти скорость каждого пешехода.
519. Моторная лодка проплыла вниз по реке а км,
а затем вверх по реке b км (а > Ь). Вся поездка про-
должалась t часов, причем остановок не было. Ско-
рость лодки в стоячей воде равна v км/ч. Определить
скорость течения реки.
§ 35. Иррациональные уравнения
Решить уравнения (520—530):
520. 1) УГ^!—Ух—10 = 3;
2) /3^1+/Г=^7— уТ^1- = 9;
3) х + У х — 1 = 2х;
4) х+ /х2+(х + 7)2= 1,8;
5) /2х—15 — УГ+Тб = -1;
6) /х+ 17 + ]/Г=7 = 5.
521. 1) /х — 10 — У 4х — 23 = У^^З;
2) У100 + У5Т+=Т = 8;
3) /Т^Тб-—£!= + /7=0;
ух — 1о
4) У7^3+Ух+5 = 2УЕ
522. 1) У94- Ух —Уэ —Ух=У2;
2) х+ Ух+ 1 = 11;
3) Ух + Ух —24 = 6;
.. X — 1 . | У X — 1
4) = 4 + -------- .
’ Ух + 1 2
523. 1) /2х — 1 + ]/'Т+2 = 4;
2) /3^7+ --= = /9^57;
у 3 — х
82
3) /10 — 5л 4- /4х — 9 = 6;
4) /22 — 13х —/2х —8 = 7.
524. 1) /2х + 5 + /Г=Л = 8;
525*.
526*.
527*.
2) /5 (х 4- 4) - /х 4- 8 — 2 = 0;
3) х2 + х + 3 4- /х24-х + 5 = 28;
4) '/(8-х)2-/(8-х) (274-л) 4- /(27 4-*?== 7.
1) /(х4- 1);+4/(х- l)-’ = 5'/F=I;
2) /Р-з/х 4-2 = 0.
1) Vх 4- /х — /х — V х = /х;
’ /7+3 /х2-9 /х-3
п 2 _ ^10х+ 2 1_ == П.
7 гт=п ______
2) Vx + aV^ — }^^-4-х = уЛ-^ —X.
528*. 1) 2/х — 7/х 4-3 = 0;
2) /Нт + У 7=7 = 2;
г I/ j л г а л
3) 1______।______6____— 1
7 VЗх + 10 ^Зх2 + 16% + 20 /х + 2 *
529*. 1) х 4xxtia —2) = За;
4 __________________
2) /Г+х 4- ]flx+X = /243х;
3) /10 —х — /з^х = 1;
4) /вЧ-х 4-/8^х = 4.
530*.
2) /4х2+ 10х4-4 4-/2х2 —5х —3 = /2х4- 1.
531. Решить следующие иррациональные уравнения
<? помощью производных пропорций:
и 1 = 2/[+ 1 .
7 Ух-2 г/г —з ’
83
a — b l^x — b a — b
а У x + b + c cfx + b a ,
aj^x + b + c — 2a c J^x + b — a
a\rx — c + b a* 1 2 3 + b2 ’
а^х-\-Ь2 bY x — a2
§ 36. Биквадратные уравнения
Решить уравнения (532—534):
532. 1) х4 — 5х2 + 4 = 0; 2) х4 — 13х2 + 36 = 0;
3) х4 —25х2+ 144 = 0; 4) х4 —41х2 + 400 = 0;
5)4х4 - 5х2 +1 = 0; 6) 9х4 — Юх2 +1=0.
533.
1) 36х4 — 25х2 + 4 = 0; 2) 2х4 — 19х2 + 9 = 0;
3) 2Х4 — ЮОх2 + 98 = 0; 4) Зх4 — 51х2 + 48 = 0;
5) ЮОх4 — 13х2 + 0,36 = 0; 6) Зх4 — 75х2 + 432 = 0.
534. 1) х4 — (а2 + 62) х2 + а262 = 0;
2) 16х4 —4(а2 + 62)х2 + а+2 = 0;
3) а2Ь2х4 — а4х2 = Ь4х2 — а2Ь2;
4) 8х4— 8а2х2 = 4х2 — 4а2;
5) 2x4 + 50m2 = 2m2x2 + 50x2;
6) 36х2 —9m2x2 —4m2x2 + m4 = 0;
7) Зба-W —464х2 —9а4х2 + а+2 = 0.
535. Решить уравнения:
1) (х2 + 5х + 8)2 — 6 (х2 + 5х + 8) + 8 = 0;
2) (/* + 2 - 3 (/*4-2 - 4-2 = 0;
3) (1/ГГз+1'/37=2)2-8(УЙ?3 + Хз7^2)4-7=0;
4) 10(х4- + -45(х 4+ + 50 = 0.
84
Решить уравнения (535—538), раскладывая их левые
части на множители:
536.
1) х3 —6х2 4- Их —6 = 0; 2) х3 —7х24- 16х— 12 = 0;
3) х3 — 2х2 — 9х +4 = 0; 4) х3 —Зх-|-2= 0;
5) х34-3х2 —4 = 0; 6) х34-х2 —2 = 0.
537. 1) х4 4-х34-х 4-1 = 0; 2) х4 4-х3 —х — 1 =0;
3) х44-х24-1=0; 4) х44-5х34-15x4-75=0;
5) х4 4- х3 4- 6х2 4- 5х 4- 5 = 0;
6) х34-8х24- 17x4- 10 = 0.
538. 1) х5 4-х44-х34-х2 4-х 4- 1=0;
2) х5 — х4 — Зх3 — 2х = 0;
3) Xs 4- 2х4 4- 2х3 4- 2х2 4- х = 0;
4) х5 — Зх4 4-х3 4-Зх2 — 2х = 0;
5) х5 — 5х4 4- 2х3 4- 20х2 — 24х = 0;
6) 5х5 — 6х4 4- 6х2 — 5х = 0.
Составить уравнения по заданным их корням хь х2,
х3, х4 (539—540):
539. 1) Xj = 1, х2 = 2, х3 = 3;
2) Xj = — 1, х2 = 2, х3 = 3;
х2 = 2, х3 = 3;
х2 =z= 2, х3 —— ~~~ 3;
х2 = 2, х3 = 3, х4 = 4;
х2 = — 2, х3 = 3, х4 = 4.
х2 = i У 2, x3 = — ty 2;
х2 = Z, х3 = — i\
х2 = 3, х3 = i У 5, х4 = — i У 5;
ЭС 2 3 1 ” ,
5) Xj = 1 4- h х2~1 — it х3 = 1 — 3/, х4 = 1 4" 3Z.
4) Xj= 1,
5) Xi = l,
6) Xj=l,
640. 1) xt = 3,
2) Xj = 3,
3) Xj = 2,
x< = 2
85
§ 37. Двучленные и трехчленные уравнения
Решить двучленные уравнения (541—546):
541. 1) %4 —4 = 0; 2) %3 4- 1=0; 3) х24-4 = 0; 4) %3— 1=0.
542. 1) %2—16 = 0; 2) %24- 16 = 0;
3) %з_|_ 8 = 0; 4) хз__ 8 = 0.
543. 1) %4 — 16 = 0; 2) %4 4- 16 = 0;
3) 8%?4-1=0; 4) 8%3— 1=0.
544. 1) %6— 1=0; 2) %64-1=0;
3) %6 —64 = 0; 4) %б —729 = 0.
545. 1) %6 4-64 = 0; 2) 16%4 —9 = 0;
3) 81%4 — 25 = 0; 4) 64%б— 1=0<
546. 1) 4%4 = 49; 2) 25%4 = 49;
3) 27%6 = 64; 4)32%5=1.
Решить трехчленные уравнения (547—552)
547. 1) (%— I)2— 5(%— 1)4-6 = 0;
2) (2% —5)2 —5(2%—5) 4-6 = 0;
3) (4% — I)2 — 4(4% — 1)4-4 = 0.
548. 1) (5% —2)2 —3(5% —2)4-1=0;
2) (0,2х 4- I)2 — 4 (0,2% 4- 1) + 3 = 0;
3) (0,3% — 2)2 — 8(0,3% — 2) 4-3 = 0.
549. 1) (% — 2)4 — 5(% — 2)24-4 = 0;
2) (% — З)4— 10(% — З)24-9 = 0;
3) 4(% — 5)4 — 5(% — 5)24- 1 = 0.
550. 1) 2(5% — 6)4— 19(5% — б)2 4-9 = 0;
2) 3(2% 4-7)4 —7(2% 4-У)2 4-2=0;
3) 3(3%4-4)4 — 28(3%4- 4)24-9 = 0.
551. 1) 8%6 —9%34- 1—0;
2) %6 — 2%34- 1 =0;
3) (%4-3)6 — 9(% 4-3)3 4-8 = 0.
552. 1) 8(3% 4-7)6 — 217 (3% 4" 7)3 4“ 27 = 0;
2) 16%8 —257%4 4-16 = 0;
3) 4- —3 = 0.
86
§ 38. Возвратные уравнения
553. Используя подстановку Л'4-~- = / и формулы
^ + v = f-2’
х3 + Л-=/3-3/,
л:4 + ~ = .'4-«! + 2,
решить следующие уравнения:
1) 12х4—16х3—Их2—16x4-12 = 0;
2) %8 + 4х6 — Юх4 + 4х2 4-1=0;
3) Юх6 4- х5 — 47х4 — 47х3 4- х2 4- Юх = 0;
4) 1 Ох6 4- 19х5 — 19х4 — 20х3 — 19х2 4- 19х 4- 10 = Qj
5) Эх6 — 18х5 — 73х4 4- 164х3 — 73х2 — 18х 4- 9 = 0.'
§ 39. Системы уравнений второй степени
с двумя и более неизвестными
Решить системы уравнений способом подстановки
(554-559):
554. (Зх2 —4у2 = —1, (2х24-3у2 = 5,
{ х4-у = 2; 2) I 2х4-/=3;
| 2х2 — Зу2 4- 5ху 4- 2х 4- Зу — 22 = 0,
3) 1х-у=1;
( х2 4- 2у2 — Зху 4- 4х — Зу — 5 = 0,
4) . о
1x4- У = о-
555.
1)
3)
I 2х2 4- У2 + Зху — 4х 4- Зу — 14 = 0,
I 2x4- У = 4;
f х2 4- у2 — 4х 4- 4у — 17 = 0,
ол у —• 13 г
1 2х24-2у2 + 8х4-8у —20 = 0,
1 6х2 — 10у = — 4;
I х24-у2 —2x4-2у— 15 = 0,
I ху = 6.
4)
87
556.
Гхг/ + х2 = 5, f х2 — ху-\-у2=Г^1
1} 1 г/ + 3х = 6,5; } (7х —8г/ = 5,7;
f х2 + г/2 + х + г/= 6,24,
' 5х + 3у = 7;
5хг/— 2х2 + 7х — 8у = 10,
4х —5у = 7.
4)
557.
1 + 1 = 1
х у 4 ’
х +г/= 18;
1 . 1
3)
558.
3)
559.
1)
3)
= 9
у + 2 20 ’
4______5 _
х — 1 у + 1
3 _ 2 .
х+ 3 ~ у ’
1 + х + X2 _ о
1 + у + у2 ’
х 4- у = 6;
х у___
—— — а,
У
1 +~хт = «2;
х — у = а(а + 1),
х = у2-,
( 1 — 1 = 1_
2) ! х У 12 ’
I у — х = 6;
Z 3 3 ______5_
4) ) х — у ‘ г/ + 3 1,33 ’
х + Г/= 5.
-------1----— = 2,
х 4" 5 ~ у — 3
4 1.
х — 2 у — 6 ’
х2 4- г/ + 1 _4.
у2 4- х 4- 1 2 ’
X — у= 1.
2)
X и "4е и ____________ g
а — b у *
х = у;
Решить системы уравнений
(560-563):
560
! x т у _п
а ~ ’
х2 4- у2 — 2а2 = 2.
используя теорему Виета
561.
( х 4- у = 8,
•Ч х9=15;
Г х + у = 6,
I ед = 8;
1)
xy = b\
x + У~
( х 4- у — 12,
I ху = 32;
4) ( х + ^ = 7’2,
’ ( ху = 0,14.
( х + у = а,
2)
( ху — — 2а2;
( х 4- у = а + 2bt
ху — — За2; I ху = ab + &2.
88
562. 1 х — у — 16, ( х — у — 3,
1) | ^ = -48; 2) 1 х— .</ = 6, ( хг/= — 2; х — г/ = л,
3) { m 4) хг/ = 16; 1 ху = Ь.
56». Ji J_= 34
1) < У ‘ х 15 ’ 2) х + у = 34; х ' у 5 ’ х J- у — 26;
3) [1-1 =0,5, „ ух 4) < х — г/ = 0,1; 1О o' 1Л II II ю | &>
Решить системы уравнений (564—566), используя
формулы а2 ± 2аЬ + = (а ± Ь)2:
564. х2 + У2 — 25, ( х2 + г/2 = 34,
1) < ху=12; 1 X2 + у2 = 29, ( ху = 15; V2_|_^2==58>
3) ‘ хг/=10; v 1 хг/ = 21.
565. х2 + г/2 = a2 J- Ь2, ( х2 + у2^4а2+Ь\
1) ху = ab", х2 J- у2 = 9а2 + 462, 1 xy = 2ab’f ( х2 + у2 = т2 + 4/г2,
3) j хг/ = 6а&; | ху = 2тп.
566.
1)
3)
х . у __ 34
У "Г” X 15 ’
X2-J- г/2 = 34;
Х_ У_= 5_
У ' х 2 ’
х2 + г/2 = 80;
2)
4)
X , у _9 1
у + X 2 2 ’
х2 + г/2 = 20;
х | у о 1
?+т=з-з.
х2 + у2 = 90.
Решить системы уравнений (567—570), используя
.подстановку y = tx'.
567.
1 х2 + %у* = Ъ\,
I 4хг/ + 5г/2 = 69;
3)
Г 2х2 — Зхг/ + у2 = 36,
I Зх2 + 4хг/ — у2 = 94;
Г 5х2 + 8хг/ —9г/2 = 27,
( Зх2 — 4хг/ + 4г/2 = 8;
Г Зг/2 —2хг/ = 4,
2) I у1— Зху — 2х3 = - 16;
Г Зх2 — 4хг/ + 2г/2 = 1,
4) I 5х2 + 8хг/ + Зг/2 = 16;
Г 7х2 — Зхг/+ 2г/2 = 53,
6) 1 2х24-5хг/— 12г/2 = 0.
89
568.
( x5 — 2xy — y- = 2,
U xz/4-z/-’ = 4;
j 5y2 -f- 5x2— 6xy = 29,
3> I 7x! + 7//!-8.«/ = 43;
f 4s/2 x2 -f xy — 6,
} l 8t/24-3x2= 14;
4)|
5xy — 4y2 + 3x2 — 38,
5x2 —'9xy — 3y2 = 15.
559.
[ x2 + x# = 36, ( x2— xy~m,
1 / I I <> j -» 2) | q
I xy + У = 4b; I «/ — xy = n;
1 x2 —2xn== 1,25, f 3(x2 — 2y-) = — 17 xy,
3) Ь2 + 4-ч/+ 1=Q; 4) ( x2=10—-4г/2.
570.
f x-~-2xz/ + y2 = 25, ( if — xy = — 12,
j 2x2 — 2xy — y2 — 11; ( x- — xy = 28;
[ 3x2 4-5xz/+ 4//2 = 12, j 4x2 — 3xy — y2 = 0,
3Ц 2x2 — 4xy — 3y2== — 5; 4Ц Зх2 4-2z/2 = 20.
Решить симметрические системы уравнений (571 —
573), используя формулы следующей таблицы:
ь h
S’^X' + U , Х + у — 'Л, xy — v
Si — х + у — и.
S2 = х2 + у2 — и2 — 2v
S3 = х3 4- у3 ~ и3 — Зии
S4 == xi + У1 ~ — 4u2v + 2и2
S5 ~ х5 + //5 = и5 — 5u3v + 5«о2
1)
j ~Ь ху 4~ у~ — 28,
[ х + ху 4- у — 14;
( х4 4- if = 97,
3) , .
I х -г У = а;
572.
5
X 4- У = у ху,
2) 1
—8|;
( X4 4- Х2у2 4- у4 = 133,
4) о , 7
I х- — ху-\-у = 7.
* х^~\~у“гх4_у === 23,
х4-// = 0,75ху;
[ х2 — ху 4- У2 = 19,
I х — ху 4- у = 7;
90
4){
х24-У24-2х4- 2//==30,
х2 + у2 + ху = 27.
Г Х2 у2 _|_^==21,
I * +*/ + *// = 9;
573.
1)
2)
Решить системы уравнений (574—581):
574.
1)
575.
1)
576.
1)
577.
1)
578.
1)
579.
1)
580.
О
581.
1)
| х2у4-х//2 = 6,
1 ху + х + у = 5;
( х2хуг/2 = 91,
I х 4~ ху -J- у = 13;
V(х 4- у)2 = 3, 2^
. /(* — //)- = 1;
Зх = -^~,
2у
. 7+7= 18^+2;
( х2#4-ху2= 12,
( ху + х + у = 7;
Г (х — у) (х2 + У2) = 447,
I ху(х — у) = 210;
( х-у2 4- х3у- =12,
( х2у3— х3г/2 = 4.
(х2+у2 = — 2(3x4-//)
I х4-у= —8.
1 । ' _ 4
, Vx V у 3 ’
ху = 9.
х2у 4- ху2 = 240,
1.1 5
х + у ~~ 12 ’
| х34-у3 = 35,
I х#(х 4-г/) = 30.
( х2 4- 2у2 = 6;
2) I х4 4.4^4 = 20.
х4 4" У4 + х2 4- у2 = ИО,
• ху=— 6;
х —У — 2 = 3,
ху 4- xz 4- yz = 11, 2)
х2 4-У2 4-г2 = 27;
( х4_^4=15
2) з 3 -
I х3у — ху3 = о.
X 4" у — z = xyz,
х — у 4“ z — xyz,
— X 4- У 4- -г = xyz.
§ 40. Задачи на составление систем уравнений
второй степени
582. Произведение двух целых чисел равно 30, а их
сумма равна 11. Найти эти числа.
583. Отношение двух целых чисел .равно 3, а их
разность равна 8. Найти эти числа.
584. Разность квадратов двух чисел равна 16,
а сумма их квадратов равна 34. Найти эти числа.
91
585. Если к первому числу прибавить удвоенное
второе число, то получится 10, а если к удвоенному
первому числу прибавить второе, то получится 11.
Найти эти числа.
586. Площадь прямоугольного треугольника равна
6 см2, а его гипотенуза равна 5 см. Найти катеты.
587. Найти диагонали параллелограмма, если они
относятся как 2:3, а его стороны равны 11 см и
23 см.
588. Определить стороны параллелограмма, если
они относятся как 2 : 3, а его 'диагонали равны 17 см
и 19 см.
589. Определить стороны параллелограмма, если
их разность равна 4 см, а диагонали равны 12 см и
14 см.
590. В параллелограмме большая сторона равна
меньшей диагонали, а разность сторон равна 3 см и
разность диагоналей равна 2 см. Определить стороны
и диагонали.
591. Основание треугольника 13 см; угол при вер-
шине 60°; сумма боковых сторон равна 22 см. Опреде-
лить боковые стороны.
592. Два тракториста должны были вспахать опре-
деленный участок колхозного поля. Проработав 4 часа,
второй тракторист прекратил работу (по техническим
причинам) и, чтобы вспахать данный участок, первому
трактористу пришлось 2 часа работать одному. За ка-
кое время каждый из них отдельно мог бы вспахать
этот участок поля, если первый мог бы вспахать его на
3 часа быстрее, чем второй?
593. Первая труба, действуя Отдельно, наполняет
бассейн на 3 часа быстрее, чем одна вторая. Чтобы
наполнить бассейн, открыли сразу обе трубы, но через
10 часов первую трубу закрыли, и после этого одна
вторая труба закончила наполнение бассейна через
5 часов 45 минут. Во сколько времени можно напол-
нить этот бассейн каждой трубой отдельно?
594. Два токаря изготовили по несколько разных;
деталей. Первый за свою работу получил 48 руб.,
а второй, сделавший на шесть деталей меньше, 27 руб*
Если бы первый токарь изготовил столько деталей,
сколько второй, а второй столько, сколько первый, то
они получили бы за свою работу поровну. Сколько
деталей изготовил каждый токарь?
92
595. Несколько токарей и несколько слесарей выпол-
няли определенное задание по изготовлению деталей.
Токарей было одним больше, чем слесарей. Каждая
бригада получила по 150 руб. Если бы каждый сле-
сарь получал столько, сколько токарь, а каждый то-
карь столько, сколько слесарь, то бригада токарей
получила бы на 67,5 руб. больше, чем бригада слеса-
рей. Определить количество токарей и слесарей, выпол-
нявших задание.
596. Чтобы изготовить некоторое число деталей,
два токаря работали вместе в течение 5 часов и сверх
того один первый токарь работал 50 минут. Сколько
времени требуется каждому токарю отдельно, чтобы
изготовить все детали данного заказа, если один пер-
вый токарь может изготовить все детали этого заказа
на 2 часа скорее, чем второй?
597. По изготовлению деталей заказа в течение
6 часов работала одна бригада токарей, после чего
к ней присоединилась другая, и тогда обе бригады
закончили заказ за 4 часа совместной работы. За
сколько часов могла бы выполнить заказ деталей каж-
дая бригада отдельно, если одной первой бригаде на это
требуется времени на 3 часа больше, чем одной второй?
598. С двух аэродромов, расстояние между кото-
рыми 2400 км, вылетели навстречу друг другу два
самолета. Скорость одного из них, вылетевшего на
40 минут раньше другого, меньше скорости другого на
60 км в час. Встреча самолетов произошла на сере-
дине пути между аэродромами. Определить скорость
каждого самолета.
599. Катер должен проплыть 25 км за определен-
ное время. Однако через 3 часа пути он был остано-
влен на промежуточном причале на 20 минут, и, чтобы
прийти вовремя в место назначения, он увеличил ско-
рость на 2 км в час. Определить первоначальную ско-
рость катера.
600. Две группы учащихся техникума купили неко-
торое количество театральных билетов. Первая группа
израсходовала на билеты 30 руб., а вторая, купившая
на 10 билетов меньше первой и по цене на 10 коп.
за билет дешевле первой, уплатила за билеты 18 руб.
Сколько билетов купила каждая группа?
601. В театральной кассе продано на 15 руб. биле-
тов в партер и на 10,8 руб. на балкон. В партер
93
продано на 5 билетов больше, чем на балкон, по цене
на 6 копеек за билет дороже, чем на балкон. По какой
цене проданы билеты в партер п на балкон?
602. Моторная лодка прошла вверх по течению
реки d км и вернулась обратно, затратив на весь путь
t часов.
Определить скорость движения лодки в стоячей воде,
км
если скорость течения реки и—.
603. Куплено некоторое количество товара первого
и второго сорта, причем товара второго сорта на а кг
больше, чем первого сорта. За товар первого сорта
заплачено b руб., а за товар второго сорта — с руб.
Один килограмм товара второго сорта стоит на d руб.
дешевле одного килограмма первого сорта. Сколько
куплено товара каждого сорта?
604. Определить стороны прямоугольника, если его
площадь равна а см2, а острый угол между диагона-
лями равен 60?.
605. Два велосипедиста выехали из пунктов А и В
навстречу друг другу. Приехав в конечные пункты,
каждый из них сейчас же возвращается обратно. Пер;
вый раз велосипедисты встретились в 40 км от В, а
второй раз через 8 часов после начала поездки — в
20 км от А. Найти расстояние от А до В и скорость
каждого велосипедиста.
606. Число а есть среднее арифметическое некото-
рых трех чисел, b — среднее арифметическое их квад-
ратов. Выразить через а и b среднее арифметическое
их попарных произведений.
ГЛАВА 4
ПРОГРЕССИИ
§ 41. Числовые последовательности
607. Написать формулу общего члена последова-
тельности:
1) 1, 2, 3, 4, 5, ...;
2) 2, 5, 8, 11,
3) 1 1 1 _L
д\ _L .2 £ £ £ £
2 ’ 3’ 4 ’ 5’ 6’ 7 ’
о £ 4 5 6
А 2 ’ 3 ’ 4 ’ 5 ’ * ’ ’ ’
1 1 1
7 1-2’ 2-3’ 3 • 4 ’
608. Выпишите последовательность {ап), если:
(а) ап = 0,5/г 4- 2, где С tn ^6;
(б) ап — — /г2 4- 1, где 1^ ^3;
(в) ал = (—1)". 2, где 1 5= ;10;
(г) «п = 4, где 1^ ;5.
609. Выпишите последовательность если
(а) ап = п2 + 2п, где 1 п 4;
(б) ап = п2 — 4п + 3, где 1 п 5.
610. Является ли бесконечная последовательность {aft}
монотонной, если:
(а) ап — Зп 4- 1, (б) ап = — 2п 4- 3,
(в) «л = » (г) «п = (« — З)2?
95
611. Выписать Аервые шесть членов последователь-
ности, общий член которой ап имеет следующий вид:
1) ап = 2п; 2) = ; 3) ап = п\
4) = J 5) «„ = — ( — 6) =
7) ап— 2 ’ 8> п(п + I) ’
9) а — п 2)
> п (п+ 1)(п + 3) *
612. Вычислить суммы внутренних углов треуголь-
ника, четырехугольника, пятиугольника. Какую после-
довательность представляют эти суммы?
613. Общий член числовой последовательности вы-
ражается формулой aft = 2n3 + 3. Узнать, являются ли
членами этой последовательности числа 5, 19, 57, 131,
178, 217, 305, и если являются, то какой порядковый
номер в этой последовательности они имеют?
614. Доказать методом математической индукции
формулу
1-2 + 2.3 + 3-4 + 4-5+ ... +«(«+!)==
= 4«(« + 1)(л + 2).
615. Общий член последовательности выражается
формулой ап = 2п2— 3. Узнать, являются ли членами
этой последовательности числа 47, 180, 197, 345, 447,
609, и если являются, то какой порядковый номер они
имеют?
616. Как называется числовая последовательность,
общий член которой выражается формулой пя = 3п + 1?
Выпишите первые 9 членов этой последовательности.
617. Написать формулу общего члена последователь-
ности:
1) 1, 4, 7, 10, 13, 16, ...;
2) 1, 2, 4, 8, 16, 32, 64, ...
§ 42. Предел последовательности
360°
618. По формуле ап= , где п — число сторон
правильного многоугольника, вычисляется величина его
центрального угла.
96
1) Какие элементы данной формулы являются по-
стоянными, а какие переменными величинами? Дайте
определение постоянной и переменной величин.
2) Укажите область изменения ап при неограничен-
ном увеличении числа сторон п (правильного много-
угольника).
3) Является ли в данном Примере а„ бесконечно
малой величиной при неограниченном увеличении числа
сторон правильного многоугольника?
619. Поясните на примерах следующей таблицы по-
ведение переменных х, 2 — х, :
X 1 1,9 1,99 1,999 1,9999 1,99999 1,999999 ...
2 — х 1 0,1 0,01 0,001 0,0001 0,00001 0,000001 ...
8 2-х 8 80 800 8 000 80 000 800 000 8 000 000 ...
Укажите пределы этих переменных величин при х->2
и дайте определение:
1) бесконечно малой;
2) бесконечно большой;
3) предела переменной величины.
620. Полагая п—\, 2, 3, ..., составить таблицу
соответствующих значений переменных:
а1 = 2", а2 = —2П, а3 = (-2Л
а4 = 2"п, а5=—2“л, аб = (-2)’п
и определить характер их изменения при п->оо.
621. Доказать, что
lim
Х->оо
5х — 2
7х
5
7 *
Указание. Составим разность —---------— = —. При
х-> оо эта разность является бесконечно малой как величина
обратная бесконечно большой величине.
622. Доказать, что lim (7х + 2) = 16.
х->2
Указание. Положим х = 2 + а и составим разность
(7х 4-2) — 16 = [7 (2-f-а) 4-2] — 16 = 7a. При х~>2 переменная
a -> 0 и разность между функцией 7х + 2 и числом 16, т. е. 7a,
будет бесконечно малой.
97
623. Найти пределы функции у = х :
1) при х->5— 0 и 2) при х—>5 + 0. Пояснить ре-
шение таблицами, как в задаче 619.
624. Пользуясь взаимной связью между бесконечно
малой и бесконечно большой величинами, а также
определением бесконечно малой величины и теоремами
о пределе, найдите пределы следующих выражений:
1) lim ——-
2) lim
П->оо
3) lim
П->оо
4)
lim
П->оо
п 4- 5 ,
п ’
16п — 1
8п 4- 2
7п + 8 .
4п + 5 ’
625. Пусть limxn = 2,
П->оо
следующих выражений:
a lim #„ = 0,3. Найти пределы
П-»оо
1) lim (хп + уп)\
2) lim(x„ — упу,
П-»оо
3) lim (х„ • уп);
П^оо
5) lim (5х„ + -^-Ь,
4“5^+7.
/) lim——— ;
rt->00 У1г
9) lim
п-> оо
ХП 4Хп + УП .
хп + 5
4) lim
Л->оо УП
е\ ! ( §хп — ^Уп I „
6) lim ——, + хп
\->оо\ Хп + Уп
10 4~ х\ 4" V»
Ю) lim x’t + ^2 .
П->оо Уп + 4
626. Найти пределы следующих выражений:
1) lim
х-»3
3) lim
х->3
х2 —- 4х 4~ 8 ф
Г+1 ’
х2 + 2х— 15 .
х2 - 9 ’
2) lim
х->1
х3 — Зх2 4- х 4- 4
2х-1 ’
4) lim
х->а
X3 — Q3 4
х2 — а2 ’
5)
6) lim
л->а
2х
х2-а2
7) lim
Л-> 1
х2 — Зх 4- 2
8) lim
—2
х3 4- х2 — х 4- 2
х 4- 2
х — 1
627. Найти пределы следующих функций:
1)
lim
л->1
Зх2 — 4х 4- 1
2х2 - х - 1 ’
2) lim
х->5
х -- 5
х3 — 8х2 4- 5х *
3)
lim
х-»2
х2 — 7х 4- Ю
х2 - 5х 4- 6
4) lim
х -> 1
X2 - 1 .
х3 — 1 ’
98
х —2 .. З.г4 —4х24-1
5) ит —•—х—; 6) пт -ч --------г-т-;
x-*i к —2 ’ 7 х->1 * —* —*+1
_ч ,. 4х2 — 4х + 1 оч .. х5 — а5
7) 1'ПЛ -4х,-_, ; 8) hm .
х~*"г
628. Найти пределы следующих последовательностей:
1) lim 1 . 2«-! ’ 2) lim 2rc — 1 . ti ’ 3) lim / 2 \\ Ш ’
4) lim оо 4n + 3 , 2n - 1 ’ 5) lim OO 1 1 -2-3. .. . •«’ 6) lim n->oo n n + 1 ’
7) lim П->оо n + 1 n ’ 8) lim П->оо n 4- 2 n, * 9) lim n->OO 2/? —4 . n. ’
10) lim П-»оо /_!_ \n. \3/ ’ 11) lim rt->oo n 2n-b 1 » 12) lim П->оо n n-j-2 ‘
629. Имеют ли следующие последовательности пре-
делы и если имеют, то найти эти пределы:
1) — 3 5 2n — 1
2 ’ 2 ’ 2 ’ • ' 2
m 3 9 27 { 3 \n
— 1 - 1
2 ’ 4 ’ 8 ’ * 1 1 • ’ \2) ’
3) - 1, I, -1, • .., (-1)"
§ 43. Арифметическая прогрессия
630. Указать, какие из следующих последователь-
ностей являются возрастающими, а какие убывающими:
1) 3; 8; 13;
2) 47; 44; 41; ...;
3) 7,5; 6; 4,5; ...;
4) -10; —7; -4;
5) 9,6; 4,6; -0,4; ...
631. Определить первый член арифметической про-
грессии, если
а12 = 104 и d = 9.
632. Найти сумму первых п нечетных чисел.
633. Из данного множества последовательностей
выписать арифметические прогрессии и указать их раз-
ности:
1) 1; 1,1; 1,2; 1,3; ...; 2) 1,5; 1,7; 1,8; 1,9; ...;
99
3) 3; 7; И; 15; ...; 4) 8; 6; 4; 2; ...;
5) 2; 6; 10; 14; ...; 6) 3; 5; 7; 9; 11;
7) 4; 11; 18; 25, ...; 8) 5; 6; 7; 8; 9;
9) 3; 6; 12; 24; ...; 10) 3,3; 6,6; 13,2; ...
634. Найти 8-й член прогрессии 4- 4; 8; ...
635. Найти 31-й член прогрессии 4-7; 11; ...
636. Найти 81-й член прогрессии 4- а, 4а, ...
637. Найти 20-й член прогрессии 4- 0.009; 0,012; ...
638. Определить последний член ап арифметической
прогрессии, если а[==7, d = 5 и п=19.
639. Определить разность d арифметической про-
грессии, если art = 80, at =—4, /г = 21.
640. Определить число членов п арифметической
прогрессии, если art = 200, 4 = 5,
641. Найти 301-й член арифметической прогрессии,
если первый ее член равен 0,8, а разность прогрессии
равна —0,4.
642. Найти 91-й член арифметической прогрессии,
если первый ее член равен 4,8 и разность прогрессии
-1,2.
643. Найти первый член арифметической прогрессии,
если 81-й ее член равен 500, а разность прогрессии
равна —6.
644. Найти разность прогрессии, если ее первый
член равен 1, а девятнадцатый член 42.
645. Найти сумму п членов арифметической про-
грессии, в которой:
1) «1 = 2, ап = 18, п = 25;
2) «1 = 14, ап — 86, п= 100:
3) = -6, ап = 106, п — 18;
4) «1 = —з, ап — 180, п — 12;
5) «1 = 15, 4=1,4, п = 50;
6) «1 = - 14,8, 4 = —2,1, п = 51.'
646. Определить первый член и сумму п членов
арифметической прогрессии, в которой:
1)4 = 2, а„ = 400, п=10;
2) d = 3, ап = 200, п = 20;
3) 4 = — у, ап = 20, п = 40;
4) 4 = — 0,25, а„ = 32, ц = 50.
100
647. Определить число п членов и сумму"#*членов
арифметической прогрессии, , в которой:
1) «! = — 4,5, d = 5,5, ап— 100;
2) «1 = 5, d = 5, ап = 40;
3) — 3, d = 4, а„ = 15;
4) ^ = 2, d — 7, ап = 30.
648. Решить следующие уравнения:
1) 1 4-5 4-9 4- ... 4-* = = 861;
2) 1 4-7 4- 13 4- ... 4- л: = 280;
3) (х 4- 2) 4- (х 4- 5) 4- ... 4- (х 4- 32) = 220.
649. В следующей таблице по данным элементам
арифметической прогрессии найти остальные:
№№ п/п а. d п ап sn
1 32 4 13
2 58 -3 10
3 24 33 240
4 7 1,5 117
5 -2 11 -10
6 2 25 150
7 10 <м [со оо сч 1 9 -1664- о
8 2 35 320
9 3,6 17 82
10 2 4 18
650. Найти арифметическую прогрессию, если:
( а2 = —5, ( а3=10, (а14-а4 = 29,
(«б_“а4 = 6; 2) 104 4~ «4 = 16; 3) | д2 4« д3 = 29;
( а2 4- а3 — а3 = 10, Г а7 — а3 = 8,
М 04 4-^6=17; '1а2-а7 = 75;
f а1 4~ «4= 16,
6) [ а2 • а3 = 60.
101
651. Сумма первого и четвертого членов арифмети-
ческой прогрессии равна 10, а разность между ее
вторым и третьим членами равна 2. Найти эту про-
грессию.
652. Найти сумму двадцати членов арифметической
прогрессии, если сумма ее первых трех членов равна
нулю, а сумма четырех первых членов равна 1.
653. Найти следующую сумму:
1002 —992-I- 982 —972 + ... + 22— I2.
654. В арифметической прогрессии сумма первого
и шестого ее членов равна —4, а произведение второго
члена на третий равно 32. Найти сумму первых семи
членов этой прогрессии, если известно, что все ее
члены — целые числа.
655. Сумма членов арифметической прогрессии, со-
стоящей из 30 членов, равна 36’45; первый член равен 20.
Чему равен седьмой член?
656. Сумма первых трех членов арифметической
прогрессии равна 66, а произведение второго и третьего
членов равно 528. Найти сумму 40 членов этой про-
грессии.
657. Выразить сумму п членов арифметической про-
грессии через at, d и п.
658. Определить сумму всех нечетных чисел:
(а) от 1 до 99; б) от 1 до 2/г—1; (в) от 1 до п.
659. Найти сумму пяти членов арифметической про-
грессии, заданной ее общим членом:
,, 3/7—1 5п + 7 8/7 — 3
1) = —б~1 2) ап = —— I 3) ап = —1>—.
660. При углублении на каждые 30,5 м внутренняя
температура Земли возрастает на ГС; если на поверх-
ности земли /=10° С, то:
1) какова температура будет на глубине 1000 м,
2) на какой глубине будет температура 100° С?
661. За какое время мотоциклист проедет 230 км,'
если в первый час он проезжает 50 км, а в каждый
следующий час на 5 км больше, чем в предыдущий?
662. Отец дарит каждому из своих пяти сыновей
в день рождения, начиная с пяти лет, столько книг,
сколько сыну лет. Года сыновей составляют арифме-
тическую прогрессию, разность которой равна 3. Сколько
102
лет было каждому сыну, когда у них составилась биб-
лиотека в 325 книг?
663. Два тела, выйдя одновременно, движутся на-
встречу друг другу из двух пунктов, находящихся на
расстоянии 200 м. Первое тело проходит 12 м в секунду,
а второе тело в первую секунду прошло 20 м и в ка-
ждую следующую секунду проходит на 2 м меньше,
чем в предыдущую. Через сколько секунд тела встретятся?
664. Стороны многоугольника составляют арифме-
тическую прогрессию. Наибольшая из сторон равна
19 см, а смежные стороны отличаются одна от другой
на 2 см. Определить число сторон этого многоуголь-
ника, если периметр его равен 84 см.
665. Куплено 10 кг товара двух сортов: за первый
сорт заплатили столько рублей, сколько членов в ариф-
метической прогрессии, имеющей первым членом ^ = 6,
разность d = 2 и сумму всех членов S„ = 266; за второй
сорт уплатили число рублей, удовлетворяющее урав-
нению 4-4— Ух — 7=1. Сколько стоил килограмм
товара каждого сорта, если 1 кг первого сорта дороже
килограмма второго сорта на столько рублей, сколько
единиц в выражении
К10- Кз
К’зб
666. Сколько надо взять членов арифметической
прогрессии 5, 9, 13, 17..., чтобы получить сумму 10877?
667. В арифметической прогрессии третий член
равен 35, а пятый член равен 55. На какое число надо
разделить сумму пяти членов этой прогрессии, чтобы
в частном получилось число, меньшее делителя на
7 единиц, а остаток от деления был равен половине
частного?
§ 44. Геометрическая прогрессия
668. Написать по шесть членов каждой из следующих
последовательностей, заданных формулой их общего
члена, и указать соответственно знаменатели этих по-
следовательностей:
1)^ = 3"; 2) а„ = (!)";
3) а„ = 2п; 4) ^ = (4)“.
103
669. Найти знаменатель геометрической прогрессии,
в которой:
1) ап==8 и ап+1 = 16; 2) а„ = 9 и ап+2== 81;
1 _ 1 .
&п + 1 4 И ^n+2 g >
.. 1 1
4) у И ^n+2 g4g •
670. Продолжить следующие прогрессии до шестого
члена:
1) 44-0,2; 0,4; ...;
2) ч-ь/2; 0,3/2; ...;
3) ^И'7; ^/7;...;
4) -№-?• 1; Ь ..
; 3 , 2 » 8 »
671. Вычислить четвертый член следующих про-
грессий:
1) 44-7; 49; ...; 2) 44-2; 8; ...;
3) 44-5,625; —3,75; 4) 44-1,4; 1,82; ...
672. Пятый член геометрической прогрессии равен
3125, а ее знаменатель равен 5. Найти эту прогрессию.
673. Найти сумму 10 членов геометрической про-
грессии 2, 8, 32, 128, ...
674. Найти первый член геометрической прогрессии,
в которой:
1) а7= 1458, <7 = 3; 2)а6 = --^-, <7 = -|;
3)ав=-^, ?=1|; 4)а9 = 768, <7 = 2.
675. Найти шестой член геометрической прогрессии
если первый ее член равен 15 и знаменатель прогрессии
равен 2.
676. Найти знаменатель геометрической прогрессии,
если первый член равен 1296, последний и сумма
19
ее членов равна 1943 ,
677. Найти число членов геометрической прогрессии,
з
если первый член равен последний 7500 и знаме-
натель прогрессии 10.
104
678. Найти число членов геометрической п^б^рессии,
в которой:
1) я1 = 2, <7 = 4, ап = 2048;
2) 04 = 32, q = 2-^> art = 7812yj
3) 04 = 3584, <7 = 4’ ап = 7.
679. Найти сумму членов геометрической прогрессии,
23
если первый член 2187, а последний 25-д-р и знаме-
2
натель равен у.
680. Найти сумму шести членов геометрической
прогрессии, если шестой член равен 2048, а знаменатель
прогрессии равен 4.
681. Найти геометрическую прогрессию, в которой:
( ai + аз~ 15, ( а5 + «! = 51,
' I а4 —-а2= 18; ' t а6 —а4 = 72;
f Лз==
' [ а6 4- а5 а4 = 168.
682. Найти сумму п членов геометрической про-
грессии, в которой:
1) at = 2, q = 2, n = 5;
2) а, = 4, ^ = 4’ n = 6’>
3) а, = 0,5, q = 3, n = 4;
4) 04 = 5,5, q = 2, n = 5.
683. Определить знаменатель и сумму п членов гео-
метрической прогрессии, в которой:
1) а, = 2, п = 7, ап= 1458;
2) 04 = 74^-, « = 6, ап = 2~\
О о
3)ae=is^, п = 6,
4)ai = -2D~, п = 5, а„ = -±.
684. Определить первый член и сумму п членов
геометрической прогрессии, в которой:
1) q= 1 п = 6, ап = 2-^;
105
2) q = 3, n = 4, ап = Ъ4',
3) q = 4, n = 8, an = 49 152;
4) q = 2-^, n = Q, an = — 3125.
685. Определить первый и последний члены геоме-
трической пр< агрессии, в которой-
1) п = 8, S — 1 — • ‘Эп — 1 б4 >
2) п = 7, ?=/2, Srt=15/2 + 14;
3) п — 9, 7 = 2, Sa = 1533;
4) п = 5, Q — 3— * ° g »
5) н= 12, q = 2, S„ = 4095.
686. В следующей таблице по данным элементам
геометрической прогрессии найти остальные:
№№ ri/n a, Q n an sn №№ n/n a, q n an sn
1 2 3 4 5 6 7 1 3 2 64 3584 1 2 2 4 3 1 2 2 1 2 1 3 6 7 6 9 4 2048 1458 768 7 8 9 10 11 12 13 14 1 5 125 1 1 81 3280,5 1 2 2 -6 1 3 7 13 3 8 64 1 405 2187 1 2 635 61 405 195
687. Н айти первые три члена возрастающей геоме-
трической прогрессии, состоящей из шести членов,
если сумма первых трех членов равна 26, а трех по-
следних 702.
688. Определить геометрическую прогрессию, со-
стоящую из девяти членов, если сумма первых трех
членов равна 21, а сумма трех последних 1344.
106
689. Разность между вторым и первым членами гео-
метрической прогрессии равна 20, а разность между
четвертым и первым ее членами 140; найти геометри-
ческую прогрессию.
690. Выписать шестой член геометрической про-
грессии, в которой произведение первых двух членов
равно —а произведение первого и пятого членов
равно
691. Сумма первых трех членов геометрической про-
грессии равна 28, а сумма следующих трех членов
равна 3,5. Найти второй член этой прогрессии.
692. Найти первый член и знаменатель возрастающей
геометрической прогрессии, состоящей из семи членов,
если сумма первых трех членов равна 26, а трех по-
следних 2106.
693. Определить первый член и знаменатель геоме-
трической прогрессии, в которой разность между пятым
и первым ее членами равна 60, а разность между
четвертым и вторым членами равна 24.
694. Найти арифметическую и геометрическую про-
грессии при условии, что сумма трех первых членов
арифметической прогрессии равна 15, а сумма трех
первых членов геометрической прогрессии равна 35,
первый член арифметической прогрессии на 2 меньше
первого члена геометрической прогрессии и второй член
арифметической прогрессии равен первому члену гео-
метрической прогрессии.
695. Сумма трех первых членов возрастающей ариф-
метической прогрессии равна 21. Если от ее членов
отнять соответственно 2,3 и 2, то получим три первых
члена геометрической прогрессии. Найти эти прогрессии.
696. Четыре числа составляют геометрическую про-
грессию. Если из них вычесть соответственно 2, 3, 7
и 17, то вновь полученные числа составят возрастающую
арифметическую прогрессию. Найти первые пять членов
каждой из этих прогрессий.
697. Четыре числа составляют убывающую геоме-
трическую прогрессию. Если от первых двух чисел от-
нять соответственно 13 и 4, а к третьему и четвертому
числу прибавить соответственно 9 и 30, то вновь полу*
ченные числа образуют арифметическую прогрессию.
Найти первые шесть членов каждой из этих прогрессий.
107
698. Даны прогрессии: 1) 4- alt а2, а3 и 2) +±b{, b2, b3,
где члены этих прогрессий — натуральные числа. Сумма
всех шести членов равна 192; bl==a2t b3 — 0^ = 102, при
этом Ь3 составлено из тех же цифр, что и а3, но между
ними вставлен нуль. Найти эти прогрессии.
699. Каждое движение поршня разрежающего на-
соса удаляет из сосуда 78 находящегося там воздуха.
Определить давление воздуха после двадцатого дви-
жения поршня, если первоначальное давление было
равно 760 мм.
700. Найти сумму ряда:
1)
2)7+1+^ + 1+<Шг + т+--”
701. Найти первый член бесконечно убывающей гео-
метрической прогрессии, в которой:
1) сумма пяти членов равна -3240» а сумма членов
4
прогрессии у’,
m 1
2) знаменатель прогрессии равен у, а сумма членов
4
прогрессии у.
702. Найти знаменатель бесконечно убывающей гео-
метрической прогрессии, в которой первый член равен 2,
о 1
а сумма членов прогрессии 3 g-.
703. Найти пятый член бесконечно убывающей гео-
метрической прогрессии, в которой знаменатель равен у,
о 3
а сумма членов прогрессии равна Зу.
704. Сумма бесконечно убывающей геометрической
прогрессии равна 25, а сумма первого и второго ее
членов 9. Найти прогрессию.
705. Найти суммы бесконечно убывающих геометри-
ческих прогрессий:
Т' 1 ' 8 ’ • • • ’ 2) з • в. 12 • • •;
3) у- 1 1 27 ’ ’ ’ ’ ; 4) I, 1, 7~2,
5) 2, 1 1 50 ’ * ’ •’ 6) 5- j. Т5Т-
108
7) /5, -4=-, 8) /7, -U, —U-, ...
5 5/5 /7 7/7
706. Каждую из следующих периодических дробей
представить в виде суммы членов бесконечно убываю-
щей геометрической прогрессии и определить предел
этой суммы:
1) 0,333 ...; 2) 0,222 ...; 3) 0,375375375 ...
707. Каждую из следующих смещанных периодиче-
ских дробей разбить на две части так, чтобы одна
из частей представляла сумму членов бесконечно убы-
вающей геометрической прогрессии, и вычислить предел
полученной суммы:
1) 4,65555 ...; 2) 7,834444 ...; 3) 0,2777 ...
708. Дан равносторонний треугольник, сторона кото-
рого а. Из высот этого треугольника строится новый
правильный треугольник, из высот второго строится
еще треугольник и т. д. Определить предел суммы
площадей всех построенных таким образом треугольни-
ков и предел суммы их периметров.
709. На стороне угла в 45° взята точка на расстоя-
нии а от вершины. Из этой точки опущен перпендикуляр
на вторую сторону, из основания этого перпендикуляра —
новый перпендикуляр на первую сторону и т. д. Найти
предел суммы длин этих перпендикуляров.
ГЛАВА 5
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ И ЛОГАРИФМЫ
§ 45. Показательная и логарифмическая функции
710. На одном чертеже начертить графики следую-
щих функций:
1) z/ = 2x, // = (4) » 2) У = ^х-
Описать: (а) общие свойства функций, (б) различие
свойств функций.
711. Построить графики следующих функций на от-
дельных чертежах:
/ Q \Х / 9 \х
1) у = ; 2) ^ = (4) ; 3) у = 4*.
712. Начертить графики следующих функций на от-
дельных чертежах:
1) у^2х+1х^ц‘, 2) у = 2х-]х-[]-, 3) z/ = 2*+l*+11.
713. Какое заключение можно сделать относительно
чисел а и b (какое из чисел больше), если:
/ 9 \а / 9 \& / Q \а / q \Ь
')({)> ({); 2) ({) >(т)
3> (4) < Ш' 4> (4) < (4)
5> (у) >(!)•- 6»(24)>Н)?
714. (а) Какое заключение можно сделать относи*
телыю показателя степени а, если
НО ,
(б) Какое заключение можно сделать относительно
положительного основания а, если:
1) а~2 > 1; 2) а~2 < 1; 3) а"3 < 1; 4) а~4 > Г?
715. Написать область допустимых значений аргу-
мента следующих функций:
5 3
1) У = ах\ 2) У = Я , 3) у — а'х\
г— 3
4) y = aVx\ 5) y = aVx-, 6) у = а^-^-ъ.
716. Следующие равенства записать с помощью лога-
рифмов:
1) 53= 125; 2) 43 = 256; 3)|jj'=-b
4) 73 = 343; 5)2"5 = -^-; 6) 3"4 = Ш.
717. Следующие равенства переписать в виде пока-
зательных:
1) log327 = 3; 2) log264 = 6; 3)log±8=-3;
2
4) logaa = — •, 5) log3 a3 fa4 = 5,7.
Va2
718. На основании определения логарифма решить
следующие задачи:
1) Какое число имеет логарифм 2 при основании 3?
2) Какое число имеет логарифм 3 при основании 4?
3) Найти логарифм числа 625 по основанию 5.
4) Найте логарифм числа 2,56 по основанию 1,6.
5) При каком основании логарифм числа 81 равен 4?
6) При каком основании логарифм числа 0,0000000032
равен 5?
Решить следующие уравнения (719—721):
719. 1) log03x = 3; 2) log02x = 4;
3) 1о^о,5х = Т; 4) log3_* = 6;
У 5
5) log Б_х=-|-; 6) log —#
а* Vas у а У а У а
7) logj_ У49 = х; 8) log, -±- = _3; 9
9) logsfx —4)(х —2)= 1.
Ill
720. 1) logx27 = 3; 2) logx64 = 3;
3) 10gx49 = 2; 4) logx4 096= 12;
5) logx 8192 = 13; 6) logx 16 384 = 14.
721. 1) log265 536 = x; 2) log2 0,78125 = x;
3) log20,0625 = x; 4) log3____
Y(a +d)2
5 ___
5) 10g^7? Va = x; 6) 10g3> T = x-
722. Используя логарифмическое тождество aloeaN=^t
найти значение каждого из следующих выражений:
1) 2!°gi7 * 9. 2) 2,og218; 3) glogj 25,
4) g2 logs 36. 5) 410®28; 6) jglog, 15.
7) 2glog5 io. 8) 36Iogs4“2; 9) g|2,5 logs 6+2.
10) y2 log, 3+1. 11) 5~21og’3; 12) 7| log, 2-1.
13) 3l+log3H^10; 2- log 2 14) 3 /3 ; 15) }72log29+2—12.
723. Сравнить расположение графиков взаимно обрат-
ных функций: у — ах и y=\ogax.
Найти область определения каждой из следующих
функций и построить их графики на отдельных черте-
жах (724-725):
724. 1) z/ = log2(x —3); 2) у = log± (— х);
3) у = log5 (2х2 + х — 3); 4) у = log± (х2 + 1).
з
725. 1) z/ = logj х — 4 [; 2) у = log3| х — 3
2
3) # = log4| х I; 4) z/ = logjx].
4
726. Используя свойства логарифмической функции,
решить следующие неравенства:
1) log3x > 0; 2) log4x>0; ' 3) lgx>0;
4) log^x > 0; 5) log^x >0; 6) Igx < o;
7) log± (x — 3) < 0; 8) log± (x — 4) < 0;
5 7
9) Iog0)5(x2-5x + 6)>0.
112
Решить уравнения (727—728):
727.
1) 1 og3 (х2 - 5х + 9) = 1; 2) log2 (х2 - 5х 4- 8) = 1;
3) log4(x2-5x+ 10)= 1; 4) log0>5 (х2-5x4-8) =-1.
728.
1) logs(х2 — 4х + 4) = 0; 2) log7 (х2 — 2х — 34) = 0;
3) log05(x2- 17x + 73) = 0;
4) log0’3(x2 —29x 4- 199) = 0.
729. Что больше:
1) log312 или log315; 2) log5 20 или logs 28;
3) log! 12 или log! 15; 4) logj 20 или log] 28?
“ТУТ
730. Решить уравнения:
О log з -^ = х; 2> 1о£ 3 х==~4;
2VT 4УГ 4
3) log 3_х=-6; 4) log0i32|/2=x;
2 У 5
5) log,4=1|; 6) log,0,125 = —2.
731. Вычислить выражения:
1) 5 logs 25 4- 8 log2 64 — 4 log3 27 4- log2 2 4- log51;
2) log2log216 —log2log381 4“ log5 5 4- 1g Ю4- Ig 1;
3^ З1-^ 7 j giog5 8+i __ 2>4Io44 10+1,
§ 46. Логарифмирование и потенцирование
Прологарифмировать следующие выражения (732—
738):
732. 1) x = 3abc; 2) х = 2а (Ь 4- с)',
3) х = 5 (а2 4- Ь2)', 4) N = а • п(т — п)\
5) 6 = a-sin а; 6) т = 5м cos 2а.
п х==2^. 91 х= 4(а + 6) •
/Ой. V х 3ab , х >
3) v = -^; 4) I = mV /(а — &)’.
113
734. 1) с = 2л/?; 2) у==4^3;
О
3) х = a~<b~ tg ₽! 4) х -
{а-Ь) 2
735.
1) х = 2аУа(а + Ь)2; 2) S = У р(р — а)(р — Ь)(р—С);
3) v — 4 cos2 4” Vsin а;
О л
2 1 4
4) х = 2а36~2 У2а2Ь2.
736.
1) х = |/~(а263 Ус) 2; 2) х — а~2 УЗа sin а :
о\ е 2р .. / р , 5а~2 У За sin2 а
3)S = -rVVtga; 4).v = - .
737. 1) x = 2sinacosa \/ Р7 ;
Юз ’
2) х — cos р ctg р cosec р (а ~Ь 6)“3 • 4 а-4;
3) х = т3п~2 ^2 cos (15° + За) sin (15° — За):
б : (tn + л)2 р 3;
4) х = а2с4 У (а3 — Ь3) с5 : Ь3.
738. 1) х = а~2Ь~4 Ус*: 7 (а ф- Ь)4;
2) х = У (г + $): {г • s)-3;
о\ («+ bYci .
Л -- 5 ______ >
У (а — 6)0,5
.. 0,5|/(а — Ь)2 о , /ол .
4) X =----- П>° +а~ C0S За *£ (30 + а)'
2 sin —--
Прологарифмировать следующие выражения, пред-
варительно приведя их к виду, удобному для логариф-
мирования (739—744):
739. 1) х = ~^4^£!24а) ;
' За У а2 + Ь2
1
пч v = a~2b2 (1 +tg3a) #
} {а + Ь)3 »
114
_____ т3п~2 J/^0,5 — sin 6a e
X ’
(tn—n)2p 3
V/l + ctgP
X --- 5___________ •
3tn~ln3 Yp3
/ У2
0,3 ----cos 4a
740. 1) x =——--------
{tn — n)2 p 3
л. V 3 — 2 cos 2a
V mj/n/p
q\ v_ МЙЕЕМ.
x ^2 ’
—g---cos a
__ 3a->d2|Za3 - b3
4) X — .
— + cos 25°
Y 2
741.
1)
(1 +tg85°)Ya2 ~b2
2)
3)
4)
a2b~3fr
1
sin a--—
x=________
2a-3Vb-‘c ’
_ cos 20+ 0,5 .
X - 4 _ ,
3a-1 Y6
3a2 (tg 30° + tg0)
0,3c ~2b3
742. 1) x= 1/a 1Va2+?2 .
r -5- + cos 40°
n\ _____ cos (15° — 20) Y<^5 — b3 .
(2 sin 40+1) a0,2 b~l ’
3) x = 3 — 4 sin2 a;
4} r — 3a 31)5 sin (a + P)
' л 1 - cos (2a + 20) *
115
_ / 1<з
2а~’ |/ sin 2а-v—~ —
743. 1) Х=*=------2------i-
(т — я)3 b 5
____ cos (а + р)/а-^ ,
> ~~ 1 + cos (2а + 20) ’
3) х — 1 —2 sin2 а;
4) г— l-cos(a + p)
? /3.a^sin^±f
744. 1)
(1 -tg433)]^2a2d~1c #
]Az2 — 62 *
sin а3 — b3
(1 — cos а) asb~2 *
|^3 а3д~'с sin -а
1 — cos (а + 0) ’
/(I — cos а) (а2 — Ь2)
2 |^3 a&“3sin’4a
Выполнить потенцирование (745—751):
745. (а) 1) logx = log + log2V2;
2) log-х = log tVi — log ?/2;
3) logx = nlog2V;
4) logx = ^logAf.
(6) 1) logx = 21oga + 31og&;
2) logx = y log a — 4 log
3) logx = — log a;
4) logx= —loga — logft.
(в) 1) logx = ploga + <?log&;
2) l0gx =
3) log x = 5 log a + log b\
4) logx = 4-log c — 31ogd.
116
746. (а) 1) logx = 4bg«;
<J
2) logx = j (log a + log ft);
3) iogx=31ogfl-(21^
4) logx ==y (41ogaylogc — log4).
(6) 1) log x = 4 log (a 4- b) — 31og(a — ft);
2) logx = — log a — 2 log ft — logc4-ylogd;
у (log a — log b) — у (log c — log d)
3) logx =-----------E-----------;
4) log x == у [log a + у (log b + 5 log c)] —
747. 1) logx = log(l—sin a) + log (1 + sin a);
2) log// = log 2 + log sin x-|-log cos x;
3) logx —logctga— log cos a 4-log sin a;
4) log x = у log tg 3a — у log ctg 3a.
748. 1) logx = —log (a 4-ft) 4-
4- log 3 — у log b 4- у (log a — у log ft);
2) log x = — у log ft 4~ у [log л —2 log c —
— log (a — b) 4- у log (a 4- ft)];
3) log x = — 3 log m4-y[l°g(m + n) +
4- у log (tn — n) — log n — у log p] •
4) logx = — у log a 4-у log (a 4- b) —
— 2 log b 4- 1,2 log с —у log cL
749. 1) logx = y logo + у log (a 4“ ft)— -rlogc+
Л w
4-У log cos 2a;
117
2) logx=^=log(a +6) —4\21oSa+ 4log&) +
+ log tg 2a;
3) logx== — “log(a —6) + 31og& — у log a 4-
-j- log (a 4- b);
4) logx=-|log(a —^)4-ylog(a4-^) —
— --log sin (a + p).
750. 1) logx = — log (a + £) + log 3 — ylog&4-
+ y(21oga —ylog&j;
2 3 Г
2) log x == — у log & + -4- [log a — 2 log c —
— 1 og (a — b) + у 1 og (a + 6)];
3) log№ — 31og/n + y[log(w + «) +
4- -j- log (m — n) — log n — у log p];
4) log x = — у log a 4- у log (a ± b) — 2 log b 4-
4- 121ogc — ylog d.
751. 1) logx = y loga 4-у log(a + —
— у log c 4- у log cos 2a;
2) log x = log (a 4-&) — у (2 log a 4-log bj 4-
4- log tg 2a;
3) log x — — у log (a — b) 4- 31og b — — log a 4-
4-log (a 4- b}\
4) logx = ylog(a-6)4-ylog(a + Z?) —
— у log sin (a 4-P);
118
5) log х =-|-(log a —log 5 + log с) —
- j l°g tg (a—
6) log x = у [log {a — b) — 7 log (a + b) 4~
+ | log (6-h c)].
§ 47. Десятичные логарифмы
752. 1) Найти логарифмы следующих чисел:
10; 100; 1000; 10000; 100000; 1024; 1039; 1033; 1036.
2) Масса земного шара равна шести секстиллионам
тонн. Чему равен логарифм этой массы, если 1g 6 =
= 0,7782?
3) Расстояние от Солнца до ближайшей звезды равно
40300 000 000000 километров. Чему равен логарифм
этого числа, если 1g 403 = 2,6053?
4) Расстояния от нас (от Земли) до самых
отдаленных светил, до туманностей, которые еле
видны в современные сверхмощные телескопы, прибли-
зительно равны двум секстиллионам километров, т. е.
2 000 000000000 000 000 000 км. Чему равен логарифм
этого числа, если 1g 2 = 0,3010?
5) Найти lg27 • 1021, если lg3 = 0,4771.
753. Найти десятичные логарифмы следующих чисел:
1) 0,1; 0,01; 0,001; 0,0001; 0,000001;
2) 10"7; 10“3; 1О“10; 10-12; 10-14.
754. Вес микроба, вызывающего туберкулез, соста-
вляет только 45 стобиллионных долей миллиграмма,
т. е. 0,00000000015 мг. Чему равен логарифм этого
числа, если 1g 3 = 0,4771, a 1g 5 = 0,6990?
755. Самый легкий из атомов водорода весит
0,00000000000000000000000165 мг. Чему равен логарифм
этого числа, если 1g 165 = 2,2175?
756. Вес электрона равен 85 • 10~29 г. Чему равен
логарифм этого числа, если 1g 5 = 0,6990, a 1g 17 =
= 1,2304?.
757. Найти логарифм числа 1001 10“7, если 1g 7 =
= 0,845, 1g 11 = 1,041, 1g 13= 1,139.
119
758. Дано: 1g-676 = 2,8299; lg 104 = 2,0170. Вычи-
слить без таблиц 1g 2 и 1g 5.
759. Следующие логарифмы выразить отрицатель-
ными числами:
1) 1,4577; 2) 4,4618; 3) 3,3046; 4) 6,1001;
5) 4,7828; 6) 3,5622; 7) 2,2673; 8) Т,8475.
760. Следующие логарифмы преобразовать в искус-
ственную форму:
1) -1,3814; 2) —2,4455; 3) -3,0692; 4) -1,1010;
5) -5,6220; 6) -0,5838; 7) —0,0483; 8) -0,1270.
761. Найти логарифмы чисел: 1) 9; 2) 17; 3) 68; 4) 141;
5) 459; 6) 640; 7) 1235; 8) 3807;
9) ЗОЮ; 10) 19,43; И) 1,05; 12) 800;
13) 0,53; 14) 0,0038; 15) 0,1007; 16) 0,00004;
17) 2174,7; 18) 2669,6; 19) 43,472; 20) 6,285;
21) 0,8793; 22) 0,05439; 23) 631,074; 24) 3,7936;
25) 0,6464; 26) 0,00237; 27) 20,00475; 28) 0,00008.
762. Найти по таблицам:
1) 1g sin 23° 23'; 2) Igsin Г 30'; 3) lgsin503 10';
4) 1g sin 72° 14'; 5) 1g cos 17° 20'; 6) lg cos 40° 20':
7) 1g cos 41° 17'; 8) 1g cos 80° 26'; 9) 1g tg 3° 20';
10) Igtg 16° 16'; 11) lgctg26°13'; 12) lgctg62°42'
763. Наити с помощью логарифмической линеики:
1) 1g sin 42° 46';
4) lgsin0°46';
7) 1g cos 84° 22';
10) lgtg54°20';
2) lgsin783 1 8';
5) 1g cos 62° 40';
8) 1g cos 70° 6';
11) lgctg0°38';
3) Igsin 10° 42';
6) 1g cos 73° 42';
9) lgtg43°4';
12) lgctg84° 17'.
764. Найти острый угол x с помощью логарифми-
ческой линейки, если дано:
(a) lgsinx = 1) 1,413; 2) 1,421; 3) 1,456;
4) Г,231; 5) Г,254; 6) Т,354;
7) 2,827; 8) 2,442; 9) 2,004;
10) 3,028; 11) 3,004; 12) 3,948.
120
(6) lgcosx== 1) 1,842;
4) 7,771;
(в) lgtgx= 1) 1,992;
4) 0,254;
(г) lgctgx= 1) 7,881;
4) 1,624;
2) 1,803; 3) 1,822:
5) 7,642; 6) 2,342.
2) 1,512; 3) 2,724:
5) 0,426; 6) 2,841.
2) 1,938; 3) 0,282;
5) 2,732; 6) 2,332
765. Найти числа, соответствующие следующим лога-
рифмам:
1) 1,9777;
5) 0,4756;
9) 7,1017;
13) 3,2648;
2) 3,6942;
6) 1,5682;
10) 4,7265;
14) 2,8176;
3) 0,9361;
7) 0,4008;
11) 3,4346;
15) 0,9236;
4) 2,7482;
8) 2,5683;
12) 7,3195;
16) 1,5419.
766. Выполнить действия над логарифмами:
1) 2,8106+ 1,5341; 2) 3,5362+ 1,6272;
3) 0,3751 + 1,3456; 4) 1,5724 + 2,7642;
5) 2,0898 — 0,1374; 6) 4,6497 — 5,7638;
7) 1,3918 — 3,4506; 8) 1,0034 — 7,9923;
9) 0,3751 — 3,6547; 10) 2,5296 — 7,7612;
11) 1 —1,5647; 12) 3 — 3,2534;
13) Г,2344-3; 14) 7,6742 - 2;
15) Г,0324 • (-2); 16) 0,3124-(-3);
17) Т,2957 • (-0,4); 18) 2,5412-(-1,2);
19) 2,5631 -(-0,6); 20) 2,3456-4; О
21) 0,5648: 1,6; 22) 4,1815:2;
23) 1,1462:2; 24) 7,1824: 3;
25) 2,3406 : 3; 26) 7,2347:3;
27) 3,3132:2; 28) 7,2439: (-2);
29) 2,3265 : (-0,8).
Вычислить при помощи таблиц логарифмов
(767 — 788):
767. 1) 0,48 • 574,5; 2) 0,039 • 2,73;
3) 0,349-0,076; 4) 12,35: 1,48;
5) 7549,6 : 23,374; 6) 0,0726 : 15,222.
121
768. 1) 3,423; 2) 0,3 264; 3) ^9976;
4) 1/^Г; 5) 289^032; 6)
' 9о1 /0,472
7) (О,ООО9)о,оооэ; 8) (0,0376)°’°Г6.
__ 1Ч 12,5-82,8 3,16-58,5
769. 1) ; 2) х = -з742 ;
__ 4,18 • 5,42 - 48,2 , .. _ 3,48 • 4,8! • 72,6 ,
°) х~~ 3,42-6,48 ’ х~ 4,24-6,82 *
2,24-/^57 сч 13,2-6,42
5) х =-------'---; 6) х =----т=— .
7,75 V 9,7
770. 1) N = 12 • sin 15°; 2) N = 16 sin 18э 14';
3) у = 24 - sin2 42'; 4) N = 3,6 sin318Э15'.
771. 1) yv = 5 1/7 cos 34°; 2) У = 14/240 cos 46°;
v------------------
3) дг = _^Zgl cos 62° sin 74°;
/542
4 / oc
4) У = |/ sin 64° cos 72°.
772. 1) N = 87,3 /562sin5T 14'tg51° 14';
2) W = 243 • 43,4 /9734 tg 72°ctg 19°.
773. Л' = 23,4 sin 61° 14'cos 52° tg 47°ctg523.
'7’7 4 M _ 0.054842 f0J445
t i ж. .'V - -----=rz~ ,
2,6792 /0,004562
.. 0,07356 • 2,6743
7/5. N = -~_
V 0,09615 • 3,1254
776. N= i/—Q’°I6125 .
У 3,615/0,2916
777 xy 6’2352 /°>^59
/о,0007617
__o .. 51,689 jXo,O5195
/ /о. /V =---------r ——. .
0.08642 /0,3973
5________
779 ДГ = 0.67912/0,004953
/з, 167-0,9186
122
780.
ъ_______
0,8754 /0,07961
1,375 / 425
_o< 62,082 /0,004812
V 0,3846- 28,642
782. Af = .12:l7£№g|
0,024172 /35,47
.. 44,28 /о,07825
N =------------s’-----
9,8722 /384,8
783.
784.
v== 0,2515 J5 / 8,0382/0,l
24,86 У ’
n /cos 8° 59' sin2 70° 38'
~ ctg33° 13'/0,0002
786, tg2 46°53z j/^ctg2 12° 9Z .
/849 sin 41° 41'
»r__ /0,0002 ctg 33° 13'
/ о / • /V /-------- •
sin2 70° 38' / cos 8° 59'
788. _t847-20'lX6g3
/cos3 28° 11'sin 77° 50'
Вычислить следующие выражения (789 — 795)’путем
логарифмирования по частям:
789 n V- /3-1^3 . /5-/7
/й». 1) х — !—0>1842 ’ “ 0,853 + 3,45 *
790. 1) х = 8 — /Тб ; 2) х= ^21^3 ~. 7.К? . t
б/б + 7/8
ю ______
791. 1) х = ]/145,272 — 124,492; 2) х=
8/15-3/2
792. х== 11,072 /б/)697— 10,25.
793. ^/=т/11|-2,05/б>2.
123
794. у 0>021 -3,81
sin2 32° 11'. 3Q,68
12,63
j/” (725-у 4235)3
------ 6 — .
/774 5645
§ 48. Показательные и логарифмические уравнения
Решить уравнения способом приведения к одинако-
вым основаниям левой и правой части уравнения
(796 — 805):
796. 1) 2х = 8; 2) 23* = 8;
3) 25х-3=16; 4) 2‘1х~3 = 64.
797. 1) 2“4х = (0,25)5х“1; 2) (0,125)3“4х = ^-;
о 4
3) 64~Ух^ = 0,5.
798. 1) 9Х = 27Х*“; 2) (4 = 814x+l;
3) 4х = /23х+1.
/ЧХ-2Ж о ,5/ г -,ч ± * “_____
799. 1) (4) =3f; 2) У 0,5 2 .]/4 = У16.
800. 1) 1253 (х2"х~2) = 25 • 0,04;
2) 0,01 • 2х- 5х = (0,01)2- 103х+3.
801. 1) 1-Зх + [0,(3)]2~х — [0,(l)f-2 =1,05: 10"2;
О
2х=15_• 7-1 \3х (81 \4х~3_ 163
ю 8 ; О) \ 16 / 274 •
х-(| —Ух) 2+Ух
802. 1) Зт • 3 1“* • 0, (3)2(’+^> =0,81 : 10“2;
2)
3)
V 2Ъх /8-1 = У16 V 8;
ysin2 х __ 4gcos х
803. 1) 25sin2x-3= 625sinx;
/4\3sin4jc_ 1,5"’
124
Г\ Зх-7_______
804. 1) У и 23x“l — /(0.125)3"* = 0;
2) aO/*-3)OZ5^7-2)__ j.
3) а^х+б+Гх-1 _ j : а~8е
one (х+7>4 (3x4-19)1 U+2)|
805. 1) а 2 = а 2 : а 2;
2) 83х~7 У V 0,53х-1
<жг=<
/ к \Х—2 Z 9\2-х
4) (у) (1т) = 125х: 343 ;
5^ 25^х2—4х+3 52 (3~4x+x2) = q.
Va+x+Va—x
6) a уа+х~уа~х — аУь = 0.
Решить уравнения с помощью таблиц логарифмов
(806 — 807):
806. 1) 15х = 238; 2) 183х+1 = 475; 3) 14х"1 = 19.
807. 1) 17х"! = 19х"3; 2) 235х+3 — 194х-1 = 0;
3) /31Х-1 = /272х~3 ;
4) 3 5254х+3 = 14 / 7833х"2.
Решить уравнения графически (808 — 809):
808. 1) 2Х=1; 2) 2Х = 2; 3) 2Х = 3; 4) 2х = 5.
809. 1) 3х = 5; 2) 3х = 7; 3) 3х"2 = 0,2;
4) Зх+1=6.
Решить уравнения способом вынесения общего мно-
жителя за скобку (810 — 813):
810. 1) 2х+2+ 2х"2 = 34; 2) 2х+2— 2х = 96;
3) 7х _ 7Х^ = 6; 4) 2х"1 + 2х"2+ 2х"3 = 896.
811. 1) 5Х+1 + 4 • 5х"2 + 5х"3 = 25"’ ♦ 646;
2) 81х + 7 • 92х + 5 • З4х"3 = 8 .
812. 1) 54х"3 — 4 • 54х-1 4-8 • 54х+1 = 24 505;
2) 5 • 32х-1 — 9х"0,5 4- 32х 4- 4 • 9х"1 = 225.
123
813. 1)4- 32х-2 + 5 • 9х = 3 • 32x-! — 9 х”0'4;
2) 3х + 3x+1 + Зх+2 = 7х + 7X+1 + 7Х+2;
3) 2 х + 2х"1 + 2Х“2 = 5х + 5х-1 + 5х-2.
Решить уравнения (814—817), приврдя их к виду
О2* ах £ — Q;
814. 1) 52x+i = 26 • 5х — 5; 2) 9х"1 + Зх+2 = 90;
3) Зх+2 + 9Х+1 = 810; 4) 3! 4-З2 т Г4-3 = 0
815. 1) 4*+Г*2-2 — 2,5 • 2х+Ух'~2 —6=0;
2) 9*4-12х = 16х; 3) /94-/6—/4 = 0.
816. 1) -3^— = 1,5;
2.З1х +1
2) 4 • 3х — 9 • 2х = 5 • Зт • 2^;
3) 2sin2* + 2COS’X = 3;
4) (/З + /в)* + (/3 —/8)Х = 2.
817. 1) 9ГР“ГГ-5 — 5 • 4-6 = 0;
2) 3----3 -——---------28 .з^7+т7=Т+! 9 ^.Q.
д_/2-л:-Ух-1 -I
3 __ 3____ 3 ________ 3 ______
3) 3 • 4|/*+17~'/ *+16_7 • 2|/*+17-1/х+16 4-2 = 0
Решить уравнения (818—819):
818. 1) 22х • 32х — 4- • 63х 4- 4 ’ 42* • 34*“2 = °;
3 4
2) хх = х; 3) хУх~ = Ух^.
819. 1) ?Л49Х+3 — /72(х+2) — 4-2x+34-2-4I+1 * = 0;
2) Xх + 139х-* — 108х-2* = 32;
X ___ 2 I х _
3) /100 4-5* — 4-^ • 10* /5 = 0.
Решить логарифмические уравнения (820—832);
820. 1) Igx = 41g24-lg3:
2) Igx+lg3 = lg27-lg9;
126
3) 21gx = lg32 + lg2;
4) у lgx = lg64 —21g4.
821. 1) 2 + lgx = lg50 + lg2;
2) 2 — 1gx = lg2 H- Ig4 4- 1g25;
JgU + 4) —]g(-r-3) __ .'
°' Jg200—lg25
л\ ]g(2x + 5) — 1g* 1 .
2 -r 1g 100 4 ’
5) lg(/x2 —7x4-18 — 7x) = Ig(24 —x2);
6) 1g x 4- 1g (2x 4- 3) = 1g (5 У 2x2 4- 3x 4- 9 — 3).
822. 1) logm(logmx)=l 4-logma — logmd;
2) log2x4-log28= 1 4-Iog25;
3) log3x 4-log3(x — 2) = 2.
823. 1) log2w 4-log4« 4-log16«= 14;
2) log2Iog3 Iog4x = 0;
3) logalog&logjogdx = m;
4) log5log1log1x = 1.
2 4
824. 1) log&x —logfi2x 4-logfilx = 0,75;
2) logo{alog&[Mogcx]} = 1;
3) log2 {2 log3 [ 1 4- n log4 (1 4-21og2x)]} = 1;
4) logo{Moge[l 4-logb(l 4-clogftx)]) = y.
2) log4x 4-logx 4 = 2;
3) log3x4-61ogx3 = 5;
4) log4_x4-log3x — log£X = 8;
Vx 3
5) log7[x 4-log2(9 —2х) 4-4]= 1;
6) log7log4Iog2(x — 7) = 0;
826.
7)
8)
1)
lg* + lg(*4-3)= lg2 4- lg(9—2|/x24-3x—6);
' 7’6+i/x __ У^з3 logj '8-»/ 76_i x )
2>ое8 (л2—Зх+9) $2 iogx Vx — i.
+ 10g3 (1 A-l)2 3.
FW- l)l2
127
3) 0,4!g’x+1 =6,252~lgx’;
.. , lglog3(logb*+4+9A') 2
4) 10 4 2 1 =^r-
827. 1) lg Ух2 —3x 4-5 = lg(7 4~ 3x —x2);
2) lg [(x2 — 7x + 18)7 — 7J = lg (2 / 6 — x) +
-Hg(2 /бН-х){
3) lg2 2x 4- lg2 3x = lg2 3 4- lg2 2;
4) xIog<* = x • 16Iog<\
828. 1) 7l°S11Zy2~9 — 2log-’<2i-x2);
2) -/a3l°g«3/5T 5 = 5 4-1/*4-^5—У%:
log ^'a+x + ^'a’~x 1
3) C _ £2 =lOgm 1;
4^ . ._ — 31g x-I __ 31gx+1—glgx-I;
5) 7,gX+1S(X+5)+^ = 343^.
829. 1) 9х • 22x — 2 • (2 • 3)3x-1 4- 32(2x”n • 42x“’ = 0;
2) log256 x2 4- logie x2 4- log4 x2 = 7 log7 7;
3) 4~ + [0>(3)]'"x —[0,(1)]' 2=35-3;
4) loga, z2 4- loga, z2 4- loga6z2 4- loga8 z2 = 25.
830. 1) Vх 4- (y)3* 4- 3 • 2х — 15,625 = - 3 • 0,5xj
2) lg84-lg20==lg54-lg2x2“5x+9;
3) 5X+2 — -^-•5X+1 — 10-5х-1 4-3-5х =-^-;
4) 2x lg3 = lg(3* 4- 2).
831. 1) log0i3x = logo131,5 —logo,31,7;
2) л210®1* =xl6log'x;
3) \ogl2°S2Xx = 1;
4) log5x = — 1 — Iog53.
832. 1) log2log3x = 0;
2) lgig*x= I;
128
3) (log5x)tog!'= 1;
4) lg-1 % = 2 + Igx-1;
5) 521gx__321gx-l — 321g *+1 _52 1gx-l.
Решить системы уравнений (833—837):
< 3х —4* = 77, ч ( \8yx — y2x =81,
833. 1) , 2)
' t (/ 3) —2* = 7; I 3x = y2;
j 2х 4-2* = 10,
S) ( _ 16 • 2К~У (2х — 2y) = 24;
834.
[ log2x4-log4y = -|,
4) I 3
[ logI6x4-Iog.tf/=-2-
fig (*2 4- У~) = lg 5 4- lg x 4- 1g У — lg 2,
I lgx4-lg£ — 21g2 = lg(x — y)\
2) lg(x4-*/) —lg*/ = lg-y-.
lg*4-lg# = 3;
835.
836.
3)
1)
3)
1)
837.
3)
1)
V2x — у =2, 4)1S = *’T>
x ( у = 4.
(2x — y) • 5* = 1000;
xy = 8, г yx — xy,
(2x)log,s = 8; 2) (xe = y*;
5x 4- 2z/ = 100, ( 1g x 1g у = 10,
lgx — 1g у = 1g l’,6; 4) I 1g21g x—lg21g y=l.
xisy=100, 2) Vx4-# = 2,
logyx = 2; (x 4-#) 7 х = 2744;
3х — 2* = 79, ( logx log2 logx у = 0,
r__ 4) {
/3х—2^ = 7; I logy9 = l.
zx = x, y4a = Zz+y,
zy = y, 2) • yz+y = za, a>0,
yv = x\ 103-^^-*> =250;
f lg(x24-*/2)=l+lg8,
I lg(x4-^) — lg 3 = lg(x — y);
129
4)
log4x2f- log16/4- log^z'^Z,
log9y2 + log81 z2 + logei x'2 = 2'°g’7,
logie Z2-Hog256 *2+bg256 y2 = 2 (log3 1 + lg 10).
Решить неравенства (838—841):
x—1 х+з
838. 1) 2x+i > 1; 2) 3X~3 > 1;
839. 1) lgf~>0; 2) !°g' j^T<0:
3
3) 1°g'.^T<°; 4)log2^|>l.
840. 1) log, > 2; 2) Ig (x - 1) < 1;
3) l°g±-7ТГ < 1; 4> lo^’-<729 > 3-
841. 1) log3(x+ 8) —log3(16 —2x) < log3x;
2) log,.» 3(x- 21) > log0.2(x2 + 4);
3) 1g 10lsl*'+211 > 1g 10 + -!^;
4> <1; 5) Ю^Г‘0>3>®'
3x+2 x-3 x—I x+3
6) (O^)*-1 < 16x+1; 7) 32 3 < 4 2 .
§ 49. Соединения
842. Имеются пять'флагов различных цветов. Сколько
различных сигналов можно сделать, поднимая по три
флага в любом порядке?
843. Сколько различных четырехзначных чисел*)
можно составить из семи цифр 1, 2, 3, 4, 5, 6, 7?
844. Сколько различных четырехзначных чисел *)
можно составить из семи цифр 0, 1, 2, 3, 4, 5, 6?
845. Сколькими способами можно выбрать четырех
лиц на четыре различные должности из девяти канди-
датов на эти должности?
*) Предполагается, что каждая цифра входит в число только
один раз.
130
846. Учащиеся изучают восемь различных предме-
тов. Сколькими способами можно составить расписание
уроков па один день, если в день можно ставить только
три предмета?
847. Сколькими способами можно разместить за
столом шесть человек?
848. Сколькими способами восемь человек, избран-
ные в местком, могут распределить между собой восемь
различных обязанностей?
849. Сколько различных трехзначных чисел*) можно
составить из цифр 2, 5, 8?
850. Сколько различных пятизначных чисел*) можно
составить из цифр 0, 1, 2, 3, 4?
851. Сколько различных четырехзначных четных чи-
сел*) можно составить из цифр 1, 2, 3, 5?
852. Из 30 учеников класса в течение урока могут
быть опрошены шесть человек. Сколько возможно ком-
бинаций?
853. Из семи кандидатов в счетную комиссию необ-
ходимо избрать трех человек. Сколькими способами
можно это сделать?
854. В шахматном турнире участвуют 12 человек.
Каждый из участников должен сыграть с каждым из
остальных по две партии. Сколько всего партий должны
сыграть участники турнира?
855. Сколько прямых линий можно провести между 15
точками, если среди них нет никаких трех точек, ле-
жащих на одной прямой?
856. Сколько различных диагоналей можно провести
в восьмиугольнике?
857. 1) Во сколько раз число Al больше числа Cs?
2) Во сколько раз число Cfo меньше числа Л10?
3) Чему равно отношение —£-?
Ст
858. Найти:
1) Число размещений из т -ф 2 элементов по 3.
2) Число размещений из п—>1 элементов по 2.
3) Число сочетаний из tn -ф 1 элементов по 4.
4) Число сочетаний из иг — 3 элементов по 2.
*) Предполагается, что каждая цифра входит в число только
один раз.
131
859. Написать формулы для:
1) Числа размещений из tn 4- 1 элементов по т.
2) Числа размещений из т 4- 3 элементов по т— 1.
3) Числа сочетаний из т 4- п элементов по п.
4) Числа сочетаний из т 4- п элементов по т 4- п — 2.
Вычислить (860 — 863):
860.
861.
1) 2) —; 3) ~
А1 Л;
1) С62; 2) С?о8о; 3)
862. 1)
863. 1)
61-4! .
3! ’
2) Aq 4~ Al 4- ^4»
' Ло Мо
Упростить следующие выражения (864 — 865):
Ап . р Р
864. 1) 2) -p^i
m-1 n-1
o\ Am + 1 ‘ Pm—n+\ , ______
Pm ’ ^ « («-!)(«-3) *
A" + A^ (m ~ 0 Anpm n -
865. 1) 2) ---- —"H?
Am Pm-l
A* - Am (Am ~ 2Лт) ’ P3
(m — 4) 4^_i ’ 6A3m (ni — 5)
866. Проверить справедливость равенств:
1) C% + С;, = ch; 2) 2 (C?5 - C?5) = Cif,;
Л8
3)Cj?=4^; 4) 12(4? + ^) = ^.
r 8
Решить уравнения (867 — 875):
867. 1) A2x = 6; 2) .4j = 72x;
3) 4^+2 = 224л: (x + 2); 4) ЛЩ = 30.
Ofift n x _ 1 . o\ 2(г-3) (г-4) __ 1 .
868. 1) ^—i2- 2) ------------------Й,
4v 3 Al
3)-ТГ^ = 4> 4) — = 20.
л;+1 4 ' x
132
д*
869. 1) -f±2- = 42; 2) /''4 = 210;
4+2
д5 __ дЗ
3) Л^+2 = 6m (m + 1); 4) *+l , = *•
Ах
дЗ Д2
870. 1) -£±2-= 8; 2) -^=0,05;
х+1 Лт
4-2.+ 4, = 4.+ Л* = 43.
"1-3 Ах
871. 1) 2) CU2:C22=11;
3) +L = 100Л*; 4) Л2-з = 2 (Зу + 13).
872. 1) 2л=1=12; 2) Ат~Ат =^89;
3) С\ + С« = 15 (4 - 1); 4) А3гг = 2А'г.
873. 1) Л?: Xj = 4.; 2)СЙ=36;
„ 1 о -/1 у Ч" Ду
3) 6СГ = 11Ап-!; 4) = 29.
Ах
874. 1) С2Х =10; 2) Ся+з = 3(х+1)(х + 2);
с^ч-с* 1 н ,2
3) -*_/=15; 4) сМ = -[2 Л«+1.
875. 1) Л^Рж_, = 42Р«_2; 4) 2^&+1 = А1;
3) ^=+ = ЛЙ1 4) оЙ±г- = 4А".
876. Число размещений из т элементов по 2 отно-
сится к числу размещений из т элементов по 4,
как 1: 12. Определить число элементов.
877. Сколько нужно взять элементов, чтобы число
размещений из них по 3 было в 12 раз больше числа
сочетаний из них по 2?
878. Число сочетаний из п элементов по 3 в пять
раз меньше числа сочетаний из п 4- 2 элементов по 4.,
Найти п.
879. Как следует определить Сп, чтобы равенство
С^ = С„”Й было справедливо и в этом случае?
133
§ 50. Бином Ньютона
880. Найти произведения следующих двучленов:
1) (х+1)(х + 2)(х + 3);
2) (х — 1)(х —2)(х —3);
3) (х—1)(х —2)(х + 3);
4) (а+1)(а + 2)(а + 3)(а + 4);
5) (а — 1) (а — 2) (а — 4) (а — 5);
6) (Z,-l)(6-2)(& + 3)(& + 4);
7) (у + l)(r/+2)(z/ + 3)(r/+4)(f/ + 5);
8) {у— !)(«/ — 2)(у — 3) {у — 4) {у — 5);
9) (х + а) (х + Ь)\
10) (х + «) (х + Ь) (х + г);
11) (х + а) (х + Ь) (х + с) (х + dy
12) как запишется выражение 11) и его произведе-
ние, если положить (a) a — b~c = d, (б) а = Ь = с —
~d—\, (в) а~ Ь — с == d— — 1?
881. Вычислить коэффициент при х2 в произведении:
(х —3) (х + 5) (х — 1)(х + 2).
882. Вычислить коэффициент при а в произведении:
(а + 1) (a 4- 2) (а 4- 3).
883. Вычислить коэффициенты при г/4 и г/° в произ-
ведении: (у + 1) (у 4- 2) (у 4- 3) (у 4- 4).
884. Написать разложения биномов:
1) (х ± у)8; 2) (а ± Ь)5; 3) (х ± I)7;
4) (1 ± г/)6; 5) (За 4- I)4; 6) (х2 —2)5;
7) (/Т + /Г)6; 8) (гуГ-х)4; 9) (1 ±
lOjfl+yT)6; 11) + 12)
13) (х 4-£/г)4; 14) (2х + 3г)4; 15) (1 ±/)’2.
885. Упростить:
n U+1)4+(х—I)4 .
х4 + 6х2-н
(а + Ь)5 + (а — b)5 — 10аЬ4
а2+1062
886. Вычислить коэффициенты второго, пятого и
шестого членов многочлена, получающегося в результате
возвышения двучлена (2,г 4- у) в седьмую степень.
134
887. Вычислить биномиальные коэффициенты вто-
рого, четвертого и пятого членов многочлена, получаю-
щегося в результате возвышения двучлена (2х— у)
в седьмую степень,.
888. Найти:
1) пятый член разложения бинома (а + I)9;
2) семнадцатый член разложения бинома (а -ф д)23;
3) шестой член разложения бинома (х3—I)8;
4) седьмой член разложения бинома (Уа—Vb) ;
5) средний член разложения бинома I — —xl ;
6) два средних члена разложения бинома 2 — у) .
889. Вычислить наибольшие биномиальные коэф-
фициенты разложений:
+ 2)(a + b)\
890. Найти:
1) член разложения (х + у)п, содержащий х7;
/ 1 \б
2) член разложения 1а ~г —) , не зависящий от а;
3) член разложения содержащий у7;
/ 1 —\9
4) член разложения —----у х3] , не зависящий
/
от х;
„ » V3 .
5) член разложения ь п—~1 , содержащий х ,
\ Vx /
6) член разложения £ -ф > содержащий
2
Ь~~-
7) член разложения (У а— а)12, содержащий а 3;
8) член разложения I-77=-—у х) , содержащий х’;
\ у х /
9) член разложения (х + а)16, содержащий х8а8;
10) члены разложения (х2— ах)24, коэффициенты ко-
торых равны числу сочетаний из 24 по 18.
891. Вычислить сумму биномиальных коэффициен-
тов членов разложения:
1) (а+ />)’; 2) (а-ЬГ, 3) (х+ //)'»; 4) (х -//)'».
135
/ 1 \П
892. Найти пятый член разложения бинома (z + —I ,
если сумма биномиальных коэффициентов равна 128.
893. Найти восьмой член разложения бинома
(а — если сумма биномиальных коэффициентов,
стоящих на нечетных местах, равна 512г
894. Найти показатель степени бинома (& Vb + l)w,
если биномиальный коэффициент третьего члена раз-
ложения бинома равен 4950.
/30 /“ 5z-\n
895. Найти показатель степени бинома 11/ — у а) ,
если шестой член разложения бинома не содержит а.
896. Найти третий член разложения бинома
(1 4-x)rt+1, если биномиальные коэффициенты четвертого
и шестого членов разложения равны между собой.
897. При каком значении х 21-й и 22-й члены раз-
ложения бинома (1 4-х)44 равны между собой?
898. Вычислить четвертый от конца член разложе-
/ 12 ! 2~\27
ния бинома (1+1/ “fy) *
899. Сумма коэффициентов при втором и третьем
(5 _________________________ J \«
у/22 4- 6- -1 равна 153.
V z /
Найти член, не содержащий г.
900. В разложении бинома а2& — 2аЬ2^ вычислить
четвертый член, если отношение биномиального коэф-
фициента третьего члена разложения к биномиальному
коэффициенту пятого члена равно 2.
901. В разложении бинома (х Ух+-^4-1 коэффици-
ент третьего члена разложения на 44 больше коэффи-
циента второго члена разложения. Найти член, не зави-
сящий от х.
902. Указать номера рациональных членов в раз-
ложениях биномов:
1) (/2 + /з)6; 2) (1 + УЗ)'0;
3) (1^- I)12; 4)(/x+fc)2’.
903. Доказать, что сумма квадратов биномиальных
коэффициентов разложения (х.+ у)п равна С2».
136
§ 51. Сложные проценты
904. Какую числовую последовательность образуют
начальный и наращенные капиталы, вычисленные по
формуле сложных процентов?
905. В какую сумму обратятся 140 руб., если они
были в обороте три месяца из 8% простых?
906. В какую сумму обратятся 840 руб., если они
были в обороте 8 месяцев из 6% простых?
907. В какую сумму обратится вклад в 1 рубль,
положенный в сберкассу на 100 лет из 8% сложных?
908. В сосуде имеется 50 л 80%-ного спирта. Сколько
литров чистого спирта останется в сосуде, если из
него 20 раз отливать по 1 л жидкости и каждый раз
добавлять по 1 л воды?
909. Известно, что некоторые болезнетворные бак-
терии делятся каждые полчаса. Сколько бактерий
могло бы быть в организме (при условии беспрепят-
ственного роста) через 24 часа после инфекции, при
которой в организм внесено 10 штук бактерий?
910. Сумма 5000 руб., отданная в сберкассу на
сложные проценты, обратилась через 7 лет в 7035 руб.
50 коп. На какие проценты была положена сумма?
911. Какую сумму надо внести в сберкассу в виде
вклада по‘ 4% сложных, чтобы по истечении 15 лет
образовалась сумма в 10 000 рублей?
912. Во сколько лет сумма 800 руб. может обра-
титься в 1680 руб., если доход составляет 3%
сложных?
913. Во сколько лет сумма 77115 рублей сможет
обратиться в 185 900 рублей при 4,5% сложных?
914. Во сколько лет сумма, отданная на р% слож-
ных, увеличится в п раз?
915. Еженедельное увеличение яиц на птицеферме
совхоза составляет 2%. Сколько яиц может продать
совхоз государству за 15 недель, если в данный момент
совхоз имеет на складе примерно 20000 яиц?
916. Если в совхозе еженедельный прирост кроли-
ков составляет 10%, то через сколько недель совхоз будет
иметь 3200 кроликов, если в настоящее время он их
имеет 2000 штук?
917. В СССР в 1948 году было выработано
66,3 млрд. квт. час. электроэнергии, а в 1963 го-
ду—412,4 млрд. квт. час. Найти средний ежегодный
137
процент роста выработки электроэнергии в СССР за
эти годы?
918. В 1952 году жилищный фонд в городах и ра-
бочих поселках СССР составлял 557 млн. кв. м.,
а в 1964 году он составлял 1182 млн. кв. м. Найти
средний ежегодный процент роста жилой площади за
указанные годы.
919. Через сколько лет жилищный фонд города
увеличится в полтора раза, если он ежегодно будет
увеличиваться на 3%?
ГЛАВА 6
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ЛЮБОГО УГЛА
§ 52. Измерение дуг и углов
920. На окружности произвольного радиуса отме-
тить точки, соответствующие:
(а) 10°, 15°, 30°, 45°, 60°, 90°, 120°, 150°, 180°, 210°,
240°, 270°, 300°, 330°, 360°;
(б) —10°, -15°, -30°, —45°, -90°, -120°, —150°,
— 180°, —270°, —300°, —360°.
921. Какая разница между дуговым и угловым гра-
дусом?
922. Почему величина отношения где 7? — ра-
диус центрального угла, I — длина дуги, служит мерой
угла?
923. Зависимость между радианной и градусной ме-
„ „ „ . „ ла° ла
рои выражается линеинои формулой: а = ра-
диан. Преобразовать все выражения задачи 920 в ра-
дианы и отметить их точками на числовой оси.
924. Заполнить следующую таблицу:
а0 57°18' 40°30' 30°30' 20° 18°39'
йрад
925. Радиус круга равен 10 см. Найти длину дуги,
содержащей 35°; 48°; 60°; 80°; 360°.
139
926. Выразить в радианах: 1) 51°; 2) 27°; 3) 76°30';
4) 12° 30' (л « 3,14159).
927. С помощью числа л составить выражения для
следующих дуг: 1) 22° 30'; 2) 36°; 3) 75°; 4) 157° 30';
5) 163°; 6) 216° 13'.
928. Выразить в градусах и минутах'углы: 1,4; 2;
„ л 2 3 3 2
0,75; то-; -т л; -х-л; 7л; —л радианов.
1о о Z 4 (
929. Металлический вал, диаметр которого равен
2,4 м, делает в минуту 800 оборотов.
1) Найти угловую скорость о одной из точек, отме-
ченной на поверхности вала.
2) Найти окружную скорость точки вала, удаленной
от его оси на 1,2 м.
3) Найти окружную скорость точки, находящейся на
расстоянии 1 м от оси вала.
.. .. радиан
Указание. Угловая скорость точки выражается в ,
секунда
а окружная скорость вращения точки равна /?<в, где R — расстоя-
ние точки от оси вращения и <о — угловая скорость точки.
930. Дополнить до прямого угла:
л л 2л л л л Зл
"з7 “Г* Т’ТГ’ 78’ Т’ 5 •
931. Почему ошибочна запись л =180°?
Рис. 5.
932. Измерить транспортиром величину углов а, 0,
у, о и выразить их в радианах (рис. 5).
140
933. Измерить транспортиром величину углов а, р,
Y, (о и выразить их в радианах (рис. 6).
Рис. 6.
934. По данному общему виду угла а написать его
частные значения в интервале 0° < а < 360° (0 < а < 2л):
1) а = 20° + 150°п; 2) а = - 20° + 150°п;
3) а = -^- + л/г, 4) а = —^- + 2л/г;
5) а = (-!)"• 30° + 180°л; 6) а = (-1)" • 4 + лп,
О
n^Q — целое число.
935. Углы треугольника относятся как 2:3:4. Вы-
разить их значение в градусах и радианах.
936. В чем разница между градусным и радианным
измерениями углов (дуг)?
937. Выразить в градусной и радианной мерах углы
правильных треугольника, четырехугольника, шести-
угольника.
938. Окружность разделена на 15 равных частей.
Найти градусную и радианную меры дуги.
939. На какой угол поворачивается минутная стрелка
за 30 минут? за 2 часа?
940. Углы четырехугольника ABCD относятся как
1 : 3 : 5 : 6. Выразить величину каждого угла в градусах
и радианах.
Найти на логарифмической линейке значение сле-
дующих тригонометрических функций острого угла пря-
моугольного треугольника:
941. 1) sin32°20'; 2) sin48°15'; 3) sin62°17';
4) sin 82° 14'; 5) sin 4° 10'; 6) sin 2° 16'.
141
942. 1) cos 52° 11'; 2) cos 30° 16'; 4) cos 14° 18'; 5) cos 84° 3';
943. 1) tg20° 11'; 2) tg 12° 14'; 4) tg47° 18'; 5) tg52° 16';
944. 1) ctg4°4'; 2) ctg44°40'; 4) ctg82° 14'; 5) ctg72°24';
3) cos 18° 12';
6) cos 2° 19'.
3) tgl3°28';
6) tg74°28'.
3) ctg58°6';
6) ctgl2’7'.
Найти на логарифмической линейке (945—948) острый
угол прямоугольного треугольника, если
945. 1) sin а = 0,432; 2) sin а = 0,252;
3) sin а = 0,941; 4) sin а = 0,0854.
946. 1) cosa = 0,231; 2) cosa = 0,342;
3) cos а = 0,547; 4) cos а = 0,822;
5) cos а = 0,0982; 6) cos а = 0,0844.
947. 1) tg а = 0,061; 2) tg а = 0,032;
3) tg а = 0,426; 4) tg а = 0,082;
5) tga= 1,582; 6) tgа = 4,831.
948. I) ctga = 0,03; 2) ctga = 0,035;
3) ctga = 0,35; 4) ctga = 0,821;
5) ctga= 1,941; 6) ctga = 2,584.
949. Найти числовые значения функций:
1) sjnl; 2) sin0,385; 3) cos5;
4) cos0,25; 5) tg0,5; 6) ctgl,2;
7) sin 3,2; 8) cos 0,7; 9) tg2,3.
950. Один угол равнобедренной трапеции содержит
48°. Выразить в радианной мере остальные углы тра-
пеции.
951. Вычислить:
. 240 . 30,25
l' tg32°57' ’ sin 38° 25'*
sin 23° 30' . 106-tg 4° 40'
tg 14° 15' ’ tg 36° 20' ’
952. Окружность морских компасов делится на 32
равные части, называемые румбами. Выразить румб
в радианах и градусах.
953. Угловая скорость якоря генератора Юл радиан
в секунду. Сколько оборотов в минуту делает якорь
генератора?
142
954. Колесо делает 20 оборотов в 1 минуту. Чему
равна угловая скорость в радианах в секунду?
955. Выразить площадь S кругового сектора через
его радиус R и Z АОВ — а (а — радианная мера угла)
(рис. 7).
956. «Лопасть винта сделала
3,2 оборота. Какой угол опи- / X.
сала лопасть винта? Построить / \
этот угол. х.
957. Вычислить радианную X.
меру внутреннего угла пра-
вильного двенадцатиуголь-
ника. Рис 7
958. Найти радианную меру
углов 1170°; 2220°; 47°?
959. Найти радианную меру углов параллелограмма,
если их отношение равно 0,5.
960. Из точки, взятой на окружности, проведен диа-
метр и хорда, равная радиусу. Найти угол между ними
и выразить его в радианах.
961. Из концов дуги, содержащей 210°, проведены
касательные до взаимного пересечения. Найти угол
между касательными и выразить его в радианах.
962. Высота ромба, проведенная из вершины его
тупого угла, делит противоположную сторону пополам.
Найти углы ромба и выразить их в радианах.
963. Вычислить длину дуги окружности радиуса
/? = 20 см, если дуга содержит 36°.
964. Радианная мера дуги радиуса 7?=12см равна
0,75. Вычислить длину дуги.
965. Вычислить периметр сектора окружности ра-
7
диуса 7? = 36 см, если дуга сектора содержит д- радиан.
966. Для измерения углов в артиллерии пользуются
единицей, называемой тысячной или делением угломера.
Эта единица равна полного угла. Выразить:
1) тысячную в минутах;
2) минуту в тысячных;
3) градус в тысячных.
967. Шкив электромотора делает 900 оборотов в ми-
нуту. Вычислить угловую скорость вращения этого*-
шкива в радианах в секунду.
143
§ 53. Изменение тригонометрических функций
с изменением угла. Знаки тригонометрических
функций
968. В какой четверти должен быть расположен
конечный радиус-вектор, чтобы синус и косинус полу-
чаемых углов были положительны? отрицательны?
Чтобы тангенс и котангенс получаемых углов были по-
ложительны? отрицательны?
969. Какие знаки имеют тригонометрические функ-
ции sin a, cos а, tga, ctg а, если а равен:
1) 80°; 2) 100°; 3) 200°;
4)-|; 5) 4я; 6)14"! 7)li"?
970. Напишите область изменения углов, для кото-
рых синус и косинус имеют одинаковые знаки.
Вычислить выражения (971—972):
071 11 4 — 2 tg 45° + tg 60°
' 3 sin 90° — 4 cos 60° + 4 ctg 45° 1
4 — tg2 _ 4- ctg4 —
2) 4---------------2----»
3 sin3 ---4 cos2 — + 4 ctg
3) (4 sin -^-)2 ~ (2 tg — (2cos-^)4 — -y)2t
972. 1) sin 2л 4- cos 4л — tg2jt;
2) ctg-^-+ cosec—+ sec0;
3) a2«sin-y- + 2ab cos л — b2 sin у л;
4) 10tg2n -J- 3cos-| л — 4tgn — 5 sinл.
973. Упростить выражения:
5 + sin 30° cos 60° — tg -j-
|\ ____________________4 .
' a + b c6s2rc — sin л *
л , .л , .
tn COS — + n Sin -7 ft tg л
2)------------;
mn + tn tg—---ctg-g-
(%a COS60°)2 — (b ctg 45°)3 + (3ab sin 18O0)2
' (It a cos 90°)'” + 2a sin 30° — 26 cos2 45d
144
974. Заполнить следующую таблицу:
№№ п/п Функции Область определения Область изменения Точки разрыва Период функции
1 sin х
2 cos X
3 tg X
4 ctg X
5 sec x
6 cosec x
975. Найти область изменения следующих функций
1) у = | sin х |;
3) у — cos х + 1;
5) у = sin2x -|- cos2x;
7) у =12 sin х — 5cosx;
9) i/ = 5sinx;
11) y= sinx 4- cosx.
2) // = cos2x;
4) # = tg2x;
6) p = cosx— sinx;
8) t/ = sinx cosx;
10) у = sin4 x -|- cos4 xj
976. Исключить периоды у следующих функций:
1) sin 370°; 2) sin 5л; 3) sin 580°; 4) sin 1500°;
5) cos 400°; 6) cos 850°; 7) .cos 7л; 8) cos 15л;
9) 1£9л; 10) tg 1850°; 11) ctg9223; 12) ctg 14,1л;
13)sec380°; 14)зес7,5л; 15) cosec4,2л; 16) cosec390°.
Чему равны периоды функций (977—979):
977. 1) i/ = sin2x; 2) t/ = sin5x; 3) t/ = siny’, >
4) i/ = sin|-x; 5)t/ = |sinx|; 6) у = | ctg у |.
978, 1) i/ = cos3x; 2) j/ = cos-|-;
3
3) у — cos у x; 4) у = | cos 2x 1.
979. 1) i/ = tgy; 2) i/ = tg4x;
3) Z/ = ctg|-x; 4) z/ = ctgy.
980. Если sin a = sin p, то можно ли утверждать,
ЧТО Я = Р?
145
981. Указать, какие из функций периодические:
О У — 1 + sinх; 2) у=1—cosx; 3) z/ = x4-cosx;
4) z/ = 2tgx—1; 5) у = sinх + cosx.
982. Указать промежутки возрастания следующих
функций:
1) z/=sin2x; 2) z/ = cosyj
3) z/ = tg3x; 4) z/ = ctg|x.
983. Указать промежутки убывания следующих
функций:
1) y = sin~; 2) z/ = cos3x;
3) # = tg-|; 4) г/ —ctg6x.
984. При каких значениях х функции t/ = sinx и
у—cosx принимают наименьшее и наибольшее значе-
ния? Написать общий вид углов.
985. При каких значениях х произведение sin 124° X
X cosx > О?
986. При каких значениях а и fi произведение
tg а tg р < О?
987. Для каких значений х, заключенных между О
и 2л, имеют смысл выражения: 3) j/cos2x;
1) 4) sin X ctg2x ’ \1 — sinx; 2) У sinx; 5) tgx;
6) У 2 — sinx;
7) У 1 -j- sinx; в) ; У sin 2x 9) У — cos x ;
Ю) 2 1 + cos X
988. Из следующего множества функций составить
два подмножества: 1) четных, 2) нечетных функций.
sinx; sin2x; cosx; cos2x; — sin2x; —cosx; tgx; ctgx;
tg2x; ctg2x; sin3x; cos3x; tg3x; ctg3x; —tgx; —ctgx;
X , x e x e COS X
sinx ’ cosx ’ tgx * sinx —cosx
989. Найти значения всех тригонометрических функ-
ций следующих углов: —90°; —30°; —45°; —60°; —180°;
-270°; -360°.
146
990. Упростить выражения:
«X sin - а) 4-2 sin а + cos (—а) — cos а
4 cos (— а) + 3 sin (— а) + 3 sin а — 3 cos а ’
2) [3mcos(-60°)|3 — 4 [m ctg (— 30°)13 4- 12 sin (-30°);
sin (— a) tg( — a) sec ( — а)
' cos (— a) ctg (— a) cosec (— а)
§ 54. Построение углов. Графики тригонометрических
функций
991. Какие тригонометрические функции являются
ограниченными и какие неограниченными?
992. Построить углы:
(а) синус каждого из которых равен:
1) 2){; 3) 4)-|; 5) -Ь 6)
(б) когинус каждого из которых равен:
1) 4: 2) -V"- 3) 4) 5> 6> “4:
(в) тангенс каждого из которых равен:
1) 1; 2) 3) 1|; 4)-|; 5)- /3; 6) — 2;
(г) котангенс каждого из которых равен:
1) f; 2) 1; 3) 3; 4) - ±; 5) -1; 6)-у5.
993. Построить графики тригонометрических функций:
1) y = sinx; 2) z/==cosx; 3) у — tg х; 4) y = ctgx и
исследовать каждую функцию по следующей схеме:
1) область определения функции,
2) область изменения функции,
3) четность функции,
4) промежутки возрастания и убывания функции,
5) каково наибольшее (максимум) значение функции
и в каких точках,
6) каково наименьшее (минимум) значение функции
и в каких точках,
7) точки, в которых функция обращается в нуль.
147
§ 55. Зависимость между тригонометрическими
функциями одного и того же угла
994. Существует ли такое значение угла х, для кото-
рого имеют место равенства:
1Ч . 12 5
1) sinx = -jg-, a cosx = -jg-;
2) sin х ==0,6, a cosx =—0,8;
3) sinx = 0,3, a tgx = ]/3;
2
4) sinx = -y, a ctgx = 3;
5) cosx = -^-, a tgx = 4,95.
Найти значения всех тригонометрических функций угла а, при выполнении следующих условий (995—996):
995. 1) 4 sin а = , ь л 2-<a < л;
2) 45 cos а 53 , 3л , a < 2л;
3) 12 sina =—jj, : лс < a 2 2 л;
4) 15 cos а = , л y<a < Л.
998. 1) tga = T, л < ' CL " 3 2 n’
2) tg а= — 2, л T < ' CL * С л;
3) tg а = — 2,4, 3л T < Z CL • < 2л;
4) ctga = — 0,5, Л ~2 < Z CL * С л;
5) ctg a = -jy, Л < ' CL * Зл в "•"2“’
6) ctg a = — 0,255, 3л 2 ' a < ' 2л;
7) ctg a = V 2, л < t a ’ Зл
Упростить следующие выражения (997—1008):
997. 1) sin a ctg a 4- cos a; 2) cosatga — sin a;
3) 1 + cos2 a — sin2 a 4) sin2 ф — 1
cos a 9 COS2 ф ‘
148
2) sin p cos p tg p ctg p sec p cosec P;
3) (sin cp 4- cos cp )2 4- (sin qp — cos qp)2;
4) tga
7 tga + ctga *
I П 1 + COS P + cos2 P t
7 1 + sec p + sec2 P *
2) sin2 у 4- sin2 у cos2 ~ 4- cos4 * у;
„V ______I_______। cos2 2a .
7 cosec2 2a — 1 ' 1 — sin2 2a ’
4)4^f| + siO;
5) (1 — cos2 x) ctg2x — 1;
6) cos4x — sin4 x + 2 sin2 x;
„к 1 — sin4 2a — cos4 2a । ,
'7 2 sin4 2a *“ 1;
8) (1 4- cos2 P) tg2 p — sec2 p.
1000
2)
л Cl <1 Ct I » Q Ct । «a
cos- cosec2-n- + sin v + cos2 -y;
Z £ Z A
cosa_________cosa I oPfo.2„.
1 + cos a 1 — cos a ‘ & »
1 + 2 sin 2x cos 2x n
-----n—j——z---------cos 2x;
cos 2x + sin 2x ’
a — sin2 a) ctg2 a 4“ cos2 a.
3)
4) (tg2
1001
1)
2)
3)
4)
1002
1)
2)
sin2 a — sin2 P , . 9 j ? n r • 9 a
——2—~nr~ 4- ctg2 a 4~ cos2 p 4~ sin2 P;
sin2 a sin2 p 1 ь । r 1
1 — 4'sin2 ф cos2 Ф I л .
-- 4“ 2 sinqp cosqp;
1 4- 2 sin ф cos ф x
cosec2 a — 1
cos2 2a — sin2 a 4- sin2 2a ’
sin3 a — cos3 a .
----------:-----h sin a cos a.
cos a — sin a
sin4 3a — cos4 3a 1 . 2
sin2 3a — cos2 3a ‘ a’
+ - ctg2 Д;
cosec2 p 4-ctg2 p ®
3) sin a (1 4- tg a) 4- cos a (1 4- ctg a);
cosec a — sin a
7 cosa
sec a — cos a
sin a
149
1003. 1)
2)
1 4- sin ct (cos a — sin a) .
1 4- ctg a ’
cosec2 a — 1 —
1
l/~sec2 a — 1
+ tg a 1/1 — sin2 a, 0 < a
л .
~2 ’
3)
4)
tg2 ф — ctg2 <p ,
tg2<p—1 ’
sin2 a sin a 4-cos a
sin a — cos a tg2 a — 1
1004. 1)
2)
3)
4)
sin a 1—cos a , sin a + cos a,
1 4- cos a sin a ‘ cos a ’
sin a 4-tg a .
----j—5-------sin a (tg a — 1);
ctg a + cosec a ' °
sec2 P — cosec2 0 ,
tg2P —ctg2P ’
tg a . о
77---7—7-----к cosz a.
tg a 4-ctg a 1
1005. 1) tg<p+ 1;
' I 4- ctg qp v 1
o\ 1 1 4- cos a Г 1 — cos a 3л .
' r 1 — cos a r 1 4- cos a ’ 11 a 2 ’
Qt (sin P 4- cos P)2 — 1 .
' ctg P — sin p cos p ’
4) ( sin a 4-tg a V
' ( cosec a 4- ctg a )
1006. i) + У Ф)’;
' Sin2 ф COS2 ф tg-^ф
(1 ~~ sin a) (1 4~ cosec a) .
' (1 — cos a) (1 4-sec a) ’
3) -ctga+l;
’ tga — 1 & 1 ’
.к 2 cos2 P — 1 cos2 P — 1
1 — 2sin2p 1 — sin2 P *
1007.
X / • \ I sin a 4-tga .
1) tg a (cos a-sin a) + ctg a + cosec a
rjx sec a 4- cosec a 1
tg a 4- ctg a sec a ’
„к 14-cos a Г j (1 — cosa)2!
' sin a I sin2 a J ’
4)
cos2 a — sin2 p
sin2 ghsin2 p
ctg2 a ctg2 0.
150
1008. 1) -----Ц—— + т------Ц—й" + 2 sin2 a cos2 а;
' (sec а ctg а)4 ' (cosec а tg а)4
2) (tg а + ctg а) (1 + cos а) (1—cos а).
Упростить выражения и вычислить результат
(1009-1010):
1009. 1) (-,-sin2AT Ч--L—cos3 0,
7 \1 — sin2р 1 cosec20—1/ 1
-а Л а _____
если sin p = -jy, g- < 0 < л;
2) (1—cosec2 a) tg a-f-sin a cos а,
Зл
если cos а = —0,8, n<a<-g-;
3) sec a (cosec а — sin а), если sec а = — У10,
4) (tg4a + tg2a)cos2actg3a,
если sec а = ]/17, ~ < а < 2л.
1010. 1) + ..
7 ctg а — sin a cos а & ’
если sec а = —1/37, ~ < а < л;
2) (1 _ +
\ 14- sma /\ 1 I — since /’
Зге
если cos а = 0,6, — < а < 2л;
гд 14- cos6 0 9 а о г»
з) T+~cos2p~ ~cos' 0» если sec 0 =3;
4) sin2 a cos2 0 — cos2 a sin2 0 + cos2 а,
если ctg 0 = /5.
Проверить равенства (1011 — 1016):
1011. 1) ,2~sec? +tg2a = —1;
' 1—2 cos2 a 1 ь ’
2) 1 4_______1 __i.
} 1 4- sin2 a ' 1 4* cosec2 a ’
3) (1 — ctg a)2 + (1 + ctg a)2 = 2 cosec2 a;
4> T^si°n2g + Ф ctS Ф = sec2 Ф-
151
1012. 1) (tga-f-ctga)2 — (tga— ctg a)2 = 4;
m cos a + ctg a . .
2) -----!—2— = 1 4- sm a;
7 cos a cosec a *
1013.
1014.
1015.
1016.
3) sin4 P — cos4 p — sin2 p -j- cos2 p = 0;
4) (cos a — sin a)2 -f- (sin a -f- cos a)2 = 2.
i \ sin a + cos a tga 4- 1 .
' sin a —cosa tga — 1 ’
2) ‘^+4L = tgatg₽;
' ctg a 4- ctg p & & r
3) cos4 a + sin2 a cos2 a -j- sin2 a + tg2 a = sec2 a;
.v 1 4~ sin a___1 — cos2 a _ sin a
J 1 — ctg a sin a (1 — ctg a) sin a — cos a
.ч 3 cos a —sin a _ 3 —tga
> 2 sin a 4- cos a 2 tg a 4- 1
2) .^°- tg2n=cosec2a;
7 1 — tg2 a
3) c?-7 r- + 7-R'4 + 2 sin2 P cos2 p = 1 j
7 ctg4 p 1 (cosec p tg P)4 1 r r >
4) (tg2 a — sin2 a) ctg2 a = sin2 a.
.. (1 — sin a — cos a) (1 — sin a 4~ cos a)_%.
J sin a (1 — sin a) ’
, sin2 a cos2 a
2) 1 —r-i—i--------m— — sm a cos a
’ 1 4- ctg a 1 4- tg a
3) ctg2 a — cos2 a = cos2 a ctg2 a;
4) 1 + sin a + cos a + tg a = (1 cosa) (14-tg a).
1) sin2 a + sin2p— sin2 a sin2 p + cos2 a cos2 p «= 1;
2) sin2 a cos2 p — cos2 a sin2 p = sin2 a — sin2 0;
3) sin2 a cos2 0 — cos2 a sin2 0 = cos2 p — cos2 a;
4) (cosa — sin a) (cosec a — seca) =
= sec a cosec a — 2;
1 — sin m cos ф sin2 ф — cos2 ф
5) 11= Sin ф.
7 cos ф (sec ф — cosec ф) sin-5 ф 4-cosd ф x
§ 56. Общий вид углов, соответствующих
данному значению тригонометрических функций.
Обратные тригонометрические функции
1017. 1) Укажите границы монотонного изменения
каждой тригонометрической функции.
2) Из промежутка от —до -у найти углы, синус
Уз „ в -
которых равен —«р. Сколько таких углов можно наити?
152
3) Из промежутка от 0 до л найти углы, косинус
которых равен —0,5. Сколько таких углов можно найти?
4) Из промежутка от —у до -у найти углы, тан-
генс которых равен У3. Сколько таких углов можно
.найти?
5) Из промежутка от 0 до п найти углы, котангенс
которых равен —^колько таких углов можно
найти?
1018. Найти угол х и записать его в общем виде,
если:
1) sinx= — 1; 2) sinx = 0;
3) sinx = 1; C4 . /2 . 5) sinx = y, • /2 4) sinx = -!y-; 6) sin x==~}
7) cosx — — 1; 8) cosx = 0;
9) cos x = 1; 1 1\ J 11) cos x = — y| 13) tgx=— 1; 10) cosx=y; 12) cosx = — ~yy~» 14) tgx = O;
15) tg x = 1; 17)tgx= 19) ctgx = 0; 21) ctg x = — У 3. 16) tgx = -y—; 18) ctgx = — 1; 20) ctg x = 1;
1019. (а) В следующих равенствах выразить х с по-
мощью обратных тригонометрических функций:
1) sinx = 4-;
О
3) sinx = 1;
3
5) COS X = — у’,
7) tgx = 2;
9) tgx = 0;
11) ctgx = — 0,3;
• 2
2) sinx = —
о
4) cos х = 0,7;
6) cos х = — 1;
8) tgx = — 1,5;
10) ctg х = 1,2;
12) ctg2x = 1;
153
13) sin Зх = ~;
15) tg(x+f) = {:
17) tg^p-=/3.
1Л\ X 1 .
14) cos y = — y*,
16) ctg(2x —l) = /2;
(б) Найти функции,
область их определения:
обратные данным, и указать
1) z/ = ysinx; 2) r/ = 2cosx;
3) 0 = ytgy; 4) г/ —2arcctgx;
5) // = arccos (2х — 1); 6) у ^arcctg-y.
(в) Вычислить:
1) arcsin у, 2) /2 . arccos -y,
3) arctg 1; 4) arcsin 1;
5) arccos 1; 6) arcctg У 3;
7) arctg (—1); 8) arcsm 1—yl;
9) arccos 1— ); io) arctg (— /3);
114 • ( • ) 11) arcsm sin—r- ' \ 4 > 12) arctg (ctg -y);
13) arcctg-—- + arctg УЗ -f- arcsin-^-; О Л
14) arctg ( l3 ) + arcctj g (— Уз) 4- arcsin (— у
1920. Обосновать справедливость равенств:
1) sin(arcsinx) = x, |х|^1;
2) cos(arccosx) = x, | х К 1;
3) tg (arctg х) = х;
4) ctg(arcctgx) = х;
5) arcsin (—х) =— arcsin х,
6) arccos (— х) — л — arccosx,
7) arctg (—х) = — arctg х;
8) arcctg(—х) = л — arcctgx.
I х К 1;
I x К 1;
154
1021. Вычислить:
1) sin (arcsin 0,5);
3) sin (arcsin 0,7);
2) cos [arccos (—0,3)];
4) ctg (arcctg 3);
5) cos (6л — arccos-^-); 6) tg(7n— arctg 1,7);
\ 10/
7) sin(12n— arcsin0,8); 8) ctg[3n—arcctg (—1,7)];
9) sin (arccos 1);
10) cos arcctg
Г/ 1/2 \1 ( 1
arccos!—y-l ; 12) tg (arcsine-
1022. Найти x:
1) arcsin (x + 0 — •£’» 2) arccos (2x + y) = -y-
3) arctg 3x = y; 4) arccos (бх— 5]/3) =
5) arctg (2x + 3) = - -J.
1023. Вычислить:
1) sin (л— 2 arcsin-y—);
2) sin (3 arctg ]ЛЗ— arccos 0);
4) cos 2 arctg (—1) — arcsin (-2/j’
5) tg (arcsin у + arccos 0^;
. 1 । П
6) sin I arcsin у + arccosy I;
7) tg (arctg /3 — arctg.
1024. Проверить справедливость равенств:
1) 2 arctg 1 = 3 arcsinу;
2) 3 arcsin-у-= arcctg (—1);
3) 3 arctg -3—= arcsin 1;
155
Z i<2 \
4) arccos(—+ arctg (—I) = arcctgO;
1 1ЛГ 1 l'<2~
5) у arcsin —h уarccos = arctg 1.
1025. Построить графики функций:
1) y = x и у = sin (arcsin x);
2) у — х и y = cos (arccos x);
3) y = — x и у = cos (arccos (—x)).
1026. (а) Указать области определения функций:
1) у== arcsin 2х; 2) у = arcsin ;
3) у = arccos Зх;
5) у = arcsin (х — 1);
7) y=arctg5x;
9) у= arcctg-^-;
11) у ~ arcsin Ух;
13) у — arcsin ]/1 — х;
15) у == ]/arccosx.
(б) Доказать:
1) sin (arccos х) = У1 -
2) cos (arcsin х) = ]/1 -
4) у = arccos-у*,
6) у — arccoslx + у I»
8) у= arctg/х; j
10) y=arcctgx— arcctg —;
12) у =-----
arcsin у x
14) у = у arcsin х;
х2, | х 1 1;
х2, | х К 1;
3) tg (arcsin х) = -j7==f» I * I < 1;
4) tg(arcctg-^ = x, x^O;
5) tg(arcsecУх) = Ух—1, x^l.
(в) Вычислить:
1) cos (arcsin 0,6);
. I 28 \
3) sin I arccos 53-1;
5) tg (arcsin 0,8);
7) cos I arctg (—2)];
2) tg (arcctg y);
t г /40
4) ctg arccos I —
6) sin (arctg 2,1);
8) tg [arcsin^—уду
.156
9) ctg [arcsin (—fof)
11) arcsin(sin-^-j;
13) arccos (cos -yj;
15) arctg (tg
17) arctg [tg (-у л)];
19) arccos[cos (—n)];
10) cos [arcsin [— gyj
12) arcsin [sin(— л
14) arccos (cos 180°);
15) arctg (tg 41°);
18) arccos (cos-p
/ 9 \
20) arcsin! sin-p л 1.
§ 57. Тригонометрические уравнения
1027. Решить тригонометрические уравнения:
(а) 1) sin Зх — 0;
3) tg 2х — 0;
5) tg (2л: + -у) = 0;
7) cos-^- = 0;
9) sin Зх = 1;
И) sinfx + =— Г,
\ /
13) cos(2x-= — 1;
15) 4sin2x = 3;
17) 1 —sin-y- = T;
19) cos(2x — 18°) = |;
21) 3cos5x— 3 = 0;
23) cos (х2) = ~;
25) 3tg(x+l)-’/3=0;
27) tg(x2)=l;
о\ • ( X Л \ __ л
2> sln(-2---6j = 0;
4) tgf = 0;
6) cos5x = 0;
8) cos (Зх = 0;
10) sin-J = — 1;
12) cos -у = 1;
14) 2sin3x —УЗ=О;
16) sin2x — = 0;
18) -Д- = 2;
20) cos (x + 2) = ± у;
22) cos (2x4-5°)—^=0;
24) 3cos2x —2 = 0;
26) tg23x=l;
28) tg (x2 4- 60°) = /3;
157
29) 2ctgx —2 = 0; 30) ctgx + 5,671 = 0;
31) ctg2x—]/3=0; 32) ctg2x—1=0.
(б) Уравнения, содержащие одну тригонометрическую
функцию одного и того же аргумента:
1) sin2х -j- 2sinx — 3 = 0;
2) sin2x — 2sinx+1 = 0;
3) 6 cos4 x = 1 + cos2 x;
ч
4) tgx + -57 = 4.
(в) Уравнения, приводимые к одной функции:
1) 2sin2x + 3cosx = 0;
2) 2tg2x + 4 = 5secx;
3) 4cos2x + 17sinx — 8 = 0;
4) tg 2x + ± ctg 2x = ;
5) sin -j- + 3 cos ;
COS-g-
6) tgx + 6ctgx — 5 = 0.
(г) Уравнения, решаемые разложением левой части
на множители:
1) sin2x — 2sinx = 0; 2) tg2x = 2tgx;
3) ctg2х + 4ctgx = 0; 4) tg2x = tgx.
(д) Уравнения, однородные относительно синуса и
косинуса:
1) ]/3sinx = cosx; 2) 2sinx = cosx;
3) sin2x — 3sinxcosx + 2cos2x = 0;
4) 2 sin2 x — 5 sin x cos x + 7 cos2 x = 1;
5) 3 sin2 x — 4 sin x cos x + 5 cos2 x = 2.
1028. Решить следующие уравнения графически:
1) sinx = а (0 < а < 1); 2)sinx = x;
3) sin2х = cosx; 4) sinx = x2.
ГЛАВА 7
ТЕОРЕМЫ СЛОЖЕНИЯ И ИХ СЛЕДСТВИЯ
§ 58. Формулы сложения
1029. Вычислить без помощи таблиц:
1) sin 105°; 2) cos 75°; 3) cos 15°.
1030. Доказать, что
1) sin 105° — sin 15° = sin 45°;
2) sin (a + 0) < sin a + sin 0,
Тде a и 0 — острые углы.
1031. Вычислить:
1) sin(a + 0)> если sin a = 0,6, sin 0 = 0,8,
0<a<f, O<0<~;
3 л
2) cos (a — 30°), если cos a =-7= и — < a < л;
7x7 K10 2
3 7
3) sin (a — 0), если sin a = у, sin 0 = — ,
0 < a < у-, л < 0 < -у;
20
4) cos(a + 0), если sina = yg-, cos 0 = —0,8,
a и 0 оканчиваются во второй четверти.
Вычислить (1032—1033):
33
1032. 1) sin а, если sin (а + 0) = у^-,
cosp = — — t 0<а<у, у < р < я;
2) cos (120° — а) + cos (а + 60°);
3) sin (120° + а) + sin (а — 60°).
159
1033. Л) cos (а — Р), если tg а = 1 ,
О
о 24 Зя л^.п^-
cosP = —2у, л<а<^-, у<р<л;
2) cos (а — р), если tga = — 2,4, tgp=ly,
ЗЯ у А J* А Зя
~2" < а < 2л, л < р < —.
1034. Вычислить:
1) sin 20° cos 25° +sin 25° cos 20°;
2) sin 43° cos 13° — sin 1 Зэ cos 43°;
3) sin 102° cos 12° — sin 12° cos 102°;
4) cos 51° cos 21° + sin 21э cos39a.
1035. Вычислить:
1) cos 15° cos 75° + sin 15° sin 75°;
2) cos 48° cos 12° — sin 48° sin 12°;
3) (cos 22° sin 80° + sin 22° sin 10°)* 1 2 3 +
+ (sin 8° cos 4® + cos 8® sin4®)2;
.ч . л я . . 8л л
4) Sin-jg COS -g- ~r sin-g- COS -j-g-.
1036. Вычислить:
.ч cos 0,3л sin 0,2л — cos 0,2л sin 0,3л t
' . я ’
sin7o"
2) cos 332° cos 207° + sin 152° cos 297°;
cos 10° 4- cos 371° cos 21° — cos 111° sin 11°
___ ;
4) sin 392° cos 3023 — sin 238° sin 778°.
1037. Выразить tg(a±p) через ctg а и ctgp.
1038. Вычислить:
1) tg(a + 45°), если tga = 3;
2) tg(a —P), если tga = —tgP=lyj
3) tg(a — 45°), если sina =--Ц-, л<а<~.
Io Z
1039. Вычислить:
n + m tg 28° + ctg 63° .
' 1 - tg 20° tg 25° ’ 1 + tg I52°tg27° ’
160
, n , , 4л
« tg-i5+lg-T5- .
1 4jt, 4tt ,
t-x 1 - ctg 72° tg 12°
' tg 198°-ctg 102° *
Упростить (1040—1042):
. tg 40° + tg 170° .
1 + tg 40°tg 190° ’
1040. 1)
2)
3)
4)
1041. 1)
2)
1^2 cos a — 2 cos (45° — а) ф
1^3 sin a — 2 sin (30° + a) ’
sin (a — 0) + 2 cos a sin ft
cos (a — 0) — 2 cos a cos 0 ’
cos (a — 0) cos (a + P) — sin (a + 0) sin (a — 0) ,
sin 2a ’
K2 cos a — 2 cos + a j
2 sin + a^ — К2 sin a
, / JX \ ( JX । \ ,
sm — + <x cos a — cos — + a sin a
\ 4 )___________\ 4 / ,
л ’
COS —r-
4
sin (a + 0) sin (a — 0)
sin a + sin 0 ’
3) (т-^Та1^-)2 4" sin4 a 4" Cos4 a + 2 sifl2 a cos2 a’
cos2 a — sin2 0 + cos2 (a — 0)
' cos a sin 0 cos (a — 0)
1049 П tg (25° + a) + tg (65° + a) .
i) i _tg (25° +a) ctg (25°-a) ’
2^ _______sin (a — 0)____.
(tga —tg0) sin(y — p)
ctg (a + 0) — ctg 0
’ ctg (a — 0) + ctg 0 ‘
Доказать тождества (1043—1044):
1043. 1) cos (x + У) cos (x— t/) = cos2?/—sin2x;
2) sin (x + У} sin (x — y) = sin2 x — sin2 y\
ctg г/ — ctg x _ sin (x — y) .
' ctg x + ctg у sin(x + z/)’
4) ~ + УУ
161
1044. 1) cos (ху) cos уsin (х-^у) sin у — cosx;
2) 4-(cosx +]/3 sinx) = cos (-J—х);
3) sin- x 4- sin2 у 4- 2 sin x sin у cos (x 4- y) =
= sin2 (x 4- y);
.. COS (jt-j-%) /Зл . \ / , .
4) т-7—;— sec Hr- 4- У = — cos (x 4- w).
’ tg(x + r/) + ctgf/ \ 2 ~
Вычислить (1045—1046):
1045. 1) sin (arcsin 4?-4-arcsin
' \ 41 1 41 j ’
ox ( • 5 . . 12 \
2) cos I arcsin-75-4~ arcsin-ту-);
у 10 1 □ j
/ 1 . 1 \
3) cos I arccos у 4-arccosy I.
1046. 1) tg (arctg 2 4~ arctg 3);
2) tg (arctg—arctg y)
/ 4 1
3) ctg I arctg у + arctg у
Проверить справедливость равенств (1047—1051):
1047. 1) «in2 (arctg 2 — arctg 5) = -^;
2) sin2 (arctg 0,2 4- arctg 0,3) = ;
ox • / • 3 . . 1 \ 3 /3 + /7 ,
3) sin arcsin -r 4- arcsin =--------5--
. ( .3 . 1 \ 6 - 4
4) sin I arcsinу— arcsin у) ==-.
1ало 1ч • ( 1 I 3\ 3K15+K7.
1048. 1) sin I arccosy 4- arccosy I =-----у--,
04 ( • 2 I 2 \ n
2) cos ^arcsin у 4-arccos yj = O;
04 ( n 7 > n 04 21 -/464T .
3) cos (arccos 0,7 4- arccos 0,3) =-,
4
4) tg (arcctg 5 4- arcctg 3) = у.
1049. 1) tg (arcctg 2 4-arcctgy^ = 5 у;
04 i I • 1 5 \ 7 КЗ -1
2) tg I arcsin у — arccos у j !-----32
162
. f . 1 \ . f 3 \ - 1
3) sin I arcsinу) + cos I arccosy I = 1
4) sin (arccos у) + cos (arcsin = 1 -.
«лел i 4. 2\ . . / . 3\ 15 +3 Из ,
1050. 1) cos arctg — + sin arctg— =------7=—;
7 \ & 3 / V & 4/ 5/13
2) tg (arctg tn) + tg (arctg ti) = tn-\-n\
3) ctg (arcctg a) 4- ctg (arcctg b) = a 4- b\
4) tg (arcctg tn) + tg (arcctg n) = ™ + " .
1051. 1) ctg (arcsin y) — tg ^arccos y^ = ~ .
2) ctg (arccos tri)— tg (arcsin tn) — 0;
. 1 , .3 . /7 + 3 /з"
3) arcsin + arcsin -5- — arcsin----.
2 о о
Решить уравнения (1052—1055):
1052. 1) sinЗхsinх — cos3xcosx=l;
2) cos 10° cos (80° -f- x) — sin 10° sin (80° 4- x) = 0;
3) sin 2x cos x cos 2x sin x = — 1;
4) sin x + -£ cos x + -5- +
4- sin(y 4-xj cos (x + y-j =y.
1053. 1) sin(3x + ^cos^ +
\ О / э
. /о . 2л \ . Зя /2"
+ cos Зх 4- sin -тг- — —n—:
\ * 5 / 5 2 ’
2) 1 + sinx sin 2x = cos x cos 2x;
3) sin (x -|- 30°) + cos (x + 60°) = 2 cos2 x;
4) sin — x) + 2 sinx = 0.
1054. 1) ==1;
7 1-/3 tgx
2) = V3;
’ 1+tgx F
3) cos (x + — ]/3 sin (n — x) — 0;
\ О /
4) cos (x + у jrj + sinx = 0.
163
1 ftKK 1 \ cos (x + 15°) + 2 sin x sin 15° ।'
' sin (x + 15°) — 2 cos x sin 15° ’
2) cos (a + x) + tg a sin (x 4“ a) = sec a;
3) 3 sin (60° — x) = sinx;
4) sin2 x — 2 ^sin cos — + cos у sin » 3,
§ 59. Формулы приведения
1056. С помощью формул синуса и косинуса суммы
и разности двух углов получить формулы приведения:
1) sin (90° ± а); 2) cos (90° ± а);
3) sin (180° ± а); 4) cos (180° ± а);
5) sin (270° ± а); 6) cos (270° ± а);
7) sin (360° ± а); 8) cos (360° ± а).
Вычислить (1057—1059):
1057. 1) tg 53° tg 37°; 2)
3) 5 sin 270° — tg 80° tg 10° tg 40° tg 50°;
4) 2 tg 180° + cos 180° — *
1058. 1) cos 120°tg 40° tg 50°;
2) tg 135° +sin 90°;
3) sin 36° 4- cos2120° 4- sin (-36°);
4) sin(--gj + tgytg-jj-.
1059. 1) cos 420° —sin2 60°;
л* / 71 \ । . / 3jT \
2) cos — V- 4~ Sin----=- .
\ 5 / \ 5 /
Следующие тригонометрические функции привести
к тригонометрическим функциям острого угла и вычи-
слить по таблицам (1060—1063):
1060. 1) sin 125°; 2) sin 249°;
3) sin 1320°; 4) sin 171° 30';
5) sin 280° 12'; 6) sin (—2012°;
7) sin 202°; 8) sin 300° 43';
9) sin (-2626°).
164
1М1. 1) cos 130°; 2) cos 305°;
3) cos 162° 18'; 4) cos 345° 16';
5) cos 193° 21'; 6) cos (-500°);
7) cos 263°; 8) cos (-3000°);
9) cos 281°.
1062. 1) tg 100°; 2) tg (—130°);
3) tg 153°; 4) tg(—238°);
5) tg200°20'; 6) tg(-546°);
7) tg2 (—1030°); 8) tg 310°;
9) tg3(-721°).
1063. 1) ctg 136°; 2) ctg (-511°);
3) ctg 198°; 4) ctg (-617°);
5) ctg 264°; 6) ctg (—5,6л);
7) ctg 2186°; 8) ctg3 (-236°);
9) ctg (5,6л).
1064. Следующие тригонометрические функции при-
вести к тригонометрическим функциям острых положи-
тельных углов, сохранив название приводимой функции:
sin 162°; cos 200°; cos 260°; sin 303°; tg 125°; ctg 159°;
cos(—602°); sin(—300°); cos885°; tg (-445°); tg(-1981°);
ctg 2012°; ctg 6,2л; cos 6,6л; sin (—8,2л); sec(—4,8л);
sin3; cos 2,5; sec(—3); cos 4.
1065. Следующие тригонометрические функции при-
вести к тригонометрическим функциям острых положи-
тельных углов, изменив название приводимой функции
на сходное:
sin 124°; sin 211° 30'; cos 252°; sin 278°; cos (— 400°);
sin 1512°; cos 1440°; tg 197°; tg (—811°); ctg612°;
ctg (—8,2л); sin (—3,83л); cos (—7,3л); sec 672°;
cosec (-3000°).
1066. Следующие тригонометрические функции при-
вести к тригонометрическим функциям положительных
углов, меньших 45°:
sin81°; sin(—6,5°); cos56°; cos(—149°); sin218°;
sin (—300°); cos 281°; cos (-340°); tg72°; ctg 80°; sec 78°;
cosec 54°; tg(—115°); ctg (—280°); sin (—5736°);
165
cos (—2562°); tgl,2rt; cos (*- 3,6 л); sin(—3); cos(—2);
tg(—5); ctg (—6).
1067. Объясните, почему для нахождения значений
тригонометрических функций при любых допустимых
значениях аргумента достаточно иметь таблицы значе-
ний этих функций для значений углов от 0° до 45°?
1068. Вычислить:
. / Зл \
1) sinl-g--си, если
2) cos (л — а), если
3) tg — а)» если
4) ctg (л — а), если
5) sin (а — л), если
12 л '
since— jy, у < а < л;
tga = yr15, л<а<-|^;
sec а = — 1^5, л<а< ;
cosec а = — ]/10, < а < 2л;
ctg а = 2 У 6, л < а < —.
Упростить (1069—1077):
1069. 1) sin 409° + sin (—49°) + cos 205° + cos 25°;
2) cos 327° — cos 17° — cos (-33°) + sin 220° +
+ cos (—377°) — sin (—40°);
3) sin (л — 2) — cos — 2^.
1070. 1) ctg 65° ctg 115э + sec 155° sec 205°;
2) sin 32° sin 148°+ tg 18° tg 288°- sin302° sin 122°;
1270 + 2330 + <-143°) ~ c[g (~37°) -'.in
’ tg 217° sin 683° (cos 217°+cos 143°) ьш/о/,
. ч sin 170° ctg 80° cos 710°
tg 190° tg 100° sin (-370°) ‘
1071.
1) 4?^!^- + sin810’-sin’1280'’;
2) [sin210° sec2 440° + cos2 (—200°) cosec2 200°] • sin2 20°;
3) [sec 352° + sin 172° ctg (—262э)] X
X [cos2140° + cos2 50°j • sec (—8°);
4) sin 750° sin 159° + cos 939° cos (—870°) +
+ tg 600° tg 1110°.
166
1072 i\ ________sin 150° — cos 240°___
1U ' ctg 730° ctg 800° + tg 730° tg 800° ’
лк 10 ctg 135° sin 210° cos 225° ,
tg 225°-ctg 315°
3) -££4^--tg210°sin315°;
’ cos 300°
4) cosec 362° sin 88° — sin 178° tg2 268°.
1073. 1) sin 450° cos 300° + tg 562° tg 788° +
4- sec 660° sec 1200°;
9 cosec (- 330°) tg 150° , cos (-135°) tg 585° .
ctg 210° cos 300° ’ sin ( — 1200°) cosec 240° ’
. - sin (-240°) ctg (-210°) . tg(-660°) sin (-855°)
£> sec 300° ctg 15° ’ cos (-600°) ctg 225° *
1074. 1) sin (2л + a) sin (3л — a) +
+ cos (3л + a) cos (5л — a);
2) — sin (л — a) + tg‘(a — л) — cos ;
/ л 1
. , \ ctg -7:— a .
qx sin (л — a) \ 2 / cos (2л — a)
' tg (л + a) , / л , \ sin (—a) ’
tgly + al
4) cos p tg (л + p) tg (-y- — p) cosec (y — ₽) •
1075. 1) sin^y—p) cosec p—tg2(p—уj sin (л — p);
2) sin (a —-yj cos (a — л) — sin (a — 2л) cos^a--------y
tg ~ a)cos a) •
' . i Зл , \ /3л \ ’
tg(~y + ay COS(y----a )
.. — COS Л
4) я ' •
sin -2 — ctg + a j tg (л + a)
1076. 1)
, / л a \ , л a \
g\2 2/“^Cg\2“^2/
(Q-r \
у-------aj [sin 2л + sin (2л — a)];
167
cos (л — a) sin I + P I
3) ____________i_z_____
’ sin (л + p) cos (4л — a) ’
(7X \
— + a 1 sin (4л — a)
-------------“Тзл---------\-‘
sin (5л + a) ctgI —-------al
/ Ятг \
1 — cos I -=-2a j + cos (2a — 4л)
IO77. 1) -----i-i-----------------у;
1 + sin (2a + 6л) — sin l-g- + 2a j
2) sin’Ox-₽) + tg2(л-₽)tg2(^ + ₽)-
— sin (4^- + ₽)cos (0 —2л);
3) sin (4л — a)tg^~---a) —
— cos (a — л) — sin (a — я).
1078. Проверить справедливость равенств:
1) cosec2 (a —y) ~’ s*n2 cosec2(y — «)— h
Г / л \~12 Г / тс \П2 л
2) sin a 4-sin I у—al + cos a — cos I у—a) — 2;
3) sin2 (y — cosec p — tg2 (p — yj sin (л —p) = 0;
4) tg2(a — л) — ctg (a —-^jctg(a— 2л) = sec2 a;
cos (2л — p) tg (л + p) — tg — p) ctg + p]
5) -----------------------/Я \ =
sin (л — P) sec (2л + P) + cos (-^— Pj ctg I — + pl cos л
= ctg p.
§ 60. Тригонометрические функции двойного
и половинного углов
1079. Выразить sin2a и cos 2a только:
1) через sin a, 2) через cos a, 3) через tga.
1080. Показать, что все тригонометрические функции
угла а выражаются рационально через tg-J.
168
1081. Что больше:
1) 2sinx или sin2x,
2) 2cosx или cos2x,
3) 2 tg x или tg 2x,
„ -л
если 0 < x < у;
если 0 < х <~2 ,
если 0 < х < у, х=/=у?
Вычислить (1082—1084):
1082. 1) sin a, cos а, tga, если sinу =0,96
л __
и -у < а < л;
2) tg 2a, если tg а = 3;
3) sin 2a, если cos а = — 0,8, у« < а < ' л;
4) cos 2a, если sin а = 0,7.
1083. 1) sina, если о 7 Зл . cos 2а —-о и -г- < о 4 Z 2а * 2л;
/ з \
2) cos (2 arccos ур г,
3) tg [2 arctg (—5)];
4) cos2 (y arcsin 0,6j — sin2 (y arcsin 0,6
ос 2
. 1084. 1) sin a, cos a, tga, если tgy = yj
2) tg2a, если sina=—=^, — < a < л;
’ & /61 2
3) sin 2a, если sin a + cos a = у.
1085. Выр азить:
1) sin За через sin а, 2) cos За через cos а, 3) tg3a
Через tga.
Вычислить (1086—1087):
1086. 1) 4 sin 15° cos 15°; 2) sin22°30'cos22o30';
3) sin 15° sin 75°; 4) 4 sin sin yp.
169
1087. 1) sin25°s^~; 2) cos2 22° 30' —sin2 22° 30';
7 cos 40 ' ’
3) cos215° — cos27S°; 4) —- 20° ~ coos2 20°
7 7 sin 50°
e> 2tgl5° . tg 22°30'
1 — tg2 15° ’ ™ 1- ctg2 67° 30' ’
Упростить (1088—1091):
1038. 1) 2sinc4oQs°iy.QL; 2)
3) -TTW: 4)
cos2 70° — cos2 35°
cos2 55° ’
2 sin 3a cos 3a
cos2 3a — cos2 — 3a
1089. 1) 2 sin (p + 45°) sin (45° — p); 2)
2 ctg a sin2 a
’ sin2 a — cos2 a ’
4) cos4 a — sin4 a.
1090. 1) /os2a 2) tg55° — tg35°;
tg y-ctgy
3) (sin 10° + sin 80°) (cos 80° — cos 10°);
.. 1 4~ sin 2a
7 (sin a + cos a)2 *
mm i\ 4 sin4 a + sin2 2a n\ • л ±
1091. 1) ----------:----------; 2) sin2a — tga
7 sin a 7 b
3) sin 3a cosec a — cos 3a sec a.
1092. Вычислить:
14 . a a , a
1) Siny, COS -g И tg-g-, (
. a a , a
2) sin у , cos у и tgy, ecj
O\ , a 161
3) ctg у» если cosa = -2gg ,
Упростить (1093—1096):
I 'm 2 sin 20° + sin 40°
1 и 93. 1) -П -. on0-. ;no ;
7 2 sin 20 — sin 40 ’
, . a
sin a + sin --
2)----------------L_
II I a
1 + cosa + cos —
170
1 — 2 cos2 (-?- + а) . 3) L ; 4) - sin а 7 / 9 а . „ а \2 cos2 sin2 — \ 4 4 /
1094. 1\ s‘n 2$ . n\ sin 2а cos а 1 4- cos 2(3 ’ "7 1 + cos а 1 + cos 2а * n\ cosec2 P s .с 1 + sin 4а 4~ cos 4а J cosec2 p — 2 ’ 7 1 + sin 4а — cos 4а sin2 -j- a i •
1095. 1) ~ft 2cos2-|-; 2) -— 7 . . p 8 7 cosa ’ 1 + cos~ 4 3) - -.--пТП---- ,7 ; 4) 2 sin’ + #)- 1. 7 cos2 a — 0,5 (1 — cos 2a) ’ 7 \ 4 1 2 ) 1 — 2 sin2 (-7- + 2a)
1096. в У L. 7 sin 2a (cos2 a — sin2 a) * .1 + cos-?- — sin 2) - ; 7 . a . a ’ 1 — COS-g— sin — 3) ctg a— 2 ctg 2a.
Проверить равенства (1097—1101):
1097. 2 —sec2 a 1) -г- ob—; rr n- = sec- a; 7 (sin2 2a + cos 4a) sec 2a 2 cos3 a — cos a 11 2 tg 1 — al snrl — + a j cos a tg a tg 2a . o 7 tg2a — tga 4) tg+ 2 sin'y ctg a = sin a.
1098. n sin2 2,5 — 4 sin2 P , 0 0 • 0 0. 1) -—2 ; гг-Лй ~ tg' P sin' P 7 sin2 2p — 4 + 4 sin1 P ° 9\ cos‘ 2P ~ sin* = 9 cfa 48- } sin2pcos2p ’ 2CTS*P’ cos 4a cos 2a + 2 sin 4a sin a cos a __ 2 ct? 2 7 sin a cos a ° * .v cos 2a cos a — 2 sin2 a cos a cos 3a
1099. j) sin (a +5) — cos a sin P = fg a- cos (a + P) + 2 sin ~ cos ~ sin P
171
2 sin a cos2 a 4- cos 2a sin a
2 sin 1,5a cos 1,5a
3) 2 sin2 pcos 2Д = 1;
*v • 1 1 ** I U»
-§- + «)-tgTsmTcosT
1100. 1)
1 — 8 sin2 a cos2 a
cos2 2a — sin2 2a
sin a (2 cos2 a 4~ cos 2a)
' sin21,5a - cos21,5a “
2 sin2 4 - 1
3) 2tg P-----g-----g - = 4 cosec 2p;
sinTcos2
4) ------—!ln.(40° +.^------ = cos (20° 4- £
4 sin I 10°+ 4) Sin I 80°-4) '
\ 4 / \ 4 /
1101. 1) -L±-S<*P +l=secp;
Ctg’f
2) sin a (sin a + sin p) + cos a (cos a + cos P) =
= 2соз!-Ц~—;
3) sin a (sin a — sin P) + cos a (cos a — cos P) =
= 2sin2^;
4) (sin a + sin p)2 + (cosa + cos P)2 = 4 cos2
5) (sin a — sin P)2 + (cos a — cos P)2 = 4 sin2 a ~
Решить уравнения (1102—1108):
1102, 1) cos3 x-j- 4 sin24 cos2cosx = 0;
2) cos2 2x — sin2 2x = —;
3) ,sin3 x + 2 sin cos = 0;
4) sin2xcos4 — 4-sin2x sin 4 е®*
<w Z £
172
1103. 1) 2 tg 2xsin ^-cos-j-sinx + tg 2х = 0;
/3
2) ' ~7TT~tgЗх~~ з :
— *6 T
3) T^7 + 2tg2-v = 3:
4) 4sin4x4* sin22x = 2.
1104. 1) tg(x + -f) + tg(x —J) = 2;
2) у(sin4x + cos4x) == sinxcosx — sin2xcos2x;
3) 4sinx + sin2x = 0;
4) cos 2x + 2 cos2 x = у.
1105. 1) 0,5 + cosx = cos2 у;
2) sinx = cos2x;
3) sin x 4- cos x ctg у = — ]/3;
lx X • л
4) Isiny — cosyl —sinx = 0.
1106. 1) arctg x— 2arctgy = 0;
2) arccos (x—1) — 2 arccos x = 0;
3) arctg (1 + x) = -y — arctg (1 — x);
4) arccos у — 2 arctg (x — 1) = 0.
1107. 1) 3 arcsin x — arcsin 2x = 0;
2) arcsin (cos x) — x = 0;
3) arcctg (tg x) — 2x = 0;
4) arcsin у — у— arcsin x.
1108. 1) 2 arcsin x + 2 }/~3 arcsin x = n;
2) arccos x — arccos (— x) = — arccos (1 — x);
3) arctg x -j- arctg 3x = -y;
4) arctg a + arctg y~- = arctg y^y.
173
§ 61. Преобразование произведения
тригонометрических функций в сумму
Преобразовать в сумму (1109—1118):
1109. 1) sin 27° sin 13э; 2) sin 28° sin 17°;
3) sin 63° sin Зэ; 4) sin 77° sin 13э.
1110. 1) cos 44° cos 46°; 2) cos 36° cos 24°;
3) cos 82° cos 8°; 4) cos 125° cos 55°.
1111. 1) sin 0,253 sin 0,257; 2) sin 0,428 sin 0,322;
3) sin0,458sin0,812; 4) sin0,712sin0,092.
1112. 1) cos 0,18 cos 0,12; 2) cos 0,142 cos 0,238;
3) cos 0,234 cos 0,326; 4) cos0,842 cos0,728.
1113. 1) 2 cos a cos 5a; 2) 2 cos 3a cos a;
3) 4 cos 5a cos 3a; 4) 8 cos 7a cos Зз.
1114. 1) sin 2a sin 4a; 2) sin 6a sin 4a;
3) sin (—7a) sin 3a; 4) 2 sin 4a sin (—5a).
1115. 1) cos (a + P) cos (a — P); 2) cos (a + P) cos a; •
3) 8 cos (a — P)cosP; 4) 4 cos 2a cos 3a.
1116. 1) 2 sin 2a cos a; 2) 3 sin 3a sin 2a;
3) 5 sin (a + p) cos (a — P); 4) 6 sin (a—P)cosp.
1117. 1) 2 sin 40° cos 10° cos 18°; 2) 4 cos 8° cos 10° cos 6°;
3) 6 cos a cos 3a cos 4a; 4) 4 sin a sin 2a sin 3a;
5) cos a sin P sin y; 6) sin a sin p sin y.
1118. 1) —sin 4a cos (2a — л); 2) 2 sin 3a cos a;
3) COS -777 Sin -T-; 4) Sin-^-COS-x-.
' 10 5 '63
§ 62. Преобразование суммы тригонометрических
функций в произведение
1119. Преобразовать в произведение:
1) sin a + sin Р; 2) sin a — sinP;
3) cos a + cos P; 4) cosa — cosP;
5) sin 40° + sin 20°; 6) sin 40° — sin 20°;
7) sin 56° 20' + sin 43° 40'; 8) sin 56° 20' — sin 43э 40';
9) cos 20° + cos 40°; 10) cos 60 — cos 20°;
11) cos 72° 20'+ cos 17° 40'; 12) cos 72° 20'— cos 17° 40'.
’ 174
1120. Следующие выражения привести к виду, удоб-
ному для логарифмирования, и вычислить с помощью
логарифмов:
1) cos 150° + cos 28°; 2) cos 46° + sin 50°;
3) sin 120° +sin 40°; 4) sin 100° — cos 20°;
5) sin 19°+sin 25°+sin6°; 6) cos 12°-2 cos 24° +cos36°.
Преобразовать в произведение (1121—.1124):
1121. 1) sin у + sin-y;
3) cos -J + cos -J;
5) tg 12° + tg32°;
7) ctg 18° +ctg 28°;
9) tg 40° + ctg 20°;
1122.
1) sin 22°30' + cos 18э 30';
3) sin-g- + cos у-;
5) tg-v-cfgf;
1123.
1) sin 2a + sin 4a;
3) tg a + tg 3a;
5) cos (40° + a)—sin (40°-
1124.
1) sin (30° + a) + sin (30°
3) cos a + sin a;
5) sin2 a — sin2 (3;
7) tg2a —tg2P;
2) sin-=- + sm-j-;
4) cos у — cos у;
z> \ । 3 jt i 2or
6) tg-^----tg—;
8) ctg 22° — ctg 46°;
10) tg 60°— ctg 40°.
2) sin 15° 46' —cos 80° 14';
л \ « JT 5T
4) -Silly — COS-у
6) tg-£-+ctg-^-.
2) cos 2a — sin 6a;
4) cos (a—p) + cos(a + p);
a); 6) sin (a + p)—sin (a—P),
-a); 2) cos ”y - + cos -y^-;
4) sin a — cos a;
6) cos2 a — cos2 P;
8) ctg2 a — ctg2p.
1125. Следующие выражения привести к виду, удоб-
ному для логарифмирования, и прологарифмировать:
1 \ sin 25° +sin 15° . cos a 4- cos р .
' sin 25° — sin 15° ’ ’ cos a — cos Р ’
sin 75° + sin 15° , . sin 7a — sin 5a .
' sin 75° — sin 15° ’ sin 7a + sin 5a ’
tg 2a tg 3a
4g 2p — tg 3p" ’
, л , л
Cig-у-Ctg у
6) ctg 0,3л 4- tg 0,2 л *
175
Преобразовать в произведение (1126—1128):
1126. 1) cos 80° + cos 79° + cos 75° + cos 74°;
2) sin 170° + sin 169° 4- sin 165° 4~ sin 164°j
3) sin a + sin 2a sin 3a 4- sin 4a;
4) cos a + cos 2a 4~ cos 3a 4~ cos 4a.
1127. 1) 14-2sina;
3) 1 — 2 cos a;
5) |/3— 2 sin a;
7) У 2 + 2 cos a;
9) 1 —sin 18°;
11) ]/2sina— 1;
13)
’ 1 4- sin a
15) 3 — 4 sin2 a;
1128.
1) 1 + sin a + cos a;
3) 1 — tg a;
5) 1 H-Ciga;
7) 1 + sin a—cos a—tga;
9) 1—sin a + cos a—tg a;
2) 1 + cos 2a;
4) 1 + cos ^a +
6) 1 4~ cos 50°;
8) 1 4- sin 40°;
10) sin20°—1;
12) 1 4- sin (a —J-Vj
\ о /
1 дч 1 + cos (a — p) ,
' 1 — cos (a — P) ’
16) 3 — 4 cos2 a.
2) 1 4- tg a;
4) 1 — cos a 4~ sin a;
6) 1 — 2 cos a 4-cos 2a;
8) 1 4- sin a 4- cos a 4" tg a:
10) cos a — cos 2a 4" cos 3a.
1129. Преобразовать в произведение с помощью вве-
дения вспомогательного угла, предполагая, что а>&>0:
1) а 4- Ь‘, 2) a — b\
3) 4)
5) У т=ь +V 7+6 •
6) У а1 4- Ь~ — %ab cos <р i
ИЗО. Привести к виду, удобному для логарифмиро-
вания:
1) (cos a 4- cos р)2 + (sin a — sin p)2;
cos (a — P) _ cos a .
t cos 2p cos P ’
cos (2P — a) + sin a . 4Hff 4.
' cos a — sin (2p — a)* to I 4 ’ 2 / to ’
6) sin2 (а + р) — sin2 а — sin2 Р; 6) 2 + tg 2а + ctg 2а;
/ cos (а- Р) cosa \ о д.
/) ------™---------------5- cos р
1 \ cos 2р cos Р ) ! ’
8) sin а + sin р + sin у — sin (а + Р + у);
q\ 1 + cos а + cos 2а + cos За t
) cos а + 2 cos2 а — 1 ’
10) sin 6а sin За — sin 9а sin 2а.
Доказать тождества (1131 — 1134):
1131. 1) sin 2a — tg a = cos 2a tg a;
2) у (cos a + /3 sin a) == cos (60° — a);
. a a
sin у — cos —
3) a--------------------a- = — sec a;
sin у + COSy
.ч sin 2a cos a _______, a
> 1 + cos a 1 + cos 2a 2 ’
5) cos2 у (1 + tg у j = 1 + sin a.
1132. 1) 4 sin a cos3 a — 4 sin3 a cos a = sin 4a;
2) + = tg a ctg ₽;
! sin (a + P) — sin (a — P) &
3) 2 sin (45° + a) sin (45° — a) = cos 2a;
л\ cos (a + P) + cos (a — P) ,
4> cos (a — P) — cos (a + P) “ Ctg a ct^
5) (cos a — cos p)2 + (sin a — sin p)2 = 4^in2 ;
6) 4 [sin2 a — 4) = 4 s*n(a +~y-jsin[a — —j;
7\ cosa ~ sin a _ 1 — sin 2a .
cos a + sin a cos 2a ’
ox sin a 4-sin 3a + sin 5a , n
8)--------±—-------— = tg3a.
’ cosa + cos3a ~r cosoa °
1133. 1) cos6 a-sin6 a = (3+CQ^a^-^ ;
2) tga + tg-y-tg(a+y) =
= — tgatgy-tg (a +-y);
3
3) sin6 a yj- cos6 a + у sin2 2a = 1;
177
1134.
4) , ;°s2° — = ' sin 2g;
7 ctg2 a — tg2 a 4
5) sin a — sin 2a + sin 3a = 4 cos у a sin a cos ;
3 + 4 cos 2a + cos 4a ,л
6) 3-4cos2a + con^==Ctg a’~
7) sin (a + P) + sin a cos a 4~ sin p cos P =
= 2 sin (a + p) cos2 a y—;
8) sin 4a + cos 4a ctg 2a =
9) У1 + cos a + У1 — cos a = 2 sin + y- j
при 0 < a < ^;
10) VT+ sin a — У1 —sin a = 2siny
при 0 < a < ;
И) tg(^~y)(l + sina) sec a 4- 2 cos 2a =
_____________________________________ sin 3a .
12) sin (a + ₽) + cos (a + (3) + 1 =
= 2/2 coscos (45’—
1) sin a (cos 4a 4- cos 6a) = у (sin 7a — sin 3a);
2) sin a (cos 2a + cos 0) = у (sin 3a 4- sin a);
3) tg a + tg P + tg у = tg a tg p tg у
при a + p + y = л;
4) cos a + cos P + cos y —
= 1 4-4 sin у sin у sin у при a 4~ P 4“ Y = л;
5) sin a 4- sin p 4- sin y = 4 cos у cos у cos y
при a 4- p 4- y = л;
6) (1 4-tga)(l 4-tgp) = 2 при a4-P = -^;
7) sin a 4~ sin p -j- sin y = 4 cos у cos у sin y
при a 4- P = Y-
178
1135. Доказать, что:
1) sin 20° sin 40° sin 60° sin 80° = yr*,
2) tg 20° tg 40° tg 60° tg 80° = 3;
3) cos 10° cos 30° cos 50° cos 70э =
7 16
.ч 2л , 4л 1
4) cos — + cos — = — у;
2л . 4л . 6л 1
5) cos — + cos — + cos — = — у;
л 2л Зл 7л о-7
6) cos^cos-iycos^... cos-|T = 2 .
§ 63. Тригонометрические уравнения
Решить уравнения (1136—1137):
1136. 1) cos Зх cos х — cos lx cos 5х;
2) cos 4х cos 2х = cos х cos 5х;
3) sin Зх sin 2х = sin 5х sin Зх;
4) sin Зх sinx = sin lx sin 5x;
5) sin 4x cos 2x == sin 5x cos x;
6) sin 8x cos 2x = sin lx cos 3x;
7) sin 4x sin 1 lx -j- sin 2x sin 5x = 0;
8) sin x cos 3x sin 2x — sinx sin 3x cos 2x = — 1;
9) sin 5x cos 2x — cos 5x sin 2x = — ~;
10) 2 sin у cos у cos 3x + sin 3x cos x = — .
1137. 1) sin22x + 2sin2x — 3 = 0;
2) 3 — 2 sin2 x — 3 cos x = 0;
3) 6 cos2 x + 5 sin x — 7 = 0;
4) sec2x — 4 = 0;
5) y<3sec2x — 4tgx = 0;
6) 2 sin2x + 3 cos x = 0;
7) 3 cos2 2x — sin 2x 1 = 0;
8) sin2 2x — 2 cos 2x 2 = 0;
9) 4 cos x — Sin2 x — 4 = 0;
10) 6sinx — cos2x — 6 = 0;
11) cos2x + sinx1 = 0;
12) cos2 x -j- 7 sin x + 7 = 0.
179
1138. Решить уравнения путем разложения левой
части на множители:
1) tg3xcosx— tg3x = 0;
2) tg3x-{- 3tgx = 0;
3) sin3 2x4- sin2x = 0;
4) 5sinx — sinxcosx = 0;
5) cos3x—cosx = 0;
6) tgy4-tgyCosx = 0;
7) cos2x 4-sinxcosx—1;
8) 2sinx — cos2xsinx = 0;
9) 14-sinx — cosx — cosxsinx = 0;
10) tg 3x (1 — cos x) 4-tg 3x — tg 3x cos x == 0.
Решить уравнения (1139— 1140):
1139. 1) sin2x—cos2x = 0;
2) cos3x 4- sin3x = 0;
3) sin2x — sinxcosx — 2cos2x = 0;
4) sin~r + *—sink-----x =0;
5) sin (x 4- 30°) 4~ cos (x 4- 30°) = 0;
6) 2sinxcosx 4- 3 cos2x = sin2x;
7) 7 sin2 x — 8 sin x cos x = 15 cos2 x;
8) V 3 cos — xj — sin (x 4--yj = 3;
9) 3sinx — 5cosx = 0;
10) cos2 2x — 3 sin 2x cos 2x 4~ 1 = O’,
11)9 sin2 x 4- 30 sin x cos x 4- 25 cos2 x — 25;
12) sin5x — cos5x = 0;
13) sin36x 4~ cos36x = 0;
14) tg у sinx — tgу cos x = 0;
15) sin2x 4-sinx cosx = 0.
1140. 1) cos (2л 4- x) 4- 2 sin 4~ = 1‘,
2) cos22x4-sin2 2x = 2sin(2л—x)4~cos
3) cos (x 4- 270°) 4- sin (x — 180°) = 2;
180
4) tg (4л — x) — ctg (у + ==
5) tg 110° tg 200° — 2 cos 2x = 0;
6) sin (2x — 2л) + cos — 2xj 4-2 = 0;
7)tg(x-f)+tg(x+^) + lX- = 0;
8) cos [x —y-j + 2 sin (x — л) = — 3;
9) cos3 (y + x) + sin3 (л + x) = 0;
10) sin2 (5л + 2x) -}- cos2 (-y- — 2xj = 2;
11) cos2 3x 4- tg [y 4~ 2xj — 2 — sin2 3x;
12) tg(x—yj —ctg(-y-4-xj~tg(y 4-x) =
• л
= siny;
13) tg24^ctg-^-4-tg(2n-f) = 0;
14) [ 1 4- sin (2л — x)] [ 1 4- sin (л — x)] = y;
15) cos2 204° 4-sin2 336° — tg2x = 0.
§ 64. Неравенства
1141. Решить неравенства:
1) cos(2x4--~)>0; 2) sin2x < — у;
3) sin(3x— л) > 0; 5) sin3x > 7) ctg (y — x j > 0; 4) sin2x>y; 6) sin3x < — -Jy-; 8) sin x 4- cos x < У 2;
9) sin x — cos x < У 2; 11) sin у > 0; 13) tgT>0; Л 10) cos x 4- cos 2x < — У 2; 12) cosy>0; 14) Igsin^y— xj < 0;
181
15) sin (л + x) < 0;
17) Igsin(у — xj > 0;
16) lg sinx <10;
18) tg 2x < sin x + tg x.
§ 65. Системы тригонометрических уравнений
1142. Найти sinx и sin у, если sin х + sin у = 0,2,
a cos х + cosy = —0,2.
1143. Найти cos х и cos у, если cos (x-f-у) = -|- (1—21^б),
a cos (х — у) = (1 + 2 ]/б),
1144. Найти tgx и tg у, если х + У = 45°, atgx +
+ tgy=10.
1145. Определить х и у, если sin(x — у) = у,
a cos (х+ ?/)= — .
1146. Решить системы уравнений:
3) I
( sinx cos у = 0,36,
I cos х sin // = 0,14;
х у Ct,
sinx -j- sin y = a\
x + У = a,
sinx sin у = a;
x + y = a,
! tgx+ tgy = cz;
( sinx sin у =0,36,
2)
( cosxcosy = 0,14;
( x-t~y = 77°,
4) <
( cos x — cos у = 0,4897;
| x — y = 31°,
6) I tgx —tgу = 0,74;
i2sin * + cos у |
IQSin2 x + cos2 у
1147. Острые углы А и В прямоугольного треуголь-
ника связаны соотношением sin Л -|- cosB = tg А. Опре-
делить эти углы.
ГЛАВА 8
ОБЗОР СВОЙСТВ И ГРАФИКОВ
ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
§ 66. Общие свойства функций
1148. Найти области определения функций:
1) У = х2; 2) У = V X",
3) у — У х2 — 9; 4) X •
У ~ X2 - 1 ’
5) 5 6) y = V4-X2;
J Ух2-25 '
7) у = ]/ х2 — 5х + 6; 8) у = У —
9) Z/ = 4x“1; 10) У = у 1 —х2;
И) 1 12) У 2х
У /1 - X2 ’ У Ух + 1 ~У х -2-
13) / X — 1 J X + 1 ’ 14) y = log7 х;
15) r/ = log2(3x — 1); 16) У = 1g (*2 — Зх + 2);
17) r/ = lg(5 + 4х — №); 18) г-Х2 У = э ;
Ух
19) у=217; 20) У = 7^;
21) у — sinx; 22) у — У sinx + cosx;
23) у = У sinx; 24) у= У tgx;
25) у — У 1 — cos 2х; 26) у = У 1 — sin х;
27) У= 1g sin х; 28) fW^lgcosy;
29) f U) = 1g tg *; 30) f(x) = lgctgx;
31) f (x) = У 1g sinx; 32) f (х) = arcsin х;
183
33) f(x) = T. 34) f(x) = arcsin (x — 3);
<21 V О ill m*A'
35) f (x) = arccos (2x + 1); 36) f (x) = |/| x | — 2;
37) f(x) = lg| l-x|.
1149. Найти области изменения функций:
1) уг=2х — 3;
з) =
5) у — х1— 6;
7) У=7Х\
9) <p(x) = cosx;
11) f(x) = ysin-|-;
13) fW = ^r:
2)
4) */ = х2;
6) у = х2— 9x4-2$;"
8) f(x) = 3"x;
Ю) f (х) == 2 cos х;
12) <р (х) = arcsin х;
14) =
Четность и нечетность функций
1150. Установить четность или нечетность функций:
1) У — х2;
3) у = х3;
5) у = 2“^;
2) у = 2xs — х4;
4) г/=1+2х2;
9) f (х) = sin 2х;
11) <р(х) = х2— cosx;
13) <р (х) = х2 sin х;
15) K=lg^.
8) f(x)==3,x|;
Ю) Hx) = cosy*.
12) qp (х) = 2 tg х 4- sin2xl
14) f(x) = -L-4;
1151. Как расположены графики четных функций
относительно осей координат?
Как расположены графики нечетных функций отно-
сительно осей координат?
1152. Какие из функций четные, нечетные или не
четные и не нечетные:
1) У = 1 lg* I; 2) у = 21х|;
184
3) У — 4) y=ysin3x;
5) у = 3х—1; 6) y = 2|sinx|;
7) у = х3— х + 1; 8) у = sinх -ф cosх;
9)^=7Т2: Ю) г/ = х3-х2 + 7.
Периодичность функций
1153. Найти периоды функций:
1) у = sinx; 2) y = cos2x;
3) У = tg х; 4) y = ctgy;
5) у = cosy; 6) у = sin у;
7) у = 2tgx-ф sin2x; 8)y=l — tgy;
9) y = |cosx|; 10) у = ctg 2x ф- tg 3x.
1154. Показать, что функции y=sin(ox, y=sin (сох-фф)
~ 2л
периодические с периодом Т — —.
1155. Показать, что следующие функции не являются
периодическими:
1) у = cosx2; 2) y = x + sinx.
1156. Найти точки пересечения графиков функций
с осью Ох:
1) у = 3х+ 2; 2) у = х2 — 1;
3) у = х24-3х—10; 4) у = —х2-ф2х—1.
1157. Найти точки пересечения графиков функций
с осью Оу:
1) х — у — 2 — 0; 2) у = х2 — Зх + 2;
3) х2 + у2 = 25; 4) у2 = 2х — 9.
1158. Указать, в каких точках функции имеютточки
разрыва:
1 \ 1 . х2 — Зх + 2 ,
1) ^ = 7’ 2) ------7+Т—’
пч X2 + X + 2 лч . 1
3) Z/ = T2_;^o-; 4) y = smx —у—*
Л Л A Olli Л
185
1159. Определить интервалы постоянства зваков
функций:
1) у = Ъх — 6; 2) = —8х Н- 7;
3) у == — х2 4- 6х — 9; 4) у — 2х2 — х;
5) у = 4х — х2; 6) r/ = sin2xp
7) у — arcsin х; 8) z/ = logi х\
9) ?/ = log2(—х); Ю) // = (% +3,5) (х~ 1);
11) z/ = (x + 8)(x~0,5)(х — 2);
12) у = {х- 1,5) (х —3) (х 4- 5).
Частные значения аргумента и функции. Возрастание
и убывание функции
1160. Вычислить частные значения функции у =
= х2— х 4- 3 для частных значений аргумента
Xi = —2, х2 = 0, х3 = у, х4=1, х5 = 2.
1161. Дана функция f (f) = 2 } . Вычислить
/(—2), f(0), f(3).
1162. Дана функция f (х) = 2 sinх. Вычислить
р С* / \ С* / «Т \ р / «ГС \ р / ЗХ \
I'\~4г Ц~Т/’ ЦУ/’ ' \ 2/*
1163. Дана функция f(x) = cos2x. Вычислить
р / л» \ р / л» А р f л» \ р I Л \
цД ц-Д МД' Л-Д-
Зх2_ |
1164. Дана функция f(x) = —2 , . Вычислить
f(2) ’
1165. Дана функция
<р (А) =х2 4- — I х 4- 4- 2.
Доказать, что
Ф М = Ф (7).
186
1166. Найти промежутки убывания и возрастания
функций:
1) У — Зх—1; 2) у = — % + 5;
3) у = I х 4) у = | х | + I;
5) У = — I х [ + 2; 6) у = — |х + 2
7) = 8) {/ = -•!;
9) у — — я2 4-2; 10) у — х2-\-х— 6.
1167. Вычислить наименьшие и наибольшие значе-
ЭДш функций:
1) у = х2 + 5х 4~ 9; 2) у = — х1 4- Зх;
3) у = 2sinx; 4) z/ = -|-cos2x;
5) // = sin2x.
Взаимно обратные функции
1168. Найти функции, обратные данным:
у = Зх; у = 2х — 5; у — -- х 4- 1; У = х3.
Построить графики данных и найденных функций.
1169. Постройте графики функций и сравните их
свойства:
1) у = 2х и z/ = log2x;
2) р==3“х и z/ = log_i_x.
з
1170. Доказать, что графики взаимно обратных
функций симметричны относительно биссектрисы I и Ш
координатных углов.
1171. Найти функции, обратные данным:
1 \ 3 х + 3 е
’ 57 ’ У ~- 2х- I ’
3) У = -~п'> 4) r/ = 2sin3x;
5) z/ = ycosx; 6) z/ = tgy.
1172. Если данная функция является возрастающей
(убывающей), то какой будет обратная ей функция.
Привести примеры.
187
Линейная функция и функции, связанные с линейной
1173. Тело движется равномерно со скоростью 40 км
в час, а до начала отсчета времени оно прошло путь
100 км. Написать формулу, выражающую путь S,
пройденный телом за t часов.
Какая из переменных величин является аргументом,
какая — функцией? Как называется полученная функ-
циональная зависимость?
1174. Дана функция у — kx 4- b. Показать, что тангенс
угла наклона прямой к оси Ох вычисляется по формуле
1175. Найти линейную функцию, переводящую ариф-
метическую прогрессию 1, 3, 5, 7, ... в арифметиче-
скую прогрессию 1, 7, 13, 19, ...
1176. Найти линейную функцию, переводящую ариф-
метическую прогрессию 0, 1, 2, 3, 4, ... в арифмети-
ческую прогрессию —1, 1, 3, 5, 7, ...
1177. Даны арифметические прогрессии —2, —12,
—22, —32, ... и —3, —1, 1, 3, ... Найти линейные
функции, переводящие первую прогрессию во вторую и
вторую в первую.
1178. При каком условии графики функций y=k{x-}-b{
и у = k2x -J- &2 пересекаются в точке, лежащей на оси Оу,
1179. Построить графики функций:
1) г/ = х; 2) г/= — х;
3) х = 2; 4) г/ = 3;
5) У = \ х |; 6) У = — | х
7) у = \х 4-2 8) у = \ х— 1 |;
9) У = \ 3 — х |; Ю) у = — 1 3 —х
И) У = \ х — 3 1— 1; 12) X
13) — X У~ |х| ’ 14) и — 1*1. 1 к\ у — — 2*
У х ’ У ’ |х| *
1180. Показать, где на плоскости расположены точки,
координаты которых удовлетворяют условиям:
1) х<1; 2) х>— 1;
3) I у I < 3; 4) | у | > 3;
5) %+ #>2; 6) К 1;
188
f x 4- у — 1, (x— z/ = 3,
(у— 2x = 2; ' [x-j-y=l.
1181. Построить графики функций:
Г 2х—1 при х < 0, Г 1 при х^>0,
( — 1 при х 0; & I 0 при х < 0.
1182. Построить графики и найти наименьшие зна-
чения функций:
1) у = }х — 1 |-ф|х — 3 |;
2) z/ = | х —2 |-ф | * + 3 |;
3) у = | х -ф 1 | -ф1 х — 2 | — 3;
4) г/ = | х | + | х— 1 | +1 х + 1
5) z/ = | х-ф 2 |-ф | х — 1 | +1 х — 3 |.
1183. Решить уравнение | х — 3 | -ф | х -ф 6 | -ф | х—8 |-ф
-ф|х-фЗ| = ЗО графически и методом интервалов. Ка-
кой из методов рациональнее?
Квадратный трехчлен
1184. Построить графики функций:
1) у = х2\ 2) у = х2~4; 3)г/ = х2ф1;
4) у = х2— Зх; 5) у — х2— 7х+10.
Найдите наименьшее значение и интервалы возраста-
ния и убывания каждой из функций.
1185. Построить графики функций:
1) у=~ х2-ф9; 2) у= — х2фх;
3) г/=_х2-ф5х —4; 4) = 2х — 3.
Найдите наибольшее значение и интервалы возраста-
ния и убывания каждой из функций.
1186. Показать, что координаты вершины параболы
у = ах2 -ф Ьх -ф с вычисляются по формулам:
__ & Ь2 — 4ас
2а ’ 4а2 *
1187. Найти уравнение параболы у — ах2 -ф Ьх -ф с,
которая пересекает ось абсцисс в точках (3; 0), (—5; 0),
а ось ординат в точке (0; 30).
1188. Найти уравнение параболы у — ах2 -ф Ьх -ф с,
если а=1 и парабола пересекает ось абсцисс в точках
(2; 0) и (5; 0).
189
1189. Построить графики функций:
1) у==-2х2 — х + 6;
3) у — \ — х2 — 2х 4~ 5
5)
7)
9)
у = 2х2 — | х |;
у = х2 — 2 |х | + 1;
2) У = J х2 + х — 2
4) */ = |х2 — х| — 3;
6) у = х2 4-| х
2х + 3 при
х2 при
8) I У 1 = х2 — 2х — 3;
х< — 1,
-1
1,
У =
X
3 — 2х при
х
1190. Решить графически неравенства:
1) х2 — Зх 4- 2 > 0; 2) 2х2 — 7х 4- 6 < 0.
§ 67. Некоторые степенные функции
1191. Построить графики функций, указать BTtfep?
валы постоянства знаков:
1) у = х3; 2) у= — х3;
3) у = (х—I)3; 4) у = (1х)3;
5) */ = |*31; 6)|у| = х3;
7)|х| = у3; 8) у = х3;
9) </=4-; 1°) у — х~3-
§ 68. Дробно-рациональные функции. Асимптоты
1192. Построить графики функций:
Рис. 8. а, Ь, с — асимптоты.
1 \ 1 2
1) У = ^> 2) у=-->
Написать уравнения их асим-
птот.
1193. Показать, что график
, 1
функции у = 2.3- получается из
графика функции У — ~ путем
сдвига его на три единицы впра-
во. Напишите уравнения асимп-
тот.
1194. Построить график функции у = 7 4- 2 и на-
писать уравнения асимптот.
190
1195. Построить график функции у = 3 + 2 и
написать уравнения асимптот.
1196. Построить график функции у = -уц- Имеет ли
эта кривая ось симметрии?
1197. Функцию у = 4^4^ привести к виду
Написать уравнения асимптот.
1198. Показать, что у гипербол, являющихся гра-
фиками дробно-линейных функций У = -~~ у > асимп-
тоты взаимно перпендикулярны.
1199. Построить графики функций:
1) У = — 1; X 2) У = 7ТТ;
3) У — —1 2- х + 1 4) У =
5) У = 1 — 2х х —2 * 6) У = 1 |х+1| •
1200. Решить уравнения аналитически и графически:
. ч х + 2 2х + 1 , л\ Зх — 4 2х — 6
Зх - 1 ’ ’ х + 3 ~~ х — Ъ*
1201. Построить график функции
X2 - 6х + з
У ~~ х - 3
§ 69. Показательная функция, логарифмическая
функция и функции, связанные с ними
1202. Какие из функций
1) у — зх’,
3) // = log5x;
5) у — 3 х+2;
2) у = 2~х;
4) y = logj_x;
з
б) У = logs (2х + 1)
возрастающие, убывающие?
1203. Построить графики функций:
1) у = 3*+'; 2) у = 3!x|+I;
З)г/ = 2Х —1; 4) у = -2"+1;
5) г/ = 2,х1; 6) у = 2~^.
Указать интервалы возрастания и убывания функций.
1204. Решить уравнения графически:
1) 2x = -i%; 2) 2х = 2х.
1205. Построить графики функций
y = \og2x и y = }og±x.
Указать общие свойства функций и их различие.
1206. Найти области определения и интервалы по-
стоянства знаков функций:
1) */ = log3(x — 2); 2) r/ = Iogj_(2x —3).
5
1207. Определить, является ли функция у =
= lg[(2— x3)(2-|-xs)] четной?
1208. Найти области определения функций:
1) */ = lgl*l; 2) r/ = lg| х—1 |; 3) г/= log2(2 — J х I).
1209. Построить графики функций:
1) z/ = 210g2X; 2) y = alos«x-
3) # = log3|x|; 4) r/ = |log2x|.
1210. Где на плоскости расположены точки, коор-
динаты
которых удовлетворяют условиям:
z/Clog^x, / ^>log9x,
3 2) / Q
y>-2; Ь<3.
§ 70. Тригонометрические функции.
Обратные тригонометрические функции
1211. Найти область определения и область измене-
ния каждой из следующих функций:
1) z/ = 3cosx; 2) z/ = cos3x;
3) У = у sinx; 4) г/= sin
5) i/ = tg2x; 6) z/ = tgx2.
192
1212. При каких значениях х каждая из следующих
функций принимает нулевые значения:
1) z/ = 2sinx; 2) y = 2sin2x;
3) i/ = cosx; 4) i/ = cos(3x — 45°);
5) y = tg^\ 6) r/ = ctgy.
Выразить формулой множество таких значений х.
1213. При каких значениях х каждая из функний^не
определена:
.v 1 + cos X i) y = ~, ; ' J I — COS X 3) j/=—4— cos lx + 1 r-\ 4 sin X- COS X o) y~— ; ’ J Sin X + COS X ’ 2 — cos x 2) у = ; ' cosx .к 1 + sin x 4) У = -\ з— ’ v 1 — sin X 2 6) Z/ = —: ; ' V sin X — cos X
7) у = tg x; 8) y = -^—\ ! J tgX
9) i/ = ctgx; 10) y=——. ’ J ctgx
1214. Найти области определения левой и правой
частей следующих выражений:
, sin х , х sin х
1) tg х =-------; 2) tg -к- = -r-г—
' ° cos х ' ° 2 1 + cos
o\ i X 1 ““ COS X «к i i x 9 9
3) tg Tf =-----------:----4) 1 4- tg2 x = sec2 x;
' b 2 sinx 7 1 b ’
5) 1 4- ctg2 x — cosec2 x; 6) ctg x = —
Какой вывод можно сделать в отношении справедли-
вости этих равенств.
1215. Из следующего множества функций:
1) y = tgx — 2; 2) у — cosx — 1;
3) у = 5 + tg х; 4) у = 8 cos х — 7;
5) £/ = x4-tgx; 6) г/= х 4-sinx;
7) у = | 2х cos х |; 8) у = | 2 cos 2х 4- 3 I
составить два подмножества: (а) ограниченных функций,
(б) неограниченных функций.
1216. Упростить:
1) sin (-60°) 4- cos (-30°) 4- tg 45° — ctg (- 45°);
2) sin -y 4-sin-2- ctgy-ctg^-yj;
193
3) sin (— a) — tg (— a) — ctg (— a) + sin a — tg a;
4) tg (x — 90°) — ctg x — ctg (x — 90°);
5) cos (x — 90°) + cos (— x) + cos (x — 360°) — cos x.
1217. Какие из следующих функций четные, нечет-
ные и какие не являются ни четными, ни нечетными:
1) У = 1 + cosx 2) У 2 sinx
1 — COS X * 1 + cos X
3) y — У sin x; 4) У = j/cos x;
5) У = lg sinx; 6) f(x) = Ig cosx;
7) f(x) = sin1 2x; 8) f(x) = tg2 X?
1218. Вычислить периоды функций:
1) у = sin (Ъх + -j) cos ^2х 4- у); 2) у = sin2 Зх;
3) y=cos (Зх — 6); 4) z/ = sin(5x+y
5) г/= sin (у — 6) y = tg^y +
7) г/= sin(4 х + -|); 8) у = tg(-|x—у);
9) !/ = ctg (у х + 7); Ю) # = cos(2yx—у).
1219. В каком промежутке функции у = sinx и
у = tg х строго монотонны (возрастающие) и имеют
обратные функции у = arcsinх, у = arctg х? Привести
примеры.
1220. (а) Найти область определения, область изме-
нения и период функции z/ = 3cosx — 4 sinx.
(б) Найти область изменения следующих функций:
1) у = 2 cos2 у + tg х ' ctg х;
2)y = ctgx.ctg(| + x +
3) у—— 2sin(x—у) + 3.
1221. Определить знак разности:
1) sin 15° — sin 5°;
3) tgl5° —tg5°;
5) sin 50° — sin 70°;
7) cos 185° —cos 350°;
9) tg 450° — ctg 87°;
2) cos 15° — cos 5°;
4) ctg 15° — ctg 5°;
6) cos 60° — cos 80°;
8) sin 365° —sin 20°;
10) sin 540° — cos 600°.
194
1222. С помощью знаков > или < записать соот-
ношение между следующими парами дуг;
1) arcsin 0,5 и arcsin 0,7;
2) arccos 0,5 и arccos 0,8;
3) arcsin 0,3 и arccos (—0,4);
4) arctg (—1,743) и arctg (—1,852).
1223. Указать промежутки монотонности функций!
1) у = sinx; 2) у = cos х;
3) y = tgx'> 4) у = [ sin х |;
5) у — | cos х |; 6) У = \ tg х |;
7) r/=3sinx; 8) qCOS X, У — о ,
9) у = ^‘; Ю) у = lg sin 2х;
11) z/ = lgcos2x.
1224. Разбить сегмент [0; 6л] на промежутки моно-
тонности функций:
1) у = sinx; 2) у = cosx;
3) # = tgx; 4) y = sin-|;
5) y==cos^x; 6)r/ = tg-|-x.
1225. Построить графики тригонометрических функ-
ций:
(а) у = A sin (kx + а) в интервале —л^х<2л при
1) А= 1, k= 1, а = 0;
2) А=1, 6=1, а = 4;
3) А=1, k=l, а = -4;
4) А = |, k = 2, а = ~;
5) А= 1, 6 = 2, а = 0°;
6) А = 2, 6 = 1, а = 0°;
7) .4=1, 6 = 1, а-03;
8) Д = 1, £=1, а = 0°.
(б) у = A cos (kx 4- а0) в интервале 0^х^2л при
1)4=1, k = l и а = 0°;
2) 4=1, k = 2 и а = 0°;
195
3) A = 2, k=l и а = 0°;
4) А = 1, k = у и а = 0°;
5)Л = у, k=l и а = 0э.
(в) В интервале —2л^х^2л
1) z/ = tgx; 2) # = ctgx.
1226. Построить график функции у= — 2cosx4-l и
исследовать функцию в промежутке от —2л до 2л.
1227. Решить графически уравнение 2 sinx =у хД-0,5.
1228. Построить график функции г/= 2sinx—1 и
исследовать функцию в промежутке от — л до 2л.
1229. Построить графики функций:
1) y=l+2cos(y + y); 2) у= 3cos(2х + -J) -• 2,
и найти интервалы постоянства их знаков.
1230. Найти наибольшее и наименьшее значение
функций:
. ч 3cosx + 3sinx sinx — cos х
1) у =------5------; 2) у =------.
1231. Построить график функции у — 3 cos х Д- 1,5
, Зл
и исследовать функцию в промежутке от — л до -у.
1232. Построить графики функций:
1) z/ = sin! g-x + yj; 2) £/ = cos|y X — yj;
3) y== arcsin x; 4) у = arccos x;
5) y— arctg x;
указать области определения и области изменения этих
функций.
1233. Решить графически уравнение ctgx = yx-|- 1.
1234. При каких значениях х функции z/= sinx и
//= cos х одновременно возрастают?
1235. Решить следующие неравенства:
1) log2sinx<0; 2) log2cosx<0;
3) log3tgx>0; 4) cosx-|-2>0;
5) cos2x — 3 cos x < 0; 6) cos 2x > --;
7) 1 cos 2x | < у; 8) | sin x ] > у;
196
9) |tg|| < 1;
11) sinxi>—
13) |tgxl>l;
10) sinx >y;
12) ctgx<X|-; .
14) cos x --g—.
§71. Разные задачи
1236. Функция у от аргумента х неявно выражается
равенством 4//— Зх = 5.
Найти явное выражение у в зависимости от х. Какая
это функция?
1237. Найти области определения каждой из функ-
ций, выразив у явно в зависимости от х:
1) x24-z/2 = 4; 2) (х-3)2 + (^-2)2=16;
5) x2~z/2 = 4; 6) г/2==4(х —2);
7) х2 = 8(у - 5).
1238. При каком значении х линейные функции
£/ = 0,6x4-5 и z/ = 2x — 2 принимают равные значения?
1239. Выразить формулой пло-
щадь заштрихованной части круга
в зависимости от радиуса этого
круга (рис. 9).
1240. Выразить объем куба как
функцию площади его боковой
грани.
1241. В каких точках график
функции
у = (х — 4) (х 4- 3) (х — 2) (2х 4- 8) Рис. 9.
пересекает ось абсцисс?
1242. у есть функция аргумента и, а и в свою оче-
редь— функция аргумента х. Найти явное выражение
функции у от х, если:
1) У= 1 — M =
2) у = У и, Зи — 2х — 3;
3) у = Зи, х—1
197
1243. В задачах на арифметическую прогрессию
обычно встречаются пять величин: alf ап, d, п, s.
1) Сколько существует независимых уравнений, свя-
зывающих эти величины?
2) Сколько из этих пяти величин нужно знать, чтобы
можно было вычислить остальные?
1244. Решить графически уравнение
2 log4x — 3 — 2х.
1245. Доказать справедливость равенства
log±x = — logax.
а
1246. При каких значениях х справедливы нераи'ен-
ства:
ч 1
1) logx 7 < logx 9; 2) logx т < logx у;
3) 1 — log3x<0; 4) 1—log£X<0.
T
1247. Решить графически уравнения:
1) х2 — 7x4-12 = 0; 2) х2 —6х —7 = 0;
3) 8х2 — 6х+ 1=0.
1248. Найти такое значение k, чтобы неравенство
kx2 + %х + 1 > 0 выполнялось при любых действитель*г
ных значениях х.
1249. Решить неравенство
Зх + 5 2х 7
х — 1 х — 1
1250. Показать, что уравнение
lgx = ]/r — х2 — Зх — 2
не имеет действительных корней.
1251. Где на плоскости расположены точки, коор-
динаты которых удовлетворяют условиям:
1)
— — <Г А
3^^2’ 2)
+ 1;
у — cosx > 0,
у — sin х < 0,
1252. Решить графически уравнение
х2— | sinx | = 0.
198
1253. Решить графически неравенство
| х 4- 2 | > | х |.
1254. Построить график функции
у = sin2 V — х 4- cos2 У — х.
1255. Найти область определения функции
У = г-,,1 2 + '8 (2х — ')•
У 2 + х — х1
1256. Решить неравенство
I Sinx |> у.
1257. Решить неравенство
logojogg-^^ < 0.
1258. При каких значениях х справедливо неравен-
ство
cos х • cos 2х > sin х • sin 2х?
1259. Решить графически систему уравнений
( * + У = 1,
1 у = х2 4- 2х — 3.
1260. Указать, начиная с какого номера члены про-
грессии 1, 6, 11, 16, ... больше 1000.
1261. Решить неравенство
0 < 1g (Зх — 1) — 1g (9 — х)< 1.
1262. Доказать, что если 0 < ср < у, то ctg у > 1 +
4-ctg<p.
§ 72. Дополнения к разделу комплексных чисел
1263. Найти модуль и аргумент комплексного числа
(2 + 3Z)(l -/)
2 44- I
199
1264. Найти модуль и аргумент каждого из слёдую-
щих чисел:
1) 2 = (-4)"; 2) г-i/^T;
5 ,----------:=- в /________
3) 2 = У — 16— 16V3Z; 4) z = V — 4+3/,
и построить найденные точки.
1265. Зная, что комплексное число
z = х + iy — г (cos ф + i sin <р) — rei<p = I z ) e! arg z,
TRex-i-iy — алгебраическая форма, r (cos<p + i sin<p) —
тригонометрическая форма, re1® — | z je’: are? — показа-
тельная форма комплексного числа z, выразить сле-
дующие числа в тригонометрической и показательной
форме:
1) г = 3 — 3/3/; 2) г = 2 + 2г;
3)2 = l + i4; 4)г = 4-±/;
ца (3 + 20(1-2/) . , (2/-1)(3 + 20
О) z— , о) Z — .
1266. Показать, что:
1) е1.2Ьл=1; 2) ez+2kni—eZ'
1267. Найти действительную и мнимую части каж-
дого из чисел:
1) е-3+2'; 2)Д‘+1; 3) е3-+
1268. Представить в показательной форме следую-
щие числа:
1) 1—z/3; 2)/3 + z;
3) 4 cos -^ + z sin ; 4) — z;
5) 2 + z /5; 6) cos л + z sin л.
1269. Преобразовать в алгебраическую фЪрму числа:
• ^5.
1) 2 = е/,2я; 2) z = e1' 2 ; 3) г = ^>30°.
200
1270. Зная, что In z — ln| z | + i arg z, найти дей-
ствительную и мнимую части каждого из чисел:
1) ln3Z; 2) In 5Z; 3) ln/2Z;
4) In (— 4ш); 5) In 1^- + j *).
1271. Представить z в показательной форме, если:
1) In г = In ]/13 + /arctg -j-;
2) 10 2 = ^1/29 — zarctg-|-.
1272. Выполнить действия:
1) 50еГ45° • ISe-*’-300 ; 2) 75еГ60°: 15е-М0°;
3) 40ег‘60° • |е-*'45°; 4) 32ег'30°: 9е-1 2'-20°.
1273. Выполнить действия:
z43(l -z)/~
Л , . . Л \3
cos-y + I sm -g I
1274. Определить действительные значения х и у,
при которых справедливо равенство:
4хе1 т = у (у/ 3 — 2Z) + /3 — 41.
1275. Определить, какое число нужно прибавить
к 2^г’300°, чтобы получить 0.
1276. Зная, что
(«1 + by) + (а2 + b2i) = г,ег<Р' + r2ei(\
построить в прямоугольной системе координат векторы
следующих комплексных чисел:
1) Zi — 2е 8 + e2+l;
1-- i
2) z2 — 2e 4 +е2+ь,
. Л t Л_
3) г3 = Зе1 4 — 2е 3;
-/ —
4) z4 = 4ея1 — 10е 6.
201
1277. Зная, что (at + bti) • (а2 + b2i) — r{r2el (чы-чМ и
(a{ + b{i): (a2 + b2i) = — ef(<₽‘_cpJ, построить векторы сле-
r 2
дующих комплексных чисел в прямоугольной системе
коо рдинат:
1) z — Zi • z2, если z{ — 5el'iy> и z2 = 15e“r30°;
2) z — z{'.z2i если Z] = 59e!''45° и z2 — 15e“*/,30°:;
3) z — u\ если и==3е‘15°.
1278. Пользуясь формулой ax = exlnat а>0 и а =/= 1,
построить векторы, соответствующие следующим ком-
плексным числам:
_£
1) z== 22г; 2) z = 2 2; 3) z = 3?+f,
представив их предварительно в показательной и три-
гонометрической форме.
1279. С помощью формул
+ e-(₽i _ е-ф/
cos <р =--2----- и sin qp =----у.---;
где qp принимает действительные значения, a z — ком-
плексные значения, вычислить значения следующих
тригонометрических функций:
1) sinz; 2) cosf;
3) sin (1 + у г); 4) cos (2 — г);
5) cos(0,5H-3z); 6) sin2z.
ГЛАВА 9
ПРЕДЕЛ ФУНКЦИИ И ПРОИЗВОДНАЯ
§ 73. Предел функции
1280. Вычислить пределы функций:
1) lim (5х3-6х2+х-5);
Х->2
2) lim (x34-x— 5);
X-»—1
3)
lim
х-»2
X2 — X -J- 1
х — 3 ’
4) lim (x-2)(x + 5)(2x-l);
x-»3
5)
lim
х-»-1
(х4-3)(х —5) .
х + 2 ’
7)
.. Зх3 + Зх2 — х — 3
2^+х-в ;
6) lim
x-»9
8) lim
x-»l
У7- 1 .
/Г+ 1 ’
x2 — 4
____ 9
9) lim (sinx — cosx);
10) lim Igx.
1281. Вычислить предел функции, когда предел дели-
теля равен 0, пределы делимого и делителя равны нулю:
1) lim — ; 2) lim ч -- ? ;
х-»2 4Х — 8 ’ 7 j Зх — 1
о\ 1- 4 лч .. Зх2 — 2х ,
2х2 + х ’ 4 *) 2х2 - 5х ’
5) lim -^2—г’» 6) lim
’ j 4х2 — 1 ’ ’ х_><1 4 — х2 ’
_ч .. Ух + 3 — 3 ОЧ .. 2х24-х—1
7)'™—^6-: 8>Лт_,-7+т-;
9) lim 10> lim ТТ4^~Т:
х-»о х х -f- ох у 1 -j. х2 _ 1
203
и)
13)
.. х2 — 7х+Ю,
х™ Х2 _ 9х + 20 ’
.. х — 4
lim
12)
И)
X
lim
х-*о ]/5-х-}<5 + х
lim
х->0
15)
17)
.. 1 — tg X
lim -=—-—;
я 2 — sec2 х
х-*т __
lim 4+^;
16)
lim
х->2
1 — cos х ф
sin2 х ’
х2 — 4
х2 - Зх + 2 ’
18)
lim
х — а
1282. Вычислить предел
1)
5
J™ 4х+3
функции:
2)
3)
4)
Зх’+1 ’•
lim -3*!~* + в
5)
7)
.. 5х
11т 37^2 *’
V->oo
.. 5п2 4- 8п — 3
lim —5-----—s—;
Л!-П + 3
6)
8)
X2
1 - Зх2 - X4 .
2х4 - х2 + 1 ’
1- 6 — z — z2 .
m 6z2 Z 1 ’
г -> оо г *
lim
9) Пт .<* + 0Ч.+.2Н* + 3).
Х->оо Х
10)
lim (2* — 3) (Зх+5) (4х —6) .
к->оо Зх3 + х 1
Н)
12) lim
Х->оо
x + (-Dx.
х - (- 1)Х ’
13)
14)
15)
16)
Пт -у-_________;
х-»оо |/ X3 + 10
Пт 2 + 4 + 6+ ... +2п
п~
и _Х гул
х — 1 \ е
X2 / ’
lim
П->оо
14-34-5+ ... 4-(2n- 1)
5п2
Вычислить предел функции (1283—1284):
1283. 1)
3)
lim
х->0
sin 5х
х ’
2)
lim
х->0
sin Зх
х
v sin5x
lim -. о , ;
х->о sin 2х
4)
.. sin8x
lim ;
х->о sin Зх
5) Вт >2/Зх
x->0 sin3f2x
6)
lim s*n лх
x->o этЗлх *
204
1284. 1) lim -—
x2
2) lim
sin x — sin a t
x — a ’
3) lim
cosx-cosa 4) lim
X — a
tg ИХ
1285. Зная,
функций:
что
— e, найти пределы
1)
3)
4)
lim (1 + sin x)x;
5)
I \n
6)
lim 1 +" '»
Xj
7)
8)
X — I \x + 2
§ 74. Приращение функции
1286. Найти приращение функции у — х2, соответ-
ствующее изменению аргумента:
1) от %] =2 до х2 = 5;
2) от хг = 3 до х2 = 3,1;
3) от Xj = 7 до х2 = 7,2.
1287. Найти приращение функции Ду и отношение ~
для следующих функций:
1) У = х2+ 1 при Дх = 1;
2) у = 2x4- 3 при Дх = 2;
3) у — 5х2 — 4 при Дх = 3;
4) у = 12х 4- 3 при Дх = 0,2.
1288. Найти приращение функции Ду и отноше-
ние , соответствующее изменению аргумента от х
до х + &х, для следующих функций:
1) у = 3x4-2; 2) у = 5х2;
3) // = 4х24'2; 4) у = 2х2 + х+ 1.
205
§ 75. Непрерывность функции
1289. Найти точки разрыва для следующих функцию
О /« = 7^7 =
2) f W = (х - 1) (х - 2) (х - 3) ‘
3) f W = 4> Их) = 77^?:
5) f (*) = -i~2tpx : 6) f (x) = x • sin x;
* l& Л
<• / \ 3x 2 г z \ 5x 4~ 4
7) f(x)= X2_5x+6; 8)f(x)=7?TT.
1290. Найти уравнения асимптот кривых:
. ч х2 — 6х + 3
’) х —3 *
§ 76. Производная функции, ее геометрический
и физический смысл
1291. Найти среднюю скорость движения точки за
промежуток времени от = 3 до t2 = 5, если путь ее
движения выражается формулой
S = 3/2 + 5t
1292. Найти производную функции f (х) = 8х2, исходя
из определения производной.
1293. Найти среднюю скорость изменения функции
у = Зх2 -|- 5х + 8 при изменении х от xt = 2 до х2 = 4.
1294. Найти производную функции у — 4х2+1, исходя
из определения производной.
1295. Найти производную функции у = ах2-\-Ьх,
исходя из определения производной.
1296. Свободное падение тела совершается по закону
а/2
S==^~~, где g — 980 см/с2. Найти среднюю скорость
движения тела за промежуток времени от ^ = 3с до
t2 — 3,5с.
206
1297. Два тела совершают движение по законам
S1(f)==2,5/2 — 6/4- 1,
S2 (/) = 0,5/2 4-2/— 3.
В какой момент времени скорость движения первого
тела будет в три раза больше скорости движения вто-
рого тела?
1298. Найти наклон кривой у = 6 — х2 в точке с аб-
сциссой х = 1.
1299. В какой точке касательная к кривой у — —х2 4"
4-4х— 3 параллельна оси Ох?
1300. в каких точках угловой коэффициент каса-
тельной к кривой у = х3 равен 3?
1301. Найти угловой коэффициент касательной, про-
веденной к параболе у — х2: (а) в начале координат;
(б) в точке х = —2.
1302. При каких значениях независимой перемен-
ной касательные к кривым у = х2 и у = х3 парал-
лельны?
1303. Написать уравнение касательной к гиперболе
у — — в точке с абсциссой х = — у.
1304. Найти угловой коэффициент касательной к ок-
ружности х24-*/2 = 25 в точке с абсциссой х = 3.
Найти производные данных функций по соответ-
ствующим формулам (1305—1306):
1305. 1) #==2х24-3х4- 1;
2) z/ = 5х3 4~ 4х2 4~ 2;
3) # = 7x3 4-2х2 4-3*4-1;
4) z/ = 5,3x44- 2,7x24- 1;
5) у = ах3 4- Ьх2 4- с;
6) # = ух54- j х4 4-у х3 4-7;
ах4 . Ьх3 , сх2 . ,
7) д= — + — + — + d’
8) У = х3 /2 + 2/7+ 1;
9) У = Vx + 4х /х + 2;
<л\ а V х .
Ю) </ = 77=- — 4-G
ух а
207
11) z/ = (1 4~ 4х) (1 — 2х);
12) t/ = (2x2— 1)(3х + 2);
13) t/ = (5x + 2)(3x—1);
14) r/= 15 (х + 4) (х2 — 2);
15) у== 18(х3+3)(х3 —7).
1306. 1) У = т^-т\ 2) г/ = 1^4
7 J 1 + X2 7 1 + X3
7)f«=4 + |. найти г(2);
8)f« = ^+-^, найти f'(l);
5 ух
9) f (х) = *+Д*2+-, найти Г (4);
Ю) = найти f (3).
§ 77. Понятие о второй производной.
Ускорение
1307. Даны законы движения двух точек; первая
точка движется по закону Si = 2/3 — 4/2 + 5Z, а вторая —
по закону S2 = 2Z3—1 >5£2, где t — время в секундах,
a Sj и S2 — пройденные пути в сантиметрах. Найти
ускорения движения точек в тот момент, когда ско-
рости их движения равны.
1308. Путь S (в метрах), пройденный телом при
прямолинейном движении в течение t секунд, задается
уравнением S~t3— t + 1. Найти ускорение в момент
времени t = 2 с.
1309. Уравнение скорости движения точки выра-
жается формулой и = 6/2— 2^+11, где v — скорость
в метрах в секунду, t — время в секундах. Написать
формулу, выражающую ускорение движения точки для
любого момента времени, и вычислить ускорение в мо-
мент времени t = 2 с.
208
1310. Найти вторую производную каждой из сле-
дующих функций:
1) ^ = 5х2 + Зх— 1;
2) г/= 7х3 4-5х2 — Зх + 2;
3) у = 1,2 г4 4- 0,5х3 + 8;
4) у = (х2 — 2)2- 5) у = (х2 4- Зх)3;
6) у=Ух-, 7) у = ]^х;
8) s = vot 4-
§ 78. Возрастание и убывание функции
1311. Исследовать следующие функции на возраста-
ние и убывание:
1) —2%2 —Зх —2; 2) у = (х — I)2 4- 1;
3) = 5х2 4- 20х — 5; 4) у = х2 —5x4-4;
5) у — х5 4- 2х; 6) у — х3 — Зх.
§ 79. Экстремумы функции
1312. Число 15 разбить на два числа так, чтобы
сумма их квадратов была наименьшей.
1313. Требуется сделать из жести коробку без крышки
с квадратным основанием, наибольшего объема, поверх-
ность которой была бы равна 12 см2. Определить раз-
меры коробки.
1314. Доказать, что из всех прямоугольных тре-
угольников, вписанных в данный круг, наибольшую
площадь имеет равнобедренный треугольник.
1315. Из всех цилиндров, имеющих полную поверх-
ность 24л см2, найти тот, который имеет наибольший
объем.
1316. Найти локальный максимум и минимум функции
1317. Найти локальный максимум и мишимум функции
уЗ **2
»=4-х-2а + ‘-
209
1318. Исследовать функцию у = на максимум
и минимум и построить примерный график функции.
1319. Следующие функции исследовать на экстремум
по второй производной и построить их примерные
графики:
1) г/ = 2х3—-Зх2; 2) г/ = 2х3-6х2-18х + 7;
3) I/= х* — 18№ + 5; 4) = (х + I)2 (х - 2);
Б) у = 0,1(х4—13х2 + 36); 6) г/ = л-3 —Зх®+ 2;
7) И= 8) и = 0,1 (х3 — 9х).
ГЛАВА 10
ПЛАНИМЕТРИЯ
ЗАВИСИМОСТЬ МЕЖДУ ЭЛЕМЕНТАМИ ТРЕУГОЛЬНИКОВ,
ЧЕТЫРЕХУГОЛЬНИКОВ И НЕКОТОРЫХ ДРУГИХ ФИГУР
§ 80. Прямоугольный треугольник
В задачах (1320—1323) по двум данным элементам
прямоугольного треугольника вычислить остальные
элементы:
1320.
1) 77 = 3, 6 = 4; 2) а=15, 6 = 20;
3) а =100, с=125; 4)6 = 65; с =169.
1321.
1) ас=12,5, 6С = 8,4; 2) ас=1,5, Ьс = 2^-,
3) /г =12, а = 13,6; 4) 6=9, 6=8^-.
1322.
1) В = 37°40', ^ = 0,65; 2) с = 21,3, А=18°40';
3) с = 39,4, 77 = 20,8; 4) 77 = 26,2, 6 = 54,5.
1323.
1) с = 20, А = 40°; 2)6 = 30, А = 70° 14';
3) с = 68,3, 77 = 39,7; 4) 77 = 3,45, 6 = 3,04.
§ 81. Равнобедренный треугольник
В задачах 1324—1326 по двум данным элементам
равнобедренного треугольника вычислить остальные
элементы;
211
1324.
1) А6 = 20, В = 36° 10'; 2) а —8, 4 = 48° 15';
3) 6 = 40, 1325. 4 = 64° 10'; 4) а = 20, В = 69° 15'.
1) а = 24, В = 69° 15'; 2) а = 50, В = 72° 30';
3) 6 = 20, 1326. В = 65° 16'; 4) hb = 40, В = 68° 14'.
1) 6 = 20, В = 48° 12'; 2) Л6 = 38, 4 = 52° 16':
3) hb= 16, 4 = 54° 35'; 4) Ла=4, 6 = 20;
5) hb = 8, 6= 16; 6) Л& = 42,8, 4 = 47° 30'.
§ 82. Косоугольные треугольники
1327. Решить треугольник, если даны его сторона и
два угла:
1) 6 = 34, С =133° 10', В = 30° 24';
2) а = 109, В = 33° 24', С = 66° 59';
3) 6 = 225,4, Л= 72° 59', С = 67° 28';
4) с =151,8, В = 48° 14', А = 64° 25'.
1328. Решить треугольник, если даны его две сто*
роны и угол, противолежащий одной из них:
1) а =19, 6 = 28,1, А = 32° 17';
2)Д = 30°, 6=100, а = 40;
3) а = 27, 6 = 32, 4=100°.
1329. Решить треугольник, если даны две его сто-
роны и угол, заключенный между этими сторонами
1) а = 10, 6= 12, С = 24°;
2) а = 2,29 , с = 1,7, В = 39° 20';
3) а = 3,4, с = 2,9, В = 108°;
4) 6 = 83, с = 36, 4= 102° 48'.
1330. Решить треугольник, если даны три его сто-
роны:
1)а=Ю, 6=15,- с = 20;
2) а = 1,23, 6 = 2,34, с = 3,48;
3) а =16,3, 6=18, с =14,5;
4) а = 423, 6 = 370, с = 545.
1331. Дано: а = 85,32 м, 4=42°20', В =72° 10'.
Найти сторону 6 и площадь треугольника.
212
1332. Дано: а = 25 см, b = 60 см, В = 68° 20'. Най-
ти сторону с и площадь треугольника.
1333. Дано: b = 12 см, с = 16 см, А = 55° 40'. Най-
ти сторону а и площадь треугольника.
1334. Дано; b = 15,6 см, А = 63°50', В = 48° 10'.
Найти сторону с и площадь треугольника.
1335. Дано: с = 10,05 м, А = 51°44', Я = 74°50'.
Найти сторону b и площадь треугольника.
1336. Дано: а = 365,5 м, В = 34° 59' и С = 45° 48'.
Найти сторону b и площадь треугольника.
1337. Определить расстояние между недоступными
точками А и В. Для этого выбрали точку С, из которой
А и В видны и доступны. ВС = 100 м; АС = 80 м и
угол между ними 40° 48'.
1338. Стороны параллелограмма равны 4 дм и
5 дм, острый угол равен 52° 30'. Определить его диаго-
нали.
1339. Верхнее основание трапеции равно Ь, ниж-
нее а, одна из боковых сторон с, угол между а и с ра-
вен а. Определить четвертую сторону и угол при осно-
вании трапеции. Вычислить при а = 10,24 см, b =
= 5,7 см, с = 12 см, а = 36° 27'.
1340. Точки А и В находятся по одну сторону реки,
точка С по другую сторону. Определить ширину реки,
если АВ = 200 м*, Z С АВ = 54° 10', Z СВ А = 70° 8'.
1341. Из точки А, лежащей на одной горизонтальной
плоскости с основанием башни, видна вершина башни
под углом в 40° 10', а приблизившись к основанию баш-
ни на 100 м, видим вершину башни под углом 74° 15'.
Определить высоту башни.
1342. Найти боковую высоту равнобедренного тре-
угольника АВС, если высота, проведенная из вершины
треугольника на основание, равна h = 4,08 и угол при
вершине В = 44° 20'.
1343. В равнобедренном треугольнике боковая сто-
рона равна 12,25 дм, угол при вершине равен 50° 20'.
Найти периметр треугольника.
1344. Высота треугольника АВС, равная 5,04 дм, де-
лит угол В на два угла, а и {3. Определить основание
треугольника АС и вычислить его, если а : В = 5 : 3 и
fZB = 65° 12'.
1345. Найти периметр прямоугольника, если его диа-
гональ равна 23,28 дм и образует с основанием угол
в 20° 14'.
213
1346. В равнобедренном треугольнике основание рав-
но 20 см, угол при вершине 66°. Определить проекцию
высоты на боковую сторону.
1347. Определить основание треугольника, если бо-
ковая сторона, лежащая против меньшего угла, равна
20 см, углы при основании равны 30° и 45°20'.
1348. Найти периметр равнобедренного треугольни-
ка, если угол при основании а = 70° 12' и радиус круга,
вписанного в треугольник, равен г = 5,75 см.
1349. Силы Р = 5Н и Q = 7Н действуют на точку.
Равнодействующая их равна ИН. Определить угол
между силами.
1350. Для определения расстояния между недоступ-
ными пунктами М и N измерили базис CD, не проходя-
щий через М и N и равный 2 км. Углы MCD = 86° 40',
NCD = 52° 40', MDC = 42°, NDC = 81° 15'. Опреде-
лить MN.
1351. Основание прямоугольника равно 50,1 м. Диа-
гональ образует с основанием угол 18° 35'. Найти пери-
метр прямоугольника.
§ 83. Площадь параллелограмма, треугольника,
трапеции и круга. Вписанные и описанные
фигуры
1352. Стороны параллелограмма равны 17,50 м и
10,20 м, угол между ними А = 4Г 15'. Найти меньшую
диагональ параллелограмма и его площадь.
1353. Вычислить меньшую сторону и площадь тре-
угольника, если а = 0,275 м, В = 36° 13', С —
1354. Диагональ прямоугольника равна 18,75 м, угол
между диагоналями 138° 20'. Определить площадь пря-
моугольника.
1355. Стороны параллелограмма равны 10,25 м и
12,75 м, угол между ними 70° 17'. Найти площадь парал-
лелограмма.
1356. Найти площадь равнобедренного треугольника
с углом при вершине 44° 52' и высотой, проведенной на
боковую сторону, равной 20,5 м.
1357. В прямоугольной трапеции диагональ равна
3
30 у дм и перпендикулярна к боковой стороне. Острый
угол трапеции 68°32'. Найти площадь трапеции.
214
1358. Вычислить площадь прямоугольной трапеции с
острым углом D = 40° 24' и высотой, в два раза большей
меньшего основания. Меньшее основание равно 12,35 м.
1359. В равнобедренной трапеции боковая сторона
равна большему основанию. Найти площадь трапеции,
если большее основание равно 13,85 дм и острый
угол а при основании равен 72° 16'.
1360. В равнобедренной трапеции меньшее основание
равно боковой стороне b = 7,35 м, острый угол а =
= 57° 18'. Найти площадь трапеции.
1361. Меньшее из оснований равнобедренной трапе-
ции и ее высота равны 10,5 дм. Острый угол трапеции
а = 37° 16'. Найти площадь трапеции.
1362. Диагонали параллелограмма а и Ь, острый
угол а. Определить площадь параллелограмма.
1363. Из общей точки М проведены к окружности
касательная МА и секущая МВС, угол М = 65° 24',
МВ = 4 м, ВС = 5 м. Определить площадь круга.
1364. Радиус окружности равен R; дуга равна а. Оп-
ределить площадь сегмента, стягиваемого дугой.
1365. Высота сегмента равна h, дуга сегмента а. Оп-
ределить площадь круга.
1366. Окружность разделена в отношении 2 : 3 : 5 : 8
и точки деления последовательно соединены между со-
бой. Определить площадь полученного четырехуголь-
ника, если площадь круга равна 314 дм2.
1367. Найти периметр прямоугольного треугольника,
если радиус описанного около него круга равен 10,02 м
и угол А = 35° 10'.
1368. Найти радиус круга, вписанного в равнобед-
ренный треугольник с боковой стороной а = 8,20 м и
ZA = 53° 16'.
1369. Найти радиус круга, описанного около равно-
бедренного треугольника с основанием, равным 20,08 м,
и углом при вершине 78° 14'.
1370. Катет треугольника АВС равен 20,05 дм и
rZ А — 36° 28'. Найти радиус круга, описанного около
этого треугольника.
1371. В треугольнике ЛВС ZX = 70° 35', ZB = 63°20S
радиус описанного круга равен 5 см. Найти стороны и
площадь.
1372. В треугольнике дано: а = 24 см, b = 45 см, ра-
диус описанного круга 28,5 см. Определить углы тре-
угольника,
215
1373. Радиус круга, описанного около равнобедрен-
ного треугольника, равен R, угол при основании а. Опре-
делить стороны и площадь.
1374. Дуга окружности равна а = 24° 20', радиус
/? = 15,6 см. Определить длину хорды.
1375. Хорда равна 30,4 см; радиус окружности
20,5 см. Определить длину дуги.
1376. Стороны треугольника 50 см. 80 см, 105 см. Оп-
ределить радиусы вписанного и описанного кругов.
1377. Найти радиус круга, вписанного в треугольник,
если а = 316,3 см, В = 94° 46', С ==26° 37'.
1378. В прямоугольную трапецию с острым углом а
вписана окружность радиуса г. Найти площадь трапе-
ции и вычислить ее при г — 6,24 дм и а — 40° 20'.
1379. Найти площадь круга, вписанного в ромб с ост-
рым углом а = 65° 30' и площадью Q = 202,5 дм2.
1380. Определить площадь круга, описанного около
прямоугольного треугольника, если катет его равен
24 см, а прилежащий к нему угол — 26° 35'.
1381. Радиус круга, вписанного в ромб, равен 3,025 м;
угол ромба 43° 16'. Определить площадь ромба.
ГЛАВА 11
СТЕРЕОМЕТРИЯ
§ 84. Перпендикуляр и наклонные к плоскости
1382. Сколько перпендикуляров можно провести из
данной точки к данной прямой, если точка находится:
(а) вне прямой, (б) на прямой?
1383. Каким ребрам куба перпендикулярна диаго-
наль его грани?
1384. Ребро куба равно 2 дм. Чему равна диагональ
его грани и диагональ куба?
1385. Провести плоскость, проходящую через концы
трех ребер куба, выходящих из одной вершины. Ребро
куба равно а. Вычислить площадь сечения куба.
1386. Из точки М (вне плоскости) проведена к пло-
скости под углом в 30° наклонная, равная 8 дм. Опре-
делить расстояние от точки М до плоскости.
1387. Из точки, лежащей вне плоскости, проведены
к этой плоскости две наклонные, сумма длин которых
равна 12 дм. Проекции этих наклонных на плоскость
1 дм и 7 дм. Найти длину каждой наклонной и угол
между плоскостью и большей наклонной.
1388. Наклонная проведена под углом 60° к плоско-
сти а и равна 1,3 дм. Найти проекцию этой наклонной
на плоскость а.
1389. Из точки А под углом 45° к плоскости а прове-
дена наклонная. Определить длину этой наклонной от А
до плоскости, если ее проекция на плоскость равна
8 дм.
1390. Из одной вершины квадрата со стороной а вос-
ставлен перпендикуляр к его плоскости, равный Ь. Точ-
ка N, лежащая на перпендикуляре, соединена с верши-
217
нами квадрата. Определить расстояния от точки N до
вершин квадрата.
1391. Что можно сказать о взаимном расположении
двух прямых в пространстве, если они имеют две об-
щие точки?
1392. Всегда ли можно провести плоскость через две
непересекающиеся прямые?
1393. Из точки N, отстоящей от плоскости а на рас-
стояние 6 дм, проведены к этой плоскости наклонные
NA, NB, NC под углами в 30°, 45° и 60° к прямой NO,
перпендикулярной к а. Определить длины проекций этих
наклонных на плоскость Л\
1394. Вне плоскости правильного треугольника дана
точка N, которая проектируется в центр треугольника.
Сторона треугольника а. Расстояние от точки N до вер-
шины треугольника равна Ь. Определить расстояние от
точки N до плоскости.
1395. Точка, удаленная от каждой вершины прямо-
угольного треугольника на 26 см, удалена от его пло-
скости на 24 см. Определить длину гипотенузы и катета,
если другой катет равен 12 см.'
1396. Два прямоугольных треугольника АВС и DBC
имеют общий катет ВС (Z. С прямой). Катет DC пер-
пендикулярен к гипотенузе АВ другого треугольника.
Найти расстояние от вершины D до вершины А, если
СВ = 12, DC = 5 и АВ = 13.
1397. Катеты прямоугольного треугольника равны
14 дм и 48 дм; перпендикуляр к плоскости треугольника,
проведенный из вершины прямого угла, равен 6 дм. Най-
ти расстояние от конца перпендикуляра до середины ги-
потенузы.
1398. Угол между перпендикуляром и наклонной,
проведенной из точки А к плоскости а, равен ср. Длина
проекции наклонной равна а. Определить длину пер-
пендикуляра.
1399. Из точки А, лежащей вне плоскости, проведен
перпендикуляр к этой плоскости длиной р; основание
его принято за центр окружности радиуса г, лежащей
в этой плоскости. Определить угол между этим перпен-
дикуляром и прямой, соединяющей точку А с любой
точкой окружности (р = 4,54; г = 8).
1400. Через центр О квадрата, сторона которого
4В == а — 30, проведен перпендикуляр к плоскости
квадрата; на нем взят отрезок ОМ = d == 20, а из М
218
проведен перпендикуляр МС на АВ. Вычислить угол х
между МС и его проекцией ОС на плоскость квадрата.
1401. Из центра О круга, вписанного в правильный
треугольник АВС, сторона которого равна а, восставлен
перпендикуляр к плоскости треугольника; на нем взята
точка М так, что отрезок МА = а, затем из М проведен
отрезок MD, перпендикулярный к АС. Вычислить уголф
между MD и плоскостью треугольника АВС.
1402. Наклонная образует с плоскостью угол а; че-
рез вершину этого угла проведена в данной плоскости
вторая прямая под углом р к проекции наклонной на
плоскость. Определить угол между этими прямыми
(а = 43° 53', 0 = 11° 10').
1403. Из центра окружности, описанной около тре-
угольника со сторонами а, b и с, восставлен к плоскости
этого треугольника перпендикуляр h. Определить углы,
образованные с этой плоскостью прямыми, соединяю-
щими вершину перпендикуляра с вершинами треуголь-
ника (А = 60; а = 30, b = 5, с — 29).
§ 85. Угол прямой с плоскостью
1404. Наклонная равна а. Чему равна проекция этой
наклонной на плоскость, если наклонная составляет
с плоскостью проекций углы: 1) 30°; 2) 45°'; 3) 60°?
1405. Точка отстоит от плоскости на расстояние h.
Найти длину наклонных, проведенных из нее под углами
к плоскости: 1) 60°; 2) 30°; 3) 45°.
1406. Длина наклонной 18 см. Угол между наклон-
ной и плоскостью 36°. Чему равна длина проекции на-
клонной на эту плоскость?
1407. Вычислить длину проекции отрезка 20 см, если
угол его наклона: 1) 0°; 2) 30°; 3) 45°; 4) 90°.
1408. Наклонная АВ составляет с плоскостью а угол
в 45°, а прямая АС, лежащая в плоскости а, составляет
угол в 45° с проекцией наклонной АВ. Определить
FZ ВАС.
1409. Из точки, лежащей вне плоскости, проведены
к этой плоскости две наклонные под углом 30°, равные
2 1^3. Их проекции образуют между собой угол 120°.
Определить расстояние между основаниями наклонных.
1410. Стороны треугольника равны 10 см, 17 см и
21 см. Из вершины этого треугольника проведен перпен-
дикуляр'к его плоскости длиной 15 см. Определить рас-
219
стояния от концов перпендикуляра до большей стороны
треугольника.
1411. Вычислить угол, под которым диагональ куба
наклонена к его грани.
1412. Из точки А, расположенной вне плоскости а,
проведены к этой плоскости наклонные АВ — с и АС —
= Ъ. Угол наклонной АС с плоскостью в три раза боль-
ше угла наклонной АВ с той же плоскостью. Найти рас-
стояние от точки А до плоскости а.
§ 86. Параллельные прямые и плоскости
1413. Из двух точек и N одной из параллельных
плоскостей проведены к другой плоскости наклонные
длиной 37 см и 125 см. Чему равна проекция второй на-
клонной на плоскость, если проекция первой 12 см.
1414. Из точки М плоскости а проведена к ней на-
клонная и на ней взяты точки В и С; МВ = 10 см;
ВС = 6 см. Разность расстояний точек В и С от пло-
скости а равна 3 см. Определить расстояния точек В
и С от плоскости.
1415. Отрезок пересекает плоскость; концы его от-
стоят от плоскости на расстояние 0,8 дм и 0,2 дм. Найти
расстояние середины этого отрезка от плоскости.
1416. Отрезок MN параллелен плоскости и равен т.
Отрезок NMiy соединяющий конец N с проекцией Л4 дру-
гого конца, составляет с плоскостью угол 60°. Опреде-
лить длину отрезка MiN.
1417. Концы отрезка MN удалены от плоскости а
на 3 дм и 5 дм. Как удалена от плоскости точка, деля-
щая данный отрезок в отношении 1 : 3?
1418. Два отрезка упираются своими концами в две
параллельные плоскости. Найти длину каждого отрезка,
если их проекции на одну из плоскостей равны b и ЗЬ,
а сумма отрезков равна ЬЬ.
1419. Отрезки АВ и CD упираются своими концами
в параллельные плоскости М и N. Угол между АВ и
плоскостью М равен 30°, АВ -J- CD = 48 см, а расстоя-
ние между параллельными плоскостями равно 12 см.
Определить угол между CD и плоскостью М.
1420. Через данную точку М, взятую вне плоско-
сти а, провести отрезок так, чтобы проекция его на
плоскость а была равна самому отрезку.
220
1421. Через точку М, взятую вне прямой АВ, прове-
дена прямая MN. В каком положении может оказаться
MN относительно Л В?
1422. Из точки, отстоящей от плоскости на 5 дм,
проведены две наклонные под углом 30° к плоскости,
причем их проекции составляют между собой угол
120°. Определить расстояние между основаниями на-
клонных.
1423. 1) Через данную точку провести плоскость, па-
раллельную данной прямой.
2) Даны плоскость и параллельная ей прямая. Че-
рез точку, взятую на плоскости, провести в этой плоско-
сти прямую, параллельную данной прямой.
1424. Нижнее основание трапеции ABCD лежит на
плоскости а, а верхнее отстоит от нее на 5 см. Найти рас-
стояние от плоскости а до точки пересечения диагона-
лей трапеции, если AD : ВС = 7:3.
1425. В плоскости а расположена одна из сторон
ромба. Расстояние противоположной стороны от той же
плоскости равно 8 см. Проекции диагоналей ромба на
плоскость а равны 4 см и 16 см. Определить площадь
данного ромба.
1426. Через катет АС прямоугольного треугольника
АВС проведена плоскость а, образующая с плоскостью
треугольника угол 45°. Определить расстояние от вер-
шины В этого треугольника до плоскости а, если из-
вестно, что катет АС = 20 см и АВ : ВС = 5:3.
1427. К плоскости равнобедренного треугольника
АВС из вершины А проведен перпендикуляр AD~
= 4}/Зсм. Определить площадь треугольника BDC,
если АВ — АС = 10 см; ВС = 16 см.
1428. Даны две параллельные плоскости а и р. Из
точек А и С плоскости а проведены две наклонные АВ
и CD к плоскости р. Определить расстояние между эти-
ми плоскостями, если АВ -{- CD = 28 см; АВ — CD —
= 4 см и AiB : CtD = 9 : 5 (Hi и Ci — проекции точек
А и С на плоскость р).
1429. Два отрезка заключены между параллельными
плоскостями. Сумма этих отрезков 12 дм. Проекции
отрезков на плоскость равны 1 дм и 7 дм. Найти
расстояние между плоскостями.
1430. Из середины стороны ромба, равной 5 см, вос-
ставлен перпендикуляр к его плоскости, верхний конец
которого отстоит от большей диагонали ромба, имею-
221
щей длину 8 см, на 2,5 см. Определить длину этого
перпендикуляра.
1431. В треугольнике АВС угол С прямой; CD — пер-
пендикуляр к плоскости треугольника. Точка D соеди-
нена с Л и В. Определить площадь треугольника ADB,
если АС = 3 дм; ВС — 2 дм и CD — 1 дм.
1432. Через вершину прямого угла С прямоугольного
треугольника АВС проведена плоскость параллельно
гипотенузе на расстоянии 1 дм от нее. Проекции кате-
тов на эту плоскость равны У3 дм и 2 V 2 дм. Опре-
делить проекцию гипотенузы на эту плоскость.
1433. Из точки N, лежащей вне плоскости а, прове-
ден к плоскости а отрезок NA. Он разделен точкой Д'
в отношении NK : КА = 4:5, и из точки К проведен
отрезок KL, параллельный плоскости а и равный 20 см.
Отрезок, соединяющий точки N и L, продолжен до пере-
сечения с плоскостью а в точке В. Определить длину от-
резка АВ.
1434. Диагональ АС квадрата ABCD равна 20 см.
Из точки М этой диагонали, отстоящей от вершины С
на 5 см, восставлен к плоскости квадрата перпендику-
ляр MN длиной 5 см. Определить расстояние от точки Af
до вершин квадрата.
1435. Отрезок длиной 10 см пересекает плоскость;
концы его удалены от плоскости на расстояние 3 см и
5 см. Найти длину проекции отрезка на плоскость.
1436. Из двух прямых, параллельных между собой и
параллельных плоскости а, одна отстоит от плоскости а
на 2,5 дм, а другая на 3 дм. Расстояние между проек-
циями этих прямых на плоскость а равно 1,2 дм. Оп-
ределить расстояние между прямыми.
1437. Из двух точек плоскости, удаленных друг от
друга на расстояние а, проведены две параллельные на-
клонные под углом (р к плоскости. Определить расстоя-
ние между ними, если расстояние между их проекциями
на плоскость равно Ь.
1438. Отрезок АВ параллелен плоскости. Из его кон-
цов проведены к плоскости две наклонные: АС = с и
BD = d. Наклонная АС составляет с плоскостью угол а.
Определить угол наклонной BD с этой плоскостью
(с = /б, d = 3, а = 60°).
1439. Из концов отрезка, параллельного плоскости,
восставлены к нему перпендикуляры под углами аир
222
(a > p) к плоскости. Длина отрезка равна а, расстоя-
ние между точками пересечения плоскости с этими пер-
пендикулярами равно Ь. Определить расстояние от пло-
скости до отрезка (два случая).
1440. Отрезки двух прямых, заключенные между
двумя параллельными плоскостями, относятся как 2:3,
а их углы с плоскостью — как 2:1. Определить эти
углы.
§ 87. Двугранные углы и перпендикулярные
плоскости
1441. Расстояние точки N от каждой грани двугран-
ного угла равно 2 дм. Определить расстояние точки N
от ребра двугранного угла, если перпендикуляры, опу-
щенные из точки N на обе грани двугранного угла, со-
ставляют углы: 1) 90°; 2) 60°; 3) 120°.
1442. Линейный угол двугранного угла равен 120°.
От вершины А линейного угла отложены три равных от-
резка: АВ и АС по сторонам линейного угла и AD по
ребру двугранного угла. Определить расстояние точ-
ки D от прямой ВС, считая, что АВ = а.
1443. Двугранный угол равен 45°. На одной из гра-
ней взята точка на расстоянии 5 см от другой грани.
Найти расстояние этой точки от ребра.
1444. А и В — точки на ребре прямого двугранного
угла, АС и BD — перпендикуляры к ребру, проведенные
в разных гранях. Найти расстояние CD, если АВ =
= 1,2 дм, АС — 0,6 дм и BD — 0,4 дм.
1445. Точка, удаленная от ребра двугранного угла
в 120° на 20 см, отстоит от каждой грани на одинако-
вое расстояние. Найти это расстояние.
1446. На одной из граней двугранного угла в 60°
взята точка, отстоящая от другой грани на 3 дм. Опре-
делить расстояние этой точки от ребра.
1447. Отрезок длиной в 7 см имеет концы на двух
взаимно перпендикулярных плоскостях и составляет
с ними углы 30° и 45°. Найти длину части ребра дву-
гранного угла, заключенного между перпендикулярами,
опущенными на него из концов отрезка.
1448. Прямоугольный треугольник АВС опирается
катетом АС на плоскость а, образуя с ней двугранный
угол в 60°. Определить гипотенузу ВС, если АС = а и
расстояние от вершины В до плоскости равно Ь.
223
1449. Дан двугранный угол а. Из точки, лежащей на
одной грани этого угла на расстоянии а от ребра, вос-
ставлен перпендикуляр до пересечения с другой гранью.
Определить длину этого перпендикуляра (а = 6,06,
а = 41° 55').
1450. Прямоугольный треугольник АВС расположен
так, что гипотенуза его АВ лежит на плоскости Р, а
катеты образуют с плоскостью Р углы аир. Определить
угол между плоскостью треугольника и плоскостью Р.
1451. В прямоугольном треугольнике даны гипотену-
за а и острый угол а. Определить расстояние от вер-
шины прямого угла до плоскости, которая проходит че-
рез гипотенузу и составляет угол (р с плоскостью тре-
угольника.
1452. Треугольник, площадь которого равна S, одной
стороной опирается на плоскость а и наклонен к этой
плоскости под углом (р. Найти площадь проекции дан-
ного треугольника на плоскость а.
1453. Проекция треугольника АВС на плоскость р
есть прямоугольный треугольник ABCi, в котором угол
Ct — прямой, угол В равен (р и катет CiB равен а. Най-
ти расстояние от вершины Ci прямого угла до плоскости
треугольника АВС, если двугранный угол равен а.
1454. Плоскость параллелограмма образует с пло-
скостью а угол ср. Найти площадь параллелограмма, если
площадь его проекции на плоскость а равна S. Вычис-
лить площадь на логарифмической линейке при (р ==.
= 30° 27' и S = 52 см2.
1455. Площадь прямоугольной прорези на скате кры-
ши для вывода трубы равна 32,6 дм2. Определить угол
наклона ската крыши к горизонту, если поперечное се-
чение трубы имеет форму квадрата со стороной 5 дм.
Вычислить на линейке.
1456. Четырехскатная крыша перекрывает площадь
в 28 м2. Все скаты крыши наклонены к потолку под
углом 32° 53'. Найти площадь крыши.
1457. Боковой скат четырехскатной крыши представ-
ляет собой равнобочную трапецию, параллельные сто-
роны которой 10 м и 6 м; высота трапеции равна 5 м.
Площадь проекции ската на плоскость потолка равна
32 м2. Найти угол наклона ската и высоту конька над
потолком.
1458. Яркость освещения зависит от угла, образуе-
мого световыми лучами с освещаемой поверхностью,
224
Пусть освещаемая площадь равна Q, а угол световых
лучей с освещаемой плоскостью а.
На какую площадь падали бы те же световые лучи,
если бы освещаемая площадь была перпендикулярна
к световым лучам? Меньше или больше предыдущей
будет эта площадь? Ярче или темнее она будет осве-
щена?
1459. Какую горизонтальную площадь можно по-
крыть крышей с наклоном в 27° 30' и с площадью
120 м2?
§ 88. Многогранные углы
1460. Прямые ОА, ОВ, ОС, выходящие из одной точ-
ки, образуют друг с другом углы 104°, 72°, 125°. В од-
ной или разных плоскостях лежат эти прямые?
1461. Можно ли составить трехгранный угол с таки-
ми плоскими углами: 1) 80°, 130°, 160°; 2) 90°, 120°, 150°;
3) 36°, 84°, 130°; 4) 50°Т 60°, 100°.
1462. Можно ли составить выпуклый четырехгран-
ный угол из плоских углов: 1) 30°, 70°, 130°, §0°; 2) 50°,
60°, 140°, 110°; 3) 160°, 30°, 110°, 45°.
1463. В трехгранном угле SABC углы BSC = 90°,
ASB = 60°, Д5С = 60°. Доказать, что ребро S/1 состав-
ляет с плоскостью BSC угол 45°.
1464. В трехгранном угле один плоский угол равен
60°, два другие по 45°. Доказать, что двугранный угол
между ними прямой.
1465. В куб с ребром а вписан правильный тетраэдр.
Выразить как функции ребра куба: 1) ребро тетраэдра;
2) расстояние от центра тетраэдра до его граней; 3) вы-
соту тетраэдра; 4) площадь одной грани тетраэдра. Оп-
ределить: (а) двугранный угол а между смежными гра-
нями тетраэдра, (б) сумму плоских углов при каждой
вершине тетраэдра и куба.
1466. Заполнить следующую таблицу:
№№ п/п Наименование элементов Куб Тетраэдр
1 2 3 4 Число граней Число вершин Число ребер Число диагоналей
235
1467. В куб с ребром а вписан правильный октаэдр
'(рис. 10). Выразить как функции ребра куба: 1) ребро
октаэдра; 2) расстояние от центра октаэдра до его гра-
ней; 3) сумму площадей всех граней октаэдра. Опреде-
лить: (а) двугранный угол а между смежными гранями
октаэдра, (б) сумму плоских углов при каждой вершине
октаэдра.
1468. Указать количественное соотношение одних и
тех же элементов октаэдра и гексаэдра.
1469. Чему равно отношение ребра октаэдра, впи-
санного в куб, к ребру этого куба?
1470. Найти отношение расстояния между противо-
положными вершинами октаэдра и диагонали описан-
ного куба.
1471. Куб вписан в октаэдр с ребром а (рис. 11). Вы-
разить как функцию ребра октаэдра: 1) ребро куба;
2) диагонали куба; 3) диагональ одной грани куба;
4) площадь одной грани куба.
1472. Дан октаэдр с ребром а. Определить площадь
его осевого сечения.
1473. Найти отношение расстояния между противо-
положными вершинами октаэдра к диагонали вписан-
ного в него куба.
1474. Найти отношение диагонали куба, вписанного
в октаэдр, к высоте грани этого октаэдра.
1475. Дан икосаэдр с ребром Ь. Определить: 1) дву-
гранный угол между смежными гранями икосаэдра;
2) расстояние между противоположными вершинами
икосаэдра; 3) расстояния от центра икосаэдра до его
граней; 4) сумму площадей всех его граней.
226
1476. В додекаэдр с ребром а вписан икосаэдр/
|!1) Заполнить следующую таблицу:
№№ п/п Наименование элементов Икосаэдр Додекаэдр
1 2 3 4 Число вершин Число граней Число ребер Число диагоналей
2) Определить: (а) сумму плоских углов при каж-
дой вершине икосаэдра и додекаэдра, (б) двугранный
угол между смежными гранями икосаэдра и додекаэдра.
3) Выразить как функцию ребра додекаэдра:
(а) расстояние между противоположными гранями
додекаэдра;
(б) расстояние от центра додекаэдра до его граней;
(в) расстояние от центра додекаэдра до его вершин;
(г) расстояние от центра додекаэдра до его ребер;
(д) расстояние от центра до граней икосаэдра;
(е) длину ребра икосаэдра;
(ж) площадь грани додекаэдра;
(з) площадь грани икосаэдра.
§ 89. Параллелепипеды и призмы
1477. Можно ли куб пересечь плоскостью так, чтобы
в сечении получить ромб, параллелограмм, трапецию?
1478. Ребро куба равно 3. Найти кратчайшее рас-
стояние от его диагонали до не пересекающего ее ребра
куба.
. 1479. Основанием прямого параллелепипеда служит
ромб. Диагонали параллелепипеда образуют с основа-
нием углы 30° и 45°. Найти острый угол ромба.
1480. Диагональ правильной четырехугольной приз-
мы равна 7 см. Диагональ боковой грани 5 см. Найти
высоту призмы.
1481. Диагональ правильной четырехугольной приз-
мы наклонена к боковой грани под углом 30°. Опреде-
лить наклон ее к основанию.
1482. В прямоугольном параллелепипеде измерения
равны 5 см, 12 см и 16 см. Концы трех ребер, выходящих
227
8*
из одной вершины, соединены. Вычислить периметр обра-
зовавшейся фигуры.
1483. Вычислить длину диагонали прямоугольного
параллелепипеда по трем его измерениям: 1) 5; 6; 7;
2) 2; 4; 6; 3) 3; 3; ]/7.
1484. Определить диагонали прямого параллелепи-
педа, каждое ребро которого равно 7 см, а один из уг-
лов четырехугольника, лежащего в основании, равен 60°.
1485. Боковое ребро прямого параллелепипеда равно
8 см, стороны основания равны 11 см и 7 см, диагональ
основания равна 14 см. Определить диагонали паралле-
лепипеда.
1486. Чему равен периметр сечения, проходящего че-
рез концы трех ребер, выходящих из одной вершины
куба, если ребро куба равно а.
1487. В прямоугольном параллелепипеде боковое
ребро равно 0,5 дм, площадь диагонального сечения
2,05 дм2, а площадь основания 3,6 дм2. Определить сто-
роны основания.
1488. В прямом параллелепипеде стороны оснований,
диагональ основания и боковое ребро соответственно
равны 2,9 дм, 3,6 дм, 2,5 дм, 4 ]/2 дм. Вычислить пло-
щадь сечения, проведенного через большую сторону ос-
нования и одну из вершин другого основания.
1489. Определить площадь сечения, проходящего че-
рез концы трех ребер, выходящих из одной вершины
куба, если ребро куба равно а.
1490. В основании наклонного параллелепипеда ле-
жит ромб ABCD со стороной а и острым углом сс. Боко-
вое ребро равно 2а и наклонно к плоскости основания
под углом 60°. Вычислить площади диагональных сече-
ний, если одно из них перпендикулярно к плоскости ос-
нования.
1491 (устно). Сколько диагоналей можно провести в
четырехугольной, пятиугольной и в треугольной призме?
1492 (устно). Сколько углов в пятиугольной призме:
(а) плоских, (б) двугранных, (в) трехгранных?
1493. Расстояния между боковыми ребрами наклон-
ной треугольной призмы равны соответственно 9 см,
12 см, 15 см. Боковое ребро призмы равно 14 см и
составляет с плоскостью основания угол 45°. Вычис-
лить высоту призмы и площадь перпендикулярного се-
чения.
228
1494. Сторона основания правильной четырехуголь-
ной призмы равна 1,5, высота призмы 2. Найти кратчай-
шее расстояние от стороны основания до не пересекаю-
щей ее диагонали призмы.
1495. Каждое ребро правильной треугольной призмы
равно а. Провести плоскость через середину бокового
ребра перпендикулярно к диагонали противолежащей
боковой грани и вычислить площадь сечения.
1496. Боковое ребро наклонной призмы равно 12 см
и наклонено к плоскости основания под углом 30°. Оп-
ределить высоту призмы.
1497. Высота правильной треугольной призмы рав-
на h. Через одно ребро основания и противоположную
ему вершину другого основания проведена плоскость.
Найти площадь сечения, если сторона основания приз-
мы равна а.
1498. В правильной четырехугольной призме прове-
дена плоскость через середину оси и середины двух по-
следовательных сторон основания. Зная, что сторона
основания равна а, а боковое ребро Ь, определить:
1) площадь полученного сечения и 2) угол между про-
веденной плоскостью и плоскостью основания.
1499. Основанием прямой призмы служит прямо-
угольный треугольник с катетами 12 см и 5 см. Через
боковое ребро, соединяющее вершины прямых углов ос-
нований, и середину гипотенузы треугольника, лежа-
щего в основании, проведена плоскость.
Доказать, что линия пересечения этой плоскости
с боковой гранью параллельна указанному боковому
ребру. Вычислить площадь сечения, если боковое ребро
призмы равно 10 см.
§ 90. Поверхность параллелепипеда и призмы
1500. Диагональ куба равна 2 1/3. Определить пол-
ную поверхность куба.
1501. Поверхность куба 54 дм2. Определить его ребро.
1502. Определить поверхность прямоугольного па-
раллелепипеда по трем его измерениям: 5 см, 11 см,
8 см.
1503. Основанием прямого параллелепипеда служит
ромб с диагоналями в 6 см и 8 см; диагональ боковой
грани 13 см. Определить полную поверхность этого па-
раллелепипеда.
229
1504. По стороне основания а и боковому ребру Ь
определить полную поверхность правильной четырех*
угольной призмы (а = 3,2 см, b = 5,1 см).
1505. Плоскость, проходящая через сторону основа-
ния правильной треугольной призмы и середину про-
тиволежащего ребра, образует с основанием угол 45°.
Сторона основания 4 см. Определить боковую поверх-
ность призмы.
1506. Одно из боковых ребер призмы равно 13 см и
составляет с каждой из двух смежных сторон основа-
ния угол 30°. Найти боковую поверхность призмы, если
основанием призмы служит правильный треугольник со
стороной в 8 см.
1507. Основанием прямого параллелепипеда служит
ромб с диагоналями 3 дм и 4 дм. Диагональ боковой
грани равна 6,5 дм. Определить полную поверхность па-
раллелепипеда.
1508. Вычислить полную поверхность призмы, осно-
вание которой есть ромб с диагоналями 16 см и 22 см;
боковые грани призмы — квадраты.
1509. Определить боковую поверхность правильной
шестиугольной призмы, если ее меньшая диагональ рав-
на п и составляет с плоскостью основания угол у.
1510. В основании прямой призмы лежит прямо-
угольный равнобедренный треугольник. Диагональ мень-
шей боковой грани призмы равна d и составляет с
основанием угол ср. Определить боковую поверхность
призмы.
1511. Меньшая диагональ прямого параллелепипеда,
в основании которого лежит ромб, составляет с пло-
скостью основания угол а. Сторона ромба равна а, ост-
рый угол р. Определить боковую поверхность паралле-
лепипеда.
1512. В прямоугольном параллелепипеде диагональ d
образует с основанием угол |3. Угол между диагональю
основания и его стороной а. Определить боковую по-
верхность параллелепипеда (а = 21° 35', р = 54° 24',
d = 17,89 м).
1513. В прямом параллелепипеде основание — ромб;
меньшая диагональ ромба равна d, а острый угол а.
Высота параллелепипеда равна-у. Найти его полную
поверхность (d = 25,87, а = 75° 20').
230
1514. Сторона основания правильной пятиугольной
призмы равна а, высота призмы равна d, где d —
диагональ основания. Вычислить полную поверхность
призмы (а = 23,79 м).
1515. Основанием прямой призмы служит равнобед-
ренный треугольник, в котором угол между равными
сторонами а равен а. Из вершины верхнего основания
проведены две диагонали равных боковых граней; угол
между ними равен 0. Найти боковую поверхность приз-
мы (а = 97,84 см, а = 63° 28' и 0 = 39° 36').
1516. В треугольной призме каждая сторона основа-
ния равна а. Одна из вершин основания имеет своей
проекцией центр другого основания. Боковые ребра на-
клонены к плоскости основания под углом а. Опреде-
лить боковую поверхность призмы.
1517. В правильной пятиугольной призме сторона ос-
нования равна а, угол наклона диагонали призмы
к плоскости основания равен а. Определить боковую
поверхность призмы.
1518. Диагональ основания прямоугольного паралле-
лепипеда составляет со стороной основания угол а, а
с диагональю параллелепипеда угол 0. Определить бо-
ковую поверхность параллелепипеда, если диагональ его
основания равна /.
1519. Проекция диагонали правильной четырехуголь-
ной призмы на боковую грань равна k и составляет
с диагональю призмы угол а. Определить боковую по-
верхность призмы.
1520. Определить боковую поверхность прямой приз-
мы, боковое ребро которой равно b и составляет с диа-
гональю большей боковой грани угол а. В основании
призмы лежит прямоугольный треугольник с острым
углом 0.
§ 91. Пирамида
1521. Высота правильной четырехугольной пирамиды
равна 14 см, а сторона основания 16 см. Найти боковое
ребро.
1522. По данной стороне а и высоте h определить
боковое ребро правильной пирамиды: 1) треугольной;
2) четырехугольной; 3) шестиугольной.
1523. Найти апофему правильной пирамиды: 1) тре-
угольной; 2) четырехугольной; 3) шестиугольной, если
231
сторона основания и высота каждой из них соответ-
ственно равны т и п (т = 6 |/3, п = 4).
1524. Дана пирамида, основанием которой является
прямоугольник, а вершина проектируется в точку пере-
сечения диагоналей основания. Все боковые ребра пи-
рамиды равны 13 см, а высота —12 см. Одна из сторон
основания пирамиды равна 8 см. Найти другую сторону
основания.
1525. Основанием пирамиды служит равнобедрен-
ный треугольник, у которого основание равно 6 см, а вы-
сота 9 см; все боковые ребра равны 13 см. Определить
высоту пирамиды.
1526. Построить сечение правильной четырехуголь-
ной пирамиды плоскостью, проведенной через середины
двух смежных боковых ребер параллельно апофеме,
расположенной в противолежащей грани. Вычислить
площадь сечения, если боковое ребро равно 5 1^34 см,
а высота пирамиды 20 см.
1527. Построить сечение правильной треугольной
пирамиды плоскостью, проведенной через середины двух
ребер основания параллельно высоте пирамиды. Вычис-
лить площадь сечения, если радиус окружности, описан-
ной около основания пирамиды, равен 6 см, а боковое
ребро 10 см.
1528. Построить сечение правильной шестиугольной
пирамиды плоскостью, проведенной через середины двух
смежных боковых ребер параллельно высоте пирамиды.
Вычислить площадь сечения, если радиус окружности,
описанной около основания пирамиды, равен 30 см, а
боковое ребро 50 см.
1529. Построить сечение правильной четырехуголь-
ной пирамиды плоскостью, проведенной через середины
двух смежных ребер основания параллельно противоле-
жащему боковому ребру (секущая плоскость не пере-
секает высоты пирамиды). Вычислить площадь сечения,
если высота пирамиды 16 см, а ребро основания
12/2 см.
1530. Построить сечение правильной четырехуголь-
ной пирамиды плоскостью, проведенной через середины
двух смежных боковых ребер параллельно высоте пира-
миды. Вычислить площадь сечения, если боковое ребро
равно 18 см, а диагональ основания 16 2 см.
232
1531. Построить сечение правильной треугольной пи-
рамиды плоскостью, проведенной через середины двух
ребер основания параллельно апофеме пирамиды. Вы-
числить площадь сечения, если ребро основания равно
Юф^З см, а высота пирамиды 12 см.
1532. В правильной четырехугольной пирамиде пло-
скость, делящая двугранный угол при основании попо-
лам, делит площадь противоположной грани в отноше-
нии 96:25 (считая от основания). Определить высоту
пирамиды, если сторона ее основания равна 3 см.
1533. В пирамиде проведено сечение параллельно ос-
нованию, которое делит высоту пирамиды в отношении
2:3 (считая от вершины). Площадь основания пира-
миды равна 100 см2. Найти площадь сечения.
1534. Высота пирамиды разделена пополам и через
точку деления проведена плоскость параллельно осно-
ванию. Площадь основания равна 50 см2. Найти пло-
щадь сечения.
1535. Высота пирамиды разделена на три равные
части и через точки деления проведены плоскости па-
раллельно основанию. Площадь основания равна
100 см2. Найти площади сечений.
1536. Высота пирамиды разделена на четыре равные
части и через точки деления проведены плоскости па-
раллельно основанию. Площадь основания равна
500 см2. Найти площади сечении.
1537. Площадь основания пирамиды равна 400 см2,
а площадь сечения, параллельного основанию, равна
80 см2. В каком отношении, считая от основания, пло-
щадь сечения делит высоту пирамиды?
1538. Высота пирамиды равна 30 см, а площадь се-
чения, параллельного основанию, относится к площади
основания как 25:64. На каком расстоянии от основа-
ния пирамиды проведено сечение?
1539. Высота пирамиды равна 16 см; площадь осно-
вания равна 512 см2. На каком расстоянии от вершины
находится сечение, параллельное основанию, площадь
которого равна 50 см2.
1540. Высота пирамиды равна /г; площадь сечения,
параллельного основанию и удаленного от вершины на
расстояние а, равна т. Определить площадь основания
пирамиды.
1541. Ребро правильного тетраэдра равно а. Найти
стороны, периметр и площадь сечения, параллельного
233
двум непересекающимся ребрам тетраэдра и отстоящего
а 1^2 \
от его центра на расстояние ~—I.
1542. Ребро правильного октаэдра равно а. Найти
стороны, периметр и площадь сечения, параллельного
грани октаэдра и отстоящего от его центра на расстоя-
ние — I.
1543. Ребро куба равно а. Найти стороны, периметр
и площадь сечения, перпендикулярного к диагонали
куба и отстоящего от его центра на расстояние р, где
Л а ]/лЗ
§ 92. Усеченная пирамида
1544. Боковое ребро правильной четырехугольной
усеченной пирамиды равно 9 см, стороны оснований
2 см и 10 см. Найти высоту этой пирамиды.
1545. Высота правильной треугольной усеченной пи-
рамиды равна 1 дм; стороны оснований 4 дм и 1 дм.
Найти боковое ребро этой пирамиды.
1546. Стороны оснований правильной четырехуголь-
ной усеченной пирамиды соответственно равны 56 см и
24 см, а высота равна 63 см. Найти апофему этой пи-
рамиды.
1547. Стороны оснований правильной четырехуголь-
ной усеченной пирамиды относятся как 3:5. Диагональ
и высота пирамиды соответственно равны 6 см и 2 см.
Найти стороны оснований.
1548. Площади диагональных сечений правильной
четырехугольной усеченной пирамиды равны 201/ 2
каждая; стороны ее оснований 8 и 2. Найти высоту этой
пирамиды.
1549. Боковое ребро правильной треугольной усечен-
ной пирамиды образует с основанием угол 45°; сто-
роны оснований соответственно равны а и b (а > Ь).
Найти площадь сечения, проведенного через боковое
ребро и ось пирамиды.
1550. Площадь диагонального сечения правильной
четырехугольной усеченной пирамиды равна 12 см2,
диагональ пирамиды равна 5 см. Найти высоту пира-
миды.
1551. В правильной треугольной усеченной пирамиде
площадь сечения, проведенного через сторону нижнего
234
основания и противоположную вершину верхнего осно-
вания, равна 24 см2, а двугранный угол между сечением
и нижним основанием равен 30°; сторона нижнего
основания пирамиды равна 8 см. Найти высоту пира.-
миды.
1552. Диагонали оснований правильной усеченной че-
тырехугольной пирамиды равны d и 3d, диагональ пира-
миды равна а.
Найти площади двух параллельных сечений, одно из
которых проходит через диагональ пирамиды парал-
лельно диагонали ее основания, а другое через сере-
дину оси.
1553. Стороны оснований правильной 6-угольной усе-
ченной пирамиды равны а и За; расстояние между двумя
параллельными ребрами, лежащими в плоскостях раз-
личных оснований и различных боковых граней, рав-
но k. В пирамиде проведены два параллельных сечения:
одно проходит через упомянутое ребро, а другое через
середину оси. Найти площади сечений.
§ 93. Поверхность пирамиды
1554. Сторона основания и апофема правильной тре-
угольной пирамиды соответственно равны 16 см и 6 см,
а боковое ребро равно 10 см. Найти боковую поверх-
ность пирамиды.
1555. Сторона основания правильной четырехуголь-
ной пирамиды равна У2 см, а боковое ребро равно
5 см. Найти полную поверхность этой пирамиды.
1556. По стороне основания а и высоте h определить
полную поверхность правильной пирамиды: 1) треуголь-
ной; 2) четырехугольной; 3) шестиугольной.
1557. Боковая поверхность правильной треугольной
пирамиды равна -±-а2У15, а сторона основания рав-
на а. Определить угол, который образует боковое ребро
пирамиды с плоскостью основания.
1558. В правильной шестиугольной пирамиде боль-
шая диагональ основания равна d, плоский угол при ос-
новании в боковой грани равен а. Определить боковую
поверхность пирамиды.
1559. Апофема правильной четырехугольной пирами-
ды равна I, двугранный угол при основании равен а.
Определить полную поверхность пирамиды.
235
1560. Определить сторону основания правильной че-
тырехугольной пирамиды по ее высоте 0,2 дм и боковой
поверхности 0,06 дм2.
1561. Вычислить высоту правильной четырехугольной
пирамиды, если апофема составляет с основанием угол
60° и полная поверхность равна 144 дм2.
1562. Вычислить полную поверхность правильной
6-угольной пирамиды, сторона основания которой равна
4 см; боковое ребро равно 5 см,-
1563. Сторона основания правильной шестиугольной
пирамиды равна а, двугранный угол при основании ра-
вен а. Определить полную поверхность пирамиды.
1564. Радиус окружности, вписанной в основание
правильной треугольной пирамиды, равен г. Двугранный
угол при основании пирамиды равен <р. Определить
полную поверхность пирамиды.
1565. Основанием пирамиды служит квадрат со сто-
роной а. Из боковых граней две перпендикулярны к ос-
нованию, а две другие образуют с ним угол а. Опреде-
лить полную поверхность этой пирамиды.
1566. Апофема правильной треугольной пирамиды
равна k и составляет с плоскостью основания угол а.
Найти полную поверхность пирамиды.
1567. Высота правильной четырехугольной пирамиды
равна h. Двугранный угол при основании равен а. Опре-
делить полную поверхность пирамиды.
1568. Определить полную поверхность правильной
четырехугольной пирамиды, боковое ребро которой рав-
но Ь, а плоский угол при вершине равен а.
1569. Определить полную поверхность правильной
треугольной пирамиды со стороной основания а, кото-
рая составляет с боковым ребром пирамиды угол а.
1570. Основанием пирамиды служит ромб с диаго-
налями в 6 см и 8 см; высота пирамиды проходит через
точку пересечения диагоналей и равна 1 см. Определить
боковую поверхность этой пирамиды.
1571. Боковая поверхность пирамиды, основанием
которой является параллелограмм со сторонами 20 см
и 36 см и площадью 360 см2, равна 768 см2. Высота пи-
рамиды проходит через точку пересечения диагоналей
основания. Определить высоту пирамиды.
1572. Дана пирамида, в основании которой лежит
параллелограмм со сторонами в 5 см и 4 см, а одна из
его диагоналей равна 3 см; высота пирамиды проходит
236
через точку пересечения диагоналей основания. Опреде-
лить высоту пирамиды, если ее полная поверхность
равна (22 + V136 ) см2.
1573. Дана пирамида, в основании которой квадрат,
высота пирамиды проходит через одну из вершин осно-
вания и равна 21 см. Боковая поверхность пирамиды
10 дм2. Определить сторону основания пирамиды.
1574. В правильной четырехугольной усеченной пи-
рамиде стороны оснований соответственно равны 8 см
и 2 см. Высота пирамиды равна 4 см. Найти полную
поверхность пирамиды.
1575. В правильной треугольной усеченной пирамиде
высота равна 10 см, а стороны оснований 60 см и 120 см.
Определить боковую поверхность пирамиды.
1576. Сторона основания правильной треугольной пи-
рамиды равна а, угол между боковыми гранями равен ср.
Определить боковую поверхность пирамиды.
1577. В правильной п-угольной усеченной пирамиде
высота равна h и стороны оснований равны а и b
(а > Ь). Определить полную поверхность этой пирамиды.
§ 94. Цилиндр и его поверхность
1578. Площадь основания равностороннего цилиндра
равна —-. Найти площадь его осевого сечения.
1579. Дан цилиндр. Площадь сечения, проведенного
параллельно оси цилиндра, равна 36 см2, высота ци-
линдра равна 6 см, а радиус основания — 5 см. Найти
расстояние от оси цилиндра до плоскости сечения.
1580. Дан цилиндр, радиус основания которого 5 см,
а высота 8 см. Расстояние от оси цилиндра до секущей
плоскости, параллельной оси цилиндра, равно 3 см. По-
казать, что это сечение есть квадрат.
1581. В правильную треугольную пирамиду вписан
равносторонний цилиндр так, что его основание лежит
в плоскости основания пирамиды. Высота цилиндра рав-
b sin 2а
на ~2^ sin (45° 4-а) * Определить боковое ребро пи-
рамиды, если оно наклонено к плоскости основания под
углом а.
1582. Площадь основания цилиндра относится к пло-
щади осевого сечения как 5:6. Определить угол между
диагоналями осевого сечения.
237
1583. Диагональ осевого сечения цилиндра равна
22,5 дм и образует с плоскостью основания угол 30°.
Определить боковую поверхность цилиндра.
1584. Найти полную поверхность равностороннего
цилиндра, если его боковая поверхность равна 80 см2.
1585. Осевое сечение цилиндра — квадрат, диагональ
которого равна 12 см. Найти полную поверхность ци-
линдра.
1586. Полная поверхность цилиндра равна
3 (5л-f-8) см2, а площадь его основания—12 см2. Опре-
делить площадь осевого сечения цилиндра.
1587. Найти боковую поверхность цилиндра, описан-
ного около правильного октаэдра так, что две вершины
октаэдра лежат в центрах оснований цилиндра, а че-
тыре вершины — на боковой поверхности. Ребро окта-
эдра равно а = 10 см.
§ 95. Конус и его поверхность
1588. Определить угол образующей равностороннего
конуса с основанием.
1589. Образующая равностороннего конуса равна
8 см. Определить высоту конуса.
1590. Площадь основания равностороннего конуса рав-
на 54 л см2. Определить площадь осевого сечения конуса.
1591. Площадь осевого сечения равностороннего
конуса равна Q. Определить площадь основания конуса.
1592. Дан конус, высота которого равна 10 см, а пло-
щадь основания равна 25 см2. Определить площадь се-
чения, параллельного основанию и удаленного от осно-
вания на 3 см.
1593. Площадь основания конуса равна ла2, а пло-
щадь сечения, параллельного основанию, равна лб2. Се-
чение отстоит от основания на расстояние с. Определить
высоту конуса. .
1594. Высота конуса разделена на шесть частей в от-
ношении 2 : 3 : 4 : 5 : 6 : 7, считая от вершины конуса.
Через точки деления проведены плоскости сечений па-
раллельно плоскости основания, площадь которого рав-
на лф. Определить площади сечений.
1595. Выразить полную поверхность равностороннего
конуса как функцию радиуса его основания.
1596. Выразить боковую и полную поверхность рав-
ностороннего конуса как функцию его образующей I.
238
1597. Выразить боковую и полную поверхность рав-
ностороннего конуса как функцию его высоты h.
1598. Боковая поверхность конуса равна 15л см2, а
его радиус равен 3 см. Найти высоту конуса.
1599. Высота конуса равна 17,1 м, а его боковая по-
верхность 250 м2. Определить радиус основания.
1600. Определить полную поверхность конуса, если
угол между образующей и плоскостью основания 60°, а
Площадь осевого сечения 10 см2.
1601. Радиус основания конуса /?, образующая накло-
нена к плоскости основания под углом а. Определить бо-
ковую поверхность конуса и площадь сечения, проходя-
щего через вершину конуса под углом р к его высоте.
1602. Боковая поверхность конуса равна Q, образую-
щая равна I. Найти угол при вершине осевого сечения
конуса (Q = 81,312 м2, / = 10 м).
1603. Боковая поверхность конуса развернута на пло-
скость и угол сектора развертки равен 216°. Радиус осно-
вания конуса 3 м. Определить высоту конуса.
1604. Угол при вершине в осевом сечении конуса ра-
вен 70° 24'. Определить угол сектора развертки его боко-
вой поверхности.
§ 96. Усеченный конус и его поверхность
1605. Радиусы оснований усеченного конуса соответ-
ственно равны 10 см и 6 см, а образующая наклонена к
плоскости основания под углом 60°. Найти высоту
конуса.
1606. Образующая усеченного конуса наклонена
к основанию под углом в 45° и_ равна 30 см, а радиус
большего основания равен 20]/2 см. Определить сумму
длин окружностей оснований.
1607. Площадь оснований усеченного конуса 4 м2
и 16 м2. Через середину высоты проведена плоскость
параллельно основанию. Найти площадь сечения.
1608. Радиусы оснований усеченного конуса и обра-
зующая соответственно равны /?, г и I. Определить бо-
ковую и полную поверхность этого конуса при R =
= 28,4 см, г — 13,8 см и Z =20 см.
1609. Высота усеченного конуса есть средняя про-
порциональная между радиусами его оснований; сумма
радиусов равна а\ угол, составленный образующей усе-
ченного конуса с плоскостью его основания, равен а.
239
Определить боковую поверхность этого усеченного ко-
нуса, если а = 45,4 см и а = 42° 30'.
1610. Радиусы оснований усеченного конуса и его
образующая относятся как 1:4:5; высота равна 8 дм.
Найти боковую поверхность.
1611. Площади нижнего и верхнего оснований усе-
ченного конуса и его боковая поверхность относятся как
а : b : с. Определить угол между образующей и пло-
скостью нижнего основания.
§ 97. Объем параллелепипеда, призмы и цилиндра
1612. Определить объем прямоугольного параллеле-
пипеда по трем его измерениям: а = 13,5 дм, b — 10,4 дм,
с = 16,8 дм.
1613. В прямоугольном параллелепипеде стороны
оснований соответственно равны 12 дм и 20 дм, а диаго-
наль параллелепипеда наклонена к его основанию под
углом 60°. Найти объем параллелепипеда.
1614. В параллелепипеде длины трех ребер, выходя-
щих из общей вершины, равны а, b и с. Ребра а и b
взаимно перпендикулярны, а ребро с образует с каждым
из них угол а. Определить объем параллелепипеда (от-
вет исследовать).
1615. Диагональ прямоугольного параллелепипеда
равна 13 см, а диагонали его боковых граней равны
4 ]z10 см и 3]/^ 17 см. Определить объем параллелепипеда.
1616. В прямом параллелепипеде стороны основания
равны а и Ь; острый угол между ними равен 60°. Боль-
шая диагональ основания равна меньшей диагонали па-
раллелепипеда. Найти объем параллелепипеда.
1617. В основании прямого параллелепипеда лежит
параллелограмм со сторонами 1 см и 4 см и острым уг-
лом 60°. Большая диагональ параллелепипеда равна
5 см. Определить его объем.
1618. Определить объем правильной шестиугольной
призмы, у которой наибольшая диагональ равна d,
а боковые грани — квадраты.
1619. Найти объем куба, если расстояние от его диа-
гонали до непересекающегося с ней ребра равно d.
1620. Основанием прямого параллелепипеда служит
ромб, площадь которого равна Q. Площади диагональ-
ных сечений равны Si и S2- Определить объем паралле-
лепипеда.
240
1621. Наибольшая диагональ правильной шести-
угольной призмы равна d и составляет с боковым реб-
ром призмы угол 30°. Найти объем призмы.
1622. Найти объем наклонной’треугольной призмы,
основанием которой служит равносторонний треуголь-
ник со стороной, равной а, если боковое ребро призмы
равно стороне основания и наклонено к плоскости осно-
вания под углом 60°.
1623. Найти объем правильной треугольной призмы,
если сторона ее основания равна а и боковая поверх-
ность равновелика сумме площадей оснований.
1624. Расстояние между непересекающимися диаго-
налями двух смежных боковых граней куба равно d.
Определить объем куба.
1625. Измерения прямоугольного параллелепипеда
равны 2 см, 3 см и 6 см. Найти длину ребра такого куба,
чтобы объемы этих тел относились как их поверх-
ности.
1626. Объем правильной восьмиугольной призмы
равен 8 м3, а ее высота равна 2,2 м. Найти боковую по-
верхность этой призмы.
1627. Площадь основания прямой треугольной приз-
мы равна 4 см2, площади боковых граней равны 9 см2,
10 см2 и 17 см2. Определить объем призмы.
1628. Основанием параллелепипеда служит ромб со
стороной а и острым углом 30°. Диагональ одной боко-
вой грани перпендикулярна к плоскости основания, а
боковое ребро составляет с плоскостью основания угол
60°. Найти полную поверхность и объем параллеле-
пипеда.
1629. Основанием прямого параллелепипеда служит
параллелограмм, один из углов которого равен 30°. Пло-
щадь основания равна 4 дм2, а площади боковых граней
параллелепипеда равны 6 дм2 и 12 дм2. Найти объем
параллелепипеда.
1630. Определить объем правильной треугольной
призмы, в которой сторона основания равна а, а диаго-
нали боковых смежных граней образуют угол а.
1631. В основании прямой призмы лежит прямо-
угольный равнобедренный треугольник с катетом а. Вы-
сота призмы равна h. Определить объем призмы.
1632. Диагональ правильной четырехугольной приз-
мы равна d и составляет с боковой гранью угол 0. Оп-
ределить объем призмы.
241
1633. Основанием прямой призмы служит равнобоч-
ная трапеция, параллельные стороны которой равны
5 см и 11 см, высота основания 4 см; боковое ребро приз-
мы равно 6 см. Вычислить полную поверхность и объем
призмы.
1634. Вычислить массу снега, выпавшего на один
гектар слоем 8 см толщиной. Плотность рыхлого снега
равна 0,17.
1635. В правильной четырехугольной призме боковое
ребро равно Ь. Диагональ призмы составляет с боковой
гранью угол р. Определить объем призмы (исследовать
ответ).
1636. Диагональ прямоугольного параллелепипеда d
составляет с плоскостью основания угол а, а с одной из
боковых граней угол р. Определить объем параллеле-
пипеда.
1637. В правильной треугольной призме отрезок, со-
единяющий центр нижнего основания с одной из вершин
верхнего основания, равен / и составляет с плоскостью
основания угол ф. Определить объем призмы.
1638. В основании прямого параллелепипеда — ромб
с углом 30°. Плоскость сечения, проходящего через два
ребра оснований, составляет с основанием угол 60°. Най-
ти объем параллелепипеда, если сторона ромба равна а.
1639. Определить объем правильной шестиугольной
призмы, если ее большая диагональ равна k и состав-
ляет с основанием угол а.
1640. В основании прямой призмы лежит четырех-
угольник с диагоналями типи углом между ними а.
Высота призмы равна среднему арифметическому диаго-
налей основания. Определить объем призмы.
1641. Радиус основания равностороннего цилиндра
равен R. Выразить объем цилиндра как функцию ра-
диуса.
1642. Чугунная труба, внутренний диаметр которой
равен 2г см, а внешний 2R см, имеет длину I см. Опре-
делить массу трубы (плотность чугуна 7,8 г/см3).
1643. Масса медной трубки, длина которой 40 см,
равна 1 кг. Определить внешний диаметр трубки, если
ее внутренний диаметр равен 3 см (плотность меди
8,9 г/см3).
1644. Объем цилиндра равен 16/л. Боковая поверх-
ность цилиндра развертывается в квадрат. Определить
сторону развертки.
242
1645. Осевое сечение цилиндра — квадрат, диагональ
которого равна 4 дм. Найти объем цилиндра.
1646. Боковая поверхность цилиндра развертывается
в квадрат со стороной 2 дм. Найти объем цилиндра.
1647. Высота цилиндрической консервной банки, ем-
кость которой равна 500 см3, равна диаметру ее дна. Вы-
числить с точностью до 0,5 мм радиус и высоту этой
банки.
1648. Диагональ осевого сечения цилиндра равна
22,5 дм и образует с плоскостью основания угол 30°.
Определить боковую поверхность и объем цилиндра.
§ 98. Объем пирамиды и конуса
1649. Боковая поверхность правильной треугольной
. пирамиды равна 18 дм. Вычислить объем этой пира-
5 миды, если высота боковой грани 4 дм.
1650. Апофема правильной четырехугольной пира-
миды равна 19 см, а диагональ основания 6 см. Найти
боковую поверхность и объем пирамиды.
1651. Длина ребра правильного тетраэдра равна а;
определить его поверхность и объем.
1652. Длина ребра правильного октаэдра равна а;
определить его поверхность и объем.
1653. Вычислить объем и полную поверхность пира-
миды, основание которой — прямоугольник со сторона-
ми 2,8 см и 4,5 см; высота пирамиды равна диагонали
основания.
1654. Основанием пирамиды служит прямоугольник
с меньшей стороной а. Найти объем пирамиды, если две
боковые грани перпендикулярны к основанию, а две
другие наклонены к основанию под углами 30° и 60°.
1655. Основанием пирамиды служит прямоугольник
со сторонами 6 см и 15 см, высота проходит через точ«
ку пересечения диагоналей основания, боковая поверх*
ность равна 126 см2. Определить объем этой пира*
МИДЫ.
1656. В правильной четырехугольной пирамиде вер*
шина основания удалена от противолежащего бокового
ребра на расстояние т. Ребро образует с основанием
угол <р. Определить объем пирамиды.
1657. Найти объем пирамиды, в основании которой
лежит параллелограмм со сторонами 12 см и 15 см и
острым углом 30°; высота пирамиды равна 30 см.
243
1658. В правильной четырехугольной пирамиде вы-
сота равна Н, угол при вершине диагонального сече-
ния 2а. Определить объем пирамиды.
1659. В основании пирамиды, боковые грани которой
наклонены к основанию под углом а, лежит прямо-
угольная трапеция с острым углом р. Определить объем
пирамиды, если ее высота равна h.
1660. В правильной треугольной пирамиде центр ос-
нования удален от боковой грани на расстояние т. Бо-
ковая грань составляет с плоскостью основания угол а.
Определить объем пирамиды.
1661. В треугольной пирамиде все боковые ребра
равны и наклонены к плоскости основания под углом р.
Две стороны основания имеют длину Ь. Угол между рав-
ными сторонами основания равен а. Определить объем
пирамиды.
1662. Боковые грани правильной четырехугольной
пирамиды наклонены к плоскости основания под уг-
лом а; радиус окружности, описанной около основания
пирамиды, равен R. Определить объем пирамиды.
1663. Образующая конуса равна 36,7 дм и составляет
с его осью угол 18°. Определить объем конуса.
1664. Площадь осевого сечения конуса 4,8 дм2; вы-
сота конуса 3 дм. Найти объем конуса.
1665. Найти объем равностороннего*конуса, если его
высота равна h — 3 дм.
1666. В равностороннем конусе сторона осевого сече-
ния равна 8 дм. Найти (с точностью до 0,1 дм) полную
поверхность и объем конуса.
1667. Образующая конуса равна 2 дм и составляет с
плоскостью основания угол 60°. Определить объем конуса.
1668. Длина образующей конуса равна 3 V3 см, а
длина окружности основания 2)^2 л см. Найти объем
конуса.
1669. Найти объем равностороннего конуса, сторона
осевого сечения которого равна 40 см.
1670. Площадь основания конуса 9л см2; полная по-
верхность его 24л см2. Найти объем конуса.
1671. Высота и образующая конуса относятся как
4 : 5, а объем конуса 96л см3. Найти его полную поверх-
ность.
1672. Высота конуса 6 см, а боковая поверхность
24л см2. Определить объем конуса.
244
§ 99. Объем усеченной пирамиды
и усеченного конуса
1673. В правильной четырехугольной усеченной пира-
миде диагонали оснований соответственно равны 8 см
и 16 см, а высота равна 9 см. Найти объем этой пира-
миды.
1674. В правильной четырехугольной усеченной пи-
рамиде стороны основания равны 12 см и 20 см; апо-
фема 5 см. Найти объем этой пирамиды.
1675. В правильной четырехугольной усеченной пира-
миде диагонали оснований 36 см и 16 см, а апофема
равна У131 см. Найти объем этой пирамиды.
1676. Объем правильной четырехугольной усеченной
пирамиды равен 10'Л м3, а стороны оснований — 5 м и
1 м. Найти боковое ребро этой пирамиды.
1677. Пирамиду, площадь основания которой 245 м2,
а высота 35 м, рассекли плоскостью, параллельной осно-
ванию, на две пирамиды — полную и усеченную. Опре-
делить объем каждой из них, если площадь основания
отсеченной полной пирамиды равна 80 м2.
1678. Объем усеченной пирамиды равен 475 м3, а вы-
сота 15 м; площади ее оснований относятся как 4 : 9.
Определить объем полной пирамиды.
1679. В правильной четырехугольной усеченной пи«
рамиде сторона нижнего основания и боковое ребро
равны а. Плоский угол боковой грани при нижнем осно-
вании равен а. Определить боковую поверхность пира-
миды.
1680. В правильной усеченной четырехугольной пира-
миде сторона нижнего основания равна 4а, боко-
вая грань наклонена к основанию под углом а. Апо-
фема пирамиды равна 2а. Определить объем пира-
миды.
1681. В правильной шестиугольной усеченной пира-
миде стороны оснований равны а и b (а^Ь), а дву-
гранный угол при основании равен а. Определить объем
пирамиды.
1682. Стороны оснований правильной треугольной
усеченной пирамиды 30 м и 20 м, а боковая поверхность
равновелика сумме площадей оснований. Определить
объем этой пирамиды.
1683. В правильной n-угольной усеченной пирамиде
стороны оснований а и Ь, а боковое ребро составляет
245
с плоскостью большего основания угол а (а > Ь). Опре-
делить объем этой пирамиды.
1684. Определить боковую поверхность и объем усе-
ченного конуса, если его образующая составляет с пло-
скостью основания угол 60°, а площади оснований рав-
ны 25л см2 и 64л см2.
1685. Радиусы оснований усеченного конуса 20 см и
10 см. Образующая наклонена к плоскости основания
под углом 45°. Найти объем конуса.
1686. Найти высоту усеченного конуса, если его
объем равен 20 дм3 и радиусы оснований 3 дм
и 1 дм.
1687. Усеченный конус, у которого радиусы основа-
ний 3 см и 5 см, и полный конус такой же высоты рав-
новелики. Чему равен радиус основания полного ко-
нуса?
1688. Высота усеченного конуса равна 3 см. Радиус
одного основания вдвое больше радиуса другого, а об-
разующая наклонена к основанию под углом 45°. Най-
ти объем этого конуса.
1689. Объем усеченного конуса равен 248л см3; его
высота 8 см, радиус одного из оснований 4 см. Опреде-
лить радиус второго основания.
1690. Радиусы оснований усеченного конуса R и г\
образующая наклонена к большему основанию под уг-
лом а Определить объем этого конуса.
1691. Отношение площадей оснований усеченного ко-
нуса равно 4; образующая равна I и наклонена к пло-
скости основания под углом а. Определить объем
конуса.
1692. В усеченном конусе помещается полный конус,
имеющий с ним общее меньшее основание, общую вы-
соту и образующие, соответственно параллельные обра-
зующим усеченного конуса. Определить объем усечен-
ного конуса, зная угол а = 65° 49' между продолжениями
его образующих, каждая из которых равна а = 24,9 дм.
§ 100. Шар и его части
1693. Радиус земного шара «6370 км. Определить
длину экватора.
1694. Радиус земного шара «6370 км. Найти длину
тропика (широта 23° 27') и полярного круга (широта
66° 33').
246
1695. Москва находится на 56° северной широты.
Зная радиус земного шара из задачи 1693, найти радиус
этого круга широты.
1696. Плоскость, перпендикулярная к диаметру шара,
делит диаметр на две части: 3 см и 9 см. На какие части
делится поверхность шара?
1697. Две параллельные плоскости, перпендикуляр-
ные к диаметру шара, делят его на три части: 2 см, 4 см
и 6 см. Определить поверхность шара, образовавшихся
сферических сегментов и сферического пояса.
1698. Поверхность шара равна 80л. Определить диа-
метр шара.
1699. Поверхность сферического сегмента, высота
которого равна 10 см, равна 200л см2. Определить ра-
диус соответствующего шара.
1700. Поверхность сферического пояса, высота кото-
рого равна 15 см, равна 900л см2. Определить радиус
соответствующего шара.
1701. Радиус сферического сектора 45 см, угол осе-
вого сечения 120°. Найти поверхность этого сектора.
1702. Поверхность сферического пояса равна
400л см2, а его высота 10 см. Определить поверхность
сферического сектора этого же шара; угол осевого сече-
ния сектора равен 60°.
1703. В шаре проведены по одну сторону от центра
два параллельных сечения; площади их равны 49л дм2
и 4л м2, а расстояние между ними 9 дм. Определить по-
верхность шара.
1704. Поверхность шара равна 324л см2. Определить
объем шара.
1705. Поверхность сферического сегмента, высота
которого 8 см, равна 32л см2. Найти объем шара.
1706. Плоскость, перпендикулярная к диаметру шара,
делит его на отрезки, равные 3 см и 9 см. На какие
части делится объем шара?
1707. Радиус шара 75 см, а радиус окружности осно-
вания сферического сектора этого шара 60 см. Опреде-
лить объем сектора.
1708. Радиусы оснований сферического сдоя 3 м и
4 м, а радиус его сферической поверхности 5 м. Опреде-
лить объем слоя (два случая).
1709. Образующая конуса составляет с его осью угол
а = 35° 18'. Определить отношение объема этого конуса
к объему описанного около него шара.
247
1710. Оцределить объем шара, описанного около усе-
ченного конуса, в котором радиусы оснований R и г,
а образующая наклонена к плоскости нижнего основа-
ния под углом а.
1711. Дуга осевого сечения сферического сегмента
а = 65° 28'; радиус шара, от которого отделен сегмент,
Я — 24 дм. Определить сферическую поверхность сег-
мента.
1712. Основанием пирамиды служит ромб со сторо-
ной а и острым углом а; двугранные углы при основа-
нии равны ф. Определить радиус шара, вписанного
в эту пирамиду.
1713. Найти радиус шара, вписанного в пирамиду,
основанием которой служит треугольник со сторонами
13 см, 14 см и 15 см; вершина пирамиды удалена от каж-
дой стороны основания на 5 см.
1714. Найти объем шара, вписанного в правильную
четырехугольную пирамиду, сторона основания которой
12 см, а высота равна 8 см.
1715. В правильную треугольную пирамиду, боковая
грань которой наклонена к плоскости основания под уг-
лом а, вписан шар, объем которого равен т дм3. Опре-
делить объем пирамиды.
§ 101. Тела вращения
1716. Прямоугольный треугольник с гипотенузой а и
острым углом а вращается вокруг гипотенузы. Опреде-
лить объем тела вращения.
1717. Ромб с меньшей диагональю d и углом а вра-
щается вокруг оси, перпендикулярной к его стороне и
проходящей через вершину острого угла. Определить
поверхность тела вращения.
1718. В основание конуса вписан квадрат со сторо-
ной а. Плоскость, проходящая через вершину конуса и
одну из сторон этого квадрата, дает в сечении треуголь-
ник, угол при вершине которого а. Найти объем ко-
нуса.
1719. Определить объем тела, полученного при вра-
щении параллелограмма вокруг большей стороны, если
известно, что меньшая сторона параллелограмма рав-
на а, острый угол равен а и угол, составленный меньшей
диагональю параллелограмма с большей его стороной,
равен 0.
248
1720. Сторона ромба равна а, острый угол 2а; этот
ромб вращается вокруг оси, проходящей через вершину
данного угла параллельно меньшей диагонали. Опреде-
лить объем тела, полученного при вращении.
1721. В треугольнике АВС даны углы аир, приле-
жащие к стороне АС, и высота h, опущенная на сто-
рону АС. Определить объем тела, образованного вра-
щением треугольника вокруг стороны АС.
1722. В треугольнике АВС даны углы аир, приле-
жащие к стороне АС, и высота h, опущенная на сторо-
ну АС. Определить объем тела, образованного враще-
нием треугольника АВС вокруг прямой, проведенной
через вершину В параллельно стороне АС.
1723. Определить поверхность тела, образуемого вра-
щением равнобедренного треугольника вокруг прямой,
параллельной основанию треугольника и проходящей
через его вершину, если известно, что высота равнобед-
ренного треугольника равна h и угол при вершине ра-
вен а.
1724. Определить отношение объемов двух тел, об-
разуемых вращением равнобедренного треугольника
с углом при основании а, вокруг одной из боковых сто-
рон и вокруг основания.
1725. Прямоугольный треугольник с острым углом а
вращается один раз вокруг катета, противолежащего
углу а, а второй раз вокруг другого катета. Найти отно-
шение поверхностей и объемов получающихся при таких
вращениях конусов.
1726. Ромб, у которого меньшая диагональ d и ост-
рый угол а, вращается вокруг стороны. Определить
объем тела вращения.
1727. Определить объем тела, полученного при вра-
щении равнобедренного треугольника с углом при
вершине а вокруг оси, проходящей через конец осно-
вания параллельного одной из боковых сторон, рав-
ной а.
1728. Параллельные стороны трапеции суть АВ == tn
и CD = п, а утлы, прилежащие к АВ, равны а и Оп-
ределить объем тела, полученного при вращении тра-
пеции вокруг стороны АВ.
1729. Тупоугольный треугольник с острым углом а
и прилежащей меньшей стороной а вращается вокруг
стороны, лежащей против тупого угла. Определить
249
объем тела вращения, если другая меньшая сторона со-
ставляет угол р с высотой, проведенной из вершины ту-
пого угла.
1730. В треугольнике даны катет а и противолежа-
щий ему угол а. Определить объем тела, полученного
при вращении этого треугольника вокруг оси, лежащей
в плоскости треугольника и проходящей вне треугольника
через вершину прямого угла под углом а к данному ка-
тету.
1731. Равнобедренный треугольник, у которого боко-
вая сторона равна Ь, а угол при вершине а, вращается
около боковой стороны. Определить объем и поверх-
ность тела вращения (а = 120°).
1732. Равнобедренный треугольник с высотой h, опу-
щенной на основание, и углом при основании а вра-
щается вокруг оси, расположенной в плоскости тре-
угольника параллельно высоте на расстоянии от
нее, равном боковой стороне. Определить объем тела
вращения.
1733. Прямоугольник вращается вокруг оси, прове-
денной через вершину параллельно диагонали; пери-
метр прямоугольника равен 2р, угол между диагональю
и большей стороной равен а. Найти поверхность тела
вращения.
1734. Сумма радиуса основания и образующей ко-
нуса равна т, а угол, составленный образующей конуса
с плоскостью основания, равен а. Вычислить полную
поверхность конуса.
1735. В треугольнике даны основание а и прилежа-
щие углы а и 90° + а- Определить объем тела, получен-
ного от вращения этого треугольника около его вы-
соты.
1736. В прямоугольном треугольнике гипотенуза рав-
на с, острый угол а. Найти объем тела, образованного
вращением этого треугольника около прямой, проведен-
ной через вершину прямого угла параллельно гипо-
тенузе.
1737. Площадь прямоугольного треугольника рав-
на S; один из острых углов равен а. Через вершину
этого острого угла проведена прямая, перпендикуляр-
ная к гипотенузе и лежащая в плоскости треугольника.
Определить объем тела, образуемого вращением тре-
угольника около упомянутой оси.
250
1738. Площадь равнобедренного треугольника Q, а
угол при вершине р. Вычислить полную поверхность
тела, образованного вращением этого треугольника
около прямой, перпендикулярной к основанию и прове-
денной через один из его концов.
1739. В треугольнике даны стороны b и с и угол
между ними а; этот треугольник вращается около оси,
которая проходит вне его через вершину угла сс и об-
разует равные углы со сторонами b и с. Определить
объем тела вращения.
ОТВЕТЫ
Глава 1
5. 1) 3; 2) 1-В-! 3) 2; 4) 5,74. 0. 1) 4-Ь 2)
3) 152,3; 4) 40,06; 5) 1-^; 6) 3-Ц. 7. 1) 4; 2) 4; 3) 1; 4) А;
5) 0,3; 6) 1—; 7) 30; 8) 75 - 10~5. 8. 1) 1,632 т; 2) 4,5 т;
о2о
4
3) « 155,5 га; 4) 64,35. 9. 51%. 10. 0,2 т. 11. 2132 12. «2,27%;
«2,55%; «3,85%; «5,31%. 13. 1) 25%; 2) 50%; 3) «38%;
4) «14,3%. 14. 1)3а2 + 5а —7; 2) х2 + 3; 3) - 4х2 + 2ху - Gy2;
4) 5а2 + За -10. 15. 1) Чу; 2) 4ху; 3) х2 + Зу2; 4) (а-6)+ 2-
16. 14 ~. 17. 12. 18. -1. 19. 1) 7a2b2(ab + 7); 2) 8//3 (2х - у};
3) 15/*(х_4); 4) (bm-cm)(bm + cm); 5) ап+2 (bm - ст) {bm+cm)\
6) a^-n-4(a2n+7_ j) 20> ц х(а_ ь)(5_3л._6х2). 2) w(x2+i)X
X (3 — 2m + 4m2); 3) 4х (а + b + с) (х + I)2; 4) 16х2 (р — q)(x+ I)2.
21. 1) (а — Ь) (х2 + х — 1); 2) (а + Ь) (х2 — х + 1); 3) х (а + b — с)Х
Х(х+1); 4) х (а + Ь 4-с) (х — 1). 22. 1) (а + b + 1) (а + b - 1);
2) (т — п + 2) (т—п— 2); 3) (3 + т—п) (3—т 4-п); 4) (2т—5п+6)Х
X (2т—5а—6); 5) (т + п+р — q) (т+п — p+q). 23. 1) (х1—х2+1)Х
X (х2 + х+ 1) (х2 — х+ 1); 2) (х2+ху+уг) (х2 — ху+у2); 3) (а+1)Х
Х(а + 2) (а + 3); 4) (а - 2) (2а2 + 5а + 6); 5) (а + 1) (а + 2) (а + 5);
6) (а2 + а + 1) (а2 + 5); 7) 2ху (6х + 5р) (35х2 - ЗОхр + 25р2);
п гЛ__h2 о 2
8)х(х-1)(х+1).24. !)—; 2) 3) 4)
25. -2 26- “W* 38’ °’0014%- 40- !>2%.41. 60кг(±1,2).
42. 0,073?6- 43. 0,003%. 44. 251 см2 (±0,85%). 45. 0,0064%.
46. 0,006%. 47. 0,064%. 48. 0,9 мм. 49. Второе. 50. Последняя
цифра 2 ненадежная. 51. 0,22%. 52. 0,16%. 53. 0,15 кг. 54. 0,3%.
55. 0,68%. 56. 0. 57. 0,1%. 58. 38,5 кг; 0,4%. 59. 24; 0,95. 60. 0,2 см;
0,05. 61. 7,93; 0,08%. 62. 0,5%. 63. 133-10 (±0,3%). 64. 8,1 (±0,079).
252
65. 76,8 см (± 0,4 см). 66. 0,33%. 67. 106,6 м (±0,05%).
68. 97 (±3,2) см3. 69. 13,333 (±0,001). 70. 28,5 (±0,1 %).
71. 22,6 (±0,1%). 72. 21,6 (±0,03) см. 73.57 см. 74. 0,2%. 75. 0,0043.
87. [2;8]. 89. {1;2;3;6;9; 18}. 91. 1) [2;5]; 2) [1;7]. 94. 1) 9,60628...;
2) 0,9453...; 3) 1,38850...; 4) 2,6007...; 5) 231,32157...; 6) 3,58765.
95.1) 371; 2) 30-|; 3)27^1; 4)1; 5)4-1 6)4±;
7) 2-у; 8) -уу. 96. 1) 3,145; 2) 3,968; 3) 5,872; 4) 7,093; 5) 2,510;
6) 1,633. 97. 1) 5,198; 2) 5,843; 3) 5,873. 98. 1) 4,60; 2) 6,00; 3) 15,00;
4) 625,00; 5) 16,00; 6) 49,00. 99. 1) 0,6; 2) 1,5; 3) 1,5. 100. 1) 0,2;
2)24,3; 3) 25. 101. 1) 11,456 ...; 2) 5,20987 ... 102. 1) 26,038...;
9
2) 0,72... 106. См. рис. 12; 10-у ед2. 108. См. рис. 13.
109. 2) См. рис. 14. 113. См. рис. 15; 18 ед2. 115. —3; 11.
9
117. (1; 2). 119. (-6; 0); (0; 3); (6; 0); (0; -3). 122. 1) -14;
О
2) у; 3) -1у. 123. 1) —4; 2) 2; 3) 1; 4) 3. 124. 1,5.
125. -5. 127. I) (2; 1); 2) (2; 1); 3) (2; 1); 4) (3; 2); 5) (3; 2);
6) (3; 2). 128. 1) ki ф k2, 2) ki = k2, b> b2, 3) = fe2, bx = b2,
129. 1) См. рис. 16; 2) см. рис. 17; 3) см. рис. 18; 5) см. рис. 19;
6) см. рис. 20; 7) см. рис. 21; 8) см. рис. 22. 139. с — —.
131. ху = 24; х>0; г/> 0. 137. См. рис. 23; ah = 18. 139. 1) См.
4
рис. 24; 2) см. рис. 25; 3) см. рис. 26. 149. 1) —1—; 2) 2.
141. 1) См. рис. 27; 2) см. рис. 28; 4) см. рис. 29; 6) см. рис. 30.
142. 1) 0; —3; 2) —3; 3) решений не имеет; 4) —6; —14-.
О
2
143. 1)—4) Решений не имеет; 5) 3—; 6) 1. 144. I) 3; 2) 4.
145. —146. Решений не имеет. 147. Нет решений.
148 П 1~т • 9) 3) + 4ч d2-n\
Ь8- '> Ь(1 +,п)’ 2) b=k’ 3> «т-1 ’ ' 2« "•
5) - * 149. 1) а+6; 2) т—сгп — л; 3) ат; 4) d — с.
3 1
159. у. 151. у. 152. 1) (3, 2); 2) (1; 1); 3) (0,2; -1); 4) (0,2;-1);
5) (2;3); 6) (2; 3). 153. 1) (5; -8); 2) (98; 164); 3)
4) (1-^-; 154. 1) (0; 1; -1); 2) (2; 2; 2); 3) (1; 2; 3); 4) (2; 1; 2);
5) (3; 2; 1); 6) (1;3;4). 155. 1) (1; 1; 1); 2) (1; 1; 1); 3) (1; 1; 1);
4) (1; 3; 2). 156. 1) (9; 7; 5; 3; 1); 2) (-За +-С ; ЗЬ 1
253
254
255
Z4
Рис. 23.
Рис. 22.
256
257
SG'5
рт ь
'внхэзкегоээн (р ![<ш (g _ > х (g ;2_r<x([ -gg^ •впхээиаоээи (р
LA £
19<х и f - > х > з- (g .~£<х (5 4>x>g‘5- (t -frgl
G
*8>й+х>-|-|г (ъ ‘.£1>/? + %>д (g ‘-£1 >/» 4-* >g‘9 (3
•‘51 >fi+x>g ([ -£si *2>x> i !g-C^<3 (£ -‘3>x> g‘o- (3
13>x>g‘O (l ’581 ‘6£ ’SHd -из !g>x> Z (£ ;8£ ’and 'из
tg— <x и 8— >x (3 '.££ -and 'на ‘д >*>£— (l *181 ’9£-ond -нэ
fg<x и I — >x (g vg -and -иэ ![ >x>-|- {— (3 i^g -and 'иэ !j <x
и y->X (l *081 ££ -Olid 'HO .‘£<x — >X (£ fj£ ’3Hd 'ИЭ
!£>X>g- (3 !{£ -OHd -из !£<X i£ - > X (1 ‘6£I !^-<X (g
g
•*y 8<* (Z 4 <x (1 -8£I -0<P = o -991 -Q<qv 'S9I '8>^>£
•££ and
t'fi ’^I’d
Игги 8>x> £ (8 ;8>x>£ (Z !8>x>£ (l ’891 ’ZI — < 8*fr— (£
133—<£3— (3.‘£3>£3 (1 '39i -1ЭЗИИ эн иияэпюа и g = v hcIu
iHUHamad оахээжонп эоньэноиээр g=? и £ = o ndjj 491 ‘(гд — zv)
,z n , n\ /„ t г<? 4~ г° t г<? 4~ gP z .( v <r_n7\ /,
•(г^ 4“ г ) (S • p _ g (l 091 \ । 4 3J
p-n (q- J. t/ q-v ( q + v\ JZ + ^ tZ~v \ ,„OI
(e •(“ <S \ ’Г •“) (l °3'
u 4- w
JUJf — qg
( ll -j- ui
' rn 4- 2/S
!хгэ1«и эн
Huaamad (3
.[ S < S
\ ^6 — 4)5 ’ ??□! — WI3
•(I U -‘I :l) (V !(l !l 4
(f, 4(<7-34-») ‘(q + ^ — °)] (8
(q-y)z {(94-p)g 1 (
Le(g-»5) s(4+»S)l
\ (7 4 pZ A (r .,Qr
) (3 p _ э ‘ P 4. Э / ‘1 ^Slt
, . , ,/______tz____t vz
'l s \?4-°5-P8 ’^ + PZ — Э£
Рис. 37.
Рис. 38.
259
4 9 19
5)х< —6. 186. 1)-п<х<-; 2) x>4 187. k == 7; 8; 9; 10;
11 О 1У
11;... 188. a = 0; x= 1; z/ = y. 189. 0; 1; 2; 3; 4; 5. 202. 1) x>4;
2)
x>2;
3)
j4
5
4)
x — 6; 5)—8) вся числовая ось.
203. 1) У a2 = | a | =
а при
— а при
0 при
3) /(- 15)2 = 15; 4) Y(- 3)2 = 3;
a> 0,
a<0, -2) //Jp = -(-l) = l;
a=0;
f 2 — x при x <2,
5) /(2-x)2 = j x — 2 при x>2,
I 0 при x = 2.
(x + 1 при X> — 1,
-(*+ I) при X< —1,
0 при x=— 1.
206. 1) 2-// 2) УЗ- 1; 3) У~2 - 1. 207. 1) /5-2;
2) 2-У5-, 3) /10-3. 208. 1) 7 —х; 2) х - 7; 3) 12-х;
2п±1_________________ 2п±1_ 3 ___ 3 ______
4) х- 12. 209. 1) У-а = - /а при а»; 2)/-10 =-/10;
3) -/15; 4) -УЗ-, 5) -/Г; 6) -/Г=Т; 7) /зх - 7 ;
8) /1х- 10. 210. 1) 4; 2) 2/2; 3) /г’; 4) /^ 211. 1) /Г;
2) У а-, 3) /а»; 4) У а. 212. 1) У аЬ2с, 2) /(a + ft)-c;
__________________ 4 _ 4 _ 6 _ 6 12 _
3) У (а- Ь}> с. 213. 1) /4 и /3; 2) /25 и /3; 3) /343 и
/12. 214. 1) У~а3 и /ft2; 2) /^з и 3) /^з и
тп_______ тп__________ втп_________________
215. 1) У(а+Ь)т и /(а+&)"; 2) У азт (Ь - с)зт и
6m п п-— 1______________ 'ti2—1_________
Уа2п (Ь — с)2п-, 3) /(2а — 1)п—1 • а””1 и /(aft2f+I;
km________ km__________
4) У\а-Ь)2т и /(а + ft)2fe. 216. 1) 2а2; 2) 3a3b; 3) 3a3b.
217 n • 9) — • 3) 2q2^c2 218 1) ____2o^bc^---
2’7. I) 42, 2) 6, 3) . 21». 1} (a+6)(fl_ft)2,
7(a + b)‘.V2 SabV
a — b ’ a + b 13 (a + ft)2
2|9 2) a02(^)VaM«-O; 3)
ya t " u) \ aujv j ci и
220. 1) УЗ-, 2) У5; 3) /7; 4) /12. 221. 1) ft2/ас; 2) /ftc2-
4__________ 5______________________ 1 4 ______—
3) Ут11(т + п). 222. 1) /(a + ft) (a - ft)2; 2) Уc3 (m - n)3;
260
5__________ V-______________________________‘
3) cd2 (a - b)Ybc2{a - ft)2; 4) V (a + b) (a - ft) (c + d).
223. 1) — ^2; 2) A /3 ; 3) A; 4) А/Г; 5) ~Уб; 6) A/7,
о □ v> *
7) A/А 8) -A-/T0. 224. 1) A/A 2) А/Ю; 3) у^21;
4 111 out
4) A/Io; 5) A/21; 6) -A-^isl 225« o 2) 1"A22;
3) A /39; 4) A/78; 5) A/246; 6) А/П. 226. 1) A/^;
2) A/^2. 3) 4) ~~Уху*; 5) —A /x2- ft2;
У У У л У^
6) —гт/а (а--ft) (а 4~ &)2. 227, 1) х х (т 4- п}; 2} А К aft + с;
a + ft ' ‘ ь ’
3) a1 /ft (a2 - ftc2). 232. 1) /2, /2, ~ /3, -А|/Т, -А/Щ
/ о О
2) А/бх//; 3) -2-А1^з^2; 4) 60а2/(а- ft) с, а> ft.
<w ао
233. 1) S^i-Га^. 2)
ас (За — 1) (2 — ft) (а — ft)
3) а2 АапЬп+[сп+\ 4) (a + ft) ftc/mft2?; 5)
2 ’ ’ v r ’ ' ft+5 (а + ft) (а — с)
X/(a + ft)2 (ft/-с) (a2_—с2). 234. I) —2) He подобны;
3) 4/а co5/а co7/а; 4) (a + ft) У a + ft co (a + ft)3/a + ft.
235. 1) 5 (a + ft) / a + ft co — 4(a + ft)2/a + ft co — (a + ft)]/ a + ft;
2) —A_ /a2 — ft2'/a2 _ ft2oo/a2 — ь2^ — aft /a2 — ft2;
a — ft ft
1 5 _____ ПЛ 5 _____ I 5 ________
3} ---------/^2 _ ^,s --------— /х2 — у2 уг-У x2 — у2;
’ x — у r u (x — у)2 2 r J ’
I m n n____ n _
4) — /^ooft« /a2co(a+ ft)3 Va2. 236. 1) - Ю- 2!/2;
d о
2) 13,41/5^ 3) 117 A//; 4) -l-A./3‘+l^-/5’,
4 Io /0
237. 1) 29a/a; 2) a ]Xa (1 - 2a + 7 f'a); 3) /a + ft (a + ft - 5).
238. 1) 1 A/6 (a-(,)+!; 2) -а/-Г/ +а<°г- '>!
3) -~Х4й3 f2a(a + i). 239, 1) ~ ‘6ail~^-3a.
4a2 x ' 4 (a —ft)
2) (a ~ 'a"L. b)Va^b - Vb (b2 - a2). 240. 1) 180; 2) -42/2';
3) 6; 4) 18; 5) /3~. 241. 1) (a + ft)2; 2) ^Ap/(«2-^2)2 («“A';
3) 4) P^ + 4).t v 242. 1) 16,5; 2) 250;
ft ’ a (1 — 4a) ’
261
3) а {(с — d} {a— b (c — rf)] + b* 2}; 4) 243. 1) a — &;
2) /оф/Р; 3) /Р-/Р; 4) a3-b3. 244. 1) 3; 2) 81
3)48/3; 4) -i/2". 245. 1) 2) (a + b)3 (a - £);
3 _____ 6 __________________ 6 _______ 4 _
3) а2Ь2Уа —b — ab. 246. 1) 2/32; 2) /3^-2‘; 3) 3/3.
247. 1) б/РР; 2) у/РР(а + Ь)5. 248. 1) 2 + 2 /2 + 2 /2 ;
4 __ 12________ 4 ___
2) 4 /200 + 5 У 2048 — /50;
С__ 6 __ 3
+ J 32 — /243 — / 6 .
6 _ з _ 6 __ _
3) 4/2 - 40 /2 +/32; 4) /0 +
249. i) /2; 2) у /4 • ЗГ7; 3) ]/3 ;
О
4) 9&/а2Р; 5) 40/«+’.
2) 413 | 2_ 10Ь ;
95 ЗаУ'аЬ
4) а ]' ЗаЬ — аУ\2аЬ3 + 2аЬ.
250. 1) т У ab (1 — т2) + т2;
3) — 4- У^Г5 + — УУ;
ЗЬ 3 За
5 ___ 8 _____ ________
251. i)/3asd + /2ad; 2) У 2а.
252. 1) Ут — Утп; 2) ]Хх.
3) —4) S)
7/5 Ь Уа ЬУ а
2) ~7~--; 3)
Ь\Уа + & + У (У а +Ь+ 1)
2 1
253. 1) ——; 2) -------
5/2 2]/3
254. I) аг + °» + ^ ..
ЗЬ (а + b + Уab)
1) (/а-6 + 1)
а\Уа— b 4-
255. ,) <£; 2) 3) 4) ф. 256. D
о О о и и
Уа + b (а—Ь)Уа+Ь' (7а+1)Уа+Ь
} а ’ 3) а-\-Ь ’ 4) а(а+Ь)
п п
257. 1) 2) 3) ]Х(а2 -9)2,
a + b a — b > v \
sn- n 2(3 + lf?). »> 5 (3 ~ /з). »> 6(5 + ;/2)
? 3 ’ ’ 6 ’ 23 •
259. 1) 5/3 +4/2; 2) + ‘^3 ;
__ _ Qm — 4n _____
(m — n) (2/m + 3/n) т + У'т2—п2
4m -9n * 2b°- 1} n------1
a — У a2 — b2 Q. m2+5+ /m4 —25 л. r—;— r-
2) --L_---. 3) ----_£-----. 4) ym + n_ym_n>
261. 1) 1; 2) —. 262. 1) 1; 2) ~У1—у2. 263. 1) У а ~УЬ}
n У 4' '
2G2
2)
265.
— — 1 X
Уу~ /х. 264. 1) —-—; 2) /ш(1 — w)
((a + ft)2 - ft2 (2a + ft)] (a + ft) t /Г(/7- l)(x2- 1)
266.
1) ---------------------------------
а2
I) У a + b — У а — Ь; 2) 1.
4х2
2) 7-тУ-
267.
268. 1) V"uv; 2)
270. 1) 1; 2) 1;
Т’ * 4>
273. I) I; 2)
а — b
3)
2)
3)
2)
1) a/1 —a2; 2) 2, если
269. 1) Y^b-,
3) —; 4) —; 5) 0,01.
2 9
272. 1) -1; 2) ~;
_й 233 5
I °; 3) 2----: 4) 22 —.
’ ’ 360 ’ ' 7
гЛ
; 3) 275. 1) 37,5;
а2 + Ь2
; 2) 2/aft (/a-/ft);
4 ’
345 10'
2аЬ (а + ft)2
а—У а2—ft2
271. 1) 1; 2) -
3) -4; 4) -64
274. 1) ;
а2о2 (а + ft)2
15
78 3) 1,74; 4) 8,5. 276. 1)
1о
277. 1) а2 + ab + ft2;
2 (а 4- Va2
279. 1) —с; 2)
281.
285.
291.
294.
1) 1; 2) 4/ft. 282. 8а /а +6.
a3b Y"b. 286. 0.
2 /х — 1, если х :
*4 '
287. —1.
2, если
2)
0.
278- ’) а>
2 (а2 + 6)
289. 1) 0; 2) — —.
283.
288.
2у(х-у). 284. ^-0-.
289.
292.
I.
2 ’
b
2
Глава 2
Я
21/3
Рис. 40.
305. АВ = | АВ |; а ~ | а [. 306. Если прямые, на которых рас-
положены векторы, параллельны или совпадают, то векторы (в этом
случае) называются коллинеарны-
ми. Направления таких векторов
могут совпадать и быть противо-
положными. 309. 1) 5; 2) 1,8;
3) 4; 4) /2?_ 5) 3/2; 6) 5/2?
310. 3/2 +/34 +8 =« 18,1.
312. JJ=Fi+F2; | Я j = j Л+Fa | =
=20. 313. См. рис. 40; АВ = | АВ |=
= 2 V5-2/3; AtBi = | ДЭ1 1 =
=1/ 28-^- — 1,5/6? x = \BBi | =
= у 22^ + ~Ув-2-уЗ-бУ2. 314.
4) 135°. 317. (а) Замкнутым векторным
1) 45°; 2) 45°; 3) 135°;
многоугольником; (б) 0;
263
(в) вектор, равный нулю. 318. | а — Ъ ] = 22. 320. | с + b j 18,3;
| Ь + d | ~ 25,7. 324. ЗОН. 325. 30°. 327. 68° 10'. 331. 12/3.
332. АВ = 9/; АО =12/. 334. АВ = 3/3"/; ВС = 7/; CD =
= 3/3(2/-/); АО = (7+б/з)/; BD = (7 + 6/3)/-3 / 3/;
АС = 7/ + 3 /3/; AM = 3,5/ + 3 /3/; AN = (7 + 3 /3) /4-1,5 / 3/;
MN = у [(7 + 6 /3) / - 3 /3/]. 335. а = axi + ayj; а = V а2х + а2.
336. ax = a-cosqp; ay = a’sin<p. 337. ах = 4; 0^=3; а = 5.
338. ах = - 3; ау = 1; /10. 340. 1) ах = 5, ау = 5 /3; 2) ах = 6 /£
ау — 6; 3) ах = ау — -^- /2; 4) ах — — 18. ау — 0; 5) ах — 0, ау = 6;
6) ах = - 2,4, ау = 2,4 /3? 341. (а) 1) 2) 10Ь-; 3) 8,2 /2;
О о
4) 12; 5) 12; 6) 7) 4. 342. (б) 1) {1; 7}; 2) {9; 1); 3) U;
О ( о о J
4) ^3; у|; 5) {25; 20}; 6) {-16; 12}; 7) {-15; -12}; 8) {16; -12};
9) 10) |-1-|-; “ф 1!> <0; 3!>- 343< ^"58; 2) 7; 3) 8;
4) 2/10. 344. 1) 7/2; 2) /То; 3) /181; 4) /бП; 5) -^-/ТЗ;
6) j/4T- 345. 1) — 2/ — /; 2) 2/ + /; 3) - / - /; 4) / +/; 5) -/;
2 3 2 3
6) 6/ - 5/. 346. I) а0 = —== i Ч-=- /; 2) а° =-— i + —= j;
/13 /13 /13 /13
2 3 2 3
3) а0 = -^=г/--—j-, 4) a° = -—==ri----------5) а° =
/13 /13 /13 /13
= j. 347. 1) W; -lyl; 2) {’4;
/41 /41 I 4 2 j ’ I 4 2 J
3) {-1|; — 7-b}; 4){-3|; 5> {5т; !4}; 6H4;~6};
7>{_^г;_34}; 8> {-r 4 9){4:24 io>{44!
3 1 I (l/3~ I 1
344. 348.4. 349. -44; 4k 350. пр. (а + & + с) = -1; np.
5 J z Z Z J
(За + 2& + с) = --|; пр. (a + 2& + 3c) = -3y; np. (2« + 3&-4c) =
= 3-|-. 352. 135°. 356. 1) 44; 2) 7; 3) 0; 4) - 16. 365. 1) 4/3 + 63Z;
2) За/7+ 2a/ai. 366. 1 - 1; 2 + /; 8 - 5/; /Г- 3/; 1.
368. 1) /TO; /5-2/5; 1; /13. 369. 1) (a) /; - i; -i\ 1; - /; 1; - 1; i;
i; —1; 1; — /; i; — г; — (—!)n г. (б) 1 — г; 2; 3 + /; — 2г — 1; 1;
-3; [(-1)”+1 + 1]/; 2) 13/13; 3) 13; 4) 26 + 74/, 2/1538.
264
/ f 1 \
370. 1) 1 — z; 2) 9+11/; 3) - 1 + 12г. 378. 1) (Л; ± ;
\ 4 О /
Ч/;/ з) (il, —4); 4) (iJL 10-U т-
\ «6 О / О / \ Z<J т’ / \ <-> /
/9 Ч \ / Ч 1Ч \ /1
2) (-9; -9); 3) (1А, 1 4) (1 2-gj). 380. 1) (ij!
/); 2) (4; 3) <5i ~2); 4) (-201-: ‘в-я-)-
ЧЯ1 n F5fl-3Z>\ д(зг> — 2) / 2a - ft2. ft).
381‘ ' [ 5a-2ft ’ 5a -2ft JJ 2) ( 2a ’ 3/’
[2a + 7ft. 2a2 + 21ft2-]i [ 3 (a + 3ft) a + 3ft~l
’ L3i-a’ ft(a —36)_T J |_2(5-a — ft) ? 4 j
382. 1) 0,9+/; 2) 1 1 + 4y /; 3) - (2I + 9 1 zj. 383. 1) 2(a + ftz);
2) — 2 (9a + 4ftz); 3) 2 (2a - 5cz). 384. 1) 10* - 4yi; 2) - x + 4yi,
386. 1) 10; 2) 6/2; 3) 28; 4) 3/; 5) 6a; 6) -aft; 7) - 6 + 10/;
8) 8-6/; 9) - 24 + 21/. 387. 1) 3-11Z; 2) /*2(l+/3*) +
+ (2-/з)/; 3) 0,4+1,9/; 4) 43-36/. 389. 1) 7 + Z/5; 2) 34;
3)9+ z/3;4)3. 391. 1)1-2/ /2; 2)-~ + y/; 3)2-3/;
4) -1-1/. 392. 1) 8+/п—1 2)^2; 3) 1-2//^ 4)
OO 1 и z
5) ~ . 6) _ 1 +2/. 393. 2/10; 2/17; /533; -^-/533?
394. 1) 1; 2) 4. 395. 1) 6/97; 2) 2 У2663 - 18/г'» 103.
396. I) 7-6//Г; 2) -у(1-//У); 3) -2(2 +г/Л.
4) “4-(1 + г/З”). 397. 1) —(49+ 12/5*); 2) - (14 + 12//2) ;
О
3) - (29-12/5); 4) -3+12//3^ 398. 1) -1(7+ 4//2*);
2) - 10 - 9//3- 3) а (а2 - 3ft2) + ft (ft2 - 3a2) /; 4) (a2 - b2) + 2afti.
399. 1) ±(2+z); 2) ± (3 - 2z); 3) ± Jy-(3~z/5*). 400. 1) - 5 +
+ 12/; 2) 5 - 12/; 3) 26 + 74/. 401. 1) (a + /) (a - /); 2) (/3 + az) X
X(/3-az); 3) (3 + ai) (3 - ai); 4) (x + yi) (x - yi}.
4
402. 1) у (cos 289° 28'+ i sin 289° 28'); 3) cos 180° + z sm 180°.
403. 1) 2 -2/; 2) 1 (1 - 2 /З) + 1 (2 + /3) /. 404. 1) -~/6;
О О Ar
2) X^-C/T+Z). 407. 1) -1 (1 +0; 2) |(!- Z/3);
□ z z
3) 1 + z/3; 4) -1(1 +z/з*). 4-408. 1) 1 - i\ 2) - 2Z; 3) 1;
265
4)l-i. 409. I) 1 G 2) -1(1 +//3).
410. 1)0,1/; 2) cos 75° + z sin 75°. 411. 1)2,5/; 2) +2(1 + /).
412. 1) -0,54(1 + //3); 2) 0,1(1 +//S’); 3) A(УЗ-i);
4) 4-(]/3+ zj. 413. 1) — 29 •/; 2) 1; 3) —f +1 /; 4) -1.
3 Z Z О
415. 1) — -~-(l+/); 2) —-^~- + l/; 3) cos-^-z’sin-^-.
415. 1) 2 У2 (1 + /), — 4 (cos 15° — / sin 15°), 4 (sin 15° — / cos 15°);
2) cos (48’ + k • 60°) + / sin (48° + k • 60°), k = 0; 1; 2; 3; 4; 5;
3) cos (7° 30'+ & • 120°)+ /sin (7° 30'+/г • 120°), k = 0; I; 2.
417. I) -iX(l+0; _1X(| + O; _15(1_Z). 15(1-0;
Z Z c Z
2) cos 15° + / sin 15°; sin 15°+/cos 15°; —-^~(1—z); — cos 15°—
— zsin 15°; — sin 15°— /cos 15°; 1T(1-/). 418. 1)
УЗ i 45° + 360°fe , . . 45° + 360°fe . n i о 4.
---2-----7’ 2 C0S-----7------Hsin----------, й = 0; 1; 2; 3;
4; 5; 6. 422. —2/; 1; 3; 423. x3 - Зх2 + 4x — 2 = 0.
Глава 3
n 4 4 ,
426. a = 2; у — 2x2. 427. a = — g-J У = — -у x •
432. 3) См. рис. 41; 4) см. рис. 42. 433. 1) h = 15 + 10/ - 4,9/2;
/ 0 I | 2 | ~3с
Л! 15 20,1 | 15,4 | 0
; 3) (a) /М c; (6) ft«20,1 m; (b) /«3 c.
434. 1) 5 =x(4 — x). 435. 1) См. рис. 43; 2) см. рис. 44;
3) см. рис. 45; 4) см. рис. 46. 437. 1) ут’п = 5 при х — — Г,
2) i/tnin = — з при X = 4; 3) ^тах = 4 при X = 1; 4) Г/тах = 8 ПРЯ
1 5 о 3
Х=у; 5) #min = — 3 при х = 4; 6) £min = —9-g- при х —— 3—.
438. (а) 1) Определена при х#=0, изменяется в интервалах
— оо < f (х) < — 2 УН и 2 V"k < f (х) < о°; 2) х = 0 — точка разрыва.
439. 1) См. рис. 47; 2) см. рис. 48. 440. 1) ±5; 2) ±7; 3) ±6.
441. 1) ±5; 2) ±4; 3) ± 442. 1) ±4; 3) ±4-/10; 4) ± У~Т0;
z 3
9 1 1 56
5) ±0.4; 6) ±15-. 443. 4) ±23-; 6) ±^; 7) ±—;
260
я
Рис. 41.
267
8) ± 0,9а. 444. 1) ± t; 2) ±5/; 3) ±5/; 5) ±-L/I33. 445. 3) 0;
1У
-4 4; 4) 0;4- 448« 3) °; -84тг; 4) 0; 50>68- 447- 0 0; ;
4 4 60 а
2)0; —; 3) 0; 4) 0; .а* ~ b . 448. 1) = х2 = 0;
’ a I — а а
х3=-|а; 2) 0; 1 4 а; 5) 0; 449. 1) jq = х2 = 2; 2) -2; 12;
J 3 2 а + о
3) 1; 3; 4) -1; 3; 7) -2; 5; 10) -1; 15. 459. 1) 2; 4; 2) -8; 12;
3) -6; 5; 4) -3; 4; 7) 1; А; 8) 2 J ; 3. 451. 1) 1; 1; 6) 0; 60.
452. 1) (б) 30; (в) -90; (г) (д) (в) 2) (а) з|;
(б) 2 4; (в) 3-|; (ж) 275. 453. 1) 5; 2) -0,7; 5; 3) 0; 4;
4 и о 2
4) -бу; 2. 458. 1) у; 6-у, 2) -у; 2. 457. 1) См. рис. 49;
2) см. рис. 50. 458. 1) 0; 2; 2) 0; -2; 3) 0; 4. 459. 2) -3; 2;
1 3
3) —2; 5. 480. См. рис. 51; 1) -5; 6; 2) -2,5; 3; 3) ——•> у,
1 а а2
4) -4-; 2. 461. 1) а- Ъ; 2а + Ь; 2) 2а; •£; 3) ; 4) ЗЬ±2а.
<5 и 2
л* -1 ah
452. 1) —2а; 2) С + rf; 3) а; 2а; 4) -1 -
453. 1) ^±1; 2) ±1/+ ; 3)
с d V с т + п т + п
464. I) —(а + 6); 6 - а; 3) ± £-. 465. 1) —-^т; 2) а;
-j——у. 466. 1) х — 6; 2) (a) Ь = — с, (б) а = с; (в) Ь = 0; (г) с = 0;
(д) 6=0; с =0; (е) 6 = ± 3 j/y • 475. 2) (ах + Ь) {Ьх + а);
4) (2х — а) (2х — 1). 476. 2) (ах - 2) (х - 3); 3) (ах - 1) (Ьх + 2).
1 3
478. 1) у = 0 при 1 <х<3; 2) # < 0 при — у < х < у; 3) # < 0
при —3<х<2,5; 4) у<0 при —-у<х<1,5. 479. 1) у <0 при
ху^ I; у = 0 при х = I; 2) у> 0 при х =£ I; у = 0 при х — 1; 3) у <0
при х — 3; у = 0 при х = — 3; 4) у > 0 при х — 3; у = 0 при
х — — 3. 480. 1) у <0 при х =# —у; у = 0 при х = —2) у> О
2 2 1
при х=£ —; у— О при х = —; 3) у>0 при х#= 1 -z-; у =0 при
о о 2
х = 1 у; 4) у> 0 при х #= 4; у = 0 при х = 4. 481. 1) у> 0 на всей
оси; 2) у на всей оси; 3) </>0 на всей оси; 4) г/ <0 на всей оси.
268
Рис. 47.
269
482. 1) z/>0 на всей оси; 2) у <0 на всей оси; 3) у>0 на всей оси;
4) у <0 на всей оси. 483. 1) у>0 в интервале — 2<х<5;
2) у <0 при х=#2; у = 0 при х — 2; 3) у>0 на всей оси; 4) у <0
при — 2 у <х < I» 5) У <0 па всей оси; 6) у <0 при — 5 <х <3 -у.
484. 1) х<—1 и х>1; 2) — 1<х<1; 3) ^<—2 и х>2;
4) —2<х<2; 5) х<—4 и х>4; 6) — |а|<х<|а|.
485. 1)х<- 18 и х> 18; 2) х<-~- их>-^-; 3) х <--
о о и
и х>—г-; 4) — (2а + 36) < х < 2а + 36. 488. I) х <0 и х>2;
от
I
2) —3<х<0; 3) х<0 и х>2; 4) х>0 и х < —-х-.
О
3 4 г---------
487. 1) 0<х<—; 2)х<0их>-?; 3) - /а2 + ab + Ъ2 <х <
( 1 э
< Vа24- ab - Ь2; 4) 0<х<-|. 488. 1) -4<х<2 и х>3;
I 2
2) х<—5 и 4<х<5; 3) —-х-<х<2; 4) х<— и х> 1;
О о
2 b
5) - 3 <х < - I у и х>2; 6) х < — и 6 < х <а. 489. I) х < — 3
О d
и х>—I; 2) — 2<х<1,5 и х>5; 3) 2<х<3 и 5<х<8;
4) ~<х < 1,5 и 1,5 <х <4; 5) х < — 3 и х > I; 6) — оо <х < 1,4;
О
1 3 3
1,4 <х<2; 3<х<5 и х>8; 7) 1— <х< I 4; 1 — <х<2,5 и х>8.
О 4 *
499. 1) х <2 и х> 3; 2) — оо <х < оо; 3) х < — I и х> 3; 4) нет
решений; 5) — оо <х < оо; 6) 6 — )^6 <х <6 + Уб\ 492. 1) х=#2;
2) —оо<х<оо; 3)х^1; 4) 1^х<4. 493. 1) — оо<х<со;
2) 0 х 1; 3) х<-2 и х>6; 4) —у х С 1; 5) х < — I и
2
х>2; 6) х<2 и х>4. 494. k <4 (k = 1, 2, 3). 495. k < — у
(/? = —1, -2, -3, ...). 496. 1) -1 и 2; 2) 3-t; 3) - 5 ± 2/То.
D *
2 2 1
497. -2-4 < a <2 -J. 499. I) 9; 2) 2; 3) 2. 509. 1) (а) а = I —;
DO •
(б) а<1у; (в) a>ly 2) при всех а корни действительны и
2 2 2
различны; 3) (а) а — — -у и а = 6; (б) — у <а <6; (в) а < —у
и а>6; 4) (а) а = (б) а=£-~. 501. 3) 0 </г < 28.
502. 1) ~4-/55<&<4-)/55; 2) k < - 6,3 и *> 1,3. 504. 1) -1
1П 3 2
и 144. 505. 4. 506. —. 507. 5 и 6. 509. 31. 510. 16. 511. 20 см.
/ о
270
512. 16 см и 12 см. 513. 50 мм. 514. 8 дн, и 12 дн.
515. 15 ч и 13 ч. 516. 18— и 24 —. 517. 48— и 36—.
ч ч _ ч ч
518. аУйуп+У^) _
т(п — т) п(п — т)
519. ~~ b^~4vt (a + b~vt) 520< 1)-2) Реше-
ний не имеет; 3) 17; 4) -55; 5; 5) 20; 6) 7,01. 521. 1)-2) Реше-
ний не имеет; 3) 25; 4) 4. 522. 1) 17; 2) 8; 3) 25; 4) 81. 523. 1) 7;
2) —3; 3) — 4) решений не имеет. 524. 1) 10; 2) 1; 3) —5; 4>
4) —19; 0. 525. 1) Решений не имеет; 2) 1; 8. 526. 1) 0; 2) 3—.
527. 1) 3; 2) а. 528. 1) и 81; 2) 3) 62. 529. 1) За;
“Та; 2) 4; 3) * 2 и 11; 4) °’ 530, 1; 2) ~т: 2- 53L Т;
1 I Л 1 л а2 + 62С / 2a2b — 2аЬ2 + Ь3 \2
2) 1+6; 3) 1-6; 4) —; 5) •
532. 1) ±2; ±1; 2) ±3; ±2; 3) ±4; ±3; 4) ±5; ±4; 5) ±1; ±
6) ±1; ±4-. 534. 1) ± а; ± Ь; 2) ±± УГ- 53S* 0 “’1
-3; -4; 2) 7; 18-1; 3) 6; 4) 1; 2. 536. 1) 1; 2; 3; 2) 2; 2; 3;
3) -I ±/2; 4; 4) -2; 1; 1. 537. 1) -1; --1/V3 ; 2) -1; 1;
rJiiKL., 3) =^VL; 4) -5; -^ГЗ;
1^15 (i ± i /з) .. -1 ± г Уз~ ,
------------5) --------------; ±гУ5; 6) -5; —2; —1.
Б38. 1) -1; I*?/3., -Г1 2) -2; 0; 1; 1; 1; 3) -1; -1;
3 + 4г
0; ± i; 4) -1; 0; 1; 1; 2; 5) -2; 0; 2; 2; 3; 6) -1; 0; 1; —=-.
540. 1) х3 — Зх2 + 2х — 6 = 0; 2) х3 - Зх2 + к - 3 = 0;
8) х4 — 5х3+ 11х2 — 25х + 30 = 0; 4) х3 - 2х2 + х - 2 = 0;
5) х4 - 4х3 + 16х2 - 24х + 20 = 0. 541. 1) ±/Г; ± г/Г; 2) -I;
И^3 ; 3) ± 2г; 4) 1; ~~1 ±2‘^-. 542. 1) ±4; 2) ± 4Z; 3) -2;
1 AZ/3; 4)2; -l±z/3*- 543. 1) ±2; ±2i; 2) ±/2(i-l);
±/2(1 + 0; 3) -Л; 4) у: • Ы4. 1) ±;;
. 1 ± ‘/з 2. + . -\f i ± i/з 47_ g 4
2 > 2 > - » - F 2
271
8) 8 » „8. „ . 3) .10 <6^Тз) fl; *
8) 4; 4,5; 5,5; 6. 551. 1) 1; 1; 3) _2;
— 1; -4±//3‘. 552. 0-2y; -ly; - ^y-^Lj
Z-.17 ^-K3 . 2) -2; -1; 1; 2; - у i; у i\ -2ц 2i; 3) -3у; 1.
553. 1) 1; 2; 2) 1; 1; -1; -1; >(1 + Г"2);
— i(l±/2); 3) 0; -1; — 1; -1; 0,4; 2,5. 554. 1) (15; -13),
(I; 1); 4) (4-1 2M (2; 1). 555. 1) (1; 2); 2) (2; -7), (5; 2); 3) (1; 1),
(~6/-34)- S5e- ° ('Г'2!)’ (2;4)! 4> <3;')
(4; -'-зй- и7- 1) (6; 12), (12; 6); 3) (2; 3), (3; 2).
\ □ ZD /
/ 2 \
558. 1) I-10; -4 уj, (3; 4); 3) (4; 2), (16; -If»; 4) (2; 1), (3; 2).
559. 3) (a2; _ a), [(a + 1)2; (a + j)]; 4) (a _ j; a + i), (a + 1; a - 1).
563. 1) (17-/274; 17 + /274), (17+ /274; 17 —/274);
2) (13-/M9; 13 + /149), (13 +/149; 13-/149). 565. 1) (a; b),
(b', a), (—a; — b), (— b\ — a). 567.
(-2; -3), (2; 3).
(/73 /75/
0<2;-2/Ю, (3; 1), (—3; — 1);
//To. ? /io'i / /То. 9 /io\
\ 5 ’ 5 \ 5 ’ 1 5 /’
n / 26 23 )
к /73 ’ /73/
568. 1) (—/2; 2/^),
2) (2;1). (-2; -j),
3) (3; 2), (2; 3), (-3; -2),
/ 1 \ / /370 . 3 /370 \
\ d; 2 J’ V 37 ’ 37 /’
57»_ 3) (_ » ),
\ /311 /311/ k/311
/370 . 3/370 \
37 ’ 37 /
-Д=Л (-1; -1), (1; 1);
}^31T /
272
-------------------------M- (-2;-2)' (2;2). 571. 3) (2;3),
\ /7 /7/ \ /7 /7 /
/Q /S + i/TsT 5- i/T5l\ /5-//ТП. 5 + Z/l5T\
2)’ к 2 ’ 2 /' \ 2 ’ 2 /’
4) (3; 2), (2; 3), (-2; -3), (-3; -2). 572. 3) (1; 4). (4; 1),
(-3 + Z/6; -3-i/6), (-3-i/6"; -3+ij/p); 4) (3; 3),
(3; 3), (-2-/15; -2 + /пГ), (—2 +/15; -2-/ИГ).
673. 1) (3; 3). (3; 3), ~3 G - О.) ),
(,-3 0-Г5~) ...-3Q +/5-) у 574 0 (1; 2) (2; 1К
[(I -г/2); (1 + //2)]. 1(1 + iV2); (1 - iV%)l 2) (1; 2) - в об-
ласти действительных чисел. 575. 1) (1; 9), (9; 1); 2) (—6; —2),
(-4; -4). 576. 1) (2; 1), (-2; -1), (1;2). (-1; -2); 2) (1; 9), (9; 1).
В77’11 (У D’ (Г; 4); 2> (_|2; 2)’(2; ~12)‘(S; 4)1 (4; 6)-
378. <) (1;3), (3;,). LZ^L; *+gL\ Mb ML);
2) (2; 3), (3; 2) — в области действительных чисел. 579. 1) (—7; —10),
(10; 7) — в области действительных чисел; 2) (—2; —1), (—2; 1),
(2; -1). (2; 1), (-/2; -/7),
(/7; /7). 580. 1) (3; -2), (-3; 2
действительных чисел; 2) (2; 1),
_2jL(1 + 0; — /2*(1 +0 ,
-0; -/г (1 -0 ,
_____________к___т/~о7
-2; ° / ; -
2) (0; 0; 0), (1; h i), (
583. (12; 4). 584. (5; 3) (—5; -3).
587. 30 см и 20 см. 588. 15 см
590. 4 см, 7 см и 9 см. 591. 15
593. 24 ч и 27 ч. 594. 24 и 18.
596. 10 ч и 12 ч. 597. 15 ч и 12
(-/2; /2), (/7; -/2),
) (2; —3), (—2; 3) — в области
(-2; -J), (2Z; 0, (-2/; - i)»
J^-(l +0; /2 (1 +i) ,
~~(l -0; /2 (1 -0 .
-5 + /2l^ (_2; -5 + /21 .
-1; _1; -1). 582. (5; 6), (6; 5).
585. (4; 3). 586. (4; 3), (3; 4)
и 10 см. 589. 11 см и 7 см.
см и 7 см. 592. 9 ч и 12 чв
595. 5 токарей и 4 слесаря.
! ч. 598. 300 км/ч и 360 км/ч.
600. 1) 30 и 20; 2) 100 и 90. 601. 30 коп. и 24 коп. или 60 коп. и 54 коп.
</ + У 6f2 + t2v2 СА_ b — с — ad + /(6 — ad — с)2 + 4abd
Ои<в« " ™ i.i.h >’ —..... .in e vCJve " ... — j
b — С + (id /(6 — ad — с)2 + 4abd
2d
605. 100 км; 22,5 км/ч; 15 км/ч. 606.
1 \______
604. -у /27а2;
За2 — 6
2 ’
4
273
Глаза 4
607. 1) «; 2) Зп- 1; 3) 4) -г^— ; 5) ^2; 5) ---------?—-.
' ' ' 2п 1 +п 7 п ’ п (/г+1)
612. 2d (п — 2). 613. Являются 1-й, 2-й, 3-й и 4-й члены. 615. 5-й
член -47; 10-й - 197; 15-й -447. 616. 4, 7, 10, ... 624. 1) 3; 2) 1;
3) 1-|-; 4) 2. 625. 1) 2,3; 2) 1,7; 3) 0,6; 4) 6-|; 5) 10,075;
6) 6 2|. 626. 1) 1; 2) 3; 3) 1 2-; 4) ~ а\ 5) 1. 627. 1) -2; 2) 0;
х-о о 2 и
2 1
3) 3; 4) —; 5) — —. 628. 1) 0: 2} 2: 3) 0: 4) 2; 5) 0: 6) 1; 7) 1;
О’ z .......................
8) 1; 9) 2. 630. 1) и 4) возрастают, остальные убывают. 631. 5.
632. п2 *. 638. 97. 639. 4,2. 640. 39. 641. —119,2. 642. —103,2.
в
643. 980. 644. 2 — . 645. 1) 250; 2) 5000; 3) 900; 4) 1062. 646. 1) 382
и 3910; 2) 143 и 3430. 647. 1) 20; 955; 2) 8; 180; 3) 4; 36; 4) 5; 80.
648. 1) 81; 3) 3. 652. 85. 653. 5050. 654. 0. 655. 62. 656. 2360.
658. (а) 2500; (б) п2. 659. 1) 6 ; 2) 36у; 3) 21. 660. 1) «43°;
2) 2745 м. 662. 5; 8; 11; 14; 17. 663. 8 с. 664. 6. 665. 7 руб и 4 руб.
666. 73. 667. 17. 668. 1) 3; 9; 27; 81; 243; 729; 2) у; 7j-; —;
-2^3 ; 669. 1) 2; 2) 3; 3) 1; 4) 1. 672. +5; 25; 125; ...
673. 699 050. 674. 1) 2; 2) 36; 3) — 1; 4) 3. 675. 480. 676. —.
677. 5. 678. 1) 6; 2) 7; 3) 10. 680. 2730. 681. 1) + -^р-; -^р-; ...
3) +3; 6; 12; ... 682. 1) 62; 2) 7-^-; 3) 20; 4) 170,5. 683. 1) 3; 2186;
О
2) 1; 147. 684. 1) -1; 6-^-; 3) 3; 65 535. 685. 3) 3; 768; 5) 1; 2048.
Л о уо
2 1 64 1
686. 1) 10-»- и 21; 8) 320 и 5; 9) и 127^+; 10) - 4 и 5;
3 64 64 3
Н) — 1,4 и 245; 0,4 и 20; 12) 3 и 3280; 13) 7 и 576; 14) 9 и 4920,5.
687. ~ 2; 6; 18. 688. + 3; 6; 12; ... 689. + 20; 40; 80; ...
690. — 691. 8. 692. 2 и 3. 693. 4 и 2. 694. ч- 3; 5; 7 и
64
~ 5; Ю; 20. 695. -г- 4; 7; 10 и + 2; 4; 8. 696. + 3; 6; 12; 24; 48 и
-н 1; 3; 5; 7; 9. 697. + —4; -8; —16; —32; —64; —128 и 4- —17.
-12; —7; -2; 3; 8. 698. -ь 6; 12; 18 и + 12; 36; 108. 699. « 53 мм.
700. 1) 2у; 2) 2^. 701. 1) Х? " V~3~) . 2) . 702.
763. 3-8-4. 704. +- 5; 4; ... 705. 1) 1; 2) 3)
274
4) 1|; 5) 2|; 6) 5^-; 7) 8) 7-£-. 70S. 1) 0,3 +
+ 0,03 + 0,003 +-..; 2) 0,2 + 0,02 +0,002 +...; 3) 0,375 +
+ 0,000375 + 0,000000375 + ... 708. а2 /3 и 6а (2 + КЗ ).
709. а(1 + /Г).
Глава 5
712. 1) См. рис. 52; 2) см. рис. 53; 3) см. рис. 54;
715. I) — оо<х<0 и 0<х<оо; 2) — оо<х<оо; 3) — оо<х<оо.
4) 0<х<°о; 5) 0<х<оо; 6) х #= 1 и х + 3. 719. 1) 0,027;
2
1 _ 7Т 2
2) 0,0016; 3) j /2; 4) 25; 5) а +6) а7; 7) - у; 8) 223; 9) 1 и 5.
729. 1) 3; 2) 4; 3) 7; 4) 2; 5) 2; 6) 2. 721. 1) 16; 2) 0,356; 3) -4.
722. 1) 7; 2) 18; 3) 25; 4) 362; 5) 64; 6) 225; 7) 100; 8)
9) 9.2<о; 10) у; II) 12) Ду-; 13) 43; 14) 2у; 15) -6.
724. 1) х>3; 2) х<0; 3) х> 1 и х<— 1у; 4) —оо<х<оо.
725. 1) —оо<х<4 и 4<х<оо; 2) —оо<х<3 и 3<х<оо
3) х=Д0 (рис. 55); 4) х=#0 (рис. 56). 728. 1) х>1; 2) к > 1;
3) х> I; 4) 0<х<1; 5) 0<х<1; 6) 0<х<1; 7) х>4; 8) х>5;
9) 1,4<х<2 и 3<х<3,6. 727. 1) 2 и 3; 2) 2 и 3; 3) 2 и 3; 4) 2 и 3.
728. 1) 1 и 3; 2) -5 и 7; 3) 8 и 9; 4) 11 и 18. 729. 1) log3 15 >
> log3 12; 2) log5 28> logs 20; 3) log i 15<log1 12; 4) log1 28 <
IT T
< 20. 730. 1) -3; 2) 1; 3) -jjL-.; 4) 5) ±-, 6) 5 /5 .
2
q
731. 1) 47; 2) 2; 3) 16 у. 732. 3) log 5 + log (а2 + 62); 4) log а +
+ logn+log(m—n). 733. 1) log 2 + log m + logn—(log3 + log a + log 6);
2) log 4+ [log 3 + log (a — &)]; 3) log 2 + log л + log R — log T.
734. 1) log 2 + log л + log R; £) log 4 — log 3 + log л + 3 log R;
3) — log a + log b + log tg p. 735. 1) log 2 + log a +
+ ^-[loga + 21og(a + b)]; 2) --Ulogp + log (p — a) + log (p — b) +
о Z
2 1 1
+ log (p — c)]; 4) log2 + — log a — — log 6 + — [log 2 + 2 log a +
<5 Z
2 / 1 \
+ 2 log 6]. 73S. 1) — — 2 log a + 3 log b —log c ; 2) —2 log a +
M \ Z /
+ 4* (log3 + log a + log sin a)—(log3 + log b + 4- log aV 3) log 2 +
+ logp— log3 + y (logp — log л) + log tga; 4) log 5 — 2 log a +
275
Рис. 52. Рис. 53.
276
+ у (log 3+ log а + 2 log sin a)
737.
1)
log 2 + log sin a + log cos a +
— [2 log a + log b +y (log a + log b) j.
2) log cos P + log ctg P — [log sin P + 3 log {a + b) + 4 log a + log 5];
4) 21oga+41ogc+y [log (a3—63)+5 log c]—3 log b. 738. 1) —2 log a—
— 4 log b + у log c — [log 7 + 4 log (a + 6)]; 2) у [log (r + s) —
— 3 (logr + logs)]; 3) 7 log (a + b) + 3 log c-- log (a — 6);
4) у log (a—6)4-logcos3a4-logtg(30° + a)—[log 4+log sin--y1 J.
739.
1)
logr2 + 2 log b + 2 log cos (45°
4-у log(a2+&2)[|; 2) —2 log a + у log&+y log 2+logsin (45°+3a) —
— [log cos 3a + 3 log (a + 6)]; 3) 3 log m — 2 log n + ~ [log 2 +
4- log cos (15° 4- 3a) 4- log sin (15° — 3a)[j — [2 log (от — n) —|- log pj;
4) y- [log 2 4- log sin (30° 4- P)] 4- log tn — [y log sin p + log 3 +
4-3 logn+y logp^j. 740. 1) log0,64-logsin^ 4-log sin —
Г 2 "1
— 2 log (от — n)—у log p ; 2) log 4 + log sin (15° + a) +
4-log sin (a — 15°) — у [log от + у ^logn+у logp^ ; 3) log0,5 +
। 2 , , ,4 [, n , , . 45° 4-a , , . a —45° 1.
4- у log (a — b) — pog 2 + log sin---g-----------F log sin-;
4) log 3 + 2 log b + 4" log (a3 — 63) — [log a + log 2 + log cos 35° +
+ log cos 10°]. 741. 2) 3 log a + log cos a - 4- log sin ——y"-------‘
~-y[logc— log 6]; 4) [log20 + 2 loga + 2 logc + logsin(30° + P)]—
ГЛ
L2
log3+ log cos P
+ log a + log cos 50° + log cos
742. 1) l[ll0g(a2 + 62)_(10g2 +
10°)l: 2) log b + Л log (a5 — 65) —
J
— [log 4 + log sin (2p + 15°) + 0,2 log a]; 3) 2 log 2 + log sin (60° + a) +
+ log sin (60°—a); 4) log3+5 log b—[log2 + y loga+logsin(a+P)[j.
743. 1) log 2 + 4- log 6+4- [log 2+log cos (a+30°)+log sin (a—30°)] —
□ 4
277
— poga+тг log (rn—n)l; 2) ^-(2 log b—log a)—[Iog2+Iog cos (a+p)];
L o J Э
3) log cos2a; 4) I log 2 + log Ъ + log sin —-—J — I — log 3 + 3 log a ).
744. 1) log sin 2° + у log 2 + ~ (log 2 + 2 log a — log 6 + log c) —
cos 43° + log (a2 — &2)1; 2) log (a3 — b3) + 2 log b —
Z J О
. Ct , „ ,
sin-g + 3 loga
+• IcgZj;
3) (y log3 + 3 log a + log c
4) |2 log sin — + 3 log b +
+ log (a2 — b2}] — log 3 + log a + log sin 4a^ 74в. (а) 1) У a2 ;
2) 3) /4) 1/(») ') ^3
F F £
747. 1) cos2a;
2) sin 2a; 3) I; 4) tg3a. 748. 3) J_ 1 A* +~.
m3 F ny p
7Л<1 n Va V (a + b)2 cos2a . (a + 6)tg2a< (a + b) b3 .
V a2 у b3
4> yot-»3V(« + Q3 . 750. 0____/(4+ ;
/sin‘(a + ₽) (a+b)Vb у \]Хб/
2)
4)
а]Л(а+ b)3 .
с2 (a — ft) ’
У (a + b}2 c12
b2 fa Vd
3 --------------5 -----------
1 “j / (m + n) ]/~(m — n)e j
F n Ур
I) a 4~ ^)2 cos 2a $
2) + 3, 4)
/vvy aV^ Va ~ b (+< (a +PT
752. 2) 21,7782; 3) 13,6033; 4) 21,301; 5) 22,4313. 754. -9,824.
755. -23,7825. 750. -27,0706. 757. -4,000. 758. lg 2 = 0,3010,
lg 5 =0,6990. 759. 1) -0,5423; 2) -3,5382; 3) -2,6^54; 4) -5,8999;
5) -3,2172; 6) -2,4378; 7) -1,7327; 8) -0,1525. 769. 1) ^,6186;
2) 3,5545; 3) 4,9303; 4) 2,8990; 5) 6,3780; 6) 1,4162; 7) 1,9517; 8)1,8730.
761. 1) 0,9542; 2) 1,2304; 3) 1,8325; 4) 2,1492; 5) 2,6618; 6) 2,8062;
278
7) 3,0917; 8) 3,5806; 9) 3,4786; 10) 1,2885; 11) 0,0212; 12) 2,9031;
13) 1,7243; 14) 3,5798; 15) Г,0039; 16) 5,6021; 17) 3,3375; 18) 3,4265;
19) 1,6382; 20) 0,7983; 21) Г,9441; 22) 2,7355; 23) 2,8001; 24) 0,5791;
25) "1,8105; 26) 3,3747; 27) 1,3010; 28) 5,9031. 762. 1)"1,5987; 2) 2,4179;
3) 1,8853; 4) 1^9788; 5) Т,9798; 6) Г,8821; 7) Г,8759; 8)1,2205; 9) 2,7652;
10) Г,4651; И) 0,3077; 12) 1~7123. 763. 1) 1,832; 2) Т,991; 3) 1,269;
4) 2,126; 5) 1,661; 6) 1,448; 7) 1,992; 8) 1,532; 9) 1,971; 10) 0,144;
11) 1,956; 12) Г,005. 764. (а) 1) 15°; 2) 15° 20'; 3) 16° 40'; 4) 9° 50';
5) 10°20'; 6) 13=3'; 7) 3=51'; 8) 1=35'; 9) 0=35'; 10) 0=4'; 12) 0=39'.
(б) 1) 46°; 2) 50° 36'; 3) 48° 24'; 4) 53° 49'; 5) 64°; 6) 83° 45'.
(в) 1) 44=23'; 2) 18=; 3) 3=2'; 4) 60’52'; 5) 69=27'; 6) 89°55'.
(г) 1) 52’45'; 2) 49°; 3) 27=36'; 4) 1°22'; 5) 0=06'; 6) 0° 16'.
765. 1) 94,99; 2) 4945; 3) 8,632; 4) 560,1; 5) 2,939; 6) 37,00; 7) 2,517;
8) 0,03701; 9) 0,1264; 10) 0,0005327; 11) 0,00272; 12) 0,2086; 13) 1840;
14) 0,06570; 15) 8,387; 16) 31,82. 766. 1) 2,3147; 2) Г,1634; 3) 1,7207;
4) 2,3366; 5) 3,9524; 6) 0,8859; 7) 3,9412; 8) 1,0111; 9) 4,7204;
10) 2,7684; 11) 1,4353; 12) 5,7466; 13) 3,7032; 14) 1,3484; 15) 1,9352;
16) 1,0628; 17) 0,2817; 18) 4,9506; 19) 0,8621; 20) 1,5637; 21) 0,353;
22) 2,0908; 23) 1,5731; 24) Г,7275; 25) 1,4469; 26) 1,7449; 27) 2,6566;
28) 0,3780; 29) 2,0919. 767. 1) 275,7; 2) 0,1065; 3) 0,02653; 4) 8,345;
5) 322,9; 6) 0,00477. 768. 1) 40,0; 2) 0,0113; 3) 21,5; 4) 0,961;
5) 142,6; 6) 0,71; 7) 0,99; 8) 0,884. 769. 1) 161,2; 2) 54,06; 3) 49,27;
4) 42,02; 5) 0,6821; 6) 173,6. 770. 1) 3,1; 2) 5,0064; 3) 0,00358;
4) 0,1105. 771. 1) 7,930; 2) 38,28; 3) 0,838: 4) 0,2443. 772. 1) 412,69;
2) 2970-102. 773. 10,58. 774. 0,005622. 775. 0,6722. 776. 0,01356-
777. 250,2. 778. 4100. 779. 0,1118. 780. 0,6308. 781. 149,1. 782. 247,1.
783. 0,0591. 784. « 0,02523. 785. 40,93. 786. 1,982. 787. 0,01976.
788. 0,0832. 789. 1) 0,3002; 2) 0,001339. 790. 1) 1,363; 2) 0,07247.
791. 1) 74,89; 2) 0,1116. 792. 61,66. 793. 0,738. 794. 5,266.
2
795. 0,0003419. 796. 1) 3; 2) 1; 3) 1—; 4)
О
3) _|®5. 798. 1)3; 2) - А-; 3) -1.
800. 1) -1; 2; 2) -0,5. 801. 1) 5; 2) 3; 3)
2) 3; 3) 2лп ± arccos — 1).
тЛГ
2) лп ± (—l)narcsin ——. 804. 1) 1
2 /— 2а Vb
805. 1) -10; 2) 1у; 3) -2,5; 3; 4) 4; 5) 1; 3; 2±/2; 6) у-р-.
2,75. 797. 1) -Х-; 2) —;
О о
799. 1) —1,5; 2) 5; -1,5.
0. 802. 1) +
803. 1)
2
— • 2) 2,2; 9; 3) 10.
279
806. 1) 2,02; 2) 0,38; 3) 2,116. 807. 1) «28; 2) « -3,17; 3) «2,43.
808. 1) 0; 2) 1; 3) 1,58. 810. 1) 3; 2) 5; 3) 1; 4) 10. 811. I) I;
2) 1,25. 812. 1) I; 2) 2. 813. 2) « - 1,75; 3) «0,37. 814. I) ± I;
2) 2; 3) 2; 4) 0; 1. 815. I) 1,5; 2) log3 2~ 1 . 816. 1) 8; 2) 4;
I
3) ntv, -y(2n+l); 4) 0. 817. 1) -8; «-7,1; «25; 27; 2) 1; 2; 10;
3) -17; -16; 818. 1) I; 2) I; 3) 1; 4. 819. 1) -2; 2) 1; 2; 3;
3) ± 1/2. 820. 1) 48; 2) I; 3) 8; 4) 16. 821. 1) I; 2) y; 3) 4; 4) y;
5) —2; 6) — 4j; 3. 822. 1) tn ' ; 2) 1 y; 3) /10 + 1. 823. I) 256;
n
m , /16-1
ham 1 ---------
2) 64; 3) dc ; 4) —. 824. I) &; 2) c; 3) 2 2 j
/2
Va
c b _ j
b -1
4) b c . 825. I) 1; 2) 4; 3) 9; 27; 4) 9; 5) 0; 3; 6) 7yj
16; 7) 2; 8) 2401. 826. 1) 2; 4; 2) 3; 3) 10; IO5; 4) 4-. 827. 1) -1;
4; 2) —2; 3) 1; 4) 1; 64. 828. I) ±3/2; 2) 25 — ; 3)
4) 100; 5) 2. 829. 1) 1; 2) ±16; 3) 5; 4) ± a12. 830. I) -1; 1; 2) 11
4; 3) -6; 4) log3 2. 831. 1) yj 2) 1 и 8; 3) 2; 4) 832. 1) 3;
2) 10; 3) 5; 4) 10; 5) 10. 833. I) (4; 1); 2) (2; 3), (2; —3), (-2; -1/3),
(-2; 1/3); 3) (1; 3), (16g2-y; log2-y-j; 4) (1; 8). 834. I) (4; 2);
2) [10 (5 +/15); 10(5 —/Т5)], [10 (5-/15); I0(5+/L5)];
3) (4 41 I 4b 4) (2: 4). 835. I) (4; 2); 2)
,(a Ф b), (1; I); 3) (16; 10); 4) (lO10; io).
(100; 10); 2) (3; 5); 3) (4; 1); 4) (3; 9).
b a '
836. I) (10“2; IO-1),
837. 1) (4; 2; /2);
2) Г 7 + /1 + 8a . -14-/14-8a. 4a 4-1~/1+8a] 3) (g; 4);
L 2 2 2 J
2L. 32\ / 2 27, 32 \ /2. _ 27
4Ц 3 ’ 8 ’ 3 /’ \3 ’ 8 ’ 3 /’ \ 3 ’ 8 ’ 3 /’ \3 ’ 8 }
32 \ / _2. 27. 32 \ ( 2 . 27 . _ 32_\ /__2. _ ^L.^X
3 /’ \ 3 ’ 8 ’ 3 M 3’8’ 3 /’ \ 3 ’ 8’3/’
-4; -4-1 ~4rb 838. 1) х<-1 И X>1; 2) x<—3 и x>3;
О о О /
280
3) х>2 4) х<—7. 839. 1) 1,5 <х <2; 2) х>2; 3) < 1;
7 1
4) 3<х<4. 840. 1) 1-~<х<2 и 4<х<4 —; 2) 1<х<11;
9 о
3) х<—2 и х>4-; 4) -2/3 <х<-/3 и /3<х<2/з'.
О
2 1
841. 1) 0,58<х<6,92; 2) х>2у; 3) 0<х<3 и х>7; 4) -1 <х<10-д-;
5) х>1; 6) х< —1 и х> 1; 7) х<7. 842. 60. 843. 840. 844. 11520.
845. 3024. 846. 335. 847. 720. 848. 81. 849. 31. 850. 96. 851. 6.
852. 853. С]. 854. 2C2i2. 855. 105. 856. С] - 8 = 20. 857. 1) 31,
2) 41, 3) k\. 858. 1) (m + 2)(m+ 1) т; 2) (n-l)(n-2);
дч (tn + 1) т (т — 1)(т — 2) . . (т — 3)(т — 4)
' 1-2-3-4 ’ 1 1-2 ’
859. 1) (т+ l)m(m- 1) ... 3-2;
3. (m + n)(m + ra— 1) ... (m+ 1). 4x
> 1-2.3... n ’ ’
860. I) 9; 2) 56; 3) 48. 861. 1) 15;
2) (m + 3) (m + 2) ... 6 • 5;
(m + n) (m + n — 1) ... 4-3
(m + ?z —2)!
2) 4950; 3) 91. 862. 1) 116;
2) 114. 863. 1) 1/30240; 2) 1/3; 3) 12. 864. 1) m; 2) n (n + Г);
3) m + 1; 4) n — 2. 865. 1) (tn — n + 2)2; 2) tn • (tn — 1); 3) tn;
4) tn —2. 867. 1) 3; 2) 10; 3) 15; 4) 5. 868. 1) 5; 2) 7; 3) 15;
4) 6. 869. 1) 7; 2) 16; 3) 4; 4) 4. 870. 1) 2; 2) 5; 3) 11; 4) 10.
871. 1) 12; 2) 10; 3) 13; 4) 14. 872. 1) 7; 2) 15; 3) 90; 4) 8.
873. 1) 23; 2) 8; 3) 11; 4) 9. 874. 1) 5; 2) 15; 3) 9; 4) 8.
875. 1) 7; 2) 8; 3) 10; 4) 10. 876. 6. 877. 8. 878. 14 и 3.
889. 1) x3 + 6x2 +llx+ 6; 2) x3 - 6x2 + 1 lx - 6; 3) x3 - 7x + 6;
4) a4 + 10a3 + 35a2 + 50a + 24; 5) a4 - 12a3 + 49a2 - 78a + 40;
6) M + 4b3 - 7b2 - 22b + 24; 7) / + 15/+ 85/+225/+274?/+120;
8) / — 15/+ 85/— 225/+ 274?/— 120; 9) x2 + (a.+ b) x + ab;
10) x3+(a+&+c) x2+(a&+ac + &c) x+a&c; 11) x4+(a+&+c+d)x3+
•¥(ab + ac-\-ad-\-bc-\-bd+cd) x2 + (abc -\-abd+acd-\-bcd) x + abed;
12) (x + a)4 = x4 + 4ax3 + 6a2x2 + 4a3x + a4, (x + I)4 = x4 + 4x3 +
+ 6x2+ 4x+l, (x- I)4 = x4 — 4x3 + 6x2 — 4x + 1. 881. -15.
882. 11. 883. 1 и 24. 884. 1) x8±8x7?/+ 28xe/±5 6x5?/3 + 70x4/±
±56x3?/5 + 28x2y6±8xy7 + у3; 2) a5±5a4& + 10a3&2± 10a2&3+5a64±+5;
3) x7 ± 7x6 + 21x5 ± 35x4 + 35x3 ±21x2 + 7x± 1; 4) 1 ±8y + 15y2 ±
± 20/+ 15z/4 ± 6/ + /; 5) 81a4 + 108a3 + 54a2 + 12a + 1;
6) x10 — 10x8 + 40xs — 80x4 + 80x2 — 32; 7) a3 + 6a2 Vab + 15a2& +
+ 20a& Vab + 15ab2 + 6&2 /Hb + b3; 8) 16x2 - 32a2 /x + 24x3 -
— 8x3/x"+x4; 9) 1 ±-+-^-±-4 + Л±-т; Ю)99±70/2;
r ’ n n2 n3 п[ 11
11) J_ + J0 Л^ _НЮ _210_ 2 +210a + 120a2 + 45a3 +
' a3 a1 a3 a2 ‘ a
281
+ 10а4+а5; 12) г4 —8х3Ух3 + 28x3Vх — 56х3Ух + 70х3 — 56х2’/х3 4-
+ 28х2 /Г - 8х2 У~х + х2; 13) (х4 - 6x2z/2 +?/') + (4х3// - 4xyz) i;
14) (16х4 -216х2 + 81) + (96x3-216x)z; 15) -64 ±1068/.
885. 1) 2; 2) 2а3. 88S. 448; 280; 81. 887. -7; -35; 35.
888. 1) ф5; 2) фЛ16; 3) - С3х6; 4) CjW; 5) - С%; 6) t/4 =
== = 889. 1) Ks = Kz = 462; 2) Z<5 = 70.
890. 1) U5 = C^y4x7; 2) ф 3) ф/; 4) Z76 = —126; 5) t713 = C?8&6x“!;
-1 5 —
G) = C<b 3; 7) Щ = Cf2a 3; 8) U5 = cf0; 9) U9 =
10) {/7 = С21Л4- и [719 = фа18х30. 891. 1) 29=512; 2) 0;
3) 210 = 1024; 4) 0. 892. -у-. 893. - C%a6 ^a. 894. 100. 895. 35.
7
896. 28x2. 897. -i-. 898. 52. 899. 6188. 900. — 20a7&8. 901. 165.
902. I) —2) нечетные; 3) l-й, 4-й, 7-й, 10-й, 13-й; 4) 1-й, 7-й, 13-й,
19-й, 25-й. 904. Геометрическую прогрессию: <7=1+-^-.
905. 142 руб. 80 коп. 906. 872 руб. 80 коп. 907. 2188 руб.
908.25,48 л. 909. 28-1014. 910.5%. 911. 5559 руб. 912. 25 лет.
913. 20 лет. 914. ------ п,—г лет. 915. 26 920. 916. 5 недель.
log (I + 0,01 р)
917. 13%. 918. 6%. 919. « 14 лет.
Глава 6
925. - см; —- см; —см; —тг— см; 20л см. 926. 1) 0,890;
1 о о о У
2) 0,471; 3) 1,335; 4) 0,218. 927. 1) ; 2) ; 3) -^; 4) -S-;
О О 1 о
5) 6) « 1,2л. 928. 80° 13'; 114° 35'30"; 42° 58'; 10°; 120°; 270°;
’ 18*J ’ ’
135°; 51° 25'40". 929. 1) 26 л — ; 2) 32л — ; 3) 26л —.
3 с с 3 с
93“- т 4’ тг Т-’ лг-9М-')ж 17°’- 320 •
2) 130’; 280°; 3) Л, ^2-; 4) 11 я; 5) 30°, 150°; 6) Л
4 4 4 о о
935. 937. 938. 24°; ~. 939. 180°, 720°.
У о У о 2 о 10
940. 24°, 72°, 120°, 144°. 941. 1) 0,535; 2) 0,746;
3) 0,885; 4) 0,991; 5) 0,073; 6) 0,040. 942. 1) 0,613; 2) 0,864; 3) 0,950;
4) 0,969; 5) 0,104; 6) 0,999. 943. 1) 0,368; 2) 0,217; 3) 0,240; 4) 1,084;
282
г) 1,292; 6) 3,598. 944. 1) 14,07: 2) 1,012; 3) 0,622; 4) 0,135; 5) 0,317;
6) 4,658. 945. 1) 25° 36'; 2) 14° 36'; 3) 70° 12'; 4) 4° 54'. 948. 1) 76° 38';
2) 70°; 3) 56° 50'; 4) 34° 42'; 5) 84° 22'; 6) 85° 9'. 947. 1) 3’30';
2) 1°50'; 3) 23’5'; 4) 4° 42'; 5) 57° 42'; 6) 78’18'. 948. 1) 88’ 18';
2) 88°; 3) 70’43'; 4) 50’37'; 5) 27° 15'; 6) 21’9'. 949. 1) 0,841; 2) 0,375;
3) 0,284; 4) 0,969; 5) 0,546; 6) 0,389; 7) -0,058; 8) 0,765; 9) -1,119.
959. 0,8378; 2,3038. 951. 1) 370: 2) 48,7; 3) 1,57; 4) 11,8.
952.0,196 рад, 11’15'. 953. 300. 954. -у у. 955. S = ~~.
956. 1152°. 957. . 958. 20,420; 38,746: 0,8203. 959.
о 3 3
л ... л ______ л 2л —„ .
9Ь0. . У61. -уг. »bz. —; • ««<5- 4Л CM. уоч. 'J см. уоу. ши см.
3 и 3 3
5 2
966. 1) 3,6'; 2) тысячных; 3) 16— тысячных. 967. 30л.
1о 3
тс
970. Положительны: 2лк < а <у Ч- 2л&; отрицательны: л Ч~ 2л/г < к <
<улЧ“2л&. 971. 1) 2 +у — ; 2) 3) -6 у. 972. 1) 1; 2) 2;
(а__4) 5 973 n 2) ^2 ^,П • 3) а2
(а Ь) , 4) 5. 973. 1) 4 (а + , 2) //г + |) > 3) а _ ь .
975. 1) 0*Сг/*С1; 2) 0С*/«С 1; 3) 0< у <2; 4) ОС */<«>; 5) 1;
6) 1у1 С^А; 7) МС13; 8) Iу I С у; 9) 0,2 С//С5; 10) 0,5Су< 1;
И) I y\<V2- 976. 1) sin 10°; 2) sin л; 3) sin 220°; 4) sin 60°; 5) cos 40°;
6) cos 130°; 7) соэл; 8) созл; 9) 1£л; 10) tg50°; 11) ctg202°;
12) ctgO.ln; 13) sec20°; 14) sec 1,5л; 15) созес0,2л; 16) coscc 30°.
977. 1) л; 2) 3) 4л; 4) -у-; 5) л; 6) 2л. 978. 1) 2) 6л;
3) -уу; 4) у. 979. 1) 2л; 2) -у; 3) 1,5л; 4) 5л. 980. Нет.
981. 1); 2); 4); 5). 982. 1) - -у Ч- л/г <х < у + nk; 2) 2л {2k - 1) <
<x<4nk; 3) ~<х 4) нет. 983. 1) -£-+ ~лк<х<
3 о 3 о 3
. л 2 2 , л 2 лк л .. .
<~2'^~Зnk', 2) У л&<х<у + у лк; 3) нет; 4) у- <х < у (1 + fe).
984. у = sinx: г/тах=1 при х = -уЧ-2л£, уты = — 1 при
х — —у Ч- 2л&; у = cos х: z/max = 1 при х = 2л&, г/mln = — 1 ПРИ
х = лЧ“2л&. 985. —•Ч-2л/г <х <Чг Ч" 2л/г. 986. лк <а <лк Ч--у>
2 2 £
л^Ч--^-<Р<л(йЧ-1) И л& Ч- лг <а < л (/г Ч- 1); л£ <₽ <л/г Ч- v*
2 2
_ .ч , л л л Зл 5л Зл 7л _ п
987. 1) х 0; у-; -у; -у-; л; ——; —у-; —у; 2л; 2) 0 С х 'Т>
283
л Зл 5л 7л ~ п
3) -г-, —у-^х^2л; 4) —оо < х < оо;
' ^^4’4^ 4 4
л Зя
5) 0<х<4г, Л=С*<~п~; 6) —оо<х<оо; 7) — оо<х<оо;
Z £
8) 0<х<у, л<х< — ; 9) 10) х^л. 993. 1) tga;
2) (9 + 32 /3) - 6; 3) tg1 а. 994. 1) Да; 2) да; 3) нет; 4) нет;
О
3 , 4 , 3 28
5) да. 995. 1) cos Cl = — -j-.lg a = —y, ctga = — T;2) sina--^,
28 45 , 5 12 5
tg a = - - « • c,Sa = ~ 28 ’ * 3) cosa = ——, tga = y, ctga = yg;
4) sin a = 8 — ; tga = 8 ctg a = — — . 996. I) sin a = -=, /61
17 15 ’ 8
6 6 2 1
cos a = — ——, ctg a = — ; 2) sina = — cos a =
/61 5 /5 T<5
ctga = — —; 3) sin a = 12 5 . 5 . 2
cosa=—, ctga = — 13 —; 4) sina = ~— 12 /5
2 13
—-=r, tga — -2; 5) 15 8 , 15
cos a = — sin a — , cos a = tga= —;
/5 17 17 8
6) sin a = 200 cos a = 51 , 200 — , tg a =— 4 1 ; 7) sin a — V-'i
/42601’
/42601 51
cos a = — •, /" 2 , 1/ — > tga _ 1_ -. 997. 1) 2 cos a; 2) 0; 3) 2 cos a; 4) — 1.
V 3 /2
998. 1) —cosec (р; 2) 1; 3) 2; 4) sin2 а. 999. 1) cos2 Р; 2) 1; 3) sec2 2а;
4) cos2 Р; 5) — sin2 г; 6) 1; 7) cosec2 2а; 8) — cos2 Р. 10,99. 1) cosec2 -у;
2) 0; 3) sin2x; 4) 1. 1001. 1) cosec2p; 2) 1; 3) cosee2 а; 4) — 1.
1002. 1) sec2 а; 2) sin2 Р; 3) cosec а Д-sec а; 4) 1. 1003. 1) sin a-cos а;
2) sin а; 3) cosee2 (р; 4) sin а + cos а. 1034. 1) 1 + tg а; 2) sin а; 3) 1;
4) 1. 1005. 1) sec2cp; 2) — 2 ctg а; 3) 2 tg2 Р; 4) tg2 а • sin2 а. 1006. 1) 2;
2) ctg3 а; 3) cosec2 а; 4) sec2 р. 1007. 1) sin а; 2) sin а; 3) 2 cosec а;
4) - 1. 1008. I) 1; 2) tga. 1009. I) - ; 2) - ; 3) 1;
4) — 0,25. 1010. 1) - 12; 2) -8-5; 3) 4) A. 1017. I) u = stax
iz ol b
Г JX
возрастает от —1 до +1 на любом из сегментов----------------+ 2л/?,
Л 1
-g-+ 2я& и убывает от 1 до —1 на любом из сегментов
["^~ + 2л&, + 2л^ ; у = cosx убывает от 1 до —1 на любом из
сегментов [2лй; л (2&+1)] и возрастает от —1 до +1 на любом
из сегментов [л (2k — 1); 2л&]; y = tgx возрастает от — оо до + оо
в каждом из интервалов (—+ лй; -f- nk\, у — ctgx убывает
284
2 / 1 \
у-; 14) 2 arccosI------yl;
от + оо до — оо в каждом из интервалов (л&; л (k + 1)); 2) 4*
3) “V-; 4) А; 5) Ю18. 1) - 4 + 2лА>; 2) л*; 3) 4 + 2л*;
4) (-l)^ + nfe; 5)(-l)fe+1 ^--W; 6) (-1)* У + nk; 7) (2*4-1) л;
8) -J + kn\ 9) 2л6; 10) ± -J + *ik', 11) ± + 2nk; 12) ± +2nfe;
2 о о 4
13) -4 + ^; 14) nk\ 15)4 + ^; 16)4 + ^; 17)-4+nfe;
4 4 О b
is) -4 + ^ 19> 4-+^ 2°) -т- + п*; 21) 4r- + ^.
4 2 4 О
1019. (a) 12) 4 arcctg 1; 13) — arcsin
2 о
15) -4 + arctg4; 16) 17) — л + 8 arctgj/’З".
О 0 z
1 X
(6) 1) у = arcsin 2x, | x | C — ; 2) у = arccos , | x | C 2;
3) у — 2 arctg 2x; 4) у = ctg; 5) y = ; 6) r/ = 3ctgx;
(в) 1) -J; 2) 4; 3) -%-; 4) A; 5) 0; 6) f; 7) -A; 8) - A;
9) 10) 11) A, 12) l3) -Si; 14) "
*± о *± ч о z
1021. 5) 4; 6) -1,7; 7) -0,8; 8) 1,7; 9) 0; 10) 11) - 1;
Io 2
12) -4-. 1022. 1) - 0,5; 2) -±; 3) 1; 4) 5) -2.
1023. 1) 2) 1; 3) -1; 4) -L; 5) -/3; 6) 1; 7) Jy-.
1026. (a) 1) |x|<y; 2) | x ]< 3; 3) |x|<l; 4) | x | < 2;
5) 0 x 2; 6) — 1,5 x 0,5; 7) — oo <x< oo; 8) x0; 9) x 0>
10) x^0; 11) 0<x<l; 12) 0<x<l; 13) 0<x<l; 14) 0<x< 1;
15) |x| <1. (в) 1) 0,8; 2) 5; 3) —; 4) - —; 5) 1 —; 6) 4L ;
53 9 3 /5,41
7) 0.2/Г; 8) 9) 10) 11) 12)
13) 4; 14) 180°; 15) A? 15 16 *) 41°; 17) 18) "^5 19) 20) T*
1027. (a) 1) -4; 2) 4(1 + 6fe); 3) 4) 3nfe; 5) (4* — 1);
6)4(1+2fe); 7) M2fe+1); 8)4(1+з1^; 9)4(1+4fe);
10)л(4А>-1); Н) -^-(-^-6 - 1); 12) Юл*; 13) -^Ц1 Ч-fc);
285
286
14) + 15) ±-"- + %; 16) ±-^ + л6;
17)[(-1)* arcsin 1 + лб^; 18) ± у + nk; 19) ± 30° +9° + 180%;
20) ± у- - 2 + nk; 21) 0,4%; 22) - 2° 30' ± 22° 30' + 180° k;
23) ±]/ 4, ±1/ ±^ + 2%(fe = l,2,...);24)±4-arccos-|-+^;
Г О у и z и
25) - 1 + у + %; 26) 15°(26+ 1); 27) ± j/"у + л6 (6 = 0, 1, 2,...);
28) ± УпИ (k = 0, 1,2,...); 29) ~ + nk; 30) л — arcctg 5,671 + nk;
31) ^(1 +6А>); 32) у(1 +2А>). (б) 1)-2) у (1 + 46); 3) у + ~;
4) 71° 34'+180%, 45°+ 180° k. (в) 1) ±-^- + 2л6; 2) ±-4 + 2%;
3 о
3) 14° 29'+360%, - 14°29'+180°(2А>+1); 4) ± -& + nk;
5) 190° 18'+ 540%, — 135° + 540%; 6) arctg2 + n&, arctg3 + n/?.
(г) 1) nk; 2) nk, 63°26'+ 180%; 3) у (2k + 1), 165°58'+ 180%;
4) nk, у + лб. (д) 1) — +nk; 2) 26°34' + 180°6; 63°26' + 180%,
45°+ 180%; 4) 71°34'+ 180°^, 63c26' + 180%; 5) 71°34'+ 180%,
45°+180°fe. 1028. 1) См. рис. 57; 2) см. рис. 58; 3) см. рис. 59;
4) см. рис. 60.
Глава 7
1029. 1) К1(/3+1); 2) ^~-(У 3-1); 3) (/3 + 1).
1031. 1)1; 2) -^(1-3/3); 3)--^; 4) 1032. 1) 0,6;
2) 0; 3) 0. 1033. 1) ~; 2) 1034. 1)J~-; 2) у; 3) 1;
Т/'ч 1 1 1 i/"9
4) -L. 1035. 1) т; 2) у; 3) 1; 4) у. 1036. 1) -1; 2)-Х-;
Z Z Z Z Z
3) 2; 4) 1. 1038. 1) -2; 2) —18; 3) ~ . 1039. 1) 1; 2) 1; 3) /3;
4) ; 5) У 3. 1040.
1) У 2 tg а; 2) — tg (а + 0); 3) ctg 2а; 4) tg а.
1041. 1) 1; 2) sin а- sin Р; 3) sec2 (а + р); 4) 2 ctg 0.1042. 1) - ctg 2а;
2) cosa; 3) -1П У ♦ 1045. 1) 1; 2) 0; 3)--|^- 1046- 0
cos (а + 0) ' ’ ’ ’ ’ 14
2) -4т; 3)-1. 1052. 1) 4(1+26); 2) nk; 3)-4+4я^
Ои 4 О и
287
4)±£ + Л 1053. 1) (-1? -^- + ^-; 2) 1Л4; 3) (1+24),
и 1О о
у (6Й+ 1); 4) у(6£- 1). 1054. 1) Л-(12А;-1); 2) 105° + 180%;
3) —^-+«fe;4)y+nfe. 1055. 1) у-|-л£; 2) 2л&; 3) arctg + ?tfe;
4) — у + 2л&. 1057. 1) 1; 2) 1; 3) -6; 4) -2. 1058. I) 0,5; 2) 0;
3)1; 4)1. 1059.
3) — И- 4\ Л 14Я-
2 ’ *'
1) —1; 2) 0. 1060. 1) 0,819; 2) -0,934;
_Л ОЯ4- лпг 7Л _ Л Я7ЛД. я\ _ л йкпя.
f о* V, * / V )<-/ I Л J, i
9) 0,9613. 1061. 1) -0,643; 2) 0,574; 3) -0,953; 4) 0,967; 5) -0,973;
6) -0,766; 7) -0,122; 8) -0,5; 9) 0,191. 1062. 1) —5,671; 2) 1,192;
3) -0,510; 4) -1,6; 5) 0,371; 6) -0,105; 7) 1,421; 8) -1,192;
9) -0,00000536. 1063. 1) —1,036; 2) 1,804; 3) 3,078; 4) -0,231;
5) 0,105; 6) 0,325; 7) 2,050; 8) -0,307; 9) -0,325. 1064. sin 18°; —cos 20°;
— cos 80°; —sin 57°; —tg55°; —ctg 21 °; —cos 62°; sin 60°;—cos 15°;
— tg85°; —tg Г; ctg 32°; —sec(rt —3); —cos (4 — л); ctg 0,2л;
— cos 0,4л; —sin 0,2л; —sec 0,2л; sin (л — 3); —cos (л —2,5).
1065. cos 34°; —cos58°30'; — sin 18°; —cos 8°; sin 50°; cos 18°; sin 90°;
ctg 73°; ctgl°; tg 18°; —tg 0,3л; соз0,33л; —sin 0,2л; cosec 42°;
—sec 30°. 1066. cos 9°; —sin6°30'; sin 34°; —cos 31°; —sin 38°; cos 30°;
sin 11°; cos20°; ctg 18°; tg 10°; cosec 12°; sec 36°; ctg 25°; tg 10°; sin 24°;
cos 42°; tg 0,2л; sin 0,1 л; — sin (л — 3); — sin ^2 — у j ; ctg ^5 —j j
5 1 1
ctg (2л-6). 1068. 1) —; 2) —; 3) 0,5; 4) 3); 5) у. 1069. 1) 0;
2) 0; 3) 0. 1070. 1) 1; 2) 0; 3)_sec37°; 4)_ sin 10°. 1071. 1) 1; 2) Ij
3) 1; 4) 2. 1072. 1) у ; 2) — ; 3) -lyt-1; 4) ctg 2° (1-cos2°).
1073. 1) -2,5; 2) -1 у; 3) -O; 4) у tg 15°; 5) V 6. 1074. 1) 1;
2) tga; 3) sin a; 4) 1. 1075. 1) 0; 2) —1; 3) tga; 4) cos2 a.
1076. 1) -1; 2) — cos a; 3) — ctgp; 4) cos a. 1077. 1) 1; 2) 2;
436 24
3) sin a. 1082. 1) 0,5376; -0,8432; 2) -0,75; 3) — -7-J
4) 0,02. 1083. 1)1; 2) ; 3) -1 ; 4) 0,8. 1084. 1)-1||
1-; 2,4; 2) -5-1; 3) -|. 1086. 1) 1; 2) 11.; 3) 4) 1.
1087. I) 1; 2) 1^-; 3) Jll; 4) -1; 5)-t=-; 6) 1. 1088. 1) lt
283
2) —1; 3) cos 2а; 4) tg6a. 1089. 1) cos 20; 2) ctg 2a; 3) —tg2a;
4) cos2a. 1090. 1) — уsin2a; 2) 2tg20°; 3) —cos20°; 4) 1.
4
1091. I) 4 sin a; 2) tga cos2a; 3) 2. 1092. 1) 0,8; —0,6; —
О
2)"‘il’ 4; 3) 1 T- 1093-!) ctg210°;2)
4) —2tg2y. 1094. 1) tgP; 2)tgy; 3)sec20;4) ctg2a. 1095. 1) -2cos|-;
2) te(if-'l);3) 4tg2a; 4) sin3?- 1096, I} “2; 2) ~cfgT;
3) tga. 1102. l)y +nk-, 2) ±y + ^k; 3) jtk; 4) nk. 1103.-1) nk;
2) fft , Jt . Jt . 3lk . . Л , , . |\ ПОД П Я t .
18 1 3 k> 8 * 2 ’ 4 4 1104’ 8 + 2 ’
2) st 3 / 3 — + nfe: 3) nk‘, 4) ± arccos — + 2nk, ± arccos —- 4 4 \ 4 ) | + 2л&.
1105. 1) ±4 + 2njfe; 2) (-l)fe-^+^, — £ + 2л/г; 3) z о z о - + 2ля;
4) (-l)*y + nfe. 1106. ±/3; 2) 0 и у; 3) ±/2;
4) Vi. 1107. 1) 0, 1, -у; 2) у; 3) 4- —• т;
4) 1/~2 (5 ~2У2)< 1108. X = sin—-—Я - ; 2) 0 Г 17 2(1+ /3) 1 и —; 2
3) 1С3-; 4) ±J^-. 1109. 1) l(cosl4°- о а z cos 40°);
2) У (cos 11° - cos 45°); 3) у (cos60° - cos 66°); 4) у cos 64°.
1110. 1) у cos 2°; 2) у (cos 12°+cos 60°); 3) у cos 74°;
4) у (cos 70°-1). 1111. 1) у (cos 0,004 — cos 0,51);
2) у (cos 0,106 — cos 0,75); 3) у (cos 0,3539 — cos 1,2701);
4) у (cos 0,62 — cos 0,804). 1112. 1) у (cos 0,06 + cos 0,3);
2) у (cos 0,096 + cos 0,38); 3) у (cos 0,092 + cos 0,56);
4) у (cos 0,144 + cos 1,57). 1113. I) cos 4a + cos 6a; 2) cos 2a + cos 4a;
3) 2 (-cos 2a + cos 8a); 4) 4 (cos4a + cos 10a).
1114. 1) у (cos 2a — cos 6a); 2) у (cos 2a — cos 10a);
3) -^-(coslOa—cos4a); 4) cos9a —cosa. 1115. 1) -^-(cos20+cos2a);
289
2) 4* (COSP + cos (2a + P)]; 3) 4 [cos a + cos (a—20)]; 4) 2 (cos a+cos 5a).
3 5
1116. 1) sin3a + sina; 2) — (cosa — cos5a); 3) — (sin2a + sin20);
4) 3 [sin a + sin (a—20)]. 1117. 1) (sin 48°+sin 32° + sin 68° + sin 12°);
3
2) cos 4° + cos 8° + cos 12° + cos 24°; 3) (cos2a+cos6a + cos 8a+l);
4) sin a + sin 2a — sin 6a; 5) -y [cos (a — 0 + y) + cos (a + 0 — y) —
—cos (a—0—y)—cos (a+0+y)]; 6) [sin (a — 0 + y)+ sin (0 — a+y) —
..... ... .. 1
— sin (a-4-0 4* y)-f-sin (a + 0 — y)]. 1118. 1) (sin 6a + sin 2a);
2) sin4a + sin 2a; 3) 7-(sin 0,3л + sin 0,1л); 4) 4-fsin-^- — sin-^H.
2 2 \ 2 b /
1\ A • a + 0 a —0 a + 0 . a —0
1119. 1) 2 sin——cos—2) 2cos—~ sin—jr-H
£2 2 2
3) 2 cos cos -a—; 4) 2 sin —sin 5) cos 10°;
6) У 3 sin 10°; 7) 2 sin 50° cos6°20'; 8) 2 cos 50° sin 6°20'; 9) У" 3 cos 10°;
10) -2 sin 40° sin 20°; 11) /2cos27°10'; 12) — / 2 sin 27°10'.
1120. 1) «0,0169; 2) «1,460; 3) «1,509;
4) « 0,045; 5) « 0,853; 6) «- 0,040. 1121. 1) 2 sin cos
4 6’
n\ n • л n 5л л 5л 2л
2) 2sin 40‘COS40 ; 3) 2cos 24 COS'24"; 4) 2 sinsin
sin 51П . 7\ sin 46° sin 24° .
cos 12° cos 32° ’ Зл 2л’ sin 18° sin 28° ’ sin 22° sin 46°’
cos -y- cos —3-
со*ч 20° 2 sin 10°
9> cos~4O°cos70° * 1122' 0 2 sin 47-cos24-30'.
2) 2 cos 12-46' sin 3°; 3) 2 sincos; 4) -2 cos sin 1
1 vl I V I £i\J I £\J
• —
r. sin0,3л c. Sin 8 ,.on _ o
5)——777-----n r, - ; 6) ------------. 1123. 1) 2 sin 3a cos a;
cos 0,6л cos 0,3л л л ’
cos -Q- cos —
o 4
2) 2 sin (45°-2a) sin (45°-4a); 3) ----Sin 4<XO- ; 4) 2 cos a cos 0;
cos a cos 3a ' r
5) 2 sin (45° + a) sin 5°; 6) 2 cos a sin 0. 1124. 1) cos a; 2) 2 cos ~ cos ~;
3) Y 2 cos (45° — a); 4) У 2 sin (a — 45°); 5) sin (a — 0) sin (a + 0);
6) sin (₽-a) sin («+₽); 7) ?" (°+P> (a-g) sin (a+B sin ф-«)
cos2 a cos2 0 sin2 a sin2 0
290
1125. 1) lg tg20° + lgctg5°; 2) lg ctg-^±-£- + lg ctg
3) -|-lg3; 4) lgctg6a + Igtga. 1126. 1) 4 cos 77° cos 2°30'cos 0°30':
2) 4 sin 13° cos 2° 30' cos 0° 30'; 3) 4 sincos a cos
.. . 5a a . 30° +a 30° — a
4) 4 cos-g-cos a cos-g-. 1127. 1) 4 sin--—cos------------;
2)2cos2a; 3) 4 sin (зо° + -£-) sin (-£-“ 30°V 4) 2 cos2 (-£- + 4-Ь
5) 4 cos ^30° + sin 30° —j ; 6) 2 cos2 25°; 7) 4 cos ^22° 30' + X
X cos ^22° 30' “ ; 8) 2 cos2 25°; 9) 2 sin2 36°; 10) -2 sin2 33°;
iM oiZn a+ 45° . a —45° / 5л a\
11) 2/2 cos------g----sin-------; 12) 2 cos2 -----— j;
13) tg2 ^45°--; 14) ctg2 a 2 -; 15) 4 sin (60° + a) sin (60° — a);
16) 4 sin (30° + a) sin (a — 30°). 1128. 1) 2/2 cos-|-cos^y — 45°];
<2 sin (45° + a) r 2 sin (45° -a) sin £ eos(-£-45°);
' cos a cos a 2 \ 2 /
f2sin(45° + a) _4cosasin, «.
’ sin a 2
2/2 sin2 -y sin (45° — a)
7)
cos a
__ П __ n
2/2 cos2 у cos (a — 45°) 2/2 cos2 sin (45° — a)
8) cos a ’ 9) cos a ’
10) 4 cos 2a sin j + 30°) sin ( 30°-f). 1129. 1) asec2<p,
где 4=‘82ф; 2) a cos2 ф, b где — = a = sin2 q>; 3) sec2p,
где A 2 — =tg2(p; 4) a sec ф, b где — a = tg ф; 5) 2 sec ф,
где b sin ф = —; 6) a /2* . ₽ sec a sin —, где . b tga = T’
cos (3 = sin 2a cos qp. , ИЗО. 1) 4 cos2 sin (a + 0) tg 0 . ' cos 20 ’
3) ctg (45°—0); 4) sec a; 5) 2 sin 0 cos (a+0) sin a;
6) 4 cosec 4a cos2 (45° — 2a); 7) sin (a + 0) sin{3 sec 20; 8) 4 sin-X
X si n a sin ft 9) 2 cos a; 10) 4 sin a sin 2a sin 3a sin 5a.
1136. 1) 2) 3) 60°-n; 4) 22°30'-n; 5) nk и %.(2k + 1);
о и и
291
6) Jtfc и “(26 4-1)', 7) 20е -п и 30°-п; 8) ± у 4-2л£;
8) (-!)‘-£ + ^: Ю) (- 1)‘т7 + -?-- 1137. I) Л +п«;
2) 2nk и ±-^- + 2nk; 3) (—Jtfe и (—l)fe arcsin + rcfe;
о О z о
, л • п 1 2л л у _ * л . . л _ у —. 2л . _
4) ± v + 2nk и ± “V + 2л&; 5) — + nk и -х- + nk\ 6) ± — + 2лй;
о о ио о
7) y-Wi 8) nk; 9) 2rtfe; Ю) у 4-2nfe; ll) - у 4- 2я£;
12) -у4-2эй. 1138. l)60°-fe и 360°. k; 2) 180°«fc; 3) 90°. k;
4) ftfe; 5) ± у4-2лй, 2nk и (2k ± 1) л; 6) 2лй; 7) nk и у (4^4-1);
8) nk-, 9) -^- + 2nk и 2nk; 10) и 2nfc. 1139. 1) -J (4k + 1);
2) Д (4fe- 1); 3) у (4fe- l)narctg2 + nk-, 4) nk; 5) -75°+ 180°• k;
6) —^4-jtfe и arctg 3-\-nk; 7) — y-f-^fe и arctg 2 у 4- nk;
8) + 9) 59° 2'+180° • k; 10) 22° 30'4-90° • k и 31°43'+90° • k;
11) 61° 55' 4- 180° -fe и 180°-k; 12) у -j-nk; 13)~ (4k - 1); 14) 2nk и
%- + nk; 15) nk и -~~}-nk. 1140. l)(2fc 4- O^i 2) — -^-~j-2nk;
3) — 4 + 2nk; 4) нет решений; 5) ± 4 4- nk; 6) — 4- jtfc;
2 о 4
7) JL4- nk; 8) 44- 2nk; 9) nk; 10) 4 + Л&; H) 67°30'+90°-k;
12) ^ + nk; 13) -^-(4^-1); 14) ±-y + 15) T № 4- 1).
1141. 1) -4-<x<4 + я/г> 2) *w4- ak<x<-^£ +nk;
3) 4<1+2£)<*<4?-(14-fe); 4) JL+nk<x<^-+nk;
О О 12 12
n , 2nk 2n , 2nk ex 4n , 2nk 5jt t 2nk
5) t + — <x<-9- + — • 6> —+ —<x<-9~ + —:
Язт
9) x ф 4- 2nk;
(k^=o), x>~4;
•Tt
x>— •
n , _ ' " n ” n ’ n ’
— — 4- 2nk у 4- 2nk
12 2 n
l3> »>x> мТ + ад Х>Г- H) -2 +2^<x<2^
7) ——I- nk x “I- от к j o) x "*7" 2nkf
O 1U 4
10) нет решений; 11) -^>х> „ ‘ эд
1 1
292
и 2л& <х <у + 2тг&; 15) 2лй <х < л (I + 2k); 16) 2л^^х^л(1 +2k);
17) нет решений; 18) (2k — 1) <х<-у-. 1142. sin х = 0,8,
sin у = — 0,6. 1143. 1) cosx = 7-, созу = -^-; 2) cos х =-
Z О Л
1 1 1 1 1
cosy = — 3) cos х = —, cosy = —; 4) cosx= ——, cosy = — —.
о о £ О +
1144. tgx = 5 + ^34, tg0 = 5—)/34; tgx = 5—1/34, tgу = 5+1/31.
1145. Xj =45°+ 180° (m + n), y^ = 15° + 180° (m — n); x2 = 105° +
4- 180° (m + n), у2 = — 45° + 180° (tn — n); x3 = — 15a + 180° (m + n)t
y3 = -45°+ 18U°(,7z-«); x4= 45° + 180°(m -|- n), 04=-lO5° +
4- 180° (/n— n). 1146. x, =21°21'+180°(m4-n), yx = 8° 39' +
+ 180° (tn — ri); x2 = 81° 21'4-180° (tn + n), y2 = 68° 39' +180° (tn — n)-t
x3 = 98° 39' + 180°(zn + n), y3 — — 6’8° 39' + 180° (tn — n); x4—
= 158° 39'+ 180° (m + n), y4 = — 8° 39' + 180° (tn — n); 2) Xj =
— 81° 21' + 180° (m + n), у, =21°21'+180°(m-n); x2 = 21°21' +
4- 180° (m+n), y2 = 8Г0 21'+ 180° (tn-n); x3 = - 21° 21' + 180° (m+n),
y3 = — 81°21'+ 18й°(т — n); x4 = — 81°21'+180° (m +n), y4 =
= — 21° 2Г + 180° (tn — n); 3) Xj = + 2 arccos-----------h 2л&,
2 . a
2s.nT
« a a a , a a . a .
w, = — — 2 arccos--------2ля; x2 = —— arccos-------------h 2лй,
y 2 o . a 2 a
2 sin у 2 sm у
a , _ a a , Г x + у a
y2 = —- + 2 arccos-------2лй указание: —~~ — —,
2 a . Ct L 2 2
2s,nT
2 sin X~a~ c°s++= “]; 4) x, = 15°21'— 360° fe, у, =61°40' +
+ 360° k; x2 = — 118° 20' — 360° k, y2 = 195° 20' + 360° k; 5) xt =
~ ’7Г + "T arccos (2a + cos a) + лй, yi~~-у arccos (2a + cos a) —
—nk; Хщ = у — у arccos (2a + cos a) + nk, y2 = у + у (2a + cos a)—
—nk [ук а за ни e: 2 sinx sin у = cos (x — y) — cos(x + у), затем под-
ставить x + y из первого уравнения]; 8) xt = 44° 20'+ 180’/г,
= 13° 20' + 180° k; х2 = — 13° 20' + 180° k, у2 = ~ 44° 20' + 180° k;
a /sin a cos a \ , .a /sin a
7) xj = у + arccos I —------g—J + 2nfe, yx =y — arccos I —-
cos a \ „ . a / sin a cos a \ , _ , a .
g—j — 2nk; x2 = y—arccos ---------— l + 2nfe, 02 = —+
,---------------------------------------/srna cos a \ n , r
+ arccos I—------—I—2лк [указание: второе уравнение
«гп(х+у) sin(x + v)
представить в виде--1----— = а, тогда —1------— — cos х cos у=
COS X COS U Of
2^3
= cos (x "Ь cos (x—£11 откуда находим x — ; 8) Xi =?
= (-l)*4 + ^’ yi = ±^- + 2nk, x2 = (-l)ft+14 +^.
о о о
у2 = ± -5- + 2лА. 1147. 60°, 30°.
О
Глава 8
1148. 1) —оо<х<оо; 2) 0^х<оо; 3) —оо<х<— 3,
3 <х<оо; 4) (— оо; — 1), (—1; 1), (1; оо); 5) (— оо; —5), (5, оо);
6) |х|<2; 7) (-оо; 2], [3; оо); 8) (-оо; 0]; 9) (-оо; 0), (0, оо);
10) [—1; 1]: II) ( — 1; 1); 12) [2: оо); 13) (—оо; — 1), [1: оо): 14) х>0;
15) ooV 16) (— оо; 1), (2; оо); 17) (—1; 5); 18) (— оо; оо);
19) [0; оо); 20) [0)3), (3; оо); 21) -оо<х<оо; 22) | — + 2л*.
+ 2л&^; 23) 2лй х л + 2л&; 24) 2л& х < -^- + 2л&;
25)—оо<х<оо; 26) — оо<.г<оо; 27) 2л£<х <л + 2лй;
23) — л + 4л/г <х< л 4-4л£; 29) nk <х<у- + nk; 30) nk<x<
<Л + я*; 31) х = у + 2л6; 32)-1<х<1; 33)-у<х<0,
0<х<-Ь 34) [2; 4]; 35) [-1; 0]; 36) (-оо; -2], [2; оо);
37) (—оо; 1), (1;оо). 1149. 1) —оо<у<оо; 2) у 0; 3) 0=Су<оо;
4) 0^у<оо; 5) — 6=Сг/<оо; 6) у — 0,25; 7) у>0; 8) //> 0;
9) -Ку<1; 10) -2<у<2; 11) -2-Сг/С 1; 12) _
О О Z
13) —1,5<г/<1,5; 14) — оо<у<0,5, 0,5<у<оо.
1150. Четные: 1), 2), 4), 5), 6), 8), 10), 11); нечетные: 3), 7), 9), 12),
13), 14), 15). 1151. 1) Симметрично относительно оси ординат;
2) симметрично относительно начала координат. 1152. 2), 3), 6)—
четные; 4) — нечетная; 1), 5), 7), 8), 9), 10) ни четные, ни нечетные.
1153. 1) 2л; 2) л; 3) л; 4) 2л; 5) 4л; 6) 6л; 7) л; 8) 2л; 9) л; 10) л.
1156. 1) о); 2) (-1; 0), (1; 0); 3) (-5;.0), (2; 0); ’4) (1; 0).
1157. 1) (0;-2); 2) (0; 2); 3) (0;-5), (0; 5); 4) (0;-3), (0; 3).
1158. 1) х = 0; 2)х = - 1; 3)х = - I, х = 2; 4)л6. 1159. 1)(-оо;2),
(2, оо); 2) (- оо; 1), (1; 7), (7; оо); 3) (- оо; 3), (3; оо); 4) (- оо; 0),
(0; 0,5), (0,5; оо); 5) (-оо; 0), (0; 4), (4; оо); 6)(л*;-£+лЙ,
\ 2 /
(у + л£; л + л/г); 7) (--^;о), (°! у)1 8) (0; 1), (1; оо);
9) (—оо; 0); 10) (-оо; -3,5), (-3,5; 1), (1, оо); 11) (—оо; - 8),
(-8; 0,5), (0,5; 2), (2; оо); 12) (- оо; -5), (-5; 1,5), (1,5; 3), (3; оо).
294
1160. 9; 3; 2v; 3; 5. 1161. — -J; 0; -L П62‘ °! V?» “
4 о о
2- -2. 1163. 01 -11 1. 1164.
1166. 1) (— oo; °°); 2) (— oo; oo); 3) (— oo; 0), (0; oo); 4) (— oo; 0),
(0; oo); 5) (— oo; 0), (0; oo); 6) (— oo; —2), (—2; oo); 7) (— oo; 0)>
(0, oo); 8) (— oo; 0), (0; oo); 9) (— oo; 0), (0; oo), 10) — oo;-
(-1; oo). 1167. 1) 2,75; 2) 2,25; 3) -2; 2; 4) -1; 1; 5) 0; I.
\ 2 / и о
1168. 1) У = ^Х\ 2) »4=1гД-95; 3) Г/ = —х-4-l; 4) = l/rzc
□ 2
3 x + 3 o. 4x + 3 .. 1 . x
1171. 1) </=57:2) -/=27^:3) »=—7-1 4) (,»yarcS1ny;
5) у = arccos 2x; 6) у = 2 arctg x. 1173. 5= 100 4-40/; линейная
1 17
функция. 1175. у = Зх— 2. 1176. у = 2х—1. 1177. у = —^-х ——;
у = — 5х — 17. 1178. bi ~ Ь2. 1180. 1) См. рис. 61; 2) см. рис. 62;
3) см. рис. 63; 4) см. рис. 64; 5) см. рис. 65; 6) см. рис. 66;
7) см. рис. 67; 8) см. рис. 68. 1181. 1) См. рис. 69; 2) см. рис. 70*
1182. 1) См. рис. 71; 2) см. рис. 72; 4) см. рис. 73; 5) см. рис. 74«
1189. См. рис. 75. 1191. 1) См. рис. 76; 3) см. рис. 77; 5) см.
рис. 78; 6) см. рис. 79; 7) см. рис. 80; 8) см. рис. 81; 9) см. рис. 82;
10) см. рис. 83. 1192. См. рис. 84. 1193. х = 3, у = 0 (рис. 85)-
1194. х = 0, у = 2. 1195. х = 3, у = 2. 1197. х = 2, у=1.
1200. 1) См. рис. 86. 1201. См. рис. 87. 1202. 1), 3), 5), 6) — воз-
растающие; 2), 4) — убывающие. 1203. Г) См. рис. 88; 2) см. рис. 89;
5) см. рис. 90; 6) см. рис. 91. 1204. 1) См. рис. 92; 2) см. рис. 93.
1206. 1) х>2; (0; 3), (3; оо); 2) х> 1,5; (0; 2), (2; оо). 1207. Да.
1208. 1) х #= 0; 2) х #= 1; 3) х #= ± 2. 1209. 1)-2) См. рис. 94;
3) см. рис. 95; 4) см. рис. 96; 1210. 1) См. рис. 97; 2) см. рис. 98.
л л/г
1211. 1) —4) определены на всей числовой оси; 5) х #= 4—g-'»
6) х=/= ± + (fe>0). 1212. 1) л£; 2) 3)^4-^;
4) 45° 4- б0°/г; 5) 2л£; 6) л 4-2л/?. 1213. 1) 2л/?; 2) j 4-л/?;
3) ^-4-nfe; 4) ^4-2л/?; 5) - 4- л/?; 6) 4-«Аг; 7)| + лй;
8) nk, у 4-л./?; 9) nk\ 10) nk, у4-^. 1214. 1) х -у 4-
2) х #= л 4- 2л/?; 3) х ф л 4- 2л/?, х =/= nk\ 4) х #= -у 4- nk’, 5) х#= nk’,
6) х =/= лб. 1215. 2), 4), 8) — ограниченные. 1216. 1) 2; 2) 0;
295
0л
J y=3
-3
as
Pile. 63. Рис. 64.
296
я
Рис. 67
Рис. 68.
Рис. 70.
Рис. 71.
2S7
Рис. 74.
298
Рис. 77.
Рис. 78. Рис. 79.
Рис. 81.
299
BOO
Рис. 89. Р“- 90. Рис- 91-
30$
ж
Рис, 98.
303
3) ctga; 4) tgx —2ctgx; 5) sinx + cosx. 1217. 1), 4), 6) — 8) — чет-
ные; 2) — нечетная. 1218. 1) 2) 3) 4) 5) 6л;
Z о О О
л\ n 8л о* 6л 8л । . 6л inin л л
6) 2л; 7) -у-; 8)—; 9)—; Ю) -у. 1219. ,
— 1220. (а) — оо<х<оо, | у | <5, 2л; (б) 1) 1<#<3;
2) — 2<//<0; 3) 1 С У 5. 1224. 1) Монотонно возрастает при
Л л Зл 5л 7л 9л 11л
О^СхС—, V^x^V1 ~2~ '~2~’ —2~^*^6л, моно-
тонно убывает
л Зл
при —
4) монотонно возрастает при О^х^л, Зл^х^бл, монотонно
убывает при л^х^Зл; бл^х^бл. 1226. См. рис. 99. 1227. См.
рис. 100. 1228. См. рис. 101. 1230. 1) г/тах = -Ц^-, ут1а « _.
О о
^2 УТ
2) 1/max = 4—> Ут1п~--------—• 1235. 1) 2л/г <х <Л + 2л&;
2)
—^- + 2л& < х < ~ + 2л&;
О \ 1 1 Л . .
3) ——|- nk < х < -g- + nk',
4) — оо<х<оо; 5)--+ 2nk <х < ~ + 2лЛ; 6)-^- + л&<
2 2 о
< х < + nk\ 7) —+л& <х < — yr+nk, ~+nk<x < 4г + л^;
8 3 6 6 3
8) —+ 2л& < х < —— + 2л£, — + 2л£ < х < + 2л&;
9) -~ + 2л^<х <-у + 2лА:; Ю) + 2л£ <х<+ 2л£;
И) -5- + 2л1г<х<-^- + 2лА!; 12) + лй><х<л + лй;
О О о
13) Y + nk < X =С-^-+л&» + nk X =с -у +
14) — + 2nk < х < + 2ak. 1236. у = 4-х+v-
7 4 4 ^44
1237. 1) | х | <2; 2) - 1<х<7; 3) |х|<4; 4) - оо<х<-5 и
5<^х<оо; 5) —оо<х=С — 2 и 2^х<оо; 6) —оо<х<оо;
7)-оо<х<оо. 1238.5. 1239. S = /?2 (л-2). 1240. V = S/S.
1241. (4;0), (-3;0), (2; 0), (-4; 0). 1242. 1) £ =
2) у = Д/ 4х-1; 3) 1/==-^—. 1243. 1) 2; 2) 3. 1244. См.
2
рис. 102. 1246. 1) х> 1; 2) 0<х<1; 3) х>3; 4) 0<х<-^-.
1248. 0<&<4. 1249. х< 1 и х>2. 1251. 1) См. рис. 103;
304
805
У A
Рис. 103.
Рис. 107.
Рис. 106.
2) см. рис. 104. 1252. См. рис. 105. 1253. х > — 1 (см. рис. 106)
[указание: построить графики функций у = | х + 21 и у=| х|].
1254. Построить график функции у=1, х^О (см. рис. 107).
1255. 4-<х <2. 1256. -%- + nk<x <~ + nk. 1257. 3<х<4и
6<Х<оо. 1258. - -у + nk < х < ~ + у nk. 1259. (1; 0),
(—4; 5) (рис. 108). 1260. Начиная с 201-го. 1261. 2,5 ^х^7.
1263.
1264.
1)
9л
” ~Г>
—; 4)
15 ’ '
arg 2 = 2л — arctg 357° 17').
। ।_, 5л ill л Зл 5л
|2| = 1, arg2=-g—; 2) |2| = 1, arg2 = —, —, — ,
11л 13л . л 4л 2л 16л 22л
—, -1--, 3) |г| = 2, argz—jg-, —, -1Г., -7Г,
|z|=/5*, argz = 23°51', 83°51', 143°51', 203°51',
5rct
3
17/442.
1265. 1) 6 f cos + i sin
\ о
ni
2) 2 Y2 ^cos -y + i sin -y j = 2 /2 e 4 ; 3) cos -y- + i sin -y = e 3 ;
tint
= e 6 ; 5) /13 (cos 1,68л + i sin 1,68л) —
/13 (cos 0,68л + i sin 0,68л) = /ТЗ e0,6SlU .
cos 114° 35' , -3 . sin 114° 35'
=-------------, b = e sin 2 =-----------s-----;
e3
2) a = e cos — 0, 6=e sin-^-== e; 3) a=e3 cos (—2)=e3cos 114° 35';
<4
263° 51',
323° 51'.
.. 11л , . . 11л
4) cos —------|- I sin —
о о
= /ТЗ е’,68п/; 6)
1267. 1) а — е-3 cos 2 =
30Г
b = e3 sin (—2) = — e3 sin 114® 35. • 1270. 1) a (in 30= In 3,
(In 3z) =~; 2) a(ln5z)=ln5, 6 (In 5z) =a-^-; 3)a(ln/2~z) =
= In УТ, b (in /2* 4) a [In (—4nz)] = In 4л, b [In (— 4л/)] =
1271. zi = /IT el •°’3t2w, z2 =/Тз е°-688л£, z3 =/IT eI131jlZ,
z4 =/l3 e1,68jl\ 1272. 1) 750ei,15°; 2) 5z; 3) 30 «e**150; 4) з|еЬ50°.
9
2)
6)
2е
е4 —
2е2
1274. 1; 1. 1275. - 1 + //3. 1279. 1) 1 z;
3) « О,99?'°’о92л; 4) « 1,24е/,0’6Эл; 5) « 10,05Ь1’84л;
1280.
Глава 9
13; 2) —7; 3) -3; 4) 40; 5) -12; 6) 7) -j-;
8) -3/2; 9) 1; 10) 1. 1281. 1) оо; 2) оо; 3) оо; 4) 5) 1,5; 6) 3;
1 2 !_ 11
7) 4-; 8) -3; 9) ~4; 10) 2; 11) 3; 12) -/5; 13) 6; 14) 4; 15)4;
О □ Z £,
16) 4; 17) 1,5; 18) 1282. 1) 0; 2) 0; 3) 5; 4) 3; 5)
£»Ск о
6) -4; 7) 5; 8)~1; 9)1о) 8: Н) 12) 1; ,3) 1; 14)
1 2 1 /— 1
15) 1; 16)-г-. 1283. 1) 5; 2) 3; 3) 2,5; 4) 2-=-; 5)4/6; 6) V
О ООО
1284. 1)1; 2) cosa; 3) - sin a; 4) л. 1285. 1) е“3; 2) efe; 3) е*; 4) е;
5)1; 6) е2; 7) в"1, 8) е~4. 1286. 1) 21; 2)0,61; 3) 1,84.
1287. 1) 2х+ 1; 2х + 1; 2) 4; 2; 3) ЗОх + 45; 10х + 15; 4) 2,4; 12.
1288. 1) ЗДх; 3; 2) ЮхДх + бДх2; Юх + 5Дх; 3) 8хДх + 4Дх2;
8х+4Дх; 4) (4х + 1) Дх + 2Дх2; 4л+1+2Дх. 1289. 1) ±2;
2) 1; 2; 3; 3) -у+ 2яй; 4) 2зхАг, 5) + 6 *) нет; 7) 2; 3: 8> нет-
1290. 1) х ~ 3, у ~ х — 3; 2) х = — 2, у = 2х — 4; 3) х = ± 1. у = х.
1291. 29. 1292. 16х. 1293. 23. 1294. 8х. 1295. 2ах+Ь. 1298.31,85 м/с.
1297. 6. 1298. —2. 1299. (2; 1). 1300. (-1; -1), (1; 1). 1301. (а) 0;
о 3
(б) -4.1302. 0 и 4- 1303. 0 = -4х-4. 1304. . 1305. 1) 4х+3;
о 4
308
2) 15х* 2 + 8х; 3)21х2+4х + 3; 4) 21,2х3 + 5,4х; 5) Зпх2 + 26х;
6) х4 + х3 + х2; 7) ах3+дх2+сх; 8) Зх2 1^2 + —L=; 9) (—• +
у х \2х /
10) (а2+х)Ух~ . Ц)2(1-8х); 12) 18х2 + 8х-3; 13) ЗОх + I;
’ 2ах2 ’
14) 15 (Зх2 + 8х — 2); 15) 108х2(х3 - 2). 1306. 1)
ОХ 6x2 . 3) 2 - 5 . 4) (х-4)/7___________1
} (1+х3)2’ ?5 2х2 ’ ) 4х* ’ ' }<7(1+)/7)2’
10) 1307. 1)4—4-; 2)9-^-. 1308. 12-^. 1309. а= 12/—2;
' 64 с2 с2 с2
22 Л- 1310- 0 /,= 10; 2) р" = 42х+Ю; 3) у" = 14,4х2 + Зх;
с2
4) у" = 12х2 - 8; 5) у" = 6х (х+3) (5х2+15x4-9); 6) у"=--1—-
4хух
2 3
7) у"—-------8) 5" = а. 1311. 1) Убывает при —оо < х < —;
9х3 у х2 4
3
возрастает при —<х<оо; 2)убывает при — оо<х< 1; возрастает
при 1<х<оо; 3) убывает при — оо<х< — 2. возрастает при
— 2<х<оо; 4) убывает при — оо<х<2,5, возрастает при
2,5<х<оо; 5) возрастает на всей числовой оси; 6) убывает при
— I <х< 1, возрастает при — оо < х< — 1 и 1<х<оо. 1312. 7,5
и 7,5. 1313. а = 2 см, h = 1 см. 1315. ^ = 2 см, h = 4 см.
2 1
1316. ртах = 3 — при X = 2, pmin — 3,5 при X = 3. 1317. ртах = 2 —
о 6
При Х=— 1, z/mln—— 2 у при X = 2. 1316. Ртах = у при X = 1,
Pmln = —у При Х=—1. 1319. 1) ртах = 0 при х = 0, рт1п = —1
при X = 1; 2) ртах =17 при Х = — 1, Рт1п = —47 при X = 3;
3) Ртах == 5 при X = 0, у mln^1 76 при х = 3, Pmhi — 76 при
х = 3; 4) Ртах = 0 при х =— I, рт1п = — 4 при х = 1; 5) ртах = 3,6
при Х = 0, Pmln = — у при х = — у’К2^, «/mln = —у при
x = yipr26"; 6) Ртах = 2 при х = 0, рт!п = —2 при х = 2;
7) Ртах ==_2 при X = — 1, Pmhi = 0 при X = 1; 8) ртах « 1,04 при
х = —ХЗ, pmiti ~ ~ 1,04 при х~УЗ.
309
Глава 10
1320. 1)с=5, а. = 1,8, Ъс = 3,2, h = 2,4, А = 36° 52', В = 53° 8';
2) с = 25, ас = 9, Ьс = 16, h = 12, А = 36° 52', В = 53° 8'; 3) b = 75,
ас = 80, Ьс = 45, h = 60, А = 36° 52', В = 53° 8'; 4) а = 156, ас = 144,
Ъс = 25, h = G0, Л = 67° 23', В = 22° 37'. 1321. 1) с =20,9, а =16,1,
6=13,2, h = /Ю5, Л = 50°39', В = 39°21'; 2) а = 2,5, 6 = 3 —
О
с = 4 4-, h = 2, Л = 36° 52', В = 53° 8'; 3) 6 = 25,5, с = 28,9, ас=6,4,
6 ' G
6С = 22,5, Л =28°4', В = 61° 56'; 4) а = 40, с =41, ас = 39^-,
6С=1.^-, Л = 77° 18', В =12° 42'. 1322. 1) Л = 52° 20', 6 = 0,397,
ас = 0,514, 6 = 0,502, с = 0,82, Ьс = 0,307; 2) В = 71° 20', а = 6,82,
6 = 20,2, ас = 2,18, 6С = 19,1, 6 = 6,46; 3) 6=33,5, ас=11,0,
6С = 28,4, 6=17,7, Л = 31° 52', В = 58° 8'; 4) с =60,4, ас=11,3,
6С = 49,1, 6 = 23,6, Л = 25° 40',’ В =64° 20'. 1323. 1) В = 50°,
а =12,9, 6=15,3, ас = 8,3, 6С = 11,7, 6 = 9,85; 2) В =19° 46',
6 = 28,2, а = 83,5, с = 88,7, ас = 78,6, Ьс = 10,1; 3) 6 = 55,6, ас=23,1,
Ьг = 45,2, 6 = 32,3, Л = 35° 32', В =54° 28'; 4) с = 4,6, ас = 2,59,
Ьс= 2,01, 6 = 2,28, Л = 48° 36', В = 41° 24'. 1324. 1) Л = 71° 55'’,
а = 21,0, 6= 13, г = 4,7, Я = 11,1, ha = 12,4, 5 = 130; 2) В = 83° 30',
hb = 5,97, 6 = 10,6. г = 2,39, R = 5,36, ha = 7,95, 5 = 31,8;
3) В = 51° 40', а = 45,9, ha = 36,0, 6Й=41,3, г =12,5, R = 25,5,
5 = 827; 4) Л = 55° 22', 6 = 22,7, ha = 18,7, hb = 16,5, r = 5,96,
R= 12,1, S = 187. 1325. 1) A = 55° 23', hb = 19,7, 6 = 27,3, r = 7,16,
Я =14,6, ha = 22,4, 5 = 269; 2) Л = 53°45', 6 = 59,1, hb = 40,3,
6a = 47,7, r=15,0, Я = 31,0, 5 = 1192; 3) Л = 57°22', a = 18,6,
6й=15,6, 6а=16,8, г = 5,47, Я =H,0, 5 = 156; 4) Л = 55°53',
а = 48,3, 6 = 54,2, ha = 44,9, г = 14,4, Я = 29,2, 5 = 1084.
1326. 1) Л = 65° 54', а = 24,6, ha = 18,2, hb = 22,4, г = 6,48, Я = 13,4,
5 = 224; 2) а = 48,1, 6а = 46,5, 6 = 58,8, В = 75° 28', 5 = 1118,
г =14,4, Я = 30,4; 3) В = 70° 50', а = 19,5, 6=22,8, ha = 18,6,
г = 5,86, Я = 12,05, 5= 182; 4) Л =11° 32', В =156° 56', а = 10,2,
hb = 2,04, 5 = 20,4± г = 1,01, R = 25,5; 5) Л = 45°, В = 90э, а = ha =
= 8 /Г, г = 8 (/2 - 1), 5 = 64, Я = 8, hb = 8; 6) В = 85°, а = 58,0,
6 = 78,4, ha = 57,8, 5 = 1718, г = 17,3, Я = 39,4. 1327. 1) Л = 16° 26',
а =19, с = 49, 5 =236; 2) Л = 79° 37', 6 = 61, с = 102, 5 = 3059;
3) в = 39° 83', а = 338,6, с = 327, 5 = 35 250; 4) С = 67° 21',
а = 148,4, 6 = 122,7, 5 = 8409. 1328. 1) с = 35,7, С = 95° 26',
В = 52° 17'; с = 12,4, С = 20°, В = 127° 43'; 2) — 3) нет решения.
1329. 1) 0 = 4,97, Л = 54°51', В =101° 9', 5 = 24,4; 2) 6 = 1,45,
Л = 92° 49', С = 47° 51', 5=1,23; 3) Л = 38° 40', С = 33° 20',
6 = 5,02, S = 4,69; 4) В = 56° 6', С = 21° 6', а = 97,5, 5 =1457.
1330. 1) Л = 29° 58', В = 46° 34', С = 104° 28', 5 = 72,6; 2) Л = 9° 16',
310
В =17° 54', С =152° 50', 5 = 0,656; 3) А = 59° 2', В = 71° 14',
С = 49° 44', 5=112; 4) Л = 50° 50', В = 42° 40', С = 86° 30',
5 = 78 100. 1331. 120,6 м, 4680 м2. 1332. 64,6 см, 750 см2.
1333. 13,54 см, 79,27 см2. 1334. 19,4 см, 135,3 см2. 1335. 12,08 м’
47,65 м2. 1336. 212,2 м, 27 820 м2. 1337. 65,5 м. 1338. 4,08 дм,
8,08 дм. 1339. 8,77 см, 125°37'. 1340. 184,6 м. 1341. 110,8 м*
1342. 3,08 м. 1343. 34,92 дм. 1344. 6,64 дм. 1345. 59,67 дм.
. , а 9 а
4r ctg y cos2 —
1346. 13 см. 1347. 38,7 см. 1348. ----------------------------— G4.7 см.
1349. 47° 49', 1.350. 1633 м. 1351. 133 9 м. 1352. 11,9 м, 117,7 м2.
1353. 0,163 м, 0,0168 м2. 1354. 116,9 м2. 1355. 123 м2. 1356. 298 м2-
1357. 346.9 дм2. 1358. 663,6 м2. 1359. 2а2 sin a sin2 ~ ~ 127,1 дм2.
1360. 2&2 sin а cos2 ~ « 70,03 м2. 1361. 255,2 дм2. 1362. 62 tga.
2 4 ь
R2
1363. «46,5 дм2. 1364. —7 (ла — 180 sin а).
иОО
1366. 141,6 дм2. 1367. 47,96 м. 1368. 2,46
1370. 16,89 дм. 1371. 9,4; 8,9; 7,2; 30,1.
1373. 2R sin 2а, 22? sin а, 22?2 sin2 a sin 2а.
1375. 34,2 см. 1376. 16,4 см, 54,45 см.
4r2 cos2 ^45° —-77) _ .
1378. ----------i------------ « 198,3 дм2. 1379. — S‘n а = 144,7 дм2,
sin а 4
4г2
1380. 180л см2. 1381. -— = 53,4 м2.
sm а
1365. ------------
4 sin4 —
4
м. 1369. 10,25 м.
1372. 24° 54', 52° 8'.
1374. 6,57 см.
1377. 61.
Глава 11
1382. (а) Один; (б) бесконечное множество. 1384. 2,8 дм,
3,5 дм. 1385. . 1386. 4 дм. 1387. 4 и 8; 28° 57'.
1388. 0,65 дм. 1389. 8/2. 1390. /а2 4- Ь2, /2а2 + Ь2 и _&•
1391. Сливаются. 1392. Если прямые параллельны. 1393. 6; 6/3 ;
2/jk 1394. j/^b2--^-. 1395. 20 и 16. 1396. 5/2".
1397. ~ 25,7 дм. 1398. a ctg ср. 1399. arctg у = 60° 26'.
1400. arctg = 53° 8'. 1401. 70° 32'. 1402. arccos (cos a cos 0) = 45°.
1403 arctg й V~(fl + ^ + с) (Д + 6 — с) (а + с — &) (^ + с — а) =
g _ а^с —
= 75° 52'. 1404. 1) 2) 3) -£• 1405. 1) 2) 2/г;
2 2 2 о
311
3) hV2. 1406. 14,56 см. 1407. 1) 20 см; 2) 10/У см; 3) 10/2 £м;
4) 0. 1408. 60°. 1409. 3/У. 1410. 8 см, 17 см. 1411. arctg
1412. У Ь (36 — с), ЗЬ>с. 1413. 120 см. 1414. 5 см и 8 см.
2о
1415. 0,3 дм. 1416. 2т. 1417. 3,5 дм и 4,5 дм. 1418. 1,6а и 3,4а.
1419. 30°. 1420-. Бесконечное множество решений. 1421. Параллельна,
пересекается, скрещивается. 1422. 15 дм. 1423. 1) Бесконечное
множество решений; 2) одно решение. 1424. 3,5 см. 1425. 80 см2.
1426. 7,5/2 см. 1427. 73,3 см2. 1428. /94 см. 1429. «3,87 дм-
1430. 2 см. 1431. 3,5 дм2. 1432. 3,6 дм. 1433. 36 см. 1434. 51/~10 см,
5/2 см, 5/6 см. 1435. 6 см. 1436. 1,3 дм. 1437. У a2 sin2 ф+&2 cos2 ф.
. c sin cl ----5 sinasinP
1438. arcsin—-z— = 45 . 1439. У b2 — a2 —r—,-если точки
d sin (a — p)
пересечения перпендикуляров с плоскостью лежат по одну сторону
от плоскости, проходящей через данный отрезок и перпендикулярной
» ----9 sin a sin Р
к данной плоскости; у Ь2 — а2 ————sr, если точки пересечения
sin (a + р)
перпендикуляров с плоскости© лежат по разные стороны от пло-
скости, проходящей через данный отрезок и перпендикулярной
к данной плоскости. 1440. 41°25' и 82° 50'. 1441. 1) 2/2 дм;
2) 2/3- дм; 3) 4 дм. 1442. -а-У5-. 1443. 5/2 см. 1444. 1,4 дм.
/4Л2 -4- Зл2
1449. a tg a = 5,44. 1450. arcsin /sin2 a -f- sjn^p. 1451. — sin 2a sin qp.
1452. S cos qp. 1453. a sin a sin ф. 1454. «60 см2. 1455. 39° 56'.
1456. 33,35 м2. 1457. 36° 52'; 3 м. 1458. Qsina; Q. 1459. 106,4 м2.
1460. В разных плоскостях. 1461. 1) Нет; 2) нет; 3) нет;
4) да. 1462. 1) Да; 2) нет; 3) да. 1465. 1) а /Г; 2) -Цр-;
3) 2a^3-; 4) ; 5) (а) 70°32'; (б) тетраэдр — 180°,
и Z
куб —270°. 1467. 1) у/2; 2) у/3-; 3) а2/3; 4) (а) а = 109° 24'1
(6) 240°. 1469. Ду-. 1470. 1 :/3. 1471. 1) 2) у/б; 3) а;
4) 1472. а2. 1473. 1474./2. 1475. 1) 138° 12'; 2) « 1,96;
2 о
3) ^~Ь-, 4) 5&2/3. 1476. 2) (а) 300°, 324°; (б) 138° 12'.
D
116’34'; 3) (а) -^-/5+/5 . (С) ^/.5 + |tl;
312
(в)|/25+^£: (r)e|A+2££: (д)^/5+|£5;
(е) "“/®±^; (ж) £ (з)
з/т
1477. Да. 1478. -. 1479. 60°. 1480. 1 см. 1481. 45°.
1482. «50 см. 1483. 10,5; 7,5; 5. 1484. «9,8 см; 14 см. 1485. 2 /65 см;
4/13 см. I486. За/2". 1487. 4 дм; 0,9 дм. 1488. 21,6 дм2..
— а а
1489. —. 1490. 2а2 У 3 cos у; 4а2 sin —. 1491. 4; 10; 0.
1492. (a) 30; (б) 15; (в) 10. 1493. 7/Т см, 54 см2. 1494. 1,2.
1495, ^К6-. Г496. & См. 1497. у/4Л2 + За2. 1498. 1) ^/2&2 + а2;
2) arctg Ь . 1499. 65 см2. 1500. 24. 1501. 3 см. 1502. 368 см2.
1503. 288 см2. 1504. 2а (а + 2£).« 85,8 см2. 1505. 48 /3 см2.
1506. 192 см2. 1507. 72 дм2. 1508. 1092 см2. 1509. я/з sin 2у.
о д_ тДГ 6 ,_
1510. —— rf2 sin 2<р; 151-1. 8а2 sin ~ tg а. 1512. d2 /2 sin 2р X
X sin (45° + а),« 393,1 м2. 1513. d2 ctg ~ 1963 м2..
1514. 5а2 ctg 36° cos2 27° « 3092 м2. 1515. 4а2 cosec cos2 (450 —X
X ]/sin sin.-^- « 34 700 см2. 1516. / а2 /Т sec а X
Х(14~/ 1 Ч-sin2 а). 1517. 10а2cos36°tga. 1518. 2/2/cos(45°—a) tgp.
1519. 3-sin22a. 1520. 2b2 /f cos ^45° - tg a cos 1521. 18 cm.
1522. 1) I/'h2+^', 2)1/h2+~-t 3) //+T2.
F O- f 2
1523. 1) / 1/ 4n2 + = 5; 2) / /4м2 + m2 « 6,56;
z г о 2
3) 4 /4п2 + 3m2 « 9,85. 1524. 6 см. 1525. 12 см. 1526. 281,25 см2.
1527. 9/3- см2-. 1528. 75/3 см2. 1529. 30 см2. 1530. 28/2 см2.
1531. -^-/Гсм2. 1532. 2 см. 1533'. 16 см2. 1'534. 12,5 см2.
4
1 4
1535. Пу см2 к 44-у см2. 1536. 31,25. см2, 125 см2, 281,25 см2,
1537. (/Г-1)с1. 1538. 11,25 см. 1539v 5 см. 1540.
1 _________ 1
1541. -уа±р/2; 2а; -у(а2 — 8р2). Указание. Проведем
прямую, соединяющую середины непересекаклцихся ребер тетраэдра
31?
/ « . <2 V 2 \
(длина этой прямой равна ——г> секущая плоскость будет пер-
пендикулярна к проведенной прямой.
При р=0 в сечении получим квадрат со стороной при
а]/"2 х aV2
р ——-— сечение обращается в отрезок прямой; при 0<р<——
сечение — прямоугольник. Для определения его сторон пайдем
сначала части ребра тетраэдра, заключенные между плоскостью
квадрата и плоскостью прямоугольника. На основании теоремы:
т/л- / & а у 2 }
циональные части» найдем у — ру2 1при у = — , р = —L—1.
1
х = — а±у. у —часть ребра тетраэдра, заключенная между пло-
скостью квадрата и плоскостью прямоугольника. 1542. -^-а ±
р/б.
2 ’
За; -Ц5-(а2 - 2р2).
Указание. В сечении получаем равно-
угольный шестиугольник (его углы равны по 120°), каждые три
несмежные стороны которого равны между собой; обозначим их
через xt и х2 (xi>x2); Xt и х2 определим способом, указанным
в предыдущей задаче. Для определения площади шестиугольника
продолжим три его равные стороны, например, три большие сто-
роны, до взаимного пересечения; тогда искомую площадь S найдем
как разность между площадью равностороннего треугольника
со стороной Х[ + 2х2 и утроенной площадью равностороннего
1/^3"
треугольника со стороной х2, S = —-—[(%! + 2х2)2 — Зх|] =
= “V" + 4хГ *2) = -qp- [(*1 + + 2XiX2] = X
X Га2 + 2(4-а2-4р2У|=-Ц^-(я2-2р2). 1543.1fl/2'± р/б;
L \ 4 4 /J о 2
3 i/'З"
За \ 2 ; —-— (а2 — 4р2). Указание. Плоскость, проходящая
через концы трех ребер, выходящих из одной и той же вершины
куба, перпендикулярна к его диагонали, выходящей из этой вер-
шины, и делит эту диагональ в отношении 1 :2. Далее см. ука-
зание к предыдущей задаче. 1544. 7 см. 1545. 2 дм. 1545. 65 см.
1547. 3 см и 5 см. 1548. 4. 1549. 4-(а2 — Ь2). 1550. 4 см.
4
1551. 2 см. 1552. ad и ^ad. 1553. У ak и ~ ak. 1554. 144 см2.
4 12 4 _ 144
1555. 16 см2. 1556. 1) ~ j/^4/i2 + у + 2) а 4/г2 + а2 + а2;Г
314
3) ^Г4/г2 + За2 + 3а2У3
2а
1559. 8/2 cos а cos2 -g-.
1557. 45°.
1560. 0,14 дм.
1558. -|-d2fga.
1561. 6 дм.
3а2/3 cos2-^-
1562. 96,6 см2. 1563. ---------------. 1564. 6г2/з" cos2 -тг sec ф.
cos а г 2
1565. 2а2 /2 cos -у cos ^45°—sec а. 1566. 6ft2/3 cosacos2-^-.
1567. 8ft2 ctga cos2 cosec а. 1568. 4ft2/2 sin—cos^45°----------
1569. -2^— sin (a + 30°) sec a. 1570. 26 cm2. 1571. 12 см.
1572. 2 см. 1573. 20 cm. 1574. 1,68 дм2. 1575. 54 дм2.
1576. ----—a\^................... — 1577. — X
8 у sin + 30°) sin (| - 30°)
, /(a-ft)2’ , 2 180° , ,, , n (a2 + ft2) , 180° л
X ]/ 2----4~ C g ~T~ + h + ~~ 4~-—' ctS * 1578' <?•
3л
1579.4 см. 1581. ft. 1582. 2arctg-jQ-. 1583. « 902,7 дм2.
1584. 120 см2. 1585. 108л см2. 1586. 15 см2. 1587. 2ла2«628 см2.
1588. 60°. 1589. 4/3 см. 1590. 54 /З^ см2. 1591.
1592. 12,25 см2. 1593. —. 1594. —
а — Ь 729 ’ 729 ’ 9 ’ 729 ’
1595. ЭД». 1595. S60K=^.; Sm„ = -^-.
_ 4лЛ2 „ 5 л/г2
1&97. 3(5ок д i ^полн— д—• 15У8. 4 см. 1599. « 4,6 м.
1600. 10л/з" см2. 1601. S6oK = л/?2 sec а; Зсеч =
=—'g ~2д~ Уcos (a + P) cos (a ~ P)- 1602. 2 arcsin-^5-я» 30°.
cos a cos2 P r nl2
1603. 4 m. 1604. 207° 30'. 1605. 4/3 cm. 1606. 50л /2 см.
1607. 9 м2. 1608. S6oK = 2650 см2; 5ПОЛН = 5782 см2. 1609. 4240 см2.
1610. 100л дм2. 1611. arccos—1612. 2360 дм3. 1613. «96 м2.
1614. abcV— cos 2а.
1617. 4/З" см3. 1618.
1615. 144 см3.
1619. 2d3/Г
10/5
1616. ~ab /баб .
О
1620. y/2S1S2Q .
1621.
64
1622. 1623.
О о
1624. 3d3/2. 1625. 3.
__ пз Т/О^
1626. 15,27 м2. 1627. 12 см3. 1628. а2 (1+2/3 +/7 ); —
315
1629. 12 /3 дм3. 1630.
sin ^30°—srn ^30°4-—j cosec
1631. 1632. d3sin2pVrcos 20. 1633.220 см2; 192 см3. 1634. 135 кг.
1635. &3 sin2 0 sec 20. 1636. V = d3 l^cos (a + 0) cos (cf — 0) sin a sin 0.
1637. 0.75Z3 yTsin qp cos2 qp. 1638. 1639. a sin a.
1640. mn (m + n) sin a. 1641. 2n7?3. 1642. л (R2 — r2) Id (d = 7,8).
1643. 3,56. 1644. 4. 1645. «18 дм3. 1646. «0,63 дм3. 1647. «4,3 см;
« 8,6 см. 1648. « 690 дм2, 3540 дм3. 1649. « 5,07 дм3. 1650. 161 см2,
113,3 см3. 1651. а2/3, —^2-. 1652. 2а2 /3,
1653. 22,26 см3; 54,94 см2. 1654. а3/3. 1655. 120 см3.
1 2
1656. — m3 cosec 2ф cosec qp. 1657. 900 см3. 1658. — № tg2 a.
6 3 _
4 / 6 \ п31^3”
1659. -х- Л3 ctg2 a cos2145°—— I cosec 0. 1660. ------------.
3 \ 2 / sin2 a cos a
ft3 a l/o"
1661. 4-sin — tg0. 1662. -J—/?3 tga. 1663. 47 м2. 1664. «4700 cm3.
6 2 а
1665. 9,42 дм3. 1666. «116,1 дм2. 1667. «1,8 дм3. 1668. «10,5 см3.
1669. «14,5 дм3. 1670. «38 см3. 1671. « 302 см2. 1672. «75 см3.
1673. 672 см3. 1674. 784 см3. 1675. 672 см3. 1676. 3 м.
1677. 533 4-м3 и 2325 м3. 1678. 675 м3. 1679. 8a2 sin2-J sin a.
о 2
9 f CL \ Q
1680. 10-g-a3 sin a (6 sin2-g-+ cos2 a j. 1681. — (a3 — Z>3) tg a.
1682. 1900 m3. 1683.
129 Уз я см3. 1685.
1688. « 198 см3.
, , . 180°
« (•a3 — &3) ctg
--------------------j-ggS---------------tga. 1684. 78л см2,
24 sin--------------
n
« 7330 см3. 1686. « 1,47 дм. 1687. 7 см.
1689. 7 см. 1690. ~(R3 — г3) tga.
О
7 7 a
1691. — л/3 sin 2a cos a. 1692. — ла3 sin a srn-77 — 28030 дм3,
б О 2
1693. 12740л км. 1694. 36710 км и 15930 км. 1695. 3562 км.
1696. 36л и 108л. 1697. 24л^48л, 72л. 1698. 4/5. 1699. 10 см.
1700. 30 см. 1701. 2025л + 1) см2. 1702 . 200 (5 - 2 Уз") л см2.
2
1703. 55л м2. 1704. 972л см3. 170S. 40 -д- я см3. 1706. 45л см3 и
243л см3. 1707. 112,5л дм3. 1708. «40 м3 и « 450 м3.
1709, 6щ2 2«cos2а ^0 2Э6< 1710. ± л /(^2+r2+2Rrcos2a)3cosec32а.
2 о
316
yjsec-y. i/z4. 2 cos a. tg^4t>“—у I ctg-у ctga.
1711. 574,6 дм2. 1712. £-sinatg-£. 1713. 1 4-. 1714. ~ 523,5 см3.
2 2 о
1715. -3.^^I-ctg3^-tga дм3. 1716. — na3sin22a. 1717. 2nrf2ctg2y.
1 , ------ а ,_,л na3 sin2 a sin (a + В)
1718. — па3 у cosa cosec -х-. 1719. ---------г-~——
12 2 smp
1720. 2яа3 sin 2а cos а. 1721. -х-я/г3 sin (а + Р) cosec a cosec р.
О
1722. | ЯЛ3 sin (а+ Р) cosec a cosec Р. 1723. 8яЛ2 sin (15° +X
1726. 0,5Я(13 cos ~ ctg -у- 1727. 4-яа381п2а. 1728. л (т — п)2У^
2 2 и о
X (m+2n) sin2 a sin2 Р cosec2 (а+р). 1729. у яа3 sin2 a cos (а — Р) sec р.
1730. -у- Яа3 cos а cosec2 а. 1731. у^/П/З +1).
1732. 2яЛ3 ctg a cosec а. 1733. яр2 УТ sin 2а cosec (45° + а).
1734. 0,5ят2 cos a sec2-у. 1735. 4" яа3 tg 2а sec 2а. 1736. 4-HC3sin22a.
2 О О’
1737. у я (1 4- cos2 а) У S3 cosec 2а » 1738. 4nQ ctg ^45°—
1739. -4 лЬс (b + с) sin a cos
о 2
ТАБЛИЦА ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
а sin а tg а ctg а cos а а
0° 0,000 0,000 1,000 90°
1° 0,017 0017 57,290 1,000 89°
2° 0,035 0,035 28,636 0,999 88’
3° 0,052 0,052 19,081 0,999 87°
4° 0,070 0,070 14,301 0,998 86°
5° 0,087 0,087 11,430 0,996 85°
6° 0,105 0,105 9,514 0,995 84°
7° 0,122 0,123 8,144 0,993 83°
8° 0,139 0,141 7,115 0,990 82°
9° 0,156 0,158 6,314 0,988 81°
10° 0,174 0,176 5,671 0,985 80°
11° 0,191 0,194 5,145 0,982 79°
12° 0,208 0,213 4,705 0,978 78°
13° 0,225 0,231 4,331 0,974 77°
14° 0,242 0,249 4,011 0,970 76°
15° 0,259 0,268 3,732 0,966 75°
16° 0,276 0,287 3,487 0,961 74°
17° 0,292 0,306 3,271 0,956 73°
18° 0,309 0,325 3,078 0,951 72’
19° 0,326 0,344 2,904 0,946 71’
20° 0,342 0,364 2,747 0,940 70°
21° 0,358 0,384 2,605 0,934 69’
22° 0,375 0,404 2,475 0,927 68°
23° 0,391 0,424 2,356 0,921 67°
24° 0,407 0,445 2,246 0,914 66°
318
Продолжение
а sin а tg а ctg а cos а а
25° 0,423 0,466 2,145 0,906 65’’
26° 0,438 0,488 2,050 0,899 64°
27° 0,454 0,510 1,963 0,891 63°
28° 0,469 0,532 1,881 0,883 62°
29° 0,485 0,554 1,804 0,875 61°
30° 0,500 0,577 1,732 0,866 60°
31° 0,515 0,601 1,664 0,857 59°
32° 0,530 0,625 1,600 0,848 58°
33° 0,545 0,649 1,540 0,839 57°
34° 0,559 0,675 1,483 0,829 56°
35° 0,574 0,700 1,428 0,819 55°
36° 0,588 0,727 1,376 0,809 54°
37° 0,602 0,754 1,327 0,799 53°
38° 0,616 0,781 1,280 0,788 52°
39° 0,629 0,810 1,235 0,777 51°
40° 0,643 0,839 1,192 0,766 50°
41° 0,656 0,869 1,150 0,755 49°
42° 0,669 0,900 1,111 0,743 48°
43° 0,682 0,933 1,072 0,731 47°
44° 0,695 0,966 1,036 0,719 46°
45° 0,707 1,000 1,000 0,707 45°
а cos а ctg а tg а sin а | а
Андрей Емельянович Рудник,
Людмила Александровна Клюева,
Мария Семеновна Мосолова
СБОРНИК ЗАДАЧ
ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ
для техникумов
М., 1974 г., 320 стр. с илл.
Редактор В. В. Донченко
Технический редактор В. Н. Кондакова
Корректор Е. А. Белицкая
Сдано в набор 15/VII 1974 г. Подписано к пе-
чати 25/Х 1974 г. Бумага 84ХЮ8‘/з2, тип. № 1.
Физ. печ. л. 10. Условн. печ. л. 16,8.
Уч.-изд. л. 16,74, Тираж 300 000 экз.
Цена книги 55 коп. Заказ Ха 257.
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени
Ленинградская типография Xs 2
имени Евгении Соколовой Союзполиграфпрома
при Государственном комитете
Совета Министров СССР по делам издательств,
полиграфии и книжной торговли.
198052, Ленинград, Л-62, Измайловский проспект, 29