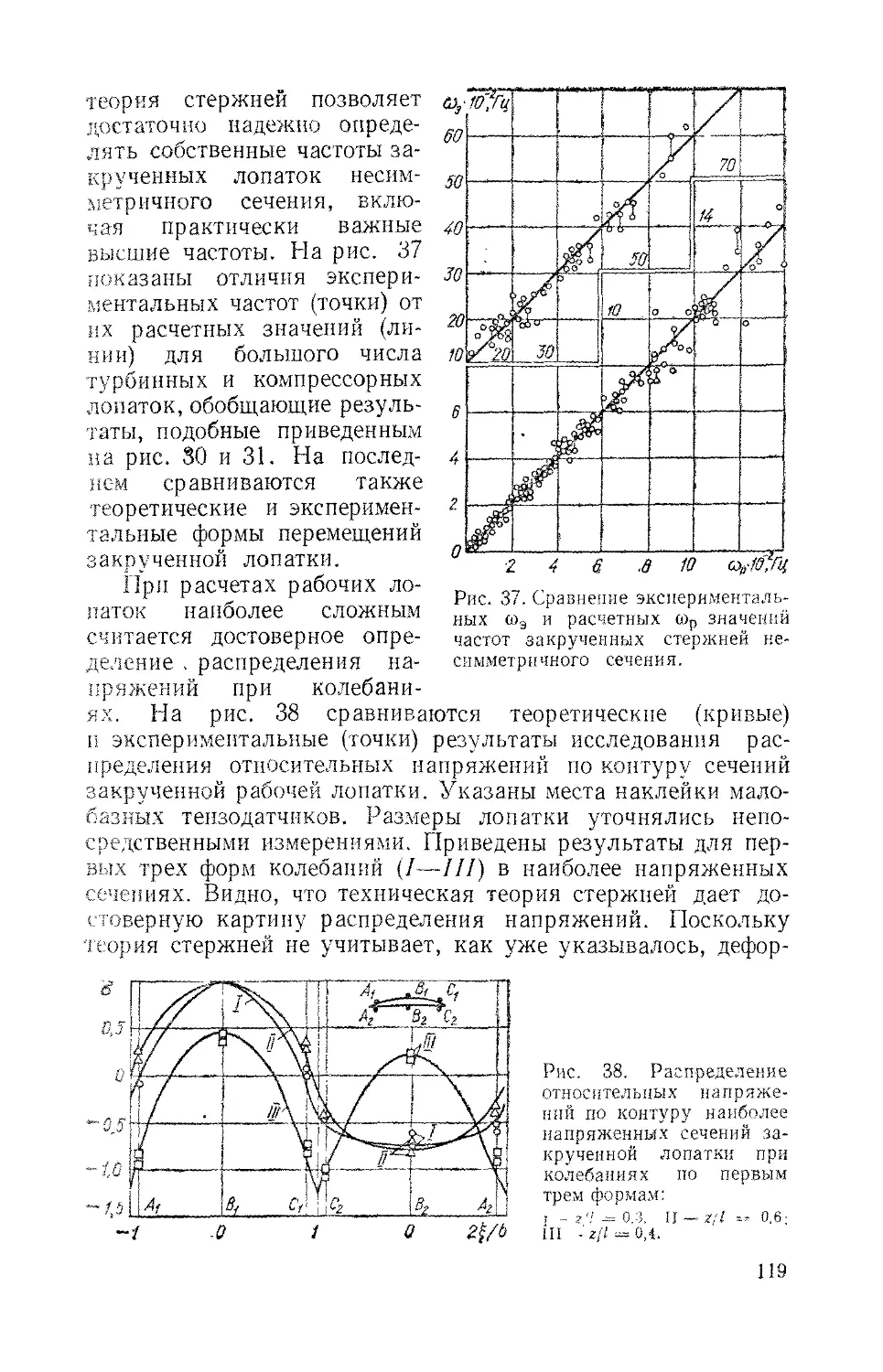
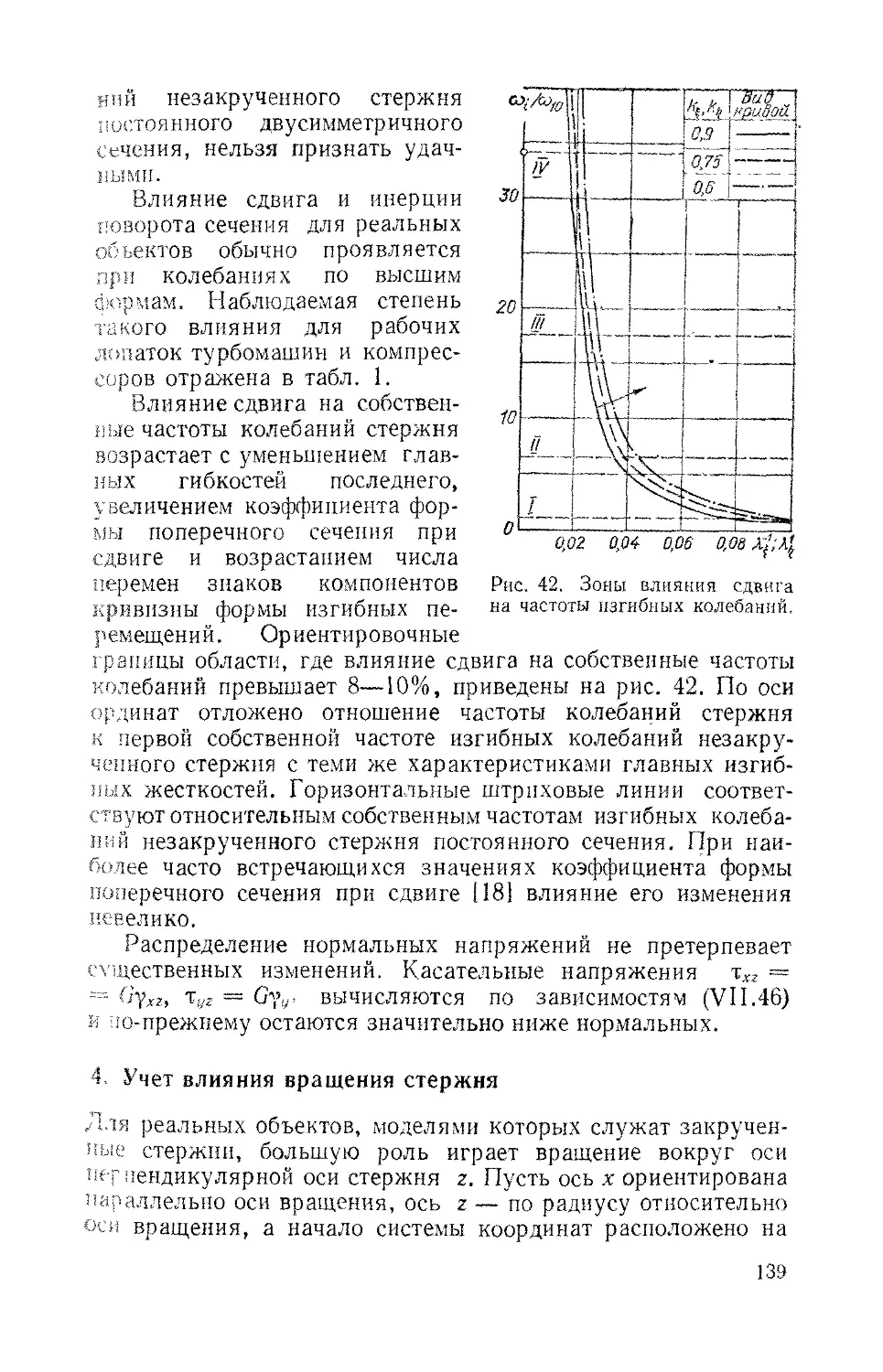
Text
АКАДЕМИЯ НАУК УКРАИНСКОЙ ССР
ИНСТИТУТ ПРОБЛЕМ МАШИНОСТРОЕНИЯ
Ю. С. ВОРОБЬЕВ, Б. Ф. ШОРР
ТЕОРИЯ
ЗАКРУЧЕННЫХ
СТЕРЖНЕЙ
КИЕВ НАУКОВА ДУМКА 1983
УДК 534.1:539.3:624.07
Теория закрученных стержней / Воробьев Ю. С, Шорр Б. Ф. Киев:
Наук, думка, 1983.— 188 с.
Изложена общая теория закрученных стержней произвольного
поперечного сечения, получившая в последнее время значительное развитие и
применение в машиностроенни и других областях техники (математические
модели рабочих лопаток паровых н газовых турбии, компрессоров,
воздушных винтов, сверл н т. д.). Приведены математическая теория и
результаты ее экспериментальной проверки в статических и динамических условиях.
Показаны особенности статической деформации н колебаний закрученных
стержней, а также влияние различных факторов: начальной закрученности,
несимметрнн сечения, соотношения главных жесткостей, депланации се-
ченнй, сдвига, осевых сил и др. Указаны области применения общей теории
и различных упрощающих предположений.
Для научных и инженерно-технических работников, занятых в области
прикладной механики.
Ил. 50. Табл. 8. Список лит.: с. 176—180 (91 назв.).
Ответственный редактор В. Л. Рвачев
Рецензенты С, И, Богомолов, А, Е. Божко
Редакция технической литературы
2105000000-084
г»
М221@4)-8з" 343-ЕЗ
@ Издательство «Наукова думка», 1983
ПРЕДИСЛОВИЕ
Развитие машиностроения связано с ростом единичной и удельной
мощности агрегатов, их быстроходности и рабочих параметров. Элементы
машиностроительных конструкций при этом подвергаются воздействию все
более интенсивных нагрузок, а их статической и вибрационной прочности
предъявляются все более жесткие требования.
Закрученные стержни являются математическими моделями ряда
ответственных элементов машиностронтельных конструкций: рабочих
лопаток паровых и газовых турбин, осевых компрессоров, лопастей воздушных
винтов, спиральных сверл, элементов измерительных приборов (трубок
Бурдона) и др. Элементы с закрученностью начинают использоваться в
строительных конструкциях. Перечисленные элементы обычно являются
одними из наиболее ответственных н наиболее нагруженных, поэтому
исследования их статической и вибрационной прочности являются весьма
актуальными. Успех таких исследований во многом зависит от достоверности
используемых математических моделей, от того, с какой степенью точности
они описывают реальные физические процессы при деформации
исследуемых элементов. Рабочие лопатки и воздушные вняты, например, можно
представить как-закрученные стержни переменного сечеиня сложной и
несимметричной формы.
Классическая теория стержней Кирхгофа — Клебша создавалась в
конце XIX ст., она не учитывает взаимосвязи различных видов деформации
в закрученных стержнях несимметричного сечения н поэтому не может
объяснить ряд экспериментально наблюдаемых явленнй. Потребности
практики обусловили развитие теории закрученных стержней. Большой вклад в
эту область механики внесли отечественные ученые П. М. Риз, С. А. Тумар-
кин, А. И. Лурье, Г, Ю. Джанелидзе, В. П. Ветчиикин, И. А, Биргер и
многие другие. Современная теория закрученных стержней обладает, с точки
зрения механики деформируемого твердого тела, достаточной строгостью,
она прошла экспериментальную проверку. Установлены области
применимости как упрощенных теорий, так и большинства уточнений.
Систематическое изложение всех положений теории закрученных
стержней, по мнению авторов, будет полезным для всех исследователей,
использующих в качестве моделей объектов закрученные стержни.
В главе Г изложены основные общие положения и понятия теории за-
крученных стержней.
Классическая теория закрученных стержней, которая находит
применение для ряда практически важных задач, изложена в главе II. Указана
область применимости этой теории и возможность ее расширения для задач
о пространственном изгибе закрученных стержней двуснмметричного се-
чення, и отражены наиболее важные результаты, полученные на основа
этой теории, в области статической деформации и колебаний стержней.
В главе III отражены результаты решений задач теории упругости о
деформации закрученных стержней, показывающие связь различных видов
деформаций вследствие начальной закрученности, которую не отражает
классическая теория. Более подробное освещение результатов,
полученных методами теории упругости в этой области, не является целью данной
монографии. Они в большинстве случаев не обеспечивают решение
практических задач, но позволяют суднть о достоверности приближенной теории.
Приближенная теория закрученных стержней произвольного сечения
рассмотрена в главе IV. В ряде частных случаев уравнения этой теории
соответствуют точным решениям. Показано, что для стержней удлиненного
поперечного сечения возможны существенные упрощения, приводящие к
технической теории закрученных стержней.
В главе V техническая теория обобщена для стержней произвольного
поперечного сечения. Исследованы статическая деформация и колебания
закрученных стержней несимметричного поперечного сечення, отражающие
связь различных видов деформаций вследствие начальной закрученности
и несимметрии сечения. Показано, что техническая теория позволяет
эффективно решать широкий круг практически важных задач.
Глава VI посвящена экспериментальной проверке технической теории
закрученных стержней и уточнению областей ее применимости.
В ряде случаев необходим учет дополнительных факторов, которыми в
теории стержней обычно пренебрегают. В главе VII рассмотрены вопросы
учета в теории закрученных стержней неравномерности депланации
поперечного сечення при кручении по длине стержня (стесненности кручения),
сдвига и инерции поворота, а также влияния вращения стержня. Показано,
что основные зависимости для тонкостенных закрученных стержней можно
получить с позиций общей теории оболочек, выделив стержень с помощью
системы ортогональных винтовых линий на поверхности оболочки и
предположив недеформируемость его сечения в своей плоскости.
Рассмотрены нелинейные задачи для случаев, когда упругая закрутка
не может считаться малой, и для сильно закрученных в начальном
положении стержней. Показаны пути учета начальной изогнутости оси
закрученных стержней.
В главе VIII приведены способы определения всех геометрических
характеристик стержней, применяемых в рассмотренных задачах. При этом
используются функции кручения и депланации сечения при сдвиге
призматического стержня, которые определяются с позиций теории упругости.
ВВЕДЕНИЕ
Во второй половине прошлого века основные соотношения
теории тонких призматических стержней A1.10) были
распространены на начально закрученные и изогнутые стержни
А. Клебшем [68] и затем А. Бэссетом, хотя в общих чертах
такая возможность указывалась еще Г. Кирхгофом [78, 791.
В 1927 г. А. Ляв [30] показал, что соотношения A1.10)
применимы для таких стержней, у которых отношения
максимального размера поперечного сечения к радиусу начальной
кривизны Ь/р0 и к обратному значению относительной начальной
закручешюсти Ы[— = Ьт0 имеют порядок упругих деформа-
ций, что позволяет пренебрегать произведениями этих
величин на упругие деформации и их квадратами. Очевидно, что эти
условия соответствуют возможности перевода
призматического стержня в сжато-изогнутое состояние и обратно линейной
(в пределах малого участка длиной А/ да Ь) и упругой
деформациями, когда квадратами углов поворота (в пределах
указанного малого участка) можно пренебрегать по сравнению
с деформациями. В течение долгого времени приложения
теории закрученных стержней опирались исключительно на
соотношения A1.10), причем на условия, ограничивающие их
применение, нередко не обращалось особого внимания.
Только после того, как опыты установили явление раскручивания
стержня при растяжении, начала развиваться специальная
теория закрученных стержней.
Закрученные стержни произвольного профиля. Первые
серьезные исследования закрученных стержней методами
теории упругости предприняты в 1939—1940 гг. П. М. Ризом
[39] и А. И. Лурье, Г. Ю. Джанелидзе [29], причем в обеих
работах начальная закрученность т0 считалась малым
параметром и решения строились с учетом членов только первого
порядка т.в.
П. М. Риз в общей форме рассмотрел задачи о растяжении
стержня (как силой на конце, так и распределенной по объему
5
в, Щ, Кг\, т, Y|. 7ti. /• Если принять Y| — Yi = d//d? = 0 и
считать а\ = Ee-l, где Е — обычный, а не приведенный мо-
дуль упругости Ех = 2G -.—я— (соответствующий абсолютно
понятному условию 8| = е" == 0), то можно показать, что для
закрученного стержня с прямой осью основные соотношения
работы 119] будут отличаться от (IV.42) только
второстепенными членами порядка (тогяJ; выражения для нормального
напряжения практически совпадут, а в выражения для
касательных напряжений (IV. 16) вместо текущего значения а* войдет
его значение в некоторой фиксированной точке. Указанное
расхождение связано как раз с тем, что при т0 Ф 0 поперечное
сечение при изгибе искажается [39].
Гипотеза о неискажаемости поперечного сечения
закрученного стержня в своей плоскости при изгибе не совместима с
требованием об отсутствии напряжений на свободной боковой
поверхности стержня. Выполнение последнего требования
также является свидетельством корректности любого варианта
теории закрученных стержней, что многие авторы, к
сожалению, не учитывают.
Техническая теория закрученных стержней в 1964 г.
обобщена Ю. С. Воробьевым для стержней произвольного
поперечного сечения с приближенным учетом сдвига и депланации
поперечного сечения [12, 13, 45]. Для определения
геометрических характеристик использовано решение задачи об изгибе
бруса с кручением [15, 17, 18]. Систематические исследования
влияния различных факторов на колебания закрученных
стержней позволили оценить области применимости
уточнений и упрощенных теорий [14, 16, 18, 45, 47, 48].
Исследованиям влияния стесненности кручения лопаток
турбомашин и компрессоров посвящены работы С. М.
Гринберга [20] и Л. Д. Магомаева [31].
Способы приближенного учета сдвига для закрученных
стержней рассмотрены в [46, 64].
Закрученные стержни удлиненного профиля. В 1929 г,
Р. Вуд и В. Перинг предложили формулу для определения
крутящего момента от продольной силы
уменьшающего начальную закрученность. Эта формула
приведена у Д. Ю. Панова, а затем, в несколько измененном
виде — у В. П. Ветчинкина [11] и, наконец, в курсе
сопротивления материалов Ден-Гартога. Однако из условий
равновесия следует, что никакого крутящего момента в растянутом
силой Pi стержне возникнуть ие может. Объяснение этому
явлению дано в работах П, М. Риза [39] и особенно четко
вскрыто И. А. Биргером, который указал на существование в
поперечном сечении закрученного стержня двух систем
касательных напряжений, крутящие моменты которых взаимно
уравновешиваются, а деформации сдвига существенно различны»
что и приводит к упругой раскрутке стержня. Что касаетсж
нормальных напряжений, то в названных работах считалось,
что они распределяются по поперечному сечению
закрученного стержня так же, как в незакрученном.
Основная формула для продольных деформаций
закрученного стержня удлиненного профиля (VII.67) и
соответствующая система соотношений (VI 1.69) (при dx/dt, — 0) получены
Б. Ф. Шорром в 1954 г. Различные варианты вывода указанных.
соотношений (или их частных случаев) приведены в [52, 53],
причем в последней переход к теории тонкостенных
закрученных стержней осуществлен с позиций теории оболочек.
Нелинейный член 0,5tV2 в связи с задачей кручения
призматических стержней (при т0 = 0) обсуждался еще С. П.
Тимошенко [43].
Повышение крутильной жесткости закрученных стержне»
рассматривалось Чэн-Чу [66], который получил для стержней
двусимметричного сечения формулу
ч
и экспериментально проверил ее для стержней с удлиненным"
прямоугольным сечением. Им же предложен приближенный
метод расчета закрученных манометрических трубок [67].
Эта формула обсуждалась Ден-Гартогом и была
экспериментально проверена другими исследователями.
Влияние начальной закрученности на жесткость стержня
на кручение и частоты крутильных колебаний изучалось
теоретически и экспериментально в разное время многими авто-
рами [3, 14, 26, 50, 61, 64, 85].
Раскрутку закрученных лопаток турбомашин под
действием центробежных сил исследовали В. П. Сухинин [36] и др.
Экспериментальное определение изгибных частот
закрученных образцов с двусиммегричными (обычно
прямоугольными) сечениями проводилось в работах С. А. Тумаркина-
[44], Д. Розарда, В. Карнеги, X. Слайпера [87], а также в
[14, 45] и др. В этом случае теория Кирхгофа — Клебша дает
правильные результаты. Проверка теории изгибно-крутиль-
ных колебаний закрученных стержней несимметричного
сечения изложена в [51, 541. Единичный опыт В, Карнеги не
выявил изменения основной частоты.
Один из вариантов вывода формулы типа (VI 1.67) при а'т/
dt, = 0 приводится Дж. Хуболтом и Г. Бруксом [74],
которые используют ее для расчета изгибных и крутильных
деформаций вращающихся лопастей винтов, полагая, однако,
что сечение лопасти симметрично относительно оси
минимальной жесткости |; при этом наиболее существенные для лопастей
винтов эффекты изгибно-крутильной связанности деформаций
выпадают из рассмотрения.
При экспериментальных исследованиях сильно
закрученных стержней с крестообразным двусимметричным сечением
обнаружено, что их изгибная жесткость уменьшается с
увеличением начальной закрученности. В работе Дж. Зикела
191] показано, что это явление объясняется увеличением
длины винтовых волокон, которое становится заметным, когда
Ро = AV)S соизмерима с единицей. Определенное влияние
оказывает также поперечная деформация сечений при
изгибе [82].
В работе Е. Вольтерра [90] развивается теория стержней,
опирающаяся на гипотезу плоских сечений, линейная
относительно начальной закрученности т0 и вместе с тем
учитывающая деформацию сдвига, что приводит к очень сложным и
ненадежным соотношениям.
Некоторые вопросы теории закрученко-изогнутых
стержней (с непрямой осью в начальном состоянии) рассмотрены
'Б. Ф. Шорром [57] и в более общей постановке Л. Д. Магомае-
вым [31] и С. Янецким [59].
Различные варианты теории изогнуто-закрученных
стержней рассматривались С. П. Вязьменским, Э, П. Аксельрадом,
А. Я- Аронсоном, Г. Б. Шашкиным, В. К. Дондошанским,
Т. Сато и др. [1, 25, 86].
Определенный интерес для теории закрученных стержней
представляют исследования по нелинейным задачам для
призматических стержней (работы В. В. Новожилова, Н. В, Зво-
линского, П. М. Риза [26], Д. Ю. Панова и др.).
Расчету закрученных лопаток турбомашин на основе
соотношений типа (V.14) посвящены работы [18, 20, 21, 36, 47,
49, 51, 55, 56, 70, 76] и др.
Совместные колебания дисков турбомашин с закрученными
лопатками изучались А, В. Левиным [28], С. И. Богомоловым
и А. М. Журавлевой [10], В. К. Дондошанским, а также в
работах [18, 46]. Колебания пакетов закрученных лопаток
рассмотрены в [18]. Показано, что начальная закрученность и
несимметрия поперечного сечения приводят к нарушению
10
симметрии форм изгибно-крутильных внутрипакетных
колебаний вдоль по пакету и перераспределению напряжений в
системе. При расстройке системы вследствие технологических
отклонений в пакетах лопаток и облопаченных дисках
начальные закрученность и несимметрия сечения вызывают
дополнительное существенное перераспределение напряжений.
Поэтому область применимости классической теории стержней
для систем закрученных стержней не расширяется, а сужается
по сравнению с областью ее применимости для единичного
стержня.
Применение теории пластин и оболочек к расчету
закрученных стержней удлиненного профиля. При большом удлинении
сечения стержня его уже необходимо рассматривать как
пластину или оболочку. Такой подход позволяет уточнить границы
применения теории тонкостенных стержней. Методы
расчета лопаток турбомашин как закрученных стержней
удлиненного профиля на основе теории пластин и оболочек
разрабатывали Б. Е. Сивчиков, И. И. Меерович [34] и Ф. С. Бед-
чер [5]. В первой работе лопатка рассматривалась как тонкая
пластинка переменной жесткости и исследовалось влияние
скосов заделки и свободного конца, а также закрученности
(приближенным способом) на прогибы и распределение
напряжений от статической поперечной и центробежной нагрузок.
Работы И. И. Меерович посвящены расчету спектра частот и
распределения динамических напряжений невращающейся
лопатки, рассматриваемой как пологая оболочка, закрученная
но линейному закону. Решения вариационным методом
получены для лопаток с сечениями частного типа при изменении
максимальной толщины и стрелы изогнутости по длине
лопатки по степенным законам, в том числе при наличии скоса
заделки. Ф. С. Бедчер обобщила эти результаты для
несимметричных профилей более общего типа, расширила число
расчетных частот от 7 до 10 и провела для ряда лонаток
расчеты на ЭВМ и сопоставление с экспериментальными данными.
В работе [40] вариационным методом решена задача о
расчете собственных частот и форм колебаний вращающейся
лопатки турбомашины, рассматриваемой как косоугольная в
плане, произвольно закрученная и изогнутая оболочка
переменной толщины.
Авторы ряда работ рассматривали закрученные пластинки
и геликоидальные оболочки постоянной толщины, учитывая
члены порядка (т0гJ по сравнению с единицей и пренебрегая
деформациями в срединной поверхности. Такой подход
использован, например, в работе Л. Маундера [82]. Я. Кноулз и
Е. Рейсснер [801 получили решение задачи о растяжении и
11
кручении геликоидальной оболочки при произвольном угле
наклона винтовых линий к оси.
В работах С. Кохановского, Я. Аргириса и Р, Хелденфел-
са, Л. Востина рассматривались нелинейные деформации
первоначально плоских пластин, что позволяет учесть начальную
закрученность как промежуточное деформированное
состояние.
Уравнення теории оболочек использовались при
разработке теории закрученных тонкостенных стержней [53].
Последние годы в ряде работ развивались численные методы
расчета закрученных стержней удлиненного профиля как оболочек
с использованием методов конечных элементов.
Сопоставление результатов, полученных на основе теории
стержней, с результатами, полученными на основе теории
пластин и оболочек, позволяют оценить область применимости
технической теории стержней (гл. V), которая для ряда
практических задач вполне достаточна.
Расчеты закрученных стержней на основе классической
теории. Несмотря на определенные ограничения, присущие
теории закрученных стержней Кирхгофа — Клебша,
полученные на базе этой теории решения в ряде случаев вполне
применимы для расчета слабо закрученных лопаток и воздушных
винтов с компактными сечениями.
Значительное число работ в .этой области представляет
большую ценность. Укажем лишь некоторые из них.
Теория закрученных стержней Кирхгофа — Клебша
достаточно полно освещена в работе А. Лява [30], а ее первые
применения к расчету лопаток и воздушных винтов — в
работах С. А. Тумаркина [44], И. А. Биргера [8, 9] и др. Расчету
закрученных лопаток на изгиб посвящены работы Н. Н. Ма-
линина, А. Ф. Гурова, В. Карнеги [64, 65] и многих других.
Широкое применение нашли методы расчета закрученных
лопаток, отраженные в [10, 58].
Глава I
ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ
ЗАКРУЧЕННЫХ СТЕРЖНЕЙ
J. Общие сведения
Стержнем принято называть деформируемое тело, у которого
один из линейных размеров значительно превышает два других.
Выделяют линию вдоль большего из размеров стержня, которую
принято называть осью стержня. Боковая поверхность
стержня может быть образована движением плоского контура вдоль
оси стержня. Часть плоскости, перпендикулярная к оси
стержня и ограниченная его боковой поверхностью,
называется поперечным сечением стержня (иногда просто сечением),
а его контур — соответственно контуром поперечного сечения.
Таким образом, стержень ограничен боковой поверхностью
и концевыми (начальным и конечным) сечениями.
Различают прямые стержни — с прямолинейной осью и
кривые стержни, оси которых искривлены по различным
законам. Длина прямого стержня определяется как расстояние
между его концевыми сечениями, длина кривых стержней —
как длина искривленной оси.
Форма поперечного сечения является важнейшей
характеристикой стержня. Выделяют сечения двусимметричные с
двумя осями симметрии, симметричные с одной осью
симметрии и несимметричные.
Если форма и величина поперечного сечения не
изменяются на протяжении всей длины стержня, то его называют
стержнем постоянного поперечного сечения. Боковая поверхность
прямого незакрученного стержня постоянного поперечного
сечения является цилиндрической. У стержня переменного
поперечного сечения величина или форма сечения может
изменяться вдоль по длине стержня непрерывно или
скачками.
Закрученными называют стержни, боковая поверхность
которых образуется винтовым движением контура плоского
поперечного сечения относительно его оси. Такие стержни
13
могут быть прямыми и кривыми,
постоянного и переменного сечения.
В настоящей работе рассматриваются
прямые или слабо искривленные
закрученные стержни, как имеющие
наибольшее практическое применение.
Чтобы подчеркнуть, что закрутка
стержня имела место до процесса
изучаемой деформации, ее называют
начальной. В ряде работ
прикладного характера начальная закручен-
ность называется естественной [3,
6, 22, 28, 29, 39, 41, 49, 61]. Такое
определение иногда подчеркивает,
что закон начальной закрученности
вызван функциональными
требованиями к соответствующему
конструктивному элементу. Например,
закрученные стержни являются
моделями лопаток осевых паровых и
газовых турбомашин, компрессоров и
воздушных винтов, законы
закрученности которых определяются
требованиями аэродинамики
соответствующих рабочих процессов. Закручен-
ность может быть равномерной по
длине (линейной) или нелинейной,
описываемой различными законами.
Закрученные стержни представляют
собой тип стержней, требующий
самостоятельного рассмотрения.
При рассмотрении прямых закрученных стержней
используются две основные системы координат: неподвижная и
подвижная (рис. 1). В качестве неподвижной примем
прямоугольную правую систему координат хуг, оси х, у, которой
расположены в плоскости начального поперечного сечения стержня,
а ось г направлена вдоль оси последнего. Оси х, у в дальнейшем
центральные, т. е. начало координат О расположено в центре
масс начального сечения. Оси |, ц подвижной системы
координат |т]? при движении вдоль оси поворачиваются вместе
с сечением, оставаясь главными центральными осями любого
сечения. Ось L совпадает с осью z и в дальнейшем не
выделяется.
Угол а (г), отсчитываемый между осями х и g против
направления вращения часовой стрелки, называется углом уста-
Рис. 1. Схема
закрученного стержня.
14
новки текущего сечения или углом начальной закрученности
стержня. Тогда соотношение между координатами
= Я
X
У
или
I
ц
х\
У
г
A.1)
Н =
где Н — матрица направляющих косинусов осей координат,
cos a sin а
— sin а cos а
cos а sin а 0
— sin а cos а 0
A.2).
О
О
Относительная закрученность (степень закрутки)
стержня в данном сечении
da/dz.
A.3)
Стержень равномерно закручен, если т0 = const. Тогда
а @ - а @)
а (г) = а @) + тог; т0 =
I
A.4)
где / — длина стержня.
Примером равномерно закрученных стержней являются
спиральные сверла и витые манометрические трубки.
Закрученность некоторых турбинных и компрессорных лопаток
близка к равномерной.
На рис. 1 ось стержня (ось закрученности ?а) совпадает
с осью г, однако в общем случае она может проходить через
точки сечения с координатами ?а, г\а. Тогда расстояние любой
точки сечения от оси закрученности ?а определяется
выражением
Га = V(l — laf + 1ц~ Т)аJ.
При смещении сечения вдоль оси на величину Дг
произойдет приращение утла закрученности и эта точка опишет в
плоскости сечения дугу длиной As = [а (г + Аг) — а (г)]га.
Основные положения линейной теории стержней применимы
к стержням, у которых (Да'ДгJ <^ 1 или
т^«1. A.5)
Можно сказать, что соответствующие точки различных
сечений закрученного стержня располагаются на винтовых
15
линиях abx, углы наклона которых по отношению к оси
стержня ро = arctg (тога). Тогда область рассмотрения стержней
может ограничиваться малыми углами наклона винтовых
линий
Ро<€1- A-6)
Это неравенство эквивалентно критерию A.5), так как при
малых углах наклона р0 *** тога-
Необходимо отметить, что понятие винтовой линии или
винтового волокна используется для наглядности и при
некоторых подходах к построению приближенной теории
закрученных стержней, но не является необходимым при построении
общей теории закрученных стержней.
Некоторые особенности поведения закрученных стержней
зависят от абсолютного угла закрученности а (от взаимного
положения сечений), другие — от степени закрутки т0 (от
скорости изменения по длине взаимного положения сечений).
2, Геометрические соотношения
Положение любого поперечного сечения стержня полностью
определяется координатой г. В теории стержней принято
рассматривать пространственные перемещения некоторой
характерной точки сечения и углы поворота сечения, которые
являются функцией одной координаты г. Перемещения же
любой точки сечения определяются линейными и угловыми
перемещениями в выбранной характерной точке сечения и
гипотезами о поведении сечения при деформировании стержня.
Например, гипотеза плоских сечений состоит в
предположении, что поперечные сечения, плоские до деформации,
остаются плоскими и после нее. Существует гипотеза,
предполагающая малые искажения плоского сечения (депланацию),
определяемые соответствующими производными перемещений
характерной точки. После введения таких гипотез трехмерная
задача о деформации стержня сводится к одномерной задаче
определения компонент перемещений характерной точки
сечения, являющихся функциями координаты г. Производные
по координате г в дальнейшем будут обозначаться штрихами.
Пусть компоненты линейных перемещений характерной
точки сечения в системе координат хуг обозначаются
соответственно и (г), v (г), w (г), компоненты угловых перемещений
сечения — ух (г), уу (г), yt (г), а компоненты перемещений
в системе координат |т)г соответственно щ (z), vn (г), ш? (г)
и у* (г), уц (г), ys (z). Тогда можно получить геометрические
J6
соотношения
Л
г
1
Уг
Tnl
Yd
w- =
Т; = Y
«i |
»Г| 1 =
= Я0
(рис
= до;
2 =
• 2)
В;
ы
V
W
A.7)
A.8)
Для компонент кривизны f/
стержня в разных системах '
координат зависимости имеют Риа % Компоненты линейных и
угловых перемещений в неподвнж-
вид
= Я!
ной и подвижной системах ко-
A.9) ординат.
Степень закрутки (относительная закрученность) стержня при
деформации
а удлинение оси
A.11)
В прямоугольной системе координат хуг компоненты
угловых перемещений
A.12)
ъ = и; ь
¦V ,
а компоненты кривизны
и"
к„
\\ + (и'J) "
При малых перемещениях
кг =
11 4
— — v".
A.13)
Тогда, воспользовавшись зависимостями A.8) и A.9), можно
получить соотношения
A.15)
= Ы| — 2т0У,, — То
2 2-1896
17
3. Уравнения равновесия
В системе координат xyz компоненты главного вектора
внутренних сил обозначаются Рх, Ру, Рг, главного момента —
Мх, Му, Mz, а компоненты распределенных внешних нагрузки
и момента соответственно qx, gy, qs и тх, пгд, тг. Тогда
уравнения равновесия элемента стержня можно записать в
обычном виде:
Px +qx = 0; Py + qv=* 0; Рг + дг = 0;
Мх - Ру + тх=* 0; Му + Рх + ту = 0;
Мг + тг = 0.
A.16)
Исключая перерезывающие силы, получаем для
изгибающих моментов уравнения
Мх — qv + тх = 0; M"v + qx + ту = 0. A.17)
В подвижной системе координат \цг компоненты главных
вектора и момента внутренних сил описываются
соотношениями
A.18)
Уравнения равновесия A.16) с учетом зависимостей A.18)
приобретают вид
pi ^ рчТо + qi = 0; Рц + РЛ + Чч = 0;
мп
мг
!
! н
1
мх
му
мг
Pi
Ръ
Рг
| — "о
1
р*\
р
Р'г + Яг = 0;
Мъ — Мг,т0 —
— Р„ + т= = 0;
ЛГЛ + /И;то + Р, + от,, = 0; Мг + тг = 0.
Для изгибающих моментов уравнения могут быть приведены
к виду
A.19)
М„ + 2т0М|
+
?т) + т; — Tomri = 0;
qi + Щ + %от = 0.
A.20)
4. Физические соотношения
и общая постановка задачи
Для решения задачи необходимо связать компоненты
кинематических характеристик деформации стержня с силовыми,
В линейной постановке задачи наиболее общий вид таких за»
18
висимостеи следующий:
Угг
Уцг
8
К:
щ
-=! аи 1
Р,
Л|
Рг
м:
м„
мг
A Г« |
У иг
W'
И
У
8'
Р
Г У
Рг
М,
A.21)
1 — Ifi ;
где yiz, ?цг и 7«, Yi/z — соответствующие деформации сдвига.
Для незакрученных стержней двусимметричного
поперечного сечения отличны от нуля только диагональные
коэффициенты ан, bu, a(t, fid и зависимости A.21) отражают
известные из теории незакрученных стержней представления о
пропорциональности деформаций сдвига перерезывающим силам,
удлинения оси продольной силе, компонент кривизны
изгибающим моментам, степени закрутки крутящему моменту.
Следовательно, недиагональные коэффициенты зависят от
начальной закрученное™ т0 и несимметрии сечения стержня.
Элементы матриц %, ац являются коэффициентами
податливосb p ф
ти, a b
Согласно
<х() =
коэффициентами жесткости упругого стержня.
б Ь Ь
теореме о взаимности работ a(j = а;-?; Ьц = Ьц\
() = ац; ${j = ft/j. Полнота матриц коэффициентов
податливости и жесткости зависит от используемой теории стержней.
Компоненты пространственного перемещения
элементарного объема стержня в направлениях хуг можно обозначить
соответственно U (х, у, г), V (х, у, z), W (х, у, z). Учитывая
особенности геометрической формы стержня (малость любого
поперечного размера по сравнению с длиной I), целесообразно
любую из этих функций представить в виде
F (х, у, z) = ]г (г) фа {х, у) + /2 (z) ф3 (х, у) + /3 (г) ср8 (х, у) К • • •
(L22)
Если задаться определенным видом функций ср,- (х, у), то
трехмерная задача сводится к одномерной. Возможен формальный
подход, когда функции ц>{ (х, у) представляют
математический ряд определенного вида (например, но степеням
неременных х и у) [7, 19, 90]. Функции /,- (г) являются неизвестными.
Обычно в качестве функций /г- (г) берутся компоненты
перемещений характерной точки сечения и их производные,
19
что обеспечивает наиболее простой переход к физическим
величинам. Второй подход предполагает использование
эвристических гипотез о виде функций ср? (х, у), основанных на
известных решениях задач о деформации стержней определенной
формы и эмпирических данных. Результаты, имеющие
прикладное значение, получены, как правило, с помощью второго
подхода.
Когда принят определенный вид функциональных
зависимостей для компонент перемещений U, V, W, методами теории
упругости можно получить зависимости для деформаций, а
затем и напряжений в стержне. Зная напряжения, всегда
можно перейти к компонентам главных вектора и момента
внутренних сил в стержне.
Однако не всегда выбранные зависимости для перемещений
позволяют получить выражения для напряжений, особенно
для касательных, с достаточной точностью отражающих
характер деформаций. Тогда вводятся дополнительные гипотезы
о виде коэффициентов в зависимостях A.21) между
кинематическими и силовыми характеристиками стержней.
Уравнения равновесия в форме A.16) или A.19) позволяют
получить уравнения статической или динамической
деформации стержней. Эти уравнения с соответствующими
граничными условиями дают возможность определить неизвестные
перемещения характерных точек сечения (функции f{ (г)). В
динамических задачах эти функции зависят от координаты г и
времени t.
Уравнения деформации стержня и соответствующие
граничные условия получают также часто с помощью
обобщенного принципа Остроградского — Гамильтона:
в П — Г ( V; qfivt + V mfy'j) dz dt, A.23)
/, l о V ^ / |
где qt, rrij — компоненты обобщенной внешней нагрузки, а
v. и у, — соответствующие им линейные и угловые
перемещения.
Потенциальная энергия деформации стержня в наиболее
общем виде выражается через напряжения и деформации [131:
i
П --, -i- ( [ @*8, 4- оугу + агъг -i- %Х1/уху -\- %хгухг -\-
0 F\z)
+ Tuzyyz)dF(z)dz, (I.24)
где F (г) — площадь поперечного сечения стержня.
20
Использование принципа Остроградского — Гамильтона
допускает также прямое решение задачи без перехода к
уравнениям деформации стержня. Независимо от метода решения
задачи каждая принятая математическая модель стержня
имеет свою область применимости, зависящую от системы
используемых гипотез. Для надежного практического применения
математической модели область ее применимости должна
уточняться путем экспериментальных исследований.
Глава II
КЛАССИЧЕСКАЯ ТЕОРИЯ
ЗАКРУЧЕННЫХ СТЕРЖНЕЙ
(ТЕОРИЯ КИРХГОФА— КЛЕБША)
J, Основные соотношения
Классическая элементарная теория основана на гипотезе
плоских сечений, согласно которой сечения, плоские до
деформации стержня, остаются плоскими и нормальными к оси и
после деформации. Сечение, таким образом, рассматривается как
недеформируемая часть плоскости. Оно поворачивается на углы
Ух> Уу относительно осей х и у, а поворот сечения в своей
плоскости 8 в общем случае происходит относительно некоторой
точки О1 — центра поворота с координатами xsys. С точностью
до бесконечно малых второго порядка перемещения любой
точки стержня в системе координат хуг согласно гипотезе
плоских сечений (рис. 3), с учетом зависимостей A.12) будут
U = и — Ьу{,
V = v + QXl;
W = w — и'х — v'y,
(ИЛ)
где хх = х — xs; уг = у — ys.
Зависимости для перемещений (IIЛ) позволяют получить
выражение для продольной деформации
ег = W' = ш' — и'х — v"y, (II.2)
Остальные деформации оказываются равными нулю.
Поскольку в элементарной классической теории стержней
напряжения от поперечного взаимодействия волокон не
учитываются, согласно закону Гука для одномерной деформации,
нормальные напряжения аг оказываются распределенными по
сечению по линейному закону
ог -= Егг = Е (ш' — и"х — v'y), (II.3)
где Е — модуль упругости материала.
22
Рис. 3. Перемещения при поворотах плоского поперечного
сечения.
Отсюда можно найти зависимости для продольной силы и
изгибающих моментов
Рг = J агс1Р
= — Elxyii
xyi
My = — J 0zxdF = ?/хгг"
?//'; i
где Ix, I — осевые, 1ху — центробежный моменты инерции,
1Х = \ уЧР; 1у = f xhiF; Ixy = \ xydF. A1.5)
При получении зависимостей (II.4) предполагалось
выполнение условий
f xdF == 0; \ ydF = 0,
(И.6)
которые определяют выбор начала координат ху в
нейтральной точке сечения, где напряжения <тг обращаются в нуль.
Геометрическое место нейтральных точек сечений является
нейтральной осью стержня. Для однородного стержня
нейтральная точка сечения совпадает с центром масс сечения.
Если нейтральная ось совпадает с осью центров масс, то ее
23
называют упругой осью стержня. Моменты инерции Ix, ly, fXff
и оси координат ху в этом случае называются центральными.
Поскольку зависимости для перемещений (II. 1) не
позволяют получить выражения для касательных напряжений,
зависимости (II.4) должны дополниться зависимостью для
крутящего момента, которая предполагается такой же, как и для
незакрученного стержня:
Af,= G/d6\ (П. 7)
где G — модуль сдвига; Id — геометрическая жесткость
стержня на кручение.
Уравнение (П.7) для крутящего момента в теории
Кирхгофа — Клебша дополняет гипотезу плоских сечений на уровне
соотношений A.21).
В подвижной системе координат щг зависимости (II.1) —
(II,3) с учетом соотношений A.8), A.9), A.12) — A.15)
приводятся к виду
(II.8)
е,-ш к^-ЩЦ; (П9>
Направление осей координат |rj выбирается так, чтобы
/|П = \ %r\dF = 0. Тогда оси |т] и соответствующие осевые
F
моменты инерции /> и /л называются главными центральными.
Выражения (II.4), (II.7) приобретают вид
Рх = EFw' = EFe;
М-Е!^ ШЛО)
В теории Кирхгофа — Клебша предполагается, что
соотношения (II.8) — A1.10) остаются справедливыми и для
закрученных стержней. Отсюда следует, что в подвижной системе
координат &)z матрицы | % || и \\b(jl зависимостей A.21) имеют
только диагональные коэффициенты, отличные от нуля, а
сами зависимости распадаются на четыре независимых
уравнения того же вида, что и для незакрученного стержня. В
системе координатхуг связь возникает согласно выражениям (II.4)
между компонентами изгибающего момента Мх, MtJ и
компонентами кривизны и", v", что отражает пространственный
характер изгиба стержня.
24
2. Пределы применимости классической теории
Если начальная закрученность стержня такова, что его
можно полностью раскрутить (перевести в незакрученное
состояние) путем упругой и линейной деформации, то соотношения
A1.10) справедливы для всех упругих деформаций стержня с
закрученностью % = тх — т0, где т0 и %г — начальная и
наибольшая конечная закрученности. Для оценки пределов
применимости классической теории можно воспользоваться
результатами решения в рамках теории упругости задачи о деформации
закрученного стержня постоянного эллиптического
сечения [381. При закручивании на относительный угол х0
стержня эллиптического сечения с отношением осей с = alb @ <С
<е<:1) максимальные деформации сдвига ут = то6с/A +
+ с2), а максимальный угол наклона продольного волокна
Р'т — 0,5т0Ь. Условие линейности деформаций требует, чтобы
было fm <?; ут или рт <^ т/Рт. откуда
Условие упругих деформаций означает, что ут < ги, где
е^ — деформация, соответствующая пределу упругости,,
имеющая порядок Ю. Следовательно, '
Для стержней с тонкими (удлиненными) сечениями (при
с < 0,1) определяющим является условие A1.11), а для
стержней с толстыми (компактными) сечениями — условие (П. 12),
В обоих случаях применение теории Кирхгофа — Клебшз
ограничивается стержнями с весьма малыми значениями
параметра Ро = Рт — хог«т (порядка 10~). При больших
значениях углов наклона винтовых волокон и соответствующих
величин начальной закрученности т0 следует использовать более
общие теории закрученных стержней, учитывающие
взаимосвязь различных видов деформаций.
В частном случае для стержней с двусимметричными
сечениями соотношения A.21) распадаются на две независимые
системы уравнений для продольно-крутильных и изгибных
деформаций, причем только последняя совпадает с
соотношениями теории Кирхгофа — Клебша для пространственною
изгиба
Му = Е {IX + lxyv").
Пределы применимости теории Кирхгофа — Клебша для этого
случая определяются условием A.6) и расширяются до
значений ро порядка 10. Поэтому классическую теорию обычно
можно использовать для решения задач о пространственном
изгибе закрученных стержней двусимметричного сечения, а
задачи растяжения и кручения закрученных стержней
необходимо рассматривать в рамках более общих теорий.
3. Пространственный изгиб закрученного стержня
двусимметричного поперечного сечения
Выражения для деформации ег (II.2), (II.9) при
пространственном изгибе приобретают вид
8г = — U"X — V"y = — Xyfe — К^Ц. A1.14)
Потенциальная энергия деформации стержня при этом в
системе координат xyz описывается выражением
П = 4- j j o2B2dFdz = 4" J J EzidFdz =
OF OF
= 4- J E [Iy (u"f + lx (v"f + 21xyu"v"\ dz, (II. 15)
о
а в системе координат 1цг —
±j(^*f)z. A1.16)
Уравнения пространственного изгиба закрученного стержня
можно получить с помощью уравнений равновесия A.17) или
A.20) с использованием зависимостей для моментов A1.13)
и компонент кривизны A.15). Эти же уравнения можно
получить с помощью обобщенного принципа
Остроградского—Гамильтона
S П — [ (qxbu + qybv + mxbv' — mybu') dz\dt =
о J
б П — {{q-bu + f?r,6fn — trilby-- — тфуц) dz
dt = 0,
Во втором случае находятся системы дифференциальных
уравнений с соответствующими граничными условиями, В си-
.26
стеме координат хуг уравнения пространственного изгиба
стержня, согласно классической теории, имеют вид
/ ft r it ( f* т l!\tt
(blxt/u + EIxv ) = qy — mx.
с граничными условиями
6u{Mv — m,}|o = O; ]
A1.17)
A1.18)
В системе координат \"г\г уравнения выглядят следующим
озразом:
д
2\
то «1
•Bт0
дг
Eh
дх„
¦tgo4
2т0
дг
да
а граничные условия
*htyWn|o
0;
¦/П|}|о==О;
== 0;
A1.20)
Для произвольно закрученного стержня, в том числе и
для стержня постоянного поперечного сечения, система
уравнений A1.17) имеет переменные по длине коэффициенты.
Система A1.19) в частном случае стержня постоянного попе-
27
речного сечения с постоянной степенью закрутки т„ = const
представляет уравнения с постоянными коэффициентами
Е [/„«|V — 2т0 (Л + /n) v"n — 2то (/„ + 2/=) щ +
+ 2то(/| + /П)У„ + 4/„и;1 = цг + тц + туп,; 9
? [/^ + 2т0 (/= + /П) «Г — 2т| (I, + 2/„) vn —
— 2то (/g + 1Ц) и -}- T(,/tt»,,] = f/r, + m? — то/ип.
Уравнения в форме A1.19) и A1.21) для решения
практических задач применяются редко.
Особенности деформации закрученного стержня будут
рассмотрены на примерах с простой загрузкой на конце. Для
решения таких задач удобно, воспользовавшись формулами A.9),
A.18) и A1.13), получить уравнения упругой линии стержня
в виде [44]
и" — к~ МХА sin a cos а + М
v" = -5- MyA sin a cos a — Mx, Pf
или
и" == — Л sin 2aMx + (В -(- Л cos 2a) М„;
A1.*;
где
л 1
2 ^ ?/л ?/.;• " - 2 [ Е1Ц ' Е/
Для стержня постоянного поперечного сечения коэффициенты
А и В являются постоянными.
Незакрученный стержень (а = 0; Iх — /j; Iy = /,,).
Уравнения A1.22) принимают вид ы" = My/EIv; v" = — MJEIx.
Стержень с равными главными местностями на изгиб (а ^=
ф 0; /, = /„ = /). При этом А = 0; В = 1/?7. Уравнения
упругой линии имеют тот же вид, что и для незакручешюго
стержня; и"— M/EI; v" = — MJEI. Закрученность в этом
случае не влияет на изгиб.
Изгиб равномерно закрученного консольного стержня
моментом М на конце (а = тог; т0 = const). Нагрузки Мх - - /VI
и Му =--- 0, граничные условия следующие : и @) = t1 @) ---
== и' @) = и' @) = 0. В этом случае в правой части уравне-
28
ш?й A1.22) функциями z являются только углы закрученнос-
тп а (г). После интегрирования этих уравнений получим
' On (/) 2 ' ' 2а2 (/) '
A1.23)
Л~~ / 1 ». h\ v '"i
1 {i R) 2a* (I) J
где v0 (I) — прогиб незакрученного стержня длиной /, vu (I) =
_i —Ml2/2EIi, к — отношение главных жесткостей стержня,
Изменения безразмерных проекций прогибов v (I) (а) и
и \1) (б) при возрастании угла закрученное™ а (I)
представлены на рис. 4. Выражения A1.23) при возрастании угла а (/)
справедливы только до таких значений т0, при которых
соблюдаются условия A.5), A.6). Поэтому предполагается, что
многократно закрученный стержень имеет соответствующую
большую длину I. При многократном закручивании (а (I) -> оо)
проекции прогибов приобретают вид и (I) -> 0; v (I) -*- (!¦+
-+- k)l2 = /|//ср, где средняя жесткость многократно
закрученного стержня стремится к Е1ср, причем средний момент инерции
A1.24)
/ 0
Многократно закрученный стержень изгибается так же,
как незакручеииый с жесткостью Ejcp. Величина 7ср иногда
называется средней гармонической величин Л, и /|. Пусть k
мало, тогда /ср г» 2/|.
Многократное закручивание стержня удлиненного
поперечного сечения увеличивает его жесткость вдвое по сравнению с
главной минимальной жесткостью. Форма упругой линии
приобретает такой же вид, как у незакрученного стержня.
Однако кривизна упругой линии многократно закрученного
стержня принципиально отличается от кривизны незакрученного.
У незакрученного стержня, изгибаемого моментом Мх = — Л-1,
только одна компонента кривизны отлична от нуля, а другая
постоянна: и" = 0; v" = MlEIt. Компоненты кривизны
многократно закрученного стержня обе не равны нулю и переменны
но длине
и" = A sin 2aM; v" = (fi — Л cos 2a) M.
Компонента v" колеблется между максимумом М/Е1-± и
минимумом M/EI-ц тем сильнее, чем больше различие главных
жесткостей. Компонента и" изменяется по длине по закону
синуса с амплитудой AM тем большей, чем больше различие
29
главных жесткостей.
При k -*¦ О амплитуда
изменения и" в 2 раза
превышает амплитуду
изменения и" по длине
стержня. Такой
характер упругой линии
многократно закрученного
стержня объясняется
тем, что направление
изгиба приходится то на
максимальную, то на
минимальную жесткость.
Поэтому участки
слабого искривления упругой
линии сменяются
участками сильного
искривления. Упругая линия
многократно
закрученного стержня стремится
к упругой линии неза-
крученного стержня при
а (I) —*¦ оо, как
вписанная ломаная линия
стремится к кривой при
увеличении числа
участков прямых. Это
необходимо учитывать при построении приближенных
методов расчета закрученных стержней. Достаточно хорошее
приближение для упругой линии закрученного стержня
не означает, что достигнуто приемлемое приближение для
кривизны.
Шгиб равномерно закрученной консоли силой на койне
D4] (а = тог; т0 = const). Пусть стержень загружен на конце
поперечной силой с проекциями Рх и Ру, которая вызывает
Рис. 4. Зависимость относительных
прогибов при изгибе закрученного стержня
моментом от угла закрученности и
отношения главных жесткостей к.
моментную нагрузку мх == — Ии (I — г); Му = Рх (I —
— г). Подставляя значения моментов в уравнения A1.22) и
интегрируя их дважды по г с учетом граничных условий,
получаем уравнения упругой линии
A1.25)
и == Рх (В% + Лп2) + РуАгп;
v = РхАщ + Ру (Вп0 — Ап2),
где п0
30
(I)
a (I) a2 тг as I;
L •* j
[a — a (/)] sin 2a + cos 2a};
...
— ail)] cos2a — sin 2a
0
/
/
t
Jrf -#<Г 5$ iffy
Рис. 5. Зависимость угла
направления осей сопротивления стержня
от угла его закрученности.
В общем случае смещение
конца закрученного стержня
не совпадает с направлением
равнодействующей сил Рх и
Ру. Введем систему координат хфг/ф) повернутую относительно
системы ху на угол <р, отсчитываемый против часовой стрелки.
Тогда зависимости между компонентами перемещений и
усилий в системах ху и хФг/ф, примут такой вид:
и — Мф cos ф — уф sin ф; Рх — Рщ cos ф — Рт sin ф;
v = йф sin ф + иф cos
Ру = Pxv sin
+ Руч, cos
С помощью этих соотношений уравнения A1.25) преобразуются
следующим образом:
«ф = Рх-,р {Вп0 + А (п1 sin 2ф -f- «2 cos 2ф)] +
+ PyqA («1 соэ2ф — n2sin29); (II.26)
V(f = РхцА (пх cos 2ф — n2 sin 2ф) +
+ Py<f \Bn0 — A (nx sin 2ф + /г2 cos 2ф)],
Отсюда видно, что при условии пх (I) cos 2ф — щ (I) sin 2ф =
= 0 или
tg 2ф = пх {1I щ (I) (II.27)
направления действия поперечной силы и смещения конца
консоли совпадают. Это условие определяет два взаимно
перпендикулярных направления, называемые осями
сопротивления закрученного стержня. Положение осей
сопротивления, как следует из условия A1.27) и выражений для л, и
щ, не зависит от формы сечения стержня и определяется
только его углом закручеиности. Зависимость угла ф от а (I)
приведена на рис. 5. Точками отмечены экспериментальные
результаты [441, При многократном закручивании стержня
(а (I) -> оо) угол ф не возрастает неограниченно, а стремится
к пределу ф» = я/4. Оси сопротивления при а (I) -*¦ оо
стремятся занять положение биссектрис главных осей инерции
защемленного сечения стержня.
0 $ 2Х Зл Лл Jjf old)
Рис. 6. Изменение относительных
коэффициентов главных
жесткостей закрученного стержня с
увеличением начальной закрученности
при различных соотношениях
главных гнбкостей ц,
1
С учетом условия A1.27)
уравнения A1.26) определяют
смещения конца консоли в
направлениях осей
сопротивления:
иФ = Р** [Вп0 (I) +
vv = Ри<е\Вп0A) —
— А Уп\ (I) + я? (/)],
Отсюда коэффициенты
главных жесткостей системы
Вп9 (/) + А У п\ (/) + ni (I)
п; (I) H- 4
A1.28)
Для незакрученного стержня kx0 = ЗЕ1уЦя; kyo = 3EIJP.
Коэффициенты главных жесткостей, согласно выражениям
A1.28), обладают следующими свойствами:
ku
Меньший коэффициент жесткости при многократном
закручивании возрастает, а больший — уменьшается согласно
отношениям
кх0
1 Ч--
Для стержня удлиненного поперечного сечения (JJly -*¦ 0)
отношение kJkya—2. Изменение относительных
коэффициентов жесткостей с увеличением закрутки стержня
представлено на рис. 6 [44],
32
4. Колебания закрученного стержня
двусимметричного поперечного сечения
Стержень, совершающий пространственные изгибные
колебания, загружен силами инерции. Поскольку в классической
теории сдвиг не учитывается, можно пренебречь и инерцией
поворота поперечных сечений при изгибе. Тогда
кинетическая энергия колеблющегося стержня
Т = -L \ р (иг + о2) Fdz = 4" J Р («I + un) Fdz- (IL29)
о о
где р — плотность материала стержня; точки над
перемещениями означают производные по времени.
Компоненты нагрузки в уравнениях A1.17), A1.19)
определяются выражениями qx — — pFu; qy = — pFv; q% = — pf%
qn r=~pFun; mx = my — пгг — /щ =0. Уравнения
колебаний закрученного стержня в системе координат xyz имеют вид
{El/ -f Elxyv")" + pF'ii = 0;
(EIxyu" + El У)" + pFv = 0. (ILg0)
Граничные условия при этом выражаются зависимостями
A1.18), а начальные условия для функций и (г, f), v (г, t)
имеют обычный вид:
и (г, t0) = и0; v (z, t0) = и0; |
и (г, t0) =t й0; у (г, /0) = у0. |
Для стержня постоянного поперечного сечения с
постоянной степенью закрутки можно записать уравнения колебаний
с постоянными коэффициентами:
(II,
Е1Ц («|V — 2т0о^'
— 2?/г (то1»п + 2то«; — toWti) + pFщ = 0;
2Е1Ц (%аиг — 2т5»г, — тг]й5) + pFvn = 0,
В этом же случае (т0 = const; /g = const; /л = const)
можно получить систему уравнений относительно изгибающих
моментов, эквивалентную системе A1.32). Для этого
необходимо в уравнение A,20) подставить компоненты нагрузки и,
3 2-] 896 33
дважды продифференцировав уравнения по г, воспользоваться
соотношениями A.15) и (П. 13):
Mlv — 4тчД1 — 6тоЛ1| + 4т30М'„ + т40М| -f -f?- Щ = 0;
л A1.33)
IV "' о * Ч " 4 0^ я'л
д^ _l. ¦eJ,'-]- j\^_^ ~~ бто/VJ 4t(v'W*' *4~ To ^W ~4" — — Ajn ;== и
) о ъ п • s-r л "г ?/| л
Эти уравнения удобны, когда граничные условия A1.20)
задаются в виде моментов и их производных. Любая из систем
уравнений A1.30), A1.32) или A1.33) вместе с
соответствующими граничными условиями описывает изгибные
колебания закрученного стержня двусимметричного поперечного
сечения.
Незакрученный стержень (а =0; 1Х — h; Iy = 1ц).
Уравнения колебаний распадаются на два независимых:
EItvw + pF'v = 0; ?/n«lv + pFu = 0.
Собственные частоты колебаний в направлениях главных жест-
костей описываются уравнениями
Тг— i2
а любая из форм колебаний определяется выражением вида
tH (г) = [С1 sin А,„-j- + С2 cosКп —- + Ca sh А,„
-f C4 ch Kn
v (z, i) = v0 (a sin co^ + b cos conf),
где значения параметров Хщ, Х| и коэффициентов Ck
определяются граничными условиями, а коэффициентов а и Ь —
начальными.
Закрученная невесомая консоль с массой на конце [44]. В
этом случае изгиб консоли в любой момент времени
описывается зависимостями A1,25), в которых силы Рх и Ру
определяются инерцией массы /га: Рх = — тй (/); Ру — —/га» (/). Тогда
уравнения колебаний массы в данном случае имеют вид
и = — т [(Вп0 + Ап2) и + Ап^о],
¦ ¦ г = I. (II.35)
V = — т \Апхи + (Вп0 — Ап2) v],
Предполагая колебания гармоническими и = «„sin©/;
v = vosinat и приравнивая нулю определитель системы
34
однородных уравнений, можно найти частотное уравнение и
значения двух собственных частот системы;
©1,2 = {т [Впй (t)±Ay n\ (I) + nl (/)]}"
или
ax = VIjm; &vYk~Jm, A1.36)
где kx и ky — коэффициенты главных жесткостей закрученной
консоли, определяемые зависимостями A1.28).
Собственные формы колебаний системы определяются
формами статической деформации консоли A1.25). Масса т при
этом перемещается в направлении, которое составляет с осью
х угол ф. Тогда v0 = uotgq>. Подставляя эту зависимость в
систему A1.35) и приравнивая нулю определитель системы,
получаем два значения угла ф, соответствующие двум
собственным частотам:
Углы фа и ф2 определяют два взаимно перпендикулярных
направления. Причем tg 2 ф1,2 = П] A)/п2A) и, следовательно,
направления собственных колебаний массы на закрученной
консоли совпадают с осями сопротивления этой консоли,
которые определяются формулой A1.27). Эти направления
не зависят от формы поперечного сечения, а зависят только
от угла начальной закрученности а (/).
Сумма квадратов периодов свободных колебаний массы на
закрученной невесомой консоли — постоянная величина, ке
зависящая от угла закрученности:
Г2 . rpl 1 , 1 с п /t\ Ml3
A1.38)
Квадраты собственных частот при закручивании консоли
сближаются так же, как коэффициенты жесткости kx и ку,
и в пределе частоты ах, &д стремятся к значению частоты
системы с бесконечной начальной закрученностью:
to» = Vef/rj/m/3 (I + k)\ k — /|//ti-
Изменения частот системы отнесенных к меньшей частоте
колебаний массы на незакрученной консоли в зависимости от угла
3* 35
щ
д
6
4
2
«я
iff
1?
Ofi
0,4
0
±
¦¦¦ I
7TZ
=33
i
1
г
_J
n
!
!
v
1
V
1
fi-10
4=
fT
Jif
5* t*(t)
Рис. 7. Зависимость
относительных собственных частот колебаний
массы на невесомой закрученной
консоли от угла закрученностн при
различных соотношениях главных
гибкостей и.
закрученности представлены
на рис, 7, откуда видно, что
значение большей частоты
падает тем сильнее, чем
больше отличаются главные из-
гибные жесткости стержня.
Равномерно закрученный
стержень постоянного
поперечного сечения (а = тог;
т0 = const; /s = const; /,, =
= const). Свободные
колебания такого стержня
описываются системой уравнений с
постоянными коэффициентами
A1.32) или A1.33), для
которых имеет место одно и то же
характеристическое
уравнение;
j — s4\
k)\ X* + ш [4а? +
+ (af — S4) (а! — ks4) = О,
где а;---а (/); k = 1/р,2 = /g//n; s — параметр в выражении
для собственной частоты колебаний
щ = D
A1.39)
Для каждой собственной частоты с номером k
характеристическое уравнение имеет четыре пары корней, половина из
которых вещественные, а половина мнимые: uIft; —ik\k\
ih2k\ —ihk', hk; —^з*; hk, —л«. Поэтому формы
перемещений и моментов представляются выражениями,
отличающимися только постоянными коэффициентами, типа
щи (z) = C\k sin %ik -j- + Oik cos X\k — + C3k sin hk — +
, cos Я2* 4- + Cok sh А,3* -у- -f Ськ ch!
A1.40)
Частотное уравнение, получаемое при удовлетворении
граничных условий, представляет собой определитель восьмого
36
порядка, элементы которого содержат трансцендентные
функции. Решение такой задачи получено в [60]. На рис. 8
представлены графики изменения параметров sk,
определяющих зависимость собственной частоты стержня от угла
начальной закрученности а (/) и соотношения главных гибкостей
стержня:
где Хщ, %i — главные гибкости: кп -¦= rn/t, Х| =/у7 (r|, Гц —
главные радиусы инерции сечений: r\ — 1%/F; Гц = In'F).
На каждом рисунке указан вид граничных условий,
которые относятся к пространственному изгибу. Например,
шарнир в сечении г — 0, означает, что щ @) = «„ @) = 0; М| @) —
-- Mr, @) = 0. Возможно также сочетание различных
граничных условий для различных направлений в плоскости ху,
но эти случаи здесь не отражены.
Характер изменения параметра sk, определяющего
собственную частоту, зависит от угла начальной закрученности
а (/), граничных условий и соотношения главных гибкостей и.
От абсолютного значения гибкостей соотношение частот и
характер их изменения не зависят.
Из кривых, приведенных на рнс. 8, видно, что собственные
частоты закрученного стержня попарно взаимодействуют и
при увеличении закрученности асимптотически сближаются.
В некоторых работах, например [44], утверждается, что
сближаются первые собственные частоты колебаний в
направлениях минимальной и максимальной жесткостей незакрученного
стержня. Такой вывод порожден аналогией с
рассмотренным выше случаем колебаний массы на невесомой
закрученной консоли, а также использованием приближенных
методик исследования колебаний закрученного стержня,
позволяющих учесть только указанные две частоты. Упругая
система массы на невесомой закрученной консоли вообще
имеет только две собственные частоты. Таким образом, вывод
о взаимодействии именно первых собственных частот
колебаний в направлениях максимальной и минимальной
жесткостей — следствие постановки или способа решения задачи,
при которых рассматриваются только эти две частоты.
Для решения задачи о колебаниях закрученного стержня
следует использовать не только приближенные, но и
аналитические методы [60]. Приведенные на рис. 8 параметры sk,
соответствующие собственным частотам колебаний
незакрученного стержня в направлении минимальной жесткости,
обозначены треугольником, а собственным частотам колебаний в
37
Рис. 8. Зависимость параметров s& собственных частот изгибных
различных соотношениях главных гибкое гей \х и граничных
а — консольный стержень; б — стержень со свободными концами; в --
оперт, другой — закреплен относительно угловых перемещений; д —
стержня закреплены относительно угловых перемещений; ж ~ один ко-
мещени.-';; з ¦— концы стержня защемлены. Треугольником обозна-
стержня в направлении минимальной жесткости, а квадратом —
колебаний закрученных стержней от угла закрученности при
условиях:
шарнирно-опертый стержень; г — один конец стержня шарнирн®
один конец стержня защемлен, другой — шарнирво оперт; е ¦— концы
нед стержня зац;емле)Ь другой — закреплен относительно угловых пере-
чеяы параметры собственных частот колебаний незакрашенного
в напразленин максимальной жесткости.
направлении максимальной жесткости — квадратом. Видно,
что попарно взаимодействуют собственные частоты в порядке
их возрастания. При этом графики изменения параметров с
увеличением угла закрученности а .'/) не пересекаются. Пока
соотношение главных гибкостей \i таково, что для незакручен-
ного стержня первая собственная частота колебаний в
направлении максимальной жесткости ниже второй собственной
частоты колебаний в направлении минимальной жесткости,
сближаются действительно первые собственные частоты
колебаний в направлениях минимальной и максимальной жест-
костей. Когда же соотношение главных гибкостей |Л возрастает
настолько, что первая собственная частота колебаний неза-
крученного стержня в направлении максимальной жесткости
становится выше второй собственной частоты колебаний в
направлении минимальной жесткости, сближаются первая и
вторая собственные частоты колебаний в направлении
минимальной жесткости.
С увеличением начальной закрученности стержня
сближаются таким образом первые две ближайшие собственные
частоты. При граничных условиях, отраженных на рис. 8,
а — г, первые две собственные частоты с увеличением угла
а (/) монотонно асимптотически сближаются. При граничных
условиях, соответствующих рис. 8, д — з, первые две
собственные частоты с увеличением угла а (I) сближаются,
расходятся и вновь сближаются, но при аA)—*-оо окончательно
асимптотически сближаются. Следующие две ближайшие
собственные частоты аналогично взаимодействуют, но перед
асимптотическим сближением графики их имеют, как правило,
большее число сближений и расхождений. Эти результаты
позволяют разобраться в поведении спектра собственных
частот стержня при его закручивании.
Приближенные методы расчета закрученных стержней на
колебания должны обеспечивать необходимую-точность
независимо от величины начальной закрученности. Такие методы
рассмотрены в работах [18, 45, 55, 56] и ряде других. В
данном случае методы расчета не рассматриваются, так как это
самостоятельная тема, а уделяется лишь внимание физике
процессов при деформации и колебаниях закрученных стержней.
В то же время используются результаты, полученные с
помощью достаточно апробированных методов.
Поведение первых шести собственных частот консольного
стержня при увеличении угла начальной закрученности а ([)
для различных значений соотношения главных гибкостей \i
показано на рис. 9. Все частоты отнесены к первой собственной
частоте колебаний иезакрученного стержня в направлении
40
—j—1—
5
V."
j
N
^о—о—<j
го
У////////////У/////Л
Г
—^
\
4
)—=#:
0 rf oC(Q
Рис. 9. Изменение относительных собственных частот консольного
стержня в зависимости от угла начальной закручепности и
соотношения главных гибкостей.
минимальной жесткости ©ю- Штриховыми кривыми
представлены частоты, которые при а (I) =0 соответствуют
собственным частотам колебаний незакрученного стержня в
направлении максимальной жесткости. Точками показаны эксперимен-
41
Рис, 10. Влияние соотношения
главных гибкостей на относительные
собственные частоты нзгибных колебаний
закрученных стержней.
тальные результаты.
Размеры поперечных сечений
указаны в миллиметрах.
Видно, что характер
кривых соответствует рис, 8, с.
Первые две собственные
частоты с увеличением угла
а (/) монотонно
асимптотически сближаются.
Сближение остальных пар
частот не носит монотонного
характера. Подобные
результаты приводятся
также в работах 163, 87],
Нелинейность закона
начальной закрученности
не вносит в картину
поведения собственных частот
качественных изменений.
Если относительная закру-
ченность т0 (г) возрастает
от корневого сечения
консольного стержня к
свободному концу, то места
сближений частот (см. рис. 8, с и 9) смещаются несколько
влево (в сторону убывания угла закрученности) по
сравнению со случаем линейного закона начальной
закрученности (т0 = const), но с тем же углом а (/). При убывании
относительной закрученности от корневого сечения к
свободному концу стержня места сближений частот несколько
смещаются вправо.
Изменение собственных частот консольных закрученных
стержней в зависимости от изменения соотношения главных
гибкостей ц показано на рис. 10. Все частоты также отнесены
к первой собственной частоте колебаний незакрученного
стержня в направлении минимальной жесткости со]О. Сплошные
горизонтальные лучи отражают спектр собственных частот
незакрученного стержня при колебаниях в направлении
минимальной жесткости, а наклонные — изменение спектра
собственных частот колебаний незакрученного стержня в
направлении максимальной жесткости при увеличении ц. Кривые
отражают изменение спектров собственных частот стержней с
различной начальной закрученностью при изменении
параметра (л. Углы а (/) указаны в радианах. При малых углах
.начальной закрученности кривые частот следуют вдоль лучей,
42
X
1У
0,4
x f
0,6 \
Л
¦0,8
0,2
X
f
/^
X
oja
в местах пересечения лучей
изгибаются и следуют
вдоль встретившегося
нового луча. С увеличением
начальной закрученности
кривые собственных частот
все больше отходят от
лучей. Совместное
использование рис. 9 и 10
позволяет представить спектр
собственных частот
консольного стержня в
широком диапазоне значений
углов начальной
закрученности и соотношения
главных гибкостей.
Изменение форм
колебаний консольного
стержня в зависимости от угла
начальной закрученности
и соотношения главных
гибкостей представлено на
рис. 11. Сплошными
кривыми показаны проекции
форм колебаний на
плоскость минимальной
жесткости, а штриховыми — на
н таскость максимальной
жесткости корневого
сечения, Указаны углы а (I)
и тон колебаний каждой формы. Даже при малых углах
начальной закрученности а (/) формы колебаний представляют
собой пространственные кривые. Это хорошо видно на рис. 12,
где приведены проекции форм колебаний стержня при
а (/) =^ яЧ, (х = 3 на плоскость ху. Отмечены 10 сечений,
расстояние которых от плоскости ху изменяется на величину,
равную 0,1 длины стержня.
Каждое сечение имеет свое направление колебаний,
которое определяется прямой, проведенной через начало
координат и соответствующую точку формы. Лишь для первой
формы можно с известным приближением говорить о
плоскости колебаний. Высшие формы колебаний представляют
собой явно выраженные пространственные кривые. Формы
колебаний закрученного стержня не имеют узлов как
неподвижных точек оси стержня, которые позволяют достаточно
Рис. 12. Проекции на плоскость хц
форм колебаний консольного стержня,
закрученного на угол а (/) = я/4 при
fi = 3.
43
Рис. 11. Проекции форм изгибиых колебаний консольного
кривые) в зависимости от угла закрученностн и солношения
о — д = 1,8; б — р. = 3;
т/т
7777?
'7777",
2-tc
стержня на плоскости хг (сплошные кривые) и уг (штриховые
главных гибкостей:
i:
V77?
'-¦//
777?
\ т / \
\
У
Ш
wr,
)
1
/2
Tt
Рис. 11. (Продолжение)
в — ц = 6; е — ц = 12.
*
fr-S,
\
У
\
Ч-.
ч
t
Ш7,
&
Ъ77>
У
^7
Ч
\ Л-
vzr.
л
У -р
О
TZ7
1Z
4
Р ~Р
20
Ж.
г
Ж
//////////У//////////л
t *-1
2*
просто классифицировать формы колебаний незакрученного
стержня.
Направление колебаний концевого сечения закрученной
консоли по первой форме колебаний составляет угол tp с осью
х (направлением минимальной жесткости). При увеличении
угла а (/) угол ср, как видно из рис. 11, стремится к величине
(piM =с л/4. Направление колебаний концевого сечения по
второй форме составляет с осью х угол ср2, который при
увеличении угла а (/) стремится к (р!оо = <р1к ± л/2. Направления
колебаний концевого сечения по высшим формам с
увеличением угла а (/) претерпевают более сложные изменения.
При классификации собственных частот и форм колебаний
закрученной консоли приведенные на рис. 9—12 зависимости
оказывают значительную помощь.
Глава III
ДЕФОРМАЦИИ ЗАКРУЧЕННЫХ СТЕРЖНЕЙ
С ПОЗИЦИЙ ТЕОРИИ УПРУГОСТИ
1. Слабо закрученные стержни
Под слабо закрученными стержнями понимают стержни,
относительная закручешгость которых значительно меньше
определяемой критериями A.5), A.6). Из задач деформации
слабо закрученного стержня методами теории упругости П. М. Риз
[39] довел до окончательных результатов задачу о растяжении
стержня силой Рг на конце. В этом случае деформации
определялись выражениями
х = о = — т,
0 GF
-1
(П1.1)
И; == «Л = О,
где 10 — полярный момент инерции; U — геометрическая
жесткость на кручение призматического незакрученного
стержня.
Напряжения в поперечном сечении имеют вид
F '
Х--, ==
= о„ =
Т|1} = о;
/'' д.
' a
(III.2)
9 5ф
I?_ |
где ф (|, 1]) — функция кручения соответствующего
незакрученного призматического стержня.
Из формул (II 1.1) следует, что при растяжении продольной
й Р й
силой Рг
закрученный стержень раскручивается, при этом
4 2-!
49
в нем кроме напряжений crz возникают, согласно зависимостям
{III.2), касательные напряжения хчг и tv-
Выражения (III.1), (II 1.2) получены в предположении, что
выполняется условие
где C81
\ = 2 A -г у) —г \1Г ~ Тг г
/r = J ridF; Тг = С [r*a -
г = J (r«
dm ,„ «. . Cro , .
ФФ = "^- (g — 6а) — -^Г- (Л — Ла).
Здесь ta и !]„ — координаты оси закрученности стержня.
Критерий (Ш.З) определяет значительно более узкую
зону применимости решений задачи, чем критерий A.6).
Касательные напряжения при кручении слабо закрученного
стержня определяются теми же выражениями, что и для
призматического. Было показано также, что для слабо закрученного и
слабо искривленного в начальном состоянии стержня, эффекты
закрученности и изогнутости могут рассматриваться отдельно,
В работе [29] с использованием неортогональных
криволинейных координат получено в общем виде решение задачи Сен-
Венана [42] для закрученного стержня. На основании этих
результатов для слабо закрученного стержня двусимметрич-
50
ного поперечного сечения в работе Г. Ю. Джанелидзе [22]
получены выражения
Р, Л'Ь / In
_ а' _
\J _
G/° ° GF
(Ш.4)
- ~ ?7, ' щ ~ EI ' (Ш.д)
Причем выражения (III.4) справедливы при условии (III.3),
а выражение (III.5) — при менее жестком условии A.6).
Таким образом, показано, что даже для слабо
закрученных стержней существует связь деформаций растяжения и
кручения. В то же время жесткости стержня на изгиб и
кручение определяются так же, как и для незакрученного
призматического стержня.
2. Произвольно закрученные стержни
Без предположения о слабой начальной закрученности до
окончательных результатов доведены лишь наиболее простые
задачи. Так, для случая растяжения силой Рг и кручения
моментом, Мг закрученного стержня удлиненного
прямоугольного сечения в работе [80] получены выражения
Рг = Ьф + 6„т; Мг = Ьтев + Ьх%, (III. 6)
где bs, bx, bex, b%e — коэффициенты в зависимостях вида
A.21) между кинематическими и силовыми характеристиками
деформаций.
При чистом растяжении Мг — 0; % = — {bxJbT) e; Рг =
= Ь?&, где «эффективная» жесткость при растяжении
4
' ЬЕ = К г—. (HI.7)
При чистом кручении Р2=0; е — — фт1Ьг)т, Мг — Ь"т%.
Эффективная жесткость при кручении закрученного стержня
теперь отличается от жесткости на кручение призматического
стержня
ь2
b'x = bx f-. (III.8)
0,3
\
К.
2
г
-f-
be
0,9
0,7 hV-rl I—
0,5-
0
0,2
0,4
Рис. 13. Зависимость относительных крутильной и
продольной эффективных жееткостей стержня
прямоугольного сечения от параметра закрученности f>nl.
Для незакрученного стержня удлиненного прямоугольного
сечения ft x 6 величины коэффициентов определяются из
выражений &so = EF = Eh8; bTo — Gl'j = -^- G/гб3.
Для закрученного стержня соответствующие жесткости
зависят от максимального утла наклона волокон рт = 0,5 х
Хто/г, соотношения сторон б'/г и коэффициента Пуассона v.
На рис. 13 [38] показано изменение эффективных жесткостей
на кручение и растяжение, отнесенных к соответствующим
жесткостям незакрученного стержня, при v == V3, blh ==0,1.
Расчеты проводились в предположении, что рт <<^ 1 и членами
порядка pi можно пренебречь (кривая 1), с учетом членов
порядка $',„ (кривая 2) и с учетом также членов порядка f>m
(кривая 5). Видно, что предположение рт <^ 1 обеспечивает
уже приемлемое приближение.
В работе В. М. Марченко рассмотрена задача о кручении и
растяжении без изгиба (что возможно для стержня двусим-
метричиого сечения) закрученного стержня. Решение доведено
до конечных результатов для стержня эллиптического
сечения. Рассмотрены продольно-крутильные колебания
вращающегося вокруг оси х стержня постоянного сечения. Показано,
что частота преимущественно крутильных колебаний
возрастает с увеличением начальной закрученности.
На основании этих результатов в работе Н. В. Алексеева
13] рассмотрена задача о продольно-крутильных деформациях
спирального сверла. Для эффективной жесткости сверла на
52
кручение получено выражение
Ьх —Ь% т
где п* = Н- _-gLj. (p0—угол наклона винтовой ка-
навки сверла к его оси; d — наименьший размер сердцевины
сверла; h — наибольший размер секущей пера сверла).
Показано, что при сжатии сверла сердцевина его сжим -
ется, а в периферийных точках сверла могут возникать
напряжения растяжения. При раскручивании сверла сердцевина
растягивается, а периферийная часть пера испытывает сжатие.
В работе [2] двумерная задача для закрученного винта
решена с помощью аналитических функций комплексного
переменного. Но при каждом конкретном расчете необходимо иметь
уравнение винтовой поверхности стержня.
В работах А. К. Рухадзе [41] и его учеников методами
математической теории упругости рассмотрены частные задачи о
растяжении и изгибе закрученного стержня как в линейной,
так и нелинейной постановке с учетом анизотропии
материала. Показана связь различных видов деформаций.
Таким образом, исследования деформаций закрученных
стержней с позиций теории упругости показали, что даже для
слабо закрученного стержня двусимметричного поперечного
сечения необходимо учитывать связь продольной и
крутильной деформаций. При несимметричном сечении возникает связь
изгиба с другими видами деформаций. Эти результаты и
определяют ограниченность области применимости классической
теории закрученных стержней. Вместе с тем методами теории
упругости доведены до практического применения лишь
простейшие частные задачи о деформации закрученного стержня.
Поэтому и возникла необходимость развития теории стержней,
учитывающей связь различных видов деформаций и в то же
время позволяющей решать достаточно сложные задачи
статики и динамики закрученных стержней.
Глава IV
ДЕФОРМАЦИИ ЗАКРУЧЕННЫХ СТЕРЖНЕЙ
ПРОИЗВОЛЬНОГО СЕЧЕНИЯ
1. Основные положения приближенной теории
закрученных стержней
Создание точной теории закрученных стержней
произвольного поперечного сечения на базе общих уравнений теории
упругости связано с большими математическими трудностями
и приводит к очень сложным решениям, вследствие чего
использовать этот путь для разработки практических методов
расчета пока не рационально.
Целесообразно построить приближенную теорию
закрученных стержней произвольного сечения, основанную на
определенных гипотезах, позволяющих разделить
компоненты напряжений и деформаций на главные и второстепенные,
которыми в ряде уравнений допустимо пренебрегать.
Достоверность приближенной теории проверяется сопоставлением с
известными для некоторых частных простых случаев точными
решениями и широким сравнением результатов расчетов с
экспериментальными данными.
Кроме системы координат |г)?, введенной в гл, I,
используется также система координат ii%?i в сечении, отстоящем
от рассматриваемого на dt,. В соответствии со способом
образования закрученного стержня, указанным в гл. I, текущая
точка поперечного сечения М, имевшая в исходном (незакру-
ченном) состоянии прямоугольные декартовы координаты | =в
— |i, г) = % или полярные координаты га -— V(I, || -\-
—j— (т] — т)-)~; \р ¦-— arctg -—z— перемещается но винтовой
? fees '
линии ММг и ее текущие координаты (рис. 14) будут
I = 1-х + (Si — fe) cos a — (t>i — %.) sin а;
г\ = г)а + (ii — 1а) sin а + (% — %) c°s а,
или ra = ra\ = const; "ф = ^ + а.
Угол наклона винтовой линии ММх к оси ?а соответствует
8„ = arctg (тога). В дальнейшем ограничимся анализом таких
54
стержней, для любой точки которых справедливо условие ро <^
< 1, т. е. (т0гаJ <1 1.
Считая стержень достаточно длинным, примем, что
объемные силы и нагрузки на боковой поверхности / (|1? %) -= О
отсутствуют, а нагрузки, приложенные по торцевым плоскостям
статически эквивалентны продольной силе N, направленной
по оси ta, изгибающему моменту с компонентами Мга, Мш
и крутящему моменту /Vfja- Для текущего сечения yV = const;
Mta — const; M|i = M|a cos a -\- Mm sin я -f- Nr\a', Mn; =
-~ —Afvxsina -f- Mi)acosa — iV|a, где Mji и Alni — моменты
относительно подвижных осей ?х и i]i.
В соответствии с принципами теории стержней
Кирхгофа, при выводе основных соотношений для закрученного
стержня достаточно рассмотреть область, непосредственно
примыкающую к сечению L = 0, для которой / соизмерима с
наибольшим размером поперечного сечения гтах. Получаемые в
дальнейшем соотношения для поперечного сечения ? = 0 будут,
естественно, справедливы для любого сечения закрученного
стержня (достаточно удаленного от торцевых плоскостей),
поскольку в качестве исходного ? = 0 можно принять любое
сечение.
При условии A.5) угол a = то? во всей указанной области
будет малым, поэтому
аг = (т0СJ^1; sina^a; cosa^l (IV. 2)
и формулы (IV. 1) принимают вид
I ---- li — (% — %) то?; г) = Tli + (li — Ы То?- (IV.3)
Тогда для любой функции f (с,х, %, ?,г) = 0 и в частности для
уравнения боковой поверхности закрученного стержня
/ Si. Ш) = 0 справедливы соотношения
h ^ /i, —
(IV. 4)
где для частных производных принято обозначение fk —
— dfldk и введена производная /^ в полярных координатах га\р:
Очевидно, что в членах с множителем т0 с принятой
точностью можно не делать различия между координатами щ
и &!% и соответствующими производными. Для уравнения
боковой поверхности /^ = 0.
55
Направляющие косинусы нормали к боковой поверхности
k, к — ?, ц, l, определяются по формулам
hi ~ 7F ft = U
Если а^ — тензор напряжений в системе координат Ету*,
то условие отсутствия напряжений на свободной боковой
поверхности имеет вид
odfi = О, k, 1 = 1, ii, ?
или
0;
= 0.
(IV.6)
где для простоты записи вместо Okk пишем ak.
Соотношения типа (IV.4), (IV.6) при ta = % = 0 исполь-
зовали П. М. Риз [39], А. И. Лурье и Г. Ю. Джанелидзе
[29J при анализе деформаций закрученного стержня с
применением полной системы уравнений теории упругости, что
естественно, приводило к весьма сложным решениям,
доведенным до конца лишь для простейших частных случаев.
Оставаясь в рамках приближенной теории, введем
понятие о главном нормальном сечении стержня, иод которым
будем подразумевать сечение, образованное некоторой
непрерывной поверхностью со следующими свойствами; главное
сечение нормально к боковой поверхности стержня во всех
точках линии пересечения этих поверхностей; главное сечение
имеет наименьшую площадь среди всех возможных
нормальных сечений. В дальнейшем указанное сечение будем называть
просто главным. Отметим, что используемые при анализе
концентрации напряжений ломаные и цилиндрические сечения
относятся к частным случаям нормальных сечений.
Очевидно, что для незакрученного стержня (т0 = 0)
главное сечение совпадает с плоским поперечным сечением ? =
= const (в частности, ^ = 0). Для закрученного стержня
уравнение главного сечения с принятой точностью можно
записать F = t, —¦ то(р (ё, ii) = 0. Вид функции ф (|, г\) будет
56
установлен ниже, исходя из определения свойств главного
сечения.
Согласно выражениям (IV.4) F% — —тоф|; Fn ——Тоф,,;
F'i = 1 и, в соответствии с первым свойством главного
сечения, для точек контура, когда / Aи %) = 0, имеем F%fi +
+ F'nfn + FE/> = 0 или при т0 ф О —
Чь/s + Фл/л + U = О- (IV-7>
Поскольку площадь главного сечения
| J Y1 + (F|J + (F'nf dgdr\ = IJ j/1 + %l \Шг + (ф',,J] <%di)t
условие ее минимума, согласно уравнению Эйлера, при
условии (IV,2) приводит к уравнению Лапласа
Фа + Флп = О- (IV.8)
С принятой точностью левая часть уравнения (IV.8) равна
удвоенной средней кривизне главной поверхности, и
равенство ее нулю означает, что главное сечение является наиболее-
плоским из всех других нормальных сечений.
Уравнением (IV.8) при граничном условии (IV.7)
определяется форма главного сечения стержня (с точностью до
несущественной постоянной). Нетрудно убедиться, что
уравнение (IV.8) и граничное условие (IV.7) совпадают с уравнением
и граничным условием для функции кручения ср0
призматического стержня того же профиля поперечного сечения
/ (s, л) = 0. полученной в предположении, что при свободном
кручении стержень закручивается относительно оси ?а.
Поэтому функции ф и ф0 совпадают с точностью до постоянной.
Приравнивая эти постоянные, получаем, что главное сечение
естественно закрученного стержня совпадает с поверхностью
депланации шф призматического стержня того же поперечного
сечения, упруго закрученного на тот же относительный угол
т0. Для определенности примем \ ydF = 0, причем в силу
F
условий (IV.5) интегрирование по площади главного сечения
можно заменить интегрированием по площади F плоского-
поперечного сечения. С принятой точностью, для главного
сечения, соответствующего поперечному сечению Z, = 0,
можно считать |] = I; г|, = ц; /ь = /?; /^ = /V
Найдем связь между компонентами тензора напряжений
ot.i для точки поперечного сечения М° (|, г\, 0) в системе
неподвижных координат (k, I = %, г\, 0 и компонентами
тензора напряжений а*ы для соответствующей точки главного
57
сечения М* (|,т1.тпф) в системе координат, связанной с
главным сечением (k, I = с*, г]*, ?*), направляющие косинусы
которой определяются соотношениями
1 0 тпср
О
1
Л
(IV.9)
т. е, ось 'Q* направлена по нормали пч. к главной поверхности,
а оси с*, i|* лежат в касательной плоскости к ней и при тв —
s= 0 совпадают соответственно с осями ?, т|.
Используя известные формулы для напряжений на
наклонных площадках и полагая а« (?, ц, тоф) =»аы (§, т], 0) +-
+ [а^г (с, 1], 0)]г то<р, получаем с принятой точностью
следующие соотношения:
•а, = а
, + т0
4 = а° - т0 {2
т?„ = ст|„
а^)? ф];
[ (IV.10)
о оч
где учтено, что вследствие уравнений равновесия (озд =
Обратные соотношения для системы (IV. 10) имеют вид
Щ — ol — т01@ц)= 4^ (оПщЫ; . . . , а напряжения в точке М*
главного сечения в системе координат cr\t, —
о, = 0> — 2т0ст^фг -- aj 4^ (ог)^т0ф; ... AV .11)
Введя выражения (IV. 11) в граничные условия (IV.6) для
точек контура главного сечения / (|, ц) = 0; 'С, = тоф, получим
}
'l'f'Jl — a,>,,/n — 0Гй (ф|/'г, 4" Фг/j) = 0.
• С учетом (IV.7) условия (IV. 12) удовлетворяются при
любой функции о-;, если
CTj = 0,! = а*п = 0; оУ* + аУ'ц = 0. (IV. 13)
Для незакрученного стержня при т0 = 0 значения а* = от0,
и из граничных условий на боковой поверхности следует
аг = а,, = 0|„ = 0; щф_ -f а„*/„ = 0.
Таким образом, граничные условия для компонент тензора
напряжения 0* в главном сечении закрученного стержня
полностью совпадают с условиями для а0 в плоском поперечном
сечении аналогичного незакрученного стержня. Условия
{IV. 13) означают, в частности, что элементы материала у
контура главного сечения не испытывают сдвигов. Особое свойство
главного сечения и заключается в том, что оно остается
нормальным к боковой поверхности после деформации
закрученного стержня.
В соответствии с общими принципами построения теории
стержней введем представление об основных и
второстепенных компонентах напряжения. К второстепенным
компонентам напряжения в главном сечении отнесем компоненты,
которые обращаются в нуль на его контуре, т. е. оч, ап и Огц,
так как в соответствии со вторым свойством главного сечения
(минимум площади) трудно ожидать, что их значения внутри
стержня станут большими.
Соответствующие компоненты в поперечном сечении <х*,
ап, О|П также должны быть малыми, а это позволяет считать
CTj»a^«a?n»0 (IV. 14)
и пренебрегать членами т()а|;ф? и тоа'^йщ по сравнению с
основными компонентами напряжений а*, а^, ст^ и ajj, a?j, o^.
Из интегральных условий равновесия
1г - 1 elndF;
(IV. 15)
Мц - - ) olUF;
F
м& = \ i<4 (l - Ы - 4 (n - na)}dF
59
и соотношений для внутренних силовых факторов при
условии (IV.2)
Pi = const; М^а = const;
следует, что изменение основных напряжений по длине
стержня должно иметь порядок т0. Поэтому соотношения (IV, 10)
с учетом условий (IV. 14) существенно упрощаются:
¦ о , о '
ЧЧЫ
(IV. 16)
Обратные соотношения приведенной системы имеют вид
4 4; аст WP;
Из трех дифференциальных уравнений равновесия (aw)/ ==
= 0; k, I = %, ц, С для основных компонент напряжения
остается одно:
(оЬ'ъ + DI + (Ад'п = 0. (IV. 17)
Представим основные компоненты напряжения в виде сумм
oli + Toa*/> причем в рассматриваемом случае (a°/)r = 0,
так что уравнение (IV. 17) с учетом (IV. 16) распадается на два;
где в соответствии с (IV. 16) принято
Здесь o\i и a^j — дополнительные касательные напряжения
сдвига, вызываемые поперечными силами Р* и Рц. Эти
напряжения, как обычно в теории стержней, отнесены к
второстепенным.
Очевидно, что первое уравнение (IV. 18) при граничных
условиях (IV. 13) соответствует задаче Сен-Венана о кручении
призматического стержня и удовлетворяется при
0,,; -= GX (фг1 +¦ S — la)
60
Здесь принято, что упругое кручение происходит относительно
оси 1а, поэтому деиланация при упругом кручении
описывается той же функцией <р, что и уравнение главного сечения.
Таким образом, распределение основных касательных
напряжений в главном сечении закрученного стержня совпадает
с распределением касательных напряжений в поперечном
сечении аналогичного незакрученного стержня при свободном
кручении. Однако зависимость относительного угла упругой
закрутки т от внешних нагрузок и величина касательных
напряжений будут другими.
Перейдем к рассмотрению деформаций и перемещений.
При условиях (IV. 14) основные деформации в главном и
поперечном сечениях соответственно
(IV. 20)
0 О/г? 0 0 ,п П О ,--,
в частности, с учетом (IV. 19)
Деформации 8t, е,,, е^ и
е?,
е?,,, связанные с
пенными напряжениями и поперечным сжатием от
напряжений ol или а*, относим, как это принято
стержней, ко второстепенным. Соотношения между
циями в главном и поперечном сечениях согласно
(IV.20) имеют вид
4 = е°;
- 2 A + v) Tn8jq)i
+ 2 A + v) то8;Фт
второстедействия
в теории
деформа(IV. 16) и
(IV.22)
Обратные им соотношения будут
•2A ~f V)TOF;V;:
-2A +v)T0e;(r.,,.
61
и соотношений для внутренних силовых факторов при
условии (IV.2)
Pi = const; Mja = const;
следует, что изменение основных напряжений по длине
стержня должно иметь порядок т0. Поэтому соотношения (IV. 10)
с учетом условий (IV. 14) существенно упрощаются:
(IV. 16)
Обратные соотношения приведенной системы имеют вид
Из трех дифференциальных уравнений равновесия (<%)/ =
= 0; k, I = |, т), ^ для основных компонент напряжения
остается одно:
D)i + D)g + («4ь = о- (iv. m
Представим основные компоненты напряжения в виде сумм
oli + ^о0*'» причем в рассматриваемом случае (o°i)r — 0,
так что уравнение (IV.17) с учетом (IV.16) распадается надва:
(^+_(^ = °;! _ # (iv. 18)
Ч [(oli)! + @«)п + К)Е — (ог>);Ф| — (o^Vpr,] =- 0,
где в соответствии с (IV. 16) принято
аш = — a?" tp| + <Т|С; апЕ = — 0Е*<рп + 4Е.
Здесь ш- и ang — дополнительные касательные напряжения
сдвига, вызываемые поперечными силами Р* и Р^. Эти
напряжения, как обычно в теории стержней, отнесены к
второстепенным.
Очевидно, что первое уравнение (IV. 18) при граничных
условиях (IV. 13) соответствует задаче Сен-Венана о кручении
призматического стержня и удовлетворяется при
ajc-GTOpg-rH-iW; AVJ9|
0П; = 64 (фП -h I Set).
60
Здесь принято, что упругое кручение происходит относительно
оси ta, поэтому депланация при упругом кручении
описывается той же функцией гр, что и уравнение главного сечения.
Таким образом, распределение основных касательных
напряжений в главном сечении закрученного стержня совпадает
с распределением касательных напряжений в поперечном
сечении аналогичного незакрученного стержня при свободном
кручении. Однако зависимость относительного угла упругой
закрутки т от внешних нагрузок и величина касательных
напряжений будут другими.
Перейдем к рассмотрению деформаций и перемещений.
При условиях (IV. 14) основные деформации в главном и
поперечном сечениях соответственно
и (IV.20)
0 /
%/
в частности, с учетом (IV.19)
Деформации ее, ет1, ее,, и е*, e^, е%ц, связанные с
второстепенными напряжениями и поперечным сжатием от действия
напряжений aj или а°, относим, как это принято в теории
стержней, ко второстепенным. Соотношения между
деформациями в главном и поперечном сечениях согласно (IV. 16) и
(IV.20) имеют вид
= Ъг]
+ v)Toe°cpj
(IV.22)
Обратные им соотношения будут
4 - еЕ;
": = е5: — 2 A + v)Top,rp;;
e;ft = е,е — 2 A + v) Toetcp,,.
61
Основные деформации г% связаны о перемещениями
б
ип обычными соотношениями:
(IV. 23)
Поскольку для призматического стержня упругие
перемещения в общем случае определяются по формулам 130, 421
Г2
иг = х„ -| т? (г]
(IV.24)
(Е, т]),
где е — удлинение; щ, нп — компоненты кривизны оси
стержня; т — относительная закрученность, то для закрученного
стержня с принятой точностью естественно искать
перемещения в виде
«I
— % (Ч — Ца) +
ъ (?, 11, 0;
; (IV.25)
(Е,
(t, л, 0>
где коэффициент k и функции Ф|, Фл, Ф{, имеющие порядок
т0, должны быть такими, чтобы удовлетворялись уравнения
(IV.21) — (IV.23). Очевидно, что компоненты деформации е,
т с принятой точностью можно считать постоянными, а
производные кривизн Х|, кщ по длине стержня имеют порядок
т0 и не зависят от ?.
Вводя в последние два уравнения системы (IV.23) значения
перемещений (IV.25) и деформаций согласно (IV.21) и (IV.22),
получаем
Ьо [(Ф?)? + (Ф*№ = — 2 A + v)
k%0 {(ФЦ + (Ф1)'п] = — 2 A + v)
(IV.26)
где (Ф0)' = Ф' (|, п> 0).
62
Прямой подстановкой легко проверить, что при т0
уравнения (IV.26) удовлетворяются, если принять
(u-)'t\ Ф;
ф еф
С учетом выражения (IV.25) для щ получим Фг =
Таким образом, окончательно имеем
1
у
Фч = —
щ = Хт| -^ т? (tj — %) +2A + v) т0Хт)?ф;
- [т — 2A + у) то8?] ф.
(IV.27)
Из формул (IV.27) видно, что в закрученном стержне депла-
нация плоского поперечного сечения связана не только с
упругим кручением, как в призматическом стержне, но и со
всеми другими видами деформации, и что при повороте сечения
относительно осей Ъ\ контур поперечного сечения
искажается, у
В соответствии с (IV.27) основные деформации в
поперечном сечении ? = 0 описываются выражениями
4; =
(Фл
+ Г|«) — 2
— la) — 2 (
V)
v)
(IV.28)
а деформации в главном сечении — условием et = е? и
формулами (IV.21). Соответственно для напряжений в
поперечном сечении
(IV. 29)
at = Е (г — х„~ -f ^i1! — То
oli = Gx (Фб — Л + Ла) — Toa^g;
a°, = Gx (ф„ + 1 — la.) — тоа^фп,
а в главном сечении
= Е (е — x^g
(IV. 30)
Рис. 14., Элемент
стержня.
закрученного
Последний член в первой
формуле системы (IV.28),
представляющий собой
дополнительную деформацию,
присущую только
закрученным стержням, можно
получить путем прямого
рассмотрения удлинения
волокна, наклонного к оси
стержня в плоскости tt, (см. рис.
14) на угол ро при деформации
кручения. Вследствие
перемещения dut = rad%
указанное волокно ММ1
повернется на угол р и получит
деформацию
Ае* =
Д (АШХ)
cos (р0 + р) cosjS0
cos
_ cos Р„ - cos ф + p0) _
cos (p + p0)
или в линейной постановке при р
0,5p),
(IV.31)
При р\> = —тпф< и р = хга получим Ле* = —тотф-ф, где
«f4 = fasp/. Однако деформация продольного волокна ММ
при том же кручении определяется относительным
продольным перемещением точек N главного сечения dw = щ-Az —
== —хохщй1, и в линейной постановке (см. рис. 14)
Л „ &(MN) _ dw _
MN
Таким образом, практически равные деформации Ле° и Ар*
получаются вследствие различных компонент перемещения
закрученного стержня при дефорхмации кручения,
64
2. Слабо закрученные стержни,
линейное по т0 приближение
Во многих исследованиях закрученных стержней в качестве
простейшего приближения принимается приближение,
линейное по т0, когда во всех уравнениях сохраняются только
члены, содержащие т0 в степени, не выше первой. В этом случае,
введя выражения (IV.29) в интегральные условия
равновесия (IV. 15), найдем после интегрирования по площади
поперечного сечения
тот
/3I;
| = Е [eS| — кп11г1 + щ1г + тот AРП —
1а) — хп (/
Рп
где
/pi = J 4
F
= J (rl
T, = | (ri + щ) %dF; Tn = ) (r« 4- Фф)
F F
. (IV.33)
Если оси координат gi] являются главными центральными
осями, то S| = 5Л = /t-i] = 0 и формулы (IV.32) принимают
вид
Л'1. = ? (х^/г, — тот AРЦ — Тп)\;
f ?ТО [Е (/р - /2) -
(П',84)
разрешив уравнения (iv.ot; относительно деформация,
получим с принятой точностью
е =
Т ==
EF
3l
HfT
s
To „,o, ^4ja;
G/»
f
f (IV.35)
Из соотношений (IV.35) видно, что в закрученном стержне
компоненты плоской деформации е, щ, щ зависят от крутящего
момента Мг^, а относительная закрутка х — от всех силовых
факторов. Для кругового цилиндра ф = 0, 1\=1 Т- =
Т / / 0
начальная закрученность не
играет никакой роли.
Нормальные напряжения в поперечном сечении согласно
(IV.29) и (IV.35) описываются уравнением
ЕМГ
м„
+ ^L
— Тп
где
F
1
¦ (Ф*)ф, (IV.36)
(IV-37)
Функция
у (ф)^ ортогональна к 1, |, г|, так что последний
член в формуле (IV.36) представляет собой
самоуравновешенную систему нормальных напряжений, возникающих в
закрученном стержне при кручении. С точностью до членов нооядка
т0 распределение нормальных напряжений от силы Pt и
моментов Mj, Мц остается таким же, как при т0 = 0.
Очевидно, что выражение для крутящего момента (IV. 15)
можно представить в виде
Mia =-- \ o%radF, (IV.38)
66
где <3ti — тангенциальная составляющая касательных
напряжений (см. рис, 14), aii ~ °>к ~~г—~ а"А —;—~ или
с учетом (IV.29)
а% = J- [От (г« + щ) — Ех0 (е — хп| + х.тО ф^) ]. (IV.39)
га
Введя в уравнение (IV.39) значения деформаций (IV.35),
найдем
а% = -L !_1-|2_ (Г| + фф) _ J± _|_ [(/ _ /2) (г„ + фф) +
(IV.40)
откуда также видно, что возникающие от действия силы Рг
и моментов Mi, Мц, касательные напряжения являются
самоуравновешенными и что с точностью до т0 распределение
касательных напряжений от крутящего момента остается таким же,
как при т0 = 0. Последнее совпадает с выводами нелинейной
теории кручения призматических стержней.
Потенциальная энергия закрученного стержня при
условиях (IV. 14) наиболее просто выражается через напряжения
в главном сечении
2
о ?
Для получения выражения П через напряжения в
поперечном сечении следует учесть второстепенные компоненты
напряжений согласно формулам (IV. 10).
Введя в формулу (IV.41) выражения (IV.30), получим
после интегрирования по площади сечения с принятой точностью
П = i J {Е [s2F + 4/, + ЩН - 2е%А + 2екн5, -
о
— 2хъхп11г1 + 2т0ет (/р — Id) — 2тохТ|т AРП — Тп) f
+ 2T0xtT (/PS — Тг) + Gx4% d'Q, (IV.42)
где учтено, тгт°
Рассмотрим два частных случая исследуемой задачи, для
которых известны доведенные до окончательного вида решения,
основанные на полной системе уравнений теории упругости
(см. гл. III).
Растяжение закрученного стержня (М\ = Мц = Мга =
-- 0; L,a — т]а = 0). Из формул (IV.35) следует
Р, Р
в =
EF '
(IV.43)
а из (IV.36) и (IV.40) —
о
а, =
Рг
Р
11
или в проекции на оси ?т] по формулам (IV.29)
0л' == —
- x<»aC | "To"
/2
(IV.44)
что полностью соответствует решению П. М. Риза (III.1).
Второстепенные напряжения о^, оп, о^п в этом случае
действительно равны нулю.
Растяжение и кручение закрученного стержня с поперечным
сечением, имеющим две оси симметрии (Mi — Мц = 0;
1х = Л, = 0; Т? = 7V, = /Р| = /рп = 0). Формулы (IV.35)
принимают вид
е ^ __
ь_
Pr
(IV. 45)
что полностью совпадает с формулами Г. Ю. Джанелидзе
A11.4), (III.5), полученными на основе решения задачи Сен-
Венана для закрученного стержня с применением полной
68
системы уравнений теории упругости в неортогональных кри-4
волннейных координатах [22].
Приведенные примеры свидетельствуют о том, что основная
гипотеза приближенной теории о второстепенном значении
напряжений а\, о*п, aln в главном сечении правильно
отражает физическую сущность особенностей напряженного
состояния в закрученных стержнях. Система уравнений (IV.34)
может рассматриваться как естественное обобщение
соотношений Кирхгофа для закрученных стержней произвольного
профиля — в отличие от обобщения Клебша, который,
распространяя соотношения A1.10) на закрученные стержни исходил
из решения задачи Сен-Венана не для закрученных, а для
призматических стержней. Хотя при решении некоторых задач
использование соотношений A1.10) 1\гожет привести и для
слабо закрученных стержней к частично правильным результатам
(расчет нормальных напряжений и изгибных деформаций при
М^а — 0; расчет касательных напряжений и угла раскрутки
при Pi — Mi = Мц = 0), но их применение для анализа
относящихся к закрученным стержням задач общего типа
является необоснованным, так как не учитывает характерную
для закрученных стержней взаимосвязь различных
деформаций и нагрузок.
3. Умеренно закрученные стержни,
нелинейное по т0 приближение
Полученные в параграфе 2 гл. IV линейные относительно
начальной закрученности т0 соотношения не отражают
экспериментально установленных фактов о том, что даже при чистом
растяжении закрученного стержня эпюра напряжений
существенно изменяется [50] и что жесткости стержня на
растяжение, изгиб и кручение также зависят от закрученности [54,
66]. Это несовершенство формул связано с формальным
пренебрежением членами порядка т5 независимо от величины
других членов, что, вообще говоря, не соответствует условиям
(IV.1) и (IV.2). По характеру влияния членов порядка т0
формулы, приведенные в параграфе 1 гл. IV. можно разделить
на три группы: I) в соотношениях чисто локального характера
основные величины (напряжения, деформации) можно
считать в общем случае одного порядка и пренебрегать членами
с множителем то, что указывает на обоснованность
завершающих формул подобного типа (IV. 16) и (IV.21) — (IV.28);
2) в формулах (IV.25) — (IV.30), содержащих компоненты
общей деформации стержня е, «•, хп, т, относительная роль
69
членов зависит от соотношения между указанными
компонентами, и поскольку член тотфф имеет, вообще говоря, тот
же порядок, что и компоненты «плоской деформации» е —
— и„| + K|ii, формулы (IV.29) целесообразно записывать
в полном виде:
<т* = Е (е — х,,! -4- ХгГ) — тотфф);
ali ~ ^х (Ф| — Т1 + %) — ^то (е — кп1 + ЩЩ — го%Щ) 4>'ь
(IV.46)
3) в формулах интегрального характера (IV. 15) роль
отдельных членов дополнительно зависит от характера
распределения соответствующих составляющих напряжений по сечению,
поэтому при интегрировании по сечению выражения (IV.46)
следует рассматривать как «точные», сохраняя все члены, в
том числе имеющие множитель to. При этом первые три
выражения систем (IV.32) и (IV.34) для Pr, Afj, Mn не изменяются,
а последние выражения (IV.32) и (IV.34) принимают вид
где
,0 Г 4 ,г>
/, = J radF\
'f
T°r = f \r'i —
(IV.47)
(IV. 48)
Основные соотношения (IV.34) с учетом (IV.47) можно
представить в виде
Ье 0 0 Ье1
о о ьп ьп%
Ьхе bxi Ьщ Ьх
где коэффициенты жесткости
be = EF; b-- = EI г; Ьц = E!n;
bx=Gld; bet = x0E(IP-Id); (IV 50
70
Разрешив систему (IV.49) относительно деформаций,
получим вместо (IV.35) соотношения
ацъ ап ацх\
ахв
ЛЬ,
где коэффициенты податливости
«,2
•ат-
Т)т .
= ат
- ат
UE11 =
а%х = —
6g,
(IV.51)
} (IV.52)
и =-= а/ь /, й = 8, 1, tj, т.
Возможны и другие эквивалентные формы записи для со-
отношений (IV.52), например, ае == 1/EF*; ац = \1Е1^\ а% =
— \IEIi, ах == \IGId, где F*, /„, /|, /^ — эффективные
геометрические жесткости закрученного стержня [54]
Формулу для G/j можно представить в виде
(IV.53)
71
где
¦г -' р к ;т| •
(IV.54)
причем
lr = f r\dF; Tr = \ [r\ - (Ф;'J1 dF;
P * AV.55)
(r, — «главное» значение квадрата полярной координаты
Лх> а Щ — «главное» значение функции ф^, определяющееся
формулой (IV.37)).
В отличие от выводов линейной относительно т0 теории,
из соотношений (IV.49), (IV.51) следует, что в закрученном
стержне все силовые факторы и все компоненты деформаций
взаимосвязаны, а также, что с увеличением начальной закру-
ченности т0 жесткость стержня на кручение возрастает, а на
растяжение и на изгиб убывает.
Нормальные напряжения в поперечном сечении согласно
(IV.29) и (IV.51) описываются выражением
Р М М.
f~f ± —- ™ >¦ 1 '— *\~\ ... ж— Т"Т"" /"f4 1 ( 1 Л / ^~\iTl i
\Jj" ¦¦ ?-, , L, j z : II Х_, t vnW'ujj i X V ,*J\J §
л " г
или
ст° г=~ _?_ 11 + ExlaT (/„ — 1% щ } —
М
¦ -, [I + Ех}дх Aрп — Тп) щ } +
л
м
+ _^ 1Ц 4- Ет1а, (IPl — /j) фф] — М^Етоатщ, AV.57)
откуда видно, что при растяжении и изгибе закрученного
стержня в нем возникает дополнительная система
самоуравновешенных нормальных напряжений, распределенных по
тому же закону щ (L ц), что и для кручения.
72
С учетом члена тохщ формула (IV.39) для тангенциальной
составляющей касательных напряжений Oti имеет вид
а
Oil = — \G% [фф + Га + 2 A + V) T5 (ффJ] —
а
— Ехо(г — хц? -f- щц) Фф). (IV.58)
откуда вместо (IV.40) получим
Га + ф* + 2A +v)
/d
''
г
п
щ)
- Тц) (А + фф) + 1'ащ Ц + Е%\а% (Im -Tn)щ}\ +
+ -j±- [(IPl — Г6) (Га + фф) + 1аЩ [Ц + ЕТопт dpi — Тъ) фф ]]
(IV.59)-
Из выражения (IV.59) следует, что даже при чистом
кручении помимо системы касательных напряжений "по Сен-Венану"
в поперечном сечении закрученного стержня возникает
дополнительная система касательных напряжений,
распределенных по сложному закону ц>^щ (|, г|), причем крутящий
момент М^а уравновешивается суммой моментов указанных
систем
ld - G/,
С увеличением закрученности роль второго члена возрастает,
что и ведет к повышению жесткости на кручение. Отметим, что
J щщйР = I, — Тг.
Выражение для потенциальной энергии закрученного
стержня (IV.41) с сохранением всех членов формул (IV.30)
7»
принимает вид
i
П = -1- j [E le*F + х*/„ + Х|/? — 28XT|Sn + 2exsS5 —
j
о
5х„/6„ + 2тоет (/„ — 1а) - 2тох„т
+ 2тох,т (/о| - 7Е) + Gt2/,} С (IV.60)
отличающийся от (IV.42) тем, что вместо Id вошла жесткость
Id, определяемая первой формулой системы (IV.48),
Как будет показано ниже, для стержней с удлиненными
сечениями, для которых влияние закрученное™, собственно,
и представляет практический интерес, соотношения (IV.49) —
(IV.52) приводят к результатам, хорошо совпадающим как с
экспериментальными данными, так и с известными более
точными решениями частной задачи о растяжении и кручении
закрученного стержня с учетом членов порядка то. Вместе
с тем указанные соотношения обладают достаточной
общностью, переходя без учета членов с то к соотношениям
линейной теории, причем для кругового цилиндра все члены,
связанные с начальной закрученностью, обращаются в нуль. Это
позволяет рассматривать формулы (IV.49) — (IV.52) как
обобщенные соотношения Кирхгофа или, иначе говоря, как
основные соотношения приближенной теории закрученных
стержней произвольного профиля.
В качестве примера рассмотрим подробнее задачу о расчете
закрученного стержня эллиптического сечения, уравнение
контура которого
где Ьь ах — полуоси эллипса, Ьг = Ь/2; ах = а/2.
Примем а ^ Ь, причем alb = с @ =$С с =$С 1). Будем считать,
что стержень закручен относительно оси, проходящей через
центр тяжести сечения, |а = % = 0.
Функция кручения для эллиптического сечения, как из-
вестно, имеет вид ф(|, ц) ——узг^^Ь так чт0 Щ ^
^
= — |^з Л! (fn = ~ ГТ75 s; Ф* = — у^ш (I2 — if)-
Вследствие симметрии эллипса /„s = IpVt = Tj = Тц ¦— 0; Ь|Т = Ьцх —
._ att = ащ — citx — а-туг = 0, а остальные геометрические ха-
74
рактеристики и коэффициенты жесткости и податливости
определяются следующими формулами:
r nb2 .
/¦=—т—с; /; =
64
с3; /п =
64
64
/I I 2\. Г° _
C(l-)-C), id —
16
64
. с%
Mr
r ~ 1024 C
/,-7,=
1024 \ 1 4- c2
1 f_ r2 j_ .,4
1 g С -г 6
2 „
с; *,= ?тз-с; 6= = E -,
яЬ4
64
nb* c3
16 1 4- c?
1 +
f с4 A —с3J
14-с2
32
4-с8 '
1 8c*
— 16<1 4-ca) 1
— ci&%s 1 4-/C '
_ 2Pm A -c2J 1
c» 1 4- К '
1 4-/С '
Л' =
1 4-
(IV.61)
где Рт— угол наклона крайнего винтового волокна | = Ъг и
т] = 0, характеризующий начальную закрученность стержня,
75
0,1
Рис. 15. Зависимость относитель- Рис. 16. Зависимость параметра
ных коэффициентов податливости упругой раскрутки от параметра
иа растяжение и кручение стержня начальной закрученности при ра-
эллиптического сечения от пара- стяжении стержня эллиптического
метра начальной закрученности и сечения с отношением осей с.
отношения осей эллипса с.
Главное значение функции щ определяется по формуле
'1 — С'Л
— Ь"
Ci) I S
"Ж
A
На рис. 15 приведены зависимости ае = aJae0 и s,-
— аТ''ато (fl.-o, aT0 ¦— значения ае, ат при Pm= 0) от угла
Р,„ для различных значений с, откуда видно, что несмотря на
удовлетворение значений рт условию рт <S 1> роль членов с
Рт = (Т<А)а является принципиально важной. С увеличением
начальной закрученности податливость стержня на
растяжение увеличивается, а на кручение — уменьшается, причем
этот эффект резко усиливается при утоньшении профиля.
Штриховые кривые соответствуют допущению 1 + с2 да 1.
Коэффициент ах изменяется значительно сильнее, чем а8
{даже при рт~*- оо и с2 <JC 1 значение lim аг ->- 2). Для
профилей, имеющих относительную толщину с > 0, 2, влиянием
закрученности на изменение жесткостей при условии рш<^ 1
практически можно пренебречь.
76
Зависимость изменения угла наклона крайнего винтового
волокна р -- xbt от угла |3Ш для различных значений с при
растяжении, когда т = апР^, приведена на рис. 16. Приняв
среднее значение напряжения сгср = Px,lF = 1МПа,
получим
ft _ ft (' -г VH' с ) ,,,
Знак минус указывает на уменьшение начальной закручен-
ности при растяжении, т. е. на "раскрутку" стержня.
При очень малых углах Рт) пока аг =& 1, зависимость р =
~- / (Рт) носит линейный характер, соответствующий формуле
(IV.43). При дальнейшем увеличении угла рш значение | р |
достигает максимума (при а% = 0,5) и затем начинает
убывать, что связано с увеличением крутильной жесткости.
Указанный характер зависимости р = / (рш) подтверждается
экспериментальными данными (см. гл. VI и работу 150]). Эффект
раскрутки под действием растягивающей силы проявляется
при любых значениях |Зт и с Ф- I, но при углах Рй <^ 1
приобретает практическое значение для профилей с толщиной с г»
«г 0,2. Штриховые кривые также соответствуют допущению
1 + С2 да 1.
Согласно теореме взаимности, зависимость осевой
деформации е от угла Рт и толщины с при действии крутящего момента
будет иметь аналогичный характер, причем положительный
крутящий момент, увеличивающий закрученность, приводит
к уменьшению длины стержня.
На рис. 17 показаны функция кручения <р, определяющая
поверхность депланации, и функция щ, характеризующая
распределение дополнительных самоуравновешенных
нормальных напряжений в поперечном сечении, максимальное
значение которых получается на концах длинной оси (Е = ±Ь%;
1] = 0).
Для эллиптического сечения при М$ — Мц = 0 и |г/ =
= "Па = 0 формулы (IV.46) для компонент касательного
напряжения приводятся к виду
[2Ml
-fv)xo(l — С2)щ;
*) Ц + Е4и, Aр - /2, щ.
77
Рис. 17. Функция кручения ф (а) Рис. 18. Функции распределения
и функция распределения допол-
нительиых нормальных иапряже- р ) (ф)ф ) ; (ф
нии (ф*)ф (б) для закрученного (б) при кручении стержня эллиптн-
дополнительных касательных иа-
пряжений —т) (ф*)ф (а) и —; (ф*п
стержня эллиптического сечения.
ческого сечения.
Функции — г)фф и —|фф, характеризующие
распределение дополнительных касательных напряжений при
кручении, показаны на рис. 18, откуда отчетливо видна внутренняя
неуравновешенность этих напряжений.
__ Зависимости а^ = / фт, с), где a-Q — отношение
максимальных дополнительных нормальных напряжений,
пропорциональных щ (?>!, 0) к среднему напряжению <тср
Р IP
при растяжении или к максимальному напряжению (сь )Un —
= MraJId (I + с%) при кручении приведены на рис, 19.
Приведенные на рисунке кривые указывают на значительное
перестроение эпюры нормальных напряжений с увеличением
закрученное™, причем дополнительные напряжения moi ут
даже превосходить напряжения аср и (а-^)тЯъ в пределе
0^ -*- (—3) при растяжении и о*-*¦ 1,21 при кручении.
На рис. 20 построены кривые для функций Оц, <т,и —
78
Рис. 19. Зависимость
максимальных относительных
дополнительных нормальных напряжений аР
(в точке /И) от параметра
начальной закручеиности, отношения осей
с при растяжении (а) и кручении
(б) стержня эллиптического се-
чения.
0J
с-0,02
0,0$
J.
——•—
—¦ -
0,1 0,2
i j
0,5 1
, j
I
/
/
.—-—-
IP
0,1
0,2 Д,
Рис. 20. Зависимость
максимальных относительных
дополнительных касательных напряжений ок
(в точке Mi) при растяжении (ф
и Оц^ (в точке М) — при кручении
(б) от параметра начальной закру-
ченности н отношения осей стержня1
эллиптического сечения.
= f фт, с), где Oif — отношение максимальных
дополнительных касательных напряжений (в точке 1=0; г\ — аг) при
растяжении к напряжению <тСр, а ст^? — отношение
дополнительных напряжений в точке ? = Ьг; г\ = 0 при
кручении к напряжению (ст^)тах.
Приведенные результаты расчета деформаций и напряжений
в закрученном стержне эллиптического сечения при произ=
вольном отношении полуосей 0 =$С с ^ 1 (в рамках
соотношений (IV.51) эти результаты являются точными) наглядно
показывают, что при типичных для закрученных лопаток значениях
угла pm ^ 0,15-г-0,20 влияние закрученности приобретает
практически важное значение для относительно тонких
профилей при с ^0,2, т. е. когда с2<^ 1. Вместе с тем для подобных
удлиненных сечении вся теория закрученных стержней
существенно упрощается.
В достаточно общем виде задача деформации закрученных
стержней рассмотрена В. Л. Бердичевским и Л. А.
Старосельским1. Результаты, полученные ими для стержней двусиммет-
ричного компактного сечения, следует сопоставлять с
приведенными выше данными для стержней произвольного
поперечного сечения. Зависимости же для стержней удлиненного
сечения, естественно, не применимы в случае стержней
компактного сечения.
4. Закрученные стержни удлиненного профиля
Из решения задачи для стержня эллиптического сечения
следует, что при значительном удлинении профиля, когда с2 <^С 1
функция кручения ср и ее производные принимают вид ф = —
— |г); фб = —г); ф„ = —ё; фф = —(I2— гJ), и следовательно,
щ = —112— yf —). При этом для большей части сечения
^за исключением области, непосредственно примыкающей к
началу координат) т) <^ |, что позволяет приближенно считать
ra^r^i. (IV.62)
Составляющие сдвигов в главном сечении в направлении
оси ц и в тангенциальном направлении t становятся
пренебрежимо малыми, так как с учетом (IV 21) е,^ = т (щ + |) дз
як 0; е*ц я» — (щ -f- r2) я» 0, что вполне естественно, если
учесть, что для удлиненного сечения направления т) и t
{см. рис. 14) на большей части сечения практически нормальны
к боковой свободной поверхности. В этом случае из выражений
{IV.38), (IV.48) и (IV.55) получим 1Р — fd » !„¦ 1;Щ — Тп »
Из формул (IV.61) также видно, что при с2 <^ 1
справедливы предельные переходы lim AР — /J) = lp\ lim (/, —
— Т°) = /?; lim (lr — Тг) = /г, т. е. при расчете этих
i±c--»i
геометрических характеристик роль центральной области
сечения, где выражения (IV.62) теряют силу, действительно
пренебрежимо мала.
1 Бердичевский В. Л,, Старосельский Л. А, К теории естественно
закрученных криволинейных стержней.— МТТ, 1979, Ла 6, с. 103—113.
«0
Штриховые кривые, приведенные на рис. 15 и 16 и
рассчитанные в пренебрежении величиной с2 но сравнению с
единицей, показывают, что даже при с = 0,2 расхождение
незначительно. В случае замены функции щ на — |2 в
формулах локального характера (при расчете распределения
напряжений) в отдельных точках (при срф да 0 или ффдаО)
расхождение становится довольно заметным, однако
максимальные значения функции щ, определяющие
максимальные дополнительные напряжения, и общий характер ее
изменения оказываются весьма близкими (даже для такого
сравнительно толстого профиля как с = 0,2 ошибка не
превышает 6,5%).
Отметим, что если при с2 <^ 1 вместо фч s=s — |2 считать
cf ф да —г2 = — (Е2 -1- tj2), то ошибка по-прежнему остается
в пределах точности расчета. Поэтому использование в
качестве функции щ значений — g2 или —г" является
вопросом удобства.
Хотя полученные упрощения непосредственно относятся
к стержню удлиненного эллиптического сечения, однако они
естественно обобщаются на стержни с удлиненными сечениями
любого профиля, если в качестве специальной гипотезы для
таких стержней принять, что для них на большей части
сечения сдвиги в поперечном и в тангенциальном направлениях
пренебрежимо малы, т. е.
s-4^8^0. AY.63)
Тогда можно считать грф =» га при га да | — ?а, что
существенно облегчает весь расчет закрученного стержня, так как
теперь не требуется предварительного нахождения функции
кручения ф и ее производных. Значение /^ для удлиненных
сечений также можно вычислить по известным приближенным
формулам без определения функции ср. Имея в виду
указанные упрощения, придем к следующей основной системе
соотношений теории закрученных стержней, которую,можно было
бы назвать технической теорией закрученных стержней
удлиненного профиля, учитывая, что основное практическое
значение эффект закрученности имеет именно для таких стержней.
Параметры деформации закрученного стержня связаны с
силовыми параметрами такими соотношениями:
' е I!
A'U
= И О |.
Хг,
(IV.64)
g 2-1896
81
Коэффициенты матрицы жесткости |Ь]| (см, выражение
(IV.49)) определяются по формулам
Ъг = EF; Ы = Eli', bn = El-ai
b% = Gld; bE% = %OE1 ; bix = to?/pS;
, , '. (IV.65)
"tit — — ТдСУр^, 0e| — 0e^ — D|n — U,
bfti = blk, k, 1-е, l, ц, т,
причем
G/d = Gfd + Exulr. (IV.66)
Коэффициенты матрицы податливости |! аы !l = fl Ь« !i"*
(см. выражение (IV.51)), определяются через коэффициенты
bki формулами (IV.52), которые можно представить в виде
ak =
bk
I
—1
g, т,;
= t;
(krl)
— CT —j~- , k = E, E, % I = T,
При этом ат =
о ,
E%iJr) ', где Ir = I°r jr- -p-
Продольная деформация определяется выражением
e^ = ej = e — xr
а нормальное напряжение —
или с учетом значения т
M,
М
(IV.67)
хо%г1 (IV. 68)
причем г^ определяется формулой (IV.55).
82
Касательные напряжения от деформации кручения в
главном сечении
a:t = — 2Стр (|, л); о^«0 (IV.69)
(р (I, ц) — расстояние от средней линии сечения до
рассматриваемой точки), поэтому
(CT;E)max = Gxh, (IV.70)
где h — максимальная толщина профиля.
Основные соотношения технической теории закрученных
стержней можно получить непосредственно, не прибегая к
общей теории, если ввести следующие допущения.
Начальная закрученность стержней удлиненного профиля
приводит к повороту элементарных площадок поперечного
сечения, нормальных к свободной боковой поверхности, на
угол р* = т,/а, поэтому на большей части площади
направление нормали С* к главному сечению практически совпадает
с направлением винтовых линий. Для удлиненного
эллиптического профиля это прямо вытекает из приведенных выше
соотношений.
Нормальное напряжение в главном сечении ст* (или, что
то же самое, в винтовом волокне) связано с деформацией этого
волокна в* формулой для одноосного напряженного состояния
ст* = ?е*.
Деформация винтового волокна, зависящая от
относительного поворота сечения т, определяется согласно рис. 14,
как ет = т%0Га. Суммируя последнее выражение с
составляющими плоской деформации е + щг\ — хГ)|, приходим к
соотношению (IV.II), а затем с помощью уравнений равновесия
(IV. 15) с учетом крутящего момента от напряжений ст* — к
основным соотношениям технической теории закрученных
стержне!! (см. гл. V).
Основные соотношения (IV,64) — (IV.70) были выведены
для равномерно закрученного стержня постоянного
поперечного сечения, нагруженного по концам продольной силой,
изгибающими и крутящим моментами. Следуя обычным
приемам сопротивления материалов, указанные соотношения
можно распространить на общий случай нагружения стержня с
переменными геометрическими характеристиками, если
считать коэффициенты жесткости Ьы и податливости аы
изменяющимися по длине стержня. В качестве оси упругого кручения
t,i берется прямая, параллельная оси стержня 'Са, проходящая
через точку Ог относительно которой момент касательных
напряжений сдвига, уравновешивающих составляющие силы Р%,
6* 83
Рп от деформации изгиба, равен нулю (центр жесткости
сечения). Координаты центра жесткости определяются теми
же способами, как для незакрученных стержней.
Выше было также принято, что упругая деформация
кручения и начальная закрученность стержня осуществляются
относительно одной и той же оси, т. е. fe3 == ?]> ца = rji- Можно
показать, что конечные результаты расчета не изменятся,
если в качестве оси начальной закрученпости для данного
сечения выбрать касательную к любому винтовому волокну
ММ1 (см, рис. 14), удовлетворяющему условию (IV. 1).
Поэтому, не ограничивая общности решения, можно принять,
что ось начальной закручеиностн стержня проходит через
центр жесткости сечения (|a = Ei, % = г),) и, следовательно,
совпадает с осью упругого кручения. При этом величины t,
кп будут представлять собой компоненты упругой кривизны
указанной оси в главных направлениях с, г\, а т„ и г —
соответственно начальную и упругую закрученности стержня
относительно той же оси.
Глава V
ТЕХНИЧЕСКАЯ ТЕОРИЯ ЗАКРУЧЕННЫХ
СТЕРЖНЕЙ
1, Основные соотношения
Для закрученных стержней несимметричного поперечного
сечения необходимо, согласно результатам гл. III и IV,
учитывать связь изгибной, крутильной и продольной
деформаций, В то же время следует обеспечить возможность достаточно
эффективного решения практических задач для стержней
неременного сечения. Стремление удовлетворить оба требования и
привело к построению технической теории закрученных
стержней.
Предполагается, что центр поворота сечения О1 в своей
плоскости совпадает с центром изгиба сечения. В каждом
сечении вводятся местные системы координат xiyl и 1;,/% с
началом в центре изгиба, оси которых паралельны осям систем ху
и Ь\ с началом в центре масс сечения. Зависимости для
перемещений любой точки стержня будут отличаться от
зависимостей A5.2) и (II.8) классической теории учетомдепланации
поперечного сечения при кручении. Эта депланация, согласно
известным решениям [4, 38, 4*2, 791 полагается
пропорциональной относительному углу упругого кручения -у- ер, где ф (|j,
1],, г) — функция кручения. Для каждого поперечного сечения
стержня она определяется как функция кручения
соответствующего призматического стержня [15, 17]. Для закрученного
стержня постоянного поперечного сечения в системе
координат ?1гI функция кручения не зависит непосредственно от
координаты г.
Перемещения любой точки стержня в системе хуг
определяются зависимостями
W^w — u'x — v'y + Q'cf. I
При определении продольной деформации гг учет
депланации сечения приводит к появлению дополнительных по
8*
-f 2т„8' (Ipw'
i
¦2тп
1
2
Л
$
0
в
И]
EF
Щ
GL
M-
M
I,, lr]/
10 GId \ F
Полярно-осевые моменты инерции в системе координат |т|
dz.
(V.9)
связаны с соответствующими характеристиками в системе ху
зависимостями
V
= я
(V.11)
В выражении (V.9) введены сила и моменты,
пропорциональные кинематическим характеристикам деформации, что
аналогично зависимостям A1.10) в классической теории;
Рг = EFw'\
Мп =
(V.I2)
Mo = GIdQ'.
Однако в технической теории закрученных стержней полные
моменты и силы внутренних напряжений определяются
взаимосвязью различных видов деформаций:
Pi = Рг + м ет„
Е1р
М? = м, + Mti% -^f- ;
/И J = Mo + т0 f P? -J?- +
Л1-
(V.13)
Введение зависимостей (V.12) упрощает некоторые
практические вычисления.
Y т т1
Величины Рг, M~z, М'ц определяются как
равнодействующие сила и моменты в поперечном сечении от нормальных
напряжений аг = Егг, где нг берется из зависимостей (V.8):
Pl = ( о/Л:] Ml = ) oz)}dF; Ml = — [ o^dF.
F F F
При определении крутящего момента Мг необходимо
учесть, что напряжения <т » <тг, действующие вдоль винтовых
волокон под углом р = хйг{ к поперечному сечению, имеют
проекцию на поперечное сечение ozx0rlt которая вызывает
дополнительный крутящий момент. Поэтому
Ml = \ (Тт,^! — Т.-гТ],) dF + %Л Q/\dF.
F F
Зависимости между силовыми и кинематическими
характеристиками деформаций A.21) в технической теории
стержней приобретают вид в системе координат |т)г:
Л!=
О
О
О
V
w
х».
где
bXTi bT
= ?/„;
(V.14)
о' !|
>r = G!d;
be = EF; Ъг = Е!ь
Для соответствующих зависимостей в системе координат
xyz с помощью выражений (V.5) можно получить
Pi
Ml
Ье
0
0
О О
bxj
Ьх
W
(V.15)
где
Ьх = Е/х
' ху>
i x, by — Ely, oXy — — E
h T pf ¦ U т F!
t-t,- — %4iCI tn Ul/T —• — XHL,I yr.
Коэффициенты матриц, входящие в (V, 14) и (V.15),
являются соответствующими эффективными жесткостяыи стержня.
Дифференциальные уравнения, отражающие совместные
деформации закрученного стержня, можно получить с помощью
уравнений равновесия A.16) или A.19), соотношений (V.15)
или (V. 14), либо с помощью принципа Остроградского —
Гамильтона A.23) и выражения для потенциальной энергии
(V.4) или (V.9). В системе координат xyz дифференциальные
уравнения выглядят следующим образом:
[Е ilvu" + lxip" — то/„,в')]' *=Ll = qB + m'x;
[Е С/,//' + Iuv" - то/„0')]" = Ll ^qx + mw;
[C/d6' + Ex0 {/pw' - Iyru" - Ixrv")\' = Ll = - m2.
Граничные условия для уравнений (V.16) будут
Ы>Р] |'о = 0;
6«{(Af»)'-mv}|o = O;
bv[{Ml)l-rax)% = (y, \ (V-l7)
= 0.
В системе координат |т]г уравнения (V. 16) приобретают вид
аг 2\ г„, г/ а2
дг
Я/,
¦ то j vn —
= (?п +
<Эг2
2\ I r^ r
— то Н ?/
- 2т0-
йг
«' дг
То 1 Vi\
р, ае
GL.
дг
дг
д%„
дг
дтв
Г] +тот;;
52
} (V.I 8)
аГ
&jd . Г/ аг
-д! 'ТУ
T0| M: -p
аг
ы.|Н = L; = —т,;
90
Граничные условия в данном случае запишутся в виде
бшР? |о = 0;
6иг {(Ml)' + том1 — тц) [о = 0;
= 0;
б (р'п + т0Н|) Мс
(V.19)
о = О;
= о.
Основные отличия технической теории закрученных
стержней от классической определяются учетом в выражениях для
продольной деформации ег (V.3), (V.8) члена О'то/1,
отражающего деформации растяжения — сжатия вследствие изменения
длины продольных винтовых волокон при кручении стержня
с начальной закрученностью. Даже для стержня с двуснммет-
ричным поперечным сечением при этом возникает связь
продольной и крутильной деформаций. У стержня с
несимметричным поперечным сечением деформации винтовых волокон
при кручении вызывают не только продольную силу, но и
изгибающие моменты. Изгиб же закрученного стержня с
несимметричным сечением за счет поперечных составляющих
деформаций винтовых волокон вызывает деформацию кручения.
Таким образом возникает связь изгибных, крутильных и
продольных деформаций {деформационная связь [54]).
Область применимости технической теории закрученных
стержней определяется критериями A.5), A.6). В практических
задачах положение оси закрученности часто неизвестно, и
тогда критерий A.5) используется в виде
(?!)'«!• (V.20)
2. Деформация закрученного стержня
Техническая теория стержней позволяет с достаточной для
практики точностью описать основные эффекты связанности
различных видов деформаций.
Крутильная и продольная деформации закрученного
стержня двусимметричного поперечного сечения. В этом случае
полярно-осевые моменты инерции 1%г = /v = 0 и
зависимости (V.14) и (V.15) распадаются на две независимые
системы уравнении. Одна из них для пространственного изгиба
стержня совпадает с зависимостями A1.13) классической
91
теории. Для крутилыго-продольной деформации
зависимости в неподвижной и подвижной системах координат имеют
одинаковый вид;
Pi = EFw' + т„?/ре'; (у21)
Ml = то?/„ш' + GJtfi'.
Пусть на стержень действует только крутящий момент
Ml = Ми Р] = 0. Тогда из первого уравнения системы (V.21)
следует w' = — т0—ё-6' —— Vp^'» гДе Г1 — полярный
радиус инерции, Гр = I /F.
Исключая ш' из второго уравнения системы (V.21), найдем
зависимость между крутящим моментом и относительной
упругой закрученностыо стержня
__ ../_. „ Ell
включающую эффективную жесткость стержня
двусимметричного сечения на кручение
Ь\ = Gld - т5 -Ж- = Gil + Ето AГ - г2р1р), (V.22)
Если ввести безразмерные параметры
63 = I°d/Ip; 8P == /,/Гр/р, (V.23)
то выражение (V.22) приобретает вид
Ъ\ - G/
Эффективная жесткость стержня на кручение линейно
зависит от квадрата степени начальной закрутки стержня, но
остается заметно меньше жесткости закрученного стержня
GIa ~ Gld + il,EIr. Попытки ввести жесткость закрученного
стержня в уравнения, где не учтена связь крутильной и
продольной деформаций, нельзя считать удачными, так как при
этом занижается степень упругой закрутки стержня. Отличие
жесткостей Ьх и Gld наибольшее для стержней удлиненного
профиля поперечного сечения. Если один из размеров сечения
значительно превышает второй, то можно положить гх я» \х.
Тогда /, — Гр/Р яа -^- /г, и коэффициент при То снижается
более, чем в 2 раза.
92
Допустим, что на стержень действует только продольная
сила Рг = Р, Мг = 0. В этом случае имеет место зависимость
El
0'--—xo-^r-w', с учетом которой Р = blsw', В этом случае
эффективная жесткость закрученного стержня двусимметрич-
ного сечения на растяжение
9/1 X. vi -rV2 1
. (V.24)
Эффективная жесткость, определяемая выражением (У,24),
ниже продольной жесткости незакрученного стержня. Это
объясняется тем, что работа продольной силы распределяется
vc-жду двумя видами деформаций. Знаки продольной и
крутильной деформаций в рассмотренных случаях
противоположны.
Выражения (V.22), (У.24) для эффективных жесткостей
закрученного стержня двусимметричиого поперечного
сечения на растяжение и кручение отличаются от зависимостей
A0,7), (III.8) учетом членов порядка малости не выше f>m
;i способом определения геометрических характеристик.
Расчеты по формулам (V.22), (V.24) соответствуют кривой 2,
приведенной на рис. 13.
Деформации закрученного стержня несимметричного по-
перэчного сечения, В этом случае следует пользоваться
зависимостями (V.14) или (V.15) без упрощений, либо одной
пз систем дифференциальных уравнений (V.16), (V.18).
Степень несимметрии поперечного сечения удобно оценивать
с помощью безразмерных параметров [161:
6= - I:r!rJp; 6„ = Iwlrnlp, (V.25)
Пусть на стержень несимметричного поперечного сечения
действует только крутящий момент: М\ -- Mt; Р' --¦- М\ —
--¦ Ml, = 0. Тогда из первых трех уравнений системы (V.14)
следуют зависимости
и/ = _ т0 -^- 0' = — vv.O';
К; = — т0 -f^- 9' = — тогр6;Э';
тогр6п9',
93
с помощью которых четвертое уравнение системы (V.14)
гтпстволится к виду Mj= bid'.
Эффективная жесткость закрученного стержня нес им-
метричного сечения на кручение определяется выражением
Ьт-и А« Ч* h* _
Ux — Пх г 7 г —
2 A + v) ^f FP - 1 - 6| - 62,)j . (V.26)
Аналогично находится эффективная жесткость закрученного
стержня несимметричного поперечного сечения на
растяжение
(V.27)
В случае двусимметричного поперечного сечения
выражения для эффективных жесткостей (V.26), (V.27) переходят в
соответствующие выражения (V.22), (V.24). Вследствие
несимметрии поперечного сечения эффективные жесткости на
кручение и растяжение уменьшаются.
Для эффективных жесткостей на изгиб в системе
координат Ъ\г подобным образом можно получить выражения
Т 9 (Е1»гУ*
Gid-r0E
/2
7Т)Г
-ЕШ
(V.28)
= Е1Ц — to
ч,
F h
2 A + v) тУд!
(V.29)
94
Для линейно закрученного vfi)
стержня постоянного
поперечного сечения коэффициенты
жесткости в зависимостях (V.14)
и эффективные жесткости в
системе координат h\z являются
постоянными. В неподвижной
системе координат хуг
коэффициенты жесткости в
формулах (V.15) и соответствующие
эффективные жесткости
являются функциями координаты г
и для стержня постоянного
сечения. Они могут выражаться
через коэффициенты
жесткости в системе координат t.r\z
и тригонометрические функции
cos a, sin а.
Пусть консольный
закрученный стержень нагружен на
конце изгибающим моментом
Ж 2Ж Jjf oCfL)
Рис. 22. Зависимость
относительного прогиба стержня в
плоскости действия
изгибающего момента от угла закру-
ченности а (/) при различных
параметрах изогнутости сече-
иия q = flh.
Мх = М. В системе координат
gtiz нагрузка определяется моментами М( — М cos а; М^ =
= — Msin а. Стержень при этом испытывает деформации
пространственного изгиба, кручения и растяжения. В частности.
для относительного прогиба стержня в плоскости действия
момента можно получить формулу
Eh,
Vo (/)
1 +
1 — cos 2a (/)
2a2 (I)
¦to-
bi 2a (/) — sin 2a (/)
ь'
a2 (I)
(V.30)
где v0 (I) — прогиб незакрученного стержня с теми же жест-
костями на изгиб. В случае двусимметричного сечения
формула (V.30) переходит во вторую из зависимостей A1.23),
полученных на основании классической теории стержней.
В качестве конкретного примера рассмотрен стержень
с поперечным сечением в виде части кругового кольца толщиной
h и хордой Ъ (рис. 22). Изогнутость срединной круговой линии
определяется значением /, а относительная изогнутость
профиля — безразмерным параметром q = f/h. Отношение
основных размеров стержня определяется соотношением b2lhl =
95
Иеснмметрия сечения возрастает с увеличением параметра
¦q. На рис. 22 показано изменение относительного прогиба
v (I) в зависимости от угла начальной закрученное™ а (I) и
параметра q.
При q = 0 поперечное сечение представляет собой
удлиненный прямоугольник и соответствующая кривая практически
совпадает с кривой прогибов v (I) стержня двусимметричного
сечения, приведенной на рис. 4, при k = 0. С увеличением угла
закрученное™ прогиб вначале уменьшается, а затем растет
и тем сильнее, чем больше несимметрия сечения. Это связано
с уменьшением эффективной изгибиой жесткости (V.28) с
ростом степени закрутки т0 и параметра несимметрии 6s.
Степень упругого закручивания при действии
изгибающих моментов определяется выражением
она пропорциональна степени начальной закрутки, а
деформация продольной оси стержня —
и пропорциональна квадрату степени начальной закрутки.
Обе величины растут с увеличением несимметрии сечения, но
имеют разные знаки,
3. Колебания закрученного стержня
несимметричного поперечного сечения
11ри колебаниях закрученного стержня каждая точка
совершает перемещения согласно зависимостям (V.l), (V.7). Но
в технической теории стержней при определении сил инерции
не учитывается инерция поворота поперечного сечения при
изгибе и инерция депланации сечения. Тогда кинетическая
энергия стержня при колебаниях:
Т = -i- f P [[w- + «2 + v2 + 26 (vxs — иу,)] F + /р02} dz =
о
= -1- j p {w2 + ы? + vl + 26 (v4t — ujTM)] F + Jpb'2} dz, (V.3J)
0
где xit y$ — координаты центра масс в системе xlyl, a ls, i|s —
в системе ^
96
Компоненты нагрузки в уравнениях (V.16), (V.18) при
колебаниях будут
Цг = — pFffl; qy = — pF (у + Qxs);
Ях — — pF (и — Qys); qz — — plpQ —
— pF (vx4 — uy%) — — p/p8 — pF (vrfes — «|T]S); \ (V.32)
дц = — pF (vrq ~f~ 6|s); <7g = — pF (u; — 0t]s);
mx = my = m; = тщ = 0.
Уравнения колебаний следуют при подстановке
инерционных нагрузок из выражений (V.16), (V.18), а соответствующие
граничные условия — из (V.17), (V.19). Кроме
деформационной связи изгибных, крутильных и продольных колебаний
имеет место, как видно из выражений инерционных
нагрузок (V.32), инерционная связь изгибных и крутильных
колебаний вследствие несовпадения центров масс и центров
изгибов несимметричных поперечных сечений.
Крутильно-продольные колебания закрученного стержня
двусимметричного поперечного сечения. Уравнения
колебаний закрученного стержня распадаются при этом на две
независимые системы уравнений. Для изгибных колебаний
имеют место уравнения, совпадающие с системами уравнений
A1.30) или A1.32) классической теории. Для крутильно-
продольных колебаний система уравнений приобретает вид
(EFw' + 4EJРВ'У - pFw - 0; ^
(x0EIDw' + G!dB'Y - pIpB - 0.
Для линейно-закрученного стержня постоянно
поперечного сечения система уравнений (V.33) имеет решение в
замкнутом виде. Собственные частоты крутильно-продольных
колебаний определяются по формуле
(«1,2)„ = -у [»п + »* ± ]/(С0п — т) + 4сОпТоГр]„, (V.34)
где (оп итк—собственные частоты парциальных продольных
и крутильных колебаний:
(«п )„ = {sn VWp)/l; (щ)п = (sn VGIJpTp)/l
(sn — собственные числа частотных уравнений парциальных
продольных или крутильных колебаний. Для консольного
стержня sf!= B/г—1)л/2, п = 1, 2, 3,...),
7 2— 1896 97
Рис, 23. Влияние связи кру-
тильных и продольных
колебаний:
а — снижение частот совместных
колебаний по сравнению с частотами
парциальных крутильных колебаний;
б — граница зоны влияния связи
продольных и крутильных колебгний.
1,6
1,3
/д
i——
/
Г
го
16
12
,о/
ip
а
if гр
\
5Г
в
ж.
\
зад/см
Взаимодействуют формы продольных и крутильных
колебаний только одного тона. Графики изменения частот в
зависимости от степени закрутки х0 для различных параметров
sn могут пересекаться. Параметр sn в формуле (V.34) можно
вынести за скобки, так как взаимосвязь продольных и
крутильных колебаний от этого параметра не зависит. Поэтому
достаточно рассмотреть влияние деформационной связи на
колебания одного любого тона.
Частоты парциальных продольных колебаний с
увеличением степени закрутки не изменяются. Частоты парциальных
крутильных колебаний возрастают в связи с ростом жесткости
на кручение Gld — Gfd -j- %\Е1г при увеличении т0. За счет
деформационной связи колебаний соответствующие частоты
крутильно-продольных колебаний растут с увеличением т0
значительно слабее. Это отражено на рис. 23, а, где штриховой
кривой показано изменение относительных частот
парциальных крутильных колебаний, сплошной кривой — частот
крутильно-продольных колебаний, а точками —
экспериментальные результаты для консольного стержня. Все частоты
отнесены к собственной частоте крутильных колебаний неза-
крученного стержня. В данном случае озп = lO,O8cofe. Частоты
крутильно-продольных колебаний, соответствующие частотам
парциальных продольных колебаний, с ростом т0
увеличиваются, но весьма мало (в реальных случаях этот рост не
всегда можно изобразить графически).
Влияние связи крутильных и продольных колебаний
зависит от степени начальной закрутки т0, значения гр и ог-
Й8
ношения парциальных частот
/ L+JL
Взаимосвязь сильнее для более близких частот. Для стержня
двусимметричного поперечного сечения увеличение значения
гп = IplF происходит при увеличении отношения главных
гпбкостей (х (при удлинении профиля поперечного сечения),
но при этом уменьшается значение 6d = l\llp, и возрастает
отношение частот. В целом с ростом ц связь продольных и
крутильных колебаний увеличивается. Увеличение т0
вызывает только повышение влияния связи колебаний.
Использование выражения жесткости закрученного
стержня на кручение (V.6) без учета связи продольных и
крутильных колебаний ведет к заметному завышению
расчетных величин собственных частот крутильных колебаний. При
fi2 ^> 1 и Ро <<^ 1 для приближенного определения крутильной
частоты можно использовать эффективную жесткость на
кручение (V.22), (V.26): (щ)п да (sn ]/^/pF)/l.
В работе [22] система (V.33) получена с учетом только
членов, линейных относительно т0, т. е. GId = GI4. Но тогда связь
продольных и крутильных колебаний приводит к понижению
собственной частоты а1 с ростом степени закрутки т0, что
противоречит экспериментальным результатам.
Собственные формы крутильно-продольных колебаний
консольного стержня имеют вид
Q п . In — 1 .2/1 — 1
в = 90 sm —щ— пг; да = да0 sin —щ— пг.
Отношение амплитуд можно найти с помощью первого из
уравнений (V.33):
EF — рр —— Ш| ,)
1
Для меньшей из частот продольно-крутильных колебаний
в реальных случаях со]/соп <^ 1, и отношение амплитуд сйо/0ояз
!^=—т0Гр, причем знаки перемещений различны. Эта форма
является преимущественно крутильной. Для большей из
частот совместных колебаний отношение Ш2/соп>1, но очень
близко к единице. Амплитуда крутильных колебаний
7* 99
1,2
0,8
пренебрежимо мала по сравнению с амплитудой
продольных колебаний, а знаки перемещений совпадают.
Колебания закрученного стержня несимметричного
поперечного сечения. В общем случае совместные изгибно-крутиль-
но-продольные колебания описываются уравнениями (V.16),
(V.18) с инерционными нагрузками (V.32). Колебания
закрученных стержней исследовались в общем случае численными
методами 118, 55],
Изменение относительных собственных частот
пространственных изгибных колебаний закрученных стержней дву-
симметричного поперечного сечения определяется, как
показано в гл. II, углом закрученности и соотношением гибкостей
и (или отношением парциальных частот изгибных колебаний
незакрученного стержня), но не зависит от абсолютного
значения гибкостей. Для стержней несимметричного
поперечного сечения деформационная связь изгибных и крутильных
колебаний возрастает с уменьшением значений Гибкостей,
Это объясняется тем, чтб с* уменьшением гибкости частоты
парциальных изгибных колебаний растут быстрее, чем частоты
парциальных крутильных колебаний. Частоты крутильных
колебаний оказываются при этом ближе к низшим частотам
изгибных колебаний, что усиливает взаимосвязь колебаний.
Изменение относительных собственных частот изгибно-
крутильных колебаний стержней несимметричного
поперечного сечения в зависимости от угла закрученности а (/) при
различных соотношениях главных гибкостей [л и параметрах
несимметрии 6t, б„ показано на рис. 24. Значение главной
гибкости Я| = 104, характерное для многих турбинных и
компрессорных рабочих лопаток, соответствует такому спектру
собственных частот стержня, когда частоты парциальных
крутильных колебаний находятся вблизи низших частот
парциальных изгибных колебаний. Все частоты отнесены
к первой собственной частоте изгибных колебаний
незакрученного стержня в направлении минимальной жесткости
<й]0. Для незакручеиных стержней относительные
собственные частоты изгибных колебаний в направлении минимальной
жесткости отмечены треугольниками, в направлении
максимальной жесткости — квадратами, а в направлении
крутильных колебаний — кружками. Штриховыми кривыми
показано изменение относительных собственных частот
пространственных изгибных колебаний стержней двусимметрич-
Рис. 24. Влияние начальной закрученности на частоты изгибло-крутиль-
ных колебаний стержней при различных значениях параметров ц, gt, б .
101
ного поперечного сечения (б* — бл = 0). Главные изгибные
жесткости стержней такие же, как и для стержней
несимметричного поперечного сечения. Эти кривые соответствуют
классической теории закрученных стержней и подобны
приведенным на рис. 9. Штрихпунктирные кривые показывают
зависимость относительных собственных частот парциальных
крутильных колебаний стержней двусимметричного поперечного
сечения от угла закрученности. Рост этих частот с углом
закрученности определяется изменением их жесткости на
кручение. Сплошные кривые и кривые, представленные
двойными штрихпунктирными линиями отражают изменение с
ростом угла закрученности относительных изгибно-крутиль-
ных колебаний стержней с различными параметрами
несимметрии 6|, бп. Для рабочих лопаток турбомашин и осевых
компрессоров параметры б|, бл могут изменяться от 0 до 2, но
в большинстве случаев изменяются от 0,1 до 1. Для воздушных
винтов величины параметров несимметрии сечения обычно-
меньше. Как правило, значения 6& и 6^ имеют разные знаки.
На рис. 24, б, г приведены кривые, соответствующие
наибольшим параметрам несимметрии 6? =—1; б^ — 1,1, а на рис. 24,
а, в — кривые, соответствующие 6| =—0,5; 8П = 0,55.
Кривые, соответствующие 6^ =—0,75; бл = 0,825
представлены на всех рисунках. На рис. 24, в, г не приведена часть
кривых, так как они располагаются слишком густо.
Деформационная связь изгибных и крутильных колебаний
приводит, как правило, к снижению собственных частот из-
гибно-крутильных колебаний по сравнению с собственными
частотами стержней двусимметричного сечения. Кривые
собственных частот изгибно-крутилышх колебаний при одних
и тех же параметрах несимметрии не пересекаются между
собой, а кривые собственных частот изгибных колебании
стержней двусимметричного сечения пересекаются с кривыми
собственных частот крутильных колебаний этих стержней.
В зоне этих пересечений различие собственных частот стержней
с несимметричными и двусимметричными сечениями
увеличивается. Вследствие деформационной связи заметно изменяются
даже первые собственные частоты совместных колебаний.
Особенно резкое снижение первой собственной частоты даже
при небольших углах закрученности (а,; ~п!8) наблюдается
при отношении главных гибкостей ц --- 24 (см, рис. 24, в, г).
Для наглядности изменение относительной первой
собственной частоты изображено в увеличенном масштабе. Увеличение
отношений гибкостей ц, как показывает сопоставление рис. 24,
а, б и в, г, усиливает влияние деформационной связи на спектр
собственных частот стержня.
102
Рис. 25. Влияние начальной закручеиности на частоты изгибно-крутнльно"
продольных колебаний стержней при различных значениях ji, б,, 6 .
Влияние продольных колебаний иллюстрируется рис.Гб.
Здесь штрихпунктирными кривыми показана зависимость
относительных собственных частот крутильно-продольных
колебаний стержня двусимметричного поперечного сечения
от угла а (I), описываемая уравнениями (V.33). Штриховые
кривые отражают изменения относительных собственных
частот пространственных изгибных колебаний стержней
двусимметричного поперечного сечения. Относительные частоты
продольных колебаний незакрученного стержня отмечены
ромбом. Сплошными кривыми показано изменение
относительных частот изгибно-крутильно-продольных колебаний. При
сопоставлении рис. 24, а и 25, а, а также рис. 24, б и 25, б
наблюдается влияние учета продольных колебаний. Хотя
собственные частоты продольных колебаний весьма высоки и,
обычно, не представляют практического интереса, но
вследствие деформационной связи продольных колебаний с
крутильными заметно изменяется весь спектр совместных колебаний.
При ц = 6 претерпевают изменение все собственные частоты,
103
5 10 15 20 Л
Рис. 26. Влияние соотношения главных
гиб костей на частоты изгибно-крутиль- Q
пых колебаний стержней.
0,25 0,50 0,7Т 4
начиная С Третьей (СМ, рис. 25, Рис- 27- Влияние несимметрии
, пл сечения на частоты колебании
fl), a при Ц = 24 заметно из- закрученных стержней,
меняется даже первая частота
(см. рис. 25, б).
Отношение главных гибкостей существенно влияет на
спектр частот совместных колебаний закрученного стержня,
что отражено на рис. 26. Тонкими сплошными лучами показано
изменение относительных частот иезакручешгого стержня с
увеличением параметра ц (см. рис. 10), кривыми — изменение
относительных собственных частот совместных колебаний
закрученного стержня несимметричного сечения. Сравнивая
рис. 26 и 10, видим, что параметр ц имеет существенное
значение для спектра собственных частот закрученного стержня
как двусимметричного, так и несимметричного сечений.
Подобные графики для других значений а (I) приведены в
[16]. При (л > 10 влияние деформационной связи колебаний
заметно сказывается даже на первые собственные частоты
стержней, закрученных на угол а (/) >¦ я/8. Поэтому
деформационная связь играет особую роль для стержней
удлиненного профиля поперечного сечения, когда справедливо
упрощенное выражение для деформации винтового волокна
iV.2), принятое в технической теории стержней.
104
i*
,#¦
2
Iff;
4
0
\\
V
203"
нр_иЬой_
Рис, 28. Зоны влияния
деформационной связи колебаний;
а — в координатах a, dt, б ; б — в
координатах a, \i. * ^
Влияние увеличения несимметрии сечения на
относительные частоты совместных колебаний закрученных стержней
наглядно представлено на рис. 27, где использован параметр
Влияние деформационной связи на колебания
закрученных стержней рассматривалось также в [62, 74, 86],
Анализ результатов большого числа расчетов, сведенных
в графики, аналогичные представленным на рис. 24—27,
позволили определить области применимости классической
теории закрученных стержней в случаях малой несимметрии
сечений или слабой закрученности. Границы таких областей
показаны на рис. 28 в зависимости от параметров а (/), б*,
Ьц, ц и /Ц. Справа вверху от соответствующих кривых влияние
деформационной связи изгибных и крутильных колебаний
превосходит 8—10%. Норма допустимого разброса частот
рабочих лопаток в результате технологических отклонений
принята в энергомашиностроении около 8—10% [18, 37, 581.
Поэтому такая величина погрешности теории при определении
частоты была принята за условную границу области
применимости теории. Следует отметить, что эта граница не означает
скачкообразного изменения влияния рассмотренных факторов,
поэтому является приближенной. При оценке необходимости
учета деформационной связи в практических расчетах исполь-
105
4
*?
1
У
А
¦
О 0,2 0,4 0,6 Pf,f-
Рис. 29. Зоны влияния
инерционной связи колебаний.
зование зависимостей,
приведенных на рис. 28, значительно
удобнее, чем на рис. 24—27. В
зависимости от конкретного случая
удобна форма представления
результатов, приведенная на рис.
28, а или б. Стрелки направлены
в область, где следует учитывать
дополнительные факторы.
На рис. 23, б представлена
область применимости технической
теории закрученных стержней без
учета связи продольных и
крутильных колебаний. Сравнение рис.
23, б и 28, б показывает, что
существует область, где необходимо переходить от классической
теории к технической, но связь продольных колебаний с
крутильными можно еще не учитывать.
Инерционная связь изгибных и крутильных колебаний за
счет несовпадения центра масс и центра изгиба сечения стержня
вызывает у незакрученного стержня снижение меньшей и
повышение большей собственных частот взаимодействующих
форм [14, 46]. Меньшими являются обычно частоты
парциальных изгибных колебаний, а большими — крутильных
колебаний. Такое же влияние инерционной связи на частоты
колебаний сохраняется и для закрученного стержня [47, 65!.
На первую и вторую собственные частоты инерционная связь,
влияет слабее, чем на высшие. Влияние инерционной связи
колебаний увеличивается с ростом расстояния между центрами
масс и изгиба сечения и в случае более близких собственных
частот парциальных изгибных юи и крутильных &>k
колебаний. Несовпадение центров масс и изгиба сечения удобно
оценивать безразмерными параметрами: р% — ?/гп; рц ~
—T]s/r?. На рис. 29 представлена граница области, где
необходим учет инерционной связи колебаний в зависимости
от параметров ps, рц и отношения частот cofe/cou.
Обработка результатов исследований колебаний серий
рабочих лопаток турбомашин и осевых компрессоров позволила
определить диапазоны относительного влияния различных
факторов на собственные частоты колебаний (табл. 1).
Компрессорные лопатки отличаются более удлиненным профилем
поперечного сечения. Наибольшее влияние на колебания таких
лопаток оказывает деформационная связь, инерционная связь,
колебаний играет большую роль для турбинных лопаток.
Несимметрия сечения во всех случаях может оказывать су-
106
Таблица 1. Влияние различных факторов на собственные частоты
колебаний рабочих лопаток
Учтенные факторы
Инерционная связь колебаний
Деформационная связь изгиба и кручения
Связь продольных и крутильных колебаний
Депланация сечения при кручении
Сдвиг и инерция поворота сечения
Изменение собственных частот
иолебаний, °~
Турбинные
лопатки
0,15 г; а <
< 1,5 рад
— 10ч-26
—12ч-25
—13-5-0
О-*-16
—28-4-0
Компрессорные лопатки,
0,2 г; а г;
^ 0,7 рад
—7-4-15
—50-4-47
—22-Т-4
0+-27
— 12-5-0
щественное влияние на колебания реальных объектов,
имеющих форму закрученных стержней. Знак минус означает
снижение частот.
Закрученные стержни несимметричного поперечного
сечения совершают совместные изгибно-продольно-крутильные
колебания. Каждая форма колебаний включает перемещения
пространственного изгиба, крутильные и продольные
перемещения. При классификации форм колебаний можно говорить
лишь о преимущественно изгибных или крутильных формах,
в зависимости от того, какие перемещения превалируют.
Для некоторых форм трудно выделить превалирующие
перемещения.
Знак угла закручешгости а (I) и знаки координат |s, rjs
мало влияют на собственные частоты колебаний стержней, но
существенно влияют на формы перемещений, которые
определяют и напряжения в сечении стержня. .
Нормальные напряжения в сечении стержня удобно
определять по формуле
р Мг AL ЕМа ,
аг = Егг = -9- + -у-в- 11 _3_ g + То _e_ rft (V.35)
где силовые параметры находятся из соотношений (V.12).
В качестве примера на рис. 30 приведены результаты
расчета компрессорной лопатки, закрученной на 0,4 рад с
отношением длины к хорде на периферии lib — 2,59. Параметр и
изменяется по длине лопатки в пределах 7,3—23. Над чертой
приведены значения частот, полученные экспериментально,
а под чертой — расчетным путем. Отмечены значения
приведенных величин и их масштабы. Хорошо видна простран-
10?
1 \# \\У (j\
i \),
№31 Z!Z4- JtJS.
4403 esof 7взб
Рис. 30. Формы перемещений (а), моментов (б) и напряжений (в)
на входной кромке (сплошные кривые), выходной кромке
(штриховые кривые) и спинке (штрихиунктирные кривые)
компрессорной лопатки.
ственность форм изгибных перемещений. Формы продольных
перемещений не нанесены. По величине они отличаются от
изгибных на 2—3 порядка и более. Третья, шестая и седьмая
формы — преимущественно крутильные, а остальные —
преимущественно изгибные, хотя для четвертой и восьмой форм
трудно выделить преобладающие перемещения. Величины
изгибающих и крутящих моментов являются в большинстве
случаев соизмеримыми. Внизу представлены формы
нормальных напряжений на входной и выходной кромках и спинке
лопатки. Максимум напряжений для ряда форм достигается
не в корне лопатки, а в промежуточных сечениях. При этом
для разных форм наибольшие напряжения могут достигаться
в любой из трех характерных точек сечения.
Для всех форм колебаний стержня в каждом поперечном
сечении известны линейные и, v и угловое В перемещения
в плоскости сечения. Это позволяет определить мгновенный
центр скоростей каждого сечения:
» v cos а -{- и sin а , _ и cos а — v sin а
** ei '; ^ ~' ё ¦
Геометрическое место центров скоростей, лежащих на
поверхности стержня, образует узловую линию для данной формы
J08
колебаний. При
экспериментальных исследованиях
узловые линии
визуализируются с помощью
песочных фигур или
методами голографии.
Практически узловые линии
образуются также
центрами скоростей, лежащими
вблизи поверхности
стержня. На рис. 31
представлены узловые линии,
полученные теоретическим и
экспериментальным путем,
на поверхности модели
рабочей лопатки,
закрученной на 1,2 рад. Над чертой
приведены
экспериментальные, а под чертой —•
теоретические значения
собственных частот.
Теория стержней не
описывает деформацию поперечного сечения в своей
плоскости. Поэтому с ее помощью нельзя получить формы узловых
линий, пересекающих одно поперечное сечение 2 раза и
более. Такие формы колебаний описываются теорией пластин
или оболочек 15, 21, 34, 40].
Для стержня весьма удлиненного поперечного сечения
(fi^> 1) и слабой закрученности (р0 <^ 1) можно пренебречь
изгибом в плоскости наибольшей жесткости и влиянием
продольной деформации при определении трех низших
собственных частот колебаний [541. Для первой частоты равномерна
закрученного стержня постоянного сечения можно
использовать приближенную формулу
г
Рис, 31. Экспериментальные
(сплошные кривые) и теоретические
(штриховые кривые) узловые линии
собственных форм закрученной лопатки.
«Ч = @1
фЕ1%, (V.36)
где ш10— первая собственная частота незакручепного стержня
того же сечения; ?ь — эффективная жесткость на изгиб (V.28).
Поскольку Ь% уменьшается с ростом начальной закручен-
иости, первая частота нзгибных колебний также падает.
Техническая теория стержней является основой для
расчета на прочность и колебания закрученных рабочих лопаток
современных турбомашин и компрессоров [18, 36, 46, 47, 54,
оо i и воздушных винтов [74].
109
Глава VI
ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА
ТЕХНИЧЕСКОЙ ТЕОРИИ ЗАКРУЧЕННЫХ
СТЕРЖНЕЙ
1. Статическая деформация закрученных стержней
Как и всякая прикладная теория, изложенная в предыдущих
главах техническая теория закрученных стержней нуждается
помимо сопоставления с некоторыми частными уточненными
решениями в прямой экспериментальной проверке. С этой
целью на специальных образцах поставлены опыты как
статического, так и динамического характера. Было изготовлено
40 закрученных образцов из листового дуралюмина Д16АТ,
отличавшихся шириной и толщиной рабочей части. В течение
1—2 ч после закалки (из температуры 500° С в воду) плоские
заготовки устанавливались на машину для испытаний на
кручение, пластически закручивались на различные углы и в
таком состоянии подвергались естественному старению в течение
четырех суток, после чего тщательно промерялись.
Закручивание образцов непосредственно после закалки, когда
материал Д16АТ имел высокую пластичность, позволило получить
на большинстве образцов весьма равномерную по длине за-
крученность, а дальнейшее естественное старение обеспечило
им необходимую упругость.
Длина рабочей части всех образцов / = 140 мм, отношения
длины к ширине изменялось в пределах lib = 3,5 4- 7,0,
относительная толщина с = 1/ц = hlb = 0,03 -г- 0,07,
абсолютная закрученность на рабочей длине до а (/) = 3,6 рад,
относительная закрученность до т0 = 0,25 рад см, параметр
закрученное™ (III.3) до р2 = 15,6. В работе 1501 приведены
фотографии нескольких образцов с закрепленными на них
зеркальцами для оптического измерения углов упругой
раскрутки.
Растягивались образцы на трехтонном прессе с помощью
специального приспособления, в котором предусматривались
две пары зажимных гаек, обеспечивающих достаточно
равномерное распределение внешней нагрузки по ширине образца,
два шариковых захвата для разгрузки образцов от изгиба и
ПО
свободно вращающаяся ~f.fozlPad/m
обойма с двумя упорными ' ¦ ,
шарикоподшипниками.
Наличие указанной обоймы,
которая даже при
максимальной нагрузке
свободно проворачивалась в обе
стороны от руки,
позволяло изменять в процессе
опыта направление
моментов трения и тем самым
находить достаточно
точное (не зависящее от
крутящего момента) значение
деформаций только от
растягивающей силы как
среднюю величину от
замеренных значений при
различных положениях
обоймы. Углы упругой
раскрутки замерялись
оптическим методом с
помощью двух зеркальцев,
закрепленных на образце на
расстоянии 100 мм друг от
друга.
На рис. 32 точками
нанесены результаты
экспериментов в виде
зависимости относительного угла
упругой раскрутки х = 6' от относительной
растягивающей силы PJP0, Рп = 1000 Н. Каждое испытание
повторялось дважды, причем углы замерялись при различных
положениях обоймы с шарикоподшипниками, а также в
процессе разгрузки, чем и объясняется некоторый разброс точек.
Как показано в гл. III—V, для данной задачи расчетную
зависимость х = f (Pz) можно представить в виде
Рис. 32. Зависимость относительной
упругой раскрутки от продольного
усилия при различной степени
начальной закрученности стержня.
т = — %()квРо,
(VI
где введены безразмерные параметры
— _i^_ _??_• Ь — (] 4-
(VI. 2)
111
Причем для стержня с удлиненным прямоугольным сечением
^ 4Gc2F 4Gc2 ! b и,
1 + V!xn_
30 I *° h
(VI.3)
Знак минус в формуле (VI. 1) указывает на уменьшение угла
при растяжении.
Линейной теории [22, 39J соответствует значение кы = 1,
что следует из формулы (III.) при /° <С /„ вследствие с ^ 1.
Если учитывается отличие угла закрутки в деформированном
состоянии а + 0 от начального а при сохранении условия
0ср = const, то значение km = A -Ь ра)™~ , что соответствует
формуле (IV.51), технической теории стержней соответствует
значение km = A + pri)~', где рн отличается от выражения,
используемого в критерии (III.3):
/2 »2 т2
р sr 1)г
/0
Для стержня с удлиненным прямоугольным сечением р,ч =
= рг и определяется по формуле (VI.3). Нелинейной задаче
соответствует значение kg. Расчетные кривые для всех
указанных методов определения коэффициента ka приведены на
рис. 32, точками указаны экспериментальные результаты.
Кривые, представленные на рис. 32, а, соответствуют
испытанию стержней с относительной начальной закрученностью
т0 = 0,0197 рад/см, на рис. 32, б — т0 = 0,0864 рад/см,
на рис. 32, в — т0 = 0,0645 рад/см, на рис. 32, г —
т0 = 0,13 рад/см. Видно хорошее соответствие результатов
технической теории стержней экспериментальным данным в
широком диапазоне степени упругой раскрутки.
На рис. 33 обобщены данные по испытаниям четырнадцати
различных образцов, для чего экспериментальные значения
безразмерного угла раскрутки
определенные при одном и том же значении параметра рв =
== 0,091, отложены в зависимости от параметра закрученнос-
ти р,. Значение 0* вычислялось по формуле 0* = —Р,&)ре,
которая вытекает из (VI.1) при учете (VI.4), причем
коэффициенты kg определялись различными методами.
112
е*
0,04
0,02
Л
к Ilk
"в/ рг
\ 1/ i
I'ff"}
№
jjf
А» ^
1°
Рис. 33. Зависимость
угла раскрутки от
параметра начальной за-
крученности стержня.
Из рассмотрения рис. 33 следует, что при % <^ 1 все
упомянутые расчетные методы дают достаточно правильные
результаты, причем учет нелинейной зависимости степени
упругой закрутки т от растягивающей нагрузки в форме km =
~ A + Ре)" является полезным. Подобные стержни можно
отнести к слабо закрученным. Когда значение §2Г соизмеримо
с единицей, линейная теория, совершенно не учитывающая
членов порядка то, оказывается несостоятельной, в то время
как техническая теория закрученных стержней (&ез)
обеспечивает хорошее совпадение расчетных и экспериментальных
углов раскрутки вплоть до значений |3; = 5, что вполне
удовлетворяет практическим требованиям. Наличие максимума
на кривых связано с возрастанием крутильной жесткости
вследствие начальной закрученности.
Наряду с изменением углов раскрутки проводилось тен-
зометрирование нескольких образцов проволочными тензодат-
чика.чи с базой 5 мм. На рис. 34 приведены экспериментальные
2%/Ь
В 2—189ft
Рис. 34.
Распределение продольных
деформаций но ширине
образца при
различных параметрах
закрученности стержня
Рг
ИЗ
Рис. 35.
Теоретические (штриховые
кривые) и
экспериментальные (сплошные
кривые) эпюры
напряжений по ширине
образца (а=--= а/аср; аср =
= 103МНа).
,2
-1.0
-OS
значения (точки) продольной деформации е^ в направлении
винтовых линий образца в нескольких точках по ширине для
трех образцов, имевших различное значение параметра за-
крученности $г, при одинаковой средней деформации. Для
этих же значений параметра закрученности линиями нанесено
распределение деформаций по ширине образцов, найденное
теоретически по формуле
12
Прямая ?? = 6-10~4 соответствует незакрученной части образца.
Значения нормальных аг и aj и касательных Т|г напряжений,
рассчитанных для одного из образцов по замеренным
деформациям в трех направлениях, приведены на рис. 35.
Штриховыми кривыми представлены расчетные эпюры напряжений
аг% T|z, вычисленных в соответствии с формулами аг =?V;
% = GvQkepeh. Совпадение расчетных и экспериментальных
значений деформаций ej и напряжений az, T|Z вполне
удовлетворительно. Напряжения <jj в технической теории не
рассчитываются как второстепенные.
Эксперименты по изгибу закрученных образцов двусим-
метричного поперечного сечения описаны в 144], а их
результаты приведены на рис. 5.
Все рассмотренные опыты проводились на стержнях с
двусимметричным сечением, для которых отсутствует связь
между продольно-крутильными и изгибными деформациями.
Результаты динамических испытаний закрученных стержней
с несимметричными сечениями, более типичными для лопаток
турбомашин, приведены ниже.
114
2. Изгибно-крутильные колебания закрученных стержней
Для исследования изгибно-крутильных колебаний
закрученных стержней несимметричного профиля изготовлялись
специальные образцы, фотографии которых приведены в 1541.
Образцы с поперечным сечением в виде дужки постоянной
толщины вырезались из изогнутых по цилиндрической
поверхности листов дуралюмина Д16АМ0 таким образом, что
продольные стороны образцов совпадали с винтовыми
линиями, наклоненными к образующим цилиндра под
небольшим углом Рт.
Закрученные образцы прямоугольного сечения получали
обрезкой одного из концов образцов, использовавшихся для
статических испытаний на растяжение. При углах Рй <^ 1
оба метода образования закрученных образцов с точки
зрения анализа в рамках стержневой теории вполне эквивалентны.
Образцы отличались друг от друга относительной закру-
ченностью т0, изогнутостью профиля q = flh, относительной
толщиной с = hlb и удлинением lib. Ислытывалиеь 16
образцов, из них 11 — закрученные с изогнутым (несимметричным)
профилем сечения, 3 — закрученные с неизогнутым
(симметричным) профилем, 2 — незакрученные (с изогнутым и
неизогнутым профилями). Каждый образец испытывался на
электродинамическом вибраторе при трех значениях длины
консольной части, опыты повторялись несколько раз, причем
в ряде опытов образцы закреплялись заново. Крепились
образцы с помощью гидравлического зажима через
специальный переходник, рабочая поверхность которого совпадала
с поверхностью образца, что обеспечивало сохранность
формы поперечного сечения в заделке (рис. 36). Основные
параметры всех образцов приведены в табл. 2.
Опыты показали, что неточность определения собственной
частоты образцов составляла примерно 1,5—2% с учетом
погрешности фиксации образца в зажиме.
В табл. 2 приведены также средние экспериментальные
значения основных собственных частот колебаний всех
образцов шэ и дано их сравнение с расчетными значениями (оь
вычисленными по зависимостям технической теории
закрученных стержней. При этом хорошие результаты дает уже
формула (V.36). Там же приведены расчетные значения щ0,
полученные без учета влияния закрученности (при т0 = 0).
Результаты всех экспериментов представлены в обобщенном
виде графически в [54].
Как следует из таблицы, при двусимметричном
поперечном сечении (образцы 14—16) начальная закрученность
8» 115
w Таблица 2, Экспериментальные и расчетные значения частот закрученных консольных образцов
га
Номер
образца
2
3
4
5
6
7
8
9
10
11
12
13
14*
15 *
16*
1
by мм
38,0
38,0
39,0
38,5
29,5
20,7
18,5
40,0
38,8
38,5
19,0
39,8
40,0
30,0
30,0
30,0
h, мм
1,92
1,45
0,93
0,46
0,46
1,92
0,93
1,92
0,93
0,46
1,92
1,92
1,45
1,45
1,45
1,90
г, • Ю=,
рад/см
5,47
5 46
5,13
5,21
5,18
5,53
5,38
2,90
2,90
2,58
2,78
0
0
9,62
10,82
3,41
щ
1,97
2,72
4,38
8,57
5,20
0,56
1,04
2,18
4,48
8,34
0,51
0
2,72
0
0
0
Собственная
/ = 16 ем
•э
ПО
97
73
46
36
70
39
134
105
72
70
60
135
—
—
—
«,
112
97
73
39
38
70
42
137
102
65
69
61
138
—
—
—
«и
139
138
137
130
80
71
43
150
140
127
69
61
138
_
_
—
частота колебаний образца, Гц, при
аэ
163
148
ill
62
58
107
60
207
156
105
104
90
200
59
60
75
/ — 13 см
и,
170
148
НО
58
57
106
63
208
155
98
105
93
208
60
60
79
1
»и
210
209
208
198
121
107
66
228
212
192
105
93
208
60
60
79
1
%
285
243
185
108
94
175
100
350
258
165
176
154
347
—
—
—
= 10 см
<*н"
288
250
186
99
96
179
107
351
262
166
177
156
353
__
_
—
«10
355
353
352
334
205
181
111
385
359
325
177
156
353
_
—
.—
I— 14 см.
Рис. 36. Изгибно-крутильная деформация
закрученного образца при колебаниях.
(вплоть до значений
угла а (I) = 1,4 рад)
практически не
повлияла на основную
частоту, что соответствует
опытам С. А. Тумаркина
144]. Если же сечения
несимметричны, то с
увеличением закручен-
ности основная частота
заметно падает
(образцы 2 и 13, 4 и 10).
Частоты
закрученного и такого же неза-
крученного образцов в
некоторых случаях
отличаются в 2—3 раза
(образцы 3—5), по мере
уменьшения
несимметрии сечения и закрученности это различие также
уменьшается.
Экспериментальные результаты подтверждают снижение
первой собственной частоты закрученного стержня
несимметричного поперечного сечения, которое отражено на рис. 24
и 25, построенных согласно технической теории стержней.
В случае стержней двусимметричного поперечного сечения
первая частота с увеличением закрученности возрастает.
В работе [54] показано, что в отдельных экспериментах
снижение первой частоты не выявлялось в связи с малой
несимметрией сечения и слабой начальной закрученностью.
При испытаниях на электродинамическом вибраторе
производился замер амплитуды углов поворота концевого
сечения фотографированием колеблющегося образца со стороны
его свободного конца. При этом весь образец и фон
окрашивались в черный цвет, а концевое сечение и линия заделки —
в белый. Поскольку выдержка при фотографировании в
несколько раз превосходила продолжительность периода
колебаний, на снимках получались довольно четкие изображения
концевого сечения образца в его крайних положениях (см.
рис. 36), что после увеличения позволяло определить
экспериментальные значения 1г/Ь, по которым затем находился
относительный угол поворота концевого сечения: 01 = 0 (/) bivn (/)«*
~ Ы1Х. Связанность изгибных и крутильных
колебаний проявляется в увеличении относительного угла В1 при
росте закрученности и несимметрии сечения. Погрешность
117
Таблица 3, Sxcnef«ментальные и расчетные значения относительных
у1лов поворота сечений при колебаниях по основной форме
Псшер
образца
1
2
3
4
5
6
7
8
9
10
11
12—16
Относительный угол поворота при
/ = 16 см
бэ
0,25
0,46
0,56
0,75
0,39
0,10
0,10
0,29
0,67
0,89
0,10
0
в1
0,26
0,37
0,53
0,62
0,43
0,020
0,048
0,25
0,62
1,00
0,007
0
<
0,28
0,47
0,64
0,95
0,52
0,10
0,10
0,31
0,83
1,20
0,10
0
3 см
в1
0,32
0,45
0,65
0,77
0,53
0,025
0,060
0,31
0,77
1,23
0,009
0
1 — 1С см
9э
0,41
0,56
0,88
0,67
0,10
0,10
0,94
1,40
0,10
0
в1
0,42
0,59
0,84
1,00
0,69
0,032
0,078
0,30
1,00
1,60
0,012
0
оценки 01 составляет около 10—15%. Средние
экспериментальные значения 0э для всех испытанных образцов и
соответствующие расчетные значения О1, определявшиеся при
расчете ф°рм по технической теории стержней, приведены в
табл. 3. Результаты экспериментов по определению О1 также
представлены в обобщенном виде графически в 154] с
использованием параметра О/гр.
Как видно из табл. 3, эффект связанности изгибных и
крутильных перемещений, определяемый параметром б1, резко
возрастает при одновременном увеличении закрученности
стержня и изогнутости сечения, причем в соответствии с
расчетными данными эта зависимость носит нелинейный
характер.
Экспериментальные исследования колебаний стержней дву-
симметричного сечения проводились на стальных образцах
прямоугольного сечения в широком диапазоне углов
закрученности. Результаты этих экспериментов представлены на
рис. 9. Результаты экспериментального исследования кру-
тильно-продольных колебаний приведены на рис. 23 [14].
Влияние начальной закрученности на колебания
турбинных и компрессорных лопаток и соответствие теоретических
результатов, согласно классической и технической теориям,
с экспериментальными приведено в [10, 46, 47, 54, 55 и др.].
Соответствие собственных частот компрессорной и
турбинной лопаток, найденных теоретически и экспериментально,
представлено на рис. 30 и 31, откуда видно, что техническая
1 18
теория стержней позволяет
достаточно надежно
определять собственные частоты
закрученных лопаток
несимметричного сечения,
включая практически важные
высшие частоты. На рис, 37
показаны отличия
экспериментальных частот (точки) от
их расчетных значений
(линии) для большого числа
турбинных и компрессорных
лопаток, обобщающие
результаты, подобные приведенным
на рис. SO и 31. На
последнем сравниваются также
теоретические и
экспериментальные формы перемещений
закрученной лопатки.
При расчетах рабочих
лопаток наиболее сложным
считается достоверное
определение . распределения
напряжений при
колебаниях. На рис. 38 сравниваются теоретические (кривые)
и экспериментальные (точки) результаты исследования
распределения относительных напряжений по контуру сечений
закрученной рабочей лопатки. Указаны места наклейки мало-
базяых тензодатчиков. Размеры лопатки уточнялись
непосредственными измерениями. Приведены результаты для
первых трех форм колебаний (/—///) в наиболее напряженных
сечениях. Видно, что техническая теория стержней дает
достоверную картину распределения напряжений. Поскольку
теория стержней не учитывает, как уже указывалось, дефор-
о
г 4 й
Рис. 37. Сравнение
экспериментальных соэ и расчетных сор значений
частот закрученных стержней
несимметричного сечения.
1!
¦ и
til
А, .
д; "
/
0,
Si
* ;¦
A
%
m~ 4
-0
Рис, 38. Распределение
относительных
напряжений по контуру наиболее
напряженных сечений
закрученной лопатки при
колебаниях по первым
трем формам:
i _ гч ^= 0,3, II — г/1 ** 0,6>
III -г/1 = 0,4.
119
мации поперечного се чения в своей плоскости, область ее
применимости ограничена частотой первой «пластиночной» или
«оболочечной» форм колебаний. Кроме того, даже при
«стержневых» формах колебаний происходит некоторая деформация
поперечного сечения в своей плоскости, что снижает
собственные частоты колебаний. В связи с этим область
применимости любой теории стержней зависит прежде всего от
параметров lib и \х. Принято считать [77], что теория стержней дает
хорошие результаты при расчете лопаток на изгибные
колебания в области lib ^ 4. Исследования, подобные
приведенным на рис. 30, позволяют уточнить эту область и расширить
ее для технической теории стержней до значений параметров
lib ^ 3, \i ^ 20. Оценке границ применимости теории
стержней посвящена работа 137], в которой показано, что при
lib ^ 4 и ц ^ 40 первые восемь расчетных частот изгибно-
крутильных колебаний закрученного стержня отличаются
от экспериментальных не более, чем на 8—10%. Границы
динамических характеристик рабочих лопаток
рассматриваются также в [33].
Глава VII
СПЕЦИАЛЬНЫЕ ЗАДАЧИ ТЕОРИИ
ЗАКРУЧЕННЫХ СТЕРЖНЕЙ
1. Учет стесненности депланации сечения при кручении
В ряде задач для закрученных стержней удлиненного
несимметричного поперечного сечения оказывается полезным учет-
стесненности депланации сечения [20, 31]. Если депланация
сечения полагается пропорциональной относительному углу
упругого кручения, то перемещения любой точки стрежня
определяются соотношениями (V.I), (V.7). Касательные
деформации по-прежнему определяются выражениями (V.3),
(V.8), а в уравнении для продольной деформации должен
учитываться член 6"<р
ег = w' — и"х — v"y + 6"ф + б'V? =
= ш' — кп1 + К|Г| + 6"ф + Q'vT. (VII. 1>
Выполнение граничного условия жесткой заделки стержня
в корневом сечении, при котором депланация отсутствует,
6@) = 0; в'@) = 0, (VII.2)
приводит к отсутствию касательных напряжений в корневом
сечении тхг = %у2 = 0 при г = 0, согласно (V.3), что
противоречит экспериментальным данным.
Выполнение условия закрепления только для угла
поворота
9@) = 0, 6'@)^=0 (VII.3)
равносильно предположению о свободной депланации
корневого сечения. Для устранения этого противоречия
предлагается иногда определять продольные перемещения вследствие-
депланации выражением |3ф [31], а соответствующую
продольную деформацию как Р' ср, где р (г, I) — функция степени
депланации сечения. При жесткой заделке в корневом
сечении о @) = р @) = 0. Такой подход при выполнении
идеализированного условия закрепления обеспечивает уточнение-
результатов, связанных со стесненностью депланации сечения
121
1311. Однако граничные условия на закрепленном конце
могут задаваться в виде
6 @) = евМпг @); 8' @) = етВв @), (VII.4)
где М" — полный крутящий момент; В — упругий бимо-
меит; ец — податливость заделки при кручении; еы —
податливость основания при депланации.
Условия (VI 1.4) являются промежуточными между
условиями (VII.2) и (VI 1.3), исходят из представления о
закреплении стержня в податливом основании и обеспечивают
уточнение результатов в специальных случаях.
С учетом зависимости для продольной деформации (VI 1.1)
выражение для потенциальной энергии стержня в
неподвижной системе координат хуг имеет вид
i
Пф = Пг + -1 J Е [/ф (в"J + 28' (Sqw' — 1щЦ' —
о
— IlJf(v" + то/Гф6')] dz, (VI 1.5)
где Пг — потенциальная энергия в технической теории
стержней (V.4). Здесь введены геометрические характеристики,
связанные с функцией депланации:
/ф = ) (p^dF; Sy = J (pdF; 1ХЧ> — \ x<pdF;
F F F
(VII. 6)
Iyv ~ \ ytpdF; /Гф = \ r%dF.
f P
В теории тонкостенных стержней 1,с называется секториаль-
ным моментом инерции, S<f — секториальныы статическим
моментом, El(f — секториальной жесткостью, а В(р — бн-
моментом, ВФ = —Е1ц'<д" [38].
В системе координат |t)z выражение потенциальной
энергии можно переписать следующим образом:
Пф = Пг + 1|?[/ф (В"J + 20" (S^w' + 1тщ — /?фх„ -г
о
-f то/гФ8')] dz = Пг + -к- ~pj г- 2 T5J
122
Геометрические характеристики
(VII.8)
связаны с соответствующими зависимостями в системе хуг
соотношениями
Нч
= Я
(\7П.9)
Зависимости (VI. 12) надо дополнить выражением для бимо-
мента
Вф = ?/Ф9". (VII. 10)
Полные моменты и силы внутренних напряжений с учетом
(V.13) и (VII. 10) выражаются в виде
т S
рч> р' i R 2_ ¦
'г — ~ 7 г & ф —} >
МЧ = Ml
= Bi
's<P
(VII. 11)
где Во — полный бимомент.
Зависимости между силовыми и кинематическими
характеристиками деформаций в системе координат 1цг
представляют матричное уравнение
м?
о о
0 h 0
0 0 Ьп
bw bx^ b
хц
bev
к,
Ьщ
Ьх<р
w'
Щ
xn
CD CD
(VII. 12)
123
дополнительные коэффициенты
где &Еф, Ь^, Ьт, Ьщ,, Ь
жесткости:
Ьщ--=хйЕ1^; &Ф = ?7Ф. (VII. 13)
В системе координат лт/г уравнениям (VII. 12)
соответствуют зависимости
О
M'f
Вв
bs
О
о
Ьех
1 ьеф
0
Ьг<р
ху @х% Uxfp
'у ЬуХ Ьит
Ьх% b,,v Ь-r Ь
Ьху
by%
Тф
(VII. 14)
Охт
Дифференциальные уравнения (V.16) дополняются
новыми членами:
Т I t i Ci f\tf\ t Г ID
+
фву = Ц
щ\
} (VII.15)
Граничные условия отличаются от выражений (V.17) тем,
что в них входят значения Р%, Mt, Ml, Mvz вместо
соответствующих величин технической теории и дополняются
условием
б8'5в|о = О. (VII. 16)
Моменты М'х и Ml связаны с моментами Mf и М®
зависимостями A.18).
Уравнения в системе |т)г с граничными условиями
можно получить с помощью выражения (VI 1.7) на основании
принципа Остроградского — Гамильтона. С учетом депланацин
поперечного сечения в зависимостях (V.1) кинетическая
энергия при колебаниях стержня определяется выражением
Tv = ТГ +
28'
1.щи'
dz.
(VII. 17)
124
о
4-Ю'-
Eф
0,02 0,04
Рис. 39. Зоны влияния депланации сечения при кручении на
собственные частоты стержней.
Тогда инерционные нагрузки при колебаниях в уравнениях
(VII. 15) будут
дг = — pFw — pSvQ';
(uys
[р(/фв#— \ (VII.18)
lmv'
Стесненность депланацни поперечного сечения повышает
жесткость стержня на кручение и собственные частоты его
крутильных колебаний, инерция денланации снижает частоты,
но б меньшей степени. Члены с характеристиками Sff, 1ХЦ,
fy.fi влияют на колебания и деформацию стержней очень слабо
и в большинстве случаев могут не учитываться.
Для оценки влияния депланации сечения удобно ввести
безразмерные параметры б| = lJIpP; 6d = IJlp. Тогда
влияние депланации сечения на частоты крутильных
колебаний можно оценить с помощью следующей формулы [14J:
где &kn — частота крутильных колебаний, найденная без
учета депланащш сечения; sn — параметр, определяющий
частоту колебаний.
125
-ist—I
0 0,2? ¦ 0,50 0.7S iOO
a
ало ojs
8
Рис. 40, Формы напряжений гю
длине лопатки в характерны*
точках сечения при колебаниях
по первой (о), второй (б) и
третьей (в) формам с учетом гли-
яния стесненности кручения
(штриховые кривые).
оло 0,7$ г/1
S
Степень влияния стесненности депланации сечения на
собственные частоты реальных турбинных и компрессорных
лопаток отражена в табл. 1, Границы областей, где влияние
депланации сечения на частоты превышает 8—10%,
показаны на рис. 39. Они зависят от параметров бФ, 8d и отношения
рассматриваемой крутильной частоты к первой крутильной
частоте незакрученного стержня, найденной без учета
депланации сечения. Горизонтальные штриховые линии
показывают расположение относительных парциальных частот
крутильных колебаний. Авторы еще раз подчеркивают
относительность понятия границы области, так как степень влияния
каждого фактора изменяется плавно.
Стесненность депланации может оказать заметное влияние
на напряжения в стержне, особенно вблизи закрепления
сечения. На рис. 40 показано распределение напряжений по
длине лопатки в характерных точках сечения, отмеченных на
рис. 38, при колебаниях по первой, второй и третьей формам.
Сплошными кривыми представлены формы нормальных
напряжений, найденные без учета стесненности кручения,
штриховыми — с учетом депланации, согласно зависимости (VII. 1),.
штрихпунктирными — формы касательных напряжений т;2г,
найденные с учетом проекций а/ГоПд. Вопрос нахождения
функции депланации рассмотрим в следующей главе.
Точками нанесены экспериментальные результаты. Влияние
стесненности кручения сказывается только непосредственно
вблизи заделки, причем теоретическое влияние его оказы^
вается завышенным. Это объясняется податливостью
реальной заделки и особенностями сопряжения пера с хвостовой
частью. Последние факторы можно оценить лишь с помощь»
эмпирических зависимостей. Касательные напряжения
значительно ниже нормальных.
2. Деформации тонкостенных
закрученных стержней
При деформациях тонкостенных закрученных стержней вли^
ние начальной закрученности и депланации сечения
проявляется наиболее сильно. Поэтому, наряду с общей теорией1
закрученных стержней произвольного сечения, представляет
интерес получение зависимостей для тонкостенных
закрученных стержней с позиций общей теории оболочек.
Проведем по поверхности цилиндра радиуса Ro (рис. 41)
две системы взаимно ортогональных винтовых линий I, s
так% чтобы угол ро между касательной к линии s = const
и осью цилиндра удовлетворял условию Ро <? 1, т. е. A.6).
127
Компоненты кривизны klt
k2 и кручение
поверхности ku ВДОЛЬ ЛИНИЙ L, S
при этом условии будут
К = Po/i?0;
k = В /R
(VII.19)
Полагая в уравнениях
общей теории оболочек
[381 для ортогональных
координат на
цилиндрической поверхности
коэффициенты первой
квадратичной формы А — В = 1,
X = л/2, опуская в
соответствии с условием A.6)
члены порядка kx, kh и
считая (#2)? = (kn)t = О,
получаем с учетом
условий Кодацци — Гаусса для закрученной оболочки
толщиной h, срединная поверхность которой совпадает с участком
указанной цилиндрической поверхности, три системы
уравнений.
Геометрические соотношения:
Рис. 41. Системы координат для
тонкостенных закрученных стержней.
Е, =
OVn
2 — Cs
К, =
д$ ' <7д
д [ дтп
Ifil i ! ,
dt ' 2 [ di
дип
ds \ ds
ds
«12 = -75Г
0'Q \ ds ' 2
(VII.
128
Уравнения равновесия, необходимые для перехода к теории
стержней:
дМ<
(VII.21)
- т
21
ким, = о.
Соотношения упругости:
Eh
,, Eh
Eh?
12 A —
(VI 1.22)
М12 =
12A
к,».
Здесь 6], ё2 — удлинения; е12 — сдвиг; у,ъ и2 — изменения
кривизн; х12 — изменение кручения срединной поверхности.
Положительные направления перемещений и0, v0, w0,
внутренних силовых факторов Nlt Мъ Мг, Мп, ... и
продольной распределенной нагрузки рг показаны на рис. 41.
В уравнениях равновесия опущены также члены, содержащие
произведение kl2 на второстепенные силовые факторы Qa
и Mt.
Переходя к закрученному тонкостенному стержню,
образованному равномерным винтовым движением произвольного
открытого удлиненного профиля относительно
прямолинейной оси ?,а, принимаем, что соотношения (VII.19) — (VII.22)
останутся приближенно справедливыми, если координату ?
отсчитывать вдоль винтовых линий на срединной
поверхности стержня или с принятой точностью вдоль оси стержня,
a s — вдоль средней линии поперечного сечения, и считать
h ¦= h (s); k% = k2 (s); kn =¦ т0 = cir (a — угол начальной
закрученности стержня, штрихами обозначаются
производные по р.
В соответствии с теорией тонкостенных стержней [38]
допустим, что при определении основных деформаций е,
X], х12 контур поперечного сечения можно считать недеформи-
руемым и пренебрегать сдвигом в срединной поверхности.
Из рис. 41 видно, что первое условие означает
Щ = «а @ is (?, s) + va (Q % (?, s) + 8 (t)
Щ = — U* (Q *]s g, S) + Va (Q & (I, S) + e {I)
[pa {s)\s,
9 Z~- 1S98
129
где м« (Q, va(t) — перемещения точки оси стержня вдоль осей
координат |, г) (перемещением <ла вдоль оси ? но
сравнению с «а, Vex пренебрегаем); 0 (Q — угол упругого поворота
сечения;
(C0a)s = (g — |о) Tfe — (т| — %) Is = (li — let) (%)s —
— % — %) m)s> ^ (VI1,24)
\ра/ s — \fe ?а/ fes ~T~ v' 1 la/ ' is —
причем
Ь7СО5Ь> %7 ''. J (VII.25)
(ij)s = cos^; (%)s = sin-ф!. J
Координаты точки в системах координат &,% и Ъ\ связаны
между собой соотношениями (IV.3) вследствие "чего |' =
= (% — Ца) т0; л' = (|х — ta) т0. Второе условие (е12 = 0)
позволяет с помощью соотношений (VI 1.20) выразить
перемещение и0 через 1»0> ^0, а именно
/0 — 2kltw0)ds, (VI 1.26)
где hs — перемещение в некоторой точке средней линии,
принятой за начало отсчета.
Введя уравнения (VII.23) в (VII.26), получим
., ,. (Т\ I,, (?~\ т п (Til E /"?" сЧ
— [v'a © + то«« (Q] ц (t, s) — В' (Q соа (s) -f 2то6 @ ра (s) (VH.27)
(функция и01 (С) включает все члены, зависящие только от
координаты ?). Подставив выражения (VII.23) и (VII.27)
в формулы (VI 1.20), найдем
«1 = ро (о -«; (91 (s, s) -1»; id л (с, s) —
— 0*(E)coa(sL-2T0e'(Dpa(s);
Xi = ьуо 4- 2^12у0 = иа (р tjs (t, s) 4- va Q & (t, s) + j f
-4- 0" (?) [pa (sIs 4" 2t00j fco2 (s)b; .
¦ i в i —
130
При выводе последнего соотношения следует учесть, что
но определению,
Ь* + k2t\s == 0; (юо)м — k% (pa)s = 0; j
=0; (ра)ss + k2 ((Da)s = 1, |
Деформация в при условиях (VII.23) также равна нулю.
Таким образом, с точностью до несущественного члена хйгг
величину к12 можно считать постоянной по сечению и равной
относительной упругой закрутке
и12»0' = т. (VII.30)
Если в формулах (VI 1,20) вообще пренебречь влиянием
тангенциальных перемещений на компоненты изгибной
деформации, т, е. считать щ да w0 (при v0 *» 0), то выражения для
Ki и Ki2 получаются в виде (VII.28), как это и сделано в [53].
В соотношениях (VII.28) удвоенная «секториальная нло-
щадь» «а = ) (wct)'s ds [38J, а pa = ] (pa)s ds = -у /?o.
0 0
Деформации в произвольной точке сечения М, удаленной
от средней линии на расстояние б, где — 0,5ft s$; б s$; 0,5ft,
связаны с компонентами деформации срединной поверхности
формулами
eie = e1(?, s)— щЦ, sN;
fe12)e = еза (С, s) — 2х« (?, s) б,
так что при подстановке выражений (VI 1.28) в (VI 1.31)
получаем
ей = е0 — иаЪй — i4il6 + 9"фб + T08'i?i (VI 1.32)
Здесь |б и Щ — координаты точки М, |s = I — r\s&', Цв =
г--= ц _j_ |sg. фа — функция кручения тонкостенного профиля,
с( 3 = —[<»a-f-(paK 6], рассматриваемого как совокупность
прямоугольных вытянутых профилей; Ra — квадрат
радиуса-вектора точки М, Rl = 2 lpa — (co3)s б],
Обозначив
щ = и'а, Щ = — Va\ T = 0', (VII.33)
найдем, что распределение продольной деформации ец
согласно (VI 1.32) отличается от (IV.67) только членом т'фа,
соответствующим учету стесненного кручения. При т0 = 0
выражение (VII.32) переходит в формулу Джанелидзе [23]. Сдвиг
(е12)д согласно уравнениям (VII.31) также совпадает со
сдвигом б|? согласно (IV.69).
9* 131
Для дальнейшего анализа целесообразно перейти от
функций (ci)a)s, pa, определенных относительно оси начальной и
совпадающей с ней оси упругой закрученности (т. е.
относительно центра жесткости сечения), к функциям ((лр)$, рр
с полюсом в некоторой другой точке ?р, г\р.
Из формул (VI 1.24) можно установить, что
(tOah = K)s + (lp — la) Ц, — (Цр — Ца) Ы
, ... ».«.,. , , , ( v 11.о4)
Pcs = Рр -Г Ир — Ы I + (lip — %t) 11 + COnst,
тогда выражения (VII.28) с учетом (VII.33) принимают вид
8j = ер — щрц — яп? —¦ т'соа + 2т0трр; г
(VII.35)
Хх = — К^рТ],; — K|pSs + Т' (pa)s + 2t0T ((Dfl)s,
где
ер == е + totJ?p; |
%> = х-; — 2тот (цр — tic); (VII. 36)
причем
i?P = у- f 1A - У8 + (Л - ^J1 ^-
F
Подставляя выражения (VII.35) при е2 = 0, щ = 0 в
соотношения (VI 1.22) и полагая в пределах точности теории
?7A — -у2) г» Е, получаем
A'i = Eh {гр — к1рц — у,пр1 — т'©а + 2т„трр);
Мг = ^- [—xnPi]s — К|РЙ + t' (pa)s + 2t0t (cop)s]
M]2 = — M21 =-~ G/i3t.
Пренебрегая в пределах точности теории проекцией
касательных напряжений сдвига на ось стержня, можно записать
первые три интегральные условия равновесия (IV. 15):
Л1, = | (Mib + iVji]) ds;
S
J
132
что после введения (VII.37) дает
Pi — E (bpF — x^pSt! — x-tpS-- — т'5ф + totSp);
М п = Е (— &pSn + пПР1п + п*Р1щ + х']фТ, — 10
М-. = — Е (— epSs + н^/|Л + Х|Р/| + т'/ф| —
где
F = J /ids; Ss = J ftT|ds; S4 = j Agds;
s s s
Sv = J hcoads; Sp = 2 ] /ippds;
s s
ф! = J A I coaTi + -jy- (pa)s 1^1 ds;
L J
/q>n =
a? Т7Г (Pa)s
/Pl = 2 J Л Гррт]
(ap)'s Щ ds;
/P4 = 2 f Л [ppl + -jl- (top
ds.
(VII.38)
ds;
(V 11.39)
Выбором начала координат в центре тяжести сечения,
главных направлений осей |т], координат полюсов Оа (ta, t)a)
и Ор (|р, т)р) и двух констант, входящих в функции ша и рр,
обеспечивается выполнение условий
S, = 5„ = Sv = Sp = /Еч == /ф| = /ФЧ = I
Pl
= О, (VII.40)
из которых, в частности, определяются координаты центра
жесткости сечения |s, т], и полюса Ор Aр, У]р):
Стоящие в числителях геометрические характеристики
соответствуют полюсу в начале координат.
133
Из соотношений (VII.39) при (VII.40) следует
= P-JEF;
(VII 42)
Формулы (VII.42) по виду совпадают с соответствующими
выражениями теории призматических стержней, но по
существу они различны, так как компоненты ър, щр, %цр не
совпадают с е, Х|, кц и являются некоторыми средними
значениями соответствующих характеристик, не относящимися к
фиксированным точкам сечения.
Уравнение крутящих моментов относительно оси ?а имеет
вид
М:а = \ [Ми + Тш (©«>; + Qt (Ш ds -Ь
5
+ % J Wl [{(Pad's}* + {(«a)s}2] —Мг ((Oafs} US.
s
Учитывая, что при свободных продольных краях
j ^21 (»a)sds = — ] (T21)s coads;
M12 (p«)ss dS = — J (M12)s (pa)s
и принимая во внимание соотношение (VII.29) и уравнения
равновесия (VI 1.21), находим
Mra = J \2Мп + [(#,)' + ft] ©а + М\ (ра)Л ^ +
;}2 + {(сОапЦ - 2М, (©„>;] dS.
Выразив Afj, Mj и Mj, согласно (VI 1.37) и учтя, что при
Sp =- 0
[(р«)Ла + K©»)d2 - 2Рр + 2с (%р - Ы + 2т) (т]„ - т|а) + ^,
получим при выполнении условий (VII.41)
+ ?т0 [epi?pF - 2х11Р (Ер - Ы /„ - 2щр (цр - п«) /5], (VII.43)
134
где
/ф = ] h \а>1 + -утр {(pa)sJl ds;
/-< i* /~<iQ i i- 2 r
Uld = bid + -CTo/r;
/S = 4-U'ds; ^ (VIL44)
, , С , Г •> , h2 ,, .',,1 ,
/, = 4 \ A l^pp + -15- {(top)sJj ds.
г
Нетрудно убедиться, что 2 [pp — (cop),6] = г, и значения
/, согласно (VII.44) и (IV.55) совпадают. Можно также
показать, что без учета эффектов стесненного кручения (/ф = О,
Рх — 0) системы (VII.42) и (VI 1.44) с учетом (VII.36)
тождественно совпадает с системой (IV.64).
Формулы (VII.39), (VII.41) и (VII.44) позволяют найти
все геометрические характеристики, необходимые для расчета
закрученных тонкостенных стержней, и в частности,
координаты центра жесткости сечения. Ряд дополнительных
вопросов, относящихся к теории тонкостенных закрученных
стержней, изложен в работах [53, 83].
3. Учет влияния деформаций сдвига
Сдвиг следует учитывать при изгибе коротких стержней и
изгибе стержня в направлении максимальной жесткости,
а также при колебаниях стержней по высшим формам. В
теории стержней принято выделять углы поворота нейтральной
оси при чистом изгибе ух\, уу\ и углы сдвига у нейтральной
оси ухо, уУ2 146]. Поворот плоского поперечного сечения
определяется углами ух\, уУ1, а деформации сдвига — углами
4x2, 1></2- Удобно ввести соответствующие обозначения для
перемещений при изгибе Mi, Vi и сдвиге ы2, v2. Тогда уу\ = щ;
уг, .-= —ц,; уу2 = ц2; ух2 = —у,, ПрИ СДВИГе ПРОИСХОДИТ
денланация поперечного сечения, пропорциональная углам
сдвига уУ2% — Тлг2*Р, где %, л? — функции депланации при
сдвиге, зависящие от формы поперечного сечения и
направления сдвига 1151.
Выражения для перемещений с учетом сдвига имеют вид
U = их + и2 — дух; V--~-vx-\- o2 + e^;|
W = w — щх — v\y -f u'2% + v'iW -f- 8'ф.1
135
Деформация соответственно
вг = ш' — щх — uji/ + «2%
&* = 8j, = 7*» = 0;
+ 8*cp + 8V?; I
ду
(VIL46)
Исследования показывают, что депланацию сечения при
сдвиге целесообразно учитывать только в выражениях для
касательных деформаций и напряжений [14].
Потенциальная энергия при деформации стержня с учетом
сдвига
i
Пс = Яф + 4" J GF ikx («гJ + ky (V2J + 2kxyu2V2\ dz, (VI1.47)
6
где Яф определяется выражением (VI 1.7).
В выражении (VI 1.47) введены безразмерные
коэффициенты формы поперечного сечения при пространственном сдвиге:
ду
dF.
(VII.48)
В системе координат h\z подстрочные индексы 1 и 2 имеют
тот же смысл, что и в системе хуг. Тогда с учетом основных
членов перемещения
а деформации
ег = w' —
в- = ел =
IV = 6'
E + %t] + 8"f -
Л.
(ЭХ-
(VI 1.49)
ax»
. (VI 1.50)
¦ l
136
Потенциальная энергия деформации принимает вид
F (kf^2 + knyl2 + 2ft|tlTtl2T|2) dz
о
4D ^ ^Ф (VIL51>
Коэффициенты формы поперечного сечения при сдвиге в
системе координат \у\ определяются по формулам,
аналогичным выражениям (VI 1.48) для kx, ky, kxu и связаны с ними
такими соотношениями!
ki — kx cos2 a -\- ku sin2 a -f- kxy sin 2a;
т, = kx sin'2 a + kx cos2 a — kxy sin 2a;
ft^ri = (kg — kx) ~j- sin 2a + kxy cos 2a.
(VII.52)
В выражение (VII.51) введены перерезывающие силы,,
пропорциональные углам сдвига,
Л = GFk,^; Рч = — GFk^j. (VII.53)
Уравнения (VII.53) дополняют зависимости (V.12) и (VII. 10).
При учете сдвига полные моменты и силы определяются
выражениями (VII.11), которые дополняются еще двумя:
Соотношения (VII.12) и (VII. 14) остаются в силе, причем
компоненты кривизны при изгибе должны иметь подстрочный
индекс 1 («si, xni,—Vu Mi). Соотношения между
перерезывающими силами н углами сдвига будут независимыми
системами соотношений!
Аналогично
Pi = GF (kxth + kxvv3);
Pi = GF (kxyu2 + kyOi).
13Г
Уравнения (VII. 15) также изменяются только вследствие
появления подстрочного индекса у перемещений и, v и
дополняются двумя уравнениями:
[GF (kxu2 + kxyv'2)\' = — qx;
с граничными условиями 6«aPi |o = 0; bv,2P\ Jo — 0.
Кинетическая энергия в данном случае учитывает инерцию поворота
поперечного сечения
{[ul + v] + ш2 — 2ucQys + 2t-0xsl F + /,92 +
+ /, (v\f + 2Itvu\v\ + /,f (Q'f + 29' (S9w —
г, (VII.55)
где ис — иг + ы2; ис = i^ + v2.
Инерционные нагрузки при колебаниях стержня
приобретают вид
qx = pF (uc — 0#s); qy = pF (vc + вх$);
q7 = — р/„8 + pF (u.u, — tuO + [p U<n®' — t
4 ... " . сУ С5;т-1р\ф i (VIL56)
В случае статической деформации стержня нагрузками, не
зависящими от перемещений, системы уравнений (VII. 15)
и (VI 1.54) могут решаться независимо. При колебаниях
стержня эти системы уравнений оказываются связанными
вследствие инерционных нагрузок^ и qy, определяемых
выражениями (VI 1.56), и составляют единую систему шести
дифференциальных уравнений.
Только в случае незакрученного стержня постоянного
двусимметричного сечения два уравнения поперечных
колебаний стержня в одной плоскости с учетом сдвига можно
свернуть в одно [13J, полученное С. П. Тимошенко. В остальных
случаях остается система уравнений. Поэтому попытки
приписать к уравнениям закрученных стержней члены, подобные
встречающимся в указанном уравнении поперечных колеба-
J38
Рис. 42. Зоны влияния сдвига
на частоты изгибных колебаний.
ний незакрученного стержня
постоянного двусимметричного
сечения, нельзя признать
удачными.
Влияние сдвига и инерции
поворота сечения для реальных
объектов обычно проявляется
при колебаниях по высшим
а'ормам. Наблюдаемая степень
такого влияния для рабочих
лопаток турбомашин и
компрессоров отражена в табл. 1.
Влияние сдвига на
собственные частоты колебаний стержня
возрастает с уменьшением
главных гибкостей последнего,
увеличением коэффициента
формы поперечного сечения при
сдвиге и возрастанием числа
перемен знаков компонентов
кривизны формы изгибных
перемещений. Ориентировочные
границы области, где влияние сдвига на собственные частоты
колебаний превышает 8—10%, приведены на рис, 42. По оси
ординат отложено отношение частоты колебаний стержня
к первой собственной частоте изгибных колебаний
незакрученного стержня с теми же характеристиками главных
изгибных жесткостей. Горизонтальные штриховые линии
соответствуют относительным собственным частотам изгибных
колебаний незакрученного стержня постоянного сечения. При
наиболее часто встречающихся значениях коэффициента формы
поперечного сечения при сдвиге 118] влияние его изменения
невелико.
Распределение нормальных напряжений не претерпевает
существенных изменений. Касательные напряжения %Х2 ~
~- Щхг, v = Gyr вычисляются по зависимостям (VI 1.46)
в ио-прежнему остаются значительно ниже нормальных.
4. Учет влияния вращения стержня
Для реальных объектов, моделями которых служат
закрученные стержни, большую роль играет вращение вокруг оси
пег иендикулярнои оси стержня г. Пусть ось х ориентирована
параллельно оси вращения, ось г — по радиусу относительно
оси вращения, а начало системы координат расположено на
139
расстоянии /? вдоль этого радиуса. В сечении 2=0 угол
между осями х и ?, называемый углом установки, а0 = а @).
Стержень вместе с системами координат хуг и t,i\z вращается
с постоянной угловой скоростью Q. Тогда перемещения
элементарного объема стержня в прямоугольной невращающейся
системе координат XYZ, ось X которой является осью
вращения, будут 118]
U а — Uo;
Va = (R + z + Wo) sin 9J + (Vo + y) cos Ш;
WQ*=(R + z + Wo) cos 0/ — (Vo + У) sin Ш,
где Uo, Vo, Wo — перемещения стержня в системе
координат хуг.
Кинетическая энергия вращающегося стержня
определяется по формуле
i
Т" = 4"
i
И Р № + ^« + ^1) dFdz =
0 F
И
0 F
+ -?- f f Р КУо + УJ + (Wo + R + г)*] dFdz +
О F
I
+ О J J р [Wo (Vo + y)-V0 (Wo -tR + z)} dFdz, (VII.57)
0 F
в которой содержатся выражения кинетической энергии
колебаний невращающегося стержня, работы центробежных сил и
работы кориолисовых сил. В последних двух выражениях
присутствуют члены, содержащие квадраты малых
перемещений и произведения перемещений на константы у и R + г.
В таких произведениях следует учитывать величины второго
порядка малости при определении перемещений Uo, Vo, Wo.
При угловом перемещении Э точка поперечного сечения
А с координатами Х\ух совершает перемещение 6гь проекции
которого на оси х и у обозначены ?«е и vo (рис. 43, а). Из
подобия треугольников ААгВ и 0$СД следует
1 1
щ Xi Т "е "в Уг г — ve
__^ = _ ; -^г-= - ,
140
Рис. 43. Перемещения второго
порядка малости при
деформации стержня.
гтхуда, пренебрегая значением 62/4 по сравнению с едини-
ц- й можно найти
ив = — (V + 4- ®
Ve = вхг — -?- d2yv (VII.58)
В результате перемещений U ш V, определяемых
формулами (VI 1.45), происходит изменение координаты z любой
точки сечения на величину (рис. 43, б)
Разложив подынтегральное выражение в ряд и удержав
величины второго порядка малости, можно найти
г
— Дг - -L I '{(u'f + (v'f + (б'J А + 2Q'v'x1 — 29'ы>,1 с!г.
(VI 1.59)
14S
При повороте поперечного сечения на углы щ, V\ за счет
изгиба перемещение W имеет проекции на оси х, у (рис. 43, в):
w±.Wuu vw=-LWv\. IV1I.60)
С учетом зависимостей (VII.58) — (VII.60) перемещения в
системе координат xyz принимают вид
Величины U, V, W в общем случае определяются
соотношениями (VII.45). Полученные зависимости подставляются в
(VII.57), При этом выражение кинетической энергии
колебаний невращающегося стержня (VII.55) с точностью до величин
второго порядка малости не претерпевают изменения.
Выражение работы центробежных сил при колебаниях стержня
имеет вид
А = -HL J р {(у2 + w* + 2vQxs) F + б2 (/„ + xlF - 1Х) +
о v
+ (ы!J1У + u\v\lxy + (в'J /ф - 2G'«i/«p + 2Q'w'S4l -
i i
- \(u'f + (v'f] J (R + z) Fdz - (%'f \{R + z) Ipdz +
г г
+ 2ы'в' J (R + z) Fysdz — 2i>'9' J (R + z) Fx.dz) dz. (VII.61)
г г
При статической деформации прямого стержня работа
центробежной силы без учета восстанавливающих моментов
второго порядка малости определяется по формуле
i
Ао = Q2 J p [QIxy + w{R + z)F] dz, (V 11.62)
о
При колебаниях стержня кориолисовы силы совершают
работу, определяемую выражением
Ак = Q ] Р {[w (v + 6xs) — w(v + вх,)] F +
U
+ (ы,'в — й[ 6) 1У + (v'td — v[Q) Ixy +
_j_ [66 — (wv\ + wv'i)] (R + zjF + (vfr —1)9') 5Ф +
+ @6' - 60') (Ixv + x.S^)} dz. (VII.63)
142
В случае статической деформации стержня в поле
центробежных сил на него будут действовать согласно (VI 1.62)
распределенные нагрузки:
дг0 = Р.2р (R + z) F; тг0 = п*р!ху. (VI 1.64)
Нагрузки от центробежных сил при колебаниях стержня на
основании (VII.61) определяются выражениями
у = п2р Aищ +
О
\ (VI 1.65)
¦в' (R + z)Fysdz\;
= — Q2p \v' j (R + z) Fdz +
+ 9'} (R + z) Fxs
m? = Q2p {(/„ + x?F — Jx) 9 + x/y —
— (/„6' — 1щщ + Svw)' + [б' { (/? + г) lpdz ¦
Г
Fxsdz .
i t
— u'\(R + z) Fysdz + v' j (R ¦
Г 2
Для нагрузок, вызываемых при колебаниях стержня кориоли-
совыми силами, согласно (VI 1.63) имеют место зависимости
ul = — 2Qp (v + Bxs) F;
/rtj = —2Йр(/в0)'; /га* = — 2Йр G^0)'; j (VII.66>
//,*:-. _ 2Qp [Fx,w — lyiii -— lxuv\ + (!xq> + х,5ф) 6'].
Нагрузки qxc, qyc, mxc, mvc относятся в выражениях (VII.68)
к системе уравнений (VI 1.54), отражающих деформации сдвига.
При колебаниях закрученного стержня центробежные силы
повышают частоты его собственных колебаний, что отражено
во многих работах [14, 18, 46, 56, 58, 59, 62]. При этом центро-
14»
с
¦ /
/
/
/
f '
—-«v
<
0,8
0,4
3 в 9 oC(i)
Рис. 44. Зависимость угла
раскрутки вращающегося
стержня от начальной закру-
ченности (а = Зба/я; 6 =
= 369/я).
бежные силы, как видно из
выражений (VII.65), создают
дополнительную связь различных видов
колебаний. Наибольшую роль при
этом играет связь крутильных и
изгибных колебаний за счет
несовпадения центра масс и центра
изгиба сечений. При крутильных
колебаниях стержня двусимметрич-
ного поперечного сечения основную
роль играет распределенный
момент О2р8'
z) Ipdz,
повышающий частоты собственных
колебаний.
При статической деформации стержня в поле центробежных
¦сил основную роль играет продольная нагрузка q^ (VI 1.67),
вызывающая упругую раскрутку стержня за счет
деформационной связи. Эту раскрутку необходимо учитывать при
расчетах лопаток турбомашин, осевых компрессоров и
воздушных винтов. Зависимость угла упругой раскрутки G (I)
конца вращающегося закрученного стержня от угла
начальной закрученности а (I) представлена на рис. 44. Характер
зависимости такой же, как и при растяжении закрученного
стержня осевой силой (см. рис. 33). Нелинейность зависимости
О (I) = f (а) отражена в выражениях (VI.1), (VI.2),
максимум которой достигается при значениях а (I),
соответствующих параметру закрученности р\. = 1.
Распределение нормальных напряжений по сечению
закрученной лопатки при действии центробежных сил
представлено на рис. 45, так же отложен масштаб <тср = Ря/F, где
Рго — полная центробежная сила, действующая на лопатку
r-J
-г
-о
Рис. 45. Распределение нормальных напряжений от центробежных сил
в сечении закрученной лопатки.
144
в данном сечении.
Максимальные напряжения достигаются
в центральной части корыта и
превосходят средние в 2,3 раза.
Сравнение теоретических и
экспериментальных
результатов по распределению
нормальных напряжений на контуре
поперечного сечения
вращающейся лопатки приведено на
й
Рис. 46. Распределение
напряжений по контуру сечения
й
рис. 46. Результаты, найденные вращающейся лопатки согласно
согласно технической теопии расчетам без учета начальной
со1ласно технической теории закрученности и по технической
закрученных стержней показа- теории.
вы сплошными линиями, а
результаты, найденные по методике, не учитывающей
начальную закрученность,— штриховыми.
Кориолисовы силы при свободных колебаниях вызывают
дополнительную связь различных видов колебаний и сдвиг
фаз между ними, что приводит к некоторому
перераспределению напряжений. При колебаниях закрученного стержня в
потоке газа сдвиг фаз между перемещениями изгиба и
кручения приводит к изменению мгновенного угла атаки и, как
следствие, к изменению аэродинамических сил, действующих
на стержень. При этом может изменяться критическая
скорость флаттера стержня в потоке [14, 48J.
5, Нелинейные задачи теории закрученных стержней
В общей теории, изложенной выше, предполагалось, что угол
упругой закрученности 0 существенно меньше начального а.
Однако возможны случаи, когда эти величины соизмеримы
(особенно при малых значениях т„ для стержней с
удлиненными сечениями). В этом случае, в соответствии с формулой
(IV.31) при фф да г|, следует считать
а; = Е [е — Кт,Н + кл] -}- т(т0 -f 0,5т)
(VII 67)
и при определении крутящего момента от напряжений <jg
полагать
Мйа =» (т0 + т) J orjodF,
F
10 2 -1898
(VII.68)
145
что приводит к системе уравнений
Pt ^ Е [sF + %(ro +0,5%) 1РУ,
Мц = Е [хп/п — т (т0 + 0,5т) 1рп]\
Мъ = Е [4h + т (т0 + 0,5т) 1РЪ]; j (VII.69)
МЕ = G/^т -f- ? (т0 + т) [е/р — к„/рт1 Ч
из которой после исключения деформаций е, х? хл
получается следующее нелинейное уравнение для угла упругой
закрутки [52J:
[Р М
l
[Р
-f-l
1
/?
+ т (т0 + 0,5т) ?/?] . (VII.70)
Введем следующие обобщающие параметры: безразмерный
параметр продольно-крутильной гибкости, характеризующий
относительную нагруженность стержня нормальными
напряжениями,
^( ^y (VH.71)
радиус приведения, учитывающий особенности геометрии
сечения,
р? = EIrIGId\ ^VII.72)
относительный угол упругой закрутки призматического
стержня того же сечения от действия крутящего момента M-q
%м = MtlG& (VII.73)
наконец, обозначим
8Г = — р^; Qm = — Pi^m- (VII.74)
Величину р? можно назвать параметром начальной закручен-
ности стержня. В других задачах роль параметра начальной
закрученности могут играть другие величины, содержащие
однако общий параметр у = %ob Ih.
С учетом введенных обозначений (VII.71) —¦ (VII.74)
уравнение (VI 1.70) можно привести к виду
9? + ЗрД2 + 2 A + ар + ; ?) 0г = 2 (ем — цД). (VI 1,75)
146
Таким образом, введение обобщающих параметров
позволяет свести задачу расчета упругой закрутки стержня к одной
зависимости 9Г = 6Г (|лр, Ом, РгЬ Рассмотрим некоторые
частные случаи приложения уравнения (VII.75).
Незакрученный стержень фг = 0). Из уравнения (VI 1.75)
следует
в? + 2A+ цр) 9, = 29м. (VII.76)
Для частных случаев осевого растяжения и кручения
стержней кругового и удлиненного прямоугольного сечений из
(VII.76) получаются формулы, совпадающие с результатами
С. П. Тимошенко [43]. При отсутствии крутящего момента
(Ом = 0) из выражения (VI 1.76) помимо тривиального
решения 9Г = 0, соответствующего незакрученной форме оси,
вытекает еще следующее:
в, = ± К—2A Н-М. (VIL77)
которое при |хр ^ —1 принимает действительное значение.
Следовательно, при \ip = —1 первоначально незакрученный
стержень теряет крутильную устойчивость под действием
одних только нормальных напряжений. Соответствующий
критический уровень нагрузок определяется по формуле
(VII.71)
—р—'р /—'рп"т 7—1р% = —ЬЦ. (VII./8)
При Mg = Мп = 0 это дает известную формулу для
критической силы
Pkp==_G/2f//p. (VI 1.79)
Крутящий момент отсутствует (9д{ = 0). Для этого
случая на рис. 47 построена зависимость 9Г = / (цр) при
различных значениях параметра рг. При \ip > 0 по мере роста
этого параметра (т. е. возрастания растягивающих нагрузок)
угол начальной закрутки убывает @, < 0), но темп
убывания замедляется с увеличением \ia, так что стержень
стремится полностью распрямиться при \ip ^> 1 + {$? (точнее,
при цр -> оо). При цр < 0 угол начальной закрутки
увеличивается с ростом абсолютного значения | цр | и особенно резко
при малых значениях рг.
Уравнение (VI 1.75) при 0д* = 0 можно записать в виде
ег = —*вцЛ. (VI 1.80)
где
ke = U+iip + ft + 0,50Г (в, + 3pr)j"!.
10* 147
Рис. 47, Зависимость параметра упругой закрутки 0Г от
параметров продольно-крутильной гибкости (хр и начальной закру-
ченности рг.
Рис. 48. Зависимость
коэффициента ?н от параметров (Зг и j.ip.
0,8:
о А
0,8
п5\
1
0,4
пЗ\
0,2
ЦП
о
\
Res
..... -
—Лр-
—1
1
0
0,1
0,2
0,3
0,4
-ОД
0?
0,7
0,8
к
ч
0.J W
Л1-
При заданных
значениях Цр, рг коэффициент
k) можно подсчитать
методом последовательных
приближений. Результаты
расчетов для наиболее
важного в практическом
отношении диапазона рг и цр
представлены на рис. 48.
При малых значениях рг
и [ip, когда lip + р2 <^ 1,
коэффициент kg ~ 1, что
соответствует линейной
теории.
Линеаризованные по %
соотношения. Линеаризуя
выражение (VI 1.70)
относительно угла т, получаем
м. . . „_ _ \
'Т1
__2L/
М-
рц~Г
148
что соответствует пренебрежению в уравнении (VII.75)
нелинейными относительно Qr членами, откуда
еЛ = h фм — иРрг) (VII.8D
при
*е = A + 1*„ + &Г1- (VI 1,82)
Как правило, выражения (VI 1.81) и (VI 1.82) дают вполне
достаточную точность для практических расчетов при р\ Ф О,
Из соотношения (VII.81) вытекает формула для
эффективной геометрической жесткости на кручение закрученного
стержня Id = h (I + \лр + %), совпадающая при \хр <5? 1 -f p? с
формулой, полученной для этого случая в [66J применительно
к пустотелым трубкам удлиненного дву симметричного сечения.
При Р? <^ 1 и Mi = Мц = М? = О из формулы (VII.81) следует
т = ^2 Т(ь Где 0ср — P^/F, что совпадает с форму-
Gl d + acpfP
лой, выведенной для этого случая И. А. Биргером.
Из уравнения (VI 1.82) видно, что роль члена цр,
отражающего нелинейную зависимость угла закрутки от
нормальной нагрузки, убывает с увеличением начальной закручен-
ности и при Цр <^ 1 + Р? вообще несущественна. Поэтому
во многих задачах, особенно по динамике лопаток, допустимо
считать k% =» A -\- р^)~' и /rf s» fd A + рг), что
соответствует выражению для коэффициента податливости ах,
согласно (IV.65).
Продольно-крутильная дефорМ11ит стержней. Из
системы (VII.69) для незакр ученного стержня двусимметричного
сечения (в частности, для круглого вала) при Мп — М| — О
имеем с точностью до т2
Pr = EFr + 0,5Е1рт2;
М^ = ?/рте + GIdx.
Отсюда следует, что под действием крутящего момента
стержень не только закручивается, но и испытывает продольную
деформацию, которая при Рт = 0 будет
GJ°dF
Использование системы (VI 1.69) для анализа связанных
продольно-крутильных колебаний роторов турбомашин с
установленными под углом к оси ротора рабочими лопатками,
149
Рис. 49. Зависимость относительного
прогиба от начальной закручепноетн
при изгибе сильно закрученных
стержней:
/ - //* = 3; 2 — 1/Ь = 7,5; 3 — 1/Ь =
= 30; 4 — 1/Ь » 40.
позволило исследовать
теоретически ряд
нелинейных эффектов, которые
наблюдались
экспериментально.
Сильно закрученные
стержни. Общая теория
сильно закрученных
стержней, у которых угол Ро
соизмерим с единицей, не
разработана. Для
приближенной оценки влияния
сильной закрученности
следует учесть, что длина
винтового волокна,
равная до деформации dl =
= cfc/cos p0, принимает
после деформации (рис. 49)
значение
A4-е — х„| + xtT)) dz
cos (р0 -i-
где в линейной постановке Pi = Р
(е — хг| + К|Г|) cos р0 X
X sin ро. Удлинение винтового волокна е* = —"^—— = Р tg Во +
-\- (е — х,|Е -f x-r\) cos2 ро. Поскольку р = xr cos2 f5n; tg Po — тог
и cos«pe~l/[r+(vn, то в* = ?=Ц?5ф?1.
Нормальное напряжение в плеском поперечном сечении
0- связано с напряжением вдоль волокна о* — Ее*
соотношением 0 * '2
0? — 0* cos'2a, поэтому
Е {е — к„14-
1 4- т0тг2)
(VI 1.83)
Изгиб сильно закрученных стержней двусимметричного
сечения. Введя формулу (VII.83) в два уравнения равновесия
(VII. 15), получим Eltxt = Mi; ?/},«,, = Мп, где /| =
F Р
Интегрирование ведется по площади плоского поперечного
сечения.
150
Для удлиненного прямоугольного сечения при h <^ Ь
значение
где
% - 0,5 cos pm | cos pm + -J^
/
m = arctg@,5x0&).
Уравнения A1.10) остаются справедливыми при замене
Л и 1Ц соответственно на /j и /ч.
На рис. 49 приведена зависимость относительного прогиба
v (I) от угла а (I) при различных значениях удлинения lib
для случая изгиба равномерно закрученного консольного
стержня моментом на конце при h <^ Ь, когда с учетом
выражений A1.23)
щ = A + _Lzi^i?/ \ 1
При сильной закрученности изгибная жесткость падает
вследствие увеличения длины и уменьшения напряженности
наиболее удаленных винтовых волокон. Участки кривых при
Р,„ <^ 1 совпадают с кривой k = 0, приведенной на рис. 4, а.
8. Закрученные стержни с изогнутой осью
В настоящее время достаточно корректные теории
разработаны только для закрученных стержней с прямой осью и для
изогнутых незакрученных стержней [381. Что касается
пространственно изогнутых и закрученных стержней, то для них
достаточно изучены и не вызывают сомнений уравнения
равновесия и геометрические соотношения. Так, для стержней
с умеренной изогнутостью в начальном состоянии,
удовлетворяющей условиям
(ЙК|оJС1; (Ь%L<1. (V 11.84)
где кр, Хпо — компоненты начальной кривизны оси
стержня "С в направлении главных осей | и *>]; Ь — максимальный
размер сечения.
Уравнения равновесия в проекциях на неподвижные оси
л, у, и г имеют вид
Qx+qx--=O; Q'y+qy^Q; Qz + qz = 0;
151
М'„А /ntf —(?,*;, +Q, = 0;
Мг + mz -f Qyxo — Qxy0 --- 0.
После исключения из последних поперечных сил Qx, Q9
(VI 1.85)
Здесь x0 (z) и yQ (z) — уравнения проекции изогнутой в
начальном состоянии оси стержня на координатные плоскости
xz и уг.
Геометрические соотношения, связывающие компоненты
упругой кривизны осп Х|, к,, и кручения т с перемещениями
оси и, у в направлении неподвижных осей х, у и с углом
поворота сечения 8 относительно оси z имеют вид [57]
Х| = и" sin а — у" cos а + вхяо;
Кг, = и" cos а + " ®
получим
Qz+ q
м"х +,
My + t
M2 +1
г == 0;
Щ—дх
+ (QzUoY
- (QzXoY
'x + tnz) X
= 0;
= 0;
о + (My
-]- my)
y'o
= 9' + и"у0 ~-v"x
0 ~vx0.
(VI 1.86)
Из этих соотношений видна дополнительная деформационная
связь, возникающая между компонентами деформации при
изогнутой оси. Более общие формулы для указанных
соотношений рассматриваются в [1, 32, 59 и др.].
Сложнее обстоит дело с уравнениями, связывающими
компоненты деформации е, Kg, Хт,, т с внутренними силовыми
факторами Qz, Ms, Мц, Мг. В большинстве работ в
качестве таких соотношений используются формулы A1.10), т.е.
представления классической теории Кирхгофа — Клебша, что
не позволяет рассматривать такие работы как «общую теорию
изогнуто-закрученных стержней».
Простейший подход к построению более общей теории
заключается в использовании в качестве соотношений упругости
соответствующих соотношений прикладной или
технической теории прямолинейных закрученных стержней,
изложенных выше (V.14). Во всяком случае, это допустимо для
умеренно изогнуто-закрученных стержней, удовлетворяющих
условиям A.5) и (VII.84). В Ш, 57] показано, что при
указанных условиях, в частности, эффекты закрученное™ и
изогнутости могут рассматриваться по отдельности, так как члены,
учитывающие их взаимосвязь, имеют второй порядок малости,
152
Кроме того, известно, что условия (VII.84) характеризуют
стержни малой кривизны, для которых соотношения
Кирхгофа — Клебша без учета закрученности остаются такими же,
как для стержней с прямой осью. На основании этого можно
считать, что зависимости (У. 14) будут справедливы для
умеренно закрученно-изогнутых в начальном положении
стержней, если в качестве оси ?, для данного сечения принимать
направление касательной к линии центров жесткости (или
приближенно центров масс), а под поперечным сечением
понимать сечение стержня плоскостью, нормальной к этой оси.
Главные оси %, ц лежат в плоскости поперечного сечения,
следовательно, также нормальны к оси ? и образуют вместе
с ней главный трехгранник. Компоненты деформации
определяются как разности между конечными (после деформации)
и начальными значениями компонент кривизны и кручения.
Указанный подход полностью соответствует
общепринятому методу исследований изогнуто-закрученных стержней
малой кривизны, но в отличие от него опирается на
соотношения упругости теории закрученных стержней.
Использование указанного подхода позволило
теоретически рассмотреть ряд особенностей поведения закрученных
лопаток турбомашин с непрямой осью (возникновение
дополнительных крутящих моментов от газовых и центробежных
сил, различные влияния для компрессорных и турбинных
лопаток наклона оси к радиальному направлению на
раскрутку лопатки в поле центробежных сил, уменьшение угла атаки
при изгибании оси лопатки в сторону спинки профиля,
влияние изогнутости оси лопатки на спектр ее собственных частот,
колебаний и пр.) [571.
Теория изогнуто-закрученных стержней привела к
принципиально новой постановке известной в турбостроении
задачи об оптимизации начальных «выносов» оси лопатки с целью-
повышения ее статической прочности при суммарном
воздействии нагрузок от газовых и центробежных сил f36, 58],
В работах Л. Д. Магомаева [32] и С. Янецкого [59, 76]
рассмотрены некоторые возможности дальнейшего развития и
обобщений теории закрученно-изогнутых стержней.
Влияние начальной кривизны на колебания закрученного
стержня рассмотрено на примере консольной компрессорной
лопатки длиной I = 18,48 см, закрученной на а = 0,942 рад.
Максимальный параметр несимметрии сечения изменяется
по длине в пределах 6j = 0,24 -~ 0,84. Смещение конца
лопатки вследствие начального изгиба составляет 0,2/, В табл. 4
приведены результаты расчета частот вращающегося и
невращающегося стержней при различных формах оси. Вари-
153
Таблица 4. Собственные частоты (Гц) колебаний стержня при
.различных формах оси
Номер
варианта
0
1
2
3
4
5
6
7
8
Q =~ С
@,
157,6
154,4
157,6
154,4
157,6
154,4
157,6
154,4
157,6
154,4
167,0
153,8
149,0
153,8
156,5
154,4
158,8
154,4
(Л,
465
639
465
639
465
639
465
639
465
639
464
637
468
637
437
639
492
639
963
778
963
778
963
778
963
778
963
778
966
825
1019
825
969
778
995
778
И — 1250 с^":
и,
290
300
290
300
284
300
289
300
291
300
308
296
273
296
285
300
293
300
(Л,
648
767
631
767
658
742
650
758
645
772
634
800
650
77)
619
756
671
775
969
852
970
870
966
870
067
853
969
854
987
91Й
1039
913
977
854
1022
851
Примечание. Над чертой приведены значения частот для закрученного
стержня, под чертой — для незакрученного.
апт 0 относится к стержню с прямой осью, варианты 1—4 —
к стержню с наклонной осью (линейный прогиб), варианты
5—8 — к стержню с изогнутой по параболе осью.
Изогнутая ось стержня лежит в плоскости гх или гу. Оси ху
являются главными осями инерции в корневом сечении. В
вариантах 1 и 5 конец стержня смещен в положительном
направлении осих (в направлении максимальной жесткости корневого
сечения), а в вариантах 2 и 6 — в противоположном
направлении. В вариантах 3 и 7 конец стержня смещен в
положительном направлении оси у, а в вариантах 4 и 8 — в
противоположном направлении. Ось вращения перпендикулярна
оси г и отстоит от корневого сечения на величину R —
-¦ 15,26 см. Частоты первой, второй и третьей форм
колебаний обозначены щ, ш2> соя-
551
Таблица 5. Соотношение крутильных и изгибных перемещений
стержня при различных формах оси
; ]омер
варианта
0
1
2
3
4
5
6
7
8
У = 0
—0,369
—0,369
—0,369
—0,369
—0,369
—0,346
—0,390
—0,375
—0,362
—0,261
—0,261
—0,261
—0,261
—0,261
—0,202
—0,338
—0,165
—0,409
—0,0122
—0,0122
—0,0122
—0,0122
—0,0122
—0,0774
—0,0480
—0,0675
0,0590
5, </)
—0,422
—0,462
—0,390
—0,411
—0,441
—0,362
—0,454
—0,428
—0,412
2= 1230 с~
5, «)
—0,210
—0,122
—0,302
—0,264
—0,169
—0,020
—0,535
—0,020
—0,648
1/5 <fl
0,0030
—0,0173
0,0244
0,0158
—0,0101
—0,0680
0,0816
—0,0412
0,0643
Видно, что наклон оси (линейный изгиб) не оказывает
влияния на частоты невращающегося стержня. Изгиб оси
стержня по параболе вызывает заметное изменение
собственных частот, причем наибольшее влияние на первую и третью
частоты оказывает изгиб оси стержня в направлении оси х,
а на вторую частоту — изгиб в направлении оси у. На частоты
колебаний вращающегося стержня оказывает влияние как
начальный изгиб оси стержня по параболе, так и наклон оси.
Начальная закрученность, начальное искривление оси и
вращение стержня несимметричного поперечного сечения
являются факторами, каждый из которых вызывает связь
тгибных и крутильных колебаний. Взаимное влияние этих
факторов и вызывает изменение частот собственных
колебаний стержня. В табл. 5 приведены отношения крутильных и
изгибных перемещений конца закрученного стержня для
рассмотренных случаев: 0 (/) = 0 (/) b (l)lvn (I), где b — хорда
профиля сечения стержня. Видно, что наклон оси невращаю-
и;егося стержня не вызывает дополнительной связи изгибных
и крутильных колебаний. В остальных случаях
дополнительная связь изгибных и крутильных колебаний ведет к
соответствующему изменению собственных частот.
Соотношения между изгибными и крутильными
перемещениями изменяются значительно больше, чем собственные
частоты стержня. В ряде случаев изменяется знак одного из
перемещений. Поэтому формы напряжений стержня в результате
начального искривления оси будут заметно изменяться даже
при малых изменениях собственных частот,
155
Экспериментальные результаты подтверждают
представленную в табл. 4 тенденцию изменения собственных частот
стержней в зависимости от вида начального искривления оси.
7. Закрученные трубчатые стержни
Для измерения давления иногда применяют закрученные
манометрические трубки Бурдона, которые имеют вид
тонкостенной полой трубки вытянутого двусимметричного (в
частности, прямоугольного) сечения с углом закрученности Да на
длине А/, т. е. с относительной закрученностью т0 = Дос/А/.
Под действием внутреннего избыточного давления р такие
трубки раскручиваются, причем при малых деформациях
угол поворота незакрепленного конца 9 (/) пропорционален
давлению. Некоторые вопросы расчета таких трубок
рассматривались в [67].
Действие внутреннего давления на полые закрученные
трубки проявляется в виде двух эффектов.
1. При наличии на незакрепленном конце торцевой
заглушки давление на нее приводит к возникновению осевого
растягивающего усилия N = pFT (FT — площадь
поперечного сечения трубки по внутреннему контуру (торцевая
площадь)). Под действием этого усилия в соответствии с
зависимостями (V.21) происходит раскрутка на угол
где F — площадь поперечного сечения стенок трубки; Ьх —
эффективная жесткость на кручение закрученного стержня,
которая для двусимметричного сечения определяется
формулой (V.22),
Геометрическая жесткость на кручение призматического
стержня I°j полого профиля с постоянной толщиной стенки б
вычисляется по формуле Id = 4Fep6/S, где Fcp — площадь
поперечного сечения трубки по среднему контуру; 5 — длина
средней линии контура.
Для вытянутого прямоугольного сечения при б2 <^ Ь% и
а2 <^ Ь2 (а и b размеры сечения по среднему контуру вдоль
осей 1] и |) соответственно имеем
FT = (b — 6) (а — б); FCp - ab; F = 2 (а + b) б;
156
"l a -j- b \ * l 90
Таким образом,
1 (a — 6) (b — 6) Ca + b) p
"l @
1 ¦ л;
2. Давление на внутренние боковые поверхности приводит
к деформации контура, который стремится стать более
выпуклым, Деформация контура сечения в своей плоскости также
оказывает некоторое влияние на раскрутку. Дополнительная
продольная деформация, связанная с поворотом наклонных
волокон закрученного стержня при кручении, определяется
формулой (IV.31), а в линейном приближении — As — рор,
где р0 — угол наклона волокна в начальном состоянии,
который определяется в общем случае как угол между
нормалями к главному и поперечному сечениям в данной точке, р0 =
Здесь щ — производная функции депланации сечения ф по
полярной координате \р.
Для вытянутых в направлении оси Е сечений ф» — Hi]
{см. гл. IV), или в полярных координатах (? = г cos \p, г\ —
— г sin \J)) op =» — 0,5r2sin 2я|) и фф = — г2 cos 2\|з, поэтому
р0 = т0 г cos 2т|>.
Изменение угла наклона волокон в результате поворота
сечений р = хг. В общем случае, когда радиус точки контура
т изменяется в процессе деформации, полное изменение угла
наклона волокна будет
р ^ хг + i|u_ дг = т, +
Полагая hr = шг, где шг — радиальное перемещение
точки контура при его деформации, связанное с
перемещениями вдоль осей с, п. соотношением
wr = Wt cos ^ ->rwn sinf, (VII.87)
получаем
P = %r -f- тошг cos 2г|).
Дополнительная деформация
Де = т0тг2 cos 2tp + x\rwr cos2 2т|). (VI1.88)
157
Для сплошных сечений wr = 0 и Ае = тотгг cos 2i|i,
Поскольку для большей части площади удлиненного сечения,
особенно при больших значениях г значение cos 2ф » 1,
для них вполне достаточную точность дает формула Де =»
я» т0тт2. Для полых профилей wr имеет наибольшие значения
именно в центральной части длинной стороны, где cos 2ij;
быстро изменяет свое значение от 1 до —1. Поскольку функция
cos2 т|з существенно положительна, приняв и в этом случае
во втором члене формулы (VI 1.88) cos 2-ф = 1, получим
физически правильные, но несколько завышенные для оценки
Де результаты. Поэтому при расчете угла раскрутки можно
считать Ае я» т0тг2 + %\rwr. Тогда нормальные напряжения
при продольно-крутильной деформации полого стержня будут
а = Е (е0 + т0тг2 + т*гм>в). (VII.89)
Введя (VI1.89) в уравнение продольного равновесия
\ adF = N, найдем
F
_ N 1Р ; Jpw
ео _ __ Т(|Т __ То __,
где /рда » \ rwrdP-
F
Следовательно
„ = ^ + Ет„ [т (г" jf) + т0 (rw - bf-) . (VII.90)
Подставив (VII.90) в уравнение крутящих моментов G/2 т +
+ \ 0^,/dF — Mz, получим в линейной по т постановке
к
Величина
Mm, = —ii\Irw — -
где /га. = \ r%w.dF\ представляет собой дополнительный
крутящий момент от нормальных напряжений, возникающих
при радиальных смещениях контура полого сечения.
Для рассматриваемой задачи о действии внутреннего
давления только на боковые поверхности полные продольная сн-
158
ла и крутящий момент равны нулю (N = Мг = 0). Тогда угол>
раскрутки на длине I определится как
M..J il
4
Перемещения контура под действием внутреннего давле-
ления могут приближенно определяться как для аналогичного
призматического стержня коробчатого сечения, что при
условии нерастяжимости стенок приводит в линейной постановке
к следующим формулам:
(b\ — ?* + \att
+ 4a,*! - 4ft?)
где /в = б8/12 A — v2); а, = а/2; Ьх = 6/2.
Для вытянутого сечения при аг <^ Ь,
? ?
Определив по (VII.87) и (VII.91) радиальное перемещение
ш, и вычислив по нему значения 1рш и /ГИ1, найдем угол
раскрутки 8а (/).
Хотя практически манометрические трубки тарируются
экспериментально, предварительная оценка их раскрутки
полезна для правильного выбора конструктивных
соотношений.
Глава VIII
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПОПЕРЕЧНОГО СЕЧЕНИЯ ЗАКРУЧЕННОГО
СТЕРЖНЯ
1. Изгиб призматического стержня с кручением
Геометрические характеристики поперечного сечения,
используемые в теории закрученных стержней, делятся на
элементарные (F, h, /т,, /0), которые отражают перемещение
плоского недеформируемого сечения, и характеристики, связанные
с особенностями распределения нормальных и касательных
напряжений при уточнении гипотезы плоских сечений.
Эти характеристики связаны с функцией кручения ф, с
функциями депланацни при сдвиге % и W. При введении этих
функций предполагалось, что их вид такой же, как и для
призматического бруса соответствующего сечения.
Справедливость такого предположения с принятой степенью точности
показана, например, для функции ср в гл. IV. Тогда для
определения функций ф, %, W достаточно решить задачу об изги-=
бе призматического бруса с кручением. При этом поперечное
сечение бруса соответствует рассматриваемому сечению
стержня. Ограничимся задачей изгиба в плоскости главной
жесткости xz, так как пространственный изгиб призматического
бруса может рассматриваться методом суперпозиции. Такая*
задача решается методами теории упругости в смысле Сеи-
Венана, если на стержень действует нагрузка в виде
сосредоточенных сил и моментов. В этом случае стержень можно
разбить на участки, на которых перерезывающие силы
постоянны, а моменты изменяются по линейному закону и,
следовательно:
«iv = u; = e" = o. (Vii i.i)
Перемещения при этом можно представить выражениями
(VII.45), в которых следует принять их = о2 = w = О и учесть
перемещения от поперечного сжатия, которые при условии
(VIII.1) принимают вид
«v = — v I &zdx = — «i -g- + Cj (f/);
tiv =s — v f е^г/ = — щху + C2 (jc).
160
Из условия отсутствия касательных напряжений на
боковой поверхности стержня туг — 0 находим Сг (у) = щ -„-;
С, (х) -- 0. Тогда перемещения призматического бруса
определяются системой зависимостей
V = 8 (х — xs) + \u\xy\
W = — Цл: -f «2X + 0'ф.
2 >
• (VIII. 2)
Здесь щ, «2 и 6 — функции только координаты г; xs, ys —
координаты центра изгиба в главной центральной
системе ху.
Деформации соответственно описываются соотношениями
8г ~ _ ихх; ех = еу = vm,x; fw ~ 0; |
. (VIII.3)
- ах
- Ц„ —г— -4- ТЫ, ХУ. !
2 ду >¦ I
Выражения {VIII.2), (VIII.3) можно привести к виду,
совпадающему с перемещениями и деформациями, полученными
Сен-Венаном для случая изгиба консольного бруса
сосредоточенной силой [42].
Функция X связана с функцией изгиба Сен-Венана соот-
Fk
ношением % = ———?_— G,с-{-ху2) — х. Однако выражения
(ViII.2), (VIII.3} являются более общими и представляют
решение для стержня, имеющего любое закрепление, под
действием нагрузок в виде сосредоточенных сил и моментов [15].
Значения щ, щ, 0 определяются методами сопротивления
материалов, и задача об изгибе стержня сводится к
отысканию функций ф и X. Поскольку решение ищется в
перемещениях, необходимо удовлетворить только уравнения равновесия
и граничные условия. Уравнения равновесия принимают вид
дг ' дг ' '
'дх "¦%'-'¦ дг '" "
И 2 -1898 101
Первые два уравнения при условии (VIII. 1) удовлетворяются
тождественно, а из третьего следует
hkx х, (VII1.4)
У2ф = 0; V2X =
Граничные условия для рассматриваемой задачи имеют вид
чхгсж(п, z) = Qnx;
V cos (п, z) = Qny; (VIII.5)
тА-г cos (я, x) + v cos (я, t/) + ог cos (re, г) = Qn2 j
где Qnx, Qnu, Qnz — проекции поверхностных сил на оси*, у, т,
п — нормаль к поверхности стержня. Причем на торцах
стержня cos (я, х) = cos (я, у) — 0; cos (я, г) = ±1, на
боковой поверхности cos (re, x) = /х; cos (n, у) = /ггх; cos (re,
г) = 0.
Граничные условия на торцах и в местах приложения
нагрузки выполняются интегрально с учетом принципа Сен-
Венана. На боковой поверхности первые два уравнения
удовлетворяются тождественно, а третье дает на контуре
поперечного сечения условия для функций ор и X.
¦(х-
ftp
ду
xs) in
ду
2
1Щ
1>
т1
vF
и +
S
S
kx
V)/,,
ftp
дп
д%
дп
S
S
-у2
2
У,) к
\ (VIII.6)
vFkr
2A +
хут1.
Уравнения (VIII.4) с граничными условиями (VIII.6)
полностью определяют функции ф и X, которые зависят только от
формы поперечного сечения стержня.
Функции ф и X могут определяться приближенно
вариационным методом. Потенциальная энергия деформации
стержня
1 1 zzzz ¦
dFdz,
Вариацию работы внешних сил можно выразить в виде
интеграла по поверхности:
6L - f \ (Qn.x?>U + Qny&V + QnMW) dS.
На основании вариационного принципа Лагранжа,
используя выражение для перемещений (VIII.2) и деформаций
162
(VI11.3), граничные условия (VIII.5) и варьируя по
неизвестным функциям ф и X, приходим к вариационным уравнениям
6JX = 0;
hi)
где
т Г Г \{ ^
1 J J I &
ЗУ. \ , ЭК
1 0*
Интегрируя выражения (VIII.7) по частям, можно
получить уравнения (VIII.4) с граничными условиями (VIII.6).
Таким образом, вариационные уравнения (VIII.7) полностью
определяют функции <р и X.
Согласно определению центра изгиба имеет место равенство
J J [(х — xs) v — {у — ys) %„} dF = 0.
При изгибе в плоскости хг на основании полученного
решения можно найти координату центра изгиба
У
дх F дх
-ij)dF. (VIII.8)
n 2A+v)Iy S
Решение задачи в замкнутом виде достигается для
полуэллипса с полуосями а и Ь. Расстояние центра изгиба от оси 2а,
ограничивающей сечение, определяется уравнением
^s"~ 15 я A + v) (За3 + й2)
При a— b = 0,5d получаем известную формулу [15] для по-
4 й 3 + 4v
перечного сечения в виде полукруга; у% = -^ —__ .
Приравнивая потенциальную энергию сдвига элемента
стержня длиной dz при отсутствии кручения и работу
поперечной силы на перемещение сдвига, можно, согласно
определению коэффициента формы поперечного сечения при сдвиге
163
Таблица 6. Значения
коэффициента формы поперечного сечения
для эллиптического сечения с
полуосями а и 6 прн v = О
[38, 46],
жение
kr = If
получить выра-
Ь/а
о
0,435
0,600
0,715
0,800
0,950
1
1,050
1,350
1,400
1,730
Согласно
формуле
(УШЛО)
0,900
0,889
0,881
0,875
0,870
0,860
0,857
0,854
0,842
0,834
0,821
Согласно
работе
184]
0,889
0,882
0,870
0,863
0,861
0,851
0,847
0,844
0,831
0,823
0,790
дх
Согласно
формуле
(VIII.11)
у (х2 — у2)
0,900
0,889
0,881
0,875
0,870
0,860
0,857
0,854
0,842
0,834
0,821
ах,
хху
2 A И- V) 1У
dF
|
(VIII.9)
где функция Ху — (X + х) -^~
определяется из вариационного
уравнения (VII 1.7) после
соответствующей подстановки.
Пренебрегая поперечным сжатием, получаем формулу для
коэффициента формы поперечного сечения при сдвиге, уже
известную по выражениям (VI 1.48):
^1- (VIIU0)
дх
ду
Используя приведенное решение задачи о деформации
бруса и переходя к функции изгиба Сен-Венана Хс [42] можно
прийти к формуле, полученной для коэффициента формы
поперечного сечения Каупером [46]:
*(}±Л!/viiT in
IV 111.1 1)
>y
xdF
Таблица 7. Значения
коэффициента формы поперечного сечения
при v= 0,3
Для бруса с прямоугольным и эллиптическим контуром
поперечного сечения вариационным методом находятся те же
решения, которые получены
Б. Сен-Венаном [42] и
Л. С. Лейбензоном [15, 45].
Без учета поперечного
сжатия для прямоугольного
сечения коэффициент формы
поперечного сечения kx =
~ 0,833..., что соответствует
результату С. П. Тимошенко
[46], а для эллиптического
контура с полуосями а и Ь
Вид сечения
Круг
Прямоугольник
о 5"^
0,92
0,86
О
К
'-2 ф
ч о
= =fT
U о—
0,930
0,872
§§?
¦- ОС
о сГ
О-&С
0,89
0,85
164
при изгибе в направлении оси 2а
Ь — 3 (За2 + &2)
Результаты для коэффициента формы поперечного сечения
(табл. 6, 7) хорошо соответствуют значениям, полученным в
17, 46, 84].
Для определения касательных напряжений при изгибе
бруса с кручением могут использоваться функции,
граничные условия для которых имеют более простой вид, Введем
функции Фи/, связанные с функциями ф и % соотношениями
_ __9Ф_ ,
У + У* — 7" *
(VIII. 12)
, v YдФ. !
ду тл ^ дх
dTTar
(VIII. 13)
ах _ df
vcxy — дх '
Ту
где с — u[lu2 =* const согласно условиям (VIII.1). Тогда
деформации сдвига
_ й, дФ , df
- а' дф '
Функции Фи/ отличаются от функций напряжения тем,
что в них не входят производные перемещений и они зависят»
таким образом, только от формы поперечного сечения.
Воспользовавшись, как и прежде, уравнениями равновесия и
граничными условиями (VIII.5), находим уравнения и
условия на контуре, определяющие функции Фи/:
У2Ф = —2; V2f**—vc2y; (VIII. 14)
Ф |s = 0; /|*-0. (VIII. 15)
Условия на контуре (VIII.15) с вычислительной точки
зрения значительно проще условий (VIII.6). Вариационные
/ 165
уравнения для функций Фи/ находятся прежними методами:
8J3 = 0; 6J4 = 0;
При использовании функций / формулы (VIII.8) и (VIII.10)
принимают вид
(VIII. 17)
ь _ ' Г f I/ # '"' ' "* ""
f J J LI <**
Если стержень слабо искривлен в начальном состоянии,
то координаты центра изгиба переменны по длине стержня.
Пусть стержень имеет начальное искривление в плоскости
yz, перпендикулярной направлению нагрузки по закону
у = 6 (г). Введем систему координат х^уъг2, оси которой
параллельны осям системы xyz, а начало координат перемещается
вдоль линии центров масс искривленного в начальном
состоянии стержня. В этом случае условие равенства нулю главного
момента касательных напряжений относительно центра
изгиба имеет вид
i - у, Ш'
о
— [х2 — xs (г)] xyz (x.2, y.2)) dFdl = 0.
Если перерезывающая сила постоянна по длине стержня и
параллельна оси х, то можно записать
1 т л-р _ п.
— %у*хч\dF =
Ниа ^ [Мй + S g) Px — ys (z) Px] dl = 0. Однако Mz2IPx ==
о
= у а) является координатой центра изгиба прямого стержня того
же поперечного сечения, что и искривленного. Тогда
координатой центра изгиба искривленного стержня будет уь ---
= у л + 4- J б (о с
о
166
Справедливость полученного результата легко проверяется на
простых опытах со стержнями из проволоки, искривленными
по различным законам.
Таким образом, зная координаты центра изгиба прямого
стержня и закон его начального искривления, можно всегда
найти центр изгиба искривленного стержня. Результаты
решения задачи об изгибе бруса с кручением определяют
функции депланации сечения при сдвиге и кручении и
показывают, что принятые гипотезы о деформации стержня
соответствуют решениям теории упругости.
2. Геометрические характеристики стержня
произвольного сечения
Форма поперечного сечения закрученных стержней на
практике обычно задается координатами точек, лежащих на
контуре сечения, либо в виде дуг окружностей и отрезков
прямых. Соответственно имеется два способа задания
исходных данных при определении геометрических характеристик.
В любом случае поперечное сечение рассматривается в
прямоугольной системе координат ху (рис. 50). Причем ось
желательно располагать приблизительно параллельно хорде
профиля.
В первом случае односвязный контур поперечного
сечения описывается с помощью массивов координат точек,
лежащих на верхней (хв., ув) и нижней (хц„ ун) кривых
профиля. Массив х{ может быть общим (х{ = хн. = XBt).
Кроме того, задается угол а между осями х и х. Массив х{
может иметь произвольный переменный шаг. Обычно у
точек А и В шаг более мелкий, а в середине профиля более
крупный. В дальнейших вычислениях координаты любых точек,
лежащих на контуре, определяются с помощью
параболической интерполяции по трем соседним точкам.
Во втором случае указываются радиусы г{ и координаты
центров окружностей xtyt, составляющих профиль. В
местах изломов задаются радиусы, равные нулю. В процессе
расчета определяются места касания окружностей различных
радиусов, окружностей с прямыми и осуществляется переход
с одного участка контура на другой [181.
Исходные данные для определения геометрических
характеристик снимаются непосредственно с рабочих чертежей
лопаток и других объектов или из приложенных к ним таблиц.
Далее обычными методами [38] определяются координаты
16?
Рис. 50. Способы задания формы про-
филя поперечного сечения.
ций депланации при сдвиге X, х?
тах удобно ввести функции
центра масс сечения хоуо,
положение главных
центральных осей сечения grj
(угол а) и элементарные
геометрические
характеристики F, /|, /,,.
Координаты точек на контуре
сечения теперь выражаются
в главной центральной
системе Ьг\:
gf = (хс — х0) cos (a — а) +
+ (iJi — У о) sin (а — а)>
Ц1 = (Ус — У о) cos (^ — а) —
— (х( — х0) sin (а — а).
Затем используется
решение задачи об изгибе бруса
с кручением, которая
сводится к нахождению функ-
и кручении <р. При расче-
Тогда вариационные уравнения для определения %х и Ч
будут содержать только уже известные характеристики /|, /
Эт)
X
дс, 2
= б
¦ = 0;
X
X
(VIII. 18)
А для определения функции ф вариационное уравнение
принимает вид
= б
(VIII. 19)
168
Задача может решаться вариационным методом [17, 18],
который обеспечивает в данном случае необходимую точность
A—5%). Вначале определяются в виде рядов функции у.) и
Vj, Это дает возможность вычислить коэффициенты формы
поперечного сечения ори сдвиге и координаты центра изгиба:
*n=!F
F
дц
дс
гМП Я атI
ax,
: __ i n -I.
(VIII.20)
2 A + v) /. 2
tf
¦ + ri — lid idf.
1 2(I-bv)/4 2 ¦¦]•
Пользуясь значениями ?s, r)S) можно на основании
вариационного уравнения (VIII. 19) найти функцию кручения ф.
Затем определить геометрическую жесткость на кручение
Г/ Лт> - . \2 / An \21
yd= ¦ ¦
*' F"
Далее находятся остальные геометрические характеристики.
Для этого требуется знать функцию ср и координаты ?х, %,
/¦]. Определяются также координаты центра л%, ys изгиба и
осевые моменты инерции 1Х, 1у, 1ху в системе координат ху.
При построении рядов, аппроксимирующих функции ср,
Xi и Yj, условия на контуре не выполнялись как
естественные. Использование аппарата ^-функций [18] позволяет
выполнить условия на контуре для областей весьма сложной
формы и решить задачу с высокой степенью точности. Введем
функции Ф, ft и f2
+ ?i5
дц
as
2 A + v) /_
169
дц
дц
2
2
A
A
V
+
V
+
V
v)
v)
Л)
4
щ2 _ |2
} (VIII.22)
д~ дц ~~ 2(I+v)/s ^ ;
Условия на контуре для этих функций согласно (VIII. 15)
следующие:
Ф|, = 0; Л|, =0; f2|s==0.
Согласно выражениям (VIII.16) эти функции определяются
вариационными уравнениями [15], следствием которых
являются уравнения (VIII.14) и граничные условия (VIII.15);
- 2ф] dF = 0;
дФ
дц
дФ
дц
дц
Mi
(l+vL fc/
(VIII.23)
j
Искомые функции аппроксимируются рядами вида со (I, ii) x
X 2BimXk (?) Yn (т)), где со (?, г|) — /^-функция для данной
области [18]. На контуре поперечного сечения она принимает
нулевые значения, а внутри контура — положительные.
Решение задачи ведется с помощью программирующей системы
«Поле», разработанной в Институте проблем машиностроения
(ИПМаш) АН УССР под руководством В. Л. Рвачева. В
качестве координатных функций использовались полиномы Че-
бышева.
Для решения задачи с помощью системы «Поле» вводится
информация о контуре поперечного сечения, составленного
из дуг окружностей и отрезков прямых, и о виде
вариационных уравнений (VIII.23). В результате появляется
возможность определить ряд геометрических характеристик на
основании выражений (VIII.12), (VIII. 13), (VIII.17), (VIII.22):
~дц~ ч
dfs E
Mi.
дц
170
= F
kn =
4IL V
дц
\ дц
} (VIII.24)
dft
_dfl
1т1я со^тветствия коэффициентов k^, kr>, кщ
вычисленных по формулам (VIII.20) и (VIII.24), необходимо положить
v =-¦= 0.
для геометрической жесткости на кручение и координат
центра нзги^а имеются приближенные формулы В. 3.
Власова 118]:
U - -г
I
(VIII. 25)
Кроме того> координаты центра изгиба могут вычисляться
также с помощью формул Джанелидзе [24]:
(VIII.26)
В раб>отах ^6, 58] предлагаются графоаналитические
методы опре^еления элементарных геометрических характеристик,
для чего сечение разбивается системой прямых, параллельных
осям х v* У- ^Ри этом координаты центра изгиба можно найти
но приб/1мжтно& формуле Грифиса и Тейлора [46], которая
получен^ в предположении параболического закона
распределения касательных напряжений,
У si
у3 (х) хйх
у* (,х) dx
(VIII. 27}
17Г
Таблица 8. Основные геометрические характеристики удлиненного по
Расчетная формула
F = kytPc
ilo = O,5ft8fe
тт = — 0,667 к,Д
а — а = kj
/. = 0,0833fe5i4c3 A + l,O676e<7)
/р sf /л = 0,0833й7й4с
I°d -= 0,3333fts6%s
Обозначение
коэффициента
*i
h
h
к,
k7
lr ^ 0,00555A12fcec A +
ax0'a% = I +0,0333 A + v) /зд2 A -{• 1,067^-'
aB;aE0 = 1 + 0,0417 (I 4^ v) кыу*ах/ат0
ац/ац0^ Н 72A -} v) knf'i% Юх0
0,0356 П -f v) feleG2Va ат
0,0356 (i
A -\- i,067i6g2) [I + 0,0333fe18 A + v) y2]
ap|/eT = 0,0222fe216vV A "f l,067Ae<?2)
о /aT
172
перечного сечення стержня
т = 1; п =
0,667
1,000
1,200
0
0,457
0,750
0,400
0,457
0,343
0
0,286
0,343
0,750
0,524
0
0,563
0,60
0,75
0
0
0,45
0
Значения коэффициентов k, для различных
]
т — 0,5; п *= *
0,693
0,858
1,143
—0,364
0,486
0,830
0,452
0,486
0,402
0,00196
0,35100
0,40900
0,84000
0,60600
1,75 -Ю-5
0,68200
0,65200
0,82800
0,00433
0,00269
0,54000
0,00359
т — 1; (t= 0,5
0,693
1,142
1,143
0,364
0,486
0,830
0,452
0,486
0,402
—0,00196
0,35100
0,40900
0,84000
0,60600
1,75-10
0,68200
0,65200
0,82800
—0,00433
—0,00269
0,54000
—0,00359
т
типоя профилей
= 0,5; п = 0,5
0,785
1,000
1,125
0
0,588
0,938
0,588
0,588
0,552
0
0,490
0,552
0,935
0,750
0
0,880
0,750
0,985
0
0
0,702
0
Л = const
1
1
1
0
1
1
1
1
1
0
1
1
1
1
0
1
!
1
0
0
1
0
12 2-1896
173
а действительная координата центра изгиба заключена в
пределах у0 — г/ч1 < у0 — ys < —рг^- (г/0 — г/si).
Результаты, определенные по формулам (VIII.20), (VIII,21),
(VIII.24) для сечений в виде эллипса, полуэллипса,
равностороннего треугольника и квадрата, практически совпадают
с результатами точных решений (погрешность менее
0,01%). Имеется хорошее совпадение с приближенными
результатами, полученными Л. С. Лейбензоном для профилей
Жуковского и параболического серна 118].
Проводилось сравнение геометрических характеристик,
найденных обычным вариационным методом, и по методике,
обеспечивающей удовлетворение граничных условий на
контуре (VIII.15) в результате применения аппарата /?-функций,
которая реализовалась с помощью системы «Поле».
Наибольшее расхождение данных составляло 6,04%. В большинстве
случаев результаты, найденные двумя методами, отличались
менее, чем на 5%.
Расчеты по приближенным формулам (VIП.25) дают
значительные погрешности даже для простейших сечений. Так,
жесткость на кручение для сечения в виде прямоугольника
определяется с погрешностью 18%, для эллипса и
полуэллипса — с погрешностью 12,5%, а координата центра изгиба для
иолуэллипса — с погрешностью 28%, Следует отметить, что
определение координат центра изгиба по формулам (VIII.26)
дает значительно лучшие результаты, но менее точные, чем по
формулам (VIII.20) или (VIII.24). Это объясняется тем, что в
методах, приведенных в [15, 17, 18], координаты центра
изгиба находятся через функции, определяющие распределение
касательных напряжений в сечении при изгибе без
кручения. Функция кручения ц> определяется с учетом положения
центра изгиба, который можно отождествлять с центром
кручения. При использовании формулы (VIII.26) функция
кручения ф должна быть найдена до определения центра изгиба,
что требует большего числа членов аппроксимирующего
ряда. Погрешности при этом возрастают с увеличением
несимметрии сечения. Формула (VIII.27) дает заметные
погрешности для аэродинамических профилей.
3. Геометрическне характеристики стержня \
удлиненного сечения
Получены сравнительно простые формулы для
геометрических характеристик удлиненного сечения, средняя линия
которого представляет собой параболу с максимальной стрелой
174
подъема f. Относительная толщина ряда типичных профилей
изменяется по следующему закону:
hit ) = h -SE-l-"I?!!- й" (i i)
где h — максимальная толщина профиля; т, п —
постоянные, значения которых приведены в табл. 8; |а = УЬ
(координата | отсчитывается вдоль хорды от точки А на входной
кромке до В на выходной кромке; Ъ — хорда профиля).
Знак параметра изогнутости q = flh положителен, если
направление стрелы прогиба противоположно оси ц. Кроме того,
в табл. 8 используются безразмерные параметры с = h/'b и
у — x0b2/h; f = fib, приведены расчетные формулы и
необходимые числовые коэффициенты для основных геометрических
характеристик и коэффициентов податливости закрученного
стержня.
При т < п сечение полнее (толще) от середины к точке А,
при т > п, наоборот, а при т = п сечение но толщине
симметрично относительно середины. Величины tM, т\10 в табл. 8
обозначают координаты центра масс. Расстояние между
центром масс и центром изгиба для таких сечений мало и при
расчетах может не учитываться.
12*
СПИСОК ЛИТЕРАТУРЫ
!. Аксельрад 9. П. Тонкостенные криволинейные стержни и трубы,—
Тр. Ленингр. ии-та инж. ж.-д. трансп.— Исслед. по стронт. механике,
1966, вып. 249, с. 147—168.
2. Александров А. Я., Соловые Ю. И. Двумерная задача для упругого
винта.— Механика твердого тела, 1974, № 1, с. 18—35.
3. Алексеев Н. В. Напряжения и деформации естественно закрученных
стержней при кручении и сжатии.— Прочность конструкций, 1977,
вып. 2, с. 106—113.
4. Арутюнян Н. X., Абрамян Б, J1. Кручение упругих тел.— М. : Физ-
матгиз, 1963,— 686 с.
5. Бедчер Ф. С. Частоты н формы колебаний компрессорных лопаток.—-
Энергомашиностроение, 1964, № 6, с. 14—19.
6. Бейлин Е. А., Левин Л. И. Задача о сжато-нзогиутом естественно
закрученном стержне.— Строит, механика н расчет сооружений, 1977,
№ 5, с. 50—53.
7. Бердичевский В. Л., Квашнина С. С. Об уравнениях, описывающих
поперечные колебания упругих стержней.— Прикл. математика и
механика, 1976, 40, вып. 1, с. 120—135.
8. Биргер И, А. Некоторые математические методы решения
инженерных задач,— М.: Оборонгнз, 1956.— 151 с.
9. Биргер И. А., Шорр Б. Ф., Шнейдерович Р. Н. Расчет на прочность
деталей машин.— М. : Машиностроение, 1966.— 616 с.
10. Богомолов С. И., Журавлева А. М. Взаимосвязанные колебания в турбо-
машннах и газотурбинных двигателях.— Харьков : Вища школа,
1373.— 179 с,
11. Ветчинкин В. П., Поляков Н. Н. Теория и расчет воздушного гребного
винта.— М. : Оборонгнз, 1940,— 520 с.
12. Воробьев Ю. С, Филиппов А. П. Свободные колебания вращающихся
стержней без гипотезы плоских сечений.— В кн.: II Всесоюз. съезд по
теорет. и прикл. механике (М., 29 янв.— 5 февр. 1964 г.): Аннот. докл.,
М. : 1964, с. 56.
13. Воробьев 10. С. Уточненные уравнения свободных колебаний
вращающихся стержней.— В кн.; Рабочие процессы в турбомашинах и
прочность их элементов, Киев : Наук, думка, 1965, с, И—27,
!4. Воробьев Ю. С, Влияние некоторых факторов на собственные
колебания стержней.— Динамика и прочность машнн, 1965, вып. 1, с. 53—61.
15. Воробьев 10, С. Изгнб стержня с учетом депланацки при сдвиге и
кручении.— Динамика и прочность машин, 1965, вып. 1, с. 125—Г31.
16. Воробьев Ю. С, Сапелкина 3. В. Колебания консольных закрученных
стержней несимметричного поперечного сечения.— Динамика и
прочность машин, 1973, вып. 18, с. 62—69.
17. Воробьев Ю. С. Определение геометрических характеристик попереч-
176
ного сечения лопаток турбомашин.— Вибрационная прочность
и надежность двигателей и систем летат. аппаратов, 1975, № 2,
с. 49—52,
18 Воробьев Ю. С, Шульженко Н. Г. Исследования колебаний систем
элементов турбоагрегатов.— Киев : Наук, думка, 1978.— 135 с.
19. Голубев О. Б. Обобщение теории тонких стержней,— Тр. Ленингр.
политехи, ии-та, 1963, № 226, с. 83—93.
20. Гринберг С. М. О роли «стесненности» кручення при расчете частот
колебаний лопаток компрессора.— Динамика и прочность авиац.
двигателей, 1966, вып. 3, с. 214—238.
21. Гринберг С, М. К расчету частот колебаний лопаток компрессора
методами теории оболочек.— Прочность и динамика авиац. двигателей,
1969, вып. 5, с. 242—255.
22. Джанелидзе Г. Ю. Соотношения Кирхгофа для естественш
закрученных стержней и их приложения.—Тр. Ленингр. политехи, ин-та, 1946,
№ 1, с. 23—32.
23. Джанелидзе Г. Ю. К теории тонких и тонкостенных стержней.— Прикл.
математика н механика, 1949, 13, вып. 6, с. 597—608.
24. Джанелидзе Г. Ю, Определение координат центра жесткости по
различным функциям напряжения при кручении.— Тр. Ленингр. политехи,
нн-та. Динамика и прочность, 1983, № 226, с. 93—102.
25. Зайцев Г. 3., Аронсон А, Я- Усталостная прочность деталей
гидротурбин.— М. : Машиностроение, 1975.— 160 с.
26. Зволинский Н. В., Риз П, М. Кручение растянутого призматического
бруса.— Докл. АН СССР, 1938, 20, № 2/3, с. 101 — 103.
27. Лазарян В, А. Техническая теория изгиба.— Киев : Наук, думка,
1976.—207 с.
28. Левин А. В, Вычисление частот собственных колебаний облопаченных
дисков с естественно закрученными лопатками.—
Энергомашиностроение, 1960, Ш 7, с. 1—5.
29. Лурье А. И., Джанелидзе Г. Ю. Задача Сен-Венана для естественно
скрученных стержней.— Докл. АН СССР, 1939, 24, № 1, с. 23—26;
№ 3, с, 226—228; № 4, с. 325—326.
30. Ляв А. Математическая теория упругости.— М. :ОНТИНар.
комиссариата тяжелого машиностроения, 1935.— 931 с.
31. Магомаев Л. Д. К теориям стесненного кручения турбинных лопаток. —
Пробл. прочности, 1972, № 9, с. 27—33.
32. /Магомаев Л. Д. К расчету напряженного состояния закрученно-изо-
гнутых турбинных лопаток.— Пробл. прочности, 1974, № 4, с. 9—16.
33. Макдэниел Т.Дж., Мэрфи В. Р. Границы динамических характеристик
вращающихся стержней.— Ракет, техника и космонавтика, 1977, 15,
№ 3, с. 183—186.
34. Меерович И. И. Колебания слабоизогнутых и закрученных
лопаток. —М. : Оборонгиз, 1956.— 56 с.
35. Меерович И. И, Распределение напряжений в компрессорных лопатках
при колебаниях.— М. ; Оборонгиз, 1961.— 107 с.
36. Напряжения н деформации в деталях паровых турбин / А. Н.
Подгорный, В. П. Сухинин, Г. М. Меллерович, В. Л. Ингульцов.— Киев :
Наук, думка, 1978.— 276 с.
37. Писаренко Г. С, Воробьев Ю. С, Ли В. А. и др. Исследование
применимости теории стержней к расчетам колебаний консольных образцов
двусимметричного сечения.— Пробл. прочности, 1975, № 10,
с. 3—7.
38. Прочность, устойчивость, колебания ; Справочник в 3-х т. / Под ред.
И. А. Бнргера, Я. Г. Пановко.— М. ; Машиностроение, 1968.— Т. 1.
831 с.
177
39. Риз П. М. Деформации естественно закрученных стержней.— Докл.
АН СССР, 1939, 23, № 1, с. 18-21; № 5, с. 441—444.
40. Рудавец В. А., Шорр Б. Ф. Расчет собственных частот и форм
пространственных колебаний закрученных компрессорных лопаток.— В кн.:
Теория оболочек и пластин : Тр. VIII Всесоюз. конф., Ростов н/Д,
16—22 сен г., 1971 г., М. : Наука" 1973, с. 550—555.
41. Рухадзе А. К- О деформации естественно закрученных стержней.—
Прикл. математика и механика, 1947. 11, вып. 5, с. 533—542.
42. Сен-Венйн Б, Мемуар о кручений призы. Мемуар об изгибе призм.—
М. : Физматгиз, 1961,— 518 с.
43. Тимошенко С. П. Сопротивление материалов : В 2-х т.— М. '.Наука,
1965.— Т. 2. 480 с.
44. Тумаркин С. А. Равновесие и колебания закрученных стержней.—
Тр. Центр, аэрогндродинам. ин-та, 1937, вып. 341,— 42 с.
45. Филиппов А. П., Булгаков В. Н., Воробьев 10. С. и др. Численные
методы в прикладной теории упругости.— Киев : Наук, думка, 1968.—
252 с.
46. Филиппов А. П. Колебания деформируемых систем.— М.:
Машиностроение, 1970.— 734 с.
47. Филиппов А. П., Воробьев К). С. Расчеты на колебания с
использованием электронно-вычислительной техники.— М. : Машиностроение,
1971.— 68 с.
48. Филиппов А. П., Кохманюк С. С, Воробьев К). С. Воздействие
динамических нагрузок на элементы конструкций.— Киев; Наук, думка,
1974.— 176 с.
49. Шорр Б. Ф. Расчет на прочность естественно закрученных лопаток,—
Тр. Ин-та им. П. И. Баранова, 1954, № 256, с. 1—18.
50. Шорр Б, Ф. К экспериментальной проверке теорий растяжения
закрученных стержней.— Изв. АН СССР. Механика и машиностроение.
1959, № 4, с. 176—178.
51. Шорр Б. Ф. Расчет основной частоты и формы колебаний закрученных
лопаток.— Тр. Ин-та им. П. И. Баранова, 1960, Ня 38, с. 61—77.
52. Шорр Б. Ф. К теории закрученных неравномерно нагретых стержней.—
Изв. АН СССР. Механика и машиностроение, I960, № 1,
с. 102—112.
53. Шорр Б. Ф. К теории закрученных тонкостенных стержней.— Изв.
АН СССР. Механика и машиностроение, 1960, № 5, с. 74—79.
54. Шорр Б. Ф. Колебания закрученных стержней.— Изв. АН СССР,
Механика и машиностроение, 1961. № 3, с. 35—39.
55. Шорр Б- Ф. Изгибно-крутильные колебания закрученных
компрессорных лопаток.— Прочность и динамика авиац. двигателей, 1964,
вып. 1, с. 15—27.
56. Шорр Б- Ф. Расчет на колебания шарнирных лопаток.— Прочность
и динамика авиац. двигателей, 1965, вып. 2, с. 292—315.
57. Шорр Б. Ф. Основы теории закрученных лопаток с непрямой осью.—
Прочность и динамика авиац. двигателей, 1966, вын. 3, с. 188—213.
58. Шубенко-Шубин Л. А., Гернер Д. М., Зельдес Н. Я- и др. Прочность
паровых турбин.— М. : Машиностроение, 1973.— 456 с.
59. Днецкий С. Влияние кинетостатических деформаций на собственные
колебания длинных лопаток турбомашин.— Динамика и прочность
машин, 1977, вып. 25, с. 66—72.
60. Anliker M., Troech В. A. Lateral vibrations of pretwisted rod with
various boundary conditions.— Z. angew. Math, and Phys., 1963, 14, N 3,
p. 218 -236.
E1. Bars С /. Torsion of ortho-tropic naturally-twisted bars.— Bui. lnst.
politelm. lasi, 1970, 66, N 1/2, p. 1353—1358.
178
62. Bossak M. A, J., Zienkiewicz 0. С. Free vibration of initially stressed
solids with particular reference to centrofugal-force effects in rotating
machinery.— J. Strain Anal., 1973, 8, N 4, p. 245—252.
63. Budansky В., Di Pritna R. S. Bending vibrations of uniform twisted
beams,—J. Math. Phys., 1960, 39, N 4, p. 237—245.
€4. Carnegie W. Vibrations of pre-twisted cantilever blading alliwing for
rotory inertia and shear deflection.— J. Mech. Eng. Sci., 1964, 6, N 2,
p. 191 — 199.
65. Carnegie It7,, Dawson B. Vibration characteristics of pre-twisted blades
of asymmetrical aerofoil cross-section.— Aeronaut. Quart., 1971, 22,
N 3, p. 257—273.
66. Chen Chu. The Effect of initial twist on the forsional regidity of thin
prismatical bars and tabular members.— In.: Proc. 1st U. S. Nat. Congr.
Appl. Mech., 1952, p. 265—269.
(J7. Chen Chu. A Theory of twisted Bourdon tubes.— In.: Proc. 1st U. S.
Nat. Congr. Appl. Mech., 1952, p. 271—280.
68. Ckbsh A. Theorie der Elastizitat fester Korper.—Leipzig, 1862.— 424 S.
69. Clebsh A. Theorie de 1'ibasticite des corps solides. Traduit par Barre de
Saint-Venant et A. Flammant.— Paris : Dunod, 1883.- 864 p.
70. Filippov A. P., Vorobjov J. S. Vyskum vibracnej pevnosti olopatkovania
turbin.— Strojn. Cas., 1975, 26, _N 5, s. 465—472.
71. Frisch-Fay R. Buckling of pre-twisted bars.— Int. J. Mech. Sci., 1973,
15, N 2, p. 171—181.
72. Friihiof J., Niordson Ph. D. Natural frequencies of rotating twisted can-
tilevered beams.— In: Proc. 2nd U. S. Nat. Congr. Mech., 1954.— 7 p.
73. Goodier J. N'., Griffin D. S. Elastic bending of pre-twisted bars.— Int.
J. Solids and Struct., 1969, 5, N 11, p. 1231 — 1245.
74. Houbolt J. G., Brooks G. W. Differential equations of motion for
combined flapwise bending, chordwise bending and torsion twisted nonuni-
form rotor blades.—In.: NASA, Techn. Note, 1958, N 3905, Rep.
N 1346.— 17 p.
75. Housner G. W., Keighiler W, 0. Vibrations of lineary tapered cantilever
beams,—J. Eng. Mech. Div. Proc. Amer. Soc. Civ.Eng., 1962, 88, N1,
p. 95—123.
76. Janecki S., Lidke M. The strength and free vibrations of the blading in
the last stages of steam turbines.— Prace IMP PAN, 1976, N 70?72,
p. 751—760.
77. Jarett G. W., Warner P. C. The vibration of rotating tapered-twisted
beams.—J. Appl. Mech., 1953, 20, N 3, p. 381—389.
78. Kirchhoff G. Uber das Gleichgevicht und die Bevegung eines unendiich
diinuen elastischen Stabis.— J. reine u. angew. Math., 1859, В 56,
S. 285—313.
79. Kirchhoff G. Vorlesungen fiber mathematische Physik. Mechanik.—
Leipzig, 1877.— 466 S.
80. Knowles J. K,., Reissner E. Torsion and extention of helicoidal shells.—
Quart. Appl. Math., 1960, 17, N 4, p. 409—422.
-81, Lisicki A. Drgania zwichrowanych lopatek wirujacvch.— Arch, budowy
masz., 1968, 15, N 3, p. 355—382.
82. Maunder L. The Bending of pretwisted thin-walled beams of symmetric
star-shaped cross section,—J. Appl. Mech., 1958, 25, N 1, p". 67—74.
83. Met Chuh. Coupled vibrations of thinwalled beams of open section using
the finite element method.— Int. J. Mech. Sci., 1970, 12, N 10,
p. 883—891,
84. Mindlin R. D., Deresiewicz i/. Timoshenko's shear coefficient for flexu-
ral vibrations of beams.— In.: Proc. 2nd U. S. Nat. Congr. Appl. Mech.,
1954, p. 175—178.
, 179
85. Rao J. S. Vibrations of pre-hvisted taperefl cantilever beams in
torsion.— Arch, budowy maszyn, 1971, 18, N 3, p. 443—448.
86. Sato Т. В, Equations of motion for curved and twisted beam with non-
coincident mass and elastic axes.— Proc. Fujihara Mem. Fac. Eng. Keio
Univ., 1958, 11, N 12, p. 66—70.
87. Slyper H. A. Coupled bending vibrations of pretwlstes cantilever beams.—
J. Mech. Eng. ScL, 1962, 4, N 4, p. 365—379.
88. Targoff W. P. The bending vibrations of a twisted rotating beam.— In.:
Proc. 3rd Midwest Conf, Solid Mech., Ann Arbor, Univ. Mich., 1957,
p. 177—194.
89. Tso W. K. On the motion of a curved and twisted rod.— Acta Mech., 1972,
N 3/4, p. 163—178.
90. Volterra E. The equations of motion for curved elastic bars deduced by
the use of «the method of internal constraints».— Ing. Arch., 1955, 23,
N 6, p. 402—409.
91. Zickel J. Pretwisted beams and columns,— J. Appl. Mech., 1956, 23,
N 2, p. 165—175.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Амплитуды перемещений:
линейных 99
угловых 99, 117
Бимомент 122
Брус 160
Влияние на колебания стержней:
депланации сечения при
кручении 125
продольной деформации 98, 103
связи деформационной 91, 101
— инерционной 106
сдвига 139
Волокно винтовое 16
Вращение стержня 139
Геометрические соотношения
между компонентами:
кривизны 17
перемещений 17
Геометрические характеристики
стержней:
произвольного сечения 65, 70,
167
тонкостенных 133, 135
удлиненного сечения 174
Гибкости стержня главные 37
Гипотеза:
неискажаемостн сечения 7
ортогональных сечений
(нормальных) 56
плоских сечений 16
Границы применимости теории
стержней:
классической 25, 105
линейной 15
технической 91, 106, 120
тонкостенного сечения 127
Депланация поперечного сечения1
при кручении 85, 121
при сдвиге 135, 160
Деформация:
винтового волокна 64, 86
призматического бруса 161
стержня в классической теории
26
— в общем случае 63
— в технической теории 87, 91
— нелинейная 70, 145
— продольная 82
— продольно-крутильная 91,
149
— с учетом депланации
сечения 121
— — — сдвига 136
— тонкостенного 132
— эллиптического сечения 74
Длина стержня 13
Жесткость:
закрученного стержня
главная 32
— — секториальная 122
— — эффективная
геометрическая 7l
— — — — на изгиб 94
— — — — на крученне 51, 92,
94
на растяжение 5!»
93, 94
сверла 53
Закрученность:
естественная 14
линейная 15
начальная 14
нелинейная 42
181
относительная 15
произвольная 51, 145
равномерная 15
сильная 150
слабая 65
умеренная 69
Изгиб;
закрученного стержня с равными
главными жесткостями на изгиб
28
— — двусимметричиого
сечения моментом 28
— _ — — силой 30
— — несимметричного сечения
93
незакрученного стержня 28
призматического бруса 160
сильно закрученного стержня
150
Колебания:
массы на закрученной консолн
изгибные 34
стержня вращающегося 143
— закрученного
двусимметричиого сечения изгибные 36
_ крутильно-продоль-
ные 97
— — несимметричного сечения
изгибно-крутильные 101
изгибно-крутильно-
продольные 103
— — с учетом депланацин
сечения 125
— — — — сдвига 138'
— незакрученного изгибные 34
•Компоненты:
кривизны 17, 152
напряжений 16, 17
перемещений линейных 16
— угловых 17
Координат система 14, 54, 85, 128,
,Г>3, 167
.Коэффициенты:
жесткости (податливости) в
общей теории стержней 70, 71
— в технической теории 89
— с учетом денланации
сечения 124
формы поперечного сечения при
сдвиге 136, 164, 169, 171
Кривизна:
в общем случае 17
многократно закрученного
стержня 29
"Кручение стержня:
в нелинейной постановке 149
двусимметричиого сечения 68,
76, 91
несимметричного сечения 93
Линеаризация задачи деформации
закрученного стержня 65, 148
Линии:
винтовые см. Волокно винтовое
узловые 108
Лопатки компрессоров, турбин 106,
119, 127, 144
Моменты:
внешних и внутренних сил 18
напряжений основных и
второстепенных 59, 70
Моменты инерции:
главные осевые 24
полярно-осевые 87, 88
Нагрузка:
внешняя 18
массовыми силами, см. Силы
Напряжения:
в классической теории 22
в общем случае 63
в призматическом брусе 161
в технической теории 87, 107
в тонкостенных стержнях 132
при больших деформациях 145
с учетом депланацни сечения 121
сдвига 136
основные и дополнительные 59
от центробежных сил 144
Нелинейные задачи теории
закрученных стержней 69, 145
Области;
влияния на колебания стержней,
см. Влияние
применимости теории стержней,
см. Границы
Оси:
закрученности стержня 15
инерции главные 24
— центральные 24
нейтральные 23
сопротивления закрученного
стержня 31
стержня 13
упругие 24
Параметр:
начальной закрученности
стержня 16, 50,75, 110, 112
несимметрии сечения 93
182
Перемещения стержня:
вращающегося 140
в классической теории 22
в общем случае 63
в технической теории 85
при учете сдвига 135
тонкостенного 129, 130
Податливости коэффициенты, см.
Коэффициенты
Профиль сечения стержня 13
Работа;
кориолисовых сил 142
центробежных сил 142
Радиус инерции сечения 37
Раскрутка стержня:
от продольного усилия 5, 7, 49,
68, 93, 111, 149
or центробежных сил 144
Растяжение стержня:
в нелинейной постановке 149
двусимметричного сечеиня 93
несимметричного сечения 94
слабо закрученного 68
Связь (связанность):
различных видов деформаций 91
колебаний деформационная 102
— инерционная 106
Сечение стержня:
поперечное 13
главное нормальное 56
двусимметричное 13
несимметричное 13
неискажаемое 8
ортогональное (нормальное) 56
переменное 13
постоянное 13
произвольное 13
симметричное 13
удлиненное 80
Си.1ы:
внешние 18
центробежные 143
инерционные 33, 97, 125, 138
кориолисовы 143
перерезывающие 137
О-отношення:
геометрические 17
физические 19
Слепень закрутки 15
Стесненность кручения 121
Стержни:
закрученные 13
закрученно-изогнугые 151
кривые 14
прямые 15
умеренно-изогнутые 151
Теория пластин и оболочек
(применение) 11, 127
Теория закрученных стержней:
классическая 22
линейная 65
произвольного профиля
приближенная 54
техническая 7, 83, 85
тонкостенных 127
удлиненного сечения 81
Трубки закрученные
малометрические 156
Угол:
начальной закрученности
стержня 15
установки стержня 15
Уравнения деформации стержней:
в технической теории 89, 90
двусимметричного сечения 27
нелинейные 70, 146
произвольного профиля 65, 70
с учетом депланации сечения 124
с учетом сдвига 137
тонкостенных 133
Уравнения равновесия 18
Условия отсутствия напряжений
на боковой поверхности стержня 56
Формы колебаний стержня:
двусимметричного сечения 36»
43, 99
несимметричного сечения 107,
117
с учетом депланации 127
Функция:
депланации при сдвиге 135, 160
кручения 85, 121
Сен-Венана 161
Характеристики:
геометрические, см.
Геометрические характеристики
вибрационные 34, 97, 115, 153
Характеристическое уравнение 36
Центр:
изгиба (жесткости) 163, 169—171
— кривого стержня 166
— тонкостенного стержня 133
масс 23
скоростей мгновенный 108
183
Частоты собственных колебаний
стержня:
вращающегося 143
двусимметричного сечения 36, 97
невесомого с массой на конце 35
незакрученного 34
несимметричного сечеиия 101, 115
с учетом депланации сечения 125
с учетом сдвига 139
Экспериментальные исследования:
деформации стержней прн изгн-
бе 31
.— растяжении ПО, 144
колебаний стержней изгибио-
крутильных 107, 115
изгибных 40
— — крутильно-продольных
98
Энергия:
кинетическая колебаний
стержня 33
— — — вращающегося 140
— — — в классической теории
33
. в технической теории 96
— — — с учетом депланации
сечения 124
_ — — — — сдвига и
инерции поворота 138
потенциальная деформации
стержня 26
— — — в классической теории
26
— — — в общем случае 74
— — — в технической теория
87
— — — слабо закрученного 67
• — — — с учетом депланации
сечения 122
— , сдвига 136
ОГЛАВЛЕНИЕ
Предисловие ,
Введение 5
Глава I. Основные положения теории закрученных стержней 13
1. Общие сведения 13
2. Геометрические соотношения 16
3. Уравнения равновесия 18
4. Физические соотношения и общая постановка задачи 18
Глава II. Классическая теория закрученных стержней (теория
Кирхгофа — Клебша) 22
1. Основные соотношения 22
2. Пределы применимости классической теории 25
3. Пространственный изгиб закрученного стержня двусимметрич-
ного поперечного сечения 26
4. Колебания закрученного стержня двусимметричного поперечного
сечення 3
Глава Ш. Деформации закрученных стержней с позиций теории
упругости ..... 49
1. Слабо закрученные стержни , 49
2. Произвольно закрученные стержни 51
Глава IV- Деформации закрученных стержней произвольного
сечения , 54
!. Основные положения приближенной теории закрученных
стержней , 54
2. Счабо закрученные стержни, линейное по т0 приближение ... 65
3. Умеренно закрученные стержни, нелинейное по т0 приближение 69
4. Закрученные стержни удлиненного профиля ......... 80
Глава V. Техническая теория закрученных стержней 65
1. Основные соотношения 85
2. Деформация закрученного стержня 91
3. Колебания закрученного стержня несимметричного поперечного
сечения . ..,.,,«.,.,,,,.., 95
185
Глава VI. Экспериментальная проверка технической теории
закрученных стержней ПО
1. Статическая деформация закрученных стержней 110
2. Изгибно-крутильные колебания закрученных стержней .... 115
Глава VII. Специальные задачи теории закрученных стержней 121
1. Учет стесненности депланации сечения при кручении ..... 121
2. Деформации тонкостенных закрученных стержней ,....., 127
3. Учет влияния деформаций сдвига 135
4. Учет влияния вращения стержня . 139
5. Нелинейные задачи теории закрученных стержней ...... 145
6. Закрученные стержни с изогнутой осью 15!
7. Закрученные трубчатые стержни 156
Глава VIII. Геометрические характеристики поперечного
сечения закрученного стержня 160
1. Изгиб призматического стержня с кручением 160
2. Геометрические характеристики стержня произвольного сечения 167
3. Геометрические характеристики стержня удлиненного сечения 174
Список литературы 176
Предметный указатель ,,. ., 181
ЮРИЙ СЕРГЕЕВИЧ ВОРОБЬЕВ
БОРИС ФЕДОРОВИЧ ШОРР
ТЕОРИЯ ЗАКРУЧЕННЫХ
СТЕРЖНЕЙ
Утверждено к печати ученым советом
Института проблем машиностроения ЛИ УССР
Редактор В В. САМОКИШ
Художественный редактор И. В. КОЗИЙ
Технический редактор И. А, РАТНЕР
Корректоры Э М. КИЯНСКАЯ, Л. Н. РЕГЕТА
Информ. бланк ?ft 5867
Сдано в набор 04.08-82. Подп. в печ. 09.02.83. БФ 00624. Формат
84Х108/зг. Бум. тип. .Ns 1. Лит. гзрн. Вые. печ. Усл. печ. л. 9,87,
Усл. кр.-отт. 10,19. Уч.-изд. л. 9,9. Тираж 1000 экз. Заказ Ш 1809.
Цена 1 руб. 70 коп.
Издательство яНаукова думка», 252601 Киев, ГСП, Репина, 3,
Отпечатано с матриц Головного предприятия республиканского-
производственного объединения «Полиграфкнига», 252087, Ки«
ев-57, Довженко, 3 во Львовской областной книжной типогра»
фии, 290000. Львов, Стефаника, 11. Зак. 3225,