ИНТЕЛЛЕКТУАЛЬНЫЕ
УПРАЖНЕНИЯ


DICK HESS
The Population
EXPLOSION
and Other Mathematical Puzzles
World Scientific
NEW JERSEY • LONDON • SINGAPORE • BEIJING • SHANGHAI • HONG KONG • TAIPEI • CHENNAI


ДИК ХЕСС
Интеллектуальные УПРАЖНЕНИЯ
Собрание математических головоломок
Перевод с английского
Н. 	А. Шиховой
Москва Лаборатория знаний


УДК 51-028.41+794 ББК 22.1я92 Х40
Хесс Д.
Х40 Интеллектуальные упражнения. Собрание математических головоломок / Д. Хесс ; пер. с англ. Н. А. Ши- ховой. — М. : Лаборатория знаний, 2019. — 192 с. : ил.
ISBN 978-5-00101-194-1
В книге собраны уникальные авторские головоломки на различные темы: логические, физические, геометрические, вероятностные, числовые и пр. Ко всем головоломкам приведены ответы, ко многим — решения.
Для всех любителей математики.
УДК 51-028.41+794 ББК 22.1 я92
Научно-популярное издание Хесс Дик
ИНТЕЛЛЕКТУАЛЬНЫЕ УПРАЖНЕНИЯ.
СОБРАНИЕ МАТЕМАТИЧЕСКИХ ГОЛОВОЛОМОК
Ведущий редактор М. С. Стригу нова. Художник В. А. Проку дин Технический редактор Т. Ю. Федорова. Корректор М. Н. Панкова Оригинал-макет подготовлен О. Г. Лапко в пакете 1ДТеХ2£ Подписано в печать 27.11.18. Формат 60x90/16.
Уел. печ. л. 12,00. Заказ 12109 Издательство «Лаборатория знаний»
125167, Москва, проезд Аэропорта, д. 3 Телефон: (499) 157-52/2, e-mail: info@pilotLZ.ru, http:/ /www.pilotLZ.ru
При участии ООО «Столица-Принт» e-mail: st.print@bk.ru Отпечатано в АО «Первая Образцовая типография», филиал «УЛЬЯНОВСКИЙ ДОМ ПЕЧАТИ». 432980, г. Ульяновск, ул. Гончарова, 14
ISBN 978-5-00101-194-1
Copyright © 2016 by World Scientific Publishing Co. Pte. Ltd.
Все права защищены. Настоящее издание, как и его любая часть, не могут быть воспроизведены в любой форме или любыми средствами, электронными или механическими, включая фотокопирование, запись или любые системы хранения или извлечения информации, известные в настоящее время или которые будут изобретены, без письменного разрешения Издателя. Русский перевод публикуется с разрешения World Scientific Publishing Co. Pte. Ltd., Сингапур
Copyright © 2016 by World Scientific Publishing Co. Pte. Ltd.
All rights reserved. This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the Publisher.
Russian translation arranged with World Scientific Publishing Co. Pte. Ltd., Singapore.
© Лаборатория знаний, 2019


Памяти моего любимого брата Роберта (Боба) Л. Хесса (9 ноября 1940—2 марта 2015)


ПРЕДИСЛОВИЕ
Эта книга— продолжение моих книг Mental Gymnastics: Recreational Mathematical Puzzles и Golf on the Moon, выпущенных издательством Dover Publishing Co. в 2011 и 2014 годах. Головоломки в этих книгах— для развлечения и удовольствия, этим удовольствием можно поделиться с друзьями. Решение головоломок развивает математическое мышление, которое включает в себя логику, озарение, владение геометрическими, аналитическими и физическими понятиями. Головоломки могут не поддаться сразу, тогда потребуется проявить настойчивость. Для решения большинства головоломок хватит карандаша и бумаги, но иногда придется прибегнуть к помощи компьютера, чтобы провести исследование или перебор вариантов или чтобы вычислить ответ. Остроумие тоже не помешает— будь к этому готов!
Идеи для головоломок я часто черпаю в бумажных изданиях или интернет-ресурсах, где есть разделы с задачами или головоломками. Среди них Crux Mathematicorum with Mathematical Mayhem, Journal of Recreational Mathematics, Pi Mu Epsilon Journal, раздел головоломок в журнале Technology Review, Ponder This и Puzzle Up. Еще один источник— устные сообщения и предложения от любителей головоломок. Я признателен всем энтузиастам, которые делятся своими новыми задачками и размышляют над моими.
Дик Хесс


ЗАДАЧИ


ГЛАВА 1. ОЗОРНЫЕ ГОЛОВОЛОМКИ
1. 	Загадочное слово
Это слово содержит 8 букв, иногда 6 букв, чаще 4 буквы, но постоянно содержит 9 букв. Что это за слово? Решение неединственно.
2. 	Тайна зарплаты
Пятеро товарищей обедали вместе, и разговор зашел о зарплате. Они решили подсчитать среднюю зарплату всех пятерых, но никто не хотел дать сведения о своей. У каждого есть карандаш и бумага, никто не помогает им в этой задаче. Как им решить проблему?
3. 	Родственники
(a) Стоят рядом два человека. Один указывает на другого и говорит: «У меня нет сыновей и дочерей, однако отец этого человека — сын моего отца». Кем друг другу приходятся эти двое?
(b) Зять Алексея — отец моего дяди Петра. Мы с Алексеем кровные родственники. Кем он мне доводится?
(c) У меня нет дочерей, племянниц и племянников, но зато есть знакомый адвокат. Свекор адвоката— сын моей свекрови.
(i) 	Догадайся, я женщина или мужчина?
(п) А адвокат?
(iii) Кем мы с адвокатом друг другу приходимся?


6. Демографический взрыв
4. 	Фишки в коробке
Всего лишь за пять ходов передвинь фишку Т в нижний правый угол коробки (рис. 1). Ходом считается перемещение одной фишки по любому пути.
Рис. 1
5. Мощная подача
Теннисист ударяет по мячу, и тот летит с огромной скоростью. Если ее выразить в километрах в час, то число будет ровно на 100 больше скорости в милях в час. Какова же скорость мяча? (1 миля = 1,6 км.)
6. Демографический взрыв
В 2015 году население Земли составляло 7,3 млрд человек. Будем считать, что средний житель Земли занимает 0,063 м3, так что общий объем, занимаемый населением, составлял 0,4599 км3.
(a) В первом приближении Земля представляет собой шар радиусом 6371 км. Равномерно распределим объем, занимаемый населением планеты, по поверхности этого шара. Какой толщины получится слой?
(b) Сейчас население растет в геометрической прогрессии, увеличиваясь на 1,14% в год. Предположим, что такая скорость роста сохранится и в будущем. Через какое время население вырастет так, что толщина слоя составит один метр? Сколько людей будет жить на Земле к тому моменту?


10 Задачи
(с) 	Пусть население Земли так и растет в геометрической прогрессии — на 1,14% в год. Через сколько лет человечество будет занимать сферу, радиус которой увеличивается со скоростью света (= 9,4605284 х1012 км/год)? Сколько людей тогда будет жить на Земле? Релятивистскими эффектами пренебречь.
7. 	Цепная линия
К верхушкам двух вертикальных десятиметровых столбов прикреплена 15-метровая цепь. Она провисает, и в нижней точке расстояние от цепи до земли 2,5 м. Чему равно расстояние d между столбами?


ГЛАВА 2. ГЕОМЕТРИЧЕСКИЕ ГОЛОВОЛОМКИ
8. Геологоразведка на Ригеле
Планета Ригель IV замечательна тем, что представляет собой абсолютно гладкую сферу радиусом 4000 миль. Как и Земля, она вращается вокруг своей оси. Как и на Земле, положение любой точки на Ригеле IV задается двумя координатами — широтой и долготой. Три геолога направили доклады в штаб разведки.
(a) Геолог А: «Из своего лагеря я отправился строго на север и прошел 1 милю в этом направлении, никуда не сворачивая. Затем я прошел 1 милю на восток. Я перекусил, а затем отправился опять на север и прошел 1 милю в этом направлении, никуда не сворачивая. Наконец, я прошел еще милю на запад и оказался в своем лагере». Где может располагаться лагерь геолога А?
(b) Геолог В: «Выйдя из своего лагеря, я прошел 1 милю на север, а затем 1 милю на восток. После этого прошел 1 милю на юг и, наконец, 1 милю на запад; после этого я оказался в собственном лагере». Где может располагаться лагерь геолога В?
(c) Геолог С: «Выйдя из своего лагеря, я прошел 1 милю на север, а затем 1 милю на восток. После этого прошел 1 милю на юг и, наконец, 1 милю на запад; после этого я оказался в точке, наиболее удаленной от моего лагеря среди всех точек, достижимых при описанных условиях». Где может располагаться лагерь геолога С и как далеко от лагеря оказался геолог в конце маршрута?
9. Соединяя точки
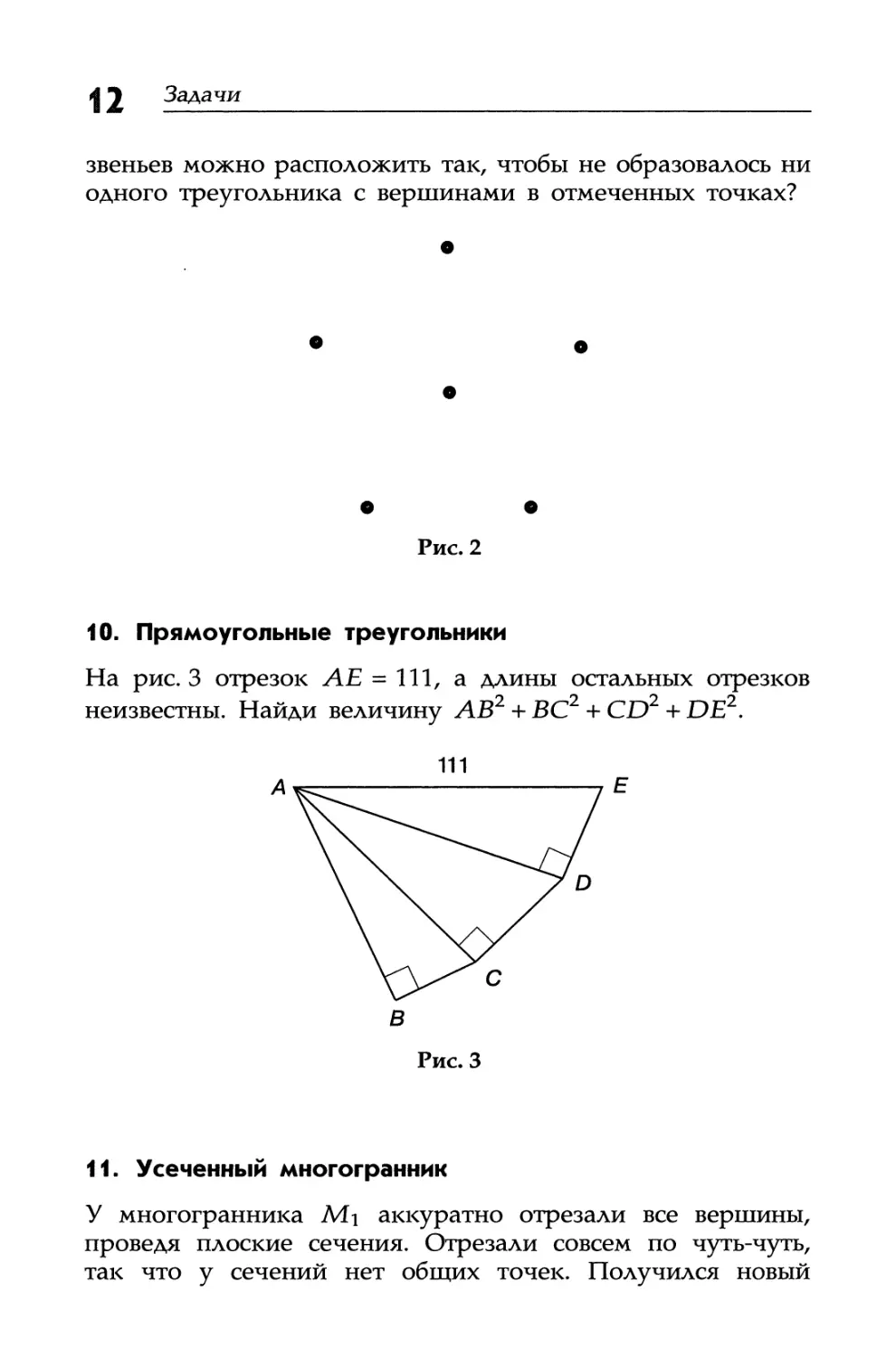
Отрезок прямой, соединяющий любые две точки из шести, изображенных на рис. 2, называется звеном. Сколько


12 Задачи
звеньев можно расположить так, чтобы не образовалось ни одного треугольника с вершинами в отмеченных точках?
Рис. 2
10. 	Прямоугольные треугольники
На рис. 3 отрезок АЕ = 111, а длины остальных отрезков неизвестны. Найди величину АВ2 + ВС2 + CD2 + DE2.
111
В
Рис. 3
11. 	Усеченный многогранник
У многогранника Mi аккуратно отрезали все вершины, проведя плоские сечения. Отрезали совсем по чуть-чуть, так что у сечений нет общих точек. Получился новый


12. Красивые коробочки
многогранник Мг, у которого Г граней, В вершин и Р ребер.
(a) Одно из чисел Г, В и Р равно 11. Каким может быть многогранник М.\ (два варианта)?
(b) Одно из чисел Г, В и Р равно 13. Каким может быть многогранник Mi (четыре варианта)?
12. 	Красивые коробочки
(a) Аня сказала своей подруге Ирине: «У меня есть прямоугольная коробка без крышки, все ее измерения — целые числа. Я обклеила коробку цветной бумагой изнутри и снаружи, всего 10 граней. Оказалось, что площадь использованной цветной бумаги в квадратных единицах равна объему коробки в кубических единицах. Более того, объем моей коробки максимально возможный при этих условиях». Ирина ответила: «Я сделала то же самое, причем у моей коробки при тех же условиях наименьший возможный объем». Каковы размеры обеих коробок?
(b) Боря сказал Кате: «У меня есть прямоугольная коробка без крышки, все размеры коробки — целые числа. Я обклеил 5 сторон коробки снаружи цветной бумагой и заметил, что площадь израсходованной бумаги в квадратных единицах равна объему коробки в кубических единицах. К тому же, хотя моя коробка не имеет форму куба, ее объем — точный куб». Катя ответила: «Я поступила так же как ты, и у меня тоже площадь израсходованной бумаги в квадратных единицах равна объему коробки в кубических единицах. При этом объем моей коробки вдвое меньше объема твоей». Каковы размеры обеих коробок?
(c) Вера сказала своему другу Леше: «У меня есть прямоугольная коробка с целыми измерениями. Я обклеила цветной бумагой все шесть граней коробки изнутри и снаружи. Оказалось, что площадь израсходованной бумаги в квадратных единицах равна объему коробки


14 Задачи
в кубических единицах. К тому же наибольшее измерение моей коробки выражается нечетным числом». Леша ответил Вере: «У меня есть коробка с такими же свойствами, но по объему она меньше твоей». Каковы размеры обеих коробок?
(d) 	Гриша сказал своему другу Мише: «У меня есть прямоугольная коробка с целыми измерениями. Я обклеил цветной бумагой все шесть граней коробки снаружи. Оказалось, что площадь израсходованной бумаги в квадратных единицах равна объему коробки в кубических единицах. К тому же все измерения моей коробки выражаются разными числами». Миша ответил: «У меня есть коробка с такими же свойствами, но по объему она вдвое меньше твоей». Каковы размеры обеих коробок?
13. 	Почти прямоугольное озеро
На рис. 4 изображено озеро ABCDEFG, берег которого — почти прямоугольник, за исключением участка DE. Пусть А\—площадь фигуры DEFG, Лг — площадь фигуры BCDE, а Аз — площадь клина ADE. Вырази Аз через А\ и Аг
Рис. 4


15. Разрезание квадрата
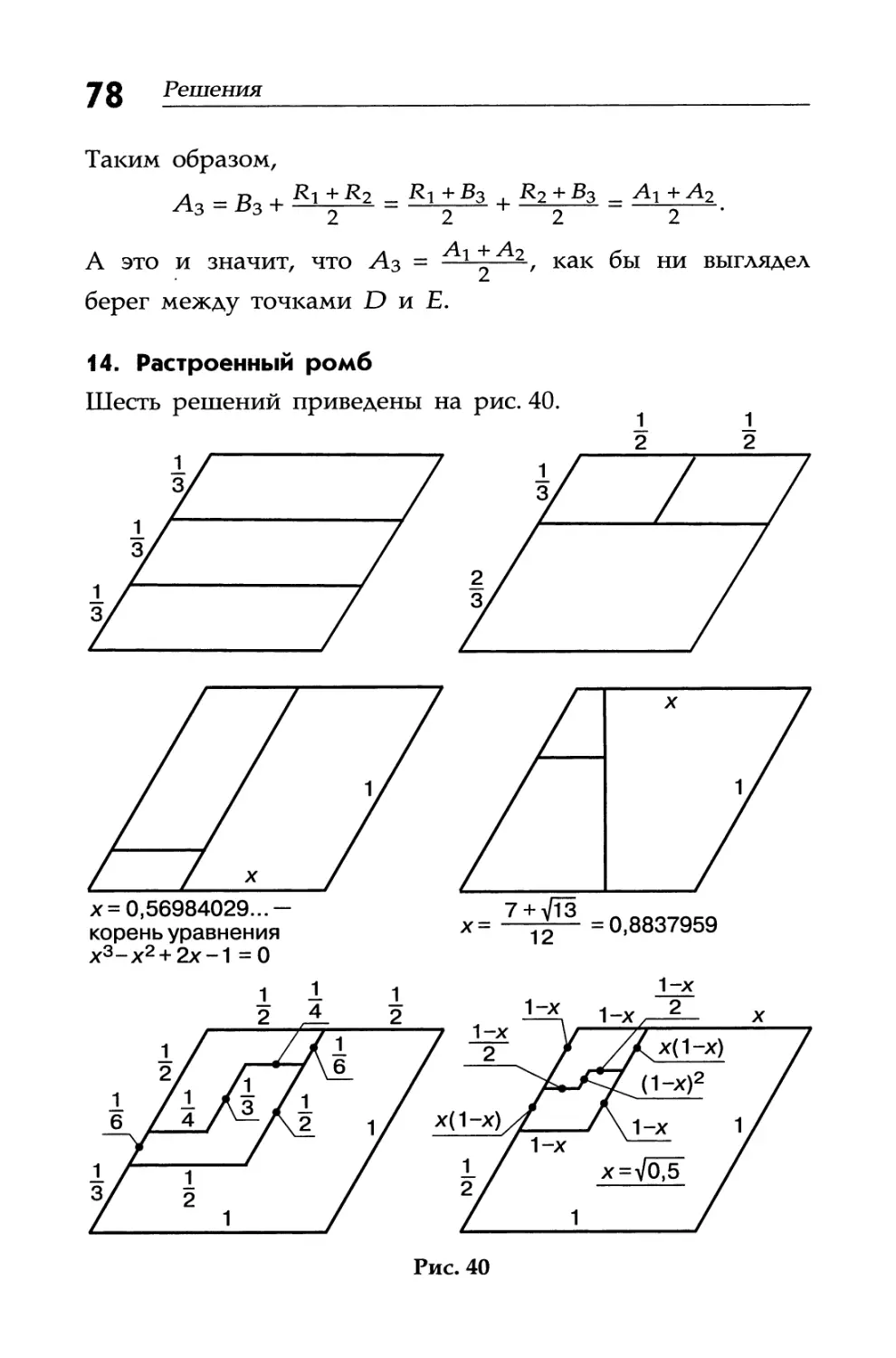
14. 	Растроенный ромб
На рис. 5 изображен ромб с углами 120° и 60°. Раздели его на три подобные друг другу части. Размеры частей могут не быть одинаковыми. Найди шесть решений.
15. 	Разрезание квадрата
Разбей квадрат на прямоугольники с целыми длинами
сторон, отношения которых равны 3 к 1. Прямоугольники не должны быть все одного размера, а их число должно быть как можно меньше.


ГЛАВА 3. ЦИФРОВЫЕ ГОЛОВОЛОМКИ
16. Всецифровые подарки
К Рождеству я купил подарки друзьям, стоимость каждого подарка в долларах выражалась точным квадратом. Когда я записал все цены на листе бумаги, то оказалось, что каждая цифра от 1 до 9 встретилась ровно по одному разу, причем мои расходы были минимально возможными при данных условиях. Сколько всего было подарков и сколько я заплатил за них?
17. Вариант су доку
Расставь в клетках таблицы на рис. 6 числа от 1 до 5 так, чтобы в каждой строке и в каждом столбце все числа были разными и чтобы все суммы в выделенных областях были различны.
V
> !
1 1
Рис. 6
18. 	Всецифровые суммы
(а) 	Обрати внимание, что в левой части равенства 87 42
^ = 1 все цифры от 1 до 9 встречаются ровно


18. Всецифровые суммы
по одному разу. Подбери такие натуральные числа а, Ъ, с, d, чтобы это свойство выполнялось для равенства
^ ^ = 1, причем:
(i) сумма а + Ъ + с + d была бы наибольшей;
(ii) сумма а + Ъ + с + d была бы наименьшей;
(iii) частное £ было бы наименьшим.
Ъ
70 143
(b) В левой части равенства — + = 1 каждая из цифр
от 0 до 9 встречается ровно по одному разу. Подбери такие натуральные числа а, Ъ, с, d, чтобы это свойство
выполнялось для равенства ^ ^ = 1, причем:
(i) сумма а + Ъ + с + d была бы наибольшей;
(п) сумма а + Ъ + с + d была бы наименьшей;
(iii) частное £ было бы наименьшим.
Ъ
4 297
(c) В левой части равенства — + = 2 все цифры от 1
до 9 встречаются ровно по одному разу. Подбери такие натуральные числа а, Ь, с, d, чтобы это свойство
выполнялось для равенства ^ ^ = 2, причем:
(i) сумма а + Ь + с + d была бы наибольшей;
(ii) сумма a + b + c + d была бы наименьшей;
(iii) частное ^ было бы наименьшим.
12 870
(d) В равенстве — + = 2 все цифры от 0 до 9
встречаются ровно по одному разу. Подбери такие натуральные числа а, Ъ, с, d, чтобы это свойство
выполнялось для равенства ^ ^ = 2, причем:
(i) сумма a + b + c + d была бы наибольшей;
(ii) сумма a + b + c + d была бы наименьшей;
(iii) частное £ было бы наименьшим.
b


18 Задачи
19. Чет и нечет
Пусть т — пятизначное число, записанное пятью разными нечетными цифрами 1, 3, 5, 7, 9 в некотором порядке; а п — пятизначное число, записанное пятью разными четными цифрами 2, 4, 6, 8, 0 в некотором порядке. Может ли п быть кратно т?
20. Странная целостность
У меня есть две разные цифры я и Ъ, и я рассматриваю целые числа, ближайшие к выражениям ~°'\/0,Ь и а.1
Оказывается, это два разных целых числа, оба они больше 10, оба записаны одними и теми же цифрами, но в разном порядке.
Чему равны а и Ь?
21. Десятизначное число
Десятизначное число записано десятью разными цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 в некотором порядке. Цифры с левого края по одной вычеркивают, и получаются числа, которые делятся соответственно на 9, 8, 7, 6, 5, 4, 3, 2 и 1.
(a) Мое число наибольшее из всех, что обладают этим свойством. Что это за число?
(b) Мое число наименьшее из всех, что обладают этим свойством. Что это за число?
1 Обозначения следуют оригиналу и будут встречаться в дальнейшем. Имеются в виду числа (0,fo)_1/0'a и (0— Прим. ред.


ГЛАВА 4. ЛОГИЧЕСКИЕ ГОЛОВОЛОМКИ
22. Дележ пирога
(a) Ася и Вася делят пирог. Сначала Ася делит пирог на две части, а затем Вася делит одну их этих частей на две. Асе достается самый большой и самый маленький из трех кусочков. Ася хочет получить как можно больше пирога. Какую наибольшую часть она может наверняка себе обеспечить?
(b) Теперь предположим, что и Ася и Вася на диете и желают получить пирога как можно меньше. Теперь Вася хочет, чтобы Ася получила как можно большую часть. Какую наибольшую часть он сможет всучить Асе?
(c) На этот раз Ася делит пирог на две части, затем Вася делит одну из этих частей на две. После этого опять Асина очередь; она делит один из трех кусочков на две части. Асе достаются самый большой и самый маленький кусочки, а Васе — два оставшихся. Какую наибольшую часть Ася может наверняка себе обеспечить и с помощью какой стратегии?
23. Побег из темницы
Злодей говорит рыцарю: «В каждом квадрате таблицы 7x17
спрятано число. (См. рис. 7.) Если ты угадаешь и сообщишь
мне сумму всех 119 чисел, тебя отпустят на свободу; если
Рис. 7


20 Задачи
нет — тебя казнят. Тебе разрешается открыть и подсмотреть число из одной клетки по выбору. На подготовку стратегии у тебя есть час». Рыцаря отвели в камеру, где охранник шепнул ему на ухо, что сумма чисел в любом прямоугольнике таблицы размером 3x4 или 4x3 равна 202. Что делать рыцарю, чтобы спастись?
24. 	Логика и геометрия
На рис. 8 изображены окружность, квадрат и равносторонний треугольник. Как ты думаешь, длина s больше или меньше радиуса окружности?
25. 	Али Баба и 10 разбойников
Десяти разбойникам, имена которых начинаются на буквы А, Б, В, Г, Д, Е, Ж, 3, И, К, нужно перебраться через реку. У них есть лодка, для которой нужны два гребца. Однако двое разбойников отказываются оставаться вместе в лодке, если первые буквы их имен не соседние по алфавиту. Из-за этого ограничения отряд разбойников не может перебраться через реку. Их главарь, чье имя начиналось на букву А, обратился за помощью к Али Бабе, и тот ответил: «Я могу помочь вам, ведь мое имя начинается на А». Какое наименьшее число раз придется пересекать реку, чтобы Али Бабе и разбойникам переправиться? (За один раз считается пересечь реку в одном направлении.)


26. Головоломки на годовщину свадьбы
26. 	Головоломки на годовщину свадьбы
Празднуя годовщину своей свадьбы, супружеская пара высказывает утверждения о возрасте своих детей. Все дети рождены в браке, поэтому их возрасты не больше чем годовщина, которую отмечают родители. В каждой головоломке супруги утверждают: «Сегодня мы уже сообщили Смитам сумму и произведение возрастов трех наших детей, но Смиты неверно определили, сколько им лет». Далее в каждой головоломке родители делают еще одно утверждение. Каждую годовщину празднуют разные пары, так что между разными головоломками нет связи. Мы считаем, что логика рассуждений Смитов, Джонсов и Браунов безупречна. В каждой головоломке требуется определить возраст детей.
(a) На 10-й годовщине свадьбы супруги А также утверждают: «Год назад Джонсы неправильно определили возраст наших детей».
(b) На 30-й годовщине свадьбы супруги В также утверждают: «Год назад Джонсы неправильно решили задачу, а 3 года назад ее неправильно решили Брауны».
(c) На 30-й годовщине свадьбы супруги С также утверждают: «Джонсы неправильно решили задачу, хотя и слышали сегодня ответ Смитов, а Брауны дали неправильный ответ 4 года назад».
(d) На 30-й годовщине свадьбы супруги D также утверждают: «Джонсы неправильно решили задачу 4 года назад, а Брауны дали неправильный ответ 7 лет назад».
(e) На 30-й годовщине свадьбы супруги Е также утверждают: «Джонсы неправильно решили задачу 5 лет назад, а Брауны — 6 лет назад».
(f) На 30-й годовщине свадьбы супруги F также утверждают: «Джонсы неправильно решили задачу 2 года назад, а Брауны —10 лет назад».
(g) На 28-й годовщине свадьбы супруги G также утверждают: «Джонсы неправильно решили задачу 2 года назад, а Брауны — 6 лет назад».


Задачи
(h) На 28-й годовщине свадьбы супруги Н также утверждают: «Джонсы неправильно решили задачу 4 года назад, а Брауны — 8 лет назад».
В следующих головоломках условия те же самые, за исключением того, что супруги сообщают Смитам и Джонсам сумму возрастов и сумму кубов возрастов своих троих детей.
(i) На 25-й годовщине свадьбы супруги I также утверждают: «Джонсы неправильно решили задачу год назад».
(j) На 20-й годовщине свадьбы супруги J также утверждают: «Джонсы неправильно решили задачу 2 года назад».
(к) На 25-й годовщине свадьбы супруги К также утверждают: «Джонсы неправильно решили задачу 3 года назад».
(1) На 25-й годовщине свадьбы супруги L также утверждают: «Джонсы неправильно решили задачу 4 года назад».
(ш) На 30-й годовщине свадьбы супруги М также утверждают: «Джонсы неправильно решили задачу 9 лет назад».


ГЛАВА 5. ГОЛОВОЛОМНЫЕ ВЕРОЯТНОСТИ
27. Сюрприз для игрока
У тебя есть 100 карточек, на 75 написано «выигрыш», а на 25 — «проигрыш». Твой начальный капитал —10000 рублей. Ты тщательно перетасовываешь карточки и ставишь 90% имеющихся денег на каждую карточку поочередно. Сколько денег у тебя останется в конце? А если бы у тебя было 80 выигрышных карточек и 20 проигрышных, сколько бы денег у тебя осталось в таком случае?
28. Игра Тензи
В игре Тензи подбрасывают 10 обычных игральных костей; то число, которое выпало наибольшее количество раз, объявляется целевым. В следующие ходы ты откладываешь в сторону те кости, на которых выпало целевое число, а оставшиеся подбрасываешь. Игра кончается, когда на всех 10 костях выпало целевое число. Каково ожидаемое число ходов в этой игре?
29. Маленькое бинго
В игре «Маленькое бинго» карточка разделена на три столбца и три строки, центральная клетка свободна (точнее, считается автоматически заполненной), на рис. 9 она отмечена звездочкой. Столбцы отмечены буквами В, N и G.
В ячейках столбца В располагаются без повторений какие-нибудь целые числа от 1 до 6; в столбце N — без повторений числа от 7 до 12, а в столбце G — от 13 до 18. Всего возможно Те = 63 х 53 х 42 = 432 000 таких карточек. Представь себе 432000 игроков, у каждого в руках карточка, все карточки
В N G
☆
Рис. 9


Задачи
разные. В ходе игры в случайном порядке выписываются числа от 1 до 18 по одному без повторений. Карточка выигрывает, если в ней выписанными к данному моменту числами заполнены строка, столбец или диагональ. Как только карточка выигрывает, ее обладатель восклицает «Бинго!» и игра заканчивается.
(a) Сколько чисел нужно выписать, чтобы наверняка выиграла хотя бы одна карточка?
(b) Когда игра заканчивается, выигравших обязательно окажется несколько. При этом есть две возможности: либо все выигравшие заполнят строку или диагональ, либо все они заполнят столбец. Назовем эти возможности «выигрывает строка» и «выигрывает столбец». Какова вероятность того, что в маленьком бинго выиграет строка?
30. 	Обычное бинго
В игре «Обычное бинго» в каждой карточке пять столбцов и пять строк, свободная центральная клетка отмечена звездочкой (рис. 10). Столбцы отмечены буквами В, I, N, G и О.
В ячейках столбца В располагаются без повторений числа от 1 до 15; в столбце I — без повторений числа от 16 до 30 и так далее; в столбце О — числа от 61 до 75. Всего возможно Т\5 = (15 х 14 х 13 х 12)5 х II4 таких карточек. Представь себе Т15 игроков, у каждого в руках карточка, все карточки разные. В ходе игры в случайном порядке выписываются числа от 1 до 75 по одному без повторений. Карточка выигрывает, если в ней выписанными к данному моменту числами заполнены строка, столбец или диагональ. Как только карточка выигрывает, ее обладатель восклицает «Бинго!» и игра заканчивается.
(a) Сколько чисел нужно выписать, чтобы наверняка выиграла хотя бы одна карточка?
(b) Когда игра заканчивается, выигравших обязательно окажется несколько. При этом есть две возможности:
☆
Рис. 10


33. Рулетка на автобус
либо все выигравшие заполнят строку или диагональ, либо все они заполнят столбец. Назовем эти возможности «выигрывает строка» и «выигрывает столбец». Какова вероятность того, что в обычном бинго выиграет строка?
31. Честная дуэль
Смит и Браун вызвали друг друга на дуэль. Они будут стрелять друг в друга по очереди, пока в кого-нибудь не попадут. Смит может попасть в Брауна в 40% случаев, он считается слабым стрелком, поэтому получает право стрелять первым. При таких условиях шансы обоих дуэлянтов равны. Какова вероятность того, что Браун попадет в Смита?
32. Золотой сет в теннисе
Золотой сет в теннисе — ситуация, когда один игрок выигрывает сет, набрав 24 очка из 24 возможных. В турнирах Большого шлема женщинам для победы в матче надо выиграть два сета из трех, а мужчинам — три из пяти. Какова вероятность золотого сета в течение матча, если очки определяются подбрасыванием монеты:
(a) для женского матча;
(b) для мужского матча?
33. Рулетка на автобус
(a) Ты оказался в Лас-Вегасе с двумя долларами в кармане. Единственный способ выбраться из города — купить билет за 4 доллара и уехать на автобусе. А добыть 4 доллара ты можешь, только поставив целое число долларов на рулетке. Какова лучшая стратегия игры для тебя и какова вероятность выехать из города?
(b) Та же задача, что в пункте (а), но вот только билет на автобус стоит 5 долларов.
Возможные ставки изображены на рис. 11.


Задачи
j- ПЯТЬ ЧИСЕЛ (1,2,3,0,00) выигрыш 6 к 1 г ДВА ПОПЕРЕЧНЫХ РЯДА (шесть чисел) выигрыш 5 к 1 г- ЧИСЛО (одно число) выигрыш 35 к 1
г- ДВА ЧИСЛА (два соседних числа) выигрыш 17 к 1
г- ПОПЕРЕЧНЫЙ РЯД (три числа в ряд) выигрыш 11 к 1
КОЛОНКА (12 чисел в колонке) выигрыш 2 к 1
J
— ДЮЖИНА (12 чисел в одной из них) выигрыш 2 к 1
'—i—L-J
L КРАСНОЕ/ЧЕРНОЕ, ЧЕТ/НЕЧЕТ, БОЛЬШЕ/МЕНЬШЕ (18 чисел) выигрыш 1 к 1
— УГОЛ (четыре числа с общим углом) выигрыш 8 к 1
Рис. 11
34. 	Цветные шарики
(a) В коробке п шариков двух разных цветов: щ шариков одного цвета и Пг — другого. В ходе эксперимента шарики наугад вынимают из коробки по одному без возвращения, пока в ней не останутся шарики только одного цвета. Каково ожидаемое количество шариков в коробке после окончания эксперимента?
(b) Теперь в коробке шарики трех разных цветов: щ шариков одного цвета, Пг — другого и Из—третьего. В ходе эксперимента шарики наугад вынимают из коробки по одному без возвращения, пока в ней не останутся шарики только одного цвета. На этом эксперимент заканчивается. До начала эксперимента вычислили ожидаемое количество шариков в коробке после его окончания. Это число оказалось целым. Кроме того, известно, что числа щ, «2 и из попарно взаимно просты. Каковы наименьшие возможные значения щ, Пг и Из при этих условиях? Каково ожидаемое количество шариков в коробке после окончания эксперимента?


35. Игра «Бродилка»
(с) 	И опять в коробке шарики трех цветов. В этой задаче эксперимент заканчивается, когда в коробке кончаются шарики какого-нибудь одного цвета. В этот момент в ней остаются шарики двух разных цветов. До начала эксперимента вычислили ожидаемое количество шариков в коробке после его окончания. Это число оказалось целым. Сколько шариков каждого цвета было в коробке изначально? Каково ожидаемое количество шариков в коробке после окончания эксперимента?
35. 	Игра «Бродилка»
У тебя есть настольная игра, в которой на игровом поле нарисована извилистая тропинка, разделенная на клетки. Тропинка начинается в клетке с номером 0, а заканчивается в клетке с номером М, которое больше 100. Ход заключается в том, что ты бросаешь обычный игральный кубик и продвигаешь фишку на столько клеток, сколько очков выпало на кубике. Игра заканчивается, когда ты достигнешь клетки М или пройдешь за нее. Ты планируешь сыграть в эту игру 21 раз. Каково ожидаемое число ходов, необходимое для завершения 21 игры? Округли его до ближайшего целого.


ГЛАВА 6. АНАЛИТИЧЕСКИЕ ГОЛОВОЛОМКИ
36. Спешка в аэропорту
В аэропорту по дороге на посадку ты замечаешь, что должен остановиться на минуту, чтобы завязать шнурки. В двух шагах впереди находится траволатор—движущийся тротуар. Где лучше завязывать шнурки — на траволаторе или нет, — чтобы быстрее попасть на посадку? Считай, что ты ходишь с постоянной скоростью — и по земле, и по траволатору.
37. Что это было!
Кевин приступил к трапезе и обратил внимание, что минутная стрелка ровно на одно деление из 60 опережает часовую стрелку. Что это было: завтрак, обед, ужин?
38. Мышиные бега
Три кошки и мышка бегают по ребрам тетраэдра. Кошки слепы, но каждая может изловить мышку, если столкнется с ней. Скорость одной из кошек на 1% больше скорости мышки, а скорости остальных двух кошек на 1% больше половины скорости мышки. Помоги кошкам — придумай, как поймать мышку.
39. Навещаем родственников
Три брата, Авдей, Бармалей и Варфоломей, собираются навестить на даче дедушку. У них есть велосипед, но ездить на нем умеет только Авдей. Зато он ездит со скоростью 40 км/ч в одиночку и со скоростью 30 км/ч, если везет кого-нибудь. Он может увезти только одного пассажира.


43. Каскад простых пифагоровых троек
Пешком Бармалей ходит со скоростью 6 км/ч, а Варфоломей— со скоростью 9 км/ч. Как далеко может быть дедушкина дача, если братья сумели добраться до нее за 3 часа?
40. Логи и рифмы
Положим х = log16 7 х log49 625. Вырази log10 2 через х, используя только целые постоянные.
41. Многочлены—1
Введем многочлены вида Р(х,у) = яо + а\Х + съу + а^х2 + + a^xy + a$y2 + ЯбХ3 + ajx^y + а$ху2 + а^у3. Известно, что
Р( 0,0) = Р(1,0) = Р(-1,0) = Р(0,1) = Р(0,-1) = Р( 1,1) =
= Р(1, —1) = Р(12,12) = 0.
Найди точку (хо,уо) = ^), где я, Ь и с > 1—целые
числа, такую, что Р(хо,уо) = 0 для всех многочленов описанного вида.
42. Многочлены—2
У уравнения ху + х + 5у + \3 = 8х3 есть целочисленное решение (х,у) = (1,-1).
(a) Сколько других целочисленных решений есть у этого уравнения (л: и у — целые)?
(b) Найди решения, где 1x1 и I у I — простые числа.
(c) Найди решения, где х и у — отрицательные целые числа.
43. Каскад простых пифагоровых троек
На рис. 12 без соблюдения масштаба изображены три пифагоровых треугольника с общими сторонами. Как показано в книге Дика Хесса All-Star Mathlete Puzzles (2009 г.), такие треугольники существуют при хо = 271, Х\ - 36 721, *2 = 674 215921.


30 Задачи
(a) Найди еще одно решение для каскада из трех простых пифагоровых треугольников.
(b) Найди пример каскада из четырех пифагоровых треугольников, в котором все числа от Хо до Х4 простые.
44. 	Разведение несушек
Авдей и Гордей разводят кур-несушек.
1 1 Авдей говорит: «В моем хозяйстве 1 j курицы несут 1 -
яиц за 11- дня».
Э
А Гордей отвечает: «А в моем хозяйстве 1 jL курицы
I 1
несут 1 - яиц за 1 - дня».
(a) В чьем хозяйстве куры лучше несутся?
(b) У Авдея 48 кур. Сколько дней ему придется ждать, чтобы получить целое число яиц в точности к концу дня? Сколько яиц за это время снесут его куры?
(c) У Гордея 300 кур. Сколько дней ему придется ждать, чтобы получить целое число яиц в точности к концу дня? Сколько яиц за это время снесут его куры?
45. 	Дилемма рыцаря
«В награду за верность, — сказал король, — я дарую тебе участок земли, который ты можешь обойти за день. Возьми с собой колышки, втыкай их в землю по дороге. Ровно


46. Наименее равносторонний треугольник
В
через 24 часа ты должен вернуться в точку старта. Вся земля внутри многоугольника с колышками в вершинах — твоя». Рыцарю требуется и секунд, чтобы воткнуть колышек в землю. Он вычислил, что площадь участка земли будет максимальна, если он будет иметь форму правильного n-угольника. Сколько земли получит рыцарь, если он двигается с постоянной скоростью 100 футов в минуту?
46. 	Наименее равносторонний треугольник
На рис. 13 изображен треугольник ABC общего вида; внутри него проведены лучи, точки пересечения которых дают треугольник А'В'С'. Углы а, р, у определяются соотношениями
а = —, /3= — и у = —,
п п п
где п — целое число, п > 2. Обрати внимание, что при и = 3 треугольник А'В'С' будет правильным вне зависимости от вида треугольника ABC. Этот факт известен как теорема Морли.
Твоя задача — подобрать углы А, В, С и целое число и так, чтобы треугольник А'В'С' как можно сильнее
отличался от правильного. Это означает, что величина


32 Задачи
где А', В' и О — углы треугольника А'В'С', максимальна.
Найди наименьшее значение верхней границы / и вычисли углы треугольника А'В'С, которые ему соответствуют.
47. 	Почувствуй себя доктором
(a) У тебя есть два пустых пузырька объемами 5 и 4 мл, запас воды, раковина и одна-единственная растворимая в воде лекарственная таблетка, которую ты можешь добавить в любой пузырек когда захочешь. Для каких положительных целых чисел п меньше 100 можно отмерить ровно п% таблетки, растворенной в воде?
Ответь на тот же вопрос, если
(b) объемы пузырьков 5 мл и 1 мл;
(c) объемы пузырьков 9 мл и 1 мл;
(d) объемы пузырьков 8 мл и 5 мл;
(e) объемы пузырьков 12 мл и 5 мл.


ГЛАВА 7. ФИЗИЧЕСКИЕ ГОЛОВОЛОМКИ
48. Лодка с сюрпризом
В плавательном бассейне находится лодка, а в ней сидит человек. Он выбросил из лодки в бассейн большой камень, при этом уровень воды в бассейне не изменился. Объясни почему.
49. Равновесие
К каждой головоломке на рисунке изображена конструкция из стержней и грузиков, подвешенная на колышек в стене. Стержни невесомые, метками они разделены на отрезки равной длины. Требуется подобрать разные целочисленные массы для грузиков так, чтобы конструкция находилась в равновесии.
(а) 	Уравновесь конструкцию на рис. 14, подобрав различные целочисленные значения грузиков от А до £ в пределах от 1 до 115.
(Ь) 	Уравновесь конструкцию на рис. 15, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 75.
I
Рис. 14


34 Задачи
(с) 	Уравновесь конструкцию на рис. 16, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 794.
(d) 	Уравновесь конструкцию на рис. 17, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 140.
I т I I I I I Г I "гтт
Рис. 17
(е) 	Уравновесь конструкцию на рис. 18, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 140.
1 1 1 1 1 1 II 1
/ГЪ
Г П'"'| 1 Г"
/с\
П Г"1 1
I I I ТН
/5 ш
Рис. 18


49. Равновесие
(f) 	Уравновесь конструкцию на рис. 19, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 135.
(g) 	Уравновесь конструкцию на рис. 20, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 190.
I I I I I I I I I
Рис. 20
(h) 	Уравновесь конструкцию на рис. 21, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 65.
Рис. 21


36 Задачи
(i) 	Уравновесь конструкцию на рис. 22, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 130.
(j) Уравновесь конструкцию на рис. 23, подобрав различные целочисленные значения грузиков от Л до £ в пределах от 1 до 30.
В следующих головоломках по-прежнему на рисунках конструкции из стержней и грузиков, но теперь каждая ячейка стержня обладает единичной массой; масса равномерно распределена в стержне.
(к) Уравновесь конструкцию на рис. 24, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 92.
I
Рис. 22
Рис. 23
/о\
Рис. 24


49. Равновесие
37
(1) Уравновесь конструкцию на рис. 25, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 800.
/f
Ж
ъ
ъ
/5
№ Рис. 25
(ш) Уравновесь конструкцию на рис. 26, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 270.
/с\
/f
1\
Рис. 26
(п) Уравновесь конструкцию на рис. 27, подобрав различные целочисленные значения грузиков от А до F в пределах от 1 до 70.
1
Ж
1\
/f
ITTei
Рис. 27


38 Задачи
50. 	Подвешенный стержень
Однородный тонкий стержень ВС длиной 3 подвешен к потолку на двух нитях: АВ длиной 2 и CD длиной 4, как изображено на рис. 28. Расстояние между точками подвеса AhD равно 5.
Рис. 28
(a) Покажи, что точка Р, в которой пересекаются продолжения линий подвеса, принадлежит линии, перпендикулярной потолку и проходящей через середину М стержня.
(b) Найди внутренние углы четырехугольника ABCD.
51. 	Падающие лестницы
Однородная тонкая лестница расположена так, как показано на рис. 29. Она наклонена под углом во к двум вертикальным стенкам, опираясь на них без трения в точках В и U. Лестница неизгибаема, находится в поле тяготения Земли, ускорение свободного падения равно g = 10 м/с2. Тяжелый брусок М подвешен к потолку на той же высоте, что и точка U. Ученикам разрешается двигать стены, чтобы изменить угол во, меняя при этом высоту бруска,


51. Падающие лестницы
Рис. 29
чтобы она совпадала с высотой более высокого конца лестницы. Три ученика рассказали об экспериментах, которые провели.
Ученик А: Я одновременно убрал обе стены и перерезал нить, на которой подвешен блок. Блок и лестница упали на землю одновременно.
Ученик В: Я одновременно убрал правую стену и перерезал нить, на которой подвешен блок. Блок и лестница упали на землю одновременно.
Ученик С: Я одновременно убрал левую стену и перерезал нить, на которой подвешен блок. Блок и лестница упали на землю одновременно.
(a) Какова была величина угла во в эксперименте ученика А?
(b) Какова была разность величин углов во в экспериментах учеников В и С?


ГЛАВА 8. ГОЛОВОЛОМКИ С ТРАПЕЦИЯМИ
В этой главе речь пойдет о равнобедренных трапециях с целыми сторонами (РТЦС). Равнобедренная трапеция — это четырехугольник, у которого две стороны параллельны, а < Ь, а две другие не параллельны, но зато одной длины с. С некоторыми головоломками этой главы поможет справиться компьютер.
РАВНОБЕДРЕННЫЕ ТРАПЕЦИИ С ЦЕЛЫМИ СТОРОНАМИ, ВПИСАННЫЕ В ОКРУЖНОСТЬ
Любую равнобедренную трапецию можно вписать в окружность, при этом центр окружности может лежать как внутри трапеции, так и вне ее, оба типа трапеций изображены на рис. 30.
Тип I Тип II
52. 	Минимальные РТЦС
(a) Найди РТЦС, которую можно вписать в окружность наименьшего радиуса.
(b) В окружность наименьшего возможного радиуса г > 1 вписали РТЦС, для которой а = 1. Каковы ее оставшиеся стороны?


56. Вытянутые РТЦС Д |
(c) В окружность наименьшего возможного радиуса г > 1 вписали РТЦС, для которой я = 1, Ъ = 2г. Каковы ее оставшиеся стороны?
(d) Найди бесконечную последовательность РТЦС таких, что я = 1 и Ъ = 2г.
53. Наименьшая окружность
(a) Найди наименьшую окружность с целым радиусом, в которую вписана РТЦС с я = 1, а Ъ и с — четные числа.
(b) Найди еще одну такую окружность со вторым по величине возможным радиусом.
54. Простые РТЦС
(a) Найди две РТЦС, у каждой из которых г, Ъ, а и с — различные простые числа.
(b) Существует ли третья такая РТЦС? (Решение неизвестно.)
(c) Найди РТЦС, у которых г, Ъ, а и с — простые числа, среди которых могут быть одинаковые.
(d) Существуют ли такие РТЦС с г ^ с? (Решение неизвестно.)
55. Плоские РТЦС
(a) Найди РТЦС, для которой с = 1иг>10.
(b) Найди бесконечную последовательность РТЦС, для которых с = 1.
56. Вытянутые РТЦС
(a) Найди наименьшее значение радиуса г для РТЦС, у которой ^ > 5.
(b) Найди наименьшее значение радиуса г для РТЦС, у которой ^ > 10.


42 Задачи
(с) 	Найди бесконечную последовательность РТЦС, для которых отношение ^ неограниченно растет.
57. Почти квадратные РТЦС
Рассмотрим РТЦС почти квадратной формы. В качестве меры близости к квадрату возьмем q = ^ ~ a + J с ~ ^ * . (Чем
меньше q, тем более РТЦС близка к квадрату.)
(a) Найди две самые маленькие РТЦС, для которых q < 0,2.
(b) Найди последовательность РТЦС, для которой q стремится к 0.
58. РТЦС с целыми высотами
Найди РТЦС минимального радиуса г, у которой расстояния ha и hb от центра описанной окружности до оснований целые.
РАВНОБЕДРЕННЫЕ ТРАПЕЦИИ С ЦЕЛЫМИ СТОРОНАМИ, ВПИСАННЫЕ В КВАДРАТЫ
Далее идут головоломки про РТЦС, которые могут быть вписаны в квадрат с целой стороной s. Это можно сделать по-разному, на рис. 31 изображены все четыре случая.
ТипА
Тип В
Тип С
Тип D
Рис. 31
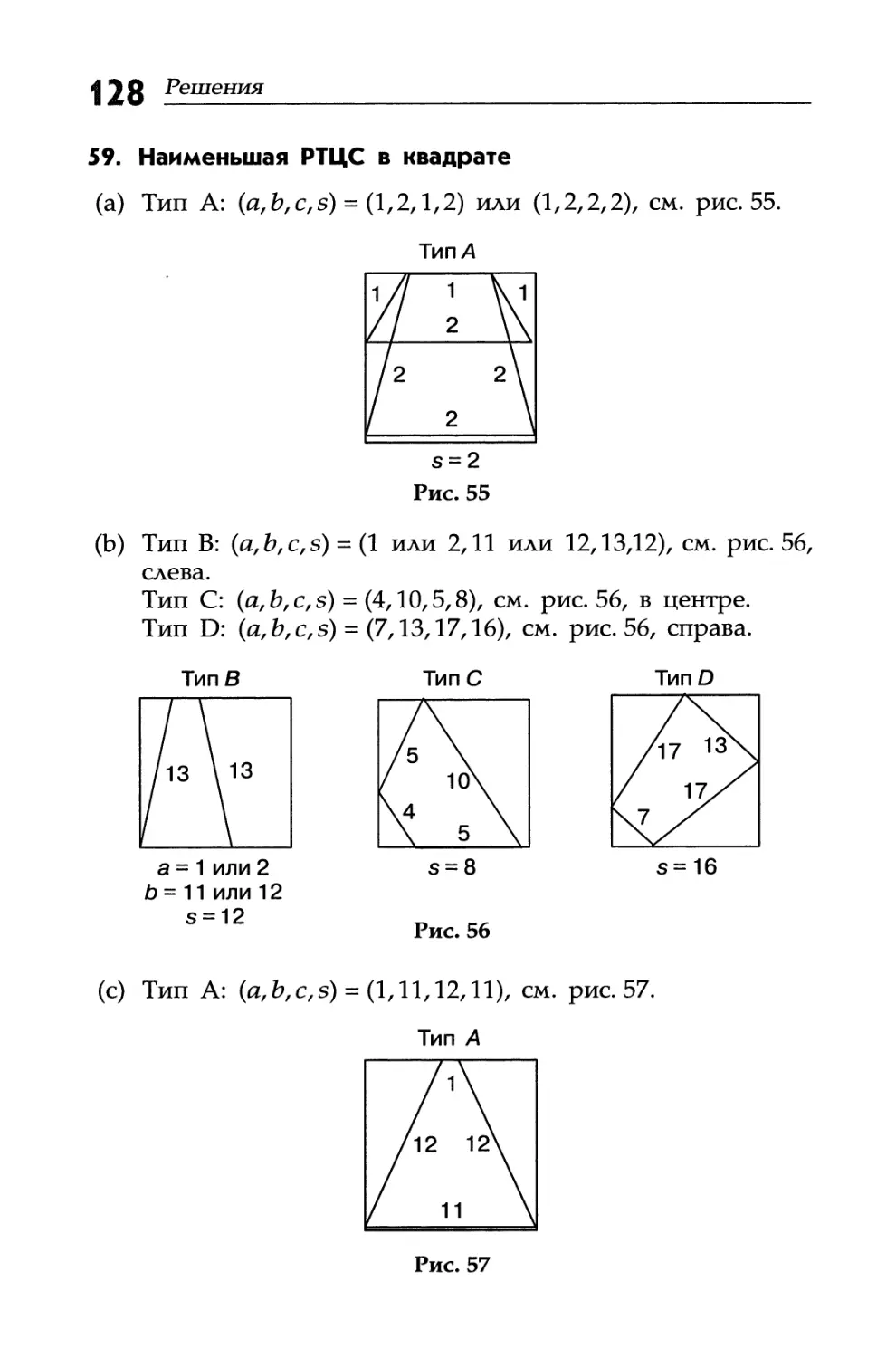
59. 	Наименьшая РТЦС в квадрате
(а) 	Найди РТЦС, которую можно вписать в квадрат с наименьшей стороной.


63. РТЦС, у которой b/s> 14 £3
(b) Найди РТЦС типов В, С и D, которые можно вписать в квадрат с наименьшей стороной.
(c) Найди РТЦС типа А с условием с > Ь, которую можно вписать в квадрат с наименьшей стороной.
(d) Найди РТЦС типа А с условием ^ ^ 0,9, которую можно вписать в квадрат с наименьшей стороной.
60. РТЦС, у которой а = 5
(a) Найди РТЦС с условием a -s, которую можно вписать в квадрат с наименьшей стороной.
(b) Найди бесконечную последовательность РТЦС с условием а = s, которые можно вписать в квадрат.
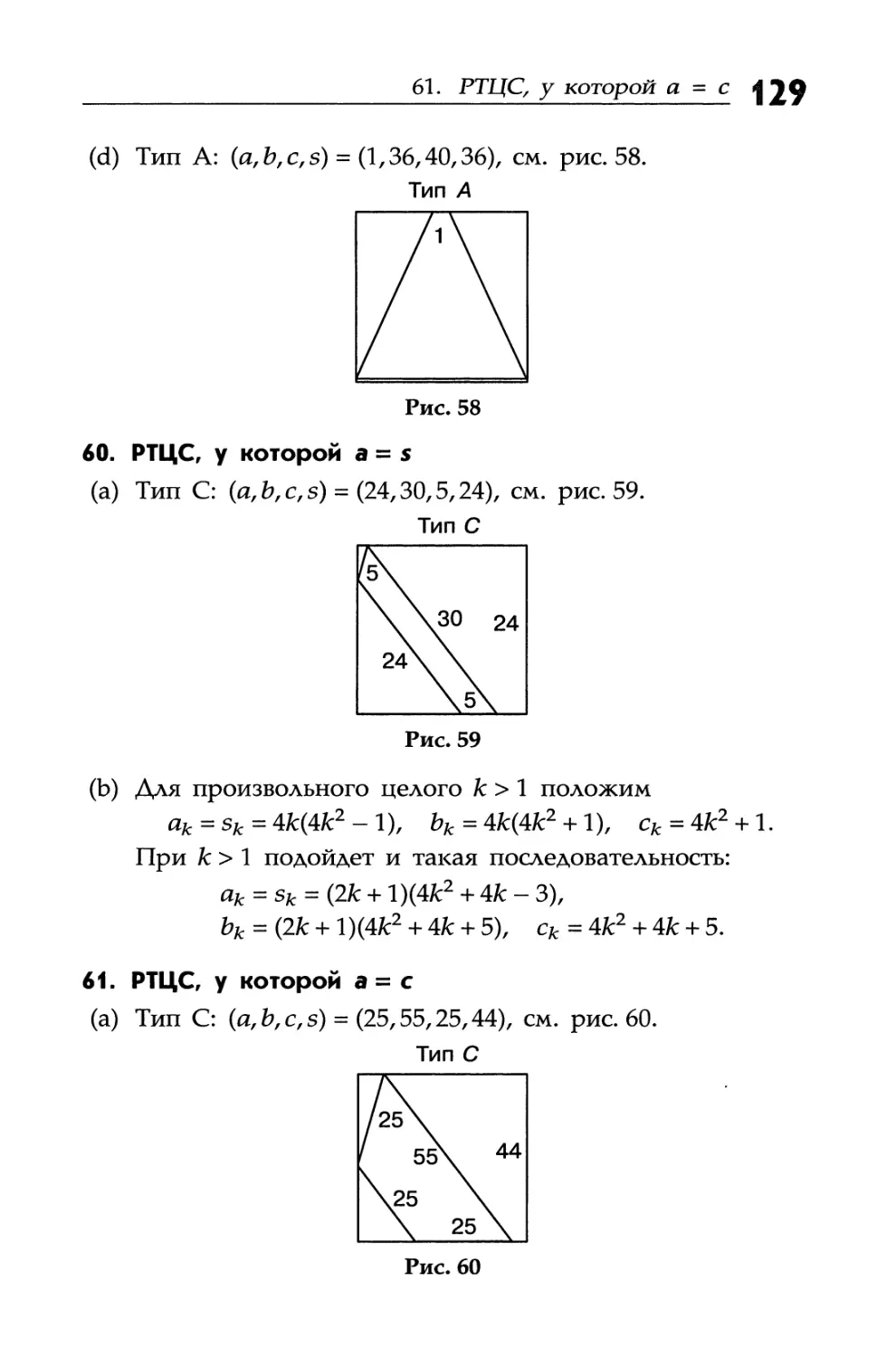
61. РТЦС у которой а = с
(a) Найди РТЦС не типа А с условием а = с, которую можно вписать в квадрат с наименьшей стороной.
(b) Найди бесконечную последовательность РТЦС не типа А с условием а -с, которые можно вписать в квадрат.
62. РТЦС у которой х = и
(a) Найди РТЦС типа С с условием х = и (рис. 32), которую можно вписать в квадрат с наименьшей стороной.
(b) Найди бесконечную последовательность РТЦС типа С с условием х = и (см. рис. 32), которые можно вписать х
в квадрат. Рис-32
63. РТЦС У которой у > 14
(a) Найди РТЦС типа С с условием ^ > 1,4, которую можно вписать в квадрат с наименьшей целой стороной.
(b) Найди бесконечную последовательность РТЦС типа С, у которых отношение ^ стремится к \/2 и которые можно вписать в квадрат.
Тип С
и


44 Задачи
(c) Найди РТЦС типа D с условием j > 1,4, которую можно вписать в квадрат с наименьшей целой стороной.
(d) Найди бесконечную последовательность РТЦС типа D, у которых отношение j стремится к у/2. и которые можно вписать в квадрат.
64. РТЦС, у которой | < 0,8, 0,75 и 0,71
(a) Найди РТЦС с условием j < 0,8, которую можно впи- сать в квадрат с наименьшей целой стороной.
(b) Найди РТЦС с условием j < 0,75, которую можно вписать в квадрат с наименьшей целой стороной.
(c) Найди РТЦС с условием j < 0,71, которую можно вписать в квадрат с наименьшей целой стороной.
65. РТЦС наименьшей площади
(a) Найди наименьший квадрат с целой стороной, в который вписана РТЦС с площадью менее 0,5000005 площади квадрата.
(b) Найди бесконечную последовательность таких РТЦС, для которых отношение площади трапеции к площади
1
квадрата стремится к
66. Наибольший квадрат
Найди наибольший квадрат с целой стороной, в который
нельзя вписать РТЦС типа D.
67. Неединственные решения
Найди наименьшую РТЦС, которую можно вписать в разные квадраты с целыми сторонами.


68. Наименьшие квадраты
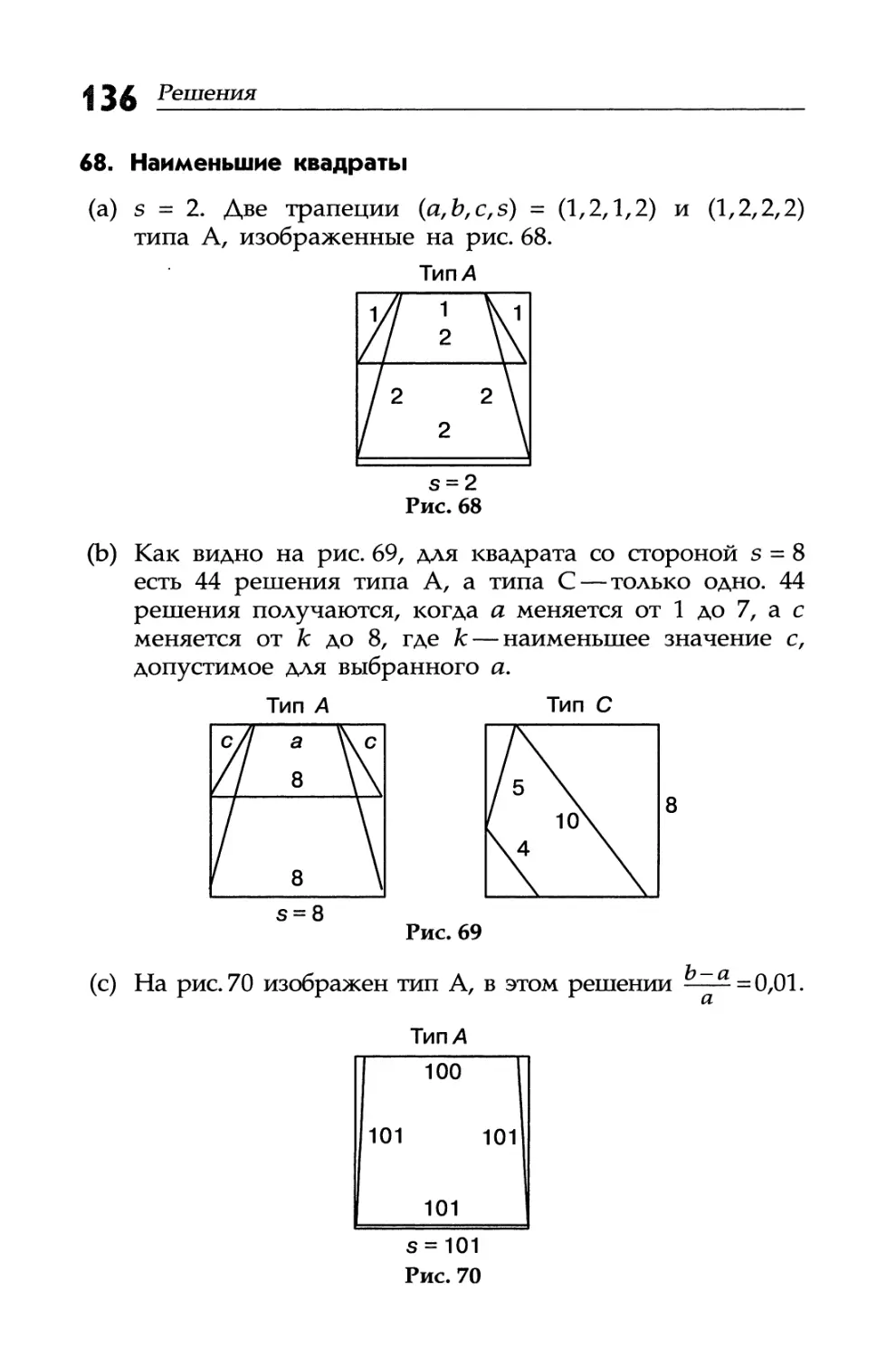
68. 	Наименьшие квадраты
(a) Найди наименьший квадрат с целой стороной, в который можно вписать более одной РТЦС.
(b) Найди наименьший квадрат с целой стороной, в который можно вписать 45 РТЦС.
(c) Найди наименьший квадрат с целой стороной, в который можно вписать такую РТЦС, что я < с ^ Ъ
и Lz* ^ 0,01.
I%
(d) Найди наименьший квадрат с целой стороной, в который можно вписать РТЦС типа D с условиями
я ^ с < Ъ и Ъ ~ a ^ 0,01. a
(e) Найди бесконечную последовательность квадратов с целыми сторонами, в которые можно вписать РТЦС
типа D, причем отношение ^ ~a стремится к 0.
(f) Какова наименьшая сторона квадрата, в который можно вписать более одной РТЦС типа С или D?
(g) Найди наименьший квадрат с целой стороной, в который можно вписать РТЦС типа D с условием Ъ = s.
(h) Найди наименьший квадрат с целой стороной, в который можно вписать две разные РТЦС типа D с условием Ъ = s.
(i) Найди два наименьших квадрата с нечетными целыми сторонами, в которые можно вписать РТЦС не типа А. Для этих двух квадратов РТЦС разные.


ГЛАВА 9. ДЖИПЫ В ПУСТЫНЕ
В задачах этой главы речь идет о колонне джипов в пустыне. Вначале они базируются в точке А, где имеется неограниченный запас топлива. Путь всех джипов завершается либо в точке А, либо в конечной точке В, которая находится как можно дальше от А. Все джипы одинаковы и расходуют топливо равномерно, пропорционально пройденному расстоянию. Расстояние, которое может проехать джип на полном баке, принимается за единицу. Один джип не может везти другой или везти топлива больше чем один бак.
69. 	Дорога в один конец на одном джипе
В этой задаче колонна состоит из одного джипа, от которого требуется удалиться от точки А на самое большое расстояние и завершить путь в наиболее удаленной точке В. Разрешается оставить в пустыне запас топлива без присмотра, чтобы воспользоваться им позднее.
(a) Как далеко можно уехать, имея в распоряжении два бака топлива?
(b) Как далеко можно уехать, имея в распоряжении 1,9 бака топлива?
(c) Сколько потребуется топлива, чтобы преодолеть 1,33 единицы расстояния?
(d) Как далеко можно уехать, имея в распоряжении три баках топлива?
(e) Как далеко можно уехать, имея в распоряжении 2,5 бака топлива?
(f) Сколько потребуется топлива, чтобы преодолеть 1,5 единицы расстояния?


71. Дорога в один конец с джипом-помощником
(g) 	Сколько потребуется топлива, чтобы преодолеть 2 единицы расстояния?
70. Дорога туда и обратно на одном джипе
В этой задаче колонна состоит из одного джипа, который должен доставить пакет в точку В, максимально удаленную от стартовой точки А, и вернуться обратно. Разрешается оставить в пустыне запас топлива без присмотра, чтобы воспользоваться им позднее.
(a) Если в твоем распоряжении только 3 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(b) Если в твоем распоряжении только 6 баков топлива, на каком наибольшем расстоянии может находиться точка В?
(c) Сколько топлива тебе потребуется, если расстояние до точки В равно 0,7?
(d) Если в твоем распоряжении только 2,5 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(e) Сколько топлива тебе потребуется, если расстояние до точки В равно 1?
(f) Сколько топлива тебе потребуется, если расстояние до точки В равно 1,5?
71. Дорога в один конец с джипом-помощником
Теперь в твоей колонне два джипа. Джип 1 должен доставить пакет в точку В, находящуюся на максимальном расстоянии от точки старта А. Джип 1 завершает свой маршрут в точке В, а джип 2 помогает ему и финиширует в точке А. Топливо можно передавать от джипа к джипу, но нельзя оставлять его запас в пустыне.
(а) 	Если в твоем распоряжении только 2 бака топлива, на каком наибольшем расстоянии может находиться точка В?


48 Задачи
(b) Если в твоем распоряжении только 2,5 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(c) Сколько топлива тебе потребуется, если расстояние до точки В равно
У
(d) Сколько топлива тебе потребуется, если расстояние до точки В равно 1,47?
(e) Сколько топлива тебе потребуется, если расстояние до точки В равно 1,489?
72. Дорога в один конец на двух джипах
В твоей колонне два джипа. Каждый из них должен доставить пакет в точку В, максимально удаленную от стартовой точки А. Оба джипа финишируют в В. Топливо можно передавать от джипа к джипу, но нельзя оставлять его запас в пустыне.
(a) Если в твоем распоряжении только 3 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(b) Сколько топлива тебе потребуется, если расстояние до
1 1
точки В равно 4j-?
(c) Сколько топлива тебе потребуется, если расстояние до точки В равно 1,23?
(d) Если в твоем распоряжении только 5 баков топлива, на каком наибольшем расстоянии может находиться точка В?
(e) Если в твоем распоряжении только 4,95 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(f) Сколько топлива тебе потребуется, если расстояние до точки В равно 1,2475?
73. Дорога туда и обратно с джипом-помощником
В твоей колонне два джипа. Один из них должен доставить пакет в точку В, максимально удаленную от стартовой


74. Дорога туда и обратно на двух джипах
точки А, и вернуться на старт. Второй джип обеспечивает поддержку первому, причем стартует и финиширует в А. Топливо можно передавать от джипа к джипу, но нельзя оставлять его запас в пустыне.
(a) Если в твоем распоряжении только 3 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(b) Если в твоем распоряжении только 3,5 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(c) Сколько топлива тебе потребуется, если расстояние до точки В равно 0,965?
(d) Сколько топлива тебе потребуется, если расстояние до
со
точки В равно —?
(e) Сколько топлива тебе потребуется, если расстояние до
СО
точки В равно ^?
(f) Если в твоем распоряжении только 7,8 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(g) Сколько топлива тебе потребуется, если расстояние до
99
точки В равно ^щ?
74. 	Дорога туда и обратно на двух джипах
В твоей колонне два джипа. Каждый из них должен доставить по пакету в точку В, максимально удаленную от стартовой точки А, и вернуться на старт. Топливо можно передавать от джипа к джипу, но нельзя оставлять его запас в пустыне.
(a) Если в твоем распоряжении только 4 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(b) Сколько топлива тебе потребуется, если расстояние до точки В равно 0,7?


50 Задачи
(c) Если в твоем распоряжении только 6 баков топлива, на каком наибольшем расстоянии может находиться точка В?
(d) Если в твоем распоряжении только 7 баков топлива, на каком наибольшем расстоянии может находиться точка В?
(e) Сколько топлива тебе потребуется, если расстояние до точки В равно 0,74?
(f) Если в твоем распоряжении только 9,2 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(g) Если в твоем распоряжении только 9,8 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(h) Сколько топлива тебе потребуется, если расстояние до
121
точки В равно j^?
75. 	Два джипа и две станции заправки
В твоей колонне два джипа. Каждый из них должен доставить по пакету в точку В, максимально удаленную от стартовой точки А. В обеих точках имеются запасы топлива. Топливо можно передавать от джипа к джипу, но нельзя оставлять его запас в пустыне.
(a) Сколько топлива тебе потребуется, если расстояние до точки В равно 1,25?
(b) Сколько топлива тебе потребуется, если расстояние до точки В равно 1,34?
(c) Если в твоем распоряжении только 5,02 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(d) Если в твоем распоряжении только 6,9 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(e) Сколько топлива тебе потребуется, если расстояние до точки В равно 1,475?


76. Дорога туда и обратно на трех джипах
(f) Если в твоем распоряжении только 8,6 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(g) Если в твоем распоряжении только 9,992 бака топлива, на каком наибольшем расстоянии может находиться точка В?
76. 	Дорога туда и обратно на трех джипах
В твоей колонне три джипа. Один из них должен доставить пакет в точку В, максимально удаленную от стартовой точки А. Два других джипа обеспечивают поддержку первому, причем все три джипа стартуют и финишируют в А. Топливо можно передавать от джипа к джипу, но нельзя оставлять его запас в пустыне.
(a) Сколько топлива тебе потребуется, если расстояние до точки В равно 1?
(b) Сколько топлива тебе потребуется, если расстояние до точки В равно 1,005?
(c) Сколько топлива тебе потребуется, если расстояние до точки В равно 1,01?
(d) Сколько топлива тебе потребуется, если расстояние до точки В равно 1,04?
(e) Если в твоем распоряжении только 4,8 бака топлива, на каком наибольшем расстоянии может находиться точка В?
(f) Если в твоем распоряжении только 5 баков топлива, на каком наибольшем расстоянии может находиться точка В?


ГЛАВА 10. ГОЛОВОЛОМКИ С ЦИФРАМИ
В 2004 году Сэм Ритчи придумал игру MathDice, которую теперь производит фирма ThinkFun. В этой игре подбрасывают игральные кости и фиксируют, сколько очков выпадает на каждой из них (от 1 до 6). Требуется составить математическое выражение из этих чисел, используя каждое ровно по одному разу. Значение выражения должно быть равно некоторому заранее заданному целевому числу.
В каждой головоломке этой главы заданы три числа (от 0 до 9). Цель — следуя определенным правилам, составить из этих чисел выражение, значение которого равно заранее заданному целевому числу.
ТРЕХЦИФРОВКИ
В первой серии задач можно использовать знаки +, -, х, 4-, степени, факториалы, скобки и конкатенацию. Последнее означает, что двумя цифрами можно записать одно число, например из цифр 1 и 2 можно составить число 21. Корни, десятичная запятая, другие математические функции недопустимы. В некоторых головоломках цифры должны идти в порядке убывания, а в других — в порядке возрастания. Выражение не должно начинаться со знака минус.
77. 	Из цифр 0, 1 и 2 в возрастающем порядке сделай число:
(a) 12;
(b) 13;
(c) 24 (2 способа).


80. Из цифр 3, 4 и 5 в возрастающем порялке
78. 	Из цифр 1, 2 и 3 сделай число:
(a) 12 (2 способа);
(b) 13;
(c) 15;
(d) 24 (3 способа);
в возрастающем порядке
(e) 27;
(f) 36 (2 способа);
(g) 64 (2 способа);
(h) 72.
79. 	Из цифр 2, 3 и 4 в возрастающем порядке сделай число:
(a) 14 (2 способа); (i) 54;
(b) 16 (3 способа); (j) 60 (2 способа);
(c) 20 (2 способа); (к) 68;
(d) 24 (2 способа); (1) 74;
(e) 30 (3 способа); (т) 83;
(f) 36 (2 способа); (п) 88;
(8) 40; (о) 96.
(h) 	47;
80. Из цифр 3, 4 сделай число:
и 5 в возрастающем порядке
(а)
12;
(Р)
39;
(Ъ)
15 (2 способа);
(q)
42;
(с)
16;
(г)
50;
(d)
17;
(S)
51;
(е)
19;
(t)
54;
(f)
22;
(и)
57;
(g)
24 (3 способа);
(V)
60
(h)
25 (2 способа);
(w)
67;
(i)
26;
(X)
76;
Ф
27;
(У)
77;
(k)
29 (2 способа);
(z)
80;
(1)
30;
(al)
86;
(m)
32 (2 способа);
(bl)
87;
(n)
35 (3 способа);
(cl)
90;
(o)
36;
(dl)
99.


Задачи
81. 	Из цифр 4, 5 и 6 в возрастающем порядке сделай число:
(a) 13; (h) 39;
(b) 20; (i) 44 (2 способа);
(c) 24 (3 способа); (j) 51;
(d) 25; (k) 54 (2 способа);
(e) 26; (1) 60;
(f) 34; (m) 80 (2 способа).
(g) 35;
82. 	Из цифр 5, 6 и 7 в возрастающем порядке
сделай число:
(a) 18 (2 способа); (h) 49;
(b) 23; (i) 53;
(c) 24; (j) 63;
(d) 27; (k) 65;
(e) 35; (1) 72;
(f) 37; (m) 77;
(g) 47; (n) 78.
83. 	Из цифр 6, 7 и 8 в возрастающем порядке сделай число:
(a) 21; (е) 59;
(b) 34; (f) 62;
(c) 48 (2 способа); (g) 75;
(d) 50; (h) 90 (3 способа).
84. 	Из цифр 7, 8 и 9 в возрастающем порядке сделай число:
(f) 70;
(g) 79;
(h) 87;
(i) 96.
(a)
(b)
(c)
(d)
(e)
24
47
63
65
69


88. Из цифр 3, 5 и 7 в возрастающем порядке
85. 	Из цифр 0, 2 и 4 в возрастающем порядке сделай число:
(a) 17; (е) 49;
(b) 23; (f) 72;
(c) 25 (2 способа); (g) 81.
(d) 30 (2 способа);
86. 	Из цифр 1, 3 и 5 в возрастающем порядке сделай число:
(a) 12; (g) 30,
(b) 15; (h) 31
(c) 16; (i) 40
(d) 19; (j) 42,
(e) 20 (2 способа); (к) 65.
(f) 29;
87. 	Из цифр 2, 4 и 6 в возрастающем порядке
сделай число:
(a) 16;
(b) 20 (2 способа);
(c) 22;
(d) 24;
(e) 26 (2 способа);
(f) 30;
(g) 32;
(h) 36 (2 способа);
(i) 	42;
(j) 48 (3 способа); (k) 54;
(1) 56;
(m) 60 (2 способа); (n) 64;
(о) 	96.
88. 	Из цифр 3, 5 и 7 в возрастающем порядке
сделай число:
(a) 13;
(b) 15;
(c) 18 (2 способа);
(d) 22;
(e) 23,
(f) 24
(g) 28
(h) 36
(i) 37
(j) 38;
(k) 41;
(1) 42 (2 способа); (m) 56;
(n) 60 (2 способа);
(о) 	63;
(P) 72;
(q) 77.


56 Задачи
89. 	Из цифр 4, 6 и 8 в возрастающем порядке сделай число:
(a) 12; (i) 54;
(b) 16 (2 способа); (j) 56;
(c) 18 (2 способа); (к) 72;
(d) 22; (1) 80;
(e) 26; (т) 90;
(f) 32 (3 способа); (п) 92;
(g) 38 (2 способа); (о) 93;
(h) 52; (р) 94.
90. 	Из цифр 5, 7 и 9 в возрастающем порядке сделай число:
(a) 21; (f) 57;
(b) 26; (g) 66;
(c) 41; (h) 68;
(d) 44; (i) 80;
(e) 48; (j) 84.
91. 	Из цифр 0, 3 и 6 в возрастающем порядке сделай число:
(a) 13; (е) 37 (2 способа);
(b) 19; (f) 42;
(c) 24 (2 способа); (g) 64.
(d) 30;
92. 	Из цифр 1, 4 и 7 в возрастающем порядке сделай число:
(a) 11 (2 способа); (g) 32;
(b) 12; (h) 35;
(c) 18; (i) 47;
(d) 21; (j) 48;
(e) 24; (k) 98.
(f) 31 (2 способа);


96. Из цифр 1, 5 и 9 в возрастающем порядке
93. Из цифр 2, 5 сделай число:
и 8 в возрастающем порядке
(а) 15;
(h) 40;
(b) 17 (2 способа);
(i) 42;
(с) 18;
(j) 56;
(d) 24;
(k) 60;
(е) 26;
(1) 80;
(f) 30;
(g) 33;
(m) 90.
94. Из цифр 3, 6 и сделай число:
9 в возрастающем порядке
(а) 18;
(g) 75;
(Ъ) 21;
(h) 81 (2 способа);
(с) 24 (2 способа);
(i) 83;
(d) 27 (2 способа);
(j) 86;
(e) 45 (3 способа);
(f) 48;
(k) 90.
95. Из цифр 0, 4 и сделай число:
8 в возрастающем порядке
(а) 13;
(e) 40;
(Ъ) 15;
(f) 48 (2 способа);
(c) 17;
(d) 33;
(g) 49.
96. 	Из цифр 1, 5 и 9 в возрастающем порядке сделай число:
(a) 15; (е) 59;
(b) 24; (f) 60;
(c) 46; (g) 80.
(d) 54;


Задачи
97. 	Из цифр 1, 2 и 3 в убывающем порядке сделай число:
(a) 11; (е) 32 (3 способа);
(b) 18; (f) 35;
(c) 23; (g) 37;
(d) 27 (2 способа); (h) 63.
98. Из цифр 1, 2 и 4 в убывающем порядке сделай число:
(а) И;
(b) 15;
(c) 18;
(d) 21;
(e) 25 (2 способа);
(f) 26 (3 способа);
(g) 30;
(h) 45
(i) 47,
(j) 64.
99. 	Из цифр 1, 2 сделай число:
(a) 11 (2 способа); (f) 40
(b) 20; (g) 51
(c) 24 (2 способа); (h) 61
(d) 26 (2 способа); (i) 99.
(e) 30;
и 5 в убывающем порядке
100. 	Из цифр 3, 5 и 6 в убывающем порядке сделай число:
(a) 12 (2 способа); (h) 42;
(b) 18; (i) 46;
(c) 21 (2 способа); (j) 48 (2 способа);
(d) 24 (3 способа); (к) 59 (2 способа);
(e) 26; (1) 66;
(f) 33 (2 способа); (ш) 90 (2 способа);
(g) 36 (3 способа); (п) 100.


104. Из цифр 3, 4 и 5 в убывающем порядке
101. Из цифр 3, 6 сделай число:
и 7 в убывающем порядке
(а) 13 (2 способа);
(g) 70 (2 способа);
(Ь) 21 (2 способа);
(h) 78;
(с) 24 (2 способа);
(i) 80;
(d) 39 (2 способа);
(j) 82;
(e) 42 (2 способа);
(f) 49;
(k) 84.
102. Из цифр 3, 6 и сделай число:
8 в убывающем порядке
(а) 14;
(g) 56;
(Ь) 24 (2 способа);
(h) 57;
(с) 28;
(i) 64 (2 способа);
(d) 48;
(j) 80;
(e) 50;
(f) 55;
(k) 96.
103. Из цифр 3, 4 и сделай число:
7 в убывающем порядке
(а) И;
(g) 35;
(Ь) 18 (2 способа);
(h) 36;
(с) 25 (2 способа);
(i) 37;
(d) 27;
(j) 70;
(e) 28 (3 способа);
(f) 31 (3 способа);
(k) 71 (2 способа).
104. 	Из цифр 3, 4 и 5 в убывающем порядке сделай число:
(a) И; (h)
(b) 12 (2 способа); (i)
(c) 15 (2 способа); (j)
(d) 16; (k)
(e) 20 (2 способа); (1)
(f) 29 (2 способа); (m)
(g) 30;
32 (2 способа); 40 (2 способа); 51;
56;
90 (3 способа); 96 (2 способа).


60 Задачи
105. 	Из цифр Зг 5 и 8 в убывающем порядке сделай число:
(a) 12; (g)
(b) 18 (2 способа); (h)
(c) 24; (i)
(d) 27; (j)
(e) 28; (k)
(f) 32;
48 (2 способа); 56;
64 (2 способа); 78;
88 (2 способа).
106. 	Из цифр 3, 7 и 8 в убывающем порядке сделай число:
(a) 14;
(b) 15;
(c) 24 (2 способа);
(d) 29 (2 способа);
(e) 49;
(f) 56;
(g) 63;
(h) 81 (2 способа);
(i) 90 (2 способа).
107. 	Из цифр 3, 4 и сделай число:
(a) 12 (3 способа);
(b) 16 (2 способа);
(c) 24 (4 способа);
(d) 28;
(e) 30;
(f) 32 (3 способа);
8 в убывающем порядке
(g) 35 (2 способа);
(h) 64 (3 способа);
(i) 72 (3 способа);
(j) 80 (2 способа);
(к) 96 (2 способа).
108. 	Из цифр 3, 4 и 6 в убывающем порядке сделай число:
(a) 18; (g) 60 (2 способа);
(b) 27 (3 способа); (h) 64;
(c) 33 (2 способа); (i) 70 (2 способа);
(d) 36 (2 способа); (j) 72 (2 способа);
(e) 40; (к) 90 (2 способа).
(f) 58;


111. Из цифр 3, 4 и 9 в убывающем порядке
109. 	Из цифр 4Г 7 и 9 в убывающем порядке сделай число:
(а) 	15;
(b) 16
(c) 18
(d) 24
(e) 26
(f) 39
(g) 48 (2 способа);
(h) 68;
(i) 73,
(j) 83 (k) 99.
110. 	Из цифр 4, 8 сделай число:
(a) 13 (2 способа);
(b) 24 (2 способа);
(c) 27;
(d) 33 (2 способа);
(e) 36 (2 способа);
(f) 41 (2 способа);
и 9 в убывающем порядке
(g) 68 (2 способа);
(h) 74;
(i) 81 (j) 93 (k) 96
111. 	Из цифр 3, 4 сделай число:
(a) 11 (2 способа);
(b) 17;
(c) 20;
(d) 21 (2 способа);
(e) 27;
(f) 33 (3 способа);
(g) 39 (3 способа);
и 9 в убывающем порядке
(h) 40;
(i) 72 (2 способа);
(j) 73;
(k) 88;
(1) 99;
(ш) 100.
ТРЕХЦИФРОВКИ — СРЕДНИЙ УРОВЕНЬ
В следующей серии задач можно использовать знаки +, х, степени, десятичные запятые, скобки и конкатенацию. Последнее означает, что двумя цифрами можно записать одно число, например из цифр 1 и 2 можно составить число 21. Ноль перед десятичной запятой писать необязательно. Корни, периодические дроби, другие математические функции недопустимы. Два выражения считаются одинаковыми, если одно из них непосредственно


61 Задачи
получается из другого. Например, одинаковыми считаются 1 -г 2-3 и 1 х 23; ,6x5-1 и 6 х ,5 - 1; 42 + 3 и 43 + 2. В этих задачах может быть несколько решений. И приготовь калькулятор, наверняка он тебе пригодится.
112. Одиозные одиночки
(По
одному
решению в каждой задачке)
(а)
Сделай
число
15, используя цифры 2, 6
и
8.
(Ь)
Сделай
число
25, используя цифры 2, 6
и
9.
(с)
Сделай
число
30, используя цифры 2, 7
и
9.
(d)
Сделай
число
7, используя цифры 2, 8 и 8.
(е)
Сделай
число
11, используя цифры 2, 8
и
9.
(f)
Сделай
число
25, используя цифры 3, 3
и
4.
(g)
Сделай
число
13, используя цифры 3, 6
и
7.
(h)
Сделай
число
17, используя цифры 3, 6
и
9.
(i)
Сделай
число
9, используя цифры 3, 7 и 8.
(j)
Сделай
число
24, используя цифры 3, 8
и
8.
(k)
Сделай
число
9, используя цифры 4, 4 и 4.
(1)
Сделай
число
16, используя
цифры 4, 5
и
5.
(m)
Сделай
число
28, используя
цифры 4, 5
и
5.
(n)
Сделай
число
30, используя
цифры 4, 5
и
8.
(o)
Сделай
число
23, используя
цифры 4, 5
и
9.
(P)
Сделай
число
64, используя
цифры 4, 5
и
9.
(q)
Сделай
число
11, используя
цифры 4, 6
и
8.
(r)
Сделай
число
18, используя
цифры 4, 9
и
9.
(s)
Сделай
число
16, используя
цифры 5, 5
и
5.
(t)
Сделай
число
11, используя
цифры 5, 5
и
6.
(u)
Сделай
число
26, используя
цифры 5, 5
и
6.
(v)
Сделай
число
11, используя
цифры 5, 8
и
9.
(w)
Сделай
число
64, используя
цифры 5, 8
и
9.


114. Трепетные трио
113. 	Пагубные парочки
(По два решения в каждой задачке)
(а
(Ь
(с
(d
(е
(f
(g
(h
(i
O'
(k
(1
(m
(n
(o
(P
(q
(r
(s
(t
(U
(V
(w
(X
(У
Сделай число 7, используя цифры 1, 2 и 2. Сделай число 18, используя цифры 1, 2 и 2. Сделай число 8, используя цифры 1, 3 и 3.
Сделай число 6, используя цифры 1, 3 и 4.
Сделай число 10, используя цифры 1, 5 и 8.
Сделай число 16, используя цифры 1, 6 и 9.
Сделай число 32, используя цифры 2, 3 и 9.
Сделай число 14, используя цифры 2, 4 и 5.
Сделай число 22, используя цифры 2, 4 и 9.
Сделай число 64, используя цифры 2, 5 и 5.
Сделай число 25, используя цифры 2, 6 и 8.
Сделай число 7, используя цифры 2, 8 и 9. Сделай число 31, используя цифры 3, 3 и 4.
Сделай число 24, используя цифры 3, 3 и 5.
Сделай число 30, используя цифры 3, 3 и 9.
Сделай число 4, используя цифры 3, 4 и 5.
Сделай число 8, используя цифры 3, 4 и 9.
Сделай число 14, используя цифры 3, 5 и 8.
Сделай число 18, используя цифры 3, 6 и 6.
Сделай число 8, используя цифры 4, 4 и 5. Сделай число 12, используя цифры 4, 4 и 5.
Сделай число 18, используя цифры 4, 5 и 5.
Сделай число 16, используя цифры 4, 5 и 6.
Сделай число 32, используя цифры 4, 5 и 8.
Сделай число 25, используя цифры 4, 5 и 9.
114. 	Трепетные трио
(По три решения в каждой задачке)
(a) Сделай число 8, используя цифры 1, 1 и 2.
(b) Сделай число 13, используя цифры 1, 2 и 8.


64 Задачи
(c) Сделай число 8, используя цифры 1, 3 и 4.
(d) Сделай число 15, используя цифры 2, 2 и 6.
(e) Сделай число 2, используя цифры 2, 3 и 8.
(f) Сделай число 10, используя цифры 2, 3 и 9.
(g) Сделай число 10, используя цифры 2, 5 и 6.
(h) Сделай число 32, используя цифры 2, 5 и 6.
(i) Сделай число 28, используя цифры 2, 5 и 7. (j) Сделай число 9, используя цифры 3, 3 и 3. (к) Сделай число 16, используя цифры 3, 4 и 6. (1) Сделай число 13, используя цифры 3, 5 и 5.
(ш) Сделай число 4, используя цифры 3, 5 и 7. (п) Сделай число 15, используя цифры 3, 5 и 7.
(о) 	Сделай число 32, используя цифры 3, 5 и 8. (р) Сделай число 10, используя цифры 4, 5 и 6. (q) Сделай число 8, используя цифры 4, 5 и 7. (г) Сделай число 9, используя цифры 4, 5 и 7. (s) Сделай число 20, используя цифры 4, 5 и 8. (t) Сделай число 25, используя цифры 5, 5 и 7. (и) Сделай число 4, используя цифры 5, 6 и 8. (v) Сделай число 25, используя цифры 5, 7 и 9.
115. 	Навязчивые нескольки
(От 4 до 7 решений в каждой задачке)
(a) Сделай число 5, используя цифры 2, 6 и 7 (4 способа).
(b) Сделай число 27, используя цифры 3, 3 и 6 (4 способа).
(c) Сделай число 32, используя цифры 3, 4 и 5 (4 способа).
(d) Сделай число 6, используя цифры 3, 5 и 9 (4 способа).
(e) Сделай число 2, используя цифры 4, 5 и 8 (4 способа).
(f) Сделай число 8, используя цифры 5, 6 и 7 (4 способа).
(g) Сделай число 6, используя цифры 5, 7 и 8 (4 способа).
(h) Сделай число 32, используя цифры 5, 8 и 8 (4 способа).
(i) Сделай число 64, используя цифры 1, 4 и 6 (6 способов).


116. Добейся максимума
(j) Сделай число 2, используя цифры 2, 4 и 8 (7 способов), (к) Сделай число 16, используя цифры 2, 5 и 5 (5 способов).
(1) 	Сделай число 32, используя цифры 2, 5 и 7 (5 способов), (ш) Сделай число 5, используя цифры 2, 5 и 9 (5 способов), (п) Сделай число 16, используя цифры 4, 4 и 8 (5 способов).
116. 	Добейся максимума
(a) Используя ровно по одному разу цифры 1, 2, 3 и 4, построй математическое выражение, значение которого максимально. Можно использовать знаки +, -, х, ч-, степени, десятичные запятые, скобки и конкатенацию. Последнее означает, что двумя цифрами можно записать одно число, например можно из цифр 1 и 2 составить число 21. Ноль перед десятичной запятой писать необязательно. Корни, факториалы, периодические дроби, другие математические функции недопустимы.
(b) То же условие, только можно использовать корни.


РЕШЕНИЯ


ГЛАВА 1. ОЗОРНЫЕ ГОЛОВОЛОМКИ
1. 	Загадочное слово
В словах «это слово» 8 букв, в слове «иногда» — 6, в слове «чаще»—4 буквы, а в слове «постоянно» — целых 9.
Еще одно решение — «тетрадка». В ней может быть записано сколько угодно букв, и это 8-буквенное слово.
2. 	Тайна зарплаты
Вот одно из решений. Первый товарищ выбирает случайное число, прибавляет его к своей зарплате, записывает сумму на листке бумаги и передает этот листок второму товарищу. Тот прибавляет свою зарплату к числу, которое видит, записывает результат на другом листке бумаги и передает третьему. То же делают остальные товарищи; пятый передает листок бумаги первому. Тот вычитает из записанного числа случайное, которое прибавлял в самом начале, делит разность на пять и сообщает результат всем остальным — это и есть их средняя зарплата. Чтобы сохранить сведения о зарплатах в тайне, все листки бумаги надо уничтожить, а все пятеро товарищей не должны рассказывать другим, какие числа были записаны.
3. 	Родственники
(a) Человек указывает на своего племянника.
(b) Алексей — мой прадед.
(c) Мы с адвокатом женщины; я ее свекровь, а она моя невестка.


6. Демографический взрыв
4. 	Фишки в коробке
Передвинь фишку 1 в нижний левый угол. Передвинь фишку Т вправо. Передвинь фишку 2 в верхний левый угол, а фишку 3 — ниже ее. Теперь передвинь фишку Т в нижний правый угол (рис. 33).
Рис. 33
5. Мощная подача
Из условия 1 миля = 1,6 км получаем скорость мяча
266,6 км/ч = 166,6 миль/ч.
6. Демографический взрыв
(a) Площадь поверхности Земли равна А = 4nR2, где R = 6371 км — радиус Земли. Объем V слоя толщины Т выражается формулой V = АТ. По условию Vо = 0,4599 км3, поэтому
Т0 = = 9,0165 х 10~4 мм.
4ttR
(b) Зависимость объема, занимаемого населением, от времени выражается формулой V(t) = Vo х 1,0114^, где время t измеряют в годах. Приравняв это выражение к 4nR2T, где Т — это 1 метр, мы получим
v(t) = ^ км3 = Vo х 1,0114',


Решения
откуда
1п(1,0114)
= 1227,91 лет.
В этот момент население достигнет 8,0963 квадриллионов1.
(с) 	При V(t) = Vо х 1,0114^ = I х nr3 мы получаем
= 9,4605284 х 1012 км/год.
Отсюда находим t = 9578,65 лет. К этому моменту население составит 1,0436 х 1048 человек, а радиус — 2,5038 х 1015 км = 264,6575 световых лет.
7. 	Цепная линия
Условиям задачи удовлетворяет только одно значение d - 0.
r(t) = (о,75 х 0^99у/3 х l,0114f/3.
Тогда
dr{t)
dt
^0,75 х 0^99 J/3 х (in i Д)Ц4) х Ь!
1,0114f/3 3
1 Квадриллион — число, которое записывается единицей с 15 ну¬
лями.— Прим. перев.


ГЛАВА 2. ГЕОМЕТРИЧЕСКИЕ ГОЛОВОЛОМКИ
8. 	Геологоразведка на Ригеле
(а) 	Лагерь А может отстоять на одно из бесконечного множества расстояний от Северного полюса, каждое из которых меньше 1 мили. Геолог А при этом отправляется на север и минует полюс. Это позволяет ему на третьем участке маршрута тоже двигаться на север и вернуться на исходную широту. Большая окружность на рис. 34 — это окружность радиусом в 1 милю с центром на Северном полюсе. Геолог А отправляется из точки А по маршруту ABCDA. Вначале его отделяет от полюса расстояние AN = s. Длина каждой из дуг АВ, ВС, CD и DAD ...к...D А должна быть равна 1 миле; здесь DAD ...к... DA обозначает маршрут с началом в D в направлении на запад; этот маршрут обходит вокруг Северного полюса к раз и приходит в А. Чтобы такой маршрут существовал, длина s
к
Sk
1 — sk
0
0,5
0,5
1
0,134435689
0,865564311
2
0,073284499
0,926715501
3
0,050245047
0,949754953
4
0,038208091
0,961791909
5
0,030818801
0,969181199
6
0,025822699
0,974177301
7
0,022219743
0,977780257
Рис. 34


Решения
должна удовлетворять соотношению
2пк = - , где R = 4000 миль.
Rsm(Rsin(l^)
Лагерь А должен находиться на расстоянии или
1 - Sk от полюса для некоторого к = 0,1,2, Первые
несколько значений s^ и 1 — sk приведены в таблице.
(Ь) 	Очевидно, геолог В мог стартовать из любой точки,
1
отстоящей на - мили к югу от экватора. Но
кроме того, лагерь В может отстоять на одно из бесконечного множества расстояний — чуть больше мили от Северного полюса или чуть меньше мили от Южного. У большого круга на рис. 35 радиус равен 1 миле, а центр расположен на Южном полюсе. Геолог В стартует в А и движется по маршруту ABCDA. Обозначим через г расстояние от лагеря В до Южного полюса. Длины дуг АВ, ВС, CD и DAD.. .к.. .DA равны по 1 миле; здесь DAD ...к... DA означает маршрут с началом в D в направлении на запад, который обходит вокруг Южного полюса к раз и заканчивается в точке А.
к
Гк
1 + гк
1
0,139652205
1,139652205
2
0,074088383
1,074088383
3
0,050501269
1,050501269
4
0,038320291
1,038320291
5
0,030877565
1,030877565
6
0,025857228
1,025857228
7
0,022241726
1,022241726
8
0,019513588
1,019513588
Рис. 35


8. Геологоразведка на Ригеле 73
Эти условия дают следующее условие на г:
2як - , где R = 4000 миль.
Rsin(£) R sin (1^Г)
Лагерь В может располагаться от Южного полюса
на расстоянии г^ для любого к = 1,2, Кроме того,
лагерь В может находится на расстоянии 1 + от Северного полюса. Это видно по рис. 35, если считать, что на нем изображен Северный полюс и маршрут CD ABC. Первые несколько значений и 1 + в милях приведены в таблице.
(с) 	На рис. 36 изображена ситуация для геолога С.
В центре — Северный полюс. Геолог стартует из точки
А на расстоянии 1 + г от Северного полюса и идет
одну милю до точки В. Затем он идет одну милю на
1
восток, перемещаясь на долготу АЛс - Rcos^—у гАе
(рв = | ^ — широта, на которой лежат точки В и С.
Затем он продвигается одну милю на юг до точки D и, наконец, одну милю до Е; при этом долгота
меняется на АЛ = ———-, где wd = — широта,
К cos (<ре)) 2. 1<
на которой лежат точки A, D и Е. Поэтому точка
Е лежит на долготе Ле = Лс — АЛ- Расстояние от А
до Е равно 2R arcsin sin cos^sj • Это расстояние
максимально, когда лагерь геолога С находится на расстоянии 1 +г = 1,2712313... миль от Северного
Рис. 36


Решения
полюса. Это максимальное расстояние между точками А и Е составляет 2,523974... миль.
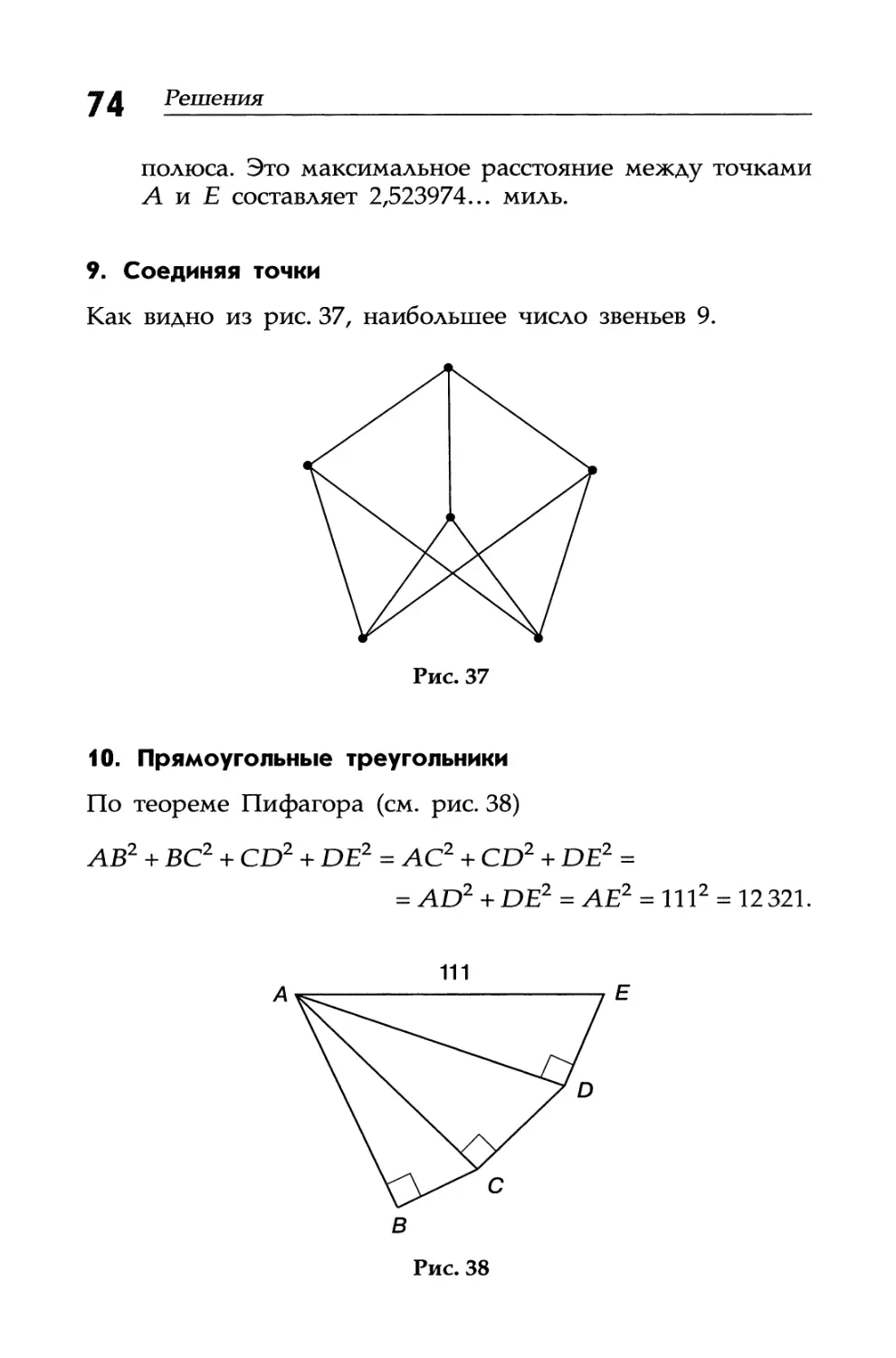
9. 	Соединяя точки
Как видно из рис. 37, наибольшее число звеньев 9.
10. 	Прямоугольные треугольники
По теореме Пифагора (см. рис. 38)
АВ2 + ВС2 + CD2 + DE2 = АС2 + CD2 + DE2 =
= AD2 + DE2 = АЕ2 = U12 = 12321.
111
В
Рис. 38


11. Усеченный многогранник
11. 	Усеченный многогранник
Когда у многогранника Mi с Г1 гранями, Bi вершинами и Pi ребрами отсекают все вершины, то получается многогранник М2, у которого Г2 = Г1+В1 граней. В каждой вершине многогранника Мг сходятся по 3 ребра, откуда
оТЭ
мы получаем соотношение Рг = Запишем для второго многогранника формулу Эйлера:
Р2 = Г2 + В2 — 2.
Отсюда следует, что
(Г2,В2,Р2) = (Г1+В1,2Р1,ЗР1).
(a) (i) Для треугольной призмы с тремя четырехуголь¬
ными гранями и двумя треугольными
(Г1,В1,Р1) = (5,6,9).
Если отрезать от нее все вершины, то получится новый многогранник, для него
(Г2,В2,Р2) = (11,18,27).
(ii) 	Для бипирамиды с 6 треугольными гранями (ri,Bi,Pi) = (6,5,9). Если отрезать от нее все вершины, то получится новый многогранник, для него (Г2,В2,Р2) = (11,18,27).
Исходные многогранники в случаях (i) и (И) двойственны друг другу.
(b) (i) Рассмотрим четырехугольник, к каждому ребру
которого примыкает по треугольной грани. Добавим к этой конструкции еще две треугольные грани, чтобы собрать ее воедино. Для такого многогранника
(ri,Bi,Pi) = (7,6,11).
Если отрезать от него все вершины, то получится новый многогранник, для него
(Г2,В2,Р2) = (13,22,33).


Решения
(ii) Теперь возьмем две треугольные грани с общей вершиной, добавим к ним четыре четырехугольные грани. Получится многогранник, для которого
(ГъВъР,^ (6,7,11).
Если отрезать от него все вершины, то получится новый многогранник, для него
(Г2,В2,Р2) = (13,22,33).
Исходные многогранники в случаях (i) и (ii) двойственны друг другу.
(iii) К одной из боковых треугольных граней четырехугольной пирамиды пристроим приплюснутый тетраэдр. Получится многогранник, для которого
(IbBbPiH (7,6,11).
Если отрезать от него все вершины, то получится новый многогранник, для него
(Г2,В2,Р2) = (13,22,33).
(iv) К двум несоседним ребрам пятиугольного основания пристроим по четырехугольной грани так, чтобы у них было одно общее ребро над этим пятиугольным основанием. Оставшиеся три грани треугольные. Для этого многогранника
(Г!, Вг, Рг) = (6,7,11).
Если отрезать от него все вершины, то получится новый многогранник, для него
(Г2,В2,Р2) = (13,22,33).
Исходные многогранники в случаях (iii) и (iv) двойственны друг другу.
12. 	Красивые коробочки
(а) 	У Ани коробочка с ребрами 5, 21 и 210, ее объем 22 050, недостающая грань коробочки имеет размеры


13. Почти прямоугольное озеро
5 х 21. У Ирины коробочка с ребрами 12, 12 и 6, объемом 864. Размеры недостающей грани —12 х 12.
(b) У Бори коробочка с ребрами 3, 6 и 12, ее объем 216. Недостающая грань — размера 3 х 12. У Катиной коробочки ребра 3, 6 и 6, объем 108. Размеры недостающей грани — 6x6.
(c) У Веры коробочка с ребрами 5, 36 и 45, объемом 8100. Лешина коробочка имеет ребра 10, 12 и 15 и объем 1800.
(d) У Гриши ребра коробочки равны 3, 8 и 24, ее объем 576. У Мишиной коробочки ребра 4, 6 и 12, объем 288.
13. 	Почти прямоугольное озеро
На рис. 39, слева, выделены пять областей озера:
R-i = EFGM, R2 = BCDM,
Bi = АЕМ, В2 = ADM и В3 = DEM.
Как видно из рис. 39, справа,
А\ = DEFG = Ri + Вз, А2 = BCDE = R2 + Вз и A3 — ADE — В\ + В2 + Вз.
Заметим, что
Bi = Ri/2 и В2 = R2/2.
Е
Е
D
А
В
С
А
В
С
Рис. 39


78
Решения
Таким образом,
л — п i^l+ ^2 _ ^1 + Дз _i ^2 + + А2
А3-Б3 + 2 2 + “г 2 •
А это и значит, что Аз = Ал *Аг, как бы ни выглядел берег между точками D и £.
14. 	Растроенный ромб
Шесть решений приведены на рис. 40.
корень уравнения х3-х2 + 2х-1 =0
1
2
1
2
Рис. 40


15. Разрезание квадрата
15. 	Разрезание квадрата
Наименьшее известное количество прямоугольников —12, они расположены в квадрате 96 х 96 так, как показано на рис. 41. Размер самого маленького прямоугольника — 1 х 3.
13x39
19x57
7x21 6x18
8x24 %
18x54
ю
X
ю
т—
9x27
27x81
32x96
Рис. 41


ГЛАВА 3. ЦИФРОВЫЕ ГОЛОВОЛОМКИ
16. Всецифровые подарки
Подарков было 5, вместе они стоили 1 + 9 + 25 + 36 + 784 = = 855 долларов.
17. Вариант судоку
Решение приведено на рис. 42.
1 I
3
5 I
4
2
5
1
4 I
2'
3
3
5
к
2
1
4
2
4
1
3
Т
4
2
3!
I*'
1
Рис. 42
18. 	Всецифровые суммы
(а)
(i)
f +
589
4123
1.
(H)
27
39
+ «- 156
= 1.
(iii)
57
864 _ ' 912
- 1.
(Ь)
(i)
7835 _ 9402
1.
(ii)
35 148 _
38
145 _
138 _
— +
135
= 1.
70
296
76
290
90
276
96
270
6
792 .
_ _4
- +
792
= 1.
534
801 "
356
801
(с)
(i)
i +
916
2748
2.
(ii)
36
24
158
= 2.
(iii)
h*
584 _ ‘ 296
= 2.
(d)
(i)
h
8930 _ 6251
2.
(ii)
45
39
176
208
= 2.
(iii)
1
238
950
476
= 2.


21. Десятизначное число
19. Чет и нечет
Это невозможно. Число m нечетно, его остаток при делении на 9 равен 7, а число п четно, и его остаток при делении на 9 равен 2. Цифровым корнем называют остаток при делении числа на 9. Это означает, что если и = km, то к = 8, но наименьшее возможное число т, умноженное на 8, даст шесть цифр.
20. Странная целостность
Это должны быть цифры 2 и 3. Тогда Е\= _о'\/0^3 = 411,52; ближайшее целое число — 412;
Е2= -°'У02 = 213,75; ближайшее целое число — 214.
21. Десятизначное число
(a) Мое число 9 876 351 240.
(b) Мое число 9123 567480.


ГЛАВА 4. ЛОГИЧЕСКИЕ ГОЛОВОЛОМКИ
22. 	Дележ пирога
(a) Ася делит пирог на две части размерами х и 1 - х,
1 2
где х ^ -. Если х > -, то Вася делит больший кусок
1 2 пополам и получает больше i пирога. Если х < |,
то Вася делит меньшую часть на части размером О
и 1 - х и все равно получает больше 1 пирога. Поэто-
2 1
му Ася делит пирог на части размерами - и -, этим
гу <3 Э
обеспечивая себе - пирога.
(b) Ася делит пирог на две части размерами х и 1 - х, где х ^ j. Васе следует делить пополам меньший кусок,
1 — X 1 4- X
тогда Асе достанется кусок размером х+ = 2
Поэтому ей нужно с самого начала делить пирог на две равные части, одну из них разделит пополам Вася,
о
оставляя Асе ^ пирога.
(c) Ася может разрезать пирог на две части размером s и 1 — s, где s < Далее возможны четыре ситуации. Наибольшая часть пирога, которую Ася сможет получить, равна
-1
1. 	При s < - Вася разрезает больший кусок пополам,
1 — S
так что получаются три куска размерами s, —^ и Затем после разреза, сделанного Асей, полу¬
чаются куски размерами s, 1 ~s, 1 ~s и 1 ~s. Ася
берет себе два куска общим размером При
1 ч
s = ^ эта часть максимальна и равна


23. Побег из темницы 83
2. При 1 <5< 1 Вася разрезает больший кусок пополам, так что получаются три куска размерами s,
и ^ 2 S' Затем после разреза, сделанного Асей,
получаются куски размерами 1 ~ s, 1 ~ s, s и ^ ~s.
Ася берет себе два куска общим размером --^7
1 3
При s = - эта часть максимальна и равна
3. При - < s < ^ Вася разрезает больший кусок пополам, так что получаются три куска размерами s,
и Затем после разреза, сделанного Асей,
получаются куски размерами —^s-, - ~-s и s.
Ася берет себе два куска общим размером При s = эта часть максимальна и равна j.
4. При ^ ^ s ^ ^ после Васиного разрезания получаются три куска размерами s, е и 1 — s — е, где е— сколь угодно малое число. Ася разрезает средний по размеру кусок и берет себе два куска общим
О
размером 1 - s. При s = j эта часть максимальна 4
и равна -.
23. 	Побег из темницы
Рыцарь разбивает большой прямоугольник десятью прямоугольниками размером 3x4 так, как показано на рис. 43.
Рис. 43


Решения
При этом два прямоугольника перекрывают центральную клетку дважды. Рыцарь решает открыть эту клетку и узнать, какое число в ней записано. Если это, например, 4, рыцарь сразу же находит общую сумму: 2016 = 10 х 202 - 4.
24. 	Логика и геометрия
В треугольнике ЛВС угол при вершине С равен 30° (рис. 44), поэтому радиус его описанной окружности равен „ . = s. А значит, ответ на логический вопрос
2 sin 30° к
должен быть таким: «s и есть радиус окружности».
25. 	Али Баба и 10 разбойников
Чтобы отряду переправиться через реку, достаточно пересечь ее на лодке 33 раза. Вместе с Али Бабой в отряде 11 человек: А, А, Б, В, Г, Д, Е, Ж, 3, И, К. Решение представлено в таблице. В общем случае, если разбойников п, потребуется пересекать реку в лодке 4и - 7 раз.
С
Рис. 44


25. Али Баба и 10 разбойников
Ход
Кто в лодке
Кто на ближнем берегу
Кто на дальнем берегу
Старт
Никого
Все
Никого
1
ААБ
ВГДЕЖЗИК
ААБ
2
АБ
АБВГДЕЖЗИК
А
3
БВ
АГДЕЖЗИК
АБВ
4
АБ
А АБГДЕЖЗИК
В
5
ААБ
ГДЕЖЗИК
ААБВ
6
БВ
БВГДЕЖЗИК
АА
7
ВГ
БДЕЖЗИК
ААВГ
8
АА
ААБ ДЕЖЗИК
ВГ
9
ААБ
ДЕЖЗИК
ААБВГ
10
БВ
БВДЕЖЗИК
ААГ
И
ДЕ
БВЖЗИК
ААГДЕ
12
АА
ААБВЖЗИК
ГДЕ
13
ААБ
ВЖЗИК
ААБГДЕ
14
АБ
АБВЖЗИК
АГДЕ
15
БВ
АЖЗИК
АБВГДЕ
16
АБ
ААБЖЗИК
ВГДЕ
17
ААБ
ЖЗИК
А АБВГДЕ
18
БВ
БВЖЗИК
ААГДЕ
19
ЖЗ
ВИК
ААГДЕЖЗ
20
АА
ААБВИК
ГДЕЖЗ
21
ААБ
ВИК
ААБГДЕЖЗ
22
АБ
АБВИК
АГДЕЖЗ
23
БВ
АИК
АБВГДЕЖЗ
24
АБ
ААБИК
ВГДЕЖЗ
25
ААБ
ИК
А АБВГДЕЖЗ
26
БВ
БВИК
ААГДЕЖЗ
27
ИК
БВ
ААГДЕЖЗИК
28
АА
ААБВ
ГДЕЖЗИК
29
ААБ
В
А АБГДЕЖЗИК
30
АБ
АБВ
АГДЕЖЗИК
31
БВ
А
АБВГДЕЖЗИК
32
АБ
ААБ
ВГДЕЖЗИК
33
ААБ
Никого
Все


86 Решения
26. 	Головоломки на годовщину свадьбы
(a) Возрасты детей — 4, 4 и 9; сумма 17, а произведение 144. Смиты дали неверный ответ (3,6,8). Год назад детям было (3,3,8), а Джонсы дали ответ (2,6,6).
(b) Возрасты детей — 6, 6 и 28; сумма 40, а произведение 1008. Смиты дали неверный ответ (3,16,21). Год назад детям было (5,5,27), а Джонсы дали ответ (3,9,25). Три года назад детям было (3,3,25), Брауны же дали ответ
(1.15.15).
(c) Возрасты детей — 6, 8 и 25; сумма 39, а произведение 1200. Смиты дали неверный ответ (4,15,20), и Джонсы дали неверный ответ (5,10,24). Четыре года назад детям было (2,4,21), а Брауны сказали, что (1,12,14).
(d) Возрасты детей — 9, 10 и 28; сумма 47, а произведение 2520. Смиты дали неверный ответ (6,20,21). Четыре года назад детям было (5,6,24), а Джонсы сказали, что (3,12,20). Семь лет назад возрасты детей были (2,3,21), а Брауны предположили, что (1,7,18).
(e) Возрасты детей —10, 12 и 21; сумма 43, а произведение 2520. Смиты дали неверный ответ (9,14,20). Пять лет назад детям было (5,7,16), а Джонсы сказали, что (4,10,14). Шесть лет назад возрасты детей были
(4.6.15), а Брауны предположили, что (3,10,12).
(f) Возрасты детей —12, 12 и 20; сумма 44, а произведение 2880. Смиты дали неверный ответ (10,16,18). Два года назад детям было (10,10,18), а Джонсы сказали, что (8,15,15). Десять лет назад возрасты детей были (2,2,10), а Брауны предположили, что (1,5,8).
(g) Возрасты детей —18, 10 и 27; сумма 45, а произведение 2160. Смиты дали неверный ответ (6,15,24). Два года назад детям было (6,8,25), а Джонсы сказали, что (4,15,20). Шесть лет назад возрасты детей были (2,4,21), а Брауны предположили, что (1,12,14).
(h) Возрасты детей —10, Ии 24; сумма 45, а произведение 2640. Смиты дали неверный ответ (8,15,22). Четыре года назад детям было (6,7,20), а Джонсы, сказали, что (4,14,15). Восемь лет назад возрасты детей были
(2.3.16), а Брауны предположили, что (1,8,12).


26. Головоломки на годовщину свадьбы
(i) 	Возрасты детей — 6, 8 и 22; сумма 36, а сумма кубов 11 376. Смиты дали неверный ответ (1,15,20). Год назад детям было (5,7,21), а Джонсы сказали, что (1,12,20).
(j) Возрасты детей — 9, 9 и 19; сумма 37, а сумма кубов 8317. Смиты дали неверный ответ (5,16,16). Два года
назад детям было (7,7,17), а Джонсы сказали, что
(3.13.15).
(к) Возрасты детей — 9, 12 и 21; сумма 42, а сумма кубов 11 718. Смиты дали неверный ответ (7,15,20). Три года
назад детям было (6,9,18), а Джонсы сказали, что
(3.15.15).
(1) 	Возрасты детей —13, 13 и 23; сумма 49, а сумма кубов 16 561. Смиты дали неверный ответ (10,17,22). Четыре года назад детям было (9,9,19), а Джонсы сказали, что
(5.16.16).
(ш) Возрасты детей —11, 19 и 25; сумма 55, а сумма кубов 23 815. Смиты дали неверный ответ (10,22,23). Девять лет назад детям было (2,10,16), а Джонсы сказали, что
(1,12,15).


ГЛАВА 5. ГОЛОВОЛОМНЫЕ ВЕРОЯТНОСТИ
27. Сюрприз для игрока
Каждый раз, когда ты выигрываешь, твой капитал увеличивается в 1,9 раз; а когда ты проигрываешь, у тебя остается 0,1 имевшихся денег.
(a) В конце у тебя станет
10 ООО х 1,975 х ОД25 = 0,80634 рубля.
(b) В конце у тебя станет
10 000 X 1,980 X 0,120 = 1 996 586,25 рубля.
28. Игра Тензи
Введем обозначения р = - и q = Вероятность того, что
при подбрасывании га костей на i из них выпадет целевое число, равна Pi = plqm~l х • Обозначим через Ет
ожидаемое количество бросков, необходимых, чтобы закончить игру при имеющихся га костях, на которых еще не выпало целевое число. Тогда
Ет — Р 0-Em + Р1 -Em—1 + • • • + Р га—1 El + 1 •
Отсюда мы находим
г г 96. г 10 566. г 728 256.
1 = 6' £2 = ТГ' £з = “ТШГ' U = "бТббГ'
и так далее до
Ею = 98 081 х 336 640 049 х
х 20 818 956 233 =
2 х З8 х 7 х И х 13 х 17 х 29 х 31 х 61 х ИЗ х 4651 х 6959
= 15,348 482 385 928 2....


29. Маленькое бинго 89
29. 	Маленькое бинго
(a) После четвертого выписанного числа обязательно выиграет хотя бы одна карточка. В наихудшем варианте среди первых трех чисел одно может оказаться в столбце N, а два других — в одном из столбцов В или G. Остальные варианты расположения трех чисел приносят какой-либо карточке выигрыш.
(b) В таблице разбирается более общий случай, когда в столбец В попадают числа от 1 до fc, в столбец N — числа от k +1 до 2к, а в столбец G — от 2к +1 до 3к. Добавим в таблицу вероятности: вероятность того, что выиграет строка, равна
р 2к(7к~3)
строка (9fc — 3)(3fc — 2)'
а вероятность того, что выиграет столбец, равна р 13к2 -21к + 6
столбец (9fc _ 3)(3fc _ 2) •
Для к = 6 получаем
Рстрока = 2Q4 = 0/57353..., а Рстолбец = 204 = 0,42647....
Первые два числа
Вероятность
Кто выигрывает
ВВ или GG
2(к -1) 9к — 3
Пока никто
BN или NB
2 к 9к — 3
Пока никто
BG или GB
2к 9к — 3
Выигрывает
строка
NN
к — \ 9к-3
Выигрывает
столбец
NG или GN
2 к 9к — 3
Пока никто


Решения
Продолжение
Третье число
Вероятность
Кто выигрывает
ВВВ или GGG
2(к — 1)(к — 2) (9к - 3)(3к - 2)
Выигрывает
столбец
BBN, BNB, NGG
6к(к — 1)
(9/с - 3)(3к - 2)
Пока никто
BBG или GGB
2к(к-\)
(9к - 3)(3к - 2)
Выигрывает
строка
BNN, NBN, GNN, NGN
4к(к — 1)
(9к - 3)(3к - 2)
Выигрывает
столбец
BNG, NBG, NGB, GNB
4/с2
(9к - 3)(3к - 2)
Выигрывает
строка
Четвертое
число
Вероятность
Кто выигрывает
BBNB, BNBB, GGNG
6/с (/с — 1) (/с — 2)
(9/с - 3)(3к - 2)(3/с - 3)
Выигрывает
столбец
BBNN, BNBN, GGNN
6/с (к — I)2 (9к - 3)(3к - 2)(3/с - 3)
Выигрывает
столбец
BBNG, BNBG, GGNB
6/с2 (к -1)
(9/с - 3)(3к - 2)(3/с - 3)
Выигрывает
строка
30. 	Обычное бинго
(a) После 16-го выписанного числа победитель определится обязательно. Распределение по столбцам первых пятнадцати чисел может оказаться таким: BBBBIIIINNNGGGG, что никого не приводит к победе, но после шестнадцатого числа обязательно найдется выигрышная карта.
(b) Полный анализ обычного бинго включает слишком много вариантов распределения чисел, чтобы его можно было включить сюда. Результат получается таким:
Рстрока = 0,737 342 369 505...,
^столбец = 0,252 657 630 494...


32. Золотой сет в теннисе
— поразительная разница! Как и для маленького бинго, вероятности Рсгрока и Рстолбец были вычислены для различных к, когда в наборе 5к чисел, в столбец В попадают числа от 1 до к, в столбец I — числа от к +1 до 2к и так далее. В общем случае получается такая формула:
Р строка =
67,2fc3^^,
где
Р (к) = 2427619к9 - 40134 267/с8+288 988 538fc7 -1186 569 792к6+ +3 051795 783к5 - 5 076 742 911к4+5 428997 681/с3- -3565395258fc2+l 284537834А:-187687500,
Q(fc) = (5к -1)(5к - 2)(5к - 3)(5к - 4)(5к - 6)(5к - 7)(5к - 8) х х (5к - 9)(5к -11)(5к -12)(5/с - 13)(5fc -14).
При к = 15 точное значение Рстрока равно р _ 924 632476 308 625
i С
строка 1 254 006 977 693 g44 •
31. Честная дуэль
Обозначим вероятность того, что Браун попадет в Смита в результате одного выстрела, буквой р, а вероятность того, что Смит победит в дуэли, обозначим S. Эта вероятность удовлетворяет соотношению S = 0,4 + 0,6(1 — p)S. Положим согласно условию справедливой дуэли, S = 0,5, тогда
получим р = - — вероятность того, что Браун попадет
в Смита в результате одного выстрела.
32. Золотой сет в теннисе
Чтобы сет оказался золотым, один из игроков должен выиграть подряд первые 24 очка. Вероятность . такого
события равна р = - 1,192092896... х 10-7.
(а) 	Половина женских матчей, которые играются по условиям задачи, будет состоять из двух сетов, а половина — из трех. Вероятность того, что не будет ни одного золотого сета в двухсетовом матче, равна (1 - р)2, а тогда вероятность золотого


Решения
сета в двухсетовом матче равна Р2 = 2р — р2. Вероятность того, что не будет ни одного золотого сета в трехсетовом матче, равна (1 - р)3, а тогда вероятность золотого сета в трехсетовом матче равна Рз = Зр - 3р2 + р3. Поэтому вероятность золотого сета в женском матче равна
Рж = р2 + рз = Ц--2р2 + ^-& 2,980 232 х 10“7.
1
(Ь) 	Когда мужчины играют по условиям задачи, то - всех
о
матчей проходит в 3 сета, матчей — в 4 сета и еще
о
о
|—в 5. Вероятность того, что в трех сетах не будет
О
ни одного золотого, равна (1 — р) , а вероятность того, что хотя бы один сет будет золотым, равна
Рз = Зр - Зр2 + р3.
Вероятность того, что в четырех сетах не будет ни одного золотого, равна (1 — р)4, а вероятность того, что один сет из четырех будет золотым, равна
Р4 ~4р- 6р2 + 4р3 - р4.
Вероятность того, что в пяти сетах не будет ни одного золотого, равна (1 — р)5, а вероятность того, что хотя бы один сет из пяти будет золотым, равна
Р5 = 5р - Юр2 + Юр3 - 5р4 + р5.
Поэтому вероятность золотого сета в мужском матче равна
Р _ 2Р3 + ЗР4 + ЗР5 _ ЗЗр 27р2 11 р3 9р4 Зр5 _ м 8 8 4 2 4 8 ~
« 4,917 383 х 10-7.
33. 	Рулетка на автобус
(а) 	Лучше всего поставить два доллара на то, что с равными шансами выиграет или проиграет (скажем, на


34. Цветные шарики
г ПЯТЬ ЧИСЕЛ (1,2,3,0,00) выигрыш 6 к 1 г ДВА ПОПЕРЕЧНЫХ РЯДА (шесть чисел) выигрыш 5 к 1 Г ЧИСЛО (одно число) выигрыш 35 к 1
г ДВА ЧИСЛА (два соседних числа) выигрыш 17 к 1
г- ПОПЕРЕЧНЫЙ РЯД (три числа в ряд) выигрыш 11 к 1
КОЛОНКА (12 чисел в колонке) выигрыш 2 к 1
J
— ДЮЖИНА (12 чисел в одной из них) выигрыш 2 к 1
/ 1—I—|—1
L КРАСНОЕ/ЧЕРНОЕ, ЧЕТ/НЕЧЕТ, БОЛЬШЕ/МЕНЬШЕ (18 чисел)
выигрыш 1 к 1 — УГОЛ (четыре числа с общим углом) выигрыш 8 к 1
Рис. 45
черное или на четное; рис. 45). При этом вероятность успеха равна Р = || = 0,473684...
(Ь) 	Лучше всего поставить любую комбинацию перекрывающихся чисел, эквивалентную одному доллару, на первую треть (см. рис. 45); а второй доллар поставить на верхнюю половину. После этого тебе повезет
12 20 с вероятностью —, с вероятностью — ты проиграешь;
и твои ставки сократятся с вероятностью Таким образом,
Р=1 *ШР' откуда Р = 1 = 0,375.
34. 	Цветные шарики
(а) 	Мы выведем общую формулу для е\ — ожидаемого числа шариков в коробке в конце эксперимента. Пусть вначале в коробке было щ белых шариков и п2 черных. Представь себе, что все вынутые шарики


Решения
выложили слева направо в линию в том порядке, в котором вынимали. Вероятность того, что какой-то фиксированный белый шарик в конце эксперимента окажется в коробке, равна вероятности того, что в линии все черные шарики лежат левее его. Эта
вероятность равна —это тот вклад, который
фиксированный шарик дает в е\. То же относится к любому другому белому шарику, поэтому вклад всех
белых шариков в е\ составляет ^ ^. Аналогичные
рассуждения годятся и для черных шариков, откуда
и получаем е\ = П1 , н—
J п2 + \ щ +1
(Ь) 	Мы выведем общую формулу для е\ — ожидаемого числа шариков в коробке в конце эксперимента. Пусть вначале в коробке было щ красных шариков, п2 белых шариков и Пз синих. Представь себе, что все вынутые шарики выложили слева направо в линию в том порядке, в котором вынимали. Вероятность того, что какой-то фиксированный красный шарик в конце эксперимента окажется в коробке, равна вероятности того, что в линии все белые и синие шарики лежат левее его. Эта вероятность равна
п +п —это тот вклад, который фиксированный
красный шарик дает в с\. То же самое относится к любому другому красному шарику, поэтому вклад
всех красных шариков в е\ составляет n + f~
Аналогичные рассуждения годятся и для белых, и для синих шариков, откуда и получаем
ел = + 52 + Ш .
П2 + Пз + 1 Щ + Пз + 1 Щ + П2 + 1
Перебором можно убедиться, что
(щ, п2, пз, е\) = (172,597,17 677,23)
— набор наименьших чисел таких, что е\ — целое число, а п\,п2,пз попарно взаимно просты.


35. Игра «Бродилка»
(с) 	Мы выведем общую формулу для е2— ожидаемого
числа шариков в коробке в конце эксперимента. Пусть
вначале в коробке было щ красных шариков, п2
белых шариков и пз синих. Представь себе, что все
вынутые шарики выложили слева направо в линию
в том порядке, в котором вынимали. Вероятность
того, что какой-то фиксированный красный шарик
в конце эксперимента окажется в коробке, равна
вероятности того, что в линии либо все белые, либо
все синие шарики лежат левее его. Эта вероятность
111 равна -н это тот вклад, который
г П2 + 1 П3 + 1 П2 + Из + 1 г
фиксированный красный шарик дает в е2. То же относится к любому другому красному шарику,
поэтому вклад всех красных шариков в с? составляет
Wl , + ni ——Аналогичные рассуждения
п2 +1 п3 +1 п2 + п3 +1 Г J
годятся и для белых, и для синих шариков, откуда и получаем
е2 = -В + -Jh т + - »2 ,,, +
7^2 + 1 Пз + 1 7^2 ^ ^1 1
+ ^2 ^2 + П3 + _Jl3 П3
Пз + 1 П1 + Пз + 1 7ti + 1 П2 + 1 Hi + П2 + 1 ’
Перебором можно найти, что
(П1,и2,и3,е2) = (4,9,25,8)
— единственный набор чисел таких, что е2 — целое число.
35. 	Игра «Бродилка»
Ожидаемое число ходов 6ЛЛ + 10. Рассмотрим более общую задачу: вместо обычного кубика бросают кость, в которой N равновероятных граней, а число М гораздо больше N. Для каждого к = 0,1,2,... ,N — 1 обозначим через вероятность того, что игра закончится на клетке с номером М + к. Вероятность попасть на любую клетку с номером


Решения
у
меньше М очень близка к —Вероятность перехода с некоторой клетки, предшествующей М, на клетку с номером М+к равна ^. Тогда Рк — это произведение этих двух вероятностей:
р _ 2 (N-k) к N(N + 1) ‘
Сумма всех кРк по к от 1 до N равна математическому ожиданию числа клеток, которые будут пройдены после М-й клетки до конца игры. Обозначим эту сумму буквой S, тогда
N(N + l)f = NS\ — S2,
где Si—сумма всех к от 1 до N, a S2 — сумма всех к2 по А: от 1 до N. При этом
КТС с _N2(N +1) (2N+ 1)N(N+ -1) _ N(N + 1)(N-1)
- Ь2 j 6 6 '
откуда S = N ~ 1.
Ожидаемое число клеток, пройденных в игре, равно М + S, а ожидаемое число ходов в одной игре равно
2(M + S) _ 2М 2(N — 1)
N +1 N +1 3 (N + 1)'
В частном случае, который относится к нашей задаче,
N = 6, а среднее число ходов за игру равно + 1^.
В 21 игре тогда ожидаемое число ходов равно 6М + 10.


ГЛАВА 6. АНАЛИТИЧЕСКИЕ ГОЛОВОЛОМКИ
36. Спешка в аэропорту
Лучше завязывать шнурки на траволаторе. Если ты сделаешь это на земле, то в течение минуты, которая на это потребуется, никуда не продвинешься. А на траволаторе за ту же минуту преодолеешь некоторое расстояние. Это станет еще понятнее, если ты сравнишь два случая: завязывать шнурки за шаг до траволатора или только что на него ступив.
37. Что это было?
Кевин обедал. Условия задачи выполняются только если часовая стрелка указывает на 11-е деление, а минутная — на 12-е. При этом часы показывают 2 часа 12 минут дня или ночи. Нормальные люди по ночам спят, так что в 2 часа 12 минут дня Кевин обедал.
38. Мышиные бега
На рис. 46 показан один из способов изобразить тетраэдр.
Рис. 46


Решения
Шустрая кошка может бегать по «квадрату» чуть быстрее мышки. Две другие кошки будут бегать туда-сюда по двум оставшимся ребрам вдвое медленнее шустрой кошки, прибегая в вершины тетраэдра одновременно с ней. Мышке некуда будет деваться — кошки обязательно ее поймают.
39. 	Навещаем родственников
На рис. 47 изображена схема движения братьев в общем виде. Варфоломей отправляется в путь пешком со скоростью v\. Авдей везет Бармалея до точки В со скоростью V3, ссаживает его, и тот продолжает путь на дачу со скоростью v2. Тем временем Авдей возвращается в точку С со скоростью V4, сажает к себе на велосипед Варфоломея, и оба они отправляются на дачу к дедушке, прибывая туда одновременно с Бармалеем.
По рисунку мы видим, что
V\t2 = У\)
v3h = уг) vz (h — h) - Уз — Vi)
V3 (h — h) - Уз — l/i;
V4(t2~t\) = У2 -1/1-
Рис. 47


41. Многочлены—1
Исключая из этих уравнений у\, у2, t\ и мы получим расстояние до дедушкиной дачи:
h Н(у4 + ^1 + *>2) - ^2(2^3 + va)\
2/3 = — 5 ■
У 4(2^3 — <7i — f2) + Щ — U2
В нашем случае по условию
{V\, v2/ v3, V4, h) = (6, 9,30,40,3), значит, расстояние до дачи равно 50 км.
40. Логи и рифмы
По условию х = log16 7 х log49 625. Введем еще обозначения V = logie 7 и q = log49 625.
Тогда 16р = 7, поэтому
log10 7 = р log1016 = 4р log10 2.
Кроме того, 49q = 625, а значит,
<7l°g1049 = log10625.
Это соотношение можно упростить:
2q\og107 = 4logw5.
Из равенства log10 5 = 1— log10 2 получаем
1о§ю 2 = 1 +2р<7 = Т+2х'
41. Многочлены—1
Мы рассматриваем многочлены
Р (х, у) = оо + а\х + агу + азх2 + а$ху +
+ а^у1 + авх3 + а.7Х2у + а&ху2 + аду3.
Упростим это выражение, воспользовавшись тем, что в некоторых точках значение многочлена равно 0.
Из условия Р(0,0) = 0 получаем До = 0, из равенств Р (1,0) = Р (-1,0) = 0 выводим «з = 0, из Р (0,1) = Р (0, —1) = 0 выводим «5 = 0.


100 Решения
Выражение для многочленов упростилось, теперь Р (х, у) = а\х + а2у + а4ху + авх3 + а?х2у + а%ху2 + аду3.
Из условия Р(1,1) + Р(1,—1) = 0 выводим соотношение а\ + «6 + as = 0, из равенства Р (1,0) = 0 получаем а\ + ав = 0, откуда as = 0 и а\ = —ав.
Из Р (0, 1) = 0 ВЫВОДИМ Яг + Я9 = 0, ИЛИ Яд - —а2.
Из Р (1, -1) = 0 получаем а2 + а4 + а7 + ад = 0, а значит,
Uy = —U4.
Выражение для многочлена можно еще упростить:
Р (х,у) = а\{х- х3) + а2(у - у3) + а4{ху - х2у).
Теперь предположим, что Р(к,к) = 0 (в нашем случае к = 12):
Р(к,к) = ai(k- к3) +а2(к- к3) + а4 (к2 - к3) = 0.
Тогда а4 = — (к + (ai + а2) = г(а\ + а2).
1 + X
При а2 — 0 мы получаем уравнение у = а при
а\ = 0 — уравнение 1 — у2 - rx{ 1 - х). Подставим выражение для у из первого во второе и получим уравнение относительно х:
(r+±)^+(^-r)*+i-1=0.
j *i "j
Его решение х = ; а тогда у - ———.
г -г + 1 г - г + 1
Вернемся к параметру к:
х= f + 1 и у= + 2fc .
3fc + 3/с +1 ЗА:2 + ЗА: + 1
И наконец, при к = 12 имеем л: = и 1/ =
г 469 ■ 469
42. 	Многочлены—2
(а) 	Запишем уравнение в общем виде: ху+ах+Ъу+с = dx3, где а, Ъ, с и d — целые числа. Решим его относительно у:
у = dx2 - bdx + b2d — а + ~ ^ f ~ с •
^ X + о


43. Каскад простых пифагоровых троек 101
В нашей задаче последнее слагаемое равно ^ ■.
Чтобы оно было целым, число 1008 должно делиться на х + 5 нацело. У этого числа 30 положительных делителей, столько же отрицательных, поэтому всего получаем 60 целочисленных решений.
(b) Есть 7 решений, в которых и л: и у— простые числа: (х,у) = (2,7), (7,227), (31,6619), (-3,-113), (-19,3919), (-23,5407), (-89,67134) и (-173,246557).
(c) Есть 4 решения, в которых и х и у отрицательны: (х,у) = (-1,-5), (-2,-25), (-3,-113) и (-4,-521).
43. 	Каскад простых пифагоровых троек
Пусть хо, у о и xi—стороны прямоугольного треугольника (пифагорова тройка) (рис. 48). Известно самое общее выражение для такой тройки:
Xo = К(ш2 — п2), т/о = 2Kmn и Х\ = К (т2 + и2), где га и и — взаимно простые натуральные числа разной четности. По условию дго и х\ — простые числа, поэтому должны выполняться условия К = 1 и п - т - 1. Отсюда
« - х% + ] X? +1 Х% +1 Хо +1
x0 = 2m-l; xi = -^—; х2 = -^—; х3 = -^—; х4 = -^—и т.д.
(a) Первые несколько примеров каскадов трех пифагоровых троек получаются при значениях (т,хо) = = (136,271), (175,349), (1501,3001), (5050,10099),
(5860,11719),....
(b) Первые несколько примеров каскадов четырех пифагоровых троек получаются при значениях
*о
Рис. 48


102 Решения
(т,х о) = (84 610,169 219), (685135,1 370 269), (2982 850,
5965 699), (7613940, 15227879), (8 875491,17 750981), (9 671 280,19 342559),....
44. 	Разведение несушек
7 ft
(a) Восемь кур из хозяйства Авдея снесут 7 х - яиц за |
7 7 /I 0/1С
дней, то есть их яйценоскость — - х - : ^ яйца от
о 6 5 2оо
курицы за день. Шесть кур из хозяйства Гордея сне- 7 8
сут 5 х - яиц за ^ дней, то есть их яйценоскость —
с 7 о ОДЪ
у х - : - = яйца от курицы за день. Значит, в обоих
6 6 7 2оо
хозяйствах куры несутся одинаково.
оде
(b) У Авдея 48 кур, в день они несут для него яиц.
Авдею придется ждать 6 дней, чтобы получить целое число яиц — 245.
(c) У Гордея 300 кур, в день они несут для него — яиц.
Гордею придется ждать 24 дня, чтобы получить целое число яиц — 6125.
45. 	Дилемма рыцаря
Рыцарю нужно обойти правильный многоугольник, в котором п сторон. Его площадь А = где s — длина
стороны, a h — расстояние от центра многоугольника до середины стороны
(рис. 49). При этом ^ = ctg Чтобы
обойти все п сторон многоугольника, потребуется ^ минут, а чтобы воткнуть колышки в его вершинах, потратив
на каждый к секунд, нужно минут. В сумме эти две
величины дают 24hr = 1440 минут, поэтому ^ = 1440 -


46. Наименее равносторонний треугольник 103
Чтобы добиться наибольшей площади, нужно фиксировать к, а затем подобрать значение и такое, что величина
(1440- ^)2 ° и 4п
максимальна. Например, для к = 10 получаем и = 31, а для Л: = 60 имеем п = 17. Перебрав другие значения А:, убеждаемся, что для к = 23 площадь максимальна при п = 23. Она равна А = 161982,4505г»2, это около 150 км2.
46. 	Наименее равносторонний треугольник
Выберем такой масштаб для рис. 50, слева, что АВ = 1. Тогда по теореме синусов для треугольника ABC имеем
ВС=^4шАС=
sin С sin С
По теореме синусов для треугольника ABC' имеем
_ АВ sin/? _ sin/? sin(or + /?) sin(ar + /?) *
По теореме синусов для треугольника А!ВС имеем
— ВС sin у _ sin Л sin у sin(/? + у) sin С sin(/? + у) *
По теореме синусов для треугольника АВ'С имеем
_ AC sin у _ sin Б sin у sin(ar + у) sin С sin (a + у) *
Отсюда получаем следующие выражения для координат точек А', В' и С':
Сх = AC' cos a = sinf cos«;
* sin (a + /?)
CV = AC sina=sinfsin<*;
у sin (a +0)
A!x = 1 — A'Bcos(B -/9 = 1- sinASinycos(B -^)
* v ^ sin С sin 03 + y)
А' = A'Bsin(B -/?) = sinAsinysin(B-/9
У v sin С sin (j8 + y)
Bi = AB' COS (A-a)= sinBsinycos(A-a) л 7 sin С sm (or + у)
В; = AB' sin (A - a) = sinBsinr sin(A-a)
У sinCsm(a-fy)


104 Решения
В
Численный анализ показывает, что мы можем сколь угодно близко подойти к верхней границе /, если положим А = 180° - 2г, В = s и С = е, где значение s может быть сделано сколь угодно малым, при этом значение п сделать неограниченно большим. Тогда
В'С = а' = ^, А'С = V = А! В' = d = s,\ +
” V я2
Предельный треугольник А'В'С' получается таким, как изображен на рис. 50, справа, где
ip = 2а tg (1) = 35,3135 743°, в = 72,34321285°.
Верхняя граница / равна 74,059 277 09°.
47. 	Почувствуй себя доктором
Далее запись (A, B,fA,fB) означает, что в большем пузырьке содержится А мл жидкости и fA таблетки, а в меньшем пузырьке содержится В мл жидкости и /В таблетки. Процедура всегда начинается с того, что в один из пузырьков наливают воду, далее перечисляются остальные действия шаг за шагом. Добавление таблетки считается отдельным шагом.
(а) 	Объемы пузырьков 5 и 4 мл. Существуют решения для п = 1-10, 12-21, 24-28, 30, 32-36, 38-40, 45, 48-52, 56, 57, 60, 61, 64-68, 70, 74-76, 80 и 85.
/ = 20% или 80% (3 шага): (5, 0, 0, 0), (5, 0, 1, 0),
(1, 4, 0,2, 0,8).


47. Почувствуй себя доктором 10 5
/ = 25% или 75% (5 шагов): (0, 4, 0, 0), (4, 0, 0, 0), (4, 4, 0, 0), (4, 4, 0, 1), (5, 3, 0,25, 0,75).
/ = 4% или 16% (6 шагов): (1, 4, 0,2, 0,8),
(1, 0, 0,2, 0), (5, 0, 0,2, 0), (1, 4, 0,04, 0,16).
/ = 64% (7 шагов): (1, 4, 0,2, 0,8), (0, 4, 0, 0,8),
(4, 0, 0,8, 0), (5, 0, 0,8, 0), (1, 4, 0,16, 0,64).
/ = 15% или 85% (7 шагов): (4, 0, 0, 0), (4, 0, 1, 0), (4, 4, 1, 0), (5, 3, 1, 0), (4, 4, 0,8, 0,2),
(5, 3, 0,85, 0,15).
/ = 5% (7 шагов): (5, 3, 0,25, 0,75), (5, 0, 0,25, 0),
(1, 4, 0,05, 0,2).
/ = 40% или 60% (7 шагов): (5, 0, 0, 0), (1, 4, 0, 0), (1, 0, 0, 0), (0, 1, 0, 0), (5, 1, 0, 0),
(5, 1, 1, 0), (2, 4, 0,4, 0,6).
/ = 32% или 68% (8 шагов): (5, 3, 0,85, 0,15),
(4, 4, 0,68, 0,32).
/ = 12% (9 шагов): (4, 0, 0,8, 0), (4, 4, 0,8, 0),
(5, 3, 0,8, 0), (4, 4, 0,64, 0,16),
(5, 3, 0,68, 0,12).
/ = 6% или 14% (9 шагов): (1, 0, 0,2, 0),
(О, 1, 0, 0,2), (5, 1, 0, 0,2), (2, 4, 0, 0,2),
(5, 1, 0,15, 0,05), (2, 4, 0,06, 0,14).
/ = 17% (9 шагов): (5, 3, 0,85, 0,15), (5, 0, 0,85, 0),
(1, 4, 0,17, 0,68).
/ = 24% или 76% (9 шагов): (4, 4, 0,68, 0,32),
(5, 3, 0,76, 0,24).
/ = 30% или 70% (9 шагов): (0, 1, 0, 0), (0, 1, 0, 1), (5, 1, 0, 1), (2, 4, 0, 1), (5, 1, 0,75, 0,25),
(2, 4, 0,3, 0,7).
/ = 34% или 66% (9 шагов): (2, 4, 0,4, 0,6),
(5, 1, 0,85, 0,15), (2, 4, 0,34, 0,66).
/ = 8% (9 шагов): (5, 3, 0,25, 0,75), (4, 4, 0,2, 0,8),
(5, 3, 0,4, 0,6), (5, 0, 0,4, 0), (1, 4, 0,08, 0,32).
/ = 49% или 51% (9 шагов): (5, 3, 0,4, 0,6),
(4, 4, 0,32, 0,68), (5, 3, 0,49, 0,51).


106 Решения
f = 50% (9 шагов): (4, 4, 0, 0), (5, 3, 0, 0),
(0, 3, 0, 0), (3, 0, 0, 0), (3, 4, 0, 0),
(3, 4, 0, 1), (5, 2, 0,5, 0,5).
/ = 3% (10 шагов): (5, 1, 0,15, 0,05), (5, 0, 0,15, 0),
(1, 4, 0,03, 0,12).
/ = 45% (10 шагов): (5, 3, 0,25, 0,75), (0, 3, 0, 0,75),
(3, 0, 0,75, 0), (3, 4, 0,75, 0), (5, 2, 0,75, 0),
(3, 4, 0,45, 0,3).
/ = 1% (10 шагов): (1, 4, 0,05, 0,2), (1, 0, 0,05, 0),
(5, 0, 0,05, 0), (1, 4, 0,01, 0,04).
/ = 33% или 67% (11 шагов): (2, 4, 0,3, 0,7),
(5, 1, 0,825, 0,175), (2, 4, 0,33, 0,67).
/ = 48% (И шагов): (2, 4, 0,4, 0,6), (0, 4, 0, 0,6),
(4, 0, 0,6, 0), (5, 0, 0,6, 0), (1, 4, 0,12, 0,48).
/ = 10% (11 шагов): (5, 2, 0,5, 0,5), (5, 0, 0,5, 0),
(1, 4, 0,1, 0,4).
/ = 65% или 35% (11 шагов): (5, 2, 0,5, 0,5),
(3, 4, 0,3, 0,7), (5, 2, 0,65, 0,35).
/ = 9% (12 шагов): (5, 3, 0,85, 0,15), (0, 3, 0, 0,15),
(3, 0, 0,15, 0), (3, 4, 0,15, 0), (5, 2, 0,15, 0),
(3, 4, 0,09, 0,06).
/ = 36% или 39% (12 шагов): (3, 4, 0,45, 0,3),
(5, 2, 0,6, 0,15), (3, 4, 0,36, 0,39).
/ = 52% (12 шагов): (3, 4, 0, 0), (5, 2, 0, 0),
(5, 2, 1, 0), (3, 4, 0,6, 0,4), (5, 2, 0,8, 0,2),
(3, 4, 0,48, 0,52).
/ = 61% (12 шагов): (5, 2, 0,65, 0,35), (3, 4, 0,39, 0,61).
/ = 18% (13 шагов): (5, 3, 0,76, 0,24), (0, 3, 0, 0,24),
(5, 3, 0, 0,24), (4, 4, 0, 0,24), (5, 3, 0,06, 0,18).
/ = 56% (13 шагов): (2, 4, 0,3, 0,7), (0, 4, 0, 0,7),
(4, 0, 0,7, 0), (5, 0, 0,7, 0), (1, 4, 0,14, 0,56).
/ = 28% (13 шагов): (2, 4, 0,4, 0,6), (2, 0, 0,4, 0),
(О, 2, 0, 0,4), (5, 2, 0, 0,4), (3, 4, 0, 0,4),
(5, 2, 0,2, 0,2), (3, 4, 0,12, 0,28).
/ = 26% или 74% (13 шагов): (3, 4, 0,48, 0,52),
(5, 2, 0,74, 0,26).


47. Почувствуй себя доктором 107
/ = 13% (13 шагов): (5, 2, 0,65, 0,35), (5, 0, 0,65, 0),
(1, 4, 0,13, 0,52).
/ = 57% (14 шагов): (0, 3, 0, 0,75), (0, 4, 0, 0,75),
(4, 0, 0,75, 0), (4, 4, 0,75, 0), (5, 3, 0,75, 0),
(4, 4, 0,6, 0,15), (5, 3, |1, ^),
(4, 4, 0,51, 0,24), (5, 3, 0,57, 0,18).
/ = 27% (14 шагов): (3, 4, 0,45, 0,3), (3, 0, 0,45, 0),
(3, 4, 0,45, 0), (5, 2, 0,45, 0), (3, 4, 0,27, 0,18).
/ = 2% (14 шагов): (1, 4, 0,08, 0,32), (1, 0, 0,08, 0),
(0, 1, 0, 0,08), (5, 1, 0, 0,08), (2, 4, 0, 0,08),
(5, 1, 0,06, 0,02).
/ = 21% (15 шагов): (2, 4, 0,3, 0,7), (2, 0, 0,3, 0),
(0, 2, 0, 0,3), (5, 2, 0, 0,3), (3, 4, 0, 0,3),
(5, 2, 0,15, 0,15), (3, 4, 0,09, 0,21).
/ = 7% (15 шагов): (5, 2, 0,5, 0,5), (3, 4, 0,3, 0,7),
(5, 2, 0,65, 0,35), (0, 2, 0, 0,35), (2, 0, 0,35, 0),
(5, 0, 0,35, 0), (1, 4, 0,07, 0,28).
/ = 19% (17 шагов): (5, 1, 0,75, 0,25), (0, 1, 0, 0,25),
(0, 4, 0, 0,25), (4, 0, 0,25, 0), (4, 4, 0,25, 0),
(5, 3, 0,25, 0), (4, 4, 0,2, 0,05), (5, 3, g, ^),
(4, 4, 0,17, 0,08), (5, 3, 0,19, 0,06).
/ = 38% (18 шагов): (5, 2, 0,5, 0,5), (0, 2, 0, 0,5),
(0, 4, 0, 0,5), (4, 0, 0,5, 0), (4, 4, 0,5, 0),
(5, 3, 0,5, 0), (4, 4, 0,4, 0,1),
(5, 3, 0,425, 0,075), (4, 4, 0,34, 0,16),
(5, 3, 0,38, 0,12).
(Ь) 	Объемы пузырьков 5 и 1 мл. Существуют решения
для п = 1-6, 8-10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32,
36, 40, 45, 48, 50, 60, 64, 75 и 80.
/ = 20% или 80% (3 шага): (5, 0, 0, 0), (5, 0, .1, 0),
(4, 1, 0,8, 0,2).
/ = 60% (5 шагов): (4, 1, 0,8, 0,2), (3, 2, 0,6, 0,4).
/ = 25% или 75% (5 шагов): (5, 0, 0, 0), (4, 1, 0, 0),
(4, 0, 0, 0), (4, 0, 1, 0), (3, 1, 0,75, 0,25).
/ = 16% или 64% (6 шагов): (4, 1, 0,8, 0,2),
(4, 0, 0,8, 0), (5, 0, 0,8, 0), (4, 1, 0,64, 0,16).


Решения
= 50% (6 шагов): (0, 1, 0, 0), (1, 0, 0, 0),
(1, 1, 0, 0), (2, 0, 0, 0), (2, 0, 1, 0),
(1, 1, ОД 0,5).
= 4% (7 шагов): (4, 1, 0,8, 0,2), (0, 1, 0, 0,2),
(1, 0, 0,2, 0), (5, 0, 0,2, 0), (4, 1, 0,16, 0,04).
= 12% или 48% (8 шагов): (3, 1, 0,6, 0,2),
(3, 0, 0,6, 0), (5, 0, 0,6, 0), (4, 1, 0,48, 0,12).
= 10% (8 шагов): (0, 1, 0, 0,2), (1, 0, 0,2, 0),
(1, 1, 0,2, 0), (2, 0, 0,2, 0), (1, 1, 0,1, 0,1).
= 15% (8 шагов): (3, 1, 0,75, 0,25), (3, 0, 0,75, 0),
(5, 0, 0,75, 0), (4, 1, 0,6, 0,15).
= 45% (9 шагов): (3, 1, 0,6, 0,2), (3, 0, 0,6, 0),
(3, 1, 0,6, 0), (4, 0, 0,6, 0), (3, 1, 0,45, 0,15).
= 5% (9 шагов): (3, 1, 0,75, 0,25), (0, 1, 0, 0,25),
(1, 0, 0,25, 0), (5, 0, 0,25, 0), (4, 1, 0,2, 0,05).
= 8% или 32% (10 шагов): (3, 0, 0,6, 0),
(2, 1, 0,4, 0,2), (2, 0, 0,4, 0), (5, 0, 0,4, 0),
(4, 1, 0,32, 0,08).
= 36% (10 шагов): (4, 1, 0,48, 0,12), (4, 0, 0,48, 0),
(3, 1, 0,36, 0,12).
= 2% (11 шагов): (1, 1, 0,1, 0,1), (1, 0, 0,1, 0),
(5, 0, 0,1, 0), (4, 1, 0,08, 0,02).
= 30% (И шагов): (3, 1, 0,45, 0,15), (3, 0, 0,45, 0),
(2, 1, 0,3, 0,15).
= 24% (12 шагов): (3, 1, 0,36, 0,12), (3, 0, 0,36, 0),
(2, 1, 0,24, 0,12).
= 9% (12 шагов): (3, 0, 0,45, 0), (5, 0, 0,45, 0),
(4, 1, 0,36, 0,09).
= 3% (12 шагов): (4, 1, 0,6, 0,15), (0, 1, 0, 0,15),
(1, 0, 0,15, 0), (5, 0, 0,15, 0), (4, 1, 0,12, 0,03).
= 6% (13 шагов): (4, 1, 0,08, 0,02), (4, 0, 0,08, 0),
(3, 1, 0,06, 0,02).
= 1% (13 шагов): (4, 1, 0,2, 0,05), (0, 1, 0, 0,05),
(1, 0, 0,05, 0), (5, 0, 0,05, 0), (4, 1, 0,04, 0,01).
= 27% (14 шагов): (3, 0, 0,36, 0), (3, 1, 0,36, 0),
(4, 0, 0,36, 0), (3, 1, 0,27, 0,09).


47. Почувствуй себя доктором 109
/ = 18% (16 шагов): (3, 1, 0,27, 0,09), (3, 0, 0,27, 0),
(2, 1, 0,18, 0,09).
(с) 	Объемы пузырьков 9 и 1 мл. Существуют решения
для п = 1-10, 12, 14-16, 18, 20, 21, 24, 25, 27, 28, 30, 32,
35, 36, 40, 42, 45, 48-50, 56, 60, 64, 70, 75 и 80.
/ = 50% (6 шагов): (0, 1, 0, 0), (1, 0, 0, 0),
(1, 1, 0, 0), (2, 0, 0, 0), (2, 0, 1, 0),
(1, 1, 0,5, 0,5).
/ = 75% (7 шагов): (9, 0, 0, 0), (8, 1, 0, 0),
(8, 0, 0, 0), (8, 0, 1, 0), (7, 1, 0,875, 0,125),
(7, 0, 0,875, 0), (6, 1, 0,75, 0,125).
/ = 25% (10 шагов): (2, 0, 0, 0), (2, 1, 0, 0),
(3, 0, 0, 0), (3, 1, 0, 0), (4, 0, 0, 0),
(4, 0, 1, 0), (3, 1, 0,75, 0,25).
/ = 20% или 80% (11 шагов): (8, 0, 0, 0), (7, 1, 0, 0), (7, 0, 0, 0), (6, 1, 0, 0), (6, 0, 0, 0),
(5, 1, 0, 0), (5, 0, 0, 0), (5, 0, 1, 0),
(4, 1, 0,8, 0,2).
/ = 60% (13 шагов): (4, 1, 0,8, 0,2), (4, 0, 0,8, 0),
(3, 1, 0,6, 0,2).
/ = 10% или 40% (15 шагов): (6, 1, 0,75, 0,125),
(6, 0, 0,75, 0), (5, 1, 0,625, 0,125),
(5, 0, 0,625, 0), (4, 1, 0,5, 0,125), (4, 0, 0,5, 0), (4, 1, 0,5, 0), (5, 0, 0,5, 0), (4, 1, 0,4, 0,1).
/ = 16% или 64% (15 шагов): (4, 0, 0,8, 0),
(4, 1, 0,8, 0), (5, 0, 0,8, 0), (4, 1, 0,64, 0,16).
/ = 15% (16 шагов): (3, 1, 0,75, 0,25), (3, 0, 0,75, 0),
(3, 1, 0,75, 0), (4, 0, 0,75, 0), (4, 1, 0,75, 0), (5, 0, 0,75, 0), (4, 1, 0,6, 0,15).
/ = 30% (17 шагов): (4, 1, 0,4, 0,1), (4, 0, 0,4, 0),
(3, 1, 0,3, 0,1).
/ = 48% (17 шагов): (4, 1, 0,64, 0,16), (4, 0, 0,64, 0),
(3, 1, 0,48, 0,16).
/ = 45% (17 шагов): (3, 1, 0,6, 0,2), (3, 0, 0,6, 0),
(3, 1, 0,6, 0), (4, 0, 0,6, 0), (3, 1, 0,45, 0,15).


110 Решения
f = 35% (19 шагов): (7, 0, 0,875, 0), (7, 1, 0,875, 0),
(8, 0, 0,875, 0), (7, 1, |, £), (7, 0, |, о),
(6' И' м)' (6' °' Й' °)' (5' И' й)'
(5, О, Ц, о), (4, 1, (4, 0, о),
(4, 1, 0), (5, О, Z, о),
(4, 1, 0,35, 0,0875).
/ = 8% или 32% (19 шагов): (4, 0, 0,4, 0),
(4, 1, 0,4, 0), (5, 0, 0,4, 0), (4, 1, 0,32, 0,08).
/ = 12% (19 шагов): (4, 0, 0,6, 0), (4, 1, 0,6, 0),
(5, 0, 0,6, 0), (4, 1, 0,48, 0,12).
/ = 5% (20 шагов): (9, 0, 0, 0), (9, О, 1, 0),
(8, 1, |, i), (О, 1, О, 1), (1, О, 1, 0),
(l, 1, 1, О), (2, О, 1, 0), (2, 1, 1, 0),
(3, О, 1, О), (3, 1, I, О), (4, О, 1, О),
(4, 1, |, о), (5, О, 1, о), (4, 1, A, i),
(4- °- °)' (3' '■ В' в)' (3' °' Ш' °)'
(3, 1, i, 0), (4, 0, i 0), (3, 1, 0,05, ±).
f = 2% (20 шагов): (7, 1, 0,875, 0,125),
(О, 1, 0, 0,125), (1, 0, 0,125, 0), (1, 1, 0,125, 0), (2, 0, 0,125, 0), (2, 1, 0,125, 0),
(3, 0, 0,125, 0), (3, 1, 0,125, 0),
(4, 0, 0,125, 0), (4, 1, 0,125, 0),
(5, 0, 0,125, 0), (4, 1, 0,1, 0,025), (4, 0, 0,1, 0),
(4, 1, 0,1, 0), (5, 0, 0,1, 0), (4, 1, 0,08, 0,02).
/ = 24% (21 шаг): (4, 1, 0,32, 0,08), (4, 0, 0,32, 0),
(3, 1, 0,24, 0,08).
/ = 70% (21 шаг): (5, 0, 0,8, 0), (5, 1, 0,8, 0),
(6, 0, 0,8, 0), (6, 1, 0,8, 0), (7, 0, 0,8, 0),
(7, 1, 0,8, 0), (8, 0, 0,8, 0), (7, 1, 0,7, 0,1).


47. Почувствуй себя доктором 111
/ = 36% / = 6% / = 4%
/ = 7% / = 9%
/ = 1%
/ = 21% / = 18% / = 56%
/ = 27% / = 3%
(21 шаг): (3, 1, 0,48, 0,16), (3, 0, 0,48, 0),
(3, 1, 0,48, 0), (4, 0, 0,48, 0), (3, 1, 0,36, 0,12).
(22 шага): (4, 1, 0,08, 0,02), (4, 0, 0,08, 0),
(3, 1, 0,06, 0,02).
(22 шага): (4, 1, 0,8, 0,2), (О, 1, 0, 0,2),
(1, 0, 0,2, 0), (1, 1, 0,2, 0), (2, 0, 0,2, 0),
(2, 1, 0,2, 0), (3, 0, 0,2, 0), (3, 1, 0,2, 0),
(4, 0, 0,2, 0), (4, 1, 0,2, 0), (5, 0, 0,2, 0),
(4, 1, 0,16, 0,04).
или 28% (23 шага): (4, 1, 0,35, 0,0875),
(4, 0, 0,35, 0), (4, 1, 0,35, 0), (5, 0, 0,35, 0),
(4, 1, 0,28, 0,07).
(23 шага): (3, 1, 0,45, 0,15), (3, 0, 0,45, 0),
(3, 1, 0,45, 0), (4, 0, 0,45, 0), (4, 1, 0,45, 0),
(5, 0, 0,45, 0), (4, 1, 0,36, 0,09).
(24 шага): (2, 0, 0,125, 0), (l, 1, i, i),
10 — 1, U, 16,
о), (l, 1,
1
16'
0), (1, 0,
1
16'
2 1 —
' 16'
0), (з, 0,
1
16'
0), (3, 1,
1
16'
4 0 —
У ' 16'
0), (4, 1,
1
16'
0), (5, 0,
1
16'
(4, 1, 0,05, i), (4, 0, 0,05, 0), (4, 1, 0,05, 0),
(5, 0, 0,05, 0), (4, 1, 0,04, 0,01).
(25 шагов): (4, 1, 0,28, 0,07), (4, 0, 0,28, 0),
(3, 1, 0,21, 0,07).
(25 шагов): (3, 1, 0,24, 0,08), (4, 0, 0,24, 0),
(3, 1, 0,18, 0,06).
(25 шагов): (4, 0, 0,64, 0), (4, 1, 0,64, 0),
(5, 0, 0,64, 0), (5, 1, 0,64, 0), (6, 0, 0,64, 0),
(6, 1, 0,64, 0), (7, 0, 0,64, 0), (7, 1, 0,64, 0),
(8, 0, 0,64, 0), (7, 1, 0,56, 0,08).
(25 шагов): (3, 1, 0,36, 0,12), (3, 0, 0,36, 0),
(3, 1, 0,36, 0), (4, 0, 0,36, 0), (3, 1, 0,27, 0,09).
(26 шагов): (4, 1, 0,04, 0,01), (4, 0, 0,04, 0),
(3, 1, 0,03, 0,01).


112 Решения
f = 14% (27 шагов): (3, 1, 0,21, 0,07), (3, 0, 0,21, 0),
(2, 1, 0,14, 0,07).
/ = 49% (29 шагов): (7, 1, 0,56, 0,08), (7, 0, 0,56, 0),
(7, 1, 0,56, 0), (8, 0, 0,56, 0), (7, 1, 0,49, 0,07).
/ = 42% (29 шагов): (4, 0, 0,48, 0), (4, 1, 0,48, 0),
(5, 0, 0,48, 0), (5, 1, 0,48, 0), (6, 0, 0,48, 0),
(6, 1, 0,48, 0), (7, 0, 0,48, 0), (7, 1, 0,48, 0),
(8, 0, 0,48, 0), (7, 1, 0,42, 0,06).
(d) 	Объемы пузырьков 8 и 5 мл. Существуют решения
для и = 1-18, 20-22, 24, 25, 27, 30, 32-36, 40, 42, 44, 45,
50-52, 56, 58, 60, 64-66, 68, 70, 72, 75, 80, 83, 85 и 88-90.
/ = 40% или 60% (5 шагов): (0, 5, 0, 0), (5, 0, 0, 0), (5, 5, 0, 0), (5, 5, 0, 1), (8, 2, 0,6, 0,4).
/ = 15% или 85% (7 шагов): (5, 5, 0, 0), (8, 2, 0, 0), (8, 2, 1, 0), (5, 5, 0,625, 0,375),
(8, 2, 0,85, 0,15).
/ = 25% или 75% (7 шагов): (8, 0, 0, 0), (3, 5, 0, 0), (3, 0, 0, 0), (0, 3, 0, 0), (8, 3, 0, 0),
(8, 3, 1, 0), (6, 5, 0,75, 0,25).
/ = 30% или 70% (9 шагов): (8, 3, 0, 0), (6, 5, 0, 0), (6, 5, 0, 1), (8, 3, 0,4, 0,6), (6, 5, 0,3, 0,7).
/ = 16% или 24% (9 шагов): (8, 2, 0,6, 0,4)
(0, 2, 0, 0,4), (8, 2, 0, 0,4), (5, 5, 0, 0,4),
(8, 2, 0,24, 0,16).
/ = 42% или 58% (10 шагов): (6, 5, 0,3, 0,7),
(8, 3, 0,58, 0,42).
/ = 6% или 9% (11 шагов): (8, 2, 0,85, 0,15),
(0, 2, 0, 0,15), (8, 2, 0, 0,15), (5, 5, 0, 0,15),
(8, 2, 0,09, 0,06).
/ = 5% (И шагов): (6, 5, 0,3, 0,7), (6, 0, 0,3, 0),
(1, 5, 0,05, 0,25).
/ = 10% (И шагов): (8, 2, 0,24, 0,16), (5, 5, 0,15, 0,25), (8, 2, 0,3, 0,1).
/ = 20% или 80% (И шагов): (8, 2, 0, 0), (0, 2, 0, 0),
(2, 0, 0, 0), (2, 5, 0, 0), (7, 0, 0, 0),
(7, 5, 0, 0), (7, 5, 0, 1), (8, 4, 0,2, 8).


47. Почувствуй себя доктором 113
f-
34%
(12
шагов):
(0, 2,
0, 0,4), (0, 5, 0, 0,4),
(5,
0,
0,4, 0), (5,
5, 0,4, 0), (8, 2, 0,4, 0),
(5,
5,
0,25,
0,15),
(8, 2, 0,34, 0,06).
f-
35%
(12
шагов):
(0, 2,
0, 0,4), (2, 0, 0,4, 0),
(2,
5,
0,4, 0), (7,
0, 0,4, 0), (7, 5, 0,4, 0),
(8,
4,
0,4, 0), (7,
5, 0,35, 0,05).
f--
36%
(12
шагов):
(8, 3,
0,4, 0,6), (0, 3, 0, 0,6),
(8,
3,
0, 0,6), (6,
5, 0, 0,6), (8, 3, 0,24, 0,36).
f-
18%
(13
шагов):
(8, 3,
0,24, 0,36), (6, 5, 0,18,
0,42).
f-
= 50%
(13
шагов):
(6, 5,
0, 0), (6, 0, 0, 0),
(1,
5,
0, 0),
(1, о,
, 0, 0), (0, 1, 0, 0),
(8,
1,
0, 0),
(8, 1,
, 1, 0), (4, 5, 0,5, 0,5).
f-
= 4%
(13
шагов):
(7, 5,
0,35, 0,05), (8, 4, 0,36,
0,04).
f-
= 90%
(13
шагов):
(7, 5,
0, 0), (8, 4, 0, 0),
(8,
4,
1, 0),
(7, 5,
0,875, 0,125), (8, 4, 0,9,
0,1).
f-
= 66%
(13
шагов):
(8, 4,
0,2, 8), (7, 5, 0,175, 0,825),
(8,
4,
0,34,
0,66).
f=
= 3%
(15
шагов):
(6, 5,
0,18, 0,42), (6, 0, 0,18,
0),
a
5,
0,03,
0,15).
f-
= 51%
(15
шагов):
(0, 3,
0, 0,6), (0, 5, 0, 0,6),
(5,
0,
0,6, 0), (5,
5, 0,6, 0), (8, 2, 0,6, 0),
(5,
5,
0,375,
, 0,225), (8, 2, 0,51, 0,09).
/ = 45% или 55% (15 шагов): (4, 5, 0,5, 0,5), (8, 1, 0,9, 0,1), (4, 5, 0,45, 0,55).
/ = 12% (15 шагов): (8, 2, 0,24, 0,16), (0, 2, 0, 0,16),
(8, 2, 0, 0,16), (5, 5, 0, 0,16),
(8, 2, 0,096, 0,064), (5, 50,06, 0,1),
(8, 2, 0,12, 0,04).
/ = 17% или 83% (15 шагов): (8, 4, 0,9, 0,1),
(7' 5' §' ш)' (8' 4' °'83' °'17)-
/ = 64% (15 шагов): (8, 4, 0,2, 0,8), (0, 4, 0, 0,8),
(8, 4, 0, 0,8), (7, 5, 0, 0,8), (8, 4, 0,16, 0,64).
/ = 11% или 89% (16 шагов): (6, 5, 0,75, 0,25),
(6, 0, 0,75, 0), (1, 5, 0,125, 0,625),
(1, 0, 0,125, 0), (0, 1, 0, 0,125),


114 Решения
(8, 1, 0, 0,125), (4, 5, 0,125), (8, 1, 0,1, 0,025), (4, 5, 0,05, 0,075), (8, 1, 0,11, 0,015).
/ = 1% (16 шагов): (1, 5, 0,05, 0,25), (1, 0, 0,05, 0),
(0, 1, 0, 0,05), (8, 1, 0, 0,05), (4, 5, 0, 0,05),
(8, 1, 0,04, 0,01).
/ = 2% (16 шагов): (6, 0, 0, 0), (6, 0, 1,0),
(1, 5, I, |), (1, 0, 1, 0), (0, 1, О, 1),
(8, 1, О, 1), (4, 5, 0, (8, 1, i),
(4, 5, i ОД), (8, 1, 11, 0,02).
/ = 14% (16 шагов): (0, 2, 0, 0,16), (2, 0, 0,16, 0),
(2, 5, 0,16, 0), (7, 0, 0,16, 0), (7, 5, 0,16, 0),
(8, 4, 0,16, 0), (7, 5, 0,14, 0,02).
/ = 88% (16 шагов): (8, 1, 0, 0), (8, 1, О, 1),
(4, 5, О, 1), (8, 1, 0,8, 0,2), (4, 5, 0,4, 0,6),
(8, 1, 0,88, 0,12).
/ = 44% или 56% (17 шагов): (8, 1, 0,88, 0,12),
(4, 5, 0,44, 0,56).
/ = 7% (17 шагов): (8, 1, 0,11, 0,015),
(4, 5, 0,055, 0,07).
/ = 8% или 72% (17 шагов): (0, 4, 0, 0,8),
(4, 0, 0,8, 0), (4, 5, 0,8, 0), (8, 1, 0,8, 0),
(4, 5, 0,4, 0,4), (8, 1, 0,72, 0,08).
/ = 33% (18 шагов): (8, 1, 0,88, 0,12), (8, 0, 0,88, 0),
(3, 5, 0,33, 0,55).
/ = 13% (18 шагов): (0, 2, 0, 0,16), (0, 5, 0, 0,16),
(5, 0, 0,16, 0), (5, 5, 0,16, 0), (8, 2, 0,16, 0),
(5, 5, 0,1, 0,06), (8, 2, 0,136, 0,024),
(5, 5, 0,085, 0,075), (8, 2, 0,13, 0,03).
/ = 68% (18 шагов): (0, 4, 0, 0,8), (0, 5, 0, 0,8),
(5, 0, 0,8, 0), (5, 5, 0,8, 0), (8, 2, 0,8, 0),
(5, 5, 0,5, 0,3), (8, 2, 0,68, 0,12).
/ = 27% (19 шагов): (7, 5, 0, 0), (7, 5, 0, 1),
(8, 4, 0,2, 0,8), (0, 4, 0, 0,8), (4, 0, 0,8, 0),
(4, 5, 0,8, 0), (8, 1, 0,8, 0), (4, 5, 0,4, 0,4),


47. Почувствуй себя доктором 115
(8, 1, 0,72, 0,08), (8, 0, 0,72, 0),
(3, 5, 0,27, 0,45).
/ = 32% (20 шагов): (4, 5, 0,4, 0,6), (4, 0, 0,4, 0),
(0, 4, 0, 0,4), (8, 4, 0, 0,4), (7, 5, 0, 0,4),
(8, 4, 0,08, 0,32).
/ = 65% (20 шагов): (8, 2, 0,68, 0,12),
(5, 5, 0,425, 0,375), (8, 2, 0,65, 0,15).
/ = 22% (21 шаг): (4, 0, 0,4, 0), (4, 5, 0,4, 0),
(8, 1, 0,4, 0), (4, 5, 0,2, 0,2), (8, 1, 0,36, 0,04),
(4, 5, 0,18, 0,22).
/ = 21% (21 шаг): (4, 5, 0,44, 0,56), (0, 5, 0, 0,56),
(5, 0, 0,56, 0), (8, 0, 0,56, 0), (3, 5, 0,21, 0,35).
/ = 52% (24 шага): (8, 4, 0,16, 0,64), (0, 4, 0, 0,64),
(О, 5, 0, 0,64), (5, 0, 0,64, 0), (5, 5, 0,64, 0),
(8, 2, 0,64, 0), (5, 5, 0,4, 0,24),
(8, 2, 0,544, 0,096), (5, 5, 0,34, 0,3),
(8, 2, 0,52, 0,12).
(е) 	Объемы пузырьков 12 и 5 мл. Существуют решения
для п = 1-10, 12-21, 24-28, 30, 32-36, 38-40, 45, 48-52,
56, 57, 60, 61, 64-68, 70, 74-76, 80 и 85.
/ = 50% (6 шагов): (0, 5, 0, 0), (5, 0, 0, 0),
(5, 5, 0, 0), (10, 0, 0, 0), (10, 0, 1, 0),
(5, 5, 0,5, 0,5).
/ = 40% или 60% (7 шагов): (10, 0, 0, 0),
(10, 5, 0, 0), (10, 5, 0, 1), (12, 3, 0,4, 0,6).
/ = 10% или 90% (9 шагов): (10, 5, 0, 0), (12, 3, 0, 0),
(12, 3, 1, 0), (10, 5, |, I), (12, 3, 0,9, 0,1).
/ = 25% или 75% (9 шагов): (12, 0, 0, 0), (7, 5, 0, 0),
(7, 0, 0, 0), (2, 5, 0, 0), (2, 0, 0, 0),
(О, 2, 0, 0), (12, 2, 0, 0), (12, 2, 1, 0),
(9, 50,75, 0,25).
/ = 15% или 85% (11 шагов): (12, 3, 0,9, 0,1),
(10, 5, 0,75, 0,25), (12, 3, 0,85, 0,15).
/ = 45% или 55% (И шагов): (12, 2, 0, 0), (9, 5, 0, 0), (9, 5, 0, 1), (12, 2, 0,6, 0,4), (9, 5, 0,45, 0,55).


116 Решения
/ = 24% или 36% (11 шагов): (12, 3, 0,4, 0,6),
(0, 3, 0, 0,6), (12, 3, 0, 0,6), (10, 5, 0, 0,6),
(12, 3, 0,24, 0,36).
/ = 35% (И шагов): (0, 3, 0, 0,6), (3, 0, 0,6, 0),
(12, 0, 0,6, 0), (7, 5, 0,25, 0,35).
/ = 30% или 70% (11 шагов): (12, 3, 0,4, 0,6),
(10, 5, 1, |), (12, 3, 0,6, 0,4),
(10, 5, 0,5, 0,5), (12, 3, 0,7, 0,3).
/ = 13% или 87% (12 шагов): (9, 5, 0,75, 0,25),
(12, 2, 0,9, 0,1), (9, 5, 0,675, 0,325),
(12, 2, 0,87, 0,13).
/ = 22% или 78% (12 шагов): (9, 5, 0,45, 0,55),
(12, 2, 0,78, 0,22).
/ = 20% (12 шагов): (12, 3, 0,24, 0,36), (10, 5, 0,2, 0,4).
/ = 4% или 6% (13 шагов): (12, 3, 0,9, 0,1),
(0, 3, 0, 0,1), (12, 3, 0, 0,1), (10, 5, 0, 0,1), (12, 3, 0,04, 0,06).
/ = 5% (13 шагов): (10, 0, 0, 0), (10, 0, 1, 0),
(5, 5, 0,5, 0,5), (5, 0, 0,5, 0), (5, 5, 0,5, 0),
(10, 0, 0,5, 0), (10, 5, 0,5, 0), (12, 3, 0,5, 0),
(lO, 5, А, X), (12, 3, 0,45, 0,05).
/ = 14% (13 шагов): (12, 3, 0,24, 0,36), (12, 0, 0,24, 0),
(7, 5, 0,14, 0,1).
/ = 16% (13 шагов): (12, 3, 0,6, 0,4), (0, 3, 0, 0,4),
(12, 3, 0, 0,4), (10, 5, 0, 0,4),
(12, 3, 0,16, 0,24).
/ = 80% (13 шагов): (12, 3, 0, 0), (0, 3, 0, 0),
(3, 0, 0, 0), (3, 5, 0, 0), (8, 0, 0, 0),
(8, 5, 0, 0), (8, 5, 0, 1), (12, 1, 0,8, 0,2).
/ = 3% (15 шагов): (12, 0, 0, 0), (12, 0, 1, 0),
(7, 5, А), (7, о, £, 0), (2, 5, 1 £).
(2, О, I, О), (О, 2, О, I), (12, 2, О, I),
(9, 5, О, I), (12, 2, 0,1, i). (О, 2, 0, ±),


47. Почувствуй себя доктором 117
(l2, 2, О, (9, 5, О,
(12, 2, 0,04, А), (9, 5, 0,03, »-).
/ = 12% или 18% (15 шагов): (12, 3, 0,7, 0,3),
(0, 3, 0, 0,3), (12, 3, 0, 0,3), (10, 5, 0, 0,3),
(12, 3, 0,12, 0,18).
/ = 9% (15 шагов): (12, 3, 0,85, 0,15), (0, 3, 0, 0,15),
(12, 3, 0, 0,15), (10, 5, 0, 0,15),
(12, 3, 0,06, 0,09).
/ = 26% (15 шагов): (12, 2, 0,78, 0,22),
(9, 5, 0,585, 0,415), (9, 0, 0,585, 0),
(4, 5, 0,26, 0,325).
/ = 29% (15 шагов): (12, 2, 0,87, 0,13),
(»■ 5' Ш' 1)' (* & <>)■
(4, 5, 0,29, |).
/ = 21% (15 шагов): (12, 3, 0,24, 0,36), (0, 3, 0, 0,36),
(3, 0, 0,36, 0), (12, 0, 0,36, 0),
(7, 5, 0,21, 0,15).
/ = 42% (15 шагов): (10, 5, 0,2, 0,4), (12, 3, 0,36, 24),
(10, 5, 0,3, 0,3), (12, 3, 0,42, 0,18).
/ = 56% (15 шагов): (3, 0, 0,6, 0), (3, 5, 0,6, 0),
(8, 0, 0,6, 0), (8, 5, 0,6, 0), (12, 1, 0,6, 0),
(8, 5, 0,4, 0,2), (12, 1, 0,56, 0,04).
/ = 54% (16 шагов): (0, 3, 0, 0,6), (0, 5, 0, 0,6),
(5, 0, 0,6, 0), (5, 5, 0,6, 0), (10, 0, 0,6, 0),
(10, 5, 0,6, 0), (12, 3, 0,6, 0), (10, 5, 0,5, 0,1), (12, 3, 0,54, 0,06).
/ = 2% (17 шагов): (12, 3, 0,45, 0,05), (0, 3, 0, 0,05),
(12, 3, 0, 0,05), (10, 5, 0, 0,05),
(12, 3, 0,02, 0,03).
/ = 7% (17 шагов): (12, 3, 0,04, 0,06),
(lO, 5, JL, А), (12, 3, 0,06, 0,04),
(10, 5, 0,05, 0,05), (12, 3, 0,07, 0,03).
/ = 8% (17 шагов): (12, 2, 0,6, 0,4), (0, 2, 0, 0,4),
(12, 2, 0, 0,4), (9, 5, 0, 0,4), (12, 2, 0,24, 0,16),


118 Решения
(9, 5, 0,18, 0,22), (9, 0, 0,18, 0),
(4, 5, 0,08, 0,1).
/ = 28% (17 шагов): (12, 3, 0,16, 0,24),
(l°, 5, А ±), (12, 3, 0,24, 0,16)
(10, 5, 0,2, 0,2), (12, 3, 0,28, 0,12).
/ = 1% (18 шагов): (0, 3, 0, 0,1), (0, 5, 0, 0,1),
(5, 0, 0,1, 0), (5, 5, 0,1, 0), (10, 0, 0,1, 0),
(10, 5, 0,1, 0), (12, 3, 0,1, 0), (10, 5, А А),
(12, 3, 0,09, 0,01).
/ = 11% (18 шагов): (12, 2, 0,78, 0,22), (0, 2, 0, 0,22), (0, 5, 0, 0,22), (5, 0, 0,22, 0), (5, 5, 0,22, 0), (10, 0, 0,22, 0), (5, 5, 0,11, 0,11).
/ = 51% (18 шагов): (12, 3, 0,54, 0,06),
(10, 5, 0,45, 0,15), (12, 3, 0,51, 0,09).
/ = 17% (19 шагов): (10, 5, 0,2, 0,4), (10, 0, 0,2, 0),
(10, 5, 0,2, 0), (12, 3, 0,2, 0), (l0, 5, 1, А),
(12, 3, 0,18, 0,02), (10, 5, 0,15, 0,05),
(12, 3, 0,17, 0,03).
/ = 27% (19 шагов): (10, 5, 0,3, 0,3), (10, 0, 0,3, 0),
(10, 5, 0,3, 0), (12, 3, 0,3, 0),
(10, 5, 0,25, 0,05), (12, 3, 0,27, 0,03).
/ = 64% (20 шагов): (9, 5, 0, 0), (9, 0, 0, 0),
(4, 5, 0, 0), (4, 0, 0, 0), (0, 4, 0, 0),
(12, 4, 0, 0), (11, 5, 0, 0), (И, 5, 0, 1),
(12, 4, 0,2, 0,8), (0, 4, 0, 0,8), (12, 4, 0, 0,8),
(11, 5, 0, 0,8), (12, 4, 0,16, 0,64).
/ = 34% (20 шагов): (0, 3, 0, 0,4), (0, 5, 0, 0,4),
(5, 0, 0,4, 0), (5, 5, 0,4, 0), (10, 0, 0,4, 0),
(10, 5, 0,4, 0), (12, 3, 0,4, 0), (lO, 5, I, i),
(12, 3, 0,36, 0,04), (10, 5, 0,3, 0,1),
(12, 3, 0,34, 0,06).
/ = 31% (21 шаг): (12, 3, 0,28, 0,12), (lO, 5, А, |),
(12, 3, 0,3, 0,1), (10, 5, 0,25, 0,15),
(12, 3, 0,31, 0,09).


47. Почувствуй себя доктором 119
/ = 33% (22 шага): (12, 3, 0,34, 0,06), (lO, 5, g, А),
(12, 3, 0,33, 0,07).
/ = 32% (24 шага): (9, 0, 0, 0), (9, 0, 1, 0),
(4' 5' I' I)' (4' °' I' °)' (°' 4' °' I)'
(12, 4, 0, |), (И, 5, 0, |), (12, 4, ± Ц),
(0/ 4, 0, If), (4, 0, If, 0), (4, 5, if, 0),
(9, 0, If, 0), (9, 5, Ц, 0), (12, 2, If, 0),
(9/ 5' 15' А)' (12, 2' °'32' гЬ)-
/ = 72% (24 шага): (0, 4, 0, 0,8), (4, 0, 0,8, 0),
(4, 5, 0,8, 0), (9, 0, 0,8, 0), (9, 5, 0,8, 0),
(12, 2, 0,8, 0), (9, 5, 0,6, 0,2),
(12, 2, 0,72, 0,08).
/ = 49% (25 шагов): (12, 4, 0,2, 0,8), (ll, 5, g, Ц),
(«■ I-1)- (
(4, 5, 0), (9, 0, %, 0), (9, 5, Щ, 0),
(12, 2, « 0), (9, 5, 0,49, ^).
/ = 48% (27 шагов): (0, 4, 0, 0,64), (4, 0, 0,64, 0),
(4, 5, 0,64, 0), (9, 0, 0,64, 0), (9, 5, 0,64, 0),
(12, 2, 0,64, 0), (9, 5, 0,48, 0,16).
/ = 68% (27 шагов): (0, 4, 0, 0,8), (0, 5, 0, 0,8),
(5, 5, 0,8, 0), (10, 0, 0,8, 0), (10, 5, 0,8, 0),
(12, 3, 0,8, 0), (10, 5, §, А),
(12, 3, 0,72, 0,08), (10, 5, 0,6, 0,2),
(12, 3, 0,68, 0,12).
О, 4, 0, | , (4, 0, %, 0 ,


ГЛАВА 7. ФИЗИЧЕСКИЕ ГОЛОВОЛОМКИ
48. 	Лодка с сюрпризом
Камень или плавает на поверхности воды, или хотя бы не тонет в воде, поэтому уровень воды в бассейне и не меняется.
49. 	Равновесие
Все решения сведены в таблицу.
A
В
С
D
E
F
(а)
14
4
105
63
1
—
(b)
2
3
40
20
70
15
(с)
35
30
520
528
792
3
(d)
22
77
18
15
72
27
(е)
25
30
119
136
4
1
(f)
30
5
70
7
3
24
(g)
35
42
33
118
188
189
(h)
5
6
22
33
14
8
(i)
40
48
22
77
36
63
(j)
12
16
29
30
25
—
(k)
11
1
46
92
91
51
(1)
71
1
21
3
785
559
(m)
17
3
1
9
234
114
(n)
35
9
38
2
8
20
50. 	Подвешенный стержень
(а) 	Обобщим задачу и положим АВ = а, ВС = b, CD = с и AD = d (рис. 51). Проекция на горизонтальную ось:
d - acosA + bcos(A + В) = ccosD. (1)


50. Подвешенный стержень 121
Рис. 51
Проекция на вертикальную ось:
bcos(A + В) - acos А = csinD. (2)
Расстояние от точки М до потолка равно MN - h = asin А — ^ sin (Л + В).
Поскольку энергия минимальна, величина h должна быть максимальной, поэтому = 0. Возьмем
производные А. 0т обеих частей равенств (1) и (2).
и А.
Исключив из них получим
-1 dB _ a sin(y4 + D) дА b sin (А + В + D)
и
2 cos A sin (А + В + D) = cos (А + В) sin(A + D).
Из этих соотношений с учетом равенства С = 2л -A-B-D
выводим
cos A sin С = sin В cos D.


122 Решения
Применим теорему синусов к треугольникам BMP и СМР:
МР = !*sinBA и МР = ,bsin^.
2cos A 2cosD
Из этих двух равенств и получаем условие того, что продолжение NM проходит через точку Р: cos Л sin С = sin В cos D, что и требовалось доказать.
(Ь) 	Преобразовав равенства (1) и (2), получим уравнение
a2 + b2 + d2_c2 lcosA = IsinAsinB.
- cos А—\ a d
cos В.
labd b a
Его можно решить численно, получив приближенные значения
(А, В, С, D) = (73°, 140°, 85°, 62°).
51. 	Падающие лестницы
(а) 	В эксперименте ученика А мы будем считать величину угла в и координаты центра масс лестницы С функциями времени (рис. 52). Обозначим массу лестницы буквой т, а ее длину буквой L. Тогда
mr 2
момент инерции относительно С равен I = При
этом координаты центра масс
Сх = ^ cosG, Су = у sin6».
Положим
d# _ rfC*
Vx~~dT и vy~~df-
в
Рис. 52


51. Падающие лестницы 123
Горизонтальные силы на лестницу не действуют, поэтому vx = 0. По закону сохранения энергии
mgL sin во = mgL sin в + mv2 + Ia>2.
Отсюда
(о = — 2 (sin во — sin в)г (1 + cos2 2.
Интеграл функции i по в от во до 0 дает время, за которое падает лестница. Время, за которое упадет
Т_
блок, равно Т = (2L^ngo)2 Интеграл можно найти
численно и добиться, чтобы он стал равен Т, подобрав подходящее значение во. Времена падения одинаковы при приближенном значении во -71°.
(Ь) 	В экспериментах учеников В и С мы примем те же обозначения, что и в экспериментах ученика А (рис. 53).
Рис. 53


124 Решения
По закону сохранения энергии
mgL sin во = mgL sin в + т (v2 + v2) + ho2.
Отсюда
(о = 2 (sin во — sin 0)2.
-1
Интеграл от функции — по в от во до 0 дает время,
за которое падает лестница. В обоих экспериментах эти интегралы одинаковые, поэтому значения во, найденные обоими учениками, равны. И этот интеграл можно найти численно. Времена одинаковые при приближенном значении во = 48°.


ГЛАВА 8. ГОЛОВОЛОМКИ С ТРАПЕЦИЯМИ
52. Минимальные РТЦС
(a) В самой маленькой РТЦС (г,Ь,а,с) = (1,2,1,1).
(b) (г, Ь, а, с) = (13,23,1,13) или (13,23,1,22).
(c) (г, Ъ, а, с) = (25,50,1,35).
(d) Подойдет такая последовательность:
^2и—1 = [(3 + л/8) н- (3 — л/8) +2j^8;
С2„-1 = [(3 + ✓в)2"-’ + (3 - V?)2"-1 + 2 ]/Ж
Вот несколько первых ее элементов: (г,а,Ь,с) = (1,2,1,1), (25,50,1,35), (841,1682,1,1189), (28561,57122,1,40391),...
53. Наименьшая окружность
(a) (г,Ъ,а,с) = (1012,2008,1,1338) или (1012,2008,1,1518).
(b) (г, Ь, а, с) = (27612,51128,1,30 798) или (27612,51 128,1,45838).
54. Простые РТЦС
(a) (г,Ь,а,с) = (7,13,2,11) или (7,13,11,2).
(b) Решение неизвестно.
(c) Таких много, например: (г,Ь,а,с) = (7,13,2,7),
(7,13,11,7), (13,23,1,13) или (19,37,11,19).
(d) Решение неизвестно, причем я не смог найти ни одного решения при г < 20 000.


126 Решения
55. Плоские РТЦС
(a) (г,Ь,а,с) = (13,23,2,1).
(b) Подойдет такая последовательность:
гп= [(3 + 2\/3)(7 + 4л/3)”- (3-2\/3)(7-4\/3)и]/(4\/3); ап= [(3 + 2\/3)(7 + 4\/3)"- (3 - 2л/3) (7 - 4\/3)и - 2 ]^4; Ъп = в-п
Вот несколько первых ее элементов: (г,Ъ,а,с) =
= (13,24,23,1), (181,314,313,1), (2521,4367,4366,1),...
56. Вытянутые РТЦС
(a) (г,Ь,я,с) = (512,141,64,1016), здесь | = 7,2.
(b) (г, Ъ, а, с) = (3523,698,157,7033), здесь | = 10,08.
(c) Подойдет последовательность
гп = и3, К = Зп2 - 1, яи = п2, с„ = 2п3 - п; здесь приближается к с ростом и.
57. Почти квадратные РТЦС
(a) (г, &, я, с, q) = (106,149,131,159, ^ = 0,1879...)
и 0r,b,a,c,q) = (125,182,175,175, ^ = 0,0769...) —две
самые маленькие РТЦС такого вида.
(b) Как мы сейчас увидим, таких последовательностей несколько.
Рассмотрим уравнения в целых числах х2 -2у„ = 1.
У них есть такие решения:
Хп = [{ 3 + V8)”+(3-V8)"]/2;
= [(3 + V8)” - (3 - \/8)” У^8.


58. РТЦС с целыми высотами 127
Тогда при гп = Уп, К = хпугп, яи = xn(yl - 1) и сп = Ъп 1
получаем qn = —.
Уп
А при г'п = хъп, Ь'п = 2у„(х2 + 2), = 2у„х* и
/ 4
получаем = — .
Хп +2
Рассмотрим еще такие уравнения в целых числах:
*1~2у1 = -*•
У них есть такие решения:
х„ = [(1 + V5) + (1 — л/2) J jl)
Уп = £(1 + V5) — (1 — V2) J j V8.
Тогда при гп = у\, Ъп = х„(у2 + 1), я„ = х„у2 и см = яи
получаем ап = —.
Уи + 1
А при г; = х%, Ь'п = 2ynxl, а'п = 2уп(хгп - 2) и
о
получаем q'n = —.
58. 	РТЦС с целыми высотами
На рис. 54 изображены четыре различные трапеции с минимальным радиусом описанной окружности г = 65. У них такие параметры: (г,Ъ,а,с) = (65,126,66,50), (65,126,66,78), (65,112,32,50) и (65,112,32,104).


128 Решения
59. 	Наименьшая РТЦС в квадрате
(а) 	Тип A: (a,b,c,s) = (1,2,1/2) или (1,2,2,2), см. рис. 55.
Тип Л
s = 2 Рис. 55
(Ь) 	Тип В: (a,b,c,s) = (1 или 2,11 или 12,13,12), см. рис. 56, слева.
Тип С: (a,b,c,s) = (4,10,5,8), см. рис. 56, в центре.
Тип D: \a,b,c,s) = (7,13,17,16), см. рис. 56, справа.
Тип В
Тип С
Тип D
а = 1 или 2 £> = 11 или 12 s = 12
Рис. 56
(с) 	Тип А: (я, Ь, с, s) - (1,11,12,11), см. рис. 57.
Тип А
Рис. 57


61. РТЦС, у которой а = с <|29
(d) 	Тип A: (a,b,c,s) = (1,36,40,36), см. рис. 58.
Тип А
60. 	РТЦС, у которой а = s
(а) 	Тип С: (я, Ь, с, s) = (24,30,5,24), см. рис. 59.
Тип С
(Ь) 	Для произвольного целого к>\ положим
ак = Sfc = 4к(4к2 - 1), bk = 4к(4к2 + 1), ск = 4к2 + 1. При А: > 1 подойдет и такая последовательность: ак = sk = (Zk + 1)(4А:2 + 4А: — 3),
Ьк = (2 к + 1)(4 к2 + 4 к + 5), ск = 4 к2 + 4к + 5.
61. 	РТЦС, у которой а = с
(а) 	Тип С: (я, Ь, с, s) = (25,55,25,44), см. рис. 60.
Тип С
Рис. 60


130 Решения
(b) 	Возьмем произвольные различные целые числа тип, т > п и положим а^- с^ = (т2 + и2)2.
Если га2 — п2 < 2тп, то положим
Ьк = (т2 + п2)(3т2 - и2)
и
sk = 2тп(3т2 - и2).
Если т2 - и2 > 2mn, то положим
frfc = (m2 + n2)(m2 + 4mn + и2)
и
Sfc = (m2 — n2)(m2 + 4 mn + n2).
62. 	РТЦС, у которой x = u
(а) 	Тип С: (a,b,c,s) = (7,25,15,20), см. рис. 61.
Тип С и = 4,2
Рис. 61
(Ь) 	Фиксируем произвольные натуральные числа к, т, п такие, что т > п, т и п взаимно просты и имеют разные четности. Пусть А — наименьшее из чисел к{т2-п2) и 2ктп, а В — наибольшее из чисел к(т2—п2) и 2ктп, С = к(т2 + п2). Тогда а = С2 - 2Л2, & - С2,
о лЗ
с = АС, х = и = АС — =0- и s = ВС.


63. РГЦС, у которой b/s > 14 131
63. 	РТЦС, у которой у > 14
(а) 	{а,Ъ,с,s) = (17,2,873,2028,2040); | = 1,408333..., см. рис. 62.
Тип С
\ 2,873 2,028
2,028 \
а = 17 s = 2,040
Рис. 62
(b) Для четных к положим o*=[(V2+l)M + (V2-l)M]/V2,
c1 = [(\/2+1)**2-(V5+1)*:+(V2-1)':-(v5-1)3':‘,2]/(4V2), st=[(\/2+l)®*2 + (V2+l)t-(4/2-l)*:-(v5-l)“',2]/V32. Для нечетных к положим a,= [(^+l)fc+1 + (V2-l)fc+1]/2,
bk=[(V2+l)3k+\(V2+l)\(V2-l)\(V2-lf+2yV32f
cfc=[(V2+l)3fc+^(V2+l)fc+(V2-l)fc-(V2-l)3fc+2]/8,
Sfc= [ (>/2+l)3fc+2+ (v/2+l)fc— (\/2-l)fc— (-y/2—i)3?C+2]/8.
(c) При к = 3 из уравнений ниже получаем
(а, Ь, с, s) = (71,16 969, И 999,12 049); | = 1,4083326..., см. рис. 63.


132 Решения
Тип D
а = 71 w = 1,43
Рис. 63
(d) 	Выберем произвольное целое к > 1. Положим а*= [(x/I + l)2*-(V2-l)a + V8]/v/8, bk = [(^-И)*’1 + + ч/8(^2 +1)2*"1 -
c* = [(x/2 +1 )**" - (V2 - I)"*1 + V8(V2 + I)2**1 +
+ V8(V2-l)“+1-2]/8, s* = [(^+ I)®*1 - (v/2-1)"*1 + (4v^-2)(v^ + 1)2*+1 + + (4v^ + 2) (V2 - l)a*’+ 21/8.
64. 	РТЦС, у которой | < 0,8, 0,75 и 0,71
Тип D: Для любого целого га > 2 положим
% = 2m2 — 4m +1, fo*. = 2m2 — 1, с*. = 2m2 - 2m +1 и Sfc — целая часть (2m (m — l)\/2). Для этой последовательности отношение - убывает и стремится к -^= с ростом га.
s V2
(а) 	При т = 9 мы получаем
(а, Ь, с, s) = (127,161,145,203) и | = 0,7931034 см. рис. 64, слева.


65. РТЦС наименьшей площади 133
Тип D
Тип D
Тип D
s = 203 iv = 43,1
s = 865 w = 219,1
Рис. 64
s= 170,469 w = 49,439
(b) При т = 18 получаем
(я, Ь, с, s) = (577,647,613,865) и | = 0,7479768
см. рис. 64, в центре.
(c) При т = 246 получаем
(я, Ъ, с, s) = (120 049,121 031,120541,170469)
см. рис. 64, справа.
65. 	РТЦС наименьшей площади
(а) 	Тип D: при к = 4 из формул ниже получаем (я, Ъ, с, s) = (409,569 737,402 845,403154). Отношение площади трапеции к площади квадрата равно 0,500000255, см. рис. 65.
Тип D
а = 409 w = 1,42
Рис. 65


134 Решения
(b) 	При различных целых к > 1 получаем последовательность трапеций, отношение площадей которых к площади квадрата убывает с ростом к:
ак = [(л/2 + 1)2* - (л/5- I)2* + ч/8]/ч/8,
Ък = [(>/5 + i)4fc+1 + (л/5- i)4fc+1 + V8(V2 + I)2*"1 - — л/8(л/5 — I)2**1 - л/8 ]/л/32, с* = [(л/5 + l)4fc+1 - (л/2-1)4А:+1 + \/8(л/2 + 1)2А:+г +
+ л/8(л/2 —1)^+1 -2]/8,
sfc = [(л/2 + l)4fc+1 - (л/5 - l)4fc+1 + (4л/2 - 2) (л/5 + 1)
+ (4л/2 + 2) (л^-1)^+г+2]/8.
2fc+l
66. 	Наибольший квадрат
Все решения для типа D получаются из прямоугольных треугольников с целыми сторонами, как видно на рис. 66.
Тип D
и
W
Обозначим стороны треугольника буквами е, h и с и положим е = К(т2 — и2), h = 2Ктп и с - К(т2 + и2). Тогда из соотношений
s = (a + e)sine + hcos6 = (а + е) cos в+ h sin в следует, что a = h — е и Ъ -h + e. Отсюда можно получить решения для всех s из промежутка от smin = int [ ^ + +1


67. Неединственные решения 13 5
до smax = int(hV2). Здесь int() обозначает целую часть числа. Численный анализ показывает, что s = 95 — сторона наибольшего квадрата, в который нельзя вписать РТЦС типа D:
пара (т,п) = (7,6) дает решения для s от 96 до 118;
пара (ш,п) = (10,1) дает решения для s от 117 до 140;
пара (т,и) = (8,7) дает решения для s от 126 до 158;
пара (m,n) = (11,2) дает решения для s от 151 до 165;
пара (т,п) = (9,8) дает решения для s от 160 до 203;
пара (m,n) = (т,т — 1) при т> 9 дает решения для s от 198 до оо;
проверка всех возможностей при К = 1 показывает отсутствие решений для s = 5, 19 или 95.
67. 	Неединственные решения
РТЦС (а,Ъ,с) = (7,31,25) типа D можно вписать в квадраты со сторонами s = 30, 31, 32 или 33, см. рис. 67.
Тип D Тип D
Тип D


136 Решения
68. 	Наименьшие квадраты
(a) 	s = 2. Две трапеции (a,b,c,s) = (1,2,1,2) и (1,2,2,2) типа А, изображенные на рис. 68.
Тип А
s = 2 Рис. 68
(Ь) 	Как видно на рис. 69, для квадрата со стороной s = 8 есть 44 решения типа А, а типа С — только одно. 44 решения получаются, когда а меняется от 1 до 7, а с меняется от к до 8, где к — наименьшее значение с, допустимое для выбранного а.
Тип А Тип С
s = 8
(с) 	На рис. 70 изображен тип А, в этом решении = 0,01.
Тип Л
s = 101 Рис. 70


68. Наименьшие квадраты 13 7
(d) Тип D: {a,b,c,s) = (81 205,81 607,81 205,81 606); ^-=-^ = 0,0099751..., см. рис. 71.
Тип D
s = 81,606 Рис. 71
(e) Построим последовательность решений, для всех к > 3 положив
ак = 2к2 -4к + -[, Ък = 2к2 - 1,
ск = 2к2 -2к + 1, sk = 2к2 - 2.
Тогда последовательность значений ^ ~а убывает:
Ьк ~ ак _ 2 ЗА: — 1
% к 2к3-4к2 +к'
(f) s = 16. Тип С: (a,b,c,s) = (14,20,5,16), (a,b,c,s) =
= (8,20,10,16), см. рис. 72, слева и в центре.
Тип D: (я, Ь, с, s) = (8,17,13,16), см. рис. 72, справа.
Тип С
Тип С
Тип D
/ о\
\ \ 20
\4 \
\ 5\
/ю\
\ 2\
\8 \
\ 10\
/13 174
\8^3
S = 16
s = 16 Рис. 72
S = 16
(g) s = 31. (а, Ь, с, s) = (17,31,25,31), см. рис. 73, слева.


138 Решения
(h) 	s = 161. (a,b,c,s) = (73,161,125,161),
(a,b,c,s) = (127,161,145,161), см. рис. 73, в центре и справа.
Тип D
Тип D
Тип D
s = 31 w= 1,24
Рис. 73
(i) 	s = 21 и 31. (a, fc, с, s) = (7,23,17,21), (a,b,c,s) = (17,31,25,31), см. рис. 74.
Тип D
s = 21
s = 31
Рис. 74


ГЛАВА 9. ДЖИПЫ В ПУСТЫНЕ
69. 	Дорога в один конец на одном джипе
(a) Расстояние равно Джип едет до точки Pi
1 1 с координатой х = -, оставляет там - бака топлива
и возвращается в точку А. Заправляет полный бак, едет в Pi, заправляется под завязку и едет до точки 4
с координатой х = -.
(b) Расстояние равно 1,3. Джип едет до точки Pi
с координатой х = 0,3, оставляет там 0,3 бака топлива и возвращается в точку А. Заправляет полный бак, едет в Pi, заправляется под завязку и едет до точки с координатой х = 1,3.
(c) Требуется 1,99 бака топлива. Джип едет до точки Pi с координатой х = 0,33, оставляет там 0,33 бака топлива и возвращается в точку А. Заправляет полный бак, едет в Р1, заправляется под завязку и едет до точки с координатой х = 1,33.
(d) Расстояние равно Джип едет до точки Рi
с координатой х = 0,2, оставляет там 0,6 бака топлива и возвращается в точку А. Заправляет полный бак, едет в Pi, заправляется под завязку (оставив там 0,4 бака топлива) и едет до точки Рг с координатой
Л 1 О -I
х = g + ^ = —, где оставляет - бака топлива. Оттуда
джип опять возвращается в точку А, по дороге долив 0,2 бака топлива в Pi и столько же там оставив. В А джип заправляет полный бак, едет в Pi, заправляется под завязку, оттуда — в Рг и там опять заправляется


140 Решения
под завязку. Ему хватает топлива, чтобы доехать до точки В с координатой х = Ц.
до
(e) Расстояние равно Джип едет до точки Pi
с координатой х = 0,1, оставляет там 0,3 бака топлива и возвращается в точку А. Заправляет полный бак, едет в Pi, заправляется под завязку (оставив там 0,2 бака топлива) и едет до точки Рг с координатой
1 1 1 О 1
•X = ^ ^ где оставляет ± бака топлива. Оттуда
джип опять возвращается в точку А, по дороге долив 0,1 бака топлива в Pi и столько же там оставив. В А джип заправляет полный бак, едет в Pi, заправляется под завязку, оттуда — в Рг и там опять заправляется под завязку. Ему хватает топлива, чтобы доехать до
_ ЛГХ
точки В с координатой х =
17
(f) Требуется — бака топлива. Джип едет до точки Р\ с координатой х = i, оставляет там 0,5 бака топлива и возвращается в точку А. Заправляет полный бак, едет в Pi, заправляется под завязку (оставив там |
бака топлива) и едет до точки Рг с координатой
111 1 х = - + - = -, где оставляет - бака топлива. Оттуда
джип опять возвращается в точку А, по дороге долив
\ бака топлива в Pi и столько же там оставив. В А
О
джип заправляет полный бак, едет в Pi, заправляется под завязку, оттуда — в Рг и там опять заправляется под завязку. Ему хватает топлива, чтобы доехать до точки В с координатой х = 1,5.
9П91
(g) Требуется 7 + бака топлива и 7 пунктов
дозаправки. Проще всего в этом убедиться, проследив за маршрутом от конца к началу; конец — в точке В с координатой х = 2. Чтобы в нее попасть, надо запасти


70. Аорога туда и обратно на одном джипе 141
бак топлива в точке Р7 с координатой х = 1. Чтобы
это топливо туда доставить, нужно иметь два бака
1
топлива и джип в точке Рв с координатой х = 1 —
А для этого потребуется три бака топлива и джип
в точке Р5 с координатой х = 1 — i Продолжая
рассуждения, приходим к выводу, что понадобится 7 баков топлива и джип в точке Pi с координатой
_ 1 1 1 1 1 1 2021
3 5 7 9 11 13 45 045'
Для этого придется сделать 7 ходок из А в Pi
и обратно, каждый раз оставляя в Pi fбака
45 045
топлива. В последний раз джип выезжает из А, заправив топливом бака.
70. 	Дорога туда и обратно на одном джипе
о
(a) Расстояние равно Джип едет до точки Pi
1 1 с координатой х = оставляет там - бака топлива
и возвращается в точку А. Заправляет полный бак, едет в Pi, заправляется под завязку (оставив там
j бака топлива) и едет до точки В с координатой
О
х = j. Оттуда он возвращается в А, дозаправившись по дороге в Pi.
(b) Расстояние равно Джип едет до точки Р\
с координатой х = оставляет там А бака топлива
и возвращается в точку А. Заправляет полный бак, едет в Pi, заправляется под завязку (оставив там
бака топлива) и едет до точки В с координатой
29
х = —. Оттуда он возвращается в А, дозаправившись по дороге в Р\.


142 Решения
(c) Требуется 1,8 бака топлива. Джип едет до точки Р\ с координатой х = 0,2, оставляет там 0,4 бака топлива и возвращается в точку А. Заправляет полный бак, едет в Р\, заправляется под завязку (оставив там 0,2 бака топлива) и едет до точки В с координатой х = 0,7. Оттуда он возвращается в А, дозаправившись по дороге в Р].
(d) Расстояние равно Джип едет до точки Pi
1 1 с координатой х = оставляет там - бака топлива
и возвращается в точку А. Заправляет полный бак,
едет в Pi и оставляет там еще - бака топлива, всего
там теперь - бака. Опять едет в А, заправляется
и держит путь в Pi. Доливает полный бак (при этом
в Pi остается Щ бака топлива) и едет до точки Р2
1 1
с координатой х = — + Оставляет там полбака
топлива и возвращается в Р\. Там заправляется под завязку (оставив А бака топлива), едет в Рг, еще
1
раз заправляется под завязку (теперь в Р2 имеется ^ бака топлива) и движется в точку В с координатой
-I -1 -1 С
x~j2+^ + ^ = ^- Оттуда он возвращается в А.
1 1
(e) Требуется у- бака топлива и 3 пункта дозаправки
111 111 (в точках с координатами —, —+ - и —+ ^+4)- Проще
всего в этом убедиться, проследив за маршрутом от конца к началу; конец — в точке В с координатой
х = 1. Чтобы в нее попасть, надо запасти | бака
л
топлива в точке Рз с координатой х - Чтобы это
топливо туда доставить, нужно иметь — бака топлива
111
и джип в точке Р2 с координатой х = - - - =
ГУ7
А для этого потребуется ^ бака топлива и джип
111 1
в точке Pi с координатой = —• Лля этого
придется сделать 3 ходки из А в Pi и обратно, каждый


71. /Хорога в один конец с джипом-помощником 143
раз оставляя в Pi | бака топлива. В последний раз джип выезжает из А, заправив топливом - бака. Всего
Оу rj -| -л
потребуется У2 + 12 = 1Г бака топлива.
(f) 	Требуется 10 + |||^ бака топлива и 10 пунктов дозаправки в точках
Рю(1); P9(l-i);
р (_J_ = 179 \
Ч 4 6 8 10 20 5040 У'
Проще всего в этом убедиться, проследив за маршрутом от конца к началу; конец — в точке В
о
с координатой х = Чтобы в нее попасть, надо запасти 1 + ^ бака топлива в точке Рю с координатой
х = Чтобы это топливо туда доставить, нужно иметь
л
2 + - бака топлива и джип в точке Р9. Продолжая
рассуждения, мы видим, что в точке Pi надо накопить 179 /"
10 + бака топлива. Для этого придется сделать
10 ходок из А в Pi и обратно, каждый раз оставляя в Р1 ^20 бака топлива. В последний раз джип
QQOO
выезжает из А, заправив топливом бака. Всего
потребуется 10 + ^~г +21 • = 10+ бака топлива.
r J 5040 5040 2520
71. 	Дорога в один конец с джипом-помощником
(а) 	Расстояние равно |. Джип 1 едет до точки Pi
с координатой х = i и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается


144 Решения
в точку А. После этого первый джип едет в точку В 4
с координатой х = -.
ос
(Ь) 	Расстояние равно Джип 1 едет до точки Р\
с координатой х = i и останавливается там. Джип 2
едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг
12 7
с координатой х = z + - - —. Джип 2 едет из А
О У lO
в Рг, дозаправляет джип 1 и возвращается в точку А.
И наконец, джип 1 едет в точку В с координатой
(с) 	Топлива потребуется 3 бака. Джип 1 едет до точки Рi с координатой х = i и останавливается там. Джип 2
едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг
с координатой х = \ + i Джип 2 едет из А
О У У
в Рг, дозаправляет джип 1 и возвращается в точку А. И наконец, джип 1 едет в точку В с координатой
(d) 	Топлива потребуется 3,69 бака. Джип 1 едет до точки Pi с координатой х = 0,23 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг с координатой х = 0,41. Джип 2 едет из А в Рг, дозаправляет джип 1 и возвращается в точку А. Теперь джип 1 едет уже в точку Рз с координатой х = 0,47. Джип 2 едет из А тоже в Рз, дозаправляет джип 1 и возвращается в точку А. И наконец, джип 1 едет в точку В с координатой х = 1,47.
(е) 	Топлива потребуется 4,609 бака. Джип 1 едет до точки Pi с координатой х = 0,203 и останавливается там.


72. Дорога в один конец на двух джипах 145
Джип 2 едет из А в Р \, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг с координатой х = 0,401. Джип 2 едет из А в Рг, дозаправляет джип 1 и возвращается в точку А. Теперь джип 1 едет уже в точку Рз с координатой х = 0,467. Джип 2 едет из А тоже в Рз, дозаправляет джип 1 и возвращается в точку А. На следующем шаге джип 1 едет в точку Р4 с координатой х = 0,489. Джип 2, как всегда, едет из А в Р4, дозаправляет джип 1 и возвращается в точку А. И наконец, джип 1 едет в точку В с координатой х = 1,489.
72. 	Дорога в один конец на двух джипах
17
(a) Расстояние равно -. Джип 1 едет до точки Pi
1
с координатой х = ^ и останавливается там. Джип 2
едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. Заправившись, джип 2 едет в Pi — там
теперь | бака топлива. Его надо разделить поровну между обоими джипами, и тогда они доберутся до
1^7
точки В, которая отстоит от А на расстояние ^ + |
Для такого путешествия надо 3 бака топлива.
(b) Топлива потребуется 4 бака. Джип 1 едет до точки Р\
-1
с координатой х = ± и останавливается там. Джип 2
едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг
с координатой х = ^. Джип 2 едет из А в Рг,
У
дозаправляет джип 1 и возвращается в точку А. Заправившись, второй джип едет в Рг — там теперь
бака топлива. Его надо разделить поровну между обоими джипами, и тогда они доберутся до точки В,


146 Решения
которая отстоит от А на расстояние ^ ^ Для
9 9 9
такого путешествия надо 4 бака топлива.
(c) Топлива потребуется 4,42 бака. Джип 1 едет до точки Р\ с координатой х = 0,14 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг с координатой х = 0,38. Джип 2 едет из А в Рг, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рз с координатой х = 0,46. Джип 2 едет из А в Рз, дозаправляет джип 1 и возвращается в точку А. Заправившись, второй джип едет в Рз — там теперь 1,54 бака топлива. Его надо разделить поровну между обоими джипами, и тогда они доберутся до точки В, которая отстоит от А на расстояние 0,46 + 0,77 = 1,23. Для такого путешествия надо 4,42 бака топлива.
67
(d) Расстояние равно Джип 1 едет до точки Pi
с координатой х = ^ и останавливается там. Джип 2
едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг
с координатой х = Джип 2 едет из А в Рг,
9
дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рз с координатой
х = Джип 2 едет из А в Рз, дозаправляет
джип 1 и возвращается в точку А. Заправившись,
второй джип едет в Рз — там теперь бака топлива.
Его надо разделить поровну между обоими джипами, и тогда они доберутся до точки В, которая отстоит
1Q АЛ £Г7
от А на расстояние ^7 + 54 = §][• Для такого путешествия надо 5 баков топлива.


72. Дорога в один конец на двух джипах 147
1339
(е) 	Расстояние равно Джип 1 едет до точки Р\
19
с координатой х = ^ и останавливается там. Джип 2
едет из Л в Рг, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг
79
с координатой х = Джип 2 едет из Л в Рг,
дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рз с координатой 2S9
* = 51Г Ажип ^ едет из А в Рз, дозаправляет
джип 1 и возвращается в точку А. Заправившись,
второй джип едет в Рз—там теперь бака топлива.
Его надо разделить поровну между обоими джипами, и тогда они доберутся до точки В, которая отстоит
от А на расстояние Щ + Для такого
путешествия надо 4,95 бака топлива.
(f) 	Топлива потребуется 6,095 бака. Джип 1 едет до точки Pi с координатой х = 0,365 и останавливается там. Джип 2 едет из А в Р\, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг с координатой х = 0,455. Джип 2 едет из Л в Рг, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рз с координатой х = 0,485. Джип 2 едет из А в Рз, дозаправляет джип 1 и возвращается в точку А. Теперь первый джип едет в точку Р4 с координатой х = 0,495. Джип 2 едет из А в Р4, дозаправляет джип 1 и возвращается в точку А. Заправившись, второй джип едет в Р4 — там теперь 1,505 бака топлива. Его надо разделить поровну между обоими джипами, и тогда они доберутся до точки В, которая отстоит от А на расстояние 0,495 + 0,7525 = 1,2475. Для такого путешествия надо 6,095 бака топлива.


148 Решения
73. 	Дорога туда и обратно с джипом-помощником
Q
(a) Расстояние равно Джип 1 едет до точки Р \
л
с координатой х = - и останавливается там. Джип 2
едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг
с координатой х = —. Джип 2 едет из А в Рг, дозаправляет джип 1 и возвращается в точку А. Далее
О
первый джип едет в точку В с координатой х = ^
и возвращается в Рг. Джип 2 привозит ему туда из А топливо на дорогу до Pi и возвращается. Первый джип едет в Pi. Второй привозит ему туда из А топливо на дорогу до А и возвращается. Первый тоже возвращается в А. Для такого путешествия надо 4 бака топлива.
1 1
(b) Расстояние равно —. Джип 1 едет до точки Pi
с координатой х = j- и останавливается там. Джип 2
едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг
11 R
с координатой х = - + ^ Джип 2 едет из А в Рг,
дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку В с координатой 1 1
л: = ^ и возвращается в Рг. Джип 2 привозит ему
туда из А топливо на дорогу до Р\ и возвращается. Первый джип едет в Pi. Второй привозит ему туда из А топливо на дорогу до А и возвращается. Первый тоже возвращается в А. Для такого путешествия надо 4,5 бака топлива.
(c) Требуется 6,11 бака топлива. Джип 1 едет до точки Pi с координатой х = 0,185 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг с координатой х = 0,395. Джип 2 едет из А в Рг,


73. Дорога туда и обратно с джипом-помощником 149
дозаправляет джип 1 и возвращается в точку А. Затем первый джип едет в точку Рз с координатой х = 0,465. Джип 2 едет из Л в Рз, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку В с координатой х = 0,965 и возвращается в Рз. Джип 2 привозит ему туда из А топливо на дорогу до Рг и возвращается. Первый джип едет в Рг- Джип 2 привозит ему туда из А топливо на дорогу до Pi и возвращается. Первый джип едет в Р\. Второй привозит ему туда из А топливо на дорогу до А и возвращается. Первый тоже возвращается в А. Для такого путешествия надо 6,11 бака топлива.
(d) Требуется 7 баков топлива. Джип 1 едет до точки Pi
-1
с координатой х = ^ и останавливается там. Джип 2
едет из Л в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг
11 д
с координатой х = g + g = ^ • Джип 2 едет из А
в Рг, дозаправляет джип 1 и возвращается в точку А. Затем первый джип едет в точку Рз с координатой
х = гт + 4т ~ Ш- Джип 2 едет из А в Рз, дозаправляет
У z/ 217
джип 1 и возвращается в точку А. После этого
53
первый джип едет в точку В с координатой х = ^
и возвращается в Рз. Джип 2 привозит ему туда из А топливо на дорогу до Рг и возвращается. Первый джип едет в Рг. Джип 2 привозит ему туда из А топливо на дорогу до Pi и возвращается. Первый джип едет в Pi. Второй привозит ему туда из А топливо на дорогу до А и возвращается. Первый тоже возвращается в А. Для такого путешествия надо 7 баков топлива.
(e) Требуется 7,3 бака топлива. Джип 1 едет до точки Pi с координатой х = 0,05 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг с координатой х = 0,35. Джип 2 едет из А в Рг,


150 Решения
дозаправляет джип 1 и возвращается в точку А. Затем первый джип едет в точку Рз с координатой х = 0,45. Джип 2 едет из А в Рз, дозаправляет джип 1 и возвращается в точку А. Теперь первый джип едет
1 29
в точку Р4 с координатой х = 0,45 + — = —. Джип 2
едет из А в Р4, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку В
с координатой х = Ц- и возвращается в Р4. Джип 2
привозит ему туда из А топливо на дорогу до Рз и возвращается. Первый джип едет в Р3. Джип 2 привозит ему туда из А топливо на дорогу до Рг и возвращается. Первый джип едет в Рг. Джип 2 привозит ему туда из А топливо на дорогу до Р\ и возвращается. Первый джип едет в Р\. Второй привозит ему туда из А топливо на дорогу до А и возвращается. Первый тоже возвращается в А. Для такого путешествия надо 7,3 бака топлива.
134
(f) 	Расстояние равно Джип 1 едет до точки Р\
с координатой х = 0,3 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Рг
о 10
с координатой х = 0,3 + ^ Джип 2 едет из А
в Рг, дозаправляет джип 1 и возвращается в точку А. Затем первый джип едет в точку Рз с координатой 1 о о 43
х = ^ + ^ = |£. Джип 2 едет из А в Рз, дозаправляет
джип 1 и возвращается в точку А. Теперь первый
43 2 133
джип едет в точку Р4 с координатой *=— + — =
Джип 2 едет из А в Р4, дозаправляет джип 1 и возвращается в точку А. После этого первый джип
144
едет в точку В с координатой х = и возвращается
в Р4. Джип 2 привозит ему туда из А топливо на дорогу до Рз и возвращается. Первый джип едет


74. Дорога туда и обратно на двух джипах 151
в Рз. Джип 2 привозит ему туда из А топливо на дорогу до Рг и возвращается. Первый джип едет в Р2. Джип 2 привозит ему туда из А топливо на дорогу до Pi и возвращается. Первый джип едет в Pi. Второй привозит ему туда из А топливо на дорогу до А и возвращается. Первый тоже возвращается в А. Для такого путешествия надо 8,8 бака топлива.
(g) 	Потребуется 8,38 бака топлива. Джип 1 едет до
точки Pi с координатой х = 0,23 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку Р2 с координатой х = 0,41. Джип 2 едет из А в Рг, дозаправляет джип 1 и возвращается в точку А. Затем первый джип едет в точку Рз
с координатой х - 0,47. Джип 2 едет из Л в Рз,
дозаправляет джип 1 и возвращается в точку А.
Теперь первый джип едет в точку Р4 с координатой х = 0,49. Джип 2 едет из А в Р4, дозаправляет джип 1 и возвращается в точку А. После этого первый джип едет в точку В с координатой х - 0,99 и возвращается в Р4. Джип 2 привозит ему туда из А топливо на дорогу до Рз и возвращается. Первый джип едет в Рз. Джип 2 привозит ему туда А топливо на дорогу до Рг и возвращается. Первый джип едет в Рг. Джип 2 привозит ему туда из А топливо на дорогу до Р1 и возвращается. Первый джип едет в Pi. Второй привозит ему туда из А топливо на дорогу до А и возвращается. Первый тоже возвращается в А. Для такого путешествия надо 8,38 бака топлива.
74. 	Дорога туда и обратно на двух джипах
о
(а) 	Расстояние равно -. Джип 1 едет до точки Pi
с координатой х = и останавливается там. Джип 2
едет из А в Pi, дозаправляет джип 1, возвращается в точку А, где заправляется и с полным баком направляется в точку Pi. Оттуда они вместе едут


152 Решения
2
в точку В с координатой х = ^ и возвращаются
в Pi. Джип 1 отправляется в Л и привозит второму джипу оттуда в Pi топливо на обратный путь. Оба возвращаются в А. Для такого путешествия надо 4 бака топлива.
(b) Потребуется 5,2 бака топлива. Джип 1 едет до точки Р1 с координатой х = 0,2 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Рг с координатой х = 0,4. Джип 2 едет из А в Рг, дозаправляет джип 1, возвращается в точку А, где заправляется и с полным баком направляется в точку Рг. Оттуда они вместе едут в точку В с координатой х = 0,7 и возвращаются в Рг. Джип 1 отправляется в А и привозит второму джипу оттуда топливо до Pi. Джип 2 едет в Pi, а джип 1 едет в А и привозит второму джипу оттуда топливо на обратный путь. Оба возвращаются в А. Для такого путешествия надо 5,2 бака топлива.
(c) Расстояние равно Джип 1 едет до точки Р \
л
с координатой х = ^ и останавливается там. Джип 2
едет из А в Pi, дозаправляет джип 1 и возвращается.
Джип 1 едет до точки Рг с координатой х = Джип 2
едет из А в Рг, дозаправляет джип 1, возвращается в точку А, где заправляется и с полным баком направляется в точку Рг- Оттуда они вместе едут
lO
в точку В с координатой х = ^ и возвращаются в Рг.
Джип 1 отправляется в А и привозит второму джипу оттуда топливо до Pi. Джип 2 едет в Pi, а джип 1 едет в А и привозит второму джипу оттуда топливо на обратный путь. Оба возвращаются в А. Для такого путешествия надо 6 баков топлива.


74. Дорога туда и обратно на двух джипах 153
79
(d) Расстояние равно ^Qg • Джип 1 едет до точки Р\
-1
с координатой х = ^ и останавливается там. Джип 2
едет из А в Pi, дозаправляет джип 1 и возвращается.
Джип 1 едет до точки Р2 с координатой х = —.
Джип 2 едет из А в Р2, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Рз
ос
с координатой х = Джип 2 едет из А в Рз,
дозаправляет джип 1, возвращается в точку А, где заправляется и с полным баком направляется в точку Рз. Оттуда они вместе едут в точку В с координатой 79
х = и возвращаются в Рз. Джип 1 отправляется
в А и привозит второму джипу оттуда топливо до Р2. Джип 2 едет в Р2, а джип 1 едет в А и привозит второму джипу оттуда топливо на дорогу до Р\. Джип 2 едет в Pi, а джип 1 едет в А и привозит второму джипу оттуда топливо на обратный путь. Оба возвращаются в А. Для такого путешествия надо 7 баков топлива.
(e) Потребуется 7,92 бака топлива. Джип 1 едет до точки Pi с координатой х = 0,32 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Р2 с координатой * = 0,44. Джип 2 едет из А в Р2, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Рз с координатой х = 0,48. Джип 2 едет из А в Рз, дозаправляет джип 1, возвращается в точку А, где заправляется и с полным баком направляется в точку Рз. Оттуда они вместе едут в точку В с координатой х = 0,74 и возвращаются в Рз. Джип 1 отправляется в А и привозит второму джипу оттуда топливо до Р2. Джип 2 едет в Р2, а джип 1 едет в А и привозит второму джипу оттуда топливо на дорогу до Рь Джип 2 едет в Pi, а джип 1 едет в А и привозит второму джипу оттуда топливо на обратный путь. Оба


154 Решения
возвращаются в Л. Для такого путешествия надо 7,92 бака топлива.
(f) Расстояние равно баков топлива. Джип 1 едет до
точки Р\ с координатой х = 0,2 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Рг с координатой х = 0,4. Джип 2 едет из А в Рг, дозаправляет джип 1 и возвращается. Джип 1 едет
1 7
до точки Р з с координатой х = 0,4 + ^ = ^5-
Джип 2 едет из А в Рз, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Р4
7 1 99
с координатой х = ^ + — = —. Джип 2 едет из А
в Р4, дозаправляет джип 1, возвращается в точку А, где заправляется и с полным баком направляется в точку Р4. Оттуда они вместе едут в точку В
f>7
с координатой х = j-r и возвращаются в Р4. Джип 1
9U
отправляется в А и привозит второму джипу оттуда топливо до Р3. Джип 2 едет в Рз, а джип 1 едет в А и привозит второму джипу оттуда топливо на дорогу до Рг- Джип 2 едет в Рг, а джип 1 отправляется в А и привозит второму джипу оттуда топливо до Р\. Джип 2 едет в Pi, а джип 1 едет в А и привозит второму джипу оттуда топливо на обратный путь. Оба возвращаются в А. Для такого путешествия надо 9,2 бака топлива.
(g) Расстояние равно Джип 1 едет до точки Pi
с координатой х = 0,3 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается.
13
Джип 1 едет до точки Рг с координатой х =
Джип 2 едет из А в Р2, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Рз
13 9 ДЗ
с координатой х = ^ Джип 2 едет из А
чЗи 4э 9U
в Рз, дозаправляет джип 1 и возвращается. Джип 1


74. Дорога туда и обратно на двух джипах 155
43 2 133
едет до точки Р4 с координатой х = ^ + — = —.
Джип 2 едет из Л в Р4, дозаправляет джип \, возвращается в точку А, где заправляется и с полным баком направляется в точку Р4. Оттуда они вместе
едут в точку В с координатой х = и возвращаются
в Р4. Джип 1 отправляется в Л и привозит второму джипу оттуда топливо до Рз. Джип 2 едет в Рз, а джип 1 едет в А и привозит второму джипу оттуда топливо на дорогу до Рг- Джип 2 едет в Рг, а джип 1 отправляется в Л и привозит второму джипу оттуда топливо до Р1. Джип 2 едет в Pi, а джип 1 едет в А и привозит второму джипу оттуда топливо на обратный путь. Оба возвращаются в А. Для такого путешествия надо 9,8 бака топлива.
(h) 	Потребуется 10 баков топлива. Джип 1 едет до
точки Pi с координатой х = i и останавливается
там. Джип 2 едет из А в Pi, дозаправляет
джип 1 и возвращается. Джип 1 едет до точки Рг
с координатой х - Джип 2 едет из А в Рг,
дозаправляет джип 1 и возвращается. Джип 1 едет до точки Рз с координатой * = i + JL = 1|.
Джип 2 едет из А в Рз, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Р4
с координатой х = Джип 2 едет из А
27 о! о!
в Р±, дозаправляет джип 1, возвращается в точку А, где заправляется и с полным баком направляется в точку Р4. Оттуда они вместе едут в точку В Л 91
с координатой х = и возвращаются в Р4. Джип 1
отправляется в А и привозит второму джипу оттуда топливо до Рз. Джип 2 едет в Рз, а джип 1 едет в А и привозит второму джипу оттуда топливо на дорогу до Рг- Джип 2 едет в Рг, а джип 1 отправляется в А и привозит второму джипу оттуда топливо до Р


156 Решения
Джип 2 едет в Pi, а джип 1 едет в А и привозит второму джипу оттуда топливо на обратный путь. Оба возвращаются в А. Для такого путешествия надо 10 баков топлива.
75. 	Два джипа и две станции заправки
(a) Потребуется 3,5 бака топлива. Джип 1 едет до точ-
Л
ки Р1 с координатой х = - и останавливается там.
Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается. Джип 1 едет до точки В с координатой
х = Джип 2 едет из А в Р\ с координатой х = 1.
Джип 1, заправившись в В, едет оттуда в Р\, дозаправляет джип 2 и возвращается в В. Джип 2 едет в В. Для такого путешествия надо 3,5 бака топлива.
(b) Топлива потребуется 4,12 бака. Джип 1 едет до точки Pi с координатой х = 0,02 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Рг с координатой х = 0,34 и останавливается там. Джип 2 едет из А в Рг, дозаправляет джип 1 и возвращается. Джип 1 едет до точки В с координатой х = 1,34. Джип 2 едет из А в Р'2 с координатой х = 1. Джип 1, заправившись в В, едет оттуда в Р'2, доставляет второму джипу топливо, чтобы доехать до точки Р\ с координатой х = 1,32, и возвращается в В. Джип 2 едет из Р'2 в Р\. Джип 1, заправившись в В, едет оттуда в Р\, доставляет второму джипу топливо, чтобы добраться до В, и возвращается в В. Джип 2 едет в В. Для такого путешествия надо 4,12 бака топлива.
(c) Расстояние равно 1,39. Джип 1 едет до точки Pi с координатой х = 0,17 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Р2 с координатой х = 0,39 и останавливается там. Джип 2 едет из А в Рг, дозаправляет джип 1 и возвращается. Джип 1 едет до точки В с координатой х = 1,39. Джип 2 едет из А


75. Два джипа и две станции заправки i 57
в Р'2 с координатой х = 1. Джип 1, заправившись в Б, едет оттуда в Р2, доставляет второму джипу топливо, чтобы доехать до точки Р\ с координатой х = 1,22, и возвращается в В. Джип 2 едет из Р2 в Р[. Джип 1, заправившись в В, едет оттуда в Р\, доставляет второму джипу топливо, чтобы добраться до В, и возвращается в В. Джип 2 едет в В. Для такого путешествия надо 5,02 бака топлива.
2 63
(d) Расстояние равно Джип 1 едет до точки Р\ с координатой х = 0,15 и останавливается там. Джип 2 едет из А в Р\, дозаправляет джип 1 и возвращает-
ся. Джип 1 едет до точки Pi с координатой х = ^
и останавливается там. Джип 2 едет из А в Р2, дозаправляет джип 1 и возвращается. Джип 1 едет до
QO
точки Рз с координатой х = и останавливается
там. Джип 2 едет из А в Рз, дозаправляет джип 1 и возвращается. Джип 1 едет до точки В с координа-
263
той л: = Джип 2 едет из А в Р3 с координатой
х = 1. Джип 1, заправившись в В, едет оттуда в Р'3, доставляет второму джипу топливо, чтобы доехать до
97
точки Р2 с координатой х = —, и возвращается в В.
Джип 2 едет из Р3 в Р2. Джип 1, заправившись в В, едет оттуда в Р^, доставляет второму джипу топли-
CQ
во, чтобы доехать до точки Р[ с координатой х =
и возвращается в В. Джип 2 едет из Р2 в Р\. Джип 1, заправившись в В, едет оттуда в Р\, доставляет второму джипу топливо, чтобы добраться до В, и возвращается в В. Джип 2 едет в В. Для такого путешествия надо 6,9 бака топлива.
(e) Топлива потребуется 7,65 бака. Джип 1 едет до точки Pi с координатой х = 0,275 и останавливается там.
Джип 2 едет из А в Pi, дозаправляет джип 1 и воз¬
вращается. Джип 1 едет до точки Р2 с координатой х = 0,425 и останавливается там. Джип 2 едет из А


158 Решения
в Р2, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Рз с координатой х = 0,475 и останавливается там. Джип 2 едет из А в Рз, дозаправляет джип 1 и возвращается. Джип 1 едет до точки В с координатой х = 1,475. Джип 2 едет из А в Р3 с координатой х = 1. Джип 1 едет из В в Р3, доставляет второму джипу топливо, чтобы доехать до точки Р'2 с координатой х = 1,05, и возвращается в В. Джип 2 едет из Р3 в Р'2. Джип 1 едет из В в Р'2, доставляет второму джипу топливо, чтобы доехать до точки Р\ с координатой х = 1,2, и возвращается в В. Джип 2 едет из Р'2 в Р\. Джип 1 едет из В в Р\, доставляет второму джипу топливо, чтобы добраться до В, и возвращается в В. Джип 2 едет в В. Для такого путешествия надо 7,65 бака топлива.
(f) 	Расстояние равно Джип 1 едет до точки Pi с координатой х = 0,1 и останавливается там. Джип 2
едет из А в Pi, дозаправляет джип 1 и возвраща-
1 1
ется. Джип 1 едет до точки Рг с координатой х = —
и останавливается там. Джип 2 едет из А в Рг, дозаправляет джип 1 и возвращается. Джип 1 едет до
точки Рз с координатой х = и останавливается там.
Джип 2 едет из А в Рз, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Р4 с координатой
х = 27Q и останавливается там. Джип 2 едет из А в Р4,
дозаправляет джип 1 и возвращается. Джип 1 едет до
точки В с координатой х = Джип 2 едет из А
в Р'4 с координатой х = 1. Джип 1 едет из В в Р'4, доставляет второму джипу топливо, чтобы доехать до
точки Р'3 с координатой х = и возвращается в В.
Джип 2 едет из Р4 в Р'3. Джип 1 едет из В в Р'3, доставляет второму джипу топливо, чтобы доехать до
точки Р'2 с координатой х = и возвращается в В.
Джип 2 едет из Р3 в Р2. Джип 1 едет из В в Р2,


75. Два джипа и две станции заправки 159
доставляет второму джипу топливо, чтобы доехать до
187
точки Р\ с координатой х = и возвращается в В.
Джип 2 едет из Р'2 в Р\. Джип 1 едет из В в Р\, доставляет второму джипу топливо, чтобы добраться до В, и возвращается в В. Джип 2 едет в В. Для такого путешествия надо 8,6 бака топлива.
3361
(g) 	Расстояние равно . Джип 1 едет до точки Р\ с координатой х = 0,332 и останавливается там. Джип 2 едет из А в Pi, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Р2 с координатой х = 0,444 и останавливается там. Джип 2 едет из Л в Р2, дозаправляет джип 1 и возвращается. Джип 1 едет до
361
точки Рз с координатой х = и останавливается
там. Джип 2 едет из А в Рз, дозаправляет джип 1 и возвращается. Джип 1 едет до точки Р4 с координа- 1111
той х = ——- и останавливается там. Джип 2 едет из А
225U
в Р4, дозаправляет джип 1 и возвращается. Джип 1
3361
едет до точки В с координатой х = . Джип 2 едет
из А в Р'4 с координатой х = 1. Джип 1 едет из В в Р'4, доставляет второму джипу топливо, чтобы доехать до
1139
точки Рз с координатой х = ——, и возвращается в В.
Джип 2 едет из Р'4 в Р3. Джип 1 едет из В в Р'3, доставляет второму джипу топливо, чтобы доехать до
11Я1
точки Р'2 с координатой х = и возвращается в В.
Джип 2 едет из Р'3 в Р2. Джип 1 едет из В в Р2, доставляет второму джипу топливо, чтобы доехать до
1307
точки Р\ с координатой х = УТ25' и возвРа1Чается в &•
Джип 2 едет из Pi, в Р[. Джип 1 едет из В в Р\, доставляет второму джипу топливо, чтобы добраться до В, и возвращается в В. Джип 2 едет в В. Для такого путешествия надо 9,992 бака топлива.


160 Решения
76. 	Дорога туда и обратно на трех джипах
(a) Топлива потребуется 4 бака. Сначала все три джипа едут до точки Р\ с координатой х = 0,25. Джипы 1 и 2 заправляются под завязку топливом из третьего джипа и едут из Pi в Рг с координатой х = 0,5. Первый джип заправляется там под завязку топливом из второго джипа, оттуда едет в точку В с координатой х = 1 и возвращается в Р2. Оттуда джипы 1 и 2, поделив топливо из второго джипа между собой, едут в Р\. Джип 3 привозит им обоим топливо из Л в Pi, после чего все три джипа возвращаются в А. Для такого путешествия требуется 4 бака топлива.
(b) Топлива потребуется 4,06 бака. Сначала все три джипа едут до точки Pi с координатой х = 0,1325. Джипы 1 и 2 заправляются под завязку топливом из третьего джипа и едут из Pi в Р2 с координатой х = 0,255. Джип 1, заполнив бак топливом из второго джипа, едет в точку Рз с координатой х = 0,505. Третий джип возвращается из Pi в А, заправляется там и едет в Р2. Джип 2 заполняет бак и едет из Р2 в Рз. Джип 1 тоже заполняет бак, едет из Рз в точку В с координатой х = 1,005 и возвращается в Рз. Джипы 1 и 2 едут из Рз в Pi, забрав топливо у третьего джипа в Р2. Джип 3 едет в А, привозит оттуда топливо в Pi, после чего все три джипа возвращаются в А. Для такого путешествия требуется 4,06 бака топлива.
(c) Топлива потребуется 4,12 бака. Сначала все три джипа едут до точки Pi с координатой х = 0,14. Джипы 1 и 2 заправляются под завязку топливом из третьего джипа и едут из Pi в Рг с координатой х = 0,26. Джип 1 едет из Рг в Рз с координатой х = 0,51. Третий джип возвращается из Pi в А, заправляется там и едет в Р2. Джип 2 заполняет бак и едет из Р2 в Рз. Там джип 1 заполняет бак, едет из Рз в точку В с координатой х = 1,01 и возвращается в Рз. Джипы 1 и 2 едут из Рз в Pi, забрав в Р2 топливо у джипа 3. Джип 3 едет из Р2 в А и привозит оттуда топливо в Pi. После этого все три джипа возвращаются в А. Для такого путешествия требуется 4,12 бака топлива.


76. Дорога туда и обратно на трех джипах 161
(d) Топлива потребуется 4,48 бака. Сначала все три джипа едут до точки Р\ с координатой х = 0,185. Джипы 1 и 2 заправляются под завязку топливом из третьего джипа и едут из Pi в Рг с координатой х = 0,29. Джип 1 едет из Рг в Рз с координатой х = 0,54. Третий джип возвращается из Pi в А, заправляется там и едет в Р2. Джип 2 заполняет бак и едет из Р2 в Рз. Там джип 1 заполняет бак, едет из Рз в точку В с координатой х = 1,04 и возвращается в Рз. Джипы 1 и 2 едут из Рз в Pi, забрав в Р2 топливо у третьего джипа. Джип 3 едет из Рг в А и привозит оттуда топливо в Pi. После этого все три джипа возвращаются в А. Для такого путешествия требуется 4,48 бака топлива.
(e) Расстояние равно —. Сначала все три джипа едут
о
до точки Р1 с координатой х = —. Джипы 1 и 2
заправляются под завязку топливом из третьего джипа
9 11 19
и едут из Pi в Р2 с координатой х = — + — =
Джип 1, заправившись топливом из второго джипа,
19 1 17
едет из Р2 в Рз с координатой х = ^ ^
Третий джип возвращается из Pi в А, заправляется
там и едет в Р2. Джип 2 заполняет бак и едет
из Р2 в Рз. Там джип 1 заполняет бак, едет из Рз
1 6
в точку В с координатой л: = ^ и возвращается
в Рз. Джипы 1 и 2 едут из Рз в Pi, забрав в Р2 топливо у третьего джипа. Джип 3 едет из Р2 в А и привозит оттуда топливо в Pi. После этого все три джипа возвращаются в А. Для такого путешествия требуется 4,8 бака топлива.
13
(f) Расстояние равно Сначала все три джипа едут
до точки Pi с координатой х = 0,25. Джипы 1 и 2 заправляются под завязку топливом из третьего джипа
1 1
и едут из Pi в Р2 с координатой х = 0,25 + — =
117
Джип 1 едет из Р2 в Рз с координатой х = - + - = —•


162 Решения
Третий джип возвращается из Р\ в А, заправляется там и едет в Р2. Джип 2 заполняет бак и едет из Р2 в Рз. Там джип 1 заполняет бак, едет из Рз
в точку В с координатой х = ^ и возвращается
в Рз. Джипы 1 и 2 едут из Рз в Pi, забрав в Р2 топливо у третьего джипа. Джип 3 едет из Р2 в А и привозит оттуда топливо в Р\. После этого все три джипа возвращаются в А. Для такого путешествия требуется 5 баков топлива.


ГЛАВА 10. ГОЛОВОЛОМКИ С ЦИФРАМИ
77. Из цифр 0, 1 и 2 в возрастающем порядке сделай число:
(a) 12 = 0 + 12;
(b) 13 = 01 + 12;
(c) 24 = (0! +1 + 2)! = [(0! + 1) х 2]!.
78. Из цифр 1, 2 и 3 в возрастающем порядке сделай число:
(a) 12 = 1 х 2 х 3! = (1 + 2)1 + 3!;
(b) 13 = 1+2x3!;
(c) 15 = 12 + 3;
(d) 24 = 1 + 23 = (12/3)! = (I2 + 3)!;
(e) 27 = (1 + 2)3;
(f) 36 = 12 х 3 = (1 + 2)! х 3!;
(g) 64 = 1 х 23! = (1 х 2)3!;
(h) 72 = 12x3!.
79. Из цифр 2, 3 и 4 в возрастающем порядке сделай число:
(a) 14 = 2 х (3 + 4) = 2 + 3 х 4;
(b) 16 = 2 х 3! + 4 = (2/3) х 4! = 23!/4;
(c) 20 = (2 + 3) х 4 = 2 - 3! + 4!;
(d) 24 = 2 х 3 х 4 = (2 + 3! - 4)!;
(e) 30 = 2 х 3 + 4! = (2 + 3)!/4 = (2 х 3)!/4!;
(f) 36 = 2 х 3! + 4! = 2 + 34;


164 Решения
(g) 40 = 23! — 4!;
(h) 47 = 23 + 4!;
(i) 54 = 2 x (3 + 4!);
(j) 60 = 2 x 3M/4! = 2 x (3! + 4!);
(к) 68 = 2x34;
(1) 74 = 2 + 3x4!;
(ш) 83 = 2 + З4;
(n) 88 = 23! + 4!;
(о) 	96 = (2 + 3)! - 4!.
80. 	Из цифр 3, 4 и 5 в возрастающем порядке сделай число:
(а)
12 = 3 + 4 + 5;
(Ъ)
15 = (3/4!) x 5! = 3! + 4 + 5;
(с)
16 = 3M/45;
(d)
17 = 3 x4 + 5;
(е)
19 = 3! x 4-5;
(f)
22 = 3 + 4!-5;
(g)
24 = (3 - 4 + 5)! = 3!! x A = 3! x 4! - 5!;
(h)
25 = 3! + 4! — 5 = 3!!/4! - 5;
(i)
26 = 3!+ 4x5;
(j)
27 = 3 x (4 + 5);
(k)
29 = 34 - 5 = 3! x 4 + 5;
(1)
30 = (3!/4!) x 5!;
(m)
32 = 3 + 4! + 5 = (3! - 4)5;
(n)
35 = (3 + 4) x 5 = 3! + 4! + 5 = 3M/4! + 5;
(o)
36 = ЗП/4/5;
(P)
39 = 34 + 5;
(q)
42 = (3 + 4)!/5!;


81. Из цифр 4, 5 и 6 в возрастающем порядке 165
(г) 50 = (3! + 4) х 5;
(s) 51 = 3! + 45;
(t) 54 = 3! х (4 + 5);
(u) 57 = 3 х (4!-5);
(v) 60 = 3x4x5 = 3!!/4 — 5!;
(w) 67 = 3x41 + 5;
(x) 76 = 34 — 5;
(y) 77 = 3x41 + 5;
(z) 80 = 311/(4 + 5);
(al) 86 = 34 + 5;
(bl) 87 = 3 x (41 + 5);
(cl) 90 = (3/4) x 51;
(dl) 99 = 3-41+51;
81. 	Из цифр 4, 5 и 6 в возрастающем порядке сделай число:
(a) 13 = 41-5-6;
(b) 20 = 41x5/6;
(c) 24 = (41 + 5!)/6 = 4 + 51/6 = 4/(51/61);
(d) 25 = 41-5 + 6;
(e) 26 = 4x5 + 6;
(f) 34 = 4 + 5x6;
(g) 35 = 41 + 5 + 6;
(h) 39 = 45-6;
(i) 44 = 4 x (5 + 6) = 41+51/6;
(j) 51 = 45 + 6;
(k) 54 = (4 + 5) x 6 = 41 + 5x6;
(1) 60 = 4 + 56;
(m) 80 = 4x51/6 = 41+56.


166 Решения
82. Из цифр 5, 6 и 7 в возрастающем порядке сделай число:
(a) 18 = 5 + 6 + 7 = (5! + 6)/7;
(b) 23 = 5x6-7;
(c) 24 = (5+ 6-7)!;
(d) 27 = 51/6 + 7;
(e) 35 = (5/6!) х 7!;
(f) 37 = 5x6 + 7;
(g) 47 = 5 + 6x7;
(h) 49 = 56 - 7;
(i) 53 = 5!-67;
(j) 63 = 56 + 7;
(k) 65 = 5 x (6 + 7);
(1) 72 = 5 + 67;
(m) 77 = (5 + 6) x 7;
(n) 78 = 5!-6x7.
83. Из цифр 6, 7 и 8 в возрастающем порядке сделай число:
(a) 21 = 6 + 7 + 8;
(b) 34 = 6x7-8;
(c) 48 = (6/7!) х 8! = 6!/(7 + 8);
(d) 50 = 6x7 + 8;
(e) 59 = 67-8;
(f) 62 = 6 + 7x8;
(g) 75 = 67 + 8;
(h) 90 = 6! х 7!/8! = 6 х (7 + 8) = 6! - 7!/8.


86. Из цифр 1, 3 и 5 в возрастающем порядке 167
84. Из цифр 7, 8 и 9 в возрастающем порядке сделай число:
(a) 24 = 7 + 8 + 9;
(b) 47 = 7x8-9;
(c) 63 = (7/8!) х 9!;
(d) 65 = 7x8 + 9;
(e) 69 = 78 - 9;
(f) 70 = 7!/8/9;
(g) 79 = 7 + 8x9;
(h) 87 = 78 + 9;
(i) 96 = 7 + 89.
85. Из цифр 0, 2 и 4 в возрастающем порядке сделай число:
(a) 17 = 0! + 24;
(b) 23 = 0!-2+ 4!;
(c) 25 = О!2+ 4! = О!+ 24;
(d) 30 = (0! + 2)! + 4! = (0! + 2)!!/4!;
(e) 49 = 0!+ 2x4!;
(f) 72 = (0! + 2) х 4!;
(g) 81 = (0! + 2)4.
86. Из цифр 1, 3 и 5 в возрастающем порядке сделай число:
(a) 12 = 1+3!+ 5;
(b) 15 = 1 х 3 х 5;
(c) 16 = 1+3x5;
(d) 19 = (1+3)!-5;
(e) 20 = (1 + 3) х 5 = (1/3!) х 5!;
(f) 29 = (1+3)!+ 5;


168 Решения
(g) 30 = 1 х 3! х 5;
(h) 31 = 1 + 3! x 5;
(i) 40 = (1/3) x 5!;
(j) 42 = (1 +3!)!/5!;
(k) 65 = 13x5.
87. Из цифр 2, 4 и 6 в возрастающем порядке сделай число:
(a) 16 = 24!/6;
(b) 20 = 2 + 4! — 6 = 2 х (4 + 6);
(c) 22 = 24 + 6;
(d) 24 = (24/6)!;
(e) 26 = 2 + 4x6 = 2 + (4!/6)!;
(f) 30 = 24 + 6;
(g) 32 = 2+ 4!+ 6;
(h) 36 = (2 + 4) х 6 = 2 х (4! - 6);
(i) 42 = 2x4!-6;
(j) 48 = 2 x 4 x 6 = 2 x (4!/6)! = 2 + 46;
(k) 54 = 2x4!+ 6;
(1) 56 = (2 x 4)!/6!;
(m) 60 = (2/4!) x 6! = 2 x (4! + 6);
(n) 64 = (2 — 4)6;
(o) 	96 = 24 x 6.
88. Из цифр 3, 5 и 7 в возрастающем порядке сделай число:
(a) 13 = 3!!/5! + 7;
(b) 15 = 3 + 5 + 7;
(c) 18 = (3! + 5!)/7 = 3! + 5 + 7;
(d) 22 = 3x5 + 7;


89. Из цифр 4, 6 и 8 в возрастающем порядке 169
(e) 23 = 31x5-7;
(f) 24 = (3! + 5 - 7)!;
(g) 28 = 35-7;
(h) 36 = 3 х (5 + 7);
(i) 37 = 3! x 5 + 7;
(j) 38 = 3 + 5x7;
(к) 41 = 3! + 5 x 7;
(1) 42 = 35 + 7 = (3!!/5!) x 7;
(m) 56 = (3 + 5) x 7;
(n) 60 = 3 + 57 = 311/(5 + 7);
(0) 63 = 31 + 57;
(p) 72 = 3! x (5 + 7);
(q) 77 = (3! + 5) x 7.
89. 	Из цифр 4, 6 и 8 в возрастающем порядке сделай число:
(a) 12 = (41/6)+ 8;
(b) 16 = 4x6-8 = (41/6)!-8;
(c) 18 = 4 + 6 + 8 = 4! х 6/8;
(d) 22 = 41 + 6-8;
(e) 26 = 41-6 + 8;
(f) 32 = 4 х 6 + 8 = (41/6) х 8 = (41/6)1 + 8;
(g) 38 = 46-8 = 41 + 6 + 8;
(h) 52 = 4 + 6x8;
(1) 54 = 46 + 8;
(j) 56 = 4 x (6 + 8);
(k) 72 = 41 + 6x8;
(1) 80 = (4 + 6) x 8;
(m) 90 = (4+ 6)1/81;
(n) 92 = 41 + 68;
(o) 	93 = (41 + 6!)/8.


170 Решения
90. Из цифр 5, 7 и 9 в возрастающем порядке сделай число:
(a) 21 =5 + 7 + 9;
(b) 26 = 5x7-9;
(c) 41 = 5! - 79;
(d) 44 = 5x7 + 9;
(e) 48 = 57-9;
(f) 57 = 51-7x9;
(g) 66 = 57 + 9;
(h) 68 = 5 + 7x9;
(i) 80 = 5 x (7 + 9);
(j) 84 = 5 + 79.
91. Из цифр 0, 3 и 6 в возрастающем порядке сделай число:
(a) 13 = 0! + 3! + 6;
(b) 19 = 01+3x6;
(c) 24 = (0! + 3) х 6 = [(0! + 3)!/6]!;
(d) 30 = (0! + 3)! + 6;
(e) 37 = 0! + 36 = 0! + 3! х 6;
(f) 42 = (0! + 3!) х 6;
(g) 64 = (0! — З)6.
92. Из цифр 1, 4 и 7 в возрастающем порядке сделай число:
(a) И = 1 х (4 + 7) = 1 х 4 + 7;
(b) 12 = 1+4 + 7;
(c) 18 = 1+41-7;
(d) 21 =14 + 7;
(e) 24 = (1 - 4 + 7)!;


94. Из цифр 3, 6 и 9 в возрастающем порядке 171
(f) 31 = 1 X 41 + 7 = (1 х 4)! + 7;
(g) 32 = 1+41 + 7;
(h) 35 = (1 +4) х 7;
(i) 47 = 1 x 47;
(j) 48 = 1+47;
(к) 98 = 14x7.
93. Из цифр 2, 5 и 8 в возрастающем порядке сделай число:
(a) 15 = 2 + 5 + 8;
(b) 17 = 25-8 = 2 + 51/8;
(c) 18 = 2x5 + 8;
(d) 24 = 25 — 8;
(e) 26 = 2 х (5 + 8);
(f) 30 = 2x51/8;
(g) 33 = 25 + 8;
(h) 40 = 25 + 8;
(i) 42 = 2 + 5x8;
(j) 56 = (2 + 5) x 8;
(k) 60 = 2 + 58;
(1) 80 = 2x5x8;
(m) 90 = (2 x 5)1/81.
94. Из цифр 3, 6 и 9 в возрастающем порядке сделай число:
(a) 18 = 3 + 6 + 9;
(b) 21=31 + 6 + 9;
(c) 24 = (36/9)1 = [(31 х 6)/9]1;
(d) 27 = 3x6 + 9 = 36-9;
(e) 45 = 36 + 9 = 3 х (6 + 9) = 31 х 6 + 9;


172 Решения
(f) 48 = 3!!/(6 + 9);
(g) 75 = 3!+ 69;
(h) 81 = (3 + 6) x 9 = 3е/9;
(i) 83 = 3 + 6!/9;
(j) 86 = 3! + 6!/9;
(k) 90 = 3! x (6 + 9).
95. Из цифр 0, 4 и 8 в возрастающем порядке сделай число:
(a) 13 = 0!+4 + 8;
(b) 15 = (0! + 4)!/8;
(c) 17 = 0!+4!-8;
(d) 33 = 0!+4!+ 8;
(e) 40 = (0! + 4) х 8;
(f) 48 = 0! х 48 = 0 + 48;
(g) 49 = 0!+48.
96. Из цифр 1, 5 и 9 в возрастающем порядке сделай число:
(a) 15 = 1+5 + 9;
(b) 24 = 15 + 9;
(c) 46 = 1+5x9;
(d) 54 = (1 + 5) х 9;
(e) 59 = 1 х 59;
(f) 60 = 1+59;
(g) 80 = (1 + 5)!/9.
97. Из цифр 1, 2 и 3 в убывающем порядке сделай число:
(a) 11 =3! х 2-1;
(b) 18 = 3 х (2 + 1)!;


99. Из цифр I, 2 и 5 в убывающем порядке 173
(c) 23 = (3! — 2)! — 1;
(d) 27 = 32+1 = 3! + 21;
(e) 32 = 32 х 1 = 32/1 = 321;
(f) 35 = З!2 - 1;
(g) 37 = З!2 + 1;
(h) 63 = 3x21.
98. Из цифр 1, 2 и 4 в убывающем порядке сделай число:
(a) 11=41/2-1;
(b) 15 = 42 — 1;
(c) 18 = 4!-(2 + 1)!;
(d) 21 = 4!-2-1;
(e) 25 = 4!+2-1 =4 + 21;
(f) 26 = 4! + 2 х 1 = 4! + 2/1 = 4! + 21;
(g) 30 = 4!+ (2 + 1)!;
(h) 45 = 4!+21;
(i) 47 = 4! x 2-1;
(j) 64 = 42+1.
99. Из цифр 1, 2 и 5 в убывающем порядке сделай число:
(a) 11 = 5 +(2 + 1)! = 5x2 + 1;
(b) 20 = 5!/(2 + 1)!;
(c) 24 = (5 — 2 + 1)! = 52 — 1;
(d) 26 = 5 + 21 =52 + 1;
(e) 30 = 5 х (2 + 1)!;
(f) 40 = 5!/(2 + 1);
(g) 51=52-1;
(h) 61 = 5!/2 + 1;
(i) 99 = 5!-21.


174 Решения
100. Из цифр 3, 5 и 6 в убывающем порядке сделай число:
(a) 12 = 6 х (5 - 3) = 6!/5! + 3!;
(b) 18 = (6!/5!) х 3;
(c) 21 = 6 + 5x3 = (6 + 5!)/3!;
(d) 24 = (6 - 5 + 3)! = 6 х 5 - 3! = 61/5/3!;
(e) 26 = 6 + 5!/3!;
(f) 33 = 6 х 5 + 3 = (6 + 5) хЗ;
(g) 36 = б5”3 = (6!/5!) х 3! = 6 х 5 + 3!;
(h) 46 = 6 + 5!/3;
(i) 48 = 6 х (5 + 3) = 6!/5/3;
(j) 59 = 6 + 53 = 65-3!;
(к) 66 = 6 х (5 + 3!);
(1) 90 = 6x5x3 = 6!/(5 + 3);
(ш) 100 = (6! - 5!)/3!.
101. Из цифр 3, 6 и 7 в убывающем порядке сделай число:
(a) 13 = 7 + (6 — 3)! = 7!/6! + 3!;
(b) 21 = 7 х (6 - 3) = (7!/6!) х 3;
(c) 24 = (7 - 6 + 3)! = (7!/6! — 3)!;
(d) 39 = (7 + 6) хЗ = 7x6-3;
(e) 42 = 7 х (6 - 3)! = (7!/6!) х 3!;
(f) 49 = 76/3;
(g) 70 = 76-3! = 7 + 63;
(h) 78 = (7 + 6) х 3!;
(i) 80 = 7!/63;
(j) 82 = 76 + 3!;
(k) 84 = 7 x (6 + 3!).


103. Из цифр 3, 4 и 7 в убывающем порядке 175
102. Из цифр 3, 6 и 8 в убывающем порядке сделай число:
(a) 14 = 8 +(6-3)!;
(b) 24 = [(8/6) х 3]! = 8 х (6 - 3);
(c) 28 = 8!/(6! + 3!!);
(d) 48 = 8 х (6-3)!;
(e) 50 = 8!/6! - 3!;
(f) 55 = (8! - 6!)/3!!;
(g) 56 = 8!/(6 — 3)!!;
(h) 57 = (8! + 6!)/3!!;
(i) 64 = 86/3 = (8 - 6)3!;
(j) 80 = 86-3!;
(к) 96 = 8 х (6 + 3!).
103. Из цифр 3, 4 и 7 в убывающем порядке сделай число:
(a) 11 = 7 + 4!/3!;
(b) 18 = (7 — 4)! х 3 = (7 - 4) х 3!;
(c) 25 = 7 + 4! — 3! = 7 х 4 — 3;
(d) 27 = (7 - 4)3;
(e) 28 = 7 + 4! — 3 = 7! х 4/3!! = 7 х 4!/3!;
(f) 31 =7x4 + 3 = 7 + (4!/3!)! = 7 + 4x3!;
(g) 35 = 7!/4!/3!;
(h) 36 = (7 - 4)! х 3!;
(i) 37 = 7 + 4! + 3!;
(j) 70 = 7 х (4 + 3!);
(k) 71 = 74 — 3 = 7 + 43.


176 Решения
104. Из цифр 3, 4 и 5 в убывающем порядке сделай число:
(a) 11 = 5!/4! + 3!;
(b) 12 = 5 + 4 + 3 = 51/(4 + 3!);
(c) 15 = 5 + 4 + 3! = (5!/4!)хЗ;
(d) 16 = (5! — 4!)/3!;
(e) 20 = 5 х 4!/3! = (5!/4!)!/3!;
(f) 29 = 5 + (4!/3!)! = 5 + 4x3!;
(g) 30 = (5!/4!) х 3!;
(h) 32 = 5 + 4! + 3 = (5! — 4!)/3;
(i) 40 = 5 х 4!/3 = (5!/4!)!/3;
0) 51 =54-3;
(к) 56 = 5! — 43;
(1) 90 = (5!/4) х 3 = 5! - 4! - 3! = 5 х (4! - 3!);
(ш) 96 = 5! - 4 х 3! = 5! - (4!/3!)!.
105. Из цифр 3, 5 и 8 в убывающем порядке сделай число:
(a) 12 = (8 - 5)! + 3!;
(b) 18 = (8 - 5)! х 3 = (8 - 5) х 3!;
(c) 24 = [8/(5-3)]!;
(d) 27 = (8 - 5)3;
(e) 28 = 8 + 5!/3!;
(f) 32 = 85/3;
(g) 48 = 8/(5!/ЗН) = 8 + 5!/3;
(h) 56 = 8!/5!/3!;
(i) 64 = 8 х (5 + 3) = 85-3;
(j) 78 = (8 + 5) х 3!;
(к) 88 = 85 + 3 = 8 х (5 + 3!).


108. Из цифр 3, 4 и 6 в убывающем порядке 177
106. Из цифр 3, 7 и 8 в убывающем порядке сделай число:
(a) 14 = 8!/7! + 3!;
(b) 15 = 8 + 71/3!!;
(c) 24 = (8 - 7 + 3)! = (8!/7!) х 3;
(d) 29 = 87/3 = 8 + 7 x 3;
(e) 49 = (8! — 7!)/3!!;
(f) 56 = 8 х 7!/ЗН;
(g) 63 = (8! + 7!)/3!!;
(h) 81 = 87 - 3! = 8 + 73;
(i) 90 = 87 + 3 = (8 + 7) х 3!.
107. Из цифр 3, 4 и 8 в убывающем порядке сделай число:
(a) 12 = (8 - 4) х 3 = (8/4) х 3! = 8 + 4!/3!;
(b) 16 = 84/3 = 8 + 4!/3;
(c) 24 = (8 - 4!/3!)! = [(8 + 4)/3]! = (8 - 4) х 3! = [(8 - 4)!/3!]!;
(d) 28 = 84/3;
(e) 30 = (8 — 4)! + 3!;
(f) 32 = 8 х 4! / 3! = 8 + 4x3! = 8 + (4!/3!)!;
(g) 35 = 8х4 + 3 = 8 + 4! + 3;
(h) 64 = (8 - 4)3 = (8/4)3! = 8 х 4!/3;
(i) 72 = (8 - 4)! х 3 = (8 + 4) х 3! = 8 + 43;
(j) 80 = 8 х (4 + 3!) = 8 + 4! х 3;
(к) 96 = 8 х 4 х 3 = (8 + 4!) х 3.
108. Из цифр 3, 4 и 6 в убывающем порядке сделай число:
(a) 18 = 6x4-3!;
(b) 27 = 6х4 + 3 = 6 + 4!-3 = 6!/4! — 3;


178 Решения
(c) 33 = 6 + 4! + 3 = 6!/4! + 3;
(d) 36 = 6 + 4! + 3! = 6!/4! + 3!;
(e) 40 = 6!/(4! — 3!);
(f) 58 = 64-3!;
(g) 60 = (6 + 4) х 3! = 6!/4/3;
(h) 64 = (6 — 4)3!;
(i) 70 = 64 + 3! = 6 + 43;
(j) 72 = 6x4x3 = 6!/(4 + 3!);
(к) 90 = (6 + 4!) х 3 = (6!/4!) х 3.
109. Из цифр 4, 7 и 9 в убывающем порядке сделай число:
(a) 15 = 9 + (7 — 4)!;
(b) 16 = (9 — 7)4;
(c) 18 = 9!/7!/4;
(d) 24 = [(9 + 7)/4]!;
(e) 26 = 9-7 + 4!;
(f) 39 = 9x7-4!;
(g) 48 = (9 - 7) х 4! = 91/71 - 4!;
(h) 68 = 9!/7! — 4;
(i) 73 = 97 - 4!;
(j) 83 = 9 + 74;
(k) 99 = 9 x (7 + 4).
110. Из цифр 4, 8 и 9 в убывающем порядке сделай число:
(a) 13 = 9 + 8 — 4 = 9!/8! + 4;
(b) 24 = (9 - 8) х 4! = [(9 - 8) х 4]!;
(c) 27 = (9/8) х 4!;
(d) 33 = 9!/8! + 4! = 9 + (8 — 4)!;


112. Одиозные одиночки 179
(e) 36 = 9 х (8 - 4) = (9!/8!) х 4;
(f) 41 =9 + 8 + 4! = 9 + 8 х 4;
(g) 68 = (9 + 8) х 4 = 9x8-4;
(h) 74 = 98-4!;
(i) 81 = 98/4;.
(j) 93 = 9 + 84;
(к) 96 = 9x8 + 4!.
111. Из цифр 3, 4 и 9 в убывающем порядке сделай число:
(a) 11 =9-4 + 3! = (9 + 4!)/3;
(b) 17 = 9 + 4!/3;
(c) 20 = (9 - 4)!/3!;
(d) 21 =9!/4!/3! = 9 + 4x3;
(e) 27 = 9 + 4! — 3!;
(f) 33 = 9 + (4!/3!)! = 9x4 — 3 = 9 + 4х3!;
(g) 39 = (9 + 4) х 3 = 9 + 4! + 3! = 9 х 4 + 3;
(h) 40 = (9 - 4)!/3;
(i) 72 = 9 х 4!/3 = 9!/(4 + 3)!;
(j) 73 = 9 + 43;
(к) 88 = 94-3!;
(1) 99 = (9 + 4!) х 3;
(гп)' 100 = 94 + 3!.
112. Одиозные одиночки
(a) 15 = 2 х 6/,8;
(b) 25 = 9 х ,6-2;
(c) 30 = 27/,9;
(d) 7 = 8-,8-,2;
(e) 11 = (9 - ,2)/,8;


180 Решения
(f)
25 = 3/03 x ,4);
(g)
13 = 6/,3 - 7;
(h)
17 = (6 — ,9)/,3;
(i)
9 = 8 + ,7 + ,3;
(j)
24 = (8 - ,8)/,3;
(k)
V
1
n—✓
II
ON
(1)
16 = 4/05 x 5);
(m)
28 = ,5-5 - 4;
(n)
30 = 4 x (8 - ,5);
(o)
23 = 9/,4+ ,5;
(P)
64 = 49'5;
(q)
11 =6+ 4/,8;
(r)
18 = 9/09 - ,4);
(s)
16 = ,5 x ,5-5;
(t)
11 =(6-,5)/,5;
(u)
26 = ,5-5 - 6;
(v)
11 = 8 + 9'5;
(w)
64 = ,5_9/8.
113. 	Пагубные парочки
(a) 7 = 1/,2+ 2 = 2 + ,2-1;
(b) 18 = 2/,1 - 2 = (2 - ,2)/,1;
(c) 8 = 3 х 3 - 1 = (3 - I)3;
(d) 6 = 4 + 3-1=3/01+,4);
(e) 10 = 8 +1/,5 = 8 + ,5-1;
(£) 16 = 1+6 + 9 = 1+9/,6;
(g) 32 = 29 + 3 = 2 + 9/,3;
(h) 14 = 4 + 2x5 = ,5_4-2;
(i) 22 = 4 + 2x9 = (9-,2)/,4;


114. Трепетные трио 181
О
(к
(1
(ш
(п
(о
(р
(q
(г
(s
(t
(U
(V
(w
(X
(У
(a
(b
(с
(d
(e
(f
(g
(h
(i
(j
(k
64 = 25/,5 = 2 x ,5-5;
25 = ,26-8 = 08 - ,6)-2;
7 = 2x8-9 = 8x,9 — ,2;
31 = 33 + 4 = 34 — 3;
24 = 3 x (3 + 5) = 3 x ,5“3;
30 = 3 x 9 + 3 = 33/,9;
4 = 3- 4 + 5 = ,5-3 -4;
8 = 3 + 9- 4 = 09- ,4) 3;
14 = 3/,5 + 8 = (5 — ,8)/,3;
18 = 6 x (6 - 3) = (6 - ,6)/,3; 8 = 4x4x,5 = 4x 4'5-,
12 = 4/,5 + 4 = ,5-4 - 4;
18 = (4 + 5)/,5 = 4 x (5-,5); 16 = ,5_6/4 = 4 + 6/,5;
32 = (8/4)5 = /5_4/'8;
25 = 5 x (9 - 4) = ,5-4 + 9.
114. 	Трепетные трио
8 = 1/Д—2 = (1— ,2)/,1 = ,1_1 — 2;
13 = 8 + 1/, 2 = 21 - 8 = 8 + ,2_1;
8 = l+ 3 + 4 = 4x(3-l) = 01+ ,4)-3;
15 = 6/(2 x ,2) = 6/(,2 + ,2) = ,6 x Д-2; 2 = 8- 2x3 = (8- 2)/3 = 3 - ,2 - ,8; 10 = 3 + 9- 2 = 32/,9 = ,9 x ,3-2;
10 = 2/,5 + 6 = 6/,5 - 2 = ,5-2 + 6;
32 = 5 x 6 + 2 = ,5 x 26 = ,5~6/2;
28 = 2 x 7/,5 = 7 x ,5~2 = 7/,25;
9 = 3 + 3 + 3 = 33/3 = (3 - ,3)/,3;
16 = (6/3)4 = 46/3 = 6/,3 - 4;


182 Решения
(1) 	13 = 3 + 5 + 5 = 5/,5 + 3 = 5 + ,5_3;
(ш) 4 = 5 + 7/3 = 5 - ,3 - ,7 = 3/,75;
(п) 15 = 3 + 5 + 7 = 3/(,7 — ,5) = 7 + ,5~3;
(0) 32 = 85/3 = ,53-8 = (,8 - ,3Г5;
(р) 10 = 5х(6-4) = -|_5 = /5-4_6;
(q) 8 = 5 + 7 — 4 = 4х(7 — 5) = ,54-7;
(г) 9 = 7 + ,4х5 = 7 + 4'5 = ,5~4 — 7;
(s) 20 = 5 х (8 - 4) = 8/,5 + 4 = ,5~4/,8;
(t) 25 = 57-5 = 5/(,7 - ,5) = ,5~5 - 7;
(и) 4 = 6/,5 - 8 = (8 - 6)/,5 = ,56~8;
(v) 25 = 59-7 = 5/(,9 - ,7) = 9/,5 + 7.
115. 	Навязчивые нескольки
(a) 5 = 2x6 — 7 = 7/(2 - ,6) = (7 - 6)/,2 = ,26~7;
(b) 27 = 3 х (3 + 6) = З6-3 = (6 - З)3 = 33-6;
(c) 32 = 4 х (3 + 5) = ,5 х 43 = 4 х ,5“3 = 43~'5;
(d) 6 = 3x5 — 9 = 9/(3 х ,5) = 3 + 9'5 = ,5 х (3 + 9);
(e) 2 = 8/5 + ,4 = ,5 х (8 - 4) = (8 - 4)'5 = ,5~4/8;
(f) 8 = 6 + 7 — 5 = 7/,5 - 6 = в/,75 = 56/7;
(g) 6 = 5 + 8 - 7 = ,8 х (7 + ,5) = 7/,5 - 8 = (5 - ,8)/,7;
(h) 32 = 5 х 8 - 8 = 5 х 8 х ,8 = (8 + 8)/,5 = ,5~8/8;
(1) 64 = 4 х 16 = 1 х 64 = 64/1 = 641 = 6/,1 +4 = (Д + ,4)'6;
0) 2 = 8-4-2 = (8—4)/2 = 24/8 = 42/8 = (2-,4)/,8 = ,2 х8+,4 = = (4 х 8)/2;
(к) 16 = ,5 х 25 = ,5_2/'5 = (,5 х ,5Г2 = ,5~5/2 = ,5 А -05~2);
(1) 	32 = 52 + 7 = 25 + 7 = 5/,2 + 7 = ,52-7 = (,7 - ,2)“5;
(ш) 5 = 9- 2/,5 = 2/(,9 - ,5) = 9/2 + ,5 = 2 + 9'5 = 9 - ,5-2;
(п) 16 = 4 + 4 + 8 = 4х(8-4) = 48/4 = (8/4)4 = 8/,4 - 4.


116. Добейся максимума 183
116. 	Добейся максимума
(a) Положим
я = , 1-4 = Ю000 и b = ,1~a = 510000.
Тогда £i = ,3~ъ — наибольшее значение; для него ln(ln£i) « 16095, где \пх — натуральный логарифм х.
(b) Положим
р = "'УД = 510 = 9765625 и q = 4Р.
Тогда £г = ,3_(? — наибольшее значение; для него In (In £2) «13 538 031.


АВТОРЫ ГОЛОВОЛОМОК
Laurie Brokenshire (1), Bob Wain wright (2, 17), Dick Hess (3, 5, 6, 8-10, 12, 14-16, 18, 20-22, 24, 26, 28, 29, 31, 32, 37, 39, 40, 42-49, 51-116), Neil Bickford (4), Joop van der Vaart (7), G. Galperin (11), Leon Bankoff (13), Задачи Всемирной олимпиады (19), Andy Liu/Dick Hess (23, 25), Joe Kisenwether (27, 30, 35), Bill Cutler/Dick Hess (33), Hirokazu Iwasawa/Dick Hess (34), Timo Jokitalo (36), Markus Gotz (38), Nick Baxter/Dick Hess (41), Charles Levitt (50).


ОГЛАВЛЕНИЕ
Предисловие 6
Задачи
Глава 1. Озорные головоломки 8
1. Загадочное слово 8
2. Тайна зарплаты 8
3. Родственники 8
4. Фишки в коробке 9
5. Мощная подача 9
6. Демографический взрыв 9
7. Цепная линия 10
Глава 2. Геометрические головоломки 11
8. Геологоразведка на Ригеле 119. Соединяя точки 1110. Прямоугольные треугольники 12
11. Усеченный многогранник 12
12. Красивые коробочки 13
13. Почти прямоугольное озеро 14
14. Растроенный ромб 15
15. Разрезание квадрата 15
Глава 3. Цифровые головоломки 16
16. Всецифровые подарки 16
17. Вариант судоку 16
18. Всецифровые суммы 16
19. Чет и нечет 18
20. Странная целостность 18
21. Десятизначное число 18
Глава 4. Логические головоломки 19
22. Дележ пирога 19
23. Побег из темницы 19
24. Логика и геометрия 20
25. Али Баба и 10 разбойников 20
26. Головоломки на годовщину свадьбы 21


186 Оглавление
Глава 5. Головоломные вероятности 23
27. Сюрприз для игрока 23
28. Игра Тензи 23
29. Маленькое бинго 23
30. Обычное бинго 24
31. Честная дуэль 25
32. Золотой сет в теннисе 25
33. Рулетка на автобус 25
34. Цветные шарики 26
35. Игра «Бродилка» 27
Глава 6. Аналитические головоломки 28
36. Спешка в аэропорту 28
37. Что это было? 28
38. Мышиные бега 28
39. Навещаем родственников 28
40. Логи и рифмы 29
41. Многочлены—1 29
42. Многочлены—2 29
43. Каскад простых пифагоровых троек 29
44. Разведение несушек 30
45. Дилемма рыцаря 30
46. Наименее равносторонний треугольник 31
47. Почувствуй себя доктором 32
Глава 7. Физические головоломки 33
48. Лодка с сюрпризом 33
49. Равновесие 33
50. Подвешенный стержень 38
51. Падающие лестницы 38
Глава 8. Головоломки с трапециями 40
Равнобедренные трапеции с целыми сторонами, вписанные в окружность 40
52. Минимальные РТЦС 40
53. Наименьшая окружность 41
54. Простые РТЦС 41
55. Плоские РТЦС 41
56. Вытянутые РТЦС 41
57. Почти квадратные РТЦС 42
58. РТЦС с целыми высотами 42


Оглавление 187
Равнобедренные трапеции с целыми сторонами, вписанные в квадраты 42
59. Наименьшая РТЦС в квадрате 42
60. РТЦС, у которой a = s 43
61. РТЦС, у которой а = с 43
62. РТЦС, у которой х = и 43
63. РТЦС, у которой b/s >  14 43
64. РТЦС, у которой b/s < 0,8, 0,75 и 0,71 44
65. РТЦС наименьшей площади 44
66. Наибольший квадрат 44
67. Неединственные решения 44
68. Наименьшие квадраты 45
Глава 9. Джипы в пустыне 46
69. Дорога в один конец на одном джипе 46
70. Дорога туда и обратно на одном джипе 47
71. Дорога в один конец с джипом-помощником 47
72. Дорога в один конец на двух джипах 48
73. Дорога туда и обратно с джипом-помощником 48
74. Дорога туда и обратно на двух джипах 49
75. Два джипа и две станции  заправки 50
76. Дорога туда и обратно на  трех  джипах 51
Глава 10. Головоломки с цифрами 52
Трехцифровки 52
77. Из цифр 0, 1 и 2 в возрастающем порядке сделай число 52
78. Из цифр 1, 2 и 3 в возрастающем порядке сделай число 53
79. Из цифр 2, 3 и 4 в возрастающем порядке сделай число 53
80. Из цифр 3, 4 и 5 в возрастающем порядке сделай число 53
81. Из цифр 4, 5 и 6 в возрастающем порядке сделай число 54
82. Из цифр 5, 6 и 7 в возрастающем порядке сделай число 54
83. Из цифр 6, 7 и 8 в возрастающем порядке сделай число 54
84. Из цифр 7, 8 и 9 в возрастающем порядке сделай число 54
85. Из цифр 0, 2 и 4 в возрастающем порядке сделай число 55


188 Оглавление
86. Из цифр 1, 3 и 5 в возрастающем порядке сделай число 55
87. Из цифр 2, 4 и 6 в возрастающем порядке сделай число 55
88. Из цифр 3, 5 и 7 в возрастающем порядке сделай число 55
89. Из цифр 4, 6 и 8 в возрастающем порядке сделай число 56
90. Из цифр 5, 7 и 9 в возрастающем порядке сделай число 56
91. Из цифр 0, 3 и 6 в возрастающем порядке сделай число 56
92. Из цифр 1, 4 и 7 в возрастающем порядке сделай число 56
93. Из цифр 2, 5 и 8 в возрастающем порядке сделай число 57
94. Из цифр 3, 6 и 9 в возрастающем порядке сделай число 57
95. Из цифр 0, 4 и 8 в возрастающем порядке сделай число 57
96. Из цифр 1, 5 и 9 в возрастающем порядке сделай число 57
97. Из цифр 1, 2 и 3 в убывающем порядке сделай число 58
98. Из цифр 1, 2 и 4 в убывающем порядке сделай число 58
99. Из цифр 1, 2 и 5 в убывающем порядке сделай число 58
100. Из цифр 3, 5 и 6 в убывающем порядке сделай число 58
101. Из цифр 3, 6 и 7 в убывающем порядке сделай число 59
102. Из цифр 3, 6 и 8 в убывающем порядке сделай число 59
103. Из цифр 3, 4 и 7 в убывающем порядке сделай число 59
104. Из цифр 3, 4 и 5 в убывающем порядке сделай число 59
105. Из цифр 3, 5 и 8 в убывающем порядке сделай число 60
106. Из цифр 3, 7 и 8 в убывающем порядке сделай число 60
107. Из цифр 3, 4 и 8 в убывающем порядке сделай число 60
108. Из цифр 3, 4 и 6 в убывающем порядке сделай число 60
109. Из цифр 4, 7 и 9 в убывающем порядке сделай число 61
110. Из цифр 4, 8 и 9 в убывающем порядке сделай число 61
111. Из цифр 3, 4 и 9 в убывающем порядке сделай число 61
Трехцифровки — средний уровень 61
112. Одиозные одиночки (По одному решению в каждой задачке) 62
113. Пагубные парочки (По два решения в каждой задачке) 63
114. Трепетные трио (По три решения в каждой задачке) 63


Оглавление 189
115. Навязчивые нескольки (От 4 до 7 решений в каждой задачке) 64
116. Добейся максимума 65
Решения
Глава 1. Озорные головоломки 68
1. Загадочное слово 68
2. Тайна зарплаты 68
3. Родственники 68
4. Фишки в коробке 69
5. Мощная подача 69
6. Демографический взрыв 69
7. Цепная линия 70
Глава 2. Геометрические головоломки 71
8. Геологоразведка на Ригеле 71
9. Соединяя точки 74
10. Прямоугольные треугольники 74
11. Усеченный многогранник 75
12. Красивые коробочки 76
13. Почти прямоугольное озеро 77
14. Растроенный ромб 78
15. Разрезание квадрата 79
Глава 3. Цифровые головоломки 80
16. Всецифровые подарки 80
17. Вариант судоку 80
18. Всецифровые суммы 80
19. Чет и нечет 81
20. Странная целостность 81
21. Десятизначное число 81
Глава 4. Логические головоломки 82
22. Дележ пирога 82
23. Побег из темницы 83
24. Логика и геометрия 84
25. Али Баба и 10 разбойников 84
26. Головоломки на годовщину свадьбы 86


190 Оглавление
Глава 5. Головоломные вероятности 88
27. Сюрприз для игрока 88
28. Игра Тензи 88
29. Маленькое бинго 89
30. Обычное бинго 90
31. Честная дуэль 91
32. Золотой сет в теннисе 91
33. Рулетка на автобус 92
34. Цветные шарики 93
35. Игра «Бродилка» 95
Глава 6. Аналитические головоломки 97
36. Спешка в аэропорту 97
37. Что это было? 97
38. Мышиные бега 97
39. Навещаем родственников 98
40. Логи и рифмы 99
41. Многочлены—1 99
42. Многочлены—2 100
43. Каскад простых пифагоровых троек 101
44. Разведение несушек 102
45. Дилемма рыцаря 102
46. Наименее равносторонний треугольник 103
47. Почувствуй себя доктором 104
Глава 7. Физические головоломки 120
48. Лодка с сюрпризом 120
49. Равновесие 120
50. Подвешенный стержень 120
51. Падающие лестницы 122
Глава 8. Головоломки с трапециями 125
52. Минимальные РТЦС 125
53. Наименьшая окружность 125
54. Простые РТЦС 125
55. Плоские РТЦС 126
56. Вытянутые РТЦС 126
57. Почти квадратные РТЦС 126
58. РТЦС с целыми высотами 127
59. Наименьшая РТЦС в квадрате 128
60. РТЦС, у которой a = s 129
61. РТЦС, у которой а = с 129
62. РТЦС, у которой х = и 130
63. РТЦС, у которой b/s >  14 131


Оглавление 191
64. РТЦС, у которой b/s < 0,8, 0,75 и 0,71 132
65. РТЦС наименьшей площади 133
66. Наибольший квадрат 134
67. Неединственные решения 135
68. Наименьшие квадраты 136
Глава 9. Джипы в пустыне 139
69. Дорога в один конец на одном джипе 139
70. Дорога туда и обратно на одном джипе 141
71. Дорога в один конец с джипом-помощником 143
72. Дорога в один конец на двух джипах 145
73. Дорога туда и обратно с джипом-помощником 148
74. Дорога туда и обратно на двух джипах 151
75. Два джипа и две станции заправки 156
76. Дорога туда и обратно на трех джипах 160
Глава 10. Головоломки с цифрами 163
77. Из цифр 0, 1 и 2 в возрастающем порядке сделай число 163
78. Из цифр 1, 2 и 3 в возрастающем порядке сделай число 163
79. Из цифр 2, 3 и 4 в возрастающем порядке сделай число 163
80. Из цифр 3, 4 и 5 в возрастающем порядке сделай число 164
81. Из цифр 4, 5 и 6 в возрастающем порядке сделай число 165
82. Из цифр 5, 6 и 7 в возрастающем порядке сделай число 166
83. Из цифр 6, 7 и 8 в возрастающем порядке сделай число 166
84. Из цифр 7, 8 и 9 в возрастающем порядке сделай число 167
85. Из цифр 0, 2 и 4 в возрастающем порядке сделай число 167
86. Из цифр 1, 3 и 5 в возрастающем порядке сделай число 167
87. Из цифр 2, 4 и 6 в возрастающем порядке сделай число 168
88. Из цифр 3, 5 и 7 в возрастающем порядке сделай число 168
89. Из цифр 4, 6 и 8 в возрастающем порядке сделай число 169


192 Оглавление
90. Из цифр 5, 7 и 9 в возрастающем порядке сделай число 170
91. Из цифр 0, 3 и 6 в возрастающем порядке сделай число 170
92. Из цифр 1, 4 и 7 в возрастающем порядке сделай число 170
93. Из цифр 2, 5 и 8 в возрастающем порядке сделай число 171
94. Из цифр 3, 6 и 9 в возрастающем порядке сделай число 171
95. Из цифр 0, 4 и 8 в возрастающем порядке сделай число 172
96. Из цифр 1, 5 и 9 в возрастающем порядке сделай число 172
97. Из цифр 1, 2 и 3 в убывающем порядке сделай число 172
98. Из цифр 1, 2 и 4 в убывающем порядке сделай число 173
99. Из цифр 1, 2 и 5 в убывающем порядке сделай число 173
100. Из цифр 3, 5 и 6 в убывающем порядке сделай число 174
101. Из цифр 3, 6 и 7 в убывающем порядке сделай число 174
102. Из цифр 3, 6 и 8 в убывающем порядке сделай число 175
103. Из цифр 3, 4 и 7 в убывающем порядке сделай число 175
104. Из цифр 3, 4 и 5 в убывающем порядке сделай число 176
105. Из цифр 3, 5 и 8 в убывающем порядке сделай число 176
106. Из цифр 3, 7 и 8 в убывающем порядке сделай число 177
107. Из цифр 3, 4 и 8 в убывающем порядке сделай число 177
108. Из цифр 3, 4 и 6 в убывающем порядке сделай число 177
109. Из цифр 4, 7 и 9 в убывающем порядке сделай число 178
110. Из цифр 4, 8 и 9 в убывающем порядке сделай число 178
111. Из цифр 3, 4 и 9 в убывающем порядке сделай число 179
112. Одиозные одиночки 179
113. Пагубные парочки 180
114. Трепетные трио 181
115. Навязчивые нескольки 182
116. Добейся максимума 183
Авторы головоломок 184