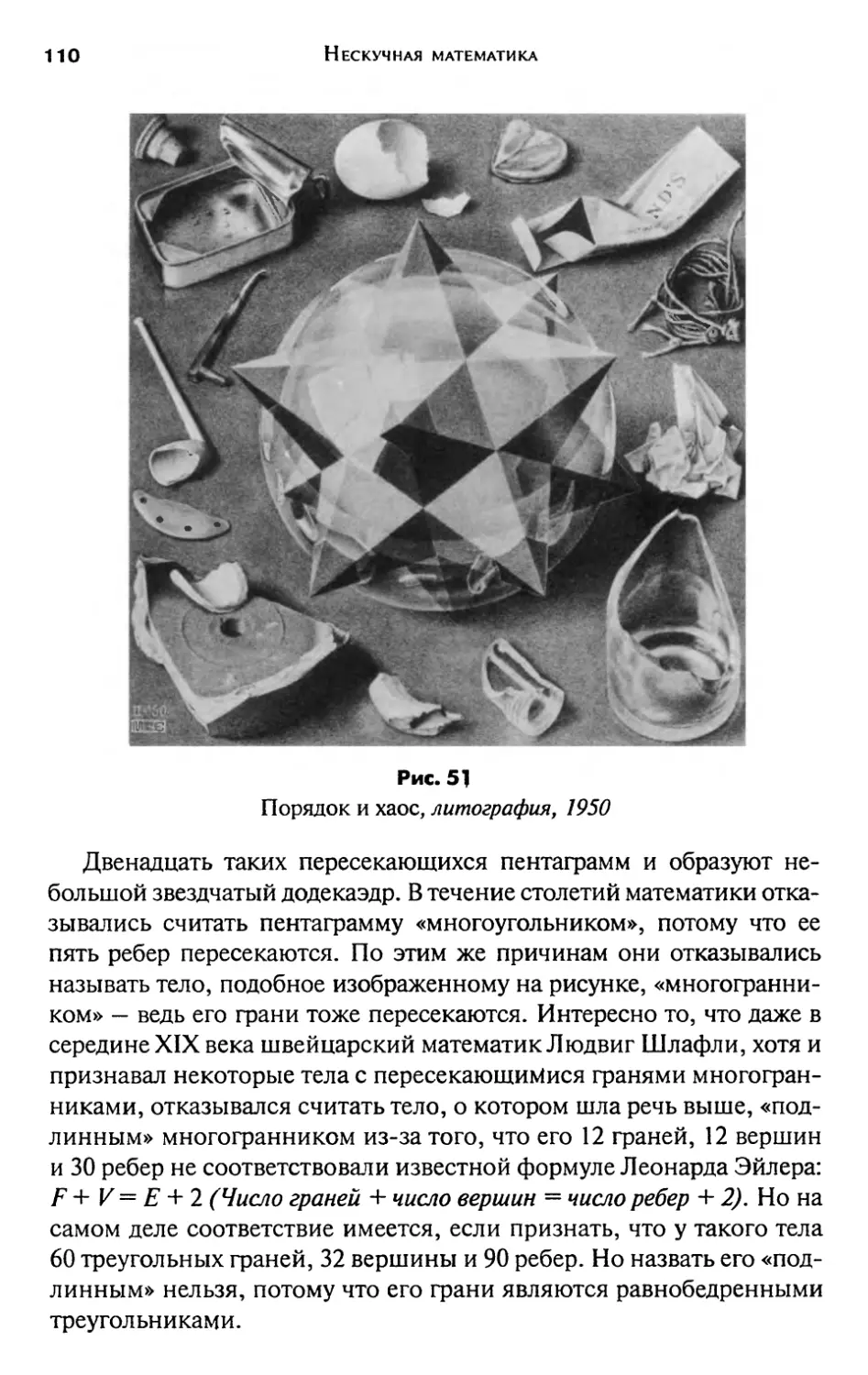
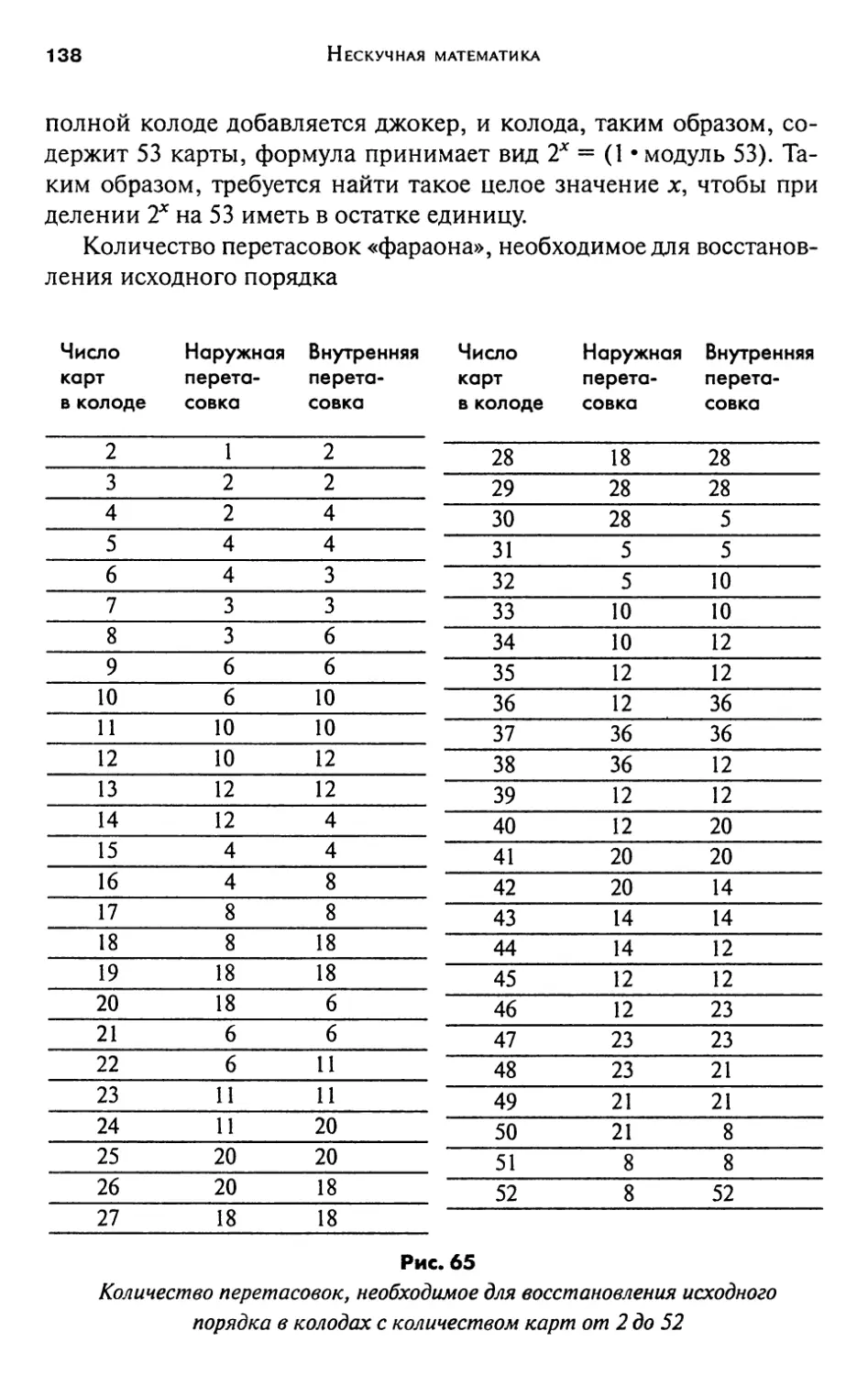
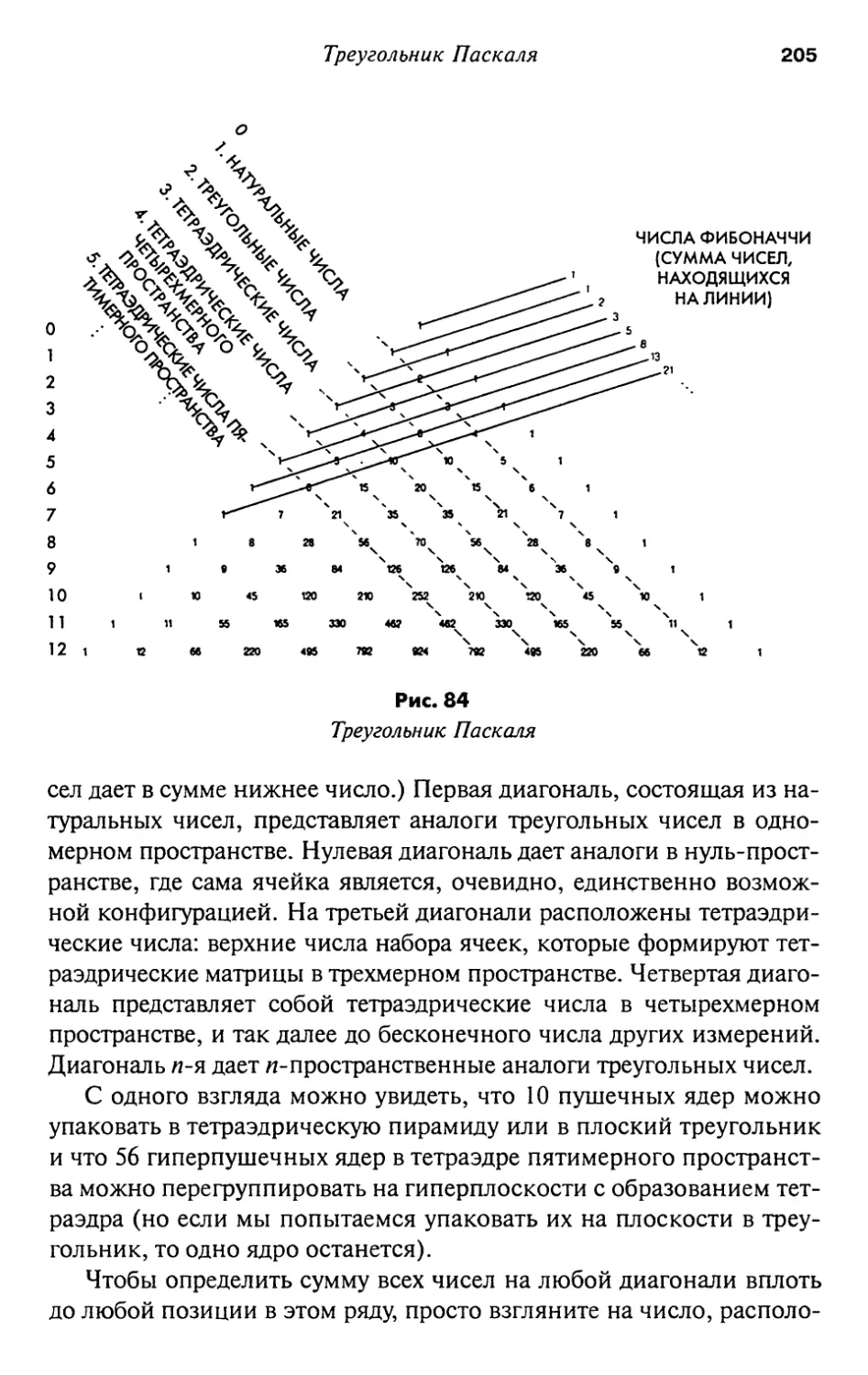
Author: Гарднер М.
Tags: настольные игры (на сообразительность, ловкость и удачу) научно-популярные издания по математике интересная математика математика арифметика математика для детей загадки математические фокусы примеры решения
ISBN: 978-5-17-049343-2
Year: 2008
МАРТИН ГАРДНЕР
НЕСКУЧНАЯ
МАТЕМА
ТИКА
Калейдоскоп
головоломок
*'*•!;
Мартин Гарднер
НЕСКУЧНАЯ МАТЕМАТИКА
Калейдоскоп головоломок
ACT • Астрель
Москва
УДК 794
ББК 22.1я92
Г20
Оригинальное издание опубликовано на англ. языке
издательством The Mathematical Association of America
под названием Mathematical Carnival
Гарднер, М.
Г20 Нескучная математика. Калейдоскоп головоломок / М.
Гарднер. — М.: ACT: Астрель, 2008. — 288 с.:ил.
ISBN 978-5-17-049343-2 (ООО «Издательство ACT»)
ISBN 978-5-271-19494-8 (ООО «Издательство Астрель»)
ISBN 0-88385-448-1 (англ.)
В этой книге, написанной ведущим автором математических игр и
развлечений, вы найдете множество задач, математических шуток, интересных
игр и головоломок. Стиль автора характеризуется доходчивостью, яркостью и
убедительностью изложения, парадоксальностью мысли, новизной и
глубиной научных идей, многие из которых стали стимулом проведения серьезных
исследований, активного вовлечения читателя в самостоятельное научное
творчество.
УДК 794
ББК22.1я92
Общероссийский классификатор продукции
ОК-005-93, том 2; 953000 - книги, брошюры
Санитарно-эпидемиологическое заключение
№ 77.99.60.953.Д.007027.06.07 от 20.06.2007 г.
Подписано в печать 25.01.2008 г. Фор мат 6 0x90/16.
Усл. печ. л. 18,0.Тираж5000 экз.Заказ № 1086.
ISBN 978-5-17-049343-2 (ООО «Издательство ACT»)
ISBN 978-5-271-19494-8 (ООО «Издательство Астрель»)
ISBN 0-88385-448-1 (англ.)
© 1965, 1966, 1967, 1975, 1989 by Martin Gardner
© ООО «Издательство Астрель», 2008
Предисловие
Мартин Гарднер — удивительный человек. Он известен как автор
колонки математических игр журнала Scientific American. Каждый
месяц тысячи читателей этого журнала с нетерпением ожидают эту
колонку в надежде узнать, что нового появилось в мире
занимательной математики. Не важно, повествует ли Мартин Гарднер от лица
остроумного весельчака доктора Матрикса или рассказывает об
итогах недавнего серьезного исследования, его заметки написаны в
неизменно легком стиле.
Мне выпала удача несколько раз пообщаться с Мартином и
Шарлоттой Гарднерами в их старом нью-йоркском доме в Гастинг-
се-на-Гудзоне. Немало счастливых часов провел я также и на самом
верхнем этаже их нового дома на авеню Евклида, знакомясь с
небезынтересным содержимым берлоги старины Мартина. Там, как в
каморке у мага, вас со всех сторон окружают загадки, игры,
механические игрушки, научные курьезы, а также целая кунсткамера
самых разных, весьма интригующих предметов. И это неудивительно.
Ведь Мартин большой любитель магии — в его библиотеке
множество книг о ней и конечно же есть полная подборка книг Л.Ф. Бау-
ма «Волшебник из страны Оз». Да и все другие книги не менее
интересны. Где еще вы можете взять с полки первую попавшуюся
книгу и обнаружить в ней рассказ, в котором совершенно не
встречается буква «е»?
Только не подумайте, что Мартин мистик. Он поразительно
рациональный человек, нетерпимый ко всякого рода обманщикам и
шарлатанам. Из-под его пера вышло много статей, разоблачающих
различные обманы. Так, в его замечательной книге Fads and Fallacies
in the Name of Science («Причуды и ошибки во имя науки») описана
история многих бытующих и по сей день спекулятивных теорий.
Книгу, которую вы держите в руках, несмотря на легкий стиль
изложения, можно отнести к серьезному исследованию, как, впрочем,
и все, что пишет Мартин Гарднер. Ведь он получил в Чикагском уни-
верситете степень доктора философии (philosophical doctor или Ph.
D. не имеет аналога в российской системе и примерно соответствует
степени кандидата наук. — Прим. перев.). Мартин Гарднер является
автором книг на самые разные темы, что кажется почти
невероятным, когда видишь перед собой этого тихого и скромного человека.
Больше всего в комнате Мартина меня заинтересовала
картотека. Мартин переписывается с разными людьми. В числе его
адресатов и профессиональные математики, и любители-энтузиасты.
Невзирая на научную глубину, все предлагаемые ему математические
идеи находят свое место в картотеке. На карточках размером
7,5x12,7 см отражено решительно все, что связано с его работой над
колонкой математических игр журнала Scientific American.
Колонка, которую ведет Мартин, повествует больше о работах
других авторов. Это может быть даже школьница из Венесуэлы,
заинтересовавшаяся математической проблемой, о которой услышала
от своих друзей. Если перебрать карточки из его архива, то можно
встретить ссылку на профессора из известного университета,
работающего в этой области. Найдя в картотеке адрес профессора,
Мартин Гарднер пересылал ему вопрос школьницы и через пару месяцев
писал в журнал материал, где объяснял этот вопрос намного проще,
чем это сделал бы университетский ученый.
Гарднер не устает повторять, что он не математик и что именно в
этом кроется секрет его способности популярно излагать
математику непосвященным. Одним из открытий Мартина стало то, что
областей применения занимательной математики не так уж и мало.
Своим творчеством он пробудил интерес к серьезной математике у
многих людей. Большая часть молодых ученых, с которыми я
общался, с энтузиазмом сообщали, что они увлеклись математикой
благодаря колонке Мартина Гарднера.
В этой книге мне многое напоминает о встречах с Гарднерами.
Лоскутное одеяло госпожи Перкинс из главы 11 этой книги стало
темой одного из моих самых первых писем к нему, а «Ростки» из
главы 7 — это та самая игра, в которую мы играли у них на кухне. За
двадцать лет, кажется, еще никто не сказал нового слова в поиске
выигрышных стратегий этой игры. До сих пор неизвестно, кто из
игроков имеет гарантированный выигрыш в базовом варианте с
семью точками или в варианте с мизером с пятью точками.
Мартин с улыбкой вручает мне мой персональный календарь
«Судного дня». Конечно, он скромно умалчивает о том, что
разработал его специально к моему двухнедельному визиту на авеню Ев-
клида. Здесь в его доме на фрагменте каменной стены среди прочих
удивительных предметов висят и парадоксальные песочные часы
(см. главу 13 этой книги).
А теперь мне бы хотелось предложить читателям идею, как без
труда компенсировать деньги, потраченные на приобретение этой
книги. Соберите десять или более человек и заключите с ними
пари. Попросите их ответить, что случится с велосипедом без
велосипедиста, если крутануть педали (естественно, в первый момент
придерживая велосипед от падения). Скажите, что заплатите 25
центов тому, кто ответит правильно. А тот, кто ответит неправильно,
заплатит вам 25 центов. Дайте людям возможность обсудить (но не
экспериментировать!). Затем найдите велосипед и проведите
эксперимент, результаты которого удивят всех (см. главу 14 этой
книги, головоломка 20). Лично я на этой шутке выигрывал всякий раз
целый доллар.
Внимательный читатель наверняка обратит внимание на то, что
это обновленное и пересмотренное издание, как и прежнее,
посвящено исключительно моей персоне. В ответ на этот комплимент
ваш покорный слуга, а также Элвин Берлекамп и Ричард Гай
посвящаем нашу новую книгу Winning Ways («Путь к победе»)
Мартину Гарднеру,
приносящему все новые сокровища математической мысли
все новым миллионам читателей.
Джон Конвей
Принстон, Нью-Джерси,
март, 1989
Содержание
Введение 13
«Ростки» и «Брюссельская капуста» 15
Ответы на странице 23
Головоломки с монетами 24
Ответы на странице 34
Алеф-нуль и алеф-один 38
Ответы на странице 51
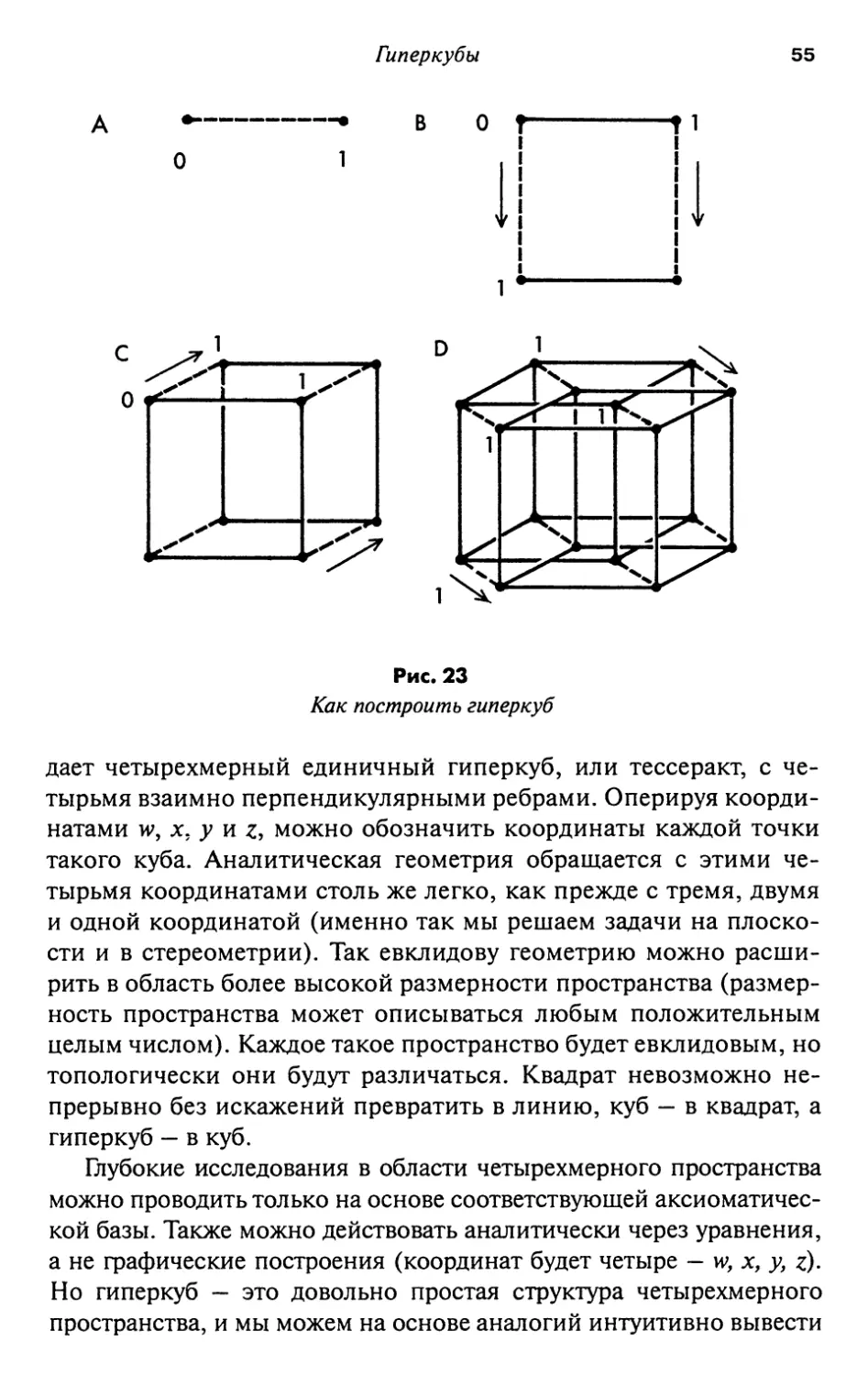
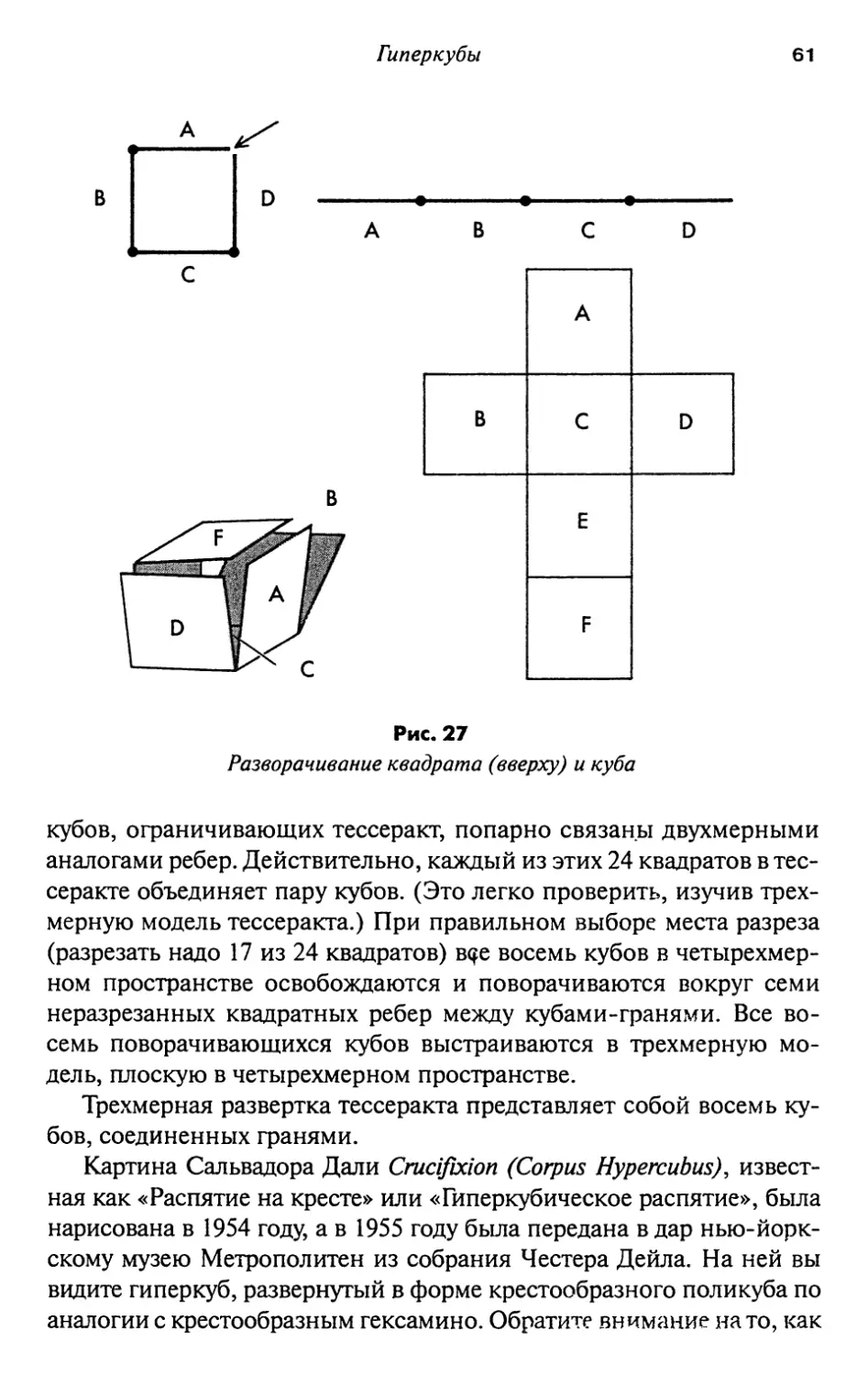
Гиперкубы 53
Ответы на странице 65
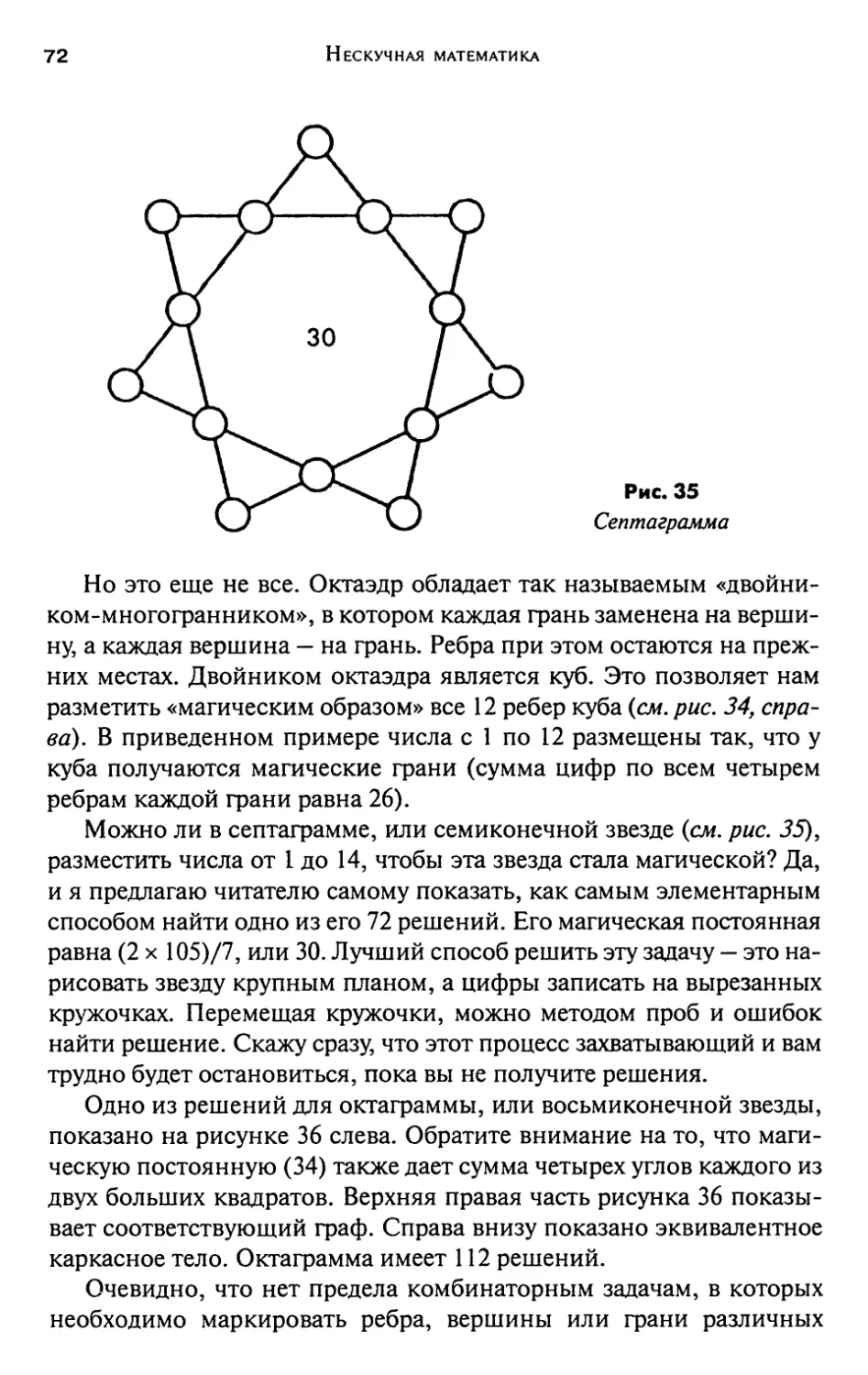
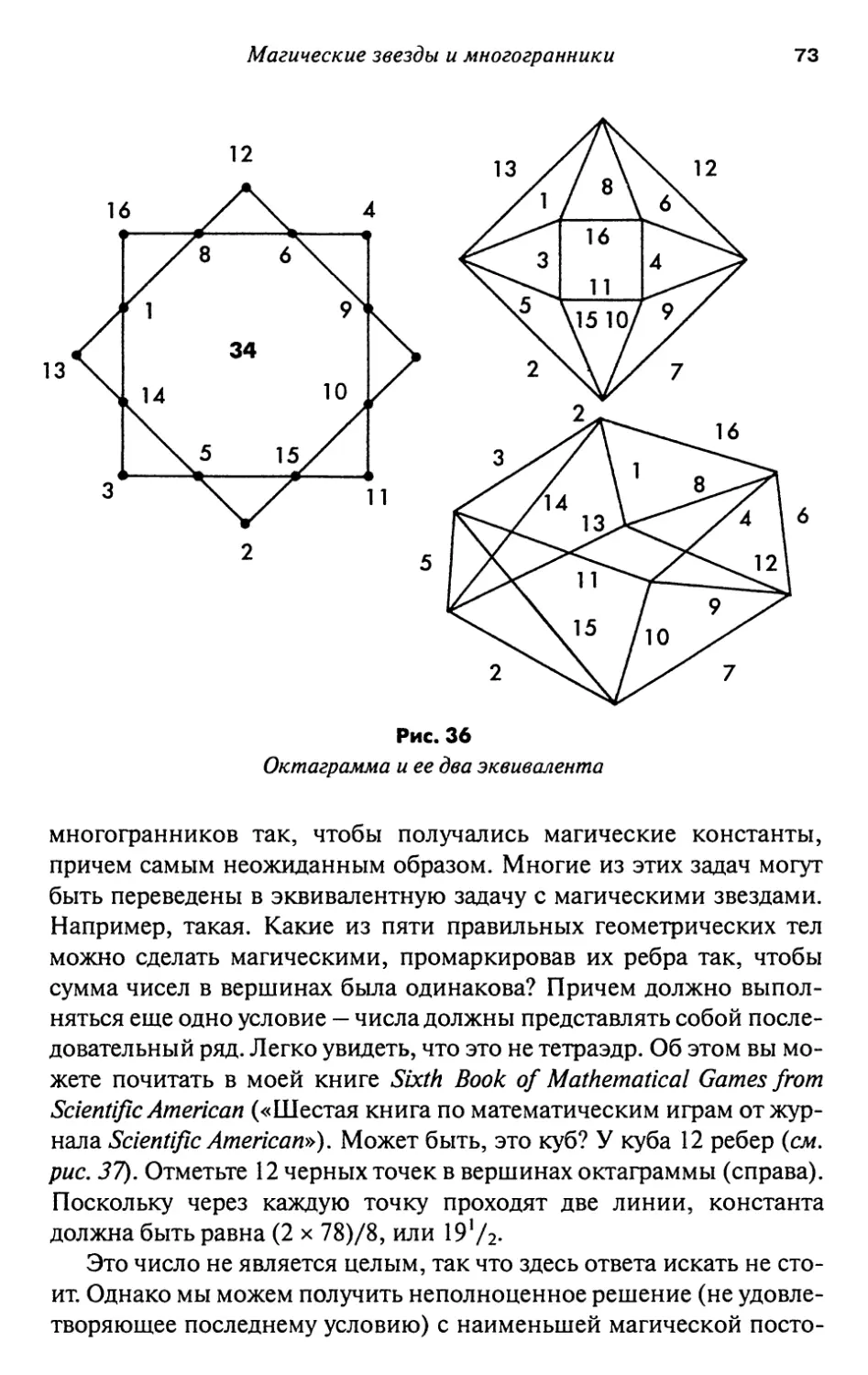
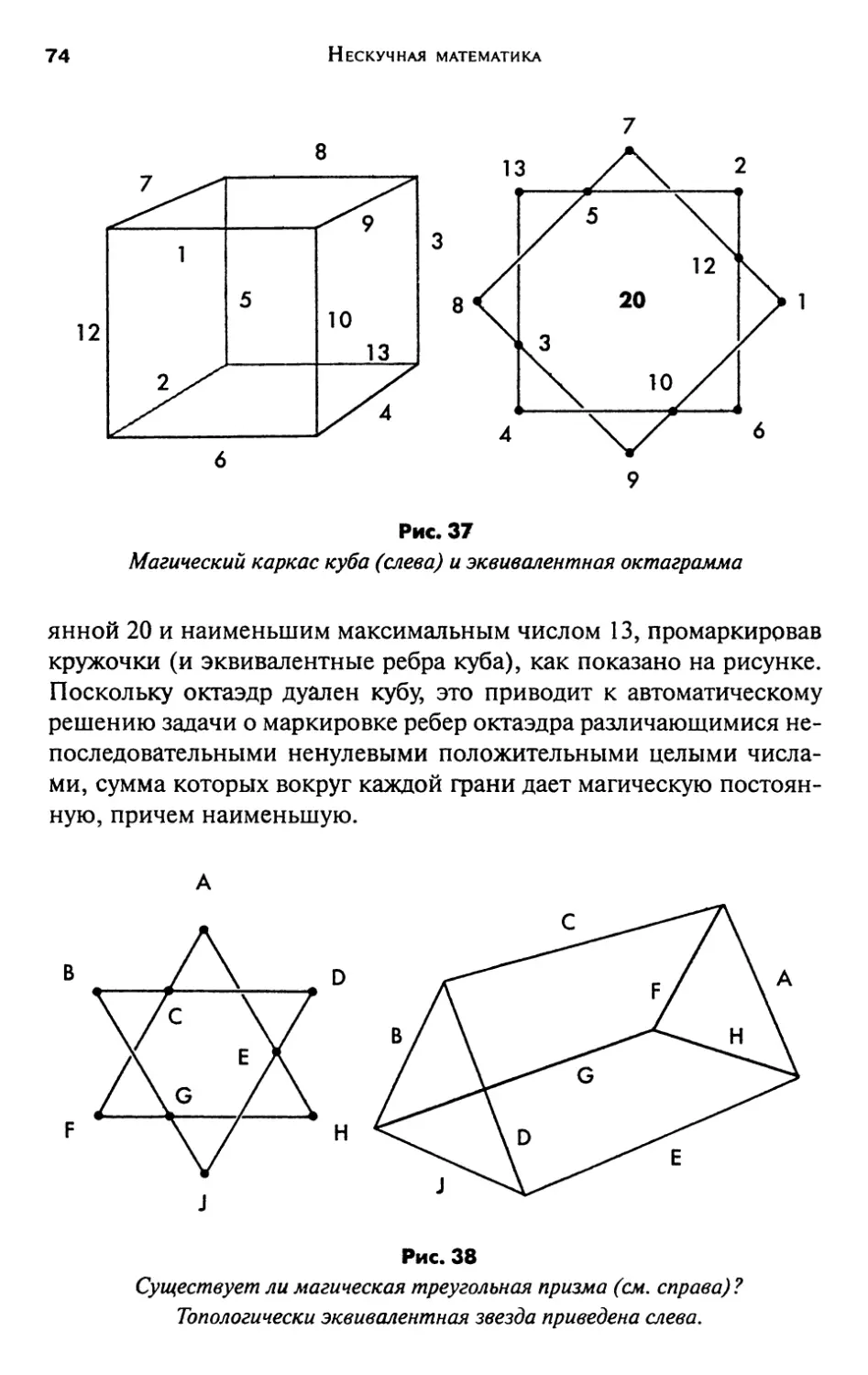
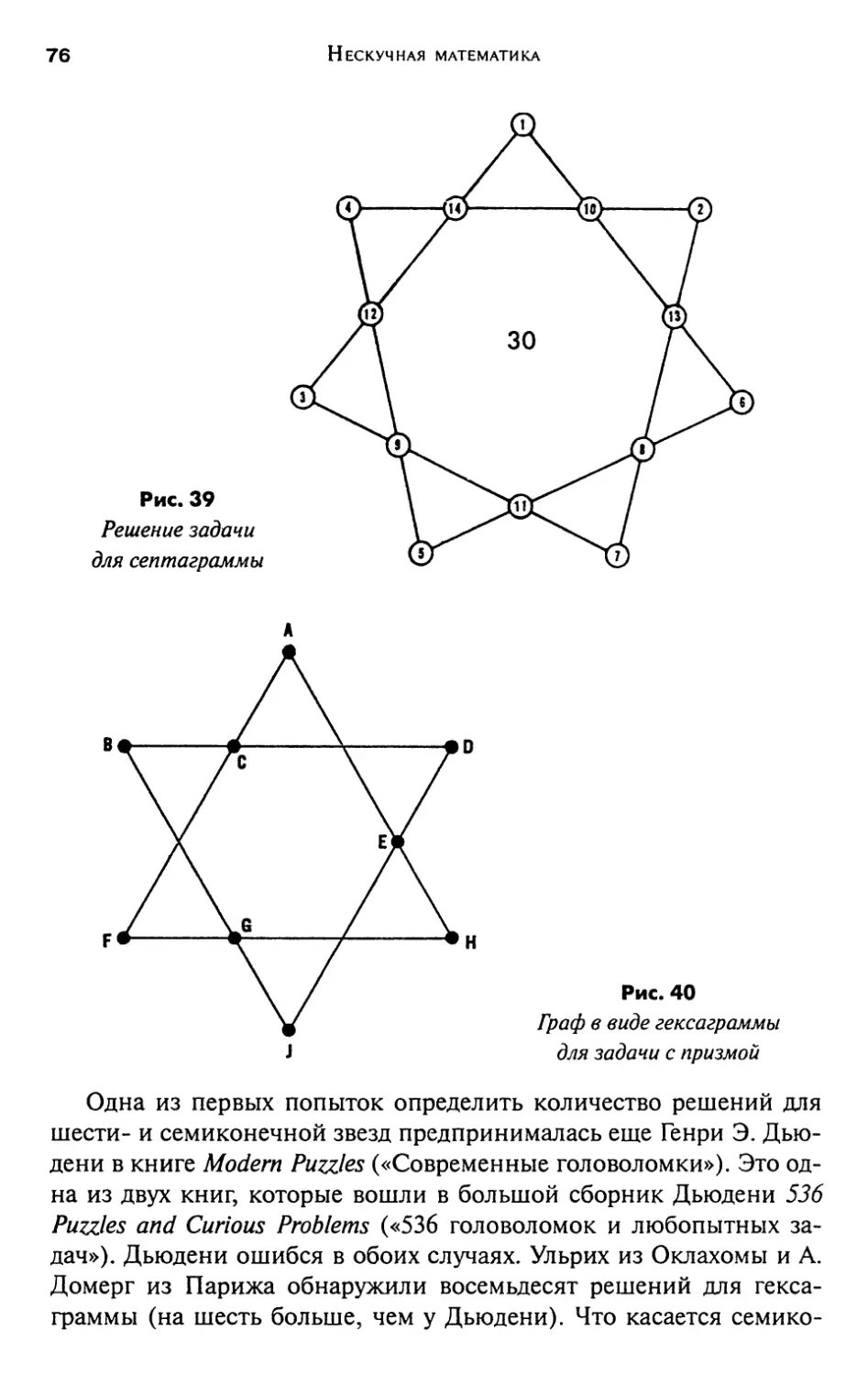
Магические звезды и многоугольники 67
Ответы на странице 77
Гении арифметики 79
Секреты молниеносных вычислений 90
Ответы на странице 101
Математическое искусство Эшера 102
Ответы на странице 115
Куб с красной гранью и другие головоломки 116
Ответы на странице 124
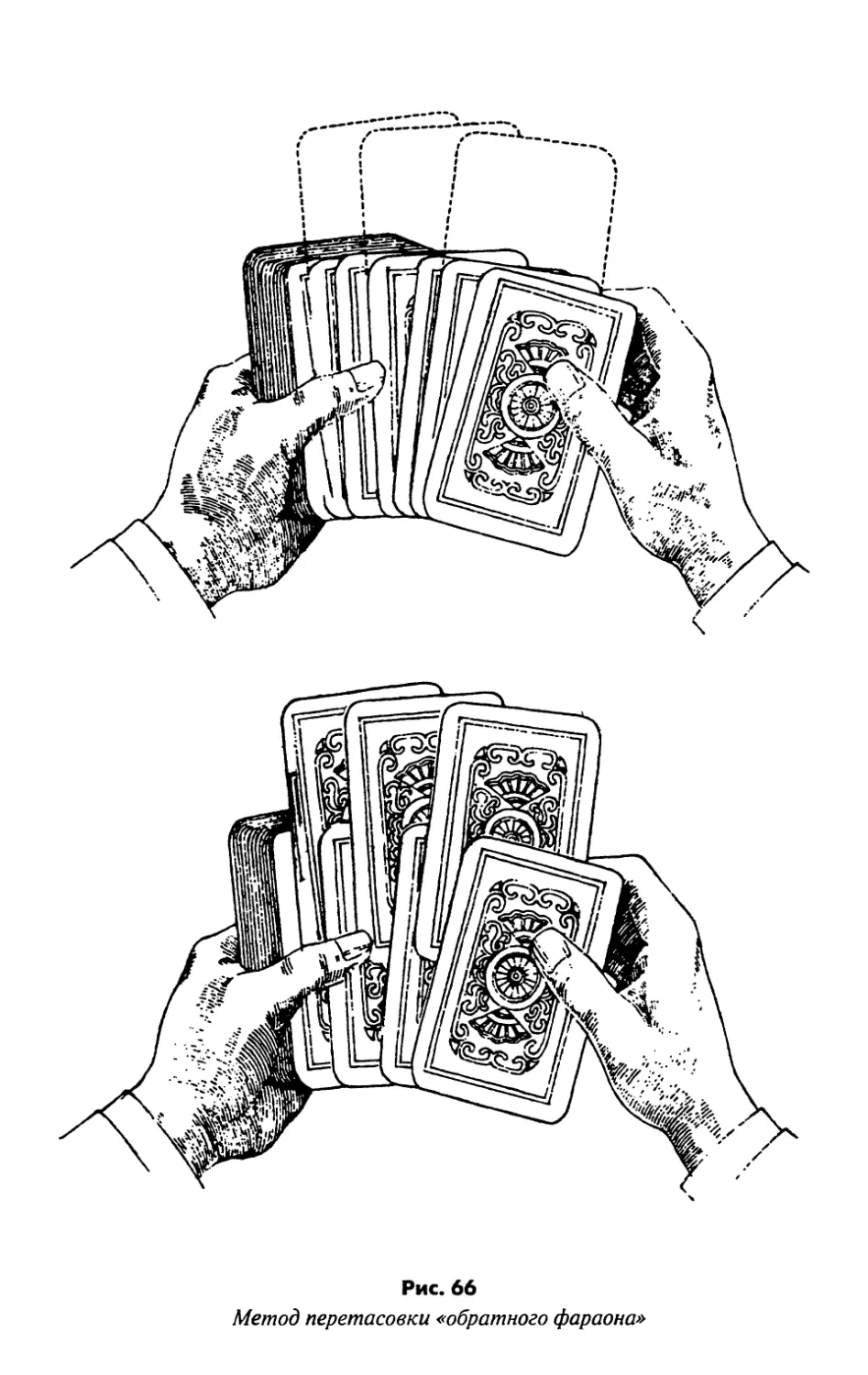
Тасовка карт 135
Ответы на странице 148
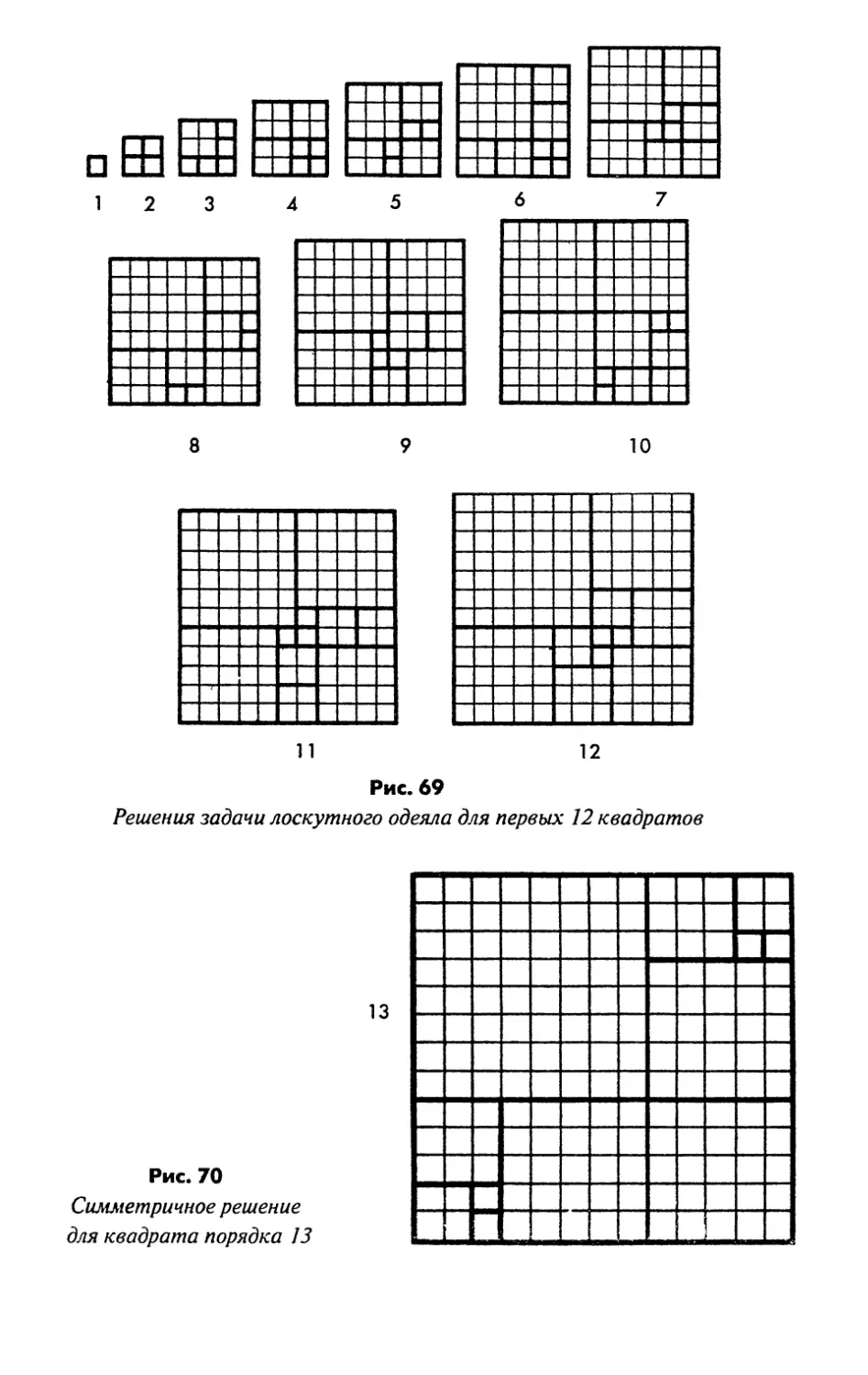
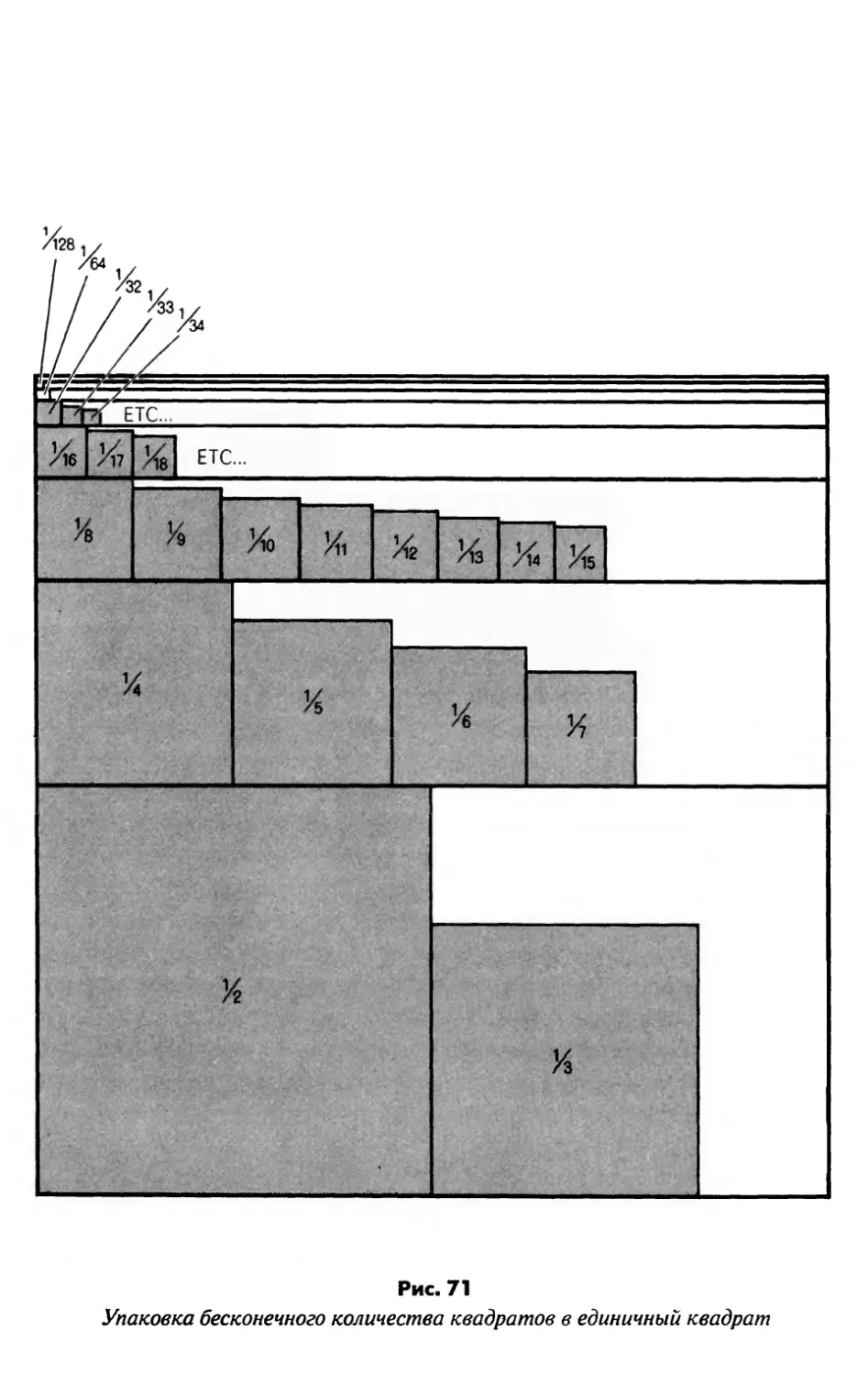
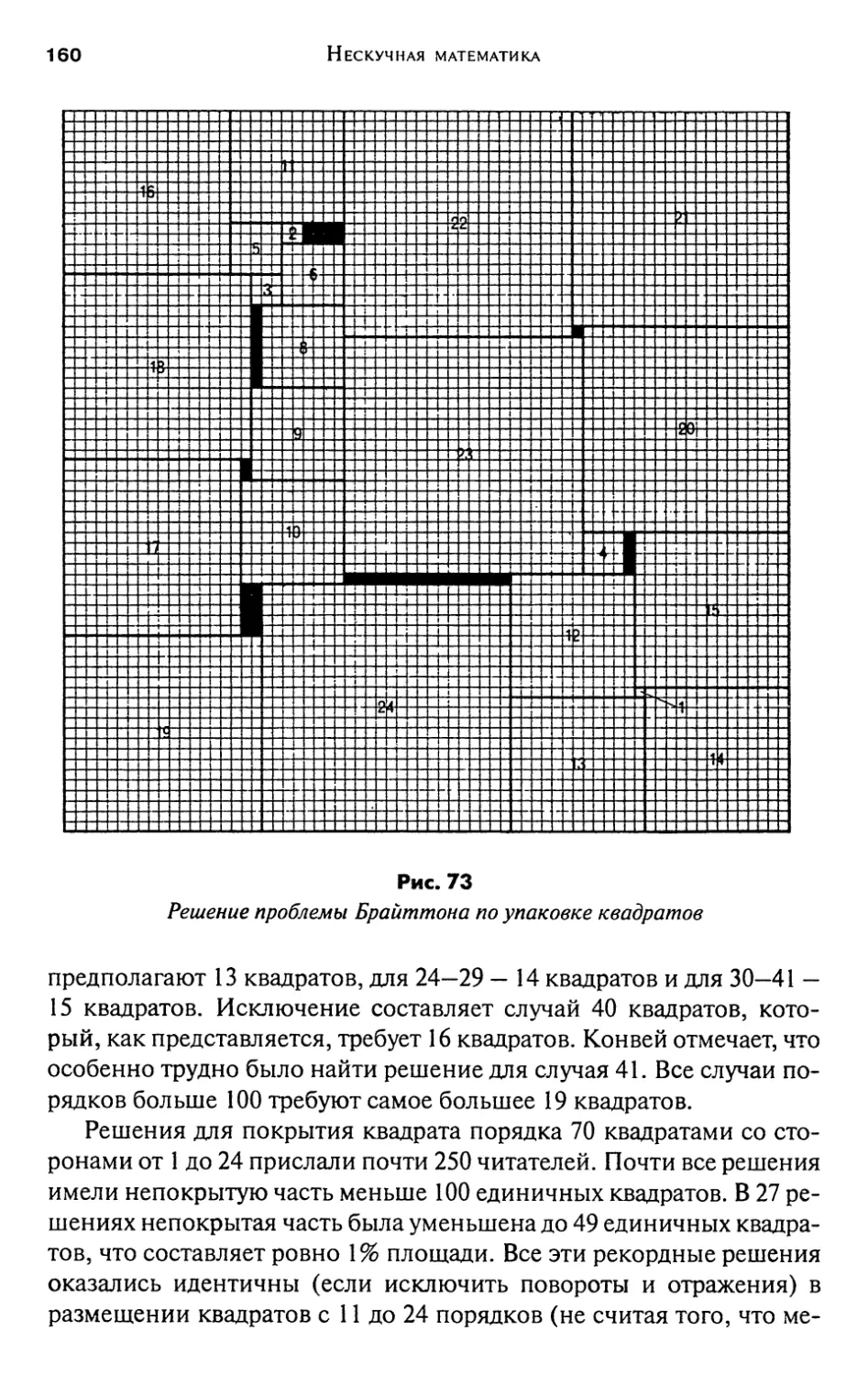
Лоскутное одеяло госпожи Перкинс
и другие упаковки квадратов 151
Ответы на странице 159
Содержание
9
12. Гадание по числам доктора Флисса 162
Ответы на странице 171
13. Случайные числа 172
Ответы на странице 181
14. Парадоксальные песочные часы
и другие физические головоломки 183
Ответы на странице 193
15. Треугольник Паскаля 202
Ответы на странице 212
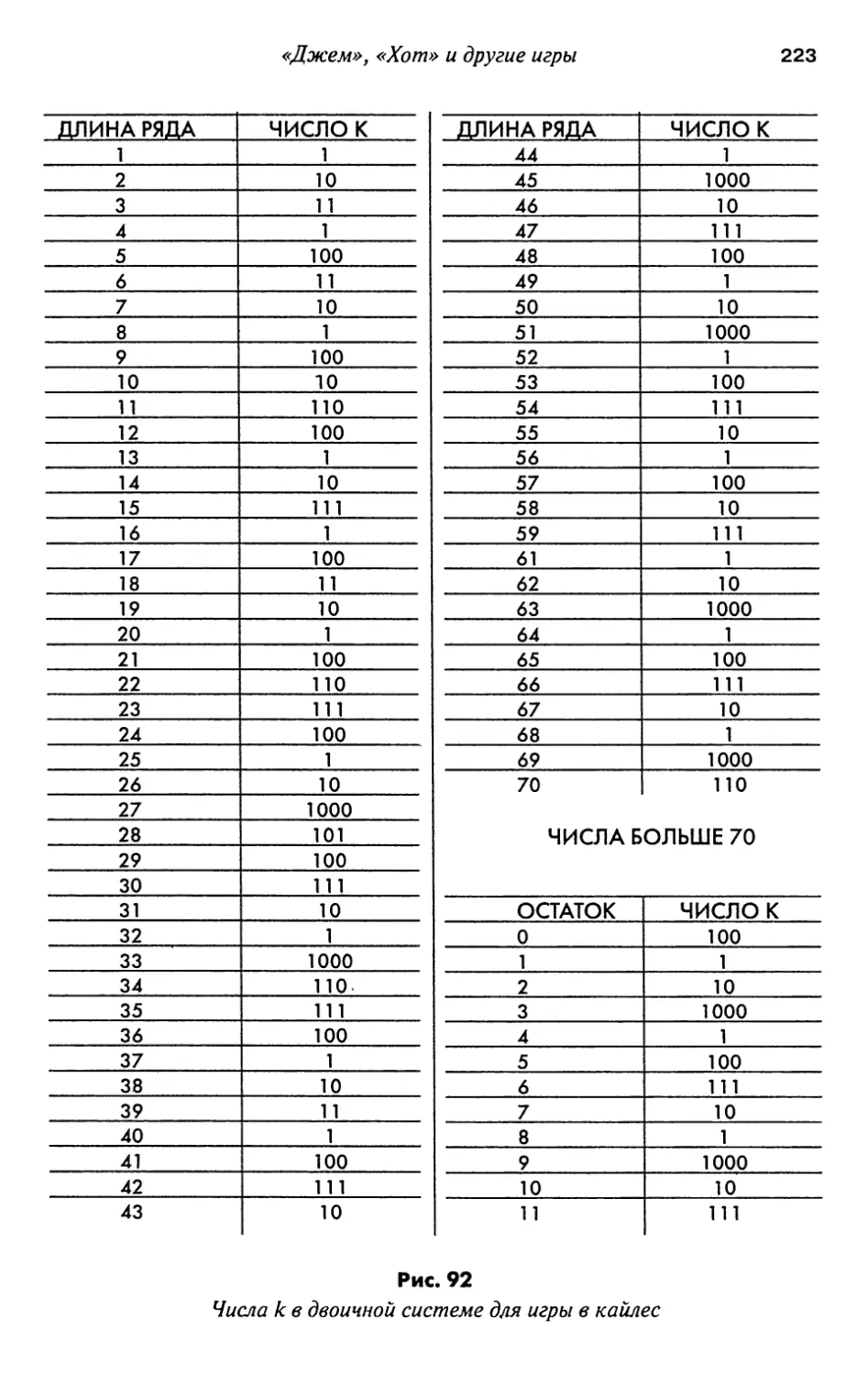
16. «Джем», «Хот» и другие игры 216
Ответы на странице 231
17. Занимательная история ошибок 234
Ответы на странице 244
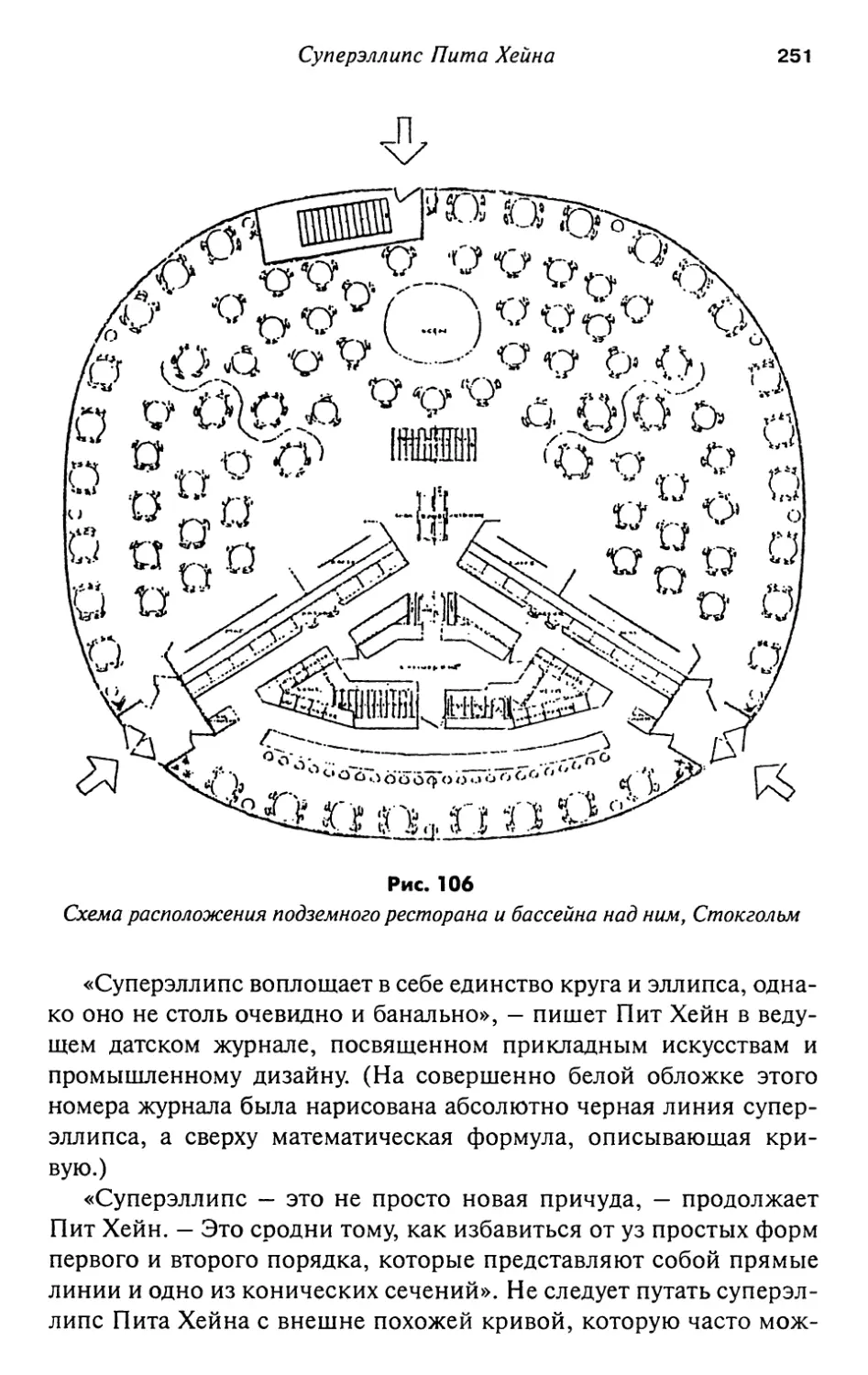
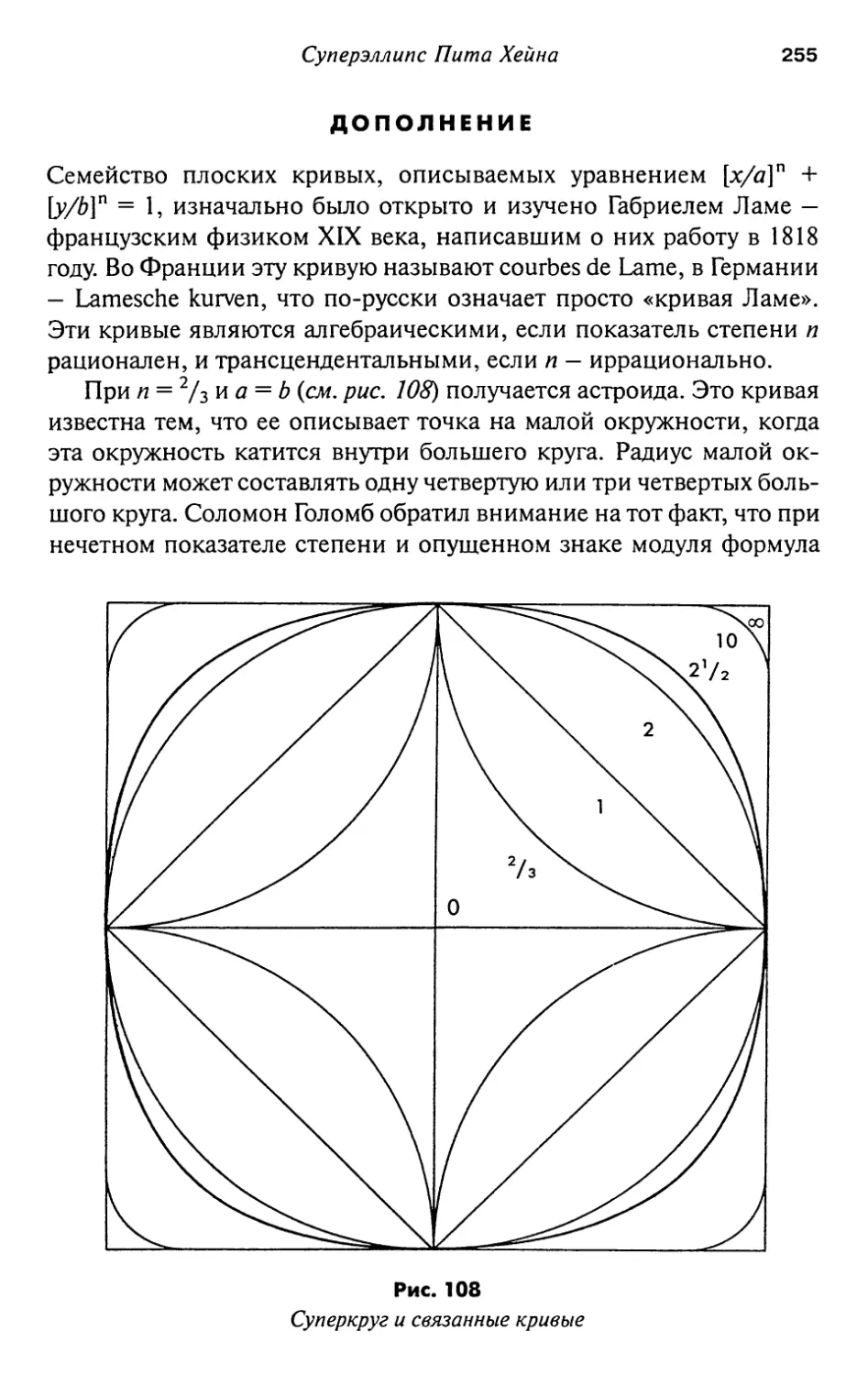
18. Суперэллипс Пита Хеша 247
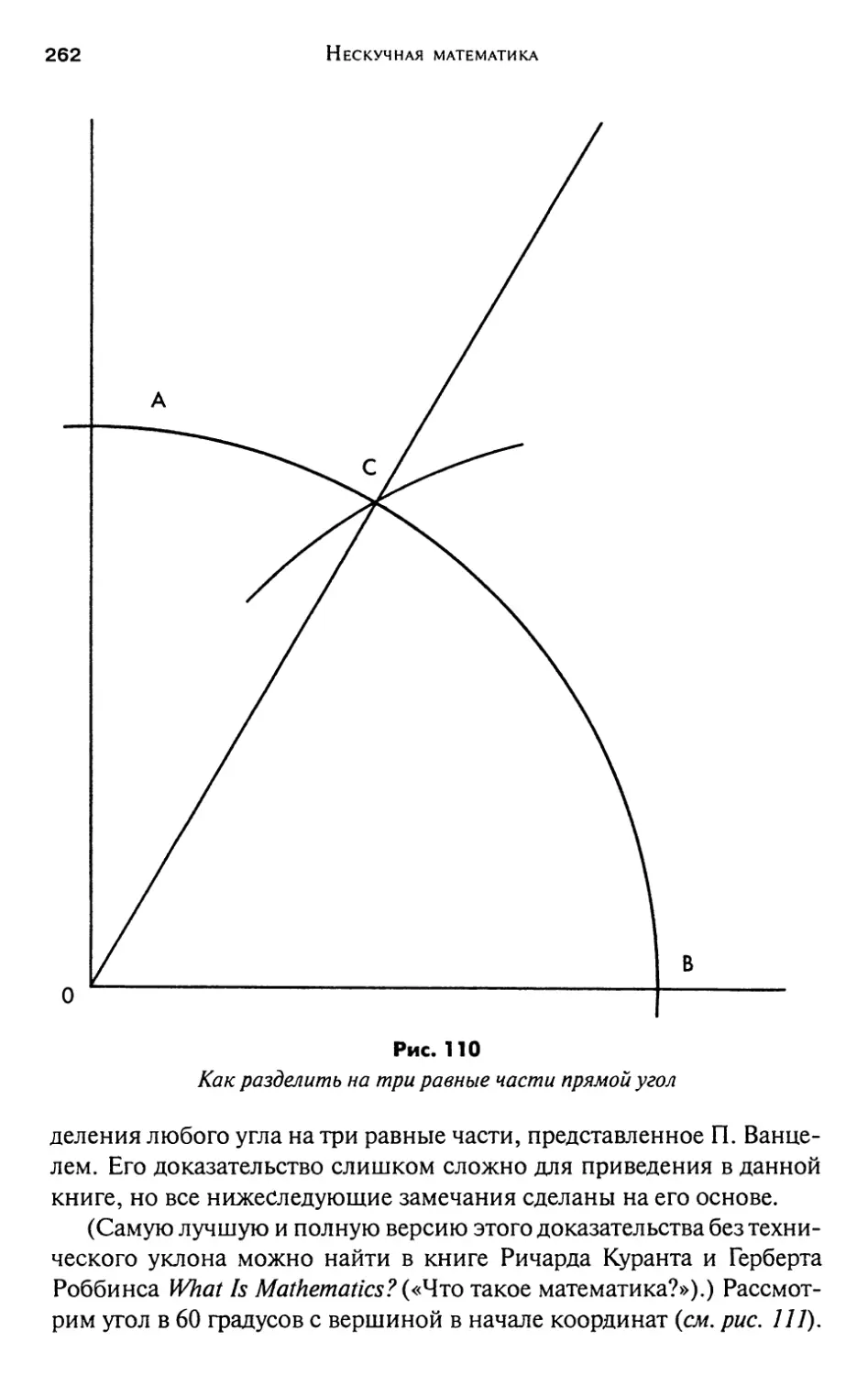
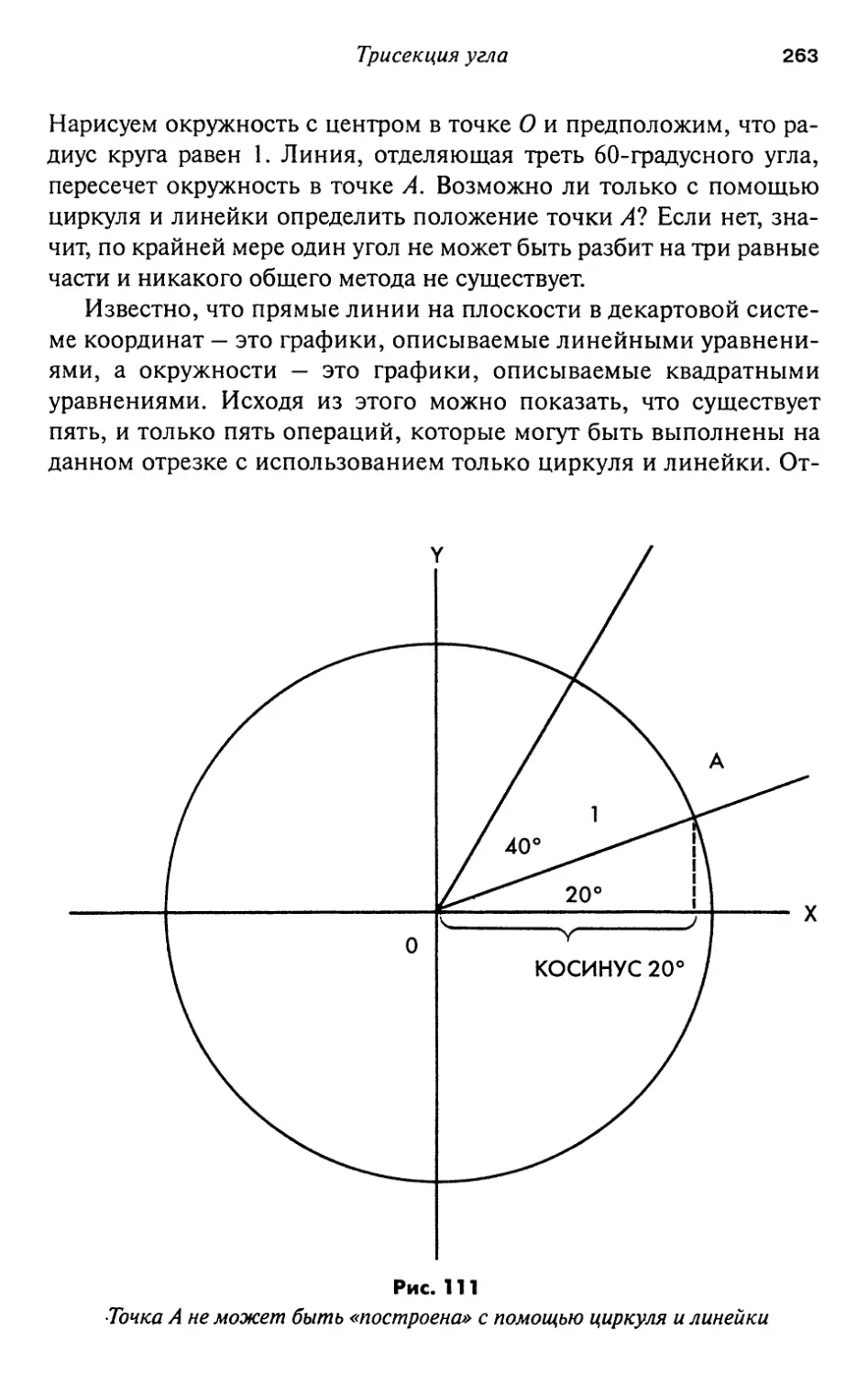
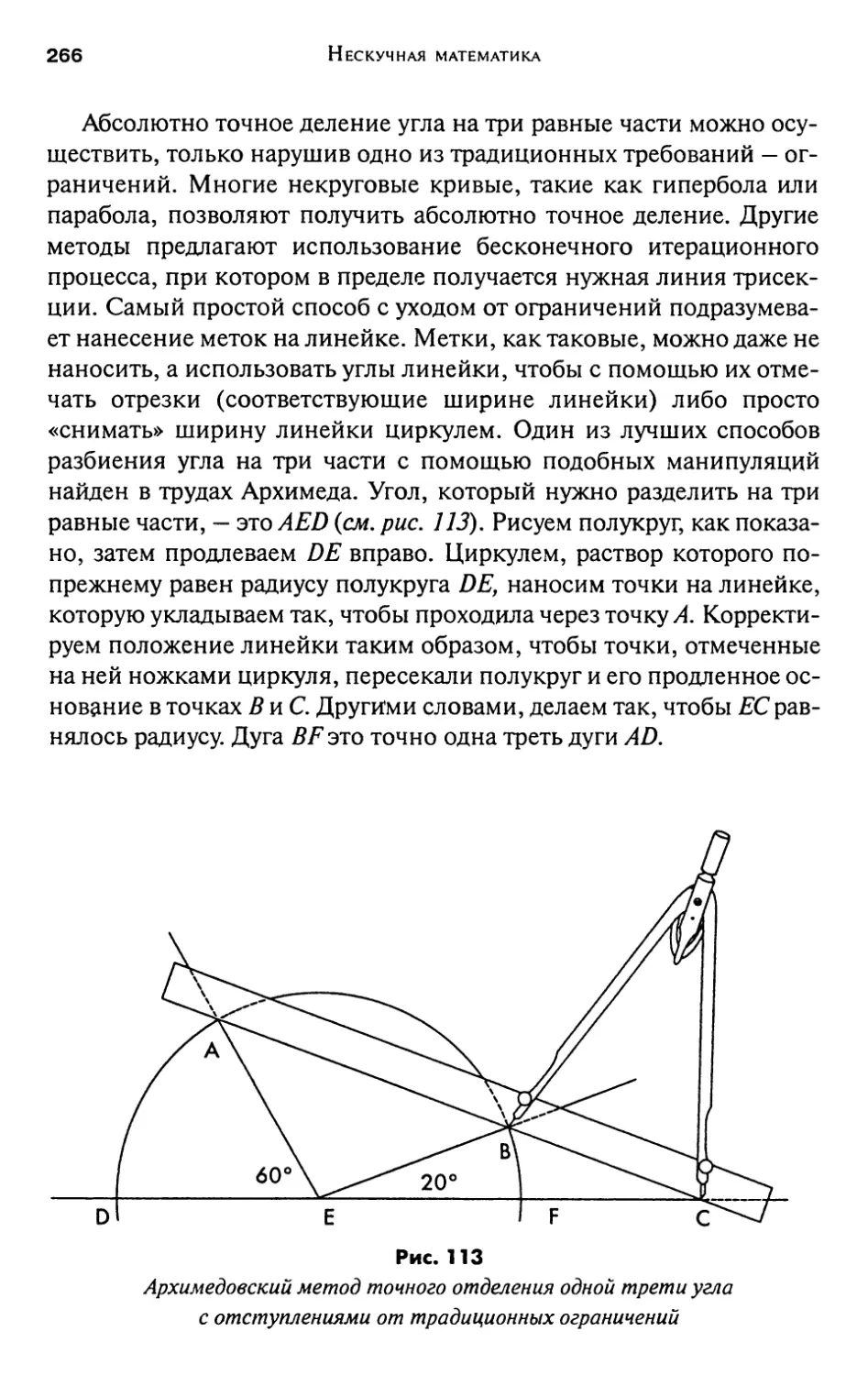
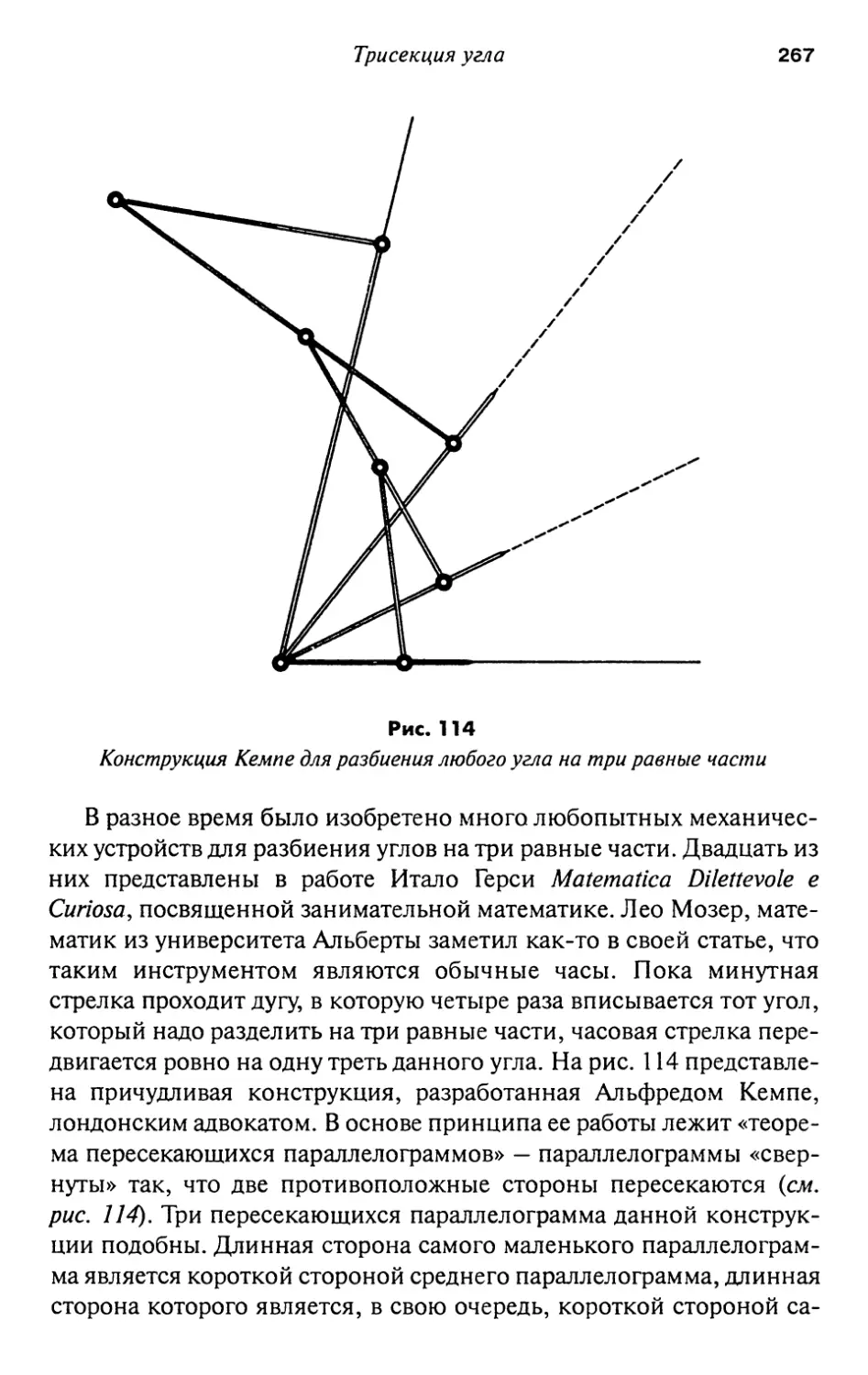
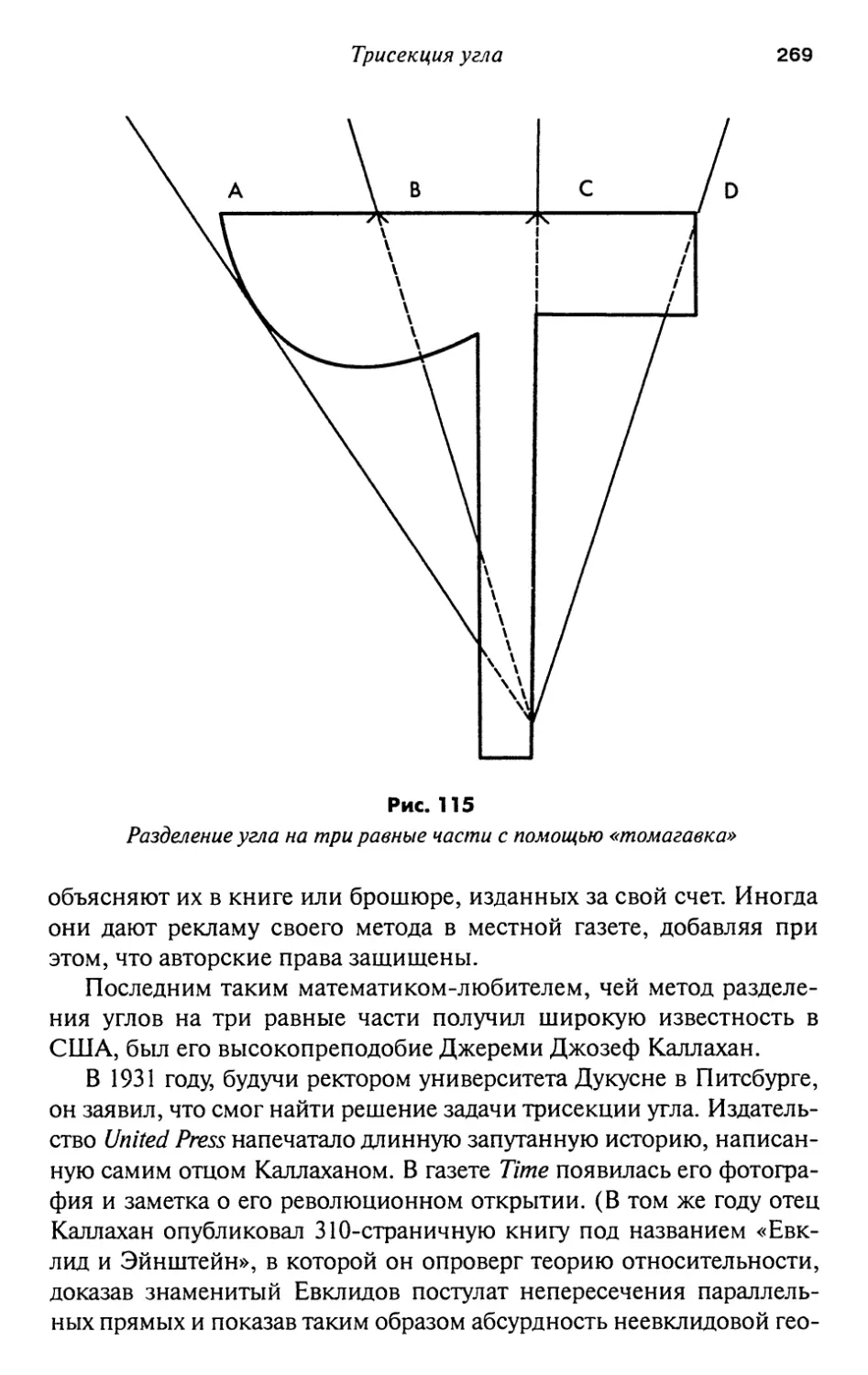
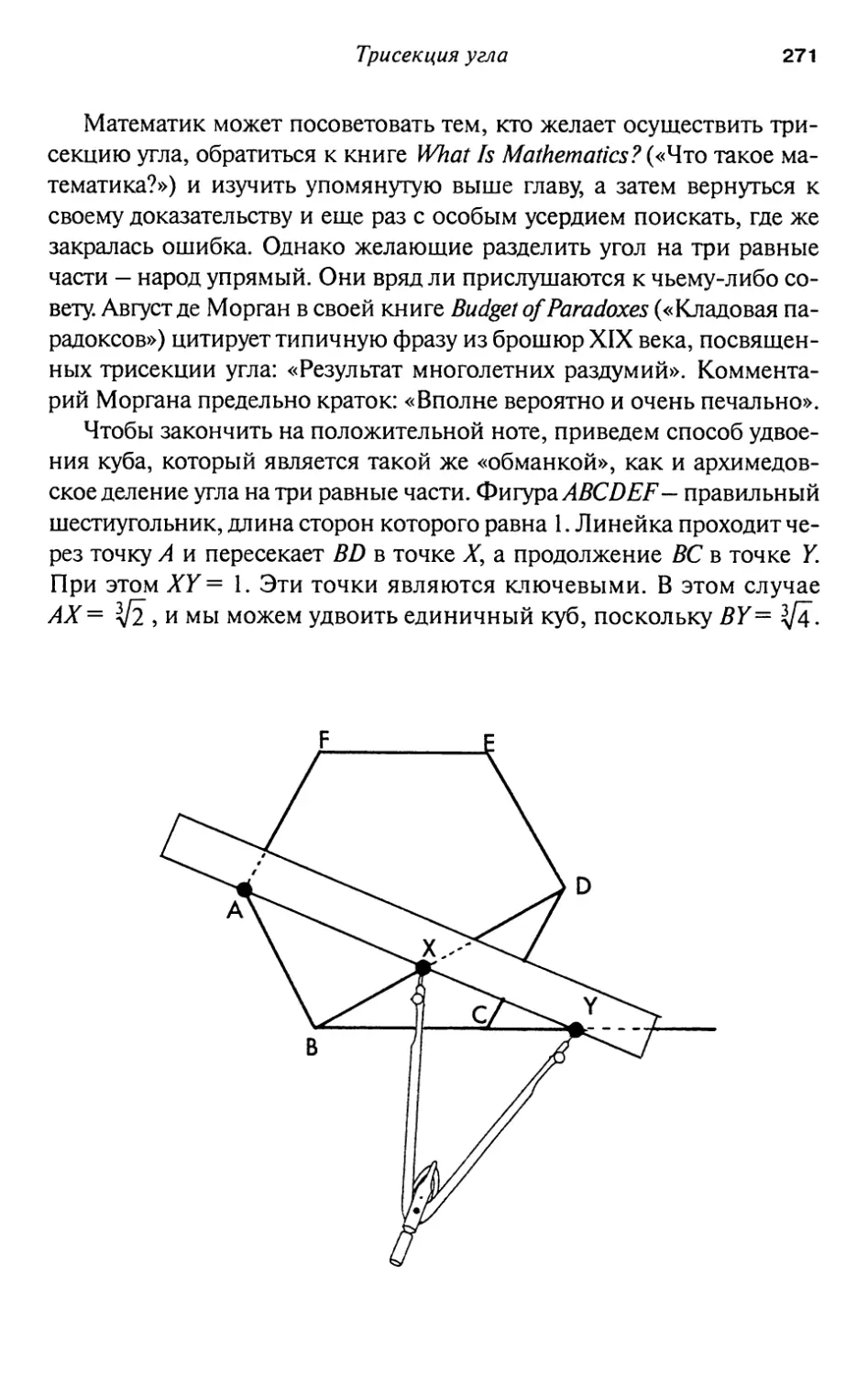
19. Трисекция угла 261
Постскриптум
272
Предисловие к изданию 1989 года
Известный издатель Алфред Абрахам Кнопф опубликовал три моих
книги по материалам колонки математических игр журнала
Scientific American. И вот все эти книги переиздаются
Американской математической ассоциацией.
Первоначальный текст, не считая небольших исправлений,
остался неизменным. Я обновил большую часть глав, добавив к ним
объемное послесловие.
Хотел бы выразить особую благодарность Джону Конвею, в
настоящее время профессору математики Принстонского
университета, за его рекомендации относительно этого издания, а также
Питеру Ренцу, моему редактору, который помог добиться единого стиля
всех трех книг и умело руководил процессом на стадии подготовки
издания.
Мартин Гарднер
октябрь, 1988
Нескучная
математика
Введение
Перед любым преподавателем математики, как бы он ни любил
свой предмет и как бы гармонично ни строил отношения со
студентами, всегда встает один и тот же вопрос: «Как сохранить
активность студентов и удержать их внимание?»
Та же проблема встала и передо мной, автором этой книги,
посвященной занимательной математике. Хотя я всеми силами уходил
от профессионального жаргона математиков и искал связи этой н&-
уки с кругом тем, интересных читателям, передо мной маячил все
тот же вопрос. Как заставить читателя перевернуть страницу?
Была разработана «новая официальная редакция» учебников
математики. Но и она не стала панацеей. Идея нового подхода
состояла в сведении на «нет» рутинной работы по запоминанию (всем
нелюбимая «зубрежка») и снижении акцента на объяснении скрытых
механизмов действия арифметических операций. Однако, по
мнению самих учащихся, изложение коммутативных, дистрибутивных
и ассоциативных законов математики стало даже более унылым,
чем таблица умножения. Та же участь постигла и сам язык
изложения элементарной теории множеств. Овладев этой «новой» наукой,
и без того посредственные преподаватели стали еще
посредственнее, а несчастным студентам пришлось изучать исключительно
терминологию — причем такую, которой не пользовался никто, кроме
придумавших ее чиновников от образования. Было даже написано
несколько книг, чтобы объяснить новый подход к математике
самим математикам. Но эти книги оказались еще более серыми и
безликими, чем прежние учебники математики. В конечном счете даже
профессиональные преподаватели стали уставать, твердя детям о
различиях между числом и цифрой. Страдающую в агонии «новую
науку математики» добил Моррис Клайн своей книгой Why Johnny
Can't Add («Почему Джонни не умеет складывать»).
Я всегда был убежден, что лучший способ сделать математику
увлекательной для студентов и интересующихся — это превратить ее в
14
Нескучная математика
игру. А вот на профессиональном уровне (особенно в применении к
прикладным задачам) математика уже может, да и должна быть
предельно серьезной.
Что же касается занимательной математики, рассчитанной на
более низкий уровень, то никакой студент не вдохновится
перспективой изучать, скажем, расширенную теорию групп. Особенно если
сказать, что ему предстоит познать все великолепие этой
замечательной теории. Та же печальная участь постигнет и часто
приводимый аргумент, что без теории групп невозможно стать
специалистом в области элементарных частиц. Естественно, лучший способ
пробудить интерес студента состоит в том, чтобы подарить ему
захватывающую математическую интригу — игру, головоломку, фокус,
шутку, парадокс. Можно просто предложить реальную модель,
прочитать лимерик или сделать что-нибудь такое, чего скучные
преподаватели математики всячески избегают, потому что это кажется им
«фривольным».
Предвидя возражения, скажу, что никто и не предлагает, чтобы
преподаватель увеселял студентов. Начальный курс математики,
который предлагает только головоломки, будет столь же
неэффективен, как и скучная монография. Очевидно, необходим компромисс
между серьезностью и фривольностью. Серьезность наполняет игру
сутью, а вот немного веселья необходимо, чтобы читатель не уснул.
Необходимое сочетание этих слагаемых успеха я и пытался
воплотить в своих колонках в журнале Scientific American, когда еще
только начинал вести эту рубрику в декабре 1956 года. Шесть
изданий по материалам этих колонок уже увидели свет. Данное издание
седьмое. Как и прежде, я пересмотрел материал колонок, дополнив
его интересными выдержками из писем читателей.
Охваченные в книге темы столь же пестры, как и шумный
карнавал. Мы надеемся, что читатель с удовольствием погрузится в
пучину этого математического карнавала и неважно, кем он будет —
профессиональным математиком или просто «интересующимся»,
которого привлекли забавы и игры. Кстати, последний может очень
даже удивиться, узнав, какое количество далеко не тривиальной
математики он усвоил, даже не прилагая к этому усилий.
Мартин Гарднер
апрель, 1975
ГЛАВА 1
«Ростки»
и «Брюссельская капуста»
Все получилось как бы само..,
-ДЖЕЙМС ДЖОЙС,
«Поминки по Финнегану»
С игрой «Ростки» меня познакомил один из моих друзей из числа
кембриджских студентов. В последнее время в Кембридже эта игра
с любопытным топологическим подтекстом стала повальным
увлечением.
А все началось в 1967 году, когда я получил письмо от Дэвида Харт-
шорна, изучавшего математику в Лидсском университете. А вскоре и
другие английские читатели начали сообщать мне о забавной игре,
для которой нужны только карандаш и бумага. Словно оправдывая
свое название, «Ростки» стремительно укоренились на
кембриджской почве.
Мне приятно сообщить вам, что я сумел проследить
происхождение «Ростков». Игра родилась в творческом союзе двух
исследователей — Джона Конвея, в то время еще преподавателя математики
колледжа Сидни-Сассекс при Кембриджском университете, и
Майкла Стюарта Петерсона, который в то время был аспирантом в
Кембридже и создавал теорию абстрактного программирования.
Игра начинается с того, что на листе бумаги ставится п точек.
Даже при трех точках анализировать новую игру сложнее, чем всем
известные «крестики-нолики». Поэтому новичкам не советуем
выбирать варианты с начальным количеством точек больше трех или
четырех. Ходом в игре «Ростки» является проведение линии через две
существующие точки и нанесение на эту линию новой точки. При
этом допускается замыкание линии на исходную точку.
16
Нескучная математика
Правила игры следующие.
1. Линии могут иметь любую форму, но не должны иметь
самопересечений, а также пересечений с ранее проведенными линиями и
не должны проходить через уже соединенные точки.
2. Из одной точки не может исходить более трех линий.
Итак, рисуя кривые, игроки по очереди соединяют точки. В
исходном варианте игры в «Ростки» (советуем начинать с нее)
победителем оказывается тот, кто сделал ход последним. Как в игре «Ним»,
здесь возможен своеобразный «мизер», когда (в карточном
варианте) нельзя брать взяток. Тогда в игре «Ростки» победителем
оказывается тот, кто не имеет хода.
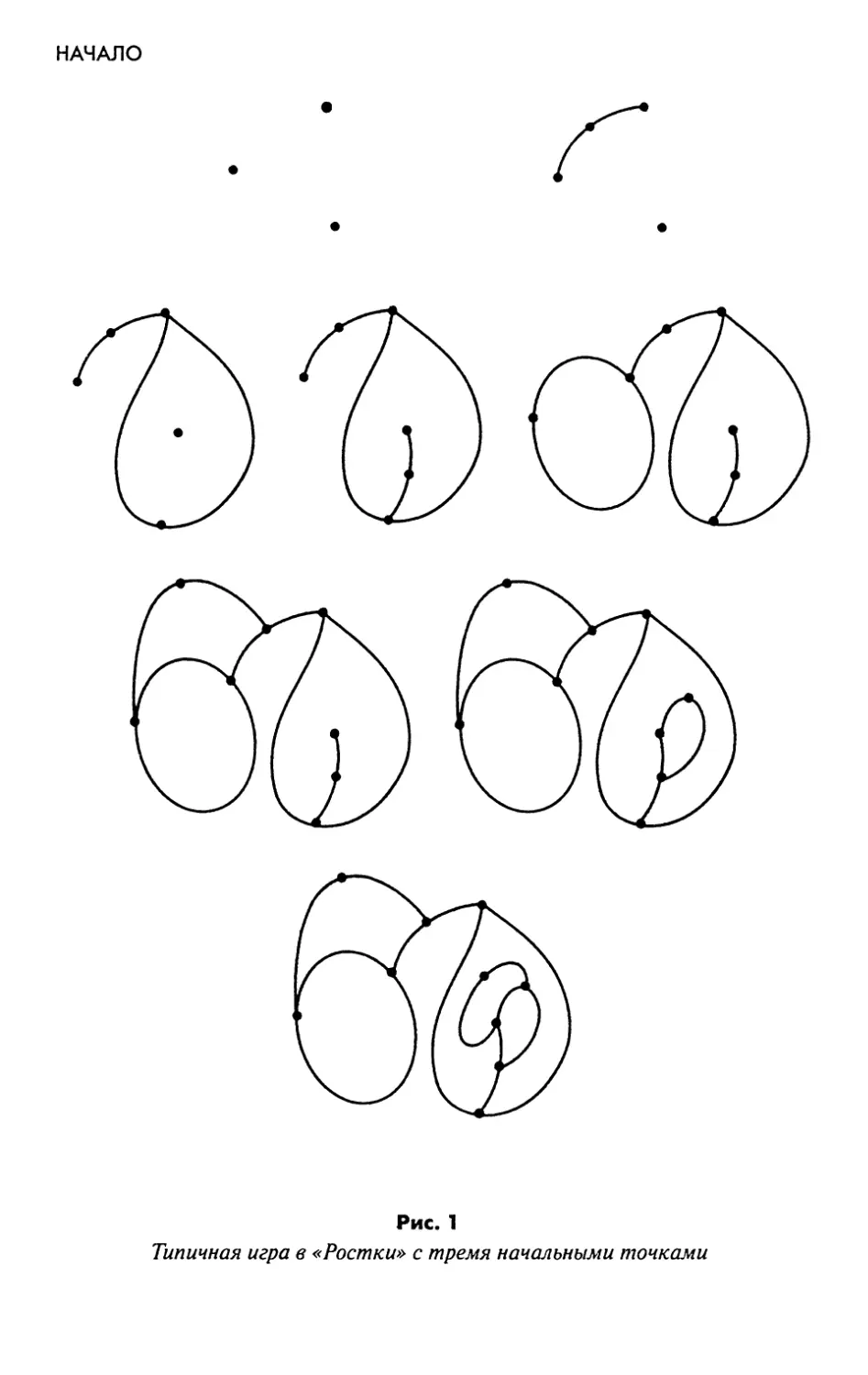
Пример типичной игры без мизера, которая началась с трех
точек и закончилась на седьмом ходу победой первого игрока,
приведен на рисунке 1. Глядя на эту партию, становится понятно, за
что игра получила такое название. Линии, словно ростки,
формируют фантастические узоры. Наибольшее восхищение вызывает
то, что в отличие от других игр с соединением точек, эта игра не
просто комбинаторная. В ней используются топологические
свойства плоскости. Если говорить языком строгой математики, то
игра построена на теореме Жордана. Ее формулировка: «плоская
простая замкнутая кривая разбивает плоскость на две связные
компоненты и является их общей границей». Проще говоря,
замкнутые кривые делят плоскость на внешнюю и внутреннюю
область.
На первый взгляд кажется, что партия в такой игре может
длиться бесконечно. Однако Конвей предложил простое доказательство
того, что партия имеет не больше (Зя — 1) ходов. Каждая точка
имеет три «жизни» — три линии, которые могут встретиться в этой
точке. Точку, из которой исходят три линии, называют «мертвой
точкой», потому что к ней проводить линию уже нельзя. Игра, которая
начинается с п точек, имеет Ъп «стартовых» жизней. Каждый ход
убивает две жизни, однако добавляет одну точку с одной жизнью.
Значит, каждый ход уменьшает количество жизней на одну.
Очевидно, что, когда останется только одна жизнь, игра продолжаться уже
не может, потому что для хода требуется «сжечь» как минимум две
жизни. Соответственно, никакая партия не может продолжаться
дольше (3/7 — I) хода.
НАЧАЛО
Рис. 1
Типичная игра в «Ростки» с тремя начальными точками
18
Нескучная математика
Также легко показать, что партия должна длиться как минимум
2п ходов. Игра с тремя точками начинается с девятью жизнями и
должна закончиться на восьмом ходу или перед ним, т. е. должна
длиться по крайней мере шесть ходов.
Игра с одной точкой тривиальна. Первый игрок имеет только
один возможный ход — соединить точку на саму себя. В этом случае
выигрывает второй игрок (или проигрывает в варианте мизера),
соединяя точки изнутри или снаружи. Оба хода второго игрока
эквивалентны, поскольку с точки зрения топологии нет ничего, что бы
отличало внутреннюю часть замкнутой кривой от наружной.
Представьте себе, что мы играем на поверхности сферы. Если мы
прокалываем поверхность во внутренней области замкнутой кривой, то
можем вывернуть эту сферу так, что все точки, ранее находившиеся
внутри кривой, оказываются снаружи и наоборот. Эквивалентность
внутреннего и внешнего с точки зрения топологии очень важна,
потому что это существенно упрощает анализ игры, начинающейся с
двух или более точек.
Если точек две, игра моментально обретает интерес. Очевидно,
что у первого игрока пять возможных ходов {см. рис. 2). Но второй и
третий, а также четвертый и пятый начала взаимно симметричны и,
соответственно, эквивалентны. Поскольку внутренняя и внешняя
части замкнутой кривой эквивалентны, то все четыре варианта (со
второго по пятый) равнозначны. Значит, требуется анализ только
двух топологически неравнозначных вариантов. Если построить
полную диаграмму всех возможных ходов в виде графа, то его
анализ покажет, что и при нормальной, и при обратной разновидности
правил выигрышная стратегия у второго игрока.
Конвей установил, что по основным правилам в варианте с тремя
точками (при правильном выборе стратегии) всегда может выиграть
первый игрок, а в варианте мизера с тремя точками гарантирован-
НАЧАЛО
АВ АВ АВ АВ А В
<Е> <5>
Ь" 'О
Рис.2
Две начальные тонки (А и В), а также возможные ходы первого игрока
в варианте игры с двумя точками
«Ростки» и «Брюссельская капуста»
19
ную победу имеет второй игрок. Студент-математик из Кембриджа
Денис Моллизон показал, что в варианте четырех и пяти точек по
основным правилам победную стратегию имеет первый игрок. Денис
заключил пари с Конвеем на 10 шиллингов, что сможет провести
анализ игры с шестью точками. Анализ Дениса занял 49 страниц и
потребовал месяца работы, а Конвей свой анализ закончить не смог.
В итоге Денис Моллизон доказал, что при шести точках и основных
правилах выигрышную стратегию имеет второй игрок. Кстати,
оказалось, что второй игрок имеет победную стратегию и в варианте
мизера с четырьмя точками. Но так и не удалось установить, кто имеет
победную стратегию в варианте мизера, если точек больше четырех.
Мне писали, что подобный анализ проводился для основного
варианта игры «Ростки» с семью и восемью точками, однако достоверной
(подтвержденной математиками) информацией я не располагаю. По
моим данным, не существует компьютерной программы, которая
позволяла бы анализировать варианты игры в общем случае.
Хотя стратегия оптимального выбора хода до сих пор не
сформулирована, к концу игры оказывается, что кривые делят плоскость
определенным специфическим образом. Характер получающегося
рисунка и подсказывает путь к победе. Возможность
стратегического планирования делает игру «Ростки» настоящей
интеллектуальной забавой и позволяет игроку бесконечно совершенствоваться. В
такой игре возможны самые неожиданные построения, для
которых, как представляется, просто не существует никакой стратегии,
которая гарантировала бы кому-либо выигрыш. По оценкам Кон-
вея, полный анализ игры с восемью точками лежит за пределами
возможности компьютеров того времени .
Игра «Ростки» была изобретена во вторник 21 февраля 1967
года, когда Конвей и Петерсон после чая развлекались в комнате
отдыха математического отдела, пытаясь придумать новую игру, в
которую можно было бы играть только с помощью карандаша и
бумаги. Конвей лишь доработал игру, идею которой предложил
Петерсон. Он занимался складыванием листов бумаги и случайно
натолкнулся на желаемый вариант игры. При выработке
оптимальных правил Петерсон предложил: «А почему бы на линию не
поместить новую точку?»
Конвей писал мне: «Как только это новое правило было
принято, все прежние правила стали просто не нужны и были
отвергнуты». Начальное положение игры свелось к п точкам, и «ростки»
стали появляться самым естественным образом.
20
Нескучная математика
Важность добавления новой точки при каждом ходе была столь
значимой, что игра даже приобрела коммерческий характер.
Выигранные средства авторы игры предполагали делить так: 3Д — Петер-
сон, 2/5 — Конвей. «Сложились довольно замысловатые правила, —
писал Конвей, - по которым мы намеревались делить полученные
от игры деньги».
«На следующий день «Ростки» вовсю пустили ростки, —
продолжает Конвей. — Казалось, что в эту игру играли все. Во время ланчей
за чаем или кофе небольшие группы людей изучали фантастические
картины из партий. Это смотрелось весьма комично. Некоторые
пытались играть на поверхности тора, бутылке Клейна (были и
другие топологические варианты). Один из сотрудников размышлял
над вариантом игры, которая бы имела большее количество
размерностей. Не избежал эпидемии и секретарский состав лаборатории.
Мы находили партии в самых неожиданных местах. Много лет
спустя, когда я кому-либо рассказывал об этой игре, непременно
оказывалось, что он уже слышал о ней. В нее играют даже мои дочери,
которым три и четыре года. Хотя обычно я у них выигрываю».
Название «Ростки» игре дал Конвей. Один из аспирантов
предложил и другое название — «корь», за ее заразительность. Однако
прижилось название Конвея. Немного позже Конвей изобрел
внешне похожую игру, которую назвал «Брюссельская капуста»
(Brussels sprouts). Но это было уже шуткой. Я опишу правила этой
игры, но решить, почему эта игра скорее шутка, предоставлю
читателю. Свою версию ответа я приведу в разделе ответов к этой главе.
Партия в «Брюссельскую капусту» начинается не с п точек, ас«
крестиков. Ход в этой игре состоит в продлении любой половинки
перекладины любого крестика в линию, которая заканчивается на
свободной половинке перекладины любого другого крестика либо
того же самого. Затем в произвольном месте создается перекладина
для образования нового креста. Две половинки перекладины нового
креста при этом получаются уже занятыми, поскольку половинка
перекладины не может использоваться дважды. Как и в игре
«Ростки», никакая кривая не может иметь самопересечений, равно как и
пересекать ранее проведенную кривую. Также она не может
проходить через ранее поставленный крест (но на себя в начальном кресте
замыкаться может). В классическом варианте игры побеждает тот,
кто последним делает ход, в мизере — тот, кто оказался без хода.
После знакомства с игрой «Ростки» новая игра поначалу
кажется более сложной и замысловатой.
«Ростки» и «Брюссельская капуста»
21
Поскольку каждый ход «убивает» две половинки перекладины и
добавляет две свободные половинки, представляется, что партия в
этой игре может длиться бесконечно. Но все игры имеют
логический конец, и в самих правилах этой игры есть намеренный изъян,
который читатель обнаружит, если проведет их анализ. Чтобы
прояснить правила игры, мы привели типичную партию классического
варианта игры. Эта партия начинается с двух крестиков и
заканчивается победой второго игрока на восьмом ходу {см. рис. 3).
Конвей в своем письме сообщает о нескольких крупных
достижениях в анализе игры «Ростки». В их число вошла концепция, которую
он сам назвал «порядок сложности терминальной позиции»
(терминальной называется конечная позиция в игре), а также
классификация терминальных позиций нулевого порядка сложности. К числу та-
Рис. 3
Типичная партия в «Брюссельскую капусту» с двумя крестиками
22
Нескучная математика
ких окончаний Конвей отнес следующие: «вошь», «жук», «таракан»,
«уховертка» и «скорпион». Более крупные насекомые могут быть
«заражены» более мелкими, такими как «вши». Мелкие «насекомые»
могут быть представлены как внутри фигуры более крупного
«насекомого», так и снаружи. Конвей нарисовал один из примеров того,
что он сам назвал «уховертка наизнанку внутри вывернутой
наизнанку вши». В одних позициях, по его мнению, больше мелких
насекомых, в других меньше. Существует теорема, получиршая в
английской литературе название FTOZOM (fundamental theorem of zero-
order moribundity, или фундаментальная теорема о терминальных
позициях нулевого порядка сложности), суть которой довольно
глубока. «Ростки» давали ростки столь стремительно, что я счел за благо
повременить со своим следующим сообщением об этой игре.
ПРИЛОЖЕНИЕ
Игра «Ростки» мгновенно захватила читателей Scientific American,
многие из которых сами предлагали различные варианты, а также
обобщения правил. Ральф Дж. Райен III предложил заменить точки
крошечными стрелками и разрешить проводить новую линию
только в сторону стрелки. Гильберт В. Кесслер объединил варианты с
точками и крестиками в новой игре под названием succotash (это
слово обозначает национальное блюдо североамериканских
индейцев из молодой кукурузы и бобов). Джордж П. Ричардсон
исследовал варианты игры в других топологиях, например на поверхности
тора. Эрик Л. Ганс рассмотрел в своем письме обобщение с игрой
«Брюссельская капуста» (сам он назвал свою игру Belgian sprouts,
что означает «Бельгийские ростки»), в которой используются
снежинки — звездочки с пересечением п перекладин. Владимир
Игнатович предложил новые правила, согласно которым игрок может
добавлять по своему выбору от нуля (ни одной!) до двух точек на
проводимой линии.
Несколько читателей высказывали сомнение по поводу того, что
партия в классическом варианте ростков должна длиться как
минимум 2/7 ходов. Они высылали мне то, что, по их мнению, было
«контрпримером», но всякий раз забывали замечать, что каждая
изолированная точка позволяет сделать два дополнительных хода.
Игровые позиции в партиях, которые длились ровно 2я ходов,
прекрасно описываются упомянутой выше теоремой FTOZOM,
предложенной Деборой Моллисон и Дж. Конвеем.
«Ростки» и «Брюссельская капуста»
23
ффон
Вошь Жук Таракан Уховертка Скорпион
Теорема FTOZOM утверждает, что партия в «Ростки»,
начинающаяся с п точек, должна продлиться как минимум 2п ходов, а также
то, что при продолжительности партии ровно 2я ходов конечная
позиция будет состоять из набора всех семи «насекомых». На рисунке
представлены пять: вошь, жук, таракан, уховертка и скорпион.
Подробнее об этом можно найти в книге Winning Ways авторов Берле-
кампа, Конвея и Гая.
ОТВЕТЫ
Почему же «Брюссельскую капусту», которая по сравнению с
игрой «Ростки» кажется более сложной, сам Дж. Конвей называл не
более чем шуткой? Ответ прост. В эту игру невозможно играть ни
хорошо, ни плохо, потому что каждая партия длится ровно (5л — 2)
ходов, где п — это начальное число крестиков. Если рассматривать
классический вариант, когда побеждает последний, сделавший
ход, то при нечетном п победителем всегда будет первый игрок,
при четном — второй. (В варианте мизера все наоборот.)
Познакомив кого-либо с игрой в «Ростки», где каждая партия проходит в
борьбе, расскажите ему о «Брюссельской капусте». Вы можете
смело делать ставки, поскольку заранее знаете, кто выиграет партию.
Возможность доказать, что каждая партия длится ровно (5я — 2)
ходов, я оставляю читателю.
ГЛАВА 2
Головоломки
с монетами
Монеты обладают множеством простых свойств, которые можно с
успехом использовать в занимательной математике. Их можно
сложить стопкой, использовать в игре в качестве фишек, они могут
служить моделью точек на плоскости, имеют замечательную круглую
форму и две различные стороны. В этой главе приведены
занимательные трюки, для которых потребуется не более 10 монеток. Эти
трюки достаточно просты и оригинальны, чтобы
продемонстрировать их в баре или за обеденным столом для развлечения гостей.
Однако основы некоторых из них ведут в глубины далеко не
тривиальной математики.
Вот одна из самых старых и, пожалуй, лучших головоломок с
монетами. Разместите восемь монеток в ряд на столе, как это
показано на рис. 4, а затем попытайтесь в четыре хода (перемещения
монетки) перестроить ряд в четыре стопки по две монеты. Еще
одно условие: на каждом ходу монета должна «перепрыгивать» ровно
через две монеты (в любом направлении) и приземляться на
ближайшую одиночную монету. При этом не важно, лежат ли монеты,
через которые перепрыгивают, рядом или друг на друге. Восемь —
это наименьшее количество монет, которое можно удвоить
подобным образом.
Рис.4
Задача на удвоение ряда
Головоломки с монетами 25
Рис.5
Задача с плотной упаковкой
Несомненно, читатель найдет эту задачу довольно простой и с
удовольствием решит ее. Но далее будет самое интересное. Предположим,
мы добавляем еще две монеты и получаем ряд из 10 монет. Можно ли
эти 10 монет удвоить за 5 ходов? Многие, успещно решив первую
задачу, пасуют перед второй. Но эта задача решается мгновенно, если вы
сможете правильно ее понять. В разделе ответов будет разъяснено, что
решение задачи для восьми монет делает тривиальным обобщение для
2л монет (п > 3), ряд которых можно удвоить за п ходов.
Когда монеты лежат на плоскости в плотной упаковке, их
центры соответствуют узлам треугольной решетки. На этом факте
строится множество головоломок с монетами. Начнем, например,
с шести монеток, плотно упакованных в ромбоидную решетку
(слева на рис. 5). Необходимо за три хода переложить их в круг
(справа на рис. 5). При этом если положить седьмую монету в
центр, то шесть других будут окружать ее в плотной упаковке. На
каждом ходу монету надо сдвигать так, чтобы она коснулась двух
других монет, которые жестко определят ее новое местоположение.
Как и в предыдущей загадке, здесь также есть хитрый момент,
которым вы можете удивить любого. Если человек отчается решить
задачу, медленно продемонстрируйте ему решение, а затем
попросите повторить. Но когда будете складывать монеты, расположите
их в зеркально-симметричной форме. Скорее всего, человек не
заметит подмены и попробует повторить ваши действия. У него
ничего не получится.
Вот неплохое продолжение к предыдущей задаче. Уложите 10
монеток в плотный треугольник (слева на рис. 6). Кстати, именно в
этой форме, известной еще древним пифагорейцам (знамени-
26
Нескучная математика
тый tetractys), устанавливаются 10 кеглей в боулинге. Задача
состоит в том, чтобы перевернуть этот треугольник (справа на рис. 6),
передвигая монетку за монеткой. Как и прежде, вы можете касаться
только тех двух монет, которые и задают новое положение монеты.
Каково минимальное количество ходов? Большинство людей
быстро находят решение в четыре хода. Но задачу можно решить и в
три хода. Она имеет интересное обобщение. Треугольник из трех
монет можно перевернуть, переместив только одну монету, а в
случае с треугольником из шести монет достаточно переместить две
монеты. Поскольку для треугольника из 10 монет достаточно трех
ходов, то можно предположить, что для переворачивания
треугольника из 15 монет, расположенных подобно шарам в бильярде в
начале партии, будет достаточно перемещения четырех монет.
Однако это не так. Потребуется пять ходов. Тем не менее существует
замечательно простой способ определись минимальное
количество монет, которые нужно переместить в треугольнике, чтобы
перевернуть его. А вы, читатель, можете найти его?
Треугольная конфигурация tetractys также является основой
занимательной логической игры типа пасьянса. Такой пасьянс,
традиционно раскладываемый на квадратной сетке, известен очень
давно, и в настоящее время ему посвящается большое количество
литературы.
А вот подобная логическая игра на треугольной решетке не
получила в литературе глубокого освещения. Даже самое простое на-
Рис. 6
Задача на переворачивание треугольника
Головоломки с монетами
27
1
Рис.7
Треугольный пасьянс
чальное положение — пифагорейский треугольник из 10 монет —
уже нетривиально. Чтобы легче было записывать ходы, нарисуйте
на листе бумаги 10 кружков таким образом, чтобы в них можно
было положить монету. Между кружками оставьте место и
пронумеруйте кружки {см. рис. 7).
Уберите с поля одну из монет, оставив «дырку». Затем
необходимо убирать монетку за монеткой, перепрыгивая через них, как в
шашках (вспомните традиционную игру «Йога»). После хода
монетка, через которую перепрыгнули, немедленно убирается.
Обратите внимание на то, что ходы здесь возможны в шести
направлениях — в обоих направлениях параллельно каждой из сторон
треугольника.
Как и в шашках, непрерывная цепочка из нескольких прыжков
считается одним ходом. Всякий, кто попытается решить эту задачу,
обнаружит, что это не так сложно. Однако истинные любители
математики не успокоятся, пока не найдут решения с минимальным
28
Нескучная математика
количеством ходов. Приведем для примера решение в шесть ходов
из позиции, в которой удалена монетка номер два.
1.7-2.
2. 9-7.
3. 1-4.
4. 7-2.
5.6-4,4-1, 1-6.
6. 10-3.
Но есть и лучшее решение — за пять ходов. Предлагаю читателю
самому найти его. А если он с этим справится, то можно
попробовать силы на треугольнике с 15 монетками. Адаме, который владеет
собственной компанией, начал продавать версию этой игры под
названием Ке Puzzle Game. Однако в комплект головоломки готового
решения не приложил.
Сколько оборотов сделает изображение на монетке, которая
катится по краю другой монетки без проскальзывания и делает полный
круг? Некоторые могут подумать, что монетка, которая катится по
краю монетки того же достоинства (и диаметра!), делает вокруг
своей оси один оборот, тогда как на самом деле таких оборотов два.
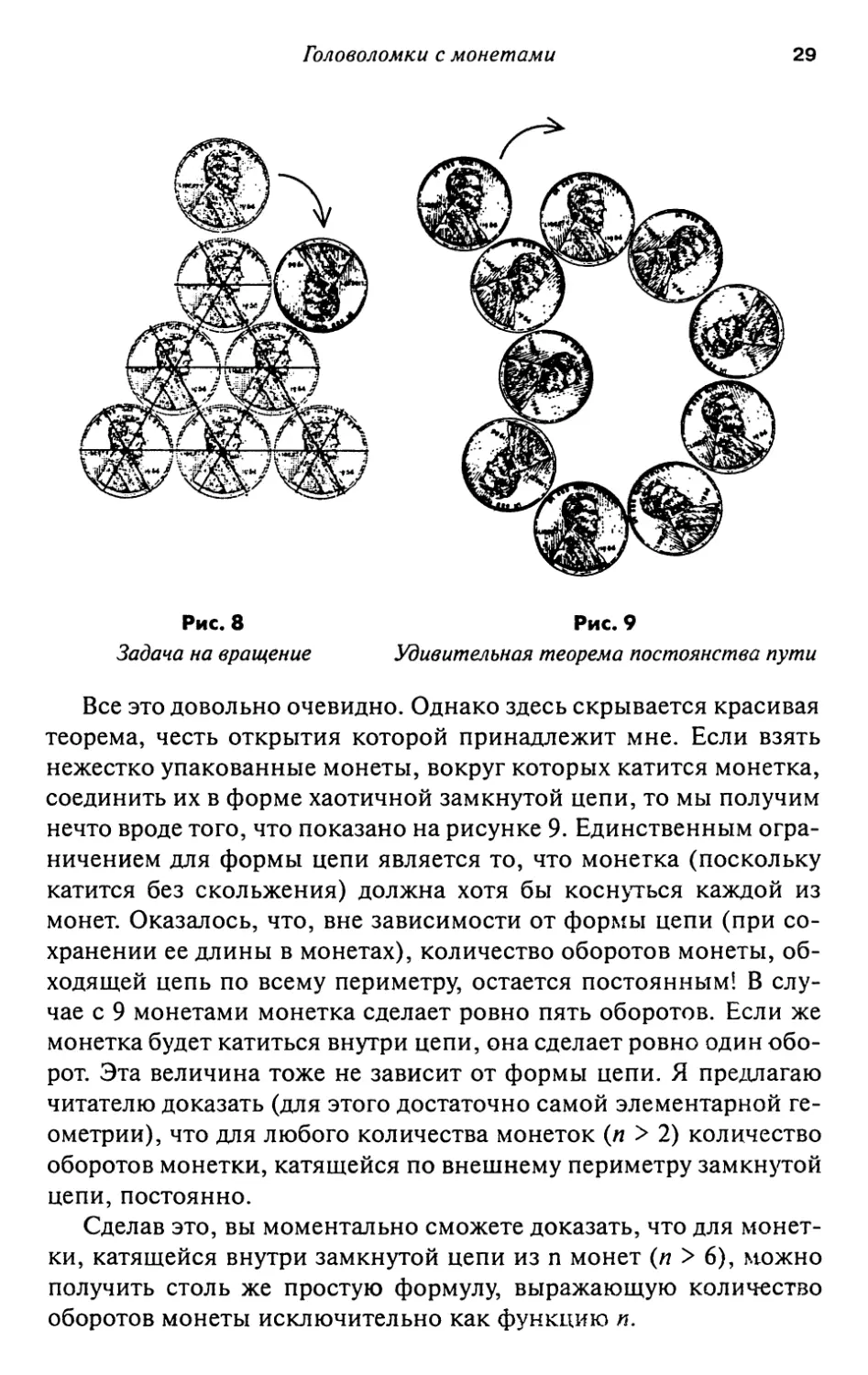
(Первый же эксперимент подтвердит это.) Вдруг этот
дополнительный поворот — постоянная добавка? Предположим, что мы катим
монетку без проскальзывания с самой вершины треугольника из
шести монет {см. рис. 8) по одной из сторон, нижней части и далее
обратно в прежнее положение. Сколько оборотов сделает монетка? По
рисунку легко увидеть, что монетка поворачивается вдоль дуг с
общим расстоянием ,2/б (выраженным в долях от полной окружности).
Это составляет два полных круга. Следовательно, монетка должна
сделать два оборота. Поскольку монетка делает полный круг, не
следует ли нам прибавить еще один оборот? Тогда мы получим три
оборота. А вот и нет! Простой эксперимент показывает, что монетка
сделает четыре оборота. Ведь на каждый градус на неподвижной
монетке подвижная монетка поворачивается на два градуса. Наи следует
удвоить длину пути, который проходит монетка по неподвижным
монетам. В итоге получаем правильный ответ в четыре оборота. Это
простое наблюдение поможет вам легко решать головоломки
подобного рода, приведенные не только в этой книге, но и во многих
других. Просто вычислите путь в градусах и умножьте на два. Вы
получите количество градусов, на которые повернется монетка.
Головоломки с монетами
29
Рис. 8 Рис. 9
Задача на вращение Удивительная теорема постоянства пути
Все это довольно очевидно. Однако здесь скрывается красивая
теорема, честь открытия которой принадлежит мне. Если взять
нежестко упакованные монеты, вокруг которых катится монетка,
соединить их в форме хаотичной замкнутой цепи, то мы получим
нечто вроде того, что показано на рисунке 9. Единственным
ограничением для формы цепи является то, что монетка (поскольку
катится без скольжения) должна хотя бы коснуться каждой из
монет. Оказалось, что, вне зависимости от формы цепи (при
сохранении ее длины в монетах), количество оборотов монеты,
обходящей цепь по всему периметру, остается постоянным! В
случае с 9 монетами монетка сделает ровно пять оборотов. Если же
монетка будет катиться внутри цепи, она сделает ровно один
оборот. Эта величина тоже не зависит от формы цепи. Я предлагаю
читателю доказать (для этого достаточно самой элементарной
геометрии), что для любого количества монеток (я > 2) количество
оборотов монетки, катящейся по внешнему периметру замкнутой
цепи, постоянно.
Сделав это, вы моментально сможете доказать, что для
монетки, катящейся внутри замкнутой цепи из п монет (п > 6), можно
получить столь же простую формулу, выражающую количество
оборотов монеты исключительно как функцию я.
30 Нескучная математика
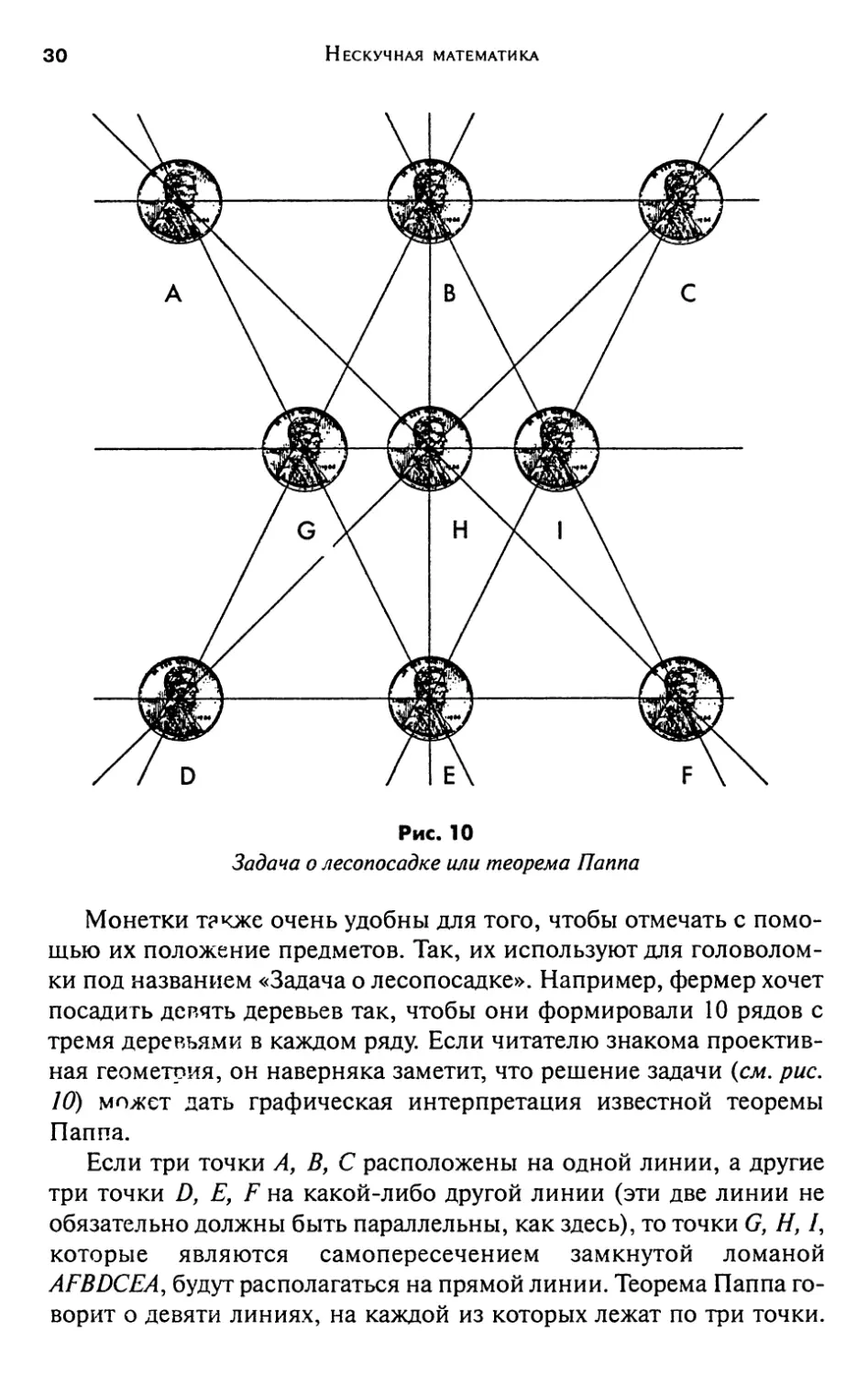
Рис. 10
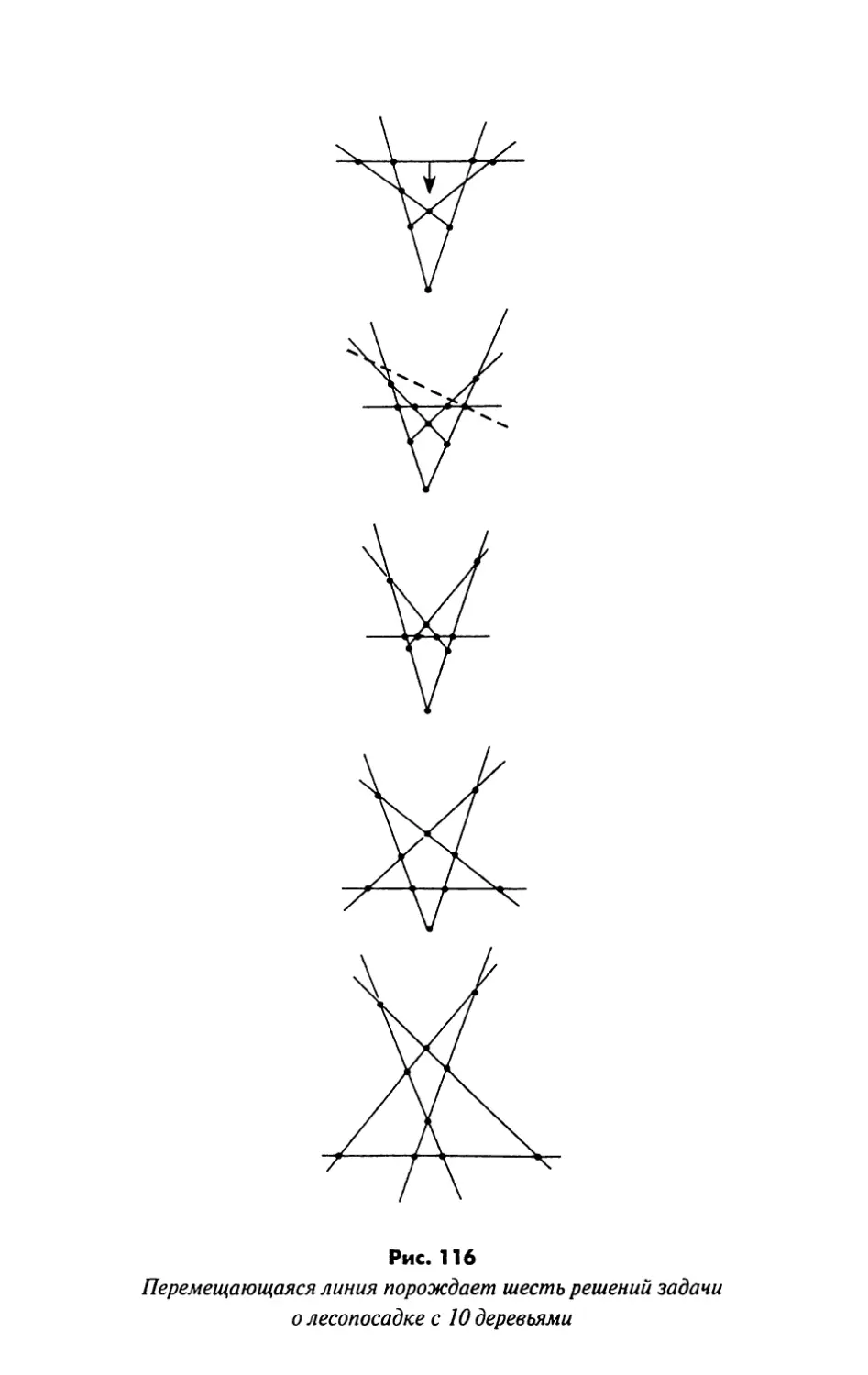
Задана о лесопосадке или теорема Паппа
Монетки также очень удобны для того, чтобы отмечать с
помощью их положение предметов. Так, их используют для
головоломки под названием «Задача о лесопосадке». Например, фермер хочет
посадить девять деревьев так, чтобы они формировали 10 рядов с
тремя деревьями в каждом ряду. Если читателю знакома
проективная геометрия, он наверняка заметит, что решение задачи {см. рис.
10) может дать графическая интерпретация известной теоремы
Паппа.
Если три точки А, В, С расположены на одной линии, а другие
три точки D, Е, F на какой-либо другой линии (эти две линии не
обязательно должны быть параллельны, как здесь), то точки G, Я, /,
которые являются самопересечением замкнутой ломаной
AFBDCEA, будут располагаться на прямой линии. Теорема Паппа
говорит о девяти линиях, на каждой из которых лежат по три точки.
Головоломки с монетами
31
Десятую линию мы добавляем, подгоняя расположение точек так,
чтобы точки В, Н, ? лежали на одной линии.
Задача о лесопосадке тесно связана с таким аспектом проективной
геометрии, как «геометрия инцидентности». (Точка считается
инцидентной к любой линии, проходящей через нее, а линия считается
инцидентной по отношению к любой точке, принадлежащей ей.)
Гарольд Л. Дорворт из Тринити-колледжа, Хартфорд, Коннектикут,
опубликовал мгновенно ставшее популярным введение в этот раздел
математики под названием The Geometry of Incidence («Геометрия
инцидентности»). Рекомендую вам почитать эту работу. В частности, он
рассказывает о двух задачах. В одной из них 25 деревьев размещены в
10 пересекающихся рядов по 6 деревьев в каждом, в другой — 19
деревьев образуют 9 пересекающихся рядов по 5 деревьев. Обе эти задачи
были решены при исследовании фигуры, получающейся при
доказательстве знаменитой теоремы проективной геометрии, носящей имя
французского математика, архитектора и инженера Жерара Дезарга
(1593—1662, по другим данным — 1591—1661). Такие задачи связаны с
комбинаторикой и еще никому не удалось выработать обобщенную
процедуру решения задач подобного рода. Так что эта ниша
математики таит в себе множество неразрешенных вопросов.
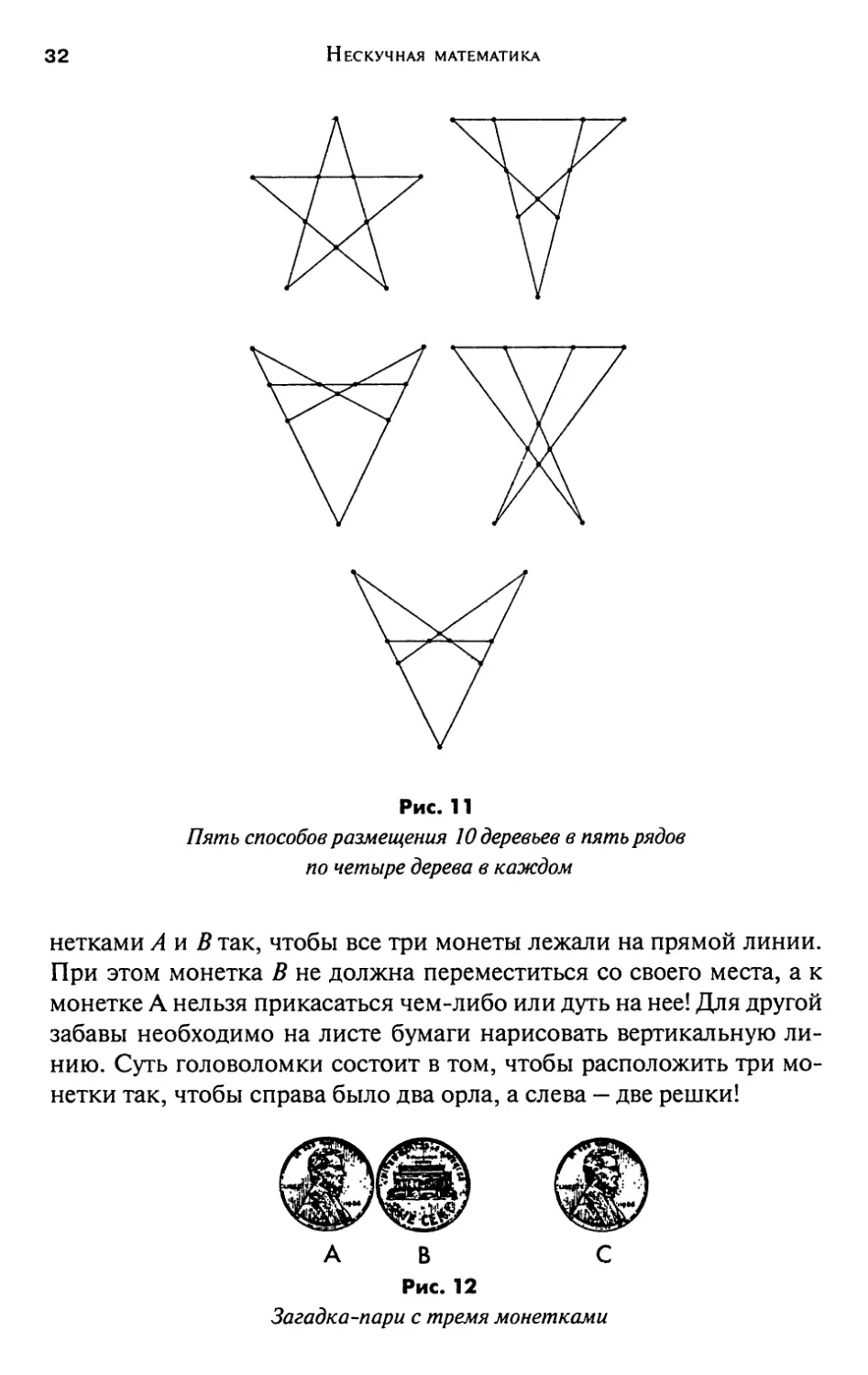
Но вернемся к нашим монеткам. Оказывается, 10 монеток
можно разместить в пять линий так, чтобы на каждой линии было по
четыре монеты. (Естественно, линия должна проходить через центры
монет.) На рисунке 11 приведено пять способов решения этой
задачи. Каждое из этих решений можно искажать до бесконечности, не
изменяя при этом топологической структуры. Решения приведены
здесь в том виде, в каком их привел знаменитый английский мастер
головоломок Генри Эрнест Дьюдени (1857—1930), чтобы
проиллюстрировать двустороннюю симметрию каждого из этих решений.
Однако есть и шестое решение, топология которого отличается от
приведенных пяти. Сможете ли вы найти его?
Многие из головоломок с монетами мало касаются математики и
больше напоминают забавы, которые прекрасно подходят для баров
и кафе. Например, расположите четыре монетки квадратом и
заключите пари, что сможете, переместив лишь одну монетку,
получить два ряда с тремя монетами в каждом. Это кажется
невозможным, но решение очень простое. Возьмите монетку и переместите ее
по диагонали, положив поверх другой монетки.
Вот еще парочка забав. Разместите три монетки, как показано на
рис. 12, и попросите кого-нибудь поместить монетку С между мо-
32 Нескучная математика
Рис. 11
Пять способов размещения 10 деревьев в пять рядов
по четыре дерева в каждом
нетками А и В так, чтобы все три монеты лежали на прямой линии.
При этом монетка В не должна переместиться со своего места, а к
монетке А нельзя прикасаться чем-либо или дуть на нее! Для другой
забавы необходимо на листе бумаги нарисовать вертикальную
линию. Суть головоломки состоит в том, чтобы расположить три
монетки так, чтобы справа было два орла, а слева — две решки!
А В С
Рис. 12
Загадка-пари с тремя монетками
Головоломки с монетами
33
ДОПОЛНЕНИЕ
Очевидно, пасьянсы по «треугольным» правилам можно
раскладывать на других матрицах, таких как шестигранная, ромбическая, в
виде шестиконечной звезды и т. д. Могут меняться и правила. Так,
можно запретить скачки, параллельные одной из сторон ячейки.
Обсуждение этого варианта пасьянса с 15 ячейками вы можете найти у Мак-
си Брука в книге Fun for the Money («Пари на деньги»). Другим
вариантом пасьянса может быть вариант, в котором допустимы не только
скачки, но и ходы, как в китайских шашках. (Китайские шашки это
«Халма» — древняя традиционная игра, в упрощенной форме
известная как «уголки». Однако для классической халмы требуется
специальная игровая доска в виде шестиугольной звезды. — Прим. перев.)
Если играть в треугольный пасьянс по классическим правилам,
допуская скачки (только скачки) во всех шести направлениях, то с
помощью изящной процедуры можно проверить, существует ли
теоретическая возможность получить из одной позиции другую. Эти
процедуры были получены по аналогии с уже известными для
квадратного пасьянса. Подробности об этом вы можете найти в моей
книге Unexpected Hanging and Other Mathematical Diversions («Галерея
сюрпризов и другие математические развлечения»), где
треугольным пасьянсам посвящена целая глава.
Как и в квадратном пасьянсе, эти процедуры не выявляют
конкретного решения, как и не доказывают, что решения существуют.
Они лишь показывают, что некоторые из задач не имеют решения.
Много неопубликованных материалов накопилось у М. Чароша,
Г. Дэвиса, Дж. Харриса и Уэйда Филпотта. Все методы
доказательства относятся к теории коммутативных групп и построены на
сопоставлении позиций.
Невозможность решения некоторых позиций можно быстро
установить, окрашивая ячейки решетки тремя цветами. Например,
гексагональное поле с вакансией в центре не может быть сведено к одной
фишке. Исключение составляет случай, когда длина стороны
шестиугольника может быть представлена в виде Ъп + 2. Четкое изложение
одной из таких процедур проверки отсутствия решения дает Ирвинг
Р. Ген цель в статье Triangular Puzzle Peg («Треугольные пасьянсы») в
журнале Journal of Recreational Mathematics, том 6, осень, 1973, стр.
280—283. Существует и более общая теория решения таких пасьянсов.
См. книгу Берлекампа, Конвея и Гая Winning Ways, постскриптум
данной книги, а также ссылку в нем на работу Дж. Д. Бизли.
34
Нескучная математика
ОТВЕТЫ
1. Чтобы удвоить ряд из восьми монеток, превратив его в четыре
стопки по две монетки, пронумеруйте монеты с первой по восьмую.
Ходы таковы: 4 на 7, 6 на 2, 1 на 3, 5 на 8. Для десяти монет просто
удвойте монетки с одной из сторон, переместив 7 на 10, а затем
решайте задачу для восьми монет, которые у вас остались. Очевидно,
что ряд в 2п монет можно удвоить за п ходов, удваивая монеты с
одного конца, пока не останется восемь монет. Решение для восьми
монет приведено выше.
2. Пронумеруйте шесть расположенных в плотной ромбоидной
упаковке монеток, которые необходимо расположить по кругу {см.
рис. 13). Затем переместите 6 до касания с 4 и 5, 5 до касания с 2 и 3
снизу и 3 до касания с 5 и 6.
Рис. 13
Задача на превращение ромбоидной упаковки в круг
3. Треугольник из 10 монет можно перевернуть, переместив три
монеты так, как показано на рис. 14. Возможно, вы поняли, что
обобщенная задача сводится к прорисовке ограничительных
треугольников (таких как рамка для построения пирамиды из 15
шаров в бильярде). Эти треугольники и предстоит переворачивать,
перемещая монетку из одного треугольника в другой. В общем
случае наименьшее количество монеток, которое необходимо
переместить, чтобы перевернуть треугольник, соответствует количеству
минимальных треугольников (по три монеты). Значит, надо
поделить количество монет на три и отбросить остаток.
4. На рисунке 7 приведен треугольник из 10 монет. Убираем
монету номер 3. Эта позиция может быть сокращена до одной монеты
за пять ходов. Вот они: 10—3, 1—6, 8-10—3,4—6—1—4, 7—2. Это
решение однозначно. Однако есть вариант с тройным скачком, который
можно сделать как по часовой стрелке, так и против. Естественно, в
Головоломки с монетами
35
Рис. 14
Как перевернуть треугольник
данном варианте вакансия может быть в любой из шести клеток
(исключая углы и центр).
Для треугольника из 15 монет минимальным является решение в
девять ходов. Вакансия должна располагаться с краю (но не в углах).
Первые два хода должны быть 1—4,7—2 (пять других пар ходов дают
симметричные эквивалентные варианты). Если рассматривать решения с
этими двумя первыми ходами, то компьютерная программа, написанная
Малкольмом Э. Джиллисом-мл. из Луизианы, дает 260 решений.
Приведенное ниже решение завершается эффектной серией из
пяти скачков. Положения монет пронумерованы слева направо и
сверху вниз: (1) 11-4, (2) 2-7, (3) 13-4, (4) 7-2, (5) 15-13, (6) 12-14,
(7) 10-8, (8) 3-10, (9) 1-4, 4-13, 13-15, 15-6, 6-4.
Мне неизвестны попытки компьютерного анализа для
треугольника из 21 и большего количества монет. Джон Харрис из Санта-
Барбары, Калифорния, доказал, что в случае с 21 монетой
необходимо как минимум девять ходов. Вот решение, которое предложил
Эдуард Мармиер из Цюриха (оно подтверждает, что девяти ходов
достаточно): (1) 1-4, (2) 7-2, (3) 16-7, (4) 6-1, 1-4, 4-11, (5) 13-6,
6-4, 4-13, (6) 18-16, 16-7, 7-18, 18-9, (7) 15-6,6-13, (8) 20-18,
18-9,9-20,(9)21-19.
36
Нескучная математика
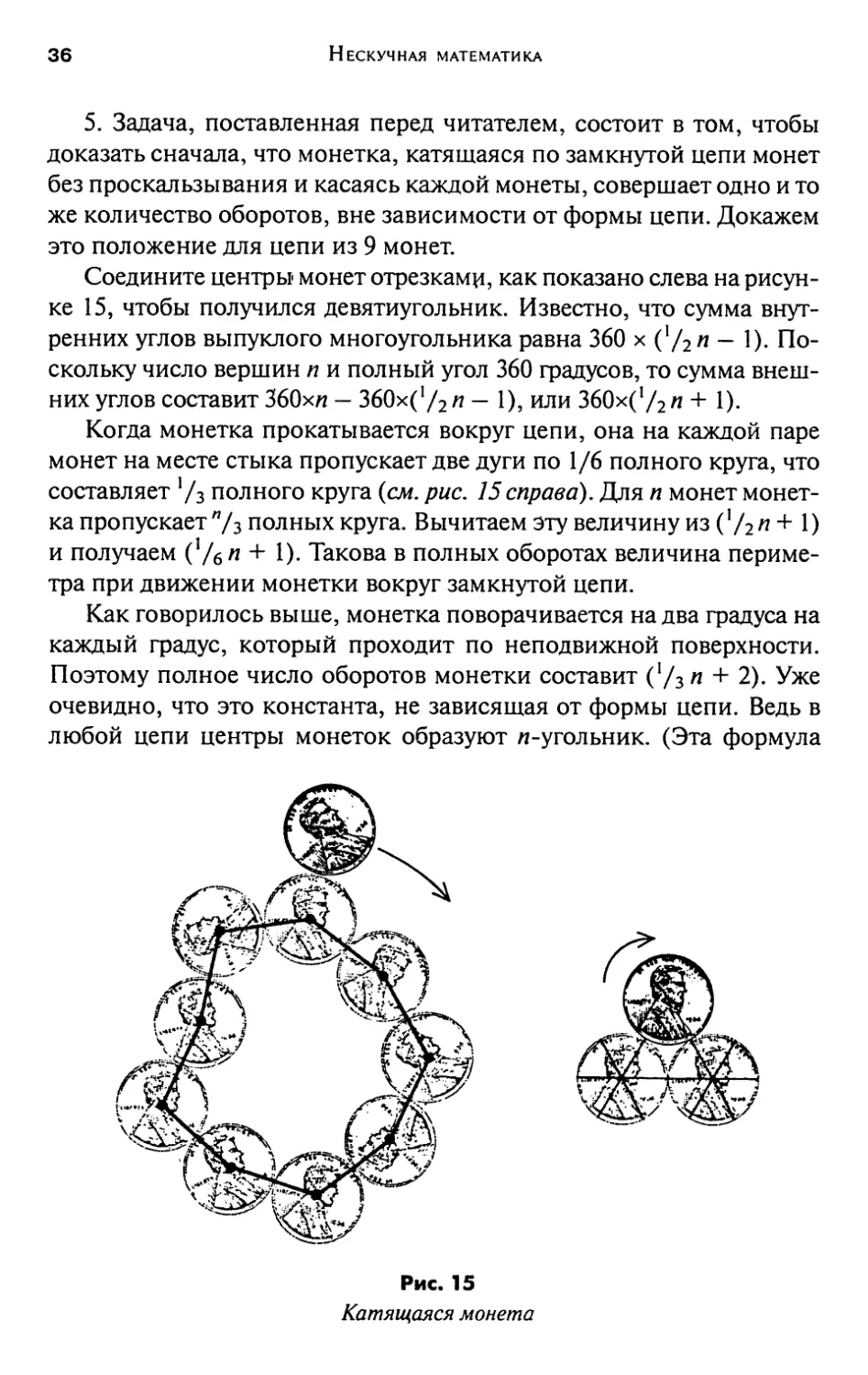
5. Задача, поставленная перед читателем, состоит в том, чтобы
доказать сначала, что монетка, катящаяся по замкнутой цепи монет
без проскальзывания и касаясь каждой монеты, совершает одно и то
же количество оборотов, вне зависимости от формы цепи. Докажем
это положение для цепи из 9 монет.
Соедините центры монет отрезками, как показано слева на
рисунке 15, чтобы получился девятиугольник. Известно, что сумма
внутренних углов выпуклого многоугольника равна 360 х ('/2 п - 1).
Поскольку число вершин п и полный угол 360 градусов, то сумма
внешних углов составит ЗбОхя — 360х(1/2п — 1), или 360х(У2я + 1).
Когда монетка прокатывается вокруг цепи, она на каждой паре
монет на месте стыка пропускает две дуги по 1/6 полного круга, что
составляет Уз полного круга (см. рис. 15справа). Для п монет
монетка пропускает"/з полных круга. Вычитаем эту величину из (Угя + 1)
и получаем (У6 п + 1). Такова в полных оборотах величина
периметра при движении монетки вокруг замкнутой цепи.
Как говорилось выше, монетка поворачивается на два градуса на
каждый градус, который проходит по неподвижной поверхности.
Поэтому полное число оборотов монетки составит (Уз п + 2). Уже
очевидно, что это константа, не зависящая от формы цепи. Ведь в
любой цепи центры монеток образуют л-угольник. (Эта формула
Рис. 15
Катящаяся монета
Головоломки с монетами
37
Рис. 16
Прямолинейная конфигурация
также верна и для вырожденной цепочки из двух монет, чьи центры
можно рассматривать как углы вырожденного многоугольника.)
При п = 2 она дает 2,6(6) оборотов.
По аналогии можно установить, что число оборотов монеты,
катящейся по внутренней стороне замкнутой цепи из п монет, равно
СУз — 2). Эта формула имеет смысл только для п > 6 и это
неслучайно. Попробуйте сами взять меньшую цепочку и поместить внутрь
монету и у вас ничего не получится. Для предельного случая (п = 6)
формула справедливо дает нулевое значение, поскольку центральная
монета касается всех шести монет. Легко показать, что для
незамкнутой цепи из п монет монетка делает при полном обходе Уз(2я + 4)
оборотов. Для проверки подставляем в нее п = 2 и получаем те же 8/з
или 2,66... оборотов монетки.
6. Шестая конфигурация 10 монет, образующих пять рядов по
четыре монеты, приведена на рис. 16.
7. Чтобы расположить монетку С между соприкасающимися
монетками А и В, не касаясь монетки А и не перемещая В, щелчком
направьте монетку С, чтобы она коснулась В. Монетка А отойдет от
монетки В (которая не переместиться из-за передачи импульса).
Теперь монетку С можно будет свободно поместить между двумя
прежде касавшимися монетками.
8. Разместить три монетки так, чтобы орлы смотрели в одну
сторону, а решки — в другую, можно следующим образом (см. рис. 17).
Рис. 17
Как разместить монетки
ГЛАВА 3
Алеф-нулъ и алеф-один
Аспирант-математик из Тринити
Бесконечность возвел в квадрат,
Но, устав записывать циферки.
Уйти в богословье был рад.
- НАРОДНОЕ ТВОРЧЕСТВО
В 1963 году математик из Стэнфордского университета Пол Джозеф
Коэн, которому тогда было 29 лет, нашел удивительное решение
одной из величайших проблем современной теории множеств. Он
положительно ответил на вопрос о существовании открытого
множества, мощность которого превышает мощность множества целых
чисел (счетное множество), но меньше мощности бесконечного
множества точек на прямой. Поскольку рассматривались открытые
множества (т. е. бесконечные), то здесь можно ввести понятие
порядка бесконечности и сказать, что Коэн открыл бесконечность
более высокого порядка. Чтобы прояснить суть открытия Коэна,
необходимо сказать несколько слов о двух самых низких порядках
бесконечности.
Тот факт, что за пределами бесконечности целых чисел может
существовать бесконечность более высокого порядка, установил Георг
Кантор. (Бесконечности целых чисел он дал имя «алеф-нуль».)
Кантор также установил, что существует бесконечное количество
бесконечностей разного порядка. Ведущие математики неоднозначно
приняли эту теоретическую работу. Так, Анри Пуанкаре, ни много
ни мало, назвал это «канторизмом» — болезнью, от которой
математике еще предстоит оправиться. А Герман Вейль иронически
называл иерархию Кантора «туманом в тумане».
С другой стороны, Дэвид Гилберт признавал, что «из рая,
который создал для нас Кантор, нас уже не изгнать». А Бертран Расселл
однажды назвал работу Кантора «величайшим достижением,
которым может похвастаться целое столетие». В наши дни о порядках
бесконечности думают лишь математики интуиционистской школы
Алеф-нуль и алеф-один
39
и еше пара философов. Интерес к ним потеряло большинство
математиков, а доказательства, с помощью которых Кантор установил
существование «ужасных династий» (так их назвал известный
аргентинский писатель Хорхе Луис Борхес), теперь по праву
украшают мировой музей истории математики.
Любое открытое множество предметов, которое можно
пересчитать, принято называть счетным множеством (в математике оно
обозначается Х0, что читается как «алеф-нуль»). Оно заключает в
себе нижнюю ступеньку лестницы Кантора — бесконечности «алеф-
нуль». Но это не означает, что элементы этого множества можно
пересчитать. Просто это множество можно поставить в поэлементное
соответствие с множеством натуральных чисел. Например,
рассмотрим бесконечное множество простых чисел. Его легко сопоставить
с бесконечным множеством целых положительных чисел:
12 3 4 5 6...
2 3 5 7 11 13...
Поэтому простые числа принадлежат уровню бесконечности
«алеф-нуль». Эти числа называют «счетным множеством», а само
множество — «исчисляемым». Вот здесь мы и сталкиваемся с
основным парадоксом открытых множеств. В отличие от них замкнутые
(конечные) множества могут быть сопоставлены в поэлементном
соответствии лишь частично. Говоря языком математики, если
мощности замкнутых множеств различаются, то одно из них
является строгим подмножеством другого. С открытыми все иначе. Хотя
простые числа — это лишь малая часть множества целых
положительных чисел, его все равно можно назвать равномощным по
отношению к последнему (тот же алеф-нуль). Точно так же целые числа
образуют лишь малую часть рациональных чисел (к ним также
относятся и дробные). Однако рациональные числа также формируют
бесконечное множество класса алеф-нуль.
Существуют разные способы доказательства равномощности
множества рациональных чисел и счетного множества. Наиболее
известный метод состоит в привязке чисел (даже целых) в виде дробей к
бесконечной квадратной решетке, а затем пересчете узлов решетки по
зигзагообразной траектории. (По одной оси откладывается числитель,
по другой — знаменатель.) Возможна и спиральная траектория, если
решетка включает в себя отрицательную область рациональных чисел.
40
Нескучная математика
Вот еще один способ упорядочить и пересчитать положительные
рациональные числа. Он был предложен американским логиком
Чарльзом Сандерсом Пирсом (1839 — 1914). (См. сборник трудов
Collected Papers of Charles Sanders Peirce, 1933 r.)
Процедура начинается с долей % и 1/о- (Вторая из этих дробей не
имеет смысла, но, учитывая бесконечность множества, этим можно
пренебречь.) Сложите пару числителей, а затем пару знаменателей.
Вы получите дробь Уь Разместите ее между предыдущей парой: °/ь
Уь Уо- Повторите эту процедуру с каждой парой соседних дробей, и
вы будете получать все новые дроби, которые будут располагаться
между ними, формируя ряд простых дробей в порядке возрастания:
1 I I I I
12 110
Эти пять простых дробей превращаются в девять:
13 2 3 12 110
В этом, не имеющем предельного элемента раду каждая
рациональная дробь появится лишь однажды и всегда будет представлена
в своей элементарной (максимально сокращенной) форме. У вас не
возникнет необходимости, как в других методах, сокращать
простые дроби типа 10/2о до наименьшего эквивалента, потому что в
этом ряду приводимая дробь не появится в принципе. Если
заполнять пробелы (назовем их так) не одновременно по всему ряду, а
слева направо, то можно пересчитать рациональные дроби, просто
рассматривая их в порядке появления.
Как показал Пирс, этот ряд имеет много любопытных свойств.
На каждом новом этапе числа над линией разделителя (если
рассматривать ряд слева направо) каждый раз повторяют предыдущую
последовательность: 01, 011,0112 и т. д. Нижние цифры на каждом
этапе получаются теми же, что и сверху, только в обратном порядке.
Как следствие, любая пара дробей, равноудаленных от значения
1/1, обратно пропорциональны. Обратите внимание также, что для
любой смежной пары (a/b, c/d) можно записать равенства: bc — ad=\
и c/d — a/b = l/bd. Эту последовательность можно признать
родственной числам Джона Фарея, английского геолога начала XIX века,
одного из пионеров геомагнитной разведки. Именно Фарей впервые
Алеф-нуль и алеф-один
41
¦D ? П
¦? D ¦
¦DID
•¦ D ?
¦ ¦
¦ ? I
¦ ¦
'III
Рис. 18
Три подмножества внутри множества
проанализировал свойства подобного ряда. В настоящее время его
теория занимает значительное место в математической литературе.
Легко показать, что существуют множества с более высокой
степенью бесконечности, чем алеф-нуль. Одним из наиболее изящных
доказательств этого положения является доказательство с помощью
игральных карт. Рассмотрим для начала замкнутое множество из
трех предметов. Назовем их ключ, часы и кольцо. Три
подмножества этого множества будут представлены тремя
последовательностями карт (см. рис. 18). Карта, обращенная лицевой стороной вверх
(она белая), указывает, что элемент выше его принадлежит
множеству. Карта, расположенная лицевой стороной вниз (черная),
указывает, что элемент выше него подмножеству не принадлежит.
42
Нескучная математика
Приведенные три ряда образуют подмножества, которые
состоят из двух типов объектов. Также они включают в себя три
подмножества самих объектов и, наконец, пустое подмножество, которое
объектов не содержит. Для любого множества количество
подмножеств соответствует 2п. (Почему так — увидеть легко. Каждый
элемент может быть либо включен в подмножество, либо нет. Так что
для одного элемента существуют два подмножества, для двух
элементов — 2x2 = 4 подмножества, для трех элементов — 2x2x2 = 8
подмножеств). Обратите внимание на то, что формула работает
даже для пустого множества, поскольку 2° = 1. Пустое множество
содержит единственное подмножество — пустое.
Результат применения данной процедуры к бесконечному (но все
же исчисляемому) множеству «алеф-нуль» приведен на рисунке 19.
Попробуем ответить на вопрос, можно ли подмножества этого
бесконечного множества поставить в поэлементное соответствие со
счетным множеством целых чисел. Предположим, что это возможно.
Пусть каждый ряд карт символически обозначает подмножество.
Только на этот раз ряды будут тянуться вправо до бесконечности.
Представьте себе бесконечное количество рядов расположенных в
произвольном порядке карт и пронумерованных 1, 2, 3... сверху вниз.
© © © © © ... © © © © © ...
Рис. 19
Таким образом можно показать, что исчисляемая бесконечность
включает в себя неисчисляемую бесконечность подмножеств (слева),
мощность совокупности которых соответствует
мощности действительных чисел (справа).
Алеф-нуль и алеф-один
43
А если мы продолжим формировать такие ряды, то можно ли
утверждать, что в конечном счете будут охвачены все подмножества?
Нет, потому что существует бесконечное количество способов
сформировать подмножества. Самый простой способ состоит в том,
чтобы рассматривать диагональные наборы карт (которые к тому же
можно инвертировать). Все карты рубашкой вверх
переворачиваются рубашкой вниз и наоборот. Каждое новое диагональное
подмножество не может быть идентично первому, поскольку его первая
карта отличается от первой карты подмножества 1. Это не может
быть и второе подмножество, поскольку его вторая карта
отличается от второй карты подмножества 2. В общем случае можно
утверждать, что новое диагональное подмножество не может быть
«энным», поскольку его энная карта отличается от энной карты
подмножества я. Поскольку мы выбираем такое подмножество,
которого не может быть в составленном нами перечне (в рядах, даже если
их количество бесконечно), то вынуждены признать, что
первоначальное предположение было ложным. Множество, составленное
из всех подмножеств порядка «алеф-нуль», — это множество с
мощностью 2 в степени, равной мощности подмножества «алеф-нуль».
Приведенное доказательство показывает, что сконструированное
таким образом множество не может соответствовать ни одному из
счетных множеств целых чисел. Значит, это более высокий ранг
бесконечности — уже «неисчислимая» бесконечность.
Знаменитое диагональное доказательство Кантора (в том виде,
как мы его привели) скрывает в себе приятный сюрприз. По сути,
оно доказывает, что совокупность всех действительных чисел
(рациональных плюс иррациональных) также образует неисчислимое
открытое множество, т. е. неприводимое к счетному ряду. Давайте
рассмотрим отрезок координатной оси от 0 до 1. Каждой точке на этом
отрезке соответствует какая-либо рациональная дробь меньше
единицы. Между любыми двумя рациональными дробями существует
бесконечное количество других рациональных дробей. Однако,
если даже их «выбрать», там останется бесконечное множество точек,
которые соответствуют непериодическим десятичным дробям,
появляющимся при решении алгебраических и других уравнений. Эти
числа называются иррациональными (такими как квадратный
корень из двух) и трансцендентальными (такими как числа к и е,
которые не могут быть корнями алгебраического уравнения). Каждая
точка на отрезке координатной оси, вне зависимости от
«рациональности», может быть представлена в виде бесконечной десятич-
44
Нескучная математика
ной дроби. Однако эти дроби можно представить не только в
десятичной системе, но и в двоичной. Таким образом, каждая точка на
линии может быть однозначно «привязана» к дроби,
представленной бесконечной последовательностью нулей и единиц.
Предположим теперь, что каждая карта рубашкой вниз в левой
части рисунка 19 соответствует единице, а перевернутая — нулю {см.
рис. 19 справа).
Разместите нули и единицы в рядах, и вы получите бесконечный
перечень бинарных дробей в диапазоне от 0 до 1. Однако после
смены каждого 0 на 1 и наоборот диагональные множества символов
оказываются уникальными по сравнению с представленными
последовательностями, так что можно говорить о существовании не-
исчисляемого открытого множества действительных чисел, а также
точек на линии. Теорема Кантора показывает, что все три
множества — совокупность подмножеств алеф-нуль, множество
действительных чисел и совокупность точек на отрезке — равномощны,
несмотря на свою бесконечность (имеют сопоставимое количество
элементов). Понятие мощности таких множеств и ввел Кантор,
называя его также «мощностью континуума» или «кардинальным
трансфинитным числом С». Он полагал, что подобная
бесконечность К (алеф-один) впервые обоснованно встала на одну
ступеньку выше бесконечности алеф-нуль.
Представив несколько вариантов простого и изящного
доказательства, Кантор также показал, что его кардинальное
трансфинитное число С определяет мощность таких бесконечных подмножеств,
как трансцендентальные числа (иррациональные числа
алгебраической природы, согласно доказательству Кантора, образуют
множество, равномощное счетному), количество точек на линии
бесконечной длины и количество точек, ограниченных любой плоской
фигурой, либо количество точек на бесконечной плоскости. Также
этому закону Кантора подчиняется и любое тело размерностью
больше двух, а вместе с ним и пространство более высоких
размерностей. Дополнительные измерения не увеличивают количества
точек. Ведь точки на отрезке (пусть даже длиной всего один дюйм)
можно поставить в поэлементное соответствие с точками тел более
высоких размерностей, а также с точками всего пространства в
целом, вне зависимости от его размерности.
Проводить грань между алеф-нуль и алеф-один (с этого момента
мы принимаем, что бесконечности класса алеф-один
характеризуются канторовским числом С) в геометрии важно тогда, когда мы
Алеф-нуль и алеф-один 45
Рис. 20
Так по спирали можно пересчитать вершины шестиугольной мозаики
на бесконечной плоскости
*+о|п
Рис.21
Пять символов «экстрасенсорного восприятия»
имеем дело с бесконечным множеством фигур на плоскости.
Можно ли их отнести к счетному алеф-нуль или нет? Представьте себе
бесконечную плоскость с шестиугольной мозаикой. Полное
количество вершин — это бесконечность типа алеф-один, или алеф-
нуль? Правильный ответ - алеф-нуль, поскольку их можно
пересчитать по спиральной дорожке (см. рис. 20). С другой стороны,
количество кругов одного (для определенности однодюймового)
радиуса, которые можно поместить на машинописный лист, — это
бесконечность типа алеф-один, потому что на участке, ограниченном
площадью листа, помещается алеф-один точек, каждая из которых
может быть центром нового круга.
Теперь взгляните на пяти символов — это своеобразный тест.
Отец парапсихологии Джозеф Бэнкс Райн (1885—1980) называл это
ESP-itcTou, или тестом на экстрасенсорное восприятие. См. рис. 21.
46
Нескучная математика
Можно ли на листе бумаги нарисовать алеф-один символов в
предположении, что линии не имеют толщины и не могут
пересекаться (и накладываться) с другими линиями? (Нарисованные
символы не обязаны быть одного размера, но они должны быть одной
формы.) Оказывается, все фигуры, кроме одной, могут быть
размещены на листе бумаги алеф-один раз. Какой же символ является
исключением?
Физик Ричард Шлегель попытался связать эти два типа
бесконечности с космологией, чтобы разрешить кажущееся
противоречие в классической теории Вселенной. Согласно теоретическим
представлениям, количество атомов во Вселенной описывается
бесконечностью типа алеф-нуль. (Вселенную мы считаем
бесконечной, несмотря на то что у нее есть «оптический горизонт» — предел
видимой части Вселенной.)
Кроме того, предполагаем, что количество атомов увеличивается
с расширением Вселенной так, чтобы ее плотность оставалась
постоянной. Бесконечное пространство можно легко приспособить
под любое конечное количество атомов, скажем, удваивая его,
поскольку умножение бесконечности уровня алеф-нуль на два (или
любое конечное число) не меняет его статуса. Если у вас яйца в
количестве алеф-нуль размещаются в коробках, количество которых
исчисляется пределом алеф-нуль, то вы всегда можете разместить
еще один алеф-нуль комплект яиц, просто переложив яйцо из
коробки 1 в коробку 2, из коробки 2 в коробку 4, из коробки п в
коробку 2п. Это освобождает все нечетные коробки, которые можно
заполнить еще одним комплектом яиц в количестве алеф-нуль. Если
рассматривать уже установившееся состояние, то в классической
теории Вселенная простирается на неограниченное время в
прошлое. Без этого условия мы не можем принять, что процесс
удвоения бесконечности алеф-нуль уже закончилось. В противном случае
это дало бы нам бесконечность типа два в степени я, где п — это
бесконечное, но счетное количество атомов. Как мы видели, в
результате получается бесконечность типа алеф-один. Даже если бы в
бесконечно отдаленное время было только два атома, то после
удвоения бесконечности алеф-нуль раз Вселенная должна была вырасти
в бесконечность алеф-один. Однако Вселенная не может содержать
бесконечность атомов алеф-один (она несчетная). Любое собрание
физических объектов (в отличие от объектов математики)
исчисляемо, и поэтому может описываться, самое большее,
бесконечностью алеф-нуль.
Алеф-нуль и алеф-один
47
В своей статье The Problem of Infinite Matter in Steady-State
Cosmology («Проблема бесконечности материи в статической
космологии») Ричард Шлегель приводит логическую цепочку,
разрешающую это противоречие. Вместо того чтобы рассматривать прошлое
как последовательность формирующихся через определенные
интервалы времени алеф-нуль множеств, мы можем взглянуть на
прошлое и на будущее состояния Вселенной как на бесконечность в
смысле отношения «низший — высший», ничего не говоря о
завершенности. (Идеальное постоянство процесса удвоения
действительно формирует континуум алеф-один, но Шлегель имел в виду
конечные временные приращения, в течение которых происходило
удвоение количества атомов.) Вне зависимости от даты рождения
Вселенной (не забывайте, что мы рассматриваем статично
расширяющуюся Вселенную, а не теорию Большого взрыва и не
осциллирующую Вселенную), мы всегда можем установить более раннюю
дату, передвинув начало в прошлое. В каком-то смысле это и есть
«начало». В данной модели Вселенная не имеет «даты рождения», так
что мы можем устанавливать ее произвольно. Есть у нашей модели
и «конец», но мы можем столь же произвольно передвинуть его в
будущее. Двигаясь в прошлое, начнем периодически уменьшать вдвое
количество атомов во Вселенной. При этом количество делений
пополам будет конечной величиной. В результате мы получим, что
количество атомов во Вселенной никогда не станет меньше
бесконечности алеф-нуль.
По мере движения вперед по шкале времени мы никогда не
удвоим количество атомов больше, чем конечное количество раз.
Поэтому количество атомов во Вселенной никогда не станет
больше бесконечности алеф-нуль. Итак, при движении в любом
направлении количество скачков по времени и удвоений никогда не
выйдет за рамки счетного множества. В результате количество
атомов не достигает мощности алеф-один, так что противоречие
снимается.
Кантор утверждал, что на основе возведения двойки в степень
мощности предыдущего класса бесконечности можно получить
новый класс бесконечности. Так формируется бесконечная иерархия
бесконечностей. Причем, по мнению Кантора, между этими
классами не может быть подклассов промежуточной мощности, как не
может быть предельного алефа, о котором Гегель говорил как об
Абсолюте. Лучшим символом Абсолюта, по утверждению Кантора,
может выступить бесконечность иерархии бесконечностей.
48
Нескучная математика
Всю свою жизнь Кантор пытался, но так и не смог доказать, что
между счетным множеством алеф-нуль и кардинальным
трансфинитным числом Сне может быть никакого континуума
промежуточной мощности. В 1938 году Курт Гедель смог доказать догадку
Кантора, позже ставшую «гипотезой о континууме», при этом избежав
конфликта с аксиоматической теорией множеств.
А в 1963 году Коэн построил контрпример гипотезы о
континууме. Можно предположить, что открытое Кантором кардинальное
трансфинитное число С не является бесконечностью алеф-один.
Это означает, что существует по крайней мере еще один алеф между
алеф-нуль и С — хотя у людей нет пока ни малейшего понятия о том,
как определить такое множество (например, в виде подмножества
трансцендентальных чисел). Это также совместимо с теорией
множеств. Гипотеза Кантора неразрешима, подобно тому как
недоказуем постулат Евклида о непересечении параллельных прямых. Это
всего лишь аксиома, которую можно принять или отклонить. Выбор
между принятием и непринятием аксиомы Евклида о параллельных
Прямых разделил геометрию на евклидову и неевклидову. Точно так
же можно утверждать, что принятие или непринятие гипотезы
Кантора разделяет теорию открытых множеств на канторовскую и не-
канторовскую. Но это еще не все! Неканторовский подход к теории
множеств открывает возможность существования бесконечной
системы теорий множеств. Причем все теории столь же
последовательны, как и общепринятая. Различия заключаются лишь в
предположениях о мощности континуума.
Конечно, Коэн всего лишь показал, что канторовская
гипотеза о континууме недоказуема в рамках стандартной теории
множеств, даже если расширить ее аксиоматическую базу. Многие
математики надеются, что некогда «самоочевидная» аксиома
Кантора, которая в принципе не может подтвердить или опровергнуть
гипотезу о континууме, будет сформулирована в новом ракурсе,
который позволит разрешить этот вопрос теории множеств. (Под
«самоочевидной» математики понимают аксиому, которая
безоговорочно принимается большинством.) Действительно, и Гедель, и
Коэн полагали, что смогли поставить финальную точку в этом
вопросе. Коэн в противовес Кантору был убежден, что смог
фальсифицировать гипотезу о континууме. Однако до сих пор эта
гипотеза остается недоказанной. Единственно бесспорно то, что в
классической теории множеств раскол. А вот чем он закончится,
никто сказать не может.
Алеф-нулъ и алеф-один
49
ДОПОЛНЕНИЕ
В бинарной версии знаменитого диагонального доказательства
Кантора, посвященного неисчисляемости множества
действительных чисел, я преднамеренно (в целях упрощения изложения) не
стал рассматривать тот факт, что дробное число меньше единицы
можно представить бесконечной двоичной дробью двумя
способами. Например, 1/4 может быть представлена как 0,01 с
последующими нулями или как 0,001 с последующими единицами. Это
увеличивает возможность того, что последовательности двоичного
представления действительных дробей могут быть организованы
таким образом, что диагонали дадут какое-либо совпадение с
одним из элементов бесконечного списка. Предположим, что
сконструированное таким образом число обладает последовательностью,
отличной от приведенных в списке последовательностей. Можно
ли тогда утверждать, что построен пример, который выражает
(только в иной форме записи) двоичную дробь, уже
представленную в списке?
Ответ — нет. В качестве доказательства можно указать, что все
теоретически существующие двоичные последовательности уже
внесены в список. Потому можно сказать, что каждая дробь уже
появляется в списке в виде каждой из двух возможных форм
представления. Из этого следует, что ни одно построенное диагональное число
не может соответствовать какой-либо дроби, представленной в
списке в обеих формах.
В любой системе счисления существует два способа выразить
дробь в виде последовательности цифр, количество которых не
превышает алеф-нуль бесконечности.
В частности, в десятичном представлении ]/4 = 0,2500000... =
0,2499999.... Хотя и нет необходимости проводить диагональное
доказательство для десятичного представления, в этом случае обычно
исключают двусмысленность, утверждая, что каждая дробь должна
быть представлена в форме с бесконечным рядом девяток. В этом
случае диагональная последовательность строится за счет замены
каждой цифры в диагональном ряду на любую другую, отличную от
нуля и девятки.
Лишь обсудив диагональное доказательство Кантора на страницах
Scientific American, я понял, насколько мощное сопротивление
пришлось ему преодолеть, причем не столько в малочисленном мире
чистых математиков, сколько в мире ученых прикладных направлений.
50
Нескучная математика
По поводу опубликованного доказательства я получил множество
писем с нападками. Вильям Дилворт, инженер-электрик, прислал мне
вырезку из газеты LaGrange Citizen, Иллиноке, от 20 января 1966 года,
в которой он высказывался ни много ни мало о «нумерологии по
Кантору» (нумерология — это гадание на числах). Дилворт был
первым, кто осудил диагональное доказательство на Международной
конференции по общей семантике (International Conference on
General Semantics), проходившей в Нью-Йорке в 1963 г.
Среди наиболее выдающихся представителей науки,
отвергнувших теорию множеств Кантора, был физик Перси У. Бриджмен. В
1934 г. он посвятил этому статью. Позже в заметке Reflections of a
Physicist (журнал Philosophical Library, 1955) он бескомпромиссно
осудил трансфинитные числа вообще и диагональное
доказательство в частности. «Лично я в этом ни на йоту не вижу
доказательства чего-либо вообще, — писал он. — Мне это представляется
совершенно бессистемным. Мой разум отказывается признавать эти
соображения, не говоря уже о том, чтобы увидеть в них
доказательство».
В основу позиции Бриджмена легла точка зрения философов
прагматической и операционалистической школ. Они утверждали,
что бесконечных чисел не существует. Это абстракция,
придуманная человеком. Действительно, любое число — это всего лишь имя
предмету, которое дает человек. Мы можем говорить о двадцати
яблоках, но не можем сосчитать бесконечное количество яблок. «Не
имеет смысла говорить о бесконечном как о существующем. Еще
меньше смысла говорить о бесконечном количестве различных
порядков бесконечности, как это делает Кантор».
«Бесконечное количество, — заключает Бриджмен, — это лишь
предел того, что производится в каком-либо процессе. Это лишь
планируемый результат».
В ответ можно лишь сказать, что Кантор действительно сумел
точно вычислить, что необходимо «сделать» для оценки величины
теоретически предсказанного кардинального трансфинитного
числа. Тот факт, что бесконечную процедуру провести невозможно,
нисколько не умаляет реальности, да и полезности открытия Кантора.
Ведь никто же не смог получить все знаки числа п. Однако его
реальность признается всеми. Вопреки убеждению Бриджмена, речь
идет не о принятии или отвержении платоновских представлений о
количестве «предметов». С точки зрения образованного
приверженца философии прагматиков (которые поставили своей целью борь-
Алеф-нуль и алеф-один
51
бу с абстракцией), теория множеств Кантора не менее значима, чем
любая другая абстрактная аксиоматическая система, такая как
теория групп или неевклидова геометрия.
ОТВЕТЫ
Вопрос состоял в том, какой из пяти символов теста на
«экстрасенсорное восприятие» невозможно нарисовать на листе бумаги в
количестве алеф-один раз. Мы предполагаем, что линии идеально
тонкие, друг на друга не накладываются и не пересекаются.
Размер фигур можно изменять, однако форма должна оставаться
постоянной.
Такой фигурой является «плюс» (или крест). На рис. 22 показано,
как нарисовать каждую из четырех других фигур алеф-один раз. На
каждом фрагменте отрезок АВ содержит в себе континуум из алеф-
один фигур (точнее континуум точек пересечения с ними).
Очевидно, что множество вложенных друг в друга или расположенных
параллельно фигур можно нарисовать так, что через каждую точку мо-
Рис. 22
Доказательство для текста на «экстрасенсорное восприятие»
52
Нескучная математика
жет проходить фигура. Таким образом, сопоставляя континуум точек
на отрезке с континуумом фигур, мы доказываем наше утверждение
о возможности нарисовать остальные четыре фигуры алеф-один раз.
Для креста не существует способа размещения, при котором одна
фигура прилегала бы к другой. Между центрами крестов должно
быть конечное расстояние (пусть даже оно будет очень мало), что
формирует на листе счетное множество алеф-нуль фигур. Возможно,
читателям будет интересно придумать формальное доказательство
того, что на листе бумаги невозможно нарисовать алеф-один
крестиков. Эта задача сходна с той, что я получил от читателя — только там
были буквы алфавита. Ее обсуждение вы можете найти в книге Uses
of Infinity («Польза от бесконечности»), автор Лео Зиппин.
Насколько я знаю, еще никто точно не сформулировал, каким
условиям должны удовлетворять фигуры, чтобы их можно было
воспроизвести на листе бумаги алеф-один раз. Некоторые фигуры
воспроизводятся «несчетное» количество раз за счет поворота или
переноса, некоторые за счет изменения размера, некоторые за счет
того и другого. Я опрометчиво сообщил в своей колонке, что любая
кривая топологически эквивалентна отрезку, а также, что любая
простая замкнутая фигура воспроизводима на листе алеф-один раз.
Однако Роберт Мак (сейчас он учится в колледже Конкорд,
Массачусетс) смог построить простой контрпример. Соедините подобно
вертикальному домино два единичных квадрата, а затем уберите
пару сегментов, чтобы осталась цифра «пять». Эту фигуру невозможно
воспроизвести на листе бумаги алеф-один раз.
Глава 4
Гиперкубы
Дети исчезли.
Они растворилисьу подобно тому, как ветер
разрывает пелену дыма, подобно тому, как сжимается
отражение в кривом зеркале. Взявшись за руки, они ушли в
направлении, о котором Парадайн мог только гадать ...
—ЛЬЮИС ПЭДЖЕТТ «Хрюкотали зелюки»
Направление, о котором Парадайн, профессор философии, «мог
только гадать», перпендикулярно трем координатным осям
пространства. Оно уходит в четвертое измерение, подобно тому как
шахматные фигурки поднимаются вертикально в третье измерение над
осями х и у шахматной доски. В великолепном
научно-фантастическом рассказе Пэджетта дети профессора философии Парадайна
находят проволочную модель тессеракта (tesseract, так называют
четырехмерный гиперкуб) с цветными бусинками, которые причудливым
образом скользят по его граням. Находка оказалась игрушечной абакой
(так называли предка обычных счет). Ее подкинули в наш мир
разработавшие машину времени ученые из четырехмерного мира. С
помощью этой абаки дети узнали, что такое четвертое измерение. В конце
рассказа благодаря подсказке, зашифрованной в «Бармаглоте»
Льюиса Кэрролла, дети вместе возвращаются в свой трехмерный мир.
Но под силу ли разуму человека представить себе четырехмерные
структуры? Немецкий физик XIX века Герман фон Гельмгольц
утверждал, что такое возможно, если дать мозгу соответствующие
исходные данные. Но к сожалению, наш опыт ограничен тремя
измерениями, и нет ни малейших научных свидетельств, что
четырехмерное пространство существует. (Не следует путать эвклидово
четырехмерное пространство с неэвклидовым четырехмерным
пространством-временем из теории относительности, в которой
четвертой координатой является время.)
54
Нескучная математика
Тем не менее при правильном подходе человек может развить
в себе способность к визуализации гиперкуба. «Если посвятить
этому жизнь, — писал Анри Пуанкаре, — то возможно прийти к
пониманию и зрительному представлению четвертого
измерения».
Чарльз Говард Хинтон — эксцентричный американский
математик, некогда преподававший в Принстоне и написавший
популярную книгу The Fourth Dimension («Четвертое измерение»), —
разработал систему цветных блоков, с помощью которых составлял
трехмерную проекцию гиперкуба в трехмерном пространстве. Хинтон
полагал, что, играя много лет с этой «игрушкой» (что-то типа
гиперкуба из рассказа Пэджетта), он смог постичь краешек
четырехмерного пространства. «Я предпочитаю осторожную оценку, — писал
он, — чтобы предостеречь других на случай, если я заблуждаюсь. Но,
по собственному убеждению, я смог выработать у себя интуицию в
этом вопросе».
Цветные блоки Хинтона слишком хитроумны, чтобы рассказать
о них здесь. Наиболее полное изложение их устройства можно
найти в книге A New Era of Thought («Новая эра мысли»). Однако в
нашей власти исследовать некоторые из наиболее простых свойств
гиперкуба — так сказать, сделать несколько шагов к вершинам
понимания Хинтона, несмотря на всю его скромность.
Давайте начнем с понятия точки и попытаемся переместить ее на
расстояние в одну условную единицу по прямой линии, как
показано на рис. 23а. Эту линию можно превратить в координатную ось с
нулем в начале и единицей в конце. Так мы идентифицируем все
точки на этом отрезке. Теперь переместим эту линию на расстояние
в одну единицу перпендикулярно оси (рис. 23Ь). Это даст нам
единичный квадрат. Отметим один из его углов цифрой 0, а затем
введем оси х и у. Теперь мы можем присвоить каждой точке квадрата
координаты. Следующий шаг также легко представить.
Переместите квадрат на расстояние в одну единицу под прямым углом к обеим
координатным осям — х и у (рис. 23с). В результате получается
единичный куб. Координатные оси jc, у и z, проведенные вдоль трех
сходящихся граней, позволяют нам присвоить каждой точке объема
куба тройку координат.
Хотя наше воображение и пасует перед следующим шагом, для
логики преград нет. Предположим, что куб можно переместить в
воображаемом направлении, перпендикулярном всем трем его
осям (рис. 23d). Пространство, образованное таким смещением,
Гиперкубы
55
Рис. 23
Как построить гиперкуб
дает четырехмерный единичный гиперкуб, или тессеракт, с
четырьмя взаимно перпендикулярными ребрами. Оперируя
координатами w, х, у и z, можно обозначить координаты каждой точки
такого куба. Аналитическая геометрия обращается с этими
четырьмя координатами столь же легко, как прежде с тремя, двумя
и одной координатой (именно так мы решаем задачи на
плоскости и в стереометрии). Так евклидову геометрию можно
расширить в область более высокой размерности пространства
(размерность пространства может описываться любым положительным
целым числом). Каждое такое пространство будет евклидовым, но
топологически они будут различаться. Квадрат невозможно
непрерывно без искажений превратить в линию, куб — в квадрат, а
гиперкуб — в куб.
Глубокие исследования в области четырехмерного пространства
можно проводить только на основе соответствующей
аксиоматической базы. Также можно действовать аналитически через уравнения,
а не графические построения (координат будет четыре — w, x, yf z).
Но гиперкуб — это довольно простая структура четырехмерного
пространства, и мы можем на основе аналогий интуитивно вывести
56
Нескучная математика
многие из его свойств. Отрезок с двух сторон ограничивают точки.
Когда отрезок перемешается, он дает квадрат, а его концы имеют
начальное и конечное положение. Следовательно, количество углов
квадрата в два раза превышает количество точек на линии
(получается четыре угла). Две двигающиеся точки производят две линии.
Эти два единичных отрезка имеют начало и конец, так что мы
должны добавить еще пару линий, чтобы получить четыре стороны,
ограничивающие квадрат.
По аналогии, когда квадрат поднимают, получается куб. Все
четыре угла квадрата имеют начало и конец. Умножаем четыре на два
и получаем восемь углов куба. Каждая из четырех точек дает
линию, однако мы должны прибавить еще другие четыре линии к
первоначальным четырем линиям квадрата. Откуда получаем 12
ребер куба (4 + 4 + 4). Четыре линии сторон квадрата формируют
четыре новые грани, которые добавляются к верхней и нижней,
откуда получаем 6 граней куба (4+1 + 1).
Теперь предположим, что куб «поднимают» на единичное
расстояние в направлении четвертой оси, перпендикулярной трем
другим. Это направление мы указать не можем, потому что
ограничены трехмерным пространством. Поскольку каждый угол куба
проходит некий отрезок и имеет начало и конец, у тессеракта (так
называют четырехмерный гиперкуб) 16 углов (2 х 8). Каждая
точка дает линию, но к этим восьми линиям мы должны прибавить
ребра начального и конечного положения кубов. У гиперкуба
будет 32 ребра (8 + 12+12). Двенадцать ребер при перемещении
дают 12 граней. Добавьте сюда еще по 6 граней от начального и
конечного положения кубов. У гиперкуба получается 24 плоские грани
(12 + 6 + 6).
Однако было бы ошибкой предположить, что гиперкуб
ограничен 24 плоскими гранями. Эти грани формируют лишь скелет
гиперкуба, как ребра у куба.
Куб ограничен квадратными гранями, а гиперкуб — кубическими
гранями. Когда куб выдвигают в четвертое измерение, каждая из его
квадратных граней проходит единичное расстояние в направлении
(не пытайтесь представить себе!), перпендикулярном всем его
граням, что приводит к формированию еще одного куба. Так что к 6
кубам, образованным 6 «восстановленными» гранями, мы должны
добавить исходный куб и куб после перемещения, что дает нам восемь
кубических граней. Эти восемь кубов и формируют
гиперповерхность тессеракта.
Гиперкубы
57
РАЗМЕРНОСТЬ, п
0
1
2
3
4
ВЕРШИНЫ
1
2
4
8
16
РЕБРА
0
1
4
12
32
ГРАНИ
0
0
1
6
24
ГИПЕРПОВЕРХНОСТИ
0
0
0
1
8
TECCEP-
АКТЫ
0
0
0
0
1
Рис. 24
Элементы структуру аналогичных кубу, в различных размерностях
Таблица 24 показывает количество кубических элементов с
размерностями от 1 до 4. Существует на удивление простой принцип, с
помощью которого таблицу можно расширить вниз, обобщив для
размерности л. Давайте зададим размерность элемента как степень
х. Тогда коэффициенты биноминального разложения (2х + 1)л дадут
нам количество элементов соответствующей размерности.
Запишите (2х + 1) и умножьте это выражение само на себя:
2х+ 1
2х+1
4х2 + 2х
2х+1
4.x2 + Ах + 1
Обратите внимание, что полученные коэффициенты
соответствуют третьему ряду таблицы. Действительно, каждое последующее
умножение полинома на (2х +1) дает нам следующий ряд.
Из чего же будет состоять пятимерный куб? Выпишите строчку
для тессеракта в виде полинома четвертой степени и умножьте ее на
(2х + 1):
16х4 + 32х3 + 24х2 + 8х+1
2х+ 1
32Х5 + 64х4 + 48*3 + 16*2 + 2х
16х4 + 32х3 + 24х2 + 8х+1
32Х5 + 80jc4 + 80х* + 40JC2 + J(k+ 1
58
Нескучная математика
Полученные коэффициенты дают пятый ряд. Итак,
пятимерный куб имеет 32 объекта нулевой размерности (вершины), 80
объектов размерности один (линии), 80 объектов размерности два
(квадраты), 40 объектов размерности три (кубы) и 10 объектов
размерности четыре (тессеракты). И наконец, один пятимерный
гиперкуб. Обратите внимание, что каждое число таблицы
соответствует верхнему, умноженному на два, плюс диагональное число
сверху слева.
Расположите проволочный скелет куба так, чтобы его тень
падала на плоскость, и попробуйте поворачивать его, наблюдая за
тенью. Если источник света располагается вблизи куба, можно
получить проекцию, приведенную на рисунке 25. Она имеет все
топологические свойства проволочного скелета куба. Например, муха не
может пройти по всем ребрам куба, не проходя дважды через какое-
либо из них. То же самое невозможно и на проекции.
Приведенная на рисунке 26 фигура — это проекция ребер
тессеракта на трехмерное пространство. Если быть более точным, это
проекция трехмерной модели на плоскость, а проекцией гиперкуба
является сама трехмерная модель. На этой проекции можно легко различить
все приведенные в таблице элементы тессеракта. Конечно, шесть из
восьми кубов претерпели перспективное искажение, так же как
искажаются четыре квадратные грани куба при проектировании на плос-
Рис. 25
Проекция куба на двухмерную плоскость
Гиперкубы
59
/-"
^
|\
\
У
^
^
-i
V
^-
^
1А
/
Рис. 26
Проекция тессеракта
на трехмерное пространство
кость. Вот эти восемь кубов: большой внешний куб, малый
внутренний куб и шесть четырехгранных усеченных пирамид (также их
можно назвать шестигранниками), окружающих малый куб.
Любознательному читателю будет интересно найти эти восемь кубов на
рисунке 23d. Это тоже проекция тессеракта, но иначе ориентированная в
пространстве. У приведенной на рисунке 26 фигуры те же
топологические свойства, что и у самого тессеракта. В данном случае муха может
обойти все его ребра, пройдя по каждому из них лишь раз. (Вообще
говоря, муха может это сделать только на гиперкубах четных
размерностей, потому что только в этом случае в углах встречается четное
количество ребер.)
Многие свойства единичного гиперкуба можно выразить в
простых формулах, применимых к любой размерности. Например,
диагональ квадрата равна квадратному корню из двух, длинная
диагональ куба — квадратному корню из трех. В общем случае диагональ
«-мерного куба равна V/2.
Квадрат со стороной х имеет площадь х2 и периметр Ах. Каков
должен быть размер стороны квадрата, чтобы его площадь
численно (не по размерности) равнялась его периметру? Уравнение х2 = Ах
дает х, равный 4 (мы берем ненулевой ответ). Объем какого куба
численно равен площади его поверхности?
После того как читатель ответит на этот простой вопрос, у него
не должно возникнуть трудностей и с еще двумя. Какого размера
должен быть гиперкуб, чтобы его гиперобъем (выраженный в
единичных гиперкубах) был численно равен его гиперповерхности
(выраженной в объемах единичного куба)? Какова формула для
величины грани я-мерного куба, у которого «-мерный объем численно
равен (п - 1)-мерной поверхности?
60
Нескучная математика
В сборниках головоломок часто задают вопросы о гиперкубах,
которые лишь кажутся простыми. Давайте рассмотрим самый
длинный отрезок, который «помещается» внутри квадрата. Очевидно,
это диагональ, и ее длина V2. Каков наибольший квадрат, который
можно вписать в единичный куб? Если читатель сумеет ответить на
этот довольно хитрый вопрос, то он сможет попробовать свои силы
и в разрешении более сложной проблемы. А именно обнаружить
наибольший куб, который можно вписать в единичный тессеракт.
Гиперкубы могут послужить интересными объектами
комбинаторных исследований, уже проведенных на квадратах и кубах.
Давайте разрежем уголок у квадрата {см. рис. 27, верхний фрагмент) и
развернем его четыре стороны, чтобы получилась одномерная
фигура. Каждая линия поворачивается вокруг вершины, пока фигура не
превратится в линию. Чтобы развернуть куб, нужно исходить из
того, что это грани соединены ребрами. Надо разрезать куб по семи
ребрам, а затем развернуть квадраты {см. рис 27, внизу), пока они не
образуют двухмерную фигуру из набора гексамино (шесть
соединенных друг с другом единичных квадратов). Разрезая разные ребра
куба, мы получаем различные фигуры гексамино. Теперь вопрос.
Сколько различных гексамино можно получить разверткой куба в
предположении того, что асимметричные формы и их зеркальные
отражения считаются как одно?
Подобным образом могут быть разрезаны и развернуты восемь
кубов, которые формируют внешнюю гиперповерхность тессеракта.
Невозможно зрительно представить себе, как четырехмерный
человек (поверхность сетчатки которого трехмерна) видит пространство
тессеракта. Однако все восемь кубов, ограничивающие тессеракт,
будут для четырехмерного человека реальной поверхностью в том
смысле, что он сможет коснуться любой точки внутри любого из
этих кубов. Причем четырехмерная булавка может пройти к любой
из этих точек, не коснувшись никакой другой точки объема кубов,
составляющих поверхность. Мы же можем коснуться булавкой
любой точки поверхности куба, не касаясь при этом никакой другой
точки поверхности?
Точки внутри кубов, окружающих тессеракт, будут внутри только
для нас. А для гиперчеловека каждая точка объемов кубов,
образующих поверхность тессеракта, будет всегда снаружи (видимой
поверхностью), как бы он ни поворачивал его своими гиперпальцами.
Трудно представить себе, как именно будут разворачиваться
кубические гиперповерхности в четырехмерном пространстве. Восемь
Гиперкубы
61
Рис. 27
Разворачивание квадрата (вверху) и куба
кубов, ограничивающих тессеракт, попарно связаны двухмерными
аналогами ребер. Действительно, каждый из этих 24 квадратов в тес-
серакте объединяет пару кубов. (Это легко проверить, изучив
трехмерную модель тессеракта.) При правильном выборе места разреза
(разрезать надо 17 из 24 квадратов) в$е восемь кубов в
четырехмерном пространстве освобождаются и поворачиваются вокруг семи
неразрезанных квадратных ребер между кубами-гранями. Все
восемь поворачивающихся кубов выстраиваются в трехмерную
модель, плоскую в четырехмерном пространстве.
Трехмерная развертка тессеракта представляет собой восемь
кубов, соединенных гранями.
Картина Сальвадора Дали Crucifixion (Corpus Hypercubus),
известная как «Распятие на кресте» или «Гиперкубическое распятие», была
нарисована в 1954 году, а в 1955 году была передана в дар
нью-йоркскому музею Метрополитен из собрания Честера Дейла. На ней вы
видите гиперкуб, развернутый в форме крестообразного поликуба по
аналогии с крестообразным гексамино. Обратите внимание на то, как
62
Нескучная математика
Дали подчеркнул контраст между плоским и объемным
пространством, подвесив поликуб над шахматной доской и нарисовав тени от
удаленного источника света, которые падают на крест от рук Христа.
Нарисовав крест в виде развернутого тессеракта, Дали хотел
символически показать, что ортодоксальное христианство зиждется на вере
в то, что смерть Христа была скорее метаисторическим событием,
имевшим место за пределами нашего времени и пространства. По
мнению Сальвадора Дали, из-за наших ограниченных возможностей
мы воспринимаем это событие только в грубой, «развернутой»
форме. Выход в эвклидово четырехмерное пространство является
символом «совершенно иного» мира, о котором уже давно говорили
оккультисты, такие как П. Д. Успенский, а также несколько ведущих
протестантских теологов, к числу которых относится немецкий
богослов Карл Хейм.
На более мирском уровне развернутый гиперкуб использовал
Роберт Хайнлайн в своем рассказе «Дом, который построил Тил».
Калифорнийский архитектор построил дом в форме развернутого
гиперкуба, только перевернутый. После небольшого землетрясения
дом сложился. Остался один-единственный куб — та кубическая
грань, которая видна в нашем пространстве. Он представлял собой
просто кубическую коробку, когда на следующее утро после сдачи
его увидели хозяева. Однако в этом доме внутри тессеракта
произошли некоторые курьезные приключения, а через некоторые окна
даже отрывались неземные виды. Следующее землетрясение
окончательно вытряхнуло этот дом из нашего пространства.
Представление о том, что часть нашей Вселенной может
находиться за пределами трехмерного пространства, не является
абсолютно беспочвенным. Выдающийся американский физик Джон А. Вил ер
высказывал вполне разумную теорию, которая могла бы объяснить те
огромные энергии, которые дают квазары.
Когда гигантская звезда претерпевает гравитационный коллапс,
ее центральная часть имеет такую невероятную плотность, что
пространство-время сжимается. Образуется сингулярность в виде
воронки. Если искривление пространства-времени достаточно
велико, воронка открывается снизу, уходя в бесконечность, и масса
проваливается за пределы пространства-времени, высвобождая
эквивалентную энергию (вспомните эйнштейновское Е = тс2).
Но вернемся к гиперкубам. Заключительный вопрос. Сколько
различных разверток восьми поликубов, образующих гиперкуб,
возможно?
Рис. 28
Сальвадор Дали, «Распятие на кресте», 1954 г ,
передана в дар нью-йоркскому музею Метрополитен
из собрания Честера Дейла в 1955 г.
64
Нескучная математика
ПРИЛОЖЕНИЕ
Хирам Бартем, инженер из Итчинхейма, Сассекс, Англия, прислал
мне вот такие «недобрые» комментарии о кубах Хинтона (согласно
Оксфордскому словарю английского языка, слово «tesseract» (тессе-
ракт) было придумано в 1888 году Чарльзом Говардом Хинтоном):
М-р Гарднер,
Когда я увидел у вас заметку о кубах Хинтона, даже вздрогнул. Я
серьезно увлекался ими, когда мне не было и двадцати. Поверьте мне —
эта забава полностью лишает разума. Единственный человек (из тех,
кого я встречал), который глубоко понял этот вопрос, это Фрэнсис
Седлак. Этот неогегелианский философ из Чехии (ему принадлежит
книга The Creation of Heaven and Earth («Сотворение небес и земли»))
жил близ городка Страуд в Глостершире в общине, напоминавшей
поселение ирокезов.
Как вы наверняка знаете, метод анализа многомерных структур
заключается в последовательном зрительном представлении
примыкающих друг к другу внутренних граней на проекции единичного гиперкуба
(для облегчения процесса они окрашиваются в разные цвета).
Результата ждать долго не приходится, но этот процесс — что-то вроде
самогипноза. Через какое-то время последовательности цветных граней
начинают проходить парадом через ваше сознание, хотите вы того или
нет. В каком-то смысле даже здорово, что я встретил в 1929 году
этого Седлака. Именно тогда я понял всю опасность «зацикливания»
процесса мышления. Спасение состоит в сознательной разработке противоси-
стемы, аналогичной по сути, но с другими цветами на гранях. Однако из
подобного состояния необходимо выходить постепенно, и я бы не
рекомендовал никому играть в своем воображении с многомерными кубами.
В 1972 году была придумана и изготовлена симпатичная
подвесная модель гиперкуба из окрашенных в черный и белый цвета
алюминиевых полосок. Автор — Эйтан Кауфман из Нью-Йорка. Модель
продавалась музеем современного искусства, и на ярлыке значилось
«тессеракт».
Насколько мне известно, до сих пор не было опубликовано ни
одного решения ни одной из предложенных задач, которые я
задумал для своей колонки (не имея при этом готового решения сам).
Первая: какова грань максимального куба, который можно вписать
в единичный тессеракт? Второй: на сколько различных поликубов
Гиперкубы
Рис. 29
Расположение максимального
квадрата в кубе
(из восьми кубов) можно развернуть тессеракт в трехмерном
пространстве? Я получил множество ответов на второй вопрос и лишь
семь на первый. К сожалению, все ответы были разными, и я не
обладаю необходимой компетенцией, чтобы оценить их. Пока ответы
на эти вопросы не опубликованы, так что обе математические
проблемы следует отнести к неразрешенным.
ОТВЕТЫ
Тессеракт со стороной х имеет гиперобъем хл. Его гиперповерхность —
&Х3. Уравнение дает ответ х = 8. В случае с кубом с л-мерным
объемом, численно равным поверхности размерностью на единицу
меньше (п — 1), ответ будет 2я.
TtJ+ff
Рис. 30
Л гексамино, из которых можно сложить куб
66
Нескучная математика
Наибольший квадрат, который можно вписать в единичный куб,
показан на рисунке 29. Каждая вершина квадрата отстоит от угла
куба на расстоянии У4. Площадь такого квадрата равна 9/8, а сторона
- 3/42- Читателям, знакомым с классической проблемой
проталкивания наибольшего куба через квадратное отверстие, эти цифры
наверняка хорошо известны. Ведь куб именно со стороной чуть
меньше 3/42 можно протиснуть через квадратное отверстие единичного
размера.
На рисунке 30 показано 11 различных гексамино, из которых
можно сложить куб. Эти гексамино входят в число «неудобных»
фигур из числа возможных 35, поскольку их нельзя сложить вместе,
чтобы получился произвольный прямоугольник площадью 66
единиц. Однако из этих гексамино можно сложить некоторые очень
интересные фигуры.
ГЛАВА 5
Магические звезды
и многогранники
— Я никогда не был силен в геометрии, — начал он ...
— Да что вы!— жизнерадостно заметил демон.
Плотоядно улыбаясь, он перешагнул нарисованную
на полу бесполезную гексаграмму, которую Генри
нарисовал по ошибке вместо защитной пентаграммы.
-ФРЕДЕРИК БРАУН,
рассказ «Медовый месяц в Аду»
В последние десятилетия в поле зрения математиков попала
комбинаторная арифметика. Вместе с этим возник интерес к
комбинаторным проблемам, которые некогда считали просто головоломками.
Герберт Дж. Райзер в своей небольшой, но превосходной книжке
Combinatorial Mathematics («Комбинаторная математика»),
изданной в 1963 году Американской математической ассоциацией,
демонстрирует магический квадрат 3x3, который был известен в
Китае за несколько веков до нашей эры. «Многие из математических
проблем, изучавшихся в прошлом ради развлечения или эстетики, в
наши дни обретают значимость не только в области чистой
математики, но и прикладной, — пишет Райзер. — Еще недавно понятие
конечной проективной плоскости рассматривалось не более чем
курьез комбинаторики. А в наши дни оно является одним из основ
геометрии и применяется при анализе и планировании
экспериментов. Новые технологии, куда прочно вошла дискретная математика,
подняли занимательную математику прошлого на новый уровень и
поставили перед ней новые цели».
Магические квадраты изучены уже довольно глубоко. В этой
главе мы рассмотрим родственные им, но менее известные магические
68
Нескучная математика
J/ >Ц Рис.31
\^) \_) Пентаграмма
звезды. Этот раздел занимательной комбинаторики неожиданным
образом связан с теорией графов и скелетной структурой
многоугольников.
Самая простая звезда — это всем знакомая пятиконечная.
Именно эту звезду (ее называют Рождественской и помещают на
макушке елки) мы детьми учились рисовать одним непрерывным
движением карандаша. В древнегреческой школе пифагорейцев эта
звезда была символом признания, а также символом здоровья. Этот
символ часто встречался и на древнегреческих монетах. В Средние
века и в эпоху Возрождения эта звезда ассоциировалась с
колдовством и называлась pentagram (пентаграмма) vuiupentalpha. Второе
название «pentalpha» связано с тем, что звезда может быть получена
наложением пяти заглавных букв «А». Три больших равнобедренных
треугольника, суперпозиция которых также дает эту звезду,
воспринимались как символ Святой Троицы, а вершины звезды часто
обозначались пятью буквами J-E-S-U-S (Иисус). Когда Фауст (в
знаменитом произведении Гете) нарисовал пентаграмму на пороге своей
комнаты, он не замкнул линию. Эта небольшая брешь позволила
Мефистофелю войти в комнату. Фауст поймал демона в ловушку,
замкнув линию пентаграммы. Позже, когда Фауст уснул, демон
приказал крысе прогрызть проход в этом пятиугольнике.
Нарисуйте кружок в каждом пересечении линий пентаграммы
(см. рис. 31). Можно ли разместить в этих кругах числа с 1 до 10
таким образом, чтобы по каждой линии сумма была одинаковой?
Легко определить, какой должна быть эта сумма. Ведь сумма цифр от 1
Магические звезды и многогранники
69
до 10 равна 55. Каждое число появляется на двух линиях и,
следовательно, сумма всех пяти линий дает удвоенное значение, а именно
110. Поскольку сумма по каждой из пяти линий должна быть
одинакова, каждая линия должна давать сумму 110/5 или 22. Если
магическая пентаграмма и существует, то сумма чисел по линиям
(магическая константа) должна равняться 22.
Тот факт, что в средневековой литературе по колдовству не было
подобных пентаграмм, является сильным доказательством
невозможности их существования. Если приложить немного
изобретательности, то можно и самим показать, что такую магическую
пентаграмму действительно нельзя построить. Смотри книгу Гарри
Лангмана Play Mathematics («Играем в математику»). Лучшее, что
можно придумать (чтобы избежать дублирования чисел или
использования нулей и отрицательных величин), — это пронумеровать
вершины числами 1, 2, 3,4, 5, 6, 8, 9, 10, 12, как показано на рисунке 32,
слева. Это исправляет дефектную пентаграмму. В данном случае
достигается наименьшая магическая константа — 24 и наименьшая
предельная цифра — 12.
Теперь давайте рассмотрим вопрос, не связанный с
пентаграммой. Можно ли промаркировать 10 ребер пентатопа (40-тетраэдра)
так, чтобы сумма на ребрах, смыкающихся в каждой вершине, была
одинаковой? Удивительно, но ответ на этот вопрос был получен
выше. С точки зрения комбинаторики этот вопрос идентичен вопросу
Рис. 32
Пентаграмма (слева), эквивалентный граф (в середине) и пентатоп (справа)
(Пентатоп (pentatope) — это наименьшая фигура в четырехмерном пространстве,
представляющая аналог тетраэдра. Приведена проекция ее трехмерной модели на
плоскость. — Прим. перев.)
70
Нескучная математика
1С
4 ) (7) (9) (b
8) 26 (Ь
MJ ПЛ Ло) Г2 )
\У Рис. 33
f о Л
ЧсУ Магическая гексаграмма
о пентафамме. Нарисуем граф (он приведен на рис. 32 в середине).
Его называют «полным графом», потому что каждая точка
соединена со всеми остальными. Если вы сравните числа на вершинах
пентаграммы с числами на линиях графа, то увидите идентичность
комбинаторной структуры. Каждая линия пентаграммы соответствует
группе из четырех чисел на ребрах, встречающихся в одной вершине.
Поскольку магическая пятиконечная звезда не существует, то не
существует и полного графа из пяти точек, соответствующих
магическим вершинам тетраэдра.
Итак, полный граф для пяти точек топологически идентичен
скелету 40-тетраэдра, в чем вы можете убедиться, сравнивая числа
на графе с числами на проекции трехмерной модели скелета
пентатопа {см. рис. 32, справа). Пентатоп с магическими вершинами не
существует. А поскольку числа, показанные на скелете пентатопа,
наносились в полном соответствии с пентаграммой, то мы можем
утверждать, что уже имеем для пентатопа решение с наименьшей
магической константой и наименьшим максимальным числом.
При переходе к гексаграмме ситуация становится более
интересной. Эта фигура довольно древняя. Когда-то она называлась
гексаграмма (hexagram), hexalpha, соломонова печать и звезда Давида (см.
рис. 33). Она занимала столь же прочное место в истории
оккультизма и суеверий, как и пентаграмма. Поскольку линий теперь шесть и
каждую пару линий объединяет одна общая вершина, а также с уче-
Магические звезды и многогранники
71
том того, что числа от 1 до 12 дают в сумме 78, мы получаем
магическую константу, равную (2 х 78)/6, или 26. Как показывает
иллюстрация, магическая гексаграмма существует.
Задача подсчета всех возможных магических гексаграмм, без
учета поворотов и отражений, не является тривиальной.
Один из способов получения новой гексаграммы состоит в том,
чтобы преобразовать гексаграмму в дуальный граф (см. рис 34,
слева), цифры на линиях которого сходящиеся в вершинах,
соответствуют рядам магической гексаграммы. Теперь становится
очевидным, что этот граф топологически эквивалентен скелету октаэдра (в
середине), одного из пяти тел Платона. Этот восьмигранник
(октаэдр) мы можем произвольным образом повернуть, а также
зеркально отразить. Затем соответствующим образом перенесем цифры
обратно на гексаграмму (картирование ребер происходит в
соответствии с начальной нумерацией). Таким образом, мы получаем новое
расположение цифр на гексаграмме.
Для получения дополнительных решений можно обратиться и к
другим преобразованиям гексаграммы, не связанным с вращением
или отражением октаэдра. Кроме того, магическая звезда имеет
своеобразное «дополнение», которое можно получить, заменив каждое
число на его разность с (п + 1), где п — наибольшее из чисел. Итак, для
гексаграммы существует 80 различных решений, 12 из которых
обладают тем свойством, что сумма внешних вершин дает магическую
постоянную (такое решение приведено в примере).
Рис. 34
Граф гексаграммы (слева), эквивалентный октаэдр (в середине)
и куб~двойник (справа)
72
Нескучная математика
Рис. 35
Септаграмма
Но это еще не все. Октаэдр обладает так называемым
«двойником-многогранником», в котором каждая грань заменена на
вершину, а каждая вершина — на грань. Ребра при этом остаются на
прежних местах. Двойником октаэдра является куб. Это позволяет нам
разметить «магическим образом» все 12 ребер куба (см. рис. 34,
справа). В приведенном примере числа с 1 по 12 размещены так, что у
куба получаются магические грани (сумма цифр по всем четырем
ребрам каждой грани равна 26).
Можно ли в септаграмме, или семиконечной звезде (см. рис. 35),
разместить числа от 1 до 14, чтобы эта звезда стала магической? Да,
и я предлагаю читателю самому показать, как самым элементарным
способом найти одно из его 72 решений. Его магическая постоянная
равна (2 х 105)/7, или 30. Лучший способ решить эту задачу — это
нарисовать звезду крупным планом, а цифры записать на вырезанных
кружочках. Перемещая кружочки, можно методом проб и ошибок
найти решение. Скажу сразу, что этот процесс захватывающий и вам
трудно будет остановиться, пока вы не получите решения.
Одно из решений для октаграммы, или восьмиконечной звезды,
показано на рисунке 36 слева. Обратите внимание на то, что
магическую постоянную (34) также дает сумма четырех углов каждого из
двух больших квадратов. Верхняя правая часть рисунка 36
показывает соответствующий граф. Справа внизу показано эквивалентное
каркасное тело. Октаграмма имеет 112 решений.
Очевидно, что нет предела комбинаторным задачам, в которых
необходимо маркировать ребра, вершины или фани различных
Магические звезды и многогранники
73
Рис. 36
Октаграмма и ее два эквивалента
многогранников так, чтобы получались магические константы,
причем самым неожиданным образом. Многие из этих задач могут
быть переведены в эквивалентную задачу с магическими звездами.
Например, такая. Какие из пяти правильных геометрических тел
можно сделать магическими, промаркировав их ребра так, чтобы
сумма чисел в вершинах была одинакова? Причем должно
выполняться еще одно условие — числа должны представлять собой
последовательный ряд. Легко увидеть, что это не тетраэдр. Об этом вы
можете почитать в моей книге Sixth Book of Mathematical Games from
Scientific American («Шестая книга по математическим играм от
журнала Scientific American»). Может быть, это куб? У куба 12 ребер (см.
рис. 37). Отметьте 12 черных точек в вершинах октаграммы (справа).
Поскольку через каждую точку проходят две линии, константа
должна быть равна (2 х 78)/8, или 191/2-
Это число не является целым, так что здесь ответа искать не
стоит. Однако мы можем получить неполноценное решение (не
удовлетворяющее последнему условию) с наименьшей магической посто-
74 Нескучная математика
Рис. 37
Магический каркас куба (слева) и эквивалентная октаграмма
янной 20 и наименьшим максимальным числом 13, промаркировав
кружочки (и эквивалентные ребра куба), как показано на рисунке.
Поскольку октаэдр дуален кубу, это приводит к автоматическому
решению задачи о маркировке ребер октаэдра различающимися
непоследовательными ненулевыми положительными целыми
числами, сумма которых вокруг каждой грани дает магическую
постоянную, причем наименьшую.
Рис. 38
Существует ли магическая треугольная призма (см. справа) ?
Топологически эквивалентная звезда приведена слева.
Магические звезды и многогранники
75
Как мы уже видели, фани октаэдра можно промаркировать
последовательными целыми числами таким образом, чтобы его
вершины стали магическими. Для икосаэдра и додекаэдра магическая
постоянная получается дробной, так что они не могут быть
решением задачи. Поскольку все многофанники имеют дуальную пару, то
среди них такого, который бы удовлетворял условиям близкой
задачи (целые, ненулевые последовательные числа, но с магическими
фанями), не существует.
Если мы разметим только 9 из вершин гексафаммы, как показано
на рисунке 38, слева, то получим звездный эквивалент задачи на
маркировку девяти ребер треугольной призмы (справа) цифрами от 1 до 9,
чтобы сделать все ее шесть вершин магическими. Магическая
постоянная при этом получается (2 х 45)/6, или 15. Существует ли такая звезда
и, соответственно, призма? Теперь это уже не столь трудный вопрос.
ДОПОЛНЕНИЕ
Я получил несколько свежих доказательств невозможности
существования магической пентафаммы. Ян Ричарде из университета
штата Миннесота подошел к этому вопросу так:
1. Числа 1 и 10 должны быть на одной линии. Каждая из двух линий,
проходящих через 1, должна включать в себя три других числа, которые
в сумме дают 21. Следовательно, сумма шести чисел должна быть 42.
Если 10 не является одним из этих шести чисел, то самая большая
сумма, которая может быть получена, — это 9 + 8 + 7 + 6 + 5 + 4 = 39.
2. Пусть L — это линия, проходящая через 1 и 10, Li — линия,
проходящая через 1, a L2 — линия, проходящая через 10.
Линия L может содержать четыре возможные комбинации.
Четверка чисел (1, 10,4, 7) не позволяет построить аналогичные
четверки для L] и L2. Три другие возможности для L, приведенные ниже,
определяют четверки на других двух линиях.
L U U
1, 10,2,9 1,6,7,8 10,5,4,3
1, 10,3,8 1,5,7,9 10,6,4,2
1,10,5,6 1,4,8,9 10,7,3,2
3. Линии Lj и L2 должны иметь одну общую цифру. Ни в одном
из трех приведенных вариантов такого числа нет. Следовательно,
магическая пятиконечная звезда невозможна.
76
Нескучная математика
Рис. 39
Решение задачи
для септаграммы
Рис. 40
Граф в виде гексаграммы
для задачи с призмой
Одна из первых попыток определить количество решений для
шести- и семиконечной звезд предпринималась еще Генри Э.
Дьюдени в книге Modern Puzzles («Современные головоломки»). Это
одна из двух книг, которые вошли в большой сборник Дьюдени 536
Puzzles and Curious Problems («536 головоломок и любопытных
задач»). Дьюдени ошибся в обоих случаях. Ульрих из Оклахомы и А.
Домерг из Парижа обнаружили восемьдесят решений для
гексаграммы (на шесть больше, чем у Дьюдени). Что касается семико-
Магические звезды и многогранники
77
нечной звезды, то она имеет 72 решения (Дьюдени насчитал 56), о
чем первым сообщил Питер Монтгомери из Миннесоты. Это
решение было подтверждено Ульрихом и Домергом, а позднее и
компьютерной программой, написанной Аланом Молдоном из
университета Ватерлоо, Канада.
Домерг сообщал о 112 решениях для восьмиконечной звезды, а
количество решений для девятиконечной звезды оценивал за две
тысячи. Результаты для шестиконечной, семиконечной и
восьмиконечной звезд были подтверждены в 1972 г. Хуаном X. Рубисеком из
Буэнос-Айреса. Эти решения исключают повороты и отражения, но
включают в себя дополнения.
ОТВЕТЫ
Первая задача, в которой требуется разместить целые числа от 1 до
14 в вершины семиконечной звезды так, чтобы каждый ряд из
четырех чисел давал в сумме 30, имеет 72 решения.
Одно из решений, с первыми семью числами на внешних
вершинах звезды, показано на рис. 39.
Суть второй задачи состоит в том, чтобы определить, возможно
ли промаркировать девять ребер треугольной призмы целыми
числами от 1 до 9 так, чтобы сумма трех ребер при каждой вершине
была равна 15. Как было показано, эта задача аналогична размещению
девяти цифр в кружках гексафаммы на рис. 40 так, чтобы суммы в
каждом ряду из трех цифр равнялись 15.
Предположим, решение существует. Тогда:
A+C+F=A+E+H
C+F=E+H (l)
B+C+D=D+E+J
В + С = Е + J (2)
F+G+H=J+G+B
F+H = J + B (3)
Объединяя (1) и (2), получаем:
(С + F) - (В + С) = (Е + Н) - (Е + J)
F-B=H-J (4)
78
Нескучная математика
Объединяя (3) и (4), получаем:
(F - В) + (F + Н) = (Н - J) + (J + В)
2F-B + H = H + B
2F = 2B
F=B
Но F не может равняться В, потому что в задаче требуется
разместить девять различных чисел. Поэтому мы можем заключить, что
исходное предположение неверно и что задача не имеет решения.
Обратите внимание, что результат доказательства оказался намного
более строгим, чем требовало условие.
Оно показывает, что невозможно построить магическую фигуру
с различающимися числами, будь они последовательными целыми,
рациональными или даже иррациональными.
ГЛАВА 6
Гении арифметики
Представляется, что способность производить в уме молниеносные
вычисления сопровождается неизменно средним интеллектом и
более чем скромной математической интуицией и творческим
потенциалом. Да, некоторые из самых вьщающихся математиков имели
проблемы со счетом в уме, а многие «профессиональные счетчики»
(но, определенно, не самые лучшие) не отличались умственными
способностями в других областях деятельности.
Однако многие великие математики также были и
великолепными «счетчиками». Карл Фридрих Гаусс, например, мог
выполнять в уме потрясающие арифметические вычисления. Сам
математик не раз говорил, что научился считать раньше, чем
разговаривать. Когда ему было три года, его отец, каменщик, составлял
еженедельную платежную ведомость для чернорабочих.
Малолетний Карл поразил его, указав на ошибку в вычислениях.
Усомнившись, отец снова просуммировал длинный столбик чисел, но сын
оказался прав. Тогда маленькому Карлу еще не преподавали
никакой арифметики.
Джон фон Нейман — это еще один математический гений,
который также был одарен этим специфическим умением вычислять без
карандаша и бумаги. В книге Brighter than a Thousand Suns, изданной
в 1956 году («Ярче тысячи солнц», Атомиздат, 1960 и 1961), Роберт
Юнг рассказывает о своих встречах в Лос-Аламосе в годы Второй
мировой войны, когда в теоретической физике властвовали фон
Нейман, Энрико Ферми, Эдвард Теллер и Ричард Файнман.
Всякий раз, когда требовалось провести математические
вычисления, в игру вступали Ферми, Файнман и Нейман. Ферми
предпочитал считать на логарифмической линейке, Файнман пользовался
арифмометром, а Нейман проделывал вычисления в уме. Цитируя
мемуары одного из физиков, Роберт Юнг отмечает, что «побеждала
всегда голова». «Было просто удивительно, насколько близко
совпадали все три ответа».
80
Нескучная математика
Вычислительные способности Гаусса, Неймана и других гениев
математики, таких как Леонард Эйлер и Джон Валлис, могут показаться
удивительными, но они бледнеют на фоне вычислительных подвигов
профессиональных артистов этого жанра, чья ментальная акробатика
процветала на сцене на протяжении всего XIX века в Европе, Англии
и Америке. Многие из них начинали свою артистическую карьеру еще
в раннем детстве. Хотя некоторые из них «щедро» писали о своих
методах тренировки и даже изучались психологами, не исключено, что
большую часть своих тайн они скрывали — либо сознательно, либо
просто сами не осознавали, как считали в уме с такой скоростью.
Первый эстрадный счетчик Зерах Колбурн родился в 1804 году в
Каботе, штат Вермонт. Как и у его отца, прабабушки и одного из
братьев, у него на каждой руке и ноге был дополнительный палец.
(Дополнительные пальцы ампутировали, когда ему было 10 лет.)
Ребенок изучил таблицу умножения от 1 до 100 еще до того, как
научился читать и писать. Его отец, бедный фермер, быстро разглядел
в этом возможность заработка и организовал турне, когда сыну
было шесть лет. Сохранилось множество воспоминаний о
выступлениях гения устного счета в Англии, когда Зераху было восемь лет. Он
почти мгновенно перемножал любые четырехзначные числа, а с
пятизначными ему приходилось немного подумать. Когда его
попросили умножить 21 734 на 543, он сразу ответил 11 801 562. На вопрос,
как он сделал это, он объяснил, что 181x3 = 543. А поскольку
умножить на 181 проще, чем на 543, он сначала перемножил 21 734 на 3, а
затем результат умножил на 181.
Вашингтон Ирвинг и другие поклонники юного гения нашли
деньги и помогли отдать его в школу сначала в Париже, а затем в
Лондоне. Впоследствии его способность к быстрому счету исчезла,
либо просто исчез интерес к таким подвигам.
В 20 лет он вернулся в Америку и еще в течение десяти лет
служил Проповедником в методистской церкви. Его довольно
экстравагантная автобиография A Memoir ofZerah Colburn: written by himself
... with his peculiar methods of calculation («Биография Зераха Колбур-
на, написанная им самим, с изложением специфических методов
вычислений») была издана в 1833 году в Спрингфилде, Массачусетс.
Он умер в возрасте 35 лет. В конце жизни он преподавал
иностранные языки в университете города Норвич, штат Вермонт. (Не
путайте Зераха с его племянником, который носил то же имя и писал
книги по механике и инженерному делу. К числу его работ относится
популярная The Locomotive Engine («Паровозные двигатели»).)
Гении арифметики
81
Параллельно с эстрадной карьерой Колбурна в Англии
расцветал талант Джорджа Паркера Биддера. Этот известный эстрадный
вычислитель родился в 1806 году в Девоншире. Рассказывают, что
математике его учил только отец, каменщик, и эта учеба
ограничилась тем, что он научил сына считать. Знание арифметики мальчик
приобрел, играя с мраморными шариками и пуговицами. А в девять
лет его отец уже организовал для гения арифметики турне. Зрители
задавали самые разные вопросы, в том числе и довольно сложные.
Например, если бы Луна находилась в 123 256 милях от Земли, а
скорость звука была 4 мили в минуту, то сколько времени шел бы
звук от Земли до Луны? Менее чем через минуту мальчик ответил:
21 день 9 часов 34 минуты. Когда Джорджа попросили извлечь
квадратный корень из 119 550 669 121, юный гений (10 лет!) ответил
345 761, на что потребовалось не более 30 секунд. В 1818 году,
когда ему было 12 лет, а Колбурну — 14, они встретились в Дербишире,
где и соревновались друг с другом. Колбурн в своих
воспоминаниях писал, что победил он, однако лондонские газеты писали о
победе Биддера.
Профессора из Эдинбургского университета убедили Биддера-
старшего позволить им обучать его сына. Мальчик превосходно
учился в колледже и в конечном счете стал одним из самых
успешных инженеров Англии. Большинство его изобретений коснулось
железнодорожного дела, но сейчас его знают в основном в связи с
том, что именно он разработал проект лондонских доков Ройал
Виктория Доке (и лично контролировал процесс строительства).
Способности Биддера к молниеносному счету не ухудшились с
возрастом. По воспоминаниям современников, незадолго до смерти
Биддера, в 1878 году, кто-то в его присутствии сказал, что в одном
дюйме помещается 36 918 волн красного цвета. Исходя из того, что
скорость света приблизительно равна в 190 000 миль в секунду,
человек пытался определить, сколько волн красного цвета достигнут
глаза человека за одну секунду.
«Не трудитесь, — заметил 70-летний Биддер. — Количество волн
составит 444 433 651 200 000».
И Колбурн, и Биддер умножали большие числа, разбивая их на
части и применяя слева направо технику алгебраического
перекрестного умножения, которую в наше время преподают в
начальных классах школы (в США. — Прим. перев.). Например,
умножение 236 х 47 превращалось в (200 + 30 + 6) х (40 + 7), а сама
операция производилась, как показано на рисунке 41. Если читатель за-
82
Нескучная математика
кроет глаза и попробует перемножить числа, то будет удивлен тем,
что это даже проще, чем традиционный европейский подход
справа налево. «Этот метод... требует намного большего количества
цифр по сравнению с классическим, — пишет Колбурн в своих
воспоминаниях. — Но не забывайте, что все действия Зерах
производит без карандаша, ручки и бумаги. Так почему же для вычислений
в уме этот метод подходит больше?» (В своей книге Колбурн пишет
о себе в третьем лице!)
Биддер дал ответ на этот вопрос в своей уникальной лекции по
методам вычислений, которая читалась в Институте для
гражданских инженеров в Лондоне (текст этой лекции был опубликован в
1856 году в 15-м томе Материалов этого института). На каждом
этапе вычислений в уме приходится держать одну и только одну цифру>
не перегружая память остальными.
Другой причиной, почему все эстрадные счетчики предпочитали
этот метод вычислений (хотя сами редко признавали это), является
т*о, что результат перемножения появляется уже в процессе
вычисления. Обычно этот прием объединяется с другими, чтобы создавать
впечатление, что время вычисления намного меньше. Например,
эстрадный артист может повторить вопрос, а затем дать «мгновен-
ЗАДАЧА: 236 х 47
236 = 200 + 30 + 6
47 = 40 + 7
1. 40x200 = 8000
2. 8000 + (40 х 30) = 9200
3. 9200 + (40 х 6) = 9440
4. 9440+ (7x200) =10 840
5. 10840 +(7x30) = 11 050
6. 11 050 + (7 х 6) = 11 092
Рис. 41
Гении арифметики
83
ный» ответ, тогда как на самом деле он начинает вычисления с
произнесения зрителем первых цифр второго числа. Иногда удается
выиграть время, если сделать вид, что не услышал вопрос, и
попросить повторить. Вспомните об этих приемах, когда будете читать
заметки журналистов о выступлении эстрадного счетчика,
демонстрирующего чудеса «мгновенного» счета.
Я намереваюсь быстро «пробежаться» по личностям
вычислителей, якобы обделенных иными талантами. Они не были настолько
глупыми, как писала о них пресса. Скорость их вычислений
заметно уступала скорости счета профессиональных эстрадных
счетчиков, но они были наделены более сильным интеллектом. Фермер
Джедедая Бакстон, живший в Англии в XVIII веке, относится к
числу самых ранних народных «талантов» в этой области. Он всю
жизнь занимался фермерством и никогда не давал представлений.
Но известность пришла сама, и однажды он был приглашен на
заседание Королевского общества в Лондон. Бакстона пригласили в
театр Друри-Лейн на постановку шекспировского «Ричарда III» с
участием Дэвида Гаррика. На вопрос о впечатлениях фермер
ответил, что актеры произнесли 14 445 слов и сделали 5202 шага по
сцене. Бакстон просто не мог не считать. Он считал шаги по полю и
мог давать необычайно точные оценки площади в квадратных
дюймах, а затем преобразовывать их в более мелкие единицы, такие как
«волос» (hairbreadth), который составлял 1/48 дюйма. При этом он
никогда не учился и не умел читать, писать и обращаться с
цифрами на бумаге.
Наверное, лучшим из лучших «новых времен» среди любителей
считать можно назвать Александра Крейга Эйткена, профессора
математики Эдинбургского университета. Эйткен родился в Новой
Зеландии в 1895 году, а в 1932 году стал соавтором учебника The Theory
of Canonical Matrices («Теория канонических матриц»), ставшего
классическим.
В отличие от большинства «молниеносных» счетчиков, он
вплоть до 13 лет в уме практически не считал. Именно алгебра, а не
арифметика пробудили его интерес к устному счету. В 1954 году,
почти век спустя после вошедшей в историю лондонской лекции
Биддера, Эйткен делал доклад в Лондонском инженерном обществе
на тему «Искусство счета в уме с демонстрацией». Этот доклад был
опубликован в материалах общества Transactions в декабре 1954 года
и стал еще одним ценным источником информации из первых рук о
том, что происходит в сознании «молниеносных счетчиков».
84
Нескучная математика
Одной из существенных предпосылок к быстрому счету является
врожденная способность легко запоминать числа. Все
замечательные вычислители демонстрировали со сцены чудеса памяти. Когда
Бидцеру было 10 лет, он просил написать и прочитать число из 40
цифр, а затем повторял его в противоположном направлении. Затем
повторял это число уже в прямом направлении. Многие из
эстрадных вычислителей могли в конце выступления повторить все числа,
которые назывались во время выступления. Да, существуют
мнемонические трюки, позволяющие превращать числа в слова, которые,
в свою очередь, запоминаются с помощью других приемов (см. мою
книгу Scientific American Book of Mathematical Puzzles and Diversions).
Но эти приемы слишком малопроизводительны для работы на
сцене, так что вряд ли мастера этого жанра прибегали к ним. «Я
никогда не пользовался мнемоникой и никогда не доверял ей, —
рассказывает Эйткен. — Она грешит чуждыми и неуместными
ассоциациями, надстраиваемыми над основой, которая должна быть чистой и
прозрачной».
Эйткен в своей лекции упоминает о том, что недавно читал о
французском счетчике Морисе Дагбере, который в процессе
запоминания 707 знаков числа, вычисленного в 1873 году Уильямом
Шэнксом, «потратил ужасно много сил и времени». «Мне стало
забавно при мысли, что я на несколько лет раньше Мориса совершил
подобное и не считаю это подвигом, — рассказывал Эйткен. — Мне
оказалось достаточным расположить цифры в ряды по пятьдесят в
каждом и каждый ряд разделить на десять групп по пять цифр, а
затем прочитать их в определенном стихотворном ритме. Это было не
только утомительно, но и бессмысленно».
А спустя двадцать лет — после того, как на компьютерах были
получены тысячи знаков числа, — Эйткен узнал, что Шэнкс ошибся в
последних 180 знаках. «Я опять получил возможность развлечься и
выучил правильную последовательность первой тысячи знаков, —
комментирует Эйткен. — И снова все получилось без проблем, за
исключением того, что пришлось искать место, с которого пошла
ошибка. Секретом к успеху этого трюка стала релаксация — полная
противоположность концентрации внимания. Необходима и
заинтересованность. Случайная последовательность цифр, не несущая
никакого арифметического или математического значения, мне бы
не понравилась. Если бы у меня возникла необходимость запомнить
ее, то и это не было бы проблемой. Но движение было бы против
течения».
Гении арифметики
85
Эйткен неожиданно прерывает лекцию, с явным ритмом
перечисляя 250 цифр числа . Его попросили начать с 301 знака. После 50
цифр его попросили перейти на 551 знак и назвать еще 150. Мэтр,
которого проверяли по таблице, не совершил ни одной ошибки.
Возможно, мастера этого жанра представляют цифры зрительно?
Не всегда. Есть и такие, которые даже не могут найти ответа на этот
вопрос. Французский психолог Альфред Бине одно время состоял в
специальном комитете Французской академии наук. Комитет
занимался исследованием умственных процессов двух известных
эстрадных вычислителей конца XIX века. Это были грек Перикл
Диаманди и итальянец Жак Эноди. В своей книге Psychologic des grands cal-
culateurs etjoueurs dechecs («Психология молниеносных
вычислителей и шахматных игроков») Бине сообщал, что Диаманди зрительно
представлял цифры, а Эноди (который считал в шесть раз быстрее)
имел выраженное слуховое восприятие и прекрасное чувство ритма.
Счетчики с выраженным зрительным восприятием почти всегда
вычисляли медленнее других, хотя к ним относились многие из
практикующих эстрадных профессионалов, таких как Дагбер, поляк
Сало Финкельштейн и замечательная француженка со сценическим
именем Мадемуазель Осака. Вычислители с выраженным слуховым
восприятием, такие как Биддер, как показали исследования,
считали быстрее. Вильям Клейн, голландский специалист по
компьютерам, который выступал под псевдонимом Паскаль, признан самым
быстрым среди ныне живущих эстрадных вычислителей (журнал
Life писал о нем 18 февраля 1952 года). Он менее чем за две минуты
способен перемножить два десятизначных числа. Этот мастер
обладает выраженным слуховым восприятием и во время выступлений
непременно бормочет на голландском языке.
Если Вильям допускает ошибку, то чаще всего из-за того, что
слова похоже звучат. Его брат Лео тоже неплохой вычислитель и
при этом обладает выраженным зрительным восприятием. Он
иногда путает числа, которые похоже выглядят.
Эйткен во время лекции сказал, что при желании может
представлять числа зрительно. На различных этапах вычисления, а
также в самом конце, когда получается ответ, цифры как бы
фокусируются перед его глазами. «Но чаще цифры словно скрыты некой
пеленой, из-под которой перемещаются в строгом порядке,
необходимом для вычислений. Я четко осознаю, как добавляю нули в
начале или конце чисел (они не появляются сами). Однако я не
могу сказать, что «вижу» цифры или «слышу» их. Образуется при-
86
Нескучная математика
чудливая смесь, которой я не могу дать разумного зрительного
представления. Хотя должен заметить, что это и не отрывки
музыкальных произведений. На уровне слуховых представлений нельзя
признать их музыкальными композициями. Также я заметил, что
временами мое сознание переполняет желание получить ответ, и я
получаю его прежде, чем даже начал вычислять. Я проверял такие
интуитивные ответы, и, к моему удивлению, они оказывались
правильными».
Мозг Эйткена можно сравнить с огромной базой данных. Все
это типично для эстрадных счетчиков. Голландский счетчик
Вильям Клейн признался, что знает таблицу умножения от 1 до 100. По
мнению некоторых журналистов, Биддер и другие мастера знали
таблицу умножения до 1000, но публично не признавали этого.
(Большие числа можно разделить на пары и тройки, с которыми
при умножении работают как с отдельными цифрами.) Наряду с
бесчисленными «цифровыми» фактами, такими как количество
секунд в году или унций в метрической тонне, в памяти счетчика
хранятся длинные таблицы квадратов, кубов и логарифмов чисел. Все
это бывает полезно, когда эстрадный вычислитель отвечает на
вопросы зрителей. Поскольку 97 — это наибольшее простое число в
пределах первой сотни, вычислителей часто просят сосчитать
цифры 96-значной повторяющейся последовательности десятичной
дроби, равной {/97. Эйткен давно запомнил эти цифры, так что
может выпалить ответ, даже не считая.
Кроме того, существуют сотни упрощенных процедур, которые
мастера этого жанра сами находят для себя. Эйткен указывает, что в
любом сложном вычислении первым делом необходимо выбрать
наилучшую стратегию.
Чтобы проиллюстрировать свои слова, он раскрывает
любопытный пример, ранее неизвестный. Предположим, вас попросили
найти обратное число (1/х) от числа, которое заканчивается на 9
(для примера, 59). Вместо того чтобы погружаться в пучину прямых
вычислений и делить 1 на 59, вы можете добавить единицу к 59,
получив 60, а затем поделить 0,1 на 6, как показано на рисунке 42.
Обратите внимание на то, что на каждом этапе деления цифры,
составляющие частное, особым образом входят в процесс деления. Это и
есть значение для х/59.
Если вас попросят вычислить 5/2з, Эйткен предлагает
следующее. Он сразу видит, что числитель и знаменатель этой дроби
можно умножить на 3. Получается эквивалентная дробь 15/б9> которая
Гении арифметики
87
очень удачно оканчивается на девятку. Затем меняем 69 на 70 и
делим, соответственно 1,5 на 7 с помощью объясненной выше
процедуры. Однако мы можем преобразовать эту дробь к65/299 и поделить
0,65 на 3 по тому же принципу.
Какая стратегия является наилучшей? По словам Эйткена, ее
надо выбирать мгновенно, следуя потом ей неукоснительно. Дело в
том, что на полпути к ответу может возникнуть озарение, что есть
стратегия лучше.
«Но подобное озарение следует решительно отметать и
продолжать ту же линию».
Эйткен возводил в квадрат числа методом, показанным на
рисунке 43. Число b должно быть небольшим и выбираться таким
образом, чтобы {а + Ь) либо {а — Ь) оканчивались на один или больше
нулей. В данном случае было выбрано значение 23. Помня наизусть
таблицу для низших квадратов, Эйткен без вычислений уже знает,
что 232 равно 529. Во время лекции ему дали семь трехзначных
чисел, каждое из которых он возвел в квадрат почти мгновенно. На два
четырехзначных числа потребовалось примерно пять секунд.
Обратите внимание, что применительно к числу, последняя цифра
которого — пять, рецепт Эйткена дает изумительную формулу, которую
следует знать наизусть. Отделите 5, первые цифры умножьте по
NWv
.10 16 9
6
4 1
3 6
5
5
6
4
2
2
9
4
ЗАДАЧА: 777 х 777
а2 = [(а + Ь) х {а - Ь)] + Ь2
7772 = [(777 + 23) х (777 - 23)] + 232
7772 = [800 х 754] + 529
7772 = 603 200 + 529
7772 = 603 729
5 4
Рис. 42
Вычисление Эйткена
значения дроби '/59
Рис. 43
Как бы Эйткен
возвел в квадрат 777
88
Нескучная математика
формуле п х (п + 1) и к результату припишите 25. Например, 85 х 85
(8 умножить на 9 дает 72, добавление справа 25 дает 7225}.
Томас X. О'Бирн, математик из Глазго, рассказывает в своем
письме, как однажды ходил вместе с Эйткеном на выставку
арифмометров. «Продавец сказал кому-то что-то вроде: «А теперь
умножим 23 586 на 71 283». Эйткен мгновенно дал ответ. Продавец был
слишком занят работой, чтобы заметить это, но присутствующий
рядом менеджер обратил внимание на реплику посетителя. Когда
же оказалось, что этот странный посетитель был прав, менеджер
онемел (впрочем, я тоже)».
Компьютеры, без сомнения, не позволяют молодым людям,
подобно Эйткену, в полной мере развить свои экзотические таланты.
Сам маэстро в конце лекции признал, что его способности стали
ухудшаться, когда он приобрел арифмометр и почувствовал,
насколько «дешевеет» его необычный дар. «Эстрадные счетчики
вымирают, как исчезают племена Тасмании и народ Мориори, — в
заключение сказал артист. — Поэтому интерес к этому жанру эстрады
теперь можно назвать больше антропологическим. Но сейчас у вас
еще есть возможность взглянуть на любопытный экземпляр.
Некоторые из сидящих здесь смогут на рубеже тысячелетий рассказать о
том, как они присутствовали на этой встрече и видели одного из
артистов подобного жанра».
В следующей главе я намерен обсудить некоторые трюки
эстрадных вычислителей, с которыми даже новичок сможет показать класс.
Помните, что даже мастера сцены порой опускались до того, чтобы
показывать людям подобные псевдовычисления со сцены. Многие
акробаты порой срывали аплодисменты за эффектные трюки,
которые не требовали никакой особой физической силы и ловкости.
ПРИЛОЖЕНИЕ
Соломон Голомб часто удивлял своих друзей, оценивая в уме
значения сложных выражений из комбинаторного анализа. Сам он
писал: «Необходимо запоминать лишь одну константу, а также
опираться на последовательность простых правил — более простых, чем
может показаться». Наиболее удачным образом Соломон пустил в
ход свое оружие еще на первом курсе колледжа. Преподаватель
биологии рассказывал классу, что существует (в то время так думали)
24 пары хромосом. Поэтому существует 224 способа выбрать
хромосомный набор из каждой пары при формировании яйцеклетки или
Гении арифметики
89
сперматозоида. «Таким образом, от одного родителя, — рассказывал
преподаватель, — количество вариантов эмбрионов 224. Знаете,
чему это равняется?»
На этот риторический вопрос Голомб немедленно ответил:
«Да, 16 777 216». Преподаватель иронически улыбнулся, заглянул
в конец страницы, где примечание, и сказал: «На самом деле это
равно...» - и замер. Затем потребовал у Соломона объяснений.
Находчивый первокурсник ответил, что это «очевидно». В группе
за Голомбом немедленно закрепилось прозвище «Эйнштейн». В
течение года некоторые в группе, а также ведущий практику
ассистент думали, что это его фамилия.
Так как же Голомб сосчитал это? Он по секрету сказал мне, что
недавно запоминал таблицу значений пп от 1 до 10. Когда преподаватель
сформулировал вопрос, Соломон быстро догадался, что 224 = 88, а
затем назвал число из короткого списка.
Современные эстрадные счетчики не делают таких заготовок,
какие делали маэстро в XIX веке. Как эстрадное направление
молниеносный счет теряет свою популярность. Уиллис Нельсон Ди-
зарт, эстрадный счетчик родом из Джорджии, некогда выступал под
псевдонимом «Вилли-волшебник» и был широко известен в США.
В Европе наиболее известны индийская «женщина-калькулятор»
Шакунтала Деви и француз Морис Дагбер. Но мои сведения
относительно мастеров этого жанра, выступающих в других странах,
скудны.
ГЛАВА 7
Секреты
молниеносных вычислений
Даже самые известные из молниеносных вычислителей, о которых
рассказывалось в предыдущей главе, при выступлении на эстраде
обычно включают в свою программу такие примеры, как
извлечение кубического корня и трюки с календарем. Эти примеры
кажутся чрезвычайно трудными, хотя на самом деле таковыми не
являются. В основе их, как и множества других — менее сложных, но столь
сильно поражающих воображение вычислений — почти всегда
лежат ловкие трюки. Некоторые из них настолько просты, что
читатель, который захочет поразить своих друзей, может освоить их за
короткое время. При этом от него потребуются только самые
элементарные счетные навыки.
Для примера рассмотрим один из трюков с умножением. Он
на удивление мало известен, хотя опубликован еще в 1747 году в
Италии. Дж. А. Альберта привел описание этого фокуса в книге
Giochi numerici:fatti arcani («Игры с числами: тайные факты»). Для
демонстрации трюка можно использовать числа любой длины,
но лучше ограничиться трехзначными, если только под рукой нет
калькулятора, на котором можно быстро проверить результат.
Попросите зрителей назвать любое трехзначное число.
Предположим, это будет 567. Напишите его дважды на доске или на листе
бумаги.
567 567
Попросите назвать еще одно трехзначное число. Напишите его в
качестве множителя под числом 567 слева. Теперь вам потребуется
еще одно трехзначное число в качестве множителя справа. Его
знаки должны представлять (хотя ваши зрители знать этого не должны)
Секреты молниеносных вычислений
91
«дополнения до 9» соответствующих знаков множителя слева, то
есть суммы соответствующих цифр этих двух множителей должны
равняться 9.
Предположим, что левый множитель — это число 382. Тогда
правый множитель должен быть 617.
567 567
382 617
Если вы показываете этот фокус в большой аудитории, то
можете попросить своего друга выступить в качестве секретного
сообщника, который и предложит этот второй множитель. При других
обстоятельствах просто напишите его сами, сделав вид, будто
выбрали его наобум. Объявите, что теперь вы намерены сосчитать в уме
эти два примера. Но вы не только перемножите, а также и
просуммируете два полученных произведения и в качестве
заключительного штриха удвоите результат. Сумму этих двух произведений вы
получите мгновенно, отняв 1 от множимого, а затем приписав
справа к трем полученным цифрам еще три, каждая из которых
является дополнением до 9 от соответствующих цифр первого числа.
В нашем случае 567 минус 1 это 566. Дополнение до 9 цифр числа
566 дает число 433. Таким образом, сумма двух произведений равна
566 433. Однако, если вы напишете этот результат внизу,
кто-нибудь из зрителей может обратить внимание на то, что он
начинается с тех же двух цифр, что и множимое. Это уже подозрительно.
Поэтому замаскируйте результат путем его удвоения. Это сделать
нетрудно. Умножая на два, записывайте цифры справа налево. Если
вы способны на большее, можно мысленно приписать к 566 433
ноль справа и разделить полученное число на 5 (так как умножение
на 10 и последующее деление на 5 это то же самое, что умножение
на 2). Но в этом случае вы должны записывать окончательный
ответ слева направо.
В чем же секрет фокуса? Сумма этих двух произведений равна
произведению 567 на 999, что, в свою очередь, может быть
получено умножением 567 на 1000 с последующим вычитанием из
произведения числа 567. Запишите это на бумаге, и вы сразу же
увидите, почему окончательный результат должен начинаться с
566 и заканчиваться дополнениями до 9 соответствующих цифр
этого числа.
92
Нескучная математика
Более изощренный принцип лежит в основе многочисленных
трюков с молниеносным умножением, в которых используются
необычные (магические) числа. На первый взгляд в них нет ничего
необычного, но на самом деле их можно быстро умножить на любое
число с тем же или большим количеством знаков. Предположим,
что фокусник просит назвать число с девятью знаками, и его
помощник в зале называет число 142 857 143. Другой девятизначный
множитель может быть любым.
Фокусник мысленно умножает эти два числа и медленно
записывает громадный результат умножения слева направо. Секрет же
на удивление прост. Нужно просто разделить второе число в
удвоенной записи на 7. Если после деления первой части появляется
остаток, его просто ставят перед следующим числом и делят столбиком
дальше. Предположим, что в качестве второго числа предложили
123 456 789. Таким образом, на 7 требуется разделить число
123 456 789 123 456 789. Результат деления на семь, равный
17 636 684 160 493 827, и будет ответом. Записанное выше число
должно разделиться на 7 без остатка. Наличие остатка указывает на
то, что при вычислении где-то была допущена ошибка.
Магическое число 142 857 143 вы можете так же легко умножить
на любое число с меньшим количеством знаков. В этом случае
просто добавьте в конец этого числа необходимое количество нулей,
чтобы получилось девятизначное число, которое вы и будете делить
на 7. Например, если множителем названо число 123 456, вам
необходимо разделить на 7 число 123 456 000 123 456. Когда будете писать
ответ, незаметно посматривайте на множитель и производите
деление в уме.
Число 142 857 143 было хорошо известно знаменитым эстрадным
вычислителям. Одним из них был уроженец штата Индиана Артур
Ф. Гриффит, умерший в 1911 году в возрасте 31 года. Он давал
эстрадные представления в Соединенных Штатах, в афишах объявлял
себя как «Непревзойденный Гриффит» и был способен
перемножить два девятизначных числа меньше чем за полминуты. Когда я в
первый раз прочел об этом, у меня возникли подозрения.
Покопавшись в библиотеке, я обнаружил свидетельство очевидца его
выступления в 1904 году перед группой студентов и преподавателей
Индианского университета. Гриффит, как говорится в сообщении,
написал на доске число 142 857 143. Одного из профессоров
попросили написать под этим числом любой девятизначный множитель.
Как только профессор начал писать этот множитель слева направо,
Секреты молниеносных вычислений
93
Непревзойденный Гриффит стал писать (тоже слева направо)
произведение. «Студенческая аудитория криками выразила свое
восхищение». О своих методах счета в уме Гриффит написал небольшую
книгу The Easy and Speedy Reckoner («Легкий и быстрый подсчет»),
изданную в Гошене, Индиана, в 1901 году. Но о числе 142 857 143 в
этой книге не сказано ни слова.
При умножении числа 142 857 143 для исполнителя возможен
один неприятный момент. Бывает, что множитель делится на 7, и
произведение «заикается». Происходит повторение группы цифр в
ответе, что выглядит подозрительно.
Конечно, исполнитель трюка может пойти на риск и продолжать
вычисления, уповая на то, что вероятность этого невелика, а также,
что аудитория не обратит на это внимания. Но если он не хочет
рисковать, то может предварительно проверить множитель, мысленно
разделив его на 7. Если при делении нет остатка (а следовательно,
будет повторение цифр), исполнитель может предпринять
некоторые шаги для предотвращения заикания. Он может объявить, что
для усложнения вычислений перевернет множитель, переставив
цифры в обратном порядке. Но это поможет только в том случае,
когда перевернутый множитель не является кратным семи. Так что
лучше, чтобы исполнитель попросил аудиторию заменить одну из цифр
якобы для того, чтобы дополнительно придать множителю
случайный характер.
Чтобы избежать «заикания», фокусник Уоллис Ли,
придумавший много замечательных математических трюков, изобрел
магическое число 2 857 143. (Это почти то же число, но у него удалены
две первые цифры.) Чтобы показать трюк с этим числом,
попросите назвать семизначный множитель, у которого все цифры не
меньше пяти. Объясните, что это делается для того, чтобы еще
больше усложнить вычисления, хотя на самом деле это упрощает
процедуру. Метод вычислений такой же, как и прежде, за
исключением того, что перед началом деления на 7 весь множитель
необходимо удвоить. Если все цифры больше 4, удвоение можно
сделать в уме в процессе вычислений цифра за цифрой, следующим
образом.
Предположим, что вторым множителем является число
8 965 797. Удвоив первую цифру и прибавив 1, получим 17. Семь
входит в 17 дважды, поэтому напишем 2 в качестве первой цифры
ответа, удерживая остаток 3 в уме. Удваивая следующее число (9) и
добавляя 1, получаем 19. Отбрасывая первую 1 и заменяя ее 3, быв-
94
Нескучная математика
шим предыдущим остатком, получаем 39. Семерка входит в 39
пять раз, так что напишем 5 в качестве второй цифры ответа,
удержав остаток 4 в уме. Удвоив следующую цифру 6 и добавив 1,
получим 13. Подставив 4 вместо 1, получим 43. Семь содержится в 43
шесть раз, так что напишем 6 в качестве третьей цифры ответа, а
остаток 1 сохраним в уме. Удваиваем следующую цифру 5,
добавляем 1 и получаем 11. Замена 1 единицей дает то же самое число 11,
так что, разделив 11 на 7, получим 1 в качестве четвертой цифры
ответа и остаток 4. Продолжаем, пока не дойдем до конца числа
8 965 797. После удвоения последней цифры 7, единицу добавлять
не нужно. В итоге получаем первые 7 цифр произведения* —
2 561 656 и остаток 2.
Цифру 2, представляющую собой остаток от последнего деления,
поставим в начало множителя перед 8. Теперь разделим на 7 число
28 965 797 обычным порядком и получаем последние семь цифр
ответа 4 137 971. Заключительный результат 25 616 564 137 971 и
является требуемым произведением.
Для опытного мастера процедура удвоения, использовавшаяся в
начале трюка, трудности не представляет. А поскольку данная
методика гарантирует отсутствие «заикания» в произведении, то секрет
выполнения трюка раскрыть гораздо труднее. Описанное
магическое число, как и предыдущее, тоже можно умножать на числа с
меньшим количеством знаков при условии, что вы мысленно
добавите к множителю нули. Можно также по просьбе зрителей не
выдвигать требование того, чтобы все цифры были больше 4. В этом
случае хорошей процедурой при определении произведения
является умножение всего числа на 10 (то есть приписка нудя справа), а
затем деление на 35. Этот процесс работает потому, что 35 равно
произведению 7 на половину 10. Конечно, вы не должны забывать, что
делитель 35 уже двузначный.
При показе обоих этих трюков ответы выражаются такими
гигантскими числами, что при отсутствии калькулятора или
карманного компьютера очень трудно подтвердить правильность
полученных вами результатов. Но существует много магических
чисел меньшей величины, которые тем не менее работают таким же
образом. Например, произведение 143 на abc получают делением
abcabc на 7 (но в произведении при этом возможно «заикание»).
Имеется еще одно число — 1667. Произведение этого числа на abc
получают следующим образом. Вначале добавляют к abc ноль и
делят число abcO на 6. Целая часть деления соответствует старшим
Секреты молниеносных вычислений
95
разрядам произведения. Затем остаток, если он имеется, делят
пополам (остаток должен иметь значение 0, 2 или 4), результат
приписывают к abc слева и производят новое деление, но уже на 3.
Если при делении на три получается двухзначный результат, то
слева дописывается ноль. Это и есть три младших разряда
произведения. Все вычисления очень легко производятся в уме.
Полученное произведение не «заикается», и зрители могут проверить
результат без помощи калькулятора. Эти достоинства позволяют
считать данный трюк наиболее подходящим «экспромтом» для
показа друзьям.
Единственной известной мне публикацией о магических числах
описанного типа является напечатанная частным образом работа
Math Miracles («Математические чудеса»). Ее автор Уоллис Ли
скончался в 1969 году. В книге приведено много занимательных
примеров молниеносных вычислений. Читателю доставят наслаждение
приведенные упражнения, где предлагается определить, как были
получены четыре магических числа, о которых я рассказал, и
почему они работают именно так, как описано.
А теперь представляю еще одно производящее глубокое
впечатление направление молниеносных вычислений — извлечение
кубических корней. При показе этого трюка вы просите зрителей
возвести в третью степень любое число от 1 до 100. Услышав результат, вы
сразу же называете кубический корень.
Для быстрого извлечения кубических корней вам необходимо
запомнить кубы чисел только первого десятка. Обратите внимание,
что все эти степени заканчиваются различными цифрами. (Для
вторых степеней такой зависимости нет — вот почему исполнителю
трюка гораздо легче извлечь кубический корень, чем квадратный).
Кубический корень заканчивается на ту же цифру, что и число, во
всех случаях, за исключением 2, 3, 7 и 8. Но и эти четыре
исключения легко запомнить, потому что в каждом случае сумма числа и
последней цифры куба равна 10.
Предположим, что вам предложили сосчитать кубический
корень числа 658 503. Мысленно отбросьте три последние цифры и
проанализируйте то, что осталось, то есть 658. Это значение
находится между кубами 8 и 9. Выберите меньшее, 8, и назовите 8 в
качестве первой цифры ответа. Последняя цифра числа 658 503 — 3, так
что вы уже знаете, что второй цифрой кубического корня будет 7.
Назовите 7. Таким образом, кубическим корнем предложенного
числа будет 87.
96
Нескучная математика
ЧИСЛО
1
2
3
4
5
6
7
8
9
10
КУБЫ
1
8
27
64
125
216
343
512
729
1000
ПЯТАЯ СТЕПЕНЬ
100 тысяч
3 миллиона
24 миллиона
100 миллионов
300 миллионов
777 миллионов
1 миллиард 500 миллионов
3 миллиарда
6 миллиардов
10 миллиардов
Рис.44
Ключевые числа для извлечения корней
Эстрадные вычислители часто исполняют трюк с извлечением
корней пятой степени. Это кажется значительно труднее, чем
извлечение кубического корня, но на самом деле легче и быстрее.
Причина заключается в том, что последняя цифра любой пятой степени
целого числа всегда совпадает с последней цифрой этого числа. Вам
опять же необходимо запомнить ключевые числа, приведенные в
таблице {см. рис. 44). Предположим, что вам предложили число
8 587 340 257. Как только услышите «восемь миллиардов», вы сразу
же определяете, что первая цифра ответа располагается между
девятой и десятой строчками таблицы. Выберите меньшее значение — 9.
Не обращайте внимания на все остальное до тех пор, пока не
услышите последнюю цифру — 7. И вот теперь можете назвать ответ 97.
Желательно не повторять этот трюк больше двух или трех раз, так
как скоро станет очевидным, что последние цифры всегда
совпадают. Профессиональные вычислители работают с третьими и пятыми
степенями не только двухзначных чисел и пользуются более
сложной системой. Я же ограничиваю объяснение простыми
двузначными корнями.
Гвоздем программы большинства великих эстрадных
вычислителей были также трюки с календарем — определение дня недели для
Секреты молниеносных вычислений
97
любой названной даты. Чтобы это выполнить, необходимо
запомнить таблицу, приведенную на рисунке 45, в которой приводятся
ключевые цифры, связанные с каждым месяцем. Для более
успешного их запоминания можно воспользоваться мнемоническими
выражениями из правого столбца таблицы.
Чтобы воспроизвести в памяти требуемый день недели,
рекомендуется следующая методика, включающая четыре шага. Конечно,
существуют и другие методики, но эта разработана специально для
быстрого счета в уме.
1. В качестве первого числа используйте две последние цифры
названного года. Разделите это число на 12 и запомните частное и
остаток. Теперь сложите три небольших числа: частное от деления (число
дюжин), остаток и число, представляющее, сколько раз входит в
остаток число 4 (частное от деления остатка на 4). В качестве примера
рассмотрим год 1910. Двенадцать не входит в 10 ни разу, так что
остаток отделения составит 10. Четверка входит в остаток дважды. Сумма
0+10 + 2 дает 12. Если сумма равна или больше 7, разделим ее на 7 и
запомним то, что останется. В нашем примере при делении 12 на 7
получается остаток 5, так что запомнить нужно только 5.
Январь 1
Февраль 4
Март 4
Апрель 0
Май 2
Июнь 5
Июль 0
Август 3
Сентябрь 6
Октябрь 1
Ноябрь 4
Декабрь 6
Первый месяц (единица)
Л-Ю-Т-О (четыре буквы)
Пусть цифру подскажет
количество букв
В апрельский день дураков
я не обманул никого (0)
«Майский день» (два слова)
Сдать семестр на пятерки
Больше никаких лекций (0)
Жар природы (три буквы)
Жуки на асфальте (6 лап)
Одинокий лист (единица)
Выпадает снег (четыре буквы)
Рождение Христа (шесть букв)
Рис. 45
Ключевые числа и мнемонические выражения для календарного трюка
98
Нескучная математика
Впредь это действие будем называть «отбрасывание семерок».
(Математик мог бы сказать, что он использовал «остаток от
деления».)
2. К результату предыдущего шага прибавим ключевое число
месяца. Если возможно, отбросим семерки.
3. К предыдущему результату прибавим день месяца. Если
возможно, отбросим семерки. Результирующая цифра обозначит нам
день недели. Соответственно 0 обозначает субботу, 1 —
воскресенье, 2 — понедельник и так далее до шестерки, которая обозначает
пятницу.
4. Если год високосный, а месяц январь или февраль, отнимите
единицу от окончательного результата.
О високосном годе автоматически предупредит вас первый шаг.
Все високосные годы делятся на 4, а любое число будет кратно 4,
если кратно 4 число, обозначенное двумя его последними цифрами.
Поэтому, если при делении на 12 или на 4 остаток равен 0,
знайте, что этот год високосный. (Однако имейте в виду, что по
григорианскому календарю 1800 и 1900 годы, хотя и кратны 4,
високосными не являются, тогда как 2000 год — високосный. Объяснение
этого заключается в том, что по григорианскому календарю годы,
заканчивающиеся двумя нудями, являются високосными только в
том случае, когда они целиком делятся на 400.)
Изложенная выше методика действительна только для дат XX
века (1900-е годы). Для дат других столетий необходима
незначительная корректировка. Даты XIX века (1800-е годы) необходимо
передвинуть на два дня вперед, а XXI века (2000-е годы) — на один день
назад. Более ранние даты лучше не определять из-за путаницы,
обусловленной переходом от юлианского к григорианскому календарю,
которое в Англии и американских колониях произошло 14 сентября
1752 года. Юлий Цезарь сосчитал, что продолжительность года
равна 365,25 дням и предложил каждый четвертый год добавлять к
февралю один день. К сожалению, год равен 365,2422 дням, так что за
прошедшие столетия накопился значительный избыток дней.
Сложилась даже ситуация, когда февраль мог обогнать Пасху (которая
«привязана» к дню весеннего равноденствия). Римский папа Григорий
XIII санкционировал решение выбросить десять лишних дней и
принять календарь с меньшим количеством високосных лет. Переход на
григорианский календарь в большинстве европейских стран был
осуществлен в 1582 году, но в англоговорящем мире изменения в кален-
Секреты молниеносных вычислений
99
дарь ввели только в 1752 году. В этом году после 2 сентября настало
сразу 14 сентября. Этим объясняется тот факт, что день рождения
Джорджа Вашингтона отмечается 22 февраля, а не 11 февраля (день
его рождения по старому стилю). Если вам придется определять дни
недели датXVIII века (1700-е годы) после смены календаря в 1752
году, необходимо вводить опережение на 4 дня.
Поясним описанную методику на примере. Предположим, что вам
необходимо определить, каким днем недели было 28 июля 1929 года.
Предположим, что это день рождения кого-то из присутствующих в
аудитории. Ваши вычисления должны быть примерно следующими:
1. В числе 29 (последние цифры 1929 года) 12 содержится
дважды с остатком 5. Четыре входит в 5 один раз. Следовательно, сумма
2 + 5+1=8. Выбрасывание семерки уменьшает это число до 1.
2. Ключевое число для июля равно 0, так что ничто не
прибавляется. Запоминаем 1.
3. Прибавляем к 1 день месяца, 28. Отбрасываем от 29 семерки.
Остаток — 1. Следовательно, загадавший это число родился в
воскресенье. (На практике этот последний шаг можно было не делать,
поскольку 28 по модулю 7 дает нуль и к предыдущей единице
ничего не прибавляется.)
Четвертый шаг опускаем, потому что 1929 год не является
високосным. Но даже если бы он был високосным, этот шаг все равно
был бы не нужен, потому что этот месяц не январь и не февраль (для
которых такая корректировка необходима).
Время от времени в печати появляются сообщения о том, что этот
календарный трюк могут выполнять некоторые «талантливые
идиоты» (умственно отсталые люди, пррявляющие незаурядные
способности в какой-либо области). Так, например, журнал Scientific
American (август 1965) писал о недавнем исследовании психиатрами
близнецов, имеющих коэффициент умственного развития 60—80.
Эти близнецы обладали способностью определять дни недели.
Маловероятно, чтобы это было проявление каких-либо таинственных
способностей. Если талантливому идиоту при определении дня
недели требуется относительно много времени, то он, вероятно, просто
запомнил первые дни каждого года и мысленно проводит
вычисления от этих ключевых дней до требуемой даты. Если же он
определяет день быстро, то его, вероятно, обучили методу, подобному тому,
который я описал, или он сам прочел о методе в книге или журнале.
В конце XIX века публиковалось много методик определения в
уме дня недели, но я не нашел ничего более раннего, чем метод,
100
Нескучная математика
изобретенный Льюисом Кэрроллом и описанный им в журнале
Nature (том 35, 31 марта 1887 года). Этот метод по существу тот же
самый, о котором я уже рассказал здесь. «Сам я не
быстродействующий компьютер, - писал Кэрролл, - и поскольку мне в среднем
нужно около 20 секунд, чтобы решить задачу подобного рода, то не
сомневаюсь в том, что компьютеру потребовалось бы 15».
ДОПОЛНЕНИЕ
Ловкий прием быстрого умножения в уме путем замены его
делением имеет множество вариантов. Один из любимых трюков
Непревзойденного Гриффита представлял собой умножение сколь угодно
большого числа на 125. А поскольку 0,125 это 1/8, то для
выполнения этого трюка нужно просто приписать к числу три нуля и
разделить его на 8.
Число 1443 можно быстро умножить на двузначное число аЬ
путем деления ababab на 7, а число 3367 можно умножить на ab путем
деления ababab на 3. (Обоснование: 1443= 10101/7, а 3367 = 10101/3.)
«Незаикающееся» магическое число 1667 является моим
собственным изобретением, так же как и число 8335. Чтобы умножить
8 335 на трехзначное число abc, припишем к abc ноль и разделим на
12. Если имеется остаток, разделим его пополам, перенесем в
начало abc и, сохраняя ноль на конце, разделим на 6. Такой порядок
действий объясняется тем, что 833,5 составляет половину числа 1667.
Могу предположить, что других четырехзначных чисел, подходящих
для таких трюков, не существует. Что касается применения этих
двух чисел в карточных фокусах, смотрите мою статью Clairvoyant
Multiplication («Умножение ясновидца») в индийском
периодическом журнале по магии Swami (Свами), март, 1972.
Эдгар А. Блэр, Мейджор Картер и Курт Эйсман независимо
друг от друга предложили способ запоминания ключевых чисел
для месяцев. Этот способ, вероятно, будет для математиков легче,
чем методы, основанные на использовании ключевых слов. Если
сгруппировать месяцы по тройкам, то числа будут представлять
следующее:
144 (январь, февраль, март);
025 (апрель, май, июнь);
036 (июль, август, сентябрь);
146 (октябрь, ноябрь, декабрь).
Секреты молниеносных вычислений
101
Обратите внимание, что первые три тройки представляют
квадраты чисел 12, 5 и 6, а последняя тройка, 146, на две единицы
больше первого квадрата.
ОТВЕТЫ
Использование в методиках молниеносного умножения магических
чисел основано на принципах, которые лучше всего объяснить на
примерах. Число 142 857 143 получено делением на 7 числа
1 000 000 001. Если 1 000 000 001 умножить на любое девятизначное
число abc def ghi, произведение, очевидно, должно быть
abc def ghi abc def ghi.
Поэтому, чтобы получить произведение чисел 142 857 143 и
abc def ghi, нужно просто разделить abc def ghi abc def ghi на 7.
Второе магическое число 2 857 143 представляет собой частное от
деления 20 000 001 на 7. Очевидно, что в этом случае перед тем, как
будет произведено первое деление на 7, семизначный множитель
числа 2 857 143 необходимо удвоить. Требованием, чтобы каждая
цифра множителя была больше 4 (а это при удвоении каждой
цифры гарантирует постоянное наличие единицы, переносимой в
другой разряд), вы обеспечиваете возможность процесса удвоения, о
котором говорилось выше. Без этого условия провести процессы
удвоения и деления в уме все-таки можно, но при этом значительно
усложняются правила.
Магические числа меньшей величины 143 и 1 667 действуют
таким же образом. Первое из них равно 1001/7, а второе — 5001/3. Во
втором случае множитель abc необходимо умножить на 5 перед тем,
как начнется первое деление на 3. А так как умножение на 5 — это то
же самое, что умножение на 10 с последующим делением пополам,
мы приписываем ноль к abc и делим на 6. Остаток необходимо
разделить пополам, чтобы превратить его из шестых долей в третьи и
поместить впереди числа перед вторым делением на 3. Тот факт, что
второе деление производится на другое число, снижает риск
повторов групп цифр в ответе. Если же умножается число 143 на
множитель abc, кратный 7, нежелательные повторы неизбежны.
ГЛАВА 8
Математическое искусство
Эшера
Все, что я создаю при свете, — всего лишь сотая
часть того, что я видел в темноте.
—М.К.ЭШЕР
Некоторые виды искусств по достаточно очевидным, но
поверхностным признакам можно отнести к математическому искусству.
Например, «опарт» (направление в графическом искусстве) является
искусством «математическим». Но считать его «новым»
направлением конечно же нельзя. Четкие ритмичные декоративные узоры
являются столь же древними, как и само искусство. Да и
современное стремление к абстракции в живописи начиналось еще с
геометрических фигур кубистов. Когда французский представитель
дадаизма художник Ханс Арп подбрасывал в воздух бумажные цветные
квадратики и приклеивал их там, куда они падали, он тем самым
протягивал мостик от прямоугольников кубизма к брызгам краски,
которые разбрасывали по холсту более поздние «воинствующие»
художники. В определенном смысле математическим можно назвать
даже абстрактное искусство экспрессионистов, так как хаос
относится к математическим понятиям.
Но при этом границы термина «математическое искусство»
расширяются до такой степени, что он теряет всякий смысл. Есть
другое, более подходящее определение этого термина. В основе
его не методы и стили изображения, а содержание изображаемых
на картине предметов. Знакомый с математикой художник может
создать композицию на математическую тему, точно так же как
художники Ренессанса создавали композиции на религиозные
темы, а современные русские художники — на политические. Но ни
Математическое искусство Эшера
103
один из современных художников не преуспел в «математическом
искусстве» так, как Морис (Мауриц) К. Эшер (Эсхер) из
Нидерландов.
«Я чувствую себя ближе к математикам, чем к своим коллегам-
художникам, — писал М.К. Эшер. — Все мои работы, по сути,
шутки. Серьезные шутки». Его литографии, гравюры по дереву, работы,
выполненные ксилографией или глубокой печатью, можно увидеть
на стенах в кабинетах математиков и ученых по всему миру.
Некоторые из его работ отличаются мрачным сюрреализмом. Но они
являются скорее изысканно философичными математическими
наблюдениями и содержат меньше сказочных фантазий, чем работы
Сальвадора Дали или Рене Магритта.
Работы Эшера намерены пробуждать то, что писавший много об
Эшере поэт Говард Немеров называл «тайной, абсурдом и иногда
ужасом» мира. Многие из его рисунков изображают те
математические структуры, которые и обсуждаются в книгах по занимательной
математике. Но прежде чем рассмотреть некоторые из них,
расскажем немного о самом Эшере.
Он родился в 1898 году в Леевардене, Голландия, и в юности
получил образование в Школе архитектуры и декоративного дизайна в
Харлеме. Десять лет Эшер прожил в Риме. Покинув в 1934 году
Италию, провел два года в Швейцарии, пять лет в Брюсселе, после чего
прочно обосновался в голландском Берне, где и умер в 1972 году. В
1954 году прошла (и не осталась незамеченной) выставка работ
Эшера в Белой галерее в Вашингтоне. Однако этот художник
больше известен не в США, а в Европе.
Большая коллекция его работ принадлежит конструктору Кор-
нелиусу ван Шак Рузвельту (он проживает в Вашингтоне и
приходится внуком президенту Теодору Рузвельту). Именно благодаря
великодушному сотрудничеству Рузвельта и разрешению Эшера в
этой книге и появились некоторые работы художника.
Среди кристаллографов Эшер больше всего известен по
многочисленным остроумным мозаичным панелям. Весьма искусными в
резьбе панелей с периодическими повторениями фигур были
испанские мавры, что доказывают орнаменты дворца Альгамбра. Но
мусульманская религия запрещала маврам изображать живые
существа. Мозаики Эшера составлены из одинаковых изображений
птиц, рыб, рептилий, млекопитающих и человеческих фигур.
Объединяя эти фигуры, он создавал разнообразные, порой потрясающие
воображение картины.
104
Нескучная математика
На литографии Рептилии (см. рис. 46), изображен только что
родившийся монстр. Его краткий жизненный цикл воплощен в
трех эпизодах. На додекаэдре рептилия находится в расцвете сил,
после чего уползает снова в безжизненную плоскость. На гравюре
по дереву День и Ночь (см. рис. 47) левая и правая стороны
изображения не только являются зеркальными отображениями, но и
представляют как бы «негативы» друг друга. Прямоугольные поля
плавно переходят в связанные друг с другом изображения птиц:
черные птицы летят к свету, белые — в темноту. На круглой
гравюре по дереву Небеса и преисподняя (см. рис. 48) переплетены фигуры
ангелов и чертей. По мере удаления от центра эти фигуры
становятся все меньше и наконец постепенно растворяются на ободке в
бесконечном множестве фигур — настолько мелких, что их
невозможно разглядеть. Эшер мог бы сказать, что Бог — это
необходимый фон для дьявола и наоборот. Такое поразительное владение
искусством мозаики основано на хорошо известной эвклидовской
модели, разработанной Анри Пуанкаре для неэвклидовой
гиперболической плоскости. Дополнительно можно об этом почитать в
книге X. Кокстера Introduction to Geometry («Введение в
геометрию»), изданной в 1961 году.
Если читатель думает, что рисунки такого рода легко создавать,
пусть попытается! Эшер говорит: «Когда я рисую, иногда ощущаю
себя медиумом, которым управляют существа, создаваемые моим
воображением. Кажется, будто они сами выбирают форму, в
которой хотят воплотиться. Чем длиннее разграничивающая две
смежные фигуры линия, выполняющая двойную функцию, тем более
сложным становится процесс ее изображения. По обе стороны этой
линии две распознаваемые фигуры. Но человеческие глаз и разум не
могут в одно и то же время заниматься двумя делами, так что
необходимо обеспечить быстрый и непрерывный переход от одной
фигуры к другой. Эта трудность, возможно, и является движущей
силой моего упорства».
Чтобы обсудить все направления, с помощью которых
фантастические мозаики Эшера иллюстрируют аспекты симметрии,
теории групп и законов кристаллографии, необходима целая книга. И
такая книга действительно была написана Каролиной X. Макгил-
лаври из Амстердамского университета: Symmetry Aspects of M. С.
Escher's Periodic Drawings («Аспекты симметрии в регулярных
рисунках М. Эшера»).
Рис. 46
Рептилии, литография, 1943
Рис. 47
День и Ночь, гравюра по дереву, 1938
Художественная галерея Микельсона. Вашингтон
106
Нескучная математика
Рис. 48
Небеса и преисподняя, гравюра по дереву, 1960
В этой книге, изданной в Утрехте Международным союзом
кристаллографов, воспроизводится 41 мозаика Эшера. Многие из
мозаик многоцветные.
Рисунки 49 и 50 иллюстрируют еще одно направление работы
Эшера — шутки с законами перспективы, а также то, что называют
«невозможными фигурами». На литографии Бельведер вы видите
брошенный на полу эскиз куба. Небольшими кружочками
обозначены два участка, где ребра куба пересекаются. В скелетной модели,
которую держит в руках мальчик, тоже есть пересечения, которые в
трехмерном пространстве реализовать нельзя. Да и сам бельведер
составлен из невозможных структур. Так, например, юноша,
стоящий на верхних ступеньках лестницы, находится снаружи
бельведера, а основание лестницы внутри. Не исключено, что мужчина в
темнице (в главной башне) сошел с ума, пытаясь разобраться в
несовместимых конструкциях этого странного мира.
Рис. 49
Бельведер, литография, 1958
Рис. 50
Восхождение и спуск, литография, I960
Математическое искусство Эшера
109
Основой для литографии Восхождение и спуск послужил
приводящей в замешательство своей невозможностью рисунок, который
вначале появился в статье Л.С. Пенроуза, британского генетика, и его сына,
математика, Роджера Пенроуза. Статья назвалась Impossible Objects: A
Special Type of Visual Illusion («Невозможные объекты: особые виды
зрительных иллюзий») и была опубликована в февральском номере
журнала British Journal of Psychology в 1958 году. Монахи неизвестной секты
заняты ежедневным ритуалом беспрерывного похода по невозможной
лестнице на крыше своего монастыря: снаружи монахи поднимаются,
внутри спускаются. «Оба направления, — комментирует Эшер, —
несмотря на кажущееся наличие цели, одинаково бессмысленны. Два
упрямца отказываются принимать участие в этом «благочестивом
ритуале». Они считают, что разбираются во всем лучше своих товарищей, но
рано или поздно они признают ошибочность своего несогласия».
Многие из картин Эшера отражают ту эмоциональную реакцию,
которая появляется у нас, когда мы смотрим на правильные и
полуправильные тела. «Среди нашего во многом хаотичного общества, —
писал Эшер, — они символизируют в не имеющем себе равным
образе действий страстное стремление человека к гармонии и порядку, но
в то же самое время их совершенство внушает нам страх по поводу
нашей собственной беспомощности. Правильные многогранники
имеют абсолютно нечеловеческие качества. Они не являются
творениями человеческого разума, поскольку существовали в виде кристаллов
в земной коре задолго до появления человечества. А что касается
сферической формы — разве мир не состоит из сфер?»
Литография Порядок и хаос {см. рис. 51) изображает «небольшой
звездчатый додекаэдр» — один из четырех «многогранников
Кеплера—Пуансо», которые вместе с пятью телами Платона составляют
девять возможных «правильных многогранников». Они были
открыты вначале Иоганном Кеплером (1571—1630), который назвал
их «ежами» и изобразил в своей работе Harmonices mundi («Гармония
мира») — фантастическом труде по нумерологии, в котором привел
основные соотношения, выведенные для музыки, и формы
правильных многоугольников и многогранников, применяющихся в
астрологии и космологии. Подобно телам Платона «ежи» Кеплера
имеют грани, которые являются правильными многоугольниками и
имеют равные углы при вершинах. Но эти грани не выпуклы и
пересекают друг друга. Представьте себе, что каждую из 12 граней
додекаэдра (как на картине Рептилии) вытягивают до тех пор, пока не
образуется пентаграмма или пятиконечная звезда.
110
Нескучная математика
Рис. 51
Порядок и хаос, литография, 1950
Двенадцать таких пересекающихся пентаграмм и образуют
небольшой звездчатый додекаэдр. В течение столетий математики
отказывались считать пентаграмму «многоугольником», потому что ее
пять ребер пересекаются. По этим же причинам они отказывались
называть тело, подобное изображенному на рисунке,
«многогранником» — ведь его грани тоже пересекаются. Интересно то, что даже в
середине XIX века швейцарский математик Людвиг Шлафли, хотя и
признавал некоторые тела с пересекающимися гранями
многогранниками, отказывался считать тело, о котором шла речь выше,
«подлинным» многогранником из-за того, что его 12 граней, 12 вершин
и 30 ребер не соответствовали известной формуле Леонарда Эйлера:
F + V = Е + 2 (Число граней + число вершин = число ребер +2). Но на
самом деле соответствие имеется, если признать, что у такого тела
60 треугольных граней, 32 вершины и 90 ребер. Но назвать его
«подлинным» нельзя, потому что его фани являются равнобедренными
треугольниками.
Математическое искусство Эшера
111
В гравюре Порядок и хаос превосходная симметрия этого тела — его
вершины, выступающие через поверхность окружающей сферы —
приходят в противоречие с тем, что Эшер называл «воплощением хаоса».
Небольшой звездчатый додекаэдр иногда используют в качестве
формы для осветительного плафона. Интересно, использовалась ли она
в качестве объемной звезды на верхушку рождественской елки? Не
представляет особого труда изготовить такую картонную модель
самому. Х.М. Ганди и А.П. Роллетв книге Mathematical Models
(«Математические модели») советуют не пытаться сложить ее полностью из одной
заготовки, а сделать вначале додекаэдр, а затем приклеить к каждой грани
пятигранную пирамиду. Между прочим, каждый линейный участок
этого тела находится (по наблюдениям Кеплера) в соотношении
«золотого сечения» с каждым следующим линейным участком большей
длины. Этому телу «дуален» так называемый «большой додекаэдр»,
образованный пересечением 12 правильных пятиугольников. Более
детальные сведения о звездчатых многофанниках Кеплера—Пуансо читатель
может получить в упомянутой книге Ганди и Роллета, а также в книге
Кокстера Regular Polytopes («Правильные политопы»).
На литофафии Рука с зеркальным глобусом (см. рис. 52)
используются свойства сферического зеркала подчеркивать то, что философ
Ральф Бартон Перри любил относить к категории эгоизма. Все
возможные знания о мире каждый человек получает из того, что входит
в его мозг через органы чувств. Создается представление, что не
существует ничего, кроме того, что лежит внутри круга его
собственных ощущений и мысленных образов. Из такой «феноменологии»
человек создает то, что, по его предположению, является внешним
миром, включая и представления о людях, которые оказываются в
затруднительном положении, подобном его собственному. Однако
доказать, что существует еще что-то, за исключением самого
человека и его меняющихся ощущений и мыслей, невозможно. Мы
видим Эшера, пристально вглядывающегося в свое собственное
отражение в сфере. Стекло отражает его окружение, сжимая все в один
совершенный круг. Куда бы ни смотрел человек, точка на
переносице между его глазами всегда остается точно в центре круга.
«Он не может оторваться от этой центральной точки, — говорит
Эшер. — Его «я» остается неколебимым центром его мира».
Приверженность Эшера к топологическим шуткам отражена
на многих его картинах. В верхней части гравюры по дереву Узлы
(см. рис. 53) мы видим два зеркально-отраженных листа
трилистника. Расположенный вверху слева узел завязан из двух длинных
112
Нескучная математика
Рис. 52
Рука с зеркальным глобусом, J 935
плоских лент, пересекающихся под прямым углом. Эта двойная
лента перед тем, как ее соединили, была скручена. Является ли
она одной односторонней лентой, которая дважды огибает узел,
пересекаясь сама с собой, или она состоит из двух отдельных, но
пересекающихся лент Мебиуса? Большой узел ниже двух
маленьких имеет структуру четырехсторонней трубы, которая была
четырежды закручена, так что муравей, ползущий внутри нее по одной
из центральных дорожек, должен сделать четыре полных круга,
прежде чем вернется в исходную точку.
Гравюра по дереву Три сферы (см. рис. 54), копия которой
принадлежит Нью-йоркскому музею современного искусства, вначале
кажется сферой, испытавшей последовательное топологическое сжатие.
Тем не менее посмотрите более внимательно, и вы увидите, что
это нечто другое.
ДОПОЛНЕНИЕ
Когда в 1972 году в возрасте 73 лет Эшер умер, он еще только
начинал приобретать мировую известность не только среди математиков
и ученых (которые оценили его первыми), но и среди широкой
публики, особенно среди молодых диссидентов.
Математическое искусство Эшера
113
Рис. 53
Узлы, гравюра по дереву, 1965
Сегодня популярность Эшера продолжает расти. Его рисунки вы
видите повсюду: на обложках математических учебников, на
альбомах рок-музыкантов, на броских афишах, полыхающих в
ультрафиолете, даже на футболках. Когда я впервые воспроизвел рисунок
Эшера в своей колонке в апреле 1961 года (журнал Scientific American
опубликовал на обложке одну из его мозаик с птицами), то
приобрел у Эшера только один отпечаток гравюры. По цене всего лишь от
40 до 60 долларов я мог купить множество картин, каждая из
которых теперь стоит тысячи. Но кто тогда мог предвидеть
ошеломляющий рост популярности Эшера?
114 Нескучная математика
Догадаетесь ли вы, читатель, что здесь с таким правдоподобием
изобразил Эшер?
Рис. 54
Три сферы, гравюра по дереву, 1945г.
Об Эшере в последние годы было написано так много, что я бы
обратил внимание лишь на несколько основных книг. Книга Абрам-
са содержит наиболее полную подборку наилучших репродукций с
работ Эшера, несколько очерков об его искусстве (один из которых
написан самим Эшером) и превосходный список отобранных
ссылок. Обширная статья Кена Вилки содержит много не публиковав-
Математическое искусство Эшера
115
шихся ранее рисунков Эшера, а также малоизвестные сведения о
частной жизни художника и о его убеждениях. Статьи об Эшере
публикует общественно-политический журнал Holland Herald,
издаваемый на английском языке в Нидерландах. Коллекция работ
Эшера, принадлежавшая Корнелиусу Рузвельту, теперь является
собственностью Национальной галереи искусств, Вашингтон, округ
Колумбия.
ОТВЕТЫ
Три Сферы — это рисунок трех плоских дисков, каждый из которых
окрашен так, чтобы имитировать сферу. Нижний диск лежит на
столе. Средний диск изогнут под прямым углом по диаметру. Верхний
диск стоит вертикально на горизонтальной половине среднего
диска. Ключи к разгадке заключены в линии сгиба среднего диска и
одинаковом затенении этих трех псевдосфер.
ГЛАВА 9
Куб с красной гранью
и другие головоломки
1. КУБ С КРАСНОЙ ГРАНЬЮ
Некоторое время назад поклонники занимательной математики
были увлечены задачами, в которых шахматная фигура обходит все
поля доски так, чтобы посетить каждое, причем только один раз.
Задачи различались накладываемыми на ходы ограничениями. Джон
Харрис изобрел новый открывающий богатые возможности класс
задач на шахматной доске (под названием «перекатывание куба»).
Если вы хотите попробовать свои силы в решении двух наиболее
впечатляющих задач Харриса, возьмите из детского набора кубик
или склейте его из картона. Его грань должна соответствовать
размеру клетки шахматной доски. Одну из граней кубика покрасьте в
красный цвет. Куб перемещается из одной клетки на другую —
соседнюю — перекатываясь ребром через линию, разделяющую
клетки. Следовательно, за один ход куб делает поворот на одну четверть
в одном из четырех направлений — на север, юг, запад или восток.
Задача 1. Расположите куб в северо-западном углу доски так,
чтобы красная грань куба смотрела вверх. Обойдите доску, проходя
каждую клетку лишь по разу, чтобы маршрут закончился в
северовосточном углу и красная грань смотрела вверх. При этом ни разу на
протяжении всего маршрута (кроме крайних точек) куб не должен
оказываться красной гранью вверх.
Задача 2. Расположите куб в любой клетке неокрашенной гранью
вверх. Проложите маршрут, посетив каждую клетку по одному разу
так, чтобы вернуться на начальную клетку. При этом куб ни разу не
Куб с красной гранью и другие головоломки
117
должен оказываться красной гранью вверх ни на одной клетке,
включая конечную.
Если исключить повороты доски и зеркальные отражения, обе
задачи имеют однозначные решения.
2. ТРИ КАРТЫ
Эту логическую головоломку придумал Джеральд Л. Кауфман,
архитектор по профессии и автор нескольких сборников головоломок.
Три игральные карты берутся из обычной колоды для бриджа и
выкладываются в ряд рубашкой вверх. Известно следующее. Справа
от короля дама или две дамы. Слева от дамы другая дама или две.
Слева от червовой масти пиковая или несколько пиковых. Справа
от пик пики или несколько пик.
Назовите эти три карты.
3. КЛЮЧ И ЗАМОЧНАЯ СКВАЖИНА
Эта запутанная топологическая проблема больше похожа на игру с
ключом и жестким шнуром длиной как минимум несколько ярдов
(1 ярд = 0,91 м). Сложите шнур вдвое и пропустите петлю через
замочную скважину, как показано вверху (см. рис. 55). Затем
проденьте оба конца шнура через петлю, как показано на среднем рисунке.
Теперь разведите концы шнура влево и вправо (нижний рисунок).
Проденьте левый конец в ушко ключа и продвиньте ключ к самой
двери. Для надежности привяжите концы шнура к чему-нибудь,
например к спинкам стульев. Шнур не должен быть натянут.
Задача состоит в том, чтобы, манипулируя ключом и шнуром,
переместить ключ из точки Р в точку Q справа. После перемещения
ключа шнур должен быть закреплен той же петлей через замочную
скважину, что и вначале.
4. СЛОВАРЬ АНАГРАММ
Николас Темперли, будучи еще студентом Кембриджа, предложил
любителям игры в слова в качестве рабочего инструмента
составлять словарь анаграмм. Каждое слово языка преобразуется в
«алфавитную анаграмму», в которой буквы слова записываются в
алфавитном порядке. Слово SCIENTIFIC (научный) превращается в
^
Q
Рис. 55
Перемещение ключа
из точки Р в точку Q
Куб с красной гранью и другие головоломки
119
CCEFIIINST Эти анаграммы затем собираются в словарь по
алфавитному принципу. Каждой алфавитной анаграмме будет
поставлено в соответствие английское слово, причем будут перечислены все
английские слова, которые могут быть сформированы из этих букв.
Так, из сочетания BDEMOOR можно получить BEDROOM
(спальня), BOREDOM (скука). Из сочетания AEIMNNOST получается
MINNESOTA (Миннесота) и NOMINATES (назначает). Некоторые
анаграммы будут иметь интересные математические сочетания.
Например, AEGILNRT дает INTEGRAL (интеграл), RELATING
(соотношение) и TRIANGLE (треугольник), а также ALTERING
(изменение). Забавно то, что анаграмма EIINNSTXY
расшифровывается и как NINETY-SIX (96) и SIXTY-NINE (69). Другая анаграмма
AGHILMORT расшифровывается как ALGORITHM (алгоритм) и
LOGARITHM (логарифм). Если в кроссворде в качестве ключа
дано слово BEAN SOUP (гороховый суп) и указания на то, что
необходимо найти анаграмму, вам следует преобразовать
последовательность букв ключа в ABENOPSU и, вооружившись словарем
анаграмм, моментально обнаружить, что это SUBPOENA (повестка в
суд). Если ключевое слово THE CLASSROOM (классная комната,
артикль считается), то отгадкой будет SCHOOLMASTER (учитель).
Большая часть анаграмм будет начинаться с букв ближе к началу
алфавита. По оценкам Темперли, более половины анаграмм будет
начинаться с буквы А. Это означает, что более половины всех
английских слов содержит букву А. (В отношении распространенных слов
это неверно, но в случае с более редкими словами, которые, как
правило, более длинные, это скорее всего так.) После буквы /
количество слов резко снизится, а после О список слов будет совсем коротким.
Предлагаю читателю, владеющему английским языком,
попытаться ответить на такие вот вопросы.
1. Какой будет последняя анаграмма словаря? (Напоминаю, что
имена, такие как Uz (Оз — волшебная страна) в словарь не
включаются.)
2. Какой будет первая и вторая анаграмма словаря?
3. Какой будет последняя анаграмма в группе, начинающейся с А?
4. Какой будет первая анаграмма в группе, начинающейся с В?
5. Расшифруйте анаграмму ABCDEFLO (начинающуюся с первых
шести букв алфавита). Какое слово она скрывает?
6. Какой будет самая длинная анаграмма, совпадающая со
словом? (Для примера назову ADDER (гадюка), AGLOW (пламенеть),
BEEFY (сильный), BEST (лучший), DIPS (макать), FORT (форт)).
120
Нескучная математика
7. Какой будет самая длинная анаграмма с неповторяющимися
буквами?
5. МИЛЛИОН ТОЧЕК
Внутри замкнутой кривой, показанной на рис. 56, лежит
бесконечное количество точек. Предположим, мы выбираем наугад миллион
точек. Вопрос в том, всегда ли возможно провести на плоскости
прямую линию так, чтобы она не проходила ни через одну точку из
выбранных и при этом делила бы множество точек так, чтобы с
каждой ее стороны лежала ровно половина точек, т. е. 500 000. Ответ на
этот вопрос положительный, а доказать это утверждение я
предлагаю читателю.
6. ЛЕДИ НА ОЗЕРЕ
Рис. 56
Головоломка с миллионом точек
Молодая женщина проводила отпуск на озере Круглом, которое
было искусственным, достаточно большим и при этом действительно
имело идеально круглую форму. За этой женщиной погнался
преступник, она, спасаясь, села в гребную шлюпку и начала грести к
центру озера, где на якорь был поставлен плот. А преследователь
остался ждать на берегу. Он знал, что женщина должна в конечном
счете вернуться на берег.
Поскольку преследователь перемещался вдоль берега в четыре
раза быстрее, чем женщина на шлюпке, то он не сомневался в том,
что сможет поймать ее, когда лодка коснется берега озера.
Но женщина оказалась сильна в математике и смогла найти
выход из затруднительного положения. Она знала, что, оказавшись на
берегу, легко опередит преследователя, так что оставалось только
Куб с красной гранью и другие головоломки
121
придумать стратегию для водной части маршрута, чтобы оказаться
на берегу с запасом времени. Вскоре женщина разработала простой
план, который спас ее.
Какова была ее стратегия? (Предполагается, что женщина всегда
точно знает свое положение на озере.)
7. ДОЛОЙ КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ
Эту безобидную задачу из комбинаторной геометрии я обнаружил
на страницах книги Sam Loyd and His Puzzles («Сэм Ллойд и его
головоломки»). Но эта задача безобидна лишь на первый взгляд. На
приведенном рисунке (см. рис. 57) сорок зубочисток образуют
подобие шахматной доски 44. Задача состоит в том, чтобы удалить
минимальное количество зубочисток, разорвав периметры всех
квадратов — не только 16 малых 1x1, но и девяти 2x2, четырех 3x3 и
одного 4x4 (всего 30 квадратов).
На произвольной квадратной шахматной доске с п2 клетками
общее количество различных прямоугольников
(к2+к)2
4 '
из которых
п(п + \)(2п + \)
6
квадраты. Британский мастер головоломок Генри Эрнест Дьюдени
писал: «Интересно то, что общее количество прямоугольников — это
всегда квадрат «треугольного» числа со стороной я». (Треугольное
число показывает количество точек в треугольнике со стороной п и равно
"¦fr + Q v
2 "'
Да, приведенное в старой книге решение задачи на разрушение
квадратов действительно правильное, и читателю не составит труда
доказать это. Но сможем ли мы пойти дальше и дать простое
доказательство того, что найденный ответ действительно минимален?
Такая постановка вопроса намного более глубокая. Очевидным
шагом будет анализ сеток по мере усложнения. Случай 1x1
тривиален. Легко показать, что для сетки 2x2 достаточно убрать три
зубочистки, а для 3x3 — шесть. Сетка 4x4 достаточно сложна для анали-
122
Нескучная математика
I
i i
! J
i
i i
i I
j i
Рис. 57
Головоломка с зубочистками
за. Очевидно, что сложность анализа стремительно нарастает с
увеличением количества клеток.
Приверженец комбинаторики вряд ли удовлетворится
качественными соображениями. Он захочет получить формулу, которая дает
минимальное количество удаленных зубочисток, как функцию
порядка сетки, а также метод построения как минимум одного решения
для произвольного порядка. Эту задачу можно расширить на
прямоугольную сетку, с которой необходимо убрать минимальное
количество линий, чтобы уничтожить все прямоугольники (включая
квадраты). Насколько я знаю, в литературе на эти вопросы ответов пока нет.
Приглашаю читателя исследовать случаи от 4x4 до 8x8. Не так'
легко найти минимальное решение для 8x8 (стандартная шахматная
доска имеет 204 различных квадрата).
3. НЕСЛУЧАЙНАЯ СЛУЧАЙНОСТЬ
Пять бумажных прямоугольников (один с оторванным углом) и
шесть бумажных кружочков случайным образом разбрасывают по
столу. Они падают, как показано на рисунке 58. Отметьте точкой
каждый угол прямоугольника, а также места пересечения границ
Куб с красной гранью и другие головоломки
123
фигур. Задача состоит в том, чтобы найти три группы по четыре
точки, лежащих на окружности.
Примером таких точек могут стать углы изолированного
прямоугольника (на рисунке 58, нижний правый угол), поскольку углы
любого прямоугольника лежат на окружности. Каковы другие три
группы? Эта и следующая головоломки были изобретены Стивеном
Барром, автором книг Experiments in Topology («Эксперименты в
топологии») и A Miscellany of Puzzles: Mathematical and Otherwise
(«Сборник головоломок: математика и не только»).
9. ОТРАВЛЕННЫЙ СТАКАН
Математики — странные люди, — сказал комиссар полиции своей
жене.
«У нас было несколько стаканов, заполненных и выстроенных в
ряд на столе на кухне гостиницы. Яд был только в одном из них, и
мы хотели узнать в каком, чтобы затем изучить на этом стакане
отпечатки пальцев. Наша лаборатория могла бы проверить жидкость в
каждом стакане, но тесты требуют времени и денег, так что мы хоте-
Рис. 58
Найдите три группы из четырех точек, принадлежащих одной окружности
124
Нескучная математика
ли, насколько это возможно, уменьшить количество тестов. Мы
обратились в университет, и нам порекомендовали профессора
математики. Он пересчитал стаканы, улыбнулся.
— Выбирайте любой. Для начала проверим его, — сказал он.
— Но не потратим ли мы зря время и химикаты? — спросил я.
— Нет, — ответил он. — Это является частью оптимальной
стратегии. Мы должны проверить один стакан, и не важно, какой стакан
это будет.
— А сколько стаканов было? — спросила супруга у комиссара.
— Не помню, где-то между 100 и 200.
Так сколько же стаканов было точно? (Предположим, что любую
группу стаканов можно анализировать одновременно, забирая
малое количество жидкости из каждого, смешивая образцы и проводя
одно исследование.)
QTBETbl
1. Решение двух задач о перекатывании куба показано на рисунке
59. В первом решении красная грань куба смотрит вверх только в
верхних углах доски. Во втором решении точка отмечает начало
движения. В этой точке красная грань смотрит вниз.
Задачи на перекатывание куба являются новой захватывающей
областью исследований, которой довольно глубоко занимался
только Джон Харрис. В этой области можно изобрести бесконечное
множество задач. Вот две из числа лучших задач Харриса.
Проложите такой замкнутый маршрут по доске, чтобы красная грань
оказывалась наверху как можно чаще. Существует ли замкнутый маршрут,
который начинается и заканчивается положением с красной гранью
наверху, однако красная грань во время всего остального пути ни
разу не оказывается верхней? Можно придумывать задачи, в которых
красным окрашено более одной грани или грани могут иметь
разные цвета. Также грань можно промаркировать буквой «А», чтобы
иметь возможность принимать во внимание ее ориентацию.
А что можно сказать о перекатывании стандартной игральной
кости, ограниченном различными условиями? Или о
перекатывании нестандартно промаркированной игральной кости? См. статью
Харриса Single Vacancy Rolling Cube Problems («Задачи на
перекатывание куба»), опубликованную в журнале Journal of Recreational
Mathematics, том 7, лето, 1974.
Куб с красной гранью и другие головоломки
125
Рис. 59
Решения задан по перекатыванию куба
В 1971 году Витман предложил новую настольную игру на
основе перекатывания кубиков. Эту игру он назвал Relate («Родство»).
Для игры используется шахматная доска 4x4. В качестве фигур
используется четыре одинаково окрашенных кубика по два на
каждого игрока. Для простоты поставим в соответствие грани куба с
игральной костью. Тогда грани 1 и 2 имели бы один цвет (первый),
3 и 5 — другой цвет (второй), 4 — третий цвет, а 6 — четвертый цвет.
Кубики одного игрока отличаются от кубиков другого игрока (на
всех гранях кубиков одного из игроков стоят черные точки).
Партия начинается с того, что кубики по очереди выставляются
на доску. При этом ориентация кубиков не важна и кубики игроков
в начале игры не должны иметь одинаковый цвет на верхней грани.
Предположим, что нумерация клеток у нас идет слева направо.
Первый игрок помещает свои кубики на клетки 3 и 4, второй — на
13 и 14. Назовем эти клетки стартовыми. Игроки по очереди
перекатывают один из своих кубиков, соблюдая три правила.
1. Оба кубика игрока всегда должны быть обращены вверх
гранями различных цветов.
i
1
126
Нескучная математика
2. Если один игрок своим ходом устанавливает цвет на верхней
грани, соответствующий верхней грани одного из кубиков
противника, то следующим ходом противник должен сделать ход этим
кубиком, чтобы на его верхней грани был другой цвет.
3. Если очередной ход не может быть сделан без нарушения
правил 1 и 2, игрок должен повернуть один из кубиков, чтобы верхняя
грань была другого цвета, при этом оставив кубик на той же клетке.
Это засчитывается как ход.
Побеждает тот, кто первым займет стартовые клетки
противника. Если один из кубиков оказался на стартовой клетке противника
и очередной ход противника требует хода этим кубиком, ход должен
быть сделан.
Я искренне обязан Джону Го из Австралии за то, что он
рассказал мне об этой игре. Как он указывал в своем письме, эта игра таит
в себе неизведанные возможности, которые выделяют ее среди
настольных игр с перекатыванием кубиков. При этом клетки могут
быть не только квадратными, но и треугольными (в последнем
случае перекатывают тетраэдры или октаэдры).
2. Первые два утверждения можно удовлетворить только двумя
сочетаниями королей (К) и дам (Д): КДД и ДКД. Вторые два
утверждения удовлетворяются лишь двумя сочетаниями червей (Ч) и
пик (П): ППЧ и ПЧП. Эти два сочетания можно объединить
четырьмя способами:
КП, ДП, ДЧ
КП,ДЧ,ДП
ДП,КП,ДЧ
ДП, КЧ,ДП
Последний набор можно исключить, так как он содержит две
дамы пик. Поскольку во всех остальных наборах встречается король
пик, дама пик и червовая дама, мы можем однозначно сказать, что на
столе именно эти карты. Точное положение карт мы сказать не
можем, но знаем точно, что первая карта это пики, а третья — это дама.
3. Чтобы переместить ключ с одной стороны двери в другую,
проденьте ключ через петлю, чтобы он висел, как показано на
рисунке 60 (слева). Зяцегште двойную петлю в точках А и 5 и протащи-
Куб с красной гранью и другие головоломки
127
те одну из петель обратно через замочную скважину наружу. Вы
получите две новые петли, выходящие из замочной скважины, как
показано на среднем рисунке. Переместите ключ вдоль шнура через
обе петли. Захватите два конца шнура с противоположных сторон и
втащите обе петли обратно внутрь замочной скважины,
восстанавливая прежнюю конфигурацию узла {см. справа). Сдвиньте ключ
направо, проденьте через петлю, и задача решена.
Один из читателей, Аллан Кайрон, в своем письме указывал, что
если шнур достаточно длинный, чтобы снять дверь с петель, то
головоломку можно было бы решить, пропустив петлю шнура над
дверью, словно дверь является кольцом.
4. Дмитрий Боргманн, автор книги Language on Vacation
(«Языковой досуг»), на мой взгляд, ответил на-эти вопросы.
Рис. 60
Решение головоломки «клюн-и-шнур»
1. Среди распространенных слов последней анаграммой будет
SU {us — «мы», косвенный падеж). Список можно продолжить
вариантами TTU {tut — «ах ты!»), TTUU {tutu — балетная пачка), TUX
{tux — разговорное название смокинга, tuxedo) и zzz (храпеть). Эти
слова Боргманн нашел во втором издании словаря The American
Thesaurus of Slang («Тезаурус американского сленга») под редакцией
Лестера Берри (Lester V. Berrey) и Мелвина Ван ден Берка (Melvin
Van Den Bark).
2. Первой и второй анаграммой словаря будут А и АА (тип
вулканической лавы). Третья анаграмма — это AAAAABBCDRR
{abracadabra — абракадабра,)
128
Нескучная математика
3. Последняя анаграмма словаря в группе «А» будет AY (ay —
«да»), если только вы не рассматриваете архаизмы: AYY{уау —
устаревший вариант «их»).
4. В группе «В» среди распространенных слов первой будет
анаграмма BBBCDEEOW (cobwebbed — затянутый паутиной). Ей
предшествует менее распространенное слово — BBBBBEEHLLUU
(hubble-bubble — журчание, а также кальян).
5. ABCDEFOL скрывает в себе boldface ("полужирное начертание
шрифта).
6. Самая длинная анаграмма, которая совпадает с формой слова, —
это billowy (холмистый). В своей книге Боргманн называет более
длинное слово такого рода aegilops (род трав).
7. Самое длинное английское слово, в котором ни одна из букв
не повторяется, — это uncopyrightables (не подпадающий под
охрану закона об авторских правах). Но Боргманн обнаружил такие
слова, как vodkathumbscrewingly (20 букв). Это слово обозначает
«применять тиски для больших пальцев, предварительно
напившись водки». А самое длинное из подобных слов содержит 23
буквы. Это редкое слово «pubvexingfjordschmaltzy» обозначает «as if in
the manner of the extreme sentimentalism generated in some
individuals by the sight of a majestic fjord, which sentimentalism is annoying to
the clientele of an English inn» (сентиментализм, порожденный
видом величественных фиордов и недостойный истинного
англичанина).
В 1964 году, вскоре после того, как Темперли предложил идею
словаря анаграмм, издательская компания Follett Publishing Company
издала словарь Follett Vest Pocket Anagram Dictionary («Карманный
словарь анаграмм») под редакцией Чарльза Герцена. Этот словарь
включает 20 000 слов с количеством букв до семи, а также
содержательное введение и полезную библиографию.
Другой словарь, Unscrambler («Дешифратор») включал в себя
13 867 анаграмм (их длина не ограничивалась семью буквами) и был
издан в 1973 году издательством The Computer Puzzle Library, Форт-
Уэрт, Техас. В 1955 году частным образом был издан словарь
анаграмм, содержащий более 3200 имен Ветхого Завета. Его издателем
является Люси Лаф, Дарьенский залив, Коннектикут. Этот словарь
называется Bible Names «De-Koder». Если читателю этот вопрос
интересен, то можно обратиться к монографии Ховарда Бергерсона
Palindromes and Anagrams («Палиндромы и анаграммы»), изданной в
1973 году издательством Dover.
Куб с красной гранью и другие головоломки
129
5. Легко показать, для любого конечного набора точек на
плоскости существует бесконечное количество прямых, которые делят
множество точек ровно пополам. Приведенное ниже
доказательство для шести точек {см, рис. 61) может быть обобщено для любого
количества точек.
Рассмотрим линии, проходящие через каждую пару точек.
Выберем новую точку у4, которая находится вне замкнутой кривой,
окружающей все остальные точки, и при этом не лежит ни на одной из
линий. Проведите линию через точку А. Поворачивая линию вокруг
точки А в показанном на рисунке направлении, мы будем
пересекать ею каждую точку по одной за раз. (Мы не можем пересечь две
точки одновременно в связи со специфическим выбором
положения точки А.) После того как линия пересечет половину точек,
ограниченных замкнутым контуром, остановим ее. Поскольку выбор
точки А произволен во всех других отношениях, то существует и
бесконечное количество таких линий.
Это решение задачи основано на беглом изложении задачи,
представленной Гербертом Виллсом в издании The Mathematical
Gazette («Математический бюллетень»).
6. Поскольку цель женщины достичь берега как можно скорее, то
наилучшей будет следующая стратегия. Сначала она держит равнение
так, чтобы центр озера, отмеченный плотом, всегда находился на
одной линии с ней и преследователем на берегу. При этом она старается
двигаться к берегу. Предположим, преследователь следует наилучшей
стратегии. Он движется вокруг озера в одном выбранном направлении
со скоростью в четыре раза выше, чем может грести женщина. Таким
Рис. 61
Доказательство существования
разделительной линии
для задачи о миллионе точек
130
Нескучная математика
образом, маршрут женщины представляет собой полукруг с радиусом
r/s> гДе г — радиус озера. В конце этого полукруга она будет на
расстоянии г/4 от центра озера. В этой точке угловая скорость, которую она
должна поддерживать, чтобы оставлять преследователя на одной
линии с плотом, не позволяет ей приближаться к берегу. (Если
преследователь меняет направление движения, то женщина может сделать то
же самое или, что лучше, зеркально отразить его.)
Как только женщина достигнет конечной точки полукруга, она
может прямо грести к берегу. Ей остается пройти расстояние Зг/4.
Преследователю необходимо пройти расстояние в яг, чтобы поймать
женщину, когда она окажется на берегу. Но женщина спасается, поскольку,
когда она достигает берега, преследователь проходит только Зг.
Но предположим, что женщина будет стремиться достичь берега
не как можно скорее, а как можно дальше от преследователя. В этом
случае ее лучшая стратегия — после того как она достигает точки на
расстоянии г/4 от центра озера, продолжать двигаться по
касательной к кругу радиусом г/4 в направлении, противоположном
направлению движения преследователя. Именно таким было первое
решение задачи, предложенное Ричардом Гаем в статье The Jewel Thief
(«Похититель жемчужин»), опубликованной в NABLA, том 8,
сентябрь, 1961, 149—150. (NABLA — это периодический бюллетень
Малайского математического общества.) А наше первое решение, где
женщина достигала берега за минимальное время, было
опубликовано в том же бюллетене в июле 1961 года.
Не прибегая к элементам анализа, Гай показал, что женщина
всегда может убежать — даже если преследователь движется более чем в
4,6 раза быстрее, чем она (на самом деле предельное соотношение
скоростей равно 3/2^- — Прим. пер.). Те же результаты получил
Томас О'Бирн (см. публикацию в The New Scientist, № 266, 21 декабря,
1961, 753), а также В. Шурман и Дж. Лоддер в статье The Beauty, the
Beast, and the Pond («Красавица, чудовище и пруд»),
опубликованной в журнале Mathematics Magazine, том 47, март, 1974, 93—95.
7. Наименьшее число фрагментов, которое необходимо удалить с
доски 4x4, — это 9. Один из вариантов решения задачи показан на
рисунке 62 (вверху).
Чтобы доказать минимальность этого решения, обратите
внимание на 8 закрашенных клеток. Эти клетки не соприкасаются, и,
чтобы разорвать периметры всех восьми клеток, необходимо удалить
по меньшей мере 8 линий. То же относится и к 8 незакрашенным
клеткам. Однако мы можем разорвать периметры всех 16 клеток те-
Куб с красной гранью и другие головоломки
131
ми же 8 линиями, если выберем их так, чтобы каждая стираемая
линия разрывала бы белую и серую клетку одновременно. Но если мы
будем формировать решение подобным образом, ни одна из
стираемых линий не будет на внешней границе, формирующей большой
квадрат. Значит надо удалить как минимум 9 линий, чтобы
уничтожить 16 маленьких квадратов 1x1 и один внешний 4x4. Как
показывает решение, эти же 9 линий убирают все 30 квадратов.
Те же соображения позволяют показать, что для любой
«четной» доски существует решение как минимум для С/гП2 + 1)
удаленных линий, где п — это порядок квадрата. Сможете ли вы
доказать это для четной доски любого порядка? Доказательство
проводятся* по индукции, что видно из иллюстрации. Мы просто
пристраиваем домино к открытой клетке на границе квадрата 4x4, а
затем выкладываем цепочку домино вокруг его границ, как показано
на рисунке сверху. Для квадрата 6x6 процедура дает минимальное
решение - 19. Для квадрата 8x8 та же процедура дает ответ 33. Оче-^
видно, эту процедуру можно повторять бесконечно, добавляя
новые клетки и перемещая открытую клетку в направлении,
показанном стрелкой.
В варианте 5x5 ситуация осложняется тем фактором, что
заштрихованных клеток на одну больше по сравнению с белыми. Чтобы
уничтожить одновременно 12 заштрихованных и 12 белых клеток,
требуется удалить 12 линий. Это решение, естественно, сформирует
12 домино. Если предположить, что оставшаяся заштрихованная
клетка выходит на внешнюю границу, то и она будет разорвана
вместе с внешним большим квадратом. Это требует как минимум одной
линии, так что для нечетной доски минимальным будет решение х/2
(п2 + 1). Однако, чтобы сконструировать такое решение, домино
следует располагать так, чтобы оно не формировало целый квадрат.
Можно показать, что это вызывает противоречие, так что
минимальное решение (1/2 (я2 + 1) + 1).
На рисунке 62 внизу показана процедура построения
минимального решения для произвольной нечетной доски.
Приведенное решение не единственное. Все прежние решения
относились только к четному или нечетному случаям. Первыми среди
читателей смогли обобщить все решения на единой диаграмме Д. Дж.
Аллен, Джордж Брюстер, Джон Диксон, Джон Харрис и Эндрю Унгар.
Дэвид Биненфельд, Джон Харрис, Мэтью Ходгарт и Уильям Но-
ултон вплотную занялись проблемой создания узора без
прямоугольников и пришли к решению через L-тримино. Эта фигура сы-
132
Нескучная математика
I I I I /
Г" I ¦" I /
* \-s\
1 х I ' 1
11 х * 1
1 х j х J
1 1 ' ' '
1 *Л * |Х
' * 1 *Ч
ГШ Ч н L
I х * I
| 1—р 1 х
Рис. 62
Решение задачи с зубочистками
грала в логике решения ту же роль, что и домино в рассмотренной
выше задаче.
Для квадратов порядка от 2 до 12 оказалось, что достаточно
убрать соответственно 3, 7, 11, 18, 25, 34, 43, 55, 67, 82, 97 линий,
чтобы лишить узор всех прямоугольных форм. Возможно,
впоследствии появятся формулы и алгоритмы, о которых я с удовольствием
расскажу. На рисунке 63 показано решения для доски 8x8.
8. Три набора из четырех точек на беспорядочно разбросанных
прямоугольниках и кругах показаны на рисунке 64 черными
точками. Четыре угла прямоугольника упоминались уже в формулировке
задачи. Четыре точки на малой окружности особых комментариев
не требуют. Третья группа из точек — А, В, С, D. Чтобы доказать
утверждение, проведите пунктиром линию BD и представьте себе, что
это диаметр круга. Поскольку углы Л и С прямые, то они должны
лежать на окружности круга с диаметром BD.
Когда я только опубликовал эту задачу, то спрашивал только о
трех группах точек. Но задача оказалась интереснее, чем
предполагалось ранее. Многие читатели тут же указали на четвертую группу
точек. Это точка А, не отмеченное на рисунке пересечение чуть правее
Куб с красной гранью и другие головоломки
133
Рис.63 L_^ I l_^ I
Как убрать все прямоугольники на доске 8х 8 | | | | |
и ниже А (назовем ее ?), точка В и не отмеченный на рисунке угол
чуть выше В (назовем ее F). Отрезок BE является диаметром
окружности, на которой лежат две другие точки, поскольку каждая из этих
точек представляет собой прямой угол, опирающийся на диаметр.
Задача с измененной формулировкой, исключающей четвертое
решение, была опубликована в книге Барра Second Miscellany of
Puzzles («Второй сборник головоломок»).
9. Вот как выглядел мой первоначальный ответ на эту задачу. При
анализе жидкого содержимого любого количества стаканов с целью
поиска одного-единственного стакана с ядом наиболее эффективен
бинарный подход. Имеющиеся стаканы делятся примерно пополам.
Проверяется одна группа стаканов (при этом смешиваются пробы
из всех стаканов в группе и проверяются за один раз). Та группа, в
которой обнаруживают яд, делится пополам и процедура повторяет-
Рис.64
Три группы точек,
лежащих на окружности
134
Нескучная математика
ся, пока отравленный стакан не находят. Если стаканов от 100 до
128, то требуется семь тестов. Если от 129 до 200 — то восемь тестов.
Цифра 128 поворотная, потому что она единственная в интервале
100-200 из ряда удвоения 1,2,4, 8, 16, 32,64,128,256 и т. д. Надо
полагать, что в гостинице было 129 стаканов, потому что только в этом
случае (а нам был задан диапазон 100—200) нас отделяет от
возможности проведения наиболее эффективной процедуры только один
стакан. Проверка 129 стаканов по такой процедуре потребует
восьми тестов. Но если сначала проверить один стакан, то оставшиеся
128 стаканов потребуют не более семи тестов, так что общее
количество тестов не меняется.
То, что вы прочитали выше, было опубликовано, и многие
читатели написали мне, что прав был скорее полицейский, чем
математик. Независимо от количества стаканов, наиболее эффективной
процедурой будет следующая: как можно более точно делить
стаканы пополам и проводить групповые анализы.
Если обратиться к теории вероятности, то ожидаемое
количество испытаний для 129 стаканов составляет 7,0155. Если же вы
проверите вначале один стакан, то ожидаемое количество испытаний
составит 7,9457. Количество испытаний получается больше, так что
комиссар полиции был прав относительно того, что предложение
математика расточительно. Однако в случае с 129 стаканами я
считаю эту ошибку простительной. Ведь правильный ответ на этот
вопрос дали даже те читатели, которые доказали неэффективность
предложения математика.
Эта задача была опубликована в книге Барра Second Miscellany of
Puzzles («Второй сборник головоломок»).
ГЛАВА 1 О
Тасовка карт
Тасовка карт — вот то единственное, что
невозможно обернуть вспять.
— СЭР АРТУР ЭДЦИНГТОН, Природа физического мира
Как же ошибался Эдцингтон. В 1964 году физики обнаружили, что
достоверные события, связанные со слабым взаимодействием
фундаментальных частиц, проявляют необратимость во времени. По-
видимому, природа разрешает для них только одно временное
направление, если только во Вселенной не существуют галактики, где
материя является зеркальным отражением нашей и имеет
противоположный зарад (то есть является антиматерией). Тогда она будет
двигаться во времени в обратном направлении. Пока никто не
знает, как эта необратимость связана (и связана ли вообще) с
макромиром, в котором процессы перемешивания обеспечивают
единственную известную физическую основу для того, что Эддингтон назвал
«стрелой времени».
Не считая недавно обнаруженных аномалий, все
фундаментальные физические законы, включая и законы квантовой физики,
обратимы во времени. Вы можете изменить знак перед t с «плюса» на
«минус», и формула опишет то, на что способна природа. Но когда
в хаотическом движении находится большое число объектов: от
молекул до звезд, статистическая теория вероятностей вводит стрелу
времени. Если газ Л и газ В находятся в одном сосуде, но разделены
перегородкой, то после удаления перегородки молекулы этих газов
начнут перемешиваться до тех пор, пока смесь не станет
гомогенной. Эта смесь никогда не разделится. Поскольку отдельные
молекулы взаимосвязаны, невозможно придать каждой из них такие
направление и скорость, которые могли бы привести смесь газов в
прежнее состояние.
136
Нескучная математика
Этого не происходит потому, что вероятность такого
распределения фактически равна нулю. Здесь Эддингтон доказывает (и
большинство физиков с ним согласны), что есть единственная причина,
почему вылитое яйцо никогда не восстановит свою форму и не
вернется назад в свою оболочку. Законы вероятности устанавливают
тот непреложный факт, что миллиарды молекул, которые
хаотически разъединены при таком событии, будут двигаться так, чтобы
увеличить энтропию (меру беспорядка) всей системы. По теории
вероятности, Вселенная движется по оси времени только в одном
направлении.
Перетасовка колоды карт, как отмечает Эддингтон, является
прекрасным примером действий Природы по перемешиванию в одном
направлении. Подготовим карточную колоду так, чтобы 26 верхних
карт были красными, а 26 нижних — черными. Эта ситуация
аналогична сосуду с двумя газами. Перемешаем колоду 10 раз, и красно-
черный порядок будет нарушен. Почему же продолжение
перемешивания не вернет разделения карт на две красно-черные половины?
Потому что существует 52! различных способов восстановить
порядок в колоде. (Восклицательный знак представляет собой знак
факториала, обозначающий произведение 1х2хЗх4х...и так далее до
52. Это произведение выражается числом с 68 знаками,
начинающимся с восьмерки.) Число перестановок, которое приводит к
полному красно-черном разделению, хотя и велико, все же составляет
такую небольшую долю от 52!, что можно продолжать
перемешивание в течение тысяч лет без надежды достигнуть хоть какого-нибудь
порядка.
Любопытно отметить то, что эффективность перемешивания, то
есть производительность по наведению беспорядка в упорядоченной
колоде, в действительности зависит от ловкости пальцев того, кто
занимается перемешиванием. До тех пор пока карты перекладываются
организованно, перемешивания на самом деле не происходит.
Рассмотрим, например, тасовку «с руки». Колода удерживается за края
правой рукой, а большой палец левой руки снимает карты снизу
небольшими пачками случайного размера. Точная тасовка с руки,
когда большим пальцем снимается по одной карте за раз, совсем не
нарушает порядка в колоде. Колода только перекладывается.
Повторение точной тасовки восстанавливает первоначальный порядок.
Наиболее привычная тасовка «перехлестыванием»,
выполняемая на столе, тоже не в состоянии выполнить эту работу, если
проводится в полной мере.
Тасовка карт
137
Идеальное перемешивание перехлестыванием карт, известное
американским фокусникам как «перетасовка фараона» и
английским фокусникам как «перетасовка переплетением», производится
сбросом карт по одной за раз поочередно двумя большими
пальцами. Перед началом перетасовки колоду необходимо разделить на
две части: при четном числе карт в колоде она делится точно
пополам, при нечетном — на две почти одинаковые части. При нечетных
колодах меньшая часть (на одну карту меньше) перемешивается с
большей половиной так, чтобы верхняя и нижняя карты большей/
половины после перемешивания оказались верхней и нижней
картами колоды. (Первый сброс производится из большей половины.)
При четных колодах есть выбор сбросить первой нижнюю карту из
любой половины. Если первой сбрасывается карта из той
половины, которая прежде в колоде была нижней, верхняя и нижняя карты
первоначальной колоды займут после перемешивания те же
положения. Фокусники называют это «наружной перетасовкой», потому
что верхняя и нижняя карты остаются снаружи. Если же первой
сбрасывается карта из той половины, которая до перемешивания
была вверху колоды, то прежде верхняя и нижняя карты окажутся в
перемешанной колоде вторыми сверху н снизу. Это фокусники
называют «внутренней перетасовкой».
Для нечетных колод «фараон» является наружной перетасовкой,
если колода снимается ниже центральной карты. При этом верхняя
карта остается в большей половине и после перетасовки становится
верхней картой колоды. «Фараон» является внутренним, если
колода снимается выше центральной карты. При этом верхняя карта
остается в меньшей половине и после перетасовки становится второй
картой колоды снизу.
Оба вида перетасовки нечетной колоды (внутреннюю и
наружную) называют «охватывающими перетасовками» (большая
половина колоды «охватывает» меньшую). Этот термин придумал Эд Марио,
знаток карт из Чикаго, который написал несколько книг по
«фараону» и изобрел много изящных карточных трюков на его основе.
Если колоду из п карт подвергнуть повторяющимся сериям
перетасовки «фараона» одного вида, то она вернется к своему
первоначальному порядку после определенного числа перемешиваний.
При нечетном п возвращение к первоначальному состоянию
колоды произойдет после х перетасовок, где jt является показателем
степени 2 в формуле 2х = (I • модуль п). «(1 • модуль я)» означает, что
это число имеет остаток 1, когда делится на п. Например, если к
138
Нескучная математика
полной колоде добавляется джокер, и колода, таким образом,
содержит 53 карты, формула принимает вид 2х = (1 • модуль 53).
Таким образом, требуется найти такое целое значение х, чтобы при
делении 2х на 53 иметь в остатке единицу.
Количество перетасовок «фараона», необходимое для
восстановления исходного порядка
Число Наружная Внутренняя Число Наружная Внутренняя
карт перета- перета- карт перета- перета-
в колоде совка совка в колоде совка совка
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
1
2
2
4
4
3
3
6
6
10
10
12
12
4
4
8
8
18
18
6
6
11
11
20
20
18
2
2
4
4
3
3
6
6
10
10
12
12
4
4
8
8
18
18
6
6
11
11
20
20
18
18
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
18
28
28
5
5
10
10
12
12
36
36
12
12
20
20
14
14
12
12
23
23
21
21
8
8
28
28
5
5
10
10
12
12
36
36
12
12
20
20
14
14
12
12
23
23
21
21
8
8
52
Рис. 65
Количество перетасовок, необходимое для восстановления исходного
порядка в колодах с количеством карт от 2 до 52
Тасовка карт
139
Если мы будем увеличивать показатель степени 2 (2,4, 8, 16, 32...),
то не достигнем числа, которое представляет значение «1 -модуль
53», до тех пор, пока не подойдем к 252. Это означает, что для
восстановления порядка в колоде из 53 карт необходимо 52 внутренних
перетасовки (или 52 наружные перетасовки).
При четном количестве карт в колоде ситуация несколько
усложняется. Количество наружных перетасовок, необходимых для
восстановления первоначального порядка, составляет 2х = (1
-модуль (я — 1)). А количество необходимых для этого внутренних
перетасовок составляет 2х = (1 • модуль (п + 1)). Иногда эти значения
различаются довольно значительно. Для обычной колоды из 52 карт
восстанавливают порядок 52 внутренние перетасовки. Но 28 =
(1 • модуль 51), так что наружных перетасовок потребуется только 8.
На рисунке 65 представлено количество перетасовок «фараона»
обоих видов, требующихся для восстановления порядка в колодах
любого размера, от 2 до 52 карт. Заметим, что для нечетной колоды
количество перетасовок всегда одинаково для перетасовок любого
вида и равно числу наружных перетасовок, требующихся для
колоды с числом карт на одну больше. А для четной колоды количество
наружных перетасовок равно количеству перетасовок внутренних
для колоды с количеством карт на 2 меньше. Это отражает тот факт,
что верхняя и нижняя карты никогда не перемешиваются при
внутренней перетасовке, так что на самом деле производится только
внутренняя перетасовка остатка колоды.
Так как безупречное тасование перехлестыванием провести даже
грубо довольно трудно (это под силу только опытному карточному
специалисту). Проверить точность сведений в приведенной выше
таблице будет проще, повернув во времени и проделав тасовку
фараона в обратном порядке. (Безупречную тасовку легко вернуть к
прежнему состоянию!) Карточные фокусники называют этот
маневр «обратным фараоном». Просто разложите колоду веером, как
показано на рисунке 66, слегка выталкивая карты поочередно вверх
из колоды (пунктирные линии на верхнем рисунке).
Напрактиковавшись, это можно проделать довольно быстро. После того как все
карты будут сдвинуты, снимите полколоды и положите на другую
половину. Если вы расположите карты так, что верхняя карта
останется сверху, вы выполните «рассортировку наружу». Если же
верхняя карта уйдет в колоду, вы проделаете «рассортировку внутрь».
Каждая из этих операций, очевидно, является обратной для
соответствующего «фараона». Теперь очень просто проверить любую
,*• i.
Рис. 66
Метод перетасовки «обратного фараона»
Тасовка карт
141
часть таблицы, так как если п «фараонов» определенного вида
восстанавливают порядок, то ясно, что п обратных «фараонов» сделают
то же самое.
Лучше провести такой эксперимент с упорядоченным набором
карт, повернув их лицевой стороной вверх, чтобы можно было
наблюдать изменения после каждой рассортировки. Обратите,
например, внимание на то, что в некоторых случаях, когда
восстанавливается порядок при четном количестве карт, карты после завершения
половины операций располагаются в обратном порядке.
Попробуйте этот трюк с 10 картами от туза до десятки, расположенными в
порядке возрастания. Десять внутренних перетасовок
восстанавливают первоначальный порядок, но после пятой перетасовки карты
располагаются в порядке убывания. Колода из 52 карт таким же
образом восстановит свой порядок после 26 внутренних перетасовок.
Отметим и такой любопытный факт: после каждой внутренней
перетасовки 52-карточной колоды 18 и 35 карты меняются местами.
Одним из первых запутанную математику «фараона» с точки
зрения фокусника исследовал Алекс Элмсли, британский программист,
который также является искусным карточным фокусником. В 1957
году в канадском журнале по магии Ibidem он рассказал, как
случайно открыл замечательную формулу. Раньше он придумал термины
«внутренняя перетасовка» и «наружная перетасовка» и в своих
записках обозначил их как I (для внутренней от «in») and О (для наружной
от «out»). В самом начале он пытался определить, какая
последовательность внутренних и наружных перетасовок наиболее эффективно
изменяет расположение верхней карты. Цель этого трюка —
расположить верхнюю карту в любое желаемое положение от вершины. К
примеру, нужно расположить верхнюю карту в полной колоде при
внутренней перетасовке «фараона» так, чтобы она оказалась на 15
месте сверху. Элмсли экспериментально определил, что это можно
достигнуть путем следующего набора фараонов: НЮ (1110). Но ведь
1110 в двоичной системе обозначает число 14, а 14 является номером
карты, которая располагается сверху заданной позиции.
Этот факт нельзя назвать случайным совпадением. Независимо
от размера колоды и того, является она четной или нечетной, всегда
выполняется следующая закономерность. Отнимите единицу от
номера позиции, в которой вы хотите видеть верхнюю карту.
Переведите результат в двоичную систему, и вы получите
последовательность внутренних и наружных перетасовок, необходимых для того,
чтобы перевести карту в нужную позицию за самое короткое время.
142
Нескучная математика
Если колода четная, вас ожидает сюрприз. Всякий раз после
завершения «фараона» чередование карт верхней половины колоды в
нижнем направлении является зеркальным отображением
чередования карт нижней половины в верхнем направлении.
В то время как карта, которая является n-Pi от вершины,
занимает положение/?, считая сверху, карта, которая является я-й от Низа,
окажется в положении/?, считая снизу. Та же самая перетасовка,
которая переводит верхнюю карту на 15 позицию вниз,
одновременно переведет нижнюю карту на 15 позицию вверх. Если колода из
52 карт упорядочена так, что каждая карта в верхней половине
колоды сочетается по значению и масти с картой, находящейся в таком
же положении в нижней половине, это сочетание никогда не
нарушится при выполнении любого количества «фараонов» любого
вида. Фокусники часто используют этот принцип. Применяющуюся
терминологию предложил его первооткрыватель, карточный
фокусник, который публиковался под именем Расдак. На принципах
зеркального отображения основано множество замечательных
карточных фокусов.
Читатель может доставить себе удовольствие проверить формулу
Элмсли, осуществив еще раз обращение по времени с
использованием внутренних и наружных перетасовок для перевода карты на
вершину колоды из любого положения в колодах любого размера.
Отнимите единицу от номера позиции, запишите результат в
двоичной форме исчисления, затем, придерживаясь обратной
последовательности двоичного обозначения, проделайте внутренние и
наружные перетасовки. В предыдущем примере, чтобы перевести 15
карту в верхнее положение в колоде, запишите 14 как 1110. Выполнив
одну наружную и три внутренних перетасовки, переведите эту
карту на вершину. Если колода четная, то 15 карта снизу одновременно
займет нижнее положение в колоде.
К нечетным колодам принцип зеркального отображения
неприменим, но есть кое-что еще более удивительное. Лучше всего это
можно пояснить на примере колоды из девяти карт одной масти:
туза, 2, 3, 4, 5, 6, 7, 8 и 9. Расположите карты по порядку лицевой
стороной вверх (туз сверху). Считайте это расположение циклическим:
верхняя и нижняя карты соединяются подобно замкнутой цепи.
Если мы разделим колоду, чтобы образовать, например, такой
порядок: 6, 7, 8, 9, туз, 2, 3, 4, 5„ то будем считать его тем же самым
циклическим. Таблица (см. рис. 65) подсказывает нам, что колода из
девяти карт вернется к своему первоначальному расположению после
Тасовка карт
143
шести перетасовок любого вида. Однако теперь вы можете снимать
колоду произвольным образом. Разделите колоду один раз или
больше, проведите перетасовку, разделите еще раз, проведите
перетасовку другого вида и продолжайте до тех пор, пока не завершите
шесть перетасовок. Больше того, вы можете произвольным образом
чередовать внутренние и наружные перетасовки. После шестой
перетасовки проверьте карты. Они сохранят тот же циклический
порядок! Это применимо к любой нечетной колоде. Перетасовки
любого вида можно чередовать при любом числе разделений колоды:
после требуемого числа перетасовок первоначальный циклический
порядок сохранится.
В процессе восстановления своего первоначального
расположения колода из девяти карт проходит через пять других состояний,
для каждого из которых имеется свой циклический порядок.
Циклические порядки этих состояний также не нарушаются при
разделении, они просто демонстрируют различные циклические
размещения в зависимости от того, какая карта находится сверху. Так как
каждое из шести состояний колоды имеет только девять различных
циклических последовательностей, общее число вариантов
расположения девяти карт, которое можно получить снятием и перета-
совками, не будет превышать 6 х 9 = 54. Это число составляет не-
большую долю от 9! вариантов (362 880), возможных при хаотичной
перетасовке 9 карт.
Поскольку перетасовки представляют собой обращение
«фараона» (движение вспять), все они применяются равным образом и к
перетасовке фараона нечетной колоды. Соломон Голомб в своей
статье Permutation by Cutting and Shuffling («Перемещение путем
разделения и перетасовки») доказал, что путем сочетания разделений
четной колоды с внутренней или наружной перетасовкой можно
достигнуть любое из возможных расположений карт. Но для всех
нечетных колод с количеством карт больше трех можно осуществить
только небольшую часть возможных размещений. Беспорядочное
разделение и перетасовка «антифараон» может привести к полному
произволу в колоде из 52 карт, так что может быть достигнуто любое
из 52! возможных размещений. Но удалим из колоды одну карту
(остается 51 карта) и произвольное сочетание перетасовок и
разделений сузит выбор до 8 х 51 = 408 размещений из общего количества
51!, которое выражается 67-значным числом.
Используя циклический характер нечетных колод, Дэй Верной,
один из ведущих национальных карточных фокусников, разрабо-
144
Нескучная математика
тал легкий для выполнения трюк. Вручите кому-нибудь из зрителей
20 карт и джокер. Попросите его перетасовать карты, при этом сами
повернитесь к нему спиной. Потом попросите вставить джокер в
колоду и запомнить две карты, между которыми находится джокер.
Повернитесь и возьмите колоду из 21 карты лицевой стороной вниз.
Проделайте «обратного фараона» (либо внутреннего, либо
наружного, значения не имеет), затем попросите зрителя снять колоду.
Повторите еще одного обратного фараона любого вида и попросите
снова снять колоду. А теперь раскройте карты веером и, удерживая
веер таким образом, чтобы зритель видел лицевую сторону, а вы нет,
попросите его удалить джокер.
Сдвиньте карты двумя группами к тому месту, где находился
джокер, затем сложите их, поменяв группы местами. Таким образом
вы снимете колоду в том месте, где находился джокер. Однако не
привлекайте к этому внимания. Аудитории должно показаться, что
вы просто сложили карты вместе, как они и лежали до удаления
джокера.
Теперь вы держите 20 карт — четное число. Сделайте две
наружных перетасовки и одну внутреннюю. Положите колоду на стол.
Попросите зрителя назвать две отобранные карты. Откройте
нижнюю карту колоды. Это будет одна из карт. Откройте верхнюю
карту колоды. Это будет другая карта.
«Фараон» является только одной из многих видов простых и
весьма характерных перетасовок, которые можно неоднократно
применять к колоде карт, достигая необычных результатов. Теперь
позвольте нам обобщить материал и определить «перетасовку» как
любое преобразование, систематизированное оно или нет. Мы
можем определить структуру перетасовки, изобразив таблицу,
подобную приведенной ниже для перетасовки пяти карт:
1-3
2-5
3-1
4-2
5-4
Таблица показывает, что первая карта займет позицию 3, вторая —
позицию 5 и так далее. Эта же перетасовка изображена в виде
диаграммы со стрелками (см. рис. 67). В расположении этих стрелок нет
никакой системы. Картина может быть совершенно случайной, как
будто бы карты перемешивали в барабане, а потом вытаскивали по
одной, чтобы сложить новую колоду.
Тасовка карт
145
ПОЛОЖЕНИЕ КАРТЫ 1 2 3 4 5
ДО ПЕРЕТАСОВКИ #^^--*^><^ ^*
ПОСЛЕ ПЕРЕТАСОВКИ щ^^^^'^^^^ ^^^^ф
Рис. 67
Диаграмма случайной перетасовки колоды из пяти карт.
Здесь отображен цикл из пяти перестановок
Предположим, что такая же перетасовка, что отображена в
таблице или на диаграмме, применяется неоднократно для колоды из п
карт. Будет ли это в конечном счете рандомизировать карты? Нет, не
будет. Независимо от картины перетасовки, карты просто пройдут
через ряд состояний, пока не вернутся к своему первоначальному
положению. Затем цикл повторится. Если колода содержит больше
двух карт, то не существует никаких перетасовок, которые,
повторяясь, прокрутят все возможные перемещения. Например, для трех
карт имеется 3!, или 1x2x3 = 6, возможных расположений.
Невозможно изобрести такую перетасовку, повторение которой потребует
шесть ступеней для завершения цикла. Самый длинный из
возможных циклов состоит только из трех ступеней.
Вот трудный, но увлекательный тест. Вообразите, что колоду из
52 карт поместили в перетасовывающую машину, которая
постоянно осуществляет одну и ту же перетасовку. Вы не можете заглянуть в
машину, поэтому не имеете никакого представления о картине
перетасовки. Каждый раз после окончания тасовки звонит
колокольчик. Каково наименьшее количество звонков, после которого вы с
абсолютной уверенностью можете сказать, что хотя бы один раз
восстановился первоначальный порядок? Пойдем другим путем:
«Какой самый длинный цикл повторения могут иметь 52 карты?»
ДОПОЛНЕНИЕ
При обсуждении повторяющейся картины тасовок я заявил без
доказательства, что подобная тасовка с уверенностью вернет колоду в
первоначальное расположение после конечного числа тасовок.
Некоторые читатели удивляются, почему же невозможно для такой
перетасовки попасть в «петлю», которая никогда не приведет к
первоначальному порядку.
146
Нескучная математика
Это не может произойти вот почему. Когда колоду неоднократно
подвергают той же самой перетасовке, она проходит через ряд
состояний: а, Ь, с, d, e... Когда тасуют, скажем, расположение Ь, это
однозначно должно привести к с. И наоборот, с может появиться
только после того, как было получено Ь. Так что, проходя конечное
число состояний, колода должна вернуться в свое первоначальное
состояние, если только что-то в этой последовательности не
нарушилось. А по условию задачи, это исключено. Ясно, что колода не
может перейти в состояние d, не побывав в состоянии с (потому что d
получается только после с). Эта цепочка замкнется только
возвращением в а.
Точно такое же объяснение применимо к любой колоде карт,
когда к ней применяется серия из п перетасовок, каждая с
различным расположением, при условии, что серии точно повторяются.
Предположим, что с колодой производят три различных
перетасовки {а, Ь, с). По сути, это постоянно повторяющийся цикл: abc, abc,
abc... Каждый триплет изменяет колоду одинаковым образом от
одного состояния до другого, так что триплет эквивалентен единой
перетасовке.
Так же легко показать, что для каждого х, где х — это
необходимое для сохранения первоначального порядка наименьшее число
повторений «фараона» одного вида, сохраняется только конечное
число колод. Например, только колоды с числом карт 4, 5, 6, 14, 15
и 16 требуют минимум 4 перетасовки для их сохранения (четыре
внешних для 5, 6, 15 и 16 и четыре внутренних для 4 и 14).Читатели
могут попытаться отыскать процедуру для определения размеров
колоды, которую можно сохранить при минимальном количестве
повторов х «фараонов» одного вида.
Одно из самых ранних упоминаний о перетасовке «фараона»
встречается в книге Джона Невила Маскелайна о карточном
жульничестве Sharps and Flats («Мошенники и карточные игры», 1894),
где эту перетасовку называют/аго dealer's shuffle (перетасовка
«фараона»). Чарльз Т. Джордан в книге Thirty Card Mysteries («Тридцать
карточных секретов») первым серьезно размышлял о том, каким
образом можно применить перетасовку в карточных трюках. Однако
фокусники начали всерьез изучать карточные перетасовки и
вскрывать их глубокие возможности только в конце пятидесятых.
«Мягкий шелест тасуемых «фараоном» карт был слышен повсюду», —
писал Джон Браун о фокусниках в своем введении к книге Пауля
Свинфорда Faro Fantasy («Фантазии на тему фараона»).
Тасовка карт
147
На каждой встрече карточных фокусников вы увидите
энтузиастов «фараона», стремящихся показать свои последние выдумки. А
также встретите картежников, которые, хотя и отлично выполняют
тасовку «фараона», избегают публично демонстрировать этот трюк с
картами. «Он снял колоду карт и сказал, что собирается показать
мне трюк с «фараоном», — писал ведущий карточный фокусник
Чарли Миллер. — Я взял ружье и выстрелил в него».
Фокусниками было обнаружено много неожиданных аспектов
«фараона». Позвольте мне напомнить только один случай. Возьмите
колоду из 32 карт (можно брать любую степень числа два) с четырьмя
тузами. Положите одного черного туза сверху колоды, другого —
снизу. Положите одного красного туза на расстоянии п, считая сверху,
другого на расстоянии п, считая снизу. Предположим, что п — 1.
Перевернем лицом вверх седьмого от верха туза. А теперь проделайте
пять обратных «фараонов», каждый раз снимая половину с
перевернутым тузом и выводя его наверх. Непременно проделайте все пять,
даже если перевернутый туз окажется на вершине уже через
несколько «фараонов». В конце красные тузы у вас окажутся наверху и внизу
колоды, а черные передвинутся на седьмые позиции сверху и снизу.
На этом принципе основано множество превосходных
карточных фокусов. В качестве примера попросите кого-нибудь
перетасовать колоду из 16 карт и передать ее вам. Незаметно для других
мельком посмотрите на верхнюю карту и запомните ее. Разверните
карты веером лицевой стороной к зрителю. Попросите его выбрать
какую-нибудь карту, запомнить ее, а также заметить, на какой
позиции от вершины колоды она находится. Проделайте четыре
обратных фараона и покажите карты веером так, чтобы он мог видеть
картинки. Перед каждым разделением колоды спрашивайте его, в
какой половине колоды находится его карта. Укладывайте эту
половину наверх. В конце попросите назвать выбранную карту и
переверните верхнюю карту, чтобы показать, что процедура
пересортировки привела эту карту наверх.
Скажите, что сейчас повторите трюк, но на этот раз попросите
его вообще не сообщать вам никакой информации. Отвернитесь,
пока он запоминает карту, находящуюся в положении, ранее занятом
картой, выбранной в первой части фокуса. Конечно, вы уже знаете
название этой карты, которую вы тайком подсмотрели, когда она
была сверху, но у него нет никаких причин подозревать, что вы это
знаете. Возьмите колоду и проделайте четыре «обратных фараона»,
на этот раз повернув карты лицевой стороной к себе и не задавая
148
Нескучная математика
никаких вопросов. Каждый раз снимайте колоду с его картой
наверх. Выровняйте карты, спросите название его второй выбранной
карты и переверните верхнюю карту. Эффект гарантирован.
Мое прежнее замечание о том, что принцип зеркального
отображения не применим к нечетной колоде, не совсем верно.
Эдвард Марио обратил внимание на то, что колода с 53 картами
с джокером сверху или снизу может быть подвергнута перетасовке
«фараона» необходимое количество раз (используя любой вид
«фараона») и разделена между перетасовками произвольное количество
раз. Если теперь джокер снимается соответственно сверху или
снизу, вы обнаружите, что колода, за исключением джокера, является
зеркально отраженной. Было разработано много необычных
карточных трюков с использованием принципа зеркального
отображения колоды с 53 картами.
Я объяснял, как можно использовать «фараон», чтобы перевести
верхнюю карту в любую желаемую позицию, и как использовать
«обратный фараон», чтобы перевести карту из любой позиции
наверх колоды. Противоположную задачу перевода карты из любой
позиции на вершину обычным «фараоном» (или сопутствующую
задачу использования «обратного фараона» для перевода верхней
карты в желаемую позицию) проанализировать гораздо труднее.
Насколько мне известно, простых формул или процедур для
выполнения этих задач с минимальным количеством перетасовок не
найдено. Предпринимались некоторые попытки разработать
результативные алгоритмы, соединяющие перетасовки различных видов, но
проблема пока еще далека от решения.
Отважившиеся окунуться в джунгли магии карт читатели найдут
ссылки на литературу в приведенной библиографии. Две
перетасовки «фараона» для 24 карт (внутренние и внешние перетасовки)
нашли неожиданное применение в теории групп. Они привели к
простому построению 12 символов Мэтью.
ОТВЕТЫ
При условии, что схема перетасовки каждый раз точно повторяется,
каково максимальное число повторений, которые необходимо
сделать, прежде чем 52-карточная колода вернется к первоначальному
порядку?
На этот вопрос лучше всего ответить, рассмотрев вначале
случайную перетасовку шести карт, схематически изображенную на рисун-
Тасовка карт
149
ке 68. Проанализировав ее, вы увидите, что схему можно разбить на
подмножества, каждое со своим индивидуальным циклом. Карта из
позиции 3 переходит в позицию 3 и таким образом образует
подмножество из одной карты с циклом I. Карты 1 и 5 обмениваются
позициями, образуя подмножество из двух карт, которые вернутся на
свои первоначальные позиции после цикла из двух перетасовок.
ПОЗИЦИИ КАРТ
1
ДО ПЕРЕТАСОВКИ
ПОСЛЕ ПЕРЕТАСОВКИ
Рис. 68
Диаграмма случайной перетасовки шести карт
Карты 2, 4 и 6 составляют подмножество, которое вернется к
своему первоначальному порядку после трех перетасовок. Таким
образом, у нас имеется три цикла длиной 1, 2 и 3. Достаточно
очевидно, что колода из шести карт вернется к своему
первоначальному положению после количества перетасовок, равного НОК
(наименьшему общему кратному) для 1, 2 и 3, которым является 6. Все
колоды при повторяющихся тасовках подразделяются на
подмножества, каждое из которых имеет цикл, равный количеству карт в
подмножестве. Чтобы определить самый длинный цикл для
полной колоды из п карт, проверим каждый возможный расклад
колоды из п карт на подмножества, чтобы определить, какой из них
дает наибольшую величину НОК. В случае шести карт имеется 11
различных раскладов:
111111
11112
1 122
222
1113
123
33
1 14
24
15
15
6
Подмножествами с наибольшим НОК являются {1, 2, 3} и {6},
оба из которых имеют в качестве НОК значение 6. Мы приходим к
выводу, что никакие перетасовки шести карт, повторяемые точно,
150
Нескучная математика
не могут иметь цикл больше 6 до того, как восстановится
первоначальный порядок.
У колоды из 52 карт так много различных составных частей, что
нужно использовать более мелкое деление, чтобы отыскать те
составные части, чьи наборы имеют самые высокие НОК. Здесь не
хватит места, чтобы все это изобразить. Я могу только отослать
читателя к статье Хадсона в сборнике Educational Times Reprints, том II
(1865), где эта проблема была разрешена, кажется, впервые.
Ни одна из составных частей 52 не имеет НОК выше 180 180,
поэтому никакая перетасовка для 52 карт не может иметь цикл
длиннее 180 180. Примером таких составных частей являются 1, 1, 1,4, 5,
7, 9, 11, 13. У читателя не должно возникнуть трудностей при
изображении диаграммы для 52-карточной перетасовки с
подмножествами, соответствующими ее составным частям, которые не могут
вернуться к первоначальному порядку до тех пор, пока перетасовка
не повторится 180 180 раз.
Необычное повторение 180 объясняется тем фактом, что
произведение составных частей 7, 11 и 13 равно 1001, а произведение
оставшихся частей 180. Любое трехзначное число abc при умножении
на 1001 дает произведение abcabc. Подмножества из единственной
карты, очевидно, не играют никакой роли в перетасовках. Поэтому
мы делаем вывод, что колоды из 49, 50 или 51 карты тоже имеют
максимальные перетасовочные циклы 180180 повторений. Добавка
джокера к колоде увеличивает максимальный цикл до 360360.
Предположим, что вместо вопроса о максимальной длине цикла
для 52 карт, мы зададим другой вопрос. Итак, машинный процесс
тасовки невозможно повернуть вспять. Мы заложили в нее колоду
из 52 карт с неизвестным расположением, и машина сделала одну
перетасовку, природа которой тоже неизвестна. Сколько
дополнительных перетасовок того же вида должна проделать машина, чтобы
у нас была полная уверенность в том, что первоначальный порядок
восстановлен?
Этот вопрос независимо друг от друга задали два читателя —
Эдвин М. Макмиллан и Дэниел Ван Арсдэйл. И сами же на него
ответили. Наименьший гарантированный цикл для восстановления
первоначального порядка равен наименьшему общему кратному всех
чисел от 1 до 52. Это число 11 х 13 х 17 х 19 х 23 х 25 х 27 х 29 х 31 х
32 х 37 х 41 х 43 х 47 х 49. Назовем его «очень большим числом N».
Если теперь машина повторит свои (7V — 1) перетасовок, мы будем
уверены, что колода вернется к своему первоначальному порядку.
ГЛАВА 1 1
Лоскутное одеяло
госпожи Перкинс
и другие упаковки квадратов
Физико-математический раздел «Материалов кембриджского
философского общества» — одного из наиболее консервативных
британских журналов — буквально поразил своих читателей в июле 1964
года, когда опубликовали заметку под названием Mrs. Perkins' Quilt
(«Лоскутное одеяло госпожи Перкинс»). Это были вполне научные
соображения кембриджского математика Джона Конвея (см. главу 1)
на тему сколь бесполезную, столь же и интригующую своей нераз-
решенностью, годящуюся, пожалуй, только для занимательной
геометрии. Рассматриваемая задача принадлежит широкому классу
комбинаторных проблем, связанных с упаковкой квадратов на
больших площадях. Наиболее известная задача такого рода — это
упаковка квадратов без зазоров и наложений (все квадраты разного
размера). Если мы представим большой квадрат в виде решетки
отдельных неравных квадратов, то самый маленький известный
квадрат, который может быть разделен подобным образом, имеет
сторону в 175 единиц. Этот квадрат можно разделить на 24 неравных
квадрата. Читатели могут найти этот квадрат в книге The 2nd Scientific
American Book of Mathematical Puzzles & Diversions («Второй
сборник математических головоломок и развлечений от Scientific
American»). Автор этой книги Вильям Татт рассказывает, как он с
друзьями воспользовался законами Кирхгофа (распределение
электрического тока), чтобы найти разгадку задачи подобного рода.
Проблема лоскутного одеяла госпожи Перкинс (так называл эту
задачу придумавший ее английский мастер головоломок Генри
Эрнест Дьюдени) — это, по сути, та же задача, которую позже решал
Татт в варианте с отсутствием ограничения на размеры квадратов.
152
Нескучная математика
Было снято требование о том, что малые квадраты не должны
повторяться. Очевидно, что любой квадрат со стороной п единиц
может быть разделен на п2 единичных квадратов. Задача состоит в том,
чтобы определить наименьшее количество квадратов, на которые
можно разделить большой квадрат. Хотя этот вариант проблемы
лоскутного одеяла госпожи Перкинс имеет меньше ограничений, его
анализ ничуть не менее сложный.
Наилучшим подходом к проблеме является поэтапный (см. рис.
69). Решения для п, равных I и 2, тривиальны. Если вращения и
отражения считать за одно решение, то для третьего порядка решение
будет единственным из всех с шестью квадратами. Поскольку
квадрат со стороной 4 имеет четыре квадрата со стороной два, то этот
вариант может выступить в качестве минимального решения. Но это
будет лишь кратный вариант решения для я, равного 2. Тогда мы
введем новое условие: порядки меньших квадратов не должны
иметь общий множитель. Это приводит к минимальному решению
из семи квадратов. Интересно то, что для меньших квадратов
подобных кратных решений не существует. Давайте назовем подобное
разбиение квадрата простым по аналогии с простыми числами,
которые не имеют делителей. Если сторона большого квадрата
представляет собой простое число, то разбиение квадрата по
определению получается простым. Если же нет, то мы должны убедиться в
том, что разбиение квадрата «простое». В противном случае это
будет тривиальное повторение решения для квадрата с порядком,
соответствующим наименьшему множителю стороны большого
квадрата. Теперь проблема лоскутного одеяла госпожи Перкинс может
быть сформулирована как нахождение минимального «простого»
разбиения для квадрата произвольного размера. На рисунке 69
показано решение для первых 12 квадратов.
Если порядок квадрата принадлежит ряду Фибоначчи (1, 1, 2, 3,
5, 8, 13 ..., каждый следующий член равен сумме двух предыдущих),
то минимальное симметричное и при этом простое решение дает та
же последовательность Фибоначчи (к ряду Фибоначчи относятся
стороны малых квадратов). Так, для 1, 2, 3, 5 и 8 ряд Фибоначчи
дает именно минимальное решение, а для п = 13 разбиение квадрата с
помощью ряда Фибоначчи получается не минимальным. На
рисунке 70 показано симметричное разбиение в соответствии с рядом
Фибоначчи для п = 13. Предлагаю читателям попытаться
уменьшить количество квадратов в разбиении с 12 до 11 (что является
минимумом). При этом от симметрии придется отступить.
ffl
12 3 4
6 7
10
11 12
Рис. 69
Решения задачи лоскутного одеяла для первых 12 квадратов
13
Рис. 70
Симметричное решение
для квадрата порядка 13
154
Нескучная математика
Конечно, было бы желательно, чтобы существовала обобщенная
процедура построения минимального простого разбиения для
квадратов произвольного размера, а также формула, которая выражала
бы минимальное количество квадратов в виде функции порядка
большого квадрата. По моим данным, ни та, ни другая задача еще не
решены. Конвей доказал, что минимальное простое разбиение
квадрата порядка п дает количество квадратов больше 6 log2Ai (оценка
снизу) и меньше буя+ 1 (оценка сверху). В 1965 году Г. Трастрам из
университета Сассекса опубликовал доказательство того, что
верхняя граница количества квадратов лежит как минимум на
уровне 6 log2tf. Для квадратов высоких порядков это большой шаг
вперед. Однако до точной формулы еще далеко.
В ранних работах Конвея, посвященных лоскутному одеялу
госпожи Перкинс, упоминается статья Лео Мозера, бывшего тогда
деканом факультета математики в университете Альберты. В своих
более поздних работах Мозер обращается к нескольким другим
задачам с упаковкой квадратов. Например, речь может идти о решении
задачи с помощью квадратов со сторонами, образующими
гармонический ряд 72 + Уз + хU + Уз--- Этот ряд расходящийся, и его
сумма не является конечным числом. Однако в случае с суммами
квадратов ситуация иная. Ряд У4 + У9 + 'Аб + У25— сходящийся и, как
ни странно, его сумма имеет предел ((п2/6) — 1). Сюрпризом здесь
является то, что неожиданно появляется число п. Значение суммы
этого ряда чуть больше 0,6. Мозер был первым, кто задался
вопросом: нельзя ли приспособить эту бесконечную последовательность,
чтобы подобрать стороны квадратов, которые бы заполняли без
наложений единичный квадрат. Ответ на вопрос оказался
положительным. На рисунке 71 показан простой алгоритм. Сначала квадрат
разделяется на полосы шириной У2, У4, Ув— Поскольку в пределе
сумма этого ряда равна единице, то бесконечное количество таких
полос без разрывов заполняет площадь единичного квадрата. Затем
в пределах каждой полосы размещаются квадраты убывающего
размера вплоть до правого края полос. Таким образом, полосы
упаковываются плотно без разрывов. Но при этом незаполненной
остается чуть меньше 40% площади квадрата.
В 1967 году Мозер вместе с коллегой из университета Альберты
Дж. В. Муном сумел поставить в этой задаче последнюю точку. Они
доказали, что бесконечный набор гармонических квадратов можно
вписать в квадрат со стороной 5/б- (Очевидно, для меньшего
квадрата это невозможно, поскольку У2 + Уз = 5/б-) Иллюстрацию бо-
Рис. 71
Упаковка бесконечного количества квадратов в единичный квадрат
156
Нескучная математика
лее компактной упаковки гармонического ряда квадратов Мозер и
Э. Майер приводят в своей статье 1968 года. Здесь незакрытая
площадь составляет приблизительно восемь процентов. Многие,
связанные с этой задачей результаты приведены в этих двух статьях,
написанных в соавторстве с Мозером. Там же можно найти
изящное доказательство того, что любым набором квадратов,
закрывающим площадь 1, можно без наложений покрыть и площадь 2.
Среди многих нерешенных проблем, которые касаются
упаковки малых квадратов в больший, есть одна, которая способна
привести любого в бешенство. Эта прежде неопубликованная
математическая задача была предложена несколько лет назад
Ричардом Б. Брайттоном из Массачусетса. Он прочитал статью Татта,
посвященную разбиению квадрата на неравные квадраты, и задался
вопросом о возможности разбиения квадрата на меньшие квадраты со
сторонами из последовательного ряда 1, 2, 3, 4, 5... Да, это было бы
возможно, если бы частичная сумма ряда 1 + 4 + 9 + 16 + 25... в
принципе могла бы быть равна квадрату целого числа. Но это так только
для первых 24 квадратов (не меньше). Сумма 12 + 22 + 32 + ... + 242
равна 4900, что соответствует 702. Любопытно, что подобное
совпадение больше никогда не повторяется.
Открытие этого уникального совпадения имеет интересную
историю, связанную с «пирамидальным числом». Пирамидальными
называются кардинальные (предельные) числа, соответствующие
количеству пушечных ядер, сложенных в правильные
четырехгранные пирамиды. Поскольку слой пирамиды квадратный, за
верхним ядром идет слой в четыре ядра, затем в девять и так далее.
Легко видеть, что пирамидальное число является частичной
суммой ряда 12 + 22 + 32 + ... + п2. Формула для такой суммы может
быть записана в виде:
я(л + 1)(2к + 1)
6
В одной старой головоломке требовалось определить
наименьшее количество пушечных ядер, сложенных в четырехугольную
пирамиду, которое может быть разложено на земле в виде правильного
квадрата. С точки зрения алгебры здесь требуется найти
минимальное решение диофантова уравнения (в целых числах):
Лоскутное одеяло госпожи Перкинс
157
Французский математик Эдуард Лукас, а позже и Дьюдени
догадались, что ответы п = 24, т =70 — это единственные
положительные числа, удовлетворяющие уравнению. Другое
решение тривиально: п = 1, т = 1. Иначе говоря, 4900 — это
единственное число больше единицы, которое является одновременно
квадратным и пирамидальным. Только в 1918 году Г. Уотсон (см.
вестник Messenger of Mathematics, том 48, с. 1—22) представил
первое в истории математики доказательство того, что это
действительно так.
Следовательно, если нам задано, что квадратная шахматная
доска может быть разделена по линиям решетки на квадраты со
сторонами 1, 2, 3..., то это должна быть доска 70x70. Я не
располагаю доказательствами того, что подобное невозможно. Да и
труды Татта и других исследователей ставят под сомнения эту
возможность, не давая при этом строгого доказательства
невозможности существования подобного разбиения. Однако вполне
возможно, что подобное доказательство не столь трудно найти.
Теперь возникает вопрос (его прежде поднимал Брайттон) о том,
какова же самая большая площадь квадрата 70x70, которую можно
закрыть квадратами из набора от 1x1 до 24x24. Конечно, не все
эти квадраты будут использованы. Предполагается, что квадраты
не выходят за рамки большого квадрата и взаимно не
перекрываются.
Подход к решению задачи покрытия квадрата 70x70 состоит в
использовании листа бумаги, разграфленного сеткой тонких линий.
Также вы можете воспользоваться подобием аппликации,
нарисовав квадрат 70x70 с сеткой единичных квадратов (каждый примерно
5 мм). Меньшие по размерам квадраты можно вырезать из тонкого
картона (три самых малых квадрата слишком малы и неудобны, так
что можно обойтись и без них). Лучшая стратегия состоит в том,
чтобы размещать вначале большие квадраты. Можете быть уверены,
что после этого останутся дырки, которые смогут заполнить
квадраты порядков 1, 2 и 3.
Начав перемещать по большому квадрату картонные
квадратики, вы вскоре почувствуете, насколько это захватывающе. Эта
задача имеет особый шарм и чем-то напоминает набивание чемодана
вещами. Только при этом требуется математическая точность.
Вначале открытое пространство с легкостью сокращается до 200
единичных квадратов, затем при значительной изобретательности
может быть уменьшено до 150 и даже меньше.
158
Нескучная математика
ДОПОЛНЕНИЕ
Задачи, представленные в этой главе, очевидно, имеют такие
аналоги, как упаковка равносторонних треугольников в равностороннем
треугольнике и упаковка кубов в большом кубе. Хотя в этих
областях мне неизвестна ни одна из работ, в варианте с треугольником
вполне применимы приемы анализа, предложенные в своих статьях
Конвеем и Трастрамом. Некоторые из читателей интересовались,
нет ли у задачи Брайттона кубического аналога. А именно:
существует ли куб, который является суммой кубов последовательных
целых чисел, начинающихся с 1? Ответ отрицательный. Нам известно,
что сочетание 3, 4, 5 — это единственный набор последовательных
целых чисел, сумма кубов которых является кубом. Дополнительно
смотрите книгу Л. Диксона History of the Theory of Numbers («История
теории чисел»).
Соломон Голомб предложил моему вниманию две задачи по
следам задачи Брайттона. Обе эти задачи не решены.
1. Существует ли квадрат пхп(п*\), для которого все квадраты
со сторонами, взятыми из ряда последовательных чисел от 1 до я,
могут покрыть большой квадрат без зазоров и наложений?
2. Можно ли покрыть плоскость квадратами со сторонами,
взятыми из ряда последовательных чисел, начиная с единицы?
Если ответ на первый вопрос отрицательный, то каков
наименьший квадрат или прямоугольник, в котором можно было бы
уложить все квадраты со сторонами из последовательного ряда от 1 до
я? В решение этого вопроса внесли вклад Конвей, Голомб и Роберт
Рейд из Лимы, Перу.
Конвей предложил для я от 1 до 17 следующую таблицу
минимальных квадратов и количество единичных квадратов,
остающихся открытыми.
п
1
2
3
4
5
6
7
8
Сторона квадрата
1
3
5
7
9
11
13
15
Избыточная
0
4
11
19
26
30
29
21
Лоскутное одеяло госпожи Перкинс
159
Сторона квадрата Избыточная площадь
9
10
11
12
13
14
15
16
17
18
21
24
27
30
33
36
39
43
39
56
70
79
81
74
56
25
64
Минимальные квадраты для п = 18 и выше неизвестны. По
оценкам Конвея, минимальный квадрат для п = 18 должен иметь
сторону 46 или 47. В квадрат со стороной 47 не так трудно упаковать эти
18 квадратов с избытком 100 единичных квадратов. Если же эти 18
квадратов упаковывать в большой квадрат со стороной 46, то
избыток составляет только 7 единичных квадратов. Это настолько мало,
что Конвей сомневается в реальности решения для стороны 46.
ОТВЕТЫ
Задача разрезания квадрата порядка 13 на 11 меньших квадратов
имеет уникальное решение, показанное на рисунке 72.
Для читателей, заинтересовавшихся исследованием квадратов
более высоких порядков, сообщу, что для случаев порядков 14-17
предполагают минимальные решения с 12 квадратами, для 18—23
Рис. 72
Решение задачи разбиения квадрата
для случая 1313
160 Нескучная математика
¦да-
РШ
1
¦Щ-
Рис. 73
Решение проблемы Брайттона по упаковке квадратов
предполагают 13 квадратов, для 24-29 - 14 квадратов и для 30-41 -
15 квадратов. Исключение составляет случай 40 квадратов,
который, как представляется, требует 16 квадратов. Конвей отмечает, что
особенно трудно было найти решение для случая 41. Все случаи
порядков больше 100 требуют самое большее 19 квадратов.
Решения для покрытия квадрата порядка 70 квадратами со
сторонами от 1 до 24 прислали почти 250 читателей. Почти все решения
имели непокрытую часть меньше 100 единичных квадратов. В 27
решениях непокрытая часть была уменьшена до 49 единичных
квадратов, что составляет ровно 1% площади. Все эти рекордные решения
оказались идентичны (если исключить повороты и отражения) в
размещении квадратов с 11 до 24 порядков (не считая того, что ме-
Лоскутное одеяло госпожи Перкинс
161
няли местами квадраты 17 и 18). Все рекордсмены единодушно
выкинули лишь один квадрат — порядка семь. Первым минимальное
решение прислал Уильям Катлер. На рисунке 73 приведено
решение, предложенное Робертом Л. Паттоном.
В 1974 Эдвард М. Рейнгольд, специалист по информатике из
университета штата Иллинойс, со своим студентом Джеймсом Бит-
нером провел исчерпывающий компьютерный анализ квадрата
порядка 70 в поисках «совершенной черепицы» из набора 24
последовательных квадратов. Поиск доказал невозможность покрытия
всеми 24 плитками. Хотя эта программа и была способна находить
максимально заполняемую плитками площадь, реально на решение
этой проблемы потребовалось бы неограниченное время.
Остается лишь гадать, можно ли уменьшить непокрытую
площадь, сделав ее меньше 49 единичных квадратов.
ГЛАВА 1 2
Гадание по числам
доктора Флисса
В Аузе я знаю замечательный лес, полный
папоротников и грибов, где вы должны раскрыть мне секреты мира
животных и мира детей. Я с нетерпением жду вашего
рассказа и надеюсь, что мир не услышит этого раньше
меня и что вместо короткой статьи вы подарите нам
через год небольшую книгу, в которой откроете секреты
периодов 23 и 28.
— ЗИГМУНД ФРЕЙД, в письме к Вильгельму Флиссу,
1897
Один из самых экстраординарных и нелепых эпизодов в истории
нумерологической псевдонауки связан с работой берлинского
хирурга Вильгельма Флисса. Флисс был одержим числами 23 и 28. Он
убедил себя и других, что в основе всех явлений живой природы, а
возможно, и неорганического мира лежат два фундаментальных
цикла: мужской цикл из 23 дней и женский из 28 дней.
Манипулируя этими двумя числами — иногда складывая, иногда вычитая их —
он был способен найти их буквально во всем. В начале XX века
большой интерес к его работе наблюдался в Германии.
Последователи продолжали разрабатывать систему и изменять ее, выпуская
многочисленные книги, брошюры и статьи. В последние годы движение
пустило корни в США.
Хотя нумерология Флисса может представить интерес для
развлекающихся математиков и собственно нумерологов, она,
вероятно, была бы уже забыта сегодня, если бы не один почти
невероятный факт — в течение 10 лет Флисс был лучшим другом Зигмунда
Фрейда. Примерно с 1890 по 1900 г., в период наибольшей творчес-
Гадание по числам доктора Флисса
163
кой активности Фрейда, который завершил публикации в 1900 году
книги «Интерпретации сновидений», они с Флиссом были связаны
странными, нервными взаимоотношениями, которые имели
сильную гомосексуальную подоплеку, что понимал и сам Фрейд. Эта
история была конечно же известна другим основателям психоанализа,
но люди, не причастные к этой сфере, ничего не слышали о ней до
публикации в 1950 году подборки писем Фрейда Флиссу. В тот год
из 284 писем, которые Флисс аккуратно сохранил, было
опубликовано 168. Впервые письма были опубликованы в Германии.
Английский перевод под названием The Origins of Psychoanalysis (Источники
психоанализа) был выпущен издательством Basic Books в 1954 году.
Фрейд был поражен, узнав, что эти письма сохранились. Он просил
их владелицу (аналитика Мэри Бонапарт) не допускать их
публикации. В ответ на ее вопрос о письмах Флисса Фрейд сказал: «Я не
знаю, уничтожил ли я их или предусмотрительно спрятал». Есть
основания полагать, что он уничтожил их. Полная история дружбы
Флисса и Фрейда описана Эрнестом Джоунсом в его биографии
Фрейда.
Когда эти двое мужчин впервые встретились в Вене 1877 году,
Фрейд, которому тогда было 31, был еще мало известен, счастливо
женат и имел довольно скромную практику в психиатрии. Флисс
работал в Берлине хирургом-отоларингологом и был гораздо более
успешен. Он был двумя годами моложе Фрейда, холост (позже он
женился на богатой женщине из Вены), красив, тщеславен,
остроумен, имел большой багаж знаний по медицине и другим наукам.
Фрейд первым начал их переписку своим лестным письмом.
Флисс ответил и прислал подарок, после чего Фрейд послал
Флиссу в ответ на его просьбу свою фотографию. К 1892 году они
перешли с официального «Sie» (по-немецки «Вы») на дружественное
«du» («ты»). Фрейд писал чаще, чем Флисс, и изводился, когда тот
медлил с ответом. Когда его жена ждала пятого ребенка, Фрейд
заявил, что его будут звать Вильгельмом.
Он бы назвал так своего ребенка и раньше, но, как отметил Джо-
унс, «к счастью, до этого у него родились две девочки».
Основы нумерологии Флисса были обнародованы в 1897 году,
когда он опубликовал свою монографию со странным названием
Die Beziehungen zwischen Nase und weibliche Geschlechtsorganen in ihrer
biologischen Bedeutungen dargestellt («Биологические аспекты
взаимосвязи носа и женских половых органов»). По утверждению Флисса,
каждый человек на самом деле двуполый. Мужская составляющая
164
Нескучная математика
управляется ритмичным 23-суточным циклом, женская - 28-суточ-
ным. (Женский цикл не надо путать с менструальным, хотя эволю-
ционно оба цикла взаимосвязаны.) У мужчин доминирует мужской
цикл, а женский — в значительной мере подавляется. У женщин все
наоборот.
Данные циклы присутствуют в каждой живой клетке и поэтому
играют свои диалектические роли в жизни любого организма. У
животных и людей оба цикла начинаются в момент рождения, пол
ребенка определяется тем циклом, который был передан первым.
Циклы продолжаются на протяжении всей жизни, проявляются во
взлетах и спадах физической и ментальной силы живого существа и
в конечном итоге определяют день его смерти. Более того, оба
цикла тесно связаны с состоянием слизистой носа. Флисс полагал, что
он обнаружил взаимосвязь раздражений слизистой носа, различных
невротических симптомов и неполадок в сексуальной сфере. Он
диагностировал подобные неполадки и заболевания, осматривая нос,
и лечил их, прикладывая кокаин к «половым точкам в носу». Он,
сообщая о случаях, когда неполадки в половой сфере были вызваны
проводимой в носу анестезией, утверждал, что посредством лечения
носа может контролировать болезненные менструации. Дважды он
оперировал нос Фрейда. Позже в своей книге он писал, что все
левши находятся во власти цикла противоположного пола. Фрейд
усомнился в справедливости этого утверждения, но Флисс заявил,
что Фрейд сам является левшой, даже не осознавая этого.
Сначала флиссовская теория циклов была расценена Фрейдом
как большой шаг вперед в биологии.
Он послал Флиссу информацию о 23- и 28-дневных периодах в
своей собственной жизни и в жизни его семьи, пытался расценивать
ухудшения и улучшения состояния своего здоровья как флуктуации
этих двух периодов. Фрейд полагал, что различие, которое он
обнаружил между неврастенией и неврозом, можно объяснить этими
двумя циклами. В 1898 году он прекратил сотрудничество с одним
журналом, потому что его редакция высказала резкую критику
относительно одной из книг Флисса и отказалась взять свои слова обратно.
Одно время Фрейд полагал, что сексуальное удовлетворение —
это высвобождение энергии 23-дневного цикла, а сексуальная
неудовлетворенность — это высвобождение энергии 28-дневного
цикла. Многие годы он думал, что умрет в возрасте 51 года, потому что
51 это сумма 23 и 28. К тому же Флисс сказал ему, что это будет его
самый критический год. «Пятьдесят один — это наиболее опасный
Гадание по числам доктора Флисса
165
возраст для человека, — написал Фрейд в своей книге о
сновидениях. — Некоторые мои коллеги совершенно неожиданно умерли в
этом возрасте. Один из них после многочисленных откладываний и
проволочек все-таки получил профессорскую степень, но это
произошло всего лишь за несколько дней до его смерти».
Принятие Фрейдом теории Флисса не показалось берлинскому
хирургу достаточно восторженным. Чрезвычайно чувствительный
даже к малейшей критике, в 1896 году Флисс узрел в одном из писем
Фрейда некоторые сомнения в построенной им системе. Это
послужило началом медленного развития скрытой враждебности с обеих
сторон. Раньше Фрейд относился к Флиссу почти как к отцу и
наставнику. Теперь же он начал разрабатывать собственные теории о
происхождении неврозов и методы их лечения. Флисс мало
разделял его идеи. Он утверждал, что предлагаемые Фрейдом методы
лечения были не чем иным, как флуктуациями умственной болезни в
повиновении мужскому и женскому ритму. Бывшие друзья явно
взяли курс на конфронтацию.
Как видно из сохранившихся писем, именно Флисс положил
начало расхождению бывших друзей. Ситуация все обострялась. Это
вызвало у Фрейда серьезный невроз, от которого он смог
избавиться только после очень длительного самоанализа. Мужчины имели
привычку часто встречаться в Вене, Берлине, Риме и в других
местах. Такие встречи Фрейд в шутку называл «конгрессами».
В 1900 году, когда трещина в отношениях была уже слишком
велика, Фрейд писал: «Не прошло еще ни одного шестимесячного
периода, чтобы я не стремился встретиться с вами и с вашей семьей...
Ваше предложение встретиться на Пасху очень взволновало меня...
Это не просто мое почти детское ожидание весны и более
красивого пейзажа; я бы охотно променял это на трехдневное пребывание
рядом с вами... Мы должны говорить разумно и с научной точки
зрения, и ваши прекрасные и меткие биологические открытия
пробудили во мне глубочайшую — хотя и неличную — зависть».
Тем не менее Фрейд не принял приглашения и мужчины
встретились только летом. Это была их последняя встреча. Флисс позже
писал, что Фрейд яростно и безосновательно нападал на него. В
течение следующих двух лет Фрейд пробовал помириться. Он
предлагал Флиссу совместную работу над книгой по
бисексуальности. В 1902 году он снова предлагал встретиться. Флисс
отклонил оба предложения. В 1904 году Флисс публично обвинил
Фрейда в том, что тот передал некоторые его идеи Герману Свободе,
166
Нескучная математика
своему молодому пациенту, который опубликовал их как свои
собственные.
Последняя ссора произошла, по всей видимости, в ресторане
«Парк-отель» в Мюнхене. Впоследствии Фрейд дважды оказывался
в этом ресторане на встречах психоаналитиков и испытывал
серьезные приступы беспокойства. Джоунс вспоминает случай,
произошедший в 1912 году, когда они с Фрейдом и Юнгом завтракали в
этом самом месте. У Фрейда и Юнга появились разногласия. Когда
мужчины начали спорить, Фрейд неожиданно упал в обморок. Юнг
отнес его на диван. «Как здорово было бы умереть», — сказал Фрейд,
когда пришел в себя. Позже он поведал Джоунсу причину
произошедшего.
Флисс написал много книг и статей о своей теории циклов, но его
главным трудом стал 584-страничный опус Der Ablauf des Lebens:
Grundlegung zur Exakten Biologie («Ритм жизни: основы точной
биологии»), изданный в Лейпциге в 1906 году (второе издание, Вена, 1923).
Основная формула Флисса может быть записана так: 23х + 28у,
где х и у — положительные или отрицательные целые числа.
Почти на каждой странице Флисс применяет эту формулу к
природным явлениям, касающимся всего: от клетки до Солнечной
системы. Например, Луна совершает оборот вокруг Земли примерно за
28 дней, полный солнечный цикл составляет почти 23 года.
Приложение книги заполнено таблицами умножения целых
чисел на 365 (количество дней в году), на 23, на 28, на 232, на 282, на
644 (произведение 23 х 28). Выделены некоторые важные
константы, например: 12167 [23 х 232], 24334 [2 х 23 х 232], 36501 [3 х 23 х
232], 21952 [28 х 282], 43904 [2 х 28 х 282] и т. д. В одной из таблиц
приведены числа от 1 до 28, выраженные разницей произведений
чисел 28 и 23 на другие целые числа [например, 13 = (21 х 28) — (25
х 23)]. В другой таблице приведены числа от 1 до 51 (23 + 28),
выраженные суммами или разностями произведений чисел 23 и 28 на
другие числа [например, 1 = (1/2 х 28) + (2 х 28) — (3 х 23)].
Фрейд во многих случаях признал, что его математические
способности были далеки от совершенства. Флисс освоил
элементарную арифметику, но не более того. Он не понял, что если заменить
числа 23 и 28 двумя другими положительными целыми числами, не
имеющими общего делителя, то можно выразить любое
положительное целое число. Немного странно, что формулу удалось так легко
приспособить для объяснения природных явлений. Это легко увидеть,
работая в качестве примера с числами 23 и 28. Сначала определим,
Гадание по числам доктора Флисса
167
каковы должны быть х и у, чтобы получилась 1. При х = 11, у = — 9,
мы получим:
(23х11) + (28х(-9)) = 1.
Посредством показанного ниже метода можно без труда
выразить любое положительное целое число.
[23 х (И х2)] + [28х(-9х2)] = 2
[23х(11хЗ)] + [28х(~9хЗ)] = 3
[23 х (И х4)] + [28х(-9х4)]=4
Как недавно показал Роланд Спрейг в своей книге головоломок,
даже если брать только положительные значения х и у, можно
выразить все положительные целые числа выше определенного значения
(целого). Какое число будет наибольшим в конечном ряду
положительных целых чисел, которые нельзя выразить с помощью этой
формулы, спрашивает Спрейг. Другими словами, каково будет
наибольшее число, которое нельзя выразить с помощью формулы 23jc +
28у, если х и у — положительные целые числа?
Фрейд в конечном итоге понял, что на первый взгляд
удивительные результаты Флисса были всего лишь очередным
нумерологическим трюком. После смерти Флисса в 1928 году (обратите внимание
на роковое 28) немецкий врач Дж. Элби опубликовал книгу, в
которой полностью опроверг нелепую теорию Флисса. Однако к тому
времени в Германии уже развился настоящий культ 23 — 28. Немало
поспособствовал этому бывший пациент Фрейда Свобода, который
прожил до 1963 года. Работая психологом в Венском университете,
он посвятил много времени исследованию флиссовской теории
циклов, много писал на эту тему. В одном из своих главных трудов,
576-страничной книге Das Siebenjahr («Один год из семи») он писал
о проведенном им изучении сотен генеалогических деревьев с
целью доказать, что такие события, как сердечные приступы, смерть,
начало серьезных заболеваний, имеют тенденцию попадать на
определенные критические дни. Эти дни можно вычислить на основе
мужского и женского циклов. Он применил теорию циклов к
анализу сновидений (хотя Фрейд в 1911 году раскритиковал в своей
книге подобное применение этой теории). Свобода также разработал
первую логарифмическую линейку, с помощью которой можно
было вычислять такие дни. Без помощи этого устройства или сложных
диаграмм производить подобные вычисления затруднительно.
168
Нескучная математика
Это может показаться невероятным, но даже в 60-х годах XX
века в Швейцарии и Германии еще находились сторонники и
почитатели теории Флисса. Доктора из нескольких швейцарских больниц
определяли благоприятные дни для проведения операций на основе
циклов Флисса. Начало этой практике положил сам Флисс. В 1925
году, когда Карлу Абрахаму, одному из основателей психоанализа,
предстояло делать операцию на желчном пузыре, он настаивал,
чтобы операция проводилась в один из благоприятных дней,
рассчитанных Флиссом.
К мужскому и женскому циклам современные последователи
Флисса добавили третий цикл, получивший название
интеллектуального. По их мнению, его продолжительность составляет 33 дня.
Швейцарской системе циклов были посвящены две книги,
выпущенные издательством Crown. Эта книга Ханса Верили Biorhythm
(«Биоритм»), изданная в 1961 году, и работа Джорджа Томмена Is
This Your Day? («Ваш ли это день?») 1964 года. Томмен является
директором фирмы, которая поставляет калькуляторы для построения
собственной таблицы циклов.
Все три цикла начинаются с момента рождения и регулярно
продолжаются на протяжении всей жизни, хотя с возрастом их
амплитуды уменьшаются. Мужской цикл управляется такими мужскими
чертами, как физическая сила, уверенность, агрессивность и
выносливость. Женский цикл управляет женскими чертами, такими как
чувственность, интуиция, творческое начало, любовь, стремление к
сотрудничеству, жизнерадостность. Недавно открытый
интеллектуальный цикл управляет умственными способностями, общими для
представителей обоих полов: интеллект, память, умение
сосредоточиваться, быстрота мышления.
В те дни, когда кривая цикла проходит выше горизонтальной
нулевой линии (оси) диаграммы, энергия, концентрируемая этим
циклом, высвобождается. Это дни наибольшей силы и
эффективности. Когда кривая цикла проходит ниже оси, энергия
накапливается. Жизнеспособность и энергичность человека в эти дни
понижена. Когда ваш мужской цикл находится высоко, а остальные
циклы низко, вы будете прекрасно справляться с физическими
задачами, но чувствительность и живость ума будут довольно слабы.
Тот день, когда высок женский цикл, а мужской — низок, идеально
подойдет, например, для посещения художественного музея, но в
такой день вы быстро утомитесь. Читатель сможет легко угадать,
какие комбинации циклов более благоприятны для различных
Гадание по числам доктора Флисса
169
жизненных событий. Я опускаю детали методов определения пола
еще не родившихся детей или установления «совместимости» двух
индивидуумов.
Самыми опасными днями считаются те, когда цикл, особенно
23-дневный или 28-дневный, пересекает горизонтальную линию.
Эти дни, когда цикл переходит из одной фазы в другую, называется
поворотными днями. Приятно, что поворотные дни 28-суточного
цикла у любого человека всегда приходятся на один и тот же день
недели, потому что этот цикл длится ровно четыре недели.
Если у вас поворотным днем 28-суточного цикла является
вторник, значит, каждый второй вторник на протяжении всей жизни
будет у вас критическим днем для женской энергии.
Естественно было бы ожидать, что при совпадении поворотных
точек двух циклов, день «вдвойне критический», а в случае трех
совпадений — «трижды критический». Книги Томмена и Верили
содержат много ритмограмм, показывающих, что дни смерти различных
знаменитых людей были днями поворотных точек двух или более
циклов. В те два дня, когда у Кларка Гэйбла были сердечные
приступы (второй из которых оказался смертельным), два цикла
находились в поворотных точках. Ага Хан умерла в трижды критический
день. Арнольд Палмер выиграл британский Открытый турнир по
гольфу во время высокого периода в июле 1962 года, а двумя
неделями позже, во время тройного спада, потерпел поражение на
профессиональном турнире по гольфу. Боксер Бенни Парет умер после
нокаута в трижды критический день. Последователям Флисса
следовало бы составить его диаграмму циклов, чтобы он мог проявлять
большую осторожность в критические дни. Однако в дело часто
вмешиваются и другие факторы, поэтому сделать предсказание со
100-процентной гарантией невозможно.
Поскольку каждый цикл имеет определенную интегральную
длину в днях, на ритмограмме каждого человека определенный
образец будет повторяться с интервалом п дней. Этот интервал будет
одинаков для всех. Например, у любого человека через п дней
после рождения все три его цикла одновременно на подъеме
пересекут нулевую линию и образец начнет повторяться снова. Два
человека, разница в возрасте у которых составляет ровно п дней, будут
жить на абсолютно синхронизированных фазах цикла. Читателям
не составит труда вычислить величину п. Это одна из важных
констант в швейцарской системе, разработанной последователями
Флисса.
170
Нескучная математика
ДОПОЛНЕНИЕ
Джордж Томмен, президент компании Biorhythm Computers,
иногда появляется на радио- и телевизионных ток-шоу, чтобы
продвигать свою продукцию. Джеймс Ранди был ведущим ночного радио-
ток-шоу.
Дважды на это шоу приглашали Том мена. Ранди рассказывал
мне, что после одного из выпусков дама из Нью-Джерси сообщила
ему дату своего рождения и попросила составить ей диаграмму ее
биоритма на следующие два года жизни. Послав ей реальную
диаграмму, но основанную на другой дате рождения, Ранди получил от
женщины восторженное письмо, в котором говорилось, что
диаграмма точно показывает все критические для нее дни. Ранди
ответил, принес извинения за то, что сделал ошибку в ее дате рождения
и приложил «правильную» диаграмму, также основанную на
неправильной дате, как и в первом случае. Вскоре он получил письмо, в
котором говорилось, что новая диаграмма даже более точная, чем
первая.
Выступая в марте 1966 года на 36-м ежегодном собрании Совета
безопасности Нью-Йорка, Томмен сообщил, что научная работа по
исследованию биоритма проводилась в университете штата
Небраска и университете штата Миннесота и что доктор Татаи,
руководитель департамента здравоохранения в Токио, опубликовал книгу
«Биоритм и человеческая жизнь» на основе системы Томмена.
Когда в феврале 1966 года в Токио разбился Boeing 727, доктор Татаи
быстро составил диаграмму пилота, утверждает Томмен, и
обнаружил, что авария пришлась на один из «низких» дней пилота.
Теория биоритма лучше прижилась в Японии, чем в США.
Согласно журналу Time от 10 января 1972 года, компания Ohmi Railway
Со. в Японии вычисляет биоритмы всех 500 водителей автобусов,
которые работают у них. Всякий раз, когда у водителя ожидается
«плохой» день, он получает предупреждение быть особенно
осторожным. Компания Ohmi сообщает о 50-процентном уменьшении
количества аварий.
В февральском номере журнала Fate за 1975 год сообщается о
конференции «Биоритм, целительство и фотосъемка ауры»,
проходивший в Эванстоне, Иллинойс, в октябре 1974 года. Майкл Заске,
который был спонсором конференции, обнаружил, что
традиционные кривые биоритма фактически являются лишь «первыми
производными» истинных кривых и что все традиционные диаграммы по-
Гадание по числам доктора Флисса
171
строены с ошибкой на несколько дней». Участники конференции
услышали также доклад, в котором говорилось о существовании
четвертого цикла и о том, что все четыре цикла «могут быть связаны
с четырьмя типами личности по Юнгу».
В журнале Science News от 18 января 1975 года размещено
большое рекламное объявление компании Edmund Scientific о новинке
Biorhythm Kit за 11,50 долларов, представляющей собой калькулятор
биоритмов. В объявлении также говорится о том, что любой
читатель, который пришлет свою дату рождения и $15,95, может
получить «точно рассчитанную персональную» диаграмму биоритма на
12 месяцев вперед. Возникает вопрос, использовала ли компания
Edmund традиционные диаграммы (с ошибкой на три дня) или
усовершенствованные по Заске.
ОТВЕТЫ
Наибольшее положительное целое число, которое не может быть
выражено суммой произведений двух неотрицательных целых чисел
а и Ь, не имеющих общих делителей, равно ab — а — Ь. В данном
случае (23 х 28) — 23 — 28 = 593. Доказательство формулы смотрите в
решении задачи 26 из книги Роланда Спрейга Recreation in Mathematics
(«Математика на досуге»).
Вторая задача состоит в том, чтобы определить, когда
биологическая диаграмма закончит полный цикл и начнет повторять тот же
самый образец. Периоды трех накладывающихся циклов
составляют 23, 28 и 33 дня. Эти числа не имеют общих делителей, поэтому
объединенный образец сможет начать повторяться только по
истечении 23 х 28 х 33 = 21 252 дней, что составляет немногим больше
58 лет. Так как система Флисса не включала 33-дневный цикл, на его
диаграммах образец будет повторяться через 23 х 28 = 644 дня.
Швейцарские последователи Флисса придавали этому периоду
особое значение. Он очень важен при расчете «биоритмической
совместимости» двух людей, т. к. два человека, разница в возрасте у
которых составляет 644 дня, синхронизованы по двум самым важным
циклам.
ГЛАВА 1 3
Случайные числа
Земля же была безвидна и пуста, и тьма над бездною,
и Дух Божий носился над водой.
БЫТИЕ, первая книга Моисея, стих 1:2
Книга A Million Random Digits with 100,000 Normal Deviates
(«Миллион случайных чисел с нормальным отклонением в 100 000») была
опубликована в 1955 году издательством Free Press, ныне входящим
в состав Macmillan. Приведенная страница состоит из
повторяющихся в различных комбинациях 10 цифр от 0 до 9. Эти цифры
организованы на странице группами по пять чисел, но сами
последовательности цифр столь хаотичны, насколько это возможно.
«Эта книга дитя двадцатого века, — писал физик Альфред Борк в
своей статье Randomness and the Twentieth Century («Хаос и двадцатый
век»), которая появилась в сборнике The Antioch Review весной 1967
года. — Она не могла появиться ни в какую другую эпоху. Я далек от
мысли, что раньше людям не позволяло сделать подобное отсутствие
необходимых знаний, но и это мнение не лишено смысла. Более
интересно то, что никогда прежде люди даже не задумывались о самой
возможности произвести на свет книгу, подобную этой. Никто преж-
деле видел ей разумного применения. Рациональный представитель
девятнадцатого века счел бы издание такое книги верхом безумия...»
Таковы были соображения Борка, озабоченного тем, что хаос все
больше проникает в культуру XX века. Однако эта проблема имела
корни в XIX веке. В первую очередь это была термодинамика, в
которой мерой хаоса выступила энтропия, а также теория эволюции, в
которой обусловленное случайными мутациями развитие
направляет естественный отбор.
В начале XX века понятие о хаосе легло в основу квантовой
механики, где неопределенность уже закладывалась изначально, причем
Случайные числа
173
в микроструктуру мира. В конечном счете может оказаться так, что
за этой неопределенностью окружающего нас мира стоят вполне
определенные законы. (Так, Эйнштейн верил, что «Бог играет в
кости».) Но в настоящее время никто не знает, как выглядят эти
законы. Если они когда-либо будут открыты, то квантовую теорию не
придется заменять на нечто иное. Борк отмечает, что влияние этих
научных идей просматривается даже в абстрактном
экспрессионизме, музыке таких композиторов, как Джон Кейдж, в случайной
игре слов таких книг, как Finnegans Wake («Поминки по Финнегану»).
Также след хаоса в искусстве мы видим в такой необычной вещи,
как перетасовывание страниц романа и публикации его в
произвольном порядке. Этим славился романист Эдгар Райе Берроуз
(1875-1950).
Возможно, некоторые художники видят в случайности спасение
от чрезмерной аккуратности современных технологий. Лорд Данса-
ни дал красивое описание (см. его рассказ о трех полусферах Tales of
Three Hemispheres) своей поездки в Нью-Йорк Сити, во время
которой он почувствовал угнетенность. Его буквально подавляла
монотонная регулярность улиц, разбивающих город на прямоугольники,
и унылые ряды окон высотных зданий. С наступлением сумерек
ночи окна хаотично начали зажигаться, оживляя картину. «Если бы
здесь приложил руку современный человек со своими умными
схемами, то единым выключателем все окна зажигались бы вместе.
Здесь же царил вольный дух, о котором рассказывают старые песни
и романы, которыми наполнены разве что горы. Вот одно окно
замерцало и погасло, а другие светят в темноту, разрушая все схемы,
которые когда-либо были созданы человеком. Мы находимся среди
огромных гор, освещенных удивительными маяками. Здесь, в Нью-
Йорке, по вечерам витает дух поэзии».
Случайный узор освещенных окон — это геометрическая аналогия
последовательности случайных цифр. Как же математически точно
определить эту последовательность? На удивление сложный вопрос.
Обычно утверждают, что конечный ряд цифр рандомизирован
(случаен), если не существует процедуры, которая бы определяла любую
неизвестную (прикрытую) цифру с вероятностью выше 1/10.
Однако это определение субъективно, и оно основывается на
нашем незнании возможных закономерностей, лежащих в основе ряда.
Существует ли какой-либо объективный способ математически
точно определить абсолютно случайную последовательность?
Очевидно, что нет. Лучшее, что мы можем сделать, это определить тес-
174
Нескучная математика
ты на различные типы хаотичности и называть ряд случайным в той
мере, в какой он проходит эти тесты. Например, можно
потребовать, чтобы ряд подчинялся следующим формальным критериям.
Каждая цифра (элементарная единица ряда) должна появляться с
частотой 1/10, каждое сочетание двух отдельных цифр — с частотой
1/100, трех цифр — 1/1000 и т. д. Дуплеты, тройки, квартеты и т.д. не
обязательно берутся из соседних цифр. При испытании на
хаотичность тройки цифр, скажем, могут браться с любыми заданными
интервалами.
Если бесконечные десятичные дроби в интервале от 0 до 1
удовлетворяют этим требованиям (на практике подобное испытание
потребовало бы бесконечное время), то говорят о «нормально
распределенных числах». Очевидно, что любая рациональная дробь в
десятичном выражении не является нормальной. Это бесконечно
повторяющаяся последовательность нескольких цифр (как в случае с
1/97, где повторяется последовательность 96 цифр) либо одной
цифры (как в случае с 1/3, где повторяется тройка). А иррациональные
числа в десятичном выражении, например 2 или знаменитые
константы к и е, считаются нормальными. Последние относятся к
трансцендентальным числам и прошли все тесты «на
нормальность». (Трансцендентальные числа являются подмножеством
иррациональных чисел и не могут быть корнями алгебраического
уравнения, появляются в пределе бесконечного сходящегося ряда.)
Было доказано, что среди бесконечного количества десятичных
дробей в диапазоне от 0 до 1 дробей с нормальным распределением
цифр бесконечно больше, чем рациональных. Выберите случайным
образом десятичную дробь, и вы получите нулевую вероятность
(здесь понятие вероятности используется в специфическом смысле)
того, что это будет дробь, распределение цифр в которой не
подчиняется нормальному. Можно ли тогда утверждать, что нормально
распределенная последовательность цифр десятичной дроби
действительно случайна? Не обязательно. Поместите десятичную точку
перед первым миллионом цифр случайно выбранной дроби, и вы
опять будете в начале бесконечной последовательности нормально
распределенных цифр.
С другой стороны, десятичная запись числа л, для которого в
1974 году было вычислено миллион знаков, прошла все проверки на
нормальность, но п все равно нельзя назвать случайной
последовательностью, поскольку оно может быть построено алгебраически в
виде простого предела. Каждая следующая цифра числа к предска-
Случайные числа
175
зуема. Следовательно, это число является высокоорганизованным,
хотя и не имеет никакой заметной регулярности.
Некоторые читатели, наверное, удивятся, узнав, что
бесконечную десятичную дробь, являющуюся иррациональной, но
имеющую очевидную закономерность, построить не так уж сложно. Вот
простой пример, как это сделать с помощью только нулей и единиц:
0,101001000100001000001...
Здесь первая единица сопровождается одним нулем, вторая —
двумя нулями, третья — тремя и т. д. Поскольку нет никакой
повторяющейся последовательности, число иррационально. Это лишь
один из множества способов записи иррациональных дробей с
простой регулярностью.
Многие числа со скрытыми последовательностями подобного
рода могут даже оказаться трансцендентальными. Действительно,
первое доказательство того, что существуют «особые» числа, дал в
XIX веке французский математик Джозеф Лиувилль, который
нашел бесконечное множество таких чисел. Их трансцендентальная
природа доказана этим математиком, и они в настоящее время
носят его имя. Интересный пример числа, которое, как было
доказано, является трансцендентальным и его цифры распределены
нормальным образом, однако все же подчиняющимся простой
закономерности, приведен ниже:
0,12345678910111213141516171819...
В настоящее время большинство математиков соглашается с тем,
что абсолютно случайная последовательность цифр — это логически
противоречивая концепция. Нет ничего более бессистемного, чем
расположение звезд на небосклоне. В обоих случаях причина
состоит в том, что последовательность цифр или точек, которая
приближается все ближе и ближе к соответствию всем тестам на
хаотичность, начинает демонстрировать очень редкий и необычный тип
статистической регулярности, которая в некоторых случаях даже
позволяет предсказывать отсутствующие части.
Для простоты предположим, что нас попросили заполнить ряд из
10 разрядов (10 цифр), причем совершенно случайным образом. Если
вы повторите одну или более цифр, то эта последовательность будет
упорядоченной, поскольку в ней будет перекос в сторону той или иной
176
Нескучная математика
цифры. Но с другой стороны, если ваш ряд не будет содержать никаких
перекосов, то он будет содержать каждую из 10 цифр. Да, такой ряд
абсолютно удовлетворил бы требование того, чтобы не было перекоса в
пользу какой-либо цифры. Но цена этого такова, что ряд получается
строго «упорядоченным» в том смысле, что содержит каждую из 10
цифр. Отсутствующую цифру вы можете восстановить со
стопроцентной вероятностью. Подобные противоречия возникают в связи с
любым случайным рядом цифр. Если он становится «слишком»
случайным, то можно уже говорить о своеобразном «рисунке хаоса».
Здесь мы сталкиваемся с любопытным парадоксом. Чем ближе
мы подходим к абсолютно хаотичному ряду, тем скорее получим ту
редкую закономерность, которую вряд ли получили бы, если бы
строили ряд более тщательно с математической точки зрения. Мы
можем говорить о случайном ряде цифр только в том смысле, что он
демонстрирует высокую степень хаотичности в тех или иных тестах
(вполне конкретных). При применении других тестов хаотичность
не гарантирована.
В этом разделе математики очень много подводных камней.
Спенсер Браун в своей книге Probability and Scientific Inference
(«Научные основы вероятности»), рассказал о некоторых глубоких
парадоксах и показал, как можно с легкостью взять таблицу случайных
чисел и найти в них порядок определенного вида, даже если эти
таблицы выглядят совершенно случайными. Многие из тестов на
экстрасенсорное восприятие, по мнению Брауна, являются примерами
закономерностей, которые неизбежно появляются в любом
достаточно длинном ряде случайных чисел. Если бы подобные
закономерности не возникали, то издатели тестов на экстрасенсорное
восприятие остались бы без работы. Если же, по мнению этих
издателей, закономерность есть, то имеет смысл и сам тест. Возможно,
если бы можно было увидеть картину полностью, то публикуемые
последовательности цифр на ее фоне стали бы менее удивительны.
Теперь я хочу объявить перерыв в курсе теории и предлагаю
читателю изучить следующую с виду бессистемную
последовательность из 10 цифр:
7480631952.
Каким правилом задается эта последовательность? Намек:
ищите цикл. Представьте себе, что начало и конец ряда соединены в
круговую последовательность.
Случайные числа
177
Конечно же нельзя исключать появление такой или любой
другой организованной последовательности из 10 цифр в наборе,
скажем, из миллиона случайных цифр. Если ряд случайных цифр
достаточно длинный, в нем должны появляться такие удивительные
последовательности. По утверждению философов некоторых школ,
в этом суть Вселенной: случайный островок порядка в бесконечном
море хаоса. Хорхе Луис Борхес придумал на эту тему короткий
метафорический рассказ под названием The Library of Babel
(«Библиотека в Вавилонской башне»). Суть мира в самых бессмысленных
сочетаниях базовых блоков нашего мира. Небольшое пятно
случайного порядка, которое является нашей Вселенной, чем-то напоминает
последовательность 123456789 в бесконечном ряде случайных цифр.
Здесь возникает древний философский софизм. Так почему же
сочетание типа 123456789 в таблице случайных чисел вызывает
«удивление»? Ведь оно не более и не менее вероятно, чем любая
другая комбинация девяти цифр. Прагматики и субъективные
идеалисты утверждают, что само понятие «порядка» или «закономерности»
не может быть определено исключительно через опыт человека.
Единственное основание, по которому мы можем утверждать, что
первый миллион десятичных знаков числа упорядочен, а
рандомизированная последовательность миллиона цифр случайна, в том,
что число — это удобная для человека константа.
«Порядок и хаос, — писал Уильям Джеймс в своем трактате
Varieties of Religious Experience («Формы проявления религиозного
опыта», кстати, позже автор сменил точку зрения), — это не что
иное, как изобретения человека. Если бы я раскидал по столу
тысячу бобов, то, несомненно, убрав часть из них, мог бы составить
практически любой геометрический узор на ваш выбор, и вы могли
бы мне возразить, что в основу этого образца лег существовавший
прежде прототип, для которого все остальные бобы были просто
упаковочным материалом.
Отношение к природе у нас во многом похожее. Для нас это
всего лишь огромная выставка картин, галереи которой тянутся,
порой теряя след, в самых различных направлениях. Некоторые из
этих галерей мы выделяем особо и даем им имена, в то время как
многие другие нами не только никак не называются, но и не пере-
считываются».
На все эти аргументы материалист ответит диаметрально
противоположно. Вместо мозга, который видит в природе собственные
закономерности, они признают иное. При рождении мозг — это
178
Нескучная математика
лишь запутанная сеть случайных связей. Способным «видеть» он
становится только после нескольких лет приобретения опыта,
который в соответствии с внешним окружением наносит свои
представления о порядке на tabula rasa (чистая доска —лат.). Конечно,
верно, что люди поражаются последовательности 123456789 в ряде
случайных цифр, потому что такая последовательность определена
математиками и используется в счете. Но в том, что эти
последовательности соответствуют структуре внешнего мира, есть свой смысл. В
далеком прошлом, до зарождения жизни, Луна уже накручивала
обороты вокруг Земли, вне зависимости от того, мог ли считать
человек их или нет. Во всяком случае, на языке науки, да и на бытовом
языке, это звучит более чем естественно. Что касается меня, то
такая формулировка только запутывает результаты исследований, в
которых пытаются приспособить язык для описания нашей
Вселенной. Ведь мы не можем говорить о ее закономерностях, которые
находятся за пределами наших наблюдений.
Давайте вернемся к менее метафизическому вопросу. Как
генерируют таблицы случайных чисел? Не имеет смысла наугад
записывать цифры. В таком ряду будет слишком много перекосов. Можно
было бы взять таблицу, скажем, логарифмов или демографический
справочник с городами Америки в алфавитном порядке и
выписывать первые цифры чисел. Однако лет двадцать назад было
обнаружено, что первые цифры любой случайно выбранной
последовательности чисел имеют определенный перекос. Чем меньше
значение цифры, тем чаще она встречается в таблице! Уоррен Вивер
прекрасно показал этот факт на страницах своей книги Lady Luck: The
Theory of Probability («Госпожа удача и теория вероятностей»).
Получить ряд случайных чисел можно с помощью физического
процесса, вовлекающего так много переменных, что следующую
цифру невозможно предсказать с вероятностью выше ]/п, где п —
основание используемой системы счисления. Подбрасывание
монетки дает случайный двоичный ряд (или бинарный). Идеальный
игральный кубик дает рандомизированную последовательность из
шести символов. Волчок с десятью положениями или игральная
кость в виде икосаэдра, у которой каждая цифра дважды появляется
на 20 ее гранях, даст случайную последовательность из 10 цифр.
Правильный додекаэдр — превосходный генератор случайных чисел
для 12-ричной системы счисления (в ней 12 цифр). Можно даже
спуститься на уровень квантовой механики и взять за основу
показания счетчика Гейгера, регистрирующего радиационный фон.
Случайные числа
179
Существует много других «генераторов» случайных чисел. В 1927
году Л. Типпет опубликовал таблицу из 41 600 случайных чисел,
просто взяв значения площадей графств Англии. В 1939 году была
опубликована таблица случайных чисел из 100 000 цифр авторов М. Кен-
далла и Бабингтона Смита. Они воспользовались рулеткой, на
внешнем ободе которой было 10 секторов. Колесо вращалось без
остановки, освещаемое стробоскопическим источником света. Те цифры,
которые высвечивались, записывали. В 1949 году Национальная
торговая комиссия США опубликовала 105 000 случайных цифр, взятых
из накладных на грузы. Случайные последовательности длиной
более одного миллиона знаков получали с помощью электронных
импульсов, генерировавших случайные двоичные числа, которые затем
преобразовывались в десятичные. Чтобы устранить небольшие
перекосы в последовательности цифр, обнаруженные углубленным
тестированием, этот первый миллион рандомизировался и дальше
путем парного сложения и отбрасывания десятков.
Когда компьютеру для решения задачи нужны случайные числа,
дешевле оказывается воспроизвести собственный случайный ряд, а
не занимать дорогостоящие модули памяти табличными
значениями. Существуют сотни способов получения на компьютере так
называемых «псевдослучайных» последовательностей. Вычисление
цифр числа или квадратного корня из трех, в силу своей малой
производительности и высоких требований к объемам оперативной
памяти, не самый лучший метод. Самая первая процедура была
предложена еще Джоном фон Нейманом и называлась она «метод
середины квадрата». Компьютер начинает с числа из п цифр, возводит
его в квадрат, берет средние п или (п + 1) цифр результата (это и
будет следующей итерацией), возводит его в квадрат и так далее.
Этот метод больше не используется, потому что с его помощью
можно получить только короткие последовательности, а также
потому, что в них обнаруживаются слишком серьезные перекосы. Бир-
гер Дженсон в своей книге 1966 года Random Number Generators
(«Генератор случайных чисел») обращает внимание на некоторые
забавные аномалии алгоритма. Если вы начнете с числа 3792 и возведете
его в квадрат, то получите 14379264 и ваш «случайный» ряд будет
выглядеть так: 3792 3792 3792... Тот же эффект получается, если вы
начнете с чисел 495475 или 971582. Современные методы генерации
псевдослучайных чисел шагнули далеко вперед и стали
фантастически производительными. Случайный ряд меняется в зависимости от
компьютера, производящего вычисления.
180
Нескучная математика
Не могу не сказать заключительное слово о все более важных
приложениях случайных чисел. Так, без случайных чисел.не обойтись
при планировании экспериментов в сельском хозяйстве, медицине и
других областях, где некоторые из переменных должны рандомизи-
роваться, чтобы обеспечить объективность. Случайные числа
используются в игровой индустрии и теории конфликтов, где лучшая
игра достигается порой хаотичным сочетанием различных стратегий.
Но прежде всего без случайных чисел не обойтись при
моделировании сложных физических процессов, в которых главную роль играют
случайные события. Как писал Роберт Конвей, математик из Ок-
риджской национальной лаборатории, «процесс генерации
случайных чисел слишком важен, чтобы пускать его по случайному руслу».
ДОПОЛНЕНИЕ
Одна из наиболее перспективных попыток дать точное определение
«случайной», или «бессистемной», последовательности цифр была
предпринята независимым образом Колмогоровым в 1965 году
(Россия) и Чайтиным в 1966 году (компания IBM). По сути, степень
случайности для последовательности цифр определяется длиной
самого короткого возможного компьютерного алгоритма,
управляющего машиной Тьюринга (идеальный исполнитель операций с
цифрами), задача которой воспроизвести эту последовательность.
Если последовательность состоит из к битов, то она может быть
получена вводом к или меньшего количества битов.
Чем больше степень упорядоченности цифр, тем меньше будет
объем программы. Если последовательность высокоупорядоченная,
типа 12121212, то она может быть получена программой намного
более короткой, чего мы не наблюдаем в случае произвольных
восьми цифр, взятых из таблицы случайных величин. Если же для
последовательности требуется программа максимальной длины, то в
такой последовательности нет никакого порядка и, соответственно,
не существует способа программу сократить. Степень
беспорядочности цепочки чисел измеряется длиной самой короткой
программы, которая воспроизводит эту последовательность. Да, никакая
конечная последовательность цифр не может быть абсолютно
бессистемна, но ведь мы говорим об абсолютном беспорядке как о
предельной концепции. К пределу беспорядка может быть
чрезвычайно близка очень длинная последовательность цифр, полученная
хорошим генератором случайных чисел.
Случайные числа
181
Если вас заинтересовал подобный подход к случайным
величинам, можно обратиться к популярному изложению Чайтина в
докладе Information-Theoretic Computational Complexity («Теоретическая
оценка сложности вычислений») из материалов конференции
Transactions on Information Theory («Транзакции в теории
информатики»), том 20, январь, 1974, с. 10—15, а также The Definition of Random
Sequences («Определение случайной последовательности»), том 9,
1966, с. 602-619. Также обратите внимание на книгу Терри Файна
1973 года Theories ofProbability: An Examination of Foundations («Теория
вероятностей: пересмотр основ»).
Важно иметь в виду, что само слово «случайный» используется,
чтобы описывать любую последовательность, полученную
генератором случайных чисел, иногда оно также используется, чтобы
описывать состояние отсутствия порядка в данной последовательности.
Это далеко не синонимы. Например, если вы шесть раз подбросите
монетку и все шесть раз выпадет орел, то этот ряд случаен в том
смысле этого слова, что сочетание шести орлов подряд столь же
вероятная комбинация, что и все остальные. Но порядок в ней
налицо. С точки же зрения машины Тьюринга можно лишь определить
степень беспорядка в плане приближения к абсолютному хаосу. Но
она мало помогает в генерации случайных чисел.
Ян Вуд из Лондона не согласен с моим утверждением, что
«Поминки по Финнегану» сдержат много случайной игры слов.
«Каждое слово этого романа, — пишет Вуд, — является плодом труда
осмотрительного Джойса».
ОТВЕТЫ
Задача состоит в том, чтобы найти правило для циклического
расположения 10 цифр в последовательности 7480631952. Начиная
слева, отсчитывайте цифры и произносите по буквам zero (ноль).
Слово закончится на нуле. Эту цифру вам необходимо вычеркнуть.
Продолжите для единицы (one), соответственно вычеркнув цифру 1.
Аналогично продолжайте с другими цифрами, записывая цифры
английскими словами и считая только оставшиеся в ряду цифры.
Не забывайте, что ряд замкнутый. Всякий раз вы будете заканчивать
на соответствующей цифре. В этом ряду спрятаны числа от нуля до
девяти в возрастающем порядке.
Набор игральных карт также можно разложить таким образом,
чтобы каждая карта могла быть найдена> если, проговаривая ее по
182
Нескучная математика
буквам, перемещать карты по одной .сверху вниз колоды. Тогда,
заканчивая называть карту, вы открываете ее. Такое расположение
карт сконструировать довольно просто, если применить процедуру
«движения в прошлое». Вы берете карты из колоды по одной в
противоположном порядке и формируете колоду в руке, перемещая
карты по одной снизу вверх колоды, каждый раз называя букву.
Чтобы проверить эту простую процедуру читатель может взять полную
колоду и сложить ее так, чтобы каждая карта «называла» свое
местоположение — начиная с туза пик и продолжая двойкой пик. За
пиками последуют другие масти в определенном порядке, и
завершится все, скажем, бубновым королем и джокером.
Многие читатели вполне корректно указывают на то, что побук-
венное произнесение цифр — это лишь одна из процедур, дающих
циклическую последовательность 7480631952. Любая подобная
вереница цифр может быть воспроизведена бесконечным набором
правил. Хотя чем длиннее последовательность, тем сложнее
правила. Если мы будем рассматривать 7480631952 как единое число, то
можно найти бесконечное количество уравнений, для которых оно
было бы решением. Хотя вряд ли они были бы простыми.
Поместите перед числом запятую, и вы получите начало бесконечного
множества десятичных дробей, каждая из которых является решением
бесконечного количества уравнений. Действительно, 0,7480631952
можно очень точно выразить так: л/10 — V2.
Мисс Майрон Милбауэр из Вилмингтона, Делавэр, обнаружила
удивительно простой способ сгенерировать последовательность
7480631952. Напишите 9 цифр треугольником:
1
2 3
4 5 6
7 8 9 0
У треугольника четыре диагонали, которые идут в
северо-западном и юго-восточном направлении (считается, что север вверху
страницы). Двигаясь налево, опуститесь вниз на две диагонали, и вы
получите 7 (первая диагональ), затем идет диагональ 4, 8.
Прибавьте к ним две следующие диагонали, беря их в обратном порядке
справа налево и вверх. Так вы получите 0, 6, 3, 1 и 9, 5, 2.
Удивительное совпадение!
ГЛАВА 1 4
Парадоксальные песочные часы
и другие физические головоломки
Задачи, которые приведены ниже, не являются математическими в
прямом смысле этого слова. При решении этих задач потребуется
логическое мышление и определенные знания законов физики (в
большинстве случаев элементарные). Так что эти задания можно
было бы даже назвать физическими головоломками. В нескольких
случаях вопросы сформулированы так, чтобы запутать читателя.
Однако все решения — серьезные. Шуточные варианты,
основанные на игре слов, исключаются. Я хочу поблагодарить Дэвида Эй-
зендрата-младшего, Джона Харта, Джерома Сални, Дейва Фальтца
и Дерека Вернера за задачи 2, 12, 15, 18 и 23.
1. 200 ГОЛУБЕЙ
В этой старой истории рассказывается о водителе, который
остановил свой крытый грузовик у небольшого шаткого мосточка, вышел
из машины и начал хлопать в ладоши у боковых сторон заднего
отсека грузовика. Фермер, стоявший на обочине дороги,
поинтересовался у водителя, зачем он это делает.
«Я везу в грузовике 200 голубей, — начал объяснять водитель. —
Это довольно большой вес. Своими хлопками я напугаю птиц, и они
начнут летать внутри. Это сделает вес груза значительно меньше.
Мостик выглядит ненадежным. Я хочу, чтобы голуби были в
воздухе, пока я буду переправляться через него».
Если исходить из того, что задний отсек грузовика плотно
закрыт, что можно сказать о рассуждениях водителя?
2. ПАРАДОКСАЛЬНЫЕ ПЕСОЧНЫЕ ЧАСЫ
В парижских магазинах можно найти в продаже необычную
игрушку — стеклянный цилиндр, заполненный водой, наверху которой
184
Нескучная математика
Рис. 74
Парадоксальные песочные часы
плавают песочные часы (см. рис. 74). Если цилиндр перевернуть,
как показано на рисунке справа, наблюдается любопытное явление.
Песочные часы остаются у основания цилиндра, пока
определенное количество песка не пересыпется в нижний отсек, затем они
начинают медленно подниматься наверх. Кажется невозможным,
чтобы просто перенос песка сверху вниз оказывал какой-либо
эффект на плавучесть часов. Можете ли вы объяснить, в чем тут дело?
Парадоксальные песочные часы
185
3. ЖЕЛЕЗНЫЙ ПОНЧИК
Кусок твердого железа в форме пончика нагревают. Станет ли
диаметр его отверстия больше или он уменьшится?
4. ПОДВЕШЕННАЯ ПОДКОВА
Из тонкого картона вырезают подкову, высота которой немного
больше высоты зубочистки (см. рис. 75). Установите подкову на
столе, наклонив и оперев ее на зубочистку, как показано на рисунке.
Ваша задача - поднять подкову и зубочистку с помощью второй
зубочистки, которую вы будете держать в руке. Вы не должны
касаться подковы или зубочистки, на которую она опирается, ничем,
кроме второй зубочистки. Вы конечно же не можете сломать
зубочистку и использовать ее части подобно палочкам для еды. Оба объекта
должны быть подняты вместе и висеть над столом. Как это сделать?
5. ПОПЛАВОК В ЦЕНТРЕ
Заполните стакан водой и опустите на поверхность воды маленький
поплавок. Он будет плавать у одной из сторон стакана, касаясь
стекла. Как можно заставить поплавок постоянно плавать в центре? В
стакане не должно быть ничего, кроме воды и поплавка.
6. МАСЛО И УКСУС
Однажды друзья собрались на пикник. «Ты взял масло и уксус для
салата?» - спросила миссис Смит у своего мужа.
Рис. 75
Подкова и зубочистка
186
Нескучная математика
«Да, — ответил мистер Смит. — И чтобы не нести две бутылки, я
налил масло и уксус в одну».
«Но это же глупо, — начала возмущаться миссис Смит. - Я
люблю много масла и мало уксуса, а Генриетта наоборот».
«Это совсем не глупо, моя дорогая», — прервал ее мистер Смит.
Он заверил жену, что нальет из одной бутылки ровно столько масла
и уксуса, сколько кому нужно. Как он сделает это?
7. ЭКИПАЖ КЭРРОЛЛА
В седьмой главе книги Льюиса Кэрролла, увидевшей свет в 1893
году Sylvie and Bruno Concluded («Заключение Сильвии и Бруно»),
немецкий профессор объясняет, что людям в его стране, чтобы
покачаться на волнах, не нужно ехать на море. Мы достигаем того же
эффекта, заменяя у телег круглые колеса овальными. Его
собеседник, Граф, заметил, что может себе представить, что овальные
колеса раскачивают телегу. «Но как они могут катиться вперед?» —
спросил он.
«Боже мой, но они же развернуты! — воскликнул профессор. —
Вытянутая часть одного колеса соответствует боковой части
противоположного колеса. Тогда вначале поднимается один бок, затем
другой. Необходимо быть хорошим моряком, чтобы ездить на
наших телегах!»
Можно ли расположить четыре овальных колеса телеги так,
чтобы она качалась и при этом ехала, как описывал профессор?
На рисунке 76 даже приведена иллюстрация и стихотворное
описание Гелетта Баргесса из The Purple Cow and Other Nonsense
(«Фиолетовая корова и другие небылицы»). Не исключено, что поэта
вдохновила телега Льюиса Кэрролла.
8. ОПРЕДЕЛЕНИЕ МАГНИТА
Вы оказались заперты в комнате, где нет никаких металлических
предметов (в том числе и на вас самих нет никакого металла),
кроме двух идентичных железных брусков. Один из них намагничен,
второй — нет. Вы можете определить, какой из них является
магнитом, подвешивая их на нитке, привязанной по центру, и
наблюдая, какой брусок будет указывать на север. Есть ли более простой
способ?
Парадоксальные песочные часы
187
Рис. 76
9. ТАЮЩИЙ КУБИК ЛЬДА
В стакане с водой плавает кубик льда, общая температура системы —
О °С. Не изменяя температуру системы, ей дали тепла ровно на
столько, чтобы растопить кубик. Уровень воды в стакане
увеличится или останется прежним?
10. КРАЖА ВЕРЕВОК
На колокольне две толстые колокольные веревки проходят через
небольшие отверстия в высоком потолке на расстоянии примерно
188
Нескучная математика
30 см друг от друга и тянутся до самого пола. Придя в колокольню,
опытный акробат, имеющий с собой нож и огромное желание
украсть эти веревки, причем как можно большей длины,
обнаруживает, что лестница, ведущая до самого потолка, спрятана за закрытой
дверью. Никаких подставок и других предметов, на которые можно
встать, также нет. Акробату остается только одна возможность —
лезть по веревке на руках и обрезать их настолько высоко,
насколько это возможно. Однако потолок очень высокий, и падение даже с
одной трети такой высоты может быть смертельно опасным. Что
ему нужно сделать, чтобы получить максимальное количество
веревки?
11. ПЕРЕМЕЩЕНИЕ ТЕНИ
Человек, идущий ночью по тротуару с постоянной скоростью,
проходит мимо фонаря. Когда его тень становится длиннее, вершина
тени двигается быстрее, медленнее или с такой же скоростью, чем
когда его тень становится короче?
Рис. 77
Парадокс садового шланга
Парадоксальные песочные часы
189
12. НАМОТАННЫЙ ШЛАНГ
Садовый шланг, намотанный на катушку диаметром примерно 1 фут
(~ 30 см), лежит на скамье таким образом, как показано на рис. 77.
Один конец шланга свисает вниз, а другой конец раскручен и
поднят на несколько футов выше катушки. Шланг пустой, в нем нет
никаких петель или препятствий. Если заливать воду в верхний конец
шланга с помощью воронки, то можно было бы ожидать, что в
конце концов вода выльется из нижнего конца шланга. Однако по мере
наливания воды увеличивается ее уровень в поднятом конце
шланга, пока она не начинает вытекать из воронки. С другого конца
шланга вода никогда литься не будет. Объясните.
13. ЯЙЦО В БУТЫЛКЕ
Если вы захотите втолкнуть через горлышко в стеклянную бутылку из-
под молока очищенное сваренное вкрутую яйцо, то не сможете сделать
этого, потому что этому будет препятствовать воздух, находящийся в
бутылке. Однако, если вы кинете в бутылку кусочек горящей бумаги
или пару зажженных спичек, прежде чем поставить яйцо на горлышко
(конечно же вертикально), горение будет нагревать и расширять
воздух. Когда же воздух охладится, образуется частичный вакуум, который
и затянет яйцо в бутылку. Но тут сам собой встает второй вопрос. Как,
не разбив бутылку и не повреждая яйцо, извлечь его наружу?
14. ПЛАСТМАССОВАЯ ЛОДКА В ВАННОЙ
Маленький мальчик катает в ванной пластмассовую лодочку,
которая заполнена всякой всячиной. Если он высыплет весь этот груз в
воду, чтобы лодочка плавала пустая, то уровень воды в ванне
поднимется или опустится?
15. ВОЗДУШНЫЙ ШАР В АВТОМОБИЛЕ
Семья едет в автомобиле в холодный день. Все вентиляционные
отверстия и окна автомобиля закрыты. Ребенок, сидящий на заднем
сиденье, держит за ниточку шарик, надутый гелием. Шарик плавает
в воздухе под самой крышей автомобиля. Когда автомобиль будет
ускоряться, что произойдет с шариком: он останется на прежнем
месте, сдвинется назад или вперед? Как шарик будет вести себя,
когда автомобиль начнет двигаться по круговой траектории?
190
Нескучная математика
16. ПОЛАЯ ЛУНА
Когда-то было высказано предположение, что в далеком будущем
станет возможным опустошить большой астероид или Луну и
использовать полое космическое тело как огромную космическую
станцию. Предположим, что такой полый астероид будет
совершенной невращающейся сферой со стенками одинаковой
толщины. Если поместить в эту сферу недалеко от стенок какой-либо
объект, он будет притягиваться гравитационным полем к стенкам
или к центру астероида? Или будет постоянно находиться на
одном месте?
17. ПТИЦА НА ЛУНЕ
Предположим, что у птицы есть за спиной маленький, легкий
баллон с кислородом, благодаря чему она сможет дышать, находясь на
Луне. Как известно, на Луне сила притяжения меньше, чем на
Земле. Скорость полета птицы на Луне будет больше, меньше или
останется такой же, как на Земле? Исходим из того, что в обоих случаях
птица несет на себе одинаковое оборудование.
18. КАМЕРА КОМПТОНА
На рис. 78 показано малоизвестное изобретение физика Артура
Холи Комптона. Стеклянный тор диаметром в несколько футов
полностью заполнен мелкодисперсной суспензией. Камера находится в
покое, пока в ней не прекратится движение жидкости, затем ее
быстро переворачивают на 180 градусов относительно горизонтальной
оси. Рассматривая взвешенные частицы в микроскоп, можно ли
определить, движется ли жидкость внутри тора?
Предположим, что камера ориентирована таким образом, что
ее вертикальная плоскость располагается с запада на восток. Так
как Земля вращается против часовой стрелки (если смотреть
сверху со стороны Северного полюса), жидкость вверху камеры
движется быстрее, чем внизу (она проходит круговой путь по
большему диаметру). Переворачивание камеры переносит жидкость,
движущуюся быстрее, вниз, создавая очень слабую циркуляцию по
часовой стрелке. Сила вращения уменьшается по мере отклонения
плоскости камеры от западно-восточного направления и
достигает нуля, когда плоскость повернута в направлении север-юг.
Исходя из этого, можно доказать, что Земля вращается, и определить
Парадоксальные песочные часы
191
направление вращения, просто устанавливая камеру в различных
направлениях и переворачивая ее, чтобы найти, где скорость
вращения максимальна.
В реальных условиях вязкость жидкости останавливает ее
циркуляцию примерно через 20 секунд или около того. Если
предположить, что камера находится на экваторе, располагается в западно-
восточном направлении и в ней совсем нет трения, за какое время
частицы жидкости совершат один оборот в камере после ее
переворота?
19. РЫБНАЯ ЗАДАЧА
Емкость, на две трети заполненная водой, стоит на весах. Если
положить в воду живую рыбку, весы покажут, что вес емкости
увеличился ровно на вес рыбы. Предположим, однако, что вы
держите рыбу за хвост и опускаете ее в воду так, чтобы над водой
оставался только кончик хвоста. Станут ли показания весов
более, чем те, что были зарегистрированы до того, как вы опустили
туда рыбку?
Рис. 78
Камера Комптона
192
Нескучная математика
20. ПАРАДОКС ВЕЛОСИПЕДА
Веревка привязана к педали велосипеда, как показано на рис. 79.
Если один человек тянет веревку назад, а другой слегка
придерживает велосипед за сиденье, чтобы он не потерял равновесие, куда
будет двигаться велосипед: назад, вперед или не будет двигаться
вообще?
21. ИНЕРЦИОННОЕ ДВИЖЕНИЕ
Если привязать к корме шлюпки веревку, сможет ли человек, стоящий
в лодке, заставить ее двигаться вперед в стоячей воде, дергая за
свободный конец веревки? Может ли космическая капсула, дрейфующая в
межпланетном пространстве, передвигаться подобным образом?
22. ЦЕНА ЗОЛОТА
Что стоит дороже — фунт золотых десятидолларовых монет или
полфунта золотых двадцатидолларовых монет?
23. ПАРАДОКС ВЫКЛЮЧАТЕЛЕЙ
Интересующая нас электрическая цепь состоит из двух маленьких
110-вольтных лампочек и двух выключателей. Для того чтобы
различать лампочки, предпочтительно, чтобы одна была матовая (назовем
ее А), другая — прозрачная (соответственно, В). Вся схема
соединяется с обычной розеткой, дающей переменный ток (см. рис. 80).
Рис. 79
Парадокс велосипеда
Парадоксальные песочные часы
193
Рис. 80
Парадокс выключателей
Когда оба выключателя включены, обе лампочки светятся. Как и
следовало ожидать, если одну лампочку вывинтить, другая гореть не
будет. Когда оба выключателя включены, обе лампочки светятся.
Когда выключены, не светятся обе. Если выключатель А включен, а. В —
выключен, светится только лампочка А. И наоборот. Короче говоря,
каждый выключатель независимо управляет соответствующей
лампочкой. Но если поменять лампочки местами, выключатель А все еще
будет контролировать лампочку А, а выключатель В — лампочку В. В
деревянном основании, на котором крепятся выключатели, патроны
лампочек и провод, ничего другого нет. В чем секрет этой цепи?
ОТВЕТЫ
1. Водитель грузовика не прав. Вес закрытого заднего отсека, в
котором находятся птицы, равен весу самого отсека в сумме с весом
птиц. Вес закрытого заднего отсека изменяется лишь в том случае,
если птицы находятся в воздухе и совершают вертикальное
движение с ускорением. Движение с ускорением вниз уменьшает вес
системы, движение с ускорением вверх увеличивает его. Если птица
находится в свободном падении, вес системы уменьшается на полный
вес птицы. Две сотни птиц, хаотично летающие внутри заднего
отсека, могут вызывать незначительные, минутные колебания веса, но
общий вес системы будет оставаться фактически постоянным.
194
Нескучная математика
2. Когда песок находится в верхней части песочных часов,
высокое положение центра тяжести заставляет часы немного
накреняться на одну сторону. В результате возникает трение между цилиндром
и часами. Силы этого трения достаточно, чтобы удерживать часы
внизу. Когда определенное количество песка пересыпается вниз,
песочные часы встанут вертикально и трение пропадет, из-за чего
часы начнут подниматься.
Если песочные часы немного тяжелее, чем вода, которую они
вытесняют, игрушка работает наоборот. То есть в нормальном
состоянии часы находятся у основания цилиндра. Когда его
переворачивают, часы какое-то время остаются наверху, начиная
опускаться лишь после того, как перемещение песка устраняет
трение.
В парижских магазинах можно найти оба варианта этой игрушки
и даже комбинированную ее форму — с двумя цилиндрами,
работающими в противоположных направлениях.
К слову сказать, игрушка была изобретена одним чехословацким
стеклодувом, который занимается изготовлением таких игрушек и
поныне. Чаще всего интерес к этой игрушке проявляют физики.
Обычно они утверждают, что «импульс падения песчинок»
удерживает часы внизу или, по крайней мере, вносит определенный вклад
в этот процесс. Однако не составит труда показать, что при
пересыпании песка вес песочных часов остается неизменным. См. статью
Weight of an Hourglass («Вес песочных часов»), Уолтер Рейд, American
Journal of Physics, том 35, апрель 1967, с. 351—352.
3. Железный пончик при нагревании расширяется, но его
пропорции остаются неизменными, поэтому отверстие тоже
становится больше. Этим принципом пользуются работники оптики, чтобы
вынуть линзы из оправы, и хозяйки, нагревающие крышки на
банках, чтобы ослабить их.
4. Вставьте зубочистку А между подковой и зубочисткой В и
немного приподнимите подкову, чтобы один конец зубочистки В лег
на зубочистку А {см. рис. 87). Осторожно поднимая А, доведите
конец В до самой подковы, а затем поднимите подкову и зубочистку,
удерживая их, как показано на рисунке внизу.
5. Пбплавок будет постоянно находиться на поверхности воды в
центре стакана только в том случае, если стакан заполнен чуть вы-
Парадоксальные песочные часы
195
ше краев. Благодаря силе поверхностного натяжения поверхность
воды в этом случае будет немного выпуклой.
Гин Линдберг и М. Гринблатт предложили второй вариант
решения. Вращайте частично заполненный стакан вокруг вертикальной
оси. Это создает вогнутую поверхность, в центре которой и будет
находиться поплавок. Есть еще более простой способ — создайте
водоворот, мешая воду ложкой.
6. Уксус и масло в бутылке разделяются, фракция масла
находится над уксусом. Чтобы налить масло, мистер Смит должен всего
лишь наклонить бутылку. Чтобы налить уксуса, он должен плотно
закрыть бутылку пробкой, перевернуть ее и затем немного ослабить
пробку, чтобы вытекло желаемое количество капель уксуса.
7. На телеге-лодке Льюиса Кэрролла большие оси каждой пары
овальных колес расположены под одним углом. Они
поворачиваются так, что длинные оси одной пары колес перпендикулярны
длинным осям другой пары. Это производит качку. Если бы
большие оси соосных овалов были бы повернуты под прямым углом, то
телега не смогла бы катиться. О^а бы поднималась и опускалась на
каждой паре диагонально расположенных колес. Однако если
связать передние и задние колеса так, чтобы по одной стороне полуоси
были под углом 45, то подобная телега могла бы мило качаться, как
на волнах. При этом колеса в четырехтактном цикле отрываются от
земли.
Рис. 81
Решение загадки с подковой
196
Нескучная математика
Майя и Николас Слейтер из Лондона писали, что если принять
условие Льюиса Кэрролла о перпендикулярности больших осей соосных
колес, то существует способ сделать так, чтобы телега катилась и
покачивалась, и все ее четыре колеса не отрывались от земли. Колеса
должны быть повернуты так, чтобы большие оси противоположных по
диагонали колес были под прямым углом. Тогда независимо от угла между
соосными передними колесами все четыре колеса будут оставаться на
земле. Если передние колеса повернуты под прямым углом, характер
качки получается один. Если большие оси одинаково ориентированы,
то характер качки другой. Все промежуточные углы дают различные
сочетания этих типов «качки». «Мы предпочитаем 45, — пишет семья
Слейтеров. — Единственная проблема — найти извозчика».
8. Коснитесь концом одного бруска середины другого. Если
появляется магнитное притяжение, тот брусок, концом которого вы
притрагивались, должен быть магнитом. И наоборот.
9. Уровень воды в стакане останется прежним. Кубик льда
плавает потому, что вода, из которой он состоит, расширилась в процессе
кристаллизации. Вес кубика равен весу воды, из которой он
сформировался. Плавающее тело вытесняет количество воды,
эквивалентное своему весу. Растаявший кубик льда даст такое же
количество воды, какое вытеснил, когда был льдом.
10. Сначала акробат связывает вместе нижние концы обеих
веревок. Затем лезет по веревке Л до самого потолка и обрезает
веревку В, оставляя немного веревки, чтобы завязать ее в петлю.
Взявшись одной рукой за эту петлю, он обрезает веревку Л у
самого потолка (проявляя большую осторожность, чтобы она не упала).
В этот момент у него в руках оказывается связанная веревка,
длина которой почти равна удвоенному расстоянию от пола до
потолка. Он перебрасывает ее конец через петлю и протягивает до
половины. Теперь он может слезть по этой двойной веревке и вытянуть
ее из петли, получив таким образом полную длину Л и почти всю
длину В.
Читатели предлагали и другие решения этой задачи. Одни
предлагали использование узлов, которые можно развязать с пола,
сильно тряся веревку. Другие предлагали немного надрезать веревку так,
чтобы она выдержала вес вора, пока он будет спускаться, но чтобы
потом ее можно было оторвать сильным и резким движением. Не-
Парадоксальные песочные часы
197
которые читатели говорили, что вор не сможет украсть нисколько
веревки, потому что начнут звонить колокола.
11. Вершина тени человека, проходящего под фонарем,
движется быстрее, чем сам человек, но скорость движения тени остается
постоянной вне зависимости от ее длины.
12. Вода, попавшая в шланг, дойдет до нижней точки первого
витка и остановится из-за образования воздушной пробки.
Находящийся в шланге воздух будет препятствовать дальнейшему
прохождению воды по первой петле.
Если верхний конец еще пустого шланга поднять достаточно
высоки, сила давления заливаемой воды превысит силу давления
воздуха, что будет препятствовать образованию «мешков» в каждом витке.
Максимальная протяженность каждого мешка примерно равна
диаметру витка. Умножив величину диаметра витка на количество
витков, можно получить примерную высоту столба воды в верхнем
конце шланга, при которой вода все-таки польется из нижнего конца.
(Это указали Джон Брайнер, Ян Лундберг и Джо Осборн.). У. Н. Гуд-
вин заметил, что если диаметр шланга 5/s дюйма или меньше, его
верхний конец достаточно поднять на высоту, равную удвоенной
высоте витков, и вода выйдет с другого конца шланга, пройдя через
целую серию витков. Причина этого пока не ясна.
13. Чтобы извлечь яйцо, наклоните голову назад, переверните
бутылку вверх дном, обхватите ее горлышко губами и энергично
выдохните. Когда вы отнимете бутылку ото рта, сжатый воздух
протолкнет яйцо через горлышко бутылки.
В присылаемых ответах к этой задаче часто встречается
распространенное заблуждение — люди считают, что яйцо втягивается в
бутылку вакуумом, созданным потерей кислорода. Кислород
действительно расходуется при горении, но эта потеря компенсируется
образованием углекислого газа и водяного пара. Вакуум создается
исключительно посредством быстрого охлаждения и сжатия воздуха
после угасания пламени.
14. Всякая всячина в игрушечном судне вытесняет количество
воды, эквивалентное своему весу. Если она опустится на дно ванны,
то вытеснит количество воды, эквивалентное своему объему. Так как
каждый предмет весит значительно больше, чем такой же объем во-
198
Нескучная математика
ды, после того как груз будет сброшен в воду, уровень воды в ванне
уменьшится.
15. Когда закрытый автомобиль, двигаясь вперед, начинает
ускоряться, сила инерции заставляет воздух в автомобиле двигаться
назад. Это сжимает воздух за воздушным шаром, выталкивая его
вперед. Когда автомобиль начнет двигаться по круговой траектории,
шарик по тем же причинам, будет перемещаться ближе к центру.
16. В любой точке полого астероида гравитационное притяжение
практически отсутствует. Объяснения смотрите в книге Германа
Бонди The Universe at Large («Вселенная крупным планом»).
Писатель Уэллс не понял этого, что видно из его романа Первые
люди на Луне. В двух местах его произведения указывается, что из-за
гравитационного притяжения внутри сферического космического
судна путешественники плавали в центре сферы. Это не согласуется
с тем фактом, что гравитационное поле, произведенное
космическим кораблем, было бы слишком слабо, чтобы каким-либо образом
влиять на путешественников.
17. Птица вообще не сможет летать на Луне, потому что там нет
воздуха, который бы ее поддерживал. Джордж Милви-младший
спрашивает у меня в письме, не позаимствовал ли я идею этой задачи у
Иммануила Канта! Во введении к «Критике чистого разума», часть 3,
Кант критикует Платона за его мысли о том, что тот добьется больших
успехов в философии, если покинет физический мир и улетит в пустое
пространство чистого разума. В ходе своей убедительной речи Кант
приводит следующую великолепную метафору: «Ясная голубка,
рассекая воздух в свободном полете и чувствуя его сопротивление, могла
бы подумать, что в пустом пространстве ее полет был бы еще легче».
18. Рассмотрим исходное состояние к частиц жидкости. Земля
несет их в пространстве против часовой стрелки (если смотреть со
стороны Северного полюса) со скоростью один оборот за 24 часа.
Однако каждая точка объема трубы, занимаемая частицей, удалена
от центра Земли на такое же расстояние, что и сама частица.
Поэтому относительная скорость циркуляции внутри трубы нулевая.
После того как трубу переворачивают, выбранные частицы продолжают
движение в пространстве против часовой стрелки с той же
скоростью. Но то, что труба переворачивается, придает им движение отно-
Парадоксальные песочные часы
199
сительно трубы по часовой стрелке (трением пренебрегаем). Это
движение длится ровно один оборот вокруг трубы, что занимает
ровно половину времени оборота Земли вокруг оси, а именно 12 часов.
Это любопытное деление на два можно лучше понять
следующим образом. Рассмотрим конкретную частицу, располагающуюся
в данный момент в верхней части трубы. Пустьх — это диаметр
Земли, г у — диаметр трубы. И частица, и часть трубы движутся на
восток со скоростью к(х + 2у) в сутки. После переворота трубы частица
продолжает движение с той же скоростью, но теперь уже находясь в
нижней части трубы, которая движется на восток с меньшей
скоростью, а именно тех в сутки. Следовательно, относительно трубы
частица перемещается со скоростью л;(;с + 2у) — юс = 2тсу в сутки.
Поскольку величина лу является длиной окружности трубы, мы видим,
что частица проходит вокруг трубы со скоростью два оборота в
сутки. Один оборот она совершает за 12 часов. Подобные вычисления
можно применить к любой частице жидкости.
Большинство людей, вычисляя идеальную скорость воды,
множитель двойку упускают из виду, предполагая, что вода будет делать
оборот за 24 часа. Эту ошибку допустил сам Комптон, опубликовав
свои ошибочные результаты в журнале Science, том 37, 23 мая, 1913,
с. 803—806. Известный физик описывал экспериментальную
установку с трубой метрового радиуса. Эта ошибка перебралась в его
следующую публикацию, появившуюся в журналах Physical Review
(том 5, февраль, 1915, с. 109) и Popular Astronomy (том 23, апрель,
1915, с. 199), где он описывает более совершенный аппарат.
Если труба находится не на экваторе, то максимального эффекта
можно добиться, если переворачивать трубу не резко, а
предварительно отклонив. Чем ближе аппарат находится к полюсу, тем
больше необходимо отклонение для того, чтобы определить широту
места. На Северном или Южном полюсе максимальный эффект будет
достигнут, если трубу наклонить горизонтально, а потом уже
перевернуть. Но для любой широты, если аппарат сориентировать по
сторонам света, а затем плоскость трубы должным образом
наклонить (чтобы получить максимальный эффект), поворот вызывает
круговое движение жидкости со скоростью два оборота в сутки.
Напомню, что это при полном отсутствии вязкости.
Полная история вопроса довольно сложна, однако можно указать
на интересную связь движения жидкости в трубе Комптона и
индукции электрического тока, текущего в проводящем кольце. В
последнем случае это кольцо переворачивают на 180 градусов в магнитном
200
Нескучная математика
поле. Информацией по этому вопросу, почерпнутой из краткой
переписки, я обязан Дэйву Фалтсу из гидродинамической лаборатории
при Чикагском университете. Фалтс объясняет вопрос в терминах
угловых скоростей и вращающих моментов, однако для читателей
это не так просто, так что я остановился на более простом (и более
грубом) объяснении с использованием линейных скоростей.
Лекцию Комптона я посетил, будучи еще на первом курсе
Чикагского университета. Комптон рассказывал о своем эксперименте.
После лекции я подошел к нему и спросил, возможно ли создать
более интенсивное движение жидкости, поворачивая трубу не только
вдоль горизонтальной, но и вдоль вертикальной оси.
Озадаченный, Комптон достал монету в 50 центов из кармана,
запустил ее по столу, что-то приговаривая. Наконец он тряхнул головой
и сказал, что скорее всего это не сработает, но он об этом подумает.
19. Вес емкости увеличится на вес количества воды,
вытесненного рыбкой, которую вы держите за хвост.
20. Когда велосипед тянут назад за нижнюю педаль, она
вращается таким образом, что велосипед должен двигаться вперед, но так
как ножной велосипедный тормоз в данный момент не
задействован, велосипед может свободно сдвигаться назад, куда его тянут.
Большой размер колес и малая передача (соотношение шестеренок)
приведут к тому, что велосипед поедет назад. Педаль движется назад
относительно земли, а относительно велосипеда она движется
вперед. Когда она поднимается достаточно высоко, срабатывает
тормоз, и велосипед останавливается. Читатели, которые не верят это-
Рис. 82
Решение головоломки об электрической цепи
Парадоксальные песочные часы
201
му, должны просто взять велосипед и провести эксперимент.
Данный парадокс объясняется во многих старых книгах. Одну из
последних работ на эту тему можно найти в журнале Mathematics
Magazine, том 45, январь, 1972, с. 1? статья автора Д. Дайкина The
Bicycle Problem («Задача велосипеда»).
21. Гребную шлюпку можно заставить двигаться вперед, дергая за
веревку, привязанную к ее корме. В стоячей воде таким образом
можно достичь скорости несколько миль в час. Когда человек
двигается вперед, к носу шлюпки, трение между лодкой и водой
препятствует значительному сдвиганию лодки назад, а сила инерции
при остановке человека достаточно велика, чтобы преодолеть
сопротивление воды и сдвинуть лодку вперед. По такому же
принципу мальчик, сидящий в коробке, может двигаться в ней по гладкому
полу, делая быстрые движения туловищем вперед. Однако в случае с
космическим кораблем такой инерционный двигатель работать не
будет, потому что почти что вакуумные условия снаружи корабля не
обеспечивают никакого сопротивления.
22. Фунт золотых 10-долларовых монет содержит в 2 раза больше
золота, чем полфунта 20-долларовых монет, поэтому фунт золотых
десятидолларовых монет стоит в 2 раза дороже.
23. В цоколях ламп и в обоих выключателях находятся
крошечные кремниевые выпрямители, которые позволяют току течь через
них только в одном направлении. В цепи, показанной на рис. 82,
стрелки указывают, в каком направлении каждый выпрямитель
позволяет течь току. Если ток течет так, что выпрямитель в цоколе
лампы «закрыт», лампочка останется темной. Не составляет труда
увидеть, что каждый выключатель включает и выключает только ту
лампочку, чей выпрямитель указывает при обходе контура то же
направление тока, что и выпрямитель в выключателе.
Кстати, многие читатели жаловались (и вполне обоснованно) на
трудность вставки крошечного диода в цоколь лампы. Р. Ален Пел-
тон счел, что рабочую модель лучше изготовить следующим
образом: «Я присоединил диод к основанию керамического гнезда,
затем сделал небольшую выемку в деревянном основании, чтобы
укрепить гнездо. В этом случае я не могу поменять схему управления,
поменяв лампочки местами, поскольку диоды не в цоколях. Моя
модель озадачивает всех, кому я показываю ее».
ГЛАВА 1 5
Треугольник Паскаля
В треугольнике Паскаля скрывается так много
соотношений, что если кто-то находит новое, то это уже не
удивляет никого, кроме самого исследователя.
ДОНАЛЬД КНУТ, Фундаментальные алгоритмы
Гарри Лорейн из Нью-Йорка, профессиональный фокусник и
демонстратор возможностей памяти, любит озадачивать друзей
необычными математическими фокусами с картами. Зрителю вручают колоду,
из которой удалены карты с картинками и десятки. Ему предлагают
разложить в ряд любые пять карт лицом вверх. Посмотрев на ряд,
Лорейн сразу же достает из колоды какую-то карту и кладет ее
лицом вниз на место выше ряда, как показано на рисунке 83. После
этого он просит зрителя выложить из карт пирамиду, выполнив
описанные ниже операции.
Вначале определяется сумма каждой смежной пары карт
выложенного ряда. Сложение карт производится с «отбрасыванием
девяток»: если полученная сумма больше 9, из нее вычитается 9. Но это
можно сделать быстрее, сложив две цифры числа, которым
записывается сумма. Поясним сказанное на примере. Сумма двух первых
карт нижнего ряда 16. Вместо того чтобы вычитать 9 из 16, тот же
результат получают сложением 1 и 6. Итоговая сумма равна 7. Получив
этот результат, зритель должен положить выше первой пары карт
семерку. Сумма второй и третьей карты ряда равна 8, так что над ними
надо положить восьмерку. Эта процедура продолжается до тех пор,
пока не будет выложен новый ряд из четырех карт, затем таким же
образом выкладывается третий ряд и так далее, пока пирамида не
приблизится к верхней, лежащей лицом вниз карте. Когда
фокусник перевернет эту карту, окажется, что она в точности
соответствует финальной сумме.
Треугольник Паскаля
203
; *
¦
¦
г
6W
А
?
V
*$
*¦
¦
¦
¦
¦
Л
г+ ¦
ф
1* п
А
<
ь
V
Рис. 83
Фокус с верхней картой
Описанный фокус можно показывать с любым количеством карт
в нижнем ряду, хотя если карт будет очень много, то колоды может
не хватить, чтобы обеспечить необходимые значения карт для
построения пирамиды. Конечно, такую пирамиду всегда можно
построить, делая записи на бумаге. Для осуществления одной из наиболее
впечатляющих разновидностей фокуса попросите кого-нибудь
бегло изобразить ряд из 10 случайных цифр.
Если секрет фокуса известен, нужную цифру верхней карты
можно быстро определить в уме, и она всегда будет правильной. Так как
204
Нескучная математика
же она определяется? Первой приходит в голову мысль, что это,
возможно, «числовой корень» первого ряда, то есть сумма цифр,
уменьшенная до одной цифры путем вычитания девяток, — но это не так.
На самом деле фокус Лорейна основан на простых формулах,
полученных при анализе одного из самых известных в истории
математики распределений чисел. Это распределение называют
треугольником Паскаля в честь французского математика и философа
XVII века Блеза Паскаля. Он был первым, кто написал научный
труд: Traite du triangle arithmetique («Трактат об арифметическом
треугольнике»). Это произведение было написано в 1654 году, но
издано только в 1665 году. Однако эта таблица распределения
чисел была хорошо известна задолго до опубликования трактата. Ее
изображение появилось в начале XVI века на титульном листе
арифметики Петруса Апиануса, астронома из Ингольштадтского
университета. Иллюстрация 1303 года в книге китайских
математиков также изображает треугольную таблицу, а последние
исследования обнаруживают ее следы еще раньше. Омар Хайям,
который был математиком, а также поэтом и философом, знал об этом
приблизительно в 1100-х годах, вероятно получив сведения из еще
более ранних китайских или индийских источников.
Таблица распределения чисел настолько проста, что ее может
изобразить 10-летний ребенок, тем не менее в ней заключено такое
неистощимое богатство и она связывает так много на вид
несвязанных аспектов математики, что, без всякого сомнения, является
одним из наиболее изящных из всех числовых множеств. Таблица
начинается с 1 на вершине (см. рис. 84). Все остальные числа
представляют суммы двух чисел, располагающихся непосредственно над
ними. (Каждую 1 вдоль боковых сторон треугольника представьте себе
как сумму 1 выше нее с одной стороны и 0, или отсутствия числа, с
другой стороны.) Данное множество является бесконечным и дву-
сторонне симметричным. На рисунке ряды и диагонали
пронумерованы обычным способом, но, начиная с 0 вместо 1, чтобы облегчить
объяснение некоторых из основных свойств треугольника.
Диагональные ряды, параллельные сторонам треугольника,
представляют треугольные числа и их аналоги в пространствах всех
измерений.
Треугольным числом называется верхнее число из набора
ячеек, формирующих треугольную матрицу. Эта последовательность
треугольных чисел (1, 3, 6, 10, 15...) располагается на второй
диагонали треугольника. (Обратите внимание, что каждая пара смежных чи-
Треугольник Паскаля
205
о
ЧИСЛА ФИБОНАЧЧИ
(СУММА ЧИСЕЛ,
НАХОДЯЩИХСЯ
НА ЛИНИИ)
Рис. 84
Треугольник Паскаля
сел дает в сумме нижнее число.) Первая диагональ, состоящая из
натуральных чисел, представляет аналоги треугольных чисел в
одномерном пространстве. Нулевая диагональ дает аналоги в
нуль-пространстве, где сама ячейка является, очевидно, единственно
возможной конфигурацией. На третьей диагонали расположены
тетраэдрические числа: верхние числа набора ячеек, которые формируют
тетраэдрические матрицы в трехмерном пространстве. Четвертая
диагональ представляет собой тетраэдрические числа в четырехмерном
пространстве, и так далее до бесконечного числа других измерений.
Диагональ я-я дает я-пространственные аналоги треугольных чисел.
С одного взгляда можно увидеть, что 10 пушечных ядер можно
упаковать в тетраэдрическую пирамиду или в плоский треугольник
и что 56 гиперпушечных ядер в тетраэдре пятимерного
пространства можно перегруппировать на гиперплоскости с образованием
тетраэдра (но если мы попытаемся упаковать их на плоскости в
треугольник, то одно ядро останется).
Чтобы определить сумму всех чисел на любой диагонали вплоть
до любой позиции в этом ряду, просто взгляните на число, располо-
206
Нескучная математика
женное непосредственно ниже и слева от последнего числа в этой
серии, оно и будет суммой. Например, какова будет сумма
натуральных чисел от 1 до 9? Опускаемся по первой диагонали до 9, затем
смотрим вниз и влево. Ответ 45. Какова сумма первых восьми
треугольных чисел? Находим восьмое число на второй диагонали,
двигаемся вниз и влево к ответу 120. Если мы соберем вместе все ядра,
требующиеся для того, чтобы сложить первые восемь треугольников,
они составят точно одну тетраэдрическую пирамиду из 120 ядер.
Суммы чисел диагоналей с меньшим наклоном, обозначенных
на рисунке сплошными линиями, формируют известную
последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13..., в которой каждое
число представляет сумму двух предыдущих чисел. (Вы можете
ответить почему?) Последовательность Фибоначчи часто встречается
в комбинаторных задачах. Чтобы привести пример, рассмотрим ряд
из п стульев. Сколько различных способов вы можете предложить
для того, чтобы усадить на эти стулья мужчин и женщин при
условии, что двух женщин рядом усаживать нельзя? Для п, равных 1, 2,
3, 4..., ответами будут 2, 3, 5, 8... и так далее в порядке Фибоначчи.
Очевидно, Паскаль не знал о том, что ряд Фибоначчи был вставлен
в треугольник; и, кажется, это не было замечено до конца XIX века.
И только недавно появилось сообщение о том, что при удалении
диагоналей с левой стороны треугольника получают частичные
суммы для ряда Фибоначчи. Это открытие было сделано Вернером Е.
Хоггатом, математиком колледжа из Сан-Хосе. Хоггат редактировал
журнал The Fibonacci Quarterly («Фибоначчи Квотерли»),
ежеквартальный занимательный журнал, в котором публиковалось много
статей о треугольнике Паскаля. Если удалить нулевую диагональ с
левой стороны, диагонали Фибоначчи дадут суммы, которые
являются частичными суммами ряда Фибоначчи (1 = 1;1 + 1=2;1 + 1 +
2 = 4;1 + 1+2 + 3 = 7ит. д.). Если с левой стороны убрать две
диагонали (обозначенные 0 и 1), то диагонали Фибоначчи дадут
частичные суммы частичных сумм (1 = 1;1+2 = 3;1+2 + 4 = 7и так
далее). В общем случае, если отрезаны к диагоналей, диагонали
Фибоначчи дают ?>свертки частичных сумм ряда Фибоначчи.
Каждый горизонтальный ряд треугольника Паскаля дает
значения коэффициентов разложения двучлена (х + у)". Например,
(х +у)3 = х3 + Ъх2у + Ъху2 + у3. Коэффициентами этого разложения
являются 1, 3, 3, 1 (коэффициент 1 обычно перед слагаемым не
ставится), что представляет третий ряд треугольника. Чтобы
определить коэффициенты разложения (х + 1)п в соответствующем поряд-
Треугольник Паскаля
207
ке, просто взгляните на я-й ряд треугольника. Это основное
свойство треугольника связывает его с элементарной комбинаторикой и
теорией вероятности таким способом, который делает треугольник
полезным инструментом вычислений. Предположим, что арабский
правитель предлагает вам любых трех из своих семи жен. Сколько
различных вариантов выбора у вас есть? Вам необходимо только
найти пересечение диагонали 3 с рядом 7, чтобы получить ответ: 35.
Если же (при стремлении быстрее получить результат) вы
совершите грубую ошибку, пытаясь найти пересечение 7-й диагонали с 3-м
рядом, то увидите, что они не пересекаются, так что этот метод
никогда не даст неверного результата. Вообще говоря, количество
способов выбора п элементов из набора г элементов определяется путем
пересечения диагонали п с рядом г.
Связь между количеством вариантов выбора и вероятностью
легко увидеть, рассмотрев восемь равновероятных результатов
выпадения орла (О) или решки (Р) при подбрасывании в воздух монеты:
000, OOP, ОРО, ОРР, POO, POP, PPO, PPP. Есть только один
вариант выпадения подряд трех орлов, три варианта выпадения двух
орлов, три варианта выпадения одного орла и один вариант вообще
без орлов. Эти числа (1,.3, 3, 1) конечно же представляют третий ряд
треугольника. Предположим, что вы хотите узнать вероятность
выпадения ровно пяти орлов при подбрасывании в воздух 10 монет.
Вначале определим, каково количество возможных вариантов, при
которых могут выпасть пять монет из 10. Пересечение 5-й
диагонали и 10-го ряда дает ответ: 252. Теперь вы должны сложить числа в
10-м ряду, чтобы получить количество равновозможных случаев. Вы
можете сделать это кратчайшим путем, вспомнив, что сумма чисел
я-го ряда треугольника Паскаля всегда равна 2п.
Достаточно очевидно, что сумма каждого ряда является
удвоенной суммой предыдущего ряда, так как каждое число передается
вниз дважды, чтобы войти в состав чисел нижнего ряда. Поэтому
суммы этих рядов образуют ряды удвоения 1, 2, 4, 8... Десятая
степень 2 составляет 1024. Вероятность выпадения пяти орлов равна
252/1024, или 63/256. Существует механическое устройство для
демонстрации вероятности, которое часто выставляется в музеях. В
этом устройстве сотни небольших шариков катятся вниз по
наклонной плоскости через гексагональный набор препятствий, чтобы
войти в щелевое устройство и образовать некоторое соответствие
колоколообразной кривой нормального распределения. В статье
Марка Каса Probability («Вероятность»), появившейся в Scientific
208
Нескучная математика
American в сентябре 1964 года, вы увидите изображение этого
устройства и познакомитесь с обсуждением того, почему треугольник
Паскаля является основой описания его работы.
Если мы обозначим каждое число треугольника небольшой
точкой, затем зачерним те точки, которые отображают числа,
делящиеся с остатком на определенное положительное целое число, то в
результате всегда получим поразительное изображение треугольника.
Изображения, полученные таким способом, таят в себе много
сюрпризов. Рассмотрим вариант, построенный для случая, когда
делителем является 2 (см. рис. 85). По направлению вниз по центру
расположены серые треугольники увеличивающихся размеров, каждый
из которых построен полностью из точек, соответствующих четным
числам. На самой вершине расположен «треугольник» с одной
точкой, затем ряд продолжается треугольниками из 6, 28, 120, 496...
точек. Из этих чисел три, а именно 6, 28 и 496, известны как
совершенные числа, потому что каждое представляет собой сумму всех
своих делителей, исключая само себя (например, 6=1+2 + 3).
Неизвестно, бесконечно ли множество совершенных чисел и есть ли
среди них нечетные. Эвклид, однако, сумел доказать, что каждое
число вида 2/7_1(2Л — 1), где (2п — 1) — простое число, является
четным совершенным числом. Много позже Леонард Эйлер показал,
что все четные совершенные числа соответствуют формуле Эвкли-
да. Эта формула эквивалентна выражению для совершенного числа:
Р(Р + \)
2 '
где Р— простое число Мерсена (простое число, имеющее вид 2Р — 1,
где р — простое число). Бывает, что вышеприведенное выражение
представляет также формулу для треугольного числа. Другими
словами, если «сторона» треугольного числа является простым числом
Мерсена, то треугольное число тоже совершенно.
Возвращаясь к треугольнику Паскаля, имеющему
четно-нечетную раскраску, можно увидеть, что формула для числа точек в п-и
центральном треугольнике, считая от вершины вниз, имеет вид
2Л_1(2Л — 1). Это формула для совершенных чисел. Поэтому все
четные совершенные числа проявляются на изображении тогда, когда
в выражении для количества точек в я-м центральном треугольнике
член 2" — 1 является простым числом. Ввиду того что 24 — 1 = 15 не
является простым числом, четвертый серый треугольник не являет-
Треугольник Паскаля
209
0 10 20 30 40 50 60 70 80 90 100
Рис. 85
Треугольник Паскаля с числами, представленными точками, —
черными точками обозначены нечетные числа.
ся совершенным. Пятый треугольник с 496 точками является
совершенным, так как 25 — 1 = 31 — простое число. (Шестой серый
треугольник несовершенный, но седьмой с 8128 точками совершенен.)
В заключение еще одно интересное свойство треугольника.
Если скомпоновать цифры каждого ряда в единое число, то для рядов
0-4 получаются числа 1, 11, 121, 1331 и 14 641. Эти числа равны
пяти первым степеням числа 11, начиная с 11° = 1. В таком случае
пятый ряд должен иметь вид 161 051, но он выглядит иначе.
Однако обратите внимание на то, что это первый ряд с двухзначными
числами. Если же представить себе десятичное число, цифры
которого могут быть двухзначными (ряд 1, 5, 10, 10, 5, 1), то пятый
210
Нескучная математика
ряд можно записать справа налево как (1 х 1) + (5 х 10) + (10 х 100)
+ (10 х 1000) + (5 х 10 000) + (1 х 100 000), что соответствует
точному значению 115. В такой интерпретации я-й ряд является
«десятичной записью» 11п. Три статьи о треугольнике Паскаля и
степени числа 11 можно найти в ежегодных выпусках Mathematics
Teacher («Учитель математики»), том 57 (1964), с. 392; том 58
(1965), с. 425, и том 59 (1966), с. 461.
Наверняка любой, кто начнет изучать этот треугольник,
обнаружит гораздо больше его свойств, но маловероятно, что они будут
новыми, так как то, что описано здесь, представляет только песчинку
обширной литературы. Сам Паскаль в своем трактате о
треугольнике сказал, что он упустил больше, чем включил. «Удивительно, -
восклицал он, — насколько этот треугольник плодороден в своих
свойствах!» Существует также бессчетные разновидности
треугольника и множество путей их обобщения, таких, например, как
построение его в тетраэдрическом виде для определения
коэффициентов трехчленных разложений.
Если читатель сможет решить следующие пять элементарных
задач, то поймет, что неплохо разобрался в структуре треугольника.
1. Какая формула дает сумму всех чисел, расположенных выше
ряда п?(Обозначение рядов приведено на рисунке 84, начиная с
нуля для верхнего числа.)
2. Сколько нечетных чисел в ряде 255?
3. Сколько чисел в 67-м ряду делится на 67 без остатка?
4. Если шашка находится на одной из черных клеток в первом
ряду пустой шахматной доски, она может двигаться (обычными для
шашек ходами) к любой из четырех черных клеток последнего
(восьмого) ряда множеством различных путей. Одна пара начальной
и конечной клеток связана максимальным числом различных
маршрутов. Определите эти две клетки и число путей, по которым
шашка может переместиться от одной клетки до другой.
5. Определите начальный ряд из п карт в фокусе с пирамидой,
который описан в начале этой главы. Каким образом по
треугольнику Паскаля можно получить простые формулы для расчета значения
верхней карты?
ДОПОЛНЕНИЕ
Ответ 5 в следующем разделе описывает, как используется
треугольник Паскаля при показе фокусов с пирамидой. Чтобы понять, как
Треугольник Паскаля
211
работает эта формула, рассмотрим треугольник, изображенный на
рисунке 83, и предположим, что смежные карты складываются без
выбрасывания девяток. Пирамида в этом случае будет выглядеть
так:
71
38 33
24 14 19
16 8 6 13
9 7 15 8
Ключевым рядом треугольника Паскаля будет пятый ряд: 1, 4,
6, 4, 1. Единицы на его концах говорят нам, что, когда мы,
складывая числа, продвигаемся наверх, значение каждой концевой карты
нижнего ряда входит в конечную сумму только один раз. Это
обусловлено тем, что для каждой из этих карт есть только один путь
наверх. Четверки, являющиеся вторыми от концов ключевого ряда,
свидетельствуют, что значение каждой второй от конца карты
входит в конечную сумму четыре раза, так как для каждой из этих карт
имеется четыре пути к вершине. И наконец, центральная шестерка
ключа отражает наличие шести путей движения центральной карты
к вершине, поэтому значение центральной карты входит в
окончательную сумму 6 раз. В соответствии с этим и определяется
значение верхнего числа: (1 х 9) + (4 х 7) + (6 х 1) + (4 х 5) + (1 х 8) = 71.
Так как описанная процедура дает значение верхнего числа, она
также может обеспечить числовой корень верхнего числа для
случая, когда при построении пирамиды отбрасываются девятки.
Фокусникам этот карточный трюк известен под названием
«Вершина» («Apex»). Он был разработан немецким фокусником
Францем Брауном, который опубликовал его описание в 1960-х годах в
своей колонке математических фокусов в немецком периодическом
издании Magie («Магия»).
Когда фокус показывается с картами, хорошо иметь под рукой
вторую колоду на тот случай, если для построения пирамиды
потребуется больше четырех карт одного значения. Но это может
быть полезным и при построении небольших пирамид. Например,
нижний ряд 4, 5, 4, 5 для заполнения структуры потребует шести
девяток.
С. Й. X. Вевере, читатель из Голландии, написал об интересной
проблеме. Если мы удалим из колоды карты с картинками и десят-
212
Нескучная математика
ки, в колоде останется 36 карт, а 36 число треугольное. Возможно
ли, спрашивает Вьюверс, сформировать ряд из восьми этих карт
таким образом, что для заполнения треугольника по правилу
вершины хватило бы только этих 36 карт? «Ясно, — пишет Вьюверс, — что
эту проблему решить нелегко, если она вообще решается. Я
убежден, что задача может быть достаточно простой, если разработать
для этого компьютерную программу...»
Размышляя над этим, я нашел, что обозначенная проблема
имеет одно изящное решение. Читатель может доставить себе
удовольствие отыскать его. Используя не обратный подсчет, а другие
методы, вы, возможно, отыщете не одно решение.
ОТВЕТЫ
1. Сумма всех чисел выше ряда п определяется по формуле 2п — 1.
2. Все числа в ряду п являются нечетными, если, и только если п
является степенью 2, уменьшенной на 1. Так как 255 = 28 — 1, все ее
числа являются нечетными.
3. Все числа в 67-м ряду, за исключением двух единиц на концах
ряда, делятся на 67 без остатка. Все числа в л-м ряду делятся без
остатка на я, если, и только если п простое число. Доказательство
этого можно найти в книге Стенли Оджилви Through the Mathescope («В
мире математики»).
4. Для быстрого решения задачи с шашкой пронумеруем клетки
так, как показано на рисунке 86. Для каждой исходной позиции
числа образуют перевернутые треугольники Паскаля, стороны
которых обрезаны доской. Каждое число указывает количество
различных путей, которыми шашка может попасть на эту клетку из
исходной позиции. Максимальное количество возможных путей
определяется клеткой, обозначенной номером 35, когда шашка
стартует с третьей черной клетки нижнего ряда.
5. Значение верхней карты в фокусе Гарри Лорейна определяется
следующим образом. Пусть п будет количеством карт в начальном
ряду. Ряд треугольника Паскаля, который содержите чисел,
обеспечивает вывод формулы для расчета вершины. Объясним это на
нескольких примерах.
Треугольник Паскаля 213
Рис. 86
Решение задачи с шашкой
Предположим, что в нижнем ряду находится шесть карт со
значениями 8, 2, 9, 4, 6, 7. Соответствующий ряд треугольника
Паскаля имеет вид: I, 5, 10, 10, 5, 1. Уменьшим десятки до их числового
корня (путем складывания их цифр), составив ряд: 1, 5, 1, 1, 5, 1.
Эти числа являются множителями для данных шести карт. Карты,
являющиеся вторыми с каждого конца, умножаются на 5,
суммируются, затем складываются со значениями оставшихся четырех карт.
Окончательная сумма, уменьшенная до ее цифрового корня, и
определяет значение верхней карты. Эту процедуру легко проделать в
уме, потому что уменьшение до цифрового корня можно
производить в процессе вычислений. Умножив вторые от конца карты на 5
и получив при этом числа 10 и 30, сразу же уменьшим их до цифро-
214
Нескучная математика
вых корней I и 3, которые дают в сумме 4. К 4 теперь прибавим
значения остальных четырех карт, уменьшая каждую сумму до ее
цифрового корня, как было только что проделано. Окончательный
результат, 5, определяет значение верхней карты.
Для пирамиды с пятью картами в нижнем ряду, изображенной на
рисунке 83, пятый ряд треугольника Паскаля дает ключ: 1, 4, 6, 4, 1.
Верхняя карта представляется цифровым корнем суммы нижних
карт после того, как центральная карта будет умножена на 6, а
каждая из ее соседок на 4. Зрителю конечно же легче выложить
пирамиду с пятью картами, а вот от исполнителя в этом случае потребуется
более интенсивная мыслительная работа, чем в случае по
сравнению с обсчетом пирамиды, имеющей в основании шесть карт.
Между прочим, удаление из колоды карт с картинками и десяток
преследует цель значительно упростить производство вычислений для
зрителя. Но этот фокус, кстати, также хорошо работает и при полной
колоде со значениями 11, 12 и 13 для валетов, дам и королей.
Нахождение вершины пирамиды наиболее легко производится
для ряда из 10 чисел. В этом случае соответствующий ряд
треугольника Паскаля, уменьшенный до цифровых корней, имеет вид 1,9,9,
3, 9, 9, 3, 9, 9, 1. Число 9 — это то же самое, что 0 (по модулю 9), так
что можно записать такую формулу: 1, 0, 0, 3, 0, 0, 3, 0, 0, 1. Так что
для определения верхнего числа необходимо только умножить на 3
четвертые от каждого конца числа, прибавить два концевых числа и
уменьшить до цифрового корня. Остальные шесть чисел можно
полностью проигнорировать. Неплохой вариант фокуса
(предложенный Л. Восбургом Лайоном) состоит в том, что зрителю
предлагают самому предсказать верхнее число, назвав любую
понравившуюся ему цифру.
Назвав ее, он пишет ряд из девяти случайных цифр, позволяя
вам добавить 10-ю цифру на любой конец ряда. Сложите три
ключевых числа формулы обычным способом, затем добавьте четвертое
число, которое необходимо, чтобы вершина соответствовала
значению, предсказанному зрителем.
Этот фокус не обязательно дополнять требованием
«отбрасывания девяток». Отбрасывать можно любое целое число. Треугольник
Паскаля с числами, уменьшенными таким же образом, обеспечит
вам требуемую формулу. Предположим, например, что фокус
начинается с восьми цифр, и пирамида формируется с отбрасыванием
семерок. Ряд треугольника Паскаля с восемью числами,
уменьшенный путем отбрасывания семерок, имеет вид 1, 0, 0, 0, 0, 0, 0, 1. Что-
Треугольник Паскаля
215
бы определить вершину, просто сложите концевые числа и, если
необходимо, уменьшите до одной цифры путем отбрасывания
семерки. Я предоставляю читателю возможность самому определить,
почему во всех таких случаях треугольник дает желаемую формулу.
Существуют замечательные соотношения между известными
конструируемыми правильными «-угольниками и треугольником
Паскаля, уменьшенным по модулю 2 так, что нечетные позиции
становятся 1, а четные становятся 0. Правильный «-угольник
поддается построению с помощью линейки и циркуля, если имеет mlk
сторон, где т равно 1 или произведению простых чисел Ферма.
Числа Ферма имеют вид Т + 1, где s равно 2Р (р — простое число).
Единственными одновременно простыми числами Ферма являются: 3, 5,
17, 257, 65 537 (остальные составные). Таким образом, известными
конструируемыми «-угольниками с нечетным количеством сторон
являются 1,3,5, 15, 17, 51, 85,... 4 294 967 295. В двоичной форме эти
числа точно соответствуют первым 32 рядам треугольника Паскаля,
уменьшенного по модулю 2. Существуют ли другие простые числа
Ферма, а следовательно, и другие «-угольники с нечетным
количеством сторон, неизвестно.
ГЛАВА 1 6
«Джем», «Хот» и другие игры
В этой главе мы приводим описание нескольких игр для двух
партнеров. Помимо старых, есть игры и новые с известной
математической стратегией. Для начала три простые игры, связанные друг с
другом интересным и неожиданным образом.
1. Для игры необходимо девять карт от туза до девятки разложить
на столе лицевой стороной вверх. Игроки берут карты по очереди.
Победителем считается тот, кто первый, взяв три карты, наберет 15 очков.
2. На карте дорог, изображенной на рисунке 87, игроки по
очереди занимают один из девяти пронумерованных участков шоссе. Это
делается путем закрашивания полной длины участка, даже если
дорога может проходить через один или два города {обозначены
кружками). Для игры используются карандаши разных цветов. Тот из
игроков, кто первым закрасит три участка, соединяющихся в одном
городе, считается победителем. Изобрел игру и назвал ее «Джем»
голландский психолог Джон А. Мишон (John A. Michon).
Написанное на английском языке («Jam»), это слово представляет инициалы
изобретателя. Интересно то, что это название отражает и суть игры
(Jam — обозначает «пробка»), целью которой является захват
пересечений дорог путем блокирования их участков.
3. На карточках напечатаны следующие слова: НОТ, HEAR, TIED,
FORM, WASP, BRIM, TANK, SHIP, WOES (в данной игре перевод слов
на русский язык не имеет смысла, потому что это полностью исказит
смысл игры. Важны не значения слова, а содержащиеся в нем буквы
английского алфавита. — Прим. перев.) Эти девять карточек лежат на
столе лицом вверх. Игроки по очереди берут карточки. Первый, кто
возьмет три карточки со словами, в которых есть одинаковые буквы,
является победителем. (Канадский математик Лео Мозер (Leo
Moser), разработавший эту игру, назвал ее «Хот» по первому слову.)
Рис. 87
Карта для игры «Джем»
218
Нескучная математика
Для каждой из описанных игр зададим один и тот же вопрос.
Если оба игрока будут делать лучшие ходы, кто из них победит:
первый, второй или игра закончится вничью? Возможно, что читатель
уже ощутил то, что психолог школы гештальттерапии назвал бы
«озарением», и понял, что все три игры по сути схожи с игрой в
крестики-нолики!
Легко увидеть, что это тот же самый случай. Для первой игры мы
составили список всех цифр, от 1 до 9, по тройкам, сумма которых
равна 15. Таких троек ровно восемь. Их можно объединить на поле,
использующемся для игры в крестики-нолики, что и показано на
рисунке 88. В результате такого объединения получается известный
магический квадрат 3x3, в котором каждый ряд, колонка и главные
диагонали составляют одну из троек. Каждая пронумерованная
карточка, выбираемая игроком в первой игре, соответствует в игре в
крестики-нолики той ячейке магического квадрата, которая имеет
ту же самую цифру. Каждый выигрышный набор троек в карточной
игре соответствует выигрышному ряду магического квадрата игры в
крестики-нолики. Таким образом, каждый, кто в совершенстве
освоил игру в крестики-нолики и кто запомнил магический квадрат,
сразу же может показать превосходную игру в карточной версии.
Карта дорог на рисунке 87 топологически эквивалентна
симметричному графу на рисунке 89 слева. Он, в свою очередь, является
топологическим двойником графа, полученного соединением центров
девяти клеток поля для игры в крестики-нолики, что изображено на
этом же рисунке справа. Каждая пронумерованная клетка
магического квадрата соответствует пронумерованному участку дороги на
карте, а каждый город на карте соответствует ряду, колонке или
главной диагонали магического квадрата. Как и в предыдущем случае,
игра с картой и игра в крестики-нолики полностью эквивалентны.
Аналогичность игры Мозера в слова и игры в крестики-нолики
становится очевидной, если эти девять слов вписать в ячейки поля
для игры в крестики-нолики, как показано на рисунке 90. Каждое из
трех слов, расположенных в соответствующем ряду, имеет общую
букву. И снова запоминание квадрата слов незамедлительно
позволит опытному игроку в крестики-нолики отлично играть в «Хот». Так
как очередность ходов при игре в крестики-нолики всегда
рационально определять по жребию, то этот же подход верен и для трех
эквивалентных игр, хотя первый игрок, естественно, имеет огромное
преимущество перед вторым, который или не понимает, что играет в
замаскированные крестики-нолики, или освоил эту игру слабо.
«Джем», «Хот» и другие, игры
219
2
7
6
9
5
1
4
3
8
Рис. 88
Представление карточной игры в виде игры в крестики-нолики
Рис. 89
Граф карты дорог игры «Джем» (слева) и его топологический двойник
из крестиков-ноликов (справа)
нот
TANK
TIED
FORM
HEAR
BRIM
WOES
WASP
SHIP
Рис. 90
Ключ к игре «Хот»
220
Нескучная математика
Тот, кто быстро воспринял идентичность трех описанных игр,
поймет, что математика изобилует «играми», которые на первый
взгляд имеют мало общего и тем не менее просто представлены
двумя различными наборами обозначений и правил для одной и той же
игры. Геометрия и алгебра, например, позволяют играть в одну и ту
же игру двумя различающимися способами. Это показало величие
открытия Декартом аналитической геометрии.
Существует много игр, в которых игроки поочередно удаляют
какой-нибудь элемент или подмножество из комплекта, причем
победителем становится тот, кому достается последний элемент.
Наиболее известной игрой такого типа является «ним», для которого
используется набор фишек, расставленных в произвольном числе
рядов с произвольным числом фишек в каждом ряду. Игрок, когда
подошла его очередь, может взять какое угодно количество фишек, при
условии, что все они находятся в одном ряду. Побеждает тот из
игроков, кто взял последнюю фишку. Совершенную стратегию этой игры
легко сформулировать в двоичной системе исчисления, что
объясняется в The Scientific American Book of Mathematical Puzzles & Diversions
(«Математические загадки и развлечения Scientific American»).
Исходная расстановка карт для нима, соответствующая тому, как
в него играли во французском фильме Last Year at Marienbad («В
прошлом году в Мариенбаде»), показана на рисунке 91.
Шестнадцать карт расположены в четырех рядах: одна, три, пять и семь карт.
(Принцип треугольной расстановки символизирует любовный
треугольник, разыгрываемый в этом фильме.) Для того чтобы
определить, кто выиграет, первый или второй игрок, запишем количество
карт в каждом ряду в двоичной системе, а затем сложим колонки.
1 1
3 11
5 101
7 Ш
224
Если сумма каждой колонки число четное (или ноль, если
сделано добавление по модулю 2), как в настоящем случае, позиция
называется «защищенной». Это означает, что первый игрок, несомненно,
проиграет мастеру, так как, независимо от того, как он сыграет, он
оставит позицию «незащищенной» (по крайней мере, с одной
колонкой, имеющей нечетную сумму), а второй игрок может обернуть
«Джем», «Хот» и другие игры
221
Рис. 91
Использовавшаяся в Мариенбаде начальная позиция карт
для «нима» или кайлеса
это к другой защищенной позиции во время своего следующего
хода. Играя всегда так, чтобы оставлять позицию защищенной, он с
уверенностью получит последнюю карту. (В кинофильме игра
заканчивается тем, что игрок, взявший последнюю карту, проигрывает. В
таком варианте придется лишь незначительно изменить стратегию в
конце игры. Победитель должен просто один раз отступить от
обычной стратегии оставлять нечетное число однокарточных рядов.)
Мишель Хенон, математик из Национального центра научных
исследований в Париже, недавно придумал очаровательный
вариант «нима», разыгрываемого с ножницами и отрезками нитей. Но
подойти к его описанию лучше всего после объяснения более
старого варианта «нима», называемого кайлесом, с которым игра с
нитями тесно связана.
Кайлес был изобретен английским мастером загадок Генри Дью-
дени, который представил его в 73-й задаче своей первой книги The
Canterbury Puzzles («Кентерберийские загадки») 1907 года. Теперь
игра называется кайлес, потому что Дьюдени представил ее связанной
с популярной в XIV веке игрой с таким названием. В ней шар
накатывался на деревянные кегли, стоящие бок о бок. Шар имел такие
222
Нескучная математика
размеры, что мог сбить или одну, или две рядом стоящие кегли.
Игроки по очереди катали шар, и тот, кто собьет последнюю кеглю
(или пару кегель), выигрывает.
В математический кайлес играть лучше всего на столе с монетами,
картами или другими предметами, просто разложив их в
произвольное число рядов точно так же, как в игре «ним», с произвольным
числом предметов в каждом ряду. Однако теперь мы должны
рассматривать каждый ряд как многозвенную цепочку. Можно удалять одно
звено или два соседних звена. Если предмет или пара предметов
удаляются изнутри цепочки, она распадается на две отдельные цепочки.
Например, если первый игрок берет центральную карту из нижнего ряда,
это разрывает семь карт на две отдельных цепочки по три звена в
каждой. Таким образом, при продолжении игры количество цепочек,
возможно, увеличится. Побеждает в игре тот, кто делает последний ход.
Кайлес также допускает двоичный анализ, но не напрямую, как
«ним». Каждая цепочка может быть представлена числом в двоичном
исчислении, но это число (за исключением трех наименьших случаев)
не является тем же, что и десятичное число, отражающее количество
карт в цепочке. На рисунке 92 представлена предложенная Хеноном
таблица, в которой приведены числа в двоичной системе (названные
здесь числами к), соответствующие целым числам от 1 до 70. После 70
появляется необычная периодичность. Если число больше 70,
разделите его на 12, определите остаток, а затем воспользуйтесь таблицей,
приведенной на рисунке 92, внизу. Чтобы определить, будет позиция
кайлеса защищенной или незащищенной, можно использовать числа
к, так же как в игле «ним» с двоичными числами.
Рассмотрим исходную позицию из фильма, которая в «ниме»
является безопасной и поэтому выигрышна для второго игрока. А
безопасна ли она в кайлесе? Подставив числа к, получим следующее:
1 1
3 И
5 100
7 Ш
122
Четными являются не все суммы, так что в кайлесе эта позиция
является незащищенной. Только один ход первого игрока переведет
позицию в защищенную, гарантирующую таким образом победу.
Может ли читатель найти э^от ход?
«Джем», «Хот» и другие игры
223
ДЛИНА РЯДА
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
ЧИСЛО К
1
10
11
1
100
11
10
1
100
10
110
100
1
10
111
1
100
11
10
1
100
по
111
100
1
10
1000
101
100
111
10
1
1000
по
111
100
1
10
11
1
100
111
10
ДЛИНА РЯДА
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
61
62
63
64
65
66
67
68
69
70
ЧИСЛО К
1
1000
10
111
100
1
10
1000
1
100
111
10
1
100
10
111
1
10
1000
1
100
111
10
1
1000
по
ЧИСЛА БОЛЬШЕ 70
ОСТАТОК
0
1
2
3
4
5
6
7
8
9
10
11
ЧИСЛО К
100
1
10
1000
1
100
111
10
1
1000
10
111
Рис. 92
Числа к в двоичной системе для игры в кайлес
224
Нескучная математика
Вывод чисел к слишком сложен, чтобы привести его здесь.
Интересующийся читатель найдет его подробное объяснение,
представленное Гаем и Смитом в Proceedings of the Cambridge
Philosophical Society (Трудах Кембриджского философского
общества), том 52, с. 516—526), а также в книге Томаса Бирна Puzzles and
Paradoxes («Головоломки и парадоксы»). Заметим, что нет чисел к,
состоящих из более чем четырех цифр. В результате мы имеем 16
различных комбинаций из четырех четных и нечетных членов,
представляющих суммы колонок, из которых только одна является четной-четной-
четной-четной. Как отмечает Хенон, это дает нам возможность
сделать вывод с высокой степенью точности о том, что если исходная
позиция кайлеса выбирается наобум из всех возможных распределений,
то вероятность того, что она будет безопасной, близка к 1/16. (При
увеличении количества рядов вероятность быстро приближается к 7i6-)
Есть полезные правила, которыми игрок в кайлес может
воспользоваться, не анализируя каждое расположение. Две
одинаковые цепочки являются защищенными, потому что независимо от
того, что ваш противник делает с одной, вы можете сделать то же
самое с другой. Например, если две цепочки представляют 5 и 5 и он
берет вторую карту из одной цепочки, вы берите вторую карту из
другой. Эти действия оставляют цепочки 1, 1, 3, 3. Если он возьмет
2 карты из тройной цепочки*, вы берите две карты из ее двойника.
Если же он возьмет однокарточную цепочку, вы берите другую. Это
приводит к тому, что, если исходная позиция представлена одной-
единственной цепочкой, первый игрок одержит легкую победу.
Если цепочка состоит из одной или двух карт, он их берет. Если же в
цепочке больше двух карт, он возьмет одну или две карты из центра,
чтобы оставить две равные цепочки, а затем продолжать игру так,
как описано. Если расположение карт имеет четное количество
цепочек одинаковой длины, позиция явно безопасная, так как, какие
бы действия ни предпринимал первый игрок по отношению к
одной цепочке, второй игрок делает то же самое с ее двойником.
Хорошо также запомнить следующие безопасные позиции для
двух или трех цепочек с количеством карт не больше девяти в
каждой. Безопасными парами (за исключением двух одинаковых
цепочек, которые безопасны сами по себе) являются 1—4, 1—8, 2—7, 3—6,
4—8 и 5—9. Безопасные тройки можно вычислить мысленно,
удерживая в памяти три следующие группы: {1,4, 8}, {2, 7} и {3, 6}.
Любая тройка, включающая по одной цифре из каждой группы,
является безопасной.
«Джем», «Хот» и другие игры
225
А сейчас позвольте вернуться к игре Хенона с нитями для двух
игроков. У нас имеется произвольное число отрезков нитей
произвольной длины. Игроки по очереди отрезают кусочки длиной один
дюйм от любого отрезка. Кусочки можно отрезать от конца или
вырезать изнутри отрезка. Во втором случае это приведет к тому, что
вместо одного отрезка получится два. Кусочек длиной в один дюйм
может быть взят без разрезания. Победителем считается тот, кому
достанется последний однодюймовый кусочек.
Длины нитей не должны быть рациональны. Рисунок 93
представляет начало игры с четырьмя нитями, имеющими длину 1, я, 30
и 50. Кто же станет победителем, если оба партнера играют
рационально? На первый взгляд это кажется необычайно трудным
вопросом, но при внимательном рассмотрении он оказывается до
смешного легким. Чтобы разрешить эту проблему, начертите четыре
прямые линии, приблизительно соответствующие требуемым длинам.
Когда все однодюймовые кусочки будут стерты, остатки линий
будут иметь как раз нужные длины.
Игра может проводиться также с замкнутыми петлями из нитей.
Предположим, что она начинается с семью такими петлями, каждая
длиной больше двух дюймов. Если об истиной длине нитей ничего
неизвестно, кто из игроков выиграет? При правильном подходе на
этот вопрос ответить даже легче, чем на предыдущий.
Наша завершающая игра взята из книги Руфуса Айзека
Differential Games («Дифференциальные игры»), опубликованной в
1965 году. Приверженцы занимательной математики могут
вспомнить, что Исаак предоставил превосходные иллюстрации для изве-
5 «i "- "- "- ^ ^
V30
з ^ ^ ^ ¦> s «cs:
V50
Рис. 93
Игра с нитями Хенона
226
Нескучная математика
стной книги Джеймса Р. Ньюмана Mathematics and the Imagination
(«Математика и воображение»), но среди математиков он более
всего известен, как специалист по анализу игр. Его книга наполнена
оригинальными методами решения трудных конфликтных игр типа
тех, которые часто встречаются в военных ситуациях, особенно игр,
имеющих отношение к преследованию и захвату. Некоторые из этих
игр обсуждаются в упрощенном, дискретном виде, который
представляет большой познавательный интерес.
Одну из основных игр, объяснение которой Исаак приводит
полностью, он назвал «игрой шофера-убийцы». Представьте
сумасшедшего шофера за баранкой автомобиля, который ведет машину
по неопределенному плану. Он движется с постоянной скоростью,
может мгновенно изменять положение своего рулевого колеса, но
угол, на который он может повернуть передние колеса автомобиля,
ограничен. Где-то в районе его движения находится одинокий
пешеход. Он может двигаться в любом направлении на любое
расстояние. Его скорость тоже постоянна, но меньше скорости
автомобиля. При каких условиях автомобиль может (допустим, в
пространстве реального окружения водителя) ударить (задеть) пешехода? При
каких условиях пешеход может постоянно избегать столкновения?
Как преследователь может уменьшить время, необходимое ему для
того, чтобы догнать намеченную жертву?
К счастью, мы не коснемся этих трудных вопросов, но
ознакомимся с более простой и в чем-то похожей игрой Исаака под
названием «Полицейский автомобиль». Вообразите город
неопределенных размеров, с улицами, которые образуют правильную
квадратную сетку. На одном из перекрестков находится полицейский
автомобиль. На другом — автомобиль злоумышленников. Полицейский
автомобиль движется в два раза быстрее этого автомобиля, но
тормозится тем, что ему необходимо соблюдать муниципальные
правила уличного движения. Эти правила запрещают левые повороты и
повороты назад, так что он может двигаться только прямо вперед
или поворачивать направо на каждом перекрестке. Автомобиль.же
преступников пренебрегает этими правилами, так что на каждом
перекрестке может поворачивать на все четыре стороны.
Для квантованной игры перекрестки заменены квадратами
бесконечной шахматной доски.
Полицейский автомобиль представлен фишкой с нарисованной
на ней стрелкой, которая указывает направление движения
автомобиля. Автомобиль преступников представлен другой фишкой. Иг-
«Джем», «Хот» и другие игры
227
роки ходят по очереди, причем начинает игру полицейский
автомобиль. Все ходы подобны ходам ладьи при игре в шахматы: вверх,
вниз, вправо или влево, но не по диагонали. Автомобиль
преступников за один ход передвигается на один квадрат. Полицейский
автомобиль передвигается за один ход на два квадрата, но только по
прямой линии, либо в том направлении, в котором двигался, либо
после правого поворота. (Он не может передвинуться на один
квадрат, затем повернуть направо и передвинуться на другой квадрат.)
Полицейские «поймают» преступников, если их автомобиль
окажется в том квадрате, где находится преследуемый автомобиль или
в соседнем квадрате в прямом или диагональном направлении.
Правила игры проиллюстрированы рисунком 94. Полицейский
автомобиль при первом ходе может передвинуться в квадраты А или
В. Из квадрата А он может переместиться в квадраты С или Z); а из В в
?или F. После каждого хода его можно повернуть (если необходимо),
так что его стрелка показывает направление, в котором был сделан
последний ход. Преступники могут передвинуться в квадраты W, X, Y
или Z Если полицейский автомобиль оказался в квадрате F, а
преступники в том же самом квадрате или в любом из восьми
закрашенных квадратов, его окружающих, они будут считаться пойманными.
В каких квадратах должен находиться полицейский автомобиль в
начале игры, чтобы одержать победу? Исаак показывает, что
окружение первоначального квадрата полицейского автомобиля представляет
асимметричную компактную область точно из 69 квадратов, каждый из
которых является роковым для преступников. Если же они стартуют в
любом квадрате, расположенном вне этой области, то могут (при
условии, что игровое поле не ограничено) всегда избежать захвата.
Читателю можно посоветовать нарисовать большую шахматную
доску, скажем, 50 на 50 квадратов (или отыскать комнату с
подходящим рисунком на полу), выбрать исходную позицию вблизи центра
для полицейского автомобиля и посмотреть, сможет ли он
определить эти 69 гибельных квадратов. Пока анализ не закончится
полностью, его проведение может доставить массу удовольствия. В свою
очередь игрок, управляющий автомобилем преступников, может
выбрать исходное положение для себя, а затем определить, сможет
ли он победить, достигнув границы до того, как будет пойман.
Играя достаточно долгое время, можно в конце концов определить
гибельную область, но есть более простой путь, благодаря которому
можно быстро сделать набросок и определить каждый из квадратов,
дающих число, указывающее количество ходов полицейского авто-
228 Нескучная математика
*
•
•
•
с
А
А
1
—>
—>
D
Б
V
F
•
—>
X*
*
Е
W
1
1
Ф
Z
*
>Y
•
_•
•
Рис. 94
//гря Исаака «Полицейский автомобиль»
мобиля, необходимое для поимки преступников, при условии, что
обе стороны будут играть рационально.
Для читателей, не склонных проводить полный анализ,
предлагаем более простую задачу. Предположим, что полицейский
автомобиль стартует из позиции, указанной на рисунке. Преступники
могут начинать игру в любом из 10 помеченных звездочками
квадратов. Стартуя из всех этих позиций, за исключением одной, они
могут постоянно избегать захвата. Какой же из помеченных квадратов
является гибельным для преступников и сколько ходов они сделают
до поимки, если начнут игру именно в этом квадрате, а оба игрока
будут делать свои лучшие ходы?
«Джем», «Хот» и другие игры
229
ДОПОЛНЕНИЕ
Джон Хортон Конвей из Кембриджского университета сообщил,
что он с несколькими друзьями увлекся составлением набора из
девяти слов, которые можно использовать при игре в «Хот» и которые
легко запомнить, поскольку их можно расположить так, чтобы
получилось предложение со смыслом. Он предложил слова, которые
помогут вам выиграть, если вы отберете три слова с одинаковыми
буквами из предложения «Count foxy words and stay awake using
lively wit» (в русском переводе это звучит так: «Сосчитай слова лисы и
выше нос»). Читатель может вставить эти слова в табличку
соответствующим образом. Наилучшим же из таких предложений,
содержащим наименьшее количество избыточных букв, считается
малоосмысленная фраза Анны Дункан: «Spit not so, fat fop, as if in pan».
To, что я назвал к числами для игры кайлес, обычно называют
числами или функциями Гранди в честь П.М. Гранди, одного из
первых, кто показал, как такие числа обеспечивают выигрышную
стратегию для большого семейства игр, подобных игре «ним» (см.
мою колонку в журнале Scientific American, январь, 1972).
Рафас Исаак показал, что полезным обобщением игр, связанных
с удалением фишек, является воображаемая большая квадратная
решетка с начальным размещением фишек по любой желаемой схеме.
Два игрока по очереди удаляют любое количество фишек при
условии, что они находятся в одном ряду или в одной колонке. Очень
много игр с удалением в таком случае можно считать
подсемейством этой обобщающей игры. Например, когда исходное
расположение фишек соответствует позиции, изображенной на рисунке 95
вверху, мы имеем марыенбадскую игру в ним. Такое расположение,
как на рисунке 95 внизу, дает марыенбадскую игру в кайлес. Если же
исходная картина расположения фишек представляет квадрат, а
удаляемые фишки на каждом ходу должны быть ортогонально
смежными, мы имеем игру в крестики-нолики Пита Хейна. Случай,
когда в каждой игре удаляются только две ортогонально смежные
фишки, соответствует «краму» (см. мою колонку в Scientific
American, февраль, 1974). Конечно, эту игру можно обобщать и
дальше, чтобы включить и другие типы решеток. Также можно провести
обобщение и в п измерениях, чтобы создать бесконечное
разнообразие игр типа «ним».
Разновидность скупого кайлеса, когда сделавший последний ход
игрок проигрывает, была полностью проанализирована Вильямом
230
Нескучная математика
¦| 1 I 1 I 1 1 1 1 1 1 1
• • •
I 1 1 1 1 1» ~
¦ •
I I 1 1 I I 1 I [¦1 I Г
~1 • •
Рис. 95
Мариенбадские версии нима (вверху) и кайпеса (внизу)
Сибертом, когда эта книга уже находилась в печати (1989 год). Этот
анализ должен появиться в совместной статье Сиберта с Джоном
Конвеем.
Некоторые читатели обращают внимание на тот факт, что в
случае, когда игра с нитями проводится с одной замкнутой петлей, она
эквивалентна замечательной игре Сэма Ллойда, описанной в его
книге Mathematical Puzzles of Sam Loyd («Математические
головоломки Сэма Ллойда»), 1960, том 2, с. 40.
«Джем», «Хот» и другие игры
231
ОТВЕТЫ
Читателей просили отыскать выигрышный ход первого игрока в
игре кайлес с начальным мариенбадским расположением одной, трех,
пяти и семи фишек в четырех рядах. Единственным выигрышным
ходом в данном случае будет удаление центральной фишки из
третьего ряда с пятью фишками.
Игра с нитями, по которой было предложено две задачи,
аналогична кайлесу! То, что нити имеют иррациональную длину,
кажется, усложняет игру, но на самом деле это не так. Доказано, что
любое «иррациональное» удлинение нити для игры не будет иметь
никакого значения. Рассмотрим отрезок нити длиной б1 /2 дюйма.
Отрезание по одному дюйму за один раз от одного конца нити
соответствует в кайлесе удалению одной фишки за ход с конца, ряда из
шести фишек. Оставшийся кусочек нити длиной 1/2 дюйма в
данном случае не играет никакой роли. Вырезание кусочка в один
дюйм внутри нити, после отрезания вначале, скажем, 3/4 дюйма
(или любого кусочка длиной между 1/2 дюйма и дюймом) с конца,
соответствует удалению в кайлесе двух фишек с конца ряда из
шести фишек. Кусочек длиной 3Д дюйма, очевидно, в дальнейшем не
будет иметь никакого значения в игре, и мы остаемся с отрезком
длиной 43Д дюйма, что в кайлесе соответствует ряду из четырех
фишек. Вырезание однодюймового кусочка из середины отрезка
длиной б1 /2 дюйма на расстоянии целого числа дюймов от конца
соответствует в кайлесе удалению одной фишки из середины ряда,
состоящего из шести фишек. Вырезание изнутри кусочка в один
дюйм на расстоянии целого числа дюймов от конца отрезка длиной
61/2 дюйма плюс кусочек длиной между ]/2 дюйма и дюймом
соответствует в кайлесе удалению двух соседних фишек изнутри ряда в
шесть фишек.
Небольшое рассуждение и практическая игра сразу убедят вас,
что каждый ход в кайлесе имеет своего двойника в игре с нитями и
наоборот. Каждый отрезок нити соответствует ряду в кайлесе с
числом фишек, равным числу целых дюймов в длине нити.
А поскольку игры оказались эквивалентными, то готов ответ и
на первый вопрос. Набор веревок 1, п (3,14), V30 (5,47), V50 (7,07)
соответствует игре, в которую играли в фильме, где
последовательность была 1, 3, 5, 7.
Первый игрок, следовательно, может победить в том случае,
если выполнит следующие операции: отрежет кусочек в один дюйм на
232 Нескучная математика
;-МШ1
1
1
0
0
0
7
10
3
2
1
1
0
•
0
4
7
8
11
8
5
4
3
1
1
0
0
0
3
4
5
8
1
11
8
/ 1
4
3
2
1
1
1
2
3
б
10
7
6
3
1
1
1
[ 3
б
9
9
б
5
2
3
4
7
8
3
4
7
10
5
8
8
11
Рис. 96
Решение для игры «Полицейский автомобиль»
расстоянии два дюйма от конца нити длиной 5,47 дюйма, затем
продолжит ходы, которые описаны ранее для стратегии кайлеса.
Если игра с нитями проводится с любым количеством замкнутых
петель, каждая из которых длиннее двух дюймов, второй игрок
легко одержит победу. Всякий раз, когда его противник открывает
петлю, вырезав из нее кусочек длиной в один дюйм, ему нужно просто
«Джем», «Хот» и другие игры
233
удалять один дюйм точно из середины той же самой нити. При этом
остаются два равных отрезка. Как и в кайлесе, это безопасная
позиция, так как в ответ на действия первого игрока с одним отрезком
второй делает то же самое со вторым. Таким образом, картина
быстро становится набором пар дублирующих друг друга нитей,
поэтому второй игрок уверенно получает последний кусочек в один
дюйм.
Если исходная позиция имеет в своем составе одну замкнутую
петлю длиной от одного до двух дюймов, первый игрок одержит
победу, взяв этот дюйм, а затем спланировав стратегию игры в
соответствии с описанной для остающихся отрезков. Легко видеть, что
первый игрок выиграет, если таких небольших петель имеется нечетное
количество, и проиграет, если количество петель четное.
На рисунке 96 показана область гибельных исходных позиций
для автомобиля преступников в игре «Полицейский автомобиль».
Полицейский автомобиль начинает игру из позиции, обозначенной
кружком с направленной стрелкой. Автомобиль преступников
может быть пойман, если стартует из любого пронумерованного
квадрата. Число в каждом квадрате обозначает количество ходов
полицейского автомобиля, необходимое для поимки в том случае, если
оба игрока делают рациональные ходы. Эта же иллюстрация дает
ответ и на последний вопрос: из десяти отмеченных звездочками
стартовых позиций для преступников гибельным квадратом является
один (серый), находящийся на расстоянии хода конем влево и вниз
от полицейского автомобиля. Если противники будут делать свои
лучшие ходы, то захват преступников произойдет через девять ходов
полицейского автомобиля.
Я предоставляю читателям возможность разработать стратегию,
посредством которой полицейский автомобиль поймает
преступников за минимальное количество ходов и посредством которой
преступники либо будут избегать захвата так долго, насколько это
возможно, либо непременно сбегут, если стартуют из
непронумерованных квадратов, или если полиция допустит грубую ошибку.
ГЛАВА 1 7
Занимательная
история ошибок
Слишком много поваров портят бульон.
— СТАРАЯ АНГЛИЙСКАЯ ПОСЛОВИЦА
Когда обнаруживается, что математическая головоломка имеет
серьезный изъян — не имеет ответа, предлагаемый ответ не подходит,
есть противоречие в условии, ответов много, либо находится
лучший ответ, — то обычно говорят, что она «плохо приготовлена».
Само английское слово «cook» (готовить) применяется не только на
кухне, но и в шахматах (Oxford English Dictionary указывает на
цитату 1899 года: «if there are two key-moves, a problem is cooked» — «если
существует два решения, то говорят, что задача опровергнута»).
О забавных эпизодах с шахматными задачами, которые позже
доведены «до ума» другими экспертами, можно написать целую
книгу. В своей книге Curious Chess Facts («Забавные факты мира
шахмат») Ирвинг Чернев цитирует одно из самых курьезных
недоразумений, которые когда-либо появлялись в литературе по шахматам.
В восьмом издании популярного в конце XIX века немецкого
руководства по дебютам Джина Дюфрена и Жака Мейсиса был приведен
следующий вариант игры для ферзевого гамбита.
БЕЛЫЕ
I.d2-d4
2. с2 - с4
3. КЫ-сЗ
4. Kgl-O
5. К f3:d4
6. К d4 - f5
ЧЕРНЫЕ
d7-d5
е7 — еб
с7-с5
c5:d4
еб — е5
е5 -е4
Занимательная история ошибок
235
БЕЛЫЕ ЧЕРНЫЕ
7. Kc3:d5 Kb8-c6
8. Odl-a4 Cc8-d7
9.е2-еЗ Kg8-e7
По мнению авторов, в этой ситуации у черных «превосходящее
преимущество». Но если внимательнее посмотреть, то белые в этой
позиции выигрывают буквально на следующем ходу. Читатель
может разыграть это начало и увидеть стремительную развязку.
Часто партии в турнирах гроссмейстерского уровня
выигрываются потому, что одному из игроков удается подготовить
стандартную линию дебюта, удерживая преимущество на своей стороне до
тех пор, пока он не сможет воспользоваться им против оппонента.
Игра шашки уже получила исчерпывающий анализ, так что многие
игры профессионалов повторяют друг друга. Если в такой партии
кто-то побеждает, значит, он смог опровергнуть знакомую всем
линию игры.
Конечно, история науки беспрестанно обогащается
всевозможными заблуждениями. Как заметил философ Карл Поппер, научная
теория тавтологична, если теоретически не существует способа
опровергнуть (или, как говорят, фальсифицировать) ее. Чем больше
возможных путей опровергнуть теорию, тем сильнее сама теория (если
только, в конце концов, она «отвечает на все вопросы и проходит все
тесты»). «Железная» определенность — это прерогатива математики,
но самим математикам ошибки не чужды. Даже в математике
доказательство порой нуждается в «социальном» одобрении со стороны
других ученых. История этой науки изобилует «доказательствами»,
авторами которых были выдающиеся математики, но тем не менее эти
доказательства были позже развенчаны. Особенно верно это в
отношении занимательной математики, где преобладают любители.
Один из наиболее известных американских авторов головоломок
Сэм Ллойд опубликовал так много шахматных задач и
математических головоломок, что огромное количество фатальных изъянов в
них не удивительно. Одну из наиболее ярких ошибок Ллойд
допустил в решении задачи о разбиении фигуры. Она опубликована в его
книге Cyclopedia of Puzzles («Энциклопедии головоломок»).
Читателя спрашивают, можно ли разбить фигуру, показанную на рисунке
97, слева (это квадрат с отсутствующей четвертинкой), таким
образом, чтобы из частей можно было собрать совершенный квадрат.
Ответ Ллойда, в котором было четыре фигуры, показан пунктиром
236
Нескучная математика
Рис. 97
Ллойдовское решение задачи (именно в нем и нашел ошибку Дьюдени)
на левом рисунке, а переставленные части — на правом.
«Существует множество способов решить эту задачу, разбивая квадрат на 5—12
частей, — писал Ллойд, — но подобный подход требует сложного
научного анализа».
Именно британский мастер головоломок Генри Эрнест Дьюдени
(а математиком он был лучшим по сравнению с Ллойдом) исправил
решение Ллойда. Известно, что прямоугольник можно с помощью
разреза «ступеньками» превратить в квадрат. Но подобный подход
«работает», только когда стороны прямоугольника находятся в
определенном соотношении, и в данном случае соотношение (три к
четырем) не позволяет это сделать. Дополнительно вы можете
почитать об этом в книге Дьюдени Amusements in Mathematics
(«Занимательная математика») в задаче 150 и в книге Modern Puzzles
(«Современные головоломки») в задаче 115. Остроумное решение Ллойда
дает квадрат, но продолговатый. Дьюдени предложил правильные
решения с пятью частями {см. рис. 98). Полагали, что решения с
четырьмя частями не существует. Однако Гарри Линдгрен в своей
замечательной книге Recreational Problems in Geometric Dissections
(«Занимательные задачи на разбиение квадрата») показывает, как
можно разделить два квадрата с вырезом, чтобы сложить из восьми
получившихся кусков два совершенных квадрата {см. рис. 99).
Иногда находят ошибки и у тех, кто сам активно опровергает
других. Англичанин Анджело Льюис, писавший книги по магии и
головоломкам под псевдонимом «Профессор Хоффман», привел
Рис. 98
Правильное решение Дьюдени с пятью частями
Рис. 99
Совместное решение для двух неполных квадратов. Автор — Линдгрен
238
Нескучная математика
вот такую головоломку с 20 точками в своей книге Puzzles Old and
New («Старые и новые головоломки») 1893 года. Глядя на крест из
точек на рисунке 100, определите, сколько различных квадратов
можно найти в различных сочетаниях из четырех точек. Хоффман
утверждает, что 17. В своей статье The Best Puzzles with Coins
(«Лучшие головоломки с монетами») в журнале The Strand Magazine, 1909,
Дьюдени дополнил его решение и привел список из 19 квадратов.
На самом деле квадратов 21.
Дьюдени привел правильное значение, когда переиздал
головоломку в одной из своих книг. Читателю не составит труда найти 21
квадрат. Однако вторая часть головоломки более сложная — удалите
6 точек так, чтобы нельзя было найти ни одного квадрата вообще.
Рис. 100
• • Двойная головоломка с точками
Большинство ошибок Дьюдени было найдено читателями в
головоломках, публикуемых в газетах и журналах. Это позволило
автору исправлять головоломки прежде, чем они появлялись в
книгах. Но даже в книгах многие головоломки оказывались
некорректными. Давайте рассмотрим одну из задач, которая
появлялась в его книгах Amusements in Mathematics (задача 244) и
Modem Puzzles (задача 161). Автомобиль начинает свой маршрут в
узле А на краю города в виде сетки кварталов 7x7
(соответственно улицы дают сетку размером 88, см. рис. 101). В другом
варианте на клетке шахматной доски, где стоит король, располагают
ладью. Однако движение вдоль разделительных линий (а не по
ним) делает вопрос о расстоянии менее однозначным. Машина
должна проехать самый длинный возможный маршрут, сделав не
более 15 поворотов и не проходя дважды ни одной части
маршрута. Также необходимо, чтобы осталось как можно меньше
пропущенных узлов.
Занимательная история ошибок
239
Рис. 101
Первое решение головоломки и два опровержения
Приведенное в книге Дьюдени минимальное решение дает 70
отрезков с 19 пропущенными пересечениями. Впоследствии
Дьюдени поправил собственное решение (см. средний маршрут). Новое
решение было опубликовано в его следующей книге Puzzles and
Curious Problems («Головоломки и любопытные задачи») под
номером 269. Теперь длина маршрута составляла 76 клеток и
пропущенными остались только три пересечения. Окончательное ли это
решение? Нет. Виктор Милли из графства Дублин, Ирландия,
прислал мне маршрут (он показан справа), который проходит
через 76 клеток, имеет 15 поворотов, и лишь один угол остается
неохваченным! Наверное, этот рекорд можно превзойти, если найти
маршрут, который проходит более чем через 76 клеток, либо тот же
маршрут, но проходящий через все пересечения. По крайней мере,
я не знаю доказательств того, что это решение окончательное.
Задача 57 из книги Puzzles and Curious Problems («Головоломки и
любопытные задачи») связана с циферблатом, на котором
изображены римские цифры. Читателю требуется разбить циферблат на
четыре части, чтобы в каждой части сумма цифр составляла 20.
Поскольку сумма цифр от 1 до 12 дает 78, необходимо поднять ее до 80.
Дьюдени не придумал ничего лучше, как перевернуть вверх ногами
IX, в результате чего получается XI. Этот трюк делает возможным
разбиение циферблата (см. рис. 102). Ллойд устранил изъян этого
решения (см. его книгу Sam Loyd and His Puzzles, 1909). Его решение
приведено на рисунке справа.
В свою очередь Ллойд сам пропустил дюжину совершенных
решений, ни одно из которых не требует, чтобы цифры читались в
противоположном направлении. Девять из них читатель построит без
240
Нескучная математика
Рис. 101
Циферблат. Первое решение головоломки и два опровержения
больших усилий, но три окажутся поистине неуловимыми. Обратите
внимание на то, что римская цифра «четыре» записана в виде НИ, а
не IV. Таковы традиции часовых дел мастеров. Цифры следует
считать частью оправы циферблата. То есть линия разделения может
разделять цифру, но не может образовывать петли, отделяющие
цифры от оправы циферблата. Если бы это было позволено, то задача
стала бы сразу неинтересной, поскольку стали бы возможны сотни
решений.
Редактируя большую ллойдовскую энциклопедию, я обнаружил
сотни ошибок, большую часть которых следует отнести на счет
наборщиков. Среди реальных ошибок мастера, которые я пропустил,
одна была для меня наиболее непростительной. Речь идет о ллой-
довской задаче с орлами на странице 117. Эту ошибку представил
моему вниманию читатель Д. Виллер из Миннеаполиса. Точно в
момент восхода солнца американский орел взлетает с вершины
Капитолия в Вашингтоне и летит на восток, пока солнце не поднимется
в зенит (для орла). Затем орел поворачивает обратно и летит на
запад, пока не увидит закат. Поскольку орел и солнце двигаются в
противоположных направлениях до полудня и в одном направлении
после полудня, очевидно, что послеобеденный полет будет более
длительным, а также что закат застанет орла к западу от точки
старта. Орел в этом месте устраивается ночевать до восхода солнца и
повторяет те же действия. Он летит на восток, пока солнце не
окажется в зените, а затем на запад, пока солнце не сядет. Так он
продолжает, пока не окажется снова над Вашингтоном. Предположим, что
длина кругового полета орла от купола Капитолия вокруг Земли с
Занимательная история ошибок
241
востока на запад составляет ровно 19 500 миль. Предположим
также, что в конце каждого дня орел оказывается на 500 миль западнее
того места, где начал полет.
Сколько дней потребуется, чтобы орел вернулся к Капитолию?
Ответ: 38 дней, который приведен в одном из первых двух выпусков
головоломок, неправильный. Как же читатель установил это?
В одном из самых красивых развенчаний головоломок свое
слово сказала география. Охотник находится в определенной точке на
земле. Посмотрев точно на юг, он видит в 100 ярдах от себя медведя.
Медведь проходит 100 ярдов на восток, в то время как охотник
остается на прежнем месте. Затем охотник направляет ружье точно на
юг, прицеливается и убивает медведя. Где стоит охотник? Конечно
же первоначальным ответом был Северный полюс. Как
объяснялось в книге The Scientific American Book of Mathematical Puzzles &
Diversions («Книга математических головоломок и развлечений от
Scientific American»), есть и другой правильный ответ. Человек мог
стоять очень близко к Южному полюсу. Причем настолько близко,
что прогулка медведя по круговой дорожке в 100 ярдов приведет его
в то же место, откуда он вышел. Ответов подобного рода
существует множество. Охотник мог вставать все ближе и ближе к Южному
полюсу и тогда медведь обходил бы его два, три и т. д. раза. Ну вот,
теперь задача решена полностью? Отнюдь нет. Бенджамин Шварц
шесть лет назад писал в математический журнал о том, что он
обнаружил еще два совершенно новых семейства решений! Прочитайте
еще раз формулировку задачи и посмотрите, нет ли у вас идей.
Мне пишут не только серьезные читатели, которые весомо
дополняют мою рубрику в Scientific American, но и, как я их называю,
«мастера каламбура». Эти люди играют значениями слов, находя
«неточности» в условиях задачу
Однажды в качестве шутки я привел в детской книге такую
задачу. Формулировка такова: обведите кружком в таблице шесть цифр
так, чтобы их сумма составила 21.
9 9 9
5 5 5
3 3 3
1 1 1
Мой ответ состоял в следующем — перевернуть таблицу вверх
ногами и обвести три шестерки и три единички. Говард Вилкерсон из
242
Нескучная математика
Сильвер Спринг, Мэриленд, восхитительно опроверг мое решение.
Не переворачивая страницы, он отметил все тройки, единицу слева,
а затем обвел кружком две другие единицы. Получилось 3,3,3,1,11,
что дает 21.
ДОПОЛНЕНИЕ
Читателям не удалось обнаружить маршрут для ладьи (или
машины), который бы имел 15 поворотов и был длиннее 76 клеток либо,
имея те же 76 клеток, проходил бы через все перекрестки. Многие
присылали мне решения с 75 клетками, но проходящими через все
перекрестки. Кстати, долгое время считалось, что 14 поворотов —
это тот минимум, который необходим, чтобы пройти через все
перекрестки сетки, и что 15 это слишком.
Задача об охоте на медведя принесла мне множество писем.
Читатели предлагали другие решения. Охотник смотрит на юг, в
зеркало, сам стоя лицом на север. Другой вариант — охотник «спокойно
стоит» на движущейся машине или лодке. Был также вариант и с
медведем, который оставался на одном месте (хотя и шел),
поскольку находился на дрейфующей льдине. А в одном из писем пуля
умудрилась обогнуть Землю. Одно из писем, от Р. Бертона из Шеппер-
тона, Англия, было опубликовано в отделе писем Scientific American
в октябре 1966 года.
Господа!
Представляю еще один бесконечный набор ответов на задачу об
охоте на медведя. Я не хотел бы более беспокоиться о несуществующем
в Антарктике роде Ursus и предлагаю следующее решение проблемы.
Хотя медведь и должен находиться в Южном полушарии, охотник
может располагаться в любом месте на той же долготе. Тогда у него
есть возможность поразить медведя с любого расстояния, как только
тот пересечет меридиан и будет на юге от охотника.
Этот метод основывается на том факте, что пуля, выпущенная из
ружья в южном направлении, получает от вращения Земли восточную
составляющую скорости.
Этот компонент соответствует линейной скорости движения
точки на экваторе, помноженной на синус широты положения
охотника. Предположим, что медведь находится на более высоких широтах
к югу от охотника, оружие которого имеет достаточно длинный ра-
Занимательная история ошибок
243
диус действия и малую скорость пули. Если охотник находится на
южной широте 89 градусов, а медведь — на широте 89 градусов и 10 минут
(что соответствует расстоянию И1/2 миль), то пуля, вылетающая
из ствола со скоростью 600миль в час, у цели будет иметь отклонение
на восток 100ярдов (91,44 м). При меньших расстояниях и на более
высоких широтах оружие может иметь меньшую скорость пули.
Эти рассуждения представляют чисто исторический интерес в
связи с событиями Первой мировой войны. Немцам приииюсь вводить
поправку на широту местности, когда они создавали артиллерию
сверхдальнего действия. Если цель располагалась на востоке,
баллистикам приходилось учитывать эффект вращения Земли.
Вот неопубликованный ответ Бенджамина Шварца.
Уважаемый Бертон!
Оценивая по достоинству ваше дополнение к вопросу, не могу не
заметить, что вы в своем решении подменили условия. В своей статье
1960 года я писал об этой задаче как о примере из сферической
математики. Конечно, персонажи задачи были введены больше для
интереса, и фундаментальная суть задачи состоит в геометрии. Обратите
внимание на отмеченные абзацы в приложенной копии.
В данном случае, чтобы остаться объективньш, необходимо
принять во внимание динамику. И тут вас ждут сюрпризы. Низкая
скорость пули не позволят ей далеко улететь. Притяжение, знаете ли.
В вашем случае пуля должна быть выпущена горизонтально на
высоте примерно 22 860 м, чтобы не удариться в землю прежде, чем она
преодолеет 18,5 км. Сопротивлением воздуха мы здесь пренебрегаем.
Я думаю, вы согласитесь, что охотник получается несколько высоко-
ватым.
Одним из вариантов преодоления этой трудности является
вариант, когда охотник стреляет навесом так, чтобы горизонтальная
составляющая скорости составляла 960 км/час (как вами было задано,
чтобы пуля поразила медведя через 69 с). Боюсь, однако, что учет
сопротивления воздуха и особенностей баллистики перечеркнет ваше
решение. Теперь вы видите, какое осиное гнездо разворошили.
Чтобы не выбрасывать эффект Кориолиса при теоретическом
рассмотрении этой проблемы, хочу вам предложить одно из «решений».
Пусть скорость пули будет 27200 км/час (этого вполне достаточно,
чтобы запустить пулю по круговой орбите на высоте 1,52 м над
Землей). Пуля будет вращаться вокруг Земли с запада на восток и, смеща-
244
Нескучная математика
ясъ, рано или поздно поразит любого медведя ростом более 1,52 м, если
только он имеет физическую ширину. (После выстрела охотнику
лучше пригнуться.)
ОТВЕТЫ
1. Мат в один ход 10. К f5 — d6 x
2. На рис. 103 показано серым цветом, как удалить шесть точек,
чтобы разом уничтожить 21 спрятавшийся квадрат. Решение
уникально, но возможны повороты и отражения.
3. Кроме решения Сэма Ллойда существует 12 других идеальных
решений {см. рис. 104). Каждый циферблат разделен на четыре
части так, что сумма чисел в каждой части составляет 20. Последние
три решения найти труднее всего.
Рис. 103
Решение головоломки с 20 точками
Рис. 104
Решения головоломки с разбиением циферблата часов
246
Нескучная математика
4. Орел Ллойда заканчивает свой полет на закате спустя 39 /2
дней.
Сам орел насчитает 38]/2 дней (от восхода до заката), но,
поскольку он движется против вращения Земли, один день для него
«теряется».
5. Предположим, что охотник и медведь находятся около
Южного полюса. Медведь в 100 ярдах к югу от человека, который
располагается так, что к моменту окончания своей прогулки на восток в 100
ярдов он будет точно с другой стороны Южного полюса. Таким
образом, когда охотник наведет свое ружье на юг и выстрелит, пуля
пролетит над Южным полюсом и поразит его. Существует бесконечное
множество решений, поскольку медведь может быть ближе к
полюсу и обойти его полтора раза или два с половиной.
Второе семейство ответов, которое легко проглядеть, зависит от
понимания фразы: «Человек смотрит на юг и видит медведя на
расстоянии 100 ярдов». Ясно, что человек и медведь могут находиться на
противоположных сторонах Южного полюса на расстоянии в 100
яров. Но человек немного дальше от полюса, чем медведь. Пройдя
сто ярдов на восток, медведь пишет полукруг и окажется на другой
стороне полюса. Конечно, охотник может немного более
отклониться от полюса, и тогда медведь может сделать один, полтора, два и так
далее полных круга, что дает бесконечное множество решений,
имеющих в пределе расположение, когда охотник окажется на
расстоянии 100 ярдов от полюса. Тогда прогулка медведя будет напоминать
пируэты на полюсе. Эти обе группы решений были приведены
Бенджамином Шварцем в статье What Color Was the Bear? («Какого
цвета был медведь?») в журнале Mathematics Magazine, том 34,
сентябрь — октябрь, 1960, с. 1—4.
ГЛАВА 1 8
Суперэллипс Пита Хейна
Самое великое из искусств— все делать безыскусно.
-ПИТХЕЙН
В современном мире человек повсюду окружен конфликтующими
формами, но редко когда замечает это. Все вокруг нас
прямоугольное либо круглое. Колеса машин, рулевое колесо круглые, а улицы
пересекаются подобно линиям прямоугольной решетки. Здания
состоят, как правило, из прямых углов, смягченных иногда округлыми
куполами и окнами. Мы сидим за прямоугольными или круглыми
столами и едим из круглых тарелок, подкладывая на колени
прямоугольные салфетки. Стаканы в своем сечении имеют круги.
Закуривая, мы подносим к цилиндрическим сигаретам спички, которые
берем из прямоугольных коробков. Расплачиваемся мы
прямоугольными банкнотами и круглыми монетами.
Даже наши игры можно описать сочетанием круглого и
прямоугольного. Большая часть спортивных состязаний проходит на
прямоугольных площадках, а играем мы круглым мячом. Настольные
игры от бильярда до шашек не исключение. Даже прямоугольные
игральные карты мы выкладываем, подобно вееру, полукругом.
Да и буквы, которыми мы пишем, — это череда прямых углов и
полукруглых дуг. Везде, куда вы ни посмотрите, вы увидите
квадраты, круги и, соответственно, прямоугольники и эллипсы. (В какой-
то мере эллипс встречается даже чаще, поскольку именно так под
углом выглядит круг.) На картинах и узорах квадраты, круги,
прямоугольник и эллипсы встречаются столь же часто, как и в нашей
повседневной жизни.
Писатель и изобретатель из Дании Пит Хейн задал себе забавный
вопрос: какова самая простая и приятная для глаза замкнутая
кривая, которая является средним между этими двумя крайностями.
248
Нескучная математика
Начав свою карьеру как ученый, Пит Хейн (он предпочитает чтобы
его имя упоминали полностью) впоследствии прославился в
Скандинавии и англо-говорящих странах огромным количеством
изящных афористичных стихов, а также заметками по научным и
гуманитарным вопросам. Тем, кто увлекается занимательной
математикой, он больше известен как изобретатель игры «Геке», кубиков
Сома и других замечательных игр и головоломок. Пит Хейн был
другом Норберта Винера, который даже посвятил ему свою последнюю
книгу God and Golem, Inc. («Корпорация Боги Голем»).
Вопрос Пита Хейна, хотя и был продиктован исключительно
любопытством ученого, впервые возник как практическая проблема
городского планирования в 1959 году в Швеции. Задолго до этого
было принято решение о сносе части старых построек Стокгольма и
реконструкции сети узких улиц в центральной части города. После1
Второй мировой войны эта масштабная и дорогостоящая
программа начала осуществляться. С севера на юг и с запада на восток город
(через самый центр) разрезали две новые транспортные артерии. А
на пересечении этих авеню образовалась большая прямоугольная
площадь (сейчас там площадь Сергельс Торг (Sergels Torg)). В ее
центре овальный остров-фонтан, окруженный овальным водоемом,
в котором несколько сотен малых фонтанов. Овальный ресторан
самообслуживания, находящийся ниже уровня тротуара, где столики
расположены овалами в несколько рядов, освещается светом,
проходящим через стеклянный потолок. Под этим рестораном
планируется поставить еще два этажа, где будут располагаться обеденные
залы, танцевальный зал, гардероб и кухня.
Планируя точную форму этого центра, архитекторы Швеции
столкнулись с неожиданной проблемой. Эллипс не подходил,
потому что его вытянутые части конфликтовали с потоком движения
машин вокруг него. Кроме того, он не гармонировал с
прямоугольником площади. Пробовали кривую, составленную из восьми круглых
дуг, однако места соединения линий имели некрасивые переходы. К
тому же план имел несколько овальных форм, вложенных друг в
друга, и кривые из восьми дуг просто отказывались вкладываться
друг в друга.
Для разрешения этой проблемы команда архитекторов
обратилась за консультацией к Питу Хейну. Это была проблема, которая
требовала не только знания математики, но и художественного
воображения, чувства юмора, гибкости творческого подхода в самых
неожиданных направлениях. Какая из кривых может быть менее
Суперэллипс Пита Хейна
249
вытянута, чем эллипс, и гармонично впишется в прямоугольник
площади, расположенной в самом сердце Стокгольма?
Давайте проследим за логикой Пита Хейна. Он рассмотрел
эллипс как частный случай более общего семейства кривых,
описываемых в декартовых координатах следующей формулой:
X
а
п
+
У
ь
где а и b — неравные друг другу параметры (произвольные
константы), которые представляют две полуоси кривой, а п — любое
положительное число. Вертикальные скобки указывают, что каждое
отношение должно быть взято по модулю (т. е. его знак надо просто
отбросить). Эти скобки в некоторых из формул будут опущены в том
предположении, что берутся абсолютные величины отношений.
При /1=2 получается эллипс с полуосями аиЬ. Говоря
современным жаргоном, множество решений уравнения {х, у} на графике
дает замкнутую кривую в виде эллипса.
При уменьшении параметра п с двух до единицы овал
становится более «угловатым» («подэллипсы», как называл их Пит Хейн).
При п = 1 кривая превращается в параллелограмм. При п < 1
стороны параллелограмма превращаются в вогнутые кривые, кривизна
которых все более увеличивается по мере приближения п к нулю.
При п — 0 кривая вырождается в пересечение двух прямых.
Если п начать увеличивать (начиная с двух), овал становится все
более похожим на прямоугольник, прижимаясь к сторонам
прямоугольника, описываемого полуосями. В пределе, когда п стремится
к бесконечности, кривая вырождается в прямоугольник. Так какая
же кривая наиболее приятна глазу? По мнению Пита Хейна, это
овал, получаемый при п = 21'/f2. На компьютере были получены 400
пар координат с точностью до 15 знаков после запятой (а иногда и
больше). Прецизионные кривые были нарисованы в самых
различных размерах, причем соотношения высоты и ширины
соответствовали размерам площади в центре Стокгольма. Эти странные овалы
оказались в меру округлыми и в меру прямоугольными, счастливым
образом сочетая в себе очарование эллипса и прямоугольника.
Более того, такие кривые прекрасно вкладывались друг в друга, как
показано на рис. 105 и 106, оставляя чувство гармонии
концентрических овалов. Пит Хейн называл такие кривые (для которых п > 2)
суперэллипсами. Архитектурная элита Стокгольма сразу же приняла
идею суперэллипса с показателем 2]/2 в качестве определяющей
250
Нескучная математика
Рис. 105
Концентрические суперэллипсы
формы нового центра. Когда было закончено обустройство центра
Стокгольма, столица Швеции обогатилась еще одной
туристической достопримечательностью (интересной, правда, для
математиков!). В настоящее время большой фонтан в форме суперэллипса
придает этому северному городу легкий математический шарм,
подобно тому, как гигантские ворота из нержавеющей стали украсили
американский город Сент-Луис.
Меж тем суперэллипс Пита Хейна заметил и с энтузиазмом
воспринял Бруно Мэтссон, известный в Швеции дизайнер мебели. Для
начала он произвел несколько вариантов столов в форме
суперэллипса (их можно увидеть во многих шведских офисах), за которыми
последовали столы для дома, стулья и кровати (кому нужны углы?).
Представители промышленности четырех стран — Дании, Швеции,
Норвегии и Финляндии обратились к Питу Хейну для решения
извечного конфликта между круглым и прямоугольным. Сейчас он
разрабатывает модели мебели, тарелок, подставок для них, ламп,
серебряных изделий, текстильных узоров и многое другое.
Столы, стулья и кровати также украсились и другим
изобретением Пита Хейна — необычными самозакрепляющимися ножками,
которые легко устанавливаются и снимаются.
Суперэллипс Пита Хейна
251
Рис. 106
Схема расположения подземного ресторана и бассейна над ним, Стокгольм
«Суперэллипс воплощает в себе единство круга и эллипса,
однако оно не столь очевидно и банально», — пишет Пит Хейн в
ведущем датском журнале, посвященном прикладным искусствам и
промышленному дизайну. (На совершенно белой обложке этого
номера журнала была нарисована абсолютно черная линия
суперэллипса, а сверху математическая формула, описывающая
кривую.)
«Суперэллипс — это не просто новая причуда, — продолжает
Пит Хейн. — Это сродни тому, как избавиться от уз простых форм
первого и второго порядка, которые представляют собой прямые
линии и одно из конических сечений». Не следует путать
суперэллипс Пита Хейна с внешне похожей кривой, которую часто мож-
252
Нескучная математика
но увидеть на лицевой панели телевизоров. Чаще всего это не
более чем путаница различных форм дуг, которую не может описать
единая математическая формула, дающая эстетическое единство
формы.
Когда оси эллипса равны, это, конечно, круг. Если в формуле
кругах2 + у2 = 1 вторую степень заменить более высокой, то
формула будет описывать, как это называет сам Хейн, «суперкруг».
При п = 211f2 получится истинный «квадрированный круг»,
поскольку графически он лежит ровно на полпути между двумя
предельными случаями. Изменение формы кривой, описываемой общей
формулой;^ +у" = 1, где п может принимать значения от 0 до
бесконечности, графически представлено на рисунке 107. Если этот график
равномерно растянуть вдоль одной из осей (одно из аффинных
преобразований), это дало бы семейство «суперэллептических» кривых
— субэллипсы, эллипсы и суперэллипсы.
Подобным образом мы можем увеличить степень в
соответствующей формуле для сферы и эллипсоида, чтобы получить
«суперсферу» и «суперэллипсоид» (как назвал бы их Пит Хейн). Если
показатель степени составит 21/2, то такое тело геометрически можно
рассматривать как нечто среднее между сферой (эллипсоидом) и кубом
(прямоугольным параллелепипедом).
Истинный эллипсоид, стремя неравными осями, можно описать
формулой
где а, Ъ и с — неравные друг другу параметры, представляющие
собой полуоси. Если эти параметры равны друг другу, то тело
вырождается в сферу. Если равны только два параметра, то получается
эллипсоид вращения, или сфероид. Его можно получить, если
вращать эллипс вокруг одной из его осей. Если это длинная ось,
получается вытянутый сфероид, напоминающий по форме яйцо. В
сечении, перпендикулярном этой оси, получается круг.
Оказывается, что вытянутый сфероид с гомогенно
распределенной плотностью нельзя заставить балансировать ни на одном
из его концов. В случае с яйцом это тоже невозможно, если только
не применить трюк, честь открытия которого приписывается
Колумбу. Христофор Колумб вернулся в 1493 году на родину в
Испанию, полагая, что открыл новый путь в Индию, обогнув Землю с
другой стороны. Однако на пути Колумба встала Америка — неиз-
Суперэллипс Пита Хейна
253
вестные прежде земли, прозванные Новым Светом. В Барселоне в
его честь давался банкет. Вот как об этом рассказывает Джироламо
Бенцони в своей книге History of the New World («Истории Нового
мира», Венеция, 1565). (Я привожу отрывок из раннего
английского перевода.)
Колумб находился в компании благородных испанцев. Один из них
спросил его: «Уважаемый, пусть вы не нашли Индии. Но мы не можем
не воздать должное человеку, который предпринял то, на что решились
вы — особенно здесь, в Испании, где так много образованных людей,
сведущих в искусстве читать по звездам».
В ответ на эти слова Колумб не проронил ни слова. Он лишь
пожелал, чтобы ему принесли яйцо, которое он положил на стол перед
собравшимися, сказав при этом: «Джентльмены, я готов заключить
пари с любым из вас, что вы не заставите это яйцо стоять на острие,
как это получится у меня. Причем сделаю я это голыми руками без
каких-либо инструментов». Гости все перепробовали, но ни у кого ничего
не получилось. Когда яйцо возвратилось к Колумбу, он немного стукнул
им по столу, расплющил один из концов и поставил. Участники пари
были посрамлены. После того как дело сделано, каждый знает, как
сделать его.
Может быть, эта история и случилась в реальности. Однако
пятнадцатью годами раньше подозрительно похожая история уже
описывалась Георгио Вазари в его знаменитой книге
«Жизнеописание наиболее знаменитых живописцев ваятелей и зодчих»
(Флоренция, 1550). Героем этой истории был молодой Филиппо Бру-
неллески — итальянский архитектор, по проекту которого
построили удивительно большой и тяжелый купол кафедрального собора
Св. Марии во Флоренции. Совет архитекторов попросил его
показать модель, но архитектор отказался, «предложив мэтрам вместо
этого... заставить яйцо стоять вертикально на совершенно плоской
мраморной плите». По словам молодого архитектора, тот, кто
сможет это, и должен строить купол, ибо обладает достаточным умом.
Именитые мастера не смогли заставить яйцо стоять на острие.
После чего Филиппо взял яйцо, незаметно стукнул им по мрамору и
поставил. Мэтры возразили, что они могли бы сделать то же самое,
на что Филиппо ответил, что всякий может поднять купол, если он
видел модель или проект. Таким образом, было принято решение,
что купол поднимает Филиппо.
254
Нескучная математика
Превосходная история. Когда большой купол был наконец
закончен (это случилось за несколько десятилетий до первого рейса
Колумба), он имел форму яйца, сплющенного в острой части.
Какое отношение это имеет к суперэллипсоиду? Пит Хейн
(насколько я знаю, именно по следам Колумба и Брунеллески) открыл,
что именно суперэллипсоид с показателем 2]/2 обладает тем
свойством, что может балансировать на любом из своих концов. Причем
без всякого обмана! Во многих домах Скандинавии можно увидеть
украшения в виде деревянных и серебряных супер-яиц, стоящих на
основании.
Посмотрите на серебряное супер-яйцо, показанное на рисунке
107. Соотношение высоты к ширине для него 4:3, а показатель
степени составляет 2'/2. Это призрачное равновесие может стать
символом хрупкого баланса между прямоугольной и круглой формой,
честь открытия которого принадлежит Питу Хейну, подружившему,
как сказал бы Чарльз Перси Сноу (1905—1980), «две культуры».
Рис. 107
Серебряное супер-яйцо, которое может стоять на любом конце
Суперэллипс Пита Хейна
255
ДОПОЛНЕНИЕ
Семейство плоских кривых, описываемых уравнением [х/а]п +
[у/Ь]п = 1, изначально было открыто и изучено Габриелем Ламе -
французским физиком XIX века, написавшим о них работу в 1818
году. Во Франции эту кривую называют courbes de Lame, в Германии
- Lamesche kurven, что по-русски означает просто «кривая Ламе».
Эти кривые являются алгебраическими, если показатель степени п
рационален, и трансцендентальными, если п — иррационально.
При п = 2/3иа = b {см. рис. 108) получается астроида. Это кривая
известна тем, что ее описывает точка на малой окружности, когда
эта окружность катится внутри большего круга. Радиус малой
окружности может составлять одну четвертую или три четвертых
большого круга. Соломон Голомб обратил внимание на тот факт, что при
нечетном показателе степени и опущенном знаке модуля формула
Рис. 108
Суперкруг и связанные кривые
256
Нескучная математика
кривой Ламе описывает другое семейство кривых, исследованное
итальянским математиком-женщиной Марией Аньези (1718—1799).
По-итальянски название кривой versiera (кривая соответственно
именовалась versiera Agnesi). Но это же слово считалось
сокращением итальянского слова avversiera — «жена дьявола».
Неправильный перевод на английский язык породил оборот «Witch of Agnesi»,
и впоследствии Марию Аньези стали величать так же (ведьма
Аньези). Мария исследовала случай для п = 3.
Уильям Хоган писал о том, что форма арок на бульваре
разрабатывалась им и другими инженерами часто с использованием кривой
Ламе с показателем степени 2,2. В тридцатые годы их бы назвали
«2,2-эллипсы».
При конструировании физических объектов в форме
суперэллипсов, когда показатель кривой Ламе больше 2, параметры а и b
можно менять в зависимости от конкретных обстоятельств и
вкуса заказчика. Для стокгольмского центра Пит Хейн использовал
такие параметры: п =21/2м а/b = в/5. Несколько лет спустя
Джеральд Робинсон, архитектор из Торонто, применил суперэллипс
при проектировании стоянки в торговом центре в Питерборо,
пригороде Торонто. Его длина и ширина соотносились как 9/7.
При данном соотношении, по мнению Джеральда, наиболее
приятный суперэллипс получается при показателе степени чуть
больше 2,7. Этот факт навел на мысль о возможности использования в
формуле иррационального числа е (так как е = 2,171828...). Как
писал Норман Гриджеман, использование Робинсоном числа е в
качестве показателя степени не прошло бесследно. Каждая точка
кривой Ламе, за исключением четырех точек, описывалась
трансцендентальным числом. Эти точки лежали на пересечении овала с
осями.
Читатели предлагали и другие параметры. Так, Дж. Тернер
предложил выбрать геометрически среднее положение между кругом и
квадратом (или прямоугольником и эллипсом). Соответственно
показатель степени должен подбираться так, чтобы по площади
фигура равнялась среднему арифметическому между двумя предельными
случаями. Мендевиль обнаружил, что показатель степени,
обеспечивающий среднюю между двумя фигурами площадь, на удивление
близок к числу я — настолько близок, что читатель задается
вопросом, не является ли это еще одной формой выражения
универсальной константы. К сожалению, нет. Нортон Блейк с помощью
компьютера установил, что эта величина чуть больше 3,17. Тернер так-
Суперэллипс Пита Хейна
257
же предложил выбирать фигуру, которая пересекает отрезок,
соединяющий угол прямоугольника с точкой пересечения эллипсом
диагонали прямоугольника, строго посередине.
И Тернер, и Блейк сошлись во мнении о том, что эстетически
наиболее приятен суперэллипс, у которого а/b соотносятся в
соответствии с золотым сечением.
Тернер утверждает, что самый приятный суперэллипс
вписывается в прямоугольник, подчиненный золотому сечению, а п = е.
Мишель Балински и Филет Холт III в своем письме, опубликованном в
New York Times в декабре 1968 года (конкретно день я не записал),
рекомендует выбрать золотое сечение и п = 2У2. Именно такой, по
их мнению, должна быть форма столов для переговоров в Париже.
Некогда дипломаты, собиравшиеся по поводу заключения
вьетнамского мира, уже ссорились по поводу формы стола. По мнению
Балински и Холта, если единства мнений по поводу формы стола
достичь не удастся, дипломатов следует поместить в полое супер-яйцо
и трясти его до тех пор, пока они не придут к «суперэллептическо-
му» соглашению.
Площадь в центре Стокгольма все еще находится в состоянии
строительства. Однако «Суперэллипс-плаца» с фонтаном уже
закончена. Расположенный под ними торговый пассаж Пит Хейн Ар-
кейд (Piet Hein Arcade) с магазинами и рестораном был закончен в
1979 году.
Супер-яйцо является особым случаем более общей формы,
описываемой суперэллипсоидом. Формула суперэллипсоида такова:
X
а
п
+
у
b
п
+
Z
С
п
= 1
При а = b = с тело представляет собой суперсферу — нечто
промежуточное между сферой и кубом. При а = b тело представляет
собой суперкруг в поперечном сечении и формула такого тела будет:
i \п
\Ц =1.
X
а
п
+
у_
а
п
+
Z
b
Супер-яйцо с круглым поперечным сечением описывается
формулой:
J
2 2
х +у
= 1.
258
Нескучная математика
Когда я писал в свою колонку о суперэллипсе, то полагал, что
любое тело данной формы при п > 2 будет балансировать на своем
конце, если только его высота ненамного больше ширины. Супер-
яйцо при показателе степени, стремящемся к бесконечности,
естественно, является правильным круглым цилиндром и будет стоять
на торце вне зависимости от пропорций.
Но если не говорить о бесконечности, то интуитивно ясно, что для
каждого показателя степени существует критическое соотношение
высоты к ширине, при которых яйцо станет неустойчивым. Я
некогда даже опубликовал следующее доказательство этого утверждения.
Если центр тяжести яйца лежит ниже центра кривизны опорной
точки основания (это центральная точка), то яйцо остается в
равновесии. Оно балансирует на этой точке, потому что любое отклонение
яйца поднимает центр тяжести. Если центр тяжести лежит выше
центра кривизны данной точки, то яйцо будет неустойчивым, потому
что малейший наклон опускает центр тяжести. Чтобы прояснить
этот момент, давайте рассмотрим сферу, показанную слева на
рисунке 109. Для сферы центр тяжести совпадает с центром кривизны. У
любой суперсферы с показателем степени выше двух (как показывает
вторая слева иллюстрация) центр кривизны выше центра тяжести,
поскольку основа менее выпукла. Чем выше показатель степени, тем
меньше кривизна центральной точки основания (соответственно,
больше радиус кривизны в этой точке).
Теперь предположим, что суперсфера равномерно растягивается
вверх вдоль вертикальной координаты, превращаясь в суперэллипсоид
вращения, или, согласно Питу Хейну, супер-яйцо. При этом центр
кривизны опускается, а центр тяжести поднимается. Очевидно, что
существует точка X, где центр кривизны и центр тяжести совпадут.
Это и будет критическая точка, определяющая предельную
устойчивость супер-яйца (показано на третьем слева рисунке). Более высокое
супер-яйцо устойчивым не будет (справа на рис. 109).
Один из моих корреспондентов, офицер ВМФ США Гремер, был
первым среди тех, кто сообщил мне об изъяне в этом
доказательстве. Интуиция нас обманула. В центральной точке основания
любого суперяйца радиус кривизны бесконечен! Если мы увеличиваем
высоту суперяйца, оставляя ширину постоянной, дно суперяйца
остается «плоским». В немецкой литературе эта точка называется
flach-punkt (точка-плоскость). Подобные «плоские» точки есть на
Суперэллипс Пита Хейна
259
Рис. 109
Иллюстрация ложного доказательства теории устойчивости супер-яйца
концах у любого суперэллипса. Другими словами, любое суперяйцо,
вне зависимости от его пропорций, получается теоретически
стабильным!
Должны существовать критические пропорции яйца, при
достижении которых предельный градус наклона (за пределами которого
наступает неустойчивость) приближается к нулю. Тогда такое яйцо
может потерять равновесие из-за мельчайшей неоднородности
поверхности, вибрации, потока воздуха. Однако в математическом
плане не существует никакого критического отношения высоты к
ширине. Как указывал Пит Хейн, теоретически можно поставить
вертикально целый лес супер-яиц, будь они хоть с дюйм шириной и
высотой с Эмпайр-стейт-билдинг. В данном случае вычисление
критического угла отклонения смысла не имеет и проблемы не
решает. Многие читатели прислали мне свои мысли по этому поводу.
Если уж говорить о равновесии обычного яйца, то не все знают,
что почти любое яйцо можно поставить на широкий конец на
гладкой поверхности. Для этого нужно лишь терпение и твердость руки.
Попытки трясти яйцо, чтобы разрушить желток, делу не помогут.
Интересно то, что можно заставить яйцо стоять и на остром конце.
Незаметно насыпьте небольшое качество соли на стол,
уравновесьте яйцо на ней, легонько сдуйте излишек соли, а затем уж зовите
зрителей. Отдельные песчинки соли невидимы, особенно на фоне
белой поверхности. Курьезно, но факт. Балансировка яйца
(естественно, на широком конце) была в 1945 году в Китае повальным
увлечением. По крайней мере, так об этом писал журнал Life в номере
от 9 апреля 1945 года.
260
Нескучная математика
Самое большое в мире супер-яйцо, сделанное из стали и
алюминия и весящее почти тонну, было установлено перед фасадом
Кельвин-холла в Глазго в октябре 1971 года в честь Пита Хейна, который
одно время выступал спикером на презентациях концептуальных
проектов жилья. Дважды суперэллипс появлялся на почтовых
марках Дании: в 1970 году на синей марке стоимостью две кроны,
посвященной Бертелю Торвальдсену, и в 1972 году на марке со
спецгашением в честь Рождества. На последней изображены портреты
королевы и ее супруга принца.
Фигуры в форме супер-яйца вы увидите в большом разнообразии
как размеров, так и материалов. Они продаются по всему миру в
магазинах, специализирующихся на необычных подарках. На ценнике
небольшой безделушки из стали в форме супер-яйца вы можете
прочитать даже назначение: executive's toy (игрушка шефа). Одна из
лучших шуток, которую можно проделать с такой игрушкой, — это
легонько толкнуть ее. Она несколько раз «перевернется и
остановится на одном из концов. Полые супер-яйца, заполненные
специальными составами, рекламируются как охладители напитков, а более
крупные безделушки выполняют функцию держателя для сигарет. В
форме супер-яйца изготавливают также и более дорогие
безделушки, которые являются уже художественным произведением.
ГЛАВА 1 9
Трисекция угла
Начиная изучать планиметрию, дети быстро узнают, как с помощью
циркуля и линейки разделить угол пополам и разделить отрезок на
любое желаемое количество равных частей. Обе эти операции столь
легко произвести, что многие ученики не могут даже предположить,
что с помощью этих двух инструментов нельзя разделить угол натри
равные части. А математически одаренные дети часто принимают
это как вызов и немедленно принимаются за работу, пытаясь
доказать, что учитель не прав.
Что-то подобное наблюдалось среди математиков на заре
развития геометрии. Еще в V веке до н. э. математики уделяли много
времени поиску способа разделения любого угла на три равные части с
помощью прямых линий и дуг. Они, конечно, знали, что некоторые
углы могут быть разделены на три равные части. В случае с прямым
углом, например, это чрезвычайно просто. Необходимо только
нарисовать дугу ЛВ {см. рис. ПО), затем, не изменяя ширины
раскрытия циркуля, поставить иглу в точку В и провести вторую дугу,
которая пересечет первую в точке С. Прямая ОС отделит одну треть угла.
(Читателям предлагается освежить свои знания по планиметрии,
доказав правильность упомянутых в этой главе методов разделения
угла на три равные части. Все доказательства^очень просты.)
60-градусный угол, в свою очередь, разделяет на три части угол в 180, а
построив биссектрису 30-градусного угла, можно получить угол,
который будет третью угла 45. Многие углы могут быть разделены на три
равные части с соблюдением всех классических требований, но
древнегреческие математики хотели найти общий метод,
применяемый к любым углам. Вместе с задачей удвоения куба и задачей о
квадратуре круга, задача трисекции угла была одной из главных
проблем, которые стояли перед математиками Древнего мира.
Только в 1837 году во французском математическом журнале
было опубликовано первое точное доказательство невозможности раз-
262
Нескучная математика
Рис.110
Как разделить на три равные части прямой угол
деления любого угла на три равные части, представленное П. Ванце-
лем. Его доказательство слишком сложно для приведения в данной
книге, но все нижеследующие замечания сделаны на его основе.
(Самую лучшую и полную версию этого доказательства без
технического уклона можно найти в книге Ричарда Куранта и Герберта
Роббинса What Is Mathematics?(«Что такое математика?»).)
Рассмотрим угол в 60 градусов с вершиной в начале координат {см. рис. 111).
Трисекция угла
263
Нарисуем окружность с центром в точке О и предположим, что
радиус круга равен 1. Линия, отделяющая треть 60-градусного угла,
пересечет окружность в точке А. Возможно ли только с помощью
циркуля и линейки определить положение точки А1 Если нет,
значит, по крайней мере один угол не может быть разбит на три равные
части и никакого общего метода не существует.
Известно, что прямые линии на плоскости в декартовой
системе координат — это графики, описываемые линейными
уравнениями, а окружности — это графики, описываемые квадратными
уравнениями. Исходя из этого можно показать, что существует
пять, и только пять операций, которые могут быть выполнены на
данном отрезке с использованием только циркуля и линейки. От-
Рис. 111
Точка А не может быть «построена» с помощью циркуля и линейки
264
Нескучная математика
резки можно складывать и вычитать, умножать и делить, также из
них можно извлекать квадратные корни. На любом данном
отрезке п можно с помощью циркуля и линейки найти квадратный
корень из я. Такую же операцию можно проделать над квадратным
корнем из я, чтобы получить его квадратный корень, который на
самом деле будет корнем четвертой степени из п. Повторяя
операцию извлечения квадратного корня конечное количество раз,
можно найти любой корень из удваивающегося ряда 2, 4, 8, 16...
Однако с помощью циркуля и линейки найти на отрезке
кубический корень невозможно, потому что число 3 не является
какой-либо степенью числа 2. Все это, вместе с аргументами аналитической
геометрии и алгебры числовых множеств, показывает, что
«построить» на плоскости можно лишь те точки, координаты х и у
которых являются реальными корнями уравнения определенного типа.
Это должно быть алгебраическое уравнение, которое является
несократимым (не может быть переведено в уравнение с более
низкими показателями степеней), имеет рациональные
коэффициенты. Порядок уравнения должен выражаться одним из чисел
удваивающего ряда 2, 4, 8...
Рассмотрим теперь координату х точки А на рис. 111 — точки,
которая отмечает на окружности треть 60-градусного угла. Она
определяет основание прямоугольного треугольника, гипотенуза
которого равна 1. Значит, величина основания равна косинусу угла
20. Проведение несложных операций с тригонометрическими
формулами покажет, что этот косинус является иррациональным
корнем несократимого кубического уравнения: 8*3 — 6х = 1. Так
как это уравнение третьей степени, точку А нельзя построить с
помощью циркуля и линейки. Значит, 60-градусный угол не может
быть разделен на три равные части при соблюдении классических
требований. С помощью похожих аргументов доказывают, что не
существует общего метода разделения с помощью циркуля и
линейки любого данного угла на 5, 6, 7, 8, 9 или любое другое
количество равных частей, которое не является членом
удваивающегося ряда 2, 4, 8, 16... Среди бесконечного количества углов
разделить на три равные части можно те, чья величина в градусах равна
360/я, где п — это 2 в какой-либо степени или 5, умноженное на 2
в какой-либо степени.
Таким образом, разделить на три равные части можно
следующие целые углы: 9, 18, 36, 45, 90 и 180. Девять градусов — это
наименьший целый угол, который можно разделить на три равные час-
Трисекция угла
265
ти. Его третья часть, трехградусный угол, не может быть разделен на
три равные части. Это значит, что единичный угол не может быть
построен с помощью циркуля и линейки. Также нельзя построить с
помощью циркуля и линейки угол величиной 2 градуса.
Есть конечно же много способов разделить угол на три равные
части приблизительно. Один из самых простых, предложенный
Хьюго Стейнаусом в своей заметке Mathematical Snapshots
(«Математические снимки»), продемонстрирован на примере
60-градусного угла на рис. 112. Сначала угол разбивается на две равные
части, затем хорда кривой половинного угла разделяется на три
равные части. Это дает точку для отделения трети исходного угла с
ошибкой меньше неизбежной погрешности, которая имеет место
быть при рисовании. В разное время были предложены многие
другие (даже еще более совершенные) способы приблизительного
деления угла на три равные части, но в массе своей они гораздо более
трудоемкие.
Рис.112
Простой способ приблизительного деления любого угла на три равные части
266
Нескучная математика
Абсолютно точное деление угла на три равные части можно
осуществить, только нарушив одно из традиционных требований —
ограничений. Многие некруговые кривые, такие как гипербола или
парабола, позволяют получить абсолютно точное деление. Другие
методы предлагают использование бесконечного итерационного
процесса, при котором в пределе получается нужная линия
трисекции. Самый простой способ с уходом от ограничений
подразумевает нанесение меток на линейке. Метки, как таковые, можно даже не
наносить, а использовать углы линейки, чтобы с помощью их
отмечать отрезки (соответствующие ширине линейки) либо просто
«снимать» ширину линейки циркулем. Один из лучших способов
разбиения угла на три части с помощью подобных манипуляций
найден в трудах Архимеда. Угол, который нужно разделить на три
равные части, — это AED {см. рис. 113). Рисуем полукруг, как
показано, затем продлеваем DE вправо. Циркулем, раствор которого по-
прежнему равен радиусу полукруга DE, наносим точки на линейке,
которую укладываем так, чтобы проходила через точку А.
Корректируем положение линейки таким образом, чтобы точки, отмеченные
на ней ножками циркуля, пересекали полукруг и его продленное
основание в точках В и С. Другими словами, делаем так, чтобы ЕС
равнялось радиусу. Дуга BF это точно одна треть дуги AD.
Рис. 113
Архимедовский метод точного отделения одной трети угла
с отступлениями от традиционных ограничений
Трисекция угла
267
Рис. 114
Конструкция Кемпе для разбиения любого угла на три равные части
В разное время было изобретено много любопытных
механических устройств для разбиения углов на три равные части. Двадцать из
них представлены в работе Итало Герси Matematica Dilettevole e
Curiosa, посвященной занимательной математике. Лео Мозер,
математик из университета Альберты заметил как-то в своей статье, что
таким инструментом являются обычные часы. Пока минутная
стрелка проходит дугу, в которую четыре раза вписывается тот угол,
который надо разделить на три равные части, часовая стрелка
передвигается ровно на одну треть данного угла. На рис. 114
представлена причудливая конструкция, разработанная Альфредом Кемпе,
лондонским адвокатом. В основе принципа ее работы лежит
«теорема пересекающихся параллелограммов» — параллелограммы
«свернуты» так, что две противоположные стороны пересекаются (см.
рис. 114). Три пересекающихся параллелограмма данной
конструкции подобны. Длинная сторона самого маленького
параллелограмма является короткой стороной среднего параллелограмма, длинная
сторона которого является, в свою очередь, короткой стороной са-
268
Нескучная математика
мого большого параллелограмма. Устройство само делит заданный
угол на три равные части, как показано на рисунке. Увеличив
количество пересекающихся параллелограммов, можно создать
инструмент, который будет делить углы на любое желаемое количество
равных частей.
Другое приспособление для деления углов на три равные части,
которое без особых усилий можно изготовить из картона, получило
название «томагавк». У него нет никаких двигающихся частей, его
использование не требует предварительного построения
каких-либо линий и может гарантировать быстрое и точное разделение угла
на три равные части {см. рис. 115). Его верхняя сторона AD
разделена точками В и С на три равные части. Изогнутая сторона
представляет собой часть окружности с радиусом АВ. «Томагавк» размещают
так, чтобы точка D находилась на одной стороне угла, полукруг
касался второй стороны угла, а правая сторона «ручки» томагавка
проходила через вершину угла. Точки В и С разбивают угол на три
равные части. Если угол слишком острый и «томагавк» не вписывается
в него, вы можете удвоить угол или проделать эту операцию
несколько раз, пока его величина не станет приемлемо большой.
Разбейте увеличенный угол, а затем разделите результат на 2 столько
раз, сколько раз вы удваивали исходный угол.
Хотя невозможность разбиения любого угла на три равные части
с помощью циркуля и линейки четко доказана, в мире все еще
находятся любители математики, которые ошибочно полагают, что им
удалось найти метод разбиения, соответствующий всем
классическим требованиям. Обычно такие люди знают геометрию не очень
глубоко. Они могут лишь проводить какие-то действия, но их
знаний недостаточно для того, чтобы в полной мере осознать
доказательство невозможности или найти ошибку в собственных
рассуждениях. Впрочем, их методы разделения обычно столь сложны, а их
доказательства столь длинны, что даже опытным математикам
нелегко бывает найти ошибку. Профессиональные математики
предпочитают не связываться с такими доказательствами. Поиски
ошибок отнимают много времени и к тому же совершенно бесполезны,
поэтому профессионалы обычно сразу отправляют такие материалы
назад, даже не пытаясь анализировать их. Это неизменно наводит
новоиспеченного «изобретателя» на мысль о том, что
профессионалы объединены в организованном заговоре и не хотят, чтобы его
открытие получило известность. Получив отказ во всех
математических журналах, куда они посылали свои «открытия», они обычно
Трисекция угла
269
Рис.115
Разделение угла на три равные части с помощью «томагавка»
объясняют их в книге или брошюре, изданных за свой счет. Иногда
они дают рекламу своего метода в местной газете, добавляя при
этом, что авторские права защищены.
Последним таким математиком-любителем, чей метод
разделения углов на три равные части получил широкую известность в
США, был его высокопреподобие Джереми Джозеф Каллахан.
В 1931 году, будучи ректором университета Дукусне в Питсбурге,
он заявил, что смог найти решение задачи трисекции угла.
Издательство United Press напечатало длинную запутанную историю,
написанную самим отцом Каллаханом. В газете Time появилась его
фотография и заметка о его революционном открытии. (В том же году отец
Каллахан опубликовал 310-страничную книгу под названием
«Евклид и Эйнштейн», в которой он опроверг теорию относительности,
доказав знаменитый Евклидов постулат непересечения
параллельных прямых и показав таким образом абсурдность неевклидовой гео-
270
Нескучная математика
метрии, на которой основана теория относительности.) Репортеры и
широкая общественность были немало удивлены тем, что корифеи
математики, даже не желая ознакомиться с моделью, предложенной
отцом Каллаханом, однозначно заявили, что она не может быть
правильной. В конечном итоге в конце года университет опубликовал
брошюру отца Каллахана The Trisection of the Angle («Трисекция угла»).
«Математики были правы, — говорит Ирвинг Адлер, который
описал эту историю в своей знаменитой книге Monkey Business
(«Мартышкин труд»). — Каллахан не разбивает угол на три равные
части». В действительности он просто взял угол, утроил его, а затем
снова нашел исходный угол.
Почтенный Даниель К. Инуи 3 июня 1960 года (позднее он стал
сенатором и членом Комитета по расследованию Уотергейта)
прочитал на 86-м конгрессе длинную речь, воздав должное Морису Кид-
желу, художнику-портретисту из Гонолулу, который не только разбил
угол на три равные части, но также нашел квадратуру круга и удвоил
куб. Киджел в соавторстве с Кеннетом Янгом написал на эту тему
книгу The Two Hours that Shook the Mathematical World («Два часа,
которые потрясли математический мир») и брошюру Challenging and
Solving the Three Impossibles («Постановка и решение трех
неразрешимых задач»). Через издательскую компанию Kidjel Ratio они
распространяли эту литературу вместе с фирменными кронциркулями,
которые обеспечивали возможность применения данной системы. В
1959 году эти двое мужчин читали лекции о своей работе в различных
городах США, а в Сан-Франциско о них сняли документальный
фильм под названием The Riddle of the Ages («Решение загадки века»).
По словам Инуи, «решения Киджела теперь преподают в сотнях
школ и колледжей на Гавайях, в США и Канаде». Остается только
надеяться, что его высказывание приукрашает действительность.
Корреспондент из Калифорнии прислал мне вырезку из
воскресной Los Angeles Times от 6 марта 1966 года, в которой
описывается 14-шаговый метод трисекции угла.
Что сегодня математик может сказать желающим найти способ
разбиения угла на три равные части. Он может напомнить им, что в
математике существуют задачи, неразрешимые в конечном,
абсолютном смысле — неразрешимые во все времена, во всех
постижимых (логически последовательных) мирах. Разделить угол на три
равные части также невозможно, как при игре в шахматы сделать
королевой такой же ход, как конем. В обоих случаях конечная причина
невозможности одинакова: действия противоречат правилам игры.
Трисекция угла 271
Математик может посоветовать тем, кто желает осуществить
трисекцию угла, обратиться к книге What Is Mathematics? («Что такое
математика?») и изучить упомянутую выше главу, а затем вернуться к
своему доказательству и еще раз с особым усердием поискать, где же
закралась ошибка. Однако желающие разделить угол на три равные
части - народ упрямый. Они вряд ли прислушаются к чьему-либо
совету. Август де Морган в своей книге Budget of Paradoxes («Кладовая
парадоксов») цитирует типичную фразу из брошюр XIX века,
посвященных трисекции угла: «Результат многолетних раздумий».
Комментарий Моргана предельно краток: «Вполне вероятно и очень печально».
Чтобы закончить на положительной ноте, приведем способ
удвоения куба, который является такой же «обманкой», как и
архимедовское деление угла на три равные части. Фигура ABCDEF— правильный
шестиугольник, длина сторон которого равна 1. Линейка проходит
через точку А и пересекает BD в точке X, а продолжение ВС в точке Y.
При этом XY = 1. Эти точки являются ключевыми. В этом случае
АХ- \J2 , и мы можем удвоить единичный куб, поскольку BY= 1[a.
Постскриптум
2. ГОЛОВОЛОМКИ С МОНЕТАМИ
Единственная ссылка на литературу, которую я смог найти,
относится к февралю 1966 года. Ею оказалась ссылка на мою
собственную колонку в Scientific American, где был опубликован памфлет
Puzzle Craft («Мастера головоломок») 1930 года под редакцией
Линн Рорбуг. Исходный материал был взят из публикации
Cooperative Recreation Service, Делавэр, Огайо. Эта публикация
описывает вариант головоломки на треугольной доске с 15
клетками с пустой 13-й клеткой и предлагает решение в 11 ходов. Однако
соавтор книги о механических головоломках Puzzles Old and New
(«Старые и новые головоломки») Джерри Слокам приводит копию
американского патента 1891 года. Предполагается, что сама идея
еще старше.
На тему задач на окрашивание было опубликовано несколько
статей. Эти задачи называют также parity checks («контроль
четности»), поскольку некоторые из подобного рода пасьянсов
неразрешимы. Пока еще нет теорий, которые определяют теоретическую
неразрешимость позиции. Головоломка с 15 клетками на
треугольной доске стала популярной и выпускается в виде деревянных
досок с колышками. Такие доски можно встретить во многих
ресторанах Америки, а несколько других форм пасьянса популярны во
всем мире.
Недавно получила популярность версия под названием Think a
Jump («Подумай и ходи»), гексагональная доска которой имеет
сторону в 4 клетки, причем одна из фишек, по каждой из сторон в
центре (по две центральные на сторону), может быть удалена.
Проверка четности показывает, что пасьянс получается неразрешимым,
если удалена центральная фишка или любая из других 12 фишек.
Кроме этих 13 ячеек, где не может находиться «дырка», все
остальные варианты делают задачу разрешимой. В книге Puzzles Old
Посткриптум
273
and New («Старые и новые головоломки») приводится вариант
условия (с решением) на треугольной доске с 15 клетками и двумя
дополнительно изъятыми фишками, так что дырки располагаются по
соседству с каждым из трех углов.
Естественно, что существуют варианты пасьянса на решетках
произвольной формы: шестиугольники, ромбоиды, звезды и многое
другое. Также можно пойти дальше и разыгрывать партии в объеме,
образованном, скажем, четырехгранниками. Правильный
шестиугольник со стороной 3 и раньше был многообещающим полем для
анализа, однако только в 1976 году Майкл Мерчант в частной
переписке доказал, что на таком поле не существует разрешимой
конфигурации, где бы ни находилась начальная «дырка». Минимальная
решетка из правильных шестиугольников, на которой пасьянс
становится разрешимым, — это поле со стороной 5 на 61 клетку. На такой
доске для любого п существуют п-п решения (начальная дырка в л,
последняя фишка в п).
Изменением правил можно получить новые головоломки.
Макси Брук в своей книге, посвященной головоломкам с
монетами, рассматривает треугольник из 15 ячеек и добавляет одно
дополнительное условие. Запрещаются горизонтальные ходы везде,
кроме нижней линии. (Сам автор приводит решение из 12 ходов.)
Дополнительно к скачкам можно разрешить ходы как в шашках.
Тогда можно будет поставить условия минимальности решения.
В статье, опубликованной в журнале Crux Mathematicorum (том 4,
1978, с. 212—216), приведен анализ треугольника из 15 ячеек,
причем вводится новое условие. Допускается ход из любого угла
в среднее гнездо противоположной стороны, если оно свободно.
Предпринимались серьезные попытки провести полный анализ
для треугольников меньшего размера. Делались попытки
определить факт существования решения пасьянса при задании начальной
и конечной позиции. Как мы видели, для треугольника из 10 клеток
разрешимой позицией является та, в которой дырка расположена в
одной из клеток 2, 3, 4, 6, 8, 9. Партия заканчивается с
единственной фишкой на соседней с дыркой позиции.
У треугольной сетки с 15 клетками существуют только четыре
начальные позиции (если не считать симметричные): 1, 2,4 и 5. Из них
возможно оставить на доске только один колышек, причем в любом
отверстии доски. Но когда в условии задаются начальная и
конечная позиции, задача существенно усложняется. Некоторые из
позиций до сих пор не решены. В своей статье Triangular Puzzle Peg («Tpe-
274
Нескучная математика
угольные пасьянсы») Генцельс показывает, что если конечная
позиция находится «внутри» позиции (клетки 5, 7 и 9), то начальная
дырка должна быть в середине одной из сторон.
Следовательно, невозможно добиться того, чтобы партия
заканчивалась там, где началась, если дырка была в одной из трех
внутренних ячеек. Но можно начать и закончить в одной ячейке из
любого внешнего отверстия. Вариант, когда дырка находится в углу,
один из самых сложных.
Я привожу минимальное решение для позиции с дыркой в
середине стороны, при условии, что в конечной позиции единственная
монетка или колышек должны оказаться именно там: 6—1,4—6,1—4,
7-2, 10-3, 13-4, 15-13, 12-14-15, 2-7, 11-4-6-1. Измените
первый ход на 3—10, и у вас получится десятиходовое решение (кстати,
минимальное) для позиции, когда начало и конец совпадают и
лежат рядом с углом.
Наиболее полный анализ возможных решений для вариантов
условий с заданными начальной и конечной позициями приведен в
статье Б. Шварца и X. Альбурга 1983—1984 годов Triangular Peg
Solitaire — A New Result («Треугольный пасьянс — новые результаты»).
Многие пары условий, такие как 4—6 (дырка в 4, последняя фишка
в 6). сразу же исключаются тестом на окрашивание. Так, авторы
показывают, что сочетание 5—5 неразрешимо. Условие 5—1, 5—7 (а
также их симметричные эквиваленты) остались без решения и,
вероятно, вообще не имеют его.
Однажды в 1984 году я обедал в ресторане, на столах которого
стояли треугольные доски с 15 клетками. Так получилось, что
компания Venture Manufacturing Company, Далтон, Джорджия,
предложила мне головоломку, которую прежде я не видел. Требовалось
начать с произвольной позиции дырки и оставить на доске ровно
восемь фишек, причем так, чтобы допускаемых правилами ходов
больше не было. Десять фишек оставить оказалось легко: 14—5,
2—9, 12—5, 9—2 (самое короткое безвыходное положение). Если
задается количество п фишек от 1 до 10, которые необходимо
оставить в безвыходном положении, то единственным значением п,
для которого решения не существует, будет число девять. Оставить
ровно восемь фишек — сложная задача, решить которую я
предоставляю читателю. Бенджамин Шварц в своей статье,
опубликованной в журнале The Journal of Recreational Mathematics («Журнал
занимательной математики») доказал, что у этой головоломки
существует единственное решение.
Посткриптум
275
С учетом поворотов и зеркальных отражений в случае с
треугольной доской на 21 клетку существует пять неэквивалентных
решений. По сути, задача решается из любой стартовой позиции. В
своем так и не опубликованном исследовании Гарри Дэвис показал, что
самое короткое решение имеет 9 ходов. Оно начинается с позиции,
в которой отсутствует фишка 13: 6—13, 7—9, 16—7, 4—11, 10—8,
21-10, 18-9, 20-18-16-7, 1-4-11-13-15-6-4-13-6-1. Все
решения из других стартовых позиций имеют в самом коротком
варианте 10 ходов.
Мне не известно ни одной опубликованной работы, где бы
рассматривались пары начальных и конечных позиций, для которых
существуют решения, не запрещенные проверкой четности.
Помимо применяемой проверки четности, была опубликована
небольшая работа для треугольной доски в 28 клеток. По данным ее
аэтора, начать и закончить в центральном отверстии невозможно.
Действительно, можно показать, что в любом треугольнике
решения типа «центр—центр» не существуют.
Гарри Дэвис совместно с Вейдом Филпоттом смогли показать, что
для треугольной доски в 36 клеток существует решение из любой
начальной позиции. Минимальное решение для такой доски имеет 14
ходов. Если изъять с поля 13 колышек, то решение выглядит так: 6—13,
1-6, 10-3, 21-10, 36-21, 4-1-6-15-28, 19-10, 11-4-6-15, 22-11,
31-16-7-9, 32-19-8-10-21-19, 24-11-13-24, 34-36-21-34-32,
29-31-18-20-33-31.
Если рассматривать на этой доске самое длинное минимальное
решение, то оно содержит 15 ходов. В приведенном решении Дэвис
начинает и завершает игру на клетке 1: 4—1, 13—4, 24—13, 20—18, 34—19,
32-34, 18-20, 30-32-19-8, 7-2, 16-7, 29-16, 15-26, 35-33-20, 6-15,
21-10, 36-21, 1-4-11-22-24-11-13-4-6-13-15-26-28-15-6-1.
Оно содержит 17 ходов.
Некоторые из читателей отмечали, что в экспериментах с
монетками лучше использовать монеты в 25 и 10 центов, а не
пенсы, поскольку последние проскальзывают. Здесь кроется новое
захватывающее направление исследований. Какие теоремы еще
появятся при исследовании замкнутой цепи монет разного
достоинства (и диаметра)? Читатели Джонатан Йех и Эрик Дрю
независимо друг от друга отметили, что все шесть решений задачи о
лесопосадке для 10 деревьев, приведенной в главе о монетах,
могут быть получены из одной базовой схемы с движущейся
линией. На рисунке 116 показано, как движущаяся горизонтальная
V
Рис. 116
Перемещающаяся линия порождает шесть решений задачи
о лесопосадке с 10 деревьями
Посткриптум
277
линия порождает пять решений. Шестое решение получается,
если наклонить линию, как показано пунктиром на второй сверху
иллюстрации.
3. АЛЕФ-НУЛЬ И АЛЕФ-ОДИН
В главе 3, говоря о трансфинитных числах Кантора, я привел
аргументацию Шлегеля, посвященную противоречию статической
теории Вселенной, не беря на себя смелость оценить ее. Несколько
читателей нашли его аргументацию ошибочной — особенно когда
речь зашла об исчисляемой бесконечности количества удвоений
атома, после которых Вселенная должна содержать неисчислимую
бесконечность атомов. Подробности вы можете найти в статье Ру-
ди Рюкера Infinity and the Mind («Бесконечность и разум»), 1982.
4. ГИПЕРКУБЫ
Обе задачи, решение которых я оставил для читателей в главе 4,
были решены. Питер Терни в своей статье 1984 года Unfolding the
Tesseract («Разворачивая тессеракт») с помощью теории графов
показал, что существует 261 вариант различных разверток.
Предложенный им метод легко применим к гиперкубам любой
размерности. Насколько мне известно, про наибольший куб, вписанный в
четырехмерный гиперкуб, так и не было публикаций. Хотя мне до сих
пор приходят ответы читателей, я вынужден признать, что единства
среди них нет.
5. МАГИЧЕСКИЕ ЗВЕЗДЫ И МНОГОУГОЛЬНИКИ
Проективные плоскости начали появляться в популярной
математической литературе еще в 1989 году, когда Клемент Лэм из Монреаля
показал подробными вычислениями невозможность существования
проективной плоскости (магической звезды) с 11 точками на линии.
Это стало неожиданностью в задачах на построение магических
фигур. Однако после того, как глава из этой книги, посвященной
магическим звездам, появилась в Scientific American, стали появляться
заметки про магические звезды с количеством лучей больше 8. В случае
с пентаграммой появилась идея задачи о наименьшей магической
сумме, которую можно получить, распределив по узлам
неповторяющиеся простые числа. Гарри Ленгман писал в журнале Play Mathematics
278
Нескучная математика
Рис. 117
13
Рис.118
(«Математические игры»), что наименьшая сумма (если 1 считать
простым числом) равна 72, но никакой аргументации не привел. Чарльз
Тригг в своей статье в журнале Crux Mathematiconim (том 5, 1977, с.
16—19) доказал, что в области простых чисел существует только два
основных решения, показанные на рис. 117. Как Тригг показал на
странице 5 того же тома, любая магическая пентаграмма может быть
переставлена 12 способами без потери своего волшебства.
Гарри Нельсон (тот же том, с. 67) сообщил о том, что провел
исчерпывающий компьютерный анализ, который показал, что если 1
Посткриптум
279
137
151
Рис.119
не является простым числом, то решение получается
единственным, с магической суммой 84. Один из 12 вариантов приведен на
рис. 118.
Гакухо Абе, специалист по магическим квадратам из Акита,
Япония, опубликовал замечательное решение для гексаграммы в
простых числах (см. Journal of Recreational Mathematics, том 16, № 2,
1983, с. 84). Его решение, приведенное на рис. 119, построено на
основе двенадцати последовательных простых чисел от 137 до 193 с
магической суммой 660.
Одно из первых доказательств того, что магическая гексаграмма,
построенная на целых числах от 1 до 12, имеет 80 основных
вариантов, было прислано мне Кристианом Тилом из Западной Германии.
Его текст был опубликован подзаголовком Ubermagische zahlensterne
(«Под магическими звездами») в немецком периодическом издании
Archimedes, том 15, сентябрь, 1963, с. 65—72.
280
Нескучная математика
11. ЛОСКУТНОЕ ОДЕЯЛО ГОСПОЖИ ПЕРКИНС
И ДРУГИЕ УПАКОВКИ КВАДРАТОВ
Несколько читателей затронули в своих письмах следующий вопрос
о стеганом одеяле госпожи Перкинс. На какое количество
квадратов, кубов или /7-мерных гиперкубов могут быть разбиты подобные,
большие по размерам фигуры в предположении, что они не обязаны
быть неповторяющимися?
Если поставить условие неодинаковости, то может быть разрезан
только квадрат. Я уже упоминал о том, что квадрат может быть
разрезан на 24 попарно неравных квадрата, однако это решение не
минимально. Доказанное минимальное решение состоит из 21
квадрата. Сообщение об этом с иллюстрацией вы найдете на страницах
Scientific American (июнь, 1978, с. 86—87). Куб или /2-мерный
гиперкуб невозможно разрезать на неравные фигуры. Доказательство
невозможности для куба (оно легко распространяется на гиперкубы)
очень изящно. Вы найдете его на странице 208 книги The Second
Scientific American Book of Mathematical Puzzles and Diversions («Вторая
книга математических головоломок и развлечений от Scientific
American») 1961 года издания.
Если «разрешить» фигурам быть одинаковыми по размерам, то
все равно невозможно разбить квадрат на 2, 3 или 5 квадратов. Но
все другие варианты разбиения существуют. Ник Лорд в своей
заметке Subdividing Hypercubes («Рассечение гиперкубов») отмечал, что
«для любой размерности количество невозможных разбиений
конечно». Однако не так легко определить то решение
(охарактеризуем его сложность количеством составляющих фигур к), для
которого существуют все более сложные разбиения. Также нелегко
определить возможные значения к, для которых существуют решения.
Лорд установил для куба нижнюю границу непрерывности
решений в 163 элемента, добавив при этом, что это решение может быть
улучшено. Коннер из Буффало, Нью-Йорк, прислал мне
доказательство с предельным значением 90. Не исключено, что этот
предел может быть понижен.
Куб можно разрезать на восемь меньших по размеру одинаковых
кубов. Поскольку любой из меньших кубов можно разделить
подобным образом, то, продолжая процесс, можно увидеть, что для
любого к, равного 1 по модулю 7 (а это 8, 15, 22, 29...), существует
разбиение. Очевидно, что к не может иметь значения 2—7, потому что
разбиение должно иметь как минимум куб в каждом из восьми углов.
Посткриптум
281
Существует решение для к — 20 (один куб объемом две единицы и 19
единичных кубов). Но можно ли найти разбиения для к в интервале
от 9 до 19 (случай к = 15 исключаем, потому что для него решение
заведомо существует)? Вероятно, нет. Но мне неизвестны
доказательства этого, за исключением случая к = 13, для которого Коннер
доказал невозможность решения.
Просто удивительно, насколько мало исследована задача
стеганого одеяла госпожи Перкинс и насколько скупо она
распространена на кубический случай. По моим данным, еще никто не смог
доказать, что 49 единичных квадратов — это наименьшая возможная
непокрытая площадь в задаче Брайттона. Хотя то, что это
минимальное решение, похоже на правду.
Когда редактировалось новое издание этой книги, Джон Конвей
отметил одно обстоятельство. Тот факт, что О2 + I2 + ... + 242 = 702,
должен найти более глубокое применение в математике, а может
быть, даже и в физике.
12. ГАДАНИЕ ПО ЧИСЛАМ ДОКТОРА ФЛИССА
С тех пор как я писал в своей колонке про Фрейда и Флисса,
появилось много сведений, касающихся странной невротической связи
между этими двумя людьми. Те, кому интересен этот вопрос, могут
заглянуть в главу Freud, Fliess, and Emma's Nose («Фрейд, Флисс и нос
Эммы») моего нового сборника The New Age: Notes of a Fringe Watcher
(1988). Эта история ужаса посвящена тому, как Флисс провел
неудачную операцию на носу одной'из пациенток Фрейда, а также
тому, как Фрейд отчаянно пытался найти оправдание хирургической
некомпетентности своего друга. _
Идея биоритмов Флисса все еще популярна. В некоторых
аэропортах имеются автоматы, которые за плату распечатывают вам
диаграмму биоритмов. В оккультных журналах вы найдете рекламу
многочисленных электронных калькуляторов для определения
хороших и плохих дней.
Было проведено множество исследований, цель которых
состояла в том, чтобы отследить корреляцию между плохими днями и
частотой несчастных случаев, смертей, самоубийств и даже неудачных
выступлений спортивных команд. И ни одно из них не показало
никакой предсказательной силы биоритмов. Как отмечали в 1978 году
в своей заметке три исследователя биоритмов и аварий на шахтах,
подобная трата времени и средств напоминает охоту на мифическо-
282
Нескучная математика
го единорога. Но истинным поклонникам этого направления
«науки», так же как и любителям астрологии, подобные исследования
неинтересны. Убедить их читать серьезную литературу столь же
сложно, как привести неверующего в церковь. В главе 12
библиографии вы найдете ссылки на некоторые критические заметки,
библиография которых, в свою очередь, позволит вам глубже
исследовать этот вопрос.
Тяжело вообразить себе теорию циклов человеческого поведения
более сумасшедшую, чем биоритмы. Однако времена таковы, что
подобная литература находит место даже у уважаемых издателей.
Так, книга Psycles («Пси-циклы») автора Дуайта Балки
отстаивает идею цикла психической активности, который длится ровно
37 часов! Теренс Хайнс по поводу этой книги опубликовал в
журнале The Skeptical Inquirer («Критические заметки»), лето, 1982, с.
60—61, свое окончательное мнение: «Эта книга представляет
читателю мешанину различных взглядов на психическую сторону
деятельности человека... Плохо написанная, логически несвязанная и
внутренне непоследовательная, это одна из самых глупых книг, сам
факт появления которой не поддается объяснению».
13. СЛУЧАЙНЫЕ ЧИСЛА
На первой странице этой главы, посвященной случайным
числам, я процитировал Альфреда Борка, который отметил, что в
наш век больше, чем когда-либо, идея случайности овладевает
умами людей. Это мнение находит свое подтверждение в
значительном интересе к идее фракталов (повторяющихся в разных
масштабах случайных узоров природы) и теории хаоса,
родившихся в 1980-е годы. Физики и математики с увлечением
погрузились в работу, связанную с поиском взаимосвязей этих двух
областей. Но не только ученым новые идеи дали пищу для
размышлений. Посвященные фракталам книги с фантастическими
картинами, которые генерирует компьютер, стали чрезвычайно
популярными, а книга 1987 года Джеймса Глюка Chaos: Making a New
Science («Хаос, на пороге новой науки») даже стала бестселлером.
15. ТРЕУГОЛЬНИК ПАСКАЛЯ
О задаче с картами, которую я привел в конце главы о треугольнике
Паскаля, но оставил без ответа, было так много писем, что здесь я счел
Посткриптум
283
нужным привести один из ответов. Не знаю, сколько решений
существует, но я нашел следующее. Нижний ряд карт: 1, 2, 3, 4, 5, 6, 7, 8.
18. СУПЕРЭЛЛИПС ПИТА ХЕЙНА
Большая часть математических идей Пита Хейна из моей колонки в
Scientific American позднее публиковались в моих книгах. Об игре
«Геке» вы можете почитать в моей книге The Scientific American Book
of Mathematical Puzzles and Diversions («Книга математических
головоломок и развлечений от Scientific American», глава 8). В главе 15
той же книги рассматривается похожая на «Ним» игра под
названием «Так-Тикс» (Tac-Tix), впоследствии получившая название
«Нимбы» (Nimbi). Знаменитые кубики Сома, которые также изобрел Пит
Хейн, стали темой главы 6 книги The Second Book of Mathematical
Puzzles and Diversions («Вторая книга математических головоломок и
развлечений от Scientific American») и главы 3 книги Фримана Knotted
Doughnuts and Other Mathematical Entertainments («Узлы, банты и дру^-
гие математические развлечения»).
В 1972 году американская фирма НиЫеу Toys, являющаяся
отделением компании Gabriel Industries, выпустила пять необычных
механических головоломок, авторство которых также принадлежит
Питу Хейну. Эти головоломки больше не выпускаются, однако я
могу процитировать то, что уже писал о них в февральском номере
Scientific American за 1973 год.
1. «Нимбы» (Nimbi). Это версия игры «Ним» Пита Хейна с 12
колышками. Колышки скользят в отверстиях. При каждом ходе
колышек (или несколько) утапливается, так что к концу партии доска
переворачивается, и можно начинать новую партию.
2. «Анагог» (Anagog). Здесь мы имеем сферического
родственника кубиков Сома. Из шести частей, представляющих собой
соединенные единичные сферы, складывают тетраэдр, в котором 20 сфер,
или два меньших тетраэдра из 10 сфер каждый. Также можно
складывать и другие фигуры на плоскости и в объеме.
3. «Кракс» (Crux). Шарнир из шести полуосей устроен так, что
каждая часть механической головоломки поворачивается отдельно.
Суть головоломки состоит в том, чтобы собрать вместе все три цвета.
4. «Твит-чит» (Twitchit). Додекаэдр имеет вращающиеся грани,
головоломка состоит в том, чтобы поворачивать их, пока три
различных символа не сойдутся вместе в каждом углу.
284
Нескучная математика
5. «Блокс-бокс» (Bloxbox). Обсуждая игру «пятнашки», Роуз Болл
писал в своей заметке 1892 года Mathematical Recreations and Essays
(«Эссе на тему занимательной математики»): «Также мы можем
вообразить себе аналогичную объемную головоломку с кубиками, но
на практике для ее решения придется перейти на язык
геометрических сечений». Спустя 81 год Пит Хейн нашел удобную
практическую форму реализации этой идеи. Семь одинаковых кубиков
располагаются внутри прозрачного пластикового куба. При его наклоне
кубики с приятным звуком опускаются в нижнюю позицию. У
каждого куба три черные и три белые грани. Суть головоломки состоит
в том, чтобы по аналогии с кубиком Рубика собрать одноцветные
грани либо выложить на них узор, скажем, в виде шахматной доски
или полос.
Можно ли считать трехмерную версию пятнашек полным
аналогом ее плоского собрата? Каково минимальное количество
ходов требуется для перехода от одного узора к другому? «Блокс-
бокс» — это не просто прозрачная коробочка, а настоящий ящик
Пандоры.
Датская компания Scantion International, специализирующаяся на
консалтинговых услугах, сделала своей эмблемой супер-яйцо. В
1982 году ее штаб-квартира переехала в Принстон, Нью-Джерси, где
теперь уже Scantion-Princeton построила роскошную гостиницу и
центр проведения международных конференций (они занимают
площадь 10 га). На площади перед гостиницей стоит огромное
каменное супер-яйцо. А в Стэмфорде, Коннектикут, чуть южнее
Выхода 25 на Мерритт Парквей из здания компании Schweppes,
располагается фигура в виде суперэллипса.
Герман Цапф придумал даже начертание шрифта (гарнитуру),
построенную на формах суперэллипса. Соответственно, этот шрифт
назвали по фамилии автора Zap/Elliptical, а сам автор дал ему
название Melior. В начертании букв этого шрифта плавные переходы
сочетают в себе округлость, среднюю между эллипсом и
прямоугольником. На страницах книги Metamagical Themas («Метамагические
темы») Дугласа Хофстэдтера вы можете увидеть подобный шрифт с
комментарием к нему.
В 1959 году компания Royal Copenhagen произвела несколько
небольших керамических мемориальных досок в форме суперэллипса,
на каждой из которых написан грук Пита Хейна с авторской
иллюстрацией. В 1988 году выдающийся специалист в области
информатики из Стэнфордского университета Дональд Кнут вместе с женой
Посткриптум
285
заказал в Кембридже в мастерской Дэвида Киндерсли, чтобы ему
высекли один из груков на куске сланца в форме суперэллипса (см.
рис. на стр. vi).
19. ТРИСЕКЦИЯ УГЛА
Когда в своей колонке в Scientific American я опубликовал заметку о
трисекции угла, то начал получать множество писем от чудаков,
которые, не поверив, убеждали меня опубликовать их метод
трисекций или указать на ошибку. Когда материал этой колонки появился
в первом издании этой книги, на меня обрушилась новая волна
подобных писем. Хочу опубликовать лишь одно из писем, которые я
написал одному из респондентов.
Не скрою у что ваше решение проблемы, перед которой пасовали
самые великие математические умы нескольких столетий, поразило
меня. Но опубликовать его теперь было бы весьма затруднительно.
Математический мир просто не поймет, как простой любитель преуспел
там, где потерпели неудачу многие великие умы. Чтобы сберечь
честолюбие больших ученых, я возвращаю вашу рукопись обратно и советую
вам сжечь ее.
А в 1983 году один джентльмен даже выслал мне чек на 100
долларов в надежде, что это «поможет» мне указать ошибки в его
доказательстве. И я нашел эти ошибки. Он немедленно выслал мне еще
одно доказательство, в котором указанный недостаток был
устранен, но появился новый. В итоге этой бесполезной переписки я
просто возвратил чек. Ответом на это стало оскорбительное письмо,
на которое я решил не отвечать.
После этого я убедился, что лучше всего в этом случае просто
возвращать доказательства с примечанием о том, что мы
некомпетентны оценить его. Если вы все же решили связаться с подобными
«трисекторами», то дайте человеку адрес другого интересующегося
этой проблемой.
Свою отнюдь не толстую папку, посвященную трисекции угла, я
выкинул, когда сортировал письма в издательство Underwood Dudley.
Именно это издательство в 1987 году публиковало некоторые из
материалов моей книги. Коллекция издательства была существенно
больше моей, и сейчас она, скорее всего, одна из самых больших
математических коллекций в мире. Дорогой читатель, если вы все же
286
Нескучная математика
сумели с помощью циркуля и линейки разделить угол на три равные
части, пожалуйста, НЕ высылайте его мне. Пошлите его в
коллекцию издательства Underwood Dudley (которая, кстати, хранится в
университете Де Пау по адресу Mathematics Department, De Pauw University,
Greencastle, Indiana 46135). Там над вами смеяться не будут.
Мартин Гарднер
НЕСКУЧНАЯ МАТЕМАТИКА
Калейдоскоп головоломок
Зав. редакцией Е. Иванова
Технический редактор Г. Этманова
Компьютерная верстка Н. Пуненковой
ООО «Издательство ACT»
141100, РФ, Московская обл., г. Щелково, ул. Заречная, д. 96
ООО «Издательство Астрель»
129085, г. Москва, пр-д Ольминского, д. За
Наши электронные адреса:
www.ast.ru E-mail: astpub@aha.ru
Отпечатано с готовых диапозитивов
в типографии ООО «Полиграфиздат»
144003, г. Электросталь, Московская область,
ул.Тевосяна, д. 25
НЕСКУЧНАЯ
МАТЕМАТИКА
Математические головоломки
Свою первую книгу Мартин Гарднер написал в 1935 году. С тех пор он не устает
очаровывать и восхищать математическими жемчужинами своих бесчисленных
поклонников. Начал свою карьеру этот популяризатор науки с колонки Mathematical Games
(«Математические игры») в журнале Scientific American, где проработал 25 лет. Именно
материал этих колонок и лег в основу многочисленных книг этого автора. Не
составляет исключения и эта книга. Мартин Гарднер написал более сорока книг. Именитый
автор был удостоен многих знаков отличия в научном мире, является почетным
доктором Бакнвльского университета, за свои труды в области науки, и математики
б частности, был отмечен премиями Американского института физики и
Американского математического общества. Является почетным членом Американской
математической ассоциации.
Отзывы о книге «Нескучная математика»
Эта книга включает в себя 19 интереснейших глав. Диапазон охвата тем простирается
от игр с монетами до анализа дизайнерских решений современной мебели, от
карточных тасовок до представления читателю недавно изобретенной логической игры.
Комментарии, сопровождающие головоломки, настолько ясны, что совершенно
не нужно быть гением, чтобы понять их.
Б. Ж Тврвил, Times, Канберра, Австралия
Те, кто устал от унылых дебатов, посвященных новым формам преподавания
математики, могут обратиться к этой превосходной книге Мартина Гарднера. Я надеюсь,
что преподаватели прочтут его книгу и найдут в ней ответ на вопрос, как «зажечь»
в своих учениках интерес к математике..
Здриан Бери, Daily Telegraph, Лондон