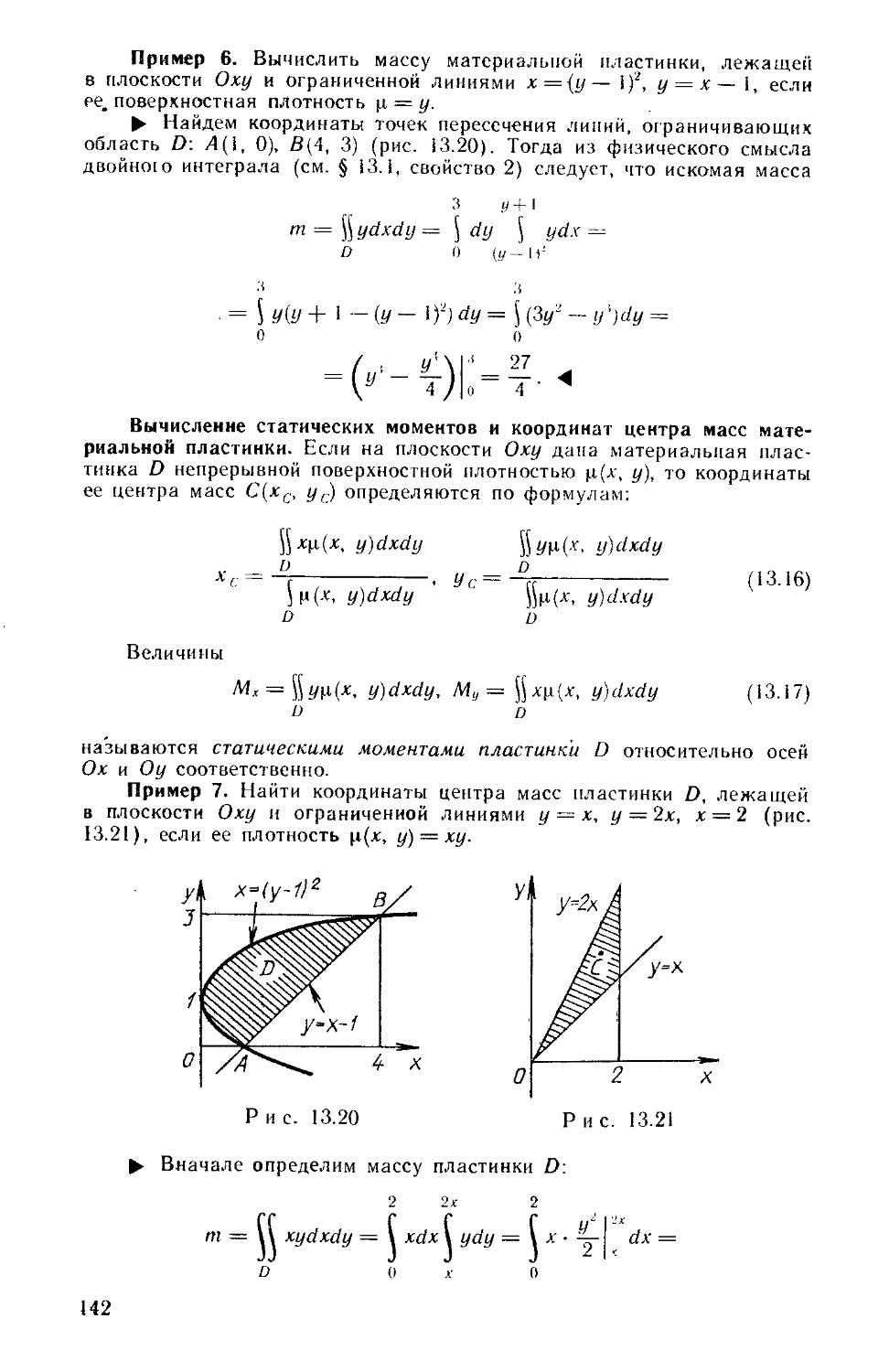
Author: Рябушко А.П. Бархатов В.В. Державец В.В. Юруть И.Е.
Tags: математика высшая математика
ISBN: 5-339-00328-0
Year: 1991
Text
СБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ
В трех частях
Под общей редакцией доктора физико-математических наук, профессора А. П. Рябушко
Часть 3
Допущено Министерством народного образования БССР в качестве учебного пособия для студентов инженерно-технических специальностей вузов
Минск «Вышэйшая школа» 1991
ББК 22.1 I я73
С23
УДК 51 (076.1) (075.8)
Авторы: А. П. Рябушко, В. В. Бархатов, В. В. Державец, И. Е. Юруть
Рецензенты: кафедра высшей математики Московского энергетического института; зав. кафедрой высшей математики Минского радиотехнического института, д-р физ.-мат. наук, проф. Л. А. Черкас
Сборник индивидуальных заданий по высшей С23 математике: Учеб, пособие. В 3 ч. Ч.З/ А. П. Рябушко, В. В. Бархатов, В. В. Державец, И. Е. Юруть; Под общ. ред. А. П. Рябушко.— Мн.: Выш. шк., 1991.—288 с.: ил.
ISBN 5-339-00328-0.
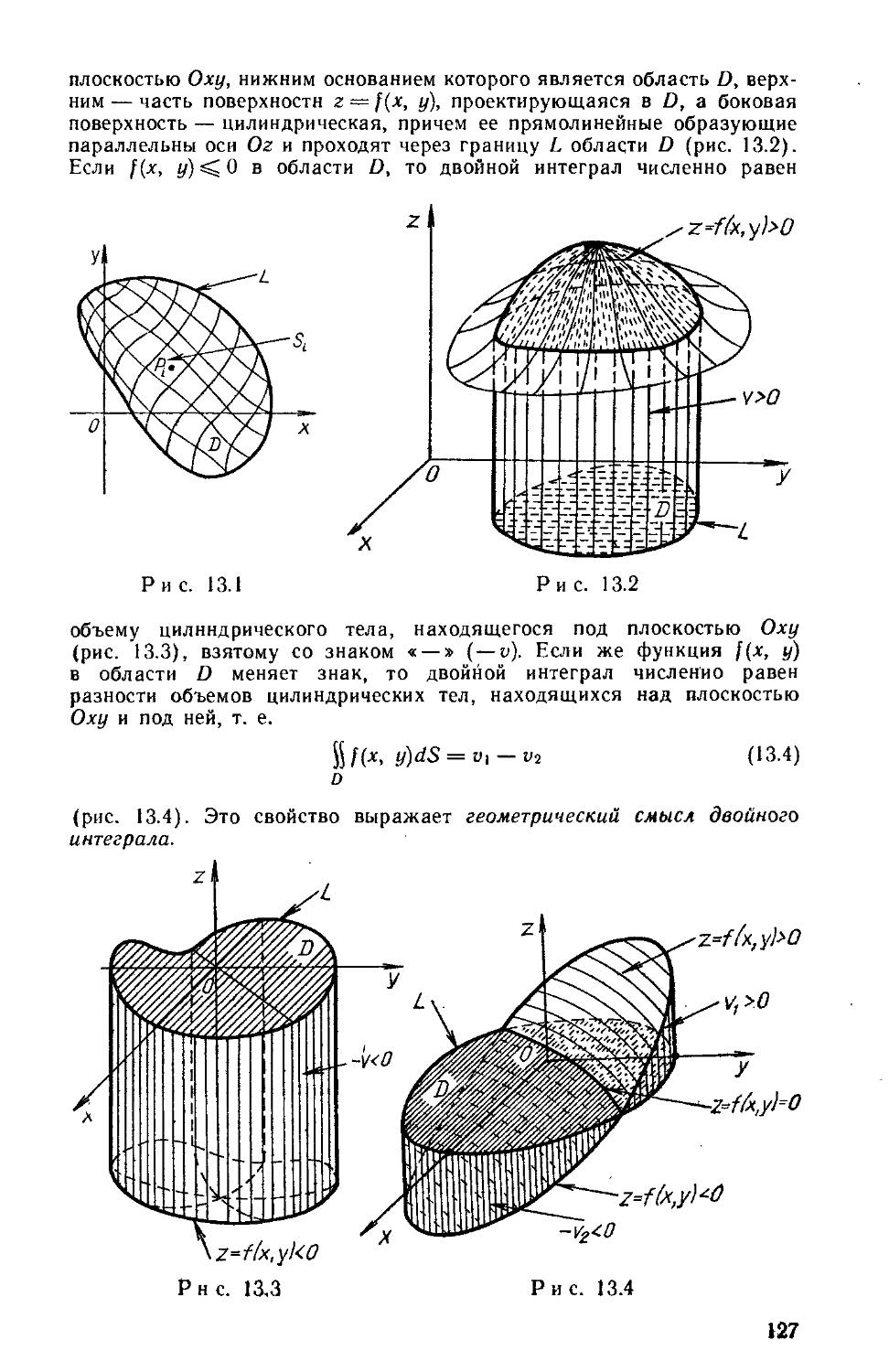
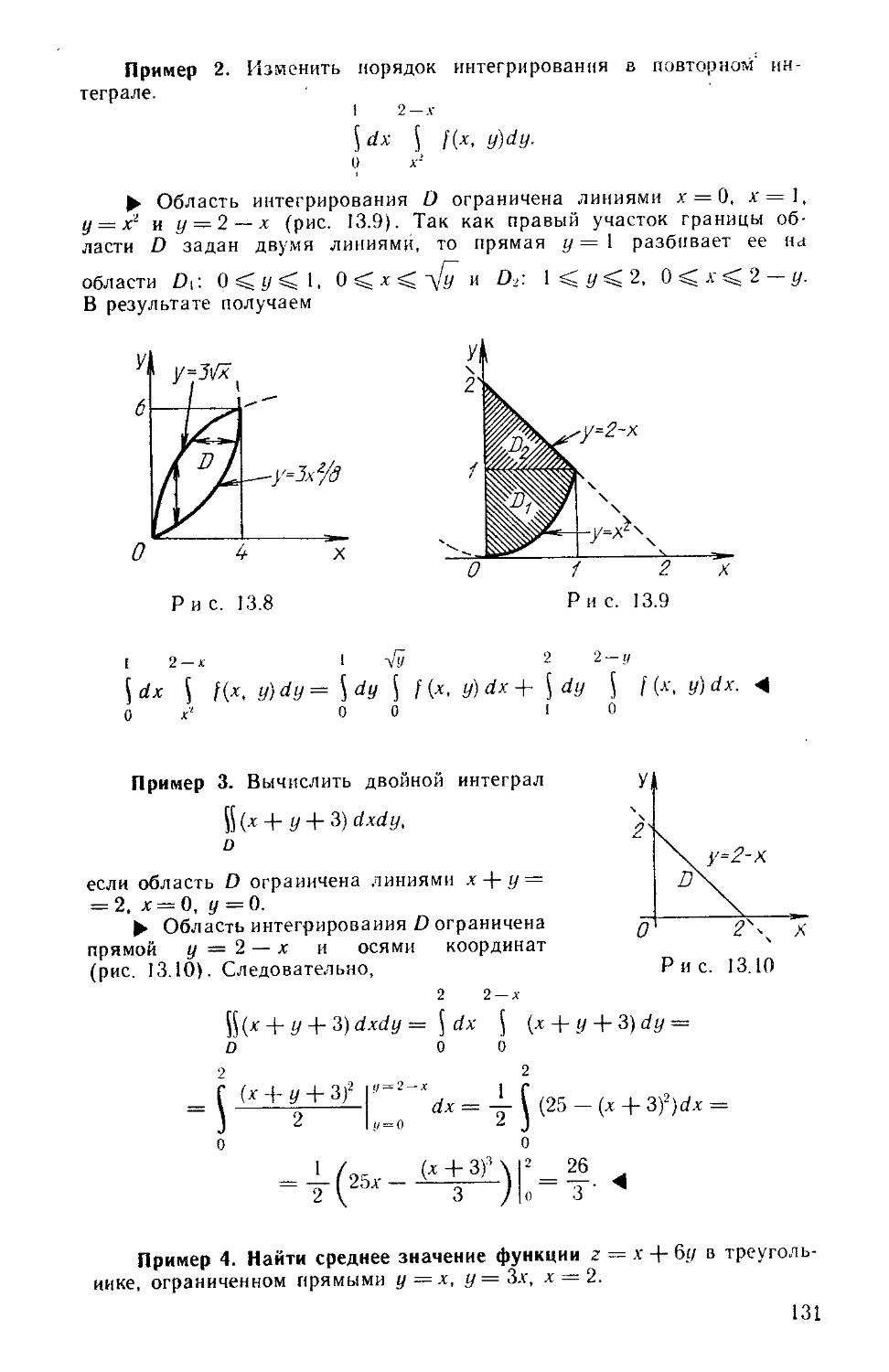
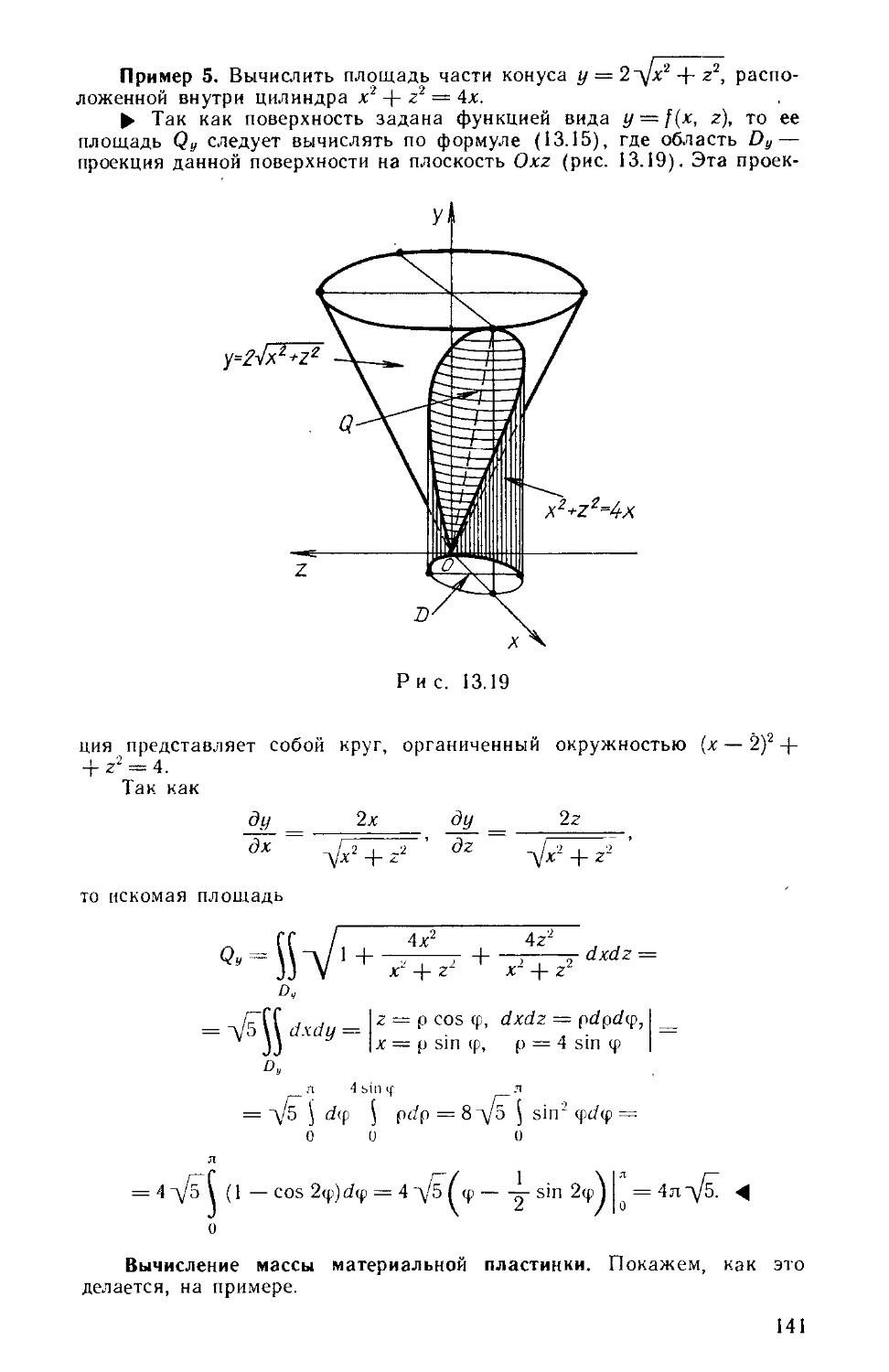
Книга является составной частью комплекса учебных пособий по курсу высшей математики, направленных на развитие и активизацию самостоятельной работы студентов вузов. Содержатся теоретические сведения и наборы задач для аудиторных и индивидуальных заданий по рядам, кратным н криволинейным интегралам и элементам теории поля.
Для студентов инженерно-технических специальностей вузов.
1602010000— 041 ______________ g_g|
М304(03)—91
ББК 22.11я73
ISBN 5-339-00328-0 (ч. 3)
ISBN 5-339-00483-Х
© Коллектив авторов, 1991
ПРЕДИСЛОВИЕ
Данная книга является третьей частью комплекса учебных пособий под общим названием «Сборник индивидуальных заданий по высшей математике», написанного в соответствии с действующими программами курса высшей математики в объеме 380—450 часов для инженерно-технических специальностей вузов. Этот комплекс также может быть использован в вузах других профилей, в которых количество часов, отведенное на изучение высшей математики, значительно меньше. (Для этого из предлагаемого материала следует сделать необходимую выборку.) Кроме того, он вполне доступен для студентов вечерних и заочных отделений вузов.
Настоящий комплекс пособий адресован преподавателям и студентам и предназначен для проведения практических занятий, самостоятельных (контрольных) работ в аудитории и выдачи индивидуальных домашних заданий по всем разделам курса высшей математики.
В третьей части «Сборника индивидуальных заданий по высшей математике» содержится материал по рядам, кратным и криволинейным интегралам и элементам теории поля. Ее структура диалогична
3
структуре предыдущих частей, а нумерация глав, параграфов и рисунков продолжает соответствующую нумерацию.
Авторы выражают искреннюю благодарность рецензентам — коллективу кафедры высшей математики Московского энергетического института, возглавляемой членом-корреспондентом АН СССР, доктором физико-математических наук, профессором С. И. Похожаевым, и заведующему кафедрой высшей математики Минского радиотехнического института, доктору физико-математических наук, профессору Л. А. Черкасу, а также сотрудникам этих кафедр кандидатам физико-математических наук, доцентам Л. А. Кузнецову, П. А. Шмелеву, А. А. Карпуку — за ценные замечания и советы, способствовавшие улучшению книги.
Все отзывы и пожелания просьба присылать по адресу: 220048, Минск, проспект Машерова, 11, издательство «Вышэйшая школа».
Авторы
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Охарактеризуем структуру пособия, методику его использования, организацию проверки и оценки знаний, навыков и умений студентов.
Весь практический материал по курсу высшей математики разделен на главы, в каждой из которых даются необходимые теоретические сведения (основные определения, формулировки теорем, формулы), используемые при решении задач и выполнении упражнений. Изложение этих сведений иллюстрируется решенными примерами. (Начало решения примеров обозначается символом ►, а конец— 4.) Затем даются подборки задач с ответами для всех практических аудиторных занятий (АЗ) и для самостоятельных (миниконтрольных) работ на 10—15 минут во время этих занятий. И, наконец, приводятся недельные индивидуальные домашние задания (ИДЗ), каждое из которых содержит 30 вариантов и сопровождается решением типового варианта. Часть задач из ИДЗ снабжена ответами. В конце каждой главы предлагаются дополнительные задачи повышенной трудности.
В приложении приведены двухчасовые контрольные работы (каждая — по 30 вариантов) по важнейшим темам курса.
Нумерация АЗ сквозная и состоит из двух чисел: первое из них указывает на главу, а второе — на порядковый номер АЗ в этой главе. Например, шифр АЗ-12.1 означает, что АЗ относится к двенадцатой главе и является первым по счету. В третьей части пособия содержится 21 АЗ и 10 ИДЗ.
Для ИДЗ также принята нумерация по главам. Например, шифр ИДЗ-12.2 означает, что ИДЗ осносится к двенадцатой главе и является вторым. Внутри каждого ИДЗ принята следующая нумерация: первое число означает номер задачи в данном задании, а второе — номер варианта. Таким образом, шифр ИДЗ-12.2:16 означает, что студент должен выполнять 16-й вариант из ИДЗ-12.2,
5
который содержит задачи 1.16, 2.16, 3.16 и т. д. При выдаче ИДЗ студентам номера выполняемых вариантов можно менять от задания к заданию по какой-либо системе или случайным образом. Более того, можно при выдаче ИДЗ любому студенту составить его вариант, комбинируя однотипные задачи из разных вариантов. Например, шифр ИДЗ-12.2:1.2; 2.4; 3.6; 4.1; 5.15 означает, что студенту следует решать в ИДЗ-12.2 первую задачу из варианта 2, вторую — из варианта 4, третью — из варианта 6, четвертую — из варианта 1 и пятую — из варианта 15. Такой комбинированный метод выдачи ИДЗ позволяет из 30 вариантов получить большое количество новых вариантов.
Внедрение ИДЗ в учебный процесс некоторых втузов (Белорусский институт механизации сельского хозяйства, Белорусский политехнический институт, Дальневосточный политехнический институт и др.) показало, что целесообразнее выдавать ИДЗ не после каждого АЗ (которых, как правило, два в неделю), а одно недельное ИДЗ, включающее в себя основной материал двух АЗ данной недели.
Дадим некоторые общие рекомендации по организации работы студентов в соответствии с настоящим пособием.
1. В вузе студенческие группы по 25 человек, проводятся два АЗ в неделю, планируются еженедельные необязательные для посещения студентами консультации, выдаются недельные ИДЗ. При этих условиях для систематического контроля с выставлением оценок, указанием ошибок и путей их исправления могут быть использованы выдаваемые каждому преподавателю матрицы ответов и банк листов решений, которые кафедра заготавливает для ИДЗ (студентам они не выдаются). Если матрицы ответов составляются для всех задач из ИДЗ, то листы решений разрабатываются только для тех задач и вариантов, где важно проверить правильность выбора метода, последовательности действий, навыков и умений при вычислениях. Кафедра определяет, для каких ИДЗ нужны листы решений. Листы решений (один вариант располагается на одном листе) используются при самоконтроле правильности выполнения заданий студентами, при взаимном студенческом контроле, а чаще при комбинированном контроле: преподаватель проверяет лишь правильность выбора метода, а студент по листу решений — свои вычисления. Эти методы позволяют проверить
6
ИДЗ 25 студентов за 15—20 минут с выставлением оценок в журнал.
2. Студенческие группы в вузе по 15 человек, проводятся два АЗ в неделю, в расписание для каждой группы включены обязательные два часа в неделю самоподготовки под контролем преподавателя. При этих условиях (которые созданы, например, в Белорусском институте механизации сельского хозяйства) организация индивидуальной, самостоятельной, творческой работы студентов, оперативного контроля за качеством этой работы значительно улучшается. Рекомендованные выше методы пригодны и в данном случае, однако появляются новые возможности. На АЗ быстрее проверяются и оцениваются ИДЗ, во время обязательной самоподготовки можно проконтролировать проработку теории и решение ИДЗ, выставить оценки части студентов, принять задолженности по ИДЗ у отстающих.
Накапливание большого количества оценок за ИДЗ, самостоятельные и контрольные работы в аудитории позволяет контролировать учебный процесс, управлять им, оценивать качество усвоения изучаемого материала.
Все это дает возможность отказаться от традиционного итогового семестрового (годового) экзамена по материалу всего семестра (учебного года) и ввести так называемый блочно-цикловой (модульно-цикловой) метод оценки знаний и навыков студентов, состоящий в следующем. Материал семестра (учебного года) разбивается на блоки (модули), по каждому из которых выполняются АЗ, ИДЗ и в конце каждого цикла двухчасовая письменная коллоквиум-контрольная работа, в которую входят 2—3 теоретических вопроса и 5—6 задач. Учет оценок по АЗ, ИДЗ и коллоквиуму-контрольной позволяет вывести объективную общую оценку за каждый блок (модуль) и итоговую оценку по всем блокам (модулям) семестра (учебного года). Подобный метод внедряется, например, в Белорусском институте механизации сельского хозяйства.
В заключение отметим, что пособие в основном ориентировано на студента средних способностей, и усвоение содержащегося в нем материала гарантирует удовлетворительные и хорошие знания по курсу высшей математики. Для одаренных и отлично успевающих студентов необходима подготовка заданий повышенной сложности (индивидуальный подход в обучении!) с перспективными по
7
ощрительными мерами. Например, можно разработать для таких студентов специальные задания на весь семестр, включающие задачи настоящего пособия и дополнительные более сложные задачи и теоретические упражнения (для этой цели, в частности, предназначены дополнительные задачи в конце каждой главы). Преподаватель может выдать эти задания в начале семестра, установить график их выполнения под своим контролем, разрешить свободное посещение лекционных или практических занятий по йысшей математике и в случае успешной работы выставить отличную оценку до экзаменационной сессии.
12. РЯДЫ
12.1. ЧИСЛОВЫЕ РЯДЫ. ПРИЗНАКИ сходимости ЧИСЛОВЫХ РЯДОВ
Выражение вида
• (12.1)
п — 1
где и„ g R, называется числовым рядом. Числа щ, и?, ..., н„, ... называются членами ряда, число и„ — общим членом ряда.
Сум-мы
S1 = U\, S? — Щ -|- Щ, ..., S„ — Щ и? ... 4- ип называются частичными суммами, a S„ — п-й частичной суммой ряда (12.1). Если lim S,, существует и равен числу S, т. е. S = lim S„, то n-*-oo п->оо
ряд (12.1) называется сходящимся, a S — его суммой. Если lim S„ п-*- оо не существует (в частности, бесконечен), то ряд (12.1) называется расходящимся. Сумма
Г п = U„+ I 4- ип-[.2 + ... 4" Ufi + k 4~ называется п-м остатком ряда (12.1). Если ряд (12.1) сходится, то
lim r„ = lim (S — S„) = 0. П —* оо л —* оо
Пример 1. Дан ряд ) —-—!—-г-. Установить сходимость .этого z_, л(л 4- 1)
п = 1 ряда и найти его сумму.
Запишем п-ю частичную сумму данного ряда и преобразуем ее:
Поскольку
S — lim S„ = lim (1--------\ = '>
П—> оо л—> оо \ п + 1 /
то данный ряд сходится и его сумма S = 1. 4 Ряд вида
а 4- aq 4- aq2 4- + аЧ" 1 4-
(12.2)
9
представляет собой сумму членов геометрической прогрессии со знаменателем q. Известно, что при |</| < 1 ряд (12.2) сходится и его сумма S = а/(1 — <?). Если |</| 1, то ряд (12.2) расходится.
Теорема 1 (необходимый признак сходимости ряда). Если числовой ряд (!2.1) сходится, то limu„ = 0.
Обратное утверждение неверно. Например, в гармоническом ряде
общий член стремится к нулю, однако ряд расходится.
Теорема 2 (достаточный признак расходимости ряда). Если lim и„ = a =f= 0, то ряд (12.1) расходится.
Сходимость или расходимость числового ряда не нарушается, если в нем отбросить любое конечное число членов. Но его сумма, если она существует, при этом изменяется.
Уп
——-——.
‘in 4- 1
Запишем общий член данного ряда:
Тогда
т. е. ряд расходится. •<
Рассмотрим некоторые достаточные признаки сходимости числовых рядов с положительными членами.
Теорема 3 (признаки сравнения). Если даны два ряда
Ul Д- и2 4“ ... 4“ Un 4“
Hi 4~ 4" 4" с'п 4"
(12.3)
(12.4)
и для всех п^гпо выполняются неравенства 0 < ип ип, то:
1) из сходимости ряда (12.4) следует сходимость ряда (12.3);
2) из расходимости ряда (12.3) следует расходимость ряда (12.4).
В качестве рядов для сравнения целесообразно выбирать ряд, оо
представляющий сумму членов геометрической прогрессии S aq\
п = 0
а также гармонический (расходящийся) ряд. Пример 3. Доказать сходимость ряда
Z1 _ 1 , 1 ,1
п-3" ~ 1-3 + 2 • З2 + + и • 3’
10
► Для установления сходимости ряда (1) венством
w„ = —!— < — (п > 2)
п 3" 3'*
воспользуемся нера
и сравним данный ряд со сходящимся рядом
Согласно признаку сравнения (см. теорему 3, и. 1), ряд (1) сходится.
Пример 4. Исследовать на сходимость ряд У —
] ] ,^2
> Так как —==^= > — для любого п 2, то члены данного / > , п
xjn — 1
ряда больше соответствующих членов расходящегося гармонического ряда. Значит, исходный ряд расходится.
Теорема 4 (признак Д'Аламбера). Пусть для ряда (12.1) и„ > О (начиная с некоторого п = п«) и существует предел
,. Mi
lim ------= q.
ll-ж Un
Тогда:
1) при q < 1 данный ряд сходится;
2) при q > ) ряд расходится.
При q = 1 признак Д’Аламбера не дает ответа на вопрос о схо-
димости или расходимости ряда: он может и сходиться, и расходиться. В этом случае сходимость ряда исследуют с помощью других признаков.
Пример 5. Исследовать на сходимость ряд
то
. п -F
► Поскольку U-; = I I — ---~
и„+1 (п + 1 )’ • 2" '
lim -----------= Inn ----------,----------
И > co Un II—>• co tl~ • 2"
Следовательно, данный ряд сходится.
Теорема 5 (радикальный признак Коши). Если, начиная с некоторого п = п0, и„ > 0 и lim \[un = q, то при q < 1 ряд (12.1) сходится, а при q > 1 расходится.
При 7=1 радикальный признак Коши неприменим.
Пример 6. Исследовать на сходимость ряд ) ( Т—
/ , \ — 1
11 = 1
► Воспользуемся радикальным признаком Кошм:
Следовательно, данный ряд сходится.
11
Теорема 6 (интегральный признак Коши). Пусть члены ряда (12.1) монотонно убывают и функция у = f(x), непрерывная при оо
такова, что f(n) — и„. Тогда ряд (12.1) и интеграл $ f(x)dx одновремен-а
но сходятся или расходятся.
Например, поскольку dx (а С R) сходится при а > 1 и расхо-
I
дится при 1, то ряд Дирихле V*— сходится при а>1 и расхо-/ , п"
дится при а 1.
Сходимость многих рядов можно исследовать путем сравнения их с соответствующим рядом Дирихле.
Пример 7. Исследовать на сходимость ряд
Z2n
(n2+ I)2 ' п= I
► Положим,
что f(x) = -------;-------. Эта
' (х2 + 1)2
функция
всем требованиям интегрального признака Коши. Тогда
удовлетворяет
несобственный
интеграл
ОО В
1 |в 1
11ГЛ —----------- = —,
оо (х2 + 1) 11 2
I I
2х . Г 2х
—------dx= 11 гл \—о---
(х2 + I)2 В^оо J (х2 + I)2
т. е. сходится, а значит, данный ряд также сходится.
Числовой ряд (12.1), члены и„ которого после любого номера N (п > N) имеют разные знаки, называется знакопеременным.
Если ряд
I «1 | -|- | Иг I -1- ... -1- I а„| -|- ... (12.5)
сходится, то ряд (12.1) также сходится (это легко доказывается) и называется абсолютно сходящимся. Если ряд (12.5) расходится, а ряд (12.1) сходится, то ряд (12.1) называется условно (неабсолютно) сходящимся.
При исследовании ряда на абсолютную сходимость используются признаки сходимости с положительными членами рядов.
Пример 8. Исследовать на сходимость ряд у --тг—(а £ R).
л= I
Рассмотрим ряд, составленный из абсолютных величин членов
Z|sin па| , -------г-- (а Е R). Так как |sin ла| С) 1, то
л= 1
члены исходного ряда не больше членов ряда Дирихле = 2).
12
который, как известно, сходится. Следовательно, на основании признака сравнениям (см. теорему 3, п. 1) данный ряд сходится абсолютно.
Ряд вида
U| — U‘2 -|- U3 — ... 4“ (— 1)” 1 Un (12.6)
где и„ 0, называется знакочередующимся рядом.
Теорема 7 (признак Лейбница). Если для знакочередующегося ряда (12.6) и, > и2 > ... > и„ > ... и lim ип = 0, то ряд (12.6) сходится п-*- оо
и его сумма S удовлетворяет условию 0 < S < и,.
Следствие. Остаток г„ ряда (12.6) всегда удовлетворяет условию I Tn I ип ।.
Например, ряд
,-т + т-т + -+(-1^'у + -
сходится, так как выполнены условия признака Лейбница. Он сходится условно, так как ряд 1 4- — -|- — -|- ... -|- -—(- ... расходится.
Абсолютно сходящиеся ряды (в отличие от условно сходящихся) обладают свойствами сумм конечного числа слагаемых (например, от перемены мест слагаемых сумма не меняется).
Верна следующая
Теорема 8. Если числовой ряд сходится условно, то, задав любое число а, можно так переставить члены ряда, что его сумма окажется равной а. Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный после перестановки, будет расходящимся.
Проиллюстрируем теорему 8 на примере. Рассмотрим условно сходящийся ряд
Переставим его члены так, чтобы после каждого положительного члена стояли два отрицательных. Получим
. 1 1,1 1 1 , 1 1 1 ,
2 4 + 3 6 8 + 5 10 12 + ~ +
1 1 1 । + 2k — 1 4k — 2 4k +"‘
Сложим теперь каждый положительный член с последующим отрицательным:
1 1 । 1 1 , 1- 1 1 1
2 - 4 + 6 ~ 8 + 10 ~ 12 + - + 4k - 2 ~ 4k+-~
= ±л_± + ±_± + ±_± + ..+
2 \ 2 .3 4^5
+ 2k — 1 ~ 2k+ “ ) = Т S'
Очевидно, что сумма исходного ряда уменьшилась вдвое!
13
Пример 9. Исследовать на сходимость ряд
У(-1Г' 2"+..!...... (!)
1 «(п + о
п = 1
► Так как члены данного знакочередующегося ряда монотонно убывают и lim —fLiJ—= 0, то, согласно признаку Лейбница, ряд n-*-oo !t{rl -р 1 )
(1) сходится.
Рассмотрим теперь ряд, составленный из абсолютных величин членов ряда (1), т. е. ояд
2n + 1
общий член которого
Найдем
оо
задается
х .. \ 2х + 1
функцией /(х) = ---.:
при
X — П,
^rfx=lim((± + -±-U =
(х 1) в—оо J \ х х 4- 1 /
1
в
= lim (In |х| 4- In |х 4- 11) |f = lim (In В (В -f- 1) — In 2) = оо. В—► оо В—*• оо
Следовательно, ряд (2) расходится, и поэтому ряд (1) сходится условно.
Пример 10. Вычислить сумму ряда-
с точностью 6 = 0,001.
► Всякая л-я частичная сумма сходящегося ряда является приближением к его сумме с точностью, не превосходящей абсолютной величины остатка этого ряда. Выясним, при каком количестве членов n-й частичной суммы выполняется неравенство |г„| 6.
Для данного ряда
= —L—4-Y+l + («+ 1)! \2/
1 (1Y+2
(п 4-2)! V 2/ +
Так как (л + 1)! < (2л + 2)! < (2л + 3)! < ..., то
Путем подбора легко найти, что гп < <0,001 при л = 4. Сле-
довательно, сумма данного ряда (с точностью 6 = 0,001)
^^-r + T + jj+ir-»-648- «
14
Пример 11. Вычислить сумму ряда
ОО
с точностью 6 = 0,001.
Так как данный ряд — знакочередующийся, сходящийся, то величина отброшенного при вычислении остатка ряда, который также является знакочередующимся рядом, не превосходит первого отброшенного члена (на основании следствия из признака Лейбница). Нужное число членов п найдем путем подбора из неравенства —-——
sj 0,001. При п = 6 последнее неравенство выполняется, значит, если отбросить в данном ряде все члены, начиная с шестого, то требуемая точность будет обеспечена. Следовательно,
S~S5=T-iV + ^-^ +W=0’449- «
АЗ-12.1
1. Доказать сходимость ряда и найти его сумму:
оо оо
у---------1——, б) у
/ . (3n-2)(3n+1) / . 10“
п = I п = 1
(Ответ: а) 1/3; Ь) 5/4.)
2. Исследовать на сходимость следующие ряды:
а) У —;
’ Д, 2п3 - 1
п-1
/2=1
ОО
д)
/1-1
3. Доказать, что:
a) lim — = 0;
Я —► со п!
Z1 / /г + 2 \«2 + 2" .
2"\ п + 1 /
б) lim = 0 при а > 1. я со ап!
4. С помощью интегрального признака Коши исследовать на сходимость следующие ряды:
15
оо
оо
а> Ivri+F’ б’ п=1 П— I
оо
В) £ Л In2 Л * = 2
Самостоятельная работа
Z3n । 5П
—-п— и найти 15
п = I
его сумму. (Ответ: 3/4)
2. Исследовать на сходимость ряд —т—
п= I
2. 1. Доказать сходимость ряда V —---------- 1 и
/ , (2л — 1)(2л + 1) /= ।
найти его сумму. (Ответ: 1/2.)
2. Исследовать на сходимость ряд > —-----------.
Z-< (и +4)
п = 1
3. 1. Доказать сходимость ряда
найти его сумму. (Ответ: 1/6.)
2. Исследовать
на сходимость
ряд
АЗ-12.2
1. Исследовать на сти следующие ряды:
условную и абсолютную сходимо-
«•2-";
л2 — 9
оо
п= [
п
6л 4- 5 ’
16
оо оо
. у cos(2ng). . у (-1)"
Д) / - п2 + 1 ’ L п - In п '
п=1 п=1
2. Составить разность двух расходящихся рядов оо оо
~2п~—Г и 2п и ИССЛеД°вать на сходимость получен-п = I п = I
ный ряд.
3. Найти сумму ряда —1 2 с точностью 6 — 0,01.
п = 1
(Ответ-. 0,58.)
4. Сколько первых членов ряда нужно взять, чтобы их сумма отличалась от суммы ряда на величину, меньшую, чем 10~6:
(Ответ: а) п = 103 * *; б) п = 106.)
Самостоятельная работа
1. 1. Исследовать на условную и абсолютную сходи-оо
мости ряд У (—1)"—А-----•
/ . п 1гг п
п~ 1 оо
2. Найти сумму ряда У (—l)"-1 , ограни-
п + 1
п = 1
чившись тремя его членами. Оценить абсолютную погреш-
ность вычислений. (Ответ: 5 = 0,266, 6 = 0,01.)
2. 1. Исследовать на условную и абсолютную сходи-оо
мости ряд
П = 1
оо
2. Найти сумму ряда ( — I)"-1 ’ огРани’
п = 1
чившись тремя его первыми членами. Оценить абсолютную погрешность вычислений. (Ответ: 5 = 0,56, 6 = 0,1.)
17
для всех х£ D, то ряд (12.7) называется равномерно сходящимся в 1>. В случае равномерной сходимости функционального ряда его п-я частичная сумма является приближением суммы ряда с одной и той же точностью для всех x(D.
Функциональный ряд (12.7) называется мажорируемым в некоторой области D, если существует сходящийся числовой ряд
ОО
2 а„ (а„ > 0), (12.9)
п = 1
такой, что для всех х£ D справедливы неравенства:
1 м*(лг)| < at (k = 1, 2, ...).
Ряд (12.9) называется мажорантным (мажорирующим) рядом. Например, функциональный ряд
cos х , cos 2х , cos Зх , , cos пх
1 + 22 + З2 + " + пг +
мажорируется рядом 1 -|—-|—^ + ... -|—— ф .... так как I cos пх\ <4 1. 2 3 ri"
Данный функциональный ряд равномерно сходится на всей оси Ох, поскольку он мажорируется при любом х.
Равномерно сходящиеся ряды обладают некоторыми общими свойствами:
1) если члены равномерно сходящегося ряда непрерывны на некотором отрезке, то его сумма также непрерывна на этом отрезке;
2) если члены ряда (12.7) непрерывны на отрезке [а; 6] и ряд равномерно сходится на этом отрезке, то в случае, когда [а; р}с[а; Ь], р оо 0
\S(x)dx = 2 \ u„(x)dx, а п = 1 а
где S(x)— сумма ряда (12.7);
3) если ряд (12.7), составленный из функций, имеющих непрерывные производные на отрезке [а; 6], сходится на этом отрезке к сумме S(x) и ряд и((х) + и'^х) -|- ... + и'п(х) 4- ... равномерно сходится на том же отрезке, то
и((х)+ «а(х)+ ... + а'„(х) + ... = S'(x).
Степенным рядом называется функциональный ряд вида
ОО
2 ап(х — xof, п=0
где До. До а„, ... — постоянные числа, называемые коэффициен-
тами ряда, х0 — фиксированное число. При х'о = 0 получаем степенной ряд вида
2 а„х". (12.10)
л=0
Теорема 1 (Абеля). 1. Если степенной ряд (12.10) сходится при некотором значении х = х, #= 0, то он абсолютно сходится при всяком значении х, удовлетворяющем условию |х| < |х, |.
19
2. Если степенной ряд (12.10) расходится при некотором значении х = хз, то он расходится при любых х, для которых |х| > | хг |.
Неотрицательное число R, такое, что при всех |х| < R степенной ряд (12.10) сходится, а при всех |х| > R — расходится, называется радиусом сходимости ряда. Интервал (— R; R) называется интервалом сходимости ряда (12.10).
Радиус сходимости степенного ряда (12.10) определяется формулой
R = lim ——— или R = lim
И-* ОО I Un + I I П-r ОС
I а„ |
(12.11)
если, начиная с некоторого п )>. п0, все а„ #= 0. (Предполагается, что указанные пределы существуют или бесконечны.) Формулы (12.11) легко получить, воспользовавшись соответственно признаком Д’Аламбера или радикальным признаком Коши.
2п • хп
Пример 2. Найти область сходимости степенного ряда S -----------—
" = '3" уп
Так как
2Л 2"+1
Лп = —, Лп -|- 1 ==: ,
3”д/« 3"+1д/«+1
то
Значит, степенной ряд сходится в интервале (— 3/2; 3/2). На концах этого интервала ряд может сходиться или расходиться. В нашем при-
ОО
мере при х ——3/2 данный ряд принимает вид
сходится по признаку Лейбница. При х = 3/2 получаем ряд
члены которого больше соответствующих членов расходящегося гармонического ряда. Значит, при х = 3/2 степенной ряд расходится. Следовательно, областью сходимости исходного степенного ряда является полуинтервал [ — 3/2; 3/2). -4
Если дан ряд вида S ап(х — хо)", то
п = 0
определяется также по формуле (12.11), будет интервал с центром в точке х=х<>: (хо— R', х» -|- R).
Пример 3. Найти область сходимости степенного ряда
его радиус сходимости R
а интервалом сходимости
(х — 2)'
п = 0
20
► Найдем радиус сходимости данного ряда:
Л =
im л/л+А = 2>
е.
ряд сходится в интервале (0; 4). При х = 0 получаем ряд
, который расходится, так как его члены больше членов
расходящегося гармонического ряда, а при х = 4—
где lim
n = o v 1
= 0, сходящийся по признаку Лейбница. Область
сходимости данного ряда (0; 4].
Zx"
—-.
► Находим радиус сходимости ряда:
Л =
Следовательно, данный ряд сходится на всей числовой прямой. Отсюда, в частности, с учетом необходимого признака сходимости ряда (см. хп
§ 12.1, теорему 1) получаем, что lim —- = 0 для любого конечного х. -4 И—* ОО fl •
На всяком отрезке [а; 0], лежащем внутри интервала сходимости, степенной ряд сходится равномерно, поэтому его сумма в интервале сходимости является непрерывной функцией. Степенные ряды можно почленно интегрировать и дифференцировать в их интервалах сходимости. Радиус сходимости при этом не изменяется.
Пример 5. Найти сумму ряда
X3 , X5 х2"-1
х + ПГ + V + - + 2^=Т + -
► При |х| < 1 данный ряд сходится (так как R = 1), значит, его можно почленно дифференцировать в интервале сходимости. Обозначив сумму ряда через S(x), имеем
S'(x) = 1 -|- Х“ -|- х1 + А'; 2 + ••
Так как |х| < 1, полученный ряд есть сумма членов убывающей геометрической прогрессии со знаменателем q = х2 и его сумма S'(x) = = ------Проинтегрировав ряд из производных, найдем сумму дан-
ного ряда:
sw=т1"It^tI (|х| < ◄
J 1 Л I Л 1 I
0
21
АЗ-12.3
1. Найти область сходимости каждого из следующих
рядов: а)
в)
Д)
ZX"
(п 4- !)• 2" ’
п = 0
у 2"х“
L, п2 + \'
п — 0
оо
у (-*• +2)"
L, (2п - 1) • 4'1 ’
И = 1
Z ^(/)‘
(Ответ: а) —2О<2;б)
— 1 <х< 1; в) -1/20
/Л /Л
1/2; г) -3/2<х<3/2; д) -8<х<2;е) -д/2/2
2. Найти область равномерной сходимости следующих рядов:
/л /л
sin их
cos их
0
3. Применив почленное интегрирование и дифференцирование, найти суммы указанных рядов:
Ответ: а)
_1П(1_Х)(-1<Х<1); б) _[ЫХ|<1)\
(х-1) /
Самостоятельная работа
1. 1. Найти область сходимости ряда V ————.........-
О, 5“лЛг —1
( Ответ: — — х < — \
2. Найти сумму ряда -—|- Д- + ~ +... + ~ ф- ... X Л” Xs ха
(Ответ: -—(|.г|>1).)
22
оо
2. 1. Найти интервал сходимости ряда \ —7 ' “ 5"“\//г3 —0,5 п — I v
и исследовать сходимость на концах этого интервала. (Ответ: (1/2; 11/2), ряд сходится при х=1/2 и х= 11/2.)
оо
2. Найти область сходимости ряда —.
« = ।
3. 1. Найти интервал сходимости ряда 10''л'" _| и
п= I
исследовать сходимость на концах этого интервала. (Ответ: (—1/10; 1/10), ряд расходится при х=±1/10.) оо
2. Найти область сходимости ряда -2-.
«=о
12.3. ФОРМУЛЫ И РЯДЫ ТЕЙЛОРА И МАКЛОРЕНА. РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ
Если функция у = fix) имеет производные в окрестности точки х = х9 до (п 4- 1)-го порядка включительно, то существует точка с = х0 -)-4- 0(х — Хо) (0 < 0 < 1), такая, что
/(X) = Дх0) + 2^1 (X - хо) + (X - х0)~’ + ... +
ДДхп!
+ (А’ —х»)" 4~ Rri(x), (12.12)
где R„(x) = (х-х,,)"1'.
у” *р I ) .
Формула (12.12) называется формулой Тейлора функции у = Дх) для точки Хо, /?„(х)—остаточным членом формулы Тейлора в форме Лагранжа. Многочлен
РДх) = Дх0) 4- (х - хо) + ... + -2^1 (х - х„)"
называется многочленом Тейлора функции у = Дх).
При х0 = 0 приходим к частному случаю формулы (12.12):
Дх.) = ДО) + m X + -И2) +... + m + Ra(л,. (, 2., 3)
/п + 1>(с) . .. ... ..
Формула (12.13) называется формулой Макларена функции У = /(х).
23
Пример 1. Разложить по степеням разности х— 1 функцию у = = х4 — Зх2 4- 2х 4- 2.
► Для того чтобы воспользоваться формулой Тейлора при х0 = 1, найдем:
1/(1) = 2, j/'(1) = (4x3-6x24-2)L=1 =0,
у"(1) = (12х2 - 12х)| V=1 =0, </"'(1) = (24х — 12)|,=, = 12,
у'1/(1) = 24, у1'(х)=0
И т. д.
Следовательно,
х4 — Зх2 4- 2х 4- 2 = 2 4- 2(х — I)3 4- (х — I)4. 4
Пример 2. Записать многочлен Тейлора функции у = в точке х0 = 1.
► Находим производные данной функции и их значения в точке х0 = 1:
= С У'(1)= - “7l^i = - -
2 1 1 . 2 • 3 I
/'0)= — = =------— =-6’
х L=i х L_i
<(1) = 2'3'4 | =24. -/'"’(I) = (-!)” =(-1)’л!.
х 1л-=1 X 1х=1
Следовательно,
Рп W = 1 - + £- (х - 1 )2 - 4г(х - 1 )3 + - +
4-(-1)«^-(х-1)"= 1-(х-1)4-(х-1)2-(х-1)34-... + (-1)'’(х-1)’>.
Остаточный член формулы Тейлора для данной функции имеет вид
g-w=|-ir' "
Сформулируем условие разложимости функции в ряд Тейлора. Если функция f(x) дифференцируема в окрестности точки х0 любое число раз и в некоторой окрестности этой точки lim /?п(х) = 0 или
lim М)
(п+1)!
ТО
Кх) — Кхо) + 11“" (х — *о) 4--" + (х — хч)" + ••• (12-15)
В частности, при х0 = 0
Кх)=/(о)+во)х+1жх2+...+ тх»+... (12.16>
Ряд (12.15) называется рядом Тейлора, а ряд (12.16)—рядом Макларена.
24
Условие (12.14) является необходимым и достаточным для того, чтобы ряд, построенный по схеме (12.15) или (12.16), сходился к функции ((х) в некоторой окрестности точки х = х0. В каждом конкретном случае необходимо находить область сходимости ряда к данной функции.
Пример 3. Разложить в ряд Маклорена функцию ch х и найти область, в которой ряд сходится к данной функции.
► Находим производные функции f(x) = chx, — sh х, ^"(х) = = ch х, = sh x, ... Таким образом, (х) = ch х, если п — четное, и f("’(x) = sh х, если п — нечетное. Полагая х0 = 0, получаем: [ (0) = 1, /'(0) = 0, /"(0)= 1, (0) = 0, ..., fw(0)=l при п четном и f"'(0) = 0
при п нечетном. Подставим найденные производные в ряд (12.16). Имеем
Воспользовавшись условием (12.14), определим интервал, в котором ряд (1) сходится к данной функции.
Если п — нечетное, то
R,, (х) =
(и + 1)!
ch Ох,
если же п — четное, то
R„ (х) =
(« + !)!
sh Ох.
Так как 0<0< 1, то | ch 0х| = (еОх -|- е "')/2 е :'! и |sh0x|^eiAl. Значит,
Но, как было установлено в примере 4 из 12.2, Нт ----------------= 0 при
И ОО (П 1 ) 1
любом х. Следовательно, при любом х lim /?„(х) = 0 и ряд (1) сходит-
П->- оо
ся к функции ch х.
Аналогично можно получить разложения в степенные ряды многих других функций:
е' = 1 + “jV + "fr + •+ +• (- оо <х< оо), (12.17)
25
т(т — !)(« — п + I)
(12.21)
Для каждого случая в скобках указана область, в которой степенной ряд сходится к соответствующей функции. Последний ряд, называемый биномиальным, на концах интервала сходимости ведет себя по-разному в зависимости от т £ R: при т^О абсолютно сходится в точках х = ± 1; при — 1 С т С 0 расходится в точке х = — 1 и условно сходится в точке х= 1; при т —1 расходится в точках %='+!.
В общем случае разложение в степенные ряды основано на использовании рядов Тейлора или Маклорена. Но на практике степенные ряды многих функций можно найти формально, используя ряды (12.17) —-(12.21) или формулу для суммы членов геометрической прогрессии. Иногда при разложении полезно пользоваться почленным дифференцированием или интегрированием рядов. В интервале сходимости ряды сходятся к соответствующим функциям.
Например, при разложении в степенной ряд функции cos х/х в формулу (12.18) вместо х подставляем х/х. Тогда
Полученный ряд сходится при любых .г Е R, но следует помнить, что функция cos х/х" не определена при х < 0. Поэтому найденный ряд сходится к функции cos х/х только в полуинтервале 0 х < 00 •
Аналогично р, , sin х и f№ =
можно записать степенные ряды функций [(х) = е 2х
Пример 4. Разложить в ряд Маклорена функцию j (х) = 3
“ (1 _Х)(| +2х)
► Разложим данную функцию на сумму простейших рациональных дробей:
3 1 г 2
(1 — ЛГ) (1 н-2лг) ~ 1— х + 1+2л-'
Поскольку
£ X" (|л-|<1), (1)
п =0
ГТ27- £ <iM< "•
п - О
(2)
26
то
-г—£ ..- + г£ л=0 п = 0
= £ (!+(-|)',2»+‘)%'1. (3)
л — О
Так как ряд (I) сходится при |х|< I, а ряд (2) — при |х| < I/2, то ряд (3) сходится к данной функции при |х| < 1/2. 4
Пример 5. Разложить в степенной ряд функцию f(x) = arctg х.
> Очевидно, что
, , = ~----;--= 1 - .v’+x'-x6+ ... + (-
l+.r I—(—Л-)
Полученный ряд сходится внутри отрезка |—1; 1], значит, его можно почленно интегрировать на любом отрезке |0; xj cz (— I; I). Следовательно,
j - '- , Ш j (-l)',~l/2(,,~1’d/,
0 () fl = 1
“ 1
-2Л-ТТ-
n = 1
т. e. получили ряд, сходящийся к данной функции при ◄
АЗ-12.4
1. Разложить по степеням х -р 1 многочлен Дх) = = х5 — 4х4 -р 2xJ -|- 2х -|- 1.
2. Разложить в ряд по степеням х функцию у = —-i-
непосредственно используя ряд Маклорена.
3. Разложить в ряд по степеням х указанную функцию и найти область сходимости полученного ряда:
а) е~' -, б) xcos2x; в) 1/д/4 — х2\
г) arcsin х; д) - , Зл + 5—; е) cos2 х.
х~ — Зх + 2
4. Разложить в ряд по степеням х *р 2 функцию /(х) =
__ 1
х2 + 4х + 7
5. Записать разложение функции у = 1п (2 -р х) в ряд
по степеням 1 -р х.
27
6. Найти первые три члена разложения в степенной ряд функции, заданной уравнением ху -ф е* = у, если известно, что у = 1 при х = 0. ( Ответ: 1 -ф 2х -ф -|- х2 -ф ...^
Самостоятельная работа
1. 1. Найти первые три члена разложения функции /(х) = д/х в ряд по степеням х—А.
2. Разложить в степенной ряд функцию f(x) = = 1п(1—Зх) и найти область сходимости этого ряда. (Ответ: —1/3 х < 1/3.)
2. 1. Найти разложение в степенной ряд функции f(x) = х sin 2х.
2. Разложить в степенной ряд функцию f(x) = о
=------------ и найти область сходимости этого ряда.
(1+х)(1—2х) '
(Ответ: |х|<1/2.)
3. 1. Разложить по степеням суммы х -ф 1 многочлен f(x) = х4 -ф Зх3 — 6х2 -ф 3.
2. Разложить в степенной ряд функцию f(x) = = 1п (1 —|—2х) и найти область сходимости этого ряда. (Ответ: -±<х^±.)
12.4. СТЕПЕННЫЕ РЯДЫ В ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЯХ
Вычисление значений функции. Пусть дан степенной ряд функции у = [(х). Задача вычисления значения этой функции заключается в отыскании суммы ряда при заданном значении аргумента. Ограничиваясь определенным числом членов ряда, находим значение функции с точностью, которую можно устанавливать путем оценивания остатка числового ряда либо остаточного члена R„(x) формул Тейлора или Маклорена.
Пример 1. Вычислить 1п 2 с точностью 6 = 0,0001
> Известно, что степенной ряд
in(i+x)=x-4+4~-+(-ir'(1)
при х=1 сходится условно (см. § 12.1, пример 8). Для того чтобы вычислить In 2 с помощью ряда (1) с точностью 6 =0,0001, необходимо взять не менее 10 000 его членов. Поэтому воспользуемся рядом, который получается в результате вычитания степенных рядов функций In (1 ф х) и In (1 — х):
1 4- х / х3 х5 х2"”1 \
ln-pt£=2(x+4- + 4-+...+ —--+...) (2)
1 — х \ 3 5 2п — 1 /
28
При |jc| < 1 ряд (2) сходится абсолютно, так как его радиус сходимости R=l, что легко устанавливается с помощью признака Д’Аламбера.
I + х
Поскольку —----— = 2 при х= 1/3, то, подставив это значение х
в ряд, получим
.„2_2(± +
5-35 +'"+ (2м — ОЗ2"-' +
Для вычисления In 2 с заданной точностью необходимо найти такое число п членов частичной суммы S„, при котором сумма остатка | rn I < < б. В нашем случае
/________!______
к (2м 4- I) • 32"+1
(2п + 3) • 32,‘ + J
(3)
Поскольку числа 2п + 3, 2м 4-5, ... больше, чем 2м 4- 1. т°, заменив их на 2м 4- 1, мы увеличим каждую дробь в формуле (3). Поэтому
Гп< 2м+1 (з2,1 + 1 + 32“ + J + "O'-
_________2_______/ 1 1 \
~ (2м + 1)-32"+' \ + 9 + 81 + -J-
= 2____________1 =__________1______
(2м + ()• З2"4 1 1-1/9 ~ 4(2м + 1) • З2"-1 ’
Путем подбора значений м находим, что для м = 3 г„ < 0,00015, при этом 1п 2 = 0,6931. 4
Пример 2. Вычислить д/е”с точностью 6 = 0,001.
► Воспользуемся разложением в степенной ряд функции (см. формулу 12.17), в котором примем х = 1 /2. Тогда получим
1 4" 4" т- 4" • • 4"-----4- •
v 2 2!-22 mI-2"
Остаток этого ряда
Z1 1 V 1 = 1
(м +k)\-2п+к < (и 4- !)!• 2" / . 2" (п 4-1) 1 • 2"
*=1
так как (м 4* 1)! < (м 4- 2)! <... При м = 4
Гл <
<0,001.
Следовательно,
е'/2~1+т + т + 1г + ^г~ 1’674-
Для определения числа членов ряда, обеспечивающих заданную точность вычисления, можно воспользоваться остаточным членом формулы Маклорена
Ох ^=W/+I>
где 0 < 0 < 1; х — 1/2. Тогда при п = 4
29
2(1/2)"+' (« + 1)!
0,001. 4
Пример 3. Вычислить sin — с точностью 6=10 3.
► Подставим в формулу (12.19) значение х = 1/2. Тогда
е [П — — ------- _1_ ------ -- -4- ( П" “ ' ----!______
.2 2 3! • 23 5! |2" " ’ (2п—1)! • 22"~'
Так как остаток знакочередующегося ряда |r„|^un+.| (см. ряд (12.6) и следствие из признака Лейбница), то достаточно найти первый член u« + i, для которого u„ + i < 6. Тогда S„ даст значение функции тре-
буемой точности. Очевидно, что уже третий член ряда
1
5! • 25
10~\
поэтому с точностью 6=10
sinT~T-4i~0’479- ◄
Пример 4. Вычислить VS" с точностью 6=10
► Очевидно, что ^/§7 = д/з2 + 2 = 2(1 + 1 /16)1'. Воспользуемся биномиальным рядом (см. формулу (12.21) при т = 1 /5, х = 1/16:
поскольку уже третий член можно отбросить в силу того, что он меньше 6 = 10" (см. следствие из признака Лейбница). Следовательно, VS= 2(1 + 1/16)1/5« 2,024. 4
Вычисление интегралов. Так как степенные ряды сходятся равномерно на любом отрезке, лежащем внутри их интервалов сходимости, то с помощью разложений функций в степенные ряды можно находить неопределенные интегралы в виде степенных рядов и приближенно вычислять соответствующие определенные интегралы.
Пример 5. Вычислить Jsin(x2)dx с точностью 6= 10'. о
► Воспользуемся формулой (12.19). Заменив в ней х на х2, получим ряд
х6 х10 х4"-2
sin(x2) = x2- — + — _... + (-!)"-' -+...
Он сходится на всей числовой прямой, поэтому его можно всюду почленно интегрировать. Следовательно,
30
Ssin ^dx=S (2; +-)
0 0
/ X3 x7 x" , x4"-' \ I1
~ \ 3 7-3! + II • 5» ~- + (_') (4n-l)(2n-l)l
= J_______। , _J_______, < । ~
3 7-3! "Г 11-5! > (4/i — 1)(2n — I)! -
як у - y-y- = 0,3333 - 0,0381 = 0,295, поскольку уже третий член полученного знакочередующегося пяла меньше 6= К)1. 4
Ssin х
—-—ах в виде степенного ряда и указать область его сходимости.
► Воспользовавшись формулой (12.19), получим ряд для подынтегральной функции
I X2 X1 rZ“~-
_sin х=[ _ _+_ 1Г. ___+...
Он сходится на всей числовой прямой, и, следовательно, его можно почленно интегрировать:
+ ( — В"-------------------к ------
г 1 (2п - 1)(2п - 1)!
Так как при интегрировании степенного ряда его интервал сходимости не изменяется, то полученный ряд сходится также на всей числовой прямой. 4
Приближенное решение дифференциальных уравнений. В случае, когда точно проинтегрировать дифференциальное уравнение с помощью элементарных функций не удается, его решение удобно искать в виде степенного ряда, например ряда Тейлора или Маклорена.
При решении задачи Коши
У'= f(x, У). У(*о) = Уо, (12.22)
используется ряд Тейлора
У«= £ -^-^-(х - х0)п, (12.23)
л=0
где у(х0) == у0, у'(Хо) = /(хц, у0), а остальные производные у(п,(хо) (п = 2, 3, ...) находятся путем последовательного дифференцирования уравнения (12.22) и подстановки начальных данных в выражения для этих производных.
Пример 7. Найти пять первых членов разложения в степенной ряд решения дифференциального уравнения у' = х2 -|- у2, если у(1)= 1
31
► Из данного уравнения находим, что у'(1) =1 + 1=2. Дифференцируем исходное уравнение:
у" = 2х + 2y/, у"(1) = 6;
у"' = 2 + 2у'2 + 2уу”, ут(1) = 22;
ylv=4y’y" +2у'у" + 2уу"’, у'1'(1)= 116
И т. д.
Подставляя найденные значения производных в ряд (12.23), получаем
</(*) = I + 2(Х — 1) + 6(Л ~ Ч2- + -у-(х - I)3 + -^-(х - I)4 +...=
= 1 +2(х- 1) + 3(х- 1)2+ -^-(х- 1)3 + ^-(х- 1)4+... 4 <5 О
Пример 8. Найти шесть первых членов разложения в степенной ряд решения дифференциального уравнения у"—(1 + х2)у = 0, удовлетворяющего начальным условиям у(0) = —2, у'(0) = 2.
> Подставив в уравнение начальные условия, получим
у"(0)= 1 -(-2)= —2.
Дифференцируя исходное уравнение, последовательно находим: у’" = 2ху + (1 + х+/, у"'(0) = 2;
ylv =2у + 2ху' + 2ху' +(l +х2)у", y'v(0) = -6;
У v = 6/ + бху" + (1 + х2)у'", у v (0) = 14.
Подставляя найденные значения производных в ряд Маклорена, получаем
у(х)= — 2 + 2х — X2 + X3 — ~х‘ + -77Г-Х5 + ... 4
3 4 bl)
Решение задачи Коши у = <р(х) для дифференциального уравнения можно также искать в виде разложения в степенной ряд
у — <р(х) = Со + Ц| (х — хо) + о2 (х — Хо)2 +... + а„(х — х0)" +... (12.24)
с неопределенными коэффициентами а,- (/ = 0, 1, ..., я, ...).
Пример 9. Использовав ряд (12.24), записать четыре первых ненулевых члена разложения решения задачи Коши у' = х + у2— 1, 4/(1) = 2.
> В ряде (12.24) х0=1. Поэтому, положив х=1, с учетом начального условия находим, что Оо = 2. Продифференцируем ряд (12.24) и подставим полученную производную у’, а также у в виде ряда (12.24) в данное дифференциальное уравнение. Тогда
у' = 01 +2а2(х —х0) + Зоо(х —х0)2 + ...=
= х— 1 + (ао + 0|(х — хо) +а2(х — хо)2 + ...)2.
Теперь в правой и левой частях последнего равенства приравняем коэффициенты при одинаковых степенях разности х—1 (т. е. при (х — 1)°, (х — I)1 и (х — I)2). Получаем простые уравнения:
а, = а,2, 2а2 = 1 + 2а0О|, Заз = а2 + 2а0а2,
из которых, учитывая, что а0 = 2, находим: а, = 4, а2 = 17/2, аз = 50/3.
32
Следовательно, искомое разложение решения имеет вид
(/ = 2 + 4(х-1)++ - ◄
АЗ-12.5
1. С помощью степенных рядов вычислить приближенно с точностью 6 = 0,001 указанные величины:
а) -д/7; б) х/\0; в) cos 10°; г) ‘^/1027; д) In 3/2.
(Ответ: а) 1,396; б) 2,154; в) 0,985; г) 2,001; д) 0,405.)
2. С помощью степенных рядов вычислить с точностью б ==0,001 следующие определенные интегралы:
a) j -д/1 -}-x3dx; о 4
в) $ el/lcdx; о
б) j cos xfxdx\ о
1/4
г) J е~*гdx. о
(Ответ: а) 0,508; б) 0,764; в) 2,835; г) 0,245.)
3. Найти неопределенный интеграл в виде степенного ряда и указать область сходимости этого ряда:
a)
J х
б) ( — dx.
1 х
4. Записать пять первых членов разложения в степенной ряд решения дифференциального уравнения, удовлетворяющего заданным начальным условиям:
а) уб) 7 = еу + ху, у(0) = 0;
б) у/ = 1+х + х2 —2у2, у(1)= 1;
в) = х2у — у', у(0)= 1, у'(0) = 0;
г) /' = •* +У2, У(0) = 0, у'(О) = 1.
Самостоятельная работа
1. 1. С помощью степенного ряда вычислить sin 1 с точностью 6 = 0,001. (Ответ: 0,841.)
2. Найти три первых члена разложения в степенной ряд решения дифференциального уравнения у’ = х2— у, если у(1) = 1.
2. 1. С помощью степенного ряда вычислить х/тО с точностью 6 — 0,001. (Ответ: 4,125.)
2. Найти четыре первых члена разложения в сте-
2—357
33
пенной ряд решения дифференциального уравнения у" = = х1 — у, если г/(0) = 1, y'(G) = 1.
3. 1. С помощью степенного ряда вычислить
0.5
j sin 2* dx с точностью 6 = 0,001. (Ответ: 0,946.) о
2. Найти три первые члена разложения в степенной ряд решения дифференциального уравнения у' = х2у 4* У3, если у(0) = 1.
12.5. РЯДЫ ФУРЬЕ
Функциональный ряд вида
4- (а„ cos пх 4- b„ sin пх), (12.25)
>1= ।
где коэффициенты а„, Ь„ (п = 0, 1, 2, ...) определяются по формулам:
Л а„ = j f(x) cos nxdx, (12 26) b„ = — \ fix) sin nxdx, л J — Л
называется рядом Фурье функции f(x). Отметим, что всегда t>0 = 0. Функция [(х) называется кусочно-монотонной на отрезке [а; Ь], если этот отрезок можно разбить на конечное число интервалов п (a; Xi), (Xi; х2), ..., (х*_ i; b) таким образом, чтобы в каждом из них функция была монотонна.
Теорема 1. Если функция f(x) периодическая (период ы = 2л), кусочно-монотонная и ограниченная на отрезке [ — л; л], то ее ряд Фурье сходится в любой точке х ( R и его сумма
s (х) = 11х о) + Кх о)
Из теоремы следует, что S(%) = /(%) в точках непрерывности функции Цх) и сумма S(%) равна среднему арифметическому пределов слева и справа функции ((х) в точках разрыва первого рода.
Пример 1. Разложить в ряд Фурье периодическую функцию (с периодом 2л):
с, (0, — л < х < 0,
^ = (х, 0<х<л.
> Так как данная функция кусочно-монотонная и ограниченная, то она разлагается в ряд Фурье. Находим коэффициенты ряда:
34
л л
1 Г ч , If, 1 X2 |Л Л ао = — \ f(x)dx = — \ xdx =-— — —
nJ nJ л2|п2
— л О
л
1 f
at! — — \ x cos nxdx =
Л J
0
и = х, dv — cos nxdx, 1 .
du = dx, v = — sin nx n
— sin nx I — \ — sin nxdx n | о J fi
0
11 r 1
=------rcosn% = ---— ((—1)"— 1),
л n Io nn
bn — — \ x sin nxdx — — (-— cos nx I + —sin nx\
nJ л \ fl Io rr Io
0
л (— 1 Yl “1
=--------cos nn = -------- (n 6 N).
л n n 1
Подставляя найденные коэффициенты в ряд (12.25), получаем
/W = т + У (------------/о 2 cos ^2п ~ ~----------sin пх
4 Л? \ л(2л — 1) п
Этот ряд сходится к заданной периодической функции с периодом 2л при всех х #= (2/г— 1)л. В точках х = (2п— 1)л сумма ряда равна
ее ряд Фурье записы-
Если функция У = 1(х) имеет период 2/, то вается в виде
f W = cos %) + b„ sin ,
п= I
(12.27)
где
(12.28)
Ьп = — J f(%) sin — xjdx. — l
35
Теорема 2. Если периодическая функция с периодом 21 кусочномонотонная и ограниченная на отрезке [ —/; /], то ее ряд Фурье (12.28) сходится для любого х £ R к сумме
S(x) = (/(x-0) + /(x+0))/2
(ср. с теоремой 1).
Пример 2. Найти разложение в ряд Фурье периодической функции с периодом 4;
. . _ J — 1 при — 2<х<0,
( 2 при О С х С 2
> Находим коэффициенты ряда:
2 0 2
а°= у j f(x)dx= у( j (— V)dx-\- 2dx^ -
— 2 — 2 О
= 4-(-*Г +2х|2')=1(-2 + 4)=1,
\ 1-2 0 "=т( 5 (-')cos{^-— 2 1 / 2 / л/г = —( sin { —-X 2 \ л/г \ 2 0 — 2 1/2 / пп = ( COS ( 2 \ л/г \ 2 3 , = (cos лп л/г 1 0 / 2 - dx ^2 cos ~ 0 )|° +—sin(^x)|2') = 0) /1—2 л/г \2 /1о/ 2 dx + ^2 sin dx^ ~ 0 \ Iе 4 \ -х| (cos л/г—1)1 = /1 _2 л/г ) _1)=_((_1Г_ 0.
36
Подставив найденные коэффициенты в ряд (12.28), получим
fW=‘ IV ^-1—
2 л / , 2п — 1 \ 2
Если периодическая функция f(x) четная, то она разлагается в ряд Фурье только по косинусам, при этом
I 2 f с / яп \ а„ = —\ f(x) cos ( — х \ dx;
о если же периодическая функция f(x) нечетная, то она разлагается в ряд Фурье только по синусам и
1
, 2 Г .... / яп \
bn = — \ f(x) sin ( —j— х jdx.
о
Так как для всякой периодической функции f(x) периода 2/ и любого XЕ R справедливо равенство
I х-н
f(x)dx = f(x)dx, — I к-1
то коэффициенты ряда Фурье можно вычислять по формулам:
а
2 /
где п = 0, 1,2, ...
Пусть функция fix) кусочно-монотонна и ограничена на отрезке [а; б] <=( — /; /). Чтобы разложить эту функцию в ряд Фурье, продолжим ее произвольным образом на интервал ( — /; /) так, чтобы она оставалась кусочно-монотонной и ограниченной в ( —/; /). Найденную функцию разложим в ряд Фурье, который сходится к заданной функции на отрезке [а; б]. Если заданную функцию продолжить на (— /; /) четным образом, то получим ее разложение только по косинусам, если же продолжить ее нечетным образом, получим разложение только по синусам.
Например, функция f(x), определенная на [а; б] <= (— /; /) и продолженная в (— /; /) в соответствии с равенствами
{О при
-ZW при О при ZW при О при
— / < х < —Ь, — b х sC —а, — а < х < а,
a sC х Ь, b < х <1,
37
разлагается только по синуса-м. Сумма 3(л) ряда Фурье такой функции равна fix') внутри отрезка |а; Z>], a S(a) = f(a)/2, S{b)=j(b')/2 согласно теореме 2 (рис. 12.3).
< г С 2).
► Так как данная функция четная, то она разлагается в ряд Фурье только по косинусам, т. е. Ь„ = 0. Далее находим:
I 2
Отсюда следует, что а„ = 0 при п четном, а„ — —8/(л2п2)при п нечетном. Искомый ряд Фурье данной функции
1
(2п- I)2
/ (2м — |)л
\ 2
Его сумма равна заданной функции на отрезке ( — 2; 2], а на всей числовой прямой эта сумма определяет периодическую функцию с периодом о> = 4 (рис. 12.4).
38
Пример 4. Разложить в ряд по на отрезке [0; 2|.
> Продолжим данную функцию образом (рис. 12.5), т. е. положим
синусам функцию /’(х) = 2 — х иа отрезок | — 2; ()| нечетным
— 2 — л- при
2 — % при
Тогда а„ = 0 при //=(), 1, 2..... а
Подставляя найденные коэффициенты в ряд Фурье, получаем
Пример 5. Разложить в ряд Фурье функцию, график которой изображен на рис. 12.6 в виде сплошной линии.
> Продолжим данную функцию на отрезок [ — 2; 0] четным образом и разложим функцию ((%) = .к, л‘ € [0; 2|, ио косинусам, т. е.
f W = -у- + cos х'}, // = 1
39
2
iZo =
xdx =
Искомый ряд Фурье имеет вид
м=
4 V cos^-'^ x
л2 / , (2п — 1г \ 2
«= 1
На отрезке |0; 2] он представляет собой заданную функцию, а на всей числовой оси — периодическую функцию с периодом ю = 4 (см. рис. 12.6, штриховая и сплошная линии). -4
Поскольку ряд Фурье сходится к значению соответствующей функции в точках, где функция непрерывна, то ряды Фурье часто используются для суммирования числовых рядов. Так, например, если в ряде Фурье функции, определенной в примере 5, положить х = 2, то получим:
(2,/- I)2
2 =
cos л,
(2и - I)2
л"
8
Пример 6. Разложить в ряд Фурье по косинусам кратных дуг функцию у = х2 на отрезке |0; л] и с помощью полученного ряда вычислить суммы числовых рядов
40
и
> Разложим данную функцию в ряд по косинусам, продолжив ее на интервал (— л; 0) четным образом и на всю числовую прямую периодически, с периодом 2л. Тогда:
Получили ряд Фурье
ОО
и*)= ~+4 £ (-'у п = 1
cos пх
п2
Так как продолженная функция непрерывна, то ее ряд Фурье сходится к заданной функции при любом значении х. Поэтому для х = 0 имеем
0=2г + 4У (-’’"-г-
3 / , п
п= I
т. е.
и — I
При х = л
п = 1 п = I
41
АЗ-12.6
1. Разложить в ряд Фурье функцию р/ х при —п < х О, 1\х) |2х при 0 < х < л,
имеющую период 2л.
/гл л 2 V-1 cos (2п — 1) х „ V , „I sin пх \
(Ответ:—------) -----i---у---р 3 > ( —I""1----.)
\ 4 л (2л — I)- Zu п /
II = I в = I
2. Разложить в ряд Фурье функцию
f, ч_(л -|- 2х при —л < х О,
1\х) (—л ПрИ 0<х^л.
(Ответ: — 4т + 2 У (--------cos (2м— 1)х---- sin пх).
\ 2 / , \ л(2н — 1)" л
3. Разложить в ряд Фурье (с периодом со = 4), если
периодическую функцию
— 2 < х 'С О,
0<х^2.
п л(2п — I)
COS —i--------
2
( Ответ:
4. Найти разложение в ряд Фурье функции у — х2 на отрезке [ — л; л]. Построить графики функции и суммы ряда. (Ответ: + 4^ (- If-СО|Л*.
п — 1
Самостоятельная работа
1. Найти разложение в ряд Фурье функции [(х) = —х. на отрезке [ — 2; 2]. Построить графики данной функции и суммы ряда. (Ответ: 2^ sin пх(^
42
2. Найти разложение в ряд Фурье функции
— 2 при
1 при
О, л.
О
Построить графики данной
функции и суммы ряда.
----------- sin (2п — 1)х.
'2п — г '
3. Разложить в ряд Фурье функцию
— х при
О при
О, л.
О
Построить графики данной
функции и суммы ряда.
—- cos пх --------— sin пх
Л/Г п ,
АЗ-12.7
и суммы
1. Разложить в ряд Фурье по синусам функцию [(х) = х2 в интервале (0; л). Построить графики данной функции
2 / / i у;
п
2. Разложить в ряд Фурье по косинусам кратных дуг (2
Ответ: — +
cos 2нх
1 - (2п);
3. Разложить в ряд Фурье по синусам кратных дуг функцию f(x)=l—х/2 на отрезке [0; 2]. (Ответ:
• ппх sin^—.
43
4. Разложить в ряд Фурье по косинусам кратных дуг функцию f(x)=l—2x на отрезке [0; 1]. (Ответ:
8 у* cos л (2п — 1) х \
л2 / , (2п — I)2 /
I
5. Пользуясь разложением в ряд Фурье по синусам кратных дуг функции f(x) = 1 на отрезке [0; л], найти сумму ряда 1-± + |-4-+... + (-1Г>-^-^+... (От-вет: л/4.)
Самостоятельная работа
1. Разложить в ряд Фурье по косинусам кратных дуг функцию f(x) = l—x на отрезке [0; 2]. (Ответ:
л2 / , (2л — I)2 2 /
п= I
2. Разложить в ряд Фурье по синусам кратных дуг функцию f(x) = n — х на отрезке [0; л]. (Ответ:
оо n sin пх \
,i=i
3. Разложить в ряд Фурье по косинусам кратных дуг функцию f(x) = ~ — у на отрезке [0; л]. (Ответ: 2 у cos ((2л — 1)х) \
л L (2П — 1)2 /
I
12.6. ИНДИВИДУАЛЬНЫЕ ДОМАШНИЕ ЗАДАНИЯ К ГЛ. 12
ИДЗ-12.1
1. Доказать сходимость ряда и найти его сумму, оо
11- У - (Ответ: 3 = 4-Л
Д л(л + 2) \ Ь )
Я — 1
44
оо
..2. Z^.(Oreer..S_|.) п = 1 оо
1.3. У -------!----. ( Ответ: S = — Л
L, (2« + 5) (2л + 7) \ 10 )
п = 0 ОО
•4- s=4-)
Л= I оо
15. У —г- . (Ответ: S = -|-Л
L-, (л + 5) (л + 6) \ 5 )
п = 0 оо
л = I оо
1,7‘ Е (2« + 7) (2л + 9) • (Ответ: S== й ) л^0 оо
1.8. У 4 ~3 . (Ответ: S = — Л
L. 12" \ 6 )
п= I оо
L9- S = 7-)
п= I
л= I
111. У -—-г- . (Ответ: S = — Л Z_/ (я + 9) (/г 10) \ 10 /
п = | оо
'’2- (о—S=l)
л= I оо
'•|з- г w7,;+8)-(°—s=io л=1
45
Л = 1 оо 1-15. У 1 . (Ответ: S=~.\
L, (n + 2)(n + 3) \ 2 /
Л=0
1J6- Ё V40re"'S=T) Л= 1 oo
1-17. У 1 . (Ответ: S=-l\
Li (п + 3) (я 4- 4) \ 3 /
п =0
1.18. Г ^L. (ответ: S =
Li 20 \ 12 /
/2=1
ОО
1-19. У 1———. (Ответ: S=— Л
L-, (п + 4) (я 4- 5) V 5 /
п= I
1.20. У ~ 4" . (Ответ: S = Л
L, 20" \ 12 7
/2 = 1 оо
1.21. У -----!-----. (Ответ' S — —
Л (2п+1)(2и + 3) \у1ве1' ° 2 у
п=0
ОО
1.22. £ Z+,3". (Ответ: <$= у.) Я=1 оо
'23- 1-гд+3)и+^ (Огеет-- s"t)
1-25. У -7Z----гг7о~ГоГ- (Ответ: S = — Л
(Зп —1)(3« + 2) V 6 )
«= 1
46
1.26. У Д+Д. (Ответ: S=*-.\ L, 24" \ 14 /
/1 = 1
1.27. У -------Д--------. (Ответ: S = Д Л
Д (Зя 4-1) (Зя 4-4) V 12 ;
/1-1
1.28. У (Ответ:
Л 24" \ 14 /
/1-1
1.29. У ----------!----. (Ответ: S= 1 Л
Д (Зя 4-2) (Зя 4-5) \ 15 )
п= ।
'•30- ) п= 1
Исследовать на сходимость указанные ряды с положительными членами.
2
2.1. _ДДДД. (Ответ: расходится.) л = 1
2.2. —L—. (Ответ: сходится.)
л = 1
2.3. (у) (-0 • (Ответ: сходится.)
« = 1
2.4. (2n + l)tg-^-. (Ответ: сходится.)
п= 1
Ей”/2
(Ответ: расходится.)
I
2-6- У 5~ 75;q6 (2я1331 • (°твет: СХОДИТСЯ.) / j О • / • У \j~fl —|— О)
п= 1
47
о*
2.7. ("Rf) п?* (®TeeT: СХ°ДИТСЯ-)
п = I
оо
7 (Ответ: расходится.)
п = 1
оо
Зп(п + 1). (Ответ: сходится.)
П=1
оо
2.Ю. + 2)! . (Ответ: сходится.)
п== 1
оо
2.11. «sin-^-. (.Ответ: сходится.)
n = t
оо
2.12. I2-+J)— (Ответ: сходится.)
z;----- I
2.13. V --. (Ответ: сходится.)
L 5"(п + 3)!
2.14. з~у~ 1 * (4"—Тр (Ответ: расходится.)
2.15. У ———. (Ответ: расходится.) L, (« + 3)!
п = I
2.16. n3tg-^-- (Ответ: сходится.)
1 оо
2.17. У (п +3) . (Ответ: сходится.) L, (« + 0!
п = 1
2.18. У -—г-. (Ответ: сходится.)
/ . (2п + 3)!
п= 1
48
2.19. (Ответ: расходится.)
л- 1 о®
2.20. У ~ . (Ответ: сходится.)
/ j о • / • 1 1 (1 J
п = 1 оо
2.21. (Зп — 1) sin (Ответ: сходится.) л- 1 оо
2.22. П^2 (Ответ: сходится.)
п— 1 оо
2.23. У 3” ~ 1 . (Ответ: сходится.) 2-', -\1п 7" п — 1 ’
оо
2.24. У ‘ 'л'! • (Ответ: расходится.)
/ J 1 • т • / (ом “ &л
л-1 оо Z5n
—. (Ответ: сходится.) п—1
2.f6 . У 1 '3'|2 ЧГ (°твет: сходится.) £ * / • J Z {Oil О)
П= 1
2.27. У п- - . (Ответ: расходится.)
Z—i 4~') •
п= 1
2.28. ' (Ответ: сходится.)
п = t
2.29.
2.30. £
п~ 1
2”
----—. (Ответ: сходится.)
2п + 1 . (Ответ: сходится.) д/пТ2л
49
3
Z1 о"
--------j—(Ответ: расходится.) «=' С21?-)
3.2. ”5~ 1 ) . (Ответ: сходится.)
л== 1
3.3.
1 \"
2n + 1 / '
(Ответ: сходится.)
3.4.
. (Ответ: сходится.)
3.5.
1 V”
arcsin —J . (Ответ: сходится.)
3.6.
п2 4- Ъп 4- 8 X” , .
—~. (Ответ: сходится.)
3.7.
I (arc,g^)' (Ответ: сходится.)
3.8.
(»/(и + 1))"'
2“
(Ответ:
сходится.)
3.9.
(Ответ:
сходится.)
3.10.
Зл
(Ответ:
сходится.)
3.11. У* ------!----. (Ответ: сходится.)
L (1п(п + 3))я v ’
п= I оо
3.12. (б”2^з” • (Ответ: сходится.)
п= I
50
з-13-1 m
. (Ответ: сходится.)
и = 1
3.14. . (Ответ: сходится.)
п = 1
3.15. + 1 ) • (Ответ: сходится.)
п= I
3.16.
4П
'((д • (Ответ: расходится.)
3J7- Г (|п(» + ))’" • {0ТвеТ: СХОДИТСЯ)
п — 1
з-18- у m
. (Ответ: сходится.)
п= 1
3-19. (arcsin-^-) . (Ответ: сходится.)
3.20. ( ”2» * ) • {Ответ: сходится.)
3-21- Ё (уУ+ з"„ + «У' <0™ет; я"т'’> п= I
3
П
Зп + 1
(Ответ: сходится.)
3.23. У' ^arcsin^-^ . (Ответ: сходится.)
оо
3-24- Ё Ш
н = 1
(Ответ: сходится.)
Ы
3.25. • (Ответ: сходится.)
\”
2~^-Т/ ’ ^твет: СХОДИТСЯ.)
3.27. (s*n'5n^pr) ’ (Ответ: сходится.)
п= I
“ 2п
3.28. У farctg- j-) • (Ответ: сходится.)
Z1 л« -------------. (Ответ: сходится.) (In (и + 5))2
(a res in 2"^35) • (Ответ: сходится.)
4
°° 9
I (^У) •
п= 1
оо
4.3. V----------L-------.
/ - (2п + l)ln3(2n+ 1)
п — I
оо
45 V 1_______
/ , (Зп + 4) In2 (Зп + 4)
п = 1
оо 2
4.7. У (-Z+2LA .
Л к 49 +и2/
п= 1
4.2.
4.4.
4.6.
4.8.
^~1 (Зп + 2) In (31! + 2)
V(4«+5)3
V(7,!-5)5
(311 — 1) In (311 - 1) '
4.11. V -® +
L—J 36 +
11= I
4.10.
1
(51! — 2) In (511 - 2) '
4.12.
52
о© оо
4.13. \/(Зп — 1 у* (п + 2),п + 2) п= 1 v' ' г- 1 ОО ОО
4.15. У ! . 4.16. У - — Zj (10«4- 5) In (10«4- 5) д^2«4-3)7
4.17. ОО у 5 +,г / , 25 4- н2 n= 1
4.18. oo («4-3) In («4-3) in (In («4-3)) n = l oo oo
4.19. У L . 4.20. У ’ . Z- (3 4- 2n) In 43 4- 2«) V(4 4-9n)5 oo oo
4.21. у ! 4 22 V —3+ ,z Z_ (9rt - 4) In2 (9« — 4) ' . 9 4- n' - 2n ' n=1 n=I oo oo
4.23. У L . 4.24. У —.1—... Zj (5n 4- 8) In (5n 4- 8) V(7,! — 5)3
4.25. OO (« 4- 4) In (n 4- 4) In (In (n 4- 4)) H = 1 oo OO
4.26. у . 4.27. У 1 (3 4- 8«) In’ (3 4- 8n) y/(4n зу n — 1 /1=1*' ' oo OO
4.28. у Ц . 4.29. У ——. Z_ (10« 4-3) In2 (IO«4-3) / . 4 4-n2 — n n 1 n = 1 oo
4.30. L-t («4-5) In («4-5) In (In («4-5)) n = 1
5
5.1. У — 1 (Ответ: сходится.)
y/n'+i
53
5.2. V —!=. (Ответ: сходится.)
У д/'г 5
5.3. 'Уру- (Ответ: расходится.) Л-— 1
5.4. У — 1 (Ответ: расходится.) п — 1 *
5.5. У — 1----. (Ответ: расходится.)
~\'П24-л
п — i '
5.6. У -—!——. (Ответ: расходится.) / j In (/I У
II ]
5.7. У —У. (Ответ: расходится.)
У п = 1 *
се
5.8. —-. (Ответ: расходится.)
и = ।
5.9. tg~y. (Ответ: сходится.)
п= I
5.10. —У~У- (Ответ: расходится.)
--1-. (Ответ: расходится.)
5.12. У ------!---. (Ответ: расходится.)
1п (п + 3)
5.13. У (Ответ: расходится.)
/ 1 Зп 5
54
5.14. ;. (Ответ: сходится.)
5.15. sin —У . (Ответ: сходится.) n - 1
5.16. . (Ответ: расходится.)
n = I
5.17. sin-|y. (Ответ: сходится.) n I
5.18. V -——1—(Ответ: сходится.) Z_, (n + 1) (n + 3) v 7
Il z_ I
5.19. У —Ут- (Ответ: сходится.) / j fl ‘ o’
I! -= I
5.2Q. £ — —J з,?' (Ответ: сходится.) tl - 1
Zn । 2
—(Ответ: расходится.) . n \/n
n = ’
5.22. sin --у | . (Ответ: расходится.) n= I
5.23. ) —. (Ответ: расходится.)
L-i + 2
n щ I
5.24. sin^-. (Ответ: расходится.)
I
5.25. —У~-j-. (Ответ: сходится.)
H = t
55
©о
5.26. V .
/ 1 2п -|- 5 л = I
(Ответ: сходится.)
5.27. У —!—. (Ответ: сходится.) ZL zr 4-4
п= 1
5.28. У -п. . (Ответ: расходится.) п2 4- 4
п = I
оо
5.29. У ------!--. (Ответ: сходится.)
Л 5п2 4- 3
п = I
5.30. У --------------• (Ответ: сходится.)
L («4-1) («4-6)
п= 1
6
ОС
ел. 1 п 6.2. £ /1= 1 1
(« 4-1)3 ' -у/п (п — 1)
оо е.з. i п= 1 2п — 1 оо ел. £ Л= 1 п(п 4-1)
2п2 4- 1 3"
оо оо
6.5. i 1 2" 6.6. £ п = 2 1
1 4- 22" ' п In7 п
оо 6.7. £ n-J п3 6.6. £ Л = 1 2
(«4- И' ’ п2 4- 3
оо оо
в.9. i п\ 6Л0. £ 1
72 (5п - 1)(6« 4- 3)
п= 1 п — 1
Z1 / « \п
«4-3/
56
6.13. оо оо У 6.14. У ЛДД. L З’+л L, п2 /1 = 1 /2 = 1 оо оо
6.15. У 6.16. у L з* Л * /1 = 1 /1=1 оо оо
6.17. У . 6.18. У /1 = 1* п = 1 оо оо
6.19. У п +- . 6.20. У 5 . ,3 = ! 2"+5 „=) -^0 + 3) оо »о
6.21. У —. 6.22. У (rt + 1)! . L, zr’+l L, (2п)! /1=1 п = 1 оо оо
6.23. У ! . 6.24. У -LM + '.V . ZL (Зп — 2) (7п - 1) / 2" к п / /2=1 /1=1 ©О «О
6.25. У —!—. 6.26. У п(~'г + °., оо оо
6.27. У /~7 . 6.28. У ! . Зп + 5п — 2 (4п-1)(4п + 5) /1 = 1 /1=1 оо оо
6.29. I ш -« 1 /1 = 1 п = 1
Исследовать на сходимость и абсолютную сходимость знакочередующиеся ряды.
7
———. (Ответ: абсолютно сходится.)
7.1. У (- 1 у +1 _ п п = I
Z(____ | у1
— . (Ответ: условно сходится.) я=0
57
Z(_______ | у! 4-1
k . (Ответ: условно сходится.)
и = 2
7.4. (—1Г +1 5 • (Ответ: расходится.)
п = I
7.5. У (—1)"——. (Ответ: абсолютно сходится.) , \1п г’
7.6. V (—1)"+'—1—. (Ответ: условно сходится.) 1>. = 1 v
7.7. (—!)"“' -С. (Ответ: абсолютно сходится.)
7.8. У (—1)',+ '-;х—Ут—• (Ответ: абсолютно схо-(2« + I) п '
11 1
дится.) оо
7.9. У (—1)"+1----!--. (Ответ: условно сходится.)
оо
Zf_____1 у ~1
-—~=^-. (Ответ: абсолютно сходится.)
, п \/п п = ’
7.11.
(Ответ: условно сходится.)
/ t \« +1 ।
L 1 ’ "("+0
п — I
(Ответ: абсолютно сходится.)
7.13. (— 1)"+1 ЗдУ t • (Ответ: расходится.)
«I
~—у. (Ответ: условно сходится.) 0=1
58
Z(_________J \'l
—--------(Ответ: абсолютно сходится.)
и = i
Z(_____। yi -'
-—. (Ответ: условно сходится.)
Il I
7.17. V (—1)" +1 2,iу 1 . (Ответ: расходится.)
7.18. 1 . (Ответ: абсолютно сходится.)
п= I
7.19. V j ~ !' . (Ответ: абсолютно сходится.)
• П ~Jfl /1=1 v
7.20. V (Ответ: абсолютно сходится.)
/ - п 5“
>1 = 1
оо
'V—< /__ J Y' “ ’
7.21. ) Д—. (Ответ: абсолютно сходится.)
7.22. у (—1)"__А__. (Ответ: условно сходится.) >1 = 1
7.23. (— 1)" + 1 (Стает: условно сходится.)
и=। оо
Е/_____ | у«+ J
У t • (Ответ: условно сходится.) оо
Е(_____ I у+ 1.
—-1------. (Ответ: абсолютно сходится.)
(2п I)"
п = I
7.26. У — Л (Ответ: условно сходится.) ~ уп 4- 5 п = 1 ’
7.27.
3'
(Ответ: абсолютно сходится.)
59
Z, 1 \
(—l^+'Z 2-—• (Ответ: абсолютно exo-
n = I
ДИТСЯ.)
oo
7.29. V . (Ответ- абсолютно сходится.)
/. (3n —2)! v
п — I
оо
7.30. £ (-1)лп ln(l +
п — 1
(Ответ: условно схо-
дится.)
8.1.
(-1Г+1
(2n — I)3 ’
8.3. £
п = I
оо
8.5. £
п = I
у1 (_____1 у» + 1 ~ 1
/2 = I
8.2. у (-'Г' .
Л (2п+1)! л = 1 оо
8.4. у (-‘Г!....
In(rt-hl)
п = 1
оо
8.б. £ (-‘г;1-2".
I
оо
8.8. £(-1)п^-±Х.
/2 = 1
8.9. у <i.
Z-/ п + 1 п — 1
1
I
8-12-п= I
оо 00
л=2 п=1
оо р
8.15. £ (-'Г^. 8.U. £(-|).+1—L^.
И=I п=I
8
60
oo
8-'7-
И= 1
oo
8.19. V -HL.
L (5n+ I)" n = I
8.21. А1’- А
8.23. £(-!)+' sin л_. п = 1 оо
8.25.
L («+ 1)(«+4) * п=1 оо
8.27. У / 1 yi — 1 2ri 4~ 1 L } «(^ + 2) 1 оо
8.29.
лУ V(«+о3
8.18. V (-l)n+l- 2"+ \ .
L, y 7 n(n + 1) n= I oo
8.20. £(-l),!Ll л = I
oo
8.22. У (-!)"+'—A_.
L, «4-1
n= 1
8'24- I (“'>*2^2 n= I
8.28. £ L.
n = 4
oo
8-3°- I ('Ат)"
n = 1
Решение типового варианта
1. Доказать сходимость ряда
2« + 1 «2(« + I)2
и найти
его сумму.
Общий член ап = — —-----
П (п + 1)
данного ряда предста-
вим в виде суммы простейших дробей:
а = 2п + 1 = А + А + с + D «2(« + 1)2 п. п2 ' /г + 1(п-р I)2 ’
2/? + 1 =Л/?(« + l)2 + S(/? + l)2 + C/?2(/? + l) + £>/?2,
п = 0
п = — 1
/г3
п
В = 1, D = -1, 0 = А + С, ч = аа-^в,
=> Л — 0, С = 0,
►
61
поэтому
Найдем сумму первых п членов ряда:
+ 1 . -4 + 4------------U = 1-------
(« — I)" /г п~ (п + 1У (н + 1р
Далее вычислим сумму ряда:
т. е. ряд сходится и его сумма 5=1. -4
Исследовать на сходимость указанные ряды с положительными членами.
Воспользуемся признаком Д’Аламбера. Имеем:
«! п _ («4-1)! iim «„+1 _ 1;т (п + 1)!п" _ —, иЯ4.| — ----------------——, liiTl -------- — ПЕП ------------—— —
n" (/I -р l)'l+ ссю a,t /!-*сю (п -р 1)"+ 'п!
= lim
(п + 1)п"
(« + !)>+ I)
= 1 im----!—- — — < 1,
И —*- оо (1 4 । / Я )П £
т. е. данный ряд сходится. -4
з. V ++4.
/ . п " • 3я
Согласно радикальному признаку Коши, имеем:
т. е. исходный ряд сходится. -4
62
оо
Воспользуемся интегральным признаком Коши. Для этого исследуем несобственный интеграл:
= Игл [ х • 2 г clx = I im f [2 г d( — х2
р-*-оо\ 2 In 2 7 I I р- *- оо \ 2 in 2 • 24 In 2 / 41п2
Поскольку данный интеграл сходится, то сходится и исследуемый ряд.
4д/п
> Исследуем данный ряд с помощью предельного признака сравнения, который состоит в следующем. Если lim — = k, k g R, k =/= 0, то ряды с такими общими чле-Л-+ оо bn
нами ведут себя одинаково в смысле сходимости: или оба сходятся, или оба расходятся. Имеем ап — tg2 л-- . В ка-4\/п
честве ряда, с которым будем сравнивать исходный ряд, возьмем гармонический расходящийся ряд с общим членом Ьп = 1/п. Тогда
lim — = lim
П-+ОО Ьп ОО / Л” \ 16
116^7 V
(Здесь мы использовали первый замечательный предел.) Итак, исследуемый ряд расходится. 4
► Для этого ряда необходимый признак сходимости рядов (lim ап — 0) не выполняется. Действительно,
63
lim an = lim fl — sin —'j = 1 =И= 0, n—► oo n-*-oo \ ft /
т. e. исходный ряд расходится.
Исследовать на сходимость и абсолютную сходимость знакочередующиеся ряды.
оо
7 V (-1Г1
Л п Г
п — 1
> Воспользуемся признаком Лейбница. Имеем:
т. е. данный ряд сходится.
Исследуем ряд, составленный из абсолютных величин членов исходного ряда:
Применим признак Д’Аламбера:
• +1 • п-7’ 1 1; п 1 . 1
lim —= lim -----------— = — lim ---= — < 1,
«-►□о an n-^oc 7 n-*- oo ti 1 7
т. e. ряд (1) сходится. Следовательно, исходный ряд абсолютно сходится. оо оо оо
* £(_|).2±^=2£^ + £1, п = 1 п = 1 п ~ I
оо | у1
выполняется признак Лейб-
оо
ница. Ряд -Г — гармонический (расходящийся). То-
п = I
Z/____ | у»
v 1 сходится условно. Сумма сходящегося
п = I
и расходящегося рядов представляет собой расходящийся ряд. Значит, исследуемый ряд расходится.
64
ИДЗ-12.2
Найти область сходимости ряда.
1
1.1.
2V пг + 1
1.2.
пх
2"~' 3"
. (Ответ: (— 6; 6).)
ОО
1.3. £ (Ответ: (-2; 2).) п= I
1-4. V —(Ответ: [ — 2; 2).) / j п • 2/(
п = I
оо
1.5. (Ответ: [—1; 1).)
п = I
оо
Ь6- У 2ТГТТ- (°твет: I-1; !)•)
п — I
п = 1 оо
1.8.
У (In х)п. f Ответ:
оо
I <0™-- ">
п= 1
оо Zr3n
WTT) 1-* 21->
п= I .
1.11. 2 (п(п-(-1)хп. (Ответ: (—1; 1).) « = 1
3—357
65
оо
l.!2.
п= I
(Ответ: ( — 2; 2).)
(Ответ:
10’
1.14. V ——. (Ответ: (~е, е).\ / , пп
п= 1
оо
1Л5- У (°твет: Г-5;5)-) / я О It
1.16. (Ответ: [—1; 1].)
п= 1 оо
1.17. £ №-^. (Ответ: ( —У?0; УТо).)
1.18. £ (1g х)". (Ответ: К)}.}
п= 1
(Ответ: ( — 5; 5).)
'•20-1
п= I
5"хп
(2п + I)2 Ут”
(Ответ: [—1; 1].)
..22.£" (Огвет..[-±;±).) п— I ’
оо
1.23. У -~х)3—• (Ответ: [-1; 1].) / 1 п
/1 = 1
66
ОО
1.24.
Ответ:
1.25. V ----. (Ответ: [-2; 2).)
- 1
п — I *
1.26.
Z2"xfl
v'2n — 1 п = I ’
( Ответ:
т: I)-)
1.27.
(n -f- 1 )~х' 2"
(Ответ: (— 2; 2).)
1-М))
п = 1 V
оо
1.29. £ x"tgy. (Ответ: [—1; 1).)
п = I
L3°- I Gm"/ v- {Ответ: (-5е; 54)
оо
2 7 V (- 1Г+1 —...........-2"~‘_____
к 1)(2п - 1)!
н= I
оо оо
67
оо во
2-I0. 1 tgJL. 2.11. У 2Z. / . nl
п = 1 п= 1
оо оо
2.12. V Z-. 2.13 У 1
2_и хп / , 3 г~- •
упх
п = t *
оо оо
2.14. У - 2 15 У
L, п(х — 2)" Ди Х" П 1П П
п = 1 п~2
оо во
2.16. У ^+..'.Г. 2.17. У -
Z1, 2Л п — 1 Злл/2п + 1
оо ОО
2.18. У —1—. 2.19. У —.
Zu (пх)п Zu Bi'
п— 1 п~ 1
оо оо
2 20 У Sln (2” ~ 0 х 2.21. У 2" sin —.
Zu (2и — 1)- Ди Зл
п = 1 п = 0
оо оо
2.22. У ~. 2.23. У -1 .
/ . х" / . п!х"
п = 1 п= 1
оо оо
2.24. У п\хп. 2.25. У —.
Zu L п."
п = 1 п = 1
оо оо
2.26. У -Sln пх . 2.27. У e~n\
La п2 Zu
п — 1 п=^ 1
оо оо
2.28. V —. / . епх 2.29. У —. Zu V
п= 1 п = 1
2.30.
3
л=|
(х — 4)2п~' 2п — 1
(Ответ: 3 х < 5.)
68
оо
———— . (Ответ: 1<х<3.) пп In (1 + 1/п) ' '
(х — 2)" 2П
(Ответ: 0 < х< 4.)
(х-1)' п2
(х + 8)'
п2 ~~
(Ответ: — 9 х — 7.)
3.6. £ (2 + х)п.
(Ответ: —3<х-<—1.)
3.7.
----(Ответ: —1 (« + 3)
3.8. V -Iх + --. (Ответ: -6<х<-4.)
Vя + >.V«2+1
3.9. £ 2"2(х + 2)п\ п = 0
(Ответ: — 2,5 < х < — 1,5.)
3.10. V —. (Ответ: —1^х<3.)
Л 2"ln(n+l) v ’
п= 1
3.11. £ 10L. (Ответ: — е — 10 < х < е — 10.)
П = 1
3.12. £ (х + 51)"1 . (Ответ: —6<х<—4.) п=0
ОО j----------
З.!3. 4 (х+ !)"• (Ответ: 0<х<2.)
п = 0
69
3.14. £ (2-х)" sin п = 0
(Ответ: 0<х<4.)
3,15. у .(3~2Л)1. (Ответ: 1<х<2.) / . п — In п
оо
ЗЛ6- I (3(П+^'~- (Ответ: 1<х<5> Z—i v* “г U *
п = 0
3.17. у (Ответ: 1<х<3.)
п = 1 оо
ЗЛ8' I ^-~1)Г2- {°ПеТ: °<*<4-> п= 1
оо з t
3.19. V (_1)«^±1(х-2)".
•*’ "Г *
п=0
(Ответ: 1<х^3.)
3.20. £ (* + 5Л...1. (Ответ: -7<х<-3.) п = 1 оо
3.21. У (2п~ |)',<х+ О” . (Ответ: — 2<х<0.) Zu z'-'n" п= 1
3.22. У (х + 3)" . (Ответ: -4<х<-2.)
Lt п2 п= 1 оо
3.23. У (*±2И. (Ответ: — 3<х<— 1.) Li п= I
3.24. у (— I)"-1 -• (Ответ: 1^х^3.)
п — 1
оо
3.25. у • (Ответ: 2<х<4.) /1=1
70
3-2в- £ (-'Г1 ,„+VnZ+l)- {ОтееТ:
Л = 1 оо
3.27. £ (Ответ: -2<х<8.)
оо
3.28. V (Ответ: -±<
(Зя —2)2" V 4
ОО
3.29. V -----. (Ответ: 2<х<4.)
l_j (п 4- 0 In (rt 4- О
n= 1
3.30. У (-1)'1-1 1А~5Г... (Ответ: 2<х<8.) / л п • 3
л= 1
Разложить в ряд Маклорена функцию f(x). Указать область сходимости полученного ряда к этой функции.
оо
4.1. f(x) = cos5x. (Ответ: У '° к . |х| < ооЛ \ L-, (2«)! /
ОО
4.2. f(x) = х3 arctg х. (Ответ: ’ 1*1^ !•)
п= 1
оо
4.3. f(x) = sinx2. (Ответ: —1)!—’ 00 •)
п= 1
—. (Ответ:
X \ л=0
оо
4.5. f(x) = cos—. (Ответ: У 'f'2^, |х| < оо
V ' 3 \ Zu 32"(2п)!
л=0
(_l)V + 2( |х| < , \
4.4. Кх)=7А.
.71
4.6. f(x) = —~. (Ответ: 2 V З^2", |x| <-!=.) 1 — 3jt \ _ /о /
n = 0 V
oo
4.7. f(x) = e3x. (Ответ: JT |x|<oo.) n = 0
4.8. f(x) = ууу- (Ответ: £ (— 1)V, W< 1.) n=0
oo
(г—ч ЛПубП
Ответ: У —, |x|<oo.
4.10. f(x)= -!=. ye1 n = 0 oo (Ответ: £ ( 2„)( , W<oo; n = 0
4.11. j(x) — sh x. । oo (Огвет: Z <2n—l)l' W<“'. 1
4.12. ^x) = e~x'. oo (Ответ: £ (-ПУ |x|<oo.' л=0
4.13. Дх) = 2-<(Ответ: £ |x| < oo.)
n = Q
oo
4.14. /(x) = 5\ (Ответ: £ --‘g'-, |x|<oo.)
n = 0
4.15. f(x) = x cos ух. (Ответ:
0 =C x < oo.)
4.16. f(x)= s!2-3*-. (Ответ:
(— l)',x', + l (2n)!
1Г1' 32"~‘ 2n-2
(2n - 1)!
| X | < oo .
72
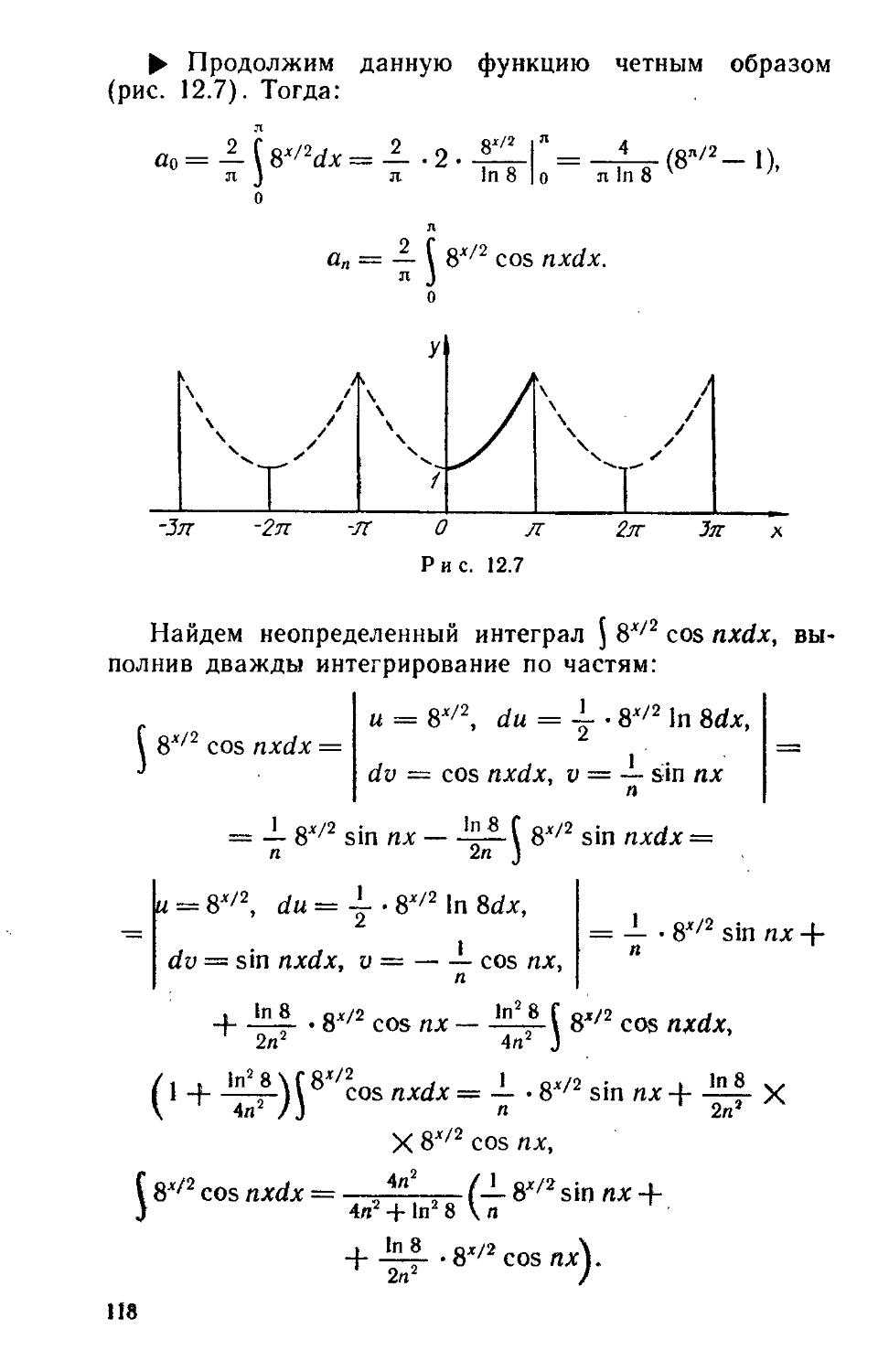
Разложить функцию f(x) в ряд Тейлора в окрестности указанной точки х0. Найти область сходимости полученного ряда к этой функции.
4.17. f(x)=-L, х0=—2. (Ответ: -± £ л —О
-4<х<0.)
4.18. f(x) = —J-т-, х0 = —2. (Ответ: 'х ' *4-3 \
п=0
-3<х< -1.)
4.19. f(x) = ex, х0 = 1. (Ответ: е^ , |х|<оо. л = 0
У (— 1 )"(х + 2)",
4.20. f(x) = хо = 3.
' v f 2х 4- 5
оо
AZf-'O't*-3)'-
л = 0
5^ 2
¥•)
< X <
4.21. f(x)= ——т> х0= 1. ( Ответ: v ' (х — З)2 \
л = 0
— 1 < X
4.22. f(x) = sin-y-, Хо = 2.
( Ответ:
Iх| <
ОО
4.23. f(x)— In (5х -j- 3), Хо = -|-.
О
оо
л= 1
73
оо
4.24. f(x) = ln l-- x0 = 1. (Ответ: V ~^{x~ x — Z X -j- Z \ / j ' I
n= I
- I)2", 0<x<2.)
4.25. f(x) = —-—. xQ = -3. у4 + *
(Ответ: 1 + £ (x + 3)", -4 < x < -2.)
4.26. f(x) = cosx, x0—
(Л , Л \ ----H « • I n
— j-----—(X-------—, | x| < OO .
/ . n! \ 4 /
n=0
4.27. f(x) = —i—. x0 = 2.
y/x- 1
(Ответ: 1 + J (x _ 2)«, I <x<3.)
(Ответ: V ((----------------Vx-f-2)Y — 5<х<1Л
\ \\6-3’ 10-5" / ' 7 / /
n=0
(, rtn\
a 4- —- j
i.M. /W = sin л, ло-u. ^y/ioei. у --------—----— (% —
n=0
— a)n, |x| < oo.^
4.30. f(x) = In (5x + 3), x0 = 1. (Ответ: In 8 +
oo
n= I
5. Вычислить указанную величину приближенно с заданной степенью точности а, воспользовавшись разложе
74
нием в степенной ряд соответствующим образом подобранной функции.
5.1. е, а = 0,0001. (Ответ: 2,7183.)
5.2. V250. а = 0,01. (Ответ: 3,017.)
5.3. sin 1, а = 0,00001. (Ответ: 0,84147.)
5.4. д/Гз, а = 0,001. (Ответ: 1,140.)
5.5. arctg^, а = 0,001. (Ответ: 0,304.)
5.6. In 3, а = 0,0001. (Ответ: 1,0986.)
5.7. ch 2, а = 0,0001. (Ответ: 3,7622.)
5.8. 1g е, а = 0,0001. (Ответ: 0,4343.)
5.9. л, а = 0,00001. (Ответ: 3,14159.)
5.10. е2, а = 0,001. (Ответ: 7,389.)
5.11. cos 2°, а = 0,001. (Ответ: 0,999.)
5.12. д/вО, а = 0,001. (Ответ: 4,309.)
5.13. In 5, а = 0,001. (Ответ: 1,609.)
5.14. arctgy, а = 0,001. (Ответ: 0,464.)
5.15. V738. а = 0,001. (Ответ: 3,006.)
5.16. а = 0,00001. (Ответ: 1,3956.)
5.17. sin 1°, а = 0,0001. (Ответ: 0,0175.)
5.18. V^36> а = 0,001. (Ответ: 2,030.)
5.19. In 10, а = 0,0001. (Ответ: 2,3026.)
5.20. arcsin-y, а = 0,001. (Ответ: 0,340.)
5.21. 1g 7, а = 0,001. (Ответ: 0,8451.)
5.22. д/ё, а = 0,0001. (Ответ: 1,6487.)
5.23. cos 10°, а = 0,0001. (Ответ: 0,9848.)
5.24. -4=з. а = 0,001. (Ответ: 0,302.)
А/зо
5.25. ^д/Т080, а = 0,001. (Ответ: 2,031.)
5.26. у, а = 0,0001. (Ответ: 0,3679.)
5.27. sin-£-, а = 0,0001. (Ответ: 0,0314.) 10U
5.28. д/эО, а = 0,001. (Ответ: 3,079.)
5.29. , а = 0,00,1. (Ответ: 0,496.)
V136
73
5.30. —, a = 0,001. (Ответ: 0,716.)
Vе
6. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.
°'25 г-
6.1. $ In(1 + -ух)dx. (Ответ: 0,070.) о
।
6.2. arctg (dL.}dx. (Ответ: 0,162.)
о 0.2
6.3. $ -yxe~xdx. (Ответ: 0,054.) о
0.5
6.4. arc*g^-dx. (Ответ: 0,487.)
О
0,2 Г-
6.5. ух cos xdx. (Ответ: 0,059.) о
0.5
6.6. J ln(l+x3)dx. (Ответ: 0,015.) о
1
6.7. $ х2 sin xdx. (Ответ: 0,223.) о
I
6.8. ^e~x2/2dx. (Ответ: 0,855.) о
6.9.
1 -}-x2dx. (Ответ: 0,480
•)
о
0.5
6.10. j (Ответ: 0,484.)
О
1
6.11. j д/1 -ф x2/4dx. (Ответ: 1,027.) О
0.5
6.12. J ~^~dx. (Ответ: 0,493.) О
76
0,1
6.13. j * 1 dx. (Ответ: 0,103.) о
0,5
6.14. j x1 cos 3xdx. (Ответ: 0,018.) 0
0,5 _
6.15. j 1п(1+*2Й*- (Ответ: 0,385.) о
0,4
6.16. j д/xe~x^dx. (Ответ: 0,159.) о
0,5
6.17. ( ±+cos.x dx. (Ответ: 2,568.) J X
0,3
0,5
6.18. ( ±rctg*2 dx (Ответ: 0,498.)
J X 0
0,8
6.19. J ~‘os* dx. (Ответ: 0,156.) 0
1
6.20. $sinx2dx. (Ответ: 0,310.) о
0,1
6.21. j dx. (Ответ: 0,098.)
о
6.22. j cos-x/xdx. (Ответ: 0,718.) 0
6.23. j^/xsinxdx. (Ответ: 0,364.) о
6.24.
dx.
(Ответ: 0,976.)
i
6.25. j cos -y- dx. (Ответ: 0,994.) о
77
6.26. arctg^-y-) dx. (Ответ: 0,318.) о
0.5
6.27. J *.^.с..е8..* dx. (Ответ: 0,039.) о
6.28.
6.29.
6.30.
0,4 ______.
J -у 1 — x3dx. (Ответ: 0,397.) о
0.5
j e~xdx. (Ответ: 0,461.) о
0.5 _______
J у1 -\-x3dx. (Ответ: 0,508.) о
. 7. Найти разложение в степенной ряд по степеням х решения дифференциального уравнения (записать три первых, отличных от нуля, члена этого разложения).
7.1. у’ = ху -ф еу, у (0) — 0. ( Ответ: у = х -ф у х2 +
7.2. у' — х2у2 -ф 1, у(0) = 1. ( Ответ: у — 1 — х -ф
7.3. у' = х2 — у2, у(0) = у. (Ответ: у =х — ~т*г+-)
7.4. / = х3 + у2, y(O) = -L. (ответ: у = ± х+
+ |х2+...)
7.5. у' = х -ф у2, у(0) = — 1. ( Ответ: у — — 1 -ф х -ф + 3х2+-) V
7.6. у' = х + х2 -ф у2, у (0) = 1. (Ответ: у = 1 -ф х -ф +Р+-)
78
7.7. if = 2 cos х — ху2, у(0) = 1. ( Ответ: у — 1 + 2х- — -1^ + -)
7.8. if = 6х — у2, у(0) = 0. (Ответ: y = x-j--^-x2 —
7.9. У' = х + у + у2, у(0) = 1. (Ответ: у = 1 + 2х + + 4?+-)
7.10. у' = х2 + у2, у(0) = 1. (Ответ: у= 1 + % + ? + ...)
7.11. у' = ?y2 + ysin х, у(0)=у. (Ответ: у = у +
+ Т*2+ Т2 +-)
7.12. у' = 2у2 + уе\ у(0) = у .(Ответ: у = А + А х+ О у О J
+ 5*2 + -)
7.13. у'= е3х+ 2ху2, у(0)=1. (Ответ: у=1+%+
+ у? + -)
7.14. у' — х + еу, у(0) = 0. (Ответ: y — x-f-x2-f
+ ух3 + ...)
7.15. у' = у cos х + 2 cos у, у(0) = 0. (Ответ: у — 2х +
4- х2 — х3 + ...)
7.16. у' = х2 + 2у2, у(0)= 0,2. (0reer:i/ = 0,2 + 0,08x + + 0,032?+.-)
7.17. у’ = х2 + ху + у1, 1/(0) = 0,5. (Ответ: t/ = 0,5 + + 0,25х + 0,375? + ...)
7.18. у'= ?пл + х, у(0) = 0. (Ответ: у = * + *2 + +4’*3+-)
7.19. if — ху — у2, у(0)= 0,2. (Ответ: у = 0,2 — 0,04% + +0,108? + ...)
7.20. у7 = 2х + у2 + ef у((f) = 1. (Ответ: у = 1 + 2х + + 3,5? + ...)
79
7.21. у'= x sin х — у2, у(0)=1. (Ответ: у = \ — х-\-+ х2 + ...)
7.22. / = 2№ — ху, у(0) = 0. (Ответ:
+ Т-)
7.23. у' = х — 2у2, у(0) = 0,5. (Ответ: у = 0,5 — 0,5х 4-+ х2+...)
7.24. у' = хе* 4- 2у2, у(0) = 0. (Ответ: у = уХ24~
+ 4-х3+|х4 + ..Л
О О /
7.25. у' = ху 4- х2 + У2, у(0) ~ 1 • ( Ответ: у = 1 х Ц-
+ ух2+...)
7.26. у' = ху + е*, у(0) = 0. (Ответ: у = х4~уХ24~
4-±х3Н-...)
7.27. у' = уех, у(0)=1. (Ответ: у — 1 4- х 4- х2 4-...)
7.28. у'= 2 sin х 4-ху, у(0) = 0. Ответ: у = х2 4*
+ *’+)
7.29. у' = х2 4* еу, у(0) = 0. ( Ответ: у = х 4~ -у х2 4~
+ 4*’+-)
7.30. у' = х2 4- у, у(0) = 1. ( Ответ: у=14~*4~^-+-)
8. Методом последовательного дифференцирования найти первые k членов разложения в степенной ряд решения дифференциального уравнения при указанных начальных условиях.
+...)
80
8.2. у' = ху 4- In {у 4- х), у(1) = 0, k = 5. (Ответ: у =
8.3. у' = х + у2,у(0) = \, k = 3.(Ответ: у = х + <^х24-+ |х3+-)
8.4. у’ = х 4- —, у(0) = 1, k = 5. ( Ответ: у — 1 4- х 4-
+Н+-)
8.5. y,v =ху-^у'х2, у(0) = /(0) = /'(0) = 1, у"'(0) = 1, (г2 к3 Л »-6 \
Ответ: ,.l + l + L + £+2.+| + „.)
8.6. у' = 2х — 0,1 у2, z/(0)=l, fe = 3. (Ответ: у={ — - 0,1х + 0,01х2 +...)
8.7. у'" = у" + у’2 +у3 + х, у(0) = 1, /(0) = 2, у"(0) =
= 0,5, fe = 6. (Ответ: у = 1 + 2х + £ + ||х3 + gx4 + у 4 12 4о
+ 8%5+-)
8.8. у' = х2 — ху, у(0) = 0,1, fe = 3. (Ответ: у = 0,1 — - 0,05х2 + О.ЗЗЗх3 + ...)
8.9. у'' = 2уу',у(0) = 0, у'(0) = 1, k — 3.(Ответ: у = х
, 2х3 . 12х5 . \
+ ~ЗГ +~5!~ +-J
8.10. у' = 2х + cos у, у(0) = 0, k — 5. ( Ответ: у — х2 —
_ £1 _ £ 4-.. \
6 4 ' /
8.11. = уех — ху'2, у(0) = 1, у'(0) = у"(0) = 1, k = 6.
(Ответ: {/=1+х+^ + £ + £+0-х5 + ...)
8.12. у' — Зх — у2, у (О') = 2, k = 3. (Ответ: у = 2 — 4х —
-т^-4
81
8.13. у" = хуу', y(ty = у'(0) — 1,6 = 6. (Ответ: у = 1 4-+ *+4 + тг + 4г+4
8.14. у' == х2 — 2у, у(0) = 1,6 = 3. (Ответ: у = 1 — 2х 4* + 2х2 + ...)
8.15. у"=Х-' у(1)=1, у'(1) = 0, 6 = 4.
У х
(О™т. + ...)
8.16. у' = х2 4~ 0,2у2, у(0) = 0,1,6 = 3. (Ответ: у = 0,1 + 4-0,002х 4-0,00004х24-...)
8.17. у" = у'2 4-ху, у(0) = 4, у'(0)=—2, 6 = 5. (Ответ: у = 4 — 2x4-2х2 — 2Х3 4-у х4 4-...)
8.18. у' = ху 4- у2, у(0) = 0,1, 6 — 3. (Ответ:у = 0,\-\-4-0,01 х 4-0,051 х2 4-...)
8.19. у" — еу sin у', у(л)= 1, у'(л) = у, 6 = 3. (Ответ: у= 1 4- у(х —л)4~ у(х —л)2 4~...)
8.20. у' = 0,2х 4- У2,У(О) = 1,6 = 3. (Ответ: у = 1 4~х 4-4-1,1 х2 4-...)
8.21. у" = х24- у2, у(—1) = 2, у'(— 1) = 0,5, 6 = 4. (Ответ: у = 2 4-у(х4-1)4~4(х4-1)24-j|(*4- 1)44-.--)
8.22. у' = х2 + ху + е~х, у(0) == 0, 6 = 3. (Ответ: у — х —
-A + ^L+\
21 ~ 3! ' )
8.23 ., у' — —|- 1, у(0) =1, 6 = 5. ( Ответ: у = 1 4-
+ 2х-х2 + ±х3-1-1-х*+...\
о У /
8.24. у" 4- у = 0, у(0) = 0, у'(0)= 1,6 = 3. (Ответ у = =—4-4+4
8.25. у" = у cos у'4-х, у(0)=1, ^(0)=-^, 6 = 3. и
(Ответ: у= 1 4~ у*4~ у *24~•••)
82
8.26. у' = cos х Н- х2, у(0) — 0, k = 3. ( Ответ: у = х 4-
8.27. у' — 4у + 2ху2 — е3х, у(0) — 2, k =4. [Ответ: у = = 2 + 9х+^-х2--У-х3+...)
8.28. (1 — х)у" + у = О, у(0) = у'(0) = 1, k = 3. [Ответ: у= 1 + х^~ у 4~...)
8.29. 4х2у"+у = 0, у(1) = 1, У'(1) = у. k = 3-
[Ответ: у= 1 4- у(х — •) ~ ~^(х~ + • )
8.30. у' = 2х2 4-у3, у(1) = 1, k = 3. [Ответ: у=14~
4-3(х— 1)4- у (х— I)2 4--. )
Решение типового варианта
Найти область сходимости ряда.
► Воспользуемся признаком Д’Аламбера:
/ ~п / рги
Un~ V4 + 1’ ,1 + 1— V (п + 1)24-1 ’
7(fl + iy + i77
= ~\[х lim
П—► оо
Интервал сходимости определяется неравенством-ух < •< 1, откуда 0 < х< 1. Исследуем граничные точки этого интервала. При х = 0 получим числовой ряд, членами которого являются нули. Этот ряд сходится, точка х = 0 входит
83
в его область сходимости. При х — 1 получим числовой ряд •о
Z.---!---. Воспользовавшись предельным признаком
, д/л2+1 п= 1 *
сравнения рядов с положительными членами, сравним этот ряд с гармоническим расходящимся рядом, общий член которого vn — 1 /п:
lim — = lim — п — 1 = k #= 0.
П->оо /1->оо -^/n2 _|_ |
Следовательно, числовой ряд\ ——------- расходится и
„41 V«2 + i
точка х — 1 не входит в область сходимости.
Таким образом, область сходимости исследуемого ря-
да — 0 С х < 1. ◄
2 У ”2 + 1 / *2 — 3* + 2
/ , п2 \ х2 + Зх + 2 / п = I
> По признаку Д’Аламбера имеем:
я2 4- 2» 4- 2 I х2 — Зх 4- 2 I"+1
lim |_Дд±2_| = lim А2.+ у +.U f + 3*+..2j— =
n-*oo I Un I л—>оо П -р 1 I X —Зх 4“ 2 Iп
~~п2 I X2 4- Зх 4- 2 I
= I х2 - Зх 4- 2 I ]im п2(«24-2« 4-2) = I х2 - Зх 4- 2 I < j
| х2 4-3x4-2 I (п24-1)(я24-2«4-1) I х2 4-Зх + 2 I
__। ,, х2 — Зх 4- 2 ,, ।
х2 4- Зх 4- 2
Решаем полученные неравенства:
। х2 — Зх 4- 2 х2 — Зх 4- 2 . । q 2х2 4~ 4 q
х2 4- Зх 4- 2 ’ х2 4- Зх 4- 2 ’ х2 4- Зх 4- 2
Отсюда
х2 + Зх 2 > 0, х £ (— оо ; — 2)U(—1; оо).
Далее,
х2 — Зх -|- 2 ,, । х2 — Зх 4- 2 _ 1^-0 — 6х___Q
X2 4- Зх 4- 2 ’ X2 4-3x4-2 ’ х2-|-Зх 4-2
84
X
х2 4- Зх + 2
Следовательно, х£( —2; —1)0(0; оо). При х = 0 получим числовой ряд , для которого
п — 1
lim ип — lim = 1 =# 0, «-►оо «-►оо п
т. е. необходимый признак сходимости не выполняется, следовательно, этот числовой ряд расходится. Область сходимости исследуемого ряда: 0<х< оо. 4
оо
3. S (3 —х2)". « = 1
> Воспользуемся радикальным признаком Коши. Находим:
ип = (3 — х2)", 1 im 13 — х21" = 13 — х21 < 1, «—► оо
-1 <3-х2< 1.
Решаем полученные неравенства:
3 —х2>—1, х2 —4<0, х6(-2; 2);
3 — х2 < 1, х2 — 2 >0, х ^ ( — оо; -V2)u(V2; оо).
Пересечение найденных решений дает интервалы сходимости исследуемого ряда xg(— 2; -V2)U(V2; 2).
Исследуем сходимость ряда на концах этих интерва-оо
лов. При х= ±2 получим числовой ряд S (—!)"• Этот п = I
знакочередующийся числовой ряд расходится, так как не выполняется необходимый признак сходимости числового ряда (lim и„ = 0). При х — ±-\/2 получаем числовой ряд «—► оо
оо
S 1", который расходится, поскольку необходимый при-п= I
знак сходимости также не выполняется. Значит, об
85
ласть сходимости исследуемого ряда: (— 2; —y2)U U(V2; 2). ◄
4. Разложить функцию z/ = cos2x в ряд Тейлора в окрестности точки х0 — л/3. Найти область сходимости полученного ряда к этой функции.
► Преобразуем данную функцию:
у — cos2 х = 4- 4- 4- cos 2х.
v 2'2
Разложим полученную функцию в ряд Тейлора. Для этого найдем значения данной функции и ее~нроизводиых до n-го порядка включительно в точке х0 = л/3:
f W = у + у cos 2х>
f'(x) = —sin 2х,
f" (х) = — 2 cos 2х,
f"'(x) = 4 sin 2х,
= j____L = ±-
2 4 4 ’
— 2 cos у = 1;
4 sin у — 2^3;
f(n)W = —2"“' sin(2x + (n- 1) Д), (Д-) =
= -2—Sin(^+(n-l)i).
Полученные числовые значения производных подставляем в ряд Тейлора при х0 = л/3:
86
Для нахождения области сходимости полученного ряда необходимо выяснить, при каких значениях х остаточный член ряда Тейлора стремится к нулю. Он имеет вид
где %о). Поскольку jsin^2g п -0| 1, достаточно
найти область сходимости ряда с общим членом 2" / л \"+ 1
( х---) . Согласно признаку Д’Аламбера,
V1 т* *)• \ J /
lim I 2,1 + 1и--я/ЗГ + 2 (« + !)! I = |im 21Х-Л/31 =0< ]
n-*oo I (л 4- 2)! • 2”(х — л/3)п 1 I п -|- 2
Полученный ряд сходится при любом х. Значит* область его сходимости к функции f(x) = cos2x такова: —оо < < х < оо.
5. Вычислить \/х[ё приближенно с точностью а = = 0,0001, воспользовавшись разложением функции у — ех в степенной ряд.
► Воспользуемся рядом (12.17). Так как \/х[ё= _ |/2, то
-'/2 = 1 _± д________!_________!____l____!__________!_
2 4-2! 8-3! 16-4! 32-5!
Получили знакочередующийся числовой ряд. Для того чтобы вычислить значения функции с точностью а = = 0,0001, необходимо, чтобы первый отбрасываемый член был меньше 0,0001 (по следствию из признака Лейбница). Имеем
С заданной степенью точности:
е->/2«1_± +±_ _L + J_____L
2 8 48 ' 384 3840 ’
-Ь « 1 — 0,5 + 0,125 — 0,02083 + 0,00260 — 0,00026 «
«0,6065. <<
87
6. Используя разложение подынтегральной функции в степенной ряд, вычислить определенный интеграл о
——— с точностью до 0,001.
► Воспользуемся биномиальным рядом (см. формулу (12.21)). Тогда
Получили бином вида (1ф.г)т, где т=—1/3, a г — = — (х/2)3. Имеем:
,69
тй-/('+1а)+//(1)+^(т)+-)=
= т(1 + + 188 + + -) ’
о о
f dx 1 f /1 . х3 . х6 . 7х9 . \ ,
) j + + W +
= _L/x + _Z_ + _^+ 7*'L_ + ...V =
2 \ ' 4•24 '7-288 ~ 10-18176 ' /|-i
- ([ - 1 I 1 7 I \
2 \ 96 ' 2016 181760
1
2016
<0,001.
С точностью до 0,001
f d* 1
V8—*3 2
— -4g- « 0,5 — 0,0052 « 0,495.
7. Найти разложение в степенной ряд по степеням х — 1 решения дифференциального уравнения у' = 2х -ф у3, z/(l)== 1 (записать три первых, отличных от нуля, члена этого разложения.)
► Точка х— 1 не является особой для данного уравнения, поэтому его решение можно искать в виде ряда:
У = Ж)+ -ф-^-1)+-ф-(х-1)2+-ф-(х-1)3 + --
88
Имеем: Д1)=1, /'(1) = 2 ф- I3 = 3, f"(x) = 2 ф- 3y2y', f"(l) = 2 + 3 • I2 • 3 = 11. Подставляя найденные значения производных в искомый ряд, получаем решение данного уравнения:
у=1 + 4(х-1)+<(%-1)2+- ◄
8. Методом последовательного дифференцирования найти первые 5 членов разложения в степенной ряд решения дифференциального уравнения 4х2у" ф- у = 0 при следующих условиях: у(1)= 1, у'(1) = 1/2-
► Ищем решение данного уравнения в виде ряда:
У = /(1) + (х- 1) + -ф- (%- I)2 ф- -ф (х- I)3 +
+ 1>(х-1)Ч...,
/(!)=!,
^/// _ __ У'%2 2ху __ (1 /2) • 1 — 2-1 __ 3 .
flv(x) = — ((z/"x2 + 2ху' — 2у — 2ху')х4 — 4х3(/х2 —
— 2ху))/(4х8); /"(!)=-2|.
Подставляя найденные значения производных в ряд, получаем искомое решение дифференциального уравнения:
z/=l + ±(x-l)-TLr(x-l)2 + ^-(x-l)3-
1 I X-1 (%— 1)2 I (X-1)3 5(x-1)4 , .
y~l + ~T~ 8 1 16 128 4
ИДЗ-12.3
1. Разложить в ряд Фурье периодическую (с периодом <о = 2л) функцию /(х), заданную на отрезке [ — л; л].
89
cos ((2k — l)x) л — 4 sin ((2k — l)x)
1.6. f« = {^+3' (Ответ:
4 у cos ((2fe— l)x) «21, (2* - I)2
Л=1
oo
+ 2(я —3) у л Z_,
k= i
sin ((2k — l)x)
2k — 1
sin (2kx) ' 2k
1.7. ?« = {“_x, (Ответ: /«= ^4
2_ у cos ((2fe — l)x) , 6 —л у sin ((2k — l)x)
л 2L (2fe — I)2 л / . 2k-}
k=l k=i
sin (2kx) 2k
k= I
1.8. /w=(j 2-
n + 4 2 у cos((2fe-l)x) . 4 + л у sin (_(2A - ])x)
2 “* л /. (2k— I)2 л 2k -1
fe=l k=l
sin (2kx)
2k
0,
4x — 3,
0<х<л.’ (Отвег: Hx) =
1.9. f(x) = {
2л —3 _ 8 у cos ((2k — t)x) .
2 я /. (2A-1)2
k= i
2(2л — 3) у sin.((2fe — l)x) , у sin (2kx) л /. 2k - 1 /. 2k
ft=i k=i
1.10. Z«={i;y- (ответ: /(x)=i±J»-
91
+
cos ((2fe — l)x) л+10 V"1 sin {{2k—l)x) (2k - l)2 я / . 2k - 1
li
•ic
8
СЧ I В
sin ((2k — l)x) _К V s'n (2^x)
II
co Qi
2(3л + 2) V sin ((2k — 1)х) (• V sin (2Лгх)
Ответ: f(x) = - ^±1 + V ' ’ 2 1 л /, (2k - I)2
1.25. f(x) — {%v_3
Ответ: f(x)= _5-л.-.3 _ 21 V
K ' 2 я ZL (2k- I)2 4
1
. 2(5n —3) у sin ((26 — l)x) If) У sin (2kx) \
Г л 26—1 *% 2k ')
6 = 1 6=1
1.26. f(x) = [l~ x/4’
'v ' 10, 0 < x CJ n.
,. f(x\ = л + 8______!_ V COS ((26-1)%)
’ 16 2л /, (26 — I)2
6= i
л +8 V sin ((26 — 1)%)
4л / , 2k — 1 6—1
sin (2kx)
26
fW={“/5-2
Ответ: f(x) = л~20 + -2- V .^k-^ 20 5л / , (2k — I)2
k= 1
. Л —20 У sin((26—l)x) 1 У sin (2kx) \
' 5л /, 2k - 1 5 /, 2k )
6=i 6=i
1.28. /(x) = {2* "
Oreer: l(X)= - ± У .c“«2t-'>4. +
2 л Z_z (2k — I у
6= i
2(л+11) у sin ((2k — l)x) __n у sin (2kx) \
я / , 2k — 1 / , 2k ')
6=i 6=i
,.29.
— л x <Z 0, 0 =C x Ci л.
Ответ: f(x) = ———
, 16 у cos ((2k — l)x)
Л L-j (2k— I)2 6 = 1
95
t 2(3 — 4л) V sin ((2/г — 1)х) ( QV sin {2kx} \
’’’ л / , 2k - 1 ° /, 2k )
A=±l k=l
1.30. ZW={£~'’
OO
(Ответ: f(x) = - + _!± V +
\ 7 4 л L {2k -I)2
k = \
7л+2 у sin ((2й — l)x) ,y sin {2kx) \
"• л / , 2k - 1 /, 2k ')
k-=t k=i
2. Разложить в ряд Фурье функцию f(x\ заданную в интервале (0; л), продолжив (доопределив) ее четным и нечетным образом. Построить графики для каждого продолжения.
2.1. f(x) = ex. (Ответ: 6х — —----!—|-
\ 11
((— 1)"е" — 1) cos пх
п sin пх
2.2.
f(x) — х2. (Ответ:
cos пх
.2 _____
k= I
Л2 —4(2fe- 1);
{2k — I)3
sin ((2k — 1 )x) —- 2л
t= ।
sin (2kx) \
2k ’)
2 л
X — —
3
2.3. f(x) = 2x. (Ответ: 2х =
2 In 2
л
2Л(- 1)"-1 n2 4- In2 2
cos nx,
oo
2, = 2_ у (-1Г + 1 5+ n sin nx\ л / , n 4- In 2 /
n = I
2.4. f(x) = ch x. (Ответ: ch x — sh ? f 1 -f-
96
oo oo
J-.(-Я ch Я rasinrax\
1 4-« /
2.5. f(x) — e (Ответ: e x=-—---------1-
J.1 V 1
Я / 1 4- n‘
= I
2
e
----n sin nx.
2.8. f(x) = (x — I)2. (Ответ: (x - I)2 = .?1~|L+3. _|_ oo oo
+ 71 W^kcos«2ft - '^)+4Г
Й=1 fe=l
00
= 7 I СтГ Г~ + sin ((2* - l)x) + 2(2 -
Л \ 2к l (2к I j /
/• = I 00
fe==l
2.7. f(x) = 3~x/2. (Ответ: 3~x/2 = 2(1 ~3 "/2) +
4 In 3 у 1 — (-If-3^л/2
я Z-i 4n2 4- (In 3)2
n= 1
3“x/2
1 — (-l)"-3~"/2
4n2 4- (In 3)2
n sin nx.
2.8. f (x) = sh 2x. ( Ответ: sh 2x = 4-
\ 2л
4 у ch 2я-(—1)' л Li 4 4- n2
<= 1
4-357
97
sh 2x = — V Л / , n = l
(-!)"+'-sh 2л
n sin nx
n2 + 4
2.9. /(x) = e2x. (Ответ: e2x = —- 4*
\ 2л
+ ± у l-Lr^l.cosrtX,
я / . 4 + «2
1 oo
<>• = А у '-l-y „ sin nx.)
Я L 4 + n2 /
« = J
2.10. f(x) = (x-2)2. (Ответ: (x-2)2 = ^~6”+,L2. 4.
4(4 — л) у cos (2fe — l)x у cos 2kx я Л (2k -I)2 L, (2k)2 ’
*=1 • *=1
00
<"-^ = 4 X +(-') 2-^-);)sinnx) n= 1
2.11. f(x) = 4x/3. (Ответ: 4Х/3 = 3(4"^~ 4-
6 In 4 я
4*/э __
(_jy.4»/3_ 1
---5------5— cos nx, 9n2 + (In 4)2
1 — (— 1Ъ4’/3
----5--1---5— П Sin
9n2 + (In 4)3
2.12. f(x) = ch4. (Ответ: ch A =-2 sh-(jl/2) 4-2 \ 2 .л
I 4 sin(n/2) у ( — 1)” cos nx л Z_, 14- 4n2
n= I
ch A = 8 ch (”/2) 2 Л
n sin nx.
2.13. f(x) = eix. (Ответ: e4x =—?—|-
(—[уе4"— 1
n2 + 16
cos nx,
98
,4х_ 2 у
~ п L
п = I
I — (—Ife4" п2 + 16
п sin пх.
2.14. f(x) = (x-f-I)2. (Ответ: (х + I)2= ” + 3” + 3
_ 4(я + 2) у cos ((2fe — 1)х) 4 у cos (2fex)
л / 1 (2/?1) (2k}2
6=1 6 = 1
_2 у (2 - п2) + (- 1Г((л - 1)2«2 - 2) , \
Л / , ГГ /
П = 1
2.15. f(x) = 5“*. (Ответ: 5~х = 1 ~ 5~- + \ л In 5
. 2 In 5 V 1—5~"(—1)" л
Н------) —->—COS ПХ,
л / . п2-f-(In 5)2
п= I
5
—2_Ц— п sin пх. П2 + (1П 5)2
2.16. f(x) = sh Зх. (Ответ: sh Зх = ch 3? ~ 1 \ Зл
(-l)" ch Зл - 1 пг + 9
cos пх,
sh Зх =
2 sh 3 л
-1)п+' п2 + 9
2.17. f(x) — е. х/4. (Ответ: е Х/А
4(1 — e—Z4)
Л
rt= t
16/l2 + 1
cos пх,
e-x/4 = 32 у 1 -(-irg-174 л / . 16л2 + 1
n = I
n sin nx.
99
2.18. f(x) = (2x - I)2. (Ответ: (2x - I)2 = 4л ~6я+3 \ 3
co
4-1 V bifclf+L cos nx>
n= 1
oo
(2x - I)2 = A £ у-8 + (-Щ8-(1-2^ sjn nx ) n= I
2.19. f(x) = 6x/4. (Ответ: 6t/4 = _i_
' ' \ Л In 6 '
I 8 In 6 V (-1)"6Л/4- 1
4------) ------4-------5- cos nx,
Л / J 16n2 4- (In 6)2
rt= I
oo
6-,< = » У n sin „,A
Л / J 16n2 (In 6)2 /
n = I
2.20. f (x) — ch 4x. (Ответ: ch 4x = -sll-4jt- 4-' ’ \ 4л
cos nx,
ch4x= — У ±-1^.4л л / . и2 + 16
n= I
2.21. f(x) = e Зх. (Ответ: e 3x = -—------1-
\ 3л
e~3x = — Л
n sin nx.
2.22. /(x) = X2 4- 1. (Ответ: x2 4- 1 = 4-
\ 3
4- 4 2^ -—p- cos nx,
n= I
X2 4- 1 = А У (^-2) + (2-л)2(лг+ 1)(—1Г
л 2_j n3
n= I
100
2.23. f(x) = 7 x/1. (Ответ: 7 x/1 —
7(1 -7~"77) л In 7
14 In 7 л
1 _ п". 7-"/7
2— — cos пх, 49л2 + (in 7)
7—‘/7 =
1 — (—1)"7_"/7
----*5------г" « SHI 49n2 -f- (In 7)2
2.24. f(x) = sh (Ответ: sh =
О \ э
(—1Г ch — i и
25л2 + 1
cos пх,
sh — = 5
50 sh4
О
л
— п sin пх.
25п2 4- 1
л
2.25. f(x) = e 2х/>. (Ответ: е 2х/3 = 211—_-1
2л
/_ lye' 2-'/3
i—-------------cos ПХ,
9п2 + 4
е-2х/3 _ 18
i-r-1--------П Sin
9л2 +4
2.26. f (х) = (х — л)2. ( Ответ: (х — л)2 == -у- -f-
оо ОО
4- 4 У ^L, (X - л)2 = У (l^KzlLzJsin пх.) / П2 Л Z_| п /
п=I . п=I
2.27. f(x)= 10 х. (Ответ: 10 х
1 - ю~" л In 10
ОО
21п)£ у I-(-1Г.10- cos rtXi л /. п2 + In2 10
л = 1
10-х
1 — (— If. IO"'1
-----1-------------п sin пх.
п2 + In2 10
101
2.28. /(х) — ch —. ( Ответ: ch — = sh 1 4-Л у л
оо
4- 2 sh 1 V — Q—. cos пх, Lu 1 4- Л Л
rt = i
ch — = 2л У 1 £h 1 л sin пх\
я / . 1 + ггя2 /
п— I
2.29. f(x) = e4*/3. (Ответ: е^/з = 3(е^~ 1) +
(-l)-eto/3 1
9л2+ 16
cos пх,
№ = 21 Г л Z-# n= t
1 — ( —1)"е4л/3 9л2+ 16
2.30. f (х) = (х - 5)2. (Ответ: (x-Sf = ”2~ '^.t75 +
У cosnx, (х —5)2 =
Л Ди Л
л== I
= 2 у ^2 -2) + (-1Г(.2-Яг(5-^ s.n пхД
я / . п3 /
п= I
3. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом <о = 2/.
3.1. f(x)= |х|, — 1 <х < 1, I = 1. (Ответ: |х|=у —
___4 у cos ((2п + 1)ях) \
л2 L (2п +1)2 7
п = 0
3.2. /(х) = 2х, — 1<х<1, /=1. (Ответ: 2х=1 — ___2 у* sin (2ялх) n= t
102
€01
j = u 1 = «
\ (nt«)uis A i (%u(i — «г))9оэ A g g OO CO
‘I >x>0 '« 1
= (*)/ :ia8io) '1=7 *0 = * ‘г/1 ?=(*)/ ’6*8
*0>*> I- ‘I )
l = «
( (g/хки) ujs "(l ) uZ 01
OO
= x — 01 iideio} -g = / *SI >x>g ‘x —01 = (*)/ *8*8
e=u
’ / г(1 + »g) Y г“ I
oo
| = U
. г(1 - »г) Y =
+ (xir(j — wg))soa A f |
co
\ ‘г > x > i 'x — g)
= (x)/ :id8J.Q ) г = 7 * I > * > О ‘X >= (x)/ те *0>*>g— ‘oj
! = «
( (xiru) uis l + "^l ) z
OO
+ z = x :-id0j.o) 1=7 *£>X>I •% = (*)/ *9-8
] = U
Л ч , г(1-иг)1Г 7 “
v(^w“) u!s + (xd-^Msoog AT-
oo
— y=(*)/ --13810) 4=7 = *5’8
/ г 6(14-иг)
l----; soo-------------------
\ xir(] + ug) |
= g—|x| :j.881O) ’Z>X>Z —
‘0- 1*1 = (*)/ *F8
+1
7 7
—— uis wir---------— soo t,
%LfW XlfW
1 = 1/
U(I-) Z Z+t)z4S = oo
= --J-aeio) 2 = 7 ‘3>*>3~ ‘^ = (*)/ "S’S
3.10. f(x)=5x—1, —5 < x < 5, I = 5. (Ответ: 5x— oo
ч=-' + тр-';;>Я
n— i
З.И. ?« = {».
I = 3. ( Ответ: f(x) = —
6 V cos ((2n — 1)лх/3) я2 / . (2л — 1 )2
n= I
oo
1 У HIT sin
л / i n 3 /
n= I
3.12. f(x) = 3 — x, —2<Zx<2,l = 2.( Ответ: 3 — x =
3.i3. /== L (°твет: f^ =
4 V1 sin ((2n-|-1 )лх) л / . 2n + 1
n = 0
3.14. f(x) = {°’ 0<x<2,’/ = 2- (°твет: U*) =
= 1 4- У ----------sin \
2-j л (2 л — 1) 2 )
n= l
( x, 0 x sC 1,
3.15. /(x) = { 1, l<x<2, / = 3. fОтвет: f(x) =
13 — x, 2 < x 3, '
__ 2 ___ 9 ’ V1 cos (2лпх/3) . 1 у cos (2лАх) \
3 2л2 / . n2 2л2 2—> k2 )
n=l *=i
3.16. f(x) == 2x — 3, —3 < x < 3, I = 3. ( Ответ: 2x —
n = 1
104
SOI
I =»W
( (g/x«w) ujs „(] —) V ~~ = co
+ЛЗ :idei(j ) Z = /'£>*> I — ‘Z + *Z = (*)/ -ggg
i =»
/ iz 7 A
\ (лигу) ujs A I oo
|=W 1=W
_______i -»г 7 А ц_ г(| -цг) 7 jA__L_ (гA“(i — «г)) ufs A s + feA“(i — «г))803 A z i
OO OO
x ‘g>x>0 ‘ZA 1
= (*)/ :id8io) z = l ‘0 = x ‘Z/l — } = (x)l 'IZS
‘Q>x>z— ‘I —J
I = w
(. u______________7 - + i
\ xuu ujs l+„(i —) Аг1 oo
= X 4- I :iaej.o) ’ I = / ‘ I > * > I — ‘x + I = (*)/ "OZ'S
I = 4
/. I — -75 7
\ (fr/xw(j — ^))ujs A fr
OO
x |=W |=W
I______________ 7 i_______;( I ~ UZ) ’’J _
(fr/rww) ujs „(I —) A (f/xw(| — «5))SO3 As 5
OO oo
x ‘^>х>0 ‘z )
= (r)/ :j.d8J.Qj f = j ‘o = x ‘j > = (*)/ -6Г₽
‘0> x> f— ‘x — J
0 = w
(___s_____so37 . A = |X,
\ %u(i 4-»г) so j А ог i I'
oo
— £:ideio) 5 = 1 *G>x>g— ‘|x| — g = (r)/ -grg
(.____L±±3__ h_)7i
\ (eA«(l +uz))so3 »'* > A t
oo
= (r)/ :ideio) •£ = / ‘g/g>x>0 ‘Ii"~} = ^^ '£re
( 3, —3<х<0, 3.23. f(x) = {3/2, x = 0.
I — x, 0 < x < 3,
I = 3. ( Ответ: f(x) =
3______6_ у cos ((2n — 1) лх/3) _ _9_ у sin ((2я-1)ях/3) .
4 л2 2_< (2n — l)2 л l_i 2n — 1
n — I n = I
। 3 V-1 sin (2лАх/3) \
+ т L 2k ) k=।
3.24. f(x)=l-|x|, -3<x<3, 1 = 3. (Ответ: 1-oo
_|Л| = -± + 4У --------------- COS<2"
2 Z. (2<i - I) 3 /
n= I
( —2, — 4<x<0,
3.25. /(x) = < — 1 /2, x = 0, I = 4. ( Ответ: f(x) — 11+x, 0 < x < 4, '
1 . 32 у cos ((2n — 1)лх/4) . 10 у sin ((2n—1)лх/4)______________
2 л2 Zj (2n — 1 )2 л Zj 2n — 1
n = I n = I
4 у sin (Алх/2)
+ / , 2k t = i
3.26. f(x) = 4x — 3, —5 <x <5, 1 = 5. (Ответ: 4x —
oo
-з^-3 + ^-У Sin-^A
л n 5 /
n=l
f x + 2, —2<x< —1,
3.27. f(x)={ 1, —1<x<1, 1 = 2.
к 2 — x, 1 <x<2,
oo
(OraCT;fW-| + 4£-<g-’W2> -
n= I 00
___8_ V1 cos(2(2fe— 1)лх/2) \
я2 zL (2(2fe-l))2 7
k=i
3.28. f(x) = { - ’/2; “oSJSe,’ l = ^(OTeeT:f(x) =
» sin(4-j)gL:
2n — I 6
( — 2x, — 2 < x < 0,
3.29. /(x)= | 2, x = 0, I = 2. (Ответ: f(x) =
[ 4, 0<x<2, '
oo oo
8 у cos ((2п — 1)лх/2) , 4 у 1 • пях \
L (2n - If Г 7 L n 2 7
n~ i n=*t
3.30. /(x)=|x|—3, —4<x<4, I = 4. (Ответ: (x(—
-3 = -1 - 4 Г —— .y cos -
я2 L. (2n - I)2 2
n = 1 OO OO
8 у sin (пях) 4 у I • (2k— l)nz
я /. 2n я /, 2k - 1 2
n=l *=1
4. Разложить в ряд Фурье функцию, заданную графически.
107
4.3
4.4.
у..
-7 -6 -5 -4 -3 -2 0 1 2 3 4 5 6 7
-1
4.5.
-1
4.6.
4.7.
108
4.8.
4.10.
4.11.
4.12.
ies
4.13.
4.14.
4.15.
4.16.
4.17.
4.18.
4.21.
4.23.
4.24.
4.27.
112
4.28.
5. Воспользовавшись разложением функции f(x) в ряд Фурье в указанном интервале, найти сумму данного числового ряда.
оо
5.1. f(x) = |x|, (-л; л), £ (2„Li)2~- (°твет: у") п = 1
5.2. f(x) = |sin х|, ( — л; л), 4п^\"' (°твет: у)
/1 = 1
оо
5.3. f(x) = х2, [ — л; л], (—1)л+1-^-. (Ответ:
п — I
113
5.12. f(x)= | sin x|,
e.o f/H-P’ -3<*<0, у 1
5.13. f(x) — 0<x<3, Д (2n — l)2
n = I
oo
5.U. ,w ={|:
5.15. f«=kl.(-i; О. 1т5^НОмет; т) n =0
5.16. Дх) = х2, (-л; л), £ (2n_^(Ответ:
( 1, -1 <x<0, “ , .
5.17. f(x)={ 1/2, x = 0, X (Ответ:
5.i8. £
n= I
1"
2n+ 1
( — X,
5.19. f(x) = l 1,
I 2,
— 4 <x<0, x = 0, 0 < x< 4,
1
(2n - I)2 ’
Ответ: —. j
8 /
520 f(x)-l U 0<^<3/2, у (-1)» (Отврт. я
&.ju . 3/2<a.<3> 2^ i^yrvraer-T
n = 1
( — 1, —2 < x < 0,
5.21. /(%) = < -1/2, x = 0, I x/2, 0 < x < 2,
l
(2n- i)2 ’
Ответ:
8
( — 2x,
5.22. f(x)=1 2,
к 4,
— 2 < x < 0, x = 0, 0 < x < 2,
I
(2n- I)2 '
Ответ:
oo
5.23. f(x) = { °’ У
к Л 1 , V л JV, £ j {Zfl — 1)
n= 1
Ответ:
5.24. /(x) = { I*•
— л<х<0, у (1 — (— l)n)
0 < x c л, / , n2 n= 1
(°твет: ^-.)
5.25. f(x) = n2 — x2, ( — л;
n= I
(-1Г
п2- 1
5.26. /(x) = xsinx, [ — л; л
5.27. /(*) = { j
О, —л^х<0, О < х < л,
2л — 1
— л<х<0, v (—1Г+' /г> л о^х<л, L ^г\Ответ: т-
5.28. f(x) = { aa’
n = 0 oo
5.29. f(x)=|cosx|, [ — л; л], n = 1
Ответ: •)
5.30. f(x) ==|cosy|, [ —л; n], n= I
Ответ: )
4n2 — 1
(-1)"
1 — 4п2
Решение типового варианта
1. Разложить в ряд Фурье периодическую (с периодом со = 2л) функцию
116
( л “I-
I o,
— л «С x < 0, 0 x sj л.
► Вычислим коэффициенты Фурье:
о
1 f / I \ J 1 (л + x)2 I 0 cio = — \ (л + x)dx - — -——
nJ л 2 I -
— Л
0
a„ = — ( (n 4- x) cos nxdx = JI 1
и = л 4- x, du — dx,
dv = cos nxdx, и — — sin nx, n
2
1 I
—r cos nx\ ЛП I —л
о
= ”n 5 (л + x) s*n =
— Л
л(2п — I)2 ’
и = л 4- x, du — dx, dv = sin nxdx, v —--------- cos nx
n
Ряд Фурье для данной функции запишется в виде
cos ((2п — 1)лх) (2n - I)2
sin (гглх) п
2. Разложить в ряд Фурье функцию f(x) = 8x/2, заданную в интервале (0; л), продолжив (доопределив) ее четным и нечетным образом. Построить графики для каждого продолжения.
П7
► Продолжим данную функцию четным образом (рис. 12.7). Тогда:
«о = - ( 8x/2dx = А . 2 . -£2-1" = —*— (8Л/2 — 1), nJ л In 8 I о л In 8
о
Найдем неопределенный интеграл $ 8Х/2 cos nxdx, выполнив дважды интегрирование по частям:
8Х/2 cos nxdx =
— • 8Х/2 sin пх 4-п
и = 8Х/2, du = у • 8х'2 In 8dx,
dv — cos nxdx, v = — sin nx n
= — 8X/2 sin nx----( 8X/2 sin nxdx =
n 2л j
и = 8х'2, du = у • 8X/2 In 8dx, dv = sin nxdx, v —-------- cos nx,
n
• 8x/2 cos nx —( 8x/2 cos nxdx,
2n 4rr J
(1 4- —t'J( cos nxdx — — • 8x/2 sin nx 4- X
\ 4n2 7J л 1 2л’
X 8X/2 cos nx,
8x/2 cos nxdx = —л—.— (— 8X/2 sin nx 4-
4n2 + In2 8 \л
4- • 8X/2 cos nx).
2л2 /
118
Вычислим коэффициенты ап:
ап =-----—-------—(— • 8х/2 sin пх 4- • 8х/2 cos пх)1
л(4п2+(1п8)2) kn 2пг /1о
_ 4 In 8(8л/2(- I)" - I)
~ л(4п2 + (1п 8)2)
Следовательно, разложение данной функции по косинусам имеет вид
8^/2 = 2(8л/2_-1). + ±1п8_ у ^•(-1Г-1_ cos пх
я In 8 лЛ 4п24-(1п8)
п = 1
Теперь продолжим данную функцию нечетным образом (рис. 12.8). Тогда:
8Х/2 sin nxdx =
и = 8х/2, du = у • 8х/2 In 8dx, dv = sin nxdx, v = — — cos nx n
=-------- 8x/2 cos nx -f- 8X/2 cos nxdx —
n 2n J
_ и = 8X/2, du= у 8X/2 In 8dx,
dv => cos nxdx, v = — sin nx n
Ц9
bn =
- — • 8X/2 cos nx -f- ’ 8X/2 sin nx —
n 2n2
—8X/2 sin nxdx, 4n2 J
----7^------г (------- 8X/2 cos nx -f-
n(4n2 + (In 8)2) \ n 2n
:8*'2 sin пх\Г = +
/10 л (4n2 + (In 8)2)
Следовательно, разложение данной функции по синусам имеет вид
со
8*'2 = _8_ у _g?^(-y п sin пх.
л 4n2 + In2 8
п= I
3. Разложить в ряд Фурье периодическую (с периодом (о — 2) функцию
1, 0,5, х,
-1 <
0<
х < 0, х = 0, х< 1.
> Вычисляем коэффициенты Фурье:
Г Г |° ^2 | 1 ] о
«о = \ dx+ \ xdx = х — = !-{- — = —-,
J J I — 1 ^10
-1 о
О I
ап = j cos (плх) dx -f- j x cos (плх) dx = -I о
_ и = x, du — dx, _
dv = cos (плх) dx, v = sin ^ПлХ). nn
=-y sin (плх)| -f- x sin (плх)|о —
— sin (плх)с?х = —cos (плх) | ° = -J-j ((— 1)" — 1), 0
an =«----—------,
л2(2п — I)2
12»
0 I
bn = J sin (ллх) dx 4- $ x sin (ллх) dx = -1 e
_ u = x, du = dx, _
dv = sin (ллх) dx, v = cos (илх)
i i0 i1
-------—- COS (плх)-----------COS (ЛЛХ) I 0 4-
I
4—— ( cos (ллх) dx =----------— (1 — (— 1)")--------— (—!)" —
* nn J x ' nn ' ' nn '
e
_ _2_ sin (плх) = =
trn2 10 nn nn nn nn
В итоге получаем следующий ряд Фурье:
cos ((2гс — 1 )лх) 1 у sin (ппх) (2п — I)2 л / . п
п~ I
4. Разложить в ряд Фурье функцию, заданную графически (рис. 12.9).
> Запишем аналитическое выражение данной функции:
/и=(Г!+1' <>-<•
Вычислим коэффициенты Фурье:
0 ' 2 2 0
= у ^у х 4“ + у 2dx = —^х)|_2^”
-2 О
+^--т<'-2)+2-4.
121
0 2
a"=T 5 (tx+ l)c°s^rfx+ Jcos^rfx =
-2 0
= u = x/2+ 1, du = ({/2)dx, =
dv = cos^dx, y = 2-sin^-
x/2 +1 ; плх 10
= ——-— sin —— ПЛ 2 I—2
пл ” 2 О
j sin-^dx4-
-2 । о . плх
= COS--------- =
О п2л2 2 1—2
2
2пл
2
+ J-sin^Ll
пл 2 I
= _!_ (С—1У+1 4-i)=___________
п2л2 ; + ' л2(2п - I)2 ’
о
ft.
2
• плх . f плх , sш —2~ ах + \ sin —— dx —
-2 0
_ и = х/2 4- 1, du = (l/2)dx, _
du = sin -s— dx, и =---------cos ——
2 пл 2
COS-^11° + —!— ( cos dx -
пл 2 | —2 2пл J 2
-2
2 плх j ”2” 0
2-((_|)"-t)_-2_c0S пл ПЛ
+ -J— sin— 1° - JL(-1)« + _1_ =
n2n2 2 1—2 пл пл
= J______L(_ 1)« = (1+2(-1Г')
пл пл ' 2 пл
Следовательно, искомый ряд Фурье
f(x) =
cos ((2n — l)nx/2) (2« - I)2
я=1
(1+Л-Г1) sin-2^.. <
п
122
на
5. Разложить в ряд Фурье по косинусам функцию
х, О
2-х, I
п —О
отрезке [0; 2] (рис. 12.10) и найти сумму ряда 1
(2п+1)2‘
Уз
2-
1
-4 -J -2 -1 О 1 2 3 4 х
Рис. 12.10
► Продолжим функцию четным образом и вычислим коэффициенты Фурье:
Яо= j xdx + (2 — x)dx — -тг))^
о I
ап =
I 2
j х cos dx-]- j (2 — x)cos dx — о I
и = x, du = dx,
dv = cos^dx, v= A sin^L 2 nn 2
и = 2 —-x, du — — dx, dU=COS^dx,
ил " 2
«л 2
= 2L sin 2£Ll1 - _2_ ( sin dx -]_ nn 2 | о nn J 2
о
n 2
sin ^-dx =
2(2 ~ *) sjn плх пя 2
= _2_sin«« + < cos-^-l --2-sin^--пл 2 и л 2 Io nn 2
123
A . 2
4т cos
пл 2 I l
4
л2(2п + I)2 ‘
Следовательно,
4 у cos (2n + 1) nx л2 / . (2n + I)2
n = Q
Полагая x = 0, получаем: oo oo
0=±-JLV________!__, V____!__=
2 л2 (2n + I)2 (2n + I)2 8
n=0 n=9
Таким образом, с помощью ряда Фурье мы нашли сумму числового ряда. Ч
12.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ К ГЛ. 12
1. Найти сумму ряда оо
£ (n + 1) (п + 2) (2n + 1) (2п + 5) ’ П — 1
(Ответ: 1/90.)
2. Исследовать на сходимость ряд
1 , 3 , / 5 \3/2 . I / 2п — 1 \«/2 ,
т + у-Ц-ioJ +- + (1ГГь) +-(Ответ: сходится.)
оо
3. Показать, что если ряд 2 абсолютно сходится, оо
то ряд п + 1 ап также абсолютно сходится.
п — I
4. Исследовать на сходимость и абсолютную схо^и-•о
__|\п+1 .3я
-i -------—. (Ответ: абсолютно сходится.)
П = 1
124
5. Показать, что ряд, полученный при перемножении оо
двух расходящихся рядов: 1 — ("^г) и +
п = 1
ОС И— 1
-|- (2Л + 2_(/г+!)), абсолютно сходится.
п= 1
оо
6. Сколько членов ряда ^(—1)'1+1 —нужно взять, п= 1
чтобы абсолютная погрешность при замене суммы S этого ряда его n-й частичной суммой Sn не превышала а = = 10~3, т. е. чтобы |S — S„| = |rn | а? (Ответ: n 7.)
oo
7. Сколько членов ряда (— l)'* + l 2n ~ 1 нужно
n= I
взять, чтобы вычислить его сумму с точностью до 0,01? (Ответ: п = 200.)
8. С помощью почленного дифференцирования и интегрирования найти сумму ряда 1 — Зх2 + 5х4 + ••• + 4-(— 1)«-’(2« — l)*2"-2. (Ответ: S(x) = ЛгД! |х|<1.)
«о
n п V cos пх Зх2 — блх 4- 2л2 ____
9. Доказать, что 5 ——-2— = -------------------, 0 <
п = I х л.
10. Подобрать два таких ряда, чтобы их сумма была сходящимся рядом, а разность — расходящимся.
11. Доказать равномерную сходимость функциональ-со
ного ряда У (— У на отрезке [0; 1].
л/п
12. Исследовать на сходимость ряд с общим членом 1/л
С yxdx / „ -- 2 \
ип= \ ------- (Ответ: сходится, —-.)
J х2 + I \ Зп3/2 /
©
00
у— является ре-
шением дифференциального уравнения / — ху = 0.
125
13. КРАТНЫЕ ИНТЕГРАЛЫ
13.1. ДВОЙНЫЕ ИНТЕГРАЛЫ И ИХ ВЫЧИСЛЕНИЕ
У f(xi. yJbSi
(13.1)
На плоскости Оху рассмотрим некоторую замкнутую область D, ограниченную замкнутой линией L. Пусть в D задана функция г = = f(x, у). Произвольными линиями разобьем D на п элементарных областей S,. площади которых AS, (Z=l.n) (рис. 13.1). В каждой области S, выберем произвольную точку Р,(х„ у,). Диаметром di области S, называется длина наибольшей из хорд, соединяющих граничные точки Si.
Выражение вида
/л =
<=1
называется п-й интегральной суммой для функции г = f(x, у) в области D. Вследствие произвольного разбиения области D на элементарные области Si и случайного выбора в них точек Pi можно составить бесчисленное множество указанных сумм. Однако, согласно теореме существования и единственности, если функция г = f{x, у), например, непрерывна в D и линия L — кусочно-гладкая, то предел всех этих сумм, найденных при условии di->-0, всегда существует и единствен.
Двойным интегралом функции г — f(x, у) по области D называется предел lim /«, обозначаемый f(x, y)dS. Таким образом, по определив D
лению п
ЭДДх, y)dS = lim 2 f(x„ y,)AS,-. (13.2)
О Л -0,^1
Здесь и далее будем предполагать, что функция г = f(x, у) непрерывна в области D и линия L — кусочно-гладкая, поэтому указанный в формуле (13.2) предел всегда существует.
Укажем основные свойства двойного интеграла и его геометрический и физический смыслы.
1. JJdS = So, где So — площадь области интегрирования D. о
2. Если подынтегральная функция z = f{x, у) = р(х, у)—поверхностная плотность материальной пластины, занимающей область D, то масса этой пластины определяется по формуле
т= йу(х, y)dS. (13.3)
D
В этом заключается физический смысл двойного интеграла.
3. Если f(x, у)>0 в области D, то двойной интеграл (13.2) численно равен объему » цилиндрического тела, находящегося над
126
плоскостью Оху, нижним основанием которого является область D, верхним — часть поверхности г = f(x, у), проектирующаяся в О, а боковая поверхность — цилиндрическая, причем ее прямолинейные образующие параллельны осн Ог и проходят через границу L области D (рис. 13.2). Если f(x, у)^0 в области D, то двойной интеграл численно равен
Рис. 13.1
Рис. 13.2
объему цилиндрического тела, находящегося под плоскостью Оху (рис. 13.3), взятому со знаком « —» (—о). Если же функция [(х, у) в области D меняет знак, то двойной интеграл численно равен разности объемов цилиндрических тел, находящихся над плоскостью Оху и под ней, т. е.
f(x, y)dS = V| — и2 (13.4)
D
смысл двойного
(рис. 13.4). Это свойство выражает
геометрический
127
4. Если функции z = fj(x, у) (j = 1, k) непрерывны в области D, то верна формула
fi(x.
y)dS.
5. Постоянный множитель С подынтегральной функции можно выносить за зиак двойного интеграла:
ЙС/(х, y)dS = С й f(x, y'jdS.
D О
6. Если область D разбить на конечное число областей Di, £>2, .... Dk, не имеющих общих внутренних точек, то интеграл по области D равен сумме интегралов по областям £>t:
й f(x, y)dS = \\f(x, y)dS + ЙКх, J/)dS+...+ \\f(x, y)dS.
D D, Di Dt
7 (теорема о среднем). Для непрерывной функции г = f (х, у) в области D, площадь которой So, всегда найдется хотя бы одна точка P(ij, л) € О, такая, что
й f(x, y)dS = f& n)S0.
D
Число /(5, л) называется средним, значением функции z = f(x, у) в области D.
8, Если в области D для непрерывных функций f(x, у), ft(x, у), fi(x, у) выполнены неравенства fi(x, y)^f(x, у)^/г(х, у), то
y)dS < \\f(xr y)dS < Sf2(x, y)dS.
D D D
9. Если функция z = f(x, у) #= const и непрерывна в области D, М = max f(x, у), m = min f(x, у), то
(х, (X.
mSu< й Кх’ y)dS < MSd-d
Замечание. Так как предел п-н интегральной суммы 1п (см. формулы (13.1), (13.2)) не зависит от способа разбиения области D на элементарные области S, (теорема существования и единственности), то в декартовой системе координат область О удобно разбивать на элементарные области S< прямыми, параллельными осям координат. Полученные при таком разбиении элементарные области S<, принадлежащие области О, являются прямоугольниками. Следовательно, dS = dxdy и
й К*. y}dS = й f(x, y)dxdy.
В В
Область интегрирования D называется правильной в направлении оси Ох (оси Оу), если любая прямая, параллельная оси Ох (оси Оу), пересекает границу L области D не более двух раз (рис. 13.5, а). Область D считается также правильной, если часть ее границы или вся граница L состоит из отрезков прямых, параллельных осям координат (рис. 13.5,6).
126
Рассмотрим методы вычисления двойного интеграла по областям, правильным в направлении координатных осей; так как практически любую область можно представить в виде объединения правильных областей (рис. 13.5, в), то, согласно свойству 6 двойных интегралов, эти методы пригодны для их вычисления по любым областям.
Для вычисления двойного интеграла нужно проинтегрировать подынтегральную функцию z = /(х, у) по одной из переменных (в пределах ее изменения в правильной области О) при любом постоянном значении другой переменной. Полученный результат проинтегрировать по второй переменной в максимальном диапазоне ее изменения в D. Тогда все произведения f(x, y)dxdy в двойном интеграле (предел суммы (13.2)) будут учтены при суммировании точно по одному разу, и мы избавимся от лишних, не принадлежащих области D, произведений.
Если область D, правильная в направлении оси Оу, проектируется на ось Ох в отрезок [а; £>], то ее граница L разбивается на две линии: АтВ, задаваемую уравнением у — (х), и АпВ, зада-
ваемую уравнением </ = <р2(х) (рис. 13.6). Тогда область D определяется системой неравенств:
D: а С х С b, <pi (х) У "С <рг(х),
и двойной интеграл вычисляется по правилу (внутреннее интегрироваиие ведется по переменной у, а внешнее — по переменной х)
b <рг (х)
^f(x, y)dxdy = dx f(x, y)dy.
D a <pi(x)
(13.5)
Если область D, правильная в направлении оси Ох, проектируется на ось Оу в отрезок [с; d], то ее граница L разбивается на две линии: CpD*, задаваемую уравнением х = (у), и CqD*, задаваемую урав-
нением x=ip2(i/) (рис. 13.7). В этом случае область D определяется системой неравенств:
О: с С у С d, ipi(i/Xx<i|>2(i/),
и двойной интеграл вычисляется по правилу (внутреннее интегрироваиие ведется по переменной х, а внешнее — по переменной у)
4'2 (У>
fif(x, y}dxdy= \dy $ /(х, y)dx.
D с у (у)
(13.6)
5-357
129
Выражения, стоящие в правых частях равенств (13.5), (13.6), называются повторными (или двукратными) интегралами.
Из равенств (13.5) и (13.6) следует, что
ft <р2(х) а *2(9)
jdx 5 f(x, y)dy = \dy j f(x, y)dx. (13.7)
u С
Переход от левой части равенства (13.7) к правой его части и обратно называется изменением порядка интегрирования в повторном интеграле.
Ри с. 13.6
Ри с. 13.7
Пример I, На плоскости Оху построить область интегрирования D по заданным пределам изменения переменных в повторном интеграле
4 За/х
I=\dx J dy. Изменить порядок интегрирования и вычислить ин-
0 Зч-'/8
теграл при заданном и измененном порядках интегрирования.
> Область интегрирования D расположена между прямыми х = 0 и х = 4, ограничена снизу параболой у = Зх2/8, сверху параболой у =
= 3да (рис. 13.8). Следовательно,
4 4
/ = j (y\\y,^)dx = j (Зд/Г—3x2/8)rfx = (2.v3/2 — r’/8)lo = 8-
о 0
С другой стороны, область интегрирования D расположена между прямыми у = 0 и у = 6, а переменная х изменяется в данной области при каждом фиксированном значении у от точек параболы х = ///9 до точек параболы х=у8у/3, т. е., согласно формуле (13.7), имеем
6 v'%7/3 6
I=\dy 5 dx=\(~\/^--¥)dy=
О i//9 О
130
Пример 2. Изменить иорядок интегрирования в повторном интеграле.
1 2-х
\dx 5 f(.x, y)dy.
О Л"’
> Область интегрирования D ограничена линиями х = 0, х=1, у = х2 и у = 2— х (рис. 13.9). Так как правый участок границы области D задан двумя линиями, то прямая у = 1 разбивает ее на
области £>i: 0 у "С 1, О
В результате получаем
<( х "С ~\[у и D>'. 1 у "С 2, О "С Л’ "С 2 — у.
Пример 3. Вычислить двойной интеграл
S(%4-#4-3) dxdy* D
если область D ограничена линиями х-\-у = = 2, х = 0, у = 0.
> Область интегрирования D ограничена прямой у = 2 — х и осями координат (рис. 13.10). Следовательно,
2 2-х
И (* + У + 3) dxdy = \dx 5 (•» + (/ + 3) dy =
О 0 0
k 4- у 4- З)2
2
2
dx = -±- j (25 — (х 4- 3f)dx —
0
(x4-3)3\f 26
3 ) |о 3
Пример 4. Найти среднее значение функции г = .г 4- бу в треугольнике, ограниченном прямыми у = х, у=3х, х = 2.
131
► Средним значением функции z = f(x, у) в области D является число (см. свойство 7 двойных интегралов)
7 = "^7 y}dxdv-
D
Вычислим сначала площадь области D:
2 Зх 2
SD = \\dxdy = \ dx \ dy = \ (Зх — x)dx = x2\l = 4.
D 0x0
Аналогично получаем
2 Зх 2
гг Г Г fl |3х
\ \ (х 4- бу) dxdy = \dx \ (х ~^6y)dy = \ — (х Ц- бу)2 dx =
D Ох 0
2 2 2
= ~ j((19*)2-(7x)2)dx= ~ ^312х2Дх = 26^х2Дх =
О 0 0
26 ,12 208
=—ч= —
Таким образом,
7 = ± 208 _ 52_ ' ~ 4 3 ~ 3 ’ *
АЗ-13.1
1. Вычислить следующие повторные интегралы:
2 I
a) J dx J (х2 + 2y)dx; о о
8 5 2 х
б) ( dy ( (х -f- 2y)dx; в) [ dx (
J J J J У
— 3 /Л —4 1 1/х
{Ответ: а) 14/3; б) 50,4; в) 2,25.)
2. Расставить пределы интегрирования в повторном интеграле для двойного интеграла §{х, у) dxdy, если из-
D
вестно, что область интегрирования D:
а) ограничена прямыми х = 1, х = 4, Зх — 2ц 4- 4 = 0, Зх- 2у- 1=0;
б) ограничена линией х1 4*у2 — 4х = 0;
в) является треугольной областью с вершинами в точках 0(0, 0), 4(1, 3), В(1, 5);
132
г) ограничена линиями у = х3-{-1, х = 0, х-(-у = 4
3. Изменить порядок интегрирования в данных повторных интегралах:
2 -/i-x! 1 5х
а) \ dx $ f(x, y)dy; б) $ dx $ f(x, y)dy; — 2 0 0 2x
1 I ~У
B) \dy J /(x, y)dx.
4. Вычислить ЭД (x2 + yjdxdy, если область D ограни-fl
чена линиями у = x2 и у2~х. (Ответ: 33/140.)
5. Вычислить ЭД x?y2dxdy, если область D ограничена о
линией х24-у2 = 9. (Ответ: 0.)
6. Вычислить ЭД х cos (x-f- yjdxdy, если область D огра-D
ничена линиями у = 0, х = л, у — х. (Ответ: — л/2.)
7. Вычислить ЭД ydxdy, если область D ограничена о
первой аркой циклоиды х = a(t — sin/), у — а(\—cos/) и осью Ох. (Ответ: -|-ла3.)
Самостоятельная работа
1. 1. Представить двойной интеграл ЭД f(x, y) dxdy в ви-о
де повторного интеграла при разных порядках интегрирования по х и по у, если известно, что область D ограничена линиями у — 2х, х = 0, г/4-х = 3.
2. Вычислить ЭД xdxdy, если область D ограничена о
линиями у — х2, у = 2х. (Ответ: 4/3.)
2. 1. Изменить порядок интегрирования в повторном интеграле
4 2х — 3
\dx $ f(x, y)dy.
0 х’/2-З
2. Вычислить ЭД xdxdy, если область D ограничена о
линиями х = 0, у— 0, у = д/4 —х2. (Ответ: 8/3.)
133
3. 1. Изменить порядок интегрирования в повторном интеграле
8 12
$ dy $ f(x, y)dx.
-4 (f/ + 4)/2
2. Вычислить ЭД x^dxdy, если область D ограничена
D
линиями у = х, у=\/х, х = 2. (Ответ: 2.)
13.2. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ. ДВОЙНЫЕ ИНТЕГРАЛЫ В ПОЛЯРНЫХ КООРДИНАТАХ
Пусть переменные х, у связаны с переменными и, v соотношениями х=<р(щ и), г/ = ф(и, и), где (р(и, о), ф(и, и)—непрерывные и дифференцируемые функции, взаимно однозначно отображающие область D плоскости Оху на область D' плоскости O'uv, при этом якобиан
J =/(х, у) =
дх ди др дГ
дх dv ду dv
сохраняет постоянный знак в D. Тогда верна формула замены переменных в двойном интеграле.
ЭД^х, у) dxdy = \\f (<р(и, v), ф(и, и)) | JI dudv. (13.8)
D D’
Пределы в новом интеграле расставляются по рассмотренному ранее правилу с учетом вида области D'.
Пример 1. Вычислить двойной интеграл
ЭД + у) dxdy
D
по области D плоскости Оху, ограниченной линиями у = х — 1, у = х 2, У= — х — 2, у — —х + 3.
> Положим
и = У — X, | У = У + -г. J
(I)
Тогда прямые у = х — 1 и у — х 4- 2 перейдут соответственно в прямые и = — 1, и— 2 плоскости O'uv, а прямые у = — х — 2, у = —х 4- 3 — в прямые v = — 2 и и = 3 этой же плоскости. При этом область D отобразится в прямоугольник D' плоскости O'uv, для которого —1 "С и 2, — 2 < v С 3.
Из системы (1) находим:
х = ( —и 4- и)/2,|
У — ( u + v)/2.j
134
Следовательно,
] = дх ду ди ди дх ду dv до = 1_ 1 — Т 2 1 1 2" 2 _ 1
а |/| = 1/2. Поэтому, согласно формуле (13.8),
(* 4- У) dxdy 6 = 55п ’ ^-dudv = О'
2 15 vdv = —
1 , 1 = \ du \ . ч
— I 2
Известно, что прямоугольные декартовы (х, у) и полярные (р, q>) координаты связаны между собой следующими соотношениями:
х = р cos <р, у = р sin <р, (р 0, 0 й/ <р < 2л).
Если в двойном интеграле перейти от декартовых к полярным координатам, то получим формулу (так как якобиан J = р)
й/(х, у) dxdy = 55 /(р cos Ф- Р s'n Ф') pdpdtp. (13.9) о О'
В обобщенных полярных координатах, для которых
х = ар cos <р, у — bp sin <р (р О О, 0 < <р < 2л), (13.10)
имеем (так как якобиан J — abp):
S К-1', У) dxdx = ab j(ap cos ср, bp sin ср) pdpdif. (13.11) D О'
Представление двойных интегралов в виде повторных в правых частях формул (13.9), (13.11) приводит к разным пределам в зависимости от того, где находится полюс О полярной системы координат’ вне, внутри или на границе области D.
1. Если полюс О полярной системы координат находится вне области D, ограниченной лучами ср = а, <р = 0 (а < 0) и линиями АтВ, АпВ (их уравнения соответственно р = р, (<р), р = рг(<р). где pi(<p), ра(ф) (pi(q>X Рг(<р))— функции, заданные на отрезке {а; 0]), то двойной интеграл в полярных координатах сводится к повторному интегралу по правилу (рис. 13.11)
Р р4<р)
55 f(x, у) dxdy = 5 dy 5 f(p COs ф. P sin <p) pdp.
O a p, (<P) 2 3
(13.12)
2. Если полюс О находится внутри области D и уравнение границы области О в полярной системе координат имеет вид р = р(ф), то в формуле (13.12) а = 0, 0 = 2л, р, (<р) = 0, рг(ф) = р(ф) (рис. 13.12).
3. Если полюс О находится на границе области D и уравнение ее границы в полярной системе координат имеет вид р = р(<р), то в формуле (13.12) р, (<р) — 0, рг(ф) = р(ф), а а и 0 могут принимать различные значения (рис. 13.13, 13.14).
135
a
5
Аналогичные формулы имеют место и для случая обобщенных полярных координат.
Пример 2. Вычислить ЭД -\/(х2 -ф у2)3dxdy, если область D — круг pa-fl
диусом R с центром в начале координат.
► Если область D — круг или его часть, то многие интегралы проще вычислять в полярных координатах. Согласно формулам (13.9) и (13.12) (случай 2), имеем:
ЭД у(х2-фу2)3dxdy = ЭД д/(р2 sin2 q> + p2 cos2 <p)3pdpd<p = fl fl
2л R
Sf f R5
p4rfpd<p = I dq> V p4dp = 2л ——.
D 0 0
Пример 3. Вычислить площадь фигуры, ограниченной эллипсом
136
> В интеграле \\dxdy, выражающем площадь эллипса в декарто-D
вой системе координат, перейдем к обобщенным полярным координатам с помощью равенств (13.10). Уравнение эллипса в обобщенных полярных координатах имеет вид р=1. Следовательно, согласно формуле (13.11), получаем
2л I
Ц dxdy — Ц abpdpdq = ab \ d<p\ pdp — nab. 4
D D‘ 00
A3-13.2
1. Вычислить \\(xy)dxdy, если область D ограни-fl
чена прямыми 2x -j-у = 1, 2x у — 3, x — y=—1, x — — y — 2. (Ответ: 2,5.)
2. Использовав полярные координаты, вычислить двойной интеграл \\(х2 + y2)dxdy, если область D огра-
D
ничена окружностью х2 -f- у2 = 4х. (Ответ: 24л.)
3. Найти площадь фигуры, ограниченной линиями х2-[-у2 = 4х, х1 + у2 = 6х, у = —!—х, у = х[3х. (Ответ: -уз
5л/6.)
4. Вычислить jjarctg — dxdy, где D — часть кольца, в х
ограниченного линиями х2 у2 = 1, х2 -f- у2 = 9, у =—— х, у = -\/Зх. (Ответ: л2/6.)
5. Найти JJ xydxdy, если область D ограничена эллип-D
сом л2 + р = 1 и прямыми х = 0, у = 0. (Ответ: а2Ь2/8.)
оо
6. Вычислить несобственный интеграл J e~x’dx, ис-— оо
пользовав значение интеграла \\е~х'~у dxdy, взятого по о
области D, ограниченной окружностью х2 + у2 = R2 {Ответ: х/я.)
Самостоятельная работа
1. Вычислить (12 — х — y)dxdy, если область D огра-
D
ничена окружностью х2 + у2 = 9. (Ответ: 108л.)
137
2. Вычислить У (6 — 2х— 3y)dxdy, если область D огра-
D
ничена окружностью х24~г/2 = 4. (Ответ: 24л.)
3. Вычислить Ц(4 — х — y)dxdy, если область D огра-
D
ничена окружностью х1 + у1 = 2х. (Ответ: Зл.)
13.3. ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ
Вычисление площадей плоских фигур. Рассмотрим несколько примеров.
Пример I. Вычислить площадь фигуры, ограниченной линиями у = к'1 — 2х, у = х.
► По уравнениям границы области D строим данную фигуру (рис. 13.15). Так как линии, ограничивающие ее, пересекаются в точках 0(0, 0) и Мо(3, 3), то в О справедливы неравенства: 0 sj х sj 3, х'2— — 2х sj у sj х. Следовательно, на основании свойства 1 двойных интегралов искомая площадь
Пример 2. Вычислить площадь фигуры, ограниченной линией (хл + у2)2 = а‘2(х'2 — уг), а > 0.
► Перейдем к полярной системе координат, в которой уравнение данной кривой примет вид:
р4 = a2p2(cos2 — sin2 <р), р2 = a2 cos 2ф, р = a л/cos 2ф.
Последнее уравнение задает кривую, которая называется лемнискатой Бернулли (рис. 13.16).
Рис. 13.15
Р и с. 13.16
Как видно из полученного уравнения и рис. 1346, кривая симметрична относительно координатных осей, и площадь S фигуры, ограниченной этой кривой, выражается двойным интегралом S =
138
= 4 ЭДpdpd<p. Здесь D— фигура (область), лежащая в первом квад-D
ранте, для которого 0^<р<л/4, 0 < р < a ycos 2<р. Следовательно, л/4 я/4 2 , /---л-
3 = 4 $ dq> $ pdp = 4 ) “ С°5*ФЛ() =
о о о 1
л /4
= 2а2 j cos 2<f>d<f> — d2 sin 2<f |j/4 = a2. ◄
о
Вычисление объемов тел. Рассмотрим следующие примеры.
Пример 3. Вычислить объем тела, ограниченного поверхностями г = х2 + у2, х + у = 1, х = 0, у = 0, г = 0.
> Данное тело ограничено координатными плоскостями, плоскостью х + у = 1, параллельной оси Ог, и параболоидом вращения г = = х2 + у2 (рис. 13.17). На основании геометрического смысла двойного
интеграла (см. § 13.1, свойство 3) искомый объем v можно вычислить по формуле
V = Эд(х2 у2) dxdy,
D
где область D ограничена треугольником, лежащим в плоскости Оху, для которого 0 С х <::: 1, 0 < sj: 1 — х. Следовательно,
Пример 4. Вычислить объем тела, ограниченного поверхностями У = 1 +х2 + г2, у =5.
139
Рассматриваемое тело ограничено параболоидом вращения с осью Оу и плоскостью у = 5, перпендикулярной к оси Оу (рис. 13.18). Его проекция на плоскость Oxz — круг, определяемый уравнениями у = 0, х2 + г2 4. Искомый объем
у = 1 — х2 — z2)dxdz = 55(4 — х2 — z2)dxdz.
D о
Перейдем в полученном интеграле к полярным координатам с помощью равенств х = р cos <р, z = р sin <р. Тогда dxdz = pdpdtf н
2л 2
v= 55(4~ p2)pdpdq>= 5 dtp 5 (4Р — р'Ир =
D 0 0
= 2nf 2p2— — M = 8л. 4 \ 4 / |o
Вычисление площадей поверхностей. Пусть в области Ог плоскости Оху задана непрерывная функция z = /(х, у), имеющая непрерывные частные производные. Поверхность, определяемая такой функцией, называется гладкой. Очевидно, что область D, есть проекция рассматриваемой поверхности на плоскость Оху. Площадь Qz поверхности z — f(x, у), (х, у) g £>г, вычисляется по формуле
о.
(13.13)
В случае, когда гладкая поверхность задана функцией x — f(y, г) (в области Dx) или функцией y = f(x, г) (в области Dy), площадь этой поверхности вычисляется по формуле
Qa=SVi+®+® dydz (|з|4)
D(
ИЛИ
Q>=fi л/1+(М+(2)dKdz- (13-15)
о,
140
Пример 5. Вычислить площадь части конуса у = 2-у/х2 -ф z2, расположенной внутри цилиндра х‘ -ф г1 = 4х.
> Так как поверхность задана функцией вида y = f(x, г), то ее площадь Q;, следует вычислять по формуле (13.15), где область Dy — проекция данной поверхности на плоскость Охг (рис. 13.19). Эта проек-
Р и с. 13.19
ция представляет собой круг, органиченный окружностью (х — 2)2 -ф ф г2 = 4.
Так как ду _______________ 2х ду _ 2z
то искомая площадь
Qy = л/1 + '4+ 2 +--4г^ dxdz =
JJ V X- + г X- -ф г2 о,
= rfvrfu =--\z = р cos (₽’ dxdz = I =
’ jJ у Iх — р sin <р, р = 4 sin <р I
D, л 4 bin л
= д/1Г J dtp J рс/р = J sin2 qdq — оо о
= 4 (1 — cos — 4 "^5 ---sin 2<р^ = 4л -у/ъ. ◄
о
Вычисление массы материальной пластинки. Покажем, как это делается, на примере.
141
Пример 6. Вычислить массу материальной пластинки, лежащей в плоскости Оху и ограниченной линиями х={у— 1)"’, у = х— 1, если ее. поверхностная плотность ц = у.
> Найдем координаты точек пересечения линий, ограничивающих область D: Л(1, 0), S(4, 3) (рис. 13.20). Тогда из физического смысла двойного интеграла (см. § 13.1, свойство 2) следует, что искомая масса
з у + I
т= §ydxdy = dy 5 У^х —
D 0 (</-н'
3 .4
.= $</(</+ 1 - (</ - I)2) dy = S (.Зу2 - y'")dy =
Вычисление статических моментов и координат центра масс материальной пластинки. Если на плоскости Оху дана материальная пластинка D непрерывной поверхностной плотностью ц(х, у), то координаты ее центра масс С(хс, ус) определяются по формулам:
й*ц(х. y)dxdy $уц(х, y)dxdy
х с = —-------------, у с = ----------— (13.16)
)ц(х, y)dxdy y)dxdy
d b
Величины
Л1х=Йуц(х, y)dxdy, Ms = $л'|т(х, y)dxdy (13.17) D D
называются статическими моментами пластинки D относительно осей Ох и Оу соответственно.
Пример 7. Найти координаты центра масс пластинки £>, лежащей в плоскости Оху и ограниченной линиями у = х, у — 2х, х = 2 (рис. 13.21), если ее плотность |х(х, у) = ху.
Рис. 13.20
Вначале определим массу пластинки D:
2 2г 2
m = xydxdy = xdx ydy = j х • 1 dx =
D о л- о
142
2
2
= 4- ( х(4х2 — x2)dx = ~Д x3dx = ,y4 I =6.
z J 2 J о |o
0 ' 0
Согласно формулам (13.16), координаты центра масс:
2 2х
х<: = Tn §Х^Х<*У ~ "(Г ydy — D Q х
2 2
1 С 2 1 /1 ’ 1 С 4 . *5Р 8
= 6- Г -T(^-^dx=-y dz=-|o=_, о о
2 2х
Ус = ^Xy2dxdy = -i- ^xdx j y2dy =
1) 0 x
2 2
1 f уЧ2< 7 f , , 112
= бГП = T8 J dX=~4^- < i) i)
Вычисление моментов инерции материальной пластинки. Моменты инерции относительно начала координат и осей координат Ох, Оу материальной пластинки D непрерывно распределенной поверхностной плотностью ц(х, у), которая лежит в плоскости Оху, вычисляются соответственно по формулам:
Л> = \\(х-+ у2)ц(х, y)dxdy,
D (13.18)
Л = $y2p(x, y)dxdy, = \\х2у.(х, y)dxdy.
D D
Пример 8. Вычислить моменты инерции относительно точки границы однородного круга и его диаметра, если радиус круга R, а вес Р.
Поместим начало координат в точке, лежащей на границе круга, а центр круга — в точке C(R; 0) (рис. 13.22). Тогда задача сведется
У..
Рис. 13.22
к нахождению моментов инерции круга относительно начала координат и оси Ох.
143
Так как круг однороден, то его плотность р постоянна и р = = P/(gnR2). Уравнение окружности в декартовой системе координат имеет вид (х— Р)2 + у2 = R, а в полярной — р = 2Р cos <р. Для данного круга выполняются соотношения —л/2 <р л/2, О^р^ 2 R cos
Следовательно, на основании формул (13.18) имеем:
= ц й(х2 4- y^dxdy = D я/2 2/?cos<p л/2
= р $ dtp $ p3dp -- р • 4/?4 J cos4 tpdtp = — л/2 0 —л/2
я/2 л/2
= (-i...+s°--s..2_4lyd(₽ = 2(i^j (1+2cos2(₽ + L+^)rfq,==
О о
/ I I \ |л/2
= 2ц/? ( ф 4- sin 2m — ф + — sin 4ф ) | =
\ * * /1 о
л/2 2/?соъф
= р §y2dxdy = р $ dtp $ р3 sin2 <pdp = о -л/2 о
л/2 л/2
. г>4 С 4 9 j n г»4 С i • 2 n 1 4“ COS 2ф
= 4ц/? \ cos ср sirr срг/ф = 8ц/? \ — sin 2ср ---------------x-dcp =
— л/2 О
л/2 л/2
= рР* sin2 2tpdtp -|- pR* J sin2 2q> cos 2q>dq> = о 0
Ot'f'2 ' /1 , , . , „4 sin3 2<p |"/2
= pR I ~2 (1 — cos 4tp)dtp + p/? --------6- 0 =
о
1 / 1 \ l-1/-' я IP
= ун/?4(^<₽-Ysin44|o =Tp/?4 = TJ/?2 ◄
A3-13.3
1. Вычислить площади фигур, ограниченных следующими линиями:
а) у =~\/х, у = с2л[х, х = 4;
б) z/2 = 10х + 25, у2 = —6х + 9; в) р = a sin 2<р, а > 0. (Ответ: а) б) -^-V15; в) -А. ла2Л \ о 3 1 /
2. Вычислить объемы тел, ограниченных указанными поверхностями:
144
а) плоскостями x = 0, y = 0„ z = 0, x — 4, у = 4 и параболоидом z = 1 + x2 + y2\
б) цилиндрами x2 + у2 = R2, x2 + z2 = /?2;
в) параболоидом z — x2-^-y2 и плоскостями z — 0. у = 1, у = 2x, y = 6 — x;
г) цилиндром x2 -j-y 2 = 4 и плоскостями z — 0, z — = х + у+10;
„2 у2
д) эллиптическим цилиндром — -ф у = 1 и плоскостями z — 12 — Зх — 4у, z=l. (Ответ: а) 186 у ; б) у в) 78г) 40л; д) 22л.)
3. Вычислить площадь части плоскости 6х + Зу 4-2z = 12, которая расположена в первом октанте. (Ответ: 14.)
4. Вычислить площадь части конуса z = д/х2 4- </2 расположенной внутри цилиндра х2 + у2 = 4х. (Ответ-4д^2л.)
5. Вычислить площадь части поверхности параболоида 2z = x2-(-y2, лежащей внутри цилиндра х2 -ф у2 = 1
(Ответ: -j-л(д^8— 1).)
6. Вычислить массу квадратной пластины со стороной а, если ее плотность в любой точке М пропорциональна квадрату расстояния от этой точки до точки пересечения диагоналей, а в угловых точках квадрата равна единице. (Ответ: а2/3.)
Самостоятельная работа
I. Вычислить площадь фигуры, ограниченной линиями у = 2 — х, у2 = 4х + 4. (Ответ: 64/3.)
2. Вычислить объем тела, ограниченного поверхностями x2-(-y2—l, z = 0, x + z/ + z = 4. (Ответ: 4л.)
3. Вычислить объем тела, ограниченного цилиндром z = y2/2 и плоскостями 2x + 3z/= 12, х = 0, у = 0, z = 0. (Ответ: 16.)
145
АЗ-13.4
1. Вычислить координаты центра масс однородной плоской фигуры, лежащей в плоскости Оху и ограниченной линиями р2 = 4х + 4, у2 = — 2х + 4. (Ответ: хс = = 2/5, ус = 0.)
2. Вычислить координаты центра масс фигуры, ограниченной линиями у = х2, у2 = х, если плотность фигуры у(х, у) = ху. (Ответ: хс = 9/14, ус = 3/56.)
3. Найти координаты центра масс однородной плоской фигуры, ограниченной кардиоидой р = а(1 + cos ср). (От-вет-.- хс = А а, ус = 0.)
4. Вычислить момент инерции относительно начала координат фигуры, ограниченной линией х2 ф- у2 — 2х = 0, если ее плотность р(х, у) = 3, 5. (Ответ: 21л/4.)
5. Вычислить моменты инерции относительно начала координат и осей координат пластины плотностью ц(х, у) = х2у, лежащей в плоскости Оху и ограниченной линиями у = х2, у — 1. (Ответ: /0 = 104/495, Л = 4/33, 1У = = 4/45.)
6. Вычислить момент инерции относительно полюса пластины, ограниченной кардиоидой р = а(1—cos q?), если ее плотность р = 1,6. (Ответ: 7па'>/2.)
7. Вычислить момент инерции относительно центра (р(х, у) = 1) эллиптической пластины с полуосями а и Ь. (Ответ: лаЬ(а2 + 62)/4.)
Самостоятельная работа
I. Вычислить момент инерции относительно начала координат фигуры плотностью ц(х, у)= 1, ограниченной линиями х У = 2, х = 2, у = 2. (Ответ: 4.)
2. Вычислить координаты центра масс однородной фигуры, лежащей в плоскости Оху и ограниченной линиями у=~х2 + 2х, у = 0. (Ответ: хс=1, ус=1/4.)
3. Вычислить момент инерции относительно точки пересечения диагоналей прямоугольной пластинки со сторонами 4 и 6, если ее плотность ц(х, у) = 2. (Ответ: 208.)
13.4. ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ
Пусть функция u = f(x, у, г) непрерывна в замкнутой области V £ RJ, ограниченной некоторой замкнутой кусочно-гладкой поверхностью S. С помощью произвольных гладких поверхностей разобьем 146
область Инал элементарных областей I', (/ = 1, л), объемы которых обозначим через Ан,. В каждой элементарной области К, выберем ПРОИЗВОЛЬНО ТОЧКу М, (х,, у,, Zi) и постооим CVMMV
Л = S /(х„ //,, z,)Ah„ (13.19)
t= I
Через d, обозначим максимальный диаметр элементарной области К.
Сумма (13.19) называется п-й интегральной суммой функции f(x, у. z) в области V.
Предел сумм (13.19). найденный при условии, что d,->-0, называется тройным интегралом функции f(x, у, z) по области V и обозначается j^/(x, у, z)dv. Таким образом, по определению и
У- z)da = lim S f(*i, y>, Zi)&Vi. (13.20)
Г d.^0 i= I
Если подынтегральная функция f(x, у, z) непрерывна в области И, то интеграл (13.20) существует и не зависит от способа разбиения V на элементарные области К и выбора точек М,.
Многие отмеченные в § 13.1 свойства двойных интегралов справедливы и для тройных интегралов, поэтому приведем только те их свойства, которые несколько отличаются от свойств двойных интегралов.
1. Если в области V f(x, у, z)= 1, то
\\\de = v, (13.21)
v
где v — объем области К
2. В случае, когда подынтегральная функция [(х, у, z) задает плотность б(х, у, z) тела, занимающего область V, тройной интеграл выражает массу этого тела:
т= Щб(х, у, z)dv. (13.22)
v
Следует подчеркнуть, что в декартовой системе координат область V удобно разбивать на элементарные области плоскостями, параллельными координатным плоскостям; при этом элемент объема dv = dxdydz.
Считаем область И правильной (т. е. такой, что прямые, параллельные осям координат, пересекают границу области И не более, чем в двух точках). Для правильной области И справедливы неравенства (рис. 13.23): а<х<&, (х)< у < <р2(х), ф|(х, «/)< z < ф2(х, у) и
следующая формула для вычисления тройного интеграла
s Ы-Ч чЧ-г,.'/)
®f(x, у, z)dxdydz = \dx j dy j f(x, y, z~)dz. I 13.23) V a y)
Таким образом, при вычислении тройного интеграла в случае простейшей правильной области V вначале интегрируют функцию [(х, у, z) по одной из переменных (например, z) при условии, что оставшиеся две переменные принимают любые постоянные значения в области интегрирования, затем результат интегрируют по второй переменной (например, у) при любом постоянном значении третьей переменной в V и, наконец, выполняют интегрирование по третьей переменной (например, х) в максимальном диапазоне ее изменения в V
Более сложные области интегрирования разбиваются на конечное
147
число правильных областей, и результаты вычисления по этим областям суммируются. В частности, если область интегрирования — прямоугольный параллелепипед, задаваемый неравенствами И = (а х 6, «С у С- d, р z то
b d q
®/(х, У, z)dxdydz — \dx\dy\f(x, у, z)dz. (13.24)
V а с p
Пример 1. Вычислить тройной интеграл I = Щ(2х 4- y)dxdydz, где v
V ограничена поверхностями: у — х, у = 0, х = I, г = I, г = 1 -|-х2 + у2.
► По заданным поверхностям строим (рис. 13.24). В области V справедливы О 'С у ’С х, 1 sj z С. 1 4- х2 у2. Тогда
область интегрирования
неравенства: OsSjxsSjl,
J48
’ г Ч-x' + i/*
/= \dx\dy J (2х + y'idz = о о I
lx lx
= \dx\(2xy)z +x’+!,’dy = \ dx\(2x ~f-y) (x2-f-y2)dy =
О 0 0 0
1 x
= 5 dx 5 (2x3 + y3 + 2xy2 4- x2y) dy =
Q 0 1
= ^2x3y+ + y^’ + T4',)|orf'V =
9
o
Пусть функции
X — <p(u, v, w), 'I
у = ф(и, v, w), I (13.25)
z = x(u, v, w). )
непрерывны, имеют непрерывные частные производные, якобиан
dx dx dx
du dv dw
dy dy dy
du dv dw
dz dz dz
du dv dw
и сохраняет знак в области V' изменения переменных и, v, w. Функции (13.25) отображают взаимно однозначно область V в область V’ Тогда верна формула
Щ/(х, у, z)dxdydz = $/(ф(и. v, w), ф(и, v, w), X(u, v, w}) |/| dudvdw. V V'
В цилиндрических координатах p, <p, z (рис. 13.25) имеем:
x = p cos <p, у = p sin <p, z = z, 'j
0 ф 2л, 0 p < oo, — oo < z < oo, (13.26)
1 = p, dxdydz = pdpdtpdz. J
В сферических координатах г, ф, 0 (г — радиус-вектор, ф — долгота, 0 — широта или склонение) (рис. 13.26) получаем:
х = г sin 0 cos ф, у = г sin 0 sin ф, z — г cos 0, 3 0^г<оо,0^ф^2л, 0 0 л, г (13.27)
1 — г2 sin 0, dxdydz — г2 sin BdrdtpdB. J
В обобщенных сферических координатах
х = ar sin 0 cos ф, у = br sin 0 sin ф, г = cr cos 0, 1
1 = abcr2 sin 0, dxdydz — abcr2 sin 0<7г<7ф<70. J '
149
Соотношения (13.26) — (13.28) позволяют осуществлять в тройных интегралах переход от - декартовых к цилиндрическим, сферическим или обобщенным сферическим координатам. Формула (13,23) для вычисления тройных интегралов в декартовых координатах справедлива также в цилиндрических и сферических координатах.
Пример 2. Вычислить / = $“\Д2 + У1’ dxdydz, если область ннте-v
грирования V ограничена поверхностями х2 + у2 = 4, z=l, z = 2 + + х + У •
► По заданным поверхностям построим область И (рис. 13.27). Перейдем в заданном интеграле к цилиндрической системе координат:
/ — $ ppdpdtfdz —
Г"
2л 2 2 + р= 2л 2
= $<Мр2^р 5 dz = $p2(i + p2w =
0 0 I 0 0
= -p !;' J (p2 + pjW = 2л (y + y) |02= 5 л- «
150
Пример 3. Вычислить /= $ \>х‘ -ф у2 -ф z'2)3 dxdydz, если область г
интегрирования V ограничена сферой х2 -ф у2 + z~ = 4 и плоскостью У = 0 (у > 0).
Область V представляет собой полушар, расположенный правее плоскости Oxz lydxOi, т. е. сферические координаты г, <р, 0 изменяются в V следующим образом: О г 2, Ossjcpssjn, 0 9 л.
Это означает, что
/ = $ r'r2 sin CWrdq>dO = v
пл 2
j dy j sin r’dr = <p|0 ’ (— cos 6) о о о
rG I - _ 64
6 |o 3
A3-13.5
1. Вычислить $ x:2y2zdxdydz, если область V опре-i'
деляется неравенствами O^x^l.O^y^x, 0 z ху. (Ответ: 1/110.)
2. Вычислить [[[---dxdydz— если область V огра-
JJJ (1 +Х + У + 2)’1
V
ничена плоскостями х = О, у = 0, z = Q, x + y + z=l. (Ответ: ±(In 2 -|).)
3. Вычислить объем тела, ограниченного поверхностями у = х2, у + z — 4, z — 0. (Ответ: 256/15.)
4. Вычислить $x2y2dxdydz, если область И ограни-г
чена поверхностями х2 + у2=1, z = 0, z — x2-\-y2. (Ответ: л/32.)
5. Вычислить объем тела, ограниченного поверхностями х2 + у2=10х, х2 + у2=13х, z = д/^х2 + у2, z = 0, у^О. (Ответ: 266.)
6. Вычислить
ffi (? + i + й d xd!ld2'
V
если область V — внутренность эллипсоида ™ + а Ь~
4-^ = 1. (Ответ: -^-лаЬс^
151
7. Вычислить объем части шара х2у2z2 — 1, расположенной внутри конуса z2 = х2 -ф- у2. (Ответ: -лр —
Самостоятельная работа
1. 1. Расставить пределы интегрирования в интеграле $f(x, у, z)dxdydz, если область V ограничена плоскостями х = 0, у = 0, z — 0, 2х + Зу + 4z = 12.
2. Вычислить \\\ух2у2 dxdydz, если область V v
ограничена поверхностями z = х2 -j- у2, z— 1. (Ответ: 4л/15.)
2. 1. Расставить пределы интегрирования в интеграле $/(х, z)dxdydz, если область V ограничена поверхностями у = х, у = 2х, z = 0, x-(-z = 2.
2. Вычислить + z2 dxdydz, если область V ограничена поверхностями y = x2-\-z2, z=\. (Ответ: 4л/15.)
3. 1. Расставить пределы интегрирования в интеграле у, z)dxdydz, если область V ограничена поверхностями у = х2, z = 0, y + z = 4.
2. Вычислить объем тела, ограниченного поверхностями х24-у2 = 9, z=l, х у z = 1 i. (Ответ: 90л.)
13.5. ПРИЛОЖЕНИЯ ТРОЙНЫХ ИНТЕГРАЛОВ
Вычисление объемов тел. Объем v области V (объем тела) обычно вычисляют по формуле (13.21), в которой в тройном интеграле можно переходить (если это удобно) к различным координатам (цилиндрическим, сферическим и др.).
Пример 1. Вычислить объем тела, ограниченного поверхностями z = 1, г = 5 — х2 — у2.
► По заданным уравнениям поверхностей в декартовых координатах строим область V (рис. 13.28). Тогда в цилиндрической системе координат искомый объем
v — Щ pdpdifdz,
V
где V: (0 «С <р 2л, 0 Р 2, 1 z 5 — р2). Следовательно,
152
2л 2 5 - р2
i>= $d<p$pdp $ dz =
О О J
2
= 2л j р(5 — р2 — I)dp = 2я^2р2 — = 8л. 4
о
Пример 2. Вычислить объем
X2 у2 Z2 ,
— + ут + — = 1.
а Ъ с
тела, ограниченного эллипсоидом
В обобщенных сферических координатах верны формулы (13.26), и поэтому искомый объем
о = Щвбсг2 s>n 9drd<pd0,
V"
где V — область, в которую отображается внутренность эллипсоида при переходе к обобщенным сферическим координатам. Уравнение поверхности, ограничивающей область V, в обобщенных сферических координатах получается путем подстановки в уравнение эллипсоида значений х, у, г из формул (13.28):
г2 sin2 0 cos2 <р + г2 sin2 0 sin2 <р + г2 cos 2 0 = I,
т. е. г= 1. Следовательно,
2л л J
Sr Г 4
d<| \ sin2 OdO \ r2dz = -у лабе. 4
I) о о
Вычисление массы тела. Масса т тела вычисляется по формуле (13.22).
Пример 3. Вычислить массу тела, ограниченного поверхностью конуса (z — 2)2 = х2 + у1 и плоскостью z = 0, если плотность тела 6(х, у, z) = г.
Вершина конуса находится в точке О,(9, 0, 2), и в сечении конуса плоскостью z = 0 получается окружность х2 + у2 = 4, г = 0 (рис. 13.29). На поверхности рассматриваемого тела z = 2 — ух2 + у2 Тогда масса
Рис. 13.29
153
m = ^zdxdydz = v
2л 2 2-p
— 5Й zpdpdqdz = \dq> $ pdp J dz — V ooo
2
= 2л ( p(2 — p)dp = 2л Л>2 — I =-4 л. 4 J \ о / j о о
о
Вычисление координат центра масс тела. Пусть в пространстве R1 задано некоторое тело V непрерывно распределенной объемной плотностью 6 = 6(х, у, z). Тогда координаты центра масс этого тела определяются по формулам:.
Щх6(л\ yt z)du у. z)dv //•
c ®6(x, y, z)dv ’ Ус Щб(л, у, z)dv c y, z)du
v v v
Величины
Mx = Щх6(х, у, z)dv, My= Щг/б(х, у, z)dv, AC = Щгб(х, у, z)du и V и
называются статическими моментами тела относительно координатных плоскостей Оуг, Охг и Оху соответственно. Если 6(х, у, z) = const, координаты центра масс не зависят от плотности тела И.
Пример 4. Вычислить координаты центра масс однородного тела И, ограниченного поверхностями х = у2 + г2, х = 4.
► Строим тело, ограниченное данными поверхностями (рис. 13.30). Область V ограничена поверхностью параболоида, отсеченного плос-
Рис. 13.30
костью х = 4. Его проекция на плоскость Oyz представляет собой круг, ограниченный окружностью у2 + г2 = 4 радиусом 2. Вычислим вначале массу тела в цилиндрических координатах, считая, что его плотность 6=1:
2л 2 4
m = dxdydz = d<^ J pdp \ dx = V 0 0 (У
2
= 2л j p(4 — p2)dp = 2n^2p'“ — ~ ®л’
о
154
Тогда
2л
4
хс — dtp pdp
V 0 0 р2
2 2
= 4- • 2я (р (4- I ,rfp=4Д р(*6—р4)^р=
ОЛ J \ Z / нг О J О О
Аналогично определяются ус и zc, но так как тело — однородное и симметричное относительно оси Ох, то можно сразу записать, что ус=0 и zc = 0. «
Вычисление моментов инерции тел. Момент инерции относительно начала координат тела V Е R3 плотностью б(х, у, г) определяется по формуле
/о = + У~ + 22)6(х, £/, z)dxdydz\
у
моменты инерции относительно координатных осей Ох, Оу, Oz соответственно:
Л = + у, z)dxdydz,
V
/,, = $(х2 + z2)6(x, у, z)dxdydz, и
Л = $(х2 +i/2)6(x, у, z)dxdydz\ .1/
моменты инерции относительно координатных плоскостей Оху, Oyz, Oxz соответственно:
!,ч = $z26(x, у, z)dxdydz, V
1уг= Щх2б(х, у, z)dxdydz, и
= ®«/26(х, у, z)dxdydz.
т
Пример 5. Вычислить моменты инерции однородного шара радиусом /? и весом Р относительно его центра и диаметра.
4
Так как объем шара v = -у л/?3, то его постоянная плотность 6 = 3P/(4gn/?3). Поместим центр шара в начале координат, тогда его поверхность будет определяться уравнением х2 + у2 + z2 — R2. Момент инерции относительно центра шара удобно вычислять в сферических координатах:
/0 = 6 ®(х2 4- у2 + z2)dxdydz = б $ г* sin QdrdtpdQ = V V
2л л R
Sr Г Р3 Р
dtp \ sin 0d0 \ rfdr = б • 2л 2 = 4----R2.
J J 5 о g
0 0 о
155
Так как вследствие однородности и симметрии шара его моменты инерции относительно любого диаметра равны, вычислим момент инерции относительно диаметра, лежащего, например, на оси Oz:
h = (> + y2)dxdydz —
v
= 6 Щ r2 sin20r2 sin OdrdqdB =
V"
2л л R
= 6 J dtp J sin3 0d0 J r*dr =
0 0 0
л
o5 p
= —62л 1 (1 — cos2 0)d(cos 0) =
D J
0
n 5 / t \ I я 9 p
= —62л( cos 0----------5-cos3 0 I = -=------R2. 4
5 \ 3 / |o 5 g
A3-13.6
1. Вычислить объем тела, ограниченного поверхностями г = д/х2 + у2, 2 — z = х2 + у2. (Ответ: 4л/3.)
2. Вычислить массу тела, ограниченного плоскостями х + у + 2=1> х = 0, у = 0, z = 0, если плотность тел; б(х, у, z) = 1 /(х + у + z + I)4. (Ответ: 1/48.)
3. Вычислить объем тела, ограниченного цилиндрол х = у2 и плоскостями x-|-z=l, z = 0. (Ответ: 8/15.)
4. Вычислить объем тела, ограниченного сферами х2 + у2 + z2 = 1, х2 -ф у2 -ф z2 = 16 и конусом г2 = х2 -ф у2 (тела, лежащего внутри конуса). (Ответ: -^у-^1 —
5. Найти координаты центра масс части однородного шара радиусом R с центром в начале координат, расположенной выше плоскости Оху. (Ответ: С^О, 0,
6. Найти координаты центра масс однородного тела, ограниченного плоскостями х у z = а, х —0, у — 0, Z = 0. ( Ответ: а> 4 а’ Т а) )
7. Вычислить момент инерции относительно оси однородного круглого прямого конуса весом Р, высотой Н и радиусом основания R. (Ответ: /?2.)
156
Самостоятельная работа
1. Вычислить объем тела, ограниченного поверхностями z = x2, Зх + 2у = 12, у = 0, 2 = 0. (Ответ: 32.)
2. Вычислить момент инерции относительно плоскости Oyz тела, ограниченного плоскостями х + 2у — z = 2, х=0, у = 0, 2 = 0, если его плотность б(х, у, z) = х. (Ответ: 4/15.)
3. Вычислить координаты центра масс однородного тела, ограниченного поверхностями 2z = 4 — х2— у2, z = = 0. (Ответ: (0, 0, 2/3).)
13.6. ИНДИВИДУАЛЬНЫЕ ДОМАШНИЕ ЗАДАНИЯ К ГЛ. 13
ИДЗ-13.1
1. Представить двойной интеграл ^/(х, y)dxdy в виде D
повторного интеграла с внешним интегрированием по х и внешним интегрированием по у, если область D задана указанными линиями.
1.1. D: у = д/4 — х2, у =~у[3х, х /э 0.
1.2. D: х2 = 2у, 5х — 2у — 6 = 0.
1.3. D: х 8 — у2, у^0, у = х.
1.4. D: х>0, у>0, у<1, у = 1пх.
1.5. D: х2 — 2 — у, х 4* у = 0.
1.6. D: у = ~\]2 — х2, у = х2.
1.7. £>: у = х2 — 2, у = х.
1.8. £>: х>0, у>1, у<3, у = х.
1.9. £>: у2 = 2х, х2 = 2у, х<7 1.
1.10. D: х /Э 0, у^х, у =д/э — х2.
1.11. D: у2 = 2 — х, у = х.
1.12. D: х = 4/2 — У2, х = у2, у>0.
1.13. D: у 0, х + 2у—12 = 0, y=lgx.
1.14. D: х^0, у 1, у < 3, у = — х.
1.15. D: у = 0, у^> х, у = —д/2 — х2.
1.16. D: у 0, х=-\/у, у = 8 — х2.
1.17. D: у——х, у2 = х + 3.
1.18. D: у =х/— х2, х^0, х=1, у = 0.
1.19. D: х= — 1, х= —2, у 0, у = х2.
1.20. £>: у<0, х2=—у, х =-\/1 — у2.
157
1.21. Dt y^Q, y< 1, y — x, x = ~xj4 — y2 •
1.22. Dt x «С 0, у = 1, у = 4, у = —x.
1.23. Dt y — 3— x2, y=—x.
1.24. Dt x = 0, x =—2, у Js- 0, у — x2 + 4.
1.25. Dt x = Q, y = Q, y=l, (x — 3)2 + y2 = 1.
1.26. Dt x = д/9 — у2, y — x, у 0.
1.27. Dt x-\-2y— 6 = 0, у = x, y^Q.
1.28. Dt y=—x, Зх + у = 3, у = 3.
1.29. Dt x^O, y=l, y —— 1, y = logi/2x.
1.30. Dt x^O, y>0, y=l, x = д/4 — y2.
2. Вычислить двойной интеграл по области D, ограниченной указанными линиями.
2.1. (х2 + у)dxdy, Dt у = х2, х — у2. и
2.2. \\xy2dxdy, Dt у = х2, у = 2х. о
2.3. §(х y)dxdy, Dt у2 = х, у = х. о
2.4. §x2ydxdy, Dt у = 2 — х, у — х, х^0. о
2.5. ЭД(х3— 2y)dxdy, Dt у = х2—1, х^0, у 0. о
2.6. ЭД (у — x)dxdy, Dt у = х, у = х2. о
2.7. ЭД(1 + y)dxdy, D: у2 — х, 5у = х. о
2.8. ЭД(х + y)dxdy, Dt у = х2—1, у = — х2 + 1. о
2.9. ЭД х(у — 1 )dxdy; D: у = 5х, у = х, х = 3. о
2.10. ЭД(х — 2)ydxdy; D: у — х, у — х, х = 2.
о 2
2.11. ЭД(х —• y2)dxdy, D: у==х2, у—1. о
2.12. §x2ydxdy, D: у = 2х3, у = 0, х=1. о
2.13. ЭД(х2 + y2)dxdy, D: х = у2, х= 1. о
2.14. ЭД xydxdy, Dt у = х3, у = 0, х^.2. о
2.15. ЭД (х -\-y)dxdy, Dt у = х3, у = 8, y = Q, х-=3. о
158
2.16. У х(2х + y)dxdy, D: y=l—x2, y^O. D
2.17. У y( 1—x)dxdy, D: y3 — x, y = x. D
2.18. $ xy3dxdy, D: y2 = 1 — x, x > 0. о
2.19. У x(y + 5)dxdy, D: y = x-\-5, x + y + 5 = 0, x^O. D
2.20. У (x — y)dxdy, D: у = x2 — 1, y = 3. о
2.21. У (x + l)y2dxdy, D: у — Зх2, у = 3. D
2.22. У xy2dxdy, D: у = x, у = 0, x = 1. о
2.23. У (x3 y)dxdy, D: x у = l,x + y = 2,x^l,x^0. D
2.24. У xy3dxdy, D: y = x3, y^Q, y = 'lx. D
2.25. У (x3 + 3y)dxdy, D: x -f- у = I, у — x2 — 1, x 0. D
2.26. У xydxdy, D; y=~yfx, у = 0, x-\-y = 2. D
2.27. {{^,dxdy, D: у = x, xy = 1, у =2. JJ x~
D
2.28. У y(l + x2)dxdy, D: y = x3, y = 3x. D
2.29. У y2(l + 2x)dxdy, D: x — 2 — y2, x — 0. D
2.30. У eydxdy, D: y = lnx, у = 0, x = 2. о
3. Вычислить двойной интеграл, используя полярные координаты.
1 I---->-г
3.1. \dx ( -J—dy.
J J V i+jc + </ у
о о
О
3.3. [dx [ + у dy
159
i
3.4. \ dx $ 1п(1 + .г2 + y2)dy. о о
2 ^-у2 .-------------
3.5. J dy J_у 1 — х2 — у2 dx.
-2 -^4-у1
yfi О
3.6. ( dx ( X!L dy.
J_ J____ x2 + y2
72
3.7. dx $ cos-yx2 4- y2dy. -r 0
R -<jR!-x2
3.8. $ dx $ tg(x2 4- y2)dy.
— R 0
R
3.9. \dx ^£_cos(x2 + t/2)dy.
R -^R2-x2 _______
3.10. J dx J_sin-yx2 + y2dy.
— R
3.11. J dx j" -\/l -f- *2 + y^dy.
-Vs 0
V2 vZ2^?'
3.12. ( dx J_(1 + X2 + y2)dy.
-V2 -V2-x2
dy
I +х2 + У2 ’
160
« о
2 х^~х“
О R2 — х2
dx
— R 0
dy
+ У2
3 0
3.17.
3.18.
3.19.
3.20.
3.21.
3.22.
3.23.
3.24.
3.25.
3.26.
3.27.
3.28.
3.29.
о 0
5 dx J_____cos(№ + y2)dy.
— R — ~^R2 — x2
o -Jr!-x-
J dx J sin(x2 + y2)dy.
-R о
1 -ф—Х2 ----------
dx J у 1 +x2 + y2dy.
~ 1 0
j dx^Yxp+P^+^dy. -2 0
\dx J ln(l -j-x2-I-y2)dy. 0 0
-J? -фг-х2
( dx e_(x +l/ 'dy.
-JV2 -xl^1
2 xfi^T2 ________________
\dx J cos-\/x2 + y2 dy. о 0
R xIR' — x2
\dx J________sin(x2 + y2)dy.
® —-yjR^ — x2
6-357
161
3.30. [dx [
J _ J_r V?+7
4. Вычислить площадь плоской области D, ограниченной заданными линиями.
4.1. D: у2 = 4х, х + у = 3, у 0. (Ответ: 10/3.)
4.2. D: у = 6х2, х -|- у = 2, х 0. (Ответ: 5/8.)
4.3. D: у2 = х-\-2, х = 2. (Ответ: 32/3.)
4.4. D: х——2у2, х=1—Зу2, х=С0, у 0. (Ответ: 16/3.)
4.5. D: у = 8/(х~ + 4), х2 = 4у. (Ответ: 2л — 4/3.)
4.6. D: у = х2-\-\, х-\-у = 3. (Ответ: 9/2.)
4.7. D: у2 = 4х, х2 = 4у. (Ответ: 16/3.)
4.8. D: y = cosx, y^x-\-i, у 0. (Ответ: 3/2.)
4.9. D: х = ^4 — у2, у=^ х 0. (Ответ: 2л — -л/з/6.)
4.10. D: у = х2 -\-2, х 0, х — 2, у — х. (Ответ: 14/3.)
4.11. D: у = 4х2, 9у = х2, у + 2. (Ответ: 20-д/2/3.)
4.12. D: у = х2, у= —х. (Ответ: 1/6.)
4.13. D: х = у2, х = ^у2+1. (Ответ: 8/3.)
4.14. D: у^х/2—х2, у = х2. (Ответ: л/2+1/3.)
4.15. D: у = х2-(-4х, у = х-\-4. (Ответ: 125/6.)
4.16. D: 2у=-\[х, х-\-у = Ь, х 0. (Ответ: 28/3.)
4.17. D: у = 2х, у = 2х — х2, х = 2, х = 0. (Ответ:
In 2 3 )
4.18. D: у = — 2х2 + 2, у^ —6. (Ответ: 64/3.)
4.19. D: у2 = 4х, х = 8/(у2 -|- 4). (Ответ: 2л —4/3.)
4.20. D: у = 4 — х2, у = х2 — 2х. (Ответ: 9.)
4.21. D: х = у2 -)- 1, х у = 3. (Ответ: 9/2.)
4.22. D: х2 = Зу, у2 = 3х. (Ответ: 3.)
4.23. D\ x = cosy, х у + 1, х 0. (Ответ: 1/2.)
4.24. D: х = 4 — у2, х — у -|- 2 = 0. (Ответ: 125/6.)
4.25. D: х = у2, х = х^2 — у2. (Ответ: л/2+1/3.)
4.26. D: ~ = 1, у х, у^0. (Ответ: л/4.)
4.27. D: у2 = 4 — х, у = х + 2, у — 2, у = —2. (Ответ: 56/3.)
162
4.28. D: у = x2, у = A x2 + 1 • (Ответ: 8/3.)
4.29. D: x — y2, y2 = 4— x. (Ответ: 16д/2/3.)
4.30. D: xy=\, x2 = y, у = 2, x = 0. (Ответ: 2/3 + +In 2.)
5. С помощью двойных интегралов вычислить в полярных координатах площадь плоской фигуры, ограниченной указанными линиями.
5.1. (х2 + у2)2 = а2(4х2 + у2).
5.2. (х2 + у2)3 = а2х:2у-.
5.3. (х2 -|- у2)3 = а2х2(4х2 + Зу2).
5.4. (х2 + у2)2 = а2(3х2 + 2у2).
5.5. х4— у4 = (х2 + у2)3 5.6. p = asin22<p.
5.7. р = a sin2 <р. 5.8. р = а( 1 —- cos ср).
5.9. (х2 + у2)2 = а2(2х2 + Зу2).
5.10. (х2 + у2)2 — а2(5х2 + Зу2).
5.11. (х2 + у2)2 = а2(7х2 + 5у2).
5.12. (х2 4- у2)2 = 2а2ху.
5.13. (х2 + у2)3 = 4х2у. 5.14. (х2 + у2)3 — а4у2.
5.15. (х2 -|-у2)3 = а4х2. 5.16. р = асоэ2ф.
5.17. р2 = а2(1 + sin2 ю). 5.18. (х2 -ф у2)3 = а2х4.
5.19. (х2 + у2)2 = 4(3х2 + 4у2).
5.20. (х2 + у2)3 = aW.
5.21. (х2 + у2 3 = а2(х’+ у4).
5.22. (х2 + у2)3 = 2ау3.
5.23. (х2 + УТ = 4а2ху(х2 — у2).
5.24. р = a sin 2<р.
5.25. р = a cos 5<р. 5.26. р.= Ч] +cos ф)-
5.27. р = 2а(2 + cos <р). 5.28. р = a cos Зф.
5.29. р = a cos 2<р. 5.30. р = a sin 3<р.
6. Вычислить объем тела, ограниченного заданными поверхностями.
6.1. z = x2+y2, х + у=1, х^О, у 0, z 0. (Ответ: 1/6.)
6.2. z = 2 — (х2 + у2), х + 2у = 1, х 0, у 0, z 0. (Ответ: 53/96.)
6.3. z = x2, х — 2у + 2 = 0, х + у — 7 = 0, z^0. (Ответ: 32.)
6.4. z = 2х2 + Зу2, у = х2, у = х, z > 0. (Ответ: 29/140.)
6.5. z = 2х2 + У^, У х, у = 3х, х = 2, z > 0. (Ответ: 152/3.)
163
6.6. z = x, у = 4, x = -y25 —у2, х>0, у >0, z > 0. (Ответ: 118/3.)
6.7. у=д/х> у = х, x + y+z = 2, z/0. (Ответ: 11/60.)
6.8. у = 1 — х2, х + у + z = 3, у О, 2^0. (Ответ: 104/30.)
6.9. z = 2x2 + y2, х + у = 4, х /2 0, у О, z /2 0. (Ответ: 64.)
6.10. 2 = 4 — х2, х2 + у2 = 4, х^О, у>0, 2/э 0. (Ответ: Зл.)
6.11. 2х-f~ Зу — 12 = 0, 2г = у2, х /2 0, у 0, 2 0.
(Ответ: 16.)
6.12. 2 = 10 + х2 + 2у2, у = х, х=1, у/г 0, г/0. (Ответ: 65/12.)
6.13. z = x2, х + у = 6, у = 2х, х О, у^О, 2/гО. (Ответ: 4.)
6.14. z = Зх2 /- 2у2 + 1, у — х2 — 1, у=1, 2^0. (Ответ: 264-д/2/35.)
6.15. 3у=д/х, у X, X Ц-у 2 = 10, У=1, 2 = 0.
1 Ответ: 303/20.)
6.16. у2 = 1 — х, х + у + z = 1, х = 0, 2 = 0. (Ответ: 49/60.)
6.17. у = х2, х = у2, z = Зх + 2у + 6, 2 = 0. (Ответ: 11/4.)
6.18. х“ = 1 — у, х Ц- у Ц- z = 3, у 0, 2 /г 0. (Ответ: 52/15.)
6.19. х = у2, х=1, x + y + z = 4, 2 = 0. (Ответ: 68/15.)
6.20. 2 = 2х2 + у’, х у = 1, х /г 0, у /г 0, 2 /г 0. (Ответ: 1/4.)
6.21. у = х2, у = 4, 2 = 2х + 5у + 10, 2/г 0. (Ответ: 704/3.)
6.22. у = 2х, х + у + 2 = 2, х 0, 2 /г 0. (Ответ: 4/9.)
6.23. у = 1 — г2, у = х,у= —х, у 0, 2/s O. (Ответ: 8/15.)
6.24. х2 + у2 = 4у, 22 = 4 — у, 2^0. (Ответ: 256/15.)
6.25. х2 + у2 = 1, 2 = 2 — х2 — у2, z 0. ( Ответ: у л.)
6.26. у = х2, 2 = 0, у + 2 = 2. (Ответ: р~\/2^
6.27. z2 = 4 —х, х2 + у2 = 4х, z^O. (Ответ: 256/15.)
|«4
6.28. z = x2 + 2y2, y = x, x 7> 0, y=l, z 2> 0. (Ответ: 7/12.)
6.29. z = y2, x-\-y—l, x^O, z 0. (Ответ: 1/12.)
6.30. y2 — x, x = 3, z = x, z 0. {Ответ: 36^3/5.)
Решение типового варианта
I. Представить двойной интеграл Ц(х, y)dxdy в виде D
повторного интеграла с внешним интегрированием по х и внешним интегрированием по у, если область D ограничена линиями x—xfy, x=xj 2 + у, х = 0, х = 2.
> Область D изображена на рис. 13.31 и ограничена дугами парабол х1 = у + 2, х2 = у и прямыми х = 0, х = 2. Следовательно,
2 х2
y)dxdy = \dx $ f(x, y)dy =
D 0 x2 —2
0 2 ~\/у + 2 4 2 _
= $ dy $ f(x, y)dx + \dy \ f(x,y)dx + \dy\j(x,y)dx.4 — 2 0 0 2 уу
2. Вычислить двойной интеграл §(х — 2y)dxdy по об-D
ласти D, ограниченной линиями х = 0, у = 7 — х, у =
= х Н- 1 •
> Область D изображена на рис. 13.32. Если выбрать внутреннее интегрирование по у, а внешнее — по х, то
У-
Рис. 13.31
Рис. 13.32
165
двойной интеграл по этой области выразится одним повторным интегралом:
4 7-х
ЭД (х — 2у) dxdy = \dx j (х — 2y)dy =
О О I
3. Вычислить двойной интеграл
используя полярные координаты. Найти его численное значение при R = 1.
► Область интегрирования D представляет собой четверть круга, расположенного во втором квадранте (рис. 13.33).
У|
р и с. 13.33
Перейдем к полярным координатам x = pcos<p, у — = р sin <р, х2 + у2 = р , где 0 < р < R; л/2 < <р < л. Тогда
л R
1= d<p^ ln(l+-£lpd<p =
\и = In(1 + р), du = dp/(i + р), [dv = dp, v = р,
166
= р
(plnU+p)
л/2\
= i(Rln(l+R)-p
К R\
+ 1п( 1 + р) ) =
о о/
= A (Z? ln(l + R)-R + ln(l +/?)).
При R = 1 получаем
/ = А(2 1п2— 1). 4
4. Вычислить площадь фигуры, ограниченной линиями у = х2 — Зх и Зх -ф у — 4 = 0.
> Данная плоская фигура ограничена снизу параболой у = х2 — Зх, сверху прямой Зх -ф у — 4 = 0 (рис. 13.34). Следовательно,
5. С помощью двойного интеграла вычислить в полярных координатах площадь фигуры, ограниченной линией (х2 -ф уу = 2ул.
► Уравнение линии в полярных координатах имеет вид р = 2 sin3 ср. Она изображена вместе с ограниченной ею областью D на рис. 13.35. Полюс О лежит на границе
167
области D, и поэтому, согласно формуле (13.12) (случай 3; см. также пример 2 из § 13.2) имеем:
я 2sin3(p л
5 = jj рг/рг/ф = j г/ф j рг/р — j б/фЕ-|^5'п =
D 0 0 0
л л
= 2 j sin6 фйф = y j (1 — cos 2ф)3 dtp —
о о
= у j (1 — 3 cos 2ф + 3 cos2 2ф — cos3 2ф)г/ф =
о
=4("-4sin4+4 V1 +cos 4<pw -о
л
— \cos2cp(l—sin2 2<р)о!<р = А л. ◄ J я
о
6. Вычислить объем тела, ограниченного поверхностями Z = ДТ— у, у — X, у — —X, 2 = 0.
Рис. 13.36
► Данное тело ограничено сверху параболическим цилиндром 2 = д/1—у (рис. 13.36), поэтому
1 у _______
v = У -д/1 — у dxdy = 2 dy \ у 1 — у dx ~
I) 0 0
I _____ | у 1 ______ ___________
= 2^1 —ух\ dy = 2\yx/T^ydy = |д/1 — у = /, о о
168
y=l—t2, dy =—2tdt, / =1 при у = 0 и / = О при у = 11 = 2j (1 — /2)/( — 2tdt) = — 4j (/2 — f)dt = о 1
= - 4(‘- - А|° = А.
\3 5/| I 15
ИДЗ-13.2
1. Расставить пределы интегрирования в тройном интеграле Щ/(х, у, zjdxdydz, если область V ограничена г
указанными поверхностями. Начертить область интегрирования.
1.1. V: х = 2, у = 4х, у = 3 \[х\ z О, 2 = 4.
1.2. V: х=1; у = Зх, у 0, 2^0, z — 2(х2 + у2).
1.3. V: х — 1, у — 4х, 2^0, г— х/Зу.
1.4. V: х = 3, у = х, у^О, 2^0, z = 3x2~]-y2.
1.5. V: у = 2х, у = 2, 2^0, 2 = 2д/х.
1.6. V: х = 0, у = х, у = 5, 2^0, z = 2х2 + у2.
1.7. V: х^О, у = 2х, у=1, 2^0, х + у -j-2 = 3.
1.8. V: х 0, у = Зх, у = 3, 2^0, х = 3д/г.
1.9. V: х — 5, у — х/Ь, у^0, 2^0, z = х2 -{- 5у2.
1.10. V: х — 2, у = 4х, z 0, у — 2-y/z.
1.11. V: х — 3, у — ~ х, у^0, 2 > 0, 2 = ~ (х2 + у2).
1.12. V: х = 4, у = х/4, 2^0, 2 = 4у2.
1.13. V: х^0, у = 3х, у — 3, z^O, z = 2(х2 + у2).
1.14. V: х^0, у = 4х, у = 8, z^0, z~3x2 -\-у2-
1.15. V: х>0, у = Ъх, у =10, 2 > 0, z = х2 + у2.
1.16. V: у=-х, у=—х, у —2, 2^0, z — 3(х2 + у2).
1.17. V' х = I, у = 2х, у = Зх, 2^0, z — 2х2 -f-у2.
1.18. V: у — х, у=—2х, у=1, 2^0 z~x2-]-4y2.
1.19. V: х 0, у^О, z^O, х-\-у=1, z — Зх2 -j- 2у2.
1.20. V: х 0, у 0, z^O, 3x-]-2i/ = 6, z = x2-\-y2.
1.21. V: х^ 0, у 0, 2^ 0, х + у = 2, z = 4 — х2 — у2.
1.22. V: х 0, у 0, z 0, х + у = 3, z = 9 — х2 — у2.
1.23. V: х>0, у>0, 2>О, Зх + 4у=12, 2 = 6 — — х2 — у2.
1.24. V: х^О, 2^0, у = х, у — 3, 2=18 — х2 — у2.
169
1.25. И:
1.26. V:
1.27. V:
1.28. V: т*2 + У2-
1.29. V: — х2 — у2.
1.30. V:
х = 2, у 0, 2^0, у = Зх, z = 4(x2 + y2).
х + 0, у = 2х, у = 4, z + О, z=10 — х~— у2.
х = 3, у + О, z + О, у - 2х, z = 4\Гу.
х 0, у + О, 2 + 0, 2х + Зу = 6, z = 3 +
X + О, У + О, 2 + О, х + у = 4, 2=16 —
х + 0, у + О, г + О, 5х + у = 5, 2 = х2 + у2.
2. Вычислить данные тройные интегралы.
2.1. ЭД (2х2 + Зу + 2~)dxdyd2, И: 2 + х + 3, — 1 + у + 2, v
О+<+4.
2.2. ЭД x2y2dxdydz, V-. —I + х + 2, 0 + у + 3, 2 + v
++ 3.
2.3. ЭД (х + у + 422)dxdyd2, V: — 1 < х + 1,0 + у + 2, -ic+l.
2.4. ЭД +'2 + у2 + z2)dxdyd2; V: 0 х 3, — 1 + у + 2, к+
2.5. ЭДx2y2zdxdydz, V: — 1+х + З, 0 <С у + 2, ~2 + v
+ z + 5.
2.6. ЭД(х + у + z)dxdydz, V'. 0<х + 1, — 1 у О, |<2<2.
2.7. $ (2х — у2 — z)dxdydz, v: 1 + х + 5, 0 + у ь'С 2, v
— 1 < 2 + 0.
2.8. $ 2xy2zdxdydz, И: 0 + х + 3, — 2 + у + О, I +
2.9. 3xyz2dxdydz, V: — 1 + х + 0, 2 + у + 3, 1 + v
+ 2 + 2.
2.10. $ (х2 + 2у2 — z)dxdydz, /: 0 + х 1, 0 + у + 3, v
— 1 + 2 + 2.
2.11. ЭД (х + 2yz)dxdydz, V: —2 + х + 0, 0 + у+ 1, v
170
2.12. yz'/dxdydz, V: 0 С хС 1, 0 С у С 2,
v
— 1 С z С 3.
2.13. -\-3z)dxdydz, V: —О С У С 1 >
2.14. Щ (ху — г2)dxdydz, у; О^х^2, О С У 1, — 1 С
<г<з/
2.15. $ (х3 + yz) dxdydz, v: — 1 С х С 2, О С у С 1, v
ос г'С 1.
2.16. Щ (х3 -(-у2 — z) dxdydz, v: О С х С 2, — 1 С У С О,
ОСгСГ
2.17. $ (2х2 + у — z3)dxdydz, к: О 1, — 2 С У Ь v
и<г< 1.
2.18. Щ x2yz2dxdydz, v: О^х^2, 1СУ'С2, —1'С v
<гСО.
2.19. $ (х + у — z) dxdydz, v: ОС^СС 1 С У С 3,
2.20. $ (х 4- 2у + 3z2) dxdydz, v: — 1 С х 'С 2, О С У С <!, 1С<2.
2.21. $ (Зх2 + 2у + г)dxdydz, v. 0С*С 1 > 0СУ^1, v
— 1 С 2 с 3.
2.22. Щ (ху — г3)dxdydz, d:0^x<1, — 1СУ 'С2, v
ОСгСЗ.
2.23. ^ipyzdxdydz, v: — 1 С^'С2, 1 СУ^З, ОС^^ 1-
2.24. Щ xy2zdxdydz, v: —2CZ:C1, О С У С2, ОС
2.25. Щ xyz2dxdydz, v: О С * 2, — 1 С У О, О С
171
2.26. ffi (x + yz) dxdydz, v: 0 x 1, — 1 у 4, 0
2.27. $ (x + y2 — z2')dxdydz, v: — 2 s/ x 0, 1 у 2,
o<2<5‘:
2.28. $ (x + у 4- z2) dxdydz, v: — 1 s/ x </ 0, 0 у s/ 1, v
2^2<3.
2.29. $ (x + y2 — 2z) dxdydz, v: 1 x 2, — 2 si у xj 3, и
0<z< 1.
2.30. Щ (x ~ У ~~ z) dxdydz, y:0^x^3, Ох/у CH v
— 2=CzC 1.
3. Вычислить тройной интеграл с помощью цилиндрических или сферических координат.
3.1. Щ (х2 + у2 + z2) dxdydz, v: х2 4- у2 z2 — 4, х>0, у>0, z^O. (Ответ: 16л/5.)
3.2. $ уд/х2 4- у2 dxdydz, v: z^0, z = 2, у ±х, z2 = v
= 4(х24-у2). ( Ответ: д/2/10.)
3.3. $ z2dxdydz, V. 1 х2 4~ у2 С 36, у х, х 0, v
z^0. (Ответ: 1555л/12.)
3.4. $ ydxdydz, v: х2 4- у2 4- z2 — 32, у2 = х2 4- z2, у > 0. и
(Ответ: 128 л.)
3.5. $ xdxdydz, v: х2 у2 z2 = 8, х2 = у2 4- z2, х 0. v
(Ответ: 8л.)
3.6. ydxdydz, v: 4 х2 4- у2 4- 22 16, у д/Зх, у 0,
2^0. (Ответ: 15л/2.)
3.7. ^ydxdydz, v: z = д/8 — х2 — у2, z = д/х2 4- у2, v
у^0. (Ответ: 8(л/2 —1).)
172
3.8. Щ ’ v- х > 0, 2 > О, у >д/Зх, 4 < х2 +
V
+ у2 + z2 36. ( Ответ: || (2л -|- Зд/З) .)
3.9. [[[ ifzdxdydz^, v. у ^(), у^-^/Зх, z = 3(x2 + y2), 'J' Л^2 + </2)3
2=3. (Ответ: 3(4л— Зд^~3)/20.)
3.10. (К x*dxdydz , V- x2 + y2 + z2=16, 2/>0. JjJ -\₽w+^)3
(Ответ: 16л/3.)
3.1 1. [[[ xzdxdydz , у: 2 = 2(х2 + У2), У^О, ys^—X, 'Р х/х2 + у2 л/з
2=18. (Ответ: 81.)
3.12. [[[ xydxdydz_ , у. z = x2 + у2, у>0, у С х, 2 = 4.
JjJ
(Ответ: 4/3.)
3.13. Hl zd.xJy^±., у. х2 + у2 = 4у. у + z = 4, z > 0. 'Р х/х2 + у2
(Ответ: 1472/45.)
3.14. $ ydxdydz^ у.х2 + у2 = 2х, x + z = 2, у^О,
2>0. (Ответ: 4/5.)
3J5 xdxdydz^ v. x2+y2==l6y> y+z= 16, Х>0,
2^0. (Ответ: 2048/5.)
3.16. ^л/х? + y2dxdydz, v: х2 + у2 = 2х, x + z = 2,
z^O. (Ответ: 128/45.)
3.17. ^xydxdydz, v: 2 < х2 + у2 + г2 < 8, г2 = х2 + у2, х^О, у/>:0, 2^0. (Ответ: 31(4д^—5)/15.)
173
3.18. ffl Jdxdydz-. v: x2 + y2 = 2y, x2 + y2 = 4y, x>0, JJJ V*2 + У
z 0, г = 6. (Ответ: 24.)
3.19. jjjx/x2 + y2 + z2 dxdydz, v: x2 4- y2 + z2 — 36, у
4^0, 2^0, у —x. (Ответ: 81л.)
3.20. Щ v, x2 _|_ = 2x, x2 + y2 = 4x, z > 0,
''' V^+y2
2 = 4, у 4s 0, y^x. (Ответ: 10д/2.)
3.21. zd^.ydL v. 1 ^x2+y2 + z2^9, y^O,
y^2-^- x, 2^0. (Ответ: 13л/8.)
л/З
3.22. $л/%2 + у2dxdydz, v: х2 —2х4-у2 = 0, у^О,
2^0, x-}-z = 2. (Ответ: 64/45.)
3.23. ^x2dxdydz, v: 1 x2 -f- y2 -f- z2 16, у 0,
y-^x, 2^0. (Ответ: 341 (л-|-2)/20.)
3-24-Щ ' v- + y + z = 4, z^O.
JJJ -Vx2+y2
(Ответ: 64/3.)
3.25. (И - yd~.ydj^ , v: 4 x2 4-z/2 4-22 < 16, y< JJJ V?T? + z2
^Сх/зх, у 0, z^O. (Ответ: 7л/3.)
3.26. 2д/х2 4- у2dxdydz, v: x2 4- у2 = 2x, у 0, 2 0,
V
z = 3. (Ответ: 8.)
3.27. ((( ... , v: 1 Cx2 + y-’ + 22<4, x>0,
'j' л/х2 + № + z!
y^x, у /s0, 2^0. (Ответ: 7д/2л/24.)
174
3.28. xdxdydz, v: x2 — 2(y2 + z2), x = 4, x 0.
(Ответ: 32л.)
3.29. : v: 1 Cx2 + y2 + z2C9, у < x,
JjJ x/x2 + y2 + z2
y^O, z^O. (Ответ: 13д/2л/2.)
3.30. jjj xdxdydz, v: z = д/18 — x2 — t/2, z = д/х2 + у2, V
x^O. (Ответ: «!(£-1).)
4. С помощью тройного интеграла вычислить объем тела, ограниченного указанными поверхностями. Сделать чертеж.
4.1. z2 = 4 —х, х2 + у2 = 4х. (Ответ: 512/15.)
4.2. z = 4 — у2, х2 -j- у2 = 4, z 0. (Ответ: 12л.)
4.3. х2-]-у2=1, z == 2 — х — у, z 0. (Ответ: 2л.)
4.4. z = у'2, х > 0, z 0, х у = 2. (Ответ: 4/3.)
4.5. у 0, z С- 0, z = x, х =л/9— у2, х = д/25 — у2. (Ответ: 98/3.)
4.6. х2 у2 = 4, z = 4 — х—у, z 0. (Ответ: 16л.)
4.7. z 0, z = х2, х — 2у 2 = 0, х -|- у = 7. (От-
вет: 32.)
4.8. х^О, z 0, z = y, х = 4, у — х( 2.3 — х2. (Ответ: 118/3.)
4.9. z 0, z = 4 — х, x — 2xfy, у = 2х[х. (Ответ: 176/15.)
4.10. у /г 0, z 0, 2х — у = 0, х + у = 9, z = x2. (Ответ: 1053/2.)
4.11. у 0, z 0, х = 4, у = 2х, z = х2. (Ответ: 128.)
4.12. х 0, 2^0, у = 2х, у = 3, z=-\[y. (Ответ:
эУз/5.)
4.13. у^О, 2^0, х=3, у = 2х, z = y2. (Ответ: 54.)
4.14. z 0, у2 = 2 — х, z = 3x. ( Ответ: 32х/2/5.)
4.15. 2^0, у —-^^ — х2, z = 2y. (Ответ: 36.)
4.16. х 0, у^О, z^O, х-(-у = 2, z = x2-}-y2-(Ответ: 8/3.)
175
4.17. 2 > О, х2 -j- z/2 = 9, z = 5 — х — у (Ответ: 45л.)
4.18. 2^0, z = x, х = ^4—у2. (Ответ: 16/3.)
4.19. у 0, 2^0, х + у = 2, 2 = х2. (Ответ: 4/3.)
4.20. у 0, 2^0, у = 4, г = х, х = ^25—у2. (Ответ:
118/3.)
4.21. 2^0, х2 + у2 = 9, 2 = у2. (Ответ: 81/8л.)
4.22. х^ 0, 2^0, у^х, 2=1—х2 — у2. (Ответ: л/16.)
4.23. 2 0, х2 +у2 = 4, 2 = х2 4- у2. (Ответ: 8л.)
4.24. 2^0, у — 2, у = х, 2 = х2. (Ответ: 4/3.)
4.25. 2^0, у 4- z = 2, х2 + у2 = 4. (Ответ: 8л.)
4.26. у 0, 2 > 0, х — у = 0, 2х-}-у = 2, 4z = у2. (Ответ: 1/162.)
4.27. х^О, у > 0, 2^0, 2х + у = 2, z = y2. (Ответ: 2/3.)
4.28. 2^0, х = у2, x = 2z/2+l, г = 1 — у2. (Ответ: 8/5.)
4.29. х>0, у 0, 2^0, у — 3 — х, z = 9 — х2. (Ответ: 135/4.)
4.30. х 0, 2 0, х + у = 4, 2 = 4~\[у. (Ответ: 512/15.)
Решение типового варианта
1. Расставить пределы интегрирования в тройном интеграле Щ Дх, у, z)dxdydz, если область V ограничена по-г
верхностями х = 1, у = х, z = 0, 2 = у2. Начертить область интегрирования.
► Согласно формуле (13.23), имеем:
I X у‘
ffi f(x> У> z) dxdydz = \ dx \ dy\ f(x, у, z)dz. V 000
Область интегрирования изображена на рис. 13.37. 4
2. Вычислить (Зх -J- 2у — 2i)dxdydz, если V: 0 х 1, г
U у ^4 2, 1 ^4 2 С 3.
► Для данной области V (рис. 13.38) на основании формулы (13.24) получаем
I 2 3
(Зх 4- 2у — 23)dxdyd2 =\ dx\ dy\ (Зх -ф 2у — z3)d2 =
V 0 0 1
176
12 з 1 2
dx 3xz + 2уг —| dy ~ dx (6x + 4y — 20)dy —
0 0 0 0
I 1
— J (6xy-f-2y2— 20y)^dx = J (12x— 32)dx = о 0
— (6x2 — 32x) | о = — 26. -<
Рис. 13.37
cp, z no област:1
3. Вычислить тройной интеграл по °^’
v
ласти, расположенной в первом октанте и ограниченной плоскостями х = 0, у = 0, z = h w конусом z2 = Д- (х2 + у2), R
с помощью цилиндрических координат.
> На рис. 13.39 изображена область интегрирования V и ее проекция D на плоскость Оху.
Перейдя к цилиндрическим координатам р, формулам (13.26), в которых для данной 0<<р< л/2, 0 С Р С R, получим:
Z2 = h‘2p2/R2,
И V
л/2 R
= J cos (pdcpj о о
л/2 R
— COS
0
z = hp/R, p2 cos qzdqdpdz
l>2 - R2
h
iw/R
i l'1
— dp = 2 Iftp//?
. p2 - R »
177
Л/2 R .
о о
л /2 У?
. 2 г г ^2 । л/2 з IR
---------l— \ cos фо!ге\ p2dp =----------------- sin <р •
2R2 J * ( J н н 2R- I о 3 I о о о
-4-Т?/г\ ◄
4. С помощью тройного интеграла вычислить объем тела, ограниченного указанными поверхностями: х — О, у = О, z = 0, х + у — 2, 2z = х1 4- у1.
► Уравнение 2z = x2-}-//2 определяет параболоид вращения, остальные поверхности — плоскости. Искомое тело изображено на рис. 13.40. Его объем и вычисляем в соответствии с формулами (13.21) и (13.23):
2 2-х (х2 + ^’)/2
и = $ dxdydz = \ dx \ dy j dz — V 000
2 2 — х 2 2— y
( f + f , 9
= J J Io dy = -2-\dx\ (x + У )dy = 0 0 0 0
2 2-x 2
=т5(^+Я1о dx=V\(x2^~x)+ о 0
2
+ 4" (2 ~ x)3) dx = 4 j ( 2x2 ~ x3 + T ~ *)3) dx =
0
=4(^3-4-4р-)‘)|И- «
1/8
ИД313.3
1. Вычислить массу неоднородной пластины D, ограниченной заданными линиями, если поверхностная плотность в каждой ее точке р = р(х, у).
1.1. D: у2 = х, х — 3, р = х. (Ответ: 36д/з/5.)
1.2. D: х = 0, у = 0, х 4- у = 1, р — х2. (Ответ: 1/12.)
1.3. D: х = 0, у = 0, 2х -f- Зу = 6, р = у2/2. (Ответ: 1.)
1.4. D: х2-(-у2 = 4х, р = 4 — х. (Ответ: 8л.)
1.5. D: х = 0, у = 1, у = х, р = х2 -f- 2у2. (Ответ: 7/12.)
1.6. D: х2 4- у2 — 1, р = 2 — х — у. (Ответ: 2л.)
1.7. D: х2 -f- у2 — 4у, р =-\/4 — у. (Ответ: 256/15.)
1.8. О: у = х, у=—х, у=\, р У- (Ответ:
8/15.)
1.9. D: х = 0, у — 2х, х -f- у = 2, р = 2 — х — у. (Ответ: 4/9.)
1.10. D: х— 1, х = у, р = 4 — х — у. (Ответ: 68/15.)
1.11. D: у = 0, х2=1~у, у = 3 — х — у. (Ответ: 14/5.)
1.12. D: у = х2, х = у2, р = Зх 4* 2у 4* 6. (Ответ: 11/4.)
1.13. D: у — х2, у = 4, р = 2х4-5у4-10. (Ответ: 752/3.)
1.14. D: х — 0, у = 0, ху = 1, р = 2х2 -f- у2. (Ответ: 1/4.)
1.15. D:x = 0, у2 = 1 — х, у = 2 — х — у. (Ответ: 32/15.)
1.16. D: у = xj~x, у = х, р = 2 — х — у. (Ответ: 51 /60.)
1.17. D: у = х2 — 1, у = 1, р = Зх2 4- 2у2 4- 1. (От-
вет: 264V2/35.)
1.18. D: х=1, у = 0, у = х, р = х2 4- 2у2 4- 10. (Ответ: 65/12.)
1.19. D: у = 0, у = 2х, х 4- у = 6, р = х2. (Ответ: 104.)
1.20. D: х 0, у^0, х24~у2 = 4, р —4 — х2. (Ответ: Зл.)
1.21. D: у = х2, у — 2, р = 2 — у. (Ответ: 32д/2/15.)
1.22. D: х = 0, у = 0, х4-у=1, р = х2 4-у2. (Ответ: 1/6-)
1.23. D: у = х24-1, х4-у = 3, р = 4х 4~ 5у 4-2. (Ответ: 351/6.)
1.24. D: у = х2—\, х4-у=1, р = 2х 4~ 5у 4~ 8. (Ответ: 45.)
179
1.25. D: х = 0, у = 0, у = 4, х=д/25 — у2, р — х. (Ответ: 118/3.)
1.26. D: х = 2, у = х, у = 3х, р = 2х2 4- у2. (Ответ: 152/3.)
1.27. D: у = х, у = х2, p = 2x-|-3y. (Ответ: 11/30.)
1.28. D: х = 0, х -f- 2у -f- 2 = 0, х 4* у = 1, р — х .
(Ответ: 32/3.)
1.29. D: х = 0, у = 0, х4-2у=1, р = 2 - (х2 + у2). (Ответ: 43/96.)
1.30. D: х = 0, у = 0, х у = 2, р = х2-|-у2- (Ответ: 8/3.)
2. Вычислить статический момент однородной пластины О, ограниченной данными линиями, относительно указанной оси, использовав полярные координаты.
2.1. D: х2 + у2 — 2ау = 0, 2.2. D: х2 4- у2 — 2ах = 0, 2.3. D: х2 4- у2 -f- 2ау = 0, 2.4. D: х2 4- у2 4- 2ах = 0, 2.5. D: х2 -j- у2 4- 2ах 0,.
2.6. D: х2 4- у2 — 2ау 0,.
2.7. D: х2 4- у2 — 2ау < 0,. 2.8. О: х2 -j- у2 — 2ах 0,. 2.9. D: х2 4- у2 — 2ах 0,.
2.10. D: х2 4-у2 4- 2ах 0,
2.11. О:х24-у2— 2ау 0,
2.12. D:x2-\-y2— 2ау 0, 2.13. D: x2-j-y2 4* 2ау = 0, 2.14. D: х2-\-у2— 2ах = 0, 2.15. D: х2 4- у2 4* 2ау = 0, 2.16. D: х2 4- у2 — 2ау = 0, 2.17. D: х2-(-у2 — 2ау = 0, 2.18. D: х2 4- у2 4* ‘2ах = 0, 2.19. D: х2-(-у2 — 2ах = 0, 2.20. D: х2 4- у2 4- 2ах — 0, 2.21. £>: х2 4-у2 4- 2ау — 0, 2.22. D: х2 4- у2 — 2ау — 0, 2.23. D: х2 4- у2 4- 2ах == 0, 2.24. D: х2 4- у2 — 2ау = 0, 2.25. D: х2 4-у2 4* 2ах = 0, 2.26. D: х2 4- у2 — 2ах = 0, 2.27. D: х24-у2 —2ах —0 2.28. D: х2 -j- у2 — 2ау = 0
х — у 0, Ох. *4-У<0, Оу. х — у > 0, Ох. х 4* У 0, Ох.
к2 4- у2 4- 2ау < 0, х < 0, Ох. г2 4- у2 4- 2ах 0, у 0, Оу. х2 4- у2 — 2ах 0, х 0, Ох. г2 4- у2 4- 2ау 0, у 0, Оу.
+ У2 + 2ау 0, х 0, Ох. х2 + У2 + ^ау 0, у < 0, Оу. х2 4- у2 4- ‘2ах 0, х 0, Ох. х2 4- У2 — ‘2ах < 0, у > 0, Оу. х2 + У2 + ау = 0, х 0, Ох. х2 у2 — ах = 0, у 0, Оу. х2 4-у2 -\-ау = 0, х>0, Ох. х2-\-у2 — ау = 0, х 0, Ох. х2 4- у2 — ау = 0, х 0, Ох.
х2 4-у2 4-ах = 0, у 0, Оу.
х2 у2 — ах = 0, у < 0, Ох.
х2 4~У2 + ах = 0, у 0, Оу.
x-J-y^O, х>0, Ох.
у — х > 0, х 0, Ох.
У — х 0, у 0, Оу.
х 4* У 0, х д' 0, Ох.
х 4- у С 0, у > 0, Оу. у — х 0, у 0, Ох.
, у — х 0, х 4~ У 0, Оу. , у — х > 0, х 4- у^О, Ох.
ISO
2.29. D: x2 4- у2 4- 2ax = 0, x 4- у 0, у — x /э 0,
2.30. D: x2-j-y2-j-2ay — 0, y —x^O, x 4-у 0,
Oy.
Ox.
3. Вычислить координаты центра масс однородного тела, занимающего область V, ограниченную указанными поверхностями.
3.1. V: х = 6(у2 4~ z2), У2 4~ z2 = 3, х = 0. (Ответ: (6, 0, 0).)
3.2. V; у = Зд/х2 4~z2, х2 4-z2 = 36, у = 0. (Ответ: (0, 27/4, 0).)
3.3. V: х = 7(у2 4- z2), х = 28. (Ответ: (56/3, 0, 0).)
3.4. V: z = 2д/х24-у2, z = 8. (Ответ: (0, 0, 6).)
3.5. V: z = 5(х2 4- у2), х2 4- у2 = 2, z = 0. (Ответ: (0, 0, Ю/З).)
3.6. V: х = 6д/у2 4-z2, у2 4- z2 = 9, х = 0. (Ответ: (27/4, 0, 0).)
3.7. V: z = 8(x24-y2), z = 32. (Ответ: (0, 0, 64/3).)
3.8. V: у = Зд/х24-z2, у = 9. (Ответ: (0, 27/4, 0).)
3.9. V: §y = x2 + z2, x24~z2 = 4, у = 0. (Ответ: (0, 4/27, 0).)
3.10. И: 3z = -\/х^4- у2, х24~ у2 = 4, z = 0. (Ответ: (0, 0, 1/4).)
3.11. V: х2 4- z2 = бу, у = 8. (Ответ: (0, 16/3,0).)
3.12. И: 8х=д/у2 + г2, х=1/2. (Ответ: (3/8, 0, 0.)
3.13. V: 2x = y24-z2, у2 4-z2 = 4, х = 0. (Ответ: (2/3, 0,0).)
3.14. V: 4у =д/х2 4-z2, х2 4- z2 = 16, у = 0. (Ответ: (0,3/8, 0).)
3.15. V: y24-z2 = 8х, х = 2. (Ответ: (4/3, 0,0).)
3.16. V: z = 9д/х2 4- у2, z = 36. (Ответ: (0, 0, 27).)
3.17. V: z--= 3(х2 4~ у2), х2 4-у2 = 9, z = 0. (Ответ: (0,0,9).)
3.18. V: х = 2д/у2 4- z2, у2 4- z2 = 4, х = 0. (Ответ: (3/2, 0,0).)
3.19. V: x24-z2 = 4y, у = 9. (Ответ: (0, 6, 0).)
3.20. V: х = 5д/у2 -f- z2, х = 20. (Ответ: (15, 0, 0).)
3.21. V: y = x'2-(-z2, x24-z2=10, у = 0. (Ответ: (0, Ю/З, 0).)
181
3.22. V: у = х2 4- г2, x2 = 22=16, у = 0. (Ответ: (0,9/2, 0).)
3.23. V: у2 + z" = Зх, х = 9. (Ответ: (6, 0, 0).)
3.24. V: у = д/х2 4- z2, у = 4. (Ответ: (0, 3, 0).)
3.25. V: x = y24~z2, у2 + z2 = 9, х = 0.
(Ответ: (3, 0, 0).)
3.26. V: х = 0, у = 0, z = 0, х + У + z = 3. (Ответ: (3/4, 3/4, 3/4).)
3.27. V: z = 2д/х2 -f- у2, х2 -f- у2 = 9, 2 = 0. (Ответ: (О, 0, 9/4).)
3.28. V: х2 -f- у = 2z, 2 = 3. (Ответ: (О, 0, 2).)
3.29. V: 2 =д/х2 4* У2, 2 = 4. (Ответ: (О, О, 3).)
3.30. V: 2 = х24-у2, х2 4- у2 = 4, 2 = 0. (Ответ: (О, О, 4/3).)
4. Вычислить момент инерции относительно указанной оси координат однородного тела, занимающего область И, ограниченную данными поверхностями. Плотность тела Ь принять равной 1.
4.1. V: у2 = х2 4- 22, у = 4, Оу. (Ответ: 512л/5.
4.2. V: х - = у2 4* 22, х = 2, Ох. (Ответ: 4л/3.)
4.3. V: у'2 = х24~22, у = 2, Оу. (Ответ: 16л/5.)
4.4. V: X - = у2 4* z2, х = 9, Ох. (Ответ: 243л/2.
4.5. V: х2 = у2 4* 22, х = 2, Ох. (Ответ: 16л/5.)
4.6. V: у-- = х24~22, у = 2, Оу. (Ответ: 4л/3.)
4.7. V: х2 = у2 4~ 22, х = 3, Ох. (Ответ: 243л/10
4.8. V: X = = у2 4* z2, х = 3, Ох. (Ответ: 9л/2.)
4.9. V-. у-- = 2~\/х2 4- 22, у = 2, Оу. (Ответ: л/5.)
4.10. V: у = х2 4- 22, у = 3, Оу. (Ответ: 9 л/2.)
4.11. V: x2 = y24-z2, у24~22=1, х = 0, Ох. (Ответ: 2л/5.)
4.12. V: х = у24~22, y24*z2--l, х = 0, Ох. (Ответ: л/3.)
4.13. V: z2 = х2 4- у2, z = 3, Oz. (Ответ: 243л/10.)
4.14. V: 2 = х24-у2, z = 3, Oz. (Ответ: 9л/2.)
4.15. V: y2 = x2 + z2, x2 + z2 = 4, у = 0, Оу. (Ответ: 64л/5.)
4.16. V: 2у = х2 4-22, у = 2, Оу. (Ответ: 16л/3.)
4.17. И: х2 = у24~22, х = 2, Ох. (Ответ: 16л/5.)
4.18. V: 2z = х2 4-у2, z = 2, Oz. (Ответ: 16л/3.)
182
4.19. V: х2 = у2 4- z2, у2 4- z2 = 4, х = 0, Ох. (Ответ: 64л/5.)
4.20. V: 2z = x2-\-y2, х2 4- у2 = 4, 2 = 0, Oz. (Ответ: 32 л/3.)
4.21. V: z = 2(х2у2), z = 2, Oz. (Ответ: л/3.)
4.22. V: х=1—у2 — zl,x = Q, Ох. (Ответ: л/6.)
4.23. V: y — 4 — x'2 — z2, у = 0, Оу. (Ответ: 32л/3.)
4.24. V: х = 3(у2г2), х = 3, Ох. (Ответ: л/2.)
4.25. V: 2 = 9— х2 — у2, z = 0, Oz. (Ответ: 243л/2.)
4.26. V: 2 = 4\Jx2 4- у2, 2 = 2, Oz (Ответ: л/80.)
4.27. V: 2 = 3(х2 4* У2)> z = 3, Oz. (Ответ: л/2.)
4.28. V: х = 2xjу2 4~ z2, х = 2, Ох. (Ответ: л/5.)
4.29. V: у = 3(х2 4- z2), у = 3, Оу. (Ответ: л/2.)
4.30. V: 2 = 3 — х2— у2, z = 0, Oz. (Ответ: 9л/2.)
Решение типового варианта
1. Вычислить массу ш неоднородной пластины D, ограниченной линиями у = 2х — х2, у = х, если поверхностная плотность в каждой ее точке ц = х2 4- 2.ху.
► Для вычисления массы ш плоской пластины заданной поверхностной плотностью р воспользуемся физическим смыслом двойного интеграла (см. § 13.1, свойство 2) и формулой m =Ц (х2 4- 2ху) dxdy, где область о
интегрирования D изображена на рис. 13.41. Это позволит легко представить записанный двойной интеграл в виде повторного:
1 2л-А-' I 2л‘ —А"’
m = \ dx J (х2 4- 2ху) dy = J (х2у 4- xy2)l dx = Ох 0 ' v
I
= $ (2х3 — х4 — х3 4- 4х3 — 4х4 4- х5 — х3) dx = о
= (х5 — 5х4 4-4х3)о!х =^-Д- —х54-х‘^| =-g-- ◄ о
2. Вычислить статический момент относительно оси Оу однородной пластины D, ограниченной линиями х2 4- у2 — — 2ах = 0, х2 + у2~ах = 0, у — х — 0, у 4~х = 0 (рис. 13.42), использовав полярные координаты. Поверхностная плотность пластины ц = 2.
183
Рис. 13.41
yi ^л/4/
p-acos'fc
О
Y-JTpt
Рис. 13.42
► Статический момент относительно оси Оу данной пластины определяется по формуле (13.17). В полярной системе координат область D преобразуется в область D': a cos фр 2а cos <р, —л/4 ^ф^ л/4. Тогда
л/4 2а cos <р
Му = 2р cos ф • prfpc/ф = 2 cos фс?ф Р2^Р =
D' — л/4 a cqs ср
”/4 .>................ .. л/4
j cos4 фо!ф —
— л/4
j 12а cos ср - з
cos ф • о!ф = 2-—
о I a cos <р о
— л/4
л/4
= J8 q3 (l +cos2<p)2
3 J 4 т
о
л/4
= а3 I (1+2 cos 2ф + cos2 2ф) с/ф = ((ф +
о J 3 V
О
л/4
IЛ//4 Г
+ sin 2q>) + \
о
=+(++)• <
3. Вычислить координаты центра масс однородного тела, занимающего область V, ограниченную поверхностями у = -^-д/х2 + z2, у = 2.
> Данное тело симметрично относительно оси Оу (рис. 13.43), поэтому хс = zc — 0, а
Ус = ® ydxdydz/ $ dxdydz. V V
184
Рис. 13.43
Переходим к цилиндрическим координатам по формулам, аналогичным формулам (13.26): х — р cos <р, z — — р sin ф, у = у. Тогда
2л 4 2
$ ydxdydz = $ ypdpdtpdy = J dq J pdp J ydy =
V V 0 0 p/2
2л 4 2л 4
=4 S p(4 - тp2)dp=4 J (2p2 - 4)|0^=
0 0 0
= 4- • 1 6w|2л = 16л, 2 Io
2л 4 2
$ dxdydz = $ pdqdpdy = J dq J pdp $ dy =
V V 0 0 p/2
2л 4 2л
= J p(2 — 4p)^P= J (p2-4 p3)|o^ = 0 0 0
Следовательно,
__ 16n • 3 ____ 3
3-H 2
и центр масс C(0, 3/2, 0). ◄
4. Вычислить момент инерции относительно оси Оу однородного тела (плотность б = const), занимающего область V, ограниченную поверхностью у = 5 — х2 — г2 и плоскостью у = 1.
> Согласно формулам (13.18), искомый момент инерции
185
/у = $ б(х, у, z) (л-2 4- z2) dxdydz = г
= 6 $ (х2 z2) dxdydz.
г
(Область V изображена на рис. 13.44.)
Переходим к цилиндрическим координатам по формулам х = р cos <р, z = р sin ф, у = у. Тогда
2л 2 5-р;
1у = б $ p2pdyd(fdy = б j dtp J p3dp J dy = lz 0 0 1
2 л 2
= 6 $
0 0
y\
2л 2
p,!rfp = 6 $ dtp $ pJ(5 —p2— l)rfp =
0 0
Ч(р*-^)1>-ч2,~т)и=т^ <
о 0
13.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ К ГЛ. 13
1. Доказать равенства:
x2dxdy = у2dxdy = у dxdy,
D о о
если область D определяется неравенствами х >• О, у > О, х2 4- у2 < а2.
2. Использовав полярные координаты, вычислить
Ц х/ а2 —~х2 — у2 dxdy, D
186
где область D — лепесток лемнискаты (х2 -ф у2)2 = а2(х2 —
-у2), х>0. (Ответ: - 16^~2-0)^.)
3. Построить область, площадь которой выражается интегралом
л/2 а( 1 -j- cos t[)
j dy j pdp. — л/2 a
4. Вычислить площадь фигуры, ограниченной линией /2 2 \ 2 2 2
-ф = — — Д-. (Ответ: 6.)
\ 4 г 2 ) 4 9 ' ’
5. Вычислить площадь фигуры, ограниченной кривыми (х2 + у2 — ах)2==а2(х2 + у2) и х2 + у2 = аух[з. (Ответ: За2х/з/2.)
6. В каком отношении гиперболоид х2 -ф у2 — z2 = d2 делит объем шара х2 -ф у2 -ф г2 гф За2? ( Ответ: Зу/з— -2/2.)
7. Доказать, что объем тела, ограниченного поверхностями z = 0 и z = е~х!~у!, равен л.
8. Вычислить координаты центра масс однородной пластины, ограниченной кардиоидой р = а(1 -ф cos <р). (Ответ: а, 0^
9. Вычислить момент инерции относительно оси Ох однородной пластины, ограниченной кривой х4 -ф у4 = = х2-ф у2. (Ответ: Зл/(2д/2).)
10. Вычислить
2 -yfax — х2 а
\ dx $ dy\ zxjx2y2dz, ООО
преобразовав его предварительно к цилиндрическим координатам. {Ответ: За2/d)
11. Вычислить
\ dx \ dy $ (х2 -ф y2)dz,
о
преобразовав его предварительно к сферическим координатам. {Ответ: 4л/?5/15.)
187
12. Вычислить массу тела, ограниченного прямым круглым цилиндром радиусом /? и высотой Н, если его плотность в любой точке численно равна квадрату расстояния от этой точки до центра основания цилиндра. (Ответ: -^-(3/?2 + 2Д2).)
13. Вычислить координаты центра масс однородного тела, ограниченного поверхностями у — х]~х, у = 2д/х, z = 0 и х + z = 6. (Ответ: (14/15, 26/15, 8/3).)
14. Вычислить координаты центра масс однородного тела, ограниченного поверхностями х2 у2 = z и х + У + + z = 0. (Ответ: (-1/2, -1/2, 5/6).)
15. Найти момент инерции относительно начала координат однородного тела, ограниченного конусом z2 = = х2 — у2 и сферой х2 -ф у2 + z2 = R2 (Ответ: 2л(2 — -V2)/?5/5.)
16. Найти момент инерции относительно диаметра основания круглого конуса, высота которого Н, радиус основания R и плотность у = const. (Ответ: nyHR2(2H2 + + 3/?2)/60.)
17. Показать, что сила притяжения, действующая со стороны однородного шара на внешнюю материальную точку, не изменится, если всю массу шара сосредоточить в его центре.
18. Дано однородное тело, ограниченное двумя концентрическими сферами. Доказать, что сила притяжения данным сферическим слоем точки, находящейся во внутренней полости тела, равна нулю.
19. Вычислить массу полушара радиусом R, если плотность распределения массы в каждой его точке пропорциональна (k — коэффициент пропорциональности) расстоянию от нее до некоторой точки О на границе основания полушара. (Ответ: 4йл/?4/5.)
20. Вычислить объем V общей части шара радиусом R и кругового цилиндра радиусом R/2 при условии, что центр шара лежит на поверхности цилиндра. (Ответ: 4Д1-Д)
21. Вычислить площадь части сферической поверхности радиусом R, которая высекается круговой цилиндрической поверхностью радиусом R/2 при условии, что центр сферы лежи' на цилиндрической поверхности. (Ответ: 2R2(n-2\)
14. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
14.1. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИХ ВЫЧИСЛЕНИЕ
Криволинейные интегралы первого рода (по длине дуги). Пусть в пространстве RJ задана гладкая дуга Lab кривой L, во всех точках которой определена непрерывная функция и = j(x, у, г). Дугу LAb про-
извольным образом разобьем на п
частей /, длиной Д/, (Z = 1, п). В каждой элементарной части L выберем произвольную ТОЧКу I/,. Z;)
(рис. 14.1) и составим интегральную сумму
п
/„=S f(x;, у;, 2,) Mt. i= 1
Тогда предел lim 1п всегда суще* д/,->0
ствует, называется криволинейным интегралом первого рода или криволинейным интегралом по длине дуги Lab от функции f(x, у, z) и обозначается $ f(x, у, z)dl.
Lab
Таким образом, по определению
п
j f(x, у, z)dl= lim S f(xt, у,, z,) Mt.
Lab max <M,^0 j=1
Если кривая L лежит в плоскости Оху и вдоль этой кривой задана непрерывная функция f(x, у), то
j f(x, y)dl— lim 2 f(x,, у,) A/,-. (14.1)
Lab max i= 1
В случае, когда гладкая кривая L задана в пространстве R3 параметрическими уравнениями х — x(t), y — y(t), z = z(t) и параметр t изменяется монотонно на отрезке |а; р] (а < р) при перемещении по кривой L из точки А в точку В, верна формула для вычисления криволинейного интеграла
₽ ________________________
5 f(x, у, z)dl = \f(x(f), y(f), z^^x'^Y+^y'^+^'^dt. (14.2) Lab a-
189
В случае плоской кривой формула (14.2) упрощается.
Р __________
5 /'(х, y)dl = \i(x(t), y(lfy(x'(t)f+(yft)fdt. (14.3) L.UJ а
Если уравнение плоской кривой р = р(<р) задано в полярных координатах р, (р, функция р((р) и ее производная р' = dp/dq непрерывны, то имеет место частный случай формулы (14.3), где в качестве параметра / взят полярный угол <р:
$ f(x,y)dl = f(p(<₽) cos q>, p(<p)sin <₽)У(У+р'*</<₽ (14.4)
L лв T.l
(фд и фв — значения <р, определяющие на кривой точки А и в).
Если плоская кривая задана непрерывной и непрерывно дифференцируемой на |<э; Z>j функцией у = у (х), где а и b — обсциссы точек А и В, то
ь
J /Д. у) dl = \i(x, у(х))д/| + (y'(x))2dx. (14.5)
Lab a
Итак, во всех случаях вычисление криволинейных интегралов первого рода сводится к вычислению определенного интеграла (см. гл. 9 во второй части настоящего пособия).
Пример 1. Вычислить 1= j (2г — д/х2 + у2) dt, где L — первый
L
виток конической винтовой линии х = t cos I, у = I sin t, z = t, 0 ci / s'; < 2л.
► Находим
dl = ^{xftf2+l,y'W + ^'(t)fdt =
= Vicos Z — Z sin If + (sin t + t cos if + 1 dt = -д/2 -f-12 dt.
Тогда
2л ______ 2л _____________
I = J' (2/ - 1} + t2 dt= \ 1^2 + I2 dt =
о 0
I i2л 2
= — (2 + Za)i/2|o = —Д-((1 +2л2)3'2- I). 4
Пример 2. Вычислить 1 = \ ---------, где L — отрезок прямой
J х + 2у 4- 5
L
у = 2х — 2, заключенный между точками А(0, —2), В(1, 0).
> Находим
dl = -д/1 + у'" dx = + 4dx = xjbdx.
190
Следовательно,
\^Г<7х
х + 2(2х - 2) + 5
1
о
dx
5х + 1
Л/5 I' л/5
= —-— In |5х + 11 = —-— In 6. ◄
5 I о 5
Так как, согласно формулам (14.2) — (14.5), криволинейный интеграл первого рода выражается через определенный интеграл, то укажем только те его свойства, которые обобщают свойства определенного интеграла.
I. j dl= l.m, где /4Я— длина дуги АВ (геометрический смысл С АВ
криволинейного интеграла первого рода).
2. Если f(x, у, г) = б(х, у, г) — линейная плотность материальной дуги Lab, то ее масса m вычисляется по формуле
пг= j б(х, у, z) dl (14.6)
Lab
(механический смысл криволинейного интеграла первого рода).
3. Координаты центра масс материальной дуги Lab, имеющей линейную плотность б = б(х, у, г), определяются по формулам:
хс — — j хб (х, у, z) dl, у,: = -L j уб (х, у, z) dl,
Lab Lab
zc = j г6(х, y, z) dl,
Lab
(14.7)
где m — масса дуги Lab-
4. Моменты инерции относительно начала координат О, осей координат Ох, Оу, Oz и координатных плоскостей Оху, Охг, Оуг материальной дуги Lab, имеющей линейную плотность б = б(х, у, z), вычисляются соответственно по формулам:
7о = J (х2 + у2 + г2) 6dl, Ix = 5 (у2 + z'2)6dl,
Lab Lab
7S = $ (х2 + 2‘) &dl, = J (-t2 + У2) ^dl,
Lab lab
I,в = $ z2§dl, /„ = y2f>dl, 7уг = j x26dl.
Lab Lab Lab
(14.8)
Моменты инерции связаны следующими соотношениями:
210 = Ix + 1в + 7г, /о = /г» + 7хг + 7уг.
Если дуга Lab лежит в плоскости Оху, то рассматриваются только моменты /о, /(, 7У (при условии, что г = 0).
191
5 Пусть функция z = f(x, у) имеет размерность длины и j(x, у) > О во всех точках плоской дуги лежащей в плоскости Оху. Тогда
$ f(x, у) dl = S,
LaB
где S — площадь части цилиндрической поверхности с образующими, параллельными оси Oz и проходящими через точки дуги Lab, ограниченной снизу дугой ЬЛв, сверху — линией пересечения цилиндрической поверхности с поверхностью z = f(x, у), а с боков — прямыми, прохо
Р и с. 14.2
дящими через точки А и В параллельно оси Oz. На рис. 14.2 изображена описанная часть цилиндрической поверхности АВВ'А'. Если /’(х, у) < О во всех точках плоской дуги Lab, то
5 /'(х, у) dl = -S
Lab
(рис. 14.3). И, наконец, в некоторых точках плоской дуги Е,1В функция /(х, у) меняет знак, тогда интеграл $ fix, у) dl выражает разность Lab
площадей частей описанной цилиндрической поверхности, находящихся над плоскостью Оху и под ней (рис. 14.4):
j /'(х, у) dl = S, — S> -|- Sj.
Lab
Пример 3. Вычислить массу т и координаты центра масс х( , ус 2 . ,,
плоской материальной дуги у = -уХ,/‘, 0 х 1, линейная плотность которой 6(х, у) = у у 1 + х.
> Согласно формулам (14.5) и (14.6), для случая плоской дуги имеем.
I I
т = j 6(х, у(х)) "71 (y'(x))2dx = j х3/2 V1 +* +xdx =
« е
19Й
Пример 4. Вычислить площадь части цилиндрической поверхности х~ //' = 4, заключенной между плоскостью Одр и поверхностью г = = 2 + лЛ’/- (рис. 14.5).
> Искомая площадь S цилиндрической поверхности выражается интегралом
S= j (2 4* д_’/2) dl,
l.
где L — окружность в плоскости Оху. х! + У~ = 4, г = 0, уравнение которой в параметрическом виде д = 2 cos t, у = 2 sin I. Тогда dl = = 2d! и
S = j (2 + ~ • 4 cos-’ 2dt =
0
2.4 2л
— 4 j (I -j- cos2 t) dl = 4 j 4- cos 2/^ dl — 12л.
о 0
7—357
193
Р и с. 14.5 р 11 с 14 6
Криволинейные интегралы второго рода (по координатам). Пусть в пространстве R’ задан вектор а = Р(х, у, z) i + Q(x, у, z) j + R(x, у, z) k, координаты которого — непрерывные функции в точках ориентированной кривой Lab- Кривую LaB разобьем в направлении от А к В на п элементарных дуг /, и построим векторы Л/, = Ax,i + Ay,j Az,к, где Ах,, Ду,, Az, — проекции векторов Л/, на оси координат. Начала этих векторов совпадают с началами элементарных дуг а концы — с нх концами (рис. 14.6). На каждой элементарной части /, выберем произвольную точку М,(х„ у,, z,) и составим интегральную сумму
п
/,,= S Р(х„ у„ z,)Ax, 4-Q(x„ у,, г,)Лу,+Л (х„ у„ г,) Az, =
<= 1
II
= S а (х/, y,, z,) • A/,. i = I
(14.9)
Предел суммы (14.9), найденный при условии, что все )Д(,|->0, называется криволинейным интегралом второго рода или криволинейным интегралом по координатам от вектор-функции а (х, у, г) по кривой Lab и обозначается
J а (х, у, z) • dl = j Р(х, у, z) dx + Q (х, у, z)dy + R(x, у, z)dz =
Lab Lab
rt
= lim S a(x„ ylt z,) -AL.
(MIO)
Если функции P (x, y, z), Q (x, y, z), R (x, у, z) непрерывны в точках гладкой кривой Lab, то предел суммы (14.8) существует, т. е. существует криволинейный интеграл второго рода (14.10).
Криволинейные интегралы второго рода обладают основными свойствами определенных интегралов (линейность, аддитивность). Непосредственно из определения криволинейного интеграла второго рода следует, например, что он зависит от направления интегрирования вдоль кривой, т е. меняет знак при изменении ориентации кривой:
j а • dl = — j а • dl.
Lab Lab
194
Если кривая интегрирования L замкнута, криволинейные интегралы второго рода обозначаются фа • dl. В этом случае через кривую L ' L
проводится ориентированная поверхность и за положительное направление обхода по L принимается такое направление, при котором область поверхности, ограниченная кривой L, находится слева, если двигаться вдоль L по выбранной стороне указанной поверхности (т. ё. обход контура L совершается против хода часовой стрелки).
Если плоскую область D, ограниченную кривой L, разбить на части, не имеющие общих внутренних точек и ограниченные з минутыми кривыми Lt и Li, то
фа-dl — фа-dl-b фа-dl, Z. Lt L3
где направления обхода по контурам L, Lt и Li — всюду либо положительные, либо отрицательные.
Если гладкая кривая Lab задана параметрическими уравнениями x = x(t), у = y(t), z = z(t), где х(0, y(t), z(t}—непрерывно дифференцируемые функции, 4(х(сс), р(а), z(a)) и В(х(Р), «/(₽). 2(Р))— соответственно начальная и конечная точки этой кривой, то верна следующая формула для вычисления криволинейного интеграла второго рода:
j Р (х, у, z)dx + Q (г, у, z)dy + R (х, у, z) dz =
Lab
= \(P(x(t), y(t), z (/)) x'(l) 4-Q (x(Z), yW. z(0)/(0 +WU14.11) a
!/(/), z(t}) z'(t)) dt.
Если кривая Lab лежит в плоскости Оху, а = Р(х, y)i-j-Q(x, у) j, то R(x, у, z)^0, z(<)=0 и формула (14.11) упрощается:
К
J Р(х, y)dx + Q(x, y)dy=\ (Р(х(<), y(0)x'(0 +
Lab а
+ Q(x(t), y(t))y'(t))dt. (14.12)
Если кривая Lab лежит в плоскости Оху и задана уравнением у — f(x), производная f'(x) непрерывна на отрезке [а; 6], а = Р (х, p)i + + Q (х. У) j. то
ь
$ Р(х, y)dx + Q{x, y)dy= $ (Р(х, /(х)) +
Lab a
4- Q(*. K*))f'(x))dx. (14.13)
Пример 5. Вычислить
/ = \ ydx + (x + z) dy + (x — y) dz,
Lab
где Lab — отрезок прямой, соединяющий точки 4(1, — 1, 1) и В(2, 3, 4).
195
► Запишем параметрические уравнения прямой АВ: х = 1 4-t, у = — 1 4-41, z = 1 4- 3t. На отрезке МВ| паоаметр 0 1 По-
этому, согласно Фоомуле (14.11),
1
/ = $ ((- 1 4- 4<) 4- (2 4- 4<) • 4 4- (2 - 30 • 3) = о
1
= 5 (13 4- 1И) dt — 18,5. о
Пример 6. Вычислить / = §ydx — x1 2dy 4- (х 4- у) dz, если L — крн-L
вая пересечения цилиндра х2 4- у2 = 4 с плоскостью х 4- у — z = 0, «пробегаемая» в положительном направлении относительно выбранной верхней стороны данной плоскости.
► Найдем параметрические уравнения кривой L. Так как проекция кривой L на плоскость Оху есть окружность х2 4- у2 = 4, z = 0, то можно записать, что х = 2 cos t, у = 2 sin t. Тогда из уравнения плоскости находим, что z = 2 (cos t 4- sin 1). Таким образом,
х = 2 cos t 'l ( dx = — 2 sin tdt
у = 2 sin t f^l dy — 2 cos tdt
z = 2 (cos t 4- sin f), t E [0; 2л], ) I dz = 2( — sin t 4- cos t) dt
Отсюда по формуле (14.11) имеем:
2л
1 = j (— 4 sin21 — 8 cos3 14- 4 (cos2 t — sin2t)) dt = 0
2л
= J ( — 2 4-2 cos 2t — 8 cos t 4- 8 sin21 cos t 4- 4 cos 2t) dt = — 4л. 4 о
Пример 7. Вычислить /= J xydx 4- (x2 4- y) dy, если линия
Lab
Lab — дуга параболы у = x2, расположенная между точками Л(0, 0) и В (2, 4).
► Так как в данном случае Дх) = х2, ('(х)=2х, х £ [0; 2], то, согласно формуле (14.13), получаем 2 2
Sr 5 12
(хх2 4- (*2 + *2) • 2х) dx = \ 5x3dx = — х4 =20. ◄
J 4 (о
о о
АЗ-14.1
1. Вычислить (———, если L — отрезок прямой у = J х У
L
= у% — 2, заключенный между точками А(0, —2) и В(4, 0). (Ответ: -д/б In 2.)
2. Вычислить§xydl, если L — контур прямоугольника
196
с вершинами в точках А(0, 0), В(4, 0), С(4, 2), £>(0, 2). (Ответ: 24.)
3. Вычислить J ^2ydl, если L — первая арка циклоиды
х = a(t — sin /), у = а( 1 — cos /) (а > 0). ( Ответ: 4ла~\[а.)
4. Вычислить $ xyzdl, если L — отрезок прямой между L
точками 4(1, 0, 1) и В(2, 2, 3). (Ответ: 12.)
5. Вычислить площадь боковой поверхности цилиндра х2 + у2 — Rx, заключенной внутри сферы х2 + у2 + z2 = У?2. (Ответ: 4R2.}
6. Вычислить J (х2 — 2ху) dx + (2ху + y2}dy, где LAB —
Lab
дуга параболы у = х2 от точки A(l, 1) до точки В (2, 4). (Ответ: 40^.^
7. Вычислить J xdx + ydy + (х + у — 1) dz, где LAB — L АВ
отрезок прямой, соединяющей точки 4(1, 1, 1) и В(2, 3, 4). (Ответ: 13.)
8. Вычислить j yzdx + zxdy xydz, где L — дуга вин-L
товой линии х = R cos /, y = Rs\ni, z = at/(2n) от точки пересечения линии с плоскостью z = 0 до точки ее пересечения с плоскостью z = а. (Ответ: 0.)
9. Вычислить J xydx + (у — x)dy, если линия LAB, со-1~АВ
единяющая точки Л (0, 0) и В(1, 1), задана уравнением: а) у = х: б) у = х2: в) у = х; г) у = хл. (Ответ: а) 1/3; б) 1/12; в) 17/30: г) —1/20.)
10. Найти координаты центра масс первой полуарки циклоиды x = a(t — sin Z), у = а(1 — cos/), t g [0; л]. (Ответ: 4а/3, 4й/3.)
Самостоятельная работа
1. Вычислить:
a) J xdl, если L — отрезок прямой, соединяющей точ-L
ки 4(0, 0) и В(1, 2);
б) J (х + у) dx + (х — у) dy, если LAB — дуга параболы L АВ
197
у = х2, лежащая между точками Л(—1, 1) и В(1, 1). (Ответ: а) д/5/2; б) 2.)
2. Вычислить:
a) J x2ydl, если L — часть окружности х2 -f- у2 = 9 ле-L
жащая в первом квадранте;
б) j (х — у) dx + (х + у) dy, если ЬАВ— отрезок прясле
мой, соединяющий точки А (2, 3) и 15(3, 5).
(Ответ: а) 27; б) 23/2.)
3. Вычислить:
a) j 7/> если — отрезок прямой у = х-)-2, соеди-
L
няющий точки Л (2, 4), В(1, 3);
б) (У + x2)dx + (2х — y)dy, если LAB — дуга парабо-
Lab
лы у = 2х — х2, расположенная между точками Л(1, 1) и 15(3, -3). (Ответ: а) (-^2/2) In 2; б) 12.)
14.2. ПРИЛОЖЕНИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
С помощью криволинейных интегралов первого рода можно вычислять длину дуги кривой, массу материальной дуги, ее центр масс, площади цилиндрических поверхностей и другие величины.
Пример 1. Вычислить массу m дуги кривой L, заданной уравнениями х = /2/2, y — t, г = t3/3, О t 2, если плотность в каждой ее точке б = 1 + 4лг у2.
► Согласно формуле (14.6), искомая масса m выражается интегралом *
__________ 2
m = j -yl + 4х2 + у2 dl = $ -0 -Н4 + t2x/t2 + 1+ I4 it =
L 0
2
= j(l -H2 + I4)d/= 116/15. -4 о
Пример 2. Вычислить координаты центра масс однородной дуги окружности х2 + у2 = R2, расположенной в первом квадранте, и моменты инерции /о, 1„ 1У.
► Так как прямая у = х является осью симметрии дуги окружности, то хс = ус. Для нахождения хс используем первую из формул (14-7):
хс = J x6dl/ \&dl = xdl/ $ dl,
L L L L
198
поскольку 6 = const. Интеграл
dl = iiR
L
определяет длину четверти рассматриваемой окружности. Вычислим (xdl, где х = R cos г; у = R sin /; 0 < t л/2;
L
dl = л/(*'(0)2+(/(0)г dt = Rdt.
Следовательно,
V2 i я/2
J xdl = j R cos IRdt = R2 sin q = R2.
l о 1°
Окончательно имеем:
R2 2R
Хс~Ус~1йй2 ~ V
При вычислении I о, lx, ly воспользуемся формулами (14.8) и (14.3) для случая плоской дуги (г sb 0) и учтем, что
л/2
10 = $ (х2 4- у2) 6Л = 6 R2Rdt = /?36л/2, L 0
л/2 л/2
Л = </2dd/= 6 R2 sin2 tRdt = j (1 — cos 2.1) dt = л/?’6/4. < to о
Криволинейный интеграл второго рода (14.9) в случае, когда а = = F — сила, под действием которой перемещается тело, определяет работу силы F иа пути Lab- В этом заключается физический смысл криволинейного интеграла второго рода.
Пример 3. Вычислить работу А силы F = yzi 4- xzj 4- хук вдоль отрезка прямой ВС, если В(1, 1, 1) и С(2, 3, 4).
Запишем параметрические уравнения прямой ВС: х = 1 4-1, у = 1 4- 2t, z = 1 + 31, где 0 t 1. Тогда работа А силы F на пути ВС вычисляется по формуле
А = j yzdx 4- xzdy 4- xydg = tec
i
= $(1 4-20(1 +3t)dt+ (1 4-0(1 + 3/) 2dt 4- (1 4-0(1+20 3Л ==
0
I
= j (1812 4- 221 4- 6) dt = 23. « о
Теорема (Грина). Если функции Р(х, у) и Q(x, у) непрерывны и меют непрерывные частные производные в замкнутой односвязной
199
области D, лежащей в плоскости Оху и ограниченной кусочно-гладкой кривой L, то
§ Pdx + Qdy dxdy,
L D
(14.14)
где интегрирование по контуру L выполняется в положительном направлении.
Формула (14.14) называется формулой Грина.
Если в некоторой области D выполнены условия теоремы Грина, то равносильны следующие утверждения.
1 §Pdx + Qdy = 0, если L — любой замкнутый контур L, располо-Ь
женный в области D.
2. Интеграл j Pdx + Qdy не зависит от пути интегрирования,
Lab
соединяющего точки А и В, где Lab ё D.
3. Pdx + Qdy = du(x, у), где du(x, у) — полный дифференциал функции и(х, у).
4. Во всех точках области D справедливо равенство dQ _ дР дх ду
(14.15)
Из формулы Грина следует, что площадь S области D можно также вычислить с помощью криволинейного интеграла второго рода:
— ydx + xdy,
L
где интегрирование ро контуру L производится в положительном направлении.
Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой /' + х* — у1 = 0 (рис. 14.7).
Рис. 14.7
200
► Из уравнения кривой получим, что у = ±х_ух4- '> т- е- кривая симметрична относительно оси Ох и пересекает ее в точках х = 0 и х=— 1; обе функции у = ±х ух 4- 1 определены при х>—1, а </->± оо при х-*оо. Перейдем к параметрическим уравнениям данной кривой, положив у = xt. Подставив у = xt в уравнение х3 4- х2— — у2 = 0, получим х3 4-х2 = х2/2, х = г— 1, у = /3—/, где для петли -1 1.
Следовательно, искомая площадь
I
S = y J [-(/3-/)2/4-(С’-1)(3/2-1)]Л = — I
(
So (С —2/24-1)Л=ч
о
Пример 5. Вычислить
/ = Ф 4/(1 — x2)dx 4- (1 4- уг) xdy,
L
где контур L — окружность х2 4~ у2 = 4, «пробегаемая» в положительном направлении обхода.
Для вычисления интеграла воспользуемся формулой Грина (14.14):
1 = S О + у2 — 1 + *2) dxdy = S (*2 + у2) dxdy, D D
где D — круг, определяемый неравенством х2 4- у2 4. Имеем
/ = К_i_ о2\иvл,, Iх = р cos <р, dxdy = pdpdcp, I
тИ) У | у = р sin <р, 0^<р^2л, 0 <1 р 21
2л 2
= Ц p3dpdq = j dtp j p'dp — 8л. < D' о о
С помощью теории криволинейных интегралов второго рода можно решить следующую задачу. Известно дифференциальное выражение Р(х, y)dx 4~ Q(x, y)dy, которое является полным дифференциалом некоторой функции и(х, у). Требуется найти эту функцию.
Решение данной задачи определяется формулой х у
U(x, у) = $ Р (X, y0)dx 4- J Q(x, у) dy 4- С (14.16) Хо уо
ИЛИ
х У
и(х, у)= 5 Р(х, y)dx+ $ Q(x0, y)dy + c, (14.17) Хо Уо
где точки Л4о(х0, у») и Л4(х, у) принадлежат области D, в которой Р(.х, У)> Q(x’ У) и их частные производные являются непрерывными функциями; С—произвольная постоянная.
201
Пример 6. Показать, что дифференциальное выражение
— dy + 67 ------- + In у} dx
у \ 1 + х1 х /
будет полным дифференциалом некоторой функции и(х, у), и найти эту функцию.
> Так как
р (*< = 7 ‘"2 - — + In у, Q (х, у) = —,
1 + X1 X у
дР 1 dQ 1 ,
то -г- = — и —7— = —. Значит, во всех точках плоскости Охи, ис-ду У дх у
ключая точки, лежащие на осях координат, данное дифференциальное выражение в силу равенства (14.14) будет полным дифференциалом некоторой функции и(х, у). Теперь воспользуемся общей формулой (14.16) или (14.17), где можно взять Л4о(1, 1).
По формуле (14.16) имеем X У
I I
= (arctg х — In |х[)| 1 + х In |у| I, 4- С =
= arctg х — In I x| + x In | у | + C,
где C — произвольная постоянная. ◄
АЗ -14.2
1. Вычислить массу дуги кривой у = In х плотностью 6 = л2, если концы дуги определяются следующими значениями х: Xi =т/з, X2=^/s. (Ответ: 19/3.)
2. Вычислить площадь поверхности, которую вырезает из круглого цилиндра радиусом R такой же цилиндр, если оси этих цилиндров пересекаются под прямым углом. (Ответ: 8R2.)
3. С помощью криволинейного интеграла второго рода вычислить площадь фигуры, ограниченной:
а) линией х = a cos31, у — a sin31 (астроида);
б) первой аркой циклоиды x = a(t— sin t), у = а(\ — — cos t) и осью Ox.
(Ответ: а) Зла2/8; б) Зла2.)
4. Найти функции и(х, у) по их полным дифференциалам:
a) du = 4(х2 — у2) (xdx — ydy)-,
б) du = (2х cos у — у2 sin x)dx ф (2у cos х — х2 sin y)dy,
в) du = (3y~ x)dx + (y — 3x)dy/(x + y)3.
'202
5. Вычислить работу силы F = (х2 + у2 + 1)i + 2xz/j вдоль дуги параболы у = х3, заключенной между точками Д(0, 0) и В(1, 1).
(Ответ: 196/105.)
6. Применив формулу Грина, вычислить
ф y2dx + (х + y)2dy, L
где L — контур треугольника АВС с вершинами в точках А(3, 0), В(3, 3) и С(0, 3). (Ответ: 18.)
7. Найти общий интеграл дифференциального уравнения (4х3у3 — у2) dx -|- (3x4z/2 — 2ху) dy = 0. (Ответ: х*у3 — — ху2 = С.)
Самостоятельная работа
1. 1. С помощью криволинейного интеграла второго рода вычислить площадь области D, ограниченной линиями у = х2 и у =~\[х. (Ответ: 1/3.)
2. Найти функцию и(х, у), если
du(x, у) = (2ху + х3 — 5) dx -|- (х2 — у3 + 5) dy.
2. 1. Вычислить площадь фигуры, ограниченной осями координат и дугой эллипса х2/а2у2/Ь2 = \, расположенной в первом квадранте. (Ответ: лаЬ/4.)
2. Найти функцию и(х, у), если
du (х, у) = (х2 + 2ху — у2) dx + (х2 — 2ху + у2) dy.
3. 1. Вычислить работу силы F(x, у) = 2xz/i + x2j, совершаемую на пути, соединяющем точки Д(0, 0) н В(2, 1). (Ответ: 4.)
2. Найти функцию и(х, у), если du = dx + (-^т +
(1 -|-х)2 Ш*2 /
14.3. ИНДИВИДУАЛЬНЫЕ ДОМАШНИЕ ЗАДАНИЯ К ГЛ. 14
ИДЗ-14.1
Вычислить данные криволинейные интегралы.
1
1.1. J (х2 — 2ху)dx + (у2 — 2ху) dy, где ЬдВ — дуга па-
Lab
203
раболы у — х2 от точки 4(—1, 1) до точки В(1, 1). (Ответ. — 6.)
. „ f x2du — u'dx ,
1.2. \ —-=—где Lab—Дуга астроиды х —
= 2 cos3 t, у = 2 sin31 от точки Л (2, 0) до точки В(0, 2). (О твет: З^л/в.)
1.3. j (х2 4- У2) dx 4- 2xydy, где LOa —дуга кубиче-Loa
ской параболы у = х3 от точки 0(0, 0) до точки 4(1, 1). (Ответ: 4/3.)
1.4. ф (х 4~ 2г/) dx 4- (х — у) dy, где L — окружность х = L
= 2 cos/, у = 2 sin t при положительном направлении обхода. (Ответ: —4л.)
1.5. ф (х2у — x)dx 4- (у2х — 2y(dy, где L — дуга эллип-L
са х = 3 cos t, у = 2 sin t при положительном направлении обхода. (Ответ: —7,5л.)
1.6. ф (ху — 1) dx 4- x2ydy, где ЬдВ—дуга эллипса Тли
x = cos/, у = 2 sin/ от точки 4(1, 0) до точки В(0, 2). (Ответ: 5/6.)
1.7. j 2xydx — x2dy, где Loba—ломаная ОБА:
0(0, 0); В(2, 0); 4(2, 1). (Ответ: —4.)
1.8. j (х2— у2) dx 4- xydy, где LAB— отрезок прямой
La в
АВ: 4(1, 1); В(3, 4). (Ответ: 11
1.9. $ cos ydx — sin xdy, где LAB — отрезок прямой
L АВ
АВ, А(2л, —2л); В(— 2л, 2л). (Ответ: 0.)
1-10. ( ydxi х<—, где Lab—отрезок прямой 4В;
J т + у-
Lab
А(1, 2); В(3, 6). (Ответ: -L 1п 3.)
1.11. j xydx 4- (у — x)dy, где Lab — дуга кубической параболы у = х3 от точки 4(0, 0) до точки В(1, 1). (Ответ: 1/4.)
204
1.12. j (x2 4- у2) dx + (x + y1) dy, где LABC— ломаная l-лвс
ABC; Л(1, 2); B(3, 2); C(3, 5). (Ответ: 64 A.)
1.13. J xt/2ofx-|- yz2dy — x2zdz, где L0B — отрезок пря-
мой OB; 0(0, 0, 0); B(-2, 4, 5). (Ответ: 91.)
1.14. J ydx -|- xdy, где L0A—дуга окружности x =
— R cos t, у = R sin t; O(R, 0); Л(0, R). (Ответ: 0.)
1.15. J xydx 4~ (y — x)dy, где L0A—дуга параболы
Loa
y2 = x от точки 0(0, 0) до точки Л(1, 1). (Ответ: 17/30.)
1.16. j xdx 4- ydy 4- (х — y-\-V)dz, где LAB— отрезок
прямой АВ; Л(1, 1, 1); В(2, 3, 4). (Ответ: 7.)
1.17. J (ху—l)dx 4- x2ydy, где LAB—дуга параболы Глв
у2 = 4 — 4х от точки Л(1, 0) до точки В(0, 2). (Ответ: 17/15).
1.18. j xydx 4- (у — х) dy, где L0B—дуга параболы
Lob
у — х2 от точки 0(0, 0) до точки B(l, 1). (Ответ: 1/12.)
1.19. j (ху — у2) dx 4- xdy, где L0B —дуга параболы
Lob
у — х2 от точки 0(0, 0) до точки B(l, 1). (Ответ: 43/60.)
1.20. j xdy — ydx, где LAB—дуга астроиды х =
Lab
= 2 cos31, у = 2 sin31 от точки Л (2, 0) до точки В(0, 2). (Ответ: Зл/4.)
1.21. (ху — x)dx 4- -L x2dy, где LAB — дуга параболы
lAb
у2 = 4х от точки Л(0, 0) до точки В(1, 2). (Ответ:0,5.)
1.22. j (ху — 1) dx 4- x2ydy, где LAB — отрезок прямой
АВ; Л(1, 6); В(0, 2). (Ответ: 1.)
1.23. j 2xydx 4- y*dy 4- z2dz, где LAB—дуга одного
Lab
витка винтовой линии x = cost, y = sint, z = 2t; Л(1, 0, 0); В(1, 0, 4л). (Ответ: 64л3/3.)
205
1.24. j X dx + xdy, где Lab — Дуга линии у = In x от Lab
точки Л(1, 0) до точки В(е, 1). (Ответ: е— 1/2.)
1.25. ф ydx — xdy, где L — дуга эллипса x = 3cos/, L
у — 2 sin/, «пробегаемая» в положительном направлении обхода. (Ответ: —12л.)
1.26. 2xydx — x2dy, где Loa—Дуга параболы у = Loa
= х2/4 от точки 0(0, 0) до точки А (2, 1). (Ответ: 0.)
1.27. \ (х2 + y2)dx(х2 — y2)dy, где LAB — ломаная
Lab
линия у= |х| от точки А( — 1, 1) до точки В(2, 2). (Ответ: 6.)
1.28. J 2xydx — x2dy + zdz, где Loa—отрезок прятал
мой, соединяющий точки 0(0, 0, 0) и А(2, 1, —1). (Ответ: 11/6.)
1.29. § xdy — ydx, где L — контур треугольника с вер-L
шинами А(—1, 0), В(1, 0), С(0, 1) при положительном на-
правлении обхода. (Ответ: 2.)
1.30. (х2 + у) dx 4- (х 4- у2) dy, где Lacb — ломаная
Lacb
АСВ; А (2, 0); С(5, 0); В(5, 3). (Ответ: 63.)
2
2.1. \^2 — z2(2z —д/х2 +y2)d/, где L — дуга кривой L
x — tcost, y = tsint, z = t, 0</<2л. (Ответ: 4л'2(1 4-
+ л2).)
2.2. ф (х2 4- у2) dl, где L — окружность х2 4- У2 = 4. L
(Ответ: 16л.)
2.3. ( . -_dl ... где Lqb — отрезок прямой, соеди-J -\fa-x2 — у2
Lob
няющий точки 0(0, 0) и В(2, 2). (Ответ: л/2.)
206
2.4. J (4-д/х — Зд/у) dl, где LAB — отрезок прямой AB;
Lab
Д(— 1, 0); B(0, 1). (Ответ: — 5^.)
2.5. i -dl-----, где Lab — отрезок прямой, заключен-
ный между точками Д(0, 4) и В(4, 0). (Ответ: 0.)
2.6. \ - - dl, где L — дуга кардиоиды р = 2(1 Д-
J V?+7
Д- cos ср), О^ср^л/2. (Ответ: 16/3.)
2.7. $ ydl, Lab — Дуга астроиды х = cos31, у = sin31, Lab
заключенная между точками Л(1, 0) и В(0, 1). (Ответ: 0,6.)
2.8. J ydl, где LOb —Дуга параболы у2 = ~х между Тов 6
точками 0(0, 0) и В(д/35/6, _\/35/3). (Ответ:
2.9. (х2 Д- у2 Д- z2) dl, где L — дуга кривой х = cos t, L
у = sin t, z = ^/it, 0 t 2л. (Ответ: 4л(1 Д- 4л2).)
2.10. jarctg-~of/, где L — дуга кардиоиды р = (1 Д-
L
Д- cos ср), 0 «С ф л/2. (Ответ: (л Д- 2)~\/2 — 8.)
2.11. \-\[2ydl, где L — первая арка циклоиды х = 2(/ — L
— sin t), у = 2(1 — cos t). (Ответ: 8л^2.)
'.12. \ , где Loa — отрезок прямой, со-
у/х2 + у2 +
единяющий точки 0(0, 0) и Л(1, 2). (Ответ: 1п((-\/5Д-+ 3)/2).)
2.13. ~y~ dl, где L — дуга кривой р = 9 sin 2<р,
L
0=С<р=Сл/4. (Ответ: —9/8.)
2.14. xydl, где Loabc — контур прямоугольника с
вершинами 0(0, 0), Д(4, 0), В(4, 2), С(0, 2). (Ответ: 24.)
207
2.15. J (x-(-y)dl, где LABo — контур треугольника с
Labo
вершинами 4(1, 0), В(0, 1), 0(0, 0). (Ответ: — -у/2.)
2.16. f z , где L — первый виток винтовой линии J * + у
L
х = 2 cos t, у = 2 sin t, z = 2t. (Ответ: у х/2л3.^
2.17. J (x-(-y)dl, где Loab — контур треугольника
с вершинами 0(0; 0), А(—1, 0), В(0, 1). (Ответ: 0.)
2.18. \(x-(-y)dl, где L—дуга лемнискаты Бернулли L
р2 = cos 2<р, —л/4 <р л/4. (Ответ: )
2.19. фд/х2 + У2 dl, где L — окружность х2-(-у2 = 2у.
L
(Ответ: 8.)
2.20. xydl, где Loabc — контур прямоугольника с
вершинами 0(0, 0), 4(5, 0), В(5, 3), С(0, 3). (Ответ: — 15.)
2.21. ф (х2 + y2)dl, где L — окружность х2 -f- у2 = 4х. L
(Ответ: 32л.)
2.22. $ (4д/х — Зх/у) dl, где Lab—дуга астроиды х = cosJ t, у = sinJ t между точками 4(1, 0) и В(0, 1). (Ответ: 1.)
2.23. J xydl, где L — контур квадрата со сторонами
х = ± 1, у = ± 1. (Ответ: 0.)
2.24. \ y2dl, где L — первая арка циклоиды x = t — I.
— sin t, у = 1 — cos t. (Ответ: 17 у
2.25. J xydl, где Labcd — контур прямоугольника с вершинами 4(2, 0), В(4, 0), С(4, 3), 0(2, 3). (Ответ: 45.)
2.26. J ydl, где L — дуга параболы у2 = 2х, отсечен-L
ная параболой х2 = 2у. (Ответ: (5х/з— 1)/3.)
208
2.27. ~Г~~у' где ^Ав — отРезок прямой, заключен-
ие
ный между точками 4(4, 0) и В(6, 1). (Ответ: In (5/4).)
2.28. j (х2 4- у2}2 dl, где L — первая четверть окруж-
L
ности р = 2. (Ответ: 16л.)
2.29. ( — dl.....—, где Lab — отрезок прямой, соеди-
няющий точки 4(1, 1, 1) и В(2, 2, 2). (Ответ: In 2.)
2.30. ф (х — у) dl, где L — окружность х2 4- у2 = 2х. L
(Ответ: 2л.)
3
3.1. ф д/2у2 4- z2 dl, где L — окружность х2 4~ у2 z2 = L
= а2, х = у. (Ответ: 2ла2.)
3.2. J xyzdl, где L — четверть окружности х2 4- у2 4~ L
-\-z2 = R2, х2-j-у2 = R2/4, лежащая в первом октанте.
(Ответ: /?4д/з/32.)
3.3. j arctg У- dl, где L — часть дуги спирали Архи-L
меда р = 2<р, заключенная внутри круга радиусом R с центром в полюсе. (Ответ: и А*2 4-4 j— 8)/12.)
3.4. J (х2 4~ у2 + z2)dl, где L — дуга кривой х = a cos t, L
у = а sin t, z — bt, 0 4 t С 2л. ( Ответ: 2лд/бГ 4~ b2 (Зй2 4~
4- 4л262)/3.)
3.5. j (2г—д/x2 4- у2) dl, где L — первый виток кони-L
ческой винтовой линии х — t cos t, у = t sin t, z — t. (Ответ: 2д/2((1 4~ 2л2)3/2 — l)/3.)
3.6. \(x-\~z)dl, где L — дуга кривой x = t, y = L
= (3/д/2)Л г = /3, O^/^l. (Ответ: (56д/7 — 1)/54.)
209
3.7. J хлД2 — y2dl, где L — кривая (x2 4- у2)2 = a2(x2 — L
— у2), x 0. (Ответ: 2а3д/2/3.)
3.8. J (x + y)dl, где L — первый виток лемнискаты p2 = L
= a2 cos 2<p. (Ответ: a2x[2.}
3.9. J xydl, где L — первая четверть эллипса x2/а2 -|-L
+ у2/Ь2 — 1. (Ответ: ab(a2 + ab 4- 62)/(3(а + 6)).)
3.10. \(x-\-y)dl, где L — четверть окружности х2 L
+ у2 + z2 = R2, у = х, лежащая в первом октанте. (Ответ: R2x[2.)
3.11.
dl
х — z
где Lab—отрезок прямой z = x/— 2,
L-АВ
у = 0, соединяющий точки Л (0, 0, —2) и В(4, 0, 0). ( Ответ: -д/51п2.)
3.12. \ x!^ydl, где L — первая арка циклоиды х = L
= a(t — sin /), у — а(1 — cos /). (Ответ: 4лод/о.)
3.13. ф (х — у) dl, где L — окружность х2 -|- у2 = ах. L
(Ответ: ла2/2.)
3.14. (—----------, где L — первый виток винтовой
J * +</ +г2
L
линии х = a cos I, у = a sin t, z = bi.
/ x/a2 + b2 . 2sib \
1 Ответ: — ---arctg-----A
3.15. J ,г , где L — первый виток винтовой ли-L Х +У
нии x = acos/, y = csin/, z = at. (Ответ: 8ал3х/2/3.)
3.16. \xlx2 + У2dl, где L — развертка окружности £
х = a(cos t + t sin Q, у = a(sin t — t cos t), 0</^2л.
(Ответ: ц2((1 4-4nj3/2— l)/3.)
210
3.17. ( —; dl - -, где LAb — отрезок прямой, соеди-няющий точки 4(0, —2) и В(4, 0). ( Ответ: 1п((3-0Г—7)/2).)
3.18. ( ——-------, где L — первый виток винтовой
J * + </ + г
L
линии x = 5cos/, y = 5sin/, z = t. (Ответ: ^|^-arctg^.)
3.19. j yzdl, где LOabc — контур прямоугольника с вершинами в точках 0(0, 0, 0), 4(0, 4, 0), В(0, 4, 2), С(0, 0, 2). (Ответ: 24.)
3.20. J x2dl, где L — дуга верхней половины окруж-L
ности х2 + у2 = а2. (Ответ: ла3/2.)
3.21. j (х2 4- у2 4- z2)dl, где L — первый виток винтовой
L
линии x = 4cos/, у = 4 sin/, г = 3/. (Ответ: 10л(48 4~ 4-36л2)/3.)
3.22. j ydl, где L — дуга параболы у2 — 6х, отсечен-L
ная параболой х2 = 6у. (Ответ: 2>(Ь-\[^— 1).)
3.23. j xdl, где Lab — Дуга параболы у = х2 от точки
4(2, 4) до точки В(1, 1). (Ответ: (— 5д/5)/12.)
3.24. $ (х 4- y)dl, где L — первый виток лемнискаты
L
р2 = 7 cos 2<р. (Ответ: 7д/2.)
3.25. ф(г2 4- y2)dl, где L — окружность z2 4- У2 = 4.
L
(Ответ: 256л.)
3.26. J y2dl, где L — первая арка циклоиды X = 3(/ — — sin /), у ~ 3(1 — cos /). (Ответ: 458
3.27. ^-^/х24- y2dl, где L — развертка окружности х~
L
= 6(cos t + t sin t\ z/— 6(sin / — / cos ^), 0 t 2л. (Ответ: 12((i 4- 4л2)3/2-1).)
211
f z^dl
3.28. k —--2, где L — первый виток винтовой линии
х = 9 cos t', у = 9 sin t, z = 9Л (Ответ: 24л3д/2.)
3.29. ф(x2 + y2)2dl, где L — окружность x = 3cosl, L
y = 3smt. (Ответ: 486л.)
3.30. \ ydl, где L — дуга параболы y2=12x, отсечен-L
ная параболой x2 == 12y. (Ответ: 12(5\/5— 1).)
4.
4.1. j (ху — y2)dx Д-xdy, где L0A—дуга параболы у = 2х2 от точки 0(0, 0) до точки Л(1, 2). (Ответ: 31/30.)
4.2. j 2yzdy — y2dz, где L0BA—ломаная ОВД-, 0(0, О, 0); 5(0^2, 0); Л(0, 2, 1). (Ответ: —4.)
4.3. j у dx 4- —dy, где L — дуга циклоиды х = L
= a(t — sin/), у = а( 1 — cos f), л/6^/^л/3. ( Ответ:
4 +
4.4. j yzdx 4- z-\IR2 — y2dy 4- xydz, где L — дуга кривой L
x — R cos t, у = R sin t, z = а//(2л), «пробегаемая» от точки пересечения ее с плоскостью z =0 до точки пересечения ее с плоскостью z = a. (Ответ: 0.)
4.5. j 2xzdy — y2dz, где L0A — дуга параболы z —
= х2/4 от точки 0(0, 0, 0) до точки Л (2, 0, 1). (Ответ: 0.)
4.6. J (х — \/y}dy, где кАВ—дуга параболы у = х2
от точки Л(1, 1) до точки В(2, 4). (Ответ: 14/3 — 1п4.)
4.7. J cos zdx — sin xdz, где LAB — отрезок прямой,
соединяющий точки Л(2, 0, —2) и В( — 2, 0, 2). (Ответ: —2 sin 2.)
4.8. J ydx — xdy, где L — четверть дуги окружности
L
x = Rcost, y = Rs'mt, лежащая в первом квадранте и «пробегаемая» против хода часовой стрелки. (Ответ: 0.)
212
4.9. (ху — x)dx 4- у dy, где ЬОд — дуга параболы
Loa
у = 2х/х от точки 0(0, 0) до точки Л(1, 2). (Ответ: 1/2.)
4.10. ф ydx — xdy, где L — дуга эллипса x = acost, L
y = bsint, «пробегаемая» против хода часовой стрелки.
(Ответ: —2лаЬ.)
4.11. <§>xdy, где L — контур треугольника, образован-L
ного прямыми у = х, х = 2, у = 0 при положительном направлении обхода контура. (Ответ: 2.)
4.12. J xdy, где L — дуга синусоиды у = sin х от точки L
(л, 0) до точки (0, 0). (Ответ: 2.)
4.13. $ y2dx + x2dy, где L — верхняя половина эллипса I.
x = acost, у = b sin t, «пробегаемая» по ходу часовой стрелки. (Ответ: 4аЬ2/3.)
4.14. J (ху — y2)dx + xdy, где Lon—дуга параболы Lon
у = 2д/х от точки 0(0, 0) до точки 5(1, 2). (Ответ: —8/15.)
4.15. $ xdx + xydy, где L - дуга верхней половины L
окружности х2 -|- у2 = 2х при положительном направлении
обхода контура. (Ответ: —4/3.)
4.16. J (х — y)dx-\-dy, где L — дуга верхней половины /.
окружности х2 у2 = Rs, «пробегаемая» в положительном
направлении обхода контура. (Ответ: nR2/2.)
4.17. ф(х2 — y)dx, где L — контур прямоугольника, образованного прямыми х = 0, у = 0, х=1, у = 2 при положительном направлении обхода контура. (Ответ: 2.)
4.18. J 4х sin2 ydx -|- у cos 2xdy, где LOn—отрезок пря-Lou
мой, соединяющий точки 0(0, 0) и В(3, 6). (Ответ: 18.)
4.19. J ydx — xdy, где L — дуга эллипса х = 6 cos t, L
y — As\nt при положительном направлении обхода контура. (Ответ: —48л.)
213
4.20. J 2xydx — x2dy, где LOa — дуга параболы x = Loa
= 2y2 от точки 0(0, 0) до точки А(2, 1). (Ответ: 2, 4.)
4.21. J xyexdx(х — l)exdy, где LAB—любая линия,
Lab
соединяющая точки Л(0, 2) и В(1, 2). (Ответ: 2.)
4.22. ф (х2 + y2)d* + (х2 — y2)dy, где L — контур треугольника с вершинами Л (0, 0), В(1, 0), С(0, 1) при положительном направлении обхода контура. (Ответ: —1/3.)
SX2
(ху — x)dx-\- у dy, где Labo—ломаная АВО Labo
(0(0, 0); Л(1, 2); В(1/2, 3)) при положительном направлении обхода контура. (Ответ: —1/2.)
4.24. j (ху — y2')dxxdy, где LOa — отрезок прямой Loa
от точки 0(0, 0) до точки Л(1, 2). (Ответ: 1/3.)
4.25. J xdy — ydx, где L0A — дуга кубической парагол
болы у = х3 от точки 0(0, 0) до точки Л(2, 8). (Ответ: 8.)
4.26. j 2ys'm2xdx — cos2xdy, где Lab —любая линия Lab
от точки Л(л/4, 2) до точки В(л/6, 1). (Ответ: —1/2.) г ,г
4.27. I (ху — x)dx + у dy, где L0B — Дуга Параболы
Lob
у = 4х2 от точки 0(0, 0) до точки В(1, 4). (Ответ: 3/2.)
4.28. J (х + y)dx + (х — y)dy, где LAB — дуга пара-
Lab
болыг/ = х2 от точки Л(—1, 1)до точки B(l, 1) (Ответ: 2.)
4.29. j xdy, где LAB — дуга правой полуокружности
Lab
х2г/2 = а2 от точки Л (0, —а) до точки В(0, а). (Ответ: ла2/2.)
4.30. $ y2dx x2dy, где L — дуга верхней половины
L
эллипса х — 5 cos/, у — 2 sin/, «пробегаемая» по ходу часовой стрелки. (Ответ: 80/3.)
214
Решение типового варианта
Вычислить данные криволинейные интегралы.
1. ф (х2 4- у2)п dl, где L — окружность х2 4- у2 = а2 L
► Запишем уравнение окружности х2-\-у2 = а2 в параметрическом виде: x = acos/, г/= a sin/, О t 2л. Тогда
x't = — a sin t, y't — a cos t, dl = x{2 4- у I2 dt, dl =x/a2sin21 4- a2 cos2 tdt — adt.
Следовательно,
2л
$(x2 + t/2)n<// = a2" + i $ dt = 2na2n + i. 4
L 0
2. j xdi, где L0B — отрезок прямой от точки 0(0, 0)
Lqb
ДО ТОЧКИ В(1, 2).
► Находим уравнение прямой ОВ по двум точкам: у = 2х. Далее имеем:
dl=^[\ 4- {y'xfdx, dl=~y[bdx,
Lqb о
3. I — <f>2x(z/ — l)rfx 4- x2dy, где L — контур фигуры, , L
ограниченной параболой у = х2 и прямой у = 9 при положительном направлении обхода.
► В соответствии со свойствами криволинейных ин-тёгралов второго рода имеем
I = \ 2х(у — 1 )dx 4- x2dy 4- $ 2х(«/ — 1 )dx 4- x2dy, L, L2
где L{—дуга параболы y = x2\ Li — отрезок прямой у = 9. Так как парабола и прямая пересекаются в точках (-3, 9) и (3, 9), то
з -з
/ = (4х3 — 2x)dx 4- 16 $ xdx = 0. ◄
-3 3
215
4. l=\(^/x + y)dx—(^[y + x')dy, где L — верхняя L
дуга астроиды х — 8 cos31, у = 8 sin31 от точки (8, 0) до точки (— 8, 0).
► Находим:
dx = 24 cos21( — sin t)dt, dy = 24 sin21 cos tdt, 0 t л.
Тогда
1 = $ (2 cos t + 8 sin3 /) (— 24 sin t cos2 t)dt — о
— (2 sin / -|- 8 cos3 /) • 24 sin21 cos tdt =
= $ ( — 48 sin / cos31 — 192 sin41 cos21 — 48 sin31 cos t — о
— 192 sin21 cos4 f)dt = [ (— 48 sin t cos t — о
— 192 sin21 cos2 t)dt = $ ( — 24 sin 2/ — 48 sin2 2t)dt = о
= 12 cos 2/|o —24^(1 — cos4/)d/ =
0
= — 24^/— sin 4/) |o = — 24л. 4
ИДЗ-14.2
1. Показать, что данное выражение является полным дифференциалом функции и(х, у). Найти функцию и(х, у).
1.1. (2х — Зу2 4* i)dx 4* (2 — 8xy)dy. (Ответ: x24-*4-
4- 2у — Зху2 4- С.)
, 2- (тти/ -3)dx+(TT^ -5>
(Ответ: In (1 -j- х2у2) — Зх — 5у 4- С.)
1.3. —-0- cos 2у 4- у sin 2х^ dx 4- (х sin 2у 4- cos2 х 4-
4- 1) dy. ( Ответ: у cos2 х — -£ cos 2у 4- у 4- С.)
1.4. (у2еху‘ 4- 3) dx 4- (2хуеху"— V)dy. (Ответ: Зх 4- еху—
-У+С.)
216
1.5. + cos х cos у — 3x2)dx + (7^ — sin x sin z/ 4-
-\-4y\dy. (Ответ: In (xу) + sin x cos у — x32y2C.)
1.6. (y/x + In у 4- 2x)dx + (In x + x/y 4- I)dy. (Ответ-x2 + у In X + X In у 4- у + с.)
1.7. (ex+y— cos x)dx + (ex+y 4- sin y) dy. (Ответ: ex+y— — cos у — sin X + C.)
1.8. (z//"\/l ~x2y2 + 2x) dx+(x/-yjl — x2y2 + 6z/) dy. (Ответ: arcsin xy + x2 4- Зу2 + C.)
1.9. (exy 4~ xyexy 4- 2)dx 4- (x2exy -\-\)dy. (Ответ: xe?y 4-4- 2x 4- у 4~ C.)
1.10. (ye*y 4- y2)dx 4- (xe“y 4- 2xy)dy. (Ответ: exy 4-+ xy2 4- C.)
1.11. (y cos (xy) 4- 2x — 3y) dx 4- (x cos (xy) — 3x 4~ ty)dy. (Ответ: sin (xy) 4- x2 — 3xy -j- 2y2 4- C.)
1.12. (y sin (x4-f/) 4- xy cos (x 4- y) — 9x2)z/x4~ (x sin (x 4-4- y) 4- xy cos (x 4- y) 4- 2y) dy. (Ответ: xysin(x + y) — -3x3 + z/2 + C.)
1.13. (5у 4- cos x 4- 6xy2) dx 4- (5x 4- 6x2z/) dy.
(Ответ: sin x 4- 3xy 4- 3x2y2 4- C.)
1.14. (y2exy — 3) dx 4- (1 4- xy) dy. (Ответ: yexy —
— Зх 4~ 0.)
1.15. (1 4~ cos (xy))ydx 4- (1 4- cos (xy)) xdy. (Ответ: xy-\-4- sin (xy) 4- C.)
1.16. (y — sin x) dx 4- (x — 2y cos y2)dy. (Ответ: cos x 4~ + xy — sin y2 + C.)
1.17. (sin 2x— —i—\ dx — —dy. ( Ответ: —L_ — к x2y / xy2 \ xy
— cos 2x 4- C.)
1.18. dx 4- y~~,x dy. (Ответ: In (xy) 4- x/y 4- C.) xy у
1.19. (20x3 — 21лЛ/ 4- 2y)dx 4- (3 4- 2x — 7x3) dy.
(Ответ: 5x4 — lx3y 4- 2xy 4- 3y 4- C.)
1.20. (yexy — 2 sin x) dx 4- (xexy 4- cos y) dy.
(Ответ: exy 4~ 2 cos x 4- sin у 4- C.)
1.21. у (exy 4- 5) dx 4- x (exy 4- 5) dy. (Ответ: exy 4-4-5xz/4-C.)
'•22' 4- p47))di + ( ~«)d«-(o™':£ +
4-arctg-^- 4-C.j
217
1.23. xln^ + j/ dx + ^lnx bx dy. (Ответ: у In x +
-I- x In у -I- C.)
1.24. ex~y(l 4-x + y)dx -|- ex~y(l — x — y)dy.
(Ответ: ex~y(x 4- y) 4- C.)
1.25. (3x2 — 2xy -|- y) dx -|- (x — x2 — 3y2 — 4y) dy.
(Ответ: x3 — x2y — y3 xy — 2y2 + C.)
1.26. (2xex‘~y* — sin x)dx -|- (sin у — 2yex‘~y,)dy. (Ответ: ex ~y‘ 4- cos x — cos у 4- C.)
1.27. (у/-V1 — x2y2 4- x2) dx 4- (х/ д/1 — x2y2 4- y) dy. (Ответ: xJ/3 4- arcsin (xy) -j- y2/2 4- C.)
1.28. —dx 4- dy. (Ответ: 4- 1 4- сЛ
X У хуг \ xy X J
1.29. (—— - —У -2\dx + (—1— ----------4-
U- 1 (x- 1/ / \x - 1 (y - 1)
4- 2y) dy. (Ответ: 4- —i-j- — 2x 4- y2 4- C.'j
1.30. (3x2 — 2xy 4- y2) dx 4- (2xy — x2 — 3y2) dy.
(Ответ: x3 — x2y 4- xy2y3 -j- C.)
2. Решить следующие задачи.
2.1. Вычислить длину дуги цепной линии у = (ех-\-4-е-х)/2, х Е [0; 1]. (Ответ: (е2 — 1)/(2е).)
2.2. Вычислить моменты инерции относительно осей координат отрезка однородной прямой 2х 4-У = 1, лежащего между этими осями. (Ответ: /х = д/5/6, 1У = д/5/24.)
2.3. Найти координаты центра масс четверти однородной окружности х2 4-у2 = а2, лежащей в первом квадранте. (Ответ: (2а/л, 2а/л).)
2.4. Вычислить массу дуги кривой у = In х, заключенной между точками с абсциссами х=д/з и х=д/8, если плотность дуги в каждой точке равна квадрату абсциссы этой точки. (Ответ: 19/3.)
2.5. Вычислить момент инерции относительно оси Оу дуги полукубической параболы у2 = х3, заключенной между точками с абсциссами х = 0 и х = 4/3. (Ответ: 1У = = 107-2'°/(105-36)« 1,13.)
2.6. Вычислить момент инерции относительно начала координат контура квадрата со сторонами х— ±а, у = = ±а. Плотность квадрата считать постоянной. (Ответ: /о = 32/3.)
218
2.7. Вычислить длину дуги кривой х = 2 — tl/4, у — = t6/6, ограниченной точками пересечения ее с осями координат. (Ответ: 13/3.)
2.8. Вычислить координаты центра масс однородной полуокружности х2 + у2 = 4, симметричной относительно оси Ох. (Ответ: (4/л, 0).)
2.9. Вычислить координаты центра масс однородной дуги одной арки циклоиды x = t — sin/, у—I—cost. (Ответ: (л, 4/3).)
2.10. Вычислить момент инерции относительно начала координат отрезка прямой, заключенного между точками А(2, 0) и В(0, 1), если линейная плотность в каждой его точке равна 1. (Ответ: /0 = 5д/5/3.)
2.11. Вычислить координаты центра масс однородного контура сферического треугольника х2 + у2 + z2 = 1, х^Ь, у^О, z^:0. (Ответ: (4/Зл, 4/Зл, 4/Зл).)
2.12. Вычислить статические моменты относительно координатных осей дуги астроиды х = 2 cos31, у — — 2 sin3/, расположенной в первом квадранте. (Ответ: Мх = 2, 4, Му — 2, 4.)
2.13. Вычислить массу отрезка прямой у— 2 — х, заключенного между координатными осями, если линейная плотность в каждой его точке пропорциональна квадрату абсциссы в этой точке, а в точке (2, 0) равна 4. (Ответ: 8-\/2/3.)
2.14. Найти статический момент относительно оси Оу однородной дуги первого витка лемнискаты Бернулли р2 = а2 cos 2<р. (Ответ: Му = а2_\/2.)
2.15. Найти работу силы F = xi + (х + у} j при перемещении точечной массы m по дуге эллипса х2/16 + + у2/9 = 1. (Ответ: 12л/п.)
2.16. Вычислить момент инерции относительно оси Oz однородной дуги первого витка винтовой линии х= = 2 cos /, у = 2 sin /, z = /. (Ответ: 7г = 8-\/5л.)
2.17. Вычислить массу дуги кривой р = 3 sin <р, <рС €[0; л/4], если плотность в каждой ее точке пропорциональна расстоянию до полюса и при <р = л/4 равна 3. ( Ответ: 9(2 — д/2) /2.)
2.18. Вычислить координаты центра масс однородной дуги первого витка винтовой линии х = cos /, у = sin /, z = 2/. (Ответ: (0, 0, 2л).)
219
2.19. Вычислить моменты инерции относительно координатных осей дуги четверти окружности х — 2 cos t, у = = 2 sin t, лежащей в первом квадранте. (Ответ: /х = 2л, 1у — 2л.)
2.20. Вычислить координаты центра масс дуги первого витка винтовой линии х = 2 cos t, у — 2 sin t, z = t, если линейная плотность в каждой ее точке пропорциональна аппликате точки и в точке t = л равна 1. (Ответ: (0, —2/л, 4л/3).)
2.21. Вычислить массу дуги четверти эллипса х2/4 4~ 4~у2=1, лежащей в первом квадранте, если линейная плотность в каждой ее точке равна произведению координат этой точки. (Ответ: 14/9.)
2.22. Вычислить работу силы F = xyi -|- (х 4- у) j при перемещении материальной точки по прямой у = х от точки (0, 0) до точки (1, 1). (Ответ: 4/3.)
2.23. Вычислить статический момент относительно оси Ох однородной дуги цепной линии у = (ех 4- е~х)/2, х£ е[0; 1/2]. (Ответ: (е — 1/е-|-2)/8.)
2.24. Вычислить работу силы F = (х — у) i -|- xj при перемещении материальной точки вдоль контура квадрата, образованного прямыми х=±1, у=±1. (Ответ: 8.)
2.25. Вычислить статический момент относительно оси Ох однородной дуги кардиоиды р = а(1 4- cos <р). (Ответ: 32а2 /5.)
2.26. Вычислить длину дуги одной арки циклоиды х = 3(t — sin t), у — 3(1 — cos f). (Ответ: 24.)
2.27. Вычислить работу силы F = (х 4- у) i — xj при перемещении материальной точки вдоль окружности х = = 2 cos t, у = 2 sin t по ходу часовой стрелки. (Ответ: 8л.)
2.28. Вычислить работу силы F = yi 4- (х 4* У) j при перемещении материальной точки из начала координат в точку (1, I) по параболе у — х2. (Ответ: 17/12.)
2.29. Вычислить работу силы F = (х — у) i 4- 2yj при перемещении материальной точки из начала координат в точку (1, —3) по параболе у =—Зх2. (Ответ: 10,5.)
2.30. Вычислить моменты инерции относительно осей координат однородного отрезка прямой у = 2х, заключенного между точками (1, 2) и (2, 4). (Ответ: /х = 28л/5/3, 1у = 7л/5/3.)
220
Решение типового варианта
I» Показать, что выражение
(—L - \\dx + (^~ - \O\dy к 1 + х2у2 ) 1 \ 1 + /
является полным дифференциалом функции и(х, у). Найти функцию и(х, у).
► Проверим, выполняется ли условие полного дифференциала == для функции и(х, у). Имеем:
Р(х, У) = -т^т - Q(*> У) = -7Т-ТТ - 10-
1 + X У 1 + Х2у2
дР д / у ________ А 1+ х2у2 — у 2х2у 1 — х2у2
~ 17 \ 1 + хУ ) (1 +х2у2)2 (1+xV)2 ’
dQ __ д / х _______ jq\ _ 1 х2у2 — х • 2ху2 _ 1 — х2у2
дх дх \ 1 + х2у'2 ) (1 + х2у2у (1 х2у2)2
Данное выражение является полным дифференциалом функции и(х, у). Положив Хо = 0, у о — 0, по формуле (14.16) найдем и(х, у):
и(х, y)=h-l)dx+{(—^r-lo\dy + C = о о
= —-Но + (arctg ху — Юу)|о + С = — х + arctg ху— - Wy + c.
(ультат вычислений верен, если
^«1 = Р(х, = Q(x, у).
Сделаем проверку:
х +arctg ху — 10у+С)= — 1 + г~,
дх 1 + х2у
— х+ arctg ху — 10у + С) = —— 10.
ду 1 + х2у2
Итак, и(х, у) = arctg ху — х — 1 Оу 4- С. ◄
2. Вычислить моменты инерции относительно осей координат однородного отрезка прямой 4х + 2у = 3, лежащего между точками (0, 3/2) и (2, —5/2).
221
► Используя общие формулы для вычисления моментов инерции, последовательно находим:
1Х = j y2dl,
L
где L: 4х -\-2у = 3, у=— 2х+-|-, dl=^fbdx.
о
_ _ -у/5 / 125 27 \ _ 49 VT
~ ~6\~8- ’““в-,) 24~’
= Iy=^5^x2dx =Л/5-^|^ = -^. « i о
14.4. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ К ГЛ. 14
1. Найти длину дуги конической винтовой линии x — ad cos t, у = ае‘ sin t, z = ае‘ от точки 0(0, 0, 0) до точки А (а, 0, а). (Ответ: сп/з.)
2. Найти массу участка цепной линии у = a ch(х/а) между точками с абсциссами Xi =0 и xz — a, если плотность линии в каждой ее точке обратно пропорциональна ординате точки, причем плотность в точке (0, а) равна у. (Ответ: уа.)
3. Определить массу эллипса х2/9 + у2/4—1, если линейная плотность в каждой его точке равна |у\. (Ответ:
4 + —arcsin-4—.) . b 3 /
4. Найти координаты центра масс первого полувитка винтовой линии х = a cos t, у = a sin t, z — bt, считая плотность в каждой ее точке постоянной. (Ответ: (0, 2а/л, 6л/2).)
5. Вычислить моменты инерции относительно координатных осей и начала координат четверти однородной окружности у = 2 cos t, z — 2 sin t, лежащей в первом квадранте плоскости Oyz. (Ответ: 1Х — 1У — 2л, /о — 4л.j
222
6. Найти момент инерции относительно оси Ох первого витка винтовой линии х — а cos t, у = а sin t, z = ht/(2fi). (Ответ: (а2/2 + А2/3)-\/4л2а2 + /г2.)
7. Проверить выполнимость формулы Грина для интеграла
ф (х + у) dx — 2xdy,
L
если L — контур треугольника со сторонами х = 0, у = 0, х + у = а.
8. Применив формулу Грина, вычислить интеграл
ф y2dx + (х + yfdy
i-ABC
по контуру треугольника АВС с вершинами Л (2, 0), В(2, 2) и С(0, 2). (Ответ: 16/3.)
9. Доказать, что
j (ух3 + еу) dx + (ху3 + хеу — 2у) dy = 0,
L
если L — замкнутая линия, симметричная относительно начала координат.
10. Доказать, что численное значение интеграла $ (2ху — у) dx Д- x2dy, L
где L — замкнутый контур, равно площади области, ограниченной этим контуром.
11. Доказать, что интеграл
J х + У2
L
где L — любой замкнутый контур, «пробегаемый» в положительном направлении и охватывающий начало координат, равен 2л.
12. Найти функцию по данному полному дифференциалу
du = ey'2dx Д- ^/г + zey'2) dy + (уеуг + e~2 -
_ {х±\}У ey/'^ dz
(Ответ: ay/z (x -J- 1) + eyz — e~г.)
15. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
15.1. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ И ГРАДИЕНТ
Отображение, которое каждому числу t £ Т £ R ставит в соответствие по некоторому правилу единственный вектор г, называется векторной функцией или вектор-функцией скалярного аргумента t. Ее принято обозначать г = г(/)- Множество Т называется областью определения функции г(/). В качестве Т обычно берут некоторый отрезок [а; Ь| или интервал (а; Ь) числовой оси. Число t также называют параметром.
Как и любой постоянный вектор, вектор-функцию скалярного аргумента г(/) при любом фиксированном значении t можно однозначно разложить по .базису i, j, k:
г = г (i) = x(t) i + у (0 j + z (0 к. (15.1)
Очевидно, что координаты х, у, г вектор-функции г = г(() в этом базисе являются функциями: х(/), у(1), z(t), область определения которых совпадает с Т. Поэтому имеют место три скалярных равенства:
х = х(/), </ = !/(/), z = z(/). (15.2)
Если вектор г откладывать из одной точки О при различных значениях t£T, то его конец M(t) опишет в пространстве, вообще говоря, линию, которая называется годографом вектор-функции г = = г(1). Точка О называется полюсом годографа. Равенство (15.1) называют в этом случае векторно-параметрическим уравнением годографа, а равенства (15.2) —его параметрическими уравнениями (рис. 15.1).
Приведем несколько примеров.
11. Годографом, задаваемым
В случае, когда t — время, длины, равенства (15.1) и (11
векторно-параметрическим уравнением вида г = г(/) = Го + s/, где Го — радиус-вектор точки Л10(х0, у0, Z(>), s — некоторый заданный вектор, является прямая в пространстве, проходящая через точку Л1о, с направляющим вектором s (см. уравнение (3.6) и рис. 3.1 в первой части настоящего пособия).
2. Годограф, задаваемый параметрическими уравнениями х = = a cos t, y = as'mt, z = bt (t C (—oo; oo), a, b — постоянные), является винтовой линией, расположенной на круговом цилиндре радиусом а с осью Oz (см. также § 4.3 в первой части пособия), а х(/), y(t), z(t) имеют размерность .2) называются соответственно век-
224
торно-параметрическим и параметрическими уравнениями движения точки, а соответствующий им годограф — траекторией ее движения.
Если
lim x(t) = Л'о, lim y(l) = y<s, limz(() = Zo, I --*( I ( -*-(o I—*- l,l
то вектор r<> = Xoi + J/nj + Zok называется пределом вектор-функции r(t) в точке I = ф. В этом случае пишут: lim г(/) = Го.
Если lim г(/)= г(Ф), то векторная функция r(t) называется непре-I -*-l II
рывной в точке t = to.
Если =# О— произвольное приращение параметра, то Лг(/) = = r(t 4- .V) — г(/) называется приращением вектор-функции г(/).
Если существует предел
Лг(/) г(( + Лф — г(/)
lim-------- = lim ----------------,
л;—о Л/ л/^о ЛЛ
то он называется производной вектор-функции г(/) в точке t и обозначается г'(0. или г((), или dr(t)/dl.
Вектор г'(/) всегда направлен по касательной к годографу функции r(t) в сторону возрастания параметра t. С механической точки зрения r'(t) есть вектор мгновенной скорости движения материальной точки по траектории, являющейся годографом функции г = г((), в момент времени t в точке Л1(1) (см. рис. 15.1).
Если существуют производные х'(t), у'(t) и z' (/), то существует г'(() и
г'(() = x'(t)i + </'(()) + z'(/)k. (15.3)
Так как вектор г'(/о) направлен по касательной к кривой в точке Л4о(Ф), определяемой уравнениями (15.2), то уравнения касательной к этой кривой в точке Л1о запишутся следующим образом:
х — Х(Ч = У ~ У(1Ф = z — z(/0) f г
х'(to) у’(to) z'(lu)
Плоскость, перпендикулярная к касательной и проходящая через точку касания /VI,цф), называется нормальной плоскостью к кривой в этой точке, а ее уравнение имеет вид
x'(tn)(x ~ х(1ф) +у'(1ф (у — у(1а)) + Х(ф)(г — z(to)-) = 0. (15.5)
Для векторных функций скалярного аргумента справедливы следующие правила дифференцирования:
') (Г|(0 + г2(())' = г'фф + г2(I);
2) (Cr(t))' = Cr'(t), С = const;
3) (г, (t) с,(1)У = г((/)- г2(() + г। (/) - ri(l);
4) (п (() X г2(7))' = г)(t) X г2(() + г!(7) X г2(().
Пример I. Найти производную вектор-функции r(() = (cos(— 1)1 + + sin2 tj + tg Ik в точке tn = л/4.
► Из формулы (15.3) следует, что
г' (/) — — sin ti + 2 sin t cos tj -|-— k.
cos t
8—
357
225
»1 . / л \ 1 .
1109T0MV Г ( ] =----— I + j 4- 2к. Ч
V 7 Л'2
Пример 2. Составить канонические уравнения касательной и уравнение нормальной плоскости к кривой, заданной параметрическими уравнениями % = (’ + (— 1, у = 2/' -ф 3/ ф- 2, г = I2 + I, в точке Мо, определяемой значением параметра /о = 1.
► Находим вектор г'(/0) = (x'(l), z'(1)) = (4, 7, 2). Параметру /о = 1 на кривой соответствует точка Л40(л'(1), у(1), z(l)), т. е. ЛФ/1 ;-.7, 2). Согласно формулам (15.4), (15.5), уравнения касательной имеют вид
х — 1 у — 7 z — 2
4 — 7 ~ 2 ’’
а уравнение нормальной плоскости
4(х- 1) + 7(</-7) + 2(г-2) =0. <4
Переходя к понятию производной функции по направлению, отметим, что направление в пространстве можно задавать единичным вектором s° = (cos a, cos 0, cos у), где а, р, у — углы, образованные вектором s° и осями Ох, Оу, Oz соответственно.
Если дана функция а = [(х, у, г), определенная в некоторой окрестности точки Л4о(л'о, уо, Zn), радиус-вектор которой г0 = (х0, у0, г0), то
Нш Kr.l + s'7)-f(r0) /^0 t
если он существует, называется производной функции и — f(x, у, z) в точке Ми(х0, у0, z0) по направлению вектора su и обозначается ди(Мо)
—т. е. по определению
ди(Мр) __ /'(,г о ф- s0/)— /(Гр)
ds 1ч-о t
Справедлива следующая формула:
ди(Ма) ди(М0') ди(М0) ди(М0) . 1СС,
---з----------=---------5—- cos а И )—- cos р Н-;—-cosy. (15.6) ds-------------------------------------------дх-ay dz 17
В случае функции двух переменных z = /’(.r, у) формула (15.6) упрощается:
dz(Mo) dz(Alo) dz(Mo)
ds dx ду ' '
где s" = (cos <z, cos 0); p = л/2 — a.
Частные производные функции и = f(x, у, z) являются производными этой функции по направлениям координатных осей. С физической точки зрения ди/дз можно трактовать как скорость изменения функции и в данной точке в заданном направлении.
Производной вдоль кривой L называют производную по направлению ориентированной касательной к кривой L, вычисленную в точке касания.
Всякой дифференцируемой функции и = [(х, у, г) соответствует вектор с координатами ди(М)/дх, ди(М)/ду, ди(М)/дг, который называется градиентом функции и в точке М и обозначается grad и. Таким образом, по определению
226
, / ди ди ди \ ди . ди . , ди , ,, _ „
grad и = — i+ ——j + — к. 1з.8)
\дх ду дг / дх ду дг
Если s° = (cos a. cos р, cosy), то из формул (15.G) и (15.8) имеем
ди(М) ds
= grad и s” = пр s« grad и (М).
Из этой связи между производной по направлению и градиентом функции u=f(x, у, г) (или г = f(x, у)) следует, что:
1) градиент функции и (или z) направлен в сторону максимального возрастания ее значений, т. е. du/ds (или dz/ds) имеет наибольшее значение в направлении градиента (рис. 15.2);
2) если единичный вектор s° перпендикулярен к grad и (или grad г), то dufds = 0 (илн dz/ds = О) (см. рис. 15.2);
3) вектор- grad (или grad z(M)) имеет направление нормали
в точке М поверхности (или линии) уровня функции и (или г) (рис. 15.3, а. б/.
М s'aulM) s
2S
Рис. 15.2
Рис. 15.3
Градиент любой дифференцируемой функции обладает следующими свойствами:
1) grad («| + их) = grad ui + grad u2;
2) grad Си = C grad и, С = const;
3) grad (mi«2) = «2 grad «i + «i grad их
Пример 3. Найти производную функции и = д/г2 -р г/2 z2 в точке Mi(— 2, 3, 6) по направлению к точке М2( — 1. 1, 4).
► Частные производные функции и в точке Mi:
du(Mi) _ х I _ 2
дХ л[х2 + у2 + z2 ' л,‘ 7 ’
227
du (Mi) _ у I _ 3
<^t/ Г~2 i > i ~ m, 7
J + У' + z
r?zt(Afi) _ г I 6
<2z / -1 . З’ф 2 II, 7
Vх + У + г
Единичный вектор, совпадающий по направлению с вектором
Л/|Мг, равен
_ ,-И,ЛЬ / I _ _2_ __ J24 f/W.Afe | ^3’ 3’ Л'
Тогда по формуле (15.6) получаем
ди (Mi) 21,3/ 2 \ , 6 / 2 \ 20
ds + + 4
Пример 4. Вычислить производную функции z = arctg (ху) в точке Л4о( 1, 1), принадлежащей параболе у = х\ по направлению этой кривой (в направлении возрастания абсциссы).
► За направление s" параболы у — х~ в точке Л4(1(1, 1) берем направление касательной к параболе в этой точке, задаваемое углом а, который касательная составляет с осью Ох. Тогда имеем:
у' (х) = 2х, tg а = у' (1) = 2,
1 1 tg а 2
cos а — —, ~ sin а - —
V1 + tg2 “ V5 vi + tg2« V5
Находим частные производные функции z в точке М<т.
dz(Md) _ у I _ 1 дг(Л4р) __ х I _ 1 дх 1 + х2у'-‘ I Л|о 2 ду 1 + хгу2 I м„ 2
Подставив полученные значения в формулу (15.7), имеем ди(М0) J_ 1 , 1 2 _ 3
ds 2 £~ ' 2 ~ п Г"
-у5 х/5 2-\'5
АЗ-15.1
1. Найти значение производной вектор-функции г = = 4(/2 + + arctg tj ф- In (1 ф- t2)k при /=1. (Ответ:
r'(i) = 12i -J—g- j + k.)
2. Дано векторно-параметрическое уравнение движения точки М: г = r(t) = (2t2 + 3) i — 3/2j -f- (4/2 — 5) k. Вычислить скорость Iv| и ускорение |w| движения точки в момент времени /=0,5. (Ответ: |v| =д/2Д |w| = = 2-729)
228
3. Дано уравнение движения материальной точки: г = 2 cos t\ + 2 sin t] + 3/k. Определить траекторию движения, вычислить скорость |v| и ускорение |w| движения этой точки в любой момент времени t. (Ответ: х = 2 cos /, у = 2 sin t, z = 3t (винтовая линия); | v| = _\/Тз", | w| =2.)
4. Записать канонические уравнения касательной прямой и нормальной плоскости к кривой г — ti -|- /2j +
, .3. , х— 1 у — 9 z —27 ,
4- гк в точке I — 3. ( Ответ: —•— = , х ±
1 у 1 6 11
+ бу + 27г = 786.)
5. Записать канонические уравнения касательной прямой и нормальной плоскости к кривой, заданной уравнениями z = x2+y2, у = х в точке Л40(1, 1, 2). (Ответ: x + y + 4z= 10)
6. Доказать, что вектор г перпендикулярен к вектору г', если | г| = const.
7. Вычислить производную функции « = 1п(3 —Х2) + + xy2z в точке М|(1,3, 2) по направлению к точке Мг(0, 5, 0). (Ответ: —11/3.)
8. Вычислить производную функции г =~\/х2 + у2 в точке М0(3, 4) по направлению: а) вектора а =(1, 1); б) радиуса-вектора точки Мо; в) вектора s=(4, 3). (Ответ: а) 7^2/2; б) 1; в) 0.)
9. Вычислить производную функции г = arctg (р//х) в точке М0(2, —2) окружности х2 + у2 = 4х вдоль дуги этой окружности. (Ответ: ±1/4.)
10. Вычислить производную функции и = 1п (ху 4* xz ф-+ yz) в точке Мо(О, 1, 1) по направлению окружности х = cos t, у = sin t, z = 1. (Ответ: ±2.)
11. Вычислить координаты единичного вектора, направленного по нормали к поверхности (г2 — x2)xyz— у2 = 5 в точке Мо(1, 1, 2). (Ответ: ±f—-—, —!—, —-—АЛ
' ' 3 д/ПГ 3 V?4 Зд/14 ' '
12. Найти grad и в точке Мо(1, 1, 1), если и — x2yz — — xy2z + xyz2. (Ответ: grad zz = 2i— 2j Д-2k.)
13. Найти угол ср между градиентами функций и = = -|- х2 + Зу2 — 2г2 и v = x2yz в точке Л4о(2, 1 /3, д/з/2). (Ответ: ср = л/2.)
229
14. Найти наибольшую крутизну подъема <р поверхности z = 2x2/yJ в точке Мо(2, 1, 8). (Ответ: tg ср = = 8д/То, Ф«87°40'.)
Самостоятельная работа
1. 1. Вычислить производную функции и ==%+ 1п (у2 -ф z2) в точке Л40(2, I, 1) в направлении вектора s = = — 2i-j-j — k. (Ответ: — -д/б/3.)
2. Вычислить координаты единичного вектора, перпендикулярного к поверхности ху -ф xz -ф yz = 3 в точке Мо(1, 1, 1). (Ответ: ±(1/д/з, 1 /дД 1/д/з).)
2. 1. Вычислить производную функции z = arctg (х2у) в точке Л4о(1, 4) параболы у = х~ в направлении этой кривой. (Ответ: ±2д/5/17.)
2. Найти наибольшую крутизну ср подъема поверхности z = 5х2— 2ху у2 в точке Л4о(1, 1, 4). (Ответ: tg ср = 8, ср « 83°.)
3. I. Записать канонические уравнения касательной прямой и нормальной плоскости к линии, заданной векторно-параметрическим уравнением г — cos2 ti 4- sin2 tj -ф -ф tg /к в точке t = л/4. (Ответ: -х °’5- =
= -Z , х' — у — 2z 4- 2 = 0.)
2. Найти наибольшую крутизну ср подъема поверхности z = х3у -ф ху2 в точке /Ио(1, 3, 12). (Ответ: tg ср = = д[373, (р«87°.)
15.2 СлАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ
Если в каждой точке М (х, у, z) пространства R3 (или его части V) определена скалярная величина и = /(х, у, z\ то говорят, что в R3 (или Г) задано скалярное поле и = и(М). Это значит, что всякая числовая функция и(М) = f(x. у, г), заданная в некоторой области V пространства R3, определяет в этой области скалярное поле. Функция двух переменных z = /(x, у) задает в некоторой области D плоскости Оху скалярное поле, называемое плоским.
Графически скалярное поле можно изображать с помощью поверхностей уровня f(x, у, z) = C или линий уровня f(x, у) = С (см. рис. 15.3).
Для всякой функции и — f(x, у, z), дифференцируемой в точке Afofxo, i/o, го), число duiM^/ds определяет скорость изменения скалярного поля в направлении s° = (cos a, cos р, cosy) (см. формулу (15.6)).
230
Если в каждой точке М(х, у, z) пространства R’ (или его части V) определен вектор а=(Р, Q, R), где Р — Р(х, у, z), Q = Q(x, у, z), R = R (х, у, z) — скалярные функции, то говорят, что в этом пространстве (или в I7) задано векторное поле а = а(Л1). Если функции Р!х, у, z), Q(x, у, z), R(x, у, z) непрерывны, то поле вектора а называется непрерывным.
Примерами векторных полей являются поле скоростей текущей жидкости, поле скоростей точек твердого тела, вращающегося с угловой скоростью w вокруг дайной оси, поле электрической или магнитной напряженности н др.
Линия, в каждой точке М которой вектор а(М) векторного поля а = а(М) направлен по касательной к линии, называется векторной (силовой) линией этого поля.
Примерами векторных линий могут служить линии тока жидкости, силовые линии магнитного поля, траектории точек вращающегося пространства.
Область пространства, целиком состоящая из векторных линий, называется векторной трубкой. В каждой точке М поверхности векторной трубки вектор а лежит в касательной плоскости в точке Л1 к этой трубке.
Векторное (или скалярное) поле, координаты которого не зависят от времени, называется установившимся или стационарным.
Если г(!) — радиус-вектор векторной линии векторного поля а = а(М), то уравнения векторных линий определяются из системы дифференциальных уравнений:
dx dp dz (15 9>
Р Q R ’
Пример 1. Найти векторную линию векторного поля 'Л(М) =
= —pi 4- xj -ф bk, проходящую через точку Л/о<1, 0, 0).
> На основании формулы (15.9) получаем систему дифференциальных уравнений
dx dy dz
— у ~ х b '
Решаем ее:
xdx + ydy = 0, х2 4- р2 — С2
илн, в параметрическом виде, х = С1 cos /, y = Ct sin t;
dz dz Ci cos tdt , ~
-1-, —r~ = —fdz = bdt, z = bt + Ci.
b b C । cos t
Так как векторная линия должна проходить через точку Л1о(1, 0, 0), то легко находим, что постоянные интегрирования Ci = I, Са = 0. Уравнения векторной линии векторного поля а = а(Л1) имеют вид х = = cos /, у — sin t, z = bt (винтовая линия).
Векторное поле, порожденное градиентом скалярного поля и(М) = = f(x, у, г) (или z(M) = f(x, у)), называется полем градиента. Согласно свойству 3 градиента, векторные линии grad и(М) (или grad z(M)) —это кривые, вдоль которых функция и -= /(х, р, г) (или z = f(x, р)) максимально возрастает (убывает) Эти линии всегда орто
231
гональны к поверхностям (или линиям) уровня скалярного поля «(Ж) (или 2(Ж)).
Дифференциальные уравнения для определения векторных линий grad и(М) имеют вид
= = (15.10)
Ux Ф 11'.
Пример 2. Найти векторные линии поля grad и, если и = (х2 3 4 ф-+ У + г~)/2-
► Согласно определению (15.8), grad и = ,ri ф- yj ф- zk, а из формул (15.10) следует, что векторные линии этого поля удовлетворяют системе дифференциальных уравнений
dx dy dz х у г '
Находим решения этой системы:
—— = In |i/| = In |х| ф-1 п Ci, у = CiX,
х у
dz dx
— = —, In |z| = in ф- In C2, z = CiX. z x
Полученные решения y = C>x, z == C-jx можно представить в виде х у z .
— = 7^ = 7^, т. е. векторные линии заданного поля grad «(Ж) пред-l Lj Ci
ставляют собой совокупность прямых, проходящих через начало координат и ортогональных множеству поверхностей уровня х2 ф- у2 ф-ф- z2 = 2С (сферы) данной функции. Ч
АЗ-15.2
1. Записать уравнения и построить поверхности уровня скалярных полей, определяемых следующими функциями:
a) u = arccos—-г - : б) и = In(х2 -ф у2 ф Z2)-, лА2+/
в) и = z/(x2 ф у2).
2. Построить линии уровня плоского скалярного поля z = xy.
3. Найти градиент скалярного поля и = с • г, где с — постоянный вектор; г — радиус-вектор точки М(х, у, z). Записать уравнение поверхностей уровня этого поля и выяснить их расположение относительно вектора с.
4. Найти производную скалярного поля и = х2у2 — — д/х2 ф z2 в точке М(— 3, 0, 4) в направлении нормали к поверхности 2х2 ф 12х ф 5у2 ф z2 — 3z — 58 = 0, образующей острый угол с осью Oz. (Ответ: —4/5.)
232
5. Найти векторные линии векторного поля а(Л1) = = (»yi + где <о 6 R, <о^0. (Ответ: х2-—у2 = С\, Z = С2.)
6. Найти векторные линии векторного поля, если:
a) a(M) = 5xi + 10t/j; б) а(М) = 4zj — 9t/k.
(Ответ: а) х2==С\у, z=C?; б) 9у2 + 4г2 — С2, х=С2.)
7. Найти векторные линии поля grad и, если и — = х2 — 2у z2. (Ответ: х = Cte~ у, z = Сге~у.)
Самостоятельная работа
1. 1. Найти векторные линии векторного поля а(Л4) = = (х + y)i — xj — xk. (Ответ: х2 + у2 -ф- z2 = Ci, у — z = = Сь)
2. Вычислить координаты единичного вектора, перпендикулярного к поверхности z — х2у2 в точке Мо( — 1, 1, 2) и образующего с осью Оу острый угол. (Ответ: ( — 2/3, 2/3, -1/3).)
2. 1. Найти векторные линии поля grad и, если и = ~х + у2. (^Ответ: х = у 1п у -ф- С\, z = С2.)
2. Вычислить координаты единичного вектора п°, перпендикулярного к поверхностям уровня скалярного поля и — 2х — Зу + 6г — 5 и образующего с осью Oz тупой угол. (Ответ: п° = (— 2/3, 3/7, —6/7).)
3. 1. Найти векторные линии векторного поля а(Л1) = = 2xi + 8zk. (Ответ: z=C\x4, у = С2.)
2. Записать единичный вектор п°, ортогональный к поверхностям уровня скалярного поля и — х2 у2 + z2 + 4. (Ответ: п° = (х/~\[х2 + у2 + z2, у/^х2 + у2 + z2, z/V^ + t^ + z2).)
15.3. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
Пусть f(x, у, г)— непрерывная функция в точках некоторой гладкой поверхности S Е R3. С помощью кусочно-гладких линий разобьем поверхность S на п элементарных площадок S,, площади которых обозначим через AS, (< = 1, гг), а диаметры — через 0 5,. На каждой площадке S, выберем произвольную точку М:1х,, у,, Zi), вычислим /(х,, г/„ г<) и составим интегральную сумму
In = X i\xi, yt, z^S,.
i= l
233
Тогда существует предел этой интегральной суммы, который называется поверхностным интегралом первого рода от функции f(x, у, г) по поверхности S и обозначается
у, z)dS = lim 2 [(х,, у„ z,)\S,. (15.Il)
s C.S.-0 <= I
Поверхностные интегралы первого рода обладают свойствами линейности, аддитивности, для ннх справедлива теорема о среднем, их величина не зависит от выбора стороны поверхности.
Очевидно, что интеграл JdS равен площади поверхности, а Цб(х, S S
у, z)dS, где 6(х, у, г) — поверхностная плотность поверхности S, — массе поверхности S.
. Если проекция D поверхности 5 на плоскость Оху однозначна, т. е. всякая прямая, параллельная оси Oz, пересекает поверхность S лишь в одной точке, то поверхность можно задать уравнением г = = F(x, у) и справедливо равенство, с помощью которого вычисление поверхностного интеграла первого рода сводится к вычислению двойного интеграла:
у, z)dS ~ у), F(x, y))Vl +№Tdxdy. (15.12)
5 D
Пример l. Вычислить Цд/х2 Ц- у2 dS, где S — часть конической
S поверхности x!-^-y2 = z2, расположенная между плоскостями z = 0 и z = 2.
► Из уравнения данной поверхности находим, что для рассматриваемой ее части z = ух2 4- у2 и проекцией ее на плоскость Оху является круг х2 у1 -С. 4. Так как
F; = x/xjx2 4- у2, Fy = у/ \х‘ 4- у2,
то из формулы (15.12) получим
(( y2dS =(( д/гДД2 ~\/I + -, Уdxdy =
JJ JJ V X2 4- (/-
s s
= ^+7dxdy =| ху=j =
D D
2л 2
д/2^ <:Лр j <rrfp = -Jv• 2л • —
О I)
Сторона гладкой поверхности S, из каждой точки которой восставлен вектор нормали п, называется положительной, а другая ее сторона (если она существует) — отрицательной. Если, в частности, поверхность S является замкнутой и ограничивает некоторую область пространства V, то положительной или внешней стороной поверхности 234
называется та ее сторона, нормальные векторы которой направлены от области И, а отрицательной или внутренней — сторона, нормальные векторы которой направлены в область V. Поверхность, у которой существуют положительная (внешняя) и отрицательная (внутренняя) стороны, называется двухсторонней. Двухсторонние поверхности характеризуются следующим свойством: если основание вектора нормали п
непрерывно перемещать по любому замкнутому контуру L, лежащую па такой поверхности, то при возвращении в исходную точку направление п совпадет с исходным (рис. 15.4). Двухсторонними поверхностями являются плоскости, все поверхности второго порядка, тор и многие другие.
Для односторонних поверхностей указанное перемещение нормали п при возвращении в исходную точку приводит к «антннормали», т е. к вектору —п. Классическим примером односторонней иоверхпост.ч является лист Мёбиуса (рис. 15.5).
Поверхность S с выбранной стороной называется ориентированной.
Если .поверхность S задана уравнением z = f(x, у), то нормальный вектор п, образующий с осью Oz острый угол у, определяется следующим образом: п = ( — f'x, —j!,, 1), а координаты единичного вектора нормали п° равны его направляющим косинусам, т. е.
пс = f-------------= (cos a, cos р, cos у),
\ |п| |п| |п1 )
ln| = Vl + /'f -Уу'а
Если поверхность 5 задана уравнением F(x, у, г) = 0, /' 0, то
гГ = ±grad F/|grad F\,
-где знак «-|~» берется в случае, когда угол у — острый, а знак <-"—» в случае, когда у — тупой.
Пусть в области V (Е RJ определена векторная функция а = Pi ф-ф- Qj ф- Лк, где Р = Р(х, у, г), Q = Q(x, у, г), Р = R(x, у, z) — функции, непрерывные в области V. Далее, пусть S — некоторая гладкая поверхность, лежащая в области V, с выбранной положительной стороной, т. е. выбранным направлением вектора п°. Разобьем поверхность S принадлежащими ей кусочно-гладкими линиями на элементарные площадки S,, площади которых AS, (Z= 1, п), и выберем в каждой из них произвольную точку М,(х,, у,, г,). Тогда существует предел
235
lim £ a(xt, у,, y,, z,)\Si, (15.13)
0AS,-*O i= 1
который называется поверхностным интегралом второго рода от функции а по поверхности S и обозначается \\a-n°dS. Таким образом, по опре-s
делению
\\а • n dS = ЭД(Р cos а + Q cos ₽ + /? cos y)dS. (15.14) з s
Поверхностные интегралы второго рода обладают свойствами линейности и аддитивности. При изменении стороны поверхности на противоположную, т. е. при замене п° на — п°, интеграл (15.14) изменяет знак.
Так как cos adS = dydz, cos (WS = dzdx, cos ydS — dxdy, то интеграл (15.14) можно записать и в виде
ЭДа • n°dS — \\pdydz Qdxdz Rdxdy. (15.15)
S S
Справедлива следующая формула, сводящая вычисление интеграла (15.14) к вычислению двойного интеграла:
ЭДа • n°dS = ЭД а(х, у, г)-п(х, у, z)dxdy, (15.16)
S D,
где область Ог является проекцией поверхности S на плоскость Оху, n = ±grad(z— /з(х, у)); поверхность S задается функцией г = f3(x, у). В двойном интеграле переменную z следует заменить на /з(х, у). Приведем еще две формулы, которые можно применять для вычисления поверхностного интеграла второго рода:
ЭДа • n°dS = ЭДа(х, у, г)-п(х, у, г)dydz =
S D,
= ЭДа(х, у, z)-n(x, у, z)dzdx, (15.17)
о,
где области Dx и О,, — соответственно проекции поверхности S на плоскости Ozy и Oxz; поверхность S задается функциями х = fi (у, г) ну = )2(х, г). В двойном интеграле по области D, следует в подынтегральном выражении заменить х функцией [i(y, z) и принять n = ±grad(x— — z''< а в двойном интеграле по Dy — заменить у функцией /2(х, г)
и взять n = ± grad(у — /г(х, z)). Отметим, что в выражениях для п знак « + » или «—» ставится в зависимости от выбранной ориентации (стороны) поверхности S.
Интегралы в правых частях формул (15.14) и (15.15) рассматривают как сумму трех интегралов, для вычисления каждого из которых можно применить одну из формул (15.16) или (15.17).
Пример 2. Вычислить
/ = ЭД zdydz — \ydzdx + 8x2dxdy, s
где S — часть поверхности z = х2-f-у2-|-1, отсеченной плоскостью z = 2, если нормаль п к поверхности S составляет с осью Oz тупой угол у.
236
► С помощью градиента находим вектор нормали к выбранной стороне данной поверхности: п = (2х, 2у, — 1), так как cos у < 0.
По условию а = (г, —4у, 8х2), поэтому, согласно формулам (15.15), (15.16), имеем (рис. 15.6):
/ = ЭД а ndxdy — ЭД(2хз — 8у~ — #x2)dxdy —
£>, D:
= ЭД(2х(х2 + у2 + 1) — 8(.г2 + у2)) dxdy = ь.
I х = р cos ((', 0 < q. < 2л I
= . , ахай — рара<р ~
I у = р sin <р, 0 Р 1, I
— ЭД(2р cos q (р2 -j- 1) — 8р2)рб/(к/(р =
Ог
I 2л I
= j рл'р j (2р cos <р(р2 +1) — 8р2)<У<р = — j 16яр3<Ур = —4л. о о о
Рис. 15.6
Пример 3. Вычислить
/ = ЭД xdydz dxdz xz2dxdy,
S
где S — внешняя сторона части сферы х2 -)- у2 -)- гг ~ I, расположенной в первом октанте.
► Если обозначить проекции поверхности S на координатные плоскости Oyz, Oxz и Оху через Dx, Du и /Л, соответственно, а данный интеграл / рассматривать как сумму трех интегралов:
/, = ^xdydz, 1-2= §dxdz, h = \\xzddxdy,
S s s
для первого из которых Р = х, Q = R = 0, для второго Q = I, Р = R = — 0 и для третьего Р = Q = 0, R = xz2, то, применив к каждому из них формулу (15.16) или (15.17), получим
/, = ЭД — у2 — z2dydz, I2 = ЭД dxdz, Is — ЭД х(1 — х2 — y2)dxdy. Dt D, D,
237
Области Dx, Dy и D. являются четвертями кругов единичного радиуса, расположенными в соответствующих координатных плоскостях, поэтому интеграл l? = SDl = л/4 (площадь четверти круга). Для вычисления интегралов h и /з перейдем к полярным координатам, положив у — р cos <р, г = р sin <р, dydz — pdpdtf для /<, х = р cos гр, у = р sin гр, dxdy = pdpdq для 1з- В обоих случаях 0 q> л/2, 0 г/р с/ I. Тогда л/2 I
li = ЭД — р2 pdpdtf = — d<f j (I — p2)l/? • -i- <7(1 — p2) = o, oo
я/2 I Sr I"
d<f 1 p cos <jp (1 — p2) pdp = sin <p|
J io
0 0- ,
2
15
Следовательно,
Если S — замкнутая гладкая поверхность, ограничивающая область V, и Р = Р(х, у, г), Q = Q(x, у, z), R — R(x, у, z)— функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области И, то справедлива формула Остроград-ского — Г аусса
ЭД Pdydz 4- Qdxdz 4- Rdxdy = з
V
или в другом виде
§(Р cos a -j- Q cos р + R cos y}dS =
V
где cos a, cos f>, cos у — направляющие косинусы внешней нормали к поверхности S.
Формула Остроградского — Гаусса позволяет упростить вычисление многих поверхностных интегралов.
Пример 4. Вычислить
/ = jj (х + y)dydz + (у + z)dxdz 4- (г 4~ x)dxdy. s
если S — внешняя сторона поверхности тела, ограниченного плоскостями х = 0, у = 0, z — 0, х 4- 2у 4- Зг — 6.
238
► Из формулы (15,18) следует, что
1 = W( 1 Н- 1 + \)dxdydz = 3 ^dxdydz — 18, V г
так как последний тройной интеграл равен объему тетраэдра (рис. 15.7).
АЗ-15.3
1. Вычислить поверхностный интеграл первого рода й xjx2 + у2 dS, если S — часть поверхности конуса s
+ yg = др , расположенная между плоскостями 2 = 0 и 2 = 3. (Ответ: 160л/3.)
2. Вычислить поверхностный интеграл первого рода й xyzds, где S — часть плоскости х + У + z = 1, лежащая s
в первом октанте. (Ответ: х/з/120.)
3. Вычислить массу полусферы z=x[a— х2— у2, если поверхностная плотность в каждой ее точке 6 = = х2у2. (Ответ: 128л/15.)
4. Вычислить массу полусферы z = х!а2 — х2 — у2, если поверхностная плотность в каждой ее точке 6 = = х2 + у2- (Ответ: 4ла4/3.)
5. Вычислить поверхностный интеграл второго рода й xdydz + ydxdz + zdxdy, s
если S — верхняя часть поверхности x-\-2y-\-z — 6 = 0, расположенная в первом октанте. (Ответ: 54.)
6. Вычислить
У (х + у)dydz + (у — x)dxdz + (z — 2)dxdy, s
239
если S — часть поверхности конуса х'2 у2 — z2 = 0, отсекаемая плоскостями 2 = 0 и 2=1, нормаль к которой образует тупой угол с осью Oz. (Ответ: 8л/3.)
7. Вычислить
jj xdydz -|- z'dxdy, s
если S — внешняя сторона сферы х’ -|- у1 + z2 = 1. (Ответ: 32л/15.)
8. Вычислить
xdydz /- ydxdz -f- zdxdy, s
если S — внешняя сторона цилиндра х2 -|-у1 = R2 с основаниями 2 = 0 и z = H. (Ответ: 3nR2H.)
9. Доказать, что объем тела, ограниченного поверхностью S,
v = у xdydz /- ydxdz + zdxdy, s
где S — внешняя сторона поверхности S.
10. Вычислить
55 уzdxdy + xzdydz -f- xydxdz, s
если S — внешняя сторона поверхности, расположенной в первом октанте и состоящей из цилиндра х2 -ф у2 = R2 и плоскостей х = 0, у = 0, z — 0, z = Н. ( Ответ: R2H2(^~ -|-+ т).)
11. Вычислить
55 уzdxdy 4- xzdydz -ф xydxdz, s
еслн S — внешняя сторона пирамиды, гранями которой ЯВЛЯЮТСЯ ПЛОСКОСТИ X = 0, 4/= 0, 2 = 0, x-f-y-(-z=l. (Ответ: 1/8.)
Самостоятельная работа
1. Вычислить 55 (У + 2z)dxdy, если S — верхняя часть s
плоскости 6х -ф Зу -ф 2z = 6, расположенная в первом октанте. (Ответ: 8/3.)
240
2. Вычислить ЭД xyzdS, если S — часть поверхности s
параболоида z = х1 у\ отсекаемая плоскостью z=l.
(Ответ: 0.)
3. Вычислить
ЭД zdydz + (Зу — x)dxdz — zdxdy, s
если S — внешняя часть поверхности тела, ограниченного поверхностями z — 0, х'1-\-у~=\, z = х~ у’ + 2. (Ответ: 5л.)
15.4. ПОТОК ВЕКТОРНОГО ПОЛЯ ЧЕРЕЗ ПОВЕРХНОСТЬ. ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ
Потоком векторного поля а(М), Л4(х, у, z)ES через поверхность S в сторону единичного вектора нормали п° = (cos a, cos 0, cos у) поверхности S называется поверхностный интеграл второго рода (15.14).
Если вектор а — (Р, Q, R) определяет векторное поле скоростей текущей несжимаемой жидкости, то интеграл (15.14) равен объему П жидкости, протекающей через поверхность S в направлении нормали п° за единицу времени (в этом заключается физический смысл интеграла (15.14)), т. е.
П= Ца(/И)- n°dS. (15.20)
х
Из формулы (15.20) ясно, что П — скаляр, и если угол ф = = (a/f'n°) < л/2, то П > 0, если же ф > л/2. то П < 0, если ф — л/2, то /7 = 0.
Прн изменении ориентации поверхности знак П меняется на противоположный (вследствие свойств поверхностных интегралов второго рода).
Пусть S — замкнутая кусочно-гладкая поверхность, единичный вектор внешней нормали к которой п°. Тогда ноток П вектора а = = (Р, Q, R) через поверхность S можно вычислить с помощью формулы Остроградского — Гаусса ([5.18):
S I-
Пусть а(Л1) — поле скоростей несжимаемой жидкости. Если П > 0, то из формулы (15.21) следует, что из области V вытекает больше жидкости, чем втекает. Это означает, что внутри области V имеются источники, т. е. точки, из которых жидкость вытекает. Если // < 0, то из области V вытекает меньше жидкости, чем втекает в нее. В этом случае говорят, что внутри области V имеются стоки, т. е. точки, в которые жидкость втекает. При П — 0 в область V втекает столько же жидкости, сколько вытекает.
Пусть в области V задано векторное поле а(Л4) = (Р, Q, R), где функции Р(х, у, г), Q(x, у, 2), R(x, у, г) имеют частные производные
241
в точке М(х, у, z) £ V по х, у, z соответственно. Тогда дивенгенцией или расходимостью векторного поля а(М) в точке М, обозначаемой div а(Л7), называется величина, равная сумме указанных частных производных, вычисленных в точке Л1, т. е. по определению
div а(,М) = (----
\ дх
dQ I
ду dz J 1л1
(15.22)
С.физической точки зрения div а(Л4) характеризует плотность источников или стоков векторного ноля а(Л1) в точке М. Если div а(Л1)> О, то точка М является источником, если div а(М) <0 — стоком. В случае, когда diva(M) = 0, в точке М нет ни источников, ни стоков.
. Перечислим основные свойства днвенгенцни векторного поля:
1) div(a 4- b) — div а + div Ь;
2) div с = 0, если с — постоянный вектор;
3) div (/а) = f div а -ф а • grad j, где j = f(x, у, z)—скалярная функция.
Из формул (15.21) и (15.22) следует, что
П = Ц а • n°dS = $div a\M)dxdydz, (15.23)
5 V
т. е. поток П векторного поля а(М) через замкнутую поверхность S во внешнюю ее сторону численно равен тройному интегралу от дивергенции этого поля по области V, ограниченной поверхностью S.
Пример 1. Вычислить дивергенцию векторного поля а(Л1)-= (.г -|-+ У) + (№ + г) j + (г2 + -t) к в точке Л1о (1, —2,3).
Согласно формуле (15.22),
div а(Л1) = = 2л- + 2// + 2г.
v дх ду дх
В точке ЛГ имеем div а(Мо) = 4 > 0, т. е. точка Мо является источником поля.
Пример 2. Вычислить поток векторного поля а = лт — 2yj ф- гк через верхнюю часть плоскости л + 2у + Зг — 6 = 0, расположенной в первом октанте.
1 2
> Из уравнения плоскости находим z — 2-----— х----—у. Нормаль-
ным вектором к этой плоскости, составляющим острый угол с осью Ог, является n = (1/3, 2/3, 1). тогда из формул (15.20) и (15.16) следует, что
П = й а • п° dS = а • n dxdy —
S Г),
= "З* (Х — + 3z)dxdy - 2 (6 — 6y)dxdy =
о, о,
3 6 — 2у 3
= 2 \ dy J (1 — y)dx = 2 $(1 — у) (6 — 2y)dy ==
0 0 о
о
= 2 \{2у~~ 8z/+ 6) = 36. 4
о
242
Пример 3. Вычислить поток векторного поля а(М) = xz'~i -ф ух-j -ф zy'k через поверхность шара № у~ -ф z‘ = а1 во внешнюю его сторону.
► Так как данная поверхность — замкнутая, то поток П векторного поля а(А4) через поверхность шара во внешнюю сторону находим по формуле (15.23):
П = ЭД а • n° dS = ЭД5 div а(М) dxdydz =
S г
= + А'2 + у-) dxdydz.
I/
Для вычисления полученного тройного интеграла перейдем к сферическим координатам по формулам:
х = р sin 0 cos tf, у — (> sin 0 sin <р. z = р cos в; dxdydz = р2 sin Odpdipdfr, Os^psCa, 2л, 0 ф 0 ф л.
Тогда
sin fWpdipc/O =
p'i/p sin (МО z/ip 0 0 о
4яа 5
Пример 4. Найти поток П электростатического ноля точечного заряда q, помещенного в центр сферы х2 ф у~ ф z2 = R'.
> Известно, что поле точечного заряда задается вектором напряженности Е = <yr/Jr|'\ где г = xi фyj ф zk. Находим направляющие косинусы вектора нормали к сфере х2 ф у1 ф z2 = /?2:
n°=n/ln|, n=(2x, 2у. 2г),
|п| = д/V Ф 4у2 ф 4z2 = 2/?, п" = (х//?, y/R, z/R),
т. е. cos а = x/R, cos (i = y/R, cos у = z/R. Поэтому на сфере
Е • n° = (q/\г|') (г • п») = (xi ф y'j + zk) • i ф j ф k} = A. \ A. t\ t\ /
= jl z!+Z±± = Л — = Л = const.
R R R' R R-
Следовательно,
П = [[ E • n"dS = {{ -Z-dS= 4л/?2 = 4яо. -4
JJ JJ R R
s s
Пример 5. Найти поток векторного поля а(М) = xi ф yj ф zk через поверхность прямого цилиндра S радиусом R и высотой Н, ось которого совпадает с осью Oz, а нижнее основание находится в плоскости Оху. Нормаль направлена во внешнюю сторону цилиндра.
► Как видно из рис. 15.8, для боковой поверхности цилиндра Si справедливо равенство а • п? = пр а = R. На верхнем основании цилиндра S? имеем а • п’ = пр а = И, а на ннжнем его основании 5з — а • п° = 0. Поэтому
243
п = fi а • n°rfS = й а n?</.S + JJ а • п5</5 + ЭД а • nUS = s Si s. s.,
= RdS + Й HdS + Й OdS = R 2ziRH + /Ул/?-’ = 3.ч/?7/. S, S3 S3
Вычисления можно значительно сократить, воспользовавшись формулой Остроградского — Гаусса (15.18). Так как объем цилиндра
v = Щ dxdydz = ^R H, v
имеем
П = ® (1 + 1 + \)dxdydz = 3nR-H. « Г
АЗ-15.4
1. Вычислить дивергенцию векторного поля а(Л4) = = (ху + z2) i + (yz 4- х2) j + (zx + у2} k в точке М (1, 3, — 5). (Ответ: —1.)
2. Вычислить поток векторного поля а(/И) = (х— — 3z) i + (х + 2у + z) j + (4х + У) к через верхнюю часть плоскости х 4- у + z = 2, лежащую в первом октанте. (Ответ: 26/3.)
3. Вычислить поток векторного поля а(/И) = 2xi 4- yj + 4* 3zk через часть поверхности эллипсоида ~ 4- у 4~ 4* jg = 1, лежащую в первом октанте, в направлении внешней нормали. (Ответ: 24л.)
4. Вычислить поток векторного поля а(/И) = (х — — у) i 4~ (Л 4~ У) j 4~ z2k через поверхность цилиндрического тела, ограниченного поверхностями х24~у2=1> z = 0 и z — 2, в направлении внешней нормали. (Ответ: —4л.)
5. Доказать, что поток П радиуса-вектора г = xi 4* yj 4~ 4-zk через внешнюю сторону поверхности, ограничивающей тело V объемом и, равен 3v.
6. Вычислить дивергенцию вектора напряженности магнитного поля Н=(2//г)( — у\ 4- xj), создаваемого то-244
ком /, проходящим по бесконечно длинному проводу. (Ответ: div Н = 0.)
7. Найти поток П векторного поля а(Л1) = x3i 4* ул] 4* + z3k через поверхность шара х2 4- у2 -j- z2 = R2 в направлении внешней нормали. (Ответ: 12л/?’/5.)
8. Вычислить поток П векторного поля а(Л1) = = 8xi 4- 1 lyj 4* 17zk через часть плоскости х 4- 2у 4- Зх = = 1, расположенной в первом октанте. Нормаль составляет острый угол с осью Ох. (Ответ: 1.)
9. Найти поток П вектора а = xi — 2yj — zk через замкнутую поверхность S, ограниченную поверхностями 1 — — х = х2 4- у2, z = 0, в направлении внешней нормали. (Ответ: —л.)
10. Найти поток П вектора а = x2i -|- z2j через часть поверхности z2 = 4—х — у, лежащую в первом октанте, и части координатных плоскостей, отсекаемых этой поверх-ностью, в направлении внешней нормали.) Ответ: 19-——.)
Самостоятельная работа
1. 1. Найти дивергенцию поля grad и, если и = In (х2 4-+ У2 4* -г2)-
2. Вычислить поток П векторного поля а(Л4) = = xi 4- 3yj -f- 2zk через верхнюю часть плоскости х 4- у 4--|-z = 1, расположенную в первом октанте. (Ответ: 1.)
2. 1. Найти дивергенцию векторного поля а(М) = — xy2i 4- x2yj 4- z3k в точке М (1, — 1, 3).
2. Вычислить поток векторного поля a(A4) = 3xi— — yj — zk через поверхности 9 — z = х2 -|- у2, х = 0, у = 0, z = 0, ограничивающие некоторое тело, в направлении внешней нормали. (Ответ: 81л/8.)
3. 1. Найти div (grad~\/x2 4-у2 4-z2)-
2. Найти поток векторного поля а(Л1) = 2xi -f- zk в направлении внешней нормали к поверхности тела, ограниченного поверхностями х = Зх2 4- 2у, х2 4- у2 = 4, z = 0. (Ответ: 20.)
15.5. ЦИРКУЛЯЦИЯ ВЕКТОРНОГО поля. РОТОР ВЕКТОРНОГО ПОЛЯ
Пусть Г — замкнутая кусочно-гладкая кривая в пространстве R’ и S — гладкая поверхность, краем которой служит кривая Г За положительное направление обхода кривой Г принимается такое на-
245
правление, при котором область, ограниченная этой кривой, будет оставаться слева на положительной стороне поверхности .S, т. с. на стороне, из точек которой восставлен единичный вектор нормали п° = = (cos a, cos р, cosy) поверхности S. Пусть, далее, в окрестности поверхности S задан вектор а = (Р, Q, R), координаты которого Р, Q, R
являются непрерывными функциями от х, у, г вместе со своими первыми частными производными. Тогда имеет место формула Стокса, связывающая криволинейный и поверхностный интегралы (рис. 15.9):
ф Pdx + Qdy + Rdz = V
где направление обхода по замкнутой кривой Г выбирается положительным.
Формула Грина (14.14) является частным случаем формулы Стокса, когда кривая Г и поверхность S лежат в плоскости Оху.
Отметим, что формула Стокса (15.24) справедлива для любой поверхности S, если ее можно разбить на части, уравнения которых имеют вид г — f(x, у).
Пример 1. Вычислить
/ = Ф (z2 — х') dx + (х- — у2) dy + (у2 — г2) dz г
по контуру х2 + у2 -|- z2 = 8, х~ + у~ = г2, г > 0, «пробегаемому» по ходу часовой стрелки с точки зрения наблюдателя, находящегося в начале координат О.
► Контур интегрирования Г — окружность х2 + у2 = 4, лежащая в плоскости г = 2, полученная в результате пересечения сферы хг -|-4- у2 -ф z2 — 8 с конусом х2 + у2 = г2 (рис. 15.10). В качестве поверх-
246
пости .S' возьмем круг с краем I’: х2 4- у2 С 4, г = 2. Далее, Р = г2 — — .г, Q = х2 — у2, Р у2 — z2,
дР dQ . дР (>Р „ dQ дР „
ду dz dz dx dx dy
Тогда в соответствии с формулой Стокса и условием задачи возьмем п°=(0, 0, 1) (этим обеспечивается положительное направление движения по [' (см. рис. 15.(0)). Имеем
х = р cos <р, dxdy = pdpdq,
у = р sin q>, 0 С ф С 2л, 0 С р С 2
D
2л 2
= 2 J cos ф</<р j p2dp = 0. о о
Если задано векторное поле а(М) — (Р, Q, R) и некоторая замкну--тая кусочно-гладкая кривая Г в пространстве R\ то криволинейный интеграл
С= фа-ЛД = §Pdx + Qdy + Rdz (15.25)
г г
называется циркуляцией векторного поля а(Л4) вдоль контура I’. Здесь т° — единичный вектор, направленный по касательной к кривой Г и указывающий направление обхода по контуру.
Если а—вектор силы, то циркуляция (15.25) равна работе этой силы вдоль замкнутой кривой Г.
Пример 2. Вычислить циркуляцию векторного поля а(М) = = xi — 2z2j 4- yk вдоль линии Г пересечения цилиндра х2/16 4- у /9 = = 1 с плоскостью z = х 4- 2у + 2 в положительном направлении обхода относительно нормального вектора плоскости п=(— 1, —2, 1).
► Пара метрические уравнения цилиндра х2/16 4-(/2/9 = 1 имеют вид х = 4 cos t, у = 3 sin t. Тогда параметрическими уравнениями кривой Г (эллипса в плоскости сечения) будут х = 4 cos t, у = 3 sin /, z — 4 cos t 4- 6 sin t 4- 2. Поэтому циркуляция векторного поля вдоль эллипса в положительном направлении обхода вычисляется по формуле
2л
С = ф xdx — 2z2dy 4- ydz = j (4 cos t (— 4 sin tdt) — г г 0
— 2 (4 cos t 4- 6 sin t 4- 2)2 3 cos tdt 4- 3 sin t (— 4 sin t 4- 6 cos t) dt) =
2л
= J (— 16 cos t sin t — 96 cos31 — 216 sin2 / cos t — 24 cos t —
0
— 288 cos21 sin t — 96 cos2 t — 144 cos t sin t — 12 sin21 4-
2л
+ 18 cos t sin t}dt — — J (96 cos21 + 12 sin2 /) dt —
о
2л 2л
= — J 48 (I 4- cos 21) dt — 6 j (1 — cos 2t) = — 48 2л — 6 • 2л = о о
= - 108л.
247
Ротором или вихрем векторного поля а(М) = (Р, Q, R) называется вектор
гМ . (А() _ № - «Л, + - «); + k. (, 5.26)
\ду dz J \дг дх) \дх ду ) '
Используя понятия ротора и циркуляции, формулу Стокса (15.24) можно записать в векторной форме:
С = §a-xQdl = ЭД rot а • nodS, (15.27)
Г S
т. е. циркуляция векторного поля а(Л4) вдоль замкнутого контура 1’ равна потоку ротора этого поля через любую гладкую поверхность S, краем которой является Г. Направление обхода по Г и сторона поверхности S одновременно или положительные, или отрицательные.
Число С(7И) = пр „" rot а(Л4)
называется плотностью циркуляции векторного поля а(Л4) в точке М в направлении вектора п°. Плотность достигает максимума в направлении rot а(Л4) и равна max С(М) = I rot а(Л4)|.
Отметим некоторые свойства ротора векторного поля:
1) rot (а -|- b) = rot а -|- rot Ь;
2) rot с = 0, если с — постоянный вектор;
3) rot (q>a) = <р rot а + grad <р • а, где <р(лг, у, г)— скалярная функция.
Если rotate, то это свидетельствует о вращении векторного поля а(Л4).
Пример 3. Найти ротор вектора линейной скорости v = ю • г
(г — (х, у, г), со = (to*, юй, ю2)) любой точки М(х, у, г) пространства. > Имеем
v =
к
i
Юх
X
}
ЮЙ
У
= (гюу — </ю,) i -|- (хюг — гюЛ) j ф- (ушЛ — хюй) к.
(02
Z
По определению ротора находим
rot v = (2юх, 2юх, 2юг) — 2ю. 4
Пример 4. Вычислить циркуляцию векторного поля a(Al)=i/i + 4- x2j — zk по окружности Г: х2 -|- у2 = 4, г — 3 в положительном направлении обхода относительно единичного вектора к двумя способами: I) исходя из определения циркуляции (15.25); 2) с помощью поверхностного интеграла, использовав формулу Стокса (15.27).
> 1. Так как при возрастании параметра t от 0 До 2л движение по окружности происходит против хода часовой стрелки относительно единичного вектора к = (0, 0, 1), то параметрические уравнения ориентированной кривой Г имеют вид х — 2 cos I, у — 2 sin t, z = 3 (t £ [0; 2nJ). Тогда
С = ф ydx -|- x2dy —- zdz = г
2л
= J 2 sin / (— 2 sin Idt) + 4 cos2 t 2 cos tdi — 3 0 = о
248
2л 2л 2л
= 8 j cos3 tdt — 4 j sin2 tdt ~ 8 j (1 — sin2 t) d (sin t) — ooo
2л
— 2 J(1—cos 2f) dt ——4л.
о
2. В качестве поверхности S, краем которой является кривая Г, возьмем круг х2 4- у2 <( 4, 2 = 3 (рис. 15.11). Тогда п° = к. Далее, rot а = (2х— - 1)к и
С— 55 rot а • n“rfS = 55 (2х — 1) dxdy =
S D
= 55 (2р cos ф — 1) pdpdq> =
D
2л 2
= 5 5 (2рcos ф —') р^р=
о о
АЗ-15.5
1. Найти ротор векторного поля а(Л4) = xi/zi-р (х+ + у + z) j + (х2 -f- у2 -f- z2) к в точке Л1(1, —1, 2). (Ответ: rot а(Л4) = — 3i — 3j — к.)
2. С помощью формулы Стокса преобразовать интеграл
ф (у2 + z2) dx + (х2 + z2) dy 4- (х2 + у2) dz, г
где Г — замкнутый контур, в интеграл по поверхности, «натянутой» на этот контур.
3. Найти циркуляцию векторного поля a(A4) = yi — — 2zj+xk вдоль эллипса, образованного сечением однополостного гиперболоида 2х2 — у2 -ф z2 — R2 плоскостью у = х. Результат проверить с помощью формулы Стокса. (Ответ: ±3л/?2.)
4, Вычислить циркуляцию векторного поля а(Л4) = = zi -ф xj -ф ук вдоль контура Г: х2 -ф у2 — 4, z ~ 0 в положительном направлении обхода относительно орта п° = к непосредственно и с помощью формулы Стокса. (Ответ: 4л-) ,
5. Найти циркуляцию векторного поля a(7W) = zi-|-+ x2j + y2k по сечению сферы х2 -ф у2 -ф z2 = R2 плоскостью х у z = R в положительном направлении обхода относительно вектора n = (l, 1, 1). (Ответ: Зл/?4/2).
249
6. Найти циркуляцию векторного поля а(Л4) = t/2i 4-+ ХУ1 + (х~ + У/ к по контуру, вырезаемому в первом октанте из параболоида х2 4- у2 = Rz плоскостями х = О, у = 0, z = R в положительном направлении обхода относительно внешней нормали поверхности параболоида. (Ответ: R3/'3.)
7. Вычислить циркуляцию векторного поля а(М) = = zy2i 4- xz2j 4- yx2k по контуру пересечения параболоида х = у2 4~ z2 с плоскостью х = 9 в положительном направлении обхода относительно орта п° = i. (Ответ: 729л.)
8. Вычислить циркуляцию векторного поля а(Л4) = = —yi 4- 2j 4- к по линии Г пересечения конуса х2 -ф-4- у2 — z2 — 0 с плоскостью z=l в положительном направлении обхода относительно орта п° = к. (Ответ: л.)
Самостоятельная работа
t. Вычислить циркуляцию векторного поля а(2И) = = yi — xj 4- zk вдоль линии Г пересечения сферы х2-(-у2-}-4- z2 = 4 с конусом ух2 4- у2 = z в положительном направлении обхода относительно орта пи = к.
2. Вычислить циркуляцию векторного поля а(М) = = yz\ 4~ 2xzj 4- y2k по линии Г пересечения полусферы z = у25 — х1 — у2 с цилиндром х2 4- у2 = 16 в положительном направлении обхода относительно орта п° = к.
3. Вычислить циркуляцию векторного поля а(Л4) = = (х — у) i 4- xj — zk вдоль линии Г пересечения цилиндра х2 + У2 — I с плоскостью z = 2, если п° = к.
15.6. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА. КЛАССИФИКАЦИЯ ВЕКТОРНЫХ ПОЛЕЙ
Дифференциальные операции. Введенные выше основные понятия векторного анализа: градиент, дивергенция, ротор — удобно описывать с помощью дифференциального оператора, который обозначается символом V (читается «набла»):
д . , д . , д ,
V —5— 14—з— J 4—л— дх ду dz
и называется оператором Гамильтона.
Выразим основные дифференциальные операции с помощью оператора V:
V ц(М) = i + j + k = grad и(М), OJC Си/ С/4.
250
V • а(Л1) = 4- = div a(Aj),
dx dy dz
i j к
д д д
V ) <а(А4) = ~дТ ду дг — rot а (А1).
Р Q R
Операции нахождения градиента, дивергенции, ротора называются дифференциальными операциями первого порядка.
Перечислим основные свойства дифференциальных операций второго порядка:
. j д2и д~и , д2н . ,,,,
div grad и(М) = --— -ф ----- ------ = Дп(Л1),
дх' ду~ дг~
д2 д2 д2 ,
где А = -----—|---—|------ = V • V = V называется оператором
дх~ ду~ дг
Лапласа;
rot grad и(М) = (V • V) и (Al) = О, div rot а(Л1) = V • (V X а(Л1)) = О, grad div a(M) = V (V • a(AJ)), rot rot a (Al) = V X (V X a (Al)) = grad div a (At) — Да (At).
Соленоидальное векторное поле. Векторное поле а(Л1) называется Соленоидальным или трубчатым в области пространства V, если в каждой точке этой области
div а(А1) = 0.
Так как div rot a(Af) = 0, то поле ротора любого векторного поля а(А1) является соленоидальным.
Поток солено'идального векторного поля а(А7) в направлении его векторных линий через каждое сечение векторной трубки, согласно формуле Остроградского— Гаусса, один и тот же. Трубчатое поле не имеет источников и стоков.
Для каждого соленоидалыюго поля а(М) существует векторное поле Ь(А1), такое, что а(А1) = rot b(Af). Вектор Ь(А1) называется вектором-потенциалом данного поля а(А1).
Потенциальное векторное поле. Векторное поле а(М) = (Р, Q, R) называется потенциальным или безвихревым в односвязной области пространства V, если в каждой точке этой области
rot а (М) = 0.
Согласно опредению ротора, необходимыми и достаточными условиями потенциальности поля а(А1) = (Р, Q, /?) являются равенства;
d±=dQ_ d^=dR_ dQ _ dP (]528)
ду dz ’ дг дх ' дх ду '
Так как rot grad и(М) = 0, то поле градиента любого скалярного поля и — и(х, у, г) — потенциальное. Для того чтобы поле а(А1) было потенциальным в области V, необходимо и достаточно, чтобы существовала дважды непрерывно диференцируемая скалярная фунция и = и(х, у, z), такая, что а = grad и(М), которая называется потенциальной функцией (потенциалом) поля а(А1).
251
Так как при выполнении условий (15.28) криволинейный интеграл второго рода не зависит от линии, соединяющей точки .VI,, и Л41, то для потенциального поля а(Л1) = Pi + Qj + Rk справедлива формула для нахождения потенциальной функции:
и(х, у, z)— J Pdx + Qdy 4- Rdz -|- С, (15.29)
М„Л1
где УИо(хо, у», zu) — некоторая фиксированная точка области И. М(х, у, г) — любая точка области V; С — произвольная постоянная.
Из формулы (15.29) следует формула для вычисления криволинейного интеграла второго рода, не зависящего от пути интегрирования:
Pdx Qdy -|- Rdz = и(В) — «(4), (15.30)
л в
где и(Л) и и(В) — значения потенциала и в начальной А и конечной В точках пути.
Гармоническое векторное поле. Векторное поле а(,М), удовлетворяющее двум условиям: diva(At) = 0 и rota(7M) = 0, называется гармоническим. Потенциал и гармонического поля является решением уравнения Лапласа
д2и
дх2
д2и д'2и
~д^~ +
0.
(15.31)
Функция и = и(х, у, z), удовлетворяющая уравнению Лапласа (15.31), иызывается гармонической.
Пример 1. Показать, что поле a(M) = {2ху г) i 4- (х2— 2у) j 4-+ хк является потенциальным, но не соленоидальным. Найти потенциал и данного поля.
> Имеем: Р = 2ху z, Q = х2 — 2у, R — х. Тогда
rot а(Л1) =
д дх 2ху 4- г
ду х2-2у
к
д ~дг
= (0-0)i + (l - 1) j + (2х -
j
д
— 2х) к = 0,
т. е. поле а(Л1)— потенциальное.
Далее имеем
div а = ~ 4- 4^- ~ 2 + 0 ¥= 0,
дх п ду 1 dz э
поэтому поле а(М) не является соленоидальным.
Согласно формуле (15.29),
ц(х, У, г) = 5 (%ху г) dx + (х2 —- 2у) dy 4- xdz + С
Мг,.М
Так как функции Р(х, у, z), Q(x, у, z), R(x, у, г) непрерывны и имеют непрерывные частные производные во всех точках пространства R3, то в качестве точки Л)о(хо, уо, го) можно взять начало координат 0(0, 0, 0), а в качестве М(х, у, г) — произвольную точку пространства. Как отмечалось ранее, криволинейный интеграл второго рода не зависит
252
от пути интегрирования, поэтому его можно вычислить по ломаной ОАВМ (рис. 15.12):
и(Х, У, Z) = J + С = i + 5 + j + С =
ОЛ1 0.1 ав вы
ОА: у = 0, z = 0, dy = 0, dz = О, 0 х -С X,
= АВ: X = X, z = 0, dx = 0, dz = 0. О у У, =
ВМ: л- = X, у = У, dx = 0, dy = О, 0 г Z
Л У 2
= i 0 • dx + S (X2 - 2у) dy + $ Xdz = А'2 У. — У2 -ф XZ.
Заменив в последнем равенстве X, У, Z на х, у, г, запишем выражение для потенциала поля:
и (х, у, г) = х2у — у2 А~ xz + С. •<
Пример 2. Проверить, является ли потенциальным поле а = (уг — — ху) i (xz — х2/2 yz2) j + (ху y2z) к, найти его потенциал и вычислить соответствующий криволинейный интеграл второго рода по линии, соединяющей точки Л(1, 1, 1) и В(2, —2, 3).
► Учитывая, что Р = yz — ху, Q = xz — х2/2yz2, R = ху А~ у2?, находим
rot a(At)=
i
д дх
yz — xy
д
dy
хг — х2/2 4- yz'
к
д
dz
ху + у2г
= (х + 2yz — х — 2yz) i + (у — у) j -ф (г — х — z -ф х) к = 0.
Следовательно, поле а — потенциальное и существует потенциал (см. формулу (15.29) и пример 1)
и(Х, У, Z) = J Pdx Qdy -|- Rdz -|- С —
ЛЛЛГ
х у г
= 0 • dx + --dy + (ху + y2z) dz + С =
оо о
= - X2 У/2 + X YZ + Y2Z2/2 + С.
253
Заменив X. Y, Z на л', у. г, окончательно получим
w = xyz х~у/'2. 4- ух/2 4~ С.
Так как в потенциальном поле криволинейный интеграл второго рода не зависит от пути интегрирования, соединяющего точки Д и В, то, согласно формуле (15.30), имеем
5 (уг — ^У) 4- (Л? — л-'/2 4- уг-) dy 4~ (ху + y2z) da =
АН
-= и(В) — и(Д) = 9. 4
Пример 3. Доказать, что функция и = \/г, где г = ух2 4- у' 4~ г?, является гармонической и векторное поле а(А4) = grad и(М)— гармоническое.
► Прежде всего следует проверить, справедливо ли. для данной функции уравнение Лапласа (15.31). Вычисляем д'и^дх2, d~u/dy?, <ru/dz~ и Хи:
Следовательно, уравнение Лапласа Хи — 0 удовлетворяется и данная функция и = 1/г — гармоническая.
Далее находим
а(Л4) = grad и(М) = — r\xi 4- yj 4- гк).
Как известно, rot а(М) = rot grad и(М) = 0 для любой функции и, т е. одно из условий в определении гармонического поля а(Л4) выполнено. Другое условие div а(Л4) — 0 также выполняется, поскольку div а = div grad и(М) = Хи{М) = 0. <
АЗ-15.6
1. Доказать с помощью формулы Стокса, что ф yzdx ф- xzdy + xydz 0, г
где Г — любой замкнутый контур. Результат проверить путем вычисления интеграла по контуру треугольника АВС с вершинами Л(0, 0, 0), В(1, 1, 0), С(1, 1, 1).
2. Найти grad div а(М), если а(Л4) = x3i -j- у3] z3k.
3. Среда вращается как твердое тело вокруг оси Oz с
254
угловой скоростью w = wk. Найти ротор поля линейных скоростей v = c6Xr, где г—радиус-вектор движущейся точки М(х, у, z). (Ответ: 2юк.)
4. Найти циркуляцию поля скоростей v, описанного в предыдущем задании, по окружности х~ 4- у — R\ z = О в положительном направлении обхода относительно орта к. (Ответ: 2n.R2.)
5. Доказать, что div rot a(M) = 0 для любого поля а(Л4).
6. Установить потенциальность поля а(Л4) и найти его потенциал и, если:
а) а(Л1) = 2xz/i 4- (х2 — 2yz) j — t/k;
б) a(M) = (3x2y— j/3)i-|-(x3— 3xy2)j;
в) а(Л4) = (у 4- 2) i (х -|- z) j -|- (у 4- х) к.
(Ответ: а) и = х2у —- y2z 4- С; б) и = х3у — ху3 -|- С; в) и == = ху -|- yz -|- xz 4- С.)
7. Проверить, является ли гармонической функция и = In г, если г = -ух2 4- у2.
8. Установить потенциальность поля а(Л1) и найти его потенциал и:
а) а(ЛД = ^4 4-(-^^
4- уе!)г 4- е J к;
б) а(Л4) = yzcos(xy)i 4- xzcos(xy)j 4- sin (ху) k. (Ответ: а) и = еу/г (х 4- 1) 4- еуг—е~г 4- С; б) и = = 2 sin (ху) 4- С.)
9. Доказать, что векторное поле а(Л4)=----~ г, где
И
г = xi 4- yj 4~ ^k, которое описывает гравитационное поле, создаваемое точечной массой т, помещенной в начало координат (у—ньютоновская постоянная тяготения), является гармоническим (потенциальным и безвихревым), найти его потенциал и и убедиться, что потенциал и удовлетворяет уравнению Лапласа. (Ответ: u = ym/\r\.)
10. Доказать, что rot grad и(М) = 0.
11. Найти потенциал и поля а(А4) = (yz 4- 1) i 4~ xzj 4~ 4-хук и вычислить
(2. 3, 2)
J (yz 4- 1) dx 4- xzdy 4- xydz.
а. г о
(Ответ: и = x 4- xyz 4~ C; 12.)
255
Самостоятельная работа
Проверить потенциальность векторного поля а(Л4), найти его потенциал и вычислить значение соответствующего криволинейного интеграла второго рода по дуге линии, соединяющей точки А и В (А — начало дуги, В — ее конец).
1. а(7И) = 2xyzi -ф x2z'] -ф x2yk, А(1, — 1, 2), б( — 2, 4, 2). {Ответ: 34.)
2. а{М) = (х2 — 2yz) i -ф {у2 — 2xz) j -ф {z2 — 2ху) k, 4'1 -1, 1), fi( —2, 2, 3). {Ответ: 92/3.)
3. а(Л4) = {2ху 4- 22) i 4- {2ху 4- %2) j 4- {2xz 4- у2) к, А (О, 1, —2), В {2, 3, 1). {Ответ: 25.)
15.7. ИНДИВИДУАЛЬНЫЕ ДОМАШНИЕ ЗАДАНИЯ К ГЛ. 15
ИДЗ-15.1
1. Дана функция u{M) = и{х, у, z) и точки Mi, М2. Вычислить: 1) производную этой функции в точке Mi по направлению вектора М1М2: 2) grad u{Mi).
1.1. u{M) = х2у -ф y2z 4- z2x, Mi (1, —1,2), Л42(3, 4, — 1).
1.2. u{M) = 5xy3z2, Mi (2, 1, —1), Л42(4, —3, 0).
1.3. u(M) = In {X2 4- у2 -ф z2), Mi (- 1,2, 1), M2{3, 1, -1).
1.4. u{M) = ze-^+^ + s, Ali(0, 0, 0), M2(3, —4, 2).
1.5. u(M) = In {xy 4- yz 4- xz), Mi( — 2; 3, —1), M2{2, 1, -3).
1.6. u{M) = ^\ +xl ^y2 -^z2, M,(l, 1, 1), M2(3, 2, 1).
1.7. u{M) = x2y 4- xz2 — 2, Afi(l, J, — I), M2{2, —1, 3).
1.8. u{M) = xe^ + Уех - г2, Mi{3, 0, 2), M2(4, 1, 3).
1.9. u(M) = 3xy2 + z2 — xyz, 44((1, I, 2), M2(3, —I, 4).
1.10. u{M) = 5x2yz — xy2z 4- yz2, 441 (1, I, 1), 442(9, -3, 9).
1.11. u{M) = x/{x2 + У2 + z2), 44,(1, 2, 2), M2(-3, 2, - I).
1.12. u{M) — y2z — 2xyz y-z2, Mi{3, 1, —I), M2{ — 2, 1, 4).
1.13. u{M) = x2 4- y2 4- z2 — 2xyz, M1 (I, —1, 2), 442(5, — 1, 4).
25®
1.14. и(Л1) = 1п(1 +x + y2 + z\ 41,(1, 1, 1), 442(3,
1.15. ы(М) = х24-2//2-422-5, 41,(1, 2, 1), M2(-3, — 2, 6).
1.16. z/(/'i4)= In (Г 4- //3 + ? + 1). Afi(l, 3, 0). 4f2(-4, 1, 3).
1.17. u(M) = x-2y + ez, 44i(-4, -5, 0), M2(2, 3, 4).
1.18. шМ) = хч-Зхуг, 44,(2, 2, -4), 442(1, 0, -3).
1.19. u(M) = 3x2yz\ 44,( —2, -3, 1), 442(5, -2, 0).
1.20. ы(Л4) = ег" + г\ 41,( —5, 0, 2), 442(2, 4, —3).
1.21. и(М) = х'';, 44,(3, 1, 4), 412(1, —1, —1).
1.22. и(М) = (хг + уг + г2)3,М1(1, 2, -1), /И2(0, -1,3).
1.23. и(М) = {х —yf, 44i(l, 5, 0), 442(3, 7, —2).
1.24. и(М) = х2у + у2г — 3z, 44((0, —2, —1), 412(12, -5, 0).
1.25. и(М)= 10/(х2 + у2 + z2 + 1), 41,(—1, 2, — 2\ 442(2, 0, 1).
1.26. и(М) = In (1 4-х2-//2 4-г2), 41,(1, 1, 1), 442(5, — 4, 8).
1.27. и(М) = zL -j- 2L _ Л, 44i(-l, 1, 1), 442(2, 3, 4).
1.28. Ы(44) = х34-%//2 — Qxyz, 41,(1, 3, —5), 442(4, 2, -2).
1.29. н(41)=— — ± —А, 441(2, 2, 2), 412( —3, 4, 1).
1.30. и{М') = ех-уг, 44,(1, 0, 3), 412(2, —4, 5).
2. Вычислить поверхностный интеграл первого рода по поверхности S, где S — часть плоскости (р), отсеченная координатными плоскостями.
2.1. ЭД (2х 4- Зу 4- 2z) dS, (р): х 4- Зу 4- z = 3. ( От-
s
ест: 15д/ТГ~/2.)
2.2. ЭД (2 у — 7л- 9z) dS, (р): 2х — у — 2г = — 2.
(Ответ: 12.)
2.3. ЭД (6% 4~ У + 4z) dS, (р): Зх 4- Зу 4- z = 3. ( Ответ: s
19VT9/6.)
9-357
257
2.4. ft (x-(-2y + 3z)dS, s
873.)
2.5. ft (3x — 2y + 6z) dS
5/2.)
2.6. ft (2x + 5y — z) dS, s
7^6/3.)
2.7. ft (5x — 8y — z) dS, s
25лМ)
2.8. ft (3y — x — z)dS, s
-20V3/3.)
2.9. ft (Зу - 2x - 2г) dS, s
в ет: 3.)
2.10. ft (2x-3y + z)rfS,
2.11. ft (5x4-у — z)dS, (j s
2.12. ft (3x + 2y + 2z)dS, s
вет: 9д/17.)
2.13. ft (2x + 3y — z)dS,
2^6.)
2.14. ft (9x + 2y + z) dS, s
40д/б.)
(p): x у + z = 2. ( Ответ:
(p): 2x 4- у -|- 2z = 2. (Ответ:
(p): x^2y + z = 2. (Ответ:
(p): 2x — 3y + z = 6. (Ответ:
(p): x — у + г• = 2. (Ответ: ip): 2x — у — 2z = —2. (0т-(p): x -/ 2y -/ z = 2. (Ответ:
): x 2y + 2z = 2. (Ответ: 5.)
(p): 3x + 2y + 2г = 6. ( От-
ip) : 2x + у 4- z = 2. (Ответ:
(p): 2x 4- у 4- 2 = 4. (Ответ:
258
2Л5. § (Ух + Sy+ 8z.dS, (ру. х + 4у + 2г = 8. ( От-
вег: 96 V^)
2.16. ЭД (4у — х 4- 4г)dS, (/?): х — 2у 4- 2г = 2. (Ответ: 8
-1.)
2.17. ЭД (ix 4- у 4~ 2г) dS, (У: Зх — 2у 4- 2г = 6. (От-8
ест: 17V1V2.)
2.18. ЭД (2х 4- Зу 4~ О dS, (р): 2х Ц- Зу -(- г = 6. ( От-
ест: 18д/Т4.)
): х — у 4~.г = 2. ( Ответ: 8д/3.)
(р): х 4~ У 4~ 2г = 2. ( Ответ:
(/?): х 4- 2у 4- 2г = 4. (От-
(р): х 4- у 4- 2г = 2. (Ответ:
(р): 2х 4- 2у -/ г = 4. (От-
(р): х 4~ 2у 4- г = 2. ( От-
(р): 2х 4- у 4- Зг = 6. ( От-
(р): х 4- 2у 4- 2г = 2. (От-
2.19. ЭД (4x-y + z)dS,(/
2.20. ЭД (6л- — у 4- 8г) dS, бд/б.)
2.21. ЭД (4х —4// — г) dS, вет: 44.)
2.22. ЭД (2л- 4- 5у + г) dS,
5д/б.)
2.23. ЭД (4л — у 4- 4г) dS,
5
вет: 44.)
2.24. ЭД (5л-4-2г/4-2г)43,
5
вет: 161/3/6.)
2.25. ЭД (2х 4- 5у 4- lOz)dS
8
вет: 56дД^)
2.26. ЭД (2x4- 15г/ + ?)dS,
8 вет: 10.)
259
2.27. ЭД(Зх-ф Юг/ — z)dS, (/?): х -ф Зу -ф 2z = 6. (От-S
вет; 35д/14.)
2.28. $ (2_r + 3i/+z)dS, (р): 2х-ф2г/-фг = 2. (От-
S
вет: 7/6.)
2.29. $ (5х — у + 5z)dS, (р): Зх + 2у + z = 6. (Ответ: s
37V14J
2.30. ЭД (х-ф Зу + 2z)dS, (р): 2x + y + 2z = 2. (Ответ:
9/2.)
3. Вычислить поверхностный интеграл второго рода.
3.1.ЭД (у2 + z2)dydz, где 3 — часть поверхности парабо-s
лоида х = 9 — у2 — 22 (нормальный вектор п которой образует острый угол с ортом i), отсеченная плоскостью х = 0. (Ответ: 81 л/2.)
3.2. ЭД z~dxdy, где 3 — внешняя сторона поверхности s
эллипсоида х2 -ф у2 -ф 2z2 = 2. (Ответ: 0.)
3.3. ЭД zdxdy -ф ydxdz -ф xdydz, где S — внешняя сто-х
рона поверхности куба, ограниченного плоскостями х = 0, у = 0, г = 0, х = i, у = i, z = 1. (Ответ: 3.)
3.4. ЭД (2 -ф 1) dxdy, где 3 — внешняя сторона поверх-.3
ности сферы л-2 -ф у2 -ф г2 = 16. (Ответ: 256л/3.)
3.5. yzdydz -ф xzdxdz -ф xydxdy, где 3 — верхняя сто-’s
рона плоскости х -ф у -ф z = 4, отсеченной координатными плоскостями. (Ответ: 32.)
3.6. ЭД x2dydz -ф y2dxdz -ф z2dxdy, где 3 — внешняя сто-s
рона сферы х2 -ф у2 -ф z2 = 16, лежащая в первом октанте. (Ответ: 96л.)
3.7. ЭД xdydz -ф ydxdz -ф zdxdy, где 3 — внешняя сто-s
рона сферы х2 -ф у2 -ф z2 = 1. (Ответ: 4л.)
3.8. ЭД xzdxdy -ф xydydz -ф yzdxdz, где S—верхняя часть s
260
плоскости х -4-z/ + г = 1, отсеченной координатными плоскостями. (Ответ: 1/8.)
3.9. yzdxdy -ф xzdydz -ф xydxdz, где S — наружная s
поверхность цилиндра х2 -ф у2 = 1, отсеченная плоскостя-
ми z = 0, z = 5. (Ответ: 25л.)
3.10. у2zdxdy -ф xzdydz -ф x2ydxdz, где S — часть по-s
верхности параболоида z = х2 -ф у2 (нормальный вектор п которой образует тупой угол с ортом к), вырезаемая цилиндром х2-\-у2=\. (Ответ: л/8.)
3.11. ЭД (х2 -ф у2) zdxdy, где S — внешняя сторона ниж-
ней половины сферы х2 -фу2 -ф z2 = 9. (Ответ: 324л/5.)
3.12. ЭД x2dydz -ф z2dxdy, где S — часть поверхности s
конуса z2 = х2 -ф у2 (нормальный вектор п которой образует тупой угол с ортом к), лежащая между плоскостями z = 0, г=1. (Ответ: —л/2.)
3.13. ЭД (2г/2— z)dxdy, где S — часть поверхности па-s
раболоида z = х2 -фу2 (нормальный вектор п которой образует тупой угол с ортом к), отсекаемая плоскостью z = 2. (Ответ: 0.)
3.14. \\— dkdy где S — часть поверхности гипер-s' + У2 — 1
болоида х1 -ф у2 = z2 -ф 1 (нормальный вектор п которой образует тупой угол с ортом к), отсекаемая плоскостями z = 0, г=х/з. (Ответ: —2л/3л.)
3.15. ЭД xydydz -ф yzdxdz -ф xzdxdy, где S — внешняя s
сторона сферы х2 -ф у2 -ф z2 = 1, лежащая в первом октанте. (Ответ: Зл/16.)
3.16. ЭД x2dydz -ф zdxdy, где S — часть поверхности s
параболоида z — x у~ (нормальный вектор п котором образует тупой угол с ортом к), отсекаемая плоскостью z = 4. (Ответ: 8л.)
3.17. ЭД x2dydz -ф у2dxdz — zdxdy, где S — часть поверх-s
ности конуса z2 — х2 -фу2 (нормальный вектор п которой
261
образует острый угол с ортом к), отсекаемая плоскостями 2=0 и 2 = 3. (Ответ: —18л.)
3.18. ЭД x2dydz — z2dxdz -ф zdxdy, где S — часть поверх-s
ности параболоида 2 = 3— х2— у2 (нормальный вектор п которой образует острый угол с ортом к), отсекаемая плоскостью 2 = 0. (Ответ: 9л/2.)
3.19. ЭД yzdydz — x2dxdz— y2dxdy, где S — часть ПО-
S'
верхностн конуса х2 -ф z2 = у2 (нормальный вектор п которой образует тупой угол с ортом j), отсекаемая плоскостями у = 0, у= \. (Ответ: л/4.)
3.20. ЭД xldydz -ф ‘2y2dxdz — zdxdy, где S — часть по-s'
верхности параболоида z = х2у2 (нормальный вектор п которой образует острый угол с ортом к), отсекаемая плоскостью 2 = I. (Ответ: —л/2.)
3.21. ЭД 2xdydz -ф(1 — zjdxdy, где S — внутренняя сто-s'
рона цилиндра х* *ф у2 = 4, отсекаемая плоскостями z — = 0 и 2=1. (Ответ: —8л.)
3.22. ЭД ‘Ixdydz — ydxdz -ф zdxdy, где S — внешняя сто-s'
рона замкнутой поверхности, образованной параболоидом Зг = х2 -ф у2 и полусферой z = д[А — х2 — у2. (Ответ: 19л/3.)
3.23. ЭД dxdydz -ф 2ydxdz — zdxdy, где S — внешняя сто-s'
рона сферы х2 -ф у2 -ф z2 = 4. (Ответ: 160л/3.)
3.24. । (х + z) dydz -ф (z -ф у) dxdy, где S—внешняя s
сторона цилиндра х2-\-у2=\, отсекаемая плоскостями 2 = 0 и 2 = 2. (Ответ: 2л.)
3.25. 55 dxdydz — ydxdz — zdxdy, где .S — часть поверх-ности параболоида 9 — z = х2 -ф у2 (нормальный вектор п которой образует острый угол с ортом к), отсекаемая плоскостью 2 = 0. (Ответ: 243л/2.)
3.26. 55 (у — x)dydz -ф (2 — у) dxdz -ф (х — z) dxdy, где s
S — внутренняя сторона замкнутой поверхности, образо
262
ванной конусом х2 = у2 -ф z2 и плоскостью х=1. (Ответ: л.)
3.27. Ц 3x2dydz — y2dxdz — zdxdy, где S — часть по-s
верхности параболоида 1 —z = x2~f-y'2 (нормальный вектор п которой образует острый угол с ортом к). (Ответ: — л/2.)
3.28. (1 + 2x~)dydz -ф y2dxdz -ф zdxdy, где S — часть s
поверхности конуса х2 -ф у2 = z2 (нормальный вектор п которой образует тупой угол с ортом к), отсекаемая плоскостями 2 = 0 и 2 = 4. (Ответ: 128л/3.)
3.29. Ц x2dydz -ф z2dxdz -ф ydxdy, где S — часть поверх-ности параболоида х2 -ф у'2 = 4 — z (нормальный вектор п которой образует острый угол с ортом к), отсекаемая плоскостью 2 = 0. (Ответ: 0.)
3.30. (у2 -ф 22) dydz — y2dxdz -ф 2yz2dxdy, где S — s
часть поверхности конуса х2 -ф z2 = у2 (нормальный вектор п которой образует тупой угол с ортом j), отсекаемая плоскостями у = 0 и у=\. (Ответ: л/2.)
4. Вычислить поток векторного поля а(Л4) через внешнюю поверхность пирамиды, образуемую плоскостью (р) и координатными плоскостями, двумя способами: а) использовав определение потока; б) с помощью формулы Остроградского — Гаусса.
4.1. а(Л4) = 3xi -ф (у -ф 2) j -ф (д' — z) к, (р): х -ф Зу ф -ф z = 3. (Ответ: 9/2.)
4.2. а(А1) = (3х — 1) i -ф (у — х -ф 2) j -ф 4zk, (р): 2х — — у — 2z = 2. (Ответ: 8/3.)
4.3. а(Л4) = xi -ф (х -ф z) j -ф (у -ф z) к, (/?): Зх -ф Зу -ф -ф z = 3. (Ответ: 1.)
4.4. а(Л4) = (х -ф z) i -ф (г — х) j -ф (х -ф 2у -ф г) к, (/?): х -ф
у z = 2. (Ответ: 8/3.)
4.5. а(М) = (у -ф 2z) i -ф (х -ф 2z) j -ф (х — 2у) к, (р): 2х -ф -фу -ф 2z = 2. (Ответ: 0.)
4.6. а(Л1) = (х -ф z) i -ф 2z/j -ф (х -фу — г) к, (р): х+2у+ -\-z = 2. (Ответ: 4/3.)
4.7. а(Л4) = (Зх — у) i -ф (2у -ф г) j -ф (2г — х) к, (р): 2х — — Зг/-фг = 6. (Ответ: 42.)
4.8. a(M) = (2z/ + z)i-ф(х — y)j — 2гк, (р): х — у -ф -фг = 2. (Ответ: —4.)
263
4.9. a(M) = (x + у) i + 3z/j + (у — z) к, (p): 2x — у — — 2z =—2. (Ответ: —1.)
4.10. a(M) = (x4p- z)i — 2yj 4-(x 4-2z) k, (p): x 4-4-2p 4- z = 2. (Ответ: 2/3.)
4.11. a(M) = (y z) i + (2x 4- y) j 4- zk, (p): 2x 4- у + 4-2 = 2. (Ответ: 4/3.)
4.12. a(M) = xi + (y — 2z) j 4- (2x — у 4- 2z) k, (p): x 4--f--2y 4- 2z = 2. (Ответ: 4/3.)
4.13. a(M) = (x + 2z) i 4- (y — 3z)j-|-zk, (p): 3x 4- 2y -|-
4- 2z = 6. (Ответ: 9.)
4.14. a(M) = 4xi 4-(x — y — z) j 4-(3y 4-2z) k, (p): 2x4-4-p-|-z = 4. (Ответ: 80/3.)
4.15. a(M) = (2z — x)i-|-(x + 2z/)j + 3zk, (p): x-4-4p-|-
4-2z = 8. (Ответ: 128/3.)
4.16. a(M) = 4zi + (x — y — z) j + (3p 4-z) k, (p): x — — 2y + 2z = 2. (Ответ: 0.)
4.17. a(M) = (x 4-p) i 4-(p 4-z) j 4-2(z 4-x) к, (p): 3x — — 2y -|- 2z = 6. (Ответ: 12.)
4.18. a(M) = (x 4~ У 4~ z) * 4" 2zj -j- (У — 7z) k, (p): 2x -|--|-3z/ + z = 6. (Ответ: —36.)
4.19. а(Л4) = (2x — z) i + (p — x) j + (x + 2z) к, (p): x — — у + z = 2. (Ответ: 20/3.)
4.20. a(M) = (2y —z)i + (x+y)j+xk, (p): x + 2p+
4- 2z = 4. (Ответ: 8/3.)
4.21. a(A4) = (2z — x) i 4-(x — p) j 4-(Зх 4-z) к, (p); x4-4~p4-2z = 2. (Ответ: —2/3.)
4.22. а(Л4) = (x 4-г) i 4-(x + 3p) j 4-£/k, (p): x 4- у 4~ 4-2z = 2. (Ответ: 8/3.)
4.23. а(Л4) = (x 4~ <) > 4~ zj 4~ (2x — p)k, (p): 2x 4-2p 4-4-z = 4. (Ответ: 8/3.)
4.24. a(M) = (3x4-p)i4-(x4-z)j4-pk, (p): x 4-2p 4-
4- z = 2. (Ответ: 2.)
4.25. a(M) = (p 4- z) i 4- (2x — z) j 4- (p 4- 3z) k, (p): 2x 4-4-p4~3z=6. (Ответ: 18.)
4.26. a(M) = (p4-z)i4-(x4-6p)j4-pk, (p): x 4-2p 4-4-2z = 2. (Ответ: 2.)
4.27. а(Л4) = (2p z) i 4~ (x 4~ 2p) j 4~ yk, (p)' x 4~ 3p 4-
4- 2z = 6. (Ответ: 12.)
4.28. а(Л4) = (p 4-z)i 4-xj 4-(p — 2z) к, (p): 2x 4-2p 4-4-z = 2. (Ответ: —2/3.)
4.29. a(M) = (x 4- z) i 4- zj 4- (2x — p) k, (p): 3x 4- 2p 4-4- z = 6. (Ответ: 6.)
4.30. a(Al) = zi 4-(x4-p)j 4-pk, (p): 2x4-p4-2z = 2. (Ответ: 1/3.)
264
Решение типового варианта
1. Дана функция u(M) — x/x/z— уу/х ф- 2xyz и точки М|(1, 1, —1), — 2, —1, 1). Вычислить: 1) производную
этой функции в точке АД по направлению вектора АД АД; 2) grad и (Mi).
> 1. Вычислим производную функции и(М) = и(х, у, z) в точке М\ по направлению вектора Л1|Л12 = ( — 3, — 2, 2):
ЦЫ(М,) = W)l .С05а + ДДЛД1 ,cos₽ +
йй; дх ду 1м-
+ -cosv’
ди(М) ______I_ . x/y 2 du(M) I = _ _3
дх 2гд/х x" ’ dx L, 2 ’
du(M) _ _ 1 2%2 ди(М) I = _ _5_
dy 2x^ ’ dy l.M, 2’
-\-2xy, I =1,
dz z2 dz I m,
2. Согласно определению,
= -4>-4)+к- •<
2. Вычислить поверхностный интеграл первого рода ЭД (Зх — y-\-z)dS по поверхности S, где S — часть пло-s
скости (/?): х ф- z — 2у = 2, отсеченная координатными плоскостями.
> Из уравнения плоскости находим:
z = 2 — х ф- 2у, z'x=—1, z'y = 2,
265
dS = д/1 + z'x2 + z’y dxdy = xj^dxdy.
Сводим вычисление поверхностного интеграла к вычислению двойного интеграла по области D, где D — треугольник АОВ, являющийся проекцией поверхности S на плоскость Оху (рис. 15.13). Тогда
ЭД (Зх — у + z) dS = ЭД (Зх — у + 2 — х + 2z/) x^Qdxdy =
S l>
-4- ^y
— ЭД (2x -4- у + 2)sJ6dxdy = $ dy J (2x + y -f- 2)dx =
I) — I 0
= Л/6 $ dy(x2 + (у + 2)-v)| =V6 $ (4 + 8t/ + 4y- +
- I 10 -1
(I
+ 2y + 2y~’ + 4 + 4y)dy = д/6 J (6y~ + 14y + 8)dy =
= 'л/б(2г/5 + 7г/2 + 8i/)| । ==3д/б.
3. Вычислить поверхностный интеграл второго рода ЭД (х2 + z2) dxdz + x~dydz — 2z~dxdy, s
где S — часть поверхности параболоида 4 — у = х2 + г2 (нормальный вектор п которой образует острый угол с ортом j), отсекаемая плоскостью у = 0.
► Представим данный поверхностный интеграл по координатам в виде суммы трех интегралов и, используя уравнение параболоида, преобразуем каждый из них в двойной интеграл по области £>т (у = 1, 2, 3) (рис. 15.14):
/ = ЭД (х2 + z") dxdz + x2dydz — 2z2dxdy = Л 4- /2 4~ Ль s
где
Л = ЭД ,Л'2 4~ Л2) dxdz\ /2 = ЭД x2dydz\ /3 = ЭД (— 2z~) dxdy. s s s
Вычислим последовательно интегралы l\, l2, ly.
/i = ЭД (x2 -j- z2) dxdz = |x = p cos q>, z = p sin <p, D,
V p 2л ., 2
dxdz = pdpdipl == \ d<o \ pJdp = w •— =8л,
J J I n 4 | о
г о
266
где область Dt —круг х2 -f- z2 = 4, у = 0, являющийся проекцией поверхности параболоида на плоскость Oxz. Перед интегралом /| ставится знак « + », так как нормаль п к поверхности образует острый угол (3 с осью Оу.
Р 11 с. 15.13 Р н с. 15.14
Далее,
Л = У x2dydz = ЭД (д/4 — у — z^dydz — ,S [)
— ЭД (—-— у — z~y~dydz — ЭД (4 — у — г2) dydz —
— ЭД (4 — (/ — Z~) dydz = 0.
D:
Координатная плоскость Oyz разбивает поверхность параболоида на две части х=^4— у — z2 и х = = —~^4 — у — z2, проекция каждой из которых па плоскость Oyz есть область Di. Поэтому интеграл 12 можно представить в виде суммы двух интегралов, перед первым нз которых надо взять знак « + », так как нормаль п к этой части поверхности параболоида образует острый угол с осью Ох, а перед вторым интегралом — знак « — », поскольку нормаль п образует с осью Ох тупой угол.
Аналогично
/3 = ЭД — 2z2dxdy = — 2 ЭД (х/4 — у — x2)2dxdy + X D,
+ 2 ЭД ( — -\/4 — у ~ x2)'2dxdy = 0. D,
267
Итак,
ЭД (х2 + z2) dxdz + x2dydz — 2z2dxdy — 8л.
5
4. Вычислить поток векторного поля а(Л4) = (х + z) i ф-+ (2у — х) j 4~ zk через внешнюю поверхность пирамиды, образуемую плоскостью (р): х — 2у + 2z = 4 и координатными плоскостями, двумя способами: 1) использовав определение потока; 2) с помощью формулы Остроградского — Г аусса.
► 1. Вычисляем поток векторного поля с помощью поверхностного интеграла
П = ЭД а • n}dS,
s
где S — внешняя сторона поверхности пирамиды АВСО (рис. 15.15).
Вначале вычислим поток через каждую из четырех граней пирамиды. Грань АОС лежит в плоскости у = О,
нормаль к этой грани п° = j, dS = dxdz. Тогда поток векторного поля а(Л4) через грань АОС
Л 2-.<72
ГЦ = — ЭД xdS = — ЭД xdxdz = — j xdx j dz —
Д.'ЮС Д/1ОС о о
268
Грань АОВ лежит в плоскости z = 0, нормаль к этой грани п12 = —k, dS = dxdy,
П2= ЭД 0 • dxdy = 0.
ДЛОЙ
Грань ВОС лежит в плоскости х = 0, нормаль к данной грани пз = —i, dS = dydz,
2 0
П3 = — ЭД zdydz = — ЭД zdz ЭД dy =
ДВОС 0 г —2
С / 3 , ,2 .
= - \ z(-z + 2)dz= +гЛ =—4-
J \ 3 ) | о 3
о
И, наконец, грань АВС лежит в плоскости х — 2у 2 г — — 4 = 0, нормаль к этой грани
nu_ i-2j + 2k _ i-2j + 2k
II4---— - zu---------z------,
д/l + 4 + 4 ‘
dS = 41 H- z'y dxdy, z = — x A~ У
2.V = — 4 ’ 4 = 1 •
11оэтому
ds =^l 1 + 4 + 1 dxdy=4 dxdy<
n4 = _L-4 Ц ((.t + z) — 2(2y — x) Ar 21) dxdy =
Д.1ЛС
== _L (x + z — 4y + 2x + 2z)dxdy =
Д.-1ИС
= _L (3x — Ay + 3z) dxdy = 4 (Зх —4y — д/1/5с д/к;в
— 4 x+зу+о) dxdy=4 (4x—у+6)dxdy=
/\AOll
0 2(/ + 'l
= 4 5dy 5 (4x ~y+6)dx=
-2 0
269
= 4 J dy(^ x‘2+(6—Aj I, = ______2
= 4 j (4(2z/ + 4J2+(6 - Д(2уД Vdy = — 2
j Цу- + 4y + 4) + I2y + 24 - 2y' - 4y^dy =
j (y2 + 20y + 36) dy = 4 (£- 4- 1 (hf + 36z/) | \ =
Далее находим поток через полную поверхность пирамиды АВСО:
п = п{ + /Д + /Л : /Л " . )
2. Вычислить поток через поверхность пирамиды АВСО по формуле Остроградского— Гаусса:
4S(£+l+£)* I
Находим
дР д(х + z) । dQ И(2у — л) OR dz । ох дх ’ ду ду с г дг
Так как интеграл ^dxdydz равен объему ирямоуголь-г
ной пирамиды АВСО, то
/7 = (1 + 2 + 1) dxdydz = 4 dxdydz = ◄
г г
ИДЗ-15.2
1. Вычислить циркуляцию векторного поля а(Л4) по контуру треугольника, полученного в результате пересечения плоскости (р): Ах + By + Cz = D с координатными
270
плоскостями, при положительном направлении обхода относительно нормального вектора п = (Л, В, С) этой плоскости двумя способами: 1) использовав определение циркуляции; 2) с помощью формулы Стокса (15.27).
1.1. а(М) = zi + (х + у)j + ук, (р): 2х + у + 2г = 2.
(Ответ: 5/2.)
1.2. а(Л4) = (х + г) i + zj + (2х — у) к, (р): Зх + 2у + + z = 6 (Ответ: —24.)
1.3. а(Л4) = (у + z) i + xj + (у — 2z) к, (р): 2х + 2у + + г = 2. (Ответ: 2.)
1.4. а(М) = (2у — z) i + (х + 2у) j + ук, (р): х + Зу + + 2z = 6. (Ответ: —12.)
1.5. а(М) = (t/ + z)i + (х —f—бу) j + ук, (р): х + 2у + + 2z = 2. (Ответ: 3/2.)
1.6. а(М) = (у + z) i + (2х — z) j + (у + 3z) к, (р): 2х ф-+ y + 3z = 6. (Ответ: 24.)
1.7. а(Л4) = (Зх —|- £/) i —j- (х -j- г) j —|- ук, (р): х 2у -J-
-(-2 = 2. (Ответ: 0.)
1.8. a(M) = (x-(-z)i-(-zj-(-(2x~y)k, (р): 2х + 2у +
+ z = 4. (Ответ: —12.)
1.9. а(М) = (х + z) i + (х + Зу) j + ук, (р): х + у + 2z = = 2. (Ответ: 4.)
1.10. а(Л4) = (2у — z)i + (х + у) j + хк, (р): х + 2у +
-|-2z = 4. (Ответ: —12.)
1.11. а(Л4) = (2г — x)i + (x — p) j + (Зх-f-г) к, (р): хф-
-|-y + 2z = 2. (Ответ: 1.)
1.12. а(Л4) = (2х — z) i + (г/— х) j + (х + 2z) к, (р): х — — у-(-2 = 2. (Ответ: 2.)
1.13. а(Л4) = (х-|-г/+ г) i-|-2zj(г/ — 7г)к, (р): 2х-(-
-|- Зу -f- z = 6. (Ответ: 0.)
1.14. а(Л1) = (х у) i (у г) j + 2(х + z) к, (р): Зх — — 2у + 2z — 6. (Ответ: — 3/2.)
1.15. a(M) = 4zi + (x —у —z)j + (3p + z)k, (р): х~ — 2у-(-2г = 2. (Ответ: —1.)
1.16. а(Л4) = (2z — х) i + (х + 2р) j3zk, (р): х-(-4у-(-
-(-2г = 8. (Ответ: 40.)
1.17. а(Л4) = 4xi + (х — р — z) j + (Зу + 2z) к, (р): 2х ф--(-у-(-2 = 4. (Ответ: 36.)
1.18. а(Л4) = (х + 2z) i + (у — 3z) j + zk, (p): 3x-(-2y-(-
-(-22 = 6. (Ответ: 39/2.)
1.19. a(M) = xi + (у — 2z) j + (2x — у + 2z) к, (p): x-(-
+ 2y + 2z = 2. (Ответ: —3/2.)
1.20. а(Л4) = (у — z)i + (2x + y)j + zk, (p): 2x + у + -(-z = 2. (Ответ: 0.)
271
1.21. а(Л1) = (х 4- у — z) i — 2yj + (x + 2z) k, (p): x 4-2y z = 2. (Ответ: —5.)
1.22. a(M) = (x 4-у) i 4-3yj + (у — z) к, (p): 2x — у — — 2z=—2. (Ответ: — 2.)
1.23. a(M) = (2y 4-z) i 4-(x — y)j — 2zk, (p): x — у + 4-z = 2. (Ответ: —4.)
1.24. a(M) = (3x-y)i + (2y + z)j + (2z-x)k, (p):
2x — 3y 4-z = 6. (Ответ: 12.)
1.25. а(Л4) = (x 4~ z) i 4- 2yj 4~ (x 4~ У z) к, (p): x 4-4-2y 4-z = 2. (Ответ: 1.)
1.26. a(A4) = (y 4-2z) i 4-(x 4-2z) j 4-(x — 2y) k, (p): 2x 4- у 4~ 2z = 2. (Ответ: — 7/2.)
1.27. a(M) = (x4~z)i4-(z — x) j 4-4-2y 4-z) k, (p): x4-y4~z = 2. (Ответ: 0.)
1.28. a(M) = xi + (x -r z) j + (y 4- z) k, (p): 3x + 3y +
4- z — 3. (Ответ: 3/2.)
i .29. a(M) = (3x - 1) i + (y - x + z) j + 4zk, (p): 2x -— y —2z=—2. (Ответ: 0.)
1.30. а(Л4) = 3xi 4- (у 4- z) j 4- (x — z) k, (p): x 4- 3y 4~
4- z = 3. (Ответ: —6.)
2. Найти величину и направление наибольшего изменения функции и(М} = и(х, у, z) в точке Л1и(х0, у0, zo).
2.1. и(М) = xuz, Л'/о(О, 1, —2). (Ответ: 2.)
2.2. и(М) = х2уг, Л4О(2, 0, 2). (Ответ: 12.)
2.3. и(М) = xy2z, Л4и(1, —2, 0). (Ответ: 4.)
2.4. u(M) = xyz'2, Л40(3, 0, Г). (Ответ: 3.)
2.5. u(M) = x2y2z, Мо(— 1, 0, 3). (Ответ: 0.)
2.6. и(М) = x2yz2, Мо(2, 1, —1). (Ответ: 4ц/б.)
2.7. и(М) = ху2г2, Мо( — 2, 1, 1). (Ответ: /33.)
2.8. u(M) = y2z — х2, Л1о’(0, I, I). (Ответ: д/5.)
2.9. и(М) = х2у 4- y~z, Л'/о(О, —2, I). ( Ответ: 4/2.)
2.10. и(М) = х(у 4- z), ЛфцО, 1, 2). (Ответ: 3.)
2.11. и(Л4) = ху —xz, Л1о(—1, 2, 1). ( Ответ: х/з.)
2.12. u(M) = x2yz, Л4,)( I, —1, 1). (Ответ: д/^-)
2.13. и(М) = xyz, Л4и(2, 1, 0). (Ответ: 2.)
2.14. u(M) = xyz2, Л40(4, 0, 1). (Ответ: 4.)
2.15. u(M') = 2x2yz, Л40( —3, 0, 2). (Ответ: 36.)
2.16. и(М) = х2уг, Л40(1, 0, 4). (Ответ: 4.)
272
2.17. и(М) = (х + у) z2, Мо(О, —1, 4). (Ответ: 24.)
2.18. и(М) = (хz)y2, Л10(2, 2, 2). (Ответ: 12д/2.)
2.19. и(М) = х2(у2 + z), Л40(4, 1, —3). (Ответ: 16^'6.)
2.20. и(М) = (х2 -j- г)у2, Л40( —4, 1, 0). (Ответ: д/33.)
2.21. и(М) = х2(г/ + z2), Л40(3, 0, 1). (Ответ: 21.)
2.22. и(М) = (х2 — у) г2, Л40(1, 3, 0). (Ответ: 0.)
2.23. и(М) = х(у2 + z2), Л40(1, —2, 1). (Ответ: д/ТА)
2.24. и(М) = х2 + Зу2 — z2, Л4о(О, 0, 1). (Ответ: 2.)
2.25. и(М) = x2z — у2, Л40(1, 1, —2). (Ответ: д/21.)
2.2S. u(M} = xz2 + у, Л40(2, 2, 1). (Ответ: Зд/2.)
2.27. и(М) = х2у — г, Л40( —2, 2, 1). (Ответ: 9.)
2.28. и(М) = ху2 — г, ЛЦ—1, 2, 1). (Ответ: д/33.)
2.29. и(М) = у(х + г), Мо(О, 2, —2). ( Ответ: 2д/3.)
2.30. и(М) = z(x + у), Л40(1, —1, 0). (Ответ: 2.)
3. Найти наибольшую плотность циркуляции векторного поля а(Л4)=(х, у, г) в точке М0(х0, у0, z0).
3.1. а(Л4) = x2i — ху2] + z2k, Л4о(0, 1, —2). (Ответ: I.)
3.2. а(Л4) = xyi + yz] + xz] + xzk, Л40(2, 0, 3). (Ответ: / 13.)
3.3. а(Л4) = xy2i + (/z2j — x2k, Л10(1, —2, 0.) (Ответ:
2/5.)
3.4. а(Л4) = xzi + z] + угк, Л4и(3, 0, 1). (Ответ: J.)
3.5. а(Л4) = xyi + xyz] — хк, Л40( — 1,0, 3.) ( Ответ: xj 2.)
3.8. а(Л4) = yzi — z2j + xyzk, М0(2, 1, —1). (Ответ:
3.7. а(Л4) = (/2i — ху] + г2к, Л4и( —2, 1, 1). (Ответ: 1.)
3.8. а(Л1) = xzi — xyz] + x2zk, Мо(0, 1, 1). (Ответ: lj
3.9. а(Л1) = xyi—y2z]—xzk, Л4и(0, —2, 1). ( Ответ:
/17-)
3.10. а(Л4) = xzi — у] — zyk, Л40(0, 1, 2). (Ответ: 2.)
3.11. a.(M) — y2i—ху2] + z2k, Л40( — 1,2, 1). (Ответ: 8.)
3.12. а(Л4) = xyi — ху‘ j — ху2] -|- г2к, Л40(1, —1, 1).
(Ответ: 2.)
3.13. а(Л4) = (х + у) i + yz] + xzk, Л4()(2, 1, 0). (От-
вет: х/2.)
273
3.14. а(Л4) = xyi — (у + z)j -f-xzk, Л4о(4, 0, 1). (Ответ: 3^2.)
3.15. a(A4) = xi — zyj + х2гк, Л4о( — 3, О, 2). (Ответ: 12.)
3.16. а(Л4) = (х + у2) i + yzj — х2к, Л4о(1, О, 4). (Ответ: 2.)
3.17. a(A4) = xzi—yj + У?к, Л4о(О, —1, 4). (Ответ: 4.)
3.48. a(M) = xyi— xj yzk, М0(2, 2, 2). (Ответ: х/\3.)
3.19. а(Л4) = (х + у) i + xyzj— хк, Л40(4, 1, —3). (Ответ: х/зз.)
3.20. а(Л4) = (х — y)i + yz'] — ук, М0(-4, 1, 0). (Ответ: х/з.)
3.21. а(Л1) = (у — z) i — z"j -j-xyzk, Л4о(3, О, 1). (Ответ: Зд/З.)
3.22. а(Л4) = yz\ — z2j + (х + у) zk, Л1о(1, 3, 0). (Ответ: 3.)
3.23. а(Л4) = z2i — xzj-j-z2k, Л40(1, —2, 1). (От-
вет: х/б.)
3.24. a(Af) = xyi + (x-z)j+ (у-х)к, Л/и(0, О, 1). (Ответ: х/б.)
3.25. а(Л4) = хг\ + (х — у) j + x2zk, Л10(1, 1, —2). ( Ответ: л/26.)
3.26. а(М) - (х — z) i + xyj y'zk, Л10(2, 2, 1). (Ответ: -д/2К)
3.27. а(Л4) = (х — г)1 + xz/zj + хк, Мо( — 2, 2, 1). (Ответ: л/24.)
3.28. а(Л4) = (у — z) i + yj — z2k, Mo{—1,2, 1). (Ответ: х/2.)
3.29. а(Л4) = (х — y)i — xj + xzk, Л4о(О, 2, —2). (Ответ: 2.)
3.30. а(Л4) = (х — z)i — yj хук, Мо(1, —1, 0). (Ответ: 0.)
4
Выяснить, является ли векторное поле а(Л4) = (х, у, г) соленоидальным.
4.1. а(Л1) = (ос — P)xi + (у — a)[j + (|3 — у)гк.
4.2. а(Л4) = х’у\ — 2xy2j 2xz/zk.
274
4.3. а(М) = (yz — 2x')i 4- (xz + 2y)j + xyk.
4.4. а(Л4) = (.v2 — z2)i — Зхг/j -f- {y~ -f- zjk.
4.5. a(M) = 2xyzi — y(yz + 1)j + zk.
4.6. a(A4) = 2x — 3wi -f- 2xyj — z2k.
4.7. a(M) = (л-2 — y~)i + (ir — z2)j + (г2 — x2)k.
4.8. а(Л4) = yzi 4- (x — y)j + z2k.
4.9. a(2W) = (z/-i;z)i + (.r + z)j +(x + y)k.
4.10. a(M) = 3x2z/i — 2xz/2j — 2xz/zk.
4.11. a(A4) = (x + t/)i — 2{y + z)j 4- (z — x)k.
Выяснить, является ли векторное поле а(М) = (х, у, г) потенциальным.
4.12. а(М) = (yz — 2х)i + (xz zy)\ + хук.
4.13. а(Л4) = yzi -j- xzj -4- хук.
4.14. а(Л4) = bxyi + (Зх2 — 2у)j 4~ zk.
4.15. а(Л4) = (2х — уz)i+ (2х — ху)] -j- yzk.
4.16. а(М) = (у — z)i + Зхг/zj + (г — х)к.
4.17. а(М) = (у - z)i + (х + z)j + (х2> - у~)к.
4.18. а(Л4) = (х + y)i — 2xzj — 3(г/ -j- z)k.
4.19. а(Л4) = 2'1 + (xz + y)j 4-х2г/к.
4.20. а(Л4) = xy(3x — 4y)i + x2(x — 4y)j + 3z2k.
4.21. a(/W) = 6x2i 3 cos (3x -f- 2z)j + cos (3г/ + 2z/k.
4.22. a(M) = (x -}- y)i (z — y)j + 2(x -|- z)k.
4.23. a(M) = 3(x — z)i + (x- — y2)j + 3zk.
4.24. a(A4) = (2x — yz)i + (xz — 2y) j -f- 2xz/zk.
4.25. a(/W) = 3x’i + 4(x — y)j (x — z)k.
Выяснить, является ли векторное поле a(/Wj = (x, у, z) гармоническим.
4.26. a(/W) = x'2zi -}- y2j — .vz2k.
4.27. а(Л4) = (x + y)i + (У + + (A‘ + 2)k.
4.28. a(A4) = ^i + |j + |k.
4.29. a(M) = yzi xzj 4- xyk.
4.30. а(Л4) = (г/ —z)i 4-(z —x)j 4-(x — y)k.
Решение типового варианта
1. Вычислить циркуляцию векторного поля а(М) = ==(х — 2z)i 4- (х 4- Зу 4- z)j 4- (5х 4- f/)k по контуру треугольника, полученного в результате пересечения плоскости (р): х 4- у 4- z — 1 с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n=(l, 1, 1) этой плоскости двумя
275
способами: 1) использовав определение циркуляции;
2) с помощью формулы Стокса (15.27).
► В результате пересечения плоскости (р) с координатными плоскостями получим треугольник АВС
Рис. 15.16
(рис. 15.16) и укажем на нем положительное направление обхода контура АВСА в соответствии с условием задачи.
1. Вычислим циркуляцию С данного поля по формуле
(15.25), в которой обозначим dl=T°d/:
С= ф а • dl = J а dl + J а • dl + $ а • dl. часа л в вс i;.t
На отрезке АВ имеем: z = 0, х-|-у=1, у=\—х, dy = -— dx,
а = xi + (х + Зу)j + (5х + у) k, dl = dxi + dy}, а • dl = xdx -ф (x ф- Зу) dy,
j a • dl = j xdx + (x + 3y)dy = j (x — x — 3(1 — x))dx =
ЛИ AH I
0 o
=--\(3x-3)dx=(^L -3x^ = 2.
На отрезке ВС верны соотношения: х=0, уА~? = 1, z = 1 — у, dz = —dy,
а = — 2zi + (Зу -f- z)j ф- yk, dl = dy'} + dzk, a - dl = (3y + z)dy +ydz, J a • dl = J (3y z)dy -ф ydz = нс нс
о о
=Ц(Зу+ 1 —y — y)dy = \)y + \)dy = = — A.
J J Л \ \ £
I 1
276
На отрезке С А имеем: у = 0, x + z=l, dz =—dx, а • dl — (х — 2z)dx + 5xdz,
J а • dl = J (х — 2z)dx + 5xdz = CA CA
2 I
= $ (x — 2 + 2x — 5x)dx = \( — 2x — z)dx =
= (x2 — 2x)|o = —3.
Следовательно,
с=4-4-з=-з.
2 . Вычислим циркуляцию данного поля с помощью формулы Стокса (15.27). Для этого определим
В качестве поверхности S в формуле Стокса возьмем боковую поверхность пирамиды ОАВС'.
S = Soca + 5олв + Sobc-
По формуле Стокса имеем
С = JJ rota • n°dS = rota • dS, s s
где
dS = dydzt + dxdz] + dxdyk, (rot a • dS) = = —7 dxdz + dxdy.
Следовательно,
C —7dxdz -j- dxdy =—7$ dxdz + $ dxdy =—3. ◄
5 StJAC SoAli
2. Найти величину и направление наибольшего изменения функции п(/Й) = 5х2г/г — lxy~z + bxyz" в точке Мо(1, 1, 1).
► Находим частные производные функции «(Л4) в любой точке Л4(х, у, г) и в точке Мо:
= l0xyz — 7y2z + 5yz2, diHMoL =10 — 7 + 5 = 8, (J Л. {уЛ.
277
= 5x2z — 14хг/г + 5xz2, ди{лМо} =5—14+5=—4,
= $x2y - 7xy2 + lOxyz, du^o} = 5 — 7+10 = 8.
Тогда в точке Л40( 1, 1, 1) имеем grad и(М0) — 8i — 4j + 8k. Наибольшая скорость изменения поля в точке Л4о достигается в направлении gradu(M()) и численно равна Igrad п(Л40)1:
du(/W0) _ <?w(Af<>)
----------- J 11 d Л д grad и-----------------ds
= Igrad u(M0)|
= ^8'2 + (-4)2 + 82= 12. 4
3. Найти наибольшую плотность циркуляции векторного поля а(М) = x(/2z2i + x2yz2\ + xyzk в точке Л+(2, -1, 1).
► Наибольшая плотность циркуляции векторного поля а(М) в данной точке Л40 достигается в направлении ротора и численно равна |rot а(Л+)|. Находим:
rot а(М) =
i
d
xy2z2
j
d
x2yz2
k
d dz xyz
= i(.V2' — 2x2(/2) — ](yz — 2xy24
rota(Mo) = lOi + 5j, |rota(AT,)| =д/102 + 52 = 5д/5. 4
4. Выяснить, является ли векторное поле а(Л4) = = (у + z)i + ху\ — xzk соленоидальным.
► Векторное поле а(М) — соленоидальное, если в каждой его точке diva(A4) = 0. Находим
div а(М) = ^+ ^+ ^= jL(z + y) + v ' дх ду dz дх ' 7
+ d7, + д; (— -v2') = 0 + -v ~~ х = 0.4
15.8. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ К ГЛ. 15
1. Найти площадь части поверхности шара х2 + у~ + + z2 = а2, расположенной вне цилиндров х2 + у2 = ±ах. (Ответ: 8а2.)
278
2. Вычислить массу поверхности куба ОСД'С? 1, 0 sC у I, О ДС С 1, если поверхностная плотность в точке Л4(х, у, г) равна xyz. (Ответ: 3/4.)
3. Вычислить координаты центра масс конической поверхности z2=x2~(-y2, 0 z 1, если ее плотность в каждой точке пропорциональна расстоянию от этой точки до оси конуса. (Ответ: (0, 0, 3/4).)
4. В каких точках пространства градиент скалярного поля и(М) = хл + у2 + z3 — Зхуг: а) перпендикулярен к оси Oz: б) равен нулю? (Ответ: a) z2 = ху, б) x = y = z.)
5. Вычислить наибольшую скорость возрастания скалярного поля и(М) = х2у -j- y2z + z2x в точке A40(2, 1, 2). (Ответ: -д/209.)
6. Показать, что в точке А(4, — 12) производная функции z — х,! ф- Зх2 + бхг/ + у2 по любому направлению равна нулю.
7. Уравнения движения материальной точки: х = t, у = I2, z = О С какой скоростью увеличивается расстояние от этой точки до начала координат? [Ответ: I +2f‘ + 3/' \
лЛ +t’ + t' ’
8. Два парохода, вышедшие одновременно из пункта А, движутся один на север, другой — на северо-восток. Скорость движения пароходов 20 км/ч и 40 км/ч. С какой скоростью увеличивается расстояние между ними? ( Ответ: 20 д/5 — 2д[2 км/ч.)
9. Записать уравнения силовых линий векторного поля а(М) = xi yj + 2гк. (Ответ: у = С\х, z — C^x2.)
10. Векторное поле определяется силой, модуль которой обратно пропорционален расстоянию от точки ее приложения до плоскости Оху. Сила направлена к началу координат. Найти дивергенцию этого поля. (Ответ: — k/(zxfх2 ф- у2 + С), где k — коэффициент пропорциональности.)
11. Твердое тело вращается вокруг оси Oz с угловой скоростью w. Вектор линейной скорости v имеет проекции на оси координат: vx ——шу, v.,= (>>x, vz = 0. Найти: а) ротор вектора v; б) циркуляцию вектора v по окружности х2 + у2 = а2 в положительном направлении обхода относительно орта к. (Ответ: а) (0, 0, 2м); б) 2ла2о>.)
279
ПРИЛОЖЕНИЕ
КОНТРОЛЬНАЯ РАБОТА «КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ» (2 ЧАСА)
1. Изменить порядок интегрирования.
2 4-х2 3 д/25-х2
1.1. \dx \ y)dy. 1.2. $ b(x, y)dy.
0 4 — 2х2 о +'9 - x2
4 л/25-i/ 1 4 —l/2
1.3. \dy b(x, y)dx. 1.4. \dy $ b (%, y)dx.
0 3VJ//2 U 2y+l
4 1-4 4 -л/25-х2
1.5. \dy j b(x, y)dx. 1.6. \dx j b'x, y)dy.
0 _v/4 + 1 0 0
2 2\M 4 y + 4
1.7. \dx j b (x, y)dy. 1.8. j dy j b (x, y)dx.
0 X-/4 -2 y‘/2
1 4 j dy\b(x, y)dx. 2 + + 2
1.9. 1.10. \dy j b(x, y)dx.
-2 1Г 0 y‘
2 x2/2 + 2 1 2-x
1.11. \dx j b(x, ij}dy. 1.12. V/.v j b{x, y)dy.
0 2x I) X1
.1/4 л/2 — у 2 12x
1.13. dy $ b(x> y)dx. 1.14. \dx $ b(x, y)dy. 0 3x2
о У
। i - У 1 X2 + 1
1.15. \dy b(x, y)dx. 1.16. \dx J b(x, y)dy.
" -Jl-y*- 0 — ]
2 i+2 1 x2 1.18. dx j J>(x, y)dy.
1.17. dx j b(x, y)dy.
1 3 —V 0 1 +y
1.19. j dy j b(x, y)dx. 1.20. j dy j b(x, y)dx.
0 2y‘- -i -i-j,
I i-y \dy j b(x, y)dx. 1 3 —x
1.21. 1.22. j b(x, y)dy.
о 0 2x2
1 2 — 21/ 4 3.W/2+4
1.23. \dy j b(x, y)dx. 0 l-y 1.24. \dy j b(x, y)dx.
0 И/2+ 1
280
1.25.
1.27.
1.29.
О l+x
j dx j b(x, ysdy.
-1 - v'7+7
i у
\dy y)dx.
0 — V?
0 2y + 1
5 dy j b(x, y)dx.
-I -i-y
4/5 3-31//2
1.26. j dy j b(x, y)dx.
о H-;/
i Vi- (r —I)2
1.28. \dx j b(x, y}dy.
о -x
3 д/4^7
1.30. jrfx j btx, y)dy.
0 0
2. Вычислить тройной интеграл по области V, ограниченной заданными поверхностями.
2.1. \§zxjx2 + у2 dxdydz-, V-. у = 0, z = 0, z = 2, x2 + y2 = ‘2x.
2.2. + z2}dxdydz, V V: у = 2, x2 + z2 — 2y.
2.3. Щ zdxdydz} V. z = xjZ + y2, z = 2.
2.4. $ ydxdydz; И: у = 4(x2 + z2), 17 = 4.
2.5. ydxdydz', V-. y2 = x2 + z2, у = 2.
2.6. Щ(4 — x — y)dxdydz, V • V\ x2 + y2 = 4, 2 = 0, 2=1.
2.7. ^dxdydz, V И: 2 = V4 — x~ — 1Д x~ + У2 = Зг-
2.8. Щ ~\jx' 4- y2 4- z~ dxdydz, V' V: x2 + y2 + z2^a2, x2 + y2 + 22< 4a2.
2.9. $ xdxdydz, V U: 2=1— xjx2 ] //’, z > 0.
2.10. Щ ydxdydz, v V: z = 1 — (x2 + y2), z > 0.
2.11. Щ dxdydz, V U: z = д/а2 — x2 — у2, z = 'y/x2 + у2.
2.12. Щ xdxdydz, V V: z = 2 - (x2 + у2), z = x2 + у2.
2.13. ® (x2 + \fxdydz, V V-. X2 + у2 = 1, z = X2 + у2, z^O.
2.14. ^(z2 + \)dxdydz, V V: г2 = х2 + у2, z^0, 2 < 1.
' ffi /+/ V V-. у2 + г2 = 1, х2 = у2 + z2, 0.
2.16. Щ (x2 -j- y2 + z)dxdydz. V'. х2 + у2 = 9, 2^0, 2 гС 3.
V
281
V X' + У*
'====.d.xdydz, V': x~ + y: -p z2 = 1, z 0. л/(х2 + I/2 + z2)1
2.18. Щ y2dxd.ydi, l'
2 19 CCC z2dxdydz
-\jx2 + y' + z2
2.20. %dxdydz,
V
221 ffC zd xdydz
JJJ д/l — A'2 — y!
2.22. Щ(х — 2)dxdydz, V
2.23. ®(y+ l)dxdydz, i'
2.24. \\\zdxdydz.
v
2.25. Щ (x + 3)dxdydz,
i-
2.26. ®(a-? + z2-)dxdydz, i'
2.27. (y2 + z’jdxdydz,
i'
2.28. Щ(А'2 + y2)dxdydz, V
2.29. \\\(x + 4)dxdydz. v
2.30. Щ'(у — 3)dxdydz,
I-': .v2 + у2 = I. z2 = .v2 + y2. z,y 0.
V: x2 4- y2 + z2 1, x2 4~ y2 + z2 'C 4, г >(>.
V : x2 + y2 = 4, z = 5 — (x2 4- y2), z > 0.
V : z = д/l — x2 — y\ z 0.
V ': x = 6(y24-z2), y2 4- z2 = 3, x = 0.
V - у ~ 3 \x~ -j~ z , x* -}- z" — 36, у = 0.
V : z = 5(л22 4- у2), л-2 4- у2 = 2, г = 0.
14 2х = у2 4- z2. у2 4- г2 = 4, х = 0.
V : у2 = л-2 4- z2, у = 4.
V : х == у2 4~ z2, х = 9.
V : 2z = х2 4- у2', л'2 4- у2 = 4. z = 0-
I': 2.v = у2 4- z2', у2 4- z2 = 4, х = 0.
V : 4у = ух2 4- г2, х2 4- z2 = 16, у = 0.
3. Проверить, является ли данное выражение полным дифференциалом функции и = и(х, у). Найти функцию и = и(х, у).
3.1. (sin2 у — у sin 2х 4- 1 /2)dx 4- (х sin 2у 4- cos2 ,v 4- V)dy.
3.2. (у/х 4“ In у 4- 2x}dx 4- (In х 4- x/y 4- l)dy.
3.3. (x2 — 2xy)dx 4- {y2 — '2xy)dy.
3.4. (у/д/1 х2У 4~ x’)rfx 4- (x/o/1 — x2y* 4- y)dy.
3.5. (4- 2хЛ dx 4- ( - „ u- „ - 2y^ dy.
\ "h / \ A” “h У /
3.6. (---l}dx+ (---------------- 10^ dy.
\ 1 4- x2y2 ) \ 1 4- x2y2 )
3.7. {y2e"J'~ 4- 3)dx 4- (2xye'-,: - 1 )rfy.
3.8. (sin x 4- cos x cos y/sin2 x)dx 4- (sin y/sin x — cos y)dy.
282
3.9. 1 , У dx + -------Д- dy.
х‘у ху
3.10. (-----—-----Ц dx + (------------- + — dy.
\ f + УУ х / \ (л- + у)' у )
3.11. (3x3iy — y2)dx + (х3, + 3xy2)dy.
3.12. (---Л') dx 4- ----------Д dy.
X У X / \х у-/
3.13. (—-----------Д dx— , dy.
X .г 4- у- / х- 4- У~
3.14. (3.V — 2ху 4~ У )dx 4" (2ху — х Зу jdy.
3.15. (sin 2а — 2 sin х sin у — 12x3y)t/x4~(sin 2</4~ 2eosxcos y — 4x2)dy.
3.16. (12x3y 4- 1 /У2','4х 4- (4x’ — 2x/y')dy.
3.17. (2xy — \/x2)dx + (x2 — '2/iffy.
3.18. (e '-----— Д/х 4- (sin 3y--------Д-Д/у.
\ -V 'y / \ x~y~ /
3.19. (2/x ’ 4- eos3 y)dx 4- (y — x sin ‘2y)dy.
3.20. (cos x — 2xy',dx 4- ( — 3 sin у — xJ)dy.
3.21. (2xy — I4<4 sin x cos x)dx 4- (x3> 4- 7e" cos3 x)dy.
3.22. (1 /cos3 x 4~ y'ldx 4~ 3xy2dy.
3.23. (1 /x 4- sin y'\dx 4- x cos ydy.
3.24. (i/x3 4- I/t/)rfx = ((l — xff)dy.
3.25. (x 4- у sin’3 y)dx 4- (1 4- x sin2 у 4~ xy sin '2y}dy.
3.26. ie' ~ 3 4- у cos xy — 6x)</x 4- (x cos xy — e' ~ ")dy.
3 27- + ’)+ ( ДД? ^8' -"+4)'
3.28. (cos у 4- У cos x — 6xy/)</x 4~ (sin x — x sin у — (ix2yfy.
3.29. (ye’-' — 2x sin(x3 — y2)',dx 4- (xe'" 4~ 2y sin(x3 — y2))dy.
3.30. (x/^'l 4- x3’ 4- if 4- 6x3//' — 3)ax 4- (п/Д1 4- x3’ + у2 /-
4- 6x‘у2 4- fi)dy.
4. Вычислить криволинейный интеграл вдоль заданной дуги L.
4.1. \xdy — ydx, L. х = a cos’ /, у = а ъ\п'I (0 С ( =С 2л).
L
4.2. J (х3 4- y2)dx 4- (х3 — iffy, L.iiy у — (л) от точки 4(— 1, 1) до I. in
точки В(2, 2).
4.3. J (х2 — 2xifdx 4- {у2 — ‘2xy)dy, L щ: у = х3 от точки А(— 1, 1) /-/it,
ДО ТОЧКИ В ( 1, 1).
4.4. j sin ydx — sin xdy, Lin', отрезок прямой, заключенной между L ill
точками 4(0, л) и В(л, 0).
4.5. j xdy —ydx, Lin'. x = a(t-smi\ y = o(l—cos/) от точки
l.-ib
4(2ла, 0) до точки В(0, 0).
283
4.6. J xdy + ydx, LAbc—контур треугольника с вершинами I-ЛВС
А(- I, 0), В(1, 0), С(0, 1).
4.7. j — dx -|- xdy, Lab- У = In х от точки А (1, 0) до точки В (е, 1). Lab х
4.8. j xex'dy + ydx, LUA: у = x'2 от точки 0(0, 0) до точки /4(1, 1).
Loa
4.9- . j (х2 y)dx -|- (х -|" у2) dy, LAB — отрезок прямой, заключенный
Lab
между точками А(1, 2) и В(3, 5).
4.10. j (ху — i)dx + x’ydy, Ьдв — отрезок прямой, заключенный
Lab
между точками /4(1, 0) и В(0, 2).
4.11. j cos ydx — sin xdy, LAB—отрезок прямой, заключенный
Lab
между точками А (2, —2) и В ( — 2, 2).
4.12. j xdy 4- ydx, Loab — контур треугольника с вершинами L ОАВ
0(0, 0), /4(3, 0), В(0, 2).
4.13. (х + у)<//, Воав—контур треугольника с вершинами Loab
0(0, 0), А (2, 0), В(0, 2).
4.14. 5(х -|- y)dl, L — первый лепесток лемнискаты Бернулли р2 = L
= a2 cos 2<р.
4.15. ф V* + у2 dl, L — окружность х2 + у'2 — ах. L
4.16. \y2dl, L — первая арка циклоиды х = a(t — sin/), у = L
= а(1 — cos /).
4.17. j xydx(у — x)dy, Lob’- У = х2 от точки 0(0, 0) до точки Lob
В(1, 1).
f dl
4.18. \ —- ---. Lot — отрезок прямой, соединяющий точки
J х/Т+у2 + 4
Loa
0(0, 0) и /4(1, 2).
4.19. $ 2xdy + ydx, LAB: х = у2 от точки /4(1, 1) до точки В(4, 2).
Lab
4.20. \—----------г, L — первый виток винтовой линии л' = 4соз/,
J х + У2 + Z-
I.
у = 4 sin /, z = 3/.
4.21. §yexdl, L — окружность х2 + у2 = 3.
284
4.22. ф(2х 4 y^dl, L — окружность ./ 4 у2 = 1.
4.23. ф(х2 4 у1) dl, L — окружность х = 2 cos t, у = 2 sin t. L
4.24. I — x dl _ — эллипс x = 4 cos t, у = sin t.
j V*2 + 161/
4.25. j (Л2 4 y~)dx 4 (x“ — y?)dy, — контур треугольника с Loa в
вершинами 0(0, 0), A (1, 0), B(0, 1).
4.26. ((arcsin у — хг)У1, L — дуга окружности x = cos t, y = L
= sin t (0 c t С л/4).
4.27. j x^ydx 4 y<?* + 2dy, Lab — отрезок прямой, заключенный Lab
между точками /4(1, 1) и В(2, 3).
4.28. V ydx 4 — dy, L,\B - дуга кривой у = е~х от точки /4(0, 1) j У
Lab
до точки В(1, 2).
4.29. j 2xydx 4- x''dy, Ьпл'. у = _т3 от точки 0(0, 0) до точки /4(1, 1). L 0/1
4.30. (ху x"ytl, L os — отрезок прямой, заключенный между
Lab
точками /4(1, 1) и В(3, 3).
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Учебники и учебные пособия
1. Бугров Я. С.. Никольский С. М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменною,- М.: I 1аука, 1981. - 448 с.
2. Жевняк Р. Л4., Карпук А. А. Высшая математика: В 5 ч.— Мн.: Выш. HIK., 1984 - 1988,— Ч. 3.-- 1985. -208 с.: Ч. 4.— 1987.--240 с.
3. Ильин В. А., Позняк Э. Г. Основы математически!о анализа: В 2 и,- М.: Наука, 1971 1973,—Ч. 2,- 1973,— 448 с.
4. Кудрявцев JI. Д. Курс математического анализа: В 2 т,- М.: Высш. П1К., 1981.-- Т. 2.— 576 с.
5. Курант Р. Kjpc дифференциального и интегрального исчислс-иия: В 2 т.-~ М : Наука, 1967 - 1970. Т. 2,— 1970. - 671 с.
6. Пискунов Н. С. Дифференциальное и интегральное исчисления: В 2 т.— М.: Наука, 1985.— 1. 2.— 576 с.
Сборники задач и упражнений
7. Берман Г. И. Сборник задач по курсу математического анализа.— М.: Наука. 1985.— 416 с.
8. Данко П. Е., Ионов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах: В 2 ч. - М.: Высш. шк.. 1986.— Ч. 2.— 464 с.
9. Кузнецов Л. А. Сборник заданий по высшей математике: Типовые расчеты.— М.: Высш, шк., 1983.— 176 с.
10. Лихолетов И. И., Мацкевич И. Г!. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике.— Мн.: Выш. шк., 1976.— 436 с.
11. Сборник задач по курсу высшей математики / Г. Ц. Кручкович, Н. И. Гутарииа, II. Е. Дюбюк и др.; Под рея. Г. Н. Кручковнча.— М.: Высш, шк., 1973.— 576 с.
12. Сборник задач но математике для втузов: В 2 ч. / В. А. Болгов. Б. П. Демидович, В. А. Ефименко и др.; Под ред. А. В. Ефимова, Б. П. Демидовича. - - М.г Паука, 1981. -- Ч. 2.— 368 е.
ОГЛАВЛЕНИЕ
Предисловие.................... .................. • • 3
Методические рекомендации .................... . . 5
12. Ряды
12.1. Числовые ряды. Признаки сходимости числовых ряд-в . . 9
12.2. Функциональные и степенные ряды......................18
12.3. Формулы и ряды Тейлора и Маклорена. Разложение функций в отепеппые ряды................................. . . 23
12.4. Степенные ряды в приближенных вычислениях . . .28
12.5. Ряды Фурье.............................. .34
12.6. Индивидуальные домашние задания к гл. 12 . . . 44
12.7. Дополни тельные задачи к гл. 12 ... . . . 124
13. Кратные интегралы
13.1. Двойные интегралы и нх вычисление...................126
13.2. Замена переменных в двойном интеграле. Двойные интегралы в полярных координатах................................. . 134
13.3. Приложения двойных интегралов . . ...........138
13.4. Тройной интеграл и его вычисление...................146
13.5. Приложения тройных интегралов . . ... ... 152
13.6. Индивидуальные домашние задания к гл. 13. . . . . . 157
13.7. Дополнительные задачи к гл. 13 . . . . . . 186
14. Криволинейные интегралы
14.1. Криволинейные интегралы и их вычисление . . .... 189
14.2. Приложения криволинейных интегралов................ 198
14.3. Индивидуальные домашние задания к гл. 14 ... . . 203
14.4. Дополнительные задачи к гл. 14 . . . ...........222
15. Элементы теории поля
15.1. Векторная функция скалярного аргумента. Производная по направлению и градиент ..... ... . . . 224
15.2. Скалярные и векторные поля . . .......... . . 230
15 3. Поверхностные интегралы......................... . 233
15.4. Поток векторного поля через поверхность. Дивергенция векторного поля............................................ 241
15.5. Циркуляция векторного поля. Ротор векторного поля . . . 245
287
15.6. Дифференциальные операции второго порядка. Классифика-
ция векторных полей...................................250
15.7. Индивидуальные домашние задания к гл. 15............256
15.8. Дополнительные задачи к гл. 15......................278
Приложение ...................... ... . 280
Рекомендуемаялитература. . . . . . 286
Учебное издание
Рябушко Антон Петрович, Бархатов Виктор Владимирович, Державец Вера Владимировна, Юруть Иван Ефимович
СБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ
В трех частях
Часть 3
Заведующий редакцией Л. Д. Дух валов. Редактор М. С. Молчанова. Младший редактор В. М. К У ш и л е в и ч. Художник переплета и художественный редактор Ю. С. Сергачев. Технический редактор Г М. Р о м а и ч у к. Корректор Т. К. Хваль
И Б № 2893
Слано в набор 18 04.90. Подписано в печать 11.04 91. Формат 84 x108/32. Бумага тип. № 2. Гарнитура литературная. Высокая печать. Усл. пен л. 15,12. Уел. кр.-отт. 15,12. Уч.-изд. л. 17,59. Тираж 15 700 экз. Заказ 357. Пена 2 р. 40 к.
Издательство « Вы ш э и t п а я школа» Государе гвснщм о комшет.ч ЬССР но печати. 220048, Минск, проспект Машсрова, I I
Минский ордена Трудового Красного Знамени полиграфкомбинат МИПО им. Я. Коласа 220005. ДХныск, ул. Красная, 23.