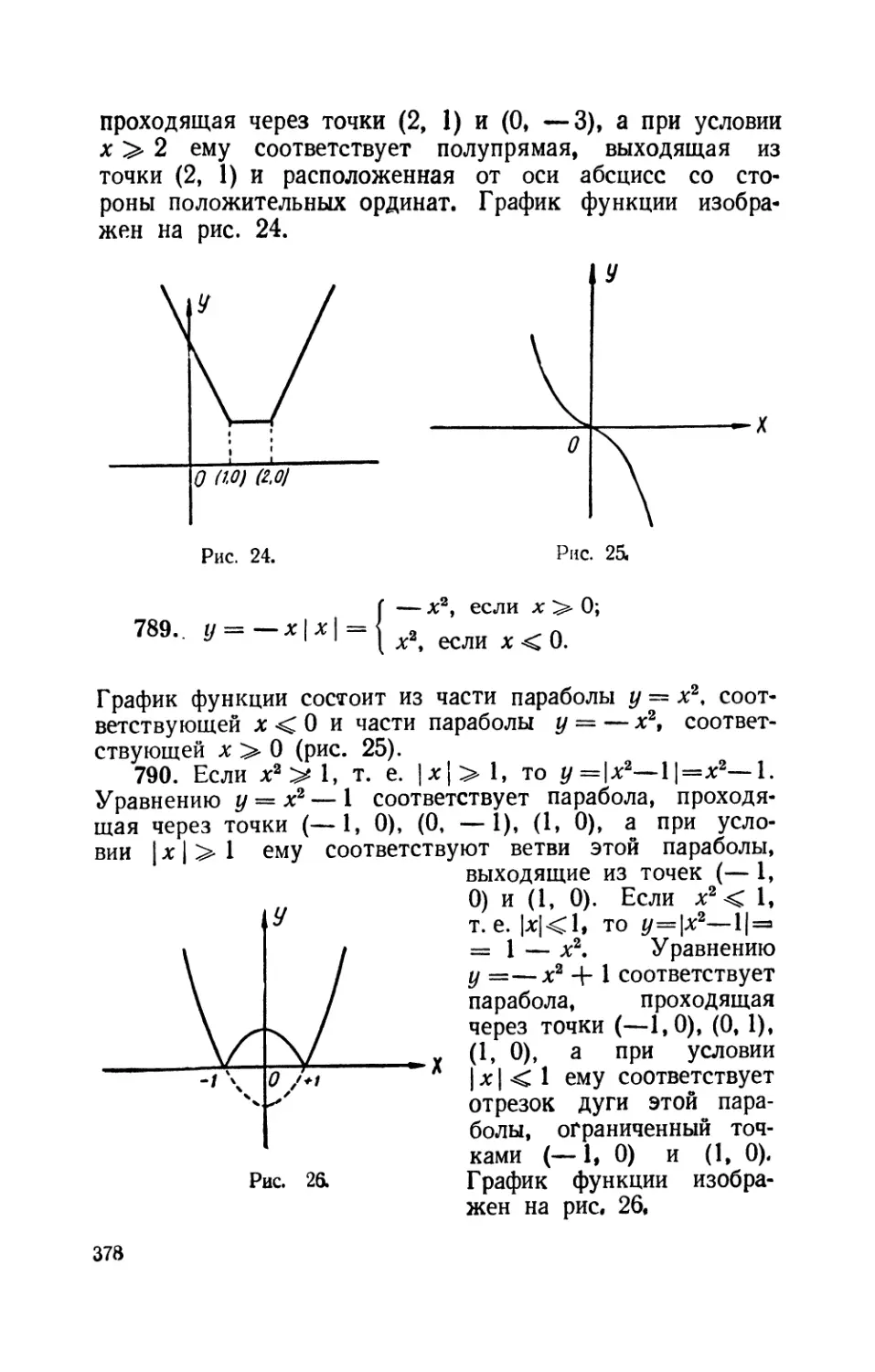
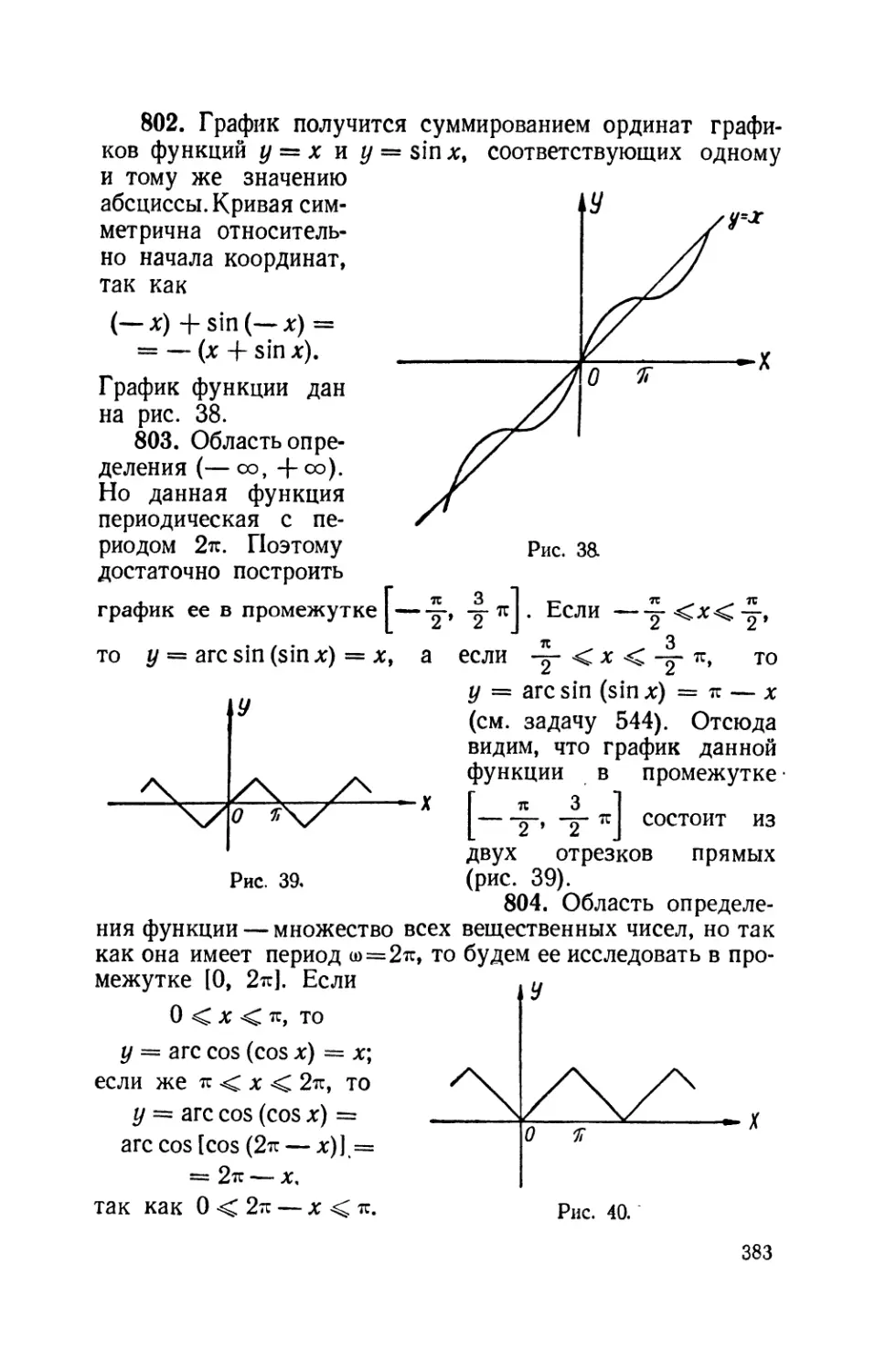
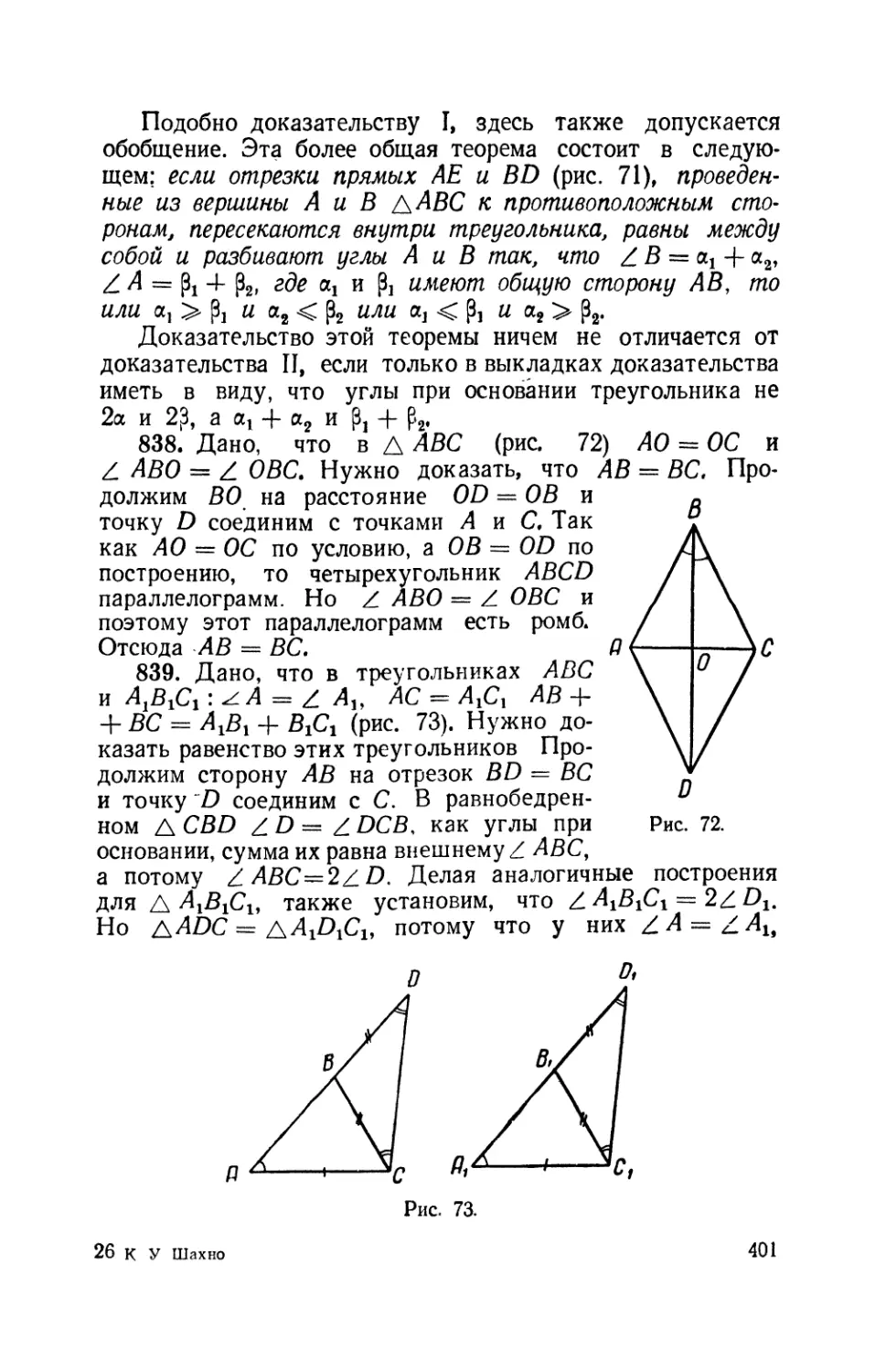
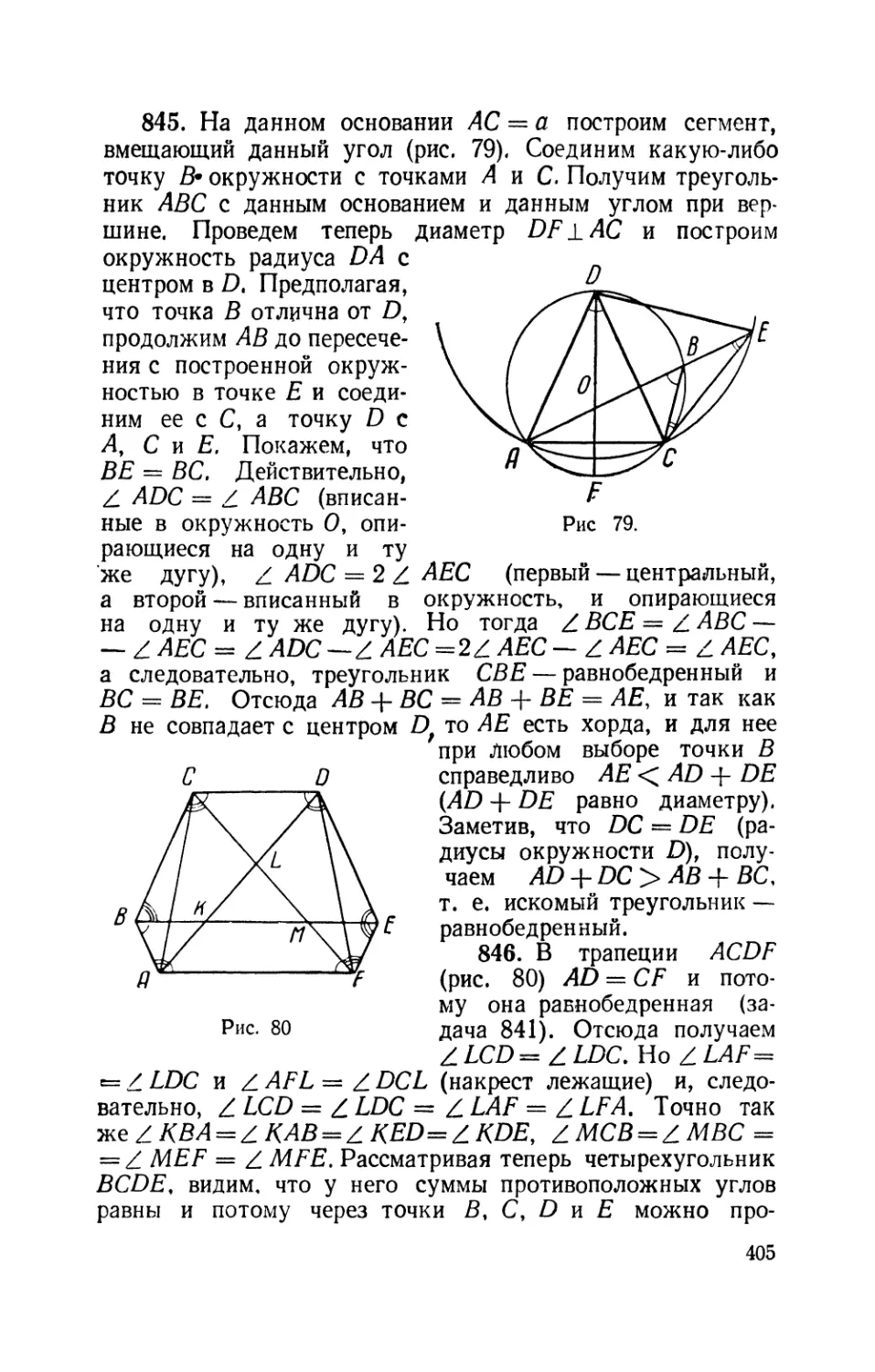
Text
^^ К. У. Шахио
и • орник
ЗАДАЧ
по
ЗЛЕМЕН АРНОЙ
МАТЕМАТИКЕ
ПОВЫШЕННОЙ
ТРУДНОСТИ
МИНСК 1965
К. У. ШАХНО
СБОРНИК ЗАДАЧ
ПО ЭЛЕМЕНТАРНОЙ
МАТЕМАТИКЕ
ПОВЫШЕННОЙ
ТРУДНОСТИ
ИЗДАНИЕ ВТОРОЕ, СТЕРЕОТИПНОЕ
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА»
МИНСК 1965
51(076)
Ш31
Сборник содержит свыше тысячи задач по элементарной
математике, главным образом повышенной трудности. Задачи, по
возможности, систематизированы и снабжены решениями. В отдельных случаях
в связи с решением задачи и там, где это уместно, приведены
вопросы теории. Иногда они предпосланы решению группы задач,
объединенных общей идеей. Даны разъяснения по вопросам теории
равносильности уравнений, построения графиков, комплексных чисел,
обратных тригонометрических функций, математической индукции и
некоторым другим вопросам.
Сборник рассчитан на лиц, окончивших среднюю школу и
желающих продолжать совершенствоваться в методах решения задач или
готовиться в вуз. Он может послужить дополнительным пособием
учителю при работе в классе, для индивидуальных заданий учащимся,
особо интересующимся математикой, студентам педагогических
институтов.
ЗАДАЧИ
I. ПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
Разложить на множители (1—15):
1. Ьс ф 4- с) + са (с — а) — аЬ (а + Ь).
2. а2Ь2 ф — а) + Ь2с2 (с — Ь)+ с2а2 (а — с).
3. 1(х2 + у2) (а2 + Ь2) + АаЬху}2 — 4[ху(а2 + Ь2) +
+ аЬ(х2+у2)]2.
4. 2а2Ь + АаЬ2 — а2с + ас2 — АЬ2с + 2Ьс2 — 4аЬс.
5. у(х — 2г)2 + 8хуг + х(у — 2г)2 — 2г (х + У)г.
6. 8х3(у + г) — у3{г+2х) — г3(2х — у).
7. х* + у* + г* — 2х2у2 — 2х2г2 — 2уЧ2.
8. х2у + хуг + х2г + хг2 + у2г + уг2 + 2хуг.
9. х2у + ху2 + *22 + хг2 + у2г + уг2 + Ъхуг.
10. х3 + 5х2 + 3х — 9.
П. а^ + 9д:24- Их —21.
12. гЧ*2 —7)2 —36*.
13. ф — с)3 + (с — а)3 + (а — Ь)3.
14. (л:2 + у2)3 + (г2 — х2)3 — (у2 + г2)3.
15. (х-\-у + г)3 — х3— у3— г3.
16. Доказать, что произведение четырех
последовательных целых чисел, увеличенное на единицу, равно
квадрату целого числа.
17. Доказать, что число 132л—1, где п — натуральное,
делится на 168.
18. Доказать, что число 721 —487 делится на 288.
3
19. Доказать, что из равенства
(а—Ь)2 + (Ь — с)2 + {с —а)2 = {а + Ъ — 2с)2 +
+ (Ь +х — 2а)2 + (с + а — 2Ь)2
следует, что а = Ь — с, если а, Ь и с — вещественны.
20. Доказать, что .если т + п + р = 0, то т3 + я3 +
+ р3 = Ътпр.
21. Разделить многочлен
у2х2 + 2ух + 1 + 2г/г*2 + г2*2 + 2гх
ка многочлен 1 + хг + ух.
22. Разделить многочлен
Зах + а?х3 — 3 — За + 2х2 + Аа2х — х* — а2х2 + 2х — а3х2
на многочлен
3 — х* + х + ах* — ах.
23. Доказать, что многочлен х* 4- у3 + г3 — Злтг/г
делится на многочлен х -{- у + г.
24. Доказать, что произведение
(хт ^ 1) (А:т-1 _ 1) (хт+\ _ 1)
делится на (х— 1) (х2— 1) (лг*— 1). Число т — целое
положительное.
25. Найти условие, при котором выражение
ат-\ + ат~2 + _ + а + 1
делится на выражение
ап-\ +ап-2+ .в#+а+ 1,
где т и п — натуральные числа.
26. Доказать, что многочлен л?* + я32 4- *28 делится на
л;2 + д: + 1, где к — натуральное число.
27. Проверить справедливость равенства
(1 +х)(1+ х2) (1 + х4) ... (1 + х2"") =
= 1 +х + х2+ ... +х2-*-
28. Найти сумму коэффициентов многочлена,
получающегося после раскрытия скобок в выражении
(1 + 4х—*4х2)11Ь (1 4- 2х)ь (1 — 3* 4- х2 + 2х*)ыК
4
29. Доказать равенство
„2 (X —Ь)(Х — С)
Ь)(а-с)
(х-
(а-
+ Ь*
(х — с){х — а)
(Ь -с)(Ь- а)
+ С
-а)(х — Ь) _ г
(с-а) (с- Ь)
30. Найти необходимые и достаточные условия того,
чтобы дробь ах , не зависела от х.
31. Найти необходимые и достаточные условия того,
чтобы дробь ах2+Ьх + с
39.
40.
41.
42.
1
1
1-х
1+*
1
1 4- х2^ 1 4- х*
1
(а — Ь)(а — с)
(Ь-
•с)(Ь
Ь2
(а
а -
-Ь)(а — с)
•Ь , Ь — с
тх2 -\- пх -\- р
Упростить выражения (32—42)
32.
33.
34.
35.
36.
37.
38.
не зависела от х.
16
1 4- *8
1 4- *10
•а)
(с-
•а)(с-
■Ь)
+
(Ь — с)(Ь-а) '
с — а , (а — Ь)(Ь
(С — а) (с — Ь)
— с) (с — а\
а + Ь^ 64 с
а + Ь
(Ь — с) (с — а) т (с — а)(а — Ь)~г
У2г2 , (У2 - Ь2) (г2 - Ь2) , 1(у2-
с 4- а "^ {а+Ь)<Ь + с){с + а)
Ь 4- с , с -\- а
{а — Ь)(Ь — с)
- с2) (г2 — с2)
ЬЧ2 ^ Ь2(Ъ2 — с2) ^ с2(с2 — Ь2)
(1 4- аЬ) [1 4- аЬ 4- (а 4- *>)*! — (а + 6)[д + 6 -НИ- а6> г] Чу/
[1 + аЬ + (а + Ь) х]2 /Ч
X
-I
л:^—(лг— I)2
(х2 4- I)2— *2
(*2 - */2)8 4- (У2 ■
а 4- 6+ (1 + аЬ)х
1 4- аб 4- (а 4- &)*
л;2_(л:2__ 1)2
л:2 (х 4- I)2—1
- г2)3 4- (г2 — х2)3
У2(л._ Х)2_ )
х4 — и 4- I)2
(х - г/)3 4- {У
а2 {с —- 6)
• г)8 4- (2 — а:)3
Ьс
Ь2 (а — с) с2 (Ь — а)
г; г
аЬ
а(с—Ь) , Ь(а—с) . с (6 — а)
Ьс
ас
аЬ
1
<х+ пи + 2)
■4-
1
(л: 4- 2) (х 4- 3)
х(*4- П
+ и 4 з^х + 4) + и + 4) с* + 5) •
+
I
43. Доказать, что
(* — ь 1 Ь-с . с-а\ (с а_ Ь_\ __ ^
V-с ^ а ^ Ь )\а-Ь~г Ь-с^ с — а)"*9
если а + Ь + с = 0.
44. Доказать, что
то
45.
1 2^3 4 ^
- 1 I 1
"" к+1 ' Л + 2
Доказать, что если
а?+а22+ .
&! + &22 + .
#А + #2^2 + •
#1 #2
•м +2^
4- 4-
■Т ••• -г
.. + йп =
.. + Ь1 =
.. +ал6я
__ «л _
1
— 1
1
2/г *
р2;
<?2;
= р<?>
я '
1
2*
если все величины, входящие в данные равенства,
вещественны.
46. Доказать, что если
й\ **2 ^П_
ьх ~~ ь2 - - ~ *>л'
то:
(а\ +а1+ ... + а1) (Ь\ + Ь\+ ... + «) =
= (аЛ + а262+ ... +аА)2-
47. Доказать, что дробь 21 4 при любом целом
п— не сократима.
48. Доказать,
49. Доказать, что
48. Доказать, что аи„ , й = —, если -—= —
о2 -\- с2 с ос
(*-)'-
СхА + с2а% + ... + ска1
сгьп1 + сшь% + - + ****'
если ~-=-^- = ••• = "^"» я съ с2> •••» с»-^любые
числа, не равные нулю одновременно.
50. Доказать иррациональность числа У~2.
51. Почему (^2~)3 = 2?
т
52. Почему: а) а0 = 1; б) ап =^0™; в) сгт =-^г>
т > 0; г) а1 = а'>
53. Чему равно арифметическое значение ]/а2 ?
54. Когда верны формулы: а) ]/~# • ]/~у =]/Л]п/;
б) # = /!; в) /?— 7"^ г)вКГ —/ОТ?
55. Доказать, что если 4г- =4г- = ••• = -гЧ то
УаА + Уафг + ... + у^Л =
= К(01 + о2 + - + а„) (6Х + 6,4-... + 6Я)
(а„>0, Ьк>0; к = 0, 1, 2, .... п).
Упростить выражения (56—112):
-2
56.
57.
58.
59.
60.
х + у
(х + У):
{х + у)' х< +у
А. А.
а3 — 8а3Ь
х + у
2_ 2_
а3 + 2У^Ь + 4Ь3
2Уху
■■{*-*№)-'*■
а — 26
У 2д26 + V 4аЬ2
У а* — у462 У а* + У\Ь* +|/ 16аЬ
а УТ + Ь\Г2Ь + Ь|/"д" + дУНгЬ *
а + 6
(д. _ у)* {\ГТ + УТ)~3 +2*/Т + у\Гу 3 (У^у -л:)
хУ х +уУ у
х — у
У аЬ —У& У&Ъ — УаЬ*
У~& —Уь*' а + Ь
(Ут - Уг) (У* + V* - У~*)
61.
(х* + уУ ху + хУху + у*)(Ух +у-у-)~2-У
ХУ
+
х — у
2Уу
62.
Ух+Уу'
(т^^ + тт^т- )(^у+гт)
\У х -Уу у х~х I
х+у- (х}/Т + уУ~у)(У~х_ + У~у)~]
' а*Ь . 1 - УаЬ \ (а — \Га_
" »/Т-1
/ УаЬ3 +У аЧ
63' ( УТ+УЬ
УаЬ
УТ + 1 )■
64.
\-У а
65
^^-у-а У«-\+1*-у-а
ут / ут^ + */жг , 4/7Г\з, Г1 ^ч
66 (4/~^+^^±^х_ -»3/*3 — 2ал;2 + а2* \~' '/— ,
67. Ь
68. Уа-
^ 2 V х х-1 '
:(у-а--\Гь)-У~а- Г!
1 + а|Ла" + в+ К"6
1 - Я/Т«
ъг— , 1 /я2
, *
1 Г^"
X
+ г*
69.
ид^Ж'-уч+^^ы^х
ХУ-(*-с)*
70.
71.
а + уЧаЧ
2х+|/л4Н*2"
1
72.
73.
74.
75.
76.
77.
78.
79.
У^ — УТх УТх )
(а + аУТ + * + хуНр2 (1 — У~х~)г
* + *
.-]
Т т/о2
+ 4а + 4*.
[*У-Ъ=ТуГ-(*+1)У(х*-1)-г]
„ ,— , х—V ах ~ ,
У х — У а
IV х +
\\ У а* + 2а*
[V а2 — 4а
ут+у*
У^Ч?Г\
Ь + 4а362
4аЬ + 4Ь2
У2Ь
Уть
У аЬ —ЬУ 2 У аЬ +ЬУ 2
У{Ъ — Ъ)УаЪ + (3 — б-1) /аЬ31
УТ-УЪ-
3/1=2
"|/ б3/ Ь2д .
(5 — 4х2) ]/" 5 — хУ(У 2 + 1)2 + (УТ— О2 — Ь(— 8л:)
X
У (5 — 4*2)2 +(4л:}/У)2
У2х + У 2а
X
1
л:+(л:2—1)
л: — Ух2^Т ~Г
х(х2-
(У~а_ + УТ)Э + 2а-
(У~а~ + У~Ь)* + 2Ь-
у-дгу + аУТ ..
аУТ+ьут-1]{1 +
Ух*—\
О +1
У'
(-4-р
+ ■
81.
1-*
/1— х* + х — 1
1
7Т 5
УТ
' X
5(а —с )
, х>0.
б6/Т
з з
а —с
ут-у~г'
82. ±.1.,у' + *+. ГД--иУ4
2 \\ + уъ+Ух,' \-у-Ь+\Гх-)\х*-
— 4х 2 + %\У 0^.
2^а?+26
84
'•[* + ■
а — Ь
■)•
85
1-2-^20+14^2 ."^6 — 4^2 +
86. э^^Тгя1- |/" з ]/^]~4-1/з-2КТХ
X К40/Т+56 : |^(К"3"+1)2 + (1/Т-1)2.
88.
|_2К(1+*)8 Т
4. */\+х(\-.х) 4
(Ш)"
М^таГ-^Г-^
90. д:}/^
+ У
Г (2л
-9^)»(^-У)
(2*-Зу)2
+
91.
2*у -1/^-уУ _ „ . -I/ (^ + У)2
+ ^"УГ (*+</)' ** У)У Х-у '
X
]/> + 1 + а
1
X
}/ а2 + 1 — а
/(
2р?
93.
р — я р + я р% — я2
1
X
■)(р+<?); Р>д>о.
1+(Ух+1)*
1
' _ Г !__
(1-}/л;)-2 |_ 2\Гх~(1-Ух)
УТ) \
1
94.
2*/ х {\ + У х) ] 2У х *-2хуг~х
8-х
2+3/Т
+
+г +пчл-;- ^г+2^г •
95. ^щ^^^-±^у,
если х = —г.
/и—1
11
96.
(I-*2) +1
+
(1-х*) --1
если х = 2к (1-М)"1 и к>\.
97. (1+ х-1)-2 + (1 — х-1)-2, если х =
_1 _ —
= (1-п-1)2(1+гГ1) \
1
1
98.
(а+х) 2(х + Ь) 2+(а — х) 2 (х - Ь)
-Т п-2
|_ (а+х) 2 (х + Ь) 2-(а-х)
(х-Ь)
если х = угаЬ и а > Ъ > 0.
[33 33
(а: + я) (* — а) + (х + а) (х — а) -
т3 + п3
если х = а-
тЛ — лл
и т > л> 0.
100
101
102.
. (хгп+хп) —4а2х
т п
если
2тп
*=(а+уг1?"=Т) .
\а + х2) 2+\а — х2) 2, если х = 4(а—1)
1) 1<а< 2; 2) а > 2.
[
(л:2 + а2) 4- (*2 — а2)
1_ 1^
(л:2 4- а2) 2 — (л;2 — а2) 2
I
, если
/ т2 + я2 \ 2 . . п
^ = аI—2^г-у и ">™>о.
и
12
103 (т + Х)
(т + х)
т > 0, 0 < п
1
2+(т-
<1.
1
-х)2
1
-*)2
если х =
2тп
Т^+1
104.
если х
= (ь3-а3)2.
,05. ** + *! , если х = ±( ЛГИ - л/±)
Х+У1+* 2\ У Ь Га)
и а>0, 6>0.
106. л:3 + 12*. если х = У 4(|/~5 + 1)— ]/ 4(]Л5— 1).
107. *» + а* + &, если * = ]/--|- + ]Л^- +-^ +
+ 1^-4-1/^+^
108. (л:-1 + а"1) (* + а) л — Ь~1х п , если
п I п п \—1
109. У2 + У~Ь~' У-М+ПУТ-тх . т/Г=^
У2+У!Г-У—38+17У1>'+тх ' * 1+пх'
если л; = — 1/ — — 1 и 0 < т < л < 2т.
110. Кл;'2 + "V а"*"* + Vап + "V хпап* — 1,
(п п \ п-\-\
111. У~акхп-к + у^а*-* л;* — 2}/1?лГ + б2, если
, , п—2к
(уЬ -УЪ-а)
2к
л—26
а
112. У(х+ \у + У{х—\)2— АУ х2— 1 + 1, если
х г__ <2 + У^У + 1
(2 + К 3)« — 1
13
Доказать справедливость равенств (113—115):
_(1^)"-Ц!±^)-_(!^)-,„_и,
туральное.
114. Ь\Г2 . 2а+ Г"*Ч1 = УЪТШ -У1^Ь)\
Уа+У~а2~Ь*
если а> \Ь\.
115. Ух + 2Ух—1 + ]/"*— 2Ух— 1=2,если*<2.
II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
116. Доказать, что уравнение шг + & = 0 при афО
имеет решение и притом единственное.
117. Доказать; что для совместности уравнений
а1х + Ь1 = 0 и а2х + Ь2 = 0, где ах -/= 0 и ^ Ф 0,
необходимо и достаточно, чтобы агЬ2 — афх = 0.
Выяснить, совместны ли уравнения (118—120):
118. х+ 1 =0 и *2 + 5л: + 4 = 0.
119. х2 + х — 20 = 0 и *2 — 6л: + 8 = 0.
120. л:2 + ал: + 1 = 0 и л;2 + а: + а = 0.
Выяснить, являются ли равносильными уравнения
(121 — 124):
121. 2х = х— 1 и 2х + л:2 + 1 = х + г8.
122. л:2-За: — 2 и гЧ Ц- = За: — 2 Н Ц~.
1 л:— 1 ' л;— 1
123. л:+1=0 и (х+ \)Ух— 1 = 0.
124. ]/(* — _б)(* — 1)=1/Т4 и ^7^6 -У~х^Х=уи.
Решить уравнения (125—134):
125. а2х = а(х + 2)~ 2.
юа х — тп . х — пгр . х — пр , ,
126. ; р-*— Н г-^- = т + Я + 0.
а, 6 и с — числа одного знака.
128. \х— 1| = 2.
129. [*—1| + |х —2| = 1.
14
130. |* — 2| + |* — 3| + |2* — 8| = 9.
131.
-1 1/ 1*1-5 14-2-иП Ы—9 7
1/ 1*1-5 14-2.|дс|\_М
'8\ 4 5 Г
4 8^ 4 5/28'
5"
132. Т*+±-х= |3*Г5
188. х- 1^=Н = 3-2-^-5.
134. у-^+^-^^ав-а».
(2т — ал;)2 + (ах — 3/г)а
135. Является ли совокупность уравнений
7х — 2у + 5 = 0;
системой?
136, В результате решения системы уравнений
Ъху _ г. 2хг __ д. уг __ ^
х+У * *+2 ' г/+2
нашли, что системе удовлетворяют следующие числа:
_ 120. __ Ш _ 120
*~~ 61 ; #~~ И» г "" 19*
Сколько это даст решений?
137. Если решение одной системы является решением
другой системы, то будут ли эти системы
эквивалентными?
138. Дана система уравнений
Г ахх + Ьху + сх = 0;
1 а2х + 62г/ + с2 = 0.
Умножаем первое уравнение на тх =^ 0, второе на
т2Ф 0 и результаты складываем; затем повторяем эту
операцию, взяв множителями числа пх Ф 0 и п2 Ф 0,
причем пхфтх и я2 =^= т2. В результате получим новую
систему
/ Ргх + Цх\) + гх = 0;
I Р2* + ЦъУ + г2 = 0.
Будет ли полученная система эквивалентна данной?
139. Доказать, что системы:
Г ахх + Ьгу + сх = 0;
1 а** + Ь2у + с2 = 0
и
Г /И! (а^ + &!# + сх) + т2 (а2х + Ь2у + с2) = 0;
\ пх (ахх + Ьху + сх) + п2 (а2х + Ь2у + с2) = 0
эквивалентны, если ШхЩ — т2пх Ф 0.
15
140. Верно ли предложение, обратное
сформулированному в задаче 139, т. е. если рассматриваемые в той
задаче системы эквивалентны, то т^ — т2пх ф 0?
141. Дана система линейных уравнений
-агх + Ьгу + сх = 0;
а2х + Ь2у. + с2 = 0.
Предполагая, что афг — афх Ф 0, будем решать ее
каким-либо способом, например способом сложения и
вычитания. Получаем:
х = С-А —^2 . и __ ад — д^
агЬ2 — афх ' ^ а^г — а2&1
Нужно ли проверять, удовлетворяют ли найденные
значения х и у данной системе?
142. Доказать, что система
ахх + Ьгу + сг= 0;
а2х + Ь2у + с2 = 0
имеет одно и только одно решение, если агЬ2—&Ф\Ф 0.
143. Равносильны ли уравнения
_^_0иР(*)«.0.
где Р(х) и С} (х) —- многочлены относительно х?
144. Равносильны ли уравнения
хт = ут и х = у?
т — натуральное число.
145. Определить число а так, чтобы система
2х + у = 5; 3* — 2у = 4; ах + Ъу = 11
была совместна.
146. При каких а и Ь система
Зх — 4у = 12; 9а: + ау = 6
будет несовместной и при каких неопределенной?
147. Определить к так, чтобы система
х + (1 + к) у - 0; (1 - *) х + ку = 1 + А;
(1 + *)*+ (12-*)у = -(1+й)
была совместна.
148. Доказать, что система
( 3* + 2у=10;
I тх-\-{т—1) г/= Зт + 1;
( 2тх + 4у ~ 7т — I
либо несовместна, либо неопределенна.
16
149. Противоречит ли равенство
а (Ь + с) — аЬ + с
равенству
а {Ъ + с) = аЬ + ас ?
Решить системы уравнений (150—154):
,5М|*+1|=4«/-4.
т-\у = 5 + \х-\\.
( 3|х| + 5у + 9 = 0;
15г- \ 2х — \у\ — 7 = 0.
153 I ^-у1 = 2:
154 ( |* + у1==1:
,54-1 1*| + |у|-1.
155. При каких целых значениях п решение системы
пх — у == 5;
2л; + Злг/ = 7
удовлетворяет условиям л; > 0, у < 0?
156. При каких значениях а и Ь многочлен
х4 — Зг> + За:2 + а* + Ь
делится на х* — Зх + 2?
157. При каких значениях а и Ь многочлен
х4 — Злг5 + Зх2 + ах + Ь
делится на х2 — Зх + 4?
158. Многочлен
хп + а1х»-1 + ... +а,,_1л: + яЛ
при делении на д: — а дает остаток Л, а при делении
на х—Ъ дает остаток В. Найти остаток от деления
этого многочлена на (х — а) (х—Ъ), если афЪ.
159. Многочлен
хп + а1хп"1 + ... + ап-1х + ап
при делении на х — а дает остаток Л, при делении на
х — ь — остаток В, при делении на х — с — остаток С.
Найти остаток от деления этого многочлена на
(х — а)(х — Ъ) (х — с), если а, Ь и с различны.
2 К. У. Шахно
17
160. При каком соотношении между ри ? многочлен
Xя + рх + Я делится (без остатка) на (х — а)2 и чему
равно в этом случае а?
161. Многочлен
х* + 2х* + ах2 + 2х + Ь
является квадратом другого многочлена. Найти этот
последний многочлен, а также числа а и Ь.
162. Определить Л, В и С так, чтобы имело место
равенство
*+3 А . Вх + С
(*+1)(*а+1) х+\ + х2+\ *
163; Убедиться, что система
2х + 3у — г + 4 = 0; 7х — 4у — Ъг + 4 = 0;
За: — У + 2г — 10 = 0; 8а: — 8у — 2г + 5 = 0
несовместна.
164. Дана система
а с Х\/ 6/'
Т+7-^('-*>
[а с р. \ ' о I
Выяснить, при каких X и ^ она совместна и
определить х, у, г.
165. Найти все решения системы
х — 2у + 4г = 0;
2х + у + Ъг = 0.
Решить системы уравнений (166—171):
166. [ х~а _ У — ь = г —г
(6 4- с)2 — а2 (с + а)2 — б2 (а + Ь)2 — с2 '
ч х + у + г = к(а + Ь + с).
167. Г х —(/ + 2 = 0;
(а + Ь)х— (а + с)# +{Ь + с)г =* 0;
аЬх — асу + Ьсг~ 1.
Числа а, Ь и с — различны,
18
168. ( ф + с) {у + г) —ах = Ь — с\
| (с + а)(г + х)~ Ьу = с — а\
\ (а + Ь) (х + у) *— сг = а— Ь,
если а + 6 + с ф 0.
169. шс + &/ + сг = Ьх + су + аг ~ сх + ау + Ъг
«= а + Ь + с.
Числа а, 6 и с — вещественные.
170.
Л#
171.
ш/ 4- 6л; С'
1 2Х _ ,,
аг + сх
уг -а
\ Ьг + су -и-
Х\ — #1 Х% — #2 __
[ хх + х2 + — + *^ == а.
™ »
тр
172. Определить вещественное число а так, чтобы один
из корней уравнения
4х2 — 15х + 4а3 = 0
был квадратом другого.
173. Составить квадратное уравнение с вещественными
коэффициентами, один из корней которого равен ' ..
174. При каких значениях а уравнение
(5а— \)х% — (5а + 2)х+3а — 2 = 0
имеет равные корни?
175. При каком вещественном значении т выражение
х2 + т(т — 1)л; + 36
есть полный квадрат?
176. При некоторых значениях р уравнение
х2 + Зх + 3 + р(х2 + х) = 0
имеет равные корни. Составить квадратное уравнение,
имеющее корнями эти значения р.
177. В уравнении
х2 — 2х + ? = 0
квадрат разности корней равен 16. Определить свободный
член уравнения.
19
178. При каких значениях т уравнение
9х2— \Ых— Ы+ 16 = 0
имеет корни, отношение которых равно двум?
179. При каких вещественных значениях т уравнение
2тх2 — 2х — Ът — 2 = 0
имеет различные корни?
180. Какими должны быть р и ц, чтобы уравнение
*2 + Рх + Я = 0
имело корнями ри??
181. При каком т уравнения
2х2 — (3т + 2)х+ 12 = 0;
4х2 — (9т — 2)х+ 36 = 0
имеют общий корень?
182. Показать, что уравнение
(х— 1) (х — 3) + т (х — 2) (х — 4) = 0
имеет вещественные корни при любом вещественном т.
183. Показать, что корни уравнения
(х — а)(х — Ь)-\-(х— Ь) (х — с) + (х — с)(х — а) =0
всегда вещественны, если а, Ъ и с — вещественны.
184. При каких целых к корни уравнения
/гх2 — (\—2к)х + к = 2
рациональны?
185. Доказать, что при нечетных р и (/ уравнение
х2 + рх + <7 = 0
не имеет рациональных корней.
186. Доказать, что уравнение
х4 + ах + 1 = 0
не имеет рациональных корней, если а — целое число,
но | а | Ф 2.
187. Доказать, что если уравнение
хт + а^-1 + а2хт~2 + ... + ат = 0
с целыми коэффициентами ах, а2, — » ат име^т
рациональный корень, то этот корень есть целое число.
188. Доказать, что если несократимая рациональная
дробь — является корнем уравнения
а0хт + агхт-1 + а2хт~2 + ... + ат = 0
с целыми коэффициентами а0, с^, а2, ... , ат, то ц есть
делитель а0, а р есть делитель ат.
20
189. Доказать, что если алгебраическое уравнение с
рациональными коэффициентами имеет корень вида
а-\-Ь]/с, где а, Ь и с — рациональные числа, причем
ЬФО, сфО и с не является квадратом рационального
числа, то оно имеет и корень вида а — ЬУс.
Решить уравнения (190—193):
190. (б* + 7)2 (3* + 4) (* + 1) = 6.
191. х2(1+л:)2-|-л:г = 8(1+л:)2.
192. х(х + 1)(х— 1)(х + 2) = 24.
193. (л-— 2)4 + (лг— З)4 = 1.
194. Решить уравнение
*■-— 21л2 + 140л:— 300 = 0,
если известно, что один из его корней вдвое больше
одного из двух других.
195. Составить алгебраическое уравнение наименьшей
степени с рациональными коэффициентами, имеющее
корнями
1 + К"3 и 2 4- У"3.
Решить системы уравнений (196—210):
196. | хг — Зл: + 2 = 0;
I х2 + 5х — 14 = 0.
197. Г хг + ху = Ъ
I у* + ху = 3.
198. | х4 + Зл:У + У* = 109;
1 л:2 + У2 + ли/=13.
199. Г (л: + У + О2 + (* + у)г = 25;
\ *• _ у2 = з.
200. Г х(у + 2) = 5;
у(г + х) = 8;
г(* + у) = 9.
л: + г/ + 2= 13;
201.
202.
л:2 + г/2-)-г2 = 61;
2«/г = х(2 + «/).
л:2 + Уг + г2 = 35;
Зл: + 2у2 — 7хг = — 14;
л-(г— 1) = 4.
21
203.
204.
205.
206.
207.
208.
209.
210.
х9 + «/2 + г2 =14;
ху + хг — уг = 7;
х + у + г = 6.
х2 + у1 — ахуг;
У2 + 22 = Ьугх;
22 + *2 = ОШ/.
а > 6 > с > 0, 6 + с > а
х2 + У2 = ^
ху + уг + гх = 47;
(г — х)(г — */) = 2.
*(л; + У + г) = а2;
У(х + у + г) = 1Р;
г (х + у + г) = с2.
а>0, 6>0, с>0.
г/ + г + #г = а;
г + х-\-гх = Ь;
х + у + ху = с.
с> —1, &> —1, с> —
л:2 = а + (г/ — г)2;
У2 = & +(г-*)2;
г2 = с + (х — г/)2.
а > 0, 6 > 0, с > 0.
#г г* х#
1.
Х» + »»+2*
Ьг + су
~ сх + аг ~~ ау+Ьх ~~ аа + Ь* + с2 '
а, 6, с — вещественны.
* + # + г = 0;
*2 4>у2 — г2 = 20;
л^ + У4 — г4 = 560.
211. Найти вещественные решения системы
Г 2х-у =1;
I 4* + */—2*г/ —г2 = 3.
Выяснить, являются ли уравнения равносильными
(212-214):
212. VР(х) =У~Щх) и Р(х)^0\х).
213. /Т^О^Г
214. У1&-
К(х) яУР(х) У<1(х) = К{х).
<Цх)
™»Ш-я(х)-
22
Решить уравнения (215—239):
215. у^х~^6 + УЮх+5 = 2.
216 (*-!)(* —2) —(*-3)(* —4) =1/-^
К*а — Зх+2 — Ух2 — 7*+12
217. л^ + З-У 2л:2-Зл: + 2 ==-|-(л;+1)-
218. ^ (7* - З)3 + 8 V (3 - 7л:)-3 - 7.
_1_ _1_
2 / \ 2
219. '
(« + 4)т+«Ыт-«-
220. (а + л:)3 + 4(а —л:)3 —5(а2—л:2)3 = 0.
V Ь-\-х ' Г а —л;
222. |/л: + 45 — Ух— 16 = 1.
224.1/1 + л: ——г4= = У"2 + л:
225. 4лг+ 1 + 2хУ2(2л:2 + 1) +
+ (2х + \)У 4л:2 + 4л: + 3 = 0.
226. 2УГ2х + У~х =31/ ^Г=^+2УГ2Х — У7'
" 2х + У х
227. У а + У~~х +
228. У~х + К 2л: — 3 == К 12 (х— 1).
229. У/~1Ъ + У~Х+УГ16 — У~Х=2.
230. К л:— 3 — 2Ух — 4 + У~х — 4 |/Т=Г4 = 1.
231. ^Ш"1^^-
/*+2 + /* —2 2
232. 1 + *-ТЛ2^:М2~ =а, У~2 + х- + УТ
1 + * + / 2* + г1 У 2 + х —У х '
233. |^1Л±^=1.
1 + ах т 1 — Ьх
23
234 г а + * 4- ^ ° + * = ^ * *
а * х ^Ь '
235. У~хп + "+^апхп* + |/а" + "Ул^ = 6,
где а > 0.
236. Уакхп~к-\-Ухкап~к = 2УШ, где л> А > О,
6>а>0.
237. ^ (х + I)2 + ^ (х — I)2 =4^"?^Л.
у а — х у а — х п Г х2
238.
239.
; + л:
У а — V х _ 1/ у а —/
Решить системы уравнений (240—243):
240. Г . т/7:
V х -
2п>
-= V х .
241.
242.
243.
х — у +
х* + у2 = 34.
х — У
■ + у
_20_
х + у'
У.*у
У~х-
■-у
■VI
1
ху2
-3.
_7_.
2 '
1^* + 0 —"К"
У~* + 7 — УТ
У х+У~У = 7.
20.
0,375;
( V х-У
\ * + У =
III. СОСТАВЛЕНИЕ УРАВНЕНИЙ
244. Турист, идущий из деревни на ж.-д. станцию,
пройдя за первый час 3 км, рассчитал, что он опоздает к
поезду на 40 мин, если будет двигаться с тою же
скоростью. Поэтому остальной путь он проходит со скоростью
4 км/час и прибывает на станцию за 45 мин до отхода
поезда. Каково расстояние от деревни до станции?
В примерах 234—239 л~ целое > 1.
24
245. Трехзначное число оканчивается цифрой 3. Если
эту цифру перенести влево (т. е. поместить вначале), то
новое число будет на единицу больше утроенного
первоначального числа. Найти это число.
246. Самолет летел сначала со скоростью 220 км/час.
Когда ему осталось пролететь на 385 км меньше, чем
пролетел, он изменил скорость и стал двигаться со
скоростью 330 км/час. Средняя скорость самолета на всем
пути оказалась равной 250 км/час. Какое расстояние
пролетел самолет?
247. Мне вдвое больше лет, чем Вам было тогда,
когда мне было столько лет, сколько Вам теперь; когда Вам
будет столько лет, сколько мне теперь, тогда сумма
наших Еозрастов будет равна 63 годам. Сколько лет
каждому?
248. Две автомашины выехали одновременно из одного
и того же пункта в одном и том же направлении. Первая
имеет скорость 50 км/час, а вторая 40 км/час. Спустя
полчаса из того же пункта выехала третья машина и,
догнав вторую, находилась в движении еще 1,5 час до
того, как нагнала первую. Какова скорость третьей
машины, если движение всех машин равномерное?
249. Пассажирский поезд идет из Л в В и после 5 мин
остановки в В идет далее в С. Спустя 14 мин после того,
как он покинул В, ему встречается скорый поезд, скорость
которого вдвое больше скорости пассажирского поезда.
Скорый поезд выехал из С в тот момент, когда
пассажирский поезд был на расстоянии 25 км от Л. Кроме того,
известно, что скорому поезду нужно 2 час, чтобы пройти
расстояние СВ, и что, если он из А сразу возвратится, то
прибудет в С на 0,75 час позже прибытия пассажирского
поезда. Сколько километров в час делает каждый поезд и
как удалены друг от друга пункты Л, В и С?
250. Некоторое количество денег было разложено на п
кучек. После этого из первой кучки переложили во вторую
— часть бывших в первой кучке денег. Затем из второй
1
кучки — часть оказавшихся в ней после перекладывания
денег переложили в третью кучку. Далее, — часть денег,
получившихся после этого в третьей кучке, переложили
в четвертую и т. д. Наконец из /г-й кучки — часть оказав-
25
шихся в ней после предшествующего перекладывания
денег переложили в первую кучку. После этого в каждой
кучке стало Л рублей. Сколько денег было в каждой
кучке до перекладывания?
251. Двое рабочих, работая вместе, могут окончить
некоторую работу в 12 дней. После 8 дней совместной
работы один из них заболел, и другой окончил работу одцн,
проработав еще 5 дней. Во сколько дней каждый из них,
работая отдельно, может выполнить эту работу?
252. Две бригады рабочих, работая одновременно, могут
выполнить некоторую работу в 8 дней. Если бы работало
2
-о- рабочих первой бригады и 0,8 второй, то работа была
бы выполнена в П-т- Дней. Во сколько дней могла бы
выполнить эту работу каждая бригада в отдельности?
253. Когда старшему брату было столько лет, сколько
сейчас среднему, тогда младшему было 10 лет. Когда
среднему будет столько, сколько сейчас старшему, тогда
младшему будет 26 лет., Сколько лет каждому брату, если
сумма лет старшего и среднего братьев в день рождения
младшего была в два раза больше числа лет младшего
в настоящее время? ;
254. Некоторый сплав состоит из двух металлов,
входящих в отношении 1:2, а другой содержит те же металлы
в отношении 2:3. Сколько частей каждого сплава нужно
взять, чтобы получить третий сплав, содержащий те же
металлы в отношении 17:27?
255. Поезд вышел со станции Л по направлению к В
в 9 час. В 15 час он остановился из-за снежного заноса.
Через 2 час путь был расчищен, и машинист, чтобы
наверстать потерянное время, повел поезд на остальном пути
со скоростью, превышающей скорость поезда до остановки
на 20%. Но поезд все же пришел с опозданием на 1 час.
На следующий день поезд, шедший по тому же
расписанию, тоже попал в занос, но на 150 км дальше от Л, чем
первый поезд. Простояв 2 час, он тоже пошел со
скоростью на 20% выше прежней, но нагнал лишь полчаса
и пришел в В с опозданием на 1,5 час. Найти расстояние
между Л и В.
256. На участке реки от Л до В течение так
медленно, что его можно принять равным нулю. На участке же
от В до С оно достаточно быстро. Лодочник проплывает
26
расстояние от А до С за 3 час, а обратно от С до А
(вверх) за 3,5 час. Если бы на всем протяжении от А
до С течение было такое же, как от В до С, то на весь
з
путь от Л до С потребовалось бы 2-т- час. Сколько
времени понадобилось бы в этих условиях, чтобы подняться
вверх от С до Л?
257. В сберкассу на книжку было положено 1640 руб.
и в конце года было взято обратно 882 руб. Еще через
год на книжке снова оказалось 882 руб. Сколько
процентов начисляет сберкасса в год?
258. Двое рабочих взялись сжать ржаное поле в
течение одного дня, причем каждый обязался сжать
половину поля. Первый начал работу на 2 час 16 мин раньше
второго. В полдень, когда ими уже было сжато 0,4 поля,
они приостановили работу для обеда и отдыха на 1,5 час.
Первый окончил свою часть в 7 час 54 мин, а второй
в 8 час 10 мин пополудни. В котором часу начал работать
каждый?
259. Два каменщика сложили вместе стену в 20 дней.
Во сколько дней выполнил бы работу каждый из них
отдельно, если известно, что первый должен работать на
9 дней больше второго?
260. Два пешехода А и В вышли одновременно друг
другу навстречу из городов М и N. Когда они
встретились, то оказалось, что А прошел на 6 км больше, чем В.
Если каждый из них будет продолжать путь с той же
скоростью, то А придет в N через 4,5 час, а В в М —
через 8 час после встречи. Определить расстояние
между М и N.
261. Два автомобиля выезжают одновременно
навстречу друг другу из А в В и из В в А. После встречи
одному приходится еще быть в пути 2 час, а другому
9
-«- час. Определить их скорости, если расстояние между
А и В равно 210 км.
262. Для печения пшеничного хлеба взято столько
килограммов муки, сколько процентов составляет припек
на эту муку. Для печения ржаного хлеба взято на 10 кг
больше муки, а именно столько килограммов, сколько
процентов составляет припек на ржаную муку. Сколько
килограммов взято той и другой муки, если всего
выпечено 112,5 кг хлеба?
27
263. Проходя первый участок пути в 24 км, паровоз
делал в час на 4 км меньше, чем когда проходил второй
участок в 39 км. На прохождение второго участка он
употребил на 20 мин больше, чем на прохождение
первого. Какова скорость паровоза на пераом участке?
264. По окружности длиною в 360 м движутся два
тела. Одно из них проходит в секунду на 4 м больше
другого и поэтому проходит всю окружность на 1 сек
скорее. Сколько метров в секунду проходит каждое
тело?
265. Окружность заднего колеса в 2 раза больше
окружности переднего. Если длину окружности заднего
колеса уменьшить на 1 м, а переднего увеличить на 1 м,
то на протяжении 60 м заднее колесо сделает на 30
оборотов больше переднего. Определить длину окружности
каждого колеса.
266. Трамвайная линия имеет длину 15 км. Если
увеличить скорость трамвая на 3 км/час, то трамвай будет
затрачивать на каждый рейс на полчаса меньше, чем
теперь (рейсом называется пробег трамвая туда и обратно).
Сколько времени затрачивает теперь трамвай и какова его
скорость?
267. В ремонте дома участвовали плотники и маляры.
Те и другие получили за работу одну и ту же сумму, но
маляров было двумя меньше, чем плотников, и поэтому
каждый маляр получил одним рублем больше плотника.
Сколько было плотников и сколько маляров, если
известно, что число рублей, уплаченных им всем, было на 26
больше утроенного числа всех рабочих?
268. От Москвы до Ленинграда 650 км.
Пассажирский поезд проходит это расстояние на 12 час скорее
товарного, так как его часовая скорость на 24 км больше.
Сколько километров в час проходит каждый поезд?
269. От дома до школы 400 м. Ученик старшего
класса делает на этом пути на 300 шагов меньше, чем ученик"
младшего класса, так как у него шаги на 30 см больше.
Определить длину шага каждого.
270. Магазин купил кусок сукна за _ 200 руб. 5 м из
этого куска остались непроданными/ а" остальное сукно
было продано за 190 руб., при этом на каждом метре
было получено 1,5 руб. прибыли. Сколько метров сукна
было в куске?
271. Куплено два сорта некоторого товара, причем
28
второго сорта на 15 кг больше первого. За второй сорт
заплачено 32 руб., а за первый 22,5 руб. Сколько
куплено килограммов того и другого сорта, если килограмм
второго сорта стоил на 10 коп. дешевле килограмма
первого?
272. При двух последовательных одинаковых
процентных повышениях заработной платы сумма в 100 руб.
обратилась в 125 р. 44 к. Определить, на сколько процентов
повышалась заработная плата?
273. В сосуде было 20 л чистого спирта. Часть этого
спирта отлили; а сосуд долили водой. Затем снова отлили
столько же литров, сколько в первый раз, и сосуд опять
долили водой. После этого в сосуде оказалось чистого
спирта втрое меньше, чем воды. Сколько спирта отлили
в первый раз?
274. У мальчика имеются двухкопеечные монеты.
Играя он укладывает их на площадке плотно одну к
другой то в виде квадрата, то в виде правильного
треугольника, используя каждый раз все монеты. В последнем
случае в стороне содержится на 2 монеты больше, чем
в первом. Какая сумма денег имеется у мальчика?
275. В шахматном турнире двое из участников
выбыли, сыграв только по три партии каждый. Поэтому на
турнире было сыграно всего 84 партии. Сколько было
участников первоначально и играли ли выбывшие
участники между собой?
276. Куплено материи двух сортов на сумму 15 р. 20 к.
Если бы цена материи первого сорта была выше, а
второго ниже на одно и то же число процентов, то первый
сорт стоил бы 15 руб. а второй 2 р. 40 к. Сколько стоил
первый сорт в действительности?
277. Из Тулы по направлению к Вязьме вышел
товарный поезд. Спустя 5 час 5 мин по той же дороге вышел
из Вязьмы в Тулу пассажирский поезд. Оба поезда
встретились на промежуточной станции. От этой станции
товарный поезд шел до Вязьмы 12 час 55 мин и от той же
станции пассажирский поезд шел до Тулы 4 час 6 мин.
Сколько времени употребил каждый поезд на
прохождение всего пути между Вязьмой и Тулой?
278. Студенты взяли на лодочной станции лодку на
прокат. Сначала они спустились на 20 км вниз по течению
реки, затем повернули обратно и вернулись на лодочную
станцию, затратив на всю прогулку 7 час. На обратном
29
пути, на расстоянии 12 км от лодочной станции, они
встретили плот, проплывавший мимо лодочной станции как
раз в тот момент, когда они отправлялись на прогулку.
Определить, с какой скоростью двигалась лодка вниз по
течению и какова скорость течения?
279. Из двух населенных пунктов выходят навстречу
друг другу два курьера и встречаются в некотором
пункте Мг. Если бы первый курьер вышел на час
раньше, а второй на полчаса позже, то они встретились бы на
18 мин раньше, чем в действительности. Если бы второй
вышел на час раньше, а первый на полчаса позже, то
они встретились бы в пункте, отстоящем отЛ^на 5600 ж.
Найти скорости обоих курьеров.
280. Несколько человек взялись вырыть канаву и
могли бы окончить работу за 24 час, если бы делали ее все
одновременно. Вместо этого они приступили к работе
один за другим через равные промежутки времени, и
затем каждый работал до окончания всей работы. Сколько
времени они рыли канаву, если первый, приступивший
к работе, проработал в 5 раз больше, чем последний?
281. Сплав из двух металлов весом в Р кг, будучи
погруженным в воду, теряет в своем весе А кг. Такой же
вес первого из двух составляющих металлов,
погруженного в воду, теряет В кг, а второй — С кг. Найти вес
составляющих сплав металлов и исследовать возможность
решения задачи в зависимости от величин Р, А, В и С.
282. От двух кусков сплава с различным процентным
содержанием меди, весящих т кг и п кг, отрезано по
куску равного веса. Каждый из отрезанных кусков
сплавлен с остатком другого куска, после чего
процентное содержание меди в обоих сплавах стало одинаковым.
Сколько весил каждый из отрезанных кусков?
283. Объем А составляет т-ю часть суммы объемов
В и С, а объем В — п-ю часть суммы объемов А и С,
Какую часть суммы объемов А и В составляет объем С?
284. Две точки движутся с постоянными скоростями
по окружности длиною Ь, Если они движутся в разных
направлениях, то встречаются каждые 1Х сек. При
движении в одном направлении одна точка настигает
другую через каждые /2 сек. Определить скорости обеих
точек.
285. Из А в В отправилась лодка. Когда лодка
прошла уже / км, из Л в В вышел пароход, который при-
30
шел в В на / час раньше лодки. Каково расстояние
между А и В, если скорость лодки составляет V км/час9 а
скорость парохода хю км/час}
286. Мастер дает сеанс одновременной игры в
шахматы на нескольких досках. В конце первых двух часов
он закончил р% партий выигрышем, а / партий
проиграл. За следующие два часа он выиграл у д%
оставшихся противников, т партий проиграл и остальные п партий
закончил вничью. На скольких досках шла игра?
287. В сосуде содержится а л р %-ного раствора
азотной кислоты. Сколько литров ц %-ного раствора той же
кислоты нужно влить в сосуд, чтобы после добавления
некоторого количества воды, доводящего общий объем
смеси до Ь л, получилась бы кислота крепостью г |%?
288. В одном сосуде находится а л р%-ного раствора
кислоты, а в другом Ь л ц ,%-ного раствора той же
кислоты. Из каждого сосуда отлили по одинаковому
количеству литров и взятое из первого вылили во второй,
а взятое из второго вылили в первый. Сколько литров
было взято из каждого сосуда, если в сосудах оказался
раствор одной и той же крепости?
289. Два велосипедиста, выехав одновременно с
разными, но постоянными скоростями из пункта А в пункт
В, достигнув его, сразу поворачивают обратно. Первый
велосипедист, обогнав второго, встречает его на
обратном пути на расстоянии а км от В, затем достигнув А
и снова повернув к В, он встречает второго
велосипедиста, пройдя к-ю часть расстояния от А до В. Найти
расстояние от А до В.
290. В некоторой точке круглого биллиарда радиуса/?
на расстоянии а от его центра находится упругий шарик.
В какую точку борта нужно направить шарик, чтобы он,
дважды отразившись от борта, вернулся в исходную
точку? Размерами шарика пренебрегаем.
291. Сферический баллон с толщиной стенки е,
изготовленный из материала плотности й, наполнен
жидкостью плотности &. Каков должен быть внутренний
радиус /? баллона для того чтобы при погружении его
в жидкость плотности Д имело место равновесие? Какому
условию должны удовлетворять плотности О и Д,
чтобы задача была возможна?
292. Средний годовой процент прироста населения из
года в год остается постоянным. Если бы годовой про-
31
цент прироста увеличился на к, то через п лет
численность населения была бы в два раза больше, чем при
нормальных условиях. Определить годовой процент прироста
населения.
293. Сосуд, наполненный последовательно двумя
жидкостями, плотности которых й и О, весит соответственно
д и ф /сг, включая сюда и вес самого сосуда. Найти вес
сосуда и его объем. Найти условия возможности задачи.
294. Два'поезда выезжают одновременно из А и В
навстречу друг другу и встречаются на расстоянии р км
от В. Через / час после встречи второй поезд,
миновав пункт Д находился в ц км от него, а первый в это
время, миновав пункт В, находился от второго поезда
на расстоянии в два раза большем, чем расстояние
между пунктами А и В. Найти скорости поездов .и
расстояние между А и В.
295. Число х в т раз больше разности чисел у и г,
а число у в п раз больше разности х и г. Найти
зависимость между тип, если известно, что г в два раза
больше разности чисел х и у. Числа х, у и г не равны нулю.
296. Часы показывают в некоторый момент на т мин
меньше, чем следует, хотя и спешат. Если бы они
показывали на п мин меньше, чем следует, но уходили бы
в сутки на I мин больше, чем уходят, то верное время они
показали бы на сутки раньше, чем покажут. На сколько
минут в сутки эти часы спешат?
297. Дети делят орехи. Первый взял а орехов и п-ю
часть остатка; второй — 2а орехов и п-ю часть нового
остатка; третий — За орехов и п-ю часть нового остатка
и т. д. Оказалось, что таким способом разделены все
орехи поровну. Сколько было детей?
298. Колхоз купил для заправки тракторов на а руб.
лигроина и на такую же сумму керосина, всего п кг.
Сколько килограммов куплено лигроина и сколько
керосина, если килограмм первого на Ь руб. дороже
килограмма второго?
299. Из пункта А в пункт В выехала машина с
почтой. Через I мин за ней выехала другая. Двигаясь со
скоростью V км/час, она нагнала первую и, передав забытый
срочный пакет, повернула назад. В пункт А вторая
машина прибыла одновременно с прибытием первой в пункт
В. С какой скоростью двигалась первая машина, если
расстояние между А и В равно й км?
32
300. Две бригады рабочих заработали по одинаковому
числу руб. В первой бригаде было на а рабочих меньше,
чем во второй, вследствие чего каждому рабочему второй
бригады досталось на Ъ руб. меньше, чем каждому
рабочему первой бригады. Число рублей, заработанных
каждой бригадой, на с больше числа рабочих в обеих
бригадах вместе. Сколько было рабочих в каждой бригаде?
301. Двое рабочих выкопали ров, работая один после
другого. При этом первый работал а дней и выполнил
часть всей работы, равную —. Если бы они работали
вместе, то ров был бы вырыт в число дней, равное
среднему арифметическому между числом дней, в течение
которых работал первый, и числом дней, в течение которых
работал второй. Сколько дней работал второй?
302. По одной и той же окружности движутся два тела
в одну и ту же сторону. Длина окружности равна а м.
Одно тело проходит окружность на р мин скорее другого
тела. Определить, сколько метров в минуту проходит
каждое тело, зная, что они при движении сходятся
каждые <7 мин.
303. Наняты двое рабочих по разным ставкам.
Первый получил а руб., а второй, работавший меньше
первого на п дней, получил с руб. Если бы первый работал
столько дней, сколько второй, а второй столько, сколько
первый, то они получили бы поровну. Сколько дней
работал каждый?
304. Группа экскурсантов должна была заплатить за
обед в ресторане а руб. Но у Ь участников не оказалось
в наличии денег и поэтому каждый из остальных внес
еще с руб. Сколько было экскурсантов?
305. Скорый поезд был задержан у семафора на
р мин и наверстал опоздание на перегоне в б, км, пройдя
его со средней скоростью на V км/час больше той, какая
полагалась по расписанию, Какова средняя скорость на
этом перегоне по расписанию?
306. Два вкладчика положили в сберкассу
одинаковые суммы. Первый взял вклад по истечении а месяцев
и получжл т руб., а второй взял вклад по истечении Ь
месяцев и получил п руб. Сколько каждый из них
положил в сберкассу и сколько процентов начисляет
сберкасса?
307. В трех сосудах находится одинаковая жидкость
3 К. У, Шахно
33
в неравных количествах. Если половину содержимого
(по объему) одного сосуда разлить поровну в два
другие, а затем половину содержимого другого сосуда,
оказавшегося после первого разлива, разлить поровну в два
другие и после этого половину содержимого третьего
сосуда разлить поровну в два другие, то во всех сосудах
окажется жидкости поровну, а именно псМб л. Сколько
было литров жидкости в каждом сосуде вначале?
(Задачу решить арифметически).
308. Товарный поезд прошел путь от Ленинграда до
Москвы со средней скоростью 20 км/час, а от Москвы до
Ленинграда со средней скоростью 30 км/час. Какова
средняя скорость поезда на всем пути (время,
потраченное на остановку в Москве, в расчет не принимается)?.
309. Доказать, что разность между любым числом и
числом, изображенным теми же цифрами, но
написанными в обратном порядке, делится нацело на 9«
IV. ПРОГРЕССИИ*
310. Могут ли числа У~Ъ> 2, У"8 быть членами (не
обязательно соседними) арифметической прогрессии?
311. Доказать, что в арифметической прогрессии аъ
а2, ... любые четыре члена ат, ал, ал, аи для которых
т + п = к + /, связаны соотношением
ам + ап = ак + а1-
312. Доказать, что три члена ап_ъ ап, ап+\
арифметической прогрессии с^, а2, ... связаны соотношением
— °п—1 "Ь ап+1
ап ~ 2
313. Найти сумму двадцати членов арифметической
прогресии аг, а2, ..., если ав + а9 + а12 + а15 = 20.
314. Найти арифметическую прогрессию а^ а2, ... ,
если а^ + а2 + а3 = 9 и ад^з = '5.
315. Найти арифметическую прогрессию, если сумма п
ее членов 5Л = 2п2 — Зп. •
316. Найти десятый член арифметической прогрессии,
если сумма п ее членов 5Л = Зп2 — 2п.
* Во всех приведенных здесь 'задачах на прогрессии
подразумевается, что члены прогрессий -~ вещественные, если специально не
оговорено противное.
34
317. Найти арифметическую прогрессию, у которой
сумма любого числа членов, начиная с первого, в четыре
раза больше квадрата числа членов.
318. Число членов арифметической прогрессии равно 10.
Сумма членов, стоящих на четных местах, равна 15, а на
нечетных—12,5. Найти все члены прогрессии.
319. Дано, что в арифметической прогрессии ар = ц,
ад = р (ап — п-и член прогрессии). Найти ат.
320. Числа а2, б2, с2 образуют арифметическую
прогрессию. Доказать, что числа
1 1 1
Ь + с * с+а* а + Ь
также образуют арифметическую прогрессию.
321. Найти сумму всех несократимых дробей со
знаменателем 3, заключающихся между целыми числами т
и-п (т < п).
322. Доказать, что если в арифметической прогрессии
8т = 8я, где 5^—сумма первых к членов прогрессии, то
323. Дано, что в арифметической прогрессии
$п ~~ л» •
Доказать, что
ат _ 2т — 1
ап 2л — 1
324. Параллелограмм пересекается двумя рядами
прямых, параллельных его сторонам. Каждый ряд состоит из
т линий. Сколько всех возможных параллелограммов
можно составить из этих линий?
325. Числа 3, 5, 9, 15, ... таковы, что разности между
ними образуют арифметическую прогрессию. Найти п-и
член этой последовательности чисел.
326. Вычислить сумму
12_22 + 32 — 42+ ... +(— 1)«-1/?А
327. Какие из последовательностей
2, 0, 0, ...
являются геометрическими прогрессиями?
328. Могут ли числа 10, 11, 12 быть членами (не
обязательно соседними) геометрической прогрессии?
3*
35
329. Доказать, что в геометрической прогрессий а»
а2, ... любые четыре члена ат, ап, ак, аь для которых
т -(- п== к-\-/, связаны соотношением
атап- акаи
330. Доказать, что три члена ап__Х1 ап> ап+\
геометрической прогрессии ах, а2> ... связаны соотношением
331. Если числа х, у, г составляют геометрическую
прогрессию, то
(х + у + г)(х — у + г) = х2 + у2 + г2.
332. Найти сумму п чисел вида
5, 55, 555, 5555, ...
333. Доказать, что
11 ... 1 55 ... 56 = 33 ... 342.
334. Сумма первых трех членов геометрической
прогрессии равна 3,5. Сумма квадратов тех же членов
равна 5,25. Найти первый член и знаменатель прогрессии.
335. В арифметической прогрессии даны ее члены
ат+п = А и ат—п = В. Найти ее члены ат и ап.
336. В геометрической прогрессии даны ее члены
= В. Найти ее члены ат и ал.
337. Доказать, что если числа а, 6, с, й составляют
геометрическую прогрессию, то
(Ь — с)2 + (с — а)2+ (й — Ь)2=(а — й)2,
338. Найти сумму
339. Доказать, что
(1 + х + х2 + ... + хп)2 — хп =
= (1+х + х2 + ... +хп~1)(1 +х + х2+ ... + *"+*)•
340. Найти произведение п первых членов
геометрической прогрессии с положительными членами, зная их
сумму 5 и сумму 51 их' обратных величин.
341. Найти сумму
х + 2х2 + З*3 + ... + пхп.
36
342. Известно, что сумма бесконечно убывающей
геометрической прогрессии еел? предел 5Л при п -> оо, где
л —-сумма первых членов прогрессии. Нужно ли это
доказывать?
343. Сумма членов бесконечно убывающей
геометрической прогрессии равна 9, а сумма квадратов ее
членов — 40,5. Найти первый член и знаменатель прогрессии.
344. Сумма членов бесконечно убывающей
геометрической прогрессии равна 3, а сумма кубов ее членов рав-
на —т~-. Написать три первых члена этой прогрессии.
345. Сумма членов бесконечно убывающей
геометрической прогрессии, стоящих на нечетных местах, равна 36,
а сумма ее членов, стоящих на четных местах, равна 12.
Найти эту прогрессию.
346. Первый член бесконечно убывающей геохметри-
ческой прогрессии равен 1. Каждый же из остальных
членов в 2-^- раза меньше суммы двух смежных с ним.
Найти сумму этой прогрессии,
347. Найти бесконечно убывающую геометрическую
прогрессию, первый член которой равен 1 и каждый член
в три раза больше суммы всех следующих за ним
членов.
348. Сумма первых четырех членов бесконечно
убывающей геометрической прогрессии равна 15. Сумма первого
и четвертого членов в 1,5 раза больше суммы второго
и третьего. Найти сумму прогрессии.
349. Найти знаменатель бесконечно убывающей
геометрической прогрессии так, чтобы сумма ее первых шести
членов составляла «^- суммы всех ее членов.
350. В арифметической прогрессии 11 членов. Первый
член равен 24. Первый, пятый и одиннадцатый члены
составляют геометрическую прогрессию. Написать все члены
арифметической прогрессии.
351. В арифметической прогрессии, состоящей из 9
членов, первый член равен 1, а сумма равна 369.
Геометрическая прогрессия тоже содержит 9 членов, причем
первый и последний члены ее совпадают с соответствующими
членами данной арифметической прогрессии. Найти
седьмой член геометрической прогрессии.
37
352. Три числа составляют геометрическую прогрессию.
Если второй член увеличить на 8, то данная прогрессия
обратится в арифметическую, но если затем третий член
будет увеличен на 64, то она опять обратится в
геометрическую прогрессию. Найти эти числа.
353. Между числом 3 и неизвестным числом вставлено
еще одно число так, что все три числа образуют
арифметическую прогрессию. Если средний член этой прогрессии
уменьшить на 6, то получится геометрическая прогрессия.
Найти неизвестное число.
354. Три числа, сумма которых 114, можно
рассматривать как три последовательных члена геометрической
прогрессии или как первый, четвертый и двадцать пятый члены
арифметической прогрессии. Найти эти числа.
355. Из точек А и В одновременно начали двигаться
два тела навстречу друг другу. Первое в первую минуту
прошло 1 м, а в каждую последующую проходило на
0,5 м больше, чем в предыдущую. Второе тело проходило
каждую минуту по 6 м. Через сколько минут оба тела
встретились, если расстояние между А и В равно
117 ж?
356. Возможны ли три таких числа ах, аг, а3, чтобы
они были одновременно первыми, вторыми и третьими
членами арифметической и геометрической прогрессии?
357. В многочлене ах* + Ь& + 4х2 -\-(1х-{-1
коэффициенты а, & и 4 образуют геометрическую прогрессию,
а 4, а и Ъ — арифметическую. Многочлен делится на
1 + х + л2- Найти частное от деления первого
многочлена на второй.
358. Даны две прогрессии: арифметическая
и геометрическая
в которых ах = Ъх и аг = &2- Обе прогрессии
возрастающие, и все члены этих прогрессий положительны.
Доказать, что все члены арифметической прогрессии, начиная
с Од, меньше соответствующих членов геометрической
прогрессии.
за
V. ЛОГАРИФМЫ
а) Общие свойства логарифмов
359. Почему а°ёаХ = х?
360. Что больше, Ь§а2 или 1о§аЗ?
361. Доказать, что \о&ьа\о*аЬ = 1.
362. Доказать, что 1о§ьа==~~.
363. Когда верна формула 1о^а2 = 2 1о§(— а)?
364. Доказать, что
, 2а-Ь36 _ 1о8 а + \оё Ь
108 5 ~~ 2 '
если 13а6 = 4а2+962.
365. Доказать, что
если а2 -{- Ь2 = 7аЬ.
366. Доказать, что
если а2 + б2 = с2.
367. Вычислить 1о§89,8, зная, что 1обю2 = а и
1°вю 7 = &-
368. Доказать, что *°|^ =1 + 1оба6,
1оёг,(1о&* Д)
369. Доказать, что а 1о& а == 1о& а.
370. Доказать, что \о§ьа = \о%ьпап.
371. Что больше, 1о&3 или 1о&169?
372. Вычислить 10^^ 8, зная, что 1о&12 3 = а.
373. Доказать, что
1°ёа1аг ... ап х = 1 1 ~ 1
1 1
374. Дано: у = 10 1-1*^; г- 10 '"Ч*"'.
Доказать: * = 10 1-1о^о^#
375. Доказать, что если а, Ь и с — три
последовательных члена геометрической прогрессии, неравные между
собой, то
Ь&> х — 1о& л: 1о& х '
376. Доказать, что если 1о§йх; Ь^г, 1о§Лх образуют
арифметическую прогрессию, то
л2*=(Ал)1(«*т.
377. Доказать, что если
ла = (*л),ов*г«>
то \о&кх; \о^тх\ \о&пх образуют арифметическую
прогрессию.
378. Найти ошибку в следующем «доказательстве»:
так как
4- < 4»то (4-.) <(4-); ,овю(4-) < 1с*1о(4-)2'
31о§104-< 21оё1о4-; 3<2.
б) Логарифмические и показательные уравнения
Выяснить, являются ли равносильными уравнения
(379—384):
379. 1о§ Р(х) = 1об<2 (а:) и Я(х) = <?(*).
380. 1о8Я(*) + 1ов<Э (*) = Я(*) и 1об[Я(х)(Цх)] = К(х).
381. 1обЯ(*) — 1ог С (*) = /?(*) и 1о8-^ = /?(*).
382. л1оеЯ(*) = <г(х) и 1о8 (Я (*)]«== (>(*); /1 —четное
число.
383. ах = а? и х = у\ (а > 0).
384. 1о& (*2 — 1) = 1 и 1о& (х— 1) + 1о& (х + 1) = 1.
385. Ученик решает уравнение 1о8(х — I)2 = 2 1о83
так! 2 1о8(х—1) = 2 1о§3; 1о§(л: — 1) = 1о83; х— 1=3;
х = 4. Нетрудно проверить, что * = 4 удовлетворяет урав-
нению. Но кроме этого корня уравнение имеет еще и
корень х = — 2. Почему он был потерян?
Решить уравнения (386 — 408):
386. (1с«, /"5)2 — 1о§, 5 ^5~+ 1,25 = 0.
387. 3 УЫх~+ 21§ ]/ 4" = 2.*
388. |Л>^5|/ЗЧ1об^5 1/5~= - Кб 1об, ^5.
389. (|^,0|Ь*-1 = 5.
390. /|^-'-51^ = 1/1о.
391. ^* + ^ + з 1 2 |
К* + 1—Т~/Т+Т+ 1
392. / 2 1ё (— х) = \§ У *Г
393. 1о§2У^= 1.
394. 1о& (л: + I)2 + 1о§21 х + 11 = 6.
395. х =9.
1ое ._<* - 2)
396. л: У* =9.
Т |0(Г/Г(Л' ~х) , а
397.* * = Л'4; (а > 0).
398. К'оёж /5^1оё5 л: = — 1.
399. 21ое,3 \о&х . з = 1о§9/гЗ.
400. V 1о§в ^"а* + 1о&г V~ах +
401. 1обл* • 1с • (1 + 1о&а) = 1о&* • 1о&* • 1о§ас.
402. 1о§3 * + 1о§/з"х + ]о8 1 * = 6-
Т
403. 1о& х + (1овв *)2 + (1о& *)3 + • • • = 4"'
404. Ю8(^±1±') = з.
1об у х — 40
__1_ 1_
405. 4 * +6 *=9~
* Знаком 1§ ж обозначается десятичный логарифм числа х.
41
406.
407.
408.
Решить
409.
410.
411.
412.
413.
414.
415.
416.
417.
418.
419.
420.
4* + / ** - 2 _ д ^ 2* _ 1 + /,* _ 2 _ (ч
27* + 12* = 2 • 8*.
системы уравнений (409 — 424):
кУ(хТ~у7=и
Г 1оеал — 1о&,.у = т;
\ \о§а*х — \о§а,у = п.
[ (1о§а х + \о%а у — 2) 1а =* — 1;
| л; + у — 5а = 0.
Г 1об/Го (л:2 + У2У= 21ое10 (2а) + 21о§100 (*» - г/2);
ху = а*.
ху = 40;
Х1«у = 4.
5** . ЗУ = 675;
1°б^(* + У) =
0*Ч-7х+12 = 1;
* + У = 6.
8* =10*/;
2х = 5у.
л;* + у = г/12;
*/* + </ = х3.
Ух + П
= у
/* + У7в,т
Хт
1обр -г =
У;
х_ _ 1оеРд;
г/ ~ \щРу •
*у = у*;
а* = ЬУ; {аф\, Ьф 1).
42
421. {
422. |
423.
хт = упт
(1 + УУ « 100;
0/4-2/+1)*-' = -|^.
г
3 16
Уу6\
424.
У «=У *,
5г = 9(1/1 +VI/).
г = у^1 + К1/;
х' = уг\
у* = х3.
VI. СОЕДИНЕНИЯ И БИНОМ НЬЮТОНА
425. Найти тип, если
С™+2 2СЙ$^С^$1 = 0,6:1:1.
426. Доказать, что
Сш ■+■ 1 • /^ш —• 1 ■ о /"»#1 >^»/п -}-1
427. Собрание, на котором присутствует 30 человек,
в том числе две женщины, выбирает четырех человек для
работы на избирательном участке. Сколько может
встретиться случаев, когда в число избранных войдут обе
женщины?
428. Нужно распределить преподавание в шести
классах между тремя преподавателями, Сколькими
способами можно произвести это распределение1 если каждый
должен получить два класса?
429. В вещевой лотерее разыгрывается 5 предметов.
Первый подошедший к урне вынимает из нее 5 билетов.
Каким числом способов он может их вынуть, чтобы 3 из
них оказались выигрышными? Всего в урне 100 билетов.
430. Экскурсанты разделились на две равные группы
для розыска заблудившегося товарища, Среди них есть
только 4 человека1 знакомых с местностью, Каким числом
43
способов они могут разделиться так, чтобы в каждую
группу вошло 2 человека, знакомых с местностью, если
всего их 16 человек?
431. Комсомольцы строительной организации
выделили в^помощь подшефному детскому дому бригаду в 5
человек. В составе комсомольской организации 25
человек, в том числе 5 маляров, 4 плотника и 2 штукатура.
Каким числом способов можно укомплектовать бригаду,
чтобы в нее вошли рабочие всех этих специальностей по
одному?
432. Для культпохода куплено 2п билетов в театр на
места, находящиеся в одном ряду партера (в ряде 2 л
мест). Сколькими способами можно распределить эти
билеты между лицами данной компании, состоящей из п
мужчин ил женщин, чтобы не сидели рядом двое
мужчин или две женщины?
433. Девять из десяти карт, среди которых есть
червонный, раздаются трем лицам так, что первый
получает 3, второй 4, а третий 2. Сколько существует
способов раздачи, при которых червонный- туз попадает к
третьему лицу?
434. Сколько различных натуральных чисел можно
составить из цифр 0, 1,2, 3, 4, если в каждое число входит
каждая из данных цифр не более одного раза?
435. Сколько различных двузначных чисел можно
составить из цифр 0, 1, 2, 3, если цифры 0, 1, 2, входят
в каждое число не более одного раза, а цифра 3 —
не более двух раз?
436. Сколько различных пятизначных чисел, больших
20 000, можно составить из цифр 1, 2, 3, 4, если цифры
2, 3, 4 входят в каждое число по одному разу, а
цифра 1 —два раза?
437. Сколько различных пятизначных чисел без
повторения цифр можно составить из цифр 1, 2, 3, 4, 5 так,
чтобы четные цифры не стояли рядом?
438. Найти коэффициент при х4 в выражении
х (1 — *)4 + х2 (1 + 2а:)8 + х* (1 + З*)12,
не выписывая лишних членов.
439. Доказать, что И10—1 делится на 100.
440. Доказать, что коэффициент при х5 в
разложении по степеням х выражения
44
[ (5— 2) X2 + ПХ — 5] (X + 1)1
равен пСгГ2.
441. Доказать, что
\* + (с1пУ + (с2пУ+ ... +КУ = сп2п.
442. В разложении^ |/* ^—^биноминальный
коэффициент третьего члена на 44 больше коэффициента
второго. Найти свободный член.
443. В разложении (]/]с-^. 3/г- ) сумма
коэффициентов на 240 меньше суммы коэффициентов разложения
{а + Ь)2п. Найти третий член первого разложения.
444. Сколько рациональных членов содержится в
разложении
(|/2 + Гз),0°?
(V
445. Найти все рациональные члены разложения
"о 1 \20
2 Т=г~\ » не выписывая члены иррациональные.
446. Найти все те значения л, при которых какие-либо
три последовательных коэффициента разложения бинома
(л: -{- а)п являются тремя последовательными членами
арифметической прогрессии.
447. Найти показатель п бинома (х + 2)", зная,
что десятый член разложения этого бинома имеет
наибольший коэффициент.
448. Доказать, что наибольший коэффициент
разложения (а + Ь)2п есть число четное.
449^ Найти наибольший член разложения(1+|/Г2)50-
450. Определить номер наибольшего члена
разложения (р -}- я)п по убывающим степеням буквы р,
предполагая, что р>0; <7>Ф Р + ?==^. При каких условиях:
а) наибольший член будет первый? б) наибольший член
будет последний? в) разложение будет содержать два
одинаковых последовательных члена, превышающих все
остальные члены разложения?
451. В разложении (*+1+—) найти свободный
член, не выписывая членов, зависящих от х.
452. В разложении (1 +х — х2)2Ь найти тот член, у
которого показатель степени х в три раза больше суммы
всех коэффициентов разложения.
45
453. Найти коэффициент при у? в выражении
(1+х)» + (1 **)* + (!+*)' + ...+.(1+*)15.
454. Доказать:
(1 + х)п + (1 + х)п~1 х + (1 +*)"-2л:2 + ... + (I + х) хп~1 +
+ ... +1,
п — натуральное число.
455. Разложить по убывающим степеням х — 2
многочлен
х* — 1IX3 + 43*2 — 72* + 45.
VII. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ
ВЫРАЖЕНИЙ
Доказать тождества (456—484):
456. 31п4а + со5'4ас1б 2а = ' ~ ^ а .
457. *е За = *8 а *8 (60° + а) *8 (60° — «)•
458.1.(35° +.а)1§(25°-а)==^;;;;0о:^:;;;.
ЛГЛ СОЗ а 4- 81П а х о I г»
459. -^— = 1& 2а + зес 2а.
СОЗ а — 51П а ь '
460. з'тх П + 1б^*б -у-) = *б*-
461. 1§3а—1е2а —1еа = 1§а1б2а1бЗа.
462. с!§а —1§а —21§2а —41е4а = 8с1й8а.
463. 1е**вР + *вР*8Т + *вТ*в*=1. а + Р + Т^-г-
464. 51П 2П0С + 31П 2я Р +• 31П 2П у =
= (— 1)п + 1 4 • 8Ш/1а 51ППР 51ППу,
если а -|- Р + Т = ^ л — целое число.
465. 1ёп<х + {&п$-{-{ёпч = {%па 1§лр 1&лт» если
л + Р + т = *• Л — целое число.
^Ь0- СО8 0-з1п* 81П(* + 0 - Т8 I* + »)•
467. соз2 а + соз2 р <» 2 соз а соз р соз (а + Р) = 81п2 (а + р).
468. соз2 (а + Р) + соз2 (а — Р) -, соз 2а соз 2р = 1.
469. 4 31П а 81П (60° — а) 31п (60° + а) ~ 31П За.
46
470. 16 зт 10° зт 30° зт 50° зт 70° зт 90° => 1.
471. зт 10° зт 20° зт 30° зт40° соз 10° соз 20° X
X соз 30° соз 40° = -Д-.
472. СОЗ-тг СОЗ —?— = -7-.
О 0 4
473. соз-^- соз * соз —^- = 0,125.
474. соз 55° соз 65° соз 175° = — 1 + ^3.
475 1 V* -4
*/0* 811110е СОЛО8""*-
.-л * 2тс 1
476. соз -с соз -е- = -у.
477. соз — + соз — + соз -у = — -^-.
478. зт47° + з1п6Г — 31п11°— зт 25° = соз 7°.
479. соз 24° + соз 48° — соз 84° — соз 12° = ~.
480. зт 10° 4* зт 20° + зт 30° + зт 40° + зт 50° =
= 51п25° зт30° созес5°.
481. ^2а *е(30°— а) + ^ 2а 1ё (60° ■« а)+
+ 1ё(60о-а)^(30°^а)- 1.
лап 1 • о п 51П 10,5л;
482. 1+2^3 7* = -;^^.
3
/ \ / \ 8Ш"2"~а
483. 4 соз 30°— 4" зт 60° ^ = \
484. зт2 а + зт2 р + зт2 у = 2 соз а соз р соз у + 2, если
а + Р + Т ~ *•
Привести к виду, удобному для логарифмирования
(485 «* 492):
485. 1в 30° + *в 40° + *8 50° + *в 60°.
486. зт2 (а + р) — зт2 а — зт2 р.
487. 3 — 4 соз 2а + соз 4а.
488. соз 11а + 3 соз 9а + 3 соз 7а + соз 5а.
489. зт 5а зт 4а + зт 4а зт За ^- зт 2а зт а.
490. 2 соз 10° соз 20° = 2 соз 30° + з*п 40°.
47
491. соз (а + Р) со$ 7 + соз а + со$р + со$ у -^
•— $т(а + р)йп'х.-
492. зт 70°+ 8 соз 20° со$40° со* 80°.
Выяснить, при каких а справедливы равенства (493
502):
493. У\ё2 а *- зт2 а ~ {§ а зт а.
494. У 1 + зт2а = зта + соза.
495. 1/ . "7 С°5 а == с!й а — созес а.
Г 1 + С05 а ь
496. I/ -г=—;—:— = созес а — с1е а.
497. У" $ес2 а + созес2 а == — (§ а — с{§ а.
498. У 1§2а +с!§2а + 2 = зеса созес а.
499. }/|_±4^ + 1/^1 = _ 2 зеса.
Г 1 — 51П а ' Г 1 + 51Па
500. У 1 — соз а + / 1 + соз а = 2 зт (-^ |-).
501. V 1 + зта + / 1—зта = — 2 зт ^
502. созесаТ/г-г-^ +,—1— У"2=а
--У~2(с1б2а + 2).
503. Доказать, что если {§ а = —'» 8*п Р ^ , то
а -[- 2р = 45° (аир — острые углы).
504. Выяснить, при каких х справедливы равенства:
а) зт х = У1 — соз2 х\ б) 1§2 х + 1 = зес2 х\
* , х этх ч • / \
В) С*б -2"=1_С03Л;; Г) ЗШ(ТГ — *) = 81П*.
505. При каких х верна формула
х т / 1 + С08 х \
С05-2-= у 2 ?
506. Что больше, зт а или 1§а? т<а<-^Д
507. Какая из тригонометрических функций (прямых)
может принять значение ■ а\— ? (я>0, 6>0).
48-
508. Что больше, зт! или зш Г?
509. Найти наименьшее значение выражения ({§* +
+ с1§а)2.
510. Что больше, 51 п (а + Р) или зта + зтр?
(0<а<-^, 0<р<-г)"
511. Что больше, 1§ 2а или 21§а? Го < а <-?-)•
512. Синусом числа х называется число, равное
синусу угла в х радианов. Это определение синуса
числа х. Можно ли было условиться называть синусом
числа х число, равное синусу угла в х градусов?
513. Правильно ли называть радианное измерение
отвлеченным?
514. В каких интервалах изменения х функция \&х
возрастает?
515. Для тангенса половинного угла существуют
следующие формулы:
16 Т" ~" ± V 1 + С05 а И 1§ ~2" — 1 + соз а '
Вторую можно получить из первой, если умножить
числитель и знаменатель подкоренного выражения на
1-|-соз а, заменить 1—соз2 а на зт2а и извлечь корень
из дроби, В результате получаем
%ё Т" ~~ ± 1 + СОЗ л *
Почему же можно не писать знаки + и — в правой
части?
516. Найти зт 18°, пользуясь равенством зт 36°= соз54°.
517. Найти сумму
51П а + 31 п 2а + зт За + ... + зт п а.
518. Найти сумму
соз а + соз2а + соз За + ... + соз па.
519. Доказать, что если
А1 — А соз2 а + В зт а соз а + С зт2 а;
Вх = 2Сз1Па соза + В (соз2 а — зт2а) — 2 А зта соз а;
Сх = А зт2 а — В зт а соз а + С соз2 а,
ТО
В\ — 4Л1С1 = 52 — 4 АС.
4 К. У. Шахно 49
520. Доказать, что если
5 51П р = 31П (2 а + Р).
то
18(« + Й _А
18* ~ 2 •
521. Дано, что'равенство
с1со5(зг1 + ?) + ^2С05(а2-Ьср)+ ... +аЛсо$(аЛ + ср) = 0
имеет место при <р = 0 и при некотором <р = <рв =^= /гя
(6 = 0, ±1, ±2, ...). Доказать, что при этих условиях
написанное равенство справедливо при всяком <р.
522. Доказать, что если
СОЗ X — С05 а _ $Шаа СОЗР
С08 X — СОЗ р "~- 31П2 Р СОЗ а *
то
523. Доказать, что если
СОЗ а = С05 Р СОЗ ср = С05 у СОЗ в; 51П а = 2 31П -7г- 31П -у,
то
1б24-с=^2-|-^2^-; («^^нг1*;*=0' ±!- ±2> •••)•
524. Доказать, что если
соз (в — а) = а и 81п (в — Р) = 6,
то
а2 — 2а&зт(а — р) + Ь2 = соз2 (а— р).
525. Доказать, что если
соз х __ соз (х + <р) __ соз (х + 2 у) _ соз (* + 3 у)
о Ъ ~~ с ~~~ й *
ТО
Д + с 6 + Л
6 "" с~"#
526. Вычислить соз (а +• Р) и 51п (а + Р), если
51Па -+■ 51П Р = р И СОЗа + СОЗ Р = <?.
"527. Доказать, что если углы а, р и у треугольника
связаны зависимостью
з
соз <х + соз р — соз (а + Р) = -^р
то треугольник правильный.
60
528. Доказать, что если стороны треугольника а> Ь, с
составляют арифметическую прогрессию, то с!^ -о-, с!§ -^
и с^-у» гДе А, В и С —углы треугольника,
противолежащие сторонам а, Ь и с, также составляют
арифметическую прогрессию.
529. Найти зависимость между углами Ау В и С, если
известно, что
Найти затем при этом условии наименьшие
положительные значения углов, если, кроме того, дано, что угол А
равен полусумме углов В и С, а угол С равен сумме
углов А и В.
530. Дано: А + В + С = *,
а 6 с
81П Л $'тВ ~~ 51ПС "
Доказать: а2 = б2 4- с2 — 2Ьс соз Л.
531. Исключить О из уравнений:
со$ (а — Зв) = т со$3 в;
81П (а — Зв) == Ш 51П3 9.
532. Исключить О и ср из уравнений
а$т2в + &С0520 = 1; асо$2ср + &зта<р = 1; а{§9 = М^<р;
а ФЬ.
533. Упростить выражение
с*еа* , *е4* , 6 4 / 1 у<\
51П2 л; "" со$2л; •" соз2* •" у $ша х ' (со52* Г
534. Доказать, что если а, р и у —острые углы и
соза + соз^ + созт = 1 + 4$'т-^ в'т -^-З1п-^-, то
а + Р + Т = *•
535. Доказать: для рациональности $тл; и созл;
необходимо и достаточно, чтобы был рационален 1?-|-.
536. Доказать, что если 0<а<-^-; 0< р <-|-;
0 < у < -?-, то равенство
С052 а -(- С052 р + С052 Т + 2 сов а со$ 49 соз у = 1
имеет место тогда и только тогда, когда а 4- Р 4~ Т = ^.
4* 51
537. Пользуясь тригонометрическими функциями,
доказать, что из равенств
а2 + Ь2 = 1 и а2 + р2 = 1
следует неравенство
|аа + Ьр|<1.
538. Главные значения Агс1§дс берутся из интервала от
Т до Т~' М°жно ли было бы взять Аля них интервал
от 0 до тс?
539. Доказать равенства:
а) агс 5Ш х + агс соз х = -^-;
б) агс 1§ х + агс с{& х = -|-.
54в. Доказать равенства:
а) агс соз (— х) = тг — агс соз дс;
б) агс с!б (— х) = те — агс с!^ л:.
541. Доказать равенства:
а) 51П (агс соз х) = соз (агс зш х) = |/ 1 — г2;
б) 51 п (агс 1§ а:) = соз (агс с1§ х) = ■
/1 + **
в) 51П (агс с1§ л:) = соз (агс 1§ х) =
г) 1б (агс 51*п а:) = .с1& (агс соз а:) = -
У\ +х*
д) 1^ (агс соз х) = с!§ (агс зш а:)
/1 — *а
е) 1е (агс с*б *) = с1§ (агс 1§ х) = —.
542. Доказать равенства (а: > 0):
а) агс 51П х = агс соз ]/ 1 — х2 = агс 1&
= агсс1е-^—- ;
V*
-1/1 х2
б) агс соз х = агс зш у 1 — а:2 = агс 1& =
= агс с!§ —р :
52
в) агс 1§ х = агс зт = агс соз
У\ + *а "|/"1 + *»
агсс1б—;
дс
г) агс с1е х = агс зт _ _ = агс соз ■ - *
' Ъ У\ + *а У\+х2
= агс(§—.
543. Чему равен агс соз (созу тс1>
544. Чему равен агсзт (зт*)?
545. Чему равен агс 1б(1б*)?
546. Доказать равенство
зт!-*- агсзт л:I = -———~- .
547. Доказать, что
. 31П X 4" СОЗ X 3
агс $т ~= = — тс — х9
У 2 4
тс . ^,5
если т < а: < - тс.
548. Доказать, что
2 агс 1& * + агс зт р^ = *.
если х> 1.
549. Доказать, что
зЫ-^- агсзтл;] =
* (1 + 2 >^1 — **)
550. Доказать, что
1*1
соз (-^- агс зт х\
V 2(1— |/"Т — х2)
551. Доказать, что соз (7 агс соз л:) есть многочлен 7-й
пени относительно х*.
Доказать равенства (552—554):
1
* Выражение вида __} соз (п агс соз дс), где п — натуральное
число, является многочленом относительно х и называется многочленом
или полиномом П. Л. Чебышева.
53
552. С08 (агс 1§ х + агс 1(* у) — — ху
У\ + х*У\ + у*
При каких х и у оно имеет смысл?
553.1§ (2агс зт х) = 2х^^х/ •
При каких х оно имеет смысл?
2х
554. зт (2 агс {§ х) = утг^ '
При каких л: оно имеет смысл?
555. Вычислить выражение
зт \2 агс *б-5~)+ соз (агс *е 2 К3~) •
556. Вычислить выражение
зт ( 2 агс 1ё -4-) + *б (4" агс51П Т§у-
557. Проверить равенство
агс соз у==. + агс 48 ~ = агс 1е ^+| .
558. Вычислить сумму
агс 1§ 2 + агс (§ 3.
559. Доказать, что сумма
агс зт х + 3 агс соз х + агс зт (2а; У 1 —= х2)
1
не
зависит от х, если х2 <
2 *
560. Доказать:
агс зт х + агс зт у = г\ агс зт (хУ^ — у2 4- У У1— *2) +
где
7] = 1, е = 0, если яг/ < 0 или х2 + у2 < 1;
71 = _ 1, 6 = ^1, если х2 + у2 > 1 и х < 0, у < 0;
7] = — 1, 6=1, если х2 + у2 > 1 и х > 0, у > 0.
561. Доказать, что
. 4 , 5 , .16 л
агс зт -у- + агс зт -^ + агс зт -^ ==> -у-.
Ь4
562. Доказать, что
агс соз х + агс соз (~ + -у У 3 — Зх2) = -|-,
если -у < х < 1.
563. Доказать:
агс 1е х + агс \&у = агс ^^| + 87Г>
где
е = 0, если яг/ < 1;
е = — 1, если ху > 1 и л: < 0;
е = 1, если ху > 1 и л; > 0.
Доказать равенства (564—569):
564. агс 51П -^ + 2 агс {& -у = -у.
565. агс *б у + агс *& -^ + агс 1& — + агс 1^ _ = -^_.
566. 4агс1§ 4"— агс*б5к = -:г.
90
567. 2 агс 1§ 10 + агс зш щ = тт.
« 1
568. агс1§л: = -2 агс!§—, если дс>0.
569. агс 1& х = -—^ агс 1§ —, если дс < 0.
VIII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Решить уравнения (570—628):
570. 5111 Л; 5117 2ЛГ 51П 3* = — 51П4#.
4
571. 3(1— 51ПА:) == 1 + соз2л:.
572. 1& -у х с!§ у х == 1 — 5ес -у- л: со5ес -у л:.
-573. 81П (х + 25°) 51п (х — 20°) = зш (70° + х) зш (65°—х).
574. 1§ (л: + 30°) *е (* — 60°) = 1.
575. 5Ш 2х + со5 2л: + зш х -)- со5 х + 1 = 0.
576. 51П х + 51П 2л: + зш Зл: = 1 + соз х + С05 2х.
577. 51П Зл: = соз х — з1п х.
55
578. соз 7х + зт2 2л: = соз2 2л: — соз х.
579. зт3л; соз х — соз3л:зт х = —.
4
580. соз 5л: + соз Зл: + зт 5л: + зт Зл: = 2 соз (~ —
581. зт х -\~ зт 2л: + зт Зх + зт 4л: = 0.
582. зтязтЗл; = -у.
583. соз3л: зт Зл: + зт3* соз Зх = —.
584. зт 2л; зт х + соз2* = зт 5л: зт Ах + соз2 Ах.
585. соз2л; + соз2 2л: + соз2 Зл; + соз2 4л; = 2.
586. 51п2л: + зт2 2л; = зт2 Зл: + зт2 4л:.
587. зт2* + зт2 2л: = зт2 Зл:.
588. 2 зт2* + зт2 2* = 2*
589. зт4 -|- + соз4 -у = -|-#
590. соз4* + зт4* — 2 зт 2* + -|- зт2 2л: = 0.
591. 2зт2* = 3(зт* + соз л;).
592. зт*-{-соз*+ 8т*соз* = 1.
593. зт10* + соз10* = -—- соз4 2х.
594. соз2* соз 2л: + соз 4л: + соз Зх соз х -\- 2 соз4* =
_ 1
~~ х
2$1П у
595. 1е 5л: = 1% х 1§ (60° — х) с1е (30° — х).
-лл , • соз 2х
596. СОЗ* 1-310* = !_зДп2х '
597. 1&х+1ё2х — {§3* = 0.
598. (1 — 1&х) (1 + зт 2х) = 1 + *б*.
599. 1% х + 1% 2*.+ 1§ Зл: + {§ 4* = 0.
600. 1§ х + с1^ х = 31 п х ( 1§ * 1§ -у- + 1).
601. зес "/7 + созес У~х = 2 |/~2.
602. 1ё(х2 — х)с1ё6= 1.
603. |зт*2| = 1.
604. 51П | л: I = 1.
605. соз** = 1.
606. фх= 'Г008,1*,1.
607. зт2л: зшбл: = 1.
608. (зес х + созес х) \/~~2 = зес2 х + созес2 х,
609. зт За: + зт 2х = т зт л;.
610. зт (-о- л соз тг л: 1 = -тр
611. зт(тгсозл:) = соз(тгзтл:).
612. 1§(^1ех) = с1е(тгс1е^).
613. *т*2У~х=±.
614. 1о§со5 х зт л: + 1о§5{п х соз х = 2.
615. л:2 + 2л: зт (л;*/) 4-1=0,
616. 2агссозл:=:6,3.
617. агс1§— + агсзтл; = -^-.
618. агс зт х + агс зт 2х = -^-.
619. 2 агс зт к = агс соз 2л:.
620. 2 агс соз х = агс зт (2л: |/ 1 — л:2).
621. агс зт л: = 2 агс зт л; 1/~2.
622. агс соз х — агс зт х = агс соз —-^—.
623. агс соз х = агс 1§ х.
624. агс 1§ (л: — 1) + агс 1§ х + агс 1§ (х + 1) = агс
625. агсзт—т=+ агсзт 1/1—# = агсзт-о-.
ЪУх 3
1 х2 2х 4
626. агс соз у-^2 + агс 1§ у—-^ = — те.
627. агс 1^ * = агс ^ -у- — агс 1§ -^^.
628. агс зт х — агс зт а + агс зт Ь.
Решить системы уравнений (629—631):
629. (ап*81пу = -§-;
630. |»1п1* + ап«у-4:
\х + у = 75°.
( 51П X = 1^ 2 51П О;
631. \_
IX. НЕРАВЕНСТВА
Решить неравенства (632 — 642):
632 тх~^~ " Рх + 9 ^ тх — п рх-
аА-Ь п. — й ^ л А 1
а + 6 а — й ^ а — Ь ' а •+ 6'
635. -1 < 4"'
636. ж3 + 5х2 + Зх — 9 > 0.
637. 2х3>х + 1.
638. !*-!!!*-!; >о.
(л; — 2) (л; — 4) "^
639. х* — бхГ+Их2 — 6х<0.
(2л; — 1) (л: + 4) (3 — л:) ^
Я41 (л;3-!) (* + 2)2 (х-5)
°41- л;2(л:2__9) (х4 + 1) ^и*
642. а:4 + х3 — 7л;2 + ах + Ь > 0, если х = 1 и л: =* — 3
являются корнями многочлена, стоящего в левой части
равенства.
643. Каково должно быть к для того, чтобы оба корня
уравнения
{к — 1) х2 — 2кх + к + 3 = 0
были положительны?
644. Каково должно быть к для того, чтобы при любом
х значение трехчлена
(2к— I) х2 + (7к + 2) х — Зк
было больше значения трехчлена
(к + 3)х* + 5(к+1)х — 4(к + 1)
при том же значении х?
58
645. Каким должно быть X, чтобы при к > 0 и при
всяком х выполнялось неравенство
2кх2 + 2Х х + Х- , ~
4г» + б* + 3 >/г'
646. Доказать, что если а, Ь и с — стороны
треугольника, то при всяком х
Ь*х2 + (Ь2 + с2 — а2) х + с2 > 0.
647. Доказать неравенство Буняковского
(я А + а А + аф3)2 < (а? + а22 + а32) ( Й + Ъ\ + ф.
648. Определить а так, чтобы все корни уравнения
X2 X2
х*-р* + я*-? ==а
были вещественные. При этом р Ф 0; <7 =?ь 0; а =?«= 0.
Решить неравенства (649—653):
649. УЦ=±>\.
650. У$^1с>х — 2.
651. }/Зд: —5> К*11"?-
652. УТТб > Т^*+7 + У2х — Ъ.
653. 4(л:— 1)< У(х+ 5) (3* + 4).
Решить системы (654—659):
(Зх—1>х + 3у,
\ х(1—3х)>4х — 3х2 — 2у.
(Зх + 2у> 7;
1 Ау + 2х > 3.
Зх+2у> 4;
* — 6#> — 5.
654
655
656.
М
5х + 3у>121;
Ь57-> 7л;+ 4*/=168.
у>*2;
*></2.
Зх + 2у = 6;
*2 + «/2>4;
лгу<1.
658.
659.
660. Доказать, что если |а|< &, то — 6 < а < &.
661. Доказать, что если — 6 < а < 6, то | а | < 6.
662. Доказать, что | а + Ь \ < | а | + | Ь |.
663. Доказать, что \а — Ь\ > |а| —16|.
664. Каково должно быть Л для того, чтобы
неравенство
2 - кх + 1
х2 + х + 1
<з
было справедливо при любом значении х?
665. Доказать, что при а > 0 и Ь > 0
а+ 6 а 6
, "^ 1 _Х г, V
1 + а + Ь ^ 1 -)- а г1 + 6*
666. Доказать, что если а > & > 0 и /л > л, то
ат — Ьт . а7 — Ъп
ат+Ьт ^ ап + Ьп '
667. Доказать, что арифметическая дробь, с
увеличением числителя и знаменателя на одно и то же
положительное число, увеличивается, если она правильная, и
уменьшается, если она неправильная.
668. Доказать, что дробь
01 + а* + - + ад
Ьх + *>2 + .« + *„
заключена между наименьшей и наибольшей из дробей
ЬЪ -&:<**>о. *-1.2 п).
Доказать неравенства (669 — 671):
669. *\+2 >2.
670. (-^)* + (-^)2 > 1^ +У>, х Ф у.
671. а)-^^>К"^;
б) ^1±^±^±^->Кад^
(ах > 0, Ог > 0, а3 > 0, а4 > 0).
60
672. Разложить данное положительное число а на
два положительных слагаемых так, чтобы их
произведение оказалось наибольшим.
673. Желают устроить прямоугольную площадку так,
чтобы с трех сторон она была отгорожена проволочной
сеткой, а четвертой стороной примыкала бы к длинной
стене. Если имеется 100 м сетки, то какими должны быть
стороны площадки с наибольшей площадью?
674. Из круговых секторов данного периметра найти
сектор наибольшей площади.
675. Окно имеет форму прямоугольника,
завершенного полукругом. Дан периметр фигуры. Каковы должны
быть ее размеры, чтобы окно пропускало наибольшее
количество света?
676. Около шара радиуса /? описать конус
наименьшего объема.
677. Данное положительное число а разложить, на
два положительных сомножителя так, чтобы их сумма
оказалась наименьшей.
678. На странице книги печатный текст должен
занимать (вместе с промежутками между строк) 216 см2.
Верхнее и нижнее поля должны быть шириною по Зсм,
а правое и левое по 2 см. Если принимать во внимание
только экономию бумаги, то каковы должны быть
наиболее выгодные размеры страницы?
679. Доказать, что
а4 + Ь4 + с4 > аЪс (а + Ь + с),
(а>0, 6>0, с>0).
680. Доказать, что если а19а2,..., ап неотрицательны, то
Уам + Уа& + ... + УЧ-1 ап < ^у~ ■(<*! +йг + ... + аа).
681. Доказать, что если ах, а2,..., ап — положительны и
а1а2...ап = 1, то
(\+а1)(\+а2)...(\+ап)>2\
682. Доказать, что если аг > 0, а2 > 0, аг > 0, то
61
683, Доказать, что
* + * + " + '« >"/адТ5;
(аг>09 а2>0, ...,ая>0).
684. Данное положительное число а разложить на п
положительных слагаемых так, чтобы их произведение
оказалось наибольшим.
685. В данный шар вписать цилиндр наибольшего
объема.
Доказать неравенства (686 — 691):
686. 2п > 1 + п У>~1; (п > 1).
687. п\ < (Ц1)"', (п > 1).
688. 1+4- + 4-+ ••• +-^Г<3-
689. 1 • 1! + 2 • 2! + ... + п - п\ < (п + 1)!
♦ 5 . .. (2п — 1) 1
2 • 4 ... 2п ^ |/~^ *
691. ^"1.2-3 ...л > |Лгг.
692. Наборщик рассыпал некоторое число,
представляющее шестую степень натурального числа. Его цифры:
О, 2; 3, 4, 4, 7, 8, 8, 9. Какое это число?
693. Газ в количестве а м3 последовательно
пропускают через п фильтров, каждый из которых поглощает
р% общего объема примесей, содержащихся в газе,
поступающем в рассматриваемый фильтр. Затем газ
поступает в резервуар, где находится Ь мъ газа, содержащего
9% (по объему) примесей. Какой процент примесей (по
объему) допустим для газа до его очистки, если число
процентов примесей в газовой смеси в резервуаре не
должно превышать г?
694. Вклад в А руб. положен в сберегательную кассу
по р % годовых. В конце каждого года вкладчик берет В
руб. Через сколько лет* после взятия соответствующей
суммы остаток будет не меньше утроенного
первоначального вклада? При каких условиях задача имеет решение?
695. Непромытый золотой песок содержит к %
чистого золота. После каждой промывки песка отходит р%
62
содержащихся в нем примесей и теряется ц \
имеющегося в песке золота. Сколько следует сделать промывок,
чтобы число процентов содержания чистого золота в
золотом песке было не меньше чем г?
696. В резервуар, содержащий А л воды, вливают
а л р%-ного (по объему) раствора спирта, а затем,
после перемешивания, через другую трубу выливают а л
образующейся смеси. Сколько раз нужно повторить эту
операцию, чтобы в резервуаре получился раствор
спирта*, крепостью не менее <7%?
697. Найти наименьшее и наибольшее значение
выражения
асо$х + Ь$\пх.
698. Найти наибольшее и наименьшее значение
выражения
а 51П2 X + Ъ $1П X СО$ X + С С052 X,
с Фа.
699. Доказать, что если А, В и С — углы
остроугольного треугольника, то
81П2 А + 81П2 В + 81П2 С > 2.
700. При каких х справедливо неравенство
51П 2Х — С05 2Х + 1 ^ ~~
81112*+ СОЗ 2Х— 1 ^ У'
701. Решить неравенство $1п(со$лг)< 0.
702. Решить неравенство 1§$т#<0.
703. Найти те значения х9 при которых со$($тл:)
положителен.
704. Найти те значения дс, при которых
агссоз [-^-агсзт*] имеет смысл.
705. Решить неравенство агс зш 1§ х > 0.
706. Решить неравенство $т —$- > 0.
707. Доказать, что если 0<а<-|-; 0<^<~;
0<Т<^- и а + р + Т = тг,
то
При каком условии будет знак равенства?
63
708. Дано: 0<а<^-, 0<$<±, 0<Т<-|-.
Доказать, что сумма а -{- р -}- ? будет острым углом тогда
и только тогда, когда выполняется неравенство
*в«*еР + *е?*вт + *вт*в«<1.
709. Доказать, что если 0 < ср < тс, то
1+с1§<р<с1§-|^.
710. Доказать, что если а, р и у — углы треугольника
и угол у— тупой, то
711. Доказать, что если а, р и у — углы треугольника,
то
з
со$2а + со$2 3 -Ь со$2 у > -г-.
712. Доказать, что если а, Р и у — углы треугольника,
то
$1П -у 51П -|- 81П -^- < -^-.
713. Доказать, что если 0<х<-^-, то
81П X < X < 1б *.
714. Доказать, что если 0<а<р<-|-< то:
а) а — $1па< р — $тр;
б) а — 1§а>р — 18р.
715. Доказать, что если 0 < а < р < -|-, то
{1 '
716. Доказать, что если 0<*<-^-, то
31П X > Ж.
*^ тс
717. Доказать, что если 0 < а < р < -^-, то
р
64
X. КОМПЛЕКСНЫЕ ЧИСЛА
718. Можно ли сказать, что число 2 + 5** больше
числа 1 + Ш
719. Является ли число —5** отрицательным?
720. Найти целое число п, если
(1+0я = (1-0я-
721. При каких вещественных х и у справедливо
равенство
* + 1 + (У - 3)/ _ , , п
722. Найти вещественные х и у из соотношения
(х + у)Ч — 4 — х = — у + 51( х + У) — 1.
723. Найти вещественные решения системы уравнений
(х — 1=у1;
\ х — Iя = 2а — у
и значение комплексного параметра а.
724. Решить уравнение \г\ —2=1+2/.
725. Решить уравнение | г | + г = 2 + и
726. Доказать тождество
|21 + 21Р + 1г1-^12 = 2(|г1|» + |гкР)|
где гх и г2 — комплексные числа.
Представить комплексное число в тригонометрической
форме (727—729):
727. 1 — соз а + I зш а, где 0 < а < тс.
728. 1 + 81П а + I соз а, где -^- < а < -^- те.
729. 1+И§а, где * < а < -|- тс.
Выяснить, где расположены точки, соответствующие
комплексным числам г = л: + и/, для которых (730 —
732):
730. а) \г\ = 2; б) 1 < |г|< 2; в) #(г2)* = 0; г) /т(г)>
. 1 ч|г —1I ^1
2+1
* Обозначения /?(г), /т(2) и аг&г означают соответственно
действительную часть, мнимую часть и аргумент комплексного числа.
5 К. У. Шахно 65
731. а)агвг-=-у; б) ^-< аг6г< \.
732. а) *<0; б) (/>0.
733. Точка 2 описывает в плоскости окружность
радиуса единица в направлении движения^асовой
^грелки. Какой путь опишет при этом точка г? (г и г —
сопряженные числа).
734. Доказать, что модуль произведения двух
комплексных чисел равен произведению модулей этих чисел,
а аргумент — сумме их аргументов.
735. Доказать, что модуль частного двух
комплексных чисел равен частному модулей делимого и
делителя, а аргумент «■ разности их аргументов,
736. Доказать формулу Муавра (п > 0):
(С08 ср + *81П <р)Л в С08 П Ср + * 81П П ср.
737. Доказать формулу Муавра (л<0):
(С08 ср + * 51П ср)" = С08 П ср + *$1П П ср.
738. Найти модуль комплексного числа
х2 — у2 + 2хщ
ЩУ"2 + *У х* + у* *
Вычислить выражения, положив со == с08 -^ + * ^п —д—
(739—741):
739. (а ш + Ь со2) (а со2 + Ь ш).
740. (а + Ь + с)> (а + Ьи> + сш2) (а + Ь<о2 + со)).
741. (а + 6<о + ссо2)3 + (а + 6(о2 + ссо)3.
742. Вычислить гш -\ зэт~» если г есть корень урав-
нения г + — = 1.
743. Выразить 81п (5 агс 8Ш х) через х.
744. Найти суммы:
а) 81п х + 81П За: + ... + зш (2л — 1) х\
б) со$* + созЗл; + ... +со8(2п— 1)л:.
745. Доказать, что если соз а + % 81п а есть решение
уравнения
хп + рхх^+ ... +рЛ = 0
и Ръ Ръ ••• » Рл*~вещественные числа, то
рх 81П а + Ра 81П 2а + ... + рЛ $т п а ~ 0.
66
746. Найти суммы:
52 = 1 — Сп + Сп — Сп + ...;
747. Найти сумму
5 = Схп — ЪС1 + 3«С5- 33С2 + ...
748. Доказать:
У 9 (С08 <р + ШП <р) = ]/ р (^ОЗ-1-^ Ь^Ш-^ р
6 = 0, ±1, ±2,...
749. Доказать:
а) У?+Ы = ± (/ЁТГ + гуТЩ. Ь > 0;
р = /а2 + Ь\
750. Вычислить: а) |/Т; б) ]/" 1 + //Т; в) ^Т
751. Доказать, что корни уравнения хп = 1 могут быть
записаны так: 1, а, а2, ..., а"-1.
752. Изобразить геометрически корни уравнения 2й = I.
Решить квадратные уравнения (753—754):
753. х2 + (21—\)х—7—1 = 0.
754. х2— (3 + 0* + 3/ = 0.
755. Решить уравнение
х6 + хь + х* + х* + х2 + х + 1 = 0.
756. Найти сумму р-х степеней всех корней
уравнения хп—1=0 (р — целое, п—натуральное).
757. Решить уравнение
(* + 0* + (х —0я = о,
п — целое положительное.
758. Решить уравнение
\1 — XI/ 1 — / 1§ а »
п — целое положительное.
5* 67
XI. МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ
759. Доказать, что в арифметической прогрессии аь
Сг, ... с разностью й любой член
ая = а1 + й(л— 1).
760. Доказать, что в геометрической прогрессии аь
0$, ... со знаменателем ц любой член
Доказать равенства (761—768):
761. Ат = т(т— 1)...(т — п+1).
762. Р„ = 1 • 2 • 3... п = 1й
-7й1 гп — т(т — 1)...(т — п+ 1)
7М. Ст 1.2.3...л *
764. (ах + а2 + ... + а„)2 = а? + а\ + ... + а% +
+ 2 (а^г + а^з + — + ап-\а„)-
7КЧ *' » 2" ■ , "* _ п(п + 1)
'°°- 1.3 "Т" 3-5 "•" — "1~ (2/1 — 1)(2п + 1) ~ 2 <2л + 1)*
766. I4 + 2*+ ... + л4 » ± п(п+1)(2п+1)(3п2+3п— 1).
767. I5 + 26 + ... + пь = -~пЦп+ I)2(2/г2 + 2л — 1).
768. 1ёх+ ±1ёЛ. + ... + ±1$-^=: ±.С1ё±^
— 2 с1§ 2ж.
у^+тЛ+у
769. К 4+ К 4+ К 4 + ,,. + 1/4 < 3.
п — четверок
770. (1 + а)п > 1 + па\ а > — 1, а =^ 0 и л —
натуральное, большее единицы.
771. Доказать, что сторона правильного, вписанного
в окружность 2*-угольника, выражается формулой
а2п
уг.
У 2+ /2+*Г+7т,
(п—2) двойки
где # —радиус этой окружности.
772. Доказать, что п прямых, пересекающихся в одной
точке и лежащих в одной плоскости, делят эту плоскость
на 2 п частей,.
68
773. Доказать, что сумма всех членов каждой
горизонтальной строки таблицы
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
равна квадрату нечетного числа.
774. Доказать, что п различных прямых, лежащих в
одной плоскости, разбивают эту плоскость на области,
которые могут быть закрашены красной и синей
красками так, что все смежные области (т. е. области,
имеющие общий отрезок прямой) будут закрашены разными
красками.
XII. ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ
ГРАФИКОВ
Найти область определения функций (775—781):
775. а) у = У<2-х\ б) у = Ух*-А; в) */=|/|±А;
г) у = Ух(х + 2)(х-3)(х-4);
776. а) у = У2 — 2-*; б) у = Ц—; в) у = х';
г) у = х~к.
777. а) у = 1о§ (х2 — 1); б) у = 1о§ (х +1) + 1об(* — 1);
в) у = 1об(х2 — Зх + 2);Гг) у = У1оёз(х—1).
778. а) у = х 1о§ л: для лг =^= 0 и г/ = 0 для х = 0;
б) I/ = -д- д: 1о§ дс2 для д: =?ь 0 и # = 0 для х = 0.
779. а) # = -г4г; б) #=1/5ш4*; в) у = зт ±;
г) у-]/Г*81х-(/3+1)*8«+Уз:
780. а) у = У1оёа&тх; б) у = \ёЫ^ёх;
в) у — 1о§ (1,5 + 51п д: + сев х).
69
781. а) г/ = агссо8—; б) г/ = агс8Ш -^у^
В) У = аГС 81П (аГС 81П X).
Найти период функций (782 — 783):
782. а) у = 81П Зг, б) у = со§ -|-;
в) у = 1§За: + 2с(§2а:; г) у = 8Ш^~- + со8-~;
Д) у = 5Ш-|- С083 -|-;
783. а) у = зт 2* а:; б) у = $т /2а: + со8УЪс.
Исследовать функции и построить их графики (784--*
812):
784.
785.
у = х* — 2л:2 + 2.
у = (х — А:)2, если А — 1 < * < А + 1 и к — О,
±2, ±4, ±6, ...
786.
787.
788.
789.
790.
791.
792.
793
1 Ок)»
794.
795.
796.
797.
798.
799.
800.
801.
802.
803.
804.
У = \х\.
у = \х + 2\.
у = \х—\\ + \х^2\.
у = —х\х\.
у = \х*-1\.
у = \х* — Зх + 2\.
о-—!—
у ~ 1 + х>-
X
11
У 1 + д-2-
У=1о§2(— х).
У=\о%2\х\.
у = \\оё2х\.
у = 2 зт 2а:.
*/ = —Зт-у.
г/ = зт 4 а: + соз 4 а:.
у==$т \х\.
у=\йпх\.
у = # + 8Ш а:.
Г/ = аГС81*п(81*ПА:).
*/ г= аГССОЗ(сОЗ#).
70
805. у — Агс соз (соз х).
806. г/= агс {§({§*).
807. г/ =
2х—\
1 *„ Л- 2* — 1
агс1§ {0
4
если х не
2 г. »"^&^б 2
равно целому числу, и у = х, если * равно целому числу.
808. у = агс 5111^1 — * + агс $1*п|/лс.
1
809. у = агс (§ х — агс с!§ —.
х
810. у = агс1§* + агс[§]-=^
811. у = агс соз
1-л:а
1 + *2 '
812. у = агс соз (2л;2 — 1) + 2агсзтл\
813. Как получить график функции у = (/(*)[, если
график функции у = !(х) известен?
814. Как получить график функции у = /(|#|), если
график функции у~[(х) известен?
Выяснить, как расположены точки плоскости,
координаты которых удовлетворяют уравнениям (815—818):
815. ху = 0.
816. \х— 2| = 1.
817. х2= у2.
818. \2у-1\ + \2у+1\ + -^=-1*1=4.
Выяснить, как расположены точки плоскости,
координаты которых удовлетворяют неравенствам (819—828):
819.
820.
821.
822.
823.
824.
825.
826.
х>~2-
|*|<з.
х + у + 1 > 0.
у — 2х + 1<0;
у — х — 3>0.
(2х + у — 2>0;
х — у< 0;
2у —л: — 2<0.
\х\ + \у\<1.
|1*+1|-|У-1||<1
71
827. у2 — х2<0.
828- Т ^п
I У — * <0.
Определить графически число вещественных корней
уравнений (829—833):
829. 51плс = лс.
830. 2х = х + 2.
831. 2*3 — 6л:2+1=0.
832. {§* = *.
833. $1п л: = —.
834. Решить графически систему уравнений
* + */2-4.
XIII. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПЛОСКОСТИ
(Планиметрия)
Доказать теоремы (835—869):
835. Треугольник, имеющий две равные высоты,—
равнобедренный.
836. Треугольник, имеющий две равные медианы,—
равнобедренный.
837. Треугольник, имеющий две равные
биссектрисы,— равнобедренный.
838. Если биссектриса угла треугольника является
одновременно его медианой, то такой треугольник —
равнобедренный.
839. Если угол, прилежащая к нему сторона и сумма
двух других сторон одного треугольника соответственно
равны у]\лу, прилежащей к нему стороне и сумме двух
других сторон второго треугольника, то такие
треугольники равны.
840. Треугольники с равными периметрами и двумя
соответственно равными углами — равны.
841. Трапеция с равными диагоналями —
равнобедренная.
842. Если в шестиугольнике противоположные
стороны равны и параллельны, то три его диагонали, сое-
72
линяющие противоположные вершины, пересекаются в
одной точке.
843. Сумма расстояний любой точки окружности до
двух ближайших к ней вершин вписанного в эту
окружность правильного треугольника равна расстоянию
взятой точки до третьей вершины треугольника.
844. Прямые, соединяющие основания высот
остроугольного треугольника, образуют треугольник,
биссектрисами которого являются высоты данного.
845. Из всех треугольников с одинаковым
основанием и одинаковым углом при вершине равнобедренный
имеет наибольший периметр.
846. Если в шестиугольнике противоположные
стороны* параллельны, а три диагонали, соединяющие
противоположные вершины, равны между собой, то вокруг
такого шестиугольника можно описать окружность.
847. Диаметры окружностей, каждая из которых
проходит через точку пересечения высот треугольника
и через две его вершины, равны между собой.
848. Прямая, проходящая через основания двух
высот остроугольного треугольника, отсекает от
треугольника подобный ему треугольник.
849. Треугольники с соответственно параллельными
сторонами подобны.
850. Радиусы окружностей, описанных около
подобных треугольников, пропорциональны сходственным
сторонам.
851. Если из точки С проведены к окружности
секущая, имеющая с окружностью точки пересечения А
и В, и отрезок СО, где О точка окружности, и если
СА • СВ = СО2, то прямая СО есть касательная к этой
окружности.
852. Если из точки, отстоящей от прямой на
расстояние а, проведены к этой прямой две наклонные, с
проекциями на нее, равными 2а и За, то сумма углов этих
наклонных со своими проекциями равна 45°.
853. Если в четырехугольнике, две противоположные
стороны которого не параллельны, отрезок прямой,
соединяющий середины этих сторон, равен полусумме двух
других сторон четырехугольника, то этот
четырехугольник4—- трапеция.
854. Длина отрезка прямой, соединяющей середину
основания треугольника с серединою отрезка высоты
73
между вершиной и ортоцентром, равна радиусу
описанного около треугольника круга.
855. Касательные к окружности, проведенные через
вершины прямоугольника, вписанного в эту окружность,
образуют ромб,
856. Прямая, проходящая через основания высот
треугольника, проведенных из двух его вершин,
перпендикулярна прямой, проходящей через его третью
вершину и центр описанного вокруг треугольника круга,
857. Биссектрисы углов, образованных
продолжениями противоположных сторон вписанного в окружность
четырехугольника, перпендикулярны между собой,
858. Диаметр вписанного в прямоугольный
треугольник круга равен разности между суммою катетов и
гипотенузой.
859. Середины оснований трапеции и точка
пересечения ее диагоналей лежат на одной прямой.
860. Если из точки Р, взятой вне окружности,
проведены к этой окружности касательные РА и РВ, где
А и В — точки касания, то отрезок перпендикуляра
АС, опущенного из точки А на диаметр ВО, делится
прямою Рй пополам. Точка С — основание
перпендикуляра, тючка О—точка окружности,
861. Расстояние от точки окружности до хорды есть
средняя пропорциональная между расстояниями от этой
точки до касательных, проведейных к окружности
в концах хорды.
862. Центр описанного около треугольника круга,
точка пересечения его высот и его центр тяжести лежат
на одной прямой.
863. Если прямая, параллельная основаниям
трапеции, проходит через точку пересечения диагоналей, то
отрезок, отсекаемый от этой прямой боковыми
сторонами трапеции, делится точкой пересечения пополам.
864. Середины диагоналей описанного около
окружности четырехугольника и центр этой окружности
лежат на одной прямой.
865. Из всех треугольников с одинаковым
основанием и одинаковым углом при вершине равнобедренный
имеет наибольшую площадь.
866. Если в равнобедренный треугольник ЛВС*
вписан полукруг, диаметр которого лежит на основании
АСУ и если к полукругу проведена касательная, пересе-
74
кающая сторону АВ в точке М, а сторону ВС в точке
М, то произведение АМ • СМ есть величина постоянная.
867. Если через точки А и В пересечения двух
окружностей проведены две секущие МАМ и РВ(2<
пересекающие одну окружность в точках М и Р, а
другую в точках Ми ($уто прямыеМР и М($ — параллельны.
868. Произведение диагоналей вписанного в
окружность четырехугольника равно сумме произведений его
противоположных сторон.
869. Куб гипотенузы больше суммы кубов катетов.
870. Найти расстояние от центра описанного около
треугольника круга до центра вписанного в этот
треугольник круга. Радиусы кругов /? и г (/?>г).
871. Доказать, что радиус вписанного в треугольник
круга не больше половины радиуса, описанного около
треугольника круга.
872. К какой вершине треугольника лежит ближе
всего центр вписанной в этот треугольник окружности?
873. Какая медиана наименьшая?
874. Будет ли вписанный равносторонний
многоугольник правильным?
875. Будет ли описанный равносторонний
многоугольник правильным?
876. Из каких равных правильных многоугольников
можно сложить паркет?
877. Вершина В треугольника АВС перемещается
так, что длина медианы АЭ остается неизменной, а
сторона АС — неподвижной. Найти геометрическое место
точек В.
878. А и В — две заданные неподвижные точки
окружности, М — подвижная точка той же окружности.
На продолжении отрезка АМ в сторону, внешнюю к
окружности, откладывается отрезок ММ = МВ> Найти
геометрическое место точек N.
8791 Найти геометрическое место вершин прямого
угла неизменяемого прямоугольного треугольника, если
две другие его вершины скользят по сторонам другого
прямого угла,
880. Одна окружность касается прямой в точке А.
Другая касается той же прямой в точке В и первой
окружности в точке М. Найти геометрическое место
точки М.
881. Найти геометрическое место точекд сумма рас-
75
стояний которых до двух данных прямых есть величина
постоянная.
882. Из точки вне окружности проведена секущая и в
точках пересечения ее с окружностью — касательные.
Найти геометрическое место точек пересечения этих
касательных,
883. Из точки В, взятой на стороне ВС
треугольника ЛВС, проводятся всевозможные прямые,
пересекающие стороны АС и АВ или их продолжения
соответственно в точках Е и Р. Найти геометрическое место
точек пересечения окружностей, описанных вокруг
треугольников СОЕ и ВОР.
884. На сторонах прямого угла отложены от его
вершины О отрезки О А и ОВ, равные между собой. Через
точки Л и Б проведены прямые, 'параллельные двум
данным взаимно перпендикулярным прямым и
пересекающиеся в точке М. Какую линию опишет точка М,
если прямой угол будет вращаться вокруг своей
вершины О?
885. В круг вписан правильный шестиугольник.
Пользуясь только линейкой, построить — часть
радиуса /?, где п = 2, 3, 4, 5,...
886. На данной прямой построить точку, сумма
расстояний которой до двух данных точек наименьшая.
887. Даны точки Л и В и между ними две
параллельные прямые МЫ и РС}. Провести между последними
в данном направлении отрезок СО так, чтобы сумма
АС + СО + ОВ была наименьшая.
888. В данный острый угол вписать треугольник
наименьшего периметра так, чтобы одна его вершина
находилась в точке, данной внутри угла, а две другие — на
сторонах угла.
889. Через три данные точки провести параллельные
прямые так, чтобы расстояния между ними были равны.
890. На продолжении диаметра построить такую
точку, чтобы длина касательной, проведенной из нее к
окружности, равнялась диаметру.
891. Из вершин треугольника как из центров
построить окружности, каждая из которых касалась бы двух
других внешним образом.
892. Построить треугольник по данной стороне с>
высоте Ъь и медиане та.
76
893. Построить треугольник, зная основания трех
его высот.
894. Провести секущую к двум концентрическим
окружностям так, чтобы хорда большего круга была
вдвое больше хорды меньшего круга.
895. На стороне данного угла найти точку,
равноудаленную от другой стороны и от данной точки внутри
угла.
896. В данный сегмент вписать квадрат так, чтобы
одна его сторона лежала на хорде (основании)
сегмента.
897. Трапецию пересечь отрезком, параллельным
основанию, так, чтобы он разделился диагоналями на три
равные части.
898. Построить окружность, проходящую через две
данные точки и касающуюся данной прямой.
899. Пользуясь только линейкой, разделить
трапецию на две равновеликие части.
900. Пользуясь только линейкой, разделить
параллелограмм на две части, площади которых
относились бы как 1:3.
901. Данный треугольник превратить в
равновеликий ему треугольник с данным основанием и общим
углом при основании, причем оба основания должны
лежать на одной прямой.
902. На данной прямой найти такую точку, чтобы
модуль разности расстояний ее от двух данных точек,
находящихся по одну сторону от прямой, был
наименьшим, а также такую точку, чтобы модуль этой разности
был наибольшим.
903. Основания трапеции равны а и 6. Найти
отрезок прямой, соединяющий середины ее диагоналей.
904. В треугольник, длины сторон которого суть а,
Ь и су вписана окружность. К окружности проведена
касательная так, что она, пересекая две первые
стороны, разделяет данный треугольник на две фигуры —
треугольник и четырехугольник. Найти периметр
полученного треугольника.
905. В треугольник вписан круг так, что две из его
т
сторон делятся точками касания в отношениях — и
—. Найти отношения сторон треугольника.
77
906. На отрезке и двух его неравных частях
построены полукруги в одну сторону, По радиусам К и г
меньших полукругов определить радиус круга, касательного
ко всем трем полукругам,
907. Площадь треугольника ЛВС равна 5. Его
стороны АВ, ВС и СА разделены точками М, N и Р так,
что АМ : МВ - 1 ! 4, ВМ х N0 *= 1 : 4 и СР г РА = 1 : 4.
Найти площадь треугольника, ограниченного отрезками
прямых АЫ, ВР и СМ.
90& В треугольник со сторонами а, Ь и с вписан
круг. Точки касания его со сторонами данного
треугольника соединены прямыми и таким образом получился
новый треугольник, стороны которого требуется
определить.
909. Основания высот остроугольного треугольника
со сторонами а, Ь и с служат вершинами другого
треугольника, Найти периметр последнего и показать, что
8 5а
он равен —г—, где 5—площадь данного
треугольника*
910. Найти радиус вписанного в прямоугольный
треугольник круга, если даны радиус /? описанного около
этого треугольника и площадь треугольника 5.
911. В треугольник со сторонами к, I и т вписана
окружность, К окружности проведена касательная так,
что отрезок ее внутри треугольника, заключенный
между точками пересечения касательной с первыми двумя
сторонами треугольника, равен а. Найти площадь
треугольника, отсеченного этой касательной от данного.
912. Прямоугольный треугольник разделен на два
треугольника перпендикуляром, опущенным из вершины
прямого угла на гипотенузу, В образовавшиеся
треугольники вписаны окружности с радиусами гг и г2.
Найти радиус круга, вписанного в данный треугольник,
913. Даны две окружности с радиусами # и г. Их
общие внутренние касательные взаимно
перпендикулярны. Найти площадь треугольника, образованного этими
касательными и общей внешней касательной
окружностей.
914. Непараллельные стороны трапеции
продолжены до взаимного пересечения и через полученную точку
проведена прямая, параллельная основаниям трапеции*
73
Найти отрезок ее, ограниченный продолженными
диагоналями, если основания трапеции а и Ъ.
915. В трапеции, основания которой а и 6, проведена
через точку пересечения диагоналей прямая,
параллельная основаниям, Найти длину отрезка этой прямой,
отсекаемого от нее боковыми сторонами трапеции.
916. Прямоугольный сектор радиуса Я разделен на
две части дугой круга того же радиуса с центром в
конце дуги сектора. Найти радиус круга, вписанного в
меньшую из этих частей.
917. Два круга радиусов гг и г2 касаются в точке С
и к ним проведена общая внешняя касательная АВ, где
А и В — точки касания, Найти длины сторон
треугольника АВС.
918. Две окружности радиусов г и К касаются
снаружи. Найти расстояние от точки касания до их общей
внешней касательной.
919. Два круга радиусов К и г внешне касательны.
Найти радиус круга, касательного к ним и к их общей
внешней касательной.
920. Три окружности радиусов а, Ь и с касаются
попарно снаружи. Найти длину хорды, отсекаемой
третьей окружностью от общей внутренней касательной
первых двух окружностей,
921. Около данного квадрата со стороною а описан
круг, и в один из полученных сегментов вписан
квадрат. Определить сторону вписанного квадрата,,
922. Два круга радиусов Я и г касаются снаружи
в точке М. На окружности радиуса г взята точка Л/,
диаметрально противоположная точке М, и в этой точке
проведена касательная. Найти радиус круга,
касательного к двум данным и к касательной, проходящей через
точку N.
923. Дан прямоугольный сектор АОВ радиуса /?.
Параллельно его хорде АВ на расстоянии т от нее
проведена секущая, пересекающая продолженные радиусы
ОА и ОВ в точках С и О, а дугу сектора — в точках
Е и Р. Из точки Я, ближайшей к С, восставлен к СО
перпендикуляр ЕМ, пересекающий ОА в точке М.
Показать, что длина отрезка ОМ не зависит от т и найти
длину этого отрезка.
924. По данным двум сторонам а и Ъ треугольника
найти третью сторону, если известно, что медианы, про-
73
веденные к данным сторонам, пересекаются под
прямым углом.
925. Найти радиус круга, зная длины а и Ь двух его
хорд, исходящих из одной точки окружности, и
расстояние й от середины первой из данных хорд до второй,
926. Через центры двух равных касающихся
окружностей радиуса г проведена окружность радиуса 2г.
Из некоторой точки, находящейся на последней
окружности, описана окружность, касательная к первым двум.
Найти ее радиус.
927. Дан прямоугольный треугольник АВС, где А —
прямой угол. Из А опущен перпендикуляр АК на
гипотенузу, а из К—перпендикуляры КР и КТ на катеты
АВ'и АС. Зная, что ВР = т и СТ = п, найти длину
гипотенузы.
928. Площадь треугольника АВС равна 5Х; площадь
треугольника АН В, где Н—точка пересечения высот,
равна 52. Найти площадь прямоугольного треугольника
АВЬ, предполагая, что точка Ь лежит на отрезке СН
или его продолжении.
929. Две стороны остроугольного треугольника —
20 см и 23,2 см. Радиус описанного около треугольника
круга равен 14,5 см. Найти радиус вписанного в
треугольник круга,
930. Катеты треугольника — 3 и 4, Через середину
меньшего катета и середину гипотенузы проведен круг,
касательный к гипотенузе. Найти площадь этого круга.
931. Две равные окружности радиуса г
пересекаются. В общую часть обоих кругов вписан квадрат. Найти
сторону этого квадрата, если расстояние между
центрами окружностей равно г.
932. На двух смежных сторонах квадрата построены
во внешнем поле два полукруга и к ним касательные,
параллельные своим диаметрам. Найти радиус круга,
касательного к этим двум полукругам и к упомянутым
касательным, если сторона квадрата равна 2а.
933. Через две смежные вершины квадрата
проведена окружность так, что касательная к ней, проведенная
из третьей вершины, равна двойной стороне квадрата.
Найти радиус этой окружности, если площадь квадрата
равна 10.
934. Окружность касается большего катета
треугольника, проходит через вершину противолежащего остро-
80
го угла и имеет центр на гипотенузе. Найти ее радиус,
если катеты равны 3 и 4.
935. Центр окружности радиуса 3 лежит на другой
окружности радиуса 5. Из центра О последней
проведен диаметр, касательный к первой, и в точку
касания—радиус, пересекающийся с общей хордой в точке
/С. Найти длину отрезка ОК.
936. Каждые две противоположные вершины
квадрата со стороною а служат вершинами двух равных
ромбов. Найти площадь, общую обоим ромбам, если
площадь каждого из них равна половине площади
квадрата.
937. Прямоугольный треугольник АВС с катетами а
и Ь разделен на две равновеликие части АМЫ и ВСМЫ
прямой МЫ, перпендикулярной к гипотенузе АВ. Найти
площадь круга, описанного вокруг четырехугольника
ВСМЫ.
938. К двум извне касающимся окружностям
радиусов /? и г проведены две общие касательные. Найти
площадь трапеции, образованной этими двумя
касательными и хордами, соединяющими точки касания.
939. В некоторый угол вписана окружность радиуса
г, а длина хорды, соединяющей точки касания, равна а.
Параллельно этой хорде проведены две касательные,
и таким образом получилась трапеция, площадь которой
требуется найти.
940. В треугольник со сторонами а, Ъ и с вписан
полукруг с диаметром, лежащим на стороне с. Найти
величину этого диаметра.
941. Найти площадь треугольника, если отрезки,
образуемые на одной из его сторон точкой касания
вписанной окружности, суть т и /ц а противолежащий ей
угол треугольника равен 60°.
942. Меньшее основание трапеции ОС = 6; большее
основание АВ — а. На продолжении меньшего основания
найти точку М при условии, чтобы прямая АМ
разделила трапецию на две равновеликие части,
943. Прямая, параллельная основанию треугольника,
делит его площадь пополам. В каком отношении она
делит боковые стороны треугольника?
944. Найти длину отрезка прямой, параллельной
основаниям трапеции и делящей трапецию на две рав-
6 К. У. Шахно
81
новеликие фигуры, заключенного между боковыми
сторонами трапеции. Длины оснований трапеции равны
а и Ь.
945. Прямая, параллельная основаниям трапеции,
разделяет ее на две части, площади которых относятся
между собой, как 7:2 (считая от большего основания).
Найти длину отрезка этой прямой, заключенного между
боковыми сторонами трапеции, если основания
трапеции равны 5 и 3.
946. Площади треугольников, образованных
отрезками диагоналей трапеции с ее основаниями, равны 5Х
и 52. Найти площадь трапеции.
947» Через некоторую точку, взятую внутри
треугольника, проведены три прямые, соответственно
параллельные сторонам треугольника. Эти прямые разделяют
площадь треугольника на шесть частей, из которых три —-
треугольники с площадями 51 52 и 53. Найти площадь
данного треугольника.
948. Прямая, параллельная основанию треугольника
с площадью 5, отсекает от него треугольник с
площадью 5ь Определить площадь четырехугольника, три
вершины которого совпадают с вершинами маленького
треугольника, а четвертая лежит на основании большого
треугольника.
949. К двум, извне касающимся в точке А
окружностям, радиусы которых 3 и 1, проведена общая внешняя
касательная ВС. Найти площадь фигуры АВСг
ограниченную окружностями и касательной.
950. По высотам Ни к2, Нъ треугольника определить
его площадь 5.
951. По медианам ти ггц* тъ треугольника определить
его площадь 5.
952.-Площадь четырехугольника равна 5. Найти
площадь параллелограмма, стороны которого равны и
параллельны диагоналям четырехугольника.
953. В равнобедренной трапеции средняя линия
равна й, а диагонали взаимно перпендикулярны. Найти
площадь трапеции.
954, В угол вписаны два внешнекасательных круга.
Хорды, соединяющие точки касания каждого круга со
сторонами угла, равны соответственно 2а и 26.
Определить угол*
82
955. В равнобедренный треугольник вписаны один
над другим два круга радиусов /? и г, касающиеся друг
друга. Найти углы при основании треугольника.
956. Точка В внутри круга радиуса Я удалена от
центра на расстояние а. Через В проведены диаметр
и две взаимно перпендикулярные хорды, одна из
которых образует угол а с диаметром. Определить
площадь вписанного в круг четырехугольника, имеющего
эти хорды диагоналями.
957. Окружности радиусов г и Я касаются прямой АО
в точке А и расположены по одну сторону от АИ.
Прямая, параллельная Л/), пересекает окружности в точках
В и С, находящихся по одну сторону от линии центров.
Найти радиус окружности, описанной вокруг
треугольника ЛВС.
958. Из вершин квадрата, сторона которого а, как
из центров, проведены окружности радиусов а. Найти
площадь, общую всем четырем построенным кругам.
959. Прямая касается окружности в точке Л.
Параллельно этой прямой проведена другая прямая,
пересекающая окружность в точках В и С, которые соединены
с точкой Л. Рассматривая площадь треугольника ЛВС
как функцию расстояния между прямыми, написать
,формулу, связывающую функцию и аргумент. Радиус
окружности равен Я*
960. Из всех прямоугольников с площадью 5 найти
прямоугольник с наименьшим периметром.
961. Треугольник ЛВС с площадью 5 и углом а при
вершине А разделен на две равновеликие фигуры АМЫ
и СМЫВ прямой МЫ, где М и N — точки на сторонах Л О
и ЛВ. Найти периметр фигуры АМЫ при условии, что
длина МЫ — наименьшая.
962. Три положительных числа а, Ь и с связаны
зависимостью
а2 = Ь2 + А
На основании каких теорем можно утверждать, что
эти числа могут быть приняты за длины сторон
треугольника и что этот треугольник прямоугольный?
о*
83
XIV, ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ В ПРОСТРАНСТВЕ
(Стереометрия)
Доказать теоремы (963—971):
963. В правильном тетраэдре сумма расстояний от
любой внутренней точки до его четырех граней есть
величина постоянная.
964. Если имеется конечное число таких прямых, что
каждые две из них пересекаются, то все они или
проходят через одну точку, или лежат в одной плоскости.
965. Любой выпуклый четырехгранный угол можно
пересечь плоскостью так, что в сечении получится
параллелограмм.
966. Куб можно пересечь плоскостью так, что в
сечении получится правильный шестиугольник.
967. Если через три вершины параллелепипеда,
являющиеся вторыми концами ребер, исходящих из одной
вершины, проведена плоскость, то треугольник,
получающийся в пересечении параллелепипеда этой
плоскостью, пересекается диагональю параллелепипеда,
исходящей из той же вершины, в центре тяжести.
968. Если все двугранные углы трехгранного угла
острые, то и все плоские углы трехгранного угла тоже
острые.
969. Если любое сечение поверхности плоскостью есть
окружность, то эта поверхность — шаровая.
970. Не существует многогранника с нечетным числом
граней, все грани которого являются многоугольниками
с нечетным числом сторон.
971. Любой плоский угол четырехгранного угла
меньше суммы трех других плоских углов.
972. Найти геометрическое место проекций данной
точки на • всевозможные плоскости, проходящие через
Другую данную точку.
973. Найти геометрическое место центров сечений
данной шаровой поверхности, плоскостями,
проходящими через данную прямую.
974. Доказать, что через любую прямую можно
провести плоскость, параллельную любой другой прямой,
если только эти прямые не пересекаются.
975. Построить общий перпендикуляр к двум
скрещивающимся прямым»
84
976. Построить прямую, параллельную данной
прямой и пересекающую две другие данные прямые.
977. Построить отрезок данной длины,
параллельный данной плоскости, так, чтобы концы его находились
на двух данных прямых.
978. Взяты такие четыре вершины куба, что
никакие две из них не лежат на одном ребре. Через каждые
три из этих четырех вершин проведена плоскость. Найти
объем тела, ограниченного проведенными плоскостями.
Ребро куба равно а.
979. Через каждые три вершины куба с ребром а,
лежащие в концах каждых трех ребер, сходящихся в
одной вершине, проведена плоскость. Найти объем тела,
ограниченного этими плоскостями.
980. От правильной четырехугольной призмы
плоскостью, проходящей через диагональ нижнего основания
и одну из вершин верхнего основания, отсечена пирамида
с полной поверхностью 5. Найти полную поверхность
призмы, если угол при вершине треугольника,
получившегося в сечении, равен а.
981. Плоские углы при вершине параллелепипеда
равны между собой и равны 45°. Длины ребер, сходящихся
в одной вершине, равны а, Ъ и с. Найти объем
параллелепипеда.
982. В параллелепипеде длины трех ребер, исходящих
из одной вершины, суть а, Ь и с. Первые два ребра
взаимно перпендикулярны, а третье образует с каждым из
них угол а. Найти объем параллелепипеда.
983. Острые углы а, р появляются плоскими углами
трехгранного угла. Найти его двугранные углы.
984. Найти объем параллелепипеда, если длины трех
его ребер, сходящихся в одной вершине, равны /, т и п,
а плоские углы при той же вершине —а, р и у, причем
все острые.
985. Через середину высоты правильной треугольной
пирамиды, параллельно ее боковой грани, проведена
плоскость. Найти площадь получившегося сечения, если
площадь боковой грани пирамиды равна 5.
986. Через центр основания правильной треугольной
пирамиды, параллельно двум непересекающимся ребрам
ее, проведена плоскость. Найти площадь получившегося
сечения, если боковое ребро пирамиды равно /, а ребро
основания а.
85
987. Боковые грани пирамиды, основанием которой
служит равнобедренная трапеция с высотой Л, одинаково
наклонены к плоскости основания. Из вершины
пирамиды опущены перпендикуляры на боковые стороны
трапеции, и основания их соединены. В полученном
треугольном сечении угол при вершине равен а, а площадь
сечения равна 5. Найти объем пирамиды.
988. Основанием четырехугольной пирамиды служит
трапеция с основаниями а и Ь (а>6) и высотой к.
Боковая грань, проходящая через меньшее основание
трапеции, перпендикулярна к плоскости основания, а
противоположная грань является равнобедренным
треугольником с углом при вершине пирамиды, равным а. Через
вершину пирамиды и точку пересечения диагоналей
трапеции проведена плоскость, параллельная основаниям
трапеции. Найти площадь образовавшегося в этой
плоскости треугольника.
989. Через сторону основания правильной
треугольной призмы проведена плоскость под углом а к
плоскости основания. Определить площадь образовавшегося
треугольного сечения, если объем пирамиды, отсеченной
плоскостью от призмы, равен V.
990. Гранями треугольной пирамиды являются
равные равнобедренные треугольники. Основание и
противолежащий ему угол каждого такого треугольника — а
и а. Найти объем пирамиды.
991. Основанием прямой призмы служит ромб КВСО
со стороною а и углом 60°. Концы В\ и й\ диагонали
верхнего основания призмы соедицены прямыми В\Е и
ОхР с серединами сторон Кй и КВ нижнего. В
пересечении этих прямых образуется угол В\Ойи равный а.
Определить объем призмы.
992. В основании прямой призмы лежит
равнобедренный треугольник, периметр которого равен 2р, а каждый
из двух равных углов равен а. Через основание этого
треугольника и конец противоположного ребра призмы
проведено сечение. Угол при основании этого
треугольного сечения равен р. Найти объем призмы.
993. Найти полную поверхность правильной
треугольной пирамиды по данному ее объему V и углу а
между боковой гранью и плоскостью основания.
994. Основанием пирамиды служит прямоугольник.
86
Длина каждого бокового ребра равна т. Плоские углы
трехгранных углов при основании пирамиды суть а, р
и 90°. Найти объем пирамиды.
995. В правильной четырехугольной пирамиде, у
которой сторона основания равна а и двугранный угол при
основании равен а, через одну из сторон основания
проведена плоскость под углом р к плоскости основания.
Определить площадь сечения.
996. Высота правильной треугольной пирамиды
равна Л, а двугранный угол при боковом ребре равен 2а.
Найти объем пирамиды.
997. В правильной я-угольной пирамиде сторона
основания равна 2ау двугранный угол при боковом ребре
равен 2а. Определить объем пирамиды.
998. Правильная треугольная пирамида пересечена
плоскостью, проходящей через вершину основания и
середины двух боковых ребер. Найти отношение боковой
поверхности пирамиды к площади основания, если
известно, что секущая плоскость перпендикулярна к одной
из боковых граней. Указать, к какой именно.
999. Основанием пирамиды служит трапеция,
боковые стороны и меньшее основание которой равны а, а
острый угол а. Боковые ребра наклонены к плоскости
основания под углом <р. Найти объем пирамиды.
1000. Из середины высоты правильной
четырехугольной пирамиды опущен перпендикуляр на боковое ребро,
равный Л, и перпендикуляр на боковую грань, равный а.
Найти объем пирамиды.
1001. Через одно из ребер основания правильной
треугольной пирамиды со стороной основания ^ проведена
плоскость перпендикулярно противолежащему боковому
ребру и делящая это ребро в отношении т : п.
Определить полную поверхность пирамиды.
1002. Вычислить объем правильной пирамиды
высоты Л, зная, что в основании ее лежит многоугольник,
сумма внутренних углов которого равна 90°п, а отношение
боковой поверхности пирамиды к площади основания
равно к.
1003. Правильная пятиугольная пирамида ЗАВСйЕ
пересечена плоскостью, проходящей через вершины А
и С основания и середины ребер 5й и ЗЕ. Найти
площадь сечения, если ребро основания пирамиды равно д,
а боковое ребро равно &«
87
1004. Через вершину правильной л-угольной
пирамиды и через две вершины многоугольника, лежащего
в основании, под углом а к плоскости основания проведена
плоскость, рассекающая основание на два
многоугольника, имеющие соответственно (г+2) вершины и (л—г)
вершин (г < п Г" ]. Найти объем пирамиды, если общая
сторона этих двух многоугольников равна Ь.
1005. Боковые ребра и две стороны основания
треугольной пирамиды равны между собой и равны Ь. Угол
между равными сторонами треугольника, лежащего в
основании, равен а. Найти объем пирамиды.
1006. Основанием пирамиды ЗАВС служит
треугольник АВС, в котором АВ я АС образуют между собой
угол а и АВ=АС = а. Грань ЗВС перпендикулярна к
плоскости основания, а грани 8ВА * и ЗСА образуют
с плоскостью основания углы ср. Определить боковую
поверхность этой пирамиды.
1007. Две правильные треугольные пирамиды имеют
общую высоту; вершина каждой пирамиды лежит в
центре основания другой; боковые ребра одной
пересекают боковые ребра другой. Боковое ребро / первой
пирамиды образует с высотой угол а, боковое ребро второй
образует с высотой угол р. Определить объем общей
части этих пирамид.
1008. Правильный октаэдр пересечен плоскостью так,
что в сечении получился правильный шестиугольник.
Все вершины этого шестиугольника соединены с одной из
вершин данного октаэдра. Найти объем образовавшегося
тела, если объем октаэдра равен V.
1009. В правильной усеченной четырехугольной
пирамиде проведена плоскость через две противоположные
вершины параллельно диагонали основания. Определить
площадь сечения, если высота пирамиды к, а стороны
оснований а и Ь.
1010. В основании пирамиды лежит ромб со
стороной а и острым углом а. Каждый из двугранных углов
при основании равен ср. Определить объем шара,
вписанного в эту пирамиду.
1011. Две равные правильные четырехугольные
пирамиды приложены одна к другой основаниями так, что
оба основания совпадают, а вершины расположены по
разные стороны от общего основания. В образованный
88
таким образом восьмигранник вписан шар. Определить
его радиус, если сторона основания каждой из пирамид
равна а, а плоский угол при вершине равен а.
1012. Шаровая поверхность касается трех ребер куба,
сходящихся в одной вершине, и трех его граней,
пересекающихся в вершине, противоположной предыдущей.
Найти часть поверхности этой сферы, лежащей вне куба,
если ребро куба равно а.
1013. Шар вписан в прямую призму, в основании
которой лежит прямоугольный треугольник. В этом
треугольнике перпендикуляр, опущенный из вершины
прямого угла на гипотенузу, имеет длину к и составляет
с одним из катетов угол а. Определить объем призмы.
1014. Ребро правильного тетраэдра равно а.
Определить радиус шара, поверхность которого касается всех
ребер тетраэдра.
1015. Двугранный угол при боковом ребре
правильной четырехугольной пирамиды равен а, а радиус шара,
вписанного в эту пирамиду, равен /?. Найти полную по-
верхность^ пирамиды.
1016. В прямой круговой конус объема V вписана
треугольная пирамида с плоскими углами при вершине,
равными а, р и у. Найти объем этой пирамиды.
1017. В шаре из точки его поверхности проведены три
равные хорды под углом 2а друг к другу. Определить их
длины, если радиус шара равен /?.
1018. В правильную четырехугольную пирамиду,
сторона основания которой равна а, а плоский угол при
вершине равен а, вписан полушар с плоскостью экватора,
расположенной в основании пирамиды. Найти объем
многогранника, четыре вершины которого находятся в
точках касания шаровой поверхности с боковыми гранями
пирамиды, а пятая — в центре полушара.
1019. Стороны равнобедренной трапеции касаются
кругового цилиндра, ось которого перпендикулярна
параллельным сторонам трапеции. Найти угол, который
образует ось цилиндра с плоскостью трапеции, если
основания трапеции суть а и 6, а ее высота равна Н.
1020. Осевое сечение конуса — две взаимно
перпендикулярные прямые. На одной и той же образующей
конуса взяты точки Л и В на расстоянии а друг от друга.
На поверхности конуса взяты еще две точки Си/) такие,
89
что АВСО — правильный тетраэдр. Найти расстояние от
вершины .конуса до ребра СО этого тетраэдра*
1021. Найти объем цилиндра, расположенного внутри
правильного тетраэдра так, что высота тетраэдра служит
осью цилиндра, окружность одного основания цилиндра
лежит в плоскости основания тетраэдра, а окружность
другого — касается остальных граней тетраэдра и
пересекает две другие его высоты. Ребро тетраэдра равно /.
1022. Радиус основания конуса равен #, а
образующая наклонена к плоскости основания под углом а.
В этом конусе проведена плоскость через его вершину
под углом ср к его высоте. Найти площадь полученного
сечения.
1023. Два конуса имеют общую высоту, но
вершины их лежат в разных концах высоты. Образующая
первого конусоравна /, а угол при вершине его осевого
сечения равен 2а. Угол при вершине в осевом сечении
второго конуса равен 2р. Найти объем общей части конусов.
1024. В трапеции одна из боковых сторон равна Ь и
образует с большим основанием, равным 2а, угол а.
Меньшее основание равно а. Определить объем тела,
образованного вращением этой трапеции вокруг данной
боковой стороны.
1025. Угол образующей а конуса с плоскостью его
основания равен а. Найти объем описанной около
конуса пирамиды, основанием которой служит ромб с острым
углом р.
1026. Около конуса описана треугольная пирамида,
причем линиями касания боковая поверхность конуса
делится на три части, относящиеся между собой, как
5:6:7. Найти отношение между частями боковой
поверхности пирамиды, ограниченными линиями касания.
1027. На плоскости лежат три равных конуса с общей
вершиной. Каждый из них касается двух, рядом
лежащих. Найти угол при вершине осевого сечения одного из
этих конусов.
1028. На высоте конуса, как на диаметре, описан
шар. Найти объем части шара, заключенной внутри
конуса, если даны высота к конуса и угол при вершине его
осевого сечения, равный 2а.
1029. Конус с углом а между осью и образующей
и радиусом основания г рассечен сферической
поверхностью, центр которой находится в вершине конуса, так
90
что объем конуса разделен пополам. Найти радиус этой
сферы.
1030. В правильную п-угольную пирамиду с ребром
основания # и боковым ребром а вписан шар. Найти его
радиус.
1031. Высота правильной четырехугольной пирамиды
равна к. Перпендикуляр, опущенный из центра шара,
описанного около пирамиды, на ее боковую грань,
образует с высотой угол а. Найти объем шара.
1032. Прямой круговой конус рассечен на две части,
равные по объему, плоскостью, проходящей через центр
вписанного шара перпендикулярно оси. Найти угол
между образующей и плоскостью основания.
1033. В прямой круговой конус, угол при вершине
осевого сечения которого равен а, вписан шар радиуса г и
затем проведена плоскость, заключающая окружность
касания поверхности конуса с поверхностью шара.
Найти объем получившегося усеченного конуса.
1034. Основанием пирамиды служит прямоугольник,
диагонали которого образуют между собой угол а, а
боковые ребра ее составляют с плоскостью основания
угол ср. Найти объем пирамиды, если известно, что
радиус описанного около нее шара равен /?.
1035. В конус вписан шар радиуса г.' Найти объем
конуса, если известно, что плоскость, касающаяся шара
и перпендикулярная к одной из образующих конуса,
отстоит от вершины конуса на расстояние й.
1036. В шар радиуса Я вписан цилиндр.
Рассматривая объем цилиндра как функцию радиуса основания
цилиндра, написать формулу, связывающую функцию
и аргумент.
1037. Можно ли определить призму как
многогранник, у которого две грани — равные многоугольники
с соответственно параллельными сторонами, а все
остальные грани — параллелограммы?
РЕШЕНИЯ
I. ПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКИХ
ВЫРАЖЕНИЙ*
% 1. А = с (Ь2 + Ьс + ас—а2) — аЬ (а + Ь) = с (Ь2 — а2) +
-5- с2 (Ь + а) — аЪ (а + Ь) = (а + Ь) (Ьс— ас + с2 — аЬ) =
= (а + Ь) [(Ьс — аЬ) + (с2 —ас)] = (а + Ь) [Ь (с — а) +
+ с(с — а)] = (а + Ь) ф + с) (с —а).
2. А = Ь2(а*Ь — а3 + с* — с2Ь) + с2а2(а — с) =
= Ь2 [(а2Ь — с2Ь) — (а3 — с8) ] + а2с2 (а — с) =
= Ь*(а2 — с2) — Ь2 (а3 — с3) + а2с2(а — с) =
*= (а — с) (Ь*а + ^с — 62а2 — &2ас — 62с2 + а2с*) =
« (а — с) [62а ф — с) + Ь*с ф — с) — а2 (Ь2 — с2)] =
= (а —с) ф — с) (Ь2а + Ь*с — а2Ь — а2с) =,
= (а — с) (6 — с)Ыф — а) + с(Ь2 — а2)]=
=(а — с) ф — с) ф — а) (аЬ + Ьс + са).
3. Выражение, стоящее в первых квадратных скобках,
легко приводится к следующему:
(ах + Ьу)2 + (ау + Ьх)2,
а второе — к такому
4 (ау + Ьх)2 (ах + Ьу)2.
Имея это в виду и воспользовавшись формулой разности
квадратов двух количеств для данного выражения А,
получаем
А = [(ах + Ьу)2 + (ау + Ьх)2]2 — 4(ау + Ьх)2 (ах + Ьу)2 =
= [(ах + Ьу)2 + (ау + Ьх)2 — 2(ау + Ьх) (ах + Ьу)] [(ах +
* Здесь выражение, подлежащее упрощению, обычно не
повторяется, а обозначается буквой А.
92
+ Ьу)2 + (ау + Ьх)* + 2 (ау + 6*) (шс + 6</)] = [(ах + 6</) -
- (ау + Ьх)]2 [(ах + Ъу)Г+ (ау + 6л;)]2 =
=[(а - 6) (х - у)? [(а + Ь)(х + у)? =
= (а - б)2 (а + б)2 (х - у)2 (х + у)2.
4. А = 2а2Ь + 4аЬ2 — а2с — 2аЬс + ас2-\-2Ьс2—
— 4Ьгс — 2аЬс = 2аЬ(а + 2Ь) — ас(а + 26) + с2(а + 26) —
— 26с (а + 26) = (а + 26) (2а6 — ас + с2 — 26с) =
= (а + 26) [а (26 — с) — с (26 — с)] =
= (а + 26) (26 —с) (а —с).
5. А = у(х— 2г)2 + Ьхуг + ху2 — Ахуг + Ахг2 — 2гх2 —
— Агху — 2гу2 = у(х — 2г)2+ (ху2 — 2гу2) — (2гл:2 — 4хг2) =
= (х — 2г) (ух — 2уг + у2 — 2хг) = (х — 2г)[х(у—2г) +
+ у(у — 2г)] = (ж —2г) (у —2г) (*+*/).
6. Л = 8ж3(у + 2) — ^2 — 2у3х — 2хг3 + г9у =
= 8г»0/ + г).-уг (у2-г2)-2х (у8 + г8) = (у + г) Г8*3-
— уг(у — г) — 2х (уг — уг + г2)] = (у + г) (8х*— уЧ + уг*—
— 2ху2+ 2хуг — 2хг2) = (у+г) [(8х9—2ху2) + (2хуг — у2г)—
— (2хг2 — уг2)] = (у + г) [2х (Ах2 — у2) + уг (2х — у) —
— г2 (2х — у)] =.(у + г) (2х — у) (Ах2 + 2ху + уг — г2) =
= (у + г) (2х - у) [(Ах2 — г2) + (2ху + уг)] =
= (у + г) (2х—у) [(2х + г) (2х — г) + у (2х + г)] =
= (у + г) (2х-у) (2х + г) (2х— г + у).
7. А = (х* + У4 — 2*У) — 2(х2 — у2) г2 + г4 — 4у2г2 =
= (л;2— у2)2 — 2(х2 — у2) г2 + г4 — 4угг2 = [(л:2 — у2) — г2]2—
— (2уг)2 = (л:2 — у2 — г2 — 2г/г) (*я — у2 — г2 + 2уг) =
= I*2- (У + г)2] 1х2- (у-г)2] = (х + у + г) (х- у-
— г) (х + у — г) (х — у + г).
8. А = (х2у + ху2) + (хг2 + у22) + (х2г + у2г + 2хуг) =
= ху (х + у) + г2 (л; + у) + г (х + у)2 = (х + у) (ху +
+ г2 + гх + гу) = (х + у) [х (у + г) + г (у + г)} =
= (х + у)(у + г)(г + х).
Замечание. Исходное выражение симметрично
относительно букв х, у, г, т. е. такое, что от замены х, у, г
соответственно буквами у, г, х не меняет своего вида.
Следовательно, если оно имеет множитель х + у, то оно
имеет также множители у + г и г + х. Таким образом,
93
после выделения множителя х + у можно было предвидеть
наличие множителей у + г и г + х в окончательном
результате.
9. А = (х*у + хуг + хуг) + (Л + хг2 + хуг) + (у2г +
-1- у г2 + хуг) = ху (х + у + г) + хг (х + у + г) + уг (х +
+ У + г) = (х + у + г)(ху + уг + гх).
10. А = (х3— 1) + (5**-^5) + (3*—3) = (*— 1) (х2 +
+ *+ 1) + 5(*- 1) (х+ 1) + 3 (ж- 1) = (*- 1) (*2 + л: +
■+- 1 + 5* + 5 + 3) = (х— 1) (х2 + 6* + 9)=(* — 1) (х + З)2.
И. А =* (х3— 1) + (9х2 — 9) + (Их— 11) = (лг— 1)(х2 +
+ *+1+9х + 9+ 11) = (л;—1)(*2+10л:+21) =
= (х-\)(х + 3)(х+7).
12.А=х\х2 (х2—7)2— 36]=л; [х (х2—7)—6] [д: (*2—7)+6]=
= *(г> — 7л: — 6) (г1 — 7х + 6)=х[(х«+ 1) —
— 7(* + 1)][(дс«— 1) —7(х— 1)] = х(х + 1) (х — I) (х2-*
— х — 6)(х2 + х — 6) = *(* + 1)(х— 1)(х — 3)(х +
+ 2)(х + 3)(х-2).
13. Воспользуемся формулой (т + я)8 = т8 + Зтп (т +
+ п) + п8 для преобразования первого слагаемого данного
выражения. Получим
А = [ф-а) + (а-с)}3 + (с-а)3 + (а-Ь)3 = ф-а)3 +
+ 3(Ь-а)(а-с)[(Ь-а) + (а-с)] + (а-с)3-^
^(а — с)3~(Ь-*а)8 = 3(а — Ь)(Ь — с)(с — а).
14. А = 3 (у2 + г2) (х2 + у2) (х — г) (х + г).
Указание. Решать так же, как задачу 13.
15. Л = [(* + 0 + г)8-л;8]-({/я + г8)=[(л: + «/ + г)-*
— х] [(х + у + г)2 + (х + у + г) х+ х2) — {у + г) (у2 —
— у г + г2) = (у + г) [ (х + у + г)2 + (х + у + г) х +
+ х2 — у2 + уг — г2].
ВмесУто того чтобы производить утомительные
выкладки для выделения других множителей способом
группировки, воспользуемся замечанием к задаче 8. Так как
данное выражение симметрично относительно х, у, г, то
наряду с множителем у + г оно имеет множители г + х
и х + у. Поэтому можно написать
(х + у + г)3-х3~-у9-г3 = (х + у)(у + г) (г + х)В,
94
где В — частное от деления данного выражения на
произведение трех выделенных множителей. Рассматривая левую
и правую части последнего равенства как многочлены
относительно х и замечая, что в равных многочленах
коэффициенты при одинаковых степенях буквы х равны,
найдем сравнением коэффициентов при х\ что В = 3.
Следовательно,
А = 3(х + у)(у + г)(г + *).
16. Пусть п — любое целое число. Тогда получим
п (п + 1) (п + 2) (п + 3) + 1 = (п2 + Ъп) (п2 + Зп + 2) + 1 =
= (п2 + Зп)2 + 2 (п2 + Ъп) + 1 = (л2 + 3п+ I)2.
17. 132*— 1 = 169Л— 1 = №(№"-1 + 1№*-*+...+ 1).
18. 721 —487 = 7-4910 —7 —480 = 7.(4910— 1) —480=
= 7-48 (499 + 498 + ... + 1) — 48-10 =
= 48 [7 (499 + 498 + ... + 1) — 10].
Так как 49 = 8-6 + 1, то 49* = 6т + 1 и выражение
в квадратных скобках будет иметь вид
7 (6л + 10) — 10 = 7-6п + 60 = 6 (7/1 + 10).
Итак,
721 — 487 = 48-6 (7л + 10) = 288 (7л + 10),
т. е. делится на 288.
19. Обозначим буквой А левую часть данного
равенства. Получим
А = (а + Ь — 2с)2 + (Ь + с — 2а)2 + (с + а — 2Ь)2 =
= [(а-с) + (Ь-с)]2 + [(Ь~а) + (с-а)]2 + [(с-Ь) +
+ (а — Ь)\2 = 2 (а — с)2 + 2(Ь — с)2 + 2 (Ь — а)2 +
+ 2(а — с)(Ь — с) + 2(Ь — а)(с — а) + 2(с — Ь)(а — Ь) =
= 2А + [(а — с)(Ь — с) + {Ь — а)(с~а)]+[(а — с)(Ь — с) +
+ (с-Ь)(а — Ь)] + [(Ь — а)(с — а) + (с — Ь)(а — Ь)] =
= 2А+ (а —с)2 + (Ь — с)2 + (а — Ь)2 = 2А + А = ЗА
Итак: Л = ЗЛ, 2А = 0, Л = 0,'т. е. (а — Ь)2 + ф — с)2 +
+ (с — а)2 = 0.
Отсюда а = Ь = с.
20. Так как из равенства т + п +• р = 0 следует, что
т = — л — р, то
т3 + п3 + Р3 = (— л — р)3 -+- л3 + р3 = — л3 — Злр (л + р)—*
— р3 + дг3 + р3 = — Злр (л + р) = Зтлр
(см. также задачу 23).
95
(у + г)х+1
(У + г)х+1
21._(у2 + 2уг + г2)х* + 2(у + г)х+1
(У2 + 2уг-^г2)х2 + (у + г)х
_(у + г)х±1
(у + г)х+1
О
22. Расположив делимое и делитель по убывающим
степеням буквы х и пользуясь известным правилом
деления многочлена на многочлен, получим
(а3-1)*3—(а*+а*-2)х*+(4а*+3а+2)х-3а~3 I (а-\)х2-(а-\)х+3
~ (д*-1)х*~(а3~1) *2 + 3 (а2 + а + 1) х (а2+а+1) х- (а+\)
— (а2—1)*2+(а2 —1)* —3(а+1)
*"" — (а2 — 1) *2 + (а2 — 0 * — 3 (а + 1)
О
23. Подставим в данное выражение вместо х величину
— у — г. Получим (— у — г)3 + у3 + г3 — 3 (— у — г) г/г =
~{У + *)8 + У* + г3 + 3</2г + 3#г2=-((/+г)3+(г/+г)3= 0.
Отсюда, на основании теоремы Безу, заключаем, что
многочлен х? + у3 + г9 — Ъхуг делится на х — (—у — г) =
=-х + у + г.
24. Среди трех последовательных натуральных чисел
одно непременно кратно 3 и одно или два четные. Тот из
двучленов хк—1(к = т+1,т— 1, т), у которого к—>
четное, разделится на х2 — 1; у которого к — кратно трем,
разделится на х3—1 и последний, при любом
натуральном к, разделится на х—1.
25. Представив данные выражения в виде ^ и
ап — 1
__ 1, видим, что вопрос сводится к выяснению признака
делимости выражений ат — 1 и ап — 1. Очевидно, для
этого необходимо, чтобы было т> п. Пусть частное и
остаток от деления т на п будут р и ^, т. е. т = пр+д.
Получим
ат — 1 апр + я — 1 апР ая — ая + ая — 1
ап — 1 ап — 1 ял — 1
Отсюда видно, что для возможности деления нацело
необходимо и достаточно, чтобы ц = 0, т. е. чтобы т было
кратно п.
96
26. Корни хх и х2 трехчлена х2 + х + 1 удовлетворяют
условиям х] + х1 + 1 = 0 и х* = 1 (/ = 1,2). Поэтому
*?* + *»» + ;* = (а:|)л+ (4)10^/+ (х;)9^=1 +х? +^=0.
Отсюда, по теореме Безу, данный многочлен делится на
х — хх и а: — лс2, а следовательно, и на их произведение
(х — хх)(х — х2) = х2 + х + 1.
27. Умножим и разделим левую часть доказываемого
равенства на 1 — х. Получим
(1-л:)(1+л:)(1+л:2)...(1+л:2"-1) _ 1—х*п _
1-х 1-х ""
= 1 +х + х2 + ... + х2П-К
28. Произведение трех данных множителей приводится
к многочлену степени 2-175 + 1 -5 + 3-149 = 802.
Поэтому можно написать
(1 + 4* — 4*2)175 (1 + 2х)ъ (1 — Ъх + х2 + 2*3)149 =
= Ахх^ + А2х»<» + ... + Л803.
Полагая в этом равенстве х = 1, получим
Ах + А2 + ... + Л803 = I175 • 3* • 1"» = 243.
29. Это равенство можно доказать путем упрощения
левой части. Но такой путь приведет к большим
выкладкам. Можно доказать короче. Известно, что если два
многочлена / (лг) и ср (л;) степени п имеют одинаковые значения
при п + 1 различных значениях х, то они тождественно
равны. В данном случае п = 2. Полагая в левой и правой
частях доказываемого равенства х = а\ х = Ь\ х = с,
получим для обеих частей соответственно а2, б2, с2. Тем самым
тождество доказано.
30. I. Необходимость. Пусть а^Х_ = К где к—
не зависит от х. Освободившись от знаменателя, получим
равенство ах +<Ь = ктх + кп. Но из равенства
многочленов следует равенство их коэффициентов при одинаковых
степенях х. Поэтому можно написать, что а=кт и Ь=^кп
или — = —. Если т = 0 (или п = 0), то пропорцию
слети а I п Ь \ гу
дует написать иначе: — = — (или — = — I. Случаи т=
= п = 0 исключается.
7 К. У. Шахно
97
II. Достаточность. Пусть — =— = А. Тогда
*. г. и йх-\-Ь ткх + пк , тхА-п и
а = тк\ Ъ = пк\ ——- = —--— = к —з— = к.
1 ' тх+ п тх + п тх+п
31. Поступая так же, как и в задаче 30, найдем, что
искомые необходимые и достаточные условия состоят в
следующем:
а _ Ь _ с
~т "*~ п ~~ р
1 , 1 (1+*)-М1—*) 2
32.
\—х « 1 + * (1 — л:) (1 -+- л:) 1— х2'
1,1,2* 2,2 4
1—* ^ 1 + х ^ 1 + х2 1 —л2 ' 1 + х2 1 —л;4'
Прибавляя к полученному результату четвертую данную
дробь, а затем пятую и шестую, получим окончательно
1 1 . 2 4 8 16 _ 32
!_* -Г 1 + Л. "Г ! +Х2~г 1 +^4-г ! -(-л:8"^ 1+*1в ~" 1— х**'
33. Приведя дроби к общему знаменателю, получим
(о^6)(б1С)(а^с)К6-С)+(С-а) + (а-^-°-
34. После приведения дробей к общему знаменателю,
получим
а2 (Ь -~ с) + б2 (с — а) 4- с2 {а — 6)
где
N = (а — Ь)(Ь — с) (а — с).
Разлагаем числитель на множители:
а2(6 —с) + 62(^~а) + с2(а-^6)=а2(6 — с) +
+ ф2с-*с2Ь) + (с2а-*Ь2а) = а2 (6 —с) + Ьс(Ь*~с)-~
^а(Ь2~с2) = (Ь — с)(а2 + Ьс — аЬ — ас)=*
«= (6 -#* с) [(а2 #-^ аб) + (^ — яс)] = (& — с) [а (а — 6) «*
^с(а — 6)] = (а — 6) (6 — с) (а — с)=#.
Ответ: -^- = I.
35. Складываем данные дроби попарно — первые две и
вторые две. Получим
98
А .^(а-Ь)(Ь + с)+ф-с)(а + Ь)
(а+Ь)(Ь + с) "Т"
(с-а)[(а + Ь)(Ь + с) + (а-Ь)(Ь-с)]
"•" (а + Ь)(Ь + с)(с + а)
_ аб — №-\-ас-~ Ьс-\-аЬ — ас-\-Ьг — Ьс .
(а + Ь)(Ь + с) "+"
. (с —а) (аЬ + Ь* + ас + Ьс + аЬ — Ь* — ас+ Ьс) _
+ (а + Ь)(Ь + с)(с + а) ~
__ 2аЬ — 2Ьс (с — а) (2аЬ + 26с) _ 26 (а — с) ,
(а + Ь)(Ь + с) "•" (а+6)(6 + с)(с + а) ~ (а + 6)(6 + с) +
. 26 (а + с) (с •*- а) _ 26(а~с) 26 (а — с) _ -
+ (а + 6)(6 + с)(с + а) - (а + 6)(6 + с) (а+6)(6 + с) _ "'
36. Приведя дроби к общему знаменателю, получим,
что данное выражение
^-(В-Ь)(б1с)(с--0)^-^ + (У-0 +
+ (С2_а2)]==0#
47 А -4*. Л- °2 (у2 * Ь2) (г* -* Ь2) * Ь* (у1"" с2) (г2 ~ с2) -
*'• Л — ^2С2 Т" Ь*С*(Ь* — С2) —
__ */222 с2#222 — сЧ%2—с2у*Ь2+с2Ь*--Ь2у2г2+Ь*с*г2+Ь2у2с2—Ь2с4 _
ЬЧ2 ^ Ь2с2 (Ь2 — с2)
1/222 С2Г/222 — 62у222 + С2Ь* -* Ь2С* */222
+
~~ 62с2 ~ &2с2 (Ь2 — с2) Ь2с2
у222 (С2 — &«) + С262 (62 ^. с2) ^ ^2 (б2 ^ С2) (~Г/222 + 62С2) __
ЬЧ2 (Ь2 — с2) *"" &2с2 ~*~ &2с2 (б2 — с2) """
— г/2г2 — г/222 + д2с2 _ у2г2 у2г2 Ь2с2 __ «
— Ь2с2 "•" &2с2 "~~ Ь2с2 Ь2с2 "•" &2с2 "" '
, (1 + ад) [\+аЬ+(а+Ь)х] - (а + 6) [а + Ь + (1 + ад)*]
оо. Л _ (1 + дЬ + (д + ц ^2 _ [а + 5 + 0 + аЬ) х}2 ^
(1 + аЬ)2 + (1 + оЬ) (а + 6) х — (а + Ь)2 — (а + Ь) (1 + ад) х
~" (1 + ад)2 — (1 + аЬ)2 х2 + (а + б)2 *2 — (а + Ь)2 ""
(1+ад)2-(а + Ь)2
(1 + ад)2 (1 — х2) — (а + Ь)2 (1 -*-*2)
(1+ад)2 —(а + д)2 1
~~ (1 — *2) [(1 + аЬ)2 — (а + д)2] 1 — **'
ЧО А = (^ — л: + 1)(л;а 4-^ — 1) , (*-** + !)(* + *2- 1)
°*# Л (х2+1—$(х2+1+х) ^ (х2 + х^ \)(х2 + х + I)"1"
(х2 — л--1)(д;2-*л:+ 1) ^а + д:^| х_^2+1
+ (л:3 — х — 1) (л:2 + ж + 1) х2 + х+1 + *2 + *+1 ~1~
я*-*х+1 __ х2 + х^1 +х^х2+1 + х2 — х+ 1
+ *2 + *+1 "" *2 + *+1
*2 + *+1 ,
99
40. Рассматривая сумму первых двух слагаемых
числителя как сумму кубов двух количеств или поступая так,
как в задаче 13, получим следующее выражение для
числителя: 3 (х2 — у2) (у2 — г2) (г2 — х2). Аналогично поступая
со знаменателем, найдем, что он равен 3(х—у) (у—г) (г—х).
Отсюда данное выражение
„ 3(*2 — у2)(у2 — г2)(г* — *а) / , х/ , ч/ , ч
4| . _ а»(с — Ь) + Ь3(а — с) + с)(Ь — а) _ М
М = а*(с — Ь) + (Ь3а — с3а) + (—63с + <*Ъ) = а3 (с — Ъ) —
— а (с3 — Ь3) + Ьс (с2 — Ъ2) = (с — 6) (а3 — ас2 — аЬс — аЬ2 +
+ Ьс2 + Ь2с) = (с — Ъ) [(а3 — аЬ2) + (— ас2 + Ьс2) +
+ (—аЬс + Ь2с)] = (с — Ь)[а (а2 — Ь2)—с2(а — Ь)^
*~Ьс (а — Ь)] = (с — Ь) (а — Ь)(а2 + аЬ — с2 — Ъс) =
= (с — Ъ) (а — Ь) [(а2 — с2) + (аЬ — Ьс)] =
= (с — Ь)(а — Ь) (а — с)(а + с + Ь).
Аналогичными преобразованиями получим, что знаменатель
N = (с — Ъ) (а — Ь) {а — с). Впрочем, эти преобразования
можно найти в решении задачи 34. Теперь получим
Л ~ "Ж ~ (с_Жа_6)(а_с) - а + ° + с-
42. Замечая, что -,—г-ггт—, . , ,ч = —г-г' , . , .,
(л: + к) (х + * + 1) * + А жНгА+1*
получим
Л = 1"Г — Т+Т/ + \Т+Т ~ Т+Т/ + [Т+Т ~~ *Тз/ +
+Р и+и и-
1 1 5
х х + 5 х(х + 5)'
43. Рассмотрим произведение первого множителя на
первое слагаемое второго множителя:
(а-Ъ + Ь-с с-а\ с , с (Ь-с
\ с ^ а ^ Ь ) а — Ь 1^а — Ь\ а ^
*)-
4 I с Ь2 — Ьс + ас—а2 __
100
, , с с(а — &) — (а2 — Ь*)
1 а — Ь аЬ
-' + т^т ■ «г^^±а -1 + -4г и- » + ад
а так как с = — (а + 6), то получим окончательно для
2с2
этого произведения 1 -\ г-. Точно также произведение
первого множителя на второе слагаемое второго множите-
2а2 2Ь2
ля будет 1 + -т— и на третье слагаемое 1 -\ .
Складывая полученные выражения и пользуясь результатом
задачи 20, получим
= 3 + ^^ = 3 + 6 = 9.
44. 1——+ -§ Г + ^ + ^Л""-"^ = 1 + Т +
+ "з" + ~ + - + 2^Л + "2Г~2 (~Т + Т" + ~б~ +
+ ... + ^) = 1 +^ + 4- + -+Т + ТТТ + ТТ2- +
+ ...+^+^-(1+4-+4-+-+4-) =
1 ' ' + +—
— ь+ 1 ^ к+ 2 ^"' ^ 2к'
45. Умножим первое равенство на ф, второе — на р2,
третье — на — 2рц и результаты сложим почленно. Получим
(ад- М2 + (ад - М2 + .- + (апя - Ьпр)* = 0.
Следовательно,
^9 — Ь\Р = ад — Кр = ... = ал9 — 6ЛР = 0,
откуда и вытекает доказываемое равенство.
46. Преобразуем заданные отношения и пользуемся
свойством равных отношений:
ахЬх _ а2Ъ2 _ _ апЬп _ а\К + афч + • • • + апЬп (\\
ъ\ ~ ь\ --- ь\ Ъ\ + ъ\ + ... + ъ\ - V
Отсюда
аА + а2Ь2 + ... + апЬп = -^ (б2 + Ь\ + ... + К). (2)
101
Аналогичными преобразованиями получим
«А + аА + -. + а„Ьп = А {а\ + а\ + ... + аД). (3)
"1
Перемножая равенства (2) и (3) почленно, найдем
(оД + о^ + - + ^А)2 = (*? + «5 + ... + я*) (^12 + Ъ\ +
+ ... + «).
47. Все общие множители числителя и знаменателя
данной дроби являются также множителями выражения
с(14л + 3) + #(21я + 4), где а и 6 —целые. Но при а=3
и6 = -2, получим 3(14л + 3) —2(21л+ 4) = 1. Таким
образом, общие множители членов дроби могут быть лишь
числа ± 1, Т. е. она не сократима.
а2 Ь2 а2 4- Ь2 Ь2
48. Так как —;. = -—, то ^^ = -у. Но из данной
пропорции имеем б2 = ас. Подставляя в правую часть по-
а2 + Ь2 ас а
лученной пропорции, найдем _Г 2 = -^ = —.
49. Из данной пропорции получаем
с&Ч сга\ скак *
ЪЬЧ сф\ скЪпк
Отсюда, пользуясь свойством равных отношений, найдем
СгаЧ + с&Ч + ... + скапк схапх
а" _ /аЛ»
50. Покажем, что никакая рациональная дробь —
(т и /г — натуральные числа) не равна "1/2. Для
доказательства допустим, что существует такая дробь , что
пг2
—2~ = 2. Предполагаем эту дробь несократимой, т. е.
т и п не имеющими общих множителей. Из соотношения
-^- = 2 вытекает, что т2 = 2п29 а это означает, что число
т есть четное. Положим т = 2р и подставив в равенство
т2 = 2л2, получим 4р2 = 2/г2 или п% = 2р2. Но в таком
* Если некоторые из ст{гп— 1,2,..., /г) равны нулю, то для
составления этих отношений используем лишь те ст, которые не
равны нулю.
102
случае число п тоже четное, чего не может быть, так как
— по предположению — несократимая дробь.
51. По определению корня кубичного из числа.
52. а) По определению нулевой степени числа (афО);
б) по определению дробной степени числа; в) по
определению отрицательной степени числа (а Ф 0); г) по
определению первой степени числа.
53. У а2 = \а |. Или иначе: У а2 — а, если а > 0; Уа?=
= — а, если а < 0.
54. а) *>0, у>0; б) х>0, у>0; в) а>0, Ь < 0,
с — любое вещественное число; г) а<0, 6>0.
55. Пользуясь свойством равных отношений, получим
% + <*2 + • • • + Л/» _ _0^
*1+*.+ ...+*я Ьг
или, извлекая квадратный корень
У~а~1 + 02 + • • ■ -Г% = К"07
К^ + ^ + .-. + б,, УТГ
С другой стороны, из данной пропорции находим
01&1 _ 02^2 _ __ С1пЬп
ь\ ы "" ь%
или
Уа^1 _ Уаф1 _^ ^ __\П^п
Ь\ Ъг "* Ьп
Отсюда получим
Уаф^+ У афч + ... + УаЦь'п _ У^\ __ У~
Ьг + Ь2 + •. • + Ьп Ьх У~ЬГ'
Сравнивая левую часть этого равенства с такою же,
полученного ранее, легко получить равенство, которое
нужно доказать
56— 115. Указание. При решении этих задач
следует помнить, что встречающиеся в них корни
предполагаются арифметическими. Поэтому важно в тех случаях,
когда наложены ограничения на параметры, уяснить себе,
где эти ограничения используются, а в прочих случаях
наложить такие ограничения, если они должны быть
наложены.
ЮЗ
56. А
-[
(УТ+УТ)2-(УхТу)
Х + У
Г (Ух+УТ)Ух+
[х+2у~зщ + у — х-
(Ух+У1)Ух~+~У ] 2Уху
2 х+у =(У^+У~у)2(*+у)
*У^У (2 К!Ю2
■у]
х + У
_ х+у (х + 2Уху + у Л_
2 У ху 2 У~х~у~ \ 2 Уху )
_ х + у
57 Л- V7 (а-*ь)
У~сё+ 2 УПЬ + 4 У~Ьг
УТ[(УТ)3-(23УТ)3]
Х + У_= (х + У)^
2У ху 2 Уху Аху
УТ-2\Г7 .«/-^
(УТ)2 + (\ГТ)(2\Гь) + (2УТ)* ух-2\Гь
= уоуа-к а = 0.
-Г3"=
г2а&
а + 6 \ |/Т+ |Л26 >^Г+ >^26
: (У^+У2Ь) =У* + 1У°Уй + уТь^ 1 =
^ Г ' Уа+\Г2Ь УТ+У2Ь
_ (УТ+УГьГ .
_(|ЛГ+^2б)2 -1'
(/?- ^ у2)« (уу+ /7)- з + 2ж уТ+ у у-у-
+ (УТ)*-(У7У _ *УТ+»/7
' У'х'+УТ _ хУТ+уУТ
зуТ _ ЗхУх — ЗхУу + ЗуУТ гут ^_
У'х'+УТ хуч+уу~у_ ут+ут
ЗУТ(х — Ух^ + у) ЗУх зУх
59. А
(УТУ+(УТ)3
У_х + Уу
ЗУ х
У х + У у
ут+уУ
0.
104
бо. л -- [^т (|лг~ УТ) У**~ Уш
■ $ГТ)*-{уТ)*
а + Ь
-[уи
(УТ-УТ)1(УТ)3 + (УТ)
УТ УёёЬ — У~а&
УТ)*] \ -
-г-
~+УТ (УТ)Ч(УТ)3
I а + 6 ]
__ (_± Л~'_ (-а ^~'_ а+Ь
— \а + Ь ) ~\а+Ь/ ~ а '
61. А = (}Г* + ^(*>/Т+ у^(]/* + У~у)~2^ху |
2К^
(УТ-УТУ
Ух* — Уху+Уу*-У~Щ1 2У~у
х — у УТ+ У~у
2/у _ ут-ут ъу-у-
уХ2-уУ2- уТ+Уу Ух + Уу у х+У у
^ У~х + УТ_ ^ !
_ (-УТ*:(УТ+ УТ) + УТ) УТ (ут+ УТ) ^
Уху
^у^у-+утут(У~х-+УП =
Уху
_ — У#у + Ух*у + УТу ^Ухм_ ь
Уху Уху
бз л._\У^(ут+ут) 1-уть 1,Гут(у*-р ,
I Уа+Уь УТЬ } ' I У~а-*-1
105
- (Г55 + ^^.)| 8^(^ + 0-^1-
1 .г г— 1
. Г \-УИ 1 ]'
Ь4, А~[(1 + УТ+ УЭ)-УТ' (1+У?):(Г^Ч-О-Ка]:
65. Л = 2
^(УП + уър + Ьх + г 2Гтуы + ь,+з
(УЫ+У~5)% .
-(КК + УТ)*
ее. и .[/ЗЗ^/^ЕВ]-'^
1 У(х* — а*)а _ 1 ■■ УУ«-Д») а 1 Т3Д*2 — ^)а п
^ 2а V х 2а V х 2а V х в а
106
= Ъ {У~а - \П> - ГН)"4 = Ь(-у~ВГ
68. А = У а —
= 6.-^ = 1.
(1 + а)(\+УТ) ,
3/—^ "Т
1-|/1Г*
1 + ^а2
у а = у~а-
1 — УТ+У^-Уа2
,2 1 '-У »-гг»—Г »- ]/~а = у-а^
+ ^а2
1 + Д
1-^"Г'' " ) 1 + УЪ
1+а + |/"а2—-а 1 — т/~сГ за— зг~ з/-—- п
"I ТТ~) [ ут(ут-ут) } г(х~а> -
^\У&+У!? | ^Т(/Т--|Г7) 15 То-_
Е=[ уТ ' ж-Уяа + а ]
_1_ _3_
= [(1^ + -^)(]^-1^)]5(^-с),0 =
X 2. ±
5 10 2 /
= (х — а) (*—*о) = (* —с) =]/* — а.
70. Л
УТБ9: [\Гьё(Угк + УТ)\ -1
ут-утх
1 }~6_ (\Лё:У!ё-\ 1 \_е_
107
г у#-у-& 1_
[уьё(\ГТ-У2х) -уъс
_ (УТ+УТх М"^ (УТ+У2х-У2х\-6_
~\ у-& уъ) \ уш I
т/ а
-6
16*4
71 л_ц*±*)ь+УЫ{1-ут%х ,
х2 — 2х + 1
*-ах]/ а2+Аах + Ах* = (а+ь-\р** х~ахУ(а + 2*)* =
= (а + х)2 х — ах (а + 2х)*= х3.
4- ±
= {^1?=ГТ:/'}?1П:=1.
73. Л =
{УТ+ \^+уТ(\Г7^уТ):(\ГТ^УТ)-УЧ
2У х+2(У* + У *)\(У а + У х)
^ (УТ+ I)2 + УТ- УТ = (УТ+ 1)г = КТ+ 1
2УТ+2 2(К*+0 2
74. Л и [^^+^+4й + </1р=?] ,
* Здесь предполагается а + 2х> 0.
108
_\*/сЦ*-*У) у-5 «я1. УТ(Уа+У2Ь-У1?+У2Ь)
-[V (а-2Ь)3 ~У а ~00 }• Т=2Ь _
г \а —26 / а —26
= ^^ТГ8р
26
а —26 1
а — 26 4 у"Т 2
й = ±}Гь{Г7=8Р.
75 .4 - ^~~362) ^а* +(3* ^!) ^а* УЖ
/ /аб (6 -. I)3 в
6-1
УШ = УШУ Ра = Уа2Ь< = Ь У а.
76. А
(Б-4*)уТ+8/Б* УТ(УТ+УТ) /—_
К (5+ 4^)* ]^Б"+]АТ К
_ (8 + ^1^^,,^^
5+4л;2
77. Л = (*-±У^, + »3р^*) : ,Я?=Г-
\* —К*2—1 *+К*2 —1/
_ (* + Ух*— I)2— (* — У^Л)8 _ 4хУх*— 1 ^ ,
[*2 — (** — 1)] У*2— 1 Ух2— 1 ~
78 Л ЛГ Я + 3^—+ 3^—+ Ь + 2а~6 1'-
^Ц о + 3|/'а26 + Зт|/'о6* + 6 + 26— а ]'
. 1У1Е.] 1/т _ Гз ут(у*+ уть+у^> ~\\ут ,/т _
•г *» / У ~5 - иупуя+Ул + Уё) \У а V а~
- (У±\\Т1ГЖ _ УЖ_ УЕ.-\
~ \ У~Ь) У а ' «3 ~ УН?' У~Ф ~
Ь 1 "" 6
109
•2
80. Из данного выражения и из условия х>0 видно,
что допустимыми значениями для х являются те числа,
которые удовлетворяют неравенствам 0<*<1. Отсюда
следует, что Ух1 = + х, а ]/(*«» I)2 = 1 **х. Имея это в
виду, преобразуем выражение так:
[утпс-гт^ъ'г ут=*~(ут=нр\I
Л / ут+и ут=и \у
*~ х) {ух + х-уг-х^ ут+~х-у\-х)
УТ+1+уТ^х д У*1— х2 — 1 _
~~ ут+~х—ут^и' х
{УТ+~х + УТ=х)2 > уГ^х^—1
~ (1 + а:)-(1^-д:) ' х "*
2 + 2У\ —х* У\—хг — \ (/1 — *г)2—1
2* ж
-л?
= —1.
81. Л =
~ *УЪ У а' УИ-УТ 2УИ 2о '
ко я- (УТ+1)(1-УТ+}Г7)+(УГ- 1)(1+ут+ УТ)
2{(1 + УТ)*-(у-5)Ч Х
х + 2УТ-4_1-5+(УТ+1)УТ+5-1+(УТ^1)УТ„
Л УТУТ 2(х+2УТ-4) Х
Х+2У1—4 _ У~х~- 2УТ .
110
83. Так как {^(9 — 4 У~5 /2 + ]/5 =
= У(9-4у-Щ(2+\Г5У= /(9-А\ГЕ)(9 + 4уТ)=*
= уГ9* — (4у"~5)2 = ^81—80 = 1,
то данное выражение
А = [2Ут(у^-УТ +у-2^ + ут) ]1
=(-2/|^)-к?(к1шьП:
= 2 1/А (У^а-Уь)2 2а
У °' \ута ' (уы-ут)*
^уТ. » .а=1.
84. А = \УГь-1 + Ь\^^-±.У±+±У±] :
1(а + УаЬ — а)(У а — У Ь) 2? а 2' ь\
Г. 2УТ(УТ+УТ)\ (у-д-+уТ а-ь\
I уя-ут* } \ут-ут^2у^ь)
. Л ■ 2УТ \ = (УТ+УТ а-ь\. У~а~+УТ
\ У~Х-УТ] \у-а~-У~ь ^ 2УаЪ}'УТ-УТ
в / У"5"+ УТ у^-УТЛ УТ-/Т = 1
V УТ— У Ь 2 УаЬ ] У а + УЬ
(УТ^-УьУ _ 2УаЬ-\-а — 2УаТ + Ь _ а+Ь
2УаЬ 2УаВ 2 УаЬ'
85. Так как ^ 20 + 14 У~2 Уб^-*У~2 =
= ^(20 + 14 У2)\6 - 4 К"2)3 =
= у/"22(10 + 7|/"2)2-23(3 —2^"2)3 =
= уГ2ь (198 + 1401/"2) (99 — 70 -/"2) =
111
= У 2в(99 + 70 7~2)(99—70У 2) =
= 2 ^ЭЭ2 —(70|/"2Т= 2 у' 9801—9800 = 2,
то данное выражение
^ = (1+1^ }Га — За + ЗУ~а— \) г
/, , УТ-1\. Уа+\ __ Уа+\ . Уа+1 _ .
-{Ч 2 )' 2 — 2 • 2 ~ ь
86. А = 9 (|/Т~54 — |Г9 • -|)~4—
— ^"(3 — 21/~2)3.82(5У"2+ 7)2:^"8=
— 2^ (99 — 70 У~2)(99 + 70]/~2):2 =
= 9 (\Гб -1/|)~4- ^99* - (70 У~2У =9 (4-/"б)~4-
^-1^9801 — 9800 = 9 (-%=)*—1=9-——1=9- — — 1 =
= 4—1=3.
_16/"16(1 —а) -ж6/ 9а3 " -.У^бр—д) 9а3 _
~~ V 9д(1 + д)" К 4(1—а2) V 9а (1 + а) ' 4(1 — д2) ~
К (1 + д)2 К 1 + а'
[.2^(1+*)3 2^(1-*)3 ] |Л-* Г 1 + *
_ 1 —х+ 1 +х 1__ )/Т^~х
2 У(\+х)*(\—х)3 " /Г^ " >/"Г+* ~~
112
2 {Л—*
1
2|/(1+*)4(1— х)*У\— х (\+х)У (1—х)*У1-х
1
~ 1 - *2 ' ^
|_ ут(ут+ ут) \у у
х9
Ш*
X*-
32
х* У~х
У х = 32*.
90. А = х(х — у)Ух — у + у(2х + Зу)Ух-у +
+ 2хуУ х — у — (х + у)2У х— у = (х2 — ху + 2ху +
+ Ъуг + 2ху — хг — 2ху — у2) Ух — у = у(х + 2у) Ух-у.
9, л_ (а+У1+аг) (а-У 1+а*)~(У 1+а*-а) (уГ\ + аг+а) =
У\ + а2 (У\ + а2 + а) (У1 + а2 — а)
(а + У\ + а3) (2а — 2 У\ + а2)
]Л + а* (а 4- /1 + а2) ()Л + а3—а) ]Л + а2 '
то |/ (р + д)2 = р + 9; V" (р — ?)2 = р — д-
Отсюда
А =
р + я
р — д
*Я
93. А
Ур — я Ур — я Ур — я
(\-ут)2 _ Г 1+|/т-1+^тТ
1
„ О-^Т)2 1
1
2Ух(\—х) 2Ух(1+х) (Х—УхТ 2Ух(\—х)
1 1 —2* __ У~х~
2Ух(\+х) 2Ух(\—х)
8 К. У. Шахно
2У х{\— х2)
*2 — 1
ИЗ
2+УТ 2+|/Т ^
У7-2 |Т(3/7+2)
8 — х 2 + уТ , з /—_ л з/—- , з ,
2 + / * 4 + 2у* + удг2
о* л ("* + *)2-1 Г2тх--1+т» + *»"Н
"°" Л"~(т-г*-1)2 Ч 2т* \ =*
__ т -|- л: + 1 . (т + х)2 — 1 _ (т + *+02 (т—1)2(т+* + I)2 =
т + х — 1 2гпх 2тпх "~~ 2/д (т — I)2 *
[тг_1 _|_(т—1)л;]2 и , 1Ч ,
* 2т(т-1)2, - Но * (т - 1) =* 1.
^ - (т2 — 1 + 1 )2 т4 т3
Поэтому Л = 2т(т-1) = 2т(т-1) = 2"(^=Т)'
96. Так как &> 1, то
V1 *> "~[/ (1 + *)2] Г (1 — Л)« 6-.1'
Поэтому
а
уК1-^) 2-П = Т^Т
Отсюда
+ ^-1=^-1(1 + ^),
97 Л-^1±1Г+Г^=-1Г~- ** + *' =
7 I ^ / + \ х ) ~ («+1)«+ (х_1)«
г (*-1)2 + (*+1)2 _ 2*»(1 + **) _ 2(п + 1)адса(1 + *2)
^Х' (л:+ 1>а(лт — I)2 — (*г-1)« "~ (л + 1)*(л;2 — 1)а
2(п+1)*Ч(я+1) + (я+1)*а]
"* 1(п + 1)*г-(«+1)Р
114
1 -1 1
Но х»=™и =Л=1, а х2(п+1) = п-1.
1 + я п+1
Поэтому
л 2(я-1)[(я+1) + (я-1)] _2(я-1)-2я , .
Л - Кя_1)_(п+1)]« 4 _ "^ ~ 1>'
98. Так как а > 0, 6 > 0 и, следовательно, Уа2 = а и
1/6* = 6, то (а + х) ф + х) = {\П$ +УаЬ){У~Ьг +У~аЬ) =,
= У~аЬ(У~а + У~Т)\ а (а-х)(х-Ь)^
<= }/"а& (У а — У~Ь)г. Так как а > Ь, то
1/( 1^й - У~Ь)2 = У~а-У~Ь.
Поэтому
л _ |У(а - х) (л: -Л) - У(о + *) (х -г 6)Т
[/(а - х) (х - Ь) + У {а + х)(х+ Ь)}
в Г ^ (1/1~ У~ь)-У&_ (У^+ /Т) Т з
в 1К^ (Кв-- У~ь) + уть (ут+ ут)\ *"
е Г (^- ^ - (*^+ ^ Т- /-2^ТУ= 1
. . т3 + я3 , т3 + я3 + т3 —я3
1 т3 — л3 ' т3 — я8
2т3« . 2я3а . х-\- а
х — а =
~ тз _ пз . * " — тз _ „з .
Поэтому данное выражение
Но т > п и, следовательно, ]/"(т — я)2 = т — я, так что
Л = 1^5.
т — п '
115
_2_
100. После вынесения хт за скобку, получим
*т (1 + * тл ) — 4а2 л: тп = *т -М.
Но * т" «(а + ]/ая- I)2 и 1 + * т* = 1 +
+ (а + 1/^Л)2 = 2а2 + 2в "^=1 = 2а (а + Уа2^!).
Поэтому
М = [2а (а + Уа2^!)]8 - 4а2 (а + /а2^!)2 =*
в= 4а2(а + Уа^П")2-4а2(а + |/"а^1)2 = Ои/. Л*«=0.
101. (а+хГГТ~ (а+У^)~Т= [а + 2 У^ГГ]~~=
- [(а- 1) + 2/а^Л + I]"5"- [(У^=Т + I)2] ~~=
(Ко-1 + 0
,-!_ 1
" /0-1 + 1*
Аналогично получим
[а-х*тК (а-У^)""2"» К/о^Т- ОТ*
Если 1) 1< а < 2, то Уа — 1< 1,
]/ (у^ГТ- 1У= 1 - 1/а^П", (а —л:2)
Поэтому данное выражение
1 ^
2
|^_1 + 1 ^ \^Уа-^\ 2-^а'
Если 2) а > 2, то У а - 1 >1, ]Л(/а - 1 - 1)2=-
1 1
= 1/7=ГГ_1((а-*2) 2 = (Уа^ГГ-1)-' =
1 А = 1 , 1 = 2/а^П
116
102. А _^ [У^^-Ух*!- а*\\
кУх*—а?+Ух*+сР)
__ ["(^л;2— д* — ух2+а2)2Т__ Г 2л;2 — 2 У(х* + а2) (х2 ^сР)
— 2а2
12
Но х2 = а2 -*^Г, (^ + а2) (*2-а2) =»
( „т2 + п* ' , \ / , т2 + л2 » \
= Г^Й-+а2Да2-2^ а] =
= "4 (т + 1^~,г)5 ^^^ ^ + а2)(,2-а^
= а2- —«р—, так как я>/л>0 и, следовательно,
У"(т2 — п*)* = п2 — т2, а Ут2п2 = тя.
Теперь можем написать, что
Л — — (п* т2 + п2 _ /,2 /г2 —/п2 \2__ / 2т2 \2_ т*
Л "" а* Г 2т/г а ' 2тп ) " \ 2тп ) ~~ /г2 *
,03 ^ = (^т + ^/т-^)2 = 2т + 2ТЛп2--л;2
(/тТ^)2- (К ^ — л;)2 2л;
л;
I/ (*) - '•
Подводя множитель х под знак радикала, мы считали
Ух2 = дс, потому что х > 0, как это следует из условия.
+1/ (" 2л ) • Но 0 < я < 1, и поэтому
гг2 + 1
2л
/с
Л2_ Л2 1 ___п2
2п ] 2л '
117
Таким образом,
2/г + 2/г 2/г /г
104. Л=[ж 3(* 3+а 3)] 2 +
+ [а 3(а 3+* 3)] 2=хЦх 3+а 3) 2 +
+ аЦх *+а 3) 2 = (х >+а 3) 2(*3+а3) =
с= [х^+а^х^а*. Но *"*"= (Д-а3^,
А. 2- Л. А .2,
:&3_а3, х3 +а3 =63.
_2_
.3 _. 3
Поэтому
_2_^^_ .2. Л. Л. Л I. Л. А _1_
Л==ф3)2(&3~а3)2а3==а3&3(&3-а3)2..
,05. А= ^ГТТЩ-Щ-^^
*= 2а V 1+х2 (К 1 + х* — х).
Но
2/аб ' ^ }/ ^иК«&/
/(
2 /об/ 2 /аТ
Поэтому
2УаЬ\2УаЪ 2}ГаЬ) УаЪ 2}ГаЬ
106. Подставляем в выражение л?+ \2х значение х и
пользуемся формулой
(ш — л)3 = т3 — Зтл (т — л) — л3.
Л - [^4(1/5"+ 1)]3-Зу/"4(]/5'+ 1) у/Т(71=-Л) *-
118
_[^4(^5— 1)]3+12д; = 41/ 5 + 4 — ЗКб4*-*
^4/"5 + 4+ 12л: = 8—12*+12* = 8.
107. Подставляем значение х в выражение хР + ах + Ь
и пользуемся формулой (т + п)3 = т3 + Зтп (т + я) + л3.
Ч1/-4+/^|)У
V—Ж
= 3 у — -^- х + ах — — ах + ах = 0.
108. Вынесем за скобки хп. Получим
■4-;сЛ.г±л.<"+'>т -6-1 ,
-^(т+«)|+«Г-1]-
-**[*(* +'Г"*]-***•
/г /г + 1
Отсюда М = ±- [(у)Л+'] "
1 = 1.Л_1в0
& а Ь Ь
Л.
119
109. Так как |/2+/ 5у^— 38+ 17/ 5 =
с=у^(2+1/"5)3(-38+171/"5') =
«= -^(38 + 171/"5) (—38+17 \Г5) =
= у/(17|/"5)2-382=1,
то данное выражение
I +т* г
1 + пх
1 + тх У 1 — шс '
Преобразуем теперь каждый множитель отдельно:
1 — тх
2т п —т ' \ —пх
/г т/"2т " -|/~2т ~
/"2т "
V I —пх п — т *
так как из условия я>т следует, что У (т — п)2=п—т.
-^——1 т-\-п у —^~— 1
итак, л = -
(/г — т)2 """ (т — /г)а
120
*/ пг / п п V
ПО. А = У хГ+ч[/1+1+ап+1)
+
П / П* / п п \
+ ]/ ап+1[ап+1+хп+Ч~1 =
п/ ~"~" ~^~ (п / """*" п/ 12Г\
= 1/ хл+1+ап+Ч1/ *Г + 1+у ал + 1]-1-
• п п п п п п
Но хп+1 = Ьп+1-ап+\ а *п+1+ап+1=^/,-'1,.
/ п \п+1
Поэтому Л = [Ьп+ V " —1=6—1.
т - , ч п—2к „ , . л—2* _
Но
2/г п—2&
*гс—Чк , \ 2п ,/-т"
а
Поэтому
+ 4»1_2.±+2]/||/1Г-1 + 1) + 6. = Л
121
112. Так как ~±±- = (2 + |/~3)",
то
х+ 1
х—1
+ 1 =
= У (х-^1)4(2+-К1)2+1-4(2+}/!)] + 1 =
«=^(л:— 1)"(4 + 41/"3 + ЗЧ-1—8— 4|/~3) +1 = 1.
^(1^1р'„(^1)"-'(^1+1)_
_ (1 - У*)"-1 0-УТ)2 = /1 + ут\п+\ п-ут\п+1
114. Воспользуемся формулой
для преобразования знаменателя лево# части
доказываемого равенства. Получим
г = 1 / <* + УЬ* , -, [а
уаЛ-у# — ъг=\/ —2—ь У ~
— /б2
2
«|Л4^+/5:
■14
Обозначая левую часть равенства буквой Л и используя
полученное выражение для знаменателя, можем написать
А^ЬУ2*
2а + УсР — Ь*
у1
+ Щ
г+/т«
26
/о+Ть! + КаН6|
122
пи (2а + Уа* - Ъ* ) (Уа + Щ -У а- \Ь\) _
м (а+\Ь\)-(а-\Ь\)
~-щ-[а + Щ + У(а + №(а-\Ь\) + а-\Ь\] {У^ТЩ-
-УТ=Щ ~^[{УЪШ~[УТ=Ш.
Если \Ь\ < а, то все выполненные выкладки будут
справедливы, так как корни являются арифметическими.
Полученное выражение равно правой части доказываемого
равенства. Действительно, при 0 < Ь < а имеем \Ъ\ = Ь и
утверждение очевидно. Если Ь < О, то \Ь\ = — 6. В этом
случае получим
_ [{у7=Ъ)* - {У^+Ъ)3} = [УТ+ь)* ~ [уТ=ъ)\
т. е. то, что требовалось доказать.
115. Пользуясь формулой преобразования радикала
у'А±УВ (см. решение задачи 114), получим
Ух+ 2 У1с^\ +Ух-*2УТ^1 =
^у-
х+2 — х ^2
Здесь мы положили у (х — 2)2 = 2 — *, так как по
условию а: < 2.
II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
116. Существование единственного решения х =
уравнения ах + Ь = 0 при а Ф 0 вытекает из однозначной
выполнимости деления в любом числовом поле.
117. I. Необходимость. Пусть данные уравнения
совместны, т. е. существует такое значение х, которое
удовлетворяет и первому уравнению, и второму. Так как
каждое из них имеет единственное решение и эти
решения суть х = -и х = -, то отсюда получаем
"1 #2
Ь1 _ ^2
или о^&о — о<Ф\ ^ 0.
#1 #2
123
II. Достаточность. Пусть выполнено условие
ахЬг — афх = 0. Из него следует, что — = —- или 1 =
= —А Но—-р и—^- являются решениями
соответственно первого и второго уравнений, в чем можно
-убедиться подстановкой этих значений в уравнения. Выходит,
что рассматриваемые уравнения имеют общее решение,
т. е. они совместны.
118. Совместны. Их общий корень * = —1.
119. Совместны. Их общий корень х = 4.
120. Вычтем из первого уравнения второе. Получим
(а— 1) (х— 1) = 0. Отсюда а = 1 или х = 1. Подставляем
х = 1 в первое уравнение. Эта подстановка дает а = — 2.
Следовательно, уравнения совместны при а = 1 и а = — 2.
124. Равносильны, так как второе получено из первого
прибавлением к обеим частям равенства одного и того же
многочлена л? + 1.
122. Не равносильны. Первое имеет корни 1 и 2, а
второе только корень 2.
123. Не равносильны. Первое имеет только один
корень х = — 1, а второе только один корень х= I. Число
— 1 не является корнем второго уравнения в области
вещественных чисел, так как Ух — 1 в этом случае не
имеет смысла.
124. Не равносильны в поле, действительных чисел.
Первое имеет корни л; = 8 и х — — 1, а второе только
х = 8.
125. а (а— I) х = 2 (а— I). Если афО и аФ\9 то
о
х = —. Если а = 0, то уравнение не имеет решений. Если
а= 1, то уравнение удовлетворяется любым значением х.
х — (тп + пр + рт) , х—(тп + пр + рт) , х—(тп+пр-\-рт) __ ~
т + п "*~ р + т "*~ п + р ~~~ '
(^+гЬ+-^)и-(т/г+йр+рт)1=0-
124
ЕслиЛГР71 + Т+т + ИТр = °' то УРавнение
удовлетворяется любым значением х.
А"-^П-^0'{а + ь+с-х)^ + т + т-
-7+Ьг^О. Множитель А -± +| + ±__*-_
не равен нулю. Действительно, пусть, например, а> Ь>
> с > О (случай отрицательных а, 6 и с легко привести к
рассматриваемому). Тогда
А _ 1 (а + Ь + с , а + Ь + с а+Ь + с Л
А - а + Ь + с \ а ' Ь | "с *) ^
так как все слагаемые в квадратных скобках положительны
( а+ > с + с > 2). Сократив последнее уравнение на этот
множитель, получим а + Ь + с — # = 0, откуда х = а +
+ Ь + с.
128. Так как \а\ = а, если а>0 и |а| =—а, если
а < 0, то данное уравнение при х > 1 приводится к
уравнению х— 1 = 2, а при *<1— к уравнению
р— (х— 1) = 2. Из первого найдем х1 = 3, а из второго
х2 = — 1.
129. Если л;< 1, то |х — 11 = 1 — х, \х-г-21 = 2 — х
и данное уравнение приводится к такому: 1 -^- х + 2 —
«» л: = 1. Из него находим х = 1. Если 1 < х < 2, то
|х—1 | = х—1 и \х—2|=2 — х. Левая часть данного
уравнения равна 1 при всяком х из рассматриваемого
промежутка, а так как правая тоже равна 1, то при всяком
х, удовлетворяющем соотношениям 1 < х < 2, уравнение
удовлетворяется. Наконец, если х > 2, то ]х— 11 = л;— 1,
\х — 21 — х — 2, и данное уравнение приводится к
уравнению х— 1 -+- л: — 2 = 1, которое не имеет решений х>2.
Итак, уравнение удовлетворяется, если 1<х<2.
130. Поступая так же, как в задаче 129, найдем, что
данное уравнение приводится к следующим смешанным
(т. е. содержащим равенство и неравенство) системам:
125
1) 2 — * + 3 — *+8 — 2* = 9, *<2;
2) л: — 2 + 3 — * + 8 — 2* = 9, 2<*<3;
3) *—2 + * —3 + 8 —2* = 9, 3<*<4;
4) л:— 2 + л: — 3 + 2* — 8 = 9, *>4.
Первое уравнение имеет корень * = 1, который
удовлетворяет неравенству *<2. Второе уравнение имеет корень
х = 0, но он не удовлетворяет неравенствам 2 < х < 3.
Третье уравнение не имеет решений, так как его левая
часть равна 3, а правая 9. Четвертое уравнение имеет ре-
шение х = -«-, которое удовлетворяет неравенству х > 4.
Поэтому данное уравнение имеет следующие решения;
131. 40(|*|— 1) — 5(|х| — 5)+ 4 (14 — 21*|) =: 80 (|*|-«
— 9)—140, 531*1=901, |*|=* 17; хх = 17, *2 = -^17.,
132. После легких преобразований получим 4*+8=э
= 5|3* — 5|. Если |Зл: —-51 = Злг —-5, т. е., если *>-§*,
то 4* +8= 15* —25 и * = 3. Если |3* —5|=5 —3*,
17
то найдем * = -у^-.
133. Поступая так же, как в задаче 132, найдем *=4.
В отличие от предыдущей задачи зд^сь только одно
решение, так как предположение |3*-^2| =а 2 -^3* приводит
к противоречию.
134. Преобразуем числитель, воспользовавшись
формулой суммы кубов двух количеств. Получим
(2т — Ъп) [(2т — а*)2 ^ (2т — ах) (ах -» Ъп) + (ах — Зл)2] _ 9 %
Если 2т— Зп ф 0, то, сократив обе части уравнения на
2т—За?, освободив уравнение от дробей и приведя
подобные, найдем (2т — ах) (ах— Зл) = 0. Отсюда хх = ,
*2 = —. Если же 2т — Ъп = 0, то уравнение
удовлетворяется любым *, не равным .
135. Является.
136. Одно, а не три, как иногда говорят учащиеся,
потому что по определению решением системы называется
126
такая совокупность численных значений неизвестных,
которая удовлетворяет каждому уравнению системы.
137. Могут быть эквивалентными, но могут и не быть.
Например, системы
х + у — 2 = 0; | Зх — у —2 = 0;
х— 3*/ + 2 = 0 И \ 6л: — 2у — 4 = 0
имеют общее решение х = у—1, но не эквивалентны.
138. Может быть эквивалентна данной системе, но
может и не быть. Так, например, взяв тх = 1, т2 = 2, /гх=2,
я2 = 4 для системы
* + 2у-4 = 0;
2х — Зу— 1 =0
получим
( Ъх — Ау — 6 = 0;
( 10*— 8у — 12=0.
Система первая не эквивалентна системе второй.
139. Если х = х0 и у = г/0 удовлетворяют первой
системе, то очевидно, что они удовлетворяют и второй
системе при всяких тъ т2, пъ п2, в частности, при таких, для
которых тхп2 — т2пх Ф 0.
Пусть теперь х = хх и у = ух есть решение второй
системы. Покажем, что оно будет решением также и первой
системы. Для этого подставим во вторую систему х = х19
у = у19 затем умножим первое уравнение на я2, а второе
на т2 и из первого результата вычтем второй. Получим
{тхп2 — т2пх) (аххх + Ъхух + с^ = 0.
Отсюда аххх + Ьхух + сг = 0, так как тх1ц — т^ =^= 0.
Умножая затем первое уравнение на пх, а второе на тх и
вычитая из второго результата первый, получим
(тхп2 -* т2пх) (а2хх + Ь2ух + с2) = 0.
А так как тхп2 — т2пх ф 0, то а2хх + Ь2ух + сх = 0.
Теорема доказана.
140. Нет не верно. В качестве примера, для которого
это утверждение не имеет места, можно взять следующую
систему уравнений:
( ах + Ьу + с = 0;
\ ах + Ьу + с = 0.
127
Однако, если в первой системе Задачи 139 а1Ь2-^а2Ь1ф01
то для такой системы, как легко показать,
сформулированное в задаче предложение верно.
141. Нужно, если предварительно не была доказана
теорема, сформулированная в задаче 139. На самом деле,
система
I афъ — афх 9
являясь выводной из данной, очевидно, удовлетворяется
теми значениями х и у, которыми удовлетворяется данная.
Но ееть ли такие числа, иначе говоря, существует ли
решение у данной системы,— из решения не вытекает.
Таким образом, можно лишь утверждать, что если данная
система имеет решение, то найденные значения х и у
дадут его. Существование решения мы докажем, если
проверим подстановкой, что найденные значения х и у
удовлетворяют данной системе.
142. Умножая первое уравнение на Ь2у а второе на
— Ъх и складывая новые уравнения, получим
(ахЬ2 — а2Ьх) х + схЬ2 — с2Ьг = 0.
Умножая первое данное уравнение на —аъ а второе на
ах и складывая, получим
(ахЬ2 — а2Ьх) у + с2аг — сха2 = 0.
Так как ахЬ2 — а2Ьг ф 0, то новая система, имеющая
единственное решение, эквивалентна данной (задача 139).
Р(х)
143. Если ^~- есть несократимая дробь, т. е. если
числитель и знаменатель ее не имеют общих множителей, то
Р(х)
уравнения ^~ = 0 и Р(х) = 0 равносильны. В общем
случае — не равносильны.
144. Корни второго уравнения, очевидно, являются
корнями первого. Однако не всякий корень первого
уравнения удовлетворяет второму. Поэтому в общем случае
они не эквивалентны.
145. Решив систему двух первых уравнений, найдем
х = 2,у=1. Подставив эти числа в третье уравнение,
получим а = 3.
123
146. Известно, что система
( ахх + Ьгу = сх;
1 а2х + Ь$ = с2
будет несовместна, если отношения коэффициентов при
одинаковых неизвестных равны, но они не равны
отношению свободных членов, т. е. если — = -—■ Ф —, и неоп-
^2 ^2 ^2
ределенна, если три коэффициента одного уравнения
пропорциональны трем соответствующим коэффициентам
другого, т. е. если — = —- = —. Применяя это к данной
системе, устанавливаем, что для неопределенности ее
нужно, чтобы у = -2- = —, т. е. чтобы а = — 12 и Ъ = 36,
а для несовместности а = — 12 и 6 =^= 36.
147. Решив первые два уравнения относительно х и */,
найдем:
(*-Ы)2 ... к+\
Х "~ Ь2 _Л_ Ь _ 1 » У ~~
Подставив найденное значение х и у в третье уравнение,
получим следующее уравнение для определения 6:
_ (1 + к)* (12-*)(*+!) _ _ м , а,ч
Л* + Л — 1 "*" № + к — 1 1 "*" ''
Из него найдем йх = — 1, й2 = 5.
148. Решая первые два уравнения, найдем, что х = 4,
у = — 1, если т =А 3 и любые х и у, удовлетворяющие
первому и второму уравнениям, если /п = 3. Подставляя
х = 4и(/ = — 1 в третье уравнение, найдем, что для
совместности требуется, чтобы т = 3. Отсюда заключаем,
что при т Ф 3 система несовместна, а при т = 3 хотя
и совместна, но неопределенна, так как приводится к
следующей:
Зх + 2у= 10;
Зх + 2у= 10;
Ъх + 4у = 20.
149. Не противоречит. Первое справедливо при с = 0
и любых а и 6, а также при а = 1 и любых 6 и с, т. е.
является уравнением. Второе же справедливо при любых
а, Ь и с и является поэтому тождеством.
9 К. У. Шахно 129
150. Из второго уравнения видно, что у— 1 =*
===== -2-1 ^:-4- 11 > 0. Поэтому |у— 11 = у*-* 1 и система
запишется так:
1|*+4 = 4*/-, 4.
Исключая | х + 11, получим 4у —* 4 + у — 1 =5. Отсюда
г/ = 2. Подставляя у <=» 2 в первое уравнение, найдем
| # -|- 1| е- 4. Если дс + 1 > 0, то получим уравнение
х + 1 с=г 4 и из него найдем х = 3. Если х + 1 < 0, то
получим уравнение — дс—I » 4 и из него найдем дс=—5.
Таким образом, система имеет решения: хх = 3, уг = 2;
х2 = —5, г/2 = 2.
151. Из второго уравнения видим, что у—*Ь*=*\х— 11>0
и, следовательно, | у — 51 =» у — 5. Теперь система
запишется так:
М*—И + 1/ —5 = 1;
Их-Ч + б-у-О.
е. а:— 1 = ± -о-. Отсюда
Из
нее
3
находим
1 #1 в У'
1*-
х% =э
-Ч
1
2»
1 =
%
1
2
, Т.
11
2'
152. Из первого уравнения находим, что Ъу = —3 | аг |—
*—9, т. е. что !/<0 и, следовательно, |*/| =— */. Из
второго —* 2х = | у | + 7, т. е. х > 0 и | # | в х. Система
принимает вид
ГЗ* + 5*/ + 9 = 0;
I 2х + У — 7 « 0.
г, 44 39
Решив ее, найдем х » у, г/ » _ у
153. Данную систему можно записать так:
г х — у «=» ± 2;
I ± х ± у =■ 4.
Во втором уравнении достаточно брать только верхние или
только нижние знаки. Решив четыре системы, найдем
следующие решения: хл = 3, г/, = 1; х2 = 1, 1/2 = 3; х3 = ■*- 3,
г/з = — 1{ *4 = — 1, уй = — 3.
130
154. 1) Пусть у>0. Тогда \у\—у и второе уравнение
будет иметь такой вид: |х| + У = 1 • Найдя из него
у =! 1 — | х | и подставив это значение у в первое
уравнение, получим |х+1 — |лс|| = 1. Отсюда х —1*1 = 0,
1 а: | = а: и, следовательно, х > 0. Итак, если у > 0, то и
а: > 0. Система же в этом случае примет такой вид:
х + У= 1.
2) Пусть у < 0. Рассуждая так же, как в первом
случае, докажем, что тогда и х < 0, а система будет иметь
вид
х + у*= — 1;
х + у = — 1.
Таким образом, системе удовлетворяет любая пара
неотрицательных чисел, сумма которых равна +1, а также
любая пара неположительных чисел, с^мма которых равна
— 1.
155. Решив систему, найдем:
— 15" + 7 . _ 7/г— 10
Х ~ 3/г2 + 2 ' У "~ Злг2 + 2 '
Так как Зп2 + 2 > 0, то для того, чтобы было х > 0, а
у < 0, необходимо и достаточно, чтобы п удовлетворяло
7 10
неравенствам \5п + 7 > 0, 7п— 10 < 0 или — у^<дг<у.
Очевидно, таких значений только два: 0 и 1.
156. Разложим трехчлен х2— За:+ 2 на множители.
Получим х2 — Зх + 2 = (х — 1) (л; — 2). Отсюда ясно, что
для того, чтобы данный многочлен делился на трехчлен
х2 — За; + 2, достаточно, чтобы он делился на х—1 и на
х—2. Но по теореме Безу остаток от деления многочлена
на двучлен х — а равен значению этого многочлена при
х^а. Применяя ее к двучленам х—1 и х — 2у получим
1—З+З+а+6 и 16 — 24 +12 + 2а + Ь. Для того
чтобы деление нацело было возможно, необходимо и
достаточно, чтобы эти остатки равнялись нулю. Отсюда
получаем систему уравнений для определения значений аи Ь
а + & = — 1;
2а + Ъ = — 4.
Решив ее, найдем а = — 3, 6 = 2.
9*
131
157. Дискриминант трехчлена х2 —3* + 4 равен
З2 — 4-4 = — 7 < 0. Следовательно, корни трехчлена
комплексные, и применять в этом случае метод, основанный
на теореме Безу (см. задачу 156), хотя и можно, не
следует, так как он приведет к большим вычислениям. Для
решения задачи другим методом будем делить данный
многочлен на данный трехчлен по правилам деления
многочленов
я4 — З*3 + Ъх2 + ах + ЬI х2— Зх + 4
*~х* — ЗгЧ-4*2 I—рЗП
— х2 + ах + Ь
~ — х2 + 3х — 4
(а— 3)х+Ь + 4
Так как в остатке получился многочлен степени более
низкой, чем степень делителя, то дальше производить
деление невозможно. Чтобы деление многочлена на трехчлен
было выполнимо нацело, нужно подобрать значения а и Ь
так, чтобы остаток стал равен нулю. Очевидно, для этого
достаточно (да и необходимо) положить а = 3 и 6 = — 4,
т. е. потребовать, чтобы коэффициент при х и свободный
член остатка обратились бы каждый в нуль, что приведет
к системе а—3 = 0, 6 + 4 = 0. Этим методом можно
было бы решить и предыдущую задачу (№ 156).
158. Остаток от деления многочлена на (х — а)(х — Ь)
будет многочленом первой степени. Обозначим его через
тх+п, а данный многочлен через /(л;). Получим
тождество.
/ (х) = (х — а)(х — Ь)у (х) + тх + п,
где <р (х) — частное. Положив в равенстве х = а и х = 6,
получим систему для определения тип
А = та + п\
В = тЬ + п.
г» „ Л — В аВ — ЪА
Решив ее, найдем, что т = г\ п = г—.
' ' а — Ь а — Ь
Отсюда искомый остаток
. А — В . аВ — ЪА я х — Ь . п х — а
тх + п= -гХ-\ г— =Л--—г +В--Г—г.
1 а — Ь 1 а—Ь а — Ь Ь — а
132
Впрочем, нетрудно и непосредственно без вычислений
сообразить, что остаток будет иметь такой вид, если учесть
теорему, сформулированную при решении задачи 29.
159. В этом случае остаток от деления будет
многочленом второй степени: тх2 + пх + р. Поэтому, поступая
как в задаче 158, найдем систему для определения чисел
т, п и р:
[ А = та2 + па + р;
| В = тЬ2 + пЬ + р;
I С = тс2 + пс + р.
Решив эту систему относительно т, п и р и подставив
найденные значения т, п и р в остаток тх2 + пл: + Р»
получим после несложных преобразований тх2 + пх + р =
= - (* — 6)(х —с) . р (* —с)(* — а) р (х — а){х—Ь)
*' (а — Ь)(а^с) ~^а' (Ь — с)(Ь — а) ~г °' (с — а) (с — 6) '
Нетрудно и без вычислений сообразить, какой будет
вид остатка, особенно если учесть теорему, приведенную в
решении задачи 29.
160. Разделив многочлен х?+рх + я на многочлен
х? — 2сах + а2, найдем остаток (р + За2)* — 2а3 + Я- Так
как остаток должен тождественно равняться нулю, то
получим уравнения р + За2 = 0 и — 2а3 + <7 = 0. Из первого
найдем, что а2 = |- или а6 = — -|~. Из второго
найдем, что а3 = -|~ или а6 = -—-. Сравнивая эти два
значения а6, получим следующее соотношение между р и (/,
которое необходимо должно выполняться для того, чтобы
деление рассматриваемых многочленов было возможно:
-|=- + -~- = 0. Значение а проще всего получить разделив
значение а3 на значение а2, найденные выше. В результате
получим а = —-—-.
161. Так как старший член данного многочлена есть х4,
то искомый многочлен имеет вид х2 + рх + ц. Отсюда
получим тождество
х4 + 2г* + ах2 + 2х + Ъ = (х2 + рх + ?)а
или
х4 + 2*3 + ах2 + 2х + 6 = х4 + 2рг* +
+ (р2 + 2<?)*2 + 2рдх + д\
133
Но в равных многочленах равны коэффициенты при
одинаковых степенях буквы х. Приравнивая коэффициенты
при г*, взятые из левой и правой частей равенства, затем
при х2 и т. д., получим следующую систему уравнений:
2 = 2р; а = р2 + 2щ\ 2 - 2рц\ Ь = ц2.
Из нее легко находим р = 1; (7=1; а = 3; 6 = 1.
Искомый многочлен имеет вид л:2 + л: + 1.
162. Освободив равенство от знаменателей, получим
тождество
(А + В) х2 + (В + С) х + Л + С = ^ + 3.
Приравняв коэффициенты при одинаковых степенях буквы
*, взятые из левой и правой частей этого равенства,
придем к системе
( А + В = 0;
| В + С=1;
[ Л + С = 3.
Из нее найдем: А = 1; 5 = — 1; С = 2.
163. Решив систему трех первых уравнений, получим
х = I, у = — 1, г = 3. Но эта тройка чисел не
удовлетворяет четвертому уравнению. Следовательно, данная система
несовместна.
Можно поступить иначе. Сложить второе и третье
уравнения и из результата вычесть первое. Получится
уравнение 8х — 8у — 2г — 10 = 0, которое противоречит
четвертому.
164. Приравнивая левые части первого и третьего
уравнений, найдем
Если X + |л ф 0 или, что одно и тоже, \Ф — ц, то у =а
= Ь • ^ТЧ . Подставляя найденное значение у в первое и
второе уравнения, получим систему для определения х и г
1—4-—— 2><*
а ~т~ с ~]Г+\'
_* г_ ___ 2
а с ~~[л + Ь*
134
Складывая, а потом вычитая почленно эти уравнения,
найдем:
ц + 1' [х + Х
Если подставить найденные значения ху у, г в
четвертое уравнение (им мы не пользовались), то получится
тождество.
Отсюда вывод: если X Ф — ц, то данная система
совместна.
185. х ——21\ у — 1\ г = 1, где / — любое число.
х — а _ у — Ь
166.
(а + Ь + с) (Ь + с — а) (а + ь + с)(с + а — Ь)'
г-—с
{а + Ь + с){а + Ь-сУ
Сделав сокращения и воспользовавшись свойством равных
отношений, получим
х — а __ у — Ь _ г—-с _ (х -4- У 4- з) -— (а + Ъ -\- с)
с + Ъ-^а а-\-с — Ь~ а -\- Ь — с а-\-Ь + с
-1)(а + Ь-
а + Ь + с
(к-\)(а + Ь + с) =к_1
Отсюда:
х = а + (к—\)(с + Ь-ау, у « Ь + {к- 1) (а + с — Ь);
г^с + (к—\){а + Ь — с).
167. Умножив первое уравнение на —а2, второе — на
ау третье — на —1 и сложив полученные уравнения,
найдем [— а2 + а (Ь + с) — Ьс]г = — 1, откуда г = (а_Ь)(а_су
Затем, умножив первое уравнение на —с2, второе — на с,
третье — на — 1 и сложив полученные результаты, найдем
х ~ ( — \(Ь— ) ' Подставляя найденные значения хну
1
в первое уравнение, получим у = , __ ^ & _ > .
168. Сложив три уравнения данной системы, получим
следующее выводное уравнение: (а + Ь + с) (л; + у + г)=0.
Так как а + 6 + с =^ 0, то оно приведется к следующему
эквивалентному: х + У + г = 0. Полученное уравнение есть
следствие уравнений данной системы и если мы добавим
его к данным трем уравнениям, то новая система из четы-
135
рех уравнений будет эквивалентна данной. Теперь
рассматриваем эту новую систему. Из четвертого уравнения
находим у + г = — х и подставляем это значение х в первое
уравнение. Получим — (Ь + с) х — ах = Ь — с, откуда
* = тТГГс' Аналогично найДем У =* 5ТтЬ
169. 1) Если а + Ь + сФО и среди чисел а, Ь и в
есть различные, то система имеет единственное решение
х = */ = г= 1. Оно найдется обычным способом
исключения неизвестных, рассмотрев, например, первые два
уравнения и уравнение х + у + г = 3, которое получится как
следствие уравнений системы, если все три уравнения
сложить почленно.
2) Если а + Ь + сфО и а = Ъ — о, то система
принимает вид
( х + у + г = 3;
\х + у + г = 3;
[ х + у + г - 3.
В этом случае любые три числа х, у и г = 3 — х — у
являются решением системы.
3) Если а -+- Ь + с = 0, но не все числа а, 6 и с равны
нулю (в этом случае любая тройка чисел удовлетворяла бы
системе), то, пользуясь равенством а -\- Ь + с = 0, можем
привести данную систему к следующей:
ах -\- Ьу — (а + Ь) г = 0;
6# — (а -{- 6) у 4- ах = 0;
— (а + 6) * + ау + Ьг = 0.
Из нее видно, что третье уравнение есть следствие
первых двух и что любые три числа, равные между собой,
будут решением системы.
Замечание. Если бы числа а, Ъ и о могли
принимать комплексные значения, то пришлось бы рассмотреть
еще один случай. Именно, если бы одновременно было
атЬ + с = 0на2 + аЬ + № = 0, то два уравнения
данной системы были бы следствием третьего. В этом можно
было бы убедиться, например, так. Положив с = — (а +■ Ь)
в первом уравнении, получим уравнение ах + Ьу —
— (а + Ь) г = 0. Умножив его на Ь и положив 62=—аЬ—а2
136
и аЬ + Ь2=* — а2, получим уравнение Ьх — (а + Ъ)\ у + аг = Оу
которое совпадает со вторым (а + Ъ = — с). Аналогично
можно показать, что и третье уравнение системы есть
следствие первого.
В рассматриваемом случае любая тройка чисел,
удовлетворяющая уравнению ах + Ьу + сг = 0 есть решение
системы.
170. Так как х, у и г не равны нулю, то система
равносильна следующей:
ау + Ьх 1_# аг + сх __ _1_# Ьг + су 1
ху ~~~ с ' гх ~~~ Ь ' уг ~сГ
или
а _&_ __ _1_. Л_ I _^_ _ _!_. ^ I с _ ^
лс *" "у с' х *~ г ~ Ь * ~у~ * ~ ~ ~сГ'
Сложим почленно последние три уравнения. Получим:
»(т + 7 + т)-Т + Т + 7«
* ^ */ ^ г 2 \а ^ Ъ ^ с)'
Это уравнение вместе с теми тремя, из которых оно
получено, образует систему, эквивалентную данной.
Вычитая из четвертого уравнения этой системы третье, найдем
а 1/1,1 1\ 2аЧс А
Т = Т (У + Т - 7> 0ТКУда х = ас + аъ-ъс • Аналогично
— 2Ь2са _ 2с2аЬ
У 'У аЬ + Ьс— са* Ьс-\-са—аЪ*
171. Обозначим равные отношения буквой I. Тогда
получим систему
Х\ — #1 #2 — #2 хр —' ар
Х1 "Т *2 "Г ••• 4" *о
или
*1 = а1 + т1^ *2 =7= а2 + я*2/;...;
*р = ар+ тр1\ хх + х2 + ... + хр = а.
Решение заданной системы и этой суть равносильные
задачи.
Подставляя значения хъ дс2,..., хр, найденные из
первых р уравнений, в последнее, придем к следующей
системе:
137
х1 = а1 + тх1\ х2 = а2 + т21\...; хр = ар + тр1\
I (щ + т2 + ... + т~) =а — а1 — а2 — ... — ар.
Введем обозначения: т1 + т2 + ... + гпр = А и а — аг—
— а2 — ... — ар = В. Тогда последнее уравнение примет вид
А=*В. Если АфО, то^4д ДЛ«ГГ^ и
данная система имеет единственное решение, которое
получим, если подставим найденное значение I в формулы
Х1 = а1 + т1^> *2 == Л2 + т2^1 •••; *р = &р + ^р^- ЕСЛИ А = О,
но В ФО, то уравнение А1 = В не имеет решений, а
следовательно, и система не имеет решений. Если Л = 0 и
Б = 0, то уравнение А1 = Б обращается в тождество.
Система в этом случае имеет бесконечное множество решений,
которые можно получить с помощью формул хх — а^ + тх1\
х2 = а2 -Ь я^'»...; Хр = а^ + т//> где ^ — любое число.
172. Если хх и х2 — корни данного уравнения, то по
условию х2=х\у а по теореме Виета хгх\ = а3 и хг + х\ =
= -^р. Отсюда: ' *х « а; а2 + а — -^- = 0; ах = -|-;
5
а, =» - «г.
173. Известно, что если алгебраическое уравнение с
вещественными коэффициентами имеет комплексный корень
а + Ы {Ъ Ф 0), то оно имеет и сопряженный ему корень
1.-х * + / (1+'*)а
а — Ы. Так как хг = . __ . = ' .2 — ь9 то второй корень
искомого квадратного уравнения будет х2 = — г. Отсюда,
пользуясь теоремой Виета, получим квадратное уравнение
х2 + 1 = 0.
174. Квадратное уравнение имеет равные корни тогда и
только тогда, когда его дискриминант равен нулю. Отсюда
получаем уравнение (5а + 2)2 — 4 (5а — 1) (За — 2) = 0 для
определения соответствующих значений а. Решаем его:
35а2 — 72а + 4 = 0; ах « 2; а2 = -^-.
175. Чтобы квадратный трехчлен был полным
квадратом, необходимо и достаточно, чтобы он имел равные
корни, что будет иметь место в том и только в том случае,
когда дискриминант трехчлена равен нулю. Поэтому
получаем [т{т— 1)]а —4-36 = 0, т(т— 1)=± 12: а) пг—т —
— 12 = 0; т1 «= 4, т2 =* — 3; б) т2 — т + 12 = 0 — дает
комплексные значения т.
138
176. Дискриминант данного уравнения должен
равняться нулю. Поэтому имеем (3 + р)2 — 4 • 3 (1 + р) = О,
р2 — 6р — 3 *= 0. Это и есть искомое уравнение. Заметим,
что находить значения р не требуется, так как уравнение
уже получено.
177. (хг — х2)2 =а 16; (^ — л;^2 » (^ + *2)2 — Ахгх2\
(хг + х2)2 — Аххх2^ 16; 22 —4^.« 16; 4^ = — 12; 9== —3.
*то о « .. I 18т 16 =— 8/п
178. В уравнения лгх + *а — -д— и хгх2 =» -
9
16 — 8т
(-тт)'
подставим хх « 2а:2. Получим Здс2 «2/п и 2л;2. =*
Сравнение х^, полученных из этих уравнений, дает
—о . Отсюда находим: 4т2 «8 — 4т; т2 +
4- т — 2 = 0; тх =» — 2; т2 = 1.
179. Чтобы квадратное уравнение имело различные
корни, необходимо и достаточно, чтобы дискриминант
уравнения был не равен нулю. Поэтому получаем соотношение
1 + 2т (Зт + 2) Ф 0 или 6т2 + 4т + 1 Ф 0. Но трехчлен
6т2 + 4т + 1 имеет комплексные корни, так как его
дискриминант отрицательный, и поэтому при любом
вещественном т он не равен нулю, а следовательно, при любом
вещественном т данное уравнение имеет различные кррни.
180. Для этого должно быть р + ^=з —р и рц — ц.
Из второго уравнения этой системы получаем ц{р—1)=0.
Отсюда или <7 *= 0, или р== 1. Но при <7 — 0 первое
уравнение дает р м 0, а при р = 1 из него получаем ^ — — 2.
Итак, имеем: рх » 0, <71 =* 0; р2 = 1, % ^ — 2 и
соответствующие им уравнения: а) & в=я 0; б) #2 + л:—2 = 0.
181. Предположим, что уравнения имеют общий корень
х = а. Тогда должно быть
Г 2а2 —(Зт + 2)а + 12 = 0;
( 4а2—(9т —2)а + 36 = 0.
Умножая первое равенство на два и вычитая из
полученного результата второе, найдем (Зт — 6) а — 12 — 0,
откуда а = ——$. Итак, необходимо, чтобы выполнялось
соотношение а = к-. Подставим это значение а в пер-
13Э
вое уравнение. Получим:
0 16 (Зт + 2)4
+ 12 = 0;
(т — 2)2 т — 2
8— (Зт + 2) (т — 2) + 3 (т - 2)2 = 0;
— 8т + 24 = 0; т = 3.
Нетрудно видеть, что при т = 3 уравнения действительно
имеют общий корень а = 4.
182. Вычисляем дискриминант и преобразовываем его:
(2 + Зт)2 - (1 + т) (3 + 8т) = т2 + т + 1 «
Последнее же выражение, как сумма положительных
величин, есть величина положительная, а в этом и состоит
необходимое и достаточное условие вещественности корней
квадратного уравнения с вещественными коэффициентами.
183. Для этого достаточно доказать, что дискриминант
уравнения неотрицательный, т. е.
4 (а + Ь + с)2 — 12 (аЬ + Ъс + са) > 0.
Покажем это:
4 (а + Ь + с)2 — 12 (аЬ + Ъс + са) = 2 (2а2 + 262 + 2с2 —
*- 2аЬ — 2Ьс — 2ас) = 2 [(а2 — 2аЬ + Ь2) + (Ь2 — 2Ьс + с2) +
+ (с2 — 2ас + а2)] = 2[(а — Ь)2 + ф — с)2+{с — а)2] > 0.
184. Для этого необходимо и достаточно, чтобы
дискриминант уравнения, равный Ак + 1, был точным
квадратом, т. е. чтобы Ак + 1 = т2, где т — целое число.
Отсюда к = т 7" = Нт-1~ ) ^ Очевидно, оба
множителя числителя должны быть четными числами. Пусть
т — 1 = 2/1 и т + 1 = 2лг + 2. Тогда Л = я (л + 1), где
л = 0, ± 1, ± 2,...
185. Так как р— нечетное, то и дискриминант р2 — 4^
тоже нечетное число. Поэтому, если есть рациональные
корни у уравнения, то должно быть
р2_4<? = (2т+ I)2.
Положив р = 2к + 1; ц = 2/ + 1, получим
(2* + I)2 _ (2т + I)2 = 4 (2/ + 1).
Преобразуем левую часть:
(2к + I)2 — (2т + I)2 « 2 (& + т + 1) 2 (* — т).
140
Это число делится ига 8, потому что числа к + т + 1
и к — т в сумме дают нечетное число 2к-\- 1 и,
следовательно, одно из них четное. Правая же часть 4(2/+ 1) не
делится на 8. Полученное противоречие доказывает
теорему.
186. Предположим, что уравнение имеет дробный
рациональный корень—, где т и п — целые числа, не
имеющие общих множителей и | п | Ф 1. Подставим его в
уравнение вместо х. Получим ^- + а»— + 1 =0. Умножим
обе части последнего равенства на п. Будем иметь —3 +
+ ат + п = 0. Но это невозможно, потому что —,—
несократимая дробь, а ат + п — целое число. Предположим,
что уравнение имеет целый корень т. Тогда, подставляя
в уравнение х = т, получим га4 + ат + 1 = 0. Разделим
на т все члены уравнения. Будем иметь т3 4- а -\ = 0.
Но если тФ ± 1, то это невозможно, потому что т3 + а
есть целое число, а нецелое. Если же т— ± 1, то
а = =р 2, что исключено. Утверждение доказано.
187. Предположим, что уравнение имеет корень х =*
= —, где р и 9—взаимно простые числа и \д\ф1.
Тогда должно быть (-^-) + ах (-^-) + а*[^ + ... +
+ ат = 0 или, после умножения на д"1"""1 >
Р-. + а1Р"-1 + а2р"-*д + ... + атдт~' = 0.
Последнее же равенство невозможно, так как первое
слагаемое есть нецелое число, а все остальные — целые.
188. Если х = — корень уравнения, то, поступая
как в задаче 187, получим следующие два равенства:
Яо^- + ^Рт~] + а2рт-2Я + ... + атдт-х = 0;
аоР"-1 + а#т~Ц + а&»*<? + ... + атч— = 0.
141
Так как в левой части первого равенства второе
слагаемое и все дальнейшие — целые числа, то и первое
слагаемое должно быть целым, иначе равенство невозможно.
Поэтому я0 должно иметь ц делителем. Аналогично, с
помощью второго равенства, докажем, что р есть
делитель ат.
189. Пусть уравнение имеет вид Р(х)—0. Выполним
деление с остатком многочлена Р(х) на произведение
(х — а — Ь У~с) (х — а + Ь ]/Т) = (х — а)2 — Ь2с.
Обозначим частное через ф(х), а остаток (он будет не выше
первой степени относительно х) через Ах + В. Тогда получим
Р(х) = (Цх) \(х — а)2 — Ь2с) + Ах+В. (*)
Так как х<=* а + ЬУ~с корень Р(х), тог положив в
равенстве (*) х «=» а + Ь У~с, получим
О = <2(х) • 0 + А (а + Ъ У"с) + В.
Но число А (а 4- Ь У^с) -\- В есть сумма рационального
числа Аа + В и иррационального числа АЬУс. Поэтому
оно может обратиться в нуль в том и только в том
случае, когда каждое из них в отдельности равно нулю, т. е.
когда АЬУ с = 0 и Аа + В =* 0. Так как по условию
6=/=Ви с^8, то из первого равенства получим А = 0, а
из второго В ?=• 0. Итак, оказывается, что многочлен Р(х)
делится на (х — а)2 — Ь2с> а следовательно, и на х —
— (а — Ь]/~с). Последнее же означает, что а — &]/ с есть
корень рассматриваемого уравнения.
190. (6* + 7)2 • -^ (6* + 8) (6л: + 6) » 6. Положим у ^
*= 6х + 7. Тогда получим: у2 (у + 1) (у — 1) « 72, у4 — у2-^
-72-0; у2 = 9, у2 = -8.
Отсюда:
а) (6*+7)2 = 9, 6* + 7« ±3; *, « ^-|-, *2=_ А;
б) (6л: + 8)2 » « 8, Ьх + 1=±2\г2 ь\
V - ~7±2УТ/
#3,4 = о .
191. л:2(1 + х)2 + х* + 2л:(1 + х)х = 8(1 + х)2 +
+ 2х2(1 + х), [*(1 + х) + х]2« 2(1 + *)14(1 + *) + **],
142
Илг + 2)]2 = 2(1 +х)(х + 2)г, х2(х + 2)2 —
— 2(1 + х)(х + 2)2 = 0, (х+2)г(х2 — 2х — 2) = 0;
х,,2 = — 2, *3,4 = 1 ± У^З.
192. (л;2 + х) (*2 + * — 2) = 24,
[(*» + *—1) + 1][(д» + х—1) —1] = 24,
(*2 + *-1)2-1=24, (гЧ*-1)2»25,
г'-Ь* — 1 = ±5; а) х2 + х — 1 = 5, л:2 + дг — 6 = 0;
*, = 2, х2 = —. 3; б) х2 + х — 1 =. — 5, х* + х + 4 = 0;
#3.4 == 2 •
,93-[(^-4)+т-]4+[(^-4)-4-]4=1-Положим
у = х —^-. Получим уравнение [у 4- -^у + [у-* -у) = 1.
Раскрывая скобки и приводя подобные, придем к
уравнению 2у* + Зу* — -|~ =* 0. Отсюда: у* = \\ у* « |-;
й = -?г; уг = «р Уз'4 ет — ^Г~ '' ПользУясь
равенством х — -тр =э у, найдем: д^ <=» 3; *2 = 2; дс3,4 = —^Х——.
Можно было бы не вводить замены х ^ ^ У> а пРе*
образовать данное уравнение к следующему квадратному!
(х2 — 5х)2 + 14 (х2 — 5х) + 48 = 0.
Оба указанные метода приложимы к любому уравнению
вида
(х — а)* + (х — Ь)*=с.
194. Пусть один корень будет ху а другой хг = 2х.
Если подставим в уравнение 2х вместо х> то получим
уравнение 8.x3 — 84х2 + 280а: — 300. Оно, вместе с данным,
образует систему, из которой можно найти корень х. Для
этого умножим данное уравнение на 2, а найденное
уравнение разделим на 4 и из первого результата вычтем
второй. Получим 21л;2 — 210*'+ 525 = 0. Отсюда (х — 5)2=0,
х = 5, хх = 10. Зная два корня кубического уравнения,
легко найти третий корень. Для этого можно, например,
воспользоваться тем, что сумма всех корней равна коэффи-
143
циенту при дс8, взятому с противоположным знаком» т. е.
х + х1 + хз = 21, так что хъ = 6.
195. Если алгебраическое уравнение с рациональными
коэффициентами имеет корни 1 + У 3 и 2 + У~3, то оно
имеет и корни 1—^3 и 2—УЪ (задача 189). Поэтому
искомое уравнение будет иметь следующий вид:
(*_ 1 _у1) (*_ 2-|/"3) (х- 1 +1ЛЗ) (*-2+1ГЗ) = 0
или после упрощений
х*-6х* + 7х2 + 6х — 2 = 0.
196. Решив каждое уравнение по формате квадратного
уравнения, найдем, что первое имеет корни 1 и 2, а
второе — 2 и — 7. Следовательно, система -имеет только одно
решение х = 2.
197. Как видно из уравнений данной системы,
значения х% у и х 4- у не равны нулю. Поэтому, разделив пер-
Еое уравнение на второе и сократив в левой части дробь
на х + у, получим уравнение х = 2у, которое является
следствием уравнений системы, т. е. уравнением, которое
удовлетворяется всеми решениями данной системы. Отсюда
следует, что система
х = 2у;
у* + ху = 3
эквивалентна данной. Подставив х = 2у во второе уравне-
нение, найдем у2 -{- 2у2 = 3 и у = ± 1. Но тогда х = ± 2.
Из уравнения х = 2у видно, что х и у одного знака.
Поэтому решения системы будут такие: хг = 2, #1 = 1;
аг2 = — 2, #2 == — * •
198. Так как первое уравнение системы приводится к
виду (х2 + У2)2 + х2У2 =109, то систему можно записать
так:
г и2 + 02= Ю9;
\ и + Vе=13,
где ис=х2 + у2 и V = лгу. Найдя и из второго уравнения,
подставляем его значение в первое и решаем: (13 —V)2 +
+ 0а«Ю9, V2— 130 + 30 = 0; ^=10, 1>2 = 3; ^ = 3,
и2 е» 10. Поэтому данная система приводится к следующим
двум: а) х2 + у2 «= 10, ху = 3; б) х2 + у2 = 3, *# = 10.
144
Решаем первую. Для этого умножаем второе уравнение на
2, и затем один раз складываем с первым, а другой раз
вычитаем из первого. В результате получаем систему
(х + г/)2= 16;
(х-*/)2- 4,
эквивалентную данной, которая приводится к следующим
четырем линейным системам:
1х + у=±4;
\ х — у=±2.
Решая их, найдем: хг = 3, уг — 1; х2 = — 3, у2 = — 1;
*8 = !. г/з = 3; х4 = — 1, */4 = — 3.
Вторая система решается аналогично. Ее решения
следующие:
_ У23 + 1УТ7 _ У23-1УТ7
хъ => § > Л ^ 2
_^"К23 —/УТ7 _ — У23+1УТ7,
Хв — 2 » Уб" 2
_ 1/23-/]/Т7 _ У23 + 1УТ7
Хт- 2 ' #7 2
х8 — ^ > #8 ^ 2 #
199. [(* + #)+1]2 + (*+*/)2==25, 2(х + у)2 +
+ 2(х + у) — 24~0, (х + у)* + (х + у)-12 = 0;
-1 ±7
х + у
2
Поэтому задача решения данной системы равносильна
задаче решения следующих двух систем: а)х + у = —4,
х2— г/2 = 3; б) х + у = 3, *2 — ^ = 3.
Решаем первую систему: х + у = — 4; (а: + у)(дс — */)=3.
з
Отсюда х— у = т", что вместе с уравнением х+у——4
19 13
дает *! = — -§-; ^ = §".
Решаем вторую систему: # + у — 3; (х + у) (х — у) = 3.
Отсюда х — у = 1, что вместе с уравнением х + у = 3
дает лг2 = 2; */2 « 1.
200. Складывая первые два уравнения и вычитая из
результата третье, найдем, что 2ху = 4 или ху = 2.
10 к. У. Шахно 145
Очевидно, всякое решение данной системы является решением
полученного уравнения. Аналогичными преобразовани ями
получим еще два уравнения уг = 6 и хг » 3, которые
также являются следствиями уравнений данной системы.
Таким образом, система ху = 2; уг = 6; хг = 3
удовлетворяется любым решением данной системы. Обратно, всякое
решение новой системы будет решением данной, так как
каждое уравнение данной системы можно получить сложив
соответствующие два уравнения новой. Следовательно,
система ху = 2; уг = 6; хг = 3 эквивалентна данной.
Перемножим все три уравнения новой системы. Получим
уравнение х2у2г2 = 36 или хуг — ± 6, которое является
следствием уравнений новой системы, и, присовокупив его к
уравнениям новой системы, получим следующую систему
из четырех уравнений: ху => 2; у г = 6; хг = 3; хуг => ± 6.
Она, как и предыдущая, также эквивалентна данной.
Решаем эту систему. Подставим в последнее уравнение
системы вместо ху число 2. Найдем, что г = ± 3.
Аналогично найдем, что х = ± 1 и */ = + 2. Учитывая первые три
уравнения, из которых видно, что ху > О, уг > 0, хг > О,
получим следующие решения данной системы:
^1=1,й = 2, гх = 3; х2 ея — 1, #2 = — 2, г2 = — 3.
201. Возведем в квадрат первое уравнение системы, из
результата вычтем второе и третье. Получим уравнение
ху + хг = 36 или х(у + г) = 36, которое является
следствием уравнений данной системы. Присовокупим это
уравнение к уравнениям рассматриваемой системы, тогда
получим систему из четырех уравнений, равносильную данной.
Найдя из четвертого уравнения у + г = — и подставив это
значение у + г в первое уравнение системы, получим
х + — = 13; х2 — 13* + 36 = 0; хг = 4; *2 => 9. Используя
эти значения х, а также третье и четвертое уравнения
системы, найдем для определения у и г следующие две
системы:
у + г = 9; | у + * = 4;
г/2-18 И Ы =18.
Решение их элементарно, а потому не приводится.
Выполнив его, получим следующие решения данной
системы:
146
х\ = 4> й = 6, гх = 3; *2 = 4, у2 = 3, г2 - 6;
*з = 9, у3 = 2 + 1УН1 г, = 2-/1/74;
*4 = 9, у4 = 2 — 1УК г4 = 2 + ^1/14.
202. Умножим первое уравнение на 2, второе — на —1,
третье — на —3 и результаты сложим. Получим:
2х2 + 2у2 + 2г2 — Зх — 2у2 + 7хг — Зхг + 3*=70 + 14 — 12;
2х2 + 2г2 + 4*г =* 72; х2 +2хг + г2 = 36; (* + г)2 = 36;
# + г = ±6.
Если к трем уравнениям данной системы присовокупить
один раз уравнение х + г = 6, а другой — уравнение х +
4- г — — 6, то получим две системы уравнений, по четыре
уравнения в каждой, которые вместе равносильны данной
системе. Беря из этих систем третьи и четвертые
уравнения, получим две системы для определения х и г:
а) х + г = 6у х(г—1) = 4; б)х + г=> — 6, х(г—1) = 4.
Решаем первую из них: г =» 6 — х\ х(6 — х — 1) = 4,
Xй — Ъх 4- 4 = О; хх = 1; л;2=х4. гх => 5, г2 = 2. Вторая система
решается аналогично. Из нее найдем: дсз.4 = ——^р-—;
23,4= к^—. Исключив произведение хг из
второго и третьего уравнений системы, получим у2 => 7 4- 2л:,
а отсюда, подставляя л^, лг2, #3» *а вместо л:, найдем:
Уг = + 3; % = ± У"15; </з = ± ^33; #4 = ± 1КЗЗ. Таким
образом, данная система имеет восемь решений.
203. Возведем в квадрат третье уравнение и из
результата вычтем первое и удвоенное второе уравнения системы.
Придем к уравнению Ауг = 8 или уг = 2, которое
является следствием уравнений данной системы, и, добавив его к
уравнениям данной системы, получим систему, равносильную
данной. Подставим вместо уг число 2 во второе уравнение
системы и рассмотрим систему из полученного уравнения
ху + хг =э 9 и третьего уравнения, т. е. следующую
систему:
(х(у + г) = 9;
\х + (у + г)~6.
Из нее находим: у + г = 6 — х;х(6 — х)==9\ х2 — 6х +
4-9 = 0; х = 3; у + г — 3. Теперь значения у и г легко
определить из системы
10*
147
уг = 2.
Решив ее, найдем для у значения 1 и 2, а для г значения
2 и 1.
Итак, хг = 3, у, =г 1, гх = 2; дс2 = 3, у2 = 2, га а= 1.
204. Сложим первое уравнение с третьим и из
результата вычтем второе. Это даст 2х2 == (а + с — 6) лгуг. Отсюда
получим л:х = 0% и 2х = (а + с — Ь) уг. Подставив в данную
систему хх — 0, найдем уг = 0, гх = 0. Аналогичными
преобразованиями получим также уравнения 2у = (6 + а—Ф*
и 2г = (с + Ъ — а) ху. Если не учитывать нулевое решение,
которое уже найдено, то полученная система
12л; = (а + с — Ь) уг\
2у = (Ь + а — с) гх\
2г = (с + Ь — а)ху
равносильна данной.
Перемножая первые два равенства этой системы и деля
результат на ху > 0, получим уравнение (а + с — Ь) (Ь 4-
+ а — с) г2 = 4. Аналогичными преобразованиями получим
также (о + а — с)(с 4- Ь—а)х2=4 и (с+Ь—а)(а+с—Ь)у2=4.
Из этих уравнений найдем:
±2 ±2
У(Ь + а — о(с+ Ь — а) ' * У (с + Ь — а) (а + с — Ь) '
±2
2 = — —.
/(а-1-е — Ь)(Ь + а — с) '
Эти формулы и дадут решения данной системы, однако,
нужно учесть, что ху у и г, как это видно из данной
системы, должны быть все положительны. Таким образом,
с учетом решения хг = ух =* гх = 0, система имеет 3 решения.
Условия, наложенные на а, Ь и с, гарантируют
вещественность найденных решений.
205. Сложим все три уравнения системы. Получим
после упрощений: х? + у2 + 2ху = 49; (х + у)2 =* 49 или
х + уя + 7. Умножим второе уравнение на 2 и сложим
результат с первым. Получим уравнение (# + у)2 +
+ 2г (х + у) = 94 + г2. Рассмотрим теперь эти два уравне-
148
ния_ и первое уравнение данной системы. Они образуют
систему
х + У=±7;
(х + у)2 + 2г(х + у) = 9А + г2\
х2 + у2 = г2,
которая, как легко доказать, равносильна данной.
Решаем эту новую систему. Подставив х + у = ±7 во
второе уравнение, найдем уравнение для определения г :
49 ± 14г = 94 + г2. Из него находим, что гх = 9; г2 = 5;
г3 = — 9; г4 =—5. Подставляя найденные значения г в
третье уравнение, получим следующие системы:
^ + ^ = 81; ( х2 + у2 = 25\
х + у= ±7 И 1 д: + у = ± 7.
Решения этих систем, приведенные в соответствие с
найденными значениями г, дадут следующие 8 решений
данной системы:
Х\ = 4, Ух — О, 2\ = 5', А^2 == ^» #2 == 4, 22 = О',
•^з == — 4, у3 = — о, г3 = — о;
*4 = —3, </4 = — 4> г^ — 5;
_ 7-/0 _ 7 + УТГЗ _ а.
#6 — 2 ' ^5 — 2 * ^б — '
_ 7 + /Ш ___ 7 — УШ _ 0.
_—7—УШ —7+УШ _ 0
*7 — 2 ' ^7 — 2 ' 2?
_-7+/ПЗ „-7-ГПЗ , _ 9
Л8 — 2 » "8 — 2 ' 8
206. Сложим три уравнения данной системы. Получим
уравнение (х + у + г)2 = а2 + Ь2 + с2. Данная система
вместе с этим уравнением образует систему, эквивалентную
данной. Подставляя в первое уравнение значение х + у +
+ г = ± У а2 + Ь2 + с2 У найдем
х = да
± У а2 + Ъ2 + с2
Аналогично получим:
Ь2 с2
и = ——' х =
± /я2 4- Ьа + с2 * * ± У а2 + Ь2 + с2 *
149
Из уравнений системы видно, что х, у> г должны быть
одного знака. Следовательно, во всех полученных
формулах нужно брать одинаковые знаки — или только знаки
плюс, или только знаки минус. Таким образом, решений
будет два.
207. Прибавив по единице к обеим частям каждого
уравнения системы и сделав несложные преобразования,
придем к следующей системе, равносильной данной:
(1+г)(1+*)=*&+1; (*)
.(1+*)О+0)«с+1.
Перемножив первые два уравнения этой системы и разде-
(а+\)(Ь+\)
лив результат на третье, подучим (1 + г)2
±т/(а+1)(6+1)
е+1
ИЛИ 2 '
о+\
1.
Аналогично найдем
/==± у (с+\)(а+1Т
У
1 и х
=±У-
+ 1)(с+1)
-1.
Ь+\ * - ~ л- р а+}
Из системы (*) видно, что знаки перед корнями нужно
взять или все верхние, или все нижние, так что
получится два решения.
208. Перенеся вторые слагаемые из правых частей
уравнений в левые и преобразовав получившиеся после этого
разности квадратов, придем к следующей системе,
равносильной данной:
[ {х + у — г)(х + г— #) = а;
(у + г — х){у + х — г) = Ь; (*)
(г + х — у)(г + у— х) = с.
Перемножив первые два уравнения этой системы и
разделив это произведение на третье уравнение, получим
(х + У — *)2 = — или х + у — г = ± ]/—-. Аналогично
С ' С
найдем еще два уравнения и составим систему
х + у—г- ± у~;
•х»±1/?; (**)
1
У + г-
г + х-
У
-±у-
а
са
Ь
150
Система (**) будет равносильна системе (*), а
следовательно, и данной, если знаки перед радикалами в правых
частях всех уравнений брать одинаковые. Это можно
усмотреть из системы (*).
Сложив два первых уравнения системы (**) и разделив
на 2, получим
у- тч± У — ± V -гг ± -2-гг+т)
и аналогично
'-±^(4-+1>.*-±^(т-+-г)-
209. Как видно из системы, ни одно из неизвестных не
может равняться нулю. На самом деле, если бы, например,
х = 0, то тогда уг = 0 и х2 + у2 + г2 = 0. Но это
невозможно, так как в этом случае было бы х = у = г = О
и отношения, входящие в систему, не имели бы числового
смысла. Поэтому система будет равносильна той, которая
получится из нее, если заменить все отношения обратными
величинами. Эта система имеет вид
а , Ъ __ Ъ , с^ _с_ , а а2 + Ь2 + с*
~Г + "У" ~~ 1Г + ~2 ~Т "*"" "Т" ~~ *а + */а + га *
Заметим, что ни одно из чисел а, 6, с не равно нулю.
Действительно, если а = 0, то из последней системы
получим— — \- — — —, откуда следует 6 = 0 и с = 0.
Но этого не может быть, так как отношения в данной
системе не имеют смысла в атом случае.
Сложим все уравнения новой системы, а затем вычтем
из полученной суммы поочередно ее первое уравнение,
второе и третье. Получим следующую систему, равносильную
данной:
^^Л^^^^^. Да + Ьг + с2
г ~~ х ~~ у 2 ' х2 + у2 + г2
или
^_ ^± __*_ _/
где * ^ 0.
Из последних равенств находим: х — сА\ д = 6/; г — с1
Ь 1 аа -4- Ьа + са
и, подставляя в равенство — = -у-, ^а Т „а Т2а » получим:
151
А. = _!. а2 + Ь\+ (? . _1_ _1_. ,
И 2 " (а2 + б2 + с2)/2 ' / 2/* '
единственное решение системы будет:
■* — 9 » У о '
210. Перепишем данную систему так:
Г г = — (х + у);
(х + у)2-2ху = г* + 20;
( (х? + у2)2 — 2х?у2 = г* + 560.
Подставляя значение * + */ =—-г из первого уравнения во
второе, получим г2— 2ху = г2 + 20, — 2ху = 20,.ху=—10.
Подставляем в третье уравнение л:2 + г/2 = г2 + 20,
полученное из второго уравнения, а также ху = —10. Это
даст: (г2 + 20)2 — 2 • (— 10)2 = г4 + 560; г4 + 40г2 + 400 —
_ 200 = г4 + 560; 40г2 = 360; г =* ± 3. Для определения
^ и (/ имеем систему
* + У = + 3;
лтг/ = — 10.
Решив ее и учитывая значения г =* + 3, получим 4
решения данной системы:
х1 = о, Ух =я — 2, 2^1 — — о; х% ==з — 2, у2 == 5, 22 = — ^»
*з =: — 5, Уз =3 2, 2з = о; #4 =э 2, у4 = — о, 24 = о.
211. Из первого уравнения находим у = 2х—1 и
подставляем во второе. Получаем:
4х + 2х — 1 — 2х (2х — 1) — г2 = 3; 4*3 — 8а: + 4 + г2 = 0;
4(а:—1)2 + г2==0.
Последнему уравнению удовлетворяют лишь х= 1, г = 0
(корни должны быть вещественными). Но тогда у=\.
Итак, система имеет единственное решение: х=\\ у = 1;
г = 0.
212—243. Указание. В элементарной математике, при
решении иррациональных уравнений и их систем, корни
четной степени считаются арифметическими. За значение
корня нечетной степени из вещественного числа
принимается его единственное вещественное значение. Основной
метод решения иррационального уравнения состоит в
исключении радикалов путем возведения обеих частей уравнения
-^-. Таким образом,
с
152
в некоторую степень с таким расчетом, чтобы после
этого уравнение перестало быть иррациональным. Иногда
такую операцию нужно повторить. В поле вещественных
чисел этот метод может привести к уравнению,
неравносильному с данным, а следовательно, и к посторонним
решениям. Поэтому при решении таких уравнений
методом исключения радикалов необходима проверка
(испытание) найденных значений путем подстановки их в
данное уравнение и те из них, которые не будут ему
удовлетворять, нужно отбросить как посторонние.
Возведение обеих частей уравнения в нечетную степень
приводит к равносильному уравнению и в этом случае
проверку производить не нужно. Все сказанное о решении
иррациональных уравнений нужно отнести к решению систем
таких уравнений.
212. В первом уравнении должно быть Р(х) > О
и ф(х) > 0, а во втором они могут быть какими угодно.
Поэтому в общем случае уравнения не равносильны.
213—214. В первом уравнении должно быть Р{х) ф(*):>0.
Во втором — Р(х) > 0 и (?(*)> 0. Поэтому в общем случае
уравнения не равносильны (см. задачу 124).
215. Так как левая часть больше двух, то уравнение
не имеет решений.
216. (*°-3* + 2)-(*»-7*+12) =^^-а—
у х* — Зх + 2 — У х* — 7х + 12
+ ухг—7х+ 12 = У% (К*2—3* + 2)2 =
= (|/~2— ]/ х2— 7х+ 12)2, х2 — 3* + 2 =
= 2—2 /2л:2— Нх + 24 + х2 — 7х + 12,
|/2лг2— 14* + 24 = 6 — 2*, 2х2 — 14* + 24 =*
= 36—24* + 4*2, 2*2 — 10* +12 = 0,
*2 — 5* + 6 = 0; хх = 2, *2 = 3.
Оба корня удовлетворяют уравнению, что легко
устанавливается проверкой.*
217. 2*2 + 6 — 3(*+ 1) — 2|/"2*2 — 3* + 2 = 0,
2*2_ 3* + 2 — 2 /2*2 — 3* + 2 + 1 =0.
Положим
)/2*2 — 3* + 2 = у.
* В тексте мы, как правило, проверку корней не приводим, а
лишь указываем, какие из найденных корней посторонние.
153
Тогда получим;
уг — 2г/+1=0, */=1; / 2л:2 — Зл: + 2 = 1,
2л:2 — Зл; + 2= 1, 2л:2 — Зл: + 1 == 0; хх «= 1, х8 = -у.
218. |/"(7л: —З)3^ .. 8 =7.
Положим
У(7х-3)*=*у.
Тогда будем иметь:
^_7у —8 = 0; {/, = -1, & = 8.
а) Г (7л: — 3)3 = — 1, 7л: — 3 = — 1, х, = -у"!
б) |/ (7л:— 3)* = 8, 7л: — 3 = 32, хг = 5.
219. 1/1±^+4=_ = 4.
1/ * + э
Положим
Тогда получим:
*/ + |-4, ^-4у + 4 = 0; */=2, |/±±± = 2,
-^-±^ « 4> * + 9 ^= 4х, л: = 3.
220. Разделим все члены уравнения на (а — х)3.
Получим следующее уравнение, эквивалентное данному:
1 а + * 1 —5 -[а^~х 1 4-4=0. Решаем это уравнение от-
(а + х\3 (а + х\3 5±3
носительно I __ 1 как квадратное: 1 __ 1 =—±—.
Отсюда: а) (-^) « 1, 2±± = 1, д + х = <* — *, д^ = 0;
6){^У = 4, ^=6^а + х~64а-64х, х2 = §*
Найденные значения х проверять не требуется.
154
п Г а у
221. Обозначим у -т—-== у. Тогда уравнение
приведется к.следующему равносильному: у + —- = 2 или у2-—
—- 2у + 1 = 0. Отсюда:
У
-''У^^'-Ш-1' *-* = ь+х>
2 '
222. |/^Т45 = 1 + ]Лс—16, (т/х+45)3 -
= (1 + у^лг^Тб)8, х + 45 = 1 + 3^—16 +
+ 3(^7=Тб)2 + * — 16, [V х— 1б)2 +
+ ^х—16 — 20 = 0; ^— 16= ~~ ^ 9 ;
а))/*—16 = 4, а:—16 = 64, ^ = 80;
б)у/х— 16 = — 5, л;—16 = —125, х2 = — 109.
223. Из уравнения видно, что допустимыми
значениями х являются лишь те, которые удовлетворяют системе
неравенств: х >0, 1 >0, что приводит к
соотношениям х > 1 или — 1 < х < 0. Поэтому у 1 — — —
арифметический, а х~ = 1 / (——) и данное уравнение
равносильно такому:
или
Отсюда:
б)УхТ~\-\ = У1~, (уТ+1-1)» =
*+1 —2/Г+Т+1 =-^±, ж2 —2* 1/7+1 +
+ * + 1 = 0, [х— Ух+ I)2 = 0, * — VТ+1 = 0,
155
х— 1
х = Ух+1, х2 = х+1, х2 — х— 1=0,
_ 1 + УТ
хг— 2 *
Значение х = ~ "— > — 1 и также корень данного
уравнения.
224. Щ^^- = У2 + х, Д_ = У2 + х,
** 2 + *, х2 = 2 + Зх + л:2, 2 + 3* = 0, х = — -|-.
, + х I ~. I ~~ I - , ~ -г «~ -. з
Но при л; = д- левая • часть уравнения меньше нуля
(там есть множитель х), а правая больше нуля (корни
арифметические). Так как все корни уравнения А —В
содержатся среди корней уравнения А2 = В2, то данное
уравнение не имеет решений.
225. [4л: + 1 +2* ]/2(2л:2+ 1)]2=
>= [— (2х + 1) |/4*2 + 4х+~3]2, (4* + I)2 +
+ 4* (4* + 1) /2(2л:2+ 1) + 8л:2 (2*2 + 1) =
= (2х + I)2 (4л:2 + 4х + 3), (4л: + I)2 +
+ Ах (4л: + 1) /2 (2л:2 + 1) + 16л;4 + 8л:2 =
«= (Ах2 + Ах + 1) (4л:2 + 4л: -+- 3), (4л: + I)2 +
+ 4л; (4л: + 1) У 2 (2л;2 + 1) + 16л;4 + 8л:2 =
= (4л: + 1) (4л;2 + 4л: + 3) + 16*4 + 16л? + 12л:2,
(Ах + I)4 + 4л; (4л; + 1) У2(2х2 + 1) =
с= (4л: + 1) (4л;2 -+- 4л; + 3) + 4л:2 (4л: + 1),
4л: (4л: + ])У2(2х2+1) = (4л: + 1) (4л:2 + 4л; + 3 +
+ 4л:2 — 4л: — 1), 4л: (4л; + 1)У2(2х2+ 1) =
= (4л: + 1) (8х2 + 2). Отсюда: а) 1 + 4л; = 0 и л: = — -Ь
б) 2л: У Ах2 + 2- Ах2 + 1, 4л:2 (4л:2 + 2) = (4л:2 + I)2,
16** + 8л;2 = 16л:* + 8л;2+1.
Последнее равенство невозможное.
Итак, уравнение имеет единственное решение х=—-^.
156
226. (2у2х + Ух-ЗУь^)Ш-
= (2У 2х—У~х)\ 4(2л:+ \Пс) — 12У~х +
+ **-=- = 4 [2х-]П)> ^-=- = 4 УТ.
2х+У х к } 2х + У х
Так как х Ф О, то, сократив на |/ л:, получим уравнение
Д = 4. Отсюда: 81/7 + 4 = 9, ]/"* = 4.
2у х+I °
_ 25
227. Возведем в куб обе части уравнения и при этом
воспользуемся формулой (т + л)3 = т3 + Зтл (т + л) + л3.
Получим:
(Уа + Ух + у/Га — У~х)3 = {У~Ъ)\ а + УН +
+*3 ^(а + У~х) (а — Уг1с) У~Ъ + а — |/~^ = 6,
2а + 3>/"а2 — а: У Ь = Ь, Уа2 — х = —
2а
Возведение уравнения в куб приводит к уравнению,
эквивалентному данному в области вещественных чисел, если
же еще учесть, что, как видно из данного уравнения, х > О,
то найденное значение х будет решением данного
уравнения тогда и только тогда, когда а2—(—"Г.— ) >0. Та-
\ ъу Ь I
ким образом, в области вещественных чисел
рассматриваемое уравнение или не имеет решения, или имеет
единственное решение.
228. Поступая так же, как в задаче 227, получим:
х + зУх(2х — 3) |/"12(лг— 1) + 2х — 3= 12(л:— 1),
х — 1 + У^(2х — 3) 12(лг— 1) = 4 (х — 1),
У\2х{х—\)(2х — Ъ) = 3(*—1), 12л: (*— 1) (2* — 3) =»
= 27(л:— I)3, (л:— 1)[4х(2х — 3) — 9(х — I)2] = О,
(л;_1)(_л:2 + 6а: — 9) = 0, (л:— 1) (л: — З)2 = 0;
Х^ = 1, Х% = о,
157
Так как уравнение было возведено в нечетную степень,
то полученное в результате этой операции новое уравнение
эквивалентно данному и найденные значения х в проверке
не нуждаются.
229. Положим у/Г16 + У7=и, ^}^16 — У1с = V.
Тогда уравнение примет вид и + V = 2. Возведем его в пятую
степень. Получим:
(и + V)5 = 32, иъ + ьъ + Ьш) (и3 + ^3) + Ю*Л2 (и + а) =*
== 32, а5 + у5 + Ът{и + у) (и2 — ш + V2) +
+ 10Л>2 (и + а) = 32, и5 + я6 + Ъш) [{и + V)2 —
— Зш] (и + у)+ \0и*хР (и + V) = 32.
Подставляя сюда и~\-ю = 2 и иъ -\-Vъ =
-(16 + У~х) + (16 — \Гх) = 32,
найдем:
32 + 5да (22 — Зио) • 2 + 10*А;а -2-32, 4ии — и2р2 =* О,
№ (4 — иу) = 0.
Отсюда:
а) ы = 0, у/~16 + |/ ~л: = 0, 16 + 1Лх=:0,
что неюзможно;
б) 0=0, 1^16 — У~х = 0, 16 — У~х = 0, х = 256.
Это значение л; является корнем данного уравнения;
в) 4 — да == 0, да = 4.
Решая систему
да = 4, а + V = 2,
получим:
а(2 —и) = 4, и2—2и + 4^0уи=1± ьУТ,
в то время как
у/Г16+ ]/"* = и
должно быть вещественным числом.
230. Положим Ух — \ = у > 0. Тогда л: = г/2 + 4 и
уравнение можно записать так:
Уу2-2у+\ + Т/у2-4у + 4 = 1
или *|/((/ — I)2 + У (у — 2)2 = 1, или, наконец, | у — 11 +
+ |0 —2| = 1. Если */< 1, то |у—1|= 1— у, |у —2|=
158
= 2 — у и уравнение примет вид 1 — у + 2 — у == 1.
Отсюда 2*/ = 2, у = 1. Если 1 < у < 2, то | у— 11 = у — 1,
| г/ — 21 == 2 — у и уравнение приведется к такому: у— \ +
-1-2 — {/=1. Но это значит, что у может быть любым.
При у > 2 будем иметь | */ — 11 = у — 1, |у — 21 = у — 2,
а данное уравнение запишется так: у—1 + у — 2=1.
Из него находим, что у =2. Итак, должно быть: 1<у<2;
1<У^Г4<2; 1<х — 4 < 4; 5<*<&\
Уравнение имеет бесконечное множество решений.
— 2*^2*, "[/"а:2 — 4 « О, х2 —4=*0* ^=2, х2 = — 2.
Первое значение * является корнем данного уравнения.
Второе должно быть отброшено, так как х=*—2 не
принадлежит области допустимых значений (х — 2 = — 4<0)#
232. Допустимыми значениями для неизвестного этого
уравнения являются х > 0, Умножим числитель и
знаменатель левой части уравнения на 2 и воспользуемся
формулами квадрата разности и квадрата суммы двух
количеств:
2 (1 + х — У 2х + *2) 2+х — 2У1Г^х'У1с-\-х __
2(\ + х + У 2х + х2) 2 + х + 2У2-\-хУ х + х
^ (У2Тх^УТ?
Тогда уравнение примет вид
'ут+~х-ут\2_^ у2+~х + ут
,У2 + х + Ух ) У2 + х — Ух
ИЛИ
'У2~+1с—У~
%1-*
кУ2 + х + У~
Извлекаем корни из обеих частей уравнения. Это даст
УТ+~х-~У~х
У2 + Х + УТ
= а. (*)
Заметим, что все примененные сейчас операции при
переходе от данного уравнения к уравнению (*), включая
операцию извлечения кубичного корня, не могут привести к
потере корней или к приобретению посторонних. Таким
15Э
образом, уравнение (*) равносильно данному уравнению.
Так как корни должны быть арифметическими, то из
полученного равенства следуют неравенства 0 < а < 1.
Действительно, числитель и знаменатель левой части
уравнения— положительные числа, причем числитель не больше
знаменателя.
Освобождая уравнение (*) от знаменателя, получим
новое уравнение, которое также равносильно данному:
У2 + х(\ — а) =: V х(1 + а). Так как а < 1, то обе
части последнего уравнения неотрицательны и возведение
его в квадрат снова приведет к уравнению,
равносильному данному. Таким образом, задача свелась к решению
следующего уравнения: (2 + х) (1 — а)2 = х (1 + а)2.
Решаем его: х [(1 + а)2 — (1 — а)2] = 2(1— а)2, Аах = 2(1— а)2,
_(1-Д)1
Х - 2а '
тл (1— я)2
Итак, уравнение имеет единственное решение *= 2 ,
если 0 < а <: 1, и не имеет решения, если а <; 0.
Замечание. В данном случае отпала надобность
в испытании найденного значения неизвестного, хотя при
решении уравнения применялась операция возведения
уравнения в квадрат, которая, вообще говоря, приводит
к посторонним корням, Объясняется это тем, что при тех
ограничениях, которые мы попутно налагали на
неизвестное (л;>0) и на параметр (0 < а <1), все производившиеся
операции приводили к уравнениям, равносильным
данному. Надо сказать, что при решении иррациональных
уравнений с буквенными коэффициентами такой путь
обычно оказывается более удобным, чем тот, при
котором мы обязаны производить испытание найденных
значений неизвестного, так как в последнем случае
приходится решать еще задачу на преобразование буквенного
выражения, иногда довольно сложного.
233. Так как корень предполагается арифметическим,
то должно выполняться условие: 1 _ , * > 0; (1 -{-Ьх)(1 —
— Ьх)>0; 1 — Ь2х2 > 0; х2 < -д?. Так как арифметический
корень есть число неотрицательное (а в данном случае
он может быть лишь положительным), то необходимо
160
(но не достаточно), чтобы было1 , ах >0;(1—ах)(1-\-ах)>
> 0; 1—а2х2 > 0; #2<—*. Если эти условия не
выполнены, то уравнение не имеет решения. Предполагая это
выполненным, мы будем иметь в обеих частях равенства
положительные величины и возведение его в квадрат
приведет к следующему уравнению, равносильному данному:
(\-ах\2 \_
\1 + ах) ' 1
+ Ьх= 1
■Ьх
Решая это рациональное алгебраическое уравнение,
получим:
(1 _ ах)2 (1 + Ьх) = (1 + ах)2 (1 — Ьх), а2Ьх? = (2а — Ь) х\
2а-
аЧ '
Очевидно, первый корень удовлетворяет уравнению.
Что касается х2 и х3, то для того, чтобы они были
корнями уравнения, должны выполняться следующие условия:
а~ > 0 (решения должны быть вещественными), #2<—
(в противном случае уравнение вообще не имеет решения,
так как левая часть его будет отрицательной, а правая
положительной), х2 < р- (корень, входящий в левую часть
уравнения, должен быть вещественным). Если эти условия
будут выполнены, то найденные значения х дадут корни
данного уравнения. Упростим эти условия. Из первого
соотношения получаем:
2<>-Ь 0 2а-Ь р 2а « 0 2а _?_ > ±
Из сопоставления первого и второго получаем:
«_2а-Ъ 1 '24-^ 12а_1 1 2а а_ 1
Х ~ а*Ь ^ а* > Ь ^ ' Ь 1^1' 6^^6Ч1•
ИЛИ, сведя два результата в один, получаем
2 ^ Ь ^ '
* За исключением х = 0, для которого а может быть любым
11 к. У. Шахно 161
Что касается условия х2 < -р-, то оно выполняется.
Действительно,
2 _1 2а~"Ь 1 _ 2а6-62 —а2 _ (а — Ь)* ^ п
* ~ б2 ^ а26 Ь2 ~~ я26а "" аЧ* ^и»
так как афЬ.
234. Если п — четное, то допустимые значения х
должны удовлетворять условиям х > О и а + х > 0. При
нечетном п эти ограничения на х налагать не требуется.
Числа а, Ь и х, очевидно, не равны нулю.
В левой части равенства вынесем за скобки /а + х.
Получаем У а + х (— + —) «■ ^-. Отсюда:}/ а + х х
х —!-— — *-г-\ I/ I—~—) ■=> у. Здесь левая часть
больше нуля, следовательно, и правая часть должна быть
больше нуля, т. е. а и Ь удовлетворяют неравенству
->адм«(^И)--|.^-(тГ-4+'-
-(#^-(|Г->--[(|Г-']^сл„
(-11 —1^=0, т. е., если афЬ, то отсюда найдем х=*
е= ^ (*). При нечетном п формула (*) всегда даст
решение данного уравнения при условии, что а и Ъ
одного знака и а Ф Ьл Кроме того, эта формула даст решение
при п нечетном и в том случае, если в знаменателе дроби
п
перед выражением (-т-1 поставить знак минус При
четном /г, кроме аЬ > О и афЬ, должно быть х > 0 и а +
+ х > 0. Из формулы (*) видно, что х будет
положительным, если: а) а> 0 и-~> 1, что приводит к сботношени-
162
ям а > Ь > 0; или б) а < 0 и 0< ~ < 1, что приводит к
соотношениям 0 > а > Ъ. Что касается а + *, то эта
сумма всегда будет положительна при положительном ху так
п
как а + х = *[-т-)
Итак, формула (*) при четном д дает единственное
решение, если а > Ь > 0 или 0 > а > 6. При иных
соотношениях между а я Ь уравнение не имеет решения.
235. Если п нечетное число, то п2 также нечетное
число, и при х < 0 корень степени п + 1 из х"ап2 даст
мнимую величину. Поэтому при нечетном п допустимыми
значениями неизвестного будут х > 0. При п четном
допустимыми значениями неизвестного х, очевидно,
будут все вещественные числа. Параметр Ъ в обоих случаях
есть величина положительная, так как Ь равняется сумме
двух арифметических корней, из которых, по крайней
мере, ОДИН не Обращается в нуль. При решении будем
считать сперва п нечетным и, следовательно, х > 0. В левой
части данного уравнения вынесем за знак первого радика-
п п
ла хп+1, а за знак второго ап+{. Получим:
<п+1 У хп+1 + ап+х + ап+{ У
п п
ап+\ _|_ хп+\ __ 6,
V Хп+
п I п п \
(п п \п-{-\ п п п
хп+\ _|_ ая+1у~-- ьу хп+1 + ап+1 = Ьп+\
п п п I п п \п-{-1
хп+\ __ 1р+1 — дп+1^ х = \Ьп+1 — ап+1) п ,
при этом, как видно из предпоследнего равенства, должно
быть Ь> а, иначе найденный х не будет решением
данного уравнения.
Из этого решения видно, что если п будет четным, то
решений будет два:
/ л_ п \п+1
Х\,2 = ±
при Ь > а и одно х = 0, если а = &.
II*
163
У Ъ — а
а
2к
2п
\ п—2к
) »
/
236. Так как п > к > 0, то уравнение имеет корень
хх = 0. Теперь можем считать, что х Ф 0. Разделим все
члены уравнения на У ап -к хк. Получим квадратное урав»
нение
п—2к п—2к
у-а(±)П -2У-Ь(±УП + У~а = 0.
Решив его, найдем:
п-2к
1х_\ 2п ^У~Ь± УУ^~а х = (У~Ь± V
\а/ УТ ' а \ У~^
2п '
*2,з = [У~Ь ± УТ=Ъ) п~2к - а2*~л .
Однако при п = 2к вычисления теряют смысл. Но х = 0
остается /корнем и в этом случае. Других же корней при
п — 2к уравнение иметь не будет, так как в этом случае
уравнение приводится к виду 2 У ах = 2 УЬх, причем по
условию аФ Ь. В заключение отметим, что, как видно из
правой части данного уравнения, допустимыми значениями
для неизвестного являются лишь х > 0. Это было
использовано и при вычислениях. Условие Ь > а гарантирует
вещественность х2 и х3.
237. Если п нечетное число, то допустимыми
значениями х являются все вещественные чиела, а при п
четном— лишь те, для которых выполняется неравенство
Разделим обе части неравенства на У(х— I)2 (х Ф 1).
Получим:
п Гх 4- 1
Решив его как квадратное относительно 1/ __,, придем
п Г X 4- 1 /
к уравнению 1/ __. = 2 ± }/ 3. Оно равносильно
данному при дополнительном условии | х | > 1 в случае п
четного. Так как 2 ± ]/~3 > 0, то возведение его в
степень п приведет к уравнению ^Ь-^.== (2 ± у 3)п, которое
164
также равносильно данному. Решив последнее, найдем
(2 ± УТ)п + 1
*1,2 == ?9—тЛП*—-Г Где В числителе и знаменателе нужно
перед V 3 брать одинаковые знаки. Оба эти корня
являются корнями данного уравнения как при п четном, так
и при п нечетном, так как, очевидно, |а:1|>1 и |х2|>1.
238. Умножим обе части уравнения на у а \х,
Получим:
х* Ух* &\ х* ~~ !'
я+1
я /" аа _ ^ Д« —*« _ ( а* — х* \ п __ 2
К *а ' а2*2 ' V *2 / "~а'
2м 2п
л: = ± — . (*)
Оба найденные значения х будут корнями данного
уравнения, правда, в случае четного п не при всяких
значениях а. Чтобы в этом убедиться, выясйим, при каких
условиях сделанные здесь преобразования будут
приводить к уравнениям, равносильным с данным, и покажем,
что эти условия выполнены. Будем сперва считать п
четным. Так как в этом случае все корни должны быть
арифметическими, то, как видно из уравнения, должно
быть а — х>0у а+*>0 или лг<а и #> — а.
Следовательно, — а < д: < а и а > 0« При этих условиях все
произведенные операции (умножение корней, деление
корней и т. д.) обратимы, т. е. их можно провести в
обратном порядке, а это гарантирует равносильность
исходных и получаемых равенств. Таким образом, данное
уравнение равносильно уравнению х = ± —. =- , одна-
V 1 + Л]
ко при условии «— а < х < а или | х | < а. Но это усло-
1 -+- а"*1 > 1,
165
Если п нечетное, то, как не трудно видеть,
уравнение (*) также будет равносильно данному, но нет
оснований требовать, чтобы было а > 0. Достаточно, чтобы
2 1
П/ П/ Л у—— П/ / Пу Л/
= а'
п, пг— 2 П/ 2 / 2 \
V а — у х -ч-п У а 1 -о-"л пг— пг—/ Т"л \
/л; у * \ /
[2 Тя Г 2 1/1
1 + а , я = а: 1 + а
а
Рассуждая так же, как в задаче 238, докажем, что
это значение х есть единственный корень данного
уравнения.
240.
т л/х — У 1/ х2 — У2 Ух2 —у*
Так как I/ —г-2- = I/ -^——~ = —^—=—у—
то первое уравнение данной системы эквивалентно сле-
~\/~ х2 ~цЪ 20
дующему: х — у + \х + у\ = Т+7* Е°ЛИ \Х+У\^Х+У*
т. е. если х + У > 0, то система эквивалентна такой:
*2 — У2 + ]/~*2 — У2 — 20 = 0; х2 + у2 = 34. Положим
У^л;2 — у2 = г > 0. Тогда первое уравнение примет вид
г2 + г — 20 = 0 и из него найдем 2Х = 4; г2 — — 5. Но
22 = — 5, как отрицательное, нужно отбросить, а тогда она
приведется к следующей, эквивалентной данной:
У х2 — у2 = 4; х2 + у2 = 34 или х2 — у2= 16; *2 + */2 = 34.
Решив ее, получим х = ± 5; г/ = ± 3. Из них только
хг = 5; ух = 3 и лг2 = 5; г/2 = — 3 являются решениями
данной системы, а лс =—5; */= ± 3 нужно отбросить,
так как при этих значениях х -\- у < 0.
Если х + у < 0, то, аналогично решая, найдем;
1/~59~- „ _ л. I/"5"
•%4 = — V ~2~у Уз<4 — ± р у•
166
241. Выполнив сокращение в первом уравнении, разделив
на У~ху и положив Т/ — —г, найдем: г + 1 -\— = у или
2г2 — 5г + 2 = 0. Решив его, получим гг = 2; г2 = у . Таким
образом, задача решения данной системы равносильна
задаче решения следующих двух систем:
и
2
3/
Решаем первую. Для этого подставляем значение \Г~х
из первого уравнения во второе. Получаем: 2У~~у—1^У =
= 3; ]Гу = 3; ух = 27; ^ = 8г/х « 216.
Так же решаем вторую систему: у У~у — У У = 3;
^ = —6; г/2- —216; х2 = ~г/2 « — 27.
242. В левой части первого уравнения уничтожаем
иррациональность в знаменателе. Тогда данная система
о ,
приводится к следующей эквивалентной: У х = у~ у; Ух+
+ У~у = 7. Подставляем значение У х из первого урав-
нения во второе: -^у + У у = 7; 3*/ + 16 |/ г/ — 112 = 0;
у у — """ ±—в Так как }/~1/— арифметический, то для
него получаем только одно значение У у = 4. Отсюда
у= 16; а: = 9.
243. (/"* — У~уУ = {2У^у)2\ х + у — 2У^у=^4ху и
на основании второго уравнения 20 — 2 |/а:г/=4а:1/; 2д;у+
+ |/^ — Ю = 0. Отсюда Уху = ~~ * * 9 ; у^ = 2; *у =
= 4. Равенство "[/"^ ~ — у — невозможное, так как
|Ло/ — арифметический. Итак, получаем систему х -\- у =
= 20; **/ = 4, которая является следствием данной
системы и потому удовлетворяется любым решением данной
167
системы, если они существуют. Решаем ее: у = 20 — х;
х(20—_х) = 4; х2 — 20л: -К4 = 0^_л; = 10±4|/^*/ = 10 Т
+ 4/6. )Ло\гх — У~у=*2Уху>0л Поэтому *>*/
(равенства быть не может) и из найденных значений нужно
взять только следующие два: л: = 10 + 4 }/ 6; (/=10 —
— 41/^ 6. Испытание х и(/ показывает, что они
удовлетворяют системе. Однако, несмотря на возведение в квадрат
уравнения, проверку можно было бы и не производить, так
как здесь выполняются условия х > 0, у > 0, х > у,
которые гарантируют обратимость указанной операции.
III. СОСТАВЛЕНИЕ УРАВНЕНИЙ
244. Пусть расстояние от деревни до станции х км.
Если бы турист шел все время со скоростью 3 км/час,
х 2
то он потратил бы на путь -^ час, что на у час больше,
чем было в его распоряжении. Таким образом, чтобы
поспеть точно к отходу поезда, он должен был затратить
времени(у—^) час. В действительности же он лишь
первый час шел со скоростью 3 км/час, а затем со
скоростью 4 км(час, что в общем составило (1 + х~ )
час, Так как он пришел за -^ час до отхода поезда, то
отсюда получаем уравнение
з — з —1 н Г~ + Т-
Решаем его:
Ах — 8 = 12 + 3*; х = 20.
245. Обозначим число десятков искомого числа
буквой хщ тогда число запишется так: 10* + 3. Число,
получающееся перемещением влево цифры 3, имеет вид
300 + х. Поэтому получим уравнение 300 + х = 3(10* +
+ 3) + 1. Решив его, получим х = 10, а искомое
число 103.
246. Обозначим расстояние, которое пролетел самолет,
через х км. Со скоростью 220 км/час он пролетел часть
* • 385 *+385
пути, большую половины на -~- км, т. е. равную-^— км,
168
х + 385 ^
затратив на нее 2' 220 час. Остальную часть пути, а
именно 2 юк» он пролетел со скоростью 330 км/часу
я —385 Лг
затратив на нее 2 330 час. Учитывая, что средняя
скорость на всем пути равна 250 км/час, можем подсчитать
все время полета. Оно равно ^ час. Отсюда получаем
уравнение 2 . 220 + 2. 33о = 250' Решив его' найдем>
что х= 1375.
247. Обозначим число лет младшего через х, а
старшего через х 4- у. Тогда для хну получим следующую
систему уравнений:
х + у = 2(х — у);
х + у + х + 2у=63.
Решив ее, найдем: * = 21; х + у = 28.
248. Пусть скорость третьей машины будет х км/час,
а число часов, за которое эта машина догнала вторую,
равно у. К тому моменту, когда третья машина догнала
вторую, первая машина прошла путь 50 (г/ + 0,5) км,
вторая 40 (у + 0,5) км, а третья ху км. К этому моменту
третья и вторая машины прошли одинаковые расстояния,
что приводит к уравнению 40 (у + 0,5) = ху, 3 первая
удалилась от второй и третьей на число километров,
равное 50 (у +- 0,5) — 40 (у + 0,5) = Юу + 5. Так как третья
машина проходит этот путь за 1,5 час, а в час пробегает
на (х — 50) км больше первой, то получаем уравнение
10г/ + 5 = 1,5 (а: — 50) или Зх — 20у— 160 = 0.
Итак, имеем систему
40 (г/+ 0,5) = **/;
За: — 20г/ — 160 = 0.
Решив ее, найдем, что х = 60.
249. Пусть скорость пассажирского поезда есть х
км/час, а скорого у км/час. Так как по условию у = 2х,
то пассажирскому поезду требуется на пробег от Л до С
столько же времени, сколько скорому-^на пробег от А
до С и обратно. Но пассажирский поезд выходит из А
169
25 . п
на — час раньше, чем скорый из С, и поэтому он,
несмотря на пятиминутную остановку в 5, приходит в С
на -т~ час раньше скорого. Отсюда получаем уравнение
25 —А о. А
Решив его, найдем дг«30. Тогда у = 60, а ВС =120 км.
Определим теперь АВ.
Пассажирский поезд шел от В до встречи со скорым
14 мин и прошел за это время -^ • 30 =» 7 (/еж).
Следовательно, скорый поезд прошел с момента выхода из С до
момента встречи с пассажирским 120 км-^7 км ^ ИЗ км,
затратив на этот путь -^ час. Пассажирский же поезд,
после того как он отошел от А на 25 км% был в пути
до момента встречи со скорым на 5 мин меньше этого
113 5 108 27 о
времени, т. е. -^ час —щ час = -щ- час = -^ час. За это
27
время он прошел 30 • -^ = 54 (км), причем 7 км из них
за пункт В. Следовательно, АВ = 72 км (25 + 54 — 7).
250. Обозначим количество денег, бывшее до
перекладывания в 1-й, 2-й,..., п-й кучках, соответственно через
*!, #2» •••» *Л> а количество денег в последней кучке,
оказавшихся в ней после перекладывания из п—1-й кучки,
но до перекладывания из нее в первую, яерез у. После
перекладывания из первой кучки во вторую в первой оста-
л—1
лось количество денег, равное хг, а после
перекладывания из я-й кучки в первую в первой их стало
—:— хх Н— у, а в последней д. После первого
перекладывания во второй кучке стало количество денег,
равное х2 + — хх% а после того, как из второй кучки
переложили в третью, во второй их оказалось п"""" (л:2-|—х\
Подобными же рассуждениями докажем, что в третьей
кучке в результате всех перекладываний количество денег
170
стало п п 1 х3 + — (дс2 + — хМ и т. д. Так как в
результате перекладываний во всех кучках стало по А руб., то
отсюда приходим к следующей системе уравнений:
/1—1
0<
Из последнего уравнения найдем у и подставив его
значение в первое уравнение, определим хг. После этого
найти *2, х9,..., #я не составит большого труда. В
результате получим: •
Л2 _ 2п + 2
ч
л (л — 2) ,
(п-1)«
*я =э Х4 =
*„« Л.
Л;
251. Пусть один рабочий может выполнить работу в х
дней, а другой в у дней. Каждый из них отдельно
выполняет в день часть работы, равную, соответственно, —
и —, а работая вместе«
12
часть. Отсюда уравнение
1 е- _, За 8 дней совместной работы они выпол-
8 2
нили -тн-« -о" все** работы, и другому пришлось еще
работать 5 дней, чтобы закончить ее. Отсюда получаем вто-
2 5
рое уравнение-у Н « 1. Итак, имеем систему
х у
» . 2 . 5 1
Решив ее. найдем х = 60; у = 15.
252. Пусть одна бригада выполняет работу в х дней,
а другая в у дней. Тогда первая в один день выполнит
171
— часть всей работы, а вторая -—. Так как, работая вме-
х у
сте 8 дней, они выполняют всю работу, то получаем сле-
8 8 2
дующее уравнение: (-— = 1. Но -^ первой брига-
X у о
2 1
ды выполняют в день лишь -= всей работы, а 0,8
второй —. Чтобы выполнить всю работу таким соста-
У
вом рабочих, нужно 11 — дня. Отсюда получаем второе
11 * 2 * , 11 1 0,8 , п
уравнение 11 -г- * ^ Ь 1*1"' ~ = * • Решив систе-
■ тг О X *Ж У
му -двух полученных уравнений, найдем, что #=12;
У =24.
253. Пусть количества лет старшего, среднего и
младшего братьев в настоящее время выражаются числами х%
у, и г. Если учесть, что (х — у) лет тому назад
младшему было 10 лет, то получим уравнение г — (х — у) = 10.
Через (х — у) лет младшему будет 26 лет. Поэтому
можно написать, что г + (х — у) = 26. В день рождения
младшего старшему было (х — г) лет, среднему (у — г) лет, а
сумма лет была 2г. Таким образом, получаем третье
уравнение х — г + у — г = 2г. Решив систему этих трех
уравнений, получим х = 40; у = 32; г = 18.
254. Обозначим число частей первого сплава и число
частей второго сплава, которые нужно взять, чтобы
получить третий сплав, через х и у. Тогда в новом сплаве
12 2 3
первого металла будет-^- х + -5-У» а второго -у х + -^-у.
Так как отношение количеств этих металлов в новом
сплаве равно 17: 27, то получим уравнение
(т^т^(т^ + т^17
27
или (5г + 6) : (Юг + 9) = 17:27, где г = -~-. Решив это
9
уравнение, найдем, что г = -д^-, т. е. первого сплава
нужно взять 9 частей, а второго 35.
255. Обозначим искомое расстояние, выраженное в
километрах, через х, а скорость поезда через у км/час.
Первый поезд шел до вынужденной остановки 6 час и прошел
да это время путь 6у км. Остальную часть пути (х — 6у) км
172
он прошел со скоростью 1,2*/ км/час, затратив на
прохождение ее х7~ у час. Всего поезд был в пути, с учетом
вынужденной двухчасовой стоянки, число часов, равное
6 + 2 + *7~п у- Это число часов на 1 больше числа часов,
положенного по расписанию и равного —. Отсюда
получаем уравнение
6+2 + ^ = ^ + 1.
Аналогично рассуждая относительно второго поезда,
получим второе уравнение
ал. 150 , о , л: —6у— 150 _ х - -
Решив систему этих двух уравнений, получим х = 600.
256. Обозначим скорость лодки в стоячей воде,
рассчитанную на час, через V1, скорость течения на участке
ВС через V2, расстояние АС через 5 и расстояние АВ
через х. 8 и х выражены в одних и тех же единицах
длины, в скоростях V1 и 1>а употреблены те же единицы
длины.
Лодочник на движение вниз по реке тратит 3 час,
причем часть этого времени, равная — час, тратится на
прохождение пути АВ, а другая, равная —-г-— час, на
^1 ~Г ^2
прохождение пути ВС. Отсюда получаем уравнение
х . 3-х _л
VI "*" ^^ + V% ~~
При движении вверх по реке лодочник тратит на про-
^ х
хождение пути ВС уже час, на прохождение пути
АВ прежнее время, т. е. -—- час, а на весь путь АС
3,5 час. Отсюда получаем второе уравнение
— + *~* = 3,5.
Если бы на всем пути АС скорость течения реки
была такая же, как и на участке ВС, то при движении
173
вниз по реке потребовалось бы на прохождение пути АО
8 '
• , час. Так как по условию это число часов равно
з
2-^-, то получаем третье уравнение
с 24-.
°1 + Я2 4
После некоторых упрощений полученных уравнений,
придем к системе
1 — Ъхъъ + 25^ « Ъх (V, — с;2); (*)
[45= 11(^ + 02).
Умножив первое уравнение на 2 и сложив полученное
уравнение со вторым, найдем 45у, = ^(13^—-г;а).
Разделив его на V^Ф0 и вычитая из результата третье
уравнение системы (*) найдем 2а, — 12у2 = 0 или ьх = 6у2.
Подставив V! с= 6у2 в третье уравнение системы (*), полу-
45
ЧИМ 1>2 ^ 77 :
Таким образом, имеем: о8 = —~,
205 ~
= -—-. Отсюда искомое время / =
77
в -н^- нас са 3 нас 51 мин.
245
С,1==="77~; ^1 —у2 =
5 5
V^-~V2 ^ 205 """
77
257. Обозначим искомое число процентов через х.
В конце первого года на книжке стало (1640 Н—ш~ х)
руб. Но с книжки было снято 882 руб., и поэтому на
следующий год осталась сумма 1640 + "шо"-^—882=758+
+ -гщ- х. К этой сумме прибавилась в конце второго года
/7СО , 1640 \ х
процентная сумма (758+ т х\ щ, после чего на
книжке снова оказалось 882 руб. Отсюда получаем уравнение
758+ 1^х + (758+ -^- х)щ-882 или 41*2+ 5995*-
— 31 000 = 0. Решив его найдем х = 5.
174
258. Обозначим число часов работы второго рабочего
через дс. Первый рабочий начал работу на 2 час 16 мин
раньше второго, а окончил лишь на 16 мин раньше его.
Значит первый работал (х+*~2) час. Второй работал после
перерыва 8 час 10 мин— 1 час 30 мин = 6 час 40 мин =а
= 6-77- час, а до перерыва 1х — б-уН час. Так как
второй за х час выполняет половину всей работы (вторую
половину выполняет первый), то в час он выполняет —
*-б-3
_2_
з
часть работы, а всего до полудня —2 . Первый
работал после перерыва 7 час 54 мин — 1 час 30 мин = 6 час
24 мин = 6-<г- час, а до перерыва (х + 2 — б -у) <тс. Так
как первый - за час выполняет часть работы, равную
1
2( , тгг, то до наступления полудня он выполняет часть
2
работы, равную 2 2—. Но вместе первый и второй
сделали до наступления полудня 0,4 всей работы.
Отсюда получаем уравнение
2 2
X 6 -7Г- ^-|-2-6т-
1. I °_ = 0 4
2х ^ 2 (ж+ 2) '
После упрощений получаем: 9л:2 — 80л;—100 = 0; х =*
~ 1 ; * — ю (отрицательный корень отбрасываем,
как не удовлетворяющий условию задачи). Следователь-
2
но, второй работал до полудня 10 час — 6-у час = 3 час
20 лшя и поэтому начал работать в 8 час 40 мин.
Первый начал работать в 6 час 24 мин.
259. Пусть второй каменщик может выполнить работу
в течение х дней. Тогда первому понадобится на нее
(л: + 9) дней. За один день первый выполнит часть
работы, равную , 0 , второй — равную —, а вместе — рав-
X ~т~ У X
ную -уг. Поэтому получаем уравнение — + х . 9 — 20 или
175
х* — 31х— 180 = 0. Из него находим, что х = 36. Итак,
первый может выполнить работу в 45 дней, а второй в 36.
260. Обозначим искомый путь в километрах через х.
Пешеход, вышедший из Л, перешел середину пути и
прошел от нее к В еще 3 км, а пешеход, вышедший из В,
не дошел 3 км до середины пути. Таким образом, к
моменту встречи первый прошел {—• + з) км, а второй
(-|—3] км. В дальнейшем первый проходит путь
(-|—з] км за 4,5 час и, следовательно, движется со
скоростью (~ з)! 4,5 км/час, а второй со скоростью
(-|- + 3) ! 8 км/час, потому что проходит путь (у + з) км
за 8 час. Зная скорость равномерного движения
пешеходов и пройденный каждым из них путь до встречи,
подсчитаем время, затраченное каждым на движение от
момента выхода до встречи. Для первого пешехода это
будет
(^-+в):[(±-з):А.ь]час,
а для второго
(-г-Ф[(-г+з)4
Так как это время одинаково, то отсюда получаем
уравнение
(т+»)=[(т-») = «Ыт.-8):[(++8)4
Решаем его:
(т+з)Ч = (-Г-з)'-8.
(-|- + 3 )• 3 — ± (-| з) - 4, 3*+18= ±(4*-24);
Х^ —— т^> Х% —— «-«
176
Второй корень^ не удовлетворяет условию задачи (путь
между М и N больше 6 км и тем более больше -у км).
Итак, М# в= 42 км.
261. Пусть скорость одного автомобиля будет х км/час.
После встречи он движется еще 2 час и, следовательно,
проходит после встречи 2х км. Другой автомобиль
проходит после встречи (210 — 2х) км, и так как он на это за-
9 9
трачивает -§- час, то скорость его равна (210 — 2х) : -^-.
Выезжают автомобили одновременно и поэтому
затрачивают одинаковое время на движение до встречи. Вычисляя
его для первого и второго автомобиля и приравнивая най-
2Ю 2х 2х
денные значения, получим уравнение = ^.
(210-2л;):-д
Решаем его: (210 — 2х)2 = -|-х2, 210 — 2*= ± -|-х, хг=*
*= 60, х2 = 420. Так как путь имеет длину 210 км, то
второй. корень должен быть отброшен, потому что в этом
случае часть пути 2х оказалась бы больше всего пути.
Итак, скорость одного автомобиля равна 60 км/час, а
другого (210— 120) : -|- = 80 км/час.
262. Пусть пшеничной муки было взято х кг. Тогда
ржаной было взято (х + 10) кг. Припек на пшеничную
муку составил щ, а на ржаную -—100 ■■ Сумма
килограммов той и другой муки вместе с припеками составляет
112,5 кг. Отсюда: * + щ + *+Ю+ ^У* *= I12,5;
*• + цо*_ 5075 = 0; * = — 55 ± 90; хг = 35; х2 = — 145.
Отрицательный корень отбрасываем. Итак, пшеничной
муки было взято 35 кг, а ржаной 35 + 10 = 45 кг.
263. Если обозначим скорость паровоза на первом
участке х км/час, то время, затраченное им,на прохождение
24
первого участка, будет равно — час. Второй участок был
пройден паровозом со скоростью (х + 4) км/час и времени
39
при этом было затрачено , . час. Но второй участок
паровоз прошел за время, которое на 20 мин, т. е. на у час
12 К. У. Шахно 177
больше времени, потраченного на прохождение первого
39 24 1
участка, и поэтому имеем уравнение = -^-,
которое приводится к такому виду: х2— 4 \х + 288 = 0.
Решив его, найдем корни хг = 32 и х2 = 9. Оба эти корня
удовлетворяют условиям задачи.
264. Пусть одно тело проходит в секуцду х м. Тогда
другое тело будет проходить в секунду (х + 4) м. Первое
360 360 и
пройдет окружность за — сек, а второе за , ,. Но
второе тратит на этот путь на одну секунду меньше первого,
360 360
и поэтому можно написать уравнение = 1.
Решаем его: 360 (х + 4) — 360* = х (х + 4), 1440 = х2 + 4*,
х* + 4х— 1440 = 0; х = 36, х + 4 = 40.
265. Пусть длина окружности переднего колеса
будет х м. Тогда окружность заднего будет 2х м. После
увеличения длины окружности переднего колеса на 1 м
и уменьшения длины окружности заднего на 1 му
переднее сделает , . оборотов на пути в 60 м9 а заднее
__ . Так как заднее при этом сделает на 30 оборотов
2 2
больше переднего, то получим уравнение ^тгу ХТ =
= 1, которое приводится после упрощений к такому:
5
2х2 + Зх — 5 = 0. Из двух его корней хг= 1 и х2 = —-^
только первый удовлетворяет условиям задачи. Итак,
длина окружности переднего колеса равна 1 м, а заднего 2 м.
266. Пусть искомое время, выраженное в часах,
будет х. Действительная скорость" трамвая на пути в 30 км
есть — км/час, а после уменьшения времени пробега на
30
0,5 час она стала равной _05 км/час. По условию
вторая скорость на 3 км/час больше первой, и поэтому мож-
30 30
но написать — + 3 = х_05 или 2х2 — х — 10 = 0.
Решив его, найдем, что время, затрачиваемое трамваем на
рейс, равно 2,5 час, а скорость движения равна 12 км/час,
267. Пусть плотников было х человек. Тогда маляров
было х — 2, а всего рабочих 2х — 2. Общее число рублей,
178
уплаченное рабочим, составило 3 (2х — 2) + 26, а так как
бригады маляров и плотников получили поровну, то на
3(2* — 2) + 26 л
долю плотника пришлось ——-—^— руб., а на долю
о /п« .__ О) «1. 96
маляра 2 0с —2)— ^' ^° п0СлеДняя сумма на 1 руб.
3 (2х 2) 1 26
больше первой, что приводит к уравнению ——<~^ (-
, . 3(2* — 2) + 26 п
+ 1 в о —2)—' Произведя упрощения, получим
уравнение х2 — 8х — 20 «0. Отсюда: х=10; х — 2 = 8.
268. Пусть скорость товарного поезда есть х км/час.
т-т 650 „
При такой скорости ему нужно — час, чтобы пройти
расстояние от Москвы до Ленинграда. Пассажирский поезд,
имеющий скорость (х + 24) км/час, проходит это расстоя-
650 |0
ние за , 24 «/ас, затрачивая при этом на 12 «оде меньше
п 650 650
товарного. Поэтому справедливо уравнение
х * + 24
с= 12. Упростив его, получим х% + 24*— 1300 = 0.
Отсюда: х = 26; х + 24 = 50.
269. Если длина шага ученика младшего класса рав-
.лл 400
на х м, то на расстоянии 400 м он сделает — шагов.
Ученик же старшего класса, имея длину шага на 0,3 м
а 400
больше, сделает на этом расстоянии только 3 шагов.
Но второй делает на 300 шагов меньше первого, и поэто-
400 400 ОЛЛ 0
му справедливо уравнение — 0 3 = 300. Выполнив
упрощения, приведем уравнение к виду 10х2 + 3х— 4 = 0.
Отсюда: х = 0,5; * +0,3 = 0,8.
270. Если в куске было х м, то покупная цена метра
равна— руб., а продажная (— + 1,5) руб. Так как
продано было лишь (х — 5) м и выручена при этом сумма
в 190 руб., то можно написать уравнение ( |-1,5](л:—5) =
= 190, которое после упрощений приводится к
следующему: Зх2 + 5х — 2000 = 0. Отсюда х = 25.
12* 179
271. Если первого сорта было куплено х кг, то цена
22 5
одного килограмма этого сорта будет—— руб. Второго
сорта было куплено (х + 15) кг, и, следовательно, цена
32
одного килограмма его будет , 15 руб. Но первая цена
на 10 коп. выше второй, что приводит к уравнению
оо 99 5
+ 0,1 = —'—- После упрощения получим х2 + 110*—
*+15 ■ "•* х
— 3375 = 0. Отсюда: х = 25; х +■ 15 = 40.
272. Обозначим искомое число процентов через х.
Тогда при первом повышении зарплата в 100 руб. повысится
на к руб. и составит сумму (100 + х) руб., а при повтор-
100 + х *
ном повышении увеличится —^ х руб. и составит
сумму П00 + л:+ Юр •*) руб., которая равна 125,44
руб. Отсюда 100 + х + 10^+* . х = 125,44. После
упрощений получим х2 + 200а: — 2544 = 0. Из него найдем,
что х = 12.
273. Если первый раз было отлито х л спирта, то
после этого в сосуде осталось (20 — х) л. Но так как сосуд
был долит водой, то в одном литре смеси уже содержа-
лось только 20 л спирта. Поэтому в х л отлитой смеси
20 — х о
содержалось чистого спирта лишь —^— х л. В
результате двух отливаний в сосуде осталось спирта 20 — х —
20 — х „ 1
20—-х. Но это составляет "т- первоначального, т. е.
5 л. Таким образом, приходим к уравнению 20 — х —
р^ • х = 5. После упрощения его получаем
уравнение х2 — 40* + 300 = 0, решив которое найдем л: = 10.
274. Обозначим буквой х число монет, уместившихся
в стороне квадрата. Очевидно, на всей площади квадрата
их разместится х2. При размещении монет в виде
правильного треугольника число монет в основании треугольника
будет х + 2, в следующем ряду х + 1, затем а: и т. д.
и, наконец, одна монета. Поэтому • получим уравнение
(х + 2) + (х + 1) + ... + 2 + 1 = х2. Оно приводится к
180
виду (* + 3Н* + 2) ^ хъ или хъ _ Ъх _ б = о. Отсюда
найдем, что * = 6, число монет *2 = 36, а сумма денег —
72 коп.
275. Пусть искомое число участников было х.
Полностью сыграли друг с другом по партии лишь (х — 2)
участников (двое выбыли) и число этих партий равно (х — 3) +
+ (х — 4)+ ... + 2+1= (*-2Н*-3>, Если выбывшие
участники турнира между собой играли, то число
различных партий, сыгранных ими, будет не 6, а 5 и в этом
случае будем иметь уравнение- -± —+5=84. Если
же выбывшие участники не играли друг с другом, то все
6 партий, сыгранных ими, будут различными, а потому
/х 2) (х 3)
уравнение для определения х будет такое: ^ +
+ 6 = 84. Первое уравнение приводится к такому:*2—
— 5х—152 = 0 и оно не имеет рациональных решений.
Второе уравнение имеет вид *2— 5*— 150 = 0. Его корень
х — 15 дает решение задачи. Итак, число участников
было 15, причем двое выбывших не играли между собой.
276. Пусть стоимость материи первого сорта есть х руб.
Тогда его стоимость после повышения на у процентов
составит * + щ> что приводит к уравнению # + щ= 15.
Первоначальная стоимость материи второго сорта равна
(15,2 — х) руб., а после понижения на у процентов
(15 2 х \ ""
15,2 — х ^—у\ руб. Но эта новая стоимость
равна 2 р. 40 к. Поэтому можно написать, что 15,2 — х —
1С О у
.——^г—у = 2,4. Итак, имеем систему уравнений
' у Л- ху - 1*
15,2-*- 15*^* у = 2,4.
Исключив из нее у, получим уравнение 2х2— 43* +
+ 228 = 0. Из него найдем: хх = 12; х2 = 9,5.
277. Пусть поезда встретились в некоторой точке пути
С (рис, 1). Обозначим число часов, затраченное товарным
поездом на прохождение пути ГС, через *, а его скорость
181
через у км/час. Время в часах, затраченное пасеажирским
поездом на прохождение пути ВС, будет равно х — 5 -у^-.
Обозначим скорость пассажирского поезда через г км/час.
Очевидно, можно написать, что ТС *=ху и ТС = 4 -^г- г.
Отсюда получаем уравнение ху =»
4 -^г г. Аналогично ВС =э
Туля Вязьме 10
Рис 1. в(*_5Т?)2 и ВС==
12^.Отсюда получаем уравнение \х — 5-^)2= \2-^у.
Перемножая эти уравнения, получим: ху[х -* 5-~\г — А-^гх
X 12-}^, *2-4* = ТГт!г; 24^-122^-1271=0.
31 1
Отсюда! хх = ^-; #2 =* 10 -^-. Первый корень не
удовлетворяет условиям задачи. Итак, товарный поезд
затратил на прохождение пути ТС 10 час 15 мин, а на
прохождение всего пути 10 час 15 мин+ 12 час 55 мин =>
— 23 час 10 лшя. Пассажирский поезд затратил на
прохождение пути ВС 10 час 15 мин-*-5 <шс 5 мин = 5 час
10 лшя, а на прохождение всего пути 5 час 10 лшя -К
+ 4 <шс 6 лшя = 9 <&с 16 иш«.
278. Если обозначить скорость лодки в стоячей воде
через х км/час, скорость течения реки и скорость
движения плота через у, то скорость лодки по течению будет
х + у, против течения х±—у, время движения лодки
20 20
по течению , час, против течения час, до встречи
х "г У х — у
20 , 8
с плотом—г 1 и, наконец, время движения плота
х "Т У х —»у
12
—. Так как прогулка длилась 7 час, то получим уравне-
20 20
ние —зц 1—^— =* 7. Так как время движения лодки
и плота до их встречи одно и то же, то получаем уравне-
20 & 12
ние —у- 1—^— «а —. Из второго уравнения находим:
20*/ (х — у) + 8у (* + </) = 12(л;2 — у2); 7ху = ЗлЛ Но х = 0
182
не удовлетворяет условиям задачи, а поэтому 1у = Зх,
7 7
# = -у у. Подставив х = уув первое уравнение, найдем
у = 3, а следовательно, # = 7. Итак, скорость лодки по
течению равна 10 км/час, а скорость течения реки
3 км/час.
279. Обозначим места первой, второй и третьей встреч
курьеров буквами М19М2,Л43 (рис. 2), скорость первого
через VI км/час, а второго через ъг
км/час. При втором движении пер-
вый курьер идет до встречи со ~ г « г « /7
вторым дольше, чем первый раз, " //$ м1 м2
на I час—18 мин = 1 аде—
—щ- аде = 0,7 час. Поэтому он Рис 2.
7
проходит больше на -т^- ох км, в то время как второй идет
1 13
меньше времени на -у- час 4- 18 >мин = -у «ас + -у^ аде =
= 0,8 час и проходит соответственно на 0,8 р2 км
меньше, чем при первом движении. Расстояние МгМ2 и есть
то дополнительное расстояние 0,7^, которое пройдено
первым, и одновременно расстояние 0,8 у2, которое не
дошел второй. Отсюда получаем уравнение 0,7^ = 0,8о2
или 7ух = 8у2.
При третьем движении второй курьер идет дольше
первого на 1,5 час и проходит за эти 1,5 час путь
1,5у2 км, в то время как первый йе доходит 5,6 км до
точки Мг и, следовательно, затрачивает времени на дви-
5,6
жение до встречи на — час меньше, чем при первом
движении. Таким образом, путь 1.5аа км, пройденный вторым
курьером за последние 1,5 час его движения до встречи,
состоит из пути МгМ3 = 5,6 км и того пути ЫМг,
который бы не дошел второй до Мъ если бы он двигался
5,6
столько же времени, сколько и первый, т. е. на —-— час
меньше, чем при первом движении. Иначе: М3#=1,5а2,
М3Мг « 5,6, М^ = ^- . ю%% а так как М^ = М3М1 +МгЫ,
56
то получаем уравнение 1,5у2 = 5,6 + — • ь%% Из первого
183
уравнения находим — =^ -д- и подставляем во второе.
Получаем 1,5о2 = 5,6 + 5,6 • -^- = 10,5.
о
Итак, у2 = 7, а тогда юх = -=- • 0а = 8.
280. Обозначим число часов работы последнего
рабочего через х, число часов работы предпоследнего через
х -\- у, а число рабочих через г. На выполнение работы
всего было затрачено число часов, равное х + (х + у) +
+ (х + 2у) + [* + (*- 1)у]=хг + у [1 + 2 + ... + (г - 1)]-
г (2—1) п
= хг + у • -1—2—-. По условию задачи это число часов
равно 24г. Отсюда получаем уравнение хг + у • 2 7" ' =
= 24г или 2лг + у(г —- 1) = 48. Но первый рабочий работал
в 5 раз больше последнего. Поэтому получим еще такое
уравнение х + (г— \)у = Ъх. Вычитая это уравнение из
первого, получим х = 48 — Ъх. Отсюда: 6х = 48; х = 8.
Так как продолжительность выполнения всей работы
равна числу часов работы первого рабочего, то,
следовательно, рабочие рыли канаву 40 час.
Замечание. Иногда решающие эту задачу
предполагают, что продолжительность работы последнего
рабочего равна промежутку времени, в течение которого
первый работал в одиночку. Тогда число рабочих
оказывается равным пяти и задача получает простое решение.
Однако такое предположение подменяет эту задачу
другой, потому что такое предположение не вытекает из
условий задачи. На самом же деле продолжительность
работы первого рабочего в одиночку будет различной и
находится в зависимости от числа рабочих, как это
видно из уравнения (г— \)у = 32. Если рабочих было
только 2, то интересующая нас продолжительность работы
будет равна 32, если число рабочих было 3, то
продолжительность равна 16 и т. д.
281. Пусть вес первого металла, входящего в сплав
веса Р, будет х кг. Тогда вес второго будет (Р — х) кг.
Килограмм первого металла теряет в весе при погруже-
В С ~
нии его в воду -р- кг, а второго р- кг. Так как
потеря в весе данного куска сплава равна сумме потерь ве-
184
сов составляющих его металлов, то получаем уравнение
хВ
+ ^^. = А.
р ~Г р
д (2
Решив его, найдем, что к = Р • в_с> а Р — х =*
= Р-*=4
г в-с
Для возможности решения задачи нужно, чтобы х
и Р — х были положительны или иначе, чтобы числители
и знаменатели найденных значений х и Р — х были одного
знака. Это приводит к таким соотношениям: С < Л < В
или В<Л<С.
282. Обозначим вес отрезанного куска через х кг, а
число процентов содержащейся в первом и втором кусках
меди соответственно через у и г. Тогда в куске,
отрезанном от первого сплава, будет содержаться щ кг ме-
Х2
ди, в куске, отрезанном от второго сплава, -^ кг, а в
остатках ^ и ^ • В новых сплавах будет
содержаться килограммов меди ^ + п ~0*)г и щ + ^йр.
Первый из новых сплавов будет весить я /сг, второй —
т кг9 а процентное содержание меди в них одинаковое.
Поэтому можно написать уравнение
ху {п — х)г хг (т~*х)у
100 + 100 в 1()0 _ 100 + 100 <00
Отсюда: ху "—~ == ** ^—-^-; хут + птг—д:гт=з
= #гл + тт/ — */!*/; хт (у — г) + хп(у — г) — тп(у — г).
Сокращая на у — г ф 0, получаем #т + хп = т/г,
откуда х = —=—.
283. Обозначим отношение объема С к сумме объемов
А п В через —. Тогда можно написать
( Ат = В +- С;
В/г = /1 4- С;
I Сх = Л + б.
185
Прибавим А к обеим частям первого равенства. Получим
А(т + 1) = А + В 4- С. Отсюда —р = А+в + с-
Аналогичными преобразованиями получим , , = А в . с и
—-|--рс= . д,с . Почленное суммирование трех пос-
1,1,1 А+В+С
ледних равенств дает ^^ + ^^рр + ^^ - 1Т^ -
= 1. Поэтому: ^-1-^-^;^==
тп-1 у , 1 = (т + 1)(п + 1), _ (т+1)(д+1)
"" (т+ 1)(л+ 1) ' "г тп — 1 * х~ тп—\
. т 4- л -4- 2 а-ч^ /-> /7Ш — 1
— 1 = - ——1—. Объем С составляет часть ; г-рг-
тп -—1 т -\- п-\- 2
суммы объемов А и В.
284. Пусть точки начали двигаться из одной точки
окружности в разных направлениях (навстречу друг
другу). Если скорость одной, рассчитанная на секунду, есть л;,
то она за время 1Х пройдет путь х11у а другая, если ее
скорость, рассчитанная на секунду, есть у, пройдет путь
у1х. Сумма их путей составит длину окружности Ь.
Поэтому получаем уравнение х1х + у1\ = ^ или х + # = -т-.
Пусть теперь точки движутся в одном направлении,
начав движение из одной и той же точки окружности.
Тогда первая за время Ь% пройдет путь х/2, а вторая за
то же время пройдет путь у12- Полагаем х > у. Тогда
первая, двигаясь быстрее второй настигнет вторую по
истечении (2 сек и, следовательно, за время /2 сек ее путь
будет на Ъ длиннее пути первой за то же время. Отсюда
получим второе уравнение х12 — у1г = Ь или х — г/= —.
Решая систему
х-у=Ь
найдем, что х = Ц%+*%)\ у= -%^~: С, > «. Следует
заметить, что раз точки при обоих движениях (т. е. в од-
186
ном направлении и в разных направлениях) сходились
через равные промежутки (г и /2, то они начинали
движение из одной и той же точки окружности, чем мы при
решении пользовались.
285. Пусть расстояние между А я В равно х км.
Лодка прошла это расстояние за — час, а пароход
за — час. Но лодка пришла в В на I час позднее
парохода и, кроме того, еще до выхода парохода она была в
движении — час. Таким образом, лодка была в движении
на(Н ) час больше, чем пароход. Отсюда получаем
уравнение — — = I -\ . Решаем его: хш— XV =
= ш1 + Ш\ х = ш(" + /); (ш > V).
286. Обозначим искомое число досок через х. В первые
два часа мастер выиграл щ партий и / проиграл.
Следующие два часа он вел игру уже на (л:—Щ^—/) досках. Из
всех партий, сыгранных за последние два часа, он
выиграл [х—щ—^)'Тоо паРт™> проиграл тип партий
свел вничью. Так как общее число партий, сыгранных за
последние два часа, составляется из всех выигранных,
проигранных и сведенных вничью партий за эти часы, то
отсюда получаем уравнение х~ щ — 1=[х—• щ ~1)щ +
п „ 10 000(т+я)+100/(100—о)
+т+п. Решив его, найдем, что а:- —(1оо_р)(100_-^-^.
287. В сосуде было чистой" (стопроцентной) кислоты
щ л. Если в сосуд добавить х л (?%-ного раствора кислоты,
то количество чистой кислоты будет доведено до
Шо^''ш)Л' ^° после Добавления туда еще воды,
раствор будет содержать чистой кислоты щ л. Поэтому по-
187
лучим уравнение %о + щ — щ* решив которое, найдем
Ьг — ар
X — - н
Я
288. Пусть из каждого сосуда отлили х л. В первом
(а — х)р
сосуде осталось чистой кислоты к . 0 ;н л, а во втором
|^0 л. Кроме того, в первый добавили ее -^ л, а во
второй щ. Так как новые смеси стали одной
концентрации, то получим:
1 Г (а — х)р хдЛ _ 1 \(Ъ — х)д хр_\
а [ 100 Ч" 100] ~~ Ъ I 100 ~*~ юо],
6р (а — л:) + б^л: = ад(Ь — х) + арх\
х(а + 6) (^ — р) = а& (^ — р).
Считая рФд и разделив уравнение на р — ? ^ 0, найдем
аЬ
Если р = 9» т0 задача имеет бесконечное множество
решений.
289. Пусть искомое расстояние есть х км, скорости
первого и второго велосипедистов у км/час и г км/час.
До первой встречи первый велосипедист проехал (х + а) км,
затратив на него х час, а второй проехал (х — а) км
у
и затратил ~~ час. Так как время их движения
одинаково, то приходим к уравнению = х~~а или
* + д = л_^ ^ моменту второй встречи, первый велосипе-
X — О, с •
диет проехал (2х + -—-) км, а второй (2л; ~) км. Таким
X X
2х + ~Т 2х~~Т
образом, получаем второе уравнение = или
2&+1
26-
188
т = —. Подставляя значение ~ из второго уравнения
в первое, получим
1+±явЩЦ,х = 2ка.
х — а 2к— V
290. Пусть в начальный момент шарик находится в
точке М (рис. 3). Так как угол падения равен углу
отражения, то / ММО = /. ОЫР = Л ЫРО = Л ОРМ, а=р,
2а = 2р и д ЛШР — равнобедренный.
Следовательно, МО 1 ЫР и
положение точки N определится
расстоянием 00 = х. По свойству
биссектрисы внутреннего угла треугольника,
0() N(1 ОС? N(1*
х2
что приводит к уравнению —г =
#а — х2 т, Рис. 3.
Из него находим:
а2 + Я2 + 2я*
*2а2 + *2#2 + 2ах* — а2 Я2 + а2х? = 0; 2ах* + 2а2х2 +
+ Я*х2 — а2Я2 = 0; 2а*2 (а + х) + Я2 (х2 — а2) = 0;
(а + х) (2ах2 + Я2* — К2а) = 0.
Так как а + хФО (х>0,а> 0), то 2а*2 + К2х — Я2а=0.
Отсюда , = :^±1^^
291. Общий вес заполненного баллона состоит из
веса
оболочки -у- тг (# + е)3 ^ тг #3 й и веса жидкости
-у-тг/?3о, наполняющей баллон. Вес жидкости, в которую
погружен баллон, вытесненной баллоном, равен у ^ (/? +
+ е)3А. Все веса предполагаются измеренными одной и
той же единицей веса. Так как погруженное тело
находится в равновесии, то получаем уравнение
[4" * (Л + е)8 — -|" *#3]<*+ -^ъКЧ = -|" * № + е)ЗД.
Решаем его:
(/? + е)»(й —А) = /?»(Л —8), (^)
4-А'
е
уШ-''
189
Условия возможности задачи получатся из требования
быть положительным /?, т. е. из условия ,_ д > 1. Если
А — Д>0, то получим: д. — 8>й — Д, 8<Д, Д<й и
8<Д<Л. Если Л —Д<0, то а — 8<й — Д, 8>Д, Д>й
ий<4<5.
292. Пусть число процентов прироста населения за
год будет х. Если к началу первого года количество
населения было А человек, то к началу второго года оно стало
Ах I х \
АХ = А+ -^ф- = А \\ + щ|, а к началу третьего А2 =
= Л(1 +Ш = А \1 +Ш/ и т* д' 0чевиДН0» к началу
п-го года количество населения будет ЛИ + щ) » а к
его концу — А(\ +щ) . При годовом приросте
населения, равном (х 4- к) процентов, общее число населения
к концу п-го года будет А 11 Н—^-1 . Во втором
случае численность населения должна быть в два раза
больше, чем в первом. Отсюда получаем уравнение
Решаем его:
1+^-!^(1+,&ИГ5-1)*-*-
— 100[}Г2 — 0 , *= —^ 100.
^ /2 — 1
Задача возможна лишь при таких кип, при которых
найденное значение для х будет положительное.
293. Если вес сосуда р, а его объем у, то при
заполнении его первой жидкостью общий вес сосуда будет
(рй + р) кеу а при заполнении второй — ^О + р. С
другой стороны, эти веса равны (/ и (}. Отсюда получаем
систему уравнений
^<1 + р^я\
из которой находим, что V = 0_а\ Р = в — л *
190
Условия возможности задачи сводятся к условиям
положительности найденных дробей для р и V. Это
приводит к требованиям, чтобы было или --т- > — > 1, или
-^-< —<1. Если хотя бы одна из дробей неположи-
тельна или если й = й, а <2 Ф А, то задача неразрешима.
Если же Б = й и ф = ц> то вес р и объем V связаны
одним соотношением Vс^ + р = ц и задача имеет
бесконечное множество решений,
294. Обозначим скорости первого и второго поездов
через VI км/час и р2 кмЦчасц а расстояние между А и В
через х км. Двигаясь после встречи в
противоположных направлениях, поезда через / час оказались на
расстоянии 2х друр от друга. До встречи они вместе
покрыли расстояние х, т. е. в два раза меньшее, чем
после встречи. Таким образом, встретились они через
-х-1 час после выезда из начальных пунктов А и В.
Поэтому можно написать следующую систему уравнений:
X — р = -у Лу,
1 ,
р=-2-^2;
I х — р+^=:V2^
Из второго уравнения находим р2 = —, а подставив это
значение у2 в третье, найдем х = 3р—-д. Теперь из пер-
2(2р — д)
вого легко находится ух = ——.
295. Как видно из условия задачи, числа х, у и г
должны удовлетворять следующей системе уравнений:
' х = т {у — 2);
у = п(х — г);
г = 2(х — у).
Решив систему первых двух уравнений относительно х
(т 4- тп)г (п + тп)г
и у, найдем, что х = тя\,| ; У = ^^ГГ> а подставив
эти значения х и у в третье уравнение, получим искомую
191
лик-
зависимость в следующем виде: г = — ^- или тп —
тп — I
— 2т + 2п—1=0.
296. Пусть часы уходят на х мин в сутки. Тогда,
чтобы они показывали правильное время, им придется
ходить -^-суток. Если бы они уходили вперед на (х + () мин
в сутки, то при отставании в данный момент на п мин
от правильного времени им пришлось бы ходить
—^-- суток или на 1 сутки меньше, чем —, чтобы
видировать это отставание. Итак, 1 = :, х? 4-
Второй корень отрицательный и его отбрасываем.
297. Пусть детей было х. Последний из них, т. е.
лг-овый получил ах орехов плюс — остатка. Но так как
это был последний из участников дележа, а орехи между
ними были поделены все, то и остатка не могло быть.
Следовательно, каждый получил по ах орехов, а всего
орехов было ах • х = ах?. Доля первого тоже была ах,
но, с другой стороны, она равна а + ~~а. Поэтому по-
, ах2 — а , , хг — 1 9 ,
лучаем: ах = а Н —, *=1Н , хг — пх + п—
« л п ± (п — 2) 1 ,
— 1=0, х= —^ -; хх = п—1, х2 = 1.
298. Пусть куплено х кг лигроина. Тогда керосина
было куплено (п — х) кг. Цена килограмма лигроина есть
— руб. и керосина п°_ руб. Так как килограмм
лигроина на Ъ руб. дороже килограмма керосина, то
получаем уравнение
_д а *
~ п — х ~~
Решаем его: а (п — х) — ах = Ьх(п — х),Ьх* — (2а + Ьп)х+
л 2а + Ьп ± V 4аа + ЬЧ* 0
+ ап = 0; х = ———^-%т — . Знак плюс перед
2Ь
192
радикалом не годится; потому что в этом случае
х был бы больше п, так как а^ь п >-—• = —■
V 4аа + ЬЧ* УЬ*п*~ _ -Ьп, _п_
И 2Ь > 2Ь ~~ 2Ь ~~ 2 '
т г 2а + Ьп — V 4а* + Ь2п*
Итак, имеем: лигроина ! ^ кг, а
керосина
2а + Ьп — V 4аа + Ь*п* Ьп — 2а + У 4а2 + Ь*п*
П
2Ь ~~ 2Ь
299. Пусть искомая скорость есть х км/час. Первая
машина проходит путь а км в — чае, а вторая
находится в пути на ( мин меньше, т. е. ( ~г-) час.
Половину времени, в течение которого вторая машина находится
в движении, она расходует на то, чтобы догнать первую,
и покрывает при этом расстояние-^-/ -^Аю км.
Первая машина прибыла в В одновременно с прибытием
второй в Л и, следовательно, после получения пакета была
в движении столько же времени, сколько и вторая, т. е.
_г \цас^ Поэтому на движение первой машины
от момента выхода из А до момента получения пакета
пошло ___(___| в_\— + —) час, за кото-
рые она прошла расстояние -у (— + -^) х км. Поэтому
получаем уравнение -^ (- ж) V = -^ [— + ж) х.
Решив его, найдем, что
— (60Л + *у) ± У(Ш + ^)а + 2404р/
X у ,
а так как скорость может быть только положительной,
то ответ будет такой:
у (ш + щ + у(щ + ы* + 24ошу км/ча0щ
13 К. У. Шахно 193
300. Обозначим число рабочих первой бригады через х.
Тогда во второй их будет х + а, а в обеих вместе 2х + а
человек. Каждая бригада получила число рублей,
превышающее число рабочих в обеих бригадах на с, т. е. 2х + а +
+ с, а следовательно, рабочий первой бригады получил
2x4- а 4-с ^ -. « „^ 2х + а-\-с *■
—-—^— руб., рабочий же второй бригады —^т^— руб.
Но рабочий второй бригады получил на Ь руб. меньше
рабочего первой бригады. Поэтому можно написать такое
2x4-а 4-с ., 2х + а + с ,-т
уравнение: —1-ц--■ Н о = —! !—. После несложных
упрощений, получим Ьх2 + {аЬ — 2а)х~а(а + с) = 0. От-
2а — аЪ± У (2а — аЬ)2 + 4аЬ(а + с) о
сюда х = г —2Ь ' ' —!—-. Знак минус
перед корнем следует отбросить, потому что
соответствующее ему решение будет отрицательным. Действительно,
12а — аЬ |< У\2а — аЬ)* + 4аЬ (а + с).
Итак,
— 2а ~~ аЬ + У (2а~~ аЬ)2 + 4аЬ (а + с)
Х~ 2Ь
301. Пусть второй рабочий работал х дней. До того
как приступил к работе второй, первый работал один
в течение а дней и выполнил часть работы, равную — всей
работы. Следовательно, первый может выполнить и
выполнил в день часть работы, равную —. Второму
пришлось выполнить оставшуюся часть работы, а именно
часть, равную 1 — = д~~~р. Отсюда видно, что второй
выполнил в день часть работы, равную я~~~р. Но в
течение ° 2 дне** Рабочие, работая вместе, могут выполнить
всю работу, поэтому имеем уравнение
Р а + х , д — р а + х __ ,
ца ' 2 "^ цх 2 '
194
Решаем его:
рх (а + х) + (<7 — р) а (а + х) = 2цах, рхг — ацх +
Оба корня удовлетворяют условиям задачи (д > р).
302. Обозначим скорость одного тела через х м/мин.
Это тело проходит окружность за — мин. Пусть другое
тело движется медленнее, тогда время, за которое
второе тело пройдет окружность, будет равно (— + р) мин,
а его скорость - м/мин. За д мин первое проходит
-т+р
путь хд м, а второе —~— ле. Но за время ц мин пер-
1Г + Р
вое тело проходит на а м больше, чем второе тело,
потому что настигает второе тело за это время. Поэтому
получаем уравнение —~ Н а = цх% решив которое,
-т+р
ар ±У а2р2 + 4а*ра „
найдем х = ——-—-^-—! —. Так как отрицательное
значение х должно быть отброшено, то получаем, что одно
тело проходит в минуту а Г м* а ДРУгое
а Ур2 + *ря~р Мш
а . 2ра
х И
303. Пусть первый работал х дней, тогда второй
работал (х — п) дней. За один рабочий день первый получал
по—руб., а второй по _^ руб. Если бы первый
работал (л: — п) дней, а второй х дней, то первый
заработал бы — (х — п) руб., а второй ^ х руб. Но в этом
13* 195
случае их заработки были бы одинаковы. Поэтому
получаем уравнение — (х — п) =—-—х. Решаем его: а(х —
— п)2 = сх2, У~а (х — п) = + хУ с. Но так как левая
часть положительна (х — л>0), то знак минус в правой
части должен быть отброшен. Поэтому получаем
х ._= * г а Второй работал число дней, равное х — я=
у а^у с
пУ а п УТ . . ч
У а—У с V а-Ус '
304. Обозначим число экскурсантов через х. Каждый
из них должен был заплатить — руб. Но из-за
отсутствия у Ь экскурсантов денег остальные х — Ъ уплатили
каждый по (— + с) руб., а все вместе, принявшие
участие в платеже, (— + с) (х — 6). Последняя сумма
составляет полный расход, т. е. а руб., и поэтому получаем
уравнение (— + с)(х — Ь) = а, решив которое, найдем
сЬ ± Ус2Ь2 + 4а Ьс о ^
х = — ^—■ Знак минус нужно отбросить, так
как в этом случае решение отрицательное (с6<|/с2Ь2+4аЬс).
305. Пусть искомая скорость есть х км/час. Скорость
же фактическая равна (х + V) км/час. Время движения
поезда по расписанию равно — час, а фактически было
затрачено —37— час, что оказалось меньше на р мин
Отсюда получаем уравнение -г— = -^-, решив ко-
X X —]~ V ОС/
торое, найдем х = — ор— —• Знак МИНУС
перед радикалом нужно отбросить, так как в этом случае
получается отрицательное решение, что невозможно,
196
306. Если сумма вклада есть х руб., а сберкасса
выплачивает у % годовых, то х и у найдутся из системы'
хуа
1200
хуЬ
= т —х\
= я— х.
1200
Разделив первое уравнение системы на второе, а
затем вычтя из первого уравнения второе, придем к
следующей системе, равносильной данной:
т — х а
п — х Ъ
ху (а — Ь)
1200
= т — я.
~ ап — Ьт 1200 (т — п)
Решив ее, получим: х= а_ь ; у = ап-Ьт •
Если учесть, что х и у должны быть положительны,
то отсюда легко получить условия возможности
задачи. Для этого должно быть -г- > — > 1 или О < —г- <
< —<1
307. Так как в третьем сосуде, как и в двух других,
после третьего разлива оказалось 16 л, то после второго
разлива в нем было 32 л и 16 из них вылито в первый
и второй по 8 л в каждый. Отсюда заключаем, что в
первый сосуд из третьего было влито 8 л. Сколько же
в него было влито из второго? После третьего разлива,
когда во второй было влито из третьего 8 л, во втором
оказалось 16 л. Следовательно, до третьего разлива,
т. е. сразу после второго, во втором сосуде также было
8 л и, следовательно, при втором разливе из второго
сосуда было перелито в первый и третий 8 л, по 4 л
в каждый. Отсюда заключаем, что в первый сосуд из
третьего и второго сосудов было перелито 8 л + 4 л =
= 12 л. При первом разливе из первого сосуда была
перелита во второй и третий половина содержимого и,
значит в нем оставалась половина количества^ литров,
бывшего там сначала. Отсюда следует, что эта
половина есть 16 л — 12 л = 4 л, а всего в первом сосуде
было 8 л. Определим теперь количество литров
жидкости, находившееся вначале во втором сосуде. В него
было влито из третьего сосуда 8 л, из первого 2 л
197
и вылито 8 л в третий и первый. Так как в результате
в нем оказалось 16 л, то, следовательно, в нем было
14 л (16 — 8 — 2 + 8). Но раз в первом было 8 л, во
втором 14 л, а во всех трех 48, то в третьем было 26 л.
308. Если путь от Ленинграда до Москвы в
километрах обозначить буквой 5, время движения поезда в часах
буквой 11У а обратно /2, то искомая скорость в км/час
28
будет такая: V = , , .—.
и , 5 , 5 25 2-60 ол
20 + 30
309. Обозначив цифру единиц первого разряда
буквой аъ цифру единиц второго разряда — буквой а2 и
т. д. по разрядам, вплоть до цифры единиц самого
высокого разряда, которую обозначим буквой ап% Само
число будем изображать так: аха2... ап-хап* Тогда
число, изображенное теми же цифрами, но
написанными в обратном порядке, будет апап-г . . .а%ах. Из
арифметики известно, что всякое число можно представить
как сумму некоторого числа кратного девяти и суммы
цифр данного числа. Поэтому каждое из написанных
выше двух чисел можно представить так:
ага2... ап^ап = 9А + ах + а2 + ... + а„_, + ап9
апап-\ ... а2ах = 9В + ап + ап^\ +. ..+а2 + а1.
Вычитая из первого равенства второе, получим
аха2... ап-\ап — апап^х... а2ах = 9А — 9В = 9(А — В),
т. е. разность чисел есть кратное девяти.
Замечание. Из этого доказательства видно, что
если второе число будет любое, но составленное из
тех же цифр, что и данное, то разность таких чисел
будет делиться нацело на 9.
IV. ПРОГРЕССИИ
310. Не могут, так как если бы было ак~УЪ,
аг =-2, ат = ")/8, то, считая для определенности &</<т,
имели бы
2 = У~3 + (/ — к) а, У "8 = V 3 + (т — к)а>
198
откуда получили бы, что
2 —/У _ 1 — к
8 — У~Ъ ~~ т — к
Но это невозможно, так как слева иррациональное число,
а справа рациональное.
311. Воспользуемся формулой
ап = а1 + а(п— 1),
где аг и й—первый член и разность прогрессии. Получим
ат + ап = аг + й (т — 1) + ах + й (п — 1) = 2аг +
+ с1(т + п — 2) = 2а1+с1(к + 1 — 2)=а1 + а(к — 1) +
+ аг + й (I — 1) = ак + а{.
312. Числа ал_ь аЛ, ап+\ являются тремя
последовательными членами арифметической прогрессии. Поэтому
ап — аЛ_, = аЛ+1 — ап или ап = ап~1 + ап+1.
313. ав + «15 = «9 + Д12 = #1 + Я20> ТаК КаК ав И Я|5»
а также а9 и а12 являются равноотстоящими от концов
прогрессии членами. Отсюда:
2 К + а20) = 20; ах + а20 = 10;
520 - (а1+2а2о)2° = 100.
314. По свойству арифметической прогрессии а2— аг =
= а3 — а2 или ах + а3 = 2а2. Заменив ах + а2 через 2а2 в
первом уравнении, получим За2 = 9, а2 = 3 и ах + а3 = 6.
Подставив значение а2 во второе уравнение, получим
30^3=15 или ага3 = 5. Итак, имеем систему а^д = 5,
#1 + аз = 6- Решив ее, получим для аг два значения: 1
и 5. Точно так же для разности прогрессии Л получим
два значения: а2 -— ах = 3 — 1 =2, а2 — аг = 3 — 5 = — 2.
Следовательно, и две прогрессии:
1, «3, о, 7,...;
5, 3, 1, -1,...
315. Положим в формуле для 5Л вместо п сперва
число 1, а потом число 2. Получим 5Х = аг = — 1, 52 =
= ау + а2 = 2. Отсюда а2 == 2 — ах = 3, й = а2 — аг = 4.
Прогрессия будет такая: —1, 3, 7, 11,...
199
316. а10 = 510 — 59 = 280 — 225 = 55.
317. Сформулированное в задаче условие можно
записать так: 5А = 4#\ где к — число просуммированных членов
прогрессии, а 8к — сумма этих к членов. Полагая в этой
формуле к = I и затем к = 2, получим:
5, = аг = 4 . I2 = 4; 52 = аг + а2 = 16.
Таким образом, имеем
а, = 4, а2 = 16 — ах = 12.
Отсюда находим разность прогрессии й = а2 — ^ == 8.
Теперь известны первый член аг = 4 прогрессии и ее
разность й — 8; следовательно, прогрессия известна. Первые
ее члены таковы: 4, 12, 20, 28, ...
318. Замечая, что в арифметической прогрессии аъ а29
..., а10, по определению арифметической прогрессии,
а2 — аг = а4 — а3 = ... = а10 — До = й, где й — разность
прогрессии, можем написать
Я2 + а4 + • • • + «Ю — «1 — «3 — • • ' — а» = (а2 — «1) +
4- (а4 — а3) + ... + (а10 —а9) = М = 15—12,5 = 2,5.
Отсюда й = 0,5. Найдем теперь первый член прогрессии
из выражения суммы ее десяти членов:
510 = 15 + 12,5 = 27,5 = 2а1+29'0'5 -10 = 5 (2а, + 4,5),
2^ + 4,5 = 5,5; аг = 0,5.
Искомая прогрессия будет такая:
0,5; 1; 1,5; 2; 2,5; 3; 3,5; 4; 4,5; 5.
319. Так как по условию ар — ц и ад = р, то ар— ад—
= ц — р. С другой стороны, используя формулу ак=а1 +
+ к(к—1), где й — разность прогрессии, получим
ар — ая = ах+й(р— 1) — ах — й(^— 1) = й(р — ?).
Сравниваем два полученных для ар — ад выражения: ^ —
— р = й (р — <7). Отсюда находим, что й = — 1. Но ат —
~-ар = (т — р)а и ат = ар + (т — р)с1 = д — т + р.
320. Для доказательства достаточно установить, что
1 1____1 1_
Ь+с а + с "~ а + с а + Ь*
200
Замечая, что числа а2, Ъ2Л с2, как образующие
арифметическую прогрессию, связаны соотношением
а*—Ь2 = Ь2 — с\
преобразуем написанные разности так:
_1 1 ^ а — Ь а* — Ь*
Ь + с а + с (Ь + с) (а+с) ~~ (а + Ь)(Ь+ с)(с +а) ч
1 1 Ь — с &а — с2
а + с а + Ь (а + с) (а + Ь) (а + Ь)(Ь + с)(а +с) '
В полученных выражениях знаменатели одинаковы и
числители равны на основании соотношения
а2 — Ь2 = Ь2 — с2.
Следовательно,
_1 !_ = _] 1_
Ь+с а + с а + с а + Ь'
321. "Дроби, сумму «5 которых нужно найти,
находятся среди следующих:
_ Ът Ът +1 Ът + 2 3/1 — 1 3/г
т ~ з • з * з » ••• • з • з ~
Эта последовательность есть конечная арифметическая
, 1
прогрессия с первым членом т и разностью а = -у.
Число к ее членов найдем из равенства
л = т+у(й-1),
откуда & = Зл — Зт+1. Следовательно, сумма этих
дробей
с (т + п) (Ъп — Ът + 1)
:>!- 2 •
Ът
Но в сумму 5! вошли также сократимые дроби
Ът + 3 ^ Зл ~"~ 3, .**" Иначе их можно записать так: /я,
3 о о
/я+1, ..., л—1, п. Этих чисел п — т+1, они
образуют арифметическую прогрессию и потому их сумма
С —. (т + п)(п — т+\)
о2 — 2 '
201
Теперь можем написать, что искомая сумма
г, о о (ет + л)(Зл — Зт+1) (т+п)(п — т+\)
Ь-Ьг— 02- ^ 2 =
= п? — т2.
322. Из равенства 8т = 5Л получаем:
+ 4(т2 —/га —п2 + л) = 0,
(т —п)[2а! + й(т + п—1)] = 0.
Или, после сокращения на т — п Ф 0, получим
гах + й^ + л— 1) = 0.
Поэтому 5т+я = 2% + ^(т + п-1){т + п) = 0.
323. Воспользуемся формулой
На основании ее и условия задачи получим
[2а!+а(т—1)]т т*_
[2ах + ^(/г— 1)]/г "" /га
или
[2а! + Л {т — 1Л п = [2ах + й (л — 1)] т.
Преобразуем последнее равенство:
2а1{т — п) + й[(п — \)т — (т — 1) п] = 0,
2ах (т — п) — й(т — п) = 0.
После сокращения на т — п Ф 0, найдем, что й = 2аг.
Теперь можем написать, что
ат ах-\- й(т — 1) ах + 2ах (т — 1) 2т — 1
~Оп аг ■+- д. (п — 1) ах + 2аг (п — 1) 2/г — 1
324. Каждый ряд из т параллельных линий вместе с
двумя сторонами параллелограмма, которым линии
соответствующего ряда параллельны, образует ряд из (т + 2)
параллельных линий. Будем их нумеровать по порядку
1, 2, 3, ..., т + 2 сверху вниз и слева направо и
называть 1, 2, 3-я, ..., (т + 2)-я по вертикали и 1, 2, 3-я,
202
... ,-(т + 2)-я по горизонтали. Первая линия поверти-
кали с каждой следующей, т. е. 2, 3-й, ..., (т + 2)-й
по вертикали образует по одному параллелограмму, а
всего (т + \) параллелограмм (рис. 4). При этом
предполагается, что т горизонтальных линий еще не
проведены. Вторая линия по вертикали образует с 3, 4-й, ...,
(т + 2)-й всего т
параллелограммов (параллелограмм, обра- / //"7 7*2
зованный ею с первой линией по */ // /~7
вертикали, учтен ранее). Третья // // / /
линия по вертикали образует с 7 // / /
каждой следующей по вертика- т+* ' ' '—^—'
ли по параллелограмму, а всего Рис. 4.
(т — 1) параллелограммов. И так
далее, вплоть до (т + 1)-й линии по вертикали, которая
образует с единственной следующей один параллелограмм.
Итак, одни вертикальные линии с двумя горизонтальными
(сторонами данного параллелограмма) образуют число
параллелограммов, равное сумме членов следующей
прогрессии: т + 1, /я, т—1, ..., 2, 1. Эта сумма равна
<"+21> + 1(«+1)-(я + 1)2(яЧЛ
причем сюда же вошел и данный параллелограмм. Проведем
теперь т горизонтальных линий и, выбрав какой-нибудь
из полученных ранее параллелограммов, будем
относительно его и (т + 2) горизонталей повторять
рассуждения, приведенные выше применительно к данному
параллелограмму и (т + 2) вертикалей. Мы убедимся, что с
помощью (т + 2) горизонталей можно из каждого ранее
^ (т + 1) (т + 2)
полученного параллелограмма образовать —-—■—~—^
параллелограммов, а следовательно, всего с помощью двух
рядов прямых, параллельных сторонам параллелограмма,
по т линий в каждом, с учетом сторон параллелограмма,
можно образовать
Г(/и+1)(т + 2)1" (т+1)*(т + 2)а
1-
4
параллелограммов.
325. Составим разности соседних членов заданной
последовательности:
^ = 5 — 3 = 2, Ь2 = 9 — 5 = 4, &3= 15 — 9 = 6, ...
203
Числа 2, 4, б, ... образуют арифметическую прогрессию
с разностью й = 2. Таким образом, член данной
последовательности равен сумме предыдущего члена этой
последовательности и того члена найденной арифметической
прогрессии, номер которого равен номеру предыдущего,
т. е.
Поэтому получим
ап = ап-\ + Ьп-\ — ап-2 + Ьп-2 + Ьп~\ = ... = ах + Ьх +
+ Ь2 + ... + Ьп-1 = 3 + 2 + 4 + ... + (2л —2) =
= 3 + 2(Г + 2 + ...+л — 1)=3 + л(л — 1) == /г2 — л + 3.
326. Если т — четное число, то искомая сумма
8т = (I2-22) + (З2-42) + ... + [(/я- I)2-т2] -
= — 3 — 7 —... — (2/гг — 1) =
(3 + 2т-1).|_ т(т+1)
— 2 — 2
Если /я — нечетное число, то
С — 9 -4- п& — (т"~1)т I т2 __ т(т + 1)
^/и — ^/и-1 "Г Л* — д "~ т ~ 2 '
327. Все четыре последовательности являются
геометрическими прогрессиями. Знаменатель первой прогрессии
1 о ,
есть <71 = о"» знаменатель второй ^2—ь знаменатель
третьей д3 = — 1, наконец, знаменатель .четвертой ^4 = 0.
328. Не могут. Для того чтобы они могли быть
членами геометрической прогрессии, должны существовать
такое число ^ и натуральные числа тип, при которых
выполнялись бы равенства:
11 = 10<Г;
12= 10(7".
Но тогда было бы Ш-] — щ") или Пл = 12т 10л—от,
что, очевидно, невозможно.
329. Воспользуемся формулой ап — а1<7л~1, где аг и ц—
первый член и знаменатель прогрессии. Получим
атап = а$т-{ а^п~х = а^"14"*"2 = а1дк+1~2 =
= а^ ахц1^ = ад.
204
330. Числа ап-и ап9 ап+\ являются последовательными
членами геометрической прогрессии. Поэтому ап : ап-\ =
= ап+\ : ап или а1 = ап^\ ап+\. В доказательстве
предполагалось, что знаменатель прогрессии ц Ф 0. Однако
справедливость доказываемого равенства для случая (7 = 0
очевидна.
331. Раскрываем скобки в левой части и пользуемся
формулой у2 = хг. Получим *
(х + г + у)(х + г-у) = (х + г)2-у2 = х2 + 2хг + г2-
— у* = х2 + 2у2+г2 — у2 = х*+у2 + г2.
332. Рассматриваемую сумму можно записать так:
,/10—1 , 10я — 1 , 1СК» — 1 \
5(-9-+—9— + ■■■ + —9—|
Так как первые слагаемые в числителях дробей образуют
геометрическую прогрессию со знаменателем 10, то
последнее выражение легко преобразуется к виду
5 Лп 10*—1 \
333. 11... 1 55... 56 = (102*-1 + 102*-2 + ... + 10 +
к к~\
+ 1) + 4 (10*-1 + 10*~2 + ... + Ю + 1) + 1 =*
= 1(^ + Ц^4-1 = ^
= -4-(10- -Н 2.10-.2 + 2^) = (^^)2= (1^^- + 1/=
[3(10*-' + 10*-2 + ... + 10 + 1) + Г]2 =
= (3- 10*-' + 3-10*-2 -Ь ... + 3-10 4- 4)2 = 33 . .. 342.
к—\
334. Обозначим первый член прогрессии через *, а
знаменатель через у. Тогда для этих трех членов х> ху и
ху2, на основании условия задачи, можно написать
х + ху + ху2 = 3,5, х2 + х2у2 + х2у* = 5,25.
Возведем в квадрат обе части первого уравнения и
разделим его после этого почленно на второе уравнение.
Получим
*2(1 +У + У2)2 _ 12,25
Х2 (1 + у2 + уА) — 5,25 '
205
Решаем это уравнение, предварительно сократив левую
часть на хг ф 0:
{\ХУ//*=-Т' 3(1+у*+у* + 2у + 2у* + 21/) =
= 7(1+г/2+ </*), 3(1+у2+у*) + 6у(1+у + у2) =
-7(1+у2 + П 6у(1+^ + 1/2) = 4(1+^ + ^),
Зу(1+У + У2) = 2[(1+у + у*У-2у(\+у + у*)1
7у(1+у + у2) = 2(1+У + У2)\ (1+у + у2)12(1+у +
+ */2)-7*/] = 0.
Но 1 + у + у2 = 0 не имеет вещественных корней.
Знаменатель прогрессии г/ определяется поэтому из
уравнения
2(1+У + У2)-7г/ = 0.
Находим:
2</2 — Ъу + 2 = 0; У1 = 2, у2 ^ 4~> *1 = ™
- 3^ - О Ч * - 3,5 _ 3,5-4 _
Итак, задача имеет два решения: *х = 0,5, г/х = 2; л;2 = 2,
#2 = 0,5.
335. Будем рассматривать ап как первый член
арифметической прогрессии. Тогда ат+п будет (т+1)-й член
этой прогрессии и будем иметь соотношение ат+п = а„ +
+ /яй. Совершенно так же, рассматривая ат как первый
член арифметической прогрессии, а ат+п как (п + 1)-й
член, получим
ат+л = ат + пй.
Наконец, рассматривая ат-п как первый член прогрессии,
а ат+п как (2п 4- 1)-й член, получим
ат+п == Ят-п + 2пй
Во всех этих равенствах й есть разность данной
прогрессии. Из этих трех уравнений находим:
ат = ат+/г — пй = Л — пй, ап = ат+„ — тй^А—тй,
1 От 4-/г — От —/г Л — /
а~~ 2/к* ~~ 2яа*
206
Подставляя значение й в первые два уравнения, находим:
г, _ л **, А —В 2пЛ — тА + тВ (2п — т)А-\-тВ ,
ап-Л-т'~ъГ^ 2~п = 2~п
336. Рассматривая ат как первый член геометрической
прогрессии, а ат+п как (п+1)-и, получим ат+п = атдп
или ат = Ад-п. Рассматривая ап как первый член
геометрической прогрессии, а ат+п как (т + 1)-й член, найдем
ат+п = йпдт или ап — Ац~т. Наконец, рассматривая ат-п
как первый член геометрической прогрессии, а ат+п как
(2п + 1)-й член, придем к соотношению аот+Л = ат-пд2п
или Л = В^2Л Во всех этих равенствах д знаменатель
данной прогрессии. Из последнего уравнения находим
И4Г
и подставляем его в первое и второе уравнения.
Получаем:
— п 1 т
*ш=а- (4Г -А-(4) 2 - ^«.-л -(4)2п
337. Обозначим знаменатель этой прогрессии буквой д
и будем число а считать первым членом этой прогрессии.
Тогда можем написать, что Ь = ад, с ^ а<?2» ^ — #<73-
Пользуясь этими формулами, получим
(Ь — с)2 + (с~ а)2 + (й — Ь)2 = (ад — ад2)2 + (ад2 — а)2 +
+ (ад3 - ад)2 = а2 (1 - ?)2 [<?2 + (? + I)2 + д2 (д + I)2] =
= ф (1 - <?)2 [?2 + <?2 + 2<7 + 1 + д* + 2д* + д2] =
= а2 (1 - д)2 [д2 + 2д (1 + д2) + (1 + <?2)2] =
= а2(\ —д)2(д + 1 + <72)2 = а2(1 — ?3)2 = (а —ад3)2 =
= (а —сО2.
338. Обозначим данное выражение буквой 3* и
воспользуемся формулой квадрата суммы двух чисел.
Получим
-Т уС "Т 2. Л хчп I == ""^ал I жал—2 г • • • + "^5" г
207
339. (1 +х + х* + ... + х«)2 — *" = (^!Г"11 )' — *" =
(хп+1—1^ — хп(\—х)2 ___ х*п+2—2хп+1+\—хп+2хп+1—хп+2
~~ (*-1)а "~ (*-1)а ~"
+ х + х2 + ... + л:л+1).
340. Дано 5 = а, + а2 4-... + ая и 5! = — + — +
4-... 4- —. Нужно найти а = аха2... ап. Пользуясь тем,
что в конечной геометрической прогрессии произведение
членов, равноотстоящих от концов, равно произведению
крайних членов (задача 329), получим
а2 = (ахаг... ап)2 = (ахап) (а2ап-х)... (апах) = {ахап)п.
С другой стороны, на основании того же свойства,
можно написать
апах
5 = а1 + аг+...+ая = ^ + ^- + .....
аП аП~ 1 а1
Поэтому
а1ая = |-, «г = (|-)Я, » = (^)2.
341. 5 = х + (*2 + х2) + (х9 + 2х?) + ... +
-+- [хп + (п — 1) хп\ = х + х* + я3 + ... + хп + х (х + 2х2 4-
+ ... + пхп) — пхп+1;
ж— 1 ' '
5 =-^-цг 1п*п+1 - (л + 1) *" + П.
208
342. Не нужно. Это определение суммы бесконечно
убывающей прогрессии, принятое в курсе элементарной
математики, а определение не доказывают.
343. Если последовательность аь а2, а3, ... есть
геометрическая прогрессия со знаменателем ц, то
последовательность а\, а\% а§, ... является также
геометрической прогрессией, но со знаменателем <72- Поэтому,
пользуясь формулой суммы бесконечно убывающей
геометрической прогрессии, можем написать следующие два
уравнения:
Подставляя значение а1 = 9(1—?), найденное из первого
уравнения, во второе, получим:
?--|"' 01-9(1 5-) = 9 — 3 = 6.
344. Если аъ о^, а3, ... есть геометрическая
прогрессия со знаменателем#, то а^, а\% а\, ...—тоже
геометрическая прогрессия, но со знаменателем ср. Поэтому
можем написать следующие два уравнения для определения
первого члена прогрессии и ее знаменателя:
1 — д ~~0>' 1 — д9 ~" 13*
Найдя из первого уравнения ^ = 3(1—^) и подставив
это значение ах во второе, получим:
27(1 — ^)3 _ 108 (1 — д)* _ _4_
1 —?3 *~ 13' \+д + Я* ~ 13*
13(1— 2<7 + <?2) = 4(1 + <7 + <72), 3^—10^ + 3 = 0,
1-Ц±1<Н = -г; о. = 3(1-4-) = 3-1 =2.
Значение цг = 3 > 1 не подходит, так как прогрессия
убывающая. Второй и третий члены прогрессии будут -д-
2
""ер
14 к. У. Шахно
209
345. Если последовательность аъ а2> а3, а4> ... есть
бесконечно убывающая геометрическая прогрессия со
знаменателем д, то последовательности аъ а3, ... и а2, а4, ...
также будут бесконечно убывающими геометрическими
прогрессиями со знаменателями д2. Поэтому можем
написать следующие два уравнения:
г^т==36; --^4=12.
Найдем из первого уравнения ах = 36(1 — д2) и подставим
это значение во второе уравнение. Учитывая, что а2 = ахду
получим:
36<? = 12, ?--~"' Л1 = 36(1 — 4")===36~4==32'
32 32
а искомая прогрессия будет такая: 32, -^-, -у,...
346. Если обозначить знаменатель прогрессии, сумму
которой нужно найти, через ду то прогрессия может быть,
записана так: 1, д, д2, ... Так как второй член
прогрессии меньше суммы смежных с ним членов 1 и (/2 в 2-у
13
раза, то получаем уравнение 1 + д2 = -^ д, решив кото-
2 3
рое найдем, что дг = -у; д2 = -у. Второй корень не
годится, так как при 9 = -у прогрессия не будет
убывающей. Находим сумму прогрессии: 5 = ^— = 3.
347. Обозначим знаменатель искомой прогрессии д.
По условию любой член прогрессии в 3 раза больше
суммы всех следующих за ним членов прогрессии. В
частности, первый член равен утроенной сумме всех членов
прогрессии без первого. Но искомая прогрессия имеет
такой вид: 1, д, д2, ... Следовательно, сумма всех членов,
начиная со второго, есть сумма бесконечно убывающей
геометрической прогрессии с первым членом д и
знаменателем д9 которая равна ^ . Отсюда получаем уравнение
1=3* -р^—, решив которое, найдем д = -г. Искомая
1 1 1
прогрессия имеет вид 1, -^-, -^р
210
348. Обозначим первый, второй, третий и четвертый
члены через аъ а2, аъ и а4, а знаменатель прогрессии —
через ц. Тогда будем иметь: а2 = ахц\ а3 — а\Ф\ #4 = ОД3-
По условию задачи ах + а4 = 1,5 (а2 + а3) или ах + й\Ф =
= 1,5 (а^ + од2). Но ах ф О, в противном случае
прогрессия имела бы вид 0, 0, 0, ... , что не может быть, так
как сумма первых четырех членов"не равна нулю. Разделив
равенство на аъ получим 1 +(/*= 1,5^(1 +?)• Решаем
это уравнение
2(1+^) = 39(1+9), 2(1+<7)(1-<7 + <72)-
-3<7(1+<7)-0,
(1+д)(2д*-5д + 2) = 0.
Но 1 + ц Ф О, иначе прогрессия не была бы убывающей
(д = — 1), поэтому 2цг — 5<7 + 2 = 0. Отсюда находим:
5±3 1 0
Я = ——; Я\ = "2"5 72 = 2-
Второе значение не даст убывающей прогрессии и
должно быть отброшено. Остается только ц = -у-. Из условия
01 + 02 + Д3 + а4 = 15, найдем аг. Действительно,
^(1-^ _ Д111--1б"]_ --
64 - —^— - — -у— - 15,
1-~ 2
-^-а1= 15, ах = 8.
о
Отсюда сумма прогрессии 5 = р- = 16.
»—г
7
349. По условию задачи имеем 56 = -о-5. Если
обозначить первый член прогрессии через ах ф 0, а
знаменатель прогрессии через цу то последнее равенство
запишется так: а1[ ~~я) = -о- • , а± . Сокращая на . а* # 0,
1 — ц о 1 — д * 1 — ц
7 1
получим 1 — 9е = "з"- Отсюда ц = ± -р=.
350. Обозначим разность этой арифметической
прогрессии буквой й. Тогда первый, пятый и одиннадцатый
члены этой прогрессии запишутся так: 24, 24 + 4с?, 24 + \Ы.
14* 211
Так как они образуют геометрическую прогрессию, то
имеет место соотношение
(24 + Щ2 = 24 (24 + 1(И).
Решаем полученное уравнение:
(6 + й)2 = 3 (12 + 5й), 36 + Ш + й2 = 36 + 15*
й2 = М; ^ = 0, </2 = 3.
Получаются две прогрессии:
24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24
и
24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54.
351. Девятый член а9 арифметической прогрессии
определится из соотношения ~^Д9 • 9 = 369. Из него
находим а9 = 81. Знаменатель ^ геометрической прогрессии
определится из равенства 81 = 1 • <78- Отсюда находим
(?2 = 3. Седьмой член геометрической прогрессии равен
сщ? = 27.
352. Обозначим первое, второе и третье числа через
аъ а2 и а3. Эти три числа составляют геометрическую
прогрессию, и поэтому можно написать, что а% = аха3.
Числа аи а2 + 8, а3 составляют арифметическую
прогрессию, и поэтому можно написать, что а2 + 8 = а± ^ 8 -
Наконец, числа а19 а2 + 8, а3 + 64 составляют
геометрическую прогрессию, и поэтому можно написать, что
(а2 + 8)2 = й1 (а3 + 64). Таким образом, имеем систему
уравнений:
а\ = сщ» а2 + 8 = Д1 + Дз , (а2 + 8)2 = аг (ц3 + 64).
Произведем умножение в третьем уравнении
а\ + 16я2 + 64 = аха3 + 64ах.
Но, на основании первого уравнения, а] = ахаъ\ поэтому
предыдущее уравнение принимает вид 1602 + 64 = 640!.
Отсюда а2 = \ах — 4. Подставляем найденное значение аа
во второе уравнение системы. Получаем:
4а1-4 + 8 = ^Чр-; 4а1+4 = -^4^-.
212
Отсюда а3 = 8 + 1ах. Найденные выражения для а2 и г3
через ах подставляем в первое уравнение системы и
решаем его относительно а±. Получаем:
(4а! - 4)2 = аг (8 + 7а,); 9а? — 40а, + 16 = 0; ах = ^— •
Если ах = ^4^" = 4' то «а = 4а,—4 = 12; а3 = 8+
+ 7^ = 36. Если ах = —^— = -д- , то а2 = 4аг — 4 =
Итак, возможны две. тройки чисел: 1) 4, 12 и 36,
о^ _4_ __20 100
^ 9 » 9 И 9 '
353. Обозначим искомое число буквой ху а другое,
вставленное между числами 3 и ху буквой у. Три числа
3, у и # образуют арифметическую прогрессию. Поэтому
3 I х
можно написать, что у = —у—. Числа 3, у — 6 и х
образуют геометрическую прогрессию, и поэтому можно
написать, что (у — б)2 = Зх. Заменив в этом уравнении
неизвестное у на основании предыдущего равенства,
получим
(Ч--б)'-з,
Решаем это уравнение:
(^^) = Зж, (х — 9)2 = 12ж, *• — 30* + 81 = 0;
Во втором случае все три числа одинаковы, так что они
образуют арифметическую прогрессию с разностью,
равной нулю. После уменьшения второго числа на 6
получим такие три числа: 3, —3, 3. Они образуют
геометрическую прогрессию со знаменателем, равным —1.
354. Обозначим первое, второе и третье числа через х,
у и г. По условию задачи имеем х + у + г = 114. Так
как эти числа образуют геометрическую прогрессию, то
имеет место равенство у2 = хг. С другой стороны, так
213
как эти числа являются, соответственно, первым,
четвертым и двадцать пятым членами арифметической
прогрессии, то, обозначая разность прогрессии буквой й,
получим у = х + Зй, у = х + 2Ы. Подставляем эти значения
у и г в полученные выше уравнения. Это приводит
к следующей системе уравнений: х + (х + 3(1) + (х + 2Ы) =
= 114; (х+ ЗА)2 = х(х + 2Ы), которая после упрощений
принимает такой вид: х + Ы = 38; сР = 2Ах. Решив ее,
найдем:хг = 38, Ах = 0ил:2 = 2, А2= 4. Итак, возможны два
решения: 38, 38, 38 и 2, 14, 98.
355. Обозначим искомое число минут через х. Второе
тело прошло за это время путь 6х м. Первое тело
проходило в каждую минуту, начиная со второй, на 0,5 м
больше, чем в предыдущую и, следовательно, общий
пройденный им путь будет равен сумме х членов
арифметической прогрессии, первый член которой есть I, а разность
0,5, т. е. — ' 2 ' ^ак как тела встРетились» то
получаем следующее уравнение:
(ь+' + оу-Ц^пу.
Отсюда
Х2 + 27* — 468 = 0; *= 12
(отрицательный корень отброшен).
356. По свойству арифметической прогрессии должно
быть а2 = а* ^ °3»а по свойству геометрической — а1=аха^
Сравнивая значения а\, взятые из этих равенств,
получаем
Отсюда находим:
(01 + а3)2 — 4а1аз __ п. (0=1 — а3)а _ п
4 ~ и> 4 "" "'
что дает аг = а3. Но тогда и а2 = 2 = ах = а3.
Итак, это возможно лишь в том случае, когда разность
арифметической прогрессии равна 0, а знаменатель
геометрической 1. Если бы эти числа были первым, вторым
и третьим членами арифметической прогрессии и первым,
214
третьим и вторым членами геометрической, то это
возможно и при неравных ах, а2 и а3. Например:
~2, ± _1(й = --|-);-2, -14(<7=-4-).
357. Должно быть Ь2 = 4а и 2а = Ь + 4. Отсюда:
62==2(6 + 4); Ь2 — 26 — 8 = 0; 6Х = 4, 6а = — 2;
«1 = 4, а2 = 1.
При а = Ь = 4 делимое будет иметь вид
4х4 + 4*3 + 4л;2 + Же + / = 4л;2 (х2 + х + 1) + их +1
Следовательно, для делимости этого многочлена на х2 +
+ х + 1 необходимо и достаточно, чтобы было й = / = 0.
В этом случае частное будет равно Ах2. При а = 1 и
Ъ = — 2 делимое имеет вид лг4 — 2х? + 4х* + их + 1и
частное от деления его на #2 + * + 1 будет многочлен второй
степени вида х2 -4- тх Ц- п. Поэтому можно написать
х* — 2*3 + 4л;2 + их +1 = (лг* + х + 1) (л;2 + тх + п) =
^х* + (т + 1)х? + (т + п+1)х2 + (т + п)х + п.
Приравнивая коэффициенты при х* из левой и правой частей
равенства, а затем при х2, придем к следующей системе:
т + 1 = — 2, т + л + 1 = 4.
Отсюда т = — 3, п = 6, а искомое частное в этом
случае будет х2 — Зх + 6.
358. Дано, что обе прогрессии возрастающие, т. е.,
что й = а2 — ах > 0, д = -^- > 1. Нужно доказать, что
ал < 6л при п > 2.
Доказательство. ая = «1 + 4(Л — 1) = 01 +
+ (01-01) (п— 1) = О! [1 + (-Ь - 1) (л- 1) ] =
= ^[1 +((/— 1)(л— 1)1«о1[1 +
+ (Я - 1) О + 1 + ... + 1)1 <
< аг [ 1 -Ь (<7 — 1) (^2 + «"-3 + ... + <7 + 1)] =
= «1 [ 1 + (7л-1 - 1)1 = ад*-1 = *Л.
215
V. ЛОГАРИФМЫ
а) Общие свойства логарифмов
359. По определению логарифма.
360. Если а> 1, то большему числу соответствует и
больший логарифм, т. е. 1о§в 2 < 1о§а 3. Если 0 < а < 17
то большему числу соответствует меньший логарифм, т. е.
1оёв2>1оёаЗ.
361. Пусть \о%ьа = х. Тогда по определению
логарифма Ъ* = а. Логарифмируя это равенство, получим х \о%аЬ =*
= '°баа> а так как х = \о&ьа и \щаа = 1, то получим
окончательно
362. Пусть \о&ь а — х и 1о§г а = у. Тогда по
определению логарифма имеем Ь* = а и су = а. Отсюда 6х = су.
Логарифмируя последнее равенство, получим х 1о§, Ъ =э
= У 1о&с с = у. Подставляем сюда вместо х и у их
выражения: 1о§^ а 1о§, 6 = 1о§, а. Отсюда \о&ь а = ^°ъ.
363. Так как под знаком логарифма должна находиться
положительная величина, то формула 1о§ а2 — 21о§ (— а)
верна, когда — а > О или а < 0. Следует также иметь в
виду, что формула 1о§ а2 = 21о& а верна лишь при а > 0.
И только формула 1о§ а2 = 21о§ | а | верна при всяком
а Ф 0.
364. Из условия
найдем, что
\Ш = 4а2 + 962
Логарифмируя последнее, найдем
Отсюда и следует доказываемое равенство.
365. Из равенства а2 + Ъ2 = 7а& следует, что
(а + *)' = 9а&, (^)2 =
аб.
Прологарифмировав последнее равенство, получим то,
что требуется доказать.
216
366. Так как а2 = (с + Ъ) (с — &), то, логарифмируя
последнее равенство сперва по основанию с + Ь, а потом
по основанию с — 6, получим
210&+* а = 1 + \о&+ь (с — Ъ) и 21о&_^ а = 1 + 1рь^(с+ 6).
Перемножаем эти равенства и производим преобразования:
41о&+* а 1о&_* а = 1 + 1оес4.ь (с — &) + 1о§г_^ (с + Ь) +
+ \о&+ь (с — Ь) 1о&_„ (с + Ь) = [ 1 + 1о&+ь (с — Ь)] +
+ 11 + 1о§^ (с + &)] = 21о&^ а + 21о§с+ь а.
367. Пользуясь соотношением \о%ьа — ^^ (см.
задачу 362), получим
8 = 1об
26 + а — 1
1по 0Я-, 1обю9,8 _ 1обю(49-0,2) _ 21о^10 7 + 1о&0 2 - 1
1°ё8*>°- 1о§1о8 - 31об102 " 31о&02
За
368. Пользуясь формулой \о&ьа = ^ ^ (см. задачу 362),
получим
1о&* (аб)
369. Пользуясь соотношениями 1о§в 6 = ^ (см.
задачу 361) иа1о&аХ <= х (задача 359), получим
1о&> (1о& а) / * \ Ь&, (1о&, а)
а 1о**а ^ у^ь а ) = ^оваЬ^Ь (1ов* а) -
370. Положим 1о§^ а — х. Тогда, по определению
логарифма, Ьх = а. Возведя последнее равенство в степень и,
получим Ьпх = ап или (Ьп)х = ап. Последнее же означает,
что \о&Ьп ап = х, а так как х = 1§^а, то \^п ап = 1§й а.
371. 1§43 = 1§4»32 = 1§1в9 (см. задачу 370).
372. Пользуясь формулами, доказанными в задачах 370
и 361, получим
кут 8 = !§з 64 - 1ь 43 « 31й 4 = 31§3 ^ -
а
217
373. Воспользуемся формулой 1о^ а = 1 , (см.
задачу 361). Получим
1облг («1^2
1 ,
Ч* * '
... ал)
1
1
«2
1о&г
-{-
^+10^^
+ *
1о§ д:
"л
+ .
•• +1°8Л,
374. Логарифмируя данные равенства, получим
(1 — 1ов1в х) 108Ю У =» 1| (1 — 1оёю */) 1о§10 2=1.
Отсюда
10ёю*=1 — 17^-77 = !
1°8ю 2
1
1 — 1о&10 г
Поэтому х = 10
375. Так как 1о^а=—р-; и Ь = )/" ас ,< то
, ^ 1 ^ 1 2
°&> * — Ь^ Ь =* ь^ у — = ^ а + Хо%х с :
21о^а х \о&с х
1о& л: + 1о& х "
Подставляя это значение 1о^л: в левую часть
доказываемого равенства, получим
1<>бд х — 1о§г, л: \о%а х (1о§а * + 1о&, х) — 21о§д * 1о&. х »
Ъ^ь х — 1о&. х ^ 21о§а х \о%с х — 1о§с х (1о&д д; + 1о^ х) "^
^ 0°3 а*)2 —*<>&,* 1о&>* Ь§а * (1о&* * — 1о& х) ^ \о^ах
^ 1о§а X \о&с X — (\о&с X)* ^ \о$с X (\0&а X — \о&с X) ^ \о$с X '
376. По определению арифметической прогрессии
можем записать
1оёт * — 1о&, х « Ьбя а: — 1о§т а:.
Пользуясь формулой 1о&,Д =1о°5^' (см. задачу 362),
преобразуем написанное выше равенство
1<>б»* _10сг х= 1о§* * 1о^ х
218
Сокращая на 1о§лх, приводя подобные члены и
потенцируя, получим:
1^=1+йёЬр 21ое^ = 1о^т(1о^Аг+ 1),
ЬбА "2 = 1оеЛ т 1о§* (лф, \оёк п2 = 1о& (лА)1о§* т,
/1« = (/1А)1ов*т.
Если 1о§Лх = 0 (на этот множитель мы сокращали), т. е.
если х = 1, то числа 1о§Л *, 1о§те дс, 1о8„ * дают
арифметическую прогрессию 0, 0, 0, при любых ку т, я, и,
таким образом, необходимость соотношения п2 = (кп)^к т
в этом случае отпадает.
377. Если х = 1, то числа 1о8Л х, \оёт х, \о&п х
образуют арифметическую прогрессию 0, 0, 0 при любых к,
т, я, в частности, и при таких, при которых выполняется
данное в задаче соотношение. Будем теперь считать,
что х Ф 1. Прологарифмировав данное равенство,
получим:
1о8Л (Ал)108* т = ЬЬ "2, 1о8л т (1 + 1оЬ л) - 21о6а п,
1 + 1о2* л _ 2 1 1 _ 2
Умножим последнее равенство на 1о8* х Ф 0. Получим
Пользуясь формулой
найдем, что
1ов„ * + 1°8* х =» 21оещ * или 1о^ * — 1о8л * «
а это и требовалось доказать.
378. При делении неравенства ЗЬ^ю-у- < 21оею 4- на
1°8ю"2" пРиДем к неравенству противоположного смысла
(3>2), так как 1о8ю-у-<0-
219
б) Логарифмические и показательные уравнения
379—381. В первых уравнениях Р(х) и С}(х) должны
быть положительны, а во вторых они могут быть одного
знака (в задаче 379 они могут также быть равными нулю).
Таким образом, рассматриваемые пары уравнений в общем
случае не равносильны.
382. В первом уравнении должно быть Р(х) > 0, а^ во
втором Р(х) может быть любым вещественным числом,
^неравным нулю. В общем случае эти уравнения не
равносильны.
383. Если х = у, то и а* = а?. Однако ах может быть
равно ау, когда хфу, если а== 1. Таким образом, если
а Ф 1, то уравнения ах = & и х = у равносильны.
384. Решаем первое уравнение: х2 — 1=8, х2 = 9,
хг = 3, х2 = — 3. Оба корня удовлетворяют этому
уравнению. Подставляем теперь х = 3 и х = — 3 во второе
уравнение и убеждаемся, что х = — 3 ему не
удовлетворяет. Следовательно, уравнения не равносильны.
385. Потому что уравнение
21ое(л:— 1) = 21о§3
не эквивалентно данному, так как
1ое(*-1)2 = 21ой|*-1|.
Оно эквивалентно данному лишь при х> 1, а при х< 1
такому: 21о§ (1 — х) = 21о§ 3.
Решив последнее, найдем х = — 2.
386—424. Указание. I. При решении логарифмических
и показательных уравнений часто приходится
логарифмировать и потенцировать обе части уравнения. Указанные
операции могут привести к уравнениям, не равносильным
данным. Это следует иметь в виду, чтобы не потерять корни
и не приобрести посторонние. Логарифмирование может
привести к потере решений, а потенцирование к
приобретению посторонних (см. задачи 379—385). Посторонние
могут быть выявлены проверкой (испытанием). Чтобы не
потерять решения, нужно стараться применять такие
операции, которые бы приводили к уравнениям, равносильным
данным или, в крайнем случае, имели бы среди своих
решений— решения данного.
II. В том случае, когда неизвестное входит и в
основание и в показатель (например: хх> (х+ 1)1обУ и т. п.),
220
допустимыми значениями букв могут быть лишь такие, при
которых основание положительно. Если же показатель не
может быть отрицательным, то основание может обращаться
и в нуль. Например, в выражении (1 + у)х должно быть
у>— 1, а если #>0, то у>— 1.
386. (^о^-^о^б+А^0' 1о^5-
— 610^5 + 5 = 0, 1о§,5 = 3 ± 2; 1о&/5 = 5, я5 = 5,
х1 = уг 5; 10^5 = 1, х2 = 5.
387. 3\^~\ёх— 1§* = 2; \&х — 3|/Тб^+2 = 0,
У~&е = -Ц1; У1Г* = 2, 1вх = 4, *х = 104 = 10000;
|/1§^ = 1, \§х=* 1, *2 = Ю. Оба корня удовлетворяют
уравнению.
388. Так как левая часть уравнения положительная, то
должна быть положительной и правая_часть, что будет
иметь место лишь тогда, когда \оцхУ 5<0, или 0<#<1.
Предполагая это условие выполненным, юзведем в квадрат
данное уравнение. Получим новое уравнение
4 1о&г5 + 3 = -|-1ой5 или 1о^5 — \оёх5 -2 = 0,
которое равносильно данному (при условии 0 < х < 1).
Решаем его:
1о&г5 = —|—; 10^5 — — 1, хх = -у-;
1°&*г 5 = 2, х2 = V 5.
Второй корень посторонний, так как ]/~5> 1.
389. Логарифмируем обе части уравнения. Получим
следующее уравнение, равносильное данному:
(Ь§5 * — ') 1°&> V* = 10& 5 или 1ов5 * — 1оь * — 2 = 0.
Решаем его:
1о& х = -Ц^; 1о& * = 2, * = 52 = 25; 1о§5 * = — 1,
_ 1
х2 —-$-.
Замечание. Равносильность данного уравнения и
полученного логарифмированием данного следует из того,
221
что основание степени У~х предполагается
положительным. Вообще, уравнение и? = до, где и > 0, как можно
показать, равносильно уравнению V \о§а и = 1о§а до.
390. Логарифмируем обе части уравнения. Получим
уравнение, равносильное данному (см. задачу 389), которое
затем решаем, как биквадратное:
(21§3х- 1,51§х)Ых = 18/10, 21§*х-^\ё*х=±,
41§4*-31й2*-1=0; \ё*х=Ц^=1, 1е ^ ==* ± 1.
х1 = 10, #2 — ~кр
391. Делаем сперва алгебраические преобразования
в правой части уравнения, затем логарифмируем обе части:
Х^х + З^х + 3^ 2
У\+х+\ у\+х—1 '
х х
хФх + Ы&х + з^^ (\ё*х + 31ёх + 3)\ёх^\ёх,
\ёх(\^х + 31ёх + 2) = 0.
Полученное уравнение равносильно данному (задача 389).
Решая его относительно 1§х, получим
1§* = 0; 1§л: = —1; 1§*=» — 2.
Отсюда
хх = 1; х2 — 0,1; х9 = 0,01.
392. Так как должно быть — х > 0, то ]/" х2 = — л:
и данное уравнение равносильно следующему:
1/21в(-*) = 1в(-*).
Возведя последнее уравнение в квадрат, получим
21ё(-х) = \ёЦ-х).
Решаем его:
18(_х)[2 —1в(-*)1 = 0; \ц(-х)=*0, 1§(-*) = 2;
^ = « 1, #2 == — Ю0.
Оба корня удовлетворяют данному уравнению.
393. Данное уравнение равносильно такому: 10&Н =1.
Отсюда | х\ =а 2; хх ~ 2, *а = — 2.
222
394. Уравнение равносильно следующему:
21ое2|*+1| + 1ое2|*+1| = 6.
Отсюда:
31о§2[л:+1| = 6, 1о8я|х+1| = 2, |*+1|=4,
х + 1 = ± 4; хг = 3, х2 = — 5.
395. Так как а}°&а г = г, то уравнение равносильно
такому: (х— 2)2 = 9 (при условии *>0, хф2). Отсюда
х — 2 = + 3, а: = 5.
396. Воспользовавшись формулой 1о§й а = \о&ьп ап (см.
задачу 370), получим
х1оё^(Х-2)=х\оих(*-2У и >(.^в91
т. е. уравнение задачи 395. Следовательно, х = 5.
397. Так как а10^* 4 = а1ов«2 = 2,
то
уЬ^- (*■ - х) ь у^ЕГГ^ 10йг (*а - х)
х —х у х г — * — #2 — х.
Поэтому уравнение принимает вид
2 = х2 — х или х2 — х — 2 = 0.
Решив его, найдем х = 2 (х =* — 1) — посторонний
корен ь.
398. Так как в правой части отрицательное число, а
корень, находящийся в левой части, — положительное
число, то множитель \о&ьх в левой части должен быть
отрицательным. Предполагая, что условие 1о§5 х < 0
выполнено, возведем обе части уравнения в квадрат.
Получим следующее уравнение, равносильное данному:
Хо^У^ЪхХо^х^ 1.
Далее преобразуем левую часть полученного уравнения,
используя формулу
Ьб* а 10а, 6 = 1.
Будем иметь:
-^ (\о%х 5 + \о%х х) 1о§| х = 1, (1о&, 5+1) 1о$ * = 2,
10^51о§52 х + 1о§| * = 2, 10&2 * + 1о&х— 2 ;= С
223
Решаем полученное квадратное уравнение относительно
1о§5#. Получаем
!<**- =±± — 2, ж-5-= •"'..
399. Преобразуем обе части уравнения, используя при
этом формулу
Будем иметь:
,0§>а = -т^т
2' *Ь ' Т^ЛЗД- = ц* (9Г5) ' 21°й (9УГ Х)
Ьбз х 1о§3 (3*), 2(1о§3 9 + 1оь /*) = 1о§3* (1о& 3 +1о& х),
2
2(2 + -о- 1°бз*) = 1о§3*(1 + 1о&*). 4 + 1об3х
<= 1о§3 х + 1о§32 х, 1о§32 * = 4.
Отсюда:
1ое3* = ± 2, хг = 9, *2 = —-.
Каждое из примененных здесь преобразований обратимо,
т. е. однозначно выполнимо в обратном порядке. Это
гарантирует равносильность всех полученных уравнений
и данного уравнения. По этой причине нет надобности
испытывать найденные значения хх и х2 — они будут
корнями данного, причем потери корней не произошло,
400. Преобразуем данное уравнение, пользуясь
соотношением
Получим:
V 41оба* "^ V А\ои* ""
Так как числители подкоренных выражений
положительны, а корни — арифметические, то должны быть и знаме-
224
натели положительными. Это значит, что должно быть
1*>0*и 1о§д*+ 1 > 1, а следовательно, данное
уравнение эквивалентно следующему:
Из него видим, что а> 1. Действительно, второе
слагаемое левой части положительно, а первое больше
единицы, так как
2У \0&а X 2}/ \о%а X
^ ЪУ\о%ах
Следовательно, если а< 1, то данное уравнение не имеет
решений. Если 1о§а*> 1, то уравнение имеет вид
-3_5Д = а или ]/ 1о^а х = а.
2 К 1о&г*
Отсюда: 1о§д л: = а2 > 1; ^ = аа\ Если 0 < 1о§а л: < 1, то
уравнение приведется к виду 1о§а х = -^ < 1 г откуда
#2 = а . Очевидно, хх и х2 являются корнями данного
уравнения, и других корней оно не имеет.
401. Пользуемся формулой \щьа=* ^? * (см.
задачу 362):
1оёа х (\оёа с + 1) = (1о§а х)2* а) 1о§а л: = 0, ^1 = 1;
б) 1о§ас + 1 = 1оеах, 1о§а х = 1о§а (ас), *а = а&
402. На основании соотношения 1о§^ а = 1о§^ ап (см.
задачу 370) данное уравнение можно записать так:
1о§3 х + 1о§3 *2 + 1обз *~* — 6.
Отсюда:
1о§3 х + 21обз х — 1о§3 * => 6; 1о§3 х = 3; * = З3 = 27.
15 К. У. Шахно 22^
403. 1о§8 х + {10& х)2 + (1о§8 х)г + ... есть бесконечная
геометрическая прогрессия с первым членом и
знаменателем, равными 1о§8лс, и раз она по условию имеет сумму,
то она убывающая. Поэтому, пользуясь формулой суммы
бесконечно убывающей геометрической прогрессии,
получим
1-1об8*~ 2 •
Решаем это уравнение:
21о§8д: = 1 — 1о§8*, 1о8в* = -~, * = 83=2.
404. Положив Ух + 1 = у > 0 и сделав некоторые
упрощения, получим'
1оё(#+1) = 1о§0/2-41).
Отсюда:
у+1=у2 —41, у* —у —42 = 0; уг = 7, у2 = — 6.
Второй корень отбрасываем, так как у2 < 0. Используя
у, = 7, найдем |/* +1 = 7, х = 48. Полученный кор%ень
удовлетворяет данному уравнению.
405. Разделим все члены уравнения на 9 х. Получим:
12 1
(4Г+(4-Я[ш Ы4Г--0,
1 ±УТ
т"7-
Но знак минус перед радикалом не годится, поэтому:
(2\ х УТ-1 ( з\х уТ-1
\3/ "* 2 ' \ 2 / ~~ 2 '
1,3 , /"5"—1 1обЗ—1о§2
х в 2 б 2 10б(|/ 5 — I)—1о^ 2
226
406. Положим х + У х2 — 2 » у. Тогда уравнение
запишется так:
4у_5 • 2У~Х = 6; 22у-4-2^6-0;
2 . 22у —5 • 2У— 12 = 0.
Решая полученное уравнение как квадратное относитель^
но 2У > 0, найдем:
2У = *±У = 4, 2У = 22, г/ - 2; х + У л;2-2 « 2,
л:9- —2 = (2 —х)2, х2 —2 = л;2 — 4х + 4, 4а: = 6, х а А.
407. Так как
У 2 + / 3 У 2 + ]/ 3
то данное уравнение эквивалентно следующему:
(|/'2 + У"з)<+ ■ ' =4 или
(V 2 + V з )
(1^2+-К^)2Л;—4(1^2+УЛ"3")Ч 1 =0.
Решая его как квадратное, получим
(1^2+У"з")* = 2 ± >гз.
Отсюда:
а) (У2+УТ)* =■ 2 + 1/"3,
(г + ^Л^^^г + ТЛз , -|- = 1, *, = 2;
б) (/~2 + У~3)* = 2 -У"3, (2 + ]АЗ)Т= (2 + У1)-\
~2~ ==: "*""" 1» %2 == *"— ^*
408. Разделив обе части уравнения на 8х, придем к
следующему уравнению, равносильному данному:
Положим у= Кг] . Тогда получим:
1? + у-2 = 0; у*-1+у-1^0; (у-1)(У* + У + 2)=0.
Но у2 4- У — 2 — 0 не имеет вещественных корней.
Поэтому:
15* 227
409. Воспользовавшись формулой
и потенцированием, приведем данную систему к
следующей, равносильной:
\х + у\= Ю; у = 2\х\. Но*/ = 2|л:|>0
и, следовательно
х + у = х + 2\х\>0.
Поэтому \х + у\ = х + у и последняя система
приводится к таким двум:
а) х + у = 10, у = 2х\ б) к + у = Ю.^г/ = — 2х.
Решив их найдем:
М 2° 1П ОЛ
*1 = X' У1 *" Т; х* = — ' у* ~ '
410. Пользуясь формулой
к>в*в = «о^л а"
и потенцируя, придем к следующей системе, равносильной
данной:
I У у *= ат\ |/~х I }/~1/ = ап или х*гу = аш\ х* : у4 » а6*.
Отсюда:
хва2(2«~3п); у_вв(—ЭД
411. Замечая, что
1о§ а
4 I 4
и производя потенцирование в первом уравнении, придем
к следующей системе равносильной данной:
Аху = 9а*; х + у = 5а.
Решив ее, найдем:
19 9 1
*1 = ха' й = "Г а; ** = Ха* #2 ** Ха'
412. Пользуясь формулой 1о§^ а = 1о§^л аЛ, приводим
логарифмы, входящие в первое уравнение, к основанию 10,
а затем потенцируем. В результате система приведется к
следующей:
(хг + у2)1 = 4а2 (х* — у% ку ~ а\
228
Замечая, что
(х2 + у2)2=*(х2 — у2)2 + 4х2у2 и х2у2 = а*,
преобразуем первое уравнение новой системы так:
(л:2 — у2)2 + 4*у - 4а2 (х2 — у2),
(х2 — у2)2 — 4а2 (х2 — у2) + 4а4 = О,
1(х2 — у2) — 2а2]2 = О, х2 — у2 = 2а2.
Таким образом, приходим к следующей системе,
равносильной данной (при условии х2 > у2 > 0):
х2 — у2 =3 2а2, хг/ = а2.
Решаем ее:
г/ = -^-, х2 — -5-= 2а2, х4 —2а2л;2 —л4 =0,
х2 = а2 + /1га4 = а2(1 + "/"2); хи 2 = ± аУ\ +У~12,
г/,2 = ,а!_= ±а]/ГуТ-1.
413. Так как здесь х>0 и у>0, то, логарифмируя
оба уравнения, придем к следующей системе,
равносильной данной:
\ё*+ 1бУ = 1б4+ 1;
ЫУ • 1§а; = 1§4.
Из первого уравнения находим выражение для 1§г/ и
подставляем его во второе уравнение:
1§*(1§4 + 1 — 1§*) = 1б4.
Решая это уравнение как квадратное относительно 1§х,
получим
18Х = 1е4 + 1 ±(1*4-1)^
Отсюда:
1§х = 1§4, \&х = 1; х, =4, х2 = 10; ух = 10, у2 = 4.
414. Из второго уравнения находим:
* + У = (К"2)в; * + </ = 4; у = 4 — х.
229
Подставив найденное значение у в первое уравнение,
получим:
5^ 34-* ^ 52. з3, З4 - 25* • 3~* = 25 . З3,
/ 25 V 25 1 0
415. Из первого уравнения следует, что должно быть
или
х2 + 7х + 12 = 0, или у = 1.
Поэтому задача решения данной системы равносильна
задаче решения следующих двух систем:
а) х2 + 7х + 12=» 0, л;+г/ = 6; б) у = 1, х + у = 6.
Их решения такие:
*! = — 3, уг =* 9; *2 = — 4, у2 » 10; *3 == 5, у3 = 1.
416. Исключив г/, получим
8* = 2 - 2* или 23* = 2х+\
откуда Зх — х -\- \, х = -к-. Подставляя л: = -^- во
второе уравнение, найдем
У—Г-2"7—В-^2".
12
417. Из первого уравнения находим у = х ,
Подставляем найденное значение у во второе уравнение.
Поре+</)2
12
лучима = х8. Следовательно, или х = 1, или
(* |*^ = 3. Если х « 1, то из первого уравнения
найдем, что г/— 1. Итак, первое решение хг » 1, ух = К
Если (* |2^)2 « 3 или (х + у)2 = 36 и х + у =* 6 (* > 0,
г/ > 0), то из любого уравнения системы получим х = у2.
Подставив в уравнение х + у = 6, придем к уравнению
у2 т|- у = 6. Отсюда
Итак, второе решение хг == 4, уа = 2.
230
418. Здесь предполагается, что л:> 0 и */>0. Из
второго уравнения находим
х — у
и подставляем в первое. Это дает
у =у .
что возможно, когда у => 1 или
Таким образом, получаем две системы:
а) {/= 1, у ==**
и
%<УТ + Г7Т -4. т- ^ V Т + VI =4-
4/ , 4/ 2
3
б) V * +- >/ у =.-*-, г/ = *
решение которых есть задача, равносильная решению
данной системы. Чтобы найти решения первой системы,
подставляем во второе уравнение у = 1 и получаем х = 1.
Итак, *! = 1, #1=1. Обращаемся теперь ко второй
системе. Подставив
в показатель левой части второго уравнения, найдем х = г/2.
Теперь для определения у имеем уравнение
Решаем его:
у1 = -э+у+48 = __1_ + _1_К57 (значение
-4— -тУЯ < о
и потому не может быть приравнено |/" г/ ).
Следовательно,
Л = (—Т + 4-1/57)*; * - (- 4" + 4-1^67)".
231
419. Так как здесь х>0 и #>0, то,
прологарифмировав первое уравнение системы, получим следующее ему
эквивалентное уравнение: т\о%рх — п\о&ру. Так как у Ф 1
(см. второе уравнение), то последнее можно записать в
виде
1о&ру ~~ ~т
при условии, что тФО. Сравнивая полученное уравнение
со вторым, видим, что
1о^Т ="^ или т1°ёрх~—т]о%рУ = п.
Таким образом, при т Ф О данная система эквивалентна
такой:
т\о&р х — п1о&р у = 0, т\о&р х — т\о&р у = п.
Вычитая из второго уравнения первое, получим
(п — т)1оёру = п
и если п ф т, то
Следовательно, в этом случае система имеет
единственное решение:
п2 п
т(п — т) п—т
* = Р • У = Р
Если п = т ф О, то ввиду положительности х и у из
первого уравнения следует # = у, что невозможно, так как
при х = у левая часть второго уравнения будет 0, а
правая 1. Таким образом при п = тФ0 система не имеет
решений. Если т = О, но п Ф 0, тогда из первого
уравнения получим */*= 1. Однако у= 1 не является
допустимым значением для второго уравнения. Следовательно,
при /п = 0и пфО система не имеет решений. Наконец
при т = п — О первое уравнение удовлетворяется
тождественно и все решения системы найдутся как решения
второго уравнения. Из второго уравнения получим
1овР* = (1о8/>* — 1оёРУ) 1оёРЛ (1°ёРУ—1) 1°ёР* = 1о$у.
232
Итак, в этом случае система удовлетворяется любой
парой таких чисел:
УФР\ * = Р
420. Допустимыми значениями неизвестных будут лишь
х > 0 и у > 0. Из этого и из второго уравнения следует,
что должно быть или а > 1 и Ь > 1, или 0 < а < 1 и
0<6< 1. Если 0<а< 1 и6>1 илиа>1 и 0<6<1,
то система не имеет решения.
Пусть теперь а > 1 и Ь > 1 (или 0 < а < 1 и
0 < 6 < 1). Логарифмируя первое и второе уравнения по
любому основанию, получим систему уравнений,
эквивалентную данной:
у\о% х = *1о§ у; *1о§ а = г/1об 6.
Перемножая уравнения полученной системы и сокращая
на ху > 0, придем к системе
1о§ а 1о§ х = 1о§ 61о§ г/; лс1о§ а = */1о§ 6,
которая также эквивалентна исходной системе. Из
первого уравнения последней системы найдем, что
Ъ&х=1щГ 1°ёУ> а х==у
Подставляя найденное значение во второе уравнение той
же системы, получим:
\о&Ь 1о& Ь ~ 1о& а
у .1о§а = г/1о§6; у ^ ~Ь§^-
Отсюда, если 1о§ Ь — 1о§ а Ф О, то
* - \1ова / ' \1<«а /
Если же \о&Ь — 1о§а = 0, то 10^6 = 1оба, а = 6 и из
второго уравнения получаем х = у. В этом случае системе
удовлетворяет любая пара положительных чисел х и г/,
равных между собой.
233
421. Здесь допустимые значения для неизвестных:
X
* > О, у > 0. Из первого уравнения находим х = у У
и, подставив найденное значение х во второе, получим
тх
у =* уп. Но последнее равенство возможно только, когда
у = 1 или — = п. Таким образом, задача решения данной
у
системы равносильна задаче решения следующих двух
систем:
а) у = 1, хт = уп и б) -у = л, х« = у*.
Подставляя у = 1 во второе уравнение первой системы,
найдем х = 1. Итак, первое решение д^ = 1, г/2 = 1.
Подставляя у = — во второе уравнение второй системы,
получим:
*-(•?)"."-(*)"*■• *-" = (тГ-
Если т — п ф 0, то найдем второе решение:
Если же т — п = 0, т. е. т = п, то из второго уравнения
получим х <= у. В этом случае система удовлетворяется
любой парой равных положительных чисел х и у.
422. Допустимые значения для неизвестных: г/> 1,
а: — любое вещественное число. Преобразуем второе
уравнение:
{у* _ 1)2,-2 в ^^, (у - 1)**-* (у + 1)2*-*= |=^-,
(у-1Г~2(У+1)2*-(у-1)2*,
(У - I)2*-2 [(У + \?х - (У - 1)21 - 0.
Полученное уравнение равносильно второму уравнению
данной системы и задача решения ее эквивалентна задаче
решения следующих двух систем:
а) {у— 1)2дг~2 = 0, (1 + у)х = 100 (при условии 2х— 2 >0)
и б) {у+1)*х — {у—1)* = 0, (1+0* «100.
234
Из первого уравнения первой системы находим у =* I и,
подставив во второе уравнение, получаем
2х = 100, х = 1о§2100> 1.
Итак, хг = 1о§2100, #1=1.
Из первого уравнения второй системы находим у—1 =(1 -\-у)х
и, пользуясь вторым уравнением, получаем:
у— 1 = 100, у = 101; 102* = 100, х » 1о§102100.
Итак, х$= 1о§102100, у2 = 101.
423. Допустимые значения неизвестных х > 0, г/ > 0,
г — любое вещественное число. Кроме того, следует иметь
в виду, что так как У~х и У~у — арифметические, то
г > 0 (это видно из третьего уравнения).
Из первого уравнения находим, что
8
52
х = у .
Подставляем это значение х во второе уравнение системы.
Это даст
Л. 16
3 1Ъг
У =У
Отсюда видим, что или у = 1, или -у = -=^-. Если у=1,
то из второго уравнения получаем х = 1, а из третьего
г = -у. Итак, первое решение
Если
Поэтому, подставив х = у2 в третье уравнение,
получим:
5
г 16
3 ~"75г"'
*1= 1. УХ= *» *1
2 16 4
3 ~~ 25 > г "" 5 ■
8
52
то л; = г/
4 , !/~ 4 Л ,/— ~1 + 3 1
у + 1/~у =4-^ +У1-^т- о, /^ —
Отсюда !/ = -<р * — У2 = зГ
235
Итак, второе решение
-Л. - * -А
Ч — ,81 ' Уг ~~ ТР *2 ~ 5 *
424. *! = 1, г/1 = 1, гг = 2; *2 = ^(]/^.-1)8,
1 /|/19 Л4 _ 4
*2" тел V 1 V • *2 ~" Т'
Решение аналогично решению задачи 423.
VI. СОЕДИНЕНИЯ И БИНОМ НЬЮТОНА
425. Воспользовавшись формулой
I и „ / »|_ 1 ._!
Ь/г = ^ • С* *
запишем данное равенство так:
Гт . л + 2 —т ^.т Л —т + 1
X
Отсюда имеем
X *~"|2 '«+2 = 0,6:1:1.
1 * /я+1 "" 5 ;
1 . /I —/Я+1 __ «
т + 2 — *
ИЛИ
г 5(т+ 1) = 3(/1 — т + 2);
1 т + 2 = гг — т + 1.
Решая последнюю систему, найдем п = 5; /л = 2.
426. Первое доказательство. Выделим какие-нибудь два
элемента из числа данных (п + 2) элементов. Тогда
сочетания цз (п + 2) элементов по (/п + 1) разделятся на
четыре группы: а) не содержащие этих двух элементов;
б) содержащие оба эти элемента; в) содержащие первый
из выделенных элементов и не содержащие второй; г)
содержащие второй из выделенных элементов и не содер-
236
жащие первый. Очевидно, группы а), б), в), г) состоят,
соответственно, из
сочетаний. Отсюда и следует тождество, которое
требуется доказать.
Второе доказательство. Имеем
Ьп +1„ + 1Ьп - (т+1)!(п_т_1)| +
, ЛЬ , о п1
(т— 1)!(л — т+ 1)! ^ т\(п — т)\
»! Г * 1 1 ,
(т—1)!(л —т—1)! [ т(т + 1) ^ (л — т)(п — т + 1) ~г
+ 2 1 = 5! Г 1_ +
~т(п — т)\ (т—1)!(л —т—1)! [ т(т + 1) ^
2п - т + 2 1 л!
Мл —т)(/1 —т +1)т ] (т — 1)! (я — т — 1)! Х
к2 + Зд + 2 = /г?(А1+ !)(/! + 2)
Х т(т+1)(л —т+1)(л —т) (т + 1)! (/г — т + 1)1 в
_ (п + 2)1 _гт+1
(т + 1)!(л —т+1)! ~"Ьл+2*
427. Очевидно, искомое число случаев равно
п2 п2 28 • 27 070
ЬЗО—2 = Ь28 = |#2 ^ *)'"#
428. Первый преподаватель может выбрать себе два
класса числом способов, равным С\. После выбора им
двух классов, из оставшихся четырех второй может
выбрать себе два класса числом способов, равным С\, а
следовательно, всего способов выбора двумя преподавателями
себе по два класса из шести равно С\ • С\. Но когда
первый и второй выберут по два класса, то останется
только два класса и поэтому третий не будет иметь
возможности выбирать. Поэтому искомое число способов
будет равно
С1'С1 = ТЪ -ТГГ = 6-5.3=90.
429. Вынуть три выигрышных билета из имеющихся
в урне пяти билетов можно числом способов,, равным С\.
Вынуть же два билета невыигрышных можно числом спо-
237
собов, равным Сшо-5 =€95. Так как каждые три
выигрышных билета могут быть соединены с каждыми двумя
невыигрышными, то общее число способов, при которых
из пяти вынутых билетов три окажутся выигрышными,
равно
430. Число способов, которыми можно распределить
четыре человека, знающих местность, на две группы по
два человека в каждой, равно С\. К каждой такой паре
можно присоединить остальных шесть человек числом
способов, равным С?б-4 —С?2. Таким образом, общее число
способов указанного в задаче разделения на группы
равно
1 /->2. Гб 1 4-3 12- 11 • 10-9.8.7 0770
-2"С4 °12 = "2 ПХ * 1 .2.3-4.5.6 в Л72'
431. Одного маляра можно ввести в состав бригады
пятью способами. К нему присоединить плотника
четырьмя способами. Поэтому общее число способов, которыми
можно выделить одного маляра и одного плотника,
равно 5 • 4. Очевидно, общее число способов, которыми можно
выделить трех человек разных специальностей (маляр,
плотник, штукатур), равно 5 • 4 • 2. Так как остальные члены
бригады не должны быть рабочими этих специальностей,
то их можно выделить числом способов, равным
гй Г& 14-13 П1
^25—11 = 014 = ^ ш 2 = ^1-
Итак, искомое число способов есть 5 • 4 • 2 • 91 = 3640.
432. Занумеруем места ряда числами 1, 2, 3, ..., 2л.
Если разместить мужчин на местах с нечетными номерами,
то каждому данному размещению мужчин соответствует
п\ размещений женщин на местах с четными номерами,
потому что это есть не что иное, как всевозможные
перестановки из п элементов. Но, в свою очередь, и мужчины
могут быть размещены на нечетных номерах п\ способами.
Итак, общее число способов, требуемых в задаче, когда
мужчины занимают места с нечетными номерами, а
женщины места с четными номерами, равно п\ п\ = (я!)2.
238
Но мужчин можно посадить и на места с четными
номерами, тогда, повторяя предыдущие рассуждения,
убедимся, что и таких способов будет (л!)3. Отсюда видно, что
полное число распределений будет равно 2(я!)2.
433. Очевидно, число способов раздачи не зависит от
порядка раздачи. Поэтому пусть сперва получит две карты
третье лицо. Одна карта у него должна быть червонный туз,
вторую карту он может взять девятью способами, поскольку
остается после изъятия червонного туза девять карт.
После того как третье лицо возьмет 2 карты, останется 8,
причем червонного туза среди них не будет, и второе лицо
может взять 4 карты числом способов, равным С|. Таким
образом, число способов, которыми^огут взять 2 карты, в
том числе червонный туз, третье лицо и 4 карты второе
лицо, равно 9С|. Но при каждом выборе этими лицами
положенного им числа карт первому предоставляется
возможность выбрать 3 карты из четырех, что можно сделать
числом способов, равным С\ = С\ ~ 4. Следовательно,
общее число способов раздачи равно 4 • 9С| — 2520.
434. Различных однозначных чисел, исключая нуль,
будет А\ = 4. Если бы среди данных цифр не было нуля,
то число различных двузначных чисел было бы равно А\.
Но так как среди них есть нуль, то в числе размещений
из этих пяти цифр по две есть однозначные числа, это те,
которые начинаются с нуля. Число их равно А\ = 4.
Значит, различных двузначных чисел получится А\ —
— А\ = 16. Аналогично найдем, что число различных
трех-, четырех- и пятизначных чисел будет равно,
соответственно,
А\ — А\=* 48, А\ — А\ = 96 и А\ — А\ = 96.
Всего получится 4 + 16 + 48 + 96 + 96 = 260 чисел.
435. Число различных двузначных чисел,
составленных из цифр 0, 1, 2, 3 так, что в каждое двузначное
число входит каждая из этих цифр не более одного раза,
равно А\—А\ = 9. Если же учесть, что цифра 3
может входить в число два раза, то к уже полученным
двузначным числам добавится число 33, а всего
получится 10 чисел.
436. Из пяти элементов можно составить Рь = 5!
различных перестановок. В этой задаче элементами являются
цифры 1, 1, 2, 3, 4 и, следовательно, каждая
перестановка даст пятизначное число, в которое войдет два раза
239
цифра 1 и по одному разу каждая из цифр 2, 3, 4.
Но среди этих цифр будут одинаковые, а также числа
меньше 20000. Выясним, сколько чисел будет различных
Если в каком-либо полученном числе поменять местами
две цифры, то получится другая перестановка. Если эти
цифры различны, то получится и другое пятизначное число.
Если же эти цифры одинаковы, то число останется
прежним. Но в каждое число входят две единицы, меняя
которые местами, мы получаем то же число, но другую
перестановку. Следовательно, различных пятизначных
чисел будет -тгРь = -о- • 5! = 60. Среди них числа,
начинающиеся с единицы, Фудут меньше 20 000. Подсчитаем
количество последних: Отбросим первый элемент. Тогда
из остальных четырех, т. е. из цифр 1, 2, 3, 4, можно
составить Р4 = 4! = 24 четырехзначных числа. Если
впереди каждого изй них приписать отброшенный ранее
элемент, т. е. цифру 1, то получатся различные пятизначные
числа, меньшие 20000. Те же самые числа получились бы,
если бы отбросить второй элемент и, составив из
оставшихся различные четырехзначные числа, приписать впереди
отброшенный ранее элемент, т. е. единицу. Но раз они
дадут те же самые числа, то их учитывать не нужно.
Все прочие числа, как пятизначные и начинающиеся
с цифр 2, 3, 4, будут больше 20 000
Итак, искомое количество чисел равно 60 — 24 = 36.
437. Из цифр I, 2, 3, 4, 5 можно составить Р5 = 5!
различных пятизначных чисел без повторения цифр. Среди
них будут и такие, которые будут иметь рядом стоящие
четные цифры 2 и 4. Подсчитаем количество последних.
Для этого рассмотрим четыре следующих элемента: 1, 24,
3, 5. Число перестановок Р4 = 4! даст пятизначные числа,
в которых четные цифры стоят рядом, причем сперва
цифра 2, а потом цифра 4. Если рассмотреть элементы 1,
3, 42, 5, то число перестановок из них также даст
пятизначные числа, в которых рядом стоят четные цифры,
причем сперва цифра 4, а потом цифра 2. Иных
пятизначных чисел, в которых бы рядом стояли четные цифры,
очевидно, нет. Поэтому искомое количество чисел равно
5! —2-4! = 72.
438. Так как при первом биноме есть множитель х,
при втором множитель х2 и при третьем л?, то из членов
разложения первого бинома нужно взять член с дг3, из
240
членов второго разложения член с лг и, наконец, из
членов третьего разложения член с х. Умножив эти члены
соответственно на х, хг, х3, получим
— *С}ж» + *2С!(2л:)2 + лг»С!2(3*).
Искомый коэффициент будет равен
— С| + 4С§ + ЗС}2 = — 4 + 4- 28 + 3- 12=144.
439. И10—1 =(10+ I)10—1 = 1010+10- 10» +
+ _!°_|.. Ю8+...+ 10- 10+1 —1 = 102(108+108 +
+ 5 • 9 • 10е + ... + 1) = 100Л,
где А — натуральное число.
440. Так'как (1 + х)п = 1 + С\х + Опх2 +...+С^+
+... + хп, то коэффициент при х* в произведении (1+х)а
на данный трехчлен равен
А, = (5 — 2) СГг + пСГ* — «С
Но Скп = с*-'. п~\+Х . Поэтому
А, = (5^- 2) СГ2+ "СГ1 -*СГ' • "~; + 1^ - 2)СГ2 +
+ СГ'(л- п + « - 1) - («- 2) СГ2 + (« - 1)СГ' =
= (з-2)СГ2 + (*-1)СГ2- ^-Т2 "
= СГ2 (« — 2 + л — * + 2) =пС1п~г.
441. С*?,, является биноминальным коэффициентом при
хп в разложении (1 + х)2п. С другой стороны,
(1 +*)2п = (1 +*)"(*+ 1)"
и тот же коэффициент можно получить, собрав
коэффициенты при х" в произведении
(1 + С\х + С2пхг + ... + Сппхп) (*" + Си*'1 +
+ С2*"-2 + ... + 1).
Он получится, если умножить первые члены этих
разложений, затем вторые и т. д., наконец, последние и
результаты сложить. Это и приведет нас к равенству
12+(^)2 + (02+... + (02=а.
16 К У. Шахно 241
442. Коэффициент третьего члена равен С2п, а
коэффициент второго Схп. По условию первый из них больше
второго на 44. Поэтому получаем уравнение
Сп — Сп = 44.
Решим его:
^И^_п==44, я'-Зл-88 = 0; « = Ц^
Знак минус перед радикалом должен быть отброшен,
потому что я>0. Получаем п ===== 11. Находим свободный
член
33-1 \к
Чтобы х был в нулевой степени, нужно, чтобы
•^-^—- == 0, т. е. к = 3. Отсюда свободный член равен
_С?1 = —165.
443. Сумма коэффициентов первого разложения есть 2",
а второго 22". По условию первая меньше второй
на 240. Поэтому получаем уравнение 22п — 2п = 240.
Решим его;
22л_2Г1-240 = 0, 2Л = Ц^.
Знак минус перед радикалом нужно отбросить, так
как 2п > 0. Получаем 2п = 16 == 24, п = 4. Находим
третий член разложения
444. Имеем
100—п п_
Гя+1 = СГоо(У^)10°"П(Гз)я = С:оо-2 2 -3*.
_ 100—/г п
Так как для рациональности члена показатели —-— и -^~
должны быть целыми числами, то число п должно Выть
кратно 3 и 2, т. е. кратно 6. Но 0 < п < 100 и числа л,
кратные шести, будут 0, 6, 12, ... , 96. Подсчитаем
число гп их. Получим:
96 = 0 + 6 (т — 1); т — 1 = 16; т == 17.
242
445. Напишем общий член данного бинома
Гя+1 = С2"0(К1)20-п(-7=)"=(-1)па • 2
40—5/1
6
Рациональными членами будут те, для которых —~
равно целому числу. Выясним, при каких п это будет
иметь место:
—"7 = т\ 40 — Ъп = 6т; 5я = 40 — 6т;
о 1
л = 8 — /га =- т.
о
Чтобы для « получались целые значения, нужно
придавать т значения; кратные пяти, но при этом такие, чтобы
число п не выходило из интервала, заключенного между
числами 0 и 20. Такие значения для т будут: —10, —5,
0, 5, а соответствующие числа для п: 20, 14, 8, 2.
Искомые члены будут:
Т21 = 2-10; Т15 = СИ • 2~б - С1о • 2~5;
Т9 = Сго; Т3 = Сго • 25.
446. По условию
С к рк— 1 л^-1-1 лк
П *-*Л е== ^Я ^П'
Воспользовавшись формулой С* =-#- и сделав не-
которые преобразования, приведем это уравнение к
такому виду:
„2 _ (4# + 1) п + 4Л2 — 2 = 0,
откуда
Так как 4к+ 1—число нечетное, а л— натуральное, то
необходимо, чтобы |/8& + 9 был нечетным числом,
т. е. чтобы 8к + 9 = (2т •+- 1)^. Отсюда находим, что
(т-1)(т + 2). _ 2(т.- \)(т + 2) + 1 ± (2т + I) .
"- — - >, п — 2 *
П1 = т2 — 2, ^ = (т + I)2 — 2.
16* 243
Выражения для пг и п2 можно объединить в одной
формуле п = т2 — 2. Так как 0 < # — 1<#<#+1<яи
, (т—1)(т + 2)
# = >-—!—^ Т0 отсюда заключаем, что т может
принимать лишь значения 3, 4, 5, ... Действительно, при
т = 1 будетч к — О, что невозможно, так как тогда
будет к — 1 < 0, что невозможно, а при т = 2
получим # = я = 2, что противоречит неравенству к + 1 < п.
447. Так как Тун = С**"-* • 2*, то должно быть
С° • 29> С* • 28и С1 • 29> Сп° • 210. Но С* = С*"!х
X ^-1—. Поэтому предыдущие неравенства примут вид
п~^ • 2 > 1 и 1 > -—^— 2. Из первого неравенства
находим: 2л — 16 > 9, 2л > 25, п > 12,5. Из второго
неравенства находим п — 9<5, л< 14. Итак, 12,5 < л < 14.
Следовательно, п= 13.
448. Наибольший коэффициент разложения (а + Ь)2п
есть коэффициент С"л У (п + 1)-го члена. Локажем, что
он — четное число:
гп __ 2/г (2/г — 1)(2/г — 2)... (2/г — /г + 1)
С2л - Ь2.3...(п-1)/1 в
2/г (2п — 1) (2/1 — 2) ...<2/г — 1 — п + 2) ___ огл-1
^ Т ' 1 . 2 ...(/г— 1) - ^2о-Ь
449. В разложении (1 + У~2)ъо общий член
гл+1==са)(1/"2)л.
Биномиальный коэффициент С50 растет с возрастанием п
от 0 до 26, а затем убывает. Множитель (|/ 2)п все
время растет с возрастанием п. Следовательно, пока п
растет от 0 до 26, растет и величина члена разложения.
Когда п станет больше 26, то биномиальный
коэффициент С"о станет убывать с возрастанием п и, хотя(1/2)п
при этом возрастает, все же не ясно, будет ли общий
член Тп+1 возрастать или убывать. Чтобы это выяснить,
исследуем отношение (п+ 1)-го члена разложения к/г-му,
т. е. отношение Тп+Х: Тп. Вначале это отношение, как мы
выяснили, больше единицы. Когда это отношение будет,
и будет ли меньше единицы?
244
Имеем
•К~2.
Решим неравенство
п> У2 =51(2-/1)
/2+1
Итак, если л > 51 (2 — /2), то отношение Тп+1: Г„
станет и будет оставаться меньше единицы. Найдем
наименьшее целое число, большее числа 51(2—/~2).
Возьмем значение / 2 по недостатку и по избытку с
точностью до одной тысячной:
1) |/"2= 1,414; 2 — /~2 = 0,586; 51(2— /~2) = 29,886;
2) /"2=1.415; 2-/^ = 0,585; 51 (2 — /"2) = 29,835.
Сопоставляя числа 29,835 и 29,886, видим, что в числе
51 (2 — V 2) содержится 29 целых и еще правильная
дробь. Значит, наименьшее целое число, которое больше
числа 51 (2 — /2), есть 30. Следовательно, начиная с
п = 30, отношение Тп+х: Тп становится меньше единицы
и значит Тз1 < Гад. При значениях п < 30 отношение
Тп+1 :Тп>1. Это означает, что Т30 > Т29 > ... > Тъ т. е.
наибольший член разложения есть
гж-сй(Г2Г=с8(Г2Г-
450. Покажем, что в разложении (р + д)п при р > 0,
<7>0 и р + <? = 1 существует наибольший член, и
найдем его номер. Для наибольшего члена должны,
очевидно, выполняться неравенства: Тк > Тк-г, Тк > Тк+г. Если
воспользоваться формулой
то неравенства примут вид
(я — к + 2) <7 1 кр .
(к-\)р * *» (п-к+1)Я^ 1'
245
Из первого найдем, что к < (п + 1)<7+ 1, а из второго
к>(пЦ- 1)<7. Объединяя, получим
(я+ 1)? <*<(* + 1)?+1.
Если (п + \)д будет целым числом, то и (п-{- \)д + 1
тоже будет .целым, и так как оба они удовлетворяют
написанным выше соотношениям для к9 то эти два числа
дадут номера наибольших членов разложения. Таким
образом, в этом случае будет два наибольших члена.
Очевидно, что для того, чтобы один из этих членов был
первым или последним (к = 1 или к = п + 1), должно быть
соответственно (п + 1) д = 1 или п + 1 — д (п + 1) + 1.
Если {п+ \)д будет нецелым числом, то, так как к не
может равняться дробному числу (п + 1) д, оно больше его, и
так как оно не может равняться дробному числу (п+1) д+1,
то оно меньше его. Такое целое число единственное. Это есть
целая часть числа (п + 1)<? + *• Таким образом, в этом
случае будет один наибольший член. Чтобы этот член
был первым или последним, очевидно, должно быть
соответственно (п + 1) д < 1 или л 4- 1 < <? (л + 1) + 1.
451. Представим выражение ( х + 1 -| ) в
следующем виде: 1 + (*+—) . Рассматривая 1 как пер-
2
вый член бинома, а х + — как второй, по формуле
общего члена можем написать:
Здесь к принимает значения 0, 1, 2, 3, 4, 5, 6.
Применяя формулу общего члена к биному \х -\ ) ,
получим для него такое выражение:
Т'т+1 = С?. хн~т- • (4)т =С? • 2т ■ я*"2*.
Таким образом, общий член разложения ( х + 1 -{ )
будет иметь вид Се • С? • 2т • хк~~2т. Здесь т принимает
значения 0, 1, ..., к. Из выражения общего члена ясно,
что свободный член получится при к — 2т = 0, т. е.
когда т = -«-. Следовательно, для получения свободного
246
члена нужно взять всевозможные четные значения для к,
а такими значениями будут числа 0, 2, 4, 6, положив
для соответствующих т значения в два раза меньше,
т. е. О, 1, 2, 3. Таким образом, свободный член
разложения (*+ 1 -\ ) будет равен
1 + С1 . С\- 2 + С\ • С%. 22 + С\ • С\. 23 =
= 1+60 + 360+160 = 581.
452. Положим (1 + х — *2)25==Лл;50 + А,*49 +...+ Л51.
При х = 1, получим
А± + А2+ ... +Л51 = 1.
Значит нужно найти член А3х3. Так как
(1 + я — *2)25 = [1 + х (1 —х)]25, то, рассматривая
последнее выражение как бином, можем написать его общий
член в виде
С другой стороны, для (1—х)к общий член будет
такой:
г;+1=с*. (-*)'.
Поэтому получим
Г,+1 = С|5.С',.(-1)'.х^.
Здесь должно быть 0 < к < 25, 0 < / < к, к + / = 3,
/ = 3 — к. Отсюда видно, что может быть только кх= 3,
к2 = 2 и, соответственно, /х = 0, /2 = 1. Заметим, что под
С& подразумевается единица.
Итак,
А3х3 = (С?5 • С§ — С& • Сх2) *3 = 1700 *3.
453. Данное выражение является геометрической
прогрессией с первым членом, равным (1 + я)3, и
знаменателем, равным 1 + х. Поэтому имеем
(1+л:)3 + (1 + л;)4+ ... + (1 + *)» =,
247
Так как в знаменателе находится х, то для получения
члена с хг нужно в числителе найти член с х4. Такой
член есть только в разложении (1 + х)16 и коэффициент
при нем
^=16;,152:^413 = 182о
является искомым.
454. Левая часть данного выражения есть
геометрическая прогрессия со знаменателем ут—•
Воспользовавшись формулой суммы членов геометрической прогрессии,
а затем формулой бинома Ньютона, получим
1У* + х; ]-=(х + 1)»+» — х"+1 = (л + 1)х" +
+ (А + ЬЦхп-1+ (Я+1).2(П3~1)^"г+- + 1-
455. Заменяя х через (х — 2) + 2, получим
х* — 11 х3 + 43а:2 — 72* + 45 = [(х — 2) + 2]4 —
—11[(* —2) +2]3+43[(х —2) + 2]2— 72[{х — 2) + 2] + 45.
Если теперь раскрыть по формуле бинома Ньютона
выражения 1(х — 2) + 2]к9 где А = 2, 3, 4, рассматривая
а; — 2 как один член, то после приведения подобных
членов получим
(х — 2)4 — 3(х — 2)3 + (* — 2)2 + 1.
Задачу можно решить, пользуясь условием равенства
многочленов и записав предварительно данный многочлен
так:
А(Х — 2)4 + В(х — 2)3 + С(х — 2)2 + й(х — 2) + Е.
VII. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ
ВЫРАЖЕНИЙ
Указание.
При решении задач этого раздела следует иметь в
виду, что, говоря о тождественности двух математических
выражений, мы исключаем из рассмотрения те значения
входящих в них букв, при которых хотя бы одно из них
теряет смысл.
248
456. $1П 4а + соз 4а с!§ 2а = $т 4а + со$ 4а
81П 4а зт 2а + со5 4а соз 2а соз (4а — 2а)
соз 2а
51п2а
■= с!§ 2а =
1
$Ш 2а
зт 2-х
соз 2т.
зт 2а
457. 1бЗа
1—3^2а
= {§а
{% 2а 21§ а '
Ьа + Ъ2а = 1&а + 1 — 1^а д
1 —1$а1б2а 21&а ^
з — <^ я _ , <е* 60° — *е2 *
1-3*б2<* "~12а* 1 —1^ 60° «в1 а
1§а
*8б0° + !8в
*б60°-1ба
= *8в*8(60° + а)18(60в—а).
А*Л *« <<**<> _1_ „\ +« /ОГ;° „\ 5Ш (35° + а) 5Ш (25° — а)
458. 1б 05 + а) 1в (25 -а) = соз (35° + а) соз (25° - а>
~2" [СОЗ (10° + 2а) — СОЗ 60°] СОЗ (10° + 2а) — -тр
-§- [соз (10° + 2а) + соз 60°] соз (10° + 2а) + -у
2соз(10° + 2а) — !
459.
2со5(10° + 2а)+1
СОЗ а + 51П а (СОЗ а + 51П а)2
СОЗ а — 31П а СОЗ2 а — 51П2 а
СОЗ2 а + 2 31П а СОЗ а + СОЗ2 а 1 + 51П 2а
СОЗ 2а
СОЗ 2а
= 1§ 2а + зес 2а.
460. <тх\\ + *е**б-тг)
СОЗ X СОЗ "Х- + 51П X 51П ~К-
= 51П X = 51П X
(«-+)
СОЗ XСОЗ '
СОЗ
СОЗ XСОЗ
зтл;-
51П*
СОЗ X
= \&х.
249
461. (§3а — 1§2а — {§а = 1бЗа —
т^Ь^(1-1ё2а18а) = ^За-^За(1-1ё2«(ба) =
= {§а1§2а{§3а.
462. с1§ а -1§ а - 216 2а - 41§ 4а = с°з8" -$1па а
ь & ь ь СОЗазШа
-2*ё2а-4{§4а - .*»* —2Ё!!* _4<§4«=
** ° зш2а соз 2а ь
___ 2 (соз2 2а — зт2 2а) д+ 4 — 4с08 4а 48*п 4а
~~ 5Ш 2а соз 2а ь "" 51П4а соз 4а ^
^_ 4 (СОЗ2 4а — 51П2 4а) _ 8соз 8а __ ,
— 51П 4а СОЗ 4а "" 5Ш 8а ~~ °С1§ ***•
463. 1§а1§р + 1§Т(1§а + 1еР)-1еа1йР +
+ *8
(а + Р) ] (*8« + *§Р) = *8а 1§р + с!§(а +
+ Р)(*8* + *8Р) = *8**8Р + \еЛ*еУ (*8* + '8р) ^
«=*8«*8Р+1— *8«*вР = 1-
464. 51Г1 2па + 51Г1 2Л Р + 51Г1 2/2 у = 2з1П П (а +
+Р) соз п (а— р) + 2зт п у соз л у = 2зт п (тс —у) соз п (а — Р)4-
+ 2зт п у соз п [тс — (а + Р)1 = 2зт (п тс — п у) соз п (а — р) -}-
4- 2$т л у соз [птс — п (а +Р)1=2-(— 1)" зт (— п у) созп(а —
— р) + 2 • (— 1)"зтлусозл(а + Р) =
с= 2 • ( — 1)пзтяу [созл(а + Р) — соз л (а — р)] =я
= 2 • (—1)"51Г1Пу • — 251Г1 П (X 51Г1 П Р =»
= (—1)п+1 4зт п а зт л р зт л у.
465. ^па + ^п$ + 1&ПЧ = 1&по1 +
+ 1^&Ъ%Пп\ (1-*8*Р*8*Т)-*8п« + 18*(т +
+ Р) (1—18/гР18пу) = 1епа + 18п(тс —а)(1~1§пр1епу) =
= 1§ я а — 1§ л а (1 —1§ л Р *8 л у) = 1^ я а 1§ л р 1§ п у.
_ зту + *\пхсоНх + у) ^у+—1вт(2х+у)^щ]
ТОО. : :—7 1 Г" ЕЯ л =
СОЗ у — 51П X 5!П (х + У) *
соз г/ -* -о" [соз */—соз(2л:-{-#)|
е. 51П # + з!п (2л; + у) __ 2з1П (л;.+ У) соз л: _ . ,
8=2 СОЗ # 4- СОЗ (2л: + */) 2С05 (Л; + У) С05Л7 ® * "Т *//•
250
467. соз2а + соз2р — 2созасозрсоз(а + р) = 1+с™2* +
+ 1 + 2°з2>3-1со5(а+Р) + соз(а-р)]соз(а + Р)^
- 1 + соз2а + с°з2? - [соз (а + р) + соз (а - р)1соз(а+Р) -
= 14-соз(а + Р)соз(а — р)— соз2(а + Р) —
— соз(а —р)соз(а + р) = 1 — соз2(а + р) = зт2(а + Р).
468. соз2 (а -}- р) + соз2 (а — р) — соз 2а соз 26 =
^1 + соз2(а + Р)+1+соз2(^Р)_^[со8(2а+2р) +
+ соз(2а-2Р)]=1+ соз2(а + Р) + соз2(а~Р) _
соз 2 (а + Р) + соз 2 (а ~ р) _ .
469. 4 зт а зт (60° — а) зт (60° + а) =»
с= 4 31П а • -н~ (соз 2а — соз 120°) = 2зт а соз 2а —
— 2з1'пасоз 120° = зтЗа— зта + зта = зтЗа*
470. 16зт 10° з1п 30° зт 50° зт 70° зт 90° =
4 • 2зт 10° соз 10° зт 50° зт 70°
8зт 10° зт50° з1п 70° = — с 1по
соз 10
4зт 20° соз 20° зт 50° 2зт 40° соз 40° зт 80°
соз 10° соз 10° зт 80°
= 1.
471. Обозначим левую часть подлежащего
доказательству тождества буквой А. Будем иметь
А = ±; зт 20° 51П 40° • ]/~3 31П 80° = ^- (соз 20° —
— соз 60°) зт 80° =, -^ (зт 80° соз 20* — -\- зт 80°) =
*= -ТЙГ(з!п 100° + 81п 60° ~ 51п 80°) =*
У1_ /.;„ ОЛО _!_ /3 _ . „в \ 3
Лт 80°+-^- —81п80°)
128 \ ' 2 *"" ^ ) 256 '
251
л тл я 2тс
472. соз-^- соз -у
2тс 2тс
81П -у СОЗ у
я тс 2гс
2 5111 -у СОЗ у СОЗ у
8Ш
4тс
тс
2зШ-у
зт
тс
тс
2зту
ТС ТС
43Ш у 451П у
473. соз
тс 4тс 5тс
у соз у соз -у- =
тс тс 4тс
2зт у соз -=- соз •'у соз
тс
2зту
2тс 4тс 2тс
31П у СОЗ у СОЗ -у-
'('-•^)
тс
2зт -у
81П
8тс
7
4тс 4тс
51П у СОЗ -у
тс
4зт -у-
81П-
ТС ТС
8$т -у 8зш у
474. соз 55° соз 65°
+ соз 10е
тс
8зту
соз 175°= у (соз 120°
°)соз5°-—!-(- !
_1_
8
= 0,125.
+
1
у соз 5° + соз 10е
ч
-±- соз 15° =— -|- соз (45° — 30°)
1
-(— соз 5° + соз 15° + соз 5°
Ч
соз 5°) =
- (соз 45° соз 30° + зт 45° зт 30°) = У-Е±
' 8 ]Л2
УТ __ 2 соз 10° — 1е 60е
от хи "СОЗ 10° ~~ 5Ш20С
__ соз 60° соз 10° — зт 60° зт 10°
■~"2' зт 20° соз 60°
475--ш^
- , 1
8 УТ *
зт 10°
= 2-
__ 9 зт 20°
~~ зт 20° соз
соз 70е
51п20° -
соз 60°
476.
ТС
СОЗ у
ЖГ д
соз 60° "~
2тс л . тс
СОЗ -у = 251П -щ 51П
Зге
10
252
Зте
Зте
2$1П -77Г СОЗ -до- • 231П -до- СОЗ
-доте
То"
10
51П
2те
10
81П
бте
10
те Зте
$1П -|Г" 8т~вГ
те / 2те 4те бте \
2зт -=-1 соз -=- 4- соз -=- + соз -у /
477. ^ - - !-!- =э
2зш-=-
/л . те 2те , 0 . те 4те ,
те I 281П -=- СОЗ -=- + 231П -«"СОЗ -=- +
зт-у- \ ' ' ' '
. л • те бте \ = ? / . Зте те
+ 251П -^=— СОЗ -=-1 те I 51П -= 81П -=- +
» ' / 2&т -у- V ' '
бте Зте , 7те . 5те \
-Н 51П-= 31П -у- + 31П -у 31П -у-1 =
2зт-
81П те — 51*П -Ч"
2зт -у-
51П
те
2зт -=г
478. зт470 + зт61° —31П 11° — зт25°=*
= 2з1п 54° соз 7° — 2зт 18° соз 7° = 2соз 7° (зт 54° —
— зт 18°) = 4соз 7° зт 18° соз 36° =
4зт 18° соз 18° соз 36° л -в 2з1п 36° соз 36°
== соз 7°
соз 18°
= соз 7° •
зт 72°
соз 7°
= соз 7°
соз 18°
зт 72°
479. соз 24° + соз 48° — соз 84° — соз 12° =»
= 2соз 36° соз 12° — 2соз 48° соз 36° = 2соз 36° (соз 12° —
~ >1оо\ л~~« одо „;« 1 о° ,;„ оло 2соз 18° зт 18° соз 36°
— СОЗ 48 ) = 4С03 дЬ 51Г1 1о 31Г1 30 = г^ =
' соз 18°
_ 2зт 36° соз 36° _ зт 72е _ 1
2соз 18° — 2зш 72° "~ Т"'
253
480. 2^п5о (2зш 5° зт 10° -Ь 2зш 5° зт 20° + ... +
+ 2зт 5° зт 50°) = 25.дУ (соз 5° — соз 15° + соз 15° —
— соз 25° + соз 25° — соз 35° + соз 35° — соз 45° +
лс° есоч соз 5° —соз 55° 2зт30о$т25°
■+- соз 45 — СОЗ 55°) = -
2зт 5° 2з1п 5°
= зт25°зт30°созес5о.
481. 1в 2а [1§ (30° - а) + 1б (60° - а)] +
+ 18 (60е-а) *в (30е-а) =
в 1е 2а <ё(30°-«) + *е(60°-«) м _ ^ (30°-
- а) 18 (60° - а)1 + 18 (60° - а) 18 (30° - а) =
= 18 2а 18 (90° — 2а) [ 1 — 1е (30° — а) 18 (60° — а)] +
+ *8 (60° — а) 1е (30° — а) = 1е 2а с1§ 2а [1 —1§ (30° —
- а) 18 (60° — а)] + 18 (60° — а) 1§ (30° — а) =
= 1-18 (30° — а) 18 (60°— а) + 18(60° — а) 18 (30° — а) = 1
482. 1 +2соз7*= 1 +*08 7*»Ш7* = шН» =
51П 7х 51П 7Х
зт 7х •+- зт 14л: 2зт 10,5лс соз 3,5до зт 10,5а?
зт 7х 2зт 3,5* соз 3,5л зт 3,5л:
483. 4соз (з0° 2») зт (б0° 2-) = 2 [зт (90° — а) +
+ 31п30°] = 2(со5а + -~|= 1 + 2соза = 1 -{-
Л- 2§Ш а СОЗ а __ . 51П 2а __ 51П а + 5"* 2а __
* С1Г1 п ' С*Г1 п С1П П
51Па
За 3
2зт ~о" а СОЗ -о- 51П -у- а
а а 1
2зт -у соз -у зт -у а
аол -ъ I • «о • -2 1 —* соз 2а . 1— соз 23
484. зт2а 4- 31П2Р + зт2у = ^ 1 §— *+"
,1 „2 о со§ 2а -|- соз 28 9
+ 1 —соз^у = 2 ~ *- — соз2т я
251
= 2 — соз (а + р) соз (а — р) — соз2 [тс — (а + р)] =
= 2 — С05 (а + р) соз (а — Р) —соз2 (а + Р) =
= 2 — соз (а + Р) [соз (а — Р) + соз (а + Р)] =
= 2 — соз (тс — 7) * 2соз а соз р = 2 + 2соз а-соз р соз у.
485. (48ЗОЧ.48бО-)+(*840°+«вБ(П --5^^- +
5т90° 1 , 1
соз 40° соз 50° соз 30° зт 30° ' соз 40° зт 40°
__ 2 2 2 (8ш 80° + 5Ш 60°) _
5111 60° ' 51П 80° 31П 60° 51П 80°
— 4з1п 70° соз 10° ___ 4соз 20°
"~ соз 30° соз 10° — соз 30° "
486. зт2 (а + р) — зт2а — зт2р = 1 — С082 (а + Р) —
1 — соз 2а 1 — соз 2Р 2 . . оч .
2 2 = —С082 (а + Р) +
, соз 2а -4- соз 23 . « , , 0\ • / I о\ / т
Л у - = —С082(а + р) + С08 (а + Р) со8 (а — Р) =
=соз (а+Р) [С08 (а — р) — соз (а + Р)] = 2соз (а + Р) зт а зт р
487. 1 + соз 4а — 4соз 2а + 2 = 2со82 2а — 4соз 2а + 2 =
= 2 (соз2 2а — 2со8 2а + 1) = 2 (1 — соз 2а)2 = 8зт4а.
488. (соз 11а + соз 5а) 4- 3 (соз 9а -+- соз 7а) =
= 2соз 8а соз За -+- бсоз 8а соз а = 2соз 8а (соз За + Зсоз а) =
= 2соз 8а (4соз3а — Зсоз а + Зсоз а) = 8соз 8а соз3а.
489. зт 5а зт 4а + зт 4а зт За — зт 2а зт а =
= зт 5а зт 4а + -у (соз а — соз 7а) ^ (соз а — соз За) =
. г • л СОЗ За — СОЗ 7а • г • л ,
= зт 5а зт 4а 4 ~ = зт 5а зт 4а 4-
4- зт 5а зт 2а = зт 5а (зт 4а + зт 2а) = 2зт 5а зт За соз а.
490. 2--у (соз 30° + соз 10°) — 2соз30° + зт 40° =
= соз 10° — соз 30° + зт 40° = 2зт 20° зт 10° +
+ 2зт20° соз 20° = 2зт 20° (зт 10° + зт 70°) =
= 4зт 20° зт 40° соз 30° = 2 ]ГЗ 5т 20° зт 40°.
256
491. [соз (а + р) соз у — 31П (а + р) 31П у] + соз а + соз р+
+ соз у = [соз (а + р + у) + соза] + (соз р 4- соз у) =
. 2соз (а + -ф-)соз 1±1 + 2со51+1 соз 1^1 =
= 2со51+1[со5(а + 1±1)+со51=х] =
= 4соз У^ ' соз-Ч[— соз ТТч
492. 51п 70° + 4 (соз 60° + соз 20°) соз 80° = зш 70° 4-
4- 2соз 80° + 4соз 20° соз 80° = $ш 70° +,2соз 80° +
+ 2соз 60е 4- 2соз 100° = соз 20° 4- 2соз 80° + 1 —
— 2соз 80° = 1 + соз 20° = 2 соз210°.
493.
г ь Г соз2а
1/Г81Паа(1 —С052а) ,лп г-«- • ,, . .
в V ТоЛ ^Ме2а51П2а=Н^аз1па|.
Но | 1§ а 51П а | == 1§ а зш а, если 1§ а зш а = -^^~ > 0 или
соз а > 0. Отсюда получаем
<4*^<а<(4*+1>«( вв(2й+1)«.
494. У 1 + 51п2а = У 31П2а + соз2а -}- 2з1П а соз а =
= ]/(зта + со$а)2 = |з1*па 4-соз а |. Но |зта + соза[ =
= зт а + соз а, если зт а + соз а = ]/^2 соз (-^ а) > 0.
Отсюда
(4*-1)я ^ « „ ^ (46+1)* __„__ (86-1)* . (8* + 3>с
2 < ~~4 ^ 2 ИЛ 4 < а < 4 *
. т/1—СОЗа _-|/(1—СОЗа)2 _ 1 /(1 — СОЗ а)2" _
<геэ. у 1 + со5 а — у 1 ___ со$2д — у 8[п2(х —
— """.со8 а = I созес а — с1& а I. Но I созес а — с(й а I =
. 1 — СОЗ а ^ ~
— с1е а — созес а, если созес а — сш а = : < 0.
ь ° 81П а
Отсюда 31П а < 0 и (2к — 1)тс < а < 2к к.
256
496. у?а-5{па =1/-1^=т/(1,-соз:>2 =
Г 1§ а + 51П а Г 1 + С05 а Г 1 — С03аа
= у ~*™ а) =У(со5ес а — с1§ д)2 = ] созес а — с!§ а |.»
Но | созес а — с!§ а | = созес а — с!§ а, если созес а — с1§ а=
= Ь^1>0. Отсюда зта>0 и 2Атс<а<(26 + 1)тс.
Однако в отличие от задачи 495 здесь доказываемое
равенство теряет смысл не только при а = к тс, но и при
а = ч—о~^' Поэтому окончательно получим:
2Ь<«<(-^;<^<а<(2Н1),.
497. |/"зес2а + созгс2а = У 1§га + 1 + с1§2а + 1 =
= 1/(1ёа + с1§а)2 = |1§а + с1еа|. Но |18« + с1б«|=»
= —1§ а — с1§ а, если 1§ а + с!§ а = Т ^ " < 0. Отсюда
498. >Л§2а + с^2а + 2 = }^(*§ а + с(§ а)2 =
VI
31П
31П
[аа4-СО$2а\ -ш / 1 .. / « «—
—— = у —^ а— = У 8ес а созес2а =
ЯП а С05 а / Г 31П2а СОЗаа г
= |зесасозеса|< Но | зес а созес а | = зес а созес а,
если зес а созес а = . ^ о— = ■ . 0— > 0.
81П а СОЗ а 81П 2а ^
Отсюда 31п 2а > 0 и & тс < а < +
2
499. ]/±±-^ + /ТЕ4"1 = т/'О+зша)»
Г 1 — 31П а 'Г 1 + 81П а Г 1 — зтаа '
-|/ (1 — 51Па)а ___ -ж/ (1 -}-5та)а -| / (1 ~ЗШа)а
+ V 1 — 8Шаа """ Г созаа "^ Г соз2а
1 + 51П а , 1 — 51П а 2 п, ,
| С08 а | ' | соз а | | соз а
Но | зес а | = — зес а, если зес а < 0, Отсюда
2 < * < 2 •
17 К. У. Шахно 257
500. У 1— со$а+]/ 1 +со$а= ]/
2з1п2-^ +
а . а
8ШТ ~НС08~Т
Так как
+ 1/2со52-^=|^2(
]/^зт^—соз-^-)== 28Ш^ ^-],
>
то доказываемое равенство будет справедливо в том и
только в том случае, когда
а
5117-
= ЗШ-^- И
СОЗ
= — СОЗ -
т. е. когда З1п -^ > 0 и соз-н- < 0. Из первого равенства
следует, что угол — должен оканчиваться в первом или
втором квадранте, а второе неравенство требует, чтобы
он оканчивался во втором или третьем квадранте.
Следовательно, угол -4- должен оканчиваться во втором
квадранте. Итак,
(2#+4-)*<-Г<(2*+ !)*• (4* + 1)* < а < (4& + 2)тг.
501. Пользуясь формулами 51п2-4- +соз2 ~ = 1
и $та = 251П-4-со8-|-, получим |/"1 + 31П.а+У 1—зта =
= у (з1П-|-+С03-|-) +у (з1П-д-— С05-|-) =
I • а I а I . I . а о!
= 31Г1-2-+СОЗ-2- + 31П-2 СОЗ-П.
Последняя же сумма будет равна — 2зт -^- тогда и
только тогда, когда
31п4-+соз4-
= — (зш-^+соз-^),
т. е.
253
51Г1-
+ соз-^<0, а
а а
31П-2 СОЗ-рр
(а а \
з,п — -соз^,
т. е.
51П ~| СО8-^-<0.
Итак, должны выполняться совместно неравенства
81П-|-+СО8-|-.<0 И 8Ш-^ СО8-|-<0.
Переписав эти неравенства в виде
со8-т(4§т- + 1)<0 ИСО5т-(12-г-1)<0»
замечаем, что одновременное выполнение их возможно
лишь в двух следующих случаях:
а) со8-^->0; *8-|-+1<0; 1е-^_1<0
или
со8-|->0; 1б-^<-1 и б) со8-|-<0; 1б-|-+1>0;
*е -| 1 >0 или со8-^-<0; 1б~§-> 1-
Рассмотрим первый случай. Если со8 -4- > 0, то угол -д-
оканчивается в первом или четвертом квадранте. Но в
этих квадрантах неравенство 1§ -^- < — 1 имеет место
лишь для углов, оканчивающихся в первой половине
четвертого квадранта, т. е. когда
Итак, имеем
(Ак — 1)тг < а < 1лк \\п.
Аналогично рассуждая, убедимся, что во втором случае
угол -4- должен оканчиваться во второй половине
третьего квадранта. Это приводит к неравенствам
2Ы ~тс<-|-<2&7г— -^- или (±к !~)тг<а<(4&— 1)*.
17* 259
Непосредственной подстановкой в равенство граничных
значений для -тг(т. е. 2Ы ^-, 2Ы ^-, 2Ы т*)
убедимся, что и при этих значениях равенство
справедливо. Поэтому можем окончательно записать
(Ак 1~У<а<(4к-±у.
502. Так как Vт-г± +1—- = ТА—*-
Г 1 + С05 а ' 1 — С05 а Г 1 — <
-V
1 + С05 а ' 1 — С05 а V \ — С052а
81П* а | 51П а
то для левой части равенства получим
1 Т/Т
81П а 81П а
Г Г \ 51П а | 51П а | /
Для того чтобы в скобках получить с!§2а + 2, нужно
положить ) 51п а | = — 51п а, т. е. считать зш а < 0.
Действительно, в этом случае выражение в скобках будет равно
1 + -^7 = 1 + созес2а - 2 + с!е2а.
Но если 81'п а < 0, то (2к + 1)тг < а < (2к + 2)те.
503. 18 Р = /1пР = I = 4~; 1б2р =
7 + 4 25
Л. Л_ 25
1_~~ 7 ' 4
Отсюда а+ 2^ = 45°+ 360°.*, где к = 0, ±1, ±2, ...,
а так как 0 < а < 45°, 0 < р < 45° и, следовательно,
0 < а + 2|3 < 135°, то А = 0 и получим а + 2р = 45°.
504. а) При 2&тг<л;<(2&+ 1)*. б) При всех лг,
исключая х = —~— те. в) При всех *, исключая л: = 2Ы.
г) При всех х.
260
505. При тех значениях, при которых со8 -§- > 0, т е.
при 2кк ^.<-|-<2^7с + -|- или (46—1)7^<л;<(4А4-
+1)1г.
506. 1§<х > 81па. Действительно, {§ а = — =
1 . .
= 81Па > 81П0С.
соза ^
507. Известно, что среднее арифметическое двух
положительных чисел не меньше среднего геометрического
этих чисел, т. е. ^ > |/а&, причем знак равенства
имеет место лишь при а = Ь. Поэтому аТ_ > 1 и при
а # 6 значение аТ— > 1 могут принять тангенс, котан-
2 у аЪ
гене, секанс и косеканс, а при а = Ь — все.
508. Синус единицы больше синуса одного градуса,
так как синус единицы по определению равен синусу
угла в один радиан, а синус одного радиана больше
синуса одного градуса.
1
509. (12 а + с!§ а)2 = . ^ = —
4 Ь ' Ь ' \ 81П а СОЗ а / 81
31П2а С052а
>4,
51П2 2а
так как 8т22а< 1. Это наименьшее значение достигается
при а = ^—^-.
510. Так как а и (3 — острые углы, то 0<соза< 1,
0 < сов р < 1. Поэтому получаем 8т (а 4- Р) = 81п а со8 (3 +
4-со8а8Шр < 81па • 1 4-1 -зт р. Итак, 8т(а 4-Р) < 8Ша ■+•
4" 51П Р.
511. 1§ 2а > 21§ а. Действительно, так как 0 < а <-|-,
то
0<1в«<1. 0<1в»а<1. 0<1-1§2а<1, ^'^ >1
и
1§2а=Т^- = 21§а--Ь=Т?7>212а-1-
261
512. Можно. Однако такое определение синуса
числа привело бы к более сложным формулам в
математическом анализе, чем принятое.
513. Неправильно. Радиан есть угол, принимаемый
за единицу при радианном измерении углов, подобно
тому, как угловой градус есть угол, принимаемый
за единицу при градусном измерении углов. И подобно
тому, как в градусном измерении угол выражается
именованным числом (числом градусов), так и при
радианном измерении угол выражается именованным числом
(числом радианов),
514. В любом интервале, в котором определена эта
функция. Так, например, \%х возрастает в интервалах
(О, -^-), (-|-, тс), но нельзя сказать, что \&х возрастает в
интервале (0, тг).
515. Задание синуса и косинуса вполне определяет, в
какой четверти оканчивается угол. Можно также
исходить из того, что
а
а 8{пТ" а а
1б -у = —♦ а 31П а = 2зш -^ соз -^
С08 —
516. 51п36° = 51п2. 18° = 2 зт 18° соз 18°; соз 54° =
= соз 3 • 18° = 4соз318° — Зсоз 18°; 2зт 18° соз 18° =
= 4со5318° — Зсоз 18°, 2зт 18° = 4 (1 — зт218°) —3,
451п218° + 2з1п18° —1 =0.
Так как зт18°>0, то из полученного уравнения
находим
5ш18°=-1+/7.
4
517. Умножим и разделим данное выражение на
2з1п -4-. Тогда, обозначая искомую сумму буквой 5,
получим
2$т
5 = ^~(2з1П-^-51Па+ 2зт-^-51п2а + ... +
2
262
+ 2$1п -|- 81П па) а. ЦНС0$ "Т ~~С08 "Т а + С08Та"~
2з!п-2
—-С08-^-а + ... + соз*"0 да — соз *" 7"' а ) =
5 _ . 2я — 1 2л + 1
-2-а + ... +соз—^—а —соз—~-
1 / а 2п+1 N 8Ш 2
па (п + \)а
81п -«г" $*л о
518. Умножив и разделив данное выражение на 2зшу
и поступая далее как в задаче 517, получим для искомой
суммы
па (П + 1)а
$1п —п- соз о
с> = ——
а
8Ш-2"
519. Пользуясь формулами косинуса и синуса
двойного угла, преобразуем выражения для Аъ Вг и Сг так:
„ л 1-|-соз2« . 0 8*п 2а , п 1 — соз 2а
Л1==Л 2 Ьи-—2—+С 2 =
— ^ +-н-8ш2аН 5— соз 2а;
— 2 -г 2 о.и^-г 2
5х=С 31п 2а +В соз 2а — А $'т 2а=В соз 2а — (Л — С) з!п 2а;
С, = ^-±^ — -|- зш 2а— ^~ соз 2а;
5? — ААгСг = [5 соз 2а — (А — С) зш 2а]2 —
— (-§- 51П 2а4- ^^ соз 2а)] = В2 соз2 2а —
— 2В(А — С) зш 2а соз 2а + (А — С)2 зш2 2а —
— [(Л + С)8 — (В 51П 2а + (А — С) соз 2а)2] «-
= В2 (соз2 2а + зш2 2а) + (А — С)8 (з1п2 2а + соз2 2а) —
— {А + С)2 = В2 + (Л —С)2 —(Л + С)2 = В2 — 4ЛС,
263
520 !б (а + ^ = ып(« + Р)созд = зш (2д + Р) + 5ш р
*8 а С08 (а -}- Р) 51П а 51П (2а + Р) — 51П р
681П Р 3
451*11 ^ 2 '
521. Для ср = 0 данное равенство приводится к виду
аг соз аг + а2 соз а2 + ... + аЛ соз аЛ =± 0.
Для ср = ср0 ф к тг его можно записать так:
(ах соз ах + ^2 соза2 + ... + йп соз аЛ) соз ср0 — (ах зт ах +
+ а2 зт а2 + ... + ап зт ая) зт ср0 = 0.
Учитывая первое равенство, а также и то, что зт ср0 ф 0,
получим равенство
ах зт ах + а2 зт а2 + ... + ап зт аЛ = 0.
Умножая теперь первое на соз ср, где ср — любое число,
а последнее на зшср и вычитая из первого результата
второй, получим
ах соз (аг + ср) + я2 соз (а, + ?) + ... + ап соз (ая + ?) = 0.
522. Находим созх из данного равенства:
81ПаВ С032а — 81Паа 51*П23
СОЗ X ==: =
51П2? СОЗ а — 31П2а СОЗ (3
(1 — С052Р) С032а — (1 — С032а) С052р ___
(1 — соз2Р)доза — (1 — соз2а)соз р ~~~
С032а — С052Э СОЗ а + СОЗ р
(соз а — соз Р) (1 + соз а соз'р) 1 -|- соз а соз р
Пользуемся формулой 1§2-тг= ^о!*'
Получим
, 2_^_ 1 + СОЗ а СОЗ Р — СОЗ а — СОЗ Р
° 2 1 + соз а соз р + соз а + соз р ==3
__ 1— соз а 1 — созр _ | 2 а 1^2 Р
= *ё2-^-*е2
1 + соз а 1 + соз р 1б 2 б 2 "
523. соз2а = 1 — зт2а = 1 — 4з1п2 -|- зт2 -|- = 1 —
— (1 — СОЗ ср) (1 — СОЗ в) = СОЗ ср + СОЗ в — СОЗ ср СОЗ в :
___ СОЗ а СОЗ а С052а
соз р соз 7 соз р соз 1 *
26^
Сокращая на соз а Ф О, найдем соза = С°$Р + С08? ,,
^ 1 + соз р соз 7
Остается, как и в задаче 522, подставить соз а в формулу
\а2~ — * ~~С08а
1ь о —
2 1 + соз а "
524. Данные равенства можно записать так:
соз 9 соз а + 31П 9 зт а = а; зт 9 соз р — соз 9 зт р = &.
Умножим первое равенство на зтр, а второе на соз а и
результаты сложим; умножим опять те же равенства —
первое на созр, а второе на зта и результаты вычтем
почленно. После этого получим
зт в соз (а — р) == а зт р + Ъ соз а
и
соз в соз (а — р) = а соз р — 6 зт а.
Возведем теперь полученные равенства в квадрат и
результаты сложим почленно. Это даст:
С052 (а — Р) (51П29 + С0520) = (а 51П р + Ь С05 а)2 +
+ (а соз р — Ь зт а)2, соз2 (а — Р) = а2 (зт2р + соз2р) —
— 2аЬ (зт Р соз а — соз р зт а) + Ь2 (соз2а + зт2а),
соз2 (а — Р) == а2 — 2аЬ зт (а — р) + Ь2.
-~- л + с __ соз х + соз (л: + 2ср) __ 2соз (л: -(- у) соз у __
Ь + й ~"~ соз (л: 4- ?) + соз (дс + 3<р) ~~" 2соз (*+2<р) соз <р ~~~
- -С05 (* + *> - А отсюда 2±± = А±1.
соз (х + 2ср) с
526. 2з1П а^ соз а ~Р = р; 2соз а"*"" соз а ~Р = <7.
Отсюда 1§ ^ =* —. Пользуясь теперь формулами зт2л;=
= 1 + *ея* и с08 = ТтФт' полУчим 8Ш (« + Р) =
= ^исоз(а + Р)=^.
527. Так как соз а + соз р = 2соз а~^Р ссз а 2 ■,
а соз (а + Р) = 2соз2 - "^ — 1, то данное равенство
можно преобразовать так:
2со5 ^-соз ^-- гсоз2-^1-А - О,
265
а-1-8 а —8 а + 8 . 1 л
соз2 -^р- —соз —^- соз —р- + -4- - О,
/ о + 8 1 а — 8 \2 . 1 1 , а — 8 л
(С03-р—2-СО8-1^]+-Г-ТСО52-2^ = 0,
(соз ^±1—1соз ^)"+ -т&[п2^Г- = °'
Но сумма квадратов вещественных чисел тогда и только
тогда равна нулю, когда каждое из этих чисел равно
нулю. Отсюда
. а —в Л а + 8 1 а — р Л
31П—2"^-- = О И СОЗ—~- 2"С08—~ = 0.
Из первого, учитывая, что а и р— углы треугольника,
получим а = р. Но тогда, подставив а = р во второе,
найдем:
\ 1 Я 1С
соз а 2~ = 0, соз а = у, а = -у. Итак, а = р = у.
Но тогда и третий угол равен -у, т. е. треугольник
правильный.
528. Стороны а, Ь и с образуют арифметическую
прогрессию и потому связаны зависимостью а — Ь = Ь — с.
Так как стороны треугольника пропорциональны синусам
противолежащих им углов, то из условия а — Ь = Ь — с
получим
51П А — 31П В = 51П В — 31П С.
Отсюда:
0. л —в А+в 0 . в—с в+с
251П—^—С08—^~~ = 2^1П—2—СОЗ 2 *
. / Л В \ тг —С . /В С\ и — А
*т[-т—2-усо8 —2- в8т 1-г—2-;со8~г-'
/ . л в л . ^ \ . с
I 31П у СОЗ ~2 СОЗ у 51П у I 51П -у =
/ . в с в . с\ . л
= I 51П у СОЗ ~2 СОЗ у 51П у I 31П у
Разделив обе части последнего равенства на положитель-
. А . в . с
ную величину зш у зт у зш у, получим
с1§4-с12 4==с12-Г~с12Т"-
2С5
529. Рассматривая данное равенство как уравнение
относительно 1§Л, определим из него 1§Л. Получим
*§ А = - У^дУс ■ - № + С) = Ц (- В - С).
Но если тангенсы равны, то углы связаны зависимостью
Л = &7г + (— В — С) или Л+В + С = /гтс, где & = О,
+ 1, ±2, ... Наименьшие положительные углы,
удовлетворяющие поставленным в задаче условиям, найдутся из
системы: Л + # + С = 2тг, 2А = В + С, С = А + В. Ре-
2 1
шив ее, найдем, что Л = -^-я, В = -^тс, С = те. Если
взять & = 1, то получили бы С = -^-, а для такого угла
данное тождество теряет смысл.
530. 51П А = 51П (7Г — 5 — С) = 51П (В + С) = 51П 5 СОЗ С +
+ созВз1пС. Но ^ = ^=^ = /. Отсюда:
51П/1 = -^-, 51*пВ = -^-, 51пС = -у-#
Подставляя в написанное выше н сокращая на /, получим
а = 6 соз С + с со5 В. Точно так же найдем 6 = с соз Л +
+ асов С и с = а соз В + 6 соз Л. Умножая первое из них
на а, второе на 6 и третье на с и вычитая из первого
результата два последних, получим
а2 — Ь2 — с2 = — 2ЬссовА или а2 = Ь2 + с2 — 2Ьссо$А.
531. Из данных равенств получаем:
соз а соз 30 + 31п а зт 30 = т соз3©;
зт а соз 30 — соз а зт 30 = т зт3©.
Умножая первое на соз 30, а второе на зшЗ© и вычитая
почленно, получим
соз а = т (соз3© соз 3© — зт3© зт 30).
Преобразуем это выражение, пользуясь формулами
косинуса и синуса тройного угла. Получим
соз а=т [соз3©(4соз3© — Зсоз О) — 31П3©(Зз1П ©—4з1П3©)] =
== т [4 (зт6© + соз6©) — 3 (зт4© + соз4©).
Возведя данные равенства в квадрат и складывая, найдем
51П6в + СОЗ6© = -V- (*)
267
Найдем теперь зш49 + со$4в.
6Ш49 + С054в = (5Ш29 + С0529)8 — 2зШ29 С0529 =
= 1—251'П2вС082в.
-^- = ЗШв9 + СО5в0 = (ЗШ29 + С0329)3 —
— Ззш29 соз2в (зт29 + соз2в) = 1 — Ззт29 со$29.
Отсюда
8т2всоз29 = ^-(1 -^)
81П
'9 + соз49 = 1 —1-(1-^-)- (**)
Пользуясь написанным выше выражением для соз а, а
также равенствами (*) и (**), получим окончательно
т2 + т соз а = 2.
532. Разделив первое уравнение на соз29, второе на
соз2ср и воспользовавшись формулой зес2* = 1 + *§2*,
найдем
(а—1)1§2в = 1-6, (6—1)1^ = 1-0,
откуда
*б2е _ /1-Й2
Но из третьего данного уравнения получим * == —^-.
Следовательно, —г- = (т——) • Так как афЬ% то =
' а2 \ 1 — а I * а
~~ -, откуда а + Ь = 2аЬ.
1-а'
Ко« со$2* $'т*х .6.4, 45Ш2*
Ь66- 'с,п4, "Г'^ев- "^Т" ме««/"Т
5Ш4ДС С05в# С052Х 5Ш2# ' С054ЛГ
1
зш4* соз6*
(соз8* + зт8* + бсоз4* зт4* + 4соз6л;з1п2л; +
+ 4С052ЛС51П6ЛС) = -—. . й ■ = —т-т г-.
534. Перенесем все члены данного равенства в левую
сторону, так что в правой будет 0, и приведем левую
часть к виду, удобному для логарифмирования. Получим
268
С08 а + С05 Р +СОЗ у — 1 г- 4з1П -^- 81П -|- 31П -— ==
= 2С08 ^ 2 5 а 2 251П2-| 4з1П^31П-~-51П-|- =
-(■
СОЗ2 -^- С082 -| 51П2 -^- 81П2 -| 31П2 -]~
С08^ тг* СОЗ4 ~
— 251П -^- 51П -у 3111 -|-) = 2
— ^81П-^81П-у- + 81П-^ I == 2 ^СОЗ-|-СОЗ-^-+
+ 31П -у 31П -~ + 31П ~- 11 СОЗ -у СОЗ-^ 31П -у 31П -д
— 51П ^") = 2 (сОЗ -^^- + 81П -^ (сОЗ ^±1 — 51П -2-) = 0.
Но первый множитель положительный в силу того, что
?-; о<р<-=-; 0<т<4
2 ~
0 < а < -^-; 0 < р < -|-; 0 < у < ~9-. Поэтому должно
быть:
СОЗ ^-—51П-у- = 0; СОЗ ^- = 31П-2-
СОЗ
Но
а для острых углов из равенства их косинусов следует
равенство углов. Поэтому
а + р
= -н ?г- И а + р + 7 = тс.
535. Достаточность. Если 1§ -^ рационален, то этого
достаточно для того, чтобы $тх и созл: были
рациональными, потому что существуют зависимости:
21*4 1-^4
51П X = ; СОЗ X =
1 + 4*4- 1 + ^24
269
Необходимость. Если $тх и создс рациональны, то
необходимо будет рациональным и ^-у» как это видно из
формулы
8 2 """ 1 + соз* '
При этом, конечно, имеются в виду такие х, при
которых существует 1ё-у, т. е. х ф (2к + 1)^.
536. Нужно доказать две теоремы:
I. Дано: 0<а<-^-, 0<р<-^-, 0<Т<-|-,
а + Р + у = тс.
Доказать: соз2а + соз2р + С052у + 2соза соз р соз у = 1.
II. Дано: 0<ос<-|-, 0<р<-|-, 0< т <-^
соз2а 4- соз2р + со52у + 2соз а соз р соз у = 1.
Доказать: а И- р + Т == те« *"
Доказательство I. Преобразуем выражение
соз2 а + соз2р + соз2 у + 2соз а соз р соз у,
соз2а + соз2р + соз2у + 2соз а соз р соз у = — 2°3 —|-
+ 1 + 2°з2,3 + соз2т + [соз (а — Р) + соз (а + р)] соз у =
= 1 + соз (а + Р) соз (а — Р) + соз (а + Р) соз у +
■+• соз (а — Р) соз у + соз2у = 1 + соз (а + Р) [соз (а — Р) +
+ соз у] + соз у [соз (а — Р) + соз у] = 1 +
+ [соз (а — Р) + соз у] [соз (а + Р) + соз у] = 1 +
+ [соз (а — р) + соз у] [соз (тг — у) -)- соз у] = 1 +
+ [соз (а — р) + соз у] (— соз у + соз у) = Ь
Доказательство II. Рассматривая равенство
соз2а + соз2р + соз2у + 2соз а соз р соз у = 1
как квадратное уравнение относительно соза, определим
из него соз а. Получим
270
= — СОЗ р СОЗ у + У С052р (С052у — 1) + 1 — С052у =
= — СОЗ Р СОЗ у ± У (1 — С052у) (1 — С052р) =
= — С05 Р СОЗ у ± ]/зШ2у 51П2р = — С05 Р СОЗ у + 51П р 51П у.
Но знак минус перед вторым слагаемым должен быть
отброшен, так как при условии 0<а<-|-, 0<р<-|-,
О < у < -у- будет соз а > 0, в то время как — со$ р соз у —
— 51прз1пу<0. Таким образом, остается только соза =
= — соз р соз у + 51п р 51'п у, что можно записать так:
соз а = — соз (Р + у) или соз а = соз [тг — (Р + у)]. Но 0 <
<Р<-Ь °<Т<тЬ Потому 0<р + у<тг, — тг<
< — (Р + у)< 0, 0 < тг — (у + р)< тг. Так как, кроме того,
О < а < -у, то из равенства косинусов углов а и тг —
— (Р + у) следует равенство этих углов, т. е. а = тг —
— (Р + у) и а + р + у = тг.
537. Из данных равенств следует, что можно
положить а = соз х, Ь = 51П х\ а = соз у, р = зш у. Но тогда
|аа + Ьр| =1со$д:со5Г/ + 51ПХ51ПГ/| = |соз(д: —г/)|< 1.
538 — 569. Указание. Напомним некоторые
определения и формулы, относящиеся к обратным
тригонометрическим функциям.
В тригонометрической функции у = $тх угол х (или
число х) является аргументом, а у — функцией. Поменяем
ролями функцию и аргумент. Тогда получим новую
функцию, которая называется обратной для данной. ^При этом
новую функцию также будем обозначать буквой у, а
аргумент— буквой х. Тогда для обратной функции получим
х = 51П у. Новая функция называется арксинусом и
обозначается так:
у = АГС 51П X.
Записи у = Атсв\пх и х = $юу равносильны, и
поэтому можно сказать, что арксинус х есть угол (или число),
синус которого равен х. Вместо слова «угол» часто
употребляют слово «дуга».
271
Так как х есть синус, то допустимыми значениями для
х являются лишь те, которые удовлетворяют неравенствам
— 1 <*< 1.
По данному синусу можно найти не один угол, а
бесконечное множество их. Поэтому говорят, что функция
у = Агс$'тх — бесконечнозначная. То ее значение уи
соответствующее данному хъ которое удовлетворяет
неравенствам —у < у1 < -|-, называется главным значением
функции Агсзшя, а если уг — угол, то главным углом.
Множество всех главных значений Агс зт*,
соответствующих всевозможным х от — 1 до + 1, называется главной
ветвью Агсзшл: и обозначается агсзшл:. Функция у =
= агс 51 п х однозначная и возрастающая в своей области
определения, т. е. в промежутке [—1, 1].
Аналогично определяются функции Агс соз*
(арккосинус х)у Агс1§д: (арктангенс х)у Агсс1§* (арккотангенс х)
и их главные значения — агс соз*, агс !§.*:, агсс1е*.
Функция у = агс соз* определена, однозначна и
убывает в промежутке [—1, 1]. Функция у = агс1§д:
определена, однозначна и возрастает в промежутке (—оо, + °°).
Функция у = агс с!§ х определена, однозначна и убывает
в промежутке (—оо, + оо).
Для обратных тригонометрических функций имеют
место следующие зависимости:
Агс 51п х = к тг + (— \)к агс зт х, |- < агс зт х < -|-;
Агс соз х = 2к тг ± агс со$ х, О < агс соз х < тг;
Агс 1е х = к тг + агс {§ х, ^- < агс 1§ х < -|-;
Агс с!§ х = к тг + агс с*е *» 0 < агс с!§ х < тг;
# = 0, ±1, ±2, ...
51п (агс 51П х) = х, соз (агс соз х) = дг,
*8 (агс (§ х) = х, с!§ (агс с(§ *) = х.
Если З1па = 51п р, причем а и р— главные значения
арксинуса, то обязательно а = р. Это следует из
однозначности функции агсзшл;. То же самое можно сказать
и о других тригонометрических функциях.
538. Можно. Однако в этом случае функция и ее
график не были бы непрерывны.
272
539. а) Положим агс зш х = а. Тогда $т а = х
и соз (-|—а) = л;. Так как по определению главного
значения арксинуса ~ < а < -|-, то |- < — а < -у- и
0<-| а < тт. С другой стороны, всегда можно
написать х = сое (агс сое х). Итак, со$ (~ — а 1 = соз (агс со$ х),
причем 0 < агс соз х < тт. Но если косинусы некоторых
углов равны и эти углы являются главными значениями
арккосинуса, то тогда и углы равны. Поэтому получим:
-^-— а = агс соз х, а + агс соз х = -^-,
агс 51п х + агс соз х = -^-.
Так же доказывается и равенство «б».
540. а) Положим агс соз (—х) = а. Тогда соза =—х
и соз (те — а) = х. Так как по определению главного
значения арккосинуса 0 < а < тс, то — тс < — а<0и0< тс—
— а < тт. С другой стороны, можно написать х =
= соз (агс соз х). Итак, соз (тс — о) = соз (агс соз х), причем
0 < агс соз х < тт. Но если косинусы некоторых углов
равны и эти углы являются главными значениями
арккосинуса, то и углы равны. Поэтому получим:
тг — а = агс соз х, а = тс — агс соз х,
агс соз (— х) = тг — агс соз х.
Аналогично доказывается равенство «б».
541. а) 51п (агс соз х) = У\ — соз2 (агс соз х) = У1 — х\
Перед корнем взят знак плюс потому, что 0< агссоз*<тс.
Таким образом, вывод этой формулы свелся к написанию
формулы 51па = |/1—соз2а, к подстановке в нее а =
= агс соз х и использованию формулы соз (агс соз х) = х.
Аналогично выводятся и все остальные формулы этой
задачи. Докажем, например, формулу «г». Пишем формулу
. 51П а
Ща = —г- » подставляем а =■= агс51 их и пользуемся
у 1 — 51П2а
формулой 51П (аГС 51П X) = X.
18 К. У. Шахно
273
Получим {§ (агс $1п *) =
У 1-х2
Перед корнем взят знак плюс потому, что когда
2~-<а<-"2"-, т0 *§а и 8*па имеют одинаковые знаки.
Для получения другой формулы, содержащейся в
равенстве «г», нужно взять формулу с{§ а = - С05 а -, поло-
У 1 — С052а •
жить в ней а = агс соз х и воспользоваться формулой
соз (агс соз х) = х.
Само собой разумеется, что каждая из формул «а» — «е»
имеет свою область допустимых значений для х. Так в «а»,
например, —1 < х < 1, в «б» и «в» — все вещественные
значения х.
542. Докажем, как образец, формулы «в». Прочие
доказываются аналогично.
I. 51П (агс {§ х) = -р=г- (см. задачу 541,6). Угол
У * ~т~ х
агс{§х заключен между 1- и-|-и имеет синус, равный
, Но в промежутке от гг До-?-, в силу одно-
значности функции арксинус, существует только один
угол, синус которого равен * %. Этот угол есть
агс5111—=* Итак, агс!§д: = агсзт—= * Получен-
У \ -\- х2 у 1 ■+■ х2
ная формула верна при любых значениях х, в частности,
при х > 0.
II. соз (агс 1§ х) = —==■ (см. задачу 541, в). Угол
у 1 ■+■ х2
атс1&х при *>0 заключен в промежутке между 0 и у
и имеет косинус, равный Но в промежутке от 0
до-^-, в силу однозначности функции арккосинус, суще-
1
ствует только один угол, косинус которого равен■ _.
У 1 4- х2
Этот угол есть агс соз —:
Итак, агс 1&х = агс соз / для х > 0.
]/ 1 -(-*а
274
III. с{§(агс{§л:) = — (см. задачу 541, е). Угол агс{§*
при х > О заключен между 0 и -~ и имеет котангенс,
1 тс
равный —. Но в промежутке от 0 до -н-, в силу одно-
значности функции арккотангенс, существует только один
угол, котангенс которого равен—, Этот угол есть
агс с!§ —. Итак, агс {§ х = агс с!§ —, если х > 0.
Требование, чтобы было х > 0, обусловлено формой
записи, а не существом дела. Так, например, если
формулы «в» записать не в виде непрерывных равенств, а
раздельно, то из трех равенств, которые только что были
рассмотрены, лишь для равенства агс (§ х = агс с!§—
требуется условие х > 0, а другие верны в более широких
пределах для х. Именно, первое верно при всех х, а
второе при х > 0.
543. агс С05 (соз -у тс 1 = агс соз соз (2тс ^тс 1 =
/4 \ 4
= агс соз (у тс I = -^ тс.
Было бы неправильно написать
/ б \ 6
агс соз I соз у тс I = -^- тс.
Равенство агс соз (соз а) = а справедливо лишь в том
случае, когда угол а заключен между 0 и тс, потому что
0 < агс соз (соз а) < тс. Если угол а не находится в
интервале [0, тс], то он является лишь одним из значений
Агс соз (соз а).
544. Так как |- < агсзш (зт*) <-?г , то: 1)
если
2~<*<~2~, Т0 агс 8*п (8*п *) == *'» 2) если-у<#<
з
< -у тс, то агс 51П (зш х) = агс зт [зт (тс — х)] = тс — х7 по-
_ _ о
тому что в этом случае 2~^тс — х ^~2~» **) еслиутс <
5
<#<-2-тс, то агсз1п(з1пл:)=:агсз1п[з1п(л: — 2тс)]=*—2тс,
18* 275
потому что —?г < * — 2* < -|-. Вообще, если ^у-^ <
<*<—2—тс или» иначе, л тс о" < ^ < «^+ -^-, то
агс 81П ($1П дс) = (— 1)*-1(&тг — *), потому что в этом слу-
5ш[(- 1 )*-'(* * — *)! = (— 1)*-*вт(кп — х) =
= (— 1)^-(— 1 )*81П (—X) - — (— 1)*-Ч— 1)*81ПХ =
- 31ПГ, ~ < (- 1)*-' (к ТС — *) < -=-.
545. Так как ^- <агс {§ ({§*)< -|-, то: 1) если
—-|- < *< 1Г. тогда агс ±ё ({ёХ>) = х; У если Т" < * <
з
< -2"«, то агс 1е (*ё *) = агс 1§ [1§ (х — тг)] = х — тс, так
как о- <С * — тс < ~2~; 3) если -~- тс < # < -~- тс, то
агс 1§(1е *) = агс 1§ [1§ (х — 2тс)] = х — 2тс, потому что
гГ<*—2тг<~Т1 4) если 2~тс<*< Г*
то
агс {§ (1§ а:) = агс 1§ И&(х + тс)] = х + тс,
так как ^- < д: + я < -^-. Вообще, если —^- тс < д: <
< 2к ^ * тс, то агс1§((§д:) = агс 1§ [!§(* — &тс)] = * — кп,
потому что ^-<^х — *тс<-?г-
546. I. Первое решение задачи будет основано на ис-
, . а У\ 4- 31П а — У 1 — 51П а
пользовании формулы зш -у = -—! т> ,
справедливой для ~ < а < -^-. Докажем ее.
У 1 + 51Па =|/51П2-^- + С032-|- + 231П-|-С08-^- =
= |/(зт-^ + С08-|-)2== ± (зш-^+СОЗ-^
276
или
С05 -|- + $1П -|- = ±]/1 +51Па.
Аналогично получим
СО$-|- —51П-|- = ±У\ — 51Па.
Но если
к тс а . • а
2" < а < -2", ТО С05-2" ± 31П "2" =
и перед радикалами нужно взять знаки плюс. Поэтому
получим
а У\ + $1*па — V1 — 51П а
8Ш -2- = Г—^ ^ •
Положив в этой формуле а = агсзтл; и воспользовавшись
равенством 5ш(агс$щ*) = х, найдем, что
1^-УТ^И
. / 1 . \ УТ
51П I -^ аГС 51П X I = 1
II. Пользуемся формулами: 51п-^-= ± ^
Л- V А*- В
Пусть а = агс 51п дг, тогда соз а = У1 — *2
У\ + /~П- (1 - ха) - "1Л— /Т-(1 -а;2)
_ л. У\ + Ух*-У\~Ух* ^ /1 + 1x1-/1-1^1
~~ - 2 "" - 2
Если х>0, то 1*1 = *, VI +х>У\ —х и а > 0.
Поэтому в правой части равенства нужно перед дробью взять
277
знак плюс. Получим
Если х < О, то |*| = —л;, |Л +* < У\—х и а < 0.
Следовательно, в правой части перед дробью нужно взять
знак минус. Получим
51П (-я- аГС 51П X) = —
У\-х-У1+х _У1+х-У1-х
2 ~~ 2
$ш д: — вт [ -—- те — х ]
сл-7 . 81ПЯ + С05ДС . \ 2 /
547. агс 51п -т=— = агс зш рк ~ =
У 2 У 2
= аГС 51П
2соз — тс 31*п [х — — к )
4 \ 4 /
. Г . / з VI з
= аГС81П 81П (-Т-ТС — *) = "л"-71 —•*%
так как при условии -^- < л: < -^- тг выполняется
соотношение ^~<~^7Г~*<~зг (задача 544).
2*
548, Положим агс 1§ л: = а, агс зт « , 2 = р и найдем
тангенс левой части доказываемого равенства. Получим
^(2а + Р)~г—Ерлр'
Но
*ба = * 1б2а= 2*6" = 2* *
1ё а — х% 1& ^а — 1 _ ^ч — 1 _ х2,
2л:
^П р = Г^2 ; С05р = + /1 -С052? -
/« 4л:2 ~ _ -[//1 - *М_ л:2- 1
1 (1+г8)2 ~" К \\ + хУ ~~*2 + 1
(так как х> 1); *8 ? = "^^ = ^ГГ7« Отсюда видим, что
*82й + «8Р = Т^?+??Твв0; *ё(2а + р) = 0
и 2а + р = /?тг. Так как *> 1, то 0<а<-^-;
278
о<К{; о<2а + к4тс-
Отсюда следует, что к = 1 и 2а + (5 = те, что и
требовалось доказать.
549. Воспользуемся формулой
$т-2-а = Ззт-^ 4з1*п3— =51п-^-(3—4$1п2-^-) =
= 5!П-|-(1 + 2соза),
положив в ней а = агс $т х. Отсюда получим $т а = х
и так как ?р<а<-^-, то со$а= +]/1—х2. Что
касается множителя 51П-|-, то для него будет следующее
выражение:
51П
1=±>/-1^211=±1/1^^! =
= ч-
1Л>(1+/1 -*а)
Когда х > 0, тогда будет и а > 0, так что в правой
части нужно взять перед дробью знак плюс. С другой
стороны, при х > 0 будет Ух2 = х и формула примет вид
2 }Л>(1 + ]/Т^Т2)'
Когда х < 0, тогда будет и а < 0 и в правой части
равенства нужно взять перед дробью знак минус, Но в этом
случае Ух2 = — х и мы приходим снова к такой же
формуле:
а х
$!П
2 У2(\ + УТ=*)
Подставляя найденные значения соза и 51п -|- в формулу
для зГп-^-а, получим
I -^-агсзшлг = , г
V2 У 1/9(1 4-1/1 - у2)
51П I „ _ , _.
V 2(1 + ут^т*)
27Э
550. Положим а = агс зш х9 где —~ < а < -^-. При
этих условиях для а будем иметь
а , 1 / 1 + соз а
К 2
С05-2>== +
соза= + / 1— зт2а=]Л — х2.
Поэтому
СОЗ (-2- аГС 51П х) = СОЗ -|- = V -
1 + СОЗ а
1 — (1 — л:а)
2 (1 — КТ^^^)
Т^Т2 Ы
1/2(1-/1-^) ^2(1 — >^1—=^з)
551. Обозначим соз (л агс соз х) = Тп. В формуле соз 2а =
= 2соз2а—1 положим а = агс соз л:. Тогда, учитывая, что
соз (агс соз х) = х, получим Т2 = 2х2 — 1. Точно так же из
формулы соз За = 4соз3а—Зсоза, найдем Т3 = 4л:3—Зх. С
помощью формулы соз (п + 1) а = 2соз п а соз а — соз (п — 1) а,
положив в ней а = агс соз л:, получим равенство Тп+\ =
= 2Тп-х — Тп-и Полагая в нем л = 3, 4, 5, 6 и
учитывая найденные значения Т2 и Г3, получим
последовательно:
Г4 = 2х (4*3 — Зх) — (2л:2— 1) = 8л:4 — 8л:2 + 1;
Ть = 16*5 — 20*3 + 5х; Тв = 32л:6 — 48л:4 + 18*2 — 1;
Т7 = соз (7агс соз х) = 64л:7 — 112л:5 + 56л:3 — 7х.
552. Пользуясь формулами задачи 541, получим
соз (агс 1§ х + агс 1§ у) = соз (агс 1§ х) соз (агс 1§ г/) —
— 31п (агс 1е х) 51П (агс 1§ г/) = г • , . —
х У 1-ху *
VI+х* VI +У2 У1+#У\+!Г
Эта формула имеет смысл при любых х и */.
* О другом способе решения см. замечание к задаче 555.
280
553. % (2агс зш х) = , «Ч***** .
2х
УТ^х~* 2хУТ^1?
х* 1-2х2 •
1 ~ 1 - ха
Здесь были использованы формулы задачи 541*.
Доказанное равенство имеет смысл, если — 1 < х < 1,
но х ф + -^=.
~У 2
554. $1п (2агс 1§ х) = 2$ш (агс 1§ #) со$ (агс 1§ х) =
— 9 * 1 __ 2х
"~ ' К ИМ* ' "К НИ** ~~ 1+*а
Здесь были использованы формулы задачи 541*.
Доказанное равенство имеет смысл при всех х.
555. Положим агс 1^-тр = #, агс 1& 2У 3 = у. Тогда,
пользуясь определением арктангенса, можем написать
Поэтому получим:
1 1 3
С05 X = ■ , г- = , = -т=,
К1 + 481* ЪЛ + — ^Ю
, 13 1
$тх = щх - совх = ,— = /— ,
6 3 У10 У10
1 1
С05 и = =— = —7=~»
У\ + (2]/Т)2 Ум
причем перед корнями берем знак плюс, так как главные
значения углов, имеющих положительные тангенсы
(4-и 2^У
являются острыми углами (углами, лежащими в первом
квадранте). Теперь будем иметь
8ш ( 2агс 1б 4") + С08 (агс *8 2^~3) = 8*п 2х +
* О другом способе решения см. замечание к задаче 5551
281
+ СО$у ев 251П ХС05 X + СО$у = 2 •
+ « = 4-+- '
Кю уТо
/13 5 уТг'
Замечание. Решение этой задачи было бы короче,
если использовать формулы задачи 541, Однако, чтобы
ими пользоваться, нужно или помнить эти формулы, или
иметь их под рукой. Задачи 552—554 были решены
именно с использованием формул задачи 541, но они могут
быть решены и способом, примененным здесь,
3 5
556. Положим агс1§-^- = #, агс81п-^=#. Тогда,
пользуясь определениями арктангенса и арксинуса, можем
написать
. з 5
*§* = -4~' 81П 0вТЗ"в
1 1 4
СО$ X = =- = >г = -*-#
Поэтому получим!
1 __
о л о
81П X, = {§ X С05 X = -^- • -у = -^-,
С05 у = VI— 5!п^ = ]/ 1—(-~)2 = -}§••
Перед корнями взяты знаки плюс, потому что 0 < х <-тр
и 0 < у < —. Теперь будем иметь
51П ( 2агс *б -§-) + ^ \"Т агс 8{п ~Ш/ = з1п 2х + *§ Т" =
-2нп*со8* + |+с^>-2-г--в- +
13('+§)
_24 , А —^1
25 "*" 25 "~ 25*
557. Положим агс соз -= = х = —, агс (§ -=. = у.
Отсюда 1§л;=1, 1§^ = -р=. Найдем теперь тангенс левой
282
части подлежащего доказательству равенства. Получим
/2"
Следовательно, х + у = к к + агс {§ - , где ^ — целое
У 2 I
число или 0. Но 0 < у < -^-, а * = -|-. Поэтому 0 < х +
+ У<у и й может быть равно только нулю. Отсюда
получаем х + у = агс {§ /— , т. е. то, что требовалось
доказать.
558. Вычислим тангенс данного выражения. Получим
(в<агс.в2 + агс.вЗ>=^||+|0||_
- 2 + 3 = — 1.
1-2-3
Следовательно, агс {§ 2 + агс {§ 3 = к те ~, где А—целое
число или 0. Но -^ < агс 1§ 2 < -|-, -~ < агс 1§ 3 < -—-
и -у- < агс {§ 2 + агс {§ 3 < те. Но между -^- и те есть
только одно число, тангенс которого равен — 1. Это число
3 3
-т-те. Поэтому получим агс {§ 2 + агс {§ 3 = -|- те.
559. Пусть агс в'тх = у. Тогда $т у = ху $т 2у =
= 251П у С05 у = 2х У1 — лс2. Отсюда
2*/ = А? те + (— 1)* агс 51П 2х V 1—х\
где Л — целое число или нуль. Но из условия х2<-9-
1^.1 те ^ . те
вытекает, что =- < *< _ , < у< —,
УТ /2 4*4
?г<2у<-7г и # = 0. Поэтому 2у = 2агс51пл: =
283
= агс 51П 2х У 1 — х2. Теперь можно написать агс $ш х +
+ Загс со$ х + агс $ш {2х УТ^~х?) = 3(агс зш х + агс соз л:) =
— 15. *
560. Положим агс зш х = а, агсзш у = р. Тогда будем
иметь: $1'па = л;, соза=+]/1—*2, зшр = у, созр =
= + У1 — #2, причем перед обоими радикалами ставим знак
плюс, потому что ~ < а < -^-, |- < Р < -у, а
косинусы таких углов положительны. Воспользуемся теперь
формулой синуса суммы двух углов. Получим
81П (агс зш х + агс 31П у) = 51П (а + Р) = $1П а соз р ■+-
+ соз а 81П р = а: У1 — у2 + У У1 — *2.
Отсюда следует, что
а + р = к к + (— 1)* агс зш (*/Г^Р"+ у У\— х2),
где &— целое число или нуль. Но
тс ^•тс те^о^те
2-<а<Т* Г<Р<Т
и сумма а 4- Р должна удовлетворять одному из
следующих соотношений:
1. _*<а + р< =-;
2
__ .^ г, л. й^Л
2. *<а+р<^
3. -5-<а + р<тс.
Легко убедиться, что при соотношениях 1, 2 и 3 будет
соответственно & = — 1, й = 0 я А = 1, так что получатся
формулы:
I. а + р » — * — агс зт (л: У1 — у2 + у/ 1 — х2);
И. а + Р = агс 31П (х У\—у2 + уУТ^Т2)-,
III. а + р = тс — агс зш [х У\—у2Л~ уУ\—х2).
Эти три формулы могут быть сведены в следующую одну:
агсзш* + агсзшу = -у] агсз1П (л: VI —у2 + уУ 1 — х2) + ек,
* Эту задачу можно решить и с помощью формулы задачи 560.
284
причем ч=1, е = 0 для соотношения 2; у\ = — 1, е = — 1
для соотношения 1; ?] = — 1; е=1 для соотношения 3.
Выясним, какие должны быть зависимости между х и у,
чтобы имели место эти формулы.
а) Пусть 4=1, е = 0, т. е. выполняется
соотношение 2. Тогда С05 (а + Р) > 0. Справедливо и обратное
утверждение: если соз (а + Р) > 0, то имеет место
соотношение 2, а следовательно, ?) = 1, е = 0. Но соз (а + р) =
= соз а соз р — 81п а зш р = У 1 — х2 ]/1 — #2 — ху.
Поэтому для того, чтобы выполнялось неравенство соз (а + 9>0,
необходимо и достаточно, чтобы
"КГ=Т21/Т^72 — *г/ > 0 (*)
Во-первых, это всегда будет. выполняться, если ху < 0.
Во-вторых, это будет выполняться и при ху > 0, если
I — х2 — у2 > 0 или х2 + у2 < 1, что становится
очевидным, если неравенство (*) переписать так:
У 1 — х2 — у2 + х2у2 > ху.
б) Пусть теперь у\ = — 1, е = — 1 или у\ = — 1, е = 1,
т. е. выполняются соотношения 1 или 3. Нетрудно
видеть, что для этого необходимо и достаточно, чтобы было
соз (а + р)< 0 или У 1-х2 У 1— у2 — ху<0. Здесь
ху > 0. Переписывая последнее неравенство в виде
У 1-х2 —у2 + х2у2 < ху,
убеждаемся в том, что I — х2 — у2 < 0 или х2 + у2 > 1.
Если же учесть, что соотношение 1 имеет место лишь
тогда, когда а и р, а следовательно, и х, и у,
отрицательны, а соотношение 3 — лишь тогда, когда а и р, а
следовательно, и х, и у положительны, то можно сказать
у\ = — 1, е = — 1, если х2 + у2 > 1 и х < 0, */<0,
а т] = — I, е = 1, если х2 + у2 > 1 и х > 0, у > 0.
4 5
561. Для упрощения выражения агсзт-у- + агсзт -^-
воспользуемся формулой задачи 560. Так как (-у) +
+ (-уз") < 1, в этой формуле нужно положить у = 1
и е = 0. Поэтому имеем
4 5
агс 51п -у + агс $т -т^ =*
285
л . ( 4 12 , 5 3 \ .63
Преобразуем полученный арксинус в арккосинус. Это мож-
но сделать с помощью формулы агс зт х = агс со$|/^ 1 — х2
со
задачи 542, так как -^ > 0- Получим
. 63 лГ~л /63\2 16
агс $1 п -^- = агс со$ у 1 — I-~-1 = агс соз -^-.
Итак, имеем
4 5 16
агс зт -^- + агс зт -^ + агс зт -^ =
16 , .16 тс
= агссо8-^ + агс81Пж = -г.
Замечание 1. Что при сложении агсзтх и агс51Пу
можно пользоваться формулой агс зт х + агс зт у =
= агс зт (хУ I —у2 + уУ 1 — х2), можно было бы
обосновать и иначе, чем сделано в решении этой задачи.
А именно: последняя формула верна, если
2~ < агс зт х + агс зт у <~|-.
В данном случае
агс зт -^- < агс зт ^-^ = -^-,
. 5 ^ .1 к
агс зт -у^- < агс зт -у = -^-
и, следовательно,
О < агс зт -рг- + агс зт -у^ < -?р
Замечание 2. Само собой разумеется, что эту
задачу можно решить без ссылки на формулу задачи 560,
а пользуясь лишь определениями обратных
тригонометрических функций и их главных значений. Для этого можно
поступить так: положить агсз1п-^ = а, агсзш -[з=^ на**~
ти 81па, соза, 51Пр, созр и воспользоваться формулой
286
синуса суммы двух углов. Это даст зт (а + (3) = -^ , отку-
да а + р =? к тс + (— 1)к агс зт -^-. Из условия же 0 < а+
+ Р < -у- установим, что к = 0. Сложив теперь по тому
.63 .16
же способу агсзш-^г- и агсзш-^-, докажем тождество.
Этим способом была решена задача 548.
562. Пользуясь формулой агс $т х + агс соз х = -|-,
можно написать агссозх + агссоз I— + -у V 3 — Зл:2] =
= тг — агсзтл:— агсзт (~- + -у ]/" 3 — ЗгЧ. Теперь
достаточно найти сумму агсзтх + агсзт(у + уУЗ—Зх2).
Воспользуемся формулой задачи 560. Для выяснения
значений г| и е вычислим величину суммы квадратов
аргументов:
*2 + (тт+4^т=~зГ2)2 = *2 + 4- + -|-"К"з=з? +
. 3 3 2 3 « ** . 'К'3" ,/"1 о^ 3 1
+4+4-(1-л;2)==-г>^
потому что из д;>-2~ вытекает, что 4л:2 > 1, З*2 > 1—л:2,
У~Зх>УТ^2и }^ хУТ^Т2 > ~(1 — х2).
Так как, кроме того, аргументы положительны, то
т] = — 1, е = 1. Итак,
агс зт х + агс зт (-тг + -тр V 3 — З*2] = тг —
— агсзт[^]/1 —(—Ч-^КЗ —3^2)2+
+ /Т=3? (т- + 4- У з-а*»)].
287
Но
1 - (-§- + 4 ухгз?)'- -1- (/** - УТ^"2)2
и так как
У~Ъх>УТ=^?< то |/1-(^ + ^>/-3-3^2=
Поэтому
агс зш * + агс $ш К- + 4" ]/"3 —3л:2) =
= тг — агс 51П [-у- ()ЛЗл: — VI—х2) +
+ (т-+4-^3_3;с2)^1Г=:Т2] =-
= тс — агс 51П !у- = тс 5- = -о~ тс-
Отсюда
(х ] \ 2 те
"2" + "2" V 3 — 3#21 =тг—д- тг = -у.
Замечание. Возможно и более короткое решение,
причем без ссылки на формулу задачи 560. Действительно,
заметив, что
. те УТ те 1 ,
51П -у = ~-9 С08 -у- = -у, С05 (аГС С05 X) = X,
51П (агс С05 х) = У 1 — л;2,
можем написать:
^+4-^з-з^-4--д:+1?-^1-л;2==
е=соз(у агс соз*]; агс соз* 4-
4- агс соз (у 4- у/З—З*2) = агс соз х +
4- агс соз соз [ у агс соз х)
4- у агс соз л: = у-,
= агс соз х +
те
283
так как
-у < х < 1, 0 < агс соз х < -|-
и
О < ~— агс соз х < —
(см. решение задачи 543).
563. Положим агс {§ х = а, агс {§ # = р. Тогда будем
иметь 1§а = *; 1§р = |/. Пользуясь формулой тангенса
суммы двух углов, получим
Ц> (агс 1Ш х + агс 1§ у) = 1§ (а + р) = /1^+^ = ^.
Отсюда следует, что
где & — целое число или нуль. Но
и сумма а + р должна удовлетворять одному из
следующих соотношений:
1. _7г<а + р<--|-;
2. —5-<в + р<-5-;
3. -|-<а + р<7г.
Легко убедиться, что при соотношениях 1, 2 и 3 будет
соответственно & = — 1, & = О и & = 1, так что получатся
формулы:
I. ?+ ? = -« +агс 1д^±|;
II в + р = агс18тУ^;
Эти три формулы могут быть сведены в следующую одну:
агс1§* + агс 1§# = агс1§^^ + агс,
19 К. У. Шахао 289
причем е = О для соотношения 2; е = — 1 для
соотношения 1; е = 1 для соотношения 3. Выясним какие должны
быть зависимости между х и у, чтобы имели место эти
формулы.
а) Пусть е = О, т. е. выполняется соотношение 2.
Тогда со5 (а + р) > 0. Справедливо и обратное утверждение:
если со5 (а + Р) > 0, то имеет место соотношение 2, а
следовательно, е = 0. Но соз (а + р) = соз а соз р— зшазтр,
а так как {§а = *, 1§Р = */, то
соз а = , = , , 51П а =8 1е а соз а =
С05 Р = 51П р =
И
С05(а + Р)-^ у 1~;'--==-.
г/ У 1 + ха)Л + г/а
Поэтому для того чтобы выполнялось неравенство
С05 (а + Р) > 0, необходимо и достаточно, чтобы было
— Х"ху >0.
У\ +х*У1+р
а это будет при 1 — ху > 0 или ху < 1.
Заметим, что при вычислении со$а перед радикалом
был взят знак плюс по той причине, что при н-<а<
< -у будет соз а > 0. То же самое можно сказать и
относительно со$р.
б) Пусть теперь е = — 1 или е = 1, т. е. выполняются
соотношения 1 или 3. Нетрудно видеть, что для этого
необходимо и достаточно, чтобы было соз (а + р) < 0 или
~"*у < 0. Последнее же будет выполняться
|Л + *а}/тт72
при 1—ху<0 пли лсу>1. Если же учесть, что
соотношение 1 имеет место лишь тогда, когда а и р, а
следовательно, и х, и у, отрицательны, а соотношение 3 — лишь
тогда, когда а и р, а следовательно, и х, и у
положительны, то можно сказать, что е = — 1, если ху > 1
и х < 0, а е = 1, если ху > 1 и х > 0.
290
9
564. Полагая в формуле задачи 563 х = у = у и за-
о
мечая, что в этом случае лг#<1, получим 2агс{§-^- =
о
+ 12 тт , 12 1 5
*= агс 1§ -Р-. Но агс 1§ -=- = агс соз —, = агс соз -т^
V 1+~25"
5 2
(см. задачу 542, в). Поэтому агс зш-т.- + 2агс 1#— =
10 ° 3
. 5 , 5 %
= агс 51п -гд- + агс соз -г=- = у.
Замечание. Эту задачу можно решить и не
пользуясь формулой сложения арктангенсов. Для этого
достаточно доказать, что зт (а + 2^) == 1, где а = агсзт-р^,
о
а р = агс 1§~з~. Отсюда будет следовать, что а -+- 2р = у.
565. Полагая в формуле задачи 563 х = -^- и у = --—
и замечая, что ху <1 1, получим
_1_ _1_
I 1 , I 1 .3 + 5 ,4
агс 1§у + агс ^-ц- = агс 1& | г = агс 1§у,
Прибавляя к этому результату агс!§у и снова пользу-
. 4 1
ясь той же формулой для х = у и у = у, получим
агс 1§у + агс !§— =агс 1§у.
7 1
Наконец, складывая агс!§у и агс!§у, получим
окончательно
агс 1§у + агс *8*5- + агс *б4" + агс 1§~8"" в
= агс1§у + агс1§у = агс 1§ 1 = у.
Замечание. Задачу можно решить не пользуясь
готовой формулой сложения арктангенсов, а применив
метод, которым была решена задача 558.
19* 291
566. Пользуемся три раза формулой суммы
арктангенсов (см. задачу 563) для случая *«/< 1. Получим:
4агс 1§-^- = 2 (агс 1§-~ + агс 1§-|-] =
«= 2агс 1§ 2 = 2агс *ё -4" = агс {б4- 4-
6('-1)
,5 , 2-5 .120
+ агс1§12- = агс1§—? Щ-=агс*§П9;
1211" ад
4агс1ё4--агс1§2^=агс1§^ + агс1§(-^)==
]20 _1_
__ . 119 ^ 239 __ . 120-239-119 _
— агс Т^ ^20 ^ —агсг§ 119-239+120 ~~
1 + 119* 239
- ягг |а П9. 239 4-239- 119 __ . 119.239+120
— ал. 1ё ид 2зд + 12() — агс 1ё П9 23д + 12() =»
= агс 1§ 1 =
тс
567. 2агс1§10 преобразуем по формуле суммы
арктангенсов, полагая в формуле задачи 563 х = у = 10 (случай
20
ху > 1, * > 0), а агсзт-щ преобразуем в арктангенс с
помощью формулы задачи 542, а. Получим
2агс 1§ 10 + агс зш ^=(агЫ§ 10 +- агс {§10) +
'»•'/<-($•
ЮГ
1- 10-10
, 20 , 10 + 10 ,
.20 . 20 , .20
+ агс 18-дд = те ~ агс 1е "99" + агс 1§~99" = 7Г-
Замечание. Задачу можно решить показав, что
20
81п (2а + Р) = 0, где а = агс {§ 10, а р = агс зт т^у.
Отсюда будет следовать равенство 2а +• [3 = к п и останется
лишь показать, что к = 0.
568. На основании формулы агс 1§ х + агс с!§ х = -^-,
292
получим агс 1§ х = -| агсс^х. Так как здесь
предполагается х > 0, то агс с!§ х = агс 1§— (см. задачу 542, г).
Теперь будем иметь агс 1§ х = -^— агс с!§ * = -|
— агс!й—■.
569. Пользуясь формулой агс 1§ л: + агс с!§ л: = ~
можем написать агс 1§ л: = -^ агс с1§ я. Но агс 1§ х = те —
— агс с1§ (— х) (см. задачу 540, б), а агс с!& (— я) =
= агс{§— (см. задачу 542, г), так как #<0 и,
следовательно, — х > 0. Теперь будем иметь:
агс с!^ х = -2 агс с^ л: = -^ Ы — агс с*& (— лг)] =
те , 1 те .1
= -2 * + агс 1§— = 2 агс 12 —•
VIII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
570. 51П х 51П 2л; зш Зх = -й- 51П 2* соз 2л;,
зт 2л; (2$1П х зт Зх — со$ 2х) = О,
ап 2л; (со5 2х — соз 4л; — соз 2х) = 0, зт 2х соз 4лс = 0.
а) зт 2л; = 0, 2х = к тс, л;х = -у-;
571. 3(1—зтл;) = 2со52л;, 3(1 — $тх) = 2(1 — зш2*),
(1—зтл;)(1—2зтл;) = 0.
а) 1 — зтл; = 0, зтл; = 1, хх = 2#тс + -тг = (—"* '*;
6)1—2зтх~0, зтл^-н-, л:2 = *тг + (— 1)* • -|-(
6
293
о с
572. $т-^-х- соз-д-х 1
51П
3 . 5 ~~ х 3 .5
СОЗ -=- X • 51П -^- X СОЗ -г- X • 51П -^ X
0 0 0 0
3.5 .3 5 ,
С05-^- X • 31П-7Г- X — $1П-рГ-Х • СОЗ -у X = 1,
. / 5 3 \ , . 16 1 16 па , *
16 46+1 15 ,„, , 1ч
1ьХ=* ^ *» *в"^(4*+ 1)*.
573. 81П (л; — 20°). соз [90° — (х + 25°)] »
= соз [90° — (70° + х)} • 51п (65° — л:),
51П (л; — 20°) • соз (65° — х) — соз (х — 20°). 51п (65е — *)= О,
81п(л; — 20° — 65° + х) = О,
31П (2х — 85°) ^ О, 2х — 85° = 180° . А,
2х = 180° к + 85°, х = 90°А + 42,5°.
574. 1§ (х + 30°) *в (х — 60°) =* с!§ [90° — (х + 30е)] X
х {§(л;_60о) = с!§(60°-х)1б(л:-60о) = - 1.
Отсюда видно, что данное уравнение не имеет решений.
575. $1П 2х + 51П х + 1 + соз 2х + соз х = О,
2 81п л; соз л: + зт х + 2 соз2 х + соз х = О,
зт х (2соз х + 1) + соз х (2соз л; + 1) = О,
(2соз х + 1) (зт л; + соз х) = 0.
1 2
а) 2соз х + 1 = 0, соз л; = ^-, д^ = 2& тс + -^- тс;
б) 51П х + соз л: = 0, 1§ х = — 1, *2 = А тс т- тс.
576. 51п 2х + 2з1П 2х соз х = соз л: + 2соз2л:,
зт 2л: (1 + 2соз х) = соз л: (1 + 2соз х),
(1 + 2 соз х) (2з1П л; соз л; — соз х) = О,
(1 + 2соз х) соз х (2з1П л; — 1) = 0.
1 2
а) 1 + 2соз х = 0, соз л: = к-, хх = 2& тс + -у тс;
*ч л 26+1
б) соз л: = О, х2 = —^— тс;
1 тс
В) 2 31П X — 1 = О, $1П X = -у, ЛГ3 = Л тс + (— \)к • —.
294
577. 81П Зх + 81П X — С08 X =а О, 231П 2х С08 X — С08 X = О,
С08 X (2з1П 2Х — 1) = О.
а) соз х = О, хг =
26+1
2
-тс:
б) 2зт2*—1 =0, яп2х=а-р2*«Ате + (—О*- -^-,
578. соз 7 * + соа* — (соз2 2л; — зш2 2х) = О,
2соз Ах соз Зл: — соз Ах = 0, соз 4* (2соз Зх — 1) = 0.
ч л„ л л 2* + 1 2Л+1
а) соз 4л: = 0, 4л: = —^— те, ^ = —~-—те;
б) 2созЗл: — 1 = 0, созЗл; = -1, Зх = 2#тс ± -|-,
2 ь , те
*з ^ ~ ТС ~ "9"*
579. 51 п х соз л: (зш2* — соз2*) = -^-,
-2-зт2л;(—соз2х) = -т-, т-зт4л; = -7-, зт4л: = —1,
л л е. тс >• 4& — 1 46 — 1
4л; = 2к тс ^-, 4л: = —^—7С» * ~ —§— те#
580. 2 соз 4х соз х + 2зш 4л; соз х = 2 (соз -^- соз 4л; +
+ зш-^- 81П Ах), соз х (соз 4л; + 81п 4л;) =»
е= 1у- (соз Ах + 51п 4л:), (соз 4л; + зш Ах) (соз х -^—)=0.
а) соз 4л; + зш 4л; = 0, {§ Ах =а — 1, 4л; = &тс ~,
46 — 1
-тс:
16
^ >^2 п "^2 0, , тс 86±1
б) СОЗ Л: — ^-у = О, С05Х = •—-, Х2 = 2А тс ± -^- = —^— тс.
581. 31П х + 51П Зх + зш 2л; + зт 4л; = О,
2з1п 2х соз х + 2з1п Зл; соз х = 0, соз л; (зт 2л: + зт Зл:) = О,
5 1
2 соз х 51п -у- л: соз -у л; = 0.
а) соз л; = 0, л;х = —~— *'•
295
б) 51П-75-л: = 0, -о-х = #1г, х2=-^-кт:\
В) СОЗ -тг- X = О, -75" X = 75"" ТС» *3 = (2^ + О 1С.
582. -у- (соз 2* — соз Ах) = -у, соз 2х — соз 4л: — 1 = О,
соз 2л; — 2соз2 2л: = 0, соз 2л: (1 — 2 соз 2х) = 0.
2* + 1
а) соз 2х = 0, 2л: = —±
тс, хл =
2* + 1
б) 1 — 2соз 2л: = 0, соз 2х = -у, 2л: = 2& тс ± -|-,
о 6к ± 1 6* ± 1
^* = о ТС, Л"2 = тд ТС.
583. соз2л; • созх • зт Зл* + зт2* «мпх- соз Зл: = —,
1 1 3
соз2л: • -у (зт Ах + 31 п 2х) + зт2* • -у (зт 4л: — зт 2 *) = -^-,
81П 4л; • (СОЗ2* + 51П2*) + 51П 2Х (С052Л: — 51П2*)
2 '
3 1 3
зт 4л; + 31 п 2х соз 2х = -у-, зт 4л: + -у зт 4л: = -у,
у-51п4* = -у, 81п4х = 1, 4л; = 2&тс-|-у,
4^ + 1
8
584. -у (соз х— соз Зх) + -у (1 + соз 2х) = -у- (соз л: —
— соз 9л:) + -у (1 + соз 8х), соз 2л: — соз Зл: + соз 9л: —
— со$8л: = 0, соз 2л: — соз 8л: + соз 9х — соз Зл: = 0,
2 зт Ъх • 81 п Зх — 2 зт 6х • зт Зл: = 0,
х 11
зт Зл: (зт 6л: — зт 5л:) = 0, 2зт Зл: . зт -у соз — х = 0.
а) зт Зл: = 0, Зх = к тс, х1 = —^-;
2
б) соз -^ л: = 0, -тг- х =
2
2к+ 1
тс, Х2 =
26 + 1
11
тс;
в) зт-у = 0, -у- = &тс, х3=2 А тт. Но при &=6/г ха=2Агтс.
296
Поэтому х3 заключается в хг и все решения уравнения
содержатся в формулах: хх = -^-, х2 =—т^— тт.
со- 1 4- соз 2х . 1 + соз 4х . 1 + соз 6* , 1 + соз 8х п
585. -2 + + 2 + 2 =2'
соз 2х + соз Ах + соз 6х + соз 8х = О,
2соз Зх • соз х + 2соз 7х • соз лс = О,
соз л: (соз Зх + соз 7х) = 0, 2соз х • соз 2х • соз 5л: = 0.
\ с л с 2& + 1 ~ 2* + 1
а) соз эл: = 0, эх = —^— тс, ха = —^— тс;
б) соз 2х = 0, л:2 = —т— тс;
\ п 2^+1
в) соз х = 0, *3 = —^— тс.
Но при к = 5п + 2 хг = —2— тс = хз- Поэтому все
решения уравнения содержатся в формулах:
2к+\ 2к+\
хх = —^— тс; х2 = —^ тс.
ГОл 1 — соз 2х , 1 — соз 4х 1 — соз 6х , 1 — соз 8х
58Ь. о 1 *-« = о Г
2^2 2 ■ 2
соз 2л: + соз 4х = соз 6л: + соз 8л:,
2соз Зх • соз * == 2соз 7х соз х, соз л: (соз Зх — соз 7х) = 0,
2соз х 81П 2* 81П 5л: = 0.
а) 31П Ъх — 0, 5л: = Л тс, л;1 = -^-;
б) 81П 2х = 0, 2х = к тс, *2 = -^;
в) соз л: = 0, л;3 = —^— тс. Но при & = 2/г + 1
#2 = —^— тс = х3. Кроме того, х2 при к = 2п дает те же
значения, что и хх при к = Ъп. Поэтому все решения
уравнения содержатся в формулах:
_ кп • _ 2&+ ]
Хх — "~5~~» *2 — 2 Л*
297
587. -1- (1 — соз 2х) + зт2 2х = -~ (1 — соз 6л:),
. « л СОЗ 2Х — СОЗ 6х /л • о л л • л г\
31п2 2х 2 = О, 31П2 2л: — 51 п 2х зт 4х = О,
81 п 2х (зт 4л: — зт 2а:) = 0, 2зт 2х • зт а: • соз За: = 0.
к к
а) зт 2а: =* 0, 2х = к тс, дгх = -у-;
б) соз ох = 0, ох = —2— тс> *2 = —ё— тс'
В) 31П X = 0, ДС3 = # 1С.
При к = 2п хг = л тс и содержится в а:3. При к = 2п + 1
^содержится в х2, если в х2 положить к = Зп+1.
Поэтому все решения уравнения содержатся в формулах:
26 + 1 ,
хх =—«—тс, А:а = #тс,
588. зт2 2а: = 2 — 2 зт2А:, 4зт2А: • соз2а: = 2соз2а:,
соз2* (2зт2х — 1) — 0, соз2* (— соз 2х) =0, соз2а: • соз 2а:=0.
а) соз*а: = 0, соз х = 0, хх = —^-^ тс;
б)соз2* = 0, 2а: = 2к + 1 тс, а:2 = 2* |* тс.
589. 51П4 у + СОЗ4 у + 251П2 ~ СОЗ2 у — 251П2 ~- СОЗ2 у =
= у, (81П2 т + СОЗ2 Т)-Т 51П2уХ = у, 1 - уЗШ2^ = у ,
. о 2 3 .2 , УТ 2 - , тс
51П2у* = -г-, 51П-д-Х = ± -Ц^—, -д- А: = #ТС ± -^-,
2 36 ± 1 36 ± 1
ТХ=—3— *• Л;==—2— **
590. соз4* + 51п4а:+2з1п2х соз2а: — 2зт2;с соз2* — 2зт 2а:+
+ -|- зт2 2а: = 0, (51П2а: + соз2а:)2 ^- зт2 2а: — 2зш 2а: +
+ -|- зт2 2а: = 0, 1 — 2зт 2х +-^ зт2 2х = 0,
5Ш22а: — 8зт2А: + 4 = 0, $1п2х = 4 — 2 ]/3" (4 + 2уТ> 1
и поэтому отброшено). 2а: = к тс + (— 1 )* • агс зт (4 — 2 У 3),
^ = -^ + 4" (- *)* агс 81п (4- 2КЗ).
298
591. 2(8ш2л;+ 1 — 1) = 3 (зшл:+соз*),
2 (2 51П X С08 X + 81П2Л: + С052ЛС — 1) = 3 (ЗШ X + С08 X),
2 [(31П X + С08 X)2 — 1 ] = 3 (ЗШ X + С08 *). ПОЛОЖИВ 81П X +
+ созх = у и сделав преобразования, придем к уравнению:
2у2 —3*/ —2 = 0, у1 = —^-, у2=2. Отсюда созл: +
+ 81п х = о- и соз х + 51п ^ = 2. Решаем первое:
д;=з
1/2зт(^+*) = --±-> 5Цх+*) = ~77г
= к тс — ( — 1 )* агс 81П —— ~, Равенство зш х 4-
х 7 2}/2 4
-(-соз* = 2 невозможно. Действительно, |.зтх + созл:| =а
= 1/Г|зт(^+х)|<уТ<2.
592. 51П* + созл; + -^-(2зт д; соз х + 1 — 1)==1, зтхЧ-
+ соз х + -у- [(31П л: + соз *)а — 1] =* 1. Положив зт х +
+ соз х = у и сделав преобразования, придем к
уравнению: у2 + 2у — 3 = 0, уг = 1, у2 = — 3. Второй корень
отбрасываем, так как | зтя + созл:] < У 2 (см. решение
задачи 591).
Итак, соз х + 51П х в 1, ]/2 соз I д; ~ ) = 1,
соз
^х—^ = у=, х 5~ =2Атг± —-; д^^г&тг,
(46+1) я
2
593. (1^^.)5 + (1±|1^)8 . 4"С054 2«
2+ 20 соз2 2* + 10 соз4 2л: 29 4 <>
" 32 = ТГ С0$ 2Х'
24соз4 2а: — 10 соз2 2х — 1 = 0, соз2 2* = -^±1 = -1-,
1,1 л 1 л п л 26+1 „ 26+1
■у+ у-соз4л: =-2", соз4* = 0, 4* =—^Г""*» х— 8 д*
299
594. Преобразуем левую часть уравнения:
соз2* со5 2х + соз Ах + соз Зл: соз х + 2 соз4л: =я
= соз2л: соз 2х + соз Ах + соз Зл: соз х + соз2л: (1 + соз 2х) =
— соз х (2соз х соз 2л: + соз Зх + соз л:) + соз 4л: =
«= соз х (соз Зл: + соз х + соз Зх + соз #) + соз 4л: =»
= соз х (2соз Зл:+2соз л:) + соз 4л: = 2соз х соз Зле +2соз2 х +
+ соз Ах = соз Ах + соз 2х + 1 + соз 2л: + соз Ах = 1 +
■+■ 2 (соз 2* + соз 4л:) = 1 + 4 соз Зл: соз х.
Теперь данное уравнение запишется так:
1
1 + 4соз Зх соз х •■
X
251П ~2~
Умножим обе части уравнения на зшл:. Получим:
31П х + 4 31П х соз х соз Зл; = —, зш х 4-
251П -о"
251П -у СОЗ -у
+ 2з1П 2л: соз Зл: = , зш х + 31П Ъх — 31П х =а
2зт -у-
= соз -~, 51П Ъх = соз -—-, соз / ~ 5л:) = соз —-,
, х я с I о *. 4& + 1 4& + 1
± "2" = "2 + ТС» ** ^ —П 7Г' *2== §—*'
Но, умножая уравнение на $тх9 мы могли ввести
посторонние корни, которые, являясь корнями уравнения
51П х = 0, имеют вид х = /г тс. Из формулы для л:х и л:2
видно, что п не может быть четным, т. е. эти формулы
не могут дать чисел вида 2т тс. Таким образом,
посторонние корни, если они есть, имеют вид (2т + 1)тс.
Приравняв значение (2т + 1) тс сперва хи а потом л:2, найдем
, 11т+ 5 , 9т + 4 п ,
к = о"1— и к = —^—. Следовательно, в формуле
. , И/я + 5 . , , 9т + 4
для хх кФ ———, а в формуле для х2 к Ф —^—,
причем в первом случае т нечетное, а во втором—-
четное.
300
595. Преобразуем правую часть уравнения:
\{>х\2(60°-х)с\2(30°-х) = 12х. ^7** X
1 + у 3 1§ х
УТ+Х&х __ Ъ\&х-\&х __ 21&х + (\ — \$*х)\%х _
X
1 — /3*б* 1-31б2* (1 — 1^а д:) — 2*б2^
2*6* , ,
1-*е2*+^* _ *е2х + се* _. «
*= 1 2*6* , 1 — *б 2х 1^ л: ~ 1*ох>
!~ 1-18»*'***
Теперь уравнение запишется так: 1§5х = 1§3х. Реша-
к к
ем его: 5х = кп + Зх, 2х = кп, х = -у. Но при
к = 2/п + 1 обе части уравнения не имеют смысла.
Следовательно, нужно считать к = 2/п и л: = /п тс.
-ЛЛ , . СОЗа X — 31П2 X
596. С05л: + 51пл;= —=—=—:-= д-: »
1 СОЗ2 X + 51П2 X — 231П X СОЗ X '
С052* — 51Па* , . СОЗ * -4- 81П ДС
СОЗ X + 51П X = "т : г-"» С08 X + $\П X = ^ ,
* (СОЗ * — 81П X)2 ' СОЗ X — 81П * '
(СОЗ X + 31П ЛГ) (СОЗ X — 51П А: — 1) = 0.
а) со5Лг+31па:=0, щх= — 1; Хх=кк — -^ = —^—тс;
б) созл; — зт* = 1, У2со$(-^- + х) = 1,
005^ + *)=-^=.; -^- + л: = 2&тс±
1_;; " + х = 2^тс±4-
|/ 2 4 — 4
46—1
Х2 = 2& тс, Х3 = 2 тс'
597. 1§л: + 1§2л: = {ёЗл:, ^^(1 - *е**б2*) =
= 1§За:, 1§Зл:(1 — 1§ л: 1§ 2л:) = 1§ Зл:,
1ё Зл: —1§ д: 1§ 2л: 1е Зл: = 4§ Зд:, 1§л:1§2л:1§3л: = 0.
а) 1елг = 0, лг2 = *тс;
б) 1§ 2л: = 0, х2 = ~^-\
в) 1§ Зх = О, *з = -у-.
301
Но при к = 3п хъ = пк = хг. Кроме того, при к = 2п
получим для х2 то же значение, что и для хг при к=3п.
Если же учесть, что х = —=— тс не может быть корнем
уравнения, то все решения содержатся в формуле
х= —
598. сс$ * "5|" х (со8«*+81п'*+2зт х соз х) = со3 * + &'т * ,
созх ч ' созх '
(СОЗ X — 31П X) (С05 X + 31П Х)г = С05 X + 51П ЛГ5
(соз # + З1п л:) (соз2л: — зт2* — 1) = О,
(соз х + $*п х) (со§ 2х — 1) = 0.
тс 46—1
тс;
а) С05Х + 5т*=0, {§* = —1; х^кп — -^
б) соз 2х — 1 =0, соз 2л: = 1; 2х = 2к тс, х2 = к тс.
599. Преобразуем левую часть уравнения:
(1в х + Ц Ах) + <48 2х + (§ Зх) = ^^ +
81П Ъх 51П Ъх (СОЗ 2х СОЗ Зх + СОЗ X СОЗ 4*) __
"• соз 2х соз Зх соз х соз 2* соз Зх соз Ах
51П Ъх [СОЗ 2Х (4С053Х — ЗС03 X) + СОЗ X СОЗ 4*]
"~~ соз х соз 2х соз Зх соз 4х
51П Ъх [соз 2х (4соз2х — 3) + соз Ах] 31П Ъх (4соз2 2х — соз 2х — 1)
6=5 соз 2х соз Зх соз 4х соз 2х соз Зх соз \х
. Приравняв это выражение нулю и освободив
полученное уравнение от знаменателя, придем к следующему
уравнению, равносильному данному:
31П Ъх (4соз2 2х — соз 2х — 1) = 0.
Решаем его:
а) З1п Ъх = 0; Ъх = к тс, хх = -^-;
б) 4соз2 2х — соз 2а: — 1 = 0; соз 2х = 1 ±*Г*7 ,
2х = 2& тс + агс соз ^ , х2 = к тс ±-2~агс соз -=-^—.
600. Преобразуем правую часть уравнения:
х 81П X 31П -о" + СОЗ X СОЗ -у
51П ^ (1§ ^ 1§ -о- + 1) = 51П X
X
СОЗ X СОЗ -тт"
302
(•-*)
С05 I X — -К- \ С05
= втх • = 51П л: • = = (& х.
X X С05* ь
С05 X С05 -о" С05 X С05 о
Следовательно, данное уравнение эквивалентно такому:
{§* + с!§л: = {§*. Прибавим к обеим частям — 1§лс,
получим уравнение с!§х = 0, которое может быть и не
эквивалентно данному, но является следствием его. Из
* 2к4- I
последнего уравнения найдем х =—т-те- Однако при
таких значениях х обе части данного уравнения теряют
смысл. Итак, уравнение не имеет решения.
601. !-=.+ 1-=г = 2}/Т, $тУТ+со$У7=*
сов ух 5ту х
*= 2)/2"51п уТсоз УТ, УЧГзш (-— + У~х) =
*= Т/2"51П 2 Т/2Х, 81П 2 1/Г= 81П (-^- + УТ).
а) 2уТ=2^тс + ^ + 'К^ У^= 8^+1 ~
4
б) 2уТ=(2А+1)тг-(-^ + ^Г), т/Г^-^+А^.
Но при к = Зп"\Гх2 — п7~— тг = У1ГУ
Поэтому все решения содержатся в формуле
(8* + 3)* 2
х ~~ 144 * '
причем & принимает лишь неотрицательные значения, т. е.
О, +1, +2, ...
602. [&(х2 — х) = *б6, л;2 —* = 6 + &7г, *2 — х —
_(6 + *гс) = 0, * = 1*^25 + 4**. здесь * = 0, ±1,±
± 2, ... и # может быть мнимым, так как х2— л: остается
вещественным при найденных значениях х.
603. Уравнение |5т;с2| = 1 равносильно следующим
двум: 81П*2 =1 и 81п х2 = — 1 или одному зт2*2 = 1.
Из последнего находим:
1-с2082*2 = 1, со5 2х2 = — 1, 2*2 = (2к + 1)те,
303
#2 =—тр— тг, х= ± |/ —т-^; * = 0, ±1, ±2, ...
604. |л;| =—^— те, или х = ± —у— тг, где-Л = 0,
+ 1, +2, ...
605. х2 = 2&тс, х =±/2*7:; # = 0, ±1, ±2,...*
606. Так как 1§2х = 1§2|*|, то уравнение можно
переписать так:
Решаем его:
1 —С052|х| 1 —СОЗ |х| 1 л о, 1 /! I к/, . . , 1Ч
1 . о =-1 . , 1 — СОЗ2 # =(1~СОЗ Ы)(1+5111 Ы),
1 — 51Па | АГ | 1—51П|*| ' I I V 11/4 1 II/»
(1 — соз | х |) (соз | х | — 51П | х |) = 0;
а) 1 — соз|л;| = 0, соз|л;| = 1, \х\ = 2/гтг, к = 0, + 1,
+ 2,... Отсюда ±х = 2кп> х=±2кп9 или х1 — 2кк,
где & = 0, ±1, ±2, ...
б) соз | х | — зш | х | = 0, 1§ | х | = 1, | х | = к тс + -^-, где
* = 0, +1» +2, ... Отсюда ± х = кп + -^-, или х2 =
4^ + 1 -_ 46 — 1 г, л 1 о
■л и х3 — 2 1с, где к = 0, 1,2, ...
607. Уравнение не имеет корней. Действительно, так
как 151П а | < 1, то произведение двух синусов может
равняться единице только в одном из следующих случаев:
а) 51П 2х = 1, зш 6х — 1; б) зт 2х = — 1, зш 6х = — 1.
Рассмотрим первый случай. Будем иметь х = —~- те
4/ -}-1 ^
и х = —^— тс. Сравнивая наиденные значения х,
получим: 4*|* тс= 4/+1 тс, 3(4/4-1) = 4/+1, 12^+3=4/4-1,
12& = 4/ — 2, 6^ = 2/ — 1. Но четное число не может
равняться нечетному, и, следовательно, первый случай
невозможен. Так же можно показать, что и второй
случай невозможен.
* Здесь, как и в задаче 602, х может быть комплексным, лишь бы
х2 был вещественным.
304
Докажем это же по-другому. Сделаем следующие пре*
образования:
1 — зт 2* зт 6х — О, 1 ^~ (соз Ах — соз 8л:) = О,
2 — соз Ах + соз 8л: = 0, 1 — соз Ах + 1 + соз 8л: = О,
2зш22л: + 2со524л: = 0.
Последнее возможно в том и только в том елучае,
когда 51 п 2л: = 0 и соз Ах = 0 совместно. Из полученных
уравнении находим, что х = -у- и х = —^— тс.
Отсюда: -у-= —тт—*; 4& = 2/ + 1, что невозможно.
51П X + СОЗ Я ч /7)" 51П2 * + С052 X
608. "п» + со»»у2-=
С1П V ГГкС V »
51П # СОЗ X ' ВШ* X СОЗ23 X
У2 (зт л: + соз х) зт # соз х =1, 2зт/~ + лпз1п*созлг=1,
зт/-^- + л:) 31П 2л: = 1. Последнее возможно тогда и
только тогда, когда: а) ^п[-^- + *) = 51п2х = 1 или
б) 51П (-^- + х) = зт 2лг = — 1. В первом случае получим:
-^- + х = 2кт: + ~^ х1 = -^-+2кк 2х = 2пк + -^-,
х2 = -~ + я *• Так как должно быть л^ = л;2, то решение
будет х = -^- + 2к тс. Во втором случае получим: -^- +
+ х = 2к тс ^-; х3 = —^— л и 2л: = 2/г тс ^-,
4п — 1 тт 4л — 1 , 8/г — 3
#4 = —^— тс. Но —^— тс Ф —^— тс, потому что в
противном случае было бы Ап — 1 = 8& — 3 или
2п = Ак—1, что невозможно. Следовательно, второй
случай отпадает, и все решения данного уравнения
содержатся в формуле х = -^- + 2к тс.
609. зт Зх + зт 2л: — т зш х = 0, зш 2л: соз х -+-
+ соз 2л: зт х + зт 2л: — т зт л: = 0, зт х (2соз2 л: + соз 2л:+
+ 2соз х — т) = 0, зт л: (4соз2 х + 2соз л: — т — 1) = 0.
20 К. У. Шахно 305
Отсюда: а)51П*=0, х=кп; б) 4со$2д;+2со$л: — т— 1=0,
1 ± V 4т+ 5 п
созл; = ^—!—.Для вещественности созл: нужно,
5
чтобы было 4т + 5 > 0, т. е. т > —. Следователь-
5
но, при т < т- уравнение 4соз2 х + 2со$ х — т — 1 =0
не имеет решения. Если /л > ^-, то еще нужно,
чтобы при этом значении т было бы |со$х| < 1, т. е.
чтобы выполнялись неравенства:
«)
1 + У 4т + 5
<1; Р)
— 1 — 1^ 4т + 5
<1.
Рассмотрим случай а). Должно быть: | — 1 + У4т + 51 <4
или — 4 < — 1 + У4т + 5 < 4, или — 3 < У 4т + 5 < 5.
Но левое неравенство всегда справедливо, а» для того,
чтобы выполнялось правое, нужно, чтобы 4т + 5 < 25,
т. е. т < 5. Если же учесть неравенство т> —, то
в рассматриваемом случае должно быть — -т- < т < 5.
Рассмотрим случай Р). Должно быть: | —1—У4т + 5 [< 4
или — 4 <— 1 — 1/4/п + 5<4, или т<1, а с учетом
5 5
т > ^-, ранее найденного, получим ^~ < ^ < 1-
Итак, уравнение имеет следующие решения:
5
1) х — кп, если т< ^~;
2) *! = 6 тг; х2 = 2А тг ± агссоз -1 ±/4т + 5 ?
5
если 4~< /п < 1;
3) хг = ктс; х2 = 2# тг ± агссоз 1—^ —»
если 1 < т < 5;
4) х = кп, если т > 5.
610. -^-т,со^т:х = кп-\- (— 1)*- -^-, со$тг^=!
= ~5" ^ + 1о ■ Так как | соз тс # |<! 1, то из всех
к = 0, ±1, ±2, ... можно взять лишь & = — 1, & = 0,
306
й=1, все же прочие дадут для |созтсл;| значение > 1,
что невозможно. При к =— 1 получим созтсх = =—
17 / 7 \
*-"-1п" = —Го"' ** = 2я тс + агссоз (—г~г), хг=2п±
± — агссоз (—го-); при к = О будем иметь: соз тс л; = -^,
тс х = 2п тс + агссоз -^, х2 = 2п ± — агссоз -^\ при к = 1
получим: соз тс л; := -^ ^- = -у, тс л: = 2п тс + -«-,
х3 = 2п± -др.
611. Уравнение можно записать так: 51п (тс соз л:) =
с= ^[у4- тсз1п дс). Пользуясь условием равенства
синусов, получим:
тс 4&4-1
а) тс соз х = 2к тс + -«■ — Л 81п * или 8*п х + С05 ^^~~?~»
б) тс соз л: = (2А + 1)тс — (-| тсзшл;] илисозл:—$тх =
4к+ 1
— 2 в
4& -4- 1
Решаем первое уравнение: зш х + соз х = —^-—,
1^2"со8 (л: у-) = -^^-, со$ (*~ ~г) ^ ^ТТ"' 0чевиА-
но, чтобы —^=- было по абсолютной величине меньше
2К 2
единицы, из всех чисел 0, ±1, ±2, ... для к нужно
1
2|/Т **
взять только нуль. Поэтому соз (л:—^-]
= 2/г тс + агссоз —— + -^-. Решаем второе уравнение:
46+1 т/о" ^ . *^ 46 + 1 / .
соз*— 51п# = —^—, у2соз(л;+-^-1 = —^—» соз 1л: +
+ -^-) =—--==--• Подобно предыдущему случаю и здесь к
может быть равно только нулю. Поэтому соз(л;+ -^-) =
1 1
= —=» #2 = 2ятс + агссоз —;=^-^-, или> объединяя
2у 2 2 2/2 4
с *!, получим л; = 2ятс + агссоз — ± -^-.
20* 307
612. Перепишем уравнение так: {§(*Н§*) =*
= 1§ [-^—тсс1&;м. Пользуясь условием равенства
тангенсов, получим:
тс1§л; = б7г + -тр — *с{§л; или {§* = & + — — с1§*. (*)
Следует иметь в виду, что те корни уравнения (*),
которые дадут тангенсу значения вида —^— или
котангенсу значения вида т (т — целое), если они вообще
существуют, не будут являться корнями данного, потому
х 2т + 1 .
что при т§ х = —2— или с*§ х = т теряет смысл левая
или правая часть данного уравнения. Такие корни
уравнения (*) при определении корней данного должны быть
отброшены.
Уравнение (*) эквивалентно следующему: {$*х = к +
+ "3 Т?ГИЛИ {^х— (*+-г)*в* + 1 = °- Решая
. 2к + 1 ± 1/(2^ + 1)2—16 п
последнее, найдем 1§х =—■ ^—!— . Для
вещественности \&х должнобыть: (2к + 1)2> 16, | 2к+1 |>4.
Следовательно, к не может быть равно 0, ±1, —2.
Кроме того, должны быть исключены те значения к,
которые дают 1§# = т~^ . Для того чтобы 1§д; = т2+ ,
необходимо, чтобы (2&+1)2—16 было квадратом
нечетного числа, т. е. чтобы (2к + I)2 — 16 = (2/ + I)2.
Отсюда получаем: (2к + I)2 — (2/ + I)2 = 16, (2к +
+ 1 +2/+ 1)(26 —2/) = 16, (к + 1+ \){к — I) = 4 или
ш) = 4, где положено и ~ к ~\-1 + I, V — к — /. Таким
образом, нужно решить в целых числах уравнение ию = 4,
причем и и V — числа различной четности, потому что
и + V = 2& + 1. Таких решений будет четыре: иг= 1, 1^=4;
ы2 = 4, 1>2=1; и3 = — 1, у3 = —4; и* = — 4, у4 = —1.
Первое и второе решения дают 2& + 1 = и + у = 5, а
последние два 2к + 1 = — 5. В первом случае к = 2, а во
5 4- 3
втором & = — 3. Но если к = 2, то {§ х = —-—, причем
только 1§ х = -о- должно быть исключено, так как левая
часть данного уравнения в этом случае не определена.
308
Второе же (1§ х = 2) приводит к решению х = пк + агс{§ 2.
5 + 3
Если к = — 3, то 1§д; = ^—, причем только
{§ х = 2~ должно быть отброшено, а 1§ х = — 2
приводит к решению х = я тс — агс{§2. Итак, данное
уравнение имеет следующие решения:
* о , * 26+1 + /(2*4- 1)2-1б
^! = птг ± агс!§ 2, *2 = я тс + агс1§ —-— 4— ;
к = + 3, ±4, ±5, ...; п = О, ±1,4 2, ...
613. -1 ^созг.г^"^^-, созг-г^^о,
26 + 1 сУ=~х 2к + 1
2.2'" =^2^*, 2Г =-±1^1с,/_х =
^10^^-^тг, }/^ = 1о§2(2*4-1)*-2,
# = — [1о§2 (2& + 1)тс — 2]2. Так как У— х —
арифметический, то 21^^> 1, т. е. ^—тс> 1. Это значит, что
к — 1, 2, 3, ..., а быть отрицательным или нулем & не
может.
614. 1о^,81п* + 1гЕ=^-2 = 0.
(1оёсо8 х 51п *)2 — 21°ёсо8 * зш * + 1 = О,
0°§соз д. 51П Л; — I)2 = 0, 10§С08 Х 51П X = 1, С05 * = 51П Л:,
{§* = 1; л; = 2к тс + -^- = —^— тс- Здесь нельзя было бы
написать * = к тс + -^-, потому что зш л: и соз х, являясь
основаниями логарифмов, должны быть положительными.
615. X2 + 2Х 81П (ОД) + 51П2 (Ху) + С052 (ОД) = О,
[х + 51п (ху)]2 + со52 (од) = 0. Следовательно, должно быть
С052 (ху) = 0, х 4- З1п (од) = 0. Из первого уравнения
находим од = к тс + -тр а тогда из второго получим
х=—зш (&тс +-у-1. Если й = 2л4-1, то хг = 1,
3
г/х = 2л тс 4- -о" тс- Если & = 2л, то *2 = — 1, у2 = — 2я тс —
^- = 2/п тс 4- -у тс; (— п = т + 1).
309
616—627. Указание. При решении уравнений, в
которых неизвестные находятся под знаком обратной
тригонометрической функции, часто приходится находить синусы
(или косинусы, тангенсы и т. д.) обеих частей равенства.
При этом следует иметь в виду, что получающиеся
уравнения, вообще говоря, не будут равносильны
исходным. Например, А = В и $т А == зт В, вообще говоря,
не равносильны. То же следует сказать об уравнениях
А = В и {§ А = 1§ В и им аналогичных.
616. Не имеет решений, так как 0 <агссозх <тс,
а здесь агссоз х = —^- = 3,15 > тс.
617. Имеем агс зт х =-т— агс*§у- Отсюдазт (агсзтл:) =
= зт (-| агс!§ -у) или х = зт -^ соз I агс!§ -у-) —
п . / . 1\ 1 1 1 1
— соз-гзт/агс^-^- =—т= • —г -= • —_ =
= -=-. Проверку найденного значения х проще всего
осуществить с помощью теоремы: если зт а = зт р,
причем а и р — главные значения арксинуса, то а = р (см.
указание к решению задач 538 — 569). В данном случае
агсзт -г- = а, а -|— агс1§ -у- = р. Так как 0< агсзт -^ <
<-Г и 0<-^^агс1ё-^<-|-, т. е. 0<а<-^
и 0 < р < -^-, кроме того, доказано, что зта = зт р, то
п • 3 тс . 1
а = р или иначе агсзт-^- = -^ агсх§-у.
618. Взяв косинус от обеих частей равенства
и воспользовавшись формулами задачи 541, получим:
соз (агсзт х -\- агсзт 2х) = соз ~,
соз (агсзт х) соз (агсзт 2х) — зт (агсзт х) зт (агсзт 2х) =
= _^э у 1-х2 У\—Ах2 — 2х2 = \, У\—х2У\—Ах2^
= 2х* + ±~, (1-х*)(1-4х*) = (2х* + ±)\ 1-5*2 +
310
х = !_1/~з-
*« 2 У Т*
Значение х2 < 0 не удовлетворяет данному уравнению,
так как в этом случае левая часть уравнения имеет
отрицательную численную величину, а правая —
положительную. Чтобы проверить первый корень хх > 0, положим
агсзш хх = а, а агсзш 2лс, = р. Так как 0 < а < -^-,
О< Р < -у, 0 < а + Р < тс и угол-^- тоже принадлежит
промежутку (0, тс), то из равенства соз (а + р) = соз -^-
следует равенство а + Р = -у-.
Замечание. Здесь была использована теорема: если
соз а = соз р, причем а и р— главные значения
арккосинуса, то а = р (см. указание к решению задач 538—569).
619. Возьмем косинус от обеих частей уравнения и,
воспользовавшись формулами задачи 541, получим:
соз (2 агсзш х)=соз (агссоз 2х), соз2 (агсзш х)—зш2(агсзш х) =э
= 2л:, (1 — х2) — х2 = 2*, 2*2 + 2* — 1 = 0; хх = ^3~! ,
я -_ _ г 3 + 1 . Второй корень посторонний (|х2| > 1).
Чтобы испытать корень хг > 0, обозначим агсзш хх = а,
а агссоз 2хх = р. Так как 0 < 2а < тс и 0 < р < тс, то из
равенства соз 2а = созр следует равенство 2а = р (см.
примечание к задаче 618).
620. Взяв синус от левой и правой частей уравнения,
получим: 81П (2 агссоз х) = зш [агсзш (2х У 1 —х2)],
2зш (агссоз х) соз (агссозх) = 2хУ\ — х2, 2х]/ 1 —х2 =
= 2х У 1 — л:2. Полученное равенство есть тождество,
однако это еще не значит, что любой х, для которого
|*| < 1» удовлетворяет данному уравнению. Так как
агссоз* всегда неотрицательный, то, как видно из
данного уравнения, 0 < агсзш (2х У 1 — х2) < -^-. Отсюда
получаем 0 < 2агссоз х < -^- или 0 < агссоз х < -^-. Следо-
вательно, —= <# < 1.
311
621. 51П (агс З1п х) = зш (2агс зш х ]/~2),
х = 2зш (агсЗ1п х)/~2) соз (агс зш ^|/"2), х=2х ]/"2 }Л—2*2.
Решив полученное иррациональное уравнение, найдем:
Л ут ут „
хг = О, х2 = —4~, х3 = т—. Корень агх, очевидно,
удовлетворяет уравнению. Испытаем корень х2. Имеем:
1/~7~
О < агс 81 п х2 < -у, агс зш *2 ]/2 = агс З1п —-г- • /2 >
> агс з1п -у- = -^-, 2агс зш х2У2 > -|-. Итак,
оказывается, что при х — х2 численная величина левой части
уравнения меньше-^-, а правой — больше-^-. Следовательно,
х2 — посторонний корень. Легко убедиться, что и х3
посторонний. Данное уравнение имеет только один корень
* = 0.
622. Запишем уравнение так: агс соз х — агс зш х = -^-.
Но агсз1пл; = -2 агс соз л: (см. задачу 539). Подставляя
это значение агсзшх в предыдущее уравнение, получим:
3 »
агс соз х — (-5 агс соз х ) = •—-, 2агс соз х =
агс соз х = -^-, ^ = соз -^- = "2~
1/1 х2
623. 1§ (агс соз х) = *е (агс *8 *)» -1—^ = х>
х2 == 1/1 — *2, х4 + *2— 1 = 0. Последнее уравнение
_1—2 '
х2 = — "V/ 2~~ . Корень х2 < 0 не удовлетворяет
данному уравнению, потому что агс соз *2> 0, а агс 1§ *2<0.
Значение х = хг удовлетворяет уравнению, так как
0< агссозх2< -^- и 0 < агс1§л;2<-^-.
624. Перенеся второй член из левой части уравнения
в правую и взяв тангенс от обеих частей уравнения,
получим
*_1+*_+1 Ъх-х или 2д:(4д:2— 1) = 0.
1_(л_1)(х+ 1) 1 +3х-х
312
Последнее уравнение имеет корни: хг = О» х2 = —,
1
х3 = о- и все они, как легко проверить,
удовлетворяют данному уравнению.
625. Взяв синус от обеих частей уравнения и
воспользовавшись формулами задачи 541, получим
Так как корни подразумеваются арифметические, то
последнее уравнение противоречиво. Следовательно, данное
уравнение не имеет решений.
626. Возьмем косинус от обеих частей уравнения и
воспользуемся формулами задачи 541. Получим:
1-х2 1 Г /х-.хя.2„
X ' 2, ,
/' + (тЫ
» 1 — х2 2
(1— л:2) 1/(1 — х2)2 _ 4хУх2 У(\ — х2)2 1_
(1+*а)а (1 +х2)2(\— х2) ~~ 2
(*)
Так как 0 < агс соз 1 ~*2 < тг и ^- < агс 1§ 1_У 2 <
< -|-, то для того, чтобы левая часть данного
уравнения была — 7г>7г, должно быть агс соз ~ *2 > -|-
и агс 1§ 1__^2 > 0. Отсюда {~^2 < 0, ^^ > 0 и,
следовательно, х2 > 1 и *•< 0.
Возвращаемся теперь к уравнению (*). Входящие
в него корни должны быть арифметическими и поэтому
У(\ — х2)2 = х2 — 1, Ух2 = — х. Теперь уравнение (*)
можно записать так: — ^ ^ — (1 + х2)2 = ^-. Но
313
это невозможно, так как левая часть равна—1, а
правая—^. Следовательно, уравнение не имеет решений.
627. Взяв тангенс от обеих частей уравнения и сделав
некоторые преобразования, получим
а а-~Ь
_ Т а + Ь __ аа + 6а _ 1
Х ~~ 1 _а_ а — Ъ ~~ Ь2 + а3 ~~ Ь
+ Ъ а + Ь
Сделаем теперь испытание найденного значения х. Левая
часть данного уравнения при х=1 дает -^-. Выясним,
даст ли правая часть-^-. Пользуясь условием равенства
тангенсов, можем написать
Замечая, что 6 Ф О (иначе данное уравнение теряет
смысл), перепишем последнее равенство так:
агс 1§ ~ + агс 1§ — = + + к я
» ь
или
агс1§г/ + агс1§т^|- = -|-4-^^ где # = -|-.
Так как —-|~<агс1§«/<-|-, ~ < агс1ег=^<-|-
и — я < агс {{*г/ + агс 1§ . ~У < тс» то к может равняться
* ~| У
только 0 или—1. Итак, получаем, что агс1&у-\-
. \ — у п . , а 1 — У 3
+ агс^т+7 = Т или агс*8» + агс18т+7в Г71'
Если 1 + у < 0, то, очевидно, ■•—^ < агс \&у < О,
^<агс1е4Д<0» -*<агс1б{/ + агс1е^<0.
Ясно, что в этом случае правая часть будет равна
т~ ^ и, следовательно, х = 1 не будет корнем
уравнения. Если 1 + у > 0, то агс1§# и агс!е 1 ~7У будут в
314
промежутке 0<у< 1 неотрицательны и их сумма может
быть только положительным числом, а в промежутках —
— 1 < */ < О и 1<#< + со они будут разных знаков,
и их сумма будет находиться между — -^- и +-?г. В этом
случае
агс*§*/ + агс*§ у^р^ = агс 1^^ агс{§т^=—.
Следовательно, при -г- > *— 1 уравнение имеет
единственное решение х~ 1. В прочих случаях уравнение не имеет
решений.
628. Взяв синус от обеих частей уравнения, получим:
81П (аГС 51П X) = 51П (аГС 51П й + ЯГС 51П Ь),
х = аУ1 — Ь2 + ЬУ1—а2.
Испытаем это значение х, подставив его в данное
уравнение. Это даст
агс 51*п {а у\ —Ь* + 6 К1 — я2) = агс зш а + агс з1п Ь,-
Последнее равенство является тождеством, если аЪ < О
или а2 + б2 < 1 (см. задачу 560). Конечно, кроме того,
предполагается, что |а| < 1 и |Ь| < 1. При указанных
ограничениях, налагаемых на а и &, найденное значение х
будет единственным решением данного уравнения. Если
а и Ъ этим соотношениям не удовлетворяют, то
уравнение не имеет решения.
629. Из второго уравнения находим произведение
созясозу, используя первое уравнение. Получим:
. х зт х&ту 3 0 1
*& X Щ У » — = -_ __ в- 3, С05 ХСО$у = -г-.
& & V со$х со8 ^ 4соз хсо5у ^4
Поэтому данная система приводится к следующей
равносильной: со5 х со5 у = -^-, 51п х 51п г/ = —. Складывая
почленно полученные уравнения, а затем вычитая их и
пользуясь формулами косинуса суммы и косинуса разности
двух углов, придем к новой системе, равносильной
данной: со5(д: — у) = 1, соз(д: + у) = ^-у- Отсюда: х^-у=
2 к
= 2т тс, * + У = 2птг + — те, * = (п + ^)^ ±"з"» У = (л —
— т)тс±-~; /п = 0, ±1, ±2, ...; я = 0, ±1, ±2, ...
315
630. 5Ш*Х + Ж*у=±, 1-соз2Ж+1-соз2у==_3_>
сое 2х + сое 2у = -2-, соз (х + у) соз {х — у)=-~,
соз 75° соз(*-</) = -!-. С05(х-У) = 1^=4Шг =
соз 15° __ соз 15° _ соз 15°
6=3 4зт15°со5 15° ~~ 2зт30° "~ 2-0,5 ~ С05 15 '
Итак, соз (х — у) = соз 15°; х — у = 360° л ± 15°,
х + (/ = 75°; *!= 180° л+ 45° = (4л+1)45°,
у1= — 180° л + 30° = (— 6л + 1) 30°; *2 = 180° л + 30° =1
= (6л + 1) 30°, у2 = - 180°л + 45° = (- 4л + 1) 45°.
631. Во втором уравнении выразим тангенсы через
синусы и косинусы и затем подставим в него значение $тх
из первого уравнения. Получим: 1§ х = ]/3~1§ у, 81П* =
-./о-зтг/ У2~$'ту Т^зГзшг/ . ,-,/оГ
= 1/3 ^-> ^ = .1 ^. 51п у (V 2 соз и —-
г соз у соз л соз # ' У1К ^
— У^Гсоз*) = 0; а) зш у = 0, ух = & тт. Подставляем в
первое уравнение зш * = 0, ^ = пк. Итак, л^лтс, ух=А л.
Следующую группу решений получим из уравнения
б) У2 соз у — ]/3 соз * = 0. Решаем его:# У2 соз у =
= 1/Тсоз х, У2~соз у = ± УЪУ\— зш2*, /"2 соз у =
= ± У1Г У 1 — 2з1п2 у. Возводим обе части уравнения в
квадрат: 2соз2 у = 3 (1 — 2зш2 у), 2соз2 */ = 3 (2соз2 у — 1),
соз2 у = -^-, соз у = ±-^2~"» Уз = т тс ± "^"- Подставляем
найденное значение соз у в первое уравнение системы.
Получим: 51п х = ± У2 ]/ 1 -^ = ± "^"» *а = / ^ ±
+ -^-. Так как мы' возводили в квадрат обе части
уравнения, то необходимо испытать значения х2 и у2.
Подставляем во второе уравнение 1§ (/тс + -^-) = уъ 1е[/П7г±
± -|-). Период тангенса есть тс, поэтому можно напи-
сать: 1ё(±х)==>А^(±Т-)> ± 1 = КЗ-- ( ± р=-).
316
Итак, уравнение удовлетворяется, если брать
одновременно верхние или одновременно нижние знаки в обеих
частях последнего равенства. Подставляем в первое
уравнение 51п (ы ±-т-) = 1/251п[ттг ±-тН- Если брать
одновременно о§а верхних или оба нижних знака, то послед-
нее равенство можно переписать так: соз / тс • —^— =
= У2 со5 т тг • —, соз / те — со5 т те, (— 1)' — (— \)т.
Отсюда заключаем, что / и т нужно брать одновременно
четные или нечетные. Поэтому система имеет следующие
решения;
*!=/г7г, Ух—кк х2=1к + ^9 У2==тт: + ^ *3=/7Г — Т'
у3 = /П7г ^-; т, я, /г, / =■ 0, ±1, ±2, ... ,
причем I и т нужно брать одновременно четные или
нечетные.
IX. НЕРАВЕНСТВА
632. После приведения к общему знаменателю получим:
(тх + п)(а — Ь) — (рх + д) (а + Ь) (тх—п) (д+ Ь)+ (рх — д) (а—Ь)
а2 — Ь2 ^ а2— Ь2
Если а2 — Ь2 > 0, то неравенство после преобразований
принимает вид (тЪ + ра)х> па — (?Ь; если а2 — Ь2 < О,
то (тЬ + ра)х<%па — цЪ. Отсюда получим х > ^Т^ »
если (а2 — б2) (тб + ра) > 0; х < ^^^ , если
(а2 — б2) (тЬ + ра)< 0.
633. 4(8* + 3)-(7*-5) п 25*+17 п
8л: + 3 ^^ 8л:+ 3 ^ и*
а) 25л; + 17>0, 8л; + 3 < 0; х>— -^-, л; < — -|-;
-"4^<;с<_4; б) 25* + 17<0' 8* + 3>0> *< — §§>
з
л: > — -тг- • Это невозможно.
317
634. 2, + 2-6 + ,-2 >()> _|^>0> 3>0.
Неравенство справедливо при всяком х ф 2.
635. ^х±<0. а) 2— *<0, 2*>0. Отсюдах> 2.
б) 2 — а: > 0, 2* < 0. Отсюда х < 0.
636. Неравенство приводится к такому: (#— 1)(* +
+3)2>0. Последнее же равносильно неравенству х —1>0,
откуда х> 1.
637. 2Х3 — л: — 1 > 0, (2*3 — 2х2) + (2х* — 2х) +
+ (х— 1)>0, (а:— 1)(2а:2 + 2х+ 1) > 0. Но 2*2 + 2* +
+ 1 = -о- [(2л: + I)2 + 1] > 0. Поэтому неравенство
равносильно такому: дс—1>0. Следовательно, л:>1.
638. Неравенство эквивалентно такому: (л;— 1) (л: —
— 2) (х — 3) (х — 4) > 0. Корни многочлена, находящегося
в левой части неравенства, будут 1, 2, 3, 4. Расположим
их в порядке возрастания. Построим интервалы:* (— оо, 1),
(1, 2), (2, 3), (3, 4), (4, + оо). Крайние интервалы есть
условная запись того факта, что в первом случае *< 1,
а в последнем х > 4. При переходе х из одного
интервала в другой, смежный с ним, многочлен меняет свой знак,
так как границею смежных интервалов служит корень
многочлена. Поэтому для всех х какого-либо из
написанных интервалов имеет место постоянство знака численной
величины многочлена и чередование знака с + на — или
с — на + при переходе из интервала в интервал.
Следовательно, раз в первом из них многочлен положительный,
что очевидно, то он будет положительным также в третьем
и пятом интервалах. Итак, должно быть х < 1 или
2 < х < 3, или х > 4.
* Если а и Ь — произвольные вещественные числа а а < Ь% та
по определению:
1) интервалом (а, Ь) называется множество всех вещественных
чисел х, удовлетворяющих неравенствам: а < х < Ь\
2) сегментом [а, Ь] называется множество всех вещественных
чисел х^ удовлетворяющих неравенствам: а < х < Ь\
3) полусегментом [а, Ь) называется множество всех вещественных
чисел х, удовлетворяющих неравенствам: а < х < Ь\
4) полуинтервалом (а, Ь] называется множество всех
вещественных чисел х, удовлетворяющих неравенствам: а < х < Ь.
Интервал, сегмент, полусегмент, полуинтервал объединяются общим
термином промежуток. При этом нередко к слову промежуток
добавляют в первом случае открытый, во втором-«замкнутый, в третьем и
четвертом — полуоткрытый,
318
639. (*4 — х*) — (Б*8 — Ъх2) + (б*2 — 6х) < О,
х(х— 1)(х2 — 5л; + 6)<0, § л;(л; — 1) (х — 2)(х — 3)< 0.
Записав теперь интервалы (—оо, 0), (0, 1), (1, 2), (2, 3),
(3, + оо) и поступая как в задаче 638, получим решения:
0 < * < 1 и 2 < * < 3.
640. Данное неравенство равносильно следующему:
^2(х + А)(х + 3){х + 2)(х+1)(х-±){х-3)>0.
Далее, поступая как в задаче 638, найдем решения:
— 4<х< — 3, — 2<л;< — 1 и-^-<л;<3.
641. Данное неравенство равносильно неравенству
(*-!)(*-5) ^ п
(* + 3)(*-3) ^">
а последнее — неравенству (л; + 3) (х —=1) (х — 3) (лг — 5)> 0.
Поступая теперь как в задаче 638, найдем решения:
х< — 3, 1<КЗих>5.
642. Пользуясь теоремой Безу, напишем остатки от
деления данного многочлена на х — 1 инах + 3 и
приравняем остатки нулю. Получим: а + Ъ — 5 = 0; — За-\-
+ Ь -*- 9 = 0. Из этой системы найдем а = — 1, Ь = 6.
Разделив теперь многочлен х* + & — 7л;2 — х + 6 на
(х—1)(х + 3), получим в частном х2 — х — 2 и,
следовательно, можем написать х*+ х*— 7л;2 — х + 6 = (х — 1) (х+
+ 3)(*2 — х — 2) = (л;—1)(* + 3)(л; — 2)(*+1)>0.
Рассматривая интервалы: (—оо, — 3), (—3, — 1), (—1, 1),
(1, 2), (2, + оо), убеждаемся, что данное неравенство
справедливо, когда х находится в первом или третьм, или
пятом интервалах, т. е. должно быть х < — 3, или
*- 1 < х < 1, или х > 2.
643. Для этого должны одновременно выполняться
неравенства: Ь2 — 4ас > 0, •— < 0, — > 0, где ау Ь, с —
коэффициенты данного уравнения. Эти неравенства
равносильны следующим: — 2к + 3 > 0, к (к — 1) > 0,
(к — 1) (к + 3) > 0. Отсюда получим: а) к < -|-> * > 0»
к > 1, 'к > — 3, что дает 1 < к < —•; б) к < -|-> * < 0.
к < 1, к < — 3, что дает к < — 3.
319
644. Составим разность трехчленов. Получим (к — 4)д^+
+ (2к — 3) х + к + 4. Этот трехчлен должен быть при
всех х положительным. Но квадратный трехчлен имеет
знакопостоянную величину при всяком х, если его корни
комплексные, т. е. дискриминант отрицательный. При этом
знак совпадает со знаком коэффициента при х2.
Следовательно, должны совместно выполняться неравенства:
(2к — З)2 — 4(к — 4)(6 + 4)<0 и к — 4>0.
Из второго получаем &>4, а из первого — 12к + 9 +
73
-|- 64 < 0, 12к > 73, к > -г^-. Отсюда видим, что должно
быть к > -уу.
645. Так как дискриминант трехчлена Ах2 + 6* + 3
Отрицательный, то он имеет знак коэффициента при х2> т. е. знак
плюс. Поэтому неравенство можно переписать так: 2к х2 +
+ 2\х + \>4кх2 + бкх + Зк или 2кх2 + 2(3к — Цх +
-4- Зк — X < 0. Но трехчлен, находящийся в левой части,
не может быть отрицательным при всех х, потому что
коэффициент 2к при х2 — положительный (см. решение
задачи 644). Таким образом, данное неравенство не имеет
решений.
646. Данное неравенство будет удовлетворяться при
всяком х, если дискриминант данного трехчлена
отрицательный, т. е. если ф2 + с2 — а2)2 — АЬ2с2 < 0. Последнее
легко преобразовать к виду — \&р (р — а) (р — Ь) (р — с) <0,
где р — полупериметр. А это неравенство очевидное.
647. Для доказательства рассмотрим неравенство
(ах + Ьх х)2 + (а2 + Ь2х)2 + (а, + Ь3х)2 > 0,
справедливое при любых х. Дискриминант квадратного
трехчлена, находящегося в левой части этого неравенства,
должен быть < 0. Отсюда и вытекает неравенство Буня-
ковского.
648. Освободив уравнение от дробей, получим
уравнение
(а — 2)х* — (а— ^(р2 + <?2)*2 + ар2ц2 = 0.
Чтобы все корни биквадратного уравнения кх* + 1х2+ т = 0
были вещественные, необходимо и достаточно, чтобы
квадраты х\ и х\ корней этого уравнения были неотрица-
320
тельны, или, чтобы совместно выполнялись неравенства:
Р — Акт > 0, -у > 0, -^- < 0. Так как последние два
можно записать в виде тк> 0 и /& < 0, то для
уравнения задачи это будет выглядеть так:
(а — I)2 (р2 + </2)2 — 4 (а — 2) а/А/2 > 0, (а — 2) ар2?2 > 0,
(а-2)(а-1)(р2 + </2)>0.
Но первое неравенство выполняется тождественно. На
самом деле, учитывая, что
(а —2)а = [(а— 1)— 1][(а— 1)+ 1] = (а— I)2— 1,
это неравенство можно записать в виде (а — I)2 (р2 — <72)2 +
+ 4р2</2 > 0. Что касается двух других, то так как р2</2> 0
и р2 + ф > 0, то их можно записать так: (а — 2) а > 0,
(а — 2) (а — 1) > 0. Отсюда: а) а — 2 > 0, а > 0, а — 1 >0,
что дает а > 2; б) а — 2 < 0, а < 0, а — 1 < 0, что дает
а < 0. Итак, а > 2 или а < 0.
649. Неравенство равносильно такому: 2 — х ^ * "или
-^—— > 0, или (4дс — 3) (х — 2)< 0. Отсюда получим
-!-<*< 2.
650. Должно быть 3 — х > 0 или л: < 3. Если д;< 2, т. е.
х — 2 < 0, то неравенство будет выполняться, потому
что 1/3 — х — арифметический. Если же 2 < х < 3, то
возведение в квадрат неравенства даст: 3 — *> х2 — 4х -\- 4,
Х--&+К0, (*_1^)(,_1±^)<0. Это
значит, что должно быть """2— < д: < 2—, а если
еще учесть, что 2 <* <3, причем """ ^— < 2, а 2— < 3,
то получим 2 < х < —— . Соединяя с ранее
полученным результатом (х < 2), видим, что решения составляют
интервал I — оо, —^—I.
651. Должно быть х — 4>0 и Зле — 5 > 0, т. е.
х > 4. Предполагая это выполненным, возведем
неравенство в квадрат. Это даст Зх — 5 > х— 4 или х > -тр
Сопоставляя с х > 4, получим окончательно л; > 4.
21 к. У. Шахно 321
652. Прежде всего должны выполняться совместно
неравенства: х + 6 > 0, х + 1 > 0, 2х — 5 > 0, что будет
иметь место, если л: > ~2-. Предполагая это выполненным,
возведем обе части неравенства в квадрат. Тогда, после
преобразований, получим ]/ (*+ 1) (2л: — 5) < 5 — х.
Следовательно, х < 5, так как левая часть положительна.
Предполагая и это выполненным, снова возведем обе части
неравенства в квадрат. Тогда придем к неравенству
х2 + 7х — 30 < 0 или (х+Щ{х — 3)< 0, которое
справедливо при —10<л:<3. Сопоставляя с ранее получен-
5
ными неравенствами -у < х < 5, видим, что для их сов-
5
местности нужно, чтобы -^ < х < 3.
653. Так как должно быть (л: -+- 5) (3* + 4) > 0, то
отсюда заключаем, что должно иметь место х < — 5 или
4
*> д-. Если, кроме того, *< 1, то левая часть будет
отрицательной и, следовательно, неравенство будет вы-
4
полняться, если х < — 5 или д- < * < 1. Если же
х> 1, то, возведя обе части данного неравенства в
квадрат, получим после упрощений 1 Зхг — 5\х — 4<0 или
13 (х + -|з")(* — 4)< 0. Последнее будет справедливо при
гг<л;<4. Сопоставляя полученные ранее для л:< 1
4
неравенства л:< —5 и д- <*< 1 с полученными
теперь для *> 1, 1 <*<4, видим, что окончательно ре-
4
шения можно записать так: 1) х <— 5; 2) -—^- < л: < 4.
654. Система приводился к виду: Зу— 2х <—1,
— 1 . 3
-3— и У>т
2х 1 з
2у — 3*>0. Из нее получим у<—^— и у>-х-х. Сле-
3 ^ ^ 2х— 1
довательно, -у х < у < —г—, а соответствующие этим
неравенствам для у значения х определятся из неравен-
з . 2х— 1 2 Тх
ства -^- х < —д—, что даст х < — -^-. Итак, получим:
^ 2 3.. 2х-— 1
*<--5". -2"*<*/<—3~>
322
655. Решая каждое неравенство относительно у, по-
Лучим у > ^ и У > 5 ' ^ТИ неРавенства ОДина"
кового смысла. Решение относительно дс привело бы также
к неравенствам одинакового смысла Полученные
неравенства показывают, что х может быть произвольным, а у
должен быть выбран больше наибольшего из значений
~ и "~ х . Чтобы выяснить, какое из этих двух
3 2х 7 Ъх
выражений больше, решим неравенство—^—>—^—,
. 11 7 — Зл^ 3 — 2х
что даст х >- -7-, а затем неравенство —^—> —т—, что
даст х< -^-. Отсюда получаем: 1) у> ~ *, если
*<~4~; 2) у>—^—, если л: >—•
656. Из первого и второго неравенств находим:
У > *=^, у < -^. Следовательно, 1=^ < у <-^.
Что касается дс, то его найдем из неравенства—-у—- <
^ I 5 7 7
< —?—. что даст ^>-уо"" Итак, окончательно: ^>-|о"»
^<„<^±5,
657. Находим у из уравнения и подставляем его
значение в неравенство, которое решаем. Получим: Ъх +
+ 3- 168~7* > 121, 20*+ 504 — 21* > 484, *<20.
Таким образом, получаем решения в виде: х > 20,
168—7х
у-—,—•
Можно было бы найти х из уравнения и подставить
его в неравенство. Тогда решения получили бы в, таком
. 7 168 — 4*/
виде: у > 7, х = ^—-.
658. Так как л; > #2> 0, то система эквивалентна такой:
У > *2, У < "К*- Отсюда *2 < у < Ух. Для этого
требуется, чтобы х удовлетворял неравенству х2 < У~х> которое
можно переписать в виде л:4 < х или х(г*— 1)< 0, или
х (д; _ 1) <; о. Из последнего находим, что 0 < х < 1.
21* 323
Следовательно, решения системы можно записать так:
0<х<1, хг<у<У7.
659. Из уравнения находим у, подставляем его в оба
неравенства и решаем совместно систему неравенств.
Получим: х2 + <6-3*>2 >4, *.!^!<1или13д:2-36л;+
+ 20>0, Зх2 — 6* + 2>0 или 1з(х— -^ (х — 2^ > О,
г(х-1^1)(х-1±1±)>0. Отсюда: а), <-§.,
х < —^у-—. Следовательно, х < —=^ , у = ~ * ;
б) х > 2, л: > —^у-—. Следовательно, л: > 2, у = "Т *.
660. а) Если а > 0, то |а|=а, и данное неравенство
запишется так: а < Ь. Кроме того, —Ь < 0, а
положительное число и нуль больше отрицательного, и поэтому
— Ь < а. Итак, если а > 0, то — Ь < а < Ь.
б) Если а < 0, то | а | = — а, и из данного
неравенства получим — а < Ь или — Ь < а. Кроме того, 6 > 0, а
отрицательное число меньше положительного, поэтому
а < Ь. Таким образом, и в этом случае — Ь < а < 6.
661. Если —6 < а < 6, то —Ь<а и а<6 или
а + 6 > 0 иа-К0. Но тогда (а -+- 6) (а — 6)< 0 или
а2 —62<0. Отсюда: а2 < б2, |а|<6.
662. Пусть а и 6 любые вещественные числа.
Очевидно, — |а|<а<|а|, —16|<6<|6|. Складывая эти
неравенства почленно, получим — (| а | + | Ь |) < а + Ь < | а \-\-
+ \Ь\. Но тогда |а + 6|<|а| + |6| (см. задачу 661).
663. Замечая, что а = (а — Ь) + Ь, можем написать
|а| = | (а — Ь) + Ь\*С\а — Ь\ + \Ь\ (см. задачу 662).
Отсюда \а — Ь\>\а\ — \Ь\.
664. Данное неравенство равносильно следующей
системе неравенств:
-3<^*+/<3'
которая, если освободится от положительного
знаменателя, приводится к следующей:
2х2 + (3 + к)х + 2>0, 4х2 — (к — 3)х + 4>0.
Чтобы эти неравенства выполнялись одновременно и
для всех х% необходимо и достаточно, чтобы дискриминанты
324
трехчленов, стоящих в левых частях неравенств, были
отрицательны, т. е. чтобы
(3 + А)»-16 = (Л + 7)(Л-1)<0,
(к — З)2 — 64 = (й + 5)(А—11)<0.
Для первого должно быть — 7<&<1, а для второго
— 5 < к < 11. Общая часть интервалов (— 7, 1) и (— 5, 11)
есть (— 5, 1). Поэтому доказываемая теорема имеет место
только для тех значений к, которые удовлетворяют
условию — 5 < к < 1.
ЙЯ5 Д+ & __ а , Ь а , Ь
писать так: тттт > тггк- Но 0<-|-<1,а т>я.
\+а + Ь 1+а + Ь ' 1+а + Ь^1+а^\ + Ь'
666. Так как а ф 0, то данное неравенство можно за-
>+(т) -+(4Г
поз-у (-ЬГ<(4)". '-(-5-Г>'-(*)"•'+
+ ( —) < 1 + (—) • Поделив почленно предпоследнее
неравенство на последнее, получим неравенство, которое
требовалось доказать.
667. Пусть -| дробь правильная и к > 0, а > О,
6 > 0. Нужно доказать, что утг^* > -т-. Так как -|
правильная арифметическая дробь, то Ь > а. Умножая это
неравенство почленно на положительную величину к и
прибавляя к обеим частям неравенства по величине аЬ,
получим аЬ + Ьк > аЬ + а/? или 6 (а + &) > я Ф + &)• Деля
теперь обе части неравенства на положительную величи-
ну Ьф + к), получимТ^->Т1Е±-Ц, или -ф;>т.
Если -| неправильная дробь и к > 0, а > 0, 6 > 0, то
неравенство ° ^ < — доказывается аналогично.
668. Пусть наименьшая из дробей -—, 4г-» ...» тт-
будет обозначена через /п, а наибольшая — через М.
а25
Тогда можно написать: т<-^<М, т<-~ < М, ...,
т<^<М. Так как Ьг>0, Ь2> 0, ..., 6Л>0, то,
освобождаясь от знаменателей, получим:
тЬ1 < аг < МЬг
тЬ2 < а2 < Ш2
тЬп < а„ < Лйл.
Суммируя почленно и вынося множители т и М за скобки,
находим т(6Х+ 62 + ... + Ь„) <аг + а2 + ... + а„< Мф1 +
+ ^2+"' + ^л)- Наконец, деля члены неравенств на
положительную величину Ьх + 62 + ... + Ьп, получаем
< Д1 + о» + - + дя <м
т< ^1 + ^2 + ... + ^ <л*'
что и требовалось доказать.
670. -^ + -^ = ^У^ =
1^ К* Уху_ _ _
-ОТ+УЮ ^-^+^ -
ЧУГ+Гу)(|^-^+уг' -
-(1/ЗГ+У7)[и- (/7^7)2]>Т/Г+1/^
671. а) а1 + °г = ^"+ *^~ 2 ^^"+ 2 ^^ в
— 2 ^ 2 — ' "]"2*
Знак равенства возможен только тогда, когда аг = а2.
б) Пользуясь только что полученным неравенством,
можно написать:
^1 + ^2 , ^3 + ^4
а\ + а2 + а3 + а4 _ 2 ~*~ 2 УЧ^г + УдзД4 ^
^ - 2 > 2 ^
> К Ка^з Уа^ > Уаха2аъа^
326
Знак равенства возможен лишь тогда, когда ах = а2 =
= а3 = а4.
672. Пусть дс и у два положительных числа, сумма
которых равна а. Так как среднее арифметическое двух
положительных чисел не меньше среднего геометрического
этих чисел (задача 671, а), то можно написать -~ > ]/**/
или ху < (-|-) . Ни при каком выборе положительных
чисел х и у произведение ху не будет больше, чем 1-|-].
С другой стороны, при х = у = -у- получается
произведение (-|-) . Следовательно, наибольшее значение ху
получит при дс = у. Нетрудно видеть, что это решение
единственное, т. е. если хфу, то *У<(-|г)#
673. Обозначим сторону площадки, перпендикулярную
стене, буквой х. Тогда параллельная стене сторона будет
100—2х, а площадь 5 = *(100— 2х). Нужно найти то
значение х, при котором 5 будет иметь наибольшее
значение. Но 5 и 25 достигают своих наибольших значений
при одном и том же значении дс. Поэтому рассмотрим
величину 25 = 2х (100 — 2х). Эта последняя является
произведением двух положительных чисел 2х и 100 — 2х,
сумма которых есть величина постоянная, равная 100.
Наибольшего значения величина 25, а следовательно, и
5, достигнет при 2х = 100 — 2х (задача 672). Отсюда *=25.
674. Пусть длина дуги сектора /, радиус г,
периметр 2р и площадь 5. Тогда: 5 = -^ г/, 2г + I = 2р,
г = -у (2р — I) и, следовательно, 5 = — (2р — 1)1.
Наибольшее значение 5 будет при том же значении /, что и
наибольшее значение 45 = (2р — /)/. Последнее же будет
при 2р — / = / (см. задачу 672). В этом случае / = р,
г = -тр Р или ^ = 2г.
675. Пусть высота прямоугольника х, его основание
и диаметр полукруга 2у, периметр всей фигуры 2р
(данная величина) и площадь фигуры 5. Тогда:
5 = 2ху + тсу\ 2х + 2у + пу=:2р; 2х = 2р — 2у — т:у
327
и, следовательно,
8 = у(2Р-2у-ку) + ку2=--у(2р-2у-т:у +
+ *У) = *У(р — У)-
Окно будет пропускать наибольшее количество света,
когда 5 будет наибольшее. Наибольшее же значение 5
наступит тогда же, когда и наибольшее значение — 5 =
= у(р-*-у). Последнее же будет при у = р— у (см.
задачу 672), т. е. при
у=-%- и х=^{2р — 2у — тсу) = ^р-'р.
676. Возьмем осевое сечение АВС (рис. 5) конуса.
Пусть высота Вй = Ну а радиус
основания СО = г. Тогда объем конуса V =
= -о-7гг2Л. Так как
ВЕ =УОВ2—ОЕ2= |/(Л — #)2 —#2 =
= /А(А — 2/?),
то из подобия треугольников ЯСГ>
и ВОЕ получим:
^ |/Л(Л —2Д)' Л-2Я'
^2 1 П2Т/ Т/ Л2
Величина V будет иметь наименьшее значение
одновременно с величиной Уг Последняя же будет
наименьшей тогда, когда у- будет наибольшей. Но
1 Л — 2Я __ 1 2/? Л 2/?\
^ ~" Л2 2/? # Л ^ Л /'
1 „ 2/? 1 2/?
и так как множитель -^ постоянный, то при -т- = 1 — -г1
величина -р- примет наибольшее значение (см. задачу 672),
а объем V — наименьшее. Найдем соответствующие
значения Л, г и V. Из равенства -у = 1 т- находим;
V = -^*Я2 • 87? = 2 • -|-1с/? = 2Кшара.
328
677. Пусть х и у — два положительных числа,
произведение которых равно а. Так как среднее арифметическое
двух положительных чисел не меньше среднего
геометрического этих чисел (см. задачу 671, а), то можно написать,
что * "I"у > У~а или * + #>2)/а. Ни при каком
выборе положительных чисел х и у сумма х + у не будет
меньше, чем 2 |/а. С другой стороны, при х = г/ = "^а
получается сумма 2 |Лх. Следовательно, наименьшее
значение х + у получит при х = у. Нетрудно видеть, что
это решение единственное, т. е. если х ф у, то
д: + у>2|/^
Замечание. В сумме х + у величина у =—.
Поэтому полученный результат можно сформулировать так:
величина и = х Н , где а > 0 и я > 0 достигает своего
наименьшего значения при х = 1/^а и только при этом
значении х.
678. Обозначим ширину печатного текста на странице
буквой х, а длину — буквой у. Тогда ширина страницы
будет х + 4, длина у + 6, площадь страницы 5 = (х +
+ 4) (у + 6). Раскрывая в последнем выражении скобки
и замечая, что ху = 2\6(по условию), получим 5 = 216+
+ 6х + 4у + 24 или 5 = 240 + 6х + 4 • ^. Нужно
найти те значения х, при которых величина 5 будет иметь
наименьшее значение. Но величины 5 = 240 + 6 ис + —)
, 144
и и = х Н достигают своих наименьших значении при
одном и том же значении х. Для величины и это
значение х равно ]/144=12 (см задачу 677), Отсюда
получаем, что ширина страницы 16 см, а длина 24 см.
679. Пользуясь соотношением среднего
арифметического и среднего геометрического двух неотрицательных чисел
(см. задачу 671, а), получим
а4 + 64 + с* = ^^ + ^^+^^>V^+
329
+ &2 .^1+^1 + С2 . ^!_+_^. > а2|ЛЬ2с2 + Ь2 ^С2а2 +
+ с2 }/а?Ь2~ = аЬс(а + Ь + с).
680. Пользуясь формулой т ^ > Ушп (см.
задачу 671, а), получим
Н 2 *" "• "• 2 —2— * * ' а2 + ••• + ап)-
681. Так как—-~- >)/гсГк или 1+аЛ>2|/а][
(задача 671, а), то получим (1 + а^ (1 + а^ ... (1 + ал) >
> 2 К^ . 2 ]/^ ... 2 ]/а^ = 2п Уарг ... а„ = 2Л.
682. Обозначим: ах = дс8, а2 = у3, а3 = г3. Тогда нера-
^з Д- и3 4- г3
венство примет вид Ч^—-— > хуг и достаточно
доказать, что х? + у3 + г3 — Зяуг>0. Но л? + у3 + г3 — Зяг/г
делится на х -{- у + г, что можно проверить по теореме
Безу, подставляя в многочлен х =э—у — г (см. решение
задачи 23). Разделив многочлен на х + У + *> получим
частное х2 + у2 + г2— ху — уг — гх. Поэтому д^ + ^ + г3 —
— Зхуг = (х + у + г)(х2 + у2 + г2 — ху — уг~ гх) = (х +
+ у + г)[±(х-у)2+±(у-г)2 + -}Г(г-х)2] (см.
решение задачи 183). Отсюда, действительно, г* + У3 + г3 —
— Зхуг > 0.
683. Справедливость этого неравенства для п = 2 была
доказана в задаче 671. Предположим, что оно
справедливо для п = к, и докажем справедливость его для п = 2&.
Действительно,
01 + а2 + °з + а4 + »■ -Ь а2&-1 + а*к _^
2к ~"
а1 + а2 , а3 + <*4 . . аъЪ-\ + л2б
о • о "т" ••• ~г о
>
-^ I/ о • о "" 2
330
Итак, если доказываемая теорема верна для п = к, то
она верна и для п = 2&, а так как она верна для п = 2,
то она верна также для п = 4, л = 8 и вообще для
п = 2т.
Пусть теперь /г не является степенью двух. Добавим
к числу п число р так, чтобы было п + р = 2т и положим
„ _я _ _„ - Д1 + Д« + ~ + Дя
"л+1 ~ "л + 2 — -• == "л+/; — „
Будем иметь
°1 + °2 +,,- + ДЯ + Д^+1 + - + Д/1+Р _ Д1 + °2+ - + 0/1 + РЯп + 1 >
п + р п + р ^
^ п+Р/~ " Нл °1 + °2 + - + Д^ + РД^ + 1 _
> ^ ага2... апаР+1 . Но ^
Д1 + Д2 + ... + йп + Р '
ап+Г "ип+У
аг + а2 + -. + Д«
п + р
(л + Р) (Д! + а2 + ... + ая) й! + а2 + - + ап
п(п + р)
, а
яуД1аа,,,ая(°1 + 0' + --- + 0я)^ Поэтому
или |Д| + "| + ^«я|^>уД1Д|<|<0д|
Возведя последнее неравенство почленно в степень
—*-*-, получим окончательно п—■—-> V а\аъ ... а„.
684. Пусть хг, х2, ..., хп — положительные числа,
сумма которых равна а. Так как среднее арифметическое
любого количества положительных чисел не меньше
среднего геометрического этих чисел (см. задачу 683), то можно
написать, что-^- > У хгх2 ... хп или хгх2 ... */!<( —) •
Ни при каком выборе положительных чисел хг, х2, ...,хп
их произведение не будет больше, чем (•—-) . С другой
331
стороны, при хг = х2 = ... — хп — — получается
произведены^ —) . Следовательно, наибольшее значение
произведение ххх2 ... хп получит при *, = х2 = ... = хп.
Нетрудно видеть, что это решение единственное, т. е.
если среди чисел х1% х2, ..., хп есть неравные, то
произведение этих п чисел будет меньше (—)
685. Обозначим радиус основания цилиндра через г,
его высоту через Л, а радиус данного шара через Я. Если
взять осевое сечение цилиндра, то из него легко установить,
что к = У{2Щ2 — (2г)2 = 2 У К2 — г\ Поэтому объем
цилиндра V = тг г2 к = 2тг г2 Ун2 — г2. Нужно найти то
значение г, при котором объем будет иметь наибольшее
значение. Но величины V и V2 достигают своих
наибольших значений при одном и том же значении г. Очевидно,
при том же значении г достигает своего наибольшего
значения и величина -^-У2^ 2г4<7?2 — г2). Последняя же
получит наибольшее значение при г2 = 2/?2 — 2г2, так как,
представив ее в виде г2-г2(2Ц2— 2г2), замечаем, что
г2 + г2 + 2Н2 — 2г2 = 2/?2, и, следовательно, наибольшее
значение произведения г2г2(2Ц2— 2г2) получится при
равенстве всех его множителей (см. задачу 684). Из
равенства г2 = 2Ц2 — 2г2 найдем значение радиуса основания
цилиндра г = Ну -тр при котором цилиндр имеет
наибольший объем.
686. 1 + (2л — 1) = 1 + (2 — 1) (2п~1 + 2п~2 + ... + 2 +
+ 1) > 1 + пУ2^ • 2"-2 ... 2 • 1 = 1 + п\[ 2^ =
= 1 + п уг2п~1 (см. задачу 683).
687. п\ ~УЩ2==У(\.п) 12-(п— 1)] [Зф—2)]... (п . 1) =
- УГПг. У2- {п— 1). УЪ*(п — 2)...У1П>
1 + гс 2 + (я — 1) 3 + (п — 2) п + \ __ (п+\\п
> 2 ' 2 ' 2 —2 \2У
(см. задачу 671).
332
688. 1 + 1+4 + Т1з-+т4гг + ... + тт|зГ<
>Ч-
= 1+2(1-^г) = 3--2^Г<3-
689. (2— 1)1! + (3—1)2! + ... + \(п+ 1) — п]п\ =
= 2! — 1! + 3! — 2!+ ... + (" + 1)! —л! = (л + 1)! — 1<
<(я+1)!
690. л _ 1 -3-5...(2п-1) _ _1_ _3_ _5_ 2я — 1
2- 4 -6...2« 2 ' 4 ' 6 ••• 2п ^*
_2_ _4_ 6 2я 1
3 5 7 ••• 2л+1 1 • 3- 5...(2л—1)(2л + 1)
2 • 4 • 6 ... 2л
А (2я + 1) ^ /4 • 2л ^ Ля
Итак, Л<4-, Л2<4-> Л< '
Ля ' ^ л ' ^ |Л„-
_ "/(1 ■/!)■ [2 . (лг — 1)] ...[*.(п-*+1)]...(/1-1)
"" V 1 • 2 • 3 ... п
Но /г(/г — к + \)=^кп — к(к—1)-=кп — п — к(к—1)+п=
= (к—\)(п — к) + п. Отсюда видцо, что при всяком к,
удовлетворяющем неравенствам 1 < к < я, выражение
к (п — к + 1) > /г. Поэтому имеем
/1 -2.3 ... „>/ГТ1Г^ = ^==.
Отсюда С/ 1 • 2 • 3 ... /г)2 > /г и ^1 • 2 • 3 ... п>У~п.
Если я > 2, то {^1 • 2 • 3 ... я > ^
692. Искомое число девятизначное. Поэтому,
обозначив его через *в, можем написать 108<*в< 109.
Извлекая корень шестой степени с точностью до единиц,
333
; получим 20 < х < 32. Но сумма цифр числа равна 45,
значит искомое число, а следовательно, и х, делится на 3.
Таких чисел, больших 20 и меньших 32, всего четыре:
21, 24, 27, 30. Рассматривая данные цифры искомого
числа, легко убедиться, что х = 27, а искомое число есть
27е = 387 420 489.
693. Если обозначить искомое число процентов
буквой х, то после прохождения газа через первый фильтр из
общего числа примесей, равного тщ ж3, будет поглощено
ахр « [ах ахр "1 о ах Л р \ ч
Ш*м*>так что останется [Ш -^ ^ илиш (1-щ) *•
Очевидно, после второго фильтра останется-^ (1—щ) ж3,
а после п'тощ{}~щ) м*- При поступлении в
резервуар к количеству \а — ш + ш (* — ш) \м* газа пРиба"
вится еще Ьм3, причем прибавится примесей щ ж3, так что
в газовой смеси в резервуаре станет ^(1—щ) + -^ ж3
примесей. Это последнее не должно превосходить г%
общего объема газа, находящегося в резервуаре. Поэтому
ах Л р \п.
искомое число х удовлетворяет соотношению -щг (1 — ткх} +
+ Ш<4[Ь + а-Ш + ш(1-Шо)]-Изнего нах°ДИм
^^К1 — таоХ1—та) +жо]<(а + 6)г-^ Так как в
левой части полученного неравенства находится
положительная величина, то при (а ^ Ь)г < Ьц неравенство,
а следовательно, и задача, не имеет решения. Если же
(а-\- 6) г > Ьд» то получим
{а + Ь) г — Ьд
х<
а[[^^)[1~й)я+Ы
694. В конце первого года к вкладу в А руб. касса
прибавила процентную сумму -щр а вкладчик взял со
334
счета В руб. Таким образом, к началу второго года
вкладчик имел на книжке сумму Ах = ЛП + ]^) — В руб.
В конце второго года были произведены такие же
операции, отчего сумма Ах руб. обратилась в сумму
А* - А>{1 + ш) ~в = А 0 + ш)2-5!1 + 0 + ш)\
В конце третьего года вместо суммы в Л2 руб. на книжке
была сумма
+ (1 + тш)2]ру*
Ясно, что в конце дг-го года вклад выражался суммой
41 + тУ-вЬ + к + т) + {1 + тУ + --- +
Выражение, стоящее в квадратных скобках, является
суммой х первых членов геометрической прогрессии с первым
членом, равным 1, и знаменателем, равным 1 + -г—.
Поэтому для суммы бклада получим
1 + 1оо —!
100В Г/, . Р У ,1 Ар— 100В Л , р \х 100В
■[(' + !&)"-'Ь^Ч'+А)'
р 1\ * 1ДО/ \ р \ ' 1Ш/ ' р
Но по условию задачи эта сумма не меньше ЗЛ. Поэтому
получаем Ар ~рШВ [{ + ^)'+ Ш- > ЗЛ. Решив это не-
равенство, найдем
1б (ЗАр — 100В) — 1б (Ар — 100 В)
Х> 1§(100 + р) —2
Так как р > 0, А > 0, 5 > 0 и, кроме того, Лр> 100В
(сумма вклада возрастала), то все выражения, находящиеся
335
под знаками логарифмов, являются положительными
величинами и выражение для х имеет смысл. С другой
стороны, если Ар < 100В, то задача не имеет решения.
695. Пусть следует сделать х промывок. В единице
непромытого песка содержится щ единиц чистого
золота и (1 — щ) единиц примесей. После одной промывки
единицы песка золота остается щ (1 — щ ) единиц, а
примесей — (1 — щ) (1 — <щ). Очевидно, после двух промывок
единицы песка число единиц золота и примесей будет
±\\ ?_ ±-(\ ?_У| = АЛ чА*
100|_ 100 100 \ 100/] 100 \ Ю0/
и (1—Шб)(1 —Шо)2'
а после х промывок, соответственно,
_к_
100
('-т^Ы'-шК'-шГ
Так как процент содержания золота после х промывок
должен быть не менее г, то отсюда получаем неравенство
100 !
V1 100/ ^ 100 [ 100 \А 100/ ~*~ \* 100 Д1 100/ ]
Решаем это неравенство: -
100 V1 100Ч 100/*" 100 \* 100 Д1 100/
А; (100 — г) (100 — д)*>г(№ — А?) (100 — р)\
I 100 — ^г V*
V 100 —р/
_г(100 —Л)
к (100 — г) '
Логарифмируем обе части неравенства, причем для
определенности будем считать основание логарифмов больше
единицы. Если ц < р, то левая часть неравенства будет
больше единицы и мы получим
ю§6(100-г) .. ю*б(Ю0-г)
* > 1 ПО - п » еСЛИ Ч > Р> Т0 Х < '
100 —</ 9^~ч^н,^~^ Ю0 — ^г
100 — р б 100
336
если ц = р, то х может равняться любому натуральному
числу, т. е. любое число промывок сохраняет процент
содержания золота. Очевидно, в этом случае задача имеет
решение лишь при к> г.
696. Первый раз влили в резервуар чистого спирта
ар
-щ- л, но после того, как из него отлили а л смеси,
чистого спирта осталось в резервуаре -щ- • -т-—— л.
Повторение этой операции привело к тому, что число литров
спирта в резервуаре стало
/ ар Л _ар\ А ар_ Г А ( А \2]
\ 100 ' А + а ~*~ 100 / А + а 100 [А + а "*" \А + а ) \
После х таких операций число литров чистого спирта в
резервуаре, очевидно, станет равным
°В- Г_±- -I- М-У 4- 4- ( А У]
100 [А + а Т\А + а) т '" ^ \А + а ) \
а общий объем смеси останется Л л. Так как процент
содержания спирта должен быть не менее ц, то отсюда
получаем неравенство
-22- Г_*_ 4- ( А У 4- 4- ( А VI > ^
1оо и+а "*■ и ч-«/ ' ^ и+«/ ] 1о° •
которое приводится к такому: р\\ — К д ) > ^. От-
сюда найдем, что а: > ^—, при этом должно быть
р> д. Если же р < д, то задача не имеет решения.
697
. асо5х + Ь$'тх = а(созлг Н зшх ) = а(созх +
+ 1§ ср 31П А:) - ^у (С05 * С05 ср + 51П X 51П ср) =
с= У а2 + б2 со5 (* — ср). Поэтому | асо$*-Ь Ь$\пх\ ~
= У а2 + Ь2\со$(х — ср)| < У а2 + &3 или _у?4г^<
< а со5 * + 6 51П х <*уЛа2 + ^2.
Следовательно, наименьшее значение данного выражения
будет — У а2 + Ь2, а наибольшее У а2 -\- б2.
22. К. У. Шахно 337
698. а5\п*х + Ь5\п хсоьх-}- ссо$*х = а ■ 1^с°52х ±
4- Ъ . — \- с • —^ = —±— + -^-[(с — а) соз 2х +
с-\- а , с — а , п , . -г>ч с + а ,
= —%— + —2~ (соз 2л; + 1е <Р яп 2х) = —^—|-
+ 2^7 (С05 2*С08 <Р + 5Ш 2*51п ?) = -Т~
+ 4" "К^2 + {с — а)2 соз (2* — <р). Если соз (2л: — 9) = 1, то
* с + а , |/"Ь2+ (с — а)2
получим наибольшее значение, равное —^ [- - Ц^ ^-»
а при соз (2* — ср) = — 1 будем иметь наименьшее значе-
с + а ]Л>2 + (с — а)2
ние, равное —^ Ц^ •
Полученный результат верен и при а = с.
699. Так как зт2Л + зт2В + зт2 С = 2соз А соз В созС+ 2
(см. задачу 484) и 2соз А соз В соз С > 0, поскольку Л, В
и С острые углы, то зт2 Л + зт2 В + зт2 С > 2.
7ПП 5*п2х--со5 2х + 1 _ 2зт х соз л + 2зт2>: _^
51П 2* + СОЗ 2х — 1 ~~ 251П X СОЗ * — 251П2 * ~~"
СОЗ Я + 51П X 1 + 1^ X т-т
е= !—:— = ■ ' .&—. Поэтому неравенство равносиль-
СОЗ X — 51П X ч 1 — 1§ X ^ Г Г
но такому ^.^ > 0 или (1 + {§ х) (1 —1§ *) > 0,
исключая л: = кк, при котором левая часть данного неравенства
теряет смысл, но которое является решением
преобразованного неравенства. Таким образом, получаем: 1 —1§2л;>0,
*8"х< 1, |*в*1<1. — К*8*<Ь Ьъ ^<х<к^
кт: <Сх<^ ~ + кт:.
701. В этом случае должно выполняться неравенство
соз х < 0. Но тогда-^- + 2кп<^ х<-к-к + 2кп.
702. Так как | зт х | < 1 и основание логарифмов
больше единицы (логарифм десятичный), то неравенство
равносильно такому: зт х > 0. Следовательно, 2к тг < х <
< (2к + 1) тт.
338
703. С05 (ЗШ X) > 0 При ЛЮбыХ X, ПОТОМУ ЧТО —1< 51П Х<
< 1, а углы, заключенные между — 1 радиан и + 1
радиан, находятся в первом и четвертом квадрантах, где
косинус положительный.
ТС 9
704. Должно быть — 1 < — агс зш х < 1 или <
I тс
2 2 2
< агс ып х < —. Отсюда — зш — < х < зш —.
тс тс тс
705. Должно быть 0 < 1§ х < 1. Отсюда 1 < х < 10.
706. Должно быть 2&7г < -^ < (2к + 1) тг, где к = 0,
1, 2, ... Если & = 0, то-^-<тг, >?>—, |х|>-р=. Это
возможно, когда: а) #> —= и б) х< 7=..Еслий=1,
V тс 1/ тс
1 1 1 *
2, 3, ..., Т0/о, , 1Ч <Х2 <-77г— ИЛИ —7= <|х|<
(2/г+1)тс^ ^ 2йтс }А(26+1)тс ' '
< г Это возможно, когда в) =■ < х < л
1/2А;тс ' У(2к+1)п У2Ьк
(х>0, \х\=х) и г)т=к==<-дг<^или
707. Так как *2-?г, *2~у"> *8"2 положительные
числа, то, пользуясь тем, что среднее арифметическое двух
положительных чисел не меньше среднего геометрического
этих чисел (см. задачу 671, а), можем написать
+4-(#4-+*Ч)+4-(^+*в,-г)>
> 1А§2-И24- + уг#4-*8'* + у&±&± -
+ *6 + (4в4-*-*8"г)в48-Г1«-Г +
22* 339
Для того чтобы имело место равенство
необходимо и достаточно, чтобы а = 9 = у = -^-.
Действительно, последнее можно записать так:
+ 4-(«'-|- + *81-г)-*в-5-*84-+*8-Г*8+ +
+ 1ё^-1ё^~ или -4-(^-| *б-|-)2-+-
+ 4(*+-*^+т(*+-*т)'-°-
Но это будет иметь место тогда и только тогда, когда
1§ -^- = 1§ -^- = 1^ "2"« а так как а» Р» у —острые углы,
сумма которых равна тс, то это приводит к условию
а = 3 = Т = -эГ-
708. Нужно доказать две теоремы:
I. Дано: 0<а<-|-, 0 < р < ^ 0 < т < ^-,
0<а + р-|-Т<-|--
Доказать: 1§а1§р + *б ? *8 Т + *8Т *2а< 1-
II. Дано: 0<а<^-, 0<р<-^-, 0 < т < ^-,
Доказать: 0<а-}Р + у< -|-.
340
Доказательство!. 0<^<-| (<* + Р)<-|-.
Поэтому 18 т < 18 [у - <« + Р)] = <*8 (« + Р) = -^^.
Итак, 1§ у < Г" ^.а*/о • Умножим обе части неравенства
на 1§а + 1§р>0. Получим 1§т(*§а + *§Р)< 1 — *8а*8 Р-
Отсюда 18а18Р + *8Р*8Т + *8Т*бв<Ь
Доказательство П. Перепишем данное
неравенство так: 1§ у ({§ а + *6 Р) < 1 —1§ а 1§ р. Отсюда видим,
что 1 —1§ а 1§ [3 > 0. Разделив обе части неравенства на
(1 — {§ а {§ Р) {§ у > 0, получим
или 1б(а + р)<18(-у — т)-
Но так как 0< а <-|-, 0 < р < -|- и 1б(* + Р)>0,
то 0 < а -+- Р < -тр. Поэтому из неравенства 1§ (а + Р) <
< 1§ (~ у) вытекает а -{- р < -^ у или 0 < а 4- Р +
709. 1 -+- с!§ ср = 1 +
1 — *§2 -5~ *§-|-+1-1б2-|-
218^- 218-Х-
■(*«НГ-*в-|- + 1-1) 2-(*«-| О"
2'8-|- 2(8Х
= с1§-| 2"с1б"|"(^"| 1) <с1§-|-, так как, при
условии 0 < <р < те, -^-с1§ -|- А§ -| 1^ > 0.
710. Раз угол 7 тупой, то 0<а4-Р<-5~и0<а<
< X ~Р <"Г. НотогАа *8« < *б(х ~Р) = С^Р = тр"
341
Итак, *ба<
*вР
Умножая обе части неравенства на
*§ Р > 0, получим 1§ а • 1§ р < 1.
711. Обозначим левую часть неравенства буквой А.
Будем иметь А = соз2а + 1 + с2°з2Р + 1+™21 = соз2а +
+1 + соз (р + т)С08 (Р — Т) = со$2 а + со8 (те ~ а)С08 (Р ~ Т) +
+ 1 = соз2 а — соз (Р — у) соз а + 1. Иначе соз2 а — соз (р —
— у) соз а + 1 — А = 0. Рассматриваем последнее как
квадратное уравнение относительно соз а. Для того чтобысоза
был вещественным, дискриминант этого уравнения должен
быть неотрицательным, т. е. должно быть соз2(Р — у)—
— 4(1—И)>0. Отсюда 4(1 — Л)< соз2(Р — т) < 1 или
1 3
1—Л<~^-. Таким образом, получаем А > —.
Отсюда же легко усмотреть, что соз2 а + соз2 р -(-
+ соз2 у = — тогда и только тогда, когда а = р = у = -|-.
712. 51П у 51П у 51П -^ =у ( СОЗ ^ СОЗ—-^)§1П-?Г ==
1/ а — р тс — 7 \ • 7 1/ а~?
— 51П
2
2 7
51П -^
1
4
СОЗ
СОЗ4
-)]~Н4
СОЗ*
-Л<4
соз*
<"8-
+4-со§2-
-(зт-1-
713. Построим острый угол АОВ (рис. 6), хорду АВ и
касательную ЛС в точке А к
окружности радиуса г с центром в вершине О
угла. Очевидно 8ааов <3Сект.олв<Здлос.
Если д; есть радианная мера угла ЛОВ,
то предыдущее неравенство можно запи-
сать так: -^- г2 зш дс < -^- г2 л; < -^- г2 {§ х
на -|- г2 > О,
Рис. 6.
2 ^ 2
или, по сокращении
31П х < * < {§ #. Следует заметить, что
неравенство зш х < л: верно при всяком
* > 0, а 181п л: | < | х | при любом
вещественном х ф 0.
342
714. а) зшр — 81па = 2з1п^^соб-Ц^<2зт^
2 2 ^--"- 2
так как 0 < соз а~Г < 1. Но известно, что если х > О,
то зтх < х. Поэтому, 2з1п ^"7* < 2 • ^ а = р — а,
(р — а> 0). Таким образом, зт р — зт а <р — а и а — зт а<
< Р — 31П Р.
^ <б(Р~а>^1+Р1Гр^ <<8Р ~ 1§а> ^ ^
0 < 1 + 1бр^а < 1в Н°' еСЛИ ° < Х < "Г» Т° *§*>*•
Поэтому 1§ р —{§ а > 1§ (Р — а) > р — а. Отсюда а —1§ а>
715. I. Обозначим р — а «= 8 > 0. Тогда -—^ — -^уЁ. =з
= -^- (Р зт а — а 31П Р) =* —- [(а + 8) зт а — а 51П (а + 8)] =
е= -^р (а зт а •{- 8 зт а — а зт а соз 8 — а соз а зт 8) =я
с=^.[азта(1-со5 8) + а8соза /^_^У|
Но оба слагаемых в квадратных скобках
положительны. Действительно, положительность первого очевидна,
а в положительности второго можно убедиться на
основании неравенств зт х < х < {§ х для 0 < х < -^- (см.
задает о\ ^& а ^ 1 п ^ 31П 5 ^. ,
чу 713), из которых следует, что ——> I, а 0<—т— < 1.
Поэтому
51П Р ^ ~ 5?П а . 51П (
II. Докажем неравенство
геометрически. Из треугольников ОС В
и ОСА (рис. 7), на основании
теоремы синусов, получим
АС 0/4 ВС _ ОБ ОЛ
8Ш [3 ~~ 5Ш С 51П а "~~ 8111 С ~~ 8111 С
Отсюда
АС
51П (3 51П а
ЛС ВС + ЛВ
ВС 51П Р
или
ВС
ВС
1 +
81П а
АВ
ВС
Г д
Рис. 7.
343
Полагая радиус окружности равным единице, можем
написать ку АР= р, ч^ ВР=а. Поэтому АВ < ^ АВ=$ — а,
БС > В5 = 1§а > а (см. задачу 713). Возвращаясь к
равенству -^~ » 1 -|- —-, заменим в нем АВ на р— а, а
БС на а, отчего получим А^- < 1 + = !-(--!- 1 =
81Па
Р .„ з!п Э зтя
:_ИЛИ-1^<-Г|
716. Возьмем любой я, удовлетворяющий условиям
т
0<л:<—. Тогда, положив в неравенстве задачи 715
тс
81П -я- п
о ТС 51П X ^ 2 ^ 2
а = #, р = -н-, получим > или зт х > — а:.
"Г
717. I. Обозначим р — а = & > 0. Тогда Ц$- ХЛ± =
р а
= ^- {а »8 (а + 8) - 1еа] - 8 *8а) «
1 / а 51П & * . \ ^ 1 /а 51П 5 & 51П а \
С= а^ ^ С05 (а -|- &) С05 а / "^" \ со$ а С08 а /
Е / 5Ш & 51П Д \
^ рсоза ^ Ь а у
а) Если 8 <а, то-^1 !Н1^>о (см. задачу 715)
и тогда-р >-~-.
б) Если & > а, то между числами аир можно вставить
ч^сла Ту, ч2, .,., т* так, чтобы было 0< а< ?, < т2<...<
< Та < Р < "7"» а разности т, — а, т2 ~ Ти •••> Р — Т*>
были бы меньше а. Тогда, на основании случая «а», по-
лучимм>ш,>...>^>^..
344
II. Дадим геометрическое доказательство. Пусть АО
и АЕ (рис. 8)— дуги окружности радиуса единица с
центром в точке О, равные, соответственно, а и р. Пусть
В и С — точки пересечения
касательной к окружности в точке А с
продолжениями радиусов СЮ и ОЕ.
Проведем через точку О прямую
ММ || АС и пусть М и N точки
пересечения ее с прямыми ОС и ОА.
Тогда можно написать
^В _ АС_ __ МЫ __ РЫ + РМ _
1с а ~~ А8 ~~ ОЛ/ ~" Я# ~~
= 1
ры
(*)
Проведем касательную ЕО к
окружности в точке О и пусть Е— точка
пересечения ее с продолжением
радиуса ОЕ. Очевидно, ОМ > ОЬ =
= *8 (? — °0 > Р — а» а ОЛ^ =- 51П а < а = ^ ОЛ
чу 713), следовательно, -у^- > „ * • Тогда
РМ
*вЭ
ства (*), получим: -р^ > 1
1-я «б9
1§<х
>^^">
«81
X. КОМПЛЕКСНЫЕ ЧИСЛА
и «меньше» неприме-
718. Нельзя. Понятие «больше»
нимо к комплексным числам.
719. Отрицательное число есть вещественное число,
которое меньше нуля. К комплексным же числам понятие
«меньше» не применимо. Поэтому нельзя число —5*'
назвать отрицательным.
720. Запишем данное равенство так:
(■тг-
1.
Но
1+/
(1 + О2
I—/2
1+2/-1
1 + 1
2
= I.
Поэтому получим ьп = 1. Отсюда п = 4к9 где к = 0, ± I,
±2, ±3, ...
345
721. Освободившись от знаменателя, получим х+1 +
+ (у — 3)/ = 2 + &\ Два комплексных числа равны, когда
равны их вещественные части и равны их мнимые части.
Поэтому имеем
/*-И=2;
10-3 = 8.
Отсюда х— 1, ^=11.
722. Умножив обе части уравнения на —и Получим
(х + у)2 + 6 + х1 = у1 + 5 (х + у) + и
Приравниваем вещественные части
(х + У)2 + 6 = Ъ{х + у) и мнимые части х = г/ + 1«
В полученной системе
(* + */)2-5(* + */)+6 = 0;
х~ у = 1
первое уравнение решаем как квадратное относительно
х + у. Получим х + у = —|—. Остается решить
системы:
а) Г х — у = 1; б) Г л: — */= 1;
I * + У = 3; I * + у = 2.
3 1
Ответ: хг = 29 уг = 1ш9 х2 = ^-9 Уг^-у-
723. Из первого уравнения находим х = 0, у = — 1.
Подставляя найденные значения х и у во второе
уравнение, получим а = 0.
724. Уравнение можно записать так: "^ л:2 + #2 —
— (х + Ч/) = 1 + 21. Отсюда "|/ л:2 + у2 — л: = 1, — */ = 2.
3 3
Решив систему, найдем: х =—» У =— 2, 2 = -^ 21.
725. ]/*2 + 02 + (^ + № = 2 +1, V х2 + у2 + х =2,
у = 1. Отсюда: * = -^ у = 1, г =-^ + I.
726. Если г1^= хх + 1уъ г2 — х2 + гуъ то *\ + г2 =
= хг + х2 + 1(ух + */2), г! — г2 = л?! — х2 + г(4/ж — </2).
Поэтому | гх + г212 + | гх — г212 = (л^ + *2)2 +
+ ЙЬ + </2)2 + (*1 — *2)2 + (Ух - У2? = 2*? + 2у? +
+ 2^ + 2у22= 2(х1+ у\) + 2(4 +У\) = 2 {\г^+ |г2|2).
346
727 — 758. Указание. В этих задачах часто
используется тригонометрическая форма комплексного числа и
его геометрическое изображение. Напомним, что любое
комплексное число а = а + Ы Ф О можно преобразовать
к виду а = р(со$ср + *' 51пср). Последнее выражение
называется тригонометрической формой комплексного числа.
Число р = У а2 + Ь2 называется модулем комплексного
числа а, а угол ср его аргументом. Аргумент определяется
формулами: соз ср =—, $т ср = —§ Модуль р > 0, а
аргумент ср может принимать бесконечное множество
значений, так как $ш ср и соз ср не меняют своей величины,
если ср изменить на 2#тг, где к— целое число. Обычно
для ср берут наименьшее по абсолютной величине
значение, т. е. такое, что —тг < ср < тт. Это значение
аргумента называется главным.
Комплексное число а = а + Ы условились
геометрически изображать точкой М, у которой в данной
прямоугольной системе координат абсцисса равна а, а
ордината Ь (рис. 9). По этой причине
ось абсцисс называется
вещественной осью, а ось ординат —
мнимой осью. Комплексное
^число также изображают
направленным отрезком ОМ, т. е.
отрезком прямой, у которого
указано, какая из
ограничивающих его точек является
началом и какая концом. В данном р 9
случае О есть начало, а М —
конец. Такой направленный
отрезок называется вектором. Вектор, имеющий началом
точку О, а концом точку М, обозначается так: ОМ.
Направление вектора указывает стрелка на его конце.
Таким образом, комплексное число а е= а + Ы изображают
вектором, начало которого совпадает с началом
координат, а конец — с точкой М (а, Ь).
Длина вектора, т. е. длина отрезка ОМ, дает
геометрическое изображение модуля числа, а угол,
образованный осью абсцисс и вектором, т. е. ^ ХОМ, дает
изображение аргумента. Очевидно, вещественным числам
соответствуют точки, лежащие на вещественной оси, а чисто
мнимым числам — на мнимой оси.
947
727. р = 1/(1—С05а)2 + 5т2а =]/ 4зт2^- =
= 2|
а 0 . а 1 — С05 а
31П -5~ = 281П -1Г, С05 ср =
2 I 2 Т а
251П-у
= 5!П-
СОЗ-
51П ср
251П-
а . тс — а
^СОЗу = 51П ^—'•
Главное значение ср =
= 231П
х(
СОЗ-
2
ТС -
а данное число г =
я — а
+ I • 81П-
728.
С05
Р=уЛ(1 + 8та)2 + соз2а=]/4со52(-^ |-) =
/тс а \ I 0 /тс а \ I + 51П а
(т-т>
в=С08(т"—1*)» 81пср =
2соз
51П
Нт-т)
Главное значение <р = -^ ?р а данное число
729.' р = 1^1 + *82 а = У ^ес2 а = | зес а | = — зес а,
созср
1
— —соза==соз(а — тс), зтср=-
{&а
зес а * " ' — зес а
51п а = 81п (а — тс), 1 + П§ а = — зес а [соз (а — тс) +
+ /31П (а — тс)].
730. а) Геометрически
модулю комплексного числа г
соответствует расстояние точки
плоскости, изображающей чис-
X ло 2, до начала координат. В
данном случае это расстояние
равно 2. Следовательно,
равенству 121 = 2 соответствуют точки
окружности ё центром в начале
координат и радиусом, равным 2
(рис. 10).
Рис. 10.
348
б) Так как равенству | г [ = 2 соответствуют точки
окружности с радиусом 2 и с центром в начале
координат, то неравенству | г | < 2 соответствуют точки круга,
ограниченного этой окружностью, исключая точки
окружности. Аналогично числам |г|>1 соответствуют точки,
расположенные вне круга, ограниченного окружностью,
радиуса единица с центром в начале координат,
исключая точки этой окружности. Поэтому числам г,
удовлетворяющим соотношениям 1 < | г | < 2, соответствуют
точки, расположенные в кольце между двумя
концентрическими окружностями радиусов / и 2 и имеющими центр
в начале координат, исключая точки этих окружностей
(рис. И).
в) Так как г2 = (х + и/)2 = х2 — у2 + 2хуьу
= х2 — у2 = (х — у) (х + у). Следовательно,
7?(г2) = 0 распадается на два: х — у = 0 и
то #(г2) ==
равенство
х + у = 0.
Рис. 11. Рис 12.
Эти уравнения являются уравнениями биссектрис
координатных углов. Поэтому точки, соответствующие
соотношению /? (г2) = 0, расположены на биссектрисах четырех
координатных углов (рис. 12).
г) Так как 1т(г)=у, то данное неравенство
запишется так: у >-<р Отсюда
видно, что точки находятся выше
прямой, параллельной оси
абсцисс и отстоящей от нее на
расстояние, равное -2~ (рис. 13).
д) |г-1|<|г+ 1 |,
|г-1|2<|г + 1
Рис. 13.
349
(х-1)2 + у2<(х+1)2 + у\ х2~2х + 1 + у*^х* +
+ 2х + 1 + *Д — 2х< 2х, Ах > 0, х > О. Отсюда
видим, что точки находятся в полуплоскости,
расположенной правее оси ординат, включая ось ординат (рис. 14).
731. а) Аргументом комплексного числа г называется
величина угла, образованного полупрямой, проведенной
из начала координат * через точку, являющуюся изобра-
Рис. 14.
Рис. 15.
жением г, с положительным направлением оси абсцисс
(вещественной оси). Поэтому равенству аг§г = -у-
соответствуют точки полупрямой, выходящей из начала
координат, наклоненной к оси абсцисс под углом -у-
(рис. 15).
б) Учитывая сказанное в пункте «а», легко убедиться,
что числам, аргументы которых удовлетворяют
соотношениям -у < аг§ г < -у,
соответствуют точки плоскости,
расположенные внутри угла,
заключенного между
полупрямой, выходящей из начала
~Х
п
Т
Рис. 16.
ложительному направлению оси
абсцисс, и положительным
направлением оси ординат. При этом
точки, расположенные на
сторонах угла, исключаются (рис. 16).
350
732. а) Во втором и третьем координатных углах,
исключая точки оси ординат (рис. 17).
б) В первом и втором координатных углах, включая
точки оси абсцисс (рис. 18).
— X
/////
ш<
0
\ч
Ш
Ш
Рис. 17.
Рис. 18.
733. Окружность радиуса 1 в направлении, обратном
движению часовой стрелки. Центр этой окружности
симметричен центру данной окружности относительно оси
абсцисс.
734. гхгг = рх (соз <рх + 151гь срх) р2 (соз ср2 + шп <р2) =>
<= Р1р2 [(СО5 ?1 С08 Ъ — §!П ?1 8*П Ъ) + * (8*П ?1 С05 ?2 +
+ СОЗ ?! 31П ср2)] = р1р2[С03 (срх + Ъ) + ' §1п (?1 + Ъ)1
735 -^- = Рх (С05СР1 + /зшуг) _
22 р2 (СОЗ <р2 + / ЗШ ср2)
р! (СОЗ Ух + ' 51П У!) (С05 <р2 — / ЗШ ср2)
^ Р2 ' СОЗ2 <р2 + 5Ш2 <р2 в
= -^ • (СОЗ (р! + I 51П срО [СОЗ (— ср2) + I 31П(— ср2)] =
Р2
с= -^- [СОЗ (?! — ср2) + I 31П (ср! — Ср2)]-
Р2
736. Так как гп = г • г ... г и аргумент произведе-
ния равен сумме аргументов сомножителей (см.
задачу 734), то отсюда и следует формула Муавра.
351
737. Так как г к = -^-, то, положив п = —т (т> 0),
получим
(С05 <р + * 31П ср)Л = (С05 ср + Г 51П ср)~ш = —. ——. — =
1 т/ N т • т/ (соз <р + / 51П срУ"
1 . .
= т-т—. = С08 /Пф — I 51П /Пер =
соз тер + * 5ш тер Т т
= соз (— т)ср + 151П (— т) ср = соз лгер + I зт тр.
738. Модуль числителя равен
У(х2-у2)2+(2ху)*= V (х2 + у2)2 = *2 + *Д
Модуль знаменателя равен
У(хуУ2)2 + (Ух* + у' )2 =/ (*2 + */2)2 = х2 + у2.
Так как модуль частного равен частному модулей
делимого и делителя, то
I хуУ 2 + сУ х* + у* \~~ х2 + у* '
739. (ао) 4- 6«>2) (аш2 + М = Л3 + а&а>2 + а&а>4 + &2и>я.
/ 2к 2я \3
Но ш3 = (СОЗ -1С- + * 31П -^-I = СОЗ 27Г + Г 51П 2тс = 1,
ш2 + «> = — 1.
Поэтому данное выражение
А = а2 + абш2 + а&а> + б2 = а2 4- аб (ш2 + а>) + Ь2 =*
= а2~аЬ + Ь\
740. Так как ш3 = 1, а ш2 + ш = — 1 (см.
задачу 739), то
(а + Ь + с) [а2 + аЬ(м2 + со) + ас (о>2 + <*>) 4-
+ Ьс(о)2 + а) • а)3) + Ь2^ + с2о)3] ^(а + Нс)(а2 + 62 +
+ сЪ — аЬ — ас — Ьс)=:а? + Ь* + с? —ЗаЬс
(см. решение задачи 682),
741. Эту задачу можно решить непосредственным
перемножением. Но такой путь длинный и утомительный.
Поступим иначе. Обозначив данное выражение буквой Ау
преобразуем его, пользуясь формулой суммы кубов двух
352
количеств и соотношением а>2 + а> = — 1 (см. решение
задачи 739). Получим
А = (а 4- Ьш + си>2 + а +Ьш2 + см) <рь
где ср1 — краткое обозначение неполного квадрата
разности данных двух количеств. Отсюда
А = (2а — Ь — с) <р1#
Но нетрудно видеть, что А симметрично относительно
а, 6 и с, т. е. не меняет своей величины от
одновременной замены а на 6, 6 на с и с на а. Действительно,
преобразуем Л, используя равенство ш3 = 1 (задача 739).
Получим
А = (ао)3 + 6и> ■+■ си2)3 + (ао)3 + 6о>2 + со>4)3 =
= и>3(6 + со) + Ян)2)3 + ®*Ф + С(1)2 + ао))8 =
= (6 + ш 4- я<*>2)3 + (& + сы2 + аш)3.
Аналогично можно показать, что
Л = (с 4- ао> 4- 6о>2)3 4- (с 4- я<о2 4- 6о>)3.
В силу этого можно утверждать, что А имеет также
множителями многочлены 26 — с — а и 2с — а — 6.
Поэтому
Л = (2а — 6 — с) (26 — с - а) (2с — а — 6) ср2,
где ср2 — частное от деления А на (2а— 6— с) (26 — с —
— а) (2с — а — 6). Замечая теперь, что коэффициент при
высшей степени а- многочлена А равен 2, устанавливаем,
на основании равенства многочленов, что <р2 = 1. Итак,
А = (2а — 6 — с) (26 — с — а)(2с — а — 6).
742. Пусть г = соза + /зша. Тогда получим
г142 + "тпг = (со5 а + 18!п а)Ш + (С08 а + ' з1п а)~142 ^
= С05 142а4-*31П 142а + соз142а —131п142а = 2соз142а.
Но из уравнения г + — = 1 получим:
г»_г4-1=0, г = ±Г±Х^-1 =
= СОз(±-|-)+ ^ш(±-§-).
23 К- У Шахно 353
Итак,
г142 + "ТЭТ" = 2с05 ^ в Эсоз-у^^ — 2соз -^ = — 1,
743. Положив в формуле Муавра (см. задачу 736)
п = 5, получим
(соз а + г 31П а)5 = соз 5а + / зт 5а
или
соз5 а + 5* соз4 а 51П а — Юсоз3 а 51П2 а — 10/ соз2 а 51П3 а +
+ 5соз а зт4 а 4- г 51П5 а = соз 5а + х зт 5а.
Приравняв мнимые части и положив в них а=агсз1п^,
найдем, что
31П (5агс зт х) = 5соз4 (агс зт х) зт (агс зт х) —
— Юсоз2 (агс зт х) зт3 (агс зт х) + зт5 (агс зт х) =
= 5 (У 1 — х2 )4 х — 10 (]/ 1 — х2 )2х* + хъ =
*= 5(1 — х2)2*— 10(1 — я2)*3 + х\
Отсюда
51п (5агс 51П х) = 16*5 — 20л? + 5*.
744. Обозначим сумму синусов буквой Л, а сумму
косинусов буквой В и, положив затем г = соз л: 4-*зт#,
получим
В + Л/ = (соз * + I зт х) + (соз Зх + Шп Зх) + ... +
+ [соз (2/г — 1)* + * зт (2п — 1) л:] = г + г3 + ... + г2"""1 =*
_ г (2а" — 1) (СОЗ X + I 51П X) (СОЗ 2ПХ + *' 5»П 2ПХ — 1)
~ 22_ 1 ' ~~ СОЗ 2Х + / 51П 2х — 1 ~~
(соз * 4 / зт *) (— 2зта пх + 2/ зт гс* соз гсх)
"" — 2зт2 х + 2/ зт # соз л:
(соз х 4 г зт #) • 2/ зт л* (соз пх + / зт пх)
2/ 51П X (СОЗ X + I 51П X)
ЗШЛХ
51ПХ
(соз/г# + /зт/гя).
Итак,
354
о , • л вт пх , . зт /где .
В 4- ь4 = — соз пх 4- ь —■— зт пх.
Отсюда:
51П X 2 51П X * 51П X
Конечно, эту задачу можно было бы решить и
способом, примененным в задаче 517.
745. Умножим обе части данного уравнения на х~п и
в полученном результате положим
ХГ* = (СОЗ а + I 81П а)~к = С05 Ы — * 81П Ы.
Получим
1 + рх х~1 + р2х~2 + ... + Рпх~1п = О, 1 + Р\ (соз а —
— I 31П а) + р2 (соз 2а — I зт 2а) + ... +
+ рп (соз па — ь 81П па) = 0.
Так как рь р2. ...» рп — вещественные, то
Р181П ах + р2 51П 2а + ... + Рп зт па = 0
как мнимая часть числа, равного нулю.
746. Так как 5! + *52 = (I + 1)\ (1 + Г)п =*
= ]/"~2~ [ соз-^- + ь зт -^- ] , то, пользуясь формулой
Л/
Муавра, можем написать 5Х + г52 = 2 2( соз-^|—|-
+ ь 31п -^т—)• Приравнивая теперь вещественные части
этого равенства, а затем мнимые, получим:
Л Л
8г = 2 соз-^-; 52 = 2 зт—^-.
747. Докажем, что 5"^ 3 является мнимой частью
выражения (1-иУ""3)л. Действительно,
(1 + 1\ГЗ)п = 1 + С\1У~Ъ + С2п 0Т"3)2+ & 0УЗ)3+...«
= 1-С'.3 + С^.32+ ... +*У"3(СЛ —СЛ-3 +
+ Сл • и —• ••• )«
23* 855
С другой стороны, пользуясь формулой Муавра, можем
написать
(1 + гу ~3)п = [ 2( соз-^ + ^!п-^)]Л -
Пя/ пк . . • пк \
в= 2Л( С08^ 1- I 31П— I.
Отсюда 5 = г 51п -^-.
1^3 -3
Любопытно отметить, что если в решении исходить
из бинома (— 1 + гУ 3)п, то ответ будет такой:
5 ==(_1Г1. 2^51п^
' ]/з 3
Полезно доказать тождественность этих двух выражений
для 5.
748. Число т называется корнем степени п из
числа г, который обозначается У г , если доп = г.
Пусть
1^ г = ^(СОЗ <р + I 51П ср) = /? (С05 Ф + I $1*П Ф).
На основании определения корня и формулы Муавра
будем иметь
Кп (С05 ПФ + I 31П /гФ) = р (С05 ср + I 31П ср).
Но если комплексные числа равны, то их модули равны,
а аргументы отличаются на число 2Ьг, где к = О, ± 1,
±2, ... Таким образом,
/?» = р, Ф = <р + 2/гтг.
Отсюда
У р(С05 ср + * 31П ср) =|/ р I С05-?-^ Ь * 31П-^*-^ I,
причем У р — арифметический.
Нет надобности придавать & всевозможные целые
значения, а достаточно брать лишь к = О, 1, 2, ... , л— 1.
Действительно, если к > п или /г < 0, то, выделив целую
часть д дроби —, получим к = цп-\-г, где
положительный остаток г < я. Но тогда
п п Ч п
356
и значения косинуса и синуса, в. силу периодичности,
будут такими же, как и при одном из к = 0, 1, 2, ...,
п— 1.
С другой стороны, при различных к, взятых из чисел
О, 1, 2, ... , п— 1, значения корней будут различными.
На самом деле, если при кх и к2, где 0 < кх < п — 1 и
О < к2 < п — 1, имеет место равенство значений корня,
то должно быть
.ГЛ. 1 -ГЛ.—2_ = 2т7Г или ^ ^ — /^^
что возможно только при т==0 (т — целое). Но тогда
кх = к2. Итак, корень степени п из комплексного числа
имеет п и только п различных значений. Исключение
представляет лишь г = 0. В этом случае все значения
корня равны между собой и равны нулю.
749. Положив У а + Ы = х + ух, получим: а + Ы =
= (х + уО2; а 4- &* = х2 — у2 + 2#у*. На основании
равенства комплексных чисел можем написать: х2 — у2 = а,
2ху = 6. Подставив у = -о-, найденное из второго
уравнения, в первое, получаем:
2
-±у-
значение а 2 р < 0 и поэтому отброшено), Тогда
Отсюда
У ~ 2* ± У2(? + а) ~ V '
у~тты- = ±уц±±1у~Ц^-.
Из равенства 2ху = 6 видно, что знаки перед радикалами
нужно взять одинаковые, если Ь > 0, и разные, если
Ь <0.
750. а) г = ^Т" = у соз-|- + / зш^- =
4к + 1 ... 4к 4- 1 у л 1 о я (
= со8—™тс + Г31П—^—тг; & = 0, I, 2; гх = со$-тг- +
357
+ /з}п-
гт
6
I 5 5
+ ~2~» 22 = С05-^-7Г + /81П -г-тг
+ -о"! 2з = С05-.-7Г + 151П-
У"з" + / .
+
кт-
В) у 1 = у СО5 0 + *81п0 =С05—н Ь 151П—г—
к = 0, 1, 2, 3, 4.
751. Корни уравнения хп = I суть ал = соз-
+ *зт , где к = 0, 1, 2, ... , /г— 1. Отсюда: а0 = 1;
2^7Г
+
2тт , . . 2п: 2кп
ах = соз— + * 51П—; ал = соз—
. . 2/гтс
* 81П =
/ 2*
2тт: , . . 2тг\л
+ * 81П—^ = а
Положив ах = а, можно записать эти корни в виде
1, а, а2,
тп—1
-г- 46+1
752. ИЗ формулы 2 = У I е= С08 ^ ТС + I
.46+1
81П
12
видно, что значение г! = соз-т^- + *$1п^у имеет модуль
р= 1, а аргумент ?=-^-.
Остальные корни г2, г3,
..., г6 также имеют
модули, равные единице, а
аргумент каждого
следующего отличается от
аргумента предыдущего на
величину -^-. Поэтому
геометрически корням 2Ъ г2,
..., г6 будут
соответствовать вершины правильного
шестиугольника,
изображенного на рис. 19.
— X
Рис. 19.
358
753. х - ~(2/~ ° ± ^(2/~ 1)Э + 4 (7 + ° =■
-(2/-1)±К25 -2/ + 1±5 , „ о , „ 9 ,
— 2 о ' '— — ' 2==— —
754 * ■-= 3 + /±^(3 + 0,-»а_ 3-И ±(3-0.
Х^ = О, Хз :=: ^#
755. Умножим обе части уравнения на х—1# Тогда
уравнение примет вид х7— 1 =0 или х1 = 1. Корни его:
хк = со5—=2—|- ь$\п—7р-% причем при к = 0 получится
*0 = 1 и этот корень посторонний для данного
уравнения. Поэтому в найденном выражении для хк нужно
положить лишь к — 1, 2, 3, 4, 5, 6,
756. Корни уравнения хп—1=0 суть 1, а, а2, ... ,
ал_1, где а = со8 \- /зт—* (задача 751). Поэтому
искомая сумма 5 = 1 4- аР 4- а2" 4- ... 4- а*"-^ =1+^4-
+ (<хр)2 4- ... + (ар)л~1. Если р делится на п, то а^ = 1 и
сумма равна п. Если р не делится на п, то <хр Ф 1 и
можно воспользоваться формулой суммы геометрической
прогрессии, Тогда для искомой суммы получим, что она
равна ^".Г/ ==0> так как *Рп — 1 =(аТ— 1 = 1—1=0.
757. Представим уравнение в виде ( _ . 1 = — 1»
(л: Ф I). Извлекая корни, найдем
■ / 26 4 1 . . . 2* + 1
-т-==С05 !—7Г + ШП !—ТС,
*•—*
где & = 0, 1, 2, ..., п— 1. Отнимем от обеих частей
равенства по 1 и после этого разделим уравнение на и
Получим
:81П-1~:~ТС + *( I — С08—^7^=3
Л . 26 4 1 26 4 1 , о • • 2 2* + 1
Л . 26 4 1 / 26 4 1 ... 26 4 1 \
= 231П -^_1С ^ СОЗ-^ 1С + I 81П -др* |
359
Отсюда
х — г =
. 26 + 1 / 26+1 , . . 26 + 1 \ '
26+1 . . 26 + 1
СОв-^с-^п-^ ,2^+1 .
.26+1 ^& 2л
Итак,
,26+1 . х 26 + 1
х—ь = с*е—2^—те—'• * = с1б~2^тс;
к = О, 1, 2 л— 1.
758. Так как
, ■ 4» = ■1-^ = соз2а + *51п2а,
1 — М§ а С05 а — I &1П а ' '
то уравнение можно записать так:
соз2а + *зт2а
(й#Г-
или, извлекая корень степени /г:
1 +*/ 2(а + 6гс) , . . 2(а+ кк)
. . = С05 х ; + Е51П '.
1 — XI п п
Прибавляя к обеим частям последнего равенства по 1,
получим
2 . , 2(а+6я) , . . 2(а+6тс) 0 ,я + Ь ,
г- = 1 + СОЗ-^— ' + I 81П-^— ' = 2С052— Н
1 —*/
о . я + 671 а + бте г» а + бл/ а + кк ,
+ 2Х51П-— СОЗ — = 2С05— СОЗ— Н
п п п \ п
1П—! .
+ Г 51П
Отсюда
1 — хг =
а + кк( а + 6л , . . а + 6тс\
СОЗ—11 СОЗ—1- Ь '51П —
а + бтс . . а + бте
СОЗ—! I 31П—• , ,
П п , . . а + кк
1 — * 18-
п
360
а + кк & п
СОЗ-
Итак,
Ж = {ё1±^; * = 0, 1, 2, ..., л- 1.
XI. МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ
759—774, Указание. Если какое-нибудь
утверждение справедливо для единицы и если каждый раз, когда
оно справедливо для какого-нибудь числа, оно
справедливо и для следующего числа, то оно справедливо для
любого числа.
Сформулированное предложение называется принципом
математической индукции.
Метод доказательства, основанный на принципе
математической индукции, называется методом
математической индукции.
Применение метода математической индукции сводится:
1) к проверке высказанного утверждения для /1=1;
2) к предположению, что утверждение верно для п = к\
3) к доказательству теоремы, что из предположения
справедливости утверждения для п = к следует его
справедливость и для п = к + 1.
Иногда пункт 1 рассматривают не с п = 1, а с какого-
нибудь другого п = т. Например, при доказательстве
свойств многогранников нам пришлось бы начинать с
/1 = 4. Однако это не умаляет общности
сформулированного выше, так как всегда можно положить п = у+т — 1
и рассматривать процесс доказательства начиная с
V = 1.
759. Для п = 1 формула справедлива, так как дает
ах = ах. Предположим, что формула верна для п = к%
т. е.
ак = ах + й (к — 1).
Тогда
акМ = ак + й = ал + й (к — 1) + й = ах + йк%
Следовательно, формула
ап = ах + й(п - I)
верна для всех п.
361
760. Формула ап = ахцп~х для п = 1 верна. Пусть она
верна для п = к, т. е. ак = а^*""1. Тогда аЛ+1 = акц =
= а^*. Следовательно, формула ал = ах <7Л~1 верна для
всех п.
761. Напомним, что размещениями из т элементов по
п называются такие соединения, из которых каждое
содержит п элементов, взятых из данных т элементов, и
которые, если отличаются одно от другого, то или
элементами, или порядком элементов.
Пусть из элементов аъ аъ ... ат составляются
различные размещения по одному. Непосредственно
очевидно, что таких размещений будет т. Таким образом,
формула
Апт = т(т— 1) ... (т — п+1) (*)
верна при п = 1.
Предположим, что формула (*) верна при п = к.
Докажем, что тогда формула (*) будет верна и при
я = к + 1, т. е.
А^1 ся т(т~\) ... (т — к\
Для доказательства возьмем какое-нибудь
размещение из т элементов по к, например, аъ а2, ..., ак, и
будем приписывать в конце его каждый из оставшихся
(т — к) элементов, т. е. будем приписывать в конце
взятого размещения поочередно и только по одному разу
элементы аЛ+1, ак+2, ..., ат. Получим (т — к)
размещений из т элементов по (к + 1). Поступая так же с
каждым из размещений из т элементов по к9 мы каждый
раз будем получать (т~ к) размещений из т элементов
по (к+ 1). А так как по предположению Акт=т(т—1)...
(т — к + 1), то число полученных описанным выше
способом размещений из т элементов по (к + 1) будет
равно
Акт(т — к) = т(т— 1) ... (т— к).
Остается выяснить, будет ли последнее выражение равно
Л/л*"1» т. е. не будет ли среди полученных размещений
одинаковых и все ли различные размещения вошли в это
число?
Допустим, что среди полученных размещений есть
два одинаковых. Назовем их Аг и А%щ Так как одинако-
362
вые размещения имеют одинаковые элементы на
одинаковых местах, то пусть на последнем месте А1 и Л2
находится элемент а{. Удалим аг^ъ А1 и Л2. Получим
два одинаковых размещения Ах и А2 из т элементов по к.
Но это невозможно, потому что мы к каждому
размещению из т элементов по к приписывали каждый из
оставшихся (т. е. не вошедших те данное размещение)
элементов только один раз.
Допустим, что некоторое размещение А из т
элементов по {к + 1) нашим способом не получено. Пусть на
последнем месте этого размещения находится элемент аь
который не совпадает ни с каким другим элементом этого
размещения, так как в размещение не входит один и тот
же элемент больше_ одного раза. Удалим а{ из Л.
Получим размещение А из т элементов по к* Значит, чтобы
получить^ размещение Л, достаточно было в конце
размещения Л приписать элемент аг, не вошедший в Л. Но мы
брали всевозможные размещения из_т элементов по к.
Следовательно, брали и размещение Л. Мы приписывали
в конце каждого такого размещения каждый из не
вошедших в него элементов,_Следовательно, мы
приписывали в конце размещения Л элемент аь и поэтому
размещение Л не может отсутствовать среди полученных.
Итак, доказано Л^1"1 « т(т— 1) ..• (т — к), если имеет
место формула Акт = т(т-* 1) ... (т — к + 1), Кроме того,
ранее было доказано, что формула (*) верна при п = I.
Следовательно, формула (*) верна при всяком п.
762. Перестановками из т элементов называются
такие соединения, каждое из которых содержит т этих
элементов и отличается от другого порядком элементов.
Очевидно, из одного элемента можно составить только
одну перестановку, т. е. Рг с= 1, так что формула Рл = л!
справедлива при я= 1.
Предположим теперь, что формула
Рп = п\ (*)
верна при п = к. Докажем, что она верна и при
п = к + 1, т. е.
Рш = (к+1)1
Для доказательства возьмем из данных (к +1)
элементов аь аг% ..., ак, ак+х какие-нибудь к элементов и
363
составим из них перестановку. В этой перестановке
поставим оставшийся к + 1-й элемент один и только один
раз перед первым элементом перестановки, затем перед
вторым и т. д., перед к-ы элементом и после к-го.
Таким образом, с помощью взятой перестановки из к
элементов получим (к + 1) перестановку из (к +. 1) элемента.
Поступая так же с каждой перестановкой из к
элементов, взятых из данных (#+1) элементов, мы каждый
раз будем получать (#+1) перестановку из (#+1)
элементов* А так как по предположению Рк — к\, то число
полученных описанным выше способом перестановок из
(к 4- 1) элементов будет равно к\ (к + 1) = (к + 1)!
Остается выяснить, будет ли полученное выражение равно /\+ь
т. е. не будет ли среди полученных перестановок
одинаковых и все ли различные перестановки вошли в это
число.
Допустим, что среди полученных перестановок еСть две
одинаковые. Назовем их рх и р2. Так как одинаковые
перестановки имеют одинаковые элементы на одинаковых местах,
то некоторый элемент аг занимает одно и то же место
как в ръ так и в р2> Пусть, например, это будет
последнее место, т. е. (к + 1)-е место. Удалим аг из р^и р2.
Получим две одинаковые перестановки рх и р2 по
к элементов в каждой. Но это невозможно, потому что мы
в каждой перестановке из к элементов ставили
оставшийся (к-{-\)-й элемент на последнее место один
и только один раз. Допустим, что некоторая
перестановка р из {к + 1) элементов нашим способом не получена.
Пусть, например, в ней'элемент аг стоит на последнем
месте. Удалим а1 из р. Получим перестановку р из
к элементов. Значит, чтобы получить перестановку р%
нужно было взять перестановку р и в конце поставить
элемент аг Но мы брали всевозможные перестановки из
к данных элементов, в том числе и перестановку р, не-
содержащую элемент аг. Мы приписывали в конце
каждой такой перестановки оставшийся (к 4- 1)-й элемент.
Следовательно, мы приписывали в конце перестановки р
элемент а1 и поэтому перестановка р не может
отсутствовать среди полученных.
Итак, доказано Рк+1 = (к -+- 1)!» если имеет место
формула Рк = к\ Кроме того, выше было доказано, что фор-
364
мула (*) верна при п=1. Следовательно, формула (*)
верна при всяком п.
763. Сочетаниями из т элементов по п называются
такие соединения, каждое из которых содержит п
элементов, взятых из данных т элементов, и отличается от
другого, хотя бы одним элементом.
Пусть из элементов аъ аъ ..., ат составляются
различные сочетания по одному. Непосредственно очевидно,
что таких сочетаний будет т. Таким образом, формула
гп __ т(т — 1) ... (т — п + 1) /3|е
Ст~ 1 • 2 ... п ('
верна для п = 1,
Предположим, что формула (*) верна для п = к
Докажем, что тогда формула (*) будет верна и для
п = к + 1, т. е.
Ът ~~ 1 . 2 ... (к + 1)
Для доказательства возьмем какое-нибудь сочетание
из т элементов по к, например ах а2у ..., ак> и будем
приписывать к нему в качестве (к + 1)-го элемента
каждый из оставшихся (т — к) элементов один и только
один раз. Получим (т — к) сочетаний из т элементов
по {к + 1)
Поступая так же с каждым из сочетаний из т
элементов по к, мы каждый раз будем получать (т — к)
сочетаний из т элементов по (/? + 1). А так как по
предположению
гъ __ т{т— 1) ... {т — к+ 1)
12- Аг
то число полученных описанным выше способом
сочетаний из т элементов по (к -\- 1) будет равно
т(т-\:2{т-к+Ь {т-к).
Нетрудно видеть, что среди подсчитанных сочетаний
есть одинаковые. Чтобы это установить, возьмем какое-
нибудь сочетание с из т элементов по (к + 1),
например аъ а2у аЗУ ..., ак+ъ и удалим из него элемент ах.
Тогда получим сочетание с1 из т элементов по к,
состоящее из элементов аъ а3, ... , ак.н, среди которых нет ах.
365
Затем из с удалим элемент а2. Тогда получим
сочетание съ состоящее из элементов аъ а3, ..., ак+г, среди
которых нет а2. Продолжая удалять из с последовательно
элементы по одному, мы, наконец, удалим из с элемент ак+1
и получим сочетание ск+г из т элементов по к,
состоящее из элементов аъ аъ ..., ак> среди которых нет
элемента ак+г. Так как мы к каждому сочетанию из т
элементов по к присоединяли каждый из оставшихся (т — к)
элементов, то мы присоединяли к сочетанию сг
элемент аъ к сочетанию с2 элемент а2 и т. д., наконец
к сочетанию ск+г элемент ак+ъ получая каждый раз одно
и то же сочетание с из т элементов по (к + 1), Отсюда
следует, что каждое сочетание из т элементов по (к -\- 1)
нами подсчитано (к + 1)раз и, следовательно, общее
число их, полученное ранее, нужно разделить на (к + 1).
Это даст
т(т — 1) ... (т — к + 1) (т — к)
1 . 2 ... к(к + 1)
Очевидно, в полученном числе сочетаний больше не
встретится одинаковых, а также не будет ни одного
пропущенного. Итак, доказано, что
гк^-\ ___ т(т — 1) ... (т — к)
Ь™ ~ Ь2...(Н1) '
если имеет место формула
гк __ т(т — 1) ... (т •— к + 1)
°т"" 1 . 2 ... к •
Кроме того, ранее • было доказано, что формула (*)
верна для п = 1. Следовательно, формула (*) верна для
всех п.
764. Так как
(аг + а2)2 = а\ + а\ + 2аха2,
то доказываемая формула верна для п = 2. Допустим, что
эта формула верна для п = к> т. е.
(аг + а2 + ... + ак)2 = а\ + а\ + ... + а\ + 25,
где 5 — сумма всевозможных попарных произведений,
составленных из чисел аь а2, ..., ак, и докажем, что
формула будет верна для п = к-{- 1,
(аг + а2+ ... +ак + аш)2 = [(аг + аа + ... + ак) + ак+1]2=
= (01 + а2 + ... + ак)% + 2{ах + а% + ... + ак) ак+ х + а2к+{ =
366
= 01 + 02 + - + а* + 28 + 2(а1ак+1 + а2ак+г + ... +
+ акак+1) + а1+: = а? + а22 + ... + а*+, + 25ь
где 5Х — сумма всевозможных попарных произведений,
составленных из чисел аг, аъ ..., ак+г. Тем самым
формула для квадрата многочлена доказана для всех п.
765. Обозначим левую часть равенства 5„. Пользуемся
методом математической индукции.
*' °! ~* 1 . 3"" 3 » 2 .(2 • 1 + 1) 2-3 ~~ 3 '
При п = 1 равенство верно.
2) Предположим, что 8к = 2 . /2^+ 1Г'
3) Докажем, что 8к+1 = (^+21?^+//+// ^
№ 4- 1)(* + 2)
в 2.(26 + 3) *
Действительно,
о __ о №+!)» __ *№+!) , (*+1)2
°А+1 — °* "Г (2^+1)(2^ + 3)"" 2(2Л-Ь1) "*" (2* + 1)(2* + 3)-~
(6+1) [6 (26+ 3)4-2 (6+1)] __ (к + 1)(262 + 56 + 2)
в 2.(26 + 1)(26 + 3) """ 2(26+0(26 + 3) ^
(6+1)(26+1)(6 + 2) __ (6+1)(6 + 2)
"^ 2(26+1) (26 + 3) 2 (2/? + 3) *
766. Обозначим левую часть формулы 5„. При л = 1
формула справедлива. Предполагая справедливость ее
при п = к — 1, докажем справедливость формулы при
/г = А.
8к = 5Л_! + А* = ±(к -\)к (2к - 1) (ЗА2- Ък - 1)+А*«
= Ж[(*~ 1} (2*- 1} (ЗА2 -ЗА- 1) + ЗОА3] =
^ ^[(й _ 1) (2к - 1) (ЗА2 + ЗА - I) - 6А(А - 1)(2Л? - 1) +
+ ЗОА3] = -^-[(А - 1) (2А - 1) (ЗА2 + ЗА - 1) +
867
+ 6*(ЗА2 + ЗА- 1)] =4-(3*2 + Зк~ !)[(*— *) №- 1) +
30'
30
+ 6А] = -^-(ЗА2 + ЗА- 1) (2А2 + ЗА + 1) =»
= 4^ + 1)(2* + 1) (ЗА1 + ЗА- 1).
30
767. Обозначим левую часть равенства 5Л. При п = 1
равенство верно. Предположим, что оно верно при
п = А — 1, и докажем справедливость его при п = А.
Получим
5, = 5,_1+А5 = -1(А-1)2А2[2(А-1)2 + 2(А-1)-
12
12*
— 1] + А6 = -1-й2 [(А — I)2 (2А2 — 2А — 1) + 12А3]
= -1-А2 [(А — I)2 (2А2 + 2А — 1) — 4А (А — I)2 + 12А3)
*= -^-А2 [(А — I)2 (2А2 + 2А — 1) + 4А (2А2 +2А — 1)] =
= -1-А2 (2А2 + 2А - 1) [(А - I)2 + 4А] -
*"(*+ 1)а(26* + 26 —1)
12
Тем самым равенство доказано для любого п.
768. Обозначим левую часть равенства 5„. При п = 1
равенство справедливо. Действительно,
1 . X 81П X , 1 — С05 X
5х = 18* + — 1ё — = —— +
2 б 2 СОЗ X 281П X
2зШаХ + С05 X — С05а X С08 X + СОЗ* X + 2зШа X — 2С05а X
2зШ X С08 X 251П X СОЗ X
соз х (1 + соз х) — 2соз 2дс соз х (1 + соз х) 2соз 2х
~~ 2зш х соз х 2зт хсоз х зт 2дг
- ЧПГГ- - 2с1^ 2*= 4" с*8-Г ~ 2с'§ 2*.
Предположим, что равенство справедливо при п — к—1,
и докажем, что при п = к оно тоже справедливо. На
самом деле,
368
+ 1>Ь ■& = 4, (2с<8 -ъ=г + Ч^) - 2с1§ 2х.
Но, положив -р- = а, получим 'для выражения
скобках
2с1§ 2а + 18 а = с1б 2а + (с*8 2а + *8 а) =
а Л , С05 2а С08 а + 8Ш 2а 81П а . п СОЗ (2а — а)
& 81П 2а С08 а в 81П 2а • С08 а
соз 2а 1 1 + С08 2а , . х
~~ "8Й+ 7ПГ2а~~~ зЛТЙ ~" СТ§а — С15^*-
Итак,
5* = -р-с*б^— 2с1ё 2л:.
Равенство доказано.
769. 1. При л = 1 неравенство справедливо, так как
У 4 < 3. 2. Если неравенство справед пиво при л = к,
то оно справедливо и при п — & + 1. Действительно,
обозначив левую часть неравенства через 5Л, будем
иметь
5,+1 = /4 + 5, < /~4~+^ - 1/"7 < 3.
770. 1. При п = 2 неравенство справедливо, так как
(1 + а)2 = 1 + 2а + а2 > 1 + 2а, (а2 > 0).
2. Пусть неравенство справедливо при п = к.
Покажем, что тогда неравенство справедливо и при я=- к +■ 1.
Действительно,
(1 + а)**1 = (1 + а)*(1 + а) > (1 + ко) (1 + а) >
>1+(*+1)а.
771. Здесь имеет смысл считать лишь_я > 2. При
л = 2 получим квадрат. Для него а4 = Н V 2, т. е.
доказываемая формула справедлива. Пусть формула
справедлива для п=к. Докажем справедливость ее длял=&+1,
пользуясь формулой удвоения. Получим
а2*+1 = У 2Я2- 2К у& - -*-
а|* =
' (6 — 2) двойки
24 К. У. Шахно 369
(к — 2) двойки
- /?]/ 2- ]/2+}Л 2 + ... + у~2 •
(к — 1) двойка
Формула доказана.
772. 1. При я= 1 утверждение справедливо, так как
прямая, проведенная на плоскости, делит эту плоскость
на две части. 2. Пусть утверждение справедливо при
п = к, т. е. плоскость разделена к прямыми на 2к
частей. Тогда (к+1)-я прямая, проходящая через ту же
точку, разделит надвое каждую из тех двух частей
плоскости, которые заключены между двумя ранее
проведенными прямыми, ближайшими к последней. Значит
плоскость будет разделена на (2к + 2) части.
773. 1. При п= 1 утверждение справедливо. 2. Пусть
при п = к эта сумма 8к=(2к — I)2. Заметим, что первый
член к-й строки равен А, число членов строки равно
(2к — 1) и последний член равен (Ък— 2). Строка
(/> + 1).я получится из строки й-й, если к каждому
члену к-й строки прибавить по единице и затем
приписать справа два следующих по порядку числа. Поэтому
получим
5Л+1 = 8к + (2к — 1) + Ък + Ък + 1 =*
= (2к— 1)2 + 8к=(2к + 1)\
Утверждение доказано.
774. Пусть в плоскости М проведена прямая АВ.
Она разделит плоскость М на полуплоскости М1 и М2.
Одну, из этих полуплоскостей можно закрасить красной
краской, а другую — синей. Таким образом, при п = 1
утверждение доказано.
Предположим, что при п = к утверждение также
справедливо. Это означает, что после проведения к
различных прямых на плоскости М плоскость так разбилась на
области, что смежные области закрашены различными
красками (красной и синей). Проведем (к + 1)-ю прямую,
которую назовем СО. Прямая СО разделит плоскость М
на полуплоскости #, и Ы2. Перекрасим полуплоскость #2
так, чтобы там, где до проведения СО было закрашено
370
синей краской, после проведения Си было бы закрашено
красной и, наоборот, где раньше было закрашено
красной краской, теперь было бы закрашено синей. В
полуплоскости N1 сохраним прежнюю окраску. Рассмотрим
теперь две произвольные смежные области Рх и Р2.
Области Рг и Р2 могут лежать по разные стороны от СО,
но могут лежать и по одну сторону от СО. В первом
случае Рг и Р2 после проведения к прямых и до
проведения прямой СЬ составляли одну область и имели
одинаковую окраску. После проведения прямой СО та часть ее
(Р1 или Р2), которая оказалась в полуплоскости Мь
сохранила свою окраску, а другая часть (Р2 или Рг), оказавшаяся в
М2, изменила свою окраску. Поэтому смежные области Рг
и Р2 в первом случае окрашены разными красками.
Во втором случае области Рг и Р2 после проведения к
прямых и до проведения прямой СО составляли две
различные области, те же, что и после проведения СО.
Если теперь они находятся в полуплоскости Иъ где
окраска сохранена прежняя, то они закрашены разными
красками, потому что раньше были закрашены разными
красками. Если теперь они находятся в
полуплоскости Л^2, где красная окраска заменена синей, а синяя —
красной, то они закрашены разными красками, потому
что до проведения СО они были закрашены разными,
хотя и другими, красками.
Таким образом, утверждение справедливо и для
п = к + 1. Следовательно, оно справедливо при любом п.
XII. ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ
ГРАФИКОВ
775—781. Указание. Областью определения
функции одного^ аргумента называется множество всех
допустимых значений этого аргумента. Для элементарной
функции, определяемой посредством математического
выражения, допустимыми считаются все те вещественные
значения аргумента, при которых математические
операции, входящие в данное выражение, имеют смысл, а
численная величина выражения является вещественным
числом. При нахождении области определения элементарных
функций следует помнить, что:
1) знаменатель дробного выражения не должен
обращаться в нуль;
24*
871
2) выражения, находящиеся под знаком корня четной
степени, должны быть неотрицательными;
3) выражения, возводимые в иррациональную степень
или в степень, содержащую в показателе аргументы,
должны быть положительными, а при положительном
показателе — неотрицательными;
4) выражения, находящиеся под знаком логарифма,
должны быть положительны;
5) выражения, находящиеся под знаком арксинуса или
арккосинуса, должны по абсолютной величине не
превосходить единицу;
6) выражения, находящиеся под знаком тангенса или
секанса, не должны равняться —^—тг, где к = О, ±1,
± 2, ... ;
7) выражения, находящиеся под знаком котангенса
или косеканса, не должны равняться /гтг, где к = О,
± 1, ±2, ...;
8) основание и показатель степенно-показательного
выражения и0 не должны одновременно обращаться в
нуль.
775. а) 2 — г^>0, х2 < 2, \х\<У~2,
— |/ 2 < л: < I/ 2 Область есть замкнутый
промежуток [— )/"2, У~2\.
б) х2 — 4 > 0, х2 > 4, \х\>2._ Область состоит из
двух промежутков: (—оо, —У 2], У 2, + оо).
в) ; о >0; л: < — 3 и х> — I. Область состоит из
двух промежутков: (—оо, —3), [—1, + °°].
г) Решив неравенство х(х + 2) (х — 3) (х — 4) > О
(см. решение задачи 638), получим: л: < —- 2, 0 < л; < 3,
х > 4. Следовательно, область состоит из трех
промежутков: (—оо, —2], [0, 3], [4, +оо).
д) х > 0, х — 1 > 0. Отсюда х > 1, а область
[1, +«>).
е) л; — 1 > 0 и х — 2\^ х — 1 > 0. Но последнее
неравенство равносильно такому: (Ух—1—1)2>0, так
что должно быть х > 1. Следовательно, область
определения есть промежуток [1, + оо)
776. а) 2 — 2~*>0, 2"*<2, — л: < 1, х > — 1.
Область есть промежуток [— 1, + оо).
372
б) х — 1 Ф 0. Область состоит из двух промежутков:
(-оо, 1) и (1, +со).
в) и г) Областью является множество всех
положительных чисел.
777. а) х*~ 1 > 0, х2> 1, |*|> 1; * < — 1 и х> 1.
Областью являются два промежутка: (—со, —1)
и (1, +оо).
б) х + 1 > 0, х— 1 > 0; х > 1 Область (1, + оо).
в) х2 — 3* + 2>0, (х— 1) (а: — 2) > 0; х < 1 и х > 2.
Область состоит из двух промежутков: (— со, 1)
и (2, + оо).
г) 1обз(*— 1) > 0- Отсюда х—\>19 а х> 2.
Областью является промежуток [2, + со).
778. а) Все неотрицательные числа, т. е. промежуток
Ю, +оо)
б) Все вещественные числа, т. е. промежуток
(— со, + со)
779. а) $\пхфО\ хфкк, где к = О, ± 1» ± 2, ...
Таким образом, область есть множество всех
вещественных чисел за исключением чисел вида кп. Иначе: область
есть множество всех промежутков вида (къ, (к 4- 1) тг),
где к = 0, ±1, ±2, ...
б) 51п Ах > 0, 2кп < Ах < (2к + 1)тс, -~- < х <
2& -4- 1
< —т-~тс- Область состоит из множества всех
промежутков вида -^-, —^-тг , где к = 0, ±1, ±2, ...
в) Множество всех вещественных чисел, исключая
а: = 0.
г) Должно быть_(§2 х — 0/~3 + 1) (§ * + уН* > 0 или
({§ * — 1) (1§ * — 1^ 3) > 0. Решение последнего
неравенства сводится к решению следующих двух неравенств:
1§ х < 1 и 1§ х > ]/~3. Из них находим, что
кп ^-<*<*тс+-^- и кп-\--^-<х<кт: + ~.
Итак, область состоит из множества всех интервалов
вида
Ш |-, Ы Л- -^ I и вида \ктс + -^-, Ы + —),
где * = 0, ±1, ±2, ...
373
780. а) Должно быть 1о§д51П*>0. Если а > 1, то
это равносильно требованию зтл:> I. Но $\пх не может
быть больше единицы, а равен единице он будет при
х = —-—тт. Таким образом, областью в этом случае бу-
\к 4- 1
дет множество всех чисел вида —?—я, где к =» 0, ±1,
±2, ... Если же 0<а<1, то это равносильно
требованию 0 < 51П х < 1 или 51п х > 0. В этом случае
областью будет множество всех промежутков вида (2#тг,
2къ + 2тг), где к = 0, ±1, ±2, ..,
б) Должно быть 1§1§*>0. Так как здесь основание
больше единицы, то последнее неравенство равносильно
такому: {§ х > 1. Отсюда кп + -^- < х < къ + -|-.
Следовательно, область состоит из множества всех
промежутков вида (&тс+~р *тс+""|")» где*в^ ± 1. ± 2, ...
в) Так как | зш х + соз х | < У 2 < 1,5 (см. решение
задачи 697), то областью является множество всех
вещественных чисел.
781. а) Должно быть — < 1. Отсюда |*|>3 или
л; < — 3 и х>3. Область состоит из промежутков:
(_оо, —3] И [3, +оо).
21x1
б) Должно быть . ' \ < 1. Но это неравенство тож-
1 ■+• X
дественное, так как 21х|< 1 + х\ 1 + х* — 21х\ > 0,
(1 — | х |)2 > 0. Поэтому областью является множество
всех вещественных чисел.
в) Должно быть — 1 < агс51пл:< 1. Область 1—зш1,
81П 1].
2п
782. а) Период со « -^-, так как
у = 51п Зх = 51П (За: + 2тг) » зт 31х + -^-тт ).
*\ п х4-8к (х . п \ х
б) со = 8тс, так как соз—^— « соз( -^ + 2п) = соз-^-.
в) Период первого слагаемого равен -у, а второго -^.
Период суммы должен содержать целое число раз как -$-,
374
так и ~. Такое наименьшее число есть тс, которое
и является периодом,
г) Рассуждая так же, как в пункте «в», убедимся,
что 12тс — период функции.
д) Так как у ~— 51п х 4--^-51п2л:, то период
функции равен 2тг.
783. а) Период функции равен -^ = 1.
. Ода
б) Период $\пу 2 х есть , а период со$]/Зл:
V ^
есть Если бы функция $1пу2 лс + со$]/ 3* была
периодической, то ее период со Ф О, как нетрудно видеть,
должен бы при делении на _ дать целое число и
точно так же при делении на Это значит, что
2Ьк 2/тс , ,
должно быть со = и ш= ■ —, где & и / какие-то
целые числа. Но тогда -— в ■ - или г =-т-, что
У 2 >^ 3 К 2 *
невозможно, так как в левой части равенства находится
иррациональное число, а в правой — рациональное.
Таким образом, рассматриваемая функция непериодическая.
784 — 812. Указание. При построении графика
функции нужно изучить свойства функции, исследовать
функцию. Построение графика функции «по точкам», без
учета ее свойств и особенностей, может привести к
грубым ошибкам. Для построения графика нужно прежде
всего найти область определения функции. Затем полезно
выяснить, не симметрична ли линия относительно оси ОУ
или начала координат, найти, по возможности, ее
наибольшее и наименьшее значения, выяснить значения
функции на границах области определения. После этого можно
взять несколько точек для уточнения линии, в частности,
точки пересечения линии с осями координат. Если
функция периодическая, то при построении можно
ограничиться любым промежутком а < лс < 6, взятым из области
определения функции, если Ъ — а = со, где со — период
функции. Полезно так же помнить, что если функция
у = 1(х) — четная, т. е. /(— х) = [(х), то ее график есть
375
линия, симметричная относительно оси ординат; если
функция у = /(*) — нечетная, т е. /(—*) = —/(*), то ее
график есть линия, симметричная относительно начала
координат.
784. Область определения — множество всех
вещественных чисел. Линия симметрична относительно оси
ординат, так как
(— х)*~ 2(— х)2 + 2=>
«*4 — 2а:2+ 2.
Поэтому достаточно
рассмотреть лишь х > 0.
Выделяя полный квадрат,
получим у = (х2 — I)2 4» 1.
Если х = 1, то у = 1.
./ Это — наименьшее
значение функции. Еслих-^-Ноо,
то (/ -* + ос. Если х = 0,
то г/ в 2* Это точка
пересечения линии с осью ОУ. С осью ОХ она не
пересекается, так как у .-= (л:2— I)2 + I > 0. Взяв еще дополни-
тельно точки для х = -у и Для * = 2, получим такую
таблицу для х > 0 (рис. 20).
ж
У
0
2
0,5
~1,5
1
1
2
10
-* -4~ оо
-► 4- оо
785. Область определения — множество всех
вещественных чисел. Но с увеличением х на 2 и к
увеличивается на 2, а поэтому
значение функции не
меняется. Значит функция
периодическая с
периодом 2. Поэтому достаточно
построить график функции'
в промежутке —1<х<1,
что соответствует к = 0.
Для этого случая у = х2
(рис. 21).
УЛЛ/
-7\П +1
Рис. 21.
376
786. Так как |х| = х для 00 и |*| = —* для
х < о, то у = а: для х > О и у = —х для х < 0. График
функции состоит из двух полупрямых, являющихся
биссектрисами первого и второго координатных углов
(рис. 22).
787. Так как |* + 2| = х + 2, если х>~2 и
| х + 2 = — (х + 2), если а: < — 2, то функцию можно
Рис. 22. Рис 2а
записать так: у = х + 2 для х> — 2 и у = — х — 2 для
л: < — 2. Функциям же у = л: + 2 и у = — х — 2
соответствуют прямые линии, из которых, первая проходит
через точки (—2, 0) и (0, 2), а вторая —через точки
(_2, 0) и (0, — 2), Поэтому искомый график состоит
из двух полупрямых, определяемых написанными выше
уравнениями. Эти полупрямые выходят из точки (— 2, 0)
и расположены от оси абсцисс со стороны
положительных ординат (рис. 23).
788. а) Если х < 1, то | * — 11 = 1 — *, \х — 2| = 2—х,
у = — 2х + 3. Этому уравнению соответствует прямая,
проходящая через точки (0, 3) и (1, 1), а при условии
х < 1 ему соответствует полупрямая, выходящая из
точки (1, 1) и расположенная от оси абсцисс со стороны
положительных ординат.
б) Если 1<д:<2, то \х— 1| = х— 1, \х — 2| =
-г 2 — х, */= 1. Этому уравнению соответствует прямая,
параллельная оси абсцисс и проходящая через точку
(1, 1), а при условии 1<х<2 ему соответствует
отрезок этой прямой, заключенный между точками (1, 1)
и (2, 1)
в)Если*>2, то \х— 1| = х— 1, \х — 2\ = х — 2,
у = 2х — 3. Этому уравнению соответствует прямая,
377
проходящая через точки (2, 1) и (0, —3), а при условии
х > 2 ему соответствует полупрямая, выходящая из
точки (2, 1) и расположенная от оси абсцисс со
стороны положительных ординат. График функции
изображен на рис. 24.
Рис. 24.
Рис. 25.
х2
2
х2, ее
— л:2, если х > 0;
если л; < 0.
График функции состоит из части параболы у = х2,
соответствующей * < 0 и части параболы у = — *2,
соответствующей х > 0 (рис. 25).
790. Если *2>1, т. е. |*|>1, то г/ =|л:2—1 |=л:2— 1.
Уравнению у = х2 — 1 соответствует парабола,
проходящая через точки (—1, 0), (0, —1), (1, 0), а при
условии | х | > 1 ему соответствуют ветви этой параболы,
выходящие из точек (— 1,
0) и (I, 0). Если *2< 1,
т. е. |*|<1, то у=\х2—1|=а
= 1 — х2. Уравнению
у ——х2 + 1 соответствует
парабола, проходящая
через точки (—1,0), (0, 1),
(1, 0), а при условии
| х | < 1 ему соответствует
отрезок дуги этой
параболы, ограниченный
точками (—1, 0) и (1, 0).
График функции
изображен на рис, 26,
-/ ч<
0 /♦/
Рис. 2а
— X
378
791. График функции получится из графика параболы
у = х2 — 3* + 2,
если часть ее,
находящуюся под осью абсцисс
(где #<0), заменить
симметричной ей линией
относительно оси абсцисс
(рис. 27).
792. Область
определения (—оо, + со).
Кривая симметрична
относительно оси ординат и
вся расположена над осью
абсцисс. При х = О функция принимает наибольшее
значение у =1. При *>1 функция убывает*, и если
х-> + оо, то у->0 (рис. 28).
Рис. 27.
Рис. 28.
793. Область определения (—оо, + оо). Кривая
симметрична относительно начала координат. Так как
У =
1 + *а
' \+х2—2*+2лГ
1
-(*—1)2+ 2*- (х— I)2
+ 2
Рис. 29.
то отсюда видно, что при
х = 1 функция имеет
наибольшее значение у = -«-.
* Функция /(*) называется убывающей (возрастающей) в
некоторой области, если она определена в этой области и если для любой
пары хх и х2 принадлежащих ей значений из хх < х2 следует
379
При х = О и у = О. Если О < х < К то функция
возрастает; если *> 1, то функция убывает. Когда х-+ + со,
1
то у =
1 + -у
О (рис. 29).
794. Функция у = 1о§2 (— х) определена для х < 0.
Ее значение при х = — а (а > 0) совпадает со значением
функции у = 1о&2 х при
х = а. Следовательно,
графики функций у=\о{У2 (—х)
ну— 1о&2 х симметричны
относительно оси ординат.
» X Но график функции у =
= 1о&2 х общеизвестен,
поэтому график данной
функции будет иметь вид,
изображенный на рис. 30.
795. Область
определения — множество всех
вещественных чисел, за исключением нуля. Кривая
симметрична относительно оси ординат, так как 1о§2|— *| = 1оё2|*|.
Но при х > 0 у = 1о§21*| = 1о&2 х, и отсюда ясно, что
Рис 30.
кУ
Рис 31.
Рис 32.
график данной функции будет состоять из графика
функции у = 1о§2 х и симметричной ему линии относительно
оси ординат (рис. 31).
796. График данной функции будет в промежутке
[I, + °°) совпадать с графиком функции у = 1о§2*» а в
380
промежутке (0, 1] являться зеркальным отображением
функции у = 1о§2 х в оси абсцисс (рис. 32).
797. Область определения функции есть промежуток
(—оо, + оо), но для .построения достаточно рассмотреть
промежуток [0, тг], потому что у = 2зт 2х имеет период
о) = тт. При х = — функция имеет наибольшее значение
у = 2, а при х = —тг — наименьшее значение у
— 2.
Рис -33.
Если у = 0, то хх = 0, #2 = ~^-
#о == 7Г.
В промежутке
О < а: <-^- функция возрастает, в промежутке ^т<.х<—т: —
убывает, в промежутке — тс < х < к — снова возрастает
(рис. 33).
798. Функция имеет период о> = 4тс, поэтому
достаточно ее исследовать в промежутке [0, 4тс]. Это
исследование проводится
аналогично исследованию, и
проведенному в зада- *
че 797. График
функции изображен на
рис. 34.
799. Период функции —
со = ~^-. Функция
приводится к виду
:'?'
у = К251п(-!- + 4*).
Рис 34
381
Исследование ее в промежутке —-^г, ^тг сходно с ис-
в задаче 797. График функции
следованием функции
см. на рис. 35.
Рис. 35.
800. График симметричен относительно оси ординат.
При х>0 график данной функции и график функции
у = $юх совпадает (рис. 36).
^ V
Рис 36.
801. Для всех лс, для которых 5т*;>0, график
данной функции и график функции у = $тх совпадают. Для
всех х, для которых зтл;<0, график данной функции
Рис. 37.
и график функции у = зт х симметричны относительно
оси абсцисс (рис. 37).
382
802. График получится суммированием ординат
графиков функций у = х и у = 51*п х% соответствующих одному
и тому же значению
абсциссы. Кривая
симметрична
относительно начала координат,
так как
(— X) + 51П (— X) =
= — (X + 51П X).
График функции дан
на рис. 38.
803. Область
определения (— со, + со).
Но данная функция
периодическая с
периодом 2тс. Поэтому Рис. за
достаточно построить
график ее в промежутке —-?-, -к- тс . Если —~ <#< ~,
то у = агс 51П ($1П х) = х, а если -^- < х < -^ тс, то
У = аГС 81П (51П X) = ТС — X
(см. задачу 544). Отсюда
видим, что график данной
функции в промежутке*
к Г п з 1
о", -о- ТС СОСТОИТ ИЗ
двух отрезков прямых
Рис. за (рис. 39).
804. Область
определения функции — множество всех вещественных чисел, но так
как она имеет период о>=2тс, то будем ее исследовать в
промежутке [0, 2тс]. Если
0 < х < тс, то
У = аГС С05 (С05 X) = Х\
если же тс < х < 2тс, то
У = аГС С05 (С05 X) =
аГС С05 [С05 (2тс — *)].=
= 2тс — х,
так как 0 < 2тс — х < тс. рис. 40.
^
^
-х
383
Отсюда видим, что график данной функции в промежутке
10, 2к] состоит из двух отрезков прямых (рис. 46).
80& Равенство у = Агс соз (соз х) равносильно
равенству соз у = соз х. Но тогда
получим у ~ 2к тг + х, где
* = 0, ±1, ±2, ...
Отсюда видим, что
х у = Агс соз (соз х) —
функция бесконечнознач-
ная. График функции
состоит из двух семейств
параллельных прямых. Одни
из них образуют с осью
абсцисс углы 45°, а
другие 135°. Расстояние между прямыми каждого семейства
равно к У 2 (рис. 41).
806. Область определения — множество всех вещест-
2к+ 1
Рис. 41.
- л, где к -
У
V / л
7Г7^~7
«-/
Рис 42
венных чисел, за исключением чисед вида-
любое целое число. Так
как данная функция
периодическая с периодом
ш = те, то достаточно
исследовать функцию в
промежутке (— у, — I.
Если ^- < х <-^-, то
у = агс 1§ (1§ х) = х.
Поэтому график данной функции в рассматриваемом
интервале состоит из отрезка прямой, ограниченного
точками (—1, — 1) и (1, 1) (рис. 42).
807. Область определения функции есть множество
всех вещественных чисел. Преобразуем выражение,
определяющее функцию. Пусть к < х < к + 1, где к — целое
число. При х = к и у = к. Пусть теперь х = к + а, где
0 < а < 1. Получим
У =
2 (к + а) — 1 1
= к +
2
2* -1
агс
*[
*е
2(к + а)—1
•]
агс
*ё(<ё2-^*)=*+
2а-
384
2а — 1 , 2а— 1
—^—т = « Н ^~
2а-1
= Ь,
О
— X
и, следовательно,
агс!§^§ а~ 7г)==~^^тс (см. задачу 545).
Итак, если &<*<&+1, то */ = &. Очевидно, для
&+1<л:<& + 2 функция у = к+1. Отсюда видим, что
график данной функции в
промежутке к < х < к + 1
представляет собой отрезок прямой,
параллельной оси абсцисс и
отсекающей на оси ординат
направленный отрезок, равный к.
Правые концы этих отрезков не
принадлежат графику (рис. 43).
808. Область определения
функции определится из
системы неравенств: 1 — х > 0, х > 0.
Это даст 0 < х < 1.
Следовательно, областью является промежуток [0, 1]. Преобразуем
данное выражение. Возьмем синус от обеих частей данного
равенства. Получим
§1П у = 51П (аГС 51П |/ 1 —X + ИГС 51П У~Х) =»
= 51П (аГС 51П У\ — X) С05 (ДГС 51П У~Х) +
+ со5 (агс 31П У\ — х) 51*п (агс 51п Ух) =
= УТ^УТ^х + У~х}Пс=1 —х + х=1.
Но так как
Рис 43.
— X
Рис. 44,
25 К. У. Шахно
У х>0 иУ1—х>0, то
0 < агс 51*п У1 — х < -^-,
0 < агс 31П У~х < -|-
и 0 < у < тс. Поэтому из
равенства 31ПГ/ = 1 следует
385
у = -у. Этот же результат можно было бы получить
и на основании задачи 560. Таким образом, графиком
данной функции является отрезок прямой, ограниченный
точками (о, -у^ и (1, у) (рис. 44).
809. Область определения — множество всех
вещественных чисел, за исключением нуля, Преобразуем
выражение, находящееся в правой части равенства, пользуясь
формулами задач 568, 539 и 569. Если х > 0, то
у = агс1§х —агсс*е— = -тр — агс1§ — агсс!§— =
= -Т ~ (агс *8 4 + агс с1§ 4) = "Г ~ "Г = °-
Если х < 0, то
у = агс {§ х — агс с*§ — = — -|- — агс 1§ — агс с{§ ~ =
ТС /х_1| х 1 \ ТС ТС
= —2--(агс1§—+ агсс1е-] = -^---г = -«.
„ Итак, графиком данной функ-
* ции будет для х > 0
положительная полуось ОХ, а для
* < 0 полупрямая,
параллельная оси ОХ, и отсекающая
на оси ОУ отрезок, величи-,
ною — тг, считая от начала
координат (рис. 45).
810. Область определения
— множество всех
вещественных чисел, за
исключением— 1. Преобразуем данное равенство. Возьмем
тангенс от обеих частей равенства. Получим
±ёУ = *§ (агс 1§ х + агс *б4т^) =
Ч (агс *2 х)+1&( агс 1ц \^)
-71
Рис. 45.
1-*8(агс*^)*8(агс*8-}+-^) 1-'"у
л: !
л -[■
1—■
\ — х
1+х
х-А^Л
х*+ 1
"" 1 + *а
+ *
386
Е
4
О
Следовательно, # = #тс+-|-. При этом, так как 1- <
<агс1§л;<-|-; — у <агс Ч\^х< |-и — тс <агс*ё* +
1 — х
4- агс 1§ { < тс, к может равняться только 0 или — 1.
Итак, получаем, что у = ~ или у = —— тс. Если 1 + * < О,
то, очевидно, — у<агс1§х<0; —~<агс1§-|^-< Ои
о
— тс < У < 0. Ясно, что в этом случае у = т- тс. Если
1 + л: > 0, то, как легко выяснить, агс {§ х и агс {§ ■
будут в интервале 0 < х < 1 положительны и,
следовательно, их сумма может
быть только
положительным числом, а в интервалах
— 1 <*<0и 1 <х< Ч-со
они разных знаков, и по-
этому их сумма будет
находиться между — ~ и + ~. д
Отсюда заключаем, что
у = ^-, если лс > — 1, и
г/ = — тс, если *< — 1, График функции состоит из
двух полупрямых, параллельных оси ОХ, из которых
одна выходит из точки!—1, -у-) и идет в сторону
положительных абсцисс, а вторая выходит из точки!—1, —-^-тс)
и идет в сторону отрицательных абсцисс. Сами точки
(— 1, -г) и (— Ь "х *)графику не принадлежат (рис. 46).
811. Область определения — множество всех вещест-
1 , » < 1 при всех х. График
функции симметричен относительно оси ОУ. Поэтому
рассматриваем только х> 0. Из данного равенства получаем
1 — х»
25* 387
-7*
3 .
Рис. 46.
Эта формула напоминает формулу, выражающую косинус
угла через тангенс половинного угла. Естественно
поэтому вычислить 1д -—-. Находим, что
1е±= Т/1-003^ = л/Т2 = х
1§ 2 У 1+созу У щ
причем перед радикалом взят знак плюс, потому что
О < */ О, 0 < -|- < у и, следовательно, 1§ -у > 0. Из
а У равенства 1§ у = х
получаем -|- = агс 1§ х или
у = 2агс1§*. Значит
—■—^ —^= график данной функции
х, \/^ для л;>0получитсяиз из-
у! * X вестного графика
функции у = агс 1§ х
удвоением ординат последне-
рис 47. ГО (рис. 47).
812. Область
определения функции промежуток [—1, 1]. Положим
агс соз (2х2—1)=г. Получим соз г= 2*2—1, причем 0<! г < тс.
Равенство созг = 2л:2—1 напоминает формулу,
выражающую косинус угла через косинус половинного угла.
Естественно поэтому вычислить соз-|-. Находим
Следовательно,
г=2агс соз х, если х > 0 и г=2агс соз ( — х)9
если х < 0. Таким образом, если
х > 0, то у = 2агс соз * 4- 2агс зт * = тс; если д: < 0? то
у = 2агссоз(— *) + 2агсзтх = 2 у — агсзт(— х)\ +
+ 2агс зт х = тс + 2 агс зт х + 2агс зт х = тс + 4агс зт х.
График функции для х > 0 есть полупрямая,
параллельная оси абсцисс, которая выходит из точки (0, тс) и идет
в сторону положительных абсцисс. График функции для
х < 0 получится из графика функции у = агс зт х, если
его ординаты увеличить в четыре раза и затем так полу-
388
Рис. 4а
ченную кривую поднять на величину те, т. е. все
ординаты увеличить на тг (рис. 48).
813. Если /(#)>0 для всей области определения, то
график функции у = \}(х)\
везде совпадает с графиком
функции у = / (х). Если же
в некоторых интервалах
/(*)<0, то график
функции у = | / (х) | в этих
интервалах симметричен с
графиком функции у = I (х)
относительно оси абсцисс, а
в прочих частях совпадает
с ним (см., например,
задачи 786, 787, 790, 791, 796,
801).
814. График функции
у = I (|я|) симметричен относительно оси ординат, причем
для х > 0 он совпадает с графиком функции у = / (х) (см.,
например, задачи 786, 795, 800). Если функция у = /(*)
определена только для х < 0 (например, /(*) = У —л:),
то выражение /(|*|) не имеет смысла.
815. Уравнение д:г/ = 0 распадается на два уравнения:
х = 0 и у = 0. Первому соответствует ось ординат,
потому что только точки, расположенные на оси ординат,
имеют абсциссы, равные нулю. Точно так же убедимся,
что второму уравнению соответствует ось абсцисс.
Поэтому уравнению ху = 0. на плоскости соответствуют все
точки, расположенные на осях координат.
816. Если х > 2, то | дг — 2| = х — 2 = 1. Отсюда * = 3
Если х < 2, то | х — 21 = 2—#— 1. Отсюда х= 1. Уравнению
х=3 на плоскости
соответствует прямая, параллельная оси
ординат и проходящая через
точку (3, 0). Уравнению х=\
на плоскости соответствует
^ прямая, параллельная оси
ординат и проходящая через
точку (1, 0). Следовательно,
уравнению |* —2| = 1 на
плоскости соответствуют все
точки расположенные на прямых
Рис. 49< х = 3 и х=1 (рис. 49)
№1
13.01
389
817. Уравнение л:2 = у2 распадается на два
независимых уравнения: у = х и у = — х. Первому соответствует
биссектриса первого и третьего координатных углов, а
второму—биссектриса второго и четвертого, Поэтому
уравнению х2 = у2 на плоскости соответствуют все точки,
расположенные на биссектрисах четырех координатных углов
(рис. 50). Л ,
818. а) Если х>0, 2у—1>0, то 2#+1>0, \х\ = х,
\2у— 11 = 2г/ — 1, |2г/+1| = 2*/+1 и уравнение
принимает вид
2*/—1+2*/+1+^=* = 4 или */ = — у=* + 1-
Этому уравнению соответствует прямая, проходящая че-
Рис. 50.
Рис. 51,
рез точку А (0, 1) и наклоненная к оси абсцисс под углом
150° (рис. 51). Но /гак как х*> 0 и у > -^-, то точки
расположатся на отрезке этой прямой, ограниченной точками
Л(0, 1)и в(^, 4)*
б) Если х> 0, 2у + 1< 0, то 2у — 1< 0, | х | = х,
12у — 11 = 1 — 2у, 12у + 11 = — 1 — 2у и уравнение примет
вид
1 — 2у— 1— 2у + ~=х = 4 или У = :р=
1.
Этому уравнению соответствует прямая, проходящая
через точку О (0, — 1) и наклоненная к оси абсцисс под
390
углом 30°, Но так как х > 0 и у < ^, то точки
расположатся на отрезке этой прямой, ограниченной точками
0(0,-1) и с(!^,-4|
в) Если *>0, 2у —1<0, 2у+1>0, то |*| = *.
12г/ — 11 = 1 — 2г/, \2у + 1\ = 2у + 1 и уравнение примет
вид
1 — 2у + 2у + 1 + 4= * = 4 или * = ^-.
уз 2
Этому уравнению соответствует прямая, параллельная оси
ут
ординат и отстоящая от нее на расстояние -Чр, считая от
начала координат в сторону положительных абсцисс. Но
так как ^- < у < -у, то точки лежат на отрезке этой
прямой, ограниченной точками В\^~-, -^) и с(^—, —-2").
Итак, при х > 0 точки, координаты которых
удовлетворяют данному уравнению, заполняют контур АВСО.
Так как подстановка в это уравнение — х вместо х не
меняет вида уравнения, то отсюда можно сделать вывод,
что и слева от оси ординат есть точки, координаты
которых удовлетворяют данному уравнению, и что они
заполняют контур ЛВхСхО,
симметричный с АВСЬ
относительно оси ординат, В
целом получится контур
правильного
шестиугольника (рис. 51).
819. Так как уравнению
х = -о- соответствует
прямая, параллельная оси
ординат и проходящая через
1
0
\У
1
2
1
I ■
I
точку
(|. о),
то точки, коор-
Рис. 52.
1
динаты которых удовлетворяют неравенству х > -у,
заполнят полуплоскость, расположенную правее этой прямой,
исключая граничные точки, т. е. точки самой прямой
(рис. 52).
391
820. Так как в этом случае выполняется соотношение
— 3 < х < 3, то точки, удовлетворяющие своими
координатами данному неравенству, расположены в полосе,
ограниченной прямыми * = 3 и * = — 3, но исключая точки
самих прямых. Эти прямые параллельны оси ординат
и отстоят от нее на расстояния, равные 3 (рис. 53).
— х
Рис. 53.
Рис. 54.
821. Точки расположены выше прямой, уравнение
которой х + у + 1 = 0 (рис. 54).
822. Выше прямой у — х — 3 = 0 и одновременно ниже
прямой у — 2х + 1 = 0 (рис. 55).
823. Выше прямых 2х + у — 2 = 0 (I) и х — у = 0 (И)
и ниже прямой 2у — х —
— 2 = 0 (III)
одновременно (рис. 56).
Рис. 55,
Рис. 5а
392
824. Данное неравенство равносильно следующим:
— 1 < х + у < 1 (см. задачу 660). Следовательно, точки
находятся в полосе между прямыми х + у — 1 = 0 и
х + у + I =0 и на ее границах (рис. 57).
825. Если х > 0, у > 0, то получим 0 < х + у < 1.
В этом случае точки находятся в прямоугольном треуголь-
Рис. 57.
Рис 58.
нике, отсеченном от первого квадранта прямой х + у = 1
(рис. 58) и на его контуре. Случаи х < 0, у < 0; х > 0,
*/ < 0; * < 0, у>0 дадут, соответственно: — 1 < х + у < 0,
0<* — у <1, — 1 < * — #<0. Очевидно, точки,
соответствующие всем этим четырем случаям, расположатся
внутри квадрата, образованного прямыми х + у=1,
х -\- у = — 1, х — У = — и х — у —\ и на его контуре.
826. Данное
неравенство равносильно
следующим:
_1<|х + 1|_|у-
— 11 < 1 (см.
задачу 660).
а) Если х + 1 > 0;
у — 1 > 0, то
— 1<х — у + 2<1.
Следовательно, в этом
случае точки
расположены выше прямой
у = 1 (/), выше
прямой х — у + 1=0 (//),
393
ниже прямой х —-у + 3 = 0 (///) и правее прямой х = — I
(IV). На рис. 59 эта область отмечена горизонтальной
штриховкой.
б) Если #+1>0, у —1<0, то — 1 <* + */< 1.
Следовательно, соответствующие точки расположены ниже
прямой у = 1 (/), ниже прямой л: + у — 1 = О (V), выше
прямой л: + у + 1 = О (У/) и правее * = — 1 (IV). На
рис. .59 эта область отмечена вертикальной штриховкой.
в) Случай я + 1 < О, у— 1 > О приведет к неравенствам
— 1 < х + У < 1, а случай дс + 1 < 0, у — 1 < 0 — к
неравенствам — 1 <х — у + 2 < 1. Очевидно,
соответствующие этим двум случаям точки расположатся в области,
симметричной заштрихованной горизонтально и вертикально
относительно прямой х = — 1 (косая штриховка).
827. Данное неравенство равносильно такому |*/| < И,
которое приводится к следующим: —| х\ < у < | х |. Если
х > О, то — а: < у < л:
1У и соответствующие точки
расположены под
прямой у=х и над прямой
г/ = — х. Если * < О,
то л; < у < — * и
соответствующие точки
расположены под прямой
у = — х и над прямой
у = х. Следовательно,
точки, координаты
которых удовлетворяют
данному неравенству,
расположены в правом и
левом углах, образованных прямыми у = х и у = — х
(рис. 60),
828. В сегменте, отсекаемом прямой у = х от
параболы, у = х2 (рис. 61).
829 — 834. Указание. Вещественные корни
уравнения / (х) = 0 можно толковать геометрически как абсциссы
точек пересечения графика функции у = [(х) с осью
абсцисс. Таким образом, число таких точек даст число
вещественных корней уравнения ^ (х) = 0. Вещественные
корни уравнения /, (х) = /2 (*) можно толковать
геометрически как абсциссы точек пересечения графиков функций
У = А (*) и У = /г (*)• Таким образом, число последних
даст число вещественных корней уравнения ^(х) =/2(*).
394
Если начерчен график функции у = / (*), то, измерив
в выбранном для построения функции масштабе отрезки,
соответствующие абсциссам точек пересечения графика
функции у = / (х) с осью абсцисс, можно приближенно
определить корни уравнения /(х) = 0. Аналогичным
способом можно
приближенно определить корни
" уравнения /, (л:) = /2 (х).
В этом состоит
графический способ решения
уравнений. Степень
точности графического
решения уравнения
существенно зависит от вь*-
бранного масштаба
построения графика. Если
вблизи точек
пересечения графиков выполнить
построение в достаточно большом масштабе, то можно
получить корни уравнения с высокой степенью точности.
829. Строим графики функций у = зт х и у = х. Они
имеют одну точку пересечения (рис. 62). Следовательно,
уравнение имеет только один корень х = 0.
Рис. 61.
у^зтх
Рис. 62.
830. Строим графики функций у *= 2* и у = х + 2.
Из рис. 63 видно, что графики пересекаются в двух
точках. Следовательно, уравнение имеет два корня. Один
корень х = 2. Другой корень, как видно из рисунка,
заключен в интервале (—2, —1). Последнее легко
проверить вычислением. Действительно, подставив в /(*) = 2* —
— х — 2 сперва х = — 2, а затем х = — 1, получим
/(—2) > 0 и /(—1) < 0. Следовательно, в интервале
(—2, —1) функция обращается в нуль.
831. Строим график функции у = 2л:3 — б*2 + 1, Из
рис. 64 видим, что график пересекается с осью абсцисс
в трех точках. Следовательно, уравнение имеет три
вещественных корня. Из рисунка также видно, что один из
корней находится в
интервале (—1, 0), другой в
интервале (0, 1) и третий в
интервале (2, 3). Последнее легко
проверить вычислением (см.
решение задачи 830). / I \ [ г. у
Рис. 64.
832. Строим графики функций у = {§х и у — х. В
силу нечетности этих функций положительному корню
уравнения соответствует равный ему по абсолютной вели-
нине отрицательный корень того же уравнения. Поэтому
интересуемся лишь корнями неотрицательными. Из рис. 65
видим, что уравнение
имеет корень х = 0, а
затем корни,
заключенные в интервалах
(*:,-2"7г], (2тг, у^, ... ,
#тс,
2к +
ч
Рис. 65
С увеличением к корень
приближается к
величине —^— тт. Таким обра-
396
зом, уравнение имеет корень х = П и бесконечное
множество корней как положительных, так и отрицательных.
833. Строим графики функций у = $т х и У=—
(гипербола). Как видно из рис. 66, уравнение имеет беско-
[У
^х
Рис. ба
нечное множество корней как положительных, так и
отрицательных. Первый положительный корень содеожится
в интервале [О, -у).' а следующие положительные близки
Рис 61
к значениям к9 2тс, Зте, ... В силу нечетности функций
у = 31П х и у = — каждому положительному корню соот-
397
ветствует равный по абсолютной величине
отрицательный.
834. Строим графики парабол у= — х2+\0 и х=4—у2
(рис. 67) и измеряем абсциссы и ординаты их точек
пересечения. Находим: #1 = 3, г/х = 1; лг2^^ 3,3, у2~ — 0,7;
х3~— 3,6, у3 ^ — 2,9; #4^ — 2,8, */4^2,6.
ХШ. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПЛОСКОСТИ
(Планиметрия)
835. Дано: в ААВС АЕ±СВ, ВО±АС, АЕ = ВО.
Доказать: АС = С В (рис. 68). ААВО = ААЕВ, потому
что у них общая гипотенуза АВ
Р и равные, по условию, катеты АЕ
А и ВО. Следовательно, равны и
углы ОАВ и ЕВА, как углы
равных треугольников, лежащих
против равных сторон ОБ и ЯЛ. Но
тогда АС=СВ, как стороны ААВС,
лежащие против равных углов ЕВА
В и ОАВ.
836. Дано: в ААВС АО = ОС,
Рис. 68, ВЕ = ЕС, АЕ = ОВ. Доказать:
АС = ВС (рис. 68), Точка
пересечения медиан О отсекает от медианы -^- часть ее, считая
2 2
от основания. Поэтому АО = -^- АЕ=-^- ВО = ВО и
А АО В — равнобедренный. Но тогда /. ОВА =* / ЕАВ,
а следовательно, и АОВА = АЕАВ, как имеющие равные
углы (/.ОВА = ^ЕАВ), заключенные между равными
сторонами (АЕ = ВО по условию, АВ — общая). Отсюда
вытекает, что АО = ВЕ% как стороны равных
треугольников, лежащих против равных углов. Но так как АО— -^ АС,
ВЕ=-~ ВС, то АС = ВС.
837. Дадим два доказательства этой теоремы.
Доказательство I. Пусть в Д ЛВС (рис. 69)
биссектрисы АО и СЕ равны. Нужнее доказать, что
ААВС—равнобедренный. Проведем третью биссектрису ВО, где О —
точка пересечения биссектрис Возьмем теперь второй
398
Рис, 69,
экземпляр этого треугольника и будем соответственные
точки обозначать теми же буквами, но снабженными
значком 1. Приложим ДЛ^А к ААВС так, чтобы
вершина Сх совпала с точкой Д
биссектриса СхЕг с О А, а вершины 5 и
Вх были расположены по одну
сторону от линии совмещения этих
биссектрис (рис. 70). В силу
равенства углов В и В{ заключаем,
что вокруг четырехугольника
АГ>ВВ1 можно описать
окружность. Покажем, что Ай || ВВХ.
Действительно, на основании
теоремы о внешнем угле
треугольника можем написать:
ЛВОО = /.ВАО + ^ОВА. Но ^ВАО== /_ВВхО
(вписанные, опирающиеся на одну и ту же дугу), а 20ВЛ =
~^ОхВхО (половины, равных углов В и Вг). Поэтому,
/: воэ = ^ вва или ^ ввл + </ воох = и.
Таким образом, вокруг четырехугольника ОВВ^Рх
можно описать окружность, а так
как у него ОгВх = ОВ, как один
и тот же отрезок биссектрисы
угла В, то дуги окружности,
описанной вокруг
четырехугольника О^ОВВц стягиваемые
хордами ОхВх и ОВ; будут равны.
В таком случае ООг \\ ВВХ или
Ай || ВВг. Итак, четырехугольник
АОВВх есть вписанная в
окружность трапеция и потому
равнобедренная трапеция. Но в
равнобедренной трапеции
диагонали АВ и ВхО равны. Отсюда
что АВ = ВС, т. е. что /\АВС — равнобедрен-
ДОУ
Рис. 70.
следует
ный.
Замечание. Так как при доказательстве было
использовано лишь условие АО = СЕ$ а то, что АО и СЕ —
биссектрисы, не было использовано, то тем самым
доказана не только сформулированная выше теорема, но и
следующая, более общая: если из двух вершин
треугольника проведены к противоположным сторонам два отрезка,
имеющие точку пересечения на биссектрисе третьего
399
Рис, 71,
угла и равные между собой, то треугольник равнобедрен-
ны&
Доказательство II, Дано, что в ААВС АЕ=ВО
и АЕ и ВО—биссектрисы углов Л и В (рис. 71). Нужно
доказать, что АС = ВС.
Проведем ВР || АЕ и АР \\ ВЕ. Пусть / ИВА = а и
/ ЕАВ = р. Рассмотрим треугольники АВО и АВР.
В этих треугольниках сторона АВ
общая, а ВР = ВО, как равные
одному и тому же отрезку АЕ (один
по построению, другой по условию).
Если допустить, что / ОБА > /. АВР,
т. е. что а>р (/АВР=/ЕАВ=$),
то сторона ЛО будет больше
стороны АР, потому что в неравных
треугольниках с двумя соответственно
равными сторонами против большего
угла лежит и большая сторона.
Итак, имеем АО>АР, если а>р.
Рассмотрим теперь А АОР, в
котором АО и АР являются сторонами.
В нем / АОР > / АР О, Действительно, / АОР = 180° —
— 23 — ,/ АМО= 180° — 2р — (а + / ВО/г)= 180° — а—
— /.ВОР — р — р; </ ЛЛЭ = 180° — </ А1Л/? — ^ АМР =
= 180° — 2а — (р + ^ ВРО) = 180° — 2а — р — ^ В ЛЭ =
= 180°— а — /ВРО— р — а. Но /ВОР= /ВРО, как углы
при основании равнобедренного АВРО (ВО = ВР).
Учитывая, кроме того, что по предположению а > р, получаем
/ АОР > / АРО. Но в треугольнике против большего
угла лежит и большая сторона, т. е. АР > АО. Однако
это противоречит полученному ранее: АО > Ар.
Итак, а не может быть больше р, а ввиду
равноправности а и р не может быть и а < р. Остается лишь а=р,
2а = 2р и, следовательно, АС = СВ.
Замечание. Доказательство II является
доказательством от противного, но оно имеет зато одно
преимущество перед доказательством I, состоящее в том, что
требует меньшего объема знаний из начального курса
геометрии, так как использует лишь теоремы о равенстве и
неравенстве треугольников и о параллельных линиях.
Измерение вписанных углов и возможность вписать
четырехугольник в окружность, используемые в доказательстве I,
здесь не требуется.
400
Подобно доказательству I, здесь также допускается
обобщение. Эта более общая теорема состоит в
следующем; если отрезки прямых АЕ и ВО (рис. 71),
проведенные из вершины А и В /\АВС к противоположным сто-
ронам, пересекаются внутри треугольника, равны между
собой и разбивают углы А и В так, что /, В = аг + я2>
^ А = рх 4- р2, где аг и фг имеют общую сторону АВ, то
или а, > р] и а2 < р2 или а} < р, и а2 > р2.
Доказательство этой теоремы ничем не отличается от
доказательства II, если только в выкладках доказательства
иметь в виду, что углы при основании треугольника не
2а и 2р, а аг + а2 и рз + Р*
838. Дано, что в Д АВС (рис. 72) ЛО = ОС и
</ Л50 = /. О ВС. Нужно доказать, что АВ = ВС,
Продолжим ВО на расстояние ОО = ОВ и
точку О соединим с точками Л и С. Так
как АО = ОС по условию, а ОВ = ОО по
построению, то четырехугольник АВСО
параллелограмм. Но А АВО = А ОВС и
поэтому этот параллелограмм есть ромб.
Отсюда АВ = ВС.
839. Дано, что в треугольниках АВС
и А&Сг :^А = А Аи АС = ЛЛ ЛВ +
+ ВС = ЛХВГ + В1С1 (рис. 73). Нужно
доказать равенство этих треугольников
Продолжим сторону АВ на отрезок ВО = ВС
и точку О соединим с С. В
равнобедренном Л СВО </ О = </ ОСВ, как углы при
основании, сумма их равна внешнему/ АВС,
а потому ,/ЛВС=2,/0. Делая аналогичные построения
для Д Л^Сь также установим, что А АХВХСХ = 2^0Ь
Но дЛОС=дЛ101Сь потому что у них /Л = ^ЛЬ
Рис. 73.
26 К У Шахно
401
АС=А1Си АВ^АВ + Вй^АВ + ВС=А1В1 + Я,С,=ЛА.
Отсюда Ю^ Юх и /. АВС ^/. АгВгС19 а тогда
равны и третьи углы данных треугольников, т. е. /. АСВ =
- 4 АгСгВг. Таким образом, в треугольниках ЛВС и АХВХС^
/ Л » ^ А19 АС = ^х^ и ^ ЛСВ = / Л^^! и,
следовательно, треугольники равны.
840. Дано, что в треугольниках АВС и Л^С,: ^ Л5С=
/ Л^Сх, / 5ЛС « ^ ВХЛ А, ЛВ + ВС + АС = Л^ +
+ 5А + Л1С1 (рис 74). Доказать равенство этих треуголь-
Рис. 74.
ников. Продолжим сторону АВ на отрезок ВО = ВС и на
отрезок ЛВ = АС и соединим точки О и В с С. В
равнобедренном треугольнике ОВС </ О = ^ ОСВ, как углы
при основании, сумма их равна внешнему углу АВС$
а потому /Ц В = -те- </ ЛВС, Точно так же докажем, что
</ Е — -^ </ ВЛС. Делая аналогичные построения для
Д А1В1С1, получим, что /Щ йг — -у- ^ Л1В1С1 и ^ Вх =*
= -у" ^ ВИ^х. Но ^ ЛВС « /: АХВХСЪ а / ВАС »
==^ В^^, поэтому ^ О = / Ох, ^ В == </ Я1§ Кроме
того, ВО = В^ — 2р и, следовательно, Л ОЕС =*
= АВгЕ^!. Из равенства этих треугольников вытекает
равенство ОС = 6^, а так как ранее было доказано, что
/.О = ,/ О^ то равнобедренные треугольники СВО
и СгВ1В1 равны. Теперь имеем в треугольниках АВС
и АгВхС{. ВС = В^ (боковые стороны в равных
равнобедренных треугольниках), /.АВС => /.А1В1С1 (по условию),
402
/.АСВ=/.А1С1В1 (как дополняющие равные величины
до 180°). Отсюда ААВС = ААгВгСг
841. Дано, что в трапеции АВСй АС = ВО. Доказать,
что АВ = С/) (рис. 75). Через вершину С проведем
прямую СЕ [| ВО до пересечения с продолжением основания
АО в точке Е. В треугольнике АСЕ АС = СЕ = ВО
(СЕ и ВО —
противоположные стороны
параллелограмма), поэтому он
равнобедренный. Но тогда /. СЕ А =а
= /. САЕу как углы при
основании равнобедренного тре- д
угольника, а так как /_ ВО А =
'/.СЕА (соответственные), то рис 75
и Л С АО = ,/ БОА. Переходя
к рассмотрению треугольников АВО и АСО> видим, что
они равны, потому что у них АС = ВО, /САО~/ВОА%
АО — общая. Но тогда АВ = СО, как третьи стороны
равных треугольников,
842. Пусть АВ = ОЕ и АВ О ОЕ (рис, 76), Соединим
А с Е и В с О. В четырехугольнике АВОЕ стороны ЛВ
и /)/: равны и параллельны, и он, следовательно, есть
параллелограмм. Но диагонали параллелограмма в точке
Рис. 76, Рис 77.
пересечения делятся пополам. Итак, диагонали ЛО и ВЕ
разделятся точкой О пополам. Но если рассмотреть теперь
четырехугольник АРОС, то также убедимся, что СР
разделится в точке О пополам. Итак, АО, ВЕ и СР
проходят через точку О.
843. Пусть правильный треугольник АВС вписан в
окружность с центром в точке О (рис. 77). Возьмем на
^
26*
403
дуге ВС точку М. Требуется доказать, что МВ + МС =
= МА. Проведем ВЭ \\ СМ, Пусть точка пересечения
прямых ВО и АМ есть Е. Покажем, что МВ == МЕ.
Действительно, углы треугольника ЛВС, как равностороннего,
равны 60°; /. АМВ = Л АСВ = 60° (вписанные,
опирающиеся на одну и ту же дугу АВ)\ л СМ А = л СВА = 60°
(вписанные, опирающиеся на одну и ту же дугу АОС)\
Л МЕВ =*Л СМ А = 60° (накрест лежащие при
параллельных СМ и ОВ и секущей АМ). Итак, в треугольнике
МВЕ два угла по 60°, следовательно, и третий также
равен 60°. Поэтому треугольник МВЕ «равносторонний и
МВ = МЕ. Покажем теперь, что МС = ЕА. Соединим
точку О с точкой А. Треугольник ОЕА —
равносторонний, потому что Л ОЕА = л МЕВ = 60° (вертикальные),
Л АОВ =з л АСВ = 60° (вписанные, опирающиеся на одну
и ту же дугу АВ), ЛОАЕ = 180°— ЛАОЕ — ЛОЕА =
= 180° — 60° — 60° = 60°. Поэтому ОЕ = АЕ. Соединим
теперь точку О с точкой С. Четырехугольник ЕОСМ есть
параллелограмм, потому что ^ СОВ =<^САВ = 60°
(вписанные, опирающиеся на одну и ту же дугу СВ), и»
следовательно, накрест лежащие углы СГ>В и иЕА при
прямых СО и АМ и секущей ОВ равны, что доказывает
параллельность СО и АМ (ОЕ [| СМ по построению). Но в
параллелограмме противоположные сторону равны и мы
имеем СМ = ОЕ = ЕА.
Окончательно АМ == АЕ + ЕМ = СМ +
+ МВ.
844. Пусть АО, ВЕ и СР —
высоты остроугольного
треугольника АВС (рис. 78). Нужно
доказать, что АО, ВЕ и СР —
биссектрисы треугольника О ЕР. Докажем,
например, что /. ЕОА = </ АОР.
Так как Л АРС =* Л ЛОС=90°, то
вокруг четырехугольника АР ОС
можно описать окружность. Тогда
убедимся, что 2. ЛОР => Л АСР,
как вписанные, опирающиеся на
одну и ту же дугу АР. Точно
так же докажем, что </ ЕОА = </ ЕВА. Но из
прямоугольных треугольников АВЕ и АСР получим Л АВЕ =»
= 90° — Л ВАС = Л АСР. Следовательно, Л ЕОА=*
= л ЛОР.
Рис. 78.
404
845. На данном основании АС — а построим сегмент,
вмещающий данный угол (рис. 79), Соединим какую-либо
точку В* окружности с точками А и С. Получим
треугольник ЛВС с данным основанием и данным углом при
вершине. Проведем теперь диаметр ОР±АС и построим
окружность радиуса ОА с
центром в О. Предполагая,
что точка В отлична от О,
продолжим АВ до
пересечения с построенной
окружностью в точке Е и
соединим ее с С, а точку О с
Л, С и Е. Покажем, что
ВЕ = ВС. Действительно,
^ АЭС = / АВС
(вписанные в окружность О,
опирающиеся на одну и ту
же дугу), ^ АЭС = 2 2 АЕС (первый — центральный,
а второй — вписанный в окружность, и опирающиеся
на одну и ту же дугу). Но тогда /.ВСЕ=^АВС —
— /. АЕС = ^ АйС — Л АЕС =2^1 АЕС— л АЕС = /. АЕС,
а следовательно, треугольник СВЕ — равнобедренный и
ВС = ВЕ. Отсюда АВ + ВС = АВ + ВЕ = АЕ, и так как
В не совпадает с центром 0} то АЕ есть хорда, и для нее
при любом выборе точки В
справедливо АЕ < АО + ОЕ
(АО + ОЕ равно диаметру).
Заметив, что ОС = ОЕ
(радиусы окружности О),
получаем АО + ОС>АВ + ВС,
т. е. искомый треугольник —
равнобедренный.
846. В трапеции АСОР
(рис. 80) АО = СР и
потому она равнобедренная
(задача 841). Отсюда получаем
^ 1СО = / ЮС. Но / ЬАР=
и </АРЬ — /, ОСЬ (накрест лежащие) и, следо-
</^С^ = /ЦОС = /ЦАР = /ИРА. Точно так
Рис. 80
*=/ЮС
вательно,
же</КВА = //КАВ = ^КЕО=/.КОЕ, ЛМСВ = /1МВС =
= / МЯ/7 = </ МРЕ. Рассматривая теперь четырехугольник
ВСОЕ, видим, что у него суммы противоположных углов
равны и потому через точки В, С, О и Е можно про-
405
Рис. 81.
вести окружность. Но тогда, в силу равенства углов СВЕ
и СРЕ, она пройдет через вершину У7, а в силу равенства
углов ОСР и ВАР — через вершину А. Теорема Доказана.
847. Пусть АО, ВЕ и СР — высоты треугольника АВС
(рис. 81), пересекающиеся в точке 0, а О К и ОЬ—
диаметры окружностей,
описанных вокруг АВ и
ВС и проходящих
через О.
Покажем, например,
что ОК = ОЬ.
Соединим Ь с В и К с 5.
Так как /ОВ/С =
= ^<т = 90°, то 15
является продолжением
В К, Но /.ОКВ=/.ОАВ,
как вписанные,
опирающиеся на одну и ту же дугу. Точно так же
А 01В =* /_ ОСВ. С другой стороны, А ОЛВ = 90°—^ АВВ=
= ^ОСВ.
Следовательно, </ ОКБ = /. ОЬВ, треугольник ОКЬ —
равнобедренный и ОК = ОЬ.
848. Пусть ВО ± АС и
АЕ±ВС (рис. 82).
Прямоугольные треугольники С/ИЭ и САЕ,
как имеющие общий уголЛСВ,
подобны. - Из их подобия по-
СГ) ВС
лучаем -^ — -^-. Таким
образом, треугольники СОЕ и
АВС имеют общий угол АСВ,
от-
Рис. 82.
заключенный между пропорциональными сторонами,
куда и следует подобие этих треугольников.
849. Известно, что углы с параллельными сторонами
или равны, или в сумме составляют два прямых. Если
допустить, что каждая пара соответственных углов
треугольников в сумме составляет два прямых, то сумма шести
углов треугольников даст шесть прямых, что невозможно.
Если допустить, что треугольники имеют только по одному
равному углу, то сумма шести углов треугольников будет
больше четырех прямых, что опять невозможно. Остается
допустить, что два угла одного треугольника равны двум
углам другого. Но тогда треугольники подобны.
406
850. Л АВС со д АгВгС19 Я и г — радиусы описанных
около этих треугольников кругов. Доказать: К:г = АС\А1С1
(рис 83). Соединим центр окружности О с точками А
и С. В треугольнике АОС АО = ОС = Я, а /ЛОС==
еэ 2^ Л15С, так как он, как центральный, измеряется
дугой АС9 в то время как
/. АВС — вписанный и
измеряется половиною
дуги АС. Соединив
центр окружности Ог
с точками Л, и С1т
также получим
равнобедренный АА101С1 с
углом при вершине АхО^Сх,
который равен
удвоенному углу А1В1С1. Но
ААВС =^А1В1С19 как
соответственные в
подобных треугольниках
АВС и А^ВхСъ поэтому ^АОС^^А^^С^ Отсюда
вытекает, что равнобедренные треугольники АОС и АгОгС1
подобны и имеет место пропорция ОС : ОхСг = АО \ АхСг
Рис. 83.
или К
851
г^АСх АгСг.
Предположим, что СО (рис. 84) не касательная.
С Тогда она будет секущей и
пусть Е вторая общая точка
прямой Си с окружностью.
Построим треугольники АЕС
и ОВС. Они подобны, так как
у них </С — общий, а углы
СВй и СЕА равны, как
вписанные, опирающиеся на одну
и ту же дугу АО. Из
подобия получим СА • СВ =
с=СО-СЕ Ф СО\ так как СЕ Ф
Ф СО (СЕ = СО + ОЕ или СЕ =
= СО — ОЕ). Но это
противоречит условию. Следовательно, СО — касательная.
852. Проведем медиану АО ААВЕ (рис. 85) и
рассмотрим треугольники АОВ и АОС. В этих треугольниках угол
О общий. Кроме того, у них отношения сторон, заключа-.
ющих этот угол, равны. Действительно, ОВ : АО =
с=а:аУИ= 1 : ]/~2, ОС \ АО = 2а : аУУ=уТ: 1. Сле-
407
Рис. 85;
довательно, Л АОВ со д/ШС. Но в подобных
треугольниках против сходственных сторон лежат равные углы.
Поэтому ^АВй= ЮАС, а IАВО + ^ АС О = ^ОАС +
-\-^АСО=^АОЕ (свойство внешнего угла треугольника).
Отсюда ^ АВО +
+ ^АСО = 45°.
853. Дано, что в
четырехугольнике АВСО
АМ = МО, В# = ЛГС7и
ММ =ЛВ+0С (рис. 86).
Нужно доказать, что
АВСО — трапеция.
Проведем отрезок
прямой ОЫ и
продолжим его на величину ЫЕ=ОЫ. Соединим точку Е с точкой А.
Получим Л АОЕ, в котором МЫ
она равна -^ Соединим
теперь точку Е с точкой
В. Получим Д ЫЕВ,
равный д ОЫС, так как у
них СМ= ЫВ (по условию),
ОЫ = ЫЕ (по построению)
и ^ СМЭ = ^ ВЫЕ как
вертикальные. Отсюда
получаем, что ВЕ = СО и, сле-
АЛМ ЛВ + ВЕ
довательно, МЫ = ъ
есть средняя линия, и
С
Рис 86.
Сравнивая с
равенством
МЫ = -*§-.
находим, что
полученным
АВ + ВЕ=*
ранее
= АЕ. Но это возможно только в том случае, когда АВ
и ВЕ лежат на одной прямой. Так как ВЕ \\ СО, то
теорема доказана.
854. Пусть О — центр
описанного около ДЛВС
круга (рис. 87); АВЧ ВЕ
иСР — его высоты; Н —
точка пересечения
высот; М, К и Ь —
середины отрезков АН, ВС
и АС. Нужно
доказать, что КМ = АО.
АОКЬ <п Д АВН в силу
Рис. 87.
408
параллельности сторон, а так как КЬ — -у АВ, то ОК =>
= -=- АН = АМ, Рассматривая четырехугольник АОКМ,
видим, что в нем противоположные стороны ОК и АМ
равны и параллельны. Поэтому АОКМ — параллелограмм
и КМ = ЛО.
855. Противоположные стороны описанного
четырехугольника попарно параллельны, так как каждая пара
сторон перпендикулярна к одной и той же диагонали
прямоугольника. Таким образом, этот четырехугольник —
параллелограмм с равными высотами. Но тогда он будет
ромб, что следует, например, из сравнения двух
выражений для его площади (аЛа = ЬНЬ).
856. Пусть в ААВС высоты АК, ВЬ, СМ
пересекаются в Я (рис. 88), Точки
/С, Ь, М лежат на
сторонах треугольника.
Проведем диаметр АО
окружности, описанной около
Л АВС, и соединим точки
М и [, Нужно доказать:
МЫ АО.
Опишем окружность
вокруг четырехугольника
АШМ. Это можно еде- д
лать, так как </ АЬН =
= </ АМН = й. Тогда
^ АНЬ = /. АМЬ
(вписанные, опирающиеся на ч^
^АЦ. Кроме того, /1 АНЬ=
= </ ВС А (взаимно
перпендикулярные стороны) и /. АйВ =я ^ АС В (вписанные,
опирающиеся на ^ АВ). Следовательно, ,/ АМЬ — /. АОВ.
Обозначим точку пересечения АО и МЬ буквой N.
В треугольниках АМЫ и АВО два угла одного равны
двум углам другого. Поэтому ^ АЬ1М = /. АВО = й, т. е.
МЬ±АО.
857. Пусть продолжения сторон АВ и СО вписанного
четырехугольника АВСО (рис.89) пересекаются в точке й,
а ВС и АО — в точке /\ Пусть биссектриса угла Е
пересекает окружность в точках К и Ьч а угла Р в
точках М и N. Пользуясь теорембй об измерении
Рис. 88
409
угла, образованного секущими с помощью дуг, можно
написать:
Е
4
==5э*"^
Рис. 89.
Складывая эти равенства почленно и сделав
преобразование, получим ^ /<7У -+- ^ МЬ в ку ЬЫ + ^ МК, что и
доказывает теорему.
858. Указание. Треугольник, одна вершина которого
совпадает с вершиной прямого угла данного треугольника,
а две другие находятся в центре окружности и в точке
касания окружности с катетом, — равнобедренный.
859. Пусть в трапеции АВСй (рис. 90) диагонали АС
и ВО пересекаются в точке О,
а точка Е есть середина
большего основания. Проведем
прямую ЕО и пусть Р будет точка
пересечения прямой ЕО с
меньшим основанием. Докажем, что
Р есть середина основания ВС.
Для этого рассмотрим
треугольники ОЕО и ВОР. Они
подобны, так как у них /1 ВОР =
вертикальные) и /. РВО = ^ ЕОО (на-
ВР ОР „
НО,
Очевиден ^ ВОЕ (как
крест лежащие).
Следовательно, -^ = -щ-.
410
но, и треугольники СРО и АЕО тоже подобны, а поэтому
РС РО ~ * вр рс г гп
-дъ = -^-. Таким образом, -^ = -^-, а так как Ей =*
«= АЕ, то ВТ7 = РС.
860. Соединим точку Л с точкой А и точку Р с
центром окружности О (рис. 91). Обозначим точку
пересечения АС и РО через Е. Так как Д#5С со дЯРЯ, то
ЕС:РВ=йС;ОВ. Так как ДЖ)С со д Р0В{^АйС «
= /.РОВ), то РВ: АС^ОВхйС. Перемножая почленно
полученные пропорции, найдем ЯС^-^-ЛС.
Рис. 91,
Рис. 92
861. Пусть ЛВ —хорда (рис. 92); ЛС и ВС
—касательные; Р — точка окружности; РД РЕ и Р/7 —
перпендикуляры, опущенные из Р на АВ, ВС и АС. Из
подобных треугольников РйВ и ЛР/7 (,/РЛ/7 = ^РВЛ как
измеряемые половиной дуги РА) найдем РО:РВ = РР:АР.
Точно так же из подобных
треугольников РАО и РВЕ
(</ РВЕ = ^ РЛВ как
измеряемые половиной дуги РВ)
получим Рй I ЛР = РЯ : РВ.
Перемножая почленно
полученные равенства, найдем РД2=з
= РР . Р5.
862. Пусть* Ох есть центр
описанного около
треугольника круга, 02 — точка пересечения его высот и 03— центр
тяжести треугольника (рис. 93). Соединим точки 01 и 03,
Рис. 93,
411
а также 03 и 02 отрезками прямых. Докажем, что ОД
и 0302 составляют одну прямую. Треугольники ОхОр и
0203В подобны. Действительно, / 0,Ш3 =/02В08, как
накрест лежащие при параллельных, ОдЪ : О-В = 1:2 —
по свойству центра тяжести треугольника, иОх: В02 =
= ОЕ : ВС = 1 : 2, так как ЕЛ есть средняя линия ДАВС<
и ДЕОхОы АС02В вследствие параллельности их сторон
(см. задачу 849), Отсюда ^ Я0302 = </Ш^ и отрезки
0г0ъ и 0302 лежат на одной прямой. При доказательстве
предполагалось, что медиана не совпадает с высотой. Но
случаи такого совпадения
соответствует равнобедренному
треугольнику, и в этом случае
теорема очевидна.
863. Нужно доказать, что
ЕО = ОЕ (рис. 94). Прове-
ж дем через точку Пересечения
^ диагоналей О высоту /СР. Так
как ЕР || АВУ то Д СОР со
слдСАВ и Л ООЕ со дОВА.
В подобных треугольниках отношение сходственных сторон
равно отношению сходственных высот, и поэтому из
первой пары подобных треугольников получаем пропорцию
-^д- = -^-, а из второй -д^ = -^р- (КР, очевидно, равна
высоте дАСВ, проведенной из вершины С, и высоте
дАОВ, проведенной из вершины Д точно так же КО для
треугольников ОСР и ООЕ).
Сравнивая написанные со-
ОР
отношения, получаем-т^-==з
-жи 0Р = Е0-
864. Пусть
четырехугольник АВСО описан
около круга с центром О,
и Е—середина его
диагонали АС (рис. 95). Нужно
доказать, что прямая ОЕ
пересекает вторую
диагональ ВО в ее середине.
Обозначим точку
пересечения ОЕ и ВО буквой Р. рис 95.
Рис. 94.
412
Обозначим радиус круга через г, а периметр и площадь
четырехугольника через 2р и 5. Так как для описанного
четырехугольника АВ +ОС =АВ + ВС = р и 5 = рг, то
можно написать, что
8лоо +8вос = '1гг(АО + ВС) = ±рг=±5. (*)
С другой стороны,
8вСЕ + 8оаЕ = -у «5/4ВС + ~2~ 8 АЭС = -у 5, (**)
Сравнивая равенства (*) и (**), найдем 8все + 8оае =*
= 8асю + 8 вое или 8 вое — 8все = 5для — 5^оо, или
8вое + 50яс = 8Аое + 8оое> Но 5оес = 8аое $ и поэтому
8вое = 8оое* Из последнего равенства находим, что ВЫ=>
= ОМ.
Рассматривая треугольники ВРN и ОМР, видим, что
они имеют по равному катету и острому углу.
Следовательно, Л РВЫ = Д РОМ и РВ= ЭР.
865. Указание, Наиболее удаленная точка
окружности от данной хорды есть точка пересечения
окружности с перпендикулярным к хорде диаметром.
866. Теорема будет сразу же доказана, если
установить, что Д АОМ со д СN0^ где О— центр полукруга
(рис. 96). В этих треугольниках
2.А—/.С, как углы при
основании равнобедренного
треугольника. Покажем еще, что /Ц МО А =
= /ОМ;. Пусть I, Р и С?-~
точки касания прямых АВ, МЬ1 и
ВС с полукругом. Так как
011.АВ и ОСЦ.ВС, то ,/10(2 =
= 180° — Л В. С другой
стороны, 180° — ^в = ^/}+/С =
=2/. А. Отсюда ^ ЮС} = 2/А Но
Л10 есть биссектриса ^ 10Р и МЭ—
биссектриса /Ц (}ОР. Поэтому
г. ьо(2 = 2 ^ молг = 2 ^ л
и ^ Ш = </ Л. Заметив, что в треугольниках АОМ
иОММтакже ^АМО=*/_ЫМО, заключаем, что и /Л10Л =
= ^ ЛШ). Так как /_ ЛМО = ^ 0#С, то / МОА =
= ^ 0#С и Д ЛОМсо дСЖ>. Из подобия получаем АМ:АО=
I ас \2
= ОС\ЫС.Отсюда АМ-ЫС = АО-ОС= АО2 = (-у-) •
413
867. Возможны два случая: а) прямые МАЫ и Р5ф
пересекаются вне данных окружностей; б) эти прямые
пересекаются внутри одной из окружностей (на рис. 97
второй случай изображен пунктиром). Разберем только
первый случай. По свойству вписанного четырехугольника
ЛЫ+ ААВС1= 180°, и
/ М+ ^АВР = 180°.
По свойству смежных
углов ^ЛВС2+/ЛВР=
= 180°, Складывая
почленно первые два
равенства и пользуясь
третьим, получим Л М+
+ /.N=180°.
Следовательно, N(2 || МР.
868. Пусть АВСО
вписанный в
окружность четырехугольник
с диагоналями АС и ВО
(рис 98), Пусть угол
АВй не меньше угла ОВС. Проведем прямую ВЕ так,
чтобы /ЦАВЕ => Л&ВС. Так как в треугольниках АВЕ и
ВОС, кроме этих равных углов,- еще равны углы ВАЕ
и ВОС, как вписанные,
опирающиеся на дугу ВС, то
ААВЕю АВОС. Поэтому
РВ _ АВ
ОС ~~ АЕ
Рис. 97.
= 4^- или йВ-АЕ
= ОС-АВ.
(*)
Подобными будут также
треугольники ВСЕ и ЛВД потому что у
них / АВй = ^ СВЕ9 как суммы
равных углов, и ^АЛВ = /.АСВ9
как вписанные, опирающиеся на
дугу АВ. Поэтому -^ = -^ или
йВ * СЕ = АВ • ВС. Складывая последнее равенство с
равенством (*), получим:
ВВ • АЕ + йВ • ЕС = ОС ЛВ + АЛ • ВС;
ЯВ (ЛЕ + ЕС) = ОС • АВ + /Ш ■ ВС;
ЭВ - АС *=* ЕЮ * АВ + АО - Вв.
414
869* Пусть длины катетов а и 6, а гипотенузы с. По
теореме Пифагора с2 = а2 + Ъ2Щ Умножим обе части
равенства на с. Получим & = с . а2 + с • б2, Но а < с и 6 < с.
Поэтому с3 е= са2 + сЬ2 > а • а2 + Ь • Ь2 = а3 + #*. Итак,
с3 > а3 + Ь\
870. Пусть Ох — центр описанного около треугольника
круга (рис. 99), а О —
центр -вписанного в * него
круга» Соединим прямой
точки В и О и пусть Э
есть точка пересечения ее
с описанной окружностью.
Проведем диаметр ОЕ =
= 27? этой окружности,
Так как ВО —
биссектриса угла ЛВС, то АО == ОС
и потому ЕО ± АС. Проведя
ОК±ЕО, найдем из
треугольника ООхО) что 00\
= 0хО2 + 0О2~ 20гО-КО.
Но ОхО = Я, КО = КЬ+ О
+ Ю=ОМ+Ш= г +Ю, Рис. 99.
где ОМ ± АС. Поэтому
00\ = Я2 + ОО2 — 27? (г+Ю) ^К2—2Кг+0О2—2Я • Ю^
= К2 — 2Яг + ОО2 — АО2, Покажем, что ОО =
= АО. Для этого рассмотрим треугольник АОО. Так как
АО — биссектриса угла ВАС и /1С АО = ^ ОВС, как
вписанные, опирающиеся на одну и ту же дугу, то
^ЯЛО= /ЮАС+ АСАО^ /ЮВС + /.ОАВ = ЛОВА +
+ </ ОАВ. Но и / АОО = А ОБА + А ОАВ, так как
2 АОО — внешний угол треугольника АВО. Из равенства
углов АОО и ОАО следует равенство АО — ОД
Поэтому получаем:
001 = К2 — 2Яп 001 = УК2 — 2%г.
Замечание. Решение задачи проведено на примере
остроугольного треугольника. Однако и способ решения
и результат будут верны для любого треугольника Если
треугольник равносторонний, то очевидно, что это
расстояние равно нулю. Впрочем, и в этом случае
полученная формула остается верной»
871. I. На основании задачи 870 квадрат расстояния
между центром описанного около треугольника круга и
415
центром вписанного в этот треугольник круга равен /?2— 2/?г,
где /? и г —радиусы описанного и вписанного кругов.
Поэтому имеем: Я2 — 2/?г > 0, 2Кг < #2, г < -~ /?. Знак
равенства будет иметь место только для равностороннего
треугольника.
II. Пусть стороны треугольника будут а, Ь и с9 а
противолежащие им углы а, р и 7. Пользуясь формулой 5=/?/-,
где 5 и р — площадь и полупериметр треугольника,
формулой 5= ^ аЬзшу, а также теоремой синусов, согласно
которой а = 2/? 51П а, 6 = 2/? зш р, с = 2/? зш у, найдем для
отношения радиусов вписанной и описанной окружностей:
г 5 аЬ $1п 7 2/? $т а 2/? зт Э зт -\
~#~ ~" "р#" "" К(а + Ь+С) ~" 2#? (81П а + 8Ш Э + 81П ?) ^
2$Ш а 51П |3 $1п 7
51П а -4" 51П р + 5Н1 *[ '
Преобразуем знаменатель полученного выражения;
251П
+ 251
ЗШСС + ЗШ? + 51'Пу =
+ 251П -1- соз-^- = 2зт (-| ^
С05-
С05
2
а —
+
- +
„(.
2
+ С05
2
* + 1
Если же учесть, что
281П а 51П Р 51П у = 1631П
-)с08+!
-] = 4соз
2соз
соз
а-Э
соз
соз
чт
СОЗ-о- 81П -7ГС08 -ЗГ 81П
СОЗ
то получим
Х = 451П-
■ 31П -н- 31П -дг < 4 • -^- =
Т51ПТ51ПТ
(см. задачу 712).
872. Пусть в треугольнике ЛВС (рис. 100) ААВС>
>/.САВ. Соединим центр
О окружности, вписанной в
треугольник, с его
вершинами Л и В и рассмотрим
треугольник АВО. Его
угол а = -о- ^ ЛВС, пото-
Рис. 100,
му что центр О лежит на
416
Рис* 101.
биссектрисе ВО угла ЛВС. Точно так же р =
= -у ^' САВ. Но тогда р < а, а так как в треугольнике
против меньшего угла лежит меньшая сторона, то ОВк^ОА
Отсюда ясно, что центр окружности, вписанной в
треугольник, лежит ближе всего к вершине того угла
треугольника, который является наибольшим углом.
873. В треугольнике ЛВС (рис. 101) проведем медиану
Вй к стороне АС, продолжим
ее на отрезок ЭЕ = Вй и
соединим точку Е с А и С. В
полученном четырехугольнике
АВСЕ диагонали в точке пере- а
сечения делятся пополам, и, ^1
следовательно, этот
четырехугольник есть параллелограмм
Отсюда получаем, что АВ =
СЕ, АЕ = ВСи (2ВЯ)2 + АС2 -
2АВ2 -\- 2ВС2. Из этого
равенства, положив в нем АВ=с, ВС=
= а. АС = Ь, ВО = ть% ^найдем
2с2 4- 2а2 Ь2 1-1
т\ = ±—А . Полученное соотношение показывает,
что медиана будет наименьшей, если она проведена к
наибольшей стороне.
874. Будет, потому что все его углы будут
вписанными, опирающимися на равные дуги, а равносторонний
и равноугольный многоугольник
есть правильный.
875. Пример ромба
показывает, что не всегда описанный
д равносторонний многоугольник
3 будет правильным. Но если он
имеет нечетное число сторон,
то он будет правильным
Докажем это.
Пусть вершины
многоугольника, имеющего (2/г -Ь 1)
сторону, будут обозначены через
Аъ А2, Л3, .., А2п+и а точки
касания сторон с окружностью
через Въ В2, В37 ..., В2п+) (рис. 102). Очевидно, 42В1=А2В2.
Но тогда, используя равенство сторон, получим, что А1В1==
Рис 102.
'/427 К. У. Шахно
417
=А3В2=А1В2п+\=А3В3, т. е, отрезки двух смежных сторон
многоугольника, сходящихся в вершине Аъ считая от
вершины до точек касания, равны таким же отрезкам сторон,
сходящимся в вершине Л3. Точно так же покажем, что они
равны отрезкам сторон, сходящимся в вершинах Л3, Аъ
...» А2п+\. Итак, отрезки сторон, примыкающие к
вершинам Лх и Л2л+1 равны, т. е. АгВ2п+\ = Дг/жЯгл+ь
Следовательно, сторона АХА2п+\ делится точкой касания пополам.
Но таким же способом убедимся, что все стороны имеют
точки касания с окружностью в серединах сторон.
Соединим точки Аь Вх и Л2 с центром 0. Очевидно А0А1В1 =
= д 0А2Въ и поэтому /. 0АхА2 ~ / 0А2Вх. Так как 0АХ
и 0А2 являются биссектрисами углов Ах и Л2, то углы
многоугольника при вершинах Ах и Л2, а значит и при
всех, равны между собой. Но равносторонний и
равноугольный многоугольник есть правильный.
876. Если из правильных одноименных
многоугольников можно сложить паркет, то необходимо, чтобы
внутренний угол такого многоугольника, повторенный
несколько раз, дал полный угол, т. е. угол в 360°. Так как
внутренний угол правильного многоугольника с п сторонами
180 (л —2)
содержит число градусов, равное у- -, то число
360 : ' должно быть натуральным Определим
из этого условия, каким должно быть п. Имеем
збо, 2« 2+ _1_ = 2+А>
180 (л —2) л —2 ^ я —2
Так как 0 < к < 4, причем к — целое, то для того чтобы
п было целым, к можно придать лишь значения делителей
числа 4, т. е. I, 2, 4. Это дает для п значения 6, 4, 3.
Итак, такими многоугольниками могут быть только
квадраты, правильные треугольники и шестиугольники.
Покажем, что этого и достаточно, т. е. что из указанных
видов многоугольников действительно можно сложить
паркет. Если провести систему равноотстоящих параллельных
прямых и пересечь ее такой же системой прямых под
углом 90°, то получится паркет, сложенный из квадратов.
Если провести систему параллельных равноотстоящих
прямых и пересечь ее такой же системой прямых под углом 60°,
418
в о
а в каждом из получившихся ромбов провести меньшую
диагональ, то получим паркет из треугольников. Паркет
из шестиугольников получится, если в паркете из
треугольников объединять подходящим образом по шесть
треугольников в один шестиугольник.
877 — 884. Указание. Геометрическим местом точек,
обладающих некоторым свойством, называется множество
всех точек, обладающих этим свойством.
Чтобы доказать, что фигура / является геометрическим
местом точек,
обладающих некоторым свойством,
достаточно доказать две
теоремы: 1) если точка
обладает указанным
свойством, то она принадлежит
фигуре /; 2) если точка
принадлежит фигуре /, то
она обладает этим свой- Рис ЮЗ.
ством.
В качестве образца подробного решения задачи на
отыскание геометрического места может служить решение
задачи 877.
877. I. Проведем прямую ВО || АО (рис. 103) до
пересечения ее с продолжением основания АС треугольника
в точке О. Точка О делит отрезок АС внешним образом
в отношении 2:1. Действительно, по свойству параллель-
ОС ВС 2
ных, пересекающих стороны угла, имеем -щ- = -^ = у =>
= 2. Следовательно, точка О неподвижна для любого
положения вершины В. Кроме того, -^ = -^- = 2, откуда
видно, что вершина В в любом положении треугольника
отстоит от неподвижной точки О на одно и то же
расстояние ВО = 2АО. Итак, вершина В находится на
окружности радиуса г = 2АО с центром в точке О,
расположенном на продолжении стороны АС за вершину А на
расстоянии ОА — АС.
II. Возьмем любую точку Вх на построенной
окружности, отличную от точек М и /V, и соединим ее с точками
Л, С и О. Проведем АВХ || ОВх. Отрезок Айг будет
медианой треугольника АВХС. Действительно, по свойству парал-
вл
лельных линии, пересекающих стороны угла, имеем с^ =
1/427*
419
=="ЛС~==Ь так что вА=А& О другой стороны,
-щ- = -щ- =» -2-» А01 = -у- 05х = Л/Э и точка Вх
является вершиной рассматриваемых треугольников. Таким
образом, найденная окружность, исключая точки М и N.
и является искомым геометрическим местом.
Рис 104,
878. Хорда АВ делит окружность на две дуги: Сх и в2
(рис. 104). Для точек М9 взятых на дуге Си
геометрическим местом точек N будет дуга другой окружности,
концы которой находятся в Л и В, расположенная от
хорды АВ по ту же сторону, что и Сг. Вписанный в эту дугу
угол, опирающийся на концы хорды ЛВ, вдвое меньше
аналогично вписанного в дугу С, угла; Для точек Мъ
взятых на дуге <22, искомым геометрическим местом будет
дуга окружности, имеющая концы Л и В, расположенная
от АВ с той же стороны, что и С2, и вмещающая
вписанный угол, опирающийся на концы хорды АВ, вдвое
меньший, чем аналогично вписанный в дугу С2 угол.
420
879. а) Пусть вершина О (рис. 105) данного прямого
угла ХОУ и вершина В прямого угла движущегося
прямоугольного треугольника ЛВС расположены по разные
стороны от гипотенузы АС. Так как /. ЛВС + /. АОС =
= 180°, то вокруг четырехугольника АВСО можно описать
окружность. Описав ее,
видим, что при любом
положении движущегося
треугольника АВС, угол АОВ
остается неизменным,
потому что ^ АОВ = ^ АСВ§
как вписанные,
опирающиеся на одну и ту же дугу
АВ. Следовательно, точка
В находится на прямой
ОМ, проходящей через
вершину О данного прямого
угла и наклоненной к
стороне ОУ этого угла под
углом ВОУ, равным углу
АСВ треугольника. Самое
близкое положение вершины В к точке О есть то
положение М, когда гипотенуза будет лежать на прямой
ОУ. Самое удаленное положение вершины В от
точки О есть положение М, при котором катеты
треугольника АВС параллельны сторонам угла ХОУ. Итак,
при любом положении треугольника АВС, скользящего
концами Л и С по сторонам угла ХОУ, вершина В его
прямого угла находится на отрезке МЫ. Справедливо и
обратное утверждение, т. е. любая точка В, взятая на
отрезке МЫ, является вершиной рассматриваемого
прямоугольного треугольника в одном из его положений. Это
легко доказать, построив окружность радиуса, равного
половине гипотенузы данного треугольника, и проходящую
через точки В и О,
Таким образом, искомое геометрическое место точек
есть отрезок МЫ диагонали ОЫ прямоугольника 0/(А^,
стороны которого КЫ и N1* равны соответственно
катетам АВ и ВС треугольника и параллельны сторонам ОХ
и ОУ угла ХОУ.
б) Пусть вершина О (рис. 106) данного прямого угла
ХОУ и вершина В прямого угла движущегося
треугольника АВС расположены по одну сторону от гипотену-
27 К. У. Шахно
421
зы АС. В этом случае, рассуждениями, сходными с
предыдущими, легко убедиться в том^ что геометрическое место
вершин В прямоугольного треугольника АВС есть отрезок
ММ, направленный по диагонали прямоугольника со
сторонами КЬ и ЬР, равными
1^ катетам АВ и ВС
треугольника АВС и
параллельными сторонам ОХ
и ОУ угла ХОУ. Этот
прямоугольник
расположен внутри угла,
смежного с данным. Отрезок
ЛШ проходит через
вершину О данного угла,
а ограничивающие его
точки М и N
соответствуют тем положениям
вершины В
движущегося треугольника ЛВС,
при которых гипотенуза
лежит, соответственно, на сторонах ОХ и ОУ угла ХОУ.
880. Соединим точку М (рис. 107) касания окружно-
Рис 107.
стей с точками А и В и проведем общую касательную МЫ
к окружностям в точке М, где Л^ —точка пересечения
прямых М№ и АВ. Так как в треугольнике АМВ отрезки
/4#, #М и ШВ равны, как отрезки касательных,
проведенных к окружностям из одной и той же точки //, то'М
422
есть центр окружности, описанной около треугольника АМВ.
Таким образом, при любых двух окружностях,
удовлетворяющих условиям задачи, точка М будет находиться на
окружности радиуса ЫМ с центром в N. Легко доказать,
что справедливо и обратное утверждение, а именно, любая
точка М окружности радиуса уЛ5с центром в N.
отличная от точек А и В, является точкой касания
некоторых двух окружностей, из которых одна касается
прямой АВ в точке А, а другая —в точке В.
Таким образом, искомым геометрическим местом будет
окружность радиуса -^- АВ с центром в середине N
отрезка АВ, исключая точки А и В.
881. а) Если прямые параллельны и расстояние между
ними а больше данной постоянной величины Ъ, то таких
точек не существует. Если а = 6, то все точри,
заключенные между этими прямыми, а также точки этих прямых
составят искомое геометрическое место точек. Если а <6,
то геометрическим местом точек будут две прямые,
параллельные данным и отстоящие от каждой данной на
расстояния, равные —^— и
Рис. юа
б) Если прямые пересекаются, то, обозначив их NР и
(?1 (рис. 108), проведем прямые АЕ и СР,
параллельные кР и отстоящие от нее на данную постоянную
величину Ь, а затем прямые ЕЕ и ВР% параллельные
прямой ОЬ и отстоящие от нее на ту же величину 6. Нетрудно
27*
423
видеть, что сумма расстояний любой точки К, взятой
внутри прямоугольника АВСО, меньше 6, а любой точки /?,
взятой вне этого прямоугольника, больше 6. Для точек же,
лежащих на контуре прямоугольника АВСО, сумма
расстояний равна Ь. На самом деле, возьмем любую точку М,
например, на стороне ВС прямоугольника. Пусть ММг и ЛШ2—
расстояния точки М от данных прямых NР и (}Ь.
Проведем ВВХ^Ь и ММ3±ВВг. Тогда ММг + ММ2 = ММг+
+ М3Вг. Но Д ММХВ = Д ЛШ3В, так как они
прямоугольные с общей гипотенузой МВ и равными углами
МВМг и ВММ3, как равные одному и тому же углу ВСВ^
Поэтому ММХ = М3В. Таким образом, получаем ЛШХ +
+ ММ2 = М3В + МдВх с= ВВХ = 6. Если возьмем точку на
какой-либо другой стороне прямоугольника, то таким же
способом докажем, что и для нее сумма расстояний до
данных прямых равна Ь. Так как для точек не
находящихся на контуре прямоугольника, как было ранее сказано,
эта сумма не равна Ь, то искомое геометрическое место
есть контур построенного прямоугольника АЗСО.
й
а ь{ р
1 о
|в
^Л/
Рис, 109,
882. Пусть ЛВС любая секущая данной окружности,
проведенная из данной точки А (рис. 109), причем В и С —
точки пересечения секущей и окружности, Пусть МВ и
МС — касательные к окружности. Проведем МР±АО и
соединим В и М с О. Обозначим точку пересечения МО и АС
буквой N. Очевидно, Д ОМР со д ОМА. Поэтому ОР\ ОМ =
*=ОМ\ОА или ОР - 0М'°" . Но из треугольника ОВМ
424
находим, что ОМ • ОУУ = ОВ2. Следовательно, ОР = -щ-.
а так как ОВ и О Л данные величины, то это означает, что
любая точка М проектируется на данную прямую ОА
в одну и ту же точку А Следовательно, точка М
находится на прямой, перпендикулярной прямой ОА и отстоящей
от центра данной окружности на величину ОР = -щ-%
Возьмем теперь любую точку М, находящуюся вне
данной окружности и расположенную на прямой,
перпендикулярной ОА и отстоящей от центра О данной окружно-
ОВ2
сти на расстояние ОР = -щ-. Проведем касательные МВ
и МС к окружности из точки М и покажем, что прямая
ВС будет проходить через точку А. Предположим, что
прямая ВС пересечет прямую ОА в некоторой точке Лг,
а ОМ в точке Л^. Тогда, замечая, что треугольники ОАхЫг
и ОМР подобны и рассуждая далее так же, как в первой
ЛП ОВ* „
части доказательства, найдем, что ОР = -туг- по тогда
ОА1 = ОЛ, а это и означает, что точки А и Ах совпадают
или что прямая ВС пройдет через точку А. Поэтому можно
сказать, что искомое геометрическое место точек суть два
луча КМ и Ш^, лежащие на прямой, перпендикулярной
данной прямой ОА и отстоящей от центра данной окруж-
/л п ОВ* п
ности на расстояние ОР = -^-, причем точка Р
находится на отрезке ОА, а не вне его.
883. Окружность, описанная вокруг треугольника ЛВС,
исключая точки В и С,
Указание. Пусть точка М
(рис. ПО) принадлежит искомому
геометрическому месту. Докажем,
что угол ВМС есть величина
постоянная, равная углу САВ.
Действительно, ^ ВМС=</ВМО-\-/1 ОМС,
^ вмо = г: вро и /_ оме =
= ^ ОЕС9 как вписанные,
опирающиеся на ^ВО и ^СО; /_ СЕО=
= АРЕА, как вертикальные;
наконец </ САВ = /. ОРВ + ^ РЕА —
по теореме о внешнем угле
треугольника. Итак, /_ САВ = /.ВМС$ а этой означает, что
точка М лежит на окружности, описанной вокруг треуголь-
-425
ника АВС. Впрочем возможно такое расположение точек Е
и Р, что угол ВМС будет не равен углу САВ, а будет
дополнять его до 180°. Но и в этом случае точка М
будет лежать на той же окружности.
884. Две прямые, параллельные биссектрисам смежных
углов, образованных данными прямыми, и проходящие
через точку О (рис. 111).
Указание. Проведем через точку О прямые ОК и
ОЬу параллельные двум
данным перпендикулярным
прямым. Проведем АМ \\ ОК и
ВМ || ОЬ, пересекающиеся в
точке М> Пусть К есть точка
пересечения ВМ и ОК и
Ь — точка пересечения АМ и
ОЦ Треугольники ОАЬ и ОКВ
равны, так как они
прямоугольные, и О А = ОВ, а
/: АОЬ = ^ КОВ, как углы
с взаимно
перпендикулярными сторонами.
Следовательно, ОЬ = ОК и точка М
лежит на биссектрисе угла
ЮК. Если бы проводить АМХ \\ 01 и ВМг II ОК то
точка Мх лежала бы на биссектрисе угла, смежного с
углом ЮК.
885. Пусть АВСйЕР — данный
центр круга (рис» 112),
Проведем АО, ВЕ> СР и
АЕ> Точка Мх разделит
радиус ОР пополам. Это
очевидно. Проведем ВМХ,
Точка М2 разделит радиус
О А в отношении 1:2, как
это видно из подобных
треугольников ВМХС и М2МхО.
Рис. 111.
шестиугольник
и О —
Итак, ОМ2
ведем СМ2,
X Л
дет
такая,
7?. Это
Про-
Точка М3 бу-
что ОМ3 =
видно из
подобных треугольников СМ,р и МгМ20. Соединяя точки
426
М3 и й отрезком прямой, получим точку М$ такую, что
0Л*4
■/? и т. д.
886. а) Если данные точки А и В лежат на данной
прямой СД то любая точка М, лежащая на отрезке АВ,
будет искомая.
б) Если точка А лежит на прямой СД а точка 5 —
вне прямой (рис. 113), то точка А и есть искомая.
Действительно, для любой точки М прямой СД отличной от А.
выполняется неравенство АМ + МВ > АВ.
Рис. 114.
в) Если А и В лежат по разные стороны от прямой СО
(рис. 114), то точка М пересечения прямых АВ и СО
будет искомой. На самом деле, для любой другой точки N
прямой СД будет АЫ + ЫВ > АВ = АМ + МВ.
г) Если точки А и В лежат по одну сторону от
прямой СО (рис. 115), то,
построив точку Лр
симметричную с А относительно
прямой СО, найдем искомую
точку, как точку М пересечения р г
прямых А^В и СО.
Очевидно для любой другой точки
N прямой СО будет
выполняться соотношение;
МА + ЫВ=МА1+ЫВ>А1В^
= АгМ + МВ = МА + МВ.
887. Пусть точка А (рис. 116) лежит ближе к ММ,
чем к Р($. Проведем через В отрезок ВЕУ равный и
параллельный СО. Соединим точки Е и А отрезком прямой и
пусть 5 есть точка пересечения прямых ЕА и МЫ.
Построив отрезок 5Г, равный и параллельный СО, где Т —
точка пересечения 5Г и РС}, найдем, что А8 + 5Г + ТВ —
наименьшее и, следовательно, положение 5Г отрезка СО—
427
искомое. Действительно, всякое иное положение З^ даст
этой сумме значение больше найденного, так как А8л +
+ 51Г1 + ТХВ = А8Х + ВЕ + Е8Х = ВЕ + (Е8Х + 8ХА) >
> ВЕ + ЕА = ВЕ + Е8 + 8А = 8Т + ТВ + А8.
Рис. на
888. Пусть треугольник ЛВ^ (рис. 117) имеет
вершины Вх и Сх на сторонах ОЫ и ОМ угла МОЫ, а третью
в данной точке Л. Построим точки Ах и Л2, симметричные
точке Л, соответственно,
относительно ОЫ и ОМ и
соединим отрезками Ах и
Вь а затем — Л2 и Сх.
Периметр треугольника
АВХСХ равен периметру
ломаной АХВХСХА2. Он
больше отрезка АХА2,
Отсюда следует, что на-
именшьий периметр будет
иметь тот из
треугольников рассматриваемого
вида, у которого вершины
будут в точках Л, В и С,
где В и С —точки
пересечения прямой АХА2 с
прямыми ОМ и ОМ. Из способа - построения ясно, что
решение будет единственное.
889. а) Пусть данные точки А, В и С (рис. 118) не
лежат на одной прямой. Предположим, что задача решена
Рис. 117.
428
Рис. 118.
и прямые ЛД ВР и ЕС — искомые. Так как ВР должна
делить расстояние между прямыми АО и СЕ пополам, то
ВР должна пройти через середину Р отрезка АС. Отсюда
следует, что одну прямую нужно направить по медиане ВР
треугольника АВС, а две
другие провести через
точки Л и С параллельно ей.
В этом случае задача
имеет три решения (три медианы),
б) Если точки лежат на
одной прямой и две из них
симметричны относительно
третьей, то любые
параллельные прямые, проходящие
через эти точки, будут
искомыми. Если же расстояния
между соседними точками
не равны, то задача не имеет решения.
890. Пусть АВ — диаметр окружности, а О — ее центр
(рис. 119). Проведем АС А. АВ и отложим АС = АВ.
Соединим С и О
отрезком прямой. Если О —
точка пересечения СО
с окружностью, то
касательная МО к
окружности в точке О
пересечет продолжение
диаметра АВ в искомой
точке М.
Действительно, Л ОСА = Л О/ИД
так как О А = ОД а
^ АОО — общий.
Отсюда ОМ = АС=АВ.
891. Искомые
окружности должны точками
касания О, Е и Р (рис. 120) разбить стороны треугольника на
отрезки АО = АР, ВО = ВЕ, СЕ =СР. Учитывая, что
отрезки касательных, проведенных из одной и той же точки
к' окружности, равны, делаем вывод, что точки Д Е и Р
будут точками касания сторон треугольника с окружностью,
вписанной в этот треугольник. Отсюда ясно, что задача
решится просто, если в треугольник АВС вписать
окружность.
Рис. 119.
429
892. Построим по гипотенузе с = АВ и катету Нъ^ВО
прямоугольный ААВй (рис. 121). Проведем ВМ\\Ай и
засечем ВМ дугой .окружности радиуса АМ = 2та с цен-
Рис, 120.
тром в точке А. Через найденную точку М проведем
СМ || АВ до пересечения с прямой АО в точке С. Точка С
будет третьей вершиной искомого Д ЛВС. Если 2та = Нь
или 2та = с, то решение будет единственное. Если 2та>кь,
м но не равно с, то два ре-
° шения. Если 2та<^Нь
или /^ < с, то задача не
имеет решения.
893. Проведем
биссектрисы внутренних
углов треугольника,
имеющего вершины в
данных точках. Проведем
через каждую вершину
*,х,^ „ЛЛ этого треугольника
прямую, перпендикулярную биссектрисе этого угла.
Построенные таким образом три прямые образуют треугольник,
который и будет искомым (см. задачу 844),
430
Рис, 121,
894, На продолжении радиуса О А (рис. 122) меньшей
окружности отложим отрезок АВ = ОАш На отрезке АВ9
как на диаметре, опишем окружность и пусть точка
пересечения ее с большей окружностью есть С. Секущая СА
и есть искомая.
Действительно, из подобных
треугольников ОгСА и ОАО видно, что
АС — АО, а
из равных
треугольников ОСА и ОБО,
что АС = ЕО. Если радиус
большей окружности больше
диаметра меньшей, то
задача не имеет решения.
895. Через данную точку
М (рис. 123) проведем
прямую ОМ, проходящую через
вершину О данного '/.АОВ.
Возьмем на стороне ОВ любую точку /С, опустим из нее на
ОА перпендикуляр КЬ и из точки /С, как из центра,
дугой радиуса КЬ засечем
прямую ОМ в точке N.
Если теперь провести
МР || Л7( до пересечения
с ОВ в точке Р, то
точка Р и будет искомая.
Действительно, проведя
РН1-ОА, видим, что
ОР _ _РК_ _ РМ_
ок ~~ кь ~~ км' а
так как КХ. = №, то
Р% = РМ. На той же
стороне найдется и еще
одна точка, удовлетворяющая условиям задачи, — это
точка пересечения стороны ОВ с прямой, проходящей
через точку М параллельно прямой /(Л^,
Если угол прямой или тупой, то точка Р найдется так:
соединяем вершину О угла АО В (рис. 124) с точкой М
отрезком прямой ОМ и проводим РЬ ± ОМ через середину Ь
отрезка ОМ. Точка Р пересечения прямых ОВ и РЬ и будет
искомая. В случае прямого угла такая точка будет
единственная на стороне ОВ. Если угол тупой, то такая точка
на стороне ОВ либо найдется одна, либо ее не будет.
431
Рис. 124.
Последнее, очевидно, будет в том случае, когда точка М
находится внутри угла АОХ или на его границах, причем
здесь ОХЮВ.
Замечание. Расстоянием от точки Р до луча О А
является длина отрезка
ОР, а не длина отрезка
Р/С, перпендикулярного
к прямой ОЛ, Длина
РК есть расстояние до
прямой О А, а не до
луча О А.
896. Проведем
радиус СЮ (рис. 125), пер-
0 пендикулярный хорде
АВ, являющейся
основанием сегмента. Пусть
С есть точка
пересечения ОО и АВ. Построим любой квадрат МЫРС},
симметричный относительно ОО, сторона которого МЫ
лежит на АВ. Проведем прямую СС1 до пересечения с
дугой сегмента в точ- п
ке 5 и прямую СРУ
пересекающую дугу
в точке /?. Из точек
5 и /? опустим
перпендикуляры на АВ
и пусть основания их
Т и I. Точки 5, /?, Ь
и Г будут вершинами
искомого квадрата.
Доказательство
правильности построения
легко привести, если
рассмотреть следующие три пары подобных
треугольников: С8Т и СС±М\ СЯЬ и СР№, С5/? и С(}Р.
Решение задачи единственное, если дуга сегмента
а < 270°. При а > 270°. задача не имеет решения.
897. Пусть в трапеции АВСО (рис. 126) построен такой
отрезок МЫ, параллельный ЛД что МК = КЬ = ^У.
Проведем прямую СЬ до пересечения ее с большим основанием
АО в точке Р. Так как К# = 2 . 1#, то АО = 2 - РО.
Следовательно, Р есть середина отрезка АО. Отсюда
вытекает, что для построения искомого отрезка, достаточно
Р
5,
/^
/ г
Г
а
\
1
и
р
/
С1
/
V
Й
1. \
О
Рис. 125.
432
провести прямую, параллельную основаниям трапеции через
точку пересечения диагонали и прямой, соединяющей
середину одного основания с концом другого, Искомый
отрезок определится точками пересечения проведенной
прямой с боковыми сторонами трапеции. Доказательство
правильности построения
легко получится, если В /? С
рассмотреть две пары
следующих
треугольников: АСР и РСД а
затем ЛВС и ОС В.
Задача имеет два
решения (см. пунктир
на рис. 126).
898. Пусть Л и В —
данные точки, а МЫ— данная прямая.
а) Если точки А и В лежат по разные стороны от
прямой МЫ или на прямой МЫ, то задача не имеет
решения.
б) Если АВ О МЫ, то существует только одно решение.
В этом случае искомая окружность проходит через
основание перпендикуляра, опущенного из середины отрезка
АВ на МЫ
в) Если А я В (рис. 127) лежат по одну сторону от
прямой МЫ и прямая АВ пересекает МЫ в некоторой
точке С, то искомая окружность проходит через такую
точку О прямой МЫ$ для которой СО есть средняя
пропорциональная между АС и ВС (см. задачу 851). В этом
случае задача имеет два решения.
433
г) Если точка А или точка В, но не обе одновременно,
лежат на МЫ, то решение единственное.
899. Продолжим боковые стороны АО и ВС (рис, 128)
данной трапеции АВСО до их пересечения в точке М и
проведем через нее и
точку О пересечения
диагоналей прямую МК,
пересекающую основания
трапеции в точках Ь и К. Эта
прямая разделит трапецию
на две равновеликие
фигуры. Действительно, пря-
1В мая МК точками [ и /(
делит основания трапеции
на равные части, откуда
и следует равновеликость
трапеций АОЕК и КЬСВ. Для доказательства того,
что К и Ь — середины оснований, проведем медиану
треугольника АМВ, выходящую из вершины М. Э^а
медиана разделит пополам и основание ОС. Но прямая,
проходящая через середины оснований трапеции, проходит
и через точку пересечения ее диагоналей (см. задачу 859).
Следовательно, проведенная медиана совпадает с прямой
МК, а точки Ь и К делят
основания трапеции пополам.
900. Проведем любую
прямую МР (рис. 129) через
точку О пересечения
диагонали данного
параллелограмма АВСО, не параллельную
его сторонам. Она разделит
параллелограмм на две
равновеликие трапеции АОЕР и
РЕСВ, где Е и Р— точки
пересечения прямой МР с
противоположными сторонами
параллелограмма.^ Продолжив
сторону АО параллелограмма до пересечения ее с прямой МР
в точке М, проведем прямую через точку М и точку N
пересечения диагоналей трапеции АОЕР. Она разделит
трапецию АОЕР на две равновеликие фигуры (см. задачу 899),
а параллелограмм на две части, отношение площадей
которых есть 1 : 3,
Рис. 129-
434
901. На основании АС данного треугольника ЛВС
отложим отрезок АО, равный данному основанию
треугольника, который нужно построить. Проведем СК II ВО до
пересечения с прямой АВ в точке /С. Эта точка и будет
третьей вершиной искомого треугольника. Доказательство
следует из равенства площадей треугольников КВй и ВСО.
902. а) Если прямая АВ, проходящая через данные
точки А и В, не параллельна и не перпендикулярна
данной прямой СО, то для точки пересечения прямой СО
с перпендикуляром к отрезку АВ в его середине выражение
| АМ — МВ | будет иметь наименьшее значение, равное
нулю, а для точки пересечения прямых АВ и СО —
наибольшее, равное длине отрезка АВ,
б) Если прямая АВ параллельна прямой СО, то
точка М, для которой | МА — МВ | имеет наименьшее значение,
является основанием перпендикуляра, опущенного из
середины отрезка АВ на СО. Этот минимум равен нулю.
Такой точки на прямой СО, для которой | АМ — МВ | было
бы наибольшим, не существует.
в) Если АВ перпендикулярна СО, то наибольшее
значение | АМ — МВ | будет для
точки пересечения АВ с
СО, Это значение равно
длине отрезка АВ, Такой точки М
на прямой СД для которой
\АМ — ВМ\ имело бы
наименьшее значение, не
существует.
903. Пусть Е и Р будут
середины диагоналей АВ и СО (рис. 130). Проведем
через точку Р прямую,
параллельную основаниям
трапеции, до пересечения ее с
боковой стороной АС в точке /С.
Очевидно, КР будет средней
линией д АСО и она пройдет
через точку Е, так что КЕ
будет средней линией Д САВ.
По свойству средней линии
треугольника можно написать
ЕР = КР — КЕ ^ ~ — 4^-«
Рис. 130.
435
904. Нужно найти периметр Д ЭСЕ (рис. 131).
Отрезки касательных, проведенных из одной и той же точки к
одной и той же окружности, равны. Поэтому ИМ = ОК,
ЕМ = ЕЕ, ВК я= ВЫУ АЕ = АЫ, а искомый периметр
2р = СО + йЕ + СЕ = СО + ИМ + МЕ + СЕ = Си +
+ фК + ЕЕ) + СЕ = (СО + ОК) + (СЕ + ЕЕ) = СК +
+ а = (СВ — ВК) + (СА-А1)=СВ + СА~(ВК+АЕ) =
= а + Ь — (ВМ + Ай)=а + Ь — ВА = а + Ь~с.
905. Положим: АО = тх, ОВ «= пх9 СЕ = р*/, ВЕ = <?#
(рис. 132).
Тогда АВ : ВС : С А = (т* + пх) : (ру + <7#) : (тх + ру).
Но по свойству отрезков касательных, проведенных к
окружности из одной и той же точки, ОВ=ВЕ или пх = ду.
Отсюда -|- = -~ и,
следовательно,
ЛВ : ВС : С А = (т^ + я?) : (рл + ?л) : (щ + рл)
- Я(т + п) : л(р + д) : (/я? + рл).
906. Пусть радиус искомой окружности есть О К = х
(рис. 133). Из треугольников 02ОхО и Ог0039 пользуясь
теоремой о квадрате стороны треугольника, получим
■ (# + х)2 = (# + г — х)2 + г2 + 2гу;
(г+х)2 - (# + г — х)2 + К2 — 2Яу,
где у = ОхА — проекция общей стороны на данный отрезок.
Умножив первое уравнение на /?, а второе — на г и сложив
результаты, получим:
(# + х)2Я + (г + х)2г = Щ + г — х)2(К + г) + г2К + г/?3;
436
Я* + 2(1? + г*)х + (К + г)х* + г*=(К + г)* — 2(11 + г)*х+
+ (/? + г)х2 + г#(# + г); 2х[г2 + /?2 + (Я +г)2] =
= (Я + г)3-^-г3 + г/? (# + г), 4*(#2 + Яг + г2) =*
= 3#г(/? + г) + Яг(# + г), 4(#2 + Яг + /-2)* =
= 4Дг(#+г), * =
/?'(/? + ')
Я2 + Яг + г* '
907. Обозначим 5Х искомую площадь Д /С/.7? (рис. 134).
Соединим точки В и К
отрезком прямой 5/С и составим
отношение площадей
треугольников СКВ и АКС,
которые будем обозначать_соответ-
ственно 52
52:53 = КС <
= В(} : АТ.
и 53. Получим
ВС} : КС-АТ =
Но Д ОД'/ со
соД АТМ, поэтому В(2:АТ =
= ВМ : МЛ = 4:1. Отсюда
52 : 53 = 4 :1. Обозначим 54
площадь Д АКВ и
составим отношение площадей 54
и 53. Получим 54 : 53 =
= ВГ)- АК:СЕ • АК=ВЪ: СЕ,
= Я#:#С=1:4
1
1
то54 :53=
прибавляя
лучим:
^2+_5з_-|- 54
ПО
а так как ВО : СЕ =
в силу подобия треугольников 50М \\СЕЫ,
с 9 1
4. Складывая равенства -^-, = 4 и -^г1 = —г- и
к обеим частям нового
равенства, по-
_5_
53
- 4 ' ^3
_4_
21
5.
Но рассуждения,
проведенные относительно ААКС,
могут быть применены и
к треугольникам СНВ и
АЬВ, так что площади
последних^ также равны
2у-5 каждая. Отсюда
51 = 5-3.-^-5
5 —
— ? 6-
28 к. У. Шахно
437
908. АМОС и А(}ОМ (рис. 135) —прямоугольные с
общим углом МО(}. Поэтому они подобны и можно
написать М(}:МО = МС\ ОС. Отсюда МЫ = 2 . М(} =
Л МС • МО тт шжг\ п г»
= 2 ^—. Но МО = /<, где /< — радиус вписанного
в А ЛВС круга;
мс + см
мс =
2 2 ~"
о + 6 — (АР + РВ) _ а + Ь^с __ (а + Ь+Ь—2с
2 2 ~~ 2
= р — с, где р — полупериметр Д Л5С;
2/? — 2с
ОС = 1/ОМ2 + МС2 = УЯ* + {р-
Следовательно,
•с)2.
абс
2^(р^с)
обе
4/р(р-
Аналогично найдем:
ЛГР =
в)(р — Жр — с)
2/? (р — 6)
#Р =
>^2 + (р-&)2'
909. Пусть Л МЫР
(рис. 136) есть тот,
периметр которого требуется
определить. Начнем с
определения стороны МЫ. Для
этого обратимся к
треугольникам МЫС и ЛВС. Они
подобны, так как у них
угол С общий, а стороны,
заключающие этот угол,
пропорциональны. Последнее
утверждение следует из
подобия прямоугольных
треугольников АМС и ВЫС, так что, действительно, -^ =
АС
= -та-. Из подобия треугольников МЫС и ЛВС имеем
^~- = -—, или ЛШ = -^-, где Я! и Я — радиусы окруж-
Рис. 136.
438
ностей, описанных вокруг этих треугольников. Радиус /?
мы можем считать известным, так как он вычисляется по
. п аЬс п ЮС
формуле /? = -т-д-, а /?! = -у-, потому что окружность,
описанная около треугольника ММС, пройдет через О
и ОМС +А ОМС = 180°), причем ОС — диаметр и ОМС=
= 90°),
Итак
.'_ сНх _с-ОС с(РС^РО) __с- РС — с - РО _
~ 2# "" 2Я ~ 2Д ""
л*лг~^-
25 — 25! _ 5 — 5!
"" 2Я ~~ Я '
где 5! — площадь А ЛВО. Аналогично получим
ЫР
■5,
и М--
где 52 и 53 —площади треугольников ВСО и АСО.
Следовательно,
2р = МЫ + ЫР + РМ - 35~~(51^,524",5з) =
35 — 5 25 85а
~~ Я — Я — аЬсщ
910. Положим ЛС = а, ВС — Ь (рис. 137). Получим
2г = СО + СЕ = ЛС — ЛЯ + СВ — ВЯ = АС — Л/4 +
+ СВ — В/7 = а + Ь — (АР + РВ) = а + Ь — 2Я =
У(а + Ь)2— 2Н = У а2 + Ь2 + 2аЬ — 2#
= уг4Я2 + 45 —2#.
Отсюда г = У К2 + 5 — /?.
Рис. 137.
Рис. 13а
28*
439
911. Нужно найти площадь «5 треугольника МСЫ
(рис. 138). Зная стороны треугольника ЛВС, легко найти
и радиус вписанной в него окружности. Поэтому будем
считать его известным и обозначим буквой г. Как видно из
рисунка,
5 = 8мсо + 8мсо — Злмо = -^ МС • г + -§- N0 • г —
+ Л4#— 2ЛГЛ0г = -^-(2р — 2а)г = (р — а)г,
где 2р — периметр д МСМ Этот периметр 2р = к +1—т
(см. решение задачи 904).
Замечание. Рассматриваемая окружность,
вписанная в д ЛВС, по отношению к Д МСЫ называется вневпи-
санной. У любого треугольника таких окружностей три.
Если стороны треугольника а, Ь и с% а радиусы
соответствующих вневписанных окружностей — га, гь и гс% то, как
показывает решение этой задачи, имеют место формулы:
5 = (р — а)га = (р — Ь)гь = (р — с)гс.
912. Пусть Оь 02 и 0« (рис. 139) —центры
кругов, вписанных в данный Д ЛВС, в Д АВВ и в АСйА,
где О — основание перпендикуляра АО, опущенного из А
на ВС. Так как Д АВ02 со д ВСОх и Д ВСОх со д АСО»
Рис 139.
то гх г /? = АВ : ВС и га: К = ЛС : СВ. Отсюда: -^ =
~~ "ВС3"» "Ж ~~ ВС* ИЛИ #а ~~ ВС2 ~" 6Са ~~ 1§
440
Итак,
/?»=г? + г|; К^УгГ+П.
913. Обозначим буквой 5 площадь Д ЛВС (рис. 140).
Соединив центры О и О! с точками касания и положив
/ ЭОЕ = а, замечаем, что /. РОхК = 90° — а. Поэтому
получим
5 - ±-АС • СВ = -1 (# + ЛЯ)(г + Я/7) -
-4(/г + /?48-г)[г + г18(450-4-)
1-й-З-
1+*8-о
Рис. 140.
914. Л ОМЕ со
со Л ЛМС, д ДЛ^со
соЛСЛ^В,
Л МАТ со д ЛСг
(рис. 141). Отсюда
получаем:
АС _ /*!_.
а ~~ Н ;
441
ев = ь^% ас_ А+А..
АС
АС
_Ьх + Ь
4^ = 1; АС= аЬ
а — Ь'
АС
а
следовательно,
Но из -^ = -~- и —- = -~ находим, что АС = ВС и,
Л5-^1С+С5 = 2ЛС
2а&
■6е
Рис. 142.
У
аЬ
Аналогично г •
2аЬ
915. Из подобия
треугольников АСО и АКО (рис. 142):
^аГ+а? Из подобия
треугольников АСВ и /ССО:
Т—АГТ*? Отсюда-«- +
Лх + А> ^ А! + Аа
Складывая, получим
обозначая искомый ра-
916. 0,01 = 0ХА2 + ОИ2, или,
диус буквой дс, получим (/? +
+ х)2 = (/? - *)2 + 02Л2; 02Л2=
= (/? + х)2 — (Я — х)2 = Щх
(рис. 143). Аналогично: 001 =
= 02В2 + ОВ2 = ОгВ2 + 02А2
или (Я — х)г = х2 + 4%х; Р.2 —
— 2Кх + х2 = х% + 4#*; Я2 =
= 6/?л:; л: = -^-.
917. Из прямоугольного
Д АВВ (рис. 144):
АВ2 = В1У — АО* = (гг +
+ /-2)а-(а-г2)а = 4г1г2.
Проведем касательную к окружности в точке С и
продолжим ее до пересечения с АВ в точке Е. Соединим
точки Е и Ох отрезком прямой. Так как АЕ = ЕС = ЕВ =
= 'К'Уа по свойству касательных, проведенных из одной
точки, то Д ОхАЕ = Д ОхЕС, ^ АОхЕ=Л СОхЕ, и, следо-
Рис, 143.
442.
вательно, прямоугольные треугольники ОгАР и ОхЕС
подобны. Поэтому
АР
ЕС
^г^. Но АО^г^ ЕС ^У7^;
ДЕВ
Рис. 144.
ОхЕ = УОхС2 4- СЕ2 = У Л + гхгг и^ = АО,
ЕС
ОгЕ
=гх. -У7^ = ^ . 1/-^— , АС = 2Л/^ = 2г, У-т- •
1 |/>2 + л^ * ' г, + г2 ' * Г /•, + гг
Аналогично получим ВС = 2/*2 • |/ _2 г . Кроме того,
ранее было найдено
ЛВ2 = 4/*!^ так что
ЛВ=2 Угхгг
918. Проведем СО ±
±АВ,ВР \\ Ог02и ЕС±
±Ог02 (рис. 145)
Получившиеся при этом
треугольники АВР и ВЕС
подобны, как
треугольники с
перпендикулярными сторонами.
Поэтому можно написать -^- = -^-. Но АВ = 2 У Кг,
СЕ = У~Кх (см. решение задачи 917), ВР = /? +г. Отсюда
Рис. 145.
СО = СЕ.
АВ
ВР
= УКг
2УЯг
2/?г
443
919. Проведем ВС || Ох02 (рис. 146). Тогда из
треугольника ЛВС по теореме Пифагора получим
АВ = У ВС2— АС2 = У(Н + г)2 — (К — г)2 = 2|/#г.
Проведем теперь ОЕ || С^Од. Из прямоугольного
треугольника АОЕ получим
АО = УЕ02-АЕ2 =У{К + х)2-(К — х)2 = 2УКх>
где л: — искомый радиус. Наконец, проведем ОР || 02Ог,
тогда из Л /Э5/7 получим
ОВ = УОГ2 — ВР2 = /(г + х)2 —(г —*)2 = 2|/7лГ
Но
Рис 146.
АВ = АО + ОВ или 2/^7=2/^ + 2/^;
/7=
^•-ь/^'
л: =
(Кя"+ КЛ2 *
Есть и еще одна окружность, которая касается данных
окружностей снизу, а прямой — правее обеих данных
окружностей. Ее радиус равен ,^~- ,—ч2-«
444
920. Проведем О^ЕХ.0^0^ 03Р±АВ и соединим прямой
центр 03 с концом А искомого отрезка АВ (рис. 147).
Очевидно,
АВ = 2АР = 2 У АО! —ГО! = 2 Ус
где х = Оз/7 = ОЕ.
Чтобы найти х,
рассмотрим треугольники 0г03Е и
0203Е, имеющие общий
катет 03Е, На основании
теоремы Пифагора
получим
ОхВ^
= 0*0\-02Е\
0,В^030\
Отсюда:
(с + а)2 — (а + х)2 =
= (Ь + с)2-ф-х)2;
(а + х)2 — ф — х)* =
= (а + с)2-(& + с)2;
(а + Ь) (а — Ь + 2х) =
= (а + Ь + 2с) (а — Ь)\
а2 — Ь2 + 2х(а + Ь) =
= а2 — Ь2 + 2с(а — Ь)\
2х (а + Ь) = 2с (а -г- Ь)\ х = с
АВ = 2/с2 — х2 =
-*/"-«,^-««УГш&
-(д-б)а
= 4с
ТЛгб
Рис. 148.
+ б)2 а + Ь '
921. Проведем ОС±ВЕ, где
О — центр окружности, и
соединим прямыми О с вершиной
А данного квадрата и с
вершиной В — вписанного (рис. 148).
Обозначим искомую сторону
через х. Из прямоугольного
треугольника ОВС имеем
О В2 = ВС2 + ОС2 = ВС2 +
+ (ОО + ОС)2 =
-(-*;-(*+'/•
445
Но ОВ = О А, и из прямоугольного треугольника ОАО
находим, что
АО2 = ОО2 + О А2 = -^ + ^ = ^
Теперь получим:
5*2 + 4а* —а2 = 0; * = -|-.
922. Таких окружностей три (одна с центром в 03,
а две другие изображены на рис/ 149 пунктиром).
Обозначим искомый радиус буквой х, а центры данных
окружностей буквами Ох и 02. Соединим прямыми 03 с Ох и 02
и опустим из 03 перпендикуляр 03А на линию О^.
Рассмотрим прямоугольные треугольники 0Х03А и 0203А,
имеющие общий катет 03Л. На основании теоремы
Пифагора получим
03А2 = 0^2 — ОгА* = 020! — 02А2 или иначе
(# + х)2 — {Я + 2г — х)2 = (г + а:)2 — (я — г)2.
Л/
Рис. 149.
Решаем это уравнение:
(2 Я + 2г) (2х — 2г) = 4гх, (# + г) (х — г) = гх,
/?* = /■(/?+/■), * = -^-(#+г).
446
Нетрудно видеть, что две другие окружности имеют
радиусы:
923. Как видно из рис. 150,
йМ « УйЕ* + МЕ2 = Уф1 + ЕЕ)2 + ЕС2 =
= |/2012 + 21Р = У~2УОЬ2 + ЬЕ2 = У~2УШ^
= /"205 = /? У 2.
Так как длина отрезка ПМ
не содержит /тг, то это и
означает, что она не зависит
от т.
А/ й С
Рис. 150.
924. Обозначим искомую сторону буквой с (рис. 151).
Так как треугольники АОВ9 ВОЕ и АОй— прямоугольные,
то по теореме Пифагора получим:
АО2 + ОО2 = ЛЯ2; ВО2 + ОЕ2 = ВЕ2; ВО2 + АО2 = А В2.
Точка О делит каждую медиану в отношении 1 к 2, считая
от основания. Поэтому, если положить Ой = х, ОЕ =у,
то АО = 2у, ВО = 2х, Так как, кроме того, ВЕ = -тр
/Ш = -|п и АВ = с, то написанные выше равенства можно
переписать так:
V + *2 = -^ 4*2 + #2 = -?-; 4*2 + 4у2 = с2.
Складывая почленно первые два уравнения, получаем
5а:2 + Ъу2 = —^— или 4х2 + 4у2 = —^—.
447
Воспользовавшись теперь третьим уравнением, найдем
=]/а-
ь2
925. Обозначим искомый радиус буквой х (рис. 152).
Так как Л АКО = 90°, то из
Д АОК находим: х = АО =
= УАК2 + /СО2; Л/С = -|-, а
длину О/С найдем из подобных
треугольников ОКО и КВЕ
(взаимно перпендикулярные стороны).
Получим
К0:0О = КВ: КЕ. Но КБ =
Рис 152.
= 4-; КЕ = (1\
ВЕ = 1//СВ2 — /СЕ2 = ]/-^- — сР; 00 = ЕР =
ВЕ = \- У*--&щ КО = ОО.^г =
= ВР
-(т-/*-*)*•
Таким образом,
# =
а
13
,/"
]/. а2 4- б2 - 26 /а2 — 4^2.
926. Таких окружностей возможно четыре — с центрами
в точках Л (две концентрические) и О (две
концентрические), из которых подробно рассмотри^ только одну с
центром в Л и радиусом Л/С = х (рис. 153). Проведя ряд
построений, понятных из рис. 153, рассмотрим треугольники
АСЕ и РСЕ. Но теореме Пифагора получим
АС2 = АЕ2 + ЕС2 = (АР + РЕ)2 + ЕС2,
но
АС = АК + КС = х + г; АР = 2г; ЕР = /ГС2 - ЕС2 =
= |/4г2 —г2 = г ]/"3; (* 4- г)2 = (2г + г ]/"3)2 + г2;
(х + г)2 = 4г2 + 4г2 |ЛЗ + Зг2 + г2, (х + г)2 = 8г2+4 У~3г2;
448
= г(2]/г2 + |ГЗ-1)=г(1Лб + )/2'-1).
Рис. 153.
Здесь была использована формула
лГа + УЖ^Е Л/а - V А* —;
У~А + УВ
2 ' ' 2
Радиусы других окружностей (две из них обозначены
пунктиром) будут:
АЬ = г(\Гб + У~2+ \)\Ш = г(\ГЪ — У~2^\)\
ОМ = г(У~6 — У~2+1).
Окончательно ответ можно записать так:
г(УЪ±У2± 1).
927. Обозначим КР = у, КГ = г (рис. 154). Пользуясь
свойством перпендикуляра,
опущенного из вершины
прямого угла на
гипотенузу, получим: у2 = тг,
г2 = пу. Отсюда находим:
у* у4 ч
г = -^-; -V = пу: у3 =
= т2я; у = Ут2п\
г = Утп2.
Рис. 154
449
Теперь, пользуясь теоремой Пифагора, вычислим
гипотенузу:
ВС2 = АВ2 + АС2 = (т + г)2 + (п + у)* = (т + УТш?)2 +
+(п+ УШЪ)2=У^(УмГ+ У^?+ УЩУЯ + Ут2)2^
= (У& + У™2)2 • (Уп?+ У&) - (Уп? + У&?-
Обозначая ВС = х, можем написать окончательно:
2 _1 Л. Л 2 Л
х,В(вЧ»,1 х = (т* + пТ)\
928. ЬКг = АК'КВ (рис. 155), где /С — проекция О
на АВ. Но Д ЛЯ/С со Д С/СЯ (взаимно перпендикулярные
стороны), поэтому А К ! ЯЙГ = СКгКВ или АК • КВ =
= С/С -Я/С. Отсюда:
ЬК2 = СК-НК; ЬК^УСК-НК или 5 = 4-^5-^=3
== _^_ лв уск-нк= У\ав-ск-\ав-нк = у'ад.
.А •
^ *—*
Рис, 155, Рис. 156,
929. Этот радиус можно найти по формуле г = -р-> если
найти третью сторону (рис. 156). Найдем ее. Пусть
треугольник с заданными сторонами есть ЛВС. Опишем вокруг
него окружность и проведем высоту его Вй и диаметр ВЕ.
Соединив конец диаметра Е с вершиной треугольника А
получим прямоугольный треугольник АВЕ, подобный
треугольнику СВй, так как ^ В ОС = ^ ВАЕ = 90% А ВСА=
= /.ВЕА. Из подобия имеем:
450
ВР
АВ
ВС
ЕВ
Вй = АВ
ВС
= 20.
.»■{-
20^
29
^-1*
ВЕ " 29
АС = АО + ОС = УАВ* — В02 + УвС^ — Вй2 =
144.
5 *
= 1/202-162+ /(х)*~ 163 = 12 + -^ =
5 = 4ЛС
/Ю-4"
144
5
16 =
1152
Р = 4-(20+Х+1г)-3^-5Л| = 6,4.
930. Соединим середину гипотенузы Е с серединой Р
катета (рис. 157), Очевидно,
ЕР || АС, а следовательно, ЕР±
±ВС. Угол ОРЕу таким образом,
является прямым вписанным
углом в окружность. Поэтому
перпендикуляр ЕО к гипотенузе в
точке касания ее с окружностью
пересечется с продолжением
катета ВС в точке Ь, находящейся на
окружности, т. е. Ей есть
диаметр. Замечая, что Д ЕВО со
со ААВС, так как они
прямоугольные и имеют общий угол ЛВС, пишем:
1ПГ = Ж-> ВЕ = ±.АВ=±УАС* + ВС* = 4г;
Рис. 157.
ВС
Рис. 158.
тт.
931. Пусть искомая
сторона будет обозначена
буквой ху а сам квадрат
занимает положение АВСВ
(рис. 158). Легко
доказать, что АО±Ох02, и на
основании теоремы о
перпендикуляре, опущенном
из точки окружности на
диаметр, можно написать
АЕ2 = ОгЕ ■ ЕР* Но АЕ = \\ ОхЕ = -^-;
451
ЕР = 0,Р — ОхЕ = 2г-
Г— X
Зг + х
—^— и поэтому
(т)^ ^ • Щ±» 2*г + 2г*-3г2 = 0, х =
г (/7-1)
/
/
\
\
\
N
\
1
к
В Е
\о/
^/ ^
V
а 1
V А
с о
Рис. 159,
932, Пусть искомая
окружность (рис, 159) имеет
центр в точке О (другая
возможная окружность
обозначена пунктиром).
Обозначим искомый радиус буквой х.
Сделаем дополнительные
построения, понятные из
рисунка. Из прямоугольного
треугольника ЕйО получим
ЕО2 = ЕО2 + ВО2 = ЕВ2 +
+ (АВ — Вй — О А)2.
Но
ЕО = а + *, ЕО = -|- ЕЬ = -±- УЕК2 + КЕ2 =
аУ~2
= ~±-Уа2 + а2 =
Вй^-^-ЕЕ--
2
а VI
, АВ = 2ЕЕ=2аУ2\
, О А = У ОС2 + АС2 =
= \/х2+х2 = хУ2у
и поэтому будем иметь
(а + х? = (^ч- (а, |/2-41 - хК1>)9.
Решаем это уравнение:
(а + х)2 = ^ + (4аТ/2-*У"2)2, а* + 2а* + л:2 =
= "т + -§-а2~6а* +2*2' *2~8ал: + 4°2 = °»
х = 2 (2 — /"3) а.
Радиус окружности, обозначенной пунктиром, равен 2а.
452
933. Обозначим искомый радиус буквой * (рис. 160).
Рассмотрим прямоугольные треугольники ОАВ и ОйР.
Применяя к ним теорему Пифагора, получим
О А2 = ОВ2 + АВ2 = (ОС — С В)2 + АВ2 = АВ2 +
+(|/0О2— йС2—СВ)2=Л52+(|/ ОЯ + Рй2 — йС2 — СВ)2.
Но
/То
ОЛ = ж; ОР = х; Рй=2\/ 10; ЯС
и равенство можно переписать так:
-; СВ = У10,
ю
*2=^ +
(}Л2 + 40 —^-|/Т0)2
Отсюда:
х* = 1° + ^2+ 40 — -^ — 2 /К)*2 + 375 + 10,
2/10л;2 + 375 = 50, Юх2 + 375 = 625, 10*а= 250, х = 5.
934. Обозначим
искомый радиус буквой г
(рис. 161). Проведем
радиус в точку касания
окружности с большим
катетом. Так как Ой \\ ВС, то ДОЛД сод5ЛС, и можно
написать^- = ~ Но Ой = г; ВС = 3; ЛВ=/9+16 =
=«5; ОЛ = 5 — г и пропорция запишется так: -г =
3 15
-^-. Отсюда находим: 5г = 15 — Зг, г = -^-.
1/а29 К. У. Шахно
453
935. Из прямоугольных треугольников АОгВ, АОВ и
СООх (рис. 162) имеем:
А0\ — ОхВ2 = АО2 — ВО2, 9 — ОхВ2 = 25 — (5 — 0ХВ)2,
0±В = -^9 СО = /00?—0^ = 4.
Из подобия треугольников Ох/СВ и 0ХС0 находим:
КВ : 0ХВ = СО : 0±С\ КВ = 0±В ~ =^ ~ - -§";
0В = 00Х — 0ХВ = 5-
Отсюда по теореме Пифагора
_9_
ю
41
10"
О К = /#В2 + ОБ2 = 4-/73.
0
Д
г)\
Рис. 162.
7 Р
Рис. 163.
В
936. Искомая площадь 5, очевидно, равна сумме
площадей треугольников АКБ, В1С, СМй и йЫА (рис. 163).
Но эти треугольники равны, и поэтому можно записать
5 = А8АКВ = 4 • 4~ • АВ • КР = 4 . ±-а • КР.
Найдем КР. Из подобия треугольников КРВ и ЯТВ
получаем
КР : КТ = РВ : ТВ и КР = КТ .
РВ
ТВ '
Так как площадь ромба равна половине площади квадрата
и одна диагональ у них общая, то вторая диагональ
ромба равна половине диагонали квадрата. После этого
нетрудно установить, что
КТ = ^гСВ=^га; ВТ = ^-. АВ =
= -т-а.
454
Что касается РВУ то ясно, что РВ = -^-а. Итак, имеем:
*Р = ЛГ.^ = 4-в--2Тз
1-4 а с , 1
а __ а2.
6 "~ 3
937. Очевидно, радиус этой окружности равен-^-ВМ
С
(рис. 164). По теореме
Пифагора получим:
ВМ2 = ВС2 + СМ2 =
= а2 + СМ2, САГ =
= ЛС — АМ = Ь— АМ.
Величину АМ найдем
из подобия
треугольников АВС и АМЫУ
после чего легко
найдутся СМ и ВМ.
Действительно:
5
АВ*
АМ2
>АВС
= 2, ЛВ2 = а2 + Ь\
а* + Ь*
АМ2
2;
ь2
ЛЛ12 = ^±^, СЛ1 = &-ЛЛ1 = &-/^4
ВМ2 = а2 + СМ2 = а2 + [ь— У ^±Щ = а2 +
+ Ь2_2ЬуЩ^+^^===^(а2+Ь2)-ЬУ2(а2+Ь2).
Искомая площадь
5 = те . М1 = 4- [3 (а2 + &2) — 26 /2 (а2 + Ь2) ].
Отметим, что вокруг
четырехугольника ВСМ&
действительно можно описать
окружность, потому что
/:ВСМ + /:ВЫМ = 180°.
938. Искомая площадь
5 = АО + вс .ВР(рис, 165).
Так как Л ЛВВ со д ЛОх/С,
то АК : ОИ = ЛВ : ВВ. Но
455
Рис. 165.
1/а29*
ОгА = К, ВЕ = К + г, АВ = УВЕг — АЕ2 =
Отсюда:
= У(Я + г)2 - (К -г)2 = 2}/Ял
2 /Л? 2/? У^
Л^ = ^-ЛД = ОхЛ
ЛВ
ВЕ
= #
/? + г
Л + г '
Аналогично
Найдем ВР:
АИ = ~
ВС =
АКУНг
К + г '
К + г *
4Яг
АВ* = ВЕ-ВР, Жг = (/? + /•)• ВР, ВР = 7^7.
Теперь можем написать:
с _ АР + ВС рр _ (2Р> + 2г)У~К~г 4Кг _ 8Кг УТг
К + г
К + г
Я + г
939. Обозначим искомую
площадь буквой 5. Проведем ОК±АВ
(рис. 166), диаметр ЕЬ и прямую
РЬ. По свойству описанного
четырехугольника йС + АВ = Ай + С В
и площадь
8^В+^ВСок^АВ + СВок^
= АО • йК = Ай . 2г,
Рис. 166. так как трапеция равнобедренная в
силу равенства углов йАВ и СВА.
Величину же В А найдем из подобных треугольников
АйК и ЕЬР (в силу перпендикулярности сторон).
Составим пропорцию:
АР
ЕЬ
ЕР '
АР
2г
2г
а
Отсюда
АО = ±!-и
а
8 = АО. 2г = -??-.
а
940. Пользуясь формулой Герона, найдем площадь
треугольника
5 = У>(р-а)(р-6)(р-с)7-
Соединим теперь центр О
(рис. 167), вписанного
полукруга с вершиной С
треугольника и вычислим
площадь А ЛВС, как
сумму площадей
треугольников АОС и ВОС.
Получим:
5 = -1- АС • ОО + -— ВС • ОЕ = -^ Ьг + -^- аг
■5-(а+ 6); '^^ТР 2г==
45
а + 6'
941. Обозначим
радиус вписанной в
треугольник окружности
буквой г. В
треугольнике ОБА (рис. 168)
гипотенуза АО =2/\ так
как Л ЕАО=30°. Поэто-
му Л5=/Л02 — ОЯ2 =
=^ г "^3=^. Заметив,
что ЕС = т и ВР = п,
подсчитаем площадь треугольника по формуле 5 = рг,
а затем по формуле Герона. В первом случае получаем
8 = рг = (т+п+г У~3) г,
а во втором —
5 = ]/р (р — а)(р — Ь) (р — с) = ]/Г(т + п + г ]/~3) тт\ ЗГ
Сравнивая правые части, предварительно возведенные в
квадрат, получаем:
(т + п + г ]/"3)2 г2 = (т + п + гУИ)тпг УТ,
(т+п + г \/~3)г = тп /~3; 5 = тп /~3.
29 к. У. Шахно 457
942. -Пусть СМ = х (рис. 169), а высоты
треугольников АВЕ и СМЕ соответственно Ах и А2. По условию
-о- а*! = -^ (а + 6) (А, + А2) или
2а
а + Ь
К + К _ 1 , к%
Но из подобных треугольников АВЕ и СМЕ имеем
~ = тт- Отсюда:
Д
Ча
а — Ь
а
И
1
и
+ ь
в
^
Рис
-1ПГ~'
С х
Ъ^
-\
а
. 169.
а
М
*2
4'
в
Рис. 170.
943. ААВС&АОВЕ (рис. 170). Но в подобных
треугольниках отношение их площадей равно квадрату
отношения сходственных сторон, и поэтому имеем
Отсюда
ло + ов
Ш
1Гз
п<
= У2.
944. Проведем йК II ВС
и МЬ || ВС (рис. 171). Если
обозначить высоты
треугольников йМК и МАЬ,
проведенные соответственно из
вершин О и М через Ах и Л2, а
искомую длину через х, то
равенство 8Мысо = $лвлш за"
Рис. 171. пишется так:
х + Ь и __ а + х
9 ' Л1 9~~
л2
458
Но, с другой стороны, ААМЬюАМйК и,следовательно,
МК А1 х — Ь а — х
—г— = -г— ИЛИ —г = —г .
Перемножая левые части полученных равенств, а затем
правые, и приравнивая результаты, получим:
х + ь
Й1
а-\- х
^2 ^ „2 .
■х\
2х2 = а2 + б2,
, *-у^
945. Решается
аналогично задаче 944. Проводим
ПК II ВС и Ш. II ВС (рис. 172).
Обозначим: М#=х, йЕ=Н19
МР = Л2. Так как
Завым • ^мысй =7:2,
то * + * Лз , Л^З ^ = 7 . 2
или 2 (5+*) Л2=7 (х+3) й^ Из
подобия треугольников АМЬ
5 ^
и ЛЮК имеем —т =
К
Перемножая левые части последних двух
равенств, а затем правые, и приравнивая результаты,
получим:
2(25
Рис. 173.
946. Проведем СЕ || ОБ (рис. 173) и обозначцм высоты
треугольников СОО и АВО через Нг и Н2. Очевидно,
искомая площадь 5 ^равна площади Д АСЕ. Поэтому, поль-
29*
459
вуясь подобием треугольников СОО и АСЕ, можем
написать
утг
- Л1
У 8 К + нг
Точно так же из подобия треугольников АВО и ЛЕС
получаем
У 8 Н{ + Н2 '
Сложив два последних равенства, найдем, что
5 = (1^57+У^)2.
947. Обозначим искомую
площадь через 5, длины
отрезков АО, ВЕ и йЕ
(рис. 174) через х, у и г.
Так как каждый из
полученных треугольников в
силу параллельности сторон
подобен основному, то
можно написать следующие три
равенства:
У Уз~3 г
У8~ х+у+г' \8 х+у+г' у8 х + у + г
Складывая почленно эти три равенства, получим
У 81 +У 81+У 8~з х + у + г
Отсюда
Или, иначе,
460
У~8 х + у + г
1/5*= уж+у^+ ук
5=(К5Г+]/57+К552.
= 1.
948. Обозначим искомую площадь буквой С}, а высоты
треугольников йСЕ и АЬр, проведенные соответственно
из вершин С и О, через кг и Л2 (рис. 175). Очевидно,
0 = 5!+ ЗяеА причем в силу
параллельности ОЕ и АВ 8 вер
не зависит от выбора точки Р на
основании АВ, Так как у
треугольников ОСЕ и РОЕ ОЕ есть
общее основание, то
5 ВЕР
ИЛИ -7г- ~
Так как АОСЕ со &АСВ9 то-^
\ 5
-_А_
жим левые части полученных
правые между собой:
/I, + Н2
равенств между
Перемно-
собой, а
51
УЗг __ Н2 + Ьх
*1
УТ
Л. + *1
= 1.
У5 -5,
= 1, (1 = У88Х.
949. Пусть точки
В и С будут точки
касания окружностей
с общей внешней
касательной, а О, и
02 — центры
окружностей (рис. 176).
Проведем СО \\ Ох02.
В прямоугольном
треугольнике ВСО
катет ВО = ВО, —
—01О = В01 — С02 =
= 3— 1 = 2, а
гипотенуза СО =0102 =
= 3 + 1 = 4. Но если катет в два раза меньше гипотенузы,
то противолежащий ему /. ВС О = 30°, а /.БОС ==/ ВОхА =
= 60° и /,С0201 = 120°. Искомая площадь 5 равна
разности между площадью трапеции Ог02СВ и суммою площадей
461
секторов АОхВ и А02С. Основания трапеции суть 3 и 1,
а высота
ВС = УСй^ — ВО* = /16 — 4 = 2 КЗ.
Поэтому
г>--^-^К<з— ^ збо + 360 /-
.,/«- 11 24/Т—11*
= 4/3-^»= §
950. Подставив в формулу Герона
_ 25_ а_^ _ 25
получим
951. Продолжим одну из медиан за основание
треугольника на отрезок, равный -=- медианы. Соединим конец
этого отрезка и точку пересечения медиан с концом
основания. При этом получится треугольник со сторонами
2 2 2
-у/Их,-д-т2, -у Щ и с площадью, в три раза меньше
искомой. Тогда, воспользовавшись формулой Герона,
получим
5= у У(тх 4-т2 + тъ) {тх + т2 — т3) (т2 + т3— тх) (т3-\-т1— т2).
952. Вычислительно это находится быстро, а именно,
если длины диагоналей суть 1Х и /2, а угол между ними а,
то площадь четырехугольника
5 = -у 'А 5*п а»
а площадь параллелограмма
ф = /1/2$1па.
Отсюда получаем (2 = 25. Этот же результат можно
получить чисто геометрически. Приведем это второе решение.
Пусть дан четырехугольник АВСО (рис. 177). Так как
462
АСРО, АВЕС и ВЕРЭ — параллелограммы, то ААВО
= АСЕР, АВСЕ = ААСВ, ААОС = АОСР. Поэтому
(2 = 8сог + 8 все + Зое/? + $всй = (8лсй + $лвс) +
+ (5лво + 5всо) = 5 + 5 == 25.
К С
Рис. 177.
953. Пусть ЕР — средняя линия трапеции (рис. 178).
Проведем высоту КХ трапеции через точку пересечения
диагоналей. Ввиду равнобедренности трапеции, точки К
и Ь будут серединами оснований. Соединим точки Е, К*
Р и Ь последовательно. Получим квадрат ЕКРЬ-
Действительно, ЕК есть средняя линия в треугольнике АОС и
Аналогично
Но в равнобедрен
ЕК = -^-АС.
ЕЬ = ^~ ЭВ.
ной трапеции диагонали равны, а
если АС = ВО, то ЕК = КР =
= РЬ = ЬЕ, т. е.
четырехугольник ЕКРЕ есть ромб, а так как
диагонали взаимно
перпендикулярны, то /.ЕКР = 90° (ЕК\\АС,
РК II ВО) и ЕКРЕ есть квадрат.
Отсюда видим, что высота
трапеции /<Х = ЕР = й.
Итак, 8 = ЕР .КЕ = &.
954. Обозначим искомый
/ ЛСВ = а, а радиусы
окружностей через т и К (рис. 179).
Проведем биссектрису СОх угла и
ЕМ || С0Х. Очевидно, /.ВЕМ =
РЬ^^АС, КР^-^ОВ,
= ^ ЕС/С =
Так как по усло-
Рис. 179.
463
вию йЕ = 2а и А В = 26, то, полагая /? > г, получим
угольники с соответственно
Поэтому
0ХВ _ АВ _/?_ _2Ь_
Отсюда
Но д ЛОхВ со д ООВ как тре-
параллельными сторонами.
Я —г 6—а
Л+г Ь+а
81П-7Г =
6 + а'
955. Обозначив искомый /. СВЛ=а (рис. 180),
поступаем далее так же, как и в задаче 954. Получим
соза =
К + г-
956. Нужно найти площадь
четырехугольника ИК1*М (рис.
181). Обозначим ее буквой 5,
а диагонали Л7, = 2х и КМ = 2у.
Выполнив дополнительные по-
Рис. 180.
строения, понятные из рисунка, получаем из
рассмотрения прямоугольных треугольников ОВА и ОАЫ:
2х = ЫЬ = 2ЛМ = 2УЫОг~ОА2 =
« 21/Л^О2 — (ОЯзша)2 =2//?2 —а251П2а.
Аналогично другая диагональ
2у = КМ = 2УК2 — а2со$2*.
464
Отсюда
8 = ±.2х.2у = 2У К2~а2$'т2аУК2 — а2С052а =
- 2 }//?4 — а2/?2 + -^ 51П2 2а.
957. Введем обозначения:
'</ СЛ5=а, ^ ВЛ/7 = р (рис. 182).
Тогда / АСВ = 90° — (а + р),
а ^ ЛВС = 180° —(90° —Р)
= 90° + р. Искомый радиус х 2*
по теореме синусов
определится так: х = -ъ~.—. По той же
25111 а
теореме можем записать
ВС АС
51П а ~" 51П (90° + 0) ^
ЛЯ
5Ш[90°~(а + Р)]
ИЛИ
ВС _ АС
51П а С05 ^
ЛЯ
СОЗ(а + р)'
Из треугольников АСР и ЛВЯ получаем
АС = 27? соз (а + р) и ЛВ = 2гсозр.
Подставляя в два последних отношения, получим:
2Н • соз (а + р) _ 2г соз р . соз2 (а + р)
созр
СОЗ (2 + р) » СОЗ2 Р
г
соз
^у-7= ]/-^ (а и а+ Р —острые углы).
созр
Отсюда
ВС 2Д соз (а 4- Р)
51П а СОЗ Ц
Следовательно,
= 2/?]/-^ = 21//?г.
* = Ш7-№-
135
958. Очевидно, искомая площадь
5 = 85омы = 8 (5амы — $амо) (рис. 183).
Так как в треугольнике АМТ катет АТ = -^-9 а
гипотенуза АМ = а, то
ААМТ = ±9 '^МАТ=±9 ^МА0 = 1>-Т = Ъ
Поэтому:
5АММ=у.Я2~ = ^, ЗаШ^-^АМ • 0А1 81П у ==
- \а • ОМ =* ^а(МГ — ОТ) = {(Шп|-|) =
а* (УТ 1 \ /Т-1 .
вт1т-т) = -8— а-
Отсюда
Рис. 183. Рис. 184.
959. Обозначим расстояние АО между параллельными
прямыми через х, а площадь А ЛВС через у (рис. 184).
Пользуясь теоремой о произведении отрезков
пересекающихся хорд, получим:
ВО.ОС = В02 = х(2К~х), ВО = Ух(2К — х).
Следовательно,
У = 1ВС. ЛО = ^- • 2ВО'АО=ВО.АО=хУх(2К~х).
466
960. Если стороны прямоугольника х и у, то его
площадь 5 = ху, а периметр Р = 2х + 2у. Используя
равенство ху = 5, преобразуем выражение для периметра.
Получим:
Р = 2* + 2*/ = 2* + 2 • -|= 2 • ^±^ =*
Отсюда видно, что наименьшее
значение для Р получится
при х = У 5, и оно равно
4 У~8. Но тогда и у = ]/"&
961. Положим ЛЛ1 = л:,
Л# = у (рис. 185). Тогда по
теореме косинусов
М№ = х2 + у2 — 2ху соз а,
а так как
Рис. 185.
115 $2
-н- ху 51П а = -н- 5; г/ = —:—, то М№ = *2 + т^
ДС51Па
Л?2 81П2 а
ь \ X 51П а / ' 51П а &
Величина Л4#2, а вместе с ней и МЫ, получит
наименьшее значение тогда, когда
' 51П а ' Г 51П а
Х$та
В этом случае
5
= 1/4-; ЛМ =* 1/4^— 25 с!ёа ■
= 2
ЗШу,
а искомый периметр
Г 5Ш
5 о тг — а
-т—С08^ -А—*
51Па 4
467
962. На основании теорем, обратных следующим:
1) сумма любых двух сторон треугольника больше
третьей; 2) Пифагора.
XIV. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ В ПРОСТРАНСТВЕ
(Стереометрия)
963. Возьмем внутри правильного тетраэдра АВСЭ
точку О (рис. 186). Соединив отрезками прямых точку О
со всеми вершинами тетраэдра,
получим четыре пирамиды:
АВСО, ВСОО, САЭО, АВЭО.
Очевидно, сумма объемов этих
четырех пирамид равна
объему данного тетраэдра.
Обозначив площадь грани
тетраэдра и его высоту через 5 и
А, а расстояние от точки О до
граней, которые являются
высотами полученных пирамид, через
Ль Л2» Л3, Л4, получим:
-у 8Н = у 8ку-1- у 8Н2+ у 5Л3+ у 5Л4
или /*!-(- А2 + Л3 + Л4 = А.
964. Если все прямые пересекаются в одной точке, то
имеет место первый случай. Если же какая-нибудь данная
прямая не проходит через точку пересечения двух других
данных прямых, то тогда она лежит в плоскости,
проведенной через эти две прямые, потому что она имеет две
общие точки с этой плоскостью, являющиеся точками
пересечения ее с прямыми,
определяющими плоскость.
Аналогично можно показать, что
всякая другая данная прямая (их
конечное множество) также
лежит в этой плоскости.
965. а) Пусть
противоположные грани четырехгранного
угла обозначены Р, (2 и /?, 5
(рис. 187). Пусть линия
пересечения первых двух есть О А, Рис. 187.
468
а вторых ОВ. Всякая плоскость, пересекающая грани
угла и параллельная плоскости, проведенной через
прямые ОА и ОВ, пересекает угол по параллелограмму.
Действительно, линии пересечения проведенной
плоскости с плоскостями Ри() параллельны ОА, а с
плоскостями /? и 5 параллельны ОВ.
б) Если плоскость Р || плоскости ф (или плоскость /? ||
|| плоскости 5), то любая плоскость, секущая грани угла и
параллельная прямой ОВ (соответственно прямой ОА),
пересечет угол по параллелограмму.
в) Если плоскость Р || плоскости ф и плоскость /? ||
II плоскости 5, то любая плоскость, секущая грани угла,
даст в сечении параллелограмм.
966. Через вершины /С, Ьу Р (рис. 188) данного куба,
проведем плоскость, а через середину А ребра
КМ—другую плоскость, параллельную первой. Сечение куба
второй плоскостью будет плоский шестиугольник АВСИЕР.
Этот шестиугольник правильный, так как все стороны его
равны между собой и равны половине диагонали грани
куба, а углы равны по 120°, потому что они имеют
стороны, параллельные сторонам правильного треугольника
КЬР.
нем
Рис. 18а Рис. 189
967. Плоскость, проходящая через ребро АО (рис. 189)
и параллельное ему ребро ЕР, пересечет сторону Д ЛВС
в середине § стороны ВС. Следовательно, диагональ ЕО
параллелепипеда пересечет плоскость Л АВС в точке /С, ле-
469
Рис. 190.
жащей на медиане А§. Проведя плоскость через ребра ВО
и МЕ, аналогично докажем, что эта диагональ проходит
и через вторую медиану д АВС> т. е. через точку
пересечения медиан.
968. Допустим противное. Пусть в трехгранном угле
О ЛВС (рис. 190) плоский
угол АОВ прямой или
тупой, а все двугранные—
острые. Пусть проекция
ребра ОС на плоскость
АОВ есть ОО. Так как
двугранные углы
предполагаются острыми, то
линия ОО пройдет внутри
угла АОВ. Через какую-
либо точку М ребра ОС
проведем плоскость, пер-'
пендикулярную к ребру
ОС. Эта плоскость будет
иметь точку пересечения <? с прямой ОО и точку
пересечения, по меньшей мере, еще с одним ребром
данного трехгранного угла. Пусть это будет точка Р ребра
ОВ. Очевидно, плоскость ОМС? _[_ (?Р и, следовательно,
М(2±С1Р и 0(}± (}Р.
Рассмотрим теперь-следующие случаи:
а) Л ОО А — острый (рис. 190);
б) Л ДОЛ —прямой (рис. 191);
в) Л ДОЛ —тупой (рис. 192).
а) В этом случае
проведенная плоскость
пересечет ребро О А.
Обозначим точку
пересечения буквой N. Отложим
С^Мх = (}М и соединим
Мх с N и Р отрезками
прямых. Так как фМ^
= С1М < ОС1, то точка
Мх будет находиться
внутри угла АОВ. На
основании теоремы о
внешнем угле
треугольника заключаем, что
Л ММгР>ЛАОВ, т. е. Рис. 191.
470
^ ЫМХР — тупой. Но это невозможно, так как, очевидно,
Д ЫМХР = А ЫМР и, следовательно, Л ЫМХР = /. ЫМР.
Последний же острый, как линейный угол острого
двугранного угла.
б) Если /.ВО А прямой, то (?Р || О А, так как 0С1±С1Р.
Отсюда следует, что и МЫ \\ С}Р. Но Л МС[Р
прямоугольный, и поэтому А МР() острый, а ',/. ЫМР тупой, что
невозможно, потому что
Л ЫМР — линейный угол
остроге) двугранного угла,
"в) Если А БОА тупой,
то, так как </ РОР
прямой, (%Р, а следовательно, Д
и МЫ пересекутся с
продолжением ребра О А в
некоторой точке А1ш
Поэтому получим (рис. 192)
/. ЫМР > А МРАг >
> I МОР « 90°, т. е.
/ ЫМР—тупой. ^Но^ этого не может быть, так как
/ ЫМР — линейный угол двугранного угла, который по
условию—острый.
Итак, наше предположение, что при всех острых
двугранных углах трехгранного угла у него есть плоские
углы не острые, приводит к противоречию, что и
доказывает теорему.
969. Пусть одно из сечений этой поверхности
плоскостью есть окружность с
центром в Ох (рис. 193). Проведем
через Ох плоскость,
перпендикулярную плоскости
полученной окружности. Эта плоскость
пересечет окружность по
диаметру АВ, а поверхность — по
новой окружности, проходящей
через точки А и В. Взяв центр
и радиус этой второй
окружности за центр и радиус сферы,
опишем сферу. Любая точкам
построенной сферы лежит на рассматриваемой
поверхности. Действительно, проведем через эту точку и через
центры двух построенных окружностей плоскость,
которая пересечет каждую из окружностей в двух точках,
471
а сферу —по новой окружности. Эта последняя, как
имеющая с поверхностью три (даже четыре!) общие
точки, лежит на поверхности, а значит, лежит на ней и
взятая точка сферы. С другой стороны, любая точка,
не находящаяся на построенной сфере, не
принадлежит к рассматриваемой поверхности. Действительно,
если бы она принадлежала поверхности, то тогда эта
точка и две точки пересечения сферы с прямой,
соединяющей центр сферы с рассматриваемой точкой, лежали бы на
одной окружности, что невозможно. Теорема доказана.
970. Допустим, что такой многогранник существует
и имеет т граней. Пусть грани имеют число сторон
Ль п2 пт- Подсчитаем число ребер этого
многогранника. Очевидно, число всех сторон всех граней в два
раза больше числа ребер многогранника, так как
одно и то же ребро служит общей стороной двум
смежным граням. Поэтому число ребер многогранника
/ = — —2 ■——. Но каждое из чисел пи п2, ..., пт —
$ нечетное и число их т тоже
нечетное, поэтому и сумма,
стоящая в числителе, тоже
нечетная и не разделится без
остатка на 2. Итак, такого
многогранника не существует.
971. Пусть в
четырехгранном угле 8АВСО наибольший
плоский угол есть А8В (рис. 194).
Проведем плоскость через
прямые 8й я 8В. Так как любой
плоский угол трехгранного угла
меньше суммы двух других, то
можем записать: / А8В< </ А3й+
+ ^ ОЗВ, г. ВЗВ < ^ В8С + ^ ВЗС. Отсюда получаем
^ А8В <*А80 +
+ Л АЗС + ^ ВЗС.
Доказательство было
проведено на примере
выпуклого угла.
Однако и теорема, и метод
доказательства
справедливы для любого
четырехгранного угла. Рис 195.
472
972. Рассмотрим какую-нибудь плоскость Р, проходя-
тую через данную точку В и не проходящую через
другую данную точку А (рис. 195). Пусть АМ ± плоскости Я
уединим В с А и М прямыми. Получим прямоугольный
оо ?па ясно' что точка М лежит на сфере
диаметра 2К = АВ с центром в середине О отрезка АВ
Нетрудно доказать, что и обратно — любая точка этой
сферы является проекцией точки А на некоторую плоскость,
проходящую через точку В, так что эта сфера является
искомым геометрическим местом.
973. Проведем через данную прямую АВ (рис. 196)
плоскость Р, пересекаю- '
щук!) данную шаровую
поверхность с центром в О
по окружности с центром
в Оъ Соединим прямой
точки О и Ох (ООх 1
плоскости Р) и через О
проведем плоскость О х АВ,
которая пересечет АВ в
точке С. Треугольник ООгС
прямоугольный и лежит в
плоскости (?. Если
плоскость Р будет вращаться
ВлКппТп АВ> пР°Д°лжая сечь шаровую поверхность то
Л оихС будет продолжать оставаться прямоугольным и
лежать в плоскости <?. Поэтому, если АВ не имеет
общих точек со сферой, то геометрическое место
точек Ох будет часть дуги
окружности диаметра ОС,
заключенная внутри данной сферы.
Если АВ касается сферы, то это
будет окружность радиуса, в
Два раза меньшего радиуса
сферы. Если АВ пересекает
сферу, то геометрическое место
точек Ох будет окружность
диаметра ОС. Во всех случаях
Рис, 196.
Я-
-В
Рис 197.
центр находится в середине отрезка ОС.
^9?^ПуСТЬ тРебУется провести плоскость через
прямую Ы* параллельно прямой АВ (рис. 197) Возможны
два случая: а) ЯР || АВ. Тогда любая плоскость^ прохо
дящая через ЕР, но не проходящая через АВ, будет па-
30 К. У. Шахно ™
473
/
•н
1 1
N
М 0
ЧЛ
й|
7?
V
раллельна АВ, потому что если плоскость проходит через
прямую, параллельную данной прямой, то она
параллельна этой прямой; б) ЕР скрещивается с АВ. Возьмем на
прямой ЕР любую точку 0 и проведем через нее прямую
СО || АВ, что по аксиоме параллельности можно сделать,
причем такая прямая будет единственная. Через
пересекающиеся прямые ЕР и СО можно провести плоскость и
притом только одну. Эта плоскость будет параллельна АВ,
потому что она проходит через прямую СД
параллельную АВ. Покажем, что такая плоскость единственная.
Предположим противное, т. е. что существует еще
плоскость, проходящая через ЕР и параллельная прямой АВ.
Тогда проведем третью плоскость, проходящую через АВ
и точку О, что можно сделать, и притом такая плоскость
будет единственная. Последняя плоскость будет
пересекать первые две по двум различным прямым, проходящим
через точку О, параллельным
АВ. Но это невозможно.
Следовательно, в этом случае
плоскость, проходящая через ЕР
параллельно АВ, единственна.
975. Пусть АВ и Си
(рис. 198) скрещивающиеся
прямые. Проведем через прямую
СО плоскость Р, параллельную
прямой АВ (задача 974), и
плоскость ($, перпендикулярную
к Р. Проведем еще через прямую
АВ плоскость /?, перпендикулярную плоскости Р и
пересекающую Р по некоторой прямой ЕР. Плоскость Р, как
перпендикулярная к
плоскостям (2 и Я, будет
перпендикулярна к линии их
пересечения МЫ. Следовательно,
МЫ перпендикулярна к СО
и ЕР. Но ЕР\\АВ и МЫ
лежит в плоскости прямых
ЕР и АВ, поэтому МЫ±АВ.
Итак, МЫ есть общий
перпендикуляр прямых АВ и СО.
976. Пусть прамые АВ и
СО (рис. 199) скрещивающиеся и ни одна из них не
параллельна третьей данной прямой МЫ. Проведем через АВ
Рис. 198.
474
плоскость Р, параллельную МЫ (задача 974). Такая
плоскость будет единственная. Проведем через СО
плоскость ф, параллельную МЫ. Такая плоскость тоже
будет единственная. Линия СВ пересечения плоскостей Р
и <2 и будет искомой. Однако может случиться, что
плоскости Р и ф параллельны. Это будет иметь место
тогда, когда прямые АВ, СО и МЫ параллельны одной
и той же плоскости* В этом случае задача не имеет
решения. Не будет решения и тогда, когда прямая
АВ или прямая СО, или обе они параллельны МЫ, Если
АВ и СО лежат в одной плоскости, но не параллельны
МЫ одновременно, то, когда плоскость Р, в которой
лежат прямые АВ и СД параллельна МЫ, — существует
бесконечное множество решений; когда эта плоскость Р
не параллельна прямой МЫ,—существует одно решение
(если прямые АВ и СО пересекаются) и ни одного (если
прямые АВ и СО параллельны или все три прямые
пересекаются в одной точке).
Рис. 200.
977. Пусть данные плоскость, прямые и длина
отрезка будут Р, АВ, СО и Л (рис, 200). Через прямую АВ
проведем плоскость а, параллельную СО, а через СО—
плоскость /?, параллельную АВ (см. задачу 974).
Очевидно, плоскости ($ и /? параллельны и данная плоскость Р
пересечет их по некоторым прямым ДХ и МЫ,
параллельным между собой. Строим отрезок ЕР = й так, что
точки Е и Р лежат соответственно на /(X и МЫ. Если
теперь провести прямую АС так, чтобы она была
параллельна прямой ЕР и пересекала прямые АВ и СО (см. задачу 976),
30*
475
то отрезок ее, заключенный между точками
пересечения Л и С, и будет искомым. Однако возможно такое
расположение плоскости Р, прямых АВ, СО и отрезка й>
а также задание длины отрезка, что задача не будет
иметь решения или будет
/7 иметь два решения, или
бесконечное множество
решений,
978. Образовавшаяся
фигура есть правильный
тетраэдр АВСО (рис^ 201) с
ребрами АВ = а ]/ 2. Его
объем 17 = а3 — 4- -^— =
В " 3-
р 2^1 979. Фигура—правильный
ис* ' восьмигранник (октаэдр) с
ребром АВ = у МЫ = ^~ (рис. 202). Он состоит из
двух равных правильных пирамид ЕАВСй и РАВСО с вы-
1 п
сотой ЕО = -у 5Т7 = у . Поэтому объем V = 2УАвсэе =
-9 * (аУ~2\* а _ а*
-*' 3 \~2~) ' У - Т'
Рис. 202.
476
980. Обозначим ребро основания буквой х, а
боковое ребро буквой у (рис. 203). Тогда 5 = у х2 + ху +
+ -о- &В • ЕР. Полная
поверхность призмы 5Л = 2х2 + 4ху.
Умножая предыдущее
равенство на 4 и сравнивая с
последним, видим, что 5Л = 45 —
~20В • ЕР. Но ЭВ = ВСУ~2=*
= х)Г2\ ЕР=РВс\ё~ =
Выразим у че-
^с^.
~~ 2
рез х:
у = ЕС = У ЕР2 — ЕС2 =
•.т/'^-.-г.т/'
Рис. 203.
С05а у — 51П2 "о"
Теперь можно найти х.
8 = ±х2+ху + ^ОВ.ЕР = \х2 +
8111» -о"
8 }Л:05 :
+
+ ±хГ*
/1
а
2 51П-2"
]/Т51П ^Г
51Пу + У^соза+созу),
25 5ш у
с* . с*
ъхп^у -\-у 2созя + С05"о"
Искомая полная поверхность
^ = 45^2;с)/1.Ц^-с1е|==4 5-2;с2с^|==
477
= 45-
45 51Пу С1§-у
а у.
51П -у+У 2С05 а + С05 "
= 45-
се .. .
зш-у + У 2соза
2 -г г ""^ «* "г «^ 2 5*п у + К 2соз а + С08-о"
981. Из прямоугольных треугольников ЛШ, ВОВ и
#Л5 (рис. 204) находим:
АО2 = /Ш2 — ВО2 = с2 — Г—*?*_ V- с2 — ^•соз45°У -
ЛСУ Л ^ ° \со5 22°30'/ ~С и§22о307 ~
= С2
со5222о30,— соз2 45°
соза 22° 30'
с*
= С*
21Л2соз*22°30''
ло =
1 + соз 45° Л_
2 ~ 2
соз2 22° 30'
с
У 2 / 2 соз 22° 30'
Рис. 204.
Поэтому искомый объем
У = 5Л = 5 • ЛО= об 81п45°-
аЬс
"К2|/Тсоз22озо'
2 У 2 соз 22° 30"
982. Искомый объем V = аЬ • ОО (рис. 205). Опустим
из О перпендикуляры /)Л и ВС на смежные ребра
основания. Так как Л ВАВ ~ Л ВСВ, как имеющие общую
гипотенузу и по равному острому углу, то АВ =5С и
прямоугольник АОСВ является квадратом. Теперь легко
найти высоту параллелепипеда:
ВО = УВВ2 — ОВ2 = УВВ2 — (АВ2 + А02) =-
478
= с У — со$ 2а.
Отсюда
V ~ аЬс У— С05 2 а.
8
Замечание, соз 2а < 0, так как 2 а > 90° (плоский
угол трехгранного угла меньше суммы двух других).
983. Через точку А (рис. 206), отстоящую на единицу
длины от вершины 5 данного трехгранного угла 8АВС,
проведем плоскость, перпендикулярную ребру ЗА. Так
цак углы рит острые, то плоскость пересечет и другие
ребра трехгранного угла. В сечении получится аАВС,
его угол ВАС и есть, очевидно, искомый. Положим
'/.ВАС = ср. Для нахождения <р выразим ВС2 с помощью
теоремы косинусов через стороны треугольников АВС и
ЗВСу и полученные выражения приравняем. Будем иметь
АС2 + АВ2 — 2АС • АВ соз ср = 5С2 + 8В2 — 28С . 5В соза
или 2АС. АВ соз ср = 25С - 5В соз а — (5С2 — АС2) — (8В2 —
— АВ2), Но из треугольников АЗС и А8В найдем: ЛС=(§ Р;
АВ=1ё т; 5С = -Ь 55 = —; 5С2 -АС2=8В2 -
& * соз [г соз 7
Поэтому получим:
-ЛЯ2 = 1.
Л1 п . 2 СОЗ а Л
21& В га т соз ср = —5 2; соз ср =
& г & * т соз р соз т ' т
соз а — соз р соз г
51П р 51П 7
479
Учитывая равноправность углов а, р, у, получим для двух
других двугранных углов следующие выражения:
СОЗ Р — СОЗ 7 СОЗ а
3111 7 31П а
СОЗ 7 — СОЗ а СОЗ Р
ЗШ 2 ЗШ В
984. Пользуясь рис. 207, можем написать, что искомый
объем V ^ 1т зш у ВО = 1т зш у • ВС зш <р = /т зш у х
X Л5 51п р з1п<р = 1тп зт р 31П -у §5п ср. В последнем
выражении неизвестна только величина зшср. Но
созср
С05 а — С05 р С08 7
810^510 7
(см. задачу 983),
, , 81П В 31П У + СОЗ а — СОЗ В СОЗ У
1 + С05 ср = 1 { . 0 . - и =я
1 Т 81П р 51П 7
= . о .— соз а — соз (3 + т)1 = ;• о •— зш 0 ' х
31Пр51П7 ' 81Пр51П7 2
X 51П^-Ч> ,
Рис 207.
Рис. 208.
и аналогично
1 — соз ср
■51П
Т + « —Р
81П
= + Р-т
2
Теперь легко
31П р 31п 7 °*1Ж 2
найдем зшу на основании формулы зш ср = ]/1 — соз2 ср
= V 1 — соз ср У 1 + соз ср, после чего получим
V = 21тп 1/зш
•±{±1й„1±|^я1„!
:Ч—зт-1^—.
480
985. Обозначим буквой о искомую площадь
треугольника МКЬ (рис. 208). На основании теоремы о свойствах
параллельных сечений пирамиды, имеем
"5
ао>
(м + \<ъ)% (4ло1 + |ло1)2
А6\
25
Отсюда о = -^ 5.
АО\
(М)'=
25
36*
986. Чтобы провести плоскость через центр
основания 0 (рис. 209) параллельно
ребрам ВС и ЛД достаточно провести
через О прямую ЬКII ВС, через
точку Ь пересечения ЬК с ребром
АС прямую Ь№ || АО и через
прямые ЬК и ЬЫ плоскость.
Последняя и будет та, о которой
говорится в задаче. Сечение ЬЫМК
есть прямоугольник.
Действительно, построенная плоскость
параллельна ребру СВ и поэтому она
пересекает боковые грани,
проходящие через это ребро по
прямым, параллельным ребру СВ, Поэтому МЫ || /,/(. Точно
также ЬЫ || М/(. Так что ЬЫМК — параллелограмм.
Кроме того, по теореме о трех перпендикулярах,
ВС ± АО и, следовательно, ЬЫМК — прямоугольник. Оче-
г /, а иско-
видно, ДХ = -%-СВ
мая площадь 5 = -«-а
|а, КМ = \Л0--
1 , 2 ,
987. Так как грани пирамиды одинаково наклонены к
плоскости основания, то в основание можно вписать
окружность, и вершина М пирамиды проектируется в центр О этой
окружности (рис. 210)* Искомый объем V = -«- 5двсэ • МО.
Определим высоту МО = У ЕМ2 — ЕС?. Из чертежа
основания АВСО видно, что А = ВК = 2 • ЕО. Следовательно,
ЕО^-^Н. Определим теперь ЕМ из /\ЕМР. Площадь
1 1 / 25
его 5 = -1ТМЕ2в'та и МЕ = I/ г—. Таким образом,
наи-
481
/25 1
^т-^—— Л2. Найдем площадь осно-
вания. Завсо = —?— ВК, а так как по свойству
описанного четырехугольника АО + ВС = АВ + СО и в силу
равнобедренности трапеции АВ=СО, то АО + ВС—2-АВ
Рис. 210.
и Здвсо — АВ • В К = АВ • А. Остается определить ЛВ. Из
подобия треугольников ЛВ/С и ЯМЭ имеем АВ : В/С =
■= Е0\ЕЫ. Но В/( = А, ЕО = 4А> поэтому АВ=ВК Е°
и?
ЕЫ
2 . &У
Из АЕМЫ находим
17*7 ПАЛ • а 1/ 25 .« -. / 25.31П»у
ВЛГ = ВЛ181П-7Г- == I/ ■: 51П-7Г=1/ _
2 У 51П а 2 |/ а а
Г 2 5Ш ~2 С05 -у
Отсюда:
лв=-
к*
У8-**т
\ 5двсо — •
к*
К5-*«т
а искомый объем
Г 31ГКХ 4 10 1/ ОС от а Г
12/25 5Ш-1'
48&
988. Пусть сечение, площадь 5 которого нужно
найти, есть КЕМ (рис. 211). Основание КЕ этого
треугольника мы найдем, воспользовавшись тем, что Д ОКВ со
со д йСВ и Д КОС со д ВАС. Получим: ^ = \\ Щ =
К „ КО х КО
= —-, а сложив эти равенства, найдем, что -—•-[- — =
= 2^" * = 1; КО = -^ту Точно так же убедимся, что
*
С Е N в О
к/^
/^°;
х!
^^ \ /
Ьг чД
а Р
Рис. 211.
/7
ОЬ = ОК =
0 , ^, так что ^ = _—. Высота
треугольного сечения ЛЮХ = УМЕ2 + Н\ » |/АГЯ — Т^2 + Л2Ь Но
Л1/^ = ^Лс1йу = ус!§у, ЁР — Н, д йх найдем из ранее
полученного соотношения — = ^, что даст Н1= — ОК =
а п> о,
Ыг
а + Ь
• Таким образом, 5 — 4-/С1 • ЛЮ2 =
х/*.*$_* +
62/е2
а + 6
X
483
989. Обозначим искомую площадь через 5, а площадь
ААВй (рис. 212) через 51в Известно, что площадь
проекции плоской фигуры равна площади проектируемой
фигуры, умноженной на косинус угла между плоскостью
проекции и плоскостью фигуры. Поэтому 5!=* 5 со8 а. Отсюда
5 = ^, где 52 = ^ = АВ • ^ ° Условию
у5гСО = К. Но так как СО = ЯЯ • {§« = ЛВ$т60о{§а =
и А8 = 2 |/ К с!§ а Поэтому искомая площадь
Рис. 212. Рис. 213.
990. Пусть ОАВС (рис. 213)—данная пирамида.
Проведем высоту ЭЕ грани ОСВ и высоту ОР пирамиды. Их
основания Е и Р} очевидно, будут лежать на высоте АЕ
треугольника АВС. Обозначим х = АЕ = ОЕ. Тогда
искомый объем V можно записать так:
V = ~ • \СВ • ЛЕ • ОР = \ах • ОР =*
«= 1 ах /ЛО2 —ЛЯ = 1 ад: У<х2 — АР2 .
Величина АР = у найдется, если сравнить два выражения
для О/72, полученные из треугольников ЛО/7 и ЕОР. Это
даст:
а2 — у2 = х2 — (х — у)2, а2 = 2х*/, у = ~, где
х = ОЕ = СЯс1§|=|с1§у.
484
Поэтому
*л/ С052^~з1п2
12 I/ . «
Г 51па_2
12 зш-^*
991. Обозначим
площадь основания и вы-
- соту призмы
соответственно 5 и Я, так что
искомый объем V =
= 5-Я=а251п60°. Я =
= ^. Из АВгЕВ
(рис. 214) получаем Я =
= Я^ = \/ВхЕ* — ВЕ\
где 5Е = /С5з1п60° =
= ^р-, а В^= ВхО + /Г Г В
+ ОЕ. Замечая, что
треугольники /СОВ и
К\0\Вх равносторонние со сторонами а и ЕР — средняя
линия Д КОВ, находим, что
В,Е =
Поэтому:
а
гиту
+
За
4 5111-
4 81П^-
и /"9а2 3 о аУ~Ъ т/3 . 2 а
У 16 зт2-^- 2 51П-2-
а V 3
2 51П-2"
1У
51П а 60° — 51П2 -
соза — соз 120°
а
251П-о-
У 51П (б0° + у) 5Ш (б0° - \) ;
У = ~~~^4г I/ 31П (б0° + -|-) 8111 (б0° - ■§-)•
43111-Й- Х ^/ V ^/
485
992. Обозначим сторону АВ (рис. 215) основания
буквой л:. Искомый объем
V = 5авс • Си = \АВ -СЕ.Сй = ^АВ . АЕ1&* • СО =
= у*-у1§а.СО = -1дгМ§а -СО.
Выразим СО через х:
СО = ]/ОЕ2 — ЕС2 =
-К(1«)"-(1 •..)"-
ДС |^51П2 В СОЗ2 а — 51П2 а СОЗ2 {3 __
2 С05 а СОЗр ~~~
X У§т (А .-)- а) 5Ш (Д — а)
Рис- 215« 2созя соз« '
Чтобы найти х, подсчитаем периметр Д АВС. Будем иметь
2р = ЛВ + ВС + С А » ЛВ + 2 СЛ = * + 2 . ^— =
2х соз2 -—
1 + соз а 2
С03,я СОЗ а
Отсюда:
СО$г-оГ
СОЗ а СОЗ «
р3 соз3 а 1& а л
^ е_ Ё_ уГв-т ф + а) 5|П (Я —а) ^
8 СОЗ6 -тт СОЗ а СОЗ р
__ РЭ 31П 2 Я У$'т О + я) 51П (3 — а)
а
16 С056 у СОЗ {1
993. Выразим полную поверхность 5 пирамиды через
сторону основания ИВ = х (рис. 216). Обозначив площадь
основания пирамиды через 5Х и пользуясь формулой пло-
486
щади проекции плоской фигуры (см. решение задачи 989),
получим
8 = 8, + Л-^Зг-!^^^^— -=—о -•
1 соз а х соз я соз а I соз я
Но
*/3
36
Х51п60Ч§а==|^а и х=2^3Ус1в«.
Подставляя значение х в найденное выражение для 5,
получим
2 ]/Т соз2 -11^9 V2 с1^а а
СОЗ а
Рис. 216,
994. Из прямоугольных треугольников ЕСВ, ЕАВ и
ЕйС (рис. 217) находим: РВ = 2СВ=2ВЕ соз а=2тсо$ а;
КВ = 2ЛВ = 2 ДЯсоз р = 2/тгсозР; ЯС =* ЯБзша=тз1па;
ЕД = )/5С2—СО^К^С2—ЛВ2=1/т251П2а —т2соз2р-
= т у З1п2 а — соз2 р = т у -^ *- =э
е= т У— соз (а + Р) соз (а — р) и искомый объем
V = ^РВ'ВК'ЕО=~т*со$асо$$У— соз (а+ р) соз (а — р).
487
Замечание, соз(а + Р)<0, так как а + Р > у
(сумма двух плоских углов трехгранного угла больше
третьего).
995. Искомая площадь 5 = ЛВ + СО . ДХ (рис. 218). По
теореме синусов из Л КРЬ находим
Лк = -М. = р1 - а
ЗШ а 51П Р 51П (180° — а — р) ~~ ЗШ (а + Р)'
Следовательно,
/(I-
а 51П а
V*. ^
азшр
5111 (а+ р)' 'х* 8111 (а+ Р)'
Из подобных треугольников ММ? и ОСЯ находим
СО : МИ = КЕ\ ЕР. Но ЫМ = а, ЕР = —
КЕ = ЕР~КР =
а 51П ?
2 соз а *
а 81П (а — р)
2соз а ЗШ (а -[- Р) 2соз а 51П (а + р)"
Рис. 219
Отсюда
г>п лл\т № азт(а— Р) • 2соз а а$'т(а—3)
31П (а + Р)
Поэтому
■Р)
2 ' А^~~ 2 Г"*~ ЗШ(а + р) ] " 5Ш(а + Р)
51П (а + 3) + 5Шт(а~-р) азш а
2 51П (а + Р)
и2 ЗШ2 а СОЗ р
$ш (а + р) "" зга2(а + р) •
488
996. Обозначим сторону основания СВ буквой х
(рис. 219). Тогда искомый объем
У=4 • 1 ВС2 з!п60° • РО - -2^
А =
8/з
А.
6 2'" 12
Из подобия треугольников Л.РО и АОЕ (прямоугольные,
имеющие общий /. РАЕ) получаем АЕ : ЭЕ = АР : РО. Но
АЕ = ЛС • 81п60°
а/з.
2 -; Ш = С5.с^а = -|с{§а;
ОР = Н и АР = Р0-4И=Н- **Т'2 = 1/"3 • А • 1§а.
КЯ
2хс1е<
Из ДЛ/^ОМ^^ЛОЧОЯ, а так как АО=^АЕ=^~х-,
ОР = Н; АР = Н У~Ъ \.%а, то (ЛУ~Ъ *§ а)2= (О^ *)* + Л2;
ЗЛМ§аа = -1л;а4-Л2; у х2 = ЗА21§ а — Л2;
*2 = 9Л2 № а - 1$ 30°) = 9Л2 зш(а + 30°)-зш(3-30°) ^
4 ь ь ' СОЗ2 а • С052 30
__ 1251П (а + 30°) • 51П (а — 30°) , 2
Итак, 1/ = ^1.Л =
__ |/Т/г3 51П (я + 30°) 81П (а — 30°)
~~ С052 а
997. На рис. 220 изображена
часть п - угольной пирамиды.
/. АСВ = 2 а есть двугранный
угол при боковом ребре. Най-.
дем площадь основания
5 = п • 5ове
1
1
П •
ВЕ - ОК =
180°
2а • а • с!§
2 * 180°
489
Определим высоту пирамиды ОМ. Из подобия
треугольников ОМЕ и СйЕ имеем 0М:СО=Е0:ЕС. Но
0Е=0В-тг = -ш* со = вг> ■ с*а =
5Ш 51П
=ВЕ-со51ВВЕ-с\%«=2асо8^-с1ёа, и^ВЕ^^КОВ);
ЕС=УЕВ*— СО* == ]/ (ЕВ З1п ^) — СО2 =
2а л Г . 2180° . о 2^80° 2~~
= -— I/ 31П2 зига— соз2 соз^а =
51П а Г П П
2а 1/ /180° , 71805 \
= -— I/ —С05 Ь» соза а .
31Па Г V П 1 I \ П )
Поэтому искомый объем
о ^ 180° 180° ^ а
па* с*в — • 2а соз — • с^* —^^г
51П ■
3 2а
2а 1/ /180° , \ /180° \
щ-а V -С05 [—+а; С051-тг -а)
х о 180О
па3 С08а-С1§2 ——
(180° \ 180°
—-—[- а I < 0, так как ——|- а > 90°.
180°
Действительно, </ 5ВО = > /. СВО, потому что
1ё^ЕВО = ^г>^г = 1ё^СВО. Отсюда ^ +
ВВ ^ ВВ
+ а > ^ СВО + ^ 5СО = 90°.
998. Плоскость сечения АЕР (рис. 221), очевидно, не
может быть перпендикулярна к грани АЭС, потому что,
опустив перпендикуляры из вершины О на линии АЕ и АР,
490
легко убедиться в равенстве их, что невозможно, так как
первый из них был бы одновременно перпендикуляром к
плоскости, а второй — наклонной к ней. Это же ясно и
из свойств симметрии:
перпендикулярность к
плоскости АЭС влечет
за собой и
перпендикулярность к
плоскости АИВ. Поэтому
плоскость сечения
перпендикулярна к плоскости
ВОС. Обозначим
сторону основания буквой
х и выразим через нее
площадь основания и
боковую п оверх н ость
пирамиды:
81 = -^АВ2^п60° =*
х*У~Ъ
~~ 4
(<$! — площадь основания).
52 = 3
Т*7'
П1
(52 — площадь боковой поверхности). Здесь ВС = х, а ЭЬ
найдем из подобных треугольников йОЬ и КАЬ (они
прямоугольные и имеют общий /_ОЬА). ОЬ:АЬ=ОЬ:КЬ- Но
АЬ=-
УТ
01.-\Л1.-^.
КЬ^^йЬ.
Поэтому
получаем:
3*2 -1_ « 4= = тЛб.
2\Г2УЪх* У 6
У 2 2/25!
999. V = у 5Авсо • ОМ (рис. 222); 5Авсо=^г^-СЯ=
= ВС + 2РЕ + ВС СЕ = (ВС+ОЕ) . ся=з
=(а + асоз а) а 81п а=а2 (1 +соза) зт а= 2а2 зт а соз2 -|-.
491
Для определения высоты ОМ пирамиды замечаем, что
ввиду одинакового наклона ребер к основанию вершина
пирамиды проектируется в центр О, описанного около
основания круга, радиус которого есть АО. Найдем этот
радиус. Для этого, описав вокруг трапеции круг,
замечаем, что так как хорды АВ, ВС и Си равны между
собой, то равны и соответствующие им дуги. Отсюда
заключаем, что центральный 2 АОВ = а, потому что
соответствующая ему у^АВ^-ъ-АС. Теперь из АОРА
получаем
Рис. 222,
Из А МО А находим
МО = АО- 1в? = —^*ё<Р-
2$1П-9"
Поэтому
1/=у. 2а251пасо52~—^-1§? = у а3со$8 у 1е<Р<
2$1П-о"
492
1000. Пусть №=Н и /а = а (рис 223). Обозначим
высоту МО буквой Я, тогда МК = у Н. Заметив, что
МИ =УМК2 — К№= ]/1 //2 — Л2 и Ж^МЯ2—ЛХ2==
«= |/-^- Н2 — а2,
воспользуемся двумя парами подоо-
ных треугольников: МОВ и
МШ МОР л МК1. Из пер-
вой пары имеем: ^ = -щг,
или ВО = МО ** -
МЫ
= //
УЧ яа ~ Ла
из второй: -^у- = -щ-, или ОР
„, /ио //
Рис. 223.
)/^//а-аа
Но так как ОР = РВ, то ОВ2 = ОР2 + РВ2 = 2 • ОР2.
Отсюда:
(^
Я/1
Яа — /1а
= 2
#а
Я5» — а*
\4 у' ^2аа —
;й2(|я>-а*у
йа
Найдем сторону основания
ВС = 2 • ВР = 2-ОР
= 2-
К
= ?.
2аЛ
а//
У>-
1 2
=3
-а2
/1а^
а2/га
2а2 — /1а~
/2аа —Ла УЛ2 —аа
Поэтому
У=\ - ВС2-Л10 = „ ^^ 2 а.
3 3 (Л2 — а2) У 2аа — Л2
31 К. У. Шахно
493
1001. Полная поверхность 5—5авс +3-$смв(рис. 224).
Но 5Авс = 4-ЛС.СВ51п60°
-*^- 8ст = ±СВ-МР
2' — ^
^\яУСМ2 — СР2 = \я У СМ2 — ^ Остается
определить СМ, Положим СО = ту, МО = пу. Так как
АМСО со &ЕСО (прямоугольные треугольники, имеющие
общий угол МСЕ),_то СЕ:СО^СМ\С0. Но СЕ^
*= СВ81п6(Г = -^р-; СО = ^СЕ =*\У~Ъ\ СО =* ту;
СМ = (т + л)у. Отсюда получаем, что СЕ*С0=СО-СМ
или
г"Кз
|-]/3 =ту(т + п)у и г/;
]/2т (/л + л)'
Таким образом,
- т Ф У2т+1п-т = ^У(т + 2п)т;
8=д^± + За* УЩШ} = + *1 [т + УЪт (т + 2п)\.
4 ' ^ Ат 4т '
1002. Сумма внутренних углов многоугольника равна
180° (т — 2)=90°я, 2(т — 2)=п9 т=у + 2. Обозначим
!^ Л4СО буквой * (рис. 225, на котором изображена — часть
494
всей пирамиды). По условию ^бок = к. Отсюда получаем:
т.^-АВ-МС МС . ОС 1
1 лп =к;-0С=к ™С08* = Ж = Т.
т -у АВ-ОС
Найдем теперь площадь основания
50сн = т -±-АВ • ОС=т • АС - ОС ^ т - ОС Л%^-ОС=*
--т • ОС2 • 1§ 360°
2/п
Из АМОС находим
ОС = ОМ с\§ х = Л с1§ л: =
Следовательно,
л + 4"
Лсозя
У 1 — соз2 х У к2 — 1'
с тН* ^ 360°
И К 6 (й2 — 1) 1ё п + 4 '
Замечание. ОС можно найти и без применения
тригонометрии. Действительно, из равенства ^ = к
находим СМ=ОС -к, а из АМОС найдем (ОС . к)2=ОС2 + Н%
1003. Найдем длины 1/С, ЛС и КР (рис. 226), нужные
Рис. 226.
31*
495
для вычисления искомой площади трапеции АЬКС. Из
подобия треугольников 51/С и 8ЕО получим: ^ = ёт? == 4"'»
1/С=у5'0==-|-. Чтобы найти АС, обращаемся к рисунку
основания. Так как А ЛВС = 108°, то ЛСВР=Ш° —
— 108°:= 72°, /.ВСР=18°. Таким образом, ВР есть
половина стороны десятиугольника, вписанного в окружность
радиуса ц. Поэтому ВР^ У Ъ~ 1 ц и ^4С8=^4В• + ВС+
ЛС = -|/2^У + 6=|-(К"5 + 1). Величину ЛС просто
вычислить и тригонометрически: АС = 2 • ЛВсо$36° =
^ 2^7С0536° = 29 • У\Л~Х = |- (К"5 + 1). Высота
/СЯ - //СС2 — РС2. Но РС = 1- (АС — ЬК)^
~\[ЦУ^+1)~\я] = ^\ КС* = КО* + СО*-
— 2 • СО • ОМ = (у) + ?2 — 2? • -|- (потому что из
подобия треугольников 8ЫО и /ШО вытекает, что
МО = ±N0 = ^00=^, т. е. /СС=^±^.
Итак,
Отсюда находим
1004. Пусть плоскость, рассекающая основание
пирамиды на два многоугольника, есть АМВ (рис. 227).
Многоугольник АВО имеет (г + 2) вершины, а АВЫЬК имеет
(я — г). Искомый объем
У=± 5 • Я = ^ /г • ^ ОВ2 • 51П ~ • ОМ -
496
-б(штсдв)5т—-°с-^а==б
251* П
180°(г + 1)
X ОС • 1§ а • 51П
360°
6 ^^(Т+1) 2
Ьс1ё^^±^Х
Х51П-
360°
^ 180°(г + 1) . 360°
1§а =
1§а
4851Пз180>+1)
Замечание. Из условия г <
- следует, что
г + 2<1 +\,ап — г>| + 1, т. е. что г + 2<л —г
и угол АОВ (см. рис. 227), соответствующий
многоугольнику с меньшим числом сторон, всегда будет меньше 180°.
1005. Обозначив площадь основания пирамиды
буквой 5, а ее высоту Н и пользуясь рис. 228, получим:
5=уу4В.ВС51па=:у6251па;
Н = 00 = У ВО2 —ВО2 = |А2 —
2соз-
005'!--! =
со5"2
"^соз2!- —соз260°
497
а
V
С05 о — С08 120^
С05Т
7уЛ8т(б0Ч|)5т(б0°-|);
СОЗТГ
у6351П^|/5щ(б0О + -^)51п(б00--^).
Рис. 230.
1006. Так как площади треугольников 8АС и ЗАВ
равны (рис. 229), то искомая боковая поверхность
(}=-\-ВС •80 + 2--тГАВ-8Е. Но АВ = а;
ВС = 2 • ВО = 2 • АВ 51п -|- = 2а зт -|-
5Е:
СОЗ<р
АОзт-т^
АВ СОЗ-о- 51П "о"
Я51П а
СОЗ <р СОЗ.ср 2С05 <р *
а 51П а а2 81П а /
+ а
2соз<р 2соз<р
(51ПУ51ПСР+ 1 ).
498
1007. Искомый объем V состоит из объемов двух
пирамид, имеющих одно и то же основание ЕСР (рис. 230)
и высоты АО и йВ. Обозначим площадь основания буквой 5.
Имеем У = -\-8-АО + ±-8 - ОВ ^±8 - (АО + ОВ)^
е= — 5 • АВ, где АВ = Л/Ссоза = /соза. Чтобы вычислить
площадь 5 правильного треугольника, найдем радиус СО
описанного около него круга:
АВ = /соза = АО +*ОВ = СО • с{§а +СО • с*еР =
с=СО(с1ба + с1§Р) = С0.54^^; СВ=/соз%51"а^^,
4 & 1 ь г/ 51П а 51П Р ' 51П (а + Р)
Отсюда
у = ±3-АВ = ±ЕС*-$!~ . ЛВ^
^±(со/~з)2.^.лв = 1^.со2. лв^
451П2 (а + р)
1008. Проведем плоскость ММР(}К8 (рис. 231) через
центр октаэдра параллельно какой-нибудь грани,
например СРО. Она образует в сечении с октаэдром шести-
Г
Рис. 231.
499
угольник с вершинами в серединах М> N. Р, <?, # и 5
шести ребер октаэдра. Этот шестиугольник правильный,
так как каждая его сторона равна половине ребра
октаэдра, а каждый угол между соседними сторонами
равен 120°, потому что стороны шестиугольника
параллельны сторонам правильного /\СйР. Соединим все вершины
этого многоугольника с вершиной В октаэдра. Получим
пирамиду с высотой ВО = -д- ВЕ = -у- А, где Н — высота
пирамиды ВСОР. Обозначим площадь многоугольника
МNР^К8 буквой а, а объем пирамиды ВСйР — буквой У2.
Тогда для искомого объема Уг найдем, что Уг = -^ а • -у к =
где а — ребро октаэдра. Итак,
1009. Из симметрии пирамиды ясно, что Кд = Ьд и
Л/С = АЬ (рис. 232). Следовательно, ЬК±Ад. Поэтому
искомая площадь 5 = -о- • КЬ • Ад. Из прямоугольного
ЛЛ<?М находим
Ад = УАМ2 + дМ2. Но дМ = Н, а АМ-=АС — СМ*
АС-
АС— Ед _ АС + Ед аУ 2 + 6 }/Т
2 ~~ 2
(а+ *>)/?
а + 6
500
Поэтому
Для вычисления отрезка КЬ заметим, что линия КЬ [| ВО,
потому что К1» и ВО лежат в плоскости ВОМР и
пересечься не могут в силу параллельности ВО и плоскости
АЬцК* Из чертежа ясно, что КЬ = ВО — РО — ВО =
= ВО — 2 ■ РО = а \/"2 — 2 . РО. Остается найти РА Так
РО ВО
как дЛМфсл /\ЬРО, то можно записать-ур- = -^. Но
аго ь пп л*г» АС — Ед аУ~2 — ЪУ~2 а — Ъ
м? = а, ^ = ^с = —2~^ = ^ ^ТТ'
1Р = ОС, а СО из подобных треугольников цАМ и (ЗЛО
определяется так:
С0__ЧМ_ пп_яМ_ Ап_ ЬУ~2 аУ~2 _ аН _тп
АО — АМ' ии ~ АМ ' ™ ~~ а + Ь ' 2 ~ а + *>
Таким образом,
рр _ ^р . /?Р __ аН . ° —6 = (а — ь)а_
Ы&~ а + Ь % У~2Н (а + Ь)У~2> а
К1 = а\ГЪ-2-РВ = аУ~2-2- {а~ ь)а_^У~*аЬ .
(а + Ч|/2 а + 6
Следовательно, площадь
_ У2аЬ -,/ (а + 6)1 , 2
"~ а + *> Г 2 ""Г" *
1010. Проведем плоскость ЮЕ (рис. 233) через
точки I и Я касания шара с двумя гранями пирамиды и его
центр О. Эта плоскость, как проходящая через
перпендикуляры ОЕ и О! к этим граням, будет перпендикулярна
к граням, а значит и к линии их пересечения. Поэтому
/_ ЬОЕ = ср, плоскость ЮЕ пересечет СР в точке Р под
прямым углом. Отсюда ясно, что отрезок РО, равный
высоте ромба, разделится точкой касания Е пополам.
Следовательно, можно написать:
а . хФт/ 4 о тг а3 . , . о ф
501
1011. Опустим перпендикуляр АО (рис. 234) на
плоскость основания пирамид. Он, очевидно, пройдет через центр
шара. Проведем апофему АВ пирамиды. Она будет
касательной к шаровой поверхности. Соединим основание О
Рис. 233. Рис. 234.
перпендикуляра АО и основание В апофемы АВ. Получим
прямоугольный треугольник АОВ и из него находим* что
радиус шара
г==ос = ов 81п ^ сво «-%- 51п /. сво =*
0
а -. / с05' Т~8Ц,Т а /"Е^
вт|/ -= №-—-•
Л соз2 -^ 2 сое -сг
1012. Искомая поверхность 5 состоит из трех равных
сегментных поверхностей. На рис. 235 эти поверхности
расположены впереди куба, ниже его и левее. Шаровая
поверхность касается ребер, сходящихся в вершине Е, и
502
граней, пересекающихся в вершине Р. Обозначая радиус
сферы г = ОА = ОЬ = ОВ и пользуясь формулой
сегментной поверхности, получим
$ = 3'27гг.СЯ = 6тгг.ЛГВ = б7гг(ЛВ — ЛАГ) = 6тгг(2г — а).
Для определения г обратимся к равнобедренному
прямоугольному Д0/(Х. Из него найдем ОЬ = ОК V 2 и так
как ОЬ^г, а ОК^ОМ = АМ — ОА = а—г, то г=^
= (а-г) 1^2, г = ^|^-а (2-/"2). Поэтому
5 = 6тгг(2г — а) = бтга2 (2 — ]Г2) (3 — 2 }/~2) а
^6тга2(10 —7>^2).
Рис. 235.
1013. 1/=5.Я=4-Л5.ВС-Е/7
1 ЯВ
/)В
2 51ГКХ СОЗа
^ =
Н*-ЕР
Н2
- 25Ша.соза ~ ^2а~ ■ ^ (Рис- 236>- Остается определить
высоту ЕР. Она равна диаметру шара КЬ, или, иначе,—
диаметру вписанного в дАВС круга. Последний можно
25
определить по формуле 2г = —. Для этого определим АС.
АС = — = ВВ
СОЗа С05 а • 51П а
-; 2р=АВ + ВС+АС =
-—-!- — + ■
С05 а ' 81П а ~ 5Ш а • СОЗ а
51П а • соз а
Л $1*па + соза + 1
$Ш*а • СОЗа
•Л:
503
а а а а а
2з1П ~2 соз "2 + 2соза ~<[ $*п ~2" + сов "о"
2$т-о- соз-п" соз а
*1™»(т + т)
ЗШ-о" • СОЗ а
31П ~п СОз а
.; ЕР=2г=- =
2Аа • гзш-тгсоза
2 К 2 А • 31П -о" • соз а
V 2 А
451П-
•С05
СОЗ а • 51П
51П 2а
^ =
1^2 А3
25ГП2а.созЛ.8т/-^ + 4-)
2 \4 2/
л 1014. Пусть АВСО
(рис. 237) данный
тетраэдр. Проведем через
ребро АВ плоскость,
параллельную
противоположному ребру СО-
Такая плоскость будет
единственная и ее
можно построить так:
взять точку К на АВ,
провести прямую С^ ||
II СД тогда плоскость,
проходящая через АВ и
СхОъ будет требуемой.
Затем таким же
способом построим
плоскость, проходящую через ребро Си и параллельную
противоположному ребру АВ. Эти две плоскости будут
параллельны. Построив для каждой пары
противоположных ребер тетраэдра параллельные плоскости, мы
получим многогранник, который, очевидно, является кубом
с диагональю грани, равной а. Шар, касающийся ребер
тетраэдра, окажется вписанным в построенный куб,
причем его диаметр будет равен ребру куба. Поэтому
искомый радиус __
* 2 т1У 2 у~2 4 '
ГХ / 1 [
1 ч X / ' •
4 X/ ' х
Ск «1
1 * ч ! х !
1).\- \1
Рис. 237.
X ш
к * /
\ ч / 1
\ \ /
Г /
А
504
1015. Обозначим буквой ср угол ОгМ8 (рис. 238) при
ребре основания данной пирамиды. Искомая полная
поверхность
АВ* = АВ2 ^ 1+созу ^
С05 ср С05 ср
О = Оосн "Т *->бок — АВ +
1 + С08 Ср
СО$ ср
•2 . С1й2 — • ! +С05СР - ЛР2<! +СОЗСР)3
Рис. 23а
Остается найти 51П ср и созср. Проведем плоскость ОЕР
через центр О шара и через точки Е и Р касания его
с двумя смежными боковыми гранями. Эта плоскость'
перпендикулярна к граням, на которых лежат точки Е и Р
и, следовательно, перпендикулярна к линии их
пересечения, т. е. к ребру 5В. Поэтому /. ЕРР = а, где Р точка
пересечения ребра 8В с построенной плоскостью* Из
четырехугольника О ЕРР находим ЕР = 2Е($ = 2Н соз -|-.
С другой стороны, четырехугольник ЕРЬК, где Ь и /С —
точки касания шара с двумя другими гранями пирамиды,
есть квадрат и поэтому
ЕР=~ ЬЕУ~2 = )Г2/?5Ш1ср= гЯсоз-^-,
605
откуда
51П <р = У 2С03 у; СОЗ ср = У\ — 81П2 ср = V 1 —
г ' ^ а
У — СОЗ а • СО$2 "Х-
2соз2| =
Рис. 239.
1016. Так как боковые
ребра ЯЛ, йВ и ОС (рис. 239)
данной пирамиды равны, то
высота ЭО проектируется в
центр О описанного около
треугольника ЛВС круга,
искомый объем У1 = — 5 • ОО,
где 5 — площадь Д АВС. По
условию задачи V = -^-тс /?2 х
X ОО, где К — радиус основа-
ЗУ
ния конуса. Отсюда ВО=^-2
и У\ = —55- Обозначим бо-
новое ребро пирамиды
буквой х. Тогда можно написать:
АВ = 2х$т-^~; ВС = 2*51п-|-; ЛС = 2*5т-|-
Воспользовавшись теперь формулами
аЬс
45
Я = 5^ и 5= /р(р-а)(р-6)(р-с).
получим
^1 =
1с • АВ* Увс*. АС* • 1653 = Т~п С08ес2 Т С08ес* 4 х
X со$ес2 -1 ]/ (згп -|- + 31п -|- + зт -|-)3 х
т// а Р Т\3 { Р Т «1»
X у ^ЗШу-}- 81П-2"—ЗШ^ • ^ЗШу+ЗШу*— 31П "2"^ X
=(•
а р \3
X 1 81П -$- + 81П ~2 ~ 81П -у I
906
1017. Если соединить концы
5, С и К (рис. 240) этих хорд
между собой, то получится
правильная пирамида,
вписанная в шар радиуса Я с
плоским углом при вершине
боковой грани 2а. Требуется
определить боковое ребро АС этой
пирамиды. Если провести
диаметр АР через центр О
основания и конец Р его соединить
с точкой С, то получится
прямоугольный треугольник.
Поэтому, приняв АС = х, получим
х2 = АР . АО = 2# У АС2 — СО2 = 2# ]/ х2 — (|- С!)2 =
= 2К\ х* — (-| • СВ ^-)2= 2/?]/д;2 — (-^= ЛС51па )* =
Итак,
Гз
С05 2а -
ут
у_г -=Р^~ = ^ }/51П (60° + а) 8>п (60° - а).
1018. Многогранник, объем V которого нужно найти,
есть пирамида. Вершины М, М, Р, ф (рис. 241) ее
основания находятся на апофемах пирамиды. Чтобы это
доказать, проведем плоскость через высоту АО пирамиды и
радиус ОР полушара, где Р — точка касания шара с
гранью ЛСД Так как АО перпендикулярна к плоскости
основания пирамиды, а ОР — к плоскости боковой грани,
то проведенная плоскость будет перпендикулярна к обеим
этим плоскостям, а следовательно, и к линии СЭ их
пересечения. А это значит, что линия АВ, являющаяся
линией пересечения проведенной плоскости с гранью САО,
перпендикулярна СД т. е. АВ, на которой находится
точка касания Р, есть апофема. Объем V = у Р0? • РЕ.
507
Для определения Р(} заметим, что Д/4Рф со ДЛВ/,, и по-
—^—, а для определе-
этому^ «^. Но 1.В = \Кй =
ния -^ положим ^ ЛОР =э ^ РВЕ = <р, после чего получим:
АР = ЛО 51П <р = АВ 81П2 ?, ^ = 51П2 <р * 1 — СОЗ2 ср =
СОЗ* у — 51П2 у
СОЗ а
С05ЯТГ
Таким образом,
РС1<=г1В • -тд =—- , & РЕ = РВ 51П ср
/Ш
2С082 —
= ОВ С08 ср 81П ср = ~
ОВ . а ДО .
8,ПСР=-2- •'Ж8,ПСР==
ля
У^С05«
Поэтому
к =
(аУ~2~соза\8т
2соз^ /
4 <8
созт
а \ СОЗ а
2
С08-
О8 СОЗ* а 5*П -о" У СОЗ а
12созв •
508
1019. Спроектируем трапецию ЛВС О (рис. 242) на
плоскость, перпендикулярную оси цилиндра. В плоскости
проекций получим трапецию А^С^х. Так как в нее
вписывается окружность и она тоже равнобедренная, то
ВгСг = А& + с& « ±+±, потому что АгВг = АВ = Ь и
СгОг = СО = а. Подсчитаем высоту трапеции: АХЕ =
- ]/(^)2-(^)" = \ГШ Отсюда 5.П х- Щ где
х — искомый угол. При этом должно быть аЬ < Л2.
Рис 242. Рис. 243.
1020. Соединим середину Ь отрезка АВ (рис. 243) с
серединой М отрезка СО. Отрезок /ЛИ является общей
медианой равнобедренных и равных между собой
треугольников СЮ и АМВ. Поэтому ЪМ. есть общий
перпендикуляр к ребрам АВ и СО тетраэдра. Найдем его
длину: 1М = УВМ2 — ВЬ2 = ]/-|- а2 — \ а2=ф=.. Проведем
через ребро СО плоскость, перпендикулярную оси
конуса. Так как осевое сечение конуса есть две взаимно
перпендикулярные прямые, то угол между проведенной пло-
32 К. У. Шахно
609
скостью и образующей АВ равен 45е. Поэтому ЬЗ =
=1М=~, а 8М = Ш/~2 = а. Но СМ2=5М.Л1^ или
^=а-МЫ. Отсюда: АГ#= |-; 0# = 5# = \(8М + МЫ)^
^Т^ + тЬт*' (°К±8МУ> КМ = КЫ-МЫ = 8К-
ОМ =
— МЫ ^ ~ а —
= Уок2+км2
_1
4
о/"34
8
бП= -д- а. Следовательно,
1021. Пусть СОР (рис. 244) есть сечение тетраэдра
плоскостью,
проходящей через его высоту
ЭО и боковое ребро
ОС, а заштрихованный
прямоугольник /(ХЛ1ЛЛ—
соответствующий разрез
цилиндра, объем V
которого требуется
определить. Здесь СО = /,
гСР = ОР
__ /У~з
как
КТ
О г N
Рис. 244.
ЫС\МЫ = ТС\ЕТ или
высоты граней
правильного тетраэдра.
Обозначим высоту цилиндра
МЫ = Л, а радиус
основания ОЫ = г# Из
подобия треугольников
ЕСТ и МЫС получим
ОС— г __ ТС
Н ~~ ТЕ
(*)
Но
ОС = 4- СР = ~ 1\ ЕТ2 = /Г • ТС (АРЕС —
прямоугольный); РТ
(±рс\2
_ГЕ» _ У )_ _ I рГ__У~Ъ .
^РС РС ~ 9 °— 18 ''
ТС = РС —
510
V-
= 1/Уз
18
/
9 ' — 9 '•
Поэтому равенство (*) можно записать так:
(«?'-')
ут
/=л-
4 Кз
/ или Н +
1
:Г=-
1
= /■
9 9 " * ' 2/2 ' ' 2^6
Из подобия треугольников /,/СР и ЕТР найдем РК'.КЬ—
по-
= РТ:ЕТ или ^р = ^. Но ОР = -^^ *"Г '•
этому получим:^/ — г)^р/=А-^/; Л + 2/"2г =
■ /;
2 1
= --= /. Решив систему: А Ч —
Уб ' 2/2
г =
2 |/~6~
А + 2)/ 2г = -^=/, найдем, что г = ^/, а А = ^А/.
Кб 7 21
Отсюда
У^тг^А^тг^/)2
21
343
1022. Соединим центр
окружности С (рис. 245) с
серединой О хорды АВ отрезком
прямой, а также соединим
точку Ь с вершиной конуса Е.
Так как Си ±АВ, а {&АОЕС=
со
= ^, то отсюда видно, что
'^ ОЁС — наименьший из всех
углов, которые образует
прямая ЕС с различными
прямыми, проведенными в данной
плоскости через вершину Е.
Следовательно, прямая ЕВ есть
проекция прямой ЕС на эту
плоскость и ^О^С=ср.
Учитывая это, найдем длины
отрезков Ей и АВ, после чего
искомую площадь 5 можно
будет легко вычислить. Имеем:
Е0=™_= ^Ч±_. АВ = 2-АО
С05 ср С08 <? '
Рис. 245.
2 У АС2 — СЯ2 =
32*
511
= 2УК2-(СЕ.\ё<?)2=2УК2-(К1ё*-1ё<?)2 =
2#|/1-{§2а1§2ср
2#
Поэтому
С05 а С05 <р
У С05 (а + ф) С05 (а — ср).
С05 а со5 ср г х ' * / у т/
"Кс052аС082ср—51П2а31П2<р=.
5 = 4г АВ-Ей = гпд"'ё°г /соз (а + <р) соз (а - <р).
Рис. 246.
1023. Искомый объем V равен сумме объемов
конусов АОЕ и АСЕ (рис. 246). Поэтому V = -|-тс. ЛВ2 • ВО +
+ _^_ гс . ЛВ2 . ВС = -^-тг-ЛВ2. (ОВ + ВС)=~тг -АВ2ОС.
Но ОС = О/7 • соз а = / соз а. С другой стороны, ОС =
= ОВ + ВС = ЛВс1&а + ЛВс1§Р или /Соза =
= ЛВ • (с1ёа + с16р) - ЛВ . "^Ц.
4 & ' ь г/ 31П а 31П Э
Отсюда
- г» ^ С05 а 81П а 51П 9 тт « л г»
^45= г—;—г-бг-^- Подставив наиденные значения АВ и
51Л (а + Р)
^^ « ^ Т7 71/3 С058 а ЗШ2 а 51П2 В
ОС в формулу объема, получим V= 351па (а + В)—•
512
1024. На рис. 247 изображено осевое сечение тела
вращения (заштрихованная фигура). Искомый объем V
равен разности между суммою объемов конуса АВЬ и
усеченного конуса ЬКйА и объемом конуса йСК. Поэтому
у=^[АР . ВР + (АР2 + АР • ОЕ + ОЕ2) • ЕР-
— йЕ2 • ЕС1 = -у [ЛР . (ВР + РЕ) + йЕ2 • (РЕ — ЕС) .+
+ АР-йЕ-ЕР] = -%- (АР-ВЕ + ОЕ2.РС + АР.ОЕ-ЕР) =
= _|_ [ЛЯ • (ВС + СЕ) + йЕ2 • (ВС — РВ) +АР -йЕх
X (ВС + СЕ — В/7)] = -у [(2а 51П а)2 (6 + а соз а) +
+ (а зш а)2 (6 — 2а соз а) + 2а 31П а - а 31П а (6+а соз а —
— 2асоза)]=^|^с(46+4асоза + 6 —2асоза +
+ 26 — 2а соза) = « .
Рис. 247.
1025. V =±8к = ±АО . СЯзтр . ОАГ=уСЯ2.(Шз1пр
(рис. 248). Но МО = Ш, зт а = а зт а, СО = -^ =
чг ' 51ПР
513
ЕР 2-ОЬ
51ПР 51П Р
2 • ЬМ С05 а
5111 Р
2а сое о ^ ^
-о—. Таким образом,
81П
17 1 /2асозсЛ2 . . 0
2а8 5Ш 2а С05 д
Ззшр
1026. Обозначим радиус основания конуса буквой г,
а его образующую — буквой / (рис. 249). Боковая поверх-
514
ность конуса образующими МК, МЬ и МЫ, по которым
касаются коническая поверхность и описанная вокруг
конуса пирамида, делится на части -^ тг г1, -^- тг г1 и -^ те г1.
Отсюда видно, что ч^ КЬ = -^ тс г, ч^ 1# = -^г- тс г,
14
ч^г Л^/С = то~7ГГ и» следовательно, ^ ЦЬ : ч^ 1М: ^ #/С=
-5:6:7, так что ^ /<т = 100% / ЮЫ = 120°,
г/ МЖ = 140°. Обозначим площади частей боковой
поверхности пирамиды, на которые ее делят
образующие МК, МЬ, МЫ, через 5Х, 52, 53.
Очевидно, 51 = 2.5мсь==С1-/ = О1.1й^1ОС-/ = г/1й50° и
аналогично 52 = г1{§ 60°, 53 = г11§ 70°. Итак, имеем
5Х: 52: 53=гЛ§50° : гП&№о:гП&Ж==\&ЫоА&&0°А&Ж.
Рис. 250.
1027. Приведенный в тексте решения рис. 250 не
соответствует действительности. Однако это искажение
позволяет лучше подметить нужные для решения зависимости.
Пусть 50 и 50х — высоты двух смежных конусов; 5/( и 5/, —
их образующие, по кбторым они касаются плоскости, и
точки А и В — проекции центров О и Ох на эти
образующие. Точка М есть точка пересечения линии ООг с
образующей, по которой эти конусы касаются. Очевидно,
^ ОМЗ = 90°. Из АОМЗ находим АВ = ООг = 2 . ОМ =
= 2 • 05 • 31п </ 05М = 2 • 05 • 31П -у-, где х — искомый
угол. Из ДЛЗС находим АВ = 2 • АС = 2 . 5Л . 5т60° =
515
=2-50-соз-2- • 51п60°. Сравнивая, находим: 2-05- эту =
= 2-05-со$|-5тб00,5т-|-=со8-|--5ш600, 1е^-=зт60°,
1028. Как видно из рис. 251, искомый объем
у = |.тсг2. кр + .1. „ . угдг. Ар_ ^ п . ^. 0р =
= |-[2г2 • /С/7 + /'Д2 • (Л/7 — 0/)1 = у (2Г2-А^ + ^2-г) =
= ^(2г-ЛТ + /Ч)а), где г ==4-:
/СР = /Ф • 51П а = 2г 81'п2 а = Л зт2 а;
У7/) = О/) • зт 2 а = г зт 2а = — зт 2а.
Отсюда
у = ^(А28ш2а + ^зт22а) = ^(1+соз2а).8т2а.
/7 О
Рис. 251. Рис. 252.
1029. Пусть искомый радиус есть х~Ой (рис. 252),
объем конуса Уг и объем шарового сектора,
заключенного внутри конуса, У2. По условию Ух = 2У2. Выразим Ух
и У2 через г, а и *. Получим:
У1 = ±ъг2.ОЕ = \ъг*с\&<х\ У2 = -|тг*2 . КМ =
516
= утгл:2- (ОК — ОМ) = ^кх2- (х — *соза) =
= -д- те Хг • (1 — С05 а) = -у- те ДГ3 31П2 -^-.
Подставим найденные значения для ^ и У2 в равенство
У\ = 2^2. Это даст-д-7г/Лс{§а=-д-7гдг351п2у.
Отсюда:
о__^С^_. Г 3 /""сТ^
^ "~ « » 2 1/ а
88111я-д- Г 51П2у
1030. Проведем плоскость через высоту МС (рис. 253)
и апофему МЕ пирамиды. Образовавшиеся при этом
треугольники МСЕ и МОО подобны. Из их подобия
находим, что СЕ\ОЭ~*МЕ: МО. Но СЕ=ВЕ • с*в ^ ЕСВ =
==Т* с1^Т~; 0О==/? (неизвестный); МЕ = УМВ2—ВЕ2=
= ]/а2 — х^2; МС = К "Ж* — Си2 =
= гА2--т—У= -Ляг • /4*2^2Т-«2;
Г 51П2 -— 28111 ——
Рис. 253.
517
мо = мс—со = тс—к.
Из предыдущей пропорции имеем:
■ у 4а251П2
Я =
СЕ-МС
СЕ + МЕ
Я;
180°
п
-<7а
2(дсо*Ж + У4^^.5тЖ)
1031. Проведем высоту С В и апофему С К пирамиды
и соединим их концы В я К (рис. 254). В полученном
АСВК /. СКВ = /. СОР = а в силу перпендикулярности
сторон. Проведем диагональ ЪО основания и соединим
точку й с концом Е диаметра СЕ. Из прямоугольного АСОЕ
получаем
ВО2 = СВ • ВЕ. Но ВО ^~Ю=\у АО2 + А12 =
= У^АО==У~2 0К==У 2
2 2
ВК=У~2-СВ. с1^а =
= К2-А-с1§а; С5 = А; ВЯ = 2# — А.
Подставив в предыдущее
равенство, получим
2А2.с^2а = А(2/? —А)^, 7?==
= А(1+2с1е2а); К-
+ 2с1е2а)3.
1032. Возьмем осевое
сечение конуса ЛВС (рис. 255).
Пусть искомый '/. ВСО = х.
Соединив центр О шара с
концом С образующей ВС и
его же с точкой касания Р
шара и образующей ВС
конуса, видим, что /_ ВОР =
= /. ВСО = х
(перпендикулярность сторон) и А ОЕР =
= /. ВСО = х (как соответственные). По условию задачи
У2 = -VIV гДе ^1 — объем данного конуса, а 72 — объем
отсеченного плоскостью конуса со стороны вершины дан-
518
ного. Обозначив радиус шара буквой г, выразим объемы
VI и У3 через г и угол х. Находим:
Ух = 1* • С/)2-50=у {Ой • с!§ /. ОСО)* • СО • \&г. ЯС1>=
у.-^-о^ов-^д^)'
тс г8
Ззта * • соз х
Подставляя найденные значения Уг и 1/2 в равенство
У2 = -2-Уь получаем:
{%хСОьХ = тс18*Т # {ёх> *'{п2х' С08* ' с1б3Т ' ^* = 2,
5Ша * СОЗ X
- у А соз 2 _ 2 - ,
„ . х х С05Х
231ПТ.С08Т
81ПТ
х 1 х 1 1
соз — = ;п=, — = агс соз тт=, дс = 2агс соз 5-7=. •
2 |/Т 2 |/Т т/Т
Рис. 256.
519
1033. Пусть ВО (рис. 256) есть высота конуса. Она
проходит через центр Ог шара и центр О основания
конуса. Опустим перпендикуляр СО из точки С касания
шара с образующей АВ на высоту ВО и центр Ог шара
соединим прямой с точкой С. Получившийся при этом
/. ОСОг = /. АВО = ~ (в силу перпендикулярности
сторон). Опустим из точки С перпендикуляр СЕ на плоскость
основания конуса. При этом получим, что </ АСЕ =
= /. АВО = ^ (соответственные). Искомый объем
у^±-к(С02 + СО- ОА + ОА2) • ВО.
Определим входящие сюда отрезки:
СО = ОхС • сое ^ йСОг = г соз -|-;
ОО = ИОх + 0±0 = ОхС • 5Ш ^ ЯСС^ + г = г М + мл ~\\
0А = АС= « - »._'(,+*т).
СОЗ / ЛСЯ а а
соз ~сг соз -9*"
Подставляя найденные величины в выражение объема,
получаем
У=-т I ( гсоз 4-1 -{-гсоз-^- — -—-^
Л[ .\- - '(1+5<пт)
т И г соз т] + г соз у -
соз» т ^
*г»(1+81п-11
X 1 — 31П2 4 + 1 + 31П ~ +
(,+-ч)'1
2 ' ' 2
1 — 81Па "2" }
-4"''(1+в1пт)'(1-
— 31П тг + 1 Н
1 — 51П 1]Г)
520
= т^(1+5тт) : =
1 — 51П -п"
= {«/•• Г—4" (з-3вш!+81п«! •
3 5!п4(1-т)
1034. По теореме синусов имеем АВ = 2/?$т ^ЛСВ =
= 2# • зш (180° — 2ср) = 2/? • 81П 2 ? (рис. 257). Высота
пирамиды С!) = /4Я 1§ «р = -^ АВ • *ё <р = /? $ш 2ср • 1§ <р.
Поэтому искомый объем
У = 4-5- Н = ]гАВ- ЕГ$та-СО = ^АВН\па.СО =
= -~- • 4#2 . 81П2 2<р • 81П а • # • 81П 2<р • 1§ <р =
Рис. 257. Рис. 258.
1035. На рис. 258 изображено сечение конуса
плоскостью, проходящей через ось конуса, и ту его
образующую, к которой перпендикулярна касательная к шару
плоскость. Следу этой плоскости на рисунке соответствует
прямая ИР. Соединим центр шара О с точкой касания С
шара и образующей МА и его же с точкой касания Р
521
шара с построенной плоскостью. Очевидно,
четырехугольник СОРО есть квадрат со стороной г. Высота конуса
МВ = ОВ+ОМ = ОВ + УОС2 + СМ2 = ОВ +
+ У0С2 + (МО — СО)2 = г + уг2 + ((1 — г)2.
Радиус основания конуса АВ определится из подобия
треугольников АВМ и ОСМ (прямоугольные, имеющие общий
угол АМВ). Имеем:
АВ:ОС = МВ:МС;АВ = ОС^=г.г-+Ц±^.
Таким образом, объем конуса
У = ±-«.АВ*-МВ = \«г*.{г + Уг^-г^\
Замечание. Возможна и другая касательная
плоскость, кроме изображенной на рисунке. Она отстоит от
построенной на расстояние, равное 2г. В этом случае
объем конуса
т/ _ И1а [г + У г* + <а + г>2]3
у "~ 3 * (4 +г)2
Рис. 259. Рис. 260.
1036. Возьмем осевое сечение цилиндра (рис. 259).
Обозначая радиус цилиндра буквой х, а объем буквой у,
можем написать у = те х2 • С б. Но из прямоугольного
треугольника СОА находим, что
СО = У АС2 —АО2 = |^4/?2 — 4х2 = 2 / #2 — х2.
Отсюда получаем формулу
у = 21гд:2//?2 — х2.
1037. Можно, но тогда придется отнести к призмам
также такие многогранники, которые не принято называть
призмами. Например, ромбический додекаэдр (см, рис. 260).
522
ОГЛАВЛЕНИЕ
Задачи
I. Преобразование алгебраических выражений . . , « . 3
II. Алгебраические уравнения 14
III. Составление уравнений ..«.»..•.»... 24
IV. Прогрессии 34
V. Логарифмы .,»*.«<»... ,39
а) Общие свойства логарифмов :«,.,*..* 39
б) Логарифмические и показательные уравнения . . « 40
VI. Соединения и бином Ньютона • . * ,.,.,.« 43
VII. Преобразование тригонометрических выражений ... 46
VIII. Тригонометрические уравнения ....«..,.. 55
IX. Неравенства ..«.».....<...«.» 58
X. Комплексные числа , . ............ 65
XI. Математическая индукция . » .-..«.•... 68
XII. Исследование функций и построение графиков ... 69
XIII* Геометрические задачи на плоскости (Планиметрия) , . 72
XIV, Геометрические задачи в пространстве (Стереометрия) 84
Решения
I. Преобразование алгебраических выражений , , » . 92
II. Алгебраические уравнения . .......... 123
III. Составление уравнений . • * . . . 168
IV. Прогрессии . . . ..,.,.«««..... 198
V. Логарифмы ... . .... . ....... . 216
а) Общие свойства логарифмов ....•«.,, 216
б) Логарифмические и показательные уравнения , . 220
VI. Соединения и бином Ньютона •«.»..*••• 236
VII. Преобразование тригонометрических выражений . , . 248
VIII. Тригонометрические уравнения .......... 293
IX. Неравенства •••....•....«...« 317
X. Комплексные числа . . . «......•„.. 345
XI. Математическая индукция ........... 361
XII. Исследование функций и построение графиков . » .371
XIII. Геометрические задачи на плоскости (Планиметрия) . . 398
XIV. Геометрические задачи в пространстве (Стереометрия) . 468
523
Шахно Константин Устинович. СБОРНИК ЗАДАЧ ПО
ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ ПОВЫШЕННОЙ ТРУДНОСТИ. Минск»
«Высшая школа», 1965.
523 стр. с илл.
Редактор Костюковвц Ф. Т. Худож. редактор Кононов А. А. Техн.
редактор Моргунова Г. М. Корректор Дубовик Л. А.
Подписано к печати с матриц 27/Ш 1965 г. Формат 84х1087з2.
Печ. л. 16.375 (26,855). Уч.-изд. л. 26.13. Изд. № 278. Тип. зак. 787.
Тираж 75 000 экз. Цена 93 коп.
Издательство «Высшая школа» Государственного комитета
Совета Министров БССР по печати. Редакция физико-математической
литературы. Тем. план. 1965 г., № 52.
Минск, ул. Кирова, 24.
Полиграфический комбинат им. Якуба Коласа Государственного
комитета Совета Министров БССР по печати.
Минск, Красная, 23,.
93 к.
> г
ч
* *