Text
Карточки
для коррекции
знаний
7 класс
Г. Г. Левитас
КАРТОЧКИ
ДЛЯ КОРРЕКЦИИ ЗНАНИЙ
ПО МАТЕМАТИКЕ
для 7 класса
«ИЛЕКСА»
Москва
2000
Левитас Г. Г.
Карточки для коррекции знаний по математике для 7 клас-
са.— М.: Илекса, 2000.— 56 с.
ISBN 5-89237-035-6
.Вашему вниманию предлагается система карточек для коррекции знаний
по курсу математики 7 класса. Каждая карточка посвящается одному отдельному
вопросу и состоит из трех частей: инструкции (формулировки правила), образца
применения этой инструкции и трех разделов заданий для учащихся.
Карточки предназначены для дополнительных занятий с учащимися
(в классе или дома). Если ученик на таком занятии правильно выполнил первый
из трех разделов заданий, этого достаточно. Если же он не смог этого сделать, то
учитель должен объяснить ему материал и дать задания из следующего раздела.
Если и эти задания ученик не может выполнить, объяснение продолжается
и решаются остальные задания.
. ЛР № 064344 от 9.12.95.
Печать офсетная. Формат 70x90/16.
Тираж 10 000 экз. Заказ 2938
ООО «Илекса», 121354, г. Москва, а/я 282.
Заказы по телефонам: в Москве (095) 365-30-55
Ордена Трудового Красного Знамени
ГУП Чеховский полиграфический комбинат
Министерства Российской Федерации по делам печати,
телерадиовещания и средств массовых коммуникаций
142300, г. Чехов Московской области
Тел. (272) 71-336. Факс (272) 62-636
ISBN 5-89237-035-6
© Левитас Г. Г., 1999
© ООО «Илекса», 1999
/
Карточка № 1. Раскрытие скобок
ПРАВИЛА ОБРАЗЦЫ ЗАДАНИЯ
Если перед скобкой стоит, плюс или не стоит никакой знак, то можно убрать скоб- ки, сохраняя знаки всех сла- гаемых, стоящих внутри скобок. Если перед скобкой стоит минус, то можно убрать скобки, меняя знаки всех слагаемых, стоящих внутри скобок. Z АЛ AA'S' 7 а .. I и I 1 1 й + <3- * И + S- + + + 7 । а 1 11 11 7? Т» I । 1 и । +. ? » + + /1 7 Л 1 ? ? ? i-" Раскрыть скобки:
.1) (х + у-г)-1; 2) х + (у - х); з) (х + у)-(х-у); 4) (х + у) - (х - у); 5) (х-y + z)-(x + у — z).
6) (а + b - с) + 2; 7) а + (Ъ - с) ; 8) а - (а - b + с); 9) (x + j)-(x-j); 10) (й-д + 1)-(а + &-1).
11) (tn + p-q)-p‘ 12) т + (р - т); 13) т - (т - р + q); 14) Cp + ?)-Cp-g); 15) (т - р + 5) - (т + р - 3).
Карточка № 2. Умножение многочленов
ПРАВИЛО ОБРАЗЕЦ ЗАДАНИЯ
Чтобы умножить многочлен на многочлен, умножь каж- дый член первого многочле- на на каждый член второго многочлена и сложи резуль- таты. (а + b - с)0 - j) = = ах - ay + bx - by - сх + су. Преобразовать произведение в многочлен:
1) (а + b)(c + d); 2) (а + 2)(Ь - с); 3) (а - 1)(а + b - 2) ; 4) (а - Ь)(а + Ь); 5) (а + Ь)(а + Ь).
6) (х + у)(г + О; 7) (x + 2)O-z); 8) 0-1)0 + у-3); 9) о-здО+у); ю) о+1)0+1) •
11) (т + ri)(p + q) ; 12) (т + 2)(л - р); 13) (т - 1)(т + п - 2); 14) (т- р)(т + р)-, 15) (т + 2)(т + 2).
Карточка № 3. График линейной функции
ТЕОРЕМА ОБРАЗЕЦ ЗАДАНИЯ
График линейной функции у = ах + b - это прямая, проходящая через точки (0,6) и (1,а + 6). Определить, к какой из следую- щих функций относится эта тео- рема и каков график этой функции: а) у = х2- 2 б) у = —, X В) у = 6 - 4х . Решение: а) Функция у = х2 - не линей- ная, теорема к ней не относится. 2 б) Функция у = "Не линей- X ная, теорема к ней не относится, в) Функция у = 6 —4х - линей- ная, теорема к ней относится. Значит ее график - прямая. Ее можно провести через точки (0,6) и (1,2). Определить, к какой из сле- дующих функций относится эта теорема и каков график этой функции:
К CS .. 1 cn 1 М £ II II II >> 'S' S S'
ч 3 а) у = ~; X б) у - 2х -1; в) J-6x2.
+ 7 к cs | к гн II II II "S' S д'
Карточка № 4. Разложение многочлена на множители вынесением за скобки
ПРАВИЛО ОБРАЗЕЦ ЗАДАНИЯ
Если у всех членов много- члена есть общий множитель, его можно вынести за скоб- ки; в скобках нужно запи- сать частные от деления каждого члена на этот множитель. ах + ау-а- а(х + у -1). Разложить на множители:
1) 2х - 2у; 2) Злу + 4xz; 3) Зх2 - 2х; 4) бху - 3xz + 9х2 ; 5) (х - 1)а + 2(х - 1)с.
6) За-З6; 7) 2ас + 5Ьс; 8) 7а2 — За; 9) 6ad + 2cd - 4J2; 10) (а + 2)х + 3(я + 2)у.
11) 4p-4g; 12) pq + 2тр; 13) q2—7q; 14) 6qy-3az + 9a2; 15) (m + 1)й + 4(m +1)6.
Карточка № 5. Свойство степени с натуральным показателем
ФОРМУЛЫ ОБРАЗЦЫ ЗАДАНИЯ |
1) атап =ат+п; CS СП II (N II Tn <N (N Выбрать нужные формулы и с их помощью упростить выражения:
2) а : а = а , если а & 0 и т > п ; 3) (ab)m = атЬт; З7 :35 = 32 =9, так как 3 Ф 0 и 7 > 5; 6т = 2“ -3"; 1) 531 :529 ; 2) (х2)3; 3) (2л)4; 4) (8л)5/(4л)5; 5) jc3jc2.
4) (a.byn=am .Ьт, если Ь Ф 0; г-\ / „т\п „тп 6) (а ) =а . 182:62 = 32 = 9, так как 6 =£ 0; (3m)2 =32т. 6) 7П:79; 7) (а3)2; 8) (За)5; 9) (6а)4/(За)4; Ю) /j-
И) 618:617; 12) (64)3; 13) (2m)3; 14) (10л)6/(5и)6; 15) аа4.
Карточка № 6. Формула квадрата суммы
ФОРМУЛА
ОБРАЗЦЫ
=/2 + 2 •/// +//\
(Зх + 4)2 =?
/=3х, 11 = 4;
ЗАДАНИЯ
Преобразовать выражение по
данной формуле, если это
возможно:
/2=(3х)2,
2-1 II = 2-Зх-4,
II2 = 42;
(Зх + 4)2 = (3х)2+2-Зх-4 + 42 =
= 9х2 +24х +16.
1)
2)
3)
4)
5)
25х2 + 10лу + у2 = 2
Z2 =25х2 =(5х)2, 1 = 5х,
II2 =у2, II = у,
2 • I • II — Юху = 2 • 5х • у,
25х2 + Юлу + у2 = (5х + у)2 .
(а + 6)2;
х2 +2ху +у2;
т2 + Зтп + п2;
(2и + 3)2;
а2 - 4а + 4.
6) (х-у)2;
7) а2 + 2аЬ + Ь2;
8) p2+4pq + q2;
9) (2 +ЗА:)2;
10) а2 + 6а + 9.
11) (c + J)2;
12) 1 + 2х + х2;
13) а2 + 8а + 16;
14) (2р + ?)2;
15) 4а2-4а + 1.
Карточка № 7. Формула квадрата разности
ФОРМУЛА ОБРАЗЦЫ ЗАДАНИЯ |
(I-II)2 =I2-2III + II2. (Зх-4)2 =? Z = 3x, // = 4; Z2=(3x)2, 2-1 11 = 2-Зх-4, II2 =42; (Зх-4)2 = (3х)2 -2-Зх-4 + 42 = = 9х2-24Х + 16. Преобразовать выражение по данной формуле, если это возможно:
1) (а-Ь}2-, 2) х2-2ху + у2; 3) т2 - Зтп + п2; 4) (2и-3)2; 5) а2 — 4а + 4.
6) (х-у)2-, 7) a2-2ab + b2; 8) p2-4pq + q2; 9) (2-ЗЛ)2; 10) а2 - 6а + 9.
N) М S S N) м и» И к, ы II И ы • и ' О II « \> о о и + + ч и 4 л ч II W - . || о -° И* х •** ” • II 14! <!к 4! И
И) (c-d)2-, 12) 1-2х + Х2; 13) а2-8а+ 16; 14) Q.p-q)2-, 15) 4а2-4а + 1.
Карточка № 8. Формула разности квадратов
ФОРМУЛА ОБРАЗЦЫ ЗАДАНИЯ
(/ + //)(/- II) = I2- II2. (2х + 3^)(2х - 3 у) = ? I = 2х, II = 3у; I2 =4х2, II2 =9 у2-, (2х + Зу)(2х - Зу) = 4х2 - 9/ . Преобразовать выражение по дан- ной формуле, если это возможно:
1) (х - У)(х + У) ; 2) а2—с2; 3) (10 + а)(а-10); 4) p2+q2; 5) 25/и2-16и2.
6) (а - Ь)(а + Ь); 7) 4а2-1; 8) (ЗГ + 2)(2-3/); 9) х2 + 4; 10) 9£2-49.
а2-25 = 2 I2=a2, II2 = 25, 1 = а, 11 = 5, а2-25 = (а + 5)(а-5).
11) (с - d)(c + d); 12) 100-х2; 13) (3 + ^-3); 14) 1 + х2; 15) т2-4.
Карточка № 9. Решение линейных уравнений
ПРАВИЛО
Чтобы решить линейное
уравнение,
1) перенеси слагаемые с не-
известным в левую часть
уравнения, меняя их знаки;
2) перенеси слагаемые без
неизвестного в правую часть
уравнения, меняя их знаки;
3) приведи в обеих частях
подобные члены;
4) раздели обе части уравне-
ния на коэффициент при х
I (если он не равен нулю).
ОБРАЗЕЦ
Решить уравнение:
2х-17 = 63 + 4х.
Решение:
1) 2х-17-4х = 63;
2) 2х-4х = 63 + 17;
3) -2х = 80;
4) х = 80:(-2),
х = -40.
Ответ: { — 40}.
ЗАДАНИЯ
Решить уравнения:
1) 4х + 5 = 2х-7;
2) 5х-7 = 13;
3) 3(х + 2) = 2(х + 2);
4) 2х - 4 = 8 + 2х;
5) 4х + 6 = 2(2х + 3).
6) Зх + 4 = 7х-8;
7) 2х-3 = 10;
8) 2(х +1) = 3(х +1);
9) Зх - 5 = 3 + Зх;
10) Зх + 6 = 3(х + 2).
11) 5х + 1 = Зх + 1;
12) 6х —1 = 11;
13) х —1 = 7(х —1);
14) х-2 = 1 + 4х;
15) 5х + 5 = 5(х-1).
Карточка № 10а. Смежные углы
ПРАВИЛО
Чтобы узнать, смежные ли два данных угла, проверь: (1) имеют ли они общую сторону, (2) обра-
зуют ли прямую две другие их стороны. Если углы смежные, то их сумма равна 180°.
ОБРАЗЕЦ
Какие их этих углов - смежные? Какова величина каждого из смежных углов?
Решение:
С Углы АВС и CBD:
\ 1) имеют общую сторону ВС,
\ 2) имеют стороны БА и BD, не образующие прямой.
\ Значит, эти углы - не смежные.
\ j) Углы АВС и BEF не имеют общей ‘стороны.
/ Значит, эти углы - не смежные.
>Ч35°\
/ . Углы АВС и АВЕ:
_ ДЮ7 1) имеют общую сторону ВА,
гХ. \ 2) имеют стороны BE и ВС, образующие прямую.
\ Значит, эти углы - смежные, их сумма равна 180°.
е Так как угол АВС равен 35°, то ХАВЕ = 180°— 35° = 145°.
Углы CBD и DBE - тоже смежные.
XCBD + XDBE = 180°.
Так как /DBE - 107°, то XCBD = 180°— 107° = 73°.
Карточка № 106. Смежные углы
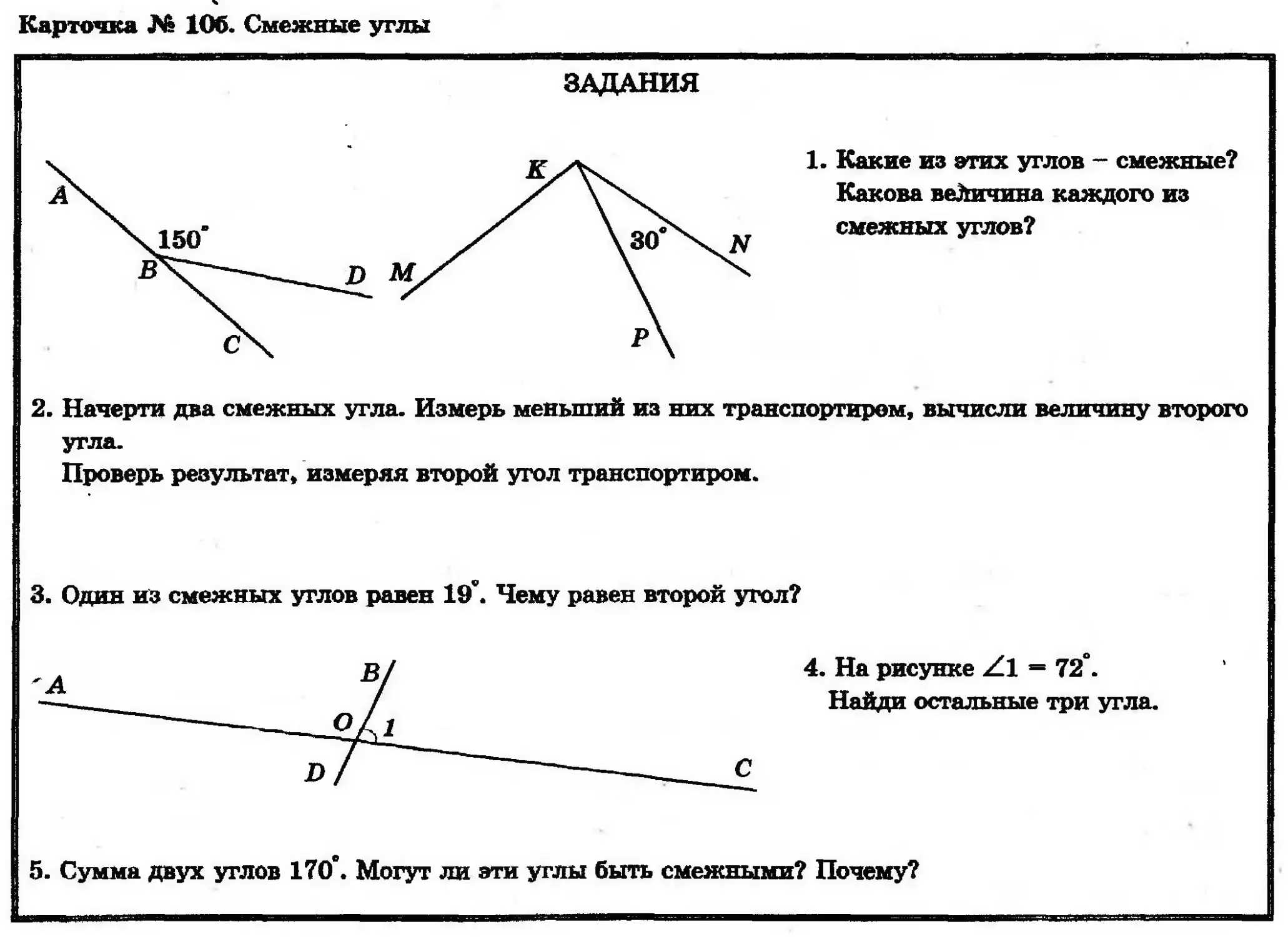
ЗАДАНИЯ
1. Какие из этих углов - смежные?
Какова веЛичина каждого из
смежных углов?
2. Начерти два смежных угла. Измерь меньший из них транспортиром, вычисли величину второго
угла.
Проверь результат, измеряя второй угол транспортиром.
3. Один из смежных углов равен 19°. Чему равен второй угол?
4. На рисунке Z1 = 72°.
Найди остальные три угла.
5. Сумма двух углов 170°. Могут ли эти углы быть смежными? Почему?
Карточка № Юк. Смежные углы
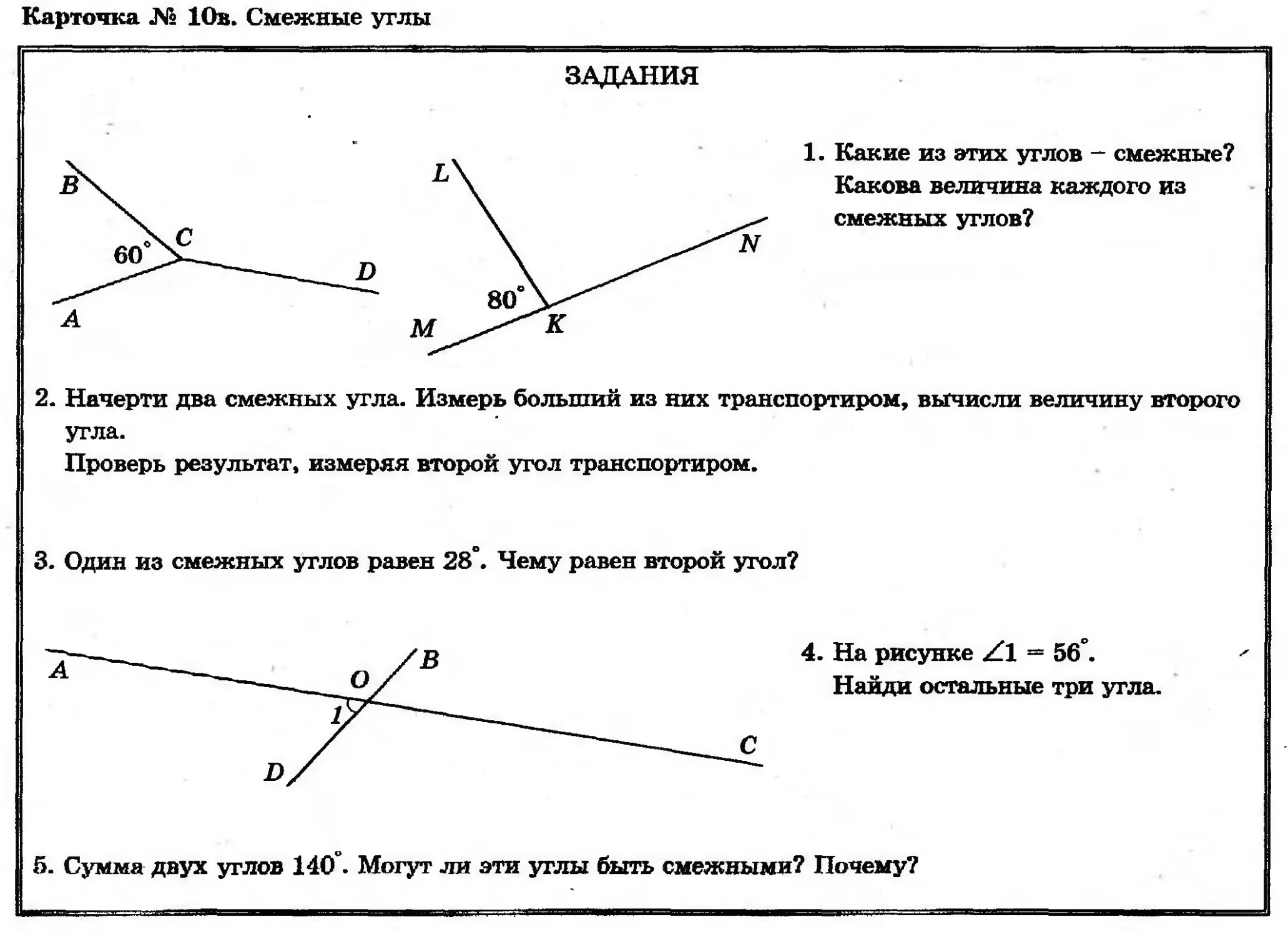
ЗАДАНИЯ
1. Какие из этих углов — смежные?
Какова величина каждого из
смежных углов?
2. Начерти два смежных угла. Измерь больший из них транспортиром, вычисли величину второго
угла.
Проверь результат, измеряя второй угол транспортиром.
3. Один из смежных углов равен 28°. Чему равен второй угол?
4. На рисунке Z1 = 56°.
Найди остальные три угла.
5. Сумма двух углов 140°. Могут ли эти углы быть смежными? Почему?
Карточка № 10г. Смежные углы
ЗАДАНИЯ
1. Какие из этих углов - смежные?
Какова величина каждого из
смежных углов?
2. Начерти два смежных угла. Измерь один из них транспортиром, вычисли величину второго
угла.
Проверь результат, измеряя второй угол транспортиром.
3. Один из смежных углов равен 19°.- Чему равен второй угол?
4. На рисунке Z1 = 88°.
Найди остальные три угла.
5. Сумма двух углов 190°. Могут ли эти углы быть смежными? Почему?
Карточка № 11а. Вертикальные углы
ПРАВИЛО
Чтобы узнать, вертикальные ли два данных угла, проверь: (1) получены ли они пересечением двух
прямых, (2) не являются ли они смежными. Если углы вертикальные, то они равны.
ОБРАЗЕЦ
Какие из этих углов - вертикальные? Какова величина каждого из них?
Решение:
а \ ’
\ Углы 1 и 2:
\ не получены пересечением двух прямых.
\ & Значит, углы 1 и 2 - не вертикальные.
1 А 8-^"
L-X""? Углы 1 и 3:
\ 4 -1Ч К
^---'2 / \ 1) получены пересечением двух прямых о ио;
/ \ 2) являются смежными.
/ \ Значит, углы 1 и 3 — не вертикальные.
/ \ Углы 1 и 4:
/ \ 1) получены пересечением двух прямых а и Ь;
/ \ 2) не являются смежными.
/ \ Значит, углы 1 и 4 — вертикальные. Поэтому Z.1 = Z4.
с \
Так как Z.1 — 90°, то z^4 = 90°.
Карточка № 116. Вертикальные углы
1. Какие из этих углов - верти-
кальные?
Какова величина каждого из них?
ЗАДАНИЯ
2. Один из вертикальных углов равен 71 . Чему равен второй угол?
3. Начерти два острых вертикальных угла. Измерь один из них транспортиром и вычисли величи-
ну второго угла. Проверь результат, измеряя второй угол транспортиром.
4. При пересечении двух прямых образовался угол в 39°. Найти остальные три угла.
5. Могут ли быть вертикальными угол в 15° и угол в 14°? Почему?
Карточка № 11в. Вертикальные углы
ЗАДАНИЯ
С
1. Какие из этих углов — верти-
кальные?
Какова величина каждого из них?
2. Один из вертикальных углов равен 48°. Чему равен второй угол?
3. Начерти два тупых вертикальных угла. Измерь один из них транспортиром и вычисли величину
второго угла. Проверь результат, измеряя второй угол транспортиром.
4. При пересечении двух прямых образовался угол в 28°. Найти остальные три угла.
5. Могут ли быть вертикальными угол в 27° и угол в 26°? Почему?
№ 11г. Вертикальные углы
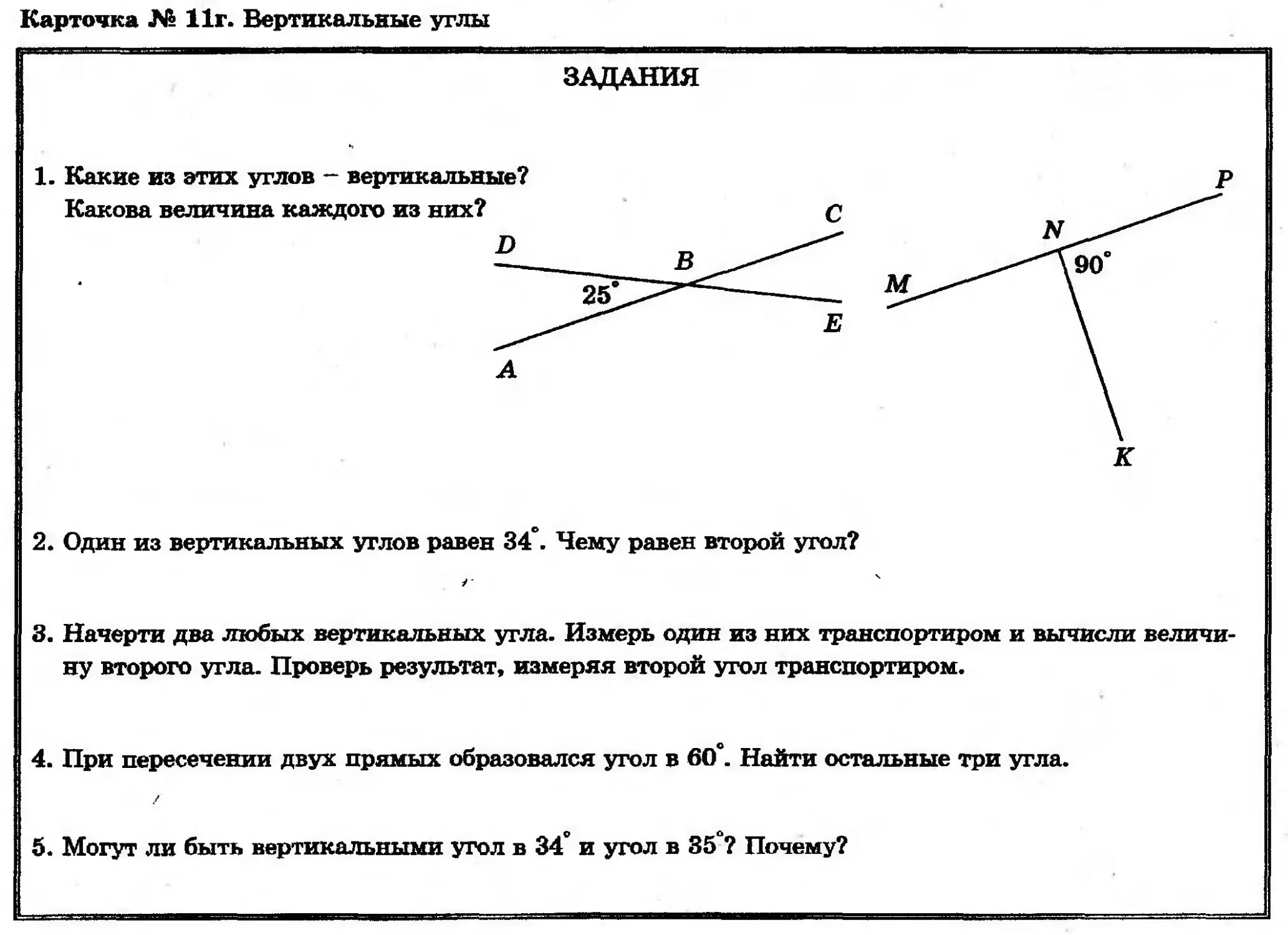
ЗАДАНИЯ
2. Один из вертикальных углов равен 34°. Чему равен второй угол?
3. Начерти два любых вертикальных угла. Измерь один из них транспортиром и вычисли величи-
ну второго угла. Проверь результат, измеряя второй угол транспортиром.
4. При пересечении двух прямых образовался угол в 60°. Найти остальные три угла.
5. Могут ли быть вертикальными угол в 34° и угол в 35°? Почему?
Карточка № 12. Свойство углов равнобедренного треугольника
ТЕОРЕМЫ ОБРАЗЕЦ
Теорема 1. У равнобедрен- ного треугольника углы при основании равны. Теорема 2. Если у тре- угольника есть равные углы, то против них лежат равные стороны, то есть этот треугольник — равнобедренный. Среди следующих треугольников найти такие, к которым относит- ся хотя бы одна из этих теорем, и сделать вывод об этих тре- угольниках. Д л лк м/_ \р
Решение: У треугольника АВС есть равные углы А и С. Значит, к нему отно- сится теорема 2. Значит, треуголь- ник АВС — равнобедренный, у него равны стороны АВ и ВС. У треугольника MNP есть равные стороны MN и NP. Значит, к нему относится теорема 1. Значит, у треугольника MNP равны углы МиР.
ЗАДАНИЯ
Среди следующих треугольников
найти такие, к которым относится
хотя бы одна из этих теорем, и сде-
лать вывод об этих треугольниках.
Е
М
Карточка № 13. Медиана, биссектриса и высота равнобедренного треугольника
ТЕОРЕМЫ ОБРАЗЕЦ ЗАДАНИЯ
Теорема 1. У равнобед- Среди следующих треугольников Среди следующих треугольников
ренного треугольника найти такие, к которым относит- найти такие, к которым относит-
совпадают медиана, бис- ся хотя бы одна из этих теорем, ся хотя бы одна из этих теорем,
сектриса и высота, прове- и сделать вывод об этих треуголь- и сделать вывод об этих треуголь-
денные к основанию. никах. никах.
Теорема 2. Если у тре- к £/\
угольника медиана совпа- \\ \ / /
дает с биссектрисой или \ \ \ / /7 м
с высотой или если его
биссектриса совпадает
с высотой, то этот тре- Решение: —
угольник — равнобедрен- У треугольника АВС есть равные В. Де7' z >Е
ный. углы А и В. Значит, он равно- A \ / /\
бедренный и к нему относится / \
теорема 1. Значит, медиана, про- / \ \/ /^м
веденная из вершины С, совпада- L -Ас \'р
ет с биссектрисой и высотой.
У треугольника MNP совпадают
медиана и биссектриса, проведен- %
ные из вершины М. Значит, к не-
му относится теорема 2. Значит, V /С\\ \\\
у треугольника MNP равны сто-
роны NM и МР. А м
№ 14а. Первый признак равенства треугольников
ПРАВИЛО
Чтобы доказать, что данные треугольники равны по первому признаку, надо:
1) найти у первого треугольника сторону, равную какой-нибудь стороне вто-
рого треугольника;
2) среди двух оставшихся сторон первого треугольника найти сторону, равную
одной из двух оставшихся сторон второго треугольника;
3) проверить, что угол между выбранными сторонами первого треугольника
равен углу между выбранными сторонами второго треугольника.
Задача 1.
Доказать, что Д АВС = Д МРК.
Доказательство:
1) В треугольнике АВС сторона
АВ = 2 см. В треугольнике МРК
такую же длину имеет сторона МР. Значит, АВ = МР.
2) Среди оставшихся сторон треугольника АВС сторона АС = 4 см. В треугольнике МРК такую
же длину имеет сторона МК. Значит, АС = МК.
3) В треугольнике АВС угол между выбранными сторонами АВ и АС равен 50°. В треугольнике
МРК угол между выбранными сторонами МР и МК тоже равен 50 . Значит, углы между
выбранными сторонами в этих треугольниках равны: Z.BAC = Z.PMK.
Вывод: Д АВС = Д МРК по первому признаку равенства.
Карточка № 146. Первый признак равенства треугольников
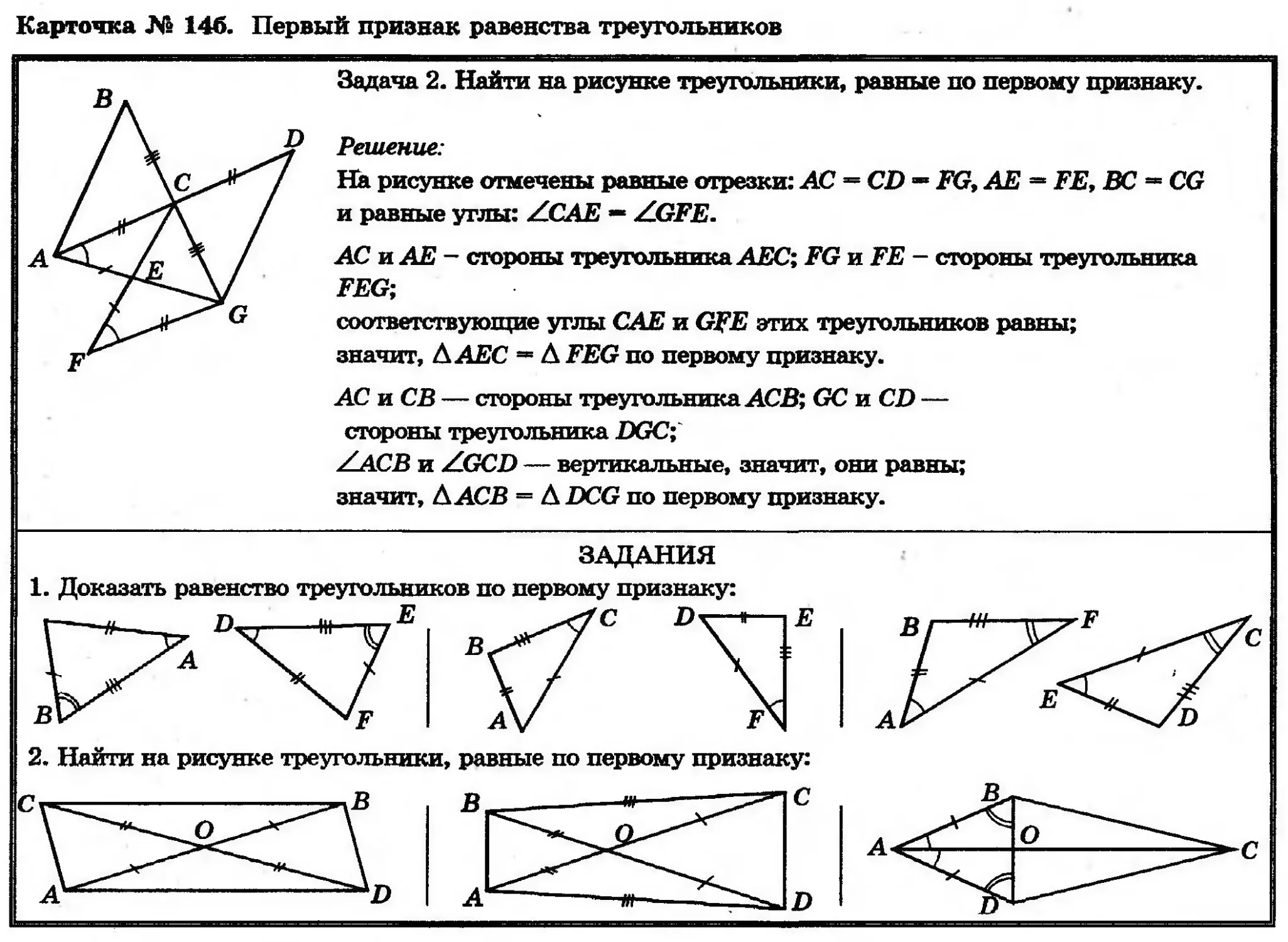
Задача 2. Найти на рисунке треугольники, равные по первому признаку.
Решение:
На рисунке отмечены равные отрезки: АС = CD — FG, АЕ = FE, ВС = CG
и равные углы: Z.CAE — ZGFE.
АС и АЕ - стороны треугольника AEC; FG W.FE- сяюроны треугольника
FEG;
соответствующие углы САЕ и GFE этих треугольников равны;
значит, Д.АЕС = Д FEG по первому признаку.
АС и СВ — стороны треугольника АСВ; GC n CD —
стороны треугольника DGC;
ХАСВ и Z.GCD — вертикальные, значит, они равны;
значит, Д АСВ = Д DCG по первому признаку.
ЗАДАНИЯ
1. Доказать равенство треугольников по первому признаку:
2. Найти на рисунке треугольники, равные по первому признаку:
Карточка. № 15а. Второй признак равенства треугольников
ПРАВИЛО
Чтобы доказать, что данные треугольники равны по второму признаку, надо: \
1) найти у первого треугольника сторону, равную какой-нибудь стороне второго А
треугольника;
2) проверить, что один из углов, прилежащих к выбранной стороне первого
треугольника, равен одному из углов, прилежащих к выбранной стороне равны
второго треугольника. .
3) проверить, что второй угол, прилежащий к выбранной стороне первого \
треугольника, равен второму углу, прилежащему к выбранной стороне , К
второго треугольника. ,
ОБРАЗЦЫ
Задача 1. 1 см
Доказать, что А АВС — А МРК. Ycm/
А./М^---------------------------------------
Доказательство:
1) В треугольнике АВС сторона АВ = 1 см. В тре-
угольнике МРК такую же длину имеет сторона МР. Значит, АВ = МР.
2) Прилежащий к стороне АВ треугольника АВС угол А равен углу М, прилежащему к стороне МР
треугольника МРК.
3) Прилежащий к стореже АВ треугольника АВС угол В равен углу Р, прилежащему к стороне МР
треугольника МРК.
Вывод: А АВС — А МРК по второму признаку равенства.
Карточка № 156. Второй признак равенства треугольников
Задача 2. Найти на рисунке треугольники, равные по второму признаку.
Решение:
На рисунке отмечены равные отрезки: АС = CD = FG, АЕ = FE, ВС = CG
и равные углы: Z.CAE — ZGFE.
В треугольниках FEG и АЕС равны стороны FE и АЕ, а также прилежащие
к ним углы: ZGFE = Z.CAE, ZGEF.^ Z.CEA (как вертикальные).
Эти треугольники равны по второму
признаку.
ЗАДАНИЯ
1. Доказать равенство треугольников по второму признаку:
Карточка № 16а. Третий признак равенства треугольников
ПРАВИЛО
Чтобы доказать, что данные треугольники равны по третьему признаку, надо:
1) найти у первого треугольника сторону, равную какой-нибудь стороне второго --*
треугольника;
равны
2) среди двух оставшихся сторон первого треугольника наити сторону, равную
одной из двух оставшихся сторон второго треугольника; .s'"
3) проверить, что оставшиеся третьи стороны первого и второго треугольни-
ков равны. —
Задача 1.
Доказать, что Д АВС = Д МРК.
Доказательство:
1) В треугольниках АВС и МРК
стороны АВ и РК равны: АВ = РК.
ОБРАЗЦЫ
2) Среди оставшихся сторон этих треугольников сторона АС равна стороне МК: АС = МК.
3) Третья сторона треугольника АВС равна третьей стороне треугольника МРК: ВС = МР.
Вывод: Д АВС = Д МРК по третьему признаку равенства.
Карточка № 166. Третий признак равенства треугольников
Задача 2. Найти на рисунке треугольники, равные по третьему признаку.
Решение:
На рисунке отмечены равные отрезки: АС = CD = FG, АЕ = FE, СЕ = EG.
АС, АЕ и СЕ - стороны треугольника АЕС;
FG, FE и GE - стороны треугольника FEG;
значит,
Д АЕС = Д FEG по третьему признаку.
ЗАДАНИЯ
1. Доказать равенство треугольников по третьему признаку:
Карточка № 17а. Признаки равенства прямоугольных треугольников
из первого признака
равенства треугольни-
ков
ПРАВИЛА
из второго признака
равенства треуголь-
ников
из теоремы о сумме углов тре-
угольников и второго признака
равенства треугольников
из теоремы о сумме углов
треугольников и второго при-
знака равенства треугольников
ОБРАЗЦЫ
Задача 1. Определить, по каким признакам равны прямоугольные треугольники на рисунках.
Решение:
а) В прямоугольных треугольниках ABD и CBD равны катеты AD и DC. В -
Катет DB у этих треугольников общий. Значит, Д ABD = Д CBD ' ------
по двум катетам.
б) В прямоугольных треугольниках АВС и EDC равны гипотенузы: АС = ЕС.
Острые углы АСВ и ECD равны как вертикальные.
Значит, Д АВС =* Д EDC по гипотенузе и острому углу.
в) В прямоугольных треугольниках АВС и EDC равны катеты: АВ — ED.
Острые углы АСВ ъ ECD 'равны как вертикальные.
Значит, Д АСВ = Д EDC по катету и противолежащему острому углу.
№ 176. Признаки равенства прямоугольных треугольников
г) В прямоугольных треугольниках АВС и EDC равны катеты: ВС = DC.
Острые углы В и D равны.
Значит, Д АВС = Д EDC по катету и прилежащему острому углу.
д) В прямоугольных треугольниках ABD и CBD равны гипотенузы:
АВ = СВ.
Катет BD у этих треугольников общий.
Значит, Д ABD = Д CBD по гипотенузе и катету.
ЗАДАНИЯ
Найти на рисунке прямоугольные треугольники, равные а) по двум катетам; б) по гипотенузе
и острому углу; в) по катету и прилежащему острому углу; г) по катету и противолежащему
острому углу; д) по катету и гипотенузе.
МАТЕМАТИКА
ISBN 5-89237-035-6