Теория сетей Петри и моделирование систем - Питерсон Дж.

Author: Питерсон Дж.

Tags: математика кибернетика моделирование вычислительная техника

Year: 1984

Similar

Сети Петри

Математическое моделирование технических систем

Имитационное моделирование систем - искусство и наука

Робототехника и гибкие автоматизированные производства. Книга 5. Моделирование робототехнических систем и гибких автоматизированных производств

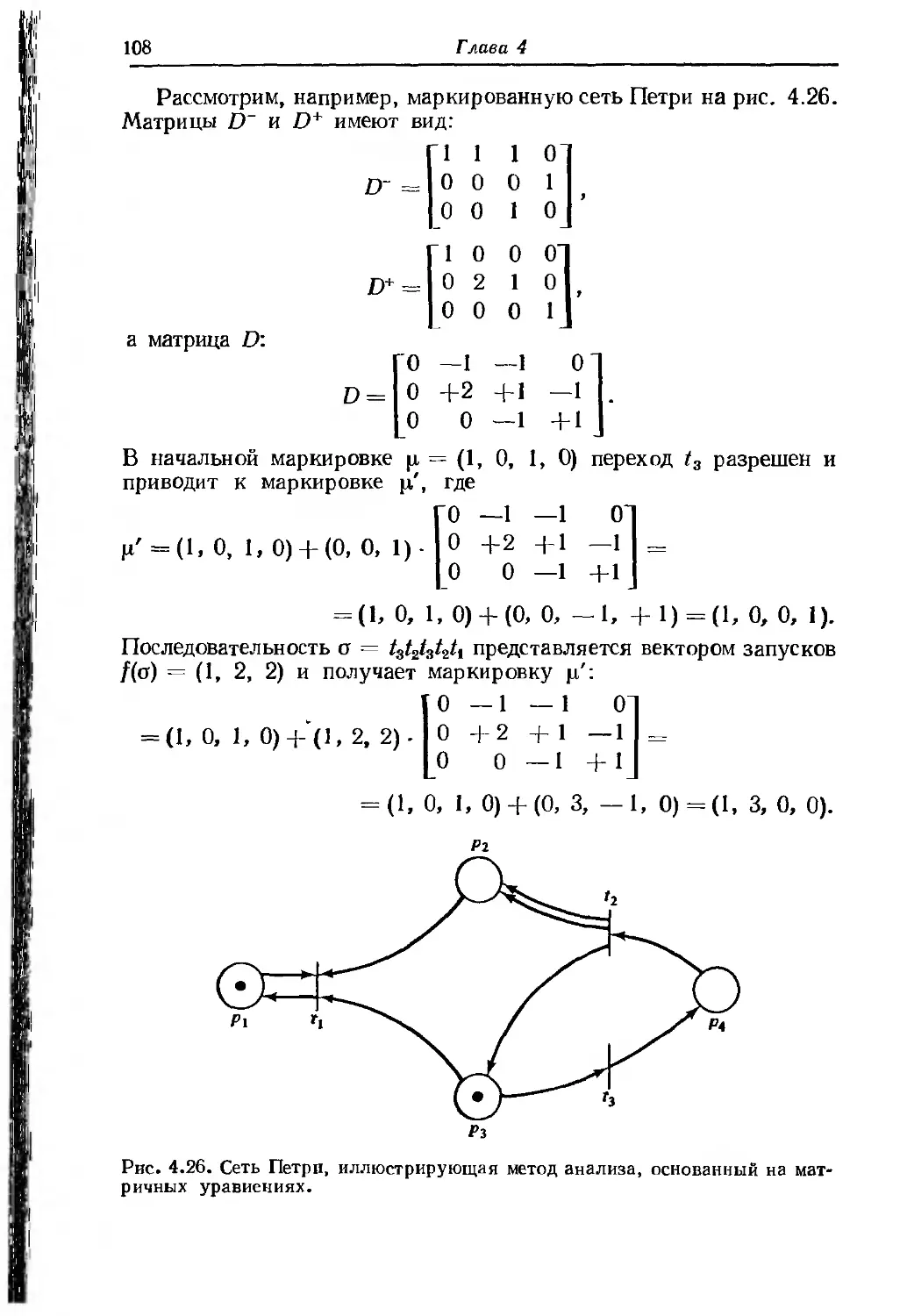
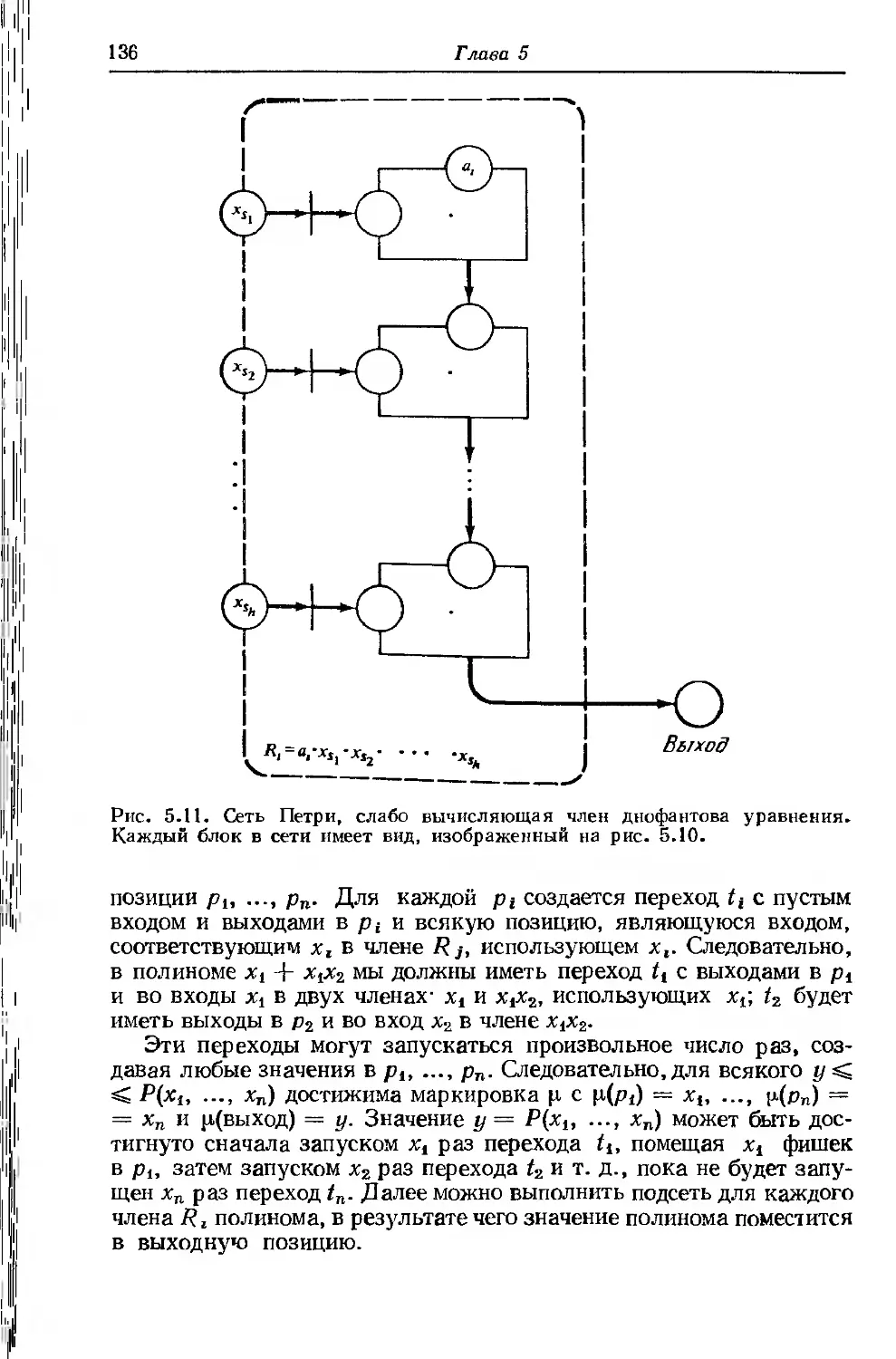
Text

НИ ДЖ. ПИТЕРСОН
ТЕОРИЯ
СЕТЕЙ ПЕТРИ
И МОДЕЛИРОВАНИЕ
СИСТЕМ
ДЖ. ПИТЕРСОН
ТЕОРИЯ
СЕТЕЙ ПЕТРИ
И МОДЕЛИРОВАНИЕ
СИСТЕМ
JAMES L. PETERSON
The University
of Texas at Austin
PETRI
NET THEORY
AND THE MODELING
OF SYSTEMS
PRENTICE-HALL, INC., ENGLEWOOD CLIFFS, N. J.
1981
АЖ. ПИТЕРСОН
теория
сетей петри
И МОДЕЛИРОВАНИЕ
систем
Перевод с английского
М. В. Горбатовой, канд. техн, наук В. Л. Торхова,
канд. техн, наук В. Н. Четверикова
под редакцией
д-ра техн, наук В. А. Горбатова
МОСКВА «МИРН984
ББК 32.816
ТЗЗ
УДК 519.95
Питерсон Дж.
ТЗЗ Теория сетей Петри и моделирование систем: Пер. с
англ. — М.: Мир, 1984. — 264 с., ил.
В книге американского ученого изложены основные понятия и результаты
теории сетей Петри, касающиеся различных аспектов вычислительной техники
и особенно систем распределенной обработки информации.
Для научных работников, аспирантов и студентов старших курсов втузов.
П
2405000000-227
041(01)-84
163-84, ч. 1
ББК 32.816
6Ф0.1
$2-
—а дЛццр« к '" |
tex гчесний иисти’С' 1
’ tioepo-^ий Филиал
Редакция литературы по новой технике
© Prentice-Hall, Inc., Englewood Cliffs, 1981
© Перевод на русский язык, «Мир», 1984
•w?*W
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
В последние годы развитие вычислительной техники харак-
теризуется не столько увеличением числа элементов, участвую-
щих в обработке данных (будь то число функциональных бло-
ков в процессоре или процессоров в вычислительной системе),
сколько усложнением структуры их взаимосвязи, управления
взаимодействием. Качественно новый характер взаимодействия
в современных вычислительных системах послужил причиной
появления новых задач, связанных с анализом, моделированием
и представлением причинно-следственных связей в сложных
системах параллельно действующих объектов. Мощным средст-
вом решения этих задач являются сети Петри — предмет данной
книги. Родившись при описании взаимодействующих автоматов,
моделирующих системы аппаратного обеспечения, они оказа-
лись очень удобными для анализа и моделирования програм-
много обеспечения, что предопределило большой интерес к ним
и быстрый прогресс в их исследовании.
Предлагаемая книга является первой переводной моногра-
фией, посвященной сетям Петри. В ней последовательно изла-
гаются основные понятия теории сетей Петри, задачи, связан-
ные с сетями Петри, методы их анализа. На протяжении всей
книги внимание читателя акцентируется на прикладных аспек-
тах теории сетей Петри. Автор определяет место сетей Петри в
ряду формальных систем, направленных на моделирование па-
раллельных процессов.
Книга написана просто и доходчиво, все излагаемые понятия
подробно обсуждаются. В ней содержится большое число при-
меров, иллюстраций, упражнений и тем для серьезных исследо-
ваний. Изложение ведется на должном уровне математической
строгости.
Автор монографии известен как специалист в области сетей
Петри, его интересы в исследовании этой области весьма мно-
госторонни. Ему принадлежат работы как обзорного плана, так
и посвященные вопросам анализа языков сетей Петри, построе-
ния иерархии моделей описания параллельных процессов и др.
Работая над переводом книги, коллектив переводчиков
осознавал ответственность, которую налагает на них издание
первой переводной монографии. Перевод не доставил особых
трудностей. Однако над системой соответствующих русских тер-
6 Предисловие к русскому изданию
минов, отвечающей требованиям концептуального единства всей
терминологии, пришлось немало потрудиться.
Предлагаемая книга будет полезна студентам и аспирантам,
специализирующимся в вычислительной технике, а также спе-
циалистам, занимающимся вопросами распределенной обработ-
ки данных.
Перевод монографии выполнен М. В. Горбатовой (гл. 1—3),
канд. техн, наук В. Л. Торховым (предисловие, гл. 4—6), канд.
техн, наук В. Й. Четвериковым (гл. 7, 8, аннотированная библио-
графия, предметный указатель).
В. А. Горбатов
ПРЕДИСЛОВИЕ
Теория сетей Петри значительно развилась со времени ее рож-
дения в диссертации д-ра Петри в 1962 г. Однако многие из публи-
каций по сетям Петри труднодоступны, поскольку оформлены, как
правило, в виде отчетов и диссертаций и рассеяны по многим ис-
точникам. И тем не менее, несмотря на трудность изучения сетей
Петри, использование их постоянно возрастает. Мы приходим к вы-
воду, что, по-видимому, каждый специалист в области вычисли-
тельной техники должен знать азы теории сетей Петри.
Эта книга собрала основные результаты теории сетей Петри,
представив их в последовательном и согласованном виде. Пред-
ставление и организация материала удобны и для индивидуального
изучения специалистом-практиком, и для организованного изуче-
ния аспирантами, специализирующимися в области вычислительной
техники. Теорию сетей Петри можно применить в безмерно боль-
шом множестве областей (как показано в гл. 3), знание основ тео-
рии сетей Петри становится обязательным для специалистов по вы-
числительной технике, системному анализу и др.
Для студентов и специалистов, желающих немедленно найти
практическое применение сетям Петри, трудно переоценить гл. 1—4
и 7. Они вполне приемлемы для самостоятельного изучения и обе-
спечивают достаточный фундамент для того, чтобы сделать возмож-
ным немедленное использование сетей Петри в самых различных
областях.
Книгу можно использовать также как учебное пособие для про-
ведения семинаров по сетям Петри для аспирантов, и если опре-
деления и приложения из первых четырех глав изучаются легко,
то оставшиеся главы подводят обучающихся к переднему краю ис-
следований. Каждая глава содержит упражнения, которые дают
возможность как практической работы с понятиями, так и закреп-
ления основ теории. Наконец, «Темы для дальнейшего изучения»
указывают новые направления исследований. Многие из этих тем
можно легко развить в диссертационную работу.
Основные понятия теории сетей Петри доступны человеку
с минимальной подготовкой. Однако сети Петри даже в большей
степени, чем множество других исследовательских тем, касаются
различных аспектов вычислительной техники и математики. Пол-
ная оценка и понимание современной теории сетей Петри требуют
хорошей подготовки в области формальных языков и автоматов,
8
Предисловие
операционных систем, архитектуры ЭВМ и линейной алгебры.
Студент последнего года обучения, специализирующийся в вычи-
слительной технике, или специалист, работающий год в этой об-
ласти, должны иметь квалификацию, необходимую для проведения
исследований с помощью сетей Петри.
Очевидно, что результатов по сетям Петри получено больше,
чем мы смогли здесь представить. Мы приветствуем дальнейшее
изучение и предлагаем библиографию, для полноты которой была
рассмотрена почти вся существующая литература.
Сообщим, что д-р Петри продолжает свои исследования. То, что
мы называем здесь теорией сетей Петри, в его терминологии назы-
вается специальной теорией сетей, являющейся только частью его
общей теории сетей [243—245, 247].
Благодарности
Своим появлением эта книга обязана многим людям. Тилак
Агервала, Мишель Хэк, Тай-Ян Хоу, К. Маттиас Лохт, Дино
Мандриоли, Джерри Ное, Гэри Натт и Вильям Риддл помогли в
изложении специальных вопросов. Дж. К- Браун, К- Мани Чэнди,
Джим Дэниел, Нэнси Итмен и Р. Т. Йе, а также кафедры вы-
числительной техники и математики Университета в Остине,
шт. Техас, и Лаборатория вычислительной техники Массачусетского
технологического института оказали техническую поддержку, поз-
волившую мне найти время и средства для того, чтобы подгото-
вить монографию.
В период написания, редактирования и корректуры источником
любви и поддержки была моя жена Жанни.
Редактирование и набор с использованием ЭВМ породили при
создании этой книги новые и уникальные трудности. Я признате-
лен издательству за поддержку, терпение и разрешение всех вопро-
сов, и особенно моему редактору, Карену Клемментсу, за муд-
рость и профессионализм.
Дж. Л. Питерсон
Остин, Техас
ГЛАВА 1
ВВЕДЕНИЕ
Сети Петри •— инструмент исследования систем. Теория сетей Петри
делает возможным моделирование системы математическим представлением
ее в виде сети Петри. Предполагается, что анализ сетей Петри поможет полу-
чить важную информацию о структуре н динамическом поведении моделируе-
мой системы. Эта информация будет полезна для оценки моделируемой систе-
мы и выработки предложений по ее усовершенствованию и изменению. Таким
образом, понятно, почему развитие сетей Петри основывалось на применении
их к моделированию и проектированию систем.
1.1. Моделирование
Применяются сети Петри исключительно в моделированииг
Во многих областях исследований явление изучается не непосредст-
венно, а косвенно, через модель. Модель •— это предетавление,
как правило, в математических терминах того, что считается наи-
более характерным в изучаемом объекте или системе. Ожидается,
что, манипулируя представлением, можно получить новые знания
о моделируемом явлении, избегая опасности, дороговизну или не-
удобства манипулирования самим реальным явлением. Моделиро-
вание применяется в астрономии (где модели рождения, смерти
и взаимодействия звезд позволяют разрабатывать теории, имею-
щие дело с большими промежутками времени и огромными количест-
вами материи и энергии), ядерной физике (где изучаемые радио-
активные атомы и элементарные частицы существуют в течение
очень коротких периодов времени), социологии (где непосредст-
венное воздействие на изучаемые группы людей связано с этиче-
скими проблемами), в биологии (где модели биологических систем
требуют для развития меньшего пространства, времени и пита-
тельного вещества) и т. д.
Как правило, модели имеют математическую основу. Характе-
ристики многих физических явлений можно описать числами, а связь
этих характеристик — уравнениями или неравенствами. В част-
ности, в естественных науках и технике уравнениями описываются
такие характеристики, как масса, положение в пространстве, мо-
мент, ускорение и силы. Однако для успешного использования
подхода моделирования необходимо знание как моделируемых
явлений, так и свойств метода моделирования. Поэтому математика
как наука развивалась частично благодаря использованию ее в
моделировании явлений, изучаемых другими науками. Так, напри-
10
Глава 1
мер, дифференциальное исчисление появилось в ответ на необхо-
димость в средствах моделирования в физике таких непрерывно
изменяющихся характеристик, как положение в пространстве, ско-
рость и ускорение.
С разработкой быстродействующих ЭВМ использование и полез-
ность моделирования значительно возросли. Представление систе-
мы математической моделью, преобразование этой модели в команды
для ЭВМ и выполнение программы на ЭВМ сделали возможным
моделирование больших и более сложных систем, чем ранее. Это
привело в результате к значительным исследованиям методов моде-
лирования на ЭВМ и самих ЭВМ, поскольку они участвуют в моде-
лировании в двух ролях: как вычислительные средства и как объект
моделирования.
1.2. Природа систем
Вычислительные системы очень сложны, часто велики, включа-
ют множество взаимодействующих компонент. Каждая компонента
также может быть очень сложной, поскольку взаимодействует с
другими компонентами системы. Это справедливо и для многих дру-
гих систем. Экономические системы, юридические системы, системы
управления дорожным движением, химические системы состоят
из многих отдельных компонент, взаимодействующих друг с другом
сложным образом.
Итак, несмотря на разнообразие моделируемых систем, выделя-
ется несколько общих черт, которые должны быть отражены в осо-
бенностях используемой модели этих систем. Основная идея заклю-
чается в том, что системы состоят из отдельных взаимодействующих
компонент. Каждая компонента сама может быть системой, но ее
поведение можно описать независимо от других компонент систе-
мы, за исключением точно определенных взаимодействий с другими
компонентами. Каждая компонента имеет свое состояние. Состоя-
ние компоненты — это абстракция соответствующей информации,
необходимой для описания ее (будущих) действий. Часто состоя-
ние компоненты зависит от предыстории этой компоненты, поэтому
оно может со временем изменяться. Понятие «состояние» очень важ-
но при моделировании компоненты. Например, в модели системы
очередей банка могут присутствовать несколько кассиров и не-
сколько клиентов. Кассиры могут быть свободны (ожидая клиента)
или заняты (обслуживая клиента). Аналогично клиенты могут быть
свободны (ожидая, когда кассир освободится для обслуживания
их) или заняты (при обслуживании их кассиром). В клинической
модели состояние пациента может быть критическим, серьезным,
удовлетворительным, хорошим или превосходным.
Действиям компонент системы присущи совмещенность или
параллелизм. Действия одной компоненты системы могут произво-
диться одновременно с действиями других компонент. В вычисли-
Введение
11
тельной системе, например, под управлением ЭВМ могут парал-
лельно действовать такие периферийные устройства, как устрой-
ства чтения с карт, построчно печатающие устройства и др. В эко-
номической системе в одно и то же время производители поставляют
одну продукцию, тогда, как продавцы сбывают другую, а покупа-
тели используют третью.
Совмещенная природа действий в системе создает некоторые труд-
ности при моделировании. Поскольку компоненты системы взаимо-
действуют, необходимо установление синхронизации. Пересылка
информации или материалов от одной компоненты к другой требует,
чтобы действия включенных в обмен компонент были во время взаимо-
действия синхронизированы. Это может привести к тому, что одна
компонента будет ждать другую компоненту. Согласование во вре-
мени действий различных компонент может быть очень сложным,
а получающиеся в результате взаимодействия между компонента-
ми трудны в описании.
1.3. Зарождение теории сетей Петри
Сети Петри разрабатывались специально для моделирования
тех систем, которые содержат взаимодействующие параллельные
компоненты. Впервые сети Петри предложил Карл Адам Петри
1241]. В своей докторской диссертации «Kommunikation mit Auto-
maten» («Связь автоматов») Петри сформулировал основные поня-
тия теории связи асинхронных компонент вычислительной системы.
В частности, он подробно рассмотрел описание причинных связей
между событиями. Его диссертация посвящена главным образом
теоретической разработке основных понятий, с которых начали
развитие сети Петри.
Работа Петри привлекла внимание А. В. Хольта и сотрудников
из Проекта Information System Theory (Теория информационных
систем) фирмы Applied Data Research (ADR). Ими была развита
большая часть начал теории, предложены обозначения и представ-
ления сетей Петри, опубликованные в окончательном отчете по этому
проекту 1128] и в отдельном отчете, имеющем название «Events and
Conditions» («События и условия») [127]. В этой работе показано,
как сети Петри можно применить к анализу и моделированию сис-
тем, включающих параллельные компоненты.
Работа Петри привлекла также внимание группы, работающей
над Проектом МАС в Массачусетском технологическом институте
(МТИ). Руководимая профессором Дж. Б. Деннисом группа вы-
числительных структур стала источником значительных исследо-
ваний и публикаций по сетям Петри, были написаны несколько
диссертаций на степень доктора философии и множество отчетов
и меморандумов (см. библиографию). Группой вычислительных
структур были проведены две большие конференции по сетям Пет-
ри: Конференция Проекта МАС по параллельным системам и па-
Глава 1
12
паллельным вычислениям в 1970 г. в Вудс Холле [73] и Конферен-
ция по сетям Петри и связанным с ними методам в 1975 г. в МТИ.
Обе эти конференции внесли вклад в распространение результатов
и методов теории сетей Петри.
За последние несколько лет использование и изучение сетей
Петри значительно расширились. В 1977 г. в Париже и в 1979 г.
в Гамбурге на лекциях по общей теории сетей проводились заседа-
ния рабочей группы по сетям Петри. В ФРГ была образована груп-
па интереса1) по сетям Петри. Исследования и применения сетей
Петри расширяют сферу действия.
1.4. Применение теории сетей Петри
Возможно несколько путей практического применения сетей
Петри при проектировании и анализе систем. В одном из подходов
сети Петри рассматриваются как вспомогательный инструмент
анализа. Здесь для построения системы используются общеприня-
тые методы проектирования. Затем построенная система модели-
руется сетью Петри, и модель анализируется. Любые трудности,
встречающиеся при анализе, указывают на изъяны в проекте. Для
их исправления необходимо модифицировать проект. Модифици-
рованный проект затем снова моделируется и анализируется. Этот
цикл повторяется до тех пор, пока проводимый анализ не приведет
к успеху. Такой подход иллюстрируется на рис.1.1. Заметим, что
его можно использовать и для анализа уже существующих'действую-
щих в настоящее время систем.
В этом общепринятом подходе использования сетей Петри в про-
ектировании требуется постоянное преобразование проектируемой
системы в модель в виде сети Петри. Можно предложить другой,
более радикальный подход, в котором весь процесс проектирования
и определения характеристик проводится в терминах сетей Петри.
Методы анализа применяются только для создания проекта сети
Петри, свободного от ошибок. Здесь задача заключается в преоб-
разовании представления сети Петри в реальную рабочую систему.
Эти два подхода использования сетей Петри в процессе проекти-
рования предлагают исследователю сетей Петри задачи разного
типа. В первом случае необходима разработка методов моделиро-
вания систем сетями Петри, а во втором случае должны быть раз-
работаны методы реализации сетей Петри системами. В обоих слу-
чаях необходимы методы анализа сетей Петри для определения
свойств модели. Таким образом, первое, чего нам необходимо кос-
нуться при рассмотрении теории сетей Петри, — это изучение
свойств самих сетей Петри.
О Эта группа провела уже три заседания: в Страсбурге (Франция),
1980 г., в Бад-Хоннефе (ФРГ), 1981 г., в Вероне (Италия), 1982 г. — Прим,
ред.
Введение
13
Рис. 1.1. Использование сетей Петри для моделирования и анализа систем.
Сначала система моделируется сетью Петрн, затем модель анализируется.
Оценка системы, являющаяся результатом анализа, приведет, как ожидается,
К лучшей системе. Необходимы исследования, направленные на разработку
автоматических методов моделирования и анализа систем сетями Петри.
1.5. Прикладная и чистая теории
сетей Петри
Развитие теории сетей Петри проводилось по двум направле-
ниям. Прикладная теория сетей Петри связана главным образом
с применением сетей Петри к моделированию систем, их анализу
и получающимся в результате этого глубоким проникновением в
моделируемые системы. Успешная работа в этом направлении тре-
бует хорошего знания области применения, сетей Петри и методов
теории сетей Петри.
Чистая теория сетей Петри занимается разработкой основных
средств, методов и понятий, необходимых для применения сетей
Петри. Хотя мотивация исследований по сетям Петри связана с
приложениями, для применения сетей Петри необходим прочный
теоретический фундамент. Большая часть работ по сетям Петри к
настоящему времени относится к фундаментальной теории сетей
Петри, развивающей средства и методы, которые окажутся некогда
полезными для применения сетей Петри к конкретным реальным
задачам. В этой книге представлены обе области теории сетей Петри
(чистая и прикладная), но внимание будет сконцентрировано глав-
ным образом на основах теории. Раскрываемые приложения пред-
назначены в основном для демонстрации широты применения и силы
теории сетей Петри и обоснования разработки методов анализа.
Мы не будем пытаться раскрыть глубоко весь диапазон тем тео-
рии сетей Петри, а скорее постараемся обеспечить прочную основу
в терминах, понятиях, методах, результатах и истории сетей Петри
для того, чтобы специалисты и аспиранты, специализирующиеся в
вычислительной технике, могли разобраться во всевозрастающем
потоке литературы по сетям Петри и были способны применить эту
теорию к еще более широкому спектру приложений. Мы начинаем
с нескольких формальных определений и примеров в гл. 2 и пока-
14
Глава 1
зываем далее в книге их силу и полезность. Заканчиваем анноти-
рованной библиографией, охватывающей большинство публикаций
по сетям Петри.
1.6. Замечания к литературе
Теория сетей Петри родилась в диссертации Петри [241], но
большинство работ в США основано на окончательном отчете по
Проекту теории информационных систем [128], в котором переведе-
на на английский язык и значительно расширена диссертация Пет-
ри. Кроме того, среди первых публикаций важную роль играет
работа Хольта и Коммонера «События и условия» [127]. Петри пред-
ставил небольшую статью на конгресс ИФИП, которая опублико-
вана в трудах конгресса [242]. Она основана на идеях, изложенных
в диссертации.
Представленный в книге подход во многом основан на работе
группы вычислительных структур МТИ и работах Денниса [72],
Патила [231] и др., кончая работой Хэка [113]. На содержание кни-
ги также оказал влияние Келлер — своим отчетом по системам
замещения векторов [150] и своей точкой зрения на моделирование
[152].
1.7. Темы для дальнейшего изучения
1. Проследите истоки и направления важных идей теории сетей
Петри. Очевидно, что исходная точка принадлежит Петри, но как
и к кому направлялись идеи дальше, как они появились в Соеди-
ненных Штатах? Куда они направились оттуда? Для определения
предшествования используйте даты и ссылки из опубликованных
отчетов, статей, диссертаций и меморандумов. Возможно, вам за-
хочется проинтервьюировать некоторых «ключевых» людей: Петри,
Хольта, Денниса, Патила и др.
ГЛАВА 2
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
В этой главе мы дадим формальные определения основных понятий сетей
Петри. Основные понятия используются на протяжении всей книги и явля-
ются необходимыми для правильного понимания.
Наш формализм основывается на теории комплектов, являющейся обоб-
щением теории множеств. Если вы не знакомы близко с теорией комплектов,
предлагаем вам прочитать приложение.
Определения, данныг здесь, по стилю подобны определениям теории ав-
томатов [130], т. е. определен новый класс машин — автоматная сеть Пет-
ри. Как мы увнднм позднее (гл. 5—8), такая точка зрения может привести к
некоторым интересным результатам в теории формальных языков и теории
автоматов.
2.1. Структура сети Петри
Сеть Петри состоит из четырех элементов: множество позиций Р,
множество переходов Т, входная функция I и выходная функция О.
Входная и выходная функции связаны с переходами и позиция-
ми. Входная функция I отображает переход tj в множество пози-
ций называемых входными позициями перехода. Выходная
функция О отображает переход tj в множество позиций 0(t j), на-
зываемых выходными позициями перехода.
Структура сети Петри определяется ее позициями, переходами,
входной и выходной функциями.
Определение 2.1. Сеть Петри С является четверкой, С — (Р, Т, I,
О). Р= {рь р2, рп} — конечное множество позиций, п > 0.
71 — {^i, ^2, im) — конечное множество переходов, т > 0. Мно-
жество позиций и множество переходов не пересекаются, Р А Т =
= 0. / : Т Р°° является входной функцией — отображением
из переходов в комплекты позиций. О : Т->- Р°° есть выходная
функция — отображение из переходов в комплекты позиций.
Мощность множества Р есть число п, а мощность множества
Т есть число т. Произвольный элемент Р обозначается символом
Pt, i~ 1, ..., п, а произвольный элемент Т — символом tj, j =
= 1,..., tn.
Примеры сетей Петри даны на рис. 2.1—2.3.
Позиция Pi является входной позицией перехода tj в том случае,
если pt Q I (tj)-, Pi является выходной позицией, если ptQ О {tj).
Входы и выходы переходов представляют собой комплекты пози-
ций. Комплект является обобщением множества, в которое вклю-
16
Глава 2
чены многократно повторяющиеся элементы — тиражированные
элементы. В приложении содержится описание теории комплектов.
Использование,комплектов, а не множеств для входов и выходов
перехода позволяет позиции быть кратным входом либо кратным
выходом перехода. Кратность входной позиции pt для перехода
tj есть число появлений позиции во входном комплекте перехода,
#(рг, I (tj)). Аналогично кратность выходной позиции pt для пе-
рехода tj есть число появлений позиции в выходном комплекте
перехода, 4ф(рь О (/;)). Если входная и выходная функции явля-
ются множествами (а не комплектами), то кратность каждой пози-
ции есть либо 0, либо 1.
Входные и выходные функции используются для отображения
позиций в комплекты переходов, а также их можно использовать
для отображения переходов в комплекты позиций. Определим, что
переход t} является входом позиции рг, если pt есть выход tj.
Переход tj есть выход позиции pit если pt есть вход tj.
Определение 2.2. Определим расширенную входную функцию /
и выходную функцию
/: Р^Т°°,
О: Р-+Т°°
таким образом, что
# (tj> I (Pi)) — # (р^ о (tj)), # (tj, ом = # (Pi, I (tj)).
Для сети Петри на рис. 2.1 расширенными входной и выходной
функциями являются:
/(й) = { },
I (Pi) = {^1» t4},
I (рз) = {^1» ^4}»
(Р&) = {^з}»
(Рз) = {^1» I?}'
О(Л) = {^},
О (рз) = {^2}»
О (Рз) — {^2> ^з}’
0(р4) = Ю»
О (Рз) = {У-
С = (Р, Т, I, О),
Р = {Pl, Pi, Рз* Pi, Рз),
г — {ti, t2, tSt ^4}»
I (G) = {Pi}. О (/j) = {p2, p3, Pb} ,
I = {d2, p3, Ps}, 0 (t2) = {p6},
Ц(з)={Рз}, 0(t3) = {Pi},
I (<4) = {Pi}, О (14) = {p2, p3}.
Рис. 2.1. Структура сети Петри представлена в виде четверки, которая состо-
ит из множества позиций (Р), множества переходов (Т), входной функции
7: Т-> Р00 и выходной функции (О: Т-»- Р00).
Основные определения
17
С = (Р, Т, I, О),
Р = {Р1, Р2, Рз, Pt, Рь, Ре),
7,= {G» ^2> ^3, ^3» 74, ^а},
7(^1) = {Р1),
/(У = {Рз}.
1<!з) = {Ръ, Рз},
1 (it) = {р4> Рз, Рз, Рз},
1 «*) = №,
О (tj) = {р2, Р3},
O(t2) = {p3, Рз, Рз},
0(i3) = {Р2, Pt},
O(tJ = (p4),
Рис. 2.2. Структура сети Петри.
С = (Р, Т, I, О),
Р = {Pi, Рг> Рз, Pt, Рь, Ре, Pi, Р», Рз),
Т~ {/i, tz, ts, 1д, t5, /е),
1 (К) = (Pi). 0(*1) = {р2. Рз).
/(« = {Р«}, оа2) = {р1, р7),
ч {Р2, Рз}, о (i3) = {p6},
1 (/4) = {Рз}, 0(/4) = {Р4},
i 4 I (tb) = {Р6. Pi),
7 Ge) = (fit, Р»}', 0(ie) = {p5i Р8}-
Рис. 2.3. Структура сети Петри.
Упражнения.
1. Найдите расширенную входную и выходную функции сетей Петри
(рис. 2.2 и 2.3).
2. Покажите, что входная и выходная функции одновременно не являются не-
обходимыми и что сеть Петри может быть определена множествами позиций,
переходов и расширенной входной (или выходной) функцией. Для этого
покажите, как расширенная выходная функция может быть определена из
расширенной входной функции и наоборот.
2.2. Графы сетей Петри
В значительной степени теоретическая работа по сетям Петри
основана на формальном определении сетей Петри, изложенном
выше. Тем не менее для иллюстрации понятий теории сетей Петри
гораздо более удобно графическое представление сети Петри. Тео-
ретико-графовым представлением сети Петри является двудольный
ориентированный мультиграф.
Структура сети Петри представляет собой совокупность позиций
и переходов. В соответствии с этим граф сети Петри обладает двумя
типами узлов. Кружок Q является позицией, а планка | — пере-
ходом. —
владимирский |
политехнический институт |
г.овг-о^сний Филиал I
г. М Б Л И С> т п ц д [
18
Глава 2
Ориентированные дуги (стрелки) соединяют позиции и переходы,
при этом некоторые дуги направлены от позиций к переходам, а
другие — от переходов к позициям. Дуга, направленная от позиции
pi к переходу tj, определяет позицию, которая является входом
перехода. Кратные входы в переход указываются кратными ду-
гами из входных позиций в переход. Выходная позиция указывает-
ся дугой от перехода к позиции. Кратные выходы также представ-
лены кратными дугами.
Сеть Петри есть мультиграф, так как он допускает существо-
вание кратных дуг от одной вершины графа к другой. Следует
добавить, что так как дуги являются направленными, то э£о ори-
ентированный мультиграф. Мы знаем, что вершины граф/1 можно
разделить на два множества (позиции и переходы) таким образом,
что каждая дуга будет направлена от элемента одного множества
(позиций или переходов) к элементу другого множества (переходов
или позиций); следовательно, такой граф является двудольным ори-
ентированным мультиграфом. В дальнейшем для простоты будем
называть его просто графом сети Петри.
Определение 2.3. Гриф G сети Петри есть двудольный ориенти-
рованный мультиграф, G = (V, Л), где V = {и1г и2, .... us} —
множество вершин, а А = {ait а2, ..., аг) — комплект направ-
ленных дуг, at = (Vj, vh), где Vj, vk £ V. Множество V может
быть разбито на два непересекающихся подмножества Р и Т, таких,
что V = Р U 7, Р (]Т = 0, к для любой направленной дуги
а* € А, если cii = (Vj, vh), тогда либо Vj £ Р и vh £ Т, либо
Vj £ 7, a vh £ Р.
Графы сети Петри, изображенные на рис. 2.4 — 2.6, экви-
валентны структурам сети Петри на рис. 2.1 — 2.3.
Для демонстрации эквивалентности этих двух представлений
сети Петри — структуры сети Петри и графа сети Петри — пока-
жем, каким образом можно преобразовать один в другой. Пред-
положим, нам дана структура сети Петри С — (Р, Т, I, О) с Р =
= {Рь Р2, •••, Рп}нТ = {ф, t2,..., tm}. Тогда граф сети Петри мож-
но определить следующим образом.
Определение 2.4. Определим V — Р U Т. Определим А как ком-
плект направленных дуг, такой, что для всех p,QP и tjQT
#Црр tj), A) = #(pi> I(tj))t
#((0> А), # (Pi, O(ti)).
G — (V, Л) есть граф сети Петри, эквивалентный структуре сети
Петри С = (Р, Т, I, О).
Обратное преобразование (от графа сети Петри к структуре)
осуществляется подобным образом, и поэтому оставим более деталь-
ное описание такого преобразования читателю. Однако при перехо-
Основные определения
19
Рис» 2.4. Граф сети Петри, эквивалентный структуре, показанной на
рис. 2.1.
Рис. 2 2* сети Петри, эквивалентный структуре, изображенной на
20
Глава 2
Рис. 2.6. Граф сети Петри, эквивалентный структуре, показанной на рис. 2.3.
де от графа сети Петри к структуре сети Петри возникает одна ин-
тересная задача: если множество вершин можно разделить на два
подмножества S и Р, то какое из этих подмножеств должно быть
позициями, а какое — переходами? Оба возможных варианта поз-
воляют определить сеть Петри, хотя в получающихся в результате
структурах позиции и переходы меняются местами.
Двойственной к сети Петри С = (Р, Т, I, О) является сеть
Петри С = (Т, Р, I, О), которая получается в результате переста-
новки позиций и переходов. Структура графа сохраняется, просто
меняются местами кружки и планки (см. упражнение 6). На рис. 2.7
Рис. 2.7. Сеть, двойственная к сети Петри, показанной на рис. 2.4.
Основные определения
21
показана сеть, двойственная к сети Петри на рис. 2.4. Двойствен-
ность — обычно полезный прием в теории графов и кажется инте-
ресным понятием для сетей Петри. Однако никакой пользы извлечь
из понятия двойственной сети Петри в исследовании этих сетей не
представляется возможным. Это объясняется в основном труд-
ностью определения сети, двойственной к маркированной сети Пет-
ри. Маркированные сети Петри мы обсудим позднее.
Упражнения
1. Постройте графы сетей Петри, двойственные к сетям Петри, показанным
на рис. 2.5 и 2.6.
2. Постройте граф сети Петри для следующей структуры сети Петри:
Р = {pi, Р2. Рз, Pt}, Т — {fi, h, 1з, М,
ад = { },
ад = (Ра.
ДУ = {Ра> Ря}.
ад = { },
ад = {рз}.
O(G)-{P,}.
ад) = {р2}.
0(t3) ~ {Pi* Рз} >
<ад = {р3}.
ад = {р4}.
3. Изобразите граф сети Петри следующей структуры:
Р = {pi, р2}, Т = {fi, f2, f3},
ад = {р1}.
/(<2) = {pi}.
ад = {р2}.
O(ti) = {Pi, Р2},
O(fa) = {pa},
ад = { }.
4. Покажите, что двойственная к двойственной сети Петри С есть сама сеть
С.
5. Определите класс сетей Петри, которые совпадают с двойственными к се-
бе. Можете ли вы дать простую характеризацию этого класса сетей Петри?
6. Если сеть, двойственная к сети Петри С = (Р, Т, I, О), определена как
С — (Т, Р, I, О), входные и выходные функции должны быть расширены
для отображения и Р, и Т. Почему? Если С — (Р, Т,1, О) имеет нерасширен-
ные входные и выходные функции, дайте определение С = (Т, Р, Г, О') с
нерасширенными входными и выходными функциями.
7. Найдите структуру сети Петри, соответствующую графу сети Петри на
рис. 2.8. Определите структуру сети Петри для графа на рис. 2.9.
8. Графы сети Петри являются мультиграфами, так как позиция может быть
кратным входом или выходом перехода. В графе это показывается несколь-
кими дугами между позицией и переходом. В то время как такой способ удов-
летворителен для дуг с малой кратностью (не более трех), он неудобен для дуг
очень большой кратности. Таким образом, в качестве альтернативного пред-
ставления структур с большой кратностью используется пучок дуг. Пучок —
это специальная дуга, которая рисуется жирной линией и помечается крат-
ностью.
₽ис. 2.10 иллюстрирует переход с входной кратностью 7 и выходной кратно-
стью 11. Нарисуйте граф сети Петри для следующей структуры:
{Pi, Pi, Рз, pt}, Т -= {fi, fa, ts, it},
ад = {}.
ДУ = {Ра}.
ДУ = {Pi, Pi, Pi, Pi, Pi, Pi},
ад = {р3, р4, р4, pj,
OCi) = {Pi. Pi, Pi, Pi, Pi},
ад = {pi. Pi. Pi. Pi» Pi. Pi. рз} .
0(f3) — {pa, Pg, Pg, Pg, Pi, P4},
ад = { }.
22
Глава 2
Рис. 2.10. Пучок дуг. Для графов с большой кратностью используется пучок
дуг, помеченный числом кратности, а не изображение всех кратных дуг.
9. Инверсная сеть Петри — С для сети Петри С — (Р, Т'I, О) определяется
перестановкой входной и выходной функций — С = (Р, Т, О, /). Как это
повлияет на граф сети Петри? В чем отличие от двойственной сети Петри?
Окажет ли влияние расширение входной и выходной функций? Изобразите
инверсную сеть Петри для сети Петри, приведенной на рис. 2.7.
2.3. Маркировка сетей Петри
Маркировка у, есть присвоение фишек позициям сети Петри.
Фишка — это примитивное понятие сетей Петри (подобно позициям
и переходам). Фишки присваиваются (можно считать, что они при-
надлежат) позициям. Количество и положение фишек при выпол-
нении сети Петри могут изменяться. Фишки используются для
определения выполнения сети Петри.
Определение 2.5. Маркировка у сети Петри С = (Р, Т, I, О) есть
функция, отображающая множество позиций Р в множество не-
отрицательных целых чисел N.
р: P-+N.
Маркировка р может быть также определена как n-вектор р =
= (pi, Иг, •••. Нп)> где п = |Р| и каждое р, € N, i — 1, ...» п. Век-
Основные определения
23
Рис. 2.11. Маркированная сеть Петри. Структура сети Петри совпадает со
структурами на рис. 2.1 и 2.4. Маркировка — (1, 2, 0, 0, 1).
Рис. 2.12. Маркированная сеть Петри. Структура аналогична структуре,
изображенной на рис. 2.11, но маркировка отличается.
тор р, определяет для каждой позиции сети Петри количество
фишек в этой позиции. Количество фишек в позиции рг есть рг,
i = 1, ..., п. Связь между определениями маркировки как функции
и как вектора очевидным образом устанавливается соотношением
Р(рг) — Цг- Обозначение ее в виде функции является несколько
более общим и поэтому употребляется гораздо чаще.
Маркированная сеть Петри М = (С, р) есть совокупность
структуры сети Петри С = (Р, Т, I, О) и маркировки р и может
быть записана в виде М — (Р, Т, I, О, р).
На графе сети Петри фишки изображаются маленькой точкой
в кружке, который представляет позицию сети Петри. На рис. 2.11
и 2.12 приведены примеры графического представления маркиро-
ванной сети Петри.
Так как количество фишек, которое может быть определено для
каждой позиции, неограниченно, то в целом для сети Петри сущест-
24
Глава 2
вует бесконечно много маркировок. Множество всех маркировок
сети Петри, обладающей п позициями, есть множество всех «-векто-
ров, Nn. Это множество, хотя и бесконечно, является счетным.
Упражнения
1. Для маркированной сети Петри (рис. 2.12) представьте маркировку как
функцию и как вектор.
2. Для структуры сети Петри (рис. 2.2) изобразите граф сети Петри и укажи-
те на графе маркировку р. = (1, 0, 1, 1, 0, 0).
3. Количество фишек в сети Петри редко превышает 5 или 6. В этом случае их
рисуют. Однако, когда маркировка имеет 10, 20 или сотни фишек, припи-
санных позиции, в кружках удобнее не рисовать фишки, а указывать их об-
щее количество, как на рис- 2.13. Используя этот способ, изобразите марки-
ровку р = (137, 22, 2, 0, 14) для сети Петри на рис. 2.12.
2.4. Правила выполнения сетей Петри
Выполнением сети Петри управляют количество и распределение
фишек в сети. Фишки находятся в кружках и управляют выпол-
нением переходов сети. Сеть Петри выполняется посредством запус-
ков переходов. Переход запускается удалением фишек из его вход-
ных позиций и образованием новых фишек, помещаемых в его вы-
ходные позиции.
Переход может запускаться только в том случае, когда он раз-
решен. Переход называется разрешенным, если каждая из его вход-
ных позиций имеет число фишек по крайней мере равное числу
дуг из позиции в переход. Кратные фишки необходимы для кратных
входных дуг. Фишки во входной позиции, которые разрешают пере-
ход, называются его разрешающими фишками. Например, если
позиции pt и р2 служат входами для перехода ?4, тогда f4 разрешен,
если pt и pz имеют хотя бы по одной фишке. Для перехода h с вход-
ным комплектом {р6,Рв, Ре} позиция рв должна обладать по крайней
мере тремя фишками, для того чтобы /7 был разрешен.
Основные определения
25
Определение 2.6. Переход tjQT в маркированной сети Петри
С == (Р, Т, /, О) с маркировкой р разрешен, если для всех Pt^P
p(Pi) > # (Pi> / (h))-
Переход запускается удалением всех разрешающих фишек из
его входных позиций и последующим помещением в каждую из его
выходных позиций по одной фишке для каждой дуги. Кратные фиш-
ки создаются для кратных выходных дуг. Переход t3 с /(/3) = {р2}
и 0(t3) = {pit Р1з) разрешен всякий раз, когда в р2 будет хотя бы
одна фишка. Переход t3 запускается удалением одной фишки из
позиции р2 и помещением одной фишки в позицию р7 и в р13 (его вы-
ходы). Дополнительные фишки в позиции р2 не влияют на запуск
/3 (хотя они могут разрешать дополнительные запуски t3). Пере-
ход в котором I(tJ = {р21, р23) и 0(12) = {р23, р25, р25}, запуска-
ется удалением одной фишки из р21 и одной фишки из р23, при этом
одна фишка помещается в р23 и две в •— р25 (так как р25 имеет крат-
ность, равную двум).
Запуск перехода в целом заменяет маркировку р сети Петри на
новую маркировку у'. Заметим также, что так как можно запус-
тить только разрешенный переход, то при запуске перехода ко-
личество фишек в каждой позиции всегда остается неотрицатель-
ным. Запуск перехода никогда не удалит фишку, отсутствующую
во входной позиции. Если какая-либо входная позиция перехода
не обладает достаточным количеством фишек, то переход не разре-
шен и не может быть запущен.
Определение 2.7. Переход t j в маркированной сети Петри с марки-
ровкой р может быть запущен всякий раз, когда он разрешен. В ре-
зультате запуска разрешенного перехода tj образуется новая мар-
кировка р', определяемая следующим соотношением: р/(рг) =
= р(р<) - #(рь /(/,-)) + #(рг,
В качестве примера рассмотрим маркированную сеть Петри,
изображенную на рис. 2.15. При такой маркировке разрешены
только три перехода: ti, t3n t4. Переход t2 не разрешен, так как ни
позиция р2, ни позиция р3, являющиеся входами перехода t2, не
содержат ни одной фишки. Так как переходы tt, t3 и /4 разрешены,
любой из них может быть запущен. Если запущен переход t4, то
происходит удаление фишки из каждого входа и помещение фишки
в каждый выход. При этом одна фишка удаляется из р3, одна
фишка помещается в р3, а количество фишек в р4 увеличивается с
двух до трех. Новая маркировка, полученная в результате запуска
перехода t4, показана на рис. 2.16.
В маркированной сети Петри, изображенной на рис. 2.16, раз-
решены только переходы t\ и t3. При запуске перехода осуществ-
ляется удаление фишки из р4 и помещение фишек в р2, р3 и р4
(в Р4 — две фишки, так как эта позиция является кратным выходом
перехода Ц). Эта операция образует маркировку, приведенную на
26
Глава 2
Рис. 2.14. Иллюстрация того, как меняется маркировка позиции, когда запу-
щен переход tj. Каждая позиция может или не может быть входом либо вы-
ходом перехода. Здесь показан случай для кратности 0 или 1.
Рис. 2.15. Маркированная сеть Петри для иллюстрации правил запуска.
Переходы ti, ta и fa разрешены.
Основные определения
27
Рис. 2.16. Маркировка, полученная в результате запуска перехода в сети
на рис. 2.15.
Рис. 2.17. Маркировка, полученная при запуске перехода fa в сети на
рис. 2.16.
Рис. 2.18. Маркировка, полученная при запуске перехода fe в сети на
Рис. 2.17.
28
Глава 2
рис. 2.17. В такой маркированной сети Петри переходы t2 и ts раз-
решены. Запуск перехода t3 образует новую маркировку (рис. 2.18),
где две фишки удалены из р4, а одна добавлена в р5.
Запуски могут осуществляться до тех пор, пока существует
хотя бы один разрешенный переход. Когда не останется ни одного
разрешенного перехода, выполнение прекращается.
Упражнения
1. Какие переходы разрешены в маркированной сети Петри на рис. 2.11,
2.12?
2. Какая маркировка получится при запуске перехода ti (рис. 2.11)? Какая
маркировка получится при запуске перехода Ц (рис. 2.12)? Какая маркиров-
ка получится в результате выполнения следующих операций: сначала — за-
пуск Ц, затем — запуск <2 (рис. 2.12)?
3. Какие переходы разрешены в сети Петри на рис. 2.13?
Какие маркировки образуются при запуске каждого из этих переходов?
4. Можно ли запустить переходы в сети Петри на рис. 2.19? Какие?
2.5. Пространство состояний сети Петри
Состояние сети Петри определяется ее маркировкой. Запуск
перехода изменяет состояние сети Петри посредством изменения
маркировки сети. Пространство состояний сети Петри, обладаю-
щей п позициями, есть множество всех маркировок, т, е. Nn. Из-
менение в состоянии, вызванное запуском перехода, определяется
функцией изменения б, которую мы назовем функцией следующего
состояния. Когда эта функция применяется к маркировке р (состоя-
нию) и переходу tjt она образует новую маркировку (состояние),
которая получается при запуске перехода i} в маркировке р. Так
как tj может быть запущен только в том случае, когда он разрешен,
то функция 6(р, tj) не определена, если tj не разрешен в марки-
Основные определения
29
повке р. Если же tj разрешен, то 6(р, tj) = р', где р' есть маркиров-
ка полученная в результате удаления фишек из входов tj и добав-
ления фишек в выходы t j.
Определение 2.8. Функция следующего состояния 6 : Nn X Т ->
для сети Петри С = (Р, Т, /, О) с маркировкой р и перехо-
дом tj G Т определена тогда и только тогда, когда р(рг)
/(tj)) для всех pt £ Р. Если 6(р, tj) определена, то 6(р, t}) = р',
где р' (Pi) = — #(Pf. I(tj)) + #(Pi, 0(h)) Для всех £ Р.
Пусть дана сеть Петри С = (Р, Т, I, О) с начальной маркиров-
кой р°. Эта сеть может быть выполнена последовательными запус-
ками переходов. Запуск разрешенного перехода tj в начальной
маркировке образует новую маркировку р1 = 6(р°, tj). В этой
новой маркировке можно запустить любой другой разрешенный
переход, например tb, образующий новую маркировку р2 = 6(р\
th). Этот процесс будет продолжаться до тех пор, пока в маркиров-
ке будет существовать хотя бы один разрешенный переход. Если
же получена маркировка, в которой ни один переход не разрешен,
то никакой переход не может быть запущен, функция следующего
состояния не определена для всех переходов, и выполнение сети
должно быть закончено.
При выполнении сети Петри получаются две последовательности:
последовательность маркировок (р°, р1, р2, ...) и последовательность
переходов, которые были запущены (ti6, t}l, tj2, ...). Эти две после-
довательности связаны следующим соотношением: 6(pft, tjk) —
— pft+1 для k = 0, 1, 2, ... . Имея последовательность переходов
и р°, легко получить последовательность маркировок сети Петри,
а имея последовательность маркировок, легко получить последо-
вательность переходов, за исключением нескольких вырожденных
случаев’). Таким образом, обе эти последовательности представ-
ляют описание выполнения сети Петри.
Пусть некоторый переход в маркировке р разрешен и, следова-
тельно, может быть запущен. Результат запуска перехода в марки-
ровке р есть новая маркировка р'. Говорят, что р' является непо-
средственно достижимой из маркировки р, иными словами, состоя-
ние р' непосредственно получается из состояния р.
Определение 2.9. Для сети Петри С = (Р, Т, I, О) с маркировкой
Н маркировка р' называется непосредственно достижимой из р,
если существует переход tj € Т, такой, что б(р, t j) = р'.
Можно распространить это понятие на определение множества
Достижимых маркировок данной маркированной сети Петри. Если
Н непосредственно достижима из р, а р" — из р', говорят, что р"
достижима из р. Определим множество достижимости Р(С, р)
) В оригинале вырожденные случаи ошибочно отнесены к первому ут-
верждению. — Прим. ред.
30
Глава 2
сети Петри С с маркировкой р как множество всех маркировок, до-
стижимых из р. Маркировка р' принадлежит 7?(С, р), если суще-
ствует какая-либо последовательность запусков переходов, изме-
няющих р на р'. Отношение «достижимости»1) является рефлексив-
ным, транзитивным замыканием отношения «непосредственной до-
стижимости».
Определение 2.10. Множество достижимости R(C, р) для сети Пет-
ри С = (Р, Т, I, О) с маркировкой р есть наименьшее множество
маркировок, определенных следующим образом:
1. р € R(C, р);
2. Если р' g R(C, р) и р" = 6(р', tj) для некоторого tjfT, то
р" eR(C, р).
Для сети Петри, изображенной на рис. 2.20, и маркировки р —
= (1, 0, 0) непосредственно достижимыми являются две марки-
ровки: (0, 1, 0) и (1, 0, 1). Из (0, 1, 0) нельзя достичь ни одной мар-
кировки, так как ни один переход не разрешен. Из (1, 0, 1) можно
получить (0, 1, 1) и (1, 0, 2). Пользуясь методами, разработанными
в гл. 4, можно показать, что множество достижимости R(C, р) имеет
следующий вид: {(1, 0, н), (0, 1, л)|п 0}.
• Рис. 2.20. Маркированная сеть Петри.
Удобно распространить функцию следующего состояния на
отображение маркировки и последовательности переходов в новую
маркировку. Для последовательности переходов (tjt, tj2, .... tjk)
и маркировки р маркировка р' = 6(р, tjt, tj2, ..., tjk) есть резуль-
тат запусков: сначала — tjlt затем — tj2 и т. д. до tjk. (Такая опе-
рация, конечно, возможна только в том случае, если каждый пере-
ход к моменту его запуска разрешен.)
Определение 2.11. Расширенная функция следующего состояния
определяется для маркировки р и последовательности переходов
от Т*I) 2~> следующими соотношениями: 6(р, tj, о) = б(6(р, tj), о),
= Н-
Обычно мы применяем эту расширенную функцию.
I) Автор имеет в виду бинарное отиошеиие иа множестве, маркировок,
такое, что (р, р') принадлежит ему тогда и только тогда, когда р' 6 /?(С, р).—
Прим. ред.
2) т* — множество всех подмножеств множества (булеан) переходов
Т. — Прим. ред.
Основные определения
31
Рис. 2.21. Маркирован-
ная сеть Петри.
Упражнения
1. Определите последовательность маркировок для маркированной сети Пет-
ри (рис. 2.21) и последовательности переходов ti, fa, fe, ti, t5. Как выглядит
соответствующая последовательность переходов для последовательности мар-
кировок (1, 0, 0), (0, 0, 1), (0, 0, 0)?
2. Ранее упоминалось, что существует несколько вырожденных случаев, при
которых последовательность маркировок не определяет единственную после-
довательность запусков переходов. Охарактеризуйте класс сетей Петри, для
которых это возможно.
3. Покажите, что U R(C, р) = Nn.
p.QNn
4. Докажите, что если р/ € R(C, р), то Д(С, р')5^Д(С, р).
5. Докажите,что p'g/?(С, р) тогда и только тогда, когда 7? (С, р') £= /?(С,р).
6. Выполняется ли равенство J?(C,p) — U$(p, 7>)?
tj^T
7. Выполняется ли равенство R(C, р) = U Д(С,5(р,/,•))?
tj 6 Т
8. В некоторых публикациях по сетям Петри множество достижимости мар-
кированной сети Петри называется ее классом маркировок. Более точно класс
прямых маркировок сети Петри есть то, что мы определили как множество до-
стижимости. Класс обратных маркировок есть множество достижимости ин-
версной сети Петри (см. упражнение 9 к разд. 2.2). Тогда класс маркировок
маркированной сети Петри есть объединение прямых и обратных классов
маркировок. Дайте формальное определение класса прямых маркировок,
класса обратных маркировок и класса маркировок сети Петри с маркировкой
р. Затем покажите, что классы маркировок сети Петри разбивают множество
всех маркировок на непересекающиеся классы эквивалентности. Для этого
требуется показать, что отношение «иметь равные классы маркировок» явля-
ется рефлексным, симметричным и транзитивным.
9. Сети Петри со своими фишками и правилами запусков во многом напоми-
нают игры, имеющие игровое поле: шашки, трик-тракЧ, ним, го и др. Можно
1) Нарды. — Прим. ред.
32
Глава 2
Рис. 2.22. Игровое поле.
придумать игру для одного—четырех человек, состоящую из игрового поля
(в качестве такого поля используется сеть Петр и) инабора пластиковых фишек.
Фишки распределены по позициям сети Петри, и игроки по очереди выбирают
разрешенные переходы и запускают их. Для разнообразия игра может быть
сделана на двадцати различных сетях Петри. Используя эти идеи, придумай-
те правила, предусматривающие следующее:
а) Как определено начальное расположение фишек? (Каждый игрок начинает
игру, имея одну фишку в «домике»; каждый игрок получ'ает «и» фишек на всем
поле по желанию и т. д.)
б) Какова цель игры? (Захватить фишки своего противника; получить наи-
большее количество фишек; как можно скорее избавиться от своих фишек и
т. д.)
в) Не нужно ли раскрасить фишки для разных игроков? (В соответствии с
этим определите правила запуска.)
г) Не стоит ли присвоить очки различным переходам? Тогда очки игрока оп-
ределятся суммой переходов, запущенных им.
д) Проанализируйте возникновение таких задач, как повторные запуски пере-
ходов, которые образуют новые фишки (выходов больше, чем входов); конеч-
ное число фишек, обеспечивающих конец игры.
Основные определения
33
После того как вы определили свою игру, попытайтесь сыграть в псе с кем-
нибудь из своих друзей. В качестве игрового поля используйте сеть Петри,
покаянную на рис. 2.22.
2.6. Альтернативные формы определения
сетей Петри
Теория сетей Петри разрабатывалась рядом авторов. У них
были различные мотивы и предпосылки. Вследствие такого раз-
нообразия многие фундаментальные понятия были определены
по-разному. Дадим некоторые из этих альтернативных определений,
чтобы показать, что между ними нет существенных различий, и
чтобы подготовить читателя к тем разнообразным представлениям,
которые могут встретиться в литературе.
Например, оригинальные сети Петри [241] не разрешают суще-
ствование кратных дуг между позициями и переходами. Это экви-
валентно определению входов и выходов переходов как множеств
(а не как комплектов) позиций. Далее, правило запуска было огра-
ничено следующим требованием: фишка есть в каждой входной
позиции для перехода, и нет ни одной фишки в выходных позициях.
Переход запускается путем удаления фишек из его входов (которые
теперь становятся пустыми) и размещением фишек в (ранее пустых)
выходах (которые теперь заполняются). Переход не может быть
запущен, если фишка уже принадлежит выходной позиции. Таким
образом, маркировка каждой позиции присваивает либо 0 фишек,
либо 1 фишку, р : Р -> {0, 1}. Теперь становится очевидным тот
факт, что сеть с п позициями имеет точно 2" возможных маркировок,
т. е конечное число состояний.
Ранние разработки Хольта по проекту теории информационных
систем [128] использовали эти же определения, но по мере продви-
жения исследований была обнаружена ограниченность такой мо-
дели. В работе Хольта и Коммонера, представленной на конферен-
ции в Вудс Холле [127], класс маркировок и правила запуска рас-
пространены на произвольные маркировки, р,: Р{О, 1, 2, ...}.
Таким образом была создана базовая модель сетей Петри в том виде,
в каком она определена сегодня (за исключением возможности
кратных дуг).
Многие из первых исследователей не давали формального опре-
деления своих моделей, а описывали неформально относящиеся к их
работе компоненты, такие, как позиции, переходы, фишки и пра-
вило запуска. Одно из первых формальных определений было дано
Патилом [231] в его докторской диссертации, в которой сеть Петри
определялась в виде четверки (7\ Р, А, В), где Т — множество
переходов, А — множество дуг, Р — множество позиций и В —
начальная маркировка. Дуги множества А соединяли либо пози-
цию с переходом, либо переход с позицией. Таким образом, A s
е (Р X Т) и (Т X Р). Многие статьи по сетям Петри основывают-
2—562
34
Глава 2
ся на этом определении и определяют сечь Петри как тройку (А Т,
А) с выделенной функцией маркировки.
Преобразование из формы (Р, Т, Л) к определению с выделением
входной и выходной функциями сравнительно просто. Множество
дуг А разбивается на множество входных дуг {(р,, tj) | (р,, tj) €
е А } и выходных дуг {(/ j, р() I (tj, Pi) € A }. Эта форма непосред-
ственно приводит к обобщению, допускающему кратные входы и
выходы. Необходимо только указывать кратность для каждой вход-
ной и выходной дуги.
Хэк [116] в конце концов остановился на определении сетей Пет-
ри в виде четверки (Р, Т, F, В), где, как обычно, Р — множество
позиций, Т — множество переходов, F и В — функции, ставящие
в соответствие позициям и переходам количество фишек, необходи-
мых для входа (F) или образованных для выхода (В). Следователь-
но, переход tj можно запустить только в том случае, если по край-
ней мере F(tj, р;) фишек находятся в каждой позиции pt Q Р. Пе-
реход запускается путем удаления F(tj, р{) фишек из каждой вход-
ной позиции и помещения B(tj, pt) фишек в каждую выходную по-
зицию. Функции F и В могут быть представлены матрицами.
Питерсон в своей диссертации [236] попытался объединить пе-
реходы и их входы и выходы, определяя переход как упорядочен-
ную пару комплектов позиций: I j Р°° х В00. Первая компонента
пары — комплект входов перехода; вторая — комплект выходов
перехода. Это сводит множество примитивных понятий теории к
позициям и фишкам, так как переходы являются структурами,
составленными из позиций. Такой подход особенно полезен для про-
стого определения переходов при построении сети Петри.
Эти определения отличаются от представленных здесь только'
разницей в обозначениях. В большинстве работ по сетям Петри
именно это имеет место: различие в определениях проявляется толь-
ко в обозначениях. Однако в некоторых случаях определения мо-
гут ограничивать класс сетей Петри тем, что не допускаются крат-
ные входные п выходные дуги или существует ограничение на форму
переходов, т. е. требуется, чтобы переходы имели непустые множе-
ства входных н выходных позиций или входные п выходные по-
зиции перехода не должны совпадать (без петель). Но, как мы по-
кажем в гл. 5, даже эти различия не имеют большого значения.
Упражнения
1. Дайте эквивалентное стандартное определение через Р, Т, I, О) дтя сети
Петри, определенной как (Р, Т, F, В). Дайте определение через (Р, Т, Г, В}
для сети Петрн, заданной как (Р, Т, I, О).
2. Почему некоторые исследователи предпочитают определение через
(Р, Т, Д)/которое объединяет входные и выходные взаимосвязи в множестве
дуг А, в то время как другие отдают предпочтение (Р, Т, I, О)? Покажите пре-
имущество н недостатки каждого.
Основные определения
35
2.7. Замечания к литературе
Для дальнейшего знакомства с сетями Петри, вероятно, лучше
всего начать с обзоров [20, 238] в Computing Surveys. Почти в лю-
бой работе несколько первых разделов посвящены основным опре-
делениям и обозначениям, поэтому, чтобы найти различия в опре-
делениях, достаточно бегло просмотреть начала некоторых из пере-
численных в библиографии. Например: [128. 127, 111, 115, 116, 152,
201, 208, 290].
2.8. Темы для дальнейшего изучения
1. Разработайте теорию сетей Петри, разрешающую существо-
вание окрашенных фишек. Рассмотрите различия в определениях
разрешенных переходов и запусков переходов. Существует по мень-
шей мере три разумных способа обобщения сетей Петри в случае
окрашенных фишек. Укажите те, которые вы сможете предло-
жить, и оцените степень их полезности.
2. Разработайте представление теории сети Петри для научных
работников, не связанных с вычислительной техникой. Сравните
ваше представление с представлением Хольта [123] и Мельдмана
[184, 185].
3. Постройте систему моделирования на ЭВМ для выполнения сети
Петри. Для удобного интерфейса пользователя с программой ис-
пользуйте стирающий графический дисплей (с электронно-лучевой
трубкой или плазменный) для изображения запусков переходов
и последовательного передвижения фишек. Это потребует решения
множества вспомогательных задач.
а) Определить язык, имеющий средства вариантов задания для за-
дания сети Петри, ее маркировок.
б) Разработать внутреннее представление сети Петри, ее маркиров-
ки и необходимые алгоритмы для моделирования.
в) Обеспечить графическую выдачу. Главная проблема здесь в дос-
тижении планарного представления сети (до разумной степени).
Следует также подумать о представлении динамических свойств
сети (движение фишек).
2
ГЛАВА 3
СЕТИ ПЕТРИ
ДЛЯ МОДЕЛИРОВАНИЯ
Сети Петри были разработаны и используются в основном для модели-
рования. С их помощью могут быть промоделированы многие системы, И осо-
бенности системы с независимыми компонентами, например аппаратное и
программное обеспечение ЭВМ, физические системы, социальные и др. Сети
Петри применяются для моделирования возникновения различных событий
в системе. В частности, сети Петри могут моделировать поток информации
или другие ресурсы системы.
В этой главе мы приведем примеры систем, моделируемых при помощи се-
тей Петри. Эти примеры дадут представление о большом классе систем, кото-
рые можно моделировать сетями Петри, об использующемся методе моделиро-
вания и о свойствах, которыми должны обладать моделируемые системы.
3.1. События и условия
Простое представление системы сетью Петри основано на двух
основополагающих понятиях: событиях и условиях. События —
это действия, имеющие место в системе. Возникновением событий
управляет состояние системы. Состояние системы может быть опи-
сано множеством условий. Условие — есть предикат или логическое
описание состояния системы. Условие может принимать либо зна-
чение «истина», либо значение «ложь».
Так как события являются действиями, то они могут происхо-
дить. Для того чтобы событие произошло, необходимо выполне-
ние соответствующих условий. Эти условия называются предусло-
виями события. Возникновение события может вызвать нарушение
предусловий и может привести к выполнению других условий,
постусловий.
В качестве примера рассмотрим задачу моделирования простого
автомата-продавца. Автомат-продавец находится в состоянии ожи-
дания до тех пор, пока не появится заказ, который он выполняет
и посылает на доставку. Условиями для такой системы являются:
а) автомат-продавец ждет; б) заказ прибыл и ждет; в) автомат-
продавец выполняет заказ; г) заказ выполнен.
Событиями будут: 1. Заказ поступил. 2. Автомат-продавец начи-
нает выполнение заказа. 3. Автомат-продавец заканчивает выпол-
нение заказа. 4. Заказ посылается на доставку.
Предусловия события 2 (автомат-продавец начинает выполнение
заказа) очевидны: (а) автомат-продавец ждет; (б) заказ прибыл и
надет. Постусловие для события 2: (в) автомат-продавец выполняет
заказ. Аналогично мы можем определить предусловия и постусло-
Сети Петри для моделирования
37
вия для других событий и составить следующую таблицу событий
и их пред- и постусловий: *
Событие Предусловия Постусловия
1 нет б
2 а, б в
3 В г, а
4 г нет
Такое представление системы легко моделировать сетью Петри.
В сети Петри условия моделируются позициями, события — пере-
ходами. При этом входы перехода являются предусловиями соот-
ветствующего события; выходы —• постусловиями. Возникновение
события равносильно запуску соответствующего перехода. Выпол-
нение условия представляется фишкой в позиции, соответствующей
этому условию. Запуск перехода удаляет разрешающие фишки,
представляющие выполнение предусловий и образует новые фишки,
которые представляют выполнение постуловий.
Сеть Петри на рис. 3.1 иллюстрирует модель приведенного выше
автомата-продавца. Мы указали каждому переходу и позиции соот-
ветствующие событие и условие.
Можно моделировать и более сложную систему. Система авто-
мат-продавец состоит из трех различных автоматов М.^ , М2 и М3
и двух операторов и F2 Оператор F- воздействует на автоматы
Mt и ТИ2, а оператор F2 — на и Л13. Заказы требуют двух стадий
обработки. Сначала они должны быть обработаны автоматом Л1,,
затем либо автоматом Л12, либо М3. Эта более сложная система бу-
дет иметь следующие условия:
а) заказ прибыл и ждет обработки автоматом
б) заказ обработан автоматом THi и ждет обработки либо автома-
том ТИ2, либо 7И3;
Начало
Заказ Заказ Выполнения
поступил ждет заказа
Завершение
Выполнения Заказ
заказа Выполнен
Рис. 3.1. Сеть Петри для простого автомата-продавца
38
Глава 3
Рис- 3.2. Сеть Петри для сложного автомата-продавца.
в) заказ выполнен;
г) автомат незанят;
д) автомат М., незанят;
е) автомат М3 незанят;
ж) оператор Ft незанят;
з) оператор F2 незанят;
и) автомат Mi находится под воздействием оператора Ft;
к) автомат М{ находится под воздействием оператора F2;
л) автомат М2 находится под воздействием оператора F,;
м) автомат М3 находится под воздействием оператора F2.
При этом могут происходить следующие события:
1. Поступление заказа.
2. Оператор Ft начинает выполнение заказа на автомате
3. Оператор Ft закончил выполнение заказа на автомате
4. Оператор F2 начинает выполнение заказа на автомате Mt.
5. Оператор F2 закончил выполнение заказа на автомате Mt.
6. Оператор Ft начинает выполнение заказа на М2.
7. Оператор Ft закончил выполнение заказа на М2.
8. Оператор F2 начинает выполнение заказа на М3.
9. Оператор Fs закончил выполнение заказа на М3.
10. Заказ посылается на доставку.
к
Сети Петри Зля моделирования
39
Рис. 3.3. Моделирова-
ние простой вычисли-
тельной системы.
Завершение
выполнения
задания
Задание
ожидает
вывода
Задание
ждет
Задание помещается
во входную очередь
Процессор
свободен
Начало
выполнения
задания
Задание
выводится
задание
обрабатывается
Пред- и постусловия каждого события:
События Предусловия Постусловия
1 нет а
2 а, ж, г и
3 и ж, г, б
4 а, з, г К
5 к б, 3, г
6 б, Ж, д л
7 л в, ж, д
8 б, е, з м
9 м в, е, з
10 в нет
Сеть Петри этой системы показана на рис. 3.2.
Аналогичный пример можно привести для вычислительной
системы, которая обрабатывает задания, поступающие с устройства
ввода, и выводит результаты на устройство вывода. Задания посту-
пают на устройство ввода. Когда процессор свободен и в устройстве
ввода есть задание, процессор начинает обработку задания. Когда
задание выполнено, оно посылается в устройство вывода; процес-
сор же либо продолжает обрабатывать другое задание, если оно
имеется, либо ждет прихода задания, если устройство ввода еще
Не получило такового. Эта система может быть промоделирована
сетью Петри, показанной на рис. 3.3.
40
Глава S
3.2. Одновременность и конфликт
Приведенные примеры иллюстрируют некоторые особенности
сетей Петри и систем, моделируемых с их помощью. Одной из осо-
бенностей является свойственный сетям и их моделям параллелизм,
или одновременность. В модели сети Петри два разрешенных не-
взаимодействующих события могут происходить независимо друг
от друга. Синхронизировать события, пока это не потребуется моде-
лируемой системе, нет нужды. Но, когда синхронизация необходи-
ма, моделировать ее легко. Таким образом, сети Петри представ-
ляются идеальными для моделирования систем с распределенным
управлением, в которых несколько процессов выполняются одно-
временно.
Другая важная особенность сетей Петри — это их асинхронная
природа. В сети Петри отсутствует измерение времени или течение
времени. Это отражает философский подход к понятию времени,
утверждающий, что одно из важнейших свойств времени, с логиче-
ской точки зрения, — это определение частичного упорядочения
событий. В реальной жизни различные события укладываются в
различные интервалы времени, и это отражено в модели сети Петри
независимостью от времени управления последовательностью собы-
*£ий. Структура сети Петри такова, что содержит в себе всю необ-
ходимую информацию для определения возможных последователь-
ностей событий. Таким образом, на рис. 3.3 событие «завершение
выполнения задания» должно следовать за соответствующим собы-
тием «начало выполнения задания». Однако нет и не требуется ни-
какой информации, связанной с количеством времени, необходи-
мым на выполнение задания.
Выполнение сети Петри (или поведение моделируемой системы)
рассматривается здесь как последовательность дискретных собы-
тий. Порядок появления событий является одним из возможных, до-
пускаемых основной структурой. Это приводит к явной недетерми-
нированности в выполнении сети Петри. Если в какой-то момент
времени разрешено более одного перехода, то любой из нескольких
возможных переходов может стать «следующим» запускаемым.
Выбор запускаемого перехода осуществляется недетерминирован-
ным образом, т. е. случайно. Эта особенность сети Петри отражает
тот факт, что в реальной жизненной ситуации, где несколько дей-
ствий происходит одновременно, возникающий порядок появления
событий — не однозначен; скорее может возникнуть любая из мно-
жества последовательностей событий. Однако частичный порядок
появления события — единственен.
Проблемы, включающие в себя эти понятия, имеют философ-
ский характер. В своей точке зрения на Вселенную я, в частности,
склонен к детерминизму: все действия предопределены состоянием
Вселенной, и никакого беспорядка не существует. Кажущийся бес-
порядок — просто результат недостатка знаний о состоянии Все-
Сети Петри для моделирования 41
ленной и ее переходов из состояния в состояние. В этом смысле
выбор для запуска одного из разрешенных переходов в моделируе-
мой системе детерминирован, но не в модели, просто потому что мо-
дель не дает полной информации о системе.
Обратимся к теории относительности. Одним из ее основных
положений является утверждение, что передача чего-либо не мо-
жет быть мгновенной. Даже информация о возникновении события
распространяется в пространстве со скоростью, ограниченной
скоростью света с. Это означает, что если два события и произойдут
i
НепримитиЬное jc
событие происходит
Начало непримитив- Конец неоримитив-
мого события него события
Рис. 3.4. Моделирование непримитивного события.
одновременно (т. е. они не имеют причинной взаимосвязи), то по-
рядок возникновения этих событий для двух разных наблюдателей
может оказаться различным. Для двух событий А и В, происходя-
щих в одно и то же время, наблюдатель, расположенный в непос-
редственной близости от события А, получит информацию, свя-
занную с событием А, прежде, чем информацию, связанную с собы-
тием В. Таким образом, наблюдатель может сделать вывод, что со-
бытие А произошло до события В. С другой стороны, наблюдатель,
расположенный в непосредственной близости от события В, отметит
прямо противоположную последовательность возникновения собы-
тий.
Такое представление, хотя и является необходимым для полноты
рассмотрения происходящего, однако влечет за собой значитель-
ные трудности при описании и анализе динамического поведения
сети Петри, когда определяется последовательность запусков пере-
ходов. Для простоты обычно вводят следующее ограничение. За-
пуск перехода (и соответствующего события) рассматривается как
мгновенное событие, занимающее нулевое время, и возникновение
двух событий одновременно невозможно. Моделируемое таким об-
разом событие называется примитивным-, примитивные события
мгновенны и неодновременны. (Иногда это обосновывается тем, что
время — это непрерывная действительная переменная. Следователь-
но, если мы присвоим каждому событию время возникновения, то
вероятность того, что любые две произвольно выбранные непрерыв-
ные действительные переменные совпадают, равна нулю, и, следо-
вательно, события неодновременны.)
42
Глава ,3
Непримитивными называются такие события, длительность ко-
торых отлична от нуля. Они не являются неодновременными и,
следовательно, могут пересекаться во времени. Так как осуществ-
ление большинства событий в реальном мире занимает некоторое
время, то они являются непримитивными событиями и поэтому
не могут должным образом моделироваться переходами в сети
Петри. Однако это не приводит к возникновению проблем при
моделировании систем. Непримитивное событие может быть пред-
ставлено в виде двух примитивных событий: «начало непримитив-
ного события», «конец непримитивного события» и условия «непри-
митивное событие происходит». Эта ситуация может быть промоде-
лирована с помощью сети, показанной на рис. 3.4
Рис. 3.5. Представление
ИеПрИМИТИБНО! о события
прямоугольник ом.
Петри и другие предложили представлягь непримитивные
события в сети Петри в виде прямоугольника [244], как
показано на рис. 3 5, а примитивные события — планками,
как мы делали это раньше. Это упростит некоторые сети Петри, на-
пример, такую, как на рис. 3 6, которая эквивалентна сети Петри,
изображенной на рис. 3.3. Но так как в принципе предложенное
понятие выражено в терминах более примитивных конструкций,
мы не будем использовать обозначение в виде прямоугольника.
Прямоугольник может иметь существенное значение при модели-
ровании сложных систем на нескольких иерархических уровнях,
так как он позволяет выделить в отдельный элемент сети целые
подсети. Это в некотором смысле подобно понятиям подпрограммы
или макроса в языках программирования.
Недетерминированность и неодновременность запусков пере-
ходов в моделировании параллельной системы показываются двумя
способами. Один из них представлен на рис. 3 7. В этой ситуации
два разрешенных перехода в любом случае не влияют друг на друга,
и в число возможных последовательностей событий входит после-
довательность, в которой первым срабатывает один переход, и по-
следовательность, в которой первым будет запущен другой пере-
ход. Это называется одновременностью.
Другая ситуация, в которой одновременное выполнение затруд-
нено и которая характеризуется невозможностью одновременного
Сети Петри для моделирования
43
Рис. 3.6. Моделирование вычислительной системы с использованием неприми-
тивного перехода.
Рис. 3.7. Одновременность. Эти два
перехода могут быть запущены в
любом порядке.
Рис. 3.8. Конфликт. Переходы ? и
находятся в конфликте, т. е. за-
пуск одного из них удаляет фишку
из р, и тем самым запрещает друюй.
44
Глава 3
возникновения событий, показана на рис. 3.8. Здесь два разре-
шенных перехода находятся в конфликте. Может быть запущен
только один переход, так как при запуске он удаляет фишку из
общего входа и запрещает другой переход.
Рассмотренные ситуации требуют внимательного изучения мо-
делируемых сетями Петри систем для правильного отображения
их поведения. К сожалению, многие работы посетим Петри исследо-
вали только свойства данной сети или класса сетей. Разработке же
методов моделирования специально для сетей Петри внимания уде-
лялось мало. Однако существуют определенные области, в которых
сети Петри представляются идеальным инструментом для моде-
лирования: это те области, в которых события происходят асин-
хронно и независимо. Для того чтобы дать представление о моде-
лировании сетями Петри, в этой главе мы проиллюстрируем исполь-
зование сетей Петри для моделирования аппаратного и программно-
го” обеспечения ЭВМ и других систем.
3.3. Аппаратное обеспечение ЭВМ
Аппаратное обеспечение ЭВМ можно рассматривать на несколь-
ких уровнях, и сети Петри могут моделировать каждый из этих
уровней. На одном уровне ЭВМ построены из простых устройств
памяти и вентилей; на более высоком уровне в качестве основных
компонент системы используются функциональные блоки и ре-
гистры. На еще более высоком уровне целые вычислительные сис-
темы могут быть компонентами сети ЭВМ. Одним из сильных свойств
сетей Петри является их способность моделировать каждый из этих
уровней. Обсудим эту способность и приведем некоторые примеры.
3.3.1. Конечные автоматы
На низком уровне вычислительные системы могут быть описаны
автоматами. Автомат — это пятерка (Q, S, А, 5, Г), где
Q — конечное множество состояний {qlt q<>, qn}\
2 — конечный входной алфавит;
А — конечный выходной алфавит;
б: Q х 2 -> Q — функция следующего состояния, отображающая
текущее состояние и текущий вход в следующее состояние; Г : Q х
X 2 -> А — функция выхода, отображающая текущее состояние
и текущий вход в выходной символ.
Автоматы часто представляют в виде графов переходов, как, на-
пример, на рис. 3.9. В графе переходов состояния представляются
кружками, являющимися вершинами. Дуга из состояния в qJt
помеченная с/b, означает, что, находясь в состоянии <уг, автомат
при входе а перейдет в состояние q j, выдавая при этом символ Ь.
Формально следовало бы записать 6(9,, а) — q} и Г (qit а) = Ь.
Сети Петри для моделирования
45
Входной алфавит определяет входы автомата из внешнего мира, а
выходной алфавит — выходы автомата во внешний мир.
В качестве примера рассмотрим автомат, изображенный на
рис. 3.9. Этот автомат преобразует двоичное число, представленное
последовательностью бит, начиная с младшего, в дополнение до
двух. В данном случае входной и выходной алфавит состоит из трех
символов: 0, 1 и R. Автомат начинает работать в состоянии ft. Сим-
вол сброса (7?) означает конец (или начало) числа и возвращает
автомат в исходное состояние. Выход автомата для символа сброса
является просто его повторением.
Рис. 3.9. Граф переходов для конеч-
ного автомата, вычисляющего допол-
нение до двух двоичного числа.
Рис. 3.10. Конечный автомат для
определения четности входного дво-
ичного числа.
Аналогичный автомат показан на рис. 3.10. При тех же самых
входах этот автомат вычисляет четность входного числа. Он начи-
нает работу в состоянии Выход копирует вход до тех пор, пока
входным символом не окажется символ сброса. Выходом для сим-
вола сброса будет 0 в случае нечетного числа и 1 — в случае чет-
ного числа.
При представлении конечного автомата сетью Петри следует об-
ратить внимание на связь между сетью Петри и внешним миром,
которая ранее не учитывалась. Моделирование взаимодействия
с внешним миром можно реализовать многими способами. В нашей
задаче мы моделируем это взаимодействие с помощью специаль-
ного множества позиций. Позициями будут представлены каждый
входной и выходной символы. Мы допускаем, что из внешнего мира
помещается фишка в позицию, соответствующую входному символу,
а затем фишка, появившаяся в позиции, соответствующей выход-
ному символу, удаляется оттуда. Эта последовательность действий
будет повторяться необходимое число раз. Общая схема проиллюст-
рирована на рис. 3.11.
Заметим, что здесь не исключена возможность путаницы в по-
нятиях, так как позиции, соответствующие входным и выходным
символам, могут быть обоснованно названы входными и выходными
Позициями сети. Однако их не следует путать с входными или вы-
46
Глава 3
Выходы
Входы
Представление
сетью Петри .
конечного
автомата
Рис. 3.11. Общий подход к мо-
делированию связи между
сетью Петри и внешним ми-
ром.
ходными позициями переходов. Несмотря на возможную путаницу,
эти термины наиболее естественны для обоих понятий.
В качестве альтернативного подхода к моделированию входов и
выходов сети могут быть использованы переходы. Для определения
следующего входного символа из внешнего мира следует выбирать
входной переходи запускать его. Сеть Петри ответит (в конце концов)
запуском соответствующего перехода из множества выходных пере-
ходов, связанного с соответствующим выходом. Затем из внешнего
мира будет запущен новый входной переход и т. д. Этот подход
проиллюстрирован на рис. 3.12. Нетрудно показать, что оба этих
подхода эквивалентны, поэтому будем использовать первый из них,
в котором входные и выходные символы моделируются позициями.
Задав представление позиций, соответствующих символам входа
и выхода, мы можем завершить построение модели системы конеч-
ных состояний. Представим каждое состояние автомата позицией
в сети Петри. Текущее состояние отмечается фишкой; все осталь-
ные позиции пусты. Теперь для определения переходов из состоя-
ния в состояние можно ввести переходы сети следующим образом.
Для каждой пары (состояние и входной символ) мы определяем
переход, входными позициями которого являются позиции, соот-
ветствующие состоянию и входному символу, а выходными пози-
циями — позиции, соответствующие следующему состоянию и вы-
ходу.
Рис. 3.12. Альтернативный
подход представления связи
между сетью Петри и внешним
миром, где вместо позиций ис-
пользуются переходы.
Сети Петри для моделирования
47
Рис. 3.13. Сеть Петри, эквивалентная автомату на рис. 3.9.
Для конечного автомата (Q, 2, А, 6, Г) мы определили сеть
Петри (Р, Т, I, О) таким образом:
P-QU2UA,
Т = Уч, = I <7 6 <2 и
1 Уч. а) = {Ч>
0{tq, 3) = {o(q, о), Г(<7, о)}.
Эта сеть Петри является моделью конечного автомата.
На рис. 3.13 изображена сеть Петри, соответствующая автомату
с рис. 3.9. На рис. 3.14—-сеть Петри, соответствующая автомату
с рис. 3.10.
При сравнении сетей Петри на рис. 3.13, 3.14 с эквивалентными
автоматами на рис. 3.9, 3.10 возникают некоторые вопросы. Преж-
де всего: почему модель сети Петри предпочтительнее описания
конечным автоматом? Описание автоматом более понятно, чем
описание сетью Петри, в которой 6 переходов, 24 дуги и 7 или 8 по-
зиций. Это верно. Однако мы показали, что сети Петри могут пред-
ставлять любую систему, представимую автоматом, и это свидетель-
ствует о больших возможностях сетей Петри.
Кроме того, следует отметить, что модель сети Петри имеет опре-
деленное преимущество при композиции автоматов. Например,
48
Глава 3
Рис. 3.14. Сеть Петри, эквивалентная автомату иа рис. 3.10.
заметим, что выходной алфавит автомата с рис. 3.9 идентичен
входному алфавиту автомата с рис. 3.10. Передавая выход автома-
та с рис. 3.9 на вход автомата с рис. 3.10, можно построить ком-
позицию автоматов, вычисляющую дополнение до двух и проверяю
Рис. 3.15. Составной’"авто-
мат, представляющий по-
следовательную компози-
цию автоматов, изображен-
ных на рис. 3.9, 3.10.
Сети Петри для моделирования
49
щую четность. Такая композиция является автоматом с составны-
ми состояниями, компоненты которых — это состояния обоих под-
автоматов. В сетях Петри такая композиция есть просто совмещение
выходных позиций первой сети с входными позициями второй. На
рис. 3.15 показана композиция автоматов, а на рис. 3.16 — со-
ставная сеть Петри.
Другое преимущество представления сети Петри связано с ины-
ми формами композиции. Например, параллельная композиция
позволяет компонентам композиции автоматов работать одновре-
менно. В этом случае вновь получаем автомат с составными состоя-
ниями, в то время как для сети Петри — это просто дублирование
фишек во входах, соответствующих входным символам, и исполь-
зование их во всех компонентах сети Петри. Наконец, на выходе
мы просто выбираем соответствующие позиции выхода. Например,
если мы хотим соединить параллельно две сети Петри (рис. 3.13
и 3.14), то в результате получим сеть Петри, подобную изобра-
женной на рис. 3.17, которая вычисляет дополнение числа до двух
и его четность. Если на входе появляется символ сброса, то выходом
является четность.
Упражнения
1. Покажите, что оба подхода к моделированию взаимодействия между сетью
Петри и ее окружением (с использованием переходов или позиций) эквива-
лентны.
3.3.2. ЭВМ с конвейерной обработкой
Возможность моделировать параллелизм и довольно простого
объединения подсистем, представленных сетями Петри, делают сети
Петри весьма полезным инструментом моделирования сложной ап-
паратуры вычислительных систем. Вычислительные системы со-
стоят из многих компонент. Это делает сеть Петри наиболее под-
ходящим средством для их представления.
На протяжении ряда лет было предпринято много попыток уве-
личения производительности вычислительных систем путем парал-
лельного выполнения нескольких функций. Примером такого под-
хода к построению высокопроизводительной ЭВМ является исполь-
зование конвейерной обработки [52]. Этот метод обработки подобен
функционированию сборочного конвейера и особенно удобен для
работы с векторами и массивами. Конвейер состоит из набора опе-
раций, которые могут выполняться одновременно. Когда операция
k завершается, она передает свой результат операции (k + 1) и
ожидает от операции (k — 1) нового задания. Если каждая операция
занимает t единиц времени и всего существует п операций, то за-
вершение обработки одного операнда потребует nt единиц времени.
Однако, если на конвейерную обработку продолжают поступать
новые операнды, результаты могут выдаваться со скоростью один
каждые t единиц времени.
Рис. 3.16. Составная сеть Петри, являющаяся последовательной композицией сетей Петри на рис. 3.13,
3.14.
Глава 3
Сети Петри для моделирования
5Г
Рис. 3.17. Параллельная композиция сетей Петри с рис. 3.13, 3.14. Необходи-
мо обеспечивать дублирование входов для обеих компонент с помощью
специальной подсети.
52
Глава 3
В качестве примера рассмотрим сложение двух чисел с плаваю-
щей точкой. Основные шаги этой операции предполагают:
1. Выделить экспоненты обоих чисел.
2. Сравнить экспоненты и изменить, если необходимо, должным
образом порядок большей и меньшей экспонент.
3. Сдвинуть точку в числе с меньшей экспонентой для их уравнения.
4. Сложить дроби.
5. Нормализовать результат.
6. Проверить экспоненту на переполнение и сформировать экспо-
ненту и дробь результата.
Каждый из этих шагов может быть выполнен отдельным вычисли-
тельным блоком, где каждый отдельный операнд передается от
блока к блоку для выполнения операции сложения. Это позволит
выполнять до шести сложений одновременно.
Координацию различных блоков можно осуществлять несколь-
кими способами. Обычно управление конвейерной обработкой яв-
ляется синхронным; время, отпущенное на выполнение каждого
шага конвейера t, постоянно и фиксированно. Каждые t единиц вре-
мени результат каждого блока перемещается по конвейеру, чтобы
стать входом для следующего блока. Однако при синхронном
подходе обработка может быть приостановлена без необходимости,
так как требуемое время может изменяться от блока к блоку, а так-
же внутри данного блока для различных входов. Например, для
выполнения шага нормализации результата при сложении чисел
с плавающей точкой может потребоваться различное количество
времени в зависимости от того, на сколько разрядов необходимо
произвести нормализующий сдвиг и в какую сторону: вправо или
влево. В этом случае, поскольку время t должно быть выбрано мак-
симальным, необходимым для самого медленного блока конвейера,
может оказаться так, что большую часть времени все единицы бу-
дут пребывать незагруженными, ожидая окончания t единиц времени.
В асинхронном конвейере в среднем процесс обработки может
быть ускорен сигнализацией о завершении каждого шага конвей-
ерной обработки и готовности передать свой операнд и получить
новый. Результат шага k конвейерной обработки может быть послан
на шаг (k + 1), как только шаг k выполнен, а блок (k + 1) свободен.
Рассмотрим произвольный шаг конвейерной обработки. Очевидно,
нужно иметь место, куда можно поместить входы и выходы в то
время, как они используются илн производятся. Обычно это пред-
полагает наличие регистров: блок использует значение своего вход-
ного (буферного) регистра для вычисления значения выходного (бу-
ферного) регистра. После этого необходимо ждать, пока (1) — вы-
ходной регистр блока не будет очищен путем пересылки
содержимого во входной регистр следующего блока и (2) — новое
входное значение не появится в его входном регистре. Таким образом,
для управления блоком k конвейера необходимо знать, когда вы-
полняются следующие условия:
Сети Петри для моделирования
53
• входной регистр заполнен;
• входной регистр пуст;
• выходной регистр заполнен;
• выходной регистр пуст;
• блок занят;
• блок свободен;
• пересылка осуществлена.
На рис. 3.18 и 3.19 показано, как можно промоделировать асин-
хронный конвейер такого типа. На рис. 3.18 приведена блок-схема
конвейера, моделируемого сетью Петри на рис. 3.19.
Отметим, что в этой модели мы промоделировали реальную ра-
боту блоков конвейера как непримитивных событий. Это позволяет
нам игнорировать на этом уровне конкретные детали того, что де-
лают блоки, и сосредоточиться на их правильном взаимодействии.
Каждая операция также может быть промоделирована сетью Петри.
Затем сети Петри для каждого блока можно внести в сеть Петри
на рис. 3.19, получив более детальную сеть. Такая возможность
моделирования системы на нескольких различных уровнях абстрак-
ции, т. е. иерархическим образом, может быть весьма полезна.
Блок k-f
Выходной регистр
блока к-1
Входной регистр
блока к
Блок к
Выходной регистр
блока к
Входной регистр
блока к+1
Рис. 3.18. Блок-схема устройства управления асинхронной ЭВМ с конвейер-
ной обработкой.
г
Б4
Глава 3
Выходной регистр
к~1 пуст
Входной регистр
к+1 заполнен
Пересыпка
из к в к+1
из к-1 В к
Блок к
занят
Блок к-1
занят
Выходной регистр
к-1 заполнен
Входной регистр
к пуст
Выходной регистр
к заполнен
Входной регистр
к+1 пуст
Рис. 3.19. Модель сети Петри устройства управления асинхронной ЭВМ с
конвейерной обработкой.
Входной регистр-
к заполнен
Пересылка
Выходной регистр
к пуст
3.3.3. Кратные функциональные блоки
Конвейерная структура управления, рассмотренная [^предыду-
щем разделе, — это один из подходов к построению очень болыпих
быстродействующих вычислительных систем. Другой подход, ис-
пользованный, например, в CDC 6600 [291] и IBM 360/91 [10],.
использует кратные функциональные блоки. В CDC 6600 имеется
10 функциональных блоков: блок ветвления (для условных пере-
ходов); булев блок (для булевых операций); блок сдвига; блок сло-
жения с плавающей точкой; блок сложения с фиксированной точ-
кой; 2 блока умножения; блок деления и 2 блока приращения
(для индексирования). Кроме того, имеется несколько регистров
для хранения входных и выходных значений функциональных
блоков. Устройство управления ЭВМ организует одновременное
функционирование нескольких независимых блоков.
В качестве примера рассмотрим следующую последовательность,
инструкций для вычислительной системы CDC 6600;
1. Умножить XI на XI, результат поместить в Х0.
2. Умножить ХЗ на XI, результат поместить в ХЗ.
Сечи Петри для моделирования
55
3. Сложить Х2 с Х4, результат поместить в Х4.
4. Сложить ХО с ХЗ, результат поместить в ХЗ.
5. Разделить ХО на Х4, результат поместить в Х6.
Для выполнения инструкций устройство управления выдает пер-
вую инструкцию в блок умножения. Поскольку существуют два
блока умножения, можно выдать также вторую инструкцию. При
этом обоим блокам доступно содержимое XI. Инструкция 3 может
быть выдана блоку сложения. Теперь, для того, чтобы выдать ин-
струкцию 4, мы должны ждать, пока инструкции I, 2 и 3 не будут
завершены, так как инструкция 4 использует блок сложения (за-
нятый выполнением инструкции 3), ХО (вычисляемый инструкцией
1) и ХЗ (вычисляемый инструкцией 2). Инструкция 5 должна ждать
выполнения инструкции 1 (вычисление ХО) и инструкции 3 (вы-
числение Х4).
Организация параллелизма этого типа (выполнение нескольких
инструкций программы одновременно) должна быть такой, чтобы
результат выполнения программы с использованием параллелиз-
ма и без него был бы одинаков. Некоторые инструкции в программе
требуют результата предыдущей инструкции до выполнения по-
следующей. Система, которая организует параллелизм в последо-
вательной программе таким способом для получения правильных
результатов, обладает свойством детерминированности. Условия
поддержания детерминированности были рассмотрены Бернстай-
ном [28]. Вот они: для двух операций а и Ь, таких, что а предшест-
вует b на линейном участке программы, b может начать выполнять-
ся прежде, чем выполнена а, тогда и только тогда, когда входные
данные b не требуют результата а и результаты b не изменят ни
входных данных, ни результатов а.
Один из методов применения таких ограничений для построе-
ния устройства управления, выдающего инструкции отдельным функ-
циональным блокам, основан на таблице резервирования. Инструк-
ция для функционального блока и, использующая регистры i, j и
k, выдается только в том случае, если ни одна из четырех компонент
не зарезервирована; при выдаче инструкции все эти компоненты
становятся зарезервированными. Если же из-за того, что либо
функциональный блок, либо один из регистров уже используются,
инструкция не может быть выдана, то устройство управления перед
переходом к следующей инструкции ожидает выполнения условий
для выдачи этой инструкции.
Схему такого типа можно промоделировать сетью Петри. Каж-
дому функциональному блоку и каждому регистру поставим в со-
ответствие позицию: если блок или регистр свободен — в позицию
будет помещена фишка, если нет — фишки в позиции не будет.
Кратные идентичные функциональные блоки показываются соот-
ветствующим числом фишек в позициях. На рис. 3.20 изображена
часть сети Петри, которая может быть использована для модели-
рования выполнения инструкции, использующей блок и и регист-
56
Глава 3
Инструкция использует
ёлок и,
регистры i,J,k
Готовность декоди-
ровать следующую
инструкцию
Выдача
инструкции
Блок и
свободен
Регистр I
свободен
Регистр j
свободен
Регистр к
свободен
Инструкция
завершена
Рис. 3.20. Часть сети Петри, моделирующая устройство управления для ЭВМ,
с кратными регистрами и кратными функциональными блоками.
ры i, j и k. Моделирование всего устройства управления, конечно
же, потребует гораздо большей сети Петри.
Схема, описанная выше, представляет собой очень простой спо-
соб введения параллелизма и не рассматривает, например, тот факт,
что кратные функциональные блоки могут использовать одновре-
менно одинаковые входные регистры. Таким образом, максимальный
параллелизм в этой схеме может быть не получен [153]. Однако
существуют другие схемы, с помощью которых это достигается. Та-
кие более сложные схемы также моделируются (более сложными)
сетями Петри. Эти сети могут быть очень велики. CDC 6600, напри-
мер, имеет 24 различных регистра и 64 различных инструкции. Если
для каждой инструкции и тройки регистров требуется позиция,
соответствующая условию «блок и оперирует регистрами i, j и &»,
то необходимо более полумиллиона позиций и переходов. Главная
трудность заключается в представлении того факта, что содержимое
внутренних регистров может определять, какие регистры и блоки
будут использоваться (индексирование).
(Однако никакая программа не использует все возможные ком-
бинации регистров и блоков. Это позволило [274] промоделировать
вычислительную систему CDC 6600 с помощью сетей Петри. Эта
модель сети Петри была затем использована для оптимальной гене-
рации кода компилятором с Фортрана, что мы увидим в разд. 3.5.)
3.4. Программное обеспечение ЭВМ
В дополнение к аппаратному обеспечению ЭВМ сетями Петри
можно моделировать и программное обеспечение. Чаще всего сети
Петри используются именно для этого, и здесь они имеют наиболь-
Сети Петри для моделирования
57
шие возможности для практического применения. В течение дли-
тельного времени разрабатывались системы для описания и моде-
лирования аппаратного обеспечения ЭВМ, но только в последние
годы такие попытки предприняты для формального моделирования
программного обеспечения ЭВМ. Большинство этих усилий связано
с анализом, спецификацией и описанием последовательных про-
грамм; системы параллельных процессов до сих пор остаются важ-
ной исследовательской проблемой. В этом разделе мы покажем,
как сети Петри могут моделировать различные системы параллель-
ных взаимодействующих процессов.
3.4.1. Блок-схемы
Вырожденным случаем параллельной системы обработки яв-
ляется система с одним процессом. Сначала рассмотрим, как сетью
Петри может быть представлен отдельный процесс, а затем путем
комбинации сетей Петри, представляющих несколько процессов,
получим систему параллельных процессов.
Отдельный процесс описывается программой. Эта программа
может быть написана на многих языках, но для удобства примем
общецелевой язык, такой, как Алгол, Фортран, PL/1, Кобол, Пас-
каль, Бэйсик или даже язык ассемблера. Программа представляет
два различных аспекта процесса: вычисление и управление. Вы-
числение связано с текущими арифметическими и логическими опе-
рациями, вводом и выводом, обычными манипуляциями над участ-
ками памяти и их содержимым. Управление же связано не со зна-
чениями или выполняемыми вычислениями, а только с порядком
их выполнения.
Сети Петри удачно представляют структуру управления про-
грамм. Сети Петри предназначены для моделирования упорядоче-
ния инструкций и потока информации, но не для действительного
вычисления самих значений. Модель системы по своей природе
является абстракцией моделируемой системы. Поэтому она игно-
рирует все возможные специфические детали. Если бы моделиро-
вались все детали, тогда модель была бы дубликатом моделируемой
системы, а не абстракцией.
Стандартный способ представления структуры управления про-
грамм — это блок-схемы. Блок-схема представляет поток управле-
ния в программе. Например, программа на рис. 3.21 представляет-
ся блок-схемой на рис. 3.22. Заметим, что блок-схема на рис. 3.22
не указывает конкретные вычисления, которые надо произвести,
а только определяет структуру программы. Такая блок-схема яв-
ляется абстрактной. Рис. 3.23 показывает, как можно проинтер-
претировать блок-схему (рис. 3.22) программы, представленной
на рис. 3.21. Каждая последовательная программа может быть
представлена в виде блок-схемы. Таким образом, показывая, как
58
Глава 3
begin
Input( _И]);
InputC y2)'-,
Уз : = 1;
while у j > о
do begin
if odd ( .у,)
then begin
Уз = Уз * Уъ
Л := Ji - 1;
end,
У 2 := У1 * У 2л
Ji := Ji - 2;
end;
Output ( j3);
end;
Рис. 3.21. Простая программа. Эта программа представлена блок-схемой на
рис. 3.22 п сетью Петри на рис. 3.25.
блок-схема может быть представлена сетью Петри, мы дадим пред-
ставление сетью Петри программы.
Оказывается блок-схема во многом подобна сети Петри: блок-
схема представима в виде узлов двух типов (принятия решения,
показанные ромбами, и вычисления, показанные прямоугольниками)
и дуг между ними. Удобный способ выполнения блок-схемы — вве-
дение фишки, которая представляет текущую инструкцию. По мере
выполнения инструкций фишка передвигается по блок-схеме. Из
сходства между графическими представлениями программы и сети
Петри может показаться, что для получения эквивалентной сети
Петри можно заменить узлы блок-схемы на позиции, а дуги — на
переходы. Такой подход использовался для превращения конеч-
ного автомата в сеть Петри (разд. 3.3.1).
Однако заметим, что в сети Петри действия моделируются перехо-
дами, тогда как в блок-схеме действия моделируются узлами. Кро-
ме того, если движение нашей фишки текущей инструкции в блок-
схеме нужно приостановить, это делается между узлами, на дугах,
а не внутри блока. Таким образом, правильный перевод блок-схемы
в сеть Петри заменяет узлы блок-схемы на переходы сети Петри,
а дуги блок-схемы — на позиции сети Петри. Каждая дуга блок-
схемы соответствует точно одной позиции в сети Петри. Узлы блок-
схемы представляются по-разному в зависимости от типа узла: вы-
числения или принятия решения. На рис. 3.24 иллюстрируются
Сети Петри для моделирования
59
Рис. 3.22. Блок-схема программы, изображенной на рис. 3.21.
Действие
а
b
с
d
е
Интерпретация
Inputfy,); Input (_у2); Уз ’•= 1;
П > О?
odd(y|) ?
Уз -=Уз* УъУ1 •= Ji - 1;
У2 = У? * Уъ У1 = У1 / 2;
Output (р3);
Рис. 3.23. Интер претация действий блок-схемы на рис. 3.22, представляющей
программу с рис. 3.21.
60
Глава 3
j а.
Вычисление
Рис. 3.24. Перевод узлов вычисления и принятия решения в блок-схеме в пе-
реходы в сети Петри.
оба способа перевода. На рис. 3.25 показан перевод блок-схемы на
рис. 3.22 в эквивалентную сеть Петри.
Необходимо сделать замечания относительно того, что означают
компоненты сети Петри на рис. 3.25. Что означают позиции? Для
ответа рассмотрим интерпретацию фишек блок-схемы счетчиком
команд. Фишка, находящаяся в позиции, означает, что счетчик
команд установлен на готовность выполнения следующей инструк-
ции. Каждая позиция имеет единственный выходной переход, за
исключением позиции, которая предшествует принятию решения;
такие позиции имеют по два выходных перехода, соответствующих
истинному и ложному значению предиката.
Переходы, очевидно, связываются с действиями программы:
вычислениями и принятиями решений. Для интерпретации сети
Петри необходимо интерпретировать каждый переход. Следует
также отметить, что переходы для вычислений имеют один вход
и один выход; переход, представляющий вычисления, не может на-
ходиться в конфликте, поскольку его входная позиция не является
входной для какого-либо другого перехода. Действие же, связанное
с принятием решения, вводит в сеть конфликт. Выбор способа раз-
решения конфликта либо недетерминирован, либо им можно управ-
лять извне (предсказателем, вычисляющим истинность или лож-
ность предиката и вынуждающим запуск нужного перехода). Раз-
личие между этими двумя способами разрешения конфликта —
методологический вопрос.
Сети Петри для моделирования
61
Рис. 3.25. Представление сетью Петри программы на рис. 3.21, полученное из
блок-схемы на рис. 3.22.
3.4.2. Параллелизм
Параллелизм (или одновременность) может быть введен несколь-
кими способами. Рассмотрим случай двух параллельных процессов,
каждый из которых может быть представлен сетью Петри. Таким
образом, составная сеть Петри, являющаяся просто объединением
сетей Петри для каждого из двух процессов, может представлять
одновременное выполнение двух процессов. Начальная маркиров-
ка составной сети Петри имеет две фишки, по одной в каждой сети,
представляя первоначальный счетчик команд процесса. Это вводит
параллелизм, который, однако, не является еще полезным.
Обычный подход основан на введении параллелизма в процесс в
вычислительной системе. Здесь имело место несколько предложе-
ний. Одно из них использует операции FORK и JOIN, впервые пред-
ложенные Деннисом и Ван Хорном [76]. Операция FORK /, выпол-
62
Глава .i
Рис. 3.26. Моделирование операций FORK п JOIN сетью Петри.
а — FORK, (выполняемая на участке i создает два новых процесса на участк к / и k),
б — JOIN (соединяет два процесса, которые заканчиваются на участка* i и >. и один
процесс, продолжающийся на участке k)
Рис. 3.27. Моделирование структуры parbegin Sl, Sz, •••> Sn parend в сети
Петри. Каждый квадрат есть представление сетью Петри утверждений Si,
S2 и т. д. Здесь иллюстрируется также иерархическая природа моделирова-
ния сетями Петри.
няемая в предложении i, приводит к одновременному выполнению
текущего процесса, начиная с предложения (i + 1), и вновь создан-
ного процесса — с предложения /. Операция JOIN соединяет два
процесса в один или, что равнозначно, уничтожает один из них.
Эти операции моделируются в сети Петри, как показано на рис. 3.26.
Другое предложение по введению параллелизма основано на
операциях parbegin и parend [79]. Структура управления была пред-
ложена Дейкстрой и имеет вид parbegin St; S2; Sn parend, где
Si — предложение. Смысл структуры parbegin!parend заключа-
ется в параллельном выполнении каждого из предложений Si, S2, ...
..., Sn. Эта конструкция может быть представлена сетью Петри, по-
казанной на рис. 3.27.
Cent Пегри дли моделирования
63
3.4.3. Синхронизация
Введение параллелизма полезно только в том случае, когда ком-
поненты процессов могуг взаимодействопать при получении реше-
ния задачи. Такое взаимодействие требует распределения ресурсов
между процессами. Для гарантии правильности работы системы
в целом распределением необходимо управлять. Проблемы синхро-
низации, возникающие при взаимодействии процессов, иллюстри-
руются многочисленными примерами, приведенными в литературе.
Среди задач синхронизации: задача о взаимном исключении [78],
производителе/потребителе [79], обедающих мудрецах [79], чге-
нии/записи [58] и др.
Эти задачи стали классическими в области синхронизации; каж-
дое новое предложение по механизму синхронизации должно решать
их. И хотя сети Петри представляют собой схему моделирования,
а не механизм синхронизации, они определенно способны модели-
ровать механизмы синхронизации. Мы представляем здесь некото-
рые решения в виде сетей Петри. Такое представление основано
частично на работе [56].
3.4.4. Задача о взаимном исключении
Предположим, что несколько процессов разделяют общую пере-
менную, запись, файл или другой элемент данных. Этот разделяе-
мый элемент данных может использоваться процессами различными
способами, упрощенно их можно классифицировать как чтение
значения элемента данных или запись нового значения. Эти две
операции являются часто единственными примитивными опера-
циями. Это означает, что для обновления разделяемого элемента
данных процесс должен сначала считать старое значение, затем вы-
числить новое и, наконец, записать его на то же место. Если два
процесса в одно и то же время пытаются выполнить такую последо-
вательность действий, то могут возникнуть трудности. Возможна
следующая последовательность:
1. Первый процесс считывает значение х из разделяемого объекта;
2. Второй процесс считывает значение х из разделяемого объекта;
3. Первый процесс вычисляет новое значение х = f(x);
4. Второй процесс вычисляет новое значение х" — g(x)-,
5. Первый процесс записывает х' в разделяемый объект;
6. Второй процесс записывает х" в разделяемый объект, уничтожая
значение х .
Результат вычисления первого процесса потерян, так как теперь
значением разделяемого объекта является g(x), в то время как им
Должно быть либо §(/(%)), либо f(g(x)). (Представьте себе, что^(х) —
«снять со счета х 1000 долл.», f(x) — «поместить на счет х 1000
Долл.», а процессы 1 и 2 — банковские операции.)
64
Глава 3
Рис. 3.28. Взаимное исключение. Управление доступом к критическим
секциям двух процессов осуществляется таким образом, что оба процесса не
могут одновременно выполнять свои критические секции.
Для предотвращения проблем такого рода необходимо обеспе-
чить механизм взаимного исключения. Взаимное исключение —
это метод создания таких программ, что одновременно не более чем
один процесс имеет доступ к разделяемому объекту данных. Участок
кода, в котором осуществляется доступ к разделяемому объекту и
который требует защиты от вмешательства других процессов, на-
зывается критической секцией. Идея состоит в том, что когда про-
цесс готов выполнить свою критическую секцию, он сначала ждет,
пока другой процесс не выполнит свою собственную критическую
секцию. Затем он «блокирует» доступ к критической секции, не
давая возможности никакому другому процессу войти в свою кри-
тическую секцию. Он входит в критическую секцию, выполняет ее
и, выйдя из нее, освобождает ее для доступа со стороны других про-
цессов.
Эта задача может быть решена сетью Петри, как показано на
рис. 3.28. Позиция т представляет собой разрешение для входа в
критическую секцию. Для того чтобы какой-либо процесс вошел в
критическую секцию, он должен иметь фишку в р^ или в р2 соот-
ветственно, свидетельствующую о желании попасть в критическую
Сети Петри для моделирования 65
секцию, а также должна существовать фишка в пг, дающая раз-
решение на вход. Если оба процесса пытаются войти в критическую
секцию одновременно, то переходы и t2 вступят в конфликт, и
только один из них сможет запуститься. Запуск Ц запретит переход
/2, вынуждая процесс 2 ждать, пока первый процесс выйдет из своей
критической секции и возвратит фишку обратно в позицию tn.
3.4.5. Задача о производителе/потребителе
В задаче о производителе/потребителе также присутствует сов-
местно используемый объект, но в этом случае разделяемый объект
точно определен и является буфером. Процесс-производитель соз-
дает объекты, которые помещаются в буфер. Потребитель ждет,
пока объект не будет помещен в буфер, удаляет его оттуда и исполь-
зует. Такая ситуация может быть промоделирована сетью Петри
так, как показано на рис. 3.29. Позиция В представляет собой бу-
фер, каждая фишка соответствует элементу данных, который про-
изведен, но еще не использован.
Один из вариантов этой задачи — это задача о нескольких про-
изводителях/нескольких потребителях. В этом случае несколько
производителей порождают элементы данных, помещаемые в общий
буфер, для нескольких потребителей. На рис. 3.30 представлено
решение этой задачи в виде сети Петри. Эта сеть совпадает с сетью
на рис. 3.29, за исключением того, что для представления s произ-
Рис. 3.29. Задача о производителе/потребителе, моделируемая сетью Петри.
3—562
66
Глава 3
Рис. 3.30. Задача о нескольких производителях/нескольких потребителях
(s производителей и t потребителей для фиксированных s и t).
Рис. 3.31. Задача о производителе/потребителе с ограниченным буфером-
Буфер, представленный позициями В и В', ограничен п ячейками.
Сети Петри для моделирования
67
д водителей и t потребителей мы начали выполнение сети с s фишка-
ми в начальной позиции процесса-производителя и t фишками в
:«i начальной позиции процесса-потребителя. Таким образом мы
представляем s производителей и t потребителей, реализуемых
’ реентерабельными совместно используемыми программами. Аль-
’ тернативой было бы дублирование программного кода для процес-
сов производителя и потребителя, однако результатом этого при
том же самом поведении была бы гораздо большая сеть.
В другом варианте задачи о производителе/потребителе исполь-
зуется буфер ограниченного размера. При такой постановке задачи
буфер между производителем и потребителем ограничен, т. е. имеет
только п ячеек для элементов данных. Следовательно, производи-
тель не может постоянно работать с той скоростью, которая ему нуж-
на, а вынужден ждать, если потребитель работает медленно и бу-
фер заполнен. На рис. 3.31 показано решение этой проблемы. Огра-
ничейному буферу сопоставляются две позиции: В представляет
< количество элементов данных, которые произведены, но еще не ис-
,< пользованы (число заполненных ячеек), В' — количество пустых
> ячеек в буфере. Первоначально В' имеет п фишек, а В фишек не
имеет. Если буфер заполнен, то В' фишек не имеет, а В имеет п
' фишек. Если теперь производитель попытается поместить еще один
элемент данных в буфер, то он будет остановлен, так как в В’ нет
фишки, делающей этот переход разрешенным.
3.4.6. Задача об обедающих мудрецах
Задача об обедающих мудрецах была предложена Дейкстрой в
[79] и связана с пятью мудрецами, которые попеременно то думали,
то ели. Мудрецы сидят за большим круглым столом, на котором
много блюд китайской кухни. Между соседями лежит одна палочка
» для еды. Однако для приема китайской пищи необходимо две палоч-
v ки, следовательно, каждый мудрец должен взять палочку слева
, и палочку справа: проблема, конечно, заключается в том, что если
все мудрецы возьмут палочки слева и затем будут яодать, когда
’ освободятся палочки с правой стороны, то они будут ждать вечно
И умрут от голода (состояние тупика).
На рис. 3.32 показано решение этой задачи с помощью сети
Петри. Позиции Cit ..., С6 представляют палочки для еды, и так
как каждая из них первоначально свободна, то в начальной мар-
кировке в каждой из этих позиций имеется фишка. Каждый мудрец
представлен двумя позициями Mt и £г для состояний размышления
и принятия пищи соответственно. Для того чтобы мудрец перешел
Из состояния размышления в состояние принятия пищи, обе па-
лочки (слева и справа) должны быть свободны. Это легко модели-
руется сетью Петри.
3‘*
Li
И
68
Глава 3
Рис. 3.32. Задача об обедающих мудрецах. Каждый мудрец представлен дву-
мя позициями: размышление (Alj), принятие пищи (£,).
3.4.7. Задача о чтении/записи
Существует несколько вариантов задачи о чтении/записи [58],
однако основная структура их остается неизменной. Имеются про-
цессы двух типов: процессы чтения и процессы записи. Все процес-
сы совместно используют общий файл или переменную или элемент
данных. Процессы чтения не изменяют объект в отличие от процес-
сов записи. Таким образом, процессы записи должны взаимно ис-
ключать все другие процессы чтения и записи, в то время как не-
сколько процессов чтения могут иметь доступ к разделяемым дан-
ным одновременно. Задача состоит в определении структуры управ-
ления, которая не приведет к тупику и не допустит нарушения
критерия взаимного исключения.
На рис. 3.33 иллюстрируется решение задачи в том случае,
когда количество процессов чтения ограничено величиной п. Если
в системе количество процессов чтения не ограничено, то только п
процессов могут выполняться в одно и то же время.
Проблема возникает в том случае, если количество процессов
чтения не ограничено и мы хотим предоставить возможность не-
I
Сети Петри для моделирования
69
« Рис. 3.33. Задача о чтении/записи в случае, когда число процессов чтения
ж ограничено величиной п. Первоначально имеются s процессов чтения и t иро-
да цессов записи.
| ограниченному количеству процессов читать одновременно. В^этом
I случае можно утверждать, что возникает необходимость хранения
количества читающих процессов. При инициализации каждого про-
f' цесса чтения в счетчик добавляется единица, а по окончании про-
i цесса единица вычитается. Это легко моделируется позицией, в
которой количество фишек равно количеству процессов чтения.
Т Однако, для того, чтобы предоставить процессу записи возможность
j- приступить к записи, необходимо, чтобы счетчик был нулевым,
, < т. е. соответствующая позиция была бы пустой. В сетях Петри нет
7’механизма, который бы осуществлял проверку на нуль неограни-
1 2 ченной позиции0. Таким образом, оказывается, что задача о чте-
f нии/записи с неограниченным числом процессов чтения не может быть
“„решена с помощью сетей Петри. Это первый случай, когда мы столк-
нулись с тем, что сети Петри не способны моделировать все системы.
* Этот вопрос заслуживает дальнейшего изучения (гл. 7).
3.4.8. Р- и V-системы
Большинство задач синхронизации не могут быть решены непо-
средственно сетями Петри, но разрешимы скорее на основе извест-
ных механизмов синхронизации. В частности, одним из самых по-
пулярных механизмов синхронизации являются Р- и V-операции
Над семафорами, впервые определенные Дейкстрой [79]. Семафор —
-Это элемент данных, который может принимать только неотрицатель-
ные целые значения. V-операция увеличивает значение на 1, а Р-
О Определения ограниченной и неограниченной позиций даны в гл. 4.—
Прим» ред.
70
Глава 3
операция уменьшает его на 1. P-операцию можно применять только
в том случае, когда значение семафора останется в результате не-
отрицательным; если же значение семафора равно 0, то Р-операция
должна ждать, пока какой-нибудь другой процесс не выполнит
V-операцию. Р- и V-операции определены как примитивные,
т. е. никакая другая операция не может изменять значение сема-
фора одновременно с ними.
Рис. 3.34. Моделирование Р-
и V-операций над семафором S.
Такие операции легко моделируются сетью Петри, как пока-
зано на рис. 3.34. Каждый семафор моделируется позицией, коли-
чество фишек в позиции показывает значение семафора. Р-опера-
ция использует позицию семафора в качестве входа, V-операция —
в качестве выхода.
Преимущество этого заключается в том, что многие системы про-
ектируются и описываются с помощью Р - и V-операций. Напри-
мер, в операционной системе Venus [179] Р- и V-операции являются
основным механизмом связи между процессами. Такие системы,
следовательно, можно промоделировать сетями Петри.
3.5. Другие системы
Описанные до сих пор системы относятся к самому очевидному
типу систем, моделируемых сетями Петри: аппаратному и про-
граммному обеспечению ЭВМ. Но в большей части эта «очевидность»
является результатом того, что сети Петри были определены и раз-
работаны главным образом для этой цели. Но они также приме-
нимы для моделирования большого числа других систем, совер-
шенно отличных от вычислительных систем. В этом разделе мы бег-
ло ознакомимся с некоторыми из них.
PERT-диаграмма давно используется для планирования боль-
ших проектов. PERT-диаграмма является графическим представле-
Сети Петри для моделирования
71
нием взаимосвязей между различными этапами, составляющими
проект. Проект представляет собой совокупность большого числа
этапов, при этом некоторые этапы должны завершиться прежде, чем
начнут выполняться другие. Кроме того, на выполнение каждого
этапа требуется определенное количество времени (иногда каждому
этапу соответствует три времени, соответствующие худшему, сред-
нему и лучшему случаям). Этапы графически представлены узла-
ми; дуги используются для отображения причинно-следственных
связей между ними.
PERT-диаграмма и сеть Петри взаимосвязаны: PERT-диаграм-
ма легко преобразуется в сеть Петри. Каждый этап PERT-диаграм-
мы представляется позицией, причинно-следственные связи — пере-
„ ходами. Диаграмма на рис. 3.35 может быть преобразована в экви-
валентную сеть Петри, изображенную на рис. 3.36.
Сеть Петри является превосходным средством для представления
। параллелизма и причинно-следственных связей PERT-диаграммы,
1но PERT-диаграмма предоставляет также информацию о времени,
используемую для определения минимального времени, необходи-
мого для выполнения проекта, —«время позднего начала» и т. д. Сеть
Петри не содержит такой информации. Добавление информации о
времени может придать сети новое мощное свойство, но это несов-
местимо с основными концепциями сетей Петри. Для такого рас-
ширения сетей Петри требуются дополнительные исследования
[277, 117].
Конвейерная обработка, описанная в разд. 3.3.2, является част-
ft ным случаем производственной системы [107]. Сборочная линия —
I другой пример производственной системы. Производственные систе-
| мы и сборочные линии могут быть промоделированы сетями Петри.
I Одно из первых применений сетей Петри — применение в ка-
S честве средства генерации оптимального кода для компилятора с
ff Фортрана CDC 6600. Подход к решению этой задачи, предложенный
Р [274], заключался в моделировании программы на Фортране
«сетью Петри способом, подобным моделированию блок-схемы
®(разд. 3.4.1). Затем отдельные операторы программы рассматри-
вались с целью определения минимального набора причинно-след-
i’ ственных связей между операторами, позволяя исключать из сети
• Петри некоторые из искусственно введенных ограничений на по-
11 следовательность операторов программы. Эти искусственные ограни-
чения введены из-за необходимости для программиста представ-
лять программу на Фортране в виде последовательности, задающей
полный порядок на множестве операторов, даже если требуется
только частичное упорядочение. В качестве примера рассмотрим
следующие три оператора:
10х’= х + 1,
20у = г/+1,
30 2 = X + у.
72
Глава 3
Водо-
отводные
канавы
Нивели-
рование
Благо-
устройство
территории
Начало
Идентификация
Котлован
Фундамент
Водопровод
f, 1
d.4
i.2
k, 10
Покраска
Окончание
Окончательные
электроработы
Штукатурные
работы
Водосточные
желоба
Окончательные
слесарно-
Водопроводные
работы
Продол-
жительность
Выполнения
работы
тия
Окончательная
отделка
Коионное
опору- 1т .
оовиние\.т'1
Р’2
Отоп-
ение
е. 6
полов
ч. 1
Рис. 3.35. PERT-диаграмма строительства дома. (Ф. Леви, Г. Томпсон, Дж.
Уист «Введение в метод критических путей», в Industrial Scheduling, edited
by John F., Muth and Gerald L. Thompson, copyright 1963, p. 335. С разреше-
ния Prentice-Hall, Inc., Englewood Cliffs, New Jersey.)
Деревянный
Кирпич- каР*ас
ная
кладка
Оконча-
тельная
обшиб,
крыши
Примерная
прокладка
злектро-
роводов
Окончательный
настил полов
деревом
Лакиро-
вание
Спецификация
работы
Между-
тажные
перекры;
Начальные
Ь, 3) слесарно-
Водои/Говодные
работы
Сети Петри для моделирования
73
Рис. 3.36. Представление PERT-диаграммы иа рис. 3.35 сетью Петри. Обра-
тите внимание на то, что введены дополнительные узлы. Онн необходимы для
адекватного отображения ограничения предшествования и точного представ-
ления ситуаций с ожиданием.
74
Глава 3
Рис. 3.37. Сеть Петри, представляющая несколько последовательностей вы-
полнения инструкции.
Они написаны таким образом, что оператор 10 предшествует опера-
тору 20, но такая последовательность вовсе необязательна. Поря-
док, в котором будут выполнены операторы 10 и 20 (или они будут
выполнены одновременно), не имеет значения для программы. Од-
нако оператор 30 должен следовать только после операторов 10 и
20. После изменения упорядочения операторов необходимо рас-
смотреть и поток управления. Этот анализ заключается в примене-
нии условий Бернстайна для обеспечения детерминированности.
Результатом такого анализа являегся сеть Петри, представляю-
щая программу с минимальными ограничениями на последователь-
ность операюров, т. е. допускающую максимальный параллелизм.
Теперь задача состоит в компиляции такой программы. Это требует
отображения переменных в регистры и упорядочения инструкций
для получения полностью упорядоченной последовательности ин-
струкций машинного языка* >. CDC 6600 — это ЭВМ с несколькими
регистрами и кратными функциональными блоками (разд. 3.3.3).
Так как функциональные блоки могут выполнять различные ин-
струкции параллельно, то очень важно порождать инструкции в
порядке, максимально увеличивающем параллелизм при работе
функциональных блоков. На это также влияет распределение пере-
менных по регистрам. Сеть Петри, моделирующая программу и
представляющая ограничения, налагаемые программой, объединя-
ется с сетью Петри, моделирующей устройство управления CDC
6600 и представляющей ограничения, налагаемые аппаратным обе-
спечением. Такая объединенная сеть представляет все возможные
последовательности инструкций, которые могут выполняться ап-
паратурой и реализовать алгоритм данной программы. Эта сеть
затем выполняется для получения всех таких последовательностей
инструкций. Две (или более) последовательности образуются вся-
*) Некоторые из которых являются инструкциями, реализующими парал-
лельную обработку. — Прим. ред.
Сети Петри для моделирования 75
кий раз, когда два (или более) перехода одновременно разрешены.
Запуск одного перехода будет порождать одну последовательность;
запуск другого перехода — другую. Например, сеть Петри на
рис. 3.37 представляв! последовательности abcdef, bacdef, abcedf,
bacedf. После того как последовательности получены, вычисляются
необходимые затраты времени на их выполнение, и наиболее быст-
рая последовательность генерируется компилятором для действи-
тельного выполнения.
Рис. 3.38. Сеть Петри, пред-
ставляющая окислительно-вос-
становительную реакцию меж-
ду щавелевой кислотой и пе-
роксидом водорода, в резуль-
тате которой получаются вода
и диоксид углерода.
Химические системы — другой пример систем, которые могут
быть промоделированы сетями Петри. Химические уравнения моде-
лируются переходами; вещества, участвующие в реакции, — по-
зициями. Количество фишек в позиции указывает на количество
данного вещества в системе. Например, сеть Петри на рис. 3.38
представляет два химических уравнения:
Н2С2О4 -* 2СОа + 2Н+ + 2е~
2е" + 2Н+ + Н2О2 -> 2НаО.
Можно представить и реакции катализа. Соединение водорода и
этилена образует этан (Н2 + С2Н4 -> С2Н6) только в присутствии
платины. Это отражено на рис. 3.39.
Мельдман и Хольт [186] выдвинули предположение, что и юри-
дические системы могут быть промоделированы сетями Петри.
В этих системах несколько действующих лиц (судьи, адвокаты, об-
виняемые, клерки и др.) могут одновременно выполнять действия,
относящиеся к конкретному длпу. Действия и их взаимосвязи могут
быть представлены сетью Петри. Например, сеть Петри на рис. 3.40
является моделью начальных стадий гражданского процесса.
76
Глава 3
Другое предложение заключается в использовании сетей Петри
для моделирования и анализа протоколов связи [194]. В сетях ЭВМ
и системах распределенных процессов необходима возможность пе-
редачи информации между ЭВМ. В этой задаче существенно при-
сутствует параллелизм, и поэтому она попадает в класс задач, для
которых определены сети Петри. Фарбер и его ученики [193, 250,
195, 251] разработали методологию для спецификации, проектиро-
вания и анализа простых протоколов связи, используя сети Петри
и подобные модели.
Рис. 3.39. Процесс получения
этана из водорода и этилена
при катализации платиной.
Другие системы, которые могли быть промоделированы сетями
Петри, включают в себя системы очередей (где очереди были бы
представлены позициями, а работы — фишками); модели мозга
(запуски нейронов могли бы моделироваться запусками переходов);
исчисление высказываний [88, 91] (позиции представляют буквы,
а переходы объединяют их для определения предложений в конъ-
юнктивной нормальной форме) и многие другие системы. Этот спи-
сок ограничен в основном временем и воображением человека, но
не свойствами сетей Петри.
Однако мы видели по крайней мере один пример (задача о чте-
нии/записи), который нельзя промоделировать с помощью сети
Петри. И хотя моделирование с помощью сетей Петри может быть
полезным при описании системы, необходимо разработать средства
анализа, которые бы позволили исследовать сеть Петри и определить
ее свойства. Обратимся к этому в следующей главе, в которой
представлены методы анализа сетей Петри.
Упражнения)
1. Промоделируйте вычислительную систему с тремя процессами и четырьмя
ресурсами: устройство чтения с карт, построчно печатающее устройство, диск
и два раздела памяти. Любой процесс может попасть в любой раздел. Исполь-
зование ресурсов тремя процессами состоит в следующем:
а) процесс 1 запрашивает устройство чтения с карт и построчно печата-
ющее устройство, а затем освобождает оба этн ресурса;
Сети Петри для моделирования
77
Клерк Выписывает вызов 6 суд
₽ис. 3.40. Сеть Петри, представляющая начальные стадии гражданского
Процесса. (Из [186], авторское право Американской ассоциации юристов,
’Отделение науки и технологии. Перепечатывается с разрешения.)
78
Глава 3
б) процесс 2 запрашивает устройство чтения с карт и диск, а затем осво-
бождает устройство чтения с карт, запрашивает построчно печатающее уст-
ройство и в конце концов освобождает и построчно печатающее устройство, н
диск;
в) процесс 3 требует все трн ресурса одновременно, и затем все нх осво-
бождает.
3.6. Замечания к литературе
Большинство исследований по сетям Петри связано с анализом,
а не с моделированием. Обзоры применений сетей Петри к модели-
рованию появились в работах [238, 6]. Моделирование аппарат-
ного обеспечения рассматривалось в [72, 132]. В работе [2741 для
реализации компилятора объединено моделирование аппаратного
и программного обеспечения. Заметки [56] связаны с моделировани-
ем программных систем сетями Петри. В диссертационной работе
Хэка [107] рассматривается моделирование производственных про-
цессов, которые включают системы типа сборочных линий.
Баер и Эллис [22] использовали сети Петри для моделирования
компилятора, а Ное [2141 и Бест [36, 37]—для моделирования
операционных систем. Ное и Кель [2231 промоделировали аппарат-
ное обеспечение вычислительной системы, Азема и др. [16, 17], Фу
и Масгрэйв [83] предложили использовать сети Петри для автома-
тизации проектирования.
Исследования Ное и Натта главным образом направлены на мо-
делирование систем для определения производительности. Их ра-
боты [214, 226, 227, 224] в конце концов привели к разработке мо-
дели Е-сетей, которая связана с сетями Петри.
3.7. Темы для дальнейшего изучения
1. Примените моделирование сети Петри для описания взаимодей-
ствия субатомных частиц в физике высоких энергий.
2. PERT-диаграммы обычно содержат информацию о времени со-
бытий. Исследуйте, каким образом можно добавить информацию
о времени в сеть Петри. Как повлияет это на правила запуска? Пред-
ложите алгоритм для вычисления минимального (максимального)
времени, требующегося для окончания процесса.
3. Выберите любую из следующих тем и исследуйте применение
сетей Петри для моделирования по темам:
а) системы операций;
б) моделирование мозга;
в) химические реакции;
г) военный конфликт;
д) политические системы;
е) экономика (в особенности макроэкономические события);
ж) транспортные потоки на дорогах и шоссе;
з) биологические популяции;
и) семантические сети для представления естественного языка.
ГЛАВА 4
АНАЛИЗ СЕТЕЙ ПЕТРИ
В предыдущей главе была продемонстрирована моделирующая мощность
сетей Петри. С помощью сетей Петри можно моделировать широкий класс сис-
тем, представляя должным образом взаимодействие различных процессов,
которые могут возникнуть. Наиболее сильны сети Петри при моделировании
систем, включающих параллельные действия, причем параллельность мо-
делируется естественным и удобным образом. Сети Петри можно использовать
для представления и сообщения о проекте параллельной системы.
Однако само моделирование малополезно. Необходимо провести анализ
' моделируемой системы. Этот анализ, можно надеяться, приведет к глубокому
проникновению в поведение моделируемой системы. Таким образом, мы по-
; дошли к необходимости рассмотрения методов анализа сетей Петри. Несколь-
ко методов анализа уже разработано, однако в области анализа сетей Петри
; существует еще много проблем. Для того чтобы лучше оценить разработанные
1’ методы анализа, рассмотрим прежде всего типы задач, которые требуют реше-
1 ния. Цель анализа сети Петри — получение ответа на вопрос о конкретной
сети Петри. Какие же вопросы о сети Петри можно задать?
' 4.1. Задачи анализа сетей Петри
В публикациях по сетям Петри рассмотрены следующие свойства
। и вопросы. (Здесь мы определим и проиллюстрируем эти свойства,
/ а во второй части главы приведем соответствующие методы ана-
L лиза.)
| 4.1.1. Безопасность
ж Одно из важнейших свойств сети Петри, которая должна моде-
KV лировать реальное устройство, — безопасность. Позиция сети Пет-
« ри является безопасной, если число фишек в ней никогда не превы-
’’ шает 1. Сеть Петри безопасна, если безопасны все позиции сети.
Определение 4.1. Позиция OiQP сети Петри С= (Р, Т, I, О)
с начальной маркировкой р является безопасной, если р'(рг) < 1
’ Для любой р' £ Р(С, р). Сеть Петри безопасна, если безопасна
Каждая ее позиция.
Безопасность — очень важное свойство для устройств аппарат-
ного обеспечения. Если позиция безопасна, то число фишек в ней
равно 0 или I. Следовательно, позицию можно реализовать одним
Триггером.
В первоначальном определении сети Петри были безопасны,
поскольку переход не мог быть запущен, если не все из выходных
80
Глава 4
позиций были пусты (а кратные дуги не были разрешены). Это объ-
яснялось интерпретацией позиции как условия. Условие, будучи
логическим высказыванием, либо истинно (представляется фишкой
в позиции), либо ложно (представляется отсутствием фишки);
кратные фишки не имеют никакой интерпретации. Таким образом,
если интерпретировать сети как условия и события, маркировка
каждой позиции должна быть безопасной.
Если позиция не является кратной входной или кратной выход-
ной для перехода, ее можно сделать безопасной. К позиции *рг,
которую необходимо сделать безопасной, добавляется новая пози-
ция p't. Переходы, в которых pt используется в качестве входной
или выходной, модифицируются следующим образом:
Если Pi€I(tj} и PitO(t}), тогда добавить р'( к
Если Pt G и Pt $ I (t j), тогда добавить p'. к
Цель введения этой новой позиции pt — представить условие
«pi пуста». Следовательно, piYipi дополнительны; pt имеет фишку,
только если р,- не имеет фишки и наоборот. Любой переход, удаля-
Рис. 4.2. Безопасная сеть Петри, эквивалентная сети, приведенной на
рис. 4.1.
Анализ сетей Петри
81
[ ющий фишку из pt, должен помещать фишку в pt-, а всякий пе-
’ реход, удаляющий фишку из pi, должен помещать фишку в р^
I Начальная маркировка также должна быть модифицирована для
, обеспечения того, чтобы точно одна фишка была либо в pt, либо
s в р'.. (Мы допускаем, что начальная маркировка безопасна.) За-
метим, что такая принудительная безопасность возможна только для
позиций, которые в начальной маркировке являются безопасными
и входная и выходная кратность которых равна О или 1 для всех
1 переходов. Позиция, имеющая для некоторого перехода выходную
кратность 2, будет получать при его запуске две фишки и, следова-
тельно, не может быть безопасной. Простая сеть Петри на рис. 4.1
преобразована в безопасную, как показано на рис. 4.2.
s 4.1.2. Ограниченность
<< Безопасность — это частный случай более общего свойства
ограниченности. Некоторые соображения относительно реального
ограничения на аппаратную реализацию позиций позволяют прий-
ти к заключению, что безопасность — необязательное требование.
Безопасность позволяет реализовать позицию триггером, но в бо-
f лее общем случае можно использовать счетчик. Однако любой
% аппаратно-реализованный счетчик ограничен по максимальному
Л числу, которое он может представить. Позиция является k-безопас-
ной или k-ограниченной, если количество фишек в ней не может
превышать целое число k.
Определение 4.2. Позиция piQP сети Петри С= (Р, Т, I, О)
с начальной маркировкой р, является k-безопасной, если у'(рг) < k
'Д для всех р,' £ R(C, р).
Ц 1-безопасная позиция называется просто безопасной. Заметим,
& что граница k' по числу фишек, которые могут находиться в пози-
ции, может быть функцией от позиции (например, позиция р± мо-
'♦ жет быть 3-безопасной, тогда как позиция р2 — 8-безопасной).
% Однако, если позиция pt Л-безопасна, то она также и ^'-безопасна
Для всех k' > k. Поскольку число позиций конечно, можно выбрать
* k, равное максимуму из границ каждой позиции, и определить сеть
‘ Петри ^-безопасной, если каждая позиция сети /г-безопасна.
Иногда нас будет интересовать только то, является число фи-
• тек в позиции ограниченным или нет, а не конкре1ное значение
границы. Позиция называется ограниченной, если она ^-безопасна
Для некоторого k\ сеть Петри ограниченна, если все ее позиции огра-
ниченны. Ограниченную сеть Петри можно реализовать аппарат-
но, тогда как сеть Петри с неограниченными позициями в общем
случае реализовать аппаратно нельзя. (Вспомним, что эти опреде-
, ления не зависят от интерпретации. В реализации позиция может
представлять некоторый объект, являющийся ограниченным, хотя
сама структура сети не отражает этот факт.)
*6
82
Глава 4
4.1.3. Сохранение
Сета Петри можно использовать для моделирования систем
распределения ресурсов. Например, сеть Петри может моделиро-
вать запросы, распределения и освобождения устройств ввода/вы-
вода в вычислительной системе. В этих системах некоторые фишки
могут представлять ресурсы. Группа из трех построчно печатаю-
щих устройств представляется позицией, имеющей в начальной мар-
кировке три фишки. Запрос построчно-печатающего устройства —
это переход, для которого данная позиция является входной; затем
устройство освобождается переходом, для которого позиция по-
строчно печатающих устройств является выходной.
Для сетей Петри такого типа помимо прочих важным свойством
является сохранение. Нам бы хотелось показать, что фишки, пред-
ставляющие ресурсы, никогда не создаются и не уничтожаются.
Простейший способ сделать это — потребовать, чтобы общее число
фишек в сети оставалось постоянным.
Определение 4.3. Сеть Петри С — (Р, Т, I, О) с начальной
маркировкой р. называется строго сохраняющей, если для всех
р G р)
S p'(pt)== S Мр,).
р^р
Строгое сохранение — это очень сильное ограничение. На-
пример, из него немедленно следует, «что число входов в каждый
переход должно равняться числу выходов, \I(t[ = |0(/ Д|. Если
бы это было не так, запуск перехода изменил бы число фишек в сети.
Однако для более общего представления о свойстве сохранения
рассмотрим рис. 4.3. Изображенная на нем сеть Петри не является
строго сохраняющей, поскольку запуск перехода или f2 умень-
шит число фишек на 1, а запуск перехода £3или /4 добавит фишку к
маркировке. Мы можем тем не менее преобразовать эту сеть Петри
в сеть на рис. 4.4, являющуюся строго сохраняющей.
Сеть Петри должна сохранять ресурсы, которые она моделирует.
Однако взаимно однозначного соответствия между фишками и ре-
сурсами нет. Фишка может представлять и один программный
счетчик или какой-нибудь другой элемент и может представлять
несколько ресурсов сразу. Во втором случае фишка позже исполь-
зуется для создания кратных фишек (по одной на ресурс) путем
запуска перехода с большим числом выходов, чем входов. В общем
следует определить взвешивание фишек. Взвешенная сумма для всех
достижимых маркировок должна быть постоянной. Фишкам, не
являющимся важными, можно присвоить вес 0; другим фишкам
можно присвоить веса 1,2,3 или любое другое целое. (Допустимы
рациональные веса, поскольку для определения целого взвешива-
ния такое взвешивание можно умножить на общее кратное. Ирра-
циональные веса не представляются необходимыми.)
Анализ сетей Петри
83
t
4
4,1
Г1
Рис. 4.3. Сеть Петри, не являющаяся строго сохраняющей.
Рис. 4.4. Строго
Иа рис. 4.3.
сохраняющая сеть Петри, эквивалентная сети, изображенной
84
Глава 4
Фишка определяется ее позицией в сети, все фишки в позиции
неразличимы. Следовательно, веса связываются с каждой пози-
цией сети. Вектор взвешивания w = (wt, w2, ..., &уп) определяет вес
wt для каждой позиции pt£P.
Определение 4.4. Сеть Петри С — (Р, Т, I, О) с начальной мар-
кировкой р называется сохраняющей по отношению к вектору
взвешивания w, w = (ш4, ш2, ..., wn), п — |Р|, wt > 0, если для
всех р' £ Р(С, р)
Z • р' (Л-) = • Р (Л)»
I I
Строго сохраняющая сеть Петри является сохраняющей по от-
ношению к вектору взвешивания (1, 1, ..., 1). Все сети Петри яв-
ляются сохраняющими по отношению к вектору взвешивания
(О, 0, ..., 0). Этот факт вносит в теорию некоторую нестройность,
поскольку нам бы хотелось определить сеть Петри как сохраняю-
щую, если она является сохраняющей по отношению к некоторому
вектору взвешивания. Однако, так как всякая сеть Петри является
сохраняющей по отношению к нулевому вектору, такое определе-
ние не является удовлетворительным. Таким образом, сеть Петри
называется сохраняющей, если она сохраняющая по отношению
к некоторому положительному ненулевому вектору взвешивания
w > 0 (с положительными ненулевыми весами, wt > 0).
Сеть Петри с рис. 4.3 является поэтому сохраняющей, посколь-
ку она сохраняющая по отношению к (1, 1, 2, 2, 1). Сеть Петри с
рис. 4.5 не является сохраняющей.
Рис. 4.5. Несохраняющая сеть Петри.
Анализ сетей Петри
85

Рис. 4.6. Распределение ресурсов для случая двух процессов (ей t) и двух
ресурсов (д (моделируется р«) и г (моделируется р5)).
4.1.4. Активность
Причиной рассмотрения сохранения в сети Петри было распре-
i деление ресурсов в операционной системе ЭВМ. Другая задача,
5 которая может возникнуть при распределении ресурсов вычисли-
1 тельной системы — тупики. Тупики служат предметом многих
исследований в области вычислительной техники [119]. Лучше
$ всего иллюстрирует задачу простой пример. Рассмотрим систему,
К включающую два различных ресурса q и г и два процесса а и Ь. Если
г, оба процесса нуждаются в обоих ресурсах, им необходимо будет
ж совместно использовать ресурсы. Для выполнения этого потребуем,
чтобы каждый процесс запрашивал ресурс, а затем освобождал
$ .его. Теперь предположим, что процесс а сначала запрашивает ре-
< суре q, затем ресурс г и, наконец, освобождает и q, и г. Процесс
i Ь работает аналогично, но сначала запрашивает г, а затем q. Сеть
Петри на рис. 4.6 иллюстрирует два процесса и распределение
«' Ресурсов между ними.
86
Глава 4
Начальная маркировка помечает ресурсы q(p^ и г(р5) доступ-
ными и указывает на готовность процессов а и Ь. Одним выполне-
нием этой сети является Другим — Ни одно из
этих выполнений не приводит к тупику. Однако рассмотрим после-
довательность, которая начинается переходами /1т t±. процесс а об-
ладает ресурсом q и хочет получить г, процесс Ъ обладает г и хочет
получить q. Система заблокирована; никакой процесс продолжать-
ся не может.
Тупик в сети Петри — это переход (или множество переходов),
которые не могут быть запущены. В сети Петри на рис. 4.6. тупик
возникает, если нельзя запустить переходы и f5. Переход назы-
вается активным, если он не заблокирован (нетупиковый). Это
не означает, что переход разрешен, скорее он может быть разре-
шенным. Переход tj сети Петри С называется потенциально запу-
стимым в маркировке р, если существует маркировка [*' € R(C, р),
в которой t j разрешен. Переход активен в маркировке р, если по-
тенциально запустим во всякой маркировке из R(C, р). Следова-
тельно, если переход активен, то всегда возможно перевести сеть
Петри из ее текущей маркировки в маркировку, в которой запуск
перехода станет разрешенным.
Существуют другие, связанные с активностью понятия, которые
рассматривались при изучении тупиков [53]. Их можно разбить на
категории по уровню активности и определить для сети Петри С с
маркировкой р следующим образом:
Уровень 0: Переход tj обладает активностью уровня 0, если он
никогда не может быть запущен.
Уровень 1: Переход tj обладает активностью уровня 1, если
он потенциально запустим, т. е. если существует такая р' G R{C, р),
что tj разрешен в р.'.
Уровень 2: Переход tj обладает активностью уровня 2, если для
всякого целого п существует последовательность запусков, в кото-
рой tj присутствует по крайней мере п раз.
Уровень 3: Переход tj обладает активностью уровня 3, если
существует бесконечная последовательность запусков, в которой
tj присутствует неограниченно часто.
Уровень 4: Переход tj обладает активностью уровня 4, если
для всякой р' € R(C, р) существует такая последовательность
запусков о, что tj разрешен в б(р', о).
Переход, обладающий активностью уровня 0, называется пас-
сивным. Переход, обладающий активностью уровня 4, называется
активным. Сеть Петри обладает активностью уровня i, если каж-
дый ее переход обладает активностью уровня i.
В качестве примера, иллюстрирующего уровни активности,
рассмотрим сеть Петри на рис. 4.7. Переход tG не может быть за-
пущен никогда; он пассивен. Переход можно запустить точно
один раз; он обладает активностью уровня 1. Переход /2 может быть
запущен произвольное число раз, но это число зависит от числа
Анализ сетей Петри
87
запусков перехода /3. Если мы хотим запустить t2 пять раз, мы
запускаем пять раз t3, затем /4 и после этого пять раз t2. Однако,
как только запустится /4 (Z4 должен быть запущен до того, как будет
запущен число возможных запусков t2 станет фиксированным.
Следовательно, t2 обладает активностью уровня 2, но не уровня 3.
С другой стороны, переход ts можно запускать бесконечное число
раз, и поэтому он обладает активностью уровня 3, но не уровня 4,
поскольку, как только запустится /4, t3 больше запустить будет
нельзя.
Рис. 4.7. Сеть Петри, иллю-
стрирующая различные уров-
ни активности.
4.1.5. Достижимость и покрываемость
Большинство задач, к которым мы до сих пор обращались,
касаются достижимых маркировок. Задача достижимости являет-
ся, по-видимому, наиболее простой (для формулировки).
Определение 4.5. Задача достижимости. Для данной сети Петри
С с маркировкой р и маркировки р' определить: р' £ R(C, р)?
Задача достижимости, быть может, основная задача анализа
сетей Петри; многие другие задачи анализа можно сформулировать
в терминах задачи достижимости. Например, для сети Петри с
рис. 4.6 тупик может возникнуть, если достижимым является со-
стояние (0, 1, 0, 0, 0, 0, 1, 0).
На рис. 4.8 показана сеть Петри, цель которой заключается в
решении задачи о взаимном исключении, — предполагается, что
позиции д4 и р9 будут взаимно исключающими. Мы хотим знать,
является ли какое-либо состояние с р(р4) > 1 и р(р9) >• 1 достижи-
мым. Эта задача аналогична достижимости, но несколько отлича-
ется; она называется задачей покрываемости. Маркировка р" пок-
рывает маркировку р', если р" > р'.
88
Глава 4
Рис. 4.8. Представление сетью Петри «решения» Химана задачи о взаимном
исключении [134]. Вследствие постоянного использования позиций kO, kl,
bl и ЬО они для удобства продублированы в графе, представляющей сеть. Все
позиции, помеченные kO, являются одной позицией.
Анализ сетей Петри
89
| Определение 4.6. Задача покрываемости. Для данной сети Петри
» С с начальной маркировкой р и маркировки у/ определить, сущест-
I вует ли такая достижимая маркировка р" С R(C, р), что у," > р'.
5 В других возможных задачах типа достижимости могло бы игно-
Т рироваться содержимое некоторых позиций и приниматься во вни-
мание сравнение или покрытие содержимого нескольких важных
позиций. Например, в сети Петри на рис. 4.8 наш интерес огра-
$ ничен позициями р4 и р9 — маркировка остальных позиций не
v важна. Таким образом, мы можем рассматривать достижимость и
® покрываемость «по модулю» множества позиций. Эти задачи назы-
« ваются задачами достижимости подмаркировки и покрываемости
У; подмаркировки.
л) Их можно еще более усложнить требованием, определить floc-
s’ тижимость и покрываемость для множества маркировок, придя
ж к задачам достижимости множества и покрываемости множества.
Ж Однако, если множество конечно, задачи можно решить обычно
w многокРатным решением задач достижимости и покрываемости
Ж для одной маркировки.
4.1.6. Последовательности запусков
Другой, предложенный к анализу подход основан не на пози-
ЯЬ циях, а на последовательностях запусков переходов, т. е. связан
Ж с активностью, поскольку уместен вопрос: может ли переход быть
Е запущен (иначе, не является ли он пассивным)? В более общем
® случае можно потребовать определить, возможна ли заданная по-
ж' следовательность запусков переходов или возможна ли какая-либо
Л, последовательность из множества последовательностей запусков.
В сети Петри на рис. 4.8, например, взаимное исключение было бы
нарушенным, если бы могла осуществиться последовательность
w ^9 или f4f10, или, более общо, если бы могла возникнуть последо-
* вательность taot9, где а — произвольная последовательность за-
Г пусков, не включающая /4. Эти вопросы анализа приводят к поня-
*. тию языков сетей Петри и будут исследованы более детально в
У гл- 6.
I *
4.1.7. Задачи эквивалентности и подмножества
, Последний класс задач порожден соображениями оптимизации.
। Пусть сети Петри присуще некоторое поведение, определяемое ее
I множеством последовательностей запусков переходов или ее мно-
, жестком достижимости. Можно ли изменить (оптимизировать) сеть
Петри, не изменяя ее поведения? Изменение означает удаление
| ? пассивных переходов (которые никогда нельзя запустить), или пас-
। сивных позиций (которые никогда не могут быть маркированы),
1 А или переопределение некоторых переходов. Можно ли показать,
90
Глава 4
что две различные маркированные сети Петри с одинаковым числом
переходов (но с различным числом позиций) будут порождать одина-
ковые последовательности запусков переходов или что две различные
маркированные сети Петри с одинаковым числом позиций (но с раз-
личным числом переходов) будут порождать одно множество дости-
жимости? Это позволило бы нам модифицировать сети Петри для
увеличения параллелизма, уменьшения стоимости реализации или
улучшения других оптимизируемых функционалов.
В этих случаях мы затрагиваем проблему определения того,
являются ли две сети Петри эквивалентными или является ли
одна из них подмножеством другой. Для точного определения по-
нятия эквивалентности или включения необходимо быть особенно
внимательным. Если мы определим эквивалентность как равенство
множеств достижимости, тогда нельзя будет изменять число пози-
ций, если потребуем равенства множеств последовательностей —
нельзя будет изменять переходы. Поэтому определение задачи,
которое мы дадим, исключительно важно.
4.2. Методы анализа
Задачи, которые были представлены здесь, являются наиболее
общими, тем не менее существует множество других задач, решение
которых может потребоваться для сетей Петри. Можно ли разра-
ботать методы анализа сетей Петри для решения этих задач? При-
чем нас интересуют особенно те методы, которые легко реализо-
вались бы на ЭВМ, что важно для осуществления автоматического
анализа моделируемых систем.
В этом разделе мы представим два основных метода анализа
сетей Петри, которые описывают механизмы решения некоторых
из уже перечисленных задач. Первый метод анализа, используемый
для сетей Петри, — это дерево достижимости, второй метод ^свя-
зан с матричными уравнениями. Обсудим каждый из них.
4.2.1. Дерево достижимости
Дерево достижимости представляет множество достижимости
сети Петри. Рассмотрим, например, маркированную сеть" Петри
на рис. 4.9. Начальная маркировка ее — (1, 0, 0). В этой началь-
ной маркировке разрешены два перехода: U и t2. Поскольку мы хо-
тим рассмотреть все множества достижимости, определим новые
вершины в дереве достижимости1) для (достижимых) маркировок,
получающихся в результате запуска каждого из этих двух пере-
ходов. Дуга, помеченная запускаемым переходом, приводит из
начальной маркировки к каждой из новых маркировок (рис. 4.10).
О Корневой (начальной) является вершина, соответствующая началь-
ной маркировке. — Прим, перев.
Анализ сетей Петри
91
Это (частичное) дерево показывает все маркировки, непосредствен-
но достижимые из начальной маркировки.
Теперь необходимо рассмотреть все маркировки, достижимые из
новых маркировок. Из маркировки (1, 1,0) можно снова запустить
ti (получая 1, 2, 0) и /2 (получая (0, 2, 1)); из (0, 1, 1) можно за-
пустить /3 (получая (0, 0, 1)). Это порождает дерево, изображенное
на рис. 4.11. Начиная с трех новых маркировок, необходимо пов-
торить этот процесс, порождая новые маркировки, которые нужно
1 Рис. 4.9. Маркированная сеть Пет- Рнс. 4.10. Первый шаг построения
ри, для которой строится дерево до- дерева достижимости.
,i стижимости.
ввести в дерево, как показано на рис. 4.12. Заметим, что марки-
ровка (0, 0, 1) пассивная; никакой переход в ней не является раз-
решенным, поэтому никакие новые маркировки из этой пассивной
1 маркировки в дереве порождаться не будут. Кроме того, необхо-
у димо отметить, что маркировка (0, 1, 1), порождаемая запуском
эд /з в (0, 2, 1), была уже порождена непосредственно из начальной
§ маркировки запуском /2.
Если эту процедуру повторять снова и снова, каждая достижи-
’> мая маркировка окажется порожденной. Однако получившееся
(1,0,0)
Рис. 4.11. Второй шаг построения дерева достижимости.
92
Глава 4
Рис. 4.12. Третий шаг построения дерева достижимости.
дерево достижимости может оказаться бесконечным. Будет порож-
дена каждая маркировка из множества достижимости, поэтому для
любой сети Петри с бесконечным множеством достижимости соот-
ветствующее дерево также должно быть бесконечным. Даже сеть
Петри с конечным множеством достижимости может иметь беско-
нечное дерево (рис. 4.13). Дерево представляет все возможные
последовательности запусков переходов. Всякий путь в дереве, на-
чинающийся в корне, соответствует допустимой последовательности
переходов. Для превращения дерева в полезный: инструмент анали-
за необходимо найти средства ограничения его до конечного разме-
ра. (Заметим, что если какое-то представление бесконечного мно-
жества конечно, то бесконечное множество маркировок должно
отображаться в такое представление. В общем случае это приведет
к потере информации и, возможно, к тому, что некоторые свойства
сетей Петри определить будет нельзя, но все зависит от того, как
представление было получено.)
Приведение к конечному представлению осуществляется не-
сколькими способами. Нам необходимо найти те средства, которые
ограничивают введение новых маркировок (называемых гранич-
ными вершинами) на каждом шаге. Здесь могут помочь пассивные
маркировки — маркировки, в которых нет разрешенных пере-
ходов. Эти пассивные маркировки называются терминальными
вершинами. Другой класс маркировок — это маркировки, ранее
Анализ сетей Петри
93
К встречавшиеся в дереве. Такие дублирующие маркировки называют-
И ся дублирующими вершинами-, никакие последующие маркировки
। рассматривать нет нужды — все они будут порождены из места
К первого появления дублирующей маркировки в дереве. Таким
5 образом, в дереве на рис. 4.12 маркировка (0, 1, 1), получившаяся
’f (1,0)
I
$ (О, I)
I Ь
St (i, о)
S г-'2 V*
i'1
S (1.0)
!'
« Рис. 4.13. Простая сеть Петри с бесконечным деревом достижимости.
! в результате выполнения последовательности tfats, не будет порож-
? дать какие-либо новые вершины в дереве, поскольку она ранее
встречалась в дереве в результате выполнения последовательности
f t2 из начальной маркировки.
Для сведения дерева достижимости к конечному представлению
[ используется еще одно средство. Рассмотрим последовательность
I запусков переходов о, начинающуюся в начальной маркировке р
и кончающуюся в маркировке р', р' > р. Маркировка р' совпадает
t с маркировкой р, за исключением того, что имеет некоторые «до-
» волнительные» фишки в некоторых позициях, т. е. р' = р + (р' —
| — р) и (р' — ф) > 0. Теперь, поскольку на запуски переходов
I лишние фишки не влияют, последовательность о можно запустить
| щюва, начиная в р', приходя к маркировке р". Так как действие
г последовательности переходов о добавило р' — р фишек к марки-
L ровке р, она добавит также р' — р фишек и к маркировке р', по-
этому р" = р'+ (р' — р) или р" = р + 2(р'—р). В общем
| можно запустить последовательность о п раз, получив в результате
L Маркировку р + и(р' — р). Следовательно, для тех позиций, ко-
| торые увеличивают число фишек последовательностью о, можно
К создать произвольно большое число фишек, просто повторяя по-
Р* следовательность о столько, сколько это нужно. В сети Петри на
94
Глава 4
рис. 4.9, например, можно запустить переход Л столько раз, сколь-
ко необходимо для того, чтобы получить произвольное число фи-
шек в р2-
Представим бесконечное число маркировок, получающихся из
циклов такого типа, с помощью специального символа со, который
обозначает «бесконечность». Для любого постоянного а определим
с» + а — о, а < о>»
с» —а = <о> <о <о.
Для построения дерева достижимости необходимы только эти опе-
рации над со.
Теперь можно точно сформулировать действительный алго-
ритм построения дерева достижимости. Каждая вершина i дерева
связывается с расширенной маркировкой p[tl; в расширенной
маркировке число фишек в позиции может быть либо неотрица-
тельным целым, либо о. Каждая вершина классифицируется или
как граничная вершина, терминальная вершина, дублирующая
вершина, или как внутренняя вершина. Граничными являются
вершины, которые еще не обработаны алгоритмом; алгоритм пре-
вратит их в терминальные, дублирующие или внутренние вершины.
Алгоритм начинает с определения начальной маркировки кор-
нем дерева, т. е. граничной вершиной. До тех пор пока имеются
граничные вершины, они обрабатываются алгоритмом.
Пусть х — граничная вершина, которую необходимо обрабо-
тать.
1. Если в дереве имеется другая вершина у, не являющаяся гра-
ничной, и с ней связана та же маркировка, р[х] = рГу], то вер-
шина х — дублирующая.
2. Если для маркировки р[х] ни один из переходов не разрешен
(т. е. 6(plx], tj) не определено для всех tj £ 7), то х — терминаль-
ная вершина.
3. Для всякого перехода tj£T, разрешенного в р [х] (т. е.
6(рЫ, t j) определено), создать новую вершину z дерева дости-
жимости. Маркировка p[z], связанная с этой вершиной, определя-
ется для каждой позиции pt следующим образом:
а) Если р[х] j = то рГг] г = о.
б) Если на пути от корневой вершины к х существует вершина
у С рГу] < 6 (рЫ, tj) и ply] г < 6 (рЫ, tj)i, ТО p[z]£ = о.
в) В противном случае р[г]г = 6(р[х], <>)г.
Дуга, помеченная tj, направлена от вершины х к вершине z.
Вершина х переопределяется как внутренняя, вершина г стано-
вится граничной.
Когда все вершины дерева — терминальные, дублирующие
или внутренние, алгоритм останавливается.
На рис. 4.14 представлено дерево достижимости для сети Петри
на рис. 4.9. Дерево достижимости сети Петри с рис. 4.15 изобра-
жено на рис. 4.16.
Анализ сетей Петри
95
(0,0,1)
(0,<о,1)
Рис. 4.14. Дерево достижимости сети Петри, приведеииой из рис. 4.9.
h
Рис. 4.15. Сеть Петри, для которой строится дерево достижимости.
1
1
Очень важным свойством алгоритма построения дерева дости-
жимости является то, что он заканчивает работу. Для доказатель-
ства этого мы должны показать, что алгоритм не может создавать
новые граничные вершины бесконечно. Доказательство основано
на трех леммах.
Лемма 4.1. В любом бесконечном направленном дереве, в котором
всякая вершина имеет только конечное число непосредственно
*
96
Глава 4
(1.0,1.0)
П
(1,0,0,1)
г?
Ъ
Рис. 4.16. Дерево достижимости сети Петри, изображенной на рис. 4.15.
последующих вершин, существует бесконечный путь, исходящий
из корня.
Доказательство. Начнем с корня в вершине х0. Поскольку имеется
только конечное число непосредственно следующих за х0 вершин,
но общее число вершин в дереве бесконечно, по крайней мере одна
из непосредственно следующих за х0 вершин должна быть корнем
бесконечного поддерева. (Если бы все поддеревья с корнями, не-
посредственно следующими за х0, были конечными, то и дерево с
корнем х0 было бы конечным.) Выберем вершину непосредст-
венно следующую за х0 и являющуюся корнем бесконечного под-
дерева. Теперь одна из непосредственно следующих за ней вер-
шин также является корнем бесконечного поддерева, выберем в
качестве такой вершины х2. Продолжая таким же образом, получим
бесконечный путь в дереве х0, xlt х2, ... . □
Лемма 4.2. Всякая бесконечная последовательность неотрица-
тельных целых содержит бесконечную неубывающую подпоследо-
вательность.
Доказательство. Возможны два случая:
1. Если какой-либо элемент последовательности встречается бес-
конечно часто, то пусть х0 является таким элементом. Бесконечная
подпоследовательность х0, х0, х0, ... является бесконечной неубыва-
ющей подпоследовательностью.
Анализ сетей Петри
97
№ 2. Если никакой элемент не встречается бесконечно часто, тогда
В всякий элемент встречается только конечное число раз. Пусть
® х0 — произвольный элемент последовательности. Существует са-
у мое большее х0 целых, неотрицательных и меньших, чем х0 (О,...,
j х0—1), причем каждый из них присутствует в последовательности
S только конечное число раз. Следовательно, продвигаясь достаточ-
f но долго по последовательности, мы должны встретить элемент
}xt, xt »х0. Аналогично должен существовать в последователь-
ности х2, х2 >> xlt и т. д. Это определяет бесконечную неубывающую
подпоследовательность х0, xt, х2... .
В обоих случаях бесконечная неубывающая последовательность
существует. □
t Лемма 4.3. Всякая бесконечная последовательность п-векторов
!• над расширенными неотрицательными целыми (неотрицательные
Ю целые плюс символ <о) содержит бесконечную неубывающую под-
• последовательность.
Доказательство. Доказываем индукцией по п, где п — размер-
юность векторного пространства.
' 1. Базовый случай (п = 1). Если в последовательности имеется
; бесконечное число векторов (<о), то они образуют бесконечную
неубывающую последовательность. В противном случае бесконеч-
л>ная последовательность, образованная удалением конечного числа
Т векторов (ю), имеет по лемме 4.2 бесконечную неубывающую под-
if последовательность.
® 2. Индуктивное предположение. (Допустим, что лемма верна для
п, докажем ее справедливость для п + 1.) Рассмотрим первую
Ьи’координату. Если существует бесконечно много векторов, имею-
щих в качестве первой координаты а, тогда выберем эту бесконеч-
ную подпоследовательность, которая не убывает (постоянна) по
'< первой координате. Если только конечное число векторов имеют
Ф в» в качестве первой координаты, то рассмотрим бесконечную по-
у следовательность целых, являющихся значениями первых коорди-
J нат. По лемме 4.2 эта последовательность имеет бесконечную не-
, убывающую подпоследовательность. Она определяет бесконечную
подпоследовательность векторов, которые не убывают по своей
* Первой координате.
, В любом случае мы имеем последовательность векторов, не-
,убывающих по первой координате. Применим индуктивное пред-
г положение к последовательности n-векторов, которая получается
В результате отбрасывания первой компоненты п + 1-векторов.
Полученная таким образом бесконечная подпоследовательность
является неубывающей по каждой координате. □
Докажем следующую теорему.
Теорема 4.1. Дерево достижимости сети Петри конечно.
Доказательство. Доказательство проводим от противного. До-
пустим, что существует бесконечное дерево достижимости. Тогда
4— 562
98
Глава 4
по лемме 4.1 в нем имеется бесконечный путь х0, xit х2, исходя-
щий из корня х0. (Число вершин, следующих за каждой вершиной в
дереве, ограничено числом переходов т.) Тогда р[х0], p[xi], р[х2],...—
бесконечная последовательность n-векторов над N U {©}, а по
лемме 4.3 она имеет бесконечную неубывающую подпоследова-
тельность |i[xto] < p[xtl] < . . Но по построению мы не мо-
жем иметь |1[хг] = р[х>], поскольку тогда одна из вершин была бы
дублирующей и не имела следующих за собой вершин. Следова-
тельно, мы имеем бесконечную строго убывающую последователь-
ность р[х1о]< ... . Но по построению, так как р[хг] <
< нам следовало бы заменить по крайней мере одну компо-
ненту p[xt], не являющуюся ы, на со в р[х,-]. Таким образом, р[хГ1]
имеет по крайней мере одну компоненту, являющуюся со, р[хг>]
имеет по крайней мере две ©-компоненты, a p[xt-n] имеет по крайней
мере п ©-компонент. Поскольку маркировки n-мерные, р[х,й] имеет
во всех компонентах ®. Но тогда р[х£/г+1] не может быть больше
p[xtn]. Пришли к противоречию, что доказывает, что наше допу-
щение относительно существования бесконечного дерева достижи-
мости неверно. □
Построение дерева достижимости было впервые описано Карпом
и Миллерам [148]. Используемый здесь вариант алгоритма был
предложен Келлером [150J. Доказательство конечности, данное
здесь, взято у Хэка [111], который принял за основу доказательство
Карпа и Миллера [148].
Дерево достижимости — очень полезный инструмент анализа
сетей Петри. В последующих разделах мы покажем, как его можно
использовать для решения некоторых задач, представленных в
разд. 4.1.
4.2.1.1. Безопасность и ограниченность
Сеть Петри безопасна, если число фишек в каждой позиции не
может превысить 1; сеть Петри ограниченна, если существует такое
целое k, что число фишек в любой позиции не может превысить k.
Оба этих свойства можно проверить с помощью дерева достижимо-
сти. Сеть Петри ограниченна тогда и только тогда, когда символ
© отсутствует в ее дереве достижимости. Присутствие символа ©
в дереве достижимости означает, что число фишек потенциально
не ограничено; существует последовательность запусков переходов,
которую можно повторить произвольное число раз, увеличивая ко-
личество фишек до произвольно большого числа. Таким образом,
если имеется символ ®, сеть неограниченна. Кроме того, поло-
жение символа о показывает, какие позиции неограниченны.
Обратное утверждение также является верным, если сеть Петри
неограниченна, то число достижимых маркировок бесконечно. По-
Анализ сетей Петри
99
(1,0. О, О)
(О, 1,0,0)
(0,0, 1,0)
(0,1. 1,0)
(О, О, 1, 0)
(0,0, 2,0)
(0,0,0, 1)
(1,0,0,0)
Рис. 4.17. Определение ограниченности для сети Петри с помощью дерева
достижимости.
скольку дерево достижимости конечно, бесконечное число дости-
жимых маркировок отражает присутствие символа ..со.
Если сеть Петри ограниченна и символ со отсутствует в дереве
достижимости, то сеть Петри представляет систему конечных сос-
тояний. Дерево достижимости, по существу, является графом состоя-
ний и будет содержать вершину, соответствующую всякой дости-
жимой маркировке. Это позволяет решить вопросы анализа простым
перебором и проверкой конечного множества всех достижимых мар-
кировок. Например, чтобы определить границу для заданной пози-
ции, нужно построить дерево достижимости и найти наибольшее
значение компоненты маркировки, соответствующей этой позиции.
100
Глава 4
Найденное значение является границей числа фишек для заданной
позиции. Если граница для всех позиций равна 1*>, сеть безопасна.
На рис. 4.17 демонстрируется использование дерева достижи-
мости для определения ограниченности.
Отметим, что по дереву достижимости даже для сетей Петри,
не являющихся ограниченными (вследствие неограниченности не-
которой позиции), можно определить границы для тех позиций,
которые являются ограниченными. Таким образом, дерево дости-
жимости позволяет эффективно решить задачи анализа сетей Петри
по определению ограниченности и безопасности для отдельных
позиций и целых сетей.
4.2.1.2. Сохранение
Сеть Петри является сохраняющей, если она не теряет и не по-
рождает фишки, а просто передвигает их. Поскольку две фишки
можно закодировать как одну фишку, которая позже вызовет за-
пуск перехода, создающего две фишки, значение фишки в каждой
позиции определяет вектор взвешивания, веса неотрицательны.
Сеть Петри является сохраняющей по отношению к вектору взве-
шивания, если взвешенная сумма фишек постоянна для всех дости-
жимых маркировок.
Свойство сохранения эффективно проверяется с помощью де-
рева достижимости. Так как дерево достижимости конечно, для
каждой маркировки можно вычислить взвешенную сумму. Если
сумма одинакова для каждой достижимой маркировки, сеть —
сохраняющая по отношению к данному весу. Если суммы не равны,
сеть — несохраняющая.
При оценке сохранения необходимо быть внимательным с сим-
волом со. Если маркировка имеет со в качестве маркировки позиции
Pt, тогда для того, чтобы сеть была сохраняющей, вес этой позиции
должен быть равным 0. Напомним, что символ со представляет бес-
конечное множество значений. Так как все веса неотрицательны,
вес должен равняться либо нулю (тем самым означая, что число
фишек в данной позиции не важно), либо быть положительным.
Если вес положителен, то сумма будет разной для двух маркировок,
различающихся в своей со-компоненте. Следовательно, если ка-
кая-либо маркировка с ненулевым весом равна со, сеть — несохра-
няющая.
Эти рассуждения относятся к сохранению по отношению к опре-
деленному взвешиванию. Сеть Петри является сохраняющей, если
она сохраняющая по отношению к некоторому вектору w, w, > 0.
Дерево достижимости можно использовать для определения того,
является сеть сохраняющей или нет, путем нахождения вектора
весов w (если он существует). Заметим прежде всего, что для того,
1) Точнее, не превышает 1. — Прим, перев.
Анализ сетей Петри
101
чтобы сеть Петрн была сохраняющей по отношению к положитель-
ному вектору весов, она должна быть ограниченной. Как было
указано выше, неограниченная позиция должна иметь нулевой вес,
что недопустимо в сети с положительным вектором весов. (Если
мы хотим допустить нулевые компоненты, нужно просто установить
веса всех неограниченных позиций равными нулю и рассматривать
после этого только оставшиеся компоненты.) Теперь, если сеть
сохраняющая, существуют взвешенная сумма, обозначим ее s, и
вектор весов w — (wt, ..., и>п). Для каждой маркировки р[х]
дерева достижимости имеем
и>1 • н W1 + “'г • В [*]г + - + • В Ип =
Это равенство определяет для k вершин дерева достижимости сово-
купность из k линейных уравнений с п + 1 неизвестными. Добавим
к ним ограничения: Wi > 0, i = 1, ..., п, в результате чего опреде-
лим ограничения для вектора весов.
Решение этой системы линейных уравнений — хорошо извест-
ная задача, имеющая множество алгоритмов решения. Можно рас-
сматривать ее как задачу линейного программирования или просто
как систему линейных уравнений. В любом случае, если решение
существует, оно будет вычислено. (Решения, получаемые этими
методами, будут, как правило, рациональными, не целыми, но веса
можно умножить на общее кратное для получения целого решения.)
Если ограничения, накладываемые на веса, являются чрезмер-
но жесткими и, следовательно, вектора взвешиваний не существу-
ет, это будет определено. В любом случае можно определить, явля-
ется или нет сеть Петри сохраняющей, и если это так, получить
вектор весов.
4.2.1.3. Покрымемость
Последняя задача, которую можно решить с помощью дерева
достижимости, — задача покрываемое™. В задаче покрываемос-
ти мы хотим для данной маркировки р' определить, достижима ли
маркировка р" > р'. Данная задача решается проверкой дерева
достижимости. Строим для начальной маркировки р дерево дости-
жимости. Затем ищем любую вершину х с р[х] > р'. Если такой
вершины не существует, маркировка р' не покрывается никакой
достижимой маркировкой; если она найдена, р[х] дает достижимую
гмаркировку, покрывающую р'.
> Путь от корня к покрывающей маркировке определяет последо-
вательность переходов, которые приводят из начальной маркиров-
ки к покрывающей маркировке, а маркировка, связанная с этой
^вершиной, определяет покрывающую маркировку. Символ со вновь
Должен рассматриваться как обозначение бесконечного множества
значений. Если компонента покрывающей маркировки — со, то в
Йпути от корня к покрывающей маркировке имеется «цикл». Для
102
Глава 4
увеличения соответствующей компоненты с тем, чтобы она была не
меньше, чем в данной маркировке, необходимо достаточное число
раз_повторить этот цикл.
Заметим, что, если несколько компонент покрывающей марки-
ровки равны со, между изменениями маркировки, получающимися
в результате прохождения циклов, возможна взаимосвязь. Рассмот-
рим сеть Петри на рис. 4.18 и ее дерево достижимости, показанное
на рис. 4.19. Согласно проведенному анализу, маркировка (0, 14,
1, 7) покрывается в множестве достижимости. Путь, порождающий
покрывающую маркировку, состоит из некоторого числа переходов 4.
за которыми следует переход t2, после которого уже следует некото-
рое число переходов 4- Задача заключается в определении того,
сколько раз нужно запустить переходы 4 и 4- Так как мы хотим иметь
в позиции р2 14 фишек, а 4 помещает в р2 одну фишку, попытаемся
(1,0,0,0)
h
(0, со, 1, со)
(0, со. 1, со)
Рис. 4.19. Дерево достижимости для сети Петри, приведенной на рис. 4.18.
Анализ сетей Петри
103
выполнить 14 ti. Однако нам необходимо выполнить 7t3, а каждый за-
пуск t3 удаляет из р2 фишку, поэтому в действительности необходимо
выполнить не менее 214, затем t2 и после этого не менее 74 (выпол-
нить 4 такое число раз, чтобы в позиции р2 осталось не менее 14
фишек). Карп и Миллер [148] предложили алгоритм, определяю-
щий минимальное число запусков переходов, необходимых для
покрытия дайной маркировки.
4.2.14. Ограниченность дерева достижимости
Как видим, дерево достижимости можно использовать для ре-
шения задач безопасности, ограниченности, сохранения и покры-
ваемости. К сожалению, в общем случае его нельзя использовать
Рис. 4.20. Сеть Петри, дерево достижимости которой представлено на
рис. 4.22.
Рис. 4.21. Вторая сеть Петри, дерево достижимости которой представлено
на рис. 4.22. Сеть Петри, изображенная на рис. 4.20, имеет в позиции р»
только четное число фишек, тогда как эта сеть Петри допускает для рг произ-
вольную маркировку.
104
Глава 4
для решения задач достижимости и активности, а также для опре-
деления возможной последовательности запусков. Решение этих
задач ограничено существованием символа со. Символ <о означает
потерю информации; конкретные количества фишек отбрасываются,
учитывается только существование их большого числа.
1,0)
Рис. 4.22. Дерево достижи-
мости для сетей Петри, приве-
денных на рис. 4.20 и 4.21.
Рассмотрим, например, сети Петри на рис. 4.20 и 4.21, дерево
достижимости которых изображено на рис. 4.22. Одно дерево
достижимости представляет эти две схожие (но различные) сети
Петри. Множества же достижимости их не совпадают. В сети Петри
на рис. 4.20 число фишек в позиции р2 всегда четно (пока не будет
запущен переход тогда как в сети Петри на рис. 4.21 оно может
быть произвольным целым. Символ to не позволяет обнаруживать
информацию такого рода, препятствуя использованию дерева до-
стижимости для решения задачи достижимости.
Аналогичная трудность существует и для задачи активности
На рис. 4.23 и 4.24 приведены две сети Петри, дерево достижимости
которых изображено на рис. 4.25. Однако сеть на рис. 4.23 может
иметь тупик (например, в результате последовательности
а сеть Петри с рис. 4.24 — нет. Дерево достижимости же вновь не
может передать различие этих двух случаев.
Заметим, что хотя дерево достижимости не обязательно содер-
жит достаточную информацию для решения задач достижимости
и активности, тем не менее в некоторых случаях это бывает возмож-
но. Сеть, дерево достижимости которой содержит терминальную
вершину (вершину, не имеющую исходящих дуг), не активна (по-
скольку некоторая достижимая маркировка не имеет последую-
щих маркировок). Аналогично маркировка р' в задаче достижимос-
ти может встретиться в дереве достижимости, и если это так, то она
достижима. Кроме того, если маркировка не покрывается некото-
рой вершиной дерева достижимости, то она недостижима.
Анализ сетей Петри
105
Рис. 4.24. Сеть Петри, в которой тупик невозможен. Эта сеть активна, хотя
ее дерево достижимости (рис. 4.25) идентично дереву достижимости неактив-
ной сети Петри, приведенной на рнс. 4.23.
Рис. 4.25. Дерево достижимос-
ти сетей Петри, изображенных
на рис. 4.23 и 4.24.
106
Глава 4
Эти условия достаточны для решения некоторых задач дости-
жимости и активности, но они не решают эти задачи в общем. Сле-
довательно, для решения этих двух задач необходимы другие
подходы.
Упражнения
1. Постройте деревья достижимости для маркированных сетей, представлен-
ных на рис. 4.1 и 4.2.
2. Напишите программу для ЭВМ, осуществляющую построение дерева до-
стижимости по описанию сети Петри и начальной маркировке.
3. Большинство формулировок алгоритма построения дерева достижимости
позволяет классифицировать вершину как дублирующую только в том случае,
если идентичная вершина встретилась на пути от корня к этой вершине. Сле-
довательно, подобные вершины, принадлежащие разным поддеревьям и
представляющие одну маркировку, будут продолжать обрабатываться алго-
ритмом. Эта модификация!) увеличивает размер поддерева, ио алгоритм за-
кончит работу, даже если дублирующие маркировки находятся в том же под-
дереве, что и первая маркировка. Докажите, что разрешение дублирующим
маркировкам быть в разных поддеревьях не вызовет в дереве потерю какой-
либо маркировки.
4.2.2. Матричные уравнения
Второй подход к анализу сетей Петри основан на матричном
представлении сетей Петри. Альтернативным по отношению к опре-
делению сети Петри в виде (Р, Т, I, О) является определение двух
матриц D~ и D+, представляющих входную и выходную функции.
(Они эквивалентны функциям F и В определения Хэка сетей Пет-
ри, см. разд. 2.6.) Каждая матрица имеет m строк (по одной на пе-
реход) и п столбцов (по одному на позицию). Определим D~[j, i] =
= #(/?,-, I(tj)), a D+ [/, i] = #(p,, 0 (tj)). D~ определяет входы в
переходы, D+ — выходы.
Матричная форма определения сети Петри (Р, Т, D~, D+) экви-
валентна стандартной форме, используемой нами, но позволяет
дать определения в терминах векторов и матриц. Пусть е[/] —
/n-вектор, содержащий нули везде, за исключением /-й компоненты.
Переход tj представляется m-вектором е[/]1 2).
Теперь переход t} в маркировке р разрешен, если р е[/] • D~,
а результат запуска перехода tj в маркировке р записывается как
8(р, tj)= р — е [у] • П- + е[/] Г+ =
= р + е |j] • (~D~ + ГР) = р 4- е [j] • D,
где D = D+ •— D~ — составная матрица изменений.
1) По отношению к описанному в этом разделе алгоритму. — Прим, перев.
2) е[/1 — вектор-строка. ~~Прим. перев.
Анализ сетей Петри
107
Тогда для последовательности запусков переходов о = tjitj,
... t; имеем
ik
8(м» °) = tji' tjt> ••• > ~
= Р 4~ е[/\] D + e [j2] -£>+-•- + e [/ft] D =
= H 4- (« [/il + e [/2] 4-be [j J) • D = p + f (o) • D.
Вектор f(o) = ef/J + Ф’г] + --• + e[/fe] называется вектором за-
пусков последовательности i-ii элемент вектора До),
До), — это число запусков перехода t, в последовательности
... tfk. Вектор запусков, следовательно, является вектором с неотри-
цательными целыми компонентами. (Вектор [(g) — это отображение
Париха последовательности [229].)
Для того чтобы показать полезность такого матричного подхода
к сетям Петри, рассмотрим, например, задачу сохранения: является
ли данная маркированная сеть Петри сохраняющей? Для того
чтобы показать сохранение, необходимо найти (ненулевой) вектор
взвешивания, для которого взвешенная сумма по всем достижимым
маркировкам постоянна. Пусть и> — п X 1 — вектор-столбец. Тог-
да, если р — начальная маркировка, ар' — произвольная дости-
жимая маркировка, необходимо, чтобы р • w = р' • w. Теперь,
поскольку р' достижима, существует последовательность запусков
переходов о, которая переводит сеть из р в р'. Поэтому
р' = 8 (р, о) = р 4- /(о) • D.
Следовательно, р • w = р' • и = (р-|- До) • D) • w = р- w +
4- До) • D • w, поэтому /(о) • D • w = 0.
Поскольку это должно быть верно для всех До), имеем
D • и> = 0.
Таким образом, сеть Петри является сохраняющей тогда и только
тогда, когда существует такой положительный вектор и>, что
D • w = 0. Это обеспечивает простой алгоритм проверки сохране-
ния, а также позволяет получать вектор взвешивания w.
Развитая матричная теория сетей .Петри является инструментом
для решения проблемы достижимости. Предположим, что марки-
ровка р' достижима из маркировки р. Тогда существует последо-
вательность (возможно, пустая) запусков переходов о, которая
приводит из р к р'. Это означает, что До) является неотрицатель-
ным целым решением следующего матричного уравнения для х:
р' = р 4- х D. (4-1)
Следовательно, если р' достижима из р, тогда уравнение (4-1)
имеет решение в неотрицательных целых; если'уравнение (4-1) не
имеет решения, тогда р' недостижима из р.
108
Глава 4
Рассмотрим, например, маркированную сеть Петри на рис. 4.26.
Матрицы D и D+ имеют вид:
11 10"
D~ = 0 0 0 1
00 1 о]’
"10 0 01
£)+„ 0 2 1 ol
ООО 1]
а матрица D:
о —1 —1 0'
D= 0 +2 +1 -1
0 0—1+1
В начальной маркировке р = (1, 0,
приводит к маркировке р/, где
1, 0) переход ts разрешен и
0 —1 —1
р' = (1, 0, 1, 0) + (0, 0, 1) -
0 +2 +1
0 0—1
о*
—1
+1
= (1, 0, 1, 0) + (О, О, — 1, + 1) =(1, О, 0, 1).
Последовательность о = представляется вектором запусков
/(о) = (1. 2, 2) и получает маркировку р':
0
О
О
= (1, 0, 1, 0) + (1, 2, 2) -
— 1—1 О"
+2 +1 -1
0—1 +1
= (1, 0, 1, 0) + (0, 3, — 1, 0) = (1, 3, 0, 0).
Рис. 4.26. Сеть Петрп, иллюстрирующая метод анализа, основанный на мат-
ричных уравнениях.
Анализ сетей Петри
109
Для определения того, является ли маркировка (1, 8, 0, 1) до-
стижимой из маркировки (1,0, 1, 0), имеем уравнение
(1, 8, 0, 1) = (1, 0, 1, 0) + х-
0 — 1
0 +2
0 0
— 1 О’
+ 1 -1
-1 +1
(0. 8, —1, 1) = х-
’0—1—1 О
О +2 +1 — 1
О 0—1+1
которое имеет решение х = (0, 4, 5). Это соответствует последова-
тельности о — tgt^tstitstitst^ts.
Далее мы можем показать, что маркировка (1, 7, 0, 1) недости-
жима из маркировки (1, 0, 1, 0), поскольку матричное уравнение
0—1—1 01
(1, 7, 0, 1)=(1, 0, 1, 0) + х-
0 —1 — 1
(0, 7,-1, 1) = х
0 +2 +1
0 0—1
О’
— 1
+ 1
не имеет решения.
Матричный подход к анализу сетей Петри очень перспективен,
но имеет и некоторые трудности. Заметим прежде всего, что мат-
рица D сама по себе не полностью отражает структуру сети Петри.
Переходы, имеющие как входы, так и выходы из одной позиции
(петли), представляются соответствующими элементами матриц
D~ и £>т, но затем взаимно уничтожаются в матрице D = £>+ — D~.
Это отражено в предыдущем примере позицией и переходом
Другая проблема — это отсутствие информации о последова-
тельности в векторе запуска. Рассмотрим сеть Петри на рис. 4.27.
Предположим, мы хотим определить, является ли маркировка
(0, 0, 0, 0, 1) достижимой из (1, 0, 0, 0, 0). Тогда имеем уравнение
-—1 2 1 0 0”
0 0 0 0 0
0 0 1 0 0
(0, 0, 0, 0, 1)=(Ь о, 0, 0, 0) + х 0 — 1 0 1 0
0 2 0 0 — 1
0 0 — 1 — 2 1_
Это уравнение не имеет однозначного решения, но сводится к мно-
жеству решений {o|f(o) = (1, х2, х6— 1, 2х6, х6 — 1, х6)}. Оно
по
Глава 4
Рис. 4.27. Другая сеть Петри, служащая для иллюстрации матричного ана-
лиза.
определяет взаимосвязь между запусками переходов. Если поло-
жим хе = 1 и х2 = 1, то f(o) = (1, 1, 0, 2, 0, 1), но этому вектору
запуска соответствуют как последовательность Д4444» так и п0‘
следовательность Следовательно, хотя и известно число
запусков переходов, порядок их запуска неизвестен.
Еще одна трудность заключается в том, что решение уравнения
(4-1) является необходимым для достижимости, но недостаточным.
Рассмотрим простую сеть Петри, приведенную на рис. 4.28. Если
мы хотим определить, является ли (0, 0, 0, 1) достижимым из
(1, 0, 0, 0), необходимо решить уравнение
Г—1 +1 —1 о
(О, 0, 0, 1)=(1, О, О, 0) + /(о). [ 0 _J +1 +1
Рз
Рис. 4.28. Сеть Петри, показывающая, что решение матричного уравнения—
необходимое, но недостаточное условие для решения задачи достижимости.
Анализ сетей Петри
111
Это уравнение имеет решение /(о) = (1, 1), соответствующее двум
последовательностям: tftz и t2tv Но ни одна из этих двух последо-
вательностей переходов невозможна, поскольку в (1,0, 0, 0) ни tif
ни 4 не разрешены. Таким образом, решения уравнения (4-1) не-
достаточно для доказательства достижимости.
Возможность недействительных решений уравнения (4-1) (ре-
шений, которые не соответствуют возможным последовательностям
переходов) стала причиной только ограниченного исследования
матричного представления сетей Петри. Лучшее исследование
этого подхода проведено Муратой [206, 208, 209].
4.3. Замечания к литературе
В публикациях Хольта и др. [128] и Хольта и Коммонера [127]
определены некоторые из первых задач анализа сетей Петри —
активность и безопасность, которые продолжают считаться основ-
ными задачами анализа. Активность изучалась Коммонером [53],
Лаутенбахом [167] и Льеном [173]. Келлер [150] вместе с другими
задачами рассматривал также и активность. Льен [173] определил
задачу сохранения.
Карп и Миллер [128] впервые описали построение дерева дости-
жимости и доказали его конечность. Задачи покрываемое™ и до-
стижимости были определены ими как если бы это были задачи
эквивалентности и включения. Последние задачи явились пред-
метом изучения в [26]. В [213] дана краткая формулировка задачи
достижимости. Хэк [Ш] рассмотрел большинство этих задач вместе
и показал, как дерево достижимости можно использовать для ре-
шения некоторых из них.
Матричный подход рассматривался Питерсоном [236], но, как
оказалось, возможности его ограничены. Мурата, имеющий боль-
шую квалификацию в линейной алгебре, достиг чуть большего
в этом подходе в [210, 206, 212, 208, 209].
4.4. Темы для дальнейшего изучения
1. Рассмотрите построение не дерева, а графа достижимости. Если
вершина х порождает последующую вершину z с p[z] — р[г/] для
некоторой неграничной вершины у, просто введите помеченную
соответствующим образом дугу из х и у. Заметим, что путь из корня
в вершину перестает быть единственным. Опишите алгоритм по-
строения графа достижимости, покажите, что он сходится, и иссле-
дуйте его свойства, сравнивая с алгоритмом построения дерева до-
стижимости.
2. Дерево достижимости нельзя использовать для решения проб-
лемы достижимости вследствие потери информации, порождаемой
символом со. Он вводится, когда мы приходим к маркировке р' и на
пути от корня к р' имеется такая маркировка р, что р' 2> р. В этом
112
Глава 4
случае можно получить все маркировки вида р + и(р' — р). Ис-
следуйте возможность использования выражения а + b • пг вме-
сто со, для того чтобы представить значения компонент. Если вы
сможете определить дерево достижимости, в котором все векторы
маркировок представляются выражениями, тогда решение задачи
достижимости определяется просто решением системы уравнений.
3. Обобщите определение сохранения, разрешая отрицательные
веса. Что можно было бы считать разумной интерпретацией отри-
цательного веса? Является ли разрешимой задача определения со-
хранения сети Петри, если разрешены отрицательные веса?
4. Разработайте с помощью матричного подхода к анализу алгоритм
определения ограниченности сети Петри [61].
5. Основная проблема матричного анализа—отсутствие информации
о последовательности и существование недействительных решений.
Однако задача достижимости является самой существенной для
сетей Петри, поэтому важно показать, что она разрешима, даже если
решения вычислительно дороги. Если задача разрешима, можно
будет искать более эффективные методы решения, но сначала не-
обходимо показать, что метод решения существует.
Для обоснования этого обозначим через Sy сумму вектора за-
пуска f по всем компонентам. Иначе говоря, если f = (ft, f2, , fm),
то Sy = ft + + ... 4- fm. Далее, если существует последова-
тельность о, переводящая сеть Петри из маркировки р в марки-
ровку р', тогда уравнение (4-1) имеет решение, являющееся векто-
ром запуска f(o) для о. Последовательность о можно определить
из вектора запуска f(a) простым перебором всех возможных последо-
вательностей длины 2f(o), стараясь, чтобы каждая из них 1) была
действительной и 2) приводила от р к р'. Для сети Петри с т пере-
ходами возможно самое большое m*~f последовательностей длины
Гу. На самом деле это число можно сократить. Поскольку нам из-
вестно, сколько раз запускается переход tt (ft), сколько раз запуска-
ется t2(f2) и т. д , то необходимо проверять не более чем Syl воз-
можных упорядочений из запусков перехода tiy fz запусков пе-
рехода t2 и т. д.
Это, казалось бы, обеспечивает процедуру решения задачи опре-
деления, является ли р' достижимой из р. Сначала решаем матрич-
ное уравнение р' = р 4- f • D. Если решения не существует, р' не-
достижима из р. Если решение f существует, проверяем все Sy!
возможных упорядочений переходов. Если какая-нибудь из этих
последовательностей действительна, то р' достижима из р, и мы
имеем последовательность переходов, переводящую из р в р'.
Имеется только одно препятствие. Решение f может быть не
однозначным, а (бесконечным) множеством векторов запусков, пред-
ставленным множеством выражений (как показано выше для примера
анализа сети Петри на рис. 4.27). Для определения возможности
доказательства достижимости в этом случае необходимы исследова-
ния В простейшем случае может оказаться, что или все решения
Анализ сетей Петри
ИЗ
представляются выражением вектора запуска, соответствующим
действительным решениям, или ни одно. В этом случае мы просто
выбираем любое решение и выполняем описанную процедуру про-
верки всех возможных упорядочений. Более вероятно, однако, что
некоторые решения будут работать, тогда как другие — нет. Так
как мы не можем испытать все решения (из, возможно, бесконечного
множества их), необходимы исследования, для того чтобы можно
было определить, какие решения необходимо проверять.
ГЛАВА 5
СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
В четвертой главе было представлено множество задач теории сетей Пет-
ри. Эти задачи касаются различных свойств структуры и поведения сетей
Петри.
Были представлены и два метода решения: подход дерева достижимости
и подход матричных уравнений. Эти методы позволяют определить свойства
безопасности, ограниченности, сохранения и покрываемости для сетей Пет-
ри. Кроме того, установлены необходимые условия для достижимости. Од-
нако эти методы анализа недостаточны для решения некоторых других задач,
в частности активности, достижимости и эквивалентности. В этой главе мы
изучим эти задачи с целью или найти их решения, или по крайней мере узнать
больше о свойствах сетей Петри.
5.1. Сводимость задач анализа
Мы будем использовать фундаментальное понятие сводимости
[146]. Решение задачи подразумевает сведение ее к другой задаче,
способ решения которой уже известен. В предыдущей главе, напри-
мер, задача определения того, является ли сеть Петри сохраняющей,
сводилась к решению системы линейных уравнений. Задача решения
системы линейных уравнений в свою очередь сводится к опреде-
ленной последовательности арифметических операций (сложение,
вычитание, умножение, деление и сравнение). Таким образом, по-
скольку арифметические операции выполнить можно, сохранение
может быть определено.
Другой пример связан с задачей равенства и задачей подмножест-
ва для множеств достижимости.
Определение 5.1. Задача равенства. Выполняется ли для двух
данных маркированных сетей Петри С, = (Рь 7\, Ilf С\) с марки-
ровкой fa и С2 = (Р2, Т2, /2, О2) с маркировкой ц2 равенство 7?(Ci,
Pi) = Р(С2, р2)?
Определение 5.2. Задача подмножества. Выполняется ли для двух
данных маркированных сетей Петри Ct = (Ръ 7\, Ilt С\) с марки-
ровкой р, и С2 = (Р2, Т2, 12, 0^ с маркировкой р2 соотношение
P(Ci, Pi)~ R(C2, р2)?
Эти задачи могут оказаться очень важными для определения,
является ли сеть Петри оптимизируемой или сравнимы ли сети
двух систем. Заметим, что если можно найти решение задачи под-
множества, то задача равенства также решается. Если необходимо
Сложность и разрешимость
115
и определить, выполняется ли R(Cit pt) = /?(С2, р2), мы сначала при-
меним алгоритм решения задачи подмножества для определения,
выполняется ли R(Ci, pje Т?(С2, р2), а затем применим тот же
В алгоритм для определения, выполняется ли /?(С2, р2)—
S Pi)- Pi) = R(C2, p2) тогда и только тогда, когда R(Cit
В Pi)s jR(C2, р2) и R(C2, рг)^ R(Ci, pt). Таким образом, за-
В дачу равенства можно свести к задаче подмножества.
-5 При рассмотрении задач анализа и сводимости важно принимать
В во внимание следующие два соображения. Во-первых, пытаясь
К найти решение, необходимо учитывать возможность того, что за-
В дача не имеет метода решения, т. е. неразрешима. Во-вторых, если
В метод решения существует, мы должны оценить его стоимость: как
S много времени и памяти требуется для решения? Для того чтобы
Зг применение сетей Петри расширялось, задачи анализа должны ре-
В шаться, а алгоритмы, осуществляющие решение, должны быть
I В не слишком дороги в смысле времени и памяти ЭВМ.
Сводимость играет большую роль для обеих из указанных проб-
В лем. Сводимость задач обычно используется для того, чтобы пока-
В зать, разрешима ли задача или неразрешима. Наш подход к теории
В разрешимости [69, 200] основан главным образом на работах Тью-
В ринга и его модели вычислений — машине Тьюринга. Значение
В машины Тьюринга состоит в том, что она служит разумным пред-
I В ставлением вычислительной машины, и можно показать*), что не
I В существует алгоритма, который бы решал определенные проблемы
1 В машины Тьюринга, в частности проблему остановки. На основе
, В этого был найден ряд неразрешимых задач. И важность этой теории—
| В в том, что невозможно создать программу для ЭВМ, которая бы
В решала эти задачи. Следовательно, для целей практического ана-
I В лиза ^обходимо избежать этих неразрешимых задач, иначе вопросы
I В анализа не получат ответа.
Ж (Здесь важно подчеркнуть, что неразрешимые задачи порожда-
j В ют вопросы, на которые не просто нет ответа, по его и не может
) В быть. Вопросы, на которые нет ответа, еще могут его получить; это
। В значит, что ответ еще никто не нашел, но он существует. Известным
I В пРимеРом является большая теорема Ферма: имеет ли решение урав-
I В неИие + Уп ~ z" Для « > 2 в классе целых чисел х, у, г? Этот
> В вопрос не получил ответа,но онего имеет. Ответом служит либо"да",
В либо "нет". Одним способом получения ответа на вопрос является
В поиск чисел х,у.гнп, удовлетворяющих условиям теоремы. Дру-
В гим будет доказательство (логический вывод) того, что таких
В х, у, z и п не существует. Никто еще не сделал этого.
» Однако предположим, что задача неразрешима. Тогда невоз-
В можно было бы определить, существуют ли x,y,z и и, решающие
’if Уравнение. Это означало бы, что мы не могли логически вывести
В их несуществование из аксиом математики и не могли получить х,у,
*) Для некоторых задач, разумеется. — Прим, перев.
116 Глава 5
г и п, которые были бы решением уравнения. Но если мы не можем
получить х, у, z и п, тогда они не должны существовать. Если же они
существуют, мы можем найти их с помощью ЭВМ. Но если х, у, z
и п не существуют, ответом на вопрос будет «нет», и, следовательно,
мы разрешили его. Это противоречит нашему предположению о
том, что вопрос неразрешим, следовательно, он разрешим.)
Теперь допустим, что задача А сводима к задаче В: конкретную
задачу А можно перевести в конкретную задачу В. Если задача
В разрешима, то разрешима и задача Л, а алгоритм решения задачи
В можно применить к решению задачи А. Конкретную задачу А
можно решить, преобразуя ее в конкретную задачу В и применяя
к ней алгоритм решения задачи В. Таким образом, если задача А
сводится к задаче В и задача В разрешима, то разрешима и задача А
Обратное также верно: если задача А сводится к задаче В и за-
дача А неразрешима, то неразрешима и задача В; если бы задача В
была разрешима,то описанная выше процедура была бы методом
решения задачи Л, что противоречит ее неразрешимости. Эти два
факта положены в основу большинства методов определения раз-
решимости. Для того чтобы показать, что задача разрешима, сводят
ее к задаче, известной как разрешимая; а для того чтобы показать,
что задача неразрешима, сводят к ней задачу, которая известна как
неразрешимая.
Мы также будем широко использовать этот подход для сокраще-
ния объема работы, которую нам необходимо выполнить. Например,
вследствие того, что задача равенства для множеств достижимости
сводится к задаче подмножества, мы хотим найти либо 1) проце-
дуру решения задачи подмножества, либо 2) доказательство того, что
задача равенства неразрешима. Если мы сможем выполнить 1), то
будем иметь метод решения обеих задач, если выполним 2), будем
знать, что обе задачи неразрешимы.
В некоторых случаях мы сможем достичь даже большего. Две
задачи называются эквивалентными, если они взаимно сводимы.
Другими словами, задача Л эквивалентна задаче В, если задача Л
сводится к задаче В, а задача В сводится к задаче Л. В этом случае
или обе задачи разрешимы, или обе неразрешимы, и мы можем рас-
сматривать любую из них. (Заметим, что в общем случае это1)
неверно Например, если бы мы показали, что задача подмножества
для множеств достижимости неразрешима, это не сказало бы нам ни-
чего о разрешимости или неразрешимости задачи равенства.)
Второе соображение по исследованию задач анализа заключает-
ся в том, что если метод решения существует, то он должен быть ра-
зумно эффективным. Это означает, что количества времени и памяти,
требуемые алгоритмом для решения конкретной задачи, не должны
быть чрезмерными. Исследование стоимости выполнения алгорит-
ма — это часть теории сложности. Теория сложности имеет дело
1) То есть то, что можно работать с любой задачей. — Прим, перев.
Сложность и разрешимость
117
с количествами времени и памяти, необходимыми для решения за-
дачи. Очевидно, что количества времени и памяти не постоянны,
а изменяются в зависимости от размерности решаемой задачи. Для
сетей Петри временные и емкостные затраты будут, по-видимому,
функцией от числа позиций и переходов. Другими факторами, вли-
яющими на время и память, будут число фишек в начальной марки-
ровке и число входов и выходов для каждого перехода и позиции
(число дуг в графе).
Требуемые время и память будут изменяться от одной задачи
к другой. Поэтому оценки сложности алгоритма могут быть даны
для наилучшего случая (нижняя граница) или наихудшего случая
(верхняя граница). Поскольку не известно, относится данный при-
мер задачи к наилучшему или наихудшему случаю, обычно прини-
мается наихудший случай, и сложность алгоритма — это времен-
ные и емкостные затраты в худшем случае как функция от размер-
ности задачи.
Анализ сложности касается главным образом сложности задачи,
а не конкретных деталей реализации какого-либо частного алго-
ритма. Поэтому в теории сложности игнорируются константы. Слож-
ность задачи размерности п определяют порядком п2 или 2я, или
п log п, допуская меньшие члены и постоянные сомножители. Осо-
бенно важны два общих класса алгоритмов: имеющих полиномиаль-
ную сложность (п, п2, п log п, п8 и т. д.) и имеющих неполиноми-
альную сложность (в частности, экспоненциальную, 2га, и факто-
риальную, п!).
Анализ сложности обычно применяют к конкретным алгоритмам,
но его можно применить также и к общим задачам. В этом случае
определяется нижняя оценка сложности из всех алгоритмов, решаю-
щих задачу. Это обеспечивает значение сложности, не зависящее
от алгоритма, и, кроме того, может оказаться полезным в доказа-
тельстве того, что данный алгоритм оптимален (с точностью до
константы), и в определении случаев, когда дальнейшая работа мо-
жет привести к лучшему алгоритму решения задачи. Например,
хорошо известно, что сортировка п чисел имеет сложность п log п.
Следовательно, алгоритмы сложности п log п нельзя значитель-
но улучшить (в асимптотически худшем случае).
При определении сложности может быть полезно сведение одной
задачи к другой. Если задачу А можно свести к задаче В и В
имеет сложность то сложность А —это, самое большее, слож-
ность В плюс стоимость преобразования из Л в В (помня, что в ре-
зультате перевода размерность задачи может измениться.) Слож-
ность преобразования является, как правило, константой или ли-
нейной функцией и поэтому часто игнорируется. Следовательно,
сведение задачи А к задаче В дает или верхнюю границу сложности
А (если известна сложность В), или нижнюю границу сложности
В (если известна сложность А). Используя снова в качестве примера
задачи равенства и подмножества, получаем, что объем вычисле-
118
Глава 5
ний, необходимый для решения задачи равенства, не больше чем
удвоенный объем вычислений для задачи подмножества. Поскольку
здесь участвует постоянный сомножитель, сложность задачи под-
множества должна совпадать со сложностью задачи равенства.
Эти два свойства задач анализа сетей Петри — разрешимость
и сложность — имеют первостепенную важность для использова-
ния сетей Петри. В этой главе представляются некоторые извест-
ные результаты. Один из используемых методов — сведение одной
задачи анализа Петри к другой.
5.2. Задачи достижимости
Задача достижимости — одна из самых важных задач анализа
сетей Петри. Она до сих пор еще не решена для различных вариаций
ее определения. Были поставлены следующие четыре задачи дости-
жимости для сети Петри С = (Р, Т, I, О) с начальной маркиров-
кой р.
Определение 5.3. Задача достижимости. Выполняется ли для дан-
ной р': p'g/? (С, р)?
Определение 5.4. Задача достижимости подмаркировки. Для под-
множества Р' е Р и маркировки р' существует ли р" 6 Р(С, р),
такая, что р"(рг) = р' (рг) для всех pt g Д'?
Определение 5.5. Задача достижимости нуля. Выполняется ли
р' g R(C, р), где р'(Рг) = 0 Для всех pi £Р? (0 g Р(С, р)?).
Определение 5.6. Задача достижимости нуля в одной позиции. Для
данной позиции р; Q Р существует ли р' g 7?(С, р) с р'(рг) = 0?
Задача достижимости подмаркировки ограничивает задачу до-
стижимости до рассмотрения только подмножества позиций,
не принимая во внимание маркировки других позиций. Зада-
ча достижимости нуля выясняет, является ли достижимой част-
ная маркировка с нулем фишек во всех позициях. Задача дости-
жимости нуля в одной позиции выясняет, возможно ли удалить
все фишки из данной позиции.
Хотя эти четыре задачи различны, все они эквивалентны. Опре-
деленные взаимосвязи очевидны сразу. Задача достижимости нуля
сводится к задаче достижимости; просто в задаче достижимости
устанавливается р' = 0. Аналогично задача достижимости сводится
к задаче достижимости подмаркировки путем установки Р’ = Р.
Задача достижимости нуля в одной позиции сводится к задаче
достижимости подмаркировки установкой Р" — {pt} и р' = 0.
Сложнее показать, что задача достижимости подмаркировки сво-
дится к задаче достижимости нуля и что задача достижимости нуля
Сложность и разрешимость
119
сводится к задаче достижимости нуля в одной позиции. Все мно-
жество взаимосвязей представлено на рис. 5.1.
Сначала покажем, что задача достижимости подмаркировки
сводится к задаче достижимости нуля. Пусть даны сеть Петри С\ =
= (Pt, Pi, Oi) с начальной маркировкой подмножество P's
£ Pi и маркировка р/. Мы хотим узнать, существует ли
р" € R(Ci, н) с р'(рг) = р"(рг) для всех pt £ Р'. Наш подход
Задача достижимости
Рис. 5.1. Сводимость задач достижимости. Дуга от одной задачи к другой оз-
начает, что первая сводится ко второй.
заключается в построении новой сети Петри С2 = (Р2, 1\, /2, 02)
с начальной маркировкой р2, такой, что маркировка р" £ R(C,, щ)
с I1'(Pt) — p"(Pi) Для всех pt Q Р' существует тогда и только тогда,
когда О£Я(Сг, р2).
Построение С2 из С4 осуществляется исключительно просто.
Начнем с С2, совпадающей с Cj. Для того чтобы позволить всякой
позиции pi вне Р' стать пустой, введем переход с входом {pi}
и пустым выходом. Этот переход можно запускать всякий раз, когда
в pi имеются фишки, чтобы изъять их, что позволяет достичь ну-
левой маркировки и тем самым игнорировать такие позиции.
Относительно pt в Р' необходимо иметь уверенность, что в pt
точно р'(рг) фишек. Для этого построим новые позиции р, для
каждой Pi£Pr с начальной маркировкой p'(P;) фишек и переход
tt с входом {pi, pt} и пустым выходом. Если в pi точно р'(рг) фи-
шек, то этот переход можно запустить точно р'(рг) раз, сокращая
маркировки pt и pt до нуля. Если число фишек в рг отлично от
р'(Рг). т0 переход можно запустить только минимальное из двух
маркировок число раз, и поэтому либо в рг, либо в pt- останутся
фишки, препятствующие достижению нулевой маркировки.
120
Глава 5
Рис. 5.2. Сеть Петри, служащая для доказательства сводимости задачи дости-
жимости подмаркировки к задаче достижимости нуля. Подмножество пози-
ций Р' будет иметь маркировку pi' в первоначальной сети тогда и только
тогда, когда в модифицированной показанным здесь способом сети будет до-
стижима нулевая маркировка.
Два типа вводимых переходов иллюстрируются на рис. 5.2.
Формально определим С2 следующим образом:
P8 = 6UUIp,-6P'},
Т2 = ли I ,
MG) = А(6) для G€M
G(G) = IpJ для рЛр’>
= |р,. р'| для р,€М
Oa(G) = °i(G) ДЛЯ G€M
о2(<)={ }ддяр,еб>
с начальной маркировкой:
Р2(Р,) = Pi(Pi)> Pi Qpi>
Р2 (рЭ = P'(Pi). Pi£p'-
Теорема 5.1. Задача достижимости подмаркировки сводится к за-
даче достижимости нуля.
Сложность и разрешимость
121
Доказательство. Покажем, что для сети Петри С2, построенной из
вышеописанным способом, 0 £ Р(С2, р2) тогда и только тогда,
когда р" С R(Ci, рЛ с p"(pf) = р'(рг) Для всех Pi С Р'
Для того чтобы показать, что 0 € Р(С2, р2) тогда и только тог-
да, когда существует р” е R(Cit р4) с р”(рг) = ц'(рг) Для pt £ Р’,
допустим сначала, что р" присутствует в R(Ci, pi). Тогда в С2 также
можно достичь маркировки р" в позициях pi € Pi запуском только
переходов из 7\. Сейчас для каждой позиции pt (= Р' можно за-
пустить ti точно р'(рг) раз, сокращая маркировку и pt, и р/ до
нуля. Затем можно запустить // для каждой pt 5 Р' столько раз,
сколько необходимо для приведения маркировки этих позиций к
нулю, поэтому О G Р(С2, р<,).
Теперь предположим, что 0 £ Р(С2, р2); тогда существует по-
следовательность запусков переходов о, переводящая р2 в 0. Эта
последовательность будет содержать точно p'(pi) запусков V { для
pt £ Р' (для удаления фишек из pt') и некоторое число запусков
tt для Pi 5 Р'. Заметим, что запуски этих переходов только уда-
ляют фишки из Ct, и поскольку 6(р', tj) определено там, где опре-
делено б(р, tj) для р' > р (лишние фишки не могут повредить за-
пуску переходов), последовательность о после удаления из нее
всех запусков tt останется действительной и будет приводить к мар-
кировке р" с точно р'(Рг) фишками в р, для р, 6 Р'. Таким обра-
зом, если 0 £ Р(С2, р2), то р" g R(Cit рО с р"(рг) = р'(Д/) Для
PitP’- □
Наша следующая задача —- показать, что задача достижимости
нуля сводится к задаче достижимости нуля в одной позиции. Дока-
зательство этого утверждения также основано на вспомогательном
построении. Пусть дана сеть Петри Ct = (Pt, Tlt /ь Ot) с началь-
ной маркировкой рь мы хотим определить, выполняется ли 0 £
€ R(Cit pi). Построим из Ct новую сеть Петри С2 с дополнительной
позицией s(P2 = Pt U {s}), такой, что маркировка р' Q R(C2, р2)
с p'(s) = 0 существует тогда и только тогда, когда 0 g R(Cit pt).
Построение С2 определяет s так, что всякий раз число фишек
в s равно сумме числа фишек в позициях Ct. Следовательно, если
p'(s) = 0, то в позициях Ct нет фишек, и наоборот. Определим
начальную маркировку р2 следующим образом:
Иа(Рг) = IhtPi) ДЛЯ PiCPlf
p<e₽i
Далее для каждого перехода t j QTt в С2 будет тот же переход, но
с добавленными дугами к позиции s. Определим
di = 2 (# (Pi, О (tj)) - # (а,7 (tj))).
р&р1
122
Глава 5
Тогда dj — это разность числа фишек после запуска перехода tj
и числа фишек до запуска t}. Теперь, если dj >0, то dj фишек
должно быть добавлено в позицию s, поэтому введем dj дуг из tj
в s, если dj<Z 0, то удалим —dj фишек из s введением —d j дуг из
s в t j.
Если dj > 0, то 4±(s, I(tj)) = 0, 4ф($, O(t j)) = dj.
Если dj< 0, то /(G)) = —dj, 4£(s, 0(G)) = 0.
Если dj = 0, то #(s, I(t})) = 0, #(s, 0(G)) = 0.
При таком построении любая последовательность запусков пе-
реходов, приводящая Ci к маркировке 0, приведет С2 к маркировке
р/ с p'(s) = 0 (а также p'(Pi) = 0), и наоборот.
Теорема 5.2. Задача достижимости нуля сводится к задаче дости-
жимости нуля в одной позиции.
Доказательство. Формальное доказательство, основанное на опи-
санной конструкции, оставляем читателю. □
На основе этих двух теорем и очевидных выводов можно заклю-
чить следующее:
Теорема 5.3. Следующие задачи достижимости эквивалентны:
1. Задача достижимости.
2. Задача достижимости нуля.
3. Задача достижимости подмаркировки.
4. Задача достижимости нуля в одной позиции.
Эти теоремы и их доказательства принадлежат главным обра-
зом Хэку [116].
5.3. Сети Петри с ограничениями
В первых работах по сетям Петри, а также в некоторых со-
временных работах сети Петри определяются в несколько более ог-
раниченной форме, чем в определении, данном в гл. 2. В частности,
иногда принимаются следующие два ограничения:
Ограничение 5.1. Кратность любой позиции равна 0 или 1. Иначе
говоря, #(/?;, /(G)) < 1 И #(/?;, 0(G)) < 1 для всех pi € Р и tj €
€ Т. Это ограничивает входные и выходные комплекты до множеств.
Ограничение 5.2. Е1икакая позиция не может быть одновременно
входом и выходом одного и того же перехода. l(tj) (\O(tj) = 0.
Это часто формулируется как #(рг, /(G)) #(Pi> 0(G)) = 0 для
всех pi и G-
Сети Петри, удовлетворяющие ограничению 5.1, называются
ординарными. Сети Петри, удовлетворяющие ограничению 5.2,
называются сетями Петри без петель, или нерефлексивными се-
тями. Сети Петри, удовлетворяющие обоим ограничениям, назы-
Сложность и разрешимость
123
ваются простыми сетями Петри^. Эти классы сетей Петри соот-
носятся так, как показано на рис. 5.3.
Подклассы модели обычных сетей Петри рассматривались по
нескольким причинам. Основная причина заключается в том, что
введение понятий сетей Петри в начале развития теории было не-
формальным. Необходимость в кратных дугах и петлях при моде-
лировании тогда отсутствовала. Кроме того, вероятно, казалось,
Обычные сети Петри
Ординарные сети Петри
(дез кратных дуг)
Сети Петри
без петель
Простые сети Петри
(без кратных дуг и петель!
Рис. 5.3. Взаимосвязи между классами сетей Петри. Дуга означает включе-
ние; дуги сводимости будут ориентированы в противоположном направлении.
что теория без этих усложнений будет проще. По мере развития тео-
рии стало ясно, что работать с более общими определениями не
труднее. Использование моделей с этими ограничениями в совре-
менных работах объясняется стремлением исследователя к более
простому и лаконичному изложению.
Однако эти ограничения не добавляют ничего к способности
анализировать сети Петри. Рассмотрим для этих классов сетей за-
дачу достижимости. Для того чтобы показать эквивалентность всех
четырех классов сетей Петри, докажем следующее:
Теорема 5.4. Задача достижимости эквивалентна для следующих
классов сетей Петри:
1. Обычные сети Петри.
2. Ординарные сети Петри.
3. Сети Петри без петель.
4. Простые сети Петри.
Доказательство. Из определений очевидны следующие сведения:
1. Задача достижимости для ординарных сетей Петри сводится к
задаче достижимости для обычных сетей Петри.
2. Задача достижимости для сетей Петри без петель сводится к за-
даче достижимости для обычных сетей Петри.
>) По аналогии с подобным понятием в теории графов. — Прим. ред.
124
Глава 5
3. Задача достижимости для простых сетей Петри сводится и к за-
даче достижимости для ординарных сетей Петри, и к задаче дости-
жимости для сетей Петри без петель.
Покажем, что обычные сети Петри можно преобразовать в про-
стые сети Петри таким образом, чтобы свести задачу достижимости
для обычных сетей Петри к задаче достижимости для простых сетей
Петри. Это покажет, что все четыре задачи достижимости экви-
валентны.
Для преобразования обычной сети Петри в простую сеть Петри
используем следующий подход. Каждая позиция в обычной сети
Петри заменяется кольцом позиций в простой сети Петри. На
рис. 5.4 показан общий вид кольца позиций. Заметим, что набор
фишек, помещенных в кольцо, может свободно двигаться по кольцу
к любой позиции в любой момент времени; все они могут сгруппи-
роваться в позиции pitl или равномерно распределиться, покрывая
все kt позиций кольца. Поэтому переход, для запуска которого
необходимы три фишки из позиции р(, может выбрать вместо всех
трех из pt по одной из р,л, pii2 и Pt,3. Аналогично переход, ис-
пользующий pt в качестве входа и в качестве выхода (петля), может
иметь вход в piA, а выход в р^, тем самым устраняя петлю.
Формально для обычней сети Петри С\ = (Рь 7\, 7Ь Oj) с мар-
кировкой [Ci определим простую сеть Петри С2 = (Р2, ^2» ^2> 02)
с маркировкой р2 следующим образом. Сначала для каждой пози-
ции Pi^Pi определим целое k{:
ki = max (# (pi, I (tj)) + # (pi,
t^T
Сеть Петри с ограничениями С2 определяется
Р2 = {А. h\Pi^Pu
^2 = 7\UVi, h | Pi. h^P^}-
Входная и выходная функции
деляются так, что
для «нормальных» переходов опре-
#(Рг.ы Ш))={
1, если 1 С h # (ft,
О, в противном случае;
+ #(А. 01 (/;)),
1, если # (рг, /1(/7))</г=с # (pt, Л(^)) +
#U-,V 02 (/;)) =
О, в противном случае;
а для «кольцевых» переходов
^г( h) ~ { Pi, h) ’
h. н) = {Pi. n |« = 1 + (Л (mod *i»J-
Сложность и разрешимость
125
Маркировка р2 определяется следующим образом:
М₽>, i) = Hi(Pi) Для pi
Pv(Pi, h) = ° Для h> 1.
Рис. 5.4. Кольцо позиций, используемое в простой сети Петри для представ-
ления позиции обычной сети Петри. Число kt позиций, представляющих по-
зицию pj, определяется максимумом сумм кратностей позиции.
Для любой маркировки р, достижимой в Ct, по построению су-
ществует такая маркировка р' в С2, что
Sp'(Pi, н) = ^(pi) для всех pt £PV
Л
в частности, в любой момент времени в С2 можно переместить все
фишки из pc,h в pi,\. Следовательно, можно определить маркировку
р' следующим образом:
l) = Р(Р‘^ ДЛЯ Pi^Pp
р' (Pi. h) = 0 ДЛЯ h > 1,
и р' становится достижимой в простой сети Петри С2 тогда и толь-
ко тогда, когда р достижима в С4. □
Таким образом, с точки зрения анализа обычные сети Петри и
три ограниченных класса обычных сетей Петри — ординарные сети
Петри, сети Петри без петель и простые сети Петри — эквивалент-
ны, всякую сеть можно преобразовать в подобную сеть другого клас-
са, сводя задачу достижимости для одной сети к задаче достижи-
мости для другой. Использованные в этом разделе конструкции
принадлежат Хэку [111].
126
Глава 5
Рис. 5.5. Сводимость задачи достижимости среди классов сетей Петри с
различными типами ограничений.
5.4. Активность и достижимость
Достижимость — важная задача сетей Петри. Другой задачей,
получившей много внимания в публикациях по сетям Петри, явля-
ется активность. Как отмечено в разд. 4.1.4, активность связана с
тупиками. Мы коснемся здесь двух задач, связанных с активностью
сети Петри С = (Р, Т, /, О) с начальной маркировкой р. Сеть Петри
активна, если активен всякий ее переход. Переход t} активен в
маркировке р, если для всякой маркировки р' £ R(C, р) сущест-
вует последовательность о, такая, что tj разрешен в 6(р', о). Пе-
реход t j пассивен в маркировке р, если не существует достижимой
маркировки, в которой бы он мог быть запущен.
Определение 5. 7. Задача активности. Активны ли все переходы
tjtT>
Определение 5. 8. Задача активности одного перехода. Активен ли
данный переход tj QT?
Очевидно, что задача активности сводится к задаче активности
одного перехода. Для нахождения решения задачи активности мы
просто решим задачу активности одного перехода для каждого t j G
€ Т; если | = т, то мы должны решить т задач активности од-
ного перехода.
Сложность и разрешимость
127
Задачу достижимости можно также свести к задаче активности.
Поскольку варианты задачи достижимости эквивалентны, мы рас-
смотрим задачу достижимости нуля в одной позиции. Если перед
нами стоят какие-либо другие задачи достижимости, их можно свес-
ти, как показано в разд. 5.2, к задаче достижимости нуля в одной
позиции. Теперь, если мы хотим определить, может ли быть позиция
pi нулевой в какой-либо достижимой маркировке для сети Петри
Ci — (Plt Тъ 7Ь Of) с начальной маркировкой то построим
сеть Петри С2 = (Р2, Т^2» 02) с начальной маркировкой р2, кото-
рая будет активна тогда и только тогда, когда нулевая маркировка
не будет достижима из р,.
Сеть Петри С2 строится из Ct введением двух позиций rt и г2
и трех переходов sit s2 и s3. Сначала модифицируем все переходы Т1г
включая /-j в качестве входа и выхода. Начальная маркировка р2
будет включать фишку в Позиция /-t — это позиция «действия»,
пока фишка остается в rt, переходы Ti могут запускаться. Следова-
тельно, любая маркировка, достижимая в С1? достижима также и в
позициях Рг в С2. Определим переход так, что его входом будет
гь а выход пуст. Это позволяет удалить фишку из rt, запрещая
запуск всех переходов в и «замораживая» маркировку Рр (За-
метим, что все переходы Tt находятся в конфликте и не только по
определению, но и по построению могут запускаться каждый раз
не более чем по одному.)
Позиция /-! и переход позволяют сети Ct достичь любой дости-
жимой маркировки, затем запуском st заморозить сеть в этой мар-
кировке. Далее необходимо проверить, является ли позиция рг-
нулевой. Введем новые позицию г2 и переход s2, имеющий в качестве
входа pt, а в качестве выхода г2. Если pt может когда-либо стать
нулевой, то этот переход не является активным. В действительнос-
ти вся сеть будет пассивной, если в этой маркировке сработает пе-
реход s,. Следовательно, если pt может быть пустой, сеть не явля-
ется активной. Если pt не может быть пустой, тогда s2 всегда мо-
жет быть запущен, помещая фишку в г2. В этом случае мы должны
будем вернуть фишку в rf и гарантировать, что все переходы в С2
активны. Необходима уверенность в том, что С2 активна, даже если
Ci не является активной. Это обеспечивается переходом s3, кото-
рый «наполняет» сеть С2 фишками, гарантируя тем самым, что, если
фишка помещена в г2, каждый переход активен. Переход s3 в ка-
честве входа имеет г2, а в качестве выхода все позиции С2 (все pi в
Сь г1 и г2). Эта конструкция иллюстрируется рис. 5.6.
Далее, если маркировка р, с ц(р,) = 0 достижима в /?(СЬ щ),
тогда С2 также может достичь этой маркировки в позициях Pi пу-
тем выполнения той же самой последовательности запусков пере-
ходов. Затем можно запустить st, замораживая подмножество Ct.
Поскольку n(pt) = 0, s2 запустить нельзя и С2 пассивна. Таким
образом, если pi может стать нулевой — С2 неактивна.
Справедливо обратное, если С2 неактивна, тогда должна быть
128
Глава 5
Рис. 5.6. Конструкция, переводящая задачу достижимости нуля в одной по-
зиции (достижима ли маркировка с p.(Pi) = О?) в задачу активности (являет-
ся ли сеть активной?).
достижима маркировка р с р(г2) = 0, из которой недостижимо
состояние с фишкой в г2. (Если в г2 есть фишка, то s3 разрешен, а
повторно запуская s3 достаточное число раз, можно разрешить лю-
бой (или все) переход, т. е. сеть активна.) Если г2 не имеет фишек
и не может их получить, тогда маркировка р, также должна быть
нулевой. Таким образом, если С2 неактивна, тогда достижима мар-
кировка, в которой маркировка pi нулевая.
На основе этой конструкции мы доказали следующую теорему.
Теорема 5.5. Задача достижимости сводится к задаче активности.
Для доказательства основного утверждения раздела покажем
следующее.
Теорема 5.6. Задача активности одного перехода сводится к задаче
достижимости.
Сложность и разрешимость
129
Доказательство того, что задача активности одного перехода
сводима к задаче достижимости, опирается на проверку достижи-
мости любой из конечного множества максимальных пассивных для
t j подмаркировок. Сеть Петри не активна для перехода tj тогда и
только тогда, когда достижима некоторая маркировка, в которой
переход t} не запускаем и не может стать запускаемым. Марки-
ровка такого вида называется пассивной для tj. Для любой марки-
ровки р можно проверить, является ли она пассивной для t j по-
строением дерева достижимости с корнем р и проверкой, можно ли
Рис. 5.7. Сеть Петри, иллю-
стрирующая пассивные мар-
кировки ДЛЯ tj.
где-либо в дереве запустить переход t}. Если нельзя, то р массивна
для tj. Проверка активности tj в таком случае требует проверки
достижимости какой-либо пассивной для tj маркировки.
В общем случае, однако, может существовать бесконечное число
пассивных для tj маркировок и бесконечное множество маркиро-
вок, в котором находятся пассивные для t} маркировки. Заметив
два свойства, сведем множество маркировок, которые необходимо
проверить для достижимости, к конечному числу. Во-первых, если
маркировка р пассивна для tj, то и любая маркировка р' р пас-
сивна для tj. (Любая последовательность запусков, возможная из
р.', возможна также из р, поэтому если р' может привести к запуску
t j, то это может и р.) Во-вторых, маркировки некоторых позиций
не будут влиять на пассивность для t} данной маркировки, поэтому
маркировки этих позиций являются «несущественными», они могут
быть произвольными. Заимствуя прием из построения дерева дости-
жимости, заменим «несущественные» компоненты на <о, показывая,
что в этих позициях может быть произвольно большое число фишек,
не влияющих на пассивность маркировки для t}. Теперь, поскольку
любая р' < р пассивна для tj, если р пассивна для t j, нам не нужно
рассматривать позиции р{ с р(рг) = со. Это означает, что мы приме-
няем задачу достижимости подмаркировки с Р' = {pt |р(рг) =/= со}.
Рассмотрим в качестве примера сеть Петри на рис. 5.7. Марки-
ровки (2, 0), (1, 0), (0, 0), (0, 1), (0, 2), (0, 3),... являются пассивными
для Ь, но их можно представить конечным образом множеством
{(2, б), (1, 0), (0, о)}.
Хэк [113, 116] показал, что для сети Петри С существует такое
конечное множество Dt маркировок (расширенных, т. е. включаю-
5—562
130
Глава 5
щих <о), что С активна тогда и только тогда, когда никакая марки-
ровка из Dt недостижима. Если маркировка из Dt содержит со,
тогда подразумевается достижимость подмаркировки.
Более того, Dt можно эффективно вычислять. Поскольку Dt
конечно, не-ы-компоненты имеют верхнюю границу Ь. Граница b
определяется как такое наименьшее число, что если пассивна для
tj любая маркировка р, такая, что р(рг) < b + 1 для всех pit то
является пассивной для tj и подмаркировка р', такая, что
И'(Pi) = p(Pi)> если p(Pi) < Ь, и р'(рг) = со, если р(рг) = b + 1.
При таком определении b можно построить Dt следующим образом.
1. Вычислить Ь. Начать с b — 0, увеличивать b до тех пор, пока
не окажется, что b удовлетворяет описанному определению
границы. Проверка каждого b требует проверки всех (Ь 4- 2)"
маркировок с компонентами, меньшими или равными Ь + 1.
2. Вычислить Dt проверкой всех маркировок и подмаркировок с
компонентами, не превышающими Ъ или равными со. Dt — это
множество пассивных для tj маркировок из множества (Ь + 2)"
маркировок.
Построив Dt, можно рассматривать задачу достижимости под-
маркировки для каждого элемента Dt. Если какой-либо элемент
Dt достижим из начальной маркировки, сеть Петри неактивна,
если же никакой элемент Dt недостижим—-сеть Петри активна.
Из доказанных теорем мы получаем следующую.
Теорема 5.7. Следующие задачи эквивалентны:
1. Задача достижимости.
2. Задача активности.
3. Задача активности одного перехода.
Более формальные доказательства сводимости активности к до-
стижимости можно найти в [ИЗ, 116].
5.5. Неразрешимые задачи
В предыдущем разделе мы показали, что многие задачи дости-
жимости и активности эквивалентны, но никакого результата от-
носительно разрешимости этих задач еще не получили. Для того
чтобы показать разрешимость, необходимо свести задачу для сетей
Петри к задаче с известным решением, а для того, чтобы показать
неразрешимость, нужно свести задачу, которая известна как не-
разрешимая, к задаче для сетей Петри. Первый важный результат
такого рода был получен Рабином [26]. Он показал неразрешимость
задачи: выполняется ли R(Clt Pi)^P(C2, р2) Для двух сетей Петри —
Ci с маркировкой pi и С2 с маркировкой р2? Позднее Хэк [114] по-
казал, что неразрешимой является и задача: выполняется ли
Д(Сь pi) = R(C2, р2)? Доказательство этих утверждений основано
на десятой проблеме Гильберта. (Д. Гильберт на конференции
математиков в 1900 г. поставил 23 проблемы, и та, на которую
опирался Хэк, была десятой в списке)
Сложность и разрешимость
131
Определение 5.9. Дан полином Р от п переменных с целыми коэф-
фициентами; существует ли такой вектор целых (хь х2, хп), что
Р(хь х2, хп) — 0? Уравнение Р(хь х2, ..., хп) = 0 называется
диофантовым.
В общем оно представляет собой сумму членов:
Р (хх, х2,..., хп) = 5 Pi (хх,
xs,..., хп),
Ri U1. х2,..., хп) = di xSi • xSt
Десятая проблема Гильберта
Задача Включения
графов полиномов
Задача подмножества для множеств
достижимости сетей Петри
Задача равенства множеств
достижимости сетей Петри
Рис. 5.8. Сведения, показывающие, что задача равенства (и подмножества)
дляжмножеств достижимости сетей Петри неразрешима.
Диофантовыми уравнениями являются xt = 0; Зх, • х2 + 6х3 =
= 0 и т. д.
В 1970 г. Матиясевич1* доказал, что десятая проблема Гиль-
берта неразрешима [70, 71]: не существует общего алгоритма, опре-
деляющего, имеет ли произвольное диофантово уравнение корень
(набор значений, для которых полином равен нулю). Этот резуль-
тат служит основой доказательства того, что задача равенства
множеств достижимости сетей Петри неразрешима. Стратегия его
заключается в построении для диофантова полинома сети Петри,
которая (в определенном смысле) вычисляет все значения поли-
нома.
5.5.1. Задача включения графов полиномов
Доказательство неразрешимости задачи равенства состоит из
трех частей (рис. 5.8). Сначала десятая проблема Гильберта сво-
дится к задаче включения графов полиномов. Затем задача включения
*) Советский математик. — Прим, персе.
132
Глава 5
графов полиномов сводится к задаче подмножества для множеств
достижимости сетей Петри. Наконец, задача подмножества для
множеств достижимости сетей Петри сводится к задаче равенства
множеств достижимости сетей Петри. Это показывает, что десятая
проблема Гильберта, известная как неразрешимая, сводится к за-
даче равенства, которая поэтому также должна быть неразреши-
мой.
Определение 5.10. Граф G(P) диофантова полинома P(xlt ..., хп)
с неотрицательными коэффициентами — это множество
G(P) = {(xv хп, i/)| у < P(xlt ..., хп1 и 0 xv ..., хп, у}.
Определение 5.11. Задача включения графов полиномов заключается
в определении для двух диофантовых полиномов А и В, выполня-
ется ли G(A) с G(B).
Покажем сначала, что десятая проблема Гильберта сводится к
задаче включения графов полиномов.
Теорема 5.8. Задача включения графов полиномов неразрешима.
Доказательство-
1. Ограничим наше доказательство задачами с неотрицательными
решениями. Если (хь ..., хТ1)— решение для Р(х1г ..., хп) =
— 0 с Xi< 0, то (хь ..., —xt, ..., хп) решение для P(xi, —х,,...,
хп) = 0. Следовательно, для определения того, является ли
(хх, ..., хп) решением произвольного полинома1’, необходимо толь-
ко проверить каждый из 2" полиномов, получающихся в резуль-
тате изменения знака у некоторого подмножества переменных для
неотрицательного решения.
2. Аналогично, поскольку P2(Xi, ..., хп) = 0 тогда и только тогда,
когда P(xlf ..., хп) — 0, необходимо рассматривать только поли-
номы, значения которых неотрицательны.
3. Сейчас можно разбить любой полином Р{х1г х2, ..., хп) на два
полинома, Qi(xb ..., хп) и Q2(x,, ..., хп), такие, что P(xi, ..., хп) =
== Qi(xt, ..., xn) — Q2(xt, хп), помещая все члены с положи-
тельными коэффициентами в (Д_, а все члены с отрицательными ко-
эффициентами в Q2. Далее, поскольку Р(х1, ..., хп) > 0 (по п. 2),
имеем, что Qifo, ..., xn) > Q2(*i, •••, хп) и P(xlt ..., хп) = 0 тогда
и только тогда, когда Q^Xj, ..., xn) = Q2(xt, ..., хп).
4. Рассмотрим два графа полиномов:
G (<3i) = {(х1(..., хп, у) |у < Qx(хх,..., xn)},
G (Q2 + 1) = {(*i. -» xn, y) ly < 1 + Q2 (xx, ..., x„)}.
1) To есть допускающего решения с отрицательными значениями пере-
менных. — Прим, перев.
Сложность и разрешимость
133
Теперь G(Q2 + l)^G(Gi) тогда и только тогда, когда для всех
неотрицательных хп и у из 1 + Gz(^i> • хп) следует, что
у Qi(Xi, ..., хп). Это справедливо тогда и только тогда, когда
не существует х4, ..., хп и у, таких, что
хп) <2 у 1 + Qa(xi’•••» хп)-
Но из п. 3 следует, что Q2, поэтому
Qi(xp..., хп) су < 1 + <22(xv •••, хп)С 1 + Qi (хР - , хп),
а поскольку все величины целые,
У ~ 1 4" <2‘/ (хР... I хп) = 1 4- Qi (х1г..., хп), |
что справедливо тогда и только тогда,когда Qi = Q2. Таким обра-
зом, мы убедились в том, что G(Q2 + l)s G(Q±) тогда и только тог-
да, когда не существует таких хь ..., хп,для которых Р(х1г ...,хп) =
= 0.
5. Итак, для определения того, что уравнение P(xlt х2, ..., хп) =
= 0 имеет решение, необходимо показать только, что не выполня-
ется G(Q2 + 1)^ GtQt). Li
5.5.2. Слабое вычисление
Теперь нам необходимо показать, что сети Петри могут (в опре-
деленном смысле) вычислять значение полинома <2(%1, х2, хп).
Мы осмотрительно ограничили полином Q до неотрицательных
значений полинома, неотрицательных коэффициентов и неотрица-
тельных значений переменных. Это позволяет нам представить зна-
чения переменных и значение полинома числом фишек в позициях
сети Петри. Общая схема показана на рис. 5.9. Входные значения
хь .... xnfпредставляются хг фишками в pt для i = 1, ..., п. Перво-
начально фишка помещается также.в позицию «действия». Выпол-
нение сети будет закончено помещением фишки в позицию остано-
ва. В это время «выходная» позиция будет иметь у фишек, где у
=С Q(xt, ..., хп).
Эта сеть Петри слабо вычисляет значение Q(xt, ...., хп). Слабое
вычисление означает, что вычисленное значение не будет превы-
шать <2(хь ..., хп), но может быть любым (неотрицательным) значе-
нием, меньшим <2(хь ••> хп). Слабое вычисление обязательно для
сетей Петри вследствие разрешающей природы запусков переходов:
сеть Петри нельзя заставить остановиться. При определении графа
полинома G(Q) это особенно учитывалось.
Сейчас мы хотим показать, что можно построить подсеть, слабо
вычисляющую функцию умножения (двух чисел). На ее основе мы
можем построить составную сеть, которая слабо вычисляет значе-
ние каждого члена полинома путем последовательной композиции
подсетей умножения. Выход подсети для каждого члена будет
134
Глава 5
помещаться в выходную позицию для полинома. Таким образом,
число фишек в выходной позиции будет суммой выходов для каж-
дого члена.
Подсеть умножения показана на рис. 5.10. Эта сеть слабо вы-
числяет произведение чисел х и у, представимых фишками в ее
входных позициях, помещая множество фишек в свой выход. Дей-
ствует сеть совсем просто. Для вычисления произведения х и у
Действие Останов
Рис. 5.9. Базовая структура сети Петри, слабо вычисляющей значение поли-
нома Q(%1, хп).
сначала запускается переход перемещая одну фишку из рх в
р2. Эта фишка разрешает запуск перехода t3, который может теперь
копировать у фишек из позиции ру, помещая их в р3 и вкладывая
в выходную позицию р* у у фишек. Теперь можно запустить t2, воз-
вращая фишку из р2 в Pi. Это разрешает запуск /4, который копи-
рует у фишек из р3 обратно в ру. Весь этот процесс можно повторить
точно х раз, помещая каждый раз в рх у у фишек. После этого мар-
кировка рх становится нулевой и сеть останавливается. Общее чис-
ло фишек в позиции рх у равно произведению х и у.
Мы описали наилучший случай в том смысле, что число выходных
фишек в точности равно х • у. Однако фишка в р2 разрешает и пере-
ход ts, и переход t2, а переход t2 можно запустить до того, как все
у фишек будут скопированы из ру в р3 и добавлены в рх у. В этом
случае число фишек, помещенных в рх у, будет меньше, чем х у.
Поскольку t3 можно запустить не более у раз для каждого запуска
ti, a ti можно запустить не более х раз, мы можем гарантировать,
что число фишек в рх у никогда не превысит х • у, но вследствие
разрешающей природы запусков переходов мы не можем гарант и-
Сложность и разрешимость
135
Выход
Рис. 5.10. Подсеть умножителя. Эта подсеть слабо вычисляет произведение
х и у.
ровать, что число фишек в рх у будет в точности равно х • у ; оно
может быть меньше. Следовательно, эта сеть Петри слабо вычисляет
произведение х и у. Теперь для того, чтобы слабо вычислить член
Ri, являющийся произведением а, • xS1 • xS2 • ... • xS/i, построим
сеть Петри показанного на рис. 5.11 вида. Поскольку каждая под-
сеть слабо вычисляет произведение двух членов, вся подсеть слабо
вычисляет значение члена Rt.
Далее на рис. 5.12 показано, как можно слабо вычислять поли-
ном Р = Rl 4- Rz + ... 4- Rh. Каждая подсеть имеет вид, изо-
браженный на рис. 5.11, и слабо вычисляет значение одного члена
полинома. Выходы k подсетей для отдельных членов объединяются
вместе, давая общее значение суммы.
Теперь для создания конкретных необходимых множеств дости-
жимости вводится несколько управляющих переходов и позиций.
Сначала необходимо обеспечить получение произвольного значения
для каждой из переменных (х1( ..., хп) и запись этого значения в
136
Глава 5
Pitc. 5.11. Сеть Петри, слабо вычисляющая член диофантова уравнения.
Каждый блок в сети имеет вид, изображенный на рис. 5.10.
позиции .... рп. Для каждой р, создается переход tt с пустым
входом и выходами в pt и всякую позицию, являющуюся входом,
соответствующим хг в члене Rj, использующем х,. Следовательно,
в полиноме Xi + хрс2 мы должны иметь переход с выходами в
и во входы Xi в двух членах- xt и хрс2, использующих xt; tz будет
иметь выходы в р2 и во вход х2 в члене х{х2-
Эти переходы могут запускаться произвольное число раз, соз-
давая любые значения в plt ..., рп. Следовательно, для всякого у С
< P(Xi, ..., хп) достижима маркировка р с р(рО = xt, ..., p(pn) =
= хп и р(выход) = у. Значение у = Pfa, ..., хп) может быть дос-
тигнуто сначала запуском xt раз перехода помещая фишек
в р^ затем запуском х2 раз перехода tz и т. д., пока не будет запу-
щен хп раз переход tn. Далее можно выполнить подсеть для каждого
члена Rt полинома, в результате чего значение полинома поместится
в выходную позицию.
Сложность и разрешимость
137
Рис. 5.12. Сеть Петри, слабо вычисляющая P(xi, х2, ..., хп путей использо-
вания набора подсетей вида, изображенного на рис. 5.11.
Для сведения задачи включения графов полиномов к задаче
подмножества выполним следующие шаги. Пусть мы хотим опре-
делить для полиномов А и В, выполняется ли б(Д)^ G(B).
1. Построим сеть Петли СА, слабо вычисляющую Д(хъ . хп), и
сеть Петри Св, слабо вычисляющую В(хЛ, . хп).
2. Если число позиций в этих сетях не равно, добавим позиции в
ту сеть, где их меньше с тем, чтобы уравнять число позиций. Эти
позиции не имеют начальной маркировки и не связаны с какими-
либо переходами в сети.
3. Теперь мы должны устранить влияние всех внутренних позиций
на множества достижимости И в СА, и в Св различимо множество
из п 4- 1 позиций — п позиций, соответствующих значениям
xt, ..., хп, и (п 4- 1)-я позиция, соответствующая выходу каждой
сети Все другие позиции являются внутренними, маркировка их
138
Глава 5
неважна. Однако может оказаться, что для внутренней позиции
pt в СА и соответствующей позиции р(- в Св существуют неравные
маркировки р в R(CA, рА) и р' в R(CB, рв), поскольку р(рг) =4=
Ik'(Pi') для всех р" в R(CB, рв).
Для того чтобы обойти это препятствие, введем по две новые по-
зиции: q и г в СА (получая Са) и qr и г' в Св (получая Св). В СА
позиции q и г не связаны с переходами и первоначально г пуста,
a q имеет одну фишку. Позиция г' в Св служит позицией «действия».
Она получает начальную маркировку0, а каждый переход модифи-
цируется с тем, чтобы включать г' в качестве входа и в качестве
выхода. Следовательно, пока фишка остается в г', сеть Св может
функционировать, как и прежде. Введем в Св новый переход,
переводящий разрешающую фишку из г' в q', запрещая все перехо-
ды С в и «замораживая» маркировку. Теперь для каждой внутрен-
ней позиции2) введем по два новых перехода.
Один из этих переходов, вводимых для каждой внутренней по-
зиции pt, маркировка которой неважна, имеет в качестве входов
позиции q' и pt, а в качестве выхода — только q' (уменьшая при
запуске на 1 маркировку в pi), другой переход в качестве входа име-
ет q', а в качестве выхода и q', и pt (увеличивая при запуске на 1
маркировку в р^. Эти переходы благодаря соответствующей после-
довательности прибавляющих или убавляющих запусков обеспе-
чивают каждой внутренней позиции возможность иметь произ-
вольную маркировку.
4. Описанная конструкция показана на рис. 5.13. Для двух сетей
Петри С а и С в с начальной маркировкой рд и рв соответственно,
6(Л)е= G(B) тогда и только тогда, когда R(CA, рд)^ R(Cb, рв).
Са и Св имеют следующие множества достижимости:
сА-. Pi • -Рп Выход г g Внутренние позиции
X] . -*п • • -хп) 0 1 Некоторая произволь- ная маркировка
С'в Pi -Рп Выход г' g' Внутренние позиции
Х1 • -Хп y<£B(xlt • - • >хп) 1 0 Некоторая произволь- ная маркировка
Х1 --^п у<В(х1, • - • >яп) 0 1 Произвольная марки - ровка
О Одну фишку. — Прим, перев.
2) f и д' не считаются внутренними. — Прим, перев.
Сложность и разрешимость
139
Рис. 5.13. Сеть Петри, построенная для проверки включения графов полино-
мов.
Следовательно, если О(Л)е G(B), то R(CA, рА)^ R(CB, рв)
и, обратно, если R(CA, рА)^ R(Cb, pi), то G(A)s G(B).
Таким образом, мы показали справедливость следующего.
Теорема 5.9. Задача включения графов полиномов сводима к за-
даче подмножества для множеств достижимости сетей Петри. До-
казательство взято из [114, 1161.
5.5.3. Задача равенства
Теперь нам осталось только показать, что задача подмножества
для множеств достижимости сетей Петри сводится к задаче равен-
ства.
Предположим, чю имеются две сети Петри Л и В, и мы хотим
определить, выполняется ли R(A, pA)s R(B, рв) (задача подмно-
жества). Покажем сейчас, что можно определить такие две сети
Петри D и Е, что R(A, Ра) — R(B, рв) тогда и только тогда, когда
₽(£>, ро) — R(E, ре). Основой построения доказательства слу-
жит тот факт, что R(A, рА) <= R(B, рв) тогда и только тогда, когда
R(B, V’b) = R(A, рА) VR(B, рБ).
D и Е строятся из общей подсети С. Сеть С представляет мно-
жества достижимости Л и В для получения их объединения. Кон-
140
Глава 5
Рис. 5.14. Построение сетей Петри С, D и Е из А и В, используемое'для до-
казательства сводимости задачи подмножества для множеств достижимости к
задаче равенства.
струкция иллюстрируется рис. 5.14. Позиции ..., рп действуют
или как позиции сети А, или как позиции сети В. Первоначально они
не имеют маскировки. Вводятся две новые позиции гА и гв, слу-
жащие позициями действия для сети А и сети В соответственно.
Все переходы сети А модифицируются с тем, чтобы включать в ка-
честве входа и выхода гА, а все переходы сети В модифицируются
с тем, чтобы включать в качестве входа и выхода гв.
Далее вводятся еще одна позиция s, и два новых перехода, tA
и tB. Начальная маркировка всей сети (включая А и В как подсети
с общими позициями; позиции гА, гв и s; переходы tA и tB) опре-
деляется одной фишкой в s и нулем в остальных. Переход tA имеет
в качестве входа s, а выход его порождает начальную маркировку
сети А плюс фишку в гА; переход7В в качестве входа также имеет s,
а выход его создает начальную маркировку сети В плюс фишку в
гв. Следовательно, если запустится tA, то подсеть А приобретает