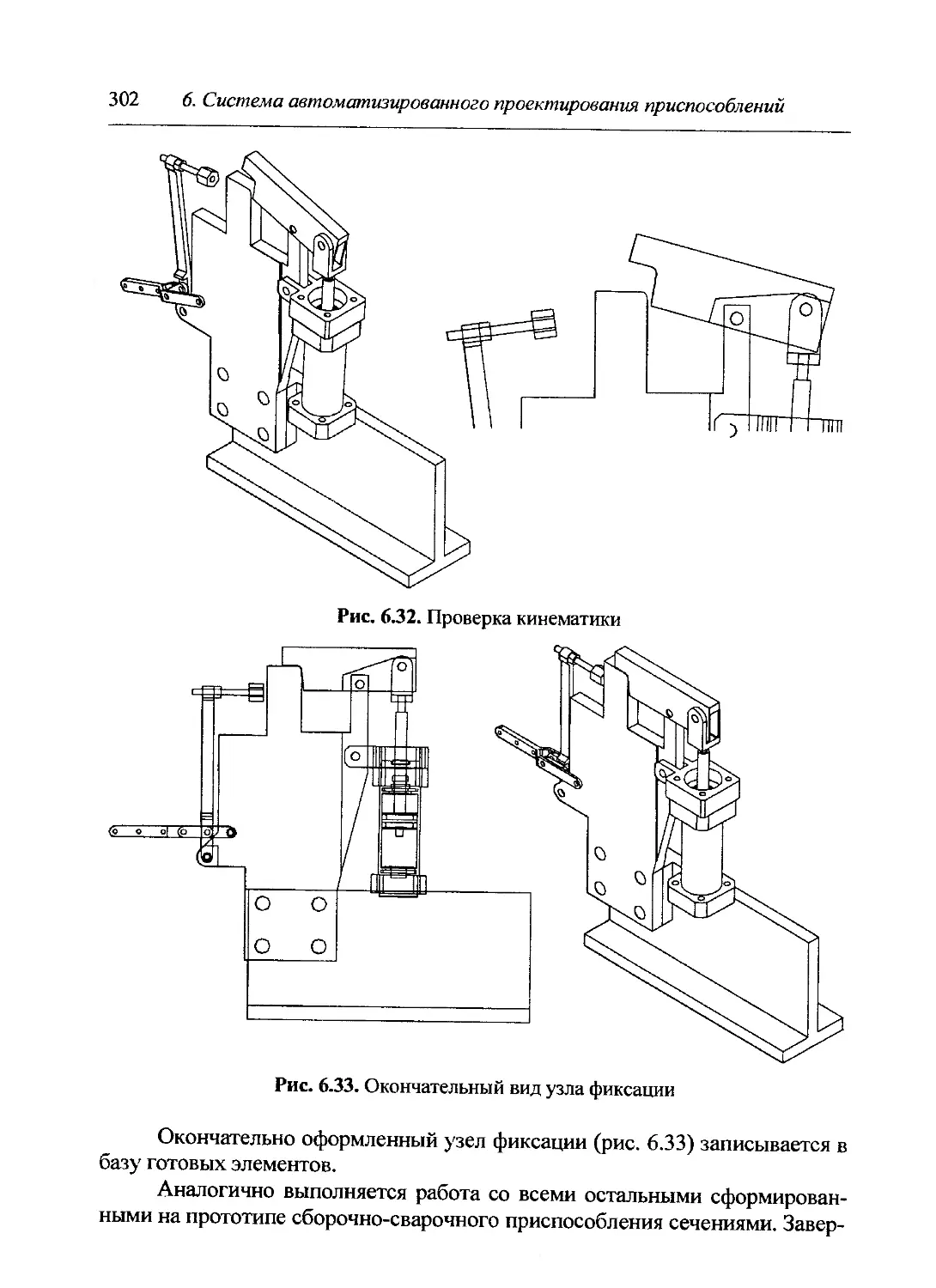
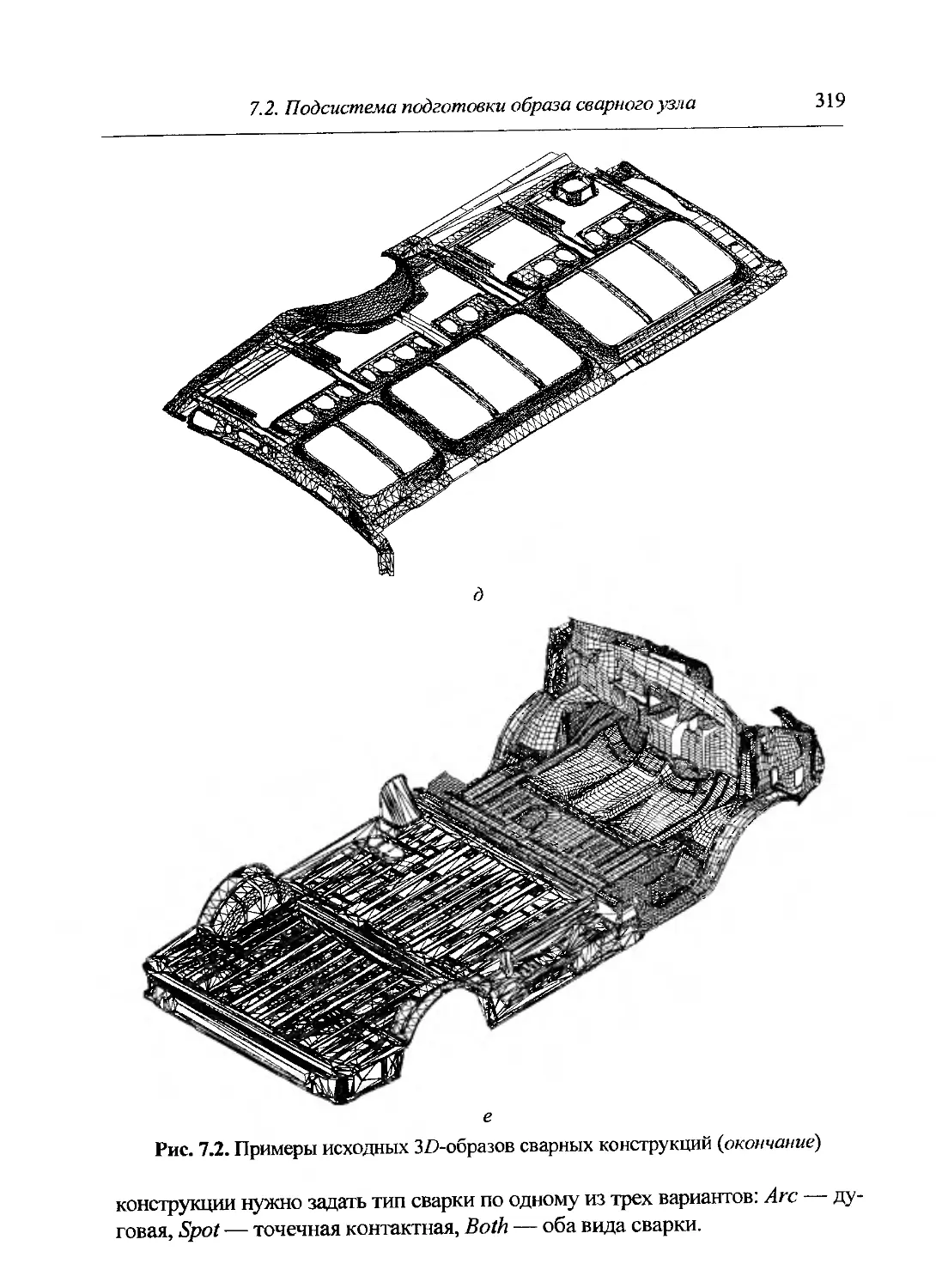
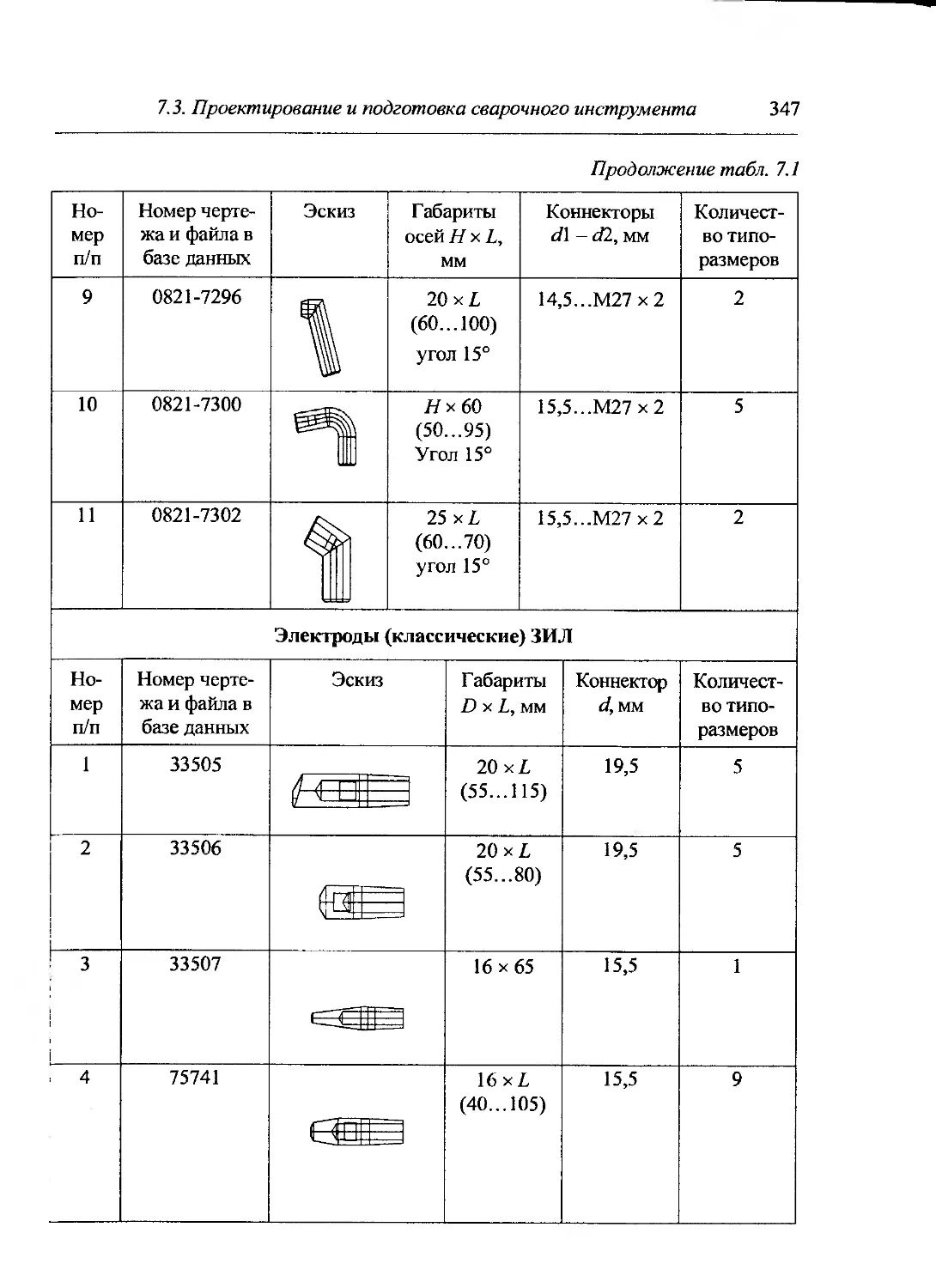
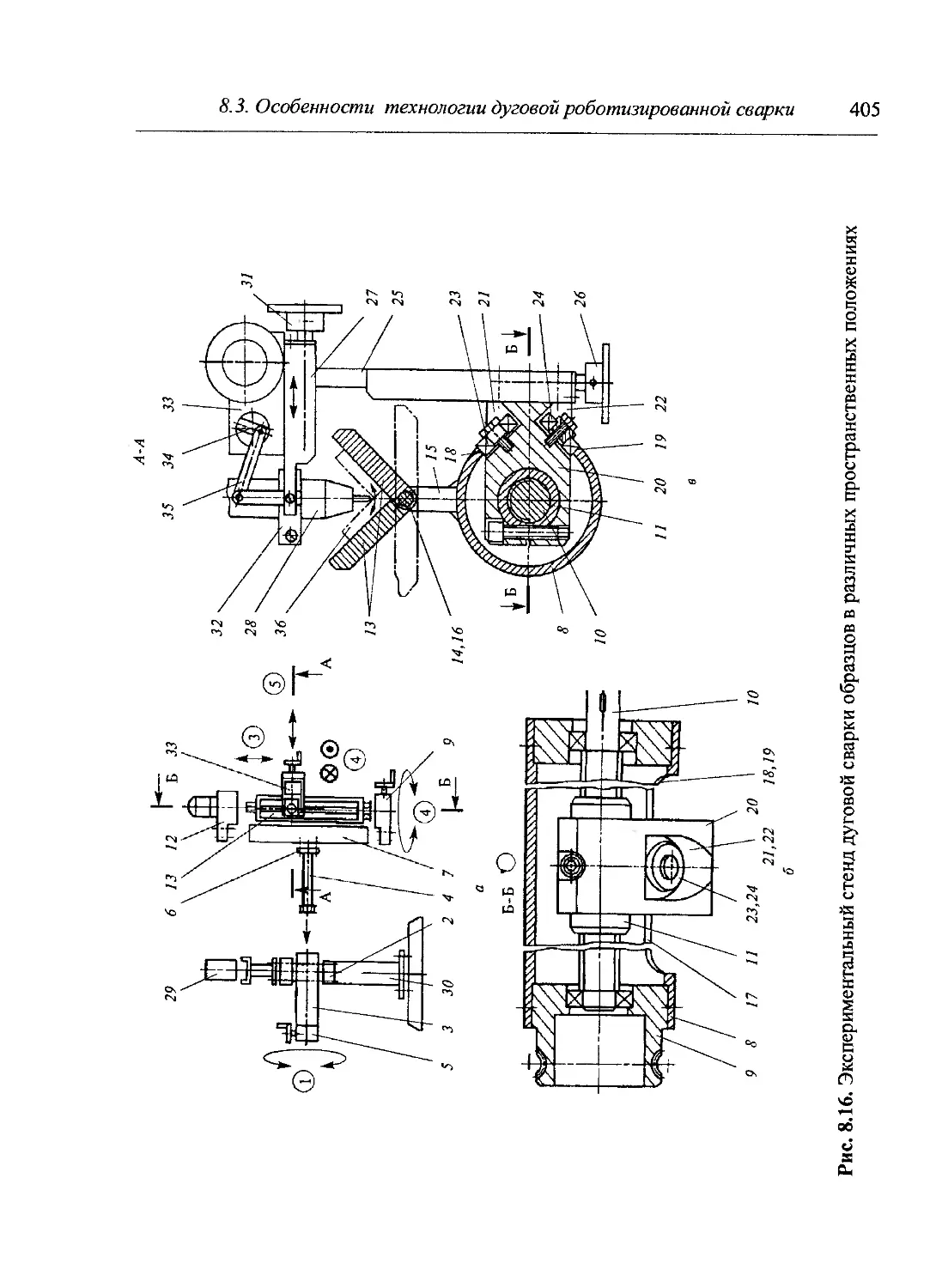
Author: Куркин С.А.
Tags: технология обработки без снятия стружки в целом: процессы, инструмент, оборудование и приспособления организация производственного процесса производственное планирование управление качеством техника и технические науки в целом компьютерные науки сварочное производство
ISBN: 5-7038-2053-7
Year: 2002
Компьютерное
проектирование
и подготовка
производства
сварных
конструкций
Под редакцией С.А. Куркина и В.М. Ховова
Рекомендовано Учебно-методическим объединением
по университетскому политехническому образованию
в качестве учебного пособия для студентов
высших учебных заведений,
обучающихся по направлению подготовки
дипломированных специалистов
«Машиностроительные технологии и оборудование»,
специальности «Оборудование и технология
сварочного производства»
Москва
Издательство МГТУ имени Н.Э. Баумана
2002
УДК 621.791:658.52.011.56 (075.8)
ББК 30.4
К 63
Федеральная целевая программа «Культура России -
(подпрограмма «Поддержка полиграфии и книгоизоания России»)
Рецензенты: кафедра «Сварка» Московского государственного
индустриального университета (зав. кафедрой проф. А.А. Антонов i:
кафедра «Технология сварки, материаловедение, износостойкость деталей
машин» Московского государственного университета путей сообщения
(зав. кафедрой проф. С.Н. Киселев)
Авторы: С.А. Куркин, В.М. Ховов, Ю.Н. Аксенов, О.Г. Касаткин.
Ал-др С. Киселев, Алекс. С. Киселев, А.В. Коновалов, А.С. Куркин, Н.С. Куркин.
А.А. Легезо, В.Ф. Лукьянов, А.В. Лыков, Ю.Г. Людмирский, Э.Л. Макаров,
В.А. Марков, С.С. Мармузевич, А.П. Пашкевич, М.В. Солтавец, А.С. Супер
Компьютерное проектирование и подготовка производства сварных
К 63 конструкций: Учеб, пособие для вузов / С.А. Куркин, В.М. Ховов,
Ю.Н. Аксенов и др.; Под ред. С.А. Куркина, В.М. Ховова. —М.: Изд-
во МГТУ им. Н.Э. Баумана, 2002. — 464 с.: ил.
ISBN 5-7038-2053-7
Рассмотрены примеры эффективного использования компьютерных
технологий на всех этапах подготовки производства сварных конструкций,
начиная от расчета и проектирования самих конструкций до моделирования
работы сварочных роботизированных технологических комплексов.
Содержание учебного пособия соответствует программам курсов лек-
дий по компьютерным технологиям сварочного производства, которые авто-
ра читают в МГТУ им. Н.Э. Баумана и других вузах.
Для студентов высших учебных заведений, обучающихся по направ-
летодготовки дипломированных специалистов «Машиностроительные
тех.-../.: гни и оборудование» по специальности «Оборудование и технология
сьарх - -: го производства». Может быть полезно руководителям подразделе-
ний то: '-толстенных предприятий.
УДК 621.791:658.52.011.56 (075.8)
ББК 30.4
© Коллектив авторов, 2002
© Издательство МГТУ им. Н.Э. Баумана. 2с
ISBN 5-“03S-2>i'53-"
Оглавление
Предисловие......................................................................5
Введение.........................................................................7
1. КОМПЬЮТЕРНЫЕ СРЕДСТВА ПРОЕКТИРОВАНИЯ И ГРАФИЧЕСКОГО
МОДЕЛИРОВАНИЯ..............................................................16
1.1. Современные технологии 11роектирования и графического моделирования.16
1.2. Принципы построения систем графического моделирования...............21
1.3. Графические стандарты...............................................31
1.4. Графические системы геометрического моделирования...................37
1.5. Пример проектирования конструкции методом трехмерного моделирования.50
2. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В МЕТАЛЛАХ СВАРНЫХ КОНСТРУК-
ЦИЙ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ.............................................70
2.1. Назначение и методы моделирования процессов, протекающих в металле.70
2.2. Метод конечных элементов для решения дифференциальных и интегральных
уравнений............................................................73
2.3. Работа программного обеспечения метода конечных элементов на примере
комплекса «СВАРКА»...................................................83
2.4. Моделирование упругопласгического поведения материала в комплексе
«СВАРКА».............................................................99
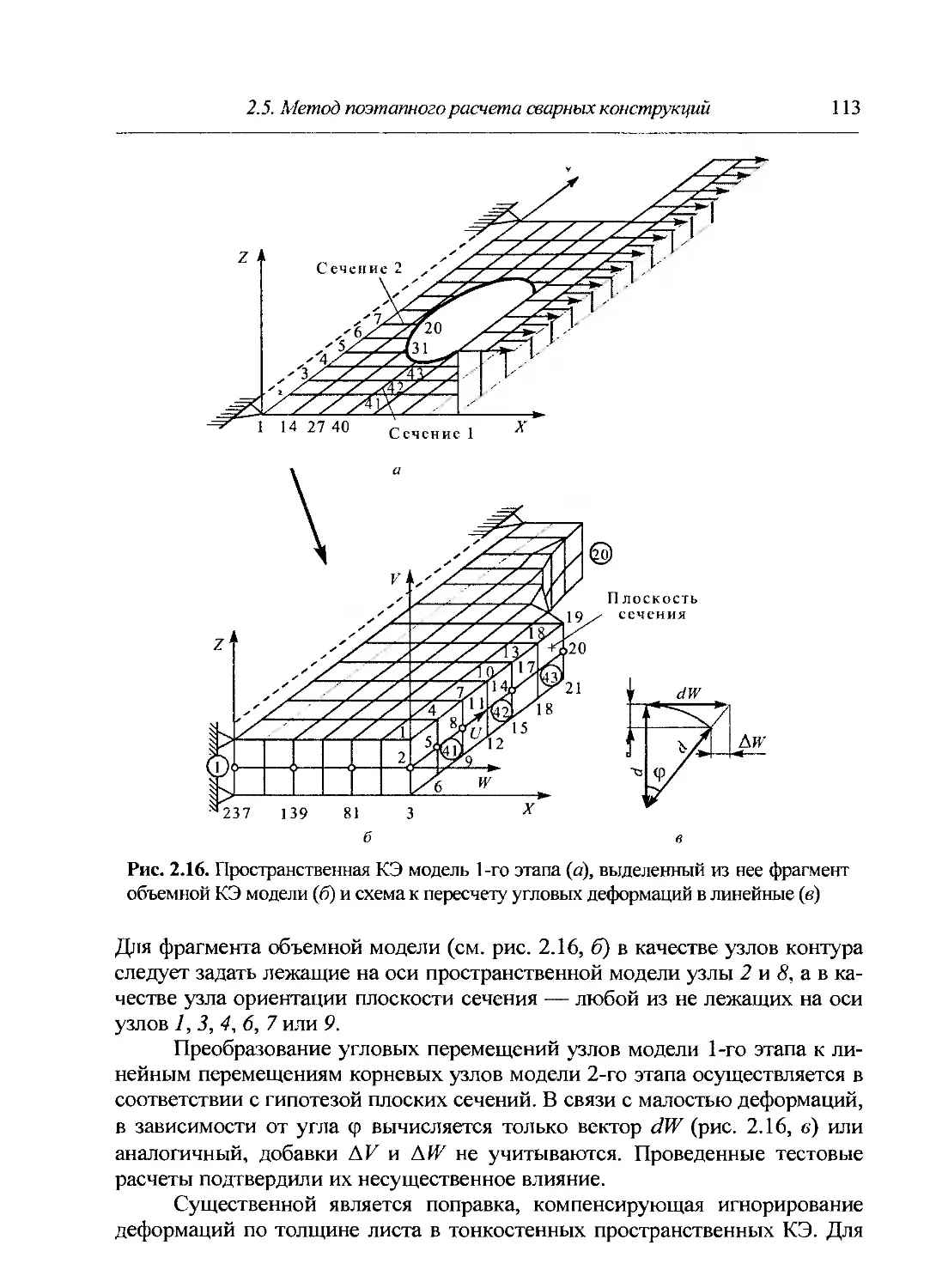
2.5. Метод поэтапного расчета сварных конструкций в комплексе «АСТРА-С».110
2.6. Суперэлементы для решения сварочных задач в комплексе «WELD3D»...120
3. ПРОЕКТНЫЕ И КОНТРОЛЬНЫЕ РАСЧЕТЫ НА ПРОЧНОСТЬ НА ОСНОВЕ
МОДЕЛИРОВАНИЯ ПРОЦЕССА РАЗРУШЕНИЯ..........................................128
3.1. Закономерности процесса разрушения сварных соединений и принципы
построения проектных и контрольных расчетов..........................128
3.2. Моделирование разрушения сварного соединения при монотонном нагружении... 140
3.2.1. Критерии наступления предельного состояния разрушения........140
3.2.2. Метод оценки работоспособности сварных конструкций...........144
3.2.3. Характеристики деформирования и пластичности конструкционных
материалов......................................................146
3.2.4. Компьютерное моделирование страгивания трещины, стабильного и
неустойчивого разрушения........................................151
3.2.5. Определение вязкости разрушения методом численного
эксперимента и ее применение в контрольном расчете..............158
3.2.6. Пример расчета корпуса ядерного реактора на «течь перед
разрушением»........................................................166
3.3. Моделирование методами механики разрушения процесса роста трещин от
дефектов при циклическом нагружении.................................172
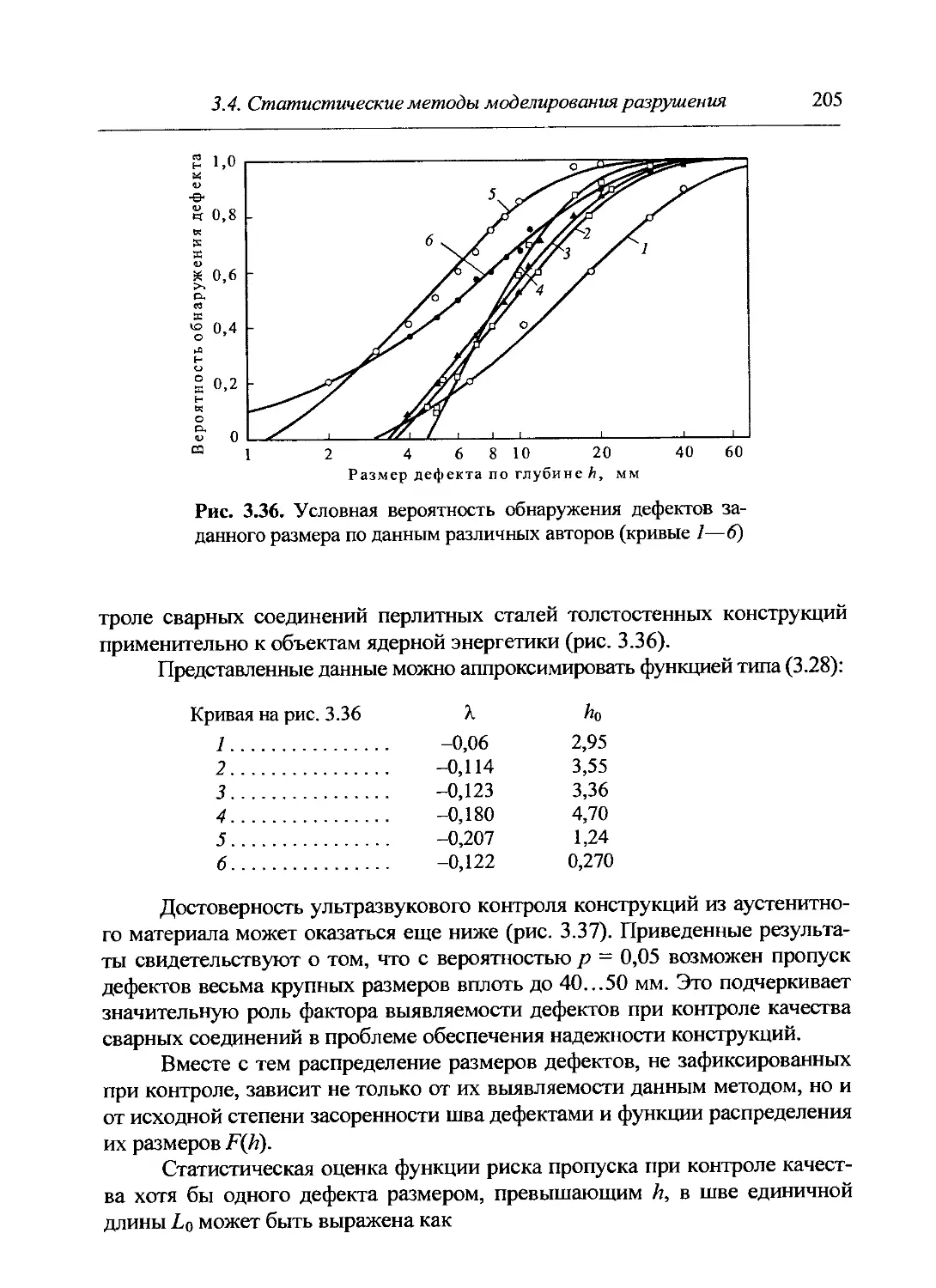
3.4. Статистические методы моделирования разрушения.....................186
3.4.1. Учет технологической наследственности сварных соединений.....186
3.4.2. Имитационное моделирование процесса разрушения при
циклическом нагружении..............................................194
3.4.3. Учет достоверности контроля качества сварных соединений......204
4
Оглавление
4. МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ В МЕТАЛЛАХ ПРИ
СВАРКЕ С ЦЕЛЬЮ ОЦЕНКИ ПОКАЗАТЕЛЕЙ СВАРИВАЕМОСТИ
И ВЫБОРА РЕЖИМОВ СВАРКИ...................................................208
4.1, Показатели свариваемости............................................208
4.2. Алгоритм компьютерной программы расчета показателей свариваемости
легированных сталей................................................209
4.3. Модели для расчета теплового поля, структуры металла, концентрации
диффузионного водорода и уровня напряжений при сварке..............211
4.4. Инженерный программный комплекс «Свариваемость легированных сталей».214
4.5. Пример компьютерного расчета показателей свариваемости легированной
стали.............................................................219
4.6. Расчетная система для выбора условий сварки низколегированных сталей в СО;. .221
5. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ ТЕХНОЛОГИИ СБОРОЧНО-
СВАРОЧНОГО ПРОИЗВОДСТВА...................................................229
5.1. Общие вопросы автоматизации проектирования сварочной технологии.229
5.2. Обработка и представление исходных данных...........................233
5.3. Формирование последовательности сборки и сварки конструкции.....241
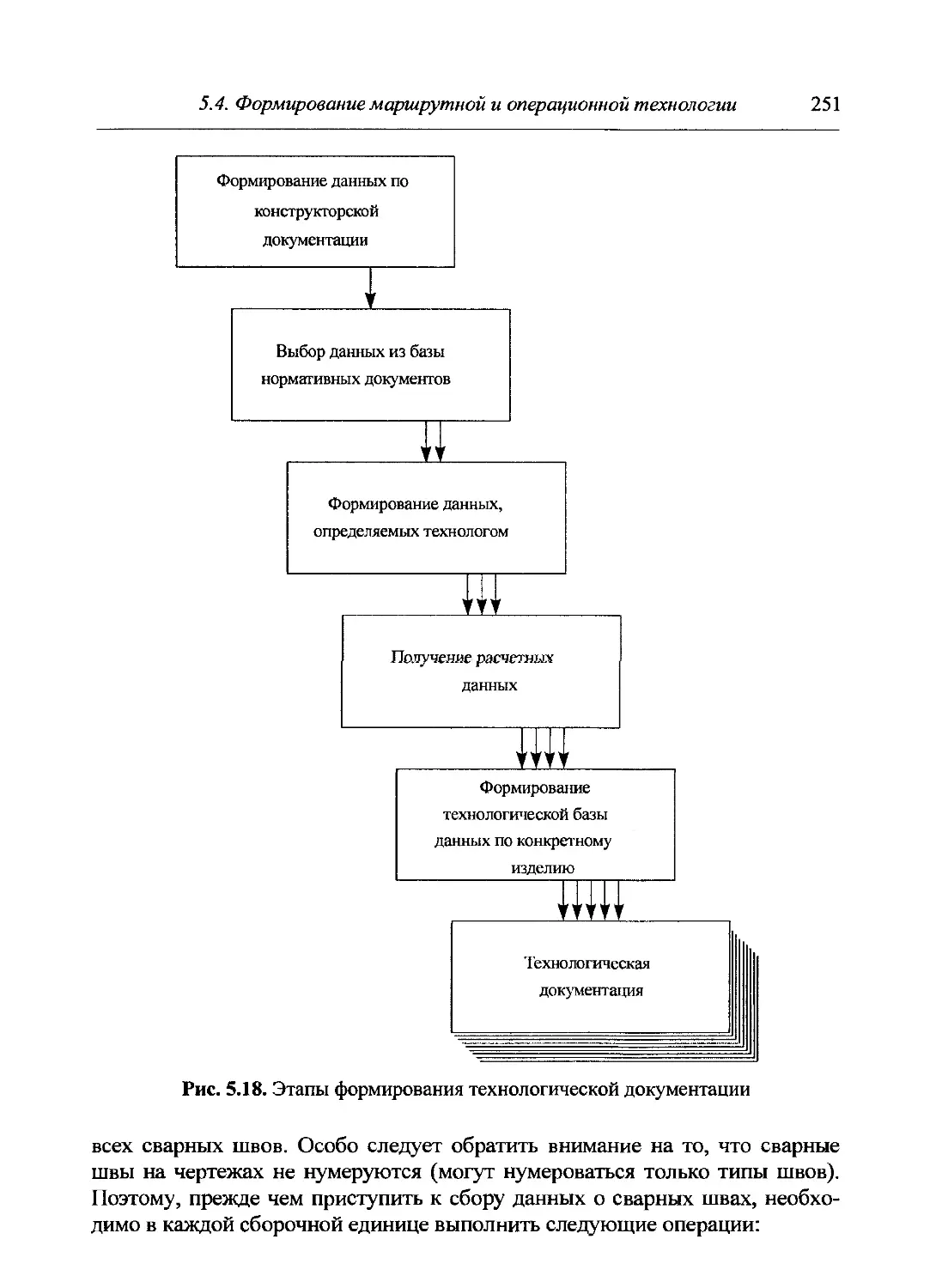
5.4. Формирование маршрутной и операционной технологии изготовления
отдельной сборочной единицы.......................................247
6. СИСТЕМА АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ СБОРОЧНО-
СВАРОЧНЫХ ПРИСПОСОБЛЕНИЙ.................................................261
6.1. Принципы проектирования.........................................261
6.2. Состав и структура библиотеки элементов.........................267
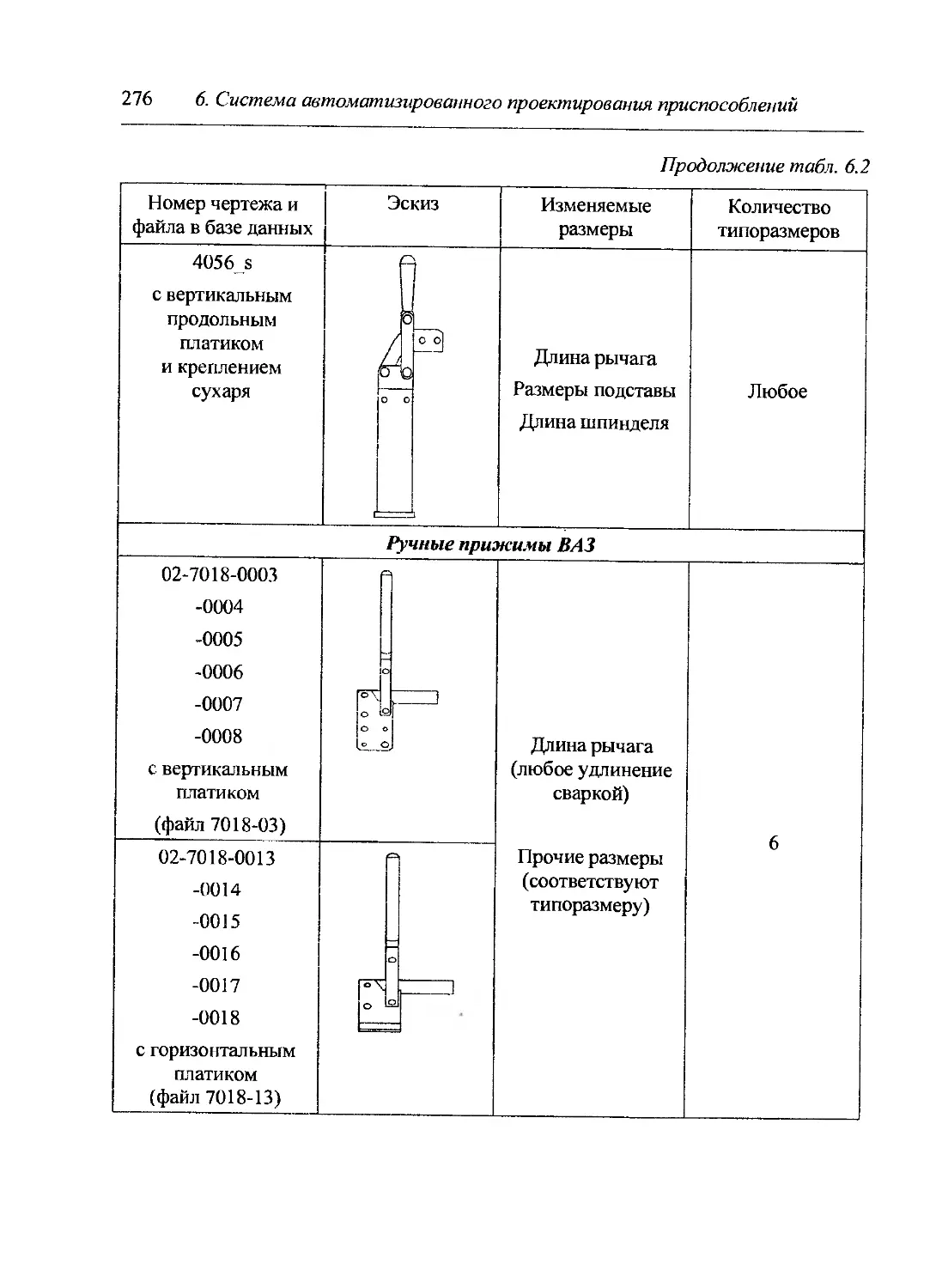
6.3. Технология автоматизированного проектирования приспособлений....281
6.4. Пример компьютерного проектирования сборочно-сварочного стенда..292
7. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ СВАРОЧНЫХ РОБОТИЗИ-
РОВАННЫХ ТЕХНОЛОГИЧЕСКИХ КОМПЛЕКСОВ.......................................307
7.1. Содержание работ и структура автоматизированной системы.........307
7.2. Подсистема подготовки образа сварного узла..........................317
7.3. Проектирование и подготовка сварочного инструмента..............323
7.4. Сборка, программирование и моделирование работы сварочного РТК......352
8. ОПЫТ ПРОЕКТИРОВАНИЯ И ИСПОЛЬЗОВАНИЯ РОБОТИЗИРОВАННЫХ
ТЕХНОЛОГИЧЕСКИХ КОМПЛЕКСОВ КОНТАКТНОЙ И ДУГОВОЙ
СВАРКИ....................................................................377
8.1. Контактная сварка кузовов автомобилей ГАЗ.......................377
8.2. РТК контактной сварки лонжеронов автомобиля ВАЗ 2110................382
8.3. Особенности технологии дуговой роботизированной сварки..........395
8.4. Роботизированный технологический участок сборки и сварки барабана
роторной жатки комбайна...........................................407
8.5. РТК сборки и дуговой сварки сложного маложесткого пространственного узла с
обеспечением заданных пределов отклонений геометрической формы....431
Заключение..................................................................461
Посвящается 100-летию со дня рожде-
ния академика Георгия Александровича
Николаева
Предисловие
Замысел настоящего издания принадлежит профессору кафедры свар-
ки МГТУ им. Н.Э. Баумана Сергею Александровичу Куркину. Быстрое раз-
витие компьютерных технологий сопровождается значительными измене-
ниями не только методик проектирования, но и самой логики решения от-
дельных задач. В связи с этим ощущается острый недостаток литературы
для студентов и специалистов, в которой был бы систематизирован и обоб-
щен появляющийся опыт разработки и использования базовых и специали-
зированных программных комплексов.
Диапазон проблем подготовки производства сварных конструкций
весьма велик и включает в себя вопросы конструкционной прочности, ана-
лиз физических и металлургических процессов в металлах при нагреве,
плавлении и кристаллизации (технологическая прочность), разработку тех-
нологической оснастки, проектирование сложнейших сварочных роботизи-
рованных автоматических линий. По каждому направлению необходим не
только ведущий специалист в своей области, но и разработчик наиболее эф-
фективных компьютерных технологий и программных комплексов, уже ис-
пользуемых промышленными предприятиями. Поэтому к работе по написа-
нию отдельных разделов этого учебного пособия были привлечены ведущие
специалисты по созданию программных средств. География представителей
авторского коллектива учебного пособия оказалась весьма обширной. Это
представители Москвы (МГТУ им. Н.Э. Баумана, МИИТ, АО «Буран», ин-
ститут атомной энергии им. И.В. Курчатова), Минска (Белорусский госу-
дарственный университет информатики и радиотехники, институт техниче-
ской кибирнетики), Киева (ИЭС им. Е.О. Патона), Ростова-на Дону (кафедра
сварки ДГУ, завод Ростсельмаш), специалисты крупнейших автозаводов
ВАЗ, ГАЗ, ЗИЛ.
При работе над текстом рукописи основное внимание было сосредо-
точено не только на описании отдельных программных комплексов, но и на
принципах, постановке и практике решения конкретных задач сварочных
технологий с использованием современных возможностей компьютерных
систем. Тем более что новые уточненные версии программных комплексов
появляются каждые 1—2 года, в то время как принципы решения задач яв-
ляются гораздо более стабильными.
6
Предисловие
Материал учебного пособия распределился между автггами следую-
щим образом:
глава 1 — А.П. Пашкевич (1.1-1.4), А.С. Супер (1.5):
глава 2 — А.С. Куркин (2.1—2.4), Ю.Н. Аксенов (2.5), Алекс. С Киселев
и Ал-др С. Киселев (2.6);
глава 3 — С.А. Куркин и В.Ф. Лукьянов (3.1), А.С. Куркин i3.2).
В.Ф. Лукьянов (3.3—3.4);
глава 4 — Э.Л. Макаров, А.В. Коновалов, О.Г. Касаткин;
глава 5 — В.М. Ховов, А.В. Лыков;
главы 6, 7 — С.С. Мармузевич, Н.С. Куркин, В.А. Марков, А.А. Леге-
зо, А.С. Супер;
глава 8 — С.С. Мармузевич, В.А. Марков, А.А. Легезо (8.1, 8.2),
Н.С. Куркин (8.3), Ю.Г. Людмирский, В.Ф. Лукьянов, М.В. Солтовец (8.4, 8.5).
Методики и технологии, приведенные в настоящем учебном пособии,
являются оригинальными разработками авторов издания, как правило, дове-
денными до широкого практического использования с помощью работников
исследовательских и производственных предприятий.
Авторы выражают благодарность за помощь и участие в работе
В.Г. Игнатову (ОКБ «Робот»), А.И. Акбулатову и В.И. Ломоносову (НПО
Автоматики приборостроения), А.Г. Андрееву (Лаб. Робототехники МГТУ-
Станкин), Н.И. Лобзину, С.М. Локшину, В.В. Голованову, В.А. Шашунькину
(ОАО ГАЗ), В.Д. Шугаеву, В.И. Баранову, В.Г. Буракову (АО АВТОВАЗ),
Г.А. Яркову, В.Г. Попову, Н.А. Зондбергу (АМО ЗИЛ), Е.П. Кукареко (Бе-
лорусский государственный!! университет информатики и радиотехники),
С.В. Медведеву (Институт технической кибернетики, Минск), К.П. Турско-
му (ИЭС им. Е.О. Патона).
В.М. Ховов
Введение
В настоящее время возможность подъема и расширения производства
сварных конструкций в значительной мере связана с объединением в еди-
ный непрерывный процесс этапов проектирования изделия и технологиче-
ской подготовки производства. Хотя в общем виде эта идея высказывалась и
даже реализовывалась давно, но лишь в условиях глобальной компьютери-
зации инженерного и производственного труда она призвана радикально
изменить традиционно сложившуюся ситуацию.
Опыт ведущих зарубежных фирм показывает, что многими своими
успехами они обязаны развитию и реализации принципа, когда широкое
применение компьютеров охватывает проектирование изделий, деталей и
технологических процессов, программирование автоматически действую-
щих устройств, планирование производства, изготовление, прием, хранение
и перевозку материалов, деталей, узлов и изделий.
Для снижения затрат ресурсов и времени на проектирование и изго-
товление сварной конструкции необходимо перейти от автоматизации про-
ектирования отдельных работ или этапов к интегрированным системам,
обеспечивающим целостную автоматизацию работ на протяжении всего
жизненного цикла проектируемого объекта от технико-экономического
обоснования и эскизного проектирования до автоматизации управления ра-
ботой оборудования, а также перейти от автоматизации отдельных рабочих
мест к автоматизации в масштабах всего проекта и предприятия и к распре-
деленному проектированию и моделированию. При этом основными стано-
вятся системы коммуникации и диспетчеризации всего проекта, которые
должны отслеживать варианты и целостность проекта, последовательность
и прохождение всех этапов, фиксировать исполнителей частей проекта и
лиц, принявших решение на той или иной стадии проектирования и подго-
товки производства.
Тесная интеграция этапов и общие базы данных делают возможным
увеличение количества итерационных циклов и обратных связей, а также по-
зволяет одновременно проектировать различные варианты с обоснованным
выбором наилучшего, что приводит к уменьшению ошибок и их исправлению
на более ранних этапах. Известно, что цена ошибки, не обнаруженной на на-
чальных стадиях, в конце проектирования и подготовки производства возрас-
тает многократно. Поэтому повышение качества принимаемых решений, уст-
8
Введение
ранение ошибок на более ранних стадиях приводит к уменьшению затрат на
последующих этапах, особенно на этапах внедрения и производства, и в ко-
нечном счете к существенному удешевлению всего проекта.
Опыт работы с наиболее совершенными компьютерными технология-
ми показывает, что автоматизированные системы необходимо и выгодно
проектировать с избыточными функциональными возможностями, опере-
жающими потребности пользователей, а также следует предусмотреть воз-
можность их модификации для решения задач, которые могут возникнуть
при эксплуатации системы.
Целью настоящего учебного пособия является анализ проблем и из-
ложение имеющегося опыта создания и использования автоматизированных
систем решения задач сварочного производства. При этом показана общая
концепция сквозного конструктивно-технологического проектирования на
базе компьютерных технологий, а также даны описания и характеристики
программных комплексов в качестве примера возможного и уже отработан-
ного варианта решения отдельных конкретных задач.
Сразу же следует отметить две особенности рассматриваемых про-
блем. Первая — это бурное развитие компьютерных технологий в последнее
десятилетие и в связи с этим возможное разнообразие решений однотипных
задач в разных организациях. Вторая особенность состоит в том, что боль-
шинство задач решалось в отрыве от остальных процессов проектирования
сварных конструкций и технологии, и только в последние годы, с появлени-
ем достаточного опыта, значительных вычислительных ресурсов компью-
терной техники и с повышением общей культуры использования форматов,
баз данных и сетевых технологий обработки данных, отдельные подсистемы
постепенно встраиваются в более мощные комплексные автоматизирован-
ные системы.
На рис. В.1 приведена структурная схема последовательности автома-
тизированного решения отдельных конструкторских и технологических за-
дач сварочного производства. Такая последовательность близка к традици-
онной, применявшейся при ручном проектировании, остается практически
неизменной и определяется последовательностью формирования данных,
получаемых на каждом отдельном этапе проектирования и необходимых
для начала реализации последующего этапа. Однако принципиальным отли-
чием и достоинством комплексной системы автоматизированного проекти-
рования является расширение использования обратных связей с предыду-
щими этапами в целях совершенствования показателей всего проекта.
Следует заметить, что обратные связи при проектировании и техноло-
гической подготовке производства действовали и раньше, когда проблемы,
возникавшие на отдельных этапах, устранялись при доработке предыдущих
этапов. Однако эти доработки, связанные с необходимостью переделки уже
Введение
9
Рис. В.1. Взаимосвязь этапов проектирования, технологической
подготовки, изготовления и эксплуатации сварной конструкции
10
Введение
завершенных и принятых этапов вместе с изменением часто обширной кон-
структорской и технологической документации, являлись скорее досадной
необходимостью, сопровождаемой незапланированными издержками вре-
мени, материальными и другими затратами, чем естественным процессом
комплексного проектирования.
В первых четырех главах рассмотрены принципы и методы моделиро-
вания сварных конструкций и процессов, протекающих при их изготовлении
и эксплуатации. В последующих главах изложены методики и дано описа-
ние конкретных компьютерных программ, используемых при проектирова-
нии конструкций и технологии изготовления. В последней главе приведены
примеры успешной разработки автоматизированных участков сварочного
производства.
Поскольку в основе потоков данных о сварной конструкции практически
для всех отдельных подсистем лежат графические данные о деталях, в главе 1
рассмотрены компьютерные средства проектирования и графического модели-
рования. В этой области за короткое время произошли существенные измене-
ния, связанные с переходом при проектировании от плоского проекционного
отображения деталей и узлов к трехмерному поверхностному и твердотельно-
му моделированию. Формирование трехмерных образов позволяет резко уско-
рить процесс проектирования, автоматически получать привычные плоские
проекционные виды и стандартные чертежи, достаточно легко проверят!, соби-
раемость и моделировать кинематические движения и связи.
В главе 2 рассмотрены принципы и приемы моделирования физиче-
ских процессов в сварных конструкциях, таких, как протекание сварочного
тока, распространение теплоты, диффузия примесей, образование деформа-
ций и напряжений, появление и развитие дефектов. Из известных методов
такого моделирования выбран наиболее гибкий и универсальный — метод
конечных элементов (МКЭ). Кроме основных положений и возможностей
самого метода приведено описание трех программных комплексов, создан-
ных для решения различных задач сварочного производства.
Глава 3 содержит описание задач расчетного анализа прочностных и
деформационных характеристик сварных конструкций. Здесь показаны не
столько простые и стандартные методы и методики расчета прочности,
сколько возможности использования более сложных методик расчета, кото-
рые учитывают наличие конструкционных и технологических концентрато-
ров напряжений и деформаций и позволяют моделировать работу и поведе-
ние сварной конструкции вплоть до начала нестабильного развития разру-
шения. Использование критерия предельной пластичности материала в
сочетании с моделированием напряженно-деформированного состояния с
помощью МКЭ практически снимает ограничения на сложность решаемых
задач как по условиям нагружения, так и по геометрии и свойствам мате-
Введение
11
риала. Это позволяет учитывать одновременно неоднородность механиче-
ских свойств материала, форму и расположение концентраторов, темпера-
турные и остаточные напряжения, т. е. все те факторы, что осложняют рас-
четы на прочность сварных конструкций.
При определении ресурса проектируемой сварной конструкции в ус-
ловиях переменного нагружения учет наличия концентраторов и дефектов
осложняется многообразием взаимодействия факторов, имеющих случай-
ный характер, что заставляет использовать вероятностные модели разрушения,
построенные на основе метода статистического моделирования. Методика
использования такого подхода и оценки ресурса оболочковых сварных кон-
струкций при малоцикловом нагружении с использованием методов меха-
ники разрушения также изложена в этой главе.
Глава 4 посвящена анализу технологических проблем сварки конст-
рукционных низколегированных сталей и сплавов. При выборе оптималь-
ных режимов сварки и оптимального состава сварочных материалов, а так-
же при оценке интервала рассеяния свойств сварных соединений, связанных
со случайными колебаниями технологических факторов, критерий опти-
мальности является комплексным и содержит требования к различным
свойствам металла (прочности, пластичности и ударной вязкости металла
шва и околошовной зоны). Изложена расчетно-экспериментальная система,
позволяющая находить оптимальные значения технологических факторов
путем использования регрессионных моделей, полученных на основе обра-
ботки значительного объема экспериментальных данных. Рассмотрена сис-
тема компьютерного анализа свариваемости и технологии сварки конструк-
ционных низколегированных сталей. Система использует полученные
экспериментальные данные для анализа структурно-водородного и напря-
женного состояния металла сварных соединений, а также для расчета конст-
руктивно-технологических параметров процесса изготовления сварных конст-
рукций, обеспечивающих как заданные механические свойства сварных со-
единений, так и отсутствие холодных трещин.
Необходимость автоматизации проектирования технологии сборочно-
сварочных операций назрела давно. Технологическая подготовка сварочного
производства в общем объеме трудоемкости иногда занимает более 60 %,
т. е., как правило, существенно превышает затраты на проектирование сварной
конструкции. Для автоматизации проектирования технологии необходимо
решить главную задачу — как наиболее эффективным способом воспользо-
ваться мощной вычислительной техникой и программными средствами.
Традиционные (ручные) методы проектирования технологии необходимо
оптимизировать для машинного проектирования.
Технология выполнения сборочно-сварочных операций включает в
себя десятки самостоятельных операций: установку и базирование загото-
12
Введение
вок, прихватку, сварку, кантовку, доварку, различные виды зачистки шва и
зоны сварки, правку, контроль, маркировку и др. Разработка технологии
предусматривает выбор схем базирования, последовательности сборки, тех-
нологической оснастки, элементов приспособлений, вспомогательного ин-
струмента и материалов. Кроме того, при разработке технологии решается
еще ряд отдельных задач:
• выбор сварочного оборудования;
• назначение параметров сварочного материала (марка и диаметр сва-
рочной проволоки, марки и характеристики защитных газов и др.);
• назначение режимов сварки (скорость, ток, напряжение);
• назначение, как правило, разнообразных методов контроля в процес-
се и после завершения сборочно-сварочных операций.
Даже из этого краткого анализа специфических особенностей техно-
логии сборочно-сварочного производства становится очевидной сложность
как ее формирования, так и в особенности автоматизации ее проектирования.
Подготовка сварочного производства имеет, во-первых, большой пе-
речень решаемых задач, таких, как анализ сварной конструкции, разработка
маршрутной и операционной технологии заготовительных и сборочно-
сварочных операций, проектирование нестандартной специализированной
оснастки и ее изготовление, проектирование отдельных автоматизирован-
ных и роботизированных комплексов, проектирование автоматизированных
технологических линий, изготовление, отладка и монтаж технологических
линий. Во-вторых, по каждой задаче обрабатывается большое количество
отдельных сварных узлов и подузлов. Большой объем работы еще увеличи-
вается при доработке конструкции и технологии ее изготовления уже в про-
цессе подготовки и отладки производства. Требование резкого сокращения
трудоемкости дополняется и существенным повышением ответственности
принимаемых решений, поскольку любые изменения на более поздних эта-
пах непременно вызовут значительные финансовые издержки.
При традиционной технике и технологии выполнения подготовки
производства, например в автомобильной промышленности, сроки работ
ранее занимали до 10 лет и более. Конечно, такие сроки подготовки произ-
водства абсолютно неприемлемы. В настоящее время имеются реальные
возможности снижения трудоемкости и сокращения сроков работ, связан-
ных с развитием компьютерной техники и технологии, примерно в 10 раз.
Вопросы автоматизации проектирования технологии сборочно-сва-
рочного производства рассмотрены в главе 5. Здесь большое внимание уделено
формированию и представлению исходных данных, организации и взаимосвязи
баз данных и пользовательскому интерфейсу для удобной и производительной
работы сварщиков-технологов по формированию маршрутной и операционной
технологии изготовления узлов сложных сварных конструкций.
Введение
13
В главе 6 рассмотрены технологии автоматизированного проектиро-
вания сборочно-сварочных приспособлений. Проектирование и изготовле-
ние сварочной оснастки — один из наиболее важных этапов организации
сварочного производства. Помимо высокой трудоемкости этого этапа, он
часто имеет определяющее значение для обеспечения точности конструк-
ций, производительности и автоматизации действующего производства.
Последовательность традиционного проектирования сборочно-свароч-
ных приспособлений обычно сводится к следующим этапам:
1) определение рационального порядка установки деталей и наложе-
ния сварных швов;
2) выбор базовых элементов и поверхностей;
3) выбор типа опорньгх и зажимных элементов;
4) разработка компоновочной схемы приспособления (в упрощенном
виде на стандартных проекциях);
5) проектирование приспособления по компоновочным схемам.
Сравнение вариантов традиционными способами не приводило к вы-
бору наилучшего, и к окончательному оформлению принимался либо пер-
вый прорабатываемый конструктором вариант, либо аналогичный имеюще-
муся на данном предприятии. Лишь с использованием информационных
технологий положение меняется.
За рубежом автоматизация проектирования сварочной оснастки раз-
рабатывается с применением весьма дорогих универсальных и специализи-
рованных программных систем на базе рабочих станций. Поиск более деше-
вых подходов без ущерба их технологическим возможностям привел к соз-
данию фирмой «Буран» (Россия) системы, использующей визуальное
моделирование взаимодействия между объемными моделями сварного узла,
сварочного инструмента, робота и сборочно-сварочного приспособления.
Однажды введенное описание ЗО-образа сварного узла многократно ис-
пользуется технологами и конструкторами по оснастке для решения необ-
ходимых задач увязки конструкции узла и технологии его изготовления, а
также автономного программирования промышленного робота.
Главы 7 и 8 посвящены применению роботов в сварочном производ-
стве, автоматизации проектирования роботизированных сварочных техно-
логических комплексов и изложению опыта применения роботов в машино-
строительном производстве и автомобилестроении. Создание роботизиро-
ванных линий и бурный рост производительности вычислительной техники
привели к появлению систем разработки сварочной технологии, основанных
на моделировании процессов работы технологического оборудования в ре-
альном режиме времени.
В настоящее время более трети от общего числа промышленных
роботов используются для сварки изделий в автомобильной промышлен-
14
Введение
ности. Первоначально область их применения ограничивалась точечной
контактной сваркой, но постепенно они стали использоваться и при ду-
говой сварке. Роботизированные комплексы дуговой сварки применяются
во многих отраслях промышленности. Наиболее широко их применяют
при производстве крупногабаритных конструкций: кузовов тяжелых гру-
зовых автомобилей, сельскохозяйственных машин, судов, железнодо-
рожных вагонов и т. д.
Опыт эксплуатации роботизированных технологических комплексов
сварки показывает, что применение роботов существенно повышает качест-
во продукции, производительность и технологическую гибкость производ-
ства. Разработка методов автоматизированного проектирования роботизи-
рованных технологических комплексов сварки представляет собой актуаль-
ную научно-техническую задачу. В западном компьютерно-интегрирован-
ном производстве широко применяют универсальные системы автоматизи-
рованного проектирования, включающие в себя множество разнообразных
программ-приложений, обеспечивающих решение практически всех про-
блем подготовки современного сварочного производства. Однако высокая
стоимость таких программных продуктов пока практически исключает воз-
можность их широкого применения в России. Использование относительно
дешевых персональных компьютеров и популярной графической системы
Autocad более доступно как в России, так и за рубежом для мелких и сред-
них фирм. Возможности персональных машин и программного обеспечения
для них в настоящее время вплотную приближаются к возможностям мощ-
ных рабочих станций. Группой российских специалистов создан пакет про-
грамм РОБОМАКС, предназначенный для конструирования, моделирования
и компьютерного программирования роботизированных комплексов и авто-
матических линий дуговой и контактной точечной сварки на базе промыш-
ленных роботов. Этот комплекс реализован на базе массовых и дешевых
моделей компьютерной техники.
В главе 7 дано описание использования пакета программ РОБОМАКС
при автоматизированном проектировании роботизированного сварочного
производства. Рассматривается ряд последовательных этапов: принятие
предварительных конструктивно-технологических решений, проектирова-
ние сварочного инструмента, выбор компонентов РТК, разработка компо-
новки РТК, его обучение и off-line-программирование. Задача проектирова-
ния РТК имеет множество вариантов решения. Программный комплекс ис-
пользует визуализацию процессов и результатов проектирования, отображая
все движения робота, манипулятора и сварочного инструмента на экране
монитора.
Опыт разработки роботизированных сварочных производств еще не-
велик. Тем не менее необходимость его обобщения и освоения не вызывает
Введение
15
сомнений, С этой целью в главе 8 изложен опыт компьютеризированного
проектирования и моделирования работы сварочных РТК на примере авто-
мобильной промышленности, а также опыт проектирования и применения
роботизированной дуговой сварки при серийном изготовлении крупногаба-
ритных сварных узлов изделий сельскохозяйственного машиностроения,
имеющих малую пространственную жесткость. Опыт создания и эксплуата-
ции РТК свидетельствует о широких возможностях роботизированной дуго-
вой сварки в обеспечении выпуска сложных сварных узлов, удовлетворяю-
щих требованиям как по точности заданных размеров и конструктивных
форм, так и по качеству выполняемых сварных соединений.
На базе приведенных в отдельных главах книги материалов возможна
постановка специальных лабораторных работ, которые могут быть полезны
как при подготовке студентов, так и при переподготовке специалистов про-
мышленных предприятий.
1. КОМПЬЮТЕРНЫЕ СРЕДСТВА ПРОЕКТИРОВАНИЯ
И ГРАФИЧЕСКОГО МОДЕЛИРОВАНИЯ
1.1. Современные технологии проектирования
и графического моделирования
Определяющими факторами успеха в промышленном производстве
являются уменьшение времени выхода продукции на рынок, повышение
качества, снижение ее стоимости. Практическая реализация этих требований
требует модернизации проектно-технологических и производственных про-
цессов как в рамках отдельных предприятий, так и в условиях «расширенно-
го предприятия», объединяющего всех поставщиков, соисполнителей и уча-
стников проектирования и производства продукции. В настоящее время
наиболее радикальным средством решения задач модернизации является
внедрение интегрированных информационных технологии на базе исполь-
зования современных средств вычислительной техники и сетевых решений.
К числу наиболее эффективных технологий, дающих весомый выигрыш в
короткие сроки, принадлежат системы автоматизированного проектиро-
вания, инженерного анализа и технологической подготовки (системы
CAD/CAM/CAE), а также системы управления производственной информа-
цией (системы PDM).
Первым, наиболее значительным результатом в области разработки
программных средств САПР является создание интерактивных графических
редакторов для работы с двумерными и трехмерными геометрическими
объектами или, иными словами, систем автоматизированного черчения
(CADD — Computer-Aided Design and Drafting). При глобальном рассмотре-
нии все графические редакторы работают одинаково: для них определены
элементарные геометрические объекты (примитивы), а также процедуры
манипулирования с этими объектами (редактирование). Поэтому в таких
редакторах реализованы упрощенные представления о процессе проектиро-
вания как о процессе создания геометрических объектов путем манипуля-
ции с набором неких элементарных геометрических объектов — геометри-
ческих примитивов. Очевидно, что такие представления недостаточно точно
отражают работу инженера-конструктора, не позволяют ему отличить ее
1.1. Технологии проектирования и графического моделирования
17
от деятельности чертежника, которая полностью ограничивается рамками
изготовления технической документации.
Специализация графических редакторов для САПР привела к появле-
нию целого ряда утилит, одни из которых встраивались в ядро редактора
(например, утилита образмеривания), а другие предполагалось применять
как независимые сервисные программы (утилита параметрического проек-
тирования и пр.). Это, безусловно, улучшило эффективность использования
САПР, но ничего не изменило принципиально. В настоящее время развитие
программных средств САПР идет в направлении решения довольно не-
большого круга проблем, к которым в первую очередь относятся: проблема
эффективности твердотельного моделирования, проблема параметриза-
ции, а также проблема ассоциативности и программного интерфейса.
Однако современное представление о процессе проектирования исхо-
дит из его «генетического» единства с процессом производства. С этой точ-
ки зрения проектирование является информационной моделью производст-
ва, а никак не процессом изготовления технической документации. Следует
отметить, что ранее конструкторы не имели инструментов для проверки
адекватности указанных процессов, поэтому и появилась специальность
технолога, который, по сути дела, осуществляет «переформатирование»
описания из форм, адекватных процессу проектирования, в форму, адекват-
ную процессу производства. Но с появлением современных средств вычис-
лительной техники стала возможна непосредственная передача информации
от компьютеров к элементам производства (к таким, например, как станки с
ЧПУ), хотя, как правило, необходимость изготовления технической доку-
ментации сохраняется.
Первые шаги в организации «единого информационного пространст-
ва» были предприняты в 1980-х годах в оборонном комплексе США, где
возникла необходимость в обеспечении оперативного обмена данными ме-
жду заказчиком, производителем и потребителем вооружений, а также в со-
кращении бумажного документопотока. Первоначально данная концепция
получила обозначение CALS (Computer Aided Logistic Support — компью-
терная поддержка поставок) и охватывала в основном фазы производства и
эксплуатации. В дальнейшем концепция CALS начала активно применяться
в промышленности, строительстве, транспорте и других отраслях экономи-
ки, расширяясь и охватывая все этапы «жизненного цикла» продукта — от
маркетинга до утилизации.
В настоящий момент CALS понимается как Continuous Acquisition and
Life Cycle Support — непрерывная информационная поддержка жизненного
цикла изделия. По своей сути CALS является глобальной стратегией повы-
шения эффективности бизнес-процессов, выполняемых в ходе жизненного
цикла изделия за счет информационной интеграции и преемственности ин-
18 1. Компьютерные средства проектирования и графического моделирования
формации, порождаемой на всех этапах жизненного цикла. Возможность
совместного использования информации определяется применением ком-
пьютерных сетей и стандартизации форматов данных, обеспечивающей их
корректную интерпретацию. Интегрированная модель продукта и обмен
конструкторскими данными между проектировщиком и производителем
является источником информации для расчета потребности в материалах,
создания электронных справочников по эксплуатации продукта и т. д.
Очевидно, что решение указанных проблем возможно только вследст-
вие унификации способов представления, интерпретации и использования
информации, которые реализованы в стандарте ISO 10303 STEP (Standard
for the Exchange of Product). Модель изделия в соответствии с этим стандар-
том включает: геометрические данные, информацию о конфигурации изде-
лия, данные об изменениях, согласованиях и утверждениях. Стандарт ISO
10303 STEP построен таким образом, что помимо базовых элементов (интег-
рированных ресурсов) в его состав входят так называемые прикладные про-
токолы, определяющие конкретную структуру информационной модели для
различных предметных областей (автомобиле- и судостроение, строительст-
во, электроника и т. п.). Стандартный способ представления конструкторско-
технологических данных позволяет решать проблему обмена информацией
между различными подразделениями предприятия, а также участниками коо-
перации, оснащенными разнородными системами проектирования.
В рамках технологии CALS развиваются современные технологии
управления производственной информацией, часто называемые PDM-сис-
темами (Product Data Management). Они следят за большими, постоянно об-
новляющимися массивами данных и инженерно-технической информации.
В отличие от баз данных, PDM-системы интегрируют информацию любых
форматов и типов, поступающую от различных источников, предоставляя ее
пользователям в структурированном виде, привязанном к особенностям со-
временного промышленного производства. Системы PDM отличаются так-
же и от интегрированных систем офисного документооборота, поскольку
текстовые документы являются далеко не самыми «нужными» на производ-
стве (куда важнее геометрические модели, данные для функционирования
автоматических линий, станков с ЧПУ и т. п.). Системы PDM обобщают та-
кие широко известные технологии, как управление инженерными данными
(Engineering Data Management — EDM), управление документами, управле-
ние информацией об изделии (Product Information Management — PIM),
управление техническими данными (Technical Data Management — TDM),
управление технической информацией (Technical Information Management —
TIM), управление изображениями и пр.
Иначе говоря, любая информация, необходимая на том или ином этапе
жизненного цикла изделия, может управляться системой PDM, которая пре-
1.1. Технологии проектирования и графического моделирования
19
доставляет корректные данные всем пользователям и всем промышленным
информационным системам. Наряду с данными, PDM управляет и проек-
том — процессом разработки изделия, контролируя собственно инфор-
мацию об изделии, о состоянии объектов данных, об утверждении вно-
симых изменений, осуществляя авторизацию и другие операции, которые
влияют на данные об изделии и режимы доступа к ним каждого конкрет-
ного пользователя.
Системы PDM играют роль связующего звена между этапом инже-
нерно-конструкторской подготовки нового изделия и системами MRP
(Manufacturing Resource Planning) или, другими словами, разного рода АСУ,
решающими задачи автоматизации управления финансами, складским хо-
зяйством, снабжением и сбытом, а также техническим обслуживанием. О
важности такого рода систем свидетельствует хотя бы такой факт, что толь-
ко 25 % рабочего времени персонала компании, начиная от проектировщика
и кончая руководителем проекта, тратится на собственно творческую рабо-
ту, а остальное — на поиск информации и стыковку потоков данных, посту-
пающих от разных подразделений. Часто оказывается, что проще заново
разработать деталь, чем найти информацию, подготовленную некоторое
время назад.
Место систем PDM в общей производственной цепочке показано на
рис. 1.1. Они занимают промежуточное положение между системами MPR и
системами CAD/CAM/CAE, которые в русскоязычной литературе называют
одним термином — интегрированные САПР. В англоязычной литературе
под указанными терминами понимают следующее:
CAD (Computer-Aided Design) — общий термин для обозначения всех
аспектов проектирования с использованием средств вычислительной техни-
ки; обычно охватывает создание геометрических моделей изделия (твердо-
тельных, трехмерных, составных), а также генерацию чертежей изделия и их
сопровождений;
САМ (Computer-Aided Manufacturing) — общий термин для обозначе-
ния программных систем подготовки информации для станков с ЧПУ; тра-
диционно исходными данными для таких систем были геометрические мо-
дели деталей, получаемые из систем CAD;
САЕ (Computer-Aided Engineering) — общий термин для обозначения
информационного обеспечения автоматизированного анализа проекта
(прочностные расчеты, коллизии кинематики и т. п.) или оптимизации про-
изводственных возможностей.
Главное направление развития современных САПР— повышение их
интеллектуальных функций, т. е. способности «понимать» намерения кон-
структоров. В простейшем случае в системе запоминается лишь «история»
или последовательность шагов, выполняемых проектировщиком. Такие сис-
20 1. Компьютерные средства проектирования и графического моделирования
CAD/CAM/CAE
Эскиз
Деталировка
Спецификация
Сборочный чертеж
Хранение
информации
Аудит
Контроль
Планирование
процессов
MRP
Финансы
Склады
Заказы
Реализация
PDM
Рис. 1.1. Взаимосвязь систем автоматизации производственных процессов
темы удобны при создании библиотек стандартных деталей и элементов, но
для более сложных ситуаций требуется более «интеллектуальная» реализа-
ция пользовательского интерфейса. Поэтому в САПР начинает все шире ис-
пользоваться объектная технология, в соответствии с которой САПР не
должны работать с файлами, они должны обрабатывать объекты. Объекты
образуют собой «целостности», включающие множественные непротиворе-
чивые представления одной и той же «сущности». Например, деталь может
представлять интерес для дизайнера с позиции эстетики формы, для инже-
нера с позиции вычислительной сложности поверхности, для технолога с пози-
ции применимости процесса штамповки для ее изготовления. Объект позво-
ляет объединить подобные представления, а это открывает прямой путь к
эффективной реализации идей С-технологии, т. е. параллельного проекти-
рования и инжиниринга (concurrent design and engineering).
С-технология (конструкторско-технологическое проектирование) —
это принципиально новый, интегрированный подход к проектированию. В
ее основе лежит идея совмещенного проектирования изделия, а также
процессов его изготовления и сопровождения, координируемых с помощью
специально создаваемой для этой цели распределенной информационной
среды. Подобная технология позволяет использовать проектные данные,
начиная с самых ранних стадий проектирования, одновременно различными
1.2. Принципы построения систем графического моделирования
21
группами специалистов. Например, в трех главных конструкторских бюро
компании Boeing действуют 220 групп «проектирование—производство»,
которые координируют параллельные разработки и состоят из специалистов
таких разнообразных областей, как конструирование, технология материа-
лов, производство и взаимодействие с клиентами. С-технология обеспечива-
ет устранение известных недостатков последовательного проектирования, в
частности, в случае, когда ошибки проекта изделия неожиданно обнаружи-
ваются на последних его стадиях. Кроме того, появляется возможность лег-
ко и быстро вносить изменения в проект, причем таким образом, чтобы из-
менения не вызывали повторного проектирования созданных деталей и уз-
лов. Сегодня «перепроектирование» продолжает оставаться существенной
затратной компонентой любой разработки.
В заключение следует обратить внимание на интересные инициати-
вы в области САПР, возникшие в Германии. Они связаны с проблемой
роста несовместимости решений, предлагаемых многочисленными про-
изводителями информационной техники, включая и CAD/CAM/CAE-
системы. Решение этих проблем стало настолько насущным, что постав-
лен вопрос о стандартизации систем CAD/CAM/CAE и информационной
техники в целом. Концерн Daimler-Benz выступил с предложением под
названием «Инициатива по передовой информационной технике», кото-
рое поддержали British Aerospace, FIAT, Renault, SAAB, Volkswagen и
многие другие компании. Другой проект под названием CAD2000 объе-
динил компании Audi, BMW, Mercedes-Benz, Porsche, Volkswagen. Эти
проекты пытаются решить громадную по масштабам и сложности про-
блему поиска стандартных решений, способных удовлетворить огромное
множество прикладных требований от проектирования до изготовления,
а также управления информационными данными и библиотеками стан-
дартных компонентов.
1.2. Принципы построения систем
графического моделирования
Двумерные графические системы широко применяются при автома-
тизации чертежных работ. Чертежи любой сложности строятся из базовых
графических элементов: точек, прямых, окружностей и других кривых. Ка-
ждый из этих элементов задается группой характерных точек, координаты
которых могут определяться в абсолютной (мировой) системе координат
или относительно предыдущей введенной точки (инкрементный ввод). При
этом используют несколько способов задания точек:
22 1. Компьютерные средства проектирования и графического моделирования
Рис. 1.2. Автоматическое построение скругления и фаски
• путем указания на экране с помощью мыши;
• путем введения чисел с клавиатуры;
• путем «привязки» к некоторому элементу чертежа, в окрестности
которого располагается указатель.
Первый способ используют в основном для создания эскизов, а второй
и третий — для построения точных изображений. Особенно удобным явля-
ется третий способ, который позволяет «захватить» ближайший к курсору
уже построенный элемент и ввести точные координаты конца или середины
отрезка, центра окружности, точки пересечения прямых и т. д.
В средствах двумерной графики обычно имеется несколько способов
построения одного и того же элемента. Например, отрезок можно построить
по двум точкам либо по начальной точке, длине и углу наклона, а окруж-
ность — по центру и радиусу, по трем точкам, по двум точкам и радиусу и
т. д. Кроме того, в таких системах имеется ряд средств, автоматизирующих
процесс черчения. Рассмотрим их подробнее.
Автоматическое построение скругления и фаски. Для получения
скругления или фаски необходимо указать мышью на стороны угла и ввести
значение радиуса скругления или размер фаски. Отрезки на стыке угла и
скругления (фаски) автоматически «срезаются» (рис. 1.2).
Автоматическая штриховка и закраска. Для получения штриховки
надо ввести угол и шаг штриховки, а затем указать мышью на внутреннюю
часть области, которую надо заштриховать. Аналогично выполняется и за-
краска (рис. 1.3).
HATCH
Рис. 1.3. Автоматическая штриховка
1.2. Принципы построения систем графического моделирования
23
200
Рис. 1.4. Автоматическая простановка размеров
Автоматическая простановка размеров. Для простановки размера
необходимо указать образмериваемые элементы и точку уровня размерной
линии. После этого система автоматически вычислит числовое значение
размера, выведет его на экране и нарисует выносные и размерные линии
(рис. 1.4).
На любом этапе выполнения компьютерного чертежа можно удалить
и модифицировать графические элементы изображения. Обычно двумерные
САПР позволяют выполнять следующие операции редактирования.
Отсечение. Эта процедура позволяет удалить лишние вспомогатель-
ные линии на чертеже. Например, после указания мышью на секущую пря-
мую и окружность из чертежа удаляется сегмент окружности. Такая же про-
цедура может быть выполнена для любой комбинации графических элемен-
тов (рис. 1.5).
«Резиновое» растяжение. Процедура растяжения позволяет пользова-
телю растягивать или сжимать изображенные на экране формы. Можно, в
частности, с помощью мыши переместить любую из вершин ломаной. При
этом в процессе редактирования перемещаемая вершина соединяется с сосед-
ними при помощи пунктирных («резиновых») линий, а сразу же после отпус-
кания кнопки мыши пунктирные линии заменяются сплошными (рис. 1.6).
Нанесение сетки. Для получения изображения с регулярной структу-
рой удобно использовать сетку, которая позволяет указывать только на те
точки экрана, в которых располагаются узлы. В таком режиме осуществля-
Рис. 1.5. Отсечение
24 1. Компьютерные средства проектирования и графического моделирования
Рис. 1.6. «Резиновое» растяжение
ется автоматический «захват» ближайшего узла и от конструктора не требу-
ется очень точного указания точки. В результате можно легко ввести точки
с заданным шагом. На твердую копию изображение сетки не выводится
(рис. 1.7).
Построение сплайнов. В большинстве двумерных пакетов имеются
средства для автоматической генерации гладких кривых (сплайнов), прохо-
дящих через заданные точки. Такие процедуры очень удобны при создании
нестандартных геометрических форм и позволяют дополнить автоматизиро-
ванное черчение элементами автоматизированного проектирования (рис. 1.8).
Увеличение и панорамирование. Средства увеличения разрешают уве-
личить или уменьшить любую область чертежа для более подробного про-
смотра или редактирования. Чтобы проанализировать другие элементы чер-
тежа, область просмотра может быть панорамирована (сдвинута) в любом
направлении, что позволяет использовать один сборочный чертеж для изде-
лий любого размера и сложности, отказавшись от множества небольших
чертежей, как принято в традиционном черчении. При необходимости мож-
но получить твердую копию любой области чертежа (рис. 1.9).
Копирование, поворот и перенос. Любой элемент изображения или
группу элементов можно скопировать, переместить и/или повернуть. Для
двумерного поворота достаточно задать положение центра вращения и угол
поворота. При переносе обычно вводятся две точки, определяющие вектор
смещения. Перенос и поворот, а также копирование широко применяются
при вставке в чертеж стандартных элементов, вызываемых из стандартных
библиотек (рис. 1.10).
SNAP ТО GRID
Рис. 1.7. Привязка к узлам сетки
1.2. Принципы построения систем графического моделирования
25
Рис. 1.8. Построение сплайна
Преобразования. Кроме поворота и переноса многие графические па-
кеты имеют и более сложные средства манипулирования изображением:
зеркальное отражение и пошаговое размножение. Используя эти средства,
очень удобно строить чертежи регулярных структур. Например, для созда-
ния чертежа зубчатой рейки достаточно построить половину профиля одно-
го из зубьев, далее применить операцию зеркального отражения, а затем
размножить полученный образ. Можно также провести масштабирование
изображения (рис. 1.11).
Выбор элементов и объединение их в группы. В большинстве графиче-
ских пакетов операции редактирования могут выполняться как над отдель-
ным элементом, так и над группой элементов. Например, для сдвига части
чертежа нет необходимости перемещать все элементы по отдельности. Вме-
сто этого достаточно «выбрать» их путем указания на каждый из элементов
либо осуществить «окнирование» (выделение на чертеже прямоугольной
области, все элементы которой выбираются автоматически). В дальнейшем
операции редактирования производятся одновременно над всеми элемента-
ми полученного набора. Можно, например, изменить цвет и тип линий всех
элементов, произвести масштабирование и т. д.
Иногда удобнее объединить выбранные элементы в группы (блоки). В
результате получается составной графический элемент, который при редак-
тировании рассматривается как единое целое. В группы можно объединять
и составные элементы, образуя многоуровневые иерархические структуры.
При необходимости можно выполнить и обратную операцию — разделить
составной элемент на отдельные составляющие.
Расслоение. Во многих двумерных САПР реализован принцип «рас-
слоения», позволяющий разделить чертеж на несколько частей, наложенных
друг на друга. С точки зрения традиционного черчения это эквивалентно
созданию нескольких чертежей, каждый из которых выполнен на прозрач-
ной пластине. Причем можно рассматривать каждую пластину по отдельно-
Рис. 1.9. Увеличение и панорамирование
26 1. Компьютерные средства проектирования и графического моделирования
Рис. 1.10. Копирование («), параллельный перенос (б) и поворот (в)
сти либо, складывая их, получать совместное изображение. При выполнении
чертежей механических конструкций можно, например, разместить все гео-
метрические элементы в одном слое, а все размеры и пояснительные надпи-
си — в другом.
Двумерные системы позволяют построить упрощенные геометриче-
ские модели реальных физических объектов, состоящие из трех независи-
мых проекций (видов). При их использовании модель куба, например, зада-
ется 12 двумерными точками с координатами XY. Поэтому при внесении
изменений конструктор должен редактировать отдельно каждую из проекций.
В трехмерных системах используются точки с тремя координатами,
что позволяет автоматически устанавливать проекционные связи. Так, в
этом случае куб описывается восемью трехмерными точками XYZ, по кото-
1.2. Принципы построения систем графического моделирования
27
MIRROR
а
ARRAY
Ж
б
SCALE
Рис. 1.11. Зеркальное отражение (а), размножение (б) и масштабирование (в)
рым находятся проекции XY, YZ и XZ. При использовании таких систем
обычно начинают с построения трехмерного изображения, а двумерные ви-
ды формируются на последнем этапе, при выводе чертежей. А в некоторых
случаях двумерные чертежи полностью заменяются трехмерной компью-
терной моделью, по которой генерируются программы для станков с ЧПУ.
Системы трехмерного моделирования широко применяются в интег-
рированных САПР/АСТПП. Они часто дополняются средствами автомати-
ческого анализа физических характеристик (вычисление массы, центра масс,
моментов и тензоров инерции и др.), а также модулями, обеспечивающими
оценку прочности и технологичности. Использование трехмерных систем в
настоящее время уже не сдерживается стоимостью программных средств и
оборудования.
28 1. Компьютерные средства проектирования и графического моделирования
Рис. 1.12. Геометрические модели трехмерных объектов:
а — каркасная (Wire-frame); б — поверхностная (Surface); в — твердотельная (Solid)
Методы трехмерного моделирования, используемые в САПР, делятся
на три группы: каркасное, поверхностное и твердотельное (сплошное) моде-
лирование (рис. 1.12).
Каркасное моделирование (рис. 1.12, а). Модель каркасного типа пол-
ностью описывается в терминах точек и линий. Ее главным достоинством
являются простота и невысокие требования к компьютерной памяти, а не-
достатки связаны с отсутствием информации о гранях, заключенных между
линиями, и с невозможностью различить внешнюю (незаполненную) и
внутреннюю (заполненную) области. Наиболее широко каркасное модели-
рование применяется при имитации несложного пространственного движе-
ния инструмента (например, при фрезеровании по трем осям).
При использовании каркасных моделей в САПР необходимо учиты-
вать следующие ограничения:
• неоднозначность — отсутствие возможности однозначно оценить
ориентацию и видимость граней, что не позволяет различать виды сверху и
снизу, а также автоматизировать удаление скрытых линий;
• приближенное представление криволинейных граней — невоз-
можность точно описать криволинейные поверхности (цилиндры, конусы
и др.), которые реально не имеют ребер; иногда для таких поверхностей
вводят фиктивные ребра, располагаемые через регулярные интервалы
(рис. 1.13);
• невозможность обнаружить столкновения — отсутствие информа-
ции о поверхностях, ограничивающих форму, не позволяет обнаружить
столкновения между объектами, что важно при моделировании роботов,
проектировании планов размещения оборудования и т. д.;
• погрешности оценки физических характеристик — возможность
некорректного вычисления массы, центра тяжести, момента инерции и
1.2. Принципы построения систем графического моделирования
29
Рис. 1.13. Приближенное представление криволинейных поверхнос-
тей в каркасных моделях (вводятся фиктивные ребра)
т. д., обусловленная недостатком информации об ограничивающих по-
верхностях;
• отсутствие средств «затенения» поверхностей — у модели, со-
стоящей только из ребер, невозможно произвести закраску поверхностей
различными цветами.
Поверхностное моделирование (рис. 1.12, 6). Модель поверхностного
типа описывается в терминах точек, линий и поверхностей. В отличие от
каркасной модели она обеспечивает:
• точное представление криволинейных граней',
• автоматическое распознавание граней и их закраску,
• автоматическое удаление невидимых линий (рис. 1.14);
• распознавание особых линий на гранях (отверстий и т. д.);
• обнаружение столкновений между объектами.
Метод поверхностного моделирования наиболее эффективен при про-
ектировании и изготовлении сложных криволинейных поверхностей (кор-
пусов автомобилей и др.). При этом можно использовать:
• базовые геометрические поверхности (плоскости, цилиндры, кубы,
результат перемещения образующей кривой в заданном направлении и т. д.,
рис. 1.15, а);
• поверхности вращения (результат вращения линии вокруг оси,
рис. 1.15, 6);
• пересечения и сопряжения поверхностей',
• аналитические поверхности (задаются математическим уравнением);
Рис. 1.14. Удаление невидимых линий при поверхностном моделировании
30 1. Компьютерные средства проектирования и графического моделирования
Рис. 1.15. Поверхностные модели, полученные путем перемещения
кривой в заданном направлении («), вращения кривой (б) и при по-
мощи сплайн-интерполяции (в)
• скульптурные поверхности или поверхности «свободных форм», ко-
торые не могут быть описаны одним математическим уравнением, а задают-
ся при помощи методов сплайн-интерполяции образующих кривых (корпуса
автомобилей, фюзеляжи самолетов, лопатки турбин, рис. 1.15, в; 1.16).
В современных трехмерных системах широко используются состав-
ные поверхности, составленные из криволинейных четырехугольников, ог-
раниченных гладкими кривыми. Внутренняя область каждого такого участ-
ка определяется путем интерполяции. При изображении составных поверх-
ностей на экране создается сетка, натянутая на многогранный каркас.
На базе методов поверхностного моделирования построен ряд
мощных графических систем, широко применяемых в промышленности.
Однако поверхностные модели имеют ряд недостатков, которые могут
быть устранены только в рамках твердотельного моделирования. К ним
относятся:
• неоднозначность при моделировании реальных твердых тел;
• сложность процедур удаления невидимых линий и отображения
внутренних областей.
Рис. 1.16. Поверхностная модель кузова
автомобиля
Твердотельное моделиро-
вание (рис. 1.12, в). Модель твер-
дотельного типа описывает трех-
мерный объем, который занимает
рассматриваемое физическое те-
ло. В отличие от каркасных и по-
верхностных моделей она обес-
печивает:
• полное описание запол-
ненного объема и возможность
разграничения внешних и внут-
ренних областей, на основе чего
автоматизируется процесс обна-
ружения столкновений;
1.3. Графические стандарты
31
• автоматизацию процесса удаления скрытых линий;
• автоматизацию процесса построения разрезов и сечений, что требу-
ется при создании сборочных чертежей сложных изделий;
• применение современных методов анализа конструкций (точное вы-
числение массогабаритных характеристик, расчет прочности и деформаций
методом конечных элементов и т. д.).
• эффективное управление цветами и источником освещения, получе-
ние тоновых изображений;
• более точное моделирование кинематики и динамики многозвенных
механизмов (роботов, станков и т. д.).
Существует целый ряд способов построения твердотельных моделей.
Однако в САПР наибольшее распространение получили два из них: метод
конструктивного представления (C-Rep) и метод граничного представления
(B-Rep). Рассмотрим их подробнее.
Метод конструктивного представления (C-Rep) основан на создании
моделей из типовых твердотельных примитивов с заданными размерами,
ориентацией и точкой привязки. При определении взаимоотношений между
соседними примитивами используются булевы операции', «объединение»,
«разность» и «пересечение». Твердотельные примитивы могут выбираться
из библиотеки или генерироваться путем движения произвольной поверхно-
сти вдоль некоторой кривой. В результате происходит «захват» (sweeping)
части трехмерного пространства, принадлежащей примитиву.
Метод граничного представления (B-Rep) также оперирует с примити-
вами, связанными при помощи булевых операций. При этом модель описы-
вается совокупностью ребер и граней, определяющих граничную поверхность
твердого тела. Эти данные дополняются информацией о топологии примитива
и особенностях его геометрии. Метод B-Rep более удобен при модификации
примитивов, но требует большего объема компьютерной памяти.
Методы твердотельного моделирования, основанные на булевых опера-
циях, особенно удобны при вычислении поверхностных и весовых характери-
стик тел, расчете напряжений, имитации операций механической обработки. В
последнем случае операции резания металла (точение, фрезерование, сверление
и т. п.) могут быть легко описаны при помощи булевой разности. Естественным
приложением булевой алгебры является также анализ столкновений (колли-
зий), которые обнаруживаются при помощи операции пересечения.
1.3. Графические стандарты
При автоматизированном проектировании металлических конструк-
ций часто возникает необходимость обмениваться графической информаци-
32 1. Компьютерные средства проектирования и графического моделирования
ей между различными подсистемами, которые в общем случае могут быть
реализованы не только в различной программной среде, но и на различных
аппаратных средствах. При этом важно правильно выбрать формат записи
данных, который, с одной стороны, должен обеспечивать минимальный
размер файлов, а с другой — сохранение точности графической модели из-
делия. Поэтому рассмотрим подробнее вопросы кодирования графической
информации или, сокращенно, графические форматы.
Для записи графической информации используются два принципи-
ально различных способа — растровый и векторный. Первый способ при-
меняется при обработке изображений, полученных при помощи сканера, а
также при редактировании фотоизображений; второй — в системах автома-
тизированного проектирования и графических пакетах.
Растровый файл описывает изображение как совокупность точек
(dots), число которых определяется разрешением, измеряемым в специальных
единицах — dpi или dpc (число точек на 1 дюйм или на 1 см соответствен-
но). Для цветных и полутоновых изображений определяется также «глубина
цвета» — число двоичных разрядов, отводимых для хранения информации о
цвете. Например, для изображений типа RGB глубина 24 разряда означает,
что на каждый основной цвет (красный — R, зеленый — G, синий — В) от-
водится по 8 разрядов и можно закодировать 224 « 16 млн цветов.
Основной недостаток растровых форматов — большой объем файлов,
описывающих изображение. Так, даже для растрового изображения со срав-
нительно невысоким разрешением 1024 х 768 точек и 256 цветами требуется
файл размером 768 кб. Поэтому в графических пакетах используются раз-
личные алгоритмы сжатия, что затрудняет преобразование растровых фор-
матов и создает множество проблем для пользователей.
Векторный файл описывает изображение как совокупность про-
стейших элементов (линия, ломаная, кривая Безье, эллипс, прямоуголь-
ник и т. д.), для каждого из которых задаются соответствующие атрибу-
ты: координаты вершин или других характерных точек, толщина и цвет
контурной линии, тип и цвет заливки и т. д. Кроме того, задается распо-
ложение элементов относительно друг друга (какой из них расположен
сверху, а какой — снизу).
Главное достоинство векторных файлов по сравнению с растровыми —
меньший размер и удобство редактирования, но при их выводе на экран
производится множество математических операций. Поэтому скорость вы-
вода векторных изображений обычно меньше, чем растровых, хотя этот не-
достаток довольно эффективно устраняется при помощи специальных про-
цессоров — графических ускорителей.
Существует целый ряд программ, переводящих графические данные
из векторного формата в растровый. Но обратная задача (перевод растровых
1.3. Графические стандарты
33
изображений в векторные) является довольно сложной и решается только в
наиболее совершенных графических пакетах. Не менее сложные проблемы
возникают и при преобразованиях одного векторного формата в другой, так
как многие графические пакеты используют уникальные математические
модели для элементов изображения. В настоящее время применяют не-
сколько десятков форматов представления графических данных. Рассмот-
рим наиболее распространенные из них.
BMP-формат реализует растровый способ представления графических
данных и поддерживается практически любым Windows-приложением. Его
главная особенность — независимость от типа адаптера и монитора при ко-
дировании цвета. Для сжатия данных используется алгоритм RLE (Run-
Length Encoded), но размер файлов довольно большой.
CGM-формат (Computer Graphics Metafile') относится к классу «ме-
тафайлов», т. е. обеспечивает кодирование как векторных, так и растровых
изображений. Его основное достоинство — независимость от аппаратных и
программных средств, что позволяет эффективно осуществлять обмен дан-
ными между различными программами и платформами. Но для хранения
чертежей и рисунков этот формат практически не применяется.
DXF-формат (Drawing eXchange Format) является векторным и под-
держивается практически всеми САПР и графическими пакетами, включая
AutoCAD. В нем реализованы многие возможности, отсутствующие в дру-
гих форматах, например хранение трехмерных объектов. Однако из-за
сложности этого формата некоторые приложения позволяют только читать
DXF-файлы, но не используют его при сохранении изображений.
EPS-формат (Encapsulated PostScript) использует как векторный, так и
растровый способы записи графических данных. Соответствующий файл
представляет собой набор команд, выполняемых интерпретатором языка
PostScript при выводе изображения. При этом EPS-файл не зависит ни от
операционной системы, ни от аппаратных средств. Однако программы, под-
держивающие этот формат, часто не обеспечивают полной совместимости.
HPGL-формат (Hewlett-Packard Graphical Language) относится к
классу векторных и является одним из основных для систем автоматизиро-
ванного проектирования. Он широко используется также при выводе черте-
жей на плоттеры и принтеры.
IGES-формат (International Graphical Exchange Standard) представля-
ет собой набор протоколов для передачи графических данных и вывода их
на экран монитора. Первоначально он применялся для поддержки удален-
ных терминалов, но в настоящее время используется в ряде CAD-приложе-
ний, оперирующих с трехмерными изображениями.
PCX-формат относится к классу растровых. Первоначально он ис-
пользовался в программе PaintBrush, но постепенно получил широкое рас-
2 6705
34 1. Компьютерные средства проектирования и графического моделирования
пространение в других графических редакторах. Его недостатком является
зависимость от типа используемого видеоадаптера. В PCX-файлах исполь-
зуется алгоритм сжатия RLE, позволяющий уменьшать размер файла на
40...70 %, если число цветов не превышает 16.
PICT-формат относится к классу «метафайл», т. е. дает возможность
кодировать как векторные, так и растровые изображения. Он ориентирован
на платформы типа Macintosh и поддерживается практически любым графи-
ческим приложением, реализованным на таких аппаратных средствах. Вви-
Рис. 1.17. Графические
стандарты, используе-
мые в САПР
ду своей сложности этот формат редко под-
держивается приложениями, работающими
на других платформах.
TIFF-формат (Tagged Image File
Format) относится к классу растровых и по-
зволяет обеспечивать переносимость графи-
ческих файлов с IBM-совместимых компью-
теров на Macintosh и обратно. Существует
несколько типов TIFF-файлов: В — черно-
белые изображения, G — полутоновые, Р —
цветные и т. д. Формат TIFF очень удобен,
но приводит к очень большим размерам
файлов (например, цветное изображение
размера А4 при разрешении 300 dpi может
занимать около 40 Мб).
WMF-формат (Windows MetaFile)
обеспечивает кодирование как векторных,
так и растровых данных и является анало-
гом формата PICT для оболочки Windows.
Он используется при обмене графическими
данными между Windows-приложениями, а
также поддерживается графическими про-
граммами, реализованными на ряде других
платформ.
При организации обмена графической
информацией в компьютерной графике раз-
личают несколько уровней графических
стандартов (рис. 1.17). Эти стандарты обес-
печивают связь между:
а) графическими утилитами и устрой-
ствами графического вывода;
б) прикладными программами и гра-
фическими утилитами;
в) различными САПР.
1.3. Графические стандарты
35
Для обеспечения связи между графическими утилитами и устройст-
вами вывода наиболее часто используется стандарт VDI (Virtual Device
Interface — интерфейс виртуального устройства), который в настоящее
время переименован в CGI (Computer Graphics Interface — интерфейс ком-
пьютерной графики).
Наиболее распространенным стандартом, обеспечивающим связь
между прикладными программами и графическими утилитами, является
GKS (Graphical Kernel System — графическая корневая система). Иногда
используется и более ранний стандарт CORE, основные функции которого
реализованы в GKS. А наиболее совершенным из стандартов этого класса
является PHIGS (Programmers Hierarchical Interface for Graphics — про-
граммистский иерархический графический интерфейс), описывающий
сложные иерархические структуры графических данных, в том числе и
трехмерные.
Для обеспечения связи между различными САПР используется ряд
стандартов, наиболее распространенным из которых является IGES (Initial
Graphics Exchange Specification — стандартный протокол обмена графиче-
ской информацией). В этом стандарте различные данные классифицируются в
терминах сущностей, которые могут принадлежать к одной из трех катего-
рий: геометрии (точки, отрезки, дуги, плоскости и т, п.), аннотации (размеры,
осевые линии, стрелки и т. п.), структуры (геометрические группы, макрооп-
ределения и т. д.). Чтобы использовать IGES, любая САПР снабжается двумя
программами — препроцессором и постпроцессором (рис. 1.18).
Международный стандарт GKS (Grapfical Kernel System) принят в
1985 г. и предназначен для обеспечения переносимости и совместимости
программных средств машинной графики. Согласно этому стандарту, любое
изображение должно строиться из типовых базовых элементов — примити-
вов вывода (рис. 1.19). В GKS определено шесть основных примитивов вы-
вода-. полимаркер, полилиния, текст, заполнение области, массив пикселей,
обобщенный примитив вывода.
Полимаркер используется для указания характерных точек на экране,
которые отображаются в виде ярких точек, крестов, квадратов и т. д. Поли-
< VT ' V САПР 1 Постпроцессор^) ! ! IGES ! ( данных J ] । ^71релроцессо|ГЧ)<^^ ! 1<^ < j ^^>(^П^1рГцсссо^ САПР 2 ( База \ ( данных ) ^Постпроцессор^ >
Рис. 1.18. Связь между двумя различными САПР через формат IGES
36 1. Компьютерные средства проектирования и графического моделирования
Рис. 1.19. Основные графические примитивы вывода GKS
линия представляет собой набор отрезков прямых (ломаную), соединяющую
заданную последовательность точек. Примитив текст — это строка симво-
лов, располагающаяся в указанной позиции.
Примитив заполнение области представляет собой многоугольник,
заполненный штриховкой, узором или фоновой окраской. Примитив «мас-
сив пикселей» позволяет задать цвет индивидуально для каждой точки неко-
торой области (пикселя). И наконец, обобщенный примитив вывода пред-
ставляет собой стандартное средство определения более сложных элементов
(прямоугольник, эллипс и т. д.), вид и количество которых зависят от спе-
цифики конкретных графических пакетов.
С каждым из примитивов в GKS связан набор параметров — атрибу-
тов, определяющих его геометрические и качественные свойства. Примеры
атрибутов для основных примитивов вывода приведены в табл. 1.1.
GKS позволяет разделить изображение на отдельные сегменты, кото-
рые могут обрабатываться и отображаться независимо друг от друга. Преду-
смотрены также средства для включения одного сегмента в другой. При
создании графической модели объекта и его изображения используются три
типа систем координат: глобальная, нормализованная приборная и собст-
венно приборная.
1.4. Графические системы геометрического моделирования
37
Таблица 1.1. Атрибуты основных примитивов вывода GKS
Примитив Атрибуты
Полимаркер Полилиния Текст Заполнение области Массив пикселей Тип маркера, его цвет и масштаб Тип, цвет и толщина линии Тип шрифта, размеры, цвет и ориентация символов Вид штриховки, цвет Цвет пикселей
Ввод в GKS определяется как связь с одним из пяти допустимых ло-
гических устройств ввода:
ЛОКАТОР — выдает положение в глобальной системе координат;
ЗНАЧЕНИЕ — выдает значение числа;
ВЫБОР — выдает целое число, определяющее один из возможных ва-
риантов ответа;
УКАЗАНИЕ — выдает имя сегмента и идентификатор примитива;
СТРОКА — обеспечивает ввод строки символов.
Ввод может происходить в одном из трех режимов: запрос, опрос, со-
бытие. Первый из указанных режимов (запрос) аналогичен операции чтения
обычных языков программирования: система ожидает, пока не произошло
событие ввода, после чего передает в программу соответствующее значение.
При этом в любой момент допустимо наличие только одного запроса на
ввод. Второй режим (опрос) применяется для ввода от таких устройств, у
которых на выходе постоянно существует какое-либо значение (например,
положение указателя мыши). А третий режим (событие) используется для
ввода от устройств, инициирующих прерывания. Эти прерывания запоми-
наются в очереди и обрабатываются в соответствии с принятой дисципли-
ной обслуживания.
Появление GKS в качестве первого международного стандарта оказа-
ло существенное влияние на развитие машинной графики и ее применение в
САПР.
1.4. Графические системы геометрического моделирования
Система DUCT. Концепция этой системы была разработана в конце
1960-х годов на инженерном факультете Кембриджского университета. Ее
промышленный вариант распространяется с 1983 г. фирмой DELCAM (Delta
Computer-Aided Manufacturing). Система DUCT позволяет конструктору
создавать трехмерные каркасные и поверхностные модели объектов, визуа-
лизировать их на экране монитора, а также вычислять площадь поверхно-
38 1. Компьютерные средства проектирования и графического моделирования
ста, объем, координаты центра тяжести объекта и генерировать сетку ко-
нечных элементов для анализа потоков и расчетов на прочность.
При помощи системы DUCT автоматизированы процессы создания
литейных форм и штампов, подготовки чертежей изделий и программ для
станков с ЧПУ. При этом учитываются припуски на толщину стенок, усад-
ки, зазоры при механической обработке.
Встроенный в DUCT каркасный редактор позволяет быстро и просто
задать форму объекта. Поверхности создаются на основе поперечных сече-
ний, определяемых набором точек. Эти сечения могут размещаться и ориен-
тироваться относительно заранее построенной кривой (сиг/на), играющей
роль «хребта», вдоль которого вытянута поверхность. Для интерполяции
поперечных сечений по заданным точкам используются кривые Безъе.
При генерации поверхности, состоящей из лоскутов, имеется возмож-
ность задавать границы в виде сложных кривых. При этом автоматически
обеспечивается гладкость поверхности между двумя любыми лоскутами.
Можно выполнить скругление угла, образованного двумя или тремя по-
верхностями, причем радиус скругления может быть как постоянным, так и
переменным. Из набора поверхностей можно создать единый объект в виде
оболочки, соединяющей в себе преимущества твердотельного и поверхностного
моделирования. При визуализации объекта, используя несколько цветов и раз-
личные источники света, генерируется цветное изображение. Если позволяет
компьютер, формируются цветные динамические модели.
Ядро системы DUCT составляет реляционная база данных, в которой
хранится вся информация о деталях и чертежах. При этом информация мо-
жет располагаться в любой из объединенных в сеть рабочих станций. Име-
ется возможность создавать параметрические чертежи. Система также имеет
библиотеку типовых деталей и интерфейсы с языками Си и Фортран.
Графический интерфейс пользователя включает в себя набор много-
уровневых меню, отображающих на экране списки параметров выбранной
команды. Пользователь может также создавать свои собственные меню и
прикладные программы. Для этого в системе имеется специальный команд-
ный язык.
Система DUCT предоставляет пользователю широкий набор методов
механической обработки. При фрезеровании можно самому задать форму
инструмента или выбрать из библиотеки шаровую фрезу, торцевую фрезу
либо торцевую фрезу со скругленными кромками. При этом осуществляет-
ся проверка на минимальный радиус кривизны поверхности. Недоступные
области высвечиваются на экране и затем могут быть обработаны инстру-
ментом меньшего радиуса. Для этого следует задать направление резания,
скорость подачи и скорость вращения шпинделя, припуск для черновой
обработки. Траектория движения инструмента генерируется, визуализиру-
1.4. Графические системы геометрического моделирования
39
ется на экране вместе с изображением инструмента и при необходимости
корректируется. Система DUCT поддерживает 2,5-, 3- и 5-координатное
фрезерование, токарную обработку и 4-координатную электроэрозионную
обработку.
DUCT может функционировать на стандартных рабочих станциях с
операционной системой UNIX. Программное обеспечение построено по мо-
дульному принципу. К числу основных модулей относятся DUCTmodel,
Advanced model, DUCTshade, DUCTnc, DUCTdraft и др. Для передачи дан-
ных используются стандарты IGES, VDA-FS и DXF. Имеются также прямые
интерфейсы с системами PDGS и С ADDS.
Система CATIA. Система CATIA, разработанная французской фир-
мой Dassault Systemes, появилась на мировом рынке САПР в 1981 г. Перво-
начально она предназначалась для самолетостроения, но постепенно нашла
применение в автомобильной промышленности и других отраслях. В на-
стоящее время система CATIA распространяется фирмой IBM и активно
используется такими фирмами, как Boeing, Chrysler, ГАЗ и ВАЗ. Большин-
ство пользователей системы CATIA использует рабочие станции IBM, но
систему можно также установить на мэйнфреймах, UNIX-станциях
RISC/6000 и рабочих станциях фирм Hewlett-Packard и Silicon Graphics.
Система содержит полные решения для автоматизированного проек-
тирования в следующих областях:
• конструирования механизмов и узлов (Mechanical Design);
• формообразования поверхностей и дизайна (Shape Design and Styling);
• анализа и моделирования (Analysis and Simulation);
• подготовки производства (Manufacturing);
• инженерных расчетов (Equipment and System Engineering).
Система CATIA обладает одной из самых совершенных методик про-
ектирования поверхностей (модули Surface Design, Advanced Surface Design,
FreeForm Design) и анализа их качества по кривизне, гладкости, непрерыв-
ности в областях сопряжения и т. д. При необходимости поверхностные мо-
дели могут быть преобразованы в твердотельные. Сложные кривые строятся
на базе кривых Безье. Поверхности, которые нельзя описать стандартными
типами элементов, могут быть аппроксимированы точками с заданными ко-
ординатами, по которым строятся бипараметрические полиномиальные
функции.
В рамках системы CATIA можно использовать целый ряд приложе-
ний, входящих в «архитектуру прикладных программ» (САА — CATIA
Application Architecture). Они позволяют выполнить динамический анализ
механизмов (CATDADS), моделирование роботизированных комплексов
(Robuse), подготовить постпроцессоры и программы для станков с ЧПУ (NC
PostProcessor Generator, CAT4AXES), создать проекты трубопроводов и
40 1. Компьютерные средства проектирования и графического моделирования
пневмосистем (3D-Tubing), а также создать фотореалистические изображе-
ния (Visualisation Studio). В результате сотрудничества IBM с фирмой BMW
создан уникальный модуль проверки собираемости изделия (Fitting Simula-
tion), который моделирует весь процесс сборки изделия с учетом доступно-
сти, способов установки и используемой оснастки. Этот же модуль позволя-
ет оценить возможность съема узла для ремонта или обслуживания.
К числу существенных достоинств системы CATIA относится совер-
шенная схема построения параметрически связанных моделей и возмож-
ность постпараметризации. Конструктор может начать построение модели,
руководствуясь лишь функциональностью и технологичностью, не занима-
ясь на первом этапе параметризацией. Далее, на любом этапе, можно опре-
делить параметры и связи между ними. При этом допускается задать лишь
наиболее существенные параметры, а остальные оставить по умолчанию.
При изменении параметров конструктор может позволить ассоциативно
распространить, изменения на все объекты либо ограничить изменения неко-
торой зоной (т. е. определить некоторые параметры как локальные). На лю-
бом этапе можно принять решение о разрыве связи. В системе САТ1А реа-
лизованы также расчеты трехмерных допусков (Functional DIMENSIONING
and 3D-Tolerancing), позволяющие рассчитать размерную цепь любой слож-
ности и оптимальные допуски, исследовать поведение механизмов при ва-
риации размеров деталей.
Новым нетрадиционным средством системы CATIA, не характерным
для других САПР, является «проектирование при помощи правил», реали-
зующее, по существу, концепцию конструктивно-технологической базы
знаний. Оно позволяет конструктору определить свои собственные правила
проектирования и использовать в повседневной работе. Например, при про-
ектировании гидро- и пневмосистем можно определить шаг расстановки
крепежа, допустимые и запретные зоны расположения, зоны безопасного
расстояния от элементов конструкции, материалы и т. д.
При помощи системы CATIA можно автоматизировать и некоторые
процессы управления предприятием (финансами, складским хозяйством,
кадрами и т. д.). Для этого используются коммерческие сетевые реляцион-
ные базы данных (Oracle, DB2) и интерфейсы с наиболее распространенны-
ми системами управления предприятиями (R3, Triton).
Системы фирмы Autodesk. Наиболее распространенным и извест-
ным программным продуктом фирмы Autodesk является пакет AutoCAD,
первые версии которого были ориентированы на двумерное черчение и вы-
пуск конструкторской документации. В процессе развития этот пакет пре-
вратился в развитую среду трехмерного моделирования и ведения проектов
в архитектуре, строительстве, машиностроении, картографии и других от-
раслях. Последние версии пакета AutoCAD могут выполняться как на пер-
1.4. Графические системы геометрического моделирования
41
сональных компьютерах под управлением DOS, Windows, Windows NT, так
и на UNIX-платформах (Silicon Graphics, Hewlett-Packard, Sun SPARC-
Station, IBM R/6000). Ядро написано на языке C++ и представляет собой
объектно-ориентированную среду, являющуюся основой для множества
прикладных программ, создаваемых как самой фирмой Autodesk, так и ее
партнерами. Число таких приложений уже превысило 5000.
Для машиностроения фирма Autodesk предлагает интегрированный
пакет Autodesk Mechanical Desktop (AMD), в который входят практически
все необходимые инженеру-конструктору средства моделирования геомет-
рических объектов. Он объединяет в себе возможности известных про-
граммных продуктов Autodesk:
• AutoCAD — в качестве графической среды;
• AutoCAD Designer — для конструирования деталей и сборочных
узлов;
• AutoSurf — для моделирования сложных трехмерных поверхностей
с использованием NURBS-геометрии;
• IGES Translator — для обмена файлами с другими системами САПР;
• MCAD — система меню для организации взаимодействия с другими
машиностроительными приложениями.
Модуль AutoCAD Designer позволяет автоматизировать процесс соз-
дания рабочих чертежей деталей и сборочных единиц. Он дает возможность
пользователю оперировать с привычными конструкторско-технологичес-
кими элементами и терминами (сопряжение, фаска, отверстие и т. д.). В нем
реализован принцип параметрического моделирования, что позволяет до-
вольно гибко вносить изменения на любой стадии проектирования.
Процесс создания трехмерных моделей в AutoCAD Designer происхо-
дит в два этапа: сначала задается плоский эскиз детали, а затем ему прида-
ется третье измерение. При конструировании сборочной единицы пользова-
телю достаточно задать параметрические связи между существующими объ-
ектами, ограничивая число степеней свободы проектируемой механической
системы. Для разработанных моделей автоматически генерируются двумер-
ные проекции (виды), причем постоянно действует двунаправленная пара-
метрическая связь модель—чертеж. Это позволяет благодаря возможностям
параметрического черчения вносить изменения как на самой трехмерной
модели, так и на ее двумерных видах путем корректировки отдельных раз-
меров. В модуле также имеются встроенные функции, обнаруживающие
взаимное пересечение деталей в сборочных единицах.
Модуль AutoSurf обеспечивает построение и редактирование фор-
мообразующих кривых и сложных поверхностей, построение на их осно-
ве новых объектов, создание каркасных (проволочных) моделей, проеци-
рование различных контуров на плоскость или поверхность. В этом мо-
42 1. Компьютерные средства проектирования и графического моделирования
дуле реализована NURBS-технология, основанная на наиболее эффектив-
ных методах работы с произвольными поверхностями, которые описы-
ваются неоднородными рациональными В-сплайнами. Поэтому AutoSurf
получил широкое распространение в автомобильной и аэрокосмической
промышленности.
IGES-транслятор используется для точного и корректного обмена
графическими моделями с другими системами CAD/CAM/CAE. Например,
dwg-файлы формата AutoCAD после обработки в AutoSurf могут переда-
ваться в другие системы, осуществляющие расчеты на прочность, генера-
цию программ для ЧПУ и т. д.
Как показывает опыт, наибольший эффект при проектировании ма-
шиностроительных конструкций может быть достигнут только при совмест-
ном использовании модулей AutoCAD Designer и AutoSurf, когда некоторые
трудности моделирования поверхностей произвольной формы в AutoCAD
Designer устраняются средствами AutoSurf, а проблемы построения проек-
ционных видов в AutoSurf решаются за счет средств AutoCAD Designer.
Объединение этих двух программ не только обеспечивает двусторонний об-
мен данными на основе формата AutoCAD (dwg-файлы), но и позволяет по-
новому организовать доступ к основным функциям AMD. В этом пакете
выделены четыре основных функциональных модуля:
1) параметрического твердотельного моделирования;
2) параметрического моделирования сборочных единиц;
3) моделирования поверхностей произвольной формы;
4) генерирования двумерных чертежей.
Первые два модуля являются составными частями программы
AutoCAD Designer, третий модуль включает основные функции AutoSurf, а
четвертый представляет собой универсальный инструмент, применимый как
для стандартных трехмерных объектов AutoCAD, так и для комбинаций
разнородных трехмерных объектов.
При создании плоского эскиза изделия используются стандартные для
AutoCAD команды рисования и редактирования двумерных объектов. При
этом от конструктора не требуется соблюдения большой точности ни в от-
ношении размеров, ни в отношении параллельности или перпендикулярно-
сти. Поэтому, в отличие от стандартных приемов AutoCAD, здесь не ис-
пользуются режимы «шаг», «сетка», а также функции объектной привязки.
Эскиз создается концептуально.
Далее выполняется профилирование эскиза, в процессе которого на
модель накладываются геометрические связи и почти горизонтальные ли-
нии становятся строго горизонтальными, почти замкнутые — замкнутыми и
т. д. При этом программа выдает сообщение о том, сколько связей или раз-
меров требуется, чтобы однозначно определить профиль.
1.4. Графические системы геометрического моделирования
43
Для простановки параметрических размеров используется единая ко-
манда, которая в зависимости от последовательности заданных точек авто-
матически определяет тип размера (линейный, угловой, радиальный и т. д.).
Если требуется указать размер, зависящий от размера других деталей, ис-
пользуются глобальные параметры.
Геометрия эскиза может быть любой сложности, но в нем должен
быть ровно один замкнутый контур. Именно этот контур используется в
дальнейшем при построении третьего измерения или создания так называе-
мой базовой формы. При этом используется один из следующих способов:
выдавливание, вращение, перемещение вдоль двумерной криволинейной
направляющей. Далее к базовой форме добавляются стандартные конструк-
торско-технологические элементы (отверстия, фаски, сопряжения) или эле-
менты произвольной формы. Следует учитывать, что базовая форма пред-
ставляет собой твердое тело и формообразование в AutoCAD Designer осу-
ществляется при помощи булевых операций над пространственными
множествами (объединение, вычитание и пересечение). Например, добавле-
ние отверстия к модели сводится к вычитанию объема, а при задании фасок
может выполняться как вычитание, так и объединение.
AutoCAD Designer поддерживает параметризацию не только на уровне
отдельной модели, но и на уровне сборочной единицы. Поэтому процесс
сборки почти полностью автоматизирован: пользователь должен только за-
дать связи, ограничивающие число степеней подвижности, а программа са-
ма генерирует сборочные чертежи и спецификации. При этом сборочная
единица представляется в виде иерархической структуры, в которой строго
заданы как взаимосвязи отдельных компонент, так и последовательность
процесса сборки.
Процесс моделирования сборочных единиц в AutoCAD Designer со-
стоит из следующих этапов:
• определение компонентов сборочной единицы;
• вставка компонентов в сборочную единицу;
• наложение и редактирование связей между компонентами;
• сборка компонентов и анализ сборочной единицы;
• создание сборочного чертежа.
Чтобы начать процесс сборки, все компоненты необходимо явно
определить как доступные для сборки («материализовать»). Вставка ком-
понентов в рабочее пространство AMD подобна вставке блоков в
AutoCAD. Причем один и тот же компонент (деталь) может использо-
ваться неоднократно. Конструктор должен строго придерживаться опре-
деленной последовательности сборки, вводя сначала «базовые» компо-
ненты, а затем «присоединяемые» к ним. При этом не требуется внима-
тельно следить за взаимной ориентацией и положением собираемых
44 1. Компьютерные средства проектирования и графического моделирования
деталей, так как в дальнейшем они скорректируются автоматически за
счет введения параметрических связей.
Введение связей производится в специальном диалоговом окне. Поль-
зователю предлагается четыре варианта связей, определяющих взаимное
расположение компонент:
• Insert (вставить соосно) — задаются цилиндрические поверхности,
которые получат общую ось, расстояние между ними и направление соеди-
нения;
• Mate (встык) — задаются сопрягаемые поверхности, линии или точ-
ки двух компонент, а также расстояние между ними (отступ);
• Flush (заподлицо) — задаются грани двух компонент, нормали к ко-
торым ориентируются параллельно в одном направлении;
• Angle (угловая зависимость) — нормали указанных граней пары
компонент ориентируются под заданным углом;
• Oppose (под углом в противоположных направлениях) — нормали
указанных граней пары компонент ориентируются в противоположных на-
правлениях под заданным углом.
После задания типа связи необходимо указать компоненты, к которым
применяется заданная связь; затем компоненты перестраиваются на экране
автоматически с учетом введенных связей, имитируя процесс сборки.
При генерации сборочных чертежей пользователь может задать лю-
бую совокупность проекционных видов и разрезов сборочной единицы, по-
зволяющих уяснить взаимное расположение компонент. Кроме того, воз-
можно построение изометрических проекций в так называемом разобранном
виде (exploded view), что удобно при подготовке руководств по сборке и
эксплуатации. В AMD имеются также средства автоматического заполнения
специфика1!ий, форма которых определяется пользователем. Спецификация
может размещаться в поле чертежа или выводиться во внешний файл.
Моделирование поверхностей в AMD осуществляется средствами
AutoSurf, во внутреннем формате которого оболочки и контуры точно опи-
сываются математическими уравнениями. Однако при выводе на экран они
преобразуются в каркасы, что существенно сокращает время регенерации
изображения. Кроме того, в AutoSurf каркасы используются как исходные
данные при построении поверхностей сложной формы. Всего в AutoSurf
существует четыре типа поверхностей:
1) элементарные;
2) вращения (получаемые перемещением элементов каркаса);
3) движения (получаемые натяжением оболочки на каркас);
4) производные (получаемые из существующих).
Для их построения можно использовать 16 различных способов, при-
меняя разные типы каркасных элементов: сплайны, полилинии, дуги, ок-
1.4. Графические системы геометрического моделирования
45
ружности, эллипсы, линии с векторами вращения. Но, несмотря на разнооб-
разие методов построения, внутренний формат представления всех без ис-
ключения поверхностей основан на одном и том же математическом аппара-
те — аппарате неоднородных рациональных В-сплайнов (NURBS). Поверх-
ности AutoSurf могут быть представлены на экране либо в тонированном
виде, либо в виде каркаса, который является лишь вспомогательным средст-
вом отображения. Для тонирования трехмерных моделей и создания фото-
реалистических изображений в стандартную поставку пакета AutoCAD
включается программа AutoVision.
Перечень дополнительных возможностей AMD по сравнению с ACAD
приведен в табл. 1.2.
Таблица 1.2. Дополнительные возможности Autodesk Mechanical Desktop
Параметрическое моделирование твердых тел на основе конструктивных элементов
Конструктивные элементы Произвольные конструктивные элементы можно моде- лировать путем выдавливания, вращения и сдвига плоско- го эскизного контура, а также путем отсечения фрагмен- тов от твердотельных объектов произвольными поверхно- стями. В конструкцию можно включать стандартные эле- менты: сопряжения (галтели), фаски и отверстия (в том числе с зенковкой, разверткой и резьбовые)
Параметриче- ские возможности Любой размер может быть переменным. Переменные могут использоваться в математических формулах. Пере- менными можно управлять при помощи таблиц
Моделирование поверхностей про- извольной формы Моделирование примитивных поверхностей (конус, шар, цилиндр) и сложных поверхностей произвольной формы. Моделирование трубчатых поверхностей, поверх- ностей натяжения, изгиба, перехода; плавное сопряжение произвольных поверхностей. Расчет площади поверхно- сти и объема
Расчет массоинер- ционных характерис- тик и анализ взаимо- действия моделей Расчет площади поверхности, массы и объема деталей и сборочных узлов. Расчет моментов инерции. Анализ взаимодействия деталей в сборочных узлах
Г еометрические зависимости Горизонтальность, вертикальность, параллельность, перпендикулярность, коллинеарность, концентричность, проекция, касание, равенство радиусов и координат X и Y. Наглядное обозначение наложенных зависимостей специ- альными символами
46 1. Компьютерные средства проектирования и графического моделирования
Окончание табл. 1.2
Средства работы с эскизами Построение и редактирование набросков стандартны- ми средствами AutoCAD
Копирование эскизов на другие грани модели
Выполнение ра- бочих чертежей Двунаправленная ассоциативная связь между моделью и ее чертежом. Автоматическое удаление штриховых и невидимых линий. Соответствие стандартам ANSI, ISO, DIN, JIS и ЕСКД. Ассоциативное нанесение размеров и выносок
Конструирование сборочных узлов
Сборка деталей в узлы Графическое и логическое представление иерархиче- ской структуры сборочного узла. Организация деталей и подузлов в виде внешних ссылок
Наложение зави- симостей на компо- ненты узлов Задание расположения деталей относительно друг дру- га по их ребрам, осям или граням. Возможность свободно- координатного расположения деталей. Графическая инди- кация степеней свободы компонентов
Выполнение сбо- рочных чертежей Выполнение схем сборки-разборки. Проставление но- меров позиций на сборочных чертежах и автоматический выпуск спецификации
Программный пакет Autodesk WorkCenter предназначен для
управления процессом создания проекта и автоматизации ведения техни-
ческой документации. Он создан в соответствии с архитектурой клиент-
сервер и позволяет работать в локальной сети рабочим группам любой
численности.
Возможности пакета включают: многопользовательский доступ к до-
кументации, выбор оптимальной структуры; использование файлов цен-
трального хранилища; «управление» версиями документов в течение их «ак-
тивной» жизни; электронное уведомление; рассылку и утверждение доку-
ментации; управление потоком необходимой информации. Он также
позволяет в процессе проектирования и просмотра документации вносить в
нее изменения, дополнения, замечания и указания. Предусмотрен просмотр
файлов более чем 100 форматов, в том числе файлов текстовой и графиче-
ской информации, файлов электронных таблиц, файлов баз данных и систем
автоматизированного проектирования.
Autodesk WorkCenter полностью интегрирован со средой AutoCAD for
Windows и совместим с программным пакетом AutoCAD* LT. Система
1.4. Графические системы геометрического моделирования
47
Autodesk WorkCenter может быть использована для обработки электронной
документации практически всех типов.
При проектировании металлических конструкций могут использо-
ваться и другие программные продукты фирмы Autodesk: AutoCAD LT —
пакет для двумерного проектирования, Autodesk View и Autodesk VQ — сис-
темы просмотра файлов, подготовленных с помощью AutoCAD и ADE,
Autodesk Mechanical Library — библиотека трехмерных конструктивных
элементов и твердотельных моделей для пакета AutoCAD Designer.
Система I-DEAS. Торговая марка I-DEAS объединяет целый ряд про-
граммных продуктов, которые можно рассматривать как интегрированный
комплекс CAD/CAM/CAE. Эти программные средства созданы фирмой
SDRC (Structural Dynamics Research Corporation) и предназначены для авто-
матизации разработки металлических конструкций в аэрокосмической, ав-
томобильной и других отраслях промышленности. Отличительной особен-
ностью I-DEAS является возможность распределения пользовательских ли-
цензий по неоднородным локальным сетям, которые содержат рабочие
станции разных производителей (HP, IBM, SUN и др.), а также наличие
встроенных средств конечно-элементного моделирования, оптимизации и
автоматизации испытаний.
Типовой набор модулей I-DEAS для решения задач проектирования
металлоконструкций (Product Design Package) включает в себя следующие
модули:
• I-DEAS Master Modeler — базовый модуль трехмерного моделиро-
вания (проволочного, поверхностного, твердотельного);
• I-DEAS Master Surfacing — модуль трехмерного моделирования де-
талей со сложными «скульптурными» поверхностями (поверхностного и
твердотельного);
• I-DEAS Master Assembly — модуль для трехмерного моделирования
сборочных узлов и простейших механизмов;
• I-DEAS Drafting — модуль создания чертежей изделия;
• I-DEAS Data Translation — модуль преобразования форматов графи-
ческих данных.
При помощи модуля I-DEAS Master Modeler создается твердотельная
геометрическая модель, которая используется в качестве исходной в боль-
шинстве других задач (при прочностном анализе, черчении, подготовке про-
грамм для ЧПУ и т. д.). В нем реализована NURBS-геометрия, а также «па-
раллельная ассоциативность», поддерживающая групповую работу несколь-
ких конструкторов. Кроме того, «история» процесса проектирования
запоминается в виде дерева, любую ветвь которого можно редактировать.
Модуль I-DEAS Master Surfacing предназначен для создания моделей
деталей со сложными («скульптурными») поверхностями. При этом предпо-
48 1. Компьютерные средства проектирования и графического моделирования
лагается, что первичный эскиз подготовлен при помощи модуля I-DEAS
Master Modeler.
В модуле Master Surfacing реализована NURBS-геометрия с двойной
точностью, а также моделирование при помощи кривых Безье высокого по-
рядка. Для контроля гладкости полученной поверхности используются спе-
циальные средства визуализации, которые позволяют выявить участки с
резкими изломами.
Модуль I-DEAS Master Assembly позволяет построить трехмерные мо-
дели сборочных узлов, состоящих из большого числа более мелких элемен-
тов, каждый из которых также может быть сборочным узлом. Для удобства
конструктора при вставке элемента в механизм не требуется точного пози-
ционирования. Достаточно лишь задать связи между элементами, по кото-
рым далее находится точное взаимное расположение деталей. Для создан-
ной сборки можно автоматически сформировать спецификацию, а для группы
сборок — построить таблицы входимости, содержащие списки сборочных
узлов, в которые входят заданные детали. Кроме того, возможны анализ со-
бираемости созданного узла и оценка допусков при помощи I-DEAS
Tolerance Analysis. При помощи модуля Master Assembly можно также по-
строить модель простейшего механизма. Но при создании моделей сложных
пространственных механизмов применяется специальный модуль I-DEAS
Mechanism Design, который также позволяет провести полный динамиче-
ский анализ (вычислить силы, моменты, перемещения, скорости, ускорения
и т. д.).
Модуль 1-DEAS Drafting предназначен для получения чертежей изде-
лия, созданного в модулях I-DEAS Master Modeler, I-DEAS Master Surfacing,
I-DEAS Master Assembly, либо применяется как самостоятельная система
двумерного черчения. Для взаимодействия с пользователем I-DEAS Drafting
использует «Динамический навигатор» — специальное средство, поддержи-
вающее как однопользовательскую, так и многопользовательскую работу.
По геометрии главной модели (мастер-модели) легко создаются проекции,
сечения, разрезы, проставляются размеры. Чертежи взаимосвязаны с глав-
ной моделью в обоих направлениях, т. е. изменение любого размера на чер-
теже сразу же отражается в мастер-модели и наоборот. В процессе черчения
также автоматически создается спецификация, которая обновляется дина-
мически при изменении числа объектов, их атрибутов и т. д.
I-DEAS Data Translation представляет собой набор модулей для чтения
и записи графических файлов в форматах IGES, STEP, VDA-FS, DXF, а также
обмен данными с пакетами Pro/ENGINEER, CATIA, CADAM, CADDS и др.
Система Unigraphics. Система Unigraphics фирмы EDS широко рас-
пространена в аэрокосмической и автомобильной промышленности, а также
в машиностроении. Ее отличительными особенностями являются наличие
1.4. Графические системы геометрического моделирования
49
средств гибридного трехмерного моделирования, ассоциативной базы дан-
ных, развитых средств моделирования сборочных узлов и создания чертежей.
В состав системы Unigraphics входит несколько десятков модулей, ос-
новными из которых являются:
• UG/Gateway — модуль, поддерживающий интерфейс системы с
пользователем и взаимодействие между ее отдельными компонентами;
• UG/Solid Modeling — базовый модуль трехмерного гибридного мо-
делирования (проволочного, поверхностного, твердотельного и их модифи-
каций);
• UG/Features Modeling -— модуль, позволяющий редактировать и па-
раметрически задавать стандартные элементы изделий, такие, как отверстия,
щели, выступы, прокладки, стержни, трубы, желоба и т. д.;
• UG/Freeform Modeling — модуль трехмерного моделирования слож-
ных «скульптурных» поверхностей;
• UG/User-Defined Features — модуль, позволяющий представлять
произвольные группы деталей в виде одного параметризованного стан-
дартного объекта, который может использоваться всеми конструкторами;
• UG/Drafting — модуль автоматизированного черчения, поддержи-
вающий все основные промышленные стандарты (ANSI, ISO, DIN, JIS) и
включающий в себя средства формирования ортогональных и изометриче-
ских проекций, разрезов, сечений и т. д.;
• UG/Assembly Modeling — модуль, позволяющий создавать ассоциа-
тивные параметрические модели сложных сборочных узлов в режиме груп-
повой работы конструкторов;
• UG/Mechanisms — модуль проектирования и моделирования дву-
мерных и трехмерных механических систем непосредственно в среде пакета
Unigraphics, позволяющий осуществить полный кинематический анализ,
оценить зазоры между элементами, выявить столкновения, вычислить силы,
моменты и т. д. (для кинематического анализа используется встроенный мо-
дуль ADAMS/Kinematis; для динамического анализа — внешний модуль
ADAMS/Solver).
Кроме этого в состав Unigraphics входит целый ряд модулей для под-
готовки автоматизированного производства, базовыми из которых являются
UG/CAM Base и UG/Postprocessor. Имеются также модули, ориентирован-
ные на конкретные технологические процессы: UG/MF-Flowcheck — для
литья; UG/Lathe — для токарных работ; UG/Planar Milling, UG/Fixed-Axis
Milling, UG/Variable-Axis Milling — для фрезерования; UG/Sheet Metal
Design, UG/Sheet Metal Fabrication, UG/Sheet Metal Nesting — для изготов-
ления изделий из листового металла. Используя средства пакета Unigraphics,
можно создавать фотореалистические изображения разрабатываемых изде-
лий (UG/Photo) и их трехмерные прототипы (UG/Rapid Prototyping).
50 1. Компьютерные средства проектирования и графического моделирования
1.5. Пример проектирования конструкции
методом трехмерного моделирования
Для последнего десятилетия характерно, что мощные графические
системы, прежде всего системы трехмерной графики, еще недавно вследст-
вие высокой стоимости аппаратно-программных комплексов доступные
лишь очень узкому кругу специалистов, теперь реализованы на дешевых и
массовых моделях компьютеров в операционной среде Windows и стали
доступными для массовых пользователей. В частности, на базе популярной
графической системы Autocad интенсивно развиваются все более мощные
версии системы Mechanical Desktop с широкими возможностями поверхно-
стного и твердотельного моделирования. Трехмерное моделирование вместе
с развитыми функциями параметризации модели многократно ускоряет
процесс проектирования конструкций.
Технику и технологию формирования трехмерных образов сборочных
узлов лучше показать на конкретном примере. Для этого рассмотрим после-
Рис. 1.20. Трехмерный
образ узла фиксации:
1 — прижим; 2 — шпин-
дель; 3 — стойка
довательность проектирования рычажного прижима
для фиксации заготовок конструкций под сварку. На
этом примере, выполняемом с использованием сре-
ды Mechanical Desktop, можно видеть, что проекти-
рование сложных конструкций часто удобно вести
путем формирования образов отдельных простых
деталей, из которых затем достаточно легко соби-
рается узел или конструкция. После завершения
формирования трехмерной модели конструкции
могут быть автоматически получены стандартные
проекционные чертежи. Следует отметить, что це-
лью рассмотрения данного примера является не
подробное изучение системы, а лишь пояснение
логики проектирования, обеспечивающей ком-
фортные условия и высокую производительность
работы проектировщика.
В состав проектируемого узла фиксации
(рис. 1.20) входят прижим 1, шпиндель 2 и стойка 3.
В состав прижима, в свою очередь, входят основа-
ние, рычаг, рукоять, шатуны и оси.
Проектирование начнем с основания прижима.
Эту деталь можно представить в виде двух параллеле-
пипедов, один из которых расположен горизонтально,
1.5. Пример проектирования конструкции
51
Рис. 1.21. Создание наброска произ- Рис. 1.22. Преобразование наброска в
вольной формы эскиз
а другой — вертикально. За базовый элемент примем горизонтальный па-
раллелепипед. Далее последовательность проектирования следующая.
Создание базового элемента. Откроем новый файл (New). Нарисуем
полилинией замкнутый контур произвольной формы (рис. 1.21). Система
автоматически преобразует набросок в эскиз (рис. 1.22) (Part\ Sketch\Profile —
здесь и далее в скобках приведены выполняемые системой команды, зада-
ваемые, как правило, указанием соответствующей пиктограммы). Каждой
линии контура автоматически присваивается собственный номер, начиная с О,
который появляется на всех элементах контура. На каждый элемент контура
система стремится наложить предварительные связи. Так, на линии, угол
наклона которых к осям на наброске не превышает 4° (устанавливается при
настройке системы), автоматически задаются условия горизонтальности и
вертикальности. Можно видеть (см. рис. 1.22), что элементы 1 и 3 автомати-
чески стали горизонтальными и на них появились служебные символы (за-
висимости) Н, которые показывают пользователю наложенные условия го-
ризонтальности.
Важно отметить, что система постоянно контролирует степень опре-
деленности эскиза и выдает сообщение о недостающем количестве размеров
или связей, необходимых для его полной определенности. В данном случае
эскизу недостает четырех зависимостей. Линии, на которые, возможно, сле-
дует наложить связи, на экране подсвечиваются пунктиром.
Задание зависимостей и простановка размеров. Условия вертикаль-
ности для двух сторон прямоугольника устанавливаются путем указания на
соответствующие линии мышью (Part\Sketch\ Add ConstraintsWertical). Они
принимают вертикальное положение, а рядом с номером линии появляется
значок зависимости, в данном случае V (рис. 1.23). Для того чтобы назна-
чить стороне прямоугольника размер (PartYAdd Dimension), нужно либо ука-
зать мышью на эту сторону и показать местоположение размера, либо
52 1. Компьютерные средства проектирования и графического .моделирования
Рис. 1.23. Задание разме-
ров и зависимостей
щелкнуть мышью на отрезках, между которыми
требуется проставить размер, и после этого ука-
зать местоположение выносной линии. Резуль-
тат действий виден на рис. 1.23.
Цосле того как установлена последняя
связь или зависимость, система выдает сообще-
ние о полной определенности чертежа и при
попытке наложить еще одну связь сообщает,
что вводимая связь является избыточной. Эскиз
определен полностью, поэтому можно присту-
пать к преобразованию плоского эскиза в трех-
мерный объект. Для этого предусмотрены такие
функции, как выдавливание, вращение, вытяги-
вание по определенной траектории или натягивание объекта между не-
сколькими сечениями. В нашем случае применяем выдавливание.
Преобразование эскиза
в 3D-образ. По команде вы-
бранной пиктограммы (Part\
Sketch FeaturesvExtrude) появ-
ляется диалоговое окно, в
котором назначается опция
выдавливания (рис. 1.24). В
данном случае это Base (ба-
зовый) и Blend (на расстоя-
ние), а в пункте SizeVDistance
указывается высота выдавли-
вания 15 мм. Система указы-
вает направление выдавлива-
ния на изображении чертежа
на экране в виде стрелки си-
него цвета и спрашивает,
нужно ли сменить направле-
ние. При ответе происходит
выдавливание эскиза на за-
данную высоту (рис. 1.25).
Дтя построения верти-
кального параллелепипеда
назначаем плоскость по-
строения на верхней грани
базового элемента, указав
выбранную грань (Part\New
Рис. 1.24. Диалоговое окно выбора параметров
преобразования эскиза в трехмерный образ
1.5. Пример проектирования конструкции
53
Рис. 1.25. Базовый трехмерный образ
Sketch Plane). Дальнейшие построения будут вестись в этой плоскости. На-
бросок контура выдавливания и преобразование его в эскиз выполняется
так же, как было показано на рис. 1.21—1.23. На короткие стороны полу-
ченного прямоугольника накладываем условия коллинеарности соответ-
ствующим граням базового элемента (рис. 1.26). Каждому размеру присваи-
вается свой уникальный номер и имеется возможность поставить один раз-
мер в зависимость от другого посредством алгебраической формулы. Полу-
ченный новый контур выдавливаем на высоту 27 мм. В окне выбора режима
выдавливания указываем Join (соединение). Результат выдавливания виден
на рис. 1.27.
Рис. 1.26. Создание эскиза на плос- Рис. 1.27. Преобразование эскиза, созданно-
кости базового элемента го на базовой плоскости, в трехмерный образ
54 1. Компьютерные средства проектирования и графического моделирования
Work Plane Feature
-г-2пЗмо®и-“-?—“5^-tj
||‘<Г.0вЕ4»^
'j' On Vertex ;
'• y । Г WarlU J ;
:. 1 'I r ri- ««,
Г Fk^'^y ’
. ::r onucs
: ry/widw 1 °-(set _ •
•'Г"“
. j flffwt |dV2 [';
' j ^S.. -H 7 У '.
.... ' °* !• Cancel.; |
Рис. 1.28. Диалоговое окно выбора рабо-
чей плоскости
плоскость построения переносится на рабочую плоскость.
В вертикальной части полу-
ченного основания должен быть
выполнен треугольный вырез. Для
его построения воспользуемся ра-
бочей плоскостью. Рабочая плос-
кость — это вспомогательный ин-
струмент, не отображаемый на
окончательном изображении, но
помогающий перенести плоскость
построения в любую удобную для
нас позицию.
На рис. 1.28 изображено
диалоговое окно (PartVWork Featu-
resVWork Plane), где нужно устано-
вить режим Planar Parallel (па-
раллельно плоскости) и Offset. Ука-
жем расстояние dl/2 и мышью —
боковую грань горизонтального
параллелепипеда. Получим рабо-
чую плоскость, и, если установлен
флажок Create Sketch Plane,
Последовательность предварительных построений рассмотрена выше.
После того как эскиз полностью определен, в диалоговом окне выдав-
ливания установим режим Cut (вырезать) и Mid Plane (от середины), а в
разделе Size — значение 24 мм. Получена заготовка детали, перейдем к
отверстиям и галтелям.
Создание конструктивных элементов. В диалоговом окне (Part\
Placed FeaturcsVFillet) (рис. 1.29) установим значение радиуса скругления, ука-
зав, что радиус постоянен по всей длине, и включим Apply. При указании
граней, между которыми нужны скругления, увидим результат (рис. 1.30).
Для получения отверстий пиктограммой откроем диалоговое окно
функции отверстий (PartVPlaced FeatureXHole). Высвечивается слайд вида от-
верстия, где имеются переключатели С’Воге (отверстие с зенковкой) и
Through (сквозное). Установим параметры, как показано на рис. 1.31, и пе-
реключатель Placement (размещение) в положение 2 Edges (от двух кро-
мок), укажем две линии и расстояние от них до центра отверстия. Результат —
на рис. 1.32. Другие три таких же отверстия создаются (Part\Placed Features\
Array) путем копирования уже сформированного отверстия. Расстояние ме-
жду отверстиями установим 40 мм, между рядами отверстий — 45 мм и
укажем объект копирования (рис. 1.33).
1.5. Пример проектирования конструкции
55
Рис. 1.29. Диалоговое окно установки значений параметров скруглений
Завершающая операция — создание еще трех отверстий. Из них два
выполним при переключателях, установленных в позиции C’Sink (отвер-
стия с цековкой), То-Plane (до плоскости) и Concentric (концентрично).
При этом укажем плоскость, от которой делается отверстие, окружность
контура, которой оно будет концентрично, и плоскость, до которой оно до-
ходит. Третье отверстие должно быть выполнено при включенных переклю-
чателях Drilled (отверстие, полученное сверлением), Through и Concentric.
Рис. 1.30. Результат скругления граней
Получено полностью готовое
основание (рис. 1.34). На рис. 1.35
показана структура объекта, ко-
торая автоматически сформиро-
вана, отображается на боковом
экране и дает возможность быст-
рого доступа к редактированию
образа и управлению видимостью
того или иного элемента. На
рис. 1.35 видно, что объект со-
стоит из трех выдавленных час-
56 1. Компьютерные средства проектирования и графического моделирования
Рис. 1.31. Диалоговое окно установки параметров отверстия
тей, одна из которых выдавлена от середины отверстий и скруглений, а
также содержит рабочую плоскость.
Сохраним спроектированную деталь обычной командой Save As под
именем, например, 4001_1. Каждую последующую отдельную деталь будем
также создавать в отдельном файле, чтобы сократить объем файла, который
будет содержать узел в сборе.
Проектирование рычага. Поскольку здесь повторяются подробно рас-
смотренные выше операции, кратко отметим лишь основные этапы. Откроем
новый файл. Нарисуем полилинией приблизительный контур рычага. Преоб-
Рис. 1.33. Создание массива отверстий
Рис. 1.32. Создание отверстия
1.5. Пример проектирования конструкции
57
разуем набросок в эскиз. Устано-
вим зависимости между линиями
контура: для дуг и смежных с ними
отрезков — зависимость Tangent
(касательность) с указанием мы-
шью на соответствующие линии,
для 0-й и 10-й линий — условие
Parallel (параллельность). Около
номера каждой линии появляются
соответствующие обозначения, на- Рис , 34 Окончательный ввд основания
пример, для линии 0 знаки Т11, Т1
и РЮ обозначают, что она касательна к линиям 11 и 1 и параллельна линии
10 (рис. 1.36).
Перед тем как перейти к простановке размеров, отметим одну особен-
ность проектируемой детали. Рычаг может иметь несколько типоразмеров
для закрепления с помощью проектируемого механизма разных заготовок.
Параметризация размеров позволяет существенно упростить процесс проек-
тирования одного универсального образа детали с большим набором полу-
чаемых типоразмеров. Параметр должен быть заранее введен в список (Part
\Design Variables). В появившемся окне (рис. 1.37) перейдем в раздел Global
(глобальные параметры), включим New, введем
имя параметра. При необходимости изменим
размер (Part\Design Variables), дважды щелкнем
клавишей мыши в разделе Equation и изменим
цифровое значение параметра. Как видим, таб-
лица параметров значительно упрощает про-
цесс изменения типоразмеров.
В диалоговом окне в разделе Table
Driven нажмем кнопки Setup и Create. На эк-
ран выводится таблица Excel (рис. 1.38), где по
горизонтали расположены названия варьируе-
мых параметров, а по вертикали — названия
вариантов типоразмеров.
Продолжая проектировать рычаг, устано-
вим недостающие до полной определенности
эскиза размеры (Part\Add Dimension), размер
dl2 поставим в зависимость от параметра 11.
Результат представлен на рис. 1.36. Преобразу-
ем эскиз в 3 D-образ (Part\Sketch Features\
Extrude), выдавив его на 24 мм.
Так как изогнутая часть рычага имеет уто-
нение, перенесем плоскость построения на одну
Б-£^4001_1
(±}-^₽PARTU
ф-йз ;KtrusionBlirid1
ЦЙЗкегсМ
--^Filled
— ••«^RectAira/l
[ J-fiTE«ru5ion^nd2
L-^[]Sketch2
— gg WorkPlanel
s-fexI xtrusionMidplanel
L-^QSketch3
-QFillet2
- fg)Hole2
— @Hole3
I—I§]Hole4
Рис. 1.35. Структура полу-
ченного элемента
58 1. Компьютерные средства проектирования и графического моделирования
Рис. 1.36. Эскиз рычага с размерами и зависимостями
Рис. 1.37. Диалоговое окно управления параметрами
1.5. Пример проектирования конструкции
59
Рис. 1.38. Таблица параметров
Рис. 1.39. Создание эскиза контура (утонения)
из боковых граней рычага (Part\New Sketch Plane). Нарисуем прямоугольник
и преобразуем его в эскиз, установим зависимости и размеры, как показано
на рис. 1.39. Выдавим полученный эскиз на 4 мм (Part\Sketch Features\
Extrude), установив режим Cut и указав направление выдавливания внутрь
тела рычага. Аналогичным образом получим углубление на противополож-
ной стороне рычага.
На боковой стороне
рычага выполним сквоз-
ное отверстие диаметром
12 мм, для этого в диало-
говом окне установим па-
раметры Drilled, Through
и Concentric. Перенесем ©
плоскость построения на
верхнюю сторону рычага
и установим рабочую
точку (рабочая точка, как
и рабочая плоскость, —
вспомогательный объект)
в нужное положение (Part\
Work Features\Work Point),
60 1. Компьютерные средства проектирования и графического моделирования
rife] Drawing]
&#DET2
Й ^PART2_1 (4001)
Й-@ТаЫв (4001J JkLS)
404001
-«4002
-[04003
р- j^ExtrusionMidplariel
i l-~frOSketchl
R-g'ExtrusionBlindl
] 1 ^QSketchZ
E 3-[^ ExtrusionBiindZ
1.$QSketch3
—Qe]Hole4
(§)Hole5
..t^WorkPointl
- ®Hole6
1 ©Fillet!
Рис. 1.40. Создание отверстия на ос- Рис. 1.41. Структура рычага с вариантами
нове рабочей точки изменения типоразмеров
определив ее местоположение относительно других элементов посредством
задания двух размеров, как показано на рис. 1.40. Создадим отверстие диа-
метром 12 мм на верхней стороне рычага, установив в диалоговом окне па-
раметры Drilled, Through, From Point (из точки). Скруглим конец рычага
радиусом 12 мм (Part\Placed Features\Fillet). Полученные готовые структура
и образы модификаций рычагов показаны на рис. 1.41, 1.42 (а, б). Заметим,
что изменение типоразмеров чертежа сведется к активизации того или иного
варианта на боковом экране (см. рис. 1.41).
Особенности проектирования шпинделя и стойки. Шпиндель в
сборе состоит из трех частей (рис. 1.43): собственно шпинделя и двух гаек.
Шпиндель создаем вращением контура (Part\Sketch Features\Revolve). После
создания, определения эскиза контура и его вращения вокруг оси получим
ЗП-образ. Длина шпинделя может быть разной и задается параметром It,
внесенным в список в разделе Global.
Для создания отдельной части проектируемого узла (Part\Part\New
Part) в командной строке укажем имя. Оно появляется на боковом экране, и
дальнейшие построения будут относиться именно к нему. Если требуется
редактирование той или иной части, делаем ее активной нажатием правой
1.5. Пример проектирования конструкции
61
кнопки мыши при указании на название в боковом экране (рис. 1.44) и в
появившемся контекстном меню даем команду Activate Part.
Гайка представляет собой шестигранник со стороной, равной dg, пре-
образованный выдавливанием в объемную фигуру. Отверстие в гайке полу-
чим путем выдавливания окружности диаметром ds, также внесенным в
список параметров. Создадим лишь одну гайку, вторую представим образ-
цом (Assembly\Assembly\Instants). Теперь при редактировании одной гайки
автоматически будут происходить изменения в другой.
После создания всех элементов (частей) шпинделя они находятся в
произвольном положении и представляют собой отдельные объекты. Уста-
Рис. 1.43. Состав шпин-
деля
Рис. 1.44. Активизация редак-
тируемой части
висимости взаиморас-
положения
62 1. Компьютерные средства проектирования и графического моделирования
новим между ними связи. В AMD предусмотрены связи че-
тырех типов: Mate (по плоскости, линии, точке и их комби-
нации), Flush (заподлицо), Angle (угловая зависимость) и
Insert (вставить). Последняя зависимость лишает объект
сразу пяти степеней свободы. По команде пиктограммы
(Assembly\Constraints\Insert) система попросит указать ци-
линдрические поверхности, для которых устанавливаются
зависимости и расстояние между ними, а направление со-
Рис. 1.46. Узел единения указывается в виде стрелок (на экране синего цве-
та) (рис. 1.45). Установив зависимости между имеющимися
частями, получим узел в сборе (рис. 1.46).
в сборе
Особенность проектирования образа стойки (рис. 1.47) состоит в том,
что она может иметь разные высоту и наклон, а также возможность наклона
площадки, на которой крепится прижим. Выполнение всех этих требований
обеспечивается введением соответствующих параметров. В данном случае в
список параметров должны быть внесены: hs (высота стойки), alfa (угол на-
клона площадки) и alia s (угол наклона стойки). Высота и углы теперь мо-
гут свободно изменяться для разных модификаций детали (рис. 1.48).
Сборка узла фиксации. После создания всех деталей проектируемого
узла переходим к его сборке. Откроем новый файл. Соберем в этом файле
ранее созданные детали (Assembly\Assembly\Attach). При вызове команды
появляется стандартное окно выбора файлов. Последовательно открывая их,
получим картинку (рис. 1.49). В состав узла входят два шатуна и две пары
СО
CU
и
Рис. 1.47. Стойка
tnJ
тз/
Рис. 1.48. Задание параметров стойки
1.5. Пример проектирования конструкции
63
Рис. 1.50. Собранный узел фиксации
осей. Поскольку они попарно одинаковы, то, вставив в
файл лишь по одной детали (Assembly\Assembly\ Ins-
tants), повторяющиеся детали получим копировани-
ем. Установим зависимости между деталями (As-
sembly\ ConstraintsMnsert) таким образом, чтобы по-
лучить окончательный вид узла фиксации (рис. 1.50)
и дерево структуры всех элементов этого узла,
фрагмент которого приведен на рис. 1.51.
Можно задать угловую зависимость между
рычагом и основанием (Assembly\Constraints\Angle)
и ее изменением моделировать работу прижима.
Для этого укажем нижнюю грань рычага и парал-
лельную ей грань основания и установим между
ними нулевой угол. Получим прижим в закрытом
состоянии. Для моделирования раскрытия прижима
на боковом экране выбираем правой кнопкой мыши
название угловой зависимости и командой Edit в
диалоговом окне Edit 3D-Constraints увеличим
значение угла раскрытия. Прижим перерисуется в
раскрытом состоянии так, как показано на рис. 1.50.
Insert
gp^S’-PARTIJ
Insert
+J-JPPART1J
^PART2_2 :
1J3J
Л 4 1
Рис. 1.51. Структура
узла фиксации
64 I. Компьютерные средства проектирования и графического моделирования
Формирование конструкторской документации. После проверки
всех принятых решений может быть сформирована конструкторская доку-
ментация. Последовательность включает в себя этапы.
1.5. Пример проектирования конструкции
65
Формирование чертежа. Перейдем в пространство листа (вкладка
Drawing на боковом экране). Выберем формат листа Al (mvsetup) из пред-
ложенного списка. На экране появятся рамка и основная надпись.
Создадим изображение главного вида (Drawing\New View) с помощью
диалогового окна формирования видов (Create Drawing View), показанного
на рис. 1.52, где выберем опции Base (основной) и Scene. Для скрытия неви-
димых линий включим кнопку Hide Hidden Lines. Коэффициент масштаби-
рования Scale установим равным единице. В пространстве модели выберем
плоскость, в которой расположены главный вид (XY) и ось (X). Положение
главного вида в поле чертежа указываем мышью (рис. 1.53) с учетом разме-
щения других планируемых видов.
Для остальных видов главный вид является исходным. После установ-
ки опции Orto (ортогонально) для вида сверху укажем в зоне чертежа кур-
сором мыши положение выше главного вида, а для вида слева — правее
(поскольку в AMD принят’американский стандарт). Получить местный раз-
рез крепежных отверстий кронштейна на виде слева можно, нажав кнопку
Section Views, в разделе Section Туре выбрать опцию Half (половина) и в
окне Section Symbol задать символ обозначения сечения А.
Чтобы изменить расположение видов (Drawing\Edit View\Attributes),
выберем редактируемую проекцию и в окне редактирования параметров
чертежа (Edit Drawing View) установим параметры так, как показано на
рис. 1.54. На виде сверху и на главном виде указываем линии выравнивания,
переносим вид сверху ниже главного вида (Edit View\Move) (для вида слева
устанавливаем в диалоговом окне опцию Align Horizontal).
Рис. 1.54. Диалоговое окно редактирования параметров проекций
3 — 6705
66 1. Компьютерные средства проектирования и графического моделирования
Рис. 1.55. Общий вид узла фиксации
рЬвефг Justification"
; l*Terrtp№14eime-'
Crente Holenote
Help»
OK
?|BUND DRILL
BLINDJ3RILLJM
THRU.DRILL
THRU_DRILL_94
Middfe of lop Line
j « t^dteof^llText
l r! Mddig of Bottom Line
Г Apply Dimension Style foTe>t Height Only
STANDARD
Рис. 1.56. Диалоговое окно задания параметров простановки размеров отверстий
1.5. Пример проектирования конструкции
67
Рис. 1.57. Оформление размеров
отверстий •
Аналогично ортогональным про-
екциям создаем изометрический вид (в
разделе Туре установим Iso). Оконча-
тельный результат создания видов по-
казан на рис. 1.55.
Окончательное оформление черте-
жа заканчивается нанесением осевых и
центровых линий (Drawing\Annotate\ Cen-
terline) с указанием окружностей и сим-
метричных элементов контура, габарит-
ных и крепежных размеров (Drawing\
Add Ref Dimension) с указанием линии,
между которыми надо проставить раз-
мер и положение самой размерной ли-
нии, размеры отверстий (Drawing\
AnnotateX Hole) Note с выбором отверстий. В диалоговом окне Create
Holenote (см. рис. 1.56) нажмем кнопку Edit Template и отредактируем
надпись. Результат оформления — на рис. 1.57.
Настройка спецификации начинается с вызова окна ВОМ (рис. 1.58)
формирования спецификации. Настройка вида спецификации (пиктограмма
Standard Properties, окно BOM Properties на рис. 1.59) заключается в ука-
зании названий разделов спецификации (Caption), ширины (Width) столб-
цов. В разделе Part List (кнопка Modify) необходимо отключить отображе-
ния заголовков спецификации (Title) и установить разделы спецификации,
перемещая названия разделов между Part List и ВОМ в разделе Columns
Рис. 1.58. Диалоговое окно формирования спецификации
з*
68 1. Компьютерные средства проектирования и графического моделирования
Рис. 1.59. Настройка вида спецификации
Parts List Properties for ANSI
Region :ASME¥H3<t-19ft9 ~
j _ P i . Inserting heading —
| | ["4’44 LUJ
deeding Gap Jo£
: | J gyL^,
Text height p
Flute
। jpartehst
* Columns to display s'-~-
BOM Columns.
Frame color:
1
LJ Eyteyer
1
Bo* Gap
Ismgle
NAME
MATERIAL
ОТ/
MASS
Parts List
| ITEM...
Linesoltext
Output direction:
P ffirep text
Punter setup т
Qefault
Рис. 1.60. Диалоговое окно выбора колонок спецификации
1.5. Пример проектирования конструкции
69
номер имя материал кол. масса
1 КРОНШТЕЙН 1
2 ОСНОВАНИЕ 1
3 ОСЬ 1 2
4 ОСЬ 2 ... 2
5 РУЧКА 1
6 РЫЧАГ 1
/ СЕРЫ А 2
8 ШПИНДЕЛЬ 1
Рис. 1.61. Пример спецификации
То Display (рис. 1.60). Полученную спецификацию (рис. 1.61) вставляем над
штампом (пиктограмма Insert Part List). Наносим номера позиций (Drawing\
Balloons And BOMs\Place Balloon). Для этого выбираем автоматический режим
и появившиеся значки, соответствующие каждой детали, разносим по чертежу,
указывая начальную точку выносной линии и расположение номера позиции.
На рис. 1.62 показан окончательный вариант оформления чертежа.
С получением комплекта стандартных проекционных чертежей заверша-
ется проектирование конструкции. Технологии трехмерного твердотельного
моделирования, рассмотренные в гл. 1, позволяют при некотором навыке рабо-
ты весь цикл проекгирования подобного узла, начиная от первых набросков
исходных плоских контуров и до получения комплекта готовых сборочных и
дет алировочных чертежей, выполнить одному человеку в течение 1 ч.
Рис. 1.62. Окончательный вид чертежа
2. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ
В МЕТАЛЛАХ СВАРНЫХ КОНСТРУКЦИЙ
МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ
2.1. Назначение и методы моделирования процессов,
протекающих в металле
При сварке различными способами происходит сложное взаимо-
действие разнообразных процессов, воздействующих на свариваемые де-
тали. Основными из них, характерными для большинства способов свар-
ки, являются:
• протекание электрического тока через сварное соединение;
• распространение теплоты от нагрева проходящим током и другими
источниками, а также при последующем охлаждении;
• диффузия примесей, структурные, фазовые и химические превра-
щения в металле шва и околошовной зоны, в том числе плавление и кри-
сталлизация;
• деформация металла под действием как нагрева, так и других техно-
логических факторов, приводящая к изменению его свойств, возникновению
напряжений, а иногда к повреждению или полному разрушению.
Эти четыре фактора могут присутствовать и в эксплуатационных на-
грузках, т. е. действовать на готовую конструкцию, влияя на ее работоспо-
собность.
Таким образом, для оценки и повышения надежности сварной конст-
рукции необходимо исследовать влияние на нее протекающих процессов.
Основным современным средством такого исследования является проведе-
ние численных экспериментов на компьютерных моделях материала и про-
цессов.
По сравнению с проведением обычных «натурных» экспериментов,
компьютерное моделирование требует предварительных усилий для созда-
ния моделей в виде программного обеспечения. Однако в дальнейшем экс-
перименты на модели оказываются гораздо более оперативными, дешевыми
и эффективными.
2.1. Назначение и методы моделирования процессов
71
Эксперименты на металлических образцах остаются необходимыми
для определения свойств материала, проверки модели, ее корректировки для
решения новых задач, но за счет применения компьютерного моделирова-
ния они резко сокращаются по объему и сложности.
Рассмотрим методы моделирования процессов на примере решения
задачи о протекании тока как наиболее простой для объяснения. Остальные
из перечисленных задач сложнее, но решаются аналогично.
Постановка задачи такова: имеется сварное соединение, к нескольким
точкам которого подведено напряжение от источника тока (потенциал этих
точек известен). По детали течет ток, плотность которого различна в разных
точках вследствие сложной формы и разного удельного сопротивления.
Требуется определить значение плотности тока (как по величине, так и по
направлению), а также электрические потенциалы в заданных точках на по-
верхности и в толще металла.
В простейшем случае (длинный ровный стержень из однородного ме-
талла) эта задача элементарна, но в реальных случаях сварных соединений
дуговой и контактной сварки она чаще всего не имеет аналитического ре-
шения. К решению задачи возможны два подхода: опираться либо на диф-
ференциальное уравнение, либо на интегральное. По своему физическому
смыслу они аналогичны, различие имеет технический характер. Для задачи
о протекании тока дифференциальным уравнением является уравнение по-
стоянства заряда в элементарном объеме металла. Это уравнение справедли-
во, если рассматривать не переходные процессы при включении тока, а его
равновесное, установившееся, медленно изменяющееся протекание. Для то-
го чтобы заряд в элементарном объеме dV= dx-dydz (рис. 2.1) не изменялся,
сумма токов, направленных внутрь элемента через все его границы, должна
быть равна нулю.
Согласно закону Ома, плотность j тока пропорциональна напряженно-
сти поля Е, т. е. градиенту потенциала U\
• 1 F 1 /О П
J=~E =——, (2.1)
р р on
где р — удельное сопротивление
вещества, п — координата, направ-
ленная по нормали к поверхности,
через которую течет ток. Знак ми-
нус означает, что ток течет в на-
правлении убывания потенциала.
Ток равен произведению плотности
тока на площадь поверхности, че-
рез которую он протекает. Суммар-
Рис. 2.1. Протекание тока в направлении
осих
72 2. Моделирование процессов в металлах методом конечных элементов
ный заряд, попадающий в элементарный объем dV через две его грани, пер-
пендикулярные к оси х, пропорционален разности токов, протекающих че-
рез левую и правую грани:
dq Т Т . . . . , , 1 82U
-T = Ixx-hi =(JXI-Jxi)dydz = ——^-dxdydz.
dt px 8x
Разность производных потенциала на двух гранях равна второй про-
, г 82U .
изводнои по координате х, умноженной на dx. Если —— >0, значит ток,
дх~
втекающий через левую грань больше, чем вытекающий через правую
Ixi, т. е. в объеме происходит накопление зарядов. Всего по трем осям получаем
dq 1 82U 1 82U 1 82U , , , „
— = (-----7- +------ +-----}dxdydz = 0.
dt px 8x2 p}. 8y pz 8z“
Это уравнение постоянства заряда (первый закон Кирхгофа) приводит
к уравнению Лапласа
1 82U 1 d2U 1 d2U „
-----г+------г +-----г = 0 (2.2)
рх 8х2 ру. 8у pz 8z2
относительно потенциала произвольной внутренней точки. Его необходимо
проинтегрировать по всему объему детали с учетом граничных условий, и
эту задачу, как отмечено выше, редко удается решить аналитически, осо-
бенно если она нелинейна (если электропроводность неодинакова в разных
точках тела, тем более если она зависит от плотности тока, т. е. от результа-
тов решения задачи).
Интегральное уравнение можно получить из условия минимума энер-
гии. Е1ри заданной разности потенциалов на границах тела выделение энер-
гии при прохождении тока обратно пропорционально сопротивлению цепи.
Ток течет по пути наименьшего сопротивления, совершая минимально воз-
можную работу. Вся работа за единицу времени может быть найдена, если
выражение закона Джоуля—Ленца проинтегрировать по объему тела:
Р=jfpdK
V
Равновесному состоянию соответствует такое распределение потен-
циалов и плотностей тока внутри сварного соединения, при котором значе-
ние интеграла минимально. Минимизируя Р, можно найти решение задачи.
Трудности решения интегральных уравнений примерно такие же, как и
дифференциальных.
2.2. Метод конечных элементов для решения уравнений
73
2.2. Метод конечных элементов для решения
дифференциальных и интегральных уравнений
Метод конечных элементов (МКЭ, по-английски FEM — Finite
Element Method) состоит в том, что все тело разбивают на некоторое коли-
чество частей (элементов) конечного (а не бесконечно малого) объема, на-
столько простых по форме и внутреннему устройству, что интегрирование
уравнений внутри каждого из них не вызывает затруднений. Для прибли-
женного решения задачи в целом необходимо обеспечить только стыковку
элементов между собой. Условия стыковки записывают в виде алгебраиче-
ских уравнений. В некоторых случаях эти уравнения независимы друг от
друга и могут быть решены по одиночке, но чаще они образуют систему
уравнений, порядок которой зависит от числа конечных элементов.
Таким образом, МКЭ состоит в замене дифференциального или инте-
грального уравнения на систему алгебраических уравнений. Существует ряд
методов, родственных МКЭ: метод конечных разностей, метод граничных
элементов и др. Каждый из них в чем-то превосходит МКЭ при решении
определенного ограниченного круга задач. МКЭ является наиболее гибким
и универсальным.
Для упрощения процедуры элемент обычно выбирают простой формы
(треугольной или четырехугольной — для плоских задач, призматической
или пирамидальной — для пространственных; рис. 2.2) и описывают рас-
пределение потенциала внутри него простой функцией (обычно полиномом
невысокого порядка). Поэтому при небольшом числе элементов решение
может получиться весьма грубым. Однако доказано математически, что при
измельчении элементов погрешность уменьшается и решение неограничен-
но приближается к точному. Чем грубее и проще элементы, тем мельче они
должны быть для достижения заданной точности.
Таким образом, наличие погрешности при использовании конечного
элемента не является свидетельством его непригодности, если эта погреш-
ность убывает при уменьшении
размеров элемента и в пределе
стремится к нулю. Это не зна- |« /
чит, что все виды элементов
равноценны. При прочих рав- ° ° /______у
ных условиях следует предпо-
читать элементы, дающие на- о---------------о а
именьшую погрешность при / / / \
данных размерах и более бы- / / / \
строе ее убывание при умень- -------<>
шении размеров. Рис. 2.2. Виды конечных элементов
74 2. Моделирование процессов в металлах методом конечных элементов
Поскольку число элементов и порядок системы уравнений для слож-
ных сварочных задач достигает десятков тысяч, решение такой большой
системы уравнений является наиболее серьезным этапом процедуры МКЭ.
Часто идут на усложнение элементов (повышение степени полинома внутри
элемента) для того, чтобы уменьшить число элементов и порядок системы
уравнений. В конкретных случаях большую экономию может дать исполь-
зование для интерполяции внутри элемента взамен полинома других функ-
ций, близких к ожидаемому решению задачи, но это снижает универсаль-
ность программного обеспечения.
На снижение порядка системы уравнений направлена и суперэлемент-
ная процедура. Несколько обычных элементов объединяют в суперэлемент,
исключая из системы уравнений неизвестные, связанные с внутренними
границами между объединяемыми элементами, и оставляя те, которые уча-
ствуют в стыковке суперэлемента с другими суперэлементами. Тогда число
уравнений в системе для суперэлементной модели уменьшается. После ре-
шения этой системы необходимо вернуться к внутреннему устройству су-
перэлемента и найти значения исключенных ранее внутренних неизвестных.
По сути дела, общее число операций не уменьшается, но задача упро-
щается за счет ее разделения на несколько этапов. Сокращение расчетов
может быть получено, если в модели много одинаковых суперэлементов.
Тогда часть операций для них можно не повторять.
Процедура МКЭ в принципе достаточно проста. Функционирующая
программа может быть написана и отлажена за неделю. Однако область
применения такой программы весьма ограничена. Программа среднего
уровня, содержащая средства подготовки данных (среду, аналогичную
AutoCAD), эффективные процедуры составления и решения уравнений и
визуальную систему анализа результатов моделирования, требует сущест-
венно больших затрат.
В мире существуют десятки коммерческих программных комплек-
сов МКЭ (наиболее известны NASTRAN, ANSYS), в том числе специали-
зированных для решения сварочных и других технологических задач
(SYSWELD, MARC). На их создание были затрачены большие усилия, и
тем не менее нельзя назвать ни одного, пригодного для решения всех
возникающих задач. Поскольку внутренняя часть программного ком-
плекса является «черным ящиком», то довольно трудно бывает самостоя-
тельно приспособить его к решению задачи, не предусмотренной разра-
ботчиками. Еще одно обстоятельство оказывается не в пользу коммерчес-
ких комплексов — огромные размеры текста программ (сотни мегабай-
тов) и обязанность поддерживать совместимость новых версий с преды-
дущими. Теряется гибкость и с трудом осваивается решение принципи-
ально новых задач, а изменения в аппаратном обеспечении (например,
2.2. Метод конечных элементов для решения уравнений
75
Рис. 2.3. Схема конечного элемента с двумя узлами 7 и 2
переход с больших ЭВМ на персональные компьютеры) имеют для таких
комплексов катастрофические последствия.
Вследствие этого создание новых комплексов МКЭ, прежде всего не
универсальных, а направленных на решение конкретного круга задач, сохраня-
ет свою актуальность. В этой главе описаны элементы трех таких комплексов,
разработанных в Москве. Их развитие продолжается и в настоящее время.
Даже если специалист не ставит перед собой задачу разработки новых
программ, а пользуется готовым комплексом МКЭ, ему полезно понимать
внутреннее устройство и механизм работы комплекса для более эффектив-
ного его применения. Под руководством разработчиков вполне осуществи-
мо добавление к работающему комплексу недостающих элементов. Некото-
рые коммерческие комплексы предусматривают для этого встроенный язык
программирования и инструкции по его применению.
Рассмотрим простейшую конечно-элементную модель (КЭМ) для
плоской пластины. Пусть имеется пластина, через которую течет ток, и на
ней обозначены точки, в которых требуется рассчитать потенциал. Разобьем
пластину на ячейки (клетки) так, чтобы границы проходили на равном рас-
стоянии от соседних точек (узлов) (рис. 2.3).
Конечный элемент (КЭ) позволяет установить, какой ток потечет из
клетки 2 в клетку 1 через их границу s, если известна разность потенциалов
между этими точками. Распределение потенциала по длине элемента ап-
проксимируем полиномом первой степени, напряженность поля во всех
„ КГ
точках элемента одинакова и равна Е = —^---. Плотность тока, согласно
Е
закону Ома (2.1), j = —, поскольку материал изотропный и сопротивление
Р
во всех направлениях одинаково. Ток через элемент равен
76 2. Моделирование процессов в металлах методом конечных элементов
Рис. 2.4. Принципиальная схема конечно-элементной модели пластины
I=js =
и2 -ц и2-и}
Таким образом, КЭ эквивалентен сопротивлению R, включенному
между узлами 1 и 2. Оно равно сопротивлению проводника из такого же ма-
териала, длиной / и сечением 5 (см. рис. 2.3). Если добавить КЭ для каждой
пары соседних узлов, то они покроют всю пластину. Если считать, что все
заряды, попавшие в одну из клеток, находятся в узле, то всю пластину мож-
но изобразить в виде принципиальной электрической схемы (рис. 2.4). Со-
гласно классификации КЭ, рассмотренный элемент следует называть стерж-
невым линейным двухузловым.
Если известны потенциалы на краях пластины и сопротивления эле-
ментов, то можно найти токи и потенциалы внутренних точек по законам
Кирхгофа, которые приводят к системе линейных уравнений, т. е. к типич-
ной процедуре МКЭ. Естественно, ввод данных, составление и решение сис-
темы уравнений и представление результатов должны быть реализованы в
компьютерной программе.
Моделирование объемных тел. Моделирование объемных тел слож-
ной формы как правило, существенно сложнее, чем плоских, и требует при-
менения более сложных элементов. Однако рассмотренный простейший
двухузловой элемент без существенных изменений может быть превращен
из плоского в объемный. На рис. 2.5 видно, что если плоский элемент со-
стоит из двух призм, высота которых равна толщине моделируемого плос-
кого тела, то объемный — из двух пирамид. Как призмы, так и пирамиды
примыкают с двух сторон к поверхности s, разделяющей соседние ячейки, а
ребра призм и пирамид соединяют точки контура поверхности s с узлами 7 и 2.
Отрезок 1—2 длиной / перпендикулярен плоскости 5, и точка пересечения с
этой плоскостью делит его пополам.
2.2. Метод конечных элементов для решения уравнений
77
Рис. 2.5. Плоский и объемный элементы
Если трехмерное тело разбить на ячейки в виде прямоугольных па-
раллелепипедов, то, соединив каждую грань, разделяющую две соседние
ячейки с узлами, расположенными в центрах ячеек, получим такой элемент.
Очевидно, что в совокупности элементы заполнят весь объем тела.
Модель протекания тока и распределения потенциалов в теле можно
представить в виде принципиальной схемы, аналогичной рис. 2.4, где каж-
дый элемент изображен в виде сопротивления, присоединенного между
двумя узлами.
Ячейки, на которые разбита модель, имеют прямоугольную форму,
если заданные точки (узлы) 7, 2, 3... расположены ровными рядами, как на
рис. 2.3. При произвольном расположении узлов на плоскости или в про-
странстве построение ячеек, границы которых равноудалены от ближайших
узлов, также возможно, хотя ячейки будут иметь более сложную форму
(рис. 2.6).
Возможность применения нерегулярной сетки, обеспечивающей за-
полнение элементами произвольной области со сложным очертанием гра-
ницы, а также сгущение сетки в отдельных местах, требующих повышения
точности расчета, является основным преимуществом МКЭ по сравнению с
более простым методом сеток.
Граничные условия.
Чтобы рассчитать токи и по-
тенциалы по модели, изобра-
женной в виде принципиаль-
ной схемы на рис. 2.4, необхо-
димы граничные условия, т. е.
параметры недостающей части
электрической цепи, присое-
диненной к модели в узлах А и
В (см. рис. 2.3 и 2.4).
При моделировании
внешние границы элементов
ничем не отличаются от внут-
ренних: через каждую из них
Рис. 2.6. Разбиение на элементы с нерегуляр-
ной сеткой
78 2. Моделирование процессов в металлах методом конечных элементов
проходит электрический ток согласно закону Ома. Однако в зависимости
от устройства внешнего участка цепи различают три рода граничных ус-
ловий.
Условие первого рода, задан электрический потенциал на границе. Это
соответствует наличию во внешней цепи стабилизированного источника
питания, поддерживающего постоянное напряжение, не зависящее от со-
противления модели. В этом случае потенциал во всех точках соответст-
вующей границы заранее известен, а плотность тока через нее зависит от
разности этого потенциала и потенциала ближайшего внутреннего узла со-
гласно закону Ома (2.1).
Условие второго рода: задан ток или плотность тока на границе. Это
соответствует наличию во внешней цепи другого источника питания, под-
держивающего постоянный ток, не зависящий от сопротивления модели. В
этом случае граница является узлом, потенциал в котором зависит от потен-
циала ближайшего внутреннего узла и определяется в ходе решения задачи.
Частным случаем такого граничного условия является нулевая плотность
тока (адиабатическая граница). Для задач электропроводности это соответ-
ствует границе проводника с изолятором. На рис. 2.3 такие условия дейст-
вуют на всех внешних границах модели, кроме граничных узлов А м В.
Условие третьего рода представляет собой наиболее общий случай,
когда ток или плотность тока на границе связаны с ее потенциалом некото-
рым уравнением. Это соответствует, например, обычному источнику пита-
ния с внутренним сопротивлением. Создаваемое им напряжение снижается
по мере увеличения тока. Очевидно, что первые два рода граничных усло-
вий являются крайними частными случаями третьего.
Нелинейные задачи. Рассмотренные уравнения протекания тока
являются линейными (зависимость тока от напряжения в законе Ома вы-
ражается уравнением прямой линии). В этом случае уравнения Кирхгофа,
из решения которых можно найти потенциалы узлов, образуют систему
линейных уравнений. Нелинейность уравнений может возникнуть в двух
случаях:
• если уравнения моделируемых физических явлений отличаются от
линейных;
• если входящие в уравнения коэффициенты не являются константа-
ми, а зависят от результатов решения (например, если удельное сопротивле-
ние проводника зависит от плотности тока).
Внимание к нелинейности вызвано тем, что методы решения системы
нелинейных уравнений гораздо сложнее и требуют большего объема вычис-
лений, чем линейных. Как правило, нелинейную систему решают итераци-
онно (методом последовательных приближений) на основе линеаризации:
кривые нелинейных уравнений заменяют прямыми, касательными к ним,
2.2. Метод конечных элементов для решения уравнений
79
или секущими и постепенно уточняют коэффициенты, входящие в уравне-
ния этих прямых.
Стационарные и нестационарные задачи. Поскольку скорость дви-
жения зарядов в проводнике велика, то переходные процессы при измене-
нии граничных условий протекают очень быстро и во многих случаях их
можно игнорировать, рассматривая только установившееся равновесное
распределение потенциалов и токов. В этом случае результат решения зави-
сит не от начального распределения зарядов и потенциалов, а от граничных
условий. Такие задачи называют стационарными или эллиптическими, по-
скольку в их основе лежит дифференциальное уравнение Лапласа эллипти-
ческого типа.
Уравнения теплопроводности и диффузии практически совпадают с
уравнениями электропроводности (вместо закона Ома в них используются
аналогичные законы Фурье и Фика). Однако скорость протекания этих про-
цессов значительно ниже. Вследствие этого не всегда можно ограничиться
расчетом установившегося поля температур или распределения примесей,
во многих случаях требуется определять распределение параметров во вре-
мя переходного процесса. В этом случае решение зависит не только от гра-
ничных условий, но и от начального состояния и времени. Соответствующее
уравнение отличается от уравнения Лапласа добавлением производной по
времени и называется уравнением параболического типа'.
82и d2U д2и ди
х дх2 ' ду2 z dz2 dt
(2.3)
Очевидно, что эллиптическое уравнение (2.2) является частным случаем
уравнения (2.3). После завершения переходного процесса скорость изменения
потенциала стремится к нулю и уравнение приобретает эллиптический вид.
Рассмотрим, как изменяется физическая картина при переходе от ста-
ционарной задачи электропроводности к нестационарной задаче теплопро-
водности. Аналогом потенциала является температура, аналогом плотности
заряда — теплосодержание, аналогом тока — поток теплоты. Если в элек-
трической задаче благодаря быстрому перемещению зарядов не происходит
их накапливание в точках тела и потенциалы этих точек сразу принимают
равновесные значения, то перемещение теплоты происходит недостаточно
быстро, теплота накапливается в одних точках и убывает из других, тепло-
содержание и температура в этих точках изменяются. Эти изменения приво-
дят к перераспределению тепловых потоков, и, лишь когда переходный
процесс завершается, наступает равновесное установившееся состояние.
Из сопоставления этих двух задач ясно, что для решения нестацио-
нарной задачи нужно к первым двум этапам (необходимым и для стацио-
нарной задачи) добавить еще два. Таким образом, имеем следующие этапы:
80 2. Моделирование процессов в металлах методом конечных элементов
1) уравнение потоков массы или энергии (закон Ома, Фурье, Фика
и т. д.);
2) граничные условия 1, 2 и 3-го рода;
3) начальные условия — исходное распределение температур или
примесей;
4) условия накопления массы или энергии.
Применительно к тепловой задаче п. 4 соответствует уравнение теп-
лоемкости, связывающее теплосодержание с температурой.
Явная и неявная схемы решения. Особенностью нестационарной
задачи является необходимость последовательного прослеживания проме-
жуточных предыдущих состояний тела для правильного расчета текущего
состояния, т. е. истории процесса, в то время как для стационарного процес-
са истории не существует, каждое состояние может быть рассчитано незави-
симо от предыдущих.
Если историю процесса прослеживать с достаточно мелким шагом во
времени, то можно пренебречь влиянием на температуру данной точки тела
температуры других точек, удаленных от нее, т. е. считать, что на каждом
шаге порция теплоты пересекает только одну границу между двумя сосед-
ними ячейками. Если найти мощности потоков теплоты через границы
ячейки на момент начала шага и считать их в течение шага постоянными, то
можно составить такую систему уравнений для расчета температур в конце
шага, в каждом из которых будет только одно неизвестное. Такая схема ре-
шения называется явной и требует существенно меньшего объема вычисле-
ний по сравнению с неявной схемой, в каждом уравнении которой несколько
неизвестных. На рис. 2.7 решение по явной схеме (1а) представляет собой
ломаную линию, начало каждого отрезка которой параллельно касательной
к кривой искомой функции. Видно, что эта ломаная с определенной точно-
стью повторяет вид кривой.
Если шаг решения недостаточно мелкий, то предположение о сохра-
нении постоянных тепловых потоков становится некорректным и приводит
к неправильному решению (ломаная 16 удаляется от кривой). Максимально
допустимый шаг во времени т пропорционален квадрату линейного размера
самого мелкого элемента I и зависит от свойств материала (для тепловой
задачи он обратно пропорционален коэффициенту температуропроводности а):
/2
г = —.
а
Поэтому при решении стационарных задач, как правило, выгоднее
один раз составить и решить систему уравнений неявной схемы, чем выпол-
нять большое число шагов явной схемы. Решение по неявной схеме (2)
представлено на рис. 2.7 ломаной, составленной из секущих, начало и конец
2.2. Метод конечных элементов для решения уравнений
81
Рис. 2.7. Работа явной (У) и неявной (2) схем решения при малом (а)
и большом (б) шаге
каждого отрезка лежат на кривой. Порядок точности явной и неявной схем
при мелком шаге одинаков. При увеличении шага при неявной схеме реше-
ние хотя и становится грубее, но остается устойчивым (ломаная 26 продол-
жает следовать за кривой). Погрешность при этом невелика, если функция
меняется медленно. Таким образом, общее правило: явная схема — для не-
стационарных переходных процессов, где большое число шагов неизбежно,
а неявная — для стационарных задач.
Напряженно-деформированное состояние. Расчет напряжений и де-
формаций во многом близок к расчету электрических потенциалов. За ис-
ключением явлений ползучести при высоких температурах и циклического
или коррозионного роста трещин, процессы деформирования металла про-
текают достаточно быстро, чтобы задачи можно было считать стационар-
ными. Сложность этих задач в том, что в каждой точке тела необходимо оп-
ределить не скалярный параметр (потенциал, температуру), а вектор пере-
мещения, имеющий величину и направление, т. е. число неизвестных для
плоских моделей удваивается, а для объемных утраивается. Сложнее стано-
вится и описание потоков энергии через границы элементов. Более нагляд-
ной является их замена условиями равновесия. Каждое уравнение системы,
полученной в соответствии с неявной схемой решения, можно трактовать
как условие равновесия соответствующего узла модели в направлении од-
ной из осей координат. В остальном все перечисленные выше положения,
82 2. Моделирование процессов в металлах методом конечных элементов
Рис. 2.8. Схема связей между процессами в металле при контактной сварке
включая граничные условия, нелинейность и т. д., в полной мере примени-
мы и к этому несколько более сложному случаю.
Связные и несвязные задачи. Процессы, протекающие при сварке и
эксплуатации конструкции, взаимосвязаны. Протекание тока вызывает на-
грев и соответственно структурные и фазовые превращения и деформации
от теплового расширения. Это не мешает моделировать процессы последо-
вательно: вначале провести моделирование процесса протекания тока и за-
писать его результаты, затем — моделирование распространения теплоты и
т. д. Результаты, полученные на одной модели, входят в начальные и гра-
ничные условия и влияют на свойства материала в следующей модели. Та-
кая последовательно решаемая задача называется несвязной. При ее реше-
нии пренебрегают обратными связями между процессами: влиянием нагрева
на протекание тока, разогревом от пластической деформации и т. д.
Примером задач, которые необходимо решать как связные, являются
задачи контактной сварки (рис. 2.8). Площадь и плотность контакта, через
который протекает ток, существенно зависят от силы сжатия и деформации
свариваемых деталей. В свою очередь, деформации зависят от изменения
предела текучести и плавления металла при его нагреве проходящим током.
Следовательно, все процессы необходимо моделировать синхронно, в рам-
ках единой связной задачи.
Связная задача требует составления единой системы уравнений для
нескольких взаимосвязанных процессов. Такой подход правильнее, но су-
щественно сложнее в реализации. Выбор связной или несвязной задачи при
2.3. Работа программного обеспечения метода конечных элементов
83
моделировании должен быть сделан на основе оценки погрешности, вноси-
мой неучетом обратных связей.
Достаточно полноценную, но менее сложную замену единой модели
можно получить при итерационном решении, если моделировать процессы
поочередно, но повторяя решение несколько раз и вводя поправки в каждую
из моделей с учетом результатов, полученных на остальных моделях при
предыдущей итерации. Сходимость, как и при решении нелинейных задач,
зависит от степени влияния обратных связей на результаты решения.
Еще более простой алгоритм можно предложить при решении мелким
шагом по явной схеме. Необходимо переходить от предыдущей модели к
последующей не после завершения всего процесса моделирования, а на ка-
ждом шаге. Тогда обратные связи между процессами будут учтены, хотя и с
запаздыванием на один шаг. При малом шаге будет получен результат,
близкий к результату решения связной задачи.
2.3. Работа программного обеспечения метода
конечных элементов на примере комплекса «СВАРКА»
Рассмотрим реализацию расчета тепловых и деформационных задач
на примере программного комплекса «СВАРКА», разработка которого на-
чата на кафедре сварки МГТУ им. Н.Э. Баумана в 1974 г. и продолжается в
настоящее время. Действующая версия 4.0 (1999 г.) ориентирована на рабо-
ту в среде Windows персонального компьютера.
Работа происходит в основном в диалоговом режиме. Основной экран,
появляющийся при запуске программы (рис. 2.9), имеет традиционное
оформление Windows с раскрывающимся меню вверху, панелью информа-
ции внизу и кнопками панелей инструментов по периметру справа и слева
(панели справа сменные). Поле экрана обычно разбито на две части: квад-
ратную слева для графических изображений и узкую справа для текстовой и
цифровой информации. Эти части относятся к одному и тому же объекту и
дополняют друг друга, редактирование данных можно проводить как в гра-
фической, так и в текстовой части окна. Возможно изменение через меню
размера всего окна и его частей в процессе рабо i ы.
Работа начинается с открытия нового или сохраненного проекта. Про-
ектом в комплексе называется совокупность исходных данных и результа-
тов моделирования для конкретной модели. При открытии нового проекта
работа с его данными начинается с самого начала (все результаты предыду-
щих расчетов стираются). При открытии сохраненного проекта восстанав-
ливается на экране то его состояние, которое было на момент прекращения
84 2. Моделирование процессов в металлах методом конечных элементов
j*' *»*4гжп<жу-» ^г<л«»\»пЧК Мэя W J64O.W ИСеСбАГК* < | >if » ;
Г;.|рьпи««К7"’Г‘“‘~~ ” jj^itraiaj>'-.Дс~
WBГ»ухж| Н(Г.\Рго^сК\и),| ДУ MkiaiO»WofO.:.| (jjAdobe Я>аи... | ^ЬниманиЬт. [ eg b4ic«JiDove..||§j СВАРКА - (С... ШФВЗИ :5К
Рис. 2.9. Диалоговое окно комплекса «СВАРКА»
предыдущего сеанса работы с ним. Можно начать работу с просмотра
полученных ранее результатов или продолжить моделирование с изме-
ненными граничными условиями от любого из уже выполненных шагов.
Построение геометрической модели. Предусмотрены две стадии по-
строения геометрической модели детали. Первая стадия выполняется ква-
лифицированным пользователем и позволяет построить любую модель.
В процессе построения определяются не только внешние контуры де-
тали, но и ее внутреннее разбиение на элементы. Одновременно вводится
информация о зонах из различных материалов в пределах детали и прово-
дился подготовка к заданию граничных условий для модели.
Второй этап предназначен для работы новичка или для выполнения
вариантов расчета на однотипных моделях. Он позволяет, выбрав одну из
уже построенных моделей, в графическом режиме редактировать ее размеры
и количество элементов в ней.
Рассмотрим структуру модели и этапы ее построения. Разбиение на
этапы позволяет выполнять построение не сразу, а постепенно, чтобы после
2.3. Работа программного обеспечения метода конечных элементов
85
каждого этапа можно было увидеть изображение построенной части модели.
Это облегчает поиск и исправление ошибок.
Основным средством построения модели является блок. Он служит
для выделения части объема модели вместе с ее содержимым (материалом).
Простой объемный блок предназначен для моделирования массивных
тел. В общем случае он имеет вид деформированного кубика, ограниченно-
го шестью гранями, каждая из которых является частью поверхности. Все
грани одного блока должны принадлежать разным поверхностям. Каждая
грань представляет собой в общем случае деформированный четырехуголь-
ник, ограниченный четырьмя ребрами, каждое из которых является частью
линии. Все ребра одной грани должны принадлежать разным линиям. Каж-
дое ребро является в общем случае пространственной кривой, вид которой
задают координаты лежащих на ней узлов. На ребрах простого блока может
быть два или три узла (два из них лежат на концах ребра и являются вер-
шинами блока, а третий — на середине ребра). В первом случае ребро
представляет собой отрезок прямой, во втором — отрезок квадратной па-
раболы, соединяющей узлы ребра. Следовательно, в частных случаях объ-
емный блок может иметь прямые ребра, быть параллелепипедом или пра-
вильным кубом.
Сложный объемный блок отличается от простого наличием дополни-
тельных узлов и линий на гранях и внутри блока. Узлов на ребре сложного
блока может быть два или любое нечетное число более двух.
Если узлов более трех, то ребро состоит из нескольких отрезков квад-
ратных парабол, каждая из которых соединяет три последовательных узла.
Для описания объемного блока (простого или сложного) необходимо
перечислить номера поверхностей, ограничивающих блок.
Поверхности перечисляются в таком порядке: 1 — нижняя, 2 — пе-
редняя, 3 — левая, 4 — задняя, 5 — правая, 6 — верхняя (если смотреть из-
нутри блока, стоя на любой его грани).
Специальные блоки отличаются числом граней, ребер и вершин. Име-
ются два вида специальных блоков: пятигранный в виде деформированной
треугольной призмы и четырехгранный в виде деформированной треуголь-
ной пирамиды (тетраэдра). Специальные блоки могут быть сложными. Для
описания этих блоков также необходимо перечислить номера поверхностей,
ограничивающих блоки.
Для четырехгранного блока порядок перечисления: 1 — нижняя по-
верхность, 2 — передняя, 3 — левая, 4 — правая. Для пятигранного блока
первые четыре такие же поверхности, а 5 — верхняя поверхность.
Пластинчатый пространственный блок предназначен для моделиро-
вания листовых конструкций и эквивалентен по виду и устройству грани
объемного блока. Простой пластинчатый блок имеет вид деформированного
86 2. Моделирование процессов в металлах методом конечных элементов
четырехугольника, ограниченного квадратными параболами. Частные
случаи — четырехугольник с прямыми сторонами, прямоугольник, квад-
рат. Каждое ребро — отрезок параболы с узлами на концах и, возможно,
в середине.
Сложный пластинчатый блок отличается наличием дополнительных
узлов и линий в пределах блока, он эквивалентен грани сложного объемного
блока. Для описания пластинчатого блока необходимо перечислить по кругу
номера четырех линий, ограничивающих блок.
Специальный пластинчатый блок имеет вид деформированного тре-
угольника и эквивалентен грани объемного четырехгранного блока, он мо-
жет быть сложным. Для его описания необходимо перечислить номера трех
ограничивающих блок линий.
Плоский блок для моделирования плосколистовых и осесимметричных
тел, а также массивных протяженных тел, имеющих в направлении третьей
координаты неизменную геометрию, неизменные граничные условия и
свойства материала. Он отличается от пластинчатого тем, что все плоские
блоки лежат в одной плоскости и их узлы имеют нулевую третью координа-
ту. При перечислении линий, ограничивающих плоский блок, следует соблю-
дать направление обхода блока против хода часовой стрелки.
Стержневой блок предназначен для моделирования стержневых кон-
струкций. Он эквивалентен ребру объемного или пластинчатого блока. Про-
стой стержневой блок имеет вид отрезка параболы или прямой с узлами по
концам и в середине отрезка.
Сложный стержневой блок имеет дополнительные узлы, соединен-
ные по три отрезками параболы, и может иметь форму любой лекальной
кривой, а также изломы в узлах.
Для описания стержневого блока необходимо перечислить номера
двух узлов на его концах.
Каждый блок, так же как каждая поверхность, линия и узел, имеет свой
номер. Все блоки нумеруются по порядку, начиная с № 1. Если в модель вхо-
дят блоки разных видов, то вначале нумеруются объемные, далее пластинча-
тые, затем стержневые блоки. В процессе построения модели номера блоков
могут измениться вследствие их разбиения на более мелкие блоки. Сложные
и специальные блоки используются для уменьшения числа вводимых блоков.
При дальнейшем построении они разбиваются на простые блоки.
Для моделирования деталей с неоднородностью может быть указан но-
мер материала каждого блока. Какой именно материал соответствует каждо-
му из номеров, уточняют на следующих этапах построения модели детали.
Отрицательные номера материалов предназначены специально для моделиро-
вания процесса многопроходной сварки. Они позволяют указать, какая группа
элементов разделки заполняется металлом при очередном проходе.
2.3. Работа программного обеспечения метода конечных элементов
87
Поверхность состоит из линий. Для описания поверхности необходи-
мо перечислить номера лежащих на ней линий (в любом порядке). Поверх-
ность может быть плоской или неплоской, в зависимости от геометрии линий.
Основное назначение поверхностей — описание объемных блоков. В
связи с этим на поверхности накладываются следующие ограничения:
• поверхность может включать одну или несколько граней объемных
блоков и пластинчатые блоки, но не должна включать две грани одного и
того же блока;
• поверхность не должна проходить дважды через одну и ту же линию
(самопересечение поверхности не допускается);
• не допускаются замкнутые поверхности (в этом случае поверхность
следует разбить на части);
• две поверхности могут иметь одну общую линию (линию пересечения);
• двойное пересечение поверхностей не допускается.
Поверхности нумеруются в произвольном порядке, начиная с № 1.
Эти номера не изменяются в процессе построения модели. Новые поверхно-
сти добавляются в конец списка.
Линия состоит из узлов. Для описания линии необходимо перечислить
номера всех ее узлов в том порядке, в котором они лежат на линии, начиная
с любого ее конца. Линия может быть прямой, кривой или ломаной в зави-
симости от координат ее узлов.
Правила описания линий:
• линия не может дважды проходить через один и тот же узел (само-
пересечение не допускается);
• замкнутая линия не допускается;
• две линии могут иметь один общий узел (точку пересечения);
• двойное пересечение линий не допускается;
• линия не может принадлежать поверхности частично, если номер
линии указан при описании поверхности, значит, этой поверхности принад-
лежат все узлы линии;
• общая линия двух поверхностей является линией их пересечения;
• линия не должна начинаться или оканчиваться внутри стержневого
блока, ребра пластинчатого или объемного блока;
• линии, ограничивающие пластинчатый блок или грань объемного
блока, должны все принадлежать одной поверхности (в плоских и осесим-
метричных моделях все линии принадлежат поверхности № 1).
Линии нумеруются в произвольном порядке, начиная с № 1. Эти но-
мера не изменяются. Новые линии добавляются в конец списка. Линии (хотя
бы одна) должны быть введены обязательно. Для ввода прямой линии
должны быть заданы два узла на ее концах; для ввода параболы необходимо
88 2. Моделирование процессов в метаплах методом конечных элементов
задать три узла: два —- по концам и один — в середине; более сложные ли-
нии могут быть описаны любым нечетным числом узлов, но практически
будут представлены в виде цепочки парабол.
Линии могут быть длинными или короткими (содержать различное
число узлов). Поверхности также могут содержать различное число линий.
Пользоваться короткими линиями и небольшими поверхностями проще, хо-
тя это несколько увеличивает количество исходных данных. Преимущество
длинных линий и больших поверхностей в том, что они позволяют описы-
вать более крупные блоки. Линии и поверхности внешнего контура узла ис-
пользуются при задании граничных условий. Поэтому те участки контура,
на которых условия могут отличаться, должны быть описаны разными ли-
ниями и поверхностями, а те, для которых условия совпадают, удобнее за-
давать целиком.
Узел представляет собой точку с тремя координатами (у плоских мо-
делей третья координата равна нулю). Расположение координатных осей
может быть любым, но одинаковым для всех узлов модели. В осесиммет-
ричных моделях первая координата направлена по радиусу, а вторая являет-
ся осью симметрии.
Основные узлы размещаются на линиях и являются узлами КЭ моде-
ли. Вспомогательные узлы служат для определения координат основных
узлов. В число узлов на линиях можно включать, кроме тех, для которых
уже заданы координаты, также узлы с последующими номерами (с неиз-
вестными пока координатами) при условии, что эти координаты будут опре-
делены в процессе составления модели к моменту их использования.
Узлы нумеруются в произвольном порядке, начиная с № 1. При со-
ставлении модели происходит добавление узлов в конец списка. Присвоен-
ные узлам номера в ходе составления модели не изменяются, за исключени-
ем узлов из конца списка, которым после вычеркивания вспомогательных
узлов присваиваются их номера.
Координаты узлов могут быть заданы с помощью смещения (размера)
по отношению к одному из ранее введенных узлов. Размеры задаются от-
дельно по каждой координате с указанием номера базового узла, имени раз-
мера (до четырех символов) и списка номеров вводимых узлов. Затем для
каждого имени задается исходное значение размера и (не обязательно) пре-
делы его возможного изменения. Если пределы заданы, то этот размер появ-
ляется на изображении модели и может быть изменен при редактировании
модели в графическом режиме на второй стадии ее построения. Такая форма
ввода облегчает параметризацию модели (обеспечивает изменение коорди-
нат нескольких узлов при изменении одного размера).
Размеры могут быть также введены от специального узла № 0 (ко-
торый не требуется вводить) с нулевыми координатами (эти размеры
2.3. Работа программного обеспечения метода конечных элементов
89
Рис. 2.10. Каркас конечно-элементной модели
равны координатам вводимых узлов). Предусмотрен также нулевой раз-
мер с именем 0.
После введения узлов и линий возможна визуализация модели в виде
каркасной («проволочной») основы (рис. 2.10).
Дальнейший процесс построения разбивки происходит автоматически
и заключается в разбиении специальных блоков на сложные, сложных — на
простые. В процессе этого разбиения в списки добавляются новые блоки,
поверхности, линии и узлы. В составленной модели все блоки простые. До-
полнительное уменьшение числа вводимых данных достигается за счет
вспомогательных операций — ввода эллипса, дробления и сгущения.
Эллипс позволяет уменьшить число вводимых координат узлов. Коор-
динаты промежуточных узлов вычисляются в программе по уравнению эл-
липса. Для ввода дуги эллипса (окружности) необходимо перечислить пять
узлов: три вспомогательных (в центре и на концах большой и малой полу-
осей) и два основных (на концах дуги). Вместо вспомогательных узлов
можно повторно использовать основные. Узлы дуги эллипса должны лежать
на одной из линий.
Дробление также имеет назначение уменьшить число вводимых коор-
динат. Координаты вычисляются по уравнению квадратной параболы.
Дробления затем видны на изображении модели и могут быть изменены при
ее редактировании на второй стадии построения модели.
Сгущение позволяет на основе ранее составленной модели получить
модель с большим количеством блоков путем их дополнительного разбие-
ния вблизи указанных узлов, линий или поверхностей. Для каждого сгуще-
ния необходимо указать внутренний радиус (радиус отверстия, создаваемо-
90 2. Моделирование процессов в металлах методом конечных элементов
Рис. 2.11. Каркас с кривыми и дроблениями
го на месте прежнего узла или линии); радиус первого яруса концентриче-
ской сетки элементов и прогрессию увеличения радиусов следующих яру-
сов. Ярусов столько, сколько помещается в исходных блоках, которым при-
надлежали узел или линия сгущения. По умолчанию внутренний радиус ра-
вен нулю, минимальный очень большой, а прогрессия со знаменателем 2.
После пост роения каркаса (см. рис. 2.10) на ребра добавляются узлы с
помощью эллипсов и дроблений. В результате некоторые ребра приобретают
криволинейную форму. Вид модели после этого этапа показан на рис. 2.11. За-
тем производится разбиение блоков на элементы (рис. 2.12). Далее на основе
полученной сетки, пред-
назначенной для расчета
напряженно-деформиро-
ванного состояния (НДС),
строится сетка для задач
тепломассопереноса
(рис. 2.13), аналогичная
сетке на рис. 2.6. Общими
у сеток на рис. 2.12 и 2.13
являются центры элемен-
тов. В сетке на рис. 2.13
центрами элементов яв-
ляются также граничные
узлы сетки на рис. 2.12.
Имеется возмож-
ность построения объем-
ной модели из плоской
Рис. 2.12. Фрагмент модели для расчета деформаций
2.3. Работа программного обеспечения метода конечных элементов
91
путем разворачивания
(движения) вдоль прямой
или окружности (рис. 2.14).
Для этого предназначен
элемент данных под име-
нем секции, указывающий
сколько слоев и какого раз-
мера нужно создать. Если
исходная модель помечена
как плоская, то информа-
ция о секциях трактуется
как линейные размеры по
третьей координате в мил-
лиметрах, а если модель
была осесимметричная —
как угловые размеры в
градусах.
Рис. 2.13. Фрагмент модели для расчета
массопереноса
Предусмотрена также библиотека готовых моделей, которую можно
просмотреть, использовать ее модели, отредактировав их размеры, или
включать эти модели на правах блоков в создаваемую новую модель.
Встроенный в программу текстовый редактор позволяет после каждо-
го этапа просмотреть отчет о ходе геометрического моделирования и пара-
метры построенной модели.
Итоговая информация о геометрии модели носит традиционный для
МКЭ вид. Ее основу составляют координаты всех узлов и список номеров
Рис. 2.14. Получение объемной модели из плоской
92 2, Моделирование процессов в металлах методом конечных элементов
узлов для каждого элемента (топология). Это позволяет импортировать моде-
ли, построенные вне комплекса, и экспортировать построенные в комплексе,
т. е. взаимодействовать с другими конечно-элементными комплексами.
Ввод свойств материала, начальных и граничных условий. Ос-
новная модель материала в комплексе «СВАРКА» представляет собой смесь
нескольких компонентов с указанием процентного содержания каждого
компонента. Свойства смеси определяются интерполяцией по свойствам
компонентов. В связи с этим в состав данных о свойствах материалов преж-
де всего входят:
• список имен компонентов;
• свойства каждого из них;
• исходный состав для каждого номера материала, введенного для
блоков при создании геометрической модели детали;
• для задач сварки — состав материала, заполняющего разделку в
процессе сварки.
Свойства компонентов хранятся в базе данных в табличном виде и из-
влекаются из нее по именам компонентов при составлении модели. Эта база
данных и система ее редактирования являются частями комплекса «СВАРКА».
Предполагается дальнейшее развитие моделей поведения компонентов ма-
териалов и их взаимных превращений, поэтому в базе данных предусмотрен
резерв для добавления новых характеристик.
Основными теплофизическими свойствами являются теплопровод-
ность и объемная теплоемкость, а также скрытая теплота при взаимном пре-
вращении таких структурных компонентов сталей, как перлит, аустенит и т. д.
Расплавленное состояние тоже может быть представлено как отдельный
компонент, что позволяет ввести в модель скрытую теплоту плавления. Ус-
ловия превращения могут быть заданы в различном виде, например в виде
температурного интервала, при прохождении которого компонент превра-
щается в другой.
Набор механических характеристик определяется тем, что в комплек-
се «СВАРКА» предусмотрено несколько различных моделей поведения ма-
териала, основными из которых являются:
• упругопластическая с произвольным законом упрочнения, с крите-
рием разрушения и постоянными механическими характеристиками;
• идеальная упругопластическая с переменными механическими ха-
рактеристиками;
• вязкоупругопластическая с характеристиками, полученными в усло-
виях программированного термодеформационного цикла;
• модель пористого материала.
Для того чтобы любая модель материала могла сочетаться с любой
геометрической моделью, предусмотрен универсальный комплект из восьми
2.3. Работа программного обеспечения .метода конечных элементов
93
механических характеристик материала, часть из которых может быть не
задействована в конкретной модели. Все они вводятся в виде таблиц. Для
каждой характеристики должно быть указано ее имя, а также ряд пар значе-
ний аргумента и характеристики, являющейся его функцией. Минимальное
количество пар — две, максимальное — не ограничено.
Список характеристик:
• деформационная характеристика в виде таблицы значений интен-
сивности напряжений, аргумент — интегральная пластическая деформация
(параметр Одквиста);
• критерий разрушения в виде таблицы значений предельной пластич-
ности, аргумент — показатель объемности напряженного состояния;
• отношение предела текучести при растяжении к пределу текучести
при сжатии, аргумент — температура;
• предел текучести при растяжении, аргумент — температура;
• модуль упругости при сдвиге, аргумент — температура;
• объемный модуль упругости, аргумент — температура;
• модуль упрочнения при ползучести, аргумент — температура;
• дилатометрическая характеристика в виде таблицы значений темпе-
ратурно-структурной объемной деформации, аргумент — температура.
Предусмотрен также материал «по умолчанию», соответствующий
стали с очень высоким пределом текучести и свойствами, не зависящими от
температуры, позволяющий пропускать ввод свойств материала в исходных
данных. Он пригоден для использования в рамках любой из перечисленных
моделей материала.
Все характеристики, являющиеся функциями температуры, должны
иметь одинаковые области определения (крайние значения аргумента).
Для каждого физического процесса предусмотрено три рода гранич-
ных условий:
1 -го рода: в точках границы задана температура в тепловой задаче или
перемещения в деформационной -— постоянные или функции от времени;
2 -го рода: задан в тепловой задаче поток теплоты, а в деформацион-
ной — распределенные или сосредоточенные силы;
3 -го рода (только для процессов энергомассопереноса): задана среда
за границей со своими параметрами и условия взаимодействия модели с
этой средой (например, коэффициент теплоотдачи с поверхности в тепловой
задаче).
Граничные условия 1-го и 2-го рода являются частными случаями ус-
ловия 3-го рода. В некоторых случаях возможно непосредственное действие
граничных условий на внутренние узлы и элементы модели (индукционный
нагрев, гравитационные, инерционные и электромагнитные силы и т. д.).
94 2. Моделирование процессов в металлах методом конечных элементов
Для моделирования сложных процессов во времени они разбиваются
на шаги (конечные элементы по координате времени). На каждом шаге пре-
дусмотрено задание граничных условий для отдельных узлов модели или
для групп узлов. Для выделения таких групп на внешнем контуре модели
служат поверхности и линии. Для векторных граничных условий (переме-
щений и сил) предусмотрено задание компонентов по осям координат, по
заданному направлению или по нормали к участку границы.
При выборе вида граничных условий следует учитывать, что сходи-
мость решения улучшается при увеличении числа узлов с заданными гра-
ничными условиями 1-го рода.
Необходимо задать начальные значения параметров для всех узлов и
элементов. Чаще всего они задаются одинаковыми для всей модели или из-
влекаются из информации, введенной при геометрическом моделировании.
Возможно также использование функций от координат узлов модели.
Составление и решение систем уравнений. На вводе граничных ус-
ловий завершается интерактивный этап моделирования, дальнейшая работа
протекает автономно с периодической информацией пользователя о ходе
работы. Все расчеты на интерактивном этапе приводят к переводу окна
пользователя в режим ожидания. В процессе длительного счета необходимо
дать ему возможность продолжать работу с моделью, просматривать порции
результатов по мере их выдачи компьютером, а при необходимости — вме-
шиваться в процесс моделирования. С этой целью в комплексе использована
многопоточная система Windows для организации дополнительного рабоче-
го потока, в котором проходит счет. В однопроцессорном персональном
компьютере запуск более одного дополнительного потока снижает произво-
дительность. Поэтому запуск еще одного экземпляра комплекса или откры-
тие одновременно нескольких проектов возможны, но нецелесообразны.
При наличии нескольких процессоров можно существенно повысить произ-
водительность решения связных задач, разделяя моделируемые параллельно
процессы между процессорами компьютера.
Этап составления системы уравнений занимает время, пропорцио-
нальное числу КЭ модели, начальный этап ее решения (прямая прогонка) —
пропорциональное кубу числа узлов, а обратная прогонка — пропорцио-
нальное квадрату числа узлов. В связи с этим операция составления матри-
цы занимает основную часть времени счета при небольшом числе элемен-
тов, а прямая прогонка — при большом числе. Объем памяти пропорциона-
лен квадрату числа узлов. Это следует учитывать при построении модели и
измельчать элементы только там, где это необходимо для обеспечения точ-
ности решения (в зонах ожидаемых больших градиентов результатов).
В комплексе «СВАРКА» предусмотрено хранение системы уравнений
в оперативной памяти. Использование виртуальной памяти на диске воз-
2.3. Работа программного обеспечения метода конечных элементов
95
можно, но при этом снижается производительность, поэтому целесообразно
иметь в компьютере оперативную память, необходимую для решаемых за-
дач (порядка 20 Мб для несложных плоских и осесимметричных задач и бо-
лее 100 Мб для объемных).
Составление и решение системы уравнений требуется только при не-
явной схеме решения, т. е. в комплексе «СВАРКА» для деформационной
задачи. Она и является критической по времени и памяти компьютера. Теп-
ловая задача может занять много времени при мелких элементах и длитель-
ном процессе вследствие большого числа шагов.
Итерационное уточнение решения. Такое уточнение проводится
всегда при неявной схеме решения, хотя реальная необходимость в нем
имеется только для нелинейных задач, для очень больших по числу элемен-
тов моделей, а также при некоторых других особенностях модели (напри-
мер, при большой гибкости элементов). Число итераций зависит от парамет-
ров точности, введенных в граничных условиях. Их три:
• абсолютная погрешность, зависящая от габаритных размеров модели;
• относительная погрешность, зависящая от изменений характеристик
модели за шаг;
• предельное число итераций.
Смысл параметров точности заключается в том, что большая точность
не требуется для крупных моделей и при крупных шагах решения, а также в
необходимости исключить зацикливание компьютера. Меняя три параметра
точности, пользователь влияет на точность решения и время его получения.
Следует отметить, что, поскольку сходимость решения обычно моно-
тонная, достигнутую точность приходится оценивать косвенно, не по по-
грешности, а по степени изменения результата решения за очередную ите-
рацию.
Итерационный процесс построен так, чтобы обеспечивать устойчи-
вость решения на каждом шаге, по мере возможности устранять все по-
грешности предыдущих шагов, как связанные с нелинейностью, так и воз-
никшие при составлении и решении уравнений.
При медленном монотонном изменении результатов итераций можно
по итогам нескольких итераций предвидеть их дальнейший ход и за счет
этого ускорить сходимость. Такой алгоритм существует и применяется в
комплексе «СВАРКА».
Пошаговое моделирование сложного процесса. Число шагов за-
висит от особенностей модели и требований, предъявляемых к результа-
там. При явной схеме решения шаг ограничен условием устойчивости
решения и зависит от размеров наименьшего элемента модели (см. рис. 2.7).
При более крупном шаге получается решение, не имеющее ничего обще-
го с реальным процессом.
96 2. Моделирование процессов в металлах методом конечных элементов
При неявной схеме, если все процессы обратимые (не было текучести
и разрушения) и нужен только окончательный результат, всегда достаточно
одного шага. Если происходят необратимые явления, влияющие на итого-
вый результат, или представляют интерес промежуточные состояния, необ-
ходимо разбивать процесс на шаги. Иногда эти шаги столь же мелкие, как и
при явной схеме, поскольку точность обеих схем имеет одинаковый поря-
док. С учетом итераций на каждом шаге время счета может оказаться очень
большим. Если нелинейность процесса невелика, то можно отказаться от
составления системы и прямой прогонки на каждом шаге, оставив матрицу
жесткости постоянной. Это обычно не препятствует получению необходи-
мой точности результатов, но увеличивает необходимое число итераций. На
каждой итерации составляется только правая часть системы уравнений и
осуществляется обратная прогонка, что требует гораздо меньшего времени.
Однако при значительной нелинейности число итераций возрастает на-
столько, что становится невыгодно использовать этот прием.
Передача данных между моделями процессов. Результаты модели-
рования каждого процесса записываются в файлы. Это позволяет не только
использовать их для моделирования другого процесса, но и просматривать,
дополнительно обрабатывать для вывода на печать или хранения, продол-
жать прерванное решение, начиная с любого из пройденных шагов.
Поскольку некоторые процессы требуют очень мелкого шага из усло-
вия устойчивости, запись производится не после каждого шага, а с перио-
дичностью, заданной в исходных данных. Граничные условия для таких
процессов также задаются не для каждого шага, а сохраняются постоянны-
ми в течение ряда шагов (стадии).
Элементы для разных процессов могут не совпадать, поэтому свя-
зующим звеном являются узлы. Результаты моделирования приводятся к
узлам и в таком виде передаются другому процессу, в котором при необхо-
димости интерполяцией определяются значения для точек внутри элементов.
Расчленение громоздких моделей. Приемы экономии времени и па-
мяти за счет разбиения сложной модели на подконструкции существуют, но
в комплексе «СВАРКА» пока недостаточно развиты. Они обсуждаются
применительно к другим комплексам в § 2.4.
Визуализация результатов решения необходима при анализе ре-
зультатов, которые МКЭ выдает в таком количестве, что их иным способом
невозможно воспринять, и помогает обнаружить ошибки, допущенные при
построении модели.
При просмотре изображения плоской модели предусмотрены опера-
ции показа номеров узлов, линий и элементов, поочередный или одновре-
менный показ линий сетки элементов для различных процессов, а также из-
менение масштаба. Номера линий контура облегчают ввод граничных уело-
2.3. Работа программного обеспечения метода конечных элементов
97
вий, правильность которых может быть затем проверена по их условным
обозначениям на изображении модели.
Для объемных моделей дополнительно необходимо удаление скрытых
линий и раскрашивание поверхностей, имитирующее их освещение источ-
ником света, а также изображение в аксонометрии с выбором точки наблю-
дения (ракурса) для лучшего представления о форме трехмерного объекта и
сетке элементов на его поверхности на двумерном экране. Необходимо так-
же изображение сечения по плоскости или по границе элементов для кон-
троля внутренней сетки элементов.
При задании граничных условий целесообразно выделение участков
внешней границы разными цветами.
При вводе таблиц свойств материалов правильность данных позволя-
ют проверить изображения графиков функций. Это относится и к парамет-
рам граничных условий, изменяющимся во времени.
Известны следующие средства изображения результатов решения
МКЭ: скалярного или векторного поля для плоской детали, а также для на-
ружной поверхности или поверхности сечения объемной детали.
Скалярный фактор может быть представлен изолиниями (разноцвет-
ными или помеченными номерами), а также в виде аксонометрического
изображения поверхности, для которой одной из координат является пред-
ставляемый фактор. Эти средства позволяют изобразить поочередно отдель-
ные компоненты векторного фактора. Кроме того, векторное поле на по-
верхности можно представить в виде рассеянных по ней стрелок, длина ко-
торых пропорциональна модулю вектора, а направление указывает линию
максимального градиента. Можно также провести силовые линии (нормаль-
ные к изолиниям), сгущающиеся в области высоких значений модуля. Под-
ведение курсора к одному из изображенных на модели узлов позволяет за-
просить информацию о значениях любых компонентов в этом узле. Поле
перемещений узлов может быть представлено в виде искаженной сетки, по-
казанной взамен или поверх исходной, причем масштаб искажений может
отличаться от масштаба координат сетки. Изображение поля искажений
можно совместить с изображением еще какого-нибудь параметра.
Если выбрать одну из линий на поверхности или в сечении детали, то
возможен одновременный просмотр сразу нескольких графиков функций
вдоль этой линии, ее проекции или развертки. Подведение курсора к точке
на линии или на графике позволяет запросить текстовую дополнительную
информацию.
Когда имеется несколько шагов решения, картину динамики его изме-
нения могут дать либо серия графиков одной функции вдоль одной линии,
4 6705
98 2. Моделирование процессов в металлах методом конечных элементов
либо графики функций для одной точки модели, аргументом которых явля-
ется время или аналогичный ему параметр, либо мультфильм с чередовани-
ем на экране изображений различных групп графиков.
Можно представить параметр в точках выбранной линии не в функ-
ции координат, а в функции другого параметра.
Все эти средства реализованы или находятся в стадии реализации в
комплексе «СВАРКА». Для управления ими используются нажатия кно-
пок на панелях инструмента, движение мыши и нажатия ее кнопок в раз-
личных частях обоих окон, а также нажатия клавиш клавиатуры. Для от-
слеживания и изменения номера шага просматриваемых результатов в
нижнем правом углу экрана появляется специальная панель, на которой
по мере решения отображается число пройденных шагов. Пример резуль-
татов показан на рис. 2.15.
Существующие программные комплексы МКЭ обычно содержат ряд
обязательных звеньев, рассмотренных в этом параграфе. Наряду с этим ка-
ждый из них ориентирован на определенный круг задач и включает допол-
нительные возможности, актуальные для этих задач. Ряд таких более слож-
ных проблем моделирования рассматривается далее на примере действую-
щих программных комплексов.
Рис. 2.15. Результаты расчета температуры при наплавке
на.железнодорожное колесо
2.4. Моделирование упругопластического поведения материала 99
2.4. Моделирование упругопластического поведения материала
в комплексе «СВАРКА»
Процесс деформирования любого материала является весьма слож-
ным, особенно вблизи концентраторов напряжения. Точность описания это-
го процесса зависит от сложности математической модели. Трудоемкость
моделирования также зависит от сложности модели и практически не имеет
верхнего предела. Однако разумная граница сложности и точности модели-
рования все же существует. Во-первых, она связана с целью получения ре-
зультатов расчета. Во-вторых, точность в принципе ограничена погрешно-
стями исходных данных. Известно, что рассеяние всех характеристик мате-
риала при современном уровне технологии может достигать 10 % как в
пределах партии деталей, так и в пределах сечения одной детали. Рассеяние
условий нагружения может быть еще больше.
Таким образом, при проектировании всегда приходится сталкиваться с
некоторой неполнотой данных для расчета. Погрешности моделирования
невозможно полностью устранить и даже оценить расчетным путем. Для их
оценки необходимо сопоставление с экспериментом. Погрешности можно
снизить и путем подгонки данных (решением так называемой обратной за-
дачи). Ориентируясь на расчетно-экспериментальный подход, следует при
выборе модели не столько стремиться к учету всех мелких деталей, сколько
следить, чтобы не был пропущен принципиально важный элемент.
Наиболее универсальной и рациональной основой уравнений МКЭ
является вариационное интегральное уравнение
JojjEydv = + j p^ds + щек = 0, (2.4)
Г V sp su
где q,,Pi — векторы* распределенных нагрузок, действующих в объеме мо-
дели V и на части ее поверхности S; nj — вектор нормали к той части по-
верхности Su, на которой заданы граничные перемещения; о.., ёу, й-, —
напряжения и скорости деформаций и перемещений в точках тела.
По своему физическому смыслу — это уравнение сохранения энергии.
Скорость изменения энергии деформаций (левая часть) равна суммарной
Здесь и далее используется тензорная форма записи для векторов и матриц. Вы-
ражение pi применяется для обозначения как компонента вектора р, так и для
обозначения всего вектора (р\,рг, ...,Pi, -,р^)- Выражение означает скаляр-
п
ное произведение векторов р и q, т. е. А 9,-
1=1
4*
100 2. Моделирование процессов в металлах методом конечных элементов
мощности объемных и поверхностных внешних сил. Равновесие во внут-
ренних и внешних точках объема V достигается путем минимизации потен-
циальной энергии системы. Исходная формулировка, основанная на законе
сохранения энергии, является принципиальной для моделирования движе-
ния трещин, так как позволяет следить за балансом энергии в конструкции
по кинетике изменения компонентов НДС в отдельных ее точках.
После подстановки в уравнение (2.4) условий связи перемещений с
деформациями Ёу = <р(й, ) и деформаций с напряжениями о- /(Ё1;) из
него может быть получена система дифференциальных уравнений равнове-
сия узлов КЭ модели.
Зависимости ср и f линейны только в случае упругого деформирования
гладкого образца. При больших деформациях и сложной форме детали их
нелинейностью нельзя пренебречь. В этом случае и система уравнений МКЭ
нелинейна. Наиболее эффективный способ ее решения итерационный, со
сведением на каждой итерации к системе линейных алгебраических уравне-
ний. Для получения такой системы необходимо перейти от скоростей к ко-
нечным приращениям перемещений и деформаций и линеаризовать выра-
жения ср и f
Согласно процедуре МКЭ, объем тела является суммой объемов эле-
ментов. Выбрав в качестве неизвестных перемещения узлов, поле переме-
щений в пределах элемента аппроксимируют полиномом, выражая прира-
щение перемещения и деформации в произвольной точке через ее координа-
ты и приращения перемещений в узловых точках ДЦт :
\ut = NmAUim,
. 1 Э(Дгт) 3(Ди)
Де,, =------—-----------
1 2
8х- дх,
= В ,
ijnm пт ’
(2.5)
(2.6)
где Nm — компоненты вектора функций формы элемента, зависящих от
координат точки и геометрии элемента (гп — номер узла в элементе); мат-
рица градиентов элемента Bijnm получается дифференцированием вектора
Nm по координатам хп. Совокупность формул (2.5) и (2.6) обеспечивает
линейность функции ср. Для функции f используют уравнение вида
+ (2-7)
Тогда система линейных уравнений относительно приращения узло-
вых перемещений за шаг Д(/„ равна:
\TJ IS _ Е’
rt^rfnm 1 пт,
(2.8)
2.4. Моделирование упругом астического поведения материала
101
где
^rtnm ~ \^ijkl^klrt^ijnm^V (2-9)
V
— матрица жесткости тела;
Fnm = \qnNmdv+ \pnNmdS-\RyBijnmdv (2.10)
Г sp V
— вектор объемных и поверхностных внешних нагрузок, включающих в
себя и составляющие от неуравновешенных начальных напряжений.
Процедура расчета НДС сводится к составлению системы уравнений
(2.8) и решению ее методом Гаусса. Вначале производится факторизация
матрицы Кппт на две треугольные матрицы, а затем умножение этих мат-
риц на вектор Fnm. Результатом решения являются приращения перемеще-
ний в узлах АСГГ, по которым могут быть найдены любые компоненты
НДС. Весь процесс нагружения разбивают на шаги по времени или другому
аналогичному параметру и итоговые деформации и перемещения определя-
ют как сумму перемещений на отдельных шагах.
На каждом этапе составления и решения системы уравнений возни-
кают погрешности, связанные как с линеаризацией, так и с ограниченной
точностью выполнения математических операций на ЭВМ. Поэтому по-
лучаемое решение Д(7Г, отличается от точного значения перемещений за
шаг. Если по найденным перемещениям вычислить деформации и напря-
жения, а затем вновь вычислить вектор правых частей системы линейных
уравнений, то компоненты этого вектора оказываются отличными от ну-
ля. Повторное решение системы дает поправку к вектору В этом
заключается процедура итерационного уточнения решения, которая мо-
жет быть продолжена до получения необходимой точности определения
перемещений. При этом скорость сходимости итераций зависит от по-
грешностей линеаризации при составлении матрицы жесткости Krtnm и от
погрешностей решения.
Предел, к которому стремятся результаты итераций, зависит практически
только от правильности вычисления вектора Fm правых частей системы, при-
чем применение при вычислении правых частей выражений любой сложности
не изменяет линейного характера системы (2.8). Таким образом, алгоритм сво-
дится к чередованию вычисления поля перемещений, обеспечивающего совме-
стность деформаций и равновесие напряжений из решения системы линейных
уравнений и вычисления по этим перемещениям поля напряжений и деформа-
ций в отдельных элементах с использованием при необходимости любых нели-
нейных зависимостей. Независимое вычисление компонентов НДС вызывает
102 2. Моделирование процессов в металлах методом конечных элементов
нарушение равновесия между элементами, которое устраняется при следую-
щем решении системы (2.8). При правильном ходе итераций компоненты век-
тора Fnm и поправки к решению A(7rt убывают. По их текущему значению
можно судить о достигнутой точности и принимать решение о завершении ите-
раций и переходе к следующему шагу изменения граничных условий.
Особенностью разработанного алгоритма является совмещение итера-
ций, устраняющих погрешности округления при решении системы уравне-
ний и обеспечивающих учет геометрической и физической нелинейности.
Использование для вычисления вектора о правых частей напряжений, а не
их приращений До.. позволяет обеспечивать равновесие напряжений в кон-
це каждого шага и автоматически корректировать погрешности в равнове-
сии тела, возникающие вследствие ограниченной точности расчета. В пра-
вой части системы появляются ненулевые коэффициенты Fnm, если в конце
шага нарушено равновесие в узлах, независимо от того, вызвано это нару-
шение изменением нагрузки, нелинейностью или погрешностями счета. Ал-
горитм обеспечивает максимальную устойчивость процесса моделирования
при любых видах нелинейности модели. Без учета нелинейности, в частно-
сти, невозможно описание процесса разрушения материала.
Геометрическая нелинейность связана с двумя явлениями при дефор-
мировании материала, не учитываемыми линейной формулой (2.6). Во-
первых, возможно вращение объема, окружающего точку, в которой произ-
водится определение деформаций, как жесткого целого относительно задан-
ной системы координат. При этом материал не деформируется, но взаимные
перемещения соседних точек происходят, и выражение (2.6) дает ненулевые
компоненты деформаций. Если отрезок АВ, направленный вначале вдоль
оси х, поворачивается вокруг точки А без изменения длины АВ, то, согласно
(2.6), деформация ехх отрезка отрицательна. Фактически (2.6) дает дефор-
мацию не самого отрезка АВ, а его проекции на ось х. При моделировании
возникновение деформаций и напряжений в жестко вращающейся части вы-
зывает изменение энергии и появление реакций, препятствующих враще-
нию, в то время как в реальности вращение жесткого тела в пространстве
при отсутствии внешних сил происходит беспрепятственно. Чтобы исклю-
чить эту погрешность, искажающую картину НДС, необходимо воспользо-
ваться более точной формулой для определения деформации
Де,,.
2
5(Дг<.) д(Л»,.) д(Дг^) S(Az^)
дх, dxi дх1 dxj
(2.U)
Сравнение выражений (2.6) и (2.11) показывает, что различие между
ними остается в общем случае существенным, даже если шаг решения стре-
мится к нулю.
2.4. Моделирование упругопластического поведения материала
103
Вторая причина геометрической нелинейности связана с изменением
базы деформации при значительных перемещениях за шаг. Поскольку коор-
динаты концов отрезка АВ являются функциями перемещений, скорость де-
формации отрезка переменна при постоянной скорости взаимного переме-
щения его концов. Если пользоваться условной деформацией, т. е. за сред-
нюю скорость принять скорость деформации в начале шага, то погрешность
будет иметь разный знак в зависимости от того, увеличивается база дефор-
мации АВ или уменьшается. В этом случае, как и в предыдущем, важен не
сам факт погрешности, которая неизбежна при применении дискретного ме-
тода решения, а ее влияние на моделирование НДС. Известно, что реальные
металлы практически несжимаемы, их объемные деформации, особенно в
пластической области, малы по сравнению с деформациями формоизмене-
ния. Достигнуть условной деформации -100 %, при которой длина образца
станет равной нулю, невозможно, для этого нужно совершить бесконечно
большую работу. Если же не учитывать изменения базы при деформации, то
эта работа окажется такой же, как при условной деформации +100 %, т. е.
при увеличении исходной длины образца вдвое. Если в модели имеются зо-
ны как растяжения, так и сжатия, то минимуму суммарной потенциальной
энергии может соответствовать состояние с деформациями сжатия более
100 %, что означает отрицательный объем, т. е. вывернутый наизнанку.
Следовательно, при деформации за шаг, соизмеримой со 100 %, в отдельных
зонах возможно нарушение условия неразрывности материала модели, за-
трудняющее продолжение моделирования.
Эту проблему можно решить без измельчения шага решения, если оп-
ределять приращение деформаций интегрированием. Для случая линейной
деформации отрезка с исходной длиной АВ, изменившего при деформации
свою длину на В.АВ, имеем условную деформацию
Деус = (2.12)
АВ
и истинную деформацию
г dAB АВ+&.АВ
Деис = ---= In-------= ln(l + Деу ).
1 АВ АВ
(2-13)
Различие между условными и истинными деформациями существует
и для компонентов сдвига, но формулы в этом случае гораздо сложнее. По-
этому' для определения компонентов тензора Де“с проще перейти к главным
осям деформаций.
Алгоритм определения истинных деформаций включает следующие
операции.
104 2. Моделирование процессов в металлах методом конечных элементов
1. Определение приращений компонентов перемещения узлов модели
за шаг. Для этого осуществляется решение системы уравнений (2.8), постро-
енной на линейных соотношениях между скоростями перемещений, скоро-
стями деформаций и напряжениями, соответствующими началу шага.
2. Определение приращений компонентов тензора условных деформа-
ций за шаг с учетом вращения, т. е. по формулам (2.11).
3. Выделение из приращений деформаций девиаторной части
Ae,-AE--8,Aem, (2.14)
Л ^^22 ^33 1 о ту
где Ает = — ---—-----—----средняя деформация; 6(J — символ Кронекера.
4. Определение приращений главных компонентов девиатора услов-
ных деформаций Ае из решения уравнения
Г>^(Ае..-8..Ае) = 0. (2.15)
5. Определение матрицы направляющих косинусов nki между осями ис-
ходной системы координат и главными осями из решения системы уравнений
(A^-8^>fa.=0, (2.16)
4+«и + «*з=1- (2.17)
6. Определение приращений главных компонентов тензора истинной
деформации за шаг. Для этого необходимо найти приращения главных ком-
понентов тензора условных деформаций Ае|с = Аед + Аеи и затем опреде-
лить Де™ по (2.13).
7. Определение приращений компонентов истинной деформации в ис-
ходной системе координат. Для этого надо воспользоваться найденными
направляющими косинусами
Ае;с=АеГ^«7*. (2.18)
Как уже было отмечено, описанный алгоритм нацелен не столько на
повышение точности решения, сколько на обеспечение разумного поведе-
ния модели в условиях огромных шагов приращения деформаций в отдель-
ных элементах. Таких мер может быть достаточно, только если состояние в
этих элементах не представляет интереса (например, это зона уже разру-
шившегося материала), а требуется точно оценить состояние в соседних
элементах с меньшими поворотами и деформациями за шаг. Для обеспече-
ния точности всей модели необходимо ограничивать шаги решения, а также
учитывать изменение матрицы градиентов Bijnm при вычислении по (2.8)
правых частей системы уравнений на каждой итерации.
2.4. Моделирование упругопластического поведения материала
105
8. Существенные погрешности могут возникнуть при переходе к сле-
дующему шагу решения. Описанная выше процедура исключает влияние
поворотов на НДС в точках модели. Это значит, что элементарный объем,
имевший в начале шага напряжение = и, = 0 и повернувшийся за
шаг как жесткое тело на 90° вокруг оси z, будет иметь то же напряжение. Но
фактически волокно, совпадавшее в начале шага с осью х, в конце шага по-
вернулось в направлении оси у, следовательно, в неподвижной системе ко-
ординат НДС в этом объеме соответствует о** = 0, о = о. Таким образом,
при переходе к следующему шагу одновременно с изменением координат
точек модели в результате их перемещений необходимо преобразовать НДС.
Эта задача распадается на две. Во-первых, необходимо определить,
как повернулся каждый элементарный объем, т. е. найти направляющие ко-
синусы между осями координат и теми волокнами, которые совпадали с
этими осями в начале шага. Направляющие косинусы любого волокна t в
конце шага
ти = (И/*Ф; ~ «9<p*)sin Aw + ср,-0(1 - cosAw) + nti cos Лео, (2.19)
Л Аш,
где 0 = «„ср,; ср,. =—— направляющие косинусы того же волокна в
Aw
начале шага. Три угла поворота элементарного объема за шаг Aw,- опреде-
ляем по формулам
5(Аг/д.) 5(Ану)
Зх- dxk
tgAw,=---------—^—4-------• (2.20)
5(Анд.) JW,)
dx; dx,.
J A
Определив девять направляющих косинусов поворота системы коор-
динат, можно найти начальные компоненты НДС следующего шага по ко-
нечным предыдущего, с учетом этого поворота
(2-21)
(2.22)
Столь подробное изложение процедуры учета геометрической нели-
нейности связано с тем, что в литературе не удалось найти достаточно пол-
ного описания, доведенного до эффективного и практически реализуемого
алгоритма. Существует также представление, что для моделирования МКЭ
геометрической нелинейности вполне достаточно вести расчет мелкими ша-
106 2. Моделирование процессов в металлах методом конечных элементов
гами и корректировать координаты узлов после каждого шага. В действи-
тельности это так, но в некоторых случаях потребуется столько шагов, что
реализация решения задачи станет нереальной.
Вопросы нелинейности деформационной характеристики в литературе
освещены более подробно. При анализе упругопластического поведения
материала применяются две основные теории: деформационная и теория
течения. Поскольку процесс нагружения при эксплуатации, а особенно при
изготовлении сварных соединений, нельзя считать простым, целесообразно
использовать модель материала, основанную на теории течения. Недостат-
ком теории течения является ограничение на размер шага. Погрешность при
замене в формулах теории течения скоростей деформаций конечными при-
ращениями невелика, если эти приращения не превышают нескольких процен-
тов от деформации предела текучести ет, т. е. имеют порядок до 10~4. Далее
погрешность резко возрастает. При деформации за шаг 2ет и более решение
по теории течения становится более грубым, чем по деформационной теории.
Предположение о линейности траектории деформаций в пределах ша-
га позволяет аналитически проинтегрировать уравнения теории течения,
ослабив тем самым ограничения на размер шага, что приводит к существен-
ному сокращению вычислительных затрат. В результате интегрирования
получаем выражение напряжений в конце шага о*. через напряжения в на-
чале шага о”, и приращение деформации за шаг. Тензор напряжений <5 у
состоит из девиатора Sy и шарового тензора т. е.
(2.23)
где среднее напряжение определяется из выражения
Я^ = ^ + Д£ -Де (2.24)
ma’ V /
а девиатор в конце упругого шага — из выражения
2G
2G'
(2.25)
и в конце упругопластического шага — из выражения
S*, S-- 2Де„
—chvK = —chvH +---------(shvK -shv11), (2.26)
о* о" ЗДе,-
2.4. Моделирование упругопластического поведения материала
107
где о*, GK, Кк — интенсивность напряжения и модуль упругости в конце
шага, а о”, G", Кн — то же в начале шага; Де,;, Деи, Де,, ДЕа — прираще-
ния девиатора и шарового тензора деформации, интенсивности деформации
и свободной температурной деформации за шаг.
Параметр vK определяется из выражения
vK = v“ + 3
Де,,
(2.27)
(G} G
где — — среднее значение отношения — за шаг;
V °, 7 °;
vH = arth
54
о" Де,. '
(2.28)
Уравнения (2.23)—(2.28) могут быть применены как для идеального
упругопластического материала, так и для материала с упрочнением. В пер-
вом случае в конце упругопластического шага интенсивность напряжения
ст* известна и равна пределу текучести о*. Во втором о,к определяется из
решения нелинейного алгебраического уравнения, в которое входит закон
упрочнения. Этот алгоритм эффективнее численного интегрирования урав-
нений теории течения, когда необходимое число шагов интегрирования
больше двух.
При переменной температуре модули упругости G и К переменны.
Это изменение, как видно из (2.24), (2.26), влияет на а,у. Свободная темпе-
ратурная деформация, а также изменение объема от структурных превраще-
ний Дест входят в Деи :
ДЕа = |аг/Т + Дест , (2.29)
дг
где а — коэффициент линейного расширения материала, зависящий от тем-
пературы.
Таким образом, приведенные уравнения выражают достаточно уни-
версальную модель поведения изотропного материала, описывающую в ча-
стных случаях:
• упругий материал при постоянной и переменной температуре;
• идеальный упругопластический материал при постоянной и пере-
менной температуре;
108 2. Моделирование процессов в металлах методом конечных элементов
• упругопластический материал с произвольным законом упрочнения
при постоянной и переменной температуре.
Последний из перечисленных случаев может быть распространен и на
вязкоупругопластический материал, что позволяет проводить расчеты НДС
с учетом ползучести. Для этого необходимо вводить в расчет свойства мате-
риала в виде изохронных кривых, т. е. зависимостей о;(е() в каждый мо-
мент времени.
В целом модель позволяет описать с достаточной для практических
целей точностью большинство деформационных процессов в металле при
изготовлении и эксплуатации сварных конструкций.
Поскольку речь идет о практическом применении при проектирова-
нии, необходимо обеспечение устойчивости и сходимости процесса модели-
рования. Существует несколько видов задач, при решении которых сходи-
мость является серьезной проблемой.
1. Модели с большим числом элементов. В этом случае причиной ите-
раций является накопление погрешностей при решении системы \ равнений
по методу Гаусса. Обычно эти проблемы возникают при десятках тысяч не-
известных, однако этот порог резко снижается, если жесткость модели су-
щественно различается при разных направлениях перемещений, например
при моделировании стержневых и листовых конструкций. Как правило, это
приводит не к увеличению числа итераций, а к полному нарушению реше-
ния. Решению этой проблемы способствует переход на решение с двойной
точностью, а также алгоритм обращения матрицы с добавлением к диаго-
нальным элементам некоторого числа. Как правило, количество итераций
при этом увеличивается, но решение становится возможным. Более карди-
нальными средствами являются переход к решению в несколько этапов на
основе применения суперэлементов или метода поэтапного расчета.
2. Нелинейные задачи. Хотя жесткость модели непрерывно изменяет-
ся, наиболее эффективным остается метод упругих решений с постоянной
матрицей Кппт. При этом число итераций можно многократно сократить,
если при вычислении вектора после очередной итерации использовать
результаты предыдущих итераций. Алгоритм такого ускорения основан на
определении суммарного перемещения /\Urt в виде линейной комбинации
приращений перемещений на итерациях:
MJrl=±c(^, (2.30)
1=1
причем коэффициенты с(,) определяются из условия минимума квадратич-
ной нормы ожидаемого приращения перемещений на следующей итерации:
2.4. Моделирование упругопластического поведения материала
109
i=l J
(2.31)
В общем случае получаем систему из и -1 линейных уравнений отно-
сительно л-1 неизвестных коэффициентов cw, при этом принимается
c(min) _ । цисло решаемых уравнений может быть уменьшено. В этом слу-
чае часть коэффициентов cw принимается равными единице и алгоритм
становится более простым, но менее эффективным.
Эффективность применения алгоритма зависит от конкретной задачи.
Обычно число итераций сокращается в 5—10 раз.
3. Нарушение устойчивости решения. Если жесткость матрицы системы
уравнений меньше, чем модели, то сходимость становится немонотонной. Если
хотя бы в одной точке модели эта погрешность матрицы превышает 200 %, то
приращения за следующую итерацию становятся больше, чем за предыдущую,
т. е. нарушается устойчивость решения и итерации расходятся.
В зависимости от причины такого поведения модели можно предло-
жить конкретные меры обеспечения устойчивости.
1. Увеличение модуля упругости материала при изменении темпера-
туры или структурных превращениях. В этом случае необходимо пересчи-
тывать матрицу Ктгт на каждом шаге или рассчитать ее для максимально
возможных значений модулей упругости.
2. Геометрическая нелинейность, в том числе связанная с моделиро-
ванием разрушения. В тех точках, где происходит укорочение, истинные
деформации по абсолютному значению больше условных, что эквивалентно
увеличению жесткости модели и ведет к нарушению сходимости. Когда ус-
ловные деформации укорочения приближаются к 100 %, жесткость стремит-
ся к бесконечности, в связи с чем необходимо ограничивать шаги решения.
Искусственно завышая модули упругости при вычислении упругой матри-
цы, можно повысить устойчивость решения, что позволит несколько увели-
чить шаг. Поскольку деформации сдвига вызывают текучесть и резкое сни-
жение жесткости, завышение необходимо только для объемного модуля уп-
ругости. Во сколько раз будет увеличен объемный модуль, во столько же
раз можно допустить превышение истинных деформаций над условными
без нарушения устойчивости решения.
3. Ускорение сходимости также может нарушать устойчивость
решения. В результате этого возможно увеличение числа итераций, поэтому
необходимо, во-первых, ограничивать значения коэффициентов с(,) (на прак-
тике ограничивали коэффициенты ускорения от -0,5 до +20) и, во-вторых,
прекращать попытки ускорения, если приращения перемещений начинают
увеличиваться от итерации к итерации.
ПО 2. Моделирование процессов в металлах методом конечных элементов
2.5. Метод поэтапного расчета сварных конструкций
в комплексе «АСТРА-С»
Для корректной оценки параметров работоспособности конструкции
необходимо не только выявление наиболее нагруженных зон исследуемого
изделия, но и проведение детального анализа кинетики напряженно-
деформированного состояния с учетом наличия локальных концентраторов
напряжений, с последующей оценкой прочности и ресурса.
Для геометрически сложных объектов, состоящих из существенно
разнотолщинных элементов, трудно за один этап решения оценить НДС не
только конструкции в целом, но и отдельных, наиболее нагруженных зон, в
частности сварных швов. Задача еще более усложняется, если приходится
учитывать упругопластическое поведение материала на основе итерацион-
ных алгоритмов,, так как при этом необходимо многократное решение сис-
темы из многих десятков или сотен тысяч уравнений. В связи с этим эффек-
тивен метод поэтапного расчета (МПР), обладающий высокой универсаль-
ностью и позволяющий резко сократить вычислительные затраты.
Сущность МПР заключается в последовательном выделении подобла-
стей со все более подробной детализацией КЭ моделей, при этом граничные
условия для каждого этапа определяют по результатам предыдущего этапа
расчета. На первом этапе проводится анализ нагруженное™ конструкции в
целом от воздействия различных эксплуатационных нагрузок. При разра-
ботке модели различные мелкие детали, не влияющие на ее глобальную же-
сткость, могут быть опущены. На следующем этапе из этой модели выделя-
ют наиболее нагруженные фрагменты и для каждого из них поочередно
проводят более точный расчет. При этом каждый фрагмент разбивается на
большее количество КЭ. При необходимости могут быть добавлены и вто-
ростепенные детали, опущенные на предыдущем этапе расчета. Условиями
нагружения фрагмента помимо усилий, приложенных непосредственно к
нему, являются перемещения на его границах, определенные на предыду-
щем этапе решения. После расчета и анализа нагруженное™ фрагмента от-
дельные его зоны могут быть преобразованы в еще более подробные моде-
ли, т. е. этапов расчета может быть несколько.
Имеется ряд программных комплексов, в которых реализован МПР.
Как правило, этапы осуществляются для однотипных КЭ сеток, т. е. с пере-
ходом от плоской модели к плоской, или от объемной к объемной. Однако
на первом этапе анализа сложных листовых сварных конструкций наиболее
эффектавны пространственные модели из пластинчатых КЭ с шестью сте-
пенями свободы в узле, а для корректной оценки НДС в зонах сварных швов
их использование неприемлемо. В этом случае необходимо применять объ-
2.5. Метод поэтапного расчета сварных конструкций
111
емные КЭ, имеющие три степени свободы в узле. Следовательно, нужен ал-
горитм МПР с переходом от пространственной модели к объемной (здесь и
далее под пространственными подразумеваются модели с использованием
пластинчатых или оболочковых КЭ, а под объемными — с использованием
объемных КЭ).
Результаты натурного обследования сварных конструкций показыва-
ют, что наибольшее внимание при оценке прочности следует уделять зонам
сварных швов, где помимо холодных и горячих трещин, связанных с техно-
логическим процессом сварки или эксплуатационными нагрузками, сущест-
вует повышенная вероятность образования трещиноподобных дефектов ти-
па несплавлений, окисных пленок, подрезов, острых переходов от наплав-
ленного к основному металлу. Такие дефекты характерны для всех видов
сварных швов, но наиболее вероятны в угловых швах.
В реальных сварных соединениях наблюдаются случайные отклоне-
ния сварного шва от идеальной формы, причем иногда в широком диапазо-
не. Возможны различные дефекты. В довольно широких пределах изменя-
ются физико-механические свойства сварного соединения, т. е. все сварные
соединения являются неоднородными областями. Указанные явления при-
водят к концентрации напряжений и снижению усталостных и прочностных
характеристик соединения и определяют избирательный характер зарожде-
ния трещин в участках с наиболее неблагоприятным сочетанием геометри-
ческих и физических свойств. Степень опасности концентраторов различна
и зависит от их относительных размеров, вида нагружения, свойств мате-
риала. В общем случае задача еще более усложняется наличием остаточных
напряжений и многоосностью напряженного состояния.
Использование МКЭ совместно с автоматизированным МПР позволя-
ет рассчитать любую сварную конструкцию практически с любой требуемой
точностью, вплоть до моделирования отдельных сварочных дефектов. Од-
нако сам процесс моделирования дефектов довольно трудоемок. Кроме того,
при оценках работоспособности сварного объекта, в связи со случайным
характером расположения дефектов, их протяженности и формы, для доста-
точной статистической представительности результатов требуется проведе-
ние многочисленных расчетов, что значительно увеличивает трудоемкость
работ по подготовке КЭ моделей сварочных дефектов. Поэтому для оценки
работоспособности сварной конструкции при наличии сварочных дефектов,
те или иные типы которых допускаются различными нормативными мате-
риалами, логическим развитием МПР является вероятностная постановка
задачи и использование алгоритма автоматической генерации дефектов, об-
ладающих заданным комплексом характерных признаков.
Основным фактором, сдерживающим применение МПР, является вы-
сокая трудоемкость определения граничных условий между этапами, свя-
112 2. Моделирование процессов в металлах методом конечных элементов
занная как с большим количеством передаваемой информации, так и со
сложностью ее интерполяции на модель последующего этапа. В связи с
этим необходима полная или частичная автоматизация МПР.
При решении реальных задач возможны различные типы перехода от
этапа к этапу. Одним из наиболее сложных является переход от пространст-
венной модели к объемной. Эту задачу можно условно разделить на две са-
мостоятельные подзадачи:
1) преобразование угловых перемещений узлов пространственной мо-
дели к линейным перемещениям соответствующих корневых (общих для
предыдущего и последующего этапов) узлов объемной модели;
2) аппроксимация перемещений для остальных граничных узлов, до-
бавляемых при дискретизации объемного фрагмента.
Первая подзадача связана как с отсутствием угловых степеней свобо-
ды в объемной модели, так и с разнотипностью напряженного состояния в
пространственных и объемных КЭ. Решение второй подзадачи необходимо
для исключения разрыва сплошности полей деформаций по поверхности
выделяемого сечения. Различные тестовые решения показали, что неучет
этого фактора приводит к резкому искажению реальной картины НДС.
На рис. 2.16, а представлена модель 1-го этапа, состоящая из про-
странственных КЭ, а на рис 2.16, б — выделенный из нее фрагмент, соот-
ветствующий модели 2-го этапа, описанный в дальнейшем объемными КЭ.
Показаны оси X, Y, Z глобальных систем координат обеих моделей, а также
оси U, V, W местной системы координат первого подсечения первого сече-
ния. Сечением 1 на рис. 2.16, а называется плоскость, проходящая через уз-
лы 40—43, параллельная оси Z КЭ модель, а сечением 2 — плоскость, па-
раллельная оси Z и проходящая через узлы 7, 20. Первое сечение включает в
себя три стороны пространственных КЭ 40—41, 41—42, 42—43 и соответ-
ственно в объемной задаче имеет три ограниченные области, называемые в
дальнейшем подсечениями. Например, первое подсечение ограничено узлами
1—3—9—7 (см. рис. 2.16, б). Корневыми называются узлы КЭ модели 2-го
этапа, соответствующие узлам КЭ модели 1 -го этапа, но не лежащие на ней-
тральной оси пространственного КЭ, например узлы 1, 3, 7 и 9, но не 2, 8 и
т. д. Обведенные кружками номера узлов на рис. 2.16, б соответствуют но-
мерам узлов КЭ модели 1-го этапа.
Вектор граничных перемещений модели 2-го этапа рассчитывается в
глобальной системе координат, но преобразование угловых перемещений в
линейные возможно только с учетом реального расположения плоскости
текущего КЭ модели 1-го этапа.
Реальное расположение плоскости текущего КЭ рассчитывается по
координатам соответствующих двух узлов контура модели 1-го этапа и до-
полнительного узла ориентации сечения, задаваемого в исходных данных.
2.5. Метод поэтапного расчета сварных конструкций
113
Рис. 2.16. Пространственная КЭ модель 1-го этапа (а), выделенный из нее фрагмент
объемной КЭ модели (б) и схема к пересчету угловых деформаций в линейные (в)
Для фрагмента объемной модели (см. рис. 2.16, б) в качестве узлов контура
следует задать лежащие на оси пространственной модели узлы 2 и 8, а в ка-
честве узла ориентации плоскости сечения — любой из не лежащих на оси
узлов 1, 3,4,6, 7 или 9.
Преобразование угловых перемещений узлов модели 1-го этапа к ли-
нейным перемещениям корневых узлов модели 2-го этапа осуществляется в
соответствии с гипотезой плоских сечений. В связи с малостью деформаций,
в зависимости от угла <р вычисляется только вектор dW (рис. 2.16, в) или
аналогичный, добавки ЛК и AW не учитываются. Проведенные тестовые
расчеты подтвердили их несущественное влияние.
Существенной является поправка, компенсирующая игнорирование
деформаций по толщине листа в тонкостенных пространственных КЭ. Для
114 2. Моделирование процессов в металлах методом конечных элементов
ее внесения рассчитываются усилия, действующие по нормали к плоскости
соответствующего пространственного КЭ и вызванные ими деформации
объемного КЭ. Расчеты без этой поправки могут приводить к заметному ис-
кажению НДС в одном или двух приграничных слоях объемных КЭ.
Исходными данными являются номера узлов моделей 1-го и 2-го
этапов, принадлежащих сечениям, по которым выделяется модель 2-го
этапа. Можно задавать не номера узлов, а только параметры секущих
плоскостей с последующей автоматической выборкой соответствующих
узлов. Это возможно в случае, когда сечение, по которому выделяется
модель 2-го этапа, является плоскостью или поверхностью второго порядка.
Для аппроксимации перемещений промежуточных узлов необходимо
установить закономерность изменения поля перемещений относительно по-
верхности сечения. Так как в область сечения может входить различное ко-
личество КЭ предыдущего этапа, то при реализации алгоритма коэффици-
енты аппроксимации определялись последовательно, для каждой пары со-
пряженных КЭ. При этом использован неполный полином 3-й степени, т. е.
решалась система уравнений вида
Ax^yt + Bx^j + Cxf + Dy? + Exiyi + Fxt + Gyt + P-q^ (2.32)
где А, В, C, D, E, F, G, P — искомые коэффициенты уравнения аппроксима-
ции перемещений; , yt — координаты узлов, в которых рассчитаны ком-
поненты перемещений q,. Система уравнений была решена аналитически и
получены зависимости для расчета коэффициентов уравнения (2.32) относи-
тельно местной системы координат текущего подсечения.
Поскольку уравнения аппроксимации строятся локально (только для
двух сопряженных подсечений), то в зонах сопряжения мотут возникать разры-
вы вследствие различия коэффициентов аппроксимации. Во избежание этого
уравнения аппроксимации строятся с перекрытием по соседним подсечениям, а
компоненты перемещений в зонах перекрытия усредняются. Подобный подход
обеспечивает однородную, достаточно точную схему аппроксимации при раз-
личной дискретизации пространственной модели 1-го этапа.
Координаты промежуточных узлов подсечения и + 1 в системе коор-
динат U, V, W и-го подсечения определяются после предварительного пово-
рота плоскости подсечения п + 1 до совпадения с плоскостью и-го подсече-
ния. Это обеспечивает возможность проведения выделяющего сечения по
произвольной ломаной линии.
В реальных задачах, например при расчете сферических или цилинд-
рических объектов относительно небольшого радиуса, может возникнуть
необходимость выделения фрагмента по кривой. В этом случае промежу-
точные узлы объемной модели могут не совпадать с гранью пространствен-
2.5. Метод поэтапного расчета сварных конструкций
115
ных КЭ. Для аппроксимации
перемещений по криволиней-
ной области определяются на-
правления осей криволинейной
системы координат R, S, Т двух
сопряженных подсечений по
координатам их корневых уз-
лов (рис. 2.17). Далее для каж-
дого подсечения рассчитывает-
ся матрица Якоби J, устанав-
ливающая связь между
производными по глобальным
координатам X, Y, Z и по кри-
волинейным координатам об-
ласти/?, S, Т:
Рис. 2.17. Схема криволинейных координат
подсечения
J д(х, у, z)
d(r,s,t)
dx dy dz
dr dr dr
dx dy dz
ds ds ds
dx dy dz
dt dt dt
(2.33)
В местной криволинейной системе координат R, S, Т находим коорди-
наты узлов модели 2-го этапа для текущей пары подсечений
{r,s,tY =J-\x,y,z}, (2.34)
где J1 — обратная матрица Якоби. Далее по перемещениям корневых узлов
в глобальной системе координат определяем перемещения всех узлов каж-
дого подсечения
Qi = + h2i4i + - + hSiq&, (2.35)
где Qi — перемещение i-ro промежуточного узла подсечения; qt... q& —
перемещения корневых узлов текущей пары подсечений; Иц ... — значе-
ния интерполяционных функций, рассчитанные для координат i-ro проме-
жуточного узла. Интерполяционные функции, соответствующие неполному
кубическому полиному (2.32), могут быть записаны в следующем виде:
hfl = 0,125(1+ Л0)(1 + 50)(1 + Т0)(Л0+50 + 7J, -2) при j = 1, 3, 5, 7; (2.36)
hjt = 0,25(1 - /?,2)(1 + 50)(1 + То) при j = 2, 6; (2.37)
116 2. Моделирование процессов в металлах методом конечных элементов
Рис. 2.18. Фрагмент КЭ модели штампосварной соединительной бал-
ки четырехосной тележки восьмиосного вагона
= 0,25(1 -S,2)(l + Яо)(1 + Го) при j = 4, 8, (2.38)
где 7?О = 7?;7?(; So = S;S/, Т0 = Т}Тр, R}., Sj, Tj — значения координаты /-го
корневого узла; R,, S,-, Tt — значения координаты z-ro промежуточного узла.
Из задач поэтапного перехода с одинаковой размерностью наиболее
сложным является переход от объемной модели конструкции к объемной
модели ее фрагмента. Такие переходы необходимы для сокращения количе-
ства параметров решаемой задачи.
На рис. 2.18 представлен фрагмент модели штампосварной балки
восьмиосного вагона с 5744 объемными 20-узловыми КЭ и с более 100000
степеней свободы. Для оценки кинетики НДС в зонах сварочных дефектов
данной конструкции необходимо дополнительное измельчение ее элементов
как минимум в 6—8 раз по каждому направлению. Это приводит к увеличе-
нию количества узлов модели и времени решения задачи на 2—3 порядка,
что даже при учете мощности современных ЭВМ явно нецелесообразно.
Проблема перехода в том, что в модели последующего этапа количе-
ство узлов на границах выделяемого фрагмента больше, чем в модели пре-
дыдущего этапа. В связи с этим необходима аппроксимация перемещений
на все узлы границы модели последующего этапа.
В алгоритме, реализующем данный тип межэтапного перехода в ком-
плексе «АСТРА-С», обеспечено автоматическое определение номеров узлов
моделей обоих этапов, попадающих в выделяющее сечение. В исходных
данных задается только минимально достаточное количество номеров узлов,
2.5. Метод поэтапного расчета сварных конструкций
117
однозначно определяющих соответствующую поверхность. Далее по коор-
динатам узлов модели и уравнению поверхности сечения определяются уз-
лы, попадающие в сечение. Допуск А на отклонение от поверхности задает-
ся в исходных данных или определяется автоматически по эмпирической
зависимости, учитывающей габаритные размеры моделируемой конструк-
ции (А, Б, С) и количество узлов модели (N);
А = 0,0 1у](А2 + Б2 + С2 )?N. (2.39)
Для расчета граничных перемещений в узлах модели последующего
этапа по их известным компонентам в узлах модели предыдущего этапа не-
обходимо установить некоторый закон, в соответствии с которым возможно
изменение поля перемещений относительно поверхности сечения. Как и при
переходе от пространственной модели к объемной, целесообразно уравне-
ния поверхности уровня компонентов перемещений строить не для всего
сечения, а локально, для подсечений.
Каждое подсечение может содержать от шести до восьми узлов моде-
ли предыдущего этапа. Поиск узлов подсечений осуществляется автомати-
чески. Для этого, если выделяющее сечение — плоскость, все координаты
узлов сечения преобразуются к системе координат секущей плоскости и ре-
шается двумерная задача принадлежности точки многоугольнику (т. е. под-
сечению). В случае криволинейного сечения по координатам узлов модели
предыдущего этапа для каждого подсечения определяется своя криволиней-
ная система координат R, S, Т. Далее для каждого подсечения рассчитывает-
ся матрица Якоби J (2.33). Пользуясь зависимостью (2.34), находим коорди-
наты узлов модели последующего этапа в местной криволинейной системе
координат R, S, Т текущего подсечения. При этом для узлов, принадлежа-
щих текущему подсечению, выполняется условие |Л, 5| < 1.
В случае, если выделяющее сечение состоит из плоскости или сово-
купности плоскостей, для аппроксимации используется неполный полином
3-й степени (2.32) или полином более низкой степени при количестве узлов
в текущем подсечении менее восьми. Для обеспечения непрерывности ап-
проксимации строятся с перекрытием по соседним подсечениям, с после-
дующим усреднением.
Если выделяющее сечение не плоскость, то для определения переме-
щений в дополнительных узлах используется зависимость
Qi =htiqt +Мг + - + (2-40)
где qt... qj — перемещения в узлах модели предыдущего этапа (у = 6...8);
hu...hji — значения интерполяционных функций, рассчитанные для коорди-
нат z-ro промежуточного узла.
118 2. Моделирование процессов в металлах методом конечных элементов
Интерполяционные функции могут быть записаны в следующем виде:
h\ = gi(g5 + g8); = gj{gj+ A + gj+ 3) при j = 2, 3, 4; hj = g7 при j = 5, 8; (2.41)
gj = G(R, Ri) • G(S, St) • G(T, Tt) при 7=1,8; (2.42)
G(P, P,) = 0,5(1 + P,P) при p,= ±1; G(P, P,) = (1 - p2) при p,= 0, (2.43)
где fi = R,S,T.
Разработанные алгоритмы автоматизированного межэтапного пере-
хода были апробированы при решении тестовых задач и расчетах реальных
сварных конструкций и показали удовлетворительные результаты.
Естественным развитием МПР является моделирование сварочных
дефектов. Для оценки работоспособности сварной конструкции при
наличии дефектов необходимы вероятностная постановка задачи оценки
работоспособности исследуемого объекта и использование алгоритма
автоматической генерации дефектов, обладающих заданным комплексом
характерных признаков.
Весьма распространен дефект в виде поры или шлакового включения.
В качестве признаков такого дефекта должен быть задан диапазон размеров
(max, min), предполагаемая вероятность его возникновения по длине и глу-
бине сварного шва, а также максимально возможное количество дефектов на
длине L. Размер поры, ее форма и место расположения являются случайны-
ми параметрами. Для генерации таких дефектов в модели использован сле-
дующий подход.
1. Исходная бездефектная модель исследуемого сварного соединения
описывается квадратичными 8-узловыми изопараметрическими КЭ.
2. Дефект моделируется в пределах одного КЭ модели. Если размер
поры больше максимального размера дефекта, который может быть разме-
щен внутри данного КЭ, то дефект моделируется в пределах нескольких
смежных КЭ.
3. Место расположения дефекта определяется с использованием стан-
дартного генератора случайных чисел.
4. Моделирование формы и размеров самой поры осуществляется ав-
томатически по программе, построенной на следующих принципах.
4.1. Универсальная модель дефекта строится на области, обладающей
8 или 16 внешними узлами (под внешними узлами подразумеваются узлы
исходной модели сварного соединения).
4.2. Универсальная модель дефекта включает фиксированное количе-
ство внутренних узлов и квадратичных 8-узловых изопараметрических КЭ
(рис. 2.19).
4.3. Основные относительные размеры КЭ внутри модели дефекта
фиксированы в ее местных криволинейных координатах -1 < \R, Sj +1.
2.5. Метод поэтапного расчета сварных конструкций
119
4.4. Максимальный диа-
метр поры в пределах исход-
ного КЭ (или совокупности че-
тырех КЭ) составляет 1/8 от
стороны КЭ (или удвоенной
стороны КЭ). Минимальный
размер не ограничен.
4.5. Выбор условия мо-
делирования поры на базе од-
ного или четырех КЭ осуще-
ствляется автоматически в за-
висимости от абсолютных
размеров текущего КЭ и мак-
симально возможного размера
поры — е/max (заданного рас-
четчиком).
4.6. Окончательная фор-
ма и размеры моделируемой
поры определяются автомати-
чески следующим образом:
Q-узлыКЭ модели предыдущего этапа
Рис. 2.19. Базовая двумерная модель
для автоматической генерации дефекта
типа поры или шлакового включения
а) устанавливается базо-
вый диаметр поры, равный 0,5dmax;
б) на окружности, моделирующей базовую форму поры, устанав-
ливаются четыре полюса, отстоящие друг от друга на 90° (или восемь полю-
сов через 45° при необходимости моделирования более сложной формы);
в) по зависимости диаметра поры dn = 0,25dmax + А определяется рас-
стояние до каждого полюса, где А = (-0,25... + 0,25)(<7max - (7mjn). Значение А
из указанного диапазона выбирается автоматически с помощью генератора
случайных чисел;
г) через полюса проводится кривая, являющаяся внешним контуром поры;
д) окончательные координаты узлов моделируемой области опреде-
ляются из соотношений между декартовой и криволинейной системой коор-
динат.
Таким образом, предлагаемая методика автоматически обеспечивает тре-
буемую изначально степень неопределенности места возникновения и формы
дефекта, которая при использовании данного алгоритма может изменяться от
круглой поры до щелевидного или точечного дефекта. Особенностью данного
алгоритма также является то, что окончательные расчеты ведутся на ограни-
ченной области с заранее известными фиксированными параметрами, т. е. по-
является возможность прогнозировать время, требуемое для проведения много-
вариантных вероятностных расчетов с требуемой точностью.
120 2. Моделирование процессов в металлах методом конечных элементов
Аналогичный подход использован при разработке универсальных
объемных моделей дефектов сварных швов, а также при моделировании де-
фектов типа подреза, наплыва и непровара корня шва.
При использовании разработанного методического и программного
обеспечения возможно решение двух задач. В первом случае, если расчетчика
интересует поверочная оценка ресурса конструкции и выявление параметров,
определяющих изучаемый процесс, предполагается, что допуски на размеры
того или иного типа дефектов известны, и при вероятностной обработке ре-
зультатов расчетов фактически проводится поверочный расчет допустимости
установленных нормативными материалами дефектов. Во втором случае реша-
ется обратная задача, т. е. при заданном ресурсе конструкции устанавливаются
закономерности влияния типа и размеров дефектов на ресурс и в результате
определяются максимально допустимые параметры дефектов.
2.6. Суперэлементы для решения сварочных задач
в комплексе «WELD3D»
Метод суперэлементов (МСЭ) целесообразно применять для расчета
конструкций, превосходящих определенную степень сложности. В этом
случае расчетная схема строится не сразу для всей конструкции (как в
обычном МКЭ), а в несколько этапов — уровней, причем описание КЭ вы-
полняется на самом нижнем уровне. Полная конструкция представляется в
виде совокупности соподчиненных подконструкций различных уровней.
Повторяющиеся части конструкции представляются типовым описанием и в
процессе расчета могут использоваться неоднократно. Такое построение
схемы позволяет сократить время, затрачиваемое на подготовку исходных
данных и выполнение расчета. Причем любое изменение местных парамет-
ров, а также замена части конструкции не требует полного пересчета всей
задачи, поскольку корректировке в таких случаях подлежат лишь описания
отдельных подконструкций.
Рассмотрим узел конструкции объемом v, для которого требуется най-
ти функцию распределения перемещений Aw(x, у, z), удовлетворяющую ус-
ловиям равновесия напряжений и совместности деформаций во внутренних
точках и заданным граничным условиям на поверхности (см. § 2.4).
Процедура МКЭ состоит в построении дискретной модели детали из
КЭ и отыскании значений функции Дг/(х, у, z) в ее узлах при заданной ап-
проксимации между' узлами.
Если разбить всю деталь на части vb г2, ..., V/, ..., v„„ то в каждой из
частей vi искомая функция локально аппроксимируется функцией вида (2.5).
2.6. Суперэлементы для решения сварочных задач
121
Если какая-то из частей имеет сложную форму, то может оказаться,
что узловых точек на ее границе недостаточно для получения необходимой
точности аппроксимации внутри нее. Тогда можно ввести в нее дополни-
тельные внутренние узлы и разбить ее на более мелкие части.
Если эти части имеют простую форму и для них удается сразу построить
непрерывную аппроксимацию искомой функции, то их можно считать КЭ.
Часть детали (подконструкция), состоящая из нескольких смежных
КЭ, может быть названа суперэлементом (СЭ).
Ключевым моментом МСЭ является возможность анализировать по-
ведение конструкции, состоящей из СЭ, взаимодействующих между собой
только в граничных узлах, без непосредственного участия данных о внут-
ренних узлах и элементах, из которых состоят СЭ. Для этого необходимо
построить полное описание поведения СЭ через параметры в его граничных
узлах.
Суперэлементный подход не препятствует заданию нагрузок во внут-
ренних узлах и различных свойств материалов во внутренних элементах.
Одной из основных задач процедуры МСЭ является учет жесткости внут-
ренних элементов при построении матрицы жесткости СЭ и перераспреде-
ление распределенных нагрузок с внутренних на граничные узлы.
Равновесие каждого СЭ, как самостоятельной единицы, описывается
через узловые параметры системой уравнений, аналогичной (2.6):
[К] {ДС7} = {F},
(2.44)
где [К], {AC/}, {F} — матрица жесткости СЭ и вектора перемещений и уси-
лий в его узлах.
Разделяя узлы СЭ на внутренние и внешние, запишем уравнение рав-
новесия СЭ в блочном виде:
ки
Ksi ’
(2.45)
где i, s — индексы внутренних и внешних (граничных) узлов.
Вектор узловых перемещений можно представить в виде суперпози-
ции двух составляющих:
{дЛ^'Ы^2}-
(2.46)
Первая из них — вектор перемещений узлов СЭ, вызванных приложе-
нием нагрузок {FJ к внутренним узлам, при неподвижных граничных узлах,
т. е. при {Д(4} = {0}; вторая — вектор перемещений всех узлов СЭ под дей-
122 2. Моделирование процессов в металлах методом конечных элементов
At/’
At/’
Н'1=
ствием перемещений граничных узлов {А 14}, но при отсутствии приложен-
ных к внутренним узлам сил: {F,} = {0}.
Разложение вектора {At/} позволяет отделить внутреннее поведение
СЭ от его взаимодействия с остальными СЭ и граничными условиями модели.
Таким образом, {At/,} = {At/’} + {At/2}; {АЦ}-{At/2}.
Аналогично: {7}}^{F2}; {Fs} = {F'} + {Fs2}.
При отсутствии перемещений в граничных узлах получаем
{а(/'}=[Хй№}, (2.47)
' {F1- (2-48)
0 J
Значения узловых перемещений во всех узлах от перемещения гра-
ничных узлов, естественно, пропорциональны перемещениям граничных
узлов, т. е. выражаются через них с помощью некоторой матрицы [А]:
{а(/2}= [A]{At/J, (2.49)
которая по аналогии с функциями формы КЭ (2.3) называется матрицей
функций формы СЭ. Из теоремы о взаимности работ следует, что та же мат-
рица позволяет перераспределить силы, приложенные ко всем узлам СЭ, на
его граничные узлы
{ЛЬМ» (2-50)
и построить матрицу жесткости СЭ, связывающую силы и перемещения в
его граничных узлах:
(2.5i)
Вектор узловых сил {/} отличается от {FJ тем, что к силам, непо-
средственно действующим на граничные узлы, добавлены составляющие от
перераспределения сил, приложенных к внутренним узлам. Аналогично
отличается от [KSJ тем, что учитывает наличие в СЭ внутренних узлов и
элементов и позволяет использовать его в составе модели без рассмотрения
внутренних узлов. В результате уравнение равновесия СЭ приведено к не-
обходимому виду:
kJk/.bU)- р-52)
Математически это эквивалентно тому, что при последовательном ис-
ключении неизвестных системы линейных уравнений методом Гаусса внут-
ренним узлам были присвоены первые номера и к моменту получения (2.52)
2.6. Суперэлементы для решения сварочных задач
123
неизвестные перемещения внутренних узлов исключены из системы урав-
нений, а граничные еще нет.
Физический смысл последовательного исключения неизвестных из сис-
темы уравнений, каждое из которых является уравнением равновесия одного из
узлов, в данном случае состоит в том, что силы, приложенные к исключаемому
узлу, переносятся на соседние узлы и соответствующим образом увеличивается
их жесткость за счет добавления жесткости элементов, примыкающих к ис-
ключаемому узлу. Из этого физического анализа ясно, что этапы составления
матрицы (добавление к модели новых частей) и исключения неизвестных (вы-
деление СЭ) можно чередовать, как это и делается в МСЭ.
Определим матрицу [7V] формы СЭ, которая является его главной ха-
рактеристикой:
Д(/'1 Где/2
о J [дс/2
(2.53)
Это матричное уравнение можно представить в виде двух уравнений:
кЛИ 1+kJW 1+kJHJ=kb (2-54)
КЙ}+ к,]{дЦ2}+ kJkt/J = {Fs}. (2.55)
Из (2.47) и (2.54) следует
{д^М^кКд^}-
Тогда
{д£/2}= = Г М{ДUs},
1 J [д(/;] [ k] J
(2.56)
где [Е] — единичная матрица порядка s (s — число неизвестных узловых
перемещений ЛЦД
Из (2.56) следует, что матрица формы СЭ
-kJ’kJ
к] .
(2.57)
Теперь легко представить зависимости для определения матрицы же-
сткости [Е| (см. уравнение (2.51)) и вектора узловых усилий {/} СЭ:
= = (2-58)
Ш = {?,} - [^ ][^й Г1 {Л } (2-59)
124 2. Моделирование процессов в металлах методом конечных элементов
Эти два соотношения описывают алгоритм построения сокращенной
алгебраической модели СЭ, если его уравнения представлены в виде (2.45).
Таким образом, СЭ, определяя поведение подструктуры через пара-
метры в граничных узлах, обладает только теми свойствами подструктуры,
которые требуются для описания взаимодействия СЭ при их сборке.
СЭ первого уровня образуются в результате группировки исходных
КЭ (они же базовые КЭ, они же СЭ нулевого уровня). Каждый СЭ представ-
ляет собой модель вполне определенной подконструкции. Матрицы жестко-
сти и вектора нагрузки СЭ вначале составляются для всех узлов, т. е. обра-
зуются простым поузловым суммированием матриц и векторов входящих в
подконструкцию элементов, как обычно в МКЭ.
Далее в целях уменьшения порядка составляющих матриц строят
сокращенные модели СЭ, включающие в себя только граничные узлы
(см. уравнения (2.44)—(2.59)). Из полученных СЭ первого уровня затем
можно собрать СЭ второго уровня и снова исключить из рассмотрения
узлы, оказавшиеся внутри СЭ. Эта процедура носит название прямого
хода в решении задачи.
Уровней может быть несколько, вплоть до сведения конструкции к
одному СЭ. Каждый переход на следующий уровень требует дополнитель-
ных операций, но позволяет понизить общее число неизвестных в системе
уравнений, требующей решения. Наибольший эффект имеет место от введе-
ния первого уровня СЭ. Каждый следующий уровень позволяет исключать
все меньшее число неизвестных. Таким образом, МКЭ можно считать част-
ным случаем МСЭ с СЭ только нулевого уровня.
Полученная модель полной конструкции представляет собой сис-
тему уравнений равновесия (2.44), в которой матрицей коэффициентов
является матрица жесткости, а вектором правых частей — вектор узло-
вых усилий подструктуры самого верхнего уровня. В результате решения
этой системы находят значения перемещений во всех узловых точках
подструктуры.
Кинематические граничные условия реализуются в виде связей, на-
кладываемых на узловые перемещения и ограничивающих свободу пере-
мещения модели в пространстве. При этом совокупность кинематических
связей должна полностью исключать перемещения модели как жесткого
целого.
Силовые граничные условия отражают внешнее нагружение конст-
рукции. Тем или иным способом внешние воздействия приводятся к эквива-
лентным узловым нагрузкам, которые в модели образуют векторы узловых
усилий.
Как силовые, так и кинематические граничные условия могут накла-
дываться в процессе прямого хода на подконструкцию любого уровня (при
2.6. Суперэлементы для решения сварочных задан
125
условии, что узловая точка, к которой приводятся граничные условия, не
была исключена на предыдущих уровнях). Распределенные и сосредоточен-
ные нагрузки, как отмечалось, приводятся к узловым. Так как при этом не-
обходимо иметь информацию о геометрических и физических параметрах
модели, а такая информация имеется в явном виде только на уровне базовых
КЭ, то введение распределенных и узловых нагрузок происходит только на
этом уровне.
Системы уравнений МСЭ (2.44) в отличие от систем уравнений МКЭ
характеризуются меньшим порядком и большей заполненностью матрицы
ненулевыми коэффициентами. Матрица жесткости остается симметричной и
положительно определенной. Диагональные коэффициенты матрицы (2.52)
преобладают над остальными.
Решение системы уравнений МСЭ дает перемещения в граничных уз-
лах СЭ верхнего уровня. Далее последовательно вычисляют перемещения
во всех внутренних узлах СЭ, исключенных из рассмотрения в процессе
уровневой сборки. Важно, что среди узлов любого СЭ присутствуют все
граничные узлы составляющих его СЭ более низкого уровня, т. е. значения
в узлах СЭ являются граничными узловыми перемещениями для СЭ преды-
дущего уровня.
При известных значениях перемещений в узлах и заданной внеш-
ней нагрузке каждый СЭ можно рассчитывать отдельно. В результате
решения таких небольших задач находят перемещения во внутренних
узловых точках. После прохода по всем уровням СЭ находят перемеще-
ния во всех узлах рассчитываемой конструкции. Этот этап решения зада-
чи называется обратным ходом. По перемещениям узлов, в соответствии
с алгоритмом МКЭ, рассчитываются деформации и напряжения (2.6,
2.11,2.13,2.24, 2.25,2.26).
При решении задач моделирования процессов сварки и наплавки
обычно имеет место повторяемость дискретной модели в направлении пе-
ремещения сварочного источника теплоты, т. е. модель можно построить
так, чтобы слои элементов полностью повторяли друг друга. В этом случае
преимущества МСЭ по сравнению с обычным МКЭ можно использовать в
полной мере. Так как все СЭ верхнего уровня имеют одинаковую внутрен-
нюю структуру, базовые матрицы жесткости вычисляются только для пер-
вого из них. Для остальных матрицы не вычисляются, а получаются копиро-
ванием или поворотом базовых матриц (операция поворота осуществляется
на порядок быстрее, чем операция составления матрицы). Вычисляются и
записываются два типа базовых матриц: — для случая, когда разделка
еще не заполнена; В2 — когда разделка заварена и остыла до температуры
Т*, ниже которой свойства материала, такие, как модуль упругости и коэф-
фициент Пуассона, можно считать неизменными. В процессе продвижения
126 2. Моделирование процессов в металлах методом конечных элементов
сварочного источника по свариваемой кромке для элементов, находящихся
перед источником, используются матрицы 51. Для элементов позади источ-
ника, остывших до температуры 7*, используются матрицы 52. Для элемен-
тов, находящихся в зоне действия источника (Г > Г*), матрицы пересостав-
ляются после каждого шага.
Если полная повторяемость слоев элементов, объединенных в СЭ, от-
сутствует и нельзя использовать базовые матрицы, суперэлементный алго-
ритм все равно дает большие вычислительные преимущества. Рассматри-
ваемые задачи являются многошаговыми, причем изменение матриц каждо-
го СЭ вследствие температурного воздействия и изменения механических
свойств имеет место только на некотором небольшом числе шагов, когда СЭ
находится в зоне влияния сварочного источника теплоты. Таким образом,
существенная экономия времени счета и оперативной памяти ЭВМ дости-
гается за счет того, что матрица жесткости конструкции на каждом шаге пе-
ресоставляется лишь частично, в то время как основная ее часть не изменя-
ется и сохраняется на внешней памяти ЭВМ. Выбор числа уровней зависит
от особенностей задачи и компьютера и обычно производится по результа-
там численных экспериментов.
Сопоставление МСЭ с МПР (см. § 2.5) показывает, что в этих двух пу-
тях сокращения вычислительных затрат много общего: конструкция разби-
вается на достаточно крупные подконструкции, поведение материала во
внутренних точках уточняется при дальнейшем расчете. Различие же их в
том, что в МПР не отслеживаются обратные связи, т. е. влияние внутренней
структуры подконструкций на перемещения их узлов. Это различие менее
существенно при внешнем нагружении конструкции. Для таких задач МПР
имеет преимущества по производительности и универсальности (сочетание
пластинчатых изгибаемых и массивных элементов). Для моделирования
сварочных процессов, в которых источником нагружения конструкции в
целом являются процессы неравномерного нагрева в зоне шва, примени-
мость МПР проблематична.
Сопоставление обоих подходов с МКЭ показывает, что эффект их
применения растет с ростом числа элементов моделей, но требует некото-
рых накладных расходов. Поэтому для небольших по числу элементов, но
сложных по форме и распределению свойств материала моделей наиболее
эффективными являются обычные модели МКЭ.
В связи с большим объемом вычислений, в МКЭ применяют целый
ряд приемов для экономии ресурсов ЭВМ. Каждый из них имеет свою об-
ласть эффективного применения. Общий принцип таков: чем сложнее про-
цесс, тем проще должен быть алгоритм моделирования. Если искомая функ-
ция имеет большие градиенты, резко изменяется во времени и уравнения
для ее определения нелинейны, то неизбежны увеличение числа элементов
2.6. Суперэлементы для решения сварочных задач
127
модели, шагов и итераций решения и соответствующий рост затрат опера-
тивной памяти и времени счета ЭВМ.
Экономия достигается за счет выявления и использования скрытой
простоты в решаемой задаче. Например, если искомая функция плавная, то
эффективно применение элементов высокого порядка; если для нее заранее
известны места с большими градиентами, то можно разбить на мелкие эле-
менты только эти части модели. Если процесс протекает плавно во времени,
то можно укрупнить шаги, перейдя от явной схемы решения к неявной. Ус-
корение сходимости итераций возможно, если процесс сходимости плавный
и монотонный. Применение МСЭ эффективно при наличии в модели повто-
ряющихся частей, а МПР — при слабом влиянии наиболее важной части
модели на поведение модели в целом. Экономия от замены решения связной
задачи последовательным решением входящих в нее подзадач возможна при
несущественном влиянии обратных связей.
Рост возможностей ЭВМ облегчает решение традиционных задач, но
одновременно открывает возможности для постановки новых задач, ранее
считавшихся неразрешимыми. Поэтому развитие программных средств мо-
делирования процессов сохраняет свою актуальность.
3. ПРОЕКТНЫЕ И КОНТРОЛЬНЫЕ РАСЧЕТЫ
НА ПРОЧНОСТЬ НА ОСНОВЕ МОДЕЛИРОВАНИЯ
ПРОЦЕССА РАЗРУШЕНИЯ
3.1. Закономерности процесса разрушения сварных соединений
и принципы построения проектных и контрольных расчетов
Важный этап проектирования конструкции — обеспечение ее работо-
способности, надежности и экономичности за счет рационального выбора
размеров и материалов для нагруженных элементов. Оптимально спроекти-
рованной можно считать такую конструкцию, которая при минимальных
затратах (металла, труда и т. д.) обеспечивает необходимые эксплуатацион-
ные показатели.
Одним из важнейших показателей качества является отсутствие раз-
рушений в течение срока эксплуатации при всех вероятных нормальных и
экстремальных нагрузках. Для этого при проектировании нужно обеспечить,
чтобы рабочее состояние конструкции, характеризуемое напряжениями и
деформациями в ее сечениях, не достигало ни одного из предельных состоя-
ний. В то же время рабочее состояние должно быть максимально приближе-
но к предельным, так как только в этом случае возможно получение конст-
рукции с минимальной массой и стоимостью.
Наиболее опасным предельным состоянием конструкции является ее
внезапное разрушение в процессе эксплуатации. В этой главе на примере
анализа этого важного предельного состояния рассмотрен подход к прочно-
стным расчетам при проектировании новых и оценке качества готовых кон-
струкций, основные этапы которого для сложных конструкций требуют
применения современных компьютерных методов.
Возможность полного использования прочности и пластичности мате-
риала с гарантией отсутствия разрушений обусловлена степенью приближе-
ния расчетной прочности к конструкционной. Под расчетной прочностью
понимают способность конструкции сопротивляться наступлению предель-
ных состояний, установленную на основе аппарата теории, характеристик
материала и условий нагружения; под конструкционной (фактической) — ту
же способность, но установленную при испытании или эксплуатации для
3.1. Закономерности процесса разрушения сварных соединений
129
Рис. 3.1. Изменение вероятности разрушения конструкции под влияни-
ем технологии изготовления: 7; 4 — идеальная технология; 2; 3 — ре-
альная технология; 3; 4 — локальные свойства
конкретной конструкции. Возможность оптимизации конструкции и техно-
логии ее изготовления с позиций прочности во многом зависит от близости
расчетной прочности к конструкционной, поэтому их сближение — одна из
важных задач производственников и проектировщиков. Расхождение между
ними связано как с несовершенством методики расчета, так и с рассеянием
значений конструкционной прочности.
Конструкционная прочность по своей природе имеет рассеяние значе-
ний, поскольку случайные колебания характерны для свойств сварного со-
единения, размеров элементов конструкций, степени засоренности дефекта-
ми, их размеров и расположения. Чтобы учесть многообразие причин сни-
жения конструкционной прочности по сравнению с расчетной, необходимо
в качестве критерия принять наступление разрушения и сопоставлять ло-
кальное НДС металла с локальными свойствами сварного соединения в
предполагаемой зоне разрушения. При этом расчеты должны строиться на
вероятностной основе.
Расчетный и фактический запасы прочности схематично показаны
на рис. 3.1. Расчетный запас прочности характеризуется взаимным рас-
положением кривых 1 и 4. Под влиянием технологического процесса в
результате искажений проектной формы и размеров сварной конструк-
ции, появления остаточных напряжений и дефектов в сварных швах, из-
менения механических свойств и возникновения механической неодно-
родности напряженность конструкции повышается, а уровень свойств
металла может снижаться. Взаимное расположение кривых 2 и 3 характе-
ризует запас конструкционной прочности. Очевидно, что он всегда
меньше запаса расчетной прочности и существенно зависит от техноло-
гии изготовления.
5 - 6705
130
3. Проектные и контрольные расчеты на прочность
В отраслях промышленности на основе статистических данных сложи-
лись определенные представления о возможностях различных способов сварки,
отражающие реальные условия конкретного производства, и выработаны нор-
мы качества, регламентирующие вид и размеры дефектов, считающихся допус-
тимыми. Применение современных методов контроля качества за счет отбра-
ковки дефектных изделий раздвигает границу между кривыми 2 и 3, но при
этом необходимо учитывать, что ни один из существующих методов контроля
не исключает существования в сварных швах дефектов, размеры которых вы-
ходят за границы норм качества. Очевидно, что современные методы расчета
прочности помимо стандартных расчетов прочности должны базироваться и на
концепции существования в сварной конструкции дефектов, в том числе тре-
щиноподобных, и, следовательно, в основе расчетов должно лежать моделиро-
вание разрушения сварного соединения.
До настоящего времени в нормах проектирования проблема безопас-
ности часто решается введением больших коэффициентов запаса. В сравни-
тельно простых случаях эти коэффициенты способны скомпенсировать не-
полноту' расчета и обеспечить разработку рациональной и безопасной кон-
струкции на основе упрощенной расчетной схемы, не учитывающей
некоторых факторов, влияющих на прочность. Для более сложных конст-
рукций и условий их работы возможна ситуация, когда влияние отдельных
факторов не находится в корреляционной связи и неучет одного из таких
факторов не может быть скомпенсирован никаким запасом по другому.
Наиболее сложными объектами являются сварные конструкции. При
их расчете возникает ряд проблем, связанных с неоднородностью свойств
материала, сложностью формы, наличием конструктивных и технологиче-
ских концентраторов напряжений, остаточных напряжений и т. д. Особую
сложность задачам анализа и обеспечения работоспособности конструкции
придает не какой-нибудь один из перечисленных факторов, а возможность
сочетания и взаимодействия сразу нескольких из них в небольшом объеме,
практически в одной точке.
При проектировании конструктор должен исходить из бездефектности
сварных соединений, иначе он с самого начала санкционирует снижение
культуры производства и увеличение массы проектируемого изделия за счет
понижения эксплуатационных напряжений. Но поскольку влияние дефектов
на работоспособность все же возможно, появляется необходимость в оценке
достаточности действующих на предприятии или в отрасли технологиче-
ских требований по допустимому размеру дефекта.
Нагружение с этой целью готовой конструкции до разрушения слишком
трудоемко и дорого, его используют редко, например при проверке новых кон-
структивных или технологических решений или для выборочного контроля
выпускаемой продукции. Расчетный подход отличается большей оперативно-
3.1. Закономерности процесса разрушения сварных соединений
131
Рис. 3.2. Схема постановки проектных и контроль-
ных расчетов сварной конструкции
стью, подробностью получаемой информации, простотой обобщения результа-
тов. При многовариантном проектировании данные расчетов могут служить
критерием оценки и оптимизации конструктивно-технологического решения.
Схема расчета сварного соединения при проектировании представлена
на рис. 3.2. Моделирование на ЭВМ процесса деформирования и разруше-
ния конструкции здесь является центральным, но не единственным звеном.
Важное значение имеет система получения исходных данных.
Набор данных для первого этапа расчета — общего анализа НДС —
состоит из трех основных групп: геометрии конструкции, свойств мате-
риалов и нагрузок. Рассмотрим каждую из них.
1. Для сварной конструкции геометрическая информация включает не
только данные о форме и размерах деталей, но и расположение и конструк-
тивное оформление сварных соединений. Поскольку целью расчета является
оценка опасности разрушения, особого внимания требуют элементы формы
деталей и швов, способные вызвать концентрацию напряжений. Такими
элементами геометрии являются, в частности, дефекты, выделенные в от-
дельную группу данных на схеме в связи с их вероятностью и опасностью
для сварных конструкций.
5*
132
3. Проектные и контрольные расчеты на прочность
Подготовка данных для учета возможных дефектов при проектиро-
вании существенно сложнее, чем в случае контрольного расчета кон-
кретного изделия, для которого все необходимые данные можно полу-
чить методами неразрушающего контроля. При проектировании возмож-
ные размеры и расположение дефектов, а также вероятные отклонения
геометрических форм сварных соединений приходится задавать, исходя
из тех предельных значений, которые считаются допустимыми в издели-
ях данного типа согласно действующим техническим нормам, или в виде
случайных величин, параметры рассеяния которых определяют на основе
собранных статистических данных. Внезапное разрушение возможно как
при монотонном нагружении, так и на очередном цикле переменной на-
грузки. В последнем случае очертания выросшей усталостной трещины,
также необходимые для расчета, могут быть получены по результатам
моделирования процесса ее роста.
2. Основными компонентами свойств материала являются деформа-
ционные характеристики о, =/(е,) основного металла и различных зон
сварного соединения при температурах эксплуатации. Установление момен-
та, когда процесс деформирования в той или иной зоне сварного соединения
прерывается образованием макротрещины, требует наличия критерия, фик-
сирующего наступление предельного состояния разрушения.
3. В состав действующих на конструкцию нагрузок для сварной кон-
струкции входят и остаточные напряжения после сварки. Уровень и распре-
деление остаточных напряжений целесообразно определять расчетным пу-
тем, исходя из параметров проектируемой технологии сварки, геометрии
сварной конструкции, механических свойств металла и послесварочной об-
работки, если она предусматривается проектом.
Перечисленные исходные данные позволяют осуществить моделиро-
вание НДС проектируемой конструкции в процессе ее деформирования по
мере увеличения нагрузки. Результатом является выявление наиболее на-
груженных мест, требующих более подробного расчета с моделированием
возможного разрушения. Кроме того, эта информация может быть исполь-
зована для оптимизации конструкции. Критерий разрушения позволяет так-
же установить уровень нагрузки, при котором в зоне концентрации напря-
жений и деформаций достигается предельное состояние разрушения, о чем
свидетельствует образование макротрещины. Считая расширение зоны, где
по мере возрастания нагрузки достигнуто предельное состояние разруше-
ния, признаком роста трещины, можно установить различия в условиях на-
ступления предельного состояния в зависимости от выбора варианта конст-
руктивно-технологического решения.
Наиболее рациональным подходом к обеспечению прочности сварных
конструкций представляется использование итерационного метода, вклю-
3.1. Закономерности процесса разрушения сварных соединений
133
чающего анализ конструкции с позиций выявления слабых мест, выработку
конструктивно-технологических решений по устранению этих недостатков
и повторную оценку конструкции с учетом ожидаемых изменений. Возмож-
ная коррекция принимаемых решений может быть организована в рамках
САПР. Проектные расчеты должны обеспечить сопоставление конструктив-
но-технологических решений при выборе наиболее работоспособного вари-
анта. Оперативное выполнение подобных расчетов возможно на основе МКЭ и
моделирования процесса деформирования с анализом изменений НДС
вплоть до наступления характерных предельных состояний разрушения. Ре-
зультаты моделирования позволяют оценить работоспособность конструк-
ции по критерию сопротивляемости разрушению. При проектировании кон-
струкции эти результаты являются основанием для внесения изменений в
проект с последующим повторным расчетом для оценки эффективности
внесенных изменений.
Для оперативности расчетов необходимо, чтобы информация о гео-
метрии конструкции генерировалась на предыдущих этапах проектирова-
ния, а свойства материала содержались в базе данных.
Решение этой задачи на основе моделирования НДС в процессе де-
формирования требует достаточно обоснованной критериальной основы
установления момента образования макротрещины. Переход к моделирова-
нию процесса разрушения позволяет установить направление и темп роста
развивающейся трещины по мере возрастания нагрузки или при повторных
нагружениях. Преимуществом МКЭ перед рядом других численных методов
расчета НДС в сварных соединениях (см. гл. 2) является возможность зада-
ния различных свойств материала как в соседних элементах, так и в преде-
лах одного элемента.
Современный уровень понимания процессов, происходящих в мате-
риале при нагружении, и воспроизведение их в расчетных методах не гаран-
тируют полного соответствия результатов расчетов реальным физическим
процессам в материале. Степень этого соответствия может быть установле-
на только из сопоставления каждого звена расчетного метода с эксперимен-
том. Следует признать целесообразным традиционно большее использова-
ние расчетов в определении параметров НДС, а экспериментов в определе-
нии критических значений этих параметров, соответствующих наступлению
предельных состояний. При этом основой системы оценки работоспособно-
сти конструкций становится расчетный подход, а функции экспериментов
включают следующее:
1) определение свойств материала (механических и теплофизических
характеристик), необходимых в качестве исходных данных для расчета МКЭ;
2) определение условий нагружения для анализируемой части конст-
рукций;
134
3. Проектные и контрольные расчеты на прочность
3) проверку соответствия результатов расчета тем параметром состоя-
ния образцов в процессе эксперимента, которые могут быть измерены непо-
средственно с помощью датчиков;
4) регистрацию момента разрушения образца и совмещение его с ре-
зультатами расчета НДС для установления критерия разрушения сварного со-
единения.
В отличие от проектных, контрольные расчеты требуют учета влияния
всех дефектов, обнаруженных в конструкции. Целью таких расчетов
является проверка работоспособности изготовленной или уже
эксплуатируемой конструкции при обнаружении отклонений от
нормативных требований. Вопросы приемки конструкции или исправления
дефектов обычно решают путем сопоставления данных контроля с норма-
тивными документами отрасли. Ограниченность такого подхода заключает-
ся в отсутствии связи между данными нормативно-технологических доку-
ментов и процессами разрушения при наличии тех или иных дефектов. По-
этому работоспособность приходится обеспечивать косвенно, на основе
регламентации уровня качества технологического процесса, а не уровня ра-
ботоспособности конструкции в условиях эксплуатации.
Соблюдение требований нормативно-технологических документов
необходимо как средство поддержания дисциплины производства, ограни-
чивающее допуск к эксплуатации по уровню дефектности. Однако этот уро-
вень условен. Иногда возникают сомнения в обоснованности браковки, осо-
бенно при браковке дорогостоящих изделий с трудноустранимыми дефек-
тами. Решение о допуске к эксплуатации без исправления дефекта может
быть принято только на основе контрольного расчета, показывающего, что в
процессе эксплуатации зарождение трещины от этого дефекта и последую-
щий ее рост не произойдут или не приведут к, наступлению предельного со-
стояния изделия в пределах заданного ресурса (срока эксплуатации). До на-
стоящего времени такие подходы в расчетах еще не получили достаточно
систематизированного изложения.
Действительную (конструкционную) прочность конкретного изделия
принято оценивать уровнем среднего напряжения ок в расчетном сечении,
при котором достигается стадия разрушения, принятая в качестве предель-
ного состояния. Наличие трещины малого размера I практически не снижает
изделия, однако по мере увеличения размера ее влияние проявляется все
сильнее (рис. 3.3). В этих условиях для сохранения работоспособности
изделия необходимо, чтобы размер трещины не превышал критического
значения /кр, вызывающего снижение прочности до уровня напряжения,
который считается допустимым [о], т. е. имеет соответствующий коэф-
фициент запаса по сравнению с от или ов.
3.1. Закономерности процесса разрушения сварных соединений
135
Для исключения от-
казов изделий в процессе
эксплуатации возможны
два подхода.
1. Периодический
контроль для выявления
растущей трещины, чтобы
устранить ее до того, как
она приведет к отказу в
работе, т. е. в период экс-
плуатации между точкой А,
Рис. 3.3. Схема снижения прочности изделия по
мере роста трещины в процессе эксплуатации
когда размер трещины
становится доступным для
обнаружения, и точкой В,
соответствующей достижению размера /кр (см. рис. 3.3).
2. Расчетная оценка достаточности сопротивляемости разрушению
рассматриваемого соединения или конструкции для исключения воз-
можности достижения трещиной размера /кр в течение заданного срока
службы.
Технологические ограничения допустимого размера дефекта /техн
(рис. 3.4) нередко назначают одинаковыми для сварных соединений, рабо-
тающих при различных уровнях напряжений и числах циклов нагружения N.
Это соответствует прямой линии АВ. Эксплуатационные требования к без-
дефектности металла сварных соединений обязательно должны учитывать
условия работы, уровень и характер действующих напряжений, свойства
металла, т.е. они должны опираться на точные количественные расчеты
прочности. Обычно уровень технологических требований оказывается до-
Рис. 3.4. Соотношение технологических и экс-
плуатационных ограничений размера дефекта
в зависимости от числа и уровня нагружений
статочным, чтобы сварная
конструкция была вполне
работоспособной, несмот-
ря на наличие в ней дефек-
тов, допустимых тех-
нологическими требовани-
ями. Иногда встречаются
такие условия эксплуата-
ции, когда технологические
требования оказываются
недостаточными (участок
ВС на рис. 3.4). Тогда всту-
пают в действие эксплуа-
тационные требования к
размерам дефектов /экспл.
136
3. Проектные и контрольные расчеты на прочность
Рис. 3.5. Схема изменения распределения напряжений при переходе от трещи-
ны к концентратору радиусом р и при развитии пластических деформаций
Описать процесс усталостного разрушения (зарождение и развитие
усталостной трещины) с единых позиций пока еще не удается. Поэтому при
анализе стадии зарождения трещины от неострого концентратора обычно
используют традиционные представления об усталости при циклическом
деформировании, тогда как анализ стадии роста трещины выполняют с по-
мощью механики разрушения.
В большинстве случаев (за исключением одиночных пор) дефекты
сварных соединений приходится рассматривать как достаточно острые над-
резы с радиусом в вершине менее 0,1...0,2 мм. Поскольку' истинное значение
остроты вершины в каждом конкретном случае неизвестно, для анализа напря-
женно-деформированного состояния с некоторой степенью консерватизма це-
лесообразно использовать методы механики трещин (механики разрушения).
Относительная простота линейной механики разрушения (ЛМР) свя-
зана с тем, что в упругом материале все компоненты напряжений и дефор-
маций в зоне перед вершиной трещин имеют аналогичное распределение, не
зависящее от формы детали с грещиной. Например, нормальные напряже-
ния на оси х, направленной в сторону продолжения исходной трещины 1
(рис. 3.5), описывает формула
yjlltX
(3-1)
Это распределение напряжений показано на рис. 3.5 эпюрой 2. В лю-
бой точке на заданном расстоянии х от вершины трещины все компоненты
НДС пропорциональны К — коэффициенту интенсивности напряжений
(КИН), который является основной характеристикой ЛМР. В тех случаях,
когда сила приложена перпендикулярно плоскости грещины и разрушение
3.1. Закономерности процесса разрушения сварных соединений
137
происходит путем нормального отрыва, КИН обозначают К\. Его значение
зависит от длины трещины и уровня номинальных напряжений сном в сече-
нии, рассчитанных без учета наличия трещины:
^,=Кпном^, (3.2)
где У — тарировочный коэффициент, определяемый расчетным путем в зави-
симости от формы фронта и относительных размеров трещины, градиента на-
пряжений в сечении и других факторов. Существуют относительно простые
формулы, позволяющие рассчитывать значения /ц в различных точках контура
трещины при условии, что фронт трещины имеет вид прямой или эллипса.
В отличие от трещин, реальные концентраторы и дефекты, даже наибо-
лее острые, имеют малый, но конечный радиус окончания с. В непосредствен-
ной близости от такого концентратора 3 напряжения ниже, чем перед фронтом
трещины 1 такой же длины 21 (рис. 3.5). По мере удаления от вершины концен-
тратора этот эффект уменьшается, и за пределами некоторой зоны а (имеющей
порядок с) распределение напряжений от концентратора (кривая 4) такое же,
как и в случае трещины (кривая 2). Отсюда следует, что условия роста трещины
зависят от формы концентратора только вблизи его вершины.
Таким образом, наличие малого радиуса с у дефекта не является пре-
пятствием для применения в качестве критерия разрушения, если распре-
деление напряжений (3.1) сохранится вплоть до начала разрушения. Однако
с ростом нагрузки в сечении начинаются пластические деформации. Внача-
ле возникает небольшая зона пластических деформаций (или пластическая
зона) 5 у вершины трещины, которая незначительно изменяет распределе-
ние напряжений в остальной части сечения (кривая 6 на рис. 3.5). Ее влия-
ние аналогично некоторому увеличению и притуплению исходной трещины
или дефекта. Дальнейший рост пластической зоны полностью изменяет рас-
пределение напряжений в сечении с дефектом.
Следовательно, условием применимости для анализа процесса раз-
рушения является ограниченное развитие пластической зоны к моменту на-
чала разрушения. Это возможно либо при малой пластичности материала
(хрупкие разрушения при низких температурах или при динамическом на-
гружении), либо при циклической нагрузке, когда номинальные напряжения
существенно ниже предела текучести.
Структуру контрольных расчетов при циклической или монотонной
нагрузке и наличии трещиноподобных дефектов поясняет диаграмма рабо-
тоспособности IgA', — 1gTV на рис. 3.6. Ниже линии ABCD — область полной
(абсолютной) работоспособности, в которой трещиноподобные дефекты не
увеличивают своих размеров. В области выше линии АВН трещины ведут
себя как нестабильные. В области между BCD и ВН трещины растут доста-
точно медленно, по мере накопления усталости металла у их вершин. Это
138
3. Проектные и контрольные расчеты на прочность
область относительной работоспособности, в которой конструкция работо-
способна, но после числа циклов, соответствующего точке F, трещина начи-
нает расти. В сосудах давления и трубопроводах рост несквозной трещины в
направлении толщины стенки может привести к образованию течи. При
этом характерны два случая: первый — когда /</кр (точка G на рис. 3.6):
трещина остается стабильной, т. е. имеется «течь перед разрушением»; вто-
рой — когда I > /кр и сквозная трещина оказывается нестабильной (точка Н
на рис. 3.6), что приводит к внезапному разрушению конструкции.
Согласно формуле (3.2), КИН пропорционален номинальному напря-
жению в сечении, причем коэффициент пропорциональности зависит от
размера трещины. Поэтому при некотором значении КИН напряжения до-
стигают предела текучести (горизонтальная пунктирная линия на рис. 3.6),
причем этот уровень может оказаться как выше, так и ниже Kic. Линейная
механика разрушения применима только при напряжениях существенно
ниже предела текучести. Таким образом, для соотношения предела текуче-
сти и вязкости разрушения, представленного на рис. 3.6, применение мето-
дов ЛМР для прогнозирования страгивания и роста усталостной трещины
(см. § 3.3) допустимо при невысоких нагрузках, соответствующих числу
циклов до разрушения, превышающему М (см. рис. 3.6). Для расчета на ма-
лоцикловую усталость и на статическую прочность необходимо привлече-
ние более сложных и точных методов, описанных в § 3.2. Такая ситуация
характерна для конструкционных сталей и сплавов при обычных условиях,
когда они обладают высокой пластичностью и выдерживают значительные
деформации до начала разрушения под действием статической (медленно и
монотонно изменяющейся) нагрузки. Увеличение опасности хрупкого раз-
3.1. Закономерности процесса разрушения сварных соединений
139
Рис. 3.7. Вид кинетической диаграммы усталостного разрушения:
1—у — участки диаграммы
рушения и соответствующее расширение области применимости методов
ЛМР возможно либо при повышении предела текучести, либо при снижении
пластичности и вязкости разрушения (оба эти явления проявляются при
снижении температуры и увеличении скорости нагружения), а также при
увеличении размеров трещин.
Исследования в области механики разрушения твердого тела при пере-
менных нагружениях позволили установить, что скорость распространения ус-
талостной трещины dl/dN при растяжении является функцией размаха коэф-
фициента интенсивности напряжений \КХ и его максимального значе-
ния К1ПИХ. В случае пульсирующего цикла (когда коэффициент асимметрии
цикла находится в интервале 0 < Ry< 0,1) имеем = А?|тах, т. е.
dl/dN = F(KlmJ. (3.3)
Эта зависимость получила название кинетической диаграммы устало-
стного разрушения (рис. 3.7). Она имеет три характерных участка.
На участке 7 при значениях меньших порогового трещина
практически не растет. Значение \Kth устанавливают экспериментально как
максимальное значение /\К., при котором скорость роста усталостной тре-
щины не превышает 3 107 мм/цикл на протяжении 106 циклов.
Условно принимают, что при ДА?( = dJCth происходит переход от пер-
вой стадии развития разрушения ко второй, причем скорость роста трещины
скачком возрастает от нуля до 5 10 5 мм/цикл.
Участок 2 кинетической диаграммы разрушения может составлять
значительную часть ресурса конструкции. Скорость роста трещины на этом
140
3. Проектные и контрольные расчеты на прочность
участке подчиняется уравнению Пэриса. Зависимость этой скорости от АХ,
степенная (в логарифмических координатах на рис. 3.7 выглядит как на-
клонный отрезок прямой).
Участок 3 кинетической диаграммы (см. рис. 3.7) — участок ускорен-
ного роста трещины (dl/dN> 10~3мм/цикл), предшествующий переходу к
скачкообразному продвижению при пределе циклической трещиностойко-
сти К]с. При приближении АД1Х к К1с скорость роста трещины неограниченно
растет. Обычно Kfc близок к вязкости разрушения К1с, однако в некоторых
случаях, например для высокопрочных сталей или сталей, нагружаемых при
криогенных температурах, можно наблюдать резкое снижение Kfc по срав-
нению с К1с. Формулы для расчета АК,, а также данные по критическим
значениям критериев ЛМР для ряда конструкционных материалов приведе-
ны в § 3.3.
Из анализа обеих диаграмм (см. рис. 3.6 и 3.7) следует, что разруше-
ние, характерное для монотонного нагружения, возможно и на очередном
цикле усталостного разрушения в результате уменьшения живого сечения и
возрастания напряжения в сечении при росте усталостной трещины. Таким
образом, методы, излагаемые в § 3.2, актуальны при любом режиме нагру-
жения конструкции.
3.2. Моделирование разрушения сварного соединения
при монотонном нагружении
3.2.1. Критерии наступления предельного состояния разрушения
Для сопоставления текущего состояния любой конструкции с пре-
дельным необходимо иметь критерий, фиксирующий его наступление. В
реальных конструкциях разрушение редко происходит в зоне с однородным
НДС. Всегда имеются ослабленные сечения с более высоким уровнем на-
пряжений, а также концентраторы напряжения, вызывающие неравномерное
распределение нагрузки по сечению. С ростом остроты концентратора про-
является так называемая ограниченная чувствительность материала к кон-
центратору. Значения напряжений и деформаций, рассчитанные для зоны
концентрации напряжений в момент разрушения, обычно оказывались су-
щественно выше, чем предельные значения для того же материала в гладком
образце. На основании этого был сделан вывод об особых свойствах мате-
риала в зоне с высокими градиентами НДС и об ограниченной применимо-
сти классической механики материалов для расчета конструкций с острыми
концентраторами, т. е. для значительной части современных металлоконст-
3.2. Моделирование разрушения при .монотонном нагружении
141
рукций. Наибольшую концентрацию
напряжений создает трещина, кото-
рая может возникнуть в процессе
изготовления конструкции (напри-
мер, при сварке) или в результате
усталости. В нахлесточных и тавро-
вых сварных соединениях наличие
трещиноподобного непровара может
иметь конструктивный характер,
т. е. быть предусмотрено проектом.
В начале XX в. А. Гриффитс
предположил, что условия разруше-
ния связаны с балансом энергии в зо-
не у концентратора. Условие неста-
бильного (хрупкого) развития трещи-
ны возникает тогда, когда упругая
энергия, выделяющаяся при разгрузке
трещины ^Wynp, при росте ее длины на dl превосходит энергию dWnos,
ходимую на образование двух новых поверхностей длиной dl. Соотношение
^p>^nOB (3-4)
Рис. 3.8. Условия применимости
линейной механики разрушения
материала у берегов раскрывающейся
необ-
определяет условия, при которых трещина, если стронется, будет продол-
жать развиваться нестабильно, без приложения дополнительной нагрузки. К
выражению, аналогичному (3.4), можно прийти и с позиций страгивания
трещины, используя в качестве критерия разрушения напряжение о. Причи-
ной получения одинаковых результатов при выборе в качестве критерия
разрушения разных параметров (энергии или напряжения) является наличие
у вершины трещины автономной сингулярной зоны Л (рис. 3.8).
Согласно теории упругости, распределение всех компонент НДС в зо-
не А практически не зависит от их распределения за пределами этой зоны и
может быть выражено через КИН Кх, Ки, Кш, пропорциональные средним
значениям компонент нагрузки на контуре зоны А о±,т±,Тц, и полярные
координаты г и <р точки в зоне А. Поскольку установлено, что наиболее
опасные, хрупкие разрушения всегда развиваются по механизму отрыва,
основным параметром признан К,, а его критическое значение в момент
страгивания трещины используется в качестве константы материала. Усло-
вие нестабильного разрушения в ЛМР имеет вид
К^К1с, (3.5)
хотя оно может быть выражено через любой параметр НДС в зоне А.
142
3. Проектные и контрольные расчеты на прочность
Фактически все рассмотренные методы механики разрушения пред-
ставляют собой обходное решение возникшей проблемы, заключающееся в
рассмотрении сингулярной высокоградиентной зоны как «черного ящика»
вместо анализа поведения металла внутри нее. Вследствие этого критерии
механики разрушения являются характеристиками не материала, а зоны,
включающей вершину острого концентратора.
Как отмечено в § 3.1, строгость применения ЛИР обеспечена в тех
случаях, когда сингулярная зона Л, в которой распределение всех компонент
НДС однозначно описывается КИН К, существует и является достаточно
обширной, чтобы контролировать начало разрушения. К сокращению зоны
А ведут две основные причины: рост внутри нее пластической зоны В, в ко-
торой не действует сингулярная формула теории упругости (3.1), и влияние
на внешнюю границу зоны А формы наружной поверхности, в том числе
угла при вершине концентратора. При сокращении зоны А НДС у концен-
тратора становится функцией не одной, а нескольких переменных. Широкое
применение ЛМР при анализе усталостного разрушения связано с невысо-
ким уровнем средних напряжений, ограничивающим рост зоны В. При мо-
нотонном росте нагрузки напряжения к моменту страгивания трещины вы-
ше, поэтому критерии ЛМР оказываются непригодными при нормальных
температурах для большинства конструкционных материалов, когда они
находятся в вязком состоянии.
Таким образом, области применимости как классической механики
материалов, так и ЛМР ограничены и не покрывают всего разнообразия ус-
ловий работы материалов в сварных конструкциях.
В классических теориях прочности делались попытки связать крите-
рии предельного состояния с каким-нибудь одним параметром тензора на-
пряжений или деформаций. По современным представлениям, разрушение
не происходит при достижении определенного критического НДС, а являет-
ся результатом накоплений повреждений, т. е. зависит от истории нагруже-
ния. В качестве показателя поврежденности можно использовать уменьше-
ние плотности материала (разрыхление), считая, что оно свидетельствует о
нарушении его сплошности (т. е. об изменении формы). При этом всесто-
роннее растяжение в процессе пластического деформирования способствует
разрыхлению, а сжатие — препятствует. Такая модель позволяет оценить
роль отдельных параметров НДС в процессе разрушения.
Исследование условий разрушения при невысоких градиентах НДС
было проведено на цилиндрических образцах, растягиваемых в камере с
жидкостью под давлением. Условие разрушения было представлено в виде
зависимости предельной интенсивности деформации (предельной пластич-
ности) ес от показателя объемности напряженного состояния j = ст1 —
отношения среднего напряжения, вызывающего изменение объема, к интен-
3.2. Моделирование разрушения при монотонном нагружении
143
сивности суммирующей компоненты напряжений, вызывающей изменение
формы:
Ес=ф(». (3.6)
Аналогичное выражение получено и теоретически для модели тела из
упругопластического материала с исходной регулярной системой одинако-
вых пор в процессе трехосного растяжения с различным соотношением
компонент напряжения, приводящим к различным показателям объемности
НДС. Разрушение материала модели происходило при разрыве перемычек
между порами в результате потери пластической устойчивости. Моделиро-
вание показало, что при нулевых значениях показателя объемности j (при
преобладании сдвига) поры вытягиваются в направлении нагрузки и не вы-
зывают разрушения вплоть до больших значений интенсивности деформа-
ций ес. Еще выше пластичность при отрицательной объемности (при пре-
обладании сжатия). При положительных j деформация всестороннего рас-
тяжения приводит к расширению пор, и в результате потери пластической
устойчивости происходит образование шеек на перемычках между порами и
разрыв их при невысоком среднем уровне вс. Методика определения и при-
менения характеристики предельной пластичности для конкретного мате-
риала рассмотрена в разд. 3.2.3.
Критерий предельной пластичности наиболее полезен при сложных
процессах нагружения, когда объемность НДС изменяется в процессе де-
формирования. В этом случае необходимо правильное суммирование по-
вреждений материала на различных этапах нагружения.
Простейшим решением является закон линейного суммирования по-
вреждений. В качестве меры поврежденное™ применяют скалярную вели-
чину' ф, изменяющуюся от нуля в исходном состоянии материала до едини-
цы в момент разрушения. Скорость роста этой меры ф является функцией
от параметров текущего состояния материала (от компонент НДС, условий
среды) и достигнутого уровня ф. Хорошее соответствие эксперименталь-
ным данным обеспечивает функция вида
Ф =-------------т, (3.7)
EC(P+1)(I-V)₽
согласно которой повреждение при простом нагружении вначале развивает-
ся с постоянной скоростью, а при приближении к разрушению резко ускоря-
ется. Выражение 1-ф носит название сплошности и характеризует уровень
остаточной прочности и пластичности материала и его способность сопро-
тивляться повреждению. При определенных условиях (при сжатии, повы-
144
3. Проектные и контрольные расчеты на прочность
шении температуры) возможно убывание у до отрицательных значений за
счет залечивания части исходных дефектов. Показана возможность распро-
странения условия накопления повреждений (3.7) на малоцикловую уста-
лость, в том числе при нерегулярном нагружении.
Экспериментальные данные о восстановлении пластичности после
термообработки позволяют установить, как развивается процесс поврежде-
ния по мере роста у. Вначале, при \|/ < 30 %, образуются неустойчивые,
полностью залечиваемые микропоры. Если на этом этапе провести термооб-
работку, то пластичность восстанавливается до исходного уровня. Повторяя
этот цикл операций, металлу можно придать любую форму (например, фор-
му тонкой проволоки) без его разрушения. При большей деформации поры
растут и становятся устойчивыми, вследствие чего пластичность можно вос-
становить лишь частично: залечиваются только первые 30 % поврежденное™, а
поврежденное™ сверх этого уровня сохраняется. При у >60 % происходит
объединение и укрупнение дефектов, термообработка почта не восстанав-
ливает пластичность на этой стадии повреждения.
При изменении объемности НДС изменяется предельная пластич-
ность, что влияет на скорость накопления повреждений согласно (3.7). Ин-
тегрируя выражение (3.7), можно определить накопленный уровень повреж-
денное™ в отдельных точках детали.
3.2.2. Метод оценки работоспособности сварных конструкций
Создание модели разрушения, пригодной для описания как крупного,
так и вязкого разрушения от концентраторов различной остроты, представ-
ляется весьма важным. Эта модель должна служить основой для подсисте-
мы прочности САПР сварных конструкций.
Несмотря на трудности, связанные с созданием такой модели на осно-
ве классической механики материалов (эти трудности обусловлены, глав-
ным образом, несовершенством расчетных методов), такой подход является
более перспективным, чем попытки построения единой модели на основе
линейной механики разрушения.
Наиболее серьезной проблемой для классической механики является
сингулярность (неограниченный рост) компонент НДС вблизи острого кон-
центратора. Но значения компонент напряжений ограничены текучестью
материала, поэтому сингулярность поля напряжений в действительности не
возникает, а в расчетах НДС является следствием неучета текучести мате-
риала и изменения остроты трещины (притупления) в процессе деформиро-
вания. Более сложную проблему создает рост деформаций. Хотя он также
ограничен, но при раскрытии трещины от исходной ширины в несколько
3.2. Моделирование разрушения при монотонном нагружении
145
микрометров до десятых долей миллиметра деформация перед ее фронтом
достигает сотен процентов. Это гораздо больше, чем пластичность металла
при растяжении гладкого образца. Однако такие большие деформации про-
исходят только в сравнительно тонком слое материала, непосредственно
примыкающем к фронту раскрывающейся трещины.
Основным допущением, позволяющим распространить классический
подход на острые концентраторы, является предположение, что материал у
концентратора подчиняется тому же критерию разрушения, что и металл
гладкого образца. Весь материал, в котором параметры НДС превысили
критический уровень, уже является разрушенным, хотя ввиду малости этого
участка наступившее продвижение трещины может быть незаметным. Такая
модель разрушения материала делает задачу анализа прочности сварной
конструкции обозримой и доступной для практического решения с учетом
всех основных факторов, так как критерии разрушения зависят только от
свойств материала и параметров НДС.
Поскольку такое расширение области применения классической меха-
ники материалов может быть достигнуто только на основе гораздо более
полного учета всех геометрических и физических факторов при моделиро-
вании НДС, для решения таких задач разработано специализированное ме-
тодическое и программное обеспечение.
При оценке работоспособности по предельным состояниям страгива-
ния и развития трещин от концентратора требуется определить НДС в ло-
кальных зонах у вершин концентраторов. Сложность решения задачи связа-
на с высокими градиентами поля в этих зонах. При этом в соответствии со
сделанным предположением о разрушении материала после превышения его
предельной пластичности процесс разрушения в зависимости от остроты
концентратора может начинаться на разных стадиях нагружения. Следова-
тельно, во-первых, повышаются требования к точности расчета. При реали-
зации численных методов это выражается в применении моделей с более
мелкой сеткой элементов вблизи концентратора, а также в учете изменения
геометрии конструкции под нагрузкой, т. е. в применении геометрически
нелинейных моделей. Во-вторых, большое значение приобретает анализ фа-
зы развития разрушения, так как начало разрушения от острого концентра-
тора возможно уже при нормальных рабочих нагрузках и в зависимости от
прогнозируемого дальнейшего хода этого процесса иногда может быть при-
знано допустимым.
В некоторых случаях анализ НДС в локальной области оказывается
недостаточным для установления наступления предельного состояния. Это
относится к случаям нарушения устойчивости развития процесса деформи-
рования и разрушения металла — к переходу к нестабильному росту трещи-
ны или к разрыву по ослабленному концентратором сечению за счет потери
146
3. Проектные и контрольные расчеты на прочность
пластической устойчивости. Существуют два способа регистрации таких
предельных состояний — по балансу энергии в детали или по кинет ике раз-
вития деформаций и перемещений в зоне разрушения. Второй подход явля-
ется разновидностью первого, так как рост от шага к шагу приращений де-
формаций в локальной области у вершины трещины свидетельствует о том,
что подводимая энергия упругих деформаций перекрывает затраты энергии
на развитие процесса. В то же время он проще реализуется (отпадает слож-
ный вопрос о размерах зоны, в которой необходимо анализировать баланс
энергии) и позволяет проследить процесс перехода в неустойчивое состоя-
ние, сосредоточив внимание на локальной зоне разрушений. Кроме того,
кинетика развития перемещений у концентратора может быть непосредст-
венно сопоставлена с экспериментом.
Таким образом, возможность решения задачи за несколько шагов при
учете изменения граничных условий и геометрии от шага к шагу и с регист-
рацией кинетики развития НДС является одним из требований к программ-
ному комплексу.
При определении НДС возможен выбор различных по сложности мо-
делей поведения материала: идеально упругого, идеально упругопластичес-
кого, упругопластического с упрочнением, анизотропного и т. д.; если про-
цесс протекает при температурах значительно ниже температуры плавления,
для большинства материалов может быть применена модель упруго-
пластического материала с упрочнением.
Характерными особенностями сварного соединения, влияющими на
его работоспособность при эксплуатации, являются неоднородность свойств
и остаточные напряжения. Учет этих факторов в рамках КЭ модели требует
исходных данных о границах зон с различными свойствами и о свойствах
материала в каждой зоне.
Анализ известных отечественных и зарубежных программных ком-
плексов показывает, что ни один из них, несмотря на объем и высокую стои-
мость, не обеспечивает решения всех перечисленных проблем, связанных с
оценкой работоспособности сварных соединений. В связи с этим в МГТУ им.
Н.Э. Баумана разработан специализированный программный комплекс
«СВАРКА», описанный в гл. 2. Особенности моделирования в этом комплек-
се упругопластически разрушающегося материала приведены в § 2.4.
3.2.3. Характеристики деформирования и пластичности
конструкционных материалов
Деформационная характеристика материала о;(еД широко применя-
ется в расчетах НДС конструкций, хотя до недавнего времени считалось,
3.2. Моделирование разрушения при монотонном нагружении
147
что для полного описания механических свойств материала достаточно ука-
зать его предел текучести сгт, предел прочности ств и относительное удли-
нение 8, которые являются частными параметрами о,(£,).
Как выяснилось из сопоставления результатов моделирования с
результатами экспериментов, методика построения о, (е;) требует сущест-
венной доработки. Обычная методика построения <?.(£,) сводится к обра-
ботке только начального участка машинной диаграммы испытания образцов
на растяжение (до образования шейки), с последующей аппроксимацией
результатов степенной функцией вида
а; = А + Въ”. (3.8)
Эту зависимость экстраполируют вплоть до точки разрушения. В некоторых
случаях коэффициенты аппроксимации уточняют с учетом результатов об-
мера разрушенного образца. Однако такое уточнение затруднено тем, что
распределение НДС после появления шейки становится неравномерным.
Шейка может появиться на любом участке гладкой части образца, что за-
трудняет решение этой сравнительно простой задачи численными методами.
До настоящего времени стандартная методика расчета НДС в шейке была
основана на аналитических решениях, которые получены с использованием
весьма грубых допущений. Одной из причин несовершенства методики сле-
дует считать отсутствие практической потребности в точном моделирова-
нии НДС при больших деформациях. Ситуация меняется при переходе к
моделированию разрушения металла.
Испытания листового материала при двухосном растяжении показали,
что использование единой степенной аппроксимации для всего участка от
площадки текучести до разрушения в принципе неверно. При двухосном
растяжении сферической оболочки внутренним давлением образование ме-
стного утонения (шейки) сопровождается выпучиванием этого участка,
уменьшением радиуса его кривизны и снижением мембранных напряжений.
Это явление позволяет обеспечить устойчивость и равномерность деформа-
ций на достаточно широком участке оболочки вдали от закреплений вплоть
до разрушения и непосредственно регистрировать изменение показателя
упрочнения п в выражении (3.8). У всех десяти испытанных марок стали
было зафиксировано изменение показателя упрочнения, причем перед раз-
рушением все они имели участок диаграммы с п = 0.
Точность моделирования на ЭВМ нагружения образцов повышается
как за счет совершенствования математической модели с учетом геометри-
ческой и физической нелинейности, так и за счет изменения конструкции
образца. Большая длина гладкой части стандартных цилиндрических образ-
цов (5 или 10 диаметров) нужна для более точного построения начальной
148
3. Проектные и контрольные расчеты на прочность
Рис. 3.9. Образцы для построе-
ния диаграмм деформирования
и пластичности материала
части деформационной характеристики (до
сть). Чем длиннее образец, тем меньшую
долю от его удлинения составляет удлине-
ние шейки. Таким образом, относительное
удлинение конструкционных материалов с
высоким значением показателя упрочнения
(п > 0,1) — это удлинение образца до обра-
зования шейки и оно не характеризует пла-
стичность к моменту разрушения. Сокраще-
ние длины гладкой части образца до 2...2,5
диаметров обеспечивает образование шей-
ки не в произвольном сечении, а всегда на
середине длины, существенно облегчает
изготовление и моделирование образца и
повышает точность построения конечного
участка деформационной характеристики. В МГТУ им. Н.Э. Баумана разра-
ботана методика построения о; (е;), основанная на решении обратной зада-
чи, т. е. на подборе такой характеристики, которая обеспечивает полное
совпадение результатов моделирования с машинной диаграммой, получен-
ной усреднением результатов испытаний нескольких образцов, от начала на-
гружения до начала разрушения.
На рис. 3.9 представлены чертежи, а на рис. 3.10 — машинные диа-
граммы растяжения образцов из стали 15Х2МФА. Удлинение определено с
помощью специального тензометра, установленного на образце, с базой из-
мерения 11 мм. Точками показаны результаты пошагового моделирования
процесса нагружения этих же образцов с помощью МКЭ.
Моделирование подтвердило независимость получаемой деформаци-
онной характеристики материала от схемы напряженного состояния. Харак-
теристика с,(е,), подобранная для гладкого образца, позволила с высокой
точностью воспроизвести и все диаграммы образцов с кольцевыми надреза-
ми радиусом R = 2, 4, 10 и 20 мм. Погрешность не превышала 5 % для стали
15Х2МФА и 1 % для стали 02Х10Н9МТ (рис. 3.11). Дополнительной про-
веркой стало сопоставление с результатами обмера шейки образцов в мо-
мент образования трещины (точки С на рис. 3.10). Погрешность расчета
диаметра шейки при соответствующих значениях нагрузки также не превы-
шала 5 % для стали 15Х2МФА и 1 % для стали 02Х10Н9МТ.
На рис. 3.11 видно, что построенная таким способом диаграмма для
стали 15Х2МФА близка к построенной по обычной методике (пунктирная
кривая) на начальном участке, но расходится с ней после образования шейки.
3.2. Моделирование разрушения при монотонном нагружении
149
Рис. 3.10. Машинные диаграммы испытаний образцов из стали 15Х2МФА
Интенсивность пластической деформации, %
Рис. 3.11. Деформационные характеристики материалов
Моделирование результатов испытаний сталей 15Х2МФА, 02Х10Н9МТ и
стали 20 показало, что на завершающем участке диаграммы при осевом рас-
тяжении, так же как при двухосном, показатель упрочнения п стремится к
150
3. Проектные и контрольные расчеты на прочность
нулю. Таким образом, разрабо танная методика обеспечивает высокую точ-
ность при одновременном снижении требований к образцам.
Основным новым элементом при переходе к моделированию процесса
разрушения является методика построения и применения характеристики
предельной пластичности ec(j).
Дальнейшая обработка машинных диаграмм позволяет построить
диаграмму пластичности (см. зависимость (3.6), рис. 3.12). Вся диаграм-
ма может быть построена на основе испытания серии образцов с различ-
ной остротой или глубиной надреза. Остановка испытаний и разрезание
образцов показали, что трещины действительно возникают от зоны с
наибольшей объемностью НДС.
Объемность напряженного состояния изменяется в широких пределах,
но для моделирования процесса разрушения наибольший интерес представ-
ляет участок диаграммы 0 < j < 3, т. е. с преобладанием растяжения. Наи-
больший показатель объемности, который можно наблюдать перед верши-
ной трещины в упрочняющемся материале, составляет 2,5...3. Образцы с
надрезами при растяжении имеют до образования трещины j = 0,33...2 в
зависимости от радиуса надреза. Для получения большей объемности можно
привлечь результаты испытаний образцов с трещиной.
На рис. 3.11 и 3.12 представлены диаграммы с,(е;) и ec(J) сталей
02Х10Н9МТ, 15Х2МФА и стали 20, а также магниевого сплава ИМВ-2.
3.2. Моделирование разрушения при монотонном нагружении
151
3.2.4. Компьютерное моделирование страгивания трещины,
етабильного и неустойчивого разрушения
Практика показывает, что в одной и той же конструкции возможно как
хрупкое, так и вязкое разрушение, поэтому необходимо обеспечить модели-
рование разрушения обоих видов. Вязким обычно называют разрушение,
сопровождаемое значительной пластической деформацией материала. Под
хрупким же в одних случаях понимают разрушение без пластических де-
формаций, в других — протекающее с большой скоростью. Однако микро-
скопические исследования показывают, что пластическая деформация со-
провождает разрушение конструкционных материалов практически всегда.
Это дает основания считать различия между видами разрушения не качест-
венными, а лишь количественными и свести начальную фазу всех видов
разрушения к одному — вязкому.
Такой подход имеет не только теоретическое, но и большое практиче-
ское значение, так как позволяет описать все виды разрушения в рамках
единой модели и единого критерия. Даже в случае некоторого усложнения
этого критерия в целом методика моделирования становится проще, чем при
использовании различных критериев для разных видов разрушения.
При анализе следующей фазы разрушения (движение трещины) более
продуктивно деление разрушения не на вязкое или хрупкое, а на стабильное
или нестабильное. Стабильный рост трещины может происходить только
при непрерывном росте нагрузки и прекращается при отсутствии ее роста.
Обычно такое развитие трещины называют вязким, так как оно, как прави-
ло, сопровождается большими пластическими деформациями. Без них ста-
бильный рост трещины наблюдается очень редко.
Нестабильное разрушение развивается за счет упругой энергии мате-
риала и не останавливается при прекращении роста нагрузки, а иногда и при
ее снижении. Такое разрушение характерно для малопластичных материа-
лов, но называть его хрупким некорректно. Во-первых, обмер разрушенных
образцов показывает наличие пластических деформаций на пути трещины.
Во-вторых, одной из разновидностей нестабильного разрушения можно счи-
тать потерю пластической устойчивости в шейке растягиваемого гладкого
образца. В большинстве случаев разрушение, называемое хрупким, также
сопровождается потерей пластической устойчивости в локальной зоне перед
вершиной трещины.
Правильность такого подхода подтверждают результаты испытаний
образцов с полуэллиптическими поверхностными трещинами. Представле-
ние результатов испытаний разных сплавов при нормальной и низких тем-
пературах на общей диаграмме в безразмерных координатах (рис. 3.13) при-
водит к выводу о единстве процесса разрушения до момента страгивания
152
3. Проектные и контрольные расчеты на прочность
Рис. 3.13. Связь характера разрушения со стадиями раскрытия по-
верхностной трещины 5:
<Tcp/onu, Еср/епц — среднее напряжение и деформация образца, отнесенные к
пределу пропорциональности материала
трещины и позволяет выделить ряд стадий этого процесса, отличающихся
размерами пластической зоны.
Если страгивание трещины происходит на первой стадии (малая пла-
стическая зона у вершины трещины, раскрытие трещины менее 0,03 мм),
оно сразу приводит к нестабильному разрушению. На второй стадии пла-
стическая зона охватывает все ослабленное трещиной поперечное сечение,
что приводит к большему расходу упругой энергии на пластическое дефор-
мирование. Поэтому трещина после страгивания вначале растет стабильно,
однако возможен переход к нестабильности после ее небольшого продвиже-
ния. Такое разрушение часто называют вязкохрупким. На третьей стадии,
при раскрытии трещины более 0,15 мм, пластическая зона распространяется
за пределы ослабленного сечения; переход к нестабильному росту трещины
возможен только при больших запасах упругой энергии (например, в сосу-
дах высокого давления) и обычно носит характер потери пластической ус-
тойчивости перемычки с превращением трещины в сквозную.
Основным препятствием при разработке единой модели разрушения
для вязкого и хрупкого разрушения от концентраторов различной остроты
является обнаруживаемое в экспериментах различие критических уровней
НДС для одного и того же материала. Этот факт привел к отказу от класси-
ческой механики материалов и к попыткам решения задачи средствами ме-
3.2. Моделирование разрушения при монотонном нагружении
153
ханики разрушения (см. разд. 3.2.1). Однако область применимости извест-
ных подходов механики разрушения также весьма ограничена. Возможно
другое решение проблемы, более эффективное при расчете сварных конст-
рукций. Для этого кроме применения описанных в разд. 3.2.1 критерия пре-
дельной пластичности и модели накопления повреждений необходимо при-
нять положения, позволяющие получить одинаковые критические значения
критерия для всех условий разрушения. Эти положения составляют основу
метода, который можно назвать прямым моделированием процесса разру-
шения.
1. Для того чтобы при моделировании зон с различными градиентами
НДС можно было использовать единые характеристики материала, необхо-
димо повысить точность моделирования НДС, учесть физическую и геомет-
рическую нелинейность у острого концентратора. Для решения этой задачи
используется специализированный программный комплекс «СВАРКА»,
описанный в гл. 2.
2. Методика получения характеристик материала должна включать
непрерывную запись регистрируемых параметров при испытаниях образцов
и компьютерное моделирование этих испытаний. Показателем точности по-
лученных характеристик материала является точность воспроизведения на
модели параметров, записанных при испытании.
3. При моделировании процесса разрушения все зоны, в которых рас-
считанные параметры НДС оказываются выше критических параметров мо-
делируемого материала, следует считать разрушенными, а материал внутри
этих зон не сплошным, а пористым (с пониженными механическими харак-
теристиками) или не существующим (с характеристиками, близкими к нулю).
Физическая достоверность третьего из выдвинутых положений требу-
ет дополнительной проверки, однако практическую ценность такого подхо-
да в качестве основы феноменологической модели можно считать доказан-
ной, поскольку он позволил с высокой точностью воспроизвести на модели
деформирование и разрушение как гладких образцов, так и образцов с раз-
личными надрезами и трещинами при растяжении и изгибе (на рис. 3.10
видно, что расчет достаточно точно воспроизводит в том числе и участок
роста трещины в шейке образца после точки С страгивания трещины).
При этом получено объяснение независимости прочности от остроты
надреза, если радиус остроты меньше критического. Моделирование пока-
зывает, что зона разрушения от острого надреза или трещины имеет малую
глубину, т. е. разрушение распространяется по внутренней поверхности
трещины, приводит к ее притуплению и тормозит увеличение ее глубины.
Обычно эта начальная фаза, на которой разрушение уже происходит, а тре-
щина почти не растет, остается незамеченной в экспериментах. При даль-
нейшем раскрытии трещины зона разрушения перед ее фронтом углубляет-
ся и вызывает рост глубины трещины.
154
3. Проектные и контрольные расчеты на прочность
Иногда углубление трещины может быть вызвано не только разделе-
нием частиц материала. Раскрытие трещины вызывает удлинение волокон
перед ее фронтом. При этом происходит их поперечная утяжка, в результате
поперечное сечение волокон перед фронтом трещины уменьшается, что
приводит к ее углублению. Приповерхностный слой у дна трещины нахо-
дится в условиях плоского напряженного состояния. К моменту достижения
разрушающей деформации, если она имеет порядок 100 %, поперечное
сечение волокон сокращается вдвое. В этом случае половина убывания
прочности волокон связана с их поперечной утяжкой перед разрывом и
только половина — с их разрывом. Продвижение трещины за счет
поперечной утяжки металла перед ее фронтом можно назвать локальной
потерей пластической устойчивости.
Прямой характер моделированию придает то, что рост трещины моде-
лируется не на основе критерия, описывающего некоторую область, содер-
жащую острый концентратор, что присуще всем критериям линейной меха-
ники разрушения, а на основе свойств, проявляемых материалом и в одно-
родном НДС. В качестве такой характеристики выбрана предельная
пластичность материала как функция показателя объемности напряженного
состояния.
Для оценки стабильности процесса разрушения применяют метод со-
поставления энергии упругих деформаций при различных продвижениях
трещины и выбирают такое продвижение, при котором энергия минимальна.
Однако этот подход осуществим на практике только в простейших случаях,
когда траектории роста трещин можно заранее предвидеть и имитировать их
рост путем освобождения узлов конечно-элементной модели. Близкий по
физическому смыслу метод прямого моделирования процесса разрешения
материала, разработанный в МГТУ им. Н.Э. Баумана, практически не имеет
ограничений по числу и сложности геометрии очагов разрушения и позво-
ляет использовать моделирование разрушения в практике проектирования
реальных сварных конструкций. Вместо перебора вариантов роста трещин
производится повторение шагов моделирования НДС при постоянной на-
грузке, с учетом на каждом шаге изменений, вызванных деформацией и раз-
рушением материала элементов. Прекращение изменений после нескольких
шагов свидетельствует о стабильности процесса, а продолжение и чекере-
ние —- о нестабильности.
Поскольку одной из причин изменения процесса разрушения при .мо-
делировании может являться неравномерность разбивки на пути трещины,
условием корректности результатов является равномерная и достаточно
мелкая сетка КЭ в местах очагов разрушения. Чем мельче размер элементов,
тем меньше может быть шаг нагружения и выше точность моделирования.
Так как размеры КЭ, как правило, существенно превышают размеры
3.2. Моделирование разрушения при монотонном нагружении
155
элементов реальной структуры
материала (зерен или атомов),
разрушение одного элемента у
фронта трещины существенно из-
меняет ее форму и тем самым
вносит искажение в процесс мо-
делирования. В этом случае уве-
личение шага нагружения приво-
дит к увеличению числа одновре-
менно разрушающихся элементов
Рис. 3.14. Образец для испытаний на изгиб
и сглаживает искажение процесса
от дискретности модели. Таким
образом, для каждой степени подробности сетки КЭ существует минимально
допустимый шаг роста нагрузки.
В остальном методика моделирования начала движения трещины, по-
ка скорость ее движения невелика, совпадает с методикой моделирования
страгивания и не требует определения дополнительных характеристик мате-
риала. При моделировании лавинного разрушения необходимо учитывать
инерцию разлетающихся частей детали и влияние скорости деформаций на
свойства материала.
Таким образом, метод прямого моделирования процесса разрушения
универсальнее и в принципе проще различных косвенных методов, хотя и
требует в сложных случаях значительных вычислительных затрат на поша-
говое моделирование с мелкой равномерной сеткой.
Разработанная методика проверена на призматических образцах из
стали 15Х2МФА с боковой трещиной при трехточечном изгибе (рис. 3.14).
Образцы сечением 100 х 100 мм, с расстоянием между опорами 400 мм име-
ли трещины глубиной L = 35 и 53 мм. Было испытано по два образца для
каждого размера трещины и кривые «усилие Р — раскрытие трещины г» у
одинаковых образцов повторялись с разбросом менее 5 %. Дополнительно
были испытаны образцы меньшей шириной В. Поскольку у образцов с оди-
наковой глубиной трещины усилие (при том же раскрытии) было прямо
пропорционально ширине, можно сделать вывод о незначительном влиянии
боковых частей образца, находящихся в условиях плоского напряженного
состояния, на усилие и о возможности моделировать весь образец по схеме
плоского деформирования. Упрощение схемы позволило сэкономить вы-
числительные ресурсы и за счет этого обеспечить равномерную и достаточ-
но мелкую (с шагом менее 0,1 мм) сетку КЭ на всем ожидаемом пути роста
трещины.
На рис. 3.15 дано сопоставление результатов моделирования с экспе-
риментами. Кривой 1 представлена экспериментальная машинная диаграм-
I
156
3. Проектные и контрольные расчеты на прочность
Рис. 3.15. Результаты испытаний (кривые 1, 2) и модели-
рования (кривые 3—7) образцов с боковой трещиной
ма Р—v для образца с начальной глубиной трещины 35 мм, кривой 3 — та
же диаграмма, полученная моделированием. Кривыми 2 и 4 представлены
экспериментальная и расчетная диаграммы для трещины глубиной 53 мм.
Погрешность при определении предельной нагрузки не превышает 2 % для
обоих размеров трещины. Важную роль в достигнутом соответствии рас-
четных и экспериментальных результатов играет моделирование процесса
разрушения. При моделировании без учета разрушения (кривая 7 для тре-
щины 35 мм) расхождение результатов расчета и эксперимента существенно
увеличивается. Кривыми 5 и б представлен рассчитанный на моделях рост
глубины трещин от исходной глубины 35 и 53 мм.
Проведенная экспериментальная проверка модели позволяет проана-
лизировать на ее основе условия страгивания и развития вязкого разруше-
ния и сделать выводы о применимости различных критериев разрушения в
этих условиях. Моделирование роста трещины в образце позволило также
достроить диаграмму пластичности стали 15Х2МФА для значений показа-
теля объемности НДС j > 2, что необходимо для моделирования процесса
разрушения реальных конструкций из этой стали.
На рис. 3.16 показано распределение компонентов НДС перед фрон-
том трещины с начальной длиной 53 мм после ее продвижения на 0,1 и 0,6
мм, а также трещины с начальной длиной 35 мм после ее продвижения на
0,1; 0,8 и 3,4 мм. При большем размере непрорезанного сечения страгивание
трещины происходит в условиях меньшего размера пластической зоны и
3.2. Моделирование разрушения при монотонном нагружении
157
Расстояние от фронта трещины, мм
Рис. 3.16. Распределение напряжений перед фронтом движущейся трещины:
1 — 53 + 0,1 мм; 2 — 53 + 0,6 мм; 3 — 35 + 0,1 мм; 4 — 35 + 0,8 мм; 5 — 25 + 1,4 мм
максимум нормального напряжения находится ближе к вершине трещины
(кривая 3). По мере развития общей текучести и приближения сечения к со-
стоянию пластического шарнира трещина несколько притупляется, а высо-
конапряженная зона расширяется, в частности максимум нормального на-
пряжения отодвигается от вершины трещины (кривая 2). Но в целом все
распределения имеют аналогичный характер и одинаковое максимальное
значение напряжения нормального отрыва. Аналогичны и распределения
остальных компонентов НДС. Это означает, что зона у вершины трещины
сохраняет автономию от остальной части сечения и состояние в этой зоне (в
системе координат, движущейся с трещиной) близко к квазистационарному.
Следовательно, для оценки условий как страгивания, так и движения тре-
щины пригодны практически любые локальные критерии, если они опреде-
лены на достаточно точной модели и не у вершины исходной трещины, а с
учетом ее продвижения. Преимущество критерия предельной пластичности
перед другими локальными критериями заключается в его применимости
для образцов как с трещинами, так и без трещин, а следовательно, для
любых острых и неострых концентраторов (надрезов различной остроты,
вырезов с различными углами при вершине, коротких и почти сквозных
трещин и т. д.).
Что касается глобальных силовых и энергетических критериев, то они
малопригодны как критерии страгивания вязкого разрушения и полностью
не пригодны как критерии его развития. На рис. 3.15 видно, что рост трещи-
158
3. Проектные и контрольные расчеты на прочность
ны вначале сопровождается ростом нагрузки, следовательно, интенсивность
напряжения и плотность энергии деформаций у вершины трещины изменя-
ются по мере ее роста. Данные рис. 3.15 позволяют также продемонстриро-
вать неоднозначность и неточность оценки условий страгивания вязкой
трещины по критерию К\. За счет высокой концентрации напряжений стра-
гивание острой трещины начинается при небольшой нагрузке (менее поло-
вины разрушающей нагрузки при глубине трещины 35 мм). Так как разру-
шение вызывает притупление трещины, ее рост происходит вначале весьма
медленно, его трудно зарегистрировать по показаниям датчика раскрытия
трещины, поэтому оценка текущего подрастания трещины может оказаться
очень приближенной. Поскольку нагрузка, а значит, и интенсивность на-
пряжений продолжают расти по мере роста трещины, найденные значения
Кс могут различаться в несколько раз в зависимости от того, насколько точ-
но будет зарегистрировано подрастание трещины, и от того, какое подрас-
тание трещины считать ее страгиванием — 0,01; 0,1 или 1 мм.
Следует отметить, что при моделировании продвижение трещины на
0,1 мм было достигнуто при одном и том же значении Ki = 189 МПа\/м для
образцов с исходными трещинами глубиной 53 и 35 мм. Это совпадение, а
также близость полученного значения к приведенным в литературе значени-
ям вязкости разрушения стали 15Х2МФА показывают, что интенсивность
напряжения может в некоторых случаях служить критерием подобия усло-
вий страгивания трещины в вязком материале, хотя границы его корректно-
го применения требуют предварительного уточнения, а считать полученное
значение константой материала нет оснований. Представленная здесь мето-
дика позволяет, в частности, рассчитать значение интенсивности напряже-
ний, при котором в конкретной детали произойдет рост трещины на задан-
ную величину, и оценить допустимость применения линейной механики
разрушения при проектировании деталей такого типа.
3.2.5. Определение вязкости разрушения методом численного
эксперимента и ее применение в контрольном расчете
Область корректного применения критериев линейной механики раз-
рушения ограничена целым рядом условий, которые полностью выполняют-
ся только при невысокой пластичности материала, значительных размерах
сечения и трещиноподобного концентратора в нем и схеме нагружения тре-
щины, близкой к нормальному отрыву. На практике бывают попытки при-
менения этих критериев за пределами области их корректности, так как в
утвержденных нормативных документах других критериев, пригодных для
3.2. Моделирование разрушения при монотонном нагружении
159
оценки опасности внезапного разрушения конструкций, практически не су-
ществует.
Таким образом, возникают две актуальные задачи:
• оценить возможную погрешность при применении в конкретных ус-
ловиях критериев ЛМР (в частности, наиболее известного из них — вязко-
сти разрушения К1с) и оценить целесообразность их применения;
• предложить методику их определения и применения, сводящую по-
грешности к минимуму.
С позиций теории ЛМР погрешности связаны с тем, что критерии
ЛМР не полностью учитывают особенности распределения НДС у концен-
тратора. Это распределение в функции расстояния от вершины концентра-
тора может быть представлено в виде степенного ряда, причем критерии
ЛМР учитывают только один, хотя и наиболее существенный, из членов ря-
да. Погрешности от неучета других членов ряда возрастают по мере умень-
шения размеров сечения, притупления концентратора, роста пластической
зоны и т. д., и их можно вычислить. Недостатком такого аналитического
подхода к оценке точности является сложность приемов решения, нарас-
тающая по мере усложнения конструкции, и неизбежность упрощений и до-
пущений, ставящих под сомнение полученный результат.
Еще одна погрешность, характерная для вязких материалов, связана с
тем, что нестабильному разрушению, для описания которого предназначена
ЛМР, может предшествовать устойчивый рост трещины от исходного де-
фекта. В этом случае использование в расчете начального размера дефекта
вносит искажение в определяемое значение критерия ЛМР.
При наличии необходимых исходных данных о геометрии конструк-
ции и концентратора, а также деформационных характеристик материалов,
из которых она изготовлена, МКЭ позволяет определить НДС с достаточной
степенью точности. Рассмотрев полученное распределение НДС у вершины
концентратора, можно сопоставить его с тем, которое дает аналитический
расчет по ЛМР. МКЭ позволяет также моделировать рост трещины в про-
цессе нагружения.
Рассмотрим вначале состояние у вершины исходной трещины в упру-
гопластическом материале (сталь 15Х2МФА) до момента ее страгивания.
Решение задачи проведено с помощью программного комплекса «СВАРКА».
Сопоставление решения с ЛМР можно проводить как по распределению од-
ного из компонентов напряжения на продолжении трещины, так и по рас-
пределению раскрытия ее берегов. Результаты такого сопоставления пока-
заны на рис. 3.17.
На рисунке видно, что профиль раскрытия берегов трещины v по МКЭ
(кривая 2) существенно отличается от квадратичной параболы, получаемой
согласно ЛМР. Однако если ввести поправку Ирвина на размер пластиче-
160
3. Проектные и контрольные расчеты на прочность
0,014
s
X 0,012
> 0,01
= 0,008
g 0,006
Ж 0,004
О
£• 0,002
о
-0,2 | |0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8
п Координата R, мм
Рис. 3.17. Проверка применимости КИН для оценки
НДС у вершины трещины
ской зоны, т. е. считать расчетную трещину несколько длиннее реальной, то
можно добиться близкого соответствия решения по ЛМР (кривая У)
2АГ,(1-ц)
G V 2л
(3.9)
с полученным решением МКЭ в некоторой зоне у вершины трещины (кри-
вая 2). Отклонение от ЛМР увеличивается как при приближении к вершине
трещины (вследствие пластических деформаций), так и при удалении от нее
(например, вследствие близости свободной поверхности детали). В формуле
(3.9) G — модуль сдвига, р. — коэффициент Пуассона, R — расстояние точ-
ки поверхности исходной трещины от ее вершины. Совмещение кривых 1 и 2 в
интервале значений R от 0,1 до 0,5 мм позволяет определить из (3.9) К\ и Rp.
На рис. 3.17 видно, что для данного случая близкое соответствие кривых
достигается при поправке Ирвина Rp = 0,1 мм.
Найденные значения Kt и Rp можно применить для А'-тарировки, т. е.
найти поправочный коэффициент Y в формуле
К, =Yuy]n(l + Rp) (3.10)
и использовать эту формулу для расчета в данном концентраторе при
других номинальных напряжениях о в сечении и других размерах трещины
У, считая Y и Rp постоянными.
Если известно, хотя бы ориентировочно, значение вязкости разруше-
ния К1е для данной марки стали, то, проведя моделирование МКЭ для уровня
нагрузки, соответствующего этому значению Kj у концентратора, можно в
первом приближении оценить корректность использования ЛМР в расчете
на прочность и необходимость соответствующих испытаний материала. Зо-
3.2. Моделирование разрушения при монотонном нагружении
161
на разрушения контролируется критериями ЛМР, если область совпадения
результатов расчета по ЛМР с результатами решения МКЭ (см. рис. 3.17)
достаточно широка и начинается достаточно близко от вершины трещины.
Обычно «достаточно близким» считают расстояние, меньшее размера
структурного элемента, который превышает на порядок размер зерна поли-
кристалла и составляет для конструкционных сплавов от десятых до сотых
долей миллиметра.
В качестве критерия механики разрушения можно принять перемеще-
ние на контуре радиусом 0,5 мм, окружающем вершину трещины. По дру-
гим данным, этот радиус для конструкционных сталей должен составлять
0,23 мм. Таким образом, в рассмотренном примере найденные значения Ki и
Rp обеспечивают необходимое соответствие моделей, что свидетельствует о
применимости критерия ЛМР для сопоставления вариантов конструктивно-
технологических решений.
Более обоснованный вывод о применимости механики разрушения к
расчету конструкции можно сделать на основе анализа процесса ее разру-
шения. Расчет по критериям механики разрушения необходим, если в про-
цессе роста трещины возможен переход к нестабильному разрушению, т. е.
к росту трещины при постоянной или снижающейся внешней нагрузке за
счет накопленной в конструкции потенциальной энергии.
При пошаговом моделировании нагружения образцов без учета их
разрушения расчетная машинная диаграмма 1 совпадает с эксперименталь-
ной 2 на начальном участке, а на завершающем проходит выше (рис. 3.18).
Характер поведения экспериментальной кривой, наличие на ней отсутст-
вующих на расчетной кривой горизонтального и спадающего участков объ-
ясняется ростом трещины. Следовательно, моментом страгивания трещины
можно считать точку Q расхождения кривых 1 и 2. Такой способ определе-
ния момента страгивания трещины при обработке результатов испытаний на
вязкость разрушения представ-
ляется более обоснованным,
чем определение по измене-
нию наклона кривой (как ре-
комендовано в стандарте), так
как искривление машинной
диаграммы не обязательно вы-
звано разрушением. Кривая 1
также изменяет наклон, хотя
построена для случая постоян-
ной длины трещины.
Значение К\ при страги-
вании трещины (А)у) может
Рис. 3.18. Сопоставление с экспериментом
результатов моделирования без учета разру-
шения
6 — 6705
162
3. Проектные и контрольные расчеты на прочность
быть принято в качестве вязкости разрушения (Kic = Kiq) только в случае,
если вслед за страгиванием сразу происходит нестабильное разрушение об-
разца (обрыв машинной диаграммы). Если нестабильному разрушению
предшествует некоторое устойчивое подрастание трещины, то правильнее
определять вязкость разрушения после этого подрастания, по последней
точке С машинной диаграммы. Однако применение модели, не учитываю-
щей роста трещины, становится все менее корректным по мере ее роста. По-
грешности можно уменьшить путем введения в длину трещины, наряду с Rp,
еще одной поправки, учитывающей ее рост.
Размер поправки должен обеспечить совпадение расчетной и экспе-
риментальной диаграмм в точке С (расчетная кривая 3). Более точным яв-
ляется постепенное увеличение размера трещины на каждом шаге модели-
рования, чтобы расчетная кривая совпадала с экспериментальной кривой 2
на всем протяжении, от начала нагружения до точки С. Найденный в ре-
зультате моделирования размер трещины может быть использован для вы-
числения Kic.
Описанная процедура моделирования процесса разрушения требует
предварительного определения только деформационной характеристики ма-
териала. Увеличение размера трещины в модели производится не на основе
анализа НДС, а из условия совмещения расчетной и экспериментальной
диаграмм. Как известно, для определения К}с требуются весьма сложные в
изготовлении образцы, а для вязких материалов — к тому же и крупногаба-
ритные. Методика моделирования процесса разрушения на основе сопос-
тавления пластической деформации металла с его предельной пластично-
стью, описанная в разд. 3.2.4, позволяет избежать испытания крупных об-
разцов как при оценке возможности нестабильного разрушения, так и при
определении критериев ЛМР.
Для моделирования процесса разрушения необходимо обеспечить
достаточно мелкую и равномерную сетку КЭ вдоль первых 1... 3 мм траек-
тории ожидаемого роста трещины. Методика моделирования включает вы-
полнение после каждого шага приращения нагрузки нескольких шагов при
постоянной нагрузке, но с учетом изменения геометрии трещины вследст-
вие деформирования и разрушения материала КЭ на предыдущем шаге. При
устойчивом характере разрушения трещина увеличивается на первых 1—2
шагах после приращения нагрузки, а затем процесс ее роста затухает. Если
рост трещины продолжается и ускоряется в процессе выполнения шагов с по-
стоянной нагрузкой, то его следует считать нестабильным. Равномерная сетка
КЭ необходима для того, чтобы изменение характера роста трещины не было
вызвано переходом к элементам другого размера. Мелкая сетка обеспечивает
разрушение на каждом шаге сразу нескольких элементов и уменьшает влия-
ние дискретности разбивки на конфигурацию фронта трещины.
3.2. Моделирование разрушения при монотонном нагружении
163
Как видно из описания методики, речь идет о прямом моделировании
процесса разрушения путем уничтожения тех элементов, в которых пара-
метры НДС превысили критический уровень, а не о косвенном моделирова-
нии путем освобождения узлов КЭ на основе критериев ЛМР, оценивающих
зону разрушения интегрально как «черный ящик». Прямое моделирование
предоставляет новые возможности при решении задач, но требует
повышения точности моделирования НДС на основе учета геометрической
и физической нелинейности поведения материала, а также определения
новой механической характеристики материала, используемой в качестве
критерия разрушения. Основные положения экспериментально-расчетной
методики определения этой характеристики, т. е. предельной пластичности
материала, и обоснование ее применения в качестве критерия разрушения
приведены в разд. 3.2.3, 3.2.4.
Преимущество предельной пластичности перед традиционными кри-
териями линейной и нелинейной механики разрушения состоит в том, что
это условие разрушения относится к точке материала, а не к зоне, содержа-
щей внутри себя острый концентратор. Поэтому условие разрушения зави-
сит только от температуры и НДС в точке. Никакое сочетание факторов в
соседних точках не оказывает влияния на условия разрушения данной точ-
ки, если в ней не изменяется температура и НДС. Это позволяет проводить
решение таких «некорректно поставленных» с позиций ЛМР задач, как рас-
чет прочности сварного соединения разнородных металлов, в том числе при
неизотермических условиях и с учетом обнаруженных дефектов.
Необходимость в большом числе элементов и шагов решения увели-
чивает вычислительные затраты на моделирование процесса разрушения
сложных деталей. Однако в том случае, когда необходимо дать консерва-
тивную оценку опасности внезапного нестабильного разрушения, можно
существенно упростить модель. При данной толщине материала такую
оценку дает концентратор в виде поверхностной трещины, глубина которой
составляет половину толщины сечения, при нагружении по схеме нормаль-
ного отрыва. Выполнение условия плоского деформирования в направлении
вдоль фронта трещины и нахождение этого фронта в максимальном удале-
нии от свободных поверхностей создают максимальную объемность НДС,
что приводит к снижению предельной пластичности и максимизирует опас-
ность нестабильного разрушения.
Осесимметричная модель сферической оболочки с кольцевой поверх-
ностной трещиной в экваториальной плоскости (рис. 3.19) позволяет ис-
пользовать двумерные КЭ и свести к минимуму их число за пределами ожи-
даемой траектории роста трещины. При этом единственным упрощающим
предположением является сохранение осевой симметрии в процессе разру-
шения.
6*
164
3. Проектные и контрольные расчеты на прочность
Рис. 3.19. Схема моделирования
роста внутренней трещины в сфе-
рической оболочке
На рис. 3.20 представлен рост L
глубины трещины от различных на-
чальных значений глубины по мере
увеличения внутреннего давления.
Размеры оболочки: R = 1700 мм. b =
= 200 мм, материал — мартенситно-
стареющая сталь 02Х10Н9МТ.
Зависимости роста глубины тре-
щины от КИН К] получены в результате
моделирования МКЭ от исходной глу-
бины трещины 10, 20 и 100 мм. Значе-
ния Ki, при которых наступило страгивание трещин глубиной 20 и 100 мм
(если за страгивание принять увеличение глубины на 0,1 мм) практически
совпали и составили 110 МПал/м. Значения К\, при которых рост этих двух
трещин стал нестабильным, также близки (около 160 МПал/м ). Следова-
тельно, критическое значение Кь найденное для трещины глубиной 100 мм,
составляющей половину толщины стенки, применимо и для других толщин
и может быть принято за характеристику материала. Значения Кх на момент
роста трещины на 0,1 мм оказались близкими к указанной в справочной ли-
тературе вязкости разрушения стали 02Х10Н9МТ (КТс = НО МПа-Ум ).
Таким образом, представленная модель сферической оболочки позволяет
по имеющимся характеристикам материала (деформационной и характе-
ристике предельной пластичности) расчетным путем определять крите-
рии ЛМР.
Модель позволяет также оценить границы применимости ЛМР для
конкретных условий. Из рассмотренного примера ясно, что внезапное раз-
Рис. 3.20. Зависимость роста глубины трещин от коэффициента
интенсивности напряжения:
L — рост трещин от различной начальной глубины; С — точки страгивания трещин
3.2. Моделирование разрушения при монотонном нагружении
165
рушение оболочки из стали 02Х10Н9МТ толщиной 200 мм возможно при
глубине трещины не только 100 мм, но и в интервале 20... 100 мм. Характер
роста трещины от исходной глубины 10 мм, также представленный на
рис. 3.20, существенно отличается от более глубоких трещин в связи с тем,
что страгивание этой трещины происходит при более высоком давлении и
после начала общей текучести оболочки. На основании этого можно сделать
вывод, что если внезапное разрушение от трещины глубиной 10 мм и воз-
можно, то произойдет оно при значении существенно превышающем Kjc.
Таким образом, для данной оболочки граница применимости ЛМР прохо-
дит между размерами глубины исходной трещины 10 и 20 мм. Продолжив
численные эксперименты, можно установить характер поведения трещин с
исходной глубиной 100...200 мм, влияние толщины материала, его марки,
формы исходного концентратора и т. д.
После проведенной проверки применимости и оценки точности расче-
та по ЛМР такой расчет может быть рекомендован как более простой взамен
моделирования процесса разрушения при проведении большого количества
расчетов типовых элементов конструкций. Проверка может служить осно-
ванием для ограниченного применения ЛМР даже в том случае, когда не
выполняются формальные признаки корректности критериев ЛМР. Следо-
вательно, ЛМР может служить «инженерной» реализацией более универ-
сальных методов моделирования процесса разрушения.
Еще одна возможная область применения имеющихся данных по кри-
териям ЛМР для вязких материалов — уточнение диаграммы пластичности
в области высокой объемности НДС. Обычные образцы с надрезами не все-
гда обеспечивают разрушение при высокой объемности НДС даже при
весьма остром исходном надрезе. В то же время регистрация данных в про-
цессе роста трещины в экспериментальном образце связана с рядом методи-
ческих трудностей. Имея результаты испытаний стандартных образцов на
вязкость разрушения, можно провести моделирование этих испытаний на
ЭВМ и уточнить характеристику предельной пластичности так, чтобы обес-
печить совпадение расчетной машинной диаграммы с экспериментом. К на-
стоящему времени накоплен значительный объем экспериментальных дан-
ных по предельной пластичности материалов, в том числе при высоких и
низких температурах, но, как правило, отсутствуют данные для высокой по-
ложительной объемности НДС.
Таким образом, можно предложить два метода проверки возможности
и необходимости применения критериев ЛМР для конкретной конструкции:
1) на основе сопоставления НДС у концентратора, описываемого ЛМР, с
точным решением, полученным с помощью МКЭ. Необходимыми характери-
стиками материала для оценки погрешности ЛМР являются деформационная
характеристика и ориентировочное значение вязкости разрушения;
166
3. Проектные и контрольные расчеты на прочность
2) на основе моделирования процесса разрушения и установления ха-
рактера разрушения. Требуется деформационная характеристика и характе-
ристика предельной пластичности, вязкость разрушения может быть найде-
на по ним в процессе моделирования. Применение ЛМР актуально для тех
конструкций, разрушение которых может стать нестабильным.
Есть и третий, традиционный способ — испытание крупногабаритных
образцов. В этом случае моделирование испытаний позволяет ввести по-
правку на устойчивый рост трещины перед нестабильным разрушением.
Накопленные справочные данные по критическим значениям пара-
метров ЛМР могут иметь следующие области применения:
1) разработка инженерных методик расчета для тех интервалов изме-
нения параметров конструкции, для которых возможность и необходимость
применения ЛМР была установлена на основе моделирования МКЭ;
2) проверка и уточнение значений характеристики предельной пла-
стичности при высокой объемности НДС. Эта характеристика затем может
быть применена для расчета любых конструкций из данного материала, как
допускающих, так и не допускающих применения ЛМР.
3.2.6. Пример расчета корпуса ядерного реактора
на «течь перед разрушением»
Концепция «течи перед разрушением» является перспективным на-
правлением в проектировании трубопроводов АЭС, разрушение которых
может повлечь за собой тяжелые последствия. Гарантия безопасности осно-
вана на том, что при всех обстоятельствах не должно произойти полного
гильотинного разрыва трубопровода, а вначале должно образоваться сквоз-
ное отверстие (течь) ограниченного размера. В этом случае появление течи
вызовет срабатывание защитной автоматики и прекращение работы, а не-
большое количество вытекших опасных веществ будет удержано защитным
кожухом установки. Важная особенность этого подхода в том, что одновре-
менно с повышением безопасности его применение позволяет получить
экономию средств при производстве АЭС и тем самым создать экономиче-
скую основу для необходимых дополнительных усилий по расчету прочно-
сти и контролю качества трубопровода.
В последние годы сделаны попытки перенести этот подход (стандар-
тизированный для трубопроводов) на корпуса сосудов давления. С позиций
механики разрушения это означает гарантию стабильного характера роста
трещины после ее превращения в сквозную. Поскольку при определенной
нагрузке и длине трещины возможно нестабильное разрушение практически
любого конструкционного материала, необходимо решить три задачи. Пер-
вая задача — обнаружение дефектов недопустимо большого размера перед
3.2. Моделирование разрушения при монотонном нагружении
\G1
началом и в процессе эксплуатации — возлагается на средства контроля и
диагностики. Методы расчета прочности должны обеспечить решение вто-
рой задачи — определение опасного размера дефекта. Методы проектирова-
ния конструкции и технологии ее изготовления должны быть нацелены на
то, чтобы размеры возникающих дефектов были как можно меньше, а кри-
тический размер дефекта был как можно больше, по крайней мере сущест-
венно больше такого, который может быть пропущен при контроле, — это
третья задача.
Таким образом, для конкретных материала, конструкции и нагрузки
требуется рассчитать минимальную длину сквозной трещины, способной
расти нестабильно, т. е. при постоянной или даже убывающей нагрузке. Эта
задача может быть решена путем компьютерного моделирования процесса
разрушения. Вначале необходимо воспроизвести на модели рост нагрузки
до уровня, который возможен в анализируемой конструкции при аварийной
перегрузке. Если трещина при этих условиях не растет, то она не является
опасной. Если трещина растет при увеличении нагрузки, это еще не означа-
ет нестабильного разрушения. В этом случае шаги моделирования нужно
продолжить при постоянной заданной нагрузке, учитывая после каждого
шага изменение формы деталей конструкции вследствие пластического де-
формирования и роста трещин. Если процесс роста трещины не затухает
после нескольких таких шагов, разрушение следует считать нестабильным,
а размер трещины — опасным.
На рис. 3.21, а схематично показана обечайка корпуса ядерного реактора
АСТ-500 из стали 15Х2МФА наружным диаметром 4950 мм, длиной 10 м,
толщиной стенки 65 мм (57 мм — толщина корпуса из стали 15Х2МФА
в
Рис. 3.21. Схема моделирования обечайки с трещиной:
а — обечайка; б — объемная модель; в — плоская модель
168
3. Проектные и контрольные расчеты на прочность
плюс 8 мм — толщина плакирующего наплавленного слоя аустенитной ста-
ли). Поскольку этот сравнительно небольшой реактор предназначен для те-
плоснабжения населенных пунктов, размещение его вблизи жилья требует
повышенной гарантии безопасности. Наибольшей возможной нагрузкой для
корпуса является внутреннее давление 6 МПа, так как при этом давлении
происходит разгерметизация фланцевых соединений. Невысокая рабочая
температура (275 °C) позволяет использовать в модели характеристики ма-
териала, полученные при комнатной температуре.
На рис. 3.21, б показана схема объемной модели оболочки с трещи-
ной. Для моделирования МКЭ потери герметичности и последующего роста
сквозной трещины необходимо воспроизвести в стенке модели исходный
полуэллиптический контур трещины, а также равномерно разбить на доста-
точно мелкие элементы область ожидаемого роста трещины. Такая наиболее
простая постановка задачи моделирования достигается ценой большого ко-
личества объемных элементов в модели и требует применения сравнительно
мощного компьютера, поэтому авторами был применен другой подход.
Объемная модель оболочки из достаточно крупных элементов нагружается
без учета декомпрессии и движения трещины и позволяет определить на-
грузку на контуре фрагмента модели (закрашен на рис. 3.21, б), содержаще-
го вершину сквозной трещины, в зависимости от длины исходной трещины.
На плоской, более подробной модели (рис. 3.21, в) решается задача о росте
трещины в толстой пластине в условиях плоского деформирования при по-
ступательном перемещении границ пластины А. Сопоставление условий на
контуре фрагмента объемной модели оболочки под давлением 6 МПа со
сквозной трещиной заданной длины L (см. рис. 3.21, а) и на контуре плоской
модели позволяет определить поведение трещины в оболочке, после того
как она внезапно превратится в сквозную. При нагружении внутренним дав-
лением деформации в направлении продольной оси цилиндрической обо-
лочки малы, поэтому показанная на рис. 3.21, в схема нагружения доста-
точно полно имитирует условия работы реального элемента оболочки с
трещиной. Наряду с геометрией конструкции и условиями ее нагруже-
ния, исходными данными для моделирования являются характеристики
деформирования и разрушения материала, методика определения кото-
рых рассмотрена в разд. 3.2.3.
На рис. 3.22 показаны результаты решения плоской задачи для фраг-
мента оболочки. После страгивания трещина растет с ускорением по мере
перемещения края А пластины. При среднем напряжении на краю модели
225 МПа, а в ослабленном сечении 1125 МПа после роста длины трещины
на 3 мм ее дальнейший рост происходит без повышения нагрузки. Для обо-
лочки это означает продолжение роста трещины при постоянном внутрен-
нем давлении, т. е. нестабильное разрушение.
3.2. Моделирование разрушения при монотонном нагружении
169
Рис. 3.22. Результаты моделирования растяжения плоской пластины (см. рис. 3.17, в):
1 — суммарная нагрузка на краю пластины А; 2 — рост трещины
Рис. 3.23. Результаты моделирования фрагмента у вершины трещины (см. рис.
3.17, в) в момент страгивания и наступления нестабильности (кривые 1, 2) и оболо-
чек с продольными сквозными трещинами различной длины (см. рис. 3.17, б)
На рис. 3.23 показаны эпюры распределения нормальных напряже-
ний вдоль края А плоской модели оболочки, параллельного трещине и
удаленного от нее на 200 мм при двух уровнях нагрузки. Начало коорди-
нат — в точке напротив вершины трещины, направление координатной
оси совпадает с направлением роста трещины. Первый уровень (кривая 7)
соответствует страгиванию трещины, а второй (кривая 2) — ее переходу
к нестабильному росту.
Тонкими линиями на рис. 3.23 показаны эпюры напряжений в сечении
А объемной модели оболочки (см. рис. 3.21, б), расположенном на том же
расстоянии (200 мм) от трещины. На каждой эпюре обозначена длина тре-
170
3. Проектные и контрольные расчеты на прочность
щины. Уровень напряжений в оболочке вдали от трещины при давлении
6 МПа составляет 222 МПа. Вследствие изгиба оболочки вокруг трещины
напряжения у ее внутренней поверхности больше, чем у наружной. На
рис. 3.23 показаны эпюры напряжений у внутренней поверхности оболочки.
Аналогичный характер эпюр, полученных на объемной и плоской моделях,
свидетельствует о корректности примененного поэтапного подхода к моде-
лированию оболочки.
Сопоставление уровней напряжений у вершины сквозной трещины в
оболочке с уровнями, при которых происходит ее страгивание и переход к
нестабильному росту, показывает, что если трещина превращается в сквоз-
ную на длине L = 400...800 мм, то возможен дальнейший рост ее длины на
1...3 мм. Если же длина образовавшейся сквозной трещины превышает
800 мм, напряжения у ее концов приближаются к уровню, при котором
дальнейший рост сквозной трещины становится нестабильным и приводит к
полному разрушению (взрыву) оболочки. Средние по толщине напряжения
в оболочке несколько ниже показанных на рис. 3.23 напряжений у внутрен-
ней поверхности, поэтому оценка критических размеров трещины является
консервативной.
Для поверхностных трещин, длина которых во много раз больше тол-
щины оболочки, можно считать глубину трещины в ее средней части посто-
янной. В этом случае модель плоского деформирования кольцевого слоя
(закрашен на рис. 3.24) позволяет оценить условия роста трещины под на-
грузкой в направлении толщины до образования течи.
При одинаковой глубине наружной и внутренней трещин условия раз-
рушения несколько различаются вследствие разного изгиба, однако влияние
этого фактора на рост трещин незначительно. На рис. 3.25 видно, что крити-
ческая глубина трещины составляет 45 мм. Длинная трещина такой глубины
прорастет насквозь при давлении 6 МПа, в то время как трещина глубиной
40 мм углубится менее чем на 1 мм. Для коротких трещин, длина которых
соизмерима с глубиной, критическая глубина трещины больше.
I
Рис. 3.24. Схемы моделирования роста наружной и внутренней тре-
щин в направлении толщины:
1 — моделируемый кольцевой слой
3.2. Моделирование разрушения при монотонном нагружении
171
Внутреннее давление, МПа
Рис. 3.25. Результаты моделирования роста глубины длинных
поверхностных трещин
Таким образом, для корпуса ядерного реактора АСТ-500 в начале срока
эксплуатации (без учета радиационного и теплового охрупчивания) опасность
течи возникает при появлении технологических или эксплуатационных трещин
глубиной более 40 мм (при толщине стенки 65 мм). Нестабильное разрушение
(взрыв оболочки) возможно, если при этом длина трещины превышает 800 мм.
Полученные критические размеры дефектов на 30...40 % меньше, чем
рассчитанные ранее по аналитическим формулам для того же реактора. Это
различие может быть связано с тем, что в модели (см. рис. 3.21) наиболее
опасное — продольное расположение трещины (поскольку окружные на-
пряжения в цилиндрической оболочке примерно в 2 раза превосходят осе-
вые). Аналитические формулы выведены для плоских пластин и к цилинд-
рической оболочке применимы только в случае поперечных трещин, пер-
пендикулярных к прямолинейной образующей.
Заключение по итогам расчета: современные средства контроля и
диагностики позволяют обеспечить безопасность эксплуатации реактора,
поскольку гарантируют обнаружение дефектов рассчитанного критического
размера.
Моделирование было проведено для стали 15Х2МФА в состоянии по-
ставки. При наличии образцов металла, испытавшего эксплуатационные по-
вреждения, разработанная методика позволяет рассчитать изменение опас-
ных размеров дефектов за время эксплуатации. Возможен также учет прак-
тически любых факторов, усложняющих условия работы конструкции
(неоднородности материала, напряжений от неравномерного нагрева, земле-
трясений и т. д.), при наличии достаточно мощного компьютера и необхо-
димых данных о свойствах материала и условиях нагружения.
Рассмотренный пример демонстрирует возможность моделирования
на персональном компьютере:
172
3. Проектные и контрольные расчеты на прочность
• страгивания и роста в глубину поверхностной трещины;
• страгивания и роста в длину сквозной трещины в оболочке;
• перехода к нестабильному росту трещин.
Моделирование позволяет проверить работоспособность оболочки
при проектных и контрольных расчетах по критерию течи перед разрушени-
ем в экстремальных условиях нагружения с учетом наличия дефектов.
3.3. Моделирование методами механики разрушения процесса
роста трещин от дефектов при циклическом нагружении
В § 3.1 показано, что область применимости линейной механики раз-
рушения (ЛМР) для расчетов усталостной прочности существенно шире,
чем для расчетов статической прочности. При циклическом нагружении
разрушение развивается при низких средних напряжениях, вследствие чего
выполняется условие ограниченности размеров пластической зоны у вер-
шины трещины, необходимое для корректного применения ЛМР. В § 3.2
рассмотрены методы численного моделирования процесса разрушения при
монотонном однократном нагружении. Их пригодность для моделирования
циклического многократного нагружения не вызывает сомнений, но для
разработки применимой в инженерной практике методики моделирования
необходимо продолжение исследований условий упрочнения материала и
суммирования повреждений в нем. Поэтому методы ЛМР, в большинстве
случаев обеспечивающие простые и достаточно точные решения задач уста-
лостной прочности, сохраняют свою актуальность.
Следует отметить, что принципиальное различие между этими подхо-
дами невелико. Большинство формул в справочниках по ЛМР получено ме-
тодами численного моделирования, в том числе МКЭ. Расчеты по формулам
ЛМР также целесообразно проводить с помощью компьютера. Поэтому
применение ЛМР для конкретной детали имеет смысл, если удается конфи-
гурацию дефектов в сечении схематизировать под одну из готовых формул
ЛМР, и если для материала детали имеются данные по критическим значе-
ниям критериев ЛМР.
В конструкциях, испытывающих 106 и более циклов нагружения, на-
личие подрастающей трещины практически любого исходного размера мо-
жет привести к такому увеличению этого размера, что КИН К\ достигнет
критического значения. Поэтому для обеспечения безотказной работы кон-
струкций при TV > 106 циклов следует исходить из условия исключения под-
растания трещины, т. е. ограничения исходного размера дефекта такими
3.3. Моделирование роста трещин при циклическом нагружении
173
пределами, при которых значение
коэффициента А) не превышает по-
рогового Kth (см. рис. 3.7).
При числе нагружений N< 106
такое условие может оказаться из-
лишне жестким. Применительно к
оболочковым конструкциям, харак-
терным является наличие стыковых
соединений и нагружение пульси-
рующим циклом растяжения в пре-
делах 102...105 циклов. Хотя в этих
условиях возможно зарождение и
последующее подрастание устало-
Рис. 3.26. Схема закономерности роста
трещины от сварочного дефекта
стных трещин от технологических
дефектов, ограниченность числа циклов нагружения позволяет обеспе-
чить безопасность работы конструкции и при наличии подрастающей
трещины, если ограничить исходные размеры дефектов условием, что их
подрастание за период эксплуатации невелико (например, не превышает
0,1...0,2 мм).
Описать процесс усталостного разрушения (зарождение и развитие
трещины) с единых теоретических позиций пока не удается. Поэтому при
анализе стадии зарождения трещины обычно используют традиционные
представления об усталости при циклическом деформировании, тогда как
анализ стадии роста трещины выполняют с помощью методов механики
разрушения. Применение такого подхода к развитию разрушения от техно-
логического дефекта существенно затрудняется тем, что влияние исходной
формы дефекта проявляется не только на стадии зарождения, но и на на-
чальной стадии роста трещины. Поэтому при моделировании этого процесса
методами механики разрушения представляется целесообразным использо-
вание схемы, представленной на рис. 3.26, где кривая 1 соответствует кине-
тической диаграмме усталостного разрушения (3.3).
Условия возникновения трещины в этом случае отражает положение
точки А с координатами lgXIycjI и 1gгде К1усл — КИН, характеризую-
щий дефект длиной 21 и подсчитанный как для трещины такой же длины, а
dlldN — скорость роста трещины от исходного дефекта. Влияние конфи-
гурации и размера этого дефекта проявляется в том, что точка А располага-
ется ниже диаграммы, т. е. начальная скорость роста трещины снижается.
По мере продвижения вершины трещины от кромки исходного дефекта это
влияние уменьшается и исчезает после выхода на кривую 1 в точке В (линия
АВ на рис. 3.26).
174
3. Проектные и контрольные расчеты на прочность
Следует заметить, что такая модель отражав! процесс усталостного
разрушения для однородного металла. Когда по той или иной причине тре-
щиностойкость металла в зоне дефекта оказывается пониженной, может
иметь место резкое ускорение роста трещины в пределах этой зоны. Такой
случай отражает кривая 2 на рис. 3.26.
Многообразие возможных вариантов страгивания и развития трещины
от конкретного дефекта, обнаруженного при неразрушающем контроле, за-
трудняет моделирование этого процесса. Трудности усугубляются ограни-
ченной достоверностью исходных данных, получаемых при неразрушаю-
щем контроле и возможными погрешностями в определении формы и раз-
меров дефекта, его расположения по толщине элемента, а также его
характера (плоский, объемный, единичный, групповой).
Поскольку при подготовке исходных данных такие погрешности
практически неизбежны и ставят под сомнение корректность выполняемых
расчетов, представляется целесообразным использовать консервативный
подход:
а ) все обнаруженные при неразрушающем контроле дефекты считать
трещиноподобными;
б ) схематизировать внутренние дефекты как эллиптические трещины,
а поверхностные дефекты как полуэллиптические трещины с такими ориен-
тацией и соотношением размеров осей, которые вызывают наибольшую
скорость роста усталостной трещины;
в ) за стадию зарождения N3 трещины от исходного дефекта, имеющего
сварочное, а не усталостное происхождение, условно принимается то число
нагружений NOj, которое необходимо для увеличения исходного размера
трещины на 0,1 мм.
Такой подход существенно упрощает расчет числа циклов до страги-
вания трещины. Обоснованность его подтверждена как экспериментами, так
и теоретическим анализом процесса усталостного разрушения. Общепри-
знанная модель описывает рост усталостной трещины как непрерывное на-
копление повреждений в высоконагруженной зоне перед фронтом трещины
с последующим разрывом поврежденного участка. Поэтому рост трещины
от трещиноподобного дефекта, имеющего усталостное происхождение, на-
чинается сразу, так как металл вокруг такого дефекта уже поврежден. От
сварочного дефекта рост трещины начинается после повреждения металла
вокруг дефекта. Повреждение накапливается с такой же скоростью, как
перед фронтом растущей трещины, и для конструкционных сталей требует
примерно столько же циклов, сколько требуется для роста этой трещины
на 0,1 мм.
Для определения NOi по кинетической диаграмме усталостного разру-
шения (3.3) достаточно иметь значения параметров уравнения Пэриса
3.3. Моделирование роста трещин при циклическом нагружении
175
dl ( К, Т
---- = И --Г >
dN \К J
(3.11)
описывающего наклонный участок диаграммы для материала той зоны соеди-
нения, где расположен дефект. Этот параметр можно использовать для сопос-
тавления стойкости материалов к страгиванию трещин от дефектов (рис. 3.27).
Если имеется уверенность, что обнаруженный дефект не испытал циклического
нагружения до начала эксплуатации конструкции, то можно дать прогноз ее
ресурса до страгивания трещин от дефекта или внести поправку в оценку ре-
сурса по предельному состоянию недопустимого роста трещин.
Процедура оценки работоспособности конструкции включает этапы:
• схематизация дефекта в сечении применительно к одной из формул
ЛМР;
• расчет текущих значений критериев ЛМР в ряде точек контура де-
фекта при рабочих нагрузках конструкции;
• определение параметров кинетической диаграммы усталостного раз-
рушения материала конструкции (см. рис. 3.7, 3.26);
• определение скорости роста усталостной трещины в точках ее контура;
• определение новых размеров и формы усталостной трещины по мере
повторения циклов нагружения вплоть до завершения запланированного
ресурса работы конструкции;
• сравнение текущего НДС в сечении со всеми возможными предель-
ными состояниями;
• выдача заключения о работоспособности конструкции.
Рис. 3.27. Сопоставление зависимостей NOj =f(Kt™d
176
3. Проектные и контрольные расчеты на прочность
в
Рис. 3.28. Схематизация
одиночных дефектов [3.6]
Контуры дефектов сварных соеди-
нений технологического происхождения
имеют сложные очертания и, как прави-
ло, известны весьма приближенно. Гото-
вые формулы и таблицы в механике
трещин имеются только для типовых
случаев. Поэтому в расчетах, основан-
ных на методах механики трещин, де-
фекты заменяют трещинами простой
формы, например: внутренней эллипти-
ческой; выходящей на поверхность по-
луэллиптической или сквозной трещи-
ной с фронтом, перпендикулярным по-
верхности сварного соединения.
На рис. 3.28 приведен пример
схематизации реальных очертаний де-
фектов сварных швов [3.6]. Ввиду того
что узкая перемычка между фронтом
трещины и поверхностью сварного со-
единения разрушается за малое число
циклов, к поверхностным полуэллип-
тическим относят все трещины, имею-
щие перемычку толщиной h < 0,0556
(рис. 3.28, б), а к сквозным — все тре-
щины, имеющие размер в глубину b > 0,75
(рис. 3.28, в). Поверхностный дефект с
соотношением ЬН < 0,01 можно рассмат-
ривать как краевой надрез неограничен-
ной длины с постоянным размером по
глубине а = Ь.
Дефекты, плоскость которых расположена не под прямым углом к
направлению действия номинальных растягивающих напряжений, заме-
няют их проекцией на площадку, перпендикулярную к линии действия
напряжений.
Рассмотрим некоторые примеры схематизации. При рентгеновском
контроле известна только протяженность дефекта I, при ультразвуковом —
для оценки размеров дефектов могут быть использованы раздельно или в
сочетании три измеряемых параметра: эквивалентная площадь дефекта Sd,
условная протяженность I (по длине) и условная ширина дефекта b (в на-
правлении толщины). Для поверхностных дефектов размер I измеряют вдоль
поверхности. Кроме того, может быть определена глубина залегания дефек-
3.3. Моделирование роста трещин при циклическом нагружении
177
та и подсчитана толщина перемычки h. Формулы для определения размеров
эквивалентной дефекту эллиптической внутренней, полуэллиптической по-
верхностной или прямоугольной сквозной трещины приведены в табл. 3.1.
Независимо от ориентации размера I большую ось эллипса располагают па-
раллельно ближайшей поверхности, так как доказано, что такое расположе-
ние наиболее опасно и приводит к наибольшему значению К\. Из тех же со-
ображений, при отсутствии данных о соотношении размеров дефекта, ши-
рину внутренней трещины принимают равной половине длины.
Таблица 3.1. Размеры трещины, принимаемые в расчет
при схематизации реальных дефектов
Размер дефекта Размер трещины, эквивалентной дефекту
Рис. 3.28, а Рис. 3.28, б Рис. 3.28, в
/, ъ Ь 1 а-—; с- — 2 2 a — b + h', с = —; если 2 а > с, то a = c = 0,8yll-(h + b) 1 а = — 2
i,sd 2’^ / <7 = с = — 71 1 2 1,4-Sd , , 1 а = -+1,27-й; с = —; 12 если а > с, то 1 а = — 2
a = c = 0,85y]Sd + 0,88-/-й
sd а = . —; с-2а Пл о = 0,54^+1,4-й-7^7; с = 2,5а а = 1,35х
х^+1,4й-^
Близко расположенные дефекты объединяют в единую трещину при
а^+а2
условии, что расстояние между ними не превышает /12 < —!где и а2 —
9а2
найденные по табл. 3.1 размеры для большего и меньшего из соседних де-
фектов. В этом случае суммарная площадь трещины
2
(с( + с2)(_/J2 + Ц + а2)
2
, ч ai
(о!]С| + а2с2) +
а<
Sd=it 1-0,5
а.
178
3. Проектные и контрольные расчеты на прочность
Рис. 3.29. Поверхность излома с метками фронта растущих трещин,
демонстрирующая этапы процесса объединения соседних поверхностных
трещин, расположенных вдоль одной линии
Если условие объединения не выполнено, взаимное влияние дефектов
не учитывают. Если дефектов больше двух, то поочередно рассматривают
каждую пару и, если условие объединения выполнено, заменяют ее суммар-
ной трещиной, затем проводят проверку на дальнейшее объединение сум-
марных трещин.
Следует отметить, что данные рекомендации чрезмерно консерватив-
ны и практическое применение их, вероятно, оправдано при моделировании
разрушения в условиях статического нагружения, когда в области перемыч-
ки между соседними трещинами можно ожидать появления больших пла-
стических деформаций, а также в тех случаях, когда нет уверенности в
достаточной точности измерения размеров дефектов. Экспериментально
установлено, что при циклическом нагружении взаимным влиянием сосед-
них трещин на скорость их роста можно пренебрегать вплоть до смыкания
их берегов.
Закономерности взаимодействия трещин исследованы главным обра-
зом применительно к случаю расположения инициаторов разрушения вдоль
одной линии. Это характерно для дефектов на линии перехода от основного
металла к усилению протяженного стыкового шва, в особенности когда
имеют место искажения геометрической формы, связанные с наличием
смещения кромок стыка. Такие искажения нередки в оболочковых конст-
рукциях и трубопроводах. Долговечность соединения в этом случае в ос-
новном определяется числом циклов, необходимых для образования отдель-
ных трещин длиной 2...5 мм, расположенных по линии сплавления. Эти
трещины сначала растут практически независимо друг от друга, но после
соприкосновения краев соседних трещин они объединяются (рис. 3.29), об-
разуя единую поверхностную трещину. К моменту нарушения герметично-
сти стенки оболочки протяженность такой образовавшейся магистральной
трещины может составлять сотни миллиметров. Процесс разрушения свар-
ного соединения от линейного инициатора определяется многообразием
3.3. Моделирование роста трещин при циклическом нагружении
179
Рис. 3.30. Схемы для расчета коэффициента интенсивности напряжений
действия ряда факторов, имеющих случайный характер. Прогнозирование
этого процесса на вероятностной основе с помощью ЭВМ изложено в § 3.4.
Известны относительно простые формулы, позволяющие рассчиты-
вать значения К\ в различных точках контура трещины (рис. 3.30). Для де-
фектов в виде внутренних эллиптических трещин (рис. 3.30, а), тарировоч-
ный коэффициент Y в формуле (3.2) подсчитывают как
л
1 + 1,464(а/с)1’65
при а < 91?, a + h <5/2, где для разных точек фронта трещины отличают-
ся коэффициенты у:
1лс a + h\ ло!л< a + h\
1а = °>5--Г" ; °’5---Г— •
\ 5 ) V. О J
При равномерном по толщине элемента распределении напряжений
180 3. Проектные и контрольные расчеты на прочность
При линейном распределении напряжений (при изгибе) в формулу
(3.2) подставляют различные значения оном для точек А и С. При изгибе с
убыванием а от точки А к точке С, а также при с < а расчетные напряжения
для этих точек
Зо . + сг а с . - —- — + — номЛ 4 с ^Л-^С, 12 '
_ сА +3ос а ^НОмС Л 4 с сл ~сс 12
При изгибе с возрастанием а от точки А к точке С при с > а расчетные
напряжения для этих точек
13о.-ог с а,-<уг
_____. /1 Lz /1 О- а
номЛ - ~ ,
_11ол+ос Зе ол-ос
°номГ 12 ~а 4 ’
Номинальное напряжение для точки D рассчитывают как среднее
арифметическое номинальных напряжений для точек А и С, а тарировочный
коэффициент — как YD = —YAYC.
V с
Для дефектов, представленных в виде поверхностных полуэллиптиче-
ских трещин (рис. 3.30, б), тарировочный коэффициент подсчитывают как
при а^с, а <0,76, где для разных точек фронта трещины отличаются ко-
эффициенты у:
Ус = 1,12-0,08—; уд =
с
1 + 0,32^ f1,23-0,09—
Ы JL с)\с
При линейном распределении напряжений в формулу (3.2) подстав-
ляют различные значения он0М для точек С и D:
° ном С — CD
+ (ос -Од)- 0,608 + 0,111—-
/ +>.75
0,282-0,536 -
k С J
/ \1,5
+ 0,254 -
ус )
а
8
°homc = 0>823od + 0,177oc.
3.3. Моделирование роста трещин при циклическом нагружении
181
Сварные соединения с конст-
руктивным непроваром рекомендует-
ся представлять в виде пластины с
центральной сквозной либо с боковой
трещиной (рис. 3.31). Коэффициент
интенсивности напряжений для пла-
стины с центральной сквозной тре-
щиной при растяжении с изгибом оп-
ределяют по формуле
„ v Г- v 3,75Ма'-5
Kt = Ypuy/ita + YM ---------,
(3.12)
Рис. 3.31. Расчетные схемы для
сварных соединений
/ \-°,5
где Yp = 0,5cos—
I 28 J
1 прио/8<0,3,
1,005
z \ "1-0.5
а )
cos—------0,3 при
215 J
0,3 <о/8< 0,85.
Здесь индексы Р и М обозначают растягивающую силу и изгибающий
момет соответственно.
Для пластины с боковой трещиной
где Yp -
1,12 + 5(о/8)4
1-а/8
KA=Yp^a+YM—-^
(р-а)’
при о/8<0,55;
(3.13)
0,303(1 + 3,03(а/8))
Yp = 4 v ” при о/8 > 0,55;
YM = 0,7?Л/1-(1-о/8)6.
Здесь Х = 1 при а/8> 0,05; X = 1,15-60(о/8)2 при о/8<0,05.
Серьезным препятствием для применения методик оценки ресурса
конструкций является отсутствие необходимых данных о свойствах мате-
риала, в частности о параметрах кинетической диаграммы усталостного раз-
рушения. Наряду с накоплением банка таких данных целесообразно разви-
182
3. Проектные и контрольные расчеты на прочность
вать альтернативные методы их определения, опираясь на их корреляцион-
ную связь с другими, более доступными характеристиками.
Пороговую интенсивность напряжения f±Kth принято рассматривать
как характеристику конструкционного материала, однако ее значение зави-
сит от толщины металла, температуры испытания, асимметрии цикла на-
гружения. Результаты испытаний ряда конструкционных сталей удовлетво-
рительно аппроксимирует формула
АЛГ,Л = 12,7 - О,ОО6со2 - (11,37 - О,ОО65с>о2Ж ,
где Rc — коэффициент асимметрии цикла. Аналогичная зависимость полу-
чена для титановых сплавов типа Ti — 6А1 — 4V:
AKlh = 6,5 - 5,6RO.
Экспериментально полученные значения \Kth обычно соответствуют
пульсирующему нагружению (7?о = 0). Для других значений Rc вносят по-
правку:
ЛКгЛ=ДК,А0(1 -Ra)\
где у = 0,5... 1,0; АК1Ю — значение AKlh при Rc = 0.
Поскольку ДДЛ имеет значительный разброс значений, рекомендуется
принимать у = 1,0.
Ввиду существенного влияния асимметрии цикла в области низких
значений АД, при моделировании разрушения необходимо учитывать оста-
точные сварочные напряжения, особенно в области Rn < 0.
Второй участок диаграммы разрушения, соответствующий устойчи-
вому росту' трещины, описывает уравнение (3.11) с параметрами v, К* и т.
Обычно применяют постоянное значение у = 10“4 мм/цикл; значения К* и т
определяют экспериментально. Для конструкционных сталей достаточно
найти т, остальные два параметра при отсутствии данных можно принять
одинаковыми для всех марок:
v - 0,553-10“4 мм/цикл; К* — 18,35 МПад/м .
На втором участке кинетической диаграммы усталостного разрушения
влияние асимметрии цикла проявляется слабее, чем на первом. Влияние
асимметрии связывают с явлением закрытия трещины. По результатам ис-
следования кинетики перемещения берегов трещины при циклическом на-
гружении Элбер установил, что вследствие образования у корня трещины
остаточных сжимающих напряжений смыкание ее берегов происходит
раньше, чем нагружение достигает нуля. Раскрытие трещины также проис-
ходит не сразу, а при некотором значении приложенных растягивающих
номинальных напряжений. Концепция Элбера состоит в невозможности
3.3. Моделирование роста трещин при циклическом нагружении
183
роста трещины в период смыкания ее берегов. Поэтому вместо размаха ЛА) в
расчет необходимо вводить эффективное значение коэффициента интенсив-
ности напряжений ДА)Эф = Kimax - А)О1|<, вычитая уровень, соответствующий
открыванию трещины. Очевидно, что влияние этого эффекта убывает с рос-
том асимметрии цикла.
Экспериментально установлено:
для алюминиевых сплавов типа Д16
ЛА)эф = (0,5 + 0,47?с)ДА) при -0,1 <ЛО< 0,7;
для алюминиевых сплавов типа 2219—Т851
ДХьф = (0,68 + 0,917?с)АЛГ[ при 0,08 <ЛО< 0,32;
для титановых сплавов типа Ti—6А1—4V
ЛКьф = (0,73 + 0,857?а)АА) при 0,08 < 7?о < 0,32.
Концепция закрытия трещины позволяет прогнозировать влияние на
скорость роста трещины одиночных перегрузок.
В работах ИЭС им. Е.О. Патона на основании сравнительного анализа
экспериментальных данных, полученных на образцах из низкоуглеродистой
и низколегированной стали при -1< Rc< 0,52, выведена формула, адекватно
описывающая влияние асимметрии цикла на скорость роста трещины:
*(«„ + !)
dl
---= VI
dN
где К.' и wj_i — параметры уравнения Пэриса, полученные для симметрич-
ного цикла, при = -1; X — характеристика чувствительности материала к
асимметрии цикла. В табл. 3.2 приведены значения этих параметров для не-
которых марок сталей.
(3-14)
Таблица 3.2. Значения параметров ти). при Rc = -1
Марка стали 002, МПа ов, МПа kJ, МПад/м т} К
СтЗ 255 460 19,8 3,96 1,05...1,18
15ХСНД 300 520 28,4 3,32 2,01...2,27
14Х2ГМР 540 735 47,7 2,63 1,04... 1,07
Остаточные сварочные напряжения, изменяя асимметрию цикла,
влияют на скорость роста трещины. На основании уравнения Пэриса выве-
дена формула
184
3. Проектные и контрольные расчеты на прочность
dN \ К* J 1-Аа J ’
(3.15)
где К1г — коэффициент интенсивности остаточных напряжений в вершине
трещины; s — определяется экспериментально (для низколегированных ста-
лей 5 = 0,25...0,5); v=v при v=------—- при Кхmax + Kv <0.
U-^a)
Основные трудности моделирования процесса разрушения сварных
конструкций с учетом собственных напряжений связаны со сложным харак-
тером распределения остаточных напряжений по сечению сварного соеди-
нения, затрудняющим вычисление К\г, с их изменением в процессе роста
трещины и изменением траектории роста трещины, а иногда и механизма
разрушения под влиянием остаточных напряжений.
Поэтому при моделировании целесообразно представить весь процесс
развития в виде серии дискретных периодов с достаточно малым подраста-
нием трещины. Основные идеи такого подхода и методические рекоменда-
ции по его реализации рассмотрены в разд. 3.4.2.
В сварных соединениях основными очагами концентрации напряже-
ний являются несплавления, плоские шлаковые включения, а также места
переходов от швов к основному металлу (рис. 3.32, а—д). Концентрация
напряжений существенно зависит от радиусов скруглений в зонах А, Б, В, Г,
в г
Рис. 3.32. Очаги концентрации напряжений в сварных соединениях
3.3. Моделирование роста трещин при циклическом нагружении
185
Рис. 3.33. Отображение роста трещин в сечении программой «РЕСУРС»:
1—4 — последовательные очертания фронта растущей трещины
Д, Е. При циклическом нагружении концентраторы напряжений могут стать
инициаторами возникновения трещин, а их взаимное расположение и ори-
ентация относительно осей главных напряжений способны в значительных
пределах снизить долговечность конструкции.
Приведенные выше формулы позволяют провести моделирование
процесса возникновения и роста усталостных трещин от исходных дефектов
при циклическом нагружении. После схематизации обнаруженных или
предполагаемых дефектов (см. рис. 3.28 и табл. 3.1) по формуле (3.2) опре-
деляют значения К\ в основных точках контура трещины (см. рис. 3.30). Да-
лее по формулам (3.11), (3.14) или (3.15), подставляя характеристики мате-
риала, взятые из справочных данных или результатов испытаний, находят
скорости роста трещины в этих точках. Считая эти скорости постоянными
на протяжении нескольких циклов, определяют приращения размеров и но-
вые размеры трещин после прохождения этих циклов. Затем проверяют ус-
ловия слияния трещин, превращения трещины из внутренней в поверхност-
ную, а затем в сквозную и вносят соответствующие изменения в количество,
форму и размеры трещин. Наибольшее значение Д сопоставляют с критиче-
ским, чтобы установить возможность внезапного хрупкого разрушения.
Процесс продолжают до завершения числа циклов, предусмотренных за
срок службы. Результатом моделирования является прогноз поведения кон-
струкции: выдержит ли она запланированный срок службы, и какого роста
трещин можно ожидать к концу срока.
В МГТУ им. Н.Э. Баумана разработана программа «РЕСУРС», кото-
рая не только выполняет моделирование, но и контролирует процесс ввода
данных, содержит пополняемую базу данных по свойствам материалов, де-
монстрирует в режиме анимации процесс роста трещин (рис. 3.33), готовит
и печатает протокол оценки ресурса и сохраняет результаты проведенных
ранее расчетов. Такая программа может служить частью более мощного
комплекса (элемента САПР) как в роли вспомогательного элемента для опе-
ративных расчетов, так и в роли центрального ядра системы контрольных
186
3. Проектные и контрольные расчеты на прочность
расчетов, в простейших типовых случаях использующей готовые формулы,
а при более сложной геометрии и условиях нагружения переходящей на мо-
делирование МКЭ.
3.4. Статистические методы моделирования разрушения
3.4.1. Учет технологической наследственности сварных
соединений
В подавляющем большинстве случаев аварийная ситуация складывается
в результате случайного сочетания нескольких неблагоприятных факторов.
Конструкционная прочность по своей природе является величиной, которая
имеет рассеяние, поскольку значения параметров, характеризующих нагружен-
ность, свойства сварного соединения, размеры элементов конструкций, степень
засоренности дефектами, их размеры и расположение в сварных швах подвер-
жены случайным колебаниям. Все это определяет необходимость использовать
вероятностные методы расчета на стадии проектирования конструкции и для
прогнозирования остаточного ресурса на стадии ее эксплуатации.
Различают два подхода к этой проблеме. Первый основан на обобще-
нии накопленного опыта проектирования, изготовления и эксплуатации кон-
струкций аналогичного типа и не ставит цель объяснить или описать сущест-
во явлений, приводящих к разрушению. Например, Управление по атомной
энергетике Великобритании (UKAEA) при оценке вероятности разрушения
сосудов атомных электростанций провело обследование 12700 неядерных
сосудов, суммарный срок эксплуатации которых составлял 100300 лет. На
основе анализа случаев разрушения сделано заключение, что до начала экс-
плуатации вероятность отказа (разрушения) за один год составляет 2,3-10-4, а
в период эксплуатации — 0,7-10'4. По данным реестра мостов федеральных
путей сообщения США, вероятность разрушения мостов составляет 9,5-10-7 в
год. Аналогичные расчеты для магистральных трубопроводов дают вероят-
ность 3-10'6разрушений в год на 1 м магистрального трубопровода.
Такой подход обеспечивает достаточно высокую достоверность оце-
нок, вместе с тем он несет в себе инерцию прошлого опыта. Как и всякая
феноменологическая модель, он может оказаться непригодным за предела-
ми области, в которой получены опытные данные, лежащие в его основе, и
поэтому мало пригоден для анализа принимаемых новых конструктивных и
технологических решений.
Более перспективен второй подход, при котором используют модели,
основанные на понимании закономерностей процесса разрушения с учетом
3.4. Статистические методы моделирования разрушения
187
статистики распределения параметров, контролирующих этот процесс. Они
позволяют прогнозировать влияние на ресурс конструктивных и эксплуата-
ционных факторов, а также учитывать технологическую наследственность
сварной конструкции.
При построении вероятностных моделей, описывающих влияние тех-
нологической наследственности на прочность конструкций, целесообразно
все расчетные величины разделить на две группы. Первая группа включает
факторы, влияющие на параметры предельного состояния конструкции,
обозначим их «обобщенная прочность» R, вторая — все факторы, влияющие
на параметры нагруженности, — «обобщенная нагрузка» Q. При разделении
на группы необходимо стремиться к тому, чтобы между параметрами, отне-
сенными к разным группам, отсутствовала корреляционная связь. Основным
условием прочности конструкции является требование удовлетворения с
некоторой достаточно большой вероятностью неравенства
R-Q>0. (3.16)
В общем случае R и Q являются случайными функциями, зависящими
от большого числа случайных и детерминированных величин, поскольку и
нагрузка, и прочностные характеристики могут существенно изменяться во
времени. Однако в тех случаях, когда изменение нагрузки во времени пред-
ставляет собой установившийся процесс, конструкционный материал не
склонен к старению и накоплением повреждений в конструкции можно пре-
небречь, R и Q рассматривают как случайные величины. Их разность Т =
= R- Q > 0 в вероятностной постановке характеризует так называемый ре-
зерв прочности.
Вероятность разрушения V можно выразить через резерв прочности
о
V=\pT(T)dT. (3.17)
—со
После преобразований получим
v = Ьо(0вй(2)б/2, (3.18)
где Pq(Q) и рт{Т) — распределение плотности вероятностей соответственно
нагруженности и резерва прочности; PR(Q) — интегральная функция рас-
пределения вероятностей обобщенного показателя прочности.
На стадии проектирования стремятся к тому, чтобы свести к миниму-
му вероятность пересечения кривых Pq(Q) и Pr(Q). Однако в процессе про-
изводства конструкция приобретает технологическую наследственность, в
результате чего кривые Pq(Q) и PR(Q) претерпевают изменения и их сосед-
188
3. Проектные и контрольные расчеты на прочность
ние ветви перемещаются навстречу друг другу как за счет изменений сред-
них значений, так и за счет увеличения дисперсии (см. рис. 3.1). Например,
остаточные сварочные напряжения изменяют среднее значение функции
Де(0; появление дефектов в сварных швах, искажение проектной формы и
размеров сварной конструкции изменяют и средние значения, и дисперсию
функции /?е(0. Во многих случаях сварка существенно влияет на локальные
механические свойства различных участков сварного соединения, и это, ес-
тественно, приводит к изменению параметров функции Pr(Q). Использова-
ние современных методов неразрушающего контроля позволяет изменить
параметры функций Pq(Q) и Pr(Q) в благоприятном направлении. В процес-
се эксплуатации развиваются эффекты накопления повреждений и старения,
в результате чего также наблюдается сближение кривых Pq(Q) и Pr(Q). Та-
ким образом, анализ уравнения (3.18) может явиться основой для выработки
управляющих и корректирующих воздействий на протяжении всего жиз-
ненного цикла сварной конструкции, т. е. на стадии проектирования, изго-
товления и эксплуатации.
В качестве случайных величин R и Q могут выступать как некоторые
усредненные параметры (например, сила, давление, средние напряжения
(величина 0, с одной стороны, и предел усталости, предел текучести или
предел прочности (величина R) — с другой), так и параметры, характери-
зующие локальное НДС и локальные свойства, например: локальные де-
формации в зоне концентрации (0 и предельное значение деформаций (R)
или коэффициент интенсивности напряжений в вершине трещиноподобного
дефекта (0 и параметр трещиностойкости (А). Следует отдавать предпочте-
ние локальным параметрам, так как они позволяют более детально анализи-
ровать различные аспекты технологической наследственности сварных кон-
струкций и прогнозировать изменение остаточного ресурса в период их экс-
плуатации. Однако практическое использование локальных параметров в
вероятностных расчетах требует большого объема исходной информации,
характеризующей технологическую наследственность. Нужны такие дан-
ные, как уровень засоренности шва дефектами, размеры дефектов, геомет-
рические характеристики сварных соединений, функции распределения ме-
ханических характеристик, в том числе трещиностойкости, и др.
Если принять, что R и Q распределены по нормальному закону с па-
раметрами R, Q, Sq соответственно, то вероятность разрушения мож-
но определить из следующего уравнения:
R-Q = ySRQ, (3.19)
где SRq = .JSR + Sq ; (3.20)
у — квантиль нормированного нормального распределения,
3.4. Статистические методы моделирования разрушения
189
R-Q
у — ------
js2R+S2Q'
(3-21)
Пользуясь таблицами нормального распределения, можно определить
вероятность наступления разрушения или другого предельного состояния,
соответствующую значению у.
Если R и Q могут быть представлены в виде функции от случайных
параметров
(3.22)
е=Ф(уьг2,...,г„),
(3.23)
то средние значения и средние квадратичные отклонения определяются по
следующим зависимостям:
- - - - I ( 8 Y
«^(Х,,^,...,^), SR= X S2, (3.24)
У
где -^- •— частная производная функции ср по фактору Xh в которую под-
дХ,
ставляют среднее значение (Xl,X2,...,Xn)-, S, — среднее квадратичное от-
клонение фактора.
При аппроксимации (3.22) и (3.23) степенной функцией вида
п
R = X?', среднее значение и коэффициент вариации соответственно рав-
/=1
ны /? = Р[АГ“' ; vR = yfiTa.2vt, при описании (3.22) и (3.23) полиномом
/=1
R = ЪХх среднее значение и коэффициент вариации соответственно равны
= v„
‘ R RV ' ‘
Значения X.; v.; S. принимают на основании результатов экспери-
ментов или по справочным данным.
Таким образом, при прогнозировании прочности элементов конструк-
ций одной из основных задач является адекватное описание функций рас-
пределения обобщенных параметров, определяющих R и Q. Кроме того, не-
обходимо иметь модели, которые позволяют получить функции типа (3.22),
(3.23) на основе параметров, характеризующих технологическую наследст-
венность.
190
3. Проектные и контрольные расчеты на прочность
Уровень дефектности и параметры технологических отклонений
сварных соединений существенно зависят от применяемого способа
сварки, технологической культуры производства, характерных особенно-
стей и технологических традиций различных отраслей промышленности
и строительства.
Интегральную функцию распределения вероятности Р(к) существова-
ния в сварном соединении к дефектов рекомендуют аппроксимировать зако-
ном распределения Пуассона
(3.25)
Параметр ц зависит от способа сварки и вида дефекта. При высо-
ком уровне технологической культуры производства р находится в пре-
делах 0,1...10 м-1, при низком — р может достигать 40 м-1 и более.
В табл. 3.3 приведены статистические данные о засоренности свар-
ных соединений дефектами.
Таблица 3.3. Уровень засоренности сварных соединений дефектами
Тип конструкции Способ сварки Тип дефекта Уровень дефектности ц, м-‘
Сельскохозяйст- венное машино- строение В среде СО2 Подрезы Трещины Поры 1,15...9,5 0,2...0,64 0,4...6,1
Корпусное энергетическое оборудование Автоматическая под флюсом Шлак Трещины 0,15 0,067
Ручная дуговая Шлак Трещины 3,5 1,6
Металлические конструкции строительных машин Автоматическая под флюсом Поры Подрезы Непровары 4,8... 10,5 0,3...0,7 0,1...1,6
В среде СО2 Поры Подрезы Непровары 13,8...44,4 1,1...3,3 1,0...1,9
Ручная дуговая Поры Подрезы Непровары Включения 0,26...4,2 0,87...1,2 1,3...2,9 0,95—1,2
Функции распределения размеров дефектов, характерных для различ-
ных отраслей промышленности, приведены в табл. 3.4 и 3.5.
3.4. Статистические методы моделирования разрушения
191
Таблица 3.4. Параметры распределения Вейбулла для размеров
дефектов сварных соединений толщиной 12...16 мм (сталь 10Г2С)
в строительных конструкциях
Способ сварки Вид дефекта Параметры распределения Вейбулла
b Ч
Механизиро- Подрезы:
ванная дуговая по длине 2,5 8,0
в среде СО2 по глубине 1,0 0,9
Непровары:
по длине 3,о 20,0
по глубине 4,0 2,5
Поры, диаметр 2,0 1,8
Автоматиче- Подрезы:
ская дуговая по длине 1,5 5,0
под флюсом по глубине 2,0 1,1
Непровары:
по длине 1,4 3,6
по глубине 4,0 2,5
Поры, диаметр 1,0 0,3
Ручная дуго- Подрезы:
вая электродом по длине 3,0 9,2
с покрытием по глубине 1,0 0,5
Непровары:
по длине 1,6 16,0
по глубине 2,0 1,6
Включения:
по длине 1,4 5,5
по глубине 2,8 1,5
Поры, диаметр 2,0 1,6
Одним из наиболее часто встречающихся дефектов сварных соедине-
ний с угловыми швами является подрез. Подрезы имеют значительный раз-
брос размеров не только по глубине, но и по значениям радиусов в вершине.
Для сварных соединений, выполненных дуговой сваркой в среде СОг, наи-
более характерными являются дефекты типа узких подрезов (шириной
b < 1,0... 1,5 мм) с малыми радиусами в вершине (г < 0,4...0,5 мм). Доля узких
подрезов в общем их количестве достигает 80 %. Относительно редко
встречаются широкие и сравнительно неглубокие подрезы (Ь > 2,5...3 мм) с
большими радиусами в вершине (г > 1...1,5 мм). Наличие таких подрезов,
по-видимому, может быть менее опасным, чем резких переходов от основ-
ного к наплавленному металлу в бездефектных швах. Однако доля этих
192
3. Проектные и контрольные расчеты на прочность
подрезов невелика (5... 10 %), и в целом подрезы в сварных узлах следует
рассматривать как трещиноподобные концентраторы. Распределения гео-
метрических параметров дефектов типа подрезов соответствуют логариф-
мически нормальному закону: для подрезов среднее значение 1пЛ» =0,117,
S2b =0,792, ЬЛ =-0,951, S2 =0,748, 1п7 =-1,780, S2 =2,14.
Таблица 3.5. Параметры распределения значений глубины непровара
Тип соединения Толщина детали, мм Выборочные характеристики распределения, мм Закон распределения Параметры распределения
^ср S
Односто- роннее без разделки кромок 6 2,24 0,884 Нормальный h = 2,24 .0 = 0,782
2,27 0,885 h = 2,27 0 = 0,785
Односто- роннее без разделки кромок на остающейся подкладке 7 2,05 0,842 h = 2,05 о = 0,709
8 2,29 0,902 h = 2,29 0 = 0,813
Односто- роннее с разделкой кромок 1,68 0,855 Логарифмический p = 0,429 5=0,417
10 1,88 1,02 Нормальный p = 0,497 5=0,517
Двусто- роннее без разделки кромок 8 1,38 0,932 Веибулла m = 2,03 /=1,63
10 1,81 0,978 m = 4,11 /=1,98
В некоторых работах глубину подрезов в тавровых соединениях реко-
мендуют аппроксимировать экспоненциальным законом. Параметр I может
колебаться в пределах 0,12 < I < 1,35 мм 1 при среднем значении глубины
подреза h = 0,75.. .0,95 мм.
При моделировании процесса зарождения разрушения при перемен-
ных нагрузках необходимо иметь информацию о концентрации напряжений
в зоне перехода от шва к основному металлу. В табл. 3.6 приведены значе-
ния коэффициентов концентрации напряжений при доверительной вероят-
ности Р = 0,5 и Р = 0,95, полученные на основании исследования сварных
узлов строительных и дорожных машин.
3.4. Статистические методы моделирования разрушения
193
Таблица 3.6. Концентрация напряжений в сварных соединениях
строительных и дорожных машин
Вид соединения Предел прочности стали, МПа Эффективный коэффициент концен- трации напряжений
Среднее значение Коэффициент вариации
400 1,05 0,16
Стыковое 600 1,10 0,11
800 1,15 0,13
400 1,35 0,11
Нахлесточное 600 1,45 0,19
800 1,55 0,22
400 1,45 0,105
Тавровое 600 1,55 0,14
800 1,65 0,17
Конфигурация зоны перехода от шва к основному металлу норматив-
ными документами не регламентируется. В то же время именно угол q пере-
хода и радиус г сопряжения шва с основным металлом оказывают более су-
щественное влияние на концентрацию напряжений, чем общие размеры
швов. Необходимо также подчеркнуть, что геометрические параметры этой
зоны не стабильны по длине шва и могут изменяться в довольно широких
пределах. Радиус перехода составляет, например, от десятых и сотых долей
миллиметра до нескольких миллиметров. Следствием этого является суще-
ственная нестабильность по длине шва концентрации напряжений, с чем
необходимо считаться при моделировании разрушения сварных соединений,
особенно работающих при переменных нагрузках.
Геометрия профиля шва в зоне перехода зависит от многих парамет-
ров: способа и режимов сварки, сварочных материалов, типа швов и др.
Результаты экспериментальных исследований распределения значе-
ний г и q профиля угловых швов тавровых соединений представлены в
табл. 3.7. Даны средние значения и в скобках 95 %-ные границы рассеяния
результатов измерений. Интегральная функция распределения хорошо ап-
проксимируется логарифмически нормальным законом.
Для сварных соединений, выполненных полуавтоматической сваркой
в среде СОг на предприятиях сельскохозяйственного машиностроения, по-
лучены следующие результаты. Для углов перехода среднее значение
9 = 65,8°; S’2 =64,7°. Радиусы перехода соответсвуют логарифмически нор-
мальному закону: среднее значение In г = -1,34°, S2=2,09°. Разброс значе-
ний имеет следующие 95 %-ные доверительные границы:
7 6705
194
3. Проектные и контрольные расчеты на прочность
радиус перехода (мм) — 0,015 < г < 4,46.
угол сопряжения (град) — 16,0° < q < 115°.
Таблица 3.7. Геометрические характеристики зоны перехода
от шва к основному металлу
Способ сварки Сварочные материалы Радиус перехода г, мм Угол сопряжения q, град
Ручная дуговая УОНИ13/45, Э42 АНО4, Э46 ЦЛ20М, Св-0941 МФ ЦМ7, Э42ГР СМИ 1,0 (0,3...3,2) 0,5 (0,2... 1,4) 1,8 (0,6...5,0) 0,8 (0,3... 1,3) 0,6 (0,3...1,1) 37 (41...42) 35 (26...47) 28 (22...43) 26(24...31)
Оплавление в Аг Без присадки 2,0 (1,1...3,6) —
Аргоно дуговая Флюс АН348А 0,9 (0,7... 1,2) 28 (26...33)
В среде СО2 Св-08Г2С 0,8 (0,4... 1,4) 46 (37...54)
Резкий переход от основного к наплавленному металлу характерен
для швов, выполненных полуавтоматической сваркой в среде СО2. Так, 67 %
общей протяженности сварных швов составляют участки с радиусом пере-
хода г < 0,5 мм и 29 % — с углом перехода q > 80°. Данные швы можно рас-
сматривать как концентраторы с нулевыми радиусами и для их расчета можно
использовать подходы, основанные на методах механики разрушения.
3.4.2. Имитационное моделирование процесса разрушения
при циклическом нагружении
В настоящее время для прогнозирования процесса разрушения конст-
рукций при циклическом нагружении используются аналитические модели,
разработанные для анализа относительно простых тел с трещинами. Нали-
чие мощного математического аппарата механики трещин и относительная
быстрота и легкость получения информации способствовали широкому рас-
пространению этих моделей и переносу основных идей аналитического мо-
делирования на случаи анализа долговечности и надежности сварных кон-
струкций. Когда закономерности процесса разрушения сварных соединений
сложны и многообразны, зачастую приходится идти на упрощения реальных
явлений. В результате этого аналитическая модель может стать слишком
грубым приближением к реальной действительности.
Имитационное моделирование значительно расширяет возможности
учета отдельных особенностей процесса развития разрушения сварных со-
единений, особенно для крупногабаритных конструкций, когда конструк-
3.4. Статистические методы моделирования разрушения
195
тивных концентраторов напряжений и очагов разрушения может быть не-
сколько.
Имитация представляет собой численный метод проведения компью-
терных экспериментов с математическими моделями, описывающими пове-
дение конструкции при заданных параметрах нагружения в течение заданного
или формируемого в ходе имитационного эксперимента периода времени.
В имитационной модели процесс разрушения описывается набором
алгоритмов, которые затем реализуют ситуации, возникающие в реальной
сварной конструкции. Моделирующие алгоритмы позволяют по исходным
данным, содержащим сведения о начальном состоянии сварного соедине-
ния, и фактическим значениям параметров сопротивления разрушению ото-
бразить реальный механизм зарождения и роста трещин в конструкции, а
также получить сведения о возможных вариантах кинетики разрушения в
данной конкретной ситуации.
Возможность описания процесса разрушения сварных соединений на
высоком уровне детализации, отсутствие ограничений на виды используе-
мых аналитических моделей и конструктивно-технологические параметры
исследуемого объекта, возможность исследования кинетики взаимодействия
отдельных очагов разрушения во времени и пространстве выдвигают ими-
тационное моделирование в число перспективных методов компьютерного
прогнозирования разрушения конструкций.
Имитационное моделирование можно рекомендовать для исследова-
ния процесса разрушения сложных объектов в случаях, когда
• аналитические методы имеются, но математические процедуры
столь сложны и трудоемки, что имитационное моделирование дает более
простой способ решения задачи;
• кроме оценки влияния конструктивно-технологических параметров
сварной конструкции на конечные результаты моделирования желательно
осуществить наблюдение за протеканием накопления повреждений и кине-
тикой развития разрушения в исследуемом объекте в течение определенного
периода;
• не существует законченной постановки задачи исследования и идет
процесс анализа объекта моделирования; имитационная модель может слу-
жить средством изучения явления;
• формирование процесса разрушения определяют несколько незави-
симых механизмов и особое значение имеет последовательность событий их
включения.
Во многих случаях имитационное моделирование оказывается един-
ственным способом исследования кинетики разрушения сложной сварной
конструкции, поскольку оно позволяет в зависимости от сложившейся си-
туации в ходе имитационного эксперимента изменять набор используемых
7*
196
3. Проектные и контрольные расчеты на прочность
аналитических моделей и/или параметров и характеристик дальнейшего
протекания процесса разрушения.
Алгоритмической основой для имитационного моделирования разру-
шения являются принципы событийности, дискретизации времени и слу-
чайности перехода модели из одного состояния в другое. Принцип собы-
тийности дает возможность процесс разрушения условно разделить на ряд
характерных состояний модели. Дискретизация времени позволяет объеди-
нить во времени и описать в рамках единого алгоритма процессы, проте-
кающие при различных состояниях модели, например зарождение разруше-
ния, развитие трещины, переход к нестабильному разрушению.
Чтобы обеспечить имитацию параллельных событий, протекающих
при одном зафиксированном состоянии модели, вводят некоторую глобаль-
ную переменную t0, которую называют модельным временем. С помощью
этой переменной организуется синхронизация всех событий в модели и вы-
полнение алгоритмов.
Корректировка временных координат нескольких параллельно проте-
кающих процессов осуществляется с помощью модельного времени сле-
дующим образом. Если в реальной системе происходит одновременно не-
сколько событий, то имитационная модель последовательно обслуживает
все алгоритмы, имитирующие процессы, совпадающие по времени выпол-
нения, при этом модельное время не меняется до окончания выполнения
всех совпавших по времени реализации алгоритмов. Таким способом после-
довательное выполнение соответствующих действий, но при неизменном
значении /0, имитирует параллельность протекания процессов.
Построение имитационной модели начинают с вербального описания
закономерностей процесса разрушения, на основании чего разрабатывают
алгоритм модели, определяют необходимый перечень аналитических моде-
лей, критерии и условия их включения в имитационную модель в ходе ма-
шинного эксперимента, задают исходные данные, характеризующие меха-
нические свойства, в том числе сопротивление разрушению.
Исходные данные по своей природе могут быть как детерминистиче-
скими, так и стохастическими. В последнем случае необходимо задать соот-
ветствующие законы распределения случайных величин и их параметры.
Необходимо установить пределы изменения значений переменных или оп-
ределить условия, ограничивающие их изменения. Они могут вводиться ли-
бо в виде исходных данных при разработке модели, либо в виде алгоритма,
устанавливающего их в ходе машинного эксперимента в зависимости от со-
стояния имитационной модели. Также должны быть установлены цели и задачи
моделирования, необходимые правила и критерии оценки их выполнения.
Рассмотрим применение метода имитационного моделирования на
примере создания модели зарождения и развития разрушения в сварных
конструкциях при циклическом нагружении.
3.4. Статистические методы моделирования разрушения
197
В сварных соединениях с механически необработанными швами уста-
лостное разрушение инициируется, как правило, в зонах концентрации на-
пряжений около линии сплавления, образуя так называемый линейный ини-
циатор. Характерной особенностью таких инициаторов является взаимное
влияние соседних очагов разрушения. Развитие разрушения в данном случае
может быть представлено в виде случайного сочетания нескольких одно-
временно развивающихся процессов: зарождение отдельных трещин на раз-
личных, не связанных между собой участках-инициаторах; их рост и появ-
ление новых трещин; объединение между собой трещин, развивающихся на
соседних участках. Такой характер разрушения назван многоочаговым раз-
рушением.
Стохастическая природа явления создает предпосылки к многовари-
антности путей и траекторий развития разрушения. Имитационная модель
предполагает последовательную пошаговую имитацию реального характера
распространения разрушения в конструкции с учетом вероятностной приро-
ды действующих факторов. Имитационное моделирование позволяет на ка-
ждом шаге оценивать сложившуюся ситуацию и в соответствии с ней опре-
делять дальнейший ход развития разрушения, учитывать влияние неизбежно
присутствующих случайных возмущений процесса. В частности, можно
учитывать акты появления новых очагов разрушения и связанное с ними
изменение НДС конструкции, объединение соседних трещин, возникнове-
ние на отдельных участках актов хрупкого разрушения или коррозионного
растрескивания и т. д. Все это позволяет учитывать в машинном экспери-
менте многовариантность путей эволюции разрушения в сложных сварных
конструкциях, приближая тем самым его к реальности.
Сценарий имитационного моделирования многоочагового разрушения
при линейном инициаторе состоит в следующем:
• в пределах одного сварного соединения наибольшее относитель-
ное колебание имеют радиус г перехода от шва к основному металлу и
угол 0 сопряжения. Именно эти два параметра оказывают главное влия-
ние на значение и характер изменения концентрации напряжений вдоль
кромки шва;
• линия перехода от шва к основному металлу представлена в виде
дискретного набора из i участков, длина /, которых изменяется случайным
образом. В пределах каждого участка очертания профиля перехода от шва к
основному металлу принимаются неизменными, а значение коэффициента
концентрации деформаций Kei, зависящее от типа соединения и локальных
параметров г и 0, постоянным (Kei = const). Интегральная функция распреде-
ления F(/,) определяется экспериментально на лабораторных образцах кон-
кретного типа соединения и технологии изготовления. Экспериментально
установлено, что для сварных соединений с механически необработанными
198
3. Проектные и контрольные расчеты на прочность
после сварки швами распределение случайной величины /, подчиняется за-
кону Вейбулла—Гнеденко
Pt = 1 - exp
6,02
(3.26)
Параметры распределения значений г и 0 завися т от типа соединения,
способа сварки, сварочных материалов и других факторов (см. табл. 3.7);
• длительность периода до зарождения трещины N3i на каждом участ-
ке рассматривается как случайная величина, зависящая от коэффициента
концентрации деформаций Kei, амплитуды номинальных деформаций еном и
свойств материала. Период N3i рассчитывается по уравнению малоцикловой
усталости в предположении, что Kei является случайной величиной, завися-
щей от функций распределения F(f) и F(&) или генерируется компьютером в
соответствии с интегральным законом распределения F(N3), подлежащим
экспериментальному определению. Принимается, что на z-м участке возни-
кает трещина длиной I, и глубиной = 0,5 мм при достижении N = N3;
• случайные величины /, и Kei являются независимыми;
• рост поверхностных трещин подчиняется законам механики разру-
шения с учетом случайной вариации параметров кинетической диаграммы
разрушения;
• в процессе подрастания трещин на отдельных участках их взаимное
влияние на скорость распространения разрушения не учитывается вплоть до
объединения соседних трещин. Объединение соседних трещин производит-
ся при выполнении условия
>*,л;
(3.27)
где X"; X" — координаты правой и левой вершин поверхностной трещины
на j-м участке в системе координат, для которой нулевая точка совмещена с
началом шва. Размер трещины вдоль малой полуоси Ь, принимается равным
наибольшему из значений для трещин, подлежащих объединению;
• в качестве модельного времени используют значение числа циклов
N, изменяют N с шагом A./V и подсчитывают характеристики нового состоя-
ния модели;
• после моделирования каждого шага A7V анализируют сложившую-
ся ситуацию с развитием разрушения и вводят корректировку в дальней-
ший ход имитационного моделирования. Например, если фронт несквоз-
ной трещины выходит на поверхность сварного соединения, то изменяют
3.4. Статистические методы моделирования разрушения
199
аналитические модели, используемые для расчета подрастания трещины;
если выполняется условие слияния соседних трещин (см. § 3.3), то про-
изводят их слияние и соответственно изменяют параметры формы фронта
трещины;
• анализируют достижение процессом заданного предельного состоя-
ния и решают вопрос о целесообразности продолжения моделирования.
Для расчета длительности периода зарождения усталостной трещины
может быть использован подход, предложенный в § 3.3. Для моделирования
роста трещины, как правило, используют кинетическую диаграмму устало-
стного разрушения (3.3). В зависимости от ситуации, складывающейся в ка-
ждый период модельного времени, управляющая программа с помощью
банка теоретических зависимостей формирует математическую модель и
включает ее в алгоритм имитационного моделирования.
Для эффективной работы имитационной модели необходимо иметь
банк исходной информации, содержащий статистически представительный
объем экспериментальных данных следующего вида:
• тип и параметры распределений, характеризующих геометрические
размеры дефектов. Сюда относятся данные о геометрии профиля перехода
от шва к основному металлу для различных технологических вариантов
сварки, данные о размерах и частоте появления внутренних дефектов (пор,
трещин, шлаковых включений) и т. д.;
• характеристики сопротивления различных участков сварного соеди-
нения зарождению разрушения, характеристики трещиностойкости сварного
соединения при циклическом и статическом нагружении на воздухе и в кор-
розионной среде.
Имитация должна предусматривать случайность и многовариантность
развития процесса разрушения. С этой целью имитационная модель задает с
помощью генератора случайных чисел координаты расположения, размеры
и вид исходного дефекта, параметры, характеризующие свойства металла,
сопротивление зарождению и росту трещины. При наличии достаточных
ресурсов компьютера в процессе машинного эксперимента может также из-
меняться случайным образом амплитуда внешней нагрузки и учитываться
эффект закрытия трещины.
Исходные данные для параметров, характеризующих процесс, должны
быть получены на основании статистического анализа результатов эксперимен-
тов и представлены в виде соответствующих законов распределения случайных
величин. Могут быть использованы данные, приведенные в разд. 3.4.1.
Имитационную модель воспроизводят на компьютере десятки и сотни
раз при различных исходных состояниях генератора случайных чисел (ГСЧ)
и статистически обрабатывают результаты моделирования.
200
3. Проектные и контрольные расчеты на прочность
Рис. 3.34. Укрупненная структурная схема алгоритма имитационного
моделирования процесса разрушения сварных соединений, работаю-
щих при циклическом нагружении
3.4. Статистические методы моделирования разрушения
201
На рис. 3.34 показана укрупненная структурная схема алгоритма ими-
тационного моделирования процесса разрушения сварных соединений, ини-
циируемого от границы перехода «шов — основной металл». Блоки 1—6
осуществляют ввод и контроль исходных данных, содержащих сведения о
типе соединения, схеме нагружения, уровне нагрузки, используемых мате-
риалах и т. д. В блоке 7 в зависимости от вида входной информации форми-
руется математическая модель расчета, в которой учитываются тип сварного
соединения, характер напряженного состояния и вид нагружения, возмож-
ность появления внешних возмущающих воздействий и т. д. Блоки 8, 9 при-
водят в исходное состояние счетчики циклов по количеству п прогонов мо-
дели и числу z участков с однородной геометрией вдоль границ шва.
В блоках 10—12 с помощью генератора случайных чисел и данных о
параметрах распределений, получаемых из информационного банка в зави-
симости от вида исходной информации, анализируется распределение гео-
метрической неоднородности вдоль зоны сплавления сварного шва и фор-
мируются выборки случайных значений долговечности до зарождения тре-
щин М на различных участках шва, длины появляющихся трещин Z, и их
глубины bi. В блоке 13 из массива {N3} определяется минимальное значение
Mmin, соответствующее длительности периода до зарождения первой тре-
щины. В блоке 14 с помощью датчика случайных чисел выбирается значе-
ние параметров функции (3.3), а в блоке 15 приводится в исходное состоя-
ние счетчик циклов, определяющий количество приращений нагружения AZV.
В блоках 16—20 реализуется моделирование процесса развития раз-
рушения. Этот этап моделирования является наиболее важным и сложным
для алгоритмизации, так как связывает неразрывно во времени, с учетом
стохастических закономерностей усталостного разрушения, две стадии, от-
личающиеся механизмами разрушения, — стадию зарождения трещин и
стадию их развития.
Алгоритм имитационной модели в данном случае организован сле-
дующим образом. В блоке 16 задается приращение числа циклов нагруже-
ния на ANj и анализируется текущее состояние накопленного уровня повре-
ждений с точки зрения размеров трещин и их расположения. Затем сорти-
руются массивы {N3}, {I,}, {bi} и выбираются такие трещины, для которых
значение N3I удовлетворяет условию N3i < N + ANj. Для периода ANj подсчи-
тывается подрастание трещин в длину AZ, и глубину А£>, и анализируется
возможность объединения двух и более трещин, расположенных рядом
(блок 20). В течение периода ANj в реальных условиях работы конструкции
одновременно протекает ряд разнообразных процессов, обслуживаемых
имитационной моделью последовательно, но благодаря введенному поня-
тию «машинное время», которое остается неизменным на протяжении АЛ} и
изменяется скачком по его истечении, в модели происходит имитация па-
202
3. Проектные и контрольные расчеты на прочность
раллельно протекающих процессов. В связи с этим на выбор значения До-
следует обратить особое внимание, поскольку его уменьшение ведет к росту
машинного времени счета, а увеличение — к снижению точности модели-
рования реальной ситуации.
В блоке 21 рассматривается возможность достижения предельного со-
стояния разрушения по условиям К, > KIc, bima > Zyp, Z,max > ZKp, и если одно из
них выполняется, то значения N3mm, предельной долговечности Np = N3min +
+ ХДА^, Ьтах и Zmax помещаются в банк результатов, а управление передается
в блок 9 на начало нового прогона модели. В ином случае изменяется со-
стояние счетчика циклов и управление передается в блок 16, осуществляю-
щий следующий шаг по приращению числа циклов нагружения на ANj.
Количество прогонов модели регистрируется в блоке 27. Опыт пока-
зывает, что в зависимости от рассеяния параметров, характеризующих слу-
чайный процесс развития разрушения, заданное число прогонов модели мо-
жет составлять 500... 1000. После завершения работы массивы результатов
счета подвергаются статистической обработке в анализаторе 29 с целью оп-
ределения средних значений N3, Np, Zmax, ftmax, их дисперсий и доверительных
интервалов, а также оценки у-процентного ресурса.
Многократная прогонка модели на компьютере при измененных со-
стояниях датчиков случайных чисел и последующая статистическая обра-
ботка результатов численного эксперимента позволяют учесть влияние слу-
чайного рассеяния параметров, характеризующих долговечность до зарож-
дения разрушения и трещиностойкость, а также случайный характер
топографии очагов разрушения и траектории роста трещин.
Рассмотрим возможности предлагаемой методики на примере анализа
кинетики разрушения и прогнозирования долговечности сварных штуцер-
ных соединений оболочковых конструкций, работающих в условиях двух-
осного поля напряжений с компонентами сц/ог - 0, 0,5 и 1,0. В расчетах бы-
ли приняты следующие исходные данные: материал — хромоникельмолиб-
деновая сталь толщиной 30 мм (р02 = 1020 МПа, о* = 1150 МПа, = 0,58);
геометрия соединения — диаметр штуцера 90 мм, катет шва, прилегающий
к стенке штуцера, — 15 мм, к стенке корпуса обечайки — 30 мм; функция
распределения коэффициентов концентрации напряжений соответствует
случаю ручной дуговой сварки аустенитными электродами; характер нагру-
жения повторно-статический, цикл пульсирующий, номинальные напряже-
ния он0м = 550 МПа. Количество прогонов модели — 500.
Имитационное моделирование выявило специфику кинетики разру-
шения, заключающуюся в том, что изменение соотношения компонент на-
пряжений (tn = O2/O1) сопровождается изменением топографии разрушения.
При о2 = О1 трещины зарождаются вдоль кромки шва с одинаковой интен-
3.4. Статистические методы моделирования разрушения
203
Рис. 3.35. Влияние соотношения компонент двухосного растяжения на рост поверх-
ностной трещины по границе кругового шва, соединяющего щтуцер с оболочкой:
1, 4 — т = 1; 2 — т = 0,5; 3 — т = 0; 1—3 — длина трешины по дуге поверхности; 4 — раз-
мер трешины по глубине
сивностью по всей окружности. Объединение отдельных трещин приводит к
образованию на некотором участке поверхностной дугообразной трещины,
длина которой интенсивно растет с увеличением числа циклов нагружения
(рис. 3.35, кривая 7). В результате этого на относительно ранних этапах на-
гружения образуется сплошная круговая трещина, которая в дальнейшем
растет в глубину.
При неравноосном нагружении поверхностная трещина охватывает
лишь часть окружности и интенсивность изменения ее длины значительно
меньше (рис. 3.35, кривые 2, 3). При определенном соотношении парамет-
ров трещины ЪН возникают условия для изменения траектории разрушения
в направлении от границы шва. Например, при глубине трещины b = 5,5 мм
угол охвата штуцера трещиной составляет 122° при о2 = 0,5сц и 84° при
о2/о1 - 0- Изменение схемы напряженного состояния от <т2 = 0,5oi до о, = сг2
приводит к уменьшению параметра N3 почти в 3 раза.
Имитационное моделирование позволяет проанализировать влияние
конструктивных параметров и схемы напряженного состояния на живучесть
сварного соединения. Анализ расчетных данных свидетельствует о том, что
увеличение диаметра шва штуцерного соединения от 150 до 350 мм (за диа-
метр шва принята сумма диаметра штуцера и удвоенного значения катета
шва) при неравноосной схеме (ст2 = 0,5о|) незначительно влияет на живу-
честь конструкции с трещиной Nc. В то время как при равноосной схеме
напряженного состояния такое же изменение диаметра приводит к умень-
шению у-процентного значения параметра N(, почти в 2 раза, а среднего зна-
чения — в 1,5 раза.
204
3. Проектные и контрольные расчеты на прочность
Закономерности развития разрушения в большинстве случаев не под-
даются умозрительному анализу. В связи с этим метод имитационного мо-
делирования целесообразно использовать на этапе проектирования для оп-
тимизации конструктивно-технологических решений с целью согласования
заданного и достижимого ресурсов сварных соединений.
Пошаговый принцип анализа развития разрушения обеспечивает гиб-
кое реагирование алгоритма модели на любые случайные возмущения и по-
зволяет, в зависимости от сложившейся ситуации, адаптировать его к изме-
нившемуся механизму. При этом важным является то обстоятельство, что
система имитационного моделирования функционирует как открытая и мо-
жет уточняться и дополняться по мере поступления сведений, отражающих
новые аспекты поведения объекта в процессе его эксплуатации.
3.4.3. Учет достоверности контроля качества сварных соединений
Достоверность контроля определяет вероятность принятия безоши-
бочных решений в отношении качества сварного соединения. С позиции
прочности конструкции, содержащей трещиноподобные дефекты, достовер-
ность контроля следует рассматривать как вероятность p(h > Лкр) пропуска
хотя бы одного дефекта размером h > hKp. Очевидно, что p(h > ht;p) непосред-
ственно связана с вероятностью обнаружения дефектов p(h), которая зави-
сит от свойств конструкционного материала, конфигурации элемента конст-
рукции, формы и местоположения дефекта, метода контроля и его реальной
чувствительности, методики и аппаратуры, квалификации оператора и дру-
гих факторов. В качестве статистической оценки p(li) обычно принимают
отношение числа обнаруженных дефектов при контроле заданным методом
к общему числу имеющихся (выявляемость дефектов).
Кривая выявляемое™ дефектов в сварных соединениях как правило
имеет вид восходящей экспоненты. Граничный размер наименьшего выяв-
ляемого дефекта ho входит в показатель экспоненты и зависит от чувстви-
тельности контроля:
р(И) = 1-ехр[Х(/?-Л0)]. (3.28)
Например, функция выявляемое™ дефектов в сварных стыковых соеди-
нениях толщиной 40 мм при ультразвуковом контроле выражается уравнением
p(s) = 1 - ехр[-0,17(5 - 9)]; при гамма-контроле — p(s) = 1 - ехр[-0,12(s - 6)],
где 5 — площадь дефекта, мм2.
В настоящее время систематазированные данные по выявляемое™
дефектов весьма ограничены. В литературе наиболее полно представлены
результаты исследования выявляемое™ дефектов при ультразвуковом кон-
3.4. Статистические методы моделирования разрушения
205
Размер дефекта по глубине Л, мм
Рис. 3.36. Условная вероятность обнаружения дефектов за-
данного размера по данным различных авторов (кривые I—6)
троле сварных соединений перлитных сталей толстостенных конструкций
применительно к объектам ядерной энергетики (рис. 3.36).
Представленные данные можно аппроксимировать функцией типа (3.28):
Кривая на рис. 3.36 X h0
1....................... -0,06 2,95
2.................. -0,114 3,55
3.................. -0,123 3,36
4.................. -0,180 4,70
5.................. -0,207 1,24
6.................. -0,122 0,270
Достоверность ультразвукового контроля конструкций из аустенитно-
го материала может оказаться еще ниже (рис. 3.37). Приведенные результа-
ты свидетельствуют о том, что с вероятностью р = 0,05 возможен пропуск
дефектов весьма крупных размеров вплоть до 40...50 мм. Это подчеркивает
значительную роль фактора выявляемости дефектов при контроле качества
сварных соединений в проблеме обеспечения надежности конструкций.
Вместе с тем распределение размеров дефектов, не зафиксированных
при контроле, зависит не только от их выявляемости данным методом, но и
от исходной степени засоренности шва дефектами и функции распределения
их размеров F(H).
Статистическая оценка функции риска пропуска при контроле качест-
ва хотя бы одного дефекта размером, превышающим h, в шве единичной
длины £0 может быть выражена как
206
3. Проектные и контрольные расчеты на прочность
Рис. 3.37. Условная вероятность обнаружения трещиноподобных дефек-
тов заданного размера в трубах ядерных реакторов:
1 — плакированные трубы диаметром 840 мм, толщина стенки 60 мм; 2 — ау-
стенитные трубы диаметром 254 мм, толщина стенки 15 мм; 3 — литые аусте-
нитные трубы диаметром 840 мм, толщина стенки 60 мм
pp(A,p,F(/z),p(/i)) = 1 - exp[-v(ft)], (3.29)
где
СО
у(й) = ц|[1-ха)1/ДОЛ; (з.зо)
h
р — математическое ожидание общего количества дефектов в шве длиной Lo;
Д/г) — плотность вероятности, соответствующая характерной для данной
технологии изготовления функции распределения размеров дефектов F(h)\
p(Ji) — условная вероятность обнаружения дефектов заданного размера И
при контроле качества (выявляемость дефектов).
Параметры, характеризующие дефектность сварных соединений ц и
F(/z) в выражении (3.30) подлежат экспериментальному определению на ос-
нове статистического анализа данных контроля в условиях штатной техно-
логии производства.
По аналогии с (3.16) вероятностную модель обеспечения трещино-
стойкости, учитывающую выявляемость дефектов при контроле можно за-
писать в виде
где Лкр — случайная величина, для которой функция распределения
pa(h,<3,Kc) подсчитывается с учетом случайного рассеяния характеристик
3.4. Статистические методы моделирования разрушения
207
статической трещиностойкости Лфакг — случайная величина, которая
подсчитывается по (3.28) с учетом случайного разброса размеров дефектов
F(h) и вероятности их обнаружения P(h) при контроле.
Следующее выражение по аналогии с (3.18) позволяет определить ве-
роятность разрушения при статическом нагружении сварного соединения с
трещиноподобными дефектами, пропущенными при выполнении контроля
качества:
R = \-— //а(Л,оЖс)Р₽(Л,ц,Г(Л),Р(Л)). (3.32)
^0 -л
Зависимость (3.29), фактически характеризующая технологическую
наследственность сварного соединения, приобретенную при изготовлении и
оставшуюся незамеченной при контроле качества, является основой для
прогнозирования ресурса конструкции при различных видах нагружения. В
частности, она может служить для имитационного моделирования процесса
разрушения при циклическом нагружении, что позволяет на вероятностной
основе учесть в совокупности такие факторы, как нагруженность, дефект-
ность и разброс характеристик трещиностойкости материала для выбранно-
го технологического процесса сварки, достоверность применяемых методов
неразрушающего контроля.
В отличие от других методов расчет на основе зависимости (3.29) дает
сравнительную количественную оценку надежности, которая в комплексе
характеризует решения, принятые на стадии проектирования и возможности
их реализации в производстве.
4. МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ
В МЕТАЛЛАХ ПРИ СВАРКЕ С ЦЕЛЬЮ ОЦЕНКИ
ПОКАЗАТЕЛЕЙ СВАРИВАЕМОСТИ
И ВЫБОРА РЕЖИМОВ СВАРКИ
4.1. Показатели свариваемости
В соответствии с ГОСТ 2600—81 свариваемость — свойство металлов
или сочетания металлов образовывать при установленной технологии свар-
ки соединения, отвечающие требованиям работоспособности и надежности
сварной конструкции и условиям ее эксплуатации. Свариваемость зависит
от состава материала, особенностей сварной конструкции, технологии свар-
ки, а также от механических, служебных свойств и качества (допустимость
дефектов), которыми должны обладать сварные соединения. Один и тот же
материал может иметь достаточную или недостаточную свариваемость в
зависимости от конкретных требований к сварной конструкции. Показате-
лями достаточной свариваемости материала являются нормативные значе-
ния свойств и качества сварных соединений, отвечающие техническим тре-
бованиям к данному типу сварных конструкций с учетом их назначения и
условий работы. В случае, если хотя бы один из показателей свариваемости
ниже нормативного значения, свариваемость материала считается недоста-
точной. Применительно к легированным сталям за показатели свариваемо-
сти приняты стойкость против образования холодных трещин и основные
механические свойства металла шва и зоны термического влияния.
Существует целый ряд экспериментальных способов оценки показа-
телей свариваемости: сварочные технологические пробы, машинные испы-
тания образцов в процессе сварки, испытания материалов в условиях моде-
лированного сварочного термодеформационного цикла. Как правило, с по-
мощью экспериментальных способов можно получить только
относительную оценку свариваемости, позволяющую сравнивать между со-
бой материалы, технологические варианты сварки. Относительные показа-
тели нельзя прямо использовать для оценки свариваемости материала при
производстве конкретных сварных конструкций при разработке технологии
их сварки. Для этого необходимы абсолютные значения показателей свари-
ваемости, которые можно получить расчетным путем.
4.2. Алгоритм программы расчета показателей свариваемости
209
4.2. Алгоритм компьютерной программы расчета
показателей свариваемости легированных сталей
Основу расчетного метода оценки свариваемости составляет анализ
физико-химических процессов в металлах при сварке, от которых зависят
показатели свариваемости. Этот анализ выполняется с учетом свойств мате-
риалов и основных конструктивно-технологических параметров процесса
образования сварных соединений. Такая система компьютерного анализа
свариваемости и технологии сварки легированных сталей разработана в
МГТУ им. Н.Э. Баумана.
В основу анализа свариваемости положены установленные опытным
путем представления о том, что показатели свариваемости сталей опреде-
ляются структурой металла сварного соединения (5Д), величиной аустенит-
ного зерна (Z)3), концентрацией диффузионного водорода (//л) и уровнем
сварочных напряжений (осв). Совокупность этих факторов принято рассмат-
ривать как структурно-водородно-напряженное состояние (СВИС) металла к
моменту завершения охлаждения после выполнения сварки.
Для анализа процесса образования холодных трещин введены понятия
о действительном и критическом СВИС металла сварного соединения. Кри-
тическое СВНС соответствует такому сочетанию факторов, при которых
металл проявляет склонность к замедленному хрупкому межкристаллитно-
му разрушению, т. е. образованию очагов холодных трещин. Сравнение ука-
занных состояний возможно по критериям действительного и критического
напряжений, что позволяет сделать вывод о возможности образования хо-
лодных трещин, если имеет место превышение действительного напряже-
ния над критическим.
В качестве объекта расчета принято элементарное типовое стыковое
соединение жестко закрепленных элементов, выполняемое одно- или много-
проходной сваркой (рис. 4.1).
Подобные соединения име-
ют сварочные жесткие тех-
нологические пробы (ГОСТ
26388—84) и многие сварные
конструкции. Этот тип со-
единений позволяет модели-
ровать локальные процессы
(тепловые, диффузионные,
сгруктурообразование) в рам-
ках единой расчетной схемы.
Конструктивные особенности
Рис. 4.1. Расчетная схема сварного соединения
210
4. Моделирование физических процессов в металлах при сварке
Н ачало
I _____________________
1. Химический состав материалов
2. Геометрия сварного соединения
3. Способ, режим сварки
4. Начальная концентрация диффу-
зионного водорода в шве
5. Жесткость сварного соединения
___________J'____________
Решение тепловой задачи
Тиш. '>|000> Z8/5’ W6/5
I
Расчет действительной
структуры
$д, £>з
Решение диффузионной
задачи перераспределения
водорода
Яд,шах>
у
Расчет механических
свойств
ав, сго.2, 8, V, HV, KCU
Рис. 4.2. Алгоритм расчета показателей свариваемости легированных сталей
изделий, определяющие уровень сварочных напряжений, учитываются задани-
ем соответствующего размера Dj, обеспечивающего эквивалентную «жесткость
закрепления» свариваемых элементов изделия. Алгоритм расчетной части
компьютерной программы приведен на рис. 4.2.
4.3. Модели для расчета структуры металла, концентрации водорода 211
4.3. Модели для расчета теплового поля, структуры металла,
концентрации диффузионного водорода
и уровня напряжений при сварке
Решение тепловой задачи выполняется аналитическим методом с
использованием теории распространения теплоты при сварке. Предвари-
тельно по эмпирическим зависимостям определяются геометрические пара-
метры сварного шва в зависимости от способа и режима его сварки и формы
разделки кромок. Затем решается задача по определению параметров моде-
ли источника теплоты из условия обеспечения заданной формы и размеров
зоны проплавления, причем в качестве моделей используются сосредото-
ченные, распределенные или комбинированные подвижные источники, дей-
ствующие в плоском слое. Полученные модели источников теплоты исполь-
зуются для последующего расчета основных параметров сварочного терми-
ческого цикла в анализируемых точках зоны термического влияния.
Экспериментальная проверка показала, что такой методический подход по-
зволяет корректно использовать аналитические решения Н.Н. Рыкалина для
анализа тепловых процессов вблизи линии сплавления (в точках околошов-
ной зоны с максимальной температурой нагрева = 1350 °C).
Расчет условного среднего диаметра аустенитного зерна (О3) вы-
полняется с использованием соотношения металлофизики:
Д = А
2 2
где Do — начальный размер зерна при 1000 °C на стадии нагрева; Т— те-
кущая температура сварочного термического цикла, К; 0 — время дости-
жения температуры 1000 °C на стадии нагрева и охлаждения соответственно;
к — постоянная Больцмана, Дж/К; А — постоянная, зависящая от поверхно-
стной энергии, см2/с; Q — энергия активации роста зерна, Дж.
Значения Do, A, Q в выражении (4.1) определяются в зависимости
от состава стали по моделям, полученным обработкой эксперименталь-
ных данных большой группы спокойных легированных сталей. Домини-
рующее влияние на эти коэффициенты оказывает содержание в стали уг-
лерода и серы.
Расчет действительной структуры металла зоны термического
влияния и шва базируется на определении критических значений скорости
охлаждения в диапазоне температур 600...500 °C, обозначаемый как W6/5,
соответствующих образованию 1 и 94 % мартенсита (Wmi и WM2). Значения
Wmi и WM2 рассчитываются исходя из предпосылки, что они являются па-
212 4. Моделирование физических прогрессов в металлах при сварке
раметрами прокаливаемое™ стали, которая может быть охарактеризована
обобщенным химическим составом с помощью эквивалента углерода (Сэкв):
WM = ^(C3KB)B, (4.2)
где А и В —- опытные коэффициенты.
Состав смешанной структуры при WM1 < W6/5 < WM2 определяется с
помощью уравнения Авраами, применяемого для оценки кинетики поли-
морфных превращений. Для более точного расчета (с учетом металлургиче-
ской природы стали) возможно использование результатов дилатометриче-
ского исследования, полученных с помощью компьютерного анализатора
материалов КАМАТ, представляющего собой светолучевой дилатометр, по-
зволяющий в образцах малого размера моделировать сварочные термиче-
ские циклы и по изменению термической и фазовой деформаций оценивать
состав структуры зоны термического влияния при сварке конкретных сталей.
При многопроходной сварке в результате многократного повторного
нагрева структура металла сварного соединения формируется в условиях
частичного отпуска структуры, образовавшейся в результате первичного
теплового воздействия. В этом случае ее состав рассчитывается с помощью
имитационной модели, описывающей кинетику процесса отпуска. В основу
расчета положена модель, определяющая скорость выделения углерода из
пересыщенного твердого раствора в зависимости от состава стали, темпера-
туры и времени. Окончательная структура после завершения сварки опреде-
ляется интегральным воздействием повторных нагревов, достижением ими
характеристических областей существования типовых структур отпуска и
временем пребывания металла в этих температурных областях.
Расчет концентрации диффузионного водорода в анализируемых точ-
ках сварного соединения выполняется путем численного интегрирования
дифференциального уравнения 2-го закона Фика, описывающего неизотер-
мическое перераспределение диффузионного водорода в металле в резуль-
тате концентрационной и термической диффузии с учетом перехода оста-
точного (металлургического) водорода в диффузионно-подвижный и обрат-
но. В инженерном варианте расчета используется интерполяционная
модель, полученная на базе результатов масштабного вычислительного экс-
перимента по расчету концентрации диффузионного водорода в околошов-
ной зоне сварного соединения, подверженной образованию холодных тре-
щин (приведены лишь первые члены модели):
Нв = (0,42 - 0,01 Тп) • Но + 0,07 • Нт + 0,006 • 5 +
+ 0,026 • h - 0,002 -h-q/v+ ..., (4.3)
4.3. Модели для расчета структуры металла, концентрации водорода 213
где Но — исходное содержание диффузионного водорода в металле шва,
определенное хроматографическим методом, мл/100 г; Нт — содержание
остаточного (металлургического) водорода в стали (определяется вакуум-
плавлением), мл/100 г; q/v — погонная энергия сварки, кДж/см; Тп — тем-
пература сопутствующего подогрева, °C; 8, h — толщина свариваемых пла-
стин и высота шва, мм.
Анализ НДС сварного соединения в условиях многопроходной
сварки выполняется на базе решения с помощью МКЭ термомеханиче-
ской задачи в соответствии с положениями неизотермической теории те-
чения. Однако такой подход не позволяет проводить оперативный анализ
технологических вариантов. Поэтому в инженерном варианте расчета
реализован подход, базирующийся на основных положениях теории сва-
рочных напряжений и деформаций. Расчет поперечной компоненты сва-
рочных напряжений выполняется с использованием балочной модели со-
единения, учитывающей размеры и условия закрепления свариваемых
элементов, положение шва в разделке, объемный эффект фазовых пре-
вращений в шве и зоне термического влияния, затрудненность усадки
шва при выполнении каждого прохода и механические свойства металла
шва и зоны термического влияния.
Уникальная модель для расчета критических (разрушающих) напря-
жений, позволяющая сделать вывод о вероятности образования холодных
трещин путем сравнения действующих сварочных напряжений с критиче-
ским значением, получена на базе результатов нескольких тысяч испытаний
образцов стали на замедленное разрушение после их обработки имитиро-
ванным сварочным термическим циклом и электролитического насыщения
водородом (приведены лишь первые члены модели):
скр = со,2 (2,68 - 5,46 • С- 0,5 • Яд- 0,004 • S, - 4,02 • D3 + ...), (4.4)
где С — содержание углерода, %; Sr — содержание мартенситной состав-
ляющей структуры, %; D3 — условный средний диаметр аустенитного зерна,
мм; Яд — концентрация диффузионного водорода, мл/100 г; Оо,2 -— услов-
ный предел текучести металла исследуемой зоны при нормальной темпера-
туре, МПа.
Учет зависимости значений критических напряжений от температуры
и времени и сопоставление их со значениями действительных сварочных
напряжений позволяют определять момент образования холодных трещин
как в процессе сварки, так и после ее завершения.
L
214
4. Моделирование физических процессов в металлах при сварке
4.4. Инженерный программный комплекс
«Свариваемость легированных сталей»
Инженерный программный комплекс «Свариваемость легированных
сталей» предназначен для оперативного анализа технологических вариантов
сварки типовых стыковых соединений жесткозакрепленных элементов из
легированных сталей (см. рис. 4.1), а также для подбора значений конструк-
тивно-технологических параметров, обеспечивающих стойкость сварного
соединения против образования холодных трещин. Комплекс реализован на
основе алгоритма, приведенного на рис. 4.2, и является плодом многолетней
работы коллектива лаборатории «Свариваемость материалов» МГТУ им.
Н.Э. Баумана.
В программном комплексе реализовано имитационное моделирование
физических процессов, протекающих в металле при сварке, на базе фунда-
ментальных законов термодинамики, металлофизики, механики с использо-
ванием статистических моделей и концептуальной модели образования хо-
лодных трещин, предложенной профессором Э.Л. Макаровым и основанной
на учете соотношений действительных и критических значений трех основ-
ных факторов:
структурного — соотношения структурных составляющих, содержа-
ния в них углерода, размера аустенитного зерна;
водородного — концентрации диффузионно-подвижного водорода;
силового —-уровня сварочных напряжений 1-го рода.
Инженерный программный комплекс «Свариваемость легированных
сталей» позволяет определить'.
• основные параметры сварочного термического цикла в анализируе-
мых точках околошовной зоны при одно- и многопроходной сварке;
• соотношение структурных составляющих и размер действительного
аустенитного зерна околошовной зоны и шва;
• комплекс механических свойств зоны термического влияния и шва;
• концентрацию диффузионного водорода в околошовной зоне;
• уровень остаточных сварочных напряжений от поперечной усадки шва;
• сопротивляемость стали замедленному разрушению (образованию
холодных трещин) в околошовной зоне и в шве сварного соединения;
• вероятность и ожидаемое время образования холодных трещин в
околошовной зоне и шве;
• стойкость сварных соединений против образования холодных тре-
щин в околошовной зоне и шве;
4.4. Программный комплекс «Свариваемость легированных сталей!
215
• необходимое время выдержки сварного изделия после сварки перед
проведением контроля на наличие трещин.
На основе полученных оценок можно установить значения конструк-
тивно-технологических параметров, обеспечивающих стойкость соеди-
нений против образования холодных трещин:
• рациональный диапазон значений погонной энергии;
• требуемой температуры предварительного или сопутствующего по-
догрева;
• допустимого исходного содержания диффузионного водорода в ме-
талле шва;
• допустимого времени перерывов между проходами при многопро-
ходной сварке;
• рациональной длительности и температуры послесварочного нагре-
ва, а также допустимого времени перерыва между окончанием процесса
сварки и началом послесварочного нагрева;
• рационального сочетания времени подогрева и послесварочного на-
грева с учетом времени возможного образования холодных трещин;
• допустимой «жесткости» сварного соединения.
Инженерный программный комплекс «Свариваемость легированных
сталей» предусматривает два варианта расчетов: исследовательский и тех-
нологический.
Исследовательский вариант выполняется для однопроходной сварки
применительно к стандартным условиям технологической пробы с перемен-
ной жесткостью (ГОСТ 26388—84). Возможна организация цикла расчетов
по изменению одного из конструктивно-технологических параметров — по-
гонной энергии, температуры подогрева, времени послесварочного нагрева,
исходной концентрации диффузионного водорода в шве, геометрии соеди-
нения. В данном случае определяются показатели свариваемости в самых
неблагоприятных условиях сварки (как это принято во всех зарубежных
стандартах). Организация цикла расчетов позволяет определять диапазоны
значений конструктивно-технологических параметров, гарантирующих
стойкость сварных соединений против холодных трещин в указанных усло-
виях сварки.
Технологический вариант выполняется для однопроходной или мно-
гослойной сварки при однократном задании исходных данных. При опреде-
лении требуемых технологических параметров имеется возможность ис-
пользовать эффект «автоподогрева», изменяя режим сварки 1, 2, 3-го и по-
следующих валиков, их длину или время между укладкой валиков (т. е.
высоту валиков и межслойную температуру). При необходимости дополни-
216
4. Моделирование физических процессов в металлах при сварке
тельно подбирают минимальную температуру подогрева (с учетом результа-
тов ее расчета в исследовательском варианте).
Эффективные вычислительные алгоритмы позволяют проводить опе-
ративный анализ технологических вариантов. Так, анализ варианта с уклад-
кой 40 валиков на компьютере С-700 требует 5...6 мин. Использование ав-
томатизированной системы позволяет значительно сократить трудоемкость
проектирования технологии сварки и подойти к решению задач оптимиза-
ции технологических параметров процесса.
Расчет показателей свариваемости возможен для сталей, имеющих
следующие пределы содержания легирующих элементов (%):
Углерод ... 0,03...0,45 Цирконий ... до 0,20
Кремний ... 0,03...1,5 Алюминий ... 0,01...1,10
Марганец ... 0,15...2,0 Кобальт ... до 0,50
Хром ... до 3,0 Бор ... до 0,008
Никель до 4,0 Сера ... 0,002...0,04
Молибден ... до 1,0 Фосфор ... 0,002...0,04
Вольфрам до 0,8 Азот ... 0,001...0,05
Титан до 0,80 Кислород ... 0,001...0,01
Медь .... до 1,20 Церий до 0,40
Ванадий до 0,80 Иттрий ... до 1,0
Ниобий .... до 0,20
Реакция стали на термодеформационный цикл сварки зависит от ее
исходного состояния (предварительной термообработки). Инженерный про-
граммный комплекс «Свариваемость легированных сталей» обеспечивает
расчет показателей свариваемости для сталей, имеющих следующие исход-
ные состояния:
горячий прокат;
нормализация;
отжиг на пластинчатый перлит;
отжиг на зернистый перлит;
закалка + низкий отпуск;
закалка + высокий отпуск (на сорбит);
закалка + высокий отпуск (на мелкозернистый перлит).
Пределы содержания легирующих элементов в сварочных материалах
(ферритно-перлитного типа) аналогичны таковым пределам для основного
металла. Для ручной сварки покрытым электродом необходимо задать хи-
мический состав наплавляемого металла; в остальных случаях — состав
сварочной проволоки.
Программный комплекс реализован в виде пакета взаимосвязанных
программных модулей.
4.4. Программный комплекс «Свариваемость легированных сталей!
217
1. Диспетчерский модуль (WELDAB.EXE). Организует взаимодейст-
вие и обмен данными между всеми остальными модулями.
2. Модуль (WELDPR.EXE) предоставляет заставку и первичную спра-
вочную информацию о возможностях комплекса «Свариваемость легиро-
ванных сталей».
3. Модуль ввода и корректировки исходных данных для расчета пока-
зателей свариваемости (INPUT.EXE).
4. Модуль построения компьютерной модели типовой диаграммы ани-
зотермического распада аустенита для выбранной стали (ARA.EXE).
5. Модуль расчета параметров физико-металлургических процессов,
показателей свариваемости и рекомендуемых конструктивно-
технологических параметров процесса сварки (ANALYSE.EXE).
6. Модули просмотра и распечатки результатов расчетов технологиче-
ского (MLTPASSR.EXE) и исследовательского (ONEPASSR.EXE) вариантов.
Кроме того, программный комплекс использует следующие файлы:
WELDPR.HLP — файл, содержащий первичную справочную инфор-
мацию о возможностях инженерного программного комплекса «Сваривае-
мость легированных сталей»; используется модулем WELDPR.EXE;
WELDPRM .CFG — файл конфигурации для INPUT.EXE;
MAINWELD.DSK — рабочий файл параметров для INPUT.EXE (ав-
томатически создается при работе комплекса);
VARIABLE.TBL — файл диапазонов переменных для INPUT.EXE;
SYS8X16.FON, SYS8X14.FON, SYS8X8.FON,
SVGA.FNT, EXOTIC.FNT — загружаемые шрифты;
ONEPASS.HLP — help-файл для ONEPASSR.EXE;
MLTPASS.HLP — help-файл для MLTPASSR.EXE;
INPUTHLP.HLP — help-файл для INPUT.EXE;
BASE.OKN — используется модулем INPUT.EXE;
VGWELDAB.PCX — используется модулем WELDPR.EXE;
INPUT.PRM — файл параметров для INPUT.EXE;
RESULT.PRM — файл параметров для ONEPASSR.EXE;
RESULTM.PRM — файл параметров для MLTPASSR.EXE.
Исходные данные для расчета включают в себя:
• химический состав и исходное состояние основного металла;
• теплофизические и механические свойства основного металла;
• концентрацию остаточного водорода в основном металле (опреде-
ленную методом «вакуум-плавления»);
• химический состав сварочных материалов (проволоки, флюса) или
наплавленного электродного металла;
• геометрические параметры сварного соединения;
• параметры технологии сварки:
218
4. Моделирование физических процессов в металлах при сварке
способ сварки;
диаметр электрода (проволоки);
параметры режима сварки;
схема заполнения разделки;
исходная концентрация диффузионного водорода в шве (определенная
хроматографическим методом);
параметры режима подогрева;
параметры режима послесварочного нагрева;
данные металлографического исследования структуры стали для
двух специально выбранных сварочных термических циклов (для выпол-
нения уточненного расчета с учетом металлургической природы иссле-
дуемой стали).
Результатами анализа технологического варианта являются:
• химический состав металла шва;
• размеры и площадь сечения сварного шва;
• параметры расхода сварочных материалов (коэффициент наплавки);
• размеры зоны термического влияния и координаты точек околошов-
ной зоны, в которых наиболее вероятно образование холодных трещин;
• параметры термического цикла многослойной сварки для каждой
опасной точки околошовной зоны и шва (корень и поверхность каждого ва-
лика):
максимальные и минимальные температуры, достигнутые за время
каждого теплового воздействия (укладки очередного валика или послесва-
рочного нагрева);
время пребывания металла выше 1000 °C (в интервале температур ин-
тенсивной гомогенизации аустенита и роста зерна) во время каждого теп-
лового воздействия;
время охлаждения от 800 до 500 °C в околошовной зоне;
скорость охлаждения околошовной зоны в интервале температур
600...500 °C во время каждого теплового воздействия;
время пребывания металла выше 200 °C;
• параметры трещинообразования для околошовной зоны и шва:
соотношение структурных составляющих;
условный средний диаметр действительного аустенитного зерна;
значения сварочных и критических (вызывающих образование холод-
ных трещин) напряжений;
распределение максимальной концентрации диффузионного водорода
в околошовной зоне и допустимая концентрация исходного водорода в шве;
вероятность образования холодных трещин;
4.5. Компьютерный расчет показателей свариваемости
219
ожидаемый момент появления холодных трещин (если они воз-
можны);
• механические характеристики металла шва и зоны термического
влияния:
условный предел текучести;
предел прочности;
твердость HV;
относительное удлинение;
относительное сужение;
ударная вязкость KCU.
Результаты анализа технологического варианта могут быть представ-
лены в виде таблиц или графиков.
4.5. Пример компьютерного расчета
показателей свариваемости легированной стали
Результаты расчета показателей свариваемости рассмотрим на приме-
ре автоматической многопроходной сварки под слоем флюса АН-17М сты-
ковых соединений низколегированной стали 12ГН2МФАЮ толщиной
30 мм. Химический состав стали и сварочной проволоки Св-08ХН2Г2СМЮ
и режимы сварки приведены в табл. 4.1 и 4.2. Длина сварного шва 1 м.
Таблица 4.1. Химический состав стали 12ГН2МФ АЮ и проволоки
СВ-08ХН2Г2СМЮ, %
Элемент С Si Мп Сг Ni Мо Си S Р
Основной металл 0,16 0,40 1,2 0,35 1,6 0,20 0,2 0,035 0,035
Электрод 0,08 0,6 1,7 0,95 2,25 0,55 — 0,03 0,03
Таблица 4.2. Режимы сварки многопроходного соединения
Проход Сварочный ток, А Напряжение на дуге, В Скорость сварки, м/ч
1 500 34 36
2 700 36 30
3—13 700 36 27
Примечание. Диаметр проволоки во всех случаях составляет 4,0 мм.
220
4. Моделирование физических процессов в металлах при сварке
Рис. 4.3. Распределение действительных и критических напряжений
при сварке без подогрева (ОШЗ — околошовная зона)
Рассмотрим два варианта выполнения указанной технологии.
Вариант 1: сварка без подогрева, время перерывов между проходами
/м п = 0,5 ч, исходный водород в шве Но = 5 мл/100 г. Возможно образование
холодных трещин в шве и зоне термического влияния как в процессе сварки,
так и после ее окончания (рис. 4.3).
Вариант 2: сопутствующий подогрев 120 °C, время перерывов между
проходами ?МГ1 = 0,5 ч, исходный водород в шве Но = 5 мл/100 г. Устойчи-
вость соединения к образованию холодных трещин обеспечена (рис. 4.4).
Справа от схемы сварного соединения на рис. 4.3 и 4.4 приведены
диаграммы, показывающие распределения поперечных сварочных и крити-
ческих напряжений, соответствующие конечному состоянию сварного со-
единения. Места возможного образования холодных трещин символически
обозначены на схеме соединения. Аналогичные диаграммы могут быть
представлены и для других факторов трещинообразования (структуры, раз-
мера аустенитного зерна, концентрации диффузионного водорода) и меха-
нических свойств зоны термического влияния и шва, причем можно просле-
дить кинетику изменения каждого параметра по мере заполнения разделки,
поскольку при выполнении каждого прохода при многослойной сварке си-
туация может существенно меняться. Это позволяет проанализировать про-
цесс формирования указанных факторов и установить влияние на них кон-
структивно-технологических параметров процесса сварки. Например, регу-
лируя режим сварки и изменяя за счет этого толщину наплавляемых слоев,
4.6. Расчетная схема для выбора условий сварки
221
Рис. 4.4. Распределение действительных и критических напряжений
при сварке с подогревом 120 °C (ОШЗ — околошовная зона)
можно оптимизировать процесс самоотпуска зоны термического влияния в
многослойном сварном соединении.
4.6. Расчетная система для выбора условий сварки
низколегированных сталей в СО2
Качественное формирование шва всегда является необходимым усло-
вием обеспечения надежной работоспособности сварной конструкции. Для
получения качественного сварного соединения низколегированных конструк-
ционных сталей необходимо главным образом обеспечить хорошее форми-
рование шва, заданные уровни механических свойств и не допустить образо-
вания холодных трещин. Задача выбора режима сварки и электродной прово-
локи, обеспечивающих получение требуемого комплекса свойств сварного
соединения, особенно высокопрочных сталей, не всегда имеет очевидное и
однозначное решение. Кроме того, точность и достоверность рекомендаций
часто зависят от квалификации и опыта сварщика-технолога.
Предлагаемая расчетная схема облегчает пользователю решение ука-
занной задачи, дает возможность сравнивать различные варианты и выби-
рать параметры технологии сварки, близкие к оптимальным.
Выбор технологии сварки должен прежде всего основываться на по-
лучении сварных швов заданной формы и размеров. При выполнении этого
222
4. Моделирование физических процессов в металлах при сварке
условия можно осуществлять оптимизацию технологии и по другим
критериям. Для решения задач оптимизации необходимы расчетные мо-
дели, описывающие зависимости свойств сварных соединений от ос-
новных технологических факторов. Сварочные процессы отличаются
сложностью и многообразием физико-химических явлений, что препят-
ствуют созданию адекватных моделей на основе лишь имеющихся фи-
зических представлений.
Площадь и размеры зоны проплавления зависят главным образом от
теплового и механического воздействия дуги на металл. Известно, что на
основе теории распространения теплоты можно относительно точно рассчи-
тать длину ванны, а также площадь проплавления. Рассчитать ширину и
глубину проплавления с достаточной точностью удается лишь в некоторых
отдельных случаях. Следует отметить, что возможности теоретического
расчета ограничиваются принятыми упрощениями характера распределения
источников теплоты, сложностью учета зависимости теплофизических
свойств металла от температуры, недостаточной изученностью процессов
теплопередачи в жидкой ванне и взаимодействия дуги с плавящимся метал-
лом. Все это вызывает серьезные трудности при решении задачи формиро-
вания шва теоретическим путем.
Еще более значительные трудности возникают при попытке построе-
ния зависимостей механических свойств сварных соединений от состава ме-
талла и основных технологических параметров сварки на основе имеющих-
ся физических представлений.
В настоящее время для описания зависимостей свойств сварных соеди-
нений от основных технологических факторов целесообразно использовать
регрессионные модели, которые достаточно хорошо отражают основные коли-
чественные соотношения и мстуг быть получены на основе обработки экспе-
риментальных данных. Однако необходимо учитывать, что эти модели имеют
локальный характер и их можно использовать лишь в той области факторного
пространства, в которой проводились экспериментальные исследования.
Предлагаемая система предназначена для выбора режима сварки в
СО2, оценки механических свойств зоны термического влияния и металла
шва, с использованием регрессионных моделей.
Система создавалась для выбора технологических параметров автома-
тизированной сварки в СО2, однако она может оказаться полезной и при
других способах сварки плавлением.
Расчетная система состоит из двух связанных между собой подсис-
тем, предназначенных для:
• выбора режима сварки из условия получения требуемых размеров шва;
• оценки механических свойств зоны термического влияния и ме-
талла шва.
4.6. Расчетная схема для выбора условий сварки
223
Рис. 4.5. Информационные связи в расчетной системе
(ЗТВ — зона термического влияния)
Структурная схема расчетной системы и информационные связи в ней
представлены на рис. 4.5.
Первая подсистема предназначена для выбора режима однопроходной
сварки из условия получения требуемых размеров шва стыковых и угловых
соединений. Свариваемый материал — листы углеродистых и низколегиро-
ванных (в том числе высокопрочных) сталей без разделки кромок толщиной
3...12 мм для стыковых и 3...20 мм для угловых соединений. Угловые соеди-
нения мотуг свариваться в горизонтальном и наклонном положениях. В по-
следнем случае сварка производится «в лодочку» на спуск, угол наклона
может изменяться от 30 до 90°.
Подсистема содержит две группы моделей. Первая используется для
оценки режима однопроходной сварки, исходя из заданных технологиче-
ских условий: вида соединения, толщины металла, зазора, диаметра элек-
тродной проволоки. Расчетные режимы сварки обеспечивают приемлемое
формирование шва. Вторая группа моделей служит для оценки размеров
швов в зависимости от технологических условий и режима сварки. Эти мо-
дели применяются, в частности, при выборе пользователем других режимов
сварки, отличных от расчетных.
Модели построены на основе обработки экспериментальных данных,
полученных при сварке образцов роботом, который с достаточной степенью
точности и стабильностью выдерживал заданные параметры технологиче-
ского процесса. Теплофизические характеристики низколегированных ста-
лей практически не зависят от их состава. Это дает возможность использо-
вать полученные модели для любых марок низколегированных сталей.
224
4. Моделирование физических процессов в металлах при сварке
Для оценки механических свойств металла шва и зоны термического
влияния (вторая подсистема) используются расчетные модели зависимостей
«состав — свойства», также построенные на основе обработки эксперимен-
тальных данных.
Основными фазовыми компонентами, оказывающими наибольшее
влияние на механические свойства зоны термического влияния, являются
мартенсит (М), бейнит (Б) и суммарное количество феррита и перлита (ФП).
В системе используются следующие модели для оценки доли фазовых ком-
понентов в структуре зоны термического влияния, полученные на основе
анализа более 100 термокинетических диаграмм распада аустенита низколе-
гированных сталей:
М(0 = [1 - F ((In t - In zM)/ln 5м)],
ФП(0 = F[(ln t - In гФП)/1п 5ФП],
Б(0= 1-М(г)-ФП(0,
где t — длительность, с, охлаждения от 850 до 500 °C; F — интегральная
функция нормального распределения; ?м и /ФП — длительность охлаждения,
при которых образуются соответственно 50 % мартенсита или ферритно-
перлитной структуры; 5М и 5Ф11 — константы, характеризующие крутизну
кривых изменения содержания мартенсита или ферритно-перлитной струк-
туры при увеличении длительности t.
Для низколегированных сталей, содержащих С < 0,3 %, Мп < 2 %,
Si < 0,8 %, Сг < 2 %, Mo < 1 %, Ni < 2 %, V < 0,3 % параметры /м, 5м, ?фп и
5ФП можно оценить следующим образом:
In tM = -2,1 + 15,5С + 0,96Мп + 0,84Si + 0,65Сг +
+ 0,5 5Ni + 0,30V - 13,5С2 - 0,55Si2,
А = 0,95, 5о = 0,70;
In 5М = 0,56 - 0,41С + ОДОМп + 0,14Сг - 0,30Мо + 1,7С • Мо,
R = 0,70, 50 = 0,32;
In ?фП = 0,34 + 5,2С + l,8Mn + 0,53Si + 0,33Cr + 2,9Мо + 0,86Ni -
-6,0С- V - 5,1С2 + 0,50Si2,
R = 0,83,50 = 0,96;
In 5ФП = 0,91 - 0,90С + 0,09Мп + 0,08Сг + 0,34Мо + 0,15Ni + 0,85 V,
R = 0,61, 50 = 0,43,
где R и 5О — соответственно величины множественной корреляции и оста-
точного отклонения.
Твердость и показатели прочности зоны термического влияния в зави-
симости от фазового состава металла можно оценить с помощью следующих
регрессионных моделей:
4.6. Расчетная схема для выбора условий сварки
225
HV = (310 + 494С + 620С2 + 18Mn) М + (234 + 122С)Б +
+ (98 + 275С + 15Мп)ФП,
R = 0,95, So = 15;
ив = (800 + 1100 VC ) М + (590 + 960С + 40 Мп + 200У)Б +
+ (300 + 1360С + бОМп + 140У)ФП,
R = 0,91, й = 140;
а0,2 = (660 + 1250С ) М + (500 + 460С - 120С2 + 150У)Б +
+ (190 + 926С + 47Мп + 90У)ФП,
Л = 0,90,5о= 100;
5 = (12,2 - 67С - 1,5Мп + 0,761п Z)M + (21,3 - 35,6С - 4,0Мп - 5,ОУ +
+ 1,81п /)Б + (36,5 - 127С + 153 С2 - 1,2Мп - 8,0V + 0,661п 0ФП,
R = 0,91, = 3,4;
\|/= (48,5 - 158С + 116С2 + l,01n Z) М + (53,3 - 132С + ЮЗС2-5,1Мп-
- 10V + 3,41п О Б + (65,4 - 88С - 82С2 - 6,7Mn + 18V + 0,61n I) ФП,
R = 0,86, So = 7,0,
где М, Б, ФП — доли мартенсита, бейнита и феррита + перлита в структуре
металла.
Для оценки механических свойств низколегированного металла шва в
относительно узком диапазоне значений длительности охлаждения от 850
до 500 °C (10...40 с) можно использовать следующие регрессионные моде-
ли, описывающие зависимость свойств от химического состава:
оЕ = 350 + 1720С + 171 Мп - 23,6Si + 202Cr + 147Мо + 97Ni + 426V +
+ 170С • Мп + 1330С • Si + 870С Cr - 160С Mo + 3 ЮС Ni -
- 694C • V - 23,5Mn • Ni + 64,5Si • Cr - 43Cr • Mo - 25,5Cr • V -
- 20,7Mo Ni - 50,7Mo V + 16,lNi • V + 86C2 - 17Mn2 - 50C? -
- 4,5Mo2 + 5,4Ni2 - 255V2 - (23,0 + 290C + 3Mn + 2,5Si + 14Cr -
- 13Mo + 10,8Ni + 13V )In Z,
R = 0,98, = 68;
o0>2 = 290,0 + 1660C + 164Mn + 17,4Si + ЮЗСг + 190Mo + 92Ni + 324V -
- 32,3C • Мп + 712C • Si + 291C • Ni + 470C • V - 24,lMn Ni +
+ 65,1 Si • Cr - 64,2Si • Ni + 201 Si V - 24Mo • Ni - 59,2Mo • V +
+ 15,3Ni • V- 161C2 - 3l,3Mn2 - 15Mo2 -4,5Ni2 - 275V2 - ( 27,5 +
+ 350C + 4,1 Mn + 4,3Cr + 3,4Mo + 2,2Ni + 6,6V )ln t,
R = 0,98, S',, = 64;
5 = 37 - ЮЗС - 3,94Mn + 1,61 Si - 8,59Cr - 9,0Mo - 20,6V + 9,2C • Mn +
+ 11C • Cr + 20C Mo - l,lMn • Si + l,64Mn Mo + 0,557Cr - Ni -
- 18(S + P) + 0,826Mo • Ni + 3,8Mo - V + 78C2 + 0,27C? + 0,686Mo2 +
+ 2,12V2 + ( 8,4C + 0,905Cr - 0,596Ni + 4,9V )ln t,
/? = 0,85,50 = 1,8;
8 6705
226
4. Моделирование физических процессов в металлах при сварке
V = 86 - 213 + 2,86Mn + 10,5 Si - 11,9Сг- 11,4Мо- 52,2V- 23(S + Р) +
+ 4,45С • Сг- 1,38Мп • Мо- 0,592Мп • Ni - 2,76Мп • V - 1,52Ni • V +
+ 110C2 + 0,31Cr2 + 4,lV2 + (-2,83 + 18,8C-l,76Mn-4,36Si + 1,76Сг +
+ 3,9Мо + 0,54Ni + 18V )ln Z,
R = 0,83, So = 3,5;
In [KCV(7)] = 0,28 + l,56Mn- 1,57Si - 0,877Cr - l,98Mo - 7,25P -
- 0,196Mn • Ni + 0,25Ni • V - 11,5C2 + 0,05 IMn2 - 0,22Mo2 +
+ 0,141Ni2 + 0,533V2 + (0,386 - 0,7C - 0,514Mn + 0,415 Si + 0,217Cr +
+ 0,703Mo - 0,12Ni + 0,715V - 8,IN - 3,440 )ln t + (0,0183 - 0,043C -
- 0,0018Mn - 0,002Mo - 0,0025Ni - 0,0068V)T+ 0,0039Tin t,
R = 0,74, So = 0,69,
где KCV — ударная вязкость в диапазоне температур Тот -30 до -70 °C.
При расчете состава металла шва учитывается доля основного металла,
которую можно оценить, исходя из размеров шва и разделки кромок.
Работа с компьютерной системой. На первом шаге пользователь вы-
бирает вид соединения, затем система требует ввода информации об исход-
ных технологических условиях. Для стыковых соединений вводятся толщина
основного металла, ширина зазора и диаметр электродной проволоки, а для
угловых — еще толщина шва и угол наклона, если сварка осуществляется в
наклонном положении. При вводе этой информации система задает ограниче-
ния на вводимые технологические факторы. Эти ограничения могут быть свя-
заны с областью действия используемых моделей, где они обеспечивают дос-
таточную точность, а также с допусками на ширину зазоров при сборке со-
единения под сварку и с рядом других технологических требований.
Например, приемлемый диапазон значений ширины зазора и длины катета
определяется главным образом толщиной основного металла, максимально
допустимый диаметр электродной проволоки зависит от длины катета и т. д.
После ввода данных об исходных технологических условиях система
рассчитывает режим сварки (сварочный ток, напряжение на дуге, скорость
сварки, скорость подачи проволоки) и ожидаемые размеры шва: глубину
проплавления, ширину и толщину шва, площадь сечения наплавленного ме-
талла, а также потери на разбрызгивание. Кроме того, система оценивает
удельные расходы электродной проволоки и защитного газа (СОг).
Естественно, что требования к размерам шва могут быть различными
в зависимости от назначения сварной конструкции. Поэтому система дает
возможность пользователю изменять режим сварки, если ожидаемые разме-
ры шва или рекомендуемый режим сварки не удовлетворяют его. Для ново-
го режима система опять оценивает ожидаемые размеры шва и дает реко-
мендации по приемлемому диапазону значений размеров шва. Для облегче-
ния подбора подходящего режима сварки предусмотрен вывод на экран
схематического изображения сечения шва.
4.6. Расчетная схема для выбора условий сварки
227
Система ограничивает пользователя при задании режима сварки. В ча-
стности, не допускаются режимы, приводящие к плохому формированию
шва (например, при очень низких значениях погонной энергии) и прожогу.
При сварке угловых швов в наклонном положении для исключения ci екания
ванны жидкого металла ограничивается ее объем.
При оценке воспроизводимости размеров шва необходимо учитывать,
что тепловая мощность дуги не дает достаточно полного представления о ее
технологических возможностях. В частности, изменение формы кривой тока
(например, при замене источника питания) может оказать существенное
влияние на глубину проплавления и разбрызгивание электродного металла.
После выбора режима сварки система переходит к решению следую-
щей задачи — оценке механических свойств металла зоны термического
влияния (твердость, временное сопротивление, предел текучести, относи-
тельное удлинение и сужение) и металла шва (временное сопротивление,
предел текучести, относительное удлинение и сужение, ударная вязкость
образцов Шарпи при отрицательных температурах). Кроме того, оценивает-
ся фазовый состав зоны термического влияния. Эти оценки рассчитываются
исходя из химического состава металла и скорости охлаждения в интервале
температур фазовых превращений.
Химические составы основного металла и электродной проволоки
пользователь может вводить поэлементно или использовать имеющийся в
системе каталог и информацию о марках и средних составах сталей и про-
волок. Если ожидаемые значения механических свойств не удовлетворяют
пользователя, он может изменить марку электродной проволоки и в опреде-
ленных пределах режим сварки, после чего получить новые расчетные
оценки свойств. Ниже приведены типовые результаты расчетов.
Исходные технологические условия:
толщина металла, мм ..................... 10,0
диаметр электродной проводки, мм ...... 1,2
зазор в соединении, мм ................ 2,0
Расчетные значения параметров
режима сварки:
сварочный ток, А......................... 251
напряжение на дуге, В ................... 25,3
скорость сварки, м/ч..................... 21,6
расчетная скорость подачи проволоки, м/ч. 441
Ожидаемые размеры шва:
глубина проплавления, мм ................ 7,5
ширина шва, мм........................... 7,8
коэффициент формы усиления шва........... 0,29
228
4. Моделирование физических процессов в металлах при сварке
потери на разбрызгивание, %................. 6
площадь сечения наплавленного металла, мм2 .... 21,8
расход электродной проволоки, кг/м ......... 0,21
расход защитного газа, л/м.................. 50 (или 18,1 л/мин)
марка свариваемой стали..................... 09Г2С
марка сварочного электрода.................. Св-08 Г2С
Ориентировочный фазовый состав
зоны термического влияния:
мартенсит, %................................ 6
бейнит, %................................... 93
феррит + перлит, % ......................... 1
Механические свойства
зоны термического влияния:
временное сопротивление, МПа................ 721
предел текучести, МПа...................... 538
относительное удлинение, % ................. 17
относительное сужение, % ................... 45
твердость, HV............................... 247
Механические свойства металла шва:
временное сопротивление, МПа................ 659
предел текучести, МПа....................... 475
относительное удлинение, %.................. 27
относительное сужение, %.................... 55
ударная вязкость, МДж/м2:
при Т= 20 °C......................... 1,33
при Г =-20 °C......................... 0,85
при Т= -40 °C......................... 0,55
По желанию пользователя на экран можно вывести графики зависимо-
стей фазового состава (содержания мартенсита, бейнита и ферритно-перлитной
структуры) и механических свойств зоны термического влияния от длительно-
сти t охлаждения от 850 до 500 °C (интервал температур фазовых превращений
в низколегированных сталях). Величина t, соответствующая выбранному ре-
жиму, на графиках указывается вертикальной стрелкой. Эти графики аналогич-
ны термокинетическим диаграммам распада аустенита, которые широко ис-
пользуются для описания свойств зоны термического влияния.
В процессе работы система дает возможность пользователю из любой
точки программы вернуться к любому предыдущему шагу расчета, скоррек-
тировать соответствующие данные и продолжить анализ. Это позволяет вы-
бирать приемлемые параметры технологии сварки для получения желаемого
комплекса свойств сварного соединения.
5. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ
ТЕХНОЛОГИИ СБОРОЧНО-СВАРОЧНОГО
ПРОИЗВОДСТВА
5.1. Общие вопросы автоматизации проектирования
сварочной технологии
Подготовка сварочного производства имеет существенные особенно-
сти, связанные с большим количеством решаемых при этом задач. Сюда
входят:
• анализ сварной конструкции;
• разработка маршрутной и операционной технологии заготовитель-
ных и сборочно-сварочных операций с определением режимов и выбором
технологического оборудования;
• проектирование нестандартной специализированной оснастки и ее
изготовление;
• проектирование отдельных автоматизированных и роботизиро-
ванных комплексов, проектирование автоматизированных технологиче-
ских линий;
• изготовление, отладка и монтаж технологических линий.
Большое количество отдельных сварных узлов и подузлов, на которые
делится конструкция, заставляют эту цепочку проходить многократно.
Большой объем работы еще увеличивается за счет возможной доработки и
изменений конструкции и технологии ее изготовления в процессе подготов-
ки и отладки производства.
Получаемая на выходе технологическая документация, как правило,
весьма объемная, так как должна описывать подробную последовательность
и содержание всех действий, включающих технологию выполнения не толь-
ко собственно сварочных операций, но и сопутствующих им операций сбор-
ки, прихватки, контроля, правки, зачистки швов и поверхностей деталей,
кантовочных и транспортных операций. Если еще к этому добавить, разно-
образие применяемых методов сварки, таких, как многие виды дуговых сва-
рочных технологий в активных и инертных газах, под флюсом, многие виды
230
5. Автоматизированное проектирование технологии
технологий контактной сварки, то очевидно, что рассматриваемая зада-
ча автоматизации проектирования сварочной технологии одновременно
является и весьма сложной и крайне необходимой для снижения ее тру-
доемкости.
Необходимость сокращения трудоемкости подготовки производства
дополняется и существенным повышением ответственности принимаемых
решений, поскольку любые изменения на более поздних этапах непременно
вызовут значительные финансовые издержки и дополнительные переносы
сроков начала производства.
При традиционной технике и технологии выполнения работ сроки
подготовки производства, например, в автомобильной промышленности ра-
нее занимали до 10 лет и более. Сегодня имеются реальные возможности
снижения трудоемкости и сокращения сроков проектирования сварочной
технологии за счет разработки и применения эффективных компьютерных
технологий. Однако традиционно высокая квалификация инженеров-техно-
логов и большая доля творческой составляющей в условиях большой воз-
можной многовариантности решений при разработке технологии делают
постановку задачи автоматизации этой работы весьма сложной. Тем не ме-
нее основные требования к этой системе очевидны. Это многократное уско-
рение работы, полное исключение или быстрое обнаружение возможных
ошибок и создание комфортной рабочей атмосферы для пользователя. В ча-
стности, автоматизированная система должна полностью исключить воз-
можность пропуска установки любой детали и сварки любого шва.
Автоматизацией разработки сварочной технологии ввиду отсутствия
эффективных и универсальных систем вынуждены заниматься самостоя-
тельно многие организации, создавая свои версии систем проектирования
сварочной технологии. Для проектирования последовательности и содержа-
ния технологии сборочно-сварочных операций различными организациями
были созданы несколько программ, которые, как правило, представляют со-
бой редакторы операций и переходов с выборкой необходимых данных в
процессе проектирования технологии из внешних баз данных или под-
ключаемых расчетных задач. Такие программы позволяют фиксировать
этапы процесса проектирования, а также все вносимые изменения техно-
логического процесса. Ведется архив технологических процессов. В не-
которых разработках существует база типовых технологических процес-
сов. На выходе системы формируется типовая технологическая докумен-
тация по ГОСТу.
Примером такой системы может служить программный комплекс
ARMSW (рабочее место технолога-сварщика), созданный на кафедре сварки
Тульского государственного технического университета под руководством
профессора В.А. Судника. Проектирование технологии начинается с выборки и
5.1. Общие вопросы автоматизации проектирования технологии
231
Спецификация сборочной единицы изделия Прицепной комбайн ПК- ЛГ: J.1100.01.000
;Поз! Обозначение | Наименование |Кол|Масса|Г.разм|Мат
2 ДП 9101.05.01.01.000 ДП 9101.05.01.00.001 Хомут Кольцо* it 2.65 1.33 5 15 Тр Тр
ЛП 9101 .05.01 . 02 . ООО I | Опора | 11 It .78 | 120
4 ДП 9101.05.01.00.032 Пояс и. 1.67 50 тр
5 ДП 9101.05.01.00.003 Труба 1 6.73 20 Тр
б ДП 9101.05.01.00.004 Ушко 1 0.4 4 ли
7 ДП 9101.05.01.20.005 Фланец 1 5.7 10 Ли
8 Стандартное изделие Болт М10 ГОСТ 7002-81 3 0.05
База: Материалы основные
Швеллер 1С-Л ГОСТ В240/ВСТЗСП2-11 ГОСТ 535
Швеллер 1Ь-П ГОСТ 8240/ВСТЗСП2-11 ГОСТ 535
Швеллер 2С ГОСТ 824Р/ВСТЗСП2-11 ГОСТ 535
Шве.иер 4D ГОСТ 8240 / ВСТЗСП 2 Н ГОСТ 535
Швеллер В100*50*4 Б ГОСТ 8278/2-СТЗКП ГОСТ 11474
Шестигранник L2-&12 ГОСТ 8560/35-В-Т ГОСТ 1051
47/ 40 |----------------------------------------------
Материал: Лист 6 ГОСТ 11234-90/Сталь 08кп ГОСТ 7112-90
|Г4-Новая трока: F6-Новый канит: F8 Уда, ппьс! року: fNTtR Bikxiii в icvituoiiik»
Рис. 5.1. Пример окна ввода спецификации
Технолошя дня имс.шя: ПринеиноП комбайн 05.00.01 000 СВ Кож\\ шн
И. | Текст описания технологии |Тшт/Кол
т 3 с 3 Тара 1-1-80-6Э-55-0.5М ГОСТ 14861-86 привезти комплектующие на рабочее место N1 20 04 1 00 9343 Сварочная #60190; #63132; #30190; #20190; Выпрямитель ВДГ-303 1.05
|D Полуатим»п А-825 'Г
1Z |.191595 4211 К 1 Поз.7 - ДП 9101.05.61.00.005; Фланеи (5.7 кп.: мм) 1
kin ми топании и $ спецификации со. с-1. ниелия: Баю: Компоненты icmio.ioihh I !рипспнои комбайн НК-3\] - Комт
В Шифры операций База данных
С Документация База данных
0 Оборудование База данных
Е Квалификация рабочего База данных
К Комплектование ! Баи данных
М Материалы вспомогател База данных
Т Инструмент; остнастка База данных
Ч 17/ 4
1 ДП 9101.05.01.0 Хомут
2 ДП 9101.05.01.0 Кольцо
4 ДП 9101.05.01.0 Пояс
3 ДП 9101.05.01.0 Опора
4 ДП 9101.05.01.0 Пояс
5 ДП 9101.05.01.00.0 Труба
6 ДП 9101.05.01.00.0 Ушко
7 ДП 9101.05.01.00.0 Фланец
14—Новая строка: F6-Новый кагалом F8-Удалим» сиюкх: EN ILK - Bucci и в 1с\ноло1ик»
Рис. 5.2. Пример окна ввода технологических параметров
звода исходных данных по изделию. Для каждой сварной конструкции сущест-
зхет перечень сборочных единиц, для которых в системе создаются специфи-
кация, графические документы и проектируется технология с печатью всей
технологической документации. На рис. 5.1 показан ввод спецификации с ис-
пользованием базы материалов. Проектирование технологии (рис. 5.2) проис-
232
5. Автоматизированное проектирование технологии
из дел ие кожух шнек а ПК- 3 И Д лО 5.0 9.01.0 0 •) СЕ
Технологический процесс
Шифр организации: 9123.12.03
Гл. инженер: Иванов
Гл. сварщик Кошкин
Начальник ОТК: Лях
Главный конструктор: Пикуль
Разработал: Ванин
Нормировал: Катин
проверил: Петин
Н.контроль: Кондаков
Литера: Р
Рис. 5.3. Окно выбора технологических документов
ходит в диалоговом режиме с использованием базы компонентов техноло-
гии и внешних программ расчета режимов и других параметров технологии.
После подтверждения окончания проектирования технологии (рис. 5.3) сис-
тема формирует весь комплект технологической документации. Формат вы-
вода представлен на рис. 5.4. Программный комплекс ARMSW охватывает
все этапы проектирования технологии сборочно-сварочных операций. Сис-
тема использует большое количество баз данных и внешних расчетных про-
граммных модулей, что в несколько раз ускоряет проектирование техноло-
гии и повышает качество принятия решений.
Дальнейшее развитие таких систем идет по пути повышения произ-
водительности работы технологов, в особенности при подготовке слож-
ных по структуре и количеству заготовок сварных конструкций. При
этом развиваются функции обработки данных для сравнительного анали-
за и обоснования выбора возможных вариантов технологических реше-
ний, автоматического контроля и исключения всех технических ошибок в
технологических документах, таких, как пропуск отдельных деталей,
сварных швов, фрагментов технологии. Но самое главное, автоматизиро-
ванные системы разработки сварочной технологии должны быть ближе
к проектированию конструкции, чтобы уже на этой стадии можно было
более полно учесть не только общие, но и специфические требования
технологии применительно к условиям конкретно существующего произ-
водства с имеющимся набором инструментов, сборочно-сварочных при-
способлений, манипуляторов изделий.
5.2. Обработка и представление исходных данных
233
ГССТ 3.1I1H-BZ форма 3
| | #0290 | | 1
9123.12.00 | Кожух шнека ПК-ЗМ | #1090 | ARMSW
| ЛП05.00.01.000 СБ |Е I | |
В | Цех I Уч I PM I Опер ! Код; наименование операции
Г | Обозначение документа
Д | Код; наименование оборудования
Е |СМ| ПРСФ | Р | УТ |КР 1КОИД| ЕН | ОП |Кшт | ТПЗ | Тшт
4
В 5
Д 6
Е 1
Е
В S
Г 10
20 2 1 00 0401 Транспортирование
Электротележка ЕП-006
130346 2 1 2 1
20 04 1 00 9043 Сварочная
#60190; #60102; «30190; #20190;
Редактирование 1-пл листа маршрутной карты
Рис. 5.4. Пример окна печати маршрутной карты
Зарубежные системы автоматизированного проектирования техноло-
гии в основном создаются для конкретных задач и основаны на собственных
разработках различных фирм. В литературе эти системы практически не ос-
вещены, и доступ к информации по технологическим САПР закрыт.
5.2. Обработка и представление исходных данных
Задача автоматизации разработки технологии сборочно-сварочных
операций требует использования большого объема данных, и только их
достаточность может обеспечить нормальное функционирование системы.
Весь объем обрабатываемой информации можно разделить на четыре груп-
пы по признакам его формирования и использования.
Входные данные — данные о конструкции, ее структуре, сборочных
единицах, деталях и сварных швах — поступают из спецификаций конст-
рукторской документации и содержат наименования деталей и узлов, значе-
ния их массы, количество, номера чертежей и другую информацию. Изуче-
ние и анализ исходных данных — начало и основа работы над формирова-
нием технологических решений.
Оперативные данные формируются для конкретного проектируемо-
го технологического процесса. Здесь собираются, хранятся и обрабатывают-
234
5. Автоматизированное проектирование технологии
ся исходные данные о конструкции, различные варианты последовательно-
сти сборки и формируемые данные о технологии и вариантах технологиче-
ских процессов.
Справочные данные — алгоритмы, база данных и знаний, в которую
включены стандарты на сварные соединения, обширные данные о материа-
лах основных и сварочных, о технологическом оборудовании, приспособле-
ниях и инструменте, справочные данные и алгоритмы расчета режимов,
нормирования и др.
Выходные данные — формируемая в процессе работы объектно-
ориентированная база данных конкретного заказа и различных вариантов
выходных форм, из которой могут быть автоматически сформированы и
распечатаны самые разнообразные варианты технологической документации.
Подготовка данных для использования в системе требует не только
решения задачи их структуризации и определения взаимосвязей, но и, что
очень важно, предоставления средств и специальных функций, обеспечи-
вающих возможность контроля и анализа их содержания. Далее будет пока-
зано, что именно наличие таких сервисных функций обеспечивает надеж-
ность и эффективность работы сложных систем.
Решение задачи структуризации данных рассмотрим на примере фор-
мирования и обработки входных данных (о сборочных единицах, деталях и
сварных швах). Поскольку сварные конструкции часто бывают весьма
сложными (количество входящих в них деталей и сварных соединений мо-
жет измеряться сотнями единиц), идею организации этих данных целесооб-
разно позаимствовать из организации файловых структур в операционных
системах вычислительной техники, в которых легко обрабатывается практи-
чески неограниченное количество входящих элементов с максимально воз-
можной глубиной вхождений. Полезность такой аналогии становится оче-
видной, если учесть следующие обстоятельства. Корневой каталог некото-
рого дискового пространства может соответствовать структуре сварной
конструкции. Отдельные каталоги и подкаталоги с любым количеством
уровней вхождения могут соответствовать отдельным сварным узлам и по-
дузлам этой конструкции. Файлы, входящие в любые каталоги, могут соот-
ветствовать отдельным деталям.
Если принять такую аналогию, то становится возможным использо-
вать большинство из уже имеющихся и привычных функций работы с фай-
ловыми системами применительно к работе с данными о сварной конструк-
ции. Так, графическое отображение дерева структуры сварной конструкции
может быть использовано для быстрого анализа и контроля правильности
ввода данных даже весьма сложных по составу изделий. В описании файло-
вых структур используется ряд полей: наименование, объем, дата последне-
го изменения, время. Этим данным могут быть близки данные об элементе
5.2. Обработка и представление исходных данных
235
Сварная конструкция
Сборочная единица
1 —Сборочная единица
<--------Деталь
М---------Деталь
------- Сборочная единица
-<---------------Деталь
-------- Деталь
«---------Деталь
<---------Деталь
Сборочная единица
---------<--------Деталь
---------<--------Деталь
Деталь
б
Рис. 5.5. Схемы древовидных структур на примере:
а — структуры каталогов; б — структуры сварной конструкции
конструкции: наименование, масса, номер чертежа, дата утверждения, время.
Имеющиеся в операционных системах функции сортировки данных (по лю-
бому параметру) будут полезными и для работы технолога со сварной конст-
рукцией. Большие возможности многооконного пользовательского интерфей-
са создают комфортные условия для технолога. Например, в левом окне —
структура узла, в правом — входящие в нее отдельные детали. Удобны функ-
ции подсчета масс групп деталей, узлов по аналогии с подсчетом размеров
групп файлов. Эффективно использование дерева структуры конструкции как
навигатора для быстрого поиска данных о нужных деталях и узлах.
Еще большие перспективы открываются при использовании других
функций операционных систем в процессе работы над технологией выполне-
ния сборочно-сварочных операций. Так, весьма полезны функции перемеще-
ния деталей и подузлов в другие сборочные единицы, функции объединения
отдельных деталей в дополнительные технологические сборочные единицы и
другие широко используемые функции файловых операционных систем.
Рассматриваемую аналогию файловой структуры и структуры сварной
конструкции можно проследить по рис. 5.5 а, б, где показаны соответствен-
но фрагмент дерева файловой структуры и структуры сварной конструкции,
состоящей из трех сборочных единиц и десяти входящих в них отдельных
деталей. Следует заметить, что графическое изображение структуры конст-
рукции (см. рис. 5.5, б) одновременно можно рассматривать и как схему по-
следовательности сборки сварной конструкции.
236
5. Автоматизированное проектирование технологии
/“] Сварная конструкция (сборочная единица)
Сборочная единица 1
Сборочная единица 2
Сварная конструкция (сборочная единица)
Сборочная единица 1
Сборочная единица 2
Деталь
<---S-L Деталь 1
Деталь 2
Деталь 2
---- Сборочная единица 2
Деталь 1
Деталь 2
Деталь 3
Деталь 4
Деталь 5
Деталь 2
Деталь 3
М-------Деталь 4
Деталь 5
Деталь 5
а
Рис. 5.6. Варианты представления сварной конструкции:
а — идеальный вариант; б — компактный вариант
Однако при очевидном внешнем сходстве в отображении структуры
связей элементов конкретной конструкции со структурой размещения фай-
лов и каталогов не следует упускать и существенных различий в характери-
стиках рассматриваемых объектов. Первое различие связано с тем, что в
сварные конструкции часто входит много одинаковых деталей и даже оди-
наковых сборочных единиц, причем одинаковые детали могут входить в
разные сборки. В отличие от файловых структур, где файл, скопированный
в другой каталог, сразу становится самостоятельным и независимым от ори-
гинала, в реальной конструкции одинаковые детали вне зависимости от их
места в структуре всегда остаются связанными друг с другом. Второе прин-
ципиальное различие связано с необходимостью отображения в системе ко-
личества ее отдельных элементов. На рис. 5.6, а показана структура некото-
рой конкретной конструкции. Если по такому принципу, когда каждый от-
дельный элемент занимает в структуре отдельную строку, отображать
реальные конструкции часто с сотнями одинаковых деталей, то эти схемы
окажутся практически неприемлемыми вследствие своей громоздкости. По-
этому на рис. 5.6, б показана структура этой же конструкции, но в компакт-
ном оформлении с указанием кратности вхождения в общую структуру от-
дельных ее элементов.
5.2. Обработка и представление исходных данных
237
Рис. 5.7. Пример листовой сварной конструкции «переходник»:
1—6 — сварные швы
Этот вариант более эффективен, так как помимо своей компактности
хорошо выделяет и показывает одинаковые элементы, которым будут соот-
ветствовать и одинаковые элементы маршрутных и операционных техноло-
гических процессов.
Более подробно методику подготовки и представления исходных дан-
ных рассмотрим на некотором примере сварного изделия (рис. 5.7). Это лис-
товая конструкция переходника, обеспечивающего плавный переход от
прямоугольного сечения к круглому и состоящего из трех отдельных узлов,
цилиндра, диффузора и короба, каждый из которых можно рассматривать
как отдельную сборочную единицу. На рис. 5.8 дан вариант структуры этой
конструкции, где указано количество входящих в каждую сборочную еди-
ницу элементов. Для разработки технологии изготовления сварного узла и
формирования технологической документации необходимо выполнить под-
готовку, сборку и сварку всех сварных швов. Для обеспечения контроля за
подготовкой технологии сварки и решения задач нормирования по каждому
отдельному сварному шву в автоматизированной системе выполнена при-
вязка швов к своим сборочным единицам. Эта привязка швов отражена в
структуре (рис. 5.9).
Для анализа конструкции и выработки технологических решений по-
мимо связей между отдельными деталями и сборочными единицами нужны
238
5. Автоматизированное проектирование технологии
Переходник
Цилиндр
1
---- Обечайка
1
---- Шов 1
Диффузор
2
----- Боковина правая
2
----- Боковина левая
2
----- Шов 2
2
----- Шов 3
Короб
2
------- Пластина большая
2
------- Пластина малая
4
---- Шов 4
Шов 5
Шов 6
Рис. 5.8. Варианты структуры сварной конструкции
«переходник»:
а — состав конструкции; б — вариант содержит сбороч-
ные единицы
Рис. 5.9. Структура сварной
конструкции «переходник»
с привязкой швов
их конкретные характеристики, прежде всего весовые, и ссылки на чертеж-
ную документацию. Поэтому типовая рабочая форма графической структу-
ры конструкции включает в себя дополнительные колонки с этими данны-
ми. Примеры структур двух сварных конструкций показаны на рис. 5.10 и
5.11, где даны взаимосвязи и порядок изготовления этих конструкций.
Естественно, что уже на стадии проектирования изделия конструктор
продумывает его узлование и последовательность сборки. Поэтому часто в
чертежной конструкторской документации сборочные узлы представляются
в виде отдельных графических листов, а каждый деталировочный чертеж
имеет собственный номер. В связи с этим оказывается, что обработка
текстовых данных листов конструкторской спецификации специальным
5.2. Обработка и представление исходных данных
239
Номера чертежей Вес, КГ Наименование чертежей
8-21293 13527,0 9=т11 корпус_барабана
3-449821 3132,0 8 !=; 1 обечайка
3-449822 2475,0 — 1 обечайка
3-449823 652,0 — 1 обечайка
3-499876 1058,0 7 != 2 обечайка
3-499877 831,0 — 1 обечайка
3-499878 224,0 — 1 обечайка
3-499879 4730,0 6 != 1 обечайка
3-499820 3713,0 — 1 обечайка
3-499881 1005,0 — 1 обечайка
2-281225 249,0 4 =j]2 рамка_люка
3-494524 116,0 5 f=r 1 фланец
4-982789 25,5 — 2 пластина
4-982790 29,5 — 2 пластина
3-494525 62,0 — 2 окантовка
2-281226 346,0 2 f=j]2 крышка_люка
3-494524-0 157,0 3 г==т|1 фланец
4-982789-0 36,5 — 2 пластина
4-982790-0 39,0 — 2 пластина
3-494526 69,0 — 2 окантовка
4-982791 20,5 — 2 ребро
4-956141 35,0 1 r=j 4 захват
4-956142 13,0 — 1 платик
4-956146 20,0 — 1 бонка
3-449820 105,0 —16 сектор
4-611247 7,6 — 4 упор
4-654383 39,0 — 4 захват
4-949050 2,2 — 8 ребро
4-951882 2,8 — 6 гайка
8-21293-13 2,6 — 4 платик
Рис. 5.10. Структура конструкторской документации
на примере сварной конструкции «корпус барабана»
240
5. Автоматизированное проектирование технологии
СТРУКТУРА КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ по цеху 00 Заказ N 000000 Изделие - Топка печи Спецификация N 1-32101 Заказчик Чертеж N 1-32101 Узел - Топка печи Вес узла N 51.4
Номера чертежей Вес, КГ Наименование чертежей
1-32101 1-32004 1-320 8 1-32103 1-32102 1-320 1 1-320 4 1-320 2 1-320 5 1-320 6 1-320 9 1-32010 1-32011 1-32012 51.4 1.0 0.5 18.3 14.9 2.6 0.9 8.7 3.4 2.6 7.0 15.5 0.6 6.4 4=j]l Топка печи 3 r=Til Топочное окно u— 2 Заготовка топочного 2 1 Колпак 1 k=rl Корпус колпака — 1 Торец задний — 1 Верх гнутый — 6 Ребро — 1 Рассекатель верхний — 1 Рассекатель нижний — 1 Стенка передняя — 1 Корпус топки — 1 Патрубок 1 Дно топки
Рис. 5.11. Структура конструкторской документации на примере свар-
ной конструкции «топка печи»
программным модулем позволяет сформировать и отобразить структу-
ры конструкций, показанные на рис. 5.10 и 5.11, в автоматическом ре-
жиме. Следовательно, для организации процесса автоматизированного
формирования технологии сборочно-сварочных операций целесообраз-
но этап ввода исходных данных из конструкторских спецификаций (ес-
ли они были оформлены вручную на бланках) отделить от этапа собст-
венно разработки технологии. В этом случае, во-первых, автоматиче-
ское формирование графических структур конструкторской докумен-
тации позволит сразу найти и устранить все возможные ошибки ввода
или исходных документов, а, во-вторых, задание на разработку техноло-
гии поступит в технологическое подразделение вместе с комплектом
чертежей, спецификаций и распечатанной наглядной структурой все-
го этого материала, что существенно упростит и ускорит работу тех-
нолога.
5.3. Формирование последовательности сборки и сварки конструкции 241
5.3. Формирование последовательности сборки
и сварки конструкции
После завершения анализа конструкторской документации первым и
принципиально важным этапом разработки технологии изготовления свар-
ной конструкции является ее деление на сборочные единицы. При этом за-
кладываются основы всей последующей технологии, по которой отдельные
узлы будут изготовляться последовательно (или параллельно) на отдельных
рабочих местах с использованием соответствующих сборочно-сварочных
приспособлений, оснастки и сварочного оборудования. В принятии решений
имеется большая доля творческой составляющей, и, как правило, наиболее
квалифицированные технологи могут предложить рациональную схему ор-
ганизации изготовления конструкции. При этом учитывается много факто-
ров, связанных с конструктивными особенностями изделия, серийностью
производства, а также возможности максимального использования уже су-
ществующих приспособлений, сроков, отведенных на подготовку производ-
ства и др. Процесс формирования структуры сборки не должен выполняться
в автоматическом режиме, а интерактивные технологии призваны обеспе-
чить высокое быстродействие выполнения всех операций и исключение всех
возможных технических ошибок. Более того, уже в процессе разработки
технологии часто возникает необходимость изменения принятой первона-
чально последовательности выполнения сборочно-сварочных операций. Это
может быть связано с возникающими трудностями сборки, точного базиро-
вания заготовок, ограниченной доступностью сварных швов, с необходимо-
стью выделения дополнительных сборочных узлов для уменьшения техно-
логического времени и синхронизации ритма работы оборудования поточ-
ных или автоматических технологических линий.
В случае изменения порядка сборки и сварки узлов при частично уже
разработанной и сформированной технологии, и особенно если такие изме-
нения произошли в завершающей стадии работы, сформированные блоки
технологического процесса, непосредственно не затронутые изменениями,
должны сохраниться и не переформировываться вновь. Достигается это
специальной системой привязки данных технологии к структуре сборочных
единиц, которая более подробно рассмотрена в § 5.4.
Технически разработку последовательности сборки и сварки конст-
рукции удобно выполнять путем видоизменения (редактирования) исходной
структуры — структуры конструкторской документации. В качестве приме-
ра для пояснения технологии формирования последовательности выполне-
ния сборочно-сварочных операций воспользуемся уже рассмотренной кон-
струкцией переходника (см. рис. 5.7). Если в конструкторской документации на
242
5. Автоматизированное проектирование технологии
Переходник
1
Цилиндр
— Обечайка
— Шов 1
Диффузор
2
Техн.сборка
----- Боковина правая
1
----- Боковина левая
——- Шов 2
2
— Шов 3
Короб
2
— Пластина большая
2 „
— Пластина малая
— Шов 4
Шов 5
Шов 6
это изделие имеется только
один сборочный чертеж, на ко-
тором изображено все изделие,
то автоматическая обработка
данных конструкторской спе-
цификации сформирует дерево
ее структуры так, как показано
на рис. 5.8, а. Для упрощения
схемы здесь пока не представ-
лены сварные швы.
В случае если в конструк-
торской документации на это
изделие помимо основного сбо-
рочного чертежа имеются от-
дельные сборочные чертежи на
цилиндр, диффузор, короб, то
система автоматически сформи-
рует структуру документации,
как показано на рис. 5.8, б. Ес-
тественно, ни первая, ни вторая
из автоматически сформирован-
ных структур документации не
обязана быть структурой про-
цесса изготовления — структу-
рой сборки конструкции в про-
изводстве, хотя, как правило,
Рис. 5.12. Вариант структуры сборки изде-
лия «переходник», включающий дополни-
тельную технологическую сборку
конструктор при выполнении
проекта определяет все отдель-
ные сборочные элементы. Тех-
нолог уточняет и окончательно
определяет структуру сборки.
Предположим, что в рассматриваемом примере процесс изготовления дол-
жен проходить так, как показано на рис. 5.12. Можно видеть, что на оконча-
тельную сборку поступают три сварных узла: цилиндр, диффузор и короб,
однако сам диффузор будет собираться и, возможно, свариваться не сразу из
четырех отдельных деталей, а из двух одинаковых технологических подсбо-
рок. При этом каждый из двух технологических сварных узлов будет вклю-
чать в себя одну боковину правую и одну боковину левую, свариваемые
швом № 2. Два собранных и сваренных технологических узла должны по-
ступить на сборку и сварку одного диффузора, где будут выполнены два
сварных шва № 3.
5.3. Формирование последовательности сборки и сварки конструкции 243
б
Рис. 5.13. Примеры окон ввода структур:
а — ввод параметров для сборочной единицы «переходник»; б — ввод пара-
метров для детали «обечайка»
Для выполнения операций преобразования исходной структуры (рис. 5.9)
в структуру сборки (рис. 5.12) в автоматизированной системе разработки тех-
нологии имеется двухоконная экранная форма (рис. 5.13). Каждой позиции де-
рева структуры в правом окне соответствуют ее характеристики в левом окне,
причем разные для сборочных единиц, деталей и сварных швов. Для сборочно-
го узла это номер спецификации, если он имеется, масса (в кг), количество та-
ких элементов в сборке более высокого уровня и общее количество таких узлов
во всей конструкции (рис. 5.13, а). Для отдельной детали помимо такого же на-
бора данных дополнительно указана марка материала (рис. 5.13, б).
При необходимости выделения в выбранной сборке новой дополни-
тельной сборочной единицы на экране (в дополнительном окне) следует
ввести наименование вновь создаваемого технологического узла и предпо-
лагаемое количество таких элементов (рис. 5.14). После ввода этой инфор-
мации в схеме структуры появляется новая строка с данными созданного
технологического узла и обновляются связи между всеми элементами. Для
перемещения в эту новую сборку нужного количества деталей их наимено-
244
5. Автоматизированное проектирование технологии
Рис. 5.14. Пример окна ввода новой сборочной единицы
Рис. 5.15. Пример окна со списком выбранных элементов конструкции
вания помечаются на схеме с помощью мыши. Выбранные детали отобра-
жаются в окне (рис. 5.15). Здесь для удобства работы показано общее коли-
чество деталей, возможное для перемещения в конкретную выбранную
сборку с учетом количества таких сборок, и имеются поля для указания
нужного количества перемещаемых деталей каждого наименования. Недо-
пустимые перемещения будут заблокированы.
После перемещения деталей измененная структура сразу видна на эк-
ране, при этом оставшиеся детали сохраняются на своих местах и все коли-
чественные и весовые характеристики всех элементов уже пересчитаны.
Точно так же перемещаются в структуре любые сборочные единицы и свар-
ные швы, причем технические ошибки исключены. Можно видеть, что из-
5.3. Формирование последовательности сборки и сварки конструкции 245
ложенная процедура изменения
структуры сборки конструкции на-
поминает работу программы «про-
водник» в Windows, с дополни-
тельным анализом количествен-
ных показателей в многоуровне-
вой системе. Следует заметить,
что происшедшие изменения при
редактировании структуры сопро-
вождаются существенным обнов-
лением связей в оперативной базе
данных и, как будет показано да-
лее, это касается не только сбо-
рочных единиц, деталей и сварных
швов, но и блоков технологиче-
ских процессов, «привязанных» к
своим сборкам.
Представленный процесс
объединения и переноса деталей с
образованием новой сборочной
единицы или перемещение дета-
лей в другие уже существующие
сборки может выполняться и в об-
ратном направлении, когда от-
дельные сборочные узлы могут
быть ликвидированы полностью,
их детали или узлы войдут в со-
став других элементов. На рис. 5.16
и 5.17 показаны структуры сборки
двух достаточно сложных сварных
конструкций. Разработанная тех-
нологами структура сборки корпу-
са барабана шахтной мельницы
массой свыше 13 т выполнена при-
менительно к единичному произ-
водству изделия с использованием
преимущественно ручной и полу-
автоматической сварки (рис. 5.16).
На рис. 5.17 показана структура
сборки сварной конструкции ото-
пительной печи массой 51,4 кг,
Номера чертежей Вес в КГ- Наименование чертежей
8-21293 13527.0 15=й1 корпус_ОараСа,на
ТС-1 6628.0 12 =j]l техн.сб.6
ТС—2 840.0 7 гехн.сб.4
3-449820 105.0 j—16 сектор
4-611241 7.6 “— 4 упор
ТС-Э 4730.0 13 Ь=?>1 техм.сб.З
3-499819 4730.0 14^=а1 обечайка
3-499820 3713.0 F— 1 обечайка
3-499881 1005.0 — 1 обечайка
ТС-4 1058.0 10^=т|1 техн.об.1
3-449876 3132.0 lllLsssgi обечайка
3-499877 831.0 !|— 1 обечайка
3-499878 224.0 “— 1 обечайка
ТС-5 5030.0 6 ==п1 техя.сб.5 |
ТС-б 840.0 7 1 техн.об.4 1
3-449820 105.0 —-16 сектор |
4-611241 1.6 " 4 упор |
ТС—7 3132.0 8 г==т11 техн. об. 2 1
п ।
3-449821 3132.0 1 обечайка '
3-449822 2475.0 j q— 1 обечайка
3-449823 652.0 I u— 1 обечайка
ТС—8 1058.0 10==п1 техн.сб.1
3-499876 1058.0 ll“=i]2 обечайка
3-499877 831.0 I]— 1 обечайка
3-499878 224.0 п— 1 обечайка
2-281225 249.0 4 рамка_люка
3-494524 116.0 5 =511 фланец
4-982789 25.5 1 —• 2 пластина
4-982790 29.5 1 — 2 пластина
3-494525 62.0 1 — 2 окантовка
2-281226 346.0 2 р=р2 жрышжа_лжяса
3-494524-01 157.0 3 (=511 фланец
4-982789-01 36.5 ir— 2 пластина
4-982790-01 39.0 — 2 пластина
3-494526 69.0 — 2 окантовка
4-982791 20.5 — 2 ребро
4-956141 35.0 1 “—^4 захват
4-956142 13.0 I— 1 платик
4-956146 20.0 U— 1 бонка 1
4-654383 39.0 —- 4 захват
4-949050 2.2 — 8 ребро
4-951882 2.8 1—- £ гайка.
8-21293-13 2.6 — 4 платик
Рис. 5.16. Пример структуры сборки
сварной конструкции «корпус барабана»
246
5. Автоматизированное проектирование технологии
СТРУКТУРА СБОРКИ по цеху 00 Заказ N 000000 Изделие - Топка печи Спецификация N 1-32101 Заказчик Чертеж N 1-32101 Узел - Топка печи Вес узла N 51.4
Номера чертежей Вес в КГ. Наименование чертежей
1-32101 ТС-1 ТС-3 ТС-2 1-32004 1-320 8 1-320 9 1-32103 1-32102 1-320 1 1-320 2 1-320 4 1-320 5 1-32010 1-320 6 1-32011 1-32012 51.4 44.4 41.8 8.0 1.0 0.5 7.0 18.3 14.9 2.6 0.9 8.7 3.4 15.5 2.6 0.6 6.4 7=п 1 Топка печи 6 1 1 Топка без днища 5 1 Топка без рассекат. 4 —1 Передняя стенка в сб 2 г=л 1 Топочное окно 11— 2 Заготовка топочного — 1 Стенка передняя 3 г—и 1 Колпак 1 —1 Корпус колпака — 1 Торец задний — 6 Ребро — 1 Верх гнутый 1 Рассекатель верхний — 1 Корпус топки — 1 Рассекатель нижний — 1 Патрубок — 1 Дно топки
Рис. 5.17. Пример структуры сборки сварной конструкции «топка печи»
которая состоит из 16 заготовок и предназначена для изготовления крупны-
ми сериями с применением как полуавтоматической сварки в смесях газов,
так и автоматической сварки на роботизированных технологических ком-
плексах. В последнем случае увеличиваются требования производительно-
сти и точности сборки и для всех семи сборочных узлов необходимо разра-
ботать специализированные сборочно-сварочные приспособления-стенды.
Наличие структуры сборки сварной конструкции позволяет присту-
пить к формированию технологических процессов изготовления отдельных
5.4. Формирование маршрутной и операционной технологии
247
сборочных единиц, однако это возможно только для тех сборок, в которые
входят одни детали или детали и сборочные единицы, для которых техноло-
гический процесс уже сформирован.
5.4. Формирование маршрутной и операционной технологии
изготовления отдельной сборочной единицы
Спецификой сварочной технологии является большой объем и разно-
образие данных но каждому сварному шву и часто большое количество
сварных швов в сварной конструкции или в узле.
Естественно, как это уже отмечалось ранее, для работы автомати-
зированной системы разработки сварочной технологии необходим пол-
ный объем всех данных о швах как по каждому отличающемуся шву
(кроме его длины), так и по количеству одинаковых швов. Однако если
по деталям и сборочным единицам исходные данные имеются в конст-
рукторской спецификации, то данные о сварных швах собирать техниче-
ски сложнее.
Часть этих данных имеется на чертежах. Здесь уместно обратить вни-
мание на тот факт, что все основные принципиальные решения по сварным
швам принимает не технолог, а конструктор — проектировщик изделия.
Именно он выполняет расчеты на прочность и единолично несет полную
ответственность за сварную конструкцию. Конструктор определяет метод
сварки, тип соединения, сечение шва, разделку кромок, необходимость за-
чистки и другие параметры, как правило даже способ сварки — ручная, ав-
томатическая.
Все эти принятые конструктором решения поступают к технологам и
контролерам из данных на обозначениях сварных швов на чертежах. При-
меры обозначений сварных швов по ГОСТ 2.312—90 показаны в табл. 5.1.
Структура данных в обозначениях сварных швов содержит:
• обозначение метода и способа сварки (например, автоматическая ду-
говая сварка в углекислом газе);
• размеры катетов угловых швов;
• длины участков прерывистых швов;
• дополнительную информацию для технологов, отображаемую с по-
мощью условных обозначений, показанных в табл. 5.2.
Данные стандарты на типы и конструктивные элементы сварных соеди-
нений устанавливают геометрию разделки свариваемых кромок, размеры и до-
пустимые отклонения на сборку стыка (эти параметры будут проверяться
контролером перед выполнением сварки стыка), а также контролируемые
248
5. Автоматизированное проектирование технологии
Таблица 5.1. Примеры условных обозначений сварных швов
Наименование шва Пример обозначения
Шов стыкового соединения с кри- волинейным скосом одной кромки, двусторонний, выполненный дуговой ручной сваркой, на монтаже изделия. Усилие снято с обеих сторон ГОСТ 5264-80-С9 (~) //
Шов таврового соединения без ско- са кромок, двусторонний, прерыви- стый, с шахматным расположением участков, выполняемый дуговой руч- ной сваркой в защитных газах плавя- щимся металлическим электродом по замкнутой линии. Катет шва 6 мм. Длина привариваемого участка 50 мм, шаг 100 мм ГОСТ 14771-76~T5-yn-A6-500zi00 /ГД
Г
Шов соединения внахлестку без скоса кромок, односторонний, выпол- няемый дуговой полуавтоматической сваркой в защитных газах плавящимся электродом. Шов по замкнутой линии. Катет шва 5 мм ГОСТ 14771-76-Н1-УП-1 5 /
Упрошенное изображение одина- ковых швов при условии полного обо- значения одного из них N 1
То же. если все швы на чертеже одинаковые
размеры геометрии готового шва. Пример данных стандарта на сварку в за-
щитных газах для стыкового шва типа Cl 1 приведен в табл. 5.3. Из нее сле-
дует, что для конкретной толщины свариваемого металла, которая указыва-
ется в сборочном или деталировочном чертеже, имеются данные, необходи-
мые для формирования технологии сборочно-сварочных операций.
Весь процесс формирования и обработки данных по каждому сварно-
му шву можно представить в виде структурной схемы (рис. 5.18). Первые
два этапа — это формирование данных, определяемых конструктором, по-
следующие этапы связаны с работой и решениями технологов.
5.4. Формирование маршрутной и операционной технологии
249
Таблица 5.2. Условные обозначения сварных соединений
Вспомогательный знак Значение вспомогатель- ного знака Расположение вспомога- тельного знака
Усиление шва снять Г'-')
Наплывы и неровно- сти шва обработать с плавным переходом к основному металлу
1 Монтажный шов
/ Шов прерывистый или точечный с цепным расположением участ- ков
Z То же, с шахматным расположением участ- ков
Q Шов по замкнутой ли- нии г
1 Шов по незамкнутой линии
Пример конкретного набора данных по одному сварному шву приве-
ден в табл. 5.4, из которой следует, что по каждому сварному шву необхо-
димо в процессе разработки технологии из разных источников собрать
большой объем данных. Необходимо отметить, что представленных в этой
таблице данных достаточно для формирования технологии сварки, но не
достаточно для разработки технологии сборки под сварку, поскольку для
этого надо знать массы и габариты сварных узлов.
250
5. Автоматизированное проектирование технологии
Таблица 5.3. Вид соединения и шва СИ
So-
—
1 е
И = 1 w
, 2±1
5 = Si h е, не более g 5 = 51 h е, не более g
12...14 5...6 18 0 5+0,5 U’U-0,5 40...42 19...20 38 0.5^
16...18 7...8 20 0 5+°’5 44...46 21...22 40 0,5+^
20...22 9...10 22 0 5*°’5 U-0,5 48...50 23...24 44 0 5*0,5 V’ -0,5
24...26 11...12 26 0,5^ 52...54 25...26 46 0 5+0’5 -0,5
28...30 13...14 28 0 5+0,5 ’ -0,5 56...58 27...28 48 О,5+0’5 “-0,5
32...34 15...16 32 0,5*^ 60 29 50 0 5+0,5
38...38 17...18 34 0 5+0’5 V’U-0,5
Полный объем данных по сварным швам для сварного узла или свар-
ной конструкции можно условно представить как некоторый массив запи-
сей, в котором каждая строка содержит информацию по одному шву и коли-
чество записей соответствует количеству сварных швов. Подготовка данных
и заполнение полей такой базы — основная и наиболее трудоемкая часть
любой САПР.
Снижению трудоемкости и повышению комфортности условий рабо-
ты технологов способствует идущий активный процесс перевода всех нор-
мативных текстовых документов в организованные электронные базы дан-
ных и знаний, обеспечивающие возможность быстрого поиска текстовой и
графической информации, ее копирование в объектно-ориентированные ба-
зы данных и дальнейшее копирование в технологическую документацию.
Так, Госстандарт Российской Федерации поставляет стандарты на методы
сварки и типы сварных швов общим объемом в многие сотни страниц в
электронном виде на компакт диске или по электронной почте, что позволя-
ет обеспечить более высокий уровень САПР технологии.
Применительно к конкретной сварной конструкции формирование ис-
ходных данных по сварным швам начинается с составления полного списка
5.4. Формирование маршрутной и операционной технологии
251
Рис. 5.18. Этапы формирования технологической документации
всех сварных швов. Особо следует обратить внимание на то, что сварные
швы на чертежах не нумеруются (могут нумероваться только типы швов).
Поэтому, прежде чем приступить к сбору данных о сварных швах, необхо-
димо в каждой сборочной единице выполнить следующие операции:
252
5. Автоматизированное проектирование технологии
Таблица 5.4. Сведения о сварном шве для операции сборки и сварки
Конструктор mtcatudsh Стандарт на метод сварки гост 14771
Тип шва У5
Способ сварки УН
Привязка Номер позиции детали (привязка) 1-2
Номер сборочного чертежа
Геометрия . Катет или толщина металла 45
Длина шва 858
Материал, Марка электрода Св-О8Г2С
Марка материала
Данные из стандар- та на метод снарки Геометрия разделки кромок
Размеры для сборки стыка
Технолог Вводимые исходные параметры Пространственное по- ложенйе сварки Пространственное положение В
Удобство выполнения работ Удобное
Необходимость кантовки Her
Требования по технике выполнения шва Способ зачистки ОШЗ Ручная
Необходимость подогрева Без
Температура окружающего воздуха Нормальная
Контроль
Испытания
Расчетная часть Оборудование Состав защитного газа
Сварочное
Сборочное
Контователь
Электрод Диаметр элекгрода(проволоки) 1.6
Режимы 1 св
V св
V под.эл.
Нд 32 В
Длина вылета электрода
Нормирование Расход проволоки 2 кг
Расход флюса
Расход защитного газа
Норма времени Гн
1) определить полный перечень типов сварных швов на узле;
2) определить по каждому типу шва количество таких швов и длины
каждого из них;
3) привязать всю информацию о сварных швах к структуре сборочной
единицы, имея при этом в виду, что сварка шва, находящегося в структуре
данной сборочной единицы может быть выполнена не обязательно в техно-
5.4. Формирование маршрутной и операционной технологии
253
Рис. 5.19. Пример сварной конструкции «фланец барабана шаровой мельницы»
логическом процессе изготовления этой сборки, а полностью или частично в
сборочных единицах более высокого уровня, вплоть до сварки на уже пол-
ностью собранном изделии.
Рассмотрим организацию ввода данных по сварным швам и их при-
вязку к структуре конструкторской документации на примере фланца ба-
рабана шаровой мельницы (рис. 5.19), который состоит из двух пластин
4-982789 и двух пластин 4-982790. Все детали соединены четырьмя стыко-
выми швами по ГОСТ 14771—90, каждый длиной по 100 мм. Все параметры
для швов одинаковые. На рис. 5.20 показана структура конструкторской до-
кументации фланца с указанием параметров деталей и сборочной единицы.
Для ввода швов и их привязки нужно указать сборочную единицу. На
рис. 5.21 показано, что курсор в структуре установлен на сборочную едини-
цу фланец, а в накладное окно вводятся количество одинаковых швов для
этой сборки и параметры шва. После ввода швы со своими параметрами по-
являются на структуре конструкторской документации (рис. 5.22).
При большом количестве швов для ускорения и удобства ввода, а
также для исключения ошибок, первоначально вводятся только обозначения
и количество швов (рис. 5.23). Остальные параметры вводятся при форми-
ровании списка швов (рис. 5.24), где видно количество одинаковых швов, а
также общее количество сварных швов в сборочной единице. Это позволяет
следить за всеми швами.
254
5. Автоматизированное проектирование технологии
Рис. 5.20. Окно формирования и редактирования структуры конструк-
торской документации фланца
Пр<кл-рапсгванноепо>ю>«еи1и
^кантовки
гмао
Рис. 5.21. Окно вставки шва № 1 для фланца с одновременным вво-
дом параметров по шву
5.4. Формирование маршрутной и операционной технологии
255
Рис. 5.22. Вид окна с обновленной структурой конструкторской
документации фланца со швом
Рис. 5.23. Окно вставки шва № 1 для фланца без ввода параметров
Завершение формирования исходных данных по сварным швам для
всей конструкции позволяет с использованием стандартных функций сорти-
ровки по всем параметрам оценить степень их разнообразия, сгруппировать
в технологически подобные группы, для которых разработать сварочную
технологию. При этом вполне может оказаться, что даже при большом ко-
личестве сварных швов и большом объеме сварочных работ режимы сварки,
оборудование и инструмент будут достаточно однотипными и при форми-
ровании технологических карт данные сварочной технологии будут легко
копироваться в разные сборочные единицы.
При разработке вариантов технологии выполнения сборочно-сва-
рочных операций для упрощения отображения информации удобно исполь-
зовать кодификатор технологических операций. Пример отраслевого коди-
фикатора операций сборочно-сварочного производства приведен в табл. 5.5.
256
5. Автоматизированное проектирование технологии
Рис. 5.24. Окно вывода списка всех швов в изделии «фланец»
С использованием кодов операций технологический процесс сборки и сварки
одного из узлов применительно к единичному производству громоздких конст-
рукций может быть представлен цепочкой операций, показанной на рис. 5.25.
которая представляет собой некоторый технологический маршрут. Формиро-
вание такой цепочки -— начало и основа построения технологии. Часто такие
цепочки могут быть достаточно длинными и сложными, однако их можно су-
щественно укоротить и упростить введением типовых комплексных операций.
Таблица 5.5. Коды операций по ОСТ 24.670.06-85
Шифр операции Наименование операции или оборудования
36 Резка газовая ручная
39 Зачистка шлака
41 Заточка переносным точилом
42 Рубка зубилом
50 Дуговая сварка покрытым электродом
54 Правка после сварки
60 Сборка
62 Маркирование
93 Сварка полуавтоматическая в среде СО2
132 Контрольная
5.4. Формирование маршрутной и операционной технологии
257
< 60>-< 36>—< 93>-< 50>—< 39>-<132>-< 50>-< 93>-< 60>-< 93>-
(->-< 42>—< 60>-< 42>—< 36>-< 39>-< 41>-< 54>-< 62>-<132>-
Рис. 5.25. Пример последовательности шифров операций для
сборки фланца
Рис. 5.26. Пример последовательности технологических операций
с использованием комплексных операций и с отображением их состава
Из анализа технологических процессов следует, что весьма часто одни
операции сопутствуют другим. Так, сборка кромок, прихватка, зачистка под
сварку, контроль перед сваркой, сварка стыка, зачистка от брызг и контроль
качества и размеров шва могут быть определены как типовая комплексная
операция, которая может быть отображена в цепочке операций специаль-
ным обозначением (рис. 5.26).
К кодам операций в технологической цепочке удобно добавить услов-
ное обозначение групп операций (табл. 5.6). Это повысит информативность,
удобство работы и анализа технологии. В этом случае цепочка операций
(см. рис. 5.26) может выглядеть так, как показано на рис. 5.27.
Таблица 5.6. Условные обозначения групп операций
Наименование групп операций Условные обозначения
Сборочная 60^-^
Контрольная 132^^
Сварочная 93
Транспортная 17
Вспомогательная 54
Комплексная 1к
Ч - 6705
258
5. Автоматизированное проектирование технологии
Рис. 5.27. Пример технологии с использованием условных обозначе-
ний групп операций
Появление в системе проектирования технологии кодов операций по-
зволяет организовать использование многочисленных баз данных и спра-
вочников (оборудования, инструмента, вспомогательных материалов, со-
держания операций и др.) при разработке операционной технологии. В этом
случае в процессе работы технолога обеспечивается выдача на экран мони-
тора только той информации, которая может понадобиться при формирова-
нии конкретной технологической операции.
Как можно видеть, основные проблемы автоматизированного форми-
рования технологии сборочно-сварочных операций связаны со сбором, вво-
дом и подготовкой большого объема исходных данных. Все эти данные ав-
томатически привязываются к деталям и сборочным единицам сварной кон-
струкции и обрабатываются при решении задач, связанных с выбором
оборудования, инструмента, определения режимов и расчета материалов,
времени и энергии. По результатам технологических решений легко могут
быть сформированы и распечатаны привычные технологические документы:
технологические карты, ведомость оснастки и др.
Однако быстрое развитие информационных технологий и особенно
возможностей отображения информации привело к тому, что введенные в
действие более 20 лет назад стандарты на формы технологических докумен-
тов подготовки сварочного производства сегодня не соответствуют ни требо-
ваниям производства, ни возможностям программно-аппаратных комплексов.
И дело здесь не только в повышении скорости и разрешающей способности
печатающих устройств. До настоящего времени практически все действующие
стандарты были построены на возможностях только алфавитно-цифровой пе-
чати, а это приводило к тому, что даже для простых технологических
Дубл.
бзам.
Подл.
1
Разраб. Иванов А.В. 37.105.11.50
— 5301СС-5601150СБ
Каркас задка 0
Н. контр
А Цех I Уч. I РМ Опер. Код, наименование операции Обозначение документа
Б Код, наименование оборудования СМ | Проф. | Р | УТ КР | КОИД ЕН ОП К шт. Т пз Тш
К/М Наименование детали, об. единицы или материала Обозначение, код ОПП ЕВ ЕН КИ Н. ро
А 01 Т005 0401 Транспортирование Инструкция ТБ Ns 37.105.55004
Б 02 Электропогрузчик М=2,5 т 11453
О 03 Транспортировать детали и сборочные единицы на участок сварки
Т 04 Т: Тара
05
А 06 0010 9011 Точечная сварка Инструкция ТБ № 37.105.55130
Б 07 34 4142 2 Машина точечная МТ- 41 4 1-1 1 1 1 1
К 08 1. Стойка задка правая/левая, сталь 08кп, 1,5 мм 5301СС-5601216/217 СБ ШТ 1 1/1
09 2. Усилитель стойки задка с пластинами 5301СС-5601208/209 СБ шт 1 1/1
10
О 11 Собрать по фиксаторам стойку задка дет.поз.1 с усилителем стойки с пластинами как показано на э
12 и сварить точечной сваркой, точками шб мм
13
Т 14 ВИ: Фиксатор 8Б Электрод С-757 Корпус С-75
15 Т:
С4 16 Fcb=3000-3500 Н; 1св= 30-35 пер; 1св=10-11 кА; tCB=10-12 пер: t=5-7 пер
Контактная точечная сварка.
мк
Рис. 5.28. Пример оформления технологической карты
260
5. Автоматизированное проектирование технологии
процессов технологические карты оказывались многостраничными с
обилием текстовых описаний, которые тем не менее часто трудно тракто-
вать однозначно. Сложная форма организации табличного материала с
многоуровневыми заголовками затрудняет понимание приведенной ин-
формации (рис. 5.28).
Известно, что мозг человека в сотни раз эффективнее обрабатывает
графическую информацию по сравнению с информацией символьно-
текстовой. Именно этим отчасти объясняется все более широкое и повсеме-
стное использование графических отображений объектов, в том числе и во
всех видах описаний. Возможности современных массовых и широко-
доступных графических систем, их высокая производительность способст-
вуют ускорению этого процесса.
С учетом сложившейся ситуации, когда выполнение требований су-
ществующих стандартов на документы технологической подготовки сва-
рочного производства является обязательным, не вызывает труда на пере-
ходный период получать из объектно-ориентированной базы данных как
традиционные формы технологических документов, так и дополнительно к
ним другие более компактные и информативные формы документов.
Это, например, могут быть рассмотренные выше (см. рис. 5.16 и 5.17)
структуры сборки, дополненные данными по режимам, оборудованию и
нормированию. Автоматизированное формирование трехмерных графиче-
ских образов сварных узлов, сборочно-сварочной оснастки, сварочного ин-
струмента и оборудования для использования их в картах эскизов рассмот-
рено в гл. 6 и 7.
6. СИСТЕМА АВТОМАТИЗИРОВАННОГО
ПРОЕКТИРОВАНИЯ СБОРОЧНО-СВАРОЧНЫХ
ПРИСПОСОБЛЕНИЙ
6.1. Принципы проектирования
Разработка, проектирование и изготовление сварочных приспособ-
лений, как правило, являются наиболее трудоемкой частью процесса под-
готовки сварочного производства. Принципы и методику автоматизиро-
ванного проектирования сборочно-сварочных приспособлений будем
рассматривать в основном на примерах задач автомобильной промыш-
ленности, где эта проблема особенно актуальна в связи с большими объ-
емами используемой оснастки и необходимостью частой модернизации
выпускаемой продукции.
Проблема собираемости кузова автомобиля решается путем стендово-
го контроля размеров штампованных тонколистовых деталей и сварных уз-
лов на всех (начиная со штамповки) этапах обработки, приводящих к их де-
формированию. Величина деформации не является стабильной, поскольку
зависит от многих факторов (свойств партии металла, номера работающего
штампа, износа оснастки и т. п.), поэтому проверка проводится периодичес-
ки. Сборка под сварку кузовных узлов осуществляется с помощью приспо-
соблений, предназначенных для фиксации штампованных деталей и обеспе-
чения при этом заданных размеров. Пробивка отверстий, завальцовка, мест-
ная выштамповка и другая обработка также зачастую выполняются вне
штампов на сборочных стендах. Суммарные объемы изготовления различ-
ных стендов кузовного сварочного производства весьма значительны. При
этом их разработка выполняется для одних и тех же изделий с использова-
нием одной и той же элементной базы. Поэтому целесообразно проектиро-
вать эти виды оснастки с помощью единой САПР.
Разновидности сборочно-сварочных приспособлений (ССП) можно
классифицировать следующим образом: по назначению, исполнению, типу
(рис. 6.1).
262
6. Система автоматизированного проектирования приспособлений
СБОРОЧНЫЕ ФИКСИРУЮЩИЕ СБОРОЧНО-
Каждая деталь, входящая в узел, базируется относительно ССП или ЗАЖИМНЫЕ, КОНТРОЛЬНЫЕ, ФИКСИРУЮЩИЕ
базовой детали, прихватывается ПРОБИВНЫЕ и другие ССП. Выполняется сборка и
сваркой (или другим способом), а затем собранный узел вынимается Базируется весь узел целиком, а ие каждая деталь обработка
а
СПЕЦИАЛЬНЫЕ ПЕРЕНАЛАЖИВАЕМЫЕ УСП
Для массового производства. Для производства двух или более наименова- Для мелкосерийного и еди-
переналадке ие подлежат, но ний однотипных изделий (со сменными упо- яичного производства, где
поддаются регулировке рами, включаемыми автоматически или вруч- ную в режиме наладки) необходима универсальность
б
в
Рис. 6.1. Типы приспособлений:
а — по назначению; б — по исполнению (в зависимости от объема производ-
ства); в — по типу; ССП — сборочно-сварочные приспособления; УСП —
универсальные сборочные приспособления; РТК — роботизированный техно-
логический комплекс
Последовательность традиционного проектирования сборочно-
сварочных приспособлений обычно сводится к следующим этапам:
• определение рационального порядка установки деталей и наложения
сварных швов;
• выбор базовых элементов и поверхностей;
• выбор типа опорных и зажимных элементов;
6.1. Принципы проектирования
263
• разработка компоновочной схемы (в упрощенном виде на стандарт-
ных проекциях);
• проектирование приспособления по компоновочным схемам.
Сравнение вариантов традиционными способами не приводило к вы-
бору наилучшего, и к окончательному оформлению принимался либо пер-
вый разработанный вариант, либо аналогичный, имеющийся на данном
предприятии. Лишь с использованием информационных технологий это по-
ложение меняется.
В СССР работы по автоматизированному конструированию сборочно-
сварочной оснастки впервые были начаты в Институте технической кибер-
нетики АН Белоруссии в 1981 г. Результатом совместной работы ИТК АНБ
и Горьковского автозавода стала система ИНСВАР автоматизированного
конструирования кузовных сборочно-сварочных приспособлений. Однако
одной системы ИНСВАР-ССП, построенной по схеме, повторяющей этапы
традиционного конструирования, было недостаточно, требовались графиче-
ское моделирование и оценка приемлемости положения сварной конструк-
ции в приспособлении в процессе сварки.
Фирма Tecnomatix Technologies (США) в составе программного ком-
плекса ROBCAD выпустила пакет Spotweld для контактной точечной свар-
ки. который снижает время подготовки работы сварочных технологических
комплексов с нескольких дней до нескольких часов. Пакет располагает мо-
дулем FIXTURES, который поддерживает обширные библиотеки элементов
оснастки и позволяет:
• собирать сварочные приспособления из стандартных элементов, до-
оавляя при необходимости компоненты, спроектированные заново (напри-
мер, ложементы);
• моделировать работу оснастки (установку детали, последователь-
ность фиксаций);
• готовить комплект конструкторской документации и программы для
нонтроллеров, управляющих оснасткой;
• автоматически формировать: сборочные чертежи стендов и устано-
--: к для контактной точечной сварки; рабочие чертежи деталей; ведомости
зтериалов; видеозапись процессов работы приспособлений с определением
.тдлкновений и оптимизацией цикла;
• формировать промежуточные файлы для системы управления робо-
-: = в формате PLC; промежуточные файлы для обработки деталей приспо-
.: Глений на станках с ЧПУ.
Интерактивное параметрическое моделирование деталей и связей ме-
ними в ROBCAD делает эту систему реальным инструментом концеп-
- данного проектирования, однако инсталляция комплекса, реализованного
264 6. Система автоматизированного проектирования приспособлений
на современных графических станциях, стоит дорого, и поэтому в сложных
экономических условиях стран СНГ комплекс практически не используется.
Поиск более дешевых подходов без ущерба их технологическим воз-
можностям привел к созданию фирмой «Буран» (Россия) аналогичной сис-
темы в составе комплекса программных средств РОБОМАКС, использую-
щего визуальное моделирование взаимодействия между объемными моде-
лями сварного узла, сварочного инструмента и сборочно-сварочного при-
способления. В качестве графической среды в настоящее время использует-
ся Mechanical Desktop (AMD) фирмы AutoDesk.
К разработке системы были привлечены квалифицированные специали-
сты, которым пришлось работать в сложных условиях. Разработка сразу же ба-
зировалась на использовании только массовых моделей персональных компью-
теров и широкодоступных недорогих универсальных графических систем. В то
время как вся САПР сварочных приспособлений изначально строилась на
принципах трехмерного моделирования, имевшиеся в 1991 г. версии базовой
графической среды AutoCad, реализованные тогда на платформе ПК 386, были
ориентированы преимущественно на плоские проекционные чертежи. В част-
ности, в версиях AutoCad еще отсутствовали такие необходимые функции, как
автоматическое построение любых плоских сечений трехмерных объектов, ав-
томатическая сборка-разборка трехмерных сборочных единиц и др. Поэтому
создаваемый программный комплекс имел многие собственные встроенные
функции, которые впоследствии появились в очередных версиях базового гра-
фического пакета. В связи с постоянным развитием систем машинной графики
естественно постоянно обновляются и версии рассматриваемой здесь САПР
приспособлений. В настоящее время установка программного комплекса тре-
бует приобретения и установки одной из последних версий известного пакета
Mechanical Desktop.
Полученное при разработке сварной конструкции описание 3 D-образа
сварного узла используется технологами и конструкторами по оснастке для
решения необходимых задач увязки конструкции узла и технологии его из-
готовления.
Автоматизированная система предназначена для формирования моде-
лей сборочно-сварочных приспособлений и применима практически для
всех их разновидностей. Она включает в себя базу данных 3£)-образов стан-
дартизованных унифицированных элементов и программные модули в со-
ставе подсистемы подготовки прототипа оснастки и подсистемы формиро-
вания 3£>-моделей узлов фиксации и самих приспособлений.
На автомобильных заводах эта система эффективно используется уже
в течение ряда лет. Последняя версия программного продукта обладает до-
полнительными возможностями. Кроме проектирования сборочно-сварочых
приспособлений САПР осуществляет проектирование контрольных и про-
6.1. Принципы проектирования
265
бивных стендов. Это определило дополнительные требования к системе как
по разнообразию типов используемых элементов, так и по возможностям их
пространственного расположения. САПР дополнена технологической под-
системой компьютерного ввода карты контроля и схем базирования узлов,
что позволило использовать ее в составе комплекса РОБОМАКС в техноло-
гических подразделениях заводов и для оперативной передачи результатов
их работы в конструкторские подразделения.
Применение данной САПР как составной части компьютерной техно-
логии подготовки производства позволяет ликвидировать «узкое место»
разработки и изготовления сварочной оснастки.
При разработке оснастки САПР обеспечивает:
• снижение трудоемкости, сроков разработки и оформления проекта;
• повышение качества документации (за счет сокращения ошибок, ис-
пользования унифицированных конструктивных решений, единообразия
оформления);
• возможность оперативного изменения схемы базирования и положе-
ния узла при сварке;
• оптимизацию решений за счет углубленной проработки вариантов;
• повышение качества результатов конструирования с автоматизиро-
ванным нормированием операций и учетом расхода основных и вспомога-
тельных материалов;
• повышение уровня нормализации и унификации конструкций;
• передачу результатов автоматизированного конструирования при-
способлений в подсистему' автономного программирования сварочных РТК;
• повышение культуры и престижности конструкторской работы.
При изготовлении и наладке САПР обеспечивает:
• сокращение сроков подготовки производства за счет использования
готовых конструктивных элементов приспособлений, хранящихся на складе,
или унифицированных элементов, изготовляемых на станках с ЧПУ по ав-
томатически подготовленным программам;
• сокращение времени наладки сборочных приспособлений за счет
использования качественных сборочных чертежей, единообразия конструк-
ций, снижения номенклатуры оригинальных деталей и повышения уровня
унификации, нормализации и культуры производства.
Объектами проектирования в САПР могут быть:
• сборочно-сварочные приспособления для ручной и роботизирован-
ной сварки;
• пробивные и комбинированные стенды;
• контрольные кузовные приспособления и стенды.
266 6. Система автоматизированного проектирования приспособлений
Проектирование приспособлений заключается в компоновке унифи-
цированных элементов относительно образа узла и в разработке оригиналь-
ных базовых, переходных и контактных элементов.
САПР имеет следующие возможности:
• в состав одинарного (унитарного) узла фиксации кроме одного под-
вижного прижима могут входить другие неподвижные элементы из базы
данных (кронштейны, фиксаторы, стойки и другие элементы);
• в состав комбинированного узла фиксации могут входить два
одинарных, причем не обязательно в одной плоскости (например, если
фиксатор вынесен в сторону от плоскости прижима, но закреплен на той
же стойке);
• многоместное сборочно-сварочное приспособление проектиру-
ется для некрупных или компактных сварных узлов, например парных
(правый-левый), где координаты расстановки сварных узлов предвари-
тельно не известны, — это выясняется в процессе проектирования.
Сборочно-сварочное приспособление с несколькими кондукторными
плитами, расположенными в разных плоскостях или под разными углами,
необходимы для главных кондукторов кузова или сборки узлов, у которых
панели находятся в разных плоскостях и в разных пространственных поло-
жениях.
Имеется возможность оснащения настольных сборочно-сварочных
приспособлений стойками, подставками под плиту и кантователями — в
этом заключается проектирование напольных стендов.
Предусмотрена возможность формирования кондукторной плиты
произвольной формы с крепежными отверстиями, отверстиями выталкива-
теля изделия, а также окнами высвобождения изделия.
Оригинальные элементы непосредственного контакта с изделием
(блочки-сухари), рычаги, стойки и кондукторная плита проектируются до
стадии рабочих чертежей с формированием соответствующей информации,
при дальнейшей разработке для станков с ЧПУ программ механообработки
поверхностей. Одновременно предусмотрен учет толщины листов фикси-
руемого соединения узла в соответствующем направлении от исходной ли-
цевой поверхности ЗВ-образа при размещении контактных поверхностей
приспособления.
При формировании одинарных и комбинированных узлов фиксации
производится проверка возможности удаления сварного узла, достаточности
хода механизма и отсутствия столкновений элементов между собой и с уз-
лом при их взаимных перемещениях.
При разработке приспособлений и стендов используется интерактив-
ное проектирование, значительно повышающее эффективность и универ-
сальность работы конструктора. Оно заключается в автоматическом форми-
6.2. Состав и структура библиотеки элементов
267
ровании варианта решения, основанного на настройке системы пользовате-
лем. При этом из всего возможного множества решений выбирается наибо-
лее соответствующее традициям предприятия и желаниям пользователя.
При необходимости разрабатываемый вариант редактируется путем замены
или пространственного перемещения базовых элементов приспособления с
сохранением их объектных связей.
6.2. Состав и структура библиотеки элементов
В базе данных имеются основные каталоги элементов, конструк-
тивных узлов и механизмов сборочно-сварочных приспособлений (табл.
6.1). В зависимости от требований производства конкретная структура и
состав базы формируются пользователем системы. Каталоги базы дан-
ных открыты не только для их пополнения, но и для изменения их со-
става самим пользователем. Однако на первом этапе работы рекоменду-
ется принять структуру базы данных, предложенную разработчиком.
Состав элементов базы данных на примере заводов ГАЗ и ВАЗ показан
на рис. 6.2.
Таблица 6.1. Основные каталоги элементов, конструктивных узлов
и механизмов сборочно-сварочных приспособлений
1 Элементы стандартизованные: блочки, пластины стоек, фланцы крон- штейнов и крепеж (болты, винты, гайки, шпонки и т. п.)
2 Элементы изменяемые: фиксаторы, упоры, стойки, кронштейны, шпиндели и т. п.
3 Пневмоцилиндры
4 Пневмозажимы и силовые головки
5 Узлы фиксации пневматические и узлы пробивки в сборе со стой- ками
6 Прижимы ручные Эйлера в сборе со стойками
7 Механизмы прочие (фиксатор выдвижной пневматический и руч- ной; зажимы ручные: струбцинный, байонетный, винтовой, накид- ной и т. п.)
8 Арматура (рама усилительная, стойка поворотная, кантователь и т. п.)
268 6. Система автоматизированного проектирования приспособлений
Рис. 6.2. Состав элементов сборочно-сварочного приспособления
Элементы, используемые в процессе формирования блоков (узлы
фиксации, узлы пробивки, узлы контроля и т. п.), можно разделить на стан-
дартизованные (например, блочок, платик, прижим, силовая головка, упор,
фиксатор), образы которых сформированы ранее, помещены в базу данных
и не подлежат изменению в процессе работы над проектом, и переходные,
формируемые в процессе разработки конкретного приспособления (напри-
мер, рычаг, пластина и т. п.). Изготовление контактных элементов (сухарей)
из блочков унифицированных типоразмеров — промежуточный случай, ко-
гда дорабатывается элемент из базы данных.
Узлы фиксации и силовые головки устанавливаются на кондуктор-
ную плиту с помощью стоек и в зависимости от направления усилия могут
занимать относительно нее разное
Рис. 6.3. Схема действия контактных
элементов
пространственное положение. Каждый
узел фиксации может иметь несколько
контактных элементов, воздействую-
щих на кромки собираемых деталей в
разных направлениях (рис. 6.3):
со стороны кондукторной плиты —
опора 1;
в противоположном направлении —
прижим 2;
в торец кромки детали вдоль ее плос-
кости — упор 3.
6.2. Состав и структура библиотеки элементов
269
Рис. 6.4. Сухарь, выполненный обрезкой блочка
Блочок — это стандартизованный элемент, имеющий ряд типораз-
меров. Он изготовляется серийно из качественного материала (металла,
полиуретана и других материалов), обладает большой точностью (имеет
шлифованные грани) и хранится на складе. Размеры блочка унифициро-
ваны (т. е. число типоразмеров ограничено, с изменением размеров по
размерному ряду). Желательно, чтобы габаритные размеры блочка и меж-
осевые расстояния были целые числа. Блочок определяется габаритными
размерами А х В х S и параметрами коннектора (совокупностью размеров
крепежных поверхностей).
Коннектор — присоединительный элемент, его форма предлагается
симметричной или кососимметричной и определяется размерами межосевых
расстояний А х В и диаметром D крепежного отверстия. Ответная часть кон-
нектора всегда соответствует его основной части (равна или зеркальна). Тол-
щина S пластины под коннектор может быть меньше габаритной толщины пла-
стины. При этом исполнение может быть как «правое», так и «левое» (рис. 6.4).
Блочок выбирается и располагается следующим образом:
• по ширине — симметрично относительно линии контакта;
• по высоте — ось коннектора блочка совмещается с осью коннектора
сухаря и излишек высоты блочка срезается при обработке торца сухаря;
270 6. Система автоматизированного проектирования приспособлений
• положение оси коннектора от линии контакта У определяется сум-
мой половины ширины коннектора, свободной высотой X и малой фаски
(рис. 6.4).
В отличие от блочка сухарь является элементом оригинальным, изготов-
ляемым специально каждый раз. Часто может изготовляться из блочка путем
механообработки контактной поверхности, причем блочок из базы данных для
конкретного сухаря выбирается как ближайший подходящий по ширине и по
длине. Если такого нет, то сухарь изображается как нестандартный.
Платик — стандартизованный элемент базы данных, служит основа-
нием конструктивного элемента (стойки), несущего сухари и зажимы через
соединительный элемент — пластину. Нижняя плоскость платика контак-
тирует с кондукторной плитой, верхняя — с пластиной.
Стандарт на блочки и платики утверждают заводы. Желательно, что-
бы их габаритные размеры и межосевые расстояния были целые круглые
числа.
Платик и пластина стойки условно рассматриваются отдельно друг от
друга. Это необходимо для построения системы, хотя они вместе составля-
Исполнение II
След пластины (или
прямоугольной трубы)
стойки
Рис. 6.5. Платик опор-стоек
6.2. Состав и структура библиотеки элементов
271
Рис. 6.6. Схемы пневматического (а) и ручного (б) прижимов
ют сборочную единицу стойка (соединяют их чаще всего сваркой). Крепле-
ние к плите производится через коннектор, расположенный по всей плоско-
сти платика. В состав коннектора входят отверстия под винты и штифты,
количество которых может быть разным. Основные варианты — это 2 + 2 и
2 + 4 (рис. 6.5).
Толщина s платика под пластину может быть меньше габаритной
толщины S при ширине паза, равной толщине пластины (он является на-
правляющим при сборке под сварку пластины и платика).
Определение конкретных размеров платков, в том числе ширины к и
положения к! торца пластины-трубы под сварку, осуществляется при подго-
товке элемента в базе данных или при выборе элементов из базы данных.
Количество типоразмеров платиков может быть ограничено (например: ос-
новной, удлиненный под широкую стойку, расширенный под головку), что
позволяет упростить простановку крепежных отверстий на кондукторной
плите.
Крепежные фланцы прочих переходных элементов (кронштейнов и
переходников) формируются аналогичным образом.
Прижимы. Прижим пневматический (рис. 6.6, а) — стандартизован-
ный элемент базы данных, в данном случае он имеет два механических
коннектора — для крепления рычага и для крепления к стойке, а также
штуцеры для подводки воздуха. Коннекторы должны быть по возможности
унифицированными, но окончательно они определяются как атрибуты ти-
поразмеров. В отличие от пневмоприжимов ручные прижимы представле-
ны в сборе с рычагом и верхним сухарём (шпинделем) и имеют чаще всего
точечный контакт (рис. 6.6, б). Основные параметры — длина рычага L
272 6. Система автоматизированного проектирования приспособлении
Рис. 6.7. Схема силовой головки
Рис. 6.8. Фиксатор
и расстояние I (независимо от исполнения) — определяются расстоянием
прижима от кромки узла. Типоразмеры подразделяются по усилию фикса-
ции (нормальное и облегченное исполнение).
Силовая головка (рис. 6.7), так же как прижим, имеет два механиче-
ских коннектора: со стойкой и с штамповой группой. Задание коннекторов
головок аналогично заданию коннекторов пневмоприжимов.
Фиксатор имеет, как правило, небольшие размеры (рис. 6.8), относи-
тельно простую форму и способы крепления, введен в систему ввиду своей
функциональной значимости. Располагается по центру элемента (пластины,
сухаря) и привязывается к базовому отверстию штампованного узла.
Пластина стойки — нестандартный переходной элемент, формируе-
мый в процессе работы системы (рис. 6.9). Является частью стойки (куда
входит также платик) и в сборе с сухарем составляет опору. Геометрия пла-
стины формируется заданием коннекторов сухарей, платика, фиксатора и
фланцев прижима. Фланец прижима обычно располагается центрально от-
носительно пластины и имеет правое или левое исполнение.
Рис. 6.9. Пластина стойки
6.2. Состав и структура библиотеки элементов
273
Варианты исполнения
пластины могут быть различ-
ными в зависимости от коли-
чества поддерживаемых ею
элементов. Это мотут быть су-
харь, прижим, фиксатор, си-
ловая головка и их комбина-
ции (например, сухарь и два
прижима; прижим и два суха-
ря и т. п.). Контур пластины
формируется как огибающая
поддерживаемых элементов,
или она может быть составной (например, используется переходной крон-
штейн от стойки к пневмоцилиндру).
Если прижим имеет нестандартное крепление на кондукторной плите
(например, крепление пневмоцилиндра в осях на двух стойках, крепление на
стойке без верхнего платика с расположением пластины по центру и т. п.),
то он изображается без стойки с последующей ручной дорисовкой переход-
ных элементов.
Рычаг является нестандартным переходным элементом, формиру-
емым в процессе работы системы (рис. 6.10). Задание геометрии рычага оп-
ределяется взаиморасположением коннекторов, высотой Н осевой линии
рычага и шириной полосы А1 (она равна нижней стороне коннектора). На-
ложение рычага на коннекторы сухаря и прижима с той или иной стороны
производится автоматически в зависимости от исполнения прижима (пра-
вый или левый). Однако, если требуется, возможна ручная установка с про-
тивоположной стороны.
При проектировании выбор конструктивных элементов сборочно-
сварочного приспособления из базы данных предоставлен инженеру-
конструктору в соответствии с техническим заданием и схемой базиро-
вания в зависимости от вида, назначения и конфигурации фиксируемого
сечения собираемой детали.
Если проектная ситуация не накладывает серьезных ограничений на
габаритные размеры приспособления, предпочтительнее использование при-
жимов с горизонтальными платиками и креплением на стойках. Прижимы с
вертикальными платиками рационально размещать по наружному контуру
узла с креплением в торец кондукторной плиты.
Примеры типоразмеров ручных и пневматических прижимов и сило-
вых головок базы данных приведены в табл. 6.2.
274 6. Система автоматизированного проектирования приспособлений
Таблица 6.2. Примеры баз данных типоразмеров ручных и пневматических
прижимов и силовых головок
Номер чертежа и файла в базе данных Эскиз Изменяемые размеры Количество типоразмеров
Ручные прижимы ГАЗ
0850-4001 с горизонтальным платиком $ Е8 Длина рычага, мм: 60 100 140 180 4
0850-4005 с вертикальным платиком
0850-4017 с горизонтальным платиком облегчен- ный s> Длина рычага, мм: 35 55 75 3
0850-4020 с вертикальным платиком облегчен- ный (S
0850-4025 с горизонтальным платиком усилен- ный ЯЛ Длина рычага, мм: 60 120 2
6.2. Состав и структура библиотеки элементов
275
Продолжение табл. 6.2
Номер чертежа и файла в базе данных Эскиз Изменяемые размеры Количество типоразмеров
0850-4056 с вертикальным продольным плати- ком и креплением сухаря t 4 о с о о] Длина рычага, мм: 60 100 180 3
Узлы фиксации в сборе Г43
4001 s нормальный с гори- зонтальным плати- ком i Длина рычага Размеры подставы Длина шпинделя Любое
4017 s с горизонтальным платиком облегчен- ный о —
4025 s с горизонтальным платиком усилен- ный f 1
276 6. Система автоматизированного проектирования приспособлений
Продолжение табл. 6.2
Номер чертежа и файла в базе данных Эскиз Изменяемые размеры Количество типоразмеров
4056 s с вертикальным продольным платиком и креплением сухаря о 3 о о] То о Длина рычага Размеры подставы Длина шпинделя Любое
Ручные прижимы ВАЗ
02-7018-0003 -0004 -0005 -0006 -0007 -0008 с вертикальным платиком (файл 7018-03) (! i 1 о ' о| о о [о 0 0 о 1 Длина рычага (любое удлинение сваркой) Прочие размеры (соответствуют типоразмеру) 6
02-7018-0013 -0014 -0015 -0016 -0017 -0018 с горизонтальным платиком (файл 7018-13) О t 1
6.2. Состав и структура библиотеки элементов
277
Продолжение табл. 6.2
Номер чертежа и файла в базе данных Эскиз Изменяемые размеры Количество типоразмеров
Ручные узлы фиксации в сборе ВАЗ
7018-0003 s в -J Д опол нител ьно: геометрия стойки (высота, вынос и наклон) Любое
7018-0013 s 1 о с L \ X \ \ \
Пневматические прижимы ГАЗ
0850-7916 -01 -02 -03 (угол и конечники) | Угол раскрытия 90 и 120° Диаметр поршня 75 мм Прочие размеры узлов фиксации
0850-7352 зеркальное -01 -02 зеркальное -03 (конечники) Угол раскрытия 120° Диаметр поршня 80 мм Прочие размеры , узлов фиксации
и 1 °®0 [О е© Л ООО о оо| ! Любое
№ 1
278 6. Система автоматизированного проектирования приспособлений
Продолжение табл. 6.2
Номер чертежа и файла в базе данных Эскиз Изменяемые размеры Количество типоразмеров
0850-7157 зеркальное -01 /Я | Угол раскрытия 108° Диаметр поршня 50 мм Прочие размеры узлов фиксации Любое
0850-7350 зеркальное -01 -02 зеркальное -03 (конечникн) ► » OI— • воо • > Pool 1
Узлы фиксации пневматические ГАЗ
7916 s II, .= Угол раскрытия 90 и 120° Диаметр поршня 75 мм Прочие размеры узлов фиксации Любое
7350_s Угол раскрытия 108° Диаметр поршня 50 мм Прочие размеры узлов фиксаци
6.2. Состав и структура библиотеки элементов
279
Продолжение табл. 6.2
Номер чертежа и файла в базе данных Эскиз Изменяемые размеры Количество типоразмеров
Головки силовые стендов ВАЗ
4211 -01 -02 -03 as а» Ход штока — 35, 50, 80 и 100 мм При диаметре поршня 125 мм 4
е[ —
4213 -01 -02 -03 -04 в CD Ход штока — 35, 50, 80, 100 и 125 мм При диаметре поршня 160 мм 5
Е _ _
4016 -01 -02 -03 & дП zih Ход штока — 35, 50, 80 и 100 мм При диаметре поршня 125 мм 4
е| — |_|
4211k_v -01 -02 -03 „Л, Высота крон- штейна — любая 4
1— й
4211k_vl -01 -02 -03 Высота и наклон кронштейна — любые Любое
280
6. Система автоматизированного проектирования приспособлений
Окончание табл. 6.2
Номер чертежа и файла в базе данных Эскиз Изменяемые размеры Количество типоразмеров
4211kg -01 -02 -03 Высота крон- штейна — любая 4
—** 1»
421l_gl -01 -02 -03 Высота и наклон кронштейна — любые Любое
Пример формирования 3/)-образа ручного прижима для занесения его
в базу данных системы рассмотрен в § 1.5. Примеры 3£)-образов пневмати-
ческих и ручных прижимов из базы данных элементов сборочно-свароч-
Рис. 6.11. Примеры 3£>-образов базы данных пневматических и ручных прижимов:
а — пневматические прижимы; б — ручные прижимы
6.3. Технология автоматизированного проектирования приспособлений 281
Рис. 6.12. Состав типового пневматического прижима
ровных приспособлений приведены на рис. 6.11. Состав деталей одного из
типовых пневматических прижимов базы данных показан на рис. 6.12.
Каждый из прижимных элементов сборочно-сварочных приспособле-
ний имеет множество конструктивных параметров, которые в определенных
пределах обеспечивают его адаптацию к фиксируемому изделию. Часть па-
раметров, определяющих подстройку под высоту прижимаемой поверхно-
сти относительно кондукторной плиты, рассчитывается системой автомати-
чески, прочие могут быть заданы пользователем.
6.3. Технология автоматизированного проектирования
приспособлений
Общая последовательность работы САПР представлена на рис. 6.13.
Подготовка к проектированию. Исходными данными для проекти-
рования служат математические модели узла и отдельных деталей. В авто-
мобильной промышленности они часто создаются в «тяжелых» графических
системах, например в CATIA, а их передача в автоматизированную систему
проектирования приспособлений производится через IGES-транслятор
AutoSurf. Кроме того, в состав исходных данных должны входить:
282 6. Система автоматизированного проектирования приспособлений
Рис. 6.13. Общая последовательность работы САПР:
ТЗ — техническое задание; ССП — сборочно-сварочное приспособление;
УФ — узлы фиксации
• техническое задание на проектирование;
• рабочие чертежи узлов и входящих деталей;
• технологический процесс сборки-сварки;
• принципиальная схема приспособления.
Техническое задание на проектирование должно содержать требова-
ния к конструкции приспособления и его отдельным элементам, характери-
стику энергоносителей (напряжение и род тока, давление воздуха), габарит-
ные размеры, производительность, перечень деталей и сборочных единиц,
условия подачи и удаления деталей и изделия, требования к управлению
(расположение пульта, необходимость дистанционного управления), требо-
вания по технике безопасности; эргономические требования.
Кроме того, техническое задание может содержать дополнительные
данные, характеризующие режим работы сборочного приспособления, воз-
можность его переналадки, степень механизации и автоматизации; надеж-
ность, унификацию и стандартизацию, связь с другими приспособлениями,
кинематические условия эксплуатации, требования к маркировке и упаковке, а
также экономические показатели использования и сведения об аналогичных
6.3. Технология автоматизированного проектирования приспособлений 283
приспособлениях, применявшихся на данном или других предприятиях для
изготовления похожих сварных узлов.
Разработка схем базирования и карт контроля. Большая интеллек-
туальная нагрузка выпадает на этап выбора схемных решений, которые оп-
ределяют качество проекта. При проектировании сборочного приспособле-
ния исходят из того, что именно конструкция сварного узла определяет
принципиальную схему приспособления. Поэтому разработка принципиаль-
ной схемы базирования осуществляются непосредственно на 3£>-модели
сварного узла, где указываются места и способы фиксации и закрепления
деталей.
В состав технического задания на проектирование могут входить сле-
дующие документы:
схема базирования — это комплект документации для разработки
приспособления. Основной из них — образ сварного узла, на котором ус-
ловными обозначениями указаны места, способы и устройства фиксации и
крепления всех деталей и подузлов для обеспечения его заданных размеров
с учетом всей гаммы технологических факторов и ограничений, действую-
щих на приспособление в процессе эксплуатации. В комплект также входят
сечения собираемого узла с обозначением формы контактных поверхностей
блочков;
карта контроля — комплект документации для разработки кон-
трольного приспособления, где кроме данных схемы базирования дополни-
тельно внесены сведения о контролируемых размерах формы детали или
узла и расположения отверстий;
принципиальная схема приспособления отличается от схемы бази-
рования наличием дополнительных сведений о способах и устройствах для
установки, манипулирования и съема деталей и узлов.
Поверхность детали, на которую она устанавливается при сборке под
сварку в определенном положении относительно сборочно-сварочного при-
способления и сварочного инструмента, называют установочной базой.
Сборочная база — совокупность поверхностей, линий и точек, которая оп-
ределяет положение детали относительно других деталей в изделии или
сборочной единице. Конструктивной базой приспособления называют сово-
купность поверхностей, линий и точек, от которых задаются размеры и по-
ложения других деталей и сборочных единиц при разработке конструкции.
Для базирования детали, имеющей развитые плоскости и цилиндриче-
ские поверхности, необходимо и достаточно шести опорных точек. Элемен-
ты с криволинейными поверхностями сложной формы, а также нежесткие
элементы базируются в приспособлениях с помощью ложементов. Детали
узла могут частично или полностью базироваться по другим элементам
сварной конструкции.
284
6. Система автоматизированного проектирования приспособлений
Ввиду сложности пространственных форм кузовных узлов невозмож-
но формализовать процесс создания схемы базирования, который заключа-
ется в указании зон предпочтительного размещения узлов фиксации. На
схеме базирования отмечаются размеры, которые следует соблюсти с осо-
бой точностью. В качестве установочных баз предпочтительно использовать
механически обработанные поверхности или отверстия деталей. При разме-
щении упоров установочных баз надо следить за тем, чтобы не происходило
защемления в приспособлении собранного и прихваченного изделия и обес-
печивался его свободный съем. В связи с этим отдельные собираемые под
сварку детали целесообразно размещать так, чтобы их ожидаемые переме-
щения от сварочных деформаций были направлены не к упорам, а в сторону
от них. В противном случае усадочные сварочные деформации с огромными
усилиями после сварки заклинят сваренное изделие в жестких базовых упо-
рах сварочного приспособления. Прижимы деталей стремятся располагать в
непосредственной близости от базовых упоров. Желательно, чтобы в проек-
тируемом сборочном приспособлении было минимальное количество типов
прижимов (лучше один-два). При этом прежде всего используют стандарти-
зованные конструктивные элементы и только в случае необходимости —
оригинальные решения.
Рациональный выбор базовых поверхностей и элементов фиксации —
важнейший фактор, определяющий качество сварного изделия.
Определение мест базирования и фиксации поверхностей сварного уз-
ла выполняется конструктором на этапе формирования прототипа проекти-
руемого приспособления в соответствии со схемой базирования. Поэтому
формирование схем базирования и карт контроля должно осуществляться
до начала проектирования самого приспособления. Лучше, если это выпол-
няется с помощью соответствующей встроенной подсистемы и точной ма-
тематической модели сварного узла специализированным технологическим
подразделением, например лабораторией собираемости и метрологии. По
сути дела, именно это подразделение должно выполнять непосредственную
разработку прототипа приспособления.
Условные обозначения опор (неподвижных, подвижных, плавающих,
регулируемых), а также зажимов одиночных и двойных регламентируются
ГОСТ 3.1107—81 и стандартом предприятия. Библиотека условных обозна-
чений элементов приспособлений присутствует в системе и открыта для
пользователя.
Разработка схемы базирования выполняется в такой последовательности:
• собираемый под сварку узел представляется схематически в виде
контуров с проемами путем обработки его ЗР-образа;
• на схему наносят условные обозначения фиксирующих, пробивных и
контрольных элементов после выбора их типов и мест установки на узле;
6.3. Технология автоматизированного проектирования приспособлений 285
• выполняются сечения в заданных местах узла и относительно них
изображается форма контактных поверхностей сухарей;
• полученные схемы дорабатывают (наносят размеры, выноски, допол-
нительные обозначения и т. п.) и включают в состав технического задания.
Основу рассматриваемой здесь концепции автоматизированного проек-
тирования сборочно-сварочных приспособлений составляет принцип двух-
этапного решения отдельных проектных задач. На первом этапе создается
условное упрощенное представление принимаемого решения (прототип схе-
мы, конструкции). С его помощью часто решается большой комплекс взаимо-
связанных с проектируемым объектом задач. После их успешного решения
уже на втором этапе наброски и, самое главное, привязка данных реализуются
при окончательном (реальном) проектировании разрабатываемого объекта. И
первый этап — создание прототипа, — и второй — проектирование объек-
та — реализованы путем создания самостоятельных подсистем САПР.
В подсистеме подготовки прототипа оснастки расстанавливаются в
виде плит-параллелепипедов прототипы кондукторной плиты и узлы фикса-
ции относительно свариваемой конструкции, а также выполняются сечения
вдоль граней прототипов узлов фиксации. Таким образом, определяются
места расположения узлов фиксации на плите, а также геометрия фиксируе-
мых поверхностей в этих местах. Поочередное формирование геометрии
самих узлов фиксации относительно сечений и их сборка воедино в приспо-
собление осуществляются позже.
При создании прототипа оснастки задается уровень размещения свар-
ного узла над кондукторной плитой. Особенно это важно для контактной
точечной сварки, когда необходимо обеспечить свободный доступ нижнего
электрода сварочных клещей к свариваемому изделию. Далее формируется
прототип кондукторной плиты, расстанавливаются прототипы прижимов и
выполняются необходимые сечения сварного узла в зонах базирования и
закрепления собираемых деталей.
Подсистема проектирования прототипов содержит программные сред-
ства, которые позволяют осуществить следующие операции:
1) вызвать на экран монитора образ узла и разместить его соответст-
вующим образом;
2) построить нормали к поверхности узла в местах приложения усилия
закрепляющих элементов;
3) создать и вставить в модель прототип кондукторной плиты;
4) расставить прототипы прижимов в соответствии со схемой бази-
рования с использованием или без использования нормалей к поверхно-
сти узла;
5) получить сечения сварного узла в зонах прототипов прижимов и
сохранить результаты работы.
286 6. Система автоматизированного проектирования приспособлений
Перечисленные пять групп операций выполняют с помощью специ-
альных меню, пиктограмм, курсора мыши, в том числе с использованием
стандартных функций графических пакетов и операционных систем (вы-
брать, передвинуть, удалить, записать полный объем информации в соответ-
ствующие каталоги на диске). Подробное описание работы подсистемы
приведено на примере проектирования конкретного сборочно-сварочного
кондуктора в § 6.4.
После того как загружен подготовленный ранее свариваемый узел, зада-
ны габаритные размеры и пространственное положение прототипов одной или
нескольких кондукторных плит и, таким образом, определены системы коор-
динат, в которых производится проектирование узлов фиксации, можно задать
габаритные размеры и пространственное положение прототипов других эле-
ментов на каждой кондукторной плите. Прототип элемента (узел фиксации,
силовая головка, контрольная поверхность) представляет собой определенный
параллелепипед в системе координат заданной плиты и определяет «чертеж-
ную плоскость» элемента при подготовке документации по проекту.
Для удобства позиционирования любых элементов на кондукторной
плите автоматически выполняется построение сетки плаза. При этом сис-
тема запрашивает плоскость проекции сетки и ее шаг. Изображение сетки
плаза показано на рис. 6.14. Сетку плаза можно наблюдать в трех плоско-
стях (в каждой плоскости отдельно или одновременно в нескольких).
Рис. 6.14. Изображение сетки плаза
6.3. Технология автоматизированного проектирования приспособлений 287
Построение нормалей к поверхности узла в точке приложения
усилия, необходимое для последующего точного расположения прототипов
пробивных и фиксирующих элементов, выполняется выбором пункта меню
и непосредственным размещением курсора мыши в точке приложения уси-
лия на поверхности узла. Для удобного позиционирования этой точки с ори-
ентацией по сетке плаза или координатам лучше предварительно разместить
обрабатываемый сварной узел в проекцию «вид сверху» или использовать
средства объектной привязки. Для большего удобства работы можно ис-
пользовать двухэкранный режим работы монитора (команда vports), когда
выполняемые действия одновременно отображаются на разных проекцион-
ных видах.
Вся работа с прототипами отдельных элементов проектируемой осна-
стки требует увязки в единой среде их взаимного расположения и организа-
ции хранения всех данных на диске. Разработана система предлагаемых
обозначений (имен) кондукторных плит, отдельных прижимов и других
элементов. Так, кондукторные плиты автоматически нумеруются в порядке
их создания Fixplate-1, Fixplate-2, отдельные прижимы — Fix-1, Fix-2 и т. д.
Удобная организация работы обеспечивает быстрое формирование прототи-
па элемента, перемещение его в требуемое пространственное положение по
трем координатам и поворот на необходимый угол.
Поскольку каждому прототипу прижима может соответствовать не
более одного реального прижима, прототипы следует расставлять везде, где
предполагаются конструктивные элементы сборочно-сварочного приспо-
собления, будь то откидывающиеся механизмы или неподвижная арматура
типа стойки. Комбинированные узлы фиксации, имеющие в своем составе
два прижима, таким образом, должны использовать не менее двух прототи-
пов, но могут использовать и три прототипа, например, для конструирова-
ния выносного фиксатора, не лежащего в плоскости узла фиксации, но за-
крепленного на его же стойке.
Если в проектируемое приспособление вставлено более одного прото-
типа кондукторной плиты, то для работы необходимо выбрать один из них в
боковом меню.
Прототип прижима еще не определяет его реальное конструктивное ис-
полнение, и для его ориентирования относительно кондукторной плиты ис-
пользуется система локальных координатных осей. Для удобства и ускорения
позиционирования прижимных элементов принято соглашение, что ось У,
обозначаемая на устанавливаемом элементе желтой линией, должна соответ-
ствовать направлению подвода рычага прижима к закрепляемой детали.
Размеры прототипа рекомендуется назначать не менее реальных раз-
меров будущего прижима, чтобы автоматически формируемый фрагмент
сечения закрепляемого узла был достаточным для определения расположе-
ния прижима.
288 6. Система автоматизированного проектирования приспособлений
Для более точного размещения прототипа относительно точки прило-
жения усилия используется автоматизированное размещение прототипа
прижима таким образом, что основание построенной заранее нормали к по-
верхности узла совмещается со средней линией прототипа.
Для автоматического построения сечений сварного узла в плоскостях
установки прижимов пользователю предоставляется возможность или са-
мому указать прототипы прижимов с помощью мыши или выбрать функцию
для построения всех сечений всех узлов, имеющихся на экране.
Для построения контактной поверхности узла фиксации (формиро-
вания контактных поверхностей торцов блочков и скоса их кромок) в
месте расположения каждого прототипа прижима строится не менее трех
сечений. Система выдает запрос требуемого количества сечений для ка-
ждого прототипа.
Подсистема формирования ЗР-модели сборочно-сварочного при-
способления предназначена для:
• размещения конструктивных элементов приспособления относи-
тельно сечений узла;
• формирования криволинейных поверхностей прижимов и их ориги-
нальных деталей, кронштейнов, стоек и т. п.;
• объединения всех элементов в единую конструкцию на кондуктор-
ной плите с рамой и поворотной стойкой, с возможностью последующего
ЗР-моделирования работы всего приспособления.
Работа подсистемы использует файлы описания сечения узла, сфор-
мированные на предыдущем этапе работы, и позволяет выполнять следую-
щие операции:
1) выбирать сечение установки прижима;
2) выбирать тип и типоразмер прижима, вызывать его на экран;
3) задавать расположение прижима относительно сечения узла и из-
менить его размеры;
4) задавать ширину, скос кромок и профиль поверхностей прижимов;
5) собирать относительно одного сечения несколько прижимов и фор-
мировать недостающие конструктивные элементы (формирование узлов
фиксации);
6) собирать воедино сборочное приспособление (как настольное, так и
напольное).
При новом сеансе работы система запрашивает имя проекта, которое
рекомендуется называть по номеру сварного узла или прототипа приспособ-
ления. Под словом «проект» понимается вся совокупность информации
(файлов), необходимой для нормального продолжения конструирования,
доводки или модернизации приспособления. В процессе разработки для ка-
ждого прототипа может быть несколько проектов, их можно сохранять, к
6.3. Технология автоматизированного проектирования приспособлений 289
работе с ними можно возвращаться,
но после того, как найдено оконча-
тельное решение, в архив должен по-
падать лишь один из них.
Меню обеспечивает выбор кон-
структивных элементов фиксации,
сечений собираемой сварной конст-
рукции, модернизацию сменных эле-
ментов узлов фиксации, дорисовку
недостающих элементов, а также
сборку нескольких элементов на од-
ном экране. Удобно диалоговое окно
выбора для работы сечений деталей
собираемого узла сварной конструк-
ции (рис. 6.15). В левой части окна
выбирается сечение для проработки
закрепления деталей. Завершенные и проработанные узлы фиксации, запи-
санные в базу готовых решений, появляются в списке правого окна.
Окно выбора из базы подходящего конструктивного элемента проек-
тируемого приспособления имеет вид, показанный на рис. 6.16. Появление
на экране изображения выбранного узла фиксации для использования его в
этом конкретном сечении собираемой под сварку конструкции автоматически
Section selection
Sections.
FIX1_2S
FIX1.3S
FIX1 4S
FIX1_5S
FIX1_6S
FIX1 7S
FIX1_8S —
FIX1_9S
FIX1J0S
FIX1 IIS-
Show<
X
loom
Vpoint
l-WS
Hide
Select
3repared:
FIX1 IP
FIX1_2P
FIX1 8P
Caned
Рис. 6.15. Диалоговое окно выбора се-
чения
Рис. 6.16. Окно выбора конструкт ивных элементов приспособления
,0 6705
290 6. Система автоматизированного проектирования приспособлений
дополняется изображением сече-
ния сварного узла в рабочей плос-
кости прижима (рис. 6.17). «Пра-
вильная» вставка узла фиксации
относительно сечения обеспечива-
ется лишь при полном выполне-
, нии правил подготовки образа
Рис. 6.17. Сечение сварного узла в рабо-
„ н / н прижима и записи его в базу дан-
чей плоскости прижима J
ных:
• прижим сохраняется в мировой системе координат, а предполагае-
мая точка контакта с закрепляемой деталью должна находиться в «нуле»;
• при этом точка фиксации образа контактного элемента также должна
совпадать с предполагаемой точкой контакта с деталью, поскольку' это важ-
но для правильного изменения типоразмеров;
• сварной узел должен сохраняться в координатах сварной конструк-
ции и прототип прижима должен быть правильно расположен относительно
его поверхности.
Далее имеется возможность выполнения любых действий по переме-
щению, редактированию и дорисовке конструктивных элементов узла фик-
сации. При этом важно отметить, что любые перемещения и изменения всех
элементов будут происходить при неизменном положении сечения сварной
конструкции. Так, положение прижима относительно закрепляемого сече-
ния свариваемой конструкции, возможно, потребует его изменения и кон-
тактный элемент (блочок, прижим и т. п.) следует перенести в нужную точку.
После того как прижим занял правильное местоположение, можно пе-
реходить к редактированию его размеров с помощью изменения цифровых
значений системы параметризации, использованной при проектировании и
формировании его ЗО-образа для базы данных. Для этого следует выбрать
пункт меню или можно использовать соответствующую пиктограмму и в
появившемся диалоговом окне менять значения варьируемых параметров.
Глобальное изменение типоразмера элемента выполняется при помощи ак-
тивизации соответствующего варианта таблицы глобальных параметров.
При редактировании размеров узла фиксации следует стремиться к тому,
чтобы
• основание стойки совпадало с плоскостью кондукторной плиты;
• другие элементы узла фиксации не касались сварного узла;
• элементы узла фиксации не сталкивались друг с другом (например,
при качании цилиндра);
• хватало хода поршня цилиндра для полного раскрытия прижима;
• обеспечивалось условие удаления сварного узла из приспособления
после сварки.
6.3. Технология автоматизированного проектирования приспособлений 291
После редактирования размеров прижима выполняются:
• формирование геометрии обрезаемых элементов узла фиксации;
• формирование контактных поверхностей прижима (рычага, ложе-
мента или блочков), в том числе и для составления программы их механиче-
ской обработки на станке с ЧПУ;
• подсборка комбинированных узлов фиксации;
• сборка окончательно подготовленных узлов фиксации, при которой
получается пространственная система, включающая в себя также кондук-
торную плиту;
• доводка конструкции кондукторной плиты путем обрезания ее кон-
тура, вырезания окон и дорисовки арматуры, а также окончательная сборка
сборочно-сварочного приспособления с усилительной рамой, подставой,
поворотной стойкой и т. п.
Для полноты картины или удобства дальнейшей работы в образ сбо-
рочно-сварочного приспособления можно вставить сварной узел и/или сетку
плаза.
Заключительный этап работы — запись результатов и формиро-
вание документации (схем, чертежей и спецификаций). Сформированная
трехмерная модель приспособления отображается в комплекте из следую-
щих чертежно-графических документов:
• схема базирования и карта контроля;
• сборочный чертеж приспособления (стенда) в двух проекциях в про-
екционной связи с обозначением координат и положения центра масс при-
способления;
• чертежи функционально завершенных узлов фиксации в стандарт-
ных проекциях;
• изображения нижних и верхних сухарей с обозначением осей кре-
пежных отверстий (для подсоединения соответственно нижнего кронштейна
и рычага пневмоприжима);
• изображения рычагов с крепежными отверстиями;
• изображения кондукторной плиты с простановкой координат от-
верстий по каждому функционально завершенному узлу фиксации; соз-
дается также специальный файл с изображением контура произвольной
формы и простановкой размеров плиты; по умолчанию толщина плиты
равна 20 мм;
• библиотека параметризованных элементов;
• технические данные приспособления (габаритные размеры, масса,
координаты центра масс и т. п.).
Формирование чертежей (размещение необходимых видов, сечений и
разрезов на формате чертежного листа и простановка размеров) выполняет-
'Т
292 6. Система автоматизированного проектирования приспособлений
ся в любой момент без затруднений путем преобразования трехмерных изо-
бражений в плоские чертежи и их редактирования с использованием воз-
можностей графической среды. Последовательность операций при получе-
нии чертежной документации рассмотрена в § 1.5. Важно еще раз заметить,
что каждому объемному изображению .dwg-файла может быть придан пло-
ский чертеж, который хранится в этом же файле и автоматически изменяет-
ся при изменении объемного изображения. Кроме того, возможно создание
любого количества дополнительных чертежей в других файлах с обрывом
всех ассоциативных связей и поэтому гораздо меньших по объему.
Более подробно вся работа по автоматизированному проектированию
сборочно-сварочного приспособления рассмотрена на конкретном примере
в § 6.4.
6.4. Пример компьютерного проектирования
сборочно-сварочного стенда
В качестве примера рассмотрим технологию проектирования сбороч-
но-сварочного приспособления для сборки под сварку каркаса задка автобу-
са ЗИЛ «Бычок», ЗР-образ которого показан на рис. 6.18. Каркас задка пред-
ставляет собой прямоугольную раму, состоящую из четырех продольных
элементов: верхней и нижней поперечин и правой и левой стоек. Каждый из
Рис. 6.18. Образ сварного узла
6.4. Пример компьютерного проектировать сборочно-сварочного стенда 293
Рис. 6.19. Сварной узел с сеткой плаза
этих элементов изготовлен из штампованных листовых заготовок толщиной
1,2 мм и имеет П-образное поперечное сечение, переменное по длине. Все
четыре продольных элемента в сборочном приспособлении должны закреп-
ляться в двух сечениях, и в каждом сечении предполагается установка одной
опоры и двух прижимов. Из них один будет с ручным приводом, другой — с
пневмоприводом. Таким образом, всего в конструкции данного приспособ-
ления должно быть установлено 16 прижимных механизмов, причем в связи
с переменными сечениями сварной конструкции у каждого прижима должна
быть спроектирована оригинальная форма контактного элемента, соответст-
вующая сложной поверхности закрепляемой в этом месте детали.
После загрузки на экран монитора образа сварной конструкции и
расположения ее в горизонтальной плоскости система автоматически
сформирует сетку плаза с выбранным нами шагом 200 мм (рис. 6.19). По
команде из меню подсистемы автоматически сформируется прототип
кондукторной плиты, который будет иметь размеры в плане немного
больше размеров изделия и по умолчанию обозначен как Fixplate-1. Рас-
стояние от изделия до базовой кондукторной плиты командой move уста-
новим 400 мм (рис. 6.20).
Установив для удобства двухэкранный режим, укажем точки закрепле-
ния деталей и расставим в этих точках нормали к поверхности детали. Для это-
го в каждом случае указываем точку и поверхность, к которой строится нор-
маль. Вид узла с восемью нормалями показан на рис. 6.21. В месте планируе-
294 6. Система автоматизированного проектирования приспособлений
Рис. 6.21. Расстановка нормалей
6.4. Пример компьютерного проектирования сборочно-сварочного стенда 295
Рис. 6.22. Прототип сборочно-сварочного кондуктора
мого размещения зажимного механизма разместим прототип прижима, при-
чем система автоматически сделает так, что его плоскость будет проходить
через нормаль, указанную мышью. Угол по отношению к изделию можно
изменять поворотом прототипа вокруг оси Z, направление размещения зада-
ем с помощью горизонтальной оси Y, отображаемой на экране желтым цве-
том (рис. 6.21). Далее расставим прототипы прижимов во всех закрепляемых
сечениях (рис. 6.22). Система автоматически их все пронумерует и обозна-
чит как Fix-1 — Fix-8.
Тип прижимного механизма в каждом сечении выберем из базы дан-
ных с помощью стандартного окна выбора файлов, в котором можно про-
смотреть обозначения и конструктивное исполнение механизма (рис. 6.23).
Выбранный прижимной механизм пока не отображается на модели проекти-
руемого приспособления, но последующая работа по проектированию узла
фиксации в данном сечении будет вестись именно с этим прижимом.
Командой меню системы сформируем сечения собираемой сварной
конструкции сразу во всех прорабатываемых узлах. Теперь они будут хра-
ниться в памяти компьютера привязанными к разрабатываемым узлам.
На этом этап подготовки прототипа завершен, нужно лишь задать его
имя и записать на диск.
296 6. Система автоматизированного проектирования приспособлений
Preww
'рО
142Ик_©п
|4211k_©v
l4211kr_n
l<11 kr_v
14213
l4213kjaw
[/Дпфяпу ~| EmdFite
«|,. / Отмуно |
Рис. 6.23. Окно выбора типа прижима
Цапка:. .|^з'силовые2гсяснвки
4016kv
4211
Кронштейны
3
401Б
4016Мд
4016k„&.rv
4016k_ev
^^».фейфек |4016k_g
Дип файлов:: |Dr<^ng(*dwg)'
Непосредственное проектирование кондуктора сначала ведется в от-
дельных сечениях, выбор которых для работы производится с помощью
диалогового окна, показанного на рис. 6.15.
В выбранном для работы сечении увидим два принятых нами ранее
зажимных механизма, закрепленных на некоторой заготовке основания
прижима (рис. 6.24). На этом и других рисунках показан не только вид
плоского сечения, но и — для ясности — существующий трехмерный образ
прорабатываемой конструкции. Отдельной командой к этому изображению
добавляется вид сформированного ранее сечения сварной конструкции и,
Рис. 6.24. Вставка прижимов
6.4. Пример компьютерного проектирования сборочно-сварочного стенда 297
что очень важно, с обозначением уровня базовой поверхности кондукторной
плиты (рис. 6.25). Автоматически собранный узел фиксации в данном слу-
чае оказался не очень правильным, поскольку вставка всех элементов ком-
плекса происходит в точку начала системы координат, привязанную к осно-
ванию нормали к поверхности. Однако теперь имеется возможность выпол-
нения любых действий по перемещению, редактированию и дорисовке
конструктивных элементов.
Положение левого и правого прижимов требует изменения. Правиль-
ное позиционирование прижимов производится путем перемещения кон-
тактных элементов в нужные точки. Правильное положение левого прижима
показано на рис. 6.26, планируемое расположение заготовки проектируемо-
го правого прижима — на рис. 6.27.
После корректировки положения каждого прижима относительно из-
делия переходим к редактированию его размеров, изменяя его варьируемые
параметры. В первую очередь, изменяя в таблице параметров необходимые
размеры, нужно дотянуть основание кронштейна до уровня кондукторной
плиты. Меняя положение отверстий на базовой пластине прижима, добива-
емся того, что ручной прижим не задевает деталь, а заготовка рычага пнев-
матического прижима накрывает сечение изделия, пересекая его.
Следующая операция — формирование контуров прямоугольной пла-
стины, на которой крепятся ручной и пневматический прижимы. Формиро-
вание образа пластины выполняется средствами Mechanical Desktop. Изме-
няемый элемент делается активным, плоскость построения располагается на
поверхности пластины, рисуется требуемый контур, устанавливаются его
298 6. Система автоматизированного проектирования приспособлений
Рис. 6.26. Перенос левого прижима относительно сечения
Рис. 6.27. Расположение заготовки правого прижима относительно сечения
6.4. Пример компьютерного проектирования сборочно-сварочного стенда 299
Рис. 6.28. Сформированная пластина узла прижима
размеры и зависимости, эскиз преобразуется в трехмерный образ. Более
подробно такие построения рассмотрены в § 1.5. Результат редактирования
базовой пластины прижима показан на рис. 6.28. Аналогичным образом
формируются и другие элементы узла фиксации.
После придания прижиму приемлемой формы необходимо сформи-
ровать контактную поверхность рычага (или верхнего блочка). Эта операция
выполняется путем удаления объема металла рычага, пересекающего по-
верхность закрепляемого узла. Поэтому обрезаемый элемент (рычаг) должен
быть наложен с запасом на фиксируемое сечение узла.
Далее необходимо выполнить ряд последовательных действий:
• сделать блочок активным;
• изменить масштаб и расположить изображение в изометрическую
проекцию, чтобы все сечения данного прототипа были отчетливо видны;
• с использованием соответствующего пункта меню последовательно
объединить отрезки линий сечения воедино (рис. 6.29);
• натянуть поверхность на линии сечений командой меню, отметив
линии сечений;
• построить по сечениям прототипа поверхность, полностью пересе-
кающую обрезаемый элемент, для чего толщина прототипа должна быть
больше толщины рычага прижима. Для контроля за выполнением этого
обязательного условия нужно расположить изображение в соответствую-
щем ракурсе (вид сверху). Если условие не выполнено, удлинить данную
300 6. Система автоматизированного проектирования приспособлений
Рис. 6.29. Объединение отрезков линий сечений
Рис. 6.30. Формирование поверхностей левого и правого прижимов
6.4. Пример компьютерного проектирования сборочно-сварочного стенда 301
Рис. 6.31. Готовая поверхность лонжерона
сторону поверхности пунктом меню, щелкнув мышью на удлиняемый край
поверхности.
Теперь необходимо выполнить сечение рычага, указав мышью секу-
щую плоскость. Появится стрелка, направление удаляемого объема, при не-
обходимости можно изменить ее направление. Результат выполнения этих
операций показан на рис. 6.30.
Для формирования контактной поверхности ложемента (нижнего
блочка) последовательность операций такая же. Различие заключается лишь
в том, что после построения секущей поверхности следует учесть толщин}'
листа сварного узла. Результат — на рис. 6.31.
Результаты формирования контактной поверхности блочков (или ры-
чага с ложементом) можно вывести для формирования программы их меха-
нической обработки на станке с ЧПУ.
Теперь имеем полностью сформированный узел фиксации. Изменяя
положения поршня пневмоцилиндра, можно открыть прижим и визуально
проверить:
• «вынимаемость» сварного узла из узла фиксации;
• отсутствие столкновений со стойкой при качании цилиндра;
• достаточность хода поршня (рис. 6.32).
302 6. Система автоматизированного проектирования приспособлений
Рис. 6.32. Проверка кинематики
Рис. 6.33. Окончательный вид узла фиксации
Окончательно оформленный узел фиксации (рис. 6.33) записывается в
базу готовых элементов.
Аналогично выполняется работа со всеми остальными сформирован-
ными на прототипе сборочно-сварочного приспособления сечениями. Завер-
6.4. Пример компьютерного проектирования сборочно-сварочного стенда 303
Рис. 6.34. Окончательный вид сборочно-сварочного приспособления:
а — без изделия; б — с изделием
304
6. Система автоматизированного проектирования приспособлений
Рис. 6.35. Чертеж сборочно-сварочного кондуктора
шение этой работы позволяет из готовых блоков собрать приспособление
целиком. Для этого с помощью диалогового окна выбирается список всех
необходимых элементов. Готовое приспособление для сборки каркаса задка
автобуса появляется на экране в изометрическом изображении (рис. 6.34, а).
Для более удобного восприятия конструкции приспособления вставим в не-
го и конструкцию собираемого под сварку узла (рис. 6.34, б).
Само сборочно-сварочное приспособление вследствие больших габа-
ритных размеров должно размещаться на поворотном столе. В системе име-
ется возможность из библиотеки имеющихся манипуляторов подобрать
подходящий поворотный стол и с помощью задания зависимостей между
столом и основанием кондукторной плиты все приспособление закрепить на
этом поворотном устройстве.
Проектируемое приспособление готово. По имеющейся его трехмер-
ной модели сформируем плоский чертеж. Процедура формирования чертежа
показана в § 1.5. Вид проекционного чертежа приспособления со вставлен-
ным в него аксонометрическим видом приведен на рис. 6.35.
После завершения работы по проектированию приспособления и
получения чертежей можно, если необходимо, продолжить корректиров-
ку размеров отдельных элементов. Например, можно уменьшить размеры
6.4. Пример компьютерного проектирования сборочно-сварочного стенда 305
Рис. 6.36. Вариант приспособления после возможной доработки
Рис. 6.37. Пример сложного приспособления
306 6. Система автоматизированного проектирования приспособлений
кондукторной плиты, воспользовавшись таблицей варьируемых параметров.
При этом и трехмерная модель и плоский чертеж сборочно-сварочного при-
способления будут автоматически перестроены. В гл. 7 изложена методика
проектирования сборочно-сварочных приспособлений с целью проверки их
функциональных возможностей в составе сварочных технологических ком-
плексов.
После проверки функциональных свойств приспособления, как прави-
ло, приходится дополнительно корректировать выполняемый проект. На-
пример, учитывая достаточно большую длин}' закрепляемых панелей, мож-
но еще добавить узлы фиксации в средней части каждого продольного эле-
мента. В этом случае приспособление будет иметь вид, показанный на
рис. 6.36. При добавлении новых элементов операцию формирования пло-
ских чертежей нужно повторить.
Изложенная здесь методика автоматизированного проектирования
сборочно-сварочных приспособлений на основе трехмерной модели сварной
конструкции является достаточно эффективной и позволяет легко проекти-
ровать сложные конструкции. В качестве примера более сложного приспо-
собления на рис. 6.37 показан сборочно-сварочный кондуктор для сборки и
сварки боковины микроавтобуса ГАЗ.
7. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ
СВАРОЧНЫХ РОБОТИЗИРОВАННЫХ
ТЕХНОЛОГИЧЕСКИХ КОМПЛЕКСОВ
7.1. Содержание работ и структура
автоматизированной системы
Применение роботов в сварочном производстве — путь эффективного
решения проблем автоматизации сварочных операций. Прежде всего это
связано с повышением качества выполнения работ, недоступного ручным
технологиям. Понятны очевидные и весомые достоинства роботизирован-
ной сварки:
• высокая точность перемещений сварочного инструмента и траекто-
рии наложения сварных швов;
• высокая точность поддержания всех технологических параметров
сварки;
• «неутомляемость» и способность работать круглые сутки.
По сравнению с другими путями автоматизации сварочных работ, та-
кими, как применение автоматических многоточечных машин в контактной
сварке, сварочных автоматов и автоматических установок при дуговой свар-
ке или термическом резании, идея роботизации выгодно отличается гибко-
стью переналадки оборудования и технологии, в том числе и возможностью
постоянного изменения программ при последовательной сварке весьма раз-
личных изделий.
Недостатки идеи роботизации сварочных технологий также имеются,
и в большинстве практических случаев они делают нереальной нарисован-
ную выше идиллическую картин}'. Эти недостатки прежде всего связаны с
чрезвычайно высокой стоимостью сварочных роботов для дуговой и кон-
тактной сварки и другого оборудования, необходимого для их успешной
работы в составе сварочных роботизированных технологических комплек-
сов (РТК). Это управляемые двух- и трехстепенные манипуляторы изделий,
гораздо более дорогой сварочный инструмент. Для успешной работы сва-
рочных РТК предъявляются существенно более высокие требования к сва-
308
7. Автоматизированное проектирование сварочных комплексов
рочным горелкам для дуговой сварки в защитных газах, механизмам подачи
сварочной проволоки, к самим сварочным проволокам, качеству их покры-
тий, качеству намотки на катушки и т. д.
Другая группа проблем промышленного использования сварочной ро-
бототехники связана с большими затратами средств и времени на подготов-
ку роботизированного сварочного производства. К ним можно отнести бо-
лее высокие требования к проектированию сварной конструкции, предна-
значенной для изготовления с применением роботов, проектирование
сборочно-сварочных приспособлений и сварочного инструмента, пригодных
для работы в составе сварочных РТК для изготовления конкретного изде-
лия. Много времени занимают программирование (обучение) сварочных
роботов, оптимизация и синхронизация их работы применительно к жест-
ким требованиям автоматических производственных линий.
Вместе с тем и первая, и, тем более, вторая группа проблем, препят-
ствующих широкому использованию сварочной робототехники в отечест-
венном сварочном производстве, может быть решена. Что касается чрез-
мерно высокой стоимости сварочных роботов, то это связано с тем, что
легкие роботы для дуговой сварки в России не производят. Роботы для
контактной сварки производят по лицензии фирмы KUKA, но системы
управления поставляются из-за рубежа. В настоящее время имеется воз-
можность организовать на отечественных заводах серийное производство
легких сварочных роботов для дуговой сварки, термического резания, ок-
раски. Разработаны и отечественные недорогие версии систем управления
роботами, реализованные с использованием массовых и дешевых плат
персональных компьютеров и работающие под управлением универсаль-
ных операционных систем.
Проблема резкого сокращения стоимости и сроков конструктивно-
технологической подготовки роботизированного производства успешно ре-
шается за счет возможного широкого применения рассматриваемых ниже
систем компьютерного проектирования и моделирования работы РТК. Та-
кие системы давно и широко применяются за рубежом, имеется успешный
опыт их использования и на крупных отечественных заводах.
Возможность и необходимость широкого применения роботизирован-
ных сварочных технологий подтверждается опытом автомобильной про-
мышленности, в которой сварочные роботы контактной сварки составляют
основу кузовного производства. Многие сотни таких роботизированных ра-
бочих мест имеются на каждом автомобильном заводе.
В роботизации дуговой сварки успехи гораздо более скромные, одна-
ко неожиданно появилось понимание того, что, как ни странно, многие
сварные конструкции сегодня вообще не могут быть изготовлены иначе, чем
с применением роботизированной дуговой сварки. Ранее некоторые такие
7.1. Содержание работ и структура автоматизированной системы 309
конструкции могли быть изготовлены с использованием ручной (или полу-
автоматической) сварки. При постоянном повышении требований точности
размеров, стабильные сварочные деформации, обусловленные большим ко-
личеством сварных швов в принципе не могут быть обеспечены при работе
сварщиков-ручников. В гл. 8 показано, что по сравнению с ручной сваркой
роботизированные сварочные технологии позволяют многократно умень-
шить разброс размеров сварных конструкций.
Основным потребителем промышленных роботов в настоящее время
является автомобильная промышленность, где они преимущественно ис-
пользуются для точечной контактной (около 80 %) и дуговой сварки. Усло-
вия жесткой конкуренции требуют от производителей как повышения каче-
ства продукции, снижения ее себестоимости, так и сокращения сроков под-
готовки производства. В связи с этим в автомобилестроении широкое
распространение получают универсальные и специализированные САПР,
которые позволяют связать воедино и автоматизировать процесс разработки
конструкции, подготовку производства и само производство. Благодаря
этому на ведущих автомобильных фирмах сроки освоения новой модели (от
дизайнерской модели до выпуска с конвейера) сократились до одного года -—
полутора лет.
При традиционном проектировании роботизированных производств,
когда указанные САПР не используются, наибольшие затраты связаны с уст-
ранением ошибок в расположении роботов. Обычно такие ошибки выявляются
уже после того, как оборудование изготовлено в металле. При этом оказыва-
ется, что некоторые точки (швы) являются недоступными д ля сварки вследст-
вие столкновений технологического инструмента с деталью либо недостижи-
мыми (при требуемой ориентации инструмента) в связи с ограничениями рабо-
чего пространства робота. Поэтому' в некоторых руководствах по
проектированию РТК сварки рекомендуется предусмотреть целую сетку кре-
пежных отверстий для основания робота, что позволяет корректировать его
расположение на фундаменте при наладке. Как показывает опыт автомобиль-
ного завода БелАЗ, устранение ошибок в проектах РТК, созданных без при-
менения специализированных САПР, может занимать до шести месяцев.
Большой трудоемкостью характеризуется и процесс программирова-
ния РТК, при котором технологические операции представляются в виде
последовательности движений робота и позиционера. Обычно каждое эле-
ментарное движение определяется как переход из одной опорной точки тра-
ектории в другую. Опорные точки задаются шестью параметрами (три де-
картовы координаты и три угла ориентации либо шесть координат звеньев).
Для каждого участка траектории задаются также способ интерполяции (ли-
нейная или круговая в системе координат звеньев) и максимальные значе-
ния скорости и ускорения. Кроме того, в программу включаются команды
310
7. Автоматизированное проектирование сварочных комплексов
управления технологическим инструментом и команды, определяющие спо-
соб сопряжения соседних участков траектории. При подготовке управляю-
щих программ для РТК используют два основных метода — ручное обуче-
ние и автономное программирование. В первом случае подготовка програм-
мы производится непосредственно на РТК, в режиме on-line-, оператор при
помощи пульта управления или задающей рукоятки последовательно пере-
водит робот из одной опорной точки в другую, записывая в каждой из них
информацию о координатах и выполняемых действиях. Во втором случае
программа создается без использования робота (в режиме off-line), а коорди-
наты опорных точек рассчитываются по чертежу или математической модели.
Программирование путем обучения на уже установленном оборудова-
нии дает удовлетворительные результаты лишь в условиях массового про-
изводства и при обработке простых деталей. Для сложных деталей, таких,
как сложная рама автомобиля, время программирования может достигать
нескольких месяцев. В некоторых случаях, например при роботизированной
сварке седлообразных патрубков, ручное обучение вовсе не позволяет дос-
тичь требуемого качества технологического процесса. Поэтому' более пер-
спективным является о^/ше-программирование, к числу достоинств кото-
рого относится возможность подготовки управляющих программ в процессе
проектирования технологических линий (задолго до того, когда роботы бу-
дут установлены в цехе) либо в процессе производства другой детали без
остановки РТК (при смене выпускаемого изделия). Однако о^/ше-програм-
мирование требует решения ряда новых задач, которые не возникают при
ручном обучении. К их числу относится обеспечение адекватности матема-
тических моделей, которая достигается путем калибровки — точной доводки
сгенерированной компьютером программы непосредственно на цеховом
производственном оборудовании.
Простейшая система р//-/л?е-программирования представляет собой
автономный модуль, включающий средства графического моделирования,
текстовый редактор и средства передачи управляющих программ роботу. Но
наибольшая эффективность от применения таких систем достигается при их
интеграции с САПР технологической подготовки производства. Поэтому
большинство специализированных САПР РТК обеспечивает и off-line-rvpo-
граммирование.
Первые специализированные САПР роботизированных технологиче-
ских комплексов появились примерно 30 лет назад. К ним относятся систе-
ма PLACE (McDonnel Douglas) в составе UNIGRAPHICS, модули
ROBOTICS в пакетах CATIA, CADDS и др. В это же время начались разра-
ботки подобных систем непосредственно в автомобильных компаниях
(Renault) и фирмах-поставщиках роботов (KUKA, FANUC), в университетах
и исследовательских центрах (Nottingham University/BYG Systems,
7.1. Содержание работ и структура автоматизированной системы 311
University of Illinois, Silma Inc.). Постепенно эти системы прошли эволюцию
от исследовательских пакетов, ориентированных на решение уникальных
задач (например, моделирования копирующего манипулятора космического
корабля Space Shuttle), до промышленных специализированных САПР, учи-
тывающих особенности конкретных технологических процессов сварки, ок-
раски, резания и т. д. и поддерживающих все имеющиеся на рынке типы
промышленных роботов и языки их программирования.
В настоящее время в зарубежной автомобильной промышленности
наибольшее распространение получили пакеты RobCAD (фирмы Techno-
matics Technologies), IGRIP (фирмы Deneb Robotics) и CimStation (фирмы
Silma).
В СССР работы по созданию САПР РТК начались в конце 1980-х го-
дов, когда фирма «Буран» предложила автомобильной промышленности
САПР РТК сварки РОБОМАКС, а фирма «Авторобот» — пакет AutoRob,
которые были ориентированы на IBM PC-совместимые компьютеры и гра-
фическую среду пакета AutoCAD фирмы Autodesk. При помощи указанных
пакетов были решены задачи технологической подготовки роботизирован-
ного сварочного производства для новых моделей автомобилей ВАЗ, ГАЗ
(пакет РОБОМАКС) и «Москвич» (АЗЛК, пакет AutoRob). В дальнейшем
работы по совершенствованию пакета AutoRob были приостановлены, а па-
кет РОБОМАКС развивается в направлении как совершенствования сущест-
вующих модулей, так и разработки новых (проектирование сварочных кле-
щей, сборочно-сварочной оснастки и др.).
На заводах России имеются инсталляции мощного пакета RobCad
американской фирмы Technomatics Technologies, включающего в себя об-
ширную, свыше 100 моделей, библиотеку роботов, развитые функции про-
ектирования сварочного инструмента, сварочной оснастки, различных робо-
тизированных комплексов. Большинство таких же функций поддерживает
отечественная разработка — программный комплекс РОБОМАКС, различ-
ные версии которого имеются на автомобильных заводах и на сварочных
кафедрах ряда вузов. Знакомство с комплексом РОБОМАКС полезно для
понимания возможностей мощных современных САПР, работающих на ос-
нове графического моделирования динамики работы технологического обо-
рудования. В связи с этим методику и технологию автоматизированного
проектирования сварочных РТК рассмотрим на примере этого программно-
го продукта, реализованного на платформах массовых моделей компьюте-
ров в операционных средах Dos и Windows. Комплекс программных средств
РОБОМАКС является инструментом для решения задач технологической
подготовки сборочно-сварочного производства. Объектами РОБОМАКС
являются РТК дуговой и точечной контактной сварки, а также линии точеч-
ной контактной сварки.
312
7. Автоматизированное проектирование сварочных комплексов
В РОБОМАКС используются понятия «проектирование изображения»
и «подготовка образа». Под «проектированием» понимается создание объ-
емного изображения объекта и готовых изображений комплектующих дета-
лей с дорисовкой недостающих элементов. «Подготовка» — это нанесение
на уже созданное изображение дополнительной информации (например,
сварных швов) и обработка графической информации, создание математи-
ческого образа изделия, с которым ведется вся последующая работа систем.
Подготовка образов всех элементов комплекса обязательна перед началом
работы расчетных программ.
Комплекс программных средств построен из нескольких систем, объ-
единенных идеей сквозного проектирования: на входе — исходные дан-
ные и образы деталей, а на выходе — готовая документация проекта и
управляющие программы работы оборудования.
Упрощенная схема взаимодействия систем и подсистем комплексов
графического проектирования и моделирования применительно к контакт-
ной точечной и дуговой сварке представлена на рис. 7.1.
Основной модуль — проектирование РТК — работает с базами дан-
ных и библиотеками
• сварочных роботов;
• управляемых манипуляторов изделия;
• сварочных клещей, горелок, резаков и другого инструмента;
• вспомогательных элементов окружения (например, ограждений,
элементов оборудования, шкафов управления);
• специально подготовленных образов свариваемых конструкций, за-
крепленных в сборочно-сварочных приспособлениях.
Другие подсистемы служат для подготовки данных этих основных
библиотек.
Подсистема, предназначенная для конструирования сварочной осна-
стки и формирования моделей, входящая в программный комплекс, но, как
и все другие подсистемы, имеющая возможность автономного использова-
ния, подробно рассмотрена в гл. 6.
Подсистема «сварочный инструмент» предназначена для подготовки
графических образов и формирования моделей сварочного инструмента,
обеспечивающих доступность к зоне сварки и исключающих столкновения
при заходе инструмента на свариваемый узел.
Подсистема «сварная конструкция» имеет целью создание образа
сварного узла из образов поверхностей и деталей, импортированных из
«внешнего» пакета (например, пакета CATIA). Детали собираются в узлы,
наносятся сварные точки и швы и готовится математический образ. Однако
возможна «сквозная» работа в среде AutoCAD с использованием пакета
AutoSURF фирмы AutoDesk без импорта данных об образе сварного узла.
Рис. 7.1. Структура программного комплекса РОБОМ АКС
7.1. Содержание работ и структура автоматизированной системы
314 7. Автоматизированное проектирование сварочных комплексов
С использованием большого объема данных вспомогательных под-
систем подсистема РТК предназначена для формирования компоновок
сварочных постов или РТК сварки. Она обеспечивает выбор модели робо-
та, манипулятора изделия, установку сварного узла вместе со сборочным
приспособлением на манипулятор, определение взаимного положения ро-
бота и манипулятора изделия относительно системы координат РТК. Вы-
полняется трехмерное моделирование как объектов РТК, так и движений
робота и манипулятора изделия со свариваемым узлом с учетом реально
действующих ограничений, накладываемых сварочной технологией, осна-
сткой, приводами подвижности робота и манипулятора. Подсистема обес-
печивает интерактивную работу с роботом при его обучении в составе
РТК. Задание и выполнение команд управления роботом и манипулятором
изделия в интерактивном режиме с графическим отображением их движе-
ний является необходимым условием эффективной работы пользователя с
системой как при компоновке РТК, так и при его программировании. Мо-
делирование обучения робота позволяет запомнить все положения робота
относительно сварного узла и включить их в технологическую программу.
Отладка технологических программ производится здесь же с использова-
нием идеальной модели РТК. Это облегчает и делает более эффективной
работу технологов-программистов. Последующую калибровку таких про-
грамм применительно к конкретному реальному технологическому ком-
плексу осуществляют на основе небольшого числа измерений, проводи-
мых с помощью самого робота на одном из сварных узлов.
Базы данных роботов и манипуляторов связаны со своими подсисте-
мами создания образов и моделей оборудования с возможностью моделиро-
вания и программирования его работы. На структурной схеме эти подсисте-
мы не показаны. При этом разработка моделей манипуляторов изделий и
запись их в базу данных доступна пользователям системы, поскольку в лю-
бом сварочном производстве, как правило, приходится разрабатывать или
покупать большое их количество самых разнообразных типов. Создание об-
разов роботов со всеми их реальными ограничениями и характеристиками, а
также с возможностью программирования ввиду сложности этой работы
остается за разработчиками системы.
Все подсистемы предназначены и для подготовки конструкторской
документации путем преобразования отработанных объемных моделей в
плоские проекции и доводки их до вида чертежей.
Структура комплекса РОБОМАКС состоит из комплекта каталогов,
подкаталогов и файлов, управление которыми осуществляется с помощью
меню и реализуется программами монитора. Примеры каталогов показаны
ниже.
РОБОМАКС — корневой каталог комплекса.
7.1. Содержание работ и структура автоматизированной системы 315
Подкаталоги:
главный системный.................................. SYSTEM
роботов..........................................ROBOT
собранных инструментов........................... TOOL
манипуляторов изделия............................POSITION
изделий.........................................WPIECE
сечений.......................................... SECTION
фурнитуры (неподвижных элементов) .................FURNITURE
прототипов приспособлений........................ FIXPROTO
пиктограмм ...................................... ICO
электродов сварочных клещей ..................... ELECTROD
электрододержателей сварочных клещей ............HOLDER
удлинителей и вылетов сварочных клещей .......... STRETCH
переходников сварочных клещей.................... TRANSIT
приводов сварочных клещей ....................... BODY
цилиндров сварочных клещей ...................... CYLINDER
сварных швов..................................... SEAMS
проектов оснастки................................FIXPROC
процессов (сведений о конкретной работе) .........PROCESS
системы столкновений ............................ IMAGE
В главном системном подкаталоге SYSTEM содержатся исполняемые
программные модули, реализующие основные функции комплекса Робо-
макс. В подкаталогах SEAMS, WPIECE и TOOL содержатся файлы исход-
ных данных сварных швов, математического образа изделия и инструмента
для решения задачи столкновений, графические образы и слайды. В катало-
ге IMAGE содержатся файлы подсистемы подготовки математических обра-
зов для задачи анализа столкновений. В подкаталоге POSITIONER содер-
жатся данные для создания моделей манипуляторов.
РОБОМАКС как система проектирования оборудования и оснастки
сварочного производства и моделирования ее работы в составе рабочей
ячейки обязана содержать прежде всего графические образы элементов и
компонентов в сборе как основу моделирования. Информация о них пред-
ставлена в различных форматах, и прежде всего 3£>-изображениями (DWG-
файлы).
Текстовая информация составляет базу данных. Она может использо-
ваться в нескольких режимах: как справочная, как поисковая для выбора
элемента и для практических расчетов различного характера. Очевидно, что
такая информация в полном объеме разнородна, велика и зачастую избы-
точна, способы ее представления разнообразны и она должна пополняться
постепенно: по мере разработки ее отдельных модулей — разработчиками,
во время практической работы — пользователями.
Виды сведений, содержащихся в базах данных:
316
7. Автоматизированное проектирование сварочных комплексов
• условные обозначения, включая габаритные контуры оборудования
и оснащения (стрелки направления движения и усилия, упоры, вентили и
точки подводки энергоносителей, проезд, тара, опоры и т. п.). Здесь содер-
жатся сведения, используемые в различных схемах: планировках, схемах
базирования, картах контроля, разводках и т. п.;
• 3£>-изображения (образы) элементов или единиц оборудования. Как
правило, они выполняют при моделировании ту же функцию, что и контуры
оборудования на неподвижных планировках, определяя габаритные размеры
и расположение элемента, но в пространстве. Поэтому ЗВ-образы обычно
имеют точные размеры, но упрощенную форму без подробностей. Здесь
очень важно специально отметить, что система, как правило, создает весьма
точные формы и размеры образов и работает с ними. Однако с целью эко-
номии вычислительных ресурсов при экранном моделировании движения
трехмерных объектов часто образы моделей на экране специально упроща-
ются, тем самым обеспечивается возможность работы системы на менее
мощных компьютерах и видеокартах;
• данные текстового или табличного типа (технические характеристи-
ки элементов, режимы, нормы, экономические сведения и т. п.), используе-
мые для выбора или расчета.
Функции базы данных:
• хранить сведения о стандартных машинах и элементах (покупных и
местных стандартизованных), реально существующих независимо от данной
системы;
• хранить справочную информацию пользователя для проведения
проектирования, расчетов, а также заказа на поставку деталей и комплект-
ного оборудования;
• накапливать результаты, полученные на разных этапах в данной сис-
теме;
• содержать сведения графического, текстового и численного характе-
ра (причем характеризующие не только элементы базы данных, но и техно-
логические режимы и нормативы);
• служить программным средством при проектировании для автома-
тизации поиска необходимых элементов сварочной оснастки по одному или
нескольким признакам (что значительно эффективнее сплошного просмотра
содержимого базы данных);
• служить программным средством для автоматизации формирования
массива исходных данных.
Каждому графическому образу элемента должны соответствовать его
технические характеристики, чертежи и контуры элементов. Технические
характеристики заполняются после создания ЗВ-образа элемента как поля
7.2. Подсистема подготовки образа сварного узла
317
данных определенных разделов и параметров. Содержание пунктов этих
полей можно редактировать.
Режимы и нормативы имеют форму таблиц и необходимы при раз-
личных расчетах (силовых характеристик, электрических параметров режи-
мов, мощностей и сечений, нормировочных расходов и экономических
сравнений).
Особенность «первичных» элементов подсистем инструмента и осна-
стки (электроды, вылеты, блочки, платики, зажимы и т. п.) заключается в
том, что они представлены лишь графическими изображениями. Готовые
компоненты (сварочные клещи, роботы, манипуляторы и т. д.) уже подго-
товлены как математические образы для работы программы анализа столк-
новений.
7.2. Подсистема подготовки образа сварного узла
Подсистема подготовки образа сварного узла (WorkPiece) предназна-
чена для подготовки графического образа и формирования математической
модели сварного узла или сварной конструкции. Эти данные будут исполь-
зоваться в подсистеме проектирования и моделирования работы РТК дуго-
вой, контактной сварки или термической резки. Следует заметить, что по-
следующее моделирование технологии полностью гарантирует ее работо-
способность и тем самым показывает возможность ее реализации как при
автоматизированных, так и при ручных операциях контактной или дуговой
сварки.
Графический ЗО-образ является исходным объектом для работы под-
системы и может формироваться в каком-либо универсальном графическом
пакете. Поскольку проектирование сварных конструкций в последние годы
все чаще выполняется с применением машинной графики, то и исходные
образы для загрузки в подсистему, как правило, имеются в наличии. Для
доступности системных функций эти образы в формате DWG должны быть
записаны в определенный каталог. Примеры исходных ЗО-образов сварных
конструкций для отработки технологии их роботизированной дуговой и
контактной сварки и лазерной резки показаны на рис. 7.2.
В подсистеме предусмотрены:
• средства нанесения и редактирования сварных швов и точек;
• база данных для хранения разработанных образов узлов и сварных
швов (точек);
• средства формирования модели для автоматического анализа столк-
новений;
318
7. Автоматизированное проектирование сварочных комплексов
г
Рис. 7.2. Примеры исходных 3£>-образов сварных конструкций:
а — задний борг грузового автомобиля ЗИЛ; б — сферический кожух; в — переходник; -
г — крыша микроавтобуса; д — боковина микроавтобуса; е — пол микроавтобуса
• функции нанесения одной или нескольких точек базирования и ко-
ординатных фреймов для точного ориентирования свариваемого изделия на
планшайбе манипулятора изделия в рабочей зоне сварочного робота.
В связи с существенной технологической спецификой дуговой и кон-
тактной сварки, связанной прежде всего с разными ограничениями отклонений
угловых параметров ориентирования сварочного инструмента относительно
поверхности свариваемого изделия, при первом определении узла как сварной
7.2. Подсистема подготовки образа сварного узла
319
е
Рис. 7.2. Примеры исходных 3£)-образов сварных конструкций (окончание)
конструкции нужно задать тип сварки по одному из трех вариантов: Аге — ду
говая, Spot — точечная контактная, Both — оба вида сварки.
320 7. Автоматизированное проектирование сварочных комплексов
После этого подготовляемое
свариваемое изделие может быть
воспринято другими подсистемами
только для работы с установлен-
ным заранее типом сварочного ин-
струмента.
Для подробного рассмотре-
ния методики подготовки образа
сварного узла воспользуемся кон-
кретным примером. Причем для
простоты и ясности описания в ка-
честве сварного узла возьмем ус-
ловную объемную конструкцию в
Рис. 7.3. Пример условной конструкции виде плоской пластины, на которой
для тестирования системы можно проварить шов как дуговой,
так и контактной точечной сваркой.
Для моделирования технологии эзу пластину удобно представить как сто-
рону прямоугольного короба, показанного на рис. 7.3. Такая условная свар-
ная конструкция удобна и для установки ее на любой сварочный стол или
манипулятор изделия.
На этом простом узле покажем методику подготовки с помощью рас-
сматриваемой подсистемы файла швов, слайдов, математических образов
для анализа столкновений и прочих сведений, необходимых для разработки
и моделирования технологии.
Как уже было сказано, ЗИ-образ сварной конструкции, записанный в
библиотеку базы данных, вызывается на экран для нанесения на него свар-
ных швов. После определения метода сварки (контактная — выбор Spot из
предлагаемого меню) активизируется специальное меню, через которое ве-
дется вся последующая работа.
Вначале на картинку узла наносятся основы для сварных швов в виде
линий или дуг в отдельном слое под названием SEAMLINE. Установка слоя,
в котором будут наноситься швы, выполняется с помощью подменю Seam
Base/Seams Layer.
Линии швов рисуются с использованием команд меню (для прямоли-
нейных — Seams Line и для круговых — Seams Аге) и привязываются к узлу
командами «объектной привязки». Для нанесения линии прямолинейного
сварного шва укажем мышью на выбранной поверхности его начальную и
конечную точки. При этом могут использоваться точки, уже имеющиеся на
этой поверхности изделия, либо указываются любые произвольные точки. В
каждой указываемой точке система ставит ее метку и формирует нормаль к
поверхности, как показано на рис. 7.4. По команде меню Seam Line и указа-
7.2. Подсистема подготовки образа сварного узла
321
Рис. 7.4. Формирование линии шва:
а — контактной сварки; б — дуговой сварки
нию крайних точек появляется на экране линия шва. Разворачивая узел в
пространстве под удобным ракурсом, можно проверить правильность поло-
жения линии шва.
Подготовленные таким образом линии основы с помощью подменю
Seam превращаются в сварные швы или в сварные точки. Для превращения
линий в швы к ним нужно добавить соответствующие атрибуты, определяе-
мые в диалоге.
Прежде всего формируемый сварной шов должен получить свое имя —
обозначение. В состав имени шва автоматически входит его тип и далее
любое удобное обозначение. Ввод имени выполняется в диалоге, но по
умолчанию система автоматически обозначает все швы, одновременно ну-
меруя их по порядку, как Arcseam-1 и т. д. или Spotseam-1 и т. д. При обо-
значении швов контактной сварки система попросит указать кромку дета-
ли, от которой впоследствии будут подходить к свариваемым точкам сва-
рочные клещи. После выполнения указанных действий вдоль шва
появляются координатные фреймы X, Y, Z, а на шве появляется надпись
Spotseam-1 (рис. 7.4, а). Ось Z, на экране зеленая, должна выходить по
нормали к поверхности узла, а ось Y, желтая, — навстречу направлению
подвода клещей. Правильность положения координатных фреймов шва
должна быть подтверждена, либо при дополнительном редактировании
следует внести необходимые изменения.
11 - 6705
322
7. Автоматизированное проектирование сварочных комплексов
Нанесенный на поверхность изделия сварной шов позволяет присту-
пить к работе с его отдельными точками. Система предлагает меню работы с
точками (Seam dots) с функциями:
добавить одну — Add;
добавить несколько — Multiple;
удалить — Remove.
Если на сварном шве нужно определить несколько сварных точек,
(выбрали Multiple), система попросит указать либо расстояние между точ-
ками, либо процент длины шва между отдельными равномерно располо-
женными точками. На запрос
Enter DISTANCE between dots, [mm or %]
введем 10 %. В этом случае 11 сварных точек будут установлены равномер-
но по длине шва (рис. 7.5).
При удалении всех или отдельных точек (Remove) список всех имею-
щихся точек автоматически помещается в боковое меню. Система просит
выбрать из бокового меню точку шва для удаления. Можно удалить и всю
линию шва. Для этого предусмотрена команда erase. Если шов сформирован
правильно, выбором пункта меню File\Date все данные о точках обрабаты-
ваются и записываются в базу данных.
Важным моментом подготовки образа сварной конструкции является
нанесение на поверхность узла точек базирования изделия на поверхности
сварочного стола или сварочного манипулятора. Их может быть несколько
для возможности переустановки свариваемой конструкции при сварке раз-
личных швов.
Рис. 7.5. Обозначение сварного шва
Для создания базовых то-
чек используется меню Base
contact\New... Система попросит
указать поверхность на сварной
конструкции, где будет распо-
лагаться точка крепления (Bot-
tom — дно, Тор — верх, Side —
сторона), задать имя этой базо-
вой точки и мышью показать
положение координатного фрей-
ма на указанной поверхности
узла. Далее система переходит к
редактированию положения точ-
ки контакта. Выводится преду-
преждение о требуемом направ-
лении Z-оси координатного
7.3. Проектирование и подготовка сварочного инструмента
323
фрейма и сообщение о возможности изменения положения точки крепления
(появляется меню с запросом о корректности положения фрейма):
Положение правильное? Move — двигать, Rotate — вращать.
Передвигая фрейм и разворачивая его, тем самым задаем точку и ось
базирования свариваемого узла и оси его ориентирования относительно
планшайбы. При подтверждении правильности позиции система рисует
специальный значок точки контакта голубого цвета.
Создание образа узла для проведения теста столкновений выполняется
через меню FileMmage... или вводом команды image в командной строке.
При этом создается DXF-файл узла и автоматически последовательно вы-
полняются стадии программы подготовки образа.
Полностью готовый графический образ узла сохраняется в базе дан-
ных системы. Он пригоден для использования его другими подсистемами
при отработке технологии сварки, проектировании и программировании ра-
боты сварочных РТК. Однако чаще всего такой подготовленный под сварку
образ реального узла или конструкции имеет мало смысла для решения
стоящих перед разработчиком реальных задач. Дело в том, что в реальных
условиях производства собранная под сварку конструкция поступает на сва-
рочный стенд вместе со сварочным приспособлением, которое, как правило,
многократно затрудняет выполнение сварочных работ. Поэтому изложенная
здесь на простом условном примере методика подготовки образа выполня-
ется обычно на изделии вместе со сварочным приспособлением. Исходный
образ весьма сложного изделия вместе со сборочно-сварочным приспособ-
лением был показан в гл. 6 (см. рис. 6.37).
7.3. Проектирование и подготовка сварочного инструмента
В составе пакета РОБОМАКС имеется САПР сварочного инструмен-
та, предназначенная для проектирования сварочных клещей и сварочных
машин контактной точечной сварки и проверки их функционирования при
выполнении технологических операций. Чаще всего это проектирование
сводится к интерактивной сборке инструмента и элементов оборудования из
набора уже имеющихся в базе данных (и в цехах) отдельных деталей. Реже,
при невозможности такого решения поставленной задачи, проектируются
оригинальные элементы с формированием конструкторской документации
для их изготовления.
От технических характеристик сварочных клещей и соответствия их
конструкции выполняемой задаче в большой степени зависит работоспо-
собность всего сварочного поста как автоматизированного, так и ручного.
и*
324
7. Автоматизированное проектирование сварочных комплексов
а б
Рис. 7.6. Сварочные клеши Х-образной конструкции:
а — общий вид; б — элементы клещей
Поэтому при проектировании роботизированного производства приходится
уделять особое внимание разработке сварочных клещей как одному из клю-
чевых моментов.
Конструкция клещей относительно проста. Встречаются два типа:
Х-образные и С-образные клещи. На рис. 7.6 приведен пример Х-образных
клещей разработки ЗИЛ для автоматизированной сварки. Конструкция кле-
щей этого типа обычно содержит кронштейн (тело) 1, рычаги 2, электродо-
держатели 3 и электроды 4 (рис. 7.6, а). Между электродом и электрододер-
жателем могут находиться удлинитель и переходник 5, а сжатие осуществ-
ляется пневмоцилиндром 6.
Все элементы сварочной оснастки имеют атрибуты (следы их обозна-
чений видны на рис. 7.6, б в виде надписей у каждого элемента), которые
при сборке проверяются и обеспечивают мгновенную автоматическую
сборку элементов в сборочный узел. Клеши собираются из образов элемен-
тов по посадочным поверхностям (коннекторам), для которых имеется оп-
ределенная дисциплина задания ориентации фреймов и их кодов. Этим
обеспечивается контроль сборки.
К механизму перемещения клещи крепятся через кронштейн 1 (см.
рис. 7.6, а), а в точку сварки подходит рабочая поверхность электрода, за-
даваемая фреймом TCP (Tool Center Point), определяющим расположение
самих клещей относительно свариваемой точки (рис. 7.7).
Конструкция клещей во многом определяет сложность манипуляций,
стабильность качества сварки и время простоя всего поста на устранение
неполадок, обслуживание и ремонт. И хотя она, как правило, не столь слож-
на, процесс проектирования клещей весьма непрост. Дело в том, что при
7.3. Проектирование и подготовка сварочного инструмента
325
Рис. 7.7. Точка сварки TCP
всей очевидности общих требований к
клещам (они должны обеспечить каче-
ственное выполнение всех «поручен-
ных» им сварных точек при макси-
мальной надежности и экономичности
работы), существует еще ряд требований.
Так, электроды, как элементы
быстро изнашиваемые, должны иметь
относительно простые формы, облег-
чающие их массовое производство,
иметь эффективное охлаждение, обес-
печивать быструю замену и обладать
стойкостью при высокотемпературном
контакте со свариваемым материалом.
При этом форма электродов должна вполне соответствовать свариваемым
кромкам узла, отбортовка которых может иметь минимально допустимые
размеры.
Другие элементы сварочной оснастки клещей — электрододержатели,
удлинители, переходники, скобы и т. п., — хотя и не являются быстроизна-
шивающимися, но также должны обладать по возможности простой формой
при минимальной массе и достаточной жесткостью для данных усилий и
вылетов при соблюдении эксплуатационных требований.
Элементы сварочной оснастки клещей должны быть максимально
унифицированы, иметь оптимальную номенклатуру, минимальную и доста-
точную для обеспечения универсальности применения, с одной стороны, но,
ограниченную для уменьшения издержек — с другой. Если номенклатура
элементов недостаточна, то нет универсальности применения и приходится
в ряде случаев проектировать оригинальные элементы, а если избыточна, то
трудно поддерживать ее в порядке — модернизировать и эффективно ис-
пользовать.
Отсутствие необходимой унификации сварочного оборудования кон-
тактной точечной сварки и составляющих его элементов приводит к значи-
тельным ежегодным издержкам на восстановление изношенных частей мед-
ных элементов клещей и машин вследствие оригинальности их конструкции
и трудностей в наладке производства этих элементов современными высо-
копроизводительными методами.
Унификация элементов сварочных клещей может быть затруднена от-
сутствием конструкторской документации или большой трудоемкостью ее
поиска в архиве, а отсутствие преемственности технических решений не
способствует повышению их качества и увеличивает сроки разработок.
Кроме того, определенную специфику накладывает применение сварочных
клещей в составе роботизированного производства.
326
7. Автоматизированное проектирование сварочных комплексов
Работа по унификации сварочной оснастки — это большой постоян-
ный труд, но он совершенно необходим для успешного проектирования.
Одной из составляющих является отработка конструкций соединений эле-
ментов оснастки. Они должны быть не только однозначно, плотно и надеж-
но состыкованы (для обеспечения точности, хорошей электропроводности и
герметичности соединения), но и прочно закреплены. Поэтому посадочные
поверхности оснастки оговариваются соответствующими дополнительными
стандартами предприятий, где приводятся их типы и размерные ряды.
Кроме поэлементного рассмотрения сварочной оснастки клещей не-
обходим анализ и расчет всей схемы механизма для обеспечения его техни-
ческих характеристик. В этом случае сварочный контур (клещевины) рас-
сматривается в паре с приводом (телом) клещей. Учитываются геометрия
клещевин и характеристики силового гидро- или пневмоцилиндра.
К телу клещей также предъявляется ряд дополнительных требований.
Оно должно не только раскрывать клещевины на определенную ширину и
сжимать их с определенным усилием, но и обеспечивать компенсацию не-
точностей положения кромок, а также быть по возможности модульным и
универсальным в плане замены или изменения положения фланца крепле-
ния к роботу или подвеске.
Полная проверка работоспособности клещей на доступность и дости-
жимость мест сварки возможна либо проверкой при отладке технологии на
реальном изделии, либо, что гораздо эффективнее, путем моделирования
работы клещей в составе сварочного поста. Необходимость ускорения под-
готовки производства при смене моделей автомобильной техники требует
мобильного решения всех задач.
САПР сварочного инструмента может использоваться для проектиро-
вания как клещей и машин для ручной сварки, так и клещей для роботизи-
рованной сварки. Проектирование — процесс творческий, все основные ре-
шения остаются за проектировщиком, но наличие ряда эффективных про-
грамм монитора значительно ускоряет и контролирует работу,
автоматизируя многие операции.
Размеры и форма элементов сварочных клещей и машин должны оп-
тимально соответствовать выполняемой технологической операции. Поэто-
му проектирование оснастки ведется путем ее набора из унифицированных
или оригинальных элементов с учетом целого ряда параметров:
• предварительного раскрытия между электродами;
• усилия их сжатия;
• положения сварного шва от кромки изделия;
• максимальной высоты сечения сварного соединения и др.
В подсистеме все разработанные блоки, детали вторичного контура и
другие детали, используемые при проектировании, хранятся в соответст-
7.3. Проектирование и подготовка сварочного инструмента
327
вующих библиотеках графических образов и базах данных текстовых и чи-
словых характеристик.
Типы сварочных клещей могут быть самыми разнообразными, хотя
избыточное разнообразие нежелательно. Их можно систематизировать по
следующим признакам:
• вид работы (роботизированная или ручная сварка);
• тип клещей (С-, Х-образные и пистолеты);
• класс (со встроенным трансформатором, без трансформатора);
• производитель (покупные, собственные);
• возможность сдвига (самоустанавливающиеся, жесткие);
• раскрытие (с дополнительным ходом, одно- и двухходовые);
• исполнение (одинарные, сдвоенные);
• привод (гидро-, пневмопривод);
• коннекторы тела клещей (цилиндрические, конические, винтовые).
Перечисленные признаки клещей присутствуют в базах данных внут-
ри сведений о каждой модели и вызываются по запросу или применяются
при поиске. Структура каталогов в этом случае используется с минималь-
ным количеством уровней с целью избежать дублирования данных и одно-
временно разделить оборудование разного типа.
Элементы сварочной оснастки клещей имеют также большое разнооб-
разие конструктивных исполнений, материалов и типоразмеров, поскольку
часто велико разнообразие свариваемых стыков. Следует заметить, что де-
ление на элементы является условным и зависит от самого пользователя,
поскольку каждый элемент в принципе можно поместить в любую из групп,
а количество групп изменить.
В базе данных имеются следующие стандартизованные элементы
клещей:
• электрод (классический и колпачковый);
• электрододержатель;
• штуцер (переходник-удлинитель);
• цилиндр (гидравлический, пневматический и пневматический встро-
енный специальный),
а также оригинальные элементы, входящие в состав клещей:
• вылет;
• рычаг-ось (для Х-образных);
• скоба (для С-образных);
• хомут-упор;
• кронштейн и т. п.
ЭЛЕКТРОД — изнашиваемый сменный элемент стандартной конст-
рукции. Контактирует с узлом и имеет один коннектор. Чаще всего воспри-
328
7. Автоматизированное проектирование сварочных комплексов
нимает центральноосевую нагрузку и имеет посадку по конусе 1:10 без до-
полнительного крепления. Для коротких электродов применяется укоро-
ченный коннектор, а для больших диаметров — конус 1:5. При экцен-
трично направленных нагрузках используют конус коннектора 1:20 без
крепления. При нагрузках, направленных под углом более 30е к оси элек-
трода, обязательно дополнительное крепление (чаще всего, это гайка). В
этом случае применяют электроды, выполняющие одновременно функ-
ции электрододержателя. Однако это вынужденный вариант, когда нельзя
применить прямой электрод стандартной конструкции, и поэтому нежела-
тельный, так как деталь, подлежащая смене при износе, оказывается бо-
лее сложной.
ЭЛЕКТРОДОДЕРЖАТЕЛЬ — не изнашиваемый элемент между
электродом и последующими элементами (вылетом, скобой, рычагом). Чаще
всего он имеет гнутую фигурную форму.
УДЛИНИТЕЛЬ — проставка между электрододержателем и элек-
тродом. Обычно прямой, того же диаметра что и электрод. Применяется для
удлинения электрода стандартной длины.
ВЫЛЕТ — не изнашиваемый элемент между электрододержателем и
рычагом; элемент не сменный, чаще всего оригинальной формы. Использу-
ют в универсальных клещах при большом полезном вылете (например, в Со-
образных клещах). Вылет может отсутствовать в составе оснастки (при обя-
зательном наличии электрододержателя и электрода), но тогда:
• удлиняют рычаг (если клещи специальные, с большим полезным
вылетом);
• удлиняют электрододержатель (если полезный вылет оснастки не-
большой).
ПЕРЕХОДНИК — это, по сути дела, такой же электрододержатель.
который используется между первым электрододержателем или колпачком
и последующими элементами для придания оснастке нужной криволиней-
ной формы или перехода с одного коннектора на другой. Для случая ис-
пользования колпачковых электродов переходник обязателен, в паре с кол-
пачком он образует единицу, сходную по размерам и функциям классиче-
скому электроду.
ПРИВОД (ТЕЛО) клещей — это клещи без оснастки. Стандартные и
унифицированные приводы можно рассматривать как элементы клешей.
Один из принципов РОБОМАКС заключается в рациональной степе-
ни подробности изображения. В рассматриваемой подсистеме, в част.-с-
сти, для ЗО-образов это выражается в весьма подробном изображении эле-
ментов клещевин (электродов, электрододержателей) и в схематичес.сш
габаритном изображении тела клещей. Делается это для достовернссти
моделирования элементов, огибающих кромки узла, и для х меньше.-:»»
7.3. Проектирование и подготовка сварочного инструмента
329
объема памяти компьютера, занятого теми элементами, для которых под-
робности не нужны, но которые требуют больших дополнительных вычис-
лительных ресурсов при моделировании динамики работы оборудования.
Однако это так лишь для 3 D-образов. После проверки они преобразуются в
ортогональные проекции для формирования чертежей. В этом случае под-
робности должны соответствовать традициям конструирования и требова-
ниям к рабочим чертежам.
Для обоснованного выбора и конструирования элементов машин не-
обходимы расчетные программы. Расчету подлежат усилия и перемещения
(расчет привода) и электрические потери во вторичном контуре при опреде-
ленном режиме сварки (расчет мощности трансформатора). Поскольку эти
параметры зависят от размеров оснастки клещей, расчет в процессе подбора
элементов приходится проводить многократно.
Предусматривается также использование нескольких расчетных про-
грамм, позволяющих определять режимы (мягкий и жесткий) точечной и
рельефной сварки в соответствии с толщиной, материалом, характером по-
крытия свариваемых листов и их количеством в пакете. Оценивается доста-
точность мощности сварочного трансформатора и развиваемого усилия для
обеспечения требуемых режимов сварки, обеспечивается получение твер-
дых копий необходимых документов (расхода ресурсов, стоимостных, вре-
менных характеристик и пр.). Реализация этих функций связана прежде все-
го с созданием ряда баз данных текстовой и числовой информации. Они
разрабатываются для тех дегалей конструкции точечных машин, клещей и
элементов вторичного контура, для которых недостаточно только графиче-
ской информации, хранящейся в библиотеках образов. Выходными доку-
ментами работы расчетных алгоритмов являются совокупности исходных
данных и результатов расчетов.
Важно отметить, что принятие принципиальных предварительных
решений, как правило, выполняется до начала работы на компьютере. Де-
лают прикидочные расчеты, подготовляют чертежи, образы и т. п. и лишь
затем приступают непосредственно к конструированию и моделированию.
Исходными данными для САПР сварочного инструмента являются:
• техническое задание на разработку (с указанием производительно-
сти линии/участка, приложением планировок, технологии и прочих основ-
ных условий заказчика);
• комплект чертежей свариваемого узла (сборочные, сварочные и де-
талировки с сечениями свариваемых стыков);
• ЗО-образы узлов, деталей и сечений стыков;
• образы и чертежи сборочно-сварочных приспособлений.
Анализ исходных данных и выработка предварительных решений по
всей гамме клещей линии/участка предусматривает:
330
7. Автоматизированное проектирование сварочных комплексов
• анализ технического задания с целью составления общего представ-
ления о задачах и специфике данного производства;
• нанесение на чертеж сварного узла:
- габаритных изображений зажимных элементов приспособления, по-
падающих в зону сварки,
- швов/точек сварки, выполняемых роботами данного участка/линии
(прочие точки данных швов, выполняемые при прихватке/доварке по-
мечаются другим цветом),
- анализ чертежей узла (прежде всего сечений свариваемых стыков и
их пространственных положений) с целью предварительного опреде-
ления габаритных размеров оснастки клещей (вылет, ход, раствор),
- определение режимов сварки на основании данных о стыках (тол-
щине листов, материале и покрытии, диаметре сварной точки): силы
тока, силы сжатия, времени цикла на точку,
- прикидочный (укрупненный) расчет трансформатора и выбор его
марки,
- расчет соотношений длин рычагов и привода; выбор его марки;
• предварительный выбор:
- типов клещей для каждого стыка,
- марки тел клещей (если клещи покупные),
- оснастки клещей (при этом предпочтение отдается опробованным,
традиционным решениям, имеющимся в наличии у заказчика);
• предварительное разбиение швов/точек:
- по каждому сварочному посту,
- по типам клещей (число типов клещей должно быть меньше числа
постов или равно ему) с учетом примерно равного числа точек на один
пост и однотипности их сечений (это — признак максимальной произ-
водительности линии), с учетом перекрытия зонами промышленных
роботов выполняемых швов и расположения роботов в РТК и т. п.
Производится заполнение соответствующей таблицы;
• анализ ранее подготовленного на компьютере образа сварного узла.
Завершение этапов принятия предварительных решений позволяет пе-
реходить собственно к проектированию инструмента с помощью рассмат-
риваемой автоматизированной системы. Организация этих работ поясняется
структурной схемой, показанной на рис. 7.8, и предусматривает следующие
варианты действий:
• поиск уже разработанных клещей для выполнения рассматриваемой
совокупности швов и точек;
• модернизацию имеющихся в базе данных клещей;
• сборку новых клещей из уже разработанных деталей для имеющейся
совокупности швов;
7.3. Проектирование и подготовка сварочного инструмента
331
Рис. 7.8. Возможные варианты работы системы автоматизированного
проектирования сварочных клещей
• проектирование недостающих деталей для выполнения сварки рас-
сматриваемых сечений и сборку их с уже имеющимися деталями.
Рассмотрим эт и варианты подробнее.
При поиске уже разработанных клещей для сварки новой совокупно-
сти швов возможны три уровня выбора клещей из базы данных.
1. Просмотр базы данных или автоматический поиск и выбор клещей
по их техническим (числовым) характеристикам: проему клещевин, усилию
сжатия и прочим параметрам.
2. В графическом режиме — по «множеству сечений», когда на экран
вызываются совмещенные по координатам сварных точек изображения сра-
зу всех сечений стыков, подлежащих сварке данным инструментом. Изо-
бражение клещей совмещается с «множеством» и становится ясно, подходят
ли они для сварки этой гаммы стыков или нет.
3. Аналитическим перебором: автоматическая «пристыковка» вы-
бранного множест ва клещей к множеству сварных точек и получение твер-
дых копий результатов перебора.
Как следует из рис. 7.8, выбор клещей в сборе завершается проверкой
их работоспособности на доступность к свариваемым стыкам, которая мо-
жет выполняться:
332
7. Автоматизированное проектирование сварочных комплексов
• по «внутреннему пространству» клещей;
• по «наружным» (для клещей) габаритам проемов узлов (окна, двери
кузова) и прочим поверхностям.
Подсистема проектирования сварочного инструмента обеспечивает
проверку доступности клещей к свариваемым соединениям (с возможно-
стью варьирования технологических параметров) и их ориентации относи-
тельно этих соединений. Математический и графический образы клещей
далее будут переданы в подсистему проектирования сварочных РТК с це-
лью проведения дополнительной проверки достижимости и отсутствия
столкновений в процессе подвода-отвода клещей и сварки с помощью робо-
та. Смысл моделирования заключается в оперативной всесторонней провер-
ке принятых конструктивных решений.
Если вновь свариваемые соединения по толщине, качеству покрытия и
количеству листов в пакете не отличаются от тех, для сварки которых была
разработана сварочная оснастка, то решается также и технологическая зада-
ча обеспечения этой оснасткой требуемых режимов сварки.
Поиск и сборка в новые клещи уже разработанных элементов (см.
рис. 7.8) во многом аналогичны рассмотренному выше варианту проверки
готовых клещей. Здесь тоже начинают с подбора готовой оснастки и, если
ни одна из них не подходит без изменений, выбирают такие элементы, из-
менение которых может быть выполнено наиболее просто. Это электроды,
переходные втулки, удлинители, электрододержатели, вылеты.
После того как на экран вызвана совокупность сечений швов и один
из вариантов оснастки, элементы, подлежащие замене, убираются и на экра-
не остаются сечения швов и та часть оснастки, которая не требует измене-
ний. Модель заносится в память как основа для новой разработки. Из соот-
ветствующих библиотек выбираются необходимые элементы и собираются
в единое целое непосредственно с сечениями узлов и имеющейся частью
оснастки, либо в некоторой промежуточной модели производится сборка в
узлы, а затем собирается все вместе.
Для подбора подходящих элементов оснастки может понадобиться
многократный перебор. Если удается подобрать имеющиеся элементы, то
такая оснастка запоминается как новая и для нее возможны все проверки,
указанные выше.
Проектирование недостающих деталей и сборка их с уже имеющими-
ся производится, если не удается подобрать подходящие элементы оснастки
из числа имеющихся. Необходимо разработать их вновь и собрать воедино.
Работа заключается в кропотливом наполнении базы данных и мобильном
опробовании получаемых вариантов решений, подходящих для конкретного
случая применения. Затем выбирается лучший из них.
7.3. Проектирование и подготовка сварочного инструмента
333
Каждый конструктивный элемент клещей должен быть подготовлен
следующим образом:
• прорисован в соответствии с требованиями подсистемы подготовки
математического образа для проведения анализа столкновений;
• сформированы фреймы концов элемента для последующей графиче-
ской сборки с другими элементами в единую конструкцию;
• сформированы коды присоединительных поверхностей элемента
(коннекторов) для последующего контроля собираемости и стыковки раз-
личных элементов;
• занесены в поля баз данных конструктивно-технологические пара-
метры элемента.
Фреймы элемента и коды присоединительных поверхностей (коннек-
торы) формируются в виде атрибутов AutoCAD и заносятся в DWG-файл
элемента программами подготовки элементов.
Каждый элемент условно имеет две стороны: верхнюю — Up-side и
нижнюю — Down-side.
В системе «сварочный инструмент» предусмотрены несколько вари-
антов ввода фреймов крепления элементов:
• ввод фрейма во вновь создаваемый элемент в режиме черчения;
• ввод фрейма в элемент, участвующий в сборке;
• трансляция фрейма с соседнего элемента в сборке с учетом согласо-
вания кодов коннекторов.
Элементы сварочной оснастки в системе хранятся порознь и могут
применяться в любом наборе. Поэтому обозначается каждый коннектор, а
не их пара. В паре должны быть внутренний и внешний коннекторы. При
этом проверяются только i юсадочные поверхности, а не крепежные.
Кроме кодов, характеризующих размеры, коннекторы обозначены
векторами систем координат (фреймами), определяющими их положение на
элементе. Фреймы задаются на этапе подготовки элементов.
Обозначение кодов:
X XX X — полное обозначение (буквы и цифры),
12 3
где 1 — внешняя или внутренняя поверхность: F -— внешняя, М — внутренняя;
2 — диаметр элемента в миллиметрах для метрической резьбы: 10, 11,
13, 16, 20, 25, 32, 40, 50 .. — натуральное число из ряда СТП ВАЗ, или 1/2,
3/8, 7/8, 1/0, 2/0... — в дюймах для дюймовой резьбы;
3 — конусность или спецсимвол (0 — цилиндрическое соединение, 1 —
конусность 1:10, 2 — конусность 1:5, 3 — конусность 1:20, К — конусность
1:10 или 1:5 короткое; М — метрическая резьба и т. п.).
Примеры обозначений, принятых на ВАЗе:
334
7. Автоматизированное проектирование сварочных комплексов
F201 — внешний диаметр 20 мм, 1:10 (для осевой нагрузки),
М322 — внутрений диаметр 32 мм, 1:5.
В рамках этих четырех символов можно закодировать различные кон-
некторы.
Конструирование элементов клещей. Поскольку создание
элементов сварочной оснастки клещей эффективнее выполнять с исполь-
зованием параметризации, то, безусловно, работать следует с применением
программного комплекса Mechanical Desktop. Последовательность действий
при рисовке в среде ACAD или AMD на конкретном примере подробно рас-
смотрена в § 1.5. Твердотельное solid-представление позволяет объединять и
вычитать объемы, строить разрезы и сечения, получать пересечения поверх-
ностей.
Сформируем в качестве примера изображение электрода диаметром
20 мм со сферическим концом и коническим коннектором. Для начала
нарисуем на листе бумаги эскиз электрода в виде набора основных
составляющих его примитивов и нанесем их размеры или координаты
относительно любых осей координат. Операции конструирования удобно
выполнять в пользовательской системе координат, совпадающей с
плоскостью экрана (о ее расположении говорит пиктограмма в углу экрана),
а примитивы изначально помещать в точке 0 системы координат.
Формирование примитива (цилиндра) выполним командами меню
Command: cylinder
EllipticaV<center point> <0,0,0>
Diameter/<Radius> 10
Center of other end/<Height> 40
Отрисуется цилиндр, у которого нижний торец расположен на
плоскости XY, а его ось совпадает с осью Z. Для формирования прими-
тива (сферы):
Command: _ sphere
Center of sphere <0,0,0>
Diameter/<Radius> of sphere: 10
Отрисуется сфера, центр которой совпадает с точкой 0 системы коор-
динат.
Для формирования примитива (конуса):
Command: _conus
Elliptical/<center point> <0,0,0>
Diameter/<Radius> 8
Apex/<Height> 20
Отрисуется конус, у которого нижний торец расположен на плоскости
XY, а его ось совпадает с осью Z.
7.3. Проектирование и подготовка сварочного инструмента
335
Фронтальная проекция изображений показана
на рис. 7.9. Командой меню поместим конус на верх-
ний торец цилиндра:
Select object: — укажем конус нажатием правой
клавиши мыши
Base point or displacement: 0,0,0
Second point of displacement: 0,0,40,
где 40 — высота цилиндра. Конус перерисуется в
другом месте.
Усечем конус, для чего зададим уровень над
его торцом 50 мм. Удалив лишнюю часть конуса и
объединив все три примитива командой меню, указав
их мышью, увидим результат выполненных операций
(рис. 7.10, а). Добавим к изображению сферического
конца электрода изображение цилиндра любого раз-
мера таким образом, чтобы он пересекал электрод
(рис. 7.10, б). Удалим объем цилиндра и получим со-
ответствующее изображение электрода (рис. 7.10, в).
Рис. 7.9. Отрисовка
конуса электрода
В другом примере изобразим электрод в виде
эксцентрично обточенного цилиндра. Для этого
сформируем два примитива: цилиндр и второй при-
митив, полученный путем вращения некоего замкнутого профиля, сформи-
рованного относительно цилиндра. Построение профиля цилиндра, обра-
Рис. 7.10. Доработка формы электрода:
а — результат построения; б — отрисовка цилиндра; в — изображение электрода
336
7. Автоматизированное проектирование сварочных комплексов
Рис. 7.11. Исходный контур
для построения электрода
зующего контура и положение оси обкручи-
вания показано на рис. 7.11. Обкручивая этот
контур вокруг оси, примитив будет отрисован
в виде «солида» (рис. 7.12, а, б). Аналогич-
ным образом можно получить и другие фор-
мы электрода, например, эксцентричной об-
точкой электрода (рис. 7.12, в).
Для иллюстрации подготовки и сборки
элементов можно взять два простых примити-
ва — цилиндра, поскольку сборка любых более
сложных объектов выполняется аналогично.
Сформировав цилиндр как описано выше, дадим команду меню для
задания фреймов присоединительных концов элемента, и появится меню
интерфейса (рис. 7.13) для установки систем координат, которые следует
расположить следующим образом:
• для «верхней» стороны элемента (Up-side): ось X — наружу от тор-
цевой поверхности элемента;
• для «нижней» стороны элемента (Down-side): ось X — внутрь эдеме! i га;
• для обеих сторон: ось Y — в направлении внутреннего проема клещей.
В нашем случае для поворота фрейма в нужном направлении отме-
тим Y. Система спросит о значении угла поворота, где зададим 90°.
Enter a angle of rotation aroud Y-axes (yellow) 90.
Обозначим элемент как Elcctrod (рис. 7.14, а), а сторону — как Up-side
(рис. 7.14, б).
Для задания второй («нижней») стороны элемента в другом меню
(рис. 7.15) отметим Origin. На запрос системы введем новые координаты:
“Enter a new position” -40,0,0.
Рис. 7.12. Получение требуемых форм электрода:
а — образующий профиль второго примитива; б — поверхность, полученная после
отрисовки; в — пример более сложной поверхности
7.3. Проектирование и подготовка сварочного инструмента
337
Select ionrf.'
Your Choise
flIternat ives:
View ’<]
x ; ;
E
£ ; »
| jDDUcs ijh
$ . Show < П OK Ы < Cancel j
Vour Choise
Alternatives?
lectrade
Holder j
Stretcher i ;
I .Transitinner
| Body _______________ £*_
A , Show < j i OK j. Canoe J |
Рис. 7.14. Меню определения параметров элемента:
Рис. 7.13. Меню установ-
ки системы координат
а — обозначение элемента; б— назначение ориентирования
В меню (см. рис. 7.14) выберем позиции Elcctrod и Down-side, а на за-
прос системы о коннекторе, введем его обозначение, например:
Enter type of the Connection : F121
На экране отразится электрод с обозначением обоих коннекторов. За-
помним образ под именем HOL01. Система автоматически загрузит поле
технических характеристик внешней базы данных. Заполним строку и вый-
дем из базы данных. Информация будет записана совместно.
Аналогичным образом сформируем образ электрододержателя Holders
в виде цилиндра с коннек-
торами М121 и F24M у
верхней и нижней сторон
соответственно и запом-
ним под именем HOL02.
Командой меню
Working\Opcn (Insert) вы-
зовем оконный интерфейс
базы данных (рис. 7.16).
Holder
Selection j
Your Choise
Alternatives:
Brig in
ipoints
Intities
lieu
| Shou < [ | OK L^| j Cancel |
! By Filter
I Open/Insert
‘ F -List 11 By Kane
[ 3D/2D |
I Too l
, Electrod
lolder
- iStretcher
J .Trans it inner
Body
Cyl inder
I OK J j Cancel | jHelp.., |
Рис. 7.15. Меню определе-
ния нижней стороны
Рис. 7.16. Оконный интерфейс базы данных
элементов сварочных клещей
338
7. Автоматизированное проектирование сварочных комплексов
Для того чтобы загрузить сформи-
рованный ранее элемент, обозначим
его группу (например, Holder), назна-
чим режим Insert, и выберем элемент
(например, HOL02). Аналогичным
образом загрузим сформированный
ранее электрод HOL01. Оба элемента
появятся на одном экране (рис. 7.17).
Соберем эти элементы воедино,
для чего на запросы системы {Select
object:) поочередно укажем объекты
щелчком мыши. Высветится меню оп-
ределения порядка сборки (рис. 7.18),
где выберем Down-Up (соединение
нижней стороны первого элемента с
верхней стороной второго). Элементы
соберутся (рис. 7.19), если их коннекто-
ры соответствуют друг другу (напри-
мер, F121 и М121). В противном слу-
Рис. 7.17. Исходные элементы чае, система сообщит о несоответствии
для сборки коннекторов с указанием их кодов.
Подготовка образа привода клещей предусматривает задание опре-
деленных атрибутов с целью упрощенного моделирования раскрытия кле-
щей и расчета усилия сжатия в зависимости от технических характеристик
цилиндра и взаимного расположения точки сжатия электродов, центрально-
го шарнира и силового цилиндра. В качестве примера здесь приводится
сварка задней стенки кабины грузовика «Газель» с использованием соответ-
ствующих сварочных клещей.
Командой меню вызовем оконный интерфейс базы данных, показанный
на рис. 7.16. С его помощью выводим на экран
графическое изображение тела клещей body —
WWW — без обозначений коннекторов и оси
вращения клещевин (рис. 7.20). Изменим ра-
курс изображения на plan и его масштаб. Ко-
мандой меню вызовем интерфейс систем коор-
динат осей «реперных» точек (рис. 7.21). В
данном случае для тела клещей body с помо-
щью команды меню зададим тип положения
оси вращения клещевин Х-образных клещей
Рис. 7.18. Меню определения
порядка сборки
как X-type. Мышью укажем положение оси на
образе тела клещей. Появится фрейм оси, ори-
7.3. Проектирование и подготовка сварочного инструмента
339
ентацию которого пока не будем менять. Ось Z должна совпадать с осью вра-
щения клещевин. Командами меню зададим фреймы присоединительных кон-
цов body в последовательности, описанной выше для электродов и электродо-
держателей, учитывая при этом следующую особенность body: оси X обоих
коннекторов (условно названных «верхним» и «нижним») должны быть распо-
ложены «наружу» от тела. Запишем образ body под именем WWM. Теперь эле-
мент будет доступен для сборки клещей.
Рис. 7.21. Меню назначения по-
ложения осей клещей
Рис. 7.20. Образ тела клещей
340
7. Автоматизированное проектирование сварочных комплексов
Рис. 7.22. Выбранные элементы клещей
С помощью диалогового окна (см. рис. 7.16) получим на экране нуж-
ные элементы клещей (рис. 7.22):
Body —WWM
Transitioner — WWW05 и WWE
Electrod — WW и WW00
Выполним сборку этих элементов, поочередно указывая сначала body, а
затем верхний (изогнутый) электрододержатель transitioner. Высветится ме-
то порядка сборки, где выберем Up-Down — соединение верхней стороны
первого элемента с нижней стороной второго. Элементы соберутся, если их
коннекторы соответствуют друг другу (М30М и F30M). Если соответствия
коннекторов нет, то элементы не соберутся и система сообщит, почему.
Если элемент присоединился неправильно в результате нарушения
последовательности сборки, необходимо повторить манипуляции. После
сборки всех элементов клещи предстанут в виде, показанном на рис. 7.23.
Специальной меткой указано положение оси вращения клещевин. Моде-
лирование раскрытия клещей можно получить, активизируя верхнюю
клещевину путем последовательного указания всех ее элементов по за-
просу системы:
What arm of Tool you want collect: :<Upper>Down/Cancel? : U
..Select the collection of upper arm.
Select objects: — укажите мышью элемент клещевины, к которому
следует присоединить другой элемент
Select objects: — укажите подвижный (присоединяемый) элемент и т. д.
Правой клавишей мыши завершается набор элементов одной клещеви-
ны. Манипуляции следует повторить для активизации и нижней клещевины.
7.3. Проектирование и подготовка сварочного инструмента
341
Рис. 7.23. Клещи в закрытом состоянии
Раскроем клещи путем поворота, например, обеих клещевин на угол а =
= 10°. По запросу системы введем значение угла раскрытия клещевин:
Enter the rotate angle around axis: 10
...Select the any body.
Select objects: — система попросит указать тело (body) данных кле-
шей, поскольку их может быть на экране несколько. Так же система дает
запрос, какие клещевины должны поворачиваться (верхняя, нижняя, обе кле-
щевины):
What element of Tool you want rotate: :Both<Upper>
Down/Cancel?:B
Клещи раскроются (рис. 7.24) в соответствии с заданными условиями.
Их можно варьировать с целью поиска наиболее приемлемого варианта.
Рис. 7.24. Клещи в раскрытом состоянии
342
7. Автоматизированное проектирование сварочных комплексов
Рис. 7.25. Изделие со сварным швом и линиями плоскостей
сечений, проходящими через свариваемые точки
Раскрытые клещи можно запомнить командой save и в таком виде использо-
вать при моделировании работы сварочного РТК.
Модернизация клещей может быть следующей ступенью работы по их
проектированию. Необходимость модернизации, как правило, появляется при
проверке возможности применения конкретного варианта сварочных клещей
для выполнения сварных швов на конкретном изделии. В качестве примера
рассмотрим возможность использования полученного выше варианта клещей
для сварки точечного сварного шва на задней стенке кабины грузовика «Га-
зель». Изделие со сварным точечным швом и сечениями, проходящими через
свариваемые точки, уже подготовлено по методике, рассмотренной в § 7.2,
имеется в базе данных и может быть загружено на экран (рис. 7.25).
Поскольку при обозначении каждой сварной точки на свариваемой кон-
струкции была использована нормаль к поверхности изделия, это позволяет
легко совместить все сечения по положению точки сварки и нормали к поверх-
ности (рис. 7.26, а). С массивом свариваемых сечений легко совместить образ
выбранных сварочных клещей, которые будем подводить в зону сварки со сто-
роны нижнего края свариваемой стенки. На рис. 7.26, б видно, что вылет кле-
щей мал и для выполнения этих работ должен быть увеличен. Наиболее рацио-
нально выполнить эту задачу, используя массивы сменных деталей клещевин в
базе данных. Детали клещевин имеются на складе и могут быть использованы
быстро и без дополнительных затрат. В табл. 7.1 приведены примеры баз
данных элементов сварочных клещевин ряда автомобильных заводов. На
рис. 7.27 можно видеть ЗР-образы некоторых этих деталей.
7.3. Проектирование и подготовка сварочного инструмента
343
Рис. 7.26. Совмещение свариваемых сечений:
а— с точками сварки: б — со сварными клещами
Рис. 7.27. Примеры ЗО-образов элементов сварочных клещей в базе данных
344
7. Автоматизированное проектирование сварочных комплексов
Таблица 7.1. Пример базы данных элементов сварочных клещей
ELECTROD — электроды (колпачки) ГАЗ
Но- мер п/п Номер чертежа и файла в базе данных Эскиз Габариты D х L, мм Коннектор d, мм Количество типоразме- ров
1 0821-4525 — 16x20 12 1
2 0821-4533 L — 16x20 12 1
3 0821-4534 i-— 16 х 20 12 1
4 0821-4534-01 — 16x20 12 1
5 0821-4541 ч — 16x20 12 1
6 0821-4596 — 16x32 12 1
7 0821-4598 - 16x25 12 1
8 0821-4607 £ в 16x25 12 1
9 0821-4626 /~Тл \1 г 15 х25 14,5 1
10 0821-4626-01 —— 15x25 14,5 1
11 0821-4626-02 — 15 х25 14,5 1
7.3. Проектирование и подготовка сварочного инструмента
345
Продолжение табл. 7.7
Но- мер п/п Номер чертежа и файла в базе данных Эскиз Габариты D x L, мм Коннектор d, мм Количество типоразме- ров
12 0821-4629 "С — 16 x 30 15,5 1
13 0821-4707 16x36 15,5 1
i.
14 0821-6206 ЕЕ — - 16x22 12 1
15 0821-6206-01 Ш— 16x30 12 1
16 0821-6209 ь / 16x30 12 1
17 0821-6210 — 16x25 12 1
TRANSIT — удлинители электродов Г АЗ
Но- мер п/п Номер чер- тежа и файла в базе данных Эскиз Габариты D x L, мм Коннекторы dl - d2, мм Количество типоразме- ров
1 0821-6712 16x£ (38...224) 12...15,5 20
1 1 Г'1'l 1 ’
2 0821-7488 [ 1 t~ 16x7 (40...113) 12...15,5 11
3 0821-6717 EzS 20xL (68... 100) 12...25 3
— i- -1
4 0821-6713 — 16 x 68 эксцен- триситет 6...12 12...15,5 2
346
7. Автоматизированное проектирование сварочных комплексов
Продолжение табл. 7.1
HOLDER — электрододержатели ГАЗ
Но- мер п/п Номер черте- жа и файла в базе данных Эскиз Габариты осей, H*L, мм Коннекторы Л - dl, мм Количест- во типо- размеров
1 0821-7291 77x60 (40...70) 11,5...М27х2 4
2 0821-7291-01 1 43,5 х 60 11,5...М27х2 1
3 0821-7292-01 -02 77x60 (20... 30) угол 15 ° 11,5...М27 х2 2
4 0821-7293 77x60 (40...145) 15,5...М27х2 9
5 0821-7293-01 60x30 15,5...М27х2 1
6 0821-7294 77x70 (40... 70) Угол 15 ° 15,5...М27х2 4
7 0821-7294-01 30x70 (40...70) угол 15 ° 15,5...М27х2 1
8 0821-7295 fl 60x20 14,5...М27х2 1
7.3. Проектирование и подготовка сварочного инструмента
347
Продолжение табл. 7.1
Но- мер п/п Номер черте- жа и файла в базе данных Эскиз Габариты осей II хЦ мм Коннекторы Л - сП, мм Количест- во типо- размеров
9 0821-7296 20x1, (60... 100) угол 15° 14,5...М27х2 2
10 0821-7300 /7x60 (50...95) Угол 15° 15,5...М27х2 5
11 0821-7302 25 х£ (60... 70) угол 15° 15,5...М27х2 2
Электроды (классические) ЗИЛ
Но- мер п/п Номер черте- жа и файла в базе данных Эскиз Габариты D х L, мм Коннектор d, мм Количест- во типо- размеров
1 33505 20 xL (55...115) 19,5 5
(/—V” Н:
2 33506 0 20 xL (55... 80) 19,5 5
4 —
3 33507 16x65 15,5 1
4 75741 16х£ (40... 105) 15,5 9
348
7. Автоматизированное проектирование сварочных комплексов
Продолжение табл. 7.1
Но- мер п/п Номер черте- жа и файла в базе данных Эскиз Габариты D x L, мм Коннектор d, мм Количество типо- размеров
5 75742 16 x L (45... 130) 15,5 7
6 75743 1—L 16 x L (36...55) 15,5 8
7 75744 —^4 =~~~j (20-40) DxL (40... 105) 15,5 7
8 75753 J j=l (20-40) DxL (70... 90) 24,5 4
9 75754 j==j 25 x L (70...90) 24,5 2
10 75755 12xL (25... 70) H,5 5
11 75756 - -J ^3 12xL (25...70) 11,5 5
7.3. Проектирование и подготовка сварочного инструмента
349
Окончание табл. 7.1
Штуцеры (переходники-удлинители) ЗИЛ
Но- мер п/п Номер чер- тежа и файла в базе данных Эскиз Габариты, D х L, мм Коннекторы dl - dl, мм Количест- во типо- размеров
1 75745 - — (27-40,6) Oxi (20...42) а) КГ(1/2; 3/4;1)" б) 11,5; 15,5; 19,5; 24,5 8
2 75788 (22; 25) Z)x£ (50... 125) а) КГ 1/2" б) 11,5; 15,5 6
3 75792 РДР “II 25 xZ, (ПО...130) а) 24,5 б) 19,5 2
Рассмотренное здесь проектирование 3/)-образов любого сварочного
инструмента дополняется и завершается формированием блока данных,
обеспечивающих использование образа этого инструмента в составе модели
универсального роботизированного сварочного технологического комплек-
са. Специальные функции подсистемы проектирования сварочных инстру-
ментов обеспечивают:
• привязку (базирование) фланцев крепления инструмента к фланцу
кисти сварочного робота, позволяющую автоматически стыковать образ ин-
струмента с образом сварочного робота;
• привязку и базирование специального координатного фрейма на ра-
бочей поверхности любого сварочного инструмента для автоматического
позиционирования сварочного инструмента относительно сварных швов и
точек свариваемого изделия;
• формирование специальной математической модели инструмента
для системы анализа столкновений инструмента с любыми элементами ком-
понентов оборудования универсального сварочного РТК.
Место контакта инструмента с фланцем робота располагается в миро-
вой системе координат с выполнением следующих правил:
• геометрический центр присоединительной плоскости фланца инст-
румента совмещается с началом мировой системы координат;
• присоединительная плоскость фланца инструмента располагается в
плоскости XY мировой системы координат;
350
7. Автоматизированное проектирование сварочных комплексов
• ось Z должна быть направлена «внутрь» инструмента;
• ось X должна быть направлена таким образом, чтобы при креплении
инструмента к фланцу робота она была направлена вниз в исходном поло-
жении робота.
При определении места контакта клещей с фланцем робота с помо-
щью меню выбора поверхности контакта задается принципиальная ориента-
ция расположения фланца на нижней, верхней или боковой поверхности
тела инструмента. После того как для крепления проектировщиком опреде-
лена, например, нижняя поверхность тела сварочных клещей, в ответ на за-
прос системы о назначении имени места контакта:
Name ofbas:<BOTTOM_l>(‘*’ to list all names)?
лучше принять предложенный при этом вариант (BOTTOM-1). Определен-
ное место контакта автоматически поместится в начало мировой системы
координат в виде значка (на экране — голубого цвета), как показано на
рис. 7.28. Обычные функции перемещения или поворота этого координатно-
го фрейма позволяют уточнить координаты крепления. Принятая классифи-
кация привязок фланца крепления инструмента позволяет на одном свароч-
ном инструменте разместить два и более фланца крепления, что позволит
при проектировании технологии роботизированной сварки конкретных
сварных конструкций проверять различные варианты установки сварочного
инструмента на роботе.
«Рабочая точка» сварочного инструмента TCP (Tool Center Point) на-
носится в виде координатного фрейма. При этом необходимо придержи-
ваться следующих правил:
• начало координатного фрейма должно находиться в точке «сжатия»
сварочных электродов или на конце вылета сварочной горелки;
Рис. 7.28. Расположение точки базирования клещей на фланце робота
7.3. Проектирование и подготовка сварочного инструмента
351
Рис. 7.29. Расположение координатных осей в зоне сварки
• ось X фрейма TCP должна быть направлена против движения верх-
него электрода к детали при контактной сварке или вдоль оси сварочной
горелки в направлении от свариваемого изделия;
• ось Z направляется «наружу» от тела инструмента;
• ось Y дополняет тройку осей до правой.
Для определения позиции и ориентации рабочей точки клещей систе-
ма запросит имя TCP инструмента:
Tool Center Point пате:<ТСР_1>(‘*’ to list all names) ?:
По умолчанию обычно задают предложенный системой вариант (в
данном случае ТСР-1). На рис. 7.29 видно, что после коррекции ось X на-
правлена в сторону «верхнего» электрода, а ось Z — от тела клещей.
Математический образ инструмента, необходимый для проведения ана-
лиза столкновений, автоматически создается программой подготовки образа в
несколько стадий. Ход выполнения программ отображается на экране. Сохра-
няется он в том же каталоге, что и графический образ инструмента.
Командой меню полностью готовый образ клещей под некоторым име-
нем записывается в базу данных инструмента, пригодного для использования в
352
7. Автоматизированное проектирование сварочных комплексов
Рис. 7.30. Пример библиотеки сварочного инструмента
составе модели сварочного РТК. Примеры таких образов — моделей сварочных
клещей — в библиотеке сварочного инструмента показаны на рис. 7.30. При не-
обходимости на любую разработанную модель, имеющуюся в библиотеке, мо-
жет быть оформлен стандартный комплект конструкторской документации.
7.4. Сборка, программирование и моделирование работы
сварочного РТК
Подсистема проектирования сварочных РТК предназначена для сбор-
ки и отладки работы оборудования при сварке конкретных сварных узлов
или конструкций. Наиболее эффективно использование подсистемы для
проектирования не одиночных изолированных комплексов, а роботизиро-
ванных технологических линий. В этом случае возникают сложные задачи
группирования сварных швов и сварных точек и распределения их сварки
по отдельным рабочим местам. Компьютерное моделирование работы обо-
рудования каждого отдельного РТК позволяет за счет быстрой проверки
большого количества возможных вариантов найти в любом случае наиболее
удачное взаимное расположение элементов оборудования и изделия, а также
технологию и организацию работы. В конечном счете это обеспечивает наи-
высшую загрузку оборудования и, как следствие, минимально необходимое
его количество для устойчивой работы производства.
Проектирование, программирование и отладка работы РТК — завер-
шающий этап подготовки роботизированного производства, в котором исполь-
зуются ранее рассмотренные этапы подготовки данных. Отладка работы РТК
1.4. Сборка, программирование и моделирование работы сварочного РТК 353
тесно связана со свариваемым изделием и с расположением на нем сварных
швов. Сварные швы определяют выбор сварочного инструмента, сварочный
инструмент определяет тип сварочного робота. Размеры и масса изделия вместе
со сварочным приспособлением определяют требования к кинематике манипу-
лятора. Все это должно быть тщательно проверено, поскольку исключительно
высокая стоимость роботизированных технологий определяет и высокую сте-
пень ответственности принимаемых решений. Следует обратить внимание на
то, что часто возможность или невозможность реализации технологии на гро-
моздких технологических комплексах определяют лишь несколько миллимет-
ров расстояний между движущимися элементами механического оборудования.
Рассматриваемая подсистема проектирования сварочных РТК исполь-
зует библиотеки:
• свариваемых конструкций или узлов в том виде, в котором они будут
реально свариваться в условиях сварочного цеха, т. е., как правило, собранны-
ми и закрепленными в сборочно-сварочных приспособлениях. На этих сварных
узлах, подготовленных в соответствующей подсистеме (см. § 7.2), имеются
обозначения сварных швов, точек и осей базирования изделий на сварочных
столах или манипуляторах. Примеры образов сварных конструкций были пока-
заны ранее на рис. 7.2 и 7.3;
• сварочных инструментов, подготовленных по методике, изложенной
в § 7.3. Примеры сварочных клещей из библиотеки сварочных инструментов
показаны на рис. 7.30;
• образов моделей сварочных роботов, примеры которых показаны на
рис. 7.31. Здесь могут быть модели роботов, как уже имеющиеся в
Рис. 7.31. Примеры базы данных сварочных роботов
12 - 6705
354 7. Автоматизированное проектирование сварочных комплексов
Рис. 7.32. Внешний вид промышленного робота «Муравей»
производственных цехах предприятия, так и планируемые к приобре-
тению и даже новые, еще только разрабатываемые модели. В частно-
сти, на рис. 7.32 показана модель перспективного легкого робота «Му-
равей» с избыточной кинематической подвижностью, разработанного
лабораторией робототехники МГТУ—СТАНКИН;
7.4. Сборка, программирование и моделирование работы сварочного РТК 355
Рис. 7.33. Примеры позиционеров свариваемых изделий
• сварочных столов и управляемых манипуляторов различных типов,
грузоподъемности, габаритов и количества степеней подвижности. Некоторые
примеры манипуляторов из базы данных показаны на рис. 7.33;
• элементов окружения сварочных РТК, таких, как ограждения
(рис. 7.34), элементы цеховых колонн, габаритов оборудования, шкафов
управления и др.
Взаимодействие подсистемы проектирования сварочных РТК с пере-
численными библиотеками базы данных видно на структурной схеме про-
граммного комплекса РОБОМАКС (см. рис. 7.1).
С использованием графических образов и данных библиотек на осно-
ве моделирования в реальном масштабе времени динамики работы оборудо-
вания подсистема проектирования РТК позволяет выполнять большой объем
работ, с которыми обычно приходится иметь дело при подготовке роботи-
зированного производства вплоть до запуска в эксплуатацию автоматиче-
ских роботизированных технологических линий.
К этим работам относятся:
• выбор отдельных компонентов РТК и их сборка в единый техно-
логический комплекс. Сюда входят установка манипулятора, установка
изделия на планшайбу манипулятора, выбор и установка сварочного ро-
бота, выбор и закрепление на кисти робота сварочного инструмента, на-
12*
356
7. Автоматизированное проектирование сварочных комплексов
пример, сварочных клещей контактной сварки или горелок для дуговой
сварки;
• определение зон возможного размещения сварочного робота относи-
тельно манипулятора и свариваемого изделия с учетом достижимости всех
необходимых для сварки сварных швов;
• перемещение и установка сварочного робота в одно из допустимых
и в то же время удобных для проекгировщика положений относительно из-
делия;
• проверка доступности сварочному инсгрументу и сварочному робо-
ту всех необходимых для сварки сварных швов с учетом установки изделия
сварочным манипулятором в заданное пространственное положение, на-
пример в положение «в лодочку», «на подъем» для дуговой сварки углового
шва под углом к горизонту 10°;
• формирование программы управления сварочным роботом и мани-
пулятором, компиляция ее в коды системы управления;
• проверка работы всего комплекса по этой программе на отсутствие
каких-либо столкновений инструмента, робота, свариваемой детали и сва-
рочного приспособления за все время технологического цикла;
7.4. Сборка, программирование и моделирование работы сварочного РТК 357
• определение времени выполнения роботом и манипулятором полу-
ченной программы (времени цикла).
Для удобства освоения методики проектирования РТК воспользуемся
\ же рассмотренным выше простейшим условным примером сварной конст-
рукции в виде плоской пластины, на которой контактной сваркой необхо-
димо выполнить точечный сварной шов (см. рис. 7.5). Образ этого условно-
го изделия с нанесенными обозначениями сварных точек и точкой базиро-
вания на поворотном столе уже находится в библиотеке подготовленных
изделий и доступен для использования в рассматриваемой здесь подсистеме.
Быстрое нахождение и выбор образа сварного узла в библиотеке свар-
ных узлов завершаются его размещением на экране в любой произволь-
но указанной точке. Это первый компонент из состава проектируемого РТК.
Точно так же из меню соответствующих библиотек в любом порядке выби-
раются и размещаются в любых произвольных точках экрана все другие
требуемые компоненты РТК, такие, как сварочные клещи, сварочные горел-
ки, сварочный робот, манипулятор изделия. Удобство выбора компонентов
обеспечивается специальными экранными меню, в которых перемещение по
спискам сопровождается сменой слайдов соответствующего оборудования
(рис. 7.35, а, б).
Пример выбора и размещения на экране компонентов сварочного
РТК показан на рис. 7.36. Здесь следует сделать несколько замечаний.
Для отслеживания процесса комплектования компонентов РТК пополне-
ние их набора, появляющегося на рабочем экране, каждый раз сопровож-
дается автоматическим масштабированием картинки комплекса. Количе-
ство отдельных компонентов проектируемого РТК часто бывает большим
и может содержать, например, несколько сварочных инструментов, не-
сколько сварочных роботов, несколько манипуляторов изделий. Так, на
рис. 7.36 можно видеть, что выбраны сразу два сварочных инструмента:
клещи для контактной точечной сварки и горелка для дуговой сварки
проволокой в среде защитных газов. На свариваемом изделии ранее были
нанесены два сварных шва: шов дуговой сварки и точечный шов кон-
тактной сварки.
При проектировании РТК можно моделировать технологию сварки
различных видов и групп сварных швов. Однако, поскольку существующие
сейчас версии системы не поддерживают моделирование параллельных
процессов, при работе над проектом задачи следует выполнять последова-
тельно, каждый раз выбирая и активизируя в специальном списке-меню од-
но свариваемое изделие и одну группу сварных швов, один робот и один
позиционер. Выполнение этих действий сразу же сопровождается автомати-
ческой сборкой РТК. Изделие установлено на планшайбе вращателя а сва-
рочные клещи закреплены на кисти робота (рис. 7.37). На рисунке также
видно, что осталась незадействованной дуговая сварочная горелка, но она
358
7. Автоматизированное проектирование сварочных комплексов
OK -I .Cancel | Щр f
б
Рис. 7.35. Меню выбора компонентов РТК:
а — выбор робота; б — выбор манипулятора
7.4. Сборка, программирование и моделирование работы сварочного РТК 359
Рис. 7.36. Набор элементов для сборки РТК
Рис. 7.37. Результат автоматической сборки компонентов сварочного РТК
360
7. Автоматизированное проектирование сварочных комплексов
легко может занять место сварочных клещей на кисти робота. Два различ-
ных сварных шва в диалоговом режиме отнесены к двум разным массивам
швов, которым система по умолчанию присвоила имена DOTS1 и DOTS2. О
наличии двух отдельно рассматриваемых системой массивов сварных
швов/точек напоминают присутствующие на экране и размещенные произ-
вольно как некоторые отдельные компоненты РТК пиктограммы DOTS1 и
DOTS2. Важно отметить, что с указанными массивами связываются не толь-
ко свариваемые точки, но и сварочный инструмент.
После автоматической сборки компонентов роботизированной техно-
логической ячейки можно приступить к решению одной из главных и наи-
более сложных задач при проектировании РТК — к поиску правильного и
рационального взаимного расположения сварочного робота и свариваемого
изделия. Следует понимать, что эта задача имеет некоторое множество воз-
можных правильных решений. Выбор варианта должен оставаться за проек-
тировщиком, поскольку он прорабатывает варианты обслуживания ком-
плекса с выделением для этого рабочих зон, обеспечивает стыковку ком-
плекса с конвейерными и другими транспортными системами.
В автоматизированной системе предусмотрено выделение рабочего
пространства, в котором может быть осуществлен поиск всех допустимых
положений сварочного робота. Поскольку здесь возможно выполнение не-
скольких этапов, система каждый раз по умолчанию или редактированием
граничных координат формирует имя очередной создаваемой зоны поиска
решений (например, AREA-1), в которой ведется анализ возможных вариан-
тов. Кроме того, в указанной зоне поиска может отдельно рассматриваться
несколько возможных процессов сварки различных массивов сварных
швов с применением различных сварочных инструментов. Поэтому систе-
ма автоматически регистрирует отдельные технологические процессы,
присваивая им соответствующие имена, например ROBPOS-1, ROBPOS-2
и т. д. Пиктограммы обозначений этих процессов также присутствуют на
рабочем экране.
Процесс автоматического поиска в заданной зоне всех возможных по-
ложений сварочного робота относительно массива точек свариваемого изде-
лия выполняется с задаваемым шагом изменения координат. Он произво-
дится с учетом достижимости точек сварного шва без столкновения между
собой отдельных компонентов комплекса. При этом для каждой отдельной
точки шва анализ ее доступности сварочному инструменту выполняется с
учетом допустимого диапазона технологических углов установки сварочно-
го электрода относительно нормали к поверхности свариваемого изделия.
При контактной сварке электроды должны располагаться к поверхности из-
делия по нормали. Диапазон возможных углов (углы у) поворота сварочных
клещей относительно нормали, при которых отсутствуют столкновения ме-
7.4. Сборка, программирование и моделирование работы сварочного РТК 361
TOOt TESTING AND SELECTION FOR THE SPOT WELDING
Name of the current welding tool 't_ciak_n', total number of seam dots current dot 17 : 17
Sean number: 1 1 1 1 1 1 1 1 1 1
Dot shift (nn): BOB 100 2001 300 i 40Of 500П 600s 700r 800 900
Ganna nin -9.0 -9.0 *Z7.0 *0.0 +Z7.0 *36.0 *0.0 *0.0 ♦0.0 *0.0
Gamma max *0.0 *18.0 *27.0 *0.0 ♦Z7.0 *36.0 *0.0 *0.0 *0.0 *0.0
Result Ok 0k Ok 0k Ok 0k 0k 0k 0k 0k
Seam number: 1 1 1 1 1 1 1
Dot shift (nnj: 1000 1100 1200 13IW 1 1400 1500 1504
Gamma nin *0.0 *9.0 *0.0 *0.0 10.0 -9.0 -27.0
Ganna nax ♦0.0 *18.0 *0.0 ♦0.0 *0.0 *9.0 *9.0
Result 0k 0k Ok Ok 0k 0k 0k
Sean number: Dot shift (ran):
Ganna nin Ganna nax
Result w~w» th 1 «1 г n UH' »ж_ « -. - -
Press ENTER key to return to AutoCAD
Рис. 7.38. Таблица возможных поворотов сварочных клещей
жду элементами сварочных клещей и сварной конструкцией, отображается
на экране в виде таблицы, показанной на рис. 7.38. Запуск процесса такого
анализа доступности производится с помощью команды меню. Если диапа-
зон по углу у существует — результат (Result) положительный (ОК), в про-
тивном случае результат отрицательный (Bad). Результаты тестирования
точек на доступность сохраняются для последующего использования при
компоновке РТК. После окончания расчета диапазонов по углам у система
производит визуальный прогон инструмента по всем доступным точкам
сварки. Функция теста столкновений оставляет только те позиции, для кото-
рых сварные точки не только достижимы, но и доступны.
Найденное множество допустимых позиций размещения сварочного
робота отображается в картинке ячейки РТК в виде осей вертикальных ци-
линдров. Вид на возможные позиции установки сварочного робота показан
на рис. 7.39 как в плане, так и в аксонометрическом изображении. Вполне
естественно, что наилучшие результаты дает расположение основания сва-
рочного робота по высоте примерно в центральной части выбранной на пла-
не оси. Это будет подтверждено при последующем моделировании работы
технологического комплекса.
Специальное экранное меню и указатель мыши позволяют установить
сварочный робот в выбранную позицию и тем самым завершить формиро-
вание РТК и подготовить его к программированию выполнения установочных
362
7. Автоматизированное проектирование сварочных комплексов
Рис. 7.39. Возможные положения робота относительно позиционера:
а — аксонометрическое изображение; б — вид в плане
О О О О О О О
7.4. Сборка, программирование и моделирование работы сварочного РТК 363
перемещений и технологических операций. Полученную версию проекти-
руемого РТК следует записать на диск под некоторым удобным именем, на-
пример RTK-3-0. Образ этого РТК появится в каталоге сформированных
технологических комплексов.
Обучение и программирование РТК предусматривает организацию ин-
терактивной работы с роботом и позволяет выполнять следующие операции:
• задавать перемещение рабочего инструмента робота в различных
системах координат (в координатах суставов, мировой системе координат,
системе координат инструмента);
• производить автоматический выход на шов (точку) сварки с задан-
ными сварочными параметрами;
• проверять достижимость и доступность сварных швов и точек сварки;
• запоминать координаты точек пространства и сварных точек для
использования их при написании технологической программы и задании
движений робота;
• задавать перемещения по степеням подвижности позиционера;
• задавать движения робота с различными способами интерполяции:
во внутренних координатах, в линейной, круговой;
• просматривать движения робота и позиционера при выполнении за-
данной технологической программы и оценивать время рабочего цикла;
• изменять вылет сварочной проволоки.
Удобство работы обеспечивается системой экранных меню, которые
- производят переинсталляцию РТК в его текущей конфигурации, на-
пример, для исключения робота из числа активных устройств. Это может
быть связано с необходимостью выполнения команд управления и обучения
инструмента после того, как РТК сконфигурирован с включением сварочно-
го робота;
- обеспечивают работу команд управления роботом или сварочным
инструментом;
- задают перемещение манипулятора изделия по отдельным степеням
подвижности;
- сохраняют координаты рабочих точек робота и манипулятора изделия;
- моделируют движение робота с интерполяцией по внутренним и
внешним координатам;
- обеспечивают выход в среду создания и редактирования технологи-
ческих программ робота и позиционера.
Технологию обучения РТК рассмотрим на уже сформированном нами
комплексе, записанном в базе данных под именем RTK-3-0 (см. рис. 7.37). В
данном случае всю последовательность операций проследим на примере
массива швов DOTS1, содержащего всего один шов контактной сварки, со-
стоящий из 11 сварных точек.
364
7. Автоматизированное проектирование сварочных комплексов
Welding seam selection
Dot subsets: D0TS1 If]
Seans: Check i ng
! — а тпнк
ipl One seam (SI Selected seams
i Weld |
j Sxit |
sHou seam < |
Zoom j Upoint | | uOptions |
Рис. 7.40. Меню выбора способа
обучения
Достижимость и доступность
отдельных точек сварного шва прове-
ряются вводом команды weld. Для пе-
ремещения клещей робота в первую
точку сварки по команде меню загру-
зится поле выбора режима анализа
достижимости (рис. 7.40), где следует
выбрать одну из позиций:
• One dot — для одной точки
сварного шва;
• One seam — для всех сварных
точек выбранного шва;
• Selected seams — для группы
выбранных швов.
При выборе позиции One dot и
включении команды Weld загрузится
меню выбора сварочных параметров
(рис. 7.41) с полями:
• Dots — список точек сварного шва, открытых для анализа достижимо-
сти и доступности. Для швов дуговой сварки это список точек начала завари-
ваемых участков. Точки удобно задавать обозначением их расстояния от начала
Welding teaching parameters
Dots: Dot parameters:
>7100 17208 ii ® Own fh| As previous -J Seans length: 1445.0854
7300 17400 !?S00 -7600 !??0o '7800 17900 ,71008 71100 >71200 (Path fron the beginning: 0 (Offset from the seam (mn): jWelding angle ALPHA (deg): Welding angle BETA (deg): (Welding angle GAMMA (deg): GAMMA angles range (deg): I ' i 1 | 1 i i i ' i I ta |j в ;shc|
Perform actions with point
| Touch <^[; approach < | Store point < [
Zoom J1 Vpoint 11 Hide
seLect another seam 11 Complete command
Рис. 7.41. Меню выбора сварочных параметров
7.4. Сборка, программирование и моделирование работы сварочного РТК 365
Рис. 7.42. Технологические
сварочные углы
шва, как сделано в данном случае, или последо-
вательными номерами;
• Seams length — текстовое поле, куда
выводится информация о длине шва (в мм);
• Path from the begining — поле зада-
ния перемещения вдоль сварного шва. При
выборе одной из точек в списке в данном
поле появляется значение ее расстояния от
начала шва;
• Offset from the seam (mm) — поле зада-
ния допустимого смещения по перпендикуля-
ру к сварному шву со стороны подхода к нему.
По умолчанию это поле устанавливается рав-
ным нулю.
Далее следуют величины технологических
сварочных углов а, р и у, которые определяют
ориентирование сварочного инструмента отно-
сительно свариваемого изделия (рис. 7.42).
Для точечной контактной сварки а —
угол между плоскостью, в которой расположе-
ны сварочные электроды, и плоскостью осей YZ
сварного шва. Для обеспечения качественной
сварки этот угол не должен превышать ±10°.
Угол Р определяется как угол между осью Z сварного шва и осью X
системы координат, связанной со сварочным электродом (в системе коор-
динат сварочного электрода ось X направлена вдоль электрода, а ось Z
«смотрит» в свободное пространство).
Для точечной контактной сварки этот угол может принимать значения
в пределах -10... 10 и 170... 190°. При этом оптимальными значениями яв-
ляются 0 и 180°.
Угол у — это угол поворота вокруг оси сварочного электрода. Этот
угол не влияет на качество сварки и является свободным параметром. При
изменении этого угла производится поиск допустимых с точки зрения дос-
тижимости и доступности конфигураций. В данном поле значение у опреде-
ляет некоторый средний угол.
GAMMA angles range (см. рис. 7.41) — поле задания полудиапазона
углов у, в которых будет вестись поиск. При этом средним будет значение,
введенное в предыдущем поле. По умолчанию полудиапазон для точечной
контактной сварки — 45°.
366
7. Автоматизированное проектирование сварочных комплексов
raMwwui?*'*'........
„ gup
qg i
о2
31
si
1
qg
out
out
out
out
out
out
out
out
out
out
out
out
out
out
FUM
вин
q2 out
q2 out
q2 out
q2 out
q2 out
q2 out
q2 out
q2 out
qg out
q2 out
q2 out
q2 out
q2 out
q2 out
qg
qg
qg
qg
qg
Qg
Qg
q?
qg
qg
out
out
out
out
out
out
out
out
out
out
out
out
out
out
ВОР
(Ж.
Ок
I
Ок
Ок
Ок
оЗ
out j out q3 out aS out q3 out q-: 3 out
out ql 3 out q3 out q3 out q3 out ql 3 out
out q; 3 out q3 out q3 out q3 out ql 3 out
out <S 3 out q3 out q3 out q3 out ql 3 out
out 3 Out qg out q3 out qg out ql 3 out
out ql L out q3 out ql out q3 out qj I out
out ql I out q3 out ql out q3 out ql I out
FOM
1a2 out
q2 out
q2 out
q2 out
q2 out
q2 out
a2 out
out
out
out
out
out
cut-
out
out
Out
out
out
out
out
out
БОН
а
а:
out
out
out
out
cut-
out
out
-Choose’-th e-ootrfi-gurat io» and feeeоагане^ет Saiwa... .
Рис. 7.43. Результат расчета достижимости и доступности
проверяемой сварной точки
Отметим точку ?0 (см. рис. 7.41) и изменим значение угла ВЕТА на
180°, после чего по команде Touch (или Enter) запускается расчетная про-
грамма, которая формирует таблицу, показанную на рис. 7.43.
Если проверяемая точка достижима и доступна, выводится результат ОК.
При наличии столкновений звеньев робота, инструмента и сварного узла выво-
дится результат Crash! Если точка не достижима, поскольку не попадает в зону
сервиса робота, то указывается, по какой оси не хватает подвижности.
Выберем одну из конфигураций (отмеченных на экране зеленым цве-
том), например FUP, GAMMA +0.0. Робот перенесет сварочные клещи в
точку 0.1 шва (рис. 7.44). Сохранение «обученной» точки производится вы-
бором из меню или вводом команды Store point в командной строке. Теку-
щее положение робота, конфигурация его суставов, координаты степеней
подвижности позиционера и дополнительных степеней подвижности (если
они присутствуют), а также номер активного инструмента и свариваемого
шва сохраняются в файле. Меню (см. рис. 7.41) появится на экране вновь. С
помощью команды меню Store point < запомним эту точку, задав ей имя «01»:
Enter the name of stored point? <Seaml_part_0.0>: 01
Продолжая обучение, запомним положения робота для других точек
сварного шва (02, 03, 04...09). При этом будем выбирать среднее значение
угла Gamma из расчетных вариантов, но ближе к нулю (см. рис. 7.43).
При «обучении» точки 10 происходит столкновение клещей с кромкой
свариваемой пластины. При этом система выдает сообщение в командной
строке и обозначает место столкновения на кромке пластины специальным
значком «царапина» (рис. 7.45, см. выноску). Выбранные сварочные клещи
7.4. Сборка, программирование и моделирование работы сварочного РТК 367
Рис. 7.44. «Обучение» начальной точки шва
Рис. 7.45. Столкновение сварочных клещей с кромкой изделия
368
7. Автоматизированное проектирование сварочных комплексов
Рис. 7.46. Траектория движения рабочей точки сварочного инструмента
имеют недостаточный вылет для сварки всех точек шва. Следовательно,
нужно выбрать другие клещи и повторить «обучение» всех точек.
В данном конкретном случае имеется возможность уже выбранными
клещами подойти к точкам 10 и 11 с другой стороны пластины. Проверим
этот вариант. После полученного сообщения о столкновении в точке 10 из-
меним сварочный угол у на 180° и повторим «обучение» точки. Аналогич-
ным образом получим последнюю точку 11 (рис. 7.46).
В системе существуют возможности для поиска положения робота
при анализе достижимости и доступности совокупности точек шва или со-
вокупности швов (рис. 7.47).
Для перемещения сварочного инструмента как при обучении, так и
при воспроизведении траектории движения имеется ряд команд. Вызов ко-
манды РТР (Point То Point — от точки к точке) производится либо выбором
из меню, либо вводом в командной строке. После выбора целевой точки ро-
бот движется в положение, соответствующее точке, сохраненной ранее под
данным именем. Интерполяция при этом осуществляется в координатах сус-
тавов. Это означает, что положение и ориентация рабочей точки инструмен-
та при движении не контролируется.
Аналогично вызывается команда Linear (перемещение по прямой
линии). В этом случае после выбора целевой точки робот движется в по-
7.4. Сборка, программирование и моделирование работы сварочного РТК 369
x
Welding possibility checking
Selected seem is:
Seams length:
Shift from the beginning (шт)
length of checked pert (mm):
Seam's weld-parameters:
SETA (deg):
fiAMMA(deg):
Perform command-
Start
Continue
2dorri
select another seam
Vpoint
sWi
1101.7659
.1101 7659
Tool walking/
P Collision
shcwlool<
slore point
Bde
Complete command,
Рис. 7.47. Окно обучения совокупности точек
и швов
•EZ
0
b
ложение, соответствующее
сохраненному ранее под
данным именем, и интер-
поляция осуществляется в
декартовых координатах.
Рабочая точка инструмен-
та движется по прямой ли-
нии. При несовпадении ори-
ентаций начальной и ко-
нечной точек движение
может осуществляться с
интерполяцией ориентации
или с постоянной ориента-
цией целевой точки.
Команда Jump (ска-
чок) после выбора целевой
точки переводит робот в
положение, соответствую-
щее сохраненному ранее
под данным именем. При
этом восстанавливаются
соответствующая конфигурация, положение манипулятора изделия, а также
номера активного инструмента и шва.
Для завершения программирования работы РТК необходимо опреде-
лить несколько дополнительных точек программируемой траектории инст-
румента путем плоскопараллельного переноса клещей (т. е. без изменения
их ориентации) из точек, ранее определенных на шве. Получим траекторию,
показанную на рис. 7.46.
Промежуточная точка pl необходима, чтобы исключить столкновение
инструмента и изделия при перемещении его из начального положения ро-
бота к первой рабочей точке. Для обучения точки pl необходимо:
• командой меню Display\Zoom\Top изменить ракурс изображения
(удобнее, если при дальнейшей работе РТК будет изображен в плане);
• командой меню Teaching\Movement\Jump вызвать меню точек и пе-
реместить клещи «скачком» в точку 01;
• с помощью команды меню TeachingVToolWiew CS задаем «промежу-
точное» положение клещей путем прямого ввода относительных координат:
Tool Center Point OFFSET in VIEW plane: @0, 500, 0
370
7. Автоматизированное проектирование сварочных комплексов
При этом перемещение будет выполнено в горизонтальной плоскости. При
выходе за пределы допустимой зоны перемещения робота система об этом
сообщит;
• запомним эту точку через пункт меню Teaching\Store point под
именем р 1.
Другие промежуточные точки траектории клещей р2, рЗ, р4 и р5 не-
обходимы для исключения столкновения клещей с изделием при их подходе
к точке 10 с противоположной стороны. После сварки точек 10 и 11 для воз-
вращения клещей в исходную точку рО необходимо задать еще две проме-
жуточные точки рб и р7 (см. рис. 7.46). Порядок обучения этих точек анало-
гичен рассмотренному выше обучению точки pl.
Off-line-программирование. Эта подсистема предназначена для ав-
тономной подготовки технологических программ робота на языке SRCL
(Siemens Control Robot Language), который является проблемно-ориенти-
рованным языком программирования роботов для системы управления
RCM. Большое количество программных команд делает возможным напи-
сание на этом языке весьма сложных технологических программ для самых
разных областей применения роботов. Подсистема позволяет:
• разрабатывать технологические программы сварочных роботов на язы-
ке SRCL с использованием многооконной интегрированной среды, включаю-
щей встроенный редактор, компилятор, окна обученных точек и команд;
• разрабатывать программы движения степеней подвижности пози-
ционера;
• производить калибровку технологических программ, созданных off-
line, в соответствии с реальным расположением оборудования в РТК;
• пересылать технологические программы в систему управления RCM
в принятом для данной системы промежуточном коде;
• принимать программы из системы управления робота и преобразо-
вывать их в текстовый формат .
В реальной системе управления роботом управляющая программа соз-
дается с помощью пульта, имеющего большое число функциональных кла-
виш (многие из которых имеют обозначение команд). При этом для выбора
различных вариантов одной и той же команды используется система меню.
Это позволяет упростить программирование, уменьшить количество синтак-
сических ошибок при наборе программы и соответственно упростить ту часть
интерпретатора, которая занимается синтаксическим анализом.
При реализации на ЭВМ системы off-line программирования, исполь-
зующей SRCL, процесс программирования неизбежно меняется, поскольку
отсутствует функциональная клавиатура, но зато используются многоокон-
ный интерфейс и разветвленная система меню, делающая систему програм-
мирования дружественной к пользователю.
7.4. Сборка, программирование и моделирование работы сварочного РТК 371
Командой меню Teaching\Program\New загрузим среду создания off-
line-программ. В отдельных окнах экрана среды имеются меню команд язы-
ка SRCL и меню записанных ранее точек. Последовательно вызывая их
мышкой, запишем программу траектории перемещения клещей, изображен-
ную на схеме (см. рис. 7.46). Сам процесс сварки занимает примерно 2 с на
точку. Эти паузы на выполнение сварки также должны быть указаны в тек-
сте управляющей программы:
DEF HP1 начало программы 1
#РТР Pl переход к промежуточной точке pl
GES BAN 6 установить скорость перемещения 6 м/мин
#LIN 01 переход по прямой к точке 01
WRT Z 2 пауза 2 с на сварку точки
#LIN 02 переход по прямой к точке 02
GES BAN3
#LIN 03
#LIN 04
#LIN 05
#LIN 06
#LIN 07
#LIN 08
#LIN 09
GES BAN 6
#LIN p2
#PTP рз
#PTP p4
#PTP P5
#LIN 09
GES BAN3
#LIN 10
#LIN 11
GES BAN 6
#LIN p6
#PTP p7
#PTP p0
END HP1 конец программы 1
Командой меню среды Compiling проведем компиляцию, а командой
Save — сохранение программы на диске.
Командой меню Teaching\Programm\Exec полученная нами программа,
отображающая все перемещения робота, будет воспроизведена на экране.
Во время моделирования работы РТК выводятся результаты:
• предупреждения о допущенных столкновениях;
• время воспроизведения и время реальной работы программы в се-
кундах — цикл работы РТК.
372
7. Автоматизированное проектирование сварочных комплексов
Командой меню Teaching\Programm\Graphics можно воспроизвести
программу в виде графиков движения робота по каждой степени свободы
или в текстовом виде пошаговых координат. Если на графиках углов нет
скачков — «перебросов» конфигурации, то это свидетельствует о непре-
рывности движения робота на протяжении рабочего цикла.
Для каждого конкретного РТК существуют свои погрешности взаим-
ного расположения робота и технологического оборудования, т. е. отличия
абсолютного положения реальных точек позиционирования робота от иде-
альных, заданных во внешних программах. Поэтому внешние программы
для каждого РТК должны быть скорректированы программой калибровки в
такой последовательности.
1. Для каждого свариваемого узла в системе off-line создается идеаль-
ная программа калибровки, которая включает команды только движения
робота: РТР, LIN (не менее 7—10 команд при условии, что количество точек
в программе сварки не меньше этого числа) и команды начала и конца про-
граммы. Такую программу удобнее всего сформировать, исключив ненуж-
ные команды в off-line-программе сварки данного узла. Необходимо остав-
лять в программе идеальной калибровки только точки, отражающие коор-
динаты швов (нельзя оставлять промежуточные точки, в которых конец
инструмента «повисает в воздухе», так как трудно получить соответствую-
щие им точки на реальном РТК).
2. Методом обучения на реальном РТК создается программа, последо-
вательность команд и обход точек в которой полностью соответствует про-
грамме идеальной калибровки. При этом координаты соответствующих то-
чек X, Y, Z будут отличаться ненамного, так как погрешности взаимного
расположения робота и технологического оборудования для реального РТК
не столь велики, что легко проверить визуально. Такую программу будем
называть реальной программой калибровки.
3. В редактор загружается программа сварки данного узла.
4. С помощью команды меню options\calibration options устанавливаются
программы идеальной и реальной калибровки для данной программы сварки.
5. С помощью команды меню file\calibration производится калибровка
данной программы сварки, т.е. координаты ее точек, и скорректированная
программа запоминается.
6. Программа реальной калибровки переносится в систему управления
робота. При этом используется команда File\Transfer.
Рассмотренная здесь методика компьютерного проектирования и отладки
работы сварочных РТК обеспечивает быстрое и качественное выполнение этой
работы. Важно еще раз отметить, что применение методики возможно и целе-
сообразно на ранних стадиях разработки проектов сварочных роботизирован-
ных производств, еще до окончательного решения вопросов закупки оборудо-
7.4. Сборка, программирование и моделирование работы сварочного РТК 373
Рис. 7.48. РТК дуговой сварки заднего борта грузового автомобиля-самосвала
вания и до изготовления заготовок сварных конструкций и сборочно-сварочной
оснастки.
Поскольку изложение основных этапов технологии проектирования сва-
рочных РТК выполнено на простейшем достаточно условном примере сварной
конструкции, покажем в качестве примера два конкретных проекта роботизи-
рованной сварки узлов автомобилей. На рис. 7.48 представлен общий вид РТК
дуговой сварки заднего борта грузового автомобиля-самосвала.
В проекте использован двухпозиционный манипулятор изделия, с тем
чтобы во время выполнения сварочных работ на одном изделии можно было
одновременно заниматься съемом уже сваренного предыдущего сварного
узла и устанавливать и готовить к сварке очередное изделие. Вследствие
больших габаритов сварного узла, превышающих размеры рабочей зоны
робота, достижимость всех сварных швов изделия обеспечивается двухсте-
пенным манипулятором, так что длинные сварные швы свариваются в два
приема. Кроме того, работа манипулятора обеспечивает возможность сварки
всех швов в наиболее удобном пространственном положении. Непрерывное
компьютерное отображение работы управляющей программы в виде от-
дельных фрагментов приведено на рис. 7.49.
На рис. 7.50 показана компоновка двухпозиционного сварочного РТК
контактной сварки крыши микроавтобуса. Два крупногабаритных изделия
7. Автоматизированное проектирование сварочных комплексов
Рис. 7.49. Экранное отображение работы управляющей программы РТК
7.4. Сборка, программирование и моделирование работы сварочного РТК 375
Рис. 7.50. РТК сварки крыши микроавтобуса
376 7. Автоматизированное проектирование сварочных комплексов
установлены на своих поворотных столах, и комплекс обслуживается двумя
сварочными роботами. Один из них оснащен сварочными клещами с очень
большим вылетом (1400 мм) для приварки листов к элементам жесткости в
средней части крыши. Другой робот — с небольшими клещами — выполняет
сварку точек по периметру изделий. Можно видеть, что работа сварочных
роботов сильно затруднена большим количеством базовых и зажимных эле-
ментов сварочных кондукторов. Компьютерное моделирование совместной
работы поворотных столов и сварочных роботов обеспечило нахождение
наиболее удачного взаимного размещения всех элементов РТК, разработку,
оптимизацию и отладку качественных управляющих программ.
8. ОПЫТ ПРОЕКТИРОВАНИЯ И ИСПОЛЬЗОВАНИЯ
РОБОТИЗИРОВАННЫХ ТЕХНОЛОГИЧЕСКИХ
КОМПЛЕКСОВ КОНТАКТНОЙ
И ДУГОВОЙ СВАРКИ
8.1. Контактная сварка кузовов автомобилей ГАЗ
В 1993—1994 гг. с использованием программного комплекса РОБО-
МАКС были разработаны проекты 35 РТК для четырех линий сборки-
сварки кабины грузового автомобиля ГАЗ-ЗЗО2 «ГАЗель». В этих линиях
выполняются операции сварки задней стенки, пола, сборки-сварки кабины и
доварки кабины в сборе. Компьютерное моделирование работы проекти-
руемых линий позволило оптимально разместить роботы, распределить ме-
жду ними точки сварки и за счет этого отказаться от закупки двух роботов
типа PR601/60, сократить время наладки линий более чем на месяц. Часть
сварных точек, первоначально предназначавшихся для ручной доварки, уда-
лось перевести на роботизированную сварку.
Задача в кратчайшие сроки разработать и освоить производство полу-
торатонного грузового автомобиля ГАЗ-3302 была поставлена перед кол-
лективом АО ГАЗ в начале 1992 г. Для этого было необходимо создать ком-
плекс линий сборки-сварки кабины, которая имеет оригинальную обтекае-
мую форму. Было принято решение автоматизировать операции сварки и
нанесения клея с помощью промышленных роботов БЕТА/KUKA. Проекти-
рование кузовного производства гребует четкого взаимодействия усилий
конструкторских и технологических служб разработчика на базе средств
вычислительной техники и соответствующего программного обеспечения,
включая всестороннюю проверку принимаемых решений путем моделиро-
вания роботизированной сварки с целью уменьшения вероятности ошибок и
резкого сокращения сроков проектирования, а также сравнения различных
вариантов проекта и выбора лучшего из них.
На рис. 8.1 и 8.2 показаны изометрические изображения линий сборки
и прихватки кабины и доварки задней стенки кабины. Для моделирования
процессов роботизированной сварки использовали графические 3£)-образы
378
8. Опыт проектирования сварочных РТК
Рис. 8.1. Линия сборки и прихватки кабины автомобиля ГАЗ-3302
Рис. 8.2. Линия сварки задней стенки кабины ГАЗ-3302
8.1. Контактная сварка кузовов автомобилей ГАЗ
379
всех элементов, которые затем «собирали» на экране монитора. Образы сва-
риваемых узлов создавали с помощью пакетов графического конструирова-
ния CATIA. После передачи образов в РОБОМАКС на поверхности узлов
наносили сварные швы и точки. Недостающие элементы сцены дорисовыва-
ли средствами пакета AutoCAD. Графические и математические модели ро-
ботов создавали и заносили в базу данных. Образы манипуляторов изделия,
сварочную оснастку, сварочный инструмент и дополнительное оборудова-
ние создавали пользователи системы.
Работе на компьютере предшествовало принятие предварительных
технологических решений по целому ряду вопросов, определяющих состав,
расположение и технологию создаваемого производства. Сначала рассмат-
ривали вопросы, относящиеся к производству сварной конструкции в целом
(планировочные решения сварочного участка, заготовительные операции,
транспортные пути, удобство обслуживания РТК, вентиляция и пр.). После
приближенного определения необходимого количества промышленных ро-
ботов, принятия планировочных решений и предварительной разработки
технологии сварки выбирали либо конструировали клещи и оснастку к ним
для всей гаммы свариваемых точек.
Использовали три уровня выбора:
I — просмотр базы данных (или автоматический поиск) и выбор сва-
рочных клещей по их техническим (числовым) характеристикам: проему
клещевин, усилию сжатия и прочим параметрам;
II — в графическом режиме — по «множеству швов» на экран вызы-
ваются совмещенные по координатам сварных точек изображения сразу
всех сечений стыков, подлежащих сварке данным инструментом. Изображе-
ние клещей совмещается с «множеством», и становится видно, подходят ли
они геометрически для сварки этой гаммы стыков;
III — аналитическим перебором: автоматическая пристыковка всего
множества клещей к множеству всех точек и получение твердых копий резуль-
татов стыковки, что дает возможность выбора тех клещей, которые подходят.
В результате работы были выбраны несколько клещей, работоспособ-
ность которых проверяли более подробно в процессе моделирования движе-
ний, после чего делали окончательный выбор. После выбора клещей для
каждой точки определяли модели ПР, распределяли сварные точки по инст-
рументам, а инструменты, в свою очередь, распределяли по постам, класси-
фицируя сварные точки и соответствующие им клещи по их пространствен-
ному расположению и ориентации. Критериями оптимальности распределе-
ния сварных швов по группам являются: во-первых, выполнимость их
соответствующими клещами, а во-вторых, время цикла работы каждого по-
ста, которое не должно сильно различаться. Это — признак максимальной
производительности данного производства.
380
8. Опыт проектирования сварочных РТК
После получения набора клещей и распределения точек надо было на-
весить клещи на ПР оптимальным образом и вставить эту сборку в техноло-
гическую ячейку, т. е. в линию. Образы ПР, клещей, узлов в приспособле-
нии и прочие эле менты оборудования и оснастки расставляли относительно
друг друга в соответствии с предварительной компоновкой. Этот процесс в
системе РОБОМАКС автоматизирован. Расчетная программа выдает мно-
жество возможных положений установки ПР, при которых обеспечиваются
достижимость и доступность каждой свариваемой точки клещами. При этом
проверяются столкновения детали не только с инструментом, но и со всеми
элементами сцены. Далее имеется возможность выбрать наилучшее поло-
жение. Приняты два критерия: минимальное закручивание последних 4, 5 и
6 степеней ПР (шланги клещей предварительно закручивают во избежание
их натяжения в какой-то момент и с целью уменьшения их износа) и мини-
мальное время выполнения движений по 1, 2 и 3 степеням ПР. На экране
отмечается точка установки ПР.
«Внешнее» программирование роботов (off-line) на специальном язы-
ке управления (для роботов БЕТА/KUKA — язык SRCL) осуществляли пу-
тем записи последовательности кантовки узла, переходов и выполнения
сварки от точки к точке, оценки доступности и достижимости мест сварки
определенным типом клещей, уточнения выбора элементов и их расположе-
ния. Если сварных точек много, то с использованием системы РОБОМАКС
определялся маршрут их обхода, назначались дополнительные опорные
точки и планировалась траектория с формированием управляющей про-
граммы сварочного робота. Полученную программу просматривали на гра-
фиках работы приводов робота либо воспроизводили в графическом режиме
и просматривали все движения робота относительно узла. На экран выводи-
ли графики переходных процессов по скорости, ускорению, значениям уг-
лов поворота и моментам в каждой из осей, а также траекторию перемеще-
ния электродов клещей в трех проекциях. Если при движении возникали
столкновения, на экране появлялось сообщение и точка столкновения отме-
чалась меткой. Необходимую коррекцию работы сварочного РТК осуществ-
ляли путем изменения положения ПР, навески клещей, выбором других мо-
делей клещей и/или роботов. В результате были получены планировки, на
которых положение ПР выверено не только «в плане», но и по высоте, а
также относительно колонн (рис. 8.3, 8.4). На основе этих планировок затем
была составлена монтажная документация фундаментов с закладными дета-
лями, порталов, силовых разводок и т. п.
Полученные на компьютере программы переносили в стойку робота и
осуществляли их калибровку с учетом реального положения ПР. Для этого в
режиме обучения инструмент на руке робота подводили к нескольким (5—7)
опорным (реперным) точкам на изделии и, вводя таким образом разность
8.1. Контактная сварка кузовов автомобилей ГАЗ
381
Рис. 8.3. Линия сборки-сварки кабины автомобиля ГАЗ-3302
Рис. 8.4. Пример оформления планировки — линия доварки
задней стенки кабины
382
8. Опыт проектирования сварочных РТК
реальных и идеальных координат его положения, обеспечивали автоматиче-
скую коррекцию off-line-программы ПР.
В 1995 г. при помощи Робомакс разработан проект роботизированного
сборочно-сварочного производства цельнометаллического кузова автомоби-
ля ГАЗ-2705 «ГАЗель». Весь комплекс включает в себя две линии сборки-
сварки боковин, два доварочных кондуктора, одну подъемно-опускную сек-
цию для навески готового узла на транспортную систему и 23 робота, об-
служивающих 890 точек сварки. В состав каждой линии входят поворотный
стол, два кондуктора на тележках, кантователь-перегрузчик готового узла и
четыре робота, сваривающих 140 сварных точек. Кроме того, роботы ис-
пользуются на линиях сборки-сварки пола, крыши, а также для доварочных
операций. В 1997 г. аналогичным образом разработан проект еще одного
автономного роботизированного сборочно-сварочного производства цель-
нометаллического кузова автомобиля ГАЗ-2217/2752 «Соболь».
8.2. РТК контактной сварки лонжеронов автомобиля ВАЗ 2110
Подготовка моделей сварных узлов выполнялась в отделе подготовки
сварочно-кузовного производства АвтоВАЗ с использованием программных
продуктов фирмы AutoDesk. При этом был использован IGES-Translator
г.5.2, обеспечивающий передачу поверхностей из других систем (CATIA,
COMPUTERVISION), сформированных с использованием NURBS-тех-
нологии.
Далее полученные поверхности сварного узла были переведены в
«фасеточное» (face) представление с точностью 0,01 мм (стандартная опция
AutoSurf) и сформированы DWG-файлы, воспринимаемые инструменталь-
ной графической средой AutoCAD (рис. 8.5).
Перевод в фасеточное представление обеспечил:
• возможность визуализации указанных моделей в режимах HIDE,
SHADE, RENDER на всех этапах проектирования;
• возможность построения произвольных сечений, разрезов, вырезов с
использованием функций программ РОБОМАКС;
• формирование математической модели для проведения теста столк-
новения между перемещающимися объектами.
ЗП-модель сборки двух изделий в сборочно-сварочном приспособле-
нии приведена на рис. 8.6.
В рамках системы РОБОМАКС к объекту «сборочно-сварочное приспо-
собление + изделие» был введен фрейм системы координатных осей, по кото-
рому производится посадка всего объекта на выбранную планшайбу поворот-
8.2. РТК контактной сварки лонжеронов автомобиля ВАЗ 2110
383
Рис. 8.5. Изображение лонжерона ВАЗ 2110 после конвертации
Рис. 8.6. Правый и левый лонжероны в сборочно-сварочном приспособлении
384
8. Опыт проектирования сварочных РТК
Рис. 8.7. Нанесение свариваемых точек и их условное изображение
ного стола (по выбранному фрейму крепления на столе). При задании сварных
точек на узле была использована сформированная в CATIA информация по
положению сварных точек на поверхности и ориентации вектора нормали в
виде линий с началом в сварной точке. Формирование фреймов сварных то-
чек произведено в соответствии с принятой в РОБОМАКС идеологией фор-
мирования фреймов, т. е. оси направлены следующим образом:
ось Z — по нормали к поверхности в сторону подхода верхнего элек-
трода сварочных клещей;
оси X и Y находятся в картинной плоскости к оси Z, причем ось Y на-
правлена в сторону предполагаемого подхода сварочных клещей (например,
ортогонально к кромке изделия);
ось X дополняет систему координат до правой.
Заданные фреймы являются базовыми: от начала фрейма, от их осей
производится отсчет таких технологических парамегров, как углы ориента-
ции сварочного инструмента относительно сварного соединения, свобод-
ный параметр у (не влияющий на технологию сварки), смещение клещей
относительно сварных точек. Пример условного обозначения и нумерации
точек приведен на рис. 8.7.
8.2. РТК контактной сварки лонжеронов автомобиля ВАЗ 2110
385
При создании моделей сва-
рочного инструмента использована
графическая модель сварочных
клещей СКП ВАЗ с креплением
торцом к фланцу робота. Подготов-
ка сварочного инструмента пред-
ставляет собой ввод фреймов креп-
ления к фланцу робота и фрейма
точки сжатия электродов (Tool
Center Point). Первый фрейм нужен
для крепления инструмента на фла-
нец робота, второй — для програм-
мирования движения инструмента в
системах координат: сварного со-
единения, мировой, инструмента,
сварочных электродов. В совокуп-
ности эти фреймы необходимы для
решения задач кинематики при ро-
ботизированной сварке изделия.
Сборка поворотного стола
(рис. 8.8) включает следующие этапы:
Рис. 8.8. Семистепенной поворотный стол
разработки ПТО ВАЗ
• подготовку графических моделей звеньев;
• задание кинематических пар (Rotor & Stator), в данном случае —
семь вращательных пар;
• задание фреймов крепления свариваемых узлов на планшайбах
стола, что обеспечивает автоматическую посадку изделия на планшайбу
с необходимой ориентацией;
• графическую сборку стола в интерактивном режиме;
• задание ограничений на кинематические параметры стола.
Для работы программы анализа столкновений были подготовлены
специальные математические модели соответствующих элементов: изделия
в сборочно-сварочном приспособлении и кондукторной плиты в сборе,
звеньев робота, звеньев стола, элементов ограждения и шкафов. Эти модели
создаются автоматически в соответствующих подсистемах РОБОМАКС.
Точность подготовки моделей можно задать в пределах 5...50 мм.
Система гарантирует отсутствие столкновений между графическими моде-
лями элементов РТК, если подсистема анализа столкновений их не обнару-
живает. Если столкновения обнаружены при точности, например, 5 мм, то
это означает, что в некоторых положениях между контролируемыми объек-
тами может быть расстояние менее 5 мм, т. е. столкновения определяются с
«запасом». Время, требуемое на анализ сцены, содержащей все элементы
13 — 6705
386
8. Опыт проектирования сварочных РТК
Рис. 8.9. Промышленный робот ПР161/60 производства ПТО ВАЗ
РТК, включая поворотный стол, пол, ограждение и анализ столкновения
клещей со звеньями собственного робота, составляет доли секунды.
Сборка РТК была произведена из подготовленных элементов по чер-
тежам АвтоВАЗ. Модель робота ПР 161/60 (без удлинителя руки) взята из
библиотеки роботов РОБОМАКС (рис. 8.9).
При проектировании РТК из четырех роботов основные проблемы
решались моделированием работы роботов № 1 и № 3, поскольку они об-
служивают сварные точки на обоих сварных узлах и для них реализуется
наиболее сложный режим по достижимости сварных точек роботами.
Для робота № 3:
• плита со свариваемой конструкцией большим измерением ори-
ентирована горизонтально и развернута поворотным столом по 1-й оси
на 240° от положения загрузки, по 2-й оси на 30° так, что правый лон-
жерон находится внизу и плита составляет с вертикальной плоскостью
угол 30°;
• робот установлен в точку с координатами 2800 мм, 810 мм, 0 и
развернут вокруг вертикальной оси на угол 210°, отсчитываемый от оси X
(рис. 8.10);
• сварочные клещи крепятся к фланцу робота с торца;
8.2. РТК контактной сварки лонжеронов автомобиля ВАЗ 2110
387
Рис. 8.10. Планировка РТК: поворотный стол установлен в точку с ко-
ординатами 0, 0, 0 мировой системы координат, робот — в точку с ко-
ординатами 2800 мм, 810 мм, 0
• робот должен сварить восемь точек, соединяющих правый лонже-
рон с правым соединителем пола (точки № 47—54), при этом правый
лонжерон находится внизу и плита составляет угол 30° с вертикальной
плоскостью;
• робот должен сварить семь точек, соединяющих левый лонжерон с
кронштейном крепления двигателя (точки № 9—13, 55, 56); при этом плита
разворачивается на 180° относительно начального положения вокруг оси
четвертого позиционера так, что левый лонжерон находится внизу и плита
составляет 30° с вертикальной плоскостью.
Для робота № 1:
• плита со свариваемой конструкцией большим измерением ориенти-
рована горизонтально и развернута поворотным столом по 1-й оси на 120°
от положения загрузки, на 30° по 2-й оси, на 180° по 4-й оси так, что левый
лонжерон находится внизу и плита составляет с вертикальной плоскостью
угол 30°;
• робот установлен в точку с координатами 2800 мм, 810 мм, 0 и раз-
вернут вокруг вертикальной оси на угол 330° относительно оси X;
• сварочные клещи крепятся к фланцу робота с торца;
• робот должен сварить восемь точек, соединяющих левый лонжерон
с левым соединителем пола (точки № 1—8);
388
8. Опыт проектирования сварочных РТК
• робот должен сварить шесть точек, соединяющих левый лонжерон с
кронштейном крепления двигателя (точки № 18—20, 25, 30, 31).
Проверка доступности сварочного инструмента к свариваемым
точкам. При проектировании РТК прежде всего проверяли доступность
сварочного инструмента к свариваемым точкам. Действительно, если
электрод не может подойти к свариваемой точке и сталкивается со свар-
ным узлом, то дальнейшее проектирование лишено смысла. Необходимо
либо выбрать или спроектировать другой сварочный инструмент, либо
изменить технологию сварки (перенести точки сварки), либо внести из-
менения в сборочно-сварочное приспособление (если столкновение про-
исходит с ним).
Поскольку роботы № 1 и 3 расположены симметрично относительно
свариваемого изделия, то проверку доступности точек, закрепленных за
этими роботами, можно моделировать на одной позиции, например на пози-
ции робота № 3. В системе РОБО МАКС для проверки доступности свароч-
ного инструмента предусмотрены следующие операции:
• позиционирование сварочного инструмента на совмещенном по
сварным точкам и нормалям к поверхности множестве сечений сварного
узла — - функция Slicing;
• автоматическая проверка позиционирования множества сварочных
инструментов на множестве сварных точек — функция Tooltry;
• моделирование подвода-отвода сварочных клещей с визуальной
и автоматической проверкой отсутствия столкновений — функция
Toolteach.
Рассмотрим все эти способы проверки доступности клещей к сварным
точкам, закрепленным для обслуживания за выбранным роботом № 3 на
правом и левом лонжеронах. Построенное множество сечений по сварным
точкам с указанными номерами точек для робота № 3 и позиционированный
к ним сварочный инструмент (базовое направление подхода клещей —
ось Y) показано на рис. 8.11.
Из этого рисунка следует, что сварные точки №47, 50, 51, 54 не
доступны вследствие пересечения сварочного инструмента с кондукторной
плитой (по базовым направлениям подхода). Точки №50, 51 желательно
сместить в направлении кромки на 2...3 мм.
Построение в точке № 54 дополнительных сечений с вариацией пово-
рота плоскости сечения относительно нормали и включение их в состав ра-
нее подготовленного множества сечений и их визуализация происходит ав-
томатически с возможностью задания цвета и расположения на заданном
слое. Можно установить, что точка № 54 будет доступна при изменении на-
правления подхода относительно базового на -30...-40°. При построении
сечения клещей и свариваемой конструкции в плоскости клещевины в точке
8.2. РТК контактной сварки лонжеронов автомобиля ВАЗ 2110
389
Рис. 8.11. Множество сечений по сварным точкам для робота №3
и сварочные клещи, подведенные к ним
№ 47, а также вида с обратной стороны кондукторной плиты можно убе-
диться в том, что эта точка недоступна.
При использовании функции Tooltry имеется возможность варьиро-
вать следующие параметры:
• угол поворота плоскости клещей относительно нормали;
• углы наклона сварочных клещей относительно нормали в пределах
технологического конуса;
• смещение точки подхода клешей в плоскости XY фрейма сварной точки.
При автоматической проверке имеется возможность задавать началь-
ное приближение и шаг поиска. При нахождении допустимого значения
сварная точка считается доступной заданному инструменту. Решение задачи
о группировании сварных точек по обслуживающим их сварочным инстру-
ментам обеспечивает выбор минимального количества типов инструмента
для обслуживания всех сварных точек.
Результаты применения приложения Tooltry совпали с результатами
анализа доступности по множеству совмещенных сечений: доступны все
сварные точки, кроме № 47 и 1.
С использованием приложения Toolteach была осуществлена проверка
не только доступности инструмента к сварным точкам, но и отсутствия
столкновений инструмента при переходе между сварными точками, а также
390
8. Опыт проектирования сварочных РТК
при выводе клещей за кромку изделия. Подключение теста столкновений
позволяет построить промежуточные точки и осуществить необходимые
операции контроля.
В системе РОБОМАКС различают понятия «доступность» и «дос-
тижимость» свариваемой точки сварочным инструментом. Доступность —
это принципиальная возможность сварки указанных точек заданными
сварочными клещами без столкновений с изделием или элементами сбо-
рочно-сварочного приспособления. Достижимость — это возможность
позиционировать в точку сварки данные сварочные клеши, определен-
ным образом закрепленные на заданном роботе. Достижимость без
столкновений включает в себя доступность и называется полной дости-
жимостью.
Для анализа достижимости в рамках приложения WORKCEEL были
сформированы четыре объекта, включающих в себя свариваемые точки
DOTS1, DOTS2, DOTS3 и DOTS4.
DOTS1 содержит точки № 47—54 и ссылку на загруженный в ячейку
сварочный инструмент (в ней может быть несколько инструментов);
DOTS2 содержит точки № 9—13, 51—54 и ссылку на загруженный в
ячейку сварочный инструмент;
DOTS3 содержит точки № 18—20, 25, 30, 31 и ссылку на загруженный
в ячейку сварочный инструмент;
DOTS4 содержит точки № 1—8 и ссылку на загруженный в ячейку
сварочный инструмент.
Выбор с помощью мыши на экране монитора графических значков,
соответствующих этим объектам, позволяет производить их редактирова-
ние: удалять или добавлять свариваемые точки и ссылки на сварочный ин-
струмент.
Анализ достижимости свариваемых точек производится в системе
РОБОМАКС с помощью команды WELD, в которой возможна настройка
параметров сварки — углов а, р, у, определяющих поворот клещей в точке
сварки вокруг осей Y, Z и X соответственно. По команде WELD система
либо проверяет заданный диапазон по углу у при фиксированных заданных
значениях углов сс и р, либо сканирует заданные диапазоны по всем трем
углам относительно заданных начальных значений в поиске достижимых
положений клещей и робота. Для решения этой задачи используются алго-
ритмы решения обратной кинематической задачи, т. е. определения обоб-
щенных координат робота по заданному конечному положению и ориента-
ции сварочного инструмента.
При моделировании работы РТК клещи в ряде случаев могут подхо-
дить к элементам сборочно-сварочного приспособления и кондукторной
плите на расстояние нескольких миллиметров (1...3 мм), при этом подсис-
8.2. РТК контактной сварки лонжеронов автомобиля ВАЗ 2110
391
тема анализа столкновений может показать наличие столкновения. В этих
случаях при необходимости можно провести дополнительный анализ с по-
мощью построения соответствующих сечений в плоскостях точек сварки
или сместить на несколько миллиметров точку позиционирования сварочно-
го инструмента командами обучения WTOOL или TOOL.
Анализ достижимости точек, предназначенных для сварки роботом
№ 3, показал, что все семь точек множества DOTS2 (9—13, 55, 56), соеди-
няющие левый лонжерон с кронштейном двигателя достижимы, однако
следует отметить близость значений обобщенных углов по осям q2 и q5 к
границе допустимого диапазона (~1...1,5°). Проверка аналогичным обра-
зом множества точек DOTS1 (точки №48—54), соединяющих правый
лонжерон и правый соединитель пола показала, что ни одна из них не дос-
тижима, так как наклон оси q2 превышает допустимые значения. Анализ
достижимости точек, предназначенных для сварки роботом № 1, показал,
что все шесть точек, соединяющие левый лонжерон с кронштейном двига-
теля, полностью достижимы и ни одна из точек множества DOTS4
(№ 1—8), соединяющих левый лонжерон и левый соединитель пола, не
достижима. Таким образом, при заданном закреплении клещей к роботу с
торца и заданном расположении роботов № 1 и 3 относительно поворотно-
го стола с изделием указанные роботы не могут полностью выполнить
поставленную задачу. Для обеспечения достижимости указанных точек
возможны следующие действия:
• изменить относительное расположение робота и поворотного стола;
• перераспределить сварные точки между роботами;
• изменить положение планшайбы поворотного стола при сварке
группы точек;
• изменить способ крепления клещей к фланцу робота.
Поскольку в соответствии с техническим заданием изменять относи-
тельное положение сварочного робота и манипулятора изделия нельзя, из-
меним способ крепления клещей к кисти робота и присоединим их со сто-
роны, обратной по отношению к силовому цилиндру. Проведем проверку
доступности точек из приведенных выше множеств DOTS3 и DOTS4 с по-
мощью команды WELD. Все точки становятся достижимыми, кроме точки
№ 1 (с учетом замечаний по точкам № 2—5, 8), однако при сварке точек,
соединяющих левый лонжерон и левый соединитель пола (№ 2—8), угол q2
находится на границе допустимого диапазона. Возможное решение этой
проблемы — развернуть плиту со свариваемой конструкцией на 5...7° так,
чтобы угол плиты с вертикальной плоскостью составил 35...37°.
Достижимость всех точек еще не гарантирует существования траекто-
рии обхода этих свариваемых точек, удовлетворяющей кинематическим и
динамическим ограничениям по осям робота и свободной от столкновений с
392
8. Опыт проектирования сварочных РТК
изделием и другими элементами сцены. Для формирования такой траекто-
рии (например, для робота № 1) следует сначала с помощью команды обу-
чения робота WELD установить роботом клещи во все свариваемые точки
рассматриваемого подмножества (выбирается одно из возможных достижи-
мых положений). После выполнения команды WELD и выбора допустимых
углов а, Р, у с помощью команды STORE необходимо сохранить положение
клещей и робота (обобщенные координаты робота и поворотного стола) для
каждой из свариваемых точек № 2—8, 18—20, 25, 30, 31. Затем для каждой
точки введем имя, например D2 х 10 и т. п. Далее запрограммируем и смо-
делируем подход клещей к точке сварки № 2. Для этого воспользуемся ко-
мандой WTOOL (TOOL) — перемещение клещей относительно системы
координат TCP. Сместим клещи в направлении подхода (по оси Y) на 70 мм
и запомним полученную точку командой STORE с именем D2 х 70. Теперь
командами LIN, РТР смоделируем перемещение клещей из этой опорной
точки в точку сварки № 2 (D2 х 10). Если столкновение не обнаружено, пе-
рейдем с помощью той же команды LIN из точки № 2 в точку № 3
(D3 х 10). При обнаружении столкновения сместим клещи в точке № 2 (или
№ 3) вдоль электродов на 2...5 мм (эта операция может потребоваться при
малом раскрытии клещевин, если расстояние между точкой TCP и каким-
либо электродом составляет несколько миллиметров). Чтобы определить
величину смещения, может потребоваться построение сечения в плоскости
клещевин (в плоскости TCP XZ). Аналогичным образом командами LIN,
РТР перейдем в точки № 4, 5-—8, из точки № 8 командой TOOL установим
смещение в направлении подхода и смоделируем командой LIN отход кле-
щей из точки № 8 в точку, смещенную на 70 мм (D8 х 70). Далее переведем
клещи в исходное положение — в точку D8z400, полученную из точки
D8 х 70 смещением на 400 мм по оси Z (команда WTOOL). Аналогичным
образом моделируется участок обхода точек № 18—20, 25, 30, 31.
Таким образом, формирование траектории обхода свариваемых точек
включает следующие основные действия:
1) позиционирование клещей в точке сварки командой WELD;
2) сохранение положения клешей, робота и поворотного стола в точке
сварки командой STORE;
3) моделирование перехода в следующую точку сварки командами
обучения LIN, РТР, ZR;
4) задание опорных точек в случае обнаружения столкновения, ис-
пользуя команды обучения в системе координат TCP (WTOOL, TOOL) или в
мировой СК (JOINT, WORLD).
5. Моделирование переходов в опорные точки командами обучения.
Формирование программы движения робота и определение вре-
мени цикла его работы. Дальнейшие действия при формировании траекто-
рии обхода точек выполняются в такой последовательности:
8.2. РТК контактной сварки лонжеронов автомобиля ВАЗ 2110
393
1) составление и компиляция «off-line» программы управления робо-
том в универсальной среде PSC (Program System Compiler);
2) проверка выполнения программы на графиках углов, скоростей и
ускорений звеньев робота;
3) 379-моделирование программы с автоматическим анализом столк-
новений.
Ниже приведен пример анализа одной из программ обхода сварных
точек для робота № 1. Плита со свариваемой конструкцией большим изме-
рением ориентирована горизонтально и развернута поворотным столом по
I-й оси на 240° от положения загрузки, по 2-й оси на 35°, по 4-й оси на 180°
так, что левый лонжерон находится внизу и плита составляет с вертикаль-
ной плоскостью угол 35°.
В процессе обхода 14 точек сварки (восемь точек, соединяющих ле-
вый лонжерон и левый соединитель пола, и шесть точек, соединяющих ле-
вый лонжерон с кронштейном двигателя, — DOTS3 и DOTS4) ориентация
плиты не изменяется. Обход точек начинается и заканчивается в одной и той
же точке D8z400.
Исходное положение робота показано на рис. 8.12, где отсутствует
изображение изделия, указано только положение сварных точек. Такой ре-
жим может использоваться при моделировании программы для ускорения
перерисовки графической модели РТК. При этом проводится анализ столк-
новений с полной моделью РТК.
Время обхода 14 точек сварки роботом (без учета времени на сварку)
составило 23,6 с. Угловые скорости звеньев робота составляли не более
30 % от максимально возможных.
Таким образом, в результате анализа достижимости точек, получены
следующие результаты:
• точки № 1 и 47 (крайние точки, соединяющие правый и левый лон-
жероны с правым и левым соединителем пола соответственно) не доступны
для сварки любым типом клещей;
• полностью достижимы семь точек (№ 9—13, 55, 56), соединяющие
левый лонжерон с кронштейном двигателя, однако значения углов по осям
q2 и q5 близки к границе допустимого диапазона;
• не достижимы восемь точек (№ 47—54), соединяющие правый
лонжерон с правым соединителем пола (ось q2 превышает допустимые
значения);
• полностью достижимы шесть точек (№ 18—20, 25, 30, 31), соеди-
няющие левый лонжерон с кронштейном двигателя;
• не достижимы восемь точек (№ 1—8), соединяющие левый лонже-
рон с левым соединителем пола (ось q2 превышает допустимые значения).
394
8. Опыт проектирования сварочных РТК
Рис. 8.12. Исходное положение ПР с рабочим инструментом относи-
тельно массива точек (изображение сварного узла отсутствует для
увеличения быстродействия моделирования)
На основании приведенного анализа предложены рекомендации по
изменению положения инструментов для роботов № 1 и 3:
1) изменить крепление клещей к ПР и присоединить их со стороны,
обратной силовому цилиндру;
2) развернуть плиту со свариваемой конструкцией на 5...7° вокруг го-
ризонтальной степени подвижности так, чтобы угол плиты с вертикальной
плоскостью составлял 35...37°;
3) исключить точки сварки № 1 и № 7;
4) желательно сместить точки сварки № 2—5, 8, 50, 51 на 2...3 мм в
сторону кромки.
В этом случае все точки, закрепленные за роботом № 1, полностью
достижимы.
Таким образом, на примере созданного в сварочно-кузовном произ-
водстве ВАЗ РТК сварки передних лонжеронов автомобиля ВАЗ 2110 про-
демонстрированы некоторые возможности САПР комплексов сварки:
8.2. РТК контактной сварки лонжеронов автомобиля ВАЗ 2110
395
• передача и конвертация моделей из других CAD-систем ( в том чис-
ле и NURBS-моделей) в систему РОБОМАКС;
• подготовка моделей элементов РТК: сварной конструкции, свароч-
ных клещей, сборочно-сварочного приспособления, поворотного стола, ро-
бота и периферийного оборудования;
• сборка сварочной ячейки;
• проверка доступности сварных точек для сварочного инструмента
различными способами, включая подвод-отвод его за кромку;
• проверка достижимости сварных точек сварочным инструментом,
закрепленным на ПР;
• формирование программ работы и моделирование работы оборудо-
вания в РТК;
• подготовка рекомендаций по результатам проектирования.
8.3. Особенности технологии дуговой
роботизированной сварки
Классификация сварных конструкций под дуговую сварку. Узлы,
изготовляемые с помощью дуговой сварки, условно можно разделить на
пять групп в зависимости от их форм и размеров (табл. 8.1). Большое разно-
образие конструкций и требований к ним не позволяет представить принци-
пы создания РТК в общем виде, поэтому их целесообразно рассматривать по
выделенным группам.
Таблица 8.1. Узлы, изготовляемые с помощью дуговой сварки
Группа Вид узлов Примеры Комментарии
I Плоские больших габаритов Рамы, плат- формы, борта, панели Их производство наи- более трудоемко
396
8. Опыт проектирования сварочных РТК
Окончание табл. 8.1
Группа Вид узлов Примеры Комментарии
II Пространствен ные больших габа, тов ЭИ- Кузова в сборе, контей- неры, вагоны, рамы тележек, надрам ники самосвалов Обычно они состоят из плоских панелей и поэтому поддаются расчленению для одновременного их изготовле- ния с последующей оконча- тельной сборкой-сваркой. При этом наиболее трудоемко про- изводство самих панелей, а не их соединение воедино
III Детали машин Картеры ве- дущих мостов, корпусы редук- торов, баланси- ры, колеса Рамы мото- циклов и складных вело- сипедов, карка- сы сидений водителей и пассажиров, Характерна работа на уста- лостную прочность и большая степень ответственности кон- струкции, при которой разру- шение сварных соединений грозит аварией. Для обеспече- ния высокого качества сварки и точности размеров свари- ваемые кромки деталей перед сборкой подвергаются механи- ческой обработке Осуществляется сварка пе- ресечений тонкостенных труб и пластин по сложной кривой. Соединения сильно нагружен- ные и ответственные, их вы- полнение зачастую возможно лишь с изменением режима
IV Трубчатые кон струкции -
V Тип< кронштейнов поручни, раз- ветвления тру- бопроводов и т.п. сварки во время движения го- релки или с непрерывным из- менением их пространствен- ных положений Малоответственные не- больших габаритов и неслож- ной формы
8.3. Особенности технологии дуговой роботизированной сварки
397
Сварочное оборудование РТК. Комплект сварочного оборудования
РТК дуговой сварки состоит из:
• сварочного источника питания;
• аппаратуры подачи сварочной проволоки;
• набора сварочных горелок;
• агрегата охлаждения горелки;
• газовой аппаратуры;
• устройства автоматической очистки горелки от брызг;
• устройства защиты горелки «антилом»;
• средства контроля положения горелки на руке ПР;
• пылесоса, коммуникаций и крепежных элементов;
• системы управления и контроля сварочным процессом.
Все эти устройства должны стабильно работать длительное время без
участия человека, управляться системой управления РТК и иметь систему
контроля параметров.
Сварочный источник питания должен обладать повышенной надеж-
ностью зажигания дуги, стабильностью поддержания заданного режима,
гибкостью управления и т. п. Современные инверторные источники питания
управляют процессом сварки на уровне объема капель и времени переноса
каждой из них, что позволяет значительно уменьшить разбрызгивание и вы-
полнять сварку в любых пространственных положениях.
Аппаратура подачи сварочной проволоки должна обеспечивать рав-
номерную и надежную подачу проволоки диаметром 0,8...2,0 мм, и при
этом отклонение ее конца не должно превышать 0,2 мм на 15 мм вылета.
Таким требованиям удовлетворяет метод «тяни-толкай», состоящий из двух
механизмов; причем толкающий — планетарный типа ИЗОПЛАН. При ра-
боте этого механизма сварочная проволока одновременно с подачей еще и
выпрямляется, тем самым достигается высокая равномерность скорости, а
значит, улучшение формы шва и уменьшение разбрызгивания. Для умень-
шения простоев РТК за счет сокращения времени заправки и увеличения
надежности работы механизмов используют катушки большой емкости или
катушки обычных размеров с фабричной намоткой проволоки.
Сварочные горелки могут быть нескольких типов: прямые, Г- и S-об-
разные; в зависимости от условий работы и режимов сварки -— как правило,
с водяным охлаждением. Они должны иметь большую жесткость и проч-
ность и не терять размеров при аварийных столкновениях до срабатывания
выключателя, быть быстроразборными и быстросъемными, сохранять по-
ложение конца проволоки относительно кисти робота в пределах допусти-
мого износа токосъемника и при повторной сборке/установке горелки. Кон-
троль точности положения конца сварочной проволоки осуществляется с
помощью специального приспособления.
398
8. Опыт проектирования сварочных РТК
Агрегат охлаждения горелки использует жидкость, не дающую наки-
пи (часто — дистиллированную воду), циркулирующую по замкнутому кон-
туру и может быть смонтирован как в источнике сварочного тока, так и от-
дельным блоком.
Газовая аппаратура обеспечивает смешивание и подачу защитного
газа (или смеси газов) с заданным расходом и составом. Поскольку газы
расслаиваются, готовые смеси, как правило, не используются, их смешива-
ют непосредственно перед использованием. Кроме этого, горелку продува-
ют сжатым воздухом для очистки и наносят противопригарную жидкость на
внутреннюю поверхность сопла.
Устройство автоматической очистки горелки от брызг (механиче-
ской «фрезой», пневматической продувкой и нанесением противопригарной
жидкости) дополняется механизмом обрезания конца электрода для повы-
шения надежности зажигания дуги.
В случае оснащения робота системой адаптации применяется прямая
горелка. Адаптация «по дуге» осуществляется во время ее горения при ис-
пользовании механизма страховки от поломок в качестве датчика «началь-
ного положения». Имеется большое разнообразие систем адаптации, однако
такая схема наиболее удобна.
Система управления сварочным процессом решает две задачи: выбор
оптимальных параметров режима в зависимости от заданных номинальных
технологических условий и их изменение или стабилизацию по определен-
ному закону в случае возмущений.
Контролируются, а иногда и регистрируются текущие значения сле-
дующих параметров: сварочного тока и напряжения, скорости сварки, ско-
рости подачи и вылета проволоки, количества израсходованной проволоки;
расхода, давления и состава газа; расхода, давления и температуры охлаж-
дающей жидкости, износа наконечника и забрызгивания сопла. Задание этих
параметров возможно как при программировании РТК, так и непосредст-
венно через регуляторы аппаратуры.
Использование манипуляторов изделия. Смысл использования ма-
нипулятора изделий состоит в том, что каждый шов может быть расположен
в наиболее благоприятном для его формирования и наиболее удобном для
робота пространственном положении. Для этого достаточно двух осей вра-
щения. А поскольку чаще всего при относительно небольшой массе узлов
(до 150...400 кг) РТК комплектуется механизмом «смены позиций», то та-
кой поворотный стол с двумя манипуляторами изделий имеет пять осей
вращения: две пары управляемых осей и одну шаговую ось. Для контактной
точечной сварки достаточно стола с одной или тремя осями. Возможны слу-
чаи, когда кантовка узла не требуется. Однако по такой схеме собирают
только относительно простые узлы с небольшим числом входящих деталей.
8.3. Особенности технологии дуговой роботизированной сварки
399
Возможны и промежуточные варианты, когда оказывается необходи-
мым поставить прихватки перед сваркой во избежание увеличения зазора в
результате тепловых деформаций, или когда сварка ведется с последова-
тельным откидыванием части прижимов после выполнения одних швов для
обеспечения доступности к другим швам, или когда на этапе сборки на при-
хватках часть коротких швов выполняется вручную.
При разработке роботизированной сварочной технологии необходимо
выбрать или определить:
• способ сварки и сварочные материалы;
• приемлемое пространственное положение каждого шва и режимы сварки;
• вероятность получения брака и пути снижения процента брака;
• последовательность сборки, сварки и кантовки изделия и т. п.
К процессу роботизированной дуговой сварки предъявляется ряд тре-
бований, невыполнение каждого из которых может привести к браку, оста-
новке работы или к другим нежелательным последствиям:
• минимальное разбрызгивание металла;
• возможность сварки в положениях, отличных от нижнего;
• широкий диапазон режимов устойчивого горения дуги;
• надежное зажигание дуги;
• качественное формирование сварного шва;
• стабильность поперечного сечения шва и его химического состава;
• надежность контакта проволоки с токосъемником и т. п.
Одним из наиболее эффективных технологических приемов влияния на
формирование шва является изменение пространственного положения стыка.
Он дает эффект даже при небольшом отклонении от «нижнего» положения
(при сварке «на спуск» до 20°). В этом случае улучшается форма шва: обеспе-
чивается плавный переход от шва к основному металлу, уменьшается расход
проволоки при повышении несущей способносности шва и увеличении скоро-
сти сварки, уменьшается опасность прожога и получения брака вследствие не-
точности расположения стыка относительно сварочной горелки. Преимуществ
много, и именно использование манипулятора изделия с соответствующим
числом осей обеспечивает получение этих преимуществ и увеличение произво-
дительности процесса роботизированной сварки. Известны и другие техноло-
гические приемы управления формированием сварного шва (наклоном элек-
трода, колебаниями горелки, изменением полярности и т. п.).
Наиболее существенным требованием при разработке технологии ро-
ботизированной сварки является уменьшение вероятности брака. Достиже-
ние максимальной производительности и экономичности процесса главным
образом достигается за счет создания условий почти непрерывной двух-,
трехсменной работы сварочных РТК.
400
8. Опыт проектирования сварочных РТК
Оценка требуемой точности положения свариваемых стыков при
роботизированной сварке. Современные промышленные роботы обладают
такими техническими характеристиками, которые способны обеспечить прак-
тически любую траекторию перемещения горелки с высокой точностью, необ-
ходимой для процесса дуговой сварки. Однако условия самого производства
далеко не всегда соответствуют этим высоким требованиям. К числу факторов,
затрудняющих применение неадаптивных роботов, следует прежде всего отне-
сти нестабильность расположения свариваемых стыков в пространстве и не-
точность сборки свариваемых кромок (табл. 8.2). Эти факторы приводят к слу-
чайным отклонениям — смещению горелки поперек стыка Т]т — и зазорам в
соединении Ь. Параметры t/np и состав газа выбраны, Si и S2 заданы, а остальные
параметры изменяются согласно технологии, в том числе и для расширения
допустимых смещений электрода и зазора в свариваемом стыке.
Таблица 8.2. Технологические параметры основных типов сварных
соединений
Группы параметров Эскиз таврового соеди- нения Эскиз нахлесточного соединения Параметр
Материалы Размеры соединения 1 5| b St 5 2 - диаметр проволоки Состав защитного газа: Si —толщина листа 1, 5? — толщина листа 2. Ь — зазор в соединении
Положение грелки относительно соединения х р \> Г|т* 1 Да. 1]т поперечное отклонение проволоки от стыка, 1 - вылет проволоки, а - поворот горелки, р - наклон горелки
сварка «углом вперед», «в угол»
Сварочный режим Лп - амплитуда колебаний, Исв - скорость сварки, /св - ток сварки, Ua - напряжение дуги
Пространст- ве иное положение соединения сварка «на спуск» «в лодочку» 57 £, - поворот соединення. у - наклон соединения
8.3. Особенности технологии дуговой роботизированной сварки
401
Существующие системы «геометрической» адаптации роботов, хотя и
расширяют допустимые пределы отклонений горелки от линии свариваемо-
го стыка, но в ограниченных пределах, не обладают универсальностью при-
менения и значительно уменьшают производительность процесса. В связи с
этим очень важно определить рациональные области использования свароч-
ных роботов без адаптации и выявить условия, при которых необходимо
применять адаптивные роботы.
В качестве наиболее простого и наглядного примера рассмотрим
среднюю часть прямолинейного шва (рис. 8.13). Здесь изображены три
линии: 1 — траектория электрода горелки, 2 — теоретическое положение
свариваемого стыка, 3 — фактическое положение стыка. Основной при-
чиной некачественного (дефектного) соединения является случайное по-
перечное отклонение г] траектории горелки от фактического положения
свариваемого стыка на величину, превышающую допустимое значение.
Это отклонение в процессе сварки получается в результате суммирова-
ния: Д1 — погрешности траектории горелки и Д2 — погрешности поло-
жения самой линии стыка.
Тот участок шва, где конец электрода отклоняется от линии стыка на
величину г] > §i (предельно допустимого смещения в данную сторону), ока-
зывается дефектным. Отсюда следует, что отклонение конца электрода не
должно выходить за пределы заштрихованной зоны шириной 5] + 52 ~ S.
Погрешности траектории горелки Д1, в свою очередь, обусловлены:
• неточностью воспроизведения траектории движения горелки ро-
ботом ДВОСпР;
• неточностью обучения робота До;
• поперечным отклонением конца сварочной проволоки относительно
оси горелки Дп.
Суммарное отклонение горелки можно представить в виде векторной
суммы этих отклонений (на рис. 8.13 изображена лишь проекция Д1).
У современных
роботов для дуговой
сварки погрешность Дв
воспроизведения граек- Г
тории электрода не пре-
вышает ±0,2 мм, и нет 10
необходимости стремить- и
ся к дальнейшему уже-
сточению этого показа-
теля, так как другие от- Рис. 8.13. Участок шва, выполняемый на РТК дуговой
клонения оказываются сварки
14 — 6705
402
8. Опыт проектирования сварочных РТК
существенно большими. Так, в реальных условиях у серийных отечествен-
ных сварочных полуавтоматов отклонение Дп сварочной проволоки на выле-
те 15 мм достигает ±1,0 мм вследствие изгиба конца и изнашивания отвер-
стия токосъемника. Неточность обучения робота, в свою очередь, также за-
висит от отклонения Ап сварочной проволоки, поскольку роботов обучают
(программируют) по концу проволоки, и от квалификации обслуживающего
персонала.
Возможны следующие пути уменьшения значений До и Дп:
• за счет обучения по концу проволоки, предварительно выпрямлен-
ной в «контрольной точке», куда переносится горелка перед обучением ро-
бота;
• за счет применения специальных подающих механизмов, выпрям-
ляющих проволоку (типа ИЗОПЛАН).
Допустимое отклонение конца сварочной проволоки с сохранением
высокого качества сварного шва может изменяться в самых широких преде-
лах и зависит прежде всего от конструкции и размеров сварного узла. По-
этому определение этой величины необходимо производить в каждом кон-
кретном случае путем предварительных расчетов или непосредственных
измерений следующих параметров:
• стабильности размеров входящих в узел деталей и их позициониро-
вания в сборочном приспособлении, а также деформаций под действием за-
жимов и прихваток;
• точности фиксации узла в сборочном приспособлении;
• точности позиционирования сварочного приспособления;
• сварочных деформаций, возникающих в процессе сварки.
Такие поэтапные замеры дают представление об основных причинах
возникновения нестабильности положения стыка и могут быть использованы
при разработке технологии роботизированной сварки. Статистическая обработ-
ка результатов замеров партии узлов и деталей позволяет установить закон рас-
пределения отклонений сварочной проволоки от оси свариваемого стыка.
Адаптация роботов. Зная значения допустимых и ожидаемых откло-
нений сварочной проволоки, можно оценить целесообразность сварки дан-
ного изделия с помощью робота без адаптации (рис. 8.14).
Уменьшить отклонение сварочной проволоки можно путем модерни-
зации конструкции узла, повышением точности изготовления его элементов
и сборки, изменением технологии сборки-сварки и прочими мероприятиями.
Если они оказываются недостаточно эффективными или экономически не-
целесообразными, то необходимо применение адаптивных роботов.
Использование систем адаптации кроме увеличения капитальных за-
трат на оборудование, усложнения (а значит, уменьшения надежности) ро-
бота и увеличения габаритных размеров инструмента (если имеется датчик
8.3. Особенности технологии дуговой роботизированной сварки
403
Рис. 8.14. Последовательность действий применительно к роботизации
дуговой сварки конкретного узла
на горелке) также уменьшает производительность работы комплекса в зави-
симости от ожидаемых погрешностей. Поэтому использование робота с сис-
темой адаптации является вынужденной мерой, к которой прибегают во из-
бежание чрезмерного процента брака сварки.
Чаще всего адаптация необходима для сварки крупногабаритных
сварных конструкций, но и она вовсе не исключает необходимости меро-
приятий по повышению точности базирования сварных швов на этапе под-
готовки производства. Из практики известно, что разброс отклонений сва-
рочной проволоки от оси свариваемого стыка путем различных усовершен-
ствований технологии был уменьшен от ±20 до ±5 мм, а затем применение
14»
404
8. Опыт проектирования сварочных РТК
Рис. 8.15. Основные условия получения качественного сварного шва:
1 — реальное положение средней линии допуска +/- доп; 2 — траектория
электрода; 3 — линия, вводимая в программу ПР
робота с системой адаптации обеспечило ведение горелки по стыку при от-
клонениях не выше ±1,0 мм.
Обычно допуск 5ДОП на поперечное отклонение конца электрода от ли-
нии стыка (рис. 8.15) для тавровых соединений принимают равным ±1,0
диаметра электродной проволоки или ±0,2 толщины свариваемого металла.
Следует отметить, что это весьма неточные ориентиры, так как допуск зави-
сит от большого количества факторов.
Для экспериментального определения зависимостей технологических
факторов при роботизированной дуговой сварке был создан стенд, позво-
ляющий вести сварку на образцах в любом пространственном положении
стыка и горелки без нарушения значений г] и b (рис. 8.16). Стенд может
Рис. 8.16. Экспериментальный стенд дуговой сварки образцов в различных пространственных положениях
8.3. Особенности технологии дуговой роботизированной сварки 405
406
8. Опыт проектирования сварочных РТК
быть использован для различных исследовательских и экспериментальных ра-
бот. В отличие от сварки с помощью ПР, он позволяет поэтапно проверить воз-
действие всех технологических факторов (режимов, положений, отклонений,
материалов и т. п.) и при этом много проще и дешевле в эксплуатации.
Методика экспериментов заключалась в сварке тавровых соединений,
у которых исследуемый параметр (т| или Ь) устанавливался переменным по
длине пластин (табл. 8.3). Эксперимент повторялся при измененных услови-
ях (например, изменяли наклон горелки).
Таблица 8.3. Методика определения предельных отклонений
Параметры
Сварка с переменными
параметрами
по длине образца
Испытание путем отгиба
пластин образца
r]T = var при Ь = 0
(от образца к образцу
изменяется один из
исходных парамет-
ров)
b = var при Г]т = 2,5 мм
(от образца к образцу
изменяется один из
исходных парамет-
ров)
По результатам экспериментов можно сделать несколько общих вы-
водов о влиянии различных технологических факторов на допустимые от-
Рис. 8.17. Положение зоны сварки
при изменении зазора
клонения и зазоры.
1. Наличие зазора в соединении
b резко сужает допуск на отклонения 8
(рис. 8.17).
2. Сварку таврового соединения
следует вести по линии, соответст-
вующей положению центральной оси
зоны допуска (т]т = 2,5 мм) (см. рис. 8.15).
3. Наиболее эффективны сле-
дующие пути расширения допустимого
смещения оси сварочной проволоки:
8.4. Роботизированный технологический участок сварки барабана жатки 407
а) наклон соединения — сварка «на спуск» (угол у до 45°),
б) поворот горелки в сторону полки (угол а до 30°).
4. Применение колебаний не эффективно, так как при толщине метал-
ла порядка 4 мм ведет к подрезам.
5. Использование смеси газов углекислоты и аргона увеличивает
жидкотекучесть металла и ужесточает допуск на позиционирование элек-
трода.
8.4. Роботизированный технологический участок сборки
и сварки барабана роторной жатки комбайна
В современных зерноуборочных машинах высокие требования к точ-
ности узлов основных агрегатов, ответственных за их технологические ха-
рактеристики, обусловлены необходимостью достижения максимальной
производительности, качества обмолота и снижения потерь зерна.
Роторная жатка ЖР-3500 (рис. 8.18) является скашивающим агрегатом
кормоуборочного комбайна Дон-680. Два барабана, вращающиеся встречно
со скоростью 2 об/с, подают стебли под ножи дисковых роторов, вращаю-
щихся соосно с барабанами со скоростью 4 об/с. Срезанные стебли подают-
ся в приемную камеру и далее в измельчитель комбайна.
Барабан диаметром 1600 мм (рис. 8.19) представляет собой сварную
обечайку, образованную четырьмя царгами — стенками 7. Жесткость обе-
чайке придают три кольцевых пояса I, II, III, каждый из которых состоит из
четырех сегментов 2, сваренных между собой встык. Фланец 5, на который
барабан устанавливается в жатке, соединен с поясами четырьмя спицами 4 и
Рис. 8.18. Роторная жатка ЖР-3500 комбайна Дон-680
408
8. Опыт проектирования сварочных РТК
Рис. 8.19. Схема конструктивно-технологического расчленения барабана
четырьмя связями 5. Перечисленные детали образуют остов барабана б, к
нижнему торцу которого приварены восемь секций съемника 7, а по высоте
цилиндрической поверхности обечайки распределены два кольцевых пояса
зубчатых сегментов 8, 9 и два пояса гребенок 10 и 11. Левый и правый бара-
баны по конструкции являются зеркальным отражением друг друга.
Четыре царги толщиной 3 мм сварены между собой встык односто-
ронними внутренними швами. Каждый пояс I, П, III приварен к обечайке
прерывистыми односторонними угловыми швами 100/200 мм, катетом 5 мм.
Съемники толщиной 7 мм приварены к нижнему поясу по периметру бара-
бана внахлестку двумя прерывистыми швами 75/150 мм, катетом 5 мм. Зуб-
чатые сегменты толщиной 5 мм и гребенки толщиной 6 мм устанавливаются
на обечайке выступами в щелевые отверстия и образуют прорезные сварные
соединения, выполняемые изнутри барабана. Соединения спиц и связей с
поясами — тавровые односторонние, а с фланцем — нахлесточные, катетом
4 мм. При изготовлении барабана выполняют 356 швов общей протяженно-
стью 21 м.
8.4. Роботизированный технологический участок сварки барабана жатки 409
Захват и подача срезанных стеблей в приемную камеру возможны
благодаря тому, что зубья гребенок и сегментов при вращении входят в со-
ответствующие прорези в боковых стенках приемной камеры. Этим и обу-
словлены жесткие требования к геометрии барабана:
• радиальное биение обечайки не более 2 мм (во избежание контакти-
рования со стенками барабана и приемной камеры);
• торцевое биение плоскости съемников не более 2 мм (во избежание
касания ротора);
• биение плоскостей сегментов и гребенок относительно плоскости
съемника не более 2 мм (во избежание заклинивания зубьев в пазах стенок
приемной камеры);
• отклонение от параллельности привальной плоскости фланца отно-
сительно плоскости съемников не более 0,8 мм.
Очевидно, что выдержать при сварке столь жесткие допуски для тон-
костенной листовой конструкции диаметром 1600 мм, имеющей такое коли-
чество сварных швов, является сложной технической задачей.
Структура роботизированного технологического участка. В про-
цессе подготовки производства жатки на заводе АО «Ростсельмаш» перво-
начально были созданы технологический процесс и сборочно-сварочная ос-
настка, предусматривающая применение полуавтоматической сварки в сре-
де углекислого газа. В кондукторе сваривали из сегментов три кольца
жесткости, на которые затем в другом приспособлении базировали четыре
стенки, обжимая их снаружи. В третьем приспособлении в полученный ба-
рабан устанавливали и приваривали спицы, связи и фланец, центрируя их
относительно обечайки. После этого, поворачивая остов на вращателе, уста-
навливали и приваривали зубчатые сегменты, гребенки и съемники, не
пользуясь оснасткой. В результате применения такой технологии брак по
геометрическим параметрам составлял около 40 %, из них половина — брак
неисправимый. Для уменьшения биений использовали механическую
правку и наложение холостых валиков на связи. Обмер партии барабанов
показал, что нарушения формы имеют случайный характер, что свиде-
тельствовало об отсутствии систематической погрешности при сборке и
нестабильности технологического процесса. Значения катетов, длины
отдельных швов и порядок их наложения имели существенные отклоне-
ния от регламентированных. В результате объем последующих доводоч-
ных работ при испытании собранной жатки на обкаточном стенде втрое
превышал длительность самой обкатки. Возникшая в производстве си-
туация потребовала создания стабильной технологии сборки и сварки
барабана, обеспечивающей его проектную точность. В связи с этим был
проведен анализ технологичности конструкции барабана с целью оценки
возможности роботизации процесса его сварки.
410
8. Опыт проектирования сварочных РТК
Вследствие значительных экономических потерь от брака главной це-
лью создания технологии роботизированной сварки является получение
конструкции, отвечающей требованиям проектной документации прежде
всего в отношении точности и стабильности геометрии, а также качества
сварных соединений. В данном случае, по-видимому, справедлив тезис
Г. Гердена о том, что применение роботов как средств автоматизации
следует предусматривать не там, где их можно использовать, а там, где
без них нельзя обойтись.
При разработке новой технологии изготовления барабана с помощью
роботов исходили из следующих соображений. Очевидно прежде всего, что
выполнение всех швов на полностью собранном барабане невозможно без
использования манипулятора. Однако габаритные размеры и масса изделия
(245 кг) требуют позиционера большой грузоподъемности, точность пози-
ционирования которого не может удовлетворить условиям применения ро-
ботизированной сварки. К тому же общее количество швов таково, что объ-
ем памяти робота, необходимый для их выполнения, намного превосходит
возможности последнего. Совместная работа внутри барабана двух роботов
проблематична, так как развести во времени и в пространстве траектории их
горелок (избежать столкновений) в столь ограниченном пространстве прак-
тически невозможно.
Таким образом, с одной стороны, очевидна необходимость расчлене-
ния изделия на отдельные технологические узлы, с другой стороны, высокая
проектная точность конструкции требовала такой схемы расчленения, при
которой узел, определяющий точность всего изделия, должен быть изготов-
лен в одном кондукторе, тем более что отсутствие переустановок изделия
уменьшает возможные отклонения электрода от оси стыка и тем самым по-
вышает качество сварных соединений. Указанные выше взаимоисключаю-
щие требования заставили искать определенный компромисс при создании
новой технологии.
Варианты расчленения на сборочные единицы анализировали с помо-
щью системы РОБОМАКС для определения доступности для робота и дося-
гаемости им всех швов. В результате анализа был принят следующий вари-
ант. Изготовление барабана осуществляется на грех РТК. На первом из них
(РТК-1) спицы 4 и связи 5 приваривают к отдельным сегментам, при этом
образуется по две сборочные единицы Т-1 и Т-2 (см. рис. 8.19) для левого и
правого барабанов.
На втором комплексе (РТК-2) изготовляют остовы левого и правого
барабанов, образуя их из стенок, сегментов, узлов Т-1, Т-2 и фланца. При
условии стационарности стенда выполнение всех сварных швов в нижнем
положении возможно только при вертикальном расположении оси барабана.
Робот, установленный на полу и расположенный вплотную к двум стоящим
8.4. Роботизированный технологический участок сварки барабана жатки 411
рядом сварочным стендам, обслуживает их поочередно. Анализ доступности
для горелки сварных швов, выполняемых на данной позиции, показал, что
на полностью собранном остове около 25 % швов оставались недоступны-
ми. Поскольку дальнейшее расчленение на сборочные единицы не целесо-
образно, было решено воспользоваться методом последовательного нара-
щивания, чередуя сборочные и сварочные операции. Моделирование такого
процесса подтвердило его приемлемость. Детально он будет рассмотрен
ниже.
Сваренные остовы левого и правого барабанов поступают на третий
роботизированный комплекс (РТК-3), где на двух стендах производится
приварка съемника, гребенок и сегментов. Для сварки всех швов в нижнем
положении ось барабана, относительно которой кантуется изделие, распола-
гается горизонтально. Робот находится между стендами и обслуживает их
поочередно. В то время как на одном стенде робот производит сварку, на
другом стенде ведется сборка. Анализ доступности швов показал, что за од-
ну установку можно сварить четверть всего количества швов при условии,
что часть их будет располагаться на цилиндрической поверхности под углом
к горизонту, достигающим 40°. Таким образом, на стенде осуществляется
четырехкратное позиционирование изделия с поворотом на 90° вокруг гори-
зонтальной оси.
Все три РТК технологически взаимосвязаны, что предполагает объ-
единение их в организационно самостоятельное производственное подраз-
деление. Предварительные технико-экономические расчеты показали, что
существенные различия длительности сборочно-сварочных операций на от-
дельных РТК делают нецелесообразным создание автоматической линии
сварки барабана с единой системой управления. Поэтому решено было ор-
ганизовать роботизированный технологический участок, объединив отдель-
ные РТК общей механизированной транспортной системой с накопителями
между ними. Для левого и правого барабанов необходимо было предусмот-
реть два отдельных грузопотока со своим технологическим оборудованием.
Учитывая сложность и высокую точность узлов и изделия в целом и
значительность потерь от возможного брака, был проведен статистический
контроль качества деталей, поступающих на участок. Результаты показали,
что для сегментов, спиц и связей, получаемых контурной вырубкой на прес-
сах, а также для фланцев, проходящих токарную обработку, брак не превы-
шает 2 %. Стенку получали контурной вырубкой с последующей гибкой на
прессе. При такой технологии брак достигал 50 %, основным дефектом было
отклонение от проектного значения радиуса гибки стенки. Местные недоги-
бы или перегибы на базе 150...200 мм вызывали неприлегание стенки к сег-
ментам. Зазоры в местах наложения швов достигали 3 мм, что не только не
позволяло выполнить качественный шов, но и вызывало недопустимое ра-
412
8. Опыт проектирования сварочных РТК
диальное биение барабана. Это потребовало усовершенствования техноло-
гии изготовления стенки, а в состав участка пришлось ввести специализиро-
ванное рабочее место для 100 %-ного входного контроля ее геометрических
размеров. Браковочным признаком являлся зазор более 1,4 мм, остающийся
между стенкой и сегментом после их закрепления в специальном приспо-
соблении. Кроме того, на участке были организованы рабочие места для
100 %-ного контроля геометрии остова барабана и место контроля и исправ-
ления брака готовой продукции.
Решение вопросов организации грузопотока и компоновки отдельных
РТК позволило приступить к разработке технологического процесса, техни-
ческих заданий и проектированию технологического оборудования.
Устройство и работа РТК-1. Поскольку технологические узлы лево-
го и правого барабанов являются зеркальным отражением друг друга, соот-
ветственно такими же являются и приспособления для их сборки. На одном
приспособлении собираются узлы Т-1 левого и Т-2 правого барабанов, на
другом — соответственно Т-2 левого и Т-1 правого барабанов (см. рис. 8.19).
Схема одного из приспособлений показана на рис. 8.20. На плоской
раме 1 закреплены опоры с установочными пальцами 2. Сегмент 3 устанав-
8.4. Роботизированный технологический участок сварки барабана жатки 413
Рис. 8.21. Схема размещения оборудования РТК-1
ливают на два пальца и закрепляют двумя клиновыми 4 и дуговыми 5 прижи-
мами. На сегмент устанавливают спицу 6 (для Т-1) или связь 7 (для Т-2), фик-
сируют с помощью съемных пальцев 8 и прижимают дуговым прижимом 9. В
месте приварки к сегменту наклонно расположенная связь заканчивается гиб-
кими усиками, которые при транспортировке деталей часто деформируются.
Для придания им перед сваркой положения, заданного чертежом, служит от-
кидной клинообразный фиксатор 10, который в рабочем положении распирает
усики до одного и того же размера, независимо от их начальной деформации.
Этим достигается точность попадания конца электрода на линию стыка дета-
лей, а значит — получение качественного шва при сварке роботом.
Наличие в приспособлении той или иной детали, правильность ее по-
ложения и качество закрепления фиксируют индукционные датчики поло-
жения 11. Они же формируют для системы управления РТК код, по которо-
му робот распознает готовность к сварке того или иного узла в определен-
ном приспособлении и вызывает соответствующую сварочную подпрограмму.
Расположение оборудования РТК-1 показано на рис. 8.21. Приспособ-
ления 1 и 2 размещены попарно на двух столах 3, которые обслуживает сва-
414
8. Опыт проектирования сварочных РТК
рочный робот 4 типа IR-161/15. Между столами установлено устройство 5
для очистки горелки робота. Каждое рабочее место имеет отдельный пульт
управления 6. Вблизи пультов расположены стойка 7 системы управления
роботом RC20/41 и источник 8 питания сварочным током типа SGL300IR.
Перед столами установлены полы безопасности 9. Каждая зона сборки име-
ет места 10 складирования и стеллажи-накопители 11 для готовых узлов.
Оператор-сборщик собирает на двух приспособлениях левого стола
узлы Т-1 и Т-2 левого барабана, нажимает кнопку «Старт» левого пульта и
переходит к правому столу. Робот поочередно анализирует коды приспо-
соблений и, если сборка произведена правильно, выполняет сварку узлов по
соответствующей подпрограмме. Затем робот и оператор обмениваются ра-
бочими местами и все операции повторяются вновь.
Устройство и работа РТК-2. Наиболее сложным и точным техноло-
гическим узлом в составе барабана является его остов. Отклонения от пра-
вильной геометрической формы, полученные при его изготовлении, лими-
тируют точность изготовления барабана. Поэтому, приступая к проектиро-
ванию сборочного кондуктора, сформулируем основные требования к нему:
• кондуктор должен быть стационарным;
• кондуктор должен обеспечивать изготовление остова при верти-
кальном расположении его оси;
• установка деталей, ответственных за точность остова барабана (сте-
нок и фланца), должна осуществляться по базовым элементам приспособле-
ния, а не по другим дсгалям;
• точность позиционирования деталей в узле должна быть достаточ-
ной для выполнения роботом качественных сварных соединений;
• жесткость кондуктора должна более чем на порядок превышать же-
сткость собираемого узла;
• конструкция кондуктора и порядок сборки должны обеспечивать
доступность для горелки робота всех сварных швов;
• базовые элементы должны быть регулируемыми, а усилия при-
жимов — достаточным, чтобы обеспечить фиксацию деталей в заданном
положении независимо от отклонений их формы;
• кондуктор должен иметь систему контроля качества сборки узла,
включенную в систему управления РТК и содержащую элементы, исклю-
чающие неправильную установку деталей;
• время сборки узла в кондукторе не должно превышать время его
сварки роботом.
В соответствии с этими требованиями процесс изготовления остова
был расчленен на три этапа (см. рис. 8.19):
8.4. Роботизированный технологический участок сварки барабана жатки 415
Рис. 8.22. Схема базирования остова барабана
этап 1 — сборка и сварка обечайки и нижнего пояса сегментов;
этап 2 — сборка и сварка среднего пояса сегментов, образованного
четырьмя узлами Т-1, и приварка его к центральному фланцу;
этап 3 — сборка и сварка верхнего пояса сегментов, образованного
четырьмя узлами Т-2, и приварка его к фланцу.
Высокие требования к точности барабана и необходимость свобод-
ного доступа горелки робота к сварным швам внутри барабана обуслови-
ли выбор системы базирования стенок по наружной поверхности и при-
жатия их к базам магнитными силами. Аналогичным образом должен
фиксироваться фланец — наиболее ответственный элемент, точность ус-
тановки и неизменность положения которого в процессе сварки опреде-
ляют торцевое и радиальное биение остова. Технологические узлы Т-1 и
Т-2 в данном случае играют роль связующих элементов. В связи с трех-
этапностью процесса сборки их положение внутри барабана необходимо
было задать специальной съемной оснасткой, а базировать — по стенкам
и фланцу. Схема базирования деталей, отражающая перечисленные тре-
бования, показана на рис. 8.22.
В соответствии с техническим заданием были созданы автоматизиро-
ванные магнитные кондукторы, конструкция которых реализует приведен-
ную схему базирования. Схема кондуктора дана на рис. 8.23. Основными
его узлами являются: основание 7; плита опорная 2; концевые 3, основные 4
и центральные 5 магнитные модули; замыкатель 6 обечайки с фиксаторами 7;
пульты 8 управления секциями; центральный пульт управления 9; прижимы
вертикальные 10 и горизонтальные 77; проставки малые 72 и большие 73;
панель 14 пневматических агрегатов.
На прямоугольном основании 7 установлена опорная плита 2 — ос-
новной несущий элемент кондуктора. Верхняя плоскость плиты обработана
механически с отклонением от плоскостности не более 1 мм. На диаметре
416
8. Опыт проектирования сварочных РТК
Рис. 8.23. Кондуктор для сборки и сварки остова барабана
1500 мм расположены шестнадцать линейных опор 15, задающих плоскость
опирания остова. Наиболее ответственными узлами кондуктора, от которых
зависит точность изготовления остова, являются стойки с магнитными мо-
дулями, расположенные по периметру кондуктора, и блок центральных маг-
нитных модулей, фиксирующих фланец. Двадцать магнитных модулей
8.4. Роботизированный технологический участок сварки барабана жатки 417
сгруппированы в четыре секции. Каждая секция содержит два концевых 3 и
три основных 4 модуля, закрепленных в соответствующих стойках. Поло-
жение модулей в стойках может регулироваться путем плоскопараллельного
радиального перемещения, а также поворотов в вертикальной и горизон-
тальной плоскостях. Для регулировки используется система направляющих
и конических упоров, перемещающихся с помощью эксцентриков.
Принцип действия всех управляемых постоянных магнитных модулей
одинаков и основан на взаимодействии магнитных полей перемагничивае-
мых и неперемагничиваемых постоянных магнитов, объединенных в мо-
дуль. Соотношение магнитных полей этих магнитов определяет одно из
двух состояний модуля: активное и пассивное.
Управление магнитным потоком перемагничиваемого магнита осуще-
ствляется с помощью охватывающей его катушки. Для приведения модуля в
активное состояние на катушку подается импульс постоянного напряжения,
доводящий материал магнита до состояния магнитного насыщения. При
этом полярность импульса такова, что магнитные потоки обоих постоянных
магнитов складываются, направляются в прилегающую к ним деталь и
практически полностью в ней замыкаются. Суммарное магнитное поле,
удерживающее деталь, остается практически неизменным более 10 сут.
Для перевода модуля в пассивное состояние на катушку перемагничи-
ваемого магнита подается электрический импульс обратной полярности.
Магнитные потоки обоих магнитов взаимно компенсируются, и сила, удер-
живающая деталь, становится близкой к нулю.
В модуль каждого магнита встроены датчики силы удержания детали
и плотности ее прилегания к полюсам. При полном прилегании стенки к
магнитам, расположенным по наружному контуру остова барабана, сила
удержания каждого модуля равна 2 кН. Усилие, развиваемое блоком цен-
тральных магнитов, удерживающих фланец, достигает 1 кН.
Левая половина стоек модулей закреплена на плите неподвижно, с
тем, чтобы рабочие поверхности полюсных наконечников образовывали ци-
линдрическую поверхность диаметром 1514 мм (наружный диаметр остова),
перпендикулярную плоскости плиты. Остальные стойки закреплены на под-
вижном сегменте 16, который скользит по плите, поворачиваясь вокруг оси
17. При замыкании происходит обжатие обечайки в тангенциальном на-
правлении и смыкание торцевых кромок стенок. Механизм замыкания при-
водится в движение пневматическим цилиндром и удерживается в заданном
положении тремя фиксаторами 7. Контроль за работой механизмов замыка-
теля осуществляется с помощью индукционных датчиков приближения.
Управление магнитными модулями каждой секции осуществляется с
отдельных пультов 8, установленных по периферии кондуктора, управление
центральными магнитными модулями и замыкателем — с центрального
418
8. Опыт проектирования сварочных РТК
пульта 9. Здесь же находятся блок связи с системой управления РТК и блоки
питания.
Если от точности фиксации в кондукторе обечайки и центрального
фланца зависит в основном геометрия остова, то качество сварных соедине-
ний, выполняемых роботами, определяется точностью и стабильностью
фиксации положения деталей, ими соединяемых. Достижению последней
цели служит дополнительная стационарная или съемная оснастка, которой
оборудован кондуктор.
На 1-м этапе сегменты нижнего пояса укладывают на опоры 15, бази-
руя каждый технологическим отверстием на один палец 18, прижимают к
обечайке эксцентриком 19, а к опорам сверху прижимами 10, через малые
12 и большие 13 проставки. Усилие прижатия достаточно, чтобы устранить
неплоскостносгь сегментов, обусловленную контурной вырубкой по криво-
линейным поверхностям. Благодаря этому отклонения линии сопряжения
деталей не превышают допустимого значения для угловых швов данного
размера (для катета шва 5 мм это значение составляет ±1,2 мм при зазоре не
более 1,5 мм). Цикл сварки начинается с постановки роботом на каждом
стыке стенок двух прихваток, придающих обечайке кольцевую жесткость.
Затем производят приварку сегментов к обечайке прерывистыми швами и в
последнюю очередь на медной подкладке выполняют 20 стыковых швов,
соединяющих сегменты между собой.
На 2-м этапе большие проставки удаляют, а на малые устанавливают
четыре узла Т-1, базируя их сегментами на обечайку, а спицами на цилинд-
рические упоры 21 и подпружиненные пяты 22. На центральные магнитные
модули укладывают фланец, базируя его по оправке 23, и фиксируют, пере-
водя магниты в активное состояние. На сегменты узлов Т-1, образующие
второй пояс жесткости, устанавливают большие проставки и прижимают
ими пояс к малым проставкам с помощью прижимов 10. Робот сначала при-
варивает сегменты к обечайке, затем сваривает их между собой и лишь по-
сле этого приваривает спицы к фланцу. Опыт показал, что указанный поря-
док выполнения швов должен строго выдерживаться. В этом случае попе-
речная усадка швов, соединяющих сегменты с обечайкой, протекает
беспрепятственно и не может вызвать отрыв стенки от магнитов. Увеличе-
ние зазоров между сегментами, вызванное некоторым их смещением от цен-
тра, не превышает допустимого значения для стыковых соединений деталей
толщиной 6 мм. Нахлесточное соединение фланца и спицы, которое выпол-
няется в последнюю очередь, практически исключает воздействие свароч-
ных деформаций ранее выполненных швов на радиальное и торцевое биение
остова барабана. Швы на фланце должны выполняться в диаметрально про-
тивоположных местах и без остановки робота. В противном случае усадка
швов приводит к появлению биения остова барабана, превышающего допус-
8.4. Роботизированный технологический участок сварки барабана жатки 419
тимое. При сварке роботом выполнение описанного порядка наложения
швов гарантировано.
На 3-м этапе откидывают прижимы 10, устанавливают цилиндриче-
ские упоры 21 и на большие проставки укладываю! четыре узла Т-2, бази-
руя их сегментами на обечайку, а связями — на фланец и цилиндрические
упоры. Сегменты прижимают к проставкам вертикальными 10, а к обечайке
горизонтальными 11 прижимами. При отработке технологии сварки остова
возникли трудности с выполнением угловых сварных соединений сегментов
с обечайкой. Вследствие малой толщины стенки металл иногда стекал по ее
наружной поверхности, и формирование шва было неустойчивым. Конст-
рукцию сварного соединения изменили, «утопив» сегменты на 4 мм и пре-
вратив тем самым угловое сварное соединение в тавровое. Качество таких
соединений значительно улучшилось. Для гарантированного прижатия свя-
зи к фланцу использовали упругость сегментов. Для этого при сборке узлов
Т-2 несколько увеличили угол между связью и плоскостью сегмента. Упру-
го деформируя последний прижимами 10, возвращали узлу Т-2 требуемую
геометрию и обеспечивали прижим конца связи к фланцу. При сварке верх-
него пояса влияние поперечной усадки швов усугублялось возможностью
появления не только радиального, но и торцевого биения, так как усадочные
силы могли действовать под острым углом к оси остова. Для повышения
точности размеров в этом случае также соблюдали описанный выше поря-
док выполнения швов.
По окончании сварки все магниты переводят в пассивное состояние,
прижимы откидывают и проставки извлекают из остова. В целях исключе-
ния их заклинивания в результате действия сварочных деформаций они бы-
ли выполнены «ломающимися». Выключив фиксаторы, подвижный сегмент
с магнитными модулями отводят от остова и извлекают из кондуктора с по-
мощью тельфера.
Система управления кондуктором связана датчиками и конечными
выключателями с системой управления комплексом, основу которой состав-
лял компьютер робота. Как и в предыдущем случае, РТК-2 имеет два иден-
тичных пульта управления для кондукторов левого и правого барабанов.
Алгоритм управления РТК построен таким образом, что при запуске с одно-
го из пультов робот обращается к программе соответствующего кондуктора,
определяет, какой из трех этапов сварки надлежит выполнить, и контроли-
рует все параметры готовности сварочной оснастки и кондуктора. Если хотя
бы на одном из магнитных модулей усилие удержания оказывается ниже
нормы, деталь недостаточно плотно прилегает к полюсным наконечникам,
замыкатель не полностью обжимает обечайку, робот не начинает сварку, а
на пультах кондуктора появляются соответствующие сигналы, то на дисплее
стойки управления появляется сообщение о причинах отказа. После их уст-
420
8. Опыт проектирования сварочных РТК
9860
Рис. 8.24. Схема расположения оборудования РТК-2:
/, 2 — кондуктор сварочный магнитный; 3 — ПР; 4 — устройство зачистки горелки; 5 —
стойка системы управления ПР; 6 — сварочный источник питания; 7 — полы безопасности;
8 - стойка защитная; 9 — пульт управления РТК; 10 — тельфер; 11 — накопитель сварен-
ных остовов, 12 — приспособление для контроля качества стенки; 13—17 — места склади-
рования для деталей и узлов, входящих в барабан; 18 — верстак
ранения робот выполняет требуемый этап сварки и запоминает его для каж-
дого из кондукторов. Очистка горелки осуществляется программно после
каждого сварочного цикла или по команде оператора с пульта управления.
Организуя роботизированный комплекс РТК-2 (рис. 8.24), два кондук-
тора 7 и 2 (для левого и правого барабанов) установили рядом и между ними
вплотную — робот 3, поочередно обслуживающий оба кондуктора. В непо-
средственной близости расположили устройство 4 для зачистки горелки,
стойку 5 системы управления, источник 6 питания сварочным током. Сбо-
рочные места ограждены полами безопасности 7, которые работают так, что
при попадании человека на них сварка прекращается. Для защиты человека
во время сборки от нештатного перемещения робо та в его сторону между
кондукторами установили стойку 8 с аварийными выключателями. Защита
срабатывает при отклонении верхнего конца стойки в любую сторону от
вертикали более чем на 10 мм. Дальнейшее выполнение программы ини-
циируется либо со стойки робота, либо с пультов 9 управления. Тельфер 10
обслуживает оба кондуктора и перемещает сваренные остовы в накопитель 11.
8.4. Роботизированный технологический участок сварки барабана жатки 421
Кроме того, в составе РТК-2 предусмотрены приспособление 12 для контро-
ля качества стенки, стеллажи 13—17 для деталей и узлов, входящих в остов
барабана, и верстак 18.
Анализ качества сварки показал, что количество дефектных сварных
соединений не превышало 5 % от их общего числа на данном узле. РТК-2
обслуживает один оператор-сборщик.
Устройство и работа РТК-3. В соответствии с принятой разбивкой на
технологические узлы (см. рис. 8.19) для завершения изготовления барабана
к его остову необходимо приварить четыре пояса зубчатых сегментов и гре-
бенок и по торцу — пояс съемников. При этом в силе остаются жесткие тре-
бования к точности геометрии барабана. В соответствии с чертежом основ-
ной базовой поверхностью узла является плоскость, образованная восемью
секциями съемника, прилегающими к нижнему торцу остова. В конечном
счете все допуски на биения барабана заданы относительно этой плоскости,
параллельно которой располагаются пояса гребенок, сегментов, а также
вращающийся ротор жатки.
Из 150 сварных швов, выполняемых на данной позиции, две трети со-
ставляют прорезные швы, прикрепляющие сегменты и гребенки к остову и
расположенные внутри него. Проект предусматривал конструкцию сварного
соединения, показанную на рис. 8.25, а. Очевидно, что такое соединение
нетехнологично по нескольким причинам. Во-первых, последовательное
выполнение двух угловых швов неизбежно вызовет остаточную деформа-
цию, нарушающую перпендикулярность относительно стенки. Учесть такое
отклонение при установке детали в стенде сложно. Во-вторых, доступ к од-
ному из двух швов затруднен даже при использовании полуавтоматической
сварки. Предварительные технологические эксперименты показали, что,
уменьшив высоту выступа, входящего в прорезь стенки, можно перейти к
конструкции сварного соединения, показанной на рис. 8.25, б. По прочности
Рис. 8.25. Конструкция сварного соединения гребенки со стенкой:
а — по проекту; б — предложенная
422
8. Опыт проектирования сварочных РТК
и объему наплавленного металла такой шов, сходный с электрозаклепоч-
ным, не уступает проектному, а по величине деформаций вследствие сварки
выгодно отличается от него.
Расположение прорезей на четырех стенках остова идентично, поэто-
му сварка прорезных швов по всему периметру обечайки выполняется при
четырехкратном позиционировании узла с поворотом его на 90° относи-
тельно горизонтально расположенной оси барабана. Необходимыми усло-
виями для этого являются доступность для горелки всех швов, достаточная
повторная точность позиционирования и получение качественных соедине-
ний на наклонной поверхности стенок.
Моделирование ситуации с помощью системы РОБОМАКС показало,
что все швы оказываются доступными при отклонении оси горелки от нор-
мали к стенке на угол до 45°. Предварительные эксперименты по сварке с
таким углом наклона показали, что в тех случаях, когда отклонение элек-
трода от оси шва не превышает 1,5 мм, сварные соединения получаются ка-
чественными, в том числе и при утапливании выступа в отверстии до поло-
вины толщины стенки, а угловая деформация практически отсутствует.
Кроме того, установили, что формирование швов, расположенных на на-
клонных (до 40°) частях стенки остается удовлетворительным при их сварке
«на спуск». В противном случае наблюдались протеки металла и прожоги.
Наибольшие трудности возникли при сварке «на весу» стыковых швов сте-
нок. В целях увеличения ширины шва использовали поперечные колебания
электродной проволоки с амплитудой 4 мм.
Учитывая сказанное выше, требования к сборочно-сварочному стенду,
предназначенному для работы в составе РТК-3, сформулировали следую-
щим образом:
• стенд должен представлять собой позиционер с горизонтальным
расположением оси вращения, имеющий четыре позиции, установка в кото-
рые осуществляется путем поворота барабана на угол 90°;
• повторная точность позиционирования изделия должна быть не ни-
же ±1,0 мм в осевом направлении и ±0,3° по углу поворота;
• базирование собранного узла необходимо осуществить по плоскости
съемника;
• система базирования гребенок и сегментов должна обеспечивать их
установку с отклонением от параллельности основной базе не более 0,3 мм;
• усилия прижимов должны быть достаточными для прижатия деталей
к базам, независимо от нарушения их проектной формы;
• элементы позиционера не должны ухудшать доступ горелки к свар-
ным швам.
8.4. Роботизированный технологический участок сварки барабана жатки 423
Рис. 8.26. Схема базирования барабана
В соответствии с данными требованиями и схемой базирования, при-
веденной на рис. 8.26, был создан позиционер, предназначенный для работы
в составе РТК-3. Основными узлами позиционера являются: основание,
держатель барабана, блок ложементов, радиальный прижим, отводная база,
торцевой прижим, блок ловителей гребенок, панель управления.
На основании 1 (рис. 8.27) расположен отводной держатель барабана,
представляющий собой пиноль 5, вращающуюся в подшипниковой опоре 4.
Передний опорный фланец служит для установки остова барабана с центри-
рованием его по отверстию фланца. На заднем фланце закреплен вращаю-
щийся пневматический цилиндр 3, соединенный со штоком 6, проходящим
внутри пиноли. На передний Т-образный конец штока надевают конусную
шайбу 7. Опора пиноли закреплена на салазках 8, приводимых в движение
пневматическим цилиндром 2.
В передней части основания, под барабаном, расположен блок ложе-
ментов, предназначенных для фиксации гребенок и сегментов в проектном
положении относительно остова. Блок состоит из четырех ложементов 11,
отдельно для каждого пояса деталей. Каждый ложемент установлен на двух
подпружиненных направляющих скалках 12, благодаря которым детали при
сборке предварительно прижимаются к остову, а их выступы остаются в па-
зах обечайки при ее повороте. Ложементы могут перемещаться с помощью не
только пружин, но и радиального прижима. Его пневматические цилиндры
13, расположенные с обеих сторон ложементов, через поперечные планки 14
прижимают все пять поясов деталей, обеспечивая их плотное прилегание к
остову перед сваркой. По ее окончании цилиндры отгягивают ложементы
вниз, освобождая приваренные детали. Для фиксации деталей в пазах
424
8. Опыт проектирования сварочных РТК
Рис. 8.27. Позиционер для сборки барабана на РТК-3
8.4. Роботизированный технологический участок сварки барабана жатки 425
служат пневматические прижимы 15. Через штоки, пропущенные сквозь
ложементы, пневматический цилиндр с помощью подпружиненных вилок
прижимает детали к базовой поверхности каждого ложемента, устанавливая
их, таким образом, в проектное положение.
Основным базовым элементом позиционера является сектор 10, на ко-
торый с помощью пальцевых фиксаторов 19 навешиваются две секции
съемника. Сектор закреплен на двух стойках с ползунами 23 и перемещается
рычагом с помощью мощного пневматического цилиндра 22. Будучи уста-
новленным в рабочую позицию, сектор в сочетании с двумя торцевыми
пневматическими прижимами 16 обеспечивает надежное базирование бара-
бана в осевом направлении. При этом в тангенциальном направлении его
положение однозначно фиксируется пальцевыми фиксаторами 19, попа-
дающими в технологические отверстия в сегментах остова. Благодаря такой
системе базирования, независимо от торцевого биения остова, достигает-
ся постоянство положения в пространстве свариваемой четверти бараба-
на, обеспечивающее попадание электрода в места расположения сварных
швов с точностью, достаточной для получения качественных сварных
соединений.
Блок ловителей гребенок предназначен для предварительного задания
положения деталей, поджима их к остову и удержания всего набора в про-
цессе сборки. Фиксаторы 19, выполненные в виде качающихся подпружи-
ненных рычагов 20 с защелками 21, установлены на общем основании в
плоскостях расположения гребенок и сегментов. При сборке барабан враща-
ется с помощью храпового механизма, который на схеме не показан. В зоне
работы оператора-сборщика расположена панель 18 с агрегатами пневмоси-
стемы. Для контроля срабатывания механизмов и правильности установки
деталей при сборке предусмотрена система индукционных бесконтактных
датчиков. Позиционер оборудован системой вытяжной вентиляции 17. Пе-
ред загрузкой остова позиционер находится в исходном положении: пиноль,
отводная база, торцевые прижимы, осевые прижимы ложементов и ловители
отведены в заднее положение, радиальный прижим удерживает блок ложе-
ментов в верхнем положении.
С помощью тельфера остов устанавливают на ложементы и выдвига-
ют пиноль, вводя центрирующий выступ опорного фланца в отверстие
фланца остова. Выдвигают вперед шток, надевают на него конусную шайбу
и, включая вращающийся пневмоцилиндр, фиксируют остов на фланце пи-
ноли. Отводят вниз блок ложементов, обеспечивая свободное вращение ос-
това. Освобождают рычаги ловителей от защелок и, установив в них первый
комплект деталей (занимает одну восьмую часть окружности остова), при-
жимают их к обечайке, следя за попаданием выступов в прорези. Затем со-
единяют остов с храповым механизмом и поворачивают его на 45°, вводя
426
8. Опыт проектирования сварочных РТК
Рис. 8.28. Схема размещения оборудования РТК-3:
1 — ПР; 2 — позиционер; 3 — пульт управления; 4 — стойка системы управления
ПР; 5 — источник сварочного тока; 6 — устройство для зачистки сварочной горелки;
7 — полы безопасности; 8 — накопитель остовов; 9 — конвейер; 10 — тельфер;
11 — места складирования деталей; 12 — верстак
детали в пазы ложементов. Аналогичным образом вводят второй комплект
деталей и фиксируют их в ложементах осевыми прижимами. На пальцевые
фиксаторы сектора отводной базы навешивают две секции съемника и пере-
водят ее в рабочее положение, добиваясь попадания фиксаторов в отверстия
остова. Остов и съемники прижимают к отводной базе с помощью торцевых
пневмоцилиндров, а затем блок ложементов с деталями — к обечайке с по-
мощью радиальных прижимов.
Предварительный расчет и хронометраж при отработке технологии
показал, что цикл сварки одной четверти барабана длится 8 мин. За это вре-
мя оператор успевает произвести сборку на позиционере такой же его части.
Поэтому в состав РТК включили два позиционера (для левого и правого ба-
рабанов), которые поочередно обслуживает один робот, расположенный
между ними. Схема размещения оборудования РТК-3 приведена на рис. 8.28.
8.4. Роботизированный технологический участок сварки барабана жатки 427
Остовы, принятые ОТК, оператор берет из накопителя 8 и с помощью
тельфера 10 поочередно устанавливает на оба позиционера 2. В процессе
установки рабочий находится между позиционером и роботом, на полу
безопасности 7. Это исключает случайный старт робота даже при нажатии
соответствующей кнопки на пульте управления. Затем оператор переходит к
одному из позиционеров и производит сборку первой четверти барабана.
Закончив сборку, он запускает робот с соответствующего пульта 3 и пере-
ходит к другому позиционеру. Система управления РТК контролирует со-
стояние робота и качество сборки на позиционере и при отсутствии откло-
нений запускает соответствующую сварочную программу. Робот последова-
тельно выполняет сварку сегментов, гребенок, стыкового шва обечайки и
съемников.
Одновременно со сваркой оператор выполняет сборку первой четвер-
ти на втором позиционере и с его пульта управления дает вызов робота. По
завершении сварки на первом позиционере производится очистка горелки
на устройстве 6, и после контроля качества сборки робот начинает сварку
первой четверти на втором позиционере. В это же время оператор собирает
вторую четверть барабана на первом позиционере. Таким образом, робот,
работая практически непрерывно, за четыре этапа осуществляет полную
сварку правого и левого барабанов на обоих позиционерах и уходит в ис-
ходную точку. Оператор снимает с них готовые изделия и укладывает на
конвейер 9, по которому барабаны передаются на место контроля и исправ-
ления брака.
Следует отметить, что количество и расположение сварных швов в
каждой четверти барабана отличаются друг от друга. Это не позволило ис-
пользовать единую сварочную программу. Поэтому алгоритм работы РТК
предусматривает последовательное подключение четырех подпрограмм и
контроль очередности их выполнения на каждом позиционере. После от-
ключения системы управления или при необходимости изменения порядка
выполнения подпрограмм номер нужной подпрограммы набирается на дис-
плее стойки управления 4. При промежуточных остановках и ручных мани-
пуляциях с роботом номер подпрограммы и место ее прерывания запомина-
ются, и при повторном старте робот продолжает сварку от места остановки.
Качество и надежность работы всех РТК на участке, в каждый из ко-
торых входят манипулятор, сварочное и технологическое оборудование или
оснастка, в значительной мере зависят от неизменности их взаимного поло-
жения, четкости и стабильности срабатывания отдельных механизмов, за-
дающих и фиксирующих в пространстве положение свариваемых деталей.
Для снижения потерь времени, вызванных сбоями в работе РТК, и поддер-
жания качества сварных соединений на заданном уровне для всех описан-
ных выше РТК, были разработаны программы оперативного технологиче-
428
8. Опыт проектирования сварочных РТК
ского контроля состояния оборудования и оснастки. Суть контроля состоит
в периодическом измерении отклонений от номинального положения в про-
странстве основных базовых и фиксирующих элементов технологического
оборудования, ответственных за точность позиционирования деталей. Для
измерений использовали робот, точность позиционирования которого со-
ставляет 0,2 мм. По окончании отладки оборудования РТК и изготовления
контрольной партии узлов в местах, доступных для горелки робота, на по-
верхностях контролируемых элементов (оснований, технологических баз,
упоров и прижимов) наносили контрольные точки в виде кернов диаметром
не более 0,5 мм. На РТК-1 такие точки располагали на рамах приспособле-
ний, закрепленных на столах, опорах жесткостей и откидном клиновом
вкладыше; на РТК-2 — на плите, подвижном сегменте и полюсных нако-
нечниках всех магнитных модулей; на РТК-3 — на основании и на концах
сектора 10 отводной базы (см. рис. 8.27). Кроме того, контрольную точку
ставили на неподвижной станине самого робота. Последняя служила для
оценки возможных отклонений конца электрода. Вместо мундштука в го-
релку вворачивали острый конусный наконечник. В ручном режиме прово-
дили обучающее программирование, подводя горелку перпендикулярно к
контролируемой поверхности так, чтобы острие наконечника коснулось дна
конусного керна, после чего горелку приподнимали на 0,5... 1,0 мм и полу-
ченную точку заносили в память робота. Перемещая горелку от одной кон-
трольной точки к другой, формировали таким образом программу контроля.
Многократно программируя одну и ту же точку, установили, что погреш-
ность работы обучающего оператора не превышает 0,3 мм, а точность изме-
рений в пределах всей программы составляет 0,5 мм. В дальнейшем подоб-
ный контроль проводили после замены горелки, подналадки или ремонта
технологического оборудования, а также при снижении точности попадания
конца электрода на линию стыка деталей. При появлении отклонений, пре-
вышающих 1 мм (их значения считывали на дисплее системы управления
роботом), находили и устраняли их причину, после чего контроль повторя-
ли. Опыт показал, что основными причинами снижения точности работы
оборудования и оснастки являются нарушение регулировок базовых эле-
ментов и изменение усилий прижатия деталей, вызванное заеданиями в под-
вижных элементах прижимов. При использовании пневматического привода
важной является стабильность давления в пневмосети.
Все три описанных РТК были объединены в отдельный участок робо-
тизированной сварки барабана. Схема размещения оборудования на участке
показана на рис. 8.29. Стандартные поддоны с деталями расставляют на
складочные места с помощью цеховой кран-балки. Технологические узлы
Т-1 и Т-2, сваренные на РТК-1, складируют в стеллажи 1 и 2 отдельно для
левого и правого барабанов. Перед сборкой остовов на РТК-2 входящие в них
8.4. Роботизгцюванный технологический участок сварки барабана жатки 429
Рис. 8.29. Схема участка роботизированной сварки барабана: обозначение
элементов оборудования соответствует рис. 8.21, 8.24
430
8. Опыт проектирования сварочных РТК
стенки проходят 100 %-ный контроль формы на приспособлении 3. Его вы-
полняет оператор, обслуживающий РТК-1.
По завершении трехэтапного процесса изготовления остовов на обоих
кондукторах изделия с помощью тельфера передаются в накопители 4. Сва-
ренные остовы устанавливают в специальный стенд 5, на котором контро-
лируют торцевое и радиальное биения, а также качество сварных соедине-
ний. Остовы барабанов, признанные ОТК годными, передаются в накопите-
ли 6. Остовы, имеющие браковочные признаки, передают в изолятор брака
7, а затем на отдельное рабочее место, где производится подварка швов либо
исправление формы путем местного нагрева соответствующих связей. Ко-
личественные результаты контроля регистрируются в специальном журнале.
Их периодическая статистическая обработка позволяет судить о стабильно-
сти технологического процесса и состоянии оборудования РТК. В случае
появления систематических отклонений, близких к предельным, устанавли-
вают причину их возникновения и производят подналадку оборудования, а
при необходимости — внеплановое техническое обслуживание и ремонт.
Следует отметить также, что результаты контроля на этой стадии не обезли-
чены и используются для оценки качества работы обслуживающих РТК
операторов.
Остовы барабанов с помощью тельфера 8 устанавливают на позицио-
неры РТК-3, где производят окончательную сварку. Готовые барабаны пе-
редаются тельфером на напольный конвейер-накопитель 9, а затем на стенд
5, где контролируют геометрические размеры и качество сварных соедине-
ний. Принятые ОТК изделия поступают на склад готовой продукции 10. Ба-
рабаны, имеющие дефекты сварных швов или формы, передаются на рабо-
чее место, укомплектованное кантователем 7 и полуавтоматом 11 для свар-
ки в среде углекислого газа, где производится устранение дефектов.
Анализ работы роботизированного технологического участка показал,
что не совмещенными во времени с процессом сварки являются в основном
транспортные операции. Их доля в общей продолжительности процесса не
превышает 10 %. Наименее загруженным является РТК-1, поэтому его опе-
ратору дополнительно поручена транспортировка узлов на всем участке.
Наиболее «узким местом» являются операции контроля. Для их сокращения
целесообразно было бы, по-видимому, автоматизировать процесс контроля
геометрии узлов и регистрации его результатов. Такт выпуска изделий со-
ставил 40 мин.
Опыт работы роботизированного технологического участка позво-
ляет заключить следующее.
1. В успешной реализации проектов роботизированной дуговой свар-
ки объемных крупногабаритных конструкций определяющую роль играет
анализ технологичности изделий, который следует проводить несколько раз,
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
431
по мере разработки и внедрения проекта. Особое значение имеет расчлене-
ние изделия на технологические узлы и анализ условий, обеспечивающих
качество сварных соединений.
2. Основными требованиями при разработке технологического обору-
дования и оснастки, входящих в состав РТК, являются:
• обеспечение доступности сварных швов, выполняемых на данном
комплексе;
• обеспечение точности и стабильности позиционирования деталей,
достаточных для получения качественных сварных соединений;
• реализация в оборудовании конструктивно-технологических реше-
ний, позволяющих исключить или учесть влияние временных и остаточных
сварочных деформаций на обеспечение заданных пределов отклонений раз-
меров и геометрической формы свариваемого изделия;
• возможность регулировки и надежная фиксация базовых элементов
оборудования;
• обеспечение усилия прижатия деталей, достаточного для исключе-
ния влияния на точность позиционирования отклонений их формы и разме-
ров от проектных значений.
8.5. РТК сборки и дуговой сварки сложного маложесткого
пространственного узла с обеспечением заданных пределов
отклонений геометрической формы
Одним из наиболее ответственных
узлов в зерноуборочном комбайне явля-
ется молотильный агрегат, схема которого
показана на рис. 8.30. Качество обмолота
зависит главным образом от дугообраз-
ного клинового зазора между барабаном
1 и решетчатой цилиндрической панелью
2, называемой подбарабаньем. На выходе
зазор между бичами 3 барабана и план-
кой подбарабанья не должен превышать
1,0 мм, а непараллельность — 0,5 мм на
длине барабана 1500 мм.
Каркас подбарабанья (рис. 8.31)
представляет собой сварную конструк-
цию, состоящую из 17 продольных пла-
нок 1, боковые грани которых должны
Рис. 8.30. Схема молотильного аг-
регата зерноуборочного комбайна:
1 — барабан; 2 — подбарабанье;
3 — бич
432
8. Опыт проектирования сварочных РТК
Рис. 8.31. Каркас подбарабанья комбайна Дон-1500:
1 — планка; 2 — втулка; 3 — боковина; 4 — ребро
располагаться по радиусу 7? = 410 мм. По торцам набор замыкают две боко-
вины 3, имеющие на концах отверстия, в которые вварены втулки 2 для
подвески подбарабанья в молотильном агрегате. По длине набор планок
скреплен шестью дугообразными ребрами 4, пропущенными в прямоуголь-
ные отверстия планок. Короткие угловые швы между элементами 1, 3 и 4
(их более 280) обеспечивают пространственную жесткость конструкции
подбарабанья. Требования к точности геометрии этого узла высоки:
• межцентровое расстояние отверстий в боковинах А = (910 ± 0,7) мм;
• радиус рабочей поверхности R - (410 ± 0,5) мм;
• отклонение от цилиндричности ± 0,5 мм;
• расстояние между любыми двумя планками b = (60 + 1) мм.
Малая жесткость конструкции и большое количество коротких сварных
швов, эксцентрично расположенных на деталях, вызывают настолько значи-
тельные сварочные деформации, что при ручной сварке обеспечить точность
таких узлов удается только механической обработкой, трудоемкость которой
иногда сопоставима с трудоемкостью всех остальных этапов изготовления.
Возможность обеспечения требуемой точности маложестких узлов с помо-
щью роботизированной дуговой сварки показывает приведенный ниже при-
мер создания и эксплуатации РТК для сварки каркаса подбарабанья.
Емкость памяти используемого робота IR161/15 недостаточна для за-
писи программы сварки всех швов каркаса, доступных для горелки, т. е.
сварка всего каркаса одним роботом не обеспечивается. В то же время одно-
временная работа двух роботов на одном изделии осложняется тем, что его
габаритные размеры и расположение швов могут вызвать столкновение кис-
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
433
тей роботов, а разводка их во времени увеличивает простои. В связи с этим
была принята схема роботизированной сварки. На двухместном позиционе-
ре два робота одновременно сваривают по половине швов на каждом из
двух каркасов, после чего они обмениваются изделиями и сваривают вто-
рую половину швов. Такая схема позволяет исключить переустановку изде-
лий в приспособлениях, не требует синхронизации работы роботов, упрощает
их рабочие программы. В то же время она предполагает создание манипуля-
тора с высокой точностью позиционирования, снабженного специальной
оснасткой, обеспечивающей требуемую точность узла после сварки и фик-
сирование в пространстве свариваемых кромок при сварке каждого углового
шва.
Практически все швы на каркасе расположены в узком пространстве
между двумя соседними планками, расстояние между которыми не превы-
шает 60 мм, поэтому доступ горелки к швам ограничен. Анализ доступности
швов для горелки, выполненный с помощью системы РОБОМАКС, показал,
что горелка между планками может располагаться только под острым углом
к оси шва. Опыты показали, что при сварке углом назад формирование шва
удовлетворительно, а глубина проплавления уменьшается незначительно.
Поэтому ориентацию горелки сочли допустимой. Кроме того, установили,
что вблизи втулок боковин расположено по четыре шва, в принципе не
доступные для горелки робота. Эти швы было решено выполнять ручной
дуговой сваркой на позиции контроля и исправления дефектов. С помощью
этой же системы определили оптимальную последовательность выполнения
швов на каждой позиции сварки.
Повторная точность позиционирования 5Р используемого робота со-
ставляет ±0,2 мм. Опыт показывает, что при тщательной наладке подающих
механизмов сварочной проволоки возможно добиться отклонения конца
электрода от оси горелки 5гор = 0,2...0,4 мм (при вылете 15... 18 мм). При
оценке погрешностей обучающего программирования робота на изделии
существенными оказываются не только квалификация, опыт и добросовест-
ность оператора — факторы субъективные, — но и тип шва, расположение
его на изделии, доступность и освещенность зоны программирования, т. е.
факторы объективные. Специальные эксперименты показали, что ошибки
программирования на тавровых и нахлесточных сварных соединениях
меньше, чем на стыковых, причем ошибки возрастают с увеличением зазо-
ра. Установлено, что в цеховых условиях, при умеренной комфортности ра-
боты оператора ошибки программирования 5П сварки стыкового соединения
без зазора и без разделки кромок не превышают 0,3 мм с доверительной ве-
роятностью 95 %. Таким образом, возможное отклонение конца электрода
составляет А1 = 0,2 + 0,3 + 0,3 = 0,8 мм.
15 — 6705
434
8. Опыт проектирования сварочных РТК
Рис. 8.32. Схема базирования деталей каркаса в сборочном стенде
Возможное максимальное смещение оси свариваемого стыка опреде-
ляется несколькими факторами. Самым существенным образом на точность
и стабильность размеров и формы деталей, поступающих на сварку, оказы-
вает технология их изготовления. Помимо механической обработки резани-
ем достаточно высокую точность обеспечивает контурная вырубка плоских
деталей в штампах.
При проектировании сборочно-сварочной оснастки важен правильный
выбор схемы базирования и закрепления деталей в приспособлении (рис. 8.32).
Эта схема, а также качество проектирования и точность изготовления осна-
стки определяют зазоры, смещения деталей и сборочные деформации. На
отклонения, вызванные несовершенством технологии изготовления деталей
и качеством оснастки, накладывается неточность позиционирования изде-
лия, связанная с характеристиками манипулятора.
Наиболее сложным и в то же время существенным для качества свар-
ных соединений является влияние сварочных деформаций. Неэффектив-
ность мер, принимаемых для предотвращения или компенсации временных
и остаточных сварочных деформаций, является одной из главных причин
неудач при создании РТК дуговой сварки неадаптивными роботами. Накоп-
ленный в этой области опыт невелик и плохо поддается обобщению. Для
установления закономерностей деформирования при сварке, как правило,
помимо предварительных расчетных оценок требуется проведение экспери-
ментальных работ в лабораторных и производственных условиях.
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
435
В совокупности все эти факторы определяют максимально возможное
смещение стыка Д2 в пространстве, которое может быть выражено следую-
щей суммой:
Д2 = 5д + 60 + 5М + &Т.Д + 5о.д,
где 5Д — смещения, связанные со схемой базирования и точностью деталей;
5О — смещения, обусловленные точностью изготовления сборочно-сва-
рочной оснастки; 5М — смещения, вызванные неточностью позиционирова-
ния манипулятора; 5ТД — смещения, вызванные временными тепловыми
деформациями; Зо д — смещения, вызванные остаточными сварочными де-
формациями.
Для оценки величины Д2 необходимо использовать схему базирова-
ния деталей (см. рис. 8.32), реализованную в сборочном стенде. В качестве
базовой плоскости приняли внешнюю поверхность А одной из боковин 1.
Каждую боковину с заранее приваренными втулками 2 устанавливают в
стенде на две цилиндрические оправки. В упор к базовой боковине устанав-
ливают торцами 17 планок 3. На рисунке для простоты показана только одна
из них. Следует отметить, что планки получают путем контурной вырубки.
За один ход пресса отрезают планку в заданный размер и одновременно
пробивают шесть прямоугольных окон по размерам, отсчитанным от базо-
вого торца, который маркируют пробивкой круглого дополнительного тех-
нологического отверстия. Этим торцом и базируют планки на боковину. Для
задания проектного положения в радиальном и тангенциальном направле-
ниях каждую нланку базируют на две регулируемые опоры 4 и на четыре
нерегулируемые опоры 5, а затем прижимают к ним отдельными прижима-
ми. Наиболее критичным в отношении точности задания положения швов,
соединяющих планки с боковинами, является смещение концов планок в
тангенциальном направлении. Для уменьшения этих смещений базы необ-
ходимо было располагать как можно ближе к концам планок. В нашем слу-
чае для свободного доступа к местам прихваток каждая планка закреплялась
на расстоянии 100 мм от торца. При допустимой неплоскостности планки
2 мм на длине 1 м возможное смещение торца планки не должно превышать
0,2 мм. С этой целью использовали специальные ловители, расположенные
под боковинами. К плоскости, образованной свободными торцами планок,
прижимают вторую боковину, зафиксированную аналогично первой. Оче-
видно, что положение в пространстве этих сварных соединений может из-
меняться от изделия к изделию случайным образом в пределах допуска на
длину планки. Благодаря контурной вырубке разброс значений длин планок
и координат прямоугольных окон не превышал 0,3 мм. Поскольку, согласно
схеме базирования, нежесткие боковины прижимаются к торцам планок,
отклонение их от плоскостности не превышает допуск на длину планки.
15*
436
8. Опыт проектирования сварочных РТК
Шесть ребер вставляют в прямоугольные окна 15 планок и замыкают по
торцам двумя крайними планками, не имеющими окон. В этом соединении
зазор между ребром и краем окна составляет 0,5 мм, а точность расположе-
ния последнего — 0,3 мм. Описанная схема базирования и соответствующие
требования были включены в техническое задание на проектирование сбо-
рочного стенда.
Точность сборочно-сварочной оснастки, как правило, на несколько
квалитетов выше, чем сварной конструкции, которую на ней собирают, т. е.
в абсолютных значениях допуски на изготовление и установку базовых эле-
ментов в 5—10 раз меньше допусков на размеры свариваемых деталей. Ре-
ально в производстве оснастки можно рассчитывать на отклонения 5О по-
рядка 0,1...0,2 мм. В тех случаях, когда обучающее программирование вы-
полняется непосредственно на сварочной оснастке, входящей в РТК, и эта
оснастка не является сменной, это отклонение можно не учитывать.
Исходя из структурной схемы РТК, специализированный манипулятор
с горизонтальной осью вращения проектировали с учетом точности пози-
ционирования свариваемого элемента на уровне точности позиционирова-
ния используемого робота, т. е. величина SM должна была оставаться в пре-
делах +0,2 мм. Кроме того, при разработке позиционера удалось найти кон-
структивное решение, позволившее практически исключить влияние вре-
менных и остаточных сварочных деформаций.
Таким образом, максимально возможное смещение стыков, связанное
с точностью изготовления деталей, сборочно-сварочной оснастки и точно-
стью позиционирования изделия, составило:
а) для швов, прикрепляющих планки к боковине,
Д2 - 8Д+ 5М= 0,3 + 0,2 = 0,5 мм;
б) для швов, соединяющих планки и ребра,
Д2 = Зд+ 6М= 0,8 + 0,2 = 1,0 мм.
В итоге максимально возможное отклонение электрода от оси шва
оказалось равным:
а) для соединений боковин с планками
г; = Д1 + Д2 = 0,8 + 0,5 = 1,3 мм;
б) для соединений планок с ребрами
т] = Д1 + Д2 = 0,8 + 0,8 = 1,6 мм.
Ширина зазора b в соединениях планки с боковиной колеблется на
одном изделии в пределах, определяемых разбросом значений длин планок,
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
437
Рис. 8. 33. Схема построения области качества таврового соединения («) и
ее реальные характеристики для катетов: 3 мм (б), 4 мм (в), 5 мм (г), 6 мм (б)
и не должна превышать 0,3 мм. В соединении планки с ребром максимально
возможный зазор Ь = 0,5 мм (разность между шириной окна и толщиной
ребра, вставленного в это окно).
Результаты экспериментов позволили установить, что тавровое свар-
ное соединение получается качественным, если зазор между кромками и
смещение электрода в реальном соединении не выходят за пределы площа-
ди фигуры, построенной в координатах «допустимое отклонение — зазор» и
ограниченной предельными значениями этих параметров. В дальнейшем
будем называть эту фигуру областью качества. Схема построения области
качества для тавровых соединений представлена на рис. 8.33, а.
В развитие этих работ проведены исследования влияния на качество
угловых швов, выполненных катетами 3, 4, 5 и б мм, отклонений А и зазора Ь.
На рис. 8.33, б—д показаны соответствующие области качества. Оказалось,
что сварные соединения каркаса подбарабанья при его сварке с помощью
неадаптивных роботов могут быть получены качественными, поскольку
рассчитанные выше значения А и b находятся в пределах области качества
для швов, выполненных катетом 5 мм.
Однако это будет возможным только в том случае, если удастся ис-
ключить влияние сварочных деформаций в процессе сварки каркаса робота-
438
8. Опыт проектирования сварочных РТК
ми. Очевидно, что при таком количестве сварных швов и малой жесткости
конструкции этот фактор может оказаться определяющим для получения не
только качественных швов, но и точности геометрии сваренного каркаса.
Поэтому уже на стадии подготовки производства, до выдачи технических
заданий на проектирование технологического оборудования, желательно
было представлять характер и закономерности деформирования каркаса в
процессе его сварки, с тем чтобы заложить в технологию решения, способ-
ные свести к минимуму влияние сварочных деформаций на геометрию под-
барабанья.
Анализ литературных данных по этой проблеме показывает, что в
конструкциях с короткими швами, которые чаще всего занимают только
часть сечения, управлять сварочными деформациями можно, изменяя на-
пряженное состояние металла, окружающего шов, причем это управление
намного эффективнее, если использовать не жесткое закрепление конструк-
ции перед сваркой, а внешнее активное нагружение. Однако вследствие
большого разнообразия форм и размеров конструкций практически невоз-
можно сформулировать общие правила использования этого метода. В каж-
дом конкретном случае приходится решать частную задачу выбора схемы и
параметров нагружения.
Эксцентричное расположение сварных швов на элементах каркаса вы-
зывает деформации сложного вида. Поэтому для создания технологического
процесса, обеспечивающего проектную точность конструкции, необходимы
сведения не только о конечных результатах деформирования, но и о причи-
нах его появления, кинетике протекания и относительном вкладе каждого
вида деформаций в общий результат. Исследования проводили в несколько
этапов.
На первом этапе исследовали кинетику и характер деформирования
каркаса в целом и отдельных элементов: боковины с приваренными к ней
планками и планки с приваренными к ней ребрами, а также выполняли экс-
перименты по оценке способов уменьшения деформаций. На втором этапе
оценивали эффективность разработанных конструктивно-технологических
приемов снижения сварочных деформаций и повышения точности каркаса в
условиях опытно-промышленного производства. На третьем этапе исследо-
вали характер деформирования, стабильность геометрии каркаса и качество
сварных соединений в процессе отладки РТК, а также оценивали эффектив-
ность его промышленной эксплуатации.
На первом этапе для анализа характера деформирования сварного узла
в целом собранный каркас устанавливали вертикально на боковину и поло-
вину швов выполняли полуавтоматической сваркой в свободном состоянии,
не используя приспособлений (рис. 8.34, а). Для сварки другой половины
швов каркас кантовали на 180°.
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
439
Рис. 8.34. Расположение швов, соединяющих планки с ребрами:
а — проектное; б — предложенное
Измерения показали, что каркас, выполненный по такой технологии,
получает следующие отклонения от проектной формы (рис. 8.35):
• межцентровое расстояние А уменьшается с 910 до 900 мм;
• радиус R уменьшается таким образом, что зазор между средними
планками и шаблоном этого же радиуса достигает 18 мм;
• длина каркаса уменьшается не более чем на 1 мм;
• диагональный перекос каркаса и отклонение от соосности отверстий
втулок достигает 12 мм;
• внутренняя рабочая цилиндрическая поверхность приобретает боч-
кообразную форму с отклонением от цилиндричности до 2 мм.
Для компенсации диагонального перекоса каркаса была предложена
схема расположения швов, соединяющих планки с ребрами (см. рис. 8.34, б).
Наибольшее влияние на геометрию каркаса оказывают изменения
межцентрового расстояния и радиуса рабочей поверхности, показанные на
рис. 8.35. Для экспериментального исследования деформаций боковин в ре-
зультате приварки к каждой из 17 планок была создана специальная уста-
новка, позволяющая накладывать на закрепленную деталь сварные швы и
измерять ее перемещения в процессе сварки. Для стабилизации параметров
режима сварки и исключения влияния случайных факторов в установке ис-
440
8. Опыт проектирования сварочных РТК
Рис. 8.35. Деформация каркаса после сварки в свободном состоянии
пользовали специальный автомат для сварки в среде углекислого газа, кон-
струкция которого позволяла быстро переустанавливать горелку в места
расположения планок и перемещать ее по радиусу вдоль торца планки с по-
стоянной сварочной скоростью. Параметры режима сварки и перемещения
боковины регистрировали. В экспериментах варьировали направление и по-
гонную энергию сварки. Помимо перемещений всей боковины в сечениях
расположения планок измеряли локальные сварочные деформации от попе-
речной усадки швов.
Не вдаваясь в детальный анализ, приведем основные результаты ис-
следования:
• уменьшение межцентрового расстояния А после приварки к бокови-
не планок является следствием увеличения ее кривизны под действием по-
перечной усадки угловых швов, расположенных эксцентрично относительно
центра тяжести боковины;
• приварка трех пар планок вблизи концов боковины на ее кривизну
практически не влияет;
• наибольшее влияние на величину искривления боковины оказывает
поперечная усадка швов, расположенных в центральной ее части;
• поперечная усадка неравномерна вдоль шва, прикрепляющего план-
ку к боковине, уменьшается от края к центру сечения и существенно возрас-
тает с увеличением длины шва и погонной энергии;
• направление сварки (от края к центру поперечного сечения бокови-
ны или наоборот) не влияет на величину поперечной усадки;
• при выполнении всех 34 швов на одной боковине без перерыва тем-
пературные деформации общего разогрева приводят к временному увеличе-
нию межцентрового расстояния А на 3 мм.
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
441
Рис. 8.36. Схема деформирования планки после приварки к ней ребер
Помимо рассмотренного соединения в каркасе содержится более 200
швов, соединяющих планки с ребрами. Схема соединения показана на рис. 8.36.
Для исследования деформаций планки в результате приварки к ней в
шести местах ребер была использована схема закрепления, позволяющая
имитировать условия, в которых деформируется планка в составе конструк-
ции. Поперечное и эксцентричное расположение швов на планке позволяло
предположить, что основными видами деформаций будут укорочение и саб-
левидность.
Измерения показали, что прогиб в результате приварки всех шести
ребер не превышает 0,4 мм, а укорочение — 1,1 мм (см. рис. 8.36), что
меньше допуска на длину каркаса подбарабанья (2 мм). Поскольку в составе
каркаса деформации планок будут протекать в условиях закрепления их
торцов на боковинах, можно было ожидать, что в этом случае они будут
значительно меньше и не повлияют на геометрию каркаса.
Установлено, что разность диагоналей каркаса, а значит и несоосность
втулок, возникает вследствие накопления угловых деформаций в соедине-
ниях планок с ребрами при выполнении швов первой очереди, которые не-
способны полностью компенсировать наложение швов второй очереди.
Бочкообразность внутренней рабочей поверхности каркаса обуслов-
лена, по-видимому, тем, что увеличение ее кривизны происходит только в
области боковин. В центре этому препятствуют ребра, придающие решетке
после сварки определенную жесткость.
442
8. Опыт проектирования сварочных РТК
Рис. 8.37. Возможные способы исправления деформаций каркаса подбарабанья:
а — жесткое закрепление; б — сварка с постоянной деформацией растяжения; в — сварка
с постоянным растягивающим усилием
Результаты проведенных исследований показали, что основной при-
чиной деформации каркаса является усадка сварных швов, крепящих набор
планок к боковинам. В связи с этим потребовалось найти способ предот-
вращения или исправления этих деформаций.
Закрепление боковины при сварке, например, базированием втулок на
неподвижные пальцы (рис. 8.37, а) позволяет уменьшить деформации лишь
на 30...40 %. При этом неизбежно возникают затруднения при снятии узла
после сварки.
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
443
Рис. 8.38. Конструкция профилометра
Жесткое нагружение растяжением перед сваркой (рис. 8.37, б) мало-
эффективно из-за релаксации растягивающих напряжений вследствие обще-
го нагрева и удлинения детали при сварке.
Конфигурация каркаса, в которой боковину можно рассматривать как
кривой брус, позволяет реализовать прием приложения постоянной силы по
линии, соединяющей центры втулок боковин (рис. 8.37, в).
Для определения растягивающего усилия, обеспечивающего сохране-
ние проектного межцентрового расстояния А, в экспериментах использовали
устройство, позволяющее регулировать усилие в заданных пределах и под-
держивать его постоянным в процессе сварки.
Отклонения формы рабочей поверхности каркаса оценивали, измеряя
радиальное перемещение каждой планки в пяти поперечных сечениях по
длине каркаса с помощью специального профилометра (рис. 8.38) с точно-
стью измерений 0,01 мм.
В экспериментах варьировали усилие растяжения, погонную энергию,
направление сварки, длину швов и порядок их выполнения. В результате
было установлено следующее:
• оптимальное значение усилия растяжения обеспечивающее после
приварки всех планок к боковине сохранение межцентрового расстояния А в
заданных пределах (910 ± 0,7) мм, составляет (7,8 ± 0,5) кН;
• при сварке с растяжением направление выполнения шва влияет на
его поперечную усадку: сварка от края к центру боковины дает меньшие
444
8. Опыт проектирования сварочных РТК
значения максимальной усадки и угла поворота, чем сварка в обратном на-
правлении;
• при сварке с растяжением сохраняется зависимость ЛА от длины на-
кладываемого шва, однако выражена она менее ярко, чем при сварке в сво-
бодном состоянии;
• порядок приварки планок к боковинам не оказывает влияния на ко-
нечное значение отклонения межцентрового расстояния ЛА.
Установлено, что после сварки с растяжением кривизна рабочей по-
верхности каркаса уменьшилась. На рис. 8.39 показаны характерные резуль-
таты измерений радиального смещения планок, полученные на одном из
каркасов как разность замеров до и после сварки. Видно, что в результате
усадки сварных швов, протекающей в условиях внецентренного растяжения
боковин, средняя часть планок приблизилась к центру, в то время как край-
ние планки удалились от него. При этом межцентровое расстояние осталось
в пределах заданного допуска. Поэтому требуемую форму поверхности кар-
каса решено было обеспечивать при сборке, смещая планки в направлении,
обратном тому, что возникает при сварке с растяжением.
При разработке стенда для сборки каркаса были учтены получен-
ные результаты измерений каркасов и реализована схема базирования
(см. рис. 8.32).
Сборка каркаса производится в два этапа. Сначала собирают на при-
хватках решетку, состоящую из планок и ребер, а затем к ней с двух сторон
прижимают и прихватывают боковины с приваренными втулками.
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
445
Рис. 8.40. Стенд для сборки каркаса
Конструкция стенда для сборки представлена на рис. 8.40.
Основными узлами стенда являются: стол 1, гребенчатый фиксатор 2,
откидной прижим 3, блок кареток 4. Стол 1 имеет раму, на которой разме-
щены поперечные балки, служащие опорой для остальных узлов. По длине
каркаса установлены четыре гребенчатых пневматических фиксатора 2.
Фиксаторы представляют собой зубчатые сегменты 5. Рабочие поверхности
зубьев являются базами для фиксируемых планок изделия. Прижим планок
осуществляется подвижными зубчатыми пластинами б, перемещающимися
446
8. Опыт проектирования сварочных РТК
в тангенциальном направлении по двум неподвижным направляющим паль-
цам 7, входящим в окна пластин. Усилие прижима на пластины передается
от двух качающихся пневматических цилиндров 8 через кронштейны 9.
Два крайних гребенчатых фиксатора максимально приближены к кон-
цам планок и несут сегменты 11, по периметру которых расположено по 17
регулируемых винтовых опор 12 планок каркаса подбарабанья 13. Это по-
зволяет целенаправленно изменять форму будущей рабочей поверхности
подбарабанья с учетом сварочных деформаций.
Откидные прижимы 3 служат для предотвращения случайного отхода
планок от регулируемых винтовых опор и несут по 17 пружинных прижи-
мов 14. Подвод и отвод откидного прижима осуществляется пневматиче-
ским цилиндром 16. Закрепление планок происходит при срабатывании
пневматических замков 15.
Каретки 4, расположенные по торцам стенда, выполняют две функ-
ции: во-первых, являются ложементами и торцевыми упорами при установ-
ке планок и сборке решетки, состоящей из 17 планок и шести дуг; во-
вторых, служат для навески и поджатия к решетке боковин с втулками. Ос-
новой каретки служит сегмент 19, по контуру которого выполнены 17 ради-
альных пазов. С одной стороны к нему прикреплена пластина 20, служащая
упором для торцов планок и несущая разрезные пальцы 21, на которые ус-
танавливают боковину с приваренными к ней втулками. С другой стороны
закреплен сегмент 18 с пазами-ловителями, в которые попадают торцы пла-
нок при поджиме к ним боковины. Каретки перемещаются по направляю-
щим скалкам 17 с помощью пневматических цилиндров 10, причем та, кото-
рую перемещает цилиндр большего диаметра, является базой при сборке
каркаса.
Приспособление для сварки каркаса с растяжением выполнено в виде
плоской прямоугольной рамы. В двух параллельных швеллерных балках /
приспособления смонтированы нагружающие устройства, показанные на
рис. 8.41. Они представляют собой пружинно-рычажный механизм с пнев-
матической разгрузкой. При установке каркаса в приспособление одна втул-
ка 3 каждой из боковин фиксируется съемным пальцем в неподвижном
кронштейне 4, другая — в отверстиях рычага 2. Рычаг, качающийся на оси
кронштейна, в нижней части поперечным пальцем соединен с тягой 9, на
которую надета пружина 8. Пружина, предварительно сжатая с помощью
регулировочных гаек 5, передает распорное усилие через упорный подшип-
ник 6 и тягу на качающийся рычаг и в конечном счете на боковину каркаса.
Для разгрузки боковины используется пневматический толкатель 7.
В процессе наладки сборочного стенда по результатам описанных
выше измерений было выполнено предварительное регулирование радиаль-
ных опор планок таким образом, что каждая планка получала радиальное
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
447
Рис. 8.41. Устройство для сварки каркаса с растяжением
смещение, по величине равное, а по знаку — противоположное полученно-
му от сварки (см. рис. 8.39). Наладка сварочных приспособлений заключа-
лась в регулировании пружин нагружающих устройств в соответствии с ус-
тановленным режимом сварки.
В процессе производства подбарабанья был проведен статистический
анализ результатов контроля геометрии 50 каркасов.
Обработка результатов показала, что выборочное среднее значение
межцентрового расстояния А после сварки составило 909,8 мм, дисперсия —
0,662 мм2, 12 % каркасов не уложилось в допуск и требовало рихтовки.
Сопоставление отклонений, полученных при сборке и сварке, позво-
лило оценить долю каждой операции в конечном результате. После сборки
разброс значений А составил (910 ± 0,6) мм. Разброс же отклонений, вы-
званных сваркой, даже с исключением бракованных каркасов, составил
910^5 з мм, что свидетельствует о нестабильности технологических парамет-
ров процесса сварки. При случайном благоприятном сочетании сборочных и
сварочных отклонений размер А укладывается в допуски. В противном слу-
чае возникают недопустимые отклонения.
Аналогичные результаты были получены при контроле геометрии ци-
линдрической рабочей поверхности каркасов. После сварки кривизна ее не-
сколько уменьшалась, а разброс измеренных значений радиуса превышал
допуск на его размер и составлял (410 ± 1) мм. Нарушения формы рабочей
поверхности устранялись последующей механической обработкой.
Контроль параметров режима сварки в процессе производства и об-
следования сваренных каркасов выявил значительные их колебания (в цехе
448
8. Опыт проектирования сварочных РТК
-S -2 -1 О 1 2 3 T.S'
Отклонение, мм
Рис. 8.42. Влияние величины сварочного тока и усилия растяжения
на межцентровое расстояние каркаса
использовалась многопостовая система питания), а также существенные от-
клонения по длине и калибру выполняемых швов. Таким образом, низкая
стабильность результатов производства явилась следствием как технологи-
ческих, так и организационных причин.
Для оценки влияния колебаний режима сварки на стабильность геомет-
рии каркасов и величины растягивающего усилия на межцентровое расстояние,
в специальном эксперименте изготавливали каркасы при повышенном и пони-
женном сварочном токе и трех уровнях растягивающей нагрузки (рис. 8.42).
Таким образом, конструкторско-технологические решения, предло-
женные для уменьшения остаточных сварочных деформаций, а также разра-
ботанные технология и оборудование обеспечивают получение проектной
геометрии каркаса подбарабанья при строгом соблюдении технологических
параметров (качества сборки, величины растягивающих усилий, режимов
сварки, размеров сварных швов и порядка их выполнения). При использова-
нии полуавтоматической сварки обеспечить требуемый уровень стабильно-
сти параметров сварки практически невозможно, тогда как использование
роботов это позволяет. В этом случае качество сварных швов подбарабанья
будет обеспечено, если удастся реализовать высокую точность позициони-
рования свариваемого элемента и исключить влияние сварочных деформа-
ций на положение швов в пространстве.
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
449
Рис. 8.43. Схема РТК сварки каркаса
В соответствии с результатами, полученными на предыдущих этапах
работы, был спроектирован и изготовлен РТК, схема которого представлена
на рис. 8.43. Манипулятор 1 изделия представляет собой позиционер с го-
ризонтально расположенной осью вращения поворотной части, на которой с
двух сторон установлены сварочные приспособления. Предварительно соб-
ранные на прихватках каркасы 2 устанавливаются в приспособлениях таким
образом, что зона, в которой расположены сварные швы, имеет практически
цилиндрическую форму.
Два сварочных робота 3 типа IR161/15 фирмы KUKA (ФРГ), имеющие
антропоморфную систему координат, шесть степеней подвижности и кон-
турную систему управления, установлены в отдельных боксах по обе сторо-
ны от позиционера. Они выполняют одновременно сварку двух каркасов в
зонах, расположенных на уровне оси вращения. Все сварные соединения
планок с боковинами и ребрами в этих зонах располагаются горизонтально,
что обеспечивает доступ к ним горелки и наилучшее качество сварного шва.
450
8. Опыт проектирования сварочных РТК
б
Рис. 8.44. Позиционер для роботизированной сварки каркаса
Поочередная переустановка планок в позицию сварки осуществляется по-
шаговым перемещением поворотной части позиционера.
В боксах помимо роботов расположены стойки 4 системы управления
роботами, источники 5 питания сварочным током и устройства 6 для очистки
горелок. С обеих сторон от позиционера, в зонах его обслуживания установле-
ны полы 7 безопасности. Пульт 8 управления модулем вынесен за его пределы
и расположен со стороны стоек управления, в зоне работы оператора.
Конструкция позиционера показана на рис. 8.44, а. Основание 8 слу-
жит опорой для поворотной части позиционера. Обе П-образные стойки ос-
нования несут цапфы 7, в которых неподвижно закреплены концы оси 3.
Поворотная часть позиционера состоит из двух сварочных приспособ-
лений 4, соединенных между собой с помощью двух поворотных опор 5,
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
451
вращающихся на оси. Приспособления одинаковы и аналогичны описанным
выше (см. рис. 8.40). На каждой из опор перпендикулярно оси закреплены
пневматические толкатели 9, разгружающие механизмы растяжения боко-
вины. Сжатый воздух к ним подается через полую ось и две вращающиеся
муфты 2.
Для поворота приспособлений на заданный угол служит храповой ме-
ханизм. Его храповое колесо 1 неподвижно закреплено на одной из пово-
ротных опор, а пневматический привод 11 — в стойке основания. Храповой
механизм снабжен бесконтактными датчиками положения, сигнализирую-
щими о начале и завершении поворота изделия на заданный угол. На проти-
воположной стойке закреплен блок программатора 6.
Требуемая точность позиционирования свариваемых элементов обес-
печивается благодаря использованию в конструкции позиционера принципа
смены баз. После поворота изделия на шаг очередные свариваемые планки
фиксируются в рабочем положении пневматическими фиксаторами 10, от
которых зависит точность позиционирования планок в положении сварки.
Принцип действия пневматических фиксаторов показан на рис. 8.44, б. Кор-
пус 12, неподвижно закрепленный на оси позиционера, является двусторон-
ним пневматическим цилиндром. Штоки 13 перемещаются в направляющих
втулках 14 и заканчиваются клиновыми пазами, в которых фиксируются
свариваемые планки при выдвижении штоков. Снизу на фиксаторах закреп-
лены блоки бесконтактных датчиков положения штоков 15.
При такой схеме базирования влияние сварочных деформаций, а так-
же неизбежных погрешностей сборки практически исключается благодаря
наличию пружинных компенсаторов 16, обеспечивающих возможность не-
зависимого перемещения каждого сварочного приспособления.
Вследствие конструктивных различий между отдельными планками
каркаса количество, размеры и расположение сварных швов на многих из
них различно, поэтому сварка их роботами ведется по семи чередующимся
подпрограммам. Оценку текущего состояния позиционера и выбор нужной
подпрограммы на каждом шаге позиционирования система управления
осуществляет с помощью электромеханического программатора, состояще-
го из перфорированного диска, закрепленного на поворотной опоре, и блока
бесконтактных датчиков, установленных на стойке основания.
Исходным состоянием позиционера является горизонтальное распо-
ложение поворотной части, зафиксированной выдвижными стопорами. Их
положение система управления определяет с помощью встроенных бескон-
тактных датчиков. Выгрузку и загрузку каркасов производят поочередно с
помощью тельфера, каркасы фиксируют в приспособлении с помощью
пальцев. Сварку каркасов производят в автоматическом режиме в соответ-
ствии с алгоритмом, заложенным в систему управления модулем.
452
8. Опыт проектирования сварочных РТК
Система управления всем комплексом оборудования на позиции робо-
тизированной сварки каркасов построена на базе компьютера одного из сва-
рочных роботов (ведущего робота 7). Робот 2 (ведомый), а также позицио-
нер обмениваются с ним информацией и выполняют его команды. При этом
робот 2 работает по собственной рабочей программе, содержащейся в памя-
ти его системы управления.
Датчики, установленные на позиционере, передают в систему управ-
ления модулем следующую информацию:
• код, определяющий состояние позиционера и подпрограммы сварки
зафиксированных планок каждым роботом;
• давление воздуха в пневматической сети;
• положение стопоров поворотной части;
• наличие растягивающего усилия в сварочных приспособлениях;
• положение толкателя храпового механизма;
• положение пневматических фиксаторов.
Кроме того, система управления контролирует нахождение роботов в
исходном положении и состояние их сварочного оборудования.
Алгоритм работы системы управления модулем роботизированной
сварки представлен на рис. 8.45. Запуск для выполнения цикла сварки двух
каркасов в автоматическом режиме осуществляется с внешнего пульта
управления нажатием кнопки «СТАРТ». По этой команде начинается вы-
полнение рабочей программы.
Обнуляются счетчики параметра X, характеризующего состояние по-
зиционера (до или после сварки), и параметра п, определяющего номер сва-
риваемой планки (от 1 до 34). Система управления проверяет, находятся ли
все компоненты модуля в исходном состоянии. Если нет, на пульт управле-
ния подается световой сигнал, а система переходит в состояние ожидания
нового старта. Оператор по сигнальным лампам определяет устройство, не
пришедшее в исходное состояние, устраняет причину сбоя и нажимает
кнопку «СТАРТ». Снова проверив исходное состояние оборудования и дав-
ление в пневматической сети, система последовательно выдает команды на
включение нагружающих устройств сварочных приспособлений и выклю-
чение стопоров поворотной части. Получив подтверждение их нормального
срабатывания, система опрашивает программатор позиционера, анализирует
полученный код U и выбирает соответствующую ему подпрограмму. Поми-
мо кодов, характеризующих исходное состояние позиционера и режим кан-
товки изделий с маршевой скоростью, имеется восемь кодов, каждому из
которых соответствует подпрограмма сварки планок, находящихся в данный
момент в пневматических фиксаторах (см. табл, на рис. 8.45).
В зависимости от содержания кода возможны три варианта действия
системы управления.
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
453
A (U = 0). Система определяет, находится ли поворотная часть в ис-
ходном горизонтальном состоянии. Если да, то проводится оценка состоя-
ния сварочного модуля: требуется ли начать сварку (X = 0) или же она за-
вершена (X = 1). Если необходимо сварку начать, храповой механизм канту-
ет изделие на один шаг и система управления снова опрашивает
программатор, на котором после первого шага устанавливается код режима
кантовки с маршевой скоростью (U = 1). Работая в цикле, система управле-
ния продолжает кантовку изделия до тех пор, пока на программаторе не
установится код, соответствующий приходу первых планок каркаса на
позицию сварки.
Б (U Ф 1). Система управления включает пневматические фиксаторы
и, если давление в пневматической сети нормальное, разрешает стартовать
роботу 2. В этот момент меняется признак состояния позиционера (X = 1) и
начинается счет сваренных планок (n = 1). Робот 2 переходит в исходное
положение (если он там не был), и система повторно опрашивает програм-
матор, определяя, по какой из шести сварочных подпрограмм должен рабо-
тать робот 2. В позиции сварки первой пары планок (U = 2) должна осуще-
ствляться сварка только на первом каркасе, так как на планке второго швы
расположены с нижней стороны. Поэтому система управления проверяет, не
нужна ли зачистка горелки робота 2, и оставляет его в исходном положении.
В это же время определяется подпрограмма сварки робота 1 и он произво-
дит сварку первой планки, после чего, проверив, не нужна ли зачистка го-
релки, возвращается в исходное положение. Система управления, убедив-
шись, что оба робота находятся в исходных точках, расфиксирует планки,
кантует изделие на шаг и снова опрашивает программатор. По коду U = 3
осуществляются фиксация и сварка второй пары планок, и система повторя-
ет описанные выше действия с тем лишь различием, что на этот раз сварку
производят оба робота, каждый по своей подпрограмме.
Сварочные циклы повторяются до тех пор, пока счетчик сварных пла-
нок не укажет, что необходима зачистка горелок. Последняя производится
на каждом роботе после сварки четырех-пяти планок. При сварке последней
пары планок работает только робот 2, так как на планке первого каркаса
швы расположены снизу.
По завершении первого цикла работы на программаторе вновь уста-
навливается код U = 1, и система управления включает режим кантовки с
маршевой скоростью, в процессе которого роботы обмениваются каркасами.
Далее при смене кода (U = 2) осуществляется сварка второй половины швов
на каждом каркасе по описанной выше процедуре, после чего на программа-
торе вновь устанавливается код U = 0.
В. Позиционер в маршевом режиме кантует изделие в горизонтальное
положение. С последним шагом меняется признак состояния сварочного
454
8. Опыт проектирования сварочных РТК
Начало
!ПУН
Внешний старт
Нет
Нет
Р1К
в исходном
сост.
1Г1УЬ
Да______
Нагружение изделий
Нет
Нет
Изделия
нагружены
Кодировка программатора
Коди Содержание кода
0 Исходное полож. позиционера
1 Маршевая кантовка
Сварка по поди эограмме
Робот 1 Робот 2
2 1 -
3 2 2
4 3 3
5 4 4
6 5 5
7 6 5
8 3 6
9 - 1
X - признак состояния РТК
Х=0-до сварки
X— I - после сварки
п - колисетво позиций сварки,
отработанных в цикле (п=0.,34)
Г~”> Нет
ШУ»-----
Опрос программатора
Да____
Расстопорение
Да
Нет
Стопор
включен
Стопорение
.Нет
1ПУ
Нет
Нет
Н=0
Да
Да
Нет
Стопор
включен
Х=0
Ж
Кантовка па шаг [—
Нет
•ПУ
Нет
U=1
Да
Дд
Нет
Кантовка
выполнена
Разгрузка изделия
1ПУ
.Нет
Нет
Нагрузка
снята
Да
I Возврат толкателя храповика —
Фиксация
Нет
Нет г
иксато
в ключе!
а вл.
Не1)ПУ|
Нет
Да
Ж.
Старт робота 2
.Нет
»пу
Нет
олкатель
В исходном
нолож
Да
Рис. 8.45. Блок-схема алгоритма работы системы управления модуля
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
455
роботизированной сварки каркаса
456
8. Опыт проектирования сварочных РТК
Рис. 8.46. Схема размещения оборудования РТК
модуля (X = I — состояние после сварки), в соответствии с которым вклю-
чаются стопора поворотной части и пневматические толкатели приспособ-
лений, разгружающие боковины изделий. Проверив выполнение этих ко-
манд, система управления переходит в состояние ожидания следующей ко-
манды «СТАРТ» с пульта управления.
Оператор со сборщиком заменяют готовые каркасы собранными, и
цикл работы модуля повторяется.
После предварительных испытаний полный комплект оборудования
РТК был смонтирован и отлажен на Урюпинском заводе «Сельхозмаш».
.Суммарная длительность операций, выполняемых на РТК, при изго-
товлении двух каркасов составляет 137,5 мин. Следовательно, трудоемкость
сборки и сварки одного каркаса составляет 68,75 мин.
Работа РТК построена таким образом, что со временем роботизиро-
ванной сварки не совмещены только транспортные операции, связанные с
загрузкой и выгрузкой изделий на позиционере, причем в этих операциях
задействованы оба работника, обслуживающие РТК.
РТК (рис. 8.46) включает в себя три рабочие позиции, объединенные
межоперационным транспортным устройством: сборки (I); роботизирован-
ной сварки (II); контроля и исправления брака (III).
Между позициями РТК предусмотрены накопители.
Сборку каркаса на прихватках осуществляет сборщик в сварочной ка-
бине на стенде 7. Здесь же, в приспособлении 2 он предварительно привари-
вает втулки к боковинам швами, не доступными для горелки робота. Сварку
и прихватку производят полуавтоматической сваркой в среде углекислого
газа, для чего кабина оборудована сварочным постом 3 и консолью для по-
дающего механизма 4. Собранный каркас с помощью тельфера 5 складиру-
ют в накопитель 6 или передают на позицию роботизированной сварки, где
сборщик вместе с оператором устанавливает и фиксирует каркас на первом
приспособлении позиционера 7, находящегося в положении загрузки. Затем
после кантовки поворотной части на 180° они загружают второй каркас.
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
457
После этого оператор с пульта управления 8 включает автоматический
цикл сварки и оба робота 9 одновременно производят сварку двух каркасов.
Стойки 10 управления роботами и источники 11 сварочного тока встроены в
кабины и лицевыми панелями обращены к оператору.
По завершении сварки позиционер переводит приспособления в гори-
зонтальное положение. Оператор вместе со сборщиком снимает сваренный
узел и устанавливает на его место новый собранный. Позиционер кантует
раму с приспособлениями на 180°, и производится перезарядка второго при-
способления. Цикл сварки повторяется.
Сваренные каркасы оператор с помощью тельфера подает в накопи-
тель 12 или на место контроля 13. Здесь за время работы роботов оператор
выполняет оставшиеся сварные швы, осматривает каркасы, исправляет брак
после роботизированной сварки и контролирует шаблонами межцентровые
расстояния на боковинах и радиус рабочей поверхности каркаса.
Готовые каркасы складируют в накопитель 14.
По завершении пусконаладочных работ оценивали качество изготов-
ляемых узлов и стабильность их геометрии. С этой целью провели обследо-
вание и контроль геометрии партии каркасов в количестве 38 штук, сварен-
ных с погонной энергией q = 6800 Дж/см и усилием растяжения боковин Р =
= 8,0 кН. Статистическая обработка результатов показала, что для межцен-
трового расстояния выборочное среднее значение составило 910,053 мм,
дисперсия — 0,333 мм2. Выход годных изделий с размерами, удовлетво-
ряющими требованиям чертежа, составил 94,3 %.
На рис. 8.47 представлены кривые распределения плотности вероят-
ности отклонений межцентрового расстояния от номинала для роботизиро-
ванной (кривая 7) и полуавтоматической (кривая 2) сварки. Последняя по-
строена по результатам обследования каркасов, приведенным выше. Кривые
наглядно демонстрируют повышение точности и стабильности результатов,
достигнутое при переходе на роботизированную сварку.
Общая картина распределения отклонений ребер планок от проектно-
го значения радиуса рабочей поверхности R = 410 мм, полученная по ре-
зультатам измерения на 38 каркасах, сваренных на РТК, представлена на
рис. 8.48. Три графика характеризуют форму рабочей поверхности каркаса
после сборки (I), после сборки и сварки (II) и отдельно — отклонения, вы-
званные сварочными деформациями (III) (получены вычитанием I из II).
График III наглядно показывает характер искажений рабочей поверхности,
вызванных сваркой с растяжением, а графики I и II иллюстрируют возмож-
ности корректировки этих искажений при сборке.
Для придания рабочим кромкам планок формы, обеспечивающей опти-
мальные условия обмолота хлебной массы, после сварки каркаса предусмотре-
на строжка боковых ребер планок, образующих рабочую поверхность.
458
8. Опыт проектирования сварочных РТК
Рис. 8.47. Распределение плотности вероятности отклонений меж-
центрового расстояния от номинала:
1 — роботизированная сварка; 2 — полуавтоматическая сварка
По базовой технологии сварные каркасы подвергали правке на гид-
равлическом прессе в целях восстановления размера (910 ±0,7) мм. При
этом радиус R = 410 мм увеличивался, в связи с чем при сборке каркаса
планки устанавливали на радиус R = 407 мм, что обеспечивало механиче-
скую обработку планок по всей рабочей поверхности каркаса.
По разработанной технологии правка после сварки не требуется. Из-
мерения формы рабочей поверхности каркаса показали, что в допуск на зна-
чение радиуса R = (410 ± 0,5) мм укладываются 92 % измеренных его значе-
ний. Это позволило уменьшить припуск на механическую обработку карка-
са до 0,6 мм. Расчет показывает, что до внедрения РТК на каждом каркасе в
стружку уходило 4,7 кг металла, после его внедрения — 0,86 кг. Соответст-
венно трудоемкость этой операции, сопоставимая со временем сборки и
сварки, сократилась в 4—5 раз.
Опыт, полученный при создании и эксплуатации РТК на Урю-
пинском заводе «Сельхозмаш», позволяет заключить следующее.
1. Стабильность режимов и строгая последовательность выполнения
швов, присущие роботизированной сварке, в сочетании со специальными
приемами уменьшения сварочных деформаций обеспечивают возможность
изготовления с заданной проектной точностью крупногабаритных, объем-
8.5. РТК сборки и дуговой сварки сложного маложесткого узла
459
Рис. 8.48. Отклонение планок от проектного положения:
I — после сборки; II — после сборки и сварки; III — в результате сварки
ных нежестких конструкций, имеющих большое количество коротких швов.
При изготовлении каркаса подбарабанья использовали следующие приемы:
• при сборке каркаса каждой планке задавали смещение от номиналь-
ного размера R = 410 мм, равное по величине и обратное по направлению
смещению, происходящему при сварке;
• при сварке к боковинам каркаса прикладывали постоянные растяги-
вающие силы, вызывающие в зонах швов деформации, обратные усадочным.
Это позволило исключить операцию правки сварных каркасов и
уменьшить на 70 % объем механической обработки после сварки.
2. Конструктивно-технологическая компоновка РТК и использование
приема смены баз, что практически исключило влияние как остаточных сва-
рочных деформаций, так и временных перемещений на точность позицио-
нирования конца проволоки относительно свариваемых стыков.
3. Трудоемкость изготовления каркаса подбарабанья на РТК состав-
ляет 1,1 чел.-ч, что в 2,4 раза меньше, чем при его изготовлении с помощью
полуавтоматической сварки в среде углекислого газа.
Снижение трудоемкости получено как результат:
460
8. Опыт проектирования сварочных РТК
• более быстрого перемещения горелки робота от шва к шву;
• оптимизации траектории перемещения горелки, выполненной с ис-
пользованием системы РОБОМАКС фирмы «Буран»;
• стабилизации номинальных размеров сварных швов с отклонением в
сторону нижнего предела поля допуска (5-0,5 мм), тогда как при полуавтома-
тической сварке швы, как правило, выполняются с завышением номиналь-
ного размера (5+1’° мм);
• уменьшения непроизводительных потерь времени.
4. Хронометраж работы РТК показал, что при такте выпуска изделий
33 мин элементы цикла изготовления каркаса в процентном отношении со-
относятся следующим образом:
• установка и съем изделия — 6,3 %;
• кантовка изделия — 5,5 %;
• перемещения горелки к местам сварки и зачистка мундштука — 17,2 %;
• горение дуги — 71 %.
Время подналадки и обслуживания оборудования РТК составляет в
среднем 15 %.
Достаточно высокая производительность РТК (14 каркасов в одну
смену) достигнута в основном благодаря рациональному совмещению во
времени основных и вспомогательных операций.
Заключение
Приведенный в настоящем учебном пособии материал охватывает
многие (но не все) направления проектно-технических работ по подготовке
производства сварных конструкций. Основное внимание уделено наиболее
сложным расчетным задачам и наиболее проблемным задачам автоматиза-
ции выполнения сварочных операций. Можно видеть, что применение мощ-
ных современных компьютерных технологий позволяет с хорошей степенью
визуализации моделировать как физико-металлургические процессы в ме-
таллах, так и работу сложного технологического оборудования. Именно на
основе весьма точного моделирования, проверяемого затем в цеховых усло-
виях, сегодня можно и нужно совершенствовать принимаемые конструктор-
ские и технологические решения. С этой целью в конструкторских и техно-
логических отделах предприятий, связанных с выпуском сварных конструк-
ций, и на кафедрах сварочной специальности необходимо изучение и
освоение эффективных программных комплексов как общесистемных, так и
по специальным направлениям. Материалы, приведенные в книге, можно
использовать при подготовке лекционно-семинарских занятий и лаборатор-
ного практикума. В последнем случае удобно использовать конкретные
примеры, достаточно подробно рассмотренные в каждой главе после изло-
жения общих принципов построения отдельных систем и подсистем.
Опыт практической работы показывает, что сложность программных
комплексов совсем не означает, что они тяжело поддаются освоению. Ско-
рее наоборот, хорошие системы, ориентированные на специалистов, могут
быть освоены ими всего за несколько часов и уже далее опыт работы будет
накапливаться в процессе конкретной практической деятельности.
В завершение необходимо отметить, что эффект применения компью-
терной техники и технологий не следует переоценивать. Снижение трудо-
емкости решения задач проектирования далеко не гарантирует легкость и
простоту получения качественных проектов. Практический опыт проекти-
рования, изложенный в §§ 8.4 и 8.5, убедительно показывает, что опреде-
ляющим фактором успеха, конечно же, является высокая квалификация спе-
циалистов предметной области. Поэтому создание комфортных условий ра-
боты для этой категории работников и разгрузка их от рутинных видов
работ с целью стимулирования творческой деятельности может быть самая
важная задача разработчиков программного обеспечения.
Список литературы
Винокуров В.А., Куркин С.А., Николаев Г.А. Сварные конструкции. Механика раз-
рушения и критерии работоспособности. М.: Машиностроение, 1996.
Карзов Г.П., Марголин Б.З., Швецова В.А. Физико-механическое моделирование
процессов разрушения. СПб.: Политехника, 1993.
Касаткин О.Г., Зайффарт П. Интерполяционные модели для оценки фазового со-
става зоны термического влияния при дуговой сварке низколегированных сталей
//Автоматическая сварка. 1984. № 1. С. 7—11.
Компьютерные технологии в сварочном производстве // Справочник. Инженерный
журнал. Приложения. 2000. № 12.
Куркин Н.С. Применение промышленных роботов для автоматизации процессов
дуговой сварки в автомобилестроении. ПРД 37.032.039—88. НПО НИИТАвто-
пром. М.: 1988.
Куркин Н.С., Кукареко Е.П., Пашкевич А.П. Комплекс программных средств
«ROBOMAX» для автоматизации проектирования сварочного производства //
Справочник. Инженерный журнал. 1997. № 1. С. 33—37.
Куркин Н.С., Легезо А.А., Марков В.А., Мармузевич С.С. САПР сварочного инстру-
мента (сварочных клещей) WTOOL // Справочник. Инженерный журнал. 1998.
№ 5. С. 12—18. 1998. № 6. С. 9—16.
Куркин С.А., Куркин А.С. Проблемы компьютерной подготовки инженеров-
сварщиков // Сварочное производство. 1996. № 1. С. 32—34.
Куркин С.А., Ховов В.М., Рыбачук А.М. Технология, механизация и автоматизация
производства сварных конструкций. Атлас. М.: Машиностроение, 1989.
Лукьянов В.Ф., Напрасников В.В. Использование имитационного моделирования
для прогнозирования характеристик надежности сварных соединений // Автома-
тическая сварка. 1989. № 1. С. 6—11.
Макаров Э.Л. Холодные трещины при сварке легированных сталей. М.: Машино-
строение, 1981.
Макаров Э.Л., Коновалов А.В. Система компьютерного анализа свариваемости и
технологии сварки легированных сталей // Сварочное производство. 1995. № 3.
С. 6—9.
Марков В.А., Куркин Н.С. Система автоматизированного проектирования комплек-
сов и технологии сварки с применением промышленных роботов // Сварочное
производство. 1991. № 7. С. 22—28.
Марков В.А., Мармузевич С.С., Ховов В.М. САПР РОБОМАКС — российским заво-
дам // Техномир. 1999. № 1. С. 17—19.
Медведев С.В. Компьютерные технологии проектирования сборочно-сварочной ос-
настки. Минск: Ин-т техн, кибернетики НАН Белоруссии, 2000.
Список литературы
463
Методические рекомендации. Расчет коэффициентов интенсивности напряжений и
коэффициентов ослабления сечений для дефектов в сварных соединениях: МР-
125-01—90. М.: ЦНИИТМАШ, 1991.
Механика разрушения и прочность материалов: В 4 т. Т. 1: Основы механики раз-
рушения / В.В. Панасюк, А.Е. Андрейкин, В.З. Партон и др. Киев: Наукова дум-
ка, 1988.
Окерблом НО. Конструктивно-технологическое проектирование сварных конст-
рукций. М.; Л.: Машиностроение, 1964.
Пашкевич А.П. Автоматизация проектирования роботизированных сварочных про-
изводств // Справочник. Инженерный журнал. 1997. № 5. С. 33—38.
Пашкевич А.П. Автоматизированное проектирование промышленных роботов и
робототехнологических комплексов для сборочно-сварочных производств.
Минск: БГУИР, 1996.
Постнов В.А., Тарануха Н.А. Метод модуль-элементов в расчетах судовых конст-
рукций. СПб.: Судостроение, 1990.
Разработка комплекса роботизированных линий сборки-сварки автомобиля ГАЗ-
3302 «Газель» с использованием САПР ROBOMAX / Н.И. Лобзин,
С.М. Локшин, С.М. Куликов, Н.С. Куркин и др. И Сварочное производство. 1995.
№ 4. С. 24—29.
Ракович А.Г. Основы автоматизации проектирования технологических приспособ-
лений. Минск: Наука и техника, 1985.
РИкович А.Г., Толкачев А.А. Автоматизация принятия проектных решений на основе
баз знаний. Минск: Наука и техника, 1989.
Расчет термонапряжений и прочности роторов и корпусов турбин // К.В. Фролов,
Ю.Л. Израилев, Н.А. Махутов и др. М.: Машиностроение, 1988.
Сварка и свариваемые материалы: Т.1: Свариваемость материалов / Под ред.
Э.Л.’ Макарова. М.: Металлургия, 1991.
Сварочные роботы / В. Геттерт, Г. Герден, X. Гюттнер и др.; Под ред. Г. Гердена;
Пер. с нем. Г.Н. Клебанова, Д.Г. Тесменицкого. М.: Машиностроение, 1988.
Сегерлинд Л. Применение метода конечных элементов. М.: Мир, 1979.
Статистические закономерности малоциклового разрушения / Н.А. Махутов,
В.В. Зацаринный, Ж.Л. Базарас и др. М., 1989.
Теория сварочных процессов / Под ред. В.В. Фролова. М.: Высшая школа, 1988.
Тихомиров В.Г. САПР роботизированных производственных систем: анализ, со-
стояние и перспективы развития (обзор) // Сварочное производство. 1994. №11.
С. 29—34.
Учебное издание
Куркин Сергей Александрович
Ховов Вячеслав Михайлович
Аксенов Юрий Николаевич
Касаткин Олег Григорьевич
Киселев Александр Сергеевич
Киселев Алексей Сергеевич
Коновалов Алексей Викторович
Куркин Алексей Сергеевич
Куркии Николай Сергеевич
Легезо Андрей Александрович
Лукьянов Виталий Федорович
Лыков Анатолий Викторович
Людмирский Юрий Георгиевич
Макаров Эдуард Леонидович
Марков Владимир Александрович
Мармузевич Сергей Серафимович
Пашкевич Анатолий Павлович
Солтавец Марат Васильевич
Супер Андрей Сергеевич
КОМПЬЮТЕРНОЕ ПРОЕКТИРОВАНИЕ И ПОДГОТОВКА
ПРОИЗВОДСТВА СВАРНЫХ КОНСТРУКЦИЙ
Редактор В.А. Козлов
Художник С.С. Водчиц
Корректор Е.В. Авалова
Компьютерная верстка С Ч. Соколовского
Подписано в печать 14.08.02. Формат 70x100/16. Печать офсетная.
Бумага офсетная. Гарнитура «Таймс». Печ. л. 29. Усл. печ. л. 37,7. Уч.-изд. л. 36,25.
Тираж 3000 экз. Заказ 6705
Издательство МГТУ им. Н.Э. Баумана.
105005, Москва, 2-я Бауманская, 5.
Отпечатано в полном соответствии с качеством предоставленного оригинал-макета
в ППП «Типография «Наука» 121699. Москва. Шубинский пер.. 6