Author: Алексеева Н.А.
Tags: авиация и космонавтика летательные аппараты ракетная техника космическая техника воздушный транспорт авиация и воздушные соединения воздушные линии и аэропорты транспорт машиностроение авиация авиастроение
ISBN: 5-217-00356-1
Year: 1989
Text
ДЛЯ ВУЗОВ
ОСНОВЫ РАСЧЕТА
И КОНСТРУИРОВАНИЯ
ДЕТАЛЕЙ
И МЕХАНИЗМОВ
ЛЕТАТЕЛЬНЫХ
АППАРАТОВ
• МАШИНОСТРОЕНИЕ*
ДЛЯ ВУЗОВ
ОСНОВЫ РАСЧЕТА
И КОНСТРУИРОВАНИЯ
ДЕТАЛЕЙ
И МЕХАНИЗМОВ
ЛЕТАТЕЛЬНЫХ
АППАРАТОВ
Под редакцией
профессора В.Н. Кестельмана
и профессора Г.И. Рощина
Допущено Государственным комитетом СССР
по народному образованию в качестве учебного пособия
для студентов высших технических учебных заведений
Москва
•Машиностроение-
1989
ББК 39.52-04-2я73
0-75
УДК 629.7.02.001.24(075.8)
Авторы: Н. А. Алексеева, | Л. А. Бони-Осмоловский/» В. В. Волгин,
П. П. Дементьев, В. В. Джамай, Н. Л. Зезин, В. Н. Кестельман,
Ю. М. Климов, В. А. Комков, Ю. Б. Михайлов, А. Д. Павлов, Г. И. Ро-
щин, Е. А. Самойлов, |М. Я. Чирсков| , В. А. Чубиков
Рецензенты: проф. Е. И. Степанычев, кафедра деталей машин
Куйбышевского авиационного института
Основы расчета и конструирования деталей и механиз-
0-75 мов летательных аппаратов: Учеб, пособие для втузов/
Н. А. Алексеева, Л. А. Бонч-Осмоловский, В. В. Волгин
и др.; Под ред. В. Н. Кестельмана, Г. И. Рощина. — М.:
Машиностроение, 1989. — 456 с.: ил.
ISBN 5-217-00356-1
Изложены критерии работоспособности деталей машин и механиз-
мов ЛА. Приведены требования к конструкционным материалам и их
характеристики, основы расчета и конструирования механических пере-
дач, их деталей и узлов; особое внимание уделено использованию ЭВМ
и САПР. Приведены примеры расчета ряда механизмов ЛА.
О
2705140400—259
038(01)—89
259-89
ББК 39.52-04-2я73
ISBN 5-217-00356-1 © Издательство «Машиностроение», 1989
ПРЕДИСЛОВИЕ
Настоящая книга является учебным пособием по ряду кур-
сов («Детали машин», «Техническая механика», «Конструиро-
вание механизмов РЭА» и др.), в которых студенты авиацион-
ных вузов изучают вопросы расчета и конструирования деталей
и механизмов летательных аппаратов (самолетов, вертолетов
и космических аппаратов различного назначения). Изучение
этих курсов завершает общеинженерную подготовку; в даль-
нейшем студенты приступают к изучению специальных дис-
циплин.
Расчет и конструирование деталей ;1|,'ие^анизмов летатель-
ных аппаратов (ЛА) связаны с процеве»м*-оптимального выбо-
ра их механизмов, материалов, технологии изготовления. При
этом следует учитывать требования к ЛА, последние дости-
жения науки и техники, состояние и перспективы развития
производства. К числу специальных требований, предъявляе-
мых к ЛА, относятся, например, минимальные масса и габари-
ты, высокие надежность, долговечность, удельная прочность,
работоспособность в различных эксплуатационных, в том чис-
ле экстремальных, условиях (низкие температуры, вакуум,
ионизирующие излучения и пр.).
Разнообразные задачи, решаемые ЛА, обусловливают слож-
ный характер нагружения деталей и механизмов. Особенности
конструкций ЛА, необходимость обеспечения высокой надежно-
сти предъявляют повышенные требования к точности расчета и
конструктивным решениям деталей и узлов.
Различным ЛА присуща своя специфика расчета и констру-
ирования как аппарата в целом, так и отдельных его узлов и
Деталей, которые рассматриваются в специальных курсах [8, 23,
3
38]. Однако во всех ЛА имеются узлы и детали общего назна-
чения: передачи (зубчатые, червячные, волновые и др.), муф-
ты, валы, подшипники, уплотнения, пружины, рессоры и др.
Механические передачи и составляющие их узлы и детали,
а также различные соединения и являются предметом рассмо-
трения данного учебного пособия.
Настоящее издание подготовлено коллективом авторов.
Н. А. Алексеева написала гл. 7, 10, разд. 12.2; В. В. Волгин —
гл. 18, разд. 25.3; В. В. Джамай — гл. 16, 17, 23; Н. Л. Зе-
зин — гл. 6, 11, 22; В. Н. Кестельман — разд. 25.2; Ю. М. Кли-
мов— гл. 15, разд. 13.1, 13.2, 25.1; В. А. Комков — гл. 19,
разд. 2.8; Ю. Б. Михайлов — гл. 20, 21; А. Д. Павлов — гл. 14;
Г. И. Рощин — гл. 1, 2 (кроме разд. 2.8), гл. 5, разд. 25.4;
Е. А. Самойлов — гл. 4, 9, разд. 5.9, 13.3, 25.5; М. Я. Чирсков —
гл. 8; В. Н. Чубиков — разд. 2.7, 12.3; Предисловие и гл. 3
написаны совместно В. Н. Кестельманом и Г. И. Рощиным;
разд. 12.1 — Н. А. Алексеевой и В. Н. Чубиковым; гл. 24 —
П. П. Дементьевым и Н. Л. Зезиным; разд. 25.6 — Г. И. Рощи-
ным и М. Я. Чирсковым.
РАЗДЕЛ I
ОБЩИЕ ВОПРОСЫ КОНСТРУИРОВАНИЯ
МЕХАНИЧЕСКИХ ПЕРЕДАЧ
ГЛАВА 1. ТИПОВЫЕ МЕХАНИЗМЫ, УЗЛЫ И ДЕТАЛИ ЛА,
УСЛОВИЯ ИХ ЭКСПЛУАТАЦИИ
1.1. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ, УЗЛЫ И ДЕТАЛИ,
ИСПОЛЬЗУЕМЫЕ В ЛА
В современной авиационной технике в основном ис-
пользуют реактивные силовые двигательные установки реак-
тивного движения. Если при использовании турбовинтовых
двигателей (ТВД) при частотах вращения газовой турбины
6000...17000 и винта 900...1100 об/мин был необходим редуктор,
то при применении прямоточных воздушно-реактивных
(ПВРД) или жидкостных ракетных (ЖРД) двигателей такая
необходимость отпадает. Однако необходимость в снижении
частоты вращения остается при отборе мощности с турбины
ТРД для стартер-генератора, генератора переменного тока,
гидронасоса и других агрегатов. Редукторы необходимы также
и в рулевом приводе, входящем в систему управления. Приво-
ды с зубчатыми передачами используют для механизации кры-
ла и хвостового оперения самолета, в механизмах триммирова-
ния, в различных авиационных приборах. В конструкциях вер-
толетов редукторы используют в приводах несущего и рулевого
винтов. В ракетах и космических аппаратах применение зуб-
чатых передач ограничено; однако зубчатые планетарные пере-
дачи применены в приводах колес луноходов, в стыковочных
узлах КА используются шарико-винтовые и другие механизмы.
Пример конструктивных решений узла коробки агрегатов двух-
роторного ТРД приведен на рис. 25.3, главного редуктора вер-
толета — на рис. 25.6.
Рычажные механизмы широко применяют в механизмах вы-
пуска и убирания шасси (рис. 1.1), в системах управления поло-
жением самолета в пространстве и изменения режима полета
(рис. 1.2), а также в некоторых приборах для преобразования
движения между входным (мембрана) и выходным (стрелка)
звеньями (рис. 1.3).
Шарико-винтовые механизмы в устройствах механизации
крыла, в механизмах триммирования преобразуют вращатель-
ное движение в поступательное и создают большие усилия (до
нескольких десятков тысяч ньютон) на выходном звене (винте).
В силовых установках ЛА и его системах управления для
приведения в движение исполнительных органов используют
5
3
Рис. 1.2. Схемы жестких рычажных механизмов (а) и их сочетания с пере-
дачами гибкой связью в бустерном (б) и безбустерном (в) вариантах в си-
стеме управления поверхностью Л:
/ — рычаг управления; 2 — тяга; 3 — ведущий шкив; 4 — направляющий ролик; 5 — ве-
домый шкив; 6 — гидроусилитель; 7 —система загрузки (бустер)
6
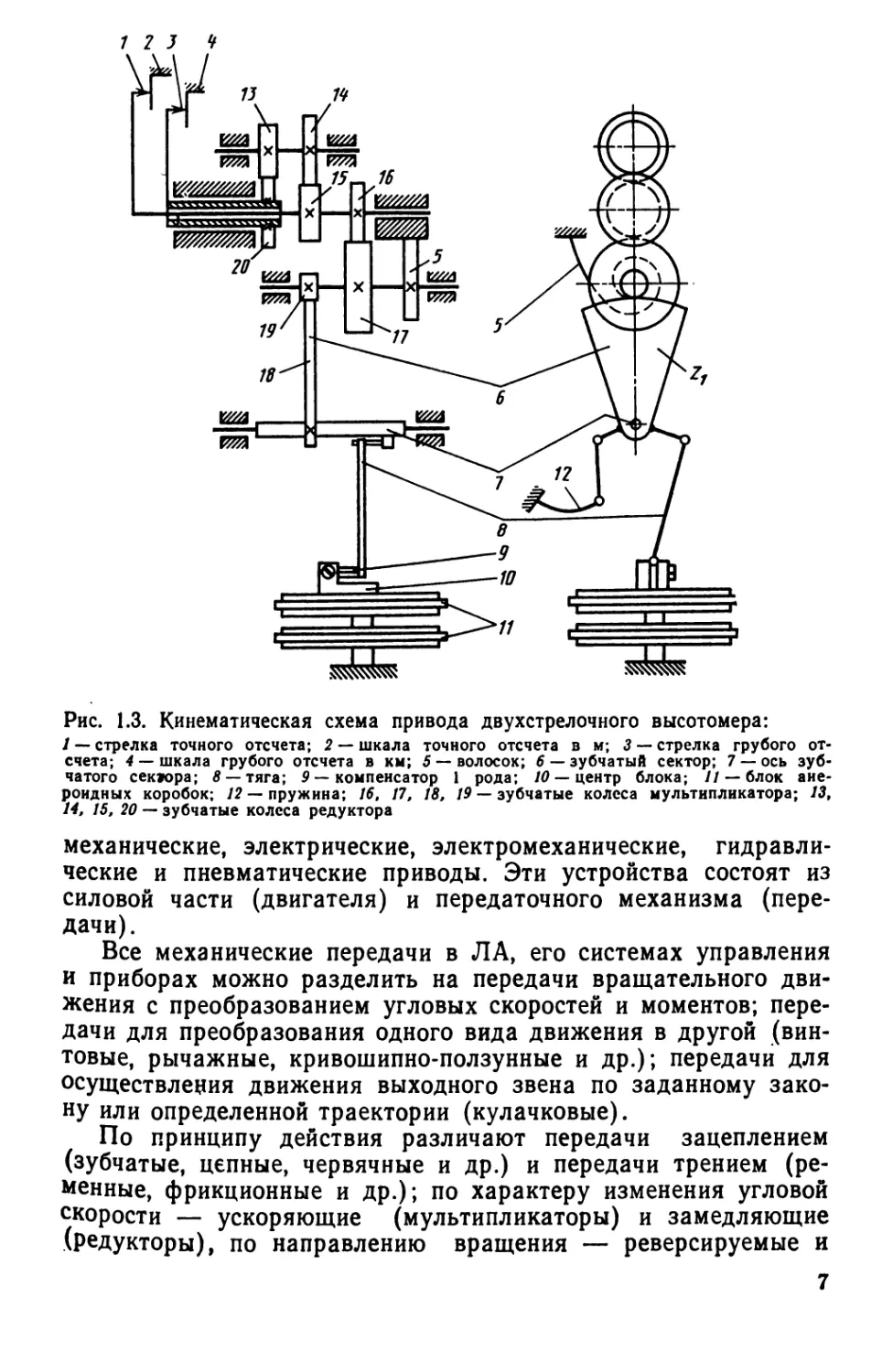
Рис. 1.3. Кинематическая схема привода двухстрелочного высотомера:
1 — стрелка точного отсчета; 2 — шкала точного отсчета в м; 3 — стрелка грубого от-
счета; 4 — шкала грубого отсчета в км; 5 — волосок; 6 — зубчатый сектор; 7 — ось зуб-
чатого сектора; в —тяга; 9 — компенсатор 1 рода; 10 — центр блока; // — блок ане-
роидных коробок; /2 —пружина; 16, 17, 18, /9 — зубчатые колеса мультипликатора; 13,
14, 15, 20 — зубчатые колеса редуктора
механические, электрические, электромеханические, гидравли-
ческие и пневматические приводы. Эти устройства состоят из
силовой части (двигателя) и передаточного механизма (пере-
дачи).
Все механические передачи в ЛА, его системах управления
и приборах можно разделить на передачи вращательного дви-
жения с преобразованием угловых скоростей и моментов; пере-
дачи для преобразования одного вида движения в другой (вин-
товые, рычажные, кривошипно-ползунные и др.); передачи для
осуществления движения выходного звена по заданному зако-
ну или определенной траектории (кулачковые).
По принципу действия различают передачи зацеплением
(зубчатые, цепные, червячные и др.) и передачи трением (ре-
менные, фрикционные и др.); по характеру изменения угловой
скорости — ускоряющие (мультипликаторы) и замедляющие
(редукторы), по направлению вращения — реверсируемые и
7
Рис. 1.4. Болтовые соединения элементов ЛА
постоянного направления вращения, по числу потоков переда-
ваемой мощности — одно- и многопоточные, а по числу сту-
пеней — одно- и многоступенчатые.
Наиболее широко используемые зубчатые передачи по вели-
чине скорости разделяют на тихоходные (о<3 м/с), среднеско-
ростные (о=3...15 м/с) и быстроходные (о>15 м/с); по виду
зуба — на передачи с прямыми, косыми, шевронными и винто-
выми зубьями; по форме кривой профиля — на передачи с
эвольвентным, круговым и специальными .(циклоидальным, ча-
совым и др.) профилем. Опоры скольжения, рассчитанные на
Рис. 1.5. Узел крыла с сотовым наполнителем:
1 — верхняя обшивка; 2 — сотовый наполнитель; 3 — нижняя обшивка
8
условие обеспечения жидкостного трения, используют в ряде
случаев в качестве опор в узлах двигателя ЛА ввиду их высо-
кой несущей способности, долговечности и надежности.
Так как механические передачи и их детали играют важную
роль в передаче и преобразовании движения, изменении сило-
вых и кинематических параметров в различных устройствах
ЛА, то их изучение является важной составной частью курса
«Детали машин».
Соединение валов в приводах обеспечивается применением
обгонных, шарнирных, зубчатых, кулачковых и фрикционных и
других муфт, как правило, с электромагнитным управлением.
Для соединения деталей узлов и механизмов широко при-
меняют различные виды соединений: резьбовые, заклепочные,
сварные, клеевые и др. На рис. 1.4 показано соединение болта-
ми двух стыковочных профилей контурного разъема крыла.
На рис. 1.5 показан узел крыла с внутренним сотовым напол-
нителем. Отдельные рифленые элементы сотового блока при-
варивают друг к другу, а сотовый блок к обшивке припаива-
ется.
1.2. ОСОБЕННОСТИ ЭКСПЛУАТАЦИИ ДЕТАЛЕЙ, УЗЛОВ
И ПЕРЕДАЧ ЛА*
Условия эксплуатации деталей машин и механизмов ЛА
очень многообразны по внешним воздействиям — механичес-
ким, климатическим, радиационным и др. Механическое воз-
действие может быть представлено силовой картиной нагру-
жения в виде статической, динамической и вибрационной со-
ставляющих. На детали ЛА воздействуют вибрации, удары,
инерционные перегрузки, вызванные линейными и угловыми
ускорениями и пр. Удары и толчки в виде отдельных неуста-
новившихся импульсов также вызывают перегрузки. Возника-
ющие при этом ускорения могут достигать десятков g (g — ус-
корение свободного падения). Опасность вибраций состоит в
том, что они постепенно приводят к разрушению конструкции,
так как даже колебания деталей с малой амплитудой могут
вызвать появление усталостных трещин. Особое влияние виб-
рации оказывают на качество соединений: ухудшается крепле-
ние деталей в узлах с резьбовыми соединениями, расшатыва-
ются заклепочные соединения, а паяные, клеевые или сварные
особо подвержены разрушению. Инерционные перегрузки могут
возникать также из-за линейных ускорений при взлете, манев-
рировании и посадке ЛА. Степень механической перегрузки
при ускорении а для ЛА оценивают величиной
J=(a-g)!g. (1.1)
9
Таблица 1.1
Ситуация, в которой возникают перегрузки Наибольшее значение перегрузки Длительность действия, с
Выход из пикирования 8...9 (до 11) 1
Вход в пикирование 4 1
Одинарная (штопорная) бочка 3 <10
Штопор 1,5 ...2 <10
Полет при болтанке 4 0,1
Посадка, пробег, разбег 3...5 0,1
Посадка гидросамолета на воду 7 0,1
Раскрытие парашюта с уменьшением скоро- сти от 60 до 5 м/с 5 0,5
Катапультирование пилота 16 0,1
Некоторые статистические данные по перегрузкам и их дли-
тельности для самолетов даны в табл. 1.1 [24].
При наличии перегрузок по трем осям х, у и z полное зна-
чение перегрузки будет равно
/= V Л+/! + >! . (1.2)
Если закон изменения вибрации имеет вид x=Aosin(Oot то
наибольшая величина ускорения будет
а- = I *max I = (1.3)
где /о=®о/2я — частота вибрации, Гц.
Вибрации вызывают увеличение амплитуды колебаний дета-
лей и ведут к возникновению дополнительных нагрузок. Осо-
бенно опасно при вибрациях появление резонанса.
Величины и вид механических воздействий зависят от мес-
та размещения детали или узла на ЛА. Так, детали шасси ис-
пытывают наибольшие механические нагрузки при взлете и
посадке, детали систем управления — при изменении направ-
ления и скорости полета, а детали двигателя — на максималь-
ных и форсированных режимах полета. Вибрации деталей ЛА,
возникающие при работе двигателей и воздействиях турбулент-
ности внешней среды, могут привести к повреждению деталей,
узлов, мест крепления, особенно на частотах, близких к резо-
нансным. Для ослабления действия вибраций и ударов на де-
тали в машинах и ЛА между источником вибрации, например
фюзеляжем самолета и размещаемым внутри него оборудова-
нием, ставятся амортизаторы. На амортизаторах устанавлива-
ется также аппаратура на приборной доске ЛА, радиоэлект-
ронная аппаратура и ряд других узлов и агрегатов.
10
Климатическое воздействие сводится к влиянию температу-
ры, влаги, давления и других факторов на работу деталей и
механизмов при их эксплуатации. При проектировании ЛА раз-
личают четыре вида климата, обладающие следующими осо-
бенностями:
умеренный .... (—45... +40) °C
Холодный .... до— (65... 70)°С
Жаркий.......... (40... 45)°С
в тени
Тропический . .. более 20°С
Относительная влажность до 80%,
солнечная радиация — умеренная
Иней, обледенение, ветер со снежной
пылью
Низкая влажность, высокая солнеч-
ная радиация, ночью возможны ми-
нусовые температуры
Относительная влажность до 100%,
ливневые дожди
Большие перепады температур могут вызывать температур-
ные деформации, а также температурные напряжения при
закреплении (заделке) детали с обоих концов. При низких
температурах (—50 °C и ниже) конструкционные стали обыч-
ного исполнения приобретают хрупкость, их механические ха-
рактеристики ухудшаются. Твердость резины обычного состава
резко увеличивается, она становится хрупкой. Увеличение вяз-
кости смазочных масел приводит к возрастанию момента соп-
ротивления или даже отказу механизма. Поэтому в этих усло-
виях применяют специальные стали и резины, низкотемпера-
турные смазочные материалы.
Высокая влажность воздуха вызывает коррозию металлов,
особенно интенсивно протекающую при наличии в эксплуата-
ционных средах растворов солей и кислот. Коррозия ухудшает
качество поверхности, механическую прочность детали, герме-
тизацию. Она особенно опасна в местах соприкосновения раз-
ных материалов, которые при наличии влаги и солей образуют
гальванические пары. Поэтому в ответственных случаях для
предотвращения коррозии используют коррозионно-стойкие ста-
ли, пластмассы, различные покрытия.
Солнечная радиация оказывает непосредственное воздейст-
вие на элементы конструкции, находящиеся на открытом воз-
духе, вызывает нагрев деталей и связанные с ним температур-
ные деформации, а также, в особенности у пластмасс, измене-
ние структуры, химического состава и механических свойств
(старение).
Радиационное воздействие большой интенсивности (10 Р/ч
и более) проявляется в космическом пространстве и связано с
наличием у Земли радиационных поясов. Радиационное воз-
действие большой и длительной интенсивности может изменять
структуру материала детали, механические характеристики, в
11
частности прочностные свойства. Поэтому для деталей, работа-
ющих в космосе, применяют материалы, стойкие к радиацион-
ному воздействию.
1.3. ФАКТОРЫ, ВЛИЯЮЩИЕ НА ПРОЧНОСТЬ
ДЕТАЛЕЙ МАШИН И МЕХАНИЗМОВ ЛА
ПРИ СТАТИЧЕСКОМ НАГРУЖЕНИИ
Оценка прочности деталей и элементов конструкции
ЛА при статическом нагружении с помощью традиционных ин-
женерных методов основана, с одной стороны, на определении
номинальных напряжений по формулам сопротивления матери-
алов, теории упругости и пластичности, теории пластин и обо-
лочек и, с другой стороны, на характеристиках прочности мате-
риалов, используемых при изготовлении деталей. При одно-
кратном нагружении стандартных образцов определяют такие
характеристики материалов, как предел прочности ов, предел
текучести от или условный предел текучести оо,2-
Различают вязкое и хрупкое разрушение. При вязком раз-
рушении деформация в момент разрушения достигает 10...20%,
при хрупком — менее 3%. Характер разрушения определяется
прежде всего свойствами материала. Вязкое разрушение свой-
ственно обычно пластичным материалам, например низкоугле-
родистым сталям, хрупкое — высокоуглеродистым сталям, чу-
гунам, керметам и др. Разделение материалов на пластичные
и хрупкие производят на основании испытаний на разрыв и на
удар по относительному удлинению б, относительному сужению
ф и ударной вязкости аи. Для пластичных материалов б>6%,
ф^ 10%, ан^50 Дж/см2, для хрупких — 6^3%, ф^6%, ан^
^30 Дж/см2. Особенно опасно хрупкое разрушение, происходя-
щее внезапно, начинаясь от зон наибольшей концентрации нап-
ряжений. Хрупкому разрушению способствуют концентрация
напряжений; работа материала при низких температурах и в
температурном интервале хладноломкости; нагружение резко
возрастающими и ударными нагрузками.
Пластичные материалы менее чувствительны к концентрации
напряжений, так как в результате пластичного течения дефор-
мации происходит перераспределение, выравнивание напряже-
ний. Поэтому для ответственных деталей применяют материа-
лы с достаточной пластичностью.
Каждый из указанных выше видов разрушения существенно
отличается по уровню номинальных и местных разрушающих
напряжений, скорости развития повреждения и виду излома
при разрушении, при этом для оценки прочности выбирают те
или иные критерии. Для деталей машин и элементов конструк-
ций ЛА, испытывающих однократное (статическое) нагруже-
ние при действии сравнительно небольших сил, при уровнях
12
Рис. 1.6. Зависимость коэффициентов влияния абсолютных размеров на
прочность Ка», К<гт и Кла от диаметра d для валов, изготовленных из углеро-
дистых (-----) и легированных (--) сталей
коэффициента запаса прочности по пределам текучести и проч-
ности в пределах 1.5...3, имеют место упругие деформации.
Критерием прочностной надежности является недопустимость
необратимых пластических деформаций в расчетных сечениях
деталей из пластичных материалов, разрушения для деталей
из высокопрочных малопластичных конструкционных сталей и
композиционных материалов, диаграммы деформирования ко-
торых близки к линейным до момента разрушения.
При недопустимости остаточных деформаций в качестве
предельных напряжений при расчетах на прочность использу-
ют пределы текучести детали при определении запаса проч-
ности по нормальным от.д и по касательным тт.д напряжениям;
в качестве предельного напряжения при хрупком разрушении
используют предел прочности детали ов.д.
При увеличении размеров поперечного сечения детали по
сравнению с сечением стандартного образца прочностные ха-
рактеристики, получаемые при статических испытаниях стан-
дартных образцов (ств, От, тв, Гт), уменьшаются.. Это учитыва-
ют с помощью коэффициентов влияния абсолютных размеров:
Kda — на предел прочности ов, Кат — на предел текучести от.
Таким образом, значения этих коэффициентов можно предста-
вить так:
Kdaz= ®в.д/°В’ Кат^=^Т,11°Т’ 0-4)
Значения этих коэффициентов для валов круглого сечения
из конструкционных углеродистых и легированных сталей при-
ведены на рис. 1.6. Снижение механических характеристик с
Увеличением размера сечения связано с неоднородностью меха-
нических свойств металла и влиянием структурных дефектов.
13
1.4. ФАКТОРЫ, ВЛИЯЮЩИЕ НА ПРОЧНОСТЬ ДЕТАЛЕЙ
МАШИН И МЕХАНИЗМОВ ЛА ПРИ ДЕЙСТВИИ
ПЕРЕМЕННЫХ НАПРЯЖЕНИИ
В процессе эксплуатации в сечениях деталей ЛА
обычно возникают напряжения, циклически изменяющиеся во
времени. Под циклом понимают совокупность последователь-
ных значений напряжений за один период их изменения при
регулярном нагружении. При воздействии переменных напря-
жений в структуре детали постепенно накапливаются повреж-
дения материала, приводящие к изменению свойств, образова-
нию трещин, их развитию и в конечном счете к разрушению
детали.
Одним из основных параметров законов изменения напря-
жений во времени (рис. 1.7) является коэффициент асиммет-
рии цикла Л = 0т1п/атах> ГДв Omfn, Отах — МИНИМЭЛЬНОе И МЭК-
симальное напряжения цикла. Для нормальных напряжений
Ra=<Jmin/Omax, Я ДЛЯ КЭСЭТеЛЬНЫХ /?т=Тт1п/Ттах. ПоСТОЯННОе ВО
времени (статическое) напряжение характеризуется коэффици-
ентом асимметрии цикла Ra— + 1, так как 0max=0min (см. рис.
1.7, а). Цикл напряжений может быть знакопостоянным с
/?„>0 (см. рис. 1.7, б) и знакопеременным с R„<.0 (см. рис.
1.7, в); при Отах=—Отт — цикл знакопеременный симметрич-
ный с Ra=—1 (см. рис. 1.7, г), а при amin=0 — отнулевой с
/?а=0 (см. рис. 1.7, д).
К параметрам цикла относятся также его амплитуда оо и
среднее напряжение ат, связанные с omin, Отах и R„ следующи-
ми зависимостями:
=0,5 (атах - вга1п)=0,5 (1 - R') стах; (1.5)
ят = 0.5 (Отах + Omin) = 0,5 (1 + Z?e) атах. (1.6)
Длительность одного цикла характеризуется периодом Т.
Тогда за время t текущее число циклов будет Nn=t/T.
Рис. 1.7. Основные виды циклов изменения напряжений
14
Рис. 1.8. Кривые усталости
Свойство материала противостоять усталости называется
сопротивлением усталости. Как известно, под долговечностью
объекта понимается свойство сохранять свою работоспособ-
ность до наступления предельного состояния при установлен-
ной системе технического обслуживания и ремонта. При цик-
лическом действии напряжений сопротивление усталости объек-
та определяется циклической долговечностью N— числом цик-
лов напряжений и деформаций, полученных нагруженным объ-
ектом до образования усталостной трещины определенной про-
тяженности или до усталостного разрушения.
Результаты испытаний на сопротивление усталости обычно
представляют в виде кривой усталости — зависимости между
максимальными напряжениями или амплитудами цикла и цик-
лической долговечностью N стандартных образцов, построен-
ной либо при от=0, либо при /?=const. Кривая усталости при
const приведена на рис. 1.8, а. Для большей наглядности
применяют также логарифмические шкалы по одной из осей
координат (оси N). В этом случае наклонный участок кривой
усталости (АВ) будет прямой линией (рис. 1.8, б). Число цик-
лов Nq, соответствующее точке перелома, представляемой дву-
мя прямыми линиями, называют абсциссой точки перелома.
Число циклов нагружений No называют базой испытаний.
Обычно для сталей средней твердости Л'о=#с=107 циклов на-
гружений, так как для них кривая усталости при числе циклов
нагружения N>N0 практически имеет горизонтальный участок.
У легких сплавов и сталей с высокой твердостью максималь-
ное напряжение непрерывно уменьшается с ростом числа цик-
лов нагружений. Поэтому за базу испытаний для них принима-
ют JVo=lO-107.
Если при начальном нагружении (W<105 циклов) имеет
Место упругопластическое деформирование, то при JV>105 воз-
никает переход' от упругопластичного деформирования к упру-
15
Рабочее сечение образца
и
Рабочее сечение kF
Образец
б
Рис. 1.9. Схемы испытаний при определении предела выносливости:
а —чистый изгиб при вращении образцов типов I, II; б — чистый изгиб в одной пло-
скости образцов типов I—-IV; в — поперечный изгиб при вращении образцов типа I, II
при консольном нагружении; г —поперечный изгиб в одной плоскости образцов типов
I—IV при консольном нагружении
тому циклическому, характеризуемому накоплением поврежде-
ний усталостного характера в виде микротрещин.
Максимальное по абсолютному значению циклическое нап-
ряжение, которое с заданной вероятностью неразрушения
может выдёржать стандартный образец при практически неог-
раниченном числе циклов (обычно за базу испытаний берется
число циклов Мо=Ю7), называется пределом выносливости и
Рис. 1.10. Рабочие части образцов для испытаний на усталость:
°— круглого сечения типа I: R>d, <1—5... 15 мм; б —круглого сечения типа II: <1—
-5... 25 мм; при d-5 мм I-5d, Я-5 мм; « — прямоугольного сечения типа III: при
изгибе в плоскости размера Л: Л<3 мм, 6—ЮЛ, R>2b; при изгибе в плоскости разме-
ра 6: Л-3... 20 мм, Ь— (0,5... 2)Л, Д>5Л; г — прямоугольного сечения типа IV: Л<3 мм,
Ь-ЮЛ, 1-5,65 bh, R>2b
16 ’ 1 ‘
при любом цикле R обозначается <jr. Обычно на стандартных
образцах определяют значение предела выносливости изгибом
при R=—1 и обозначают его о-ь
Варианты схем испытаний различных образцов (рис. 1.10)
при определении предела выносливости при изгибе приведены
на рис. 1.9 (ГОСТ 25.502—79).
Исследование чувствительности материалов к концентрации
напряжений и влияние формы и абсолютных размеров детали
на предел выносливости проводят на образцах с кольцевой
выточкой (тип V), с боковыми надрезами (тип VI), с цент-
ральным поперечным круглым отверстием (тип VII) и кольце-
вой выточкой круглого профиля (тип VIII). При этом рабочие
части образцов всех типов должны быть изготовлены по точ-
ности не ниже 7-го квалитета с шероховатостью поверхностей
рабочей части Яа=0,32...0,16 мкм. Построение кривой устало-
сти и определение предела выносливости ведут при испытании
не менее 15 образцов с вероятностью неразрушения 50%.
Поэтому приводимые в справочниках значения er—i даются с
вероятностью 0,5.
При циклической долговечности N<No максимальное по
абсолютному значению циклическое напряжение, соответствую-
щее этой долговечности, носит название предела ограниченной
выносливости и в общем виде обозначается orn для стандарт-
ного образца и orna для детали. Наклонный участок кривой
усталости аппроксимируется зависимостью
const. (1.7)
Тогда предел ограниченной выносливости равен:
для стандартного образца
aRN=aR^o.\ (1-8)
для детали
вЯАГд = aRn V N0^ = ц» (1-9)
где Kn=7N0/N.
Если N>N0, то принимают Кц=1.
Величина т зависит от механических характеристик мате-
риала (о«, от), его числа твердости (НВ), вида деформации
образца при проведении испытаний (растяжение—сжатие, из-
гиб). Для сталей при изгибе при твердости менее 350 НВ при-
нимают т=6, при твердости, большей или равной 350 НВ,
принимают т=9.
Однако при переходе от стандартных образцов к детали,
имеющей конструктивные формы и размеры, отличные от стан-
дартного образца, orka будет отличатьря от оду, ТЯ1Г, при “увели-
п
Рис. 1.11. Напряжения в зоне концентратора-галтеля ступенчатого вала:
а —эпюры аи и атах к по галтели; б — зависимость от pid при различных D/d
чении размеров сечения детали по сравнению с сечением стан-
дартного образца предел выносливости снижается. При расче-
тах это учитывают коэффициентом влияния абсолютного
размера детали при действии нормальных ^а=а_]д/з_1 и ка-
сательных ^Т=т_1д/г_1. Здесь о-1д и т-1д — пределы вынос-
ливости детали круглого, сечения соответственно при действии
нормальных и касательных напряжений (см. рис. 1.6). При рас-
четах обычно принимают Kde=Kdv
Форма детали также оказывает влияние на сопротивление
усталости. Это влияние проявляется в местах изменения фор-
мы— у галтелей, отверстий, проточек, в резьбе, в шлицах
и т. д., где возникают повышенные местные напряжения — кон-
центрация напряжений. Конструктивные элементы, вызываю-
щие ее, называют концентраторами напряжений. Например,
номинальное напряжение пи=Л1и/1Ги при действии изгибающе-
го момента Ми в плоскости чертежа (рис. 1.11, а), вычислен-
ное по формулам сопротивления материалов, у детали в зоне
концентратора — галтели радиуса р — увеличивается до Отахк-
Отношение максимального местного напряжения Отахк к дя
называют теоретическим коэффициентом концентрации напря-
жений и обозначают для нормальных <х« (рис. 1.11, б) и для
касательных а,. Для большинства концентраторов значения а,
и а» можно найти в справочной литературе. Поскольку а, и
ат получены для абсолютно упругих материалов, а материал
деталей обладает пластичностью, поэтому это не отражает
истинной картины распределения напряжений по сечению.
Из этих соображений при расчетах на прочность деталей из
пластичных материалов при переменных напряжениях сниже-
ние сопротивления усталости в зоне концентрации напряжений
оценивается эффективным коэффициентом концентрации напря-
жений К«=а-1/о-1к, где о-щ — предел выносливости образца
18
Тип A
Тип В
Рис. 1 .12. Зависимости эффективных коэффициентов концентрации напряжений Ка и Кх от
предела прочности материала огв:
а, б —для ступенчатых валов [p/d=var, Я2=10 мкм, d=15 мм, £>/d=2 (a), D/d-1,4 (6)]; в — для вала со шпо-
ночными пазами (R2=\0 мкм, а — 15 мм)
Рис. 1.13. Зависимость коэффи-
циента чувствительности стали к
концентрации напряжений q от ра-
диуса выкружки р
с концентратором напряжений
(для касательных напряжений
/С^т-j/t-ik). ГОСТ 25.504—82
содержит данные по величи-
нам эффективных коэффициен-
тов концентрации напряжений
Ка и Кх для валов е различны-
ми видами концентраторов на-
пряжений (рис. 1.12).
В расчетах на прочность К„
и Кх можно также определить
по значениям а0 и ат из соот-
ношений Ко= 1 + <7(а0—1) и Лг=1+<7(ат—1), где q — коэффи-
циент чувствительности металла к концентрации напряжений
(рис. 1.13).
Приближенно для стали принимают q=0,0008ав; для
алюминиевых деформируемых сплавов 7 «0,3 ...0,5.
Шероховатость поверхности детали существенно влияет на
сопротивление усталости, поскольку возникновение и развитие
усталостных трещин связано с микрогеометрией поверхностно-
го слоя. Оставшиеся после обработки поверхности микронеров-
ности способствуют повышению напряжений в поверхностном
слое, являясь как бы их микроконцентраторами. Влияние
качества поверхности на предел выносливости оценивается
коэффициентом влияния шероховатости поверхности: при
нормальных напряжениях ^o = c_lf/a_1, при касательных
ATf x = r_lF/r_i,
где ct-if и т-if — пределы выносливости образцов с заданной
шероховатостью.
Значения коэффициентов К Fa и Kfx в зависимости от шеро-
ховатости поверхности могут быть определены по формулам
KF.= (1 +
KF^a+anT-i/lO4)-1,
(1.10)
где о-] и т-1 — пределы выносливости, МПа; ап — коэффици-
ент, зависящий от вида обработки (шероховатости) поверхно-
сти (табл. 1.2).
Наиболее сильное снижение сопротивления усталости из-за
ухудшения качества поверхности наблюдается при наличии
коррозии; ее влияние оценивается коэффициентом Ккор—
= <т-1дкор/о-1д. где ст- 1дкор — предел выносливости детали, име-
ющей коррозионное повреждение поверхности. В авиационных
механизмах особенно опасна фреттинг-коррозия, возникающая
в соединениях деталей (шлицевое, заклепочное и др.) при нали-
чии коррозионной среды и микроперемещениях одной из дета-
20
Таблица 1.2
Вид обработки Шероховатость, Ra или Rz, мкм Од
Электрополирование или механическое Яа=0,08... 0,16 0
полирование высокой чистоты
Механическое полирование средней чи- Яа = 0,32...0,16 0,5
стоты
Шлифование или шевингование тонкое Яа=0,63 ...0,32 2...3
Шлифование обычное Яа=2,5... 1,25 4
Резание тонкое Яг=20... 10 5
Резание обычное (чистовое) =40 ...20 6
Резание получистовое, штамповка, про- Яг=80... 40 10
кат, фрезерование Наличие окалины, следы коррозии
— 20
лей относительно другой. В расчетах влияние коррозии оцени-
вается снижением коэффициента Кр.
Для повышения несущей способности деталей широко ис-
пользуют технологические процессы, ведущие к упрочнению
поверхности деталей и повышению ее прочностных свойств бла-
годаря появлению в поверхностном слое остаточных напряже-
ний сжатия. Такими технологическими процессами являются
дробеструйный наклеп, накатка роликами, поверхностная за-
калка, химико-термические способы упрочнения поверхности.
Влияние этих факторов может быть учтено коэффициентом
упрочнения /Сь=о-1д.у/о-1д, где о-1д.у и о—1Д— соответственно
пределы выносливости детали, подвергнутой упрочнению, и без
упрочнения. Упрочнение особенно эффективно в местах кон-
центрации напряжений, так как Kv увеличивается с ростом /Са.
В табл. 1.3 приведены значения коэффициента Kv при различ-
ных способах упрочнения деталей. В числителе приведены Kv
для образцов без концентратора напряжений, а в знаменате-
ле — с концентратором.
Влияние анизотропии на предел выносливости учитывают с
помощью коэффициента анизотропии fta=o-inon/a-inp, где
а-inon — предел выносливости образцов, вырезанных из заготов-
ки в направлении, перпендикулярном направлению волокон,
образующихся при прокатке или других технологических про-
цессах; а_1пр — предел выносливости образцов, вырезанных из
заготовки в направлении волокон. Для деталей из стали Ка
зависит от Ов’ при ов=600..,900 МПа ^a=0,86, при ов=900...
1200 МПа 7(а=0,83, при ав>1200 МПа Ка=0,8. Влияние ани-
зотропии при растяжении, сжатии и изгибе учитывают, если
главное напряжение o-i в зоне его действия перпендикулярно
волокнам. При кручении влияние анизотропии не учитывается.
21
Таблица 1.3
Способ упрочнения поверхности d, мм
7 ... 20 8 ... 15 30 ... 40
Закалка ТВЧ, глубина закаленного слоя 0,9... 1,5 мм Обкатка роликом Обдувка дробью Азотирование при глубине слоя 0,1... 0,4 мм, твердости слоя (730... 970) НВ Цементация при глубине слоя 0,2 мм 1,3 ...1,6 1,15... 1,25 1,2... 1,5
1,6... 2,8 1,2... 1,4 1,5... 2,5 1,10... 1,25
1,5 ...2,20 1,10... 1,30 1,30... 1,80 1,10... 1,20
1,40... 2,5 1,10... 1,50 1,10... 1,15
1,90... 3,00 1,20 ...2,10 1,3 ...2,00 1)10... 1,50
1,50... 2,50 1,20... 2,00
Влияние всех факторов на сопротивление усталости детали
учитывают с помощью коэффициента снижения предела вынос-
ливости К, величина которого при известных значениях коэф-
фициентов Kda, Ка, Kfo, Kv и Ка определяется по формулам:
для нормальных напряжений
Н—----1"|—!—;
для касательных напряжений
---------------------------1)—— .
к 5,-----------------------МЛа
(1-И)
(М2)
ГЛАВА 2. ОСНОВНЫЕ КРИТЕРИИ РАБОТОСПОСОБНОСТИ
ДЕТАЛЕЙ МАШИН И МЕХАНИЗМОВ ЛА
И ПУТИ ИХ ОБЕСПЕЧЕНИЯ
Для обеспечения работоспособности машины или ме-
ханизма ее детали, узлы и конструкция должны удовлетворять
ряду требований. Важнейшими из них для деталей ЛА явля-
ются прочность, жесткость, износостойкость, теплостойкость,
виброустойчивость, надежность и ряд специальных требований.
Значение и первостепенность каждого из них для конкретной
детали определяются требованиями к конструкции машины в
22
целом и условиями ее эксплуатации. Так, для вала редуктора
вертолета первостепенным является требование прочности, для
подшипника скольжения — его износостойкость и т. д.
2.1. ПРОЧНОСТЬ
Под прочностью понимается способность детали вы-
держивать приложенные нагрузки без разрушения. Различают
прочность объемную и поверхностную (контактную). При недо-
статочной объемной прочности деталь разрушается по всему
сечению (поломка зуба шестерни, поломка вала, разрыв бол-
та), при недостаточной контактной прочности происходит раз-
рушение (выкрашивание) поверхности контакта (выкрашива-
ние поверхности зуба у зубчатых колес, рабочей поверхности
колец у подшипников качения).
Различают разрушение под действием однократного нагру-
жения и при действии переменных нагрузок. Нагрузкой Q на
деталь, например вал редуктора, может быть сила F, изгибаю-
щий Ми и крутящий Л!к моменты. Они могут быть сосредото-
ченными и распределенными. При циклическом нагружении
плавное изменение нагрузки Q за какое-то время цикла дейст-
вия нагрузки /ц обычно при расчетах заменяют ступенчатым
путем вписывания прямоугольников со сторонами Qi, t\; h:
Qk, tk (рис. 2.1). Применительно к передаточному механиз-
му зубчатого редуктора интервалам времени ti, tz, ..., tk соот-
изменения нагрузки Q и частоты вращения от вре-
РЦс> 2.1. Зависимости
Мевд п
23
Рис. 2.2. Приведенный закон изменения нагрузки Q и числа циклов нагру-
жений Яц
ветствуют средние значения частоты вращения th, пг,...,пк вала
механизма (см. рис. 2.1). Максимальную нагрузку Q и соот-
ветствующее время ее действия t отмечают индексом 1; после-
дующие значения нагрузок по убывающей и соответствующие
им времена их действия обозначают индексами 2, 3 и т. д.
Изменение нагрузки за цикл можно изобразить в виде диаг-
раммы (рис. 2.2), где /ц=/1-Н2+- + ^- Тогда долговечность
механизма L может быть задана в виде произведения времени
цикла действия нагрузки /ц на число циклов нагрузки Уц.н:
L,=tyN ц.н-
Число циклов нагружений какой-либо детали механизма за-
висит от его кинематики и ряда других факторов. Для вала
зубчатого редуктора число циклов изменения напряжений Nn
при однократном его изменении за один оборот вала будет
равно
ЛГц=60Л'ц.),2'Мр (2.1)
i=i
где rii — частота вращения вала, об/мин; t, — длительность дей-
ствия нагрузки, ч.
При расчетах на прочность заданную переменную нагрузку
Qi, Q2, Qk обычно заменяют постоянной Qp, равноценной по
ее влиянию на прочность детали. Задавая нагрузку Qp=Qmax=
= Qi, находят эквивалентное ей число циклов нагружений
Ne<Nq (см. рис. 2.2), при котором Qp=Qi оказывается равно-
ценной по ее влиянию на прочность заданной переменной наг-
рузке. Возможен также вариант, когда по расчетному числу
циклов изменения нагружений N* находят эквивалентную ему
24
нагрузку Qe, которая оказывает
то же влияние на усталостную
прочность, что и заданная пере-
менная нагрузка.
Методика определения экви-
валентного числа циклов нагру-
жений Ne, при котором постоян-
ная нагрузка QP=Qi оказывает-
ся равноценной по влиянию на
прочность детали заданной пере- Рис. 2.3. Кривая усталости для
менной нагрузке, базируется на определения QP и Ne
зависимости (1.7). Показатель т
в этом случае заменяется на m'=mlv, где v — коэффициент, оп-
ределяемый зависимостью между нагрузкой Q и напряжением
о или т: Q=o)av, или Q=o)Tv, где со — постоянный коэффициент.
При расчетах на изгиб, кручение, растяжение и сжатие прини-
мают v=I, при расчетах зуба на контактную прочность v=2.
Для кривой усталости в координатах (рис. 2.3) можно за-
писать
• (2.2)
где Qi — нагрузка на t-м цикле; Мщ- — число циклов изменения
нагрузки Qi.
Тогда
л
^=a-i2[(Q//Qp)m'^«J, (2.3)
i=i
где а — поправочный коэффициент, зависящий от характера
изменения нагрузки, его величина при спектре нагружения с
резкими перегрузками и малыми продолжительными нагрузка-
ми снижается и может быть значительно меньше единицы.
Под влиянием циклических напряжений разрушение детали
носит усталостный характер, характеризуемый постепенным
накоплением повреждений. Сопротивление усталости детали
значительно снижается при наличии концентраторов напряже-
ний (проточек, галтелей, шпоночных канавок, отверстий под
штифты и заклепки, резьбы и др.), обусловленных ее конст-
руктивной формой.
Для оценки прочности детали используют ряд способов.
Один из них состоит в использовании для этой цели неравен-
ства <т^[сг] при расчете по нормальным или т<[т] при расчете
по касательным напряжениям. Здесь о и т — номинальные
(расчетные) напряжения, [о] и [т] — допускаемые напряжения.
Величины [о] и (т] могут задаваться в виде табличных значе-
ний, полученных в результате испытаний деталей, или опреде-
25
ляться расчетом как часть разрушающего (предельного) нап-
ряжения. Однако эта форма оценки прочности не позволяет
получить в явном виде соотношение между номинальным (рас-
четным) и предельным напряжениями. Поэтому при инженер-
ных расчетах наибольшее распространение получила проверка
по запасу прочности:
Лв=<’11тд/’ >[«];
(2.4)
«г = Т|1тд/Т >[«],
где па и п, — запасы прочности по нормальным и касательным
напряжениям; огптд и тнтд — предельные напряжения детали
при действии нормальных и касательных напряжений; [п] — до-
пустимый запас прочности.
Предельные напряжения детали ацтд и тнтд определяются
как напряжения, при которых происходит разрушение детали
или возникают остаточные пластические деформации. При дей-
ствии переменных напряжений и работе на выносливость в ка-
честве сгцтд и тнтд используют ее усталостные характеристи-
ки; при действии постоянного по времени напряжения расчет
на прочность ведут по зависимости (2.4), используя при опре-
делении оптд и тнтд пределы прочности Ов или текучести ат.
С учетом влияния размеров детали при расчетах на статиче-
скую прочность на основании (1.4) оцтд—от^йт для пластич-
ных материалов при недопустимости остаточных деформаций
и опт л=ОвК<1в — для хрупких материалов.
В отдельных случаях (в местах конструктивной концентра-
ции напряжений, в сварных швах, в заклепочных соединениях,
при действии температурных напряжений) под действием экс-
плуатационных статических нагрузок могут возникать локаль-
ные или общие пластические деформации. Тогда изменение
номинальных и местных напряжений при увеличении действу-
ющих нагрузок происходит не пропорционально этим нагруз-
кам. В результате при переходе из упругой области в упруго-
пластическую эксплуатационные номинальные и местные нап-
ряжения увеличиваются на 5...15% при возможном возрастании
деформаций в 1.5...3 раза. Поэтому в этих случаях результаты
расчетов прочности по номинальным или местным напряжени-
ем становятся недостаточными и могут заменяться или допол-
няться проведением расчетов по предельным нагрузкам. В прак-
тике расчета таких деталей ЛА, как правило, используют зави
симости вида
^*р -^разр ИЛИ Ср ®разр’ (2.5)
Расчетное значение нагрузки Fp и расчетное напряжение аР
определяются по формулам
26
о₽ = °э/. (2.6)
где F3, (Уз — эксплуатационная нагрузка и эксплуатационное
напряжение; f — коэффициент безопасности, согласно нормам
прочности для основных деталей ЛА он изменяется от 1,3 до
2 с учетом характера действия нагрузки, ее повторяемости,
требований надежности и условий эксплуатации.
Одним из условий применения этого метода для расчета
деталей ЛА является использование норм прочности, в кото-
рых рассмотрены возможные режимы нагружения ЛА при экс-
плуатации, которые являются наиболее опасными для прочно-
сти его деталей и определяют величины эксплуатационных
нагрузок. Эти случаи нагружения выбраны на основе летных
испытаний, лабораторных и теоретических исследований, а так-
же обобщения опыта эксплуатации ЛА. Для типовых схем наг-
ружения в нормах прочности приведены величины эксплуата-
ционных нагрузок на ЛА и его части, а также их направление
и распределение.
Величины разрушающих нагрузки Гразр и напряжения
Стразр. полученные путем экспериментальных испытаний узлов
и деталей, приводятся в справочниках в виде нормируемых
показателей прочности. При отсутствии экспериментальных
данных разрушающую нагрузку можно ориентировочно опре-
делить расчетным путем:
^’разр = 0в'-*раб^> (2-7)
где 5Раб — площадь рабочего сечения; 6 — коэффициент ослаб-
ления сечения, учитывающий концентрацию напряжений, шеро-
ховатость поверхности и другие факторы, если нагружение но-
сит циклический характер, для деталей ЛА 6=0,85...0,95.
При расчетах деталей ЛА по запасу прочности принимают
допускаемый запас прочности [п]=1,3 ...2 в зависимости от
достоверности используемых в расчетах значений исходных
данных, точности расчетной методики, проверки расчетов экс-
периментом. Надежность ответственных деталей авиационных
конструкций подтверждают, проверяя результаты расчета экс-
периментально и проводя их натурные испытания. Поскольку
Для современных конструкционных материалов, используемых
в ЛА, ов/от= 1,25...1,3, то эта величина и обосновывает выбор
(п]= 1,25...1,3, как обеспечивающего достаточную прочность
по от.
Возможно также при расчетах на прочность применение
Других критериев: проведение расчета по эквивалентному запа-
су длительной прочности, по эквивалентному времени работы
И Другим критериям [6].
Расчеты на прочность при многоцикловом нагружении.
Многоцикловая область сопротивления усталости начинается с
27
Af>105 и характеризуется накоплением усталостных поврежде-
ний. Рассмотрим расчет на сопротивление усталости при изги-
бе с кручением, который характерен для некоторых деталей
машин и механизмов ЛА, например валов. В этом случае про-
верка прочности ведется по запасу прочности:
п п
О Т
п
[«].
V nl + n^
(2-8)
где л0, пх определяют по формулам (2.4); оцтд> титд — пре-
дельные нормальные и касательные напряжения для расчетно-
го сечения детали при цикле с коэффициентом асимметрии R
и циклической долговечности N.
Для деталей машин и механизмов ЛА коэффициент асим-
метрии цикла R определяется по циклограмме нагружения. При
переменных напряжениях для наиболее типичных циклов R =
=—1и7?=0.
Рассмотрим определение предельного напряжения детали
при действии переменных напряжений с коэффициентом асим-
метрии R. При R=—1 ог-1д обычно в 2...6 раз меньше, чем
о-ь Эта разность характеризуется коэффициентом снижения
предела выносливости К, отражающим влияние всех конструк-
тивных и технологических факторов на сопротивление устало-
Рис. 2.4. Диаграммы предельных амплитуд цикла для образца (/) и де-
тали (2)
28
сти детали. При растяжении — сжатии, изгибе и кручении ко-
эффициент К рекомендуется определять по формуле (1.11) для
нормальных и (1.12) —для касательных напряжений. Коэффи-
циенты, входящие в выражения (1.11) и (1.12), учитывают
влияние на сопротивление усталости детали концентрации нап-
ряжений (Ка, Кх), масштабного фактора (Kdo, Ках), шерохова-
тости поверхности (К Fa, Kfx) и технологических методов по-
верхностного упрочнения (Kv)- Предельное напряжение ацт и
оптд Для любого R применительно к нормальным напряжени-
ям можно найти с помощью диаграммы предельных амплитуд
<ja—От (рис. 2.4). Экспериментальное получение такой кривой
(часть ее показана пунктирной линией) для стандартных об-
разцов по ряду значений a_i>aa^0 требует длительных испы-
таний. Поэтому ее построение по точкам заменяют прямой 1,
проходящей через точку А с координатами 0; <у_i и точку В с
координатами <То/2; <т0/2, где а0 — предел выносливости, при
R„=0 (через точку В проходит прямая с Ra=0). Для луча с
Ra=0 для стандартного образца
«а = в-1 - °т = 3-1 - °® tg « =
DC
= а-1 —°m(—?~*~ао )=e-i —(2.9)
где согласно основным терминам сопротивления усталости
фа= (2о_1—Оо)/оо — коэффициент чувствительности к асиммет-
рии цикла напряжений.
Из (2.9) следует, что при оа=0 ат=<У-1/^>а соответствует
абсциссе точки D. Тогда можно принять о_1/ф0=от.и.
Для детали прямую 2 предельных напряжений построим по
о-1д. Эта прямая пересекает ось от в точке D\, причем
OZ?i/OZ) = СГт.и.дК^т/От.и == KdT* Отсюда ODi = (Jx.nKdr^= (<Т-1/фа)Кат.
Тогда для детали аад=<т-1д—<Jmp)ga', где 1£а'=У„/(КатК),
К=0-1/(Т-1д.
Для детали получим
<’ад = а-1д-а®дФ,/(^Л). (2.10)
По (1.5) И (1.6) И рис. 2.4 получим (Ja/(Jm = (1— Ra)l(l +
+/?«)=tg₽.
Тогда для детали
(2.Н)
Подставив (2.11) в (2.10), получим для детали
Одд-.’-1 д ’ад .
29
откуда
______Q-iC1 -Я„)______
0-*a)K+('+'W^ ‘
Предельное напряжение детали <тцт д для цикла Ra при чис-
ле циклов напряжений N равно
а =--------ЯЛ2--.=---------*=1"-----------, (2.13)
Итд 0,5(1-Я.) (i_^)K4-(14-/?e)V^t
где a-iN — ограниченный предел выносливости для цикла с
Re=—1, равный на основании (1.7)
т/~^0 /0 14\
о—i№a_j 1/ — < ат. (2.14)
Тогда запас прочности по нормальным напряжениям с уче-
том (1.5) и (1.6) будет равен
л _ »11тд _____________________2д-1.у__________
’ °тах [(1 - Я,) К + (1+Я.) ’max
_______________^3-\N_____________
/ ’а к , ’т )
0,5отах Л 0,5атах Kdt I таХ
ИЛИ
*,= (2-15)
'аК + Om’P./KdT
(2.12)
Для касательных напряжений получим
nt=---------------------------. (2.16)
Рекомендуется величину ф0 определять по формуле
Ф/= 0,02-|-2-10“4зв, и фх = 0,5ф3, где ав, МПа.
При расчетах в среднем принимают для деталей, изготовленных из
Ф, Фг
углеродистых мягких сталей................. 0,05 0
среднеуглеродистых сталей.................. 0,15 0,05... 0,1
хромоникелевых и аналогичных легированных ста-
лей при ов>800 МПа......................... 0,3... 0,4 0,15... 0,2
легированных сталей, подвергнутых цементации . 0,6 0,4
легированных сталей, подвергнутых азотированию 0,8 0,5
Величину допустимого коэффициента запаса прочности
можно определить так:
1п] = [«1][п2] [л3].
(2.17)
30
где [«iL [/hl [«з! — коэффициенты достовернос'ги расчетных наг-
рузок, однородности механических характеристик, точности
расчетной методики и особых требований безопасности, [«i]=
U 1,0... 1,5, («2]= 1,2...1,5, [л3]= 1,0...1,5.
Принятые величины [П1], [п2], [п3] в предположении неблаго-
приятного сочетания всех трех факторов приводят к увеличе-
нию массы и габаритных размеров детали. Поэтому при отсут-
ствии точных значений частных коэффициентов пользуются
следующими рекомендациями:
[«]
Применение методики расчета, обеспечивающей повышенную
достоверность результатов, с учетом основных и дополнительных
нагрузок; контроль расчетов натурными испытаниями ответствен-
ных деталей и узлов ЛА и стабильности механических характери-
стик материала ...................................... 1,2... 1,45
Расчеты с приближенным учетом динамических нагрузок, не-
полным контролем прочности путем натурных испытаний .... 1,5... 2
Применение методики расчета, дающей приближенную точ-
ность результатов без проведения натурных испытаний, а также
при расчете деталей из хрупких и анизотропных материалов
(пластмассы, керамика)............................... 2... 3
Особенности расчета на прочность при малоцикловом нагру-
жении. Разрушение от малоцикловой усталости — это разру-
шение в условиях повторного упругопластического деформи-
рования с числом циклов (к моменту образования макротре-
щины или окончательному разрушению) до 5-(Ю^.-Ю5) циклов.
Это число циклов является условной границей между мало-
цикловой и многоцикловой усталостью для пластичных сталей
и сплавов и определяет среднее число циклов для зоны пере-
хода от упругопластического к упругому деформированию.
Зависимость между деформацией и напряжением при
малоцикловом нагружении обычно изображают в виде диаг-
раммы о—е, где о — напряжение, е — деформация. Размах
пластической деформации для каждого полуцикла k обозна-
чается 8(Ч
Нагружение при исследовании малоцикловой усталости мо-
жет быть жестким и мягким. Жесткое нагружение (рис.
2.5, а) — циклическое нагружение, при котором в процессе
испытания среднее значение и размах e(ft) циклических
Деформаций сохраняют свои исходные значения. Мягкое нагру-
жение (рис. 2.5, б) — циклическое нагружение, при котором в
процессе испытания средние и амплитудные значения цикличе-
ских напряжений сохраняют свои исходные значения, их раз-
мах S(*)=const.
Циклическое деформирование в упругопластической области
® жестком и мягком режимах сопровождается образованием
Петли гистерезиса, характеризующей работу упругопластиче-
ского деформирования за полный цикл изменения усилий. Диа-
31
Рис. 2.5. Диаграммы циклического упругопластического деформирования
грамма циклического деформирования отражает зависимость
напряжения о от деформации е при различном числе полуцик-
лов нагружения k (рис. 2.6). Исходное нагружение описывает-
ся в соответствии с диаграммой статического деформирования,
проходящей через точки А, В, С с началом в точке 0. Исход-
ное нагружение доводят до определенного значения напряже-
ний и деформаций, характеризуемых в этом полуцикле (как
нулевом) точками А, В, С. Для этих точек напряжения исход-
ного нагружения составляют о/0*, ог(0) и а3(0), а деформации
е/0), е2(°) и е3<°>. После разгрузки остаются пластические дефор-
мации еР1(0\ ер2(0) и ер3<°>. Деформация, соответствующая преде-
лу пропорциональности оПц, обозначена еПц. Исходное нагруже-
ние и разгрузка образуют нулевой (k=Q) полуцикл нагру-
жения.
Реверс нагружения про-
исходит по своей диаграмме,
достигая, например, состоя-
ний, характеризуемых точ-
ками D, К, N, соответствую-
щих напряжениям —o-i(1),
—О2(1), —о3(1). Реверсивное
нагружение и последующая
разгрузка образуют первый
(6=1) полуцикл нагруже-
ния; совокупность нулевого
и первого полуциклов обра-
зуют первый цикл нагруже-
ния.
Рис. 2.6. Обобщенная диаграм-
ма циклического деформирования
a S
Рис. 2.7. Диаграммы деформирова-
ния циклически упрочняющегося (/),
циклически разупрочняющегося (//)
и циклически стабилизирующегося
(III) материалов при мягком нагру-
жении от числа циклов нагружений
для различных материалов
Характеристиками циклической диаграммы являются упру-
гая е/к\ пластическая ер^ и упругопластическая e^=eew+
+ер<*> деформации в полуциклах нагружения, максимальные
напряжения и амплитуда напряжений в цикле 0а(Л)> ширина
петли гистерезиса 6<Л), модуль разгрузки т, определяемый как
тангенс угла наклона прямой, соединяющей точки диаграммы,
соответствующие началу и концу разгрузки.
В зависимости от структурного состояния материалы могут
быть упрочняющимися, разупрочняющимися или циклически
стабильными. При малоцикловом нагружении они ведут себя
по-разному.
У циклически упрочняющихся материалов ширина петли
гистерезиса при мягком нагружении уменьшается (рис. 2.7,
а), а максимальные напряжения цикла при жестком нагру-
жении увеличиваются (рис. 2.7, I б), показатель упрочнения
от цикла к циклу возрастает. У циклически разупрочня-
ющихся материалов ширина петли гистерезиса при мягком на-
гружении увеличивается (рис. 2.7, II а), а отах при жестком
нагружении уменьшаются (рис. 2.7, // б); m(h) от цикла к цик-
лу снижается. У циклически стабилизирующихся материалов
ширина петли гистерезиса при мягком (рис. 2.7, III а) и жест-
(рис. 2.7, III б) нагружениях, а также mw остаются прак-
тически постоянными.
Материалам, находящимся в упрочненном состоянии, кото-
Рое характеризуется высокими ов и от, свойственно разупроч-
нение. Материалам с низкими механическими характеристика-
2—1085 33
Рис. 2.8. Зависимость деформации при
мягком нагружении от числа циклов нагру-
жений для различных материалов
ми и высокими пластическими свой-
ствами присуще упрочнение. Ука-
занным свойствам соответствуют
характерные особенности их диа-
грамм статического разрушения.
Материалы, у которых упругая де-
формация невелика, склонны к цик-
лическому разупрочнению. Мате-
риалы с большой равномерной де-
формацией упрочняются, а мате-
риалы, у которых упругая деформа-
ция и удлинения на стадии образо-
вания шейки приблизительно рав-
ны, имеют циклическую стабиль-
ность. Циклически анизотропные
материалы, в отличие от цикличе-
ски изотропных, имеют неодинаковое сопротивление цикличе-
скому деформированию во время четных и нечетных полуциклов
нагружения.
В зависимости от изотропных свойств материала, характе-
ра изменения свойств при малоцикловом нагружении, режима
испытаний односторонние деформации либо накапливаются,
либо отсутствуют. Для циклически упрочняющихся материа-
лов накопление односторонних деформаций носит затухающий
характер с увеличением числа циклов нагружений. Для цикли-
чески разупрочняющихся и стабилизирующихся материалов
возможно прогрессирующее либо стабилизирующееся с числом
циклов нагружений накопление односторонних деформаций.
Односторонне накопленную деформацию определяют по вели-
чине упругопластической eW или пластической дефор-
мации, достигнутой в процессе циклического нагружения после
k-ro полуцикла.
На рис. 2.8 показан характер изменения односторонних де-
формаций от числа циклов нагружения для циклически изо-
тропных упрочняющихся (а), разупрочняющихся (б) и стаби-
лизирующихся (в) материалов. В процессе малоциклового на-
гружения возможны накопление односторонних деформаций в
направлении как четных, так и нечетных полуциклов, смена
направления процесса накопления деформаций, а также умень-
шение накопленных односторонних деформаций. В зависимо-
сти от значений и характера накопленных односторонних де-
формаций различают квазистатическое, усталостное и смешан-
ное малоцикловое разрушение.
34
Квазистатическое малоцикловое разрушение происходит пре-
мущественно вследствие одностороннего накопления деформа-
ий равных деформациям при статическом разрыве. При этом
накопленная упругопластическая деформация на k-м полуцик-
ле доходит до (0,9... 1,0) ев, пластическая деформация на
том же полуцикле — до (0,9... 1,0) 67, где ей и ef — дефор-
..апии соответствующие соответственно пределу прочности и
статическому разрыву.
Усталостное малоцикловое разрушение происходит без вы-
раженного накопления односторонних деформаций, при этом
e(ft)<0,l<?z, 4ft)<0,le?„.
При смешанном малоцикловом разрушении значения одно-
сторонне накопленных деформаций имеют широкий предел из-
менения:
е?(й) = (0,1.. .0,9) ев; =(0,1.. .0,9) ef.
Диапазон квазистатических малоцикловых разрушений зани-
мает область от однократного статического разрыва до 103 цик-
лов и зависит от типа и состояния материала, а также от
режима нагружения. Смешанное малоцикловое нагружение
занимает область от десятков до нескольких тысяч циклов и
наблюдается в переходной области долговечностей между ква-
зистатическим и усталостным типами разрушения.
Уравнение кривой усталости при мягком нагружении имеет
вид
(2.18)
где v=lg(oB/o-i)/lg^o-iWB); NB и W0-i— число циклов до
разрушения соответственно на уровнях пределов прочности ов
и выносливости о-1 материала.
При расчетах принимают jVb~10 и Na-i« 106. Тогда v=
e0.21g(aB/o-i), и при o-i«0,4 ов зависимость (2.18) преобра-
зуется к виду
a№’06=auNB’06. (2.19)
Экспериментальные данные (рис. 2.9) [24] подтверждают,
что для большинства материалов формула (2.19) обеспечивает
хорошее совпадение с экспериментальными данными.
Таким образом, использование зависимости (2.19) право-
мерно для большинства материалов, имеющих or-i«0,4oB.
Расчет малоцикловой долговечности выполняется на осно-
вании анализа местных деформаций при условиях нагружения,
к°гда максимальные деформации достигают 0,5...1%. Кривую
Малоцикловой усталости строят по результатам испытаний
Серии образцов при жестком нагружении. Основным видом
Рис. 2.9. Кривая малоцикловой
усталости при мягком нагружении
нагружения является растяже-
ние-сжатие, хотя возможно
испытание на изгиб и кручение
основных образцов типов I и
II (см. рис. 1.10) диаметром 5;
7,5; 10 и 12 мм. Испытания
проводятся на испытательных
машинах, обеспечивающих тре-
буемый режим нагружения,
с регистрацией результатов с
допустимой погрешностью. Ре-
зультаты представляются в
виде зависимости долговечно-
сти N от циклической упруго-
пластической e(ft) или пласти-
ческой деформаций.
Аналитически кривую малоцикловой усталости при жест-
ком нагружении можно описать уравнениями:
размах пластической деформации в Л-м полуцикле
^}=cN~mP\
(2.20)
размах упругопластической деформации
= (2.21)
где с=0,51п(1—фв)-1, или с=0,51п(1—ф)"1.
Показатели т и тр для конструкционных сталей и сплавов
в первом приближении равны 0,5...0,6. Кривые усталости (рис.
2.10) строят обычно по формулам (2.20), (2.21) в двойных
логарифмических координатах: зависимости размаха упругоплас-
тической деформации е, размаха пластической деформации гР
и размаха упругой деформации ге от числа циклов Nf. Испы-
Рис. 2.10. Зависимость долговеч-
ности от величины упругопластиче-
ской деформации при е(*>=const
лости при жестком нагру-
жении в зависимости от ве-
личины средней деформа-
ции ет
36
ния проводят до образования трещины длиной 0,5...1,0 мм,
Тпоеделяемой визуально или с помощью оптических средств.
Попускается продолжение испытаний до разрушения образца.
При жестком нагружении, когда статическая составляющая
еформации в цикле жесткого нагружения равна примерно
половине значения пластичности при статическом разрыве об-
оазца материала, имеет место снижение долговечности. Так,
для стали с содержанием Ni до 2,5%, Сг и Мо до 1% (24] при
увеличении среднего значения деформации гт от 20 до 40%
долговечность по числу циклов снижается до пяти раз (рис.
2.И).
Аналитически долговечность в циклах при этом виде нагру-
жения описывается уравнением
= (2.22)
Оценку прочности при малоцикловом нагружении элемен-
тов конструкций для заданных условий эксплуатации проводят
по критериям квазистатического и усталостного разрушения.
Квазистатические разрушения возникают вследствие накопле-
ния в процессе нагружения односторонних пластических дефор-
маций, равных деформациям при однократном статическом раз-
рушении. Усталостные разрушения — разрушения с образова-
нием трещин — происходят из-за накопления усталостных пов-
реждений.
Несущую способность по долговечности рассчитывают на
основании данных по предельным (соответствующим образова-
нию трещин) местным деформациям еа или напряжениям оа
для чисел циклов, равных эксплуатационным. При расчете
местных предельных деформаций используют кривые цикличе-
ского деформирования, полученные по данным испытаний стан-
дартных образцов.
Значения местных эксплуатационных деформаций еа3 или
напряжений оа9 в элементах конструкций определяют их изме-
рением на моделях или на натурных образцах при заданных
эксплуатационных нагрузках.
В результате расчета на прочность получают коэффициен-
ты запаса прочности по деформациям пе или напряжениям па
в виде
пе=еа/еа; n,=oaha. (2.23)
Коэффициент запаса по долговечности nw определяют путем
олучения данных по разрушающему числу циклов N для де-
формации еа или напряжений аа и эксплуатационному числу
nN=N!N3.
(2.24)
37
Для трубопроводов, листовых конструкций, корпусов допус-
каемые запасы прочности {ne]=[nj=2, [ллг]= 10; для деталей
машин (сварных, резьбовых соединений и др.)
К]=К1=1.5, ы=з.
Если испытанию при эксплуатационных нагрузках подвер-
гают натурные конструкции или полномасштабные модели, то
при расчете по моменту образования трещин принимают
[«е1 = [«Л'=1,25, а [л„]>2,1.
Контактная выносливость. Рассмотрим причины разрушения
контактирующих поверхностей и пути обеспечения их выносли-
вости. При контактном взаимодействии двух тел нормальная
сила действует на малый участок поверхности в зоне контакта,
образующейся при соприкосновении сферических и цилиндри-
ческих тел с плоскими, сферическими и цилиндрическими по-
верхностями. Размеры площадки соприкосновения зависят от
упругости материалов и формы контактирующих поверхностей.
В зоне контакта при отсутствии деформирующего усилия со-
прикасание тел происходит в точке или по линии (рис. 2.12).
После приложения усилия в результате деформирования тел
образуется площадка контакта, форма которой зависит от гео-
метрии соприкасающихся тел. При контакте двух цилиндров по
образующей в результате их деформирования силой Fn обра-
зуется площадка шириной 2Ьн (см. рис. 2.12, в). Интенсивность
сил, нормальных к сопряженным поверхностям, характеризу-
i
Рис. 2.12. Точечный (а, б) и линейный (в) контакт двух тел
38
максимальным контактным напряжением он в зоне кон-
еТ та деталей, распределенным по эллиптическому закону. Мак-
ТЯмальное значение контактного напряжения сн используется
сИкаЧестве критерия работоспособности сопряженных поверхно-
В ей при условии, что величина оя не превышает допустимого
качения, полученного экспериментально при аналогичных ус-
3оВИях в’ зоне контакта. Касание по линии в зоне контакта
характерно для зубчатых передач, роликовых подшипников и
других случаев. Величина ан в зоне контакта определяется
Формулой Герца—Беляева, полученной из решения контактной
задачи теории упругости для контакта двух цилиндров по об-
щей образующей, имеющих модули упругости Е\ и £2, радиусы
и /?2 и длину линии контакта 1К:
ан
-----------------------------------, (2.25)
л[е2(1 - h)2 + £i(i - ^)2] рпр
где qH=FnilK — удельная контактная нагрузка; щ, ц2 — коэф-
фициенты Пуассона материалов цилиндров; рпр — приведенный
радиус кривизны, pnp=/?i/?2/(^2±^i) (знак плюс принимают
при внешнем касании, знак минус — при внутреннем касании).
Для стали при ц=0,3 получим
ая = 0,418]/ ^£пр/Рпр , (2.26)
где £Пр=2£1£2/ (£1+ Е2)— приведенный модуль упругости.
В реальных конструкциях, как правило, в зоне контакта
происходит относительное движение контактирующих поверх-
ностей, а нагрузка действует циклически. Это искажает кар-
тину распределения напряжений в зоне контакта, которая име-
ет место при статическом сжатии.
Процесс усталостного разрушения контактирующих поверх-
ностей при нагружении зоны контакта циклически действую-
щей нагрузкой состоит в зарождении первичных трещин в зоне
действия максимальных касательных напряжений на глубине
нескольких десятков микрометров от поверхности. Постепенно
Развиваясь, эти трещины выходят на поверхность, отдельные
точечные дефекты сливаются, материал в зоне трещин отслаи-
вается, а крупные частицы выкрашиваются, в результате чего
Деталь выходит из строя. Поскольку разрушение поверхностно-
го слоя детали в зоне контакта зависит от числа циклов нагру-
жений, можно в этом случае говорить о контактной выносли-
вости детали. Типичным примером контактного разрушения
является выкрашивание рабочих поверхностей зубьев зубчатых
°Дес, которое сосредоточивается на участках зуба, близких к
ячальной окружности. Это объясняется изменением направле-
Ия сил трения в этой зоне, а также тем, что на этих участках
агрузку несет один зуб, а участки, близкие к головке и нож-
39
ке, менее нагружены, так как нагрузка здесь распределяется
на два зуба. Кроме того, при высоких давлениях в зоне кон-
такта масло, внедряясь в вышедшие на поверхность детали от
зоны наибольших касательных напряжений микротрещины,
вызывает процесс ускоренного выкрашивания материала.
Действительная картина нагружения в зоне контакта зубь-
ев гораздо сложнее, вследствие чего зависимости (2.25) ц
(2.26) носят в определенной степени условный характер. Однако
их использование для оценки контактной выносливости зубьев
по условию оя<[оя] правомерно, если принятые при определе-
нии вн и (ая] условия достаточно хорошо будут соответство-
вать истинной картине.
2.2. ЖЕСТКОСТЬ
Жесткость — способность детали сопротивляться об-
разованию деформации под действием нагрузок. Если действу-
ющая нагрузка при этом не меняется во времени, то говорят
о статической жесткости. Виброжесткость — способность дета-
ли сопротивляться деформации при вибрации определенной час-
тоты и амплитуды, под крутильной жесткостью понимается
способность детали иметь в определенных пределах деформа-
цию кручения под действием приложенного крутящего момен-
та определенной частоты. При резонансе деформации возрас-
тают до опасных пределов.
Расчеты на статическую жесткость сводятся к определению
линейных f и угловых 0 прогибов при изгибе, удлинения А/ при
растяжении и угла закручивания <р при кручении. При этом
используют зависимости из курса «Сопротивление материалов»
и сравнивают результаты расчета с допускаемыми значениями.
При каждом виде деформации жесткость можно характе-
ризовать коэффициентом жесткости c=dFidb, где F—воздей-
ствующая сила; б — деформация. Тогда при растяжении стерж-
ня cP=ES/l, при кручении с = GJPH, а при изгибе cK=kElх/13,
где Е — модуль упругости при растяжении; G — модуль упру-
гости при сдвиге; S — площадь сечения стержня; ]р и Jx — по-
лярный и осевой моменты инерции; I — длина стержня; k — ко-
эффициент, зависящий от схемы нагружения и способа задел-
ки концов. Величина, обратная коэффициенту жесткости, назы-
вается коэффициентом податливости е= \jc.
2.3. износостойкость
Износ — изменение размеров, формы, массы тела или
состояния поверхности разрушения поверхностного слоя изде-
лия. Износ обычно проявляется при трении, которое возникает
при относительном перемещении (скольжении) поверхностей.
40
этом происходит как бы снятие неровностей, расположен-
ПРИ на СОПрИкасающихся поверхностях; попадание абразивных
НЫ тин и продуктов изнашивания в область трения усиливает
ЧЭоцесс износа. Износ является результатом не только меха-
Пического, но также теплового, химического и молекулярного
нзаимодействия вершин неровностей трущихся поверхностей.
В Для уменьшения износа, происходящего при соприкоснове-
нии вершин неровностей, следует трущиеся поверхности обиль-
но смазывать, а поверхности контакта должны иметь весьма
малую высоту неровностей. Это приближает работу трущихся
поверхностей к условиям жидкостного трения, когда между
поверхностями трения всегда находится слой смазочного мате-
риала и износ практически не имеет места.
Н Под износостойкостью понимают свойство материала оказы-
вать сопротивление изнашиванию в определенных условиях
трения. Ее оценивают величиной, обратной скорости изнашива-
ния или интенсивности изнашивания. При этом значение изно-
са может выражаться в единицах длины, объема, массы и др.
Скорость изнашивания оценивают отношением значения
износа к интервалу времени, в течение которого он возник, а
интенсивность изнашивания — отношением значения износа к
пути, на котором происходило изнашивание, или объему выпол-
ненной работы:
Jh=hLlL, (2.27)
где hL— толщина слоя, снятая в результате изнашивания;
L — перемещение точки поверхности, на которой фиксировал-
ся износ.
Различают следующие виды изнашивания: механическое
(абразивное, усталостное), коррозионно-механическое и моле-
кулярно-механическое.
Абразивное изнашивание возникает при попадании твердых
частиц абразива и продуктов изнашивания в зону трения. Внед-
ряясь в менее твердую поверхность, частицы абразива движут-
ся вместе с ней и при скольжении одной поверхности относи-
тельно другой действуют на более твердую поверхность как ре-
зец. Эффективное средство уменьшения абразивного износа —
защита зоны трения от попадания частиц абразива с помощью
специальных уплотнений, а для защиты зон трения от продук-
тов изнашивания при использовании жидкой смазки — очистка
сМазки с помощью специальных фильтров.
Усталостное выкрашивание, причины которого выявлены
пРи рассмотрении контактной выносливости, сначала проявля-
ется на участках с перегрузкой контактной поверхности. Воз-
Икающие в результате перегрузки выкрашивание микрообъе-
°в металла и отслаивание отдельных частиц с увеличением
пела циклов нагружений прогрессируют и ведут к ускорению
41
разрушения поверхности от усталости и пластическому дефор.
мированию.
Если в зоне контакта имеет место скольжение профилей,
как, например, в зубчатой паре при зацеплении зубьев, то, как
правило, сопротивление усталостному выкрашиванию у опере-
жающей поверхности выше, чем у отстающей. Одно из объясне-
ний этого — снижение коэффициента трения скольжения в свя-
зи с ростом суммарной скорости для опережающей поверхно-
сти; это ведет к росту толщины масляного слоя, разделяющего
соприкасающиеся поверхности.
Коррозионно-механическое изнашивание характерно для
процесса разрушения поверхностных слоев контактирующих по-
верхностей деталей под действием нормальных сил, микропе-
ремещений и связанных с ними сил трения; оно возникает при
наличии в зоне контакта смазок с поверхностно активными при-
садками, в условиях высоких местных давлений и высоких ло-
кальных температур в зоне контакта. Образующиеся в этих ус-
ловиях на поверхности металла поверхностные пленки разру-
шаются и снова образуются. Одним из видов такого изнаши-
вания является окислительное изнашивание — разрушение не-
прерывно восстанавливающихся окисных пленок.
Коррозионно-механическое изнашивание, обусловленное
очень малыми колебательными относительными перемещения-
ми сопряженных поверхностей, возникающих из-за деформаций
и зазоров в соединении при наличии взаимного перемещения,
называется фреттинг-коррозией. Относительные микропереме-
щения контактных поверхностей вследствие контактного трения
ведут к разрушению окисных контактных пленок и их после-
дующему восстановлению под действием агрессивных составля-
ющих окружающей среды, что нарушает прочность соединения.
Этот вид изнашивания характерен для шлицевых и шпоночных
соединений, соединений с натягом, зубчатых муфт, рессор.
Молекулярно-механическое изнашивание проявляется при
разрушении защитных пленок на контактирующих поверхно-
стях, в результате чего приходят в действие силы молекуляр-
ного сцепления. Это явление называется схватыванием, а про-
цесс возникновения трения на этой основе — заеданием. Его ин-
тенсивность растет с увеличением удельного давления, скоро-
сти скольжения и температуры в зоне контакта. Разновидно-
стью этого вида изнашивания является задир — повреждение
поверхности контакта в виде борозд глубиной до 100... 200 мкм
в направлении вектора скорости относительного движения. Про-
цесс схватывания обычно происходит при значительной скоро-
сти скольжения и больших усилиях поджатия контактирующих
поверхностей. Уменьшение схватывания достигается изготовле-
нием поверхностей трения из разных материалов и применени-
ем смазок с антизадирными присадками. Наличие износа удо-
42
жает эксплуатацию машин, увеличивает простои в связи с
Р°монтом, проверкой и наладкой, что снижает их производи-
^льность. Износ снижает также точность механизма, его КПД,
ТовЫшает ШУМ> создаваемый им, и может служить причиной
поломки. Основными критериями оценки износостойкости для
случая полужидкостного трения являются ограничения по ус-
ловному удельному давлению: р< [р]; по тепловыделению (на-
гоеву): pv^[pv], где р —удельное давление, МПа, v — ско-
иость скольжения, м/с. Значения [р] и [ри] для подшипников
скольжения с различными материалами вкладыша приведены
в табл. 14.1.
Обеспечение жидкостного трения на основе использования
гидродинамического эффекта состоит в получении минималь-
ной толщины масляной пленки ho при определенном значении
нагрузки Fr, скорости скольжения t»s, динамической вязкости
смазки ц, температуре t и приведенной кривизне сопряженных
поверхностей рпр, т. е. ho=f(Fr, vs, ц, t, рпр). Расчет парамет-
ров подшипников скольжения исходя из этого условия приве-
ден в гл. 14.
Одним из главных путей уменьшения износа является при-
менение соответствующих смазок для разделения поверхностей
трения. Применяемые при этом смазочные материалы разделя-
ют на газообразные, жидкие, пластичные и твердые. Для смаз-
ки узлов трения в механизмах ЛА используются жидкая, пла-
стичная и твердая смазки. Жидкая смазка в зону трения может
подаваться разбрызгиванием, под давлением или благодаря
гидродинамическому эффекту. Этот эффект используется в под-
шипниках скольжения жидкостного трения. Условия такого тре-
ния обеспечиваются при заданной нагрузке на подшипник и
частоте вращения вала выбором определенного зазора между
валом и подшипником, вязкости масла, шероховатости и мате-
риалов поверхностей вала и подшипника.
В качестве жидкой смазки (для деталей и узлов редукторов
авиационных двигателей) при принудительной ее подаче в зо-
ну трения используются высококачественные масла, способные
Длительное время работать в условиях разнообразных режимов
трения, высоких температур, нагрузок и скоростей. Их приме-
нение уменьшает трение и износ деталей, обеспечивает отвод
от них тепла, предохраняет от коррозии, удаляет твердые вклю-
чения и частицы износа от пар трения. К качеству масел предъ-
являются требования высокой смазывающей способности, хо-
роших вязкостно-температурных характеристик (для обеспече-
ния надежной работы при низких температурах), отсутствия
Коррозионного воздействия на соприкасающиеся с маслом де-
али. В авиационных редукторах и узлах трения ГТД и ТВД
спользуют масла СМ-4,5; СМ-8; СМ-11,5; МН-7,5 и синтетиче-
к°е масло Б-ЗВ; последнее имеет противозадирную и анти-
43
окислительную присадки; стабильно до 200°С, имеет темпера,
туру застывания —60°С и обладает высокой смазывающей спо-
собностью.
Пластичные смазки являются продуктами загущения смазоч-
ных нефтяных или синтетических масел загустителями и вве-
дения в них присадок, придающих им коллоидную структуру ц
дополнительные свойства, определяющие их назначение и ка-
чество. По внешнему виду пластичные смазки представляют
собой мази различных консистенций и цвета. Наиболее приме-
нимы в узлах трения ЛА следующие виды антифрикционных
смазок.
Тугоплавкая самолетомоторная (СТ) — высокотемператур-
ная пластичная смазка темно-зеленого цвета. Смазка работо-
способна при температуре от —15 до +200°С. Она предназна-
чена для смазывания подшипников шасси и других узлов са-
молета.
Универсальная среднеплавкая (УС) (солидол жировой)—
водостойкая антифрикционная и консервационная смазка. Для
подшипников качения и зубчатых редукторов ЛА используют
солидол марки УС-2, работоспособна при температуре от —40
до +70°С.
ЦИАТИМ-203 — антифрикционная смазка темно-коричнево-
го цвета; предназначена для смазывания механизмов, работаю-
щих при высоких удельных нагрузках и температуре от —50 до
+90°С.
ЦИАТИМ-221 — высокотемпературная водостойкая смазка;
мягкая мазь белого или светло-серого цвета. Работоспособна
при температуре от —60 до 150°С.
ОКБ-122-7 — мягкая мазь желтого или светло-коричневого
цвета; работоспособна при температуре от —60 до + 120°С.
Твердые смазки применяются при работе в условиях низ-
ких (ниже —100°С) и высоких (выше 300°С) температур для
смазывания подшипников и узлов трения. Наиболее часто при-
меняют коллоидальный графит (до /<350°С), дисульфид мо-
либдена (M0S2) и нитрид бора (BNO2). Дисульфид молибдена
сохраняет в атмосфере свои смазывающие свойства до темпе-
ратуры 400°С; при более высокой температуре образуется окись
молибдена, обладающая абразивными свойствами. В вакууме
и в инертных газах дисульфид молибдена сохраняет свои сма-
зочные свойства до 800... 1150°С.
2.4. ТЕПЛОСТОЙКОСТЬ
Нагрев деталей машин, обусловленный рабочим про-
цессом и трением в узлах, может вызывать следующие явления,
отражающиеся на надежности их работы.
44
1. Снижение прочностных характеристик материала и появ-
ление при напряженных температурных режимах явления пол-
зучести, характеризуемого изменением характеристик ползуче-
сти, а также возникновением с течением времени остаточных
деформаций. Для деталей из конструкционных легированных
сталей это наблюдают при температурах свыше 300... 400°С,
для алюминиевых сплавов — при 150...200°С. Применение жа-
ропрочных сплавов титана повышает эти температуры до 450...
55{гС, для легких жаропрочных сплавов — до 250... 300°С и бо-
лее, а У стальных жаропрочных — до 1000°С и более. Ползу-
честь особенно опасна для узлов, где возможна выборка зазора
при вращающихся или поступательно движущихся деталях.
В затянутых соединениях явление ползучести может вызвать
снижение усилия затяжки.
Работоспособность материала при повышенной температуре
оценивается пределами ползучести и длительной прочности.
Обозначение предела ползучести сопровождается двумя индек-
сами: например, Оод/юо, где первый индекс означает остаточ-
ную деформацию в процентах (в данном случае 0,1%), вто-
рой— время в часах, за которое получается эта деформация,
для соответствующей температуры материала.
2. Повышение износа или появление заедания ввиду нару-
шения нормальной работы масляного слоя. Расчет зубчатых
колес на заедание в этом случае основан на предположении по-
тери смазкой смазывающих свойств.
Приводящее к заеданию повышение температуры рабочих
поверхностей зубчатых колес лежит для закаленных сталей в
пределах 200... 350°С.
3. Изменение зазоров в узлах машин ввиду температурной
деформации деталей (в опорах скольжения и качения, в турби-
не между лопатками и корпусом газотурбинного двигателя
и др.) может быть причиной (при уменьшении зазора до нуля)
выхода из строя подшипников и поломки лопаток. При опреде-
лении изменения величины зазора в качестве исходной зависи-
мости используют формулу температурного изменения длины
Детали при нагреве ее на Д/ градусов Д//=а«Ш, где at — тем-
пературный коэффициент линейного расширения материала де-
тали.
4. Возникновение температурных напряжений и деформаций
ПРИ жесткой заделке концов детали или при ее неравномерном
иагреве.
Появление температурных деформаций и температурных на-
пряжений может являться причиной снижения прочности дета-
ли или узла и должно учитываться при расчете. В точных ме-
ханизмах, часто являющихся составной частью приборов, они
*°гут служить причиной появления погрешностей измере-
45
2.5. ВИБРОУСТОИЧИВОСТЬ
В связи с высокими частотами колебаний деталей ма-
шин и большими диапазонами их изменения имеется опасность
их разрушения от возникающих колебаний, амплитуда которых
может возрастать под действием возмущающей силы, что осо-
бенно опасно на частотах, близких к резонансным. Это явле-
ние наступает, когда частота возмущающей силы совпадает с
частотой собственных колебаний детали. При возрастании ам-
плитуды колебаний напряжения в детали резко увеличиваются,
в результате чего может произойти ее разрушение. Под вибро-
устойчивостью понимается способность детали сохранять рабо-
тоспособность в требуемом диапазоне режимов угловых скоро-
стей, создающих определенную частоту возмущающей силы без
появления недопустимых амплитуд колебаний. При эксплуата-
ции деталей машин, а также узлов и агрегатов ЛА наиболее
возможными видами колебаний являются вынужденные коле-
бания и автоколебания. Причинами первых могут быть дина-
мическая неуравновешенность вращающихся частей, периодич-
ность действия внешних возмущающих сил и другие факторы.
Автоколебания, являющиеся самовозбуждающимися, возни-
кают при достижении равенства между энергией демпфирова-
ния и энергией возбуждения, поступающей в колебательную
систему. Демпфирование может быть, например, аэродинамиче-
ским при колебаниях лопаток компрессора двигателя. Оно мо-
жет создаваться благодаря изменению сил трения или других
периодически изменяющихся внутренних факторов.
Частота f (Гц) собственных колебаний балки постоянного
поперечного сечения под действием собственного веса, вызы-
вающего статический прогиб бет, определяется по формуле
/= (2.28)
Для консольной балки постоянного поперечного сечения с
моментом инерции /з и длиной I при нагрузке на конце Q бСт=
= Q/3/(3EJ). В практике расчетов, например, лопаток ГТД
формула собственной частоты учитывает распределенную массу
лопатки как консольной балки.
Для консольной балки
8СТ=11/140 [qWJ)];
(2-29)
где ?=pS— масса единицы длины балки; S — площадь сече-
ния; р — плотность материала.
46
р!з (2.29) видно, что частота f зависит от Е/р (см. табл.
3 2 и 3.14). Зависимости для определения бет для различных
конструктивных схем и сечений балок рассматривается в курсе
«Сопротивление материалов».
В авиационных конструкциях расчет деталей ЛА на коле-
бания имеет особо важное значение в связи с периодичностью
действия возмущающих сил, широким диапазоном частот их
действия и применительно к ряду деталей и узлов ЛА рассмат-
ривается в специальных курсах.
2.6. ТЕХНОЛОГИЧНОСТЬ
Под технологичностью конструкции понимается ис-
пользование при ее разработке таких конструктивных решений,
которые обеспечивают наиболее быстрое и экономичное освое-
ние этой конструкции в производстве с современными техноло-
гическими процессами. Технологичность конструкции подразу-
мевает возможность применения при изготовлении высокопро-
изводительных и наиболее прогрессивных способов формообра-
зования при минимальных затратах рабочей силы, рациональ-
ного использования производственного оборудования, материа-
лов; исключает сложную подготовку производства; позволяет
осуществить автоматизацию производственных процессов и
контроль при выпуске изделия.
Детали машин очерчиваются чаще всего цилиндрическими
и коническими поверхностями, получаемыми на токарных, свер-
лильных, расточных, кругло- и внутришлифовальных станках,
плоскостями, обрабатываемыми на фрезерных, строгальных и
плоскошлифовальных станках, а также винтовыми и эвольвент-
ными поверхностями, получаемыми на винторезных, резьбофре-
зерных, резьбошлифовальных и зуборезных станках.
Литые детали должны быть легко формируемыми, качество
отливки должно быть высоким; детали должны быть удобны
Для последующей базировки и механической обработки.
Штампованные детали должны иметь форму, обеспечиваю-
щую хорошее растекание металла в штампе, и уклоны, обеспе-
чивающие удаление детали из штампа.
Технологичность конструкции тесно связана с серийностью:
изделие, изготовленное в условиях мелкосерийного производст-
®а, может оказаться нетехнологичным для крупносерийного.
Технологичные конструкции подразумевают широкое внед-
рение стандартизации, нормализации и унификации, использо-
Иание полуфабрикатов и рекомендованных к использованию
Материалов, а также типизацию технологических процессов.
47
2.7. НАДЕЖНОСТЬ
Перечень требований, обеспечивающих работоспособ-
ность, будет неполным, если его не дополнить требованием на-
дежности. Надежность — свойство объекта сохранять во време-
ни в установленных пределах значения всех параметров, ха-
рактеризующих способность выполнять требуемые функции в
заданных режимах и условиях применения, технологического
обслуживания, ремонта, хранения и транспортирования. На-
дежность состоит из сочетаний свойств безотказности, долговеч-
ности, ремонтопригодности и сохраняемости. При этом безот-
казность определяется как свойство объекта непрерывно сохра-
нять работоспособное состояние в течение некоторого времени
или некоторой наработки. Долговечность — свойство объекта
сохранять работоспособное состояние до наступления предель-
ного состояния при установленной системе технического обслу-
живания и ремонта. Ремонтопригодность заключается в при-
способленности объекта к предупреждению и обнаружению
причин возникновения отказов, повреждений и поддержанию и
восстановлению работоспособного состояния путем проведения
технического обслуживания и ремонтов. Сохраняемость — свой-
ство сохранять значения показателей безотказности, долговеч-
ности и ремонтопригодности в течение и после хранения и тран-
спортировки.
Для конкретных объектов и условий их эксплуатации эти
свойства имеют различную относительную значимость. Так, для
некоторых неремонтируемых объектов (самолетные электро-
двигатели, стрелочные приборы, турбина ГТД и пр.) основным
свойством в полете является их безотказность. Для ремонтируе-
мых объектов (ячейки памяти стационарной ЭВМ, электродви-
гателя привода самолетной радиолокационной антенны) одним
из важнейших свойств является ремонтопригодность. Парамет-
рами, характеризующими способность выполнять требуемые
функции, являются кинематические и динамические характери-
стики, показатели точности функционирования, скорости и т. п.
С течением времени значения этих параметров могут изменять-
ся. При изменениях, превышающих допустимые пределы, про-
исходит переход объекта в неработоспособное состояние. Коли-
чественно надежность объекта оценивается с помощью показа-
телей, которые выбирают и определяют с учетом его особенно-
стей, режимов и условий его эксплуатации и последствий отка-
зов. Значения этих показателей определяют для заданных ре-
жимов и условий применения, технического обслуживания, ре-
монтов, хранения и транспортировки.
Причиной ненадежной работы является отказ — событие,
заключающееся в полной или частичной утрате машиной, меха-
низмом или изделием работоспособного состояния. Отказ как
48
ачественный показатель надежности зависит от многих случай-
ных величин (качества материала изделия, состояния оборудо-
вания и инструмента при обработке, изменений температуры
и т. д), поэтому при расчете надежности используются методы
теории вероятностей.
Причинами отказов могут быть: 1) конструктивные ошибки
и недоработки, снижающие надежность изделия (недостаточ-
ная прочность деталей, плохая защита от влаги, пыли, неучтен-
ные механические и температурные деформации); 2) производ-
ственные дефекты (раковины, трещины, включения примесей,
пониженные физико-механические характеристики материала);
3) неправильная эксплуатация изделия; 4) плохой ремонт и по-
вреждения; 5) естественный износ, старение, потеря усталост-
ной прочности детали.
Одним из путей повышения надежности деталей и механиз-
мов ЛА является разработка такой конструкции, которая ис-
ключала бы появление таких отказов. Повышение надежности
возможно также за счет резервирования и восстановления. Ре-
зервирование— применение дублирующих средств или возмож-
ностей с целью сохранения работоспособности; восстановле-
ние— устранение отказов в изделии во время эксплуатации пу-
тем ремонта или замены вышедшей из строя детали.
При оценке надежности механизмов ЛА наиболее часто
определяют наработку, технический ресурс, срок службы. На-
работка— продолжительность или объем работы объекта. Тех-
нический ресурс — наработка объекта от начала его эксплуата-
ции или после ремонта определенного вида до перехода в пре-
дельное состояние. Срок службы — календарная продолжитель-
ность работы объекта от начала эксплуатации или после ре-
монта до перехода в предельное состояние. При этом под пре-
дельным понимают такое состояние объекта, при котором его
дальнейшее применение по назначению, а также и восстановле-
ние, недопустимо или нецелесообразно.
Для оценки надежности могут использоваться такие харак-
теристики, как Р(/)—вероятность безотказной работы в тече-
ние заданного отрезка времени t\ Х(/) —интенсивность отказов;
Тер—среднее время безотказной работы.
Вероятность безотказной работы Р(/) есть вероятность того,
что в заданном интервале времени не возникает отказа объек-
та или что его параметры не будут выходить за границы задан-
ных допусков (при заданных условиях эксплуатации), 0^
^р(0^1; Р(0) = 1; Р(оо)=0.
Вероятность безотказной работы изделия (точечная оценка)
спытаний некоторого числа изделий в течение заданного про-
е5кутка времени можно определить по формуле
Р (/)=N (t)/N0=(N0-n (2.30)
49
где No — общее число испытанных изделий; N(t), n(t) — число
изделий, исправно работавших и вышедших из строя за время
испытаний.
Наряду с вероятностью безотказной работы для характери-
стики надежности можно пользоваться также вероятностью от-
каза Q(f)—ненадежностью. Так как безотказная работа и от-
каз есть несовместимые и противоположные события, то
Q(/)==l— Р(/). (2.31)
Интенсивность отказов %(/) или К — условная плотность ве-
роятности возникновения отказа невосстанавливаемого объекта,
определяемая для рассматриваемого момента времени при ус-
ловии, что до этого момента отказ не возник. Условной эту
плотность называют потому, что она не обладает необходимым
«•
свойством плотности распределения: dt ф 1*
о
Интенсивность отказов за время испытаний М примерно
можно оценить по формуле
Х(О=л(/да(/)Д/). (2.32)
Средним временем безотказной работы называется величи-
на, равная площади, ограниченной кривой надежности и осями
координат:
Тср= [P(/)J/.
(2.33)
При оценке надежности используют различные законы рас-
пределения частоты отказов, например экспоненциальный, Вей-
булла, нормальный, логарифмически нормальный (рис. 2.13).
Для экспоненциального закона распределения (см. рис.
2.13, a) k(t) =Хо=const,
Р (/)==ехр (—ty)=exp (—х), (2.34)
где X—М;
Рис. 2.13. Экспоненциальный (а), Вейбулла (б) и нормальный (в) законы
распределения
50
Таблица 2.1
4 6 8 * 0 2
0,0 1,000 0,980 0,961 0,942 0,923 0,6 0,549 0t538 0,527 0,517 0,507
0,1 0,905 0,887 0,869 0,852 0,835 0,7 0,500 0,487 0,477 0,467 0,458
0,2 0,819 0,803 0,787 0,771 0,756 0,8 0,449 0,440 0,432 0,423 0,415
0,3 0,741 0,726 0,719 0,688 0,684 0,9 0,407 0,398 0,391 0,383 0,375
0,4 0,670 0,657 0,644 0,631 0,619 1,0 0,368 0,361 0,353 0,346 0,340
0,5 0,607 0,595 0,583 0,571 0,560 1,1 0,333 0,326 0,320 0,314 0,307
/(/)=~4г₽=х°е~ч
(2.36)
Значения ехр(—х) приведены в табл. 2.1.
Этот закон справедлив для описания потока отказов с по-
стоянной интенсивностью, когда время появления отказа не
связано с предыдущей наработкой изделия. Этому закону под-
чиняются отказы по причинам усталостного разрушения, раз-
рушение от сочетания неблагоприятных факторов в процессе
эксплуатации изделия и др.
Распределение Вейбулла (см. рис. 2.13, б) используют для
статистических моделей надежности в первый период эксплуа-
тации, когда возможны так называемые приработочные отка-
зы. Он имеет следующие характеристики:
P(O=e-um; (2.37)
/(/)= __±L = X/n/’B-,e-x/m; (2.38)
X(/)=^L=kznf'n-’. (2.39)
Здесь m>0; при 0<т<1 интенсивность отказов со време-
нем убывает, что характерно для «приработочных» отказов.
Нормальный закон распределения (см. рис. 2.13, в) имеет
следующие характеристики:
/(0= Jy- exp [ —(/—а)2/(2э2)], (2.40)
а У ЛЛ
где а и а—соответственно среднее значение времени наработ-
ки до отказа и среднее квадратическое отклонение;
51
Таблица 2.2
Z Ф(г) % риска 2 Ф(2) % риска Z Ф(г) % риска
0,1 0,0398 92,04 1,6 0,4452 10,96 2,6 0,4953 0,94
0,5 0,1915 61,7 1,8 0,4641 7,18 2,8 0,4974 0,52
1,0 0,3413 31,74 2,0 0,4772 4,56 3,0 0,4986 0,27
1,2 0,3849 23,02 2,2 0,4861 2,78 3,2 0,4993 0,04
1,4 0,4192 16,16 2,4 0,4918 1,64 3,6 0,4998 0,03
(2.41)
- / t — а\
где Ф ------- =
\ а /
J
о
(<—а)1
2’’ di — функция Лапласа, зна-
чения которой приводятся в справочниках (табл. 2.2). В табл. 2.2
также приводится для каждого значения z процент риска, т. е.
процент изделий, надежность которых не обеспечена.
Нормальному закону распределения подчиняются отказы,
связанные с износом детали.
Выбор вероятностной модели может быть произведен толь-
ко на основании статистического анализа функционирования
данного класса объектов при испытаниях или эксплуатации и
не может быть обоснован математическими выкладками. Мате-
матические модели надежности, хотя и являются в значитель-
ной мере идеализацией реальных законов надежного функцио-
нирования объектов, в ряде случаев позволяют получать вполне
достоверные оценки параметров. При этом степень идеализации
модели определяется требованием простоты ее использования.
Так, сложная модель надежности часто требует настолько боль-
шого объема выборки для оценки ее параметров, что ее ис-
пользование становится невозможным. И наоборот, использо-
вание простой модели может не согласовываться с реальными
О
ч
Рис. 2.14. Зависимость
ности отказов от времени
результатами эксплуатации
объекта.
Физическая природа при-
работочных отказов (рис. 2.14)
заключается в неидеальности
технологии изготовления дета-
лей, сборки узлов и агрегатов,
контроля качества изготовлен-
интенсив- ных изделий. Не замеченные
наработки при изготовлении изделия де-
52
фекты являются концентраторами напряжений различного ро-
да, что приводит к уменьшению запаса прочности и разрушению
даже при более низких уровнях нагрузки в течение короткого
периода. Закон распределения отказов в этот период может
быть самым различным, однако из рис. 2.14 видно, что он дол-
жен отражать уменьшение интенсивности отказов до постоянно-
го значения в течение сравнительно короткого периода 0—Л.
В этот период надежность изделия определяется, главным обра-
зом, интенсивностью приработочных отказов, снизить которые
можно разработкой методов их устранения.
Внезапные отказы (отрезок Л—/г) считаются неустранимы-
ми при приработке и возможными при эксплуатации изделия,
но они должны быть минимальными. Причина таких отказов
связана с тем, что при эксплуатации существует вероятность
появления внезапной концентрации нагрузки, ведущей к сниже-
нию запаса прочности ниже допустимого значения. При этом
закон распределения вероятности появления критических на-
грузок может быть описан моделями, основанными на статис-
тических теориях их значений.
Износовые отказы (при отражают естественные про-
цессы разрушения объектов при их нагружении и взаимодейст-
вии со средой. Для механических объектов износовые отказы
основываются в основном на недостаточной длительной объем-
ной и поверхностной прочности. Эти процессы по скорости раз-
рушения могут быть быстро текущими (например, поломка зу-
ба шестерни в результате превышения изгибных напряжений
от динамических нагрузок), средней скорости (например, по-
степенное снижение параметров изделия от изменения темпе-
ратуры) и медленно текущие (например, отказ от усталости,
коррозии, ползучести материала). Построение модели отказов
конкретно для определенного класса изделий позволяет оцени-
вать их надежность и должно базироваться на физических про-
цессах разрушения. В механических объектах объемное и по-
верхностное разрушения имеют наибольшее значение и явля-
ются причиной 80 ...85% отказов.
Особенно большое число отказов, т. е. снижение надежно-
сти, связано с недооценкой внешних условий, например влия-
ния на надежность механических и температурных воздействий.
Так, вибрации ведут к появлению в материале усталости, от
ударов возникают местные перенапряжения; стали при низких
температурах становятся хрупкими, обычные резины теряют уп-
ругость, а смазки — пластичность. Причем, эти процессы могут
быть как быстротекущими (мгновенная повреждаемость в виде
поломки), так и медленно текущими (постепенное накопление
микродефектов или изменение свойств). Задача конструктора
при создании изделия — исключить в пределах заданного ре-
сурса появление отказов обоснованным выбором соответствую-
53
щих материалов, смазки, методов упрочнения и защиты от
влияния внешних условий, учетом в методике расчета всех фак-
торов, влияющих на надежность. Большое влияние на повыше-
ние надежности изделия имеет выбор рациональных техноло-
гических процессов изготовления, завершаемого техническим
контролем.
Вероятность безотказной работы системы, состоящей из п
элементов, зависит от способа соединения их между собой. При
последовательном соединении отказ хотя бы одного элемента
ведет к отказу всей системы. В этом случае вероятность без-
отказной работы такой системы будет
Л
Рпосл W=P1 (О Р2 (О • • • р„ (0= п Р/ (О, (2.42)
i-i
При экспоненциальном законе распределения вероятность
безотказной работы системы, состоящей из п элементов, с ин-
тенсивностью отказов каждого элемента If будет равна
РпосЛ(О= ПехР(“ М)=ехр(-М), (2.43)
Z-1
п
где Xs=^kz — интенсивность отказов всей системы.
При наличии в системе (или ее узле) п параллельно соеди-
ненных элементов, обеспечивающих резервирование,
п
Р(/)Ъ=1- П[1-Р/(0]. (2.44)
i-i
Если рассматриваемый элемент механической системы ис-
пользуется не на номинальную нагрузку, то, исходя из условий
работы, определяют коэффициент нагрузки по мощности: kw=
= И7раб/^ном или ПО напряжению: t/раб/t/ном, где Wpa6 и
Whom — рабочая и номинальная мощности; 1/раб и t/H0M — рабо-
чее и номинальное напряжения.
Для приближения интенсивности отказов к реальным усло-
виям работы вводят также поправочный коэффициент k\, учи-
тывающий место размещения объекта. Для лабораторных по-
мещений 1, для наземных стационарных устройств &=10,
для самолетов /г»=120... 150. С учетом этих поправок интенсив-
ность отказов i-ro элемента будет равна
У-1 — (2.45)
где Хо — интенсивность отказов элемента при kv=\, ki—1.
54
Пример 2.1. Наработка механизма до отказа подчиняется экспоненциаль-
ному распределению с параметром Хо=1О“4 ч-1. Определить среднее время
наработки до отказа и вероятность безотказной работы механизма в течение
400 ч при номинальной нагрузке в лабораторных условиях.
Среднее время наработки до отказа согласно (2.36) Тср=1/Хо=1О4 ч.
Вероятность безотказной работы по (2.34) Р(0 = Р(400) =ехр(—М) =
=ехр(— 10”4-400)=ехр(—0,04); нз табл. 2.1 определяем Р(/) = 0,961.
Пример 2.2. Определить интенсивность отказов, время наработки до от-
каза и вероятность безотказной работы механизма высотного корректора само-
лета за время эксплуатации /о=ЗОО ч, если механизм состоит из двигателя
ДИД-0,5, трехступенчатой зубчатой передачи, электромагнитной муфты сцеп-
ления и потенциометра обратной связи, имеющих за время /=106 ч соответ-
ственно интенсивности отказов Х4 = 8,6; Х2=0,12; Х3=0,6; Х4=4,4 ч-1. Дви-
гатель в работе используется на 0,25 мощности; запас прочности зубчатой
передачи принять 1,2, а передаваемый муфтой момент — не более 0,5 номи-
нального. Потенциометр нагружен мощностью не более 0,2 номинальной.
Определить, как изменится вероятность безотказной работы, если осущест-
вить трехкратное резервирование.
С учетом коэффициентов загрузки элементов механизма по мощности
4Г1=0,25; Лт2=(1,2)“1; £уз=0,о; ЛУ4=0,2 и коэффициента £х=120, учи-
тывающего летную эксплуатацию, согласно (2.43) за время /=10в ч средняя
интенсивность отказов всего механизма будет равна ХЕ = (8,6 0,25+0,12Х
хз- ^г-^о.б-о.б+м-о.г) • ю-в-120=0,435- ю-3 ч-1.
Среднее время наработки до отказа согласно (2.36) составит
Тср = I/Хд = 1 /(0,435• 10-3) = 2300 ч.
Вероятность безотказной работы одного механизма корректора в течение
заданных 300 ч согласно (2.43) и табл. 2.1 составит
(300) = ехр (- 0,435-10-3.300) = ехр ( - 0,13) = 0,88.
При трехкратном резервировании вероятность безотказной работы со-
гласно (2.44) будет равна
р<3> (300) = 1 - [I - pj.‘> (ЗОО)]3 = I - (I -0,88)3 = 0,998.
т. е. значительно возрастет.
2.8. ПРИМЕНЕНИЕ ВЕРОЯТНОСТНЫХ МЕТОДОВ
В РАСЧЕТАХ ДЕТАЛЕЙ МАШИН
При решении многих прикладных задач проектирова-
ния и изготовления деталей машин и механизмов ЛА необходи-
мо использовать вероятностные методы расчета. Это обуслов-
лено тем, что оценка их работоспособности основана на исполь-
зовании данных о физических свойствах материалов в виде тех
или иных характеристик, которые по своей природе являются
случайными величинами. Кроме того, технологические процес-
сы обработки деталей также представляют собой случайные
процессы, характеризуемые случайными величинами.
Применение вероятностных методов расчета позволяет ре-
шать следующие задачи:
оценивать вероятности неразрушения или безотказной ра-
боты;
55
оценивать влияние внешних силовых воздействий на вероят-
ность безотказной работы;
выработать способы обеспечения требуемой работоспособ-
ности на стадии проектирования и изготовления.
Таким образом, использование вероятностных статистиче-
ских методов создает базу для научно обоснованного выбора
наиболее эффективных конструктивно-технологических путей
повышения работоспособности деталей машин и механизмов
ЛА.
Физические свойства материалов, применяемых при изготов-
лении деталей, изменение этих свойств при получении загото-
вок и обработке, влияние условий эксплуатации — все это обыч-
но случайные функции времени или случайные величины. Слу-
чайные величины не имеют постоянного знака и величины и,
хотя значение каждой из них при разовом появлении не пред-
сказуемо, при многократном появлении они подчиняются опре-
деленным законам.
К случайным величинам обычно относятся такие, которые
могут принимать то или иное заранее неизвестное значение.
К ним могут быть отнесены значения механических характери-
стик материала (ов, От, o-i и др.), получаемые в результате
опыта, отклонения действительных размеров детали от номи-
нала, значения коэффициента трения, величины эксплуатаци-
онных нагрузок и т. д.
Противоположностью случайным величинам являются детер-
минированные, т. е. такие, значения которых известны заранее
с определенной точностью. К таким величинам могут быть от-
несены площадь круга радиуса R, момент инерции сечения с
размерами b%h и т. д.
Законы, которым подчиняются случайные величины, рас-
сматриваются в теории вероятностей. Так, если случайная ве-
личина X в процессе испытаний принимает значения Xi,x2.хп,
образующие конечную или бесконечную последовательность чи-
сел, то она называется дискретной. В противном случае — не-
прерывной.
Вероятность непревышения случайной величиной X задан-
ного уровня х — доля значений случайных величин в совокуп-
ности, не превышающих этот уровень.
Для нее выполняются условия
О< Р {X< х} < i.
Функция распределения случайной величины
Fx(x)=P{Z<x} (2.46)
описывает зависимость вероятности непревышения случайной
величиной X заданного уровня х. Fx(x) является функцией ар-
56
гумента х. Индекс х означает ее принадлежность к заданной
случайной величине и обычно опускается.
Функция распределения однозначно задает распределение
случайных величин в общей совокупности. Например, функция
распределения предела прочности ав записывается так: F0)t(3).
Соотношение F,я(540) = 0,1 означает, что 10% значений ав не
превосходит величины 540 МПа. Все остальные характеристи-
ки распределения выражаются через функцию распределения.
Квантиль распределения случайной величины определяется
соотношением
Fx(xp) = p, (2.47)
или в соответствии с (2.46)
Р{х<хр}=р.
Квантиль хр уровня р представляет собой значение случай-
ной величины, вероятность непревышения которой равна р.
Квантиль хо,з уровня р=0,5 называется медианой распределе-
ния. Так, квантиль распределения предела прочности ав уровня
р обозначается как [ав]р. Соотношение [ов]о,о5 = о означает,
что значения ав, не превышающие о, составляют 5% всей сово-
купности.
Характеристикой случайных величин с вероятностной точки
зрения является функция распределения Fx(x), определяющая
вероятность попадания величины х в какой-то промежуток от
Х\ ДО Х2.
Производная от функции распределения Fx(x) по парамет-
ру х есть плотность вероятности fx(x), т. е.
Л(х)=-^^-). (2.48)
Математическое ожидание случайной величины определяет-
ся соотношением
М{Х}= J xf (x)(x)dx=a. (2.49)
— 00
Математическое ожидание дискретной случайной величины
представляет собой среднее арифметическое ее значений.
Дисперсия случайной величины определяется соотношением
D {%} = +j (х - М {X})*fx (х) dx. (2.50)
— 00
Дисперсия дискретной величины представляет собой сред-
нее арифметическое значение квадрата отклонения случайной
величины от ее математического ожидания.
57
Среднее квадратичное отклонение случайной величины оп-
ределяется соотношением
а{Х}=]/ЩЛ}=3 (2.51)
и характеризует отклонение значений случайной величины от
математического ожидания.
Коэффициент вариации случайной величины определяется
соотношением
у{Х) = а {X}IM {X} = ala (2.52)
и характеризует относительное отклонение значений случайной
величины от математического ожидания.
Поведение случайной величины X может моделироваться
рядом законов распределения, причем на практике при расче-
тах обычно пользуются нормальным распределением, называе-
мым также Гауссовым, которому подчиняется целый ряд слу-
чайных величин. Применительно к механическим характеристи-
кам материала закон нормального распределения означает, что
отклонение этих характеристик от математического ожидания
можно представить в виде суммы элементарных отклонений,
каждое из которых вызвано случайным изменением какого-ли-
бо фактора от одного испытания к другому. Например, приме-
нительно к пределу прочности ов в качестве таких факторов
выступают содержание химических элементов, разнозерни-
стость, шероховатость поверхности и т. д. Рассмотрим основные
зависимости, характеризующие закон нормального распределе-
ния:
/(х)=—2»» . (2.53)
з у
Функция распределения для закона нормального распреде-
ления имеет вид
(2.54)
\ а /
х - —
где t=±^, а Ф(х)=—(’ е 2 dt-
О /2я J
— со
функция Лапласа, значения которой для некоторых величин х
приведены в табл. 2.3.
Квантиль нормального закона распределения
jCp=a-f-zpa, (2.55)
где zp — квантиль нормированного нормального распределения
уровня р,
Ф(£р)=р.
58
Таблица 2.3
X Ф(Х) X Ф(х) X Ф(х) * Ф(х)
0,0 0,5000 1.1 0,8643 2,2 0,9861 3,3 0,9995
0,1 0,5398 1,2 0,8849 2,3 0,9893 3,4 0,9996
0,2 0,5793 1,3 0,9032 2,4 0,9918 3,5 0,9997
0,3 0,6179 1,4 0,9192 2,5 0,9938 3,6 0,9998
0,4 0,6554 1,5 0,9332 2,6 0,9953 3,7 0,9999
0,5 0,6915 1,6 0,9452 2,7 0,9965 3,8 0,9999
0,6 0,7258 1,7 0,9554 2,8 0,9974 3,9 0,9999
0,7 0,7580 1,8 0,9641 2,9 0,9981 4,0 0,9999
0,8 0,7881 1,9 0,9713 3,0 0,9987
0,9 0,8159 2,0 0,9773 3,1 0,9990
1,0 0,8414 2,1 0,9821 3,2 0,9993
Значения zp уровня р приведены в табл. 2.4.
Оценки параметров а и а нормального распределения по
данным эксперимента вычисляют по формулам
(2.56)
где xi — значение измеряемой величины при испытании i-ro
объекта; п — число испытаний объектов.
Оценки вероятности Рх непревышения заданного уровня х
и квантиля хр уровня р вычисляют на основе функции нор-
мального распределения по следующим формулам:
Рж = ф( х~а xf=a-\-z^s. (2.57)
Поскольку приведенные оценки вычисляют на основе слу-
чайной выборки, то они имеют случайные отклонения от ис-
Таблица 2.4
Р Р
0,00 0,55 0,13
0,05 —1,64 0,60 0,25
0,10 —1,28 0,65 0,39
0,15 —1,04 0,70 0,52
0,20 —0,84 0,75 0,67
0,25 —0,67 0,80 0,84
0,30 —0,52 0,85 1,04
0,35 —0,39 0,90 1,28
0,40 —0,25 0,95 1,64
0,45 —0,13 0,999 3,09
0,50 0,00
59
тинных значений оцениваемых характеристик распределения;
возможные отклонения от истинных значений характеризуются
доверительными границами.
Верхняя доверительная граница Р1в). для вероятности Рх
превышения заданного уровня х отвечает соотношению
Р{Р'в)>Рж) = р, (2.58)
где р<1—доверительная вероятность.
Соотношение (2.58) означает, что при статистической обра-
ботке каждых ста совокупностей результатов измерений в сред-
нем до 100 р совокупностей измерений истинное значение Рх не
будет превышать оценки Р1в)
Верхняя доверительная граница АрВ) для квантиля хр уров-
ня р отвечает соотношению
Р {Хрв>>хр)=р. (2.59)
Нижняя доверительная граница X™ для квантиля хр уров-
ня р отвечает соотношению
PMf’<xpl=p. (2.60)
Очевидно, что
Р {X <Х(РИ)} < р, (2.61)
т. е. с вероятностью 0 доля измерений во всей совокупности,
меньших А'рк), не превзойдет уровня р.
Для нормального распределения верхнюю и нижнюю одно-
сторонние доверительные границы квантиля уровня р вычисля-
ют по формулам
Хрв)=а-|-/р[п—1; Vnz ]а/Уп;
(2.62)
А’рН)=а-|-/1_р[/г—1; Vn.zp] а/У~п ,
где /т[£, и]—квантиль уровня у(у=₽ или у=1—0) нецент-
рального распределения Стьюдента с k степенями свободы и с
параметром нецентральности u=zpV7i. Здесь zp— квантиль
уровня р стандартного нормального распределения. Верхнюю
доверительную границу вероятности непревышения уровня вы-
числяют по формуле
р^ = ф(и/|/й), (2.63)
где и вычисляют как корень уравнения
Л-р [п - 1, и] = . (2.64)
О
во
Рассмотрим примеры применения вероятностных методов к
расчетам деталей ЛА.
Пример 2.3. Определить предел текучести материала детали с заданной
вероятностью Р=0,08, если предел текучести ат изменяется в интервале
560... 585 МПа и подчиняется нормальному закону распределения.
Определим величину oTpmin, при которой вероятность неравенства а<
<Отртш равна заданному значению Р=0,08. Из (2.52) и (2.53) получим
°Tpmin = °i ^Р°»т= О’® (втт1п "I" °гтах) + ~ •
При Р=0,08 по табл. 2.4 определяем, что ?₽«=—1,41. Тогда
585 — 560
erpmin == 0,о(560 585) — 1,41 = 566,63 МПа.
Вероятность того, что <тт>Отрт1п будет равна Р(ат><Ттрт»х) = 1—0,08=
=0,092, т. е. 92%.
ГЛАВА 3. КОНСТРУКЦИОННЫЕ МАТЕРИАЛЫ ДЕТАЛЕЙ
МЕХАНИЗМОВ ЛА
3.1. ТРЕБОВАНИЯ К КОНСТРУКЦИОННЫМ МАТЕРИАЛАМ
И ИХ ХАРАКТЕРИСТИКИ.
Выбор материалов для деталей машин и механизмов
ЛА определяется назначением конструкции, условиями ее экс-
плуатации и технологическими возможностями производства.
Поэтому технологические свойства материала при его выборе
определяют как возможность его модификации с целью улучше-
ния или придания изготовленной из него детали специальных
свойств; при этом трудоемкость и стоимость ее изготовления в
конкретных условиях производства должна быть оптимальной.
Основными характеристиками конструкционных материалов
являются:
1. Прочность, показателями которой являются: пределы
прочности св, текучести от и Сто,2, выносливости o-i; для жаро-
прочных материалов при высоких температурах показателями
являются: предел ползучести ое//, вызывающий деформацию е
(%) за t ч при температуре Т, предел длительной прочности одл,
или ot, т. е. предел прочности, вызывающий разрушение за t ч,
при температуре Т.
2. Контактная выносливость, показателями которой являют-
ся предел контактной выносливости онитв для базового числа
Циклов перемены напряжения NHo, а также твердость поверх-
ности по Бринеллю (НВ) или по Роквеллу HRC.
3. Жесткость, характеризуемая величиной модуля продоль-
ной упругости Е.
61
Таблица 3.1
Материал р, кг/м’-Ю-3 ав, МПа £• 10-4, МПа Коэффициент теплопровод- ности X, Вт/(м«С)
Сталь конструкцией- 7,8 320... 750 . 35
ная углеродистая каче-
ственная
Сталь конструкционная
легированная:
качественная 7,8 700... 1500 (20 ...21)
особо прочная 7,8 2000... 3000
Сплавы титана 4,54 800... 12000 11,5 7,5
Сплавы меди 8,8 300... 500 11 380
Алюминиевые сплавы 2,7 200... 500 7,1 120—170
Магниевые сплавы 1,8 100... 280 4,2 —
Текстолит ПТК 1,35 100 — —
Стеклопластики 1,6... 1,9 200... 950 — —
4. Ударная вязкость ая, показателем которой является
удельная работа по разрушению образца в поперечном сечении.
5. Пластичность материала, характеризуемая относительны-
ми удлинением б и сужением ф.
6. Износостойкость, косвенно характеризуемая твердостью
поверхности НВ или HRC и допускаемым давлением [р].
7. Фрикционные свойства, характеризуемые коэффициентом
трения f, допускаемым давлением [р] и скоростью скольжения
Ы-
8. Плотность р.
9. Удельные показатели прочности стт/р, ударной прочности
ств2/(2Ер), жесткости Е/р, Е/пв.
Таблица 3.2
Материал ат/р (^в/2ЕР)-103 (£/р)-103 (£/св).Ю-3
Сталь углеродистая обыкновенного качества 3,1 . .. 3,9 17,5... 29 2,7 3,3... 5,5
Сталь углеродистая 2,4.. ,. 18,8 11 ... 66 2,7 1,2... 6,6
конструкционная каче- ственная Сталь конструкцион- ная легированная 5,7.. .. 19,1 61 ...71 2,7 1,1... 3,5
Коррозионно-стойкие 3,6.. . 18,1 24 ...610 2,7 1,2... 11,0
жаропрочные и жаро- стойкие стали
Алюминиевые сплавы 4,1 . .. 22,5 3... 102 2,5-2,7 1,0... 4,4
Магниевые сплавы 4,7.. .. 13,8 44... 368 2.5-2,6 1,3... 3,5
Титановые сплавы 8,9.. , 32,2 1450... 1840 2,4-2,7 0,7... 0,8
62
10. Коррозионная стойкость, характеризуемая обычно поте-
рей массы, определяемой на единицу поверхности в единицу
времени.
11. Теплофизические свойства — теплостойкость, хладнолом-
кость, теплопроводность, удельная теплоемкость, термостабиль-
ность, определяемая коэффициентом линейного расширения
и др.
При изготовлении деталей машин общего назначения наи-
более широко используют металлы, сплавы цветных металлов,
пластмассы. В конструкциях современных ЛА применяют, глав-
ным образом, легкие алюминиевые сплавы, титан и его сплавы,
стали и их сплавы, пластмассы, древесину, композиционные ма-
териалы, керамико-металлические материалы (керметы) и др.
В табл. 3.1 и 3.2 приведены некоторые характеристики основ-
ных конструкционных материалов.
3.2. ЧЕРНЫЕ МЕТАЛЛЫ
К черным металлам относят железо и его сплавы:
чугун, сталь, сплавы, состоящие из легирующих элементов и
железа, в которых железа менее 50... 55%.
Чугун — сплав железа с углеродом (свыше 2%), обладаю-
щий хорошими литейными свойствами. Из-за недостаточной ме-
ханической прочности серые и ковкие чугуны с легирующими
добавками в авиационной технике применяют лишь в отдель-
ных случаях. Для деталей машин применяют серый и высоко-
прочный чугуны.
Конструкционные стали содержат углерода не более
0,7%, по химическому составу делятся на две основные груп-
пы: углеродистые, и легированные. Углеродистая делится на
обыкновенного качества и качественную. Легированная сталь
делится на низколегированную (легирующих элементов менее
3%), среднелегированную (легирующих элементов 3...5,5%) и
высоколегированную с содержанием легирующих элементов
свыше 5,5%.
Для исключения вредных примесей и повышения механиче-
ских характеристик стали и сплавов применяют улучшающую
обработку: электрошлаковый переплав, электронно-лучевой пе-
реплав, плазменно-дуговую плавку и др. Стали, полученные
указанным способом, используют для изготовления деталей и
узлов повышенной надежности, например подшипников каче-
ния авиационных двигателей.
Стали конструкционные углеродистые обыкновенного каче-
ства марок подразделяют на группы А, Б и В в зависимости
от нормируемых показателей. Они широко используются при
Изготовлении сортового и листового проката, а малоуглероди-
стые сорта хорошо свариваются.
63
Таблица 3.3
Марка стали Термообработка МПа ат, МПа МПа НВ (HRC) Примеры применения
Нормализа- ция 590 315 255 180 Стаканы подшип- ников качения, штиф-
45, 45А Термоулуч- шение 690 490 325 Не менее 220 ты, болты, винты, шпильки, гайки, ва- лы, полумуфты и др.
Закалка, средний отпуск Закалка ТВЧ 880 880 635 635 390 390 Не менее 270 (Не ме- нее 52)
65 Закалка, средний отпуск 980 635 490 290 Пружины, рессоры, диски и др.
65Г То же 1470 1270 580 440 То же и пружинные шайбы, стопорные кольца
10, 10А Нормализа- ция 335 205 157 130 Оггибные шайбы, шплинты, регулиро-
15, 15А > 370 225 175 137 вочные прокладки, заклепки, гнутые де- тали
20, 20А Нормализа- ция 410 245 195 145 Гнутые, сварные и штампованные дета- ли, крепежные дета- ли
45Л Нормализа- ция 540 295 235 153 Станины, корпусы, муфты, водила, ры- чаги и др.
Стали углеродистые качественные при С<0,3% отличаются
хорошей пластичностью и вязкостью, хорошо свариваются и
куются, однако не подвергаются закалке. Увеличение содержа-
ния С приводит к повышению прочностных характеристик, но
к снижению пластичности. Свойства стали повышают термиче-
ской обработкой. Углеродистые стали используются для дета-
лей малой и средней напряженности в общем машиностроении,
а в ЛА применяются ограниченно. Некоторые марки и меха-
нические характеристики приведены в табл. 3.3.
Сталь легированная конструкционная содержит примеси ле-
гирующих элементов, каждый из которых имеет условное бук-
венное обозначение (например, X — хром, М — молибден, С —
кремний, Н — никель, Г — марганец, Ю — алюминий, Т — титан,
Ф — ванадий, Р — бор). Легированные стали применяют при
требованиях высокой прочности или специальных свойств: теп-
лостойкости, жаропрочности, коррозионной стойкости, износо-
64
Таблица 3.4
Марка стали Термообработка <ТВ, МПа сгт, МПа <7-1. МПа НВ Применение
38ХА Закалка, высо кий отпуск - 930 785 420 300 Зубчатые коле- са, червяки, звез- дочки, валы и оси, водила, ходовые винты, кулачки, пальцы, вилки, бол- ты, винты, гайки и др.
15ХА Закалка, низки? отпуск Цементация, за калка, низкий от пуск 685 685 490 . 490 315 390 220 560
ЗОХГСА Нормализован- ные Термоулучшение Поверхностная* закалка ТВЧ, вы- сокий отпуск Закалка, низкий отпуск 685 910 1080 1660 490 765 830 1560 360 440 470 570 230 290 320 500 Клепаные и тон- костенные узлы из листов и труб, ка- чалки, рычаги, оси, валы, стаканы под- шипников, зубча- тые колеса и др.
20ХНЗА Закалка, высо- кий отпуск Цементация, по- верхностная за- калка, низкий от- пуск 930 930 735 735 410 520 280 560 Высокоответст- вённые и высоко- напряженные де- тали, испытываю- щие вибрационные и . динамические нагрузки, обла- дающие повышен- ной термостой- костью и прокали- ваемостью
12ХНЗА Термоулучшение Закалка, низкий отпуск Цементация, за- калка, низкий от- пуск 880 930 930 685 735 735 350 370 490 260 280 560
18Х2Н4МА 1 1 Закалка, высо- кий отпуск Закалка, низкий отпуск . Цементация, за- калка, низкий от- пуск Азотация после закалки и высоко- го отпуска 1030 ИЗО 1175 1030 785 835 980 785 510 550 610 570 290 320 560 580
38Х2Ю Закалка, отпуск Азотирование 900 750 430 • 210 Азотируемые и лиловые детали, >аботающие на из- ю с и выносли- вость
500 с
38Х2МЮА Закалка, отпуск Азотирование 1000 850 500 - Г 260 i 500 Е
3—1085
65
стойкости и др. Эти стали обычно эффективны после термиче-
ской обработки.
Хромистые стали (15ХА, 38ХА, ШХ15) обладают повышен-
ной прочностью, износостойкостью; при содержании хрома бо-
лее 13% являются коррозионно-стойкими.
Хромоникелевые стали (12ХНЗА, 12Х2Н4А, 20ХНЗА) соче-
тают высокую прочность и износостойкость с повышенной вяз-
костью, хорошо подвергаются закалке. Стали с молибденом или
вольфрамом (18Х2Н4ВА, 40ХНМА, 25ХНВА) обладают высо-
кими механическими и технологическими свойствами. Их при-
меняют для ответственных деталей, например валов редукто-
ров, турбин и компрессоров, шестерен, болтов и шпилек.
Хромомарганцево-кремнистые низколегированные стали ма-
рок 20ХГСА, 25ХГСА, ЗОХГСА обладают повышенной прочно-
стью и умеренной вязкостью. Они используются в сварных кон-
струкциях и при обработке деталей резанием; при содержании
углерода более 0,25% хорошо подвергаются отпуску и закалке.
Для азотируемых деталей используют хромоалюминиевые ста-
ли (38Х2ЮА) и стали с добавками молибдена (38Х2МЮА) и
ванадия (40ХФА).
Хромоникелевые коррозионно-стойкие (нержавеющие) стали
имеют высокую коррозионную стойкость (2X13, 4X13); жаро-
стойкие стали (1Х17Н2, Х18Н9, Х18Н9Т) обладают стойкостью
против химического разрушения поверхности.
Марки, механические характеристики и области применения
некоторых сортов легированных конструкционных сталей при-
ведены в табл. 3.4.
3.3. ТИТАН И ЕГО СПЛАВЫ
Титан обладает высокими прочностью, вязкостью с
малой, по сравнению со сталью, плотностью (4,5 г/см3) при
высокой коррозионной и повышенной термостойкости. Ряд спла-
вов титана обрабатываются давлением, свариваются аргонно-
дуговой и контактной сваркой, удовлетворительно обрабатыва-
ются резанием. Сплавы титана обладают высокой коррозион-
ной стойкостью. Это определило их применение в авиационной
технике. Напримёр, замена стальных валов на титановые в
главном приводе вертолета УС400 и зубчатых колес в плане-
тарном редукторе вертолета ВА105 позволила снизить массу и
повысить ресурс этих деталей. Зубчатые колеса из титановых
сплавов широко применяют во вспомогательных агрегатах вер-
толетов и самолетов. В США 45% общего объема сплавов ти-
тана используют в авиадвигателях и 35% — в вертолетах и са-
молетах. В перспективе сплавы из титана будут составлять 15%
всех применяемых в авиационной технике материалов, спла-
вы алюминия — 45%. К недостаткам титана и его сплавов сле-
66
дует отнести низкие теплопроводность и модуль упругости
(11,5-Ю4 МПа), плохие антифрикционные свойства. В конст-
рукциях ЛА используют сплавы титана с алюминием, марган-
цем, хромом, железом. Сплавы титана с дорогими и дефицит-
ными элементами (цирконием, ниобием, оловом и др.) исполь-
зуют при работе в агрессивных средах, при температурах жид-
кого гелия, а также в условиях высоких нагрузок и темпера-
тур. Они используются для изготовления обшивки высокоско-
ростных самолетов (М=3...4), передних кромок крыльев, ста-
билизатора, лонжеронов, нервюр, шпангоутов, перегородок, топ-
ливных баков, тяг, а также высоконагруженных болтов и шпи-
лек. Сплавы титана широко используют в двигателестроении
ЛА для изготовления деталей компрессора, камеры сгорания,
корпусных деталей и др.
По технологии изготовления титановые сплавы делят на де-
формируемые и литейные, а по механическим характеристи-
кам— на сплавы нормальной прочности, высокопрочные, жаро-
прочные, повышенной пластичности. Некоторые сплавы могут
упрочняться путем термической обработки (ВТ6, ВТ8, Вт9,
ВТ14, ВТ15, ВТ16). В табл. 3.5 приводятся марки и механиче-
ские характеристики некоторых деформируемых титановых
сплавов.
Таблица 3.5
Вид сплава Марка сплава ав, МПа ат, МПа а_р МПа Рабочая тем- пература, °C
Пластичные средней проч- ности ОТ4-1 ОТ4 ВТ5 600... 750 700... 900 700... 950 470... 650 550... 650 600... 850 210...250 240... 300 ДО 500 200... 300 до 400
Конструкци- онные повы- шенной прочно- сти ВТ5-1 ВТ4 ОТ4-2 ВТ6 750... 950 850... 1050 950... 1000 1100... 1150 650... 850 700... 800 900 1000... 1050 240... 300 до 500 300... 400 300... 400 400... 450,
Высокопроч- ные коррозион- но-стойкие и жаропрочные ВТЗ-1 ВТ8 ВТ9 1000... 1200 1000... 1150 1140... 1300 850 ...1100 850... 1050 1000 ...1150 260... 340 310 ...350 330... 370 600... 700 600... 700 600... 700
Высокопроч- ные, термически и механически обрабатывае- мые ВТ14 ВТ15 ВТ16 1150... 1400 1300... 1500 1250 ...1450 1080... 1300 1180... 1400 1100... 1200 340... 370 300... 400 300... 350 300... 400
3* 67
Таблица 3.6
Марка сплава ав, МПа б. % ан, Н-м/см2
ВТ1 400—600 15—23 50
ВТ5Л 700—900 6—12 30—35
ВТЗ-1Л 1000—1100 4—6 30
ВТЛ1 900—1000 5-10 15
ВТ21Л 1000—1100 4—7 20
Сплавы ВТ5 и ВТ5-1 имеют высокий предел ползучести, хо-
рошо свариваются аргонно-дуговой и контактной сваркой, удов-
летворительно обрабатываются резанием, хорошо работают при
низких температурах. Сплав ВТ4 имеет хорошую пластичность,
удовлетворительно сваривается. Сплав ВТ6 с повышенной жа-
ропрочностью имеет хорошую пластичность при 950... 980°С, но
плохо сваривается. Он используется для изготовления крепеж-
ных деталей и деталей обшивки ЛА. Сплавы ВТ8, ВТ 14, ВТ 15,
ВТ 16 деформируются в горячем состоянии, свариваются кон-
тактной сваркой и обрабатываются, прокатываются.
Литейные титановые сплавы имеют хорошие литейные ка-
чества (высокую жидкотекучесть и плотность) и используются
для изготовления заготовок и фасонных отливок. Ввиду склон-
ности к поглощению газов и взаимодействию с формовочными
материалами плавку и разливку их ведут в вакууме или в среде
нейтральных газов.
3.4. МЕДЬ И ЕЕ СПЛАВЫ
Медь отличается высокой электропроводностью и теп-
лопроводностью, диамагнитными свойствами, хорошим сопро-
тивлением коррозии, пластичностью. В механизмах ЛА приме-
няются сплавы меди: бронзы и латуни.
Бронзой называют сплавы меди с различными элементами,
кроме цинка (некоторые специальные сплавы меди с марган-
цем и никелем также имеют другие названия). В обозначение
марки бронзы входят буквы Бр, а также обозначения А — алю-
миний, Б — бериллий, Ж— железо, К — кремний, Мц — марга-
нец, Н — никель, О — олово, Ц — цинк, Ф — фосфор. Бронзы
обладают хорошими антифрикционными, антикоррозионными и
литейными свойствами, а ряд марок (бериллиевые)—и упру-
гими. Они применяются для изготовления опор с трением сколь-
жения, венцов червячных колес, гаек винтовых передач, пружин
(табл. 3.7).
Оловянистые бронзы, содержащие 4... 12% олова, хорошо ра-
ботают при высоких скоростях скольжения без заедания. Вви-
68
Таблица 3.7
Марка сплава Вид полуфаб- риката °в. МПа °Т’ МПа Е, МПа Свойства
БрОФ 6,5-0,15 Прутки, ПОКОВКИ 420 300 1,12-10’ Хорошая прира- батываемость и об-
БрОЦ4-3 То же 440 310 1,1-10’ рабатываемость резанием, высокие антифрикционные свойства (без смазки f=0,l ... 0,12)
БрАЖ9-4 Прутки, поковки 440 340 1,14-10’ Повышенная прочность, пригод- ность к повыше-
БрАЖМц 10-3-1,5 Прутки, лента 590 315 1,08-10’ нию твердости и прочности термо- обработкой; при-
БрКМцЗ-1 Полоса, лента 620 240 1,04-10’ рабатываемость и антифрикционные свойства хуже, чем
БрБ2 То же 980 360 1,35-10’ у оловянистых бронз (без смазки f=0,18... 0,2)
БрАЖ9-4П Литье в кокиль 500 250 1,1-10’ Хорошие литей- ные свойства:
БрАЖН10-4-4П То же 600 350 1,16-10’ литье в песчаные формы, в кокиль
Таблица 3.8
Марка Состояние поставки ов, МПа б. % Область применения
ЛАЖ60-1- 1Л Литье в кокиль 420 18 Арматура, втулки, подшип- ники
ЛС59-1Л Литье под дав- лением 200 6 Детали, изготовляемые лить- ем под давлением: арматура,
ЛМцОС58-2- 2-2 Литье в кокиль 294 4 втулки, сепараторы подшипни- ков, зубчатые колеса
Л63 Прессованные прутки 300 30 Детали, изготовляемые реза- нием, штамповкой, вырубкой:
ЛСбЗ-З Тянутые твер- дые прутки 600 1 платы, втулки, крепежные де- тали, шестерни, пружины
Л63 7 о же 450 9
ЛАЖ60-1-1 Прессованные прутки 450 18
69
ду дефицитности применение оловянных бронз ограничено.
Бронзы безоловянистые имеют более высокие механические
характеристики по прочности, твердости, упругости. Однако они
хуже работают на скольжение, возможны заедания.
Латуни — сплавы на основе меди и цинка — немагнитны, об-
ладают высокими механическими и технологическими свойст-
вами. Латуни также обладают высокой коррозионной стойко-
стью и используются для изготовления арматуры, втулок, пру-
жин и других деталей в авиационном приборостроении. Постав-
ляются в виде прутка, лент, полос, проволоки, труб, а литей-
ные— в чушках (табл. 3.8).
3.5. АЛЮМИНИЯ. МАГНИЙ И ИХ СПЛАВЫ
Алюминий в чистом виде (марки АДО, АД1 с содер-
жанием алюминия более 99,5%) ввиду его низкой механиче-
ской прочности практически используется мало. Применяют в
основном сплавы алюминия с медью, кремнием, марганцем и др.
Для некоторых марок алюминиевых сплавов удельные показа-
тели прочности выше, чем у стали. Поэтому сплавы алюминия
применяют в ЛА, летающих на дозвуковых и умеренных сверх-
звуковых скоростях при температурах нагрева не свыше 150...
200°С. Сплавы алюминия обладают высокой коррозионной стой-
костью, хорошо обрабатываются резанием и давлением, свари-
ваются, паяются, ряд сплавов обладает хорошими литейными
свойствами. По технологическим свойствам различают сплавы
алюминия литейные и деформируемые, а по основным компо-
нентам— силумины (в основном алюминий — кремний) и дю-
ралюмины (в основном алюминий — медь — марганец). Литей-
ные алюминиевые сплавы АЛ предназначены для фасонного
литья и разделяются на пять групп в зависимости от основы:
I —Al—Si; II —Al—Mg; III —Al—Си; IV —Al—Si—Си; V —
Al—Ni—Zn—Fe (табл. 3.9).
Таблица 3.9
Марка сплава ав, МПа б, % Твер- дость, НВ Марка сплава ав, МПа б, % Твер- дость, НВ
АЛ2 130 6,0 50 АЛЮ 320 8,0 80
АЛ4 180 3,0 60 АЛЮ 360 5,0 100
АЛ4 260 4,0 70 АЛ32 270 3,0 80
АЛ5 220 1,0 80 ВИ11-3 240 3,0 95
АЛ7 220 8,0 65 В-300 180 ’0,6 —
АЛ7 250 ’ 5,0 80 В-300 220 0,6 —
АЛ8 АЛ9 320 200 12,0 6,0 70 55 В14А 170 0,8 —
70
АЛ4 и АЛ5 являются сплавами повышенной прочности. Они
применяются для изготовления корпусных деталей крупных и
средних двигателей, подверженных значительным нагрузкам.
Выдерживают температуры до 200... 250°С. Сплавы АЛЗ и АЛб
имеют хорошие литейные свойства, среднюю механическую
прочность. Они применяются для средних и мелких деталей
двигателей и механизмов ЛА, не подверженных значительным
нагрузкам.
АЛ7, АЛ8, АЛ9 используют для литья деталей типа крон-
штейнов, корпусов редукторов, качалок, педалей и др.
Сплав ВИ-11-3 обладает высокой коррозионной стойкостью,
хорошими литейными свойствами (литье в землю, кокиль или
под давлением) и повышенной прочностью; удовлетворительно
сваривается аргонно-дуговой сваркой и хорошо обрабатывает-
ся резанием.
Сплав АЛ 19 обладает высокими механическими характери-
стиками, жаропрочностью, однако имеет низкую коррозионную
стойкость и невысокие литейные качества. Он хорошо сварива-
ется и обрабатывается резанием; применяется для деталей ЛА,
работающих при 175... 300°С.
Деформируемые алюминиевые сплавы (табл. 3.10) поставля-
ются в виде листового проката, проволоки, фасонного профиля
и труб, в основном изготовленных прессованием. Сплавы по-
ставляются повышенного качества (А), мягкими отожженными
(М), полунагартованными — степень обжатия 40% (П) и нагар-
тованными — степень обжатия 80% (Н).
Сплав АМц обладает высокой пластичностью в отожженном
состоянии (АМцМ) и низкой — в нагартованном состоянии
(АМцН), хорошо сваривается, подвергается ковке и штамповке.
Сплав АМг также обладает хорошей пластичностью, хорошо
сваривается. Сплав АВ имеет высокую пластичность в отож*
женном состоянии и среднюю после закалки и старения, хоро-
шо сваривается точечной и атомно-водородной сваркой, куется
и штампуется при 470... 475°С. Сплав Д16 — дюралюмин повы-
шенной прочности. В отожженном состоянии он имеет сред-
нюю пластичность и пониженную обрабатываемость, в закален-
ном и нагартованном состояниях — обрабатываемость удовлет-
ворительная. Хорошо работает при низких температурах. Сплав
применяют для изготовления силовых элементов конструкции
ЛА.
Сплав В95 — высокопрочный после термической обработки,
среднепластичный в отожженном и свежезакаленном состояни-
ях; хорошо обрабатывается резанием и сваривается точечной
сваркой.
Алюминиевые сплавы для ковки и горячей штамповки обоз-
начаются АК (АК4, АК6, АК8). К этой группе относится так-
же сплав Д20. Жаропрочный сплав АК4 удовлетворительно
71
Таблица 3.10
Марка ав, МПа <тт, МПа 6, % Область применения
АДО АД1 60 — 25 Ненагруженные детали, требующие материала с вы- сокими пластическими свой- ствами
АМц 100 — 20 Детали, изготовляемые глубокой вытяжкой и гиб- кой
АДЗЗ 180-270 ПО... 230 15... 10 Профили сложной формы, требующие высокого преде- ла текучести
АМгЗ АМг5 АМгб 180 250... 270 290... 320 80 ПО... 120 120... 160 13 10... 15 11... 15 Сварные мало- и средне- нагруженные детали
АВ 180... 300 — 12... 14 Средненагруженные дета- ли высокой пластичности
Д1 360... 380 200... 220 10... 12 Детали средней прочности
Д16Т 400... 430 250... 300 6... 10 Детали повышенной проч- ности при переменных на- грузках и низких темпера- турах
В95 500... 540 400... 430 4... 6 Нагруженные детали, дли- тельно работающие при 120°С, клепаные конструк- ции
АК4 320... 360 — 8 Штампованные и кованые детали, работающие при повышенных температурах (до 350°С)
АК8 420... 460 200 10 Высоконагруженные штампованные детали
72
сваривается атомно-водородной сваркой. АК6 — сплав с хоро-
шей пластичностью; применяются для изготовления штампо-
ванных и кованых деталей сложной формы. АК8— сплав с
большой прочностью, обрабатывается давлением в горячем со-
стоянии.
Сплавы магния благодаря малой плотности, высокой удель-
ной прочности, хорошим литейным качествам используют в
авиационном приборостроении для литья корпусов, крышек, ар-
матуры и других деталей. Магниевые сплавы склонны к по-
верхностному окислению, поэтому требуют защиты поверхности
от разрушения. Для этой цели используются специальные виды
покрытий. Сплавы магния делятся на деформируемые и литей-
ные. Деформируемые сплавы марок MAI, МА2, МА5, МА8 наи-
более распространены и поставляются в виде плит, полос и
горячепрессованных профилей.
Литейные магниевые сплавы марок МЛ2, МЛЗ и МЛ4 ис-
пользуют для деталей средней нагруженности, МЛ5 и МЛ6 —
для высоконагруженных деталей, в том числе корпусов редук-
торов ЛА. Магниевые сплавы МЛ 12 и МЛ 15 (ов=250...
290МПа) могут также работать при 200... 250°С.
Сверхлегкие магниево-литиевые сплавы марок ИМВ1.ИМВ2,
ИМВЗ с р=1,4... 1,65 г/см3 хорошо обрабатываются давлением
и свариваются аргонно-дуговой сваркой.
3.6. КОМПОЗИЦИОННЫЕ ПОЛИМЕРНЫЕ МАТЕРИАЛЫ
В настоящее время требования к летно-техническим
характеристикам ЛА опережают темпы развития традиционных
конструкционных материалов: физико-механические характери-
стики традиционных конструкционных материалов улучшились
незначительно. Так, прочность алюминиевых сплавов за послед-
ние 20... 25 лет возросла на 100... 150 МПа. Прочность конструк-
ционной стали и титановых сплавов повысилась на 300 МПа.
Этим объясняется повышенный интерес к композиционным по-
лимерным материалам (КПМ), механические характеристики
которых в ряде случаев выше, чем у алюминиевых и титановых
сплавов. Применение КПМ для изготовления деталей ЛА име-
ет также следующие преимущества: низкая трудоемкость и воз-
можность автоматизации производства деталей и программно-
го управления; меньшие капитальные затраты на организацию
участков и цехов по производству изделий из КПМ; высокий
коэффициент использования материала, близкий к 1; повыше-
ние технического уровня и качественных показателей деталей
благодаря снижению массы, повышению коррозионной стойко-
сти, долговечности, расширению функциональных возможно-
стей. Их особенностью является и то, что при создании деталей
из КПМ можно исключить стадию получения исходного мате-
73
Таблица 3.11
Материал р, г/см® Разрушающее напряжение. МПа Д-10-®, МПа Теплостойкость*. Способ пере- работки**
при растяже- нии ав при сжатии °В.СЖ при изгибе
морозостойкость °C
Полиэтилен высокой плотности 0.95 22... 30 25... 60 20... 35 при изгибе 0,55... 0,75 128 —60 1—7
Фторопласт-4 2.19 21... 25 12 14 0.5... 0,8 250 (М) —269 2,6
Поливинилхлорид Полиметилметакрилат 1,4 1.18 40... 70 42... 70 70 ...130 100... 120 90... 120 2... 3,5 60... 80(B) —10 70 —40 4, 6, 7, 8 2, 4, 5, 6, 7
Полиамиды 610 кпс-зо 1,2 1.36 50... 90 130 80 ...90 195 70... 100 245 1,2... 1,9 8.3 70(М) — (40 .'.60) 200 (М) —2 1-7 1-7
Полиамиды ПМ-67 1.39... 1,41 100... 130 200... 230 180... 230 2...3 280(B) 1» 2
ПМ-69 1,38... 1,41 90... 125 210... 240 180... 230 2...3 280(B) 1, 2
Поликарбонаты 1,4 90 ...ПО 120... 140 150... 200 2,2... 2,4 150(р) —60 1, 4—7
Гетинакс 1,3... 1,45 70... 100 — 105... 125 1,2... 2,1 150 -60 2, 4, 5, 6, 7
Текстолит ПТК 1,3 ...1,4 68... 100 120... 180 120... 160 4... 6,5 130 —60 2, 4, 5, 7
Стеклотекстолит КАСТ 1,8 150... 250 — — 1,6 ...2 250 —60 2, 4, 5, 7
Волокниты 1,7... 1,9 78... 80 по... 12а ПО... 120 34,3 280 —60 2, 4, 5
Аминопласты А, Б, В 1,6 ...1,8 32... 38 90... 100 60... 70 7,4 ... 9,8 100... 140(М) 2
• М — по Мартенсу, В — по ВИка, р — температура работоспособности. 1—литье под давлением; 2 —прессова-
ние; 3 — экструзия; 4 — штамповка; 5 — механическая обработка; 6 — сварка; 7 — склеивание.
сл _________________________________________________________________________________________________________________________
риала, совместив ее со стадией формирования конкретной де-
тали. Для такой детали можно определить оптимальную струк-
туру армирующих волокон и связующего, качественное и коли-
чественное их соотношение, упаковку и ориентацию волокон,
оптимальные параметры технологического процесса получения
деталей из КПМ.
КПМ представляют собой композиции на основе полиме-
ров— высокомолекулярных органических и элементоорганиче-
ских соединений, включающие в себя наполнители, стабилиза-
торы, пластификаторы, красители и другие компоненты. Термо-
пластичные полимеры способны многократно размягчаться. Ре-
актопласты под влиянием нагрева необратимо отверждаются
и не могут быть использованы повторно. К термопластичным
пластмассам относятся полиэтилен, винипласт, ряд марок фто-
ропласта, полиметилметакрилат (оргстекло), полиамиды, поли-
имиды, поликарбонаты (табл. 3.11). Наполнителем в них служит
бумага, ткани, древесный шпон, волокна (текстильные, стек-
лянные, асбестовые) или мелкие частицы в виде муки (древес-
ной, минеральной и др.). Широкое применение пластмасс свя-
зано с их технологическими преимуществами и широким диа-
пазоном физико-механических свойств. К недостаткам КПМ от-
носят низкие теплопроводность и теплостойкость, старение, ани-
зотропность, ползучесть.
Полиэтилен и поливинилхлорид (винипласт)—материалы с
высокой химической стойкостью; они используются при невысо-
ких температурах в виде прокладок, труб, пленок. Фторопласт
имеет ряд модификаций; основные из них фторопласт-4 (отно-
сящийся к термореактивным пластмассам), фторопласт-40,
фторопласт-42. Фторопласт-4 отличается высокой химической
стойкостью, повышенными тепло- и морозостойкостью, малым
коэффициентом трения (может работать без смазки), при дли-
тельном нагружении склонен к ползучести. Фторопласт-40 и
фторопласт-42 имеют повышенные механическую прочность, ра-
диационную стойкость и ползучесть.
Полиметилметакрилат (оргстекло) — прозрачный полимер,
изготовляемый обычно в виде листов толщиной 0,8... 24,0 мм.
Полиамиды — литьевые пластмассы, допускающие наполне-
ние стекловолокном (КПС-30), графитом, тальком, дисульфидом
молибдена и другими наполнителями, придающими им повы-
шенные триботехнические и прочностные свойства. Полиамиды
применяют для изготовления подшипников, уплотнений, зубча-
тых колес, роликов, муфт, звездочек, втулок, блоков и других
деталей. Литые детали из полиамидов используются как амор-
тизаторы, снижающие вибрацию машин.
Полиимиды — термостойкие пластмассы, используемые в ка-
честве прессовочных и литьевых материалов (ПМ-67 и ПМ-69).
Допускают с целью снижения коэффициента трения наполне-
76
ние графитом (ПМ-67-Г-40) и дисульфидом молибдена
(ПМ-67-ДМ-3). Коэффициент трения без смазки 0,15...0,2, со
смазкой 0,05... 0,12.
Поликарбонаты для повышения механических свойств на-
полняют стекловолокном (СТН-30).
Свойства термопластов можно регулировать пластификаци-
ей, ориентационной вытяжкой и другими способами.
К реактопластам относят фторопласт-4, гетинакс, текстолит,
стеклотекстолит, волокниты, аминопласты и др.
Гетинакс состоит из наполнителя в виде бумаги, пропитан-
ной фенолформальдегидной смолой; в текстолите наполнителем
является хлопчатобумажная ткань, а в стеклотекстолите — стек-
лоткань. Изготовляются эти пластмассы методом горячего
прессования в виде листов, блоков, прутка, труб. Волокниты
имеют наполнитель в виде крошки, волокон, нитей. Аминопла-
сты имеют минеральный или органический наполнитель и ле-
Таблица 3.12
Детали
Зубчатые и червячные колеса
Шкивы, маховички, ступицы
Подшипники скольжения, вкладыши
Детали шарикоподшипников
Тормозные колодки, накладки
Облицовка барабанов, шкивов трения
Трубы, фитинги, детали арматуры, фильтры,
вентили и другие детали масляных и водных си-
стем
Уплотнения (манжеты, прокладки, сальниковые
набивки), мембраны, антикоррозионные покрытия
металлических деталей, облицовка аппаратуры
Износоустойчивые покрытия металлических из-
делий
Рукоятки, штурвалы, кнопки, колпачки
Пружины, рессоры
Кулачковые механизмы, клапаны и другие де-
тали машин, воспринимающие ударные нагрузки
Крупногабаритные элементы конструкций, несу-
щие нагрузки корпуса, емкости и т. д.
КПМ*
1, 9, 10, 11, 16, 17, 20, 21
4, 9, 11, 12, 14-18, 20
1, 3, 11, 12, 14, 17
1, 9, 11 ♦
15, 22
5, 15, 20, 22
1, 7, 9, 12, 13, 18
1—5, 8, 9
1, 3, 7, 8, 9, 10, 11
4, 6, 7, 11—14, 16, 18
24, 25
1, 6, 9Г—11, 14
20, 23, 24, 25
* 1 — полиамиды; 2 — полиэтилены; 3 — фторопласты; 4 — винипласты
жесткие; 5 —винипласты пластифицированные; 6 — полистирол и его сополи-
меры; 7 — акрипласты; 8"— эпоксипласты; 9 — пентапласты; 10 — поликарбо-
наты; 11 — полиформальдегиды; 12—пресс-порошки фенольные; 13 — пресс-
порошки карбамидные; 14 — волокниты; 15 — асбоволокниты; 16 — стеклово-
локниты; 17 — текстолитовая пресс-крошка; 18 — древесная пресс-крошка;
19 — гетинакс; 20 — древесно-слоистые пластики; 21 — текстолит; 22 — асбо-
текстолиты; 24 — угле- и стеклопластики; 25 — стеклопластики листовые, на-
мотанные из стекломатов на связующем контактного типа.
77
Таблица 3.13
Материал р, г/см’ <тсж. МПа ар, МПа £, МПа <Ур/р, МПа-см’/г Е/р. МПа*см’/г
Сталь ЗОХГСА 7,85 1200 1050 210 155 25
Титановый сплав ВТ-4 4,50 1800 1800 ПО 400 25
Алюминиевый сплав АМг-6 Стеклопластик на основе: 2,70. 320 320 70 120 . * 26
хаотичных воло- кон АГ-4С 1,75 270 200 24 150 14
ткани ТС 8/3 1,80 500 300 25 240 11,5
однонаправлен- ных волокон ВМП 2,21 1600 700 66 724 27,1
Углепластик ВМП-5 1,5 1100 200 170 733 ИЗ
Боропластик 2,0 1200 800 200 600 100
Органопластик 1,35 1500 200 80 1100 59,7
гирующие добавки. Прессовочные массы пластмасс поставля-
ются в виде порошков, крошки, пучков. Для изготовления де-
талей в зависимости от вида и марки пластмасс могут исполь-
зоваться литье под давлением, прессование, напыление, экстру-
зия, выдувание, механическая обработка, сварка и склеивание.
Области использования КПМ для деталей ЛА приведены в
табл. 3.12.
Таблица 3.14
Материал Р, г/см8 ар. МПа МПа Е, МПа Gp/plO-’, МПа*см’/г £/р-10-\ МПа*см’/г ь.108 Е
Сталь с упроч- нением термооб- работкой Алюминиевый 7,85 1100 300 210000 153 267 1,43
2,77 393 72000 145 267 —
сплав 2024-76
Стеклопластик «Э> 1,85 380 — 27500 206 149 ——
Стеклопластик ЭФ 32-301 1,85 500 120 35000 270 189 1,9
Стеклопластик СК-5-2113 1,95 1000 180 50000 513 256 3,6
Углепластик КМУ-3 1,4 800 — 120000 570 857 3,0
Орга нит 7Т 1,25 520 — 30000 416 240 —
Боропластик 2,0 1300 400 260000 » 650 1300 1,54
78
Особенностью КПМ является возможность достижения и
обеспечения наиболее полного соответствия их свойств характе-
ру и условиям работы деталей ЛА. Используя различные мат-
рицы, вырьируя содержание армирующих волокон, их ориен-
тацию, сочетая в одной матрице волокна с различными упруго-
прочностными свойствами, можно создавать материалы с за-
данным комплексом свойств.
В табл. 3.13 и 3.14 для сравнения приведены свойства неко-
торых металлических сплавов и композиционных материалов
на основе тканых наполнителей. Из таблиц видно, что КПМ
имеют высокие показатели удельной прочности и жесткости.
Кроме того, они обладают низкой чувствительностью к концент-
раторам напряжений, высокой стойкостью к воздействию ат-
мосферы, хорошие удельные прочности и жесткости.
Эффективность применения тех или иных конструкционных
материалов наиболее наглядно можно оценить по возможности
снижения массы агрегатов ЛА при сохранении показателей
прочности или уменьшения трудоемкости изготовления. Иссле-
дования показали эффективность применения для изготовления
деталей ЛА КПМ на основе стеклянных, углеродных, органиче-
ских волокон и полимерных матриц.
3.7. АНТИФРИКЦИОННЫЕ И ФРИКЦИОННЫЕ
МАТЕРИАЛЫ
Антифрикционные и фрикционные материалы, исполь-
зуемые в узлах трения машин, должны обладать свойствами
минимизации или максимизации коэффициента трения и по-
вышенной износостойкостью при длительной безотказной рабо-
те узла трения. При этом антифрикционные (подшипниковые)
материалы, предназначенные для работы в узлах трения сколь-
жения, должны обладать наименьшими коэффициентом трения
и износом, а фрикционные (тормозные), применяемые в тор-
мозах, фрикционных передачах, муфтах, требуют материалов
с высоким коэффициентом трения и минимальным изнашива-
нием.
Для подшипников тихоходных и слабо нагруженных пере-
дач применяются латуни и бронзы. Для подшипников и подпят-
ников при больших скоростях и нагрузках применяют специаль-
ные антифрикционные сплавы:
алюминиевые — АОЗ-7, АО9-2, АО6-1 и др.;
баббиты оловянные, свинцовые и кальциевые марок Б88,
Б83, БКА и др.;
цинковые ЦАМ9-1, ЦАМ10-5Л и др.; антифрикционная ме-
таллокерамика (железографитовая и меднографитовая). Марки
и свойства металлокерамических материалов приведены в табл.
79
Таблица 3.15
Марка ме- таллокера- мики Допускаемое удельное давление, МПа Твердость, НВ Материал контртела Коэффициент трения f
со смазкой без смазки
Железо- графитовые МФ-15 0,5 130... 160 чугун СЧ — * 0,26... 0,45
МП-11 1,0 15... 20 18..,. 40 НВ 250... 270 Ст35 0,10... 0,13 0,3
Медногра- фитовые МК-5 15... 20 стали 0,08... 0,12 0,16... 0,32
ФАБ-1 40 80 ...90 65Г; 45 То же 0,08... 0,9 —
углеродные (углеграфитные) антифрикционные материалы,
работающие в интервале температур от —200 до 2000°С при
скоростях скольжения до 100 м/с и в агрессивных средах. Ма-
териалы имеют плотность 1,65... 3,1 г/см3, предел прочности
LOO... 200 МПа в зависимости от марки материала. Углеродные
обожженные материалы марок АО-1500, АО-600 и графитизи-
рованные марок АГ-1500 и АГ-600 могут пропитываться бабби-
том Б83 и сплавом СО5 (95% РЬ и 5% Sn).
Графитофторопластовые антифрикционные материалы яв-
ляются полимерными композициями фторопласта-4 и углерод-
ных наполнителей (марки 7В-2А, АФГМ и АФГ-80ВС).
Графитопластовые антифрикционные материалы на эпоксид-
но-кремнийорганическом связующем работают при температу-
рах до 200°С (АМС-1, АМС-3, АМС-5), антифрикционные час-
тично графитизированные материалы работают в агрессивных
средах при температурах до 300°С, высоких скоростях и дав-
лениях (НИГРАН, НИГРАН-В).
Применяют новые композиционные материалы на основе
алюминия или бронзы, содержащие дисперсный порошок либо
нитевидные криста'ллы графита как твердую смазку.
Эксплуатация машин с узлами трения при низких и высоких
температурах и в вакууме требует соответствующих антифрик-
ционных покрытий. Эти покрытия представляют собой пленки,
образующиеся после высыхания суспензии антифрикционных
порошков и пленкообразующей композиции, которые обладают
свойствами твердых смазочных материалов. К ним относятся:
дисульфидмолибденовое антифрикционное покрытие ВНИИ
НП-209 на основе кремнийорганического связующего. Предназ-
начено для узлов трения с возвратно-поступательным движени-
80
Таблица 3.16
Марка материала р, г/см3 ап.сж» МПа ап н, МПа Ор, МПа £-10-з, МПа
АО-1500 1,65... 1,7 150... 180 60 ... 80 16
АГ-1500 1,7... 1,8 80... 100 40... 50 13
АПГ 1,8... 1,9 85... 105 45... 55 20... 25 11
Химанит-Т 1,85... 1,9 130... 170 — 32... 38 —
ем. Работоспособно при температурах от —70 до 850°С и в ва-
кууме до 900°С;
дисульфидмолибденовое антифрикционное покрытие ВНИИ
НП-230 на основе эпоксидной смолы. Используется для раз-
личных узлов трения скольжения в условиях радиационного об-
лучения. Работоспособно при температурах от —60 до 250°С;
дисульфид молибдена — эффективная твердая смазка для
узлов трения, работающих в жестких условиях. Может исполь-
зоваться в смеси со связующими материалами;
твердые смазки на основе мягких металлов — золота, сереб-
ра, индия, фториды вида CaFr, BoFr.
Для деталей узлов трения, работающих в сложных усло-
виях, применяют самосмазывающиеся антифрикционные мате-
риалы на основе углерода, которые имеют повышенные плот-
ность, твердость и теплопроводность (табл. 3.16).
Фрикционные материалы применяются, главным образом,
в различного вида тормозных устройствах. Изыскание фрикци-
онных материалов с большим коэффициентом трения, высоки-
ми износоустойчивостью, теплостойкостью, надежностью акту-
ально для современного самолетостроения. Так, для обеспече-
ния нормальной посадки самолета один тормоз за 25... 30 с дол-
жен совершить работу до 107 Н-м. Для решения этих задач
могут использоваться следующие материалы:
ретинакс — асбосмоляная композиция с включением латун-
ной проволоки (тип А); в паре с чугуном 4НМХ допускает тем-
пературу трения до 1100°С при скорости скольжения до 50 м/с
и давлении до 2,5 МПа. Коэффициент трения меняется в зави-
симости от температуры: /=0,4 при t= (100... 300)°С, /=0,3...
0,2 при /= (300... 500)°С;
металлокерамические материалы на основе железа исполь-
зуются в тормозных устройствах в паре с чугуном ЧНИМХ или
сталью 3X13: ФМК8, ФМКИ, ФМКПМ, МКВ50А и др. Пере-
численные материалы допускают удельную мощность трения
300 Н-м/см2, давление 130 Па, объемную температуру 500°С,
скорость скольжения 30 м/с и удельную работу трения 5Х
ХЮ3 Н-м/см2 (табл. 3.17).
81
Таблица 3.17
Пара тревия Коэффициент трения f Твердость диска, НВ
Твердость контртела, НВ
ФМК8-ЧНМХ 0,16... 0,2 60-85
160... 220
фмки—чнмх 0,25... 0,29 65... 95
160... 220
фмким—чнмх 0,22... 0,27 65... 95
160... 220
ФМК11—3X13 0,18... 0,22 65... 95
270 - 300
МКВ50А—ЧНМХ 0,34... 0,38 70... 85
160... 220
3.8. НОВЫЕ МАТЕРИАЛЫ ДЛЯ ДЕТАЛЕЙ ЛА,
РАБОТАЮЩИХ В ЭКСТРЕМАЛЬНЫХ УСЛОВИЯХ
Детали ЛА могут эксплуатироваться в экстремаль-
ных условиях:
при температурах —(80... 50)°С и ниже;
при кратковременном нагреве до температуры 500... 1000°С
и длительном—до температуры 300... 500°С;
в вакууме;
при радиационном воздействии на материалы.
Для обеспечения надежной работы деталей в таких усло-
виях требуются материалы, обладающие соответствующими
свойствами. При снижении температуры у конструкционных ма-
териалов (стали, титановые и алюминиевые сплавы) величины
<Гв, От, 1 и Е могут несколько повышаться, однако ударная
вязкость при этом снижается, причем особенно резко при тем-
пературах ниже —60°С. Снижение ударной вязкости при этих
температурах у легированных сталей зависит от ее марки и
может составлять 25% и более. Поэтому для изготовления де-
талей, работающих при низких температурах, рекомендуются
материалы с высокой ударной вязкостью (стали марок 12ХНЗА,
Х18Н10Т, 18Х2Н4ВА, ОН6А, ОН9А, сплавы титана ВТ6, ВТ5-1,
алюминиевые сплавы Д16Т, АМгб и др.).
Для изготовления деталей, работающих при 500°С, исполь-
зуются жаропрочные и теплостойкие стали, а также специаль-
ные сплавы, композиционные материалы и металлокерамика.
Так, жаропрочный деформируемый сплав ЭП-800 может дли-
82
тельное время работать в нагруженном состоянии при темпе-
ратурах до 80(гС, имея при 200°С ав=1150 МПа, а при 800...
850°С ов=750... 950 МПа; его предел длительной прочности за
время, соответствующее 20-103 циклов при 800°С, более
900 МПа. Сплавы 75Х28Л и 185Х34Л также отличаются высо-
кими жаростойкостью (до 1100°С) и прочностью.
На основе алюминия используются спеченные сплавы, об-
ладающие высокими жаропрочностью и коррозионной стойко-
стью. Так, деформируемый жаропрочный сплав САП из алю-
миниевого порошка, получаемый прессованием со спеканием
при 500... 600°С, может длительно работать при ЗОО...55О°С и
кратковременно — при 700... 1100°С (у сплава САП-3 ав=
= 130 МПа при 500°С).
На основе алюминия изготовляются также композиционные
материалы, имеющие волокнистые или нитевидные наполнители
из окиси алюминия, углерода, вольфрама, бора и др. Так, сплав
ВКА-1 на основе алюминия с волокнами бора имеет при тем-
пературе 500°С предел прочности в 2...3 раза выше, чем у
обычных алюминиевых сплавов (ов=600 МПа при 400°С).
Металлокерамика обладает высокими химическими и тер-
мохимическими свойствами при высоких температурах. Карби-
ды, бориды, нитриды, силициды и другие окислы, входящие в
состав металлокерамики, придают им жаростойкость, а ме-
таллы— жаропрочность. Наиболее качественны такие материа-
лы на основе алюминия, циркония, бериллия и других метал-
лов (железа, кобальта, никеля, хрома) с характеристиками:
св=1225 МПа при 980°С, ов=490 МПа при 1200°С. Исполь-
зуется также волокнистая металлокерамика на основе нитевид-
ных волокон из алюминия, меди, коррозионно-стойкой стали.
ГЛАВА 4, ИСПОЛЬЗОВАНИЕ ЭВМ И САПР
ПРИ КОНСТРУИРОВАНИИ И РАСЧЕТАХ
ДЕТАЛЕЙ МЕХАНИЗМОВ ЛА
4.1. ЗАДАЧИ ПРОЕКТИРОВАНИЯ, РЕШАЕМЫЕ
С ПОМОЩЬЮ ЭВМ И САПР
Развитие авиационной техники сопровождается ус-
ложнением всех систем самолета и его элементов. Возрастает
и трудоемкость создания современных ЛА при одновременном
повышении требований к их качеству, эффективности, сокра-
щению сроков разработки и промышленного освоения. Выпол-
нение этого комплекса задач базируется на широком внедре-
нии в проектирование вычислительной техники. Основное на-
правление— создание систем автоматизированного проектиро-
83
вания (САПР), позволяющих повышать качество, сокращать
сроки проектирования, снижать трудоемкость и стоимость про-
ектных разработок [33].
Использование САПР сокращает сроки проектирования и
доводки самолетов в 2...3 раза, а подготовки производства —
в 3...5 раз. Так, с помощью специальной САПР, разработан-
ной фирмой «Локхид», компоновочные чертежи небольшой слож-
ности выполняются в 10... 13 раз быстрее, а выпуск деталиро-
вочных чертежей — в 10... 17 раз. На фирме «Боинг» автомати-
зированное проектирование составляет более 60% общего
объема работ.
При традиционных методах работы проектировщиков толь-
ко 10% затраченного времени используется на творческую ра-
боту, а 90%—на поиск нужной информации, вычисления,
оформление документации. При автоматизированном проекти-
ровании (АП) эта часть работы осуществляется ЭВМ, причем
намного быстрее и качественнее.
Использование САПР также позволяет исключить субъекти-
визм при принятии решений и реализовать выбор оптимально-
го варианта конструкции.
Автоматизация проектирования не только повьцпает произ-
водительность труда конструктора, но и делает его труд более
привлекательным. ЭВМ осуществляет размножение документа-
ции, вычерчивание деталей и сборок по заданным типовым об-
разцам, использование автоматизированных каталогов норма-
тивных материалов и стандартных изделий, деталировку черте-
жей, построение графиков, таблиц и т. д.
Переход от набора средств для автоматизации отдельных
конструкторских операций к разработанным на базе современ-
ных технических средств системам, включающим правила взаи-
модействия их элементов друг с другом, порядок выполнения
работ и обработки документации, определяет использование
САПР.
САПР — это организационно-техническая система, состоя-
щая из комплекса средств автоматизации проектирования, вза-
имосвязанного с подразделениями проектной организации, и
выполняющая автоматизированное проектирование.
При автоматизированном проектировании отдельные преоб-
разования описаний объекта и(или) алгоритма его функциони-
рования или алгоритма процесса, а также представление опи-
саний на различных языках осуществляются взаимодействием
человека и ЭВМ.
При работе человека в режиме диалога с ЭВМ целесооб-
разно следовать следующему правилу: всю рутинную работу —
ЭВМ, а творческую — конструктору. Это требует более высокой
квалификации проектировщика.
Однако разработка САПР требует проведения комплекса
84
научных исследований и использования сложных вычислитель-
ных устройств — ЭВМ второго и третьего поколений.
Автоматизированное проектирование позволяет совершенст-
вовать процесс создания изделия в следующих основных на-
правлениях:
1. Повышение качества проектирования за счет увеличения
числа анализируемых конструкторских решений; более деталь-
ного и всестороннего анализа каждого проектного решения;
решения принципиально новых задач, связанных с моделиро-
ванием на ЭВМ сложных процессов функционирования элемен-
тов; обеспечения конструктора современными техническими
средствами, расширяющими его возможности при разработке
новой конструкции.
2. Сокращение срока разработки конструкции за счет ав-
томатизации выполнения чертежных работ; совершенствования
расчетных операций и операций по обработке графической ин-
формации, автоматизации использования информации; механи-
зации процесса выпуска чертежно-технической документации и
процесса изготовления изделия.
3. Уменьшение стоимости проектных работ путем сокраще-
ния числа специалистов, особенно занятых рутинной работой по
проведению вычислений и обработке графической и текстовой
информации; замены ряда экспериментальных работ на натур-
ных объектах и установках моделированием на ЭВМ.
Основными структурными звеньями САПР являются под-
системы. Подсистемой называют выделенную по некоторым
признакам часть САПР, обеспечивающую получение закончен-
ных проектных решений и соответствующих проектных доку-
ментов.
Различаются объектно ориентированные (объектные) и объ-
ектно независимые (инвариантные) подсистемы САПР. Объ-
ектные подсистемы предназначены для выполнения процедур,
специфичных для конкретного объекта. Инвариантные рассчи-
таны на выполнение типовых проектных процедур и использу-
ются для более широкого ряда объектов.
•В САПР выделяют компоненты, выполняющие определенные
функции в подсистемах и являющиеся элементами средств обе-
спечения САПР. Различают компоненты методического, прог-
раммного, технического, информационного и организационного
обеспечения.
Компонентами методического обеспечения являются доку-
менты, в которых изложены: теории, методы, способы, матема-
тические модели, алгоритмические языки для описания объек-
тов, терминология, нормативы, стандарты и другие данные, обе-
спечивающие методологию проектирования в подсистемах САПР.
Из состава методического обеспечения выделяют компоненты
математического и лингвистического обеспечения.
85
Компонентами программного обеспечения являются доку-
менты с текстами программ, программы на машинных носите-
лях и эксплуатационные документы, обеспечивающие функциони-
рование соответствующих подсистем САПР. Программное обе-
спечение подразделяется на общесистемное и прикладное. Ком-
понентами общесистемного программного обеспечения являются,
например, операционные системы, трансляторы с алгоритмиче-
ских языков. Компонентами прикладного программного обе-
спечения являются программы и пакеты прикладных программ,
предназначенных для получения проектных решений.
Компонентами технического обеспечения являются устрой-
ства вычислительной и организационной техники, средства пе-
редачи данных, измерительные и другие устройства или их со-
четания, обеспечивающие функционирование соответствующих
подсистем САПР. Совокупность компонентов технического обе-
спечения образует комплекс технических средств САПР.
Компонентами информационного обеспечения являются до-
кументы, содержащие описания стандартных проектных проце-
дур, типовых проектных решений, типовых элементов, комплек-
тующих изделий, материалов и другие данные, а также файлы
и блоки данных на машинных носителях с записью указанных
документов, обеспечивающие функционирование соответствую-
щих подсистем САПР. Совокупность компонентов информаци-
онного обеспечения образует информационную базу (базу дан-
ных) САПР.
Компонентами организационного обеспечения САПР явля-
ются методические и руководящие материалы, положения, ин-
струкции и другие документы.
В развитии САПР механизмов можно выделить три этапа:
использование ЭВМ для выполнения расчетов; ввод-вывод
информации (включая графическую) . в диалоговом режиме;
комплексная автоматизация проектирования. На последнем
этапе результаты могут выдаваться в виде сборочных и рабочих
чертежей, программ для станков с программным управле-
нием.
Одной из основ методики автоматизированного проектиро-
вания является системный подход. Его главными задачами яв-
ляются исследование специфических связей, присущих отдель-
ным типам систем, и разработка на этой основе определенных
методов их описания и изучения. При системном подходе иссле-
дуется структура объекта (системы) и свойства его частей в
их взаимосвязи. Система состоит из подсистем, элементов и т. д.
Такое деление отображает иерархическую (ступенчатую) струк-
туру САПР.
При таком подходе механизм рассматривается как совокуп-
ность сборочных единиц и деталей, которые находятся в опре-
деленной взаимосвязи и обеспечивают требуемое функциониро-
86
ванне (рис. 4.1). На схеме видна иерархичность уровней. Низ-
ший иерархический уровень включает в себя поверхности дета-
ли, которые рассматриваются как базовые элементы, не под-
лежащие дальнейшему делению. Например, для зубчатого ко-
леса такой поверхностью является рабочая поверхность зуба.
Следующим уровнем является часть детали и т. д. Такая си-
стематизация используется при расчетах рабочей поверхности
зубьев на контактную прочность, на основании которых опре-
деляется геометрия части детали — зубчатого венца колеса.
Зубья проверяются на изгибную прочность. На следующем
уровне идет формирование конструкции детали, в которую мо-
гут входить ее части: зубчатый венец, обод, диск, ступица.
Можно в качестве базового элемента использовать и другой
объект, например деталь. Это реализуется при укрупненном
рассмотрении. Использование в схеме декомпозиции — разбив-
ки— каждого уровня на ряд составных частей (блоков) дает
возможность раздельного (поблочного) проектирования на
каждом уровне.
В САПР системный подход используется при выделении ха-
рактерных подсистем, элементов, рассмотрении связи между
ними, изучении влияния отдельных компонентов на функциони-
рование всей системы, анализе возможности внесения измене-
ний в функционирование системы и процесс проектирования.
Составной частью системного подхода является разработка
структуры системы, рассматриваемого изделия, что учитывает-
ся при классификации. Под классификацией понимают процесс
распределения объектов и их элементов в соответствии с уста-
новленными признаками сходства. Классификация связана с
Рис. 4.1. Структурная схема механизма
87
теми требованиями, которые к ней предъявляются. Основные
требования делятся на эксплуатационные и производственно-
технологические.
Эксплуатационные требования — это требования функциони-
рования; выполнения штатных работ; технологии и организации
обслуживания; технологии и организации ремонта. Основными
являются требования функционирования, которые отражены в
эксплуатационных характеристиках машин и указаны в техни-
ческом задании (ТЗ) на проектирование.
Создаваемая конструкция должна удовлетворять и произ-
водственно-технологическим требованиям: технологического и
вспомогательного процессов, их обслуживания и организации
производства.
Обычно детали механизмов классифицируют по функцио-
нальным признакам: корпусные детали, соединения, передачи,
валы, оси, подшипники и т. д. Иногда используют и производ-
ственно-технологические признаки, например детали классифи-
цируют по способу изготовления на литые, механически обра-
ботанные, штампованные и т. д. В соответствии с классифика-
цией по функциональным признакам в курсе «Детали машин»
отдельно рассматривают каждый элемент механизма, особенно-
сти его конструирования и расчета. Однако проектировщики
ЛА дополнительно, кроме зубчатых и червячных передач, раз-
рабатывают рычажные, кулачковые, гидравлические, пневмати-
ческие механизмы и характерные для них детали: тяги, качал-
ки, кронштейны, подвижные соединения и т. д.
При составлении программ для автоматизированного проек-
тирования пользователь составляет лишь головную программу,
используя готовые подпрограммы (модули), хранящиеся в па-
мяти ЭВМ. Такие модули разработаны в ряде организаций для
передач и других типовых деталей, выделенных по функцио-
нальным признакам. Проектирование каждого элемента обеспе-
чивается рядом модулей, выполняющих расчеты поверхностей,
частей, формирование конструкции и ее изображения и воспро-
изведение чертежа. Например, модули DET составляют пакет
прикладных программ кафедры «Детали машин» МАИ. Они
обеспечивают автоматизированное проектирование зубчатых пе-
редач, валов, осей, соединений вал — ступица и других де-
талей.
При подготовке модулей DET использована методика рас-
чета и конструирования, изложенная в настоящей книге. По
ней составлены алгоритмы и программы счета на ЭВМ на язы-
ке ФОРТРАН-IV.
Совершенствование конструкции при проектировании обеспе-
чивается ее оптимизацией по одному или нескольким крите-
риям. Для механизмов ЛА критериями эффективности конст-
рукции могут являться высокая надежность, минимальные мас-
88
са, габаритные размеры и стоимость, наибольший КПД, высо-
кая точность и др. При этом часто критерии могут быть про-
тиворечивыми.
Различают два направления оптимизации механизмов:
структурное, включающее в себя оптимизацию структуры; пара-
метрическое, обеспечивающее оптимальные параметры элемен-
тов заданной структуры.
При оптимизации используют исходные условия (данные),
управляющие параметры — варьируемые параметры, сущест-
венно влияющие на показатели качества, ограничения. При па-
раметрической оптимизации управляющими параметрами, на-
пример, зубчатых приводов могут быть: распределение переда-
точных отношений по ступеням, относительная ширина колес,
материал колес, геометрия зацепления, частота вращения дви-
гателя и др.
При структурной оптимизации можно анализировать раз-
личные типы редукторов, например многоступенчатый цилинд-
рический, планетарный, волновой, комбинированный.
Исходные данные при проектировании механизмов в соот-
ветствии с ТЗ могут включать в себя следующие характери-
стики: мощность, скорость, ход, ресурс, режим работы, цикло-
грамму нагружения и др.
Ограничения разделяют на кинематические (по передаточ-
ному отношению одной пары, предельным окружным скоро-
стям); прочностные (по условию контактной и изгибной проч-
ности зубчатых колес); конструктивные (по габаритным разме-
рам, условию размещения элементов, их взаимодействию и
соединению) и др.
При оптимизации по одному критерию задача решается наи-
более просто. Например, решение можно получить перебором
различных вариантов конструкции и выбором наилучшего.
Решение многокритериальных задач более сложно. Много-
критериальную оптимизацию используют, когда одного крите-
рия для оценки качества проектируемой системы недостаточно.
Например, когда стоит задача обеспечения максимальной на-
дежности и минимальной массы при создании редуктора.
Рассмотрим некоторые методы решения многокритериальных
задач оптимального проектирования.
Первая группа классических методов включает в себя метод
множителей Лагранжа, вариационное исчисление, принцип мак-
симума Понтрягина, линейное программирование, нелинейное
программирование и другие. Например, для решения задач с
несколькими переменными, когда известно аналитическое вы-
ражение целевой функции и ограничения на переменные в ви-
де равенств, можно использовать метод множителей Лагранжа.
Группа методов связана с вычислением на каждом шаге
Движения к оптимальному решению значения функции цели.
89
Наиболее простым является метод прямого перебора, или ме-
тод сканирования, который можно использовать при малом чис-
ле переменных. Однако он требует больших затрат времени.
В более эффективных методах осуществляется выбор направле-
ния поиска оптимума по результатам последовательных вычис-
лений целевой функции. Отличие методов случайного поиска
заключается в том, что большинство шагов формируется с ис-
пользованием случайных чисел.
Группа методов решения многокритериальных задач связа-
на с использованием различных приемов, которые преобразу-
ют их в одну либо несколько однокритериальных. Обычно для
этого применяют метод ограничений, обобщенные критерии или
критерии более высокого уровня. В первом, наиболее распро-
страненном, случае на все целевые функции, кроме одной, вво-
дят ограничения типа неравенств. Задача сводится к определе-
нию максимума этой функции при принятых ограничениях. Во
втором — множество критериев сводится в один обобщенный
критерий. При этом необходимо установить коэффициенты обоб-
щенного критерия, которые выбирают на основании расчетов
аналогичных наиболее совершенных конструкций. Решение за-
дачи сводится к определению экстремальных значений обоб-
щенного критерия. Третий поясним на примере. Если оптималь-
ные значения некоторых параметров задаваемого механизма ЛА
зависят от массы и от стоимости, то, вводя критерий более вы-
сокого уровня — стоимость, сводим задачу к однокритериаль-
ной.
К группе компромиссных методов также относится метод по-
следовательных уступок, метод Парето и другие. Метод после-
довательных уступок применяют, когда показатели эффективно-
сти могут быть расположены в порядке убывания их важности.
В этом случае находят последовательно экстремум для каждо-
го показателя и назначают уступку (величину допускаемого от-
клонения от максимума). При заданных значениях уступок на-
ходят оптимальную величину варьируемого параметра.
Метод Парето основан на следующих допущениях: степень
достижения общей цели возрастает, если увеличивается эффек-
тивность всех частных показателей по сравнению с некоторыми
начальными условиями; степень достижения общей цели уве-
личивается, если возрастает один или несколько показателей, а
остальные не изменяются. Состояние, при котором нельзя боль-
ше увеличивать хотя бы один из критериев качества, не умень-
шая хотя бы один из остальных, свидетельствует о достижении
оптимума Парето.
Большое распространение при оптимальном проектирова-
нии механизмов и их деталей также получили методы услов-
ной оптимизации: геометрического программирования и штраф-
ных функций.
90
В настоящее время имеется много математических методов
оптимизации систем. Поэтому возникает вопрос о выборе луч-
шего математического метода для решения каждой конкретной
задачи исследования системы.
4.2. ТЕХНИЧЕСКИЕ СРЕДСТВА ДЛЯ АВТОМАТИЗАЦИИ
ПРОЕКТИРОВАНИЯ
Существует два направления выбора и использова-
ния технических средств для САПР. Первое направление осно-
вано на использовании универсальных ЭВМ средней или боль-
шой мощности, оснащенных наряду с основными традиционны-
ми устройствами специальными устройствами ввода и вывода
графической информации. Второе направление — использование
мини-машинных комплексов с графическими устройствами. Для
автоматизированного проектирования механизмов целесообраз-
но использовдть первое направление, а при решении частных
задач — второе.
К устройствам для ввода и вывода графической информации
относятся: графические дисплеи, графопостроители и устройст-
ва для ввода графической информации.
Устройства для ввода графической информации. Автомати-
ческие устройства графического ввода информации, преобра-
зующие в цифровой код ЭВМ начертания линий, символов, на-
несенных на бумагу или другой носитель, разделяют на скани-
рующие и следящие. В сканирующих устройствах поле чертежа
просматривается построчно с помощью развертывающих систем,
в следящих — отслеживаются линии чертежа. Автоматические
следящие устройства обычно используют для ввода в ЭВМ от-
носительно несложной информации.
Более широкое распространение получили устройства полу-
автоматического ввода графической информации. Оператор,
анализируя чертеж, выделяет элементы, подлежащие кодирова-
нию, устанавливает рабочий орган устройства в определенные
точки чертежа. После этого по его сигналу автоматически вы-
числяются их координаты и представляются в цифровом коде.
Так по точкам осуществляется ввод графической информации
в ЭВМ.
Разработаны разные конструкции машин для полуавтомати-
ческого ввода информации, отличающиеся методами выполне-
ния основных процессов и техническими принципами реализа-
ции этих методов. Распространены устройства ввода графиче-
ской информации, использующие электромагнитный принцип.
Он используется в полуавтомате кодирования графической ин-
формации (ПКГИО) (рис. 4.2), который входит в состав авто-
матизированного рабочего места (АРМ). Рабочим полем полу-
автомата является планшет 2 с координатной сеткой. При на-
91
Рис. 4.2. Полуавтомат кодирования гра-
фической информации
жатии магнитным карандашом 3
на точку планшета определяются
ее координаты. Эти координа-
ты запоминаются и высвечиваются
на индикаторах 4. С помощью
пульта 1 пользователь кодирует тип
линии: сплошная, основная, штри-
ховая, размерная стрелка и др. На полуавтомате имеется план-
шет символов 5. При касании магнитным карандашом какого-
либо символа планшета символ вводится в устройство для даль-
нейшего воспроизведения на чертеже.
Устройство вывода графической информации. Графопострои-
тели воспроизводят графическую информацию, рисуют точки,
линии и символы изображения на различных бумажных и син-
тетических носителях. Графопостроители могут работать в ав-
тономном режиме или в режиме ввода-вывода по каналу, со-
пряженному с ЭВМ. В автономном режиме графическая инфор-
мация выводится с ЭВМ на магнитную ленту или перфоленту,
с которых затем вводится с помощью магнитосчитывающего
или фотосчитывающего устройства в графопостроитель, который
воспроизводит изображение на носителе.
В ЕС ЭВМ применяются планшетные (ЕС-7051, ЕС-7054) и
рулонные (ЕС-7052, ЕС-7053) графопостроители. В графопо-
строителях планшетного типа (рис. 4.3, а) носитель закрепля-
ется на планшете 1, вдоль которого в двух взаимно перпенди-
кулярных направлениях хну перемещается пишущий узел 2.
На нем закреплены пишущие устройства, воспроизводящие
Рис. 4.3. Графопостроители планшетного (а) и рулонного (б) типов
92
изображение. Принцип действия исполнительного блока графо-
построителя рулонного типа (рис. 4.3, б) отличается от план-
шетного тем, что пишущий узел 2 перемещается по направляю-
щим только вдоль оси х, а ведущий барабан перемещает носи-
тель 1 вдоль оси у. Носитель сматывается с рулона, укреплен-
ного на ведомом барабане.
Исходная информация поступает в графопостроитель в ви-
де совокупности следующих групп данных. Первая включает в
себя приказы, определяющие режим работы графопостроителя,
а вторая — данные, характеризующие исполняемый чертеж и
представляющие собой координаты узловых точек перемещения
пишущего устройства. В первую группу входят приказы, опре-
деляющие выбор пишущего устройства, его состояние (опуще-
но или поднято), режим работы (линейной интерполяции, кру-
говой интерполяции), тип линии и др. Приказы позволяют вы-
чертить всевозможные комбинации линий различной толщины и
прерывности.
Графические приказы для графопостроителей ЕС ЭВМ фор-
мируются с помощью базисного программного обеспечения.
Входящие в состав ОС ЕС ЭВМ базисные подпрограммы для
графопостроителей позволяют с помощью средств алгоритмиче-
ского языка ФОРТРАН-IV описывать практически любые гра-
фические изображения. Базисными эти подпрограммы называ-
ются потому, что на их основе разрабатывают функциональные
и проблемно ориентированные программы.
Базисное программное обеспечение состоит из шести под-
программ, которые вызываются с помощью оператора CALL.
Подпрограмма PLOTS выдает данные, по которым графопо-
строитель выполняет вычерчивание. PLOTS имеет восемь вход-
ных точек; используя их, оператор управляет типом вычерчива-
емых линий, масштабом чертежа, состоянием пишущего узла,
сменой пишущих элементов, сменой систем координат и др.
(см. разд. 13.3).
Диалоговые устройства (терминалы) используют для ввода-
вывода информации, что обеспечивает диалог пользователя с
ЭВМ. Они обычно имеют клавиатуру с алфавитно-цифровыми
и символьными знаками. Для вывода информации используются
электронно-лучевые трубки и печатающие устройства. Диалого-
вые устройства с выводом информации на экран называют дис-
плеями.
Дисплеи делятся на алфавитно-цифровые и графиче-
ские. Последние позволяют выводить на экран графическую ин-
формацию и работать с ней.
В графическом дисплее ЕС-7064 (размер рабочего поля эле-
ктронно-лучевой трубки 250x250 мм) световое перо, выведенное
из корпуса, позволяет выполнять редактирование изображения
на экране. Другой вариант светового пера — введение светового
93
маркера (знака плюс, треугольник и др.), который с помощью
специальных устройств перемещается по экрану, например, с
помощью дискретных переключателей. После установки марке-
ра по команде с пульта осуществляется преобразование ука-
занной информации.
В состав графического дисплея кроме электронно-лучевой
трубки и пульта с символьной и функциональной клавиатурой
входят генераторы знаков и векторов, буферная память, свето-
вое перо, устройство управления. В системе автономного проек-
тирования графический дисплей должен взаимодействовать с
мини-ЭВМ. Графические дисплеи осуществляют прием инфор-
мации из вычислительного комплекса, работу с графической и
алфавитно-цифровой информацией на экране, обработку инфор-
мации с помощью оперативных диалоговых средств и устройств
ввода-вывода.
Диалоговые системы обеспечивают обратную связь — реак-
цию одного из партнеров (пользователя или ЭВМ) на действия
другого в процессе их взаимодействия до логического заверше-
ния проектирования.
Взаимодействие в процессе автоматизированного проектиро-
вания можно рассматривать как последовательность запросов
и ответов. Инициатором взаимодействия может быть любой из
партнеров — как оператор, так и ЭВМ. Системы, обеспечиваю-
щие такой вид взаимодействия, называются интерактивными.
Значение таких систем велико. Оперативный диалог проекти-
ровщика и ЭВМ необходим, так как проектирование включает
в себя трудно формализуемые этапы, требующие вмешательст-
ва оператора, принятия им тех или иных решений. В таких си-
стемах имеется возможность просмотреть за короткое время
множество вариантов конструктивных решений и выбрать опти-
мальное. Ускоряется поиск научно-технической и нормативно-
справочной информации. Характерно и то, что диалог может
осуществляться быстро и в наиболее удобной форме. Есть пред-
положение, что в будущем все большее значение будут
приобретать методы диалога с помощью графических изобра-
жений.
Для автоматизированного проектирования разработаны спе-
циализированные графические системы. Комплекс АРМ-М—ав-
томатизированное рабочее место конструктора изделий машино-
строения. Он создан на базе малых ЭВМ, оснащенных внешни-
ми устройствами, обеспечивающими разностороннюю обработку
текстовой и графической информации. Для работы с графиче-
ской информацией комплекс имеет графический дисплей УПГИ
(рабочее поле электронно-лучевой трубки 210X297 мм), полу-
автомат кодирования графической информации ПКГИО и план-
шетный графопостроитель АП-7251. Предусмотрена связь с
ЭВМ.
94
4.3. ИСПОЛЬЗОВАНИЕ ЭВМ И САПР
ПРИ ПРОЕКТИРОВАНИИ ДЕТАЛЕЙ И МЕХАНИЗМОВ ЛА
Важным этапом автоматизированного проектирова-
ния является формирование исходного изображения, которое
может реализоваться различными способами. Один из спосо-
бов основан на использовании базового образа. На экран вы-
водится изображение проектируемой типовой детали или меха-
низма. Это изображение вызывается на экран из банка дан-
ных или вводится с помощью устройства для ввода графиче-
ской информации. Затем пользователь редактирует изображе-
ние путем изменения на экране отдельных элементов, устране-
ния ненужных, добавления других элементов. ЭВМ получает
исходную информацию и выполняет необходимые расчеты, ре-
зультаты которых выдаются пользователю.
Другой способ связан с синтезом конструкции из отдель-
ных типовых элементов. ЭВМ также должна воспринимать ин-
формацию и выдавать результаты расчетов. Использование это-
го способа требует решения более сложных задач. Автоматизи-
рованное проектирование зубчатого колеса по последнему спо-
собу используется, например, в подпрограмме DET 29, которая
воспроизводит изображение зубчатых венцов по результатам
расчета на прочность, построение ступиц насаживаемых на вал
зубчатых колес в зависимости от диаметра вала, а для колес
большого диаметра осуществляет построение обода и диска с
отверстиями.
При интерактивном автоматизированном проектировании
процесс создания конструкции протекает при постоянном взаи-
модействии человека и машины. ЭВМ демонстрирует результа-
ты и по указанию пользователя осуществляет корректировку
исходных данных и текущих результатов, ставит вопросы о не-
достающей информации по ходу решения задачи, о продолже-
нии или окончании выполнения задания. Основной элемент диа-
логовой системы — точка диалога. Она определяет и регламен-
тирует момент взаимодействия пользователя и машины (см.
рис. 5.18).
В настоящее время САПР широко используются при созда-
нии самолетов, что привело к существенному изменению мето-
дов работы конструктора. Чертежную доску он сменил на си-
стему интерактивной графики, где используются графический
терминал со световым пером и алфавитно-цифровая клавиату-
ра. Способность ЭВМ выполнять намеченную задачу во много
раз быстрее, чем человек, наличие большого объема памяти для
хранения информации и способность графически воспроизво-
дить эту информацию позволяют конструктору выпускать ком-
поновочные схемы и чертежи во много раз быстрее, чем это
делается на чертежной доске. В то же время все большее рас-
95
пространение находит автоматизация изготовления деталей ЛА.
Наибольший эффект дает объединение разрозненных автомати-
зированных гнетем и создание системы, в которой проектиро-
вание и изготовление деталей осуществляются с помощью ЭВМ.
Такие работы проводятся в СССР и за рубежом. Американ-
ские фирмы все больше используют объединенные системы
проектирования и изготовления при создании самолетов. На-
пример, система CAD/CAM обеспечила возможность процесса
производства с прямым доступом к результатам проектирова-
ния. Использование CAD/CAM позволяет после завершения
разработки узловых и деталировочных чертежей через базу
данных передать их специалистам по подготовке производства
и программированию для станков с ЧПУ, которые разрабаты-
вают управляющие программы для оборудования, изготавли-
вающего детали.
Проведенные фирмой «Локхид» исследования показали, что
производительность системы типа CAD/CAM в 4... 17 раз выше,
чем при использовании старых способов проектирования. Уве-
личение производительности в 4 раза характерно при выполне-
нии чертежей компоновки механических узлов и подготовке уп-
равляющих программ для станков с ЧПУ, а в других случаях
больше. Эта система, в частности, может применяться при раз-
работке принципиальных схем систем и механизмов, кинемати-
ческом анализе, разработке схем гидросистем и т. д.
В СССР также осуществляется разработка таких систем и
для других отраслей машиностроения.
РАЗДЕЛ II
ОСНОВЫ РАСЧЕТА И КОНСТРУИРОВАНИЯ
МЕХАНИЧЕСКИХ ПЕРЕДАЧ
ГЛАВА 5. ЗУБЧАТЫЕ ЦИЛИНДРИЧЕСКИЕ ПЕРЕДАЧИ
6.1. ВИДЫ ЗУБЧАТЫХ ПЕРЕДАЧ И ИХ ПРИМЕНЕНИЕ
В ЛА. КОНСТРУКЦИЯ ЗУБЧАТЫХ КОЛЕС
Зубчатые передачи наиболее широко применяются
для передачи вращательного движения в широком диапазоне
мощностей и окружных скоростей. Передачи для понижения уг-
ловых скоростей называют редукторами, а для повышения —
мультипликаторами. Зубчатые передачи используют, например,
в двигателях, системах управления ЛА, механизмах радиолока-
ционных антенн. Их достоинства: высокая несущая способность,
технологичность, надежность, высокий КПД. Недостатки: огра-
ниченность передаточного отношения в одной ступени (не бо-
лее шести), появление шума при больших окружных скоростях,
износ.
В двигателестроении зубчатые передачи носят название
авиационных: они обеспечивают передачу крутящего момента
от ротора ТВД к его винту и привод к различным агрегатам
двигателя, передачу крутящего момента от двигателя к валам
несущего и рулевого винтов вертолета, применяются в приводе
изменения стреловидности крыла у самолета й т. д. t помощью
редукции передачи увеличивают крутящий момент двигателя в
десятки раз при высокой надежности работы, малых массе и
габаритных размерах, высоком КПД.
По назначению авиационные зубчатые передачи делят на
следующие четыре группы: 1) зубчатые передачи основной ки-
нематической цепи главных и промежуточных редукторов вер-
толетов; 2) зубчатые передачи редукторов ТВД; 3) зубчатые
передачи силовых установок самолетных и вертолетных агре-
гатов; 4) передачи трансмиссий самолетов и прочие передачи,
в том числе кинематические.
Первые две и частично третья группа передач являются вы-
соконапряженными, а часть из них также и высокоскоростны-
ми. Улучшение характеристик этих передач — повышение несу-
щей способности, снижение массы и габаритных размеров, уве-
личение срока службы и повышение КПД являются задачами
авиационного редукторостроения.
При параллельных валах используют передачи с цилиндри-
ческими зубчатыми колесами с прямым (рис. 5.1, а) и косым
4—1085 97
Рис. 5.1. Зубчатые передачи
(рис. 5.1, б) зубом. Косозубые передачи применяются при по-
вышенных скоростях (о>5 м/с). При пересекающихся валах
применяются передачи с коническими зубчатыми колесами, ко-
торые могут иметь прямые (рис. 5.1, в), тангенциальные и кру-
говые зубья (рис. 5.1, г).
Меньшее зубчатое колесо в передаче называют шестерней,
а большее — колесом. Термин зубчатое колесо является общим.
Зацепление двух зубчатых колес может быть как внешним, так
и внутренним (см. рис. 5.1, а). Основной характеристикой за-
цепления является стандартизованный модуль т (мм) *:
Первый ряд (предпочти-
тельный) ............ 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0.4; 0,5; 0,6; 0,8; 1,0;
1,25; 1,5; 2,0; 2.5; 3,0; 4,0; 5,0; 60 и т. д.
Второй ряд........... 0,14; 0,18; 0,22; 0.28; 0,35; 0,45; 0.55; 0,7; 0,9;
1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5 и т. д.
Форма зубчатых колес в большинстве случаев определяется
технологическими соображениями, зависящими от способа по-
лучения заготовки, а также требований прочности и жесткости.
В свою очередь, способ получения заготовки зависит от мате-
риала и размеров зубчатого колеса, масштаба производства.
Зубчатые колеса механизмов ЛА выполняют обычно из легиро-
ванных сталей с соответствующей термообработкой, что обе-
спечивает необходимую прочность при минимальных габарит-
ных размерах; в отдельных случаях, особенно в приборах, мо-
гут применяться бронзы и пластмассы. Зубчатые колеса изго-
товляют из круглого проката (прутка) и заготовок, получаемых
ковкой, штамповкой и литьем. Шестерня изготовляется заодно
с валом (вал-шестерня), если ее диаметр da близок к диаметру
вала dB. Зубья нарезают на выступающем венце (рис. 5.2, а).
При диаметре венца, большем или равном диаметру вала,
зубья углубляются в тело вала частично или полностью (рис.
• Для цилиндрических косозубых и шевронных колес значения модуля
относят к нормальному сечению.
98
Рис. 5.2. Конструкции зубчатых
колес, выполненных совместно с ва-
лом
5.2, б); зубья в этом случае нарезаются червячной фрезой. Из-
готовление шестерни заодно с валом при da>2dB возможно пу-
тем глубокой горячей высадки заготовки, обеспечивающей ма-
лоотходную технологию обработки (рис. 5.2, в). Цилиндриче-
ские зубчатые колеса, насаживаемые на вал, можно выполнять
со ступицей (рис. 5.3, а) и в виде сплошного диска, где заго-
товка выполнена штамповкой (рис. 5.3, б) или точением (рис.
5.3, в). В отдельных случаях два смежных зубчатых колеса
выполняются в виде блока (рис. 5.3, г). Для соединения зубча-
тых колес с валом используется шпоночное или шлицевое (зуб-
чатое) соединение.
Конструктивные параметры. Основными конструктивными
размерами цилиндрических зубчатых колес являются наруж-
ный диаметр da и ширина колеса Ь. Рекомендации по выбору
размеров других элементов цилиндрических зубчатых колес за-
висят от назначения конструкции, вида заготовки, требований
по жесткости, массе, точности. Для снижения массы в переда-
точных механизмах ЛА зубчатое колесо делают часто с более
тонким диском и облегченным ободом; для облегчения и удоб-
ства транспортировки в диске делают отверстия.
Рекомендации по выбору размеров отдельных элементов
цилиндрического зубчатого колеса общего применения следую-
щие (см. рис. 5.3): /CT=(0,7...1,7)rf,,; rfCT=(l,35...l,55)rfB; 8 =
= (2...3)m; £>o=(rfa+dcT)/2; d0= Pi—dCT)/(3...4); е=0,25й;
c=(0,15...0,3) 6; f—Q,5m.
Надежное базирование зубчатого колеса на валу обеспечи-
вает достаточная длина /ст посадочного отверстия. При lc-r<dB
применение шлицевого соединения улучшает центрирование. Ис-
пользование одной или двух дополнительных цилиндрических
поверхностей повышает точность центрирования; шлицы тогда
передают только крутящий момент.
4» 99
Вид посадки зубчатого колеса на вал по центрирующему
диаметру зависит от величины передаваемой нагрузки, требо-
ваний точности работы и монтажа. При постоянных нагрузках
в неподвижных соединениях используют посадки H7/h6; H7/k6.
Посадки Н7/р6; Н7/гб; H7/s6 используют при циклических на-
грузках и наличии осевых сил. Для стабильности соединения
возможно применение более высоких квалитетов.
Шероховатость посадочных мест (среднее арифметическое
отклонение профиля Ra) обычно для седьмой степени точности
зубчатого колеса составляет 1,25 мкм, для шестой 0,63 и
0,32 мкм, а для профилей зубьев соответственно 0,63 и 0,32 мкм
(рис. 5.3, е). Кроме того, у цилиндрических зубчатых колес ог-
раничивают: предельное отклонение диаметра вершин зубьев,
радиальное биение вершин зубьев, биение торцевой поверхности
венца, если эта поверхность является базой при нарезании
зубьев (эти величины должны соответствовать стандартам).
Для отверстия в ступице, которое является технологической
и конструкторской базой, указывают также предельное отклоне-
100
ние формы цилиндрической поверхности — допуск на некруглость
и нецилиндричность отверстия, а также торцевое биение.
Особенностями авиационных зубчатых колес являются малая
относительная масса и ажурность конструкций. В редукторах и
приводах авиационных конструкций подавляющее большинство
цилиндрических зубчатых передач являются прямозубыми с пере-
даточным числом в одной ступени не более четырех, с числом
зубьев у первой ступени 25^2^45, у зубчатых колес внутрен-
него зацепления 81 ^z^ 127, модуль т=2,25... 8 мм, числа зубь-
ев z^20 применяются редко.
Конструктивными параметрами зубчатого колеса, непосред-
ственно влияющими на прочность, являются коэффициенты
tyba=bw/aw, tybd=bw/mz и tybm—bw/m. Авиационные зубчатые ко-
леса относятся к категории колес с узким зубчатым венцом. Это
обеспечивает снижение неравномерности распределения нагрузки
по длине зуба. С целью снижения неравномерности распределе-
ния нагрузки по длине зуба в авиационных редукторах старают-
ся избегать консольного расположения зубчатых колес. Неравно-
мерность распределения нагрузки по длине зуба при несиммет-
ричном расположении зубчатого колеса относительно опор уме-
ньшают модификацией — приданием зубу бочкообразной формы.
Обод и диск зубчатого колеса (соединение обода со ступицей)
при значительных окружных скоростях проектируют так, чтобы
исключить резонансные колебания. Для снижения неравномер-
ности распределения нагрузки вдоль линий контакта стремятся
к симметричности конструкции колеса, а для выравнивания жест-
кости зубчатого колеса по его ширине внутреннюю поверхность
обода часто выполняют криволинейной (рис. 5.3, д). Толщина
обода оценивается коэффициентом фОб=(^а—£>i)/(2m). У высо-
конапряженных колес 2,3фоб 6,8; среднее значение фоб.с₽=
=4,5. Уменьшение толщины обода требует более тщательной
обработки самого обода и зубчатого венца для повышения его
надежности.
На жесткость зубчатого венца существенно влияет толщина
диска с, которую оценивают коэффициентом ^с=с/.Ь; 0,1^фс^
^0,5. Переход от диска к ступице и к ободу делают плавным,
радиусом не менее 1,5 мм. Обычно коэффициент длины ступицы
фст ^ст/^в 1 •
Кроме профильной модификации, величина которой зависит
от нагруженности и точности изготовления зубчатого колеса и
узла в целом, у авиационных зубчатых колес у вершины профиля
зуба снимается фаска (фланкирование зуба), что смягчает или
исключает кромочный контакт зубьев и обеспечивает благопри-
ятные условия для формирования масляного слоя. Фаски сни-
маются также по контуру торцевой поверхности зубьев. При
цементировании зуба глубина слоя берется примерно Д= (0,15...
0,3) т, но не менее 0,5... 0,6 мм.
101
8.2. МАТЕРИАЛЫ, ТЕРМИЧЕСКАЯ ОБРАБОТКА
И ОСОБЕННОСТИ ТЕХНОЛОГИИ ОБРАБОТКИ
ЗУБЧАТЫХ КОЛЕС
Авиационные зубчатые колеса изготавливают из вы-
соколегированных и цементируемых высоколегированных сталей
электрошлакового или вакуумного переплава.
Для изготовления зубчатых колес используют хромоникеле-
вые стали марок 12Х2Н4А, 14ГСН2МА, 18Х2Н4ВА, 14ХГСН2МА
и др. Для зубчатых пар с повышенной рабочей температурой (до
300°С) используют сталь 20ХЗМВФА; при рабочих температурах
в зоне контакта до 350...400°С рекомендуют теплопрочные це-
ментируемые стали марок 16ХЗНВФМБ, 13ХЗНВМГФ и др. Вве-
дение небольшого количества ниобия в сталь способствует из-
мельчению зерна и повышению теплопрочности цементирован-
ного слоя до 500°С.
Зубчатые передачи четвертой группы изготовляют из легиро-
ванных конструкционных сталей 20Х, 20ХФ, 12ХНЗА, 20X13,
16Х16НЗМА и др. При упрочнении поверхностного слоя азотиро
ванием используют стали 38ХМЮА, 35ХМЮА, 30ХН2МФА.
Для получения высокой несущей способности применяют хи-
мико-термическую обработку стали, заключающуюся в нагреве
детали, выдержке при высокой температуре (85О...95О°С) в ак-
тивных газовых, жидких или твердых средах, последующем ох-
лаждении, отпуске. При этом регламентируются процентное
содержание углерода в поверхностном слое, однородность и мел-
козернистость структуры, глубина химико-термического слоя, его
твердость и изотропность. Это приводит к изменению химическо-
го состава, структуры и свойств поверхностных слоев. Результа-
том является повышение поверхностной твердости (более
HRC60) при твердости сердцевины HRC (31... 41), износостой-
кости, усталостной прочности. Оцениваются также величина и
характер распределения остаточных сжимающих напряжений,
влияющих на выносливость зуба.
Используются следующие виды химико-термического упроч-
нения.
Цементация — газовая в шахтных печах, в твердом карбюри-
заторе и нитроцементация. Для авиационных зубчатых колес
наибольшее применение получила газовая цементация, осуществ-
ляемая подачей в зону цементации жидкого карбюризатора и га-
зовой среды в виде светильного или природного газа. Нитроце-
ментация используется в основном для авиационных зубчатых
колес малого модуля. Ее проводят в муфельных печах в смеси
жидких или газообразных карбюризаторов с аммиаком при
850... 900°С.
В зависимости от марки стали для получения необходимой
структуры металла используют закалку, отпуск и обработку
102
холодом при —(50... 100)°C. В результате этого может быть по-
вышена пластичность и снижены остаточные напряжения.
Технология изготовления авиационных зубчатых колес наряду
с конструкцией играет важную роль в обеспечении их высокой
эксплуатационной надежности. Технологический процесс состоит
из следующих операций: 1) получение заготовки из проката, по-
ковки или штамповкой; 2) обдирка заготовки; 3) нормализация
для снятия внутренних напряжений и улучшения структуры ме-
талла; 4) предварительная механическая обработка посадочных,
базовых и других точных поверхностей и окончательная — вспо-
могательных поверхностей; 5) нарезание зубьев; 6) зачистка за-
усенцев и скругление острых кромок; 7) цементация; 8) механи-
ческая обработка нецементируемых поверхностей; 9) закалка;
10) окончательная механическая обработка; И) зубошлифова-
ние, отделка зубьев и контроль.
Нарезание зубчатых колес с внешними зубьями производится
червячными фрезами. В процессе обработки зуба получают три
вида впадин зубчатого венца: 1) шлифованные по поверхности
впадины и по всему контуру зуба; 2) шлифованные с уступом,
где качество поверхности впадины определяется зубофрезерова-
нием, когда этот процесс является чистовой операцией; 3) с под-
нутрением оснований зубьев (см. рис. 5.3, е). Поднутрение вы-
полняется в две операции (черновое и чистовое), для чего исполь-
зуются два типа фрез. Для особо ответственных колес вводится
дополнительная операция по отделке дна впадин — полирование.
Шлифование профиля зуба является отделочной операцией,
обеспечивающей высокую точность зубчатых колес. Уменьшая
шероховатость поверхности [/?а= (0,20... 1,20) мкм], оно из-за
интенсивного тепловыделения в зоне резания способно изменить
структуру, твердость, напряженное состояние, т. е. работоспособ-
ность зубчатых колес. Наибольшее отрицательное влияние ока-
зывают прижоги в слое толщиной 20... 25 мкм, вызывающие
структурные изменения. Шлифование изменяет также напряжен-
ное состояние. До шлифования в поверхностном слое зуба имеют
место остаточные напряжения сжатия. При шлифовании слой с
остаточными напряжениями сжатия частично или полностью сре-
зается, что приводит к перераспределению напряжений. При
шлифовании с прижогами в большинстве случаев на поверхности
зуба формируются остаточные напряжения растяжения, выра-
стающие с увеличением дефектного слоя, что снижает прочност-
ные показатели зубчатых колес.
Для повышения эксплуатационных (прочностных) свойств мо-
гут использоваться различные методы поверхностного пластиче-
ского деформирования. К ним относятся обкатка роликами, об-
дувка дробью; особенно эффективно их сочетание с электрополи-
рованием. Кроме электрополирования в качестве финишной
операции повышения точности зубчатых колес применяют при-
103
тирку пастами с использованием притиров, а также хонингова-
ние, позволяющие снимать тонкий дефектный слой, оставшийся
после термообработки, шлифования и травления для выявления
прижогов.
6.3. КРАТКИЕ СВЕДЕНИЯ ПО КИНЕМАТИКЕ
И ГЕОМЕТРИИ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ
ПЕРЕДАЧ
Зацепление двух зубчатых колес с числами зубьев z\
и z2 можно представить как качение без скольжения двух окруж-
ностей диаметрами dw] и dw2, называемых начальными. Эти ок-
ружности определяют диаметры двух цилиндров, называемых на-
чальными (рис. 5.4). Параметрам шестерни согласно стандартам
присваивают индекс «1», а параметрам колеса — «2». У парамет-
ров зубчатых колес индекс «о»» относится к начальной поверхно-
сти (окружности), «а»— к поверхности (окружности) вершин и
к головке зуба, — к поверхности (окружности) впадин и нож-
ке зуба, «Ь» — к основной окружности.
При эвольвентном профиле зубьев траектория точки контак-
та двух сопряженных профилей зубьев во время зацепления
представляет собой прямую линию и называется линией зацеп-
ления.
Рис. 5.4. Схема зацепления зубчатых колес
104
Делительная
Рис. 5.5. Влияние числа зубьев и смещение рейки на форму зуба
Точка касания начальных окружностей и одновременно точка
пересечения линии центров с линией зацепления называется по-
люсом зацепления.
Угол между нормалью к линии центров, проведенной через
полюс зацепления, и линией зацепления называют углом зацеп-
ления aw, для стандартного зацепления а»=20°.
Окружность зубчатого колеса, делящуюся при его нарезании
на равное число частей длиной Р, называемых шагами, и имею-
щую стандартный модуль, называют делительной. Диаметр такой
окружности находят из равенства Pz—nd, откуда d=P/(jtz) =
= mz.
Зубчатые колеса с модулем т менее 1 мм называются мелко-
модульными. Для снижения номенклатуры и унификации режу-
щего и мерительного инструментов модули стандартизированы
(см. разд. 5.1).
Отношение угловых скоростей ведущего <oi и ведомого ©2 зуб-
чатых колес называют передаточным отношением: i=a>i/<x>2.
В редукторах (понижающих угловую скорость передачах)
(02<Wi и »>1, в мультипликаторах <В2>ш1 и i<l.
В зубчатой паре отношение чисел зубьев зубчатого колеса Z2
и шестерни z\ называют передаточным числом: u=zzlz\. Так как
всегда Z2>zb то и>1. В силовых передачах наибольшее значение
передаточного числа 6, в отдельных случаях, особенно в кинема-
тических передачах, оно может доходить до 10... 12.
При нарезании на зубчатом колесе зубьев профиль в зави-
симости от их числа при одном модуле меняется (рис. 5.5,а).
С уменьшением z его толщина у основания и вершины уменьшэ
ется, что приводит к уменьшению прочности зуба. При стандарт-
ных параметрах зуба при некотором z<zmm=17 происходит
подрезание ножки зуба, что ведет к снижению его прочности,
105
а искажение профиля нарушает правильность зацепления. При
нарезании зубчатого колеса рейкой без смещения начальная и
делительная прямые рейки совпадают (рис. 5.5,6). Для исклю-
чения подрезания ножки зуба и в отдельных случаях для повы-
шения несущей способности зуба режущий инструмент при наре-
зании смещают. В этом случае делительная прямая рейки (рис.
5.5, в) или делительная окружность долбяка смещаются от цент-
ра зубчатого колеса на величину хт (положительное смещение),
которое обычно применяется к зубчатому колесу зубчатой пары
с меньшим числом зубьев; возможно также отрицательное сме-
щение к центру на величину —хт. Здесь х — коэффициент
смещения исходного контура. Как видно из рис. 5.5, в, смещение
инструмента от центра зубчатого колеса (положительное сме-
щение) приводит к изменению формы зуба; увеличивается его
толщина у основания и заостряется головка. Отрицательное сме-
щение вызывает обратную картину. При этом для шестерни бе-
рут Х]>0, а для колеса х^<0.
Суммарное смещение передачи из двух зубчатых колес равно
Хх=Х1+Х2-
При хх=0 (при Xj=—х2) начальные dw и делительные d ок-
ружности совпадают: dWi=dit dw2=di; межосевое расстояние
будет равно aw=0,5/n(zi4-Z2); диаметр вершин зубьев da=d+
+2m(ha*+x); диаметр впадин df=d—2m(ha*+c*—х); высота
зуба h=m(2ha*+c*), где ha* — коэффициент высоты головки
зуба; с* — коэффициент радиального зазора. Для зубчатых ко-
лес при т^1 мм Ла*=1, с*=0,25. Исходный контур производя-
щей инструментальной рейки имеет стандартный угол профиля
а=20°.
При хх=^0 (обычно Хх>0 при Xi>0 и х2>0) делительные и
начальные окружности зубчатых колес не совпадают, причем
начальные окружности становятся больше делительных. При
этом увеличивается угол наклона линии зацепления как общей
касательной к основным окружностям, т. е. увеличивается угол
зацепления а», что ведет к снижению коэффициента перекрытия.
Смещения Xi и х2 при этом изменяют большее число параметров
зацепления. В этом случае
межосевое расстояние опреде-
ляется по формуле:
ao,=m(0,5zI+x1—Ах/), где
Xx=z( + z2;
At/ — коэффициент уравни-
тельного смещения. Рекомен-
дации по выбору смещений Xi
и Хг для различных случаев и
определению At/ приведены в
ГОСТ 16532—70.
Ширина венца зубчатого
Рис. 5.6. Исходный производящий
реечный контур авиационных зубча-
тых колес
106
колеса b (bw — рабочая ширина зубчатого венца) определяется
как произведение межосевого расстояния aw, делительного диа-
метра d или модуля т на соответствующий коэффициент ширины
зубчатого венца: &=фьаДи>=фм^==фьотт, причем фьй=фьа(и±
±1)/2. Значения фг>а при фьт — 8 ... 12 для различных условий
применения приведены ниже.
Кинематические и легконагруженные передачи . ...... 0,01 ...0,1
Легко- и средненагруженные передачи при повышенной жест-
кости валов............................................... 0,1... 0,25
Передачи повышенной и высокой нагруженности при доста-
точной жесткости валов и точности зубчатых колес ....... 0,25... 0,35
Передачи авиационные высоконапряженные и высокоскоро-
стные (требуют достаточной жесткости валов и высокой точности
зубчатых колес)...........................................0,08... 0,45
Особенности геометрии авиационных зубчатых колес. Пара-
метры исходного производящего реечного контура (ИПК) высо-
конапряженных авиационных зубчатых колес (рис. 5.6) в основе
соответствуют стандарту (табл. 5.1).
Здесь ha* и hf* — коэффициенты высоты головки и ножки,
ра* — коэффициент радиуса кривизны скругления головки, са*
и Cf* — коэффициенты высоты скругления головки и ножки.
Этот ИПК обеспечивает высокую контактную и изгибную
прочность, а также стойкость против заедания поверхностей зубь-
ев. Этот контур использован при изготовлении ряда редукторов
ТВД: АИ-20, АИ-24, главного редуктора Р-26 вертолета и др.
Применение ИПК с углами профиля, превышающими стандарт-
ный (а=20°), приводит к увеличению угла зацепления aw и
уменьшению коэффициента перекрытия ев, увеличению толщины
гидродинамической пленки, росту
контактной прочности зубьев
и стойкости их поверхностей к за-
еданию; облегчает изготовление у
зуба поднутренного основания.
Рассмотрим особенности гео-
метрии косозубых цилиндриче-
Рис. 5.8. Схема распределения на-
грузки по профилю зуба за время
зацепления
Рнс. 5.7. Косозубое зацепление
(а) и эквивалентное зубчатое коле-
со (б)
107
Таблица 5.1
а® Ла* ¥ Ро* са* <7*
25 1,0 1,0 0,35208 0,20328 0,20328
28 0,9 0,9 0,34754 0,18438 0,18438
ских колес.. У косозубых колес направление зуба с образующей
делительного цилиндра составляет некоторый угол 0 (рис. 5.7, а).
В косозубых передачах зубья нагружаются постепенно по мере
захода в зацепление, причем в отличие от прямозубых передач
в зацеплении всегда находится минимум две пары зубьев. По-
этому косозубое зацепление снижает шум и уменьшает допол-
нительные динамические нагрузки. Это качество особенно суще-
ственно при больших окружных скоростях, поэтому при i»>5 м/с
часто переходят на применение косозубых передач.
Профиль зуба косозубого колеса в нормальном сечении п—п
совпадает с профилем прямого зуба (см. рис. 5.7, а), и модуль
тп в этом сечении берется по ГОСТу. В торцовом сечении t—t
модуль m< = mn/cos0, соответственно шаг P<=Pn/cos0, диа-
метр делительной окружности d=mtz=mnzl cos 0.
Оценку прочности зуба косозубого зубчатого колеса ведут в
нормальном сечении, рассматривая в этом случае эквивалентное
прямозубое зубчатое колесо (рис. 5.7,6) с диаметром dv=2rv=
=<//cos2 0.
Нормальное к зубу сечение образует эллипс с полуосями а=
=d/(2cos0) и 6 = d/2; радиус кривизны (относительно малой
оси) эллипса rv=a2/b=d/ (2cos2 0). Тогда число зубьев для эк-
вивалентного колеса будет равно
z -з — d — т‘г — z .
v тп тп cos2 ? «/cos3? cos3?
Увеличение dv и zv по сравнению с d и z ведет к повышению
прочности косозубых колес.
В прямозубой передаче линия контакта пары зубьев переме-
щается по линии зацепления на отрезке qa — рабочем уча-
стке линии зацепления (рис. 5.8,а). Торцевой коэффици-
ент перекрытия Za.=qalPb, где Рь— основной шаг. Для
обеспечения непрерывности зацепления и плавности работы
передачи необходимо, чтобы еа>1. Поэтому при работе
прямозубой передачи в начале зацепления (рис. 5.8, б) участок
зуба 1—1' будет зоной двухпарного зацепления с нагрузкой на
зуб Fn/2. Участок Г—2 — зона однопарного зацепления с нагруз-
кой на зуб Fn, участок 2—2' — зона двухпарного зацепления с
нагрузкой Fn/2. Зона однопарного зацепления зависит от коэф-
фициента торцевого перекрытия ев. Рекомендуется для прямозу-
108
бых передач еа^1,2, для косозубых еа>1. Величина ев зависит
от числа зубьев и увеличивается при возрастании г. Для передач
без смещения
еа = [1,88 — 3,2(-— ± —Y| cos
I \ *1 *2 /J
Здесь знак « + » соответствует внешнему, «—» внутреннему
зацеплению. Увеличение угла наклона зуба 0 снижает еа и уве-
личивает осевую силу; это ограничивает использование у зубча-
тых колес больших 0.
В косозубой передаче в любой момент времени в зацеплении
находятся одновременно несколько зубьев. Кроме того, в косо-
зубой передаче зубья нагружаются постепенно по мере захода в
поле зацепления, что обеспечивает плавность работы косозубого
зацепления, снижает шум и дополнительные динамические на-
грузки. Это преимущество особенно заметно в быстроходных пе-
редачах, так как динамические нагрузки пропорциональны квад-
рату скорости.
Осевое перекрытие в косозубой передаче определяется коэф-
фициентом осевого перекрытия e₽=6u,tg fi/Pbt, где Ры — шаг за-
цепления по торцу. При перемещении точки контакта зубьев по
линии зацепления при зацеплении пары зубьев имеют место их
перекатывание и скольжение, причем скорость скольжения vs
уменьшается по мере приближения точки контакта профилей к
полюсу зацепления, в котором она становится равной нулю, а
затем меняет знак. Таким образом, максимальное скольжение
имеет место на ножках и головках зубьев, и при наличии сил
трения вызывает их износ и снижает КПД.
5.4. ТОЧНОСТЬ ИЗГОТОВЛЕНИЯ ЗУБЧАТЫХ КОЛЕС
Погрешности изготовления зубчатых колес приводят
к повышению динамических нагрузок, вибрации, шума и нагрева
силовых передач. Те же погрешности в кинематических переда-
чах нарушают согласованность движения ведущих и ведомых
звеньев ввиду нестабильности передаточного отношения и в пре-
делах одного оборота. Основными погрешностями изготовления
зубчатых колес являются погрешности шага и формы профиля
зубьев, ошибки направления зубьев.
Точность изготовления зубчатых колес и передач регламен-
тируется соответствующими ГОСТами, предусматривающими для
их оценки двенадцать степеней точности, причем для каждой из
них устанавливаются нормы на кинематическую точность, плав-
ность работы и контакта зубьев.
Норма кинематической точности регламентирует наибольшую
погрешность передаточного отношения или полную погрешность
угла поворота в пределах одного оборота.
109
Рис. 5.9. Виды сопряжений и гарантированные боковые зазоры в передаче
при т^1 мм (а) и т<1 (б)
Норма плавности работы определяет величину повторяющей-
ся циклической ошибки передаточного отношения в пределах
одного оборота. Норма контакта зубьев определяет величины
ошибок изготовления зубьев, влияющих на размеры пятна кон-
такта зубьев в зацеплении при сборке.
•Критериями оценки точности зубчатых колес в передаче, ис-
ходя из вида сопряжения, считают норму на боковой зазор /п,
допуск на него 7/ и допуск на межосевое расстояние ±fa.
Для цилиндрических передач (при т^1 мм) (рис. 5.9, а)
установлено шесть видов сопряжений: Н, Е, D, С, В, А и восемь
видов допусков на боковой зазор Г/: h, d, с, b, а, х, у, г. Сопря-
жение Н имеет гарантированный боковой зазор /ппнп=0. При
ш<1 мм (рис. 5.9,6) установлено пять видов сопряжений: Н, G,
F, Е и D и четыре вида допусков 7/: h, g, f, е. Сопряжения Н и
G — с малым боковым зазором — требуют для избежания закли-
нивания зубьев стабильного температурного режима. Для высо-
коскоростных передач (о>15...25 м/с) и точных кинематических
цепей применяют 5 и 6-ю степени точности (при и>25 м/с — ко-
созубые передачи), для передач с повышенными скоростями и
умеренными нагрузками или при повышенных нагрузках и уме-
ренных скоростях—7-ю степень точности (i»=10... 17 м/с); для
передач, не требующих особой точности,—8-ю степень точности.
При выполнении рабочего чертежа зубчатого колеса точность его
изготовления записывается в зуборезной таблице, выполняемой
по ГОСТу. Так, точность изготовления зубчатого колеса для пе-
редачи с модулем т^1 мм, имеющей 7-ю степень точности по
всем трем нормам и сопряжение D, будет обозначено 7-D
(ГОСТ 1643—81).
Выбор степени точности зубчатого колеса определяют вели-
чина окружной скорости в зацеплении и требования к кинемати-
110
ческой точности, плавности ра- боты и пятну контакта. С ро- стом окружной скорости повы- шаются требования к точности передачи, так как динамиче- ские нагрузки, вызванные по- грешностями зубчатых колес, пропорциональны скорости. Ориентировочные значения предельных окружных скоро- стей в зависимости от степени Таблица 5.2
Степень точности Окружная скорость в зацеплении, м/с
прямозубом косозубом
5 и более 6 7 8 15 до 15 до 10 до 6 30 до 30 до 15 до 10
точности и вида передачи приведены в табл. 5.2.
Вид сопряжения, определяющий величину бокового зазора
/п, выбирается в зависимости от рабочей температуры передачи
и исключает возможность заклинивания передачи от температур-
ных деформаций деталей передачи и корпуса.
Увеличение ресурса у высокоресурсных и высоконапряженных
авиационных зубчатых колес достигается их выполнением по
4-й степени точности по нормам плавности и контакта зубьев.
Однако в ряде случаев повышение точности до приведенных зна-
чений не всегда является целесообразным, поскольку на факти-
ческое распределение нагрузки влияют жесткость сопряженных
зубьев и всей системы в целом. Зубчатые авиационные передачи
средней нагруженности изготавливают с точностью 6-5-5-В или
7-6-6-В.
6.5. УСИЛИЯ, ДЕЙСТВУЮЩИЕ в зацеплении,
влияние погрешностей изготовления зубчатых
КОЛЕС И ДЕФОРМАЦИИ ВАЛОВ НА РАБОТУ ПЕРЕДАЧИ
В прямозубой цилиндрической передаче (см. рис. 5.4)
нормальная сила Fn в любой точке контакта зубьев направлена
по линии зацепления как общей нормали к рабочим поверхностям
зубьев. Перенося эту силу в полюс зацепления П, разложим ее
на окружную силу Ft и радиальную Fr. При известном вращаю-
щем моменте Мх и диаметре di зубчатого колеса
Ft=2Mx/dx; Fr=Fttgaw-, Fn=Ft/(cos aw). (5.1)
В косозубой передаче (рис. 5.10) сила Fn раскладывается на
три составляющие: окружную Ft, осевую Fa и радиальную Fr:
Ft=2Tx/dc, Fa=FM-,
Fr=Ft tg aw=Fztgaw/cosP; (5.2)
Fn=Fdcos aw=FJcos % cos p.
При расчете зубчатых колес на контактную и изгибную проч-
ность обычно имеют дело с расчетной нагрузкой, под которой
Ш
понимается значение удельной нагрузки q, распределенной по
линии контакта зубьев, учитывающее перекрытие зубьев, нерав-
номерность ее распределения по ширине венца колес и влияние
динамических составляющих:
q = ^-K?Kv
•к
cos aw ’
(5.3)
Здесь /K=&w^ea/cos р — суммарная длина контактных ли-
ний, зависящая от коэффициента торцевого перекрытия еа и его
эффективности, оцениваемой коэффициентом К,. Величина Kt
зависит от степени точности зацепления, Ке=0,8 ...1,0, в среднем
принимают Ке=0,9. l/Keee=Ka учитывает распределение на-
грузки между зубьями; К» — неравномерность распределения
нагрузки по ширине венца колеса, Kv— дополнительную дина-
мическую нагрузку, возникающую в зацеплении при работе
передачи. Параметр
(Ftibw)K$Kv=wt (5.4)
называют удельной окружной динамической силой, имеющей
размерность Н/мм.
При расчете зуба на контактную прочность параметрам Ка,
К», Kv и Wt добавляется индекс Н, а при расчете на изгиб — ин-
декс F.
Введение в (5.3) коэффициента неравномерности нагрузки по
ширине венца колеса К» связано с прогибами валов и деформа-
циями опор, корпуса и зубьев зубчатых колес. Так, в зависимо-
сти от положения зубчатых колес относительно опор наблюда-
ется перераспределение нагрузки вдоль образующей зуба, вы-
зывающее в отдельных местах ее концентрацию. При симметрич-
ном расположении зубчатых колес относительно опор (рис.
5.11, а) прогиб валов почти не
Рис. 5.10. Схема сил на косозу-
бом колесе
изменяет распределение на-
грузки по длине зуба (концен-
трация минимальная); несим-
метричное (рис. 5.11,6) и кон-
сольное (рис. 5.11,4) располо-
жение зубчатых колес относи-
тельно опор вызывает их вза-
имный перекос и ведет к пере-
распределению нагрузки от но-
минального значения q=Ft/bw
(рис. 5.11, а) до значения <7шах=
= q+q' (рис. 5.11,6). Концент-
рация нагрузки увеличивает
контактные напряжения и на-
пряжения изгиба у краев зуба
в месте <7тах- Приработка зуба
112
Рис. 5.11. Схемы расположения зубчатых
нагрузки (г, д) по длине зуба
г д
колес (а, б, в) и концентрации
при невысокой твердости зубчатых колес и применение тонких
колес уменьшает это явление. Для зоны концентрации
^тах = ^ + ^ = ^(1+^) = Л (5.5)
где К» — коэффициент концентрации нагрузки по длине зуба.
При расчете зуба на контактную прочность для определения Кн»
можно воспользоваться графиками в приложении к ГОСТ
21354—75 *. Его величину оценивают также по формуле
(14-Се/^С^Ся), (5.6)
где С,, Се, Си, СОб— коэффициенты, учитывающие наклон зуба,
расположение зубчатых колес относительно опор, твердость зуб-
чатых колес и жесткость обода соответственно.
Таблица 5.3
Коэффициент Cq при расположении колеса
Расположение ше- стерни относительно опор симметричном несимметричном консольном !=—=
Симметричное 0,1 0,2 0,2 0,45 0,45
Несимметричное 1= 0,2 0,3 0,15 0,4 0,4
I Консольное 0,45 0,5 0,5 0,6 0,35
113
Рис. 5.12. Схема зацепления
двух зубчатых колес с ошиб-
ками по шагу
Для прямозубых колес. Сц=1,
для косозубых Cf=l,2 . Выбор Се
осуществляется по табл. 5.3.
Коэффициент Сн учитывает воз-
можность приработки зубчатых ко-
лес при понижении твердости и оп-
ределяется по формуле
С
н—
HBt нв2
600 600 ’
где HBi и НВ2 — соответственно
твердости шестерни и колеса. Коэф-
фициент СОб учитывает податливость обода; при жестком ободе
СОб=1, при ободе с утонченными краями СОб=0,9.
Введение в (5.3) коэффициента Kv объясняется возникнове-
нием при работе передачи динамической составляющей нагрузки,
связанной с ошибками зацепления. Одной из причин ее появле-
ния является ошибка основного шага бРь=Ры—Рьг, где Ры и
Pi>2 — основные шаги шестерни и колеса (рис. 5.12). Если Ръг>
>Ры, то вторая пара зубьев вступает в зацепление в точке Ь' до
выхода на линию зацепления в точке Ь. При этом изменяется
мгновенное значение передаточного отношения и происходит кро-
мочный удар (при Pb2<.Pbi — срединный удар). Величина этой
нагрузки зависит также от скорости v, размеров передачи и. ряда
других факторов. Удельная нагрузка на зуб с учетом ее концент-
рации по длине зуба и динамической составляющей от погреш-
ности зацепления будет равна
^max^wH-^— 9max^w П 4~Рд/0?max^w)] —t^- Hv (5-7)
где ^max&w — статическая составляющая нагрузки (окружная си-
ла) с учетом концентрации; КяР= l + fA/(^max^w ) — коэффициент
динамической нагрузки, учитывающий появление динамической
составляющей Fn от динамического момента Т. = J„ м ——-;
di
г du>2
•'в.м и -----момент инерции и угловое ускорение вращающих-
ся ведомых масс. Возникновение динамической составляющей
F^ связано с погрешностью основного шага зубчатых колес, вы-
зывающего кромочный удар при dd)2/^^=0. Таким образом:
(5.8)
где WHi>—Fnlbw — удельная окружная динамическая сила, Н/мм;
Т\ — вращающий момент на шестерне, Н-мм.
114
Таблица 5.4
Твердость поверхности зуба, Нв Виды зубьев
Не менее 350 HBi или 350 НВ2 Прямые без модификации головки 0,006
Прямые с модификацией головки 0,004
Косые 0,002
Более 350 HBt и 350 НВг Прямые без модификации головки 0,014
Прямые с модификацией головки 0,010
Косые 0,004
Удельная окружная динамическая сила оценивается также по
формуле
=Ънёо10 Vaw/U <wHvUm, (5.9)
где дн — коэффициент, учитывающий вид зуба и твердость мате-
риала колес (табл. 5.4) (ГОСТ 21354—75*); go — коэффициент,
учитывающий погрешность зацепления по шагу; при т<3,5 мм
для 6-й степени точности go=38, для 7-й — go=47, для 8-й —
go=56.
Если значения whv, вычисленные по (5.9), превышают шн«ит
(табл. 5.5), то их следует при /п<3,5 мм принимать равными
Whv Иш-
5.6. ДЕФЕКТЫ И РАЗРУШЕНИЯ ЗУБЧАТЫХ КОЛЕС
Причиной выхода из строя зубчатых колес являются
неправильные условия эксплуатации, выбор материала и ошибки
в конструкции. Основными видами разрушения являются кон-
тактные разрушения, износ, задиры по боковым поверхностям
зубьев и разрушение (поломка). Контактные разрушения зубьев
являются основной причиной отказов быстроходных зубчатых
колес. Они проявляются в выкрашивании материала на контакт-
Таблица 5.5
Степень точности wBv 11m- tlm- W““ Степень точности w/fpllnv “'follm- Н/ММ
4 32 7 240
5 85 8 380
6 160 9 700
115
ной поверхности и могут быть ограниченными и прогрессирую-
щими. Прогрессирующее выкрашивание проявляется, как пра-
вило, у зубчатых колес с твердыми зубьями и развивается со
временем до значительных размеров. Может также наблюдаться
глубинное контактное разрушение в виде отслаивания сравни-
тельно крупных участков упрочненного (цементированного) слоя
металла.
Основными причинами контактных разрушений зубьев явля-
ются: концентрация нагрузки по длине и профилю зубьев, осо-
бенно проявляющаяся при твердых зубьях ввиду их плохой при-
рабатываемости; дефекты изготовления деталей передачи и их
сборки; неблагоприятные упругие деформации деталей, обуслов-
ленные их недостаточной жесткостью; неблагоприятное воздей-
ствие на зубья смазки. Концентрация нагрузки проявляется в
большинстве случаев у одного из краев зубьев, вызывая разру-
шение поверхности в этом месте. Особенно часто это проявляется
у конических зубчатых колес. Неблагоприятное воздействие смаз-
ки проявляется в эрозионных повреждениях поверхности, что ве-
дет к повышению местных контактных напряжений и разруше-
нию. Изнашивание и заедание зубьев по их боковым поверхно-
стям происходит из-за недостаточной несущей способности
масляного слоя, разрывов масляной пленки в местах контакта,
отсутствия и прекращения подачи смазки, несоответствия сорта
смазки режиму работы и др. Износ зубьев является причиной
отказа зубчатых колес как открытых, так и закрытых передач,
работающих в среде, засоренной абразивными частицами. Износ
связан с работой сил трения в зоне контакта.
Задиры возникают вследствие молекулярного сцепления ма-
териалов на участках разрыва пленки и вырыва частиц материа-
ла. Это происходит обычно при сочетании высоких давлений в
зоне контакта и больших окружных скоростей.
Разрушение (излом) зубьев является распространенным ви-
дом выхода из строя зубчатых колес. Оно обычно является уста-
лостным. Излом начинается, как правило, на переходной поверх-
ности зуба. При наличии у зуба локальных механических дефек-
тов (раковин, включений) разрушение может начинаться от этих
дефектов. Причиной поломки зуба может быть также значитель-
ная концентрация нагрузки на отдельные участки зуба, особен-
но по его краям.
6.7. ОСНОВЫ РАСЧЕТА ЗУБЬЕВ ЦИЛИНДРИЧЕСКОЙ
ПЕРЕДАЧИ НА КОНТАКТНУЮ ВЫНОСЛИВОСТЬ
Расчет на контактную выносливость прямозубых и ко-
созубых эвольвентных цилиндрических передач (ГОСТ
21354—75*) предусматривает предотвращение усталостного вы-
116
крашивания активных поверхностей зубьев. Рассмотрим основы
этого расчета с некоторыми упрощениями.
Расчет зубьев ведут в полюсе П контакта (см. рис. 5.4), по-
скольку околополюсная зона обладает наименьшей контактной
прочностью ввиду того, что нагрузка здесь наибольшая, а сколь-
жение зубьев выше и ниже этой зоны способствует развитию
микротрещин и выкрашиванию частиц металла.
Контакт зубьев с радиусами кривизны р! и р2 рассмотрим как
контакт двух цилиндров с радиусами =pi и #2=рг; для опре-
деления контактных напряжений, возникающих в зоне контакта
под действием нагрузки Fn, используем формулу Герца (2.25).
Удельная нагрузка q—Fnllv, распределенная по линии контакта
зубьев /к, с учетом перекрытия зубьев, неравномерности распре-
деления нагрузки по ширине венца колеса и влияния динамиче-
ских составляющих на основании (5.3) и (5.4) будет равна
' д^К„,К„.= , (5.10)
th COS dm К. * COS
где 'wHt=^ntl^,u)^H^nv (5.П)
В общем случае для косозубой передачи радиусы кривизны по
диаметрам dv эквивалентных прямозубых колес будут равны (см.
рис. 5.7)
Pi =0,5rfl,1 sin aw; p2=0,5rft,2 sin аю.
Тогда
1 1,1 2 cos2? , 2 cos2? 2(«±l)cos2? ,C1O.
' I* “““““ 1 i* j (U. 1 & J
рлр Pi P2 rfisinatp d2 sin aw rftasinaw
где знак «+» соответствует наружному, а «—» — внутреннему
зацеплению.
Подставляя в (2.25) значение q из (5.10), 1/рПр из (5.12) и
заменяя cos aw sin aw на 0,5sin 2a®, получаем
a 1/ wHt 2(a±l)cos2? £np
9fi V sin2aa,rf1u л(1— n2)
Обозначив Zh— V 2 cos2 p/sin 2a„, — коэффициент, учиты-
вающий форму сопряженных поверхностей зубьев; ZM=
— У £пр/л (1 — р2) — коэффициент, учитывающий механические
свойства материалов сопряженных зубчатых колес; Z,=
= V 1/(Л\еа)— коэффициент, учитывающий суммарную длину
контактных линий, получим зависимость для проверки контакт-
ной выносливости зубчатой пары в виде
a„=Z^Z Z 1/ wff‘ “ 1
° Я— I/-------
И di и
aHp<
(5.13)
где внр — допускаемое контактное напряжение.
117
6»
tfvilm
0
"на Nhq ^u,
Рис. 5.13. Зависимость предельных кон-
тактных напряжений owim от числа цик-
лов N
Для передачи без смещения или при смещении Xi+X2=*x=0
и aw=a=20°, Zh— 1,76 cos р, для стальных зубчатых колес ZM=
=275 МПа1/2, для прямозубых передач Z,= l, для косозубых —
При проектном расчете, когда необходимо определить разме-
ры передачи из условия контактной выносливости, зависимость
(5.13) решают относительно aw или dt. При определении aw,
заменяя FHt=2Ti/dwl; b=^baOw и dwi=2aw/u±l, получим:
... _ ± Ч
wHt—------1-----"--------i 72 ’
"w rbaaw
Обозначив 0,5(ZHZuZt)2=Ka, получим после преобразо-
вания
(5-14)
। Для стальных зубчатых колес при прямых зубьях и aw=20°
Ла=48,5 МПа1/3.
Допускаемое контактное напряжение определяют, используя
кривую предельных контактных напряжений (рис. 5.13) по фор-
муле
. _ °Я111П _ °Я11т» £Л
ЯНр—----------------A HL'
SH SH
(5.15)
Здесь (Гнить — предел контактной выносливости поверхностей
зубьев, соответствующий базовому числу циклов перемены на-
пряжений Nho', Sh — коэффициент безопасности, Khl — коэффи-
циент долговечности, стя um а — верхний предел контактной вынос-
ливости, он um — предел контактной выносливости, соответствую-
щий числу ЦИКЛОВ Nhu<Nh<NhO-
Предел контактной выносливости он нт ь и базовое число цик-
лов перемены напряжений Л/яо зависят от твердости рабочих по-
верхностей зубьев; анить определяется по табл. 5.6, а Nho — по
рис. 5.14 и в зависимости от твердости колеблется в пределах от
ЛГяо=1О7 (200 НВ) до#яо=12-10г (550 НВ).
118
Nuo, или. циклов
Рис. 5.14. Зависимость базового числа циклов перемены напряжений Nho
от твердости
Коэффициент безопасности для материала зубчатых колес
с однородной структурой (при нормализации, термоулучшении
или обычной закалке) $н=1,1; для зубчатых колес с поверхност-
ным упрочнением (поверхностная закалка, цементация, азотиро-
вание) $я=1,2. Для передач, выход из строя которых связан с
тяжелыми последствиями, $н=1,25... 1,35.
Коэффициент долговечности Khl учитывает влияние срока
службы и режима нагружения. Его расчет основан на исполь-
Таблица 5.6
Материал Способы термической или термохимической обработки Твердость поверхности
Углеродистая или легированная сталь Отжиг, нормализация или термоулучшение Объемная закалка со средним или низким от- пуском Поверхностная закал- ка Цементация и нитро* цементация Азотирование не более 350ЯВ 38... 50HRC 40... 56HRC 56... 64HRC 550... 750ЯУ 2НВ+70 18ЯЯС+150 17Я/?С+200 23HRC 1050
Безоловянистая бронза Закалка с отпуском не менее 80ЯВ 2НВ
Оловянистая бронза Закалка с отпуском не менее 60Я® 2,ЗЯВ
119
зовании кривой выносливости (см. рис. 5.13), для которой на
участке Nna^Nfi^Nno справедлива зависимость
^н(аНМп)6 = ^Яо(аЯНт»)в==СОП5^ (5.16\
Тогда можно записать, что
аЯПтв °ЯПт — aHlImft
6 Г ft я
I / НО ____„ is
I/ “77---—°ЯНт6/'//£»
Г п н
(5.17)
где при ./Vtf^lO5 2,4>ЛГЯД= 1/ но > 1; при поверхност-
F NH
ном упрочнении 1,8>Кк>1.
При расчетах на контактную выносливость авиационных зуб-
чатых передач, с учетом того, что они изготавливаются из опре-
деленной группы сталей и к ним предъявляются жесткие требо-
вания, допускаемые напряжения в области NH=5-107 циклов
могут доходить до Олр=1500 МПа. Для обеспечения высокой
контактной выносливости и износостойкости поверхности зуба
твердость цементируемой стали должна быть не менее HRC 60
при твердости сердцевины HRC 30... 42.
Определение Nh зависит от срока службы и режима нагруз-
ки. При постоянных режимах нагрузки, к которым обычно от-
носят режимы с отклонениями до 20% от номинального, расчет-
ное число циклов перемены напряжений
NH = 60nthc, . (5.18)
где л — частота вращения колеса, по материалу которого опре-
деляют допускаемое напряжение, об/мин; th — время работы пе-
редачи (ресурс), ч; с — число зацеплений зуба за один оборот
колеса.
При переменных режимах нагрузки (рис. 5.15) расчет Khl
ведут по эквивалентному чис-
лу циклов Nhe<Nh- Методика
его расчета базируется на тео-
рии суммирования поврежде-
ний. Ведя расчет на контакт-
ную выносливость, в этом слу-
чае по максимальному моменту
циклограммы Ть используя за-
висимость (5.16), получим
= вя.1т/Уя£=const. (5.19)
Рис. 5.15. Циклограмма нагруже- Здесь —SA/нь где
ния при переменном режиме S/Vjh — число циклов действия
120
некоторого предельного напряжения Онить например ан iimi,
Он 11т 2 И Т. Д.
Так как контактные напряжения согласно (5.13) пропорцио-
нальны корню квадратному из нагрузки в виде момента Т, по-
лучим, используя (2.3) при m'=mjv=3 и а= 1, зависимость для
подсчета эквивалентного числа циклов
ЛГя2?=60с (5.20)
Г-1
где — частота вращения i-ro вала редуктора, об/мин; ti — дли-
тельность действия момента, ч.
При расчете на контактную выносливость не принято учиты-
вать кратковременные перегрузки, поскольку ввиду малости чис-
ла циклов они ее не снижают.
5.8. РАСЧЕТ ЗУБЬЕВ НА ВЫНОСЛИВОСТЬ
ПО НАПРЯЖЕНИЯМ ИЗГИБА
При работе передачи зуб испытывает сложнонапря-
женное состояние; при этом наибольшие напряжения возникают
у корня зуба в месте перехода эволь-
вентного профиля в' галтель. В этом
же месте возникает и концентрация
напряжений. Расчетная схема на-
пряжений в прямозубой цилиндриче-
ской передаче приведена на рис.^
5.16. При расчете принимают сле-
дующие допущения: 1) вся нагрузка
в зацеплении воспринимается одним
зубом и приложена к его вершине;
2) зуб рассматриваем как консоль-
ную балку, для расчета которой
справедливы методы сопротивления
материалов. Полученные зависимо-
сти, являющиеся приближенными,
уточняем введением коэффициентов.
Нагрузку на зуб в виде силы Fn
по линии действия переносим в точ-
ку А, лежащую на оси симметрии
зуба, и раскладываем на составляю-
щие Ft'=Fncosaw и Fr'=Fncosaa>,
принимая а'=Оа>. Наибольшее зна-
чение напряжения в зоне растяну-
Рис. 5.16. Эпюры напряжений в
опасном сечении зуба
121
тых волокон, где обычно возникают трещины:
--вц ®СЖ
Ма
«"и
сж
S
6f'tl
^Х
F'r
Ьп$х
где sx — размер зуба в сечении, расположенном вблизи основной
окружности; Wn — момент сопротивления изгибу.
С учетом концентрации напряжения у корня зуба получим
а/7=олав=
QF’tl
sx2
tg и»
&wsx
а.
Используя геометрическое подобие зубьев различного модуля,
положим 1=Гт-, sx=s'xm, где I' и s'x—безразмерные коэффи-
циенты. Тогда с учетом дополнительной динамической нагрузки в
зацеплении, ее распределения по ширине венца зубчатого колеса
и наличия перекрытия, принимая F/=F/tgaw, получим
д __ Pt^p^F^Pv Г 6/'_________tg aw
Р bwm I (s^)2 s’x
Параметр yP=
называют коэффици-
ентом формы зуба. Принимая в запас прочности Ft'=Ft, полу-
чим условие изгибной выносливости зуба:
°р — Ур
Ft^F^F^Fo
bwm
(5.21)
где gfp — допускаемое напряжение на выносливость при изгибе.
Обозначая wFt=-----‘ Рл ? (удельная расчетная окруж-
bw
ная сила), преобразуем зависимость (5.21) с учетом наклона
зуба:
яр—УрУ»У^
wpt
т
(5.22)
где yt=l/ea — коэффициент, учитывающий перекрытие зубьев;
ffo=l—Р/140 — коэффициент, учитывающий наклон зубьев; для
прямозубой передачи yt=yfi=\.
Безразмерный коэффициент ур зависит только от формы зуба
(размеров I и $я) и формы галтели у его основания, вызывающей
концентрацию напряжений (учитывается коэффициентом eta).
Величину ур в зависимости от эквивалентного числа зубьев zv—
=z/cos3p и коэффициента смещения х определяют по рис. 5.17. Ко-
эффициент Kf» зависит от тех же факторов, что и Кн»- При рас-
четах принимают Кр^=К.нь. Коэффициент Kpv определяют по
122
Рис. 5.17. Зависимость коэффициента Y? от эквивалентного числа зубьев
z0 и коэффициента смещения х
(5.8) с учетом (5.9) путем замены в (5.8) буквы Н на F. При
этом для прямозубых передач без модификации головки бр=
=0,016, с модификацией головки 6f=0,011, для косозубых и
шевронных передач 6f=0,006. Предельные значения wFv цщ даны
в табл. 5.5. Если значения wFv, вычисленные по (5.8), превыша-
ют Wviim, их принимают равными этим предельным значениям.
Вводя вспомогательный коэффициент Кт и принимая Kf*=
=Л’р1>=1, после преобразований (5.22) получим ориентировоч-
ное значение модуля зацепления:
-у,*)''’. (5.23)
Величину коэффициента фм берут в пределах 0,3... 0,6, при-
чем меньшие значения назначают тогда, когда возможна боль-
шая концентрация нагрузки по длине зуба (консольное располо-
жение зубчатых колес); принимают Л'т«1,4 для прямозубых,
Кт» 1,12 для косозубых передач.
Допускаемые напряжения изгиба при расчете на выносли-
вость при de<300 мм определяют по формуле
(5.24)
SF
123
Таблица 5.7
Стали Способ термической или термохимиче- ской обработок зубьев Твердость зубьев аП1тЪ> МПа
поверхности сердцевины
Углероди- стые и леги- рованные (40, 45, 40Х, 40ХН, 40ХФА, 40ХН2МА, 18Х2НЧВА и др.) Нормализация, термоулучшение Объемная закал- ка с применением средств против обезуглерожива- ния То же при воз- можном обезугле- роживании 180... 300ЯВ 45... 55ЯЯС 180... 300ЯВ 45... 55ЯЯС 1,8 НВ 600
Содержа- щие алюми- ний Азотирование зубьев на глубину 0,1... 0,2m 700...950ЯУ 24... 40HRC 12ЯЯС+300
Прочие легирован- ные То же 550... 750ЯИ 24... 40HRC
Легиро- ванные всех марок Цементация на глубину не менее 0,2m с последую- щей закалкой без обезуглерожива- ния 56... 63ЯЯС 30... 45HRC 800... 950
где предельное напряжение при изгибе aFiim=OFiim
X KpcKpl.
Значения базового предела выносливости для отнулевого цик-
ла в зависимости от вида термической или термохимической об-
работки приводятся в табл. 5.7.
Для зубчатых колес с нешлифованной переходной поверхно-
стью КР<=1; при шлифовании с наличием шлифовочных прижо-
гов и острой шлифовочной ступеньки Kpg=0,75... 0,8.
Коэффициент Kpd учитывает деформационное упрочнение, при
его отсутствии Kpd=l. Коэффициент Крс учитывает снижение
Of ишь в случае двухстороннего приложения нагрузки; в этом
случае Kfc=0,65... 0,8 (большие значения берутся при повышен-
ной вязкости стали).
Коэффициент долговечности Kfl= (Npo/Npe)'1”1, где т — не-
который коэффициент, /и=6 для зубчатых колес со шлифованной
переходной поверхностью, т=9 при нешлифованной переходной
поверхности. При m=6 2,8^KfL^;l, при т=9 1,63>Хм>1.
124
Базовое число циклов Уко=4-106, а эквивалентное число цик-
лов перемены напряжений определяется по циклограмме в за-
висимости от нагружения. При постоянном режиме нагружения
Nfe определяется по (5.18), а при переменном режиме по ана-
логии с (5.20) по формуле
(5.25)
Для нормализованных и улучшенных сталей т=6, для за-
каленных сталей /п=9.
Коэффициент безопасности Sp= 1,75... 2,2. Большие значения
Sf берутся при обеспечении надежности свыше 0,99.
Коэффициент у3 учитывает чувствительность материала к кон-
центрации напряжений и зависит от модуля т (табл. 5.8).
Коэффициент ун учитывает шероховатость переходной поверх-
ности, при шлифовании и зубофрезеровании ун= 1; при полиро-
вании в зависимости от способа термического упрочнения при-
нимают: при цементации и азотировании (полирование до хими-
ко-термической обработки) «/я=Г,05; при закалке ТВЧ, когда
закаленный слой повторяет очертания зуба, уд=1,05.
Расчет на малоцикловую выносливость при изгибе. При мало-
цикловом нагружении (JV< 10s) прочность зубьев лимитируется
их изгибной выносливостью. Предотвращение излома зубьев от
малоцикловой усталости при плавном и ударном нагружении с
заданной степенью вероятности гарантируется при соблюдении
неравенства
aFL ~ УрУзУ$ —-iL -С aFPL‘ (5.26)
tn
Здесь коэффициенты ур, у„ У» вычисляются аналогично рас-
чету на выносливость при изгибе. Удельная расчетная окружная
сила вычисляется по формуле
р __ M\fil г f // 97 \
wFtL—г FtL----------------——К.pj\ р$'\(5-27)
Оу
За расчетную нагрузку Tifii, при ступенчатой циклограмме
принимают каждую из ступеней с соответствующим ей на цик-
Таблица 5.8
т, мм Уя т, мм Уя
1 м 5 0,96
2 1,03 6 0,94
3 1,0 7 0,93
4 0,98 8 0,92
125
КЗ о>
Стали Способ и вид термической или химико- термической обработок Твердость аяи
поверх- ности сердце- вины 10»
Легирован- ные, содер- жащие никель более 1% Цементация. Закалка с применением средств про- тив обезуг- лероживания 57...62ЯЯС 30...45ЯЯС 2650 2100
Прочие ле- гированные
Легирован- ные, содер- жащие никель более 1% Цементация. Закалка в ус- ловиях, допу- скающих обез- углерожива- ние 56...62ЯЯС 2650 2100
Прочие ле- гированные
Легирован- ные, содержа- щие молибден (25ХГМ и др.) Нитроцемен- тация. Закал- ка с примене- нием средств против обез- углерожива- ния, деаэоти- зация 57...62ЯЯС (азота 0,15...0,5% 2650
Прочие ле- гированные 57...62ЯДС (азота 0,15...0,5%)
Легирован- ные, содержа- щие алюминий Азотирован- ные 700...950ЯУ 24...31ЯЯС 32...40ЯЯС 1700 1800
Таблица 5.9
mL. МПа, при числе циклов KPLg при числе циклов при числе циклов при ве- роятности неразрушения
10s 10< 105 10я и 10s 10‘ 10® 102 и 10» 10< 10® 0,99 свыше 0,99
2150 1750 1650 1350 1100 1000 1,1 0,9 0,85 0,95 1,05 1,1 1,55 1,98
2100 1700 1450 1250 1000 900 — 1,15 1,3 1,75 2,2
220 1700 1350 0,95 0,85 0,75 0,95 1,05 1,1 1,55 1,95*
1,0 1,3 1,6
1300 1400 1000 1100 750 850 - — — — — 1,75 2,2
Рис. 5.18. Структурная схема автоматизированного проектирования зубча-
тых колес
лограмме числом циклов, если оно не превышает 10s; при этом
производится проверка по каждой ступени. При плавной цикло-
грамме нагружения расчет производят при числах циклов, рав-
ных 103, 104 и 105, принимая за исходные те расчетные нагрузки,
которые на циклограмме нагружения соответствуют указанным
числам циклов.
При проектировании зубчатой передачи в случае ее работы
на малоцикловую выносливость модуль зацепления по исходным
данным определяют, используя (5.26), подбирая затем его бли-
жайшее большее значение по стандарту.
Допускаемое напряжение определяется отдельно для шестер-
ни и колеса по формуле
у,Кг. (5.28)
SFL
Предельное напряжение аршпь, не вызывающее излома зуба
при малоцикловой усталости, а также коэффициенты KvLg, Кыл
и sfL определяют в зависимости от способа термической или хи-
мико-термической обработки и числа циклов перемены напряже-
ний (табл. 5.9).
5.9. ИСПОЛЬЗОВАНИЕ ЭВМ ПРИ ПРОЕКТИРОВАНИИ
ЗУБЧАТОЙ ПЕРЕДАЧИ
Кратко рассмотрим один из возможных вариантов диа-
логово-автоматизированного проектирования цилиндрической
зубчатой передачи (рис. 5.18). В точке диалога Д-1 на экран
дисплея выводится опросный бланк, заполнение которого поль-
зователем обеспечивает ввод числовых значений исходных дан-
ных, а при повторном счете — их редактирование. После выпол-
нения проектных расчетов цилиндрической зубчатой передачи
127
Таблица 5.10
Идентифи- катор Обозначение величины Единица измерения Наименование величины Тип переменной
Zl; Z2 Zt; Z2 — Число зубьев шестерни и колеса REAL
НВ1; НВ2 НВс нв2 — Твердость рабочей по- верхности зубьев шестер- ни и колеса REAL
Е Е МПа Модуль упругости ста- ли REAL
SAI; SB1 GFllmai; ОЛ1тМ МПа Верхний и нижний пре- делы выносливости .зуба шестерни при изгибе REAL
SA2; SB2 <JFIlma2> ОЯ1тЬ2 МПа Верхний и нижний пределы выносливости зуба колеса при изгибе REAL
KD Кд — Коэффициент динамич- ности REAL
Т1 Т1 Н-мм Расчетный момент на ведущем валу REAL
AW aw мм Межосевое расстояние REAL
М т мм Модуль REAL
SIPH Онр МПа Допускаемое контакт- ное напряжение REAL
КНА — Коэффициент, учиты- вающий распределение нагрузки между зубьями REAL
кнв Коэффициент, учиты- вающий неравномерность распределения нагрузки по длине зуба REAL
BW bw мм Рабочая ширина венца REAL
ATW O>tw градус Угол зацепления REAL
DA1 DA2 dal da2 мм мм Диаметры вершин зубьев шестерни и коле- са REAL
SIH ОН МПа Расчетное контактное напряжение зубьев REAL
L — — Число, обозначающее диапазон твердости ра- бочих поверхностей зуба INTEGER
L1 — — Число, обозначающее модификацию головок зуба Степень точности пе- редачи по нормам плав- ности INTEGER
L2 — — INTEGER
N1 ni об/мин Частота вращения ве- дущего вала REAL
NHE1 Nhei — Расчетное число цик- лов контактных напря- жений зуба шестерни REAL
NFE1 Nfei — Расчетное число цик- лов изгибных напряже- ний зуба шестерни REAL
128
Продолжение табл. 5.10
Идентифи- катор Обозначение величины Единица измерения Наименование величины • Тип переменной
W1 wt кВт Мощность на ведущем валу REAL
в 3 градус Угол наклона зуба REAL
PSIA 1|>а — Относительная ширина колес REAL
CQ — Коэффициент, учиты- вающий влияние прогиба валов REAL
ЕА еа — Коэффициент торцево- го перекрытия REAL
XI Х2 Xi Х2 Коэффициент смеще- ния исходного контура зубьев шестерни и коле- са REAL
SF SF — Коэффициент без- опасности REAL
(блок 1) в точке Д-2 результаты расчетов (геометрические ха-
рактеристики зубчатого венца) выводятся на экран дисплея и
при необходимости уточняются. В блоке 2 выполняются прове-
рочные расчеты цилиндрической передачи, и результаты выво-
дятся на экран (блок 3). На основании анализа полученных ре-
зультатов в точке Д-З принимается решение об окончании рас-
четов и переходе к воспроизведению детали или повторении счета
с соответствующим уточнением данных в Д-1. Далее осуществля-
0001
0002
оооз
0004
0005
QQQ6
0009
0010
0011
0012
0015
0014
0015
0016
0017
COMMON LI.L2.N1.W1,SA1,SB1.SB2.В,Z1.Z2.H1.Н2.
Е,NHE1.NP4l.fSlA.Ci.EA.X1,a2,SF. YR1.YR2,К D,STHP
L]KHA.£HB.F fe,AW.6w,ft,AtW, t)A1 ,DA2,Slfi,T1
rSal Й1 .nAeiInpSi,i(D’KHA,KHB’M. _
NAMELlSt/РНОёКТ/ 1Л ,Lf,N1]W1.SAI.SB1,
SA2.SB2,B,Z1,Z2.H1,H2XE,NHE1.NFE1,
PSlA.CQ eA.x! .X^.SP1 ,Yrt1 ,YR2,?.D
READ (5.PR6EKT)
CALL DET71 ,, „
Л?У1Ж9**7*К1)/(5-1416*М1)
v A Jj-Li Ub 1 I c.
CALL DET73
AW=0.8~' ^'
•PSIA*
Ms 2* AW
PRINT '
FORMAT
CALL DL_. .
iw=few*pl|/siHP)»»2
CALL DET76
CALL DET77
3
М
0018 STOP
0019 END
Рис. 5.19. Головная программа расчета цилиндрической зубчатой передачи
5—1085
129
' Г
DET76 Для изгива зувьев опреде лаются расчетные напряже чип Ъ-Шв . допускаемые напряжения Проверка бр « бРР Проверка по изгибу
SFZ7.SFP7.5FZZ.SFPZ
0ЕТ77 Проверка резупьтав расчета | \Расчетные значения |M,fllKBW.Z7.ZZ.Dfl7.DflZ,X7,XZ..
Рис. 5.20. Алгоритм расчета цилиндрической зубчатой передачи
130
ется формирование изображения (блок 4), которое требует ввода
дополнительных исходных данных в точке Д-4 (диаметр вала,
характер соединения, вид конструкции). В точке Д-5 изображе-
ние выводится на экран, и в конструкцию могут вноситься из-
менения. В точке Д-6 принимается решение о повторении счета
или формировании изображения с необходимыми изменениями.
Уточнение данных выполняется в точках Д-1 и Д-4.
Более подробно рассмотрим расчет на ЭВМ цилиндрической
зубчатой передачи. При составлении программы применяется мо-
дульное программирование, которое связано с использованием
готовых подпрограмм (модулей). Расчет может выполняться как
в диалоговом режиме, так и с вводом информации с перфокарт.
В основной программе используются идентификаторы (табл.
5.10).
На рис. 5.19 приведена головная программа расчета цилинд-
рической зубчатой передачи, а на рис. 5.20 — ее алгоритм.
В заключение отметим, что использование ЭВМ позволяет
быстро выполнить расчет для ряда вариантов зубчатых передач
и выбрать из них оптимальный, что повышает качество конструк-
ции. Еще больший эффект дает автоматизация проектирования.
5.10. ЛЮФТОВЫБИРАЮЩИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
Наличие бокового зазора /п между зубьями в ревер-
сивных передачах вызывает погрешность мертвого хода и появ-
ление дополнительных динамических нагрузок. Особенно это от-
носится к передачам авиационного приборостроения, в которых
ошибка мертвого хода снижает их точность и в некоторых.случа-
ях должна быть сведена к нулю.
Погрешность мертвого хода бфм (рад) на валу зубчатого ко-
леса оценивают по формуле
8?H=/n/(rcosaw), (5.29)
где аш — угол зацепления; /п, мм; г — радиус начальной окружно-
сти зубчатого колеса, мм.
При aw=20° и величине /п, выраженной в микрометрах и оп-
ределяемой по ГОСТу в зависимости от вида сопряжения, по-
грешность мертвого хода на валу зубчатого колеса в угловых
минутах определяется так:
8<рм=7,4/л/(/п,г). (5.30)
Величина суммарного или приведенного к входному или вы-
ходному валу многоступенчатой (трехступенчатой) зубчатой пе-
редачи (рис. 5.21) при мертвом ходе на валу 2 — 6фм2, на валу
3— бфмз и на валу 4 — бфМ4, определяемых по формуле (5.30) в
5* 131
Рис. 5.21. Схема трехступенчатой зубчатой передачи
зависимости от величины бокового зазора /я, будет
движном входном вале):
—+-^+8?м4=
«2-3«3-4 «3-4
_&Рм2«1—2 ^?м3«1-3 I
«1-4 «1-4 М4’
или в общем случае при п валах
п
8?мл = —— У 8?м*
И1-Л «
(при непо-
(5.31)
(5.32)
Здесь «1-2, «2-з. «(n-i)-n — передаточные числа между ва-
лами 1, 2,п.
При приведении к валу 1 получим
п
8?м1= 28?m*«i-s.
»=2
(5.33)
Для уменьшения погрешности мертвого хода на основании
зависимостей (5.32) и (5.33) следует разбивку передаточного
числа редуктора выполнить согласно условию Ы1-2<«2-з< — <
<«(П-1)_П, т. е. увеличивая передаточные числа последних ступе-
ней за счет уменьшения начальных.
132
Для устранения погрешности мертвого хода применяют люф-
товыбирающие (разрезные) зубчатые колеса с пружинами растя-
жения или сжатия (рис. 5.^2, а) или с моментной пружиной кру-
чения (рис. 5.22, б). Их основой является сдвоенное зубчатое
колесо, одна половина которого неподвижна, а другая может
перемещаться, выбирая боковой зазор либо за счет пружины
растяжения или сжатия, либо за счет усилия, создаваемого ото-
гнутым концом моментной пружины кручения.
Расчет усилия на пружине растяжения или сжатия (рис.
5.22, в) ведется по формуле
(5<34)
где Тк — момент на колесе; г' — расстояние от оси колеса до
пружины; п — число пружин; 0=1,5...3 — коэффициент запаса
по моменту.
Деформация пружины ДЯ, создаваемая силой Fnp смещением
подвижного колеса на kz зубьев (kz=3 ...6), будет равна
ДА/=kznmr'lr. (5.35)
По величинам ГПр и ДЯ ведется расчет пружины.
Рис. 5.22. Конструкции разрезных
зубчатых колес
133
Рис. 5.23. Конструкции мелкомодульных зубчатых колес
Возникновение у разрезных зубчатых колес дополнительной
силы на рабочей и нерабочей поверхностях зуба от усилия пру-
жины заметно снижает их КПД. Он падает до 0,3 и менее с уве-
личением р и уменьшением окружной силы Ft.
Конструкция мелкомодульных зубчатых колес зависит от их
размеров, метода изготовления и материала. При конструирова-
нии им стремятся придать такую форму, которая удовлетворяла
бы требованию жесткости, малой массы, технологичности и др.
При d<40... 50 мм и Ь^З мм используют форму, приведенную на
рис. 5.23, а. При больших размерах для облегчения делают двух-
сторонние выточки (рис. 5.23, б) или предусматривают отверстия
(рис. 5.23, в). Односторонние выточки делают тогда, когда для
компактности внутрь колеса помещают какую-либо деталь (рис.
5.23, г, д, е). Ступица зубчатого колеса по соображениям техно-
логичности делается обычно односторонней. Двухсторонняя сту-
пица (рис. 5.24) допускается в случае, если для компактности
Рис. 5.25. Конструкции сборных зубчатых колес
Рис. 5.24. Зуб-
чатое колесо с
двухсторонней сту-
пицей
134
она соединяется с другими вращающимися деталями колеса или
при необходимости использования торца ступицы в качестве упо-
ра при посадке на вал другой детали.
При d^50 мм и небольшой ширине венца (6^6 мм) изготов-
ление колес из одной заготовки становится экономически невы-
годным и их делают сборными: тело колеса выполняют из листо-
вого материала и напрессовывают на ступицу (рис. 5.25, а) или
на вал-шестерню, предварительно срезав часть зуба (рис. 5.25, б).
Они могут также соединяться со ступицей на винтах (рис. 5.25, в).
Основной способ крепления мелкомодульных колес на ва-
лах— штифтовое (коническим штифтом). Для его осуществления
в ступице под углом 90° делают два односторонних отверстия:
под стопорный винт с резьбой и гладкое, диаметр которого равен
меньшему диаметру штифта. При сборке колесо фиксируют на
валу винтом, а через гладкое отверстие в ступице делают сквоз-
ное отверстие через вал и другую сторону ступицы. Затем это
отверстие развертывается под штифт, после чего штифт забива-
ется, а стопорный винт удаляется; от выпадания штифт стопо-
рится.
ГЛАВА 6. ЗУБЧАТЫЕ ПЕРЕДАЧИ С ЗАЦЕПЛЕНИЕМ
НОВИКОВА
6.1. ОБЩИЕ СВЕДЕНИЯ
В 1954 г. М. Л. Новиков предложил зацепление с кру-
говым профилем зубьев, имеющее точечный контакт и отличаю-
щееся высокой несущей способностью. Зубья передачи Новико-
ва располагаются по винтовым линиям и имеют профиль, вы-
полненный по дугам окружностей (рис. 6.1). В зацеплении Но-
викова контакт зубьев перемещается не по боковдму профилю,
как в прямозубой эвольвент-
ной передаче, а вдоль зуба
по линии, параллельной оси
колеса. Так как скорость пе-
ремещения контакта vK—
= »ctg₽ (где v — окружная
скорость; р — угол наклона
зубьев) и угол давления ад
остаются постоянными, то
профили зубьев шестерни и
колеса могут быть очер-
чены несопряженными кри-
выми — дугами окружно-
стей с близкими радиусами
кривизны.
Рис. 6.1. Цилиндрическая переда-
ча Новикова
135
Рис. 6.2. Исходные кон-
туры передачи Нови-
кова с одной (а) и с дву-
мя (б) линиями зацепле-
ния
В связи с тем, что точка контакта зубьев перемещается вдоль
линии, параллельной оси колес, коэффициент торцевого пере-
крытия еа в передаче Новикова равен нулю. Следовательно, для
обеспечения постоянства передаточного отношения ii2=coi/®2=
=d,2ld\=zzlzi необходимо, чтобы коэффициент осевого перекры-
тия es=&w//3o=bw sin sin р/лтп был больше единицы.
В этих выражениях d\ и dz— диаметры делительных окружно-
стей колес; Zi и Zz — числа зубьев колес; bw — ширина колес;
Рп и тп — шаг зацепления и модуль в нормальном сечении.
В основном применяют два вида зубчатых передач Новикова:
с выпуклым профилем зубьев шестерни и вогнутым профилем
зубьев колеса (рис. 6.2, а); с выпукло-вогнутым профилем зубь-
ев шестерни и колеса (рис. 6.2, б). У передач первого вида од-
на линия зацепления. При ведущем зубчатом колесе с выпуклым
профилем зубьев линия зацепления расположена за полюсом за-
цепления по направлению вращения ведущего колеса. При ве-
дущем зубчатом колесе с вогнутым профилем зубьев линия за-
цепления располагается до полюса зацепления по направлению
вращения ведущего колеса (рис. 6.3, а, б). У передач второго
вида две линии зацепления: одна располагается до полюса, дру-
гая,, за полюсом — такие передачи получили название дозапо-
136
люсных (рис. 6.3, в). Дозаполюсные передачи наиболее распро-
странены. Их несущая способность больше, чем у передач с од-
ной линией зацепления, так как число точек начального контак-
та при двух линиях зацепления больше, чем при одной. Кроме
того, зубья шестерни и колеса в этом случае можно нарезать
одним и тем же инструментом.
Радиусы кривизны профилей зубьев шестерни и колеса в пе-
редачах Новикова выбирают близкими по значению и после при-
работки зубья соприкасаются по всей их высоте. В плоскости,
перпендикулярной линии соприкосновения зубьев, в связи с боль-
шими радиусами кривизны винтовых поверхностей зубьев их
касание происходит на значительной длине. Нагрузка распреде-
ляется на значительную площадку контакта (см. рис. 6.3), что
является причиной высокой нагрузочной способности зацепления
Новикова. Допускаемая нагрузочная способность по условию
контактной прочности зубьев передач Новикова в 1,7...2 раза
больше, чем для эвольвентных передач. Благодаря большой на-
грузочной способности передачи Новикова по сравнению с пе-
редачами эвольвентного зацепления более компактны и допус-
кают большие передаточные отношения. Благодаря образова-
нию режима жидкостного трения уменьшается износ зубьев и
повышается КПД передачи.
Недостатком таких передач является значительное уменьше-
ние контактной площадки при перекосах зубчатых колес и из-
менении межосевого расстояния в результате погрешностей из-
готовления и сборки.
Для деталей передач Новикова применяются те же материа-
лы, что и для эвольвентных — стали с твердостью рабочих по-
верхностей менее 350 НВ. Это связано с тем, что в переда-
чах Новикова контактная и изгибная прочности достигаются
не увеличением твердости поверхности, а увеличением площади
пятен контакта. Применение материалов с высокой твердостью
поверхности здесь менее эффективно, так как снижается способ-
ность к приработке профилей зубьев в зубчатой паре.
12 1^2 2 1
Рис. 6.3. Линии зацепления, контактные линии и площадки контакта в пере-
дачах Новикова:
а — выпуклый зуб; б — вогнутый зуб; в — выпукло-вогнутый зуб; 1 — след линии зацеп-
ления; 2 — контактная линия; 3 — площадка контакта
137
В нашей стране и за рубежом передачи Новикова с заполюс-
ным и дозаполюсным зацеплением находят применение и в авиа-
ции. Так, в вертолете «Lynx-13» в силовом редукторе использо-
вано зацепление Новикова, позволившее вдвое повысить нагру-
зочную способность nd сравнению с эвольвентными передачами,
облегчить конструкцию вертолета и существенно улучшить его
летно-тактические данные.
в.2. ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ
ПЕРЕДАЧИ
Для цилиндрических зубчатых передач Новикова с
одной и двумя линиями зацепления стандартизованы модули
зацепления по нормальному шагу ГОСТ 14186—69. Исходный
контур для колес с одной линией зацепления установлен из
условия прочности нормалью.
Геометрические соотношения для определения основных гео-
метрических размеров цилиндрических передач Новикова сле-
дующие:
для одной и двух линий зацепления
dx=/n2:t/cos Р; rf2= /nzj/cos р;
aw=0,5/n (Zj -f-z2)/cos P; Pa=л/n/sin P;
(6.1)
й2=^— 4pa\
e?: 1,1...1,3; 2,1...2,3; 3,1...3,3; 4,1...4,3;
для одной линии зацепления для двух линий зацепления
^ei=rfi4"2Ael; da\=d\-\-2ha\
dai=d2 — 2c-, dtt2=d2-[:2ha;
(O.v
df\=d\—2йд; dfi=di 2(йв-]-с);
dj2^d\ — 2йу2; df2=d2—2(йв-|-с).
6.3. РАСЧЕТ НА ПРОЧНОСТЬ
При проектировочном расчете на контактную и изгиб-
ную прочность определяют основные геометрические размеры
передачи. Затем проводят уточненный проверочный расчет
зубьев.
В случае необходимости вносят изменения в размеры переда-
чи, полученные при проектировочном расчете.
При проектировочном расчете диаметр d\ определяют по фор-
муле
(64)
’яр » Kfv-ma
138
Рис. 6.4. Зависимость* коэффи-
циентов /(в, /С» от р и фк от Де
проверочный расчет проводят
сначала из условия обеспече-
ния контактной прочности:
= 1 | /7^я^//Л,(ц+1) <
V КуРти
< аНр’ (6-5)
где « 2 • 10-5 1 /МПа — коэф-
фициент исходной рейки, ха-
рактеризующий конкретный
исходный контур зацепления, а
также величину приведенного
модуля упругости; Kt — коэф-
фициент, учитывающий особен-
ности контактирования зубьев
в передачах Новикова (рис.
6.4); р, — величина, зависящая
от осевого коэффициента пере-
крытия ер (если ер=2,3, то р.=2)
Значения Кнь Khv, Онр передач Новикова принимают таки-
ми же, как для эвольвентных передач.
При проектировочном расчете на изгибную прочность рас-
считывают модуль
(6.6)
проверочный расчет проводят из условия изгибной прочности:
аР\
*1‘рУ₽1'»3
(6.7)
где ofi и ofp — расчетное и допускаемое напряжения для зубьев
шестерни на изгибную прочность; Кт— коэффициент, учитыва-
ющий влияние угла 0 на изгибную прочность; фк=/(Ае)—экс-
периментальный коэффициент, учитывающий отличие объемного
напряженного состояния в зубьях передач Новикова от плос-
кого (см. рис. 6.4); Ае — коэффициент, зависящий от коэффи-
циента осевого перекрытия ер. Так, если ер=2,3, то Ае=0,3. Зна-
чения коэффициента формы зуба t/p для зубьев с контуром по
ГОСТ 15023—76 приведены ниже:
2, 10 11 12 13 14 15 16 18 20 22 24 26 28 30
Др 0,79 0,83 0,87 0,89 0,92 0,93 0,95 0,97 0,99 1,02 1,03 1,04 1,05 1,05
139
Эквивалентное число зубьев zo=z/cos3p.
Допускаемое напряжение при расчете на изгиб:
при односторонней нагрузке на зубья
0,54а_! (N FJN рЕ)1!т\ (6.8)
при двухсторонней нагрузке на зубья
Ofp ^0,34а_1 (6.9)
где а_1 — предел выносливости материала зубьев при изгибе;
Npo — базовое число циклов напряжений (рекомендуется при-
нимать JVfo=107); Npe — расчетное число циклов напряжений;
т — показатель степени корня, для зубьев со шлифованной пе-
реходной поверхностью т = 6, для нешлифованной переходной
поверхности т = 9.
ГЛАВА 7. КОНИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
7.1. ВИДЫ КОНИЧЕСКИХ ПЕРЕДАЧ И ОБЛАСТИ
ИХ ПРИМЕНЕНИЯ В ЛА
Конические зубчатые колеса используют в передачах,
где оси ведущего и ведомого валов пересекаются в пространст-
ве под некоторым углом S. Наиболее часто встречаются переда-
чи с 2=90° — ортогональная передача (рис. 7.1). В ЛА полу-
Рис. 7.1. Ортогональная коническая передача
140
чили распространение кони-
ческие зубчатые колеса с
прямыми и круговыми зубь-
ями. В прямозубых колесах
(рис. 7.2, а) линии зубьев со-
впадают с образующими де-
лительного конуса; круговой
зуб (рис. 7.2, б) располага-
ется по дуге окружности. С
увеличением угла наклона
Рис. 7.2. Коническое зубчатое ко-
лесо с прямыми (а) и круговыми (б)
зубьями
зуба рт передача работает
более плавно; рекомендует-
ся выбирать рт=35°. Колеса
с круговыми зубьями при
одинаковых габаритных размерах передачи имеют в 1,5 раза
большую несущую способность по сравнению с прямыми зубья-
ми; передача с такими зубьями работает плавно и бесшумно да-
же при повышенных окружных скоростях (до 100 м/с). Это объ-
ясняется многопарностью зацепления, постепенным входом зубь-
ев в зацепление, начиная с контакта в точке, что делает их ма-
лочувствительными к динамическим нагрузкам. Это обусловило
применение конических передач с круговыми зубьями, например,
в приводе винтов вертолетов. Такая коническая передача в транс-
миссиях вертолетов, если рассматривать ближайшую перспекти-
ву, сможет передавать мощность до 6000 кВт.
Тяжелые вертолеты одновинтовой схемы могут быть трех-
двигательными (рис. 7.3, а). При этом возможна передача мощ-
Рис. 7.3. Схемы трансмиссий вертолетов:
а — одновинтовая; б — продольная; в — поперечная
141
ности от каждого двигателя через двухпоточный зубчатый ре-
дуктор, состоящий в каждом потоке из конической пары z\—z<i
и цилиндрической z%—Z3. Следовательно, максимальная мощ-
ность, передаваемая от трех двигателей через шесть пар кони-
ческих колес, может доходить до 36 000 кВт.
Вертолет продольной схемы может иметь два синхронизиру-
ющих вала, которые обеспечивают синхронное вращение несу-
щих винтов с взаимным перекрытием, а также в случае отказа
одного из двигателей обеспечивают равномерное перераспреде-
ление мощности между винтами (рис. 7.3, б). При этом макси-
мальная мощность, передаваемая от двух двигателей к двум
несущим винтам двумя двухпоточными редукторами через четы-
ре пары конических колес, составит 24 000 кВт.
Вертолет поперечной схемы может иметь четыре двигате-
ля (рис. 7.3, в). Передача мощности к двум несущим винтам
ведется через четыре двухпоточных редуктора (восемь пар ко-
нических колес). Поэтому максимальная передаваемая мощность
у такого вертолета — 48 000 кВт.
Конические передачи широко используют также в системах
управления рулевыми поверхностями ЛА, в механизмах прибор-
ных устройств, в различных механизмах ЛА, условия компонов-
ки которых требуют передавать движение между валами, пересе-
кающимися в пространстве.
Нагрузочная способность конических передач составляет
около 0,85 от нагрузочной способности цилиндрических передач.
Это объясняется, в частности, сложностью изготовления, монта-
жа и обеспечения требуемой точности, наличием осевых сил в
зацеплении, неравномерностью распределения нагрузки по дли-
не зуба. Конические передачи в вертолетных редукторах ис-
пользуют чаще на быстроходной ступени, что приводит к упро-
щению конструкции опорных узлов.
7.2. ГЕОМЕТРИЯ КОНИЧЕСКИХ ЗУБЧАТЫХ ПЕРЕДАЧ.
СИЛОВОЙ РАСЧЕТ. ПОНЯТИЕ ОБ ЭКВИВАЛЕНТНОМ
ЗУБЧАТОМ КОЛЕСЕ
Конические зубчатые колеса изготовляют с тремя
различными осевыми формами зубьев: 1) пропорционально по-
нижающиеся зубья, вершины делительного конуса и конуса впа-
дин сходятся в одной точке; 2) понижающиеся зубья, вершины
конусов делительного и впадин не совпадают. Толщина зуба по
делительному конусу растет пропорционально расстоянию от вер-
шины. Эта форма позволяет обрабатывать одним инструментом
обе поверхности зуба. Ширина дна впадин здесь постоянна;
3) равновысокие зубья. Образующие конусов вершин, делитель-
ного конуса и конуса впадин параллельны.
Первая форма является основной для прямозубых и косозу-
142
бых передач и, частично, — для передач с круговыми зубьями
при Zz=20... 100. Вторая форма является основной для колес
с круговыми зубьями. Третья форма применяется также для кру-
говых зубьев при гх^40. Остановимся на передачах с наиболее
распространенными зубьями первой формы.
По аналогии с цилиндрическими передачами вводится поня-
тие начальных и делительных конусов (обычно они совпадают)
(см. рис. 7.1): dm\=d\ — для шестерни, dm2—(fa—для колеса.
Угол делительных конусов шестерни бь колеса бг, 2=61+62.
Эвольвентная форма зубьев получается на развертке дополни-
тельного конуса, образующие которого перпендикулярны обра-
зующим делительного конуса. Сечение зуба дополнительным де-
лительным конусом называют торцевым; параметрам зубчато-
го колеса в этом сечении присваивается индекс ”t". Выделяют
внешнее торцевое сечение ”/е”, среднее ”/т” и внутреннее
Ширину зубчатого венца bw измеряют по образующей
делительного конуса, а высоту зуба h — по внешнему торце-
вому сечению. Участки образующей дополнительного ко-
нуса, ограниченные по длине внешней de и средней dm делитель-
ными окружностями, называются внешним Re и средним Rm де-
лительными конусными расстояниями. Делительные диаметры
в торцевом сечении определяют из соотношений:
<4=/n„z; dm=mtaz‘ /п/т=от/е(1+0,5фл),
где z— число зубьев шестерни или колеса; mte—средний
и внешний торцевые модули; фя=bv>IRe — относительная шири-
на зубчатого венца.
Для колес с прямыми зубьями стандартизирован внешний
торцевой модуль т<е; величина конусного расстояния равна
Re=^V ; (7.1)
тогда Rm=Re—0,5bw.
Высоту головки hae и ножки hfe зуба по внешнему торцу при-
нимают равными hae=mte, hfe=l,2mte — ДЛЯ прямого зуба; hfe =
— 1,25т/е — для кругового.
Для круговых зубьев стандартизирован средний нормальный
модуль mnm:
I* tn = ж мп/COS (7.2)
Передаточное число конической передачи:
“=^m2/^mi=22/2i=sin 82/sin 8i-
При 2=90° получим u=tg62=ctg6i. Этим выражением при за-
данном и пользуются для вычисления углов di и бг.
Для. повышения сопротивления заеданию рекомендуют шес-
терню выполнять с положительным смещением хь а колесо —
с отрицательным х2=—хг, тогда Xz=Xi+*2=0 и а»=а=20°.
143
Рис. 7.4. Усилия, действующие в коническом зацеплении
В отличие от величины смещения для цилиндрических колес
(у которых обычно Xi = + 0,3, х2=—0,3) у конических колес рас-
ширена область целесообразного применения высотного корри-
гирования. Коэффициенты смещения Xi для прямых зубьев и xni
для круговых с округлением до 0,1 определяют по формуле
х1=хщ = 2(1—u2/cos3 Pm/zi)- Тогда внешний диаметр колес dae=
=de+2hae cos б, высота головки зуба hae = mte{h*te -f-xcos
где h*te=cospm. Основные геометрические размеры вычисляют
для шестерни и колеса.
В зацеплении'прямозубой конической передачи действуют
окружная Ft, радиальная Fr и осевая Fa силы. Если силы при-
ложены к шестерне (рис. 7.4), между ними можно установить
зависимости. Нормальную силу в зацеплении Fn раскладывают
на Ft и Fr', a FT' — на Fo и FT. Тогда
Р.
Fn=Ftlcosa', Fr=Fttga;
Fr = Fr cos 8! —Ft tg a cos 8! I
fe=y/sin &i=Ft tg a sin 8P ’
Для колеса направление действия сил противоположно:
^2“ 3 P{fi^ Fn.
Силы в зацеплении конической передачи с круговыми зубья-
ми определяются по формулам
Ft^TJd^-,
(1А)
Fr=(Ft/cos pm) (tg a cos 8! ± sin sin 8t);
Pa = (F-t/cos POT) (tg a sin 8! ± sin cos 8J.
144
Знаки в последних двух формулах означают: плюс — при сов-
падении направления момента (при наблюдении с внешнего тор-
ца) и винтовой линии зуба, минус — при несовпадении.
Профиль зубьев конических колес близок к эвольвентному
профилю зубьев цилиндрического колеса, образованному раз-
верткой среднего дополнительного конуса (см. рис. 7.1). Такое
цилиндрическое колесо называется эквивалентным. При этом
диаметр начальной окружности эквивалентного колеса dv равен
длине образующей среднего дополнительного конуса: dv —
=dm/cosd. Число зубьев эквивалентного прямозубого колеса
или шестерни:
zv=djmtm=zlcos 8.
Для конических колес с круговыми зубьями производится
двойной переход к биэквивалентному колесу: в нормальном се-
чении среднего дополнительного конуса к профилю прямозубых
колес с числом зубьев
^OT=2/(cos8cos3?m).
Передаточное число эквивалентной передачи равно
uv=--Zv2 = Znv2 = (cos S^cos 82) (z2/zl)=w2.
zvl znvl
Параметры биэквивалентных и эквивалентных колес исполь-
зуются в расчетах на прочность.
7.3. УЧЕТ ДИНАМИЧЕСКИХ НАГРУЗОК
И ДРУГИХ ФАКТОРОВ ПРИ РАСЧЕТАХ ЗУБА
НА ПРОЧНОСТЬ
Удельная расчетная окружная сила при определении
контактных напряжений в зубе с рабочей шириной зуба bw=bi =
— b2 равна:
(7.5)
где Ft=2Tildm\ — расчетная окружная сила на шестерне; dmi =
= monZi — средний диаметр конической шестерни; Кна — коэффи-
циент, учитывающий распределение нагрузки между зубьями
(см. разд. 5.5); — коэффициент, учитывающий неравномер-
ность распределения нагрузки по ширине зубчатых венцов;
K.hv — коэффициент, учитывающий дополнительную динамиче-
скую нагрузку: Khv = l+wHvbw/Ft, при проектировочных расче-
тах в первом приближении можно принять 2СнР=1; whv — удель-
ная окружная динамическая сила, W№=8//g0'D]/rfff,1(a4-l)/(2«)^
^O’wuiim; v=ndminif(60-103)—окружная скорость в среднем
сечении конических колес; бя и Whv 11m определяются по
145
табл. 5.4 и 5.5, go—аналогично зубчатой цилиндрической пере-
даче.
Удельная расчетная окружная сила при определении изгиб-
ных напряжений в зубе
(7.6)
гдеЖр«— коэффициент, учитывающий распределение нагрузки
между зубьями (см. разд. 5.5).
Коэффициент торцевого перекрытия еа определяют через чис-
ло зубьев эквивалентных zv или биэквивалентных Zm колес (см.
разд. 5.3); коэффициент Кр» учитывает неравномерность распре-
деления нагрузки по длине зуба, Кп=*Кн£ коэффициент Кр0,
учитывающий возникающие дополнительные динамические на-
грузки, вычисляют по формуле (5.8).
Окружная динамическая сила равна
(« + 1У(2«) < ®>₽Пп..
где бк=0,016 для прямых зубьев без модификации головки; ду=
=0,006 для круговых зубьев, величины g0, выбираются
так же, как при расчете на контактную прочность цилиндриче-
ских передач.
7.4. ОСНОВЫ РАСЧЕТА КОНИЧЕСКОЙ ПЕРЕДАЧИ
С ПРЯМЫМИ И КРУГОВЫМИ ЗУБЬЯМИ
Контактные напряжения в конических зубьях рассчи-
тывают по формуле
9h=ZhZmZ, У wh Vu2 +1 +2а cos S/(0,85udml), (7.7)
где zw= 1,76 cos pm (при xx=0 и отсутствии смещения инстру-
мента); Zm=270 МПа,/2— для стальных колес; Z,= (К,ев)-1/2;
ев определяется по формуле, приведенной в разд. 5.3, исходя из
числа зубьев эквивалентного и биэквивалентного колес, a Kt—
согласно рекомендациям, приведенным в разд. 5.5.
Условие контактной прочности зубьев конической передачи:
(7.8)
Рекомендации по расчету допускаемых величин контактных
напряжений оНр аналогичны .приведенным в разд. 5.7 для пря-
мозубой передачи. Следует отметить, что в случае невыполне-
ния условия прочности (7.8) для конических передач нельзя ог-
раничиваться увеличением расчетной ширины зубчатых колес bw,
как это делают в цилиндрических передачах, так как это ведет
к изменению многих геометрических параметров зацепления.
Возможно (до 10... 15%) увеличить ширину венца bw, но только
в сторону внутреннего торца; при этом конусное расстояние R»
146
не изменится. Если этого недостаточно, то следует перейти на
ближайший больший стандартный модуль и повторить расчеты
основных геометрических размеров и проверочные расчеты. При
недогрузке передачи можно уменьшить ширину зубчатого венца
bw, но также только в сторону внутреннего торца.
Поскольку за критерии работоспособности авиационных ко-
нических передач принимается контактная выносливость, то про-
ектировочный расчет конусного расстояния Re (мм) проводят
по формуле
Re >0,82.r“2+l+2“cosS .1/ ./(?). (7.9)
Vasias У 9hp^ (1 “ 0 ’ 5’^)
При расчете прямозубых колес f(p) = l, а для колес с кру-
говым зубом f(P) =cos2pm/(£i8a). Коэффициент эффективности
торцевого перекрытия ki зависит от степени точности:
Степень точности 4 5 6 7 8 9
kt 0,99 0,97 0,93 0,87 0,80 0,70
После вычисления в первом приближении конусного расстоя-
ния Re по (7.9) из (7.1) определяют в первом приближении тор-
цевой внешний модуль mte (мм)
mte=2Re sin 2 /zl-[-Z2-\-2zlZ2Cos'£l. (7.10)
Далее mte округляют до стандартного значения (см. разд.
5.1). Для передач с круговым зубом стандартизуют нормальный
модуль тпт (построением дополнительного конуса в среднем
сечении зуба). Тогда mnm=/nte(l—0,5фьн)соз рт; затем округ-
ляют его до ближайшего большего стандартного значения. Ве-
личина торцевого модуля rn(e=mnm/[(l—0,5фьд)соз рт].
В соответствии со стандартным значением модуля определя-
ют основные геометрические параметры конических зубчатых
колес, используя зависимости разд. 7:2.
Проверка изгибной прочности производится для зубьев шес-
терни и колеса отдельно.
Напряжения изгиба в зубе конической передачи вычисляют
аналогично напряжениям в зубе цилиндрической передачи, при-
нимая его параметры по среднему сечению зуба. Путем приве-
дения конического колеса к биэквивалентному получим следу-
ющую расчетную формулу:
°г=УрУ№Р11((),85гппт). (7.11)
Здесь wFt и тпт определяют по (7.6) и (7.2) соответственно;
Уе — коэффициент формы профиля конических зубьев — опреде-
ляют в среднем нормальном сечении (см. рис. 5.16) с подста-
новкой числа зубьев биэквивалентного колеса отдельно для шес-
терни и колеса; у^— коэффициент, учитывающий наклон ли-
147
нии зуба, t/s=l для прямых зубьев, —₽т/140°^0,7 — для
круговых зубьев.
Условие изгибной прочности зубьев конической передачи
(7.12)
Допускаемое изгибное напряжение ofp выбирают согласно
рекомендациям, приведенным в разд. 5.8.
ГЛАВА 8. ПЛАНЕТАРНЫЕ И ДИФФЕРЕНЦИАЛЬНЫЕ
ПЕРЕДАЧИ
8.1. ОБЩИЕ СВЕДЕНИЯ. КИНЕМАТИКА.
ОСНОВНЫЕ СХЕМЫ ПЛАНЕТАРНЫХ ПЕРЕДАЧ
У рассмотренных ранее зубчатых передач оси колес
в пространстве не перемещались. Зубчатые передачи, имеющие
зубчатые колеса с перемещающимися осями, называются пла-
нетарными (рис. 8.1). Эти зубчатые колеса называются сателли-
тами; деталь Н, на которой закреплены оси сателлитов, назы-
вается водилом. Зубчатые колеса, вокруг которых обкатываются
сателлиты, называются центральными; неподвижное централь-
ное колесо называется опорным.
Используя различные схемы расположения зубчатых колес,
можно обеспечить этому виду передач широкие кинематические
возможности, компактность и малую массу. Наиболее часто при-
меняют в механизмах ЛА, приборах и радиоэлектронной аппа-
ратуре (РЭА) ЛА следующие схемы планетарных передач. В си-
ловых передачах используют однорядную планетарную (см.
рис. 8.1, а, схема 1), двухрядную (см. рис. 8.1, б, схема 2) и од-
Рис. 8.1. Кинематические схемы планетарных передач
148
Таблица 8.1
Число сателлитов Степень точности зубчатых колес
5 6 7
2 1,19 > 1,31 1,50
3 1,25 1,42 1,65
норядную многоступенчатую (см. рис. 8.1, в, схема 3) передачи.
В несиловых передачах, достоинством которых является воз-
можность получения больших передаточных чисел, используют
двухрядную схему наружного (см. рис. 8.1, г, схема 4) и внутрен-
него (см. рис. 8.1, д, схема 5) зацеплений. Однако они имеют су-
щественные недостатки — низкий КПД, уменьшающийся с увели-
чением i, и динамическую неуравновешенность из-за возможно-
сти размещения только одного сателлита. Число сателлитов в си-
ловых передачах берется не менее двух и в отдельных конструк-
циях доходило до 24 (редуктор привода авиационного поршне-
вого двигателя). Расположение сателлитов по окружности рав-
номерное, что позволяет разгрузить опоры от радиальных на-
грузок и распределить мощность по нескольким потокам. Вмес-
те с тем из-за погрешностей изготовления зубчатых колес и мон-
тажа некоторая неравномерность распределения по сателлитам
остается. Ее можно оценить коэффициентом неравномерности
Kti=Ft'/Ft, где Ft' — действительная нагрузка; Ft — номиналь-
ная нагрузка. Значения коэффициента Кя в зависимости от чис-
ла сателлитов и степени точности изготовления колес приведе-
ны в табл. 8.1.
Для более равномерного распределения нагрузки между са-
теллитами рекомендуется центральные зубчатые колеса делать
самоустанавливающимися, без жестких радиальных опор, с по-
датливым ободом. Кроме того, следует обеспечивать высокую
точность изготовления деталей и монтаж их с подбором сател-
литов по величине бокового зазора в зацеплении с центральны-
ми зубчатыми колесами.
Для исследования кинематики движения планетарных пере-
дач используется метод остановленного водила (метод Вилли-
са), механизм с остановленным водилом называют приведен-
ным. Планетарной передаче условно сообщают вращение с час-
тотой вращения водила, но в обратном направлении. Тогда
водило останавливается, а частоту вращения зубчатых колес при-
веденного механизма определяют с учетом его останова. При
определении передаточного отношения каждой пары колес знак
<+» при i ставят при одинаковых направлениях их вращения
149
(внутреннее зацепление), а знак «—» — при различных (внеш-
нее зацепление).
Схема 1 (см. рис. 8.1, а). Передаточное отношение при оста-
новленном водиле (приведенный механизм) равно
(8.1)
*1*2 *1
У реального механизма л3 = 0, следовательно, из (8.1) полу-
чим
—-—, откуда L-н=— =i3i-H = 1 +— • (8.2)
пн Z1 пн Zl
КПД такой передачи t)i-h=0,98, а рациональные пределы
передаточных отношений i3i-H=4 ... 8.
Схема 2 (см. рис. 8.1, б). Передаточное отношение равно
= l + (8.3)
пН г\г2
Рациональные пределы /1-я=8 ... 16, а т] 1-н=0,96 ... 0,98.
Схема 3 (см. рис. 8.1, в). При последовательном соединении
п входных и выходных валов ступеней общее передаточное от-
ношение равно
А-н=(/;-н)я. (8.4)
где i'i-н — передаточное отношение одной ступени.
Схемы 4 и 5 (см. рис. 8.1, г, д). При передаче движения от
водила Я к зубчатому колесу z\ (при п3=0) передаточное отно-
шение равно
/н-1 = М—(8-5)
\ г'г‘2 /
Большое i получаем, если ZtZzKziZz)»1; тогда одновременно
КПД снижается до 0,5 и менее.
8.2. ОСОБЕННОСТИ ГЕОМЕТРИИ. ВЫБОР ЧИСЕЛ ЗУБЬЕВ
И МАТЕРИАЛА ЗУБЧАТЫХ КОЛЕС
Планетарные передачи являются соосными и много-
сателлитными, что накладывает дополнительные требования на
выбор чисел зубьев зубчатых колес. Если для обычной переда-
чи без смещения числа зубьев выбираются только из условия
неподрезания (zmin>-17) и обеспечения заданного I, то для пла-
нетарных должны выполняться дополнительные условия: сосед-
ства, соосности и собираемости.
150
Условие соседства должно обеспечить гарантированный за-
зор между сателлитами. Для этого необходимо, чтобы АБ>
>R<a (си. рис. 8.1, а), где АБ=ОА sin p=0,5/n(zi+z2)sin р;
7?а2 = 0,5/П (z24-2) .
Тогда формула для проверки условия соседства принимает
вид
(Zj+<г2) sin л/с > z2-{-2.
Это условие можно проверить и графически.
Условие соосности соблюдается при равенстве межосевых
расстояний между зацепляющимися парами зубчатых колес:
схема 1
аа,1_2=л1г2_з; Zi+z2=z3—z2, или Zi+2z2=z3; (8.6)
схема 2
аа,1_2=а«й»_з; m1(z1-|-z2)=/n2(z3 —z2); (8.7)
схема 4
awl_2=aw2x_3; /n^Zj—z2)=/n2(z3—z2); (8.8)
схема 5
а®1-2=л«й'-з; /n1(Zi+z2)=/n2(z3-|-z2). (8.9)
Для схемы 3 условия для каждой ступени определяются
по (8.6).
Условие сборки должно обеспечить свободный вход зубьев
сателлитов во впадины между зубьями центральных колес. Это
достигается определенным угловым размещением зубьев и впа-
дин колес.
Зависимости для проверки условия сборки имеют вид
схема 1
(zt+«,)/<: (8.10)
схема 2
(ztz2 -|- z2z3)/(cd)=N; (8.11)
схемы 4, 5
(,zlZ2—z2z3)/(cd)=N, (8.12)
где N — целое, положительное или отрицательное, число; d—на-
ибольший общий делитель чисел и z2'.
Для схемы 3 условие сборки каждой пары определяют
по (8.10).
В авиационных редукторах рубчатые колеса изготавливаются
из легированных конструкционных сталей марок 12ХНЗА,
18Х2Н4МА, 38Х2Ю, 38Х2МЮА с заналкой до твердости 320...
151
450 НВ. Для зубчатых колес механизмов систем управления
и РЭА используют стали ЗОХГСА, 38ХА, 40ХН с твердостью
280 ...320 НВ, что позволяет производить термическую обработ-
ку заготовки до зубонарезания (см. табл. 3.4).
8.3. СИЛОВОЙ И ПРОЧНОСТНОЙ РАСЧЕТЫ
ПЛАНЕТАРНОЙ ПЕРЕДАЧИ
На рис. 8.1 показаны также силы, действующие на
элементы планетарной передачи: Ft — усилие в зацеплениях,
Fh — усилие на водиле (радиальные силы Fr на схемах не пока-
заны).
Для рассматриваемых схем планетарных передач окружное
усилие в зацеплении пары колес zt—Z2 при заданном крутящем
моменте 7\ с учетом неравномерности распределения нагрузки
равно
27-1(1-ПИ„
где П — коэффициент потерь на трение в опорах качения пер-
вого вала, П — 0,001... 0,008.
Для нахождения остальных сил, используя уравнения стати-
ки = TtT0(Fi)—Q, получаем:
схема 1
Ft\—2=Ft2-i, FF(8.13)
схема 2
F a—2—Kff2T1/(dtC')', F fj = F д—2
FtV-3=F Hd2/(d2-\-d2); (8.14)
схемы 4, 5
F H = T 2» F t\—2 — F /y</2'/(^2' — d2)',
F t2'—3=LF tx-id^ld1!. (8.15)
Для схемы 3 силы, действующие в каждой ступени, опреде-
ляют по (8.13).
При расчете на контактную и изгибную выносливость зуба
зубчатых колес zt—z2 номинальный крутящий момент, переда-
ваемый этим зацеплением, равен
Т[ = Тх(\-П)Кн!с-, (8.16)
крутящий момент на водиле —
F H==Fxix~IIr^_n. (8.17)
152
Рис. 8.2. Схема нагружения центральных валов дополнительной нагрузкой
Окружная скорость vHi_2 (м/с) в зацеплении при определе-
нии коэффициента определяется в относительном движении:
viL2=ndt (пх — пя)/(60-1000).
Дополнительная радиальная нагрузка Д7?1 от неравномерности
ее распределения по сателлитам, для схемы 1 на вал централь-
ного зубчатого колеса 2\ равна (рис. 8.2)
A/?i = 47\ — l)/(^iawi-2 cos aw). (8.18)
При расчете вала водила Н нагрузка на вал, как результат
неравномерности распределения нагрузки по сателлитам, будет
WH = <2TH[KH-V)l(awc). (8.19)
8.4. ПРОЕКТНЫЙ РАСЧЕТ ПЛАНЕТАРНЫХ РЕДУКТОРОВ
Рассмотрим пример расчета однорядного и двухрядного планетарных ре-
дукторов (см. рис. 8.1, а и б).
Исходные данные. Мощность на ведущем валу IFi, Вт; частота вращения
выходного вала привода пн, об/мин; расчетная долговечность — число циклов
нагрузки Nh.h — определяется по нагрузочному графику Г(/) (рис. 8.3),
здесь /ц.н — длительность цикла нагрузки, с.
Порядок расчета.
1. Определение передаточного отношения и-я привода. По формулам
(8.2) и (8.3) в зависимости от схемы.
2. Разбивка общего передаточного отношения и выбор чисел зубьев:
схема 1
Z«_2 = ----1; _; (8.20)
2 ll-H
схема 3, передаточное отношение каждой ступени будет равно
«Я.
где п — число ступеней.
Разбивка далее идет по (8.11);
схема 2
/Г_2 = /^-1; = (8.21)
По полученным значениям передаточных отношений выбираются числа зубьев
зубчатых колес, удовлетворяющие требованиям соседства, соосности и соби-
раемости.
153
Рис. 8.3. Циклограмма нагружения
входного вала редукюра
3. Определение примерного значения межосевых расстояний по формуле
„ 0.82-^- (8.22)
у uH V ^Hp^fba
Здесь знак «+> берут для расчета awi-г, знак <—»— а^,^; T't опре-
/ к
деляют по (8.16) при расчете awi-2; при определении а= Т—IL-;
с
=1,05; Кн = 1,1; К„в = 1.05,
/IV ПЛ г пр
Величину ОнР определяют аналогично прямозубым цилиндрическим пере-
дачам (см. гл. 5). При этом число циклов нагружений Nhe при одностороннем
вращении определяется в относительном движении для зубчатого i-ro колеса:
NНЕ — (л/ л/у)^ц.нс • (8.23)
где /Р— рабочая длительность одного цикла изменения нагрузки на деталь;
щ—пн=*П1н — частота вращения i-ro зубчатого колеса при остановленном
водиле; с' — число контактов с одной стороной поверхности зуба за один
оборот колеса.
Для центрального зубчатого колеса при с=3 с'=3, для сателлитов
с'=1, так как в каждом из зацеплений зубья работают разными сторонами.
У передачи по схеме 2 для сателлитов с'=1.
4. Определение примерного значения модуля зацепления по формуле
/я = 4* *к)» (8.24)
где zm, zK — числа зубьев шестерни и колеса.
Затем полученное значение модуля in определяется до ближайшего стан-
дартного значения (см. разд. 5.3).
5. Определение окончательного значения межосевого расстояния:
aw =, 0,5m (гш 4- zK). (8.25)
Для двухрядной передачи из условия соосности в конструкции .принима-
ется большее из двух значений awl_2 и ^w2/_3.
6. Определение значений относительных угловых (об/мин) и линейных
(м/с) скоростей:
„н _ „н _ ”1 . ,,Н _ (Я1 Яя) .
”2 ~Я2'~ Z«_2 • Vl-2 - 60.1000 ’
v£_3 = Л<*2 (f>2 - пн)/(60-1000).
154
8.6. ДИФФЕРЕНЦИАЛЬНАЯ ПЕРЕДАЧА
Рассмотренные выше планетарные передачи являют-
ся механизмами с одной ступенью свободы. Если в таких пе-
редачах, например в однорядном планетарном редукторе (см.
рис. 8.1, а), освободить неподвижное опорное колесо z3 и предо-
ставить ему возможность вращаться в подшипниках, то полу-
чится планетарная передача с двумя степенями свободы. Такой
механизм называется дифференциальной передачей (дифферен-
циалом). С его помощью можно суммировать два движения или
разделять одно движение на два.
Например, для схемы 1, пользуясь понятием приведенного
механизма, получим:
/ь-з=(о>1— шя)/(шз — <•>//). (8.26)
где iBi-з — передаточное отношение от колеса г\ к колесу 2з в
движении относительно водила Я. Из этой формулы
ш3= [Ш1 + ({’Г_з - 1) шя]//Г-3. (8.27)
Углы поворота фЬ ф2, фя тех же звеньев будут связаны соотно-
шением
?з=[?1 + (/Г-з-1)?я]//Г-з. (8.28)
Таким образом, задаваясь углами поворота ф1 и фн, можно
по (8.28) определить угол поворота ф3. Из (8.28) можно также
получить зависимость^ =/(ф2. <Рн> ii-з)-Таким образом диф-
ференциальный зубчатый механизм можно применять для сум-
мирования двух движений.
На рис. 8.4 показана схема использования однорядного пла-
нетарного редуктора для вращения двух воздушных винтов (си-
дящих соответственно и 8
оси водила и оси зубчато-
го колеса z3) с равными
УГЛОВЫМИ СКОРОСТЯМИ (Obi
и Шв2 в противоположные
стороны от ведущего вала
/. При вращении воздуш-
ных винтов в противопо-
ложные стороны с одина-
ковыми угловыми скоро-
стями Пв1 = Пп И «В2=л3 =
»—Пн получим П$1Пн =
=—1.
Рис. 8.4. Схема дифферен-
циального редуктора с двумя
соосными воздушными винтами
155
Моменты на валах найдем из уравнений равновесия сил на
сателлите (см. рис. 8.1, а):
Th=Fн (di-^-dz)/^', T$=F2—з^2)х= //(0,5 d\-\-d2),
так как Гн=2Гг-з. отношение моментов на валах будет равно
тн °’5Гя <rfi + dx + di i (8 29ч
2"з (Кб-/*1 (0,5rf[ 4- г/2) 0,5<fi 4-4/2
Это значит, что при ыз=—ыя момент сопротивления на первом
воздушном винте должен быть больше, чем на втором, что может
быть достигнуто изменением угла установки винта.
ГЛАВА 9. ВОЛНОВЫЕ ПЕРЕДАЧИ
9.1. ОБЩИЕ СВЕДЕНИЯ
Принцип действия волновых передач основан на из-
менении параметров движения вследствие волнового деформи-
рования одного из звеньев механизма.
Основные достоинства зубчатой волновой передачи:
1. Малые масса и габаритные размеры при большой нагру-
зочной способности. Это связано с тем, что одновременно в за-
цеплении находится 20...40% общего числа зубьев, а нагруз-
ки на налы и опоры невелики.
Масса волнового редуктора при i=80...300 меньше, чем
планетарного и многоступенчатых зубчатых передач. В неко-
торых конструкциях при переходе от планетарной к волновой
передаче удается снизить массу вдвое.
2. Высокая кинематическая точность, которая обеспечивает-
ся многопарностью зацепления и наличием нескольких зон кон-
такта зубьев.
3. Большое передаточное отношение одной ступени (t=80...
300).
4. Возможность передачи движения из герметизированного
пространства.
5. Достаточно высокий КПД (т]=0,8... 0,9) при работе пе-
редачи в качестве редуктора. КПД волновой и планетарной пе-
редач близки при одинаковых передаточных отношениях.
6. Возможность использования не только в качестве редукто-
ра или мультипликатора, но и в качестве дифференциала.
К недостаткам волновых передач можно отнести: сложность
изготовления гибкого колеса и генератора волн, большое зна-
чение минимального передаточного отношения.
Достоинства волновой передачи делают целесообразным ее
широкое использование на ЛА в механизмах с большим пере-
даточным отношением и в устройствах с повышенными требо-
156
Рис. 9.1. Волновая передача с роликовым генератором волн
ваниями к герметичности и кинематической точности. Напри-
мер, герметичную волновую передачу успешно использовали на
луноходе LRV (см. разд. 25.5).
Волновая передача (рис. 9.1) состоит из трех основных звень-
ев: генератора волн h, гибкого колеса g и жесткого колеса Ь.
Зубчатый венец гибкого колеса деформируется генератором
волн и входит в зацепление с центральным жестким колесом,
имеющим делительный диаметр db, в зонах у точек А и С. Гиб-
кое колесо изготовляется в виде стакана с фланцем. Зубча-
тый венец на гибком колесе нарезан снаружи в середине ста-
кана; его стенка имеет малую толщину, что позволяет ему лег-
ко деформироваться при воздействии вставленного внутрь гене-
ратора волн. Двухволновой генератор состоит из водила с дву-
мя роликами. Наружный .размер генератора по оси АС (боль-
шая ось генератора) больше внутреннего диаметра цилиндра
на 2о»о, где w0 — радиальное перемещение стенки гибкого коле-
са по большой оси генератора. При установке генератора внутрь
Рис. 9.2. Радиальные перемещения гибкого колеса
157
гибкого колеса происходит увеличение делительного диаметра
гибкого колеса dg по большой оси на величину
db — dg=2w0. (9.1)
При вращении генератора волн волна деформации переме-
щается по окружности гибкого колеса. На рис. 9.2, а показан
график радиальных перемещений w(t) гибкого колеса по длине
окружности. Любая точка цилиндрической поверхности гибкого
колеса перемещается и совершает у двухволновой передачи два
колебания за один оборот генератора волн (рис. 9.2, б). При
вращении генератора две волны бегут по окружности гибкого
колеса независимо от частоты его вращения. В точках А и С
зубья гибкого колеса зацепляются по всей рабочей высоте, а в
точках В и Е находятся на некотором расстоянии друг от друга.
За один оборот генератора волн зоны зацепления зубьев у то-
чек А и С также совершают один оборот, в результате чего про-
исходит поворот одного колеса относительно другого на число
угловых шагов, равное разности их чисел зубьев.
Если три основных звена волновой зубчатой передачи враща-
ются, то она имеет две степени свободы и называется дифферен-
циальным механизмом. Чаще используются волновые передачи, в
которых одно из основных звеньев (гибкое или жесткое колесо)
остановлено. Тогда механизм имеет одну степень свободы. Если
ведущим является генератор волн, то механизм работает как ре-
дуктор, а если генератор является ведомым, то как мультипли-
катор.
В трехволновых передачах генератор волн имеет три ролика
и образует на гибком колесе три волны деформации. Напряжения
изгиба в таком гибком колесе выше, чем в двухволновой пере-
даче, поэтому эти передачи применяют редко.
Различают волновые передачи: зубчатые, фрикционные и
типа винт — гайка; с различными генераторами волн: механи-
ческим, электромагнитным, гидравлическим.
Работоспособность гибкого колеса определяется, в первую
очередь, его прочностью, а в передачах с кулачковым генерато-
ром волн — и прочностью гибких подшипников.
9.2. КИНЕМАТИКА И ГЕОМЕТРИЯ ВОЛНОВОЙ ПЕРЕДАЧИ
Рассмотрим волновую передачу, у которой ведущим
является генератор, а ведомым гибкое колесо при остановлен-
ном листком или жесткое колесо при остановленном гибком.
За один оборот генератор волн поворачивается на угол ул =
= 2л. При этом из-за разности чисел зубьев происходит пово-
рот ведомого колеса zB.M относительно остановленного z0 на угол
Yb.m = С^в.м — z0) pl(0,5do), (9.2)
158
где zb.m и zo — числа зубьев ведомого и оставленного колеса;
р — шаг зубьев по делительной окружности; do — делительный
диаметр остановленного колеса.
В общем случае передаточное отношение для волновой пере-
дачи
Z=-^- = Zn* . (9.3)
¥а.м гв.ы .го
Из (9.1) и (9.3) получим
при неподвижном гибком колесе (ng=0)
*1»=— = —= 'db ; (9.4)
пц zb — zg do — dg 2»о
при неподвижном жестком колесе (пь=0)
/£ =• - -2L =-----—=---------=--------, (9.5)
ng Zb — Zg db — dg 2w0
где tih, ng, nb— соответственно частоты вращения генератора
волн, гибкого и жесткого колес.
Знак минус в (9.5) указывает на разные направления вра-
щения генератора волн и гибкого колеса.
Для обеспечения условия сборки разность зубьев колес долж-
на быть равна или кратна числу волн, возбуждаемых генерато-
ром:
I хлМ—г0 | —kV, или zb — Zg=kV, (9.6)
где k — коэффициент кратности, k=l, 2, 3...; обычно для умень-
шения напряжений при деформации гибкого колеса принимают
k=l; V—число волн деформации (число зон зацепления).
Из (9.3) и (9.6) получим
I =^.м/(А V)=rfB.M/(2w0), (9.7)
или
ilt=ZbKkV) при ng=0, ikg=~~Zgl(kV) (9.8)
при «»=0.
Из (9.7) видно, что с уменьшением i увеличивается а>о, что
приводит к увеличению ои стакана гибкого колеса, т. е. при ма-
лых i увеличивается опасность его усталостного, разрушения,
что ограничивает минимальное значение i.
С увеличением i число зубьев у колес становится больше.
Это приводит к возрастанию требований к точности их изготов-
ления и увеличению габаритных размеров и массы передачи.
Числа зубьев гибкого г» и жесткого zg колес согласно (9.6)
и (9.7) будут равны zB.M=ifcV, или
159
zb=ilbkV\ zg=zb-kV при n^=0; (9.9)
zg = ibgkV-, zb=zg-\-kV при nb=0. (9.10)
Модуль зацепления при известных dg и zg или db и хь будет
равен
m=dglzg=dblzb.
(9.П)
Затем значение т округляется до ближайшего стандартного
значения.
В волновых передачах используют несколько профилей зубь-
ев. Наиболее распространены эвольвентные зубья с исходным
контуром а=20°. При z> 150 форма эвольвентного зуба близка
к трапецеидальной.
На рис. 9.3 показаны три положения зуба гибкого колеса
g относительно зуба жесткого колеса b при различных углах по-
ворота генератора (положение 1: <р = 0; положение 2: 0<ф<90°;
положение 3: ф = 90°). Из диаграммы видно, что в положении 2
происходит интерференция: зубья гибкого и жесткого колес упи-
раются друг в друга поверхностями вершин, генератор волн
сжимается, жесткое колесо деформируется в радиальном на-
правлении, что приводит к проскакиванию зубьев, т. е. наруша-
ется зацепление. Это может также вызвать разрушение дета-
лей передачи, поэтому интерференция зубьев не допускается.
Устранение интерференции можно осуществить путем умень-
шения высоты зуба. Так, на диаграмме после уменьшения вы-
соты зуба жесткого колеса с йы до йь2 интерференция не наб-
людается. Одновременно с уменьшением высоты зуба уменьша-
ется глубина захода с hd\ до h^. Это нежелательно, так как при
малой величине hd возможно проскакивание зубьев передачи
под нагрузкой. Для устранения ин-
терференции выгоднее уменьшать
высоту зуба гибкого колеса при од-
новременном увеличении ширины
впадины (рис. 9.4).
Модифицированные таким спо-
собом зубья называются зубьями с
широкой впадиной. Зубья жесткого
колеса имеют только ножки, а гиб-
кого— только головки. Высота зу-
ба уменьшается на (0,5... 1,0)/п
(Ad2~w). Положительный эффект от
такой модификации зубьев заключа-
Рис. 9.3. Взаимное положение зубьев
жесткого и гибкого колес
ло
Рис. 9.4. Зацепление зубьев жесткого и гибкого зубчатых колес на большой
оси генератора:
а — немодифицированные зубья; б — модифицированные зубья с широкой впадиной
ется и в том, что увеличивается гибкость гибкого колеса и в
нем снижается уровень напряжений от деформации изгиба.
Различают свободную и принудительную деформации гибко-
го колеса, вызываемые генератором волн. При принудительной
деформации ее форма определяется профилем кулачка или дис-
ка генератора на участках их контакта с гибким колесом. При
действии нагрузок, возникающих в зоне зацепления, форма де-
формации на этих участках изменяется мало. Свободная дефор-
мация происходит на тех участках, где перемещение гибкого ко-
леса не ограничено. Поэтому при действии нагрузки первона-
чальная форма меняется. Наиболее распространены формы де-
формации гибкого колеса под действием двух или четырех сил,
по дугам окружностей или контуру кулачка (см. рис. 9.5).
9.3. КОНСТРУКЦИЯ ВОЛНОВОЙ ПЕРЕДАЧИ
Генераторы волн. Форма гибкого колеса волновой
передачи при деформации его генератором волн определяется
конструкцией последнего. Различают генератор с двумя ролика-
ми (рис. 9.5, а); генератор с четырьмя роликами (рис. 9.5, б);
дисковый генератор (рис. 9.5, в); кулачковый генератор (рис.
9.5, г). Кулачковый генератор дает возможность получить лю-
бую форму гибкого колеса.
Роликовый генератор со свободной деформацией не обеспе-
чивает под нагрузкой сохранения гибким колесом первоначаль-
но заданной формы. В зоне за катящимся роликом имеет место
контакт по всей высоте зуба, перед роликом резко меняется кри-
визна цилиндрической поверхности гибкого колеса, а в некото-
рых случаях и ее знак. Это снижает прочность гибкого колеса.
Возможность изменения начальной формы у дисковых генерато-
ров весьма ограничена.
Роликовые генераторы применяют в малонагруженных пере-
дачах, например во фрикционных, в которых зубья на жестком
6—1085 161
£
Рис. 9.5. Деформирование гибких колес при различных конструкциях гене-
раторов волн (/ — эксцентриситет)
и гибком колесе отсутствуют, а передача нагрузки осуществля-
ется силами трения.
Форма деформирования гибкого колеса четырьмя силами
принята в передачах общего назначения с кулачковым генерато-
ром волн. Окружные напряжения изгиба в гибком колесе за-
висят от угла р между вертикальной осью и вектором силы F,
вызывающей деформацию (см. рис. 9.5, б). При р = 25° напря-
жения минимальны, при р>35° они резко возрастают. Поэто-
му для снижения уровня напряжений в гибком колесе рекомен-
дуется использовать форму деформации с углом р = 25 ... 35°, вы-
бираемым в зависимости от передаточного числа и из условий
обеспечения минимума напряжений в гибком колесе и достаточно
большого числа зубьев, находящихся в одновременном зацепле-
нии:
и 60... 100 100... 130 130
₽ 25е ' 30е 35°
Кулачковый генератор волн лучше сохраняет форму дефор-
мации гибкого колеса под нагрузкой (рис. 9.6). Он состоит из
кулачка 1 и напрессованного на него гибкого подшипника 2 с
меньшей толщиной колец и особой конструкцией сепаратора.
Форма профиля кулачка должна быть эквидистантной к за-
данной форме деформации гибкого колеса. При определении фор-
мы профиля кулачка следует учитывать величину зазора в раз-
мерной цепи кулачок — гибкое колесо.
У дискового генератора (рис. 9.7) деформирование гибкого
колеса происходит по дугам окружности у большой оси генера-
162
тора (см. рис. 9.5, в). Для каждой зоны контакта длина дуги
соответствует углу 2у. Минимальные окружные напряжения из-
гиба на гибком колесе возникают при у=20 ... 40°, исходя из чего
определяют радиус диска и эксцентриситет.
Диски 1 и 2 генератора (см. рис. 9.7) установлены на втулках
3 и 4, внутренние отверстия которых имеют эксцентриситет е по
отношению к наружной поверхности. Втулки 3 и 4 обрабатывают
как одну деталь с общими эксцентриситетом и шпоночным па-
зом, а затем разрезают на две части и при сборке поворачивают
одну относительно другой на 180°. Аналогично вместо шпоноч-
ного соединения втулок 3 и 4 с валом 5 можно использовать шли-
цевое с четным числом зубьев. Для предохранения гибкого ко-
леса с толщиной Л] от раскатывания опорной поверхности уста-
навливают стальное подкладное кольцо толщиной Лк=1,5Ль
Кольцо изготавливают из стали ШХ15 или другой с твердостью
50... 58 HRC. Твердость рабочей поверхности стальных дисков
48 ...50 HR С.
Конструкция дискового генератора волн проще, чем кулачко-
вого: нет специальных подшипников и кулачков со сложным про-
филем. Момент инерции массы дискового генератора относи-
тельно оси вращения значительно ниже, чем кулачкового, так
как частота вращения диска пд значительно меньше, чем часто-
та вращения кулачка пк. Так, при остановленном гибком колесе
па=п*,11гд. Дисковые генераторы предпочтительнее при индиви-
дуальном и мелкосерийном производстве. Однако при специа-
лизированном массовом производстве кулачковый генератор из-
готавливать проще и дешевле.
В волновых передачах применяют жесткое или подвижное
соединение генератора с валом. При жестком креплении тре-
бования к точности изготовления повышаются, так как несоос-
ность звеньев передачи приводит к неравномерности распреде-
Рис. 9.6. Кулачковый гене-
ратор волн
6*
163
ления нагрузки по зонам за-
цепления. Подвижное соедине-
ние компенсирует несоосность
генератора, гибкого и жесткого
колес. Такое крепление обеспе-
чивают с помощью упругих эле-
ментов (резиновых упругих ко-
лец, муфт).
Гибкие колеса. Гибкое коле-
со волновой передачи под дей-
ствием генератора волн под-
в нагружен-
Рис. 9.8. Напряжения
ном гибком колесе
вергается циклическому нагру-
жению при деформации его цилиндрической части, а также
нагружению от окружных сил в зацеплении. При этом значения
окружных напряжений at, вызванных изгибом гибкого колеса, и
напряжений растяжения ор, вызванных окружными силами, вы-
соки (рис. 9.8). Одновременно это колесо подвергается нагру-
жению крутящим моментом, который вызывает касательные на-
пряжения т. Кроме того, на зубчатом венце возникает концент-
рация напряжений. Поэтому гибкое колесо является одним из
слабых звеньев волновой передачи. При проектировании необхо-
димо проводить проверочный расчет его на прочность.
Передача движения может осуществляться через герметич-
ную стенку (рис. 9.9, а). В такой конструкции деформация гиб-
кого колеса ограничивается по краям с одной стороны фланцем,
а с другой — днищем, что оказывает влияние на его напряжен-
ное состояние. Для снижения влияния краевого эффекта и уров-
ня напряжений принимают /^(1... 1,25)£> и снижают жесткость
переходных участков от цилиндра к фланцу и днищу. Обычно
они делаются той же толщины, что и стенка цилиндрической
части гибкого колеса.
В негерметичных волновых передачах (рис. 9.9, б) правая
часть стакана не нужна, и тогда 1\ = (0,7... 1,0)£>. Жесткость
крепления стакана можно уменьшить, заменяя фланцевое сое-
Рис. 9.9. Волновые передачи
164
динение шлицевым. Это приводит к снижению о< и возможности
уменьшения
В негерметичных волновых передачах (рис. 9.9, в) возмож-
но дальнейшее уменьшение 1\. Гибкое колесо выполнено здесь
в виде кольца с двумя зубчатыми венцами. При zi=z2 эта пе-
редача аналогична двум другим (см. рис. 9.9), но КПД снижа-
ется на 20... 25% и примерно вдвое уменьшается допускаемый
крутящий момент на тихоходном валу. При zj>z2 и г4>гз по-
лучаем двухступенчатую волновую передачу с максимальным i=
=3000... 8000, однако с очень низким КПД. Так, при i>4000
т] <0,05. Одна из причин снижения КПД заключается в том, что
обе ступени нагружены максимальным моментом.
Во всех рассмотренных случаях использование гибких колес
с зубьями, имеющими широкую впадину, приводит к снижению
их жесткости, что вызывает уменьшение а<. Для увеличения ре-
сурса гибкого колеса его изготавливают с повышенной точно-
стью, а шероховатость поверхности должна быть не ниже 6 клас-
са. На основные размеры устанавливают допуски по 6—8-му ква-
литету, а допуск на некруглость, нецилиндричность и несоос-
ность цилиндрической поверхности должен быть не более 0,01...
0,05 мм.
Жесткие колеса. Конструкция их аналогична колесам с внут-
ренними зубьями цилиндрических и планетарных передач. Сое-
динение жесткого колеса с корпусом осуществляется по посадке
Hlljjo с дополнительной фиксацией штифтами или винтами. Ши-
рину зубчатого венца жесткого колеса делают на 2... 4 мм боль-
ше, чем гибкого.
Толщину жесткого колеса h выбирают так, чтобы его мак-
симальное радиальное перемещение wOb под нагрузкой от сил в
зацеплении удовлетворяло неравенству:
®>0й<(0,05...0,02) w0. (9.12)
Это обеспечивается при толщине стенки
Л = (0,17...0,18)£>. (9.13)
Материалы гибкого и жесткого колес. Тяжелонагруженные
гибкие колеса при малом передаточном отношении i и допускае-
мом напряжении при смятии [оСм]^20 МПа изготовляют из кон-
струкционных сталей с повышенной вязкостью марок 40ХНМА,
38ХМЮА, так как они менее чувствительны к концентрации на-
пряжений. Средне- и легконагруженные гибкие колеса общего
назначения (i> 100, [аСм]<20 МПа) изготовляют из более деше-
вых сталей ЗОХГСА и ЗОХМА. Гибкие колеса подвергают термо-
обработке— улучшению (280 ...320 НВ) (табл. 9.1).
Напряжения в жестком колесе волновой передачи значитель-
но ниже, чем в гибком. Поэтому жесткое колесо изготовляют из
165
Таблица 9.1
Марка стали Термообработка и упрочнение Твердость Механические характеристики, МПа Удельная ударная вязкость он, Дж/см2
сердцевины, НВ поверх- ности, HRC стт a-i
ЗОХГСА Улучшение 280... 320 1100 850 420 40
ЗОХГСА Улучшение + -{-дробеструй- ный наклеп 280... 320 28... 32 1100 850 48С 40
ЗОХГСА Улучшение 4- +азотирование 280... 320 50... 54 1100 850 600 90
38ХМЮА Улучшение . 320 — 1000 850 450 90
38ХМЮА Улучшение+ +азотирование 320 65... 70 1000 850 620 80
40ХНМА Улучшение 320 —. 1100 950 480 80
Х18НЮТ Состояние поставки 180... 220 — 600 350 280 ПО... 250
конструкционных сталей 45, 40Х, ЗОХГСА с твердостью НВ на
20 ...30 единиц ниже, чем у гибкого колеса.
9.4. РАСЧЕТ ВОЛНОВЫХ ПЕРЕДАЧ
Рассмотрим пример расчета основных параметров герметичной волновой
передачи (гибкое колесо неподвижно) с дисковым и кулачковым генератором
волн.
Исходные данные. Мощность на ведущем валу Wh, Вт; частота вращения
ведущего вала п*, об/мин; частота вращения ведомого вала пь, об/мин; коэф-
фициент динамичности внешней нагрузки Ад; ресурс /, ч.
Порядок расчета.
1. Передаточное отношение волновой передачи
1ы> = пьШь-
2. Задаваясь числом волн У=2, из (9.8) при £=1 находим число зубьев
гибкого и жесткого колес
zb = 2ihb< Zg = zi>-2. (9.14)
3. Выбираем материал и вид термообработки зубчатых колес (см.
табл. 9.1) и определяем [<тСм]. Рекомендуется выбирать [аСм]= 10... 30 МПа
для стальных зубчатых колес (с числом твердости порядка 300 НВ) быстро-
ходных и среднескоростных передач; [<уСм]=60... 100 МПа для режимов с
кратковременными перегрузками и тихоходных передач.
4. Диаметр делительной окружности зубчатого венца гибкого колеса
dg (мм) определяем из условия обеспечения прочности рабочих поверхностей
зубьев на смятие:
dg = V ЮГ»/[«см]фл , (9.15)
где Ть~ расчетный крутящий момент на жестком колесе, Н-мм,
^ = л:а/^га,
где Th — крутящий момент на ведущем валу;
166
[сГсм] — допускаемые напряжения смятия на рабочих поверхностях зубьев;
^a=bgldg — коэффициент ширины зубчатого венца, рекомендуется принимать
фв=0,1...0,3 (меньшие значения для малых i и малонагруженных передач).
По (9.15) определяем наименьший допустимый диаметр dg.
5. Определяем модуль Ч
m^dglzg}
По табл. 9.2 выбираем гибкий подшипник (см.
рис. 9.6); полагая, что dg=D (D — внутренний
диаметр гибкого колеса, равный наружному диа-
метру подшипника), получим
m—DIzt.
Выбираем ближайшее значение стандартного модуля т (табл. 9.3) (обыч-
но берут ближайшее большее значение):
Уточняем число зубьев гибкого колеса по
формуле
zg=D!m\
принимаем целое число, зубьев гя и уточняем
гь и i*hb, используя (9.4), (9.14).
6. Выбираем основные геометрические параметры зацепления при нареза-
нии зубьев стандартным инструментом с а = 20°, xq = 0,3 и радиальное пере-
мещение стенки гибкого колеса wQ.
Задаем значение у для Задаем значение 0 для кулачкового генератора:
дискового генератора: р = 25... 35° (см. с. 162)
у=20... 40° (ббльшие
значения для больших
О.
Принимая £=1, находим w0, хв, he, hd (рис. 9.10) в соответствии с
рекомендациями: w0= (1,05... l,2)m (меньшие значения для меньших 0;
Таблица 9.2
Условное обозначе- ние под- шипника Размеры, мм Радиальный зазор б, мм Число шариков Z Пре- дельная частота враще- ния п-10-’. об/мин
d D В г
806 30 42 7 0,5 3,969 0,01...0,024 21 3
808 40 52 8 0,5 3,969 0,012...0.026 23 3
809 45 62 9 0,5 5,953 0,012...0,029 21 3
812 60 80 13 0,5 7,144 0,013...0,033 .23 3
815 75 100 15 1,0 9,128 0,014...0,034 21 3
818 90 120 18 1,0 11,113 0,016...0,040 23 3
822 110 150 24 1,0 14,288 0,02...0,046 21 1,5
824 120 160 24 1,0 14,288 0,02...0,046 23 1,5
826 150 200 30 1,0 19,05 0,023...0,058 23 1,5
1 Слева приводим расчет волновой передачи с дисковым генератором,
справа — с кулачковым.
167
Таблица 9.3
Модуль, мм Номинальный делительный диаметр, мм Коэффи- циент высоты головки зуба h*e0
ряд 40 64
1-й 2-й Число зубьев *0 Диаметр вершин зубьев do0' мм Число зубьев 2о Диаметр вершин зубьев do0. “«
0,2 200 40,67 320 64,67 1,5
0,22 182 40,77 290 64,53 1,5
0,25 160 40,82 256 64,82 1,5
0,28 140 40,12 228 64,76 1,5
0,3 132 40,59 212 64,59 1,5
0,35 114 40,05 182 64,85 1,5
0,4 100 41,32 160 65,32 1.5
0,45 90 41,98 144 66,28 1.5
0,5 80 41,65 128 65,65 1,5
0,55 72 41,41 116 65,61 1,35
0,6 66 41,58 108 66,78 1,35
0,7 56 41,51 90 65,31 1,35
0,8 50 42,64 80 66,64 1,35
0,9 44 42,57 72 67,77 1,35
коэффициент смещения хв— 3 ... 4; высота зубьев hg= (1,5 ... l,8)m; глубина
захода hd= (1,3... 1,5)/п, предпочтительнее использовать большие значения
hg и hdf так как при малых hd возможно проскакивание зубьев под нагрузкой.
7. Уточняем и определяем геометрические параметры зацепления dfgt хе,
dag и размеры гибкого колеса Л, г, D, нарезаемого червячной фрезой. Задаем
hi (см. рис. 9.10, а); рекомендуется hi = (0,005 ... 0,015)dg.
Определяем диаметр окружности впадин гибкого колеса (см. рис. 9.10, а):
d/g=dg—2 (h*o—xg) т=
=m(zg—2ft *Q+2xg);
определяем внутренний диаметр гиб-
кого колеса
D=dfg—2Ль
dfg=D~i“2hif
(9.16)
уточняем коэффициент смещения гиб-
кого колеса
xg=d/g/(2m) — zg/2+ft*0, (9.17)
где fta0 — коэффициент высоты го-
ловки зуба долбяка (см. табл. 9.3).
Определяем диаметр окружности вершин зубьев гибкого колеса:
dag~djg + 2hg. (9.18)
Находим радиус срединной поверхности до деформации:
r = (D + ^!)/2. (9.19)
8. Находим параметры зубчатого венца жесткого колеса, нарезаемого
долбяком. После определения коэффициента смещения жесткого колеса
xb = xg — [т — (wQ/k)]/mt (9.20)
168
Рис. 9.10. Геометрия зубчатых колес волновой передачи
вычисляем
inv tfWo = 2 [(х* — хй)/(гь — z0)l tg а — inv а, (9.21)
где а=20в; хо=О,3; г» — число зубьев долбяка, а» — угол зацепления в ста-
ночном зацеплении с долбяком.
Найдя а»о по таблице invaw, определяем межосевое расстояние в ста-
ночном зацеплении с долбяком:
я w0 = т (2ъ — z0) cos a/(2 cos а®0). (9.22)
Найдем:
диаметр окружности впадин жесткого колеса (см. рис. 9.10, б)
dp = 2(awo + 0,5dfl0)> (9.23)
где dao —диаметр окружности выступов долбяка;
диаметр окружности вершин жесткого колеса
dab = dag + 2wQ — 2hd. (9.24)
9. Проверяем отсутствие интерференции, определив для гибкого колеса
‘g «I = ‘g a — 4 (Л*о - Ро - Xg)/(zg sin 2a), (9.25)
где ро ^0,35 —коэффициент высоты скругленного участка вершины зуба
инструментальной рейки.
Найдем диаметр окружностей граничных точек гибкого колеса:
dig = mzg cos a/ cos а/. (9.26)
Определим для жесткого колеса:
cos аа0 = mzQ cos a/daQ; (9.27)
tg Чь = tg aw0 + z^zb (tg %0 - tg
Найдем диаметр окружности граничных точек жесткого колеса
dib = тгь cos a/ cos а/^. (9.28)
Проверяем условие отсутствия интерференции:
dag<dlb — 2w0; dab>dig + 2w$. (9.29)
Если эти условия не выполняются, то уменьшаем и hd.
10. Выбираем и рассчитываем геометрические параметры конструкции.
Ширина зубчатого венца гибкого колеса bg=dg^a , жесткого колеса
~bg + (2...4) мм. Для гибкого колеса (см. рис. 9.1) />(1... 1,25)D.
169
По формуле, полученной из вы-
ражений, описывающих форму дефор-
маций, определяем радиус диска Rg
и величину эксцентриситета е:
fig = R—0,5/t 1—hm\
e=r+wQ—R, (9.30)
где А =
=л/2—sin у cos у—у; В = (4/л) X
X(cos у+у sin у)—2sin у.
Толщину диска принимаем рав-
ной: Ь«0,1Л<.
Значение радиуса-вектора профи-
ля кулачка найдем по формуле
Р (ф) = 0,5d—wK (<р), (9.31)
где Шк(ф)=шок/(ф); приращение ра-
диуса-вектора кулачка по большой
оси шок определяем с учетом зазоров
и деформаций,
Ш0к=Шо+бэ+бу,
где ба — средняя величина зазора в
размерной цепи кулачок — гибкое ко-
лесо (зазоры в подшипнике и его
посадке); бу — упругое сближение
колец подшипника под нагрузкой.
Расчет профиля кулачка упро-
щаем 1 * путем использования таблиц
значений шк(ф)/шОк при заданном
угле 6.
Толщину кулачка принимаем рав-
ной Ь»В.
11. Рассчитываем гибкое колесо на прочность.
Определим напряжения, действующие на гибкое колесо (см. рис. 9.8):
а) напряжения изгиба о/ в окружном направлении, связанные с дефор-
мацией гибкого колеса генератором волн (/?а=—1):
a/ = XEAr-2Wo; /(=СУг,
(9.32)
где Yz =1,26... 2,35 — коэффициент, учитывающий влияние зубчатого веица на
прочность гибкого колеса:
hi/m 1 1,5 2 2,5 3
Yz 2,35 1,85 1,52 1,36 1,26
С9 — коэффициент, величина которого зависит от формы деформации (при
деформировании по форме w=w0 cos 2ф С9 = 1,5):
у, ° 20 30 40 50 I ₽,° 25 30 35
С9 1,41 1,4 1,51 1,72 I С9 1,45 1,55 2,0
б) напряжения растяжения оР от окружных сил в зацеплении (7?в=0).
Они максимальны у большой оси генератора волн:
9ртах = 0, $Tbl(Dbghy, (9.33)
в) напряжения кручения (/?т = 0)
тк=Т^/(2лг2А). (9.34)
Проверочный расчет на прочность выполняется по формуле
« = W ( Л» + л«)~1/2 > М ’ <9-35)
где
„ а-1У X.-\N . ЯР .
’ K.’a + V/» ’ + • °а 9,+ 2 '
1 Иванов Н. М., Иванов В. Н. Детали машин: Курсовое проектирование.
М.: Машиностроение, 1985. 516 с.
170
\ ~~ 2 ’ Ха ~ Хт ~~ 2
Прочность гибкого колеса проверяется в двух сечениях: А — А — на
краю зубчатого венца и В — В — на цилиндрической части стакана (рис. 9.11).
Для сечения А—А принимают Ко = 1,8... 2; = (0,7 ... 0,8)Ко; =
а=0,15; фх=0,1; A=Ai.
Для сечения В — В (сгр=О) принимают КО=КТ=1; фо=0,15; фт=0,Г,
Yz=l,h = h3.
Из (9.32) — (9.34) видно, что с увеличением h напряжение ст/ увеличива-
ется, а Ор и тк уменьшаются. Поэтому существует оптимальная толщина
стенки Л, которая обеспечивает максимальный запас прочности Птах. Для
определения оптимального значения повторяем проверочные расчеты, зада-
ваясь несколькими значениями Л, и строим график зависимости п от h. Из
графика определяем оптимальную толщину А, при которой получаем лШах.
ГЛАВА 10.ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
10.1. ВИДЫ ЧЕРВЯЧНЫХ ПЕРЕДАЧ
И ОБЛАСТИ ИХ ПРИМЕНЕНИЯ
Червячные передачи относят к категории зубчато-
винтовых. Они применяются для передачи движения в тех слу-
чаях, когда оси ведомого и ведущего валов перекрещиваются
в пространстве. Угол перекрещивания чаще всего равен 90°.
Передача состоит из двух звеньев — червяка 1 и червячного
колеса 2 (рис. 10.1).
Червячные передачи классифицируют по форме поверхности
червяка, на которой нарезается резьба: различают передачи с
цилиндрическими (см. рис. 10.1, а) и глобоидными (см. рис.
10.1, б) червяками. Глобоидные червяки обладают более высо-
кой несущей способностью, но сложнее в изготовлении и экс-
плуатации. Цилиндрические
профиля резьбы в торцевом
сечении на архимедовы, кон-
волютные и эвольвентные.
Архимедовы червяки, как
наиболее экономичные и тех-
нологичные в изготовлении,
применяют с нешлифованны-
ми витками при числах твер-
дости не более 350 НВ. Для
повышения работоспособно-
сти уменьшают шерохова-
тость и увеличивают твер-
дость до чисел не менее 45
HRC. В этом случае приме-
червяки подразделяют по форме
Рис. 9.11. Элемент конструкции
гибкого колеса
171
Рис. 10.1. Червячные передачи
няют эвольвентные червяки, так как они шлифуются плоской
стороной шлифовального круга, что является их существенным
преимуществом. В передачах с эвольвентными червяками, по
сравнению с другими червяками, улучшен геометрический кон-
такт, повышены контактная прочность, КПД и износостойкость.
Это достигается, в частности, при выборе угла профиля ап от
14,5 до 30°.
В ЛА широко применяют цилиндрические червячные пере-
дачи с архимедовым червяком. Такие червяки являются винта-
ми с трапецеидальным профилем резьбы в осевом сечении, в
торцевом — витки очерчены архимедовой спиралью. Касание зу-
ба колеса с витком червяка происходит по контактной линии,
благодаря чему у таких передач более высокая по сравнению с
винтовой несущая способность.
Основные достоинства червячной передачи следующие: ра-
циональность компоновки и минимальные габаритные размеры
всего механизма для передачи движения между перекрещиваю-
щимися осями, возможность получения больших передаточных
чисел (до 100, чаще всего 10... 50), плавность зацепления и бес-
шумность работы, высокая кинематическая точность, возмож-
ность самоторможения (под действием вращающего момента
со стороны червячного колеса червяк остается неподвижным).
К недостаткам относят низкий КПД из-за больших потерь
на относительное скольжение под нагрузкой сопряженных про-
филей червяка и колеса. Нагрев, износ и склонность к заеда-
нию при больших скоростях скольжения обусловливают особые
требования к материалам, шероховатости рабочих поверхностей,
точности, что повышает стоимость передачи. В передачах для
изготовления червячных колес используют дорогостоящие
бронзы.
В авиации червячные передачи применяют для передачи не-
больших мощностей (5... 10 кВт), а также при кратковремен-
ной работе или в слабонагруженных кинематических механиз-
мах, где не требуется специальных охлаждающих устройств,
172
гДе необходимы высокая точность и плавность работы: в меха-
низмах систем управления рулевыми поверхностями, в РЭА
ЛД; в самолетах вертикального или укороченного взлета и по-
садки для поворота закрепленных в крыле мотогондол, крыла
вместе с двигательной установкой, воздушных насадков в дви-
гательных установках; в некоторых типах ЛА для поворота си-
ловых установок, стабилизаторов струйных рулей, створок во-
дяные и масляных радиаторов.
।
10.2. ГЕОМЕТРИЯ, КИНЕМАТИКА И ТОЧНОСТЬ
Геометрические расчеты аналогичны расчетам зубча-
тых передач, так как червяк является подобием косозубого
эвольвентного колеса, у которого число зубьев равно числу вит-
ков резьбы. По числу винтовых линий резьбы червяк может
быть однозаходным и многозаходным. С увеличением числа за-
ходов возрастает угол подъема винтовой линии и повышается
КПД передачи. Однозаходные червяки применяют, когда необ-
ходимы большие передаточные числа или самоторможение. Чер-
вяки имеют обычно правую нарезку, кроме случаев, обусловлен-
ных требованиями кинематики. В зависимости от положения
червяка относительно червячного колеса передачи бывают с
верхним и нижним расположением червяка. При нижнем рас-
положении условия для смазки лучше.
Основные геометрические параметры червячной передачи:
модуль т=Р1п\ коэффициент диаметра червяка q; Р — шаг
резьбы червяка в осевом сечении. Делительный диаметр червя-
ка di связан с модулем т коэффициентом диаметра червяка:
q=d\lm. Для многозаходных червяков ход Рг связан с шагом Р
соотношением: P2—Pzi, где Zi— число витков (заходов) червя-
Рис. 10.2. Геометрия червяка и червячного колеса
173
ка. Угол подъема винтовой линии определяют из соотношения
tg y = nmzxlnd^=mzxldi—zjq.
В цилиндрических передачах с архимедовым червяком шаг
червяка Р и шаг зубьев червячного колеса совпадают. Гео-
метрические размеры червяка и червячного колеса (рис. 10.2)
приведены в табл. 10.1 (z2— число зубьев колеса).
В целях ограничения номенклатуры стандартного инстру-
мента для нарезания червячных колес и червяков значения т,
q, Zi стандартизированы. Рекомендации по выбору т, q, z при-
ведены ниже (угол профиля в осевом сечении также стандарти-
зирован: а=20°):
т, мм 1,0; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3
q 6,3: 8; 10 (кроме т=2); 12,5 (кроме т=2,5); 16; 20
zt 1; 2; 4
Таблица 10.1
Параметры Обозначение Расчетные соотношения
Червяк
Диаметр делительный вершин витков впадин червяка di dal du (при d{ — mq dai=di—2t4m d/\ = dl—2,4m радиальном зазоре 0,25 мм)
Длина нарезной части червяка bl bi> (ll+0,06z2)m при 21 = 1 И 2 (1,25 + 0,0922)т при 21=4
Высота витка головки витка ножки витка hi hai hn Л1=2,2т ha2 = m hf[ = \,2m
Червячное колесо
Диаметры делительный вершин зубьев впадин зубьев наружный Высоты зуба головки зуба ножки зуба Ширина венца Угловая ширина чер- вячного венца ^2 da2 djz davi2 h2 hat Л/2 26 62 d2 — ^TlZz daz=mz2-^2m df2=tnz2—2,4m daMZ^daZ^~^f^l (^1 + 2) h2=2,2m ha2=rn hf2 = l,2m f 0,75dai при 2i=l и 2 ( 0,67dai при Zi = 4 90... 110° —для силовых передач 75... 90° — для приборных передач
174
\ Из опыта проектирования рекомендуется выбирать: Zi = l
паи i>=40; Zi=2 при t=18...4O; Z\=4 при t=10... 18; q^
;5a0,25z2 (во избежание сильных прогибов червяка); z2^28 (по
условию неподрезания зубьев).
1Межосевое расстояние червячной передачи равно
\ aw=0,5m(z2-\-q).
При нарезании червячных колес со смещением х, а червяка
без смещения получаем следующие соотношения:
aw=0,5.71 (^ + z2+2х); da2=m(z2-j-2-j-2x);
dJ2=m(z2 — 2,4 -f- 2x).
Коэффициент смещения профиля зубьев червячного колеса:
—0,7^х^4-0,3. Отрицательное смещение профиля уменьшает
размер и момент инерции червячного колеса, улучшает условия
смазки и зацепления.
Таким образом, изменяя параметры т, q, х, можно вписать
в заданные габаритные размеры механизма (ада) червяки и
червячные колеса с различными z\ и z2, получая требуемые пе-
редаточные отношения.
Рассмотрим кинематику передачи. В червячной передаче на-
чальные делительные цилиндры не обкатываются, а скользят
друг по другу. Окружные скорости червяка vt и червячного ко-
леса v2 не совпадают (рис. 10.3). Поэтому передаточное отноше-
ние не может быть определено отношением делительных пара-
метров, а определяется так:
. <>! п; nd2 ятг2 г2
о>2 л2 л/п*! amzi z\
Так как Zi = l; 2; 4, то в червячной передаче могут быть
реализованы большие значения передаточных отношений. Аб-
солютные значения скоростей червяка t»i и червячного колеса
Vi, относительная скорость скольжения vs в зацеплении опре-
деляются следующим образом:
‘O1 = niZ1/i1/60; v2—nd2n2/(60-103);
v-i/vi=tg YI 4=^ +^2 =i»t/cos y-
Точность изготовления червячных передач регламентируется
стандартом. Однако по сравнению с зубчатыми цилиндрически-
ми передачами, ошибки в межосевом расстоянии, а также в по-
ложении средней плоскости колеса относительно червяка более
существенно влияют на распределение нагрузки по длине зуба.
175
Рис. 10.3. План скоростей в чер-
вячном зацеплении:
/ — зуб колеса; 2 — резьба червяка
Рис. 10.4. Схема сил, действующих в
червячном зацеплении
Поэтому назначают более жесткие допуски на нормы точности
и монтажа передачи. Конструкция передачи должна обеспечи-
вать возможность регулирования взаимного положения червяка
и червячного колеса. Стандарт устанавливает 12 степеней точ-
ности червячных передач. В ЛА используют передачи 5, 6-й сте-
пеней точности.
10.3. СИЛЫ В ЗАЦЕПЛЕНИИ. КПД. САМОТОРМОЖЕНИЕ
Для упрощения расчетов будем полагать, что распре-
деленное давление в зоне контакта червяка с червячным коле-
сом можно заменить сосредоточенной и нормально приложенной
в полюсе зацепления силой Fn. В червячной передаче действуют
окружная Ft, радиальная Fr и осевая Fa силы. Окружная сила
на червяке Fn (рис. 10.4) равна осевой силе на червячном ко-
лесе: Fti=Fa2=2T\/d\, где Т\ — вращающий момент на червя-
ке. На рис. 10.4 изображено осевое сечение витка червяка. Ок-
ружная сила колеса Ft2 равна осевой силе червяка Fai: Ft2 =
=Fat=2T2/d2, где Т2 — расчетный момент на колесе. В осевом
сечении червяка силы Ft2 и Fr являются составляющими силы
Fc (проекция суммарной силы Гс=^п+Лр на осевую плос-
кость, где Г— приведенный коэффициент трения). Радиальна?
сила Fr=r(2tga; нормальная сила Fn=Ft2/(cos a cos у). По
аналогии с передачей винт — гайка окружная сила на червяке
связана с окружной силой на колесе соотношением Fti=
=Ft2 tg(y-l-<p')> гДе ф'— приведенный угол трения, <p'=arctgf'.
КПД червячного зацепления ниже, чем зубчатого за счет
больших потерь на скольжение. КПД определяют, как в паре
винт — гайка. При ведущем червяке КПД T)=tg y/tg (qp'+y),
при ведущем червячном колесе r|,=tg (V—фЭ/tg У- Если у^ф',
то движение от колеса к червяку невозможно, так как rfs^O.
Такая пара называется самотормозящейся, и при движении
от червяка к колесу для нее т)^0,5 (при у^ф'). Но для обе-
176
ёпечения надежности самоторможения, особенно в условиях
вибрации, выбирают у<0,5ф'.
\ При проектировочных расчетах, когда геометрия передачи
еще неизвестна, КПД ориентировочно определяют по следую-
щим рекомендациям: при Zi=l т)=0,7...0,75; при Zi=2 т) =
= 0,75... 0,82; при Zi=4 т]=0,87 ... 0,92.
КПД передачи растет с увеличением у и с уменьшением ф'.
Приведенный коэффициент трения f' зависит не только от ма-
териала зубьев колес и червяка, но и от скорости скольжения
в зацеплении. Он существенно снижается при увеличении vs,
что связано с улучшением условий смазки трущихся поверхно-
стей.
Выбор материалов червячной передачи в основном опреде-
ляется скоростью скольжения vs. При проектировочных расче-
тах червячной передачи vs можно предварительно определить
по эмпирической формуле vs^Q,02nl у Т2, где Т2—в Н-м.
Червяк изготавливается из легированных сталей ЗОХГСА,
40ХН, 20Х и др. Поверхность витков термообрабатывают (це-
ментация, закалка ТВЧ), а затем шлифуют и притирают. Чер-
вячные колеса при vs< 10 м/с изготавливают из безоловянистых
бронз (БрАЖ9-4) и малооловянистых бронз (БрОЦС-б-б-3,
БрОЦС-4-4-17 и др.), а при vs>10 м/с —из высокооловянистых
бронз (БрОФЮ-1, БрОФб), которые дефицитны и дороги.
10.4. ОСНОВЫ РАСЧЕТА НА ПРОЧНОСТЬ
Основные виды повреждений червячных передач — это
износ и заедание, а не усталостное выкрашивание зубьев, как
у зубчатых передач. Это вызвано спецификой передачи, высоки-
ми скоростями скольжения и неблагоприятными условиями для
смазки. Выбор антифрикционных материалов для изготовления
червяка и червячного колеса (сталь — бронза) снижает заеда-
ние, но не ликвидирует износ. Однако на практике основным
критерием работоспособности передачи считают контактную вы-
носливость, а расчет изгибных напряжений делают провероч-
ным. Стальной червяк всегда значительно прочнее бронзового
колеса, поэтому червяк на прочность не рассчитывают. В осно-
ву расчета положены соотношения, используемые при расчетах
на прочность косозубых колес с поправками, учитывающими
форму зубьев и положение контактных линий. Условие контакт-
ной прочности зуба колеса:
4.65
Q ГГ - --
Н (?2/q)
где Ещ> — приведенный модуль упругости, Enp=2EiE2/(Ei+
+£2); Z2 — число зубьев колеса; Кяр= 1,05 ... 1,1 ввиду хорошей
177
72£пр(г2/4 +
------------------------о
(ЮЛ)
(28)°а®
Таблица 10.2
Материал зубчатого венца червячного колеса Предельное контактное напряжение
ан Нт а °'н пт °Я Пт Ъ
Бронзы оловянистые Бронзы безоловянистые 0,95о. 0,8ов 0,85Ов 0,7(Тв 4Z V 1+V. 0,55о. 0,5(Гв
прирабатываемости зацепления; Khv — коэффициент, учитываю-
щий дополнительную динамическую нагрузку, Кяо=1 +
+wHv6w/Ft2, где б® — ширина зуба по дуге делительной окруж-
ности, 5a=ndi(26)7360°; Whv— удельная окружная динамиче-
ская сила,
O’vKz.Jq) < wWtIllm;
6н — коэффициент, учитывающий тип зуба, 6н=0,002.
Коэффициент go, учитывающий погрешность шага в зацеп-
лении, и предельную величину удельной окружной динамиче-
ской силы и'яонщ выбирают по табл. 5.5 и рекомендациям, при-
веденным в разд. 5.5. Допускаемое контактное напряжение авр
определяется, как и для зубчатой передачи (см. гл. 5):
°Hp~aHHmlSH'i aHUma aHUm~aHUmV WIN
Для определения граничных значений контактных напряже-
ний и значения аниш можно воспользоваться табл. 10.2.
Если условие контактной прочности не выполняется, не-
большая перегрузка устраняется путем увеличения угловой ши-
рины 26°. При значительной перегрузке нужно пересчитать ос-
новные геометрические размеры передачи при большем стан-
дартном модуле, повторить проверочные расчеты.
Преобразуя условие контактной прочности (10.1), получают
формулу для проектировочного расчета межосевого расстояния
червячной передачи а®, мм:
3 Л-
aw > 2,9-Z2/g±j- 1/ . (10.2)
to/?)2/3 V 'HpW
При проектировочном расчете, выбрав материал червяка и
червячного колеса, необходимо определить передаточное отно-
шение червячной передачи i, расчетный момент на колесе Т2 и
допускаемое контактное напряжение материала колеса онР. Ве-
личины Zi и q стандартизированы; z2=zii (округляется до бли-
жайшего целого числа). При проектировочном расчете прини-
мают Кя0=1. Угловая ширина червячного венца (26°) для
178
Рис. 10.5. Номограмма для определения
в зависимости от zt, т и i
силовых передач — 90... 110°, в при-
борных передачах может снижаться
до 75°.
После определения приближен-
ного значения межосевого расстоя-
ния aw находят величину осевого
модуля червяка (торцевого модуля
червячного колеса) m^2aw/ (z2 + q).
Эту величину округляют до ближай-
шего большего стандартного значе-
ния. Далее переходят к расчету гео-
метрических размеров червячной пе-
редачи.
Для выбора zi, z2, i при различ-
ных т можно воспользоваться но-
мограммой (рис. 10.5). Три наклонные прямые внизу характе-
ризуют зависимость Z2 от i, вверху — зависимость aw от i при раз-
личных т. Если, например, (=24 и т=1 мм, то, проводя вер-
тикальные прямые, получаем: z2 = 48 и aw=32 мм. Заметим, что
точка i=24 лежит в зоне zi=2. Это значит, что число заходов
червяка следует брать Z] = 2.
Наибольшее разнообразие передаточных чисел можно реали-
зовать в червячном редукторе с aw=24... 25,2 мм. Так, для ре-
дуктора с aw=24 мм возможны следующие параметры:
т, мм
1
0,8
0,6
Q zi z2
16 4,2,1 32
18 4,2,1 42
20 4,2,1 60
I
8, 16,32
10,5; 21; 42
15, 30,60
Условие изгибной прочности зуба червячного колеса:
^=УрУ^р,1шп<оРр. (Ю.З)
Здесь of — расчетное местное напряжение изгиба у основа-
ния зуба со стороны растяжения; ур— коэффициент формы зу-
ба, который выбирается по табл. 10.3 в зависимости от эквива-
лентного числа зубьев
zo = z2/cos3y; Y=arctg (zJqY,
Ун — коэффициент, учитывающий наклон зуба,
^ = 1-у7140в>0,7;
wf— удельная расчетная окружная сила при расчете на изгиб,
. (Ю.4)
bw
179
Таблица 10.3
zv Ур zv Ур zv Ур zv Ур
20 1,98 30 1,76 40 1,55 80 1,34
24 1,88 32 1,71 45 1,48 100 1,30
26 1,85 35 1,64 50 1,45 150 1,27
28 1,80 37 1,61 60 1,40 300 1,24
Кра — коэффициент, учитывающий торцевое перекрытие в
червячной передаче, Kfa=l/ee£'; еа — торцевой коэффициент
перекрытия в средней плоскости зацепления, для передач с ци-
линдрическим червяком еа= 1,8... 2,2; — коэффициент, учиты-
вающий уменьшение суммарной длины контактных линий вслед-
ствие того, что зуб колеса соприкасается с витками червяка не
по полной дуге обхвата, |'=0,75; Kf» — коэффициент, учиты-
вающий неравномерность распределения нагрузки по дуге зуба,
Kfo=Kho= 1,05... 1,1; Kfv — коэффициент, учитывающий допол-
нительную динамическую нагрузку на зуб, Лр»=14-и’£О&«/^2;
wf«— удельная окружная динамическая сила,
V ?2iq
(10.5)
6f=0,006; go и выбираются согласно рекомендациям
разд. 5.5 с подстановкой нормального модуля тп в среднем се-
чении зуба; орр — допускаемые напряжения изгиба,
aFll.nM*
(10.6)
Предел изгибной выносливости зубьев червячного колеса оп-
ределяется по неравенству
1,2ат> аГ11П1 = 1 > l,7s_j,
где а-1 — предел выносливости материала червячного колеса.
Методика определения уr, ys, Sf и Nfb приведена в разд. 5.8.
При этом при вычислении ys вместо осевого значения модуля
т используют величину модуля в нормальном сечении тп—
=/ncos у.
Если условие изгибной прочности не выполняется, то нужно
повторить проверочные расчеты передачи при большем значе-
нии стандартного модуля.
180
ГЛАВА 11.ПЕРЕДАЧИ ВИНТ—ГАЙКА
11.1. ВИДЫ ПЕРЕДАЧ ВИНТ-ГАИКА И ОБЛАСТИ
ИХ ПРИМЕНЕНИЯ В ЛА
Передачи винт —гайка предназначены для преобра-
зования вращательного движения в поступательное. Их широко
применяют в механизмах управления ЛА. Так, они использу-
ются в механизмах управления внутренними и внешними за-
крылками, предкрылками, рулями высоты и направления, в ме-
ханизмах изменения стреловидности крыла, выпуска шасси
и т. п. Передачи винт — гайка при значительной несущей спо-
собности имеют небольшие габаритные размеры и массу, позво-
ляют с малым вращающим моментом создать большую осевую
силу и обеспечивают высокую точность требуемого закона дви-
жения.
Передачи винт — гайка по характеру движения звеньев раз-
деляют на:
передачи с ведущим вращающимся винтом, совершающим
одновременно осевое перемещение. Такие передачи применяют
при незначительных перемещениях, например в измерительной
технике;
передачи с вращающимся винтом и ведомой, поступательно
перемещающейся гайкой (рис. 11.1). Такая схема обычно ис-
пользуется в силовых передачах при больших перемещениях,
например в механизме изменения стреловидности крыла само-
лета (см. рис. 11.5). Такие передачи в механизмах управления
ЛА обычно применяют одновременно с зубчатой передачей, по-
нижающей частоту вращения винта;
передачи с вращающейся гайкой и ведомым поступательно
перемещающимся винтом (рис. 11.2). Такие передачи применя-
ются при небольших перемещениях и значительных осевых си-
лах на винте, например в механизмах управления стабилиза-
торами ЛА (см. рис. 11.3).
Передачи винт — гайка по виду трения делятся на передачи
скольжения и качения.
Рис. 11.1. Схема передачи винт —гайка с вращающимся винтом и посту-
пательно перемещающейся гайкой
181
Рис. 11.2. Схема передачи винт — гайка с вращающейся гайкой и посту-
пательно перемещающимся винтом
11.2. ПЕРЕДАЧИ ВИНТ—ГАЙКА С ТРЕНИЕМ
СКОЛЬЖЕНИЯ
Эти передачи при значительной несущей способности,
небольших габаритных размерах и массе конструктивно просты
и технологичны в изготовлении. Для механизмов управления
ЛА важно, что при однозаходной резьбе такие передачи обе-
спечивают самоторможение.
На рис. 11.3 в качестве примера использования передачи
винт — гайка скольжения показан подъемник стабилизатора
современного самолета. Движение от гидромотора передается
к вращающейся гайке 2 через понижающий частоту вращения
двухступенчатый цилиндрический редуктор 4, 5. С помощью
трапецеидальной резьбы вращение гайки преобразуется в по-
ступательное движение винта /, который, в свою очередь, через
карданный узел 6 перемещает стабилизатор. Гайка фиксирует-,
ся в корпусе подъемника 3 радиальными 8 и упорными 7 шари-
коподшипниками.
Недостатками передач винт — гайка с трением скольжения
являются низкий КПД (0,25... 0,40 при однозаходных резьбах)
и невозможность использования ее при высоких скоростях по-
ступательного движения гайки или винта, так как скорость
скольжения витков гайки относительно витков винта в 10...40
раз превышает скорость осевого перемещения, что ведет к по-
вышенному износу и перегреву механизма.
В силовых реверсивных передачах винт — гайка скольжения,
характерных для механизмов управления ЛА, чаще всего при-
меняют трапецеидальную резьбу (рис. 11.4, а), обладающую
высокой прочностью витков, технологичностью изготовления и
меньшими по сравнению с метрической треугольной потерями
на трение. Метрическую резьбу мелкого шага (рис. 11.4, б) при-
меняют для получения точных перемещений в механизмах при-
боров.
Резьба характеризуется наружным d(D), внутренним di(Di)
и средним d2(D2) диаметрами (d относится к винту, D — к гай-
ке); шагом резьбы Р; теоретической высотой профиля Н;
рабочей высотой профиля Н\\ углом профиля а; числом
182
Рис. 11.3. Подъемник стабилизатора самолета
Рис. 11.4. Трапецеидальная (а) и метрическая (б) резьбы
в
заходов z, ходом резьбы Рг—Рг, углом подъема резьбы ф. Для
трапецеидальной резьбы профиль и основные ее размеры тести-
рованы: а=30°; Я1 = 0,5Р; di—d—0,5Р; dmin=8 мм; Ртш=
= 1,5 мм.
Для метрической резьбы эти параметры даны в ГОСТ 8724—
71. Для каждого диаметра резьбы указаны основной и мелкий
шаги. Резьба ходовых винтов и гаек в зависимости от назначе-
ния передачи может быть правой и левой, одно- или многоза-
ходной.
Ходовые винты передач винт — гайка скольжения изготов-
ляют из сталей, обладающих высокой прочностью и износостой-
костью. При числах твердости поверхности не более 350 НВ —
из сталей 45, 50 и др.; при числах твердости не менее 50 ЯРС—
из сталей 65Г, 45Х, 40ХН, 12ХНЗА и др. Для уменьшения по-
терь на трение гайки выполняют из антифрикционных оловяни-
стых (БрОФЮ-1, БрОЦС6-6-3) и безоловянистых (БрАЖ9-4,
БрАЖМцО-3-1,5) бронз, способных воспринимать большие удель-
ные нагрузки и обладающих антикоррозионными свойствами и
хорошей прирабатываемостью. Оловянистые бронзы применяют-
ся при окружных скоростях 0,2... 0,25 м/с. При окружных скоро-
стях, меньших 0,2 м/с, применяют безоловянные бронзы, кото-
рые менее дефицитны, но имеют по сравнению с оловянными
бронзами больший коэффициент трения в паре со сталью.
Расчет передачи винт —гайка с трением скольжения. При проектирова-
нии передачи задают величину перемещений гайки или винта L (мм), время
перемещения t (с) и силу на гайке или винте F(a). Зависимость между пере-
мещением, временем, частотой вращения винта п, (об/мин) и параметрами
резьбы имеет вид
L=PznBt/60, (11.1)
откуда
лв=60£/(РгО;
(И.2)
184
поступательная скорость перемещения гайки v (мм/мин) равна
v = 6QL/t = Ргпв. (11.3)
Формула (11.3) может быть использована также для выбора Риги для
определения пв при выбранных г и Р.
Поскольку основным видом разрушения в передачах винт —гайка с тре-
нием скольжения является износ резьбы, то в качестве критерия работоспо-
собности таких передач принимается износостойкость. Давление q между вит-
ками резьбы винта и гайки не должно превышать допускаемого [<?], завися-
щего от материала винтовой пары и условий ее эксплуатации. Условие изно-
состойкости:
g = Fe/(rtrf2Hi?B) < (11.4)
где zB — число витков резьбы гайки, связанное с высотой гайки Нг соотноше-
нием
гв = Нг/Р. (11.5)
Подставляя (11.5) в (11.4) и учитывая, что /71=0,5Р, получаем формулу
для проверочного расчета винта и гайки на износостойкость резьбы
q=2Fa/(nd2HT)< [д]. (11.6)
При проектировочном расчете средний диаметр определяют из (11.6):
^2 = V2Ffl/(ny [g]), (11.7)
где y=Hr/d2— коэффициент высоты гайки, у выбирают из конструктивных
соображений в пределах 1,2... 1,5; большие значения у назначают для резьб
малых диаметров.
При трении закаленной стали по бронзе рекомендуют выбирать [<?]=
= 10... 13 МПа; при незакаленной стали по бронзе — [?]=8... 10 МПа. Если
изнашиваемость резьбы в процессе работы передачи необходимо уменьшить,
то принимают М=4 ...6 МПа.
По найденному значению среднего диаметра резьбы d2 по соответствую-
щему ГОСТу находят размеры всех параметров резьбы: di(Di); ^2(^2);
d(D); Hi; Р. Угол подъема резьбы ф определяют по формуле:
tg^ = Pz/(nrf2)-
После выбора параметров производят проверочные расчеты резьбы гайки
на срез, а стержня винта на прочность при действии осевой силы и крутя-
щего момента. Прочность витков резьбы гайки на срез проверяют по соот-
ношению
^ср.г = Ft^cp.rl » (11*6)
где Тср.г — расчетное напряжение на срез в витках гайки; 5 — коэффициент
полноты резьбы, показывающий отношение высоты витка в опасном сечении
к шагу резьбы (для трапецеидальной резьбы £=0,65); [тср.г] — допускаемое
напряжение на срез резьбы гайки, [тсР.г]= (0,2... 0,3) огт.
Так как ресурс ЛА в настоящее время приближается к десяткам тысяч
часов, а передачи винт —гайка в механизмах управления ЛА работают в ре-
версивном режиме, то число циклов изменения напряжений в этих передачах
достигает значений W=104... 105. Это дает основание вести расчет на проч-
ность стержня винта с учетом усталостного характера разрушения. В этом
случае определяют коэффициент запаса прочности винта в опасном сечении
по формуле
п = nent/V л’+л’ > (л), (11.9)
где [л] — допускаемый коэффициент запаса прочности, для ходовых винтов
ЛА [л]=1,3... 1,5; п9 и пх —коэффициенты запаса прочности по нормальным
и касательным напряжениям,
185
па— allm д/°р(сж)’ — ^Пшд/^к»
где огцтд и тцтд — предельные напряжения для расчетного сечения винта
(см. гл. 2); Ор(сж) и тк — рабочие напряжения растяжения (сжатия) и кру-
чения,
а₽(сж)=4^^^ <11Л°)
тк - 0,5^2 tg (ф + ?')/(0,2<ф, (11.11)
где ф' — приведенный угол трения, ф'=агс!д/'; f'— приведенный коэффи-
циент трения, f'=f/cos(a/2); / — коэффициент трения в резьбе; для пары
сталь — бронза при пластичной смазке /=0,08 ... 0,10.
В случае Af<103 циклов стержень винта на прочность рассчитывают по
формуле
®экв = J/’p+3tk < [’р] . (4.12)
где Оэкв — эквивалентное напряжение в опасном сечении винта; [сгР] — допу-
скаемое напряжение на растяжение для винта, [aP]=aT/l,5.
Винт, нагруженный сжимающей силой Fa, проверяют также на продоль-
ную устойчивость по запасу устойчивости по формуле
Пу = Fакр/Fа > [лу] > (11.13)
где пу — коэффициент запаса устойчивости; Fa к₽ — критическая сила; [лу] —
допускаемый коэффициент запаса устойчивости, обычно [пу]=2,5... 5; меньшие
значения (2,5... 4) для вертикальных, большие (3,5... 5) для горизонтальных
винтов.
По формуле Эйлера при X=p//i^Xnp
FaKP = n2£//(|A/)2r (Ц.14)
где Е —модуль упругости материала винта; / — приведенный момент инерции
сечения винта, /= (ndi4/64) (0,4+0,6d/cG); р, — коэффициент приведения дли-
ны винта, зависящий от условий закрепления винта (табл. 11.1); I — длина
сжатого участка винта; X, ХПр — гибкость и предельная гибкость винта; для
углеродистых и легированных сталей Хпр«90, i — радиус инерции сечения
винта (i«dj/4).
Таблица 11.1
Примечание. Опоры скольжения при l/di^2 и опоры качения с од-
ним подшипником эквивалентны шарнирной опоре; гайки с опорой рассматри-
ваются как заделка.
186
Для винтов любой гибкости удобно пользоваться объединенным условием
прочности и устойчивости
AFal(nd\) < [iclt()Ty, (11.15)
где [Осж] — допускаемое напряжение для винтов передач, [аСж]=От/3; фу—
коэффициент понижения допускаемых напряжений на сжатие, выбираемый в
зависимости от параметра гибкости:
X 10 20 30 50 60 80 100 120 140 160
Фу 0,98 0,95 0,91 0,86 0,82 0,70 0,52 0,37 0,29 0,24
КПД винтовой пары в случае преобразования вращательного движения
в поступательное равен
’) = tg+/tg(«|/+v'). (П-16)
КПД передач винт — гайка с трением скольжения невысок. При ф=
= 2... 20° и ф'=5 ... 6° т]=0,25... 0,70.
Условие самоторможения в винтовых передачах ф^ф' выполняется
только в винтовых передачах с однозаходными резьбами.
11.3. ПЕРЕДАЧИ ВИНТ—ГАЙКА С ТРЕНИЕМ КАЧЕНИЯ
Передачи винт — гайка с трением качения широко
применяют в силовых и приборных механизмах ЛА. Усилие
между винтом и гайкой передается через шарики, которые пе-
ремещаются в винтовых дорожках качения, выполненных на
винте и в гайке. Скорость перемещения этих шариков отлича-
ется от скорости ведущего и ведомого звеньев, поэтому для
обеспечения непрерывной циркуляции шариков концы рабочей
части резьбы в гайке соединены возвратным каналом. Шарико-
винтовые механизмы (ШВМ) применяются для рабочих нагру-
зок от сотен до сотен тысяч ньютон. Средние диаметры винтов
в этих механизмах 5... 150 мм, диаметры шариков 1...20 мм.
На рис. 11.5, а показан шарико-винтовой механизм, приме-
няющийся в узле изменения стреловидности крыла современно-
го сверхзвукового самолета (рис. 11.5, б). Движение к вращаю-
щемуся винту 6 передается от конического двухпоточного ре-
дуктора через зубчатую цилиндрическую передачу 2, понижаю-
щую частоту вращения винта. С помощью винтовой резьбы и
шариков 4- вращение винта в ней преобразуется в поступатель-
ное перемещение гайки 5. Непрерывность циркуляции шариков
обеспечивается перепускным каналом 3, выполненным в гайке.
Узлом крепления 7 гайка связана с крылом самолета. Винт в
корпусе ШВМ 1 фиксируется радиальными 9 и радиально-упор-
ными 10 шарикоподшипниками. Для предохранения пары
винт—гайка от загрязнения в конструкции ШВМ предусмот-
рен защитный кожух 8.
ШВМ имеют ряд преимуществ перед обычными передачами
винт — гайка скольжения: малые потери мощности на трение
качения, позволяющие повышать КПД механизма до 0,9; низкий
187
a
Рис. 11.5. Шарико-винтовой меха-
низм в узле изменения стреловидно-
сти крыла
6
Рис. 11.6. Профили резьбы в шарико-винтовых механизмах
в
е
приведенный коэффициент трения покоя и, следовательно, высо-
кая кинематическая чувствительность; малый износ рабочих
винтовых поверхностей винта и гайки, обеспечивающий высо-
кую точность и равномерность поступательного движения с со-
хранением стабильности этих параметров в процессе эксплуа-
тации; надежная работа в широком диапазоне температур и
вакууме.
К недостаткам ШВМ относят относительную сложность и
трудоемкость изготовления. Особенно трудоемкой является опе-
рация шлифования специального профиля резьбы гайки и хо-
дового винта. Однако с появлением станков для шлифования
профиля резьбы винта и гайки и разработкой более совершен-
ных методов обработки деталей этот недостаток устраняется.
В ШВМ различного назначения применяют криволинейные
профили резьбы винта и гайки (рис. 11.6, а, в), прямолинейные
(рис. 11.6, г, д, е) и комбинированные (рис. 11.6, б). Для си-
ловых ШВМ, применяемых в ЛА, рекомендуют полукруглые
профили с двухточечным контактом и углом контакта ак=45°
(см. рис. 11.6, а). Прямолинейный профиль резьбы (треуголь-
ный, трапециевидный) является наиболее технологичным, но
значительно уступает по нагрузочной способности криволиней-
ному. Это объясняется тем, что допускаемая нагрузка на ша-
рик, находящийся в желобе с профилем в виде дуги окружно-
сти, более чем в три раза выше допускаемой нагрузки на ша-
рик, лежащий на плоской поверхности трапецеидального или
треугольного профиля. Прямолинейный профиль резьбы приме-
няют в ШВМ для восприятия небольших осевых нагрузок, на-
пример в приборах. В измерительных устройствах с высокими
189
требованиями к точности перемещения узла рекомендуются
ШВМ с прямоугольным профилем и трехточечным контактом
между шариком и элементами винта и гайки (см. рис. 11.6, г,
д). При таком контакте положение шарика определяется одно-
значно.
Высокий КПД, надежность ШВМ в значительной степени
зависят от конструкции и качества изготовления перепускного
канала. Каналы должны быть просты в изготовлении и допус-
кать регулировку элемента, направляющего шарики из резьбо-
вой канавки в возвратный канал; иметь плавный переход резь-
бовой канавки в возвратный канал; обеспечивать минимальный
путь возврата шарика при малом числе поворотов. Одним из
распространенных способов перепуска является перепуск шари-
ков по изогнутой трубке, соединяющей начало и конец винто-
вой канавки гайки (рис. 11.7, а). Шарики направляются в
трубку либо концом самой трубки, либо специальными отража-
телями в корпусе гайки около концов трубки. Существенным
недостатком таких конструкций возврата шариков является уве-
личение радиальных размеров гайки.
Более рациональной является конструкция, в которой воз-
врат шариков осуществляется с помощью специальных вклады-
шей, вставленных в окна гайки по диагонали и соединяющих
соседние винтовые канавки ее резьбы (рис. 11.7, б). Обычно в
гайке предусматривают три вкладыша, которые располагают
под углом 120°, причем шарики разделены на три независимо
циркулирующие группы.
Твердость контактирующих поверхностей резьбы винта и
гайки определяет нагрузочную способность и долговечность
ШВМ. Она должна быть не ниже 60 HRC. В случае поверхно-
стного упрочнения (азотирования, объемной закалки после це-
ментации или закалки ТВЧ) толщина слоя должна быть доста-
точной для восприятия высоких контактных напряжений.
Винты изготовляют из сталей ХВГ и 7ХГ2ВМ с объемной
закалкой, 8ХВ с закалкой при индукционном нагреве и
20ХЗМВФ с азотированием поверхности. Для гаек применяют
Рис. 11.7. Шарико-винтовые механизмы с перепуском шариков с помощью
трубки (а) и с помощью вкладышей (б)
190
Рис. 11.8. Шариковая пара винт — гайка
стали марок 9ХС, ШХ15 с объемной закалкой и цементируемые
стали 18ХГТ, 12ХНЗА, 18ХНВА и др. Шарики обычно изготав-
ливают из стали ШХ15, ШХ15СГ. Твердость поверхности шари-
ков должна быть не ниже 63 HRC.
Расчет шарико-винтового механизма. Расчет силовых ШВМ существен-
но отличается от расчета передач винт-—гайка с трением скольжения. Его
геометрические размеры определяют исходя из нагрузочной способности, осно-
вываясь на зависимости размеров механизма в зоне контакта шариков от ве-
личины допускаемых контактных напряжений и числа циклов нагружения.
Диаметр винта выбирают, прежде всего, из условия устойчивости винта.
Внутренний диаметр резьбы винта di определяют по формуле
dI = l,2^Fe[ny]((i/)2/fi- (11.17)
При проектном расчете диаметр шарика dmt шаг резьбы Р, средний диа-
метр резьбы d0, наружный диаметр резьбы гайки Di, радиус профиля каналов
в винте и гайке гп; угол подъема винтовой линии резьбы ф на среднем диа-
метре (рис. 11.8) можно выбирать в зависимости от d\ по табл. 11.2. Для
полукруглого профиля ак=45 . Диаметр отверстия в гайке D и наружный
диаметр резьбы винта d находят по формулам
£> = Г>2-2Л; d = 6f14-2A, (11.18), (11.19)
где A, dm— глубина профиля резьбы у винта и гайки, Л= (0,3 ... 0,35); меньшее
значение h принимают для ШВМ, воспринимающих небольшие осевые нагруз-
ки, большие — для механизмов со значительными осевыми нагрузками.
Ходовой винт ШВМ проверяют на прочность при сложном напряженном
состоянии. Определяют крутящий момент Тк, приложенный к ходовому винту
для преодоления осевой нагрузки. В ШВМ учитывают момент трения в шари-
коподшипниках винта Топ, который сравним по величине с моментом трения
в резьбе шарико-винтовой пары Тв. Тогда
Тк = Тв+Топ, (11.20)
где Тв=О,5Та^о1д(ф+ф'к); Ton==T0+l,5k'Fad'o/d'm; <рк — приведенный угол
трения качения, <p'K=arctg kl(dm cos d*)\ k — коэффициент трения качения в
Шариковинтовой паре, А=0,01... 0,015 мм; А'— коэффициент трения качения
в шарикоподшипниках винта, А'=0,005... 0,007 мм; То —момент трения нена-
груженного шарикоподшипника, Н-мм, To=O,OO4d'oFa; d'o — средний диаметр
Шарикоподшипника, d'o= (D'4-d')/2; d'w — диаметр шарика шарикоподшип-
ника; d't D' — внутренний и наружный диаметры подшипника.
191
Таблица 11.2
do. мм di. мм D,. мм ^Ш’ ММ Р, мм гп> мм ф
10 6,98 13,02 3,000 4,00 1,54 7° 19'
17 13,80 20,20 3,175 5,0 1,68 5°22'
20 16,80 23,20 3,175 5,0 1,68 4°33'
22 18,80 25,20 3,175 5,0 1,68 4°08'
25 21,80 28,20 3,175 5,0 1,68 5°06'
30 25,20 34,80 4,763 4° 15'
36 31,20 40,80 4,763 7,0 2,45 3°32'
36 29,60 42,40 6,350 8,5 3,27 4°18' ,
40 33,60 46,40 6,350 8,5 3,27 3°52'
40 33,60 46,40 6,350 10,0 3,27 4°33' 1
40 32,20 44,80 4,763 7,0 2,45 3°11'
45 40,20 49,80 4,763 7,0 2,45 2°50'
45 38,60 51,40 6,35 7,0 2,45 3°26'
50 43,60 56,40 6,350 8,5 3,27 3°06'
50 41,93 58,07 8,000 12,0 4,12 4°22'
55 48,60 61,40 6,350 10,0 3,27 3°19'
55 47,79 62,21 7,144 12,0 3,68 3°58'
60 53,60 66,40 6,350 10,0 3,27 3°02'
Проверка винта на продольную устойчивость производится аналогично
методике, приведенной в разд. 11.2.
КПД ШВМ при преобразовании вращательного движения в поступатель-
ное определяется по формуле (11.16) с заменой ф' на ф'к. Так как ф'к<ф,
то КПД шариковой передачи даже при малых углах подъема винтовой линии
достигает 80... 90%.
У ШВМ, работающих при значительных нагрузках, деформация его эле-
ментов вызывает наряду с трением качения трение скольжения. В этом слу-
чае действительные значения КПД будут на 6... 8% ниже. Влияние трения,
скольжения на КПД тяжелонагруженного ШВМ можно учесть с помощью
коэффициента kc: = £<:?«• Величина kc зависит от нагрузки и твердости
контактирующих тел, 1,5 ... 3.
Условие самоторможения в ШВМ имеет вид
Расчеты ШВМ с параметрами, указанными в табл. 11.2, показывают, что
все ШВМ не являются самотормозящимися.
Грузоподъемность и долговечность ШВМ можно определять по соответст-
вующим формулам для радиально-упорного шарикоподшипника, нагруженного
осевой силой, поскольку условия работы шариков в них близки.
Грузоподъемность ШВМ при выбранных диаметрах ходового винта и
шарика зависит о г числа шариков, одновременно воспринимающих нагрузку,
и от твердости контактирующих поверхностей резьбы и шарика.
Наибольшие контактные напряжения на площадке контакта для сопри-
касающихся поверхностей шарик — поверхность резьбы ходового винта опре-
деляется по формуле Герца
о
’я = a v FnE* (2гп - *ш)2/(*шП.)2 < ’ О L22)
где Fn — нагрузка на шарик, действующая по нормали к площадке контакта;
£ —приведенный модуль упругости материалов шарика и ходового винта;
192
рис. П«9. График для выбора ко-
эффициента а
а — коэффициент, зависящий от от-
ношения рпр max/Рпр mln (рис. 11.9);|
рпр max, Рпр min — НЗИбОЛЬШИЙ И НЗИ-
меньший приведенные главные ра-
диусы кривизны площадки контакта
шарика с резьбой ходового винта,
рпр шах = ^шГп/(2Гп—dui)'t рпр mln =
ss={/ni^i/[2 (^ш COS (Хк4*^1)1
Для ШВМ ЛА при числах твердо-
сти соприкасающихся поверхностей
более 60 Н/?С рекомендуют <УнР =
= 2500... 4000 МПа, при кратковре-
менной работе он5000 МПа. При
числах твердости менее 60 HRC при-
нятое значение ОяР следует снижать,
умножая его на коэффициент /Ст, за-
висящий от числа твердости HRC\
HRC 29 35 40 45
Хт 0,38 0,415 0,5 0,6
49 54 58 62
0,69 0,79 0,89 1
Из (11.23) при выбранных значениях радиуса профиля резьбы гп и
СнР определяют допускаемую нагрузку, действующую на шарик по нормали
к поверхности контакта:
'•frM®3*2 (2rn - • (1L23)
Действующая нагрузка на шарик равна
Нп = Fal(zk sin ак cos Р) < [/=*„], (11.24)
где z — число рабочих шариков в гайке; X — коэффициент, учитывающий не-
равномерность распределения нагрузки между шариками, Х=0,8, отсюда
минимальное число рабочих шариков равно
z = Fa/([Fn] * sin ак cos р); (11.25)
минимальное число рабочих витков в гайке
^niln — Р/(Л^о)- (11.26)
В ШВМ из условия равномерности нагружения общее число рабочих ша-
риков, находящихся между витками резьбы и в перепускном канале, не долж-
но превышать 125 для каждой замкнутой цепи, а максимальный путь, прохо-
димый шариками под нагрузкой, не должен превышать четырех витков резь-
бы. Если по расчету z> 125, то следует увеличить диаметр шарика.
Общее число витков в гайке пОбщ зависит от конструкции перепускного
канала — числа рабочих витков nmfn:
Hmin 1,5 2,5 3,5 4
Побщ 3 4,5 5,5 6
Высоту гайки в ШВМ вычисляют по формуле:
Яг = [^общ +(!...!, 5)] Р. (11.27)
Полученные зависимости применимы для расчета как однозаходной, так
и многозаходной резьбы.
7—1085 193
Долговечность ШВМ рассчитывается по методике расчета радиально-
упорного подшипника. Отличие в расчете ШВМ состоит лишь в расчете дина-
мической грузоподъемности по формуле:
С = fc (г cos Ок)0’7 <^8, (11.28)
где fe — коэффициент, зависящий от геометрии ШВМ:
dmcosax/do 0,05 0,06 0,07 0,08 0,09 0,10 0,12 0,14 0,16 0,18
fc 46,7 49,1 51,1 52,8 54,3 55,5 57,5 58,8 59,6 60,0
ГЛАВА 12.РЫЧАЖНЫЕ ПЕРЕДАЧИ
12.1. НАЗНАЧЕНИЕ И ОСНОВНЫЕ СХЕМЫ РЫЧАЖНЫХ
ПЕРЕДАЧ. ОБЛАСТИ ПРИМЕНЕНИЯ В ЛА И ПРИБОРАХ
Рычажные передачи широко применяют в системах
управления и в приборах ЛА для передачи и преобразования
движений, перемещений, скоростей, силовых воздействий, вы-
полнения некоторых математических операций, воспроизведения
функций и т. д.
В составе систем управления рулевыми поверхностями ЛА
применяются: механические передачи, называемые силовыми
механическими проводками, обеспечивающие дистанционную пе-
редачу управляющих воздействий в виде перемещений и усилий;
суммирующие устройства или механизмы дифференциального
управления, осуществляющие алгебраическое суммирование или
разделение управляющих воздействий на узлы ЛА; устройства
регулирования или механизмы изменения передаточного числа,
корректирующие величины управляющих воздействий на узла
ЛА за счет изменения линейных размеров (плеч) звеньев меха-
нической проводки.
Эти механизмы включают в себя такие конструктивные эле-
менты, как тяги, качалки, рычаги. Поэтому они получили наз-
вание механической передачи типа качалка — тяга. Входные
Рис. 12.1. Кинематическая схема механической проводки
194
Нейтральное
положение
руля
управляющие усилия для работы
передачи качалка — тяга могут
создаваться непосредственно лет-
чиком через рычаг управления
(штурвал), а также различными
автоматическими системами (ав-
топилотом, автоматом коррекции
траектории, рулевой машинкой),
соединенными с входным звеном
механизма. Закон управления ру-
левыми поверхностями, реализуе-
мый механизмом, зависит от ре-рис 12.2. Схема передачи усилия
жима полета ЛА. По результатам^ тяге
сравнения текущей информации о
траектории движения с требуемой формируется входное воздей-
ствие в виде перемещения рычага управления (входного звена)
механизма качалка — тяга. Далее механизм преобразует это пе-
ремещение в соответствующие отклонения органов управления
(рулей). На рис. 12.1 изображен вариант кинематической схемы
механической проводки. Управляющее воздействие Fq-i с рычага
управления 0—2 (входное звено) передается на руль 11 с помо-
щью возвратно-поступательного движения тяг 2—3, 4—5, 6—10,
качательного движения рычага 1—2 и поворотных качалок 12, 13.
Направляющие устройства (ролики) 7 и 9 используют для
подвески тяг и создания требуемого направления сил в пере-
даче.
В схеме передачи усилия по тяге (рис. 12.2) рулевая ма-
шинка (РМ) 3 сообщает возвратно-поступательное движение
тяге 2, а она, в свою очередь, через рычаг 1 поворачивает вал
руля 4. Угол р поворота рычага может быть любым, а угол у
должен быть близок к прямому при среднем (нейтральном) по-
ложении руля. Этим достигается одинаковый поворот вала ру-
ля в обе стороны от нейтрального положения при одинаковом
ходе тяги. Изменение величины и направления управляющего
воздействия, передаваемого на тягу 2 в механизме качалка —
тяга (рис. 12.3), осуществляется силовой (поворотной) качал-
кой 3 треугольной формы. Управляющие усилия передаются тя-
гой 1 через качалку 3 на тягу 2. Силовая качалка крепится к
каркасу летательного аппарата 4 с помощью кронштейна 5.
Разворот тяг 1 и 4 (рис. 12.4) друг относительно друга на 180°
обеспечивает коромысловая качалка 3, которая крепится к кар-
касу 5 с помощью кронштейна 2.
Величину входного воздействия на рычаг управления, а так-
же значения ходов (перемещений) рычага управления и руле-
вой поверхности задают как исходные данные при проектиро-
вании согласно установленным нормам.
7*
195
Рис. 12.3. Конструкция силовой (поворотной) качалки
Ход или перемещение рулевой поверхности следует понимать
как перемещение выходной тяги 6—10 (см. рис. 12.1), соеди-
ненной с валом руля через одноплечий выходной рычаг. Анали-
зируя возможную трассу прокладки механической проводки по
ЛА (с учетом накопленного опыта проектирования и эксплуа-
тации), выбирают рациональные значения перемещений проме’-
жуточных тяг, рычагов и качалок. При этом выделяют три ха-
рактерных положения рулевой поверхности — два крайних и
нейтральное. Для определения управляющих усилий, передавае-
мых в нейтральном положении любым из промежуточных, а
также выходным звеном, рекомендуют пользоваться соотноше-
Рис. 12.4. Конструкция коромысловой качалки
196
нием: F0-iH0=F(n-i')-nHn-i, где Fo-i — входное усилие (входное
воздействие); Но — суммарное перемещение (в обе стороны)
входного звена 0—1 в точке приложения силы Fq-i, мм (см.
рис. 12.1); F(n-i)-n — усилие, передаваемое тягой (п—1)—п ме-
ханизма; Hn-i — суммарное перемещение (в обе стороны) соот-
ветствующего звена, п=3,5,.„ ,2^4-1; k — номер звена, fe=O,
1,... ,т.
Исходя из требований прочности, для равномерного нагру-
жения звеньев механизма ограничивают величину радиуса R
рычагов и качалок: Rmin^Hn-i. Выполнение условия ограниче-
ния усилия в крайних положениях FKVH на любом звене приб-
лиженно определяют из соотношения Лфи/Ли-^ 1,15, где FHT —
усилие в нейтральном положении.
Для более точного определения передаваемых усилий по
трассе механической проводки необходимо проанализировать
кинематику механизма в двух крайних и нейтральном положе-
ниях. При известном входном усилии Fo-i значения усилий
F2-3, —, F(n-iy-n, передаваемых тягами механической проводки
(см. рис. 12.1), будут зависеть от величин плеч п,...,Г(П-о соот-
ветствующих рычагов и качалок и определяются из равенств:
F2-3 = ^o-iri/r2< F= F2—згз1г^--->
^(n-i)-n—^(n—3)—(n—2)r‘n—2lrn-l'
Величины плеч различны в крайних и нейтральных положе-
ниях механизма. Используя вышеуказанные равенства, опреде-
ляют максимальные значения передаваемых усилий в тягах,
которые затем используются как эксплуатационные нагрузки
при расчете на прочность тяг, рычагов и качалок.
В нейтральном положении рулевых поверхностей передаточ-
ное отношение I механизма качалка — тяга приближенно опре-
деляется так: io-(n-\)—Ho/Hn-\. После проведения кинетостати-
ческого анализа, в результате которого находят величины уси-
лие. 12.5. Аксиальный (а) и дезаксиальный (б) кривошипно-ползунные ме-
ханизмы:
1 — ползун; 2 — шатун; 3 — кривошип
197
Рис. 12.6. Кулисный механизм:
1 — кривошип; 2 — кулиса
Рис. 12.7. Поводковый ме-
ханизм:
1,2 — поводки; 3, 4 — валики
лий в крайних положениях механизма, передаточное отношение
можно определить более точно:
*0—(л—1) = ^0—1)-л- (12.1)
В авиационных приборах применяют кривошипно-ползунный
(рис. 12.5), кулисный (рис. 12.6), поводковый (рис. 12.7, 12.8),
синусный и тангенсный (рис. 12.9) механизмы. В приборных
рычажных механизмах вращающиеся звенья (а^2л) называ-
ются кривошипами, качающиеся (а<л) — коромыслами,
звенья, совершающие плоскопараллельное движение,— шатуна-
ми, а движущиеся поступательно — ползунами. Звенья, образую-
щие с ползунами поступательные пары, называют направляю-
щими; подвижные направляющие — кулисами.
Кривошипно-ползунные механизмы (см. рис. 12.5) предназ-
начены для преобразования возвратно-поступательного движе-
ния во вращательное и наоборот. Они широко применяются в
манометрических авиационных приборах (барометрических вы-
сотомерах, указателях скорости, варио-
метрах и др.). Например, в передаточ-
ном механизме вариометра (рис. 12.10)
ползуном является жесткий центр 2
мембранной коробки 1, шатуном — тя-
га 3, а кривошипом — стержень 5.
Кулисные механизмы (см. рис.
12.6) предназначены для передачи
вращательного движения с одной оси
на другую, обеспечивая определенную
величину передаточного отношения.
Например, применение кулисного ме-
ханизма в вариометрах обеспечивает
возможность применения затухающей
шкалы, что позволяет повысить точ-
ность измерения при малых значениях
скоростей спуска и подъема ЛА.
Рис. 12.8. Конструкция
механизма высотомера:
1 — манометрическая коробка;
2, 3 — поводковые передачи;
4 — зубчатая передача; 5 —
стрелка
198
Рис. 12.9. Синусный (а) и тангенсный (б) механизмы:
/ — толкатель; 2 — рычаг
Поводковый механизм (см. рис. 12.7, 12.8) является про-
странственным механизмом и предназначен для преобразования
вращательного движения из одной плоскости в другую.
Синусные и тангенсные передачи (см. рис. 12.9) служат для
преобразования поступательного движения во вращательное.
Рис. 12.10. Передаточный механизм вариометра с затухающей шкалой:
' — мембранная коробка; 2 — жесткий цен гр; 3 —тяга; 4 — штифт; 5 — кривошип; б
винт; 7 — валик; 8 — рычаг; 9 — поводок; 10 — кулиса; 11 — зубчатый сектор; 12
трнбка; 13 — волосок; 14 — стрелка; 15 — шкала
199
В них перемещение толкателя пропорционально синусу или тан-
генсу угла поворота рычага.
Основные достоинства рычажных передач — простота конст-
рукции, малогабаритность, надежность в работе, универсаль-
ность, малые потери на трение и более высокий, чем у зубча-
тых и кулачковых передач, КПД. Рычажные механизмы преоб-
разуют движение с высокой точностью, так как элементы их
кинематических пар — простые поверхности (плоскость, ци-
линдр или сфера).
К недостаткам рычажных передач можно отнести ограничен-
ность угловых и линейных перемещений, зазоры в шарнирах
снижающие точность передачи.
12.2. РЫЧАЖНЫЕ МЕХАНИЗМЫ СИСТЕМ УПРАВЛЕНИЯ ЛА.
ОСНОВЫ РАСЧЕТА
Рассмотрим механизм дифференциального управле-
ния, осуществляющий алгебраическое суммирование или разде-
ление управляющих воздействий на рулевые поверхности. Боль-
шую роль в информации, получаемой летчиком об изменении
режима полета и о действии органов управления, играют физи-
ческие ощущения перегрузок и изменения усилий на рычагах
управления. Причем изменение и точность дозирования усилий
Рис. 12.11. Кинематическая схема дифференциальной качалки
200
существенно выше точности дозирования перемещений. Резкое
возрастание аэродинамических вращающих моментов на руле-
вых поверхностях для скоростных самолетов привело к увели-
чению потребной мощности для передачи движения на органы
управления. Физических возможностей человека при этом не-
достаточно, поэтому для сохранения «чувства управления» в
механизмах управления и создания дополнительных усилий на
рычагах управления стали вводить специальные загрузочные
устройства, а также различные дифференциальные механизмы,
которые формируют или корректируют управляющие воздейст-
вия совместно с летчиком или независимо от него. На рис.
12.11 изображен дифференциальный механизм качалка — тяга,
позволяющий создавать это дополнительное усилие. Две вход-
ные /, 3 и выходная 2 тяги шарнирно соединены со сложной
пространственной качалкой. Дифференциальная качалка служит
для того, чтобы управляющие воздействия, создаваемые авто-
матическими системами управления, передавались только в
сторону рулевых поверхностей через звенья механической про-
водки и не передавались в сторону рычага управления (штур-
вала). В качестве автоматической системы может быть исполь-
зован, например, рулевой агрегат системы демпфирования ко-
роткопериодических колебаний ЛА, работающий по сигналам
от автомата продольной устойчивости (АПУ). Дифференциаль-
ная качалка состоит из двух качалок — внешней 4 (V-образной
формы) и внутренней — рычага 6. Верхний конец внешней ка-
чалки установлен на кронштейне 7, а к нижнему присоединена
входная тяга 1, усилие на которую через звенья механической
проводки передается от штурвала. Внутренняя качалка 6 уста-
новлена на оси 5 внутри большой качалки и к ней присоедине-
ны две тяги: к верхнему концу — тяга 3 от АПУ, а к нижне-
му— выходная тяга 2, передающая усилия на рулевую поверх-
ность.
Когда не работает АПУ, верхний конец внутренней качалки
6 перемещаться не может. При отклонении тягой 1 внешней ка-
чалки 4 внутренняя качалка отклоняется вместе с ней как еди-
ное целое и перемещает выходную тягу 2. При работе только
АПУ перемещается тяга 3, а тяга 1 неподвижна (т. е. внешняя
качалка также неподвижна); при этом внутренняя качалка по-
ворачивается вокруг своей оси на угол, заданный АПУ, и пере-
мещает выходную тягу 2 в точку С'. Таким образом, перемеще-
ние от АПУ благодаря дифференциальной качалке в сторону
штурвала (тяги /) не передается. При одновременной работе
АПУ (тяга 3) и летчика (тяга /) внутренняя качалка отклоня-
ется на суммарный угол, заданный АПУ. Усилия на выходной
тяге 2 при этом алгебраически суммируются. В нейтральном
положении усилия в тяге 2 при заданных усилиях в тягах 1 и
5 определяются из равенств:
201
F2==F1/?3/^4 при работе только тяги /;
F'2=F3RilR2 ПРИ работе только АПУ;
F2=F2 ± F’2 при совместной работе летчика и АПУ .
Радиусы R\, R2, R3, R* качалки выбирают из конструктив-
ных соображений с учетом указанных выше рекомендаций.
Точные значения усилий в крайних положениях определяют
после кинетостатического анализа.
На рис. 12.12 представлена конструкция дифференциального
механизма качалка — тяга. Входные и выходные тяги механиз-
ма выполнены в виде трубчатых стержней цилиндрической
формы. Для шарнирного соединения с качалкой тяги на концах
имеются стандартные наконечники типа «уха» или «вилки». На-
конечник— отдельная деталь, привариваемая к концу тЯг или
ввинчиваемая в них. Наконечники могут быть фиксируемые и
регулируемые. Регулировка длины тяги облегчает сборку меха-
низма. Тяги и нерегулируемые наконечники делают обычно из
стали ЗОХГСА или алюминиевых сплавов Д1Т, Д16Т, регули-
руемые наконечники — из стали ЗОХГСА (для повышения проч-
ности резьбы).
Конструирование тяг сводится к определению длины и сече-
ния трубчатой части тяги исходя из трассы прокладки механи-
Рис. 12.12. Конструкция дифференциальной качалки
202
рис. 12.13. Конструкции тяг с одной (а) и двумя (б) пружинами
ческой проводки, а также к выбору способа сборки этой части
со стандартными наконечниками. Трубы тяг подбирают из ус-
ловия устойчивости по усилию: Fp=F3Kf, где Fp и F3K— расчет-
ное и эксплуатационное усилия, f — коэффициент безопасности,
/=2. Эксплуатационное усилие — максимальное усилие, пере-
даваемое тягой. При известных длине тяги L и критическом
усилии FKp, принимаемом равным Fp (рис. 12.13), подбирают
сечение трубы dX6, где d — диаметр трубы, мм, б — толщина
трубы, мм (рис. 12.14).
Расчет тяг на устойчивость проводят по формуле л = °кр/о^
^1, где я — коэффициент запаса прочности при расчете ЛА по
разрушающим нагрузкам; окр— критическое напряжение при
потере устойчивости тяги при заданных длине L и радиусе инер-
ции сечения трубы i, оКр=ф(Ь/7); о — расчетное напряжение
при растяжении в трубе с площадью сечения S, <j—Fp/S. На
рис. 12.4, б изображен наконечник тяги с двойной проушиной.
Трубы тяг также рассчитывают на растяжение по условию проч-
ности я=^в/о^1.
203
Рис. 12.15. Наконечники тяг
На рис. 12.15 показаны варианты сочетания тяг с различны-
ми наконечниками: с шариковым подшипником /, с шаровым
шарниром 2 и с наконечником в виде простой вилки 3. Конт-
ровочная шайба 4 служит для стопорения резьбы наконечников
тяг. Для стопорения резьбовых соединений регулируемых нако-
нечников часто используют гайки с отгибной шайбой. Для из-
готовления качалок, рычагов используют алюминиевые дефор-
мируемые сплавы (ВМ65, Д19, Д20, Д1Т, АК4 и др.), а также
Таблица 12.1
с-х/у b/d К для материалов при ав, МПа
Д1Т (350 ... 400) Ст45 (650 ... 800) ЗОХГСА 1200
1 2 0,706 0,946 0,820
1 2,5 0,535 0,886 0,766
1 2,5 0,585 0,805 0,716
1 2,75 0,555 0,796 0,675
1 3 0,530 0,786 0,655
1 3,5 0,500 0,755 0,630
1 4 0,500 0,746 0,620
1,2 2 0,765 0,930 0,910
1,2 2,25 0,760 0,916 0,850
1,2 2,5 0,660 0,890 0,810
1,2 2,75 0,630 0,870 0,786
1,2 3 0,616 0,857 0,750
1,2 3,5 0,585 0,830 0,730
1,2 4 0.580 0,810 0,726
1,4 2 0,846 1,0 1,00
1,4 2,25 0,786 0,985 0,945
1,4 2,5 0,740 0,966 0,905
1,4 2,75 0,715 0,945 0,875
1,4 3 0,695 0,925 0,860
1,4 3,5 0,675 0,895 0,830
1,4 4 0,575 0,87 0,810
204
магниевые литейные сплавы
(МЛ5-Т4 и др.) - Проушины кача-
лок рассчитывают на разрыв и
смятие.
Условие прочности проушины
на разрыв: г)=Хств/<Тразр> 1, где
К — коэффициент снижения пре-
дела прочности, учитывающий
концентрацию напряжений вбли-
зи отверстия (табл. 12.1), оразр=
=FX/S — расчетное напряжение
при расчете на разрыв; S =
= (b—d)6 — площадь разрыва
(рис. 12.16); Fx— проекция рас-
четного усилия Fp на ось х проу-
шины; <Тв — предел прочности на
Рис. 12.16. Проушина
растяжение.
Условие прочности проушины на смятие: t)=£i(Tb/<Tcm^1,
где ki — коэффициент, выбираемый в зависимости от степени
подвижности соединения: £i=l,3 (неподвижное соединение),
£1=0,65 (малоподвижное); £1=0,2 (подвижное) ов— предел
прочности на смятие, стСм — расчетное напряжение смятия, аСм=
^Fx/Sck, SCM — площадь смятия, 5См=^б.
Тело внутренней качалки, представляющее собой тонко-
стенную конструкцию с ребрами жесткости, рассчитывается на
изгиб по опасным сечениям А—А и Б—Б (см. рис. 12.12) по
формуле я=0Гв.и/<Ти^ 1, где <тв.и— предел прочности при изгибе,
ов.и«1,2ов; Пи — расчетное напряжение изгиба в опасных сече-
ниях; <3u=MyjWyA-Mz/Wz\ Му — расчетный изгибающий момент
от боковой силы, которую при проектировании задают равной
3% от Fy\ Fy — проекция расчетной силы Fp на ось у, Мг —
расчетный изгибающий момент от силы Fy (см. рис. 12.16); Wy,
Wz—моменты сопротивления изгибу опасных сечений (Л—А,
Б—Б на рис. 12.12).
Для внешней качалки расчет проводится по сечению В—В
на изгиб, по сечению Г—Г — на изгиб и кручение (см. рис.
12.12).
Расчет на прочность по сечению Г—Г состоит в определении
запаса прочности по разрушающим нагрузкам:
- аЯ.И 3Я.И |
°зкв +
где п=3 для стали, п=4 для цветных металлов; тк— касатель-
ные напряжения при кручении в сечении Г—Г, возникающие
под действием крутящего момента от силы Fy/2.
205
12.3. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ И ВЫБОР
ПАРАМЕТРОВ РЫЧАЖНЫХ ПЕРЕДАЧ В ПРИБОРАХ ЛА
Основной особенностью характеристик рычажных пе-
редач в приборах ЛА является непостоянство передаточного от-
ношения; постоянным его можно считать только с определенной
степенью точности на определенном интервале работы при за-
ранее установленных размерах отдельных деталей и узлов, их
соотношениях, расположении и т. д.
Для определения передаточного отношения рычажной пере-
дачи составляют уравнение функциональной связи между вы-
ходными и входными параметрами; при этом ведущее звено
передачи выбирается в зависимости от требований конструкции.
Кроме проведения кинематических расчетов в процессе проек-
тирования требуется проводить как силовые, так и динамиче-
ские расчеты. При этом необходимо учитывать, что рычажная
передача будет осуществлять заданное теоретическими расчета-
ми передаточное отношение только тогда, когда ее конструкция
разработана и выполнена в строгом соответствии с геометриче-
ской схемой, а все узлы и элементы имеют достаточные проч-
ность и жесткость.
Рассмотрим методику расчета характеристик и выбора па-
раметров типовых рычажных механизмов, применяемых в авиа-
ционных приборах.
Рассмотрим дезаксиальный кривошипно-ползунный меха-
низм (см. рис. 12.5, б). В таком механизме ползун движется
в плоскости, которая смещена относительно оси вращения кри-
вошипа на величину d, называемую дезаксиалом. В манометри-
ческих приборах ползун 1 обычно является ведущим звеном, не-
посредственно связанным с жестким центром упругого чувстви-
тельного элемента, перемещение которого передается ведомому
звену — кривошипу 3. Характеристикой механизма, выражаю-
щей функциональную связь между входной и выходной величи-
нами, в данном случае является зависимость перемещения w
ползуна от угла поворота а кривошипа. В результате геометри-
ческих расчетов получаем характеристику механизма w=f(a)
в следующем виде:
w=(a sin a —sin a0) — b(]^l — A — К1 — &), (12.2)
где A=[(acosa—d)/b}2\ B=[(acosao—d)/b}2\ a —радиус
кривошипа; b — длина шатуна, ao — начальный угол кривоши-
па; a — угол кривошипа при перемещении ползуна на w.
Передаточное отношение механизма при ведущем ползуне
можно получить из
• 14 U I /
----=la cos a
d w-I \
a sin 2a — 2d cos a XI-1
2b /]
(12.3)
206
В авиационных приборах наиболее часто применяются кон-
струкции механизмов, имеющих Ь/а~^7 и data. Тогда характе-
ристика и передаточное отношение с достаточной для практики
точностью будут равны:
wssa(sina — sina0); i ss l/(acosa). (12.4), (12.5)
Как видно из (12.4) и (12.5), i не является постоянным и
зависит от а; плавность изменения i зависит также от соотно-
шения а и Ь, определяющих размеры механизма, а введение
дезаксиала d вызывает более резкое уменьшение передаточно-
го отношения на малых углах а. Таким образом, регулировка
кривошипно-ползунного механизма может производиться изме-
нением а, b и d.
Рассмотрим кулисные рычажные механизмы (см. рис. 12.6)
с вращающейся (а) и качающейся (б) кулисами. В таких ме-
ханизмах кривошип 1 считается ведущим звеном, а кулиса 2 —
ведомым. Из Д О АВ и Д АВО' имеем:
tg?=/sin а/[с —/cosaj, (12.6)
где a — угол поворота ведущего звена кривошипа /; 0— угол по-
ворота кулисы 2; I—длина кривошипа, с — расстояние между
осями вращения кривошипа и кулисы.
Отсюда характеристика механизма имеет вид:
P=arctg [I sin аЦс—l cos a)], (12.7)
а передаточное отношение равно
1=^-= У 7 "‘°’° , , (12.8)
da л2 — 2л cos a + 1
где п=1/с.
Из (12.8) видно, что /—величина переменная, зависящая от
угла а поворота кривошипа и отношения 1/с. Регулировка ку-
лисного механизма может осуществляться изменением расстоя-
ния с между осями вращения кривошипа и кулисы и изменени-
ем угла а между кривошипом и кулисой в начальном положе-
нии, если кулиса при работе поворачивается на ограниченный
угол. Радиус кривошипа в этом случае остается неизменным, а
изменяется величина 1/с, что используется для выбора требуе-
мого характера изменения i от а. В некоторых приборах пре-
дусматривается возможность изменения радиуса кривошипа.
Рассмотрим поводковый рычажный механизм. Элементами
поводковой передачи (см. рис. 12.7) являются поводки 1 и 2,
укрепленные на валиках 3 и 4. При повороте валика 3 на угол
а поводок 1 будет давить на поводок 2 и поворачивать валик
4 на угол р. Здесь поводок 1 считается ведущим, а 2—ведо-
мым. Расстояния от осей вращения валиков до точки А сопри-
косновения поводков называются плечами поводков. Из рисун-
207
ка видно, что а — плечо ведущего звена, b — ведомого. Посколь-
ку траектории точек касания А ведущего звена atga и ведо-
мого b tg р одинаковы, характеристика поводкового механизма
запишется в виде
|3 = arctg[(a/£)tga], (12.9)
а передаточное отношение —
b 1 + sin2a(a2/*2_ 1) ' ' ‘ '
Из (12.10) следует, что при а=Ь, при всех a 1=1. В ос-
тальных случаях передача обладает переменным i, что исполь-
зуется в ряде конструкций приборов. В механизме высотомера
(см. рис. 12.8) регулировка поводковых передач может осущест-
вляться либо изменением плеч поводков и установкой нужного
начального положения передачи, либо изгибом ведущего повод-
ка на определенный угол <р (см. рис. 12.7). В этом случае ха-
рактеристика имеет вид
р = arctg {a tg a/[b -{-(a/cos a) tg ?]}, (12.11)
а передаточное отношение —
I = = а (6 + д cos a tg <р) . (12 12)
da (i cos a + a tg <р)2-j-(a sin a)2
Для того чтобы поводки для изменения длины плеч можно
было легко изгибать при точной настройке механизма, их обыч-
но делают из мягкой латунной проволоки. Иногда требуется,
чтобы передаточное отношение менялось более резко или более
плавно в крайних положениях передачи. В этих случаях изги-
бают конец поводка, как это, например, показано на рис. 12.8
во второй поводковой передаче 3 при затухающей шкале.
В синусном механизме (см. рис. 12.9, а) при поступательном
движении толкателя 1 длина а рычага 2 практически остается
постоянной. При этом зависимость между ходом толкателя w
и углом поворота рычага а имеет вид:
w=a(sin a—sin а0). (12.13)
Следовательно, характеристика механизма при ведущем тол-
кателе имеет вид
a=arcsin(w/a-|-sin a0). (12.14)
Передаточное отношение механизма равно
/ = —=-------!---. (12.15)
dw a cos a
208
Определив cos а из (12.13) и подставив в (12.15), найдем
выражение передаточного отношения через ход толкателя:
i=a~iyrl — (wM4-sin а0)2. (12.16)
В тангенсном механизме (см. рис. 12.9, б) длина рычага 2
изменяется, а расстояние а остается неизменным, следова-
тельно,
w=a(tga — tga0). (12.17)
Характеристика механизма при ведущем толкателе имеет
вид
a=arctg(w/a + tgao). (12.18)
а передаточное отношение —
i, = ^ = JK.!ia=1r Л +iyi. (|2.19)
dw a a L \ a / J
Пример 12.1. Расчет вариометра на основании следующих исходных дан-
ных: максимальный прогиб центра манометрической коробки Хтах при макси-
мальных скоростях спуска и подъема — не более ±2 мм; максимальный угол
поворота стрелки прибора утах=±180°; начиная с Л = ±1,2 мм, цена деления
шкалы должна возрасти в три раза.
1. Анализ основных характеристик рычажных, зубчатых и других передач
показывает, что в качестве передаточного механизма целесообразно применять
дезаксиальную кривошипно-ползунную, кулисную и зубчатую передачи (см.
рис. 12.10). Это обусловлено тем, что дезаксиальная кривошипно-ползунная
передача наилучшим образом может быть использована для преобразования
линейного перемещения центра мембранной коробки во вращательное движе-
ние стрелки 14. Кулисная передача чаще всего используется для получения
неравномерных шкал, а зубчатая передача служит для получения необходи-
мой величины общего передаточного отношения. Ползуном кривошипно-пол-
зунной передачи является верхний жесткий центр 2 манометрической коробки
1, перемещающейся при изменении давления р. В начальном положении, когда
манометрическая коробка не нагружена, тяга 3 и кривошип 5 должны быть
взаимно перпендикулярны (или близки к этому). Из конструктивных сообра-
жений для устойчивой работы длину а кривошипа выбирают не менее 4 мм,
а длину b тяги —не менее 16 мм. Выберем а = 5 мм, приняв d = at а из усло-
вия bla^l следует д = 35 мм.
2. Определим углы at- поворота кривошипа 5 по формуле (12.4) при про-
гибах X/ от нуля до Атах, например, через ДА=0,4 мм. Принимая ао = О, по-
лучим Qi = arcsin Ai/a = arcsin 0,4/5 = 4°34'. Аналогично определяем значения
углов а2|..., as и заносим их в табл. 12.2.
3. Исходя из заданной неравномерности шкалы определим размеры кулис-
ного механизма. Из (12.8) для ао = О и аз = 13°50' (см. табл. 12.2) получим
следующие передаточные отношения:
л2 — л л (л — 1)_____л '
° = л2-2л + 1 = (л-1)2 = л-1 ’
Л2-ЛС03 13°15у________л2-0,9708л
3~ л2 —2лсоз 13°15'+1 “ л2-1,9416л+ 1
209
Таблица 12.2
i 1 2 3 4 5
М, мм 0,4 0,8 1,2 1,6 2
а/ 4°34' 9° 14' law 18°45' 23о40'
₽< 29°46' 50°56' 64°48' 74°22' 81°04'
Y< 66°05' 113°04' ИЗ^О7 165°06' 180°
Поскольку на основании исходных данных необходимо обеспечить
=3, получаем п= 1,1627. Приняв из конструктивных соображений длину ры-
чага 8 равной 28 мм, определим расстояние с между осями кулисы и рычага:
с =//л = 28/1,1627 » 24 мм.
4. Из (12.7) определим углы 0 поворота кулисы для всех заданных точек,
результаты заносим в табл. 12.2. Например, для а5=атм=23°40' получим
₽5 = Ртах=arctg 6,36=81 °04'.
5. Определим параметры зубчатой передачи, исходя из условия, что ее
передаточное отношение «з.п в первом приближении равно передаточному
числу иа.п:
/з.п = Ymax/Pmax = 180°/81 °04' » 2,22 » tf3,n »Z\\J Z\%9
где Zh и Z|2 — соответственно числа зубьев сектора 11 и трибки 12. Принимая
£12=18, получим 211=212Кэ.п = 18-2,22»40. Уточненное передаточное число
Ma.n=211/zi2=40/18=2,22. Приняв модуль зубчатой передачи т=0,3 мм,
получим размер диаметра сектора </j1=mzH=0,3-40=12 мм, а диаметр
трибки di2=mz12=0,3-18=5,4 мм.
6. Определим углы у поворота стрелки 14 по формуле у=иэ.пР и значе-
ния у при различных i также занесем в табл. 12.2.
Из-за неточностей расчетов, различной жесткости мембранных коробок и
других факторов характеристика реального механизма может несколько от-
личаться от требуемой. Для этого в конструкции, изображенной на рис. 12.10,
показаны возможные методы некоторых регулировок, например, изменением
длины а кривошипа 5 с помощью винта 6, перештифтовкой тяги 3 штифтами
4 и др.
РАЗДЕЛ III
ДЕТАЛИ И УЗЛЫ ПЕРЕДАЧ ЛА
ГЛАВА 13.ВАЛЫ И ОСИ В ПЕРЕДАЧАХ ЛА
13.1. КОНСТРУКЦИИ ВАЛОВ И ОСЕЙ. МАТЕРИАЛЫ,
ИСПОЛЬЗУЕМЫЕ ДЛЯ ИХ ИЗГОТОВЛЕНИЯ
Вал — деталь, вращающаяся в подшипниках, служащая
опорой и передающая крутящий момент. Ось только поддержи-
вает детали, но крутящий момент не передает. Валы (оси) могут
совершать вращательное или качательное движения (например,
в передаче качалка — тяга). Некоторые валы предназначены
только для передачи вращающих моментов (валы трансмиссий
ЛА, торсионные и гибкие).
Валы при работе испытывают действие вращающих и изгиба-
ющих моментов, поперечных и осевых нагрузок — от усилий в
зацеплениях, аэродинамических нагрузок на несущие и хвосто-
вые винты вертолетов, от угловых и линейных ускорений при
эволюциях ЛА. Отдельные конструктивные элементы валов
(осей) такие, как буртики, уступы, торцы кольцевых канавок
и др., могут испытывать также напряжения среза и смятия.
В передачах ЛА используют валы с постоянной формой гео-
метрической оси — прямые и с изменяемой формой геометриче-
ской оси — гибкие, по конструкции они могут быть гладкими,
ступенчатыми и выполненными заодно с зубчатыми и червячны-
ми колесами и другими деталями, по форме сечений участков
вала — круглыми, профильными, со шлицевыми участками. Валы
(оси) могут быть сплошными и пустотелыми. Пустотелые валы
наиболее широко применяют в передачах ЛА, так как при почти
одинаковых со сплошными валами моментах сопротивления
изгибу и кручению и равной жесткости дают значительный выиг-
рыш в массе.
Конструктивные формы валов передач ЛА разнообразны
(рис. 13.1) и зависят от многих факторов: назначения механиз-
ма, вида нагрузки и характера ее распределения по длине вала,
способа передачи крутящего момента, формы сопряжения участ-
ков насадных деталей, способов осевой фиксации деталей и вала
в корпусе, условий сборки, технологии получения заготовок
(поковка, штамповка и др.), способа центрирования деталей на
валу, конструкции стопорящих устройств и др.
Выходной вал редуктора вертолета имеет ступенчатую форму
(см. рис. 13.1, а). Такая форма объясняется неравномерностью
211
Рис. 13.1. Валы и оси передач ЛА:
а — выходной вал главного редуктора вертолета; б — промежуточный вал авиационного
редуктора; в — вал механизма управления рулем высоты; г — вал привода лунохода;
д — вал-винт; е — вал-шестерня; ж — вал углового редуктора; з — вал-червяк; и — вал-
шестерня привода агрегатов; к — вращающаяся ось; л — невращающаяся (неподвижная)
ось
212
распределения нагрузки по его длине и необходимостью провод-
ки насадных деталей при сборке до посадочных мест без заеда-
ний и повреждений других участков. Промежуточный вал
авиационного редуктора выполнен заодно с зубчатым колесом
(см. рис. 13.1, б). Такая конструкция повышает усталостную
прочность и жесткость вала. Составная конструкция вала с по-
саженными на нем зубчатыми (червячными) колесами обуслов-
ливает более быстрое коррозионно-механическое изнашивание
соединения, увеличение массы узла и стоимость его изготовле-
ния, усложнение производства. У реверсивного вала циклические
деформации изгиба усиливаются деформациями кручения, вызы-
вая микроперемещения поверхностей вала и посаженной на него
детали. Поэтому вал выполняют заодно с деталями во всех
случаях, когда это позволяют технология и условия сборки.
Если вал (ось) с минимальной прочностью сечений не удов-
летворяет требованию поперечной жесткости или продольной
устойчивости, то его делают сплошным целиком или на отдель-
ных участках (см. рис. 13.1, в). Допускаемые прогибы и углы
поворота в опорах определяют исходя из условия исключения
защемления тел качения в подшипниках.
Конструкция отдельных участков вала определяется их на-
значением. Можно выделить, например, следующие функцио-
нальные участки: опорные (под подшипники), для соединения с
различными деталями, для центрирования, под уплотнения под-
шипниковых узлов.
Опорные участки валов и осей на концах вала называют
цапфами. Они имеют, как правило, цилиндрическую форму. В пе-
редачах приборов и радиотехнических конструкциях для под-
шипников скольжения применяют также конические и сфериче-
ские цапфы. Посадочные диаметры под подшипники качения
выбирают из стандартного ряда (по справочникам)—для диа-
метров 3... 10 мм — через 1 мм; 10...20 мм — через 2...3 мм;
20... ПО мм — через 5 мм; ПО... 200 мм — через 10 мм. Шерохо-
ватость опорных поверхностей выбирается в зависимости от
характера сопряжения с кольцом подшипника, диаметра цапфы
и класса точности подшипника.
Рис. 13.2. Переходные участки валов и осей
213
Переходные участки валов и осей для устранения или умень-
шения концентрации напряжений в месте изменения диаметров
выполняют по радиусу (галтельный переход). Для плотного
упора ступицы детали или кольца подшипника в торец уступа
вала берется г<гь г<с (рис. 13.2, а, б). В противном случае
между этим торцом и деталями образуется осевой зазор, что
недопустимо.
На свободных переходных участках (для исключения кон-
центрации напряжений) r>0,ld, где d — наименьший диаметр в
месте перехода. Для увеличения гх рекомендуется вводить про-
ставку с внутренней фаской (рис. 13.2, в) или применять галтель
с поднутрением (рис. 13.2, г).
Высота уступа (буртика) для упора внутреннего кольца
подшипника должна быть такой, чтобы подшипник можно было
снимать при демонтаже. При передаче больших осевых усилий
высота уступа выбирается из условия прочности торцевой по-
верхности на смятие, а ширина буртика — из условия прочности
на соез.
При необходимости шлифования на валу посадочных мест,
примыкающих к уступу (буртику), рядом с ним вместо галтели
может выполняться канавка для выхода шлифовального круга
(рис. 13.2, д). Размеры и форма канавок стандартизированы. На
валах диаметром d^lO мм они имеют ширину 1 ... 2 и глубину
0,15 мм, при d=10... 50 мм соответственно 3 и 0,25 мм, при d=
=50 ... 100 мм — ширину 5 мм и глубину 0,5 мм. Однако наличие
канавки вызывает в этом месте концентрацию напряжений, что
существенно снижает циклическую (усталостную) прочность
валов.
Участки соединения валов с различными деталями имеют
форму, необходимую для соединения их со ступицами насажи-
ваемых деталей и зависящую от вида соединения. Для передачи
вращающих моментов в передачах ЛА используют шлицевые,
шпоночные, фланцевые и другие соединения (см. гл. 21 и 22).
Участки перехода шлица в вал выполняют с закруглениями
радиуса г при центрировании по D (рис. 13.3, а) или с выкруж-
ками при центрировании по d (рис. 13.3, б). Это делают для
снижения концентрации напряжений. Для предохранения наруж-
ных кромок шлицев от скалывания на них выполняют фаски.
Прочность шлицевых участков вала повышают за счет приме-
нения шлицев с внутренним диаметром, равйЪш диаметру вала
или больше него, а также плавного выхода шлицев на поверх-
ность вала (рис. 13.3, в). Диаметр фрезы £>фР (мм) подбирают
по соотношению
£)фр^0,65Р4-15, (13.1)
где D — наружный диаметр шлицев вала; при шлифовании шли-
цов выход инструмента /вых увеличивают на 4... 5 мм.
214
f*450
f*45'
Ряс. 13.3. Участки валов для соединения со ступицами
Шлицевые пазы изготовляются протяжкой (более произ-
водительный способ), долблением или прошивкой. При изготов-
лении долблением или прошивкой предусматривается канавка
для выхода долбяка (рис. 13.3, г).
Для передачи вращающих моментов с помощью шпонки на
валу выполняют паз (рис. 13.3, д). Паз ослабляет сечение вала,
уменьшает его площадь и создает концентрацию напряжений в
месте перехода паза в тело вала. Для уменьшения концентрации
напряжений рекомендуется делать в этом месте скругление
радиусом т. Невозможность передачи значительных вращающих
моментов, снижение прочности сечений вала и недостаточно
высокая точность центрирования насаживаемых деталей по
цилиндрической поверхности вала ограничивают применение
шпоночных соединений в силовых передачах ЛА.
Форма паза определяется типом шпонки (призматическая,
сегментная, круглая, клиновая). Длина шпонки (паза на валу)
выбирается в соответствии с длиной ступицы насаживаемой дета-
ли (на 5... 10 мм меньше) из стандартного ряда длин шпонок.
При циклическом нагружении валов ступицы детали со
шпоночным пазом имеют посадку с натягом (например, Я7/р6),
а при действии еще и значительной осевой нагрузки (валы
червячных колес) —с гарантированным натягом. При этом натяг
создает на валу дополнительную концентрацию напряжений.
215
Поэтому при значительных нагрузках в передачах ЛА шпоноч-
ное соединение применяется редко и заменяется шлицевым.
Участки вала для крепления на них колец подшипников с
фиксацией в осевом направлении с помощью гайки имеют резьбу
(рис. 13.4, а). Для выхода резьбонарезного инструмента на валу
предусматривают кольцевые проточки. Ширина, глубина и фор-
ма проточки стандартизированы. Для стопорения гайки с по-
мощью стопорных шайб, имеющих внутренние выступы, на валу
выполняется продольный паз. Для уменьшения концентрации
напряжений выход паза должен иметь радиус R>0,ld.
Для осевой фиксации подшипников на валу применяют раз-
резные пружинные шайбы (рис. 13.4, б). Они вставляются в
кольцевые канавки, диаметр dj и ширина b которых стандарти-
зированы.
Для центрирования деталей, например зубчатых колес, на
валу при повышенных требованиях к точности вала предусмат-
ривают специальные пояски (рис. 13.4, в). Два разнесенных по
краям ступицы пояска обеспечивают более надежную продоль-
ную устойчивость насаженной детали.
Ширина центрирующих поясков зависит от диаметра вала.
Для облегчения сборки посадка детали по пояску меньшего диа-
метра производится с меньшим натягом, а по большему диамет-
ру— с большим натягом. При этом с увеличением натяга
снижается усталостная прочность вала из-за концентрации на-
пряжений, а также под воздействием переменных напряжений,
трения между сопряженными поверхностями и коррозии. На
участки вала, охватываемые уплотнительными устройствами,
указывается допуск цилиндричности поверхности. Наиболее рас-
пространены в передачах ЛА резиновые манжеты и лабиринтные
уплотнения, а в отдельных случаях — войлочные. Поля допусков
на номинальный диаметр участка под уплотнение обычно /8
или Й8.
Конструктивные элементы валов (осей) для осевой фиксации
деталей и передачи осевых усилий выполняют в виде уступов
(буртиков) с высотой, зависящей от диаметра вала. Диаметр
уступа (буртика) при отсутствии осевой нагрузки ориентиро-
вочно определяют по зависимости
Рис. 13.4. Участки валов для фиксации и центрирования деталей
d' ^rf+(3...4)/,
(13.2)
где f — размер катета фаски детали, мм.
Буртики увеличивают диаметр заготовки и снижают коэффи-
циент использования металла. Для уменьшения высоты бурти-
ков рекомендуют применять кольца или втулки (проставки), уве-
личивающие торцевую поверхность соприкосновения кольца или
втулки с деталью (см. рис. 13.2, в).
Для облегчения сборки насаживаемых на вал деталей и
устранения опасности скалывания острых кромок и поврежде-
ния рук рабочего кромки на выступах и на торцах валов выпол-
няются с фасками (см. рис. 13.1, а, б, рис. 13.4, а, б). Они слу-
жат также направляющими, облегчая сборку деталей. Размеры
фасок зависят от величины диаметра участка вала и стандарти-
зированы.
Ширина участков вала под ступицы деталей определяется
длиной ступиц, зависящей от диаметра вала d. Для кованых
и штампованных зубчатых колес длина ступицы /Ст= (0,8...
l,5)d; для колес, соединяемых с валом при помощи шлицев,
/ст= (0,8... 1,4)4/.
Развитие авиации сопровождается увеличением передавае-
мой мощности и частот вращения валов. Это приводит к увели-
чению нагрузок и, соответственно, напряженности элементов
валов передаточных механизмов ЛА при жестких ограничениях
массы.
При выборе материала вначале учитывают условия работы
вала (оси), возможные виды напряженного состояния и изнаши-
вания конструкции вала. При выполнении валов со шлицами
заодно с зубчатыми колесами материал выбирают по критериям
износостойкости и прочности зубьев. Для увеличения износо-
стойкости и стойкости к фреттинг-коррозии, а также снижения
массы вала материал должен обладать высокой твердостью.
Поэтому в ряде случаев марка материала назначается с учетом
проведения последующей термообработки и получения необхо-
димой твердости. Для избежания фреттинг-коррозии обеспечи-
вается высокая твердость в местах сопряжения с другими
деталями.
Выбор материала вала производится с учетом его механиче-
ских характеристик. Однако при работе валов в сложных усло-
виях нагружения (на различных режимах и при случайном
характере изменения нагрузок) кроме стандартных механиче-
ских характеристик следует учитывать весь комплекс свойств
материала, в том числе таких, которые определяют накопление
повреждений и характер его разрушения при различных видах
н характере нагружения (стационарном, нестационарном, слу-
чайном).
217
У валов передач ЛА возможны повреждения материала, ве-
дущие к его разрушению. Недопустимыми повреждениями
являются остаточная деформация или значительные прогибы;
износ; трещины; контактное выкрашивание; коррозия. В разных
условиях работы один и тот же вид нагружения может вызвать
различные виды повреждений: в одних условиях возникает
хрупкое, а в других — вязкое разрушение. Повторно статическое
нагружение может вызвать статическую и усталостную трещину.
Это объясняется многообразием и сложностью микромеханизмов
разрушения. При возникновении в сечениях вала объемного на-
пряженного состояния валы склонны к хрупкому разрушению, в
особенности при понижении температуры. Поэтому при выборе
материала вала (оси) следует учитывать его чувствительность к
трещинообразованию.
Наиболее полно требованиям к материалу валов и осей
передач ЛА удовлетворяют стали. В малонагруженных переда-
чах возможно применение конструкционных сталей марок
45А, 50. Для средне- и тяжелонагруженных валов применяют
легированные стали 40Х, 40ХН, 40ХН2МА, ЗОГСА и др. Для
валов и осей кинематических (несиловых) передач применяют
конструкционные стали и цветные сплавы.
Валы из легированных сталей подвергают улучшению, закал-
ке с высоким отпуском; для повышения износостойкости отдель-
ные места подвергаются поверхностной закалке ТВЧ.
Цапфы валов и осей под подшипники скольжения механиз-
мов с большим ресурсом для повышения износостойкости реко-
мендуется цементировать. Выбор твердости и вида термообра-
ботки осуществляется в соответствии с маркой стали (цементи-
руемой или позволяющей азотирование). Для получения высокой
износостойкости вала применяют хромоникелевые стали или
хромируют шейки вала (хромирование может увеличить ресурс
в 3 ... 5 раз).
Валы и оси изготавливают из проката, особо ответственные
валы — из поковок. Малонагруженные валы и оси (для прибор-
ных передач и механизмов следящих систем) могут изготавли-
ваться из штампованных заготовок или из труб.
Посадочные места валов и осей после токарной обработки
обязательно шлифуют. Особо ответственные валы рекомендуется
шлифовать по всей поверхности, а высоконапряженные участки
подвергать полированию даже на несопряженных поверхностях.
В процессе циклического знакопеременного нагружения вала
неровности, как микроконцентраторы напряжений, являются
источником усталостных трещин. Шлифование, полирование и
термическая обработка снижают величину неровностей и увели-
чивают долговечность валов. Шероховатость поверхностей вала
должна быть не ниже /?а=2,5 мкм, а под подшипники качения —
не ниже /?а=0,63 мкм.
218
• Прочность валов и осей, их долговечность и надежность в
эксплуатации зависят не только от механических свойств мате-
риала, но и от состояния поверхностного слоя наиболее напря-
женных участков, а также от микрогеометрии, остаточной
напряженности поверхности после механической, термической
и термохимической обработки. Для уменьшения возможных по-
вреждений поверхностного слоя после механической обработки
и повышения прочности валы, применяющиеся в авиационной
технике, подвергаются поверхностному пластическому деформи-
рованию (ППД). К таким методам относят дробеструйную об-
дувку, обработку шариками на вибростенде (виброупрочнение и
виброшлифование), раскатывание поверхности после чистовой
обработки, пневмодинамический наклеп и др. Они являются
высокоэффективными средствами повышения чистоты поверхно-
сти, создания сжимающих остаточных напряжений, повышения
твердости поверхностей и их контактной выносливости и износо-
стойкости.
Обкаткой роликами, чеканкой галтельных переходов можно
упрочнить участок вала и повысить его несущую способность
в 1,5 ... 2 раза. Вибрационной обработкой (шариками) шлицевых
участков вала значительно повышают их усталостную прочность.
Некоторые особо ответственные валы подвергаются алмазному
выглаживанию.
13.2. ОСНОВЫ РАСЧЕТА ВАЛОВ И ОСЕЙ НА ПРОЧНОСТЬ
И ЖЕСТКОСТЬ
Проектировочный расчет валов и осей. На валы пере-
даточных механизмов действуют поперечные силы от зацеплений
зубчатых и червячных колес (червяков) и в ряде случаев про-
дольные силы. На валы редукторов вертолетов могут действо-
вать также поперечные и продольные составляющие тяги винта,
а на валы передач винт — гайка — значительные осевые нагруз-
ки. При эволюциях ЛА добавляются инерционные нагрузки и
гироскопические моменты.
На начальной стадии проектирования передаточных механиз-
мов данные о распределении нагрузок по длине вала обычно
отсутствуют. За исходный размер для конструирования вала
(вращающейся оси) принимают диаметр предполагаемого наи-
более нагруженного его участка. Расположение этого участка
можно приближенно оценить по кинематической схеме.
При отсутствии данных об изгибающих моментах ориентиро-
вочный диаметр вала можно определить по величине вращающе-
го момента, принимая в условии прочности
где [тк]=т-,/[п]. При t-i«0,6o-i получим
d^lTy^l-c4)]!’73, (13.3)
219
где d — наружный диаметр вала; ТР — расчетная величина
вращающего момента, 7’р=7’н/Сд; Тк — номинальное значение
вращающего момента, Ун=9550 W/n; W — передаваемая валом
мощность; п — частота вращения вала; Кл — коэффициент дина-
мичности приложенной нагрузки (задается в ТУ на проектируе-
мый объект, /Сд=1,0... 1,3; верхнее значение выбирают при не-
стабильности подводимой к механизму мощности или возмож-
ном росте сопротивления в исполнительном органе); o-i — пре-
дел выносливости материала вала при изгибе; c=dold— отно-
шение диаметра отверстия do к наружному диаметру d участка
вала (для сплошных валов с=0); с=0,7...0,85 (нижнее значе-
ние принимают при ограничении жесткости вала). К.— коэффи-
циент, учитывающий влияние изгибающего момента на проч-
ность сечения вала.
Ниже приведены значения К в зависимости от положения
зубчатых колес относительно опоры и типа вала:
Положение зубчатых Быстроходный вал Тихоходный вал
колес
симметричное 3,8 3,0
несимметричное 4,0 3,1
консольное 4,4 3,2
Для вала, не работающего на изгиб, К. оценивают по пока-
зателю асимметрии цикла изменения вращающего момента
Rx—T'min/T'max:
Я, 4-1 0 —1
К 2 2,4 2,8
После проверочного расчета геометрия сечения обычно коррек-
тируется. Это объясняется тем, что в (13.3) используется предел
выносливости а-i, а не предел ограниченной выносливости, и
эта формула лишь приближенно учитывает действие изгибаю-
щего момента. При наличии концентраторов напряжений, кото-
рые не учитываются выражением (13.3), окончательный запас
прочности тяжелонагруженных валов может оказаться ниже
допускаемого.
Диаметры валов, работающих только на кручение и жестко
ограниченных по массе, рекомендуется оценивать исходя из
условия крутильной жесткости с учетом допускаемого угла за-
кручивания по формуле
d > 16,4 3/Г/(п [?]), (13.4)
где W—мощность, передаваемая валом; п — частота вращения
вала; [<р] — допускаемый угол закручивания на 1 м длины ва-
ла> °. [ф]=0,25... 1,5° (верхние значения соответствуют длинным
трансмиссионным валам и торсионным валикам).
220
Приближенный диаметр невращающихся осей (например, в
коробках приводов агрегатов ВРД) можно оценить исходя из
прочности на изгиб:
d^lOAlu/K]₽» (13.5)
где Ми — максимальный изгибающий момент, определяемый по
эпюре Ми при примерных длинах участков и ориентировочных
значениях нагрузок; [ии] — допускаемое напряжение на изгиб.
После оценки диаметра вала (оси) разрабатывают его конст-
руктивную форму.
Проверочный расчет валов и осей. В сечениях вала возника-
ют напряжения, переменные по величине и направлению. Ряд
механизмов ЛА периодического действия (управления стабили-
затором, элеронами и др.) являются реверсивными. Для боль-
шинства передаточных механизмов характерна работа на разных
режимах нагружения.
При постоянной внешней нагрузке F и действии распределен-
ной нагрузки от силы тяжести узла вала с насаженными деталя-
ми (рис. 13.5, а) упругая линия вала деформируется; при этом
напряжения сжатия будут в одной части сечения, а растяже-
ния— в другой. В крайней точке 2 сечения вращающегося вала
за один оборот напряжение изгиба сти изменяется по симметрич-
ному циклу (Ra——1). Если в сечении действует продольная си-
ла, вызывающая напряжения сжатия аСж или растяжения оР, то
Ra определяется по формуле
=(’и — 3р)/(3иН-3?) ИЛИ Ra (Зи 0сж)/(3иЗсж)*
Амплитудное значение напряжения аи в точке А в любой
момент времени I равно:
®в=(ДХи) sin W=aHmax sin <
где Мк — изгибающий момент в сечении; 1ГИ— момент сопротив-
ления сечения изгибу; со — угловая скорость вала.
Напряжения кручения в сечениях вала (оси) изменяются в
зависимости от характера изменения вращающего момента во
времени и от направления вращения вала (рис. 13.6). При вра-
Рис. 13.5. Схема вала (а) и цикл изменения напряжения аи (б)
221
Рис. 13.6. Циклограммы нагружения зубчатых колес
щении вала в одном направлении (валы редукторов вертоле-
тов, приводы агрегатов ВРД) с остановками между полетами
принимают Rx=0.
Расчетные схемы валов и осей. При расчете валов (осей) на
прочность необходимо знать фактические нагрузки. Но при
сложных спектре нагружения и характере распределения на-
грузки по сопряженным поверхностям действительные условия
нагружения и работы вала (оси) заменяют условными и состав-
ляют расчетные схемы. Нагрузки на валы и оси передаются от
насаженных деталей, соединительных муфт и в виде реакций
связей. Расчетная схема представляет собой упрощенное изобра-
жение реальной схемы нагружения вала. Приближенные расче-
ты затем уточняют по результатам натурных испытаний и дан-
ным эксплуатации.
В расчетных схемах опоры валов считают либо шарнирно-
неподвижными, либо шарнирно-подвижными. Если опора вала
закреплена и допускает небольшой поворот вала, то ее можно
считать шарнирно-неподвижной. Подшипники, одновременно вос-
принимающие радиальные и осевые нагрузки, схематизируют
как шарнирно-неподвижные, а воспринимающие только радиаль-
ные нагрузки и имеющие возможность перемещения — как шар-
нирно-подвижные.
Нагрузки, передаваемые валам и осям от насаженных дета-
лей и являющиеся распределенными (примерная эпюра
интенсивности нагрузки q(x) вдоль ступицы показана на рис.
13.7, а), в первом приближении заменяют сосредоточенными
силами F, приложенными в середине ступицы. Распределенные
нагрузки, действующие в зубчатых и червячных зацеплениях,
при расчетах заменяют сосредоточенными силами Ft, Fr, Fa, при-
ложенными в середине длины зубьев (рис. 13.7, б, в).
При составлении расчетной схемы вала в виде балки силы
переносят на ее ось. При приведении действующих в зацеплении
сил к оси балки в точке приведения возникают сосредоточенные
изгибающие моменты: MK=Fadwl2 от силы Fa (см. рис. 13.7, б),
Мив и Л4иг от сил Fa и Fr в вертикальной и горизонтальной
плоскостях (см. рис. 13.7, в); MnB—Fadm/2—Frl; MaT=Ftl,
где I — плечо силы Fr и Ft при их переносе на ось вала. От
силы Ft при переносе на ось балки возникает также крутящий
момент TK=0,5Ftdw и TK—0,5Ftdm (см. рис. 13.7, в).
222
Валы и оси, вращающиеся в опорах качения, рассчитывают
на изгиб как балки на шарнирных опорах. В случае радиальных
подшипников условную опору помещают посередине подшипника
(рис. 13.8, а). В случае радиально-упорного подшипника поло-
жение условной опоры определяют с учетом угла контакта а как
точку пересечения нормали к площадке контакта с осью вала
(рис. 13.8, б). Для увеличения грузоподъемности опоры при
ограничении размеров в радиальном направлении применяют
опору из двух подшипников. При приближенном расчете услов-
ную опору помещают посередине общей ширины двух подшип-
ников (рис. 13.8, в), при уточнении расчета — на одной трети
общей ширины, но ближе к нагруженной части вала (рис.
13.8, г). При точном расчете тяжелонагруженных валов и осей
условную опору размещают под каждым подшипником (рис.
13.8, д), а реакции в опорах находят путем решения статических
уравнений равновесия и уравнений деформаций.
^нс. 13.8. Схемы расположения опор
223
Ftf Рис. 13.9. Расчетная схема вала
На рис. 13.9 показан промежуточный вал двухступенчатого
редуктора с прямозубым (Zi) и косозубым (z2) цилиндрически-
ми зубчатыми колесами, с опорами в виде радиально-упорных
подшипников и его расчетная схема. Для удобства построения
эпюры изгибающего момента от усилий в зацеплениях Fa, Fr
и Ft зубчатых колес усилия спроецированы на две взаимно пер-
пендикулярные плоскости хоу и xoz. Суммарный изгибающий
момент в сечениях равен Afz= где Му и Мг соот-
ветственно изгибающие моменты в горизонтальной и вертикаль-
ной плоскостях.
Крутящие моменты от сил Ft\ и Ftz будут соответственно
равны:
7'к1=0,5/7tidwi', 7’К2=0,5/7tidW2-
Кроме изгибающего и крутящего моментов, возникающих
при работе передаточных механизмов, на валы передач могут
действовать при эволюциях ЛА перегрузки, инерционные силы
и гироскопические моменты, а от неуравновешенности узла ва-
ла— инерционные силы и моменты.
Величины этих дополнительных нагрузок оцениваются сле-
дующими зависимостями:
Fu=mf^, Ма—кРл1-, MT=aJрч>^ Мл=те<^1. (13.6)
Здесь Ги — инерционная сила, возникающая при эволюции
ЛА и действующая по радиусу кривизны в направлении от цент-
ра; т — масса узла вала; р — радиус кривизны траектории
ЛА; Йэ — угловая скорость эволюции ЛА; — инерцион-
224
Рис. 13.10. Прецессионное движение вала
ная сила от неуравновешенности ротора; со — угловая скорость
вала; е — эксцентриситет (смещение центра масс ротора от оси
вала); Мп— изгибающий момент от перегрузки; k — коэффи-
циент перегрузки (для истребителей 6=8, для вертолетов k=2);
Fg — сила тяжести узла вала; I — плечо силы; Мг — гироско-
пический момент, возникающий при эволюции ЛА; а — ко-
эффициент, учитывающий влияние угла поворота воздушного
или несущего винта на Мг (а=2 для выходных валов с двух-
лопастным винтом, а= 1 для винтов с тремя и более лопастями,
а.также для валов с массивными зубчатыми колесами и дисками
любых передач ЛА); /р — полярный момент инерции винта, ко-
леса или диска; Мл — инерционный момент от неуравновешен-
ности ротора.
Для получения минимальной массы валы передач ЛА вы-
полняют пустотелыми с минимальными запасами прочности в
сечениях. Такие валы становятся податливыми и прогибаются
под нагрузкой. Из теории колебаний известно, что прогнувший-
ся вал может вращаться вокруг оси вращения со скоростью й,
отличной от скорости собственного вращения вала со. Такое дви-
жение называют прецессионным (рис. 13.10). В плоскости А
лежит упругая линия вала, которая вращается со скоростью й
или в ту же сторону, что вал (прямая прецессия), или в проти-
воположную сторону (обратная прецессия). При этом на вал
от насаженных зубчатых колес действует результирующий изги-
бающий момент
M^=AJ^Wa, (13.7)
где А — коэффициент прецессии; А = 1—2со/й, /л — экваториаль-
ный (диаметральный) момент инерции диска; а — угол поворота
сечения вала в месте закрепления сосредоточенной массы.
Наибольший момент возникает при со/Й= —1 (обратная
синхронная прецессия).
Момент Мрез, а также другие нагрузки, вычисленные по
(13.6), являются исходными данными для проектирования валов
при точных расчетах. При приближенных расчетах их учитыва-
ют в эквивалентной нагрузке или путем увеличения исходного
8—1085 225
диаметра вала по данным прототипов и некоторым завышением
запасов прочности при проверочных расчетах.
Расчет на усталостную прочность. При действии циклических
и вибрационных нагрузок, инерционных сил и моментов, кратко-
временных перегрузок в материале валов и осей накапливаются
необратимые микроповреждения, приводящие к зарождению в
поверхностном слое микроскопических трещин. Их развитие
приводит после определенного числа циклов изменения нагрузок
к появлению макротрещин критического размера и последую-
щему разрушению усталостного характера. Для валов и осей
передач ЛА этот вид разрушения является основным.
При расчете на усталостную прочность принимают следую-
щие допущения: вал заменяют балкой на шарнирных опорах;
при расчете используют статические и усталостные характеристи-
ки стандартных образцов материала; распределенные нагрузки
заменяют сосредоточенными; влиянием силы тяжести валов
(осей) и насаженных деталей пренебрегают; расчет ведут с уче-
том конструктивных и технологических факторов, влияющих на
прочность и выносливость сечения (введением коэффициентов
влияния размеров, формы, состояния поверхности, упрочняющей
технологии и др.); учет'гироскопического эффекта и перегрузок
производят для передач маневренных ЛА (истребителей, верто-
летов, КА), а также для валов редукторов ТВД.
Расчет на усталостную прочность целесообразно производить
в таком порядке:
1. Составить расчетную схему вала (оси) (см. рис. 13.9).
2. Определить реакции опор, использовав уравнения равно-
весия балки.
3. Построить эпюры изгибающих и крутящих моментов.
4. Выявить сечения, где ожидаются наименьшие запасы проч-
ности, учитывая величину нагрузок по эпюрам и наличие кон-
центраторов напряжений (галтелей, отверстий, пазов, шлиц, ка-
навок, резьбы и т. п.).
5. Определить амплитудные и средние значения напряжений
изгиба и кручения, используя зависимости, приведенные в курсе
сопротивления материалов. При одновременном действии в рас-
четном сечении изгибающего момента и продольной силы N
суммарное максимальное напряжение равно:
(13.8)
где для валов момент сопротивления круглого сечения изгибу
U7H~0,lrf3(l — с4); c=ddd.
При наличии концентраторов напряжений, уменьшающих пло-
щадь сечения вала, момент сопротивления сечения изгибу
вычисляется по следующим формулам:
226
а) в случае сплошного вала и поперечного отверстия диамет-
ром
Wp=^-(l-dk/dy, (13.9)
32 10
б) в случае участка вала со шпоночным пазом шириной b
и глубиной t
^H=n</3/32-W-/W; Wp=nd3n^-bt(d-t)/2d. (13.10)
6. Определить коэффициенты запаса прочности по изгибу па
и по кручению на основании формул (2.15) и (2.16), учитывая
что при оценке o-in по (2.14) при переменном режиме нагруже-
ния вместо N для о нужно подставить эквивалентное число
циклов Ne, а в правой части (2.14) вместо предела текучести
при растяжении от подставить предел текучести при изгибе
(Гт.и=1,2от. При оценке формула (2.14) принимает вид
г_1ЛГ=т_1 < тт, (13.11)
где t-i«0,6q_i; тт~0,6от. При переменном режиме нагружения
вместо N нужно определить Ne-
В общем случае числа циклов изменения ои и тк будут раз-
ными. При постоянной нагрузке и заданной долговечности в
часах число циклов изменения ои равно
^=60л/А, (13.12)
где п — число циклов изменения ои в минуту, равное частоте
вращения вала (подвижной оси) в об/мин (см. рис. 13.5); th —
долговечность (ресурс), ч.
При вращении вала в одну сторону Nx равно числу циклов
нагружения механизма за весь срок эксплуатации, а для валов
редукторов вертолетов и ТВД — числу запусков двигателя.
7. При совместном действии изгиба и кручения определить
общий коэффициент запаса прочности и сравнить его с допускае-
мой величиной
п=п„пх / (13.13)
где [п] выбирают согласно рекомендациям, приведенным в
разд. 2.1 в зависимости от точности расчета и полноты проверки
прочности вала натурными испытаниями.
В (2.15) и (2.16) входят коэффициенты К, учитывающие
влияние конструктивных и технологических факторов на сопро-
тивление усталости детали и определяемые по (1.11) и (1.12).
Эффективные коэффициенты концентрации напряжений К,
и Кх для различных концентраторов напряжений определяют по
графикам или таблицам. Для ступенчатых валов с галтелями
и проточками значения Ка при D/d=2 и Kt при D/d=l,4 в за-
«* 227
Кб
J
г
1
г
Рис. 13.11. Зависимость коэффи-
циентов К, и Кт поправочных коэф-
фициентов а и Ь от p/d для валов с
галтелью
висимости от отношения p/d и предела прочности материала ов
приведены на рис. 1.12, а и рис. 13.11, а, б. Для значения D/d<2
при определении Ка и Кх можно использовать поправочные ко-
эффициенты а и b (рис. 13.11, в, г):
Ka — (Ka)D/d-l(l\ К\=(К\)D/d-l,4b. (13.14)
Для концентратора напряжений в виде кольцевой канавки зна-
чения Ко в зависимости от отношения радиуса канавки р к диа-
метру канавки d и высоты h к р приведены в табл. 13.1, значения
Кх в зависимости от p/d— в табл. 13.2.
Коэффициенты Ко и Кх для шлицевых участков валов приве-
дены в табл. 13.3, а для сечений валов с поперечным отверстием
диаметром d* в табл. 13.4. При расчете малонагруженных вали-
ков при ов^700 МПа и любых валов с промежуточными значе-
ниями Ов величины Ко и Кх оценивают по рис. 13.12.
Для резьбовых участков вала, испытывающих изгиб, значе-
ния Ко приведены ниже:
о,, МПа 500 600 700 800 900 1000 1200
К, 1,8 1,95 2,20 2,30 2,45 2,60 2,90
Валы передач винт — гайка в ряде механизмов (например,
изменения геометрии крыла) имеют резьбовые участки, испыты-
вающие растяжение или сжатие.
228
Таблица 13.1
оа, МПа P/d
0,01 0,02 0,03 0,05 0,1 0,01 0,02 0,03 0,05
й/р=0,5 Л/р = 1
700 2,05 1,95 1,85 1,75 1,55 2,25 2,15 2,1 1,95
900 2,15 2,05 1,95 1,9 1,6 2,4 2,3 2,2 2,1
1200 2,3 2,2 2,1 2,05 1,75 2,6 2,5 2,35 2,25
Л/р=2 л/1 р=5
700 2,5 2,4 2,3 2,65 2,5
900 2,65 2,5 2,4 — — 2,8 2,65 —
1200 2,85 2.7 2,6 — — 3,05 2,85 — —
Таблица 13.2
аВ’ МПа Pld
0,01 0,02 0,03 0,05 0,1
700 1,9 1,75 1,65 1,5 1,25
900 2,1 1,95 1,8 1,65 1,3
< 1200 2,4 2,2 2,05 1,8 1,4
Таблица 13.3
<jb, МПа К а К для шлицев т
прямобочных эвольвентных
700 1,60 2,45 1,49
800 1,65 2,55 1,52
900 1,70 2,65 1,55
1000 1,72 2,70 1,58
1200 1,75 2,80 1,60
229
Таблица 13.4
<*В’ МПа К t
dA/d-0,05...0,l dk/d-0,15.. .0,25 0,05...0,25
<700 2,00 1,80 1,75
900 2,15 1,90 1,90
>1100 2,35 2,10 2,00
В месте посадки насаженных деталей на вал возника!ет кон-
центрация напряжений, зависящая от абсолютных размеров
сечения. Поэтому при расчете валов на таком участке использу-
ются отношения KaIKda и KxIKdx (табл. 13.5), учитывающие
в расчете сразу два фактора.
После оценки усталостной прочности вала путем сравнения п
с [п] в наиболее напряженных местах уточняют диаметр внут-
реннего отверстия или наружный диаметр вала с целью получе-
ния минимальных массы и размеров, соответствующих п=[л]
во всех сечениях вала. Для ускорения расчетов при большом
числе сечений целесообразно применять ЭВМ.
Расчеты валов на жесткость. Нагрузки на валы в виде сил
и моментов при минимальных запасах прочности в сечениях
вызывают прогибы валов и повороты сечений. Упругие попереч-
ные перемещения валов вызывают перекос зубчатых колес в
пространстве и увеличивают концентрацию нагрузки по ширине
зубьев, а при значительных углах поворота упругой линии вала
приводят к защемлению тел качения подшипников (особенно
роликовых). При высоких частотах вращения возникает опас-
ность появления колебаний вала (вызванных неуравновешенно-
стью, возрастающей с увеличением прогиба) и роста напряжений
в сечениях по сравнению с расчетными. При вращении валов в
подшипниках скольжения прогиб вызывает увеличение неравно-
мерности распределения нагрузки по опоре. В приборных устрой-
ствах прогибы валиков приводят к снижению точности изме-
рений.
Рис. 13.12. Зависимости
К и К от о, для валов с
поперечным отверстием
230
Таблица 13.5
диаметр вала, мм Посадка * ав, МПа
700 800 900 1000 1200
I 3.0 3,25 3,50 3,75 4,25
30 II 2,25 2,44 2,63 2,82 3,19
III 1,95 2,11 2,28 2,44 2,76
I 3,66 3,96 4,28 4,60 5,20
50 II 2,75 2,97 3,20 3,45 3,90
III 2,38 2,57 2,78 3,0 3,40
100 и более I 3,94 4,25 4,60 4,90 5,60
II 2,96 3,20 3,46 3,98 4,20
III 2,56 2,76 3,0 3,18 3,64
I 2,20 2,35 2,50 2,65 2,95
30 II 1,75 1,86 1,98 2,09 2,31
III 1,57 1,67 1,77 1,86 2,06
I 2,60 2,78 3,07 3,26 3,62
50 II 2,15 2,28 2,42 2,57 2,74
III 1,83 1,95 2,07 2,20 2,42
100 и более I 2,76 2,95 3,16 3,34 3,76
II 2,18 2,32 2,48 2,80 2,92
III 1,94 2,06 2,20 2,31 2,58
* I —посадки с гарантированным натягом; II — переходные посадки;
Ш — посадки типа H/h.
Допускаемые прогибы и углы поворота зависят от требований
К жесткости вала, обеспечивающей нормальную работу зацепле-
ний и подшипников, и требований по точности балансировки узла
вала с насаженными деталями.
Изгибная жесткость оценивается стрелой прогиба у и углом
Наклона упругой линии вала 0 (рис. 13.13). Крутильная жест-
кость оценивается углом закручивания фо на единицу длины
вала или общим углом закручивания ф.
Прогибы и углы наклона упругой линии вала определяют
Методами, изложенными в курсе сопротивления материалов.
231
Рис. 13.13. Прогиб и угол поворота упругой линии вала
Жесткость вала проверяется условиями
У—\У\\ 0<[9]- (13.15)
При расчете прогибов у и углов поворота 0 в любых точках
вала можно использовать упрощенные формулы сопротивления
материалов (табл. 13.6). Для увеличения жесткости участка
вала и уменьшения его прогиба опоры располагают ближе к
плоскости действия сосредоточенной нагрузки. Уменьшению
прогибов вала от инерционных нагрузок способствуют современ-
ные методы балансировки вращающихся деталей на рабочих
частотах вращения в собственных подшипниках [37] и высокие
требования к точности изготовления деталей. К деталям тяжело-
нагруженных роторов предъявляются следующие требования к
погрешностям формы и взаимного расположения поверхностей:
овальность цапф вала под подшипники качения должна быть не
более 0,005 мм; биение поверхности цапф друг относительно
друга — не более 0,02 мм; торцевое биение упорных буртиков,
в которые упираются подшипники качения,— не более 0,02 мм;
разностенность колец подшипника — не более 0,005 мм, разно-
размерность роликов в подшипнике — не более 0,003 мм; торце-
вое биение зубчатых колес — не более 0,02 мм; радиальное бие-
ние— не более 0,01 мм.
В каждой конкретной конструкции прогибы валов зависят от
величины нагрузки, размеров участков вала, расположения на-
грузок относительно опор. Норм на допускаемые прогибы и
углы поворота не существует. Но статистика опасных прогибов
позволила получить эмпирические рекомендации по величине
допускаемых прогибов [у] и углов [0] в местах расположения
зубчатых колес, опор и в месте максимального прогиба вала.
Для валов зубчатых передач стрела прогиба в месте посадки
колеса ограничивается величиной, определяемой в зависимости
от модуля зацепления т и типа передачи: 0,01т — для
цилиндрических передач; [t/] 0,005m— для конических, гипо-
идных и глобоидных передач. Угол наклона упругих линий валов
в месте расположения колес [0]^О,ОО1 рад. Максимальный про-
гиб вала
!/тзх<М-0.0003/, (13.16)
где I — расстояние между опорами.
232
Таблица 13.6
Углы поворота упругой линии вала Прогибы Ур
0В e.
Frab(l + д) 6£/о/ Ffab(a — b) 3EJU. FfaW 3E/Ul
Fa (d/2) (a^—ab—0,5 №) Fa (d/2) (дз л- V) Fa(d/2)ab(ai-bi)
3EJJ 3EJal2 3EJal2
frel 3EJa Frc(2l + 3c) 6£/a Frc^l -j- c) 3£/B
Fad/2 ‘ (4^ + c) Fq(d!2)l 3EJa Fad/21 I c \ 1 — 4- — 1 c EJU\3 2 )
Для обеспечения нормальной работы подшипников без за-
щемления тел качения и заклинивания допускаемые углы накло-
на [0] не должны превышать величин: в шарикоподшипниках
0,005 рад; в сферических шарикоподшипниках 0,05 рад; в роли-
ковых подшипниках 0,002 рад; в игольчатых подшипниках
0,0005 рад; в подшипниках скольжения 0,002 рад.
При недостаточной крутильной жесткости валов зубчатых
передач концентрация нагрузки по ширине зубьев может увели-
чиваться, а длинные валы трансмиссий могут разрушиться;
При оценке крутильной жесткости (преимущественно валов
трансмиссий, соединительных и торсионных) определяют угол
закручивания и сравнивают его с допускаемым значением:
?=7’,//(О/р<[?], (13.17)
где Тк — крутящий момент; / — длина участка вала; G — модуль
сдвига; Jp — полярный момент инерции сечения.
Если участки ступенчатого вала нагружены различными
крутящими моментами, то после определения <р на каждом уча-
стке их величины суммируются.
Допускаемые углы закручивания [<р0] различных валов могут
резко отличаться по величине. Например, торсионные валики
и соединительные рессоры допускают углы закручивания не бо-
лее 30° на 1 м длины, а валики в приводах следящих систем —
не более нескольких секунд. Поэтому для валов определенного
типа [ф0] должны уточняться при натурных испытаниях или за-
даваться в технических условиях.
Для оценки крутильной жесткости участков вала, ослаблен-
ных шпоночными пазами, галтелями, шлицами, натягом и дру-
гими концентраторами используют специальные рекомендации.
13.3. ПРИМЕНЕНИЕ ЭВМ И САПР
ПРИ ПРОЕКТИРОВАНИИ ВАЛА
В авиационных механизмах валы обычно испытывают
комплекс нагрузок с переменными режимами и имеют различные
ресурсы. Валы механизмов ЛА обычно рассчитывают на проч-
ность лишь в опасных сечениях. Поэтому в других сечениях
коэффициенты запаса прочности п часто завышены, что приводит
к увеличению вала.
Использование ЭВМ позволяет быстро провести расчеты
вала на прочность для большого числа сечений. За счет соот-
ветствующего изменения конфигурации вала можно разработать
близкую к равнопрочной конструкцию с заданным запасом проч-
ности п и спроектировать оптимальный по массе вал.
Применение ЭВМ также позволяет получить подробную ин-
формацию о жесткости валов, определить прогибы и углы
наклона упругой линии по всей его длине.
234
Таблица 13.7
Иденти- фикатор Обозначение величины Единица измерения Наименование величины
J / — Число точек, в которых заданы внешние силовые факторы, опоры, на- чало и конец вала
X(J) X ММ Массив координат точек, в которых задаются внешние силовые факторы, опоры и торцы вала
F(J. 3) F H Массив величин внешних сил, осе- вых и перпендикулярных оси вала в плоскостях хоу и xoz в точках с коор- динатой X
M(J,3) 1\ Н-мм Массив вращающих и изгибающих моментов в плоскостях хоу и xoz в точках с координатой х
JA; JB /a; js — Номера точек, в которых располо- жены опоры вала
К k Число интервалов деления вала с постоянным шагом h
X4(K) Xi мм Массив координат точек, заданных с постоянным шагом h
QY(K) Qv Массив поперечных сил в плоско-
QZ(K) Qz Н стях хоу и xoz в точках с координа- той х4
MY(K); MZ(K) Mv-, мг Н-мм Массив изгибающих моментов в плоскостях хоу и xoz в точках с ко- ординатой Xi
MS(K) Н-мм Массив суммарных изгибающих мо- ментов в точках с координатой х4
N(K) N Н Массив нормальных сил в точках с координатой х4
MK(K) Тц Нмм Массив крутящих моментов в точ- ках с координатой х4
R(2) R Н Массив полных реакций в опорах
N1 ni Число расчетных сечений
X4(N1) *4 мм Массив координат расчетных се- чений
D(N1); DO(N1) d; d0 мм Массив наружных и внутренних диаметров вала в расчетных сечени- ях
K(N1); KN(NI) К; Kn мм Массив величин, учитывающих ос- лабление сечений вала при изгибе и растяжении
KS(N1); KT(N1) К; К — Массив коэффициентов снижения предела выносливости при изгибе и кручении Массив коэффициентов влияния абсолютных размеров
KDT(Nl) KdT —
K2 hi — Число точек, определяющих кон- фигурацию вала
X2(K2) Xi мм Массив координат точек, определя- ющих конфигурацию вала
235
Продолжение табл. 13,7
Иденти- фикатор Обозначение величины Единица измерения Наименование величины
Dl (К.2); DO1(K2) TY(K); TZ(K); TS(K) Y(K); Z(K); PR(K) м s O’ T- О N O’ ММ ММ Массив наружных и внутренних диаметров вала в сечениях с коор- динатой Х2 Массив углов наклона упругой ли- нии в плоскостях хоу и xoz и сум- марных в точках k Массив прогибов вала в плоско- стях xoyt xoz и суммарных в точ- ках k
S(8) 0's, От, O—i МПа Механические характеристики ма- териала
Npa, NPx Расчетное число циклов нагруже- ний
№ Коэффициент асимметрии цикла
[«] Допускаемый коэффициент запаса прочности
E МПа Модуль упругости материала
С помощью ЭВМ можно провести дополнительные исследо-
вания, повышающие качество проектируемого вала; провести
оптимизацию по массе, сделать вероятностный расчет на проч-
ность, исследовать динамику и устойчивость. Рассмотрим состав-
ленную на языке ФОРТРАН-IV программу расчета на ЭВМ
прочности и жесткости вала. При составлении ее используется
модульное программирование. Основная программа составляется
пользователем с применением готовых подпрограмм (модулей)
«DET».
Характерной особенностью программы является ее универ-
сальность. Ее можно использовать для расчета двухопорных
валов любой расчетной схемы. Программа позволяет оптимизи-
ровать вал по массе при заданных ограничениях. Геометрические
ограничения в основном распространяются на участки наружной
конфигурации вала.
В табл. 13.7 приведено описание идентификаторов, исполь-
зуемых в программе расчета вала. Для идентификаторов J, JA,
JB, К, Nl, К2 тип переменной INTEGER, а для всех остальных —
REAL.
Для вала (рис. 13.14) на рис. 13.15 приведен алгоритм голов-
ной программы, в которой производится расчет вала на проч-
ность и жесткость. В этой программе (рис. 13.16) сокращена
236
Рис. 13.14. Схема нагружения вала
часть, в которой дается описание идентификаторов и выполняет-
ся присвоение им числовых значений в соответствии с исходны-
ми данными.
На рис. 13.14 Fj2=FTi; Fj3=Fti', F(j+i)2=Fr2; F(/+i)3=^t2;
Мц=T\=Ft\d/2‘, F(j+i)i=—М2=—F<2^2/2.
Поясним каждую из подпрограмм DET, используемую в про-
грамме расчета вала. В подпрограмме DET61 по действующим
на вал внешним нагрузкам определяются реакции в опорах и
распределение внутренних силовых факторов по длине вала.
Могут рассчитываться лишь двухопорные статически определи-
мые валы.
Рис. 13.15. Алгоритм программы расчета вала на прочность и жесткость
237
ООО1
0002
ООО?
0004
0005
REAL Х(6/0,,10,.35..60,,85,.95./. ,
INTEGER J/б/,JA/2/,j6/5/,N1 / 2/.К/200/,
CALL DET61(X> ,M.J IJA.JB, К, КГ, Й,
QY.QZ.MY.MZ.MS1MK.X4.RJ
CAtL f)ET^9(i4. ЙЗ.ЙК.Й ,К,ХЗ, D, DO,
K.KN.KS.KT.KDt.NI.S)
cAll рв;341MYxAzxbiadoi.k.ja.jb.x2.
... -x -X _x Y 2 ,f>R,14 ,§Y ,SZ,
* с
* DLiTS
* SY1 Зь ।
CALL DET?8(X2,D1,D01,DL,K4)
STOP
END
0006
0007
0008
Рис. 13.16. Программа расчета вала на прочность и жесткость
Для определения реакций
уравнения равновесия:
п
2^)=°;
в опорах используются четыре
п
(13.18)
n
Z-l
Два неиспользованных уравнения равновесия должны учиты-
ваться при определении крутящих моментов и нормальных сил.
Из (13.18), (13.19) определяются реакции в опорах Л и В:
^Ау = 2 Мвг (/Г‘)/(хл “ :
/-1
/-1
n
2 ^(Л)=о.
(13.19)
(13.20)
#ву = 2 ~ ^А«' ^Вг (г) “ ^Al’
/-1 Z-1
где Ха, Хв — координаты опор; MBy(Fi), MBz(Fi)—моменты в
плоскости хоу и xoz относительно точки В.
Суммарные реакции в плоскости yoz будут равны
^a=/>2a,+/?L; %B=VJ&y+Rb. (13.21)
Внутренние силовые факторы определяются методом сечений:
т=1т'-
Z-1
0.=%Г,Ю; ЛГ=2ЛГ,;
1-1 1 — 1
(13.22)
238
х т кт
My = j Qydx +2 Му1; М, = $ Qtdx +2 Mtl,
О 1-1 О 1-1
где МУ1 и MZi — внешние сосредоточенные моменты в плоскостях
Хоу и xoz.
Для уменьшения погрешности при интегрировании нужно
разбивать вал не менее чем на 100 участков (k~^ 100).
Суммарный изгибающий момент
MZ=V МУ+Mi
(13.23)
В подпрограмме выводятся на печать величины опорных
реакций и их составляющие: Ra, Rb, Rab, Rey, Raz, Rbz- Можно
также выводить на печать массивы внутренних силовых факто-
ров и в графическом виде их эпюры.
В подпрограмме DET39 проверяется прочность вала в рас-
четных сечениях и проводится оптимизация его по массе путем
изменения внутренней конфигурации. Наружную конфигурацию
нельзя менять, так как имеется ряд ограничений: в местах уста-
новки подшипников, уплотнений, зубчатых колес и т. д.
В подпрограмме выводятся на печать для каждого сечения
исходные данные (геометрия сечения, внутренние силовые фак-
торы и коэффициенты, используемые в расчетах), а также
результаты расчетов. В ней дается информация о прочности
вала: «БОЛЬШОЙ ЗАПАС ПРОЧНОСТИ» при л>1,2[л];
«НЕПРОЧНО» при п<[п]; «ПРОЧНОСТЬ В НОРМЕ» при
При большом запасе прочности размер отверстия последова-
тельно увеличивается, пока не будет удовлетворено условие
1,2[п]. При недостаточной прочности конструкции, на-
оборот, размер отверстия уменьшается.
В подпрограмме DET34 анализируется жесткость вала. Углы
наклона и прогибы упругой линии вала определяются по фор-
мулам:
dx-\-Ci\
Qy-
о
dx J
о
(13.24)
о о
о о
239
Постоянные интегрирования Ci определяют из граничных
условий в опорах вала: у=0 и z=0 при х=Ха и х=хв.
Из граничных условий и (13.24) получаем
J Ef J J £/
о оо
(^А— ХВУ,
„ СА СА Мд
£2 — ) j £/ " ^1Ха'
о о
dx—С3хА.
(13.25)
Суммарные прогибы и углы наклона упругой линии равны
08=^+0-
Для уменьшения погрешности при интегрировании нужно
разбивать вал на 200 или больше участков (Л^200).
В подпрограмме можно вывести на печать массивы координат
точек по шагам интегрирования и значения в них прогибов и
углов наклона или их значения в точках приложения внешних
силовых факторов и у опор или построить графики /х и 0г.
В подпрограмме DET38 определяется масса вала и печатается
ее величина. Полученную из расчетов оптимальную конструкцию
вала пользователь должен оценить с точки зрения возможности
конструктивной реализации внутренней конфигурации вала.
В случае необходимости можно провести корректировку не толь-
ко внутренней, но и наружной конфигурации вала путем измене-
ния исходных данных и проведения повторного счета. При
выполнении таких изменений нужно определить возможность их
реализации на участках, где имеются геометрические ограниче-
ния, например в местах установки подшипников и уплотнений.
Дальнейшая автоматизация проектирования вала связана с
формированием данных для геометрических построений и вос-
произведением чертежа на графопостроителе. Разработанные
программы предназначены для выполнения упрощенного черте-
жа, в котором следует осуществить выбор баз, проставить разме-
ры, допуски, посадки, шероховатость поверхностей, сформулиро-
вать технические требования.
Алгоритм головной программы, в которой производится рас-
чет соединений вал — ступица и выполняется воспроизведение
чертежа, приведена на рис. 13.17. В программу входит подпро-
240
Рис. 13.17. Алгоритм расчета шпонки и формирования изображения вала
со шпоночными пазами
грамма DET40, которая выполняет построение наружной и внут-
ренней конфигурации вала по исходным данным, используемым
для проверочного расчета. Однако этого изображения недоста-
точно для выполнения чертежа.
Для отдельных участков вала может возникнуть необходи-
мость более подробного воспроизведения ряда конструктивных
элементов: переходных участков (галтелей, канавок...), элемен-
тов соединения вал — ступица (шпоночных, штифтовых, шлице-
вых...). Тогда в программу вводятся подпрограммы, выполняю-
щие дополнительные построения. Так, в основную программу
для вала с двумя пазами (рис. 13.18) под сегментные шпонки
включены подпрограммы DET158, которая выполняет расчет
0001
0002
ООО?
0004
0005
0006
0007
REAL X2(6)/0.,
* MK.D,LST,STS"
CALL DET40(X
CALL DET156(i
♦ DSHR.TSHR) k
2(6)/0.,2*20..2*75..95./
mi^,d’lst,st,bshr,hshr,
VU ГI П у ЮПП/
STOP
END
Рис. 13.18. Программа расчета шпонки и формирования изображения ва-
ла со шпоночными пазами
241
Таблица 13.8
Иденти- фикатор Обозначение величины Единица измерения Наименование величины
BSHR Ь СМ Ширина шпонки
HSHR Л > Высота >
DSHR d > Диаметр >
TSHR t > Глубина паза под шпонку
LST » Длина ступицы
Ml; М2 — — Масштабы вала и сечения
LK /к СМ Расстояния от края паза шпонки
до торца выступа вала
ST Or МПа Предел текучести материала вала
обоих шпоночных соединений, и DET159, используемая дважды
для изображения шпоночных пазов.
В табл. 13.8 приведено описание идентификаторов, используе-
мых в программе для воспроизведения изображения элементов
вала.
Поясним подпрограммы, используемые в основной программе
(см. рис. 13.18). Подпрограмма DET158 осуществляет расчет
сегментной шпонки на прочность по заданным силовым факто-
рам, геометрическим параметрам и механическим характеристи-
кам материала. На АЦПУ печатается обозначение шпонки по
ГОСТу. В подпрограмме DET159 по геометрическим данным для
вала и результатам расчета формируется и воспроизводится
изображение шпоночного паза на валу и выносного сечения.
Подпрограмма DET40 выполняет построение вала с количе-
ством узловых точек К2. Каждая из них задается двумя коор-
динатами. Точки наружного контура Х2, D1/2, а внутреннего
Х2, DO1/2. Эти точки координат верхней половины вала графо-
построитель в соответствии с программой соединяет отрезками
прямой, а затем вычерчивает изображение симметричной ей
нижней половины. Обращение к подпрограмме DET40:
CALL DET40 (Х2-, DI, DOI, К2).
У графопостроителей ЕС ЭВМ имеется базовое обеспечение,
позволяющее использовать язык графических приказов. Проил-
люстрируем его использование на фрагменте из подпрограммы
DET40 (рис. 13.19) при построении контура вала (см. рис. 13.14).
В ней выполняются следующие операции: строка 1 — заголовок
подпрограммы, строка 2 — описание области ввода в основной
памяти для накопления данных и других массивов; строка 3 —
обращение к графопостроителю.
Оператор CALL PLOT (X, Y, К) осуществляет перевод пера
графопостроителя из предыдущего положения в точку с коорди-
натами X, Y. Если К=2, то линия вычерчивается, а если К=3,
то перо поднято.
242
Строка 4 — оператор перевода пера в новое начало коорди-
нат О (К= —3). Строка 5 — определение нового типа линии —
«щтрихпунктирная». Строка 6 — перевод пера в исходное поло-
жение для вычерчивания осевой линии (точка /о). Строка 7 —
вычерчивание осевой линии от точки /о до 20. Строка 8 — пере-
род пера в начало координат (точка О). Строка 9 — определение
типа линии — «сплошная», строки 10—12 — вычерчивание в
цикле отрезков верхней половины контура вала. Соединяются
отрезками точки 0—1, 1—2, 2—3,.... 5—6. Последний отрезок от
точки 6 до 7 вычерчивается по отдельной команде. Строка 13 —
перевод пера в начало координат (точка О). Строки 14 и 15 —
вычерчивание верхней половины внутреннего контура (отвер-
стия) вала. Отрезками последовательно соединяются точки
0—Ь, 1 ь—4ь... Строка 16 — перевод пера в начало координат О.
Далее аналогично вычерчивается нижняя половина вала (строки
17-24).
Переход к автоматизированному проектированию связан с
объединением программ расчета и воспроизведения вала. Вхо-
дящие в нее отдельные блоки уже рассмотрены. Для полной
автоматизации проектирования вала программу нужно допол-
нить блоком, выполняющим проектные расчеты и формирую-
щим конструкцию. Это не представляет трудностей при заданной
схеме конструкции после проведения расчетов зубчатых передач.
Для других конструкций вала подпрограммы DET158 и
DET159 заменяются на другие, выполняющие расчеты и воспро-
0001 0002 0003 0004 0005 888$ ооой 88?8 0012 0013 0014 88! S 0017 0018 0019 0020 0021 SUBROUTINE DET40(ХЗ.D.DO.N) REAL BUP£2000J ,хШ). D(N), D0( N CALL PLOTSCBUP 12000JO) 8® Жг - Шййййл’о.д CALL PLOT(O*,0.,3) CALL TYPLM J 6 (Fall PLot(X3(j),d(j)/2.,2) CALL PLOT X3 NO.,2) CALL PLOT(O.,0.,3) 5 йй Й^ОЬТ172-’2’ call plot(o.,o; 3) DO 3 J=1,N
0022 0023 0024 0025 0026 3 CALL PL0T(X3(J),-D0(J)/2. ,2) CALL PL0TlX3(N)!0.,2) CALL PL0T(-7.,-20.,-3) STOP END
Рис. 13.19. Фрагмент подпрограммы DET 40
243
Рис. 13.20. Схема диалогово-автоматизированного расчета вала
изводящие другие конструктивные элементы вала и соединений
вал — ступица.
Рассмотрим методику интерактивного диалогово-автоматизи-
рованного проектирования детали на примере разработки опти-
мального по массе вала (рис. 13.20). В точке Д-1 на экран
дисплея выводится опросный бланк, который с помощью клавиа-
туры заполняет пользователь, обеспечивая тем самым ввод
числовых значений исходных данных или при повторном счете
их корректировку. В точке диалога Д-2 выбирается контур опти-
мизации— наружный или внутренний. При счете на ЭВМ раз-
меры выбранного контура меняются по длине вала до получения
равнопрочной конструкции с заданным коэффициентом запаса
прочности, что обеспечивает получение конструкции минималь-
ной массы. В блоках 1 и 4 вычисляются внутренние силовые
факторы.
Оптимизация путем изменения внутреннего контура преду-
смотрена в программе расчета вала на прочность (блок 2). По-
сле окончания счета программа выводит на печать данные по
внутреннему контуру, а с помощью блока 3 определяется его
масса.
При оптимизации путем изменения наружного контура
после каждого расчета вала на прочность (блок 5) результаты
выдаются на экран (блок 6). После анализа последних в точке1
диалога Д-З пользователь решает и дает указание о необходи-
мости определения массы (блок 7), а в точке Д-4 — окончить
счет или провести его повторно. В последнем случае в точке Д-1
проводится корректировка размеров наружного контура с уче-
том заданных ограничений — диаметров отверстий ступиц, под-
шипников и т. д. Этот процесс, используя итеративный метод,
нужно повторять до тех пор, пока не будет получен минималь-
ной по массе вариант конструкции.
244
При автоматизированном проектировании должны не только
выполняться расчеты, но и создаваться конструкции и воспро-
изводиться их изображения. Это требует формирования изобра-
жения и подготовки данных для вычерчивания детали на графо-
построителе.