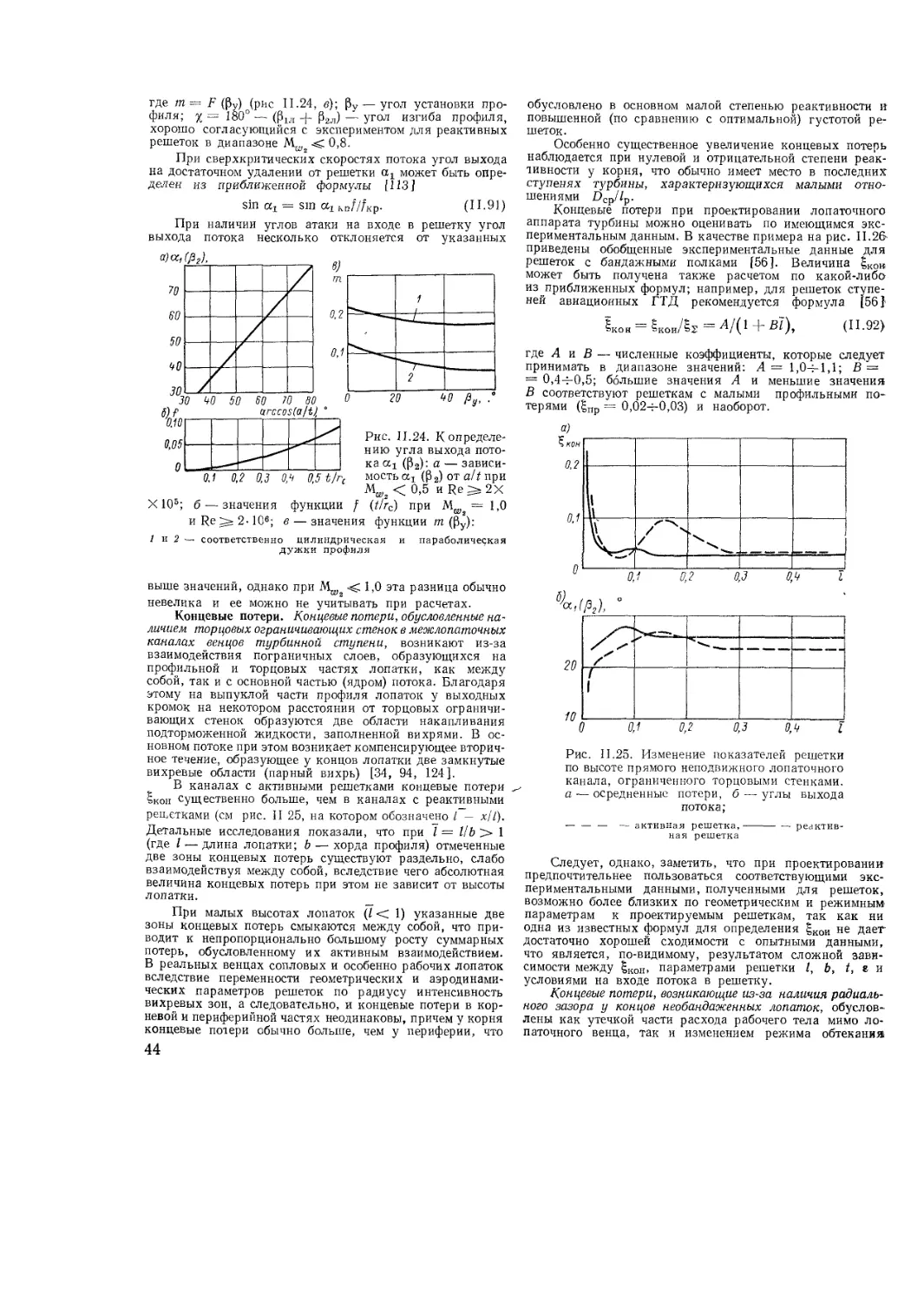
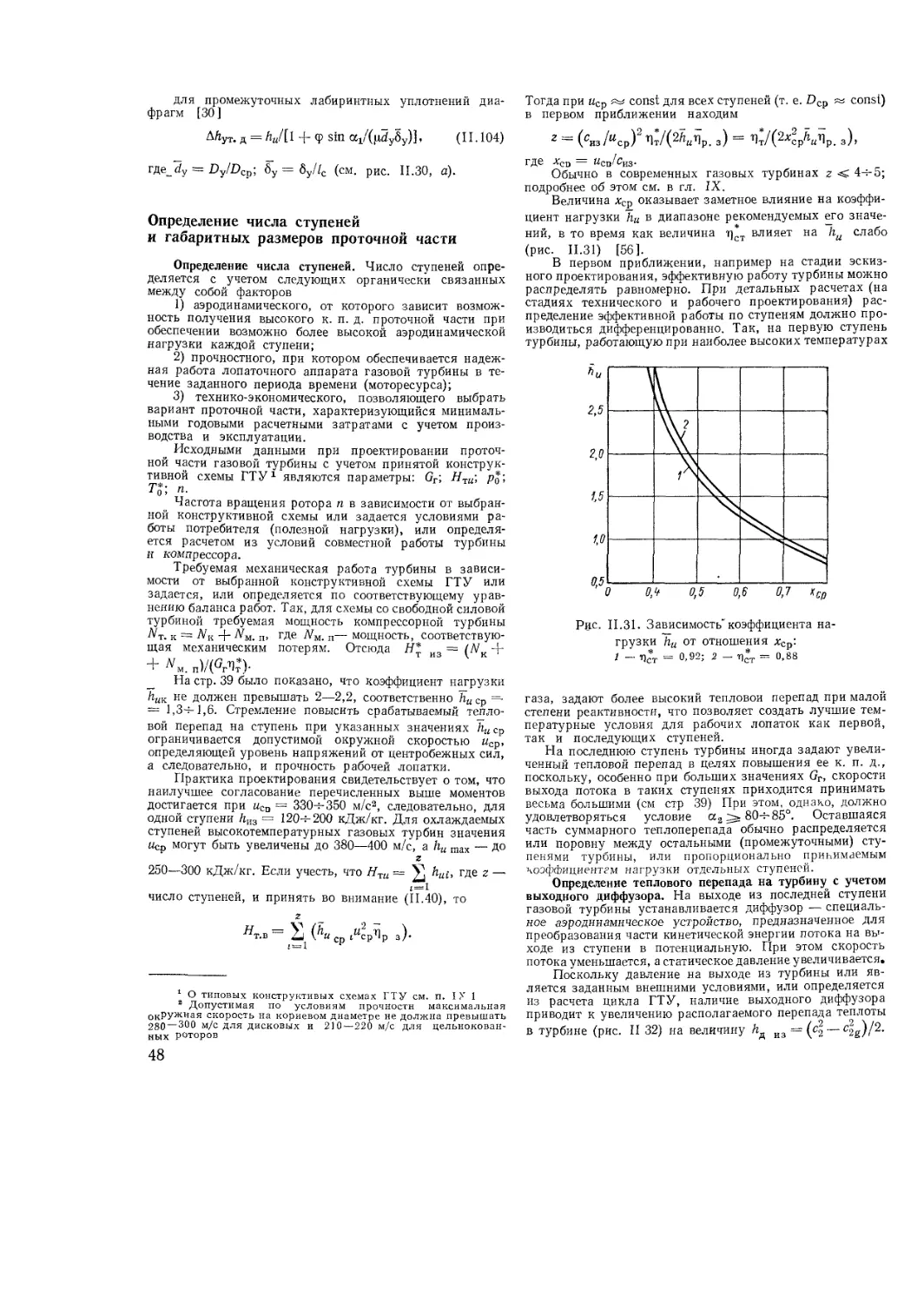
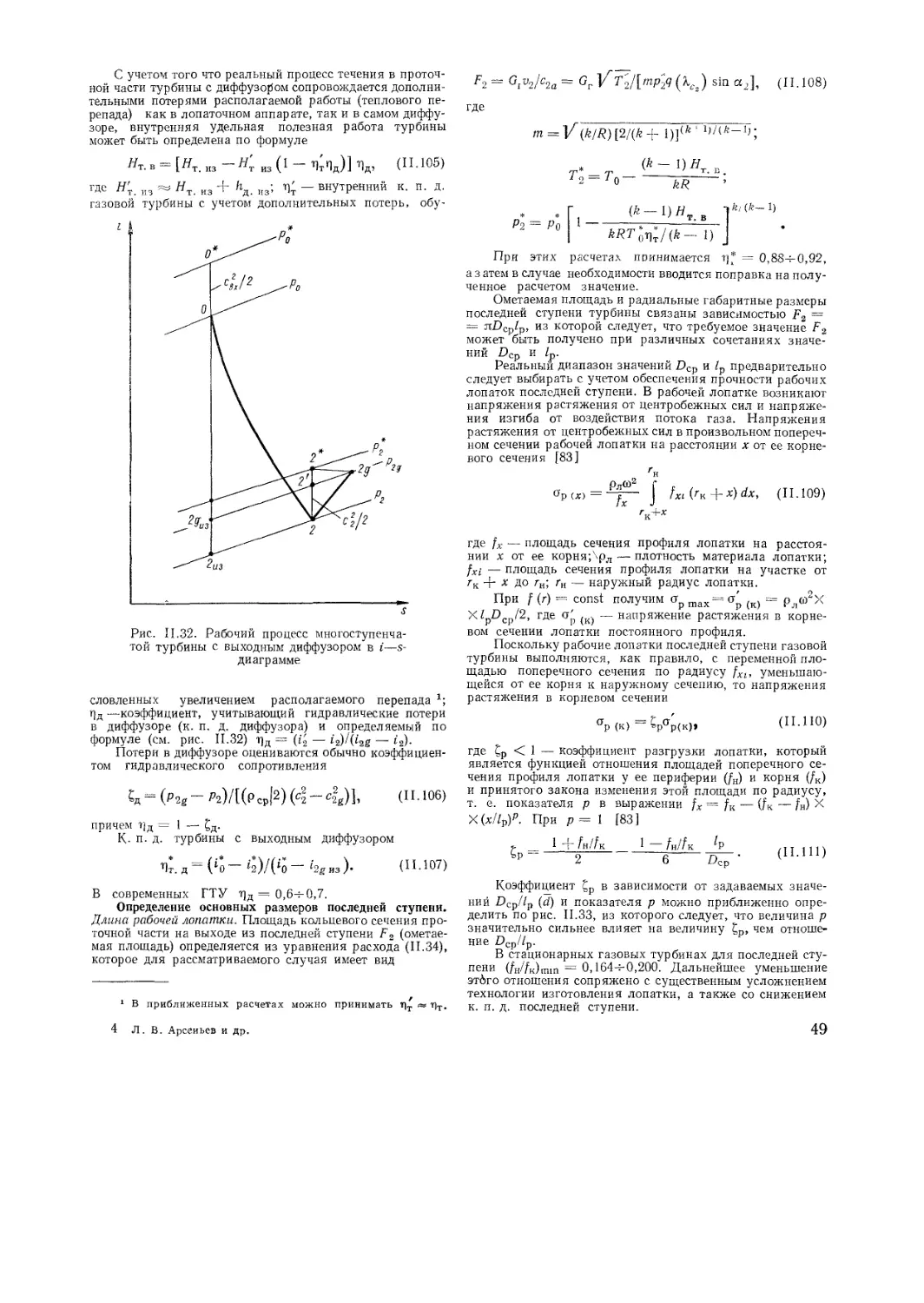
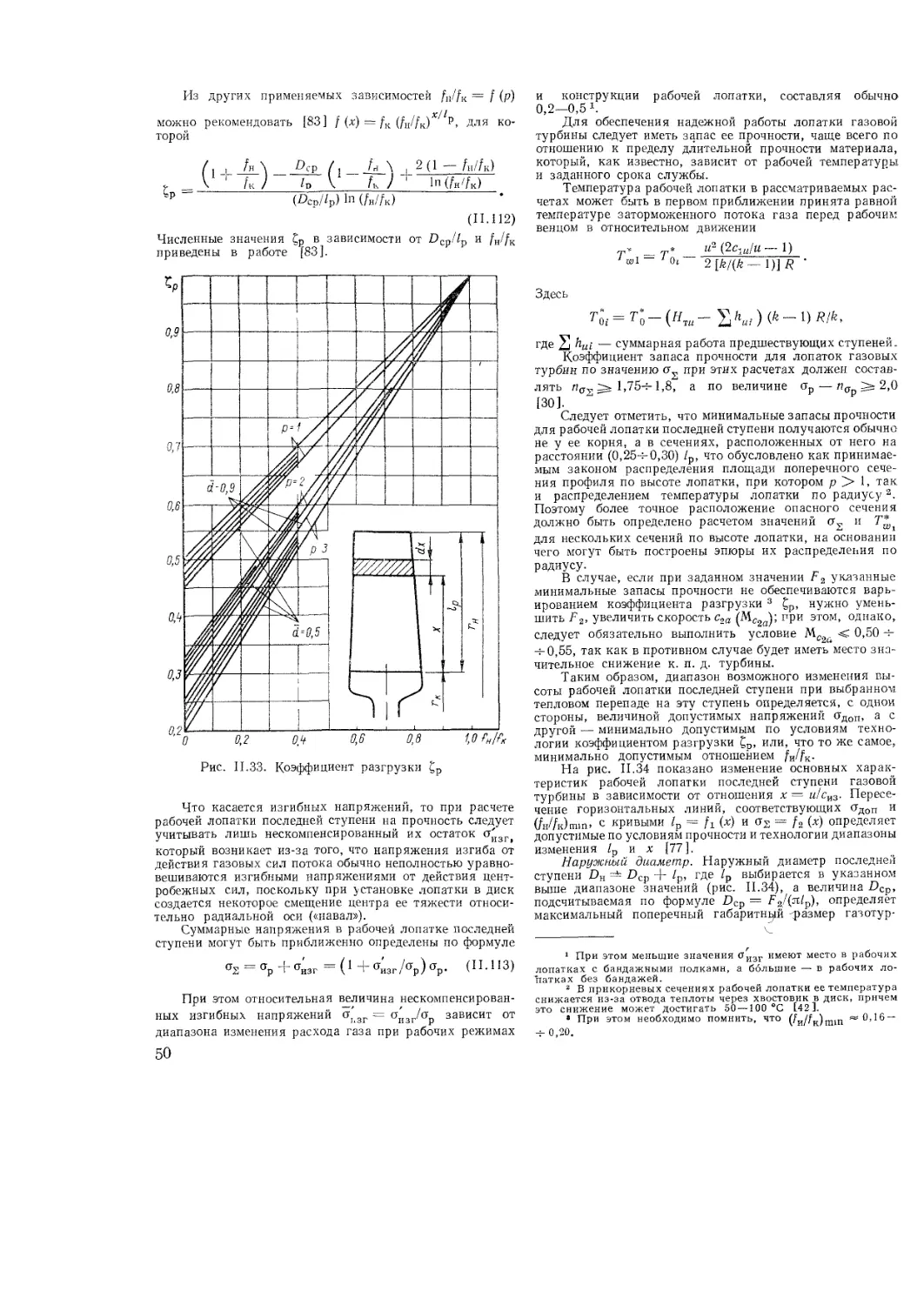
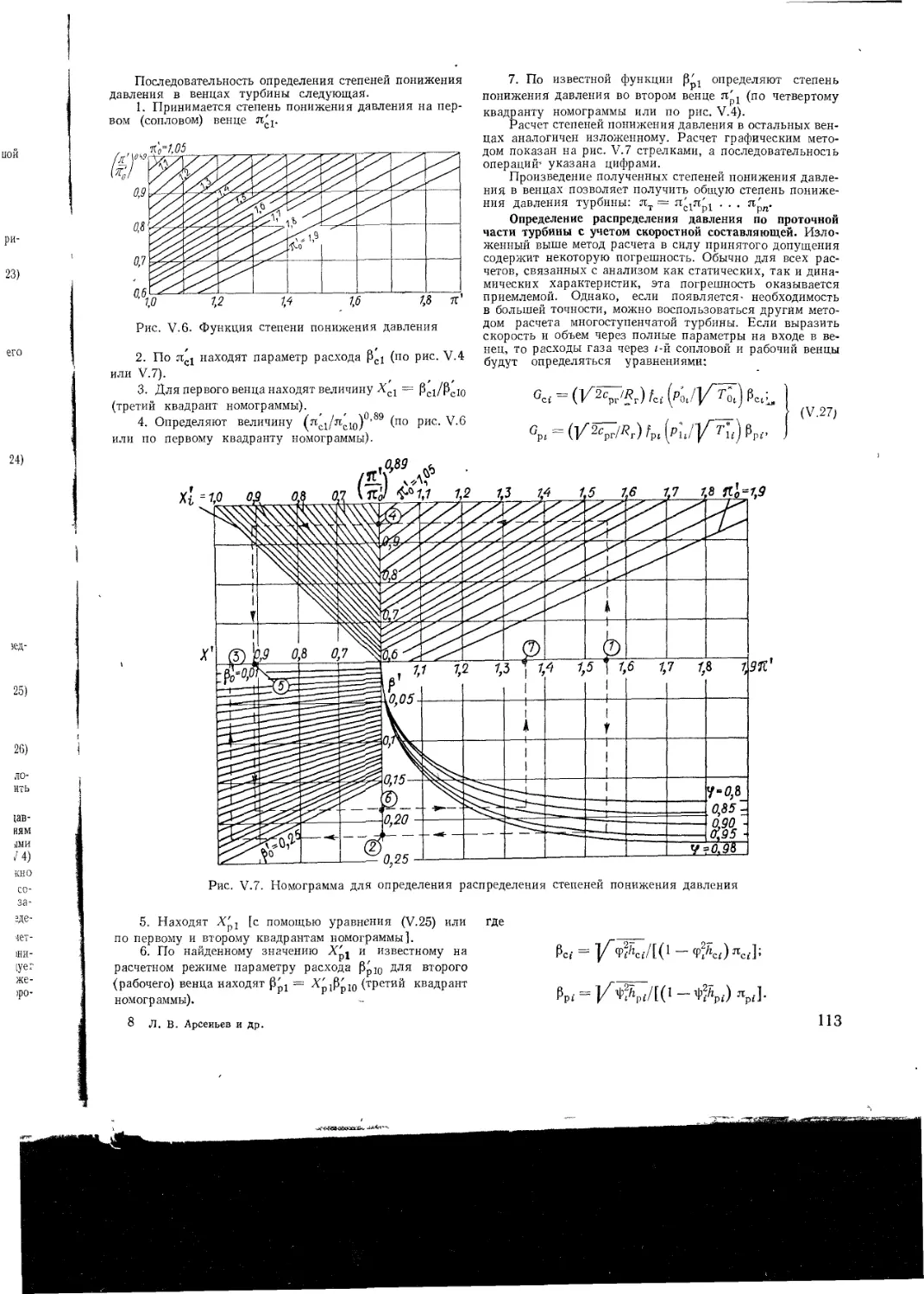
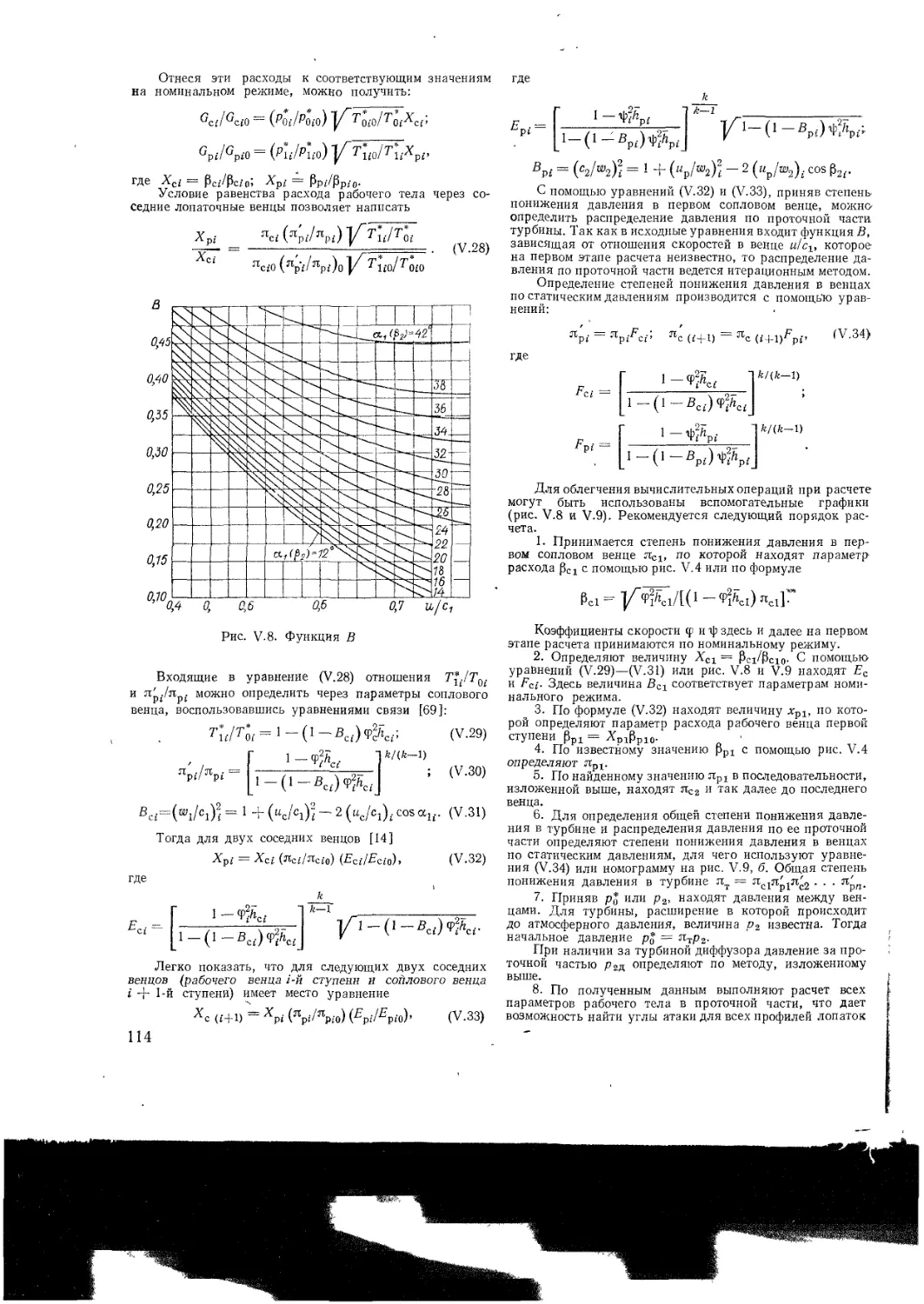
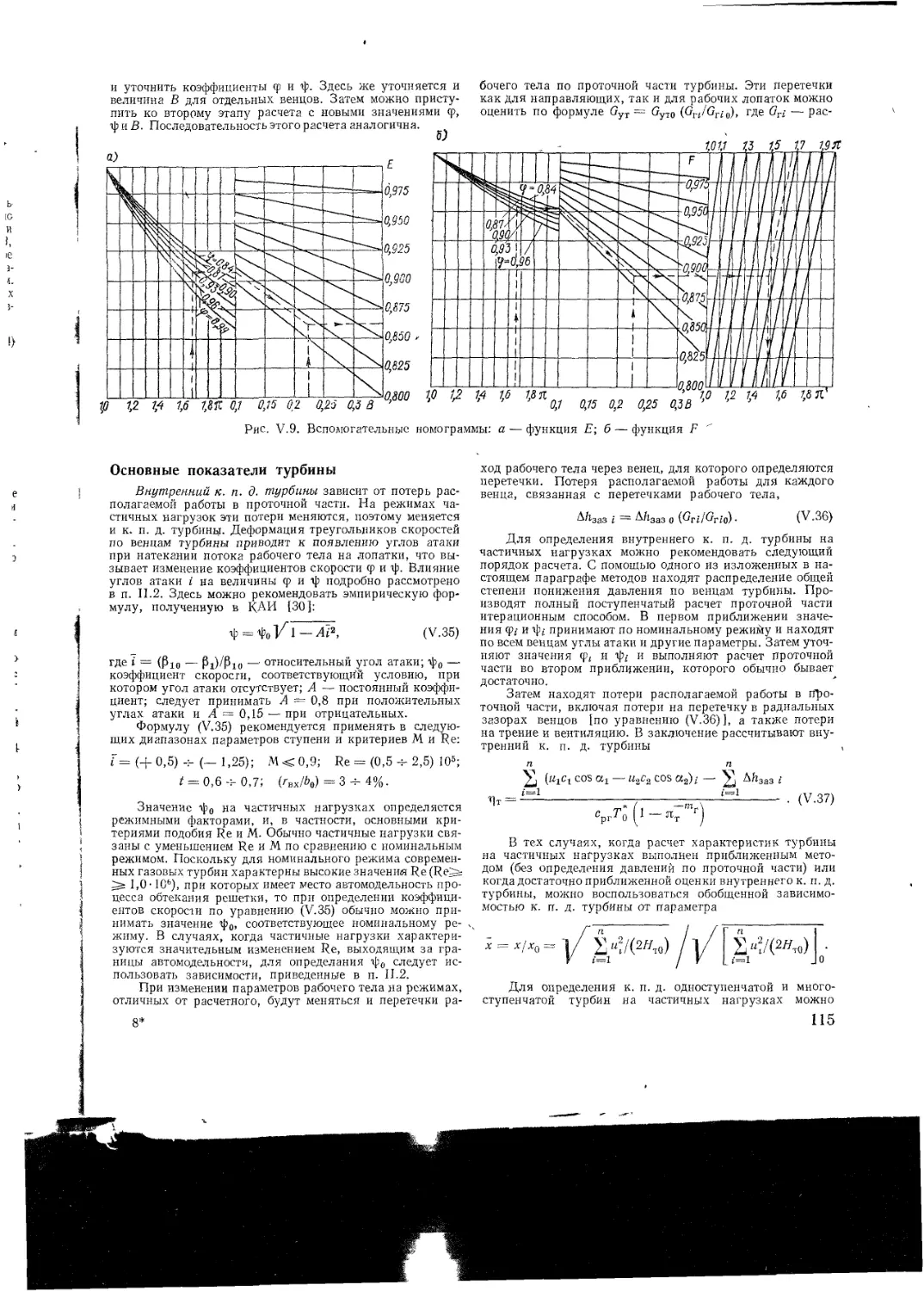
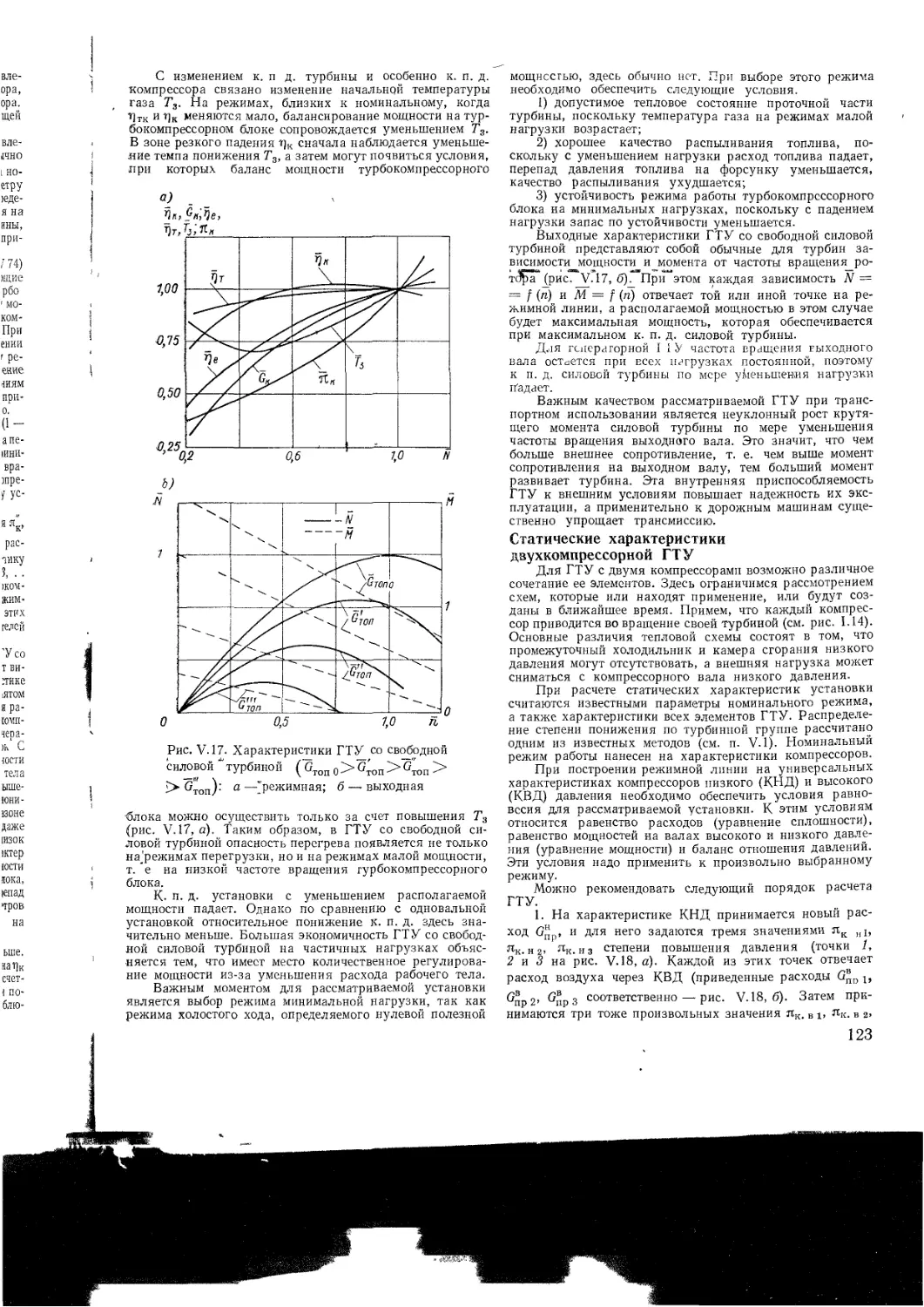
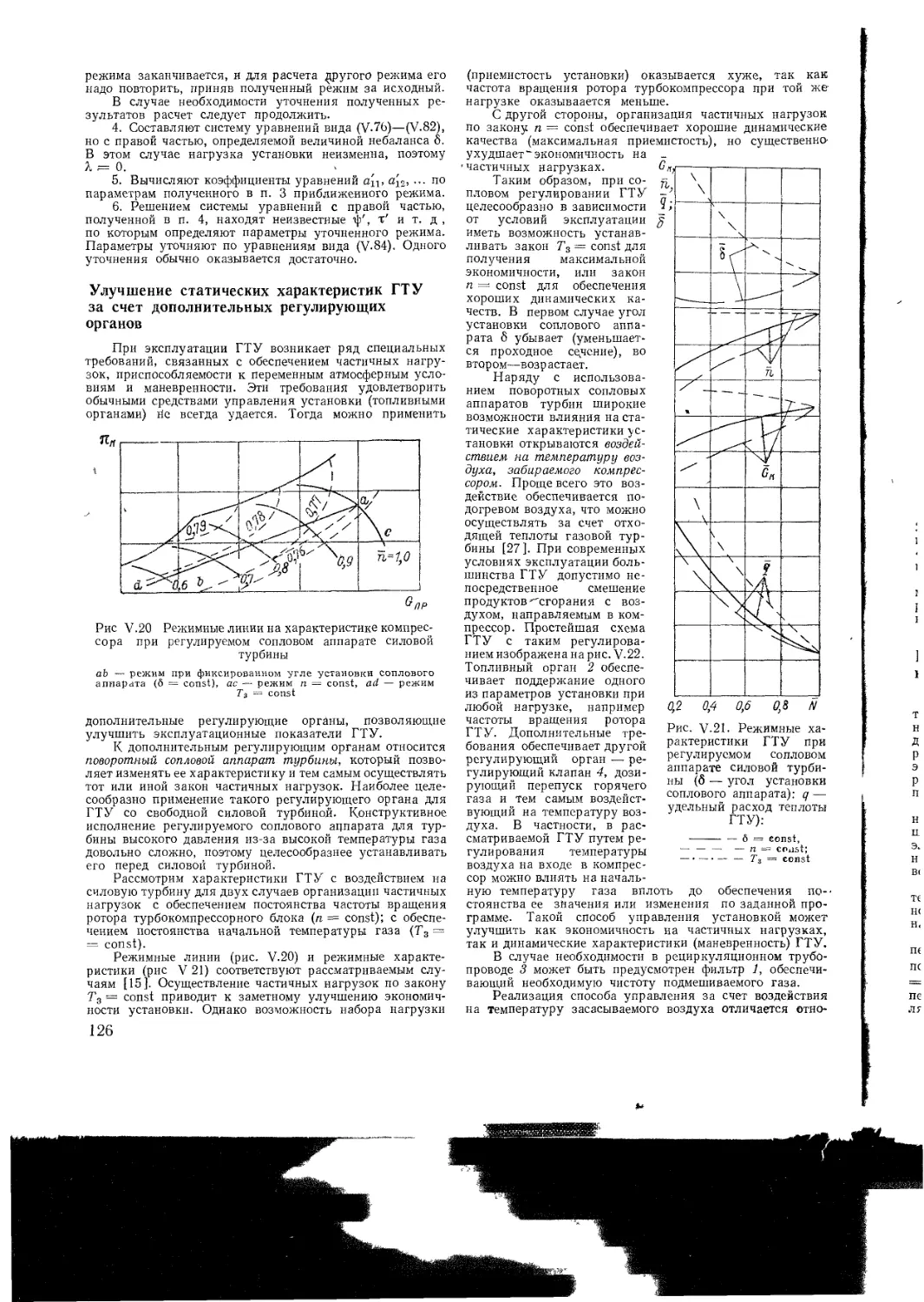
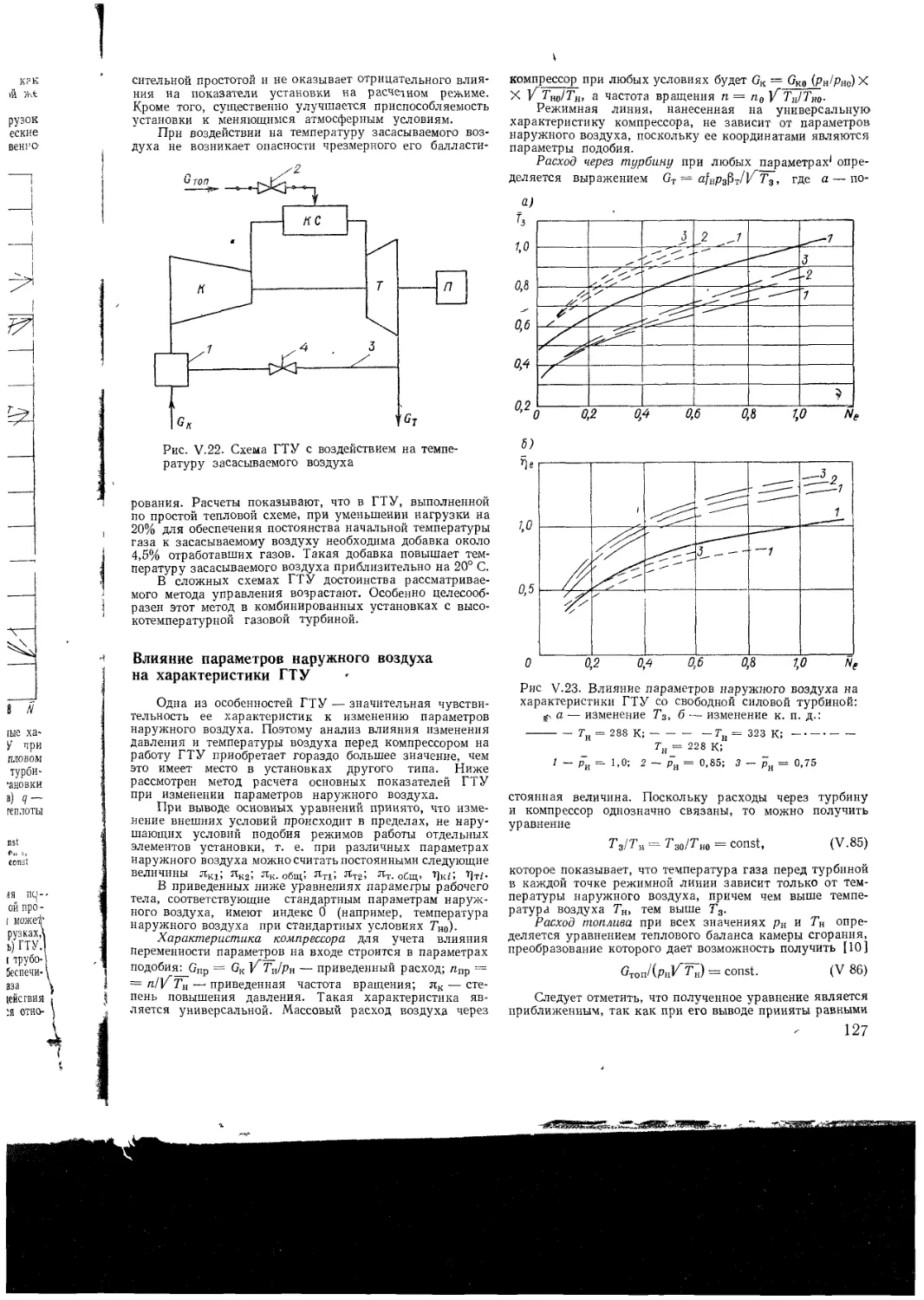
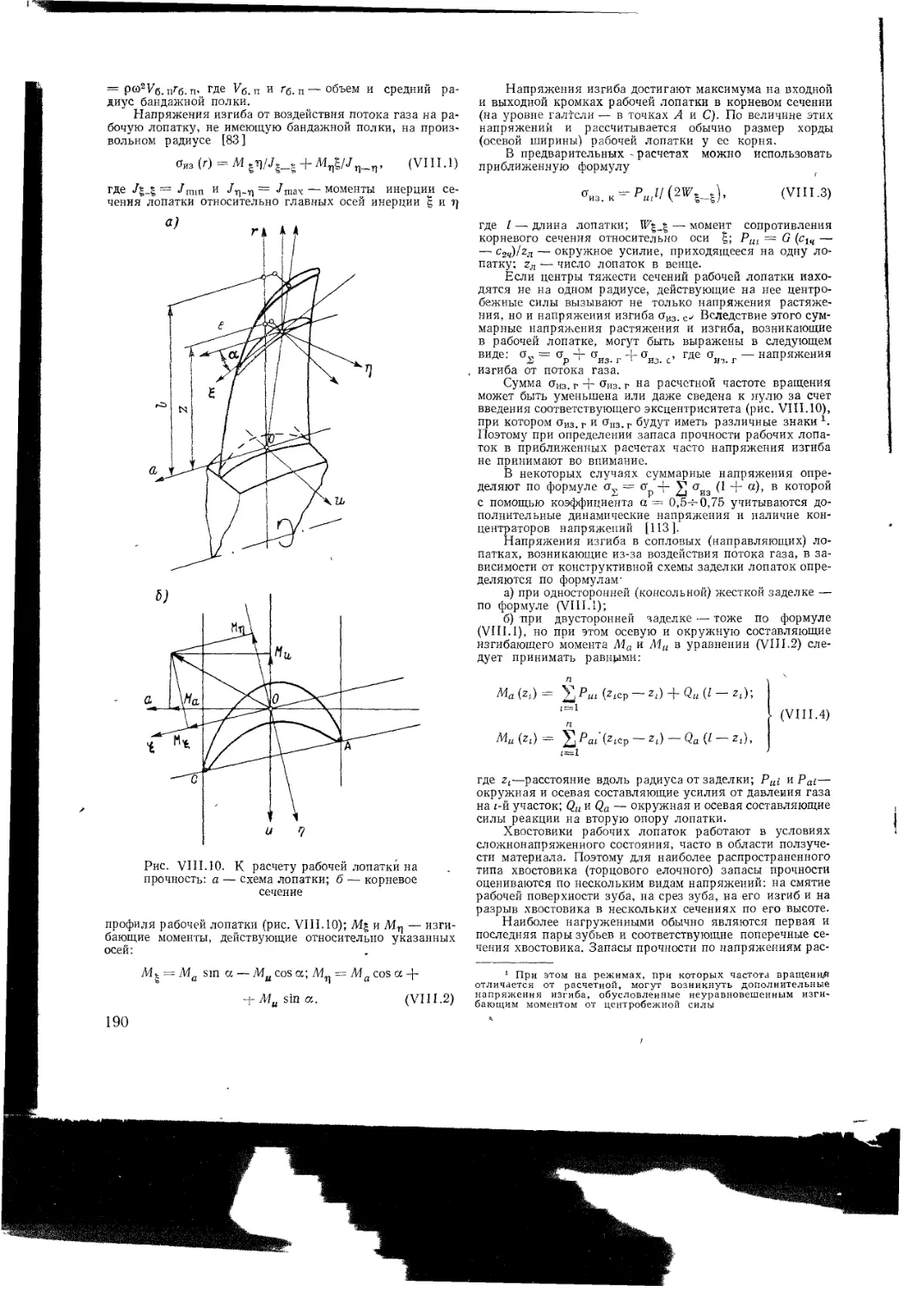
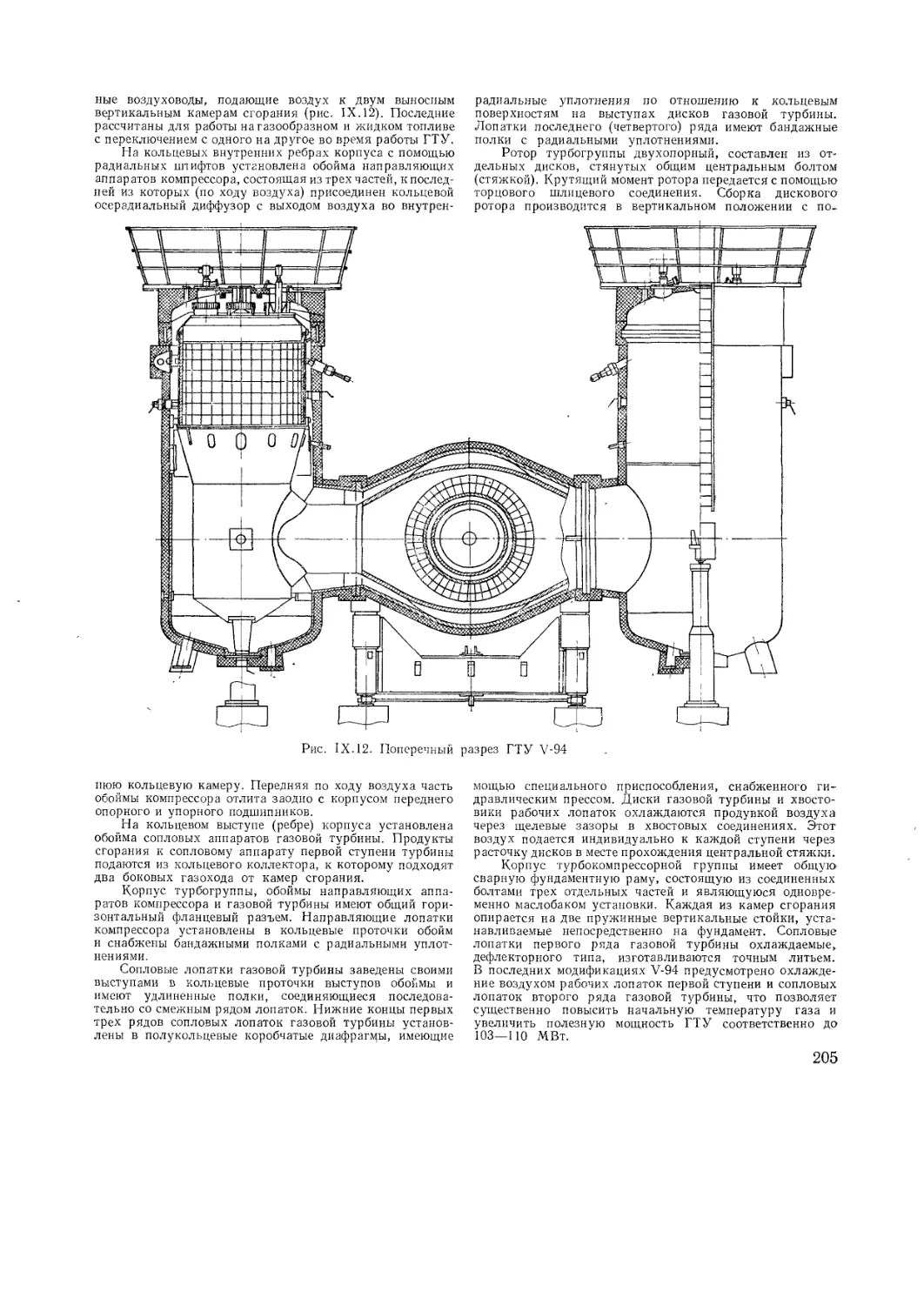
Text
ГАЗОТУРБИННЫЕ
УСТАНОВКИ
КОНСТРУКЦИИ И РАСЧЕТ
СПРАВОЧНОЕ ПОСОБИЕ
Под общей редакцией
Л. В. АРСЕНЬЕВА и В. Г. ТЫРЫИЖИНА
ЛЕНИНГРАД
«МАШИНОСТРОЕНИЕ»
ЛЕНИНГРАДСКОЕ ОТДЕЛЕНИЕ
1978
ФБ СПбГТУ
ШНИIIIIII
0000201035
ББК 31.363
ПЗ
УДК 621.5-843.8.001.2 (031)
АВТОРЫ: Л. В. АРСЕНЬЕВ, Ф. С. БЕДЧЕР, И. А. БОГОВ,
Е. Е. ЛЕВИН, В. Г. ТЫРЫШКИН, Е. А. ХОДАК
Рецензент д-р техн, наук А. А. КАНАЕВ
Газотурбинные установки. Конструкции и расчет: Справочное пособие/
ПЗ Под общ. ред. Л. В. Арсеньева и В. Г. Тырышкина( —Л.: Машиностроение. Ленингр
отд-ние, 1978. — 232 с., ил.
В пер.: 2 р. 20 к.
В справочном пособии приведены основные сведения по конструкции и рас-
чету газотурбинных установок — стационарных (энергетических и газоперека-
чивающих) и транспортных. Приведены тепловые расчеты схем ГТУ, а также
методы расчета их основных элементов. Описаны конструкции основных элемен-
тов ГТУ и дан анализ конструктивных решений узлов газовых турбин, компрес-
соров и теплообменных аппаратов. Приведены конкретные рекомендации по выбору
их параметров. Изложены принципы построения систем регулирования, рас-
смотрены системы топливоподачи, масляные системы и вспомогательное оборудо-
вание ГТУ.
Справочное пособие предназначено для инженерно-технических работни-
ков, занимающихся расчетом и проектированием как газотурбинных установок,
так и их основных элементов. Оно может быть использовано также студентами
втузов, изучающими газотурбинные установки и турбомашины.
30305—155
038(01)—78
155—78
ББК 31.363
6П2.23(083)
ИБ № 777
Леонид Васильевич АРСЕНЬЕВ, Фрида Соломоновна БЕДЧЕР,
Игорь Александрович БОГОВ, Евгений Ефимович ЛЕВИН,
Всеволод Георгиевич ТЫРЫШКИН, Евгений Александрович ХОДАК
ГАЗОТУРБИННЫЕ
УСТАНОВКИ
Конструкции и расчет
Справочное пособие
Редактор издательства В. М. Рошаль Переплет художника В. Э. Н ефед ов и ч а
Технический редактор Л. В. Щетинина
Корректоры А. И. Лавриненко н Н. Б. Семенова
Сдано в набор 17.04.78. Подписано в печать 04.11.78. М-09653. Формат 84Х1081/1в.
Бумага типографская № 2. Гарнитура литературная. Печать высокая.
Усл. печ. л. 24,36. Уч.-изд. л. 32,77. Тираж 7000 экз. Зак. 900. Цена 2 р. 20 к.
Ленинградское отделение издательства «МАШИНОСТРОЕНИЕ»
191065, Ленинград, Д-65, ул. Дзержинского, 10
Ленинградская типография № 6 Союзполиграфпрома
при Государственном комитете СССР по делам
издательств, полиграфии и книжной торговли
193144, Ленинград, С-144, ул. Моисеенко, 10
© Издательство «Машиностроение» , 1978 г .
ОГЛАВЛЕНИЕ
Предисловие
Основные условные обозначения
Глава 1 Схемы и циклы ГТУ , .
I 1 Схемы и идеальные циклы
I 2 Основные соотношения термодинамики для
идеальных газов
I 3 Простая тепловая схема ГТУ
Идеачьный цикл
Реальный цикл ,
Анализ параметров реальной ГТУ
I 4 ГТУ с регенерацией
Идеальная ГТУ Степень регенерации
Анализ параметров реальной ГТУ
I 5 ГТУ с промежуточным охлаждением и подо-
гревом рабочего тела
Изотермическое сжатие и расширение
Промежуточное охлаждение и промежуточ
ный нагрев рабочего тела
Анализ сложных схем ГТУ
I 6 ГТУ с охлаждаемой турбиной
Показатели турбины с закрытой системой
охлаждения
Показатели турбины с открытой системой
охлаждения
Характеристики ГТУ с охлаждаемой тур-
биной
’ 7 ГТУ с утилизацией теплоты уходящих
газов
ГТУ с подогревателями сетевой воды
Применение ГТУ для повышения маневрен-
ности паросиловых блоков
Получение пара за счет теплоты уходящих
газов ГТУ
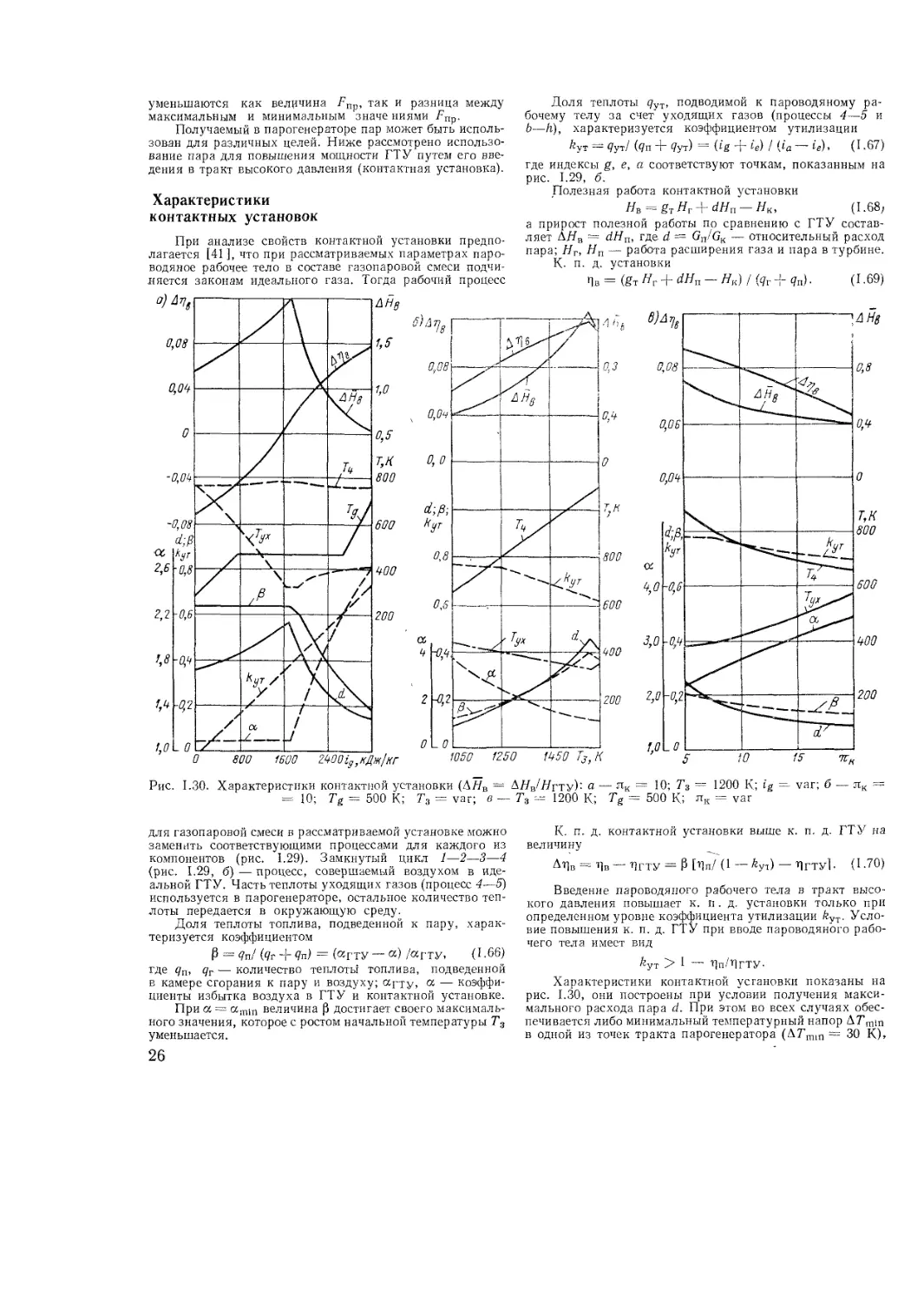
Характеристики контактных установок
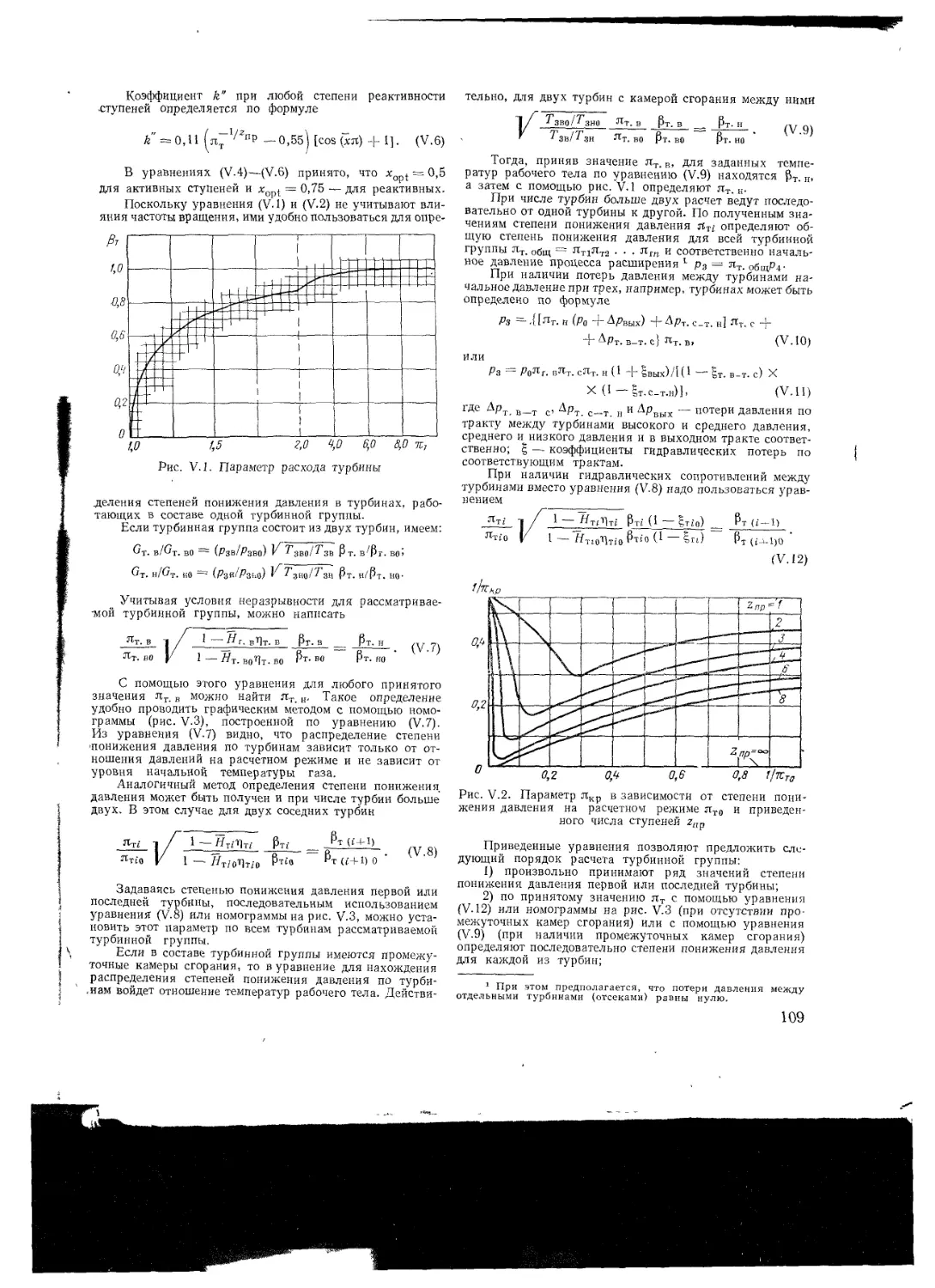
I 8 Расчет тепловых схем ГТУ
Расчет характеристик ГТУ с учетом зави-
симости теплоемкости газов от температуры
Тепловой баланс камеры сгорания
Кпд турбомашин
Глава II Газовые турбины . .
II 1 Теоретические основы газодинамического
расчета проточной части
II 2 Газодинамический расчет одномерного по-
тока
Одномерный сжимаемый поток
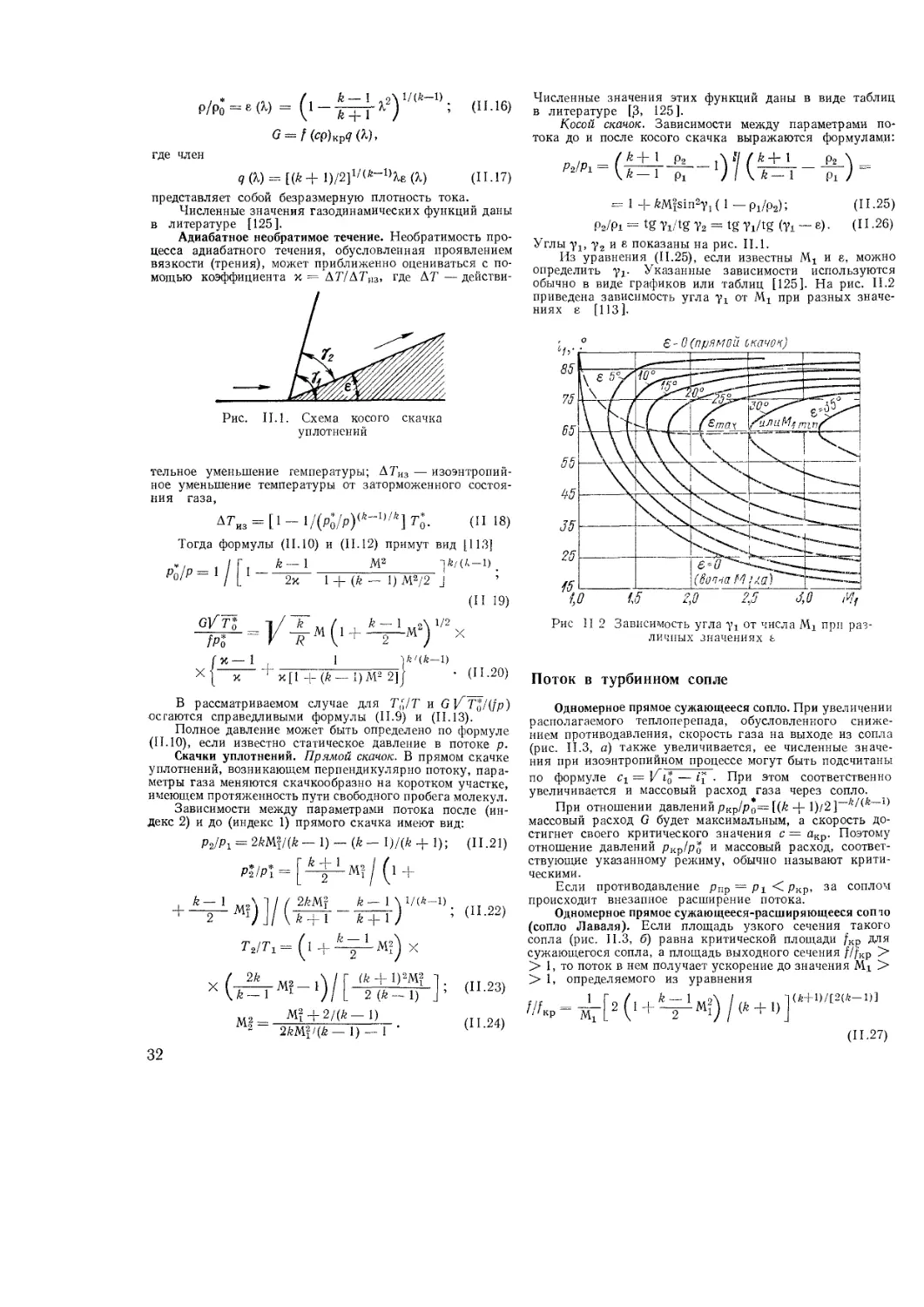
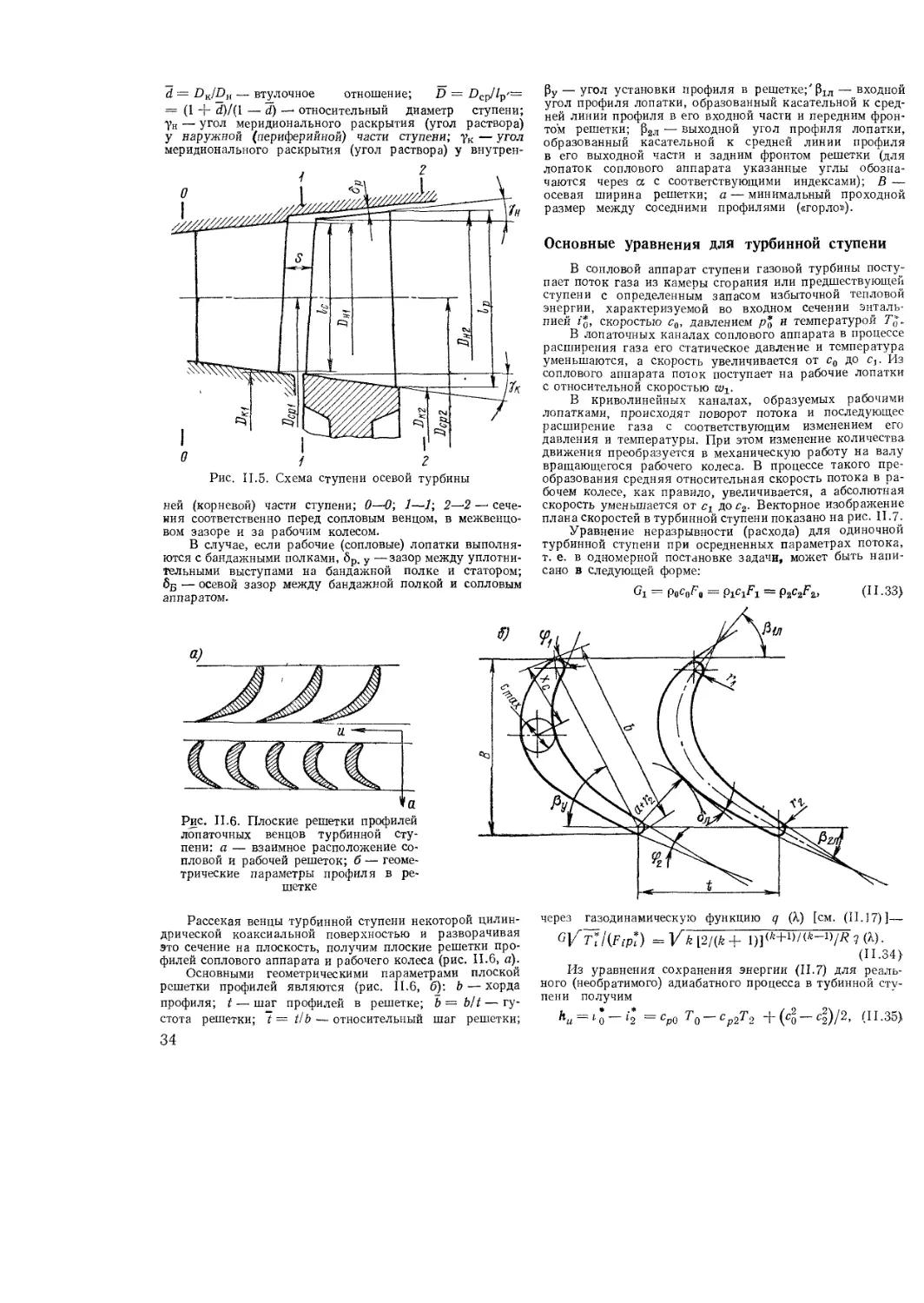
Поток в турбинном сопле
Основные геометрические параметры сту-
пени осевой турбины
Основные уравнения для турбинной ступени
Коэффициент полезного действия ступени
и турбины
Коэффициент возврата теплоты в многосту
пенчатой турбине
Степень реактивности
Коэффициент нагрузки ступени
Скорость и направление выхода потока из
турбинной ступени
По1ери в турбинной ступени
Определение числа степеней и габаритных
размеров проточной части
Газодинамический расчет турбины по сред-
нему диаметру
ИЗ Газодинамический расчет пространствен-
ного потокi в турбиннон ступени
II 4 Профилирование лопаток
Общие положения
Графические способы построения профилей
Построение профилей путем изгиба исход
ного профиля
Аналитические методы расчета профилей
Построение профильной чаети лопатки
И 5 Охлаждение газовых турбин
1*
5
6
8
9
12
13
15
16
19
20
21
22
23
24
26
27
28
29
30
31
32
33
34
35
36
37
40
41
48
53
54
58
59
62
64
65
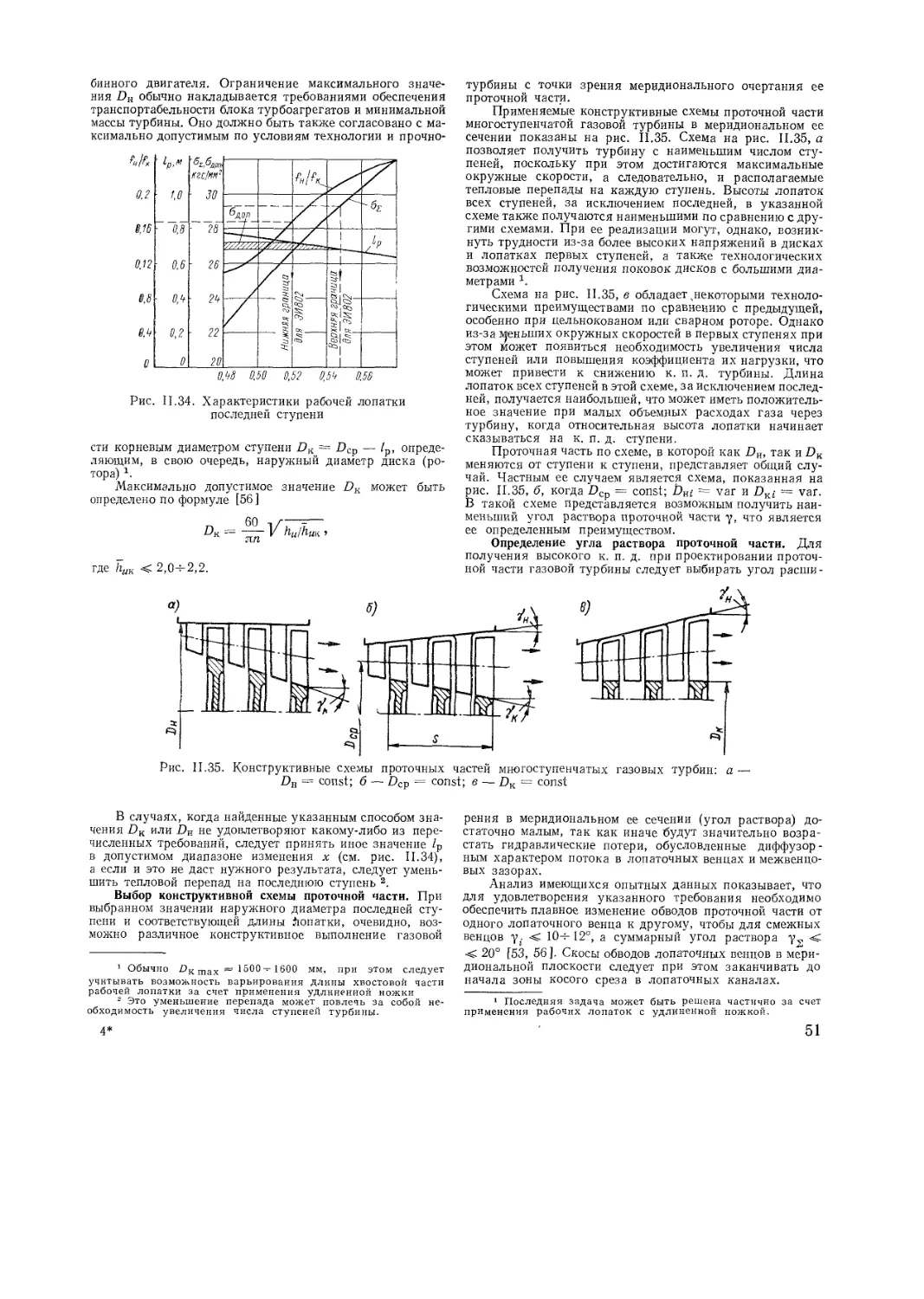
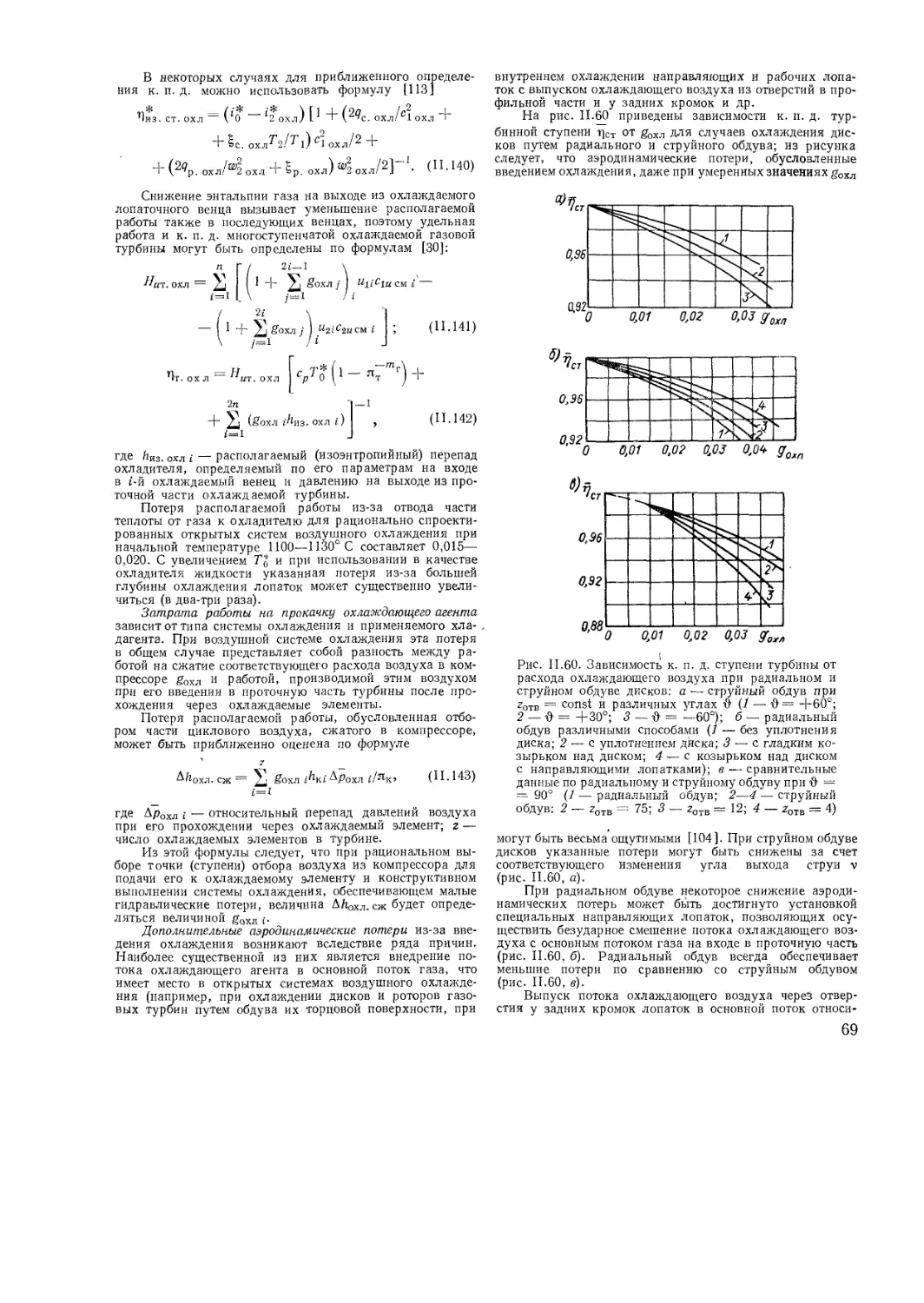
Системы охлаждения деталей газовых турбин
Газодинамический расчет охлаждаемых
турбин
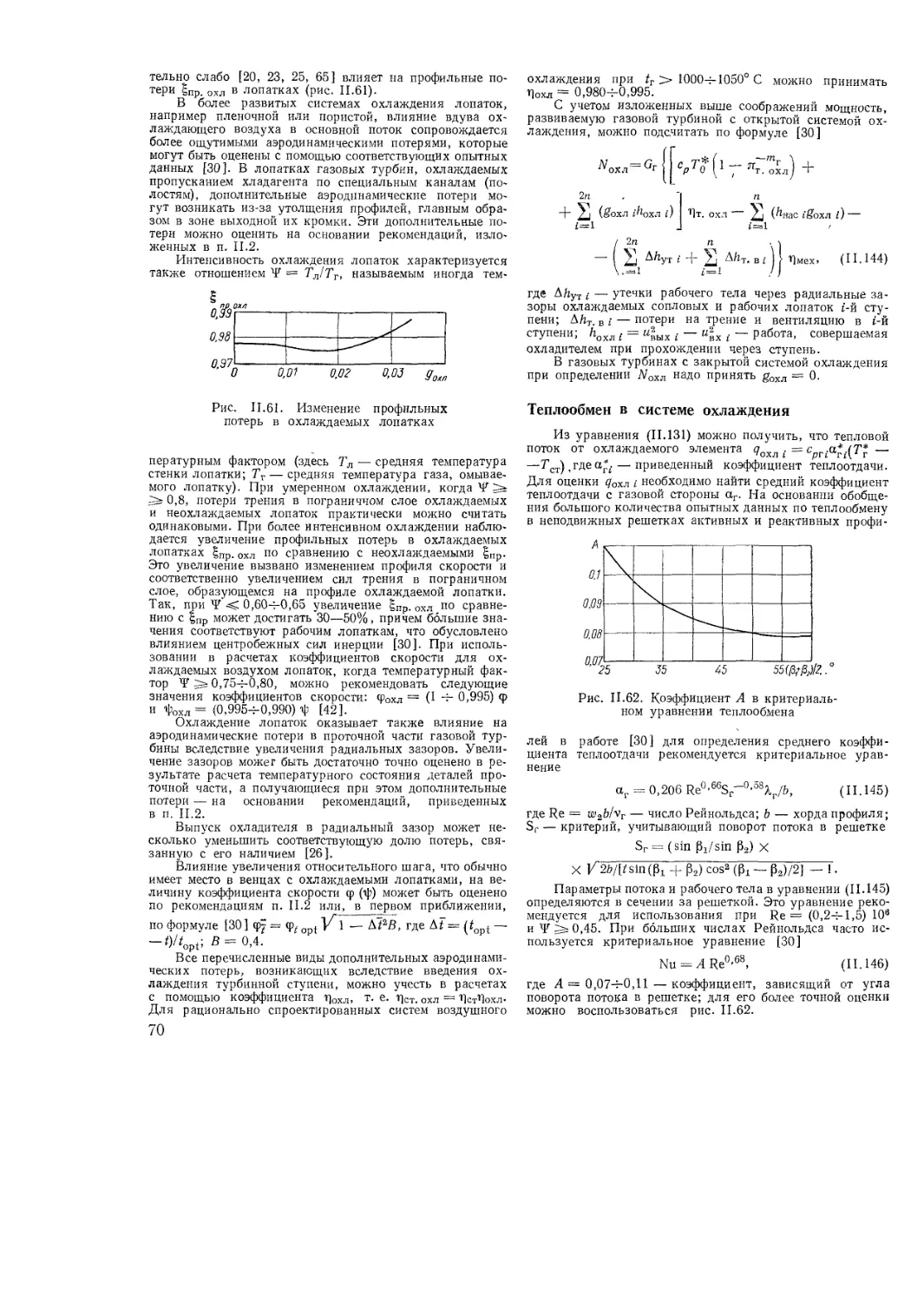
Теплообмен в системе охлаждения
Глава III Осевые компрессоры
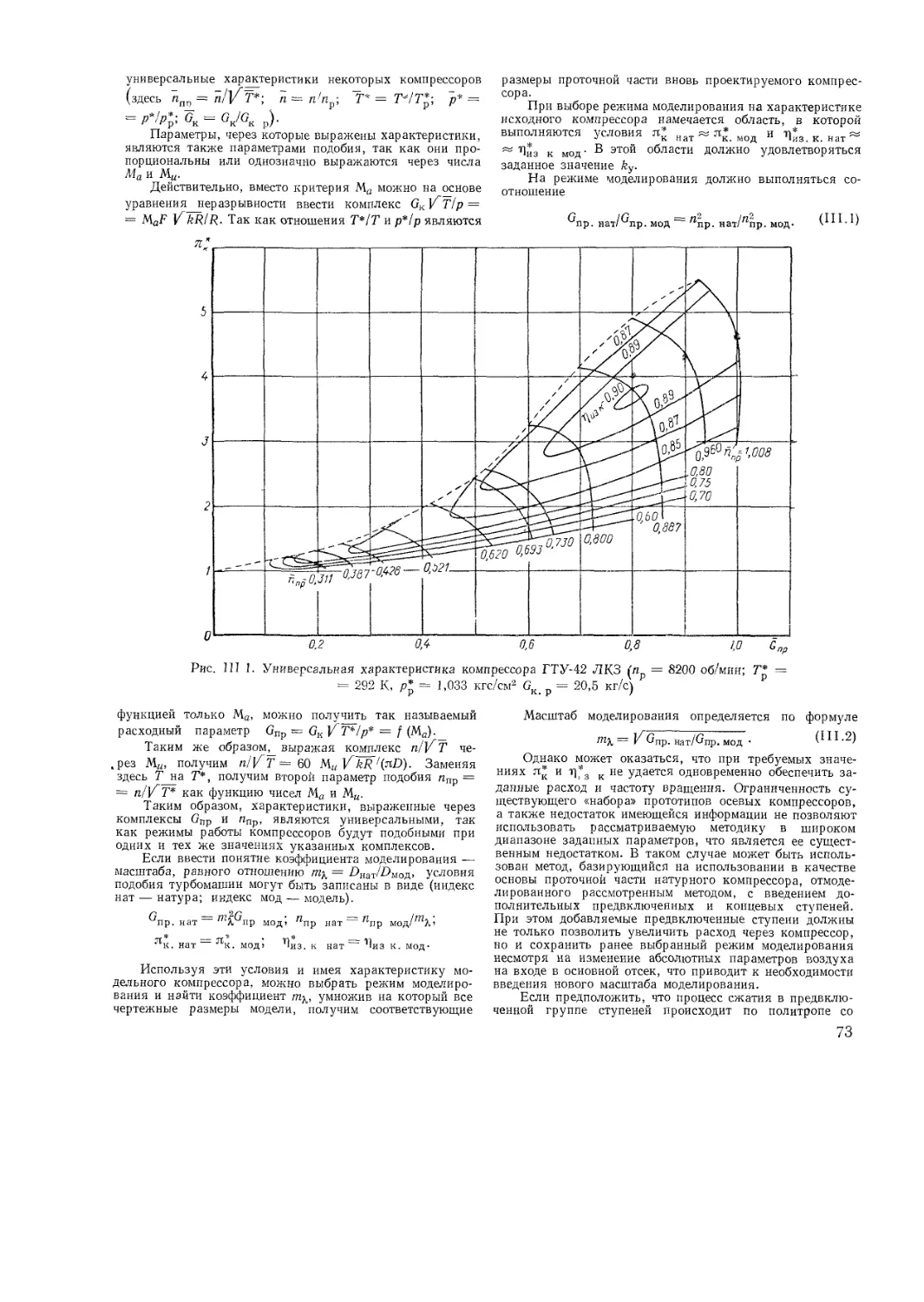
III 1 Методы газодинамического расчета
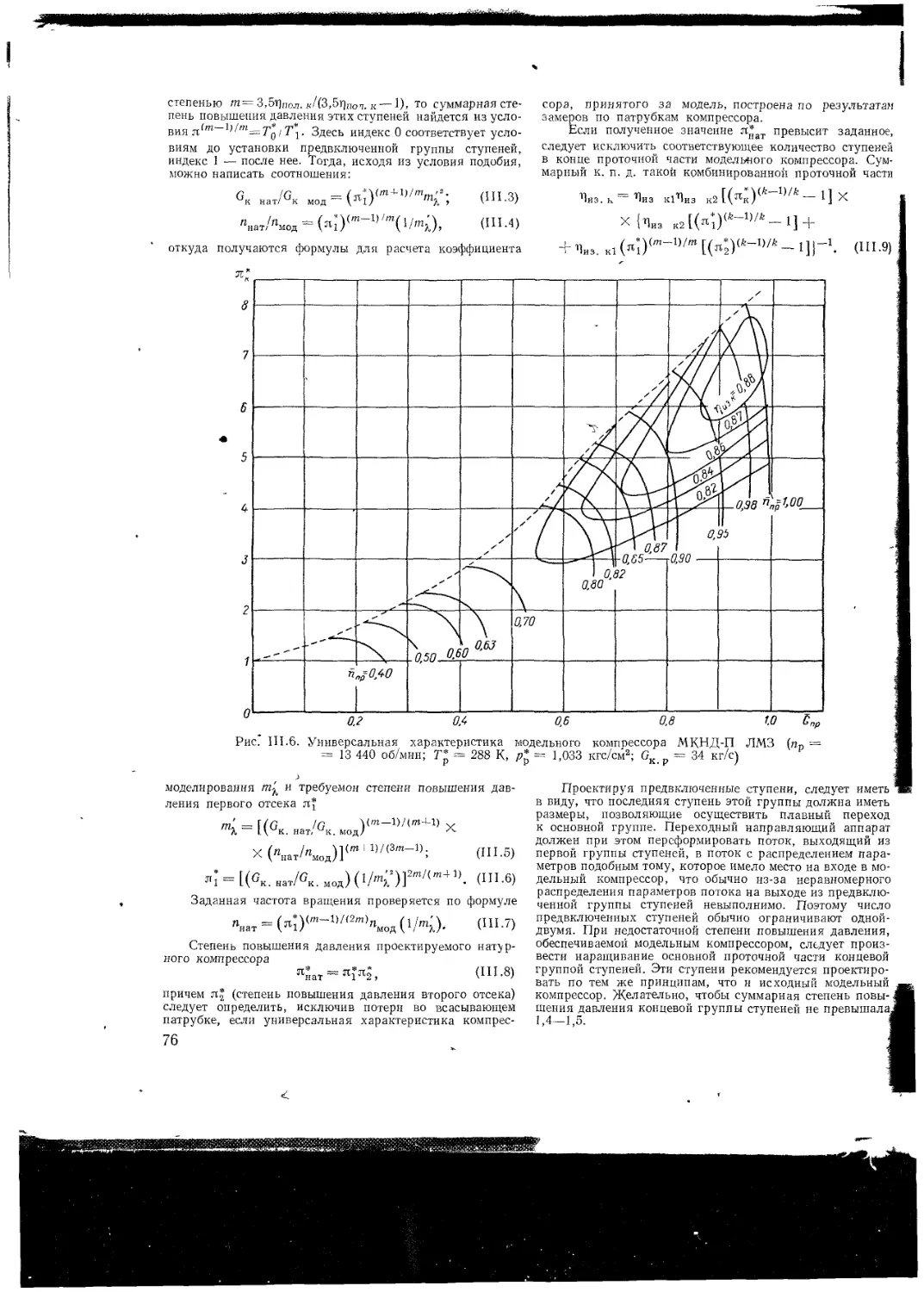
III 2 Метод полного моделирования
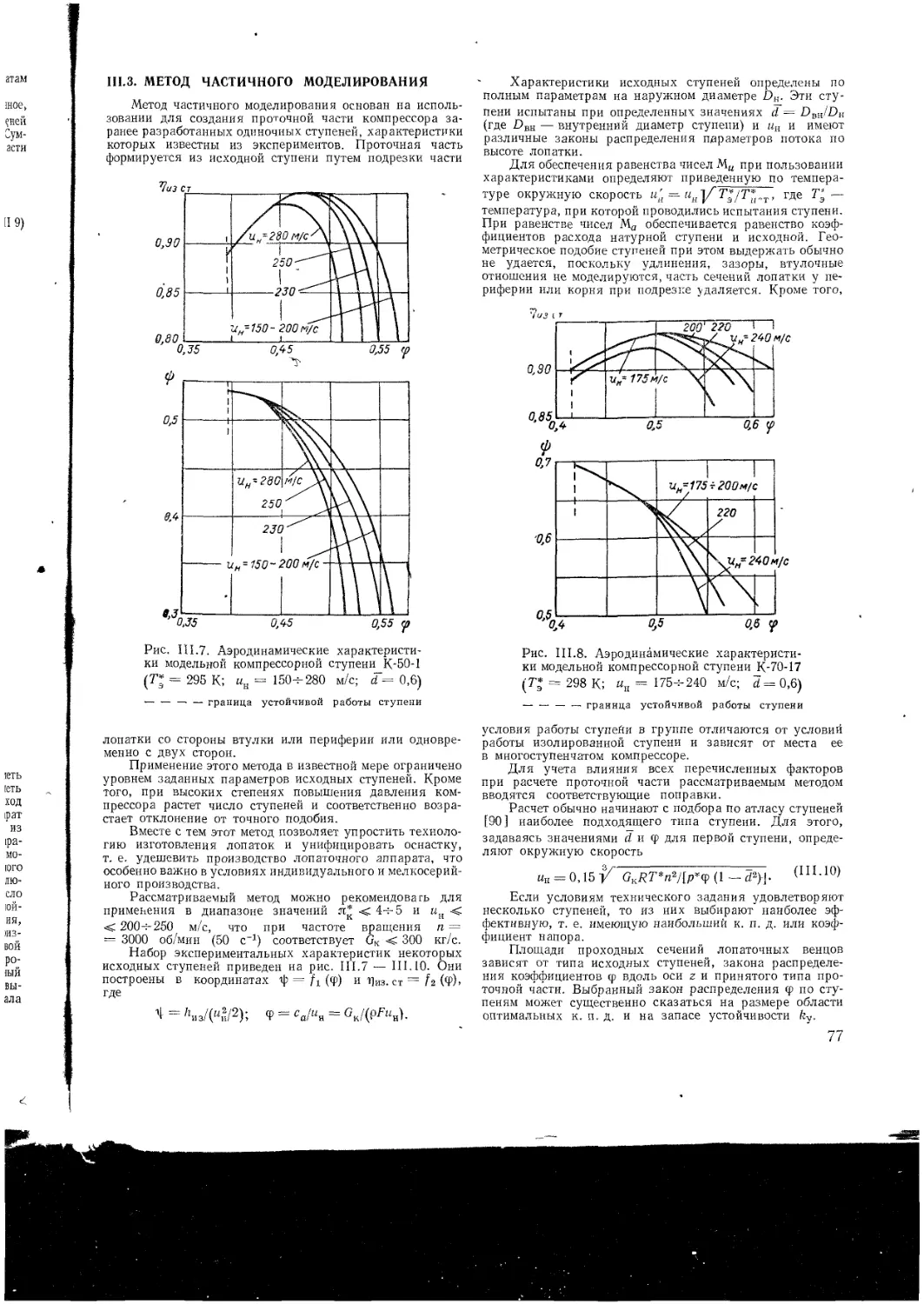
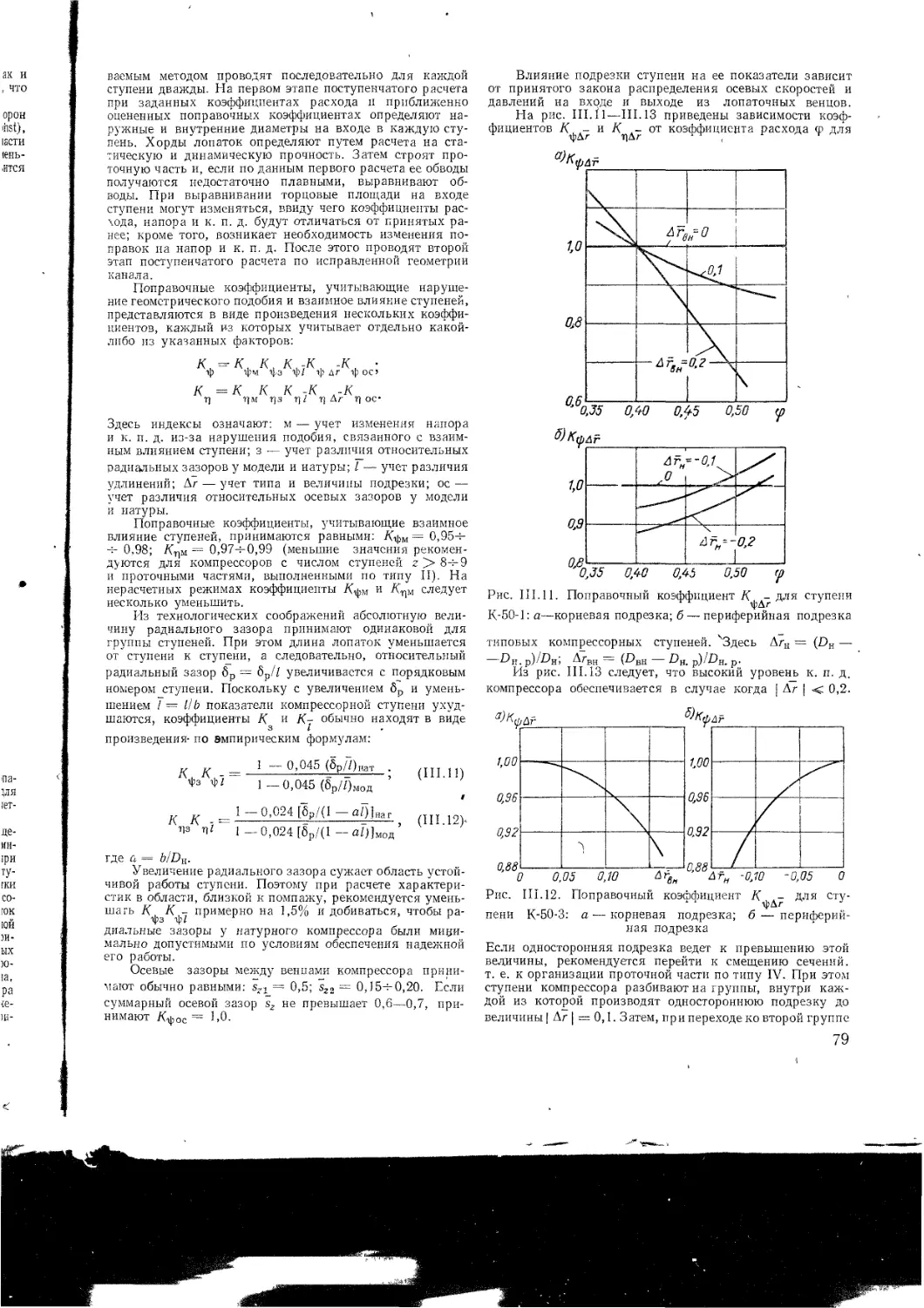
III 3 Метод частичного моделирования
III 4 Расчет характеристик компрессора
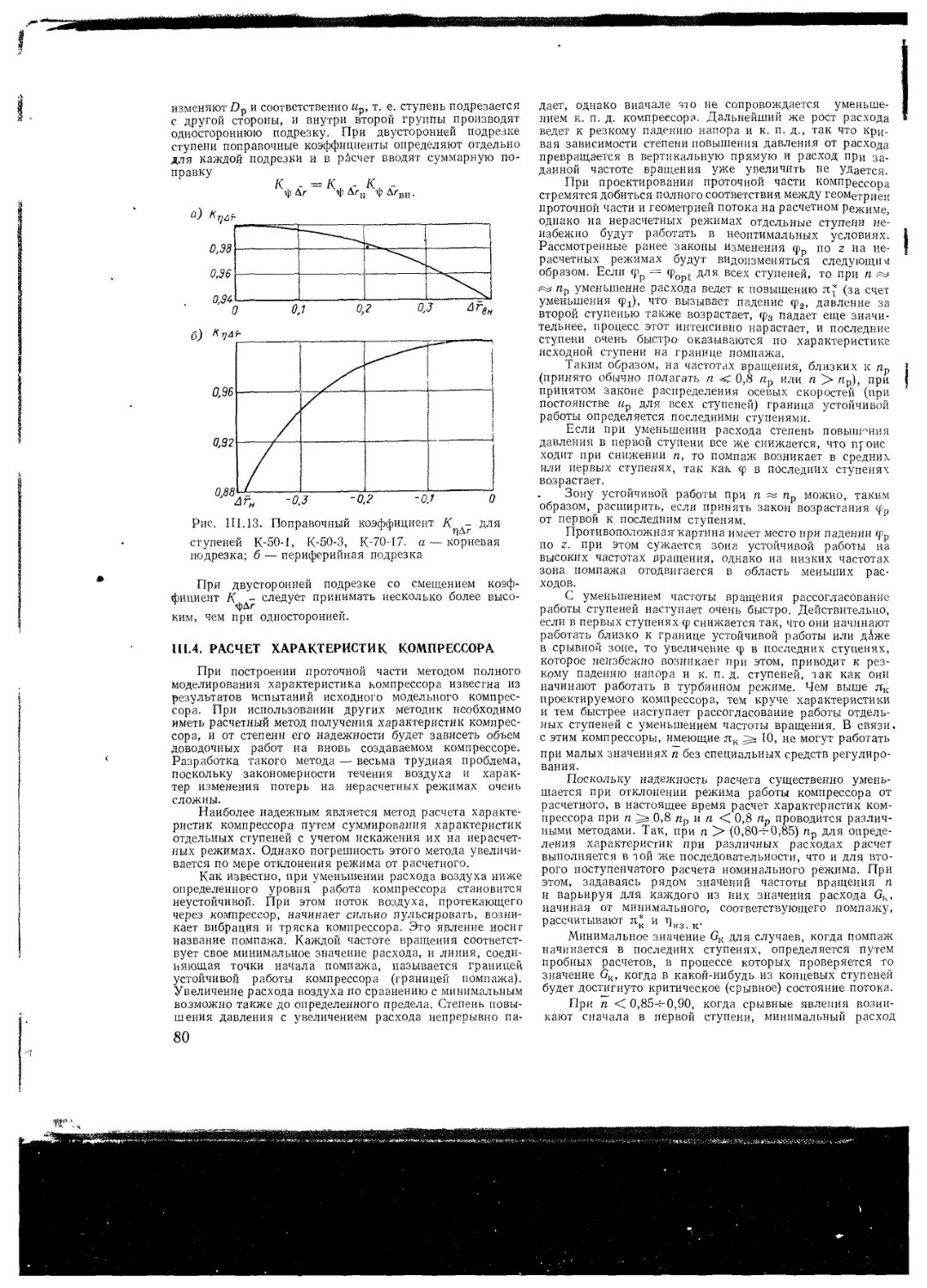
III 5 Метод расчета проточной части компрес
сора по результатам исследования пло
скнх решеток профилей
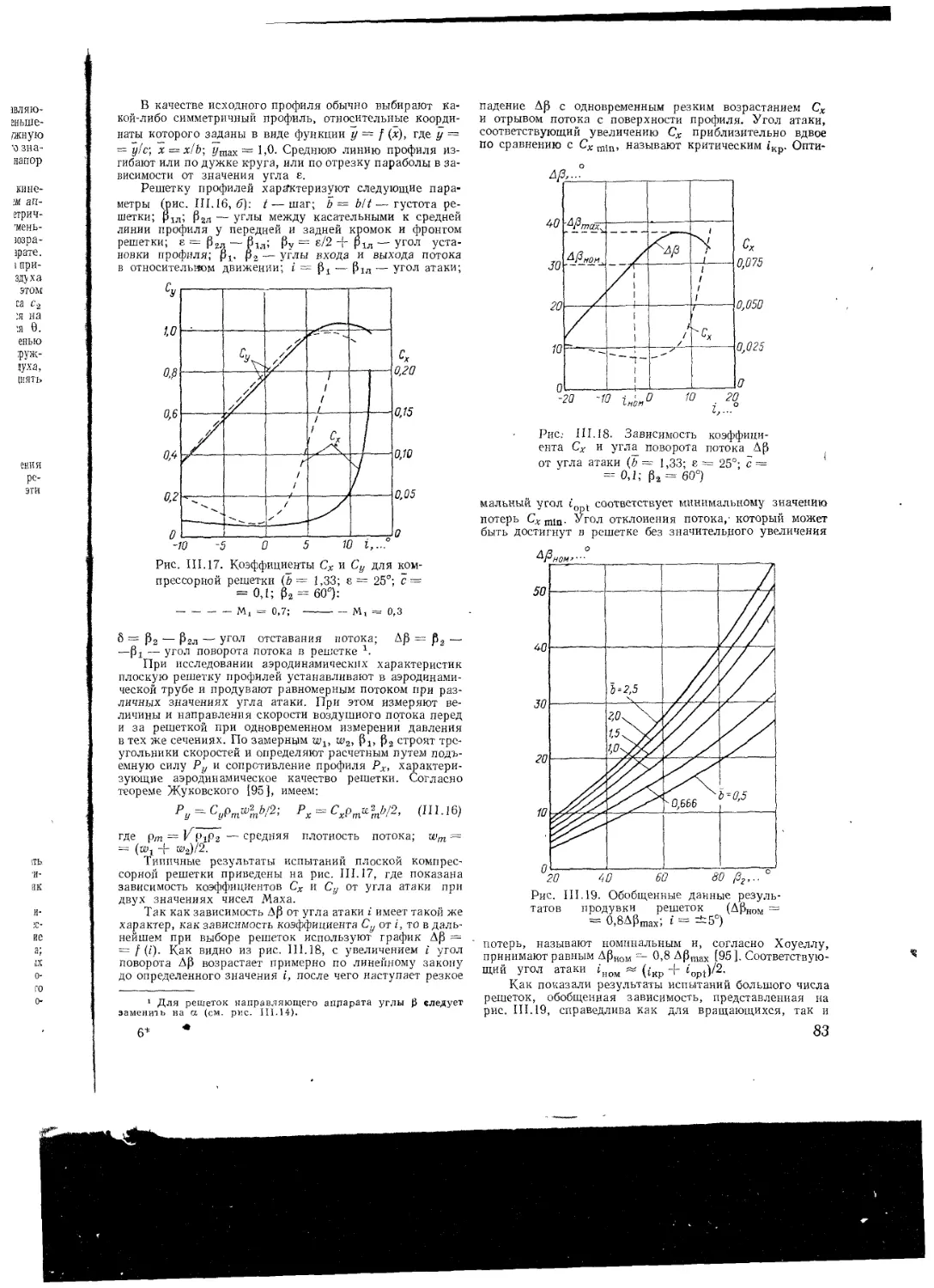
Общие положения
Кинематика потока в компрессорной ступени
Аэродинамические характеристики плоских
компрессорных решеток
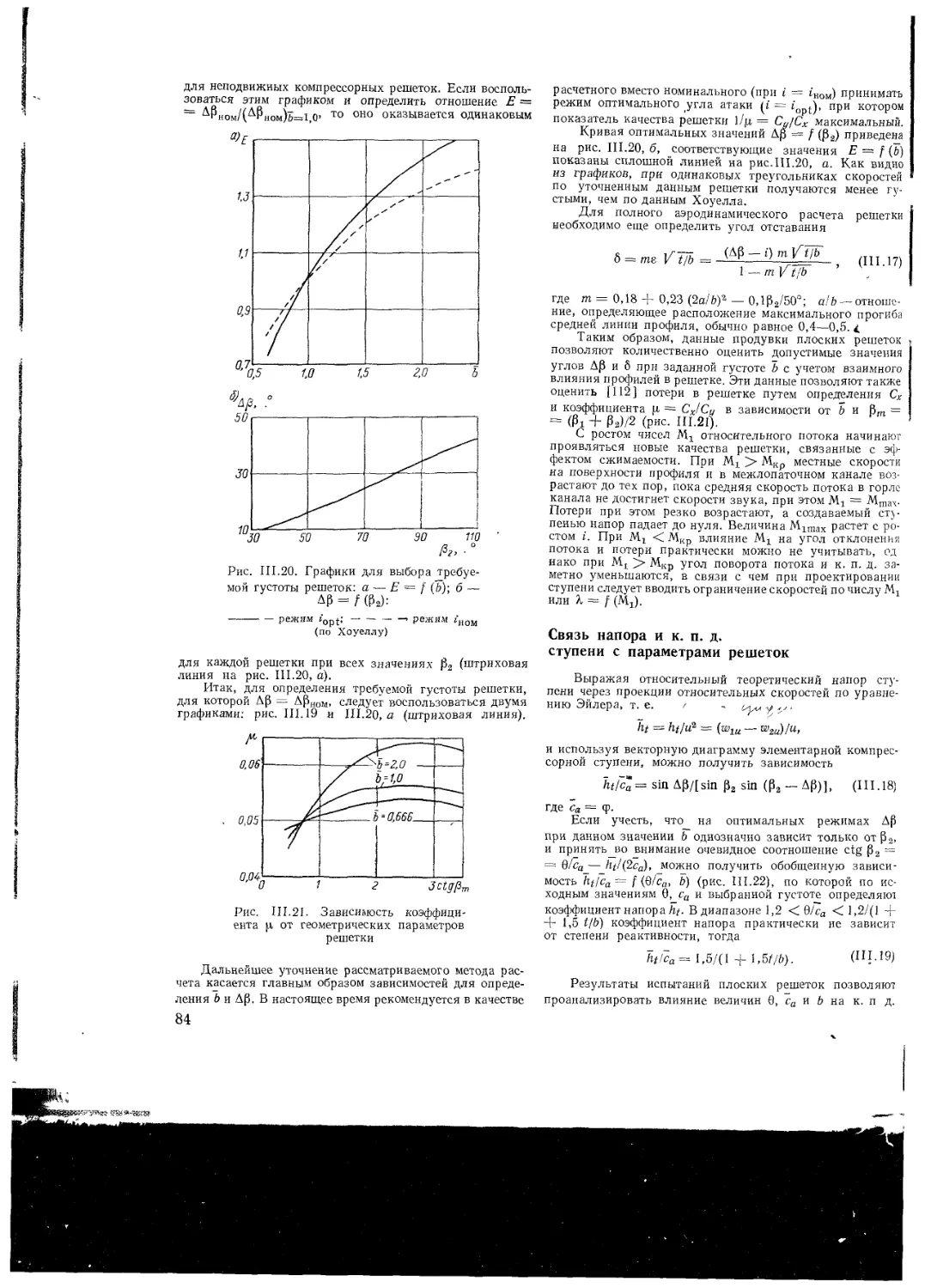
Связь напора н к п д ступени с пара
метрами решеток
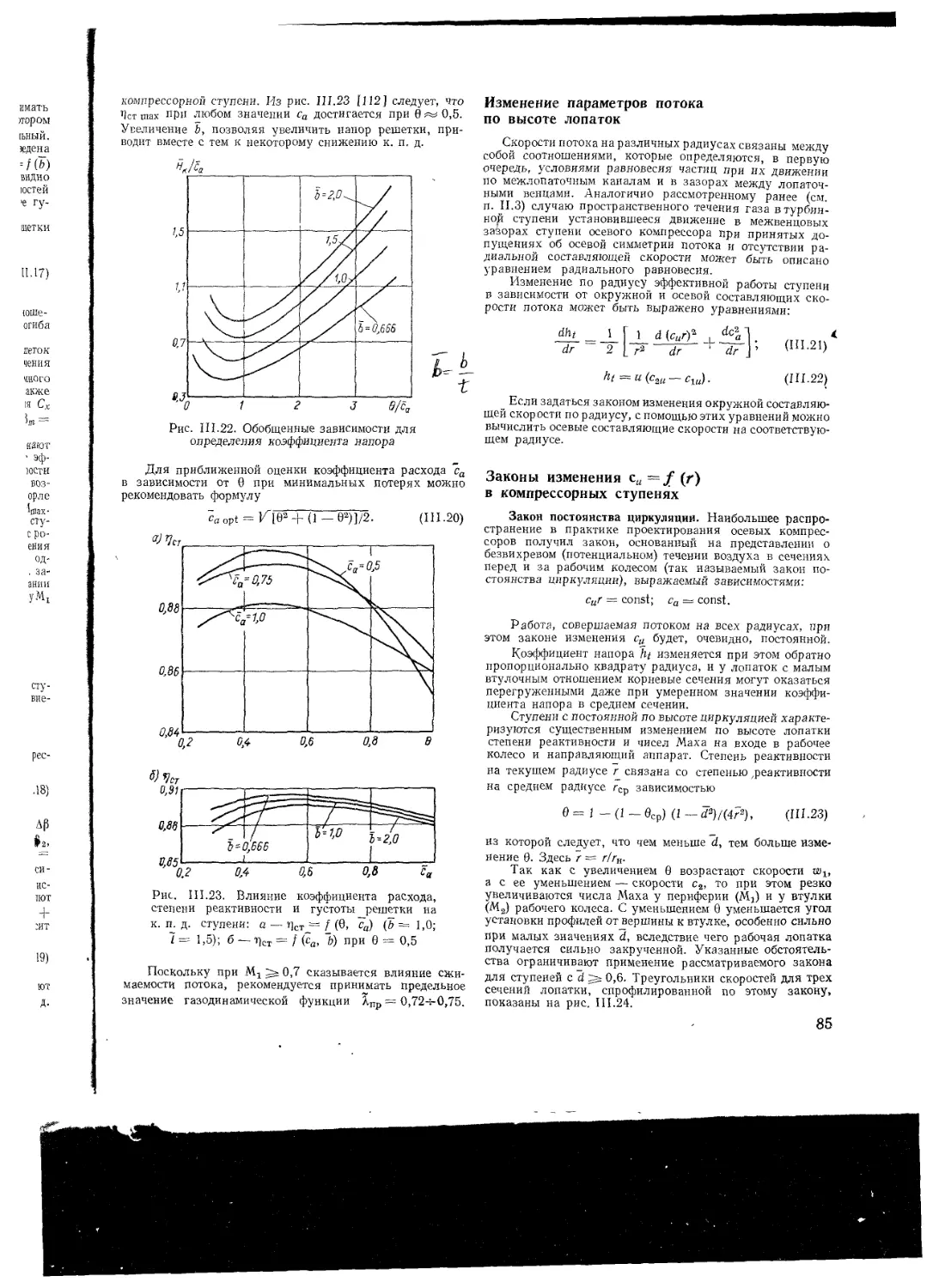
Изменение параметров потока по высоте
лопаток
Законы изменения си = f (г) в компрес-
сорных ступенях
Определение осевых составляющих скоро-
стей по радиусу
Расчет ступени по среднему радиусу
Расчет треугольников скоростей по вы-
соте лопаток
Профилирование лопаток
Глава IV Камеры сгорания и теплообменные аппа-
раты ГТУ
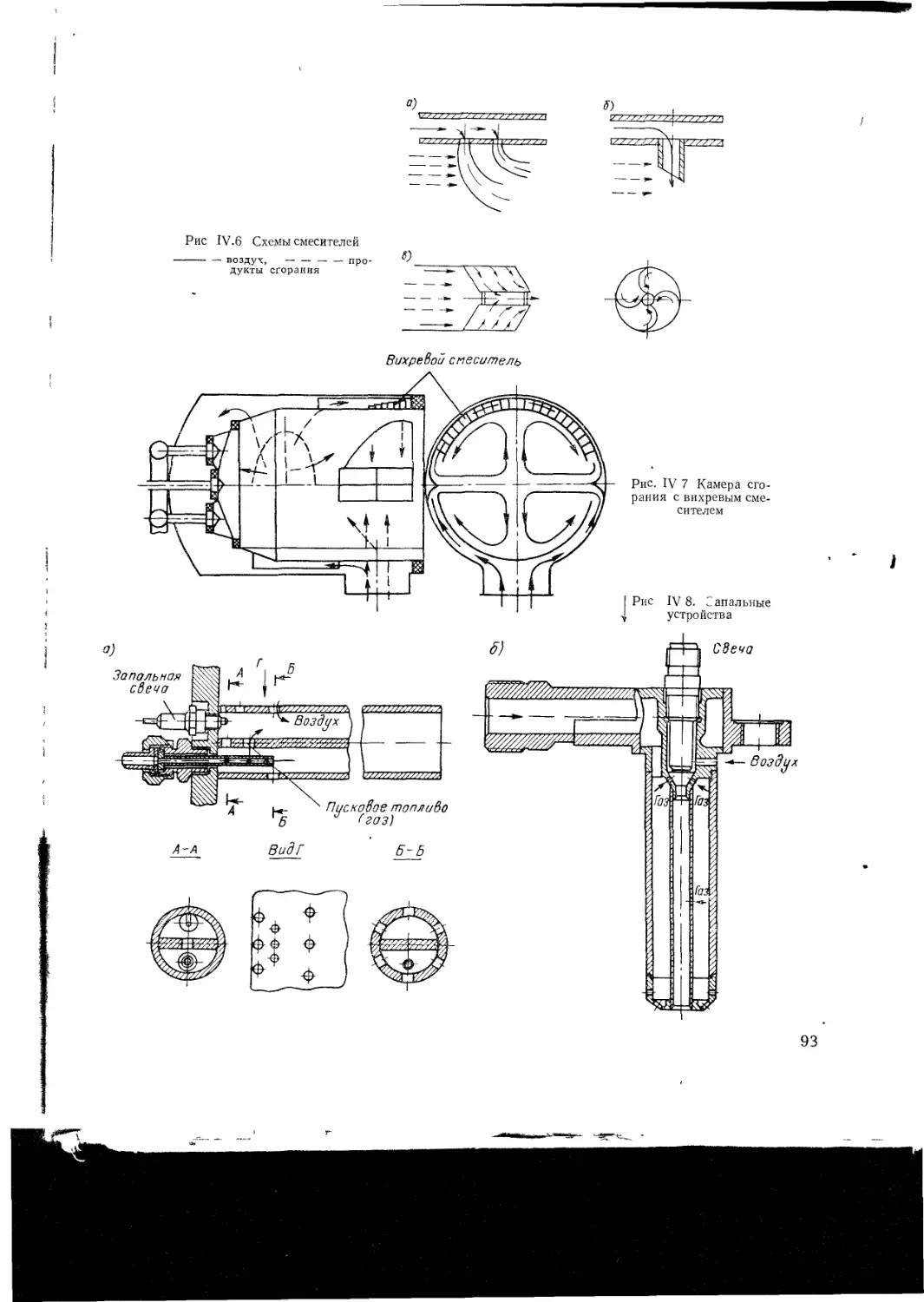
IV 1 Камеры сгорания
Общие сведения
Основные элементы камер сгорания
Основные характеристики камер сгорания
Конструкция основных элементов камер
сгорания
Расчет основных параметров камер сго-
рания
IV 2 Теплообменные аппараты ГТУ (ТОА)
Классификация теплообменных аппаратов
Тепловой расчет
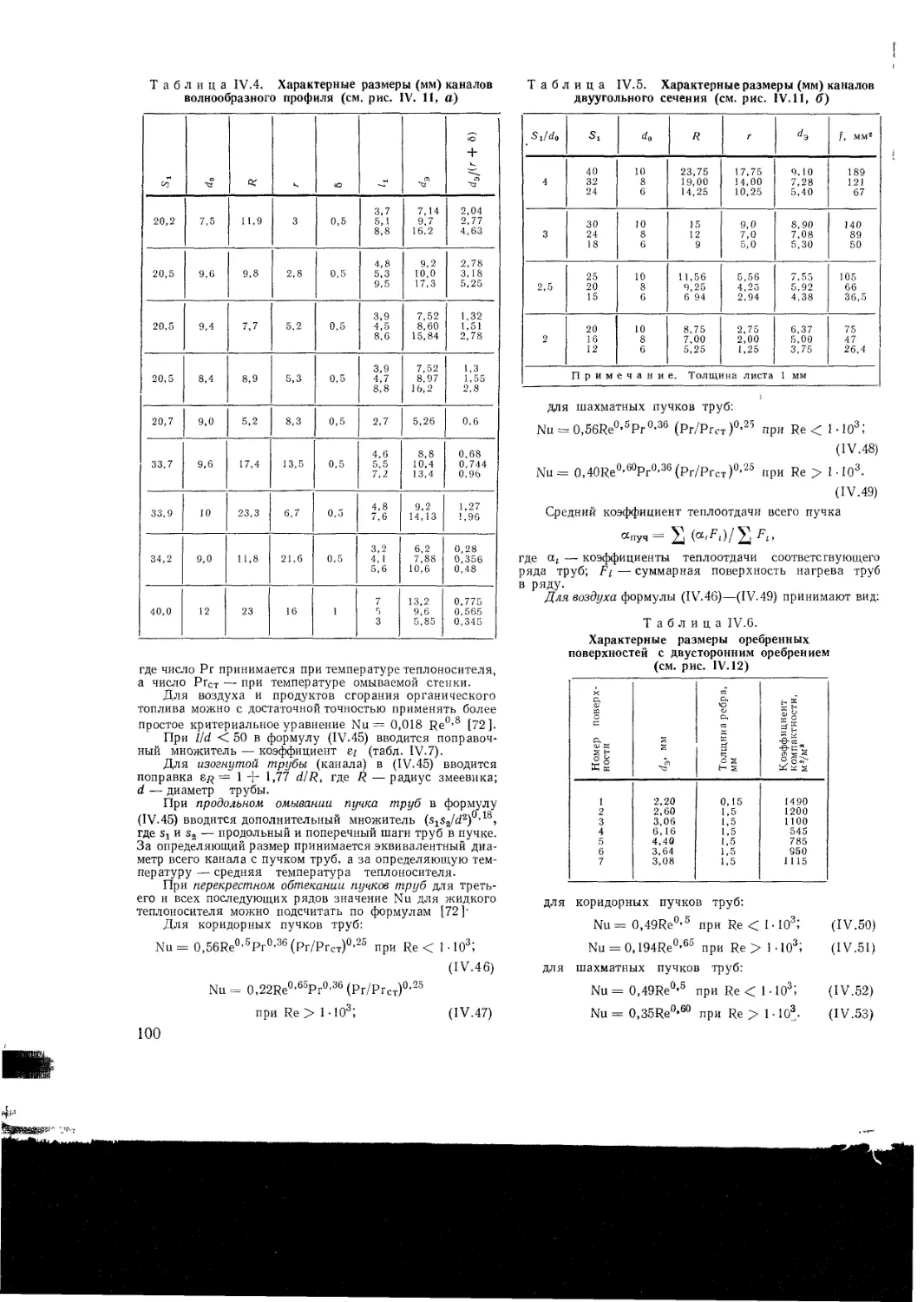
Теплопередача через оребренную поверх-
ность
Использование теории подобия при расчете
ТОА
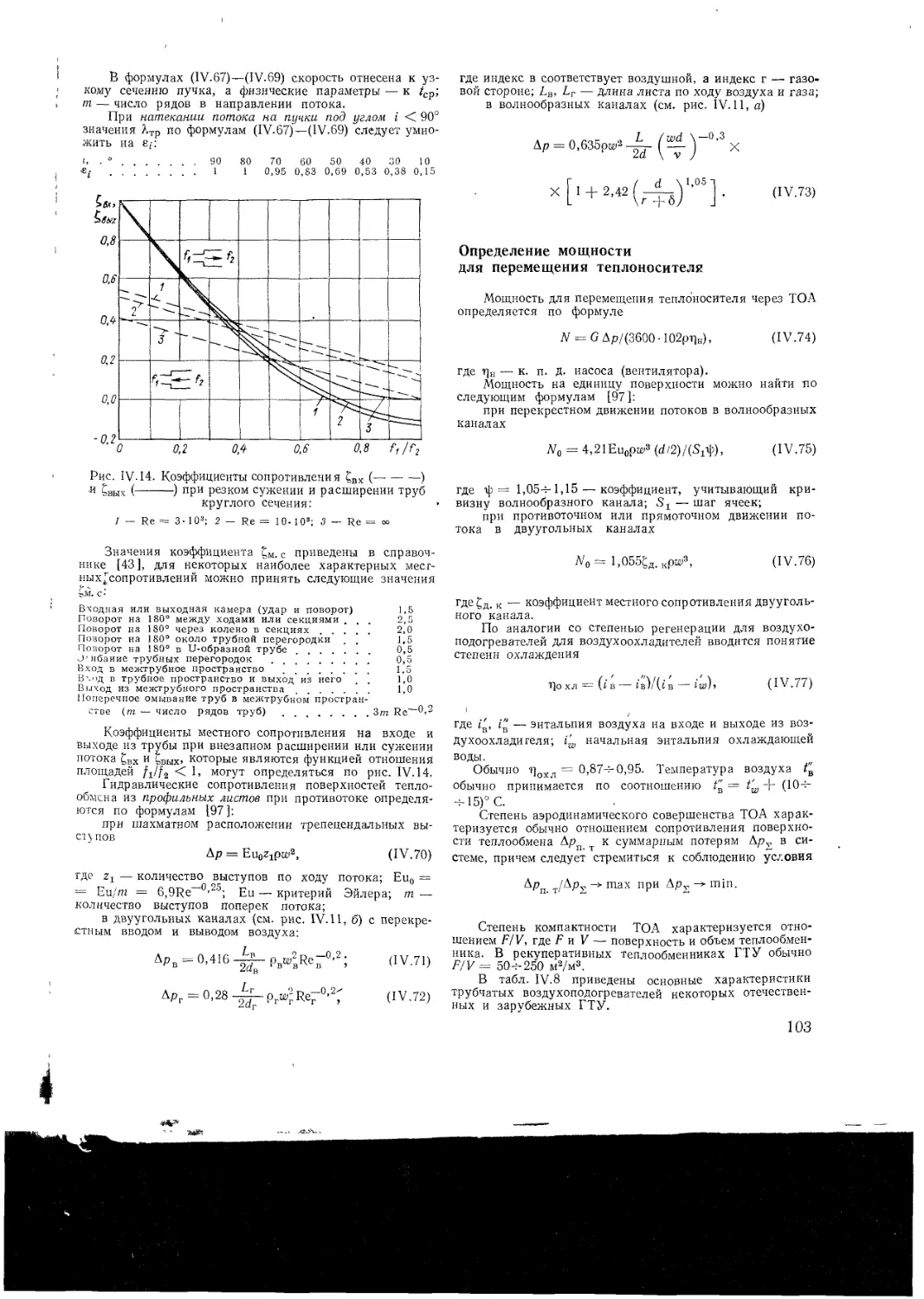
Гидравлический расчет
Определение мощности для перемещения
теплоносителя
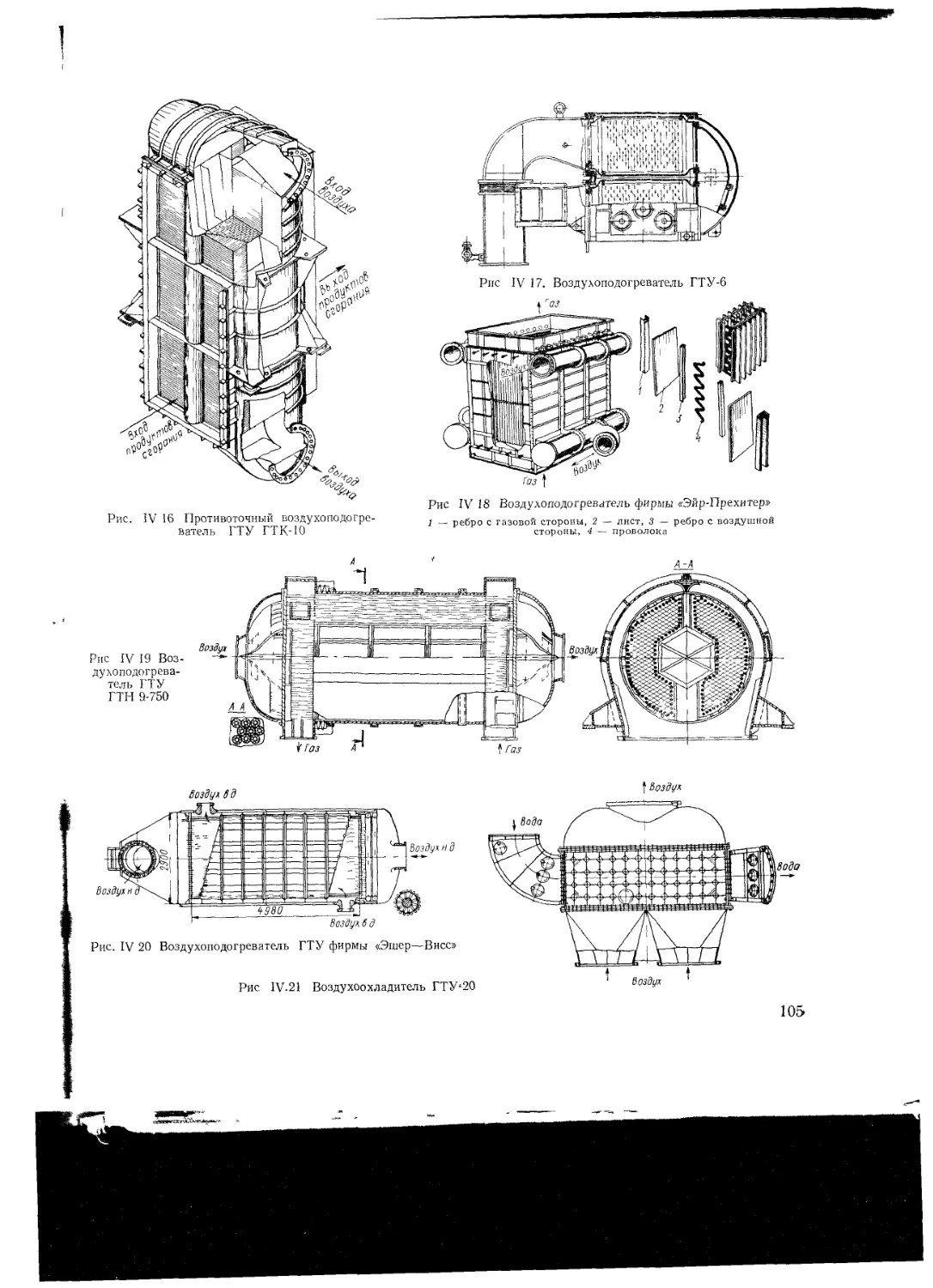
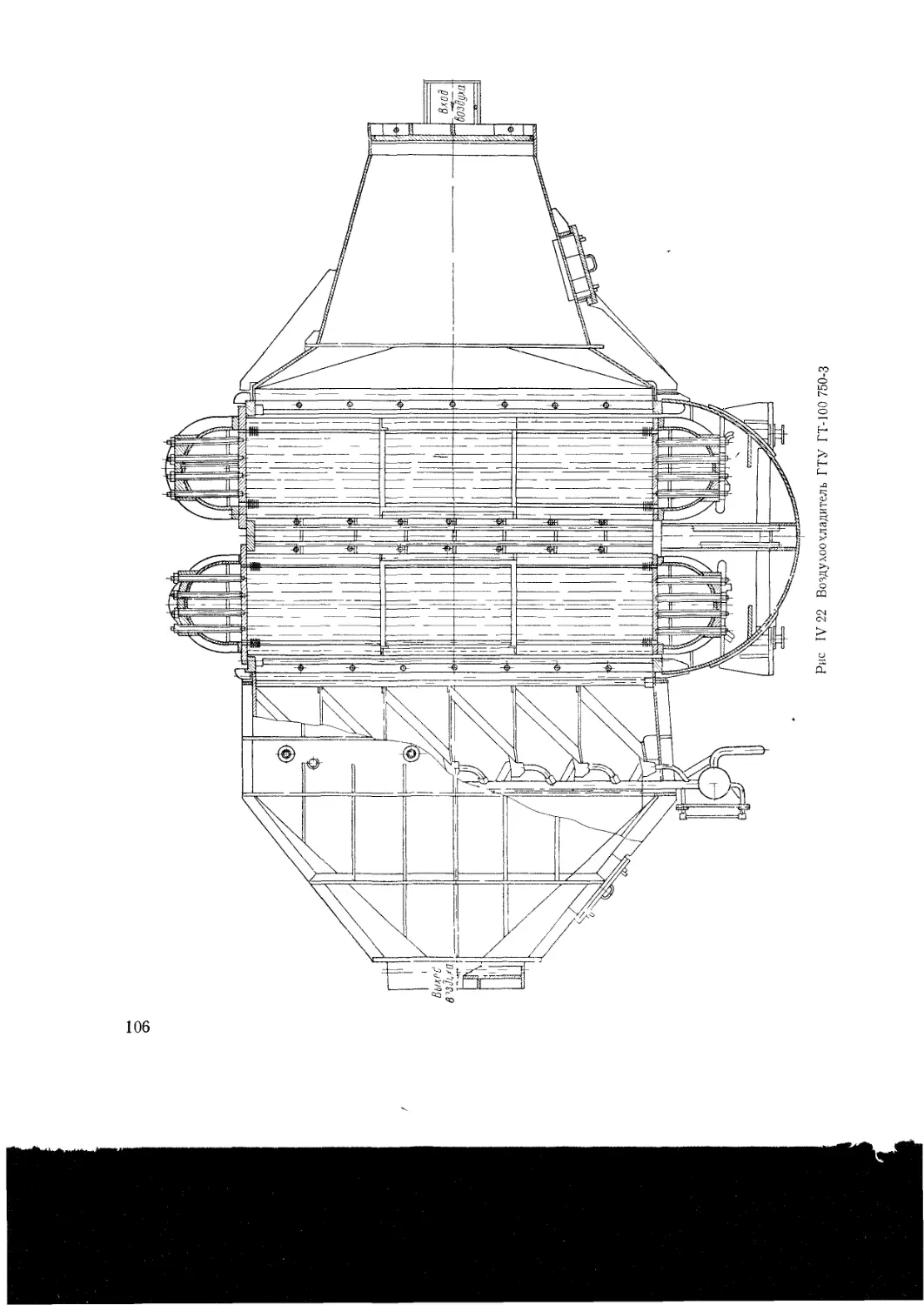
Конструкции теплообменных аппаратов ГТУ
Глава V Режимы работы i азотурбннных установок
на частичных нагрузках
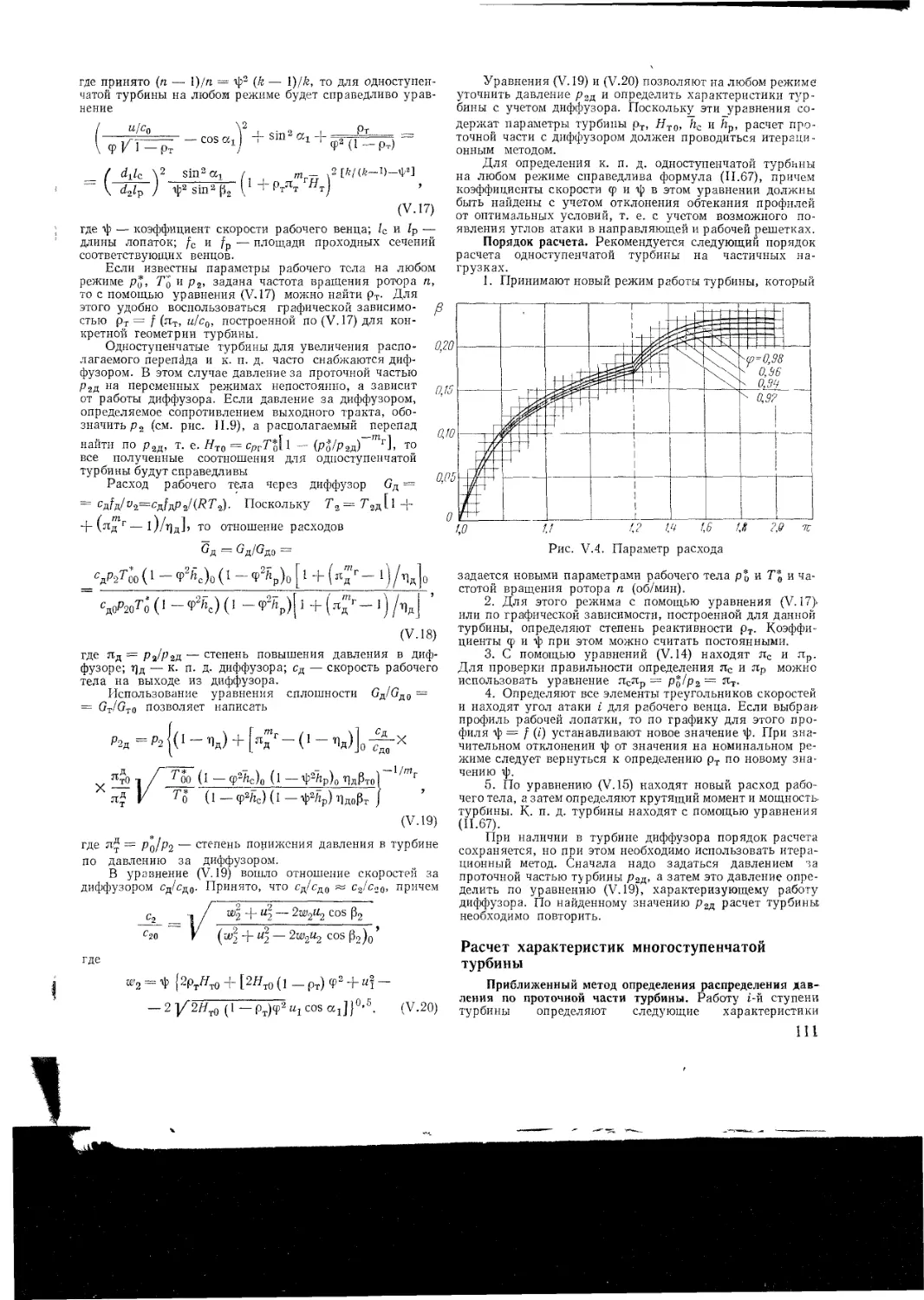
V 1 Работа турбины на частичных нагрузках
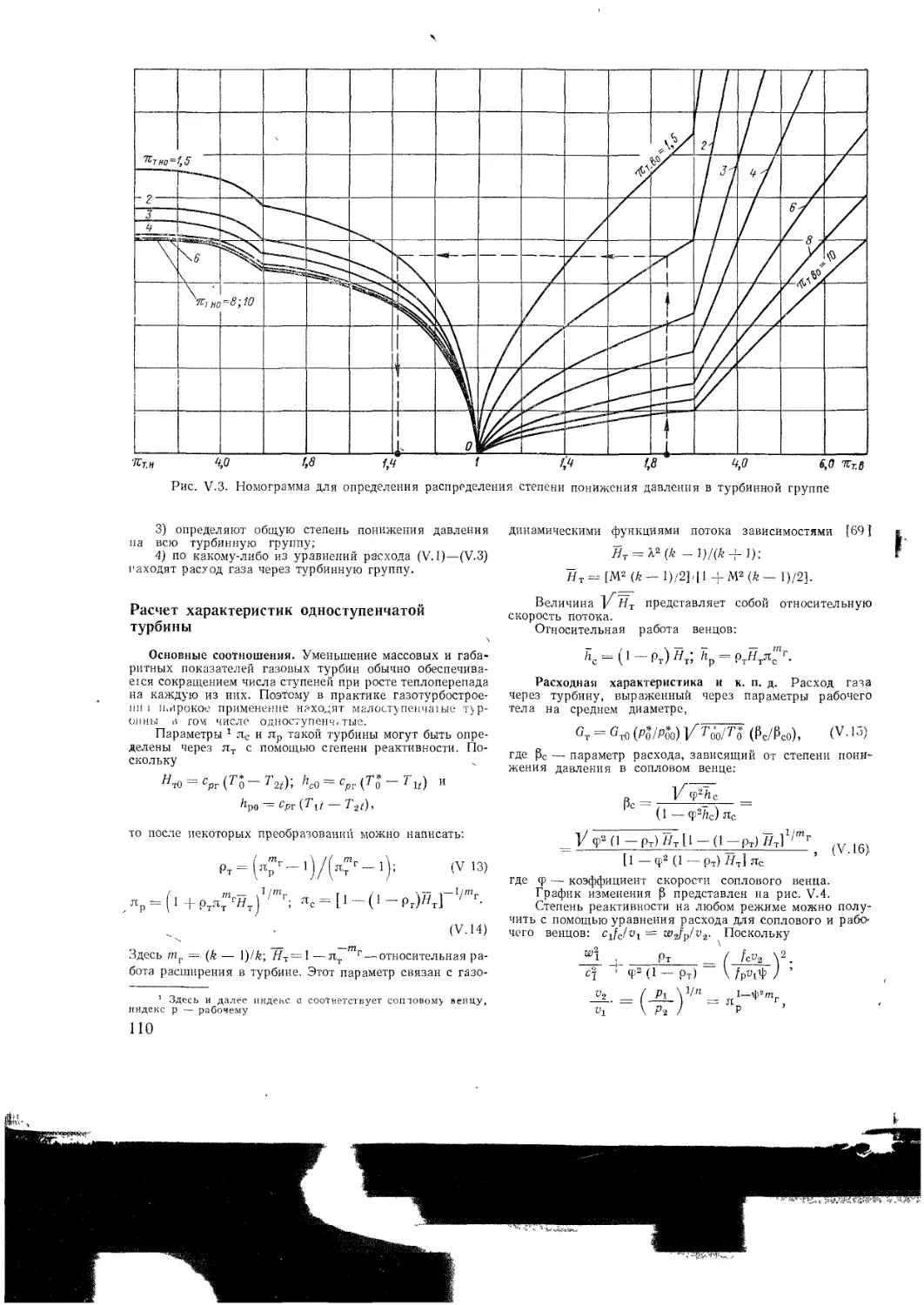
Приближенные методы расчета турбин
Расчет характеристик одноступенчатой тур-
бины
Расчет характеристик многоступенчатой тур
бины
Основные показатели турбины
V 2 Работа камеры сгорания и теплообменных
аппаратов на частичных нагрузках
Камера сгорания
Регенератор
Воздухоохладитель
V3 Согласование параметров элементов ГТУ
Основные уравнения
Гидравлические потерн в трактах ГТУ
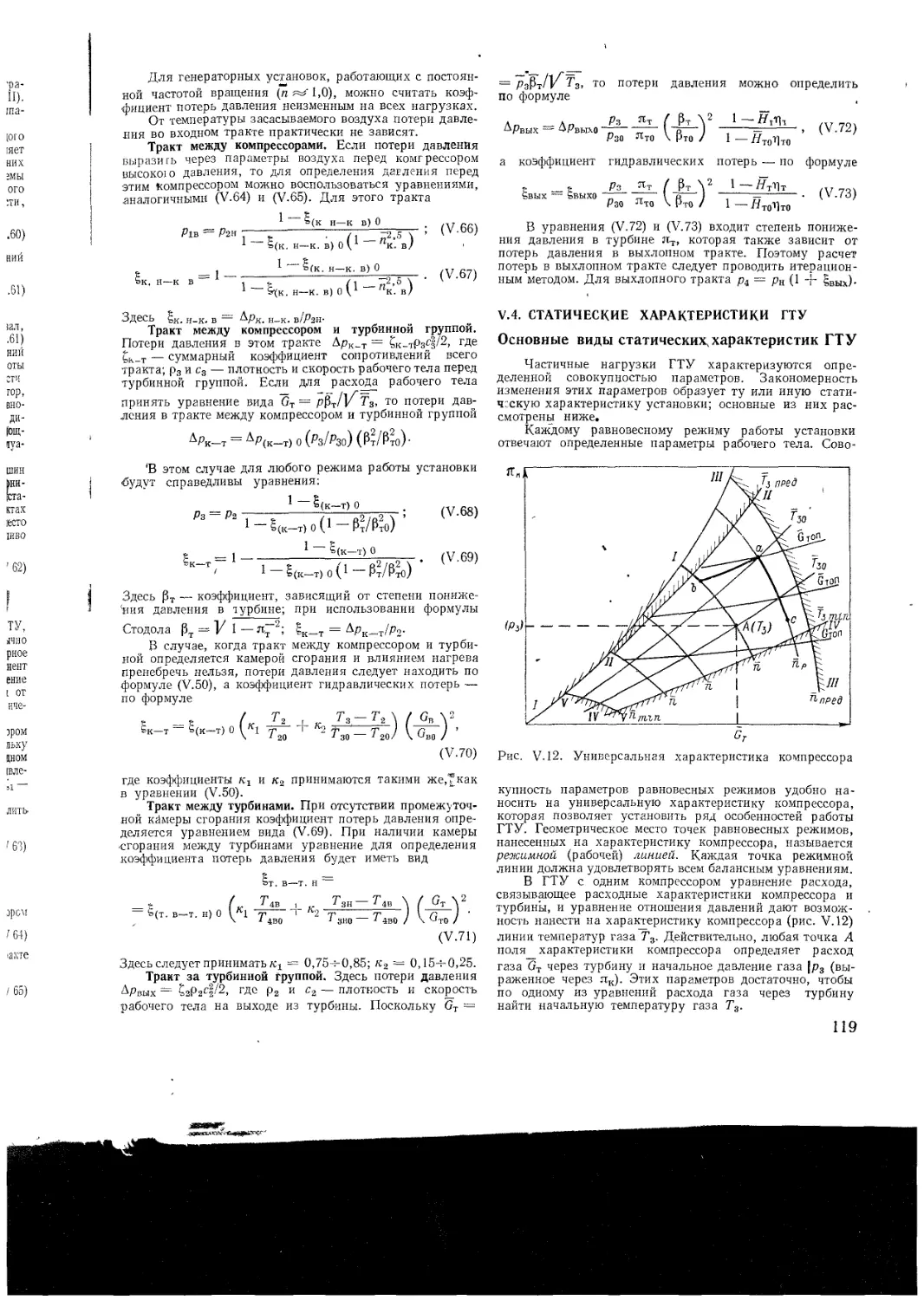
V 4 Статические характеристики ГТУ
Основные внды статических характеристик
I ГУ
Статические характеристики одновальной
1 ТУ
65
66
70
72
77
80
81
82
84
85
86
87
88
89
90
91
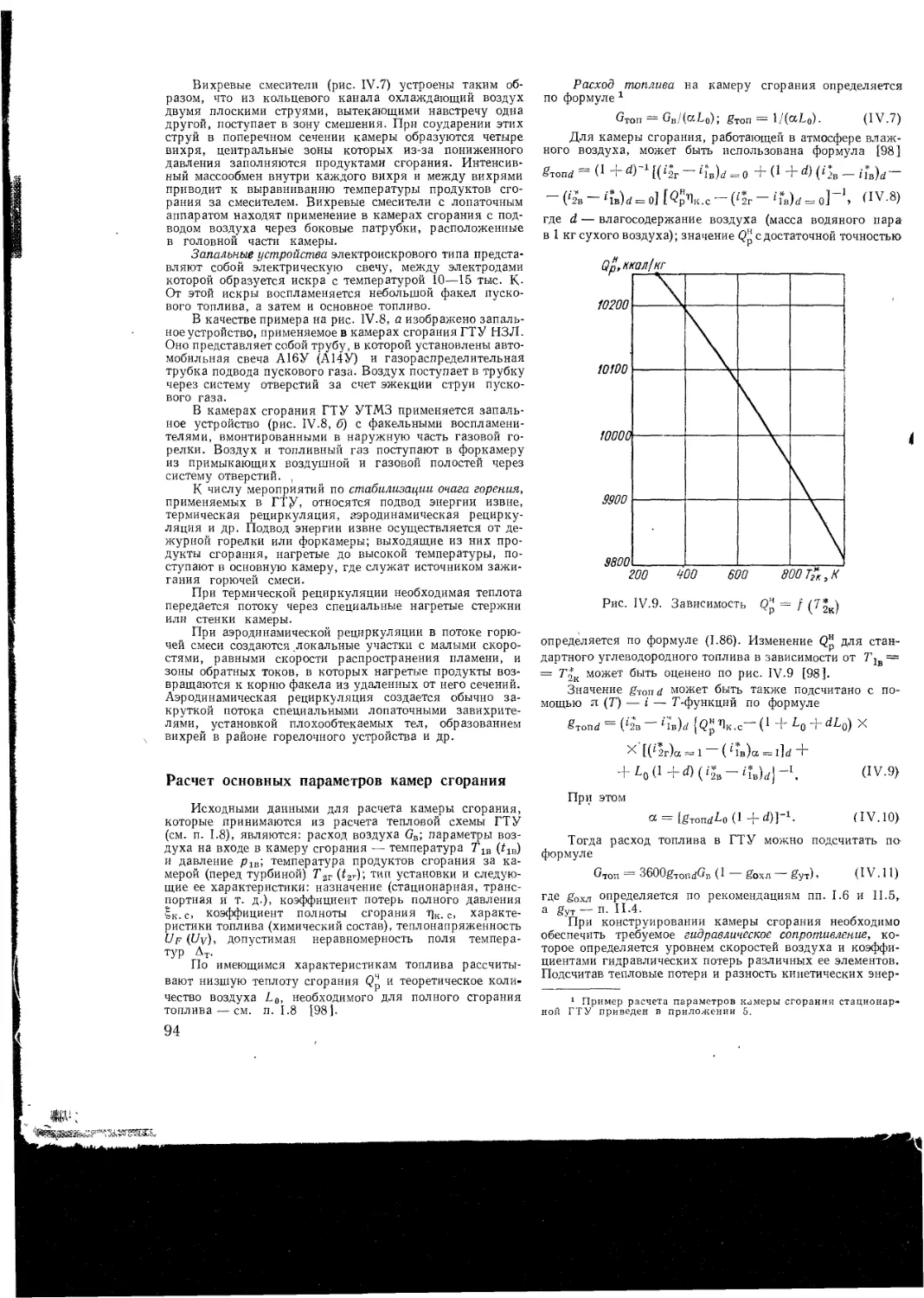
94
97
98
102
103
104
108
110
111
115
116
119
120
Статические характеристики однокомпрес-
сорной ГТУ со свободной силовой турбиной
Статические характеристики двухкомпрес
сорной ГТУ
Улучшение статических характеристик ГТУ
за счет дополнительных регулирующих ор
гаиов
Влияние параметров наружного воздуха на
характеристики ГТУ
Глава VI Динамические характеристики ГТУ и си
стемы автоматического регулирования
управления и защиты . . .
VI 1 Основные уравнения движения
Уравнения движения роторов ГТУ
Уравнения движения аккумулятора мате
риальной среды
Уравнения движения аккумулятора тепло
вой энергии
Системы дифференциальных уравнений двн
жения для ряда схем ГТУ
VI 2 Динамические характеристики
Анализ устойчивости
Построение графика переходного процесса
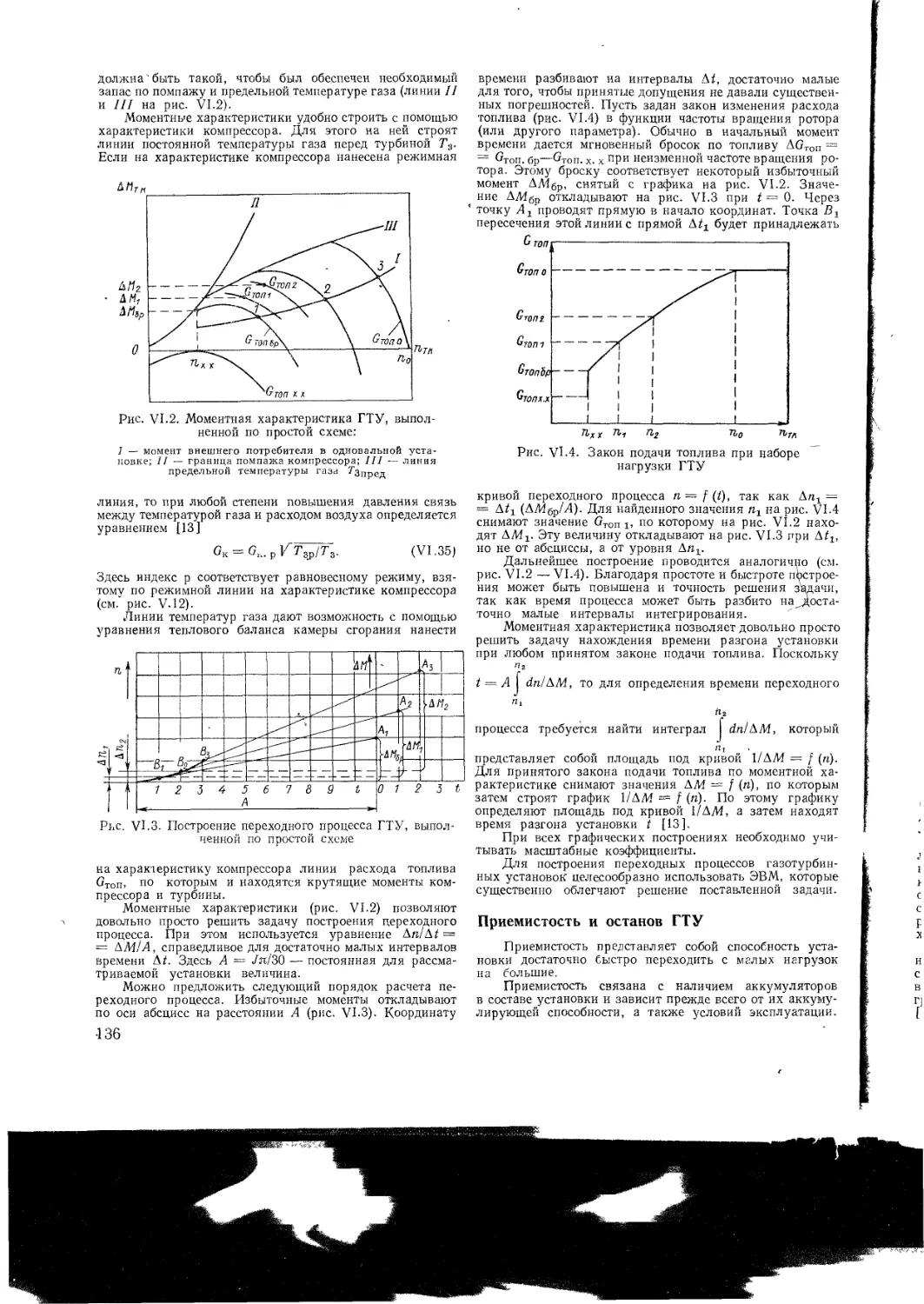
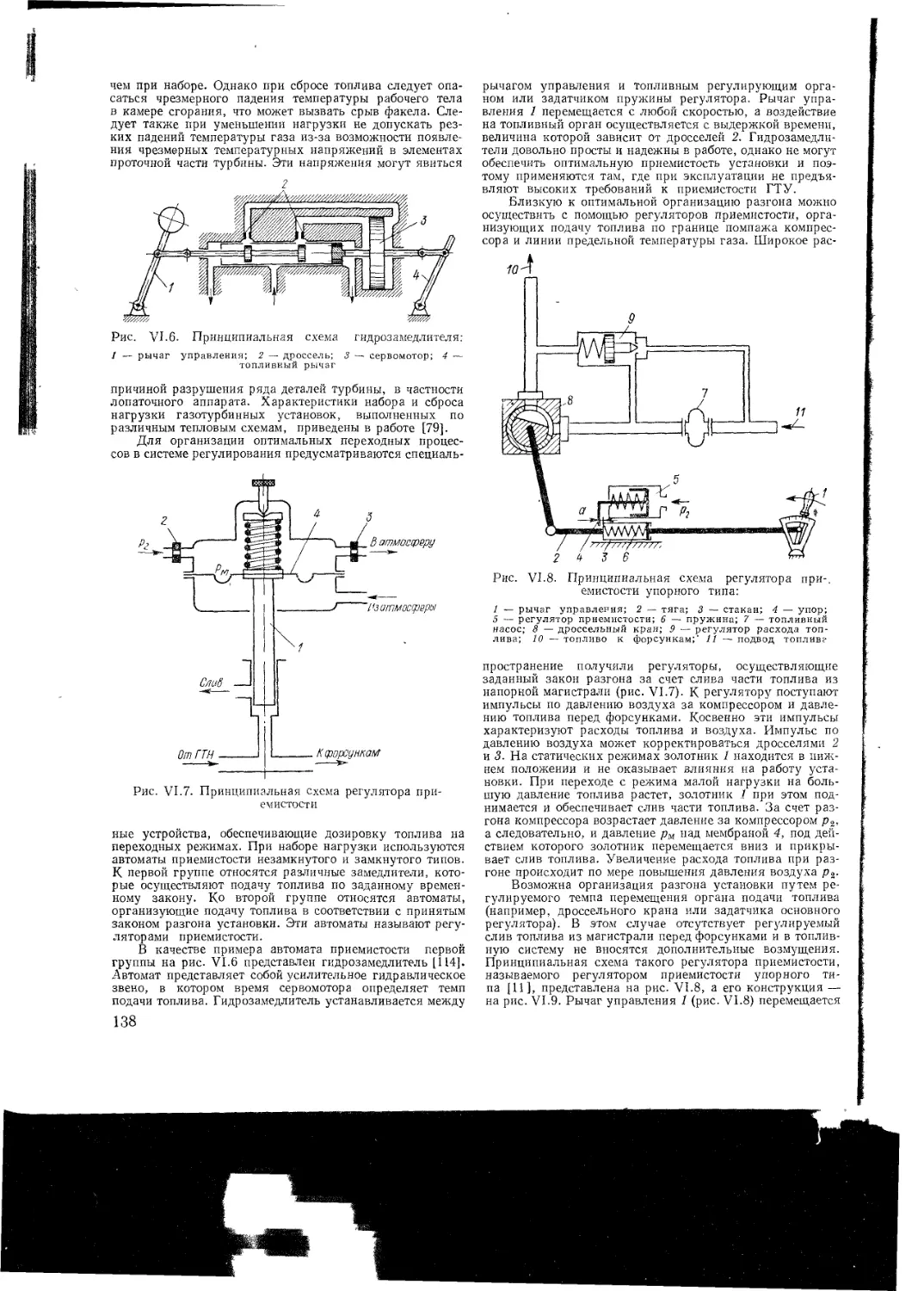
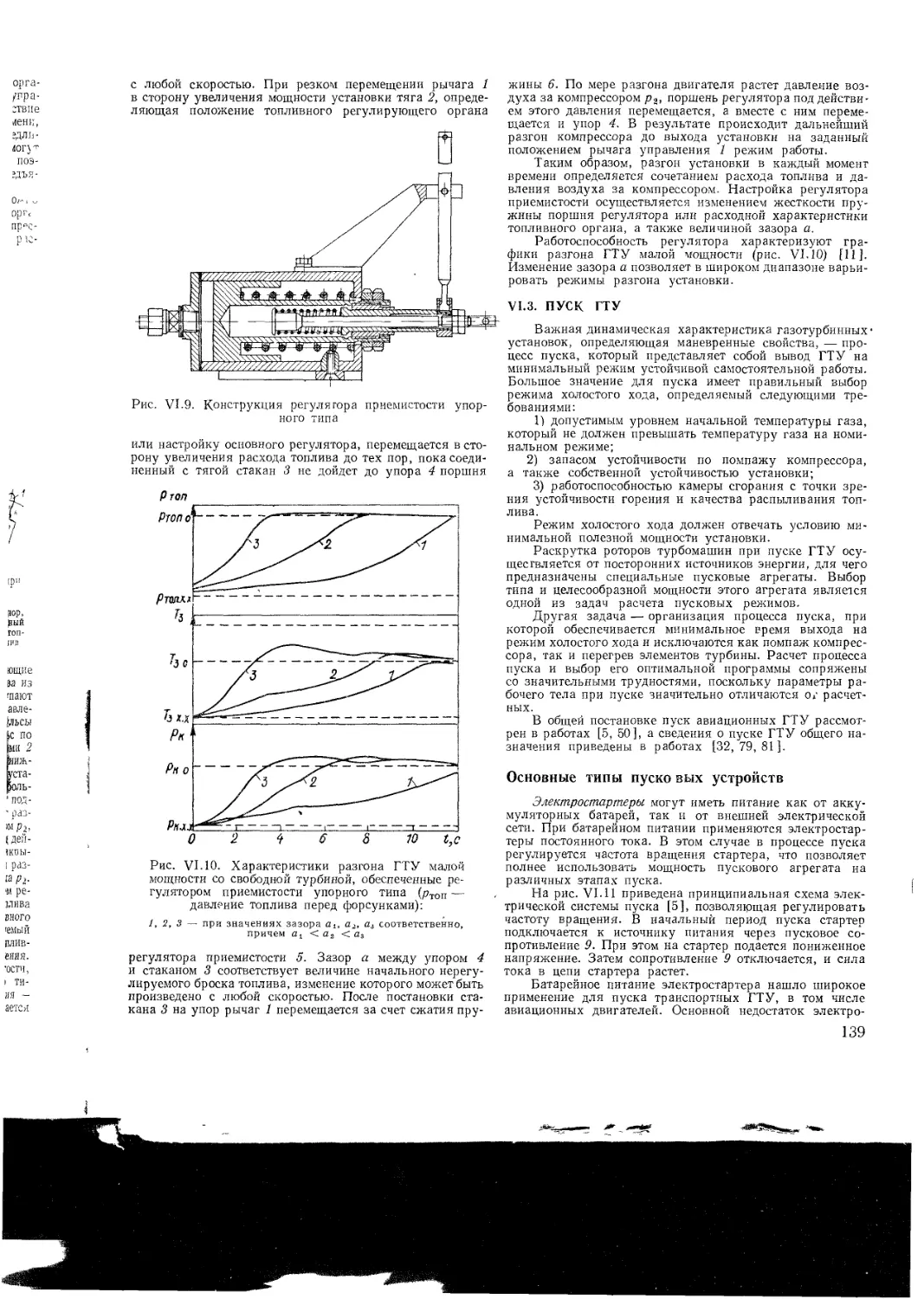
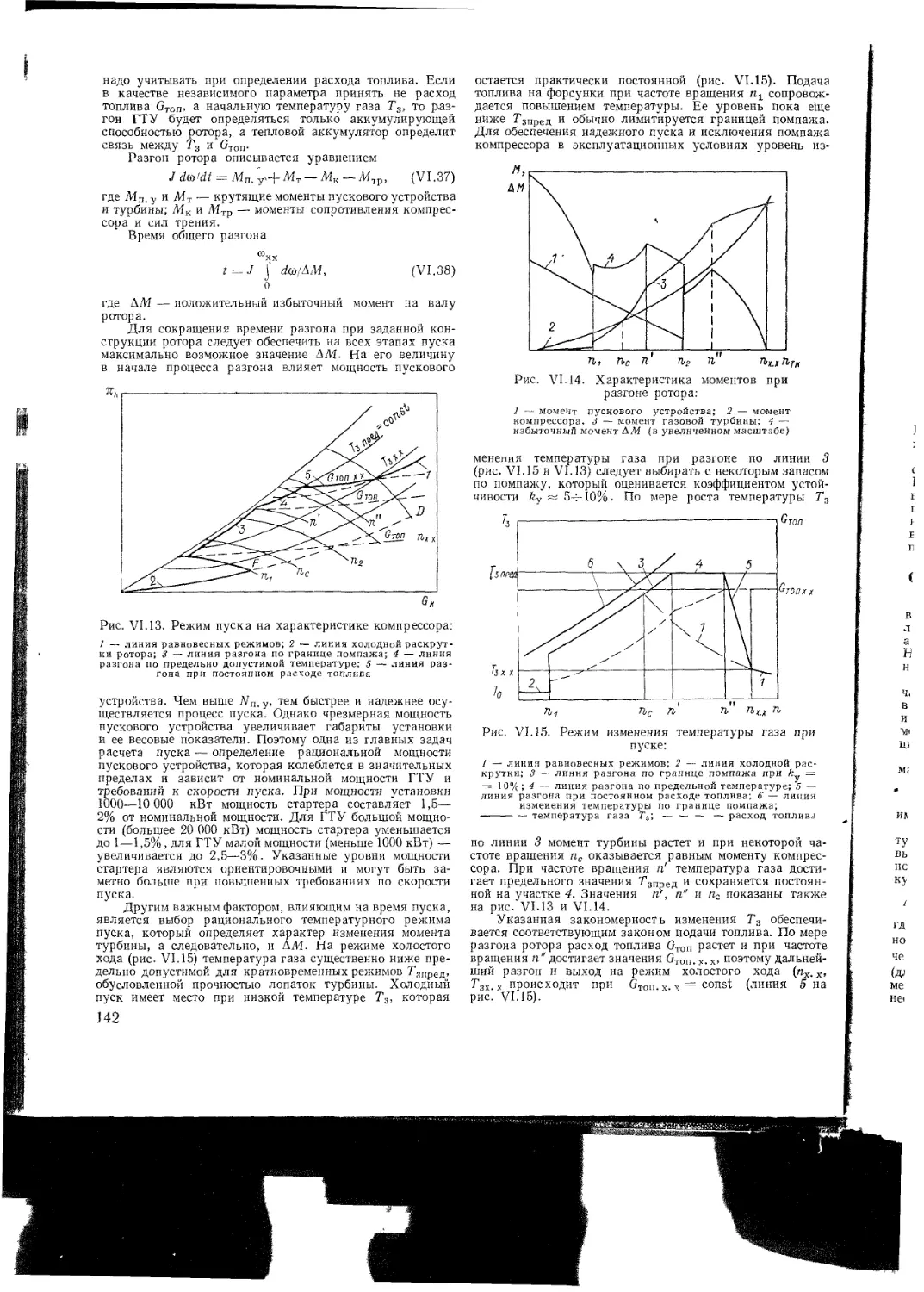
Приемистость и останов ГТУ
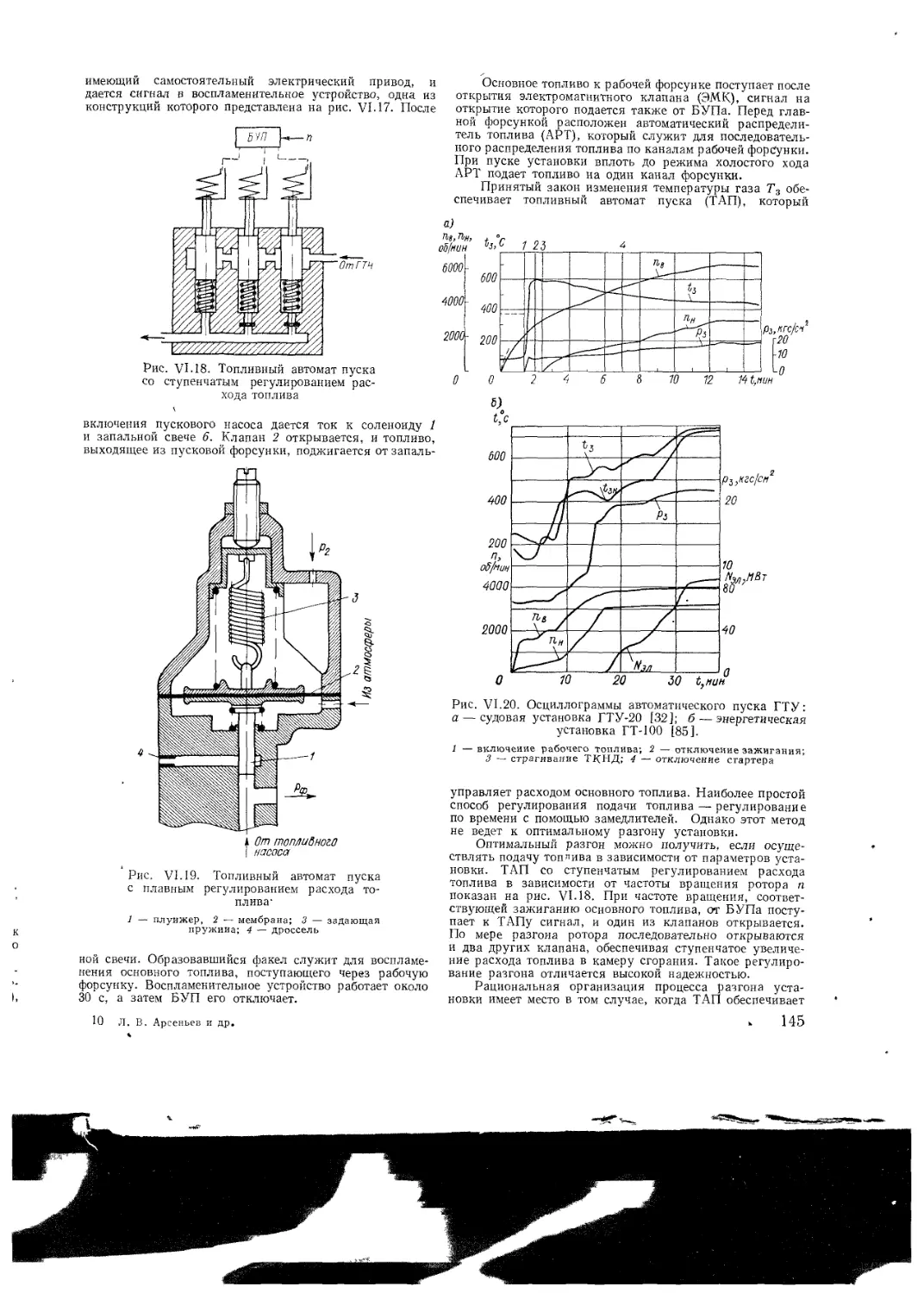
VI 3 Пуск ГТУ
Основные типы пусковых устройств
Процессы, происходящие при пуске
Основы расчета процесса пуска
Управление пуском
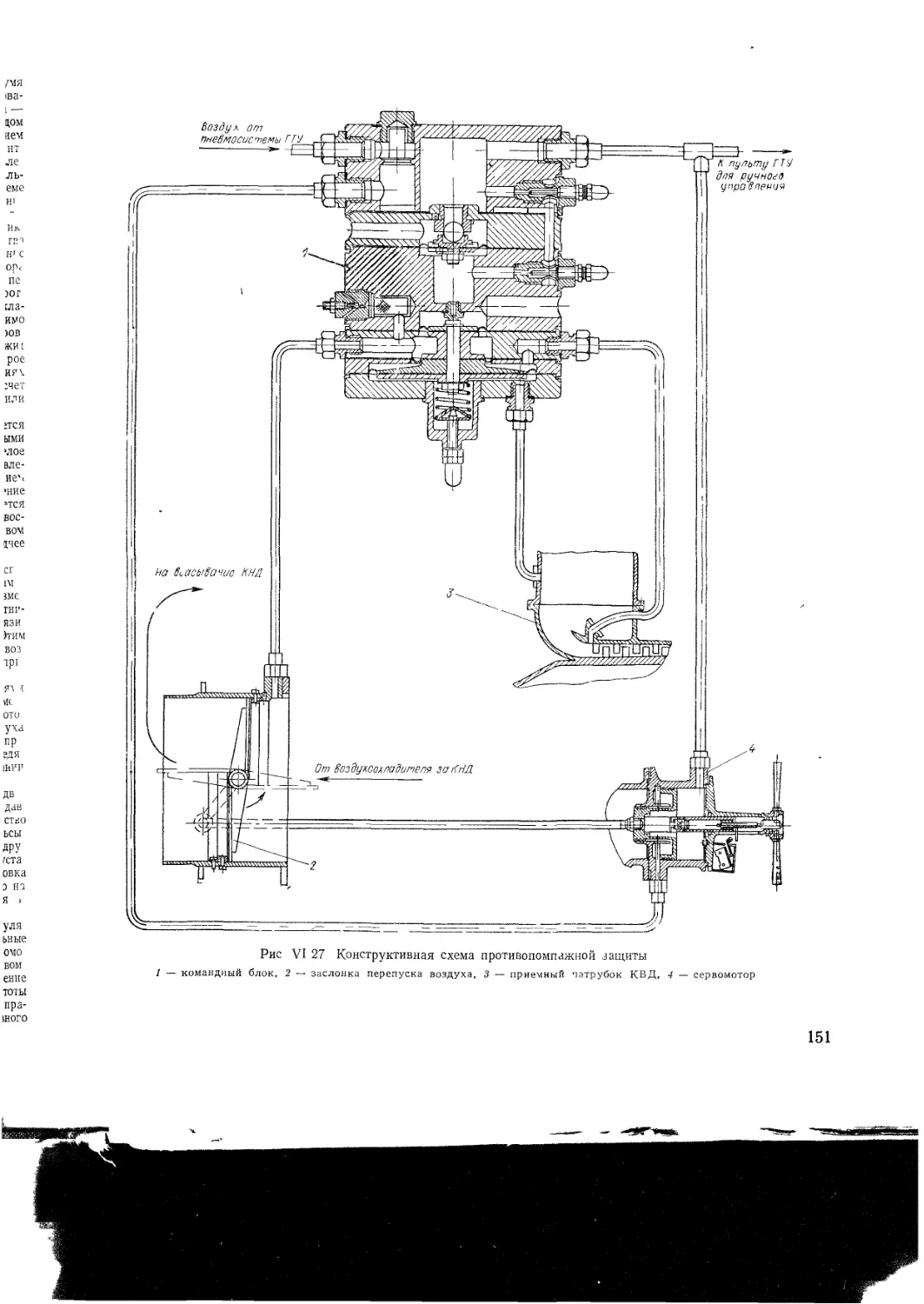
VI 4 Устройства защиты ГТУ
Защита по частоте вращения
Защита по начальной температуре газа
Протнвопомпажная защита
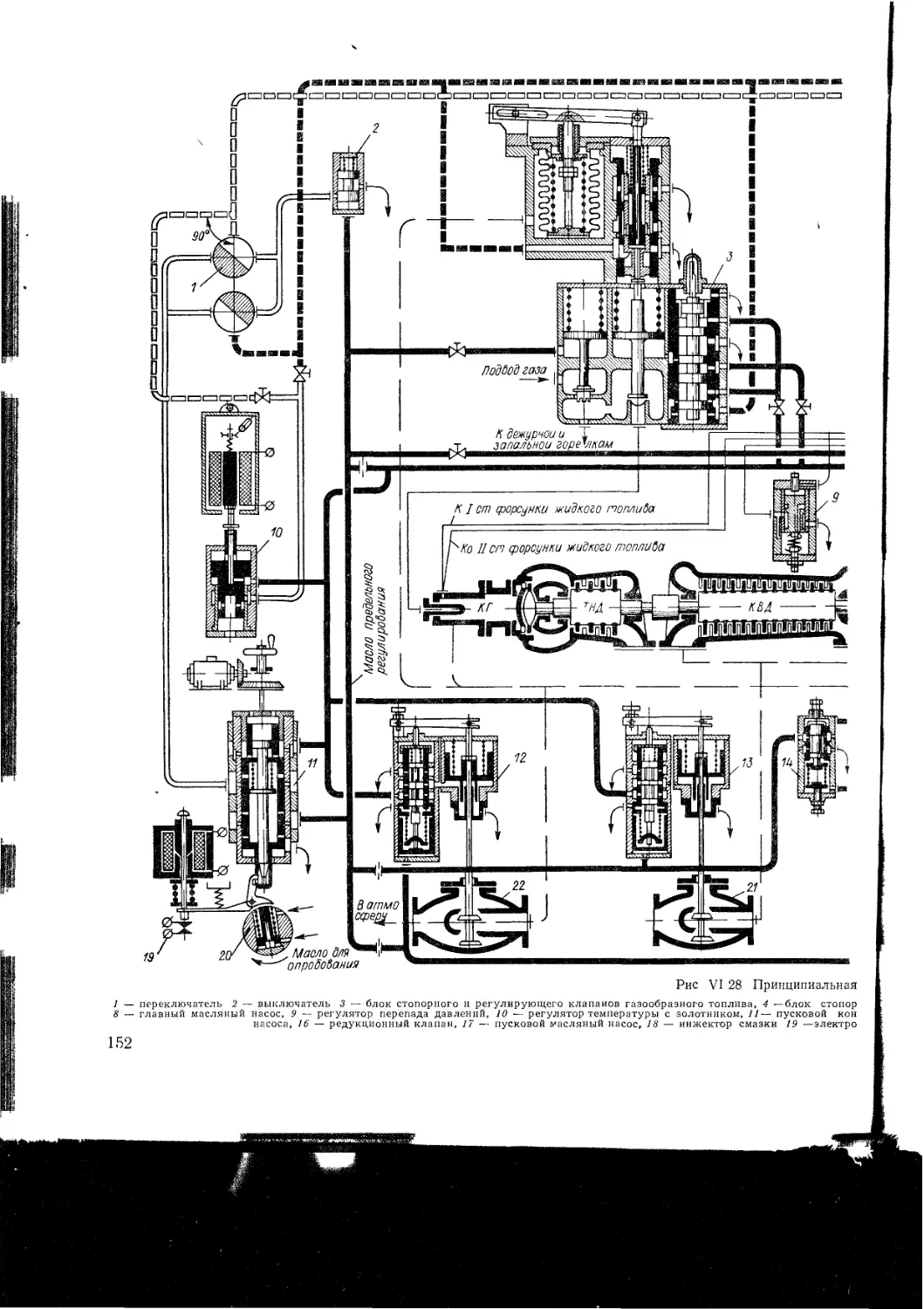
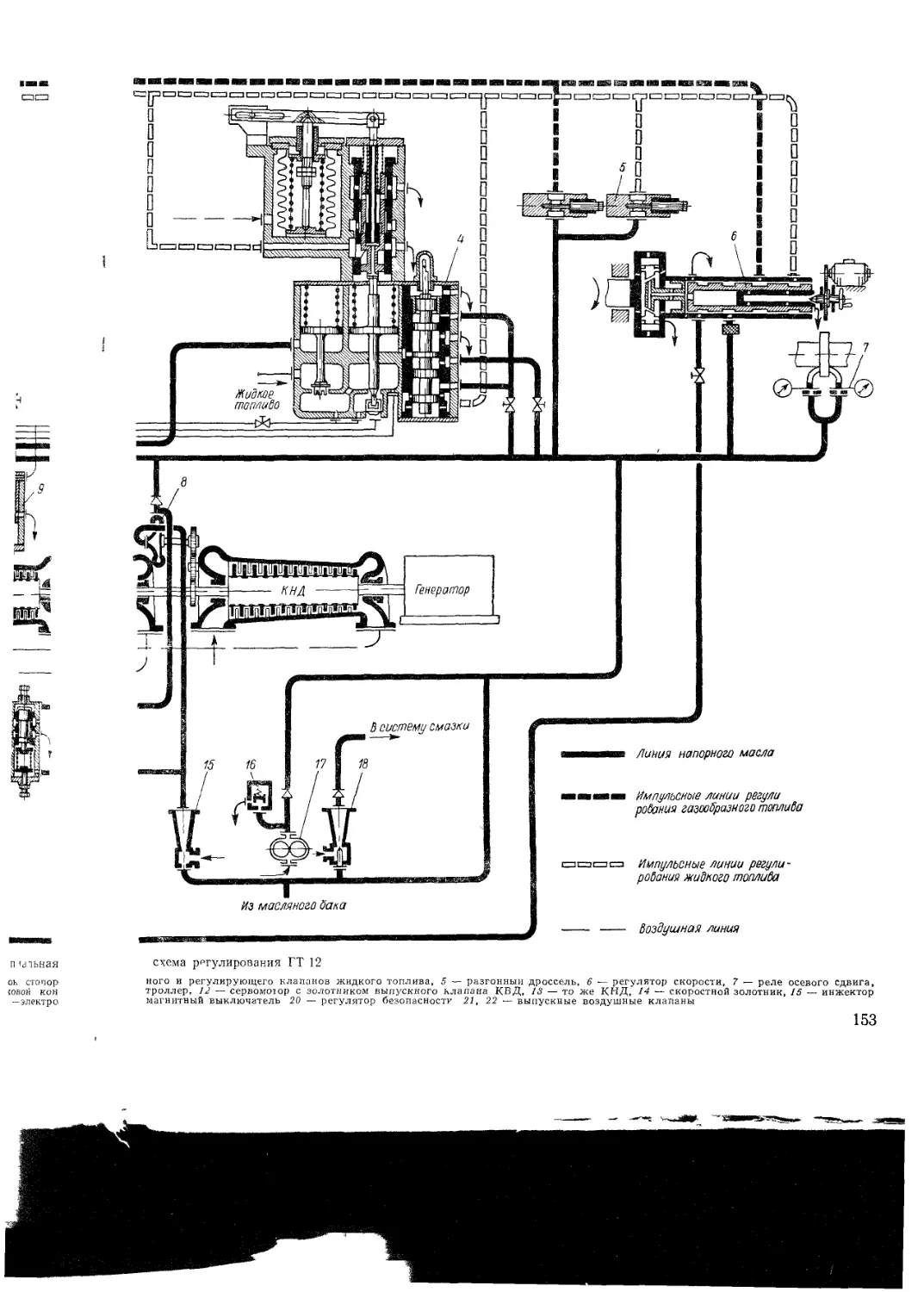
V I 5 Системы автоматического регулирования
ГТУ
Регулирование энергетических ГТУ
Регулирование ГТУдля газоперекачивающих
станций
Регулирование транспортных ГТУ
Глава VII Системы топлнвоподачи и маслоснабжения
Вспомогательное оборудование
VI I 1 Топливная система
Топливо для ГТУ
Системы подачи жидкого топлива
121
123
126
127
129
130
131
133
134
135
136
139
140
143
144
146
147
149
150
162
Системы подачи газообразного топлива
VII 2 Система маслоснабжения
VII 3 Вспомогательное оборудование
Воздухоочистительные устройства
Устройства для глушения шума
Устройства для охлаждения и подогрева
засасываемого воздуха
Охладители масла и охлаждающего воздуха
Противопожарная система
Источники питания электроэнергией для
собственных нужд
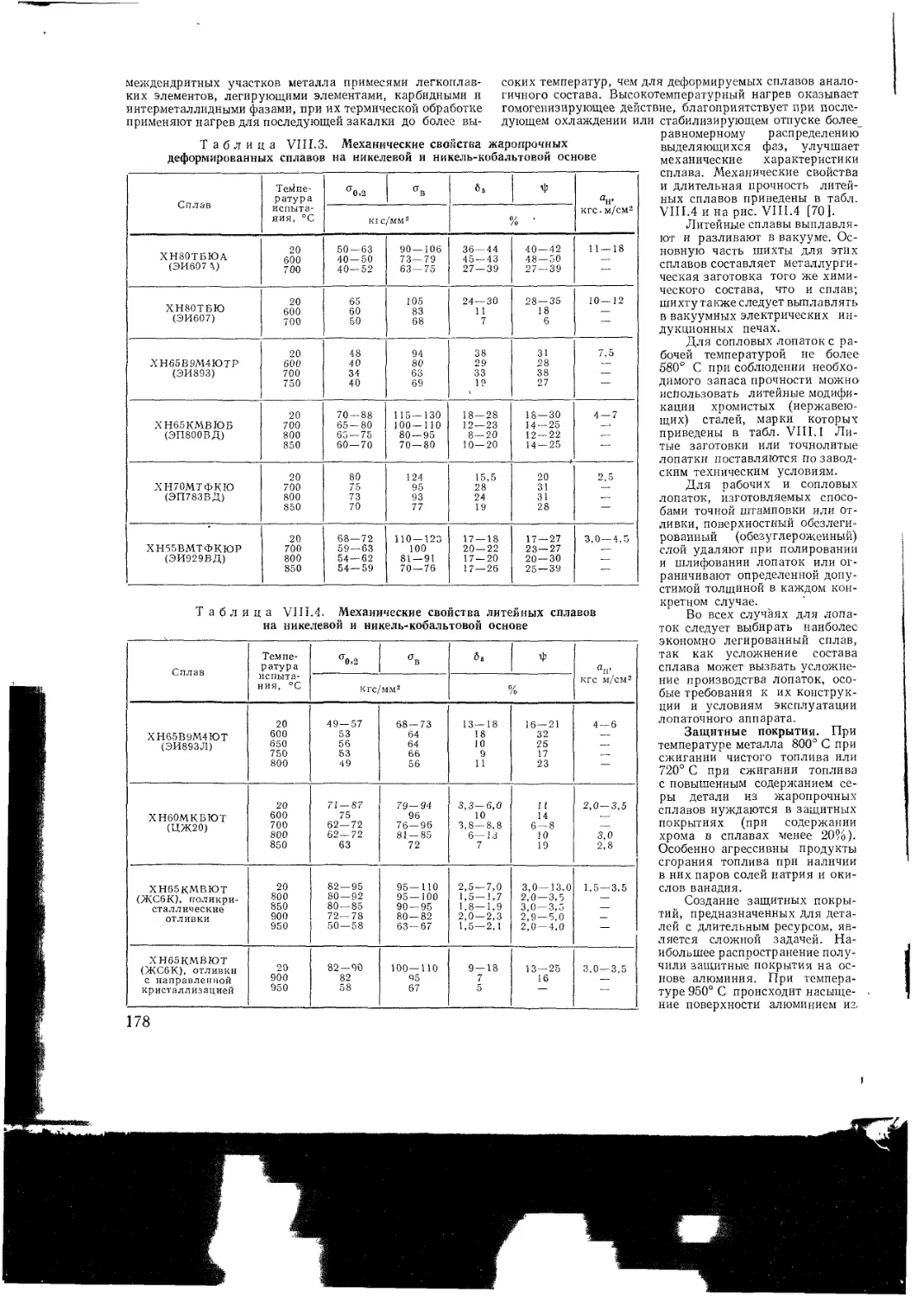
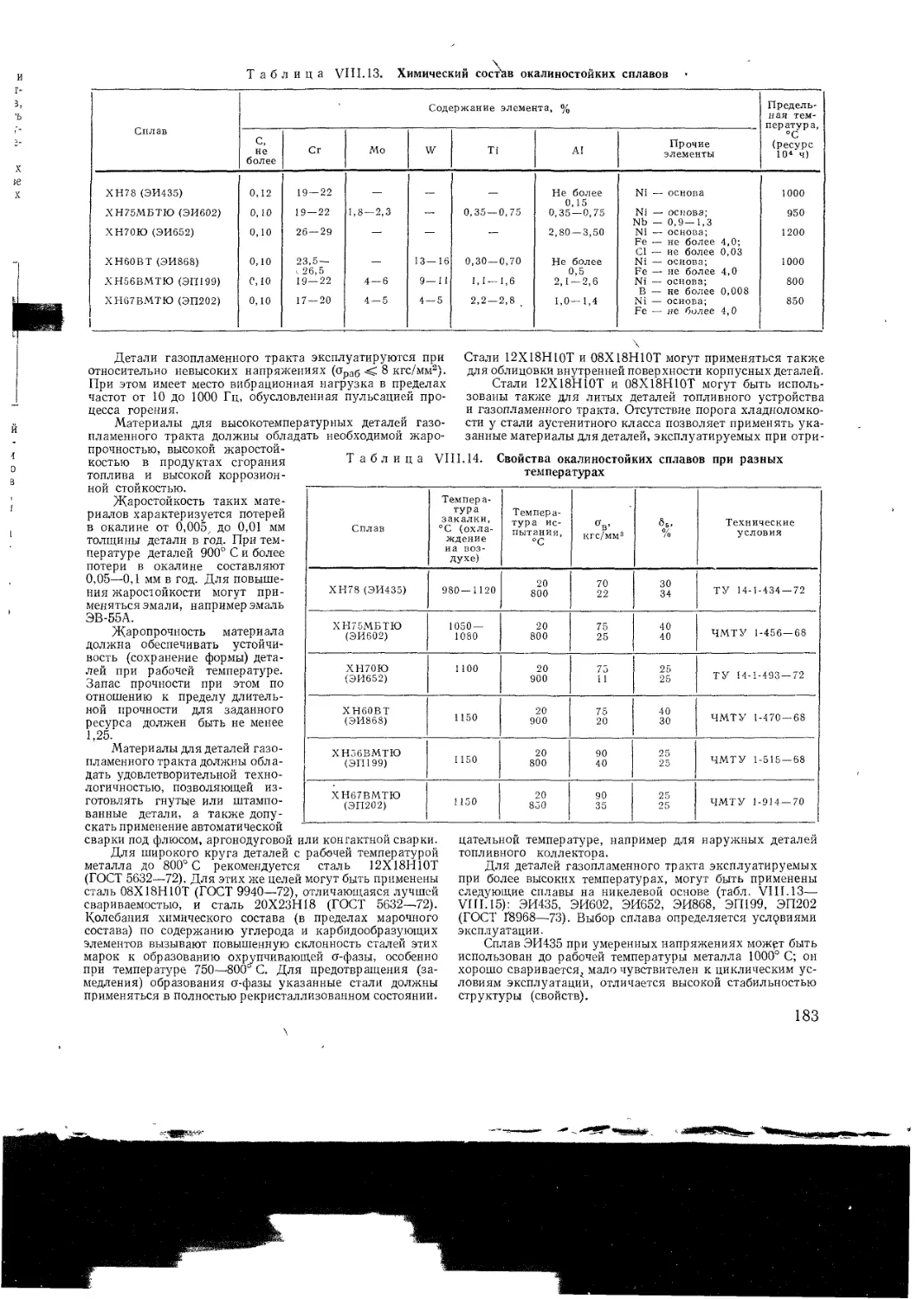
Глава VIII Материалы в газотурбостроении
VII I 1 Материалы для лопаток газовых турбин
VI II 2 Материалы для лопаток осевых компрес
соров
VII I 3 Материалы для роторов и дисков га
зовых турбин и компрессоров
VIII 4 Материалы для деталей камер сгора
ния и газопламенного тракта
VIII 5 Материалы для деталей корпусов га
зовых турбин и компрессоров
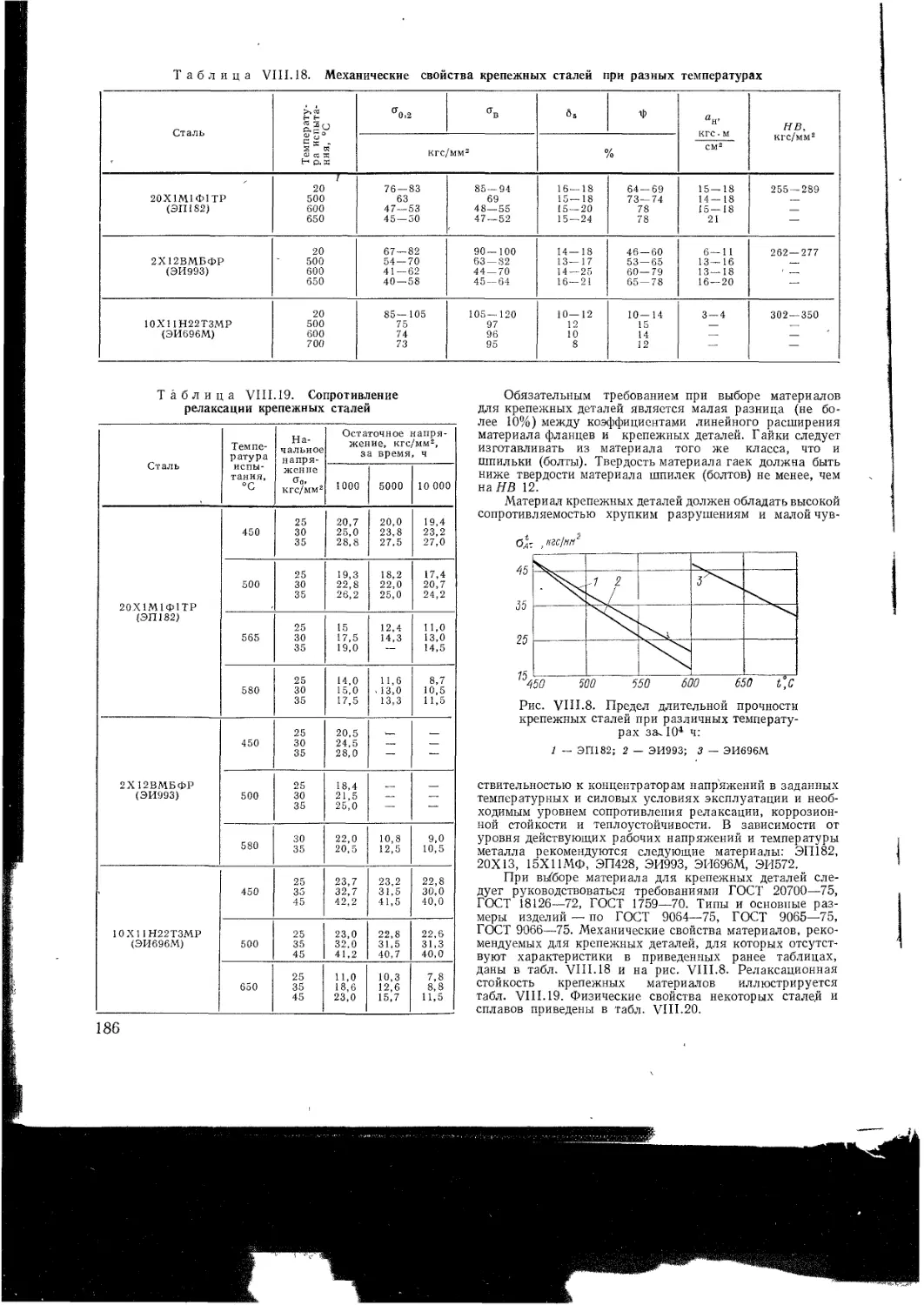
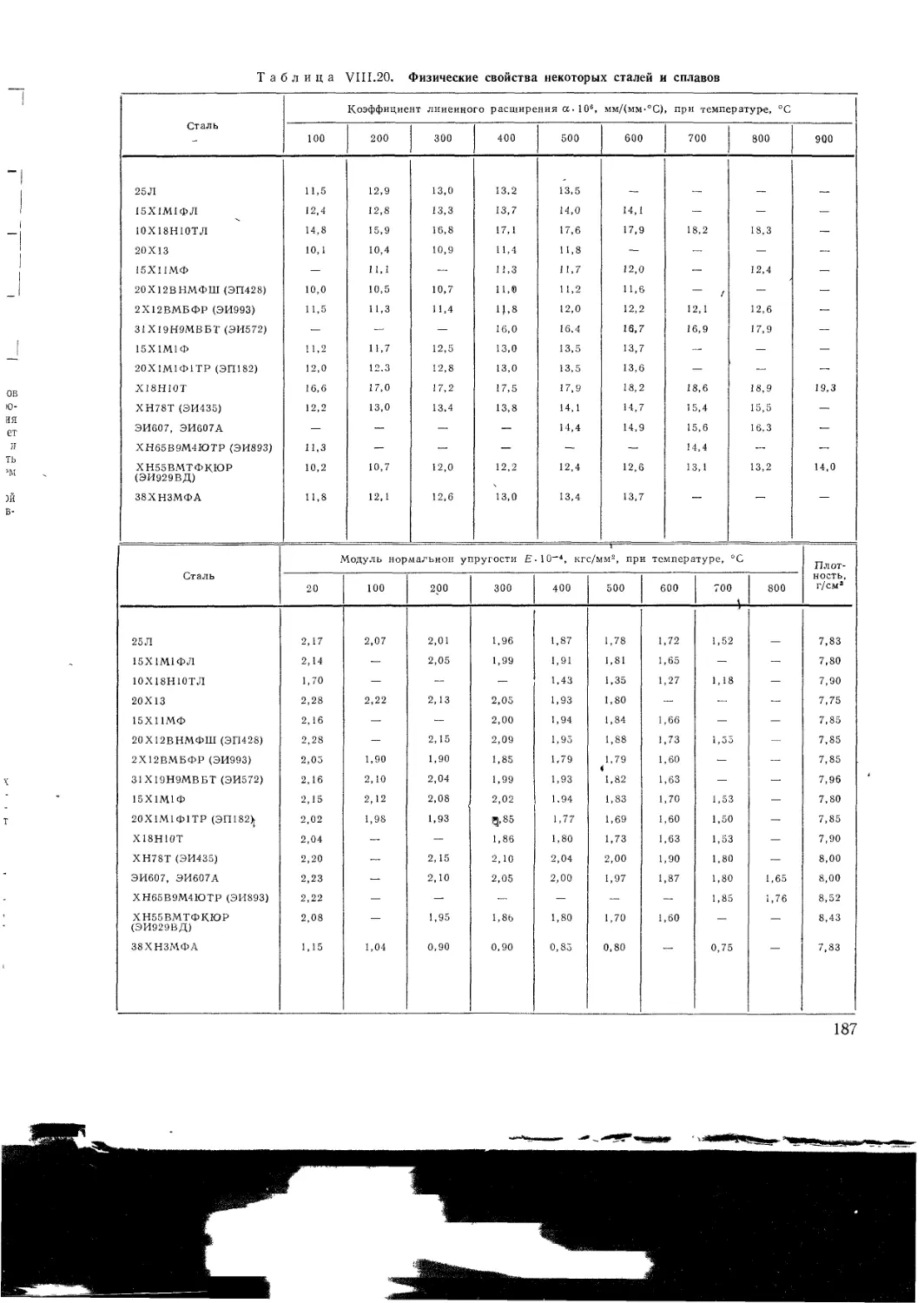
VII I 6 Материалы для крепежных деталей
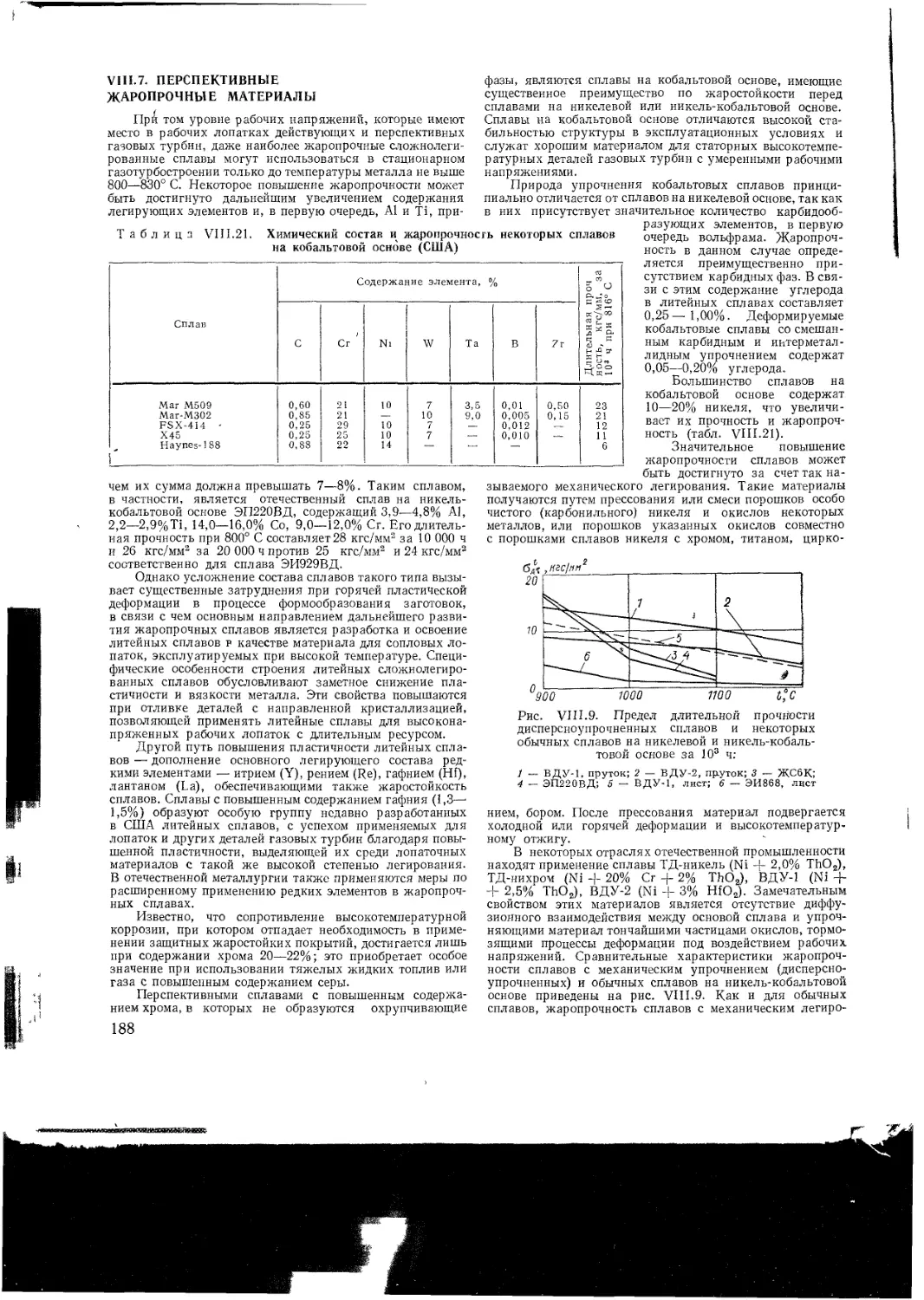
VI II 7 Перспективные жаропрочные материалы
VII I 8 Напряжения в основных деталях ГТУ
Напряжения в лопатках
Напряжения в дисках я роторах
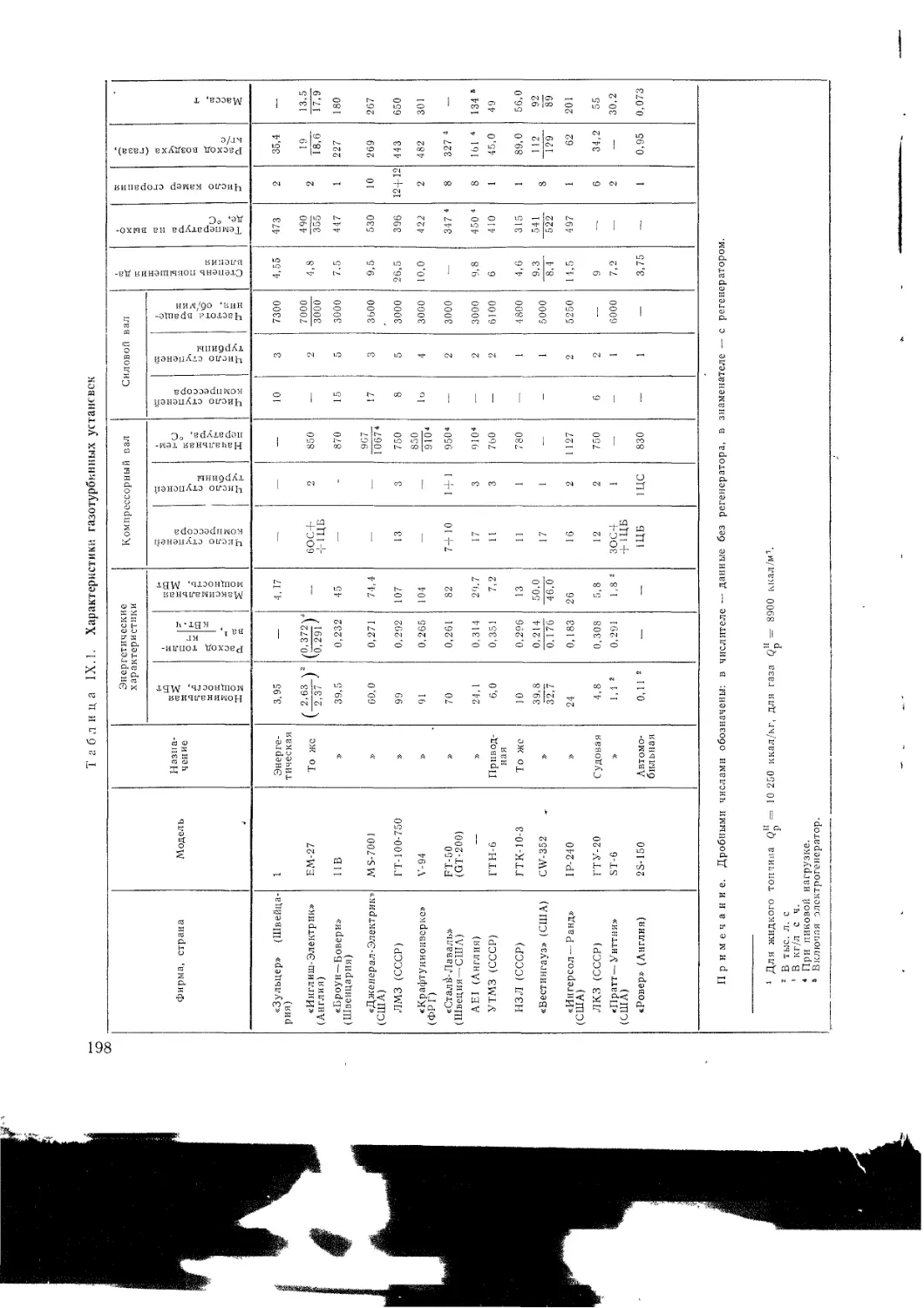
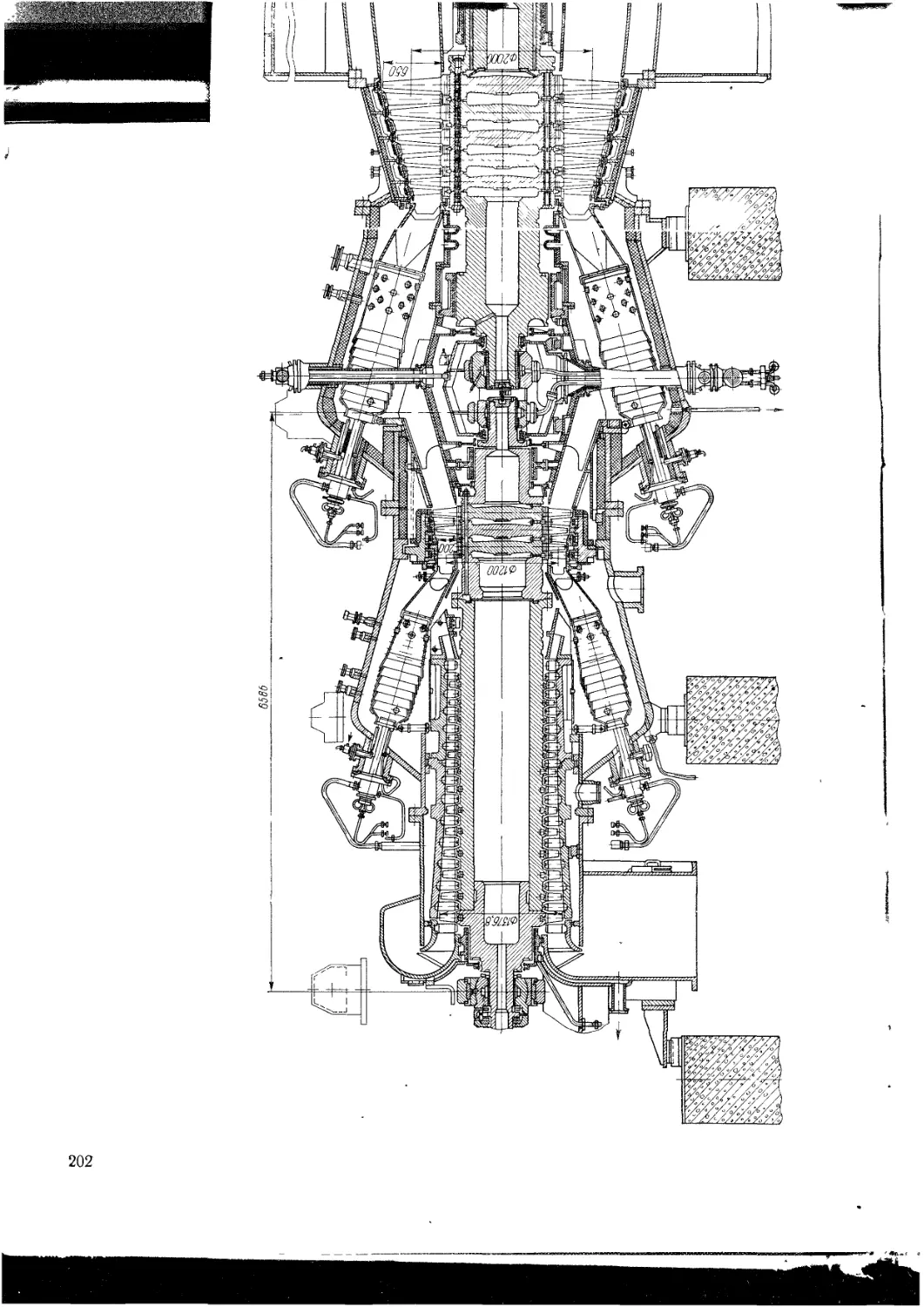
Глава IX Конструкции современных ГТУ
IX 1 Типовые конструктивные схемы
1X2 Общие вопросы проектирования
1X3 Конструкции отдельных типов ГТУ
Энергетические ГТУ
Приводные ГТУ
ГТУ, используемые в схемах ПГУ
Транспортные ГТУ
Приложение 1 Теплофнзическне характеристики не
которых газов
Приложение 2 Порядок расчета тепловой схемы ГТУ
Приложение 3 Расчет проточной части осевого ком
прессора методом частичного моделирования
Приложение 4 Расчет проточной части осевого ком
прессора методом продувок плоских решеток
163 Список литературы
167
166
170
171
172
173
174
179
181
182
184
185
188
189
W
193
194
196
208
214
215
220
222
224
225
231
ПРЕДИСЛОВИЕ
Последние годы характеризуются быстрым развитием газотурбинных уста-
новок для самых различных областей применения. Именно этим обстоятельством
объясняется тот повышенный интерес, который проявляется в широких кругах
специалистов к газовым турбинам.
Несмотря на то что по рассматриваемому вопросу в отечественной и зарубеж-
ной литературе опубликовано большое количество монографий, статей и учебных
пособий, существует потребность в обобщающем труде, в котором приводились бы
апробированное практические методы расчетов и проектирования отдельных
элементов ГТУ и всей установки в целом.
Предлагаемое справочное пособие является попыткой решить эту задачу.
В нем последовательно рассмотрены различные применяемые и перспективные
схемы ГТУ, методы расчета параметров этих схем, методы газодинамического
и теплового расчета лопаточных аппаратов газовых турбин и компрессоров, ка»
мер сгорания, теплообменных аппаратов (как на номинальном, так и на про-
межуточных режимах), методы расчета характеристик систем автоматического ре-
гулирования газотурбинных агрегатов. Приведены расчеты характеристик си-
стем топливоподачи, маслоснабжения и вспомогательного оборудования ГТУ.
Значительное внимание в справочном пособии уделено расчету тепловых
схем ГТУ, вопросам проектирования и расчета охлаждаемых лопаток высокотем-
пературных газовых турбин. Даны также рекомендации по применению материа-
лов для различных элементов ГТУ и основные характеристики этих материалов.
Проведен анализ конструкций наиболее типичных образцов современных
ГТУ, выпускаемых отечественными и зарубежными предприятиями.
Вопросы прочности основных деталей газовых турбин рассмотрены лишь
в минимально необходимом объеме, так как более подробно они освещены в соот-
ветствующей специальной литературе.
При изложении ряда разделов книги использованы результаты исследований,
выполненных при участии авторов на кафедре турбиностроения ЛПИ им. М. И. Ка-
линина и в ЦКТИ им. И. И. Ползунова.
По конкретным вопросам приведена библиография.
В приложениях даны необходимые справочные материалы общего характера,
а также примеры расчета отдельных элементов ГТУ по рекомендуемым методам.
Гл. I написана Е. А. Ходаком (за исключением п. 1.6, который раписан
Л. В. Арсеньевым и Е. А. Ходаком совместно), главы II (за исключением п. II.5,
написанного совместно с Л. В. Арсеньевым), VII и IX — В. Г. Тырышкиным,
гл. III — Ф. С. Бедчер, гл. IV — И. А. Боговым, главы V и VI — Л. В. Арсенье-
вым, гл. VIII — Е. Е. Левиным (за исключением п. VIII. 8, написанного В. Г.Ты-
рышкиным).
Все замечания и пожелания по содержанию книги просим присылать на
адрес издательства: 191065, Ленинград, ул. Дзержинского, 10.
ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Параметры установки
N — мощность (вид мощности — эффективная,
внутренняя и другие — определяется
подстрочным индексом)',
т] — к. п. д. (вид к. п. д. — электрический, эф-
фективный, внутренний и т. д. — опреде-
ляется подстрочным индексом);
М — вращающий (крутящий) или тормозной
момент сопротивления;
Н — удельная работа турбомашины;
л — степень повышения (понижения) давле-
ния;
G — массовый расход;
g — относительный массовый расход;
q — удельная теплота;
п — частота вращения;
О (р) — степень реактивности;
г — степень регенерации.
Параметры потока
Т; t — температура;
р — давление;
р — плотность;
i — энтальпия;
s — энтропия;
а — скорость звука;
с; w, и — абсолютная, относительная и окружная
скорости;
а; р — направление потока в абсолютном и отно-
сительном движении;
R — газовая постоянная;
k — показатель изоэнтропы;
п — показатель политропы;
Ср, Срт — удельные истинные и средние теплоемкости
при постоянном давлении;
v — удельный объем.
Термодинамические характеристики турбомашин
П — перепад энтальпий на турбину (компрес-
сор), корпус, отсек ступеней;
По (Яиз) — изоэнтропийный перепад энтальпий от
полного давления перед проточной частью
р* до статического давления за проточной
частью р2;
Нц (Н*3) — изоэнтропийный перепад энтальпий от
полного давления перед проточной
частью р*0 до полного давления за проточ-
ной частью р?;
h — перепад энтальпий в ступени, сопловом
(направляющем) или рабочем венце.
Индексы параметров в различных сечениях ГТУ 1
О — сечение, характеризующее невозмущен-
ное состояние наружного воздуха (напри-
мер, давление и температура наружного
воздуха);
1 — при входе в компрессор;
2 — при выходе из компрессора 2;
3 — при входе в турбину;
4 — при выходе из турбины;
5 — при выходе воздуха из регенератора;
6 — при выходе газа из регенератора.
Индексы параметров в различных сечениях турбины,
корпуса, отсека ступеней, ступени 3
О — перед проточной частью (перед первым
сопловым венцом);
2 — за проточной частью (за последним рабо-
чим венцом);
1 — между сопловым аппаратом и рабочим
колесом;
1с — за сопловым аппаратом;
1р — перед рабочим колесом.
Индексы параметров установки и ее характеристик
* — параметры заторможенного потока;
т — параметры в турбине (т. н — низкого дав-
ления; т. в — высокого давления);
г. т — параметры в газовой турбине;
п. т — параметры в паровой турбине;
к — параметры в компрессоре (к. н — низ-
кого давления; к. в — высокого давле-
ния);
г — параметры газа;
ух — параметры уходящих газов;
в — параметры воздуха;
вод — параметры воды;
топ — параметры топлива;
охл — параметры, связанные с охлаждением;
кр — критические параметры;
с (и) — сопловая (направляющая) лопатка;
р —• рабочая лопатка;
ст — ступень в целом;
1 В сложных схемах ГТУ к индексу сечения добавляется
буквенное обозначение компрессора или турбины. Например,
давление воздуха за компрессором высокого давления обозна-
чается р в, а давление рабочего тела за турбиной низкого давле-
ния — р4и и т. д.
2 Если требуется выделить сечение иа входе в камеру
сгорания и иа выходе нз нее, то рекомендуются индексы 2к. с
и Зк. с.
2 При рассмотрении промежуточной ступени в многосту-
пенчатой проточной части к индексу сечения добавляется буква I
или номер ступени. Например, параметры рабочего тела перед
сопловым аппаратом третьей ступени будут иметь подстрочный
индекс 03.
6
t — теоретический;
эф — эффективный;
в — внутренний;
пол — политропический;
э — электрический; эквивалентный;
из — изоэнтропийный.
Основные сокращения элементов ГТУ
ГТУ — газотурбинная установка;
ГТЭ — газотурбинная установка для привода
электрического генератора;
ГТН — газотурбинная установка для привода на-
гнетателя компрессорной станции газо-
провода;
ГТД — газотурбинный двигатель;
ПГУ — парогазовая установка;
ЗГТУ — замкнутая газотурбинная установка;
ГТ — газовая турбина х;
К — компрессор 1;
КС — камера сгорания х;
3 При нескольких турбинах, компрессорах или камерах
сгорания в схеме ГТУ к ним добавляются буквы, обозначающие
уровень давления в элементе (например, турбина высокого да-
вления— ТВД и т. д ).
ВО — воздухоохладитель;
Р — регенератор;
П — потребитель мощности (полезная на-
грузка).
Основные сокращения организаций
ЛМЗ — Ленинградский металлический завод;
НЗЛ — Невский машиностроительный завод
им. В. И. Ленина;
ХТГЗ — Харьковский турбинный завод
им. С. М. Кирова;
УТМЗ — Уральский турбомоторный завод
им. К- Е. Ворошилова;
Л КЗ — Ленинградский Кировский завод;
ЦКТИ — Центральный котлотурбинный институт
им. И. И. Ползунова;
ЛПИ — Ленинградский политехнический ин-
ститут им. М. И. Калинина;
МВТУ — Московское высшее техническое училище
им. Н. Э. Баумана;
ВТИ — Всесоюзный теплотехнический институт
им. Ф. Э. Дзержинского;
ИТТФ — Институт технической теплофизики АН
УССР;
МЭИ — Московский энергетический институт;
КАИ — Казанский авиационный институт.
Глава I
СХЕМЫ И ЦИКЛЫ ГТУ
1.1. СХЕМЫ И ИДЕАЛЬНЫЕ ЦИКЛЫ
Идеальный цикл ГТУ непрерывного горения, так назы-
ваемый цикл Брайтона (рис. 1.1), состоит из обратимого
процесса адиабатного сжатия газа в компрессоре от дав-
ления pt до давления р2 (линия 1—2), процесса подвода
теплоты от горячего источника к газу при постоянном дав-
лении р2=р3 (линия 2—3), вследствие чего удельный объем
Рис. 1.1. Идеальный цикл ГТУ непрерывного горения: а —
в Т—s-диаграмме; б — в р—а-диаграмме
и температура газа возрастают до значений, соответствую-
щих точке 3, обратимого процесса адиабатного расширения
газа в турбине от давления р3 до давления р4 (линия 3—4)
и процесса отвода теплоты к холодному источнику при
постоянном давлении газар4=р! (линия 4—1). Расширяясь
в газовой турбине, рабочее тело развивает механическую
Рис. 1.3. Схема простей-
шей открытой ГТУ непре-
рывного горения
Рис. 1.2. Схема замкнутой
ГТУ непрерывного го-
рения:
1 — поверхностный нагре-
ватель газа; 2 — поверхност-
ный охладитель газа
работу, достаточную как для обеспечения процесса сжа-
тия газа в компрессоре, так и для получения полезной
механической работы, передаваемой потребителю.
На рис. 1.1 изображен идеальный цикл замкнутой
ГТУ. В этой установке (схема — на рис. 1.2) теплота от
8
горячего источника подводится к рабочему телу в поверх-
ностном тейлообменнике /, а отвод теплоты в окружающую
среду происходит в поверхностном теплообменнике 2.
Рабочим телом в замкнутой ГТУ может быть не только
воздух, но и другие газы (например, гелий, углекислый
газ, азот и др.). Давление рабочего тела, поступающего
в компрессор, может быть более высоким, чем давление
окружающей среды (атмосферное давление). При неиз-
менной степени повышения давления в цикле, характери-
зуемой отношением р2/р1; возрастает давление газа и перед
турбиной. Вследствие повышения плотности рабочего
тела габариты компрессора и газовой турбины при одной
и той же полезной мощности будут снижаться по мере
увеличения рг.
Большинство современных ГТУ выполняется по откры-
той схеме непрерывного горения (рис. 1.3). В такой ГТУ
рабочее тело (воздух) сжимается в компрессоре и через
камеру сгорания нагнетается в газовую турбину. В ка-
меру сгорания непрерывно вводится топливо, при окисле-
нии которого кислородом воздуха выделяется теплота,
обеспечивающая повышение температуры рабочего тела
до необходимого уровня. Отработавший в газовой турбине
газ выбрасывается в окружающую среду. Если принять,
что процесс рассеивания теплоты в окружающую среду
эквивалентен процессу теплообмена в поверхностном тепло-
обменнике 2 (см. рис. 1.2) замкнутой установки, и прене-
бречь изменением теплофизических свойств рабочего тела
в камере сгорания, то идеальный цикл открытой ГТУ не-
прерывною горения в диаграммах состояния будет иметь
такой же вид, как идеальный цикл замкнутой ГТУ
Предложен ряд схем полузамкнутых ГТУ непрерыв-
ного горения, в которых рабочим телом является воздух.
Принципиальная схема одной из таких установок при-
ведена на рис. 1.4 [52]. Полузамкнутая ГТУ состоит из
основной замкнутой ГТУ, выделенной на рис. 1.4 штрихо-
вым контуром, и дополнительной открытой ГТУ, которая
служит для поддержания постоянного расхода рабочего
тела в замкнутом контуре и подачи воздуха, используе-
мого для окисления топлива, в камеру сгорания.
Известны также открытые ГТУ прерывистого горения,
или пульсирующие ГТУ (рис. 1.5). Камера сгорания та-
кой ГТУ снабжена тремя клапанами. При закрытых вы-
пускном 3 и топливном 2 клапанах в камеру сгорания ком-
прессором закачивается порция воздуха. При полном
давлении нагнетания впускной клапан 1 закрывается,
а клапан 2 открывается, и в камеру сгорания подается
порция топлива, которая воспламеняется с помощью элек-
трозапала. Температура и давление газа при этом мгно-
венно повышаются, открывается клапан 3, рабочее тело,
проходя через газовую турбину, расширяется, а затем
выводится в окружающую среду. Давление в камере сгора-
ния и перед турбиной быстро падает. После того как дав-
ление станет несколько ниже давления нагнетания ком-
прессора, открывается клапан 1, воздух прокачивается
через камеру сгорания, и цикл повторяется. Его отличие
от цикла Брайтона состоит в том, что подвод теплоты к ра-
бочему телу осуществляется по изохоре 2—3 (рис. 1.6).
Пульсирующая ГТУ может быть выполнена и без компрес-
сора. В этом случае изохорический процесс подвода теп-
лоты начинается от атмосферного давления. Тогда точки 1
и 2 на рис. 1.6 совпадают.
Рис. 1.4. Схема полузамкну-
той ГТУ непрерывного горе-
ния:
Рис. 1.5. Схема открытой
ГТУ прерывистого горе-
ния
1 — вспомогательная газовая
турбина; 2 — вспомогательный
воздушный компрессор
Несмотря на то что теоретически к. п. д. идеального
цикла ГТУ прерывистого горения является более высоким
по сравнению с ГТУ непрерывного горения, такие уста-
новки пока не нашли практического применения. Это объ-
ясняется тем, что к. п. д. реального цикла ГТУ преры-
вистого горения обычно существенно ниже, чем к. п.
Д-
цикла с изобарическим под-
водом теплоты, что, главным
образом, обусловлено неэко-
номичной работой турбины
Рис. 1.6. Идеальный цикл ГТУ прерывистого
горения: а — в Т—s-диаграмме; б — в р—v-
диаграмме
из-за переменности во времени параметров поступающего
газа, в нее. Кроме того, конструктивно ГТУ со сгоранием
при v = const значительно сложнее, чем ГТУ непрерыв-
ного горения.
По указанным причинам газотурбостроение разви-
вается в настоящее время исключительно на базе ГТУ
непрерывного горения, поэтому в дальнейшем изложении
будут рассматриваться установки только этого типа.
1.2. ОСНОВНЫЕ СООТНОШЕНИЯ ТЕРМОДИНАМИКИ
ДЛЯ ИДЕАЛЬНЫХ ГАЗОВ
Уравнение состояния однокомпонентного идеального
газа pv=RT. Уравнение состояния смеси идеальных
газов pv = RCMT, где RZM = У gtR;; gj — массовая доля
1
/-го компонента газа; R, — газовая постоянная /-го ком-
понента газа.
Удельная теплоемкость смеси газов сСм = S gjCj,
1
где с, — удельная теплоемкость /-го компонента газа
т
Энтальпия газа di = ср dT, или i — i0 = j" ср dT,
То
2 Л. В Арсеньев и др.
где То—’температура начала отсчета энтальпии газа.
При Т = То имеем i ~ i0 — 0. При ср = const имеем
i = ср (Т—То). Если 7’0 принимается по температуре
плавления льда при нормальных условиях, то То =
= 273,15 К, Т — То = t и i = cpt.
Полезная работа непрерывного потока газа dH =
Pi
= —v dp, или Н = j v dp.
Р2
Уравнение первого закона термодинамики для потока
газа dq = di — v dp, или q = z2 — гх + H.
Уравнение второго закона термодинамики для обра-
тимых процессов dq = Т ds, или s2— sx = J dq!T.
о
Изменение энтропии газа s2 •— sx = R In (px/p2) —
— cp In (T-JT2).
Термодинамическое тождество T ds = di — v dp.
Обратимый адиабатный процесс характеризуется соот-
ношениями:
dq = 0; ds = 0; с = 0; pvk = const;
7’2/л = («1м)/г“1 = (р2/р1)'п;
ff = pxnx[l —(p2/px)m]//n =
— СрТг [1 — (Рг/Рх)"2] — cp (^1 — Тг),
где с — удельная теплоемкость процесса; k = cplcv; m =
= (k— l)/k.
Для процесса сжатия Н < 0, для процесса расшире-
ния Н > 0.
Изотермический процесс . характеризуется соотноше-
ниями:
dT = 0; с = оо ; dH = dq = — vdp = Тds;
pv = const; qHRT) = H/(RT) = (s^—s^/R = In (px/p2).
При подводе теплоты к газу q > 0 и s2 — sx>0;
при отводе теплоты от газа q < 0 и sa — sx < 0.
Изобарический процесс характеризуется соотноше-
ниями:
dp = O; с = ср; v/T = const; dq = di;
H = 0; q = (2 — ix = cp(T2 — T1);
s2 —sx = Cpln (Tz/TJ.
Политропический процесс характеризуется соотно-
шениями:
с = const; pan — const; Та'2-1 = const; Tnpl'~'1 = const;
n — (.Cp — с)/(c0 с); Т2/= (цх/п2) =
= (p2/Pi)(^1)/n; sa-sx = cln(7’2/7’x);
H = рЛ [1 - (p2/px)(n-1)/n] n/(n - 1).
Необратимый адиабатный процесс характеризуется
тем, что часть развиваемой (подводимой) работы необра-
тимо превращается в теплоту (например, вследствие тре-
ния). Такой процесс может быть условно представлен
в виде последовательности некоторого числа политропиче-
ских процессов, в каждом из которых теплоемкость имеет
постоянное осредненное значение. Показатель политропы/!
на каждом участке вычисляется по параметрам в начале
и конце участка:
п = (In рх — In р2) /(In v2 — In nx).
При анализе ГТУ часто необратимый адиабатный про-
цесс в турбомашинах представляют как политропический
9
10
11
процесс с показателем степени, приближенно определяемым
из выражений
(п l)/n = Лпол ’ ^тПпол /77т
при расширении газа в турбине и из выражений
(П~ 1)/П= (Й — 1)/(Ипол) = ^к/Ппол = тк
при сжатии газа в компрессоре, где '>]пол — политропиче-
ский к. п. д. соответствующих процессов.
Для необратимого адиабатного процесса сжатия газа
Нк — РА [ 1 — (Р2/Р1)тк]/тк =
— — (Р2/Р1) К].
В расчетах ГТУ работу сжатия в компрессоре Нк принято
считать положительной. Если p2lpi = як> то
Нк = срТ;(я^-1)^срТ1Як,
где /7К — относительная работа сжатия газа.
Для необратимого адиабатного процесса расширения
газа при р,/р2 = лт
Дт = W1 (1 _ я~шт)Дт = _ я-тт^ =
— РрГ 1-Дт»
где Нт — относительная работа расширения газа.
Величины /7К и //т для обратимого и необратимого
адиабатных процессов удобно определять с помощью гра-
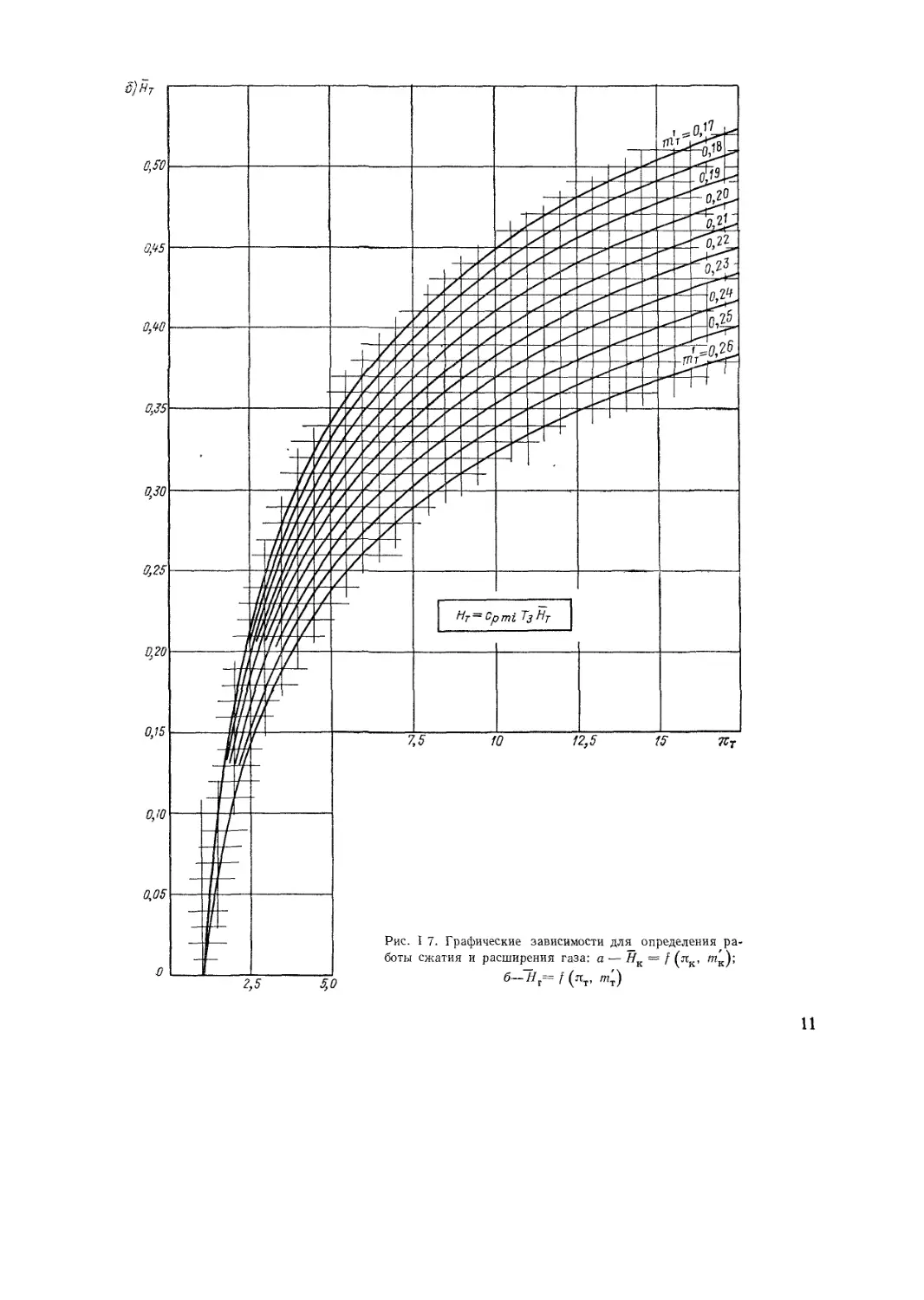
фических зависимостей, приведенных на рис. 1.7.
1.3. ПРОСТАЯ ТЕПЛОВАЯ СХЕМА ГТУ
Идеальный цикл
В идеальной ГТУ, выполненной по простой тепловой
схеме, принимается ср= const; k = const; р3/р4 = р2/рг =
= л (обозначения точек приняты в соответствии с рис. 1.1)
Полезная удельная работа Н ~ НТ — Нк, или для обра-
тимых адиабатных процессов сжатия и расширения
И = срГ3(1 — л-т)(1 — т.тт), (II)
где т = Tx/Tg — отношение характерных температур ра-
бочего тела.
Рис. I 8. Характеристики идеального цик-
ла простейшей ГТУ
Относительная полезная работа Н = Н/(срТ3) обра-
щается в нуль при двух значениях л (рис. 1.8) = 1 и
л2 = (1/т)1/т. Между этими двумя значениями имеется;
оптимальное л = при котором величина Н
достигает максимального значения Дщах = (1 — Кт)2.
12
Термический к. п. д. газотурбинной установки
(1.2)
где qL = Ср (Т3— Т2) — затраты теплоты на подогрев
1 кг рабочего тела. Тогда
T]Z=I— n~m, (1.3)
т. е. зависит только от л и физических свойств газа,
характеризуемых показателем ш. Термический к. п. д.
идеальной ГТУ монотонно возрастает при увеличении л
ОТ Т)< mm = о при Л = Лх ДО Т]< max = 1 —• Т при Л = Л2
(рис. 1.8). Максимальное значение к. п. д. цикла Брайтона
соответствует значению к п. д. цикла Карно, однако в этом
предельном случае Н = 0 и <?!= 0. При Н = Ятах к. п. д.
ГТУ в _1 + Кт раз меньше к. п. д. цикла Карно и равен
1 — Кт.
Степень совершенства идеального цикла ГТУ, вы-
полненной по простой схеме, может характеризоваться
также коэффициентом полезной работы, определяемым как
отношение удельной полезной работы установки к удель-
ной работе газовой турбины.
<р = Н/Нт = 1 — хлт. (1.4)
При л = л, коэффициент полезной работы достигает
максимального значения <ршах =1 — т; при л = л2 =
= (I/t)1^"1 получается ср = 0. Между этими предельными
значениями величина ср монотонно убывает (рис. 1.8).
При Н '= /7Шах имеем ср = 1 — Кт.
Рассмотренные характеристики цикла Брайтона свя-
заны между собой соотношением
Я=<ртц. (1.5)
Реальный цикл
В реальных условиях все процессы в ГТУ являются
необратимыми, что оказывает большое влияние на харак-
теристики установки. Необратимость реальных процессов
вызвана
а) потерями располагаемой работы в турбине и ком-
прессоре, которые оцениваются внутренними к. и. д.
турбомгшин Т]т ч тк,
б) потерями давления рабочего тела в тракте ГТУ,
которые определяются коэффициентом гидравлических
потерь.
Если приближенно считать расход рабочего тела оди-
наковым в любой точке тракта ГТУ, то реальный цикл
с учетом этих потерь может быть построен в тепловых
диаграммах. На рис. 1.9 действительный процесс расшире-
ния изображен линией 3—4, а действительный процесс
сжатия — линией 1—2. Точками 2t и 4t отмечено состоя-
ние газа соответственно в конце изоэнтропийного расшире-
ния и сжатия 1, точкой 0 — параметры окружающей среды.
Внутренняя удельная работа ГТУ определяется по
формуле
/7в = (1 + ётоп) Нт Нк • йтопНтоп, (1-6)
где Нтоп — удельная работа сжатия топлива; gron —
— GTon/GK — расход горючего GTOn, отнесенный к рас-
ходу рабочего тела GK, поступающего в компрессор.
Если ГТУ работает на жидком топливе, то работа,
затрачиваемая на его сжатие, составляет менее 1%
от работы расширения и ее целесообразно отнести
к внешним потерям энергии и учитывать при опреде-
лении механического к. п д. [52]. Если горючий газ
1 Поскольку при анализе схем ГТУ давление рабочего
тела целесообразно задавать как давление адиабатного торможе-
ния во всех точках тракта, то индекс * у параметров в даль-
нейшем опускается
поступает в ГТУ уже сжатым, затраты на сжатие входят
в стоимость топлива и учитываются в технико-s кономи-
ческих расчетах.
Если горючий газ сжимается в специальном компрес-
соре, то работа на его сжатие может быть значительной.
В этом случае при анализе циклов ГТУ принимается [52],
что GK — сумма расходов воздуха и горючего газа. По-
скольку топливный компрессор при малом расходе горю-
чего газа может иметь значительно более низкий к. п. д.,
чем основной компрессор, внутренний к. п. д. процесса
-сжатия рабочего тела и топлива в расчетах следует при-
нимать несколько меньшим. В уточненных расчетах ра-
Рис. 1.9. Реальный цикл ГТУ:
а — в i—s-диаграмме; б — в р—^-диаграмме
боту на сжатие горючего газа следует вычислять особо,
пользуясь уравнением (1.6).
Вследствие потерь давления в тракте ГТУ степень
повышения давления в компрессоре лк = p2<Pt больше,
чем степень понижения давления в турбине ят = р3/р^
Обозначим лт — vnK, где v — коэффициент, харак-
теризующий общие потери полного давления. Для ГТУ,
выполненной по простой схеме,
v = (1 — SIix) (1 — §к. т)/( 1 Ч- §вых) >
где в соответствии с обозначениями на рис. 1.9, б
^ВХ == Лрвх/Ро’ ёк. Т = Арк. т/р2> ёвых ~ ^Рвых/Ро-
При сделанных предположениях внутренняя удель-
ная работа ГТУ может быть представлена в виде
"в = ЙтСртТ3 [1 - ('’ЯкГтТ ) 'Пт -
(!-7)
где gT = GT/GK.
Внутренний к. п. д. ГТУ
т)в = //в/<71> (1-8)
где 71 — удельный расход теплоты в камере сгорания,
определяемый из уравнения ее теплового баланса
‘71 = ёгт(3-1'1-срк'Г1 (якК- 0Лк- (!-9)
Коэффициент полезной работы реальной ГТУ
или
m
<р=1------—1----------Як ~ 1--------1. (1.Ю)
Срт gT i-(VJlK) т'г т1тТ1к
Анализ циклов ГТУ часто производится в широком
интервале изменения лк. При этом следует иметь в виду,
что политропические к. п. д. турбины т]пол. т и компрес-
сора т)пол. к в меньшей степени зависят от л, чем адиабат-
ные к. п. д. этих турбомашин. Поэтому если зависимость
адиабатных к. п. д. от параметров цикла не задана, в рас-
четы могут быть введены политропические к. п. д. турбо-
машин, которые приближенно принимаются не зависящими
от л. При использовании политропических к. п. д. турбо-
машин основные расчетные формулы принимают вид:
Нв = ^рт^З [1 - (™к)~тт] -
(1.11)
<?! = «т'з - h ~ сркГ1 (,якК~ О’
(1.12)
Помимо потерь связанных с
необратимостью процессов в ГТУ
и оказывающих непосредственное
влияние на состояние рабочего
тела, имеются внешние потери
энергии, уменьшающие полезную
работу, но не изменяющие состоя-
ния рабочего тела (потери от тре-
ния в подшипниках, потери вслед-
ствие утечек рабочей среды через
концевые уплотнения, затраты
энергии на привод топливного и
масляного насосов и др.1). Удель-
ная эффективная работа ГТУ Не определяется по формуле
Не = Нв-Нм, (1.13)
где Нм — сумма внешних потерь'располагаемой работы.
Эффективный к. п. д. ГТУ г]г — отношение эффек-
тивной работы Не, отдаваемой двигателем потребителю,
к действительному количеству затраченной теплоты:
пе = не1я\, (1-14)
где q\— удельный расход теплоты с учетом потерь Д<?
в камере сгорания, так что = <71 + Л<7-
Если ввести механический к. п. д. ГТУ т]м = Не!Нв
и к. п. д. камеры сгорания г]к. с = q-Jq'i, эффективный
к. п. д. может быть представлен в виде
Пе = Пв'Пм'Пк. с- (1-15)
Механический к. п. д. ГТУ связан с механическим
к. п. д. турбины т]м. т и компрессора г]м. к зависи-
мостью [52]
Пм = г]м.т/ф — (1— <р)/(ФПм. к). (1-16)
где т)м. Т (^T * ^М. t)/^ Ям. К == (^К Hyi. к)»
/7М. т и //м. к — механические потери энергии соответ-
ственно в турбине и компрессоре.
Анализ параметров реальной ГТУ
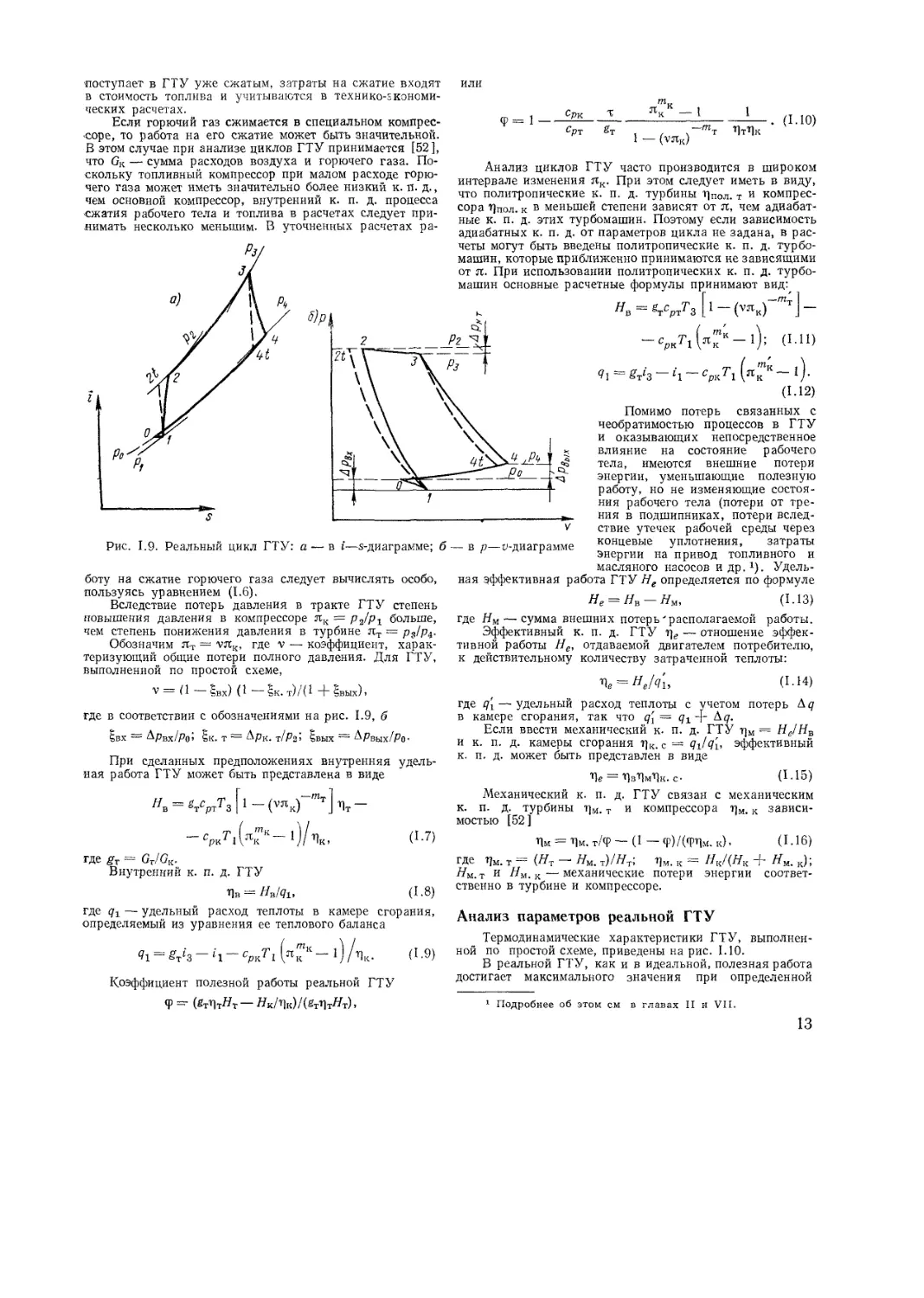
Термодинамические характеристики ГТУ, выполнен-
ной по простой схеме, приведены на рис. 1.10.
В реальной ГТУ, как и в идеальной, полезная работа
достигает максимального значения при определенной
<р — (йтЛт^Т--Лк/Як)/(&гЯтЛт)>
1 Подробнее об этом см в главах II и VII.
13
степени повышения давления воздуха в компрессоре пк =
= лкн. Если полагать, что т)т и т]к не зависят от л, то
_ / 7?т gT ПтПк \V(«T+mK) ,т 17,
Як№ D т т • I1-17)
I ‘'•к V т L /
Рис. 1.10. Характеристики ГТУ, выполненной по про-
стой тепловой схеме (т)пол. т=0,85; г]ПОл. к = 0,89; v =
= 0,93; 7\ = 288 К): а — т]в = f (Нв, t3) (точками на-
несены значения лк); б — <|- - / (лк, /3):
1 — fs = 1050° С; 2 — t3 = 950° С, 3 — t3 = 850° С; 4 —
= 750° С
При использовании политропических к. п. д. турбо-
машин
«г
l/(m'+mB)
(1-18)
К. п. д. реальной ГТУ достигает максимального зна-
чения при некотором значении лк = лК1). Если принять,
14
что 1]т и 7]к не зависят от л, то
_ Г RT gT ПтПк 11/(тт+тк)
КТ| vmT т(1- Т]в)
(I.19)
или, если использовать политропические
к- п. д.,
. _Г2?т йт Дпол. тПпол. к |
К11“ rk < т(1-пв)
V
1/(т'+«к) -
(1.20)
Оптимальные значения лкн и лКГ| свя-
заны между собой зависимостью
i/(mT+mK)
= ’ <L21>
Из приведенных формул видно, что-
снижение параметра т вызывает увеличе-
ние лкя и лКт). При неизменной темпера-
туре воздуха перед компрессором сниже-
ние т происходит за счет повышения тем-
пературы газа перед турбиной Т3. Рост t3
от 850 до 950° С вызывает увеличение лкя
примерно от 8 до 10, а лКТ1 — от 15,7
до 21 (рис. 1.10).
Температура геза Т3 оказывает боль-
шое влияние на к. п. д. и полезную ра-
боту установки. В рассмотренном интер-
вале температур при лк = 10 относительное повышение
к. п. д. составит 5,3%, а полезной работы — 27%.
Кривые на рис. 1.10 построены при фиксированных,
значениях т]Пол. т> т1пол. к и других параметров. Изме-
нение т]в и ЯЕ при небольшом отклонении этих пара-
метров может быть оценено по следующим приближенным
зависимостям:
ДЯВ (Т3)/ЬТз — ДЯВ (т]т)/ДЛт —
= Дт)в (Пт)/Д’Пт= 1/<р;
ДЯВ (v)/Av = Дт)в (v)/Av =
= (т;/<Р)[(^лк)тт-1]“1;
Д#В (Т]к)/Д'Пк ~ Дт]в (11к)/[ДТ|к (1 Лв)] =
= -дяв(Л)/ДЛ=-(1-ф)/ф;
Дт]в (т)/Дт= — (1/<р— 1/71),
(1.22)
где ДЯВ = ДЯ/ЯВ, Дг)в = Дг]/т)в — относительное изме-
нение соответственно полезной работы и к. п. д.; Д73^
ДТ1!, Д1]т, Дт)к, Av, Дт—относительное изменение иссле-
дуемого параметра; 7j= qj(.g-гСртТз) —-относительный рас-
ход теплоты в камере сгорания.
Из этих формул видно, что небольшое отклонение
выбранных при расчете параметров может существенно
повлиять на характеристики установки. Так, при Т.>--
— 1223 К и пк= 10 имеем ср =~ 0,418. Относительное от-
клонение к. п. д. турбины па 1% от расчетного значения
вызовет относительное изменение к. п. д. и полезной ра-
боты ГТУ на 2,4%. Аналогичное отклонение к. п. д. ком-
прессора вызовет изменение полезной работы на 1,4% и
к. п. д. установки примерно на 1% при расчетном уровне
к. п. д. 30,3%.
Уменьшение температурного коэффициента т приводит
к росту к. п. д. ГТУ г]в, причем небольшое изменение
температуры Tj вызывает повышение к. п. д. в несколько
раз большее, чем такое же изменение температуры Т3.
Так, при т= 0,25 понижение температуры 1\ на 1 К
равносильно повышению температуры Т3 на 4 К.
Так как лК|1 значительно больше, чем лкн, то при
лк — лкТ) происходит существенное снижение полезной
работы ГТУ по сравнению с ее максимальным значением.
Так, при t3 = 950° С снижение полезной работы проис-
ходит примерно на 14%. Аналогично при лк = лки про-
исходит снижение к. п. д. по сравнению с его максималь-
ным значением. В рассмотренном примере относительное
снижение к. п. д. составляет 9,2%.
Величину л,, следует выбирать в зависимости от на-
значения ГТУ и режима ее работы. Для пиковых энерге-
тических ГТУ и ГТУ вспомогательного назначения значе-
ние лк выбирают близким к лк//, а для ГТУ, работающих
в базовом режиме, и транспортных установок целесообраз-
ный уроень лк приближается по величине к лК11-
1.4. ГТУ С РЕГЕНЕРАЦИЕЙ
Идеальная ГТУ. Степень регенерации
Одним из средств повышения к. п. д. ГТУ является
применение регенеративного подогрева воздуха перед его
поступлением в камеру сгорания. Повышение темпера-
туры воздуха осуществляется в специальном теплообмен-
нике— регенераторе (рис. 1.11, а). Количество теплоты,
передаваемой воздуху в
регенераторе, характери-
зуется степенью (коэффи-
циентом) регенерации г,
которая представляет со-
бой отношение действи-
тельного значения повы-
шения энтальпии воздуха
в регенераторе (z5—/2) к
максимально возможному
<'4в—Д)1' т- е-
Рис. 1.11. ГТУ с регенерацией: а —
тепловая схема; б — характеристики
идеальной установки
г = ('5 - «-2)/(йв - г'2) - (Т5 - Г2)/(Г4 - 7%). (1.23)
С ростом лк температура за компрессором увеличи-
вается, а за турбиной — падает. При фиксированном зна-
чении коэффициента г количество теплоты, сообщаемой
воздуху, будет уменьшаться. При некотором значении
лк = лкг имеем Т2 = Т4, и осуществление регенерации
становится невозможным. В идеальной ГТУ равенство
температур Т2 и возникает при лкг = лки, поэтому
в такой схеме регенерация возможна в диапазоне измене-
ния лк от 1 до лкн.
1 Энтальпия воздуха определяется по температуре Tt.
К- п. д. идеальной ГТУ с регенерацией
т] = тц/[1 — г (1 — т]//ф)], (1-24)
где т|/ — к. п. д. цикла Брайтона.
При г = 1 получим г] = <р. Значение лк = лкг1, при
котором к. п. д. ГТУ достигает максимального значения,
определяется по формуле
{(1 — гт])/[1 — т] (1 — г)]}1/,(2т). (1.25)
Отсюда следует, что лкт) = лкп при г = 0,5. При г > 0,5
выполняется условие 1 с лКт) <: лкн, а при г < 0,5 к. п. д.
достигает максимального значения при лк = лкн-
Характеристики идеальной ГТУ с регенерацией по-
казаны на рис. 1.11,6 Применение регенерации в ГТУ,
выполненной по простой схеме, целесообразно только при
относительно низких значениях лк (при лк < лкн и вы-
соких значениях г.
Анализ параметров реальной ГТУ
В реальной ГТУ температура воздуха за компрессо-
ром 7’2 будет равна температуре газа за турбиной Т4 при
условии
Як = лкг = (1.26)
Сравнивая и из формул (1.26) и (1.18), по-
лучим зависимость
1ХкН= М^поЛ.т%оЛ.Л/ЯК) >
из которой видно, что в реальной ГТУ всегда лкг > лкя.
К. п. д. ГТУ с регенерацией определяется по формуле
г1в = (§Лт-/7к)/[§т13- 11-Як-г(цв- i2)].
(1-27)
Величина лк = лкт), при которой к. п. д. ГТУ дости-
гает максимума, определяется из выражения
_ — Г 1 ^'Пвсрк/(^тсрт) *]
ЛКГ| 1-(1-Г)Т1в J
. (1.28)
Применение регенерации значительно понижает ве-
личину лкг1, а при г > 1/[1 + Срк/^тСрт)] 0,5 имеем
Величина степени регенерации оказывает большое
влияние на размеры теплопередающей поверхности регене-
ратора Fp. Относительную поверхность регенератора
можно приближенно определить по формуле
/р —
ф/гР
срк^к
11.29)
где йр — средний коэффициент теплопередачи в регенера-
торе; ф — поправочный коэффициент для теплообменника
с перекрестным током воздуха и газа [72 ], для теплообмен-
ника с продольным током ф = 1; с = cPKGKl(cPTGT) —1 от-
ношение полных теплоемкостей воздуха и газа.
В ГТУ без отборов воздуха на охлаждение газовой
турбины можно принять с 1, и в этом случае fp = г/(1 —
— г). С ростом г относительная поверхность регенератора
увеличивается, стремясь к бесконечности при г ->• 1.
Включение регенератора в схему ГТУ вызывает до-
полнительные потери давления, которые также зависят от
степени регенерации. Согласно [66], относительные по-
тери давления со стороны нагреваемого воздуха
Др2/р2 = Рк^/и — г), (1-30)
а со стороны горячего газа
Др4/р4 = ₽тгД1 — г), (1-31>
15
где Pf; = ш2с/;к/(27?'Л|'/грл d2z), С — коэффициент гид-
равлического сопротивления, ш — средняя скорость воз-
духа, Т — средняя температура воздуха; d —• диаметр
трубок регенератора; z — число трубок регенератора,
через которые протекает 1 кг/с нагреваемого воздуха.
Коэффициент рт определяется аналогично по соответ-
ствующим параметрам.
Общий коэффициент потерь давления в регенера-
торе 1 — gp можно найти как отношение степени пониже-
Рис. 1.12. Характеристики ГТУ с регенерацией
СПпол. т = 0,85, т]пол. к — 0,89; Рр = 0,025):
----------— t3 = 850° С, --- — t3 = 1150° С
ния давления газа в ГТУ с регенератором лт к степени по-
нижения давления газа в ГТУ без регенератора лт0-
1 — |р = лт/лт0 = (1 — Др2/р2)/(1 + bpiJPt), (1.32)
или
ёр » Ьръ1р2 + Др4/р4 = Эр^/(1 — г), (I 33)
где Рр = Рк + Рт — обобщенный коэффициент. В ориен-
тировочных расчетах можно принимать Рп = 0,024-0,04.
С учетом (1.30) коэффициент v = лт/лк, характеризу-
ющий общие потери полного давления в ГТУ с реге-
нерацией, определяется по формуле
v = (1 - §Вх) (1 - Ь) (1 - U т)/(1 + UJ. (1-34)
Потери давления в регенераторе вызывают снижение
полезной работы ГТУ, особенно сильное при больших зна-
чениях г. Целесообразная величина степени регенерации
зависит от як и ts и при ts - 850° С составляет г — 0,75-*-
-0,80, а при t3 = 1150° С- г = 0,80-0,85.
Зависимость т]в ГТУ с регенерацией от г и лк при-
ведена на рис I 12, из которого видно, что при правиль-
ном выборе параметров применение регенерации может
существенно повысить к. п д установки. Однако в каж-
дом конкретном случае вопрос о применении регенерации
должен решаться на основе результатов технико-экономи-
ческого анализа с yt-етом удельных затрат на топливо
и стоимости регенератора
1.5. ГТУ С ПРОМЕЖУТОЧНЫМ ОХЛАЖДЕНИЕМ
И ПОДОГРЕВОМ РАБОЧЕГО ТЕЛА
Изотермическое сжатие и расширение
Идеальный цикл ГТУ с изотермическим сжатием и рас-
ширением в Т—-s-диаграмме приведен на рис. I 13. Про-
цесс сжатия рабочего тела изображается изотермой 1—2',
а процесс расширения — изотермой 3—4’. По сравнению
с политропическим процессом 1—2 удельная работа при
изотермическом сжатии уменьшится на величину
ДЯК = сркТ1 [(<К - 1) - 1П лк К]>
а удельная работа расширения увеличится по сравнению
с политропическим процессом 3—4 на величину
ДНт = СртТ3[1п<5-(1 - <<)],
и соответственно удельная полезная работа цикла возра-
стет на Д//в = ДЯК + ДЯТ. В то же время затраты удель-
ной теплоты, подводимой к рабочему телу, увеличатся
на величину
д? 1 = сркТг (<к - 1) + сртт3 In п^.
Если сравнить идеальный цикл Брайтона 1—21—
3—41 и дополнительные циклы с обратимыми изотерми-
ческими процессами сжатия l—2’—2t и расширения 3—
4’—4t, то можно показать [47 ], что всегда к п. д допол-
нительных треугольных циклов ниже, чем к. п. д. основ-
ного цикла 1—21—3—4t. Поэтому термический к. п. д.
идеального цикла с обратимыми изотермическими процес-
сами сжатия и расширения всегда меньше термического
’ж п. д. цикла Брайтона.
Если же сопоставить реальный цикл простой ГТУ 1—
2—3—4 и дополнительные циклы с необратимыми изотер-
Рис 1.13 Цикл ГТУ с изотермиче-
скими процессами сжатия и расшире-
ния
мическими процессами сжатия 1—2'—2 и расширения 3—
4'—4, то, так как к. п. д треугольного цикла т] доп моно-
тонно возрастает с ростом лк, а к. п. д ГТУ, выполненной
по простой схеме, имеет максимальное значение при лк =
= лКТ), всегда может быть найдено такое значение лк,
при котором т]доп > Лв Следовательно, при относительно
высоких значениях лк к. п д цикла с изотермическими
процессами сжатия и расширения может превосходить
к п. д реальной ГТУ, выполненной по простой тепловой
схеме.
Промежуточное охлаждение
и промежуточный нагрев рабочего тела
Применение изотермического сжатия в компрессоре
и изотермического расширения в турбине теоретически
позволяет получить увеличение полезной работы ГТУ,
а при высоких значениях лк возрастает и к. п. д уста-
новки. Однако эти процессы практически не могут быть
реализованы.
Известным приближением к указанным процессам яв-
ляется введение промежуточного охлаждения при сжатии
и промежуточного подогрева при расширении рабочего
тела Это достигается разделением компрессора и турбины
на отдельные отсеки (корпуса) с включением между ними
соответственно промежуточных охладителей или проме-
жуточных подогревателей рабочего тела.
Применение промежуточных охлаждения и подогрева
рабочего тела существенно усложняет конструкцию ГТУ,
поэтому в настоящее время практически применяют не
16
более одного или двух промежуточных охладителей и
одного промежуточного подогревателя.
В качестве примера на рис. 1.14, а изображена схема
ГТУ с двумя ступенями сжатия (КНД, КВД, один проме-
жуточный охладитель воздуха ВО) и двумя ступенями
расширения (ТВД и ТНД) х.
Для общего случая — схемы 2-2 — формула для вну-
тренней полезной работы ГТУ может быть написана в виде
«В — gT. в (г3 — Ч) + йт. н (1’з — й) ~
(''2 *1) (!2 Ч)- (1.35)
Удельное количество теплоты, подведенной к уста-
новке, определяется по формуле
‘71 = (gT. в'з-Ч) + (8т Л~«т. bU), d-36)
а внутренний к. п. д. ГТУ —
по формуле
Пв = ^в/?1- (J-37)
При анализе схемы 2-2
в качестве независимых пе-
ременных обычно принимают-
ся (обозначения точек см.
на рис. 1.14, б) Т3, тт =
= Т3/Т3, тк = Т'1/Т1 и т=
= Ti/Tg. Величины лт. Е =
~Р3 ЛТ. н Pz^Pit Дк. н —
= p'4Jpr и Лк.в'= ра/р{свя-
заны с общей степенью по-
вышения давления цикла лк
и максимального к. п. д. при
Лк. ВТ) [(ткТ]к в/Т]к, н) (1 — Т]в) ]
(1.39)
2. В установках с промежуточным подогревом рабо-
чего тела (схемы 1-2 и 2-2) распределение степени пони-
жения давления газа лт между турбинами ТВД и ТНД
обеспечивает получение максимальной полезной работы
при
лт. Лт1ттйт. нПт. HZ(gT. вПг. в)] ( 1-40)
и максимального к. п. д. при
.--(Г / , 1 /(2tfZ )
Л-т. н п ~ V лт нЛ г. н/(§т. вПт. в)1 U ~ Пв) I
(I 41)
3. В установке, выполненной по схеме 2-2, степень
повышения давления Лк, при которой к. п. д. и полезная
работа достигают максимальных значений, будет
В Rt. в
Rk. в
St. ~
Т|т. вНк. в
ттк
/тт. в
(1.42)
Рис. 1.14. ГТУ с промежуточными охлажде-
нием и подогревом рабочего тела: а — тепло-
вая схема; б — цикл ГТУ
Это выражение позволяет определить лкт)н при про-
извольно выбранных значениях лт. н и лк. в. Если при
этом ят, н = Лт, нН и лк. в = лк. в и, то совокупность
величин лк, определенной по формуле (1.42), лт.Нн и
лк. в Н обеспечит получение максимально возможной при
данных параметрах полезной работы. А если лт. н =
= лт. и,) и лк. в = лк. вЛ, то совокупность величин лк,
лт. н г| и лк. в обеспечит получение максимально возмож-
ного к. п. д. установки.
Принимая лк. в = лк и тк = 1, можно получить ве-
личину лкт|н для схемы 1-2, а при лт. Н=1 — величину
лкн для схемы 2-1. Для этой схемы величина лкг) опре-
деляется по формуле
Л-КТ]
„ -тк. в St ПтПк
к' 3 i Rk vmr Т(1— Т]в)
1 /тт
11.43)
По схеме 2-2 выполнена двухвальная энергетическая
газотурбинная установка ГТ-100-750 ЛМЗ. В этой уста-
новке компрессор высокого давления КВД и турбина вы-
сокого давления ТВД выделены на отдельный высоко-
оборотный вал, с которого полезная мощность не сни-
мается, и соотношение между лк. в и лт. н устанавливается
из баланса мощности этого вала:
зависимостями. в*^т. н — *^т '— *^к. н*^к» в — где
суммарные гидравлические сопротивления
ятк.в _1Г/т'
I _ Ср к, в 31к. в
Ср г. в С (т) Т)мех
т. в
, (1.44)
v — (1 ^вх) (1 н_к# в) (1 • в_т. в) X
X (1 £т, В-т. н)/(1 4~ 5вых) •
Исследование системы уравнений (1.35)—(1.37) по-
казывает следующее.
1. В установках с промежуточным охладителем (схемы
2-1 и 2-2) распределение степени повышения давления воз-
духа лк между компрессорами КНД и КВД обеспечивает
получение максимальной полезной работы при
--- 1 /(2тк)
Лк. вН ~ 1' ЛЕ (ТкЛк. в/Лк. н) (I -38)
где с (т) — gT. вт]т> вт]к. в/С^к)-
Совместное решение (1.42) и (1.44) дает
__ Г , а Лмех^р т. в !ср к, в Vе (iQ / 1
к- в цН — [ Т|мехт,;. в/тт. в + 1
к. в
(1.45)
Оптимальное значение лк, при котором к. п. д. и по-
лезная работа ГТУ по схеме 2-2 с выделенным валом до-
стигают максимальных значений, составит
1 Для удобства изложения ниже вводится следующее
условное обозначение схем ГТУ: схема с двумя ступенями
сжатия и расширения — схема 2-2, схема с двумя ступенями
сжатия и одной ступенью расширения — схема 2-1; схема
с одной ступенью сжатия и двумя ступенями расширения —
1-2, простая тепловая схема с одной ступенью сжатия и расши-
рения — схема 1-1.
_ -- ( ~ тк. н_тт. tl Rr^jt St. к
лкпН I Лк. в Ят. в Z?K.H H
Пт. нНк. нуАтт. н+тк. н)
т’
(1.46)
2 Л. В. Арсеньев и др
17
одо
0,35
0,30
200/® /80
1—J / © /50 150 i 20 J ®т зо/ш /^1 20* ?0< 1 -J /зо 30/ /60 '50 9П& 3/>' (^\ /80 00 зокт/ ТОк 81/, г® "200
60/^
(45Х 30/- — 1 20 3- 20/00 У OOs'2 '—2 20 ^2
l!J^ 15* ,Л(0 '150 20» 20"'
"ft К rf*'Kuh /за- /^3 30 80J 20 S
10 е
ООО
050
300
350
250
200
ЬОО Hg, кДж/кг
Рис. 1.15. Характеристики ГТУ с промежуточным охлаждением воздуха и промежуточным подогревом газа
(^1пол. т = 0,85, т]пол. к = 0,89; v = 0,88; 7\ = 288 К; тк = тт = 1):
1 ~ «К. В = ЯК. ВТ)’ ЛТ. И = "т. НТ)’ 2 ~ пк. в = як. вН- Лт. Н = ЯТ.11Н’- 3 ~ "к. в = "т. в*>
--------t3 = 750° С;---------73 = 850° С;---------/3 = 950° С;----------t, = 1 050° С
Рис. 1.16. Характеристики ГТУ с промежуточным охлаждением
воздуха (т]пол. т = 0,85; т]Пол. к = 0,89; v = 0,91; 7\ = 288 К;
тк= 1,0);
ЛК.В ~ •rtK.BTp ЛК,В = лк вН
Рис. 1.17. Оптимальные зна-
чения лк для различных схем
ГТУ:
/ — Я’К'П//’ схема 2-2; 2 — ЛкТр
схема 2-1; 3 — Якх]Н> схема 2-2
при 7VK Е = NT в; 4 - пкЯ,
схема 2-1; 5 — лКГр схема 1-1»
— ^кН' схема 1-1
18
где величина лт. в = лт/лт. и определяется из фор-
мулы (1.44).
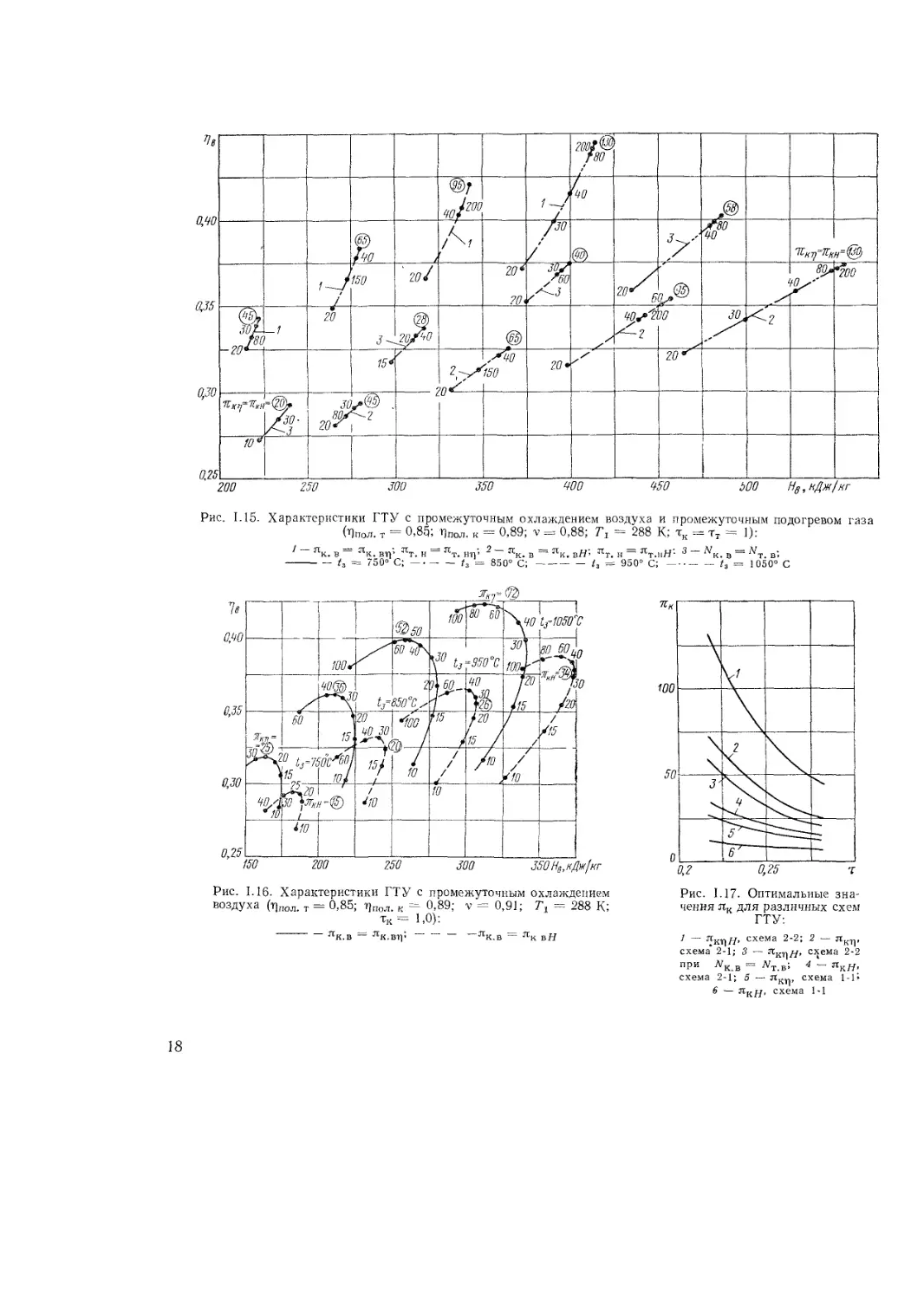
На рис. 1.15 показаны зависимости Т]Е = f (Нв) ГТУ
по схеме 2-2, построенные из условия получения макси-
мальных значений Цв (кривые 7) и Нв (кривые 2) при каж-
дом лк для нескольких значений температуры газа Т3
при тт= тк = 1 и ?!= 288 К. Точками на кривых обо-
значены соответствующие значения лк.
Для кривых 2 соблюдаются условия лк, и = лк.в и
лт. в = ят. и> в то время как для кривых 1 лт, н >• ят. Е
и лк. в>лк.н. Из анализа графиков на рис. 1.15 сле-
дует, что применение промежуточного подогрева и проме-
жуточного охлаждения приводит к заметному увеличе-
нию Н,, и Т)в по сравнению с ГТУ, выполненной по про-
стой тепловой схеме (см. рис. 1.10, о). Однако при этом
требуются значительно большие степени повышения дав-
ления лк.
На этом же рисунке нанесены кривые 3 для ГТУ по
схеме 2-2 с выделенным свободным валом. Их сравнение
с кривыми 1 и 2 показывает, что в такой установке уже
не представляется возможным получить такие же боль-
шие приращения величин к. п. д. и полезной работы.
Так, при t3 -= 1050° С и як = 40 к. п. д. ниже максималь-
ного примерно на 2%, а удельная работа — на 10%. Раз-
ница возрастает еще больше, если сравнение производить
при оптимальных значениях лк. При t3 = 1050° С и
Лк = лкт|// к. п. д. ниже максимального при этой темпера-
туре газа на 3%, а удельная работа — на 13%.
Аналогичные семейства кривых т]в -= f (Нв) для ГТУ
по схеме 2-1, построенных исходя из условия получе-
ния 77вп]ах 11 Чвшах при каждом значении лк и нескольких
значениях Т3, приведены на рис. 1.16. ГТУ с промежуточ-
ным охлаждением воздуха обеспечивает повышение удель-
ной работы и к. п. д. по сравнению с установкой, выпол-
ненной по простой схеме (см. рис. 1.10, а), однако это
повышение несколько меньше, чем в ГТУ по схеме 2-2.
Оптимальные значения лк для различных схем ГТУ
в зависимости от т приведены на рис. 1.17. Применение
промежуточного охлаждения и промежуточного подогрева
рабочего тела существенно повышает оптимальные зна-
чения лк по сравнению с ГТУ, выполненной по простой
схеме.
для силового вала
~т- и Ллк %- ^- н Ал,
Ж.:. п л _
н д ___ д гт .
в
уравнение теплового баланса
Л к + Ж7Т к-в к +
J^11! Анк. в = А?1-
Тогда приращение к. п. д. установки
Решение этих уравнений дает возможность получить:
А77в — Н, Алк -ф- Н2 Алк. в, Аг|е = В± Алк -J- В2 Апк. в.
Здесь коэффициенты ТУф, Н2, Bv В2 выражаются через
частные производные. Знаки при этих коэффициентах
указывают на целесообразное направление изменения Ллк
и Апк. в При достижении оптимума соответствующие
коэффициенты превращаются в нуль.
1.6. ГТУ С ОХЛАЖДАЕМОЙ турбиной
Анализ различных схем ГТУ показывает, что повыше-
ние удельной работы и к. п. д. ГТУ связано с увеличением
начальной температуры газа, что требует совершенство-
вания конструкционных материалов, а также применения
интенсивного охлаждения лопаток и других элементов
газовых турбин.
Известны различные системы охлаждения, которые
могут быть разделены на открытые и закрытые системы.
Анализ сложных схем ГТУ
Оптимальные параметры сложных схем ГТУ удобно
определять методом малых отклонений при линеаризации
исходных зависимостей, впервые предложенным С. А. Кан-
тором [45]. При расчете этим методом в первом прибли-
жении задаются рядом параметров, которые позволяют
получить основные характеристики установки с помощью
системы следующих уравнений: для свободных валов
S — £ HTi = 0; для силового вала S 77т* — S 7/,,ц. =
= Нв; к. п. д. установки Г|в = 77в/£ qr
Входящие в эти уравнения величины Нк, Нт и q
являются функциями параметров установки. Поэтому
характер влияния этих параметров может быть определен
по уравнениям равновесия в конечных разностях, коэф-
фициентами которых являются частные производные функ-
ций по варьируемым параметрам. Например, для уста-
новки по схеме 2-2 со свободным валом при варьировании
лк и лк. в уравнения равновесия имеют следующий вид:
для свободного вала
Рис. 1.18. Схемы ГТУ: а — с открытой системой охлажде-
ния; б — с закрытой системой охлаждения;
/ — охлаждаемая газовая турбина; 2 — трубопровод для под-
вода охлаждающего воздуха; 3 — трубопровод для отвода
охлаждающего воздуха
2*
ЭНТ. в
Алк '
дПт.в
Элк. в
Алк. в
дНк.„
дпв
Длк —
дНл.в
длк. в
Алк. в — 0»
Открытые системы (рис. 1.18, а) характеризуются тем, что
теплоноситель после прохождения тракта охлаждения
выводится в проточную часть и, расширяясь в последую-
щих ступенях турбины, участвует в выработке полезной
работы. Чаще всего в этих системах в качестве теплоноси-
теля используется цикловой воздух, подаваемый компрес-
сором. Однако могут применяться и другие агенты.
В закрытых системах тракт охлаждения конструк-
тивно выполняется герметичным. Здесь охлаждающий агент
может использоваться многократно, для чего выделяется
отдельный контур охлаждения. Это позволяет включать
газовую турбину в комбинированную установку, одно из
рабочих тел которой служит теплоносителем в системе
охлаждения. Такое решение обеспечивает эффективное
19
использование теплоты системы охлаждения, что повы-
шает к. п. д. установки. Принцип закрытого охлаждения
положен в основу газопаровой установки по схеме ЦКТИ—
ЛПИ [29], в которой для охлаждения газовой турбины
используется пар.
В закрытой системе охлаждения возможно примене-
ние циклового воздуха, который после системы охлажде-
ния может быть возвращен в цикл (рис. 1.18, б). Охлажде-
ние по этой схеме иногда называют полузамкнутым.
Показатели турбины
с закрытой системой охлаждения
Процесс расширения газа в охлаждаемой турбине
условно изображен на рис. 1.19. Состояние газа в конце
адиабатного процесса расширения с трением отмечено
точкой 4а, а в конце процесса расширения с трением и
охлаждением — 4q. На Т—s-диаграмме площадь 4а—
Рис. 1.19 Процесс расширения
газа в газовой турбине при за-
крытой системе охлаждения
I—k—4q соответствует снижению энтальпии газа за тур-
Синои вследствие охлаждения.
Удельная работа расширения Hq определяется по
уравнению первого закона термодинамики
Hq = Срт (Тз Tiq) <7охл> (1-47)
1де Сохл — удельное количество теплоты, отводимой от
газа при охлаждении.
Можно показать, что [111]
Tw = Тю [1 -Уохл/^рт^)], (1.48)
где Тв = S 7^<7Охл /S Сохл / ~ средняя температура ра-
„ 7 ' »
бочего тела, при которой отводится теплота охлаждения;
Tqj, <7охл у — параметры /-го охлаждаемого элемента про-
точной части.
Если На — работа неохлаждаемой турбины, то
Hq=Ha ХдУохл, (П49)
где xQ = 1 — Tia/Tq = 1 — Т3лт тг\тч — коэффициент,
харг; тсризуюшки относится;ьую потерю полезной ра-
боты вследствие охлажусь; я.
Количество теплоты ?охл t, отведенной от поверхности
охлаждаемого элемента, определяется по формуле
9охл у = а/ Срт 3] ст),
где Тст — средняя температура стенки; а* = —
приведенный коэффициент теплоотдачи, характеризую-
щий I онструктивное исполнение охлаждаемого элемента
и режим теплообмена; — осредненный коэффициент
теплоотдачи от газа к охлаждаемой поверхности F j (под-
робнее об этом см. в гл. II.6).
20
Используя уравнение сплошности и критериальное
уравнение теплообмена Nu = cRem, приведенный коэф-
фициент теплоотдачи в охлаждаемом лопаточном венце
можно записать в виде
“*=cV(sin ₽;Pr/Re J_m), G-5°)
где Nu, Pr, Re — критерии Нуссельта, Прандтля и Рей-
нольдса; f--Fi'S— приведенная охлаждаемая поверх-
ность венца; S — ометаемая площадь; р — угол между
векторами относительной и окружной скоростей потока
газа.
Для энергетических газовых турбин можно прини-
мать f = 4<-5; Re = 5- 105<-3- 10е, а в качестве крите-
риального уравнения теплообмена использовать зависи-
мость, рекомендованную Авиамоторным институтом
им. П. И. Баранова [30]- Nu = cRe0,6S, где с = 0,07<-
-<-0,11 —коэффициент, зависящий от угла поворота по-
тока в решетке (рг + ра)/2. В указанном диапазоне из-
менения параметров охлаждаемого венца а* = 0,01<-
<-0,03, причем большие значения относятся к малорас-
ходным турбинам.
Коэффициент а? зависит главным образом от расхода
рабочего тела и в пределах проточной части изменяется
незначительно. Это позволяет в расчетах приведенный
коэффициент теплоотдачи приближенно принимать по-
стоянным по проточной части:
GC 1 — ОС — GC ~ — СС
1 / £
В результате суммирования qj .от j = 1 до / — г, где
z— чис.,о охлаждаемых венцов, общее удельное коли-
чество теплоты, отводимой от охлаждаемых элементов
протонной части газовой турбины, будет раьно
Vox.n = а*сртга (Т3 Т’с,), (К51)
где
а = 1 - [(г - 1)/(2г)] [(Т3 - Т4?)/(Т3 - Тст)].
При вариантных расчетах целесообразно использо-
вать характеристики ранее отработанной охлаждаемой
ступени (индекс 0). Тогда приближенно
= [GToMGTra)l1-m-
Величина </охл приближенно можег быть оценена
с помощью графика на рис. 1.20, а, который рассчитан
по приведенным выше соотношениям.
Температура Tq определяется по формуле [1111 (если
считать Тч. = Т3/)
Tq=Tsl\~b(Ts-T„)ITs], (1.52)
где
Если z = 1, то а = 1 и b = 0. Если (Т3 — Tiq)/(T3 —
— Т’ст) = 1, то а = (г+ 1)/(2г) и 6 = (г — 1)/(Зг). При
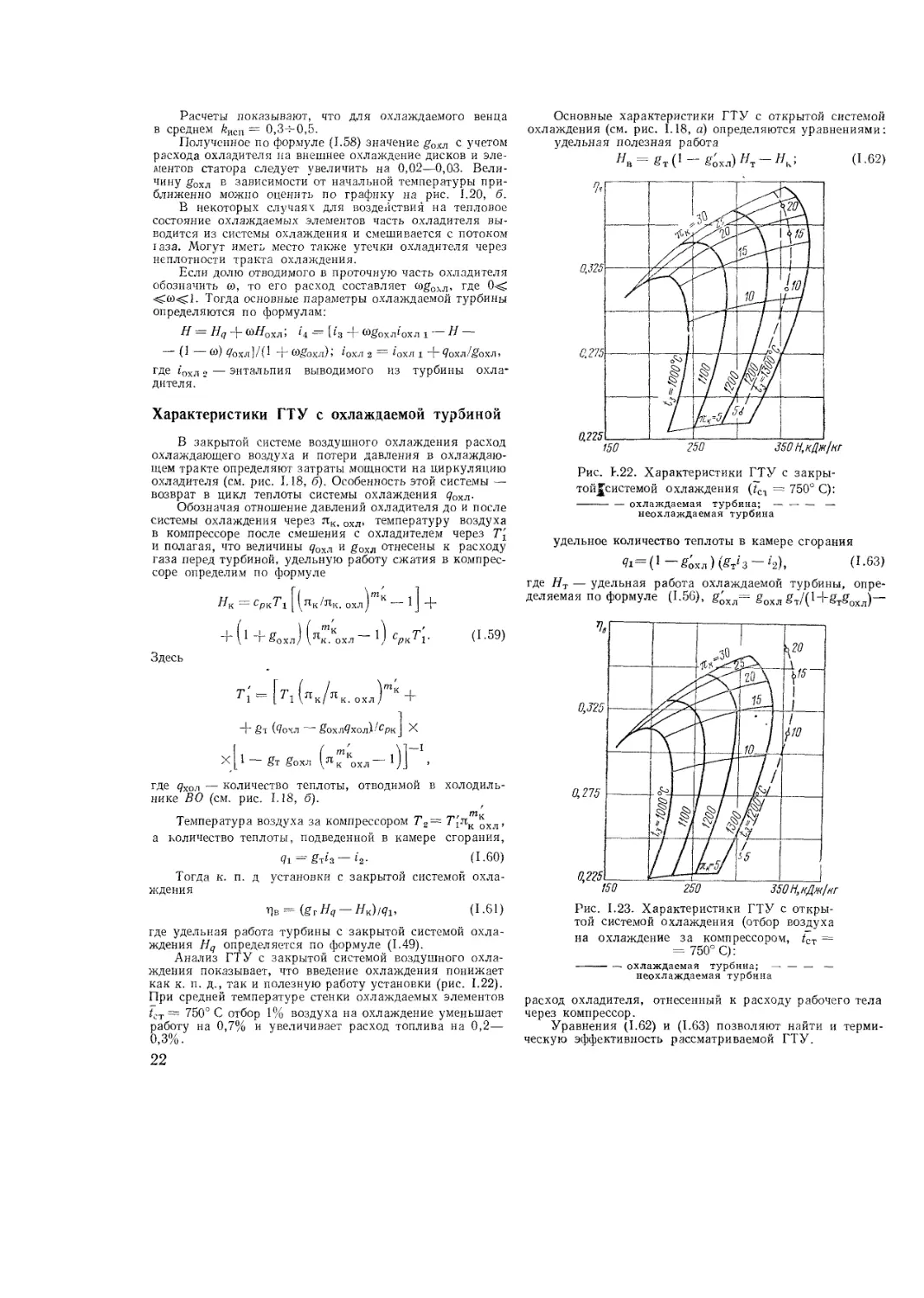
этом, если г -> оо, то а -> 0,5, а Ь -> 1/3. Как видно из
рис. 1.21, коэффициенты а и b в многоступенчатой турбине
мало зависят от числа венцов. В приближенных расчетах
можно принимать
7’? = 7’3[1-(7’з-7ст)/(ЗТ3)].
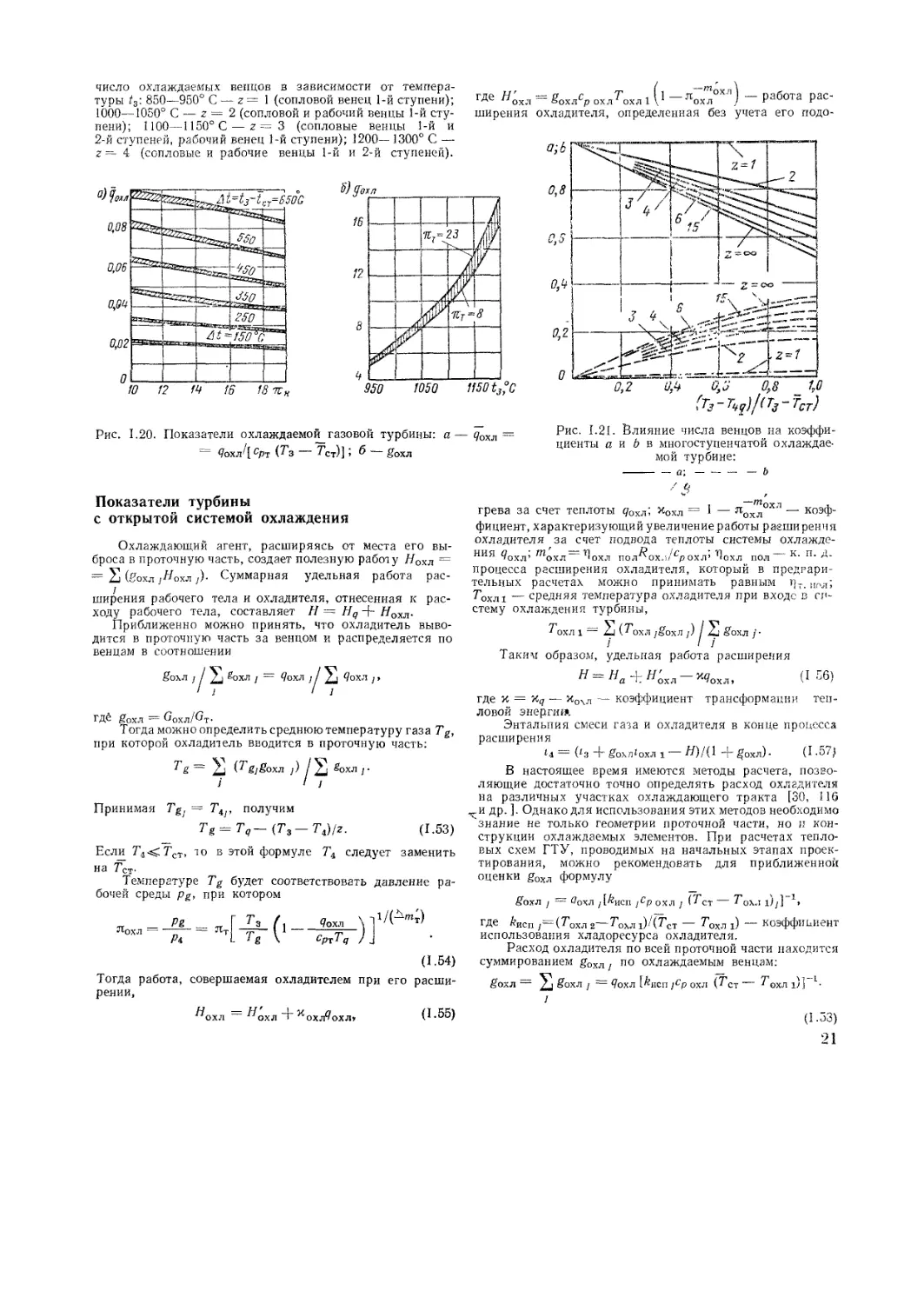
На величину </охл большое влияние оказывает число
охлаждаемых венцов z. Имея в виду современные тенден-
ции применения высоконагруженных ступеней, можно
для приближенных расчетов рекомендовать следующее
число охлаждаемых венцов в зависимости от темпера-
туры 13: 850—950° С — z = 1 (сопловой венец 1-й ступени);
1000—1050° С — z = 2 (сопловой и рабочий венцы 1-й сту-
пени); 1100—1150° С — z=3 (сопловые венцы 1-й и
2-й ступеней, рабочий венец 1-й ступени); 1200— 1300° С —
z = 4 (сопловые и рабочие венцы 1-й и 2-й ступеней).
Рис. 1.20. Показатели охлаждаемой газовой турбины: а —
= ?охл'[ срт (7з Т’ст)] > б ёохл
Показатели турбины
с открытой системой охлаждения
Охлаждающий агент, расширяясь от Места его вы-
броса в проточную часть, создает полезную работу /70ХЛ =
= S (Лохл у^охл /)• Суммарная удельная работа рас-
I
ширения рабочего тела и охладителя, отнесенная к рас-
ходу рабочего тела, составляет Н = Hq-\- Нохл.
Приближенно можно принять, что охладитель выво-
дится в проточную часть за венцом и распределяется по
венцам в соотношении
8оХЛ у! У| бохл у — ?ОХЛ У 9охл у >
ГДё Рохл — Сохл/Ст.
Тогда можно определить среднюю температуру газа 7g
при которой охладитель вводится в проточную часть:
Т g ~~ У (^giSoxn у) /2| 8°хл Г
i I 1
Принимая Tft, = TtJ, получим
7’g = 7’9-(7’3-T4)/z. (1.53)
Если 7,<7'ст. то в этой формуле 7’4 следует заменить
на Тст-
Температуре Tg будет соответствовать давление ра-
бочей среды pg, при котором
Pg Г Т’з (1
Этохл = —р- = лт —±- ( 1
Pt L I g \
а ' 11 / (^'"т)
_____Чохл \ '
Cp-tTq / J
(1.54)
Тогда работа, совершаемая охладителем при его расши-
рении,
^охл ^охл “Г к охл?охл»
(1.55)
гда яохл
ширения
= §охлср охл^охл 1 0 - яохлОХЛ) - РабоТа Рас-
охладителя, определенная без учета его подо-
= Рис. I.2I. Влияние числа венцов на коэффи-
циенты а и b в многоступенчатой охлаждае-
мой турбине:
-------а-,-------— Ь
ц
грева за счет теплоты <уОхл; «охл = 1 — ^охл0*1 — коэф-
фициент, характеризующий увеличение работы раеши рения
охладителя за счет подвода теплоты системы охлажде-
ния ?охл, тохл ^охл пол^ох.|/срохл’ ^охл пол к' п' 4-
процесса расширения охладителя, который в предвари-
тельных расчетах можно принимать равным ,юл;
7охл1 — средняя температура охладителя при входе в си-
стему охлаждения турбины,
Т’охл 1 — 2 (Т’охл у&>ХЛ у) I 2 8оХЛ ]
Таким образом, удельная работа расширения
н = На + Н'охл - х?охл> (I 56)
где х = — хохл — коэффициент трансформации теп-
ловой энергии.
Энтальпия смеси газа и охладителя в конце процесса
расширения
Н — 0з Ч~ &х/Цохл г Н)/(Д _1” §охл) (I -57)
В настоящее время имеются методы расчета, позво-
ляющие достаточно точно определять расход охладителя
на различных участках охлаждающего тракта [30, 116
,_и др. ]. Однако для использования этих методов необходимо
знание не только геометрии проточной части, но и кон-
струкции охлаждаемых элементов. При расчетах тепло-
вых схем ГТУ, проводимых на начальных этапах проек-
тирования, можно рекомендовать для приближенной
оценки £охл формулу
8оХЛ у = Цохл у [(гИСП уСр ОХЛ у (Тст Т охл 11 у] \
где &исп у~(Т’охл2 ^'охл1)/(7’Ст Т’охл i) коэффициент
использования хладоресурса охладителя.
Расход охладителя по всей проточной части находится
суммированием g0XJI; по охлаждаемым венцам:
йохл = У 8охл у — <7охл [^ИСП 1Ср ОХЛ (ТСТ Т’охл 1)] 1-
1
(1.53)
Расчеты показывают, что для охлаждаемого венца
в среднем йисп = 0,3а-0,5.
Полученное по формуле (1.58) значение gOXJi с учетом
расхода охладителя на внешнее охлаждение дисков и эле-
ментов статора следует увеличить на 0,02—0,03. Вели-
чину goxn в зависимости от начальной температуры при-
ближенно можно оценить по графику на рис. 1.20, б.
В некоторых случаях для воздействия на тепловое
состояние охлаждаемых элементов часть охладителя вы-
водится из системы охлаждения и смешивается с потоком
I аза. Могут иметь место также утечки охладителя через
неплотности тракта охлаждения.
Если долю отводимого в проточную часть охладителя
обозначить со, то его расход составляет <ogOXJ1, где 0<:
<со<1. Тогда основные параметры охлаждаемой турбины
определяются по формулам:
Н = Hq -ф <оЯохл; С4 = [i3 -ф <0£охл(охл 1 Н
(1 СО) <7охл]/( 1 + ®&>хл) ; с'охл 2 = с'охл 1 -ф <?охл/&хл,
где сохл; — энтальпия выводимого из турбины охла-
дителя.
Характеристики ГТУ с охлаждаемой турбиной
В закрытой системе воздушного охлаждения расход
охлаждающего воздуха и потери давления в охлаждаю-
щем тракте определяют затраты мощности на циркуляцию
охладителя (см. рис. 1.18, б). Особенность этой системы —
возврат в цикл теплоты системы охлаждения ?0Хл-
Обозначая отношение давлений охладителя до и после
системы охлаждения через лк, охл, температуру воздуха
в компрессоре после смешения с охладителем через
и полагая, что величины уохл и gQxli отнесены к расходу
газа перед турбиной, удельную работу сжатия в компрес-
соре определим по формуле
Нк.— СрК7\ Цлк/лк. охл) к 1J +
+ (1+^охл)(<Кохл-1)^к7’;. (1.59)
Здесь
Л “ [л(лк/як.охл) К +
+ gl (</охл ёохл9хол)/Срк] X
х[1 — ёт£охл 1лк’охл~|)|
где <7Хол — количество теплоты, отводимой в холодиль-
нике ВО (см. рис. 1.18, б).
Температура воздуха за компрессором Т’2= Тг^кохл’
а количество теплоты, подведенной в камере сгорания,
<71 = ^т»з—»2- (Г60)
Тогда к. п. д установки с закрытой системой охла-
ждения
= (£гЯч-Як)/<71, (1.61)
где удельная работа турбины с закрытой системой охла-
ждения Hq определяется по формуле (1.49).
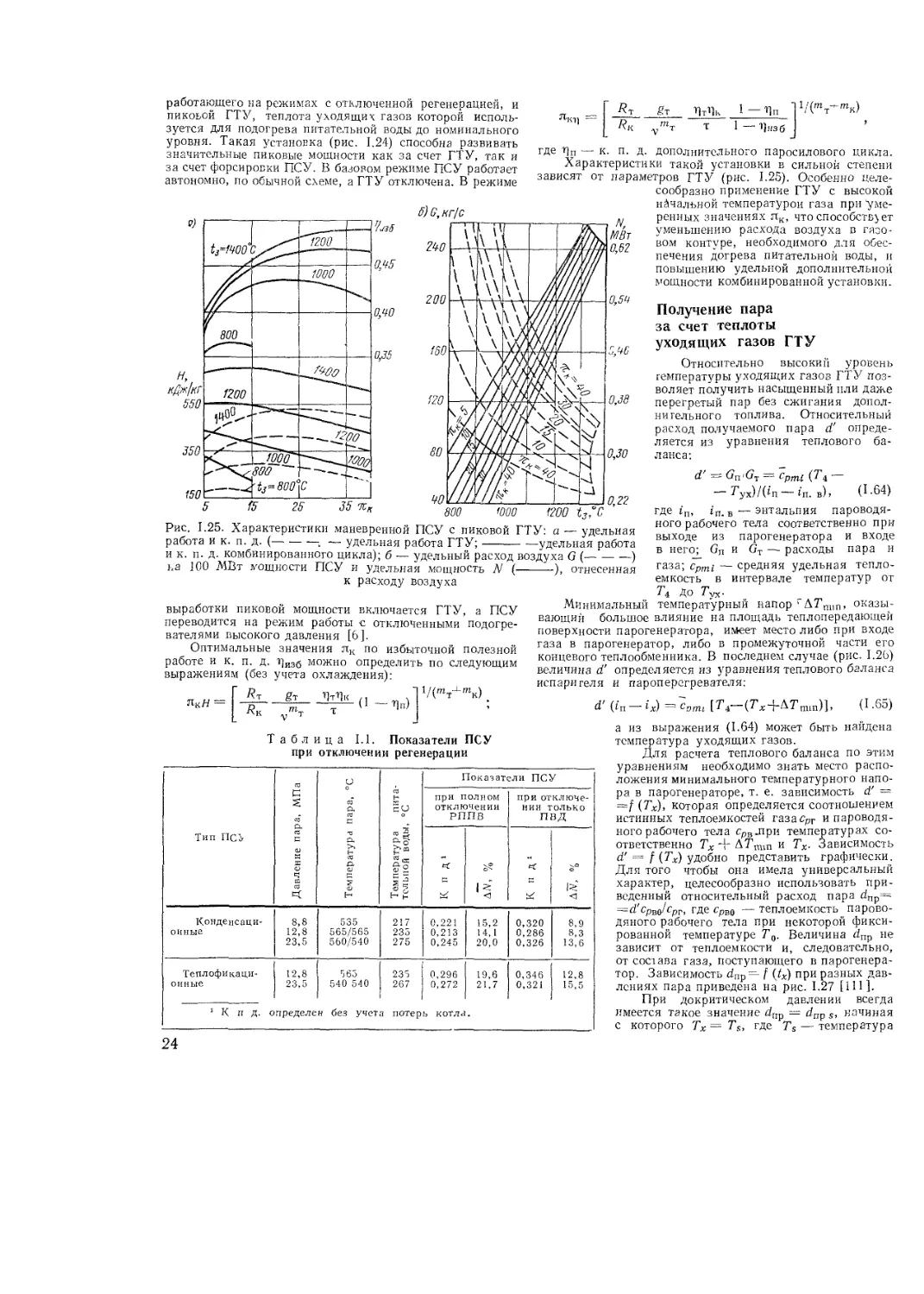
Анализ ГТУ с закрытой системой воздушного охла-
ждения показывает, что введение охлаждения понижает
как к. п. д., так и полезную работу установки (рис. 1.22).
При средней температуре стенки охлаждаемых элементов
Гст — 750° С отбор 1% воздуха на охлаждение уменьшает
работу на 0,7% и увеличивает расход топлива на 0,2—
0,3%.
Основные характеристики ГТУ с открытой системой
охлаждения (см. рис. 1.18, а) определяются уравнениями:
удельная полезная работа
wB = gT(>-g;x.n)wT-^; (1-62)
Рис. Е22. Характеристики ГТУ с закры-
той^системой охлаждения (/С1 = 750° С):
-------охлаждаемая турбина; —-----—
неохлаждаемая турбина
удельное количество теплоты в камере сгорания
<7i= (1 — ^охЛ) (й'т'з ~ г'г), (1.63)
где Нт — удельная работа охлаждаемой турбины, опре-
деляемая по формуле (1.56), £;хл= £охл£т/(1+£т£охл)~
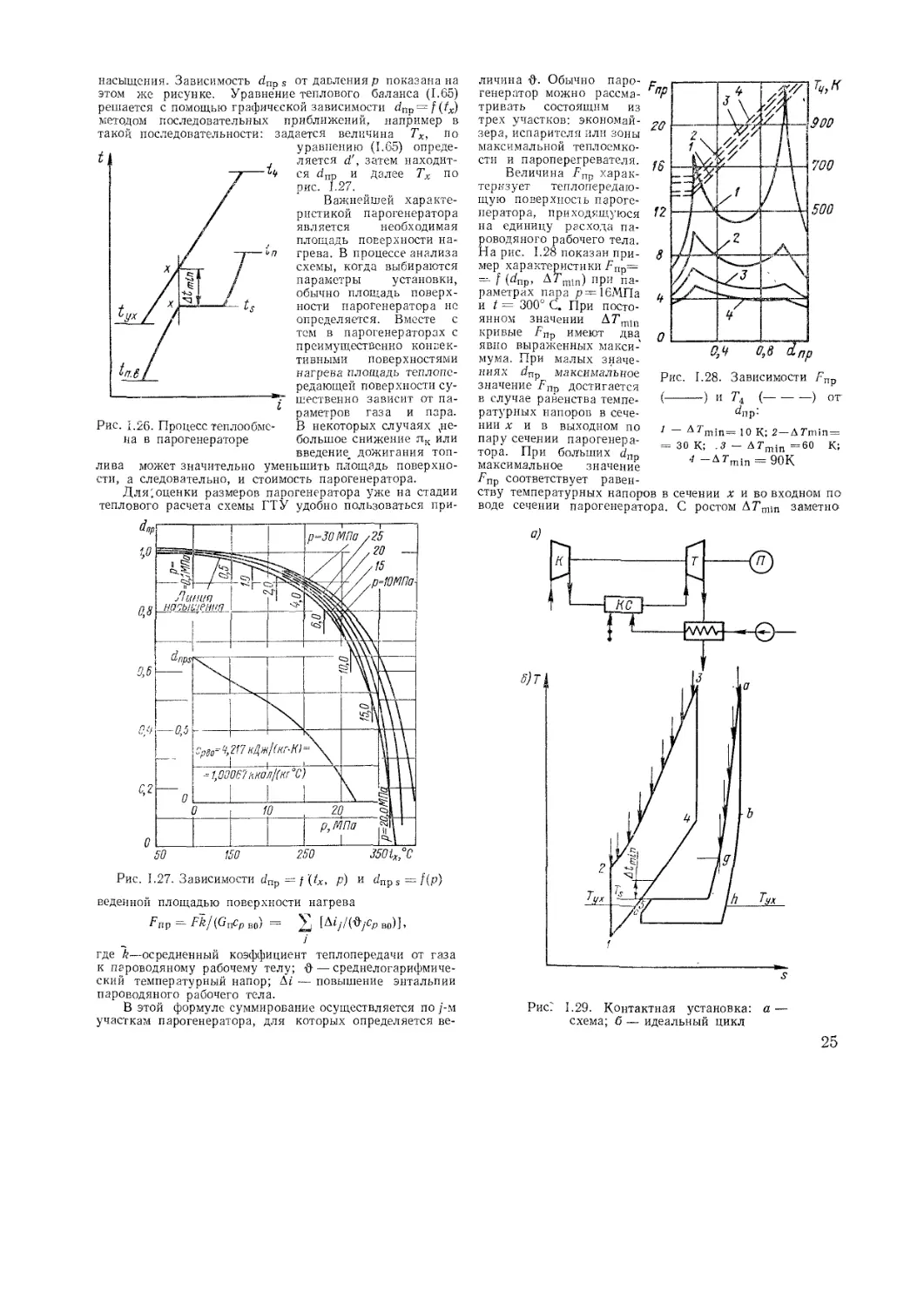
Рис. 1.23. Характеристики ГТУ с откры-
той системой охлаждения (отбор воздуха
на охлаждение за компрессором, гст =
= 750° С):
-------охлаждаемая турбина; — — — —
неохлаждаемая турбина
расход охладителя, отнесенный к расходу рабочего тела
через компрессор.
Уравнения (1.62) и (1.63) позволяют найти и терми-
ческую эффективность рассматриваемой ГТУ.
22
В открытой системе отбор воздуха на охлаждение су-
щественно сказывается на показателях установки
(рис. 1.23). В этом случае отбор 1% воздуха на охлажде-
ние уменьшает полезную работу на 1,5—2% и повышает
удельный расход топлива на 0,3—0,6% .
1.7. ГТУ С УТИЛИЗАЦИЕЙ
ТЕПЛОТЫ УХОДЯЩИХ ГАЗОВ
Теплоту уходящих из ГТУ газов можно использовать
для генерации пароводяного рабочего тела, которое,
в свою очередь, применяется для различных целей: тепло-
фикации, получения полезной мощности в паровой тур-
бине, форсировки ГТУ путем введения воды или пара
в тракт высокого давления, охлаждения газовой тур-
бины и др.
Сравнительно высокий уровень коэффициента из-
бытка воздуха в ГТУ позволяет сжигать большое коли-
чество дополнительного топлива в среде продуктов сгора-
ния, что обеспечивает повышение параметров и расхода
пара. Для этого применяются парогенераторы с развитой
радиационной поверхностью нагрева. В таких установках
пар используют для получения полезной мощности в паро-
вой турбине (до 80—85% общей полезной мощности).
В зависимости от места включения парогенератора в схему
установки различают высоконапорный (ВПГ) и низкона-
порные (НПГ) парогенераторы. ВПГ включаются в тракт
высокого давления ГТУ перед газовой турбиной. Теплоту
уходящих газов ГТУ при этом используют для подогрева
питательной воды в экономайзере. НПГ устанавливаются
за газовой турбиной при давлении продуктов сгорания,
близком к атмосферному. Известны также комбинирован-
ные установки со средненапорными парогенераторами
(СПГ) [82], которые включаются между турбинами вы-
сокого и низкого давления.
В соответствии с типом парогенератора перечислен-
ные установки называют парогазовыми установками с ВПГ,
НПГ или СПГ.'Подробный термодинамический и технико-
экономический анализ таких установок представлен в ра-
ботах [8, 41, 44].
Ниже рассматриваются газотурбинные и парогазовые
установки, в которых подогрев пароводяного рабочего тела
осуществляется в основном за счёт теплоты уходящих га-
зов в теплообменных аппаратах с преимущественно кон-
вективными поверхностями нагрева. При этом в газоходе
между турбиной и теплообменным аппаратом можно до-
жигать небольшое количество топлива.
ГТУ с подогревателями сетевой воды
Использование теплоты уходящих газов для отопле-
ния и горячего водоснабжения — один из наиболее про-
стых и распространенных способов повышения технико-
экономических показателей ГТУ. Так, установки ГТ-25-700
ЛМЗ снабжены сетевыми подогревателями производитель-
ностью около 125 ГДж/ч при температуре наружного воз-
духа —50° С [85].
Количество теплоты, которое может быть получено
в сетевом подогревателе, Qc. п = <3Т (Ц— 1ух)- Тем-
пература газа после сетевого подогревателя назначается
исходя из температуры Т1В (%. = 45-ь 70° С) воды, по-
ступающей в сетевой подогреватель, и вида топлива, при-
мененного в камере сгорания. Последний фактор часто1
играет решающую роль при выборе величины Туу с точки
зрения предотвращения низкотемпературной ’ коррозии
поверхностей нагрева. Расход сетевой воды Gc. в =
= Qc. п'^'гв — Цв)- Максимальная температура воды за
подогревателем 150—160° С.
Поверхность нагрева сетевого подогревателя F =
= Qc. П/(А), где k — коэффициент теплопередачи от газа
к воде, определяемый по рекомендациям [96]; О =
-= [(Л - Г2в) - (Гух - Г1В)]/[1П(74 - Г2в)/(ГУх-
— Г1В)] — среднелогарифмический температурный напор.
Подогрев сетевой воды уходящими из ГТУ газами
может быть учтен при выборе степени повышения давле-
ния лк. В качестве примера рассмотрим случай, когда
сетевой подогреватель ГТУ частично или полностью вы-
тесняет водогрейный котел. Тогда с учетом экономии топ-
лива в водогрейном котле расход теплоты на производство
полезной работы в ГТУ с сетевым подогревателем (ПСВ)
составит q = ?к.сА)к. с — е?с, гАв. к> где т]в. ,( - к. п. д.
водогрейного котла; е — отношение годового числа часов
работы ПСВ к годовому числу часов работы ГТУ. Тогда
величина лк, обеспечивающая максимальный к. п. д., мо-
жет быть определена по формуле
7?т
Т]тПк
1 — АЧа. к
1/(тк+тт)
1 — Не/ Пк с
При е = 1 величина лКГ| существенно пойижается и ста-
новится даже ниже, чем пкн-
Применение ГТУ для повышения
маневренности паросиловых блоков
Для быстрого наращивания пиковых и полупиковых
мощностей в настоящее время рассматривается возмож-
ность повышения маневренности мощных паросиловых
блоков. Широкие возможности в этом направлении откры-
ваются при форсировке паросиловой установки (ПСУ) за
счет пропуска через ее цилиндры части пара регенератив-
ных отборов. В табл. 1.1 приведены значения дополни-
тельной мощности ДА, которые могут быть получены при
ПСУ
Рис. 1.24. Схема маневренной ПСУ с пиковой ГТУ:
1 — паровая турбина; 2 — конденсатор; 3 — конденсат-
ный насос, 4 — подогреватели питательной воды низкого
давления; 5 — деаэратор; 6 — подогреватели питательной
воды высокого давления; 7 — питательный насос; 8 — па-
рогенератор; 9 — водоподогреватель
полном или частичном отключении регенеративных подо-
гревателей питательной воды (РППВ) как в конденсацион-
ных, так и в теплофикационных ПСУ. При полном отклю-
чении РППВ дополнительная пиковая мощность обеспе-
чивается главным образом за счет отборов пара высокого
давления. Имеется и ряд других преимуществ отключения
только подогревателей высокого давления (ПВД).
Таким образом, при наличии у паросиловых блоков ре-
зерва по прочности имеется возможность выработки до-
полнительной мощности с хорошими маневренными харак-
теристиками. Турбостроительные заводы предусматри-
вают во вновь проектируемых ПСУ режимы работы с от-
ключенными подогревателями питательной воды.
Существенное улучшение показателей выработки ма-
невренной мощности может быть достигнуто в комбиниро-
ванной установке, состоящей из паросилового блока,
23
работающего на режимах с отключенной регенерацией, и
пикоьой ГТУ, теплота уходящих газов которой исполь-
зуется для подогрева питательной воды до номинального
уровня. Такая установка (рис. 1.24) способна развивать
значительные пиковые мощности как за счет ГТУ, так и
за счет форсировки ПСУ. В базовом режиме ПСУ работает
автономно, по обычной схеме, а ГТУ отключена. В режиме
Рис. 1.25. Характеристики маневренной ПСУ с пиковой ГТУ: а —- удельная
работа и к. п. д. (----, — удельная работа ГТУ;---------удельная работа
и к. п. д. комбинированного цикла); б — удельный расход воздуха G (--)
на 100 МВт мощности ПСУ и удельная мощность N (-----------), отнесенная
к расходу воздуха
выработки пиковой мощности включается ГТУ, а ПСУ
переводится на режим работы с отключенными подогре-
вателями высокого давления [6].
Оптимальные значения лк по избыточной полезной
работе и к. п. д. цизб можно определить по следующим
выражениям (без учета охлаждения):
11/(тта'тк)
ЛкН =
vmr т ( !п)
Таблица 1.1. Показатели ПСУ
при отключении регенерации
Тип ПС;, Давление пара, МПа Температура пара, °C Температура пита- тельной воды, °C Показатели ПСУ
при полном отключении РППВ при отключе- нии только пвд
! V и У1 ДА/, % , V 11 У1 № О
Конденсаци- 8,8 535 217 0,221 15,2 0,320 8,9
онные 12,8 565/565 235 0,213 14,1 0,286 8,3
23,5 560/540 275 0,245 20,0 0,326 13,6
Теплофикаци- 12,8 565 235 0,296 19,6 0,346 12,8
они ые 23,5 540 540 267 0,272 21,7 0,321 15,5
1 К п д. определен без учета потерь котла.
—
Кт Р.т Вт Л К ------Лп
Кк vmT Т 1 — Лизб
где Лп — к. п. д. дополнительного паросилового цикла.
Характеристики такой установки в сильной степени
зависят от параметров ГТУ (рис. 1.25). Особенно целе-
сообразно применение ГТУ с высокой
начальной температурой газа при уме-
ренных значениях лк, что способстгл ет
уменьшению расхода воздуха в газо-
вом контуре, необходимого для обес-
печения догрева питательной воды, и
повышению удельной дополнительной
мощности комбинированной установки.
Получение пара
за счет теплоты
уходящих газов ГТУ
Относительно высокий уровень
температуры уходящих газов ГТУ поз-
воляет получить насыщенный пли даже
перегретый пар без сжигания допол-
нительного топлива. Относительный
расход получаемого пара d' опреде-
ляется из уравнения теплового ба-
ланса;
тГ = Gn*GT = (7\
-Тух)/(тп-1п. в), (1.64)
где in, 1п. в — энтальпия пароводя-
ного рабочего тела соответственно при
выходе из парогенератора и входе
в него; Gn и GT — расходы пара и
газа; cpmi — средняя удельная тепло-
емкость в интервале температур от
Д до Тух •
температурный напор оказы-
влияние на площадь теплопередающей
Минимальный
вающий большое
поверхности парогенератора, имеет место либо при входе
газа в парогенератор, либо в промежуточной части его
концевого теплообменника. В последнем случае (рис. 1.26)
величина d' определяется из уравнения теплового баланса
испарителя и пароперегревателя:
d' (t'n — ix) = Сопи (Гх+ДТпип)],
а из выражения (1.64) может быть
температура уходящих газов.
Для расчета теплового баланса
(1.65)
найдена
по этим
уравнениям необходимо знать место распо-
ложения минимального температурного напо-
ра в парогенераторе, т. е. зависимость d' —
=) (Тх), которая определяется соотношением
истинных теплоемкостей газасрг и пароводя-
ного рабочего тела СрВ.при температурах со-
ответственно Тх -ф АТтш и Тх. Зависимость
d' = f (Тх) удобно представить графически.
Для того чтобы она имела универсальный
характер, целесообразно использовать при-
веденный относительный расход пара dnp=
= d'CpB0/cpr, где СрВ0 — теплоемкость парово-
дяного рабочего тела при некоторой фикси-
рованной температуре 7’0. Величина dnp не
зависит от теплоемкости и, следовательно,
от состава газа, поступающего в парогенера-
тор. Зависимость dnp=- f (Д) при разных дав-
лениях пара приведена на рис. 1.27 [111].
При докритическом давлении всегда
имеется такое значение dnp = dnp s, начиная
с которого Тх = Ts, где Ts — температура
24
насыщения. Зависимость dnp s от давления р показана на
этом же рисунке. Уравне'ние теплового баланса (1.65)
решается с помощью графической зависимости dnp=f(tx)
методом последовательных приближений, например в
такой последовательности: задается величина Тх, по
уравнению (1.65) опреде-
ляется d', затем находит-
ся dnp и далее Тх по
Рис. 1.26. Процесс теплообме-
на в парогенераторе
рис. 1.27.
Важнейшей характе-
ристикой парогенератора
является необходимая
площадь поверхности на-
грева. В процессе анализа
схемы, когда выбираются
параметры установки,
обычно площадь поверх-
ности парогенератора нс
определяется. Вместе с
тем в парогенераторах с
преимущественно конвек-
тивными поверхностями
нагрева площадь теплопе-
редающей поверхности су-
щественно зависит от па-
раметров газа и пара.
В некоторых случаях ,не-
болыпое снижение лк или
введение, дожигания топ-
личина '0. Обычно паро-
генератор можно рассма-
тривать состоящим из
трех участков: экономай-
зера, испарителя или зоны
максимальной теплоемко-
сти и пароперегревателя.
Величина Гпр харак-
теризует теплопередаю-
щую поверхность пароге-
нератора, приходящуюся
на единицу расхода па-
роводяного рабочего тела.
На рис. 1.28 показан при-
мер характеристики Гпр=
= f (rfnD, дЛтШ1) при па-
раметрах пара р—16МПа
и t = 300° С. При посто-
янном значении ДТт1п
кривые Гпр имеют два
явно выраженных макси-
мума. При малых значе-
ниях d,-[p максимальное
значение ГПр достигается
в случае равенства темпе-
ратурных напоров в сече-
Рис. 1.28. Зависимости Тфр
(------) и 7’, (---------) от
<^пр:
лива может значительно уменьшить площадь поверхно-
сти, а следовательно, и стоимость парогенератора.
Для?оценки размеров парогенератора уже на стадии
теплового расчета схемы ГТУ удобно пользоваться при-
НИИ X и в выходном по 1
пару сечении парогенера- =
тора. При больших dno ~~
максимальное значение
Г'пр соответствует равен-
ству температурных напоров в
воде сечении парогенератора.
— Azmin= 10 К; 2 — ATmin =
30 К; .3 - АТфнп = 60 К;
4 ~Armin = 90K
сечении х и во входном по
С ростом ATmin заметно
веденной площадью поверхности нагрева
Fпр — Fkl(G-nCp во) = , [^IjK^jCp во)] >
i
где k—осредненный коэффициент теплопередачи от газа
к пароводяному рабочему телу; б)— среднелогарифмиче-
ский температурный напор; Ai — повышение энтальпии
пароводяного рабочего тела.
В этой формуле суммирование осуществляется по /-м
участкам парогенератора, для которых определяется ве-
Рис? 1.29. Контактная установка: а —
схема; б —- идеальный цикл
25
уменьшаются как величина Гпр, так и разница между
максимальным и минимальным значе ниями F
Получаемый в парогенераторе пар может быть исполь-
зован для различных целей. Ниже рассмотрено использо-
вание пара для повышения мощности ГТУ путем его вве-
дения в тракт высокого давления (контактная установка).
Характеристики
контактных установок
При анализе свойств контактной установки предпо-
лагается [41 ], что при рассматриваемых параметрах паро-
водяное рабочее тело в составе газопаровой смеси подчи-
няется законам идеального газа. Тогда рабочий процесс
Доля теплоты цут, подводимой к пароводяному ра-
бочему телу за счет' уходящих газов (процессы 4—5 и
b—h), характеризуется коэффициентом утилизации
йут = <7ут/ (?п 4" ?ут) = (г'й + le) / (t'a — l’e)> (1.67)
где индексы g, е, а соответствуют точкам, показанным на
рис. 1.29, б.
Полезная работа контактной установки
WB = gT^r + rfWn-WK, (1.68;
а прирост полезной работы по сравнению с ГТУ состав-
ляет А//в — dHn, где d = GnCiK — относительный расход
пара; Нг, Нп — работа расширения газа и пара в турбине.
К- п. д. установки
Пв = (ёт "г + — Нк) / (</rJ- ?г1). (1.69)
Рис. 1.30. Характеристики контактной установки (Л/7„ = А//в///рту): а — лк = 10; Т3 = 1200 К; tg =- var; б — лк =
= 10; Tg = 500 К; Т3 = var; в — Т3 1200 К; Tg = 500 К; лк = var
для газопаровой смеси в рассматриваемой установке можно
заменить соответствующими процессами для каждого из
компонентов (рис. 1.29). Замкнутый цикл 1—2—3—4
(рис. 1.29, б) — процесс, совершаемый воздухом в иде-
альной ГТУ. Часть теплоты уходящих газов (процесс 4—5)
используется в парогенераторе, остальное количество теп-
лоты передается в окружающую среду.
Доля теплоты топлива, подведенной к пару, харак-
теризуется коэффициентом
₽ = <7п/ (?г Ч- <7п) = («гту — а) /аггу, (1-66)
где <7п> <7г — количество теплоты топлива, подведенной
в камере сгорания к пару и воздуху; арту, а — коэффи-
циенты избытка воздуха в ГТУ и контактной установке.
При а = ат1п величина Р достигает своего максималь-
ного значения, которое с ростом начальной температуры Т3
уменьшается.
26
К. п. д. контактной установки выше к. п. д. ГТУ на
величину
Ails = Лв — Пгту = ₽ [Пп/ (1 —*yi) — ПгтуЪ (I-70)
Введение пароводяного рабочего тела в тракт высо-
кого давления повышает к. п . д. установки только при
определенном уровне коэффициента утилизации йут- Усло-
вие повышения к. п. д. ГТУ при вводе пароводяного рабо-
чего тела имеет вид
/гут > 1 — Чп/Нгту-
Характеристики контактной установки показаны на
рис. 1.30, они построены при условии получения макси-
мального расхода пара d. При этом во всех случаях обес-
печивается либо минимальный температурный напор АГтш
в одной из точек тракта парогенератора (А7га1П = 30 К),
-либо минимально допустимый коэффициент избытка воз-
духа в камере сгорания (amin = 1,1). Максимальная тем-
пература подогрева пара принята равной 773 К-
Проведенный анализ не учитывает дополнительных
гидравлических потерь в тракте парогенератора, которые
приводят к снижению полезной работы установки. По
сравнению с ГТУ без парогенератора потери мощности,
связанные с повышением противодавления турбины, со-
ставляют АЯ, и увеличение удельной полезной работы
в этом случае будет Л//, = dHn — АН. Тогда прираще-
ние А1]Е, определяемое по формуле (1.70), снизится на
величину Ai] (1 — Р), где Ат] = AHlqT.
Выше были рассмотрены условия, позволяющие по-
лучить максимальную мощность. Вместе с тем ощутимый
эффект может быть достигнут при вводе Ограниченного
количества пароводяного тела.
1.8. РАСЧЕТ ТЕПЛОВЫХ СХЕМ ГТУ
Расчет характеристик ГТУ с учетом
зависимости теплоемкости газов
от температуры
В п. 1.2 приведены основные термодинамические соот-
ношения, полученные в предположении ср — const. Такое
допущение дает приемлемую погрешность при расчете
процессов в относительно небольшом интервале темпера-
тур. Непрерывный рост лк и 7’:) в современных ГТУ при-
вел к тому, что температурный интервал процесса расшире-
ния газа в турбине возрос до 500—600 К- В этих условиях
допущение ср = const вносит в расчет значительную по-
грешность. В работе [125] предложен способ построения
таблиц термодинамических свойств газов, удобный для
расчетов изоэнтропийных процессов. Такие таблицы [86,
98] нашли довольно широкое распространение. Методика
расчета, приведенная ниже, позволяет рассчитывать как
адиабатные процессы (обратимые и необратимые), так и
политропические процессы.
В большинстве случаев рабочее тело в ГТУ может
рассматриваться как газ, подчиняющийся уравнению
Клапейрсна—Менделеева. Для такого газа истивнея
удельная изобар.я-сск; я тсгшосмкость хожет быть задана
в .виде темпеш'.тргого уя^а
/
Если за начало отсчета энтальпии газа принять То —
— 273,15 К, то при температуре Т имеем
т
t — [ cpdT = Cpmi (Т То),
Параметры изоэнтропийного процесса определяются
по уравнению
Л
Р1/Р2 = j cpd.T / (RT) = (TJT^P^, (1.73)
Г 2
где cpms — удельная среднелогарифмическая изобариче-
ская теплоемкость газа в интервале температур ог Т\ до Т2,
Показатель степени в уравнении (1.73) может быть вы-
ражен через показатель адиабаты, зависящий от соотно-
шения среднелогарифмических теплоемкостей газа ks =
~ CpmJCvms, где cvms — Coms — R — удельная изохориче-
ская теплоемкость газа. Тогда
Cpms — (*s l)/^s = ^s*
Если по-прежнему в качестве начала отсчета принять тем-
пературу газа Т0, то среднелогарифмическая теплоемкость
в интервале температур от Т до То будет зависеть только
от температуры Т, т. е.
и может быть затабулирована. В этом случае среднелога-
рифмическая теплоемкость в интервале температур от
7\ до Г2
Cpms = [Cpms (Тi) In (Т^/То)
-cpms (Г2)1п (Г2/Го)]/1п (Л/ГД. (1.76)
Удельная работа обратимого адиабатного сжатия или
расширения потока газа
Н — i-i i2 = Cpmi (Н)П Cpmi Да) — Cpmi 1 Г2),
(1.77)
где Cpmt = (t’i — 1^(71 — T’a) — средняя удельная изо-
барическая теплоемкость газа в интервале температур от
Тi до Т2.
Величину Н можно также представить в виде
н = CpmiTr [1 - (р2/Р1)^]- (1.78)
Эта работа будет положительной для процесса рас-
ширения и отрицательной для процесса сжатия газа.
Уравнение обратимого адиабатного процесса может
быть записано в виде
Cpms (Тi) In (Т-JTд) R In (Pi/Pg) =
= Cpms (Т2) In (T2IT0) - R In (p2/p0), (1.79)
где pn 0,1 МПа — давление газа, принятое за начало
отсчета.
Величина cpms (Г) In (777’0) = s (Г) определяет при-
ращение энтропии при изменении температуры от То до Т
при постоянном давлении, а величина R In (Р/Ро)—при-
ращение энтропии при изменении давления от рд до р
при постоянной температуре газа. Если принять в точке
начала отсчета s = s0 = 0, то уравнение обратимой адиа-
баты может быть представлено в обычном виде:
s (Т, р) •= s (TJ — s (Р1) = s(T2) — s (р2) = const.
По уравнению (1.79) температура газа в конце изо-
энтропийного процесса определяется следующим образом.
Сначала вычисляется величина s(T2) = cpms (Тг) X
X In (TjTg)—R In (P1/p2), а затем - температура T2 из
уравнения s (Г2) = cpms (Г2) In (Т21Т^). Решение этого
уравнения осуществляется или итерационным методом,
или по таблицам, если функция s (Т) затабулирована.
Если необратимый адиабатный процесс заменя-
ется политропическим процессом, то справедливы урав-
нения:
для процесса расширения
Т’г/Т’г = (Pi/p2) s пол-т; s (Тт]пол. ts (Pi) = 1 (1.80)
= s (Т’з) — т]пол. ts (Ра)‘>
для процесса сжатия
= (р1/р2)т5'/’1пол-к:
S (Тi) S (Р1)/1)поЛ. К — S (Т2) S (р2)/г]пол. к-
(1.81)
27
Тогда энтропия газа в начале процесса s (Т1У рг) ~
—- s (7J — s (fl); в конце процесса расширения
s (Т2,р2) = s (^1) 11пол. ts (Pi) ~ s (Т2) ^ПОЛ. TS (Р2)>
в конце процесса сжатия
s Р2) — S (i j) S (Р1)/Т]пол. к = s (Т'г) ' ® (Р2)Alnoa. к,
т. е. необратимый адиабатный процесс представлен как
совокупность изотермического процесса дросселирования
с изменением энтропии от з, до s2 и обратимого адиабат-
ного процесса при s2 -= const. Порядок вычисления тем-
пературы 72 остается таким же, как и в случае изоэн-
тропийного процесса.
В табл. 1.1 приложения 1 приведены коэффициенты
уравнения (1.71) для наиболее распространенных в газо-
урбостроении газов. Для сухого воздуха и водяного пара
в табл. 1.2 приложения 1 приведены значения српи, coms
и s (7). Пересчет срт (7) и s (7) для влажного воздуха
осуществляется по формуле
а (Т) sB (7) ___cpm (Т) сРтв (Т)_____ d
sn (7) sB (7) Cpmn (7) (7) 1 d ’
где cp,n (T), cpmp (T), cpmn (T) — удельная теплоемкость
влажного воздуха, сухого воздуха и пара; s(7),sB(7),
sn (Т) — удельная энтропия влажного воздуха, сухого
воздуха и пара; а— отношенье массы влаги к м..ссе
сухого всздуха. Иногда задается относительная влажность
воздуха ф, связанная с величиной d зависимостью
d = 0,622фр5/(р — <pps),
где ps —* давление насыщенного пара при температуре
воздуха 7; р — давление влажного воздуха.
Поскольку при анализе схем ГТУ состав применя-
емого топлива зачастую неизвестен, величину Q” для
газотурбинных топлив и теплофизические характеристики
их продуктов сгорания можно принимать такими же, как
для стандартного углеводорода, содержащего по массе
85% углерода и 15% водорода [109].
В табл. 1.2 приложения 1 приведены теплофизические
характеристики продуктов сгорания такого топлива'
при различных значениях коэффициента избытка воздуха а.
Пересчет cpm (Г), s (7) и R при произвольном коэффици-
енте избытка воздуха осуществляется по формуле
s (Г) sB (7) ___cpm (Т) срп№ (Т)____
sa=l Cpm (a=l) сртв
__ R Rb ________Гр % 1
“ =aLo + 1 ’
где Lg — теоретическое количество воздуха, необходи-
мого для полного сгорания 1 кг топлива.
Примерный порядок расчета тепловой схемы ГТУ
приведен в приложении 2.
Тепловой баланс камеры сгорания
Для расчета характеристик топлива и продуктов
сгорания, поступающих из камеры сгорания в газовую
турбину, должны быть известны состав топлива и воздуха
в массовых или объемных долях. Характеристики топлива
и продуктов сгорания определяются по следующим фор-
мулам РТМ 24. 022.11—74 (в пересчете на систему СИ).
Низшая теплота сгорания для газообразного топлива
(кДж/м3)
Q" = 359,62СН4 %- 598,86C2H44-231,28H2S Д-
+ 108,05Н2 + 127.47СО-]----,
где СН4, С2Н4, H2S, Н2, СО и т. д. — объемные доли
составляющих горючего газа в топливе, %; коэффици-
енты — значения теплоты сгорания соответствующих со-
став, якщнх горючего 1аза.
28
Для жидкого топлива (кДж/кг)
Q” = 4,1868 [8ICP %- 246ДР — 26 (О₽ — Sp) — 6WP],
где Ср, Н\ Ор, Sp, Wp—массовые доли компонентов
в рабочей массе топлива, %.
Последней формулой можно пользоваться и для газо-
образного топлива, если его содержание задано массовыми
долями компонентов. Более точно теплота сгорания опре-
деляйся экспериментально в кг лоримст рст ссксй бомбе.
Теоретическое количество воздуха, необходимого для
полного сгорания 1 кг твердого или жидкого топлива
(при коэффициенте избытка воздуха а = 1),
Lo =' 0,115СР -L 0,342Нр % 0,043 (Sp — Ор).
Для газообразного топлива
Lo = 0,00628 [0,5СО + 0,5Н2 + 2СН4 + 1,5H2S +
% [(от ~г'Ч)/4]СпНт —О2]/р,
где р — плотность, горючего газа.
Количество, состав (массовый) и теплоемкость про-
дуктов сгорания при а = 1 определяются по следующим,
формулам.
Количество трехатомных газов (кг/кг):
для жидкого топлива
grd2 = 0,0371(Ср +0,375Sp);
для газообразного топлива
grc,2 = o,oi [ сн4 + со + h2s + со2+
+ У1 pRC>2/p.
Количество водяных паров (кг/кг):
для жидкого топлива
GH,o = 0,09Нр % 0,01 Wp % 0,0161 Lq % Орасп,
где Gpacn — содержание воды в распыливающем агенте-
на 1 кг топлива;
для газообразного топлива
gh2O =°>01 [2СН4+ Н2+ H2S-|-0,124dr +
+ ^(«72)CnHm]pH2O/p+0,0161L0,
где dr — влажность газообразного топлива.
Количество азота (кг/кг)
GN2 = O,768Lo + NP.
Суммарное массовое количество газов при а= 1 (кг/кг)
Gr = gro2 + gh2o + gn2-
Массовые доли каждого компонента:
SrO2 = GRO2/Grl §11,0 = GH2o/Grl £n2 ~= GN2/Gr-
Средняя массовая теплоемкость продуктов сгорания
Cpni = cpmi (Н2О)£Н2О + Cpmi (RO2) £rG>2 +
+ cpmi (N2) £n2.
Аналогично определяется газовая постоянная R.
В приложении 1 приведены характеристики продук-
тов сгорания при различных коэффициентах избытка
воздуха для стандартного углеводородного топльвг.
В общем случае массовая доля воздуха в газе, посту-
пающем в i-ю камеру сгорания, определяется по формуле
х = Lo (ai-i— l)/(a/-iGo + О- (1-82)
Относительное количество воздуха gB, содержащегося
в продуктах сгорания за камерой сгорания, определяется
из уравнения теплового баланса:
Ов 1GpHk. с + гтоп "Ь
— (£0/х + 1) zs]/(z2 — й)> (’-83)
где — энтальпия газа перед камерой сгорания; i'2 —
энтальпия продуктов сгорания при а = 1 и Т = Т
1'2 — энтальпия газа при а = и Т = Tg, »топ — эн-
тальпия топлива при Т = 7’Т()П (в большинстве случаев
допустимо считать (топ «=* 0).
Для первой (одиночной) камеры сгорания получаются
следующие сооотношения при к = 1:
а = (LogB)/L0', (1-84)
gB = [ОрПк. с + ‘топ + Loli — (Lo + 0 г’2]/(12— й)-
(1.85)
Температура t0, при которой определена величина Q&,
должна совпадать с температурой начала отсчета энталь-
пии воздуха и продуктов сгорания. Если эти температуры
не совпадают, то величину Q” определяют по формуле
Qp = ^рО — WBi) + ( ^0 + 1 ) ‘о — гтоп о, (1-86)
где Q“o, tTOn 0, гв0, i'o — параметры топлива, воздуха и
продуктов сгорания при температуре /0.
При подмешивании к газу воздуха, например из
-системы охлаждения газовой турбины или из уплотнений,
коэффициент избытка воздуха увеличивается. Если ин-
дексом i—1 обозначить параметры газа до смешения с воз-
духом, a i — после смешения, то
а, = а«-г[1 +&gBi (а(_1Л0+ ОЛсЧ-Л)], (1-87)
где &.gBi — доля воздуха, подмешиваемого к газу.
Расход количества теплоты высокого потенциала
(теплоты топлива), подведенной от первой камеры сгора-
ния к данному сечению тракта ГТУ, определяется по
формуле
?,• = (СтопСр), = (1 - U GkC/(«A), (I 88)
где — массовая доля от общего расхода воздуха, по-
ступившая в газовый тракт за расчетным (г-м) сечением;
а( — коэффициент избытка воздуха в расчетном (г-м)
сечении.
К- п. д. турбомашин
К- п. д. турбины определяется как отношение дей-
ствительной работы Яг к теоретической Ят/ при равенстве
входных и выходных параметров газа реальной и идеаль-
ном турбин:
Чт = = (i3 — 14)/(»3 — iit).
При расчете циклов ГТУ можно пользоваться при-
ближенной формулой 1
1-89)
Величину т)пол т, входящую в показатель степени
тт = ттт]пол. т, можно определить по параметрам сту-
пени, воспользовавшись формулой (1.89), записанной
для ступени. При этом т)т заменяется на Т]ст, а ят —на
2/2
лст = лт > где г — число венцов турбины
1 Эта формула получена при условии с = const, лт—
2 /2 * Р
= и Пст^ const
Для неохлаждаемых турбин величину г]* можно
определять по рис. 1.31, а1.
Для турбин низкого давления в расчетах можно
принимать к. п. д. по статическим параметрам потока
на выходе: г]т 0,86-:-0,88 (подробнее об этом см. в пп. 11.2
и П.5).
К. п. д. компрессора определяется как отношение тео-
ретической работы сжатия HKt к действительной работе
сжатия Нк:
'Нк ~ ^Kt/^к — (12< 11)/(12 й )•
Рис. Е31. Номограммы для определения к. п. д.:
а — турбины (?]*); б — компрессора (rj*)
При расчете циклов ГТУ можно пользоваться при-
ближенной формулой 2
Пк = 1) / — 1) •
(I 90)
Аналогично предыдущему случаю величину т]п->ъ к
можно определить по формуле (1.90), используя параметры
* 2/2
ступени компрессора rjCT и лст = .
Величина Т]* может быть определена также по
рис. 1.31, б3.
1 При этом Ппол т можно определить также по рис I 31, а
по значениям и т}ст или принимать НПол т “ 0,86 — 0,89.
2 Эта формула получена пои условии ср — const, лк =
г/2 *
= Лс'т и Т)ст = cons^
3 При этом т)пол к можно определять также по рис 131,6
2т!г '
по значениям лк и т)ст
29
Глава II
ГАЗОВЫЕ ТУРБИНЫ
11.1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ГАЗОДИНАМИЧЕСКОГО РАСЧЕТА
ПРОТОЧНОЙ ЧАСТИ
Применяемые в ГТУ компрессоры и турбины пред-
ставляют собой машинь'1, в которых передача механиче-
ской энергии рабочему телу осуществляется в процессе
взаимодействия потока газа с лопатками специальной
формы, установленными на вращающемся роторе. Другим
основным элементом турбомашины является неподвиж-
ный статор, в котором размещаются направляющие ло-
патки (сопла), преобразовывающие потенциальную эпер-
нию потока газа в кинетическую и придающие ему целе-
сообразное направление перед входом на вращающиеся
лопатки.. Лопаточный аппарат компрессора или турбины
совместно с входным и выходным устройствами образуют
их проточную часть. Сочетание последовательно распо-
ложенных направляющего (соплового) аппарата и рабочего
колеса, т. е. вращающегося диска с установленными на
нем рабочими лопатками, называют ступенью. Совокуп-
ность отдельных ступеней образует лопаточный аппарат
турбомашины.
В зависимости от формы меридионального обвода
проточной части и направления движения газа все турбо-
машины'подразделяют на осевые и радиальные. В прак-
тике стационарного газотурбостроения повсеместное рас-
пространение находят осевые турбомашины, в транспорт-
ных ГТУ малой мощности часто применяют радиальные
турбомашины.
Проектирование лопаточного аппарата турбомашин
представляет собой одну из наиболее ответственных и в то
же время сложных задач, возникающих при создании
газотурбинной установки. Сложность эта обусловлена
необходимостью комплексного решения вопросов газо-
динамики, конструктивной прочности и технологии обра-
ботки лопаток.
Газодинамический расчет лопаточного аппарата тур-
бомашины основан на применении следующих основных
законов механики сплошной среды: сохранения массы,
изменения количества движения, изменения момента
количества движения, сохранения энергии, первого и
второго законов термодинамики.
Уравнения, описывающие указанные законы, связы-
вают характеристики потока жидкости (газа) с действием
внешних сил и моментов, а также с подводом (отводом)
энергии от внешнего источника.
Уравнение сохранения массы (неразрывности) ’
dp/dt + <> dive = 0. (И.1)
Уравнение количества движения
pdcldt =_- pF -ф- Div Р > (I I-2)
где F — плотность распределения объемных сил, Р
тензор напряжений.
Уравнение динамики движения вязкого газа в форме
Навье—Стокса [63]
pdadi = pF — g.ad (р 4- (2/3) р div с] 4- 2 Div (pS), (11.3)
30
где S — тензор скорости деформаций.
Уравнение (II.3) составлено с учетом следующих
общепринятых допущений:
1) газ является совершенным, т. е. описывается за-
коном Клапейрона—Менделеева
р'р --RT; (II.4)
2) газ подчиняется обобщенному закону Ньютона,
связывающему напряжения трения и скорость дефор-
мации, причем характеризующий вязкость динамический
коэффициент р, = f (7);
3) теплоемкости газа ср, cv, а следовательно, и по-
казатель k = cp!cv не зависят от 7;
4) коэффициент теплопроводности газа X связан с ii со-
отношением цср/Х = const.
Уравнение баланса сохранения энергии в движущемся
газе
р—4- с2/2) = pFc 4^ dp !dt 4- div ^2pcS —
----pc div с -4 grad Л . (11.5)
3 Cp J
Система уравнений (II. 1)—(II.5) принципиально мо-
жет быть‘решена при задании соответствующих гранич-
ных и начальных условий. Однако получение конкретного
конечного ее решения пока практически неосуществимо
из-за значительных математических трудностей. Поэтому
возникает необходимость введения дополнительных упро-
щающих допущений, при которых, однако, должны со-
храняться основные особенности, характеризующие поток
газа в турбомашине. Одно из таких допущений состоит
в том, что газ предполагается идеальным, т. е. в нем не
возникает касательных напряжений, обусловленных вяз-
костью.
Подобный подход позволяет с достаточной точностью
вывести зависимости между основными параметрами
пространственного потока для центральной области про-
точной части турбомашины, в которой затрата (потеря)
располагаемой работы, обусловленная проявлением вяз-
кости, относительно мала.
В краевых областях потока, т. е. у периферии и корня
проточной части, где становится заметным проявление
вязкости, принятие указанного допущения является не-
оправданным и должен быть использован принципиально
иной подход при описании потока жидкости, например
применение модели пространственного пограничного слоя
и т. п.
Используя допущение об идеальности газа, можно
написать уравнения (II.3) и (II.5) в следующем виде.
1. Уравнение динамики в форме Эйлера
dc/dt 4- (eV) с =---— grad р 4- F, (II.6)
Р
в форме Громэко—Лэмба —
dc/dt -4 grad (с2/2) -4 rot с х с --— grad р 4- F. (П ,6а)
Р
Для наиболее распространенного случая баротроп-
ного движения, т. е. когда плотность является функцией
только давления (р) = Jdp/pj, а объемные силы F
имеют потенциал (F = —grad 77), уравнение (II.6) при-
нимает вид
dcjdt + grad Е ф- rot с X с = О, (II.66)
где
р
Е~ са/2 ф— J" dp/p-f-77.
¥
Ро
2. Уравнение сохранения (баланса) энергии
d (i ф- c'/ty/dt =-- Fc ф — dpjdt ф- q. (I I-7)
P
При движении реального газа через проточную часть
турбомашины часть располагаемой механической энергии
(работы) превращается в тепловую в результате трения.
Этот процесс, хотя и является необратимым, в случае,
если количество теплоты, образующейся в результате
работы сил трения, относительно мало, с достаточной
для практических целей точностью может быть условно
сведен к некоторому обратимому политропическому про-
цессу с подводом извне соответствующего количества
теплоты (т. е. с показателем политропы п < k). Тогда
уравнение (II.7) может быть написано в, виде [63]
d (i ф- с?/2)/dt = Fc ф- — dp/dt — dqxjdt, (II.7а)
Р
где qx — удельное количество теплоты, выделившейся
в результате работы сил трения (вязкости).
В большинстве задач течение газа в проточной части
турбомашины можно считать установившимся, т. е. такие
характеристики потока, как масса, количество движения,
энтальпия и энтропия, не изменяющимися во времени.
При таком допущении соответствующие члены уравнений
(II. 1)—(II.7), содержащие d/dt, исключаются.
При проектировании лопаточного аппарата турбома-
шины обычно возникает необходимость решать две раз-
личные задачи:
1) расчет профильной части лопаток при заданных
массовом расходе рабочего тела, располагаемой тепловой
энергии, габаритных размерах и частоте вращения ро-
тора — обратная задача;
2) расчет параметров потока, проходящего через ло-
паточный аппарат турбомашины при заданных его раз-
мерах и профилях лопаток, частоте вращения ротора,
а также соответствующих граничных и начальных усло-
виях — прямая задача.
Вследствие того что точное решение исходной системы
уравнений (II. 1)—(II.7) как для обратной, так и для
прямой задач даже при допущении об идеальности газа
не представляется пока возможным, обычно вводится
дополнительное допущение об осесимметричности потока
в осевых зазорах между лопаточными венцами.
Решение задач для трехмерного (пространственного)
потока при этом может быть сведено к решению двух дву-
мерных задач на криволинейных поверхностях тока Sj
и 32 [131].
Однако даже с использованием всех указанных выше
допущений точное решение как прямой, так и обратной
задач для пространственного потока в общем виде пока
не получено из-за значительных математических трудно-
стей. Поэтому на практике решение указанных задач осу-
ществляется для каждого конкретного случая путем
численного решения системы уравнений (II.1)—(11.7)
с помощью ЭВМ, чго требует значительных затрат вре-
мени и квалифицированного труда.
Поэтому наряду с указанными общими методами
газодинамического расчета широко применяются более
простые приближенные методы, например, расчет пара-
метров одномерного потока газа, а также двумерного
плоского и пространственного потоков только в межвен-
цовых зазорах ступени.
Ниже изложены перечисленные приближенные методы
расчета применительно к проточной части газовой турбины.
Газодинамический расчет осевых компрессоров ГТУ
приведен в гл. III.
II.2. ГАЗОДИНАМИЧЕСКИЙ РАСЧЕТ
ОДНОМЕРНОГО ПОТОКА
Одномерный сжимаемый поток
Изоэнтропийное течение (расширение). Примени-
тельно к рассматриваемому случаю с учетом допущений
об идеальности газа и установившемся характере движе-
ния исходная система уравнений газодинамики (II.1)—
(II.7) может быть записана в следующем виде: уравнение
неразрывности pfe = G, уравнение сохранения энергии
Н ф- с2/2 = const, уравнение изоэнтропийного процесса
течения ppk = const.
Система этих уравнений является достаточной для
решения одномерной задачи о течении газа по каналу
произвольной формы, если заданы параметры на входе
(р/; р*; Т*; ir0) и известен закон изменения площади по-
перечного сечения канала по длине.
При расчетах изоэнтропийных процессов течения
обычно используют следующие безразмерные газодина-
мические характеристики, число Маха М = da, где а =
= (dp/dp),/2 = kRT ; число X = с/акр, где акр =
= V2kRT^/(k + 1). Связь между М и X выражается фор-
мулой
("s>
Функциональные зависимости между параметрами
изоэнтропийного потока и числом М имеют вид:
То*/Т= 1 +^-2 М2; (II.9)
* / (1 । — 1 л<2\ 1^ 1) /т । ,
*/ Л , k— 1 9\1/(А-1), ...
Ро/р ” Н-----§—ДО ) ’ (И-11)
G]/^/(K) =
= »/(1 +A1llM2)(ft+1)/t2<^1)];(II.12)
G^KKfp) = VldRd / (1 + м2)1/2 • (I I • 13)
Численные значения этих функций даны в литературе
[3, 125].
Аналогичные зависимости между параметрами изоэн-
тропийного потока и числом X, называемые газодинами-
ческими функциями, выражаются формулами:
т/П =т(Х) = 1Т (Ц-14)
р/р* = П (К)= (l — Х2у/{к ° ; (11.15)
31
p/p* = eW = (11.16)
G — f (ф)кР<7 (h) >
Численные значения этих функций даны в виде таблиц
в литературе [3, 125].
Косой скачок. Зависимости между параметрами по-
тока до и после косого скачка выражаются формулами:
где член
q (X) =-- [(6 + (%) (11.17)
представляет собой безразмерную плотность тока.
Численные значения газодинамических функций даны
в литературе [125].
Адиабатное необратимое течение. Необратимость про-
цесса адиабатного течения, обусловленная проявлением
вязкости (трения), может приближенно оцениваться с по-
мощью коэффициента х = Д77ДТНЗ, где ДТ —действи-
Рис. II.1. Схема косого скачка
уплотнений
тельное уменьшение температуры; ДТИз — изоэнтропий-
ное уменьшение температуры от заторможенного состоя-
ния газа,
дгиз = [! - 1/(Ро/р)<А"1,М] то- (II 18)
Тогда формулы (11.10) и (11.12) примут вид [113]
,, __ / Г £—1 М2 .
Ро/Р-11[1 2х 1 _)_ „ 1) М2/2 j ;
_ (П 19)
^ = /тм(1 + А^>му\
/Но * /\ \ 2 /
fx—1 1 W(fc-i)
х| х х[1 4-(6—1)М2 2]j • (11-20)
, /64-1
Р2
Р1
Р-2 X
Р1 /
= 1 +6M?sin2yI( 1 — Pi/p2); (11.25)
Р2/Р1 = tg Tx/tg ?2 = tg Yi/tg (Yi — e). (II .26)
Углы y1; y2 и e показаны на рис. II.1.
Из уравнения (11.25), если известны Mt и е, можно
определить уг. Указанные зависимости используются
обычно в виде графиков или таблиц [125]. На рис. II.2
приведена зависимость угла от М; при разных значе-
ниях е [113].
Рис II 2 Зависимость угла у-, от числа М, при раз-
личных значениях ь
Поток в турбинном сопле
В рассматриваемом случае для T[JT и G
остаются справедливыми формулы (II.9) и (11.13).
Полное давление может быть определено по формуле
(11.10), если известно статическое давление в потоке р.
Скачки уплотнений. Прямой скачок. В прямом скачке
уплотнений, возникающем перпендикулярно потоку, пара-
метры газа меняются скачкообразно на коротком участке,
имеющем протяженность пути свободного пробега молекул.
Зависимости между параметрами потока после (ин-
декс 2) и до (индекс 1) прямого скачка имеют вид:
P2/Pj = 26М2/(6 - 1) - (k- 1)/(6 + 1); (II.21)
= j (1 +
т2п\ = (1 + X
X ( 2k № 1V Г (k + 1)2М" 1 • (II 231
Х\6—1M1 L 2(6—1) J’ (П-23)
Одномерное прямое сужающееся сопло. При увеличении
располагаемого теплоперепада, обусловленного сниже-
нием противодавления, скорость газа на выходе из сопла
(рис. II.3, а) также увеличивается, ее численные значе-
ния при изоэнтропийном процессе могут быть подсчитаны
по формуле Ci = Kto — 1’1 • При этом соответственно
увеличивается и массовый расход газа через сопло.
При отношении давлений рКр/р*= [(6 + 1)/2 ]—
массовый расход G будет максимальным, а скорость до-
стигнет своего критического значения с = акр. Поэтому
отношение давлений ркр1р% и массовый расход, соответ-
ствующие указанному режиму, обычно называют крити-
ческими.
Если противодавление рпр = Pi < рКр, за соплом
происходит внезапное расширение потока.
Одномерное прямое сужающееся-расширяющееся сошо
(сопло Лаваля). Если площадь узкого сечения такого
сопла (рис. II.3, б) равна критической площади /кр для
сужающегося сопла, а площадь выходного сечения f/fKP >
> 1, то поток в нем получает ускорение до значения Мх >
> 1, определяемого из уравнения
м,_ М? + 2/(6-1)
2 26М^/(6 — 1) — 1 •
(11.24)
(11.27)
32
При этом расчетное отношение давлений
р>1 = [1 + (й- (11.28)
Если противодавление будет равно расчетному до-
звуковому давлению, заданному уравнением (11.28),
то в сужающейся части поток будет ускоряться до /VIг = 1
(в сечении /кр) с соответствующим снижением давления
До Ркр, а в расширяющейся части — замедляться.
Из уравнения неразрывности (II. 1), применяя его
к сечениям АС и BD (для сопла единичной высоты) и при-
нимая во внимание, что f = \ АВ sin а,' и f = i АД sin а,
получим 1
sin (а{ -|- 6) = f sin ajZ/кр = sin a-J q(E),
откуда угол отклонения потока в косом срезе [1 ]
6 « arcsin [sin а,/р (Z.)] — К1. (11.29)
Подсчитанные по формуле (11.29) углы 6 оказы-
ваются несколько меньшими по сравнению с дей-
ствительными, в основном за счет неучитываемого
влияния участка ВС косого среза сопла
Г. Ю. Степановым [94] предложена фор-
мула для определения угла 6, полученная из рас-
смотрения плоского течения идеального газа через
решетку пластин:
Pf/Po
Рис. II.3. Одномерные прямые сопла: а — сужающееся; б —
сужающееся-расширяющееся:
[1 ~-^(W(l)]2/7(1) + 180
2k п ft) [1 + ^-zrO(Z.)/n(l)] tg Й1 Л •
(П.ЗО)
Когда граничная звуковая волна совпадет с
фронтом сопла АВ (рис. II.4), расширение потока
в косом срезе будет исчерпано и угол выхода по-
тока будет равен а1пр = а' + 6 = arc sin (1/MJ), где
Mj соответствует выходному сечению сопла, а пре-
дельный угол отклонения [1 ] составит
1 - PjPo > Ркр/Р0-' 2 — Р1/Р0 = Ркр/РО— 0,576; З—Pl/po < Ркр/PQ
'-’пр а1пр а1 —
Расширение потока в косом срезе. Прямые сужаю-
щиеся-расширяющиеся сопла находят ограниченное при-
менение, например во вспомогательных ГТУ малой мощ-
ности. При установке оси сопла под некоторым углом
к оси турбины в выходной его части за узким сечением /кр
образуется особый участок АВС (рис. II.4), называемый
Рис. II.4. Схема расширения потока в ко-
сом срезе сопла
косым срезом. Поток в подобных соплах при прспиво-
давлении рпр < ркр обладает следующими особенностями:
поскольку в'точке А давление газа практически мгновенно
внижается до противодавления рпр, а вдоль участка
сопла ВС понижение давления происходит постепенно,
струя газа отклоняется от ее первоначального направле-
ния. Здесь, таким образом, имеет место как бы внезапное
расширение при обтекании сверхзвуковым потоком угла
FAE. При этом угловая точка А служит источником воз-
никновения в потоке звуковых волн.
3 Л. В. Арсеньев и др.
(sin а.])2 (* —1)/(Н-1)
1- -т-т—r(sin а,)2 «-!)/(*+’)
(11.31)
Минимальное давление рх mln, при котором исчерпы-
вается расширительная способность косого среза, может
быть найдено из уравнения
Plmin/Ро = [2/(k + l)]^"1’ (sin ai)2A/(A+1) =
= pKp (sin
(11.32)
из которого следует, что с уменьшением а± предельная
расширительная способность косого среза сопла увели-
чивается.
Если давление за соплом падает ниже того значения,
которое соответствует предельной расширительной спо-
собности косого среза, дальнейшее расширение потока
происходит вне косого среза и сопровождается волно-
выми колебаниями с образованием скачков уплотнения.
Составляющая скорости вдоль фронта сопла при этом
сохраняется практически постоянной.
Перерасширение потока при pt <plmln сопровожда-
ется дополнительными потерями, обусловленными как
уменьшением полного давления в системе возникающих
при этом многочисленных скачков уплотнения, так и
взаимодействием этих скачков с пограничным слоем на
стенках сопла.
Основные геометрические параметры
ступени осевой турбины
Введем следующие обозначения (рис. II.5): DH —
наружный диаметр; DK — корневой (внутренний) диаметр;
Е>ср = (Он + Ок)/2 — средний диаметр; /с — длина (вы-
сота) сопла; /р — длина (высота) рабочей лопатки; 6р —
радиальный зазор между вершинами рабочих лопаток
и статором; s — осевой зазор между лопаточными венцами;
33
d = DK!Dn — втулочное отношение; D = Dcvll-p'=
= (1 + d)/(l — d) — относительный диаметр ступени;
ун — угол меридионального раскрытия (угол раствора)
у наружной (периферийной) части ступени; ук — угол
меридионального раскрытия (угол раствора) у внутрен-
£
Рис. II.5. Схема ступени осевой турбины
ней (корневой) части ступени; 0—0; 1—7; 2—2 — сече-
ния соответственно перед сопловым венцом, в межвенцо-
вом зазоре и за рабочим колесом.
В случае, если рабочие (сопловые) лопатки выполня-
ются с бандажными полками, 6Р. у —зазор между уплотни-
тельными выступами на бандажной полке и статором;
6Б — осевой зазор между бандажной полкой и сопловым
аппаратом.
Ру — угол установки профиля в решетке;'Р1Л — входной
угол профиля лопатки, образованный касательной к сред-
ней линии профиля в его входной части и передним фрон-
том решетки; Р2Л — выходной угол профиля лопатки,
образованный касательной к средней линии профиля
в его выходной части и задним фронтом решетки (для
лопаток соплового аппарата указанные углы обозна-
чаются через а с соответствующими индексами); В —
осевая ширина решетки; а — минимальный проходной
размер между соседними профилями («горло»).
Основные уравнения для турбинной ступени
В сопловой аппарат ступени газовой турбины посту-
пает поток газа из камеры сгорания или предшествующей
ступени с определенным запасом избыточной тепловой
энергии, характеризуемой во входном сечении энталь-
пией z*, скоростью с0, давлением р* и температурой
В лопаточных каналах соплового аппарата в процессе
расширения газа его статическое давление и температура
уменьшаются, а скорость увеличивается от с0 до с3. Из
соплового аппарата поток поступает на рабочие лопатки
с относительной скоростью aij.
В криволинейных каналах, образуемых рабочими
лопатками, происходят поворот потока и последующее
расширение газа с соответствующим изменением его
давления и температуры. При этом изменение количества
движения преобразуется в механическую работу на валу
вращающегося рабочего колеса. В процессе такого пре-
образования средняя относительная скорость потока в ра-
бочем колесе, как правило, увеличивается, а абсолютная
скорость уменьшается от лд до с2. Векторное изображение
плана скоростей в турбинной ступени показано на рис. II.7.
Уравнение неразрывности (расхода) для одиночной
турбинной ступени при осредненных параметрах потока,
т. е. в одномерной постановке задачи, может быть напи-
сано в следующей форме:
Gi = PqCoF0 - 1 = а.» (11.33)
Рис. II.6. Плоские решетки профилей
лопаточных венцов турбинной сту-
пени: а — взаимное расположение со-
пловой и рабочей решеток; б — геоме-
трические параметры профиля в ре-
шетке
Рассекая венцы турбинной ступени некоторой цилин-
дрической коаксиальной поверхностью и разворачивая
это сечение на плоскость, получим плоские решетки про-
филей соплового аппарата и рабочего колеса (рис. II.6, а).
Основными геометрическими параметрами плоской
решетки профилей являются (рис. II.6, б): b — хорда
профиля; t —• шаг профилей в решетке; Ь = bit — гу-
стота решетки; t = t/b — относительный шаг решетки;
34
через газодинамическую функцию q (X) [см. (П.17)]—
= Vk\2/(k+ 1)]<H-1W-D/.?? ? (Л).
(11.34)
Из уравнения сохранения энергии (II.7) для реаль-
ного (необратимого) адиабатного процесса в тубинной сту-
пени получим
Ли = 1о 12 = сро Т'о +(со (П-35)
где hu — тепловой перепад, срабатываемый на окружности
рабочего колеса.
Из-за различного рода потерь, обусловленных прояв-
лением вязкости, протечек и т. п., работа в турбинной
ступени уменьшается по сравнению с таковой для изо-
энтропийного процесса течения идеального газа, а следо-
Рис. П.7. План (треугольники) скоростей
турбинной'ступени -
вательно, полная энтальпия потока на выходе из реальной
турбинной ступени I* будет больше на величину указан-
ных потерь.
С учетом высказанных выше соображений рабочий
процесс в реальной турбинной ступени условно может
быть изображен в i—s-диаграмме так, как показано на
рис. II.8.
Рис. II.8. Рабочий
процесс в турбин-
иой ступени в
i—s-диаграмме
Для соплового аппарата i* = !*, тогда скорость ис-
течения газа из соплового аппарата
= <pl/2cX[l-(Pi/Po)(^W], (П-36)
где tp = Ci/c1H3 — коэффициент скорости; <?1из =
Для рабочего колеса из уравнения сохранения энер-
гии следует, что в абсолютном движении ftp = =
= срТ* — СрТ?,, в относительном движении
= Ч’/[ 1 (II.37)
где ф = —коэффициент скорости. *
Уравнение (11.35) может быть написано также в виде
Лв = ^и3-АЛг.п-(с2-О2’ <П-38)
где Дйг. п — доля располагаемой работы, затраченной
на преодоление гидравлических потерь.
Из уравнения (II.6) при сделанных допущениях можно
получить
и (сш -|- ^2и) * (11.39)
Так как в реальной ступени имеется радиальный зазор
между рабочим колесом и статором, а также существует
трение диска рабочего колеса о i аз, внутренняя работа
турбинной ступени может быть выражена формулой
А3 — Аг/Г|р. з АЛтр. д, ' (11.40)
где т)р. з — коэффициент, учитывающий наличие радиаль-
ного зазора; ДАтр. д — работа, затрачиваемая на трение
диска; согласно [53],
ААтр д= рРн.д(ын.д/Ю0)3р, (11.41)
где £>н. д и ин. д — наружный диаметр диска и окружная
скорость на этом диаметре.
Коэффициент [< следует принимать равным 0,5—1,0
в зависимости от ширины полости, в которой вращается
диск.
Коэффициент полезного действия ступени
и турбины
Эффективность турбинной ступени, равно как и сово-
купности ступеней, т. е. лопаточного аппарата турбины,
оценивается ее коэффициентом полезного действия, пред-
ставляющим собой отношение полезной работы на окруж-
ности колеса к располагаемой работе в изоэнтропийном
процессе при допущении равенства начальных параметров
газа и равенства конечного давления в реальной и идеаль-
ной ступенях (турбинах):
Лет — Ав//1из > (II. 42)
Лт = (11.43)
Различают два основных характерных случая изо-
энтропийного расширения: до некоторого значения вы-
ходной скорости и до состояния, соответствующего ну-
левой выходной скорости. Тогда к. п. д. одиночной тур-
бинной ступени (см. рис. II.8) по параметрам затормо-
женного потока
Лет (*0ст г2ст)/(г0ст ” ^2из ст)’ (11.44)
по статическим параметрам потока на выходе из ступени
Лет Оост ' 'О'ост ' ^2из ст)’ (11.45)
Аналогично для многоступенчатой турбины к. п. д.
по заторможенным параметрам потока (рис. II.9)
. (п.46)
по статическим параметрам на выходе из турбины
Л? ~ (‘о ~~ 'г)/(1о ~~ *2из)’ (И.47)
Этот к. п. д. часто называют мощностным, поскольку
он характеризует степень использования располагаемой
энергии для получения работы (мощности) на валу тур-
бины в реальном процессе расширения газа с учетом всех
потерь, в том числе потерь с выходной скоростью. Иногда
для оценки гидравлического совершенства лопаточного
аппарата турбины определяют изоэнтропийный ее к. п. д.
по параметрам незаторможенного потока на выходе (как
идеальной, так и реальной турбин):
Лиз. т = (<* У/(ГО ггиз) • (11.48)
35
Зависимость между nJ, Пт и Пиз.т может быть выРа’
жена формулой [56]
Пт = Пг/Ът + О -Пиз. т)]- <IL49)
Если принять во внимание, что полезная работа много-
ступенчатой турбины представляет собой сумму полезных
работ, создаваемых отдельными ступенями, и использо-
вать приближенную формулу [113]
Пст~ (10ст — ^2ст)/[(г0ст г2из ст )l‘ (Свх. ст С2ст)/2] ,
Рис. II.9. Рабочий процесс в много-
ступенчатой турбине в i—5-диаграмме
то к. п. д. турбины
Нг^^т
<0 --- *2ИЗ
. *
10 — (2из
Ост *2из
Е(4.ет-4т)/2
1_____________
*0 - 12й3
(11.50)
Аналогично [113]
Коэффициент возврата теплоты
в многоступенчатой турбине
Турбина с бесконечно большим числом ступеней.
Реальный процесс течения газа через лопаточный аппарат
турбинной ступени характеризуется тем, что часть рас-
полагаемой работы, затрачиваемая на преодоление гид-
равлических сопротивлений и протечки через зазоры,
необратимо преобразуется в тепловую энергию. В много-
ступенчатой турбине из-за наличия нескольких последо-
вательно расположенных ступеней эта дополнительно
сообщенная газу теплота может быть частично преобра-
зована в полезную работу, развиваемую в последующей
ступени, т. е. как бы возвращена последующим сту-
пеням.
В i—s-диаграмме отмеченное явление выражается
в том, что благодаря различному наклону изобар, завися-
Рис. 11.10. Коэффициент возврата теплоты
для многоступенчатой турбины при г = оо
щему от абсолютной температуры газа, величина первого
слагаемого в формулах (11.50 и (11.51) будет больше еди-
ницы, т. е.
2 (1'о ст из. ст)/(*0 *2 из) ,
и поэтому nJ > Пст-
Величину 1 -]- а называют коэффициентом возврата
теплоты.
Если ввести понятие к. п. д. элементарной (беско-
нечно малой) ступени, называемого обычно политропиче-
ским к. п. д. х
Ппол ст « Лг’о/(Л‘из + Дс2/2) = Д‘о/(^Р + Дс72),
(11.52)
и предположить, что ср = const при Ар -> 0 и Ас2/2 -+ 0,
можно получить зависимость Ппол. ст = cpdT/(vdT).
Тогда коэффициент возврата теплоты для многоступен-
1 Зависимость между Ппол.ст и Чт рассмотрена в п. 1.2.
36
чатой турбины с бесконечно большим количеством эле-
ментарных ступеней
(1 со Д*из. ст/(*0 ^2 из)
1 1^ (Р2/Ро)(Л~1)11пол-стМ ,П5 )
Ппол.ст 1 - (p2/p0)<k~^k 1 ’
Значения (1Ц-а)<х> в зависимости от р0/р3 = лт при
различных т|пол. ст приведены на рис. 11.10 1113].
Турбина с конечным числом ступеней. Если предпо-
ложить, что в многоступенчатой турбине с числом ступе-
ней z для каждой из них отношение давлений Poilp2t — лст
одинаково, то л,г = л|т.
Пренебрегая разностью кинетических энергий, со-
ответствующих скоростям на входе и выходе из ступени,
а также учитывая, что
«о- h = срт0[1 - Ст/(М ];
получим
= (1 - Я^пол. ст)/(1 - Л71)
или приближенно
^Ict ^лол.стС^т (ят 0 Лет!' (11.54)
Тогда коэффициент возврата теплоты для многоступенча-
той турбины
1 _ n~(k-D/(kz'l
° + “)г = 1- я-^пол.ст^-ПД**) Х
1 _ ^пол. ст^—
X - ! L ’ {П'55)
где Лгюл. ст определяется1 из формулы (11.54).
Степень реактивности
Термодинамическая степень реактивности представ-
ляет собой отношение располагаемых изоэнтропийных
перепадов энтальпии в рабочем колесе и турбинной ступени:
0Т ^р. ИЗ 7иЗ*
В ряде случаев используется понятие кинематиче-
ской ci епени реактивности
0К 1 (с1ц -ф- с2ц) /(2u) X
~~ (с1и ~ с2и^/[2(а1с1и ~~ и2с2и)Г (И.56)
В отличие от 0Т величина 0К определяется по кинемати-
ческим характеристикам действительного процесса те-
чения газа в ступени, т. е. с учетом потерь располагаемой
работы.
Связь между 0К и 0Т может быть выражена формулой
[112]
ек = ет11р.з+ sin2«2(1 — С1а/С2а)], (П-57)
где 0т = 1 — d (1 — 6Т)/(С1изг?из.ст).
1 При расчетах можно принимать Т)пол ст ~ 0,86^0,89.
Поскольку при обычных соотношениях между с1а
и с2а величина, стоящая в квадратных скобках формулы
(11.57), близка к нулю, в приближенных расчетах можно
принимать 0К 0тТ]р. з-
Связь между 0Т и кинематическими параметрами по-
тока для изоэнтропийного течения выражается формулой
(при с1а= с2а= са) [113]
От = са [(ctg р2 — ctg ₽!)/2]/и = са ctg ₽m/u, (И.58)
где = (₽i 4- р»)/2.
Отношение eJu называют коэффициентом расхода
ступени и обозначают <рр.
С увеличением 0Т или 0К возрастает степень расшире-
ния газа в рабочем колесе и соответственно степень кон-
фузорности каналов рабочих лопаток.
При расчете одномерного потока по среднему сечению
обычно принимают следующую классификацию ступеней
по величине 0:
а) 0 = 0 — активная ступень, в которой расширение
происходит только в сопловом аппарате; в рабочем колесе
давление не изменяется;
С) =0,5— реактивная (конгруэнтная) ступень,
в которой степень расширения в сопловом аппарате и ра-
бочем колесе одинакова.
Поскольку степень реактивности, как правило, ме-
няется по высоте лопатки, уменьшаясь от периферии сту-
пени к ее корню, могут возникнуть условия, особенно
при переменных режимах, когда в корневых сечениях
появится отрицательная реактивность. Появление отри-
цательной степени реактивности сопровождается повы-
шенными потерями располагаемой работы, и поэтому
ее следует избегать, особенно на расчетных режимах.
Чтобы не допускать этого, выбирают среднюю величину
0ср = 0,15=0,50, причем большие значения рекоменду-
ются для ступеней с малыми отношениями Оср/1р (от 3
до 3,5), а меньшие — для первых ступеней (в том числе
охлаждаемых) при Z?cp//p 10=12.
Коэффициент нагрузки ступени
Коэффициент нагрузки ступени характеризуется сра-
батываемым в ней тепловым перепадом hu, отнесенным
к квадрату окружной скорости вращения рабочего колеса:
hu = hu!u*. (11.59)
Газодинамическая нагрузка ступени часто харак-
теризуется также отношением и/сИз = х, где сиз — ско-
рость (условная) потока, кинетическая энергия которого
равна располагаемой (теоретической) работе расширения
т- е- сиз/2 = ^из- _ /ч
Зависимость между hu, х и к. п. д. ступени т]ст [см.
(11.45)] выражается формулой [56]
hu = т]ст/(2^2)- (11.60)
Аналогично для к. п. д. ступеней Т|из ст и т]*т можно
получить формулы:
чИз.сГ = 2М2 + ^7(2Лиз); (Ц.6!)
Пет = 2V2/[1 - с|/(2Лиз)] ~ 2^Ар. з- (П-62)
Используя очевидные соотношения:
с2и = ф cos ₽2]Лw\ + 2ftp — u2;
W1 — ci + “i — 2Mici cos ai»
из формул (11.45), (11.61) и (II.62) можно получить раз-
вернутую функциональную зависимость между к. п. д.
37
h^hu/u2
Рис.11.11. Коэффициент нагрузки ступени hu
при изоэнтропийном процессе течения (е =
= ₽i+₽2) [113]: а —0 = 0; 6 — 0 =
= 0,5 (ах = р2), в — а2 = 90°
38
турбинной ступени при заданных значениях ах, ф, ф и сте-
пенью реактивности 0Т [56]:
, Т|ст = 2х [ф cos ах У1 — 9т +
+ ф cos ₽2Кет -f- ф2 (1 — 0т) — ’ ’ ’
— 2хф cos йх ]/” 1 — 9Т + х2 — х; (11.63)
Пиз. Ст ~ ф2ф2 (1 -- 9Г) ф29т -----
— (I — ф2) (х2 — 2хф cos йх УТ— 9Т); (II.64)
Рис. 11.12. Зависимость к. п. д. ступени
коэффициента нагрузки hu при 0 = 0,5 и
них значениях ах
Лет от
различ-
й
^ст '
ф2 9Т
Ф2 1—0.
4- (1 — ф2) (2xjcos aj — х2)
где хх = и/сг = и/[ф К2 (1 — 9Т) Лиз. стЬ
В формулу (11.63) входит угол р2, зависящий от боль-
шого количества параметров (и, ах, 9Т и др.). Предполо-
получить
(11.65)
жив, что ф и ф не зависят от х — и/сяз, можно
приближенные формулы, связывающие между
собой коэффициенты hu, х и к. п. д. ступени
для некоторых наиболее характерных случаев.
1. - ~ ”
При изоэнтропийном процессе течения, т. е. когда
ф = ф = 1 (рИс. П.11, а) [113],
= 2са ctg р2/и = 2фр ctg Р2. (Н.71)
Если при этом выходная скорость с2 имеет осевое направ-
ление, т. е. а2 = 90°, то ctg р2 = ц/с2Д и hu — 2.
2. 0 = 0,5. При изоэнтропиийном процессе течения,
т. е. когда <р = ф= 1 (рис. (П.11, б),
hu = Тш "Ь ^2и)/м = 2сй ctg р2/и — 1 “
= 2са ctg йх/и — 1. (П.72)
3. Скорость потока на выходе из ступени направлена
вдоль оси, т. е. ctg a2 = 0. При изоэнтропийном течении
(рис. 11.11, в):
ctg Р2 = w/c2a, hu — У^2а/У (и/с%а) 1 — 1, (11.73)
т. е. изменение окружной составляющей абсолютной ско-
рости в ступени равно средней окружной скорости.
Учитывая наличие потерь, характеризуемых коэф-
фициентами ф и ф, и полагая их не зависящими от х, можно
получить зависимости г]ст, г]‘т и т]из ст в функции от hu
и х, аналогичные предыдущему случаю. В качестве при-
мера на рис. И. 12 приведен график т]*т = / (/ги) при
различных значениях ах и постоянных коэффициентах
скорости ф и ф [56]. В действительности коэффициенты ф
и ф зависят от hu и х, причем зависимость эта является
сложной. Поэтому на практике целесообразно исполь-
зовать имеющиеся экспериментальные зависимости Т|*т =
~ f (hu> х).
На рис. 11.13 приведены зависимости [56] Т)*т —
= 'Пст/’Пст max = ffruK’ “1- у которых аргументом яв-
ляется коэффициент нагрузки 1г!1К на корневом диаметре
ступени, где обычно наблюдаются максимальные значе-
ния числа и угла поворота потока в каналах лопаток
рабочего колеса [56]. '
9Т = 0. Учитывая, что при этом =
получим
hu — (1 + Ф) (fpcosaj — х)/х, (11.66)
достаточно широком диапазоне углов ах
величина hu изменяется незначительно и яв-
ляется однозначной функцией _ ц/сиз.
Соответственно:
Пет = 2х [<р cos <*! 4- ф (<р cos ах — х) — х];
(11.67)
Лиз. ст - Ф2Ф2 + (1 — Ф2) (2хф cos aj — х2);
(11.68)
т. е. в
Рис. 11.13. Зависимости т]*т = f (hUK, MCJ: а — а.
б — а1ср = 30-4-36°
1СР = 18-25°;
Т|ст
'и
2
(11.69)
(1 + ф)2 ф2 cos3
Из формул (11.67) и (11.68) следует, что максимумы
к. п. д. т]ст и Т]из. Ст достигаются при различных значениях
параметра х. Максимальное значение т]*т будет достигаться
яри [56]
4. Когда скорость потока на выходе из ступени на-
правлена вдоль оси, ctg р2 = и!с^а. При изоэнтро-
пийном течении:
0т = с2а [и/саа — ctg рх]/(2«) = 1 /2 — с2 ctg ₽i/(2u);
(I I-74)
hu = Acu/« = са ctg а^/и =
= 2 + са (ctg Рх — ctg p2)/x.
(11.75)
Ьц. opt -
+ ф)2 — <1 + 1 — Ф2)ф2 COS2 «х
। 1 — ф21|;2
(П.70>
Отсюда следует, что максимальное значение коэффи-
циента нагрузки hu = 2 достигается при осевом выходе
потока из ступени и нулевой степени реактивности.
39
Дальнейшее увеличение hu может быть получено лишь
при отрицательном значении 9Т, что вызывает, однако,
существенное снижение к. п. д. ступени.
Скорость и направление выхода потока
из турбинной ступени
При изоэнтропийном течении газа, как следует из
(11.44) и (11.45), г)*т = 1, а величина т]ст будет изменяться
в зависимости от степени реактивности и аэродинамиче-
ской нагрузки на ступень из-за потери располагаемой
работы с выходной скоростью. О количественном влиянии
выходной скорости на к. п. д. Т]ст можно судить по рис.
зывалось выше, используется также отношение х = и/сиз.
Из рис. 11.15 1 [112] следует, что с увеличением 9 макси-
мум к. п. д. ступени смещается в сторону больших зна-
чений х.
Для оптимальных условий работы ступени имеется
однозначная связь между фр и ах. Так, в ступенях, пред-
Рис. 11.15. Зависимость к. п. д. сту-
пени т]ст, г]*т, т]из. стот х=«/сизпри
cCicp — 22 :
' ®ср “0» 0ср = 0,3;
-------0ср = 0,5
назначенных для больших расходов (фр), направляющие
лопатки следует проектировать с большими углами вы-
хода ах и наоборот. В реальных условиях, когда процесс
течения в ступени сопровождается гидравлическими
потерями располагаемой работы
\hr_ п = (1 - ф2) cf/2 + (1 - ф2) ш|из/2, (11.78)
Рис. II.Независи-
мость коэффициен-
та нагрузки hu =
= hjti1 от коэффи-
циента расхода
фр = са'и при Раз-
личной степени ре-
активности (ср =
= ф = 1)- а —
0=0; б — е =
= 0,5; в — а2 =
= 90°
зависимости т]*т =J (ф, Ф, \ ) имеют вид [56]:
при 9 = 0
, 2ф2ф2 — ф2
'Пет k 1 2 , 2 2
-Rk/(k - 1)
-1 X2
(11.79)
-(1
— ф2) J^L------L I ф2.
2ЙИ
11.14, из которого следует, что в ступени с 9 = 0 значение
Т]ст = 1,0 достигается при = 2 (х = 0,5) и <рр = 0,
в ступени с 9 = 0,5 — соответственно при hu = 1 (г =
= l/KSl и фр = 0, в ступени с осевым выходом потока
Чет = 1,0 — при всех значениях Ии (х), когда фр -> 0.
При конечной величине фр максимум Т|ст достигается
при значениях hu, соответственно равных [113]:
для ступени с 9 = 0
йи=2]Л + Фр; л-= 1/^2 (1 + 4ф2); (П.76)
для ступени с 9 = 0,5
hu = /1+4фр2; х = 1/]/'2(1 + 4ф2)1/4. (11.77)
При этом на выходе из ступени имеет место закрутка
потока, противоположная направлению вращения рабо-
чего колеса.
В практике стационарного газотурбостроения в ка-
честве характеристик нагруженности ступени, как ука-
40
при 9 = 0,5
*
Чет
МН 1Л ’'''
Г Rk/(k —1)
ф2 (1 + Ф2)
(11.80)
k — 1
1 к.
Ci
.. ,21 2Ли — 1
— (1 — ф2)—у---
+ 2
В этих формулах коэффициент нагрузки hu = с1и/и,
т. е. предполагается, что с2и = 0.
Данные рис. 11.16, полученные при коэффициентах
скорости ф — 0,98 и ф = 0,97 и hu/T2— 200, позволяют
1 Кривые кпд на рисунке подсчитывались соответ-
ственно по формулам (II 67)-—(II 69)
судить об относительном изменении т]*т в зависимости
от величины выходной скорости с2 (Мс j и 0* [56].
Рис. 11.16. Зависимость к. п. д. сту-
пени Тст = Т]*т/Г)*т. тах от МС2:
Г ®ср “О’ 2 ®ср = 0.5
Потери в турбинной ступени
Классификация потерь. Все потери располагаемой
работы, возникающие в реальной ступени, могут быть раз-
делены на внутренние и внешние.
К внутренним относят потери, сопровождающиеся
изменением теплового состояния рабочего тела, при воз-
растании его энтропии, потери на трение потока вязкого
сжимаемого газа о поверхности, ограничивающие про-
точную часть турбины, профильную поверхность направ-
ляющих и рабочих лопаток; на взаимное трение отдель-
ных слоев потока, движущихся с различными скоростями;
потери из-за турбулентности. Сюда же относят потери,
обусловленные наличием зазоров между движущимися и
неподвижными частями турбины, нестационарными яв-
лениями в проточной части и др.
К внешним потерям располагаемой работы относят
такие, которые не оказывают влияния на тепловое состо-
яние рабочего тела в турбине: на трение в опорных и упор-
ных подшипниках, на привод вспомогательных механиз-
мов и органов регулирования, потери из-за утечки рабо-
чего тела через концевые лабиринтные уплотнения и др.
Внутренние потери, обусловленные трением потока
о профильную часть лопаток, называют профильными
потерями. Они включают в себя: потери от трения и вих-
реобразования в пограничном слое на профильной по-
верхности направляющих и рабочих лопаток; потери
от вихреобразования в вихревом закромочном следе;
потери в скачках уплотнении, взаимодействующих с по-
граничным слоем, образующимся на поверхности лопаток
Потери, обусловленные наличием торцовых огра-
ничивающих поверхностей в ступени, а также радиаль-
ных зазоров у вершин лопаток, обычно объединяют
и называют концевыми (вторичными) потерями.
Третью группу внутренних потерь составляют потери,
возникающие за пределами лопаточных венцов от трения
и вихреобразования в межвенцовых зазорах, в том числе
у торцовых стенок, от трения дисков о газ, от смешения
основного потока газа с потоком охлаждающего воздуха
и др.
Для оценки потерь в турбинной ступени могут исполь-
зоваться следующие коэффициенты:
а) коэффициенты потерь ?, представляющие собой
отношение потерь располагаемой работы к располагае-
мой изоэнтропийной работе (перепаду энтальпии) в сту-
пени:
для сопловых лопаток
Sc = ДЛс/йиз, или ДЛС = ccCj нз/2; (11.81)
1 В ступенях газовых турбин обычно = 180- 200
для рабочих лопаток
Ер = Айр/йиз, или Айр = из/2; (11.82)
суммарная относительная потеря располагаемой работы
для каждого из венцов
Ед Епр ~i~ Екон>
где fenp — коэффициент профильных потерь; Щон — коэф-
фициент концевых потерь;
б) коэффициенты скорости ф и ф;
в) коэффициенты потерь полного давления (для соп-
ловых и рабочих лопаток соответственно):
у<=(Ро-Р1ЖЛ-Р1У,
^р ' (.Р1 отн Р'г отн)/(Р2 отн ^г),
г) коэффициенты профильного сопротивления реше-
ток (для сопловых и рабочих лопаток) [ИЗ, 120]:
^с = <7тР. с/(рсрссР6с/2); (11.83)
Схр =^тР"р/(Рср^рЬр/2), (П.84)
где <?Тр i — сила трения на единицу длины решетки; —
хорда профиля.
Различные коэффициенты для сопловой решетки
связаны Л зависимостями:
сс — 1 — ф2, или <р = V1 — Ес;
кс«§c(i +*м?/2);
= 2ДрХ sin 3аср/(Рсрс16с sin Ч),
где аср = (явх 4- ctj)/2.
Аналогичные формулы могут быть написаны и для
рабочей решетки.
Профильные потери. Влияние геометрических па-
раметров. Теоретические и экспериментальные исследо-
вания свидетельствуют о том, что на профильные потери
влияют такие геометрические параметры сопловых и
рабочих решеток, как угол поворота потока, относитель-
ный шаг, форма и размеры входных и выходных кромок,
относительная толщина профиля.
Профильные потери в решетках чаще всего находят
экспериментально (при продувке плоских решеток), опре-
деляя их суммарную величину £Пр = Етр + Екр-
Расчетные методы предусматривают раздельное опре-
деление потерь на трение 4р и кромочных потерь ?кр.
На рис. 11.17 приведены расчетные значения $тр.
для плоских решеток с оптимальной относительной тол-
щиной профиля стах в зависимости от суммы углов рх + р2,
связанной с углом поворота потока Ар соотношением Ар =
= 180° —- (pj + р2), и от типа решетки, характеризу-
емого отношением k — sin px/sin р2 (величина k равна
также отношению площадей сечений струи на входе и
выходе из решетки [94]).
Из рис. 11.17 следует, что значения feTp уменьшаются
с увеличением k и Рх 4- р2, т. е. с уменьшением угла по-
ворота потока Ар. Это обусловлено тем, что в активных ре-
шетках (k 1) имеется развитая диффузорная область
потока за входной кромкой и на выходном участке спинки
профиля, а скорость потока на спинке профиля значи-
тельно больше средней скорости. С увеличением k, т. е-
с увеличением степени реактивности, протяженность ука-
занной области уменьшается, давление по обе стороны
выходной кромки выравнивается, а разница в максималь-
ной и средней скорости потока уменьшается.
Оптимальная относительная толщина профиля сгаах =
= ctnax/b (см. рис. II.6, б) также зависит от угла поворота
41
потока и типа решетки. Ее можно оценить по прибли-
женной формуле, предложенной Г. Ю. Степановым [94],
Стах — (cmax/^)opt ~ 1 4 Pi, (11.85)
где А = 0,84-1,0 для активной и А= 1,04-1,1 для реак-
тивной решеток.
Кромочные потери £кр возникают из-за взаимодей-
ствия пограничных слоев, сходящих с вогнутой и выпук-
лой частей профиля у задней кромки. Они зависят от ре-
Рис. 11.17. Зависи-
мость коэффициен-
та потерь на трение
от угла поворота
потока для плоской
решетки турбинных
профилей
жима течения в пограничном слое, существенно возра-
стая при его отрыве. Приближенно можно считать [94]
gKp = 0,2d2/(F sin р2Э) = 0,2d2/a, (11.86)
где d2 = d2/b — относительная толщина выходной кромки;
sin Р2Э = alt (см. рис. II.6, б).
Рис. 11.18. Зависи-
мость коэффициен-
та кромочных по-
терь от угла Р2Э
(7= 0,6; 0,03)
Из рис. 11.18 следует, что с увеличением углов р2Э
в применяемом на практике диапазоне их значений (10—
30°) величина |!(р существенно уменьшается. Для при-
ближенной оценки профильных потерь в решетках при
дозвуковых скоростях потока в области автомодельности
по критерию Рейнольдса Re и при оптимальных-значе-
ниях tl могут быть использованы {[112] зависимости
'фпр = f (Pl н- р2, k ) (рис. 11.19).
Многочисленными опытами показано наличие опти-
мального шага решетки Zopt, при котором профильные
потери в ней имеют минимальное значение. Величина iopt
зависит от угла поворота потока, толщины профиля сшах
и типа решетки. Для приближенной оценки ? t можно
Подробнее об этом см. на стр. 43.
рекомендовать эмпирическую формулу В. И. Дышлев-
ского [56]
F0pt = 0,55 (180й/[180-(|31 + р2)]}1/3 (1 - Стах)-
(11.87)
Характер влияния относительного шага решетки t
на коэффициент профильных потерь Snp при различных
углах выхода потока ах (р2) при безударном входе на ре-
шетку показан на рис. 11.20 [113].
Рис. 11.19. Зависимость приведенного коэффициента ско-
рости фпр от рх + р2 при различных значениях k
Поскольку, как следует из рис. 11.20, при увеличе-
нии t потери в решетке увеличиваются менее интенсивно
при t > tQpi, чем при t < £opt, в ряде случаев по конструк-
тивным соображениям целесообразно принимать более
редкие решетки по сравнению с оптимальными. Для ло-
Рис. 11.20. Зависи-
мость коэффициента
профильных потерь
в решетке от t = t!b
при различных углах
выхода потока и без-
ударном входе на ре-
шетку: а — сопловая
решетка; б — рабочая
решетка
паточных венцов ступеней газовых турбин на их среднем
диаметре можно рекомендовать следующие значения:
'’opt С =0,64-0,95; 70ptp = 0,54-0,8.
Влияние режима течения. Параметрами, характери-
зующими режим течения, являются скорость на выходе
из турбинной решетки и угол атаки I = рх —• р1л.
Потери 1отр, возникающие из-за угла атаки, обуслов-
лены отрывом потока от входных кромок и профильной
42
части лопатки, несплошным заполнением межлопаточных
каналов и т. д. Поэтому коэффициент профильных потерь
при наличии углов атаки §пр = >тр ф. gKp g0Tp
В области положительных значений i их влияние
на величину Епр оказывается значительно более интенсив-
ным [94] как для активной, так и для реактивной тур-
бинных решеток (рис. 14.21) [113].
Для реактивной решетки изменение дпр в зависимости
от i является менее интенсивным по сравнению с актив-
ной решеткой. В некоторых случаях представляется
целесообразным задавать на расчетном режиме неболь-
шие положительные углы атаки i, так как при этом из-за
увеличения конфузорности межлопаточного канала до-
Рис. 11.21. Зависимость коэффициента
профильных потерь Ёпр (------) и угла
выхода потока (р2) (-----------) от
угла атаки i.
1 — активная решетка; 2 — реактивная
решетка
Приближенно профильные потери при наличии углов
атаки на входе в решетку можно оценить по формуле [94 ]
sm Ар sin р2\ 2
sm рх sm р10/
(11.88)
где А = | ; В = 0,058; С — 0,265; р10 соответствует
углу атаки i = 0.
Влияние скорости выхода потока из решетки оцени-
вается по значениям критериев Re = w2blv и МЮ2 =
= w2la. Изменение числа Re влияет на профильные по-
тери лишь в области малых его значений [Re< Репред ~
« (1,2-?2,0)106], причем реактивные решетки менее
чувствительны к влиянию Re по сравнению с активными
решетками [34, 94, 113]. При числах Ре<Репред их
влияние на с„р можно оценивать по рис. II.22.
Влияние числа Ма,2 (К,,.,) на профильные потери в ре-
шетке оценивают обычно по величине скорости на выходе
из решетки с, (о>2). В реактивных решетках при углах
атаки I, близких к расчетным, коэффициент скорости ф
мало изменяется вплоть до значений Л г=а 0,8 (рис. II.23).
На* нерасчетных углах обтекания влияние сжимаемости
начинает сказываться при меньших значениях
В решетках малой реактивности профильные потери
более существенно зависят от М (л), достигая максимума
при М^р-аО.8, что обусловлено возникновением местных
сверхзвуковых скоростей на профиле, и несколько умень-
шаясь до Мш «а 1,0, а затем снова растут при
МШ1>1 [112]1.
Рис. 11.22. Влияние числа Рейнольдса на относи-
тельные профильные потери в решетке §пр = §пр/?пР
(^-значение £рр при Re — 1,2 • 106):
1 — по Доллину при В = 8 мм; 2 - тоже при В = 19 мм;
3 — по Содербергу; 4 — по Аккерету
Сверхзвуковые скорости (Mffli>l) могут возникать на
входе в решетку, например в корневых сечениях ступеней,
где степень реактивности близка к нулю. При этом во
входном сечении решетки возникает сложная система
скачков уплотнений, сопровождающихся ростом профиль-
ных потерь. В таких случаях для уменьшения потерь
требуется специальное профилирование решетки, напри-
мер с сужающимися-расширяющимися каналами
Другой важной характеристикой турбинной решетки
является угол выхода потока. Для малых, дозвуковых
скоростей (М„,2 С 0,5) с достаточной степенью точности
можно считать, что при безударном входе для решеток
профилей, выходная часть спинки которых очерчена
прямой, угол выхода потока ах (р2) изменяется пропор-
ционально величине arcsm (alt) (рис. II. 24, а) с некоторым
отставанием от нее [56, 113]. В диапазоне 0,5 < М„, <
<1,0 для таких решеток sin 04 — alt.
Рис. II.23. Зависимость коэффициента скорости ф от
при различных углах атаки для реактивных решеток
Для профилей, участок спинки которых у выходной
кромки очерчивается кривой радиусом гс, угол аг при
<0,5 оказывается меньшим, чем по рис. II.24, а;
соответственно при М„, ш 1,0
г
04 arc sin (a/t) —fare sin (a>t), (11.89)
где f=F (tire) (рис. 11.24, б) [113].
Угол отставания Ар = р2Л — |32 можно приближенно
определить по какой-либо из эмпирических формул,
например [ИЗ]
А₽ = туУТ, (11.90)
43
где т = F (ру) (рис 11.24, в); [Зу— угол установки про-
филя; х = 180° — (|31л 02л) — угол изгиба профиля,
хорошо согласующийся с экспериментом для реактивных
решеток в диапазоне М^, С 0,8.
При сверхкритических скоростях потока угол выхода
на достаточном удалении от решетки аг может быть опре-
делен из приближенной формулы {113]
sin а, = sin а, кп///кр. (II.91)
При наличии углов атаки на входе в решетку угол
выхода потока несколько отклоняется от указанных
и Re >; 2- 10е; в — значения функции т фу):
1 и 2 — соответственно цилиндрическая и параболическая
дужки профиля
выше значений, однако при МШг 1,0 эта разница обычно
невелика и ее можно не учитывать при расчетах.
Концевые потери. Концевые потери, обусловленные на-
личием торцовых ограничивающих стенок в межлопаточных
каналах венцов турбинной ступени, возникают из-за
взаимодействия пограничных слоев, образующихся на
профильной и торцовых частях лопатки, как между
собой, так и с основной частью (ядром) потока. Благодаря
этому на выпуклой части профиля лопаток у выходных
кромок на некотором расстоянии от торцовых ограничи-
вающих стенок образуются две области накапливания
подторможенной жидкости, заполненной вихрями. В ос-
новном потоке при этом возникает компенсирующее вторич-
ное течение, образующее у концов лопатки две замкнутые
вихревые области (парный вихрь) [34 , 94, 124].
В каналах с активными решетками концевые потери
§кон существенно больше, чем в каналах с реактивными
решетками (см рис. II 25, на котором обозначено / — х//).
Детальные исследования показали, что при 7 = llb> 1
(где I — длина лопатки; Ь — хорда профиля) отмеченные
две зоны концевых потерь существуют раздельно, слабо
взаимодействуя между собой, вследствие чего абсолютная
величина концевых потерь при этом не зависит от высоты
лопатки.
При малых высотах лопаток (I < 1) указанные две
зоны концевых потерь смыкаются между собой, что при-
водит к непропорционально большому росту суммарных
потерь, обусловленному их активным взаимодействием.
В реальных венцах сопловых и особенно рабочих лопаток
вследствие переменности геометрических и аэродинами-
ческих параметров решеток по радиусу интенсивность
вихревых зон, а следовательно, и концевые потери в кор-
невой и периферийной частях неодинаковы, причем у корня
концевые потери обычно больше, чем у периферии, что
обусловлено в основном малой степенью реактивности и
повышенной (по сравнению с оптимальной) густотой ре-
шеток.
Особенно существенное увеличение концевых потерь
наблюдается при нулевой и отрицательной степени реак-
тивности у корня, что обычно имеет место в последних
ступенях турбины, характеризующихся малыми отно-
шениями Оср/1р.
Концевые потери при проектировании лопаточного
аппарата турбины можно оценивать по имеющимся экс-
периментальным данным. В качестве примера на рис. 11.26
приведены обобщенные экспериментальные данные для
решеток с бандажными полками [56]. Величина £ков
может быть получена также расчетом по какой-либо
из приближенных формул; например, для решеток ступе-
ней авиационных ГТД рекомендуется формула [56}
1коН = ?кои/Ь=^/(1 + ^Х (П.92>
где А и В — численные коэффициенты, которые следует
принимать в диапазоне значений: А= 1,04-1,1; В =
= 0,44-0,5; большие значения А и меньшие значения
В соответствуют решеткам с малыми профильными по-
терями (Епр = 0,024-0,03) и наоборот.
Рис. 11.25. Изменение показателей решетки
по высоте прямого неподвижного лопаточного
канала, ограниченного торцовыми стенками.
а — осредненные потери, б — углы выхода
потока;
— — — — активная решетка,----------- реактив-
ная решетка
Следует, однако, заметить, что при проектирований
предпочтительнее пользоваться соответствующими экс-
периментальными данными, полученными для решеток,
возможно более близких по геометрическим и режимным
параметрам к проектируемым решеткам, так как ни
одна из известных формул для определения |кои не дает
достаточно хорошей сходимости с опытными данными,
что является, по-видимому, результатом сложной зави-
симости между ёкои. параметрами решетки I, b, t, в и
условиями на входе потока в решетку.
Концевые потери, возникающие из-за наличия радиаль-
ного зазора у концов необандаженных лопаток, обуслов-
лены как утечкой части расхода рабочего тела мимо ло-
паточного венца, так и изменением режима обтекания
44
верхних концов лопаток по сравнению с расчетным.
Это изменение выражается главным образом в том, что
под влиянием геретекания рабочего тела через торец
лопатки с вогнутой части профиля на выпуклую на спинке
лопатки у ее верхнего конца возникает интенсивный
отрыв, сопровождающийся необратимым преобразованием
части кинетической энергии потока в тепловую энергию
диссипирующихся вихрей и изменением углов выхода из
решетки [105].
Потери располагаемой работы в ступенях с лопатками
рассматриваемого типа зависят от ряда факторов: отно-
сительного радиального зазора, геометрических пара-
метров решеток профилей, степени реактивности в кон-
цевых частях лопатки, критериев подобия М и Re, пара-
метров потока в пристенном (пограничном) слое на входе
в зазор. Эти потери могут быть оценены как с помощью
потери располагаемой работы, обусловленные наличием
как торцовых стенок, так и радиального зазора 6р.
Положительная перекрыта между входными кром-
ками рабочих и выходными кромками направляющих
лопаток может привести к уменьшению потерь в радиаль-
ном зазоре, особенно при малых степенях реактивности
у периферийной части ступени с относительно корот-
кими лопатками. Опыты показали» что существует опти-
мальное значение такой перекрыши A/opt, которое зависит
от ряда факторов: осевого и радиального зазоров, степени
реактивности 0, угла а1н, числа Мс и др., причем с увели-
чением 0 величина AIopt уменьшается [53].
Некоторое снижение потерь в радиальном зазоре
может быть также получено при отрицательной перекрыше
на выходе из рабочего колеса [56].
6)
Рис. 11.26. Концевые потери в решетках с бандажными полками: а — сопловая решетка; б — рабочая
решетка
соответствующих опытных данных, полученных при ис-
следованиях на модельных ступенях [56], так и расчетом
по какой-либо из известных приближенных полуэмпири-
ческих формул, например [105]
Пр.з = Лр. 3/’Нбр=о= 1 ~km’ (П-93)
где
m=(6p//)[M(/cpsinp2)]; й = /(0). (11.94)
Рекомендуется принимать k = 0,454-0,55, причем
меньшие значения соответствуют большим значениям
степени реактивности 0 и наоборот.
Эта формула дает удовлетворительное согласование
с экспериментом при t ~ £opt; 6р = 6р/1 <: 0,025 4-
4-0,05 и относительно длинных лопатках.
Для приближенной оценки потерь из-за наличия
радиального зазора для ступеней с DZpll = 54-12 может
быть использована формула [38]
Чр. з = РсС0 з. с (1 — lc/DCp) 6р. с +
Ч-Ррсаз.р(1 ^р/^ср) бр. р, (11.95)
где рс и Цр — коэффициенты расхода через радиальный
зазор у сопловых и рабочих лопаток; са з. с = саз.с/с1аср;
<4гз.р ^аз.р/^гаср-
'Расход протечек газа через радиальный зазор у вер-
шины необандаженной лопатки составляет прибли-
женно [30]
gnp — Gnp/Gr ~ 6Р (DH/£>cp)(l -|- 0,&bKl sin р2) Рн/Рср-
(11.96)
Следует заметить, что при использовании указанных
формул получают, как правило, суммарные концевые
Потери располагаемой работы из-за радиального
зазора зависят также от конструктивного выполнения
верхнего конца лопатки, который обычно делается за-
остренным в виде относительно тонкой дужки. Влияние
это, однако, невелико, и для ступеней газовых турбин
с относительно длинными лопатками им можно пренебречь.
При установке на концы лопаток бандажных полок
потери, связанные с существованием радиального зазора,
уменьшаются, что происходит главным образом вслед-
ствие устранения той их составляющей, которая обус-
ловлена перетеканием газа с вогнутой стороны профиля
в торцовой части лопатки на выпуклую.
В рассматриваемом случае определяющую долю
потерь составляют утечки газа через кольцевые щели
в зазорах1. Эти потери зависят от относительного зазора
6б=6б//р и 6р. у = бр. yilp, степени реактивности 0
(рис. 11.27). Они могут быть существенно снижены уст-
ройством развитого лабиринтного уплотнения над бандаж-
ной полкой (ср. варианты I и II на рис. 11.27) [102].
Потери из-за наличия радиального зазора 6р. у в сту-
пени с бандажированными лопатками зависят также от
относительной высоты лопатки DZp/l, причем степень
этого влияния различна в зависимости от принятого кон-
структивного выполнения бандажной полки (рис. II.28).
Потери в межвенцовом осевом зазоре. Возникновение
этих потерь обусловлено рядом факторов, основными из
которых являются трение потока газа на ограничивающих
торцовых стенках в межвенцовом зазоре и турбулентное
перемешивание в завихренных зонах потока, где наиболее
1 При этом возникает дополнительная потеря из-за взаи-
модействия потока утечек с замкнутыми вихревыми областями
в полости над бандажными полками, а также из-за смешения его
с основным потоком на выходе из венца [53].
45
интенсивно проявляется вязкость (закромочный след,
пристеночные области в корневой и периферийной частях
ступени и т. д.). В свою очередь, на интенсивность тур-
булентного перемешивания потока в межвенцовом зазоре
влияют режим обтекания решеток профилей, степень
неравномерности распределения параметров потока по
радиусу и шагу на выходе из лопаточного аппарата и др.
поскольку неравномерность потока за направляющими
лопатками по шагу уменьшается, а следовательно, сни-
жаются и потери в рабочем колесе, а потери на трение
о торцовые поверхности, ограничивающие межвенцовый
зазор, при этом невелики. Для таких ступеней потери
на трение о торцовые поверхности, ограничивающие меж-
венцовый зазор, могут быть приближенно оценены пс
Рис 11.27. Ступень турбины с бандажированными лопат-
ками а — конструктивные варианты выполнения бан-
дажа, б — зависимость к п. д. ступени рст fflax от величи-
ны зазора 6р. у(6б):
1 — бандаж по варианту 1; 5^ = 0,01; 6р.у = var; 1' — бандаж по варианту I; 6б = 0,03, 6,. у=0,006;
2 — бандаж по варианту II; бр.у = 0,015, 6g — var, 2’ — бандаж по варианту II; у = 0,006; 6g =
— var; 3— гладкий бандаж, 6g— var
Как показали соответствующие опыты, потери рас-
полагаемой работы в осевом зазоре при расчетных режимах
обтекания зависят от ширины зазора, угла выхода потока
а1 (Рг), толщины выходных кромок лопаток, степени
реактивности в корневой части ступени, относительной
длины лопаток, степени уплотнения осевого зазора,
значений критериев М и Re и др. [103, 118].
Рис. 11.28. Изменение к. п. Д. Дт)ст max
в зависимости от Dc-p/l для ступени
с бандажированными рабочими лопат-
ками (см. рис. II 27)-
1 — гладкий бандаж, 2 — бандаж по ва-
рианту I; 3 — бандаж по варианту II
На рис. 11.29 показаны зависимости относительного
изменения потерь в осевом зазоре от величины s= s//c
при различных значениях степени реактивности у корня
0К (от —0,15 до +0,04), построенные по опытным данным
для модельных турбинных ступеней с длинными лопатками
(Dcp/Z < 4-т-10) [103].
Наличие sopf при 0к > 0 на этих кривых обусловлено
тем, что увеличение осевых зазоров в области их малых
значений приводит к снижению суммарных потерь §оС,
46
формуле
^c = 2(^/Re°’139)(s/smc61); А «0,022, (11.97)
которая (см. рис. 11.29) удовлетворительно согласуется
с опытной зависимостью в области практически приме-
няемых осевых зазоров [28 ].
При большой неравномерности распределений па-
раметров потока по радиусу на выходе из лопаточного
венца увеличение осевого зазора может привести к более
интенсивному увеличению потерь по сравнению с тем,
которое приведено на рис. 11.29, особенно на начальном
участке изменения s, что обусловлено существенной пере-
стройкой структуры потока по направлению его движения,
сопровождающейся значительным изменением степени
реактивности 0 и углов выхода потока а1 (|32) вдоль оси.
Рис. JI 29.’Потери в осевом межвенцовом за-
зоре турбинной ступени:
1 — 9К > 0; 2 — 0К < 0, 3 — расчет по (11.96)
Потери в осевом зазоре существенно зависят также
от степени его уплотненности. Так, при подсосе (обычно
в корневых сечениях ступени) или утечках (в периферий-
ной части) зависимость изменения этих потерь может
отличаться-от приведенной на рис. 11.29 [67].
Потери, связанные с установкой перед решеткой или
в ее пределах некоторых тел. К таким телам относятся
ребра, связывающие корпус турбины с блоком внутрен-
них подшипников, перегородки между жаровыми трубами
в сборном коллекторе, корпуса различных измеритель-
ных устройств, а также скрепляющая (бандажная) прово-
лока, устанавливаемая для снижения уровня динамиче-
ских напряжений в лопатках, и др. Наличие в потоке
таких обычно плохо обтекаемых тел сопровождается воз-
никновением за ними обширных зон (следов), заполненных
вихрями, взаимодействующими с основным потоком,
что приводит в конечном счете к увеличению гидравличе-
ских потерь в проточной части турбины, а также к изме-
нению некоторых кинематических характеристик потока.
Эти дополнительные потери при неблагоприятном рас-
положении ребер и перегородок и большой их относитель-
ной толщине d = d/tc (где d — толщина ребра) могут
быть достаточно большими и сопоставимыми с профиль-
ными потерями [56].
5)
средней окружности колеса; т — 1,0ч-2,5 — поправочный
коэффициент, принимаемый в зависимости от степени
диффузности канала и угла атаки.
Потери с утечками через лабиринтные уплотнения.
Лабиринтные уплотнения применяются для уменьшения
утечек рабочего тела через кольцевые зазоры между вра-
щающимся ротором и неподвижными частями турбины
под действием соответствующего перепада давлений.
Схема типового лабиринтного уплотнения показана
на рис. 11.30, а. При протекании через узкую кольцевую
щель шириной бу под действием перепада давлений газ
приобретает значительную скорость, которая гасится
в камере уплотнения А за счет вихреобразования и удара
струи о стенки камеры. При распределении всего распо-
лагаемого перепада давлений Др = pj — р, (рис. II.30, б)
между несколькими камерами перепад давлений на каждую
/ / / / ъу
Рис. II.30. Лабиринтное уплотнение; а — конструктивная схема; б — процесс истечения в i—s-
диаграмме (условно)
Соответствующим выбором места установки ребер
и перегородок (непосредственно против входных кромок
сопловых лопаток), а также уменьшением ~d указанные
дополнительные потери могут быть доведены на расчетных
режимах обтекания до 0,2—0,3% от к. п. д. ступени
Йи нерасчетных режимах эти потери возрастают до
-0,8%).
Дополнительные потери, обусловленные наличием
скрепляющей проволоки, зависят от ее относительного
диаметра, места расположения проволоки по высоте
и глубине межлопаточного канала, степени конфузор-
ности (реактивности) и режима течения. При установке
двух н более рядов скрепляющей проволоки в одном
межлопаточном канале возникающие при этом дополни-
тельные потери непропорционально увеличиваются из-за
взаимного влияния рядов.
Для приближенной оценки потерь при установке
одного ряда скрепляющей проволоки можно рекомендо-
вать формулу [53]
ДЛс.п = ?с.п<п/2- (П-98)
Здесь шс. п = wt sin рх/вх/\ас, п1вых) — скорость потока
перед проволокой; /вх, /вых — высота лопатки на входе
и выходе из потока; ас. п — ширина канала на среднем
диаметре вблизи плоскости установки, проволоки; £с. п —
коэффициент местных потерь проволоки,
(1,15тСх/с. п//м. к) (1— ‘l&r/l} /
Sc- П ~ ~ (1-/с.п//м.к)3 ’ (11'99)
где сх — коэффициент лобового сопротивления проволоки;
/с. п — площадь миделевого сечения проволоки; /м. к —
площадь сечения межлопаточного канала в месте установ-
ления проволоки; Аг — расстояние от оси проволоки до
щель уменьшается, что обусловь ив ет снижение скорости
газа, а следовательно, и расхода утечек.
Процесс истечения через многокамерные лабиринт-
ные уплотнения может быть условно изображен в i—s-диа-
грамме так, как показано на рис. 11.30, б. Поскольку
при этом энтальпия рабочего тела i* остается практически
постоянной, процесс расширения в лабиринтном уплот-
нении представляет собой многократное дросселирование.
Расход утечек рабочего тела через такое уплотнение
[130, 35]
GyT = —Р2)/(гРЛ), (П.100)
где и. — коэффициент расхода, зависящий в основном от
конструкции уплотнения и соотношения его геометриче-
ских параметров 1 [35]; f — площадь поперечного сечения
кольцевой щели; г — число гребней (щелей).
Если в какой-либо из щелей, обычно в последней
по ходу газа, возникает критическая скорость, то при
р2 < Ркр следует применять формулу [30]
GyT = |т//р,/[(г+ 1,1) vj- (11.101)
Критическое давление можно подсчитать по формуле
[35]
ркр^0,77Р1/Уг + 1,1. (11.102)
Потери располагаемой работы, обусловленные утеч-
кой газа, могут быть подсчитаны по формулам:
для концевых лабиринтных уплотнений (т. е. внеш-
ние потери)
к — 1?ут-^тг/» (II. 103)
1 В лабиринтных уплотнениях газовых турбин можно
принимать м = 0,65 — 0,80.
47
для промежуточных лабиринтных уплотнений диа-
фрагм [30]
АЛут. д = Аи/[1 4~ ф sin otj/(|xdy6y)], (II. 104)
где_б(у =-DyZ-Dcp; бу = 6y/Zc (см. рис. 11.30, а).
Определение числа ступеней
и габаритных размеров проточной части
Определение числа ступеней. Число ступеней опре-
деляется с учетом следующих органически связанных
между собой факторов
1) аэродинамического, от которого зависит возмож-
ность получения высокого к. п. д. проточной части при
обеспечении возможно более высокой аэродинамической
нагрузки каждой ступени;
2) прочностного, при котором обеспечивается надеж-
ная работа лопаточного аппарата газовой турбины в те-
чение заданного периода времени (моторесурса);
3) технико-экономического, позволяющего выбрать
вариант проточной части, характеризующийся минималь-
ными годовыми расчетными затратами с учетом произ-
водства и эксплуатации.
Исходными данными при проектировании проточ-
ной части газовой турбины с учетом принятой конструк-
тивной схемы ГТУ1 являются параметры: Gr; Нти; р$;
Го; п.
Частота вращения ротора п в зависимости от выбран-
ной конструктивной схемы или задается условиями ра-
боты потребителя (полезной нагрузки), или определя-
ется расчетом из условий совместной работы турбины
и компрессора.
Требуемая механическая работа турбины в зависи-
мости от выбранной конструктивной схемы ГТУ или
задается, или определяется по соответствующему урав-
нению баланса работ. Так, для схемы со свободной силовой
турбиной требуемая мощность компрессорной турбины
Л/т. к = ZVK + ?/м. п, где Л1М. п— мощность, соответствую-
щая механическим потерям. Отсюда Н* из = (У,с +
+ n)/(GXy
_ На стр. 39 было показано, что коэффициент нагрузки
hUK не должен превышать 2—2,2, соответственно hu Ср =-
= 1,34-1,6. Стремление повысить срабатываемый тепло-
вой перепад на ступень при указанных значениях /гМСр
ограничивается допустимой окружной скоростью иср,
определяющей уровень напряжений от центробежных сил,
а следовательно, и прочность рабочей лопатки.
Практика проектирования свидетельствует о том, что
наилучшее согласование перечисленных выше моментов
достигается при исп = 3304-350 м/с2, следовательно, для
одной ступени йиз = 1204-200 кДж/кг. Для охлаждаемых
ступеней высокотемпературных газовых турбин значения
«ср могут быть увеличены до 380—400 м/с, a hu max — до
z
250—300 кДж/кг. Если учесть, что Нти = У йи(-, где г —
число ступеней, и принять во внимание (11.40), то
г _
•^Т.В = (^« ср iUcpTlp з)*
О типовых конструктивых схемах ГТУ см. п. IУ 1
2 Допустимая по условиям прочности максимальная
окРУЖНая скорость на корневом диаметре не должна превышать
280 — 300 м/с для дисковых и 210 — 220 м/с для цельнокован-
ных роторов
48
Тогда при мср const для всех ступеней (т. е. Оср ~ const)
в первом приближении находим
2 = (Сиз/Мср)21ь/(2МР. з) = </(2*срМр. з),
где хсо — Wcn/1-из*
Обычно в современных газовых турбинах г < 44-5;
подробнее об этом см. в гл. IX.
Величина хср оказывает заметное влияние на коэффи-
циент нагрузки hu в диапазоне рекомендуемых его значе-
ний, в то время как величина Т]ст влияет на 1ги слабо
(рис. 11.31) [56].
В первом приближении, например на стадии эскиз-
ного проектирования, эффективную работу турбины можно
распределять равномерно. При детальных расчетах (на
стадиях технического и рабочего проектирования) рас-
пределение эффективной работы по ступеням должно про-
изводиться дифференцированно. Так, на первую ступень
турбины, работающую при наиболее высоких температурах
Рис. 11.31. Зависимость'коэффициента на-
грузки 1ги от отношения хСр:
/ — 'Чет = О,®2: 2 — т)*т ~ °-
газа, задают более высокий тепловой перепад при малой
степени реактивности, что позволяет создать лучшие тем-
пературные условия для рабочих лопаток как первой,
так и последующих ступеней.
На последнюю ступень турбины иногда задают увели-
ченный тепловой перепад в целях повышения ее к. п. д.,
поскольку, особенно при больших значениях Gr, скорости
выхода потока в таких ступенях приходится принимать
весьма большими (см стр 39) При этом, однако, должно
удовлетворяться условие а2 80-4-85°. Оставшаяся
часть суммарного теплоперепада обычно распределяется
или поровну между остальными (промежуточными) сту-
пенями турбины, или пропорционально принимаемым
коэффициентам нагрузки отдельных ступеней.
Определение теплового перепада на турбину с учетом
выходного диффузора. На выходе из последней ступени
газовой турбины устанавливается диффузор — специаль-
ное аэродинамическое устройство, предназначенное для
преобразования части кинетической энергии потока на вы-
ходе из ступени в потенциальную. При этом скорость
потока уменьшается, а статическое давление увеличивается.
Поскольку давление на выходе из турбины или яв-
ляется заданным внешними условиями, или определяется
из расчета цикла ГТУ, наличие выходного диффузора
приводит к увеличению располагаемого перепада теплоты
в турбине (рис. II 32) на величину Лд из = (с2 — c2g)/2-
С учетом того что реальный процесс течения в проточ-
ной части турбины с диффузором сопровождается дополни-
тельными потерями располагаемой работы (теплового пе-
репада) как в лопаточном аппарате, так и в самом диффу-
зоре, внутренняя удельная полезная работа турбины
может быть определена по формуле
Ят.в = [//Т. изиз 0 - ЛтПд)]1)д, (И.105)
где Н'т из Нт из + Яд из; >); — внутренний к. п. д.
газовой турбины с учетом дополнительных потерь, обу-
Рис. 11.32. Рабочий процесс многоступенча-
той турбины с выходным диффузором в i—s-
диаграмме
словленных увеличением располагаемого перепада *;
т)д —коэффициент, учитывающий гидравлические потери
в диффузоре (к. п. д. диффузора) и определяемый по
формуле (см. рис. 11.32) т]д = (ig — izWzg — is)-
Потери в диффузоре оцениваются обычно коэффициен-
том гидравлического сопротивления
?Д = (P2g - Р2)/[(рср|2) ” 4g) L (П 106)
причем т]д = 1 — £д.
К- п. д. турбины с выходным диффузором
Лт. д — (*0— 'г)/(‘о — '2g из)- (11.107)
В современных ГТУ т]д = 0,6-ь 0,7.
Определение основных размеров последней ступени.
Длина рабочей лопатки. Площадь кольцевого сечения про-
точной части на выходе из последней ступени F2 (сметае-
мая площадь) определяется из уравнения расхода (11.34),
которое для рассматриваемого случая имеет вид
В приближенных расчетах можно принимать Т]т « т)т.
4 Л. В. Арсеиьев и др.
F2 = = Gr sin а2], (II. 108)
где
т = ]/'(й//?)[2/(й+ i)> •
, , Г (6—1)/Д » Г'^-1)
* * 1 z т. в
Р2 - Р0 I , * Т——----—
kFT С)Пт/(й— О
При этих расчетах принимается ц* = 0,88-1-0,92,
а з атем в случае необходимости вводится поправка на полу-
ченное расчетом значение.
Ометаемая площадь и радиальные габаритные размеры
последней ступени турбины связаны зависимостью F2 =
= лОср/р, из которой следует, что требуемое значение F2
может быть получено при различных сочетаниях значе-
ний Пер и Ip.
Реальный диапазон значений ОСр и Zp предварительно
следует выбирать с учетом обеспечения прочности рабочих
лопаток последней ступени. В рабочей лопатке возникают
напряжения растяжения от центробежных сил и напряже-
ния изгиба от воздействия потока газа. Напряжения
растяжения от центробежных сил в произвольном попереч-
ном сечении рабочей лопатки на расстоянии х от ее корне-
вого сечения [83]
2 ГН
<7р (х) = j J fxi (гк -ф- я) dx, (II.109)
где fx — площадь сечения профиля лопатки на расстоя-
нии х от ее корня;\рл—плотность материала лопатки;
fxt — площадь сечения профиля лопатки на участке от
гк + х до гн; гн — наружный радиус лопатки.
При f (г) = const получим Op тах= Ор (к) = рлсо2Х
XZpDcp/2, где о' — напряжение растяжения в корне-
вом сечении лопатки постоянного профиля.
Поскольку рабочие лопатки последней ступени газовой
турбины выполняются, как правило, с переменной пло-
щадью поперечного сечения по радиусу fxi, уменьшаю-
щейся от ее корня к наружному сечению, то напряжения
растяжения в корневом сечении
°р (к) = ^рстр(к), (II.ПО)
где ?р < I — коэффициент разгрузки лопатки, который
является функцией отношения площадей поперечного се-
чения профиля лопатки у ее периферии (/н) и корня (/.<)
и принятого закона изменения Этой площади по радиусу,
т. е. показателя р в выражении fx= fK — (fK — in) х
X (x/Zp)p. При р = I [83]
г 1+/н//к I —/н//к Ip /ТТ 1111
SP“ 2 (НИИ)
Коэффициент д, в зависимости от задаваемых значе-
ний Dcp/Zp (d) и показателя р можно приближенно опре-
делить по рис. 11.33, из которого следует, что величина р
значительно сильнее влияет на величину £р, чем отноше-
ние DCD/Zp.
В стационарных газовых турбинах для последней сту-
пени (^н//к)тт = 0,164-3-0,200. Дальнейшее уменьшение
этдго отношения сопряжено с существенным усложнением
технологии изготовления лопатки, а также со снижением
к. п. д. последней ступени.
49
Из других применяемых зависимостей fn/fK = f (р)
х! I
можно рекомендовать [83] f (х) = (Zh/Zk) р, Для ко-
торой
/ < j_ /н \ _ Рср /, _______ fa \ . 2(1 — Zh/Zk)
\ ~ hj 1О \ к ) 1п(А,7к)
(77ср//р) In (Zh/Zk)
(11.112)
Что касается изгибных напряжений, то при расчете
рабочей лопатки последней ступени на прочность следует
учитывать лишь нескомпенсированный их остаток <т'зг
который возникает из-за того, что напряжения изгиба от
действия газовых сил потока обычно неполностью уравно-
вешиваются изгибными напряжениями от действия цент-
робежных сил, поскольку при установке лопатки в диск
создается некоторое смещение центра ее тяжести относи-
тельно радиальной оси («навал»).
Суммарные напряжения в рабочей лопатке последней
ступени могут быть приближенно определены по формуле
о2 = ар+<зг =(1 +CTH3r/CTp)ffp- (П.113)
При этом относительная величина нескомпенсирован-
ных изгибных напряжений аьзг = оизг/<тр зависит от
диапазона изменения расхода газа при рабочих режимах
50
и конструкции рабочей лопатки, составляя обычно
0,2— 0,5 Ч
Для обеспечения надежной работы лопатки газовой
турбины следует иметь запас ее прочности, чаще всего по
отношению к пределу длительной прочности материала,
который, как известно, зависит от рабочей температуры
и заданного срока службы.
Температура рабочей лопатки в рассматриваемых рас-
четах может быть в первом приближении принята равной
температуре заторможенного потока газа перед рабочим
венцом в относительном движении
т’ = т* — “1 2 (2с™1и~ О
ш1 01 2 [k/(k — 1)] 7? ‘
Здесь
T*Oi=T*o-(HTU- ^Лы?)(й-1)
где S hut — суммарная работа предшествующих ступеней.
Коэффициент запаса прочности для лопаток газовых
турбин по значению при этих расчетах должен состав-
лять 1,754-1,8, а по величине ор — па Зд 2,0
[30].
Следует отметить, что минимальные запасы прочности
для рабочей лопатки последней ступени получаются обычно
не у ее корня, а в сечениях, расположенных от него на
расстоянии (0,254-0,30) /р, что обусловлено как принимае-
мым законом распределения площади поперечного сече-
ния профиля по высоте лопатки, при котором р > 1, так
и распределением температуры лопатки по радиусу2.
Поэтому более точное расположение опасного сечения
должно быть определено расчетом значений <7V и Г*
для нескольких сечений по высоте лопатки, на основании
чего могут быть построены эпюры их распределения по
радиусу.
В случае, если при заданном значении указанные
минимальные запасы прочности не обеспечиваются варь-
ированием коэффициента разгрузки 3 £р, нужно умень-
шить F2> увеличить скорость с2а ГРИ этом, однако,
следует обязательно выполнить условие МС2& <: 0,50 4-
4-0,55, так как в противном случае будет иметь место зна-
чительное снижение к. п. д. турбины.
Таким образом, диапазон возможного изменения вы-
соты рабочей лопатки последней ступени при выбранном
тепловом перепаде на эту ступень определяется, с одной
стороны, величиной допустимых напряжений Одоп, а с
другой — минимально допустимым по условиям техно-
логии коэффициентом разгрузки £р, или, что то же самое,
минимально допустимым отношением fw/fK.
На рис. 11.34 показано изменение основных харак-
теристик рабочей лопатки последней ступени газовой
турбины в зависимости от отношения х = и/сиз. Пересе-
чение горизонтальных линий, соответствующих <тДоп и
(faWmw с кривыми lp = (х) И о2 = /2 (х) определяет
допустимые по условиям прочности и технологии диапазоны
изменения /р и х [77].
Наружный диаметр. Наружный диаметр последней
ступени Он — Оср + /р, где /р выбирается в указанном
выше диапазоне значений (рис. 11.34), а величина Оср,
подсчитываемая по формуле Dcp = Р21(л,1р), определяет
максимальный поперечный габаритной -размер газотур-
1 При этом меньшие значения Оизг имеют место в рабочих
лопатках с бандажными полками, а большие — в рабочих ло-
патках без бандажей.
2 В прикорневых сечениях рабочей лопатки ее температура
снижается из-за отвода теплоты через хвостовик в диск, причем
это снижение может достигать 50 —100 ®С [42].
8 При этом необходимо помнить, что (ZH/fK)min
0,20.
бинного двигателя. Ограничение максимального значе-
ния £>н обычно накладывается требованиями обеспечения
транспортабельности блока турбоагрегатов и минимальной
массы турбины. Оно должно быть также согласовано с ма-
ксимально допустимым по условиям технологии и прочно-
Рис. 11.34. Характеристики рабочей лопатки
последней ступени
сти корневым диаметром ступени Рк = Рср — /р, опреде-
ляющим, в свою очередь, наружный диаметр диска (ро-
тора) А
Максимально допустимое значение Ок может быть
определено по формуле [56]
DK — ~ hu/huK >
где hUK « 2,04-2,2.
турбины с точки зрения меридионального очертания ее
проточной части.
Применяемые конструктивные схемы проточной части
многоступенчатой газовой турбины в меридиональном ее
сечении показаны на рис. 11.35. Схема на рис. 11.35, а
позволяет получить турбину с наименьшим числом сту-
пеней, поскольку при этом достигаются максимальные
окружные скорости, а следовательно, и располагаемые
тепловые перепады на каждую ступень. Высоты лопаток
всех ступеней, за исключением последней, в указанной
схеме также получаются наименьшими по сравнению с дру-
гими схемами. При ее реализации могут, однако, возник-
нуть трудности из-за более высоких напряжений в дисках
и лопатках первых ступеней, а также технологических
возможностей получения поковок дисков с большими диа-
метрами х.
Схема на рис. 11.35, в обладает некоторыми техноло-
гическими преимуществами по сравнению с предыдущей,
особенно при цельнокованом или сварном роторе. Однако
из-за меньших окружных скоростей в первых ступенях при
этом может появиться необходимость увеличения числа
ступеней или повышения коэффициента их нагрузки, что
может привести к снижению к. п. д. турбины. Длина
лопаток всех ступеней в этой схеме, за исключением послед-
ней, получается наибольшей, что может иметь положитель-
ное значение при малых объемных расходах газа через
турбину, когда относительная высота лопатки начинает
сказываться на к. п. д. ступени.
Проточная часть по схеме, в которой как £>„, так и £>к
меняются от ступени к ступени, представляет общий слу-
чай. Частным ее случаем является схема, показанная на
рис. 11.35, б, когда £>Ср = const; Ощ == var и £>кг- = var.
В такой схеме представляется возможным получить наи-
меньший угол раствора проточной части у, что является
ее определенным преимуществом.
Определение угла раствора проточной части. Для
получения высокого к. п. д. при проектировании проточ-
ной части газовой турбины следует выбирать угол расши-
Рис. 11.35. Конструктивные схемы проточных частей многоступенчатых газовых турбин: а —
£>н = const; б — Dcp = const; в — DK = const
В случаях, когда найденные указанным способом зна-
чения DK или £>н не удовлетворяют какому-либо из пере-
численных требований, следует принять иное значение /р
в допустимом диапазоне изменения х (см. рис. 11.34),
а если и это не даст нужного результата, следует умень-
шить тепловой перепад на последнюю ступень 1 2 *.
Выбор конструктивной схемы проточной части. При
выбранном значении наружного диаметра последней сту-
пени и соответствующей длины йопатки, очевидно, воз-
можно различное конструктивное выполнение газовой
1 Обычно DK max & 1500— 1600 мм, при этом следует
учитывать возможность варьирования длины хвостовой части
рабочей лопатки за счет применения удлиненной ножки
2 Это уменьшение перепада может повлечь за собой не-
обходимость увеличения числа ступеней турбины.
рения в меридиональном ее сечении (угол раствора) до-
статочно малым, так как иначе будут значительно возра-
стать гидравлические потери, обусловленные диффузор-
ным характером потока в лопаточных венцах и межвенцо-
вых зазорах.
Анализ имеющихся опытных данных показывает, что
для удовлетворения указанного требования необходимо
обеспечить плавное изменение обводов проточной части от
одного лопаточного венца к другому, чтобы для смежных
венцов yt- < 10т-12°, а суммарный угол раствора у2 С
С 20° [53, 56]. Скосы обводов лопаточных венцов в мери-
диональной плоскости следует при этом заканчивать до
начала зоны косого среза в лопаточных каналах.
1 Последняя задача может быть решена частично за счет
применения рабочих лопаток с удлиненной ножкой.
4*
51
В качестве примера на рис. II.36 показана зависимость
изменения вторичных потерь в решетке турбинных лопа-
ток от угла у. Уровень дополнительных потерь, обусловлен-
ных наличием угла раствора, остается практически неиз-
менным в диапазоне чисел с 0,44-0,9. Угол у опре-
деляется принятой схемой проточной части, а также осе-
вой шириной лопаточных венцов и межвенцовых осевых
зазоров. Осевая ширина лопаточных венцов, в свою оче-
редь, определяется допустимым запасом прочности по
Рис. 11.36. Зависимость вторичных
потерь р решетке от угла раствора у
величине изгибающих напряжений, которые возникают от
действия газового потока, а для рабочих лопаток — и от
центробежных сил.
На предварительной стадии проектирования, когда
выбирается схема проточной части и определяются ее
основные габаритные размеры, еще не имеется данных газо-
динамического расчета и геометрических профилей ло-
паток. Поэтому ширина лопаток определяется прибли-
женно. Для лучшего приближения следует использовать
данные по лопаткам выполненных ступеней газовых тур-
бин аналогичного типа.
При сравнительно небольшом отличии геометричес-
ких размеров проектируемых и выполненных ступеней
можно принимать одинаковой их относительную ширину
в корневом сечении1: Вк = Вк/1.
Для рабочих лопаток стационарных газовых турбин
средней и большой мощности можно рекомендовать в пер-
вом приближении Вр. к = 0,24-0,4, причем меньшие
значения соответствуют последним ступеням с малым от-
ношением Dcpll, а большие — первым ступеням турбины.
На наружном диаметре последней ступени осевая ши-
рина профиля рабочей лопатки Вр. н = Вр. H/Zp может при-
ниматься в диапазоне 0,15—0,30, причем меньшие значения
соответствуют ступеням с малым отношением D^/l.
Осевой зазор между лопаточными венцами выбирается
по рекомендациям, приведенным на стр. 46 в зависимости от
Zc, причем в целях снижения вибрационных напряжений
в рабочих лопатках желательно задаваться передним осе-
вым зазором в пределах Sj 0,24-0,4 (большее значение
относится к первым ступеням газовой турбины, сопло-
вые лопатки которых охлаждаются воздухом). Задний
осевой зазор можно принимать s2 = (1,24-1,8) sr
Осевая ширина сопловых лопаток в их корневых сече-
ниях может приниматься равной Вс. к = (I,2’’’1,5) Вр, к.
Осевое расстояние между ступенями Lt- можно прове-
рять, определив Lt_r = При у- 7-:~10° обычно
'Ll = 0,654-0,80; при у = 154-20° — Lt = 0,554-0,70.
Откладывая последовательно от оси рабочего колеса
последней ступени полученные отрезки Lt, можно в первом
приближении определить расстояние между осями рабочих
колес первой и последней ступеней, а следовательно, и
осевой габаритный размер проточной части /.п ч
(рис. 11.37).
Для определения угла раствора у при выбранном типе
проточной части необходимо определить длину сопловой
лопатки первой ступени /щ. Это можно приближенно вы-
полнить следующим образом. Поскольку параметры газа
перед первой ступенью известны из расчета цикла ГТУ,
а располагаемый тепловой перепад на нее ZiH3 i мы выби-
раем исходя из соображений, приведенных на стр. 49, то,
задаваясь степенью реактивности на среднем диаметре
первой ступени в диапазоне 0ср i = 0,154-0,25, можно
определить все необходимые параметры потока на выходе
из соплового аппарата на диаметре £>ср i: Pii; Т\ из j;
clt. Тогда
Zci = Gj/(nDcP ipicn sm a, cp i).
Рис. П.37. Схема построения меридиональных раз-
меров проточной части многоступенчатой турбины
(индекс п. с. обозначает последнюю ступень)
Задаемся alcpi = 154-25° х.
По выбранной схеме проточной части турбины опре-
деляются значения £>Ср i и £>Ki (DHi), причем Dcp j =
= DKi + Zci, иди Оср ] = DHl — Zcj.
После этого следует проверить получающиеся для
первой ступени значения коэффициентов: хср = иср i/cH3i;
йиК1 = Желательно получить xCD = 0,46 4- 0,50
и 7iUKj < 2,04-2,2. Отмечая размер Zcj/2 по радиусу (по
обе стороны от Оср ;) и соединяя линиями точки А 2 и С1( а
также А 2 и С2, расположенные на концах выходных кро-
мок сопловой лопатки первой ступени и рабочей лопатки
последней ступени (с учетом радиального зазора 6Р. п. ст),
можно получить габаритные очертания проточной части
проектируемой газовой турбины в меридиональной пло-
скости, которые определяют ее углы раствора у (корневой
ук и наружный ун).
Если окажется, что у > 20°, в целях получения высо-
ких к. п. д. целесообразно или несколько увеличить осе-
вые размеры, или использовать другую исходную конструк-
тивную схему проточной части. В некоторых случаях может
оказаться необходимым пойти на увеличение числа ступе-
ней турбины.
1 15 сопловых лопатках за такое сечение следует принимать
ближайшее к месту их крепления сечение, где заканчивается
галтель.
1 В турбинах малой мощности из-за нежелательности по-
лучения малых длин лопаток можно принимать ajcp j = 124-13°.
52
Газодинамический расчет турбины
по среднему диаметру
В результате этого этапа расчета определяются:
параметры потока в межвенцовых зазорах каждой ступени
на ее среднем диаметре; углы выхода потока из лопаточных
венцов на среднем диаметре, при этом уточняются высоты
и средние диаметры лопаточных венцов; к. п. д. отдельных
ступеней и всей турбины; удельная работа (мощность)
турбины.
Рис. 11.38. Показатель изоэнтропы k и удельная тепло-
емкость ср для воздуха и продуктов сгорания стан-
дартного углеводородного топлива
В качестве расчетного принимается режим, соответ-
ствующий номинальной мощности агрегата, для которого
из расчета цикла ГТУ являются известными Gr, р*, Т*,
р2т (Яти), п. Для отдельных лопаточных венцов при этом
должна учитываться возможная добавка охлаждающего
воздуха к основному потоку газа.
Кроме того, в результате предварительного этапа рас-
чета, как указывалось выше, производится выбор кон-
структивной схемы проточной части, числа ступеней, а
также распределение располагаемого теплового перепада
по ступеням, т. е. давления и температуры в заторможенном
потоке газа за каждой ступенью на среднем диаметре.
В результате построения габаритных очертаний про-
точной части в меридиональном ее сечении определяются
в первом приближении средние диаметры и длины лопаток
каждого из венцов (рис. 11.37). Дальнейший расчет каждой
ступени по среднему диаметру может производиться не-
сколькими различными способами в зависимости от до-
полнительно задаваемых исходных данных.
Рассмотрим некоторые из наиболее распространенных
способов этого расчета на примере первой ступени турбины
[56, 112].
Способ 1. Заданы Оср, /с, МСг, а2. Расчет ведется
в следующей последовательности.
1. Абсолютная температура и давление в заторможен-
ном потоке за ступенью:
T2 = T“0-hu/[Rk/(k- 1)];
Р2 = р*о {1 - VRTqtictW - 1)]}
где k определяем по рис . 11.38, величиной т)*т задаемся
в пределах 0,87—0,91 (меньшие значения следует прини-
мать для первых, а также для последних ступеней много-
ступенчатой турбины).
2. Ометаемая площадь на выходе из ступени (рабочего
колеса) F2 = л£>Ср1р> где £>ср — задано; Zp определяется
по принятой схеме проточной части.
к. v 3. Газодинамическая функция q ) [см. формулу
(Н.17)]
q (ЛС2) = GT VT2/(mF2p2 sin а2).
По значению q (<2), задаваясь величиной а2 = 70-г-
-т-90°, из таблиц [3] находим лС2 и определяем скорость
с2 по формуле с2 = /.с.2 V2kRT*l(k + 1).
4. Скорости для рабочего колеса:
^*2’ =::=: ^2 COS 0&21
^Ср. р — JtDCpM/60j. ~ ^2U ^Ср. р»
w2 = Vcla + wla •
5. Ометаемая площадь на выходе из соплового аппа-
рата Ах = лОСр/с, где £>Ср — задано; Zc определяется по
схеме (предварительному чертежу) проточной части.
6. Окружная составляющая скорости
с 1и~ \^и иср. pC2«]/Ucp. с?
где h'u = т) 3 = 0,98ч-0,95 — коэффициент, учи-
тывающий потери в радиальном зазоре.
Рис. 11.39. Потери полного давления
в сопловом аппарате
7. Угол aj и абсолютная скорость газа сх находятся
путем решения системы уравнений:
sina!= GrVT^JlmF^q XC1 = Xc^/cosap
(11.114)
где v* — Pq/P*c— коэффициент потери полного давлен ия
в сопловом аппарате, значением которого задаются в ди-
апазоне 1,01—1,03 или находят по рис. 11.39.
Указанная система может быть решена как аналити-
чески, так и графически1, откуда с1а = сг Sinar.
Если газодинамический расчет различных вариантов
турбинных ступеней проводится с использованием ЭВМ,
относительную скорость обычно целесообразно находить
методом «дробных шагов» из условия равенства углов вы-
хода потока и а{, определяемых из уравнений (11.114).
Приемлемая точность вычисления ХС1 определяется нера-
венством |ах—а{ | < 0,003. * ____________
.8 . Относительная скорость газа = ]/"cl—2u1clu-[-ul.
9. Статическое давление и абсолютная температура
потока на выходе из соплового аппарата:
Р1с = /’1ся(Ч)= Роя(Ч)Л*; T1=Tot(^C1),
1 При Кс >1 необходимо учитывать отклонение потока
в косом срезе сопловых решеток (см. стр. 33) .
53
где газодинамическая функциях (ХС1) [см. формулу (11.14)]
находится по таблицам [3].
10. Температура в заторможенном потоке на входе
в рабочее колесо T^w = Т\ + [2Rk/(k— 1)].
11. Углы входа и выхода потока из рабочего колеса:
tg Pl = cla/(clu — tg P2 == C2a/(C2U + uz)-
12. Располагаемый тепловой перепад в рабочем колесе
Аиз. р = Низ - да21)/2 = (а’з/^)2/2 - wl/2-
13. Давление, абсолютная температура и плотность
газа на выходе из рабочего колеса:
Р2 = Pi [ 1 ^из. р I । J ,
Т2 = - (wl - wl)/[2Rk/(k - !)]; р2 = р2/(Т?Т2).
14. Осевая составляющая абсолютной скорости газа
на выходе из рабочего колеса с2а == Gr/(P2p2)-Это значе-
ние с2а сопоставляется с ее значением, полученным в п. 4.
При расхождении более 1% следует повторить расчет,
начиная с п. 2, вводя соответствующую корректировку
в значения /р и Dcp.
15. Температура и давление в заторможенном потоке
на выходе из рабочего колеса:
T* = T2+cl/[2Rkl(li-l)]-,
Р2 = Pzn (т'г)/3'1 * *
где л (Г) находится из таблиц или номограмм [98].
16. Степень реактивности1 0рр = /ip//iH3, где /гиз
или задается при распределении общего располагаемого
перепада по ступеням, или (если задано р2/Р1) определяется
по формуле
Лиз=Т^Т^0[1-(Р2/Р1)(^1)/Й1-
17. К-п. д. ступени т)*т = hu/hH3. Это значение со-
поставляем я с заданным (см. п. 1); При расхождении более
0,5% расчет следует повторить, начиная с п. 1, задаваясь
новым значением т)* .
Газодинамический расчет второй и последующей
ступеней турбины ведется по такой же методике, как и
первой ступени. Исходными для этого расчета являются
давление и температура в заторможенном потоке на выходе
из предшествующей ступени:
П = Р2 l/vn. у> ^0 II ~ Г0 IVOT>
где V* у — коэффициент потери полного давления переход-
ного участка между предшествующей и данной ступенями
(значение v* можно получить газодинамическим расче-
том или задаться им в диапазоне 1,00—1,01); Уот — коэф-
фициент, учитывающий отвод теплоты в соответствующий
охлаждаемый элемент проточной части (определение см.
в п. 11.5).
При расчете промежуточных ступеней значения чисел
Маха и углов а2 следует задавать в указанном выше диа-
пазоне (см. стр. 39), последовательно увеличивая их от
ступени к ступени. Углыа1; |32, а также 0ср при этом также
будут увеличиваться от ступени к ступени.
Способ 2. Заданы Лик, Мс , а2. Расчет ведется в
следующей последовательности.
1 По этому значению 6Ср на следующем этапе расчета
(проектирования профильной части лопатки по радиусу) прове-
ряется степень реактивности в корневом сечении ступени 6К.
54
1. Абсолютная температура и давление в заторможен-
ном потоке за ступенью — см. способ 1, п. 1.
2. Площадь проходного сечения на выходе из рабочего
колеса (ступени)
F2 = GrVT2/[mPS‘/ (М sin аа],
где <? (%CJ — газодинамическая функция, определяемая
из таблиц [3] по величине %С2 = c^j/^RTzk/ (fe — 1) .
3. Окружная скорость у корня рабочей лопатки
мк. р — Vh/huK, где коэффициент нагрузки hUK прини-
мают в диапазоне 2,0—2,2.
4. Диаметры ступени: Ок. р = 60ик. р/(ля); DH, р =
= У^.р + 4^; оср. р = рн р+пк р)/2.
После этого уточняются соответствующие размеры
предварительно спроектированной проточной части. При
значительном их различии по сравнению с первона-
чально принятыми задаются другим значением ftUK. Да-
лкс расчет ведется в той же последовательности, что и по
способу 1, начиная с п. 6.
Способ 3. Заданы/iUK, МС2а, 0ср. Расчет ведется в сле-
дующей последовательности.
1. Площадь проходного сечения Г2> а также наружный
и внутренний диаметры ступени — см. пп. 2—4 предыду-
щего расчета.
2. Статическое давление и располагаемый изоэнтро-
пийный перепад в ступени:
hH3 = RT* [ 1 - (p2M) .
3. Изоэнтропийная работа расширения в сопловом
аппарате йиз. с = (1 — 0ср) йиз; скорость истечения газа
из соплового аппарата сх= <р V2/гиз. с = <р]/"2(1 —9ср) Лиз-
4. Углы выхода потока ах — по подсчитанной сме-
таемой площади на выходе из соплового аппарата.
Далее определяются все параметры, как и в преды-
дущих способах. Обычно в практике проектирования газо-
вых турбин проводятся расчеты для нескольких исходных
вариантов схемы (габаритных очертаний) проточной части
и соответственно нескольких значений углов выхода по-
тока ах (Р2) с последующей проверкой запасов прочности
лопаток. Окончательный вариант для дальнейшего про-
ектирования выбирается на основе анализа результатов
указанных выше вариантных расчетов.
Необходимо провести также дополнительные расчеты
по определению степени реактивности у корня ступени 0к.
а также углов выхода потока из ступени в ее корневом и
наружном сечениях.
Следующим этапом проектирования является профи-
лирование лопаток, т. е. построение их профилей как в рас-
четном сечении на среднем диаметре, так и по всей высоте
лопатки.
П.З. ГАЗОДИНАМИЧЕСКИЙ РАСЧЕТ
ПРОСТРАНСТВЕННОГО ПОТОКА
В ТУРБИННОЙ СТУПЕНИ
'' Реальный поток, проходящий через лопаточные венцы
ступени осевой турбины, имеет пространственный харак-
тер, т. е. его параметры изменяются не только в осевом,
но и в окружном направлениях и по радиусу. Интенсив-
ность этого изменения обусловливается рядом факторов,
к числу которых относятся изменение окружной скорости
в рабочем колесе по радиусу, меридиональное раскрытие
проточной части, поворот потока в лопаточных каналах,
•образованных профилями с конечной толщиной выходной
кромки, вязкость жидкости, проявляющаяся в пристен-
ном пограничном слое, взаимодействующем с основным
потоком, и др.
В ступенях газовых турбин, имеющих относительно
длинные лопатки, наибольшее влияние на структуру про-
странственного потока оказывают изменение окружной
скорости и закрутка потока по радиусу.
Известные приближенные методы расчета параметров
пространственного потока в турбинной ступени основы-
ваются на применении гипотезы установившегося течения
идеального газа и равномерного распределения параметров
в окружном направлении. Большинство таких приближен-
ных методов расчета используют в качестве дополнитель-
ного условия так называемую гипотезу цилиндрических
сечений, согласно которой предполагается, что газ через
лопаточные венцы ступени движется по соосным цилиндри-
ческим поверхностям тока, а следовательно, радиальная
составляющая скорости сг равна нулю. Распределение па-
раметров потока вдоль радиуса при этом рассчитывается
только для сечений 0—0, 1—1, 2—2, расположенных в пре-
делах межвенцовых зазоров (см. рис. II.5).
Теоретические соображения и имеющиеся опытные
данные позволяют утверждать, что подобная схема расчета
пространственного потока дает достаточно точные резуль-
таты до значений Dep/l 4,0-ь4,5 и у <20° [91, 101].
За пределами этих диапазонов Dcp!l и у может возникнуть
необходимость учета сг, для чего следует или использовать
гипотезу конических сечений, в которой учитывается
только наклон меридиональных линий тока, а кривизна
линий тока предполагается равной нулю, или задаться
кривизной линий тока в пределах межвенцового зазора
[113, 129]. Необходимость учета сг может возникнуть
также при значительном отклонении режимов работы сту-
пени от расчетного [113].
При дииндрическом течении газа относительно конт-
рольных сечений в межвенцовых зазорах ступени, т. е.
при сг = 0, основополагающим является уравнение ра-
диального равновесия частицы под действием центробеж-
ной силы и гидродинамического давления, которое для рас-
сматриваемого случая может быть написано в форме
(1/р) dp/dp = cl/r. (11.115)
Это уравнение, очевидно, справедливо и для необра-
тимого процесса течения газа при условии сг = 0. Для ука-
занного общего случая, используя уравнения второго за-
кона термодинамики в виде Tds = di — (1/р) dp и пред-
полагая, что энтальпия и энтропия заторможенного потока
постоянны и равны их значениям на входе в ступень,
можно получить уравнение радиального равновесия в
упрощенной форме, связывающее окружную и осевую
составляющую скорости потока [91]:
+ = (11.116)
Для сечения 1—1 (см. рис. II.5) с учетом того, что
потери в сопловом аппарате могут быть выражены форму-
лой Дйпот, с = (1/ф2 — 1) cJ/2, при <р (г) = const можно
получить уравнение связи между с1а и с1и [91 ]:
(1 /ф2) (с1а dclafir + clu dClu/dr) 4“ с1и/г = °- (НИ?)
Задаваясь законом изменения вдоль радиуса г одной
из составляющих скорости с, из этого уравнения можно
найти закон изменения по г дугой ее составляющей, а
следовательно, и изменение всех других аэродинамических
параметров потока по радиусу в рассматриваемом сечении.
Ниже рассматриваются некоторые, наиболее распро-
страненные способы задания указанных зависимостей.
1. clur = const, т. е. обеспечивается постоянство
циркуляции скорости сх по радиусу [107]. Из уравнения
(11.117) находим
dcja (2 - l/cp2)/dr + Д±ДП-РГс;’12 (1/<р2 — 1) = 0.
После интегрирования от г до гсР получим
откуда следует, что осевая составляющая скорости с1а для
рассматриваемого случая будет переменной по радиусу,
причем для ф = 0,97 и Dcpll 4 разница в значениях с1а
может достигать 10—12%. При Dcpll > 8-ь-10 эта разница
будет составлять не более 3—5% , и в первом приближении
ее можно не учитывать [56, 112].
2- cia = const. Из исходного уравнения (11.117) мо-
жно получить зависимость
clur4’2/(2(₽2-I) = const. (11.119)
3. (г) = const. Искомая зависимость может быть
найдена из дифференциального уравнения
d ] = 0, (11.120)
из которого после интегрирования получается:
С1ЫГФ cOs == const; Clar®' C°S2 “l = const.
В общем случае закон изменения окружной составля-
ющей cllt по радиусу можно представить формулой
clurm = const [34, 55]. Тогда зависимости между осевой
составляющей с1а и углом выхода потока а*, с одной
стороны, и радиусом г — с другой — имеют вид [56, 112]:
с1а -- V 1 4- [(1 - Ф2» (1 - l/T^J/tg2^ ср; (11.121)
tg И1 = 7« /tg2 К1 ср + (1 — ф2/щ) (1 — 1/72"2), (11.122)
где г — радиус, отнесенный к его значению в выбранном
контрольном сечении.
Аналогичные зависимости могут быть получены для
сечения 2—2 на выходе из рабочего колеса (см. рис. II.5).
При этом обычно на поток накладывается дополнительное
требование. Так, задаваясь обобщенным законом1 изме-
нения с1и по г в виде clurm = const, будем полагать, что
отдаваемая работа остается постоянной по радиусу.
Это условие равносильно исключению дополнительных
потерь, которые возникают из-за обмена энергией в потоке
газа между его отдельными трубками тока, т. е. hu (г) =
= const, откуда
~ Ср (t/г 1 /гт) -ф C-2U Ср (1 /г) • (II . 123)
Используя эту зависимость, а также уравнение энер-
гии для трубки тока между сечениями ступени 0—0 и 2—2
и уравнение радиального равновесия (11.115), в сечении
2—2 можно получить дифференциальное уравнение, свя-
зывающее между собой с2м и с2а [56]:
dc1aldr + dc2uldr + (^Ф2 - t) (dAa/dr + *!«/*) “Н
4“ Ф ^c'2ulr 4* (1 — Ф2) d (^с2ци + 11 }!dr =
1 Закон изменения сли по г часто называют законом за-
крутки потока (лопаток).
55
отсюда после интегрирования можно получить интересую-
щую нас зависимость с2а = f (г), где с2а — составляющая
скорости, отнесенная к ее значению в выбранном контроль-
ном сечении.
Рис. 11.40. Изменение с1и по г
Рис. П.41. Изменение с1а по г:
— <р = 0,97;---------— ф = 1,0
Рис. 11.42. Изменение аг по г:
-----ф = 0,97;-------— ф = 1,0
При осевом выходе потока из рабочего колеса на сред-
нем радиусе
С2О = 1 + (1 - Й) Ctg2₽2 ср [(1 - Г2) -
-2йиср (1 -Й~т)] +hu ср ctg2|3 2Ср { (1 - ф2) (1 - 1/F2)-
— 2 [1 — 2ф2/(от + 1)] (1 — 1/7'"11} +
4- (1 —ср2ф2/т) (1 — l/r2m)],
где
'ги ср = hu ср/иср “ clu cp^S Pzcp/^a ср-
Соответственно изменение углов выхода р2 и <х2 по
радиусу для рассматриваемого случая определяется фор-
мулами [56]:
Рг “ tg Рз срС2аг/1Ли ср (1 — rm ') /"],
tg <Z2 = ГС2а/[(С1и ср/с2а ср) (1 1/гт )] -
Используя уравнение связи между степенью реактив-
ности ступени 0 и составляющими скорости си [см. (11.56) ],
можно получить зависимость [56]
Рис. 11.43. Изменение с2а по г
Рис. II.44. Изменение р2 по г
пользуясь которой, легко определить степень реактивности
в корневом сечении ступени 0К при заданных 0,-п и т.
Если окажется, что 0к с 0, то следует задаться другими
значениями 0ср или т.
Количественное влияние т на некоторые характерные
параметры ступени турбины иллюстрируется графиками,
приведенными на рис. 11.40—П.44 для ступени с а1ср =
= 27°30'; ₽2ср = 37°10'; ф = 0,97 и ф = 0,95 [56, 112],
из которых следует, что это влияние при малых отноше-
ниях DCp/l весьма велико. Несколько меньшее влияние
показатель т оказывает на степень реактивности 0.
Малые значения т приводят к существенному возраста-
нию угла закрутки в рабочем колесе и соответственно-
к уменьшению угла а2, а также к увеличению неравномер-
йб
ности распределения осевых составляющих скоростей с1а
и cia по радиусу.
Указанные обстоятельства могут привести к появле-
нию значительных радиальных составляющих скорости
из-за несоответствия между расходом газа через каналы
сопловых и рабочих лопаток, особенно в их корневых и
периферийных сечениях. С другой стороны, значения
т > 1 соответствуют более интенсивному изменению сте-
пени реактивности по радиусу, особенно в корневой части
ступени, и большей степени неравномерности распределе-
ния осевой составляющей скорости по радиусу, что неже-
лательно с точки зрения возможного ухудшения экономич-
ности ступени.
Наименьшие (теоретически нулевые) радиальные пере-
течки обеспечивает закон закрутки потока, характеризуе-
мый уравнением clag = const, что соответствует посто-
янству удельного массового расхода вдоль радиуса1.
Используя это условие и традиционную систему урав-
нений движения, сохранения энергии и неразрывности,
можно получить следующие зависимости с1а = (г) и
cia = f-2 0 при указанном законе закрутки [17, 101 ].
Для сечения 1—1 (см. рис. II.5):
C1U = - (Мо2/2) - 1 ’
= {[1-т+т / [i
(11.125)
/г— 1
k + 1 Х
X 0 ~Мо)ЛЛкр]>
(11.126)
где Мъ — число Маха на входе в ступень; йкр =
Лкр — тепловой перепад, соответствующий скорости акр.
В рассматриваемом случае за контрольное принято корне-
вое сечение ступени.
Для сечения 2—2 (см. рис. II.5):
с — (М + [ф (г) — ик/(с1и кг)]2 — гик/с1и к .
\ ' (1 к)2 ик/с1и к
(11.127)
С2О —
1 “ -ТТТ (1 ~ мо) ЧIеЛ/(1 - ек»
(11.128)
Отдаваемая удельная механическая работа, изменяю-
щаяся по радиусу, для закона закрутки сор = const
hu(r) — hu/hucp =
(11.129)
1 Для всех приведенных выше законов закрутки должно,
очевидно, иметь место радиальное смещение линий тока при
прохождении через лопаточные венцы
В этих формулах
г2 (М^/2) [г2 — 1 ] йкр
т (Ь = [г2 d-Mo) _ м2 (?2 -1) йкр/2]-т;
v(/7p) = {1-м2[1-К(;)()-М2) +
+ (1-М2)ГгДр])Яр.
Уравнения (11.125)—(11.129) целесообразно решать
численным способом с использованием ЭВМ. Как показы-
вают расчеты, изменение отдаваемой работы ступени по
радиусу при реальных значениях параметров ик!с1ил,
йкр и Л1о сравнительно невелико и даже для малых зна-
чений DCp/l не превышает 2—3%.
Рассмотренный закон закрутки может быть приведен
к обобщенному виду, когда т = f (Мо, йкр). Вместе с тем
закон закрутки сар — const в контрольных сечениях 1—-1
и 2—21 позволяет получить, как показывают более деталь-
ные расчеты, меньшие углы поворота потока в каналах
сопловых и рабочих лопаток вдоль их высоты (радиуса)
по сравнению с законами cur = const и са = const, причем
эта разница увеличивается с повышением числа Маха [17 ].
Приведенные зависимости между основными кинема-
тическими и геометрическими параметрами для различ-
ных законов закрутки потока по высоте лопаток турбинной
ступени позволяют выбрать какой-либо из них в основном
из конструктивно-технологических соображений, а также
исходя из некоторых качественных представлений о струк-
туре потока. Что касается к. п. д. ступени, то приведен-
ный анализ не дает возможности судить о преимуществах
в этом отношении какого-либо из рассмотренных законов
закрутки. Более того, опыты, проведенные на модельных
и натурных вращающихся турбинных ступенях, показы-
вают, что вплоть до значений £>Ср/1 3,5-г- 4,0 все рас-
смотренные законы оказываются примерно равноценными
в отношении достижимого уровня к. и. д. [1011-
Таким образом, для указанных условий основным тре-
бованием, обеспечивающим получение высоких к. п. д.
турбинных ступеней, является, по-видимому, достаточно
удовлетворительное согласование углов а1( р, и р2 во
всех сечениях по высоте лопатки с соответствующими гео-
метрическими углами решеток профилей.
При £>cp/Z < 3,54-4,0, как и при углах раствора
у > 20°, необходимо использовать усовершенствованные
методы расчета пространственного потока [37, 91, 131 ],
в которых находит отражение дополнительный учет таких
факторов, как радиальная составляющая скорости потока,
изменение потерь располагаемой работы вдоль радиуса,
сжимаемость рабочего тела, силовое воздействие потока
на лопатки и др. Уравнение связи между параметрами
пространственного потока в этих методах выводится не
только для межвенцовых зазоров, но и для областей, заня-
тых лопатками.
Основой для разработки большинства указанных ме-
тодов явилась предложенная By [131 ] схема расчета по-
тока на системе пересекающихся криволинейных поверх-
ностей тока Si и S2 (рис. II.45), когда для каждой из них
получаются дифференциальные уравнения вида
(б2ф/<5х2) -ф J (д^/дх) + К (<?2ФМа) -+- L (<?ФЖ) = N,
где Z—'угловая координата для поверхности Sx;
х— линейная координата для поверхности S2; J, К,
* В предположении, что это условие удовлетворяется и на
входе в ступень, т. е. в сечении 0 — 0.
57
L, N — функции от t, и x, в которые входят также задавае-
мое изменение энтальпии заторможенного потока, энтро-
пии и момента количества движения.
В нашей стране наиболее полную разработку указан-
ные методы получили в известных работах [91, 94 и др. ].
Рис. 11.45.” Расчетная схема пространственного по-
тока в турбинной ступени на поверхностях тока Sx
и 32
В них представляется также возможным учитывать тол-
щину профиля лопатки и тангенциальный ее наклон.
Решение соответствующей системы уравнений в этих ме-
тодах производится численным способом с использованием
быстродействующих ЭВМ, обладающих достаточно боль-
шой оперативной памятью.
11-4. ПРОФИЛИРОВАНИЕ ЛОПАТОК
Общие положения
Цель этого этапа проектирования турбины состоит
в том, чтобы построить профильную часть лопатки, т. е.
«материализовать» полученные при газодинамическом рас-
чете углы входа и выхода потока из лопаточных венцов
каждой ступени по высоте профильной их части для обе-
спечения высоких к. п. д. и полезной работы и требуе-
мого расхода рабочего тела.
Практически профилирование лопаток сводится к
построению решеток для нескольких выбранных контроль-
ных сечений по радиусу, включая расчетное (обычно сред-
нее) сечение, после чего решетки в указанных сечениях со-
прягаются между собой плавными переходами малой кри-
визны.
Сами профили, которые образуются в указанных конт-
рольных сечениях, в большинстве случаев проектируются
графическим методом с последующей экспериментальной
проверкой. Последнее время все большее распространение
при проектировании профилей получают аналитические
методы расчета [9].
На основании приведенных в п. II.2 соображений по
поводу получения минимальных профильных потерь
(включая кромочные потери) при построении профилей
турбинной лопатки в каждом контрольном сечении необ-
ходимо руководствоваться следующими основными пра-
вилами.
1. Относительный шаг профилей в решетке должен
£ыть принят возможно более близким к оптимальному.
58
Рекомендации по выбору /opt в зависимости от угла пово-
рота потока, диапазона изменения углов атаки, режима
обтекания и т. п. приведены в п. II.2. В первом прибли-
жении для выбора 7opt можно пользоваться эмпирической
формулой В. И. Дышлевского (11.87).
При построении профильной части лопаток, особенно
с малым отношением Dcp/l, часто возникает необходимость
отступать от указанных выше значений t t, причем в кор-
невых сечениях — в сторону уменьшения (/ < /орЦ, а
в наружных—• в сторону увеличения (£ > £opt). При от-
клонениях t от /opt следует учитывать не только измене-
ние профильных потерь, но и
изменение угла выхода по-
тока ах (Р2)Ч
2. Углы атаки i = р1л—
— Рх на расчетном режиме
выбираются дифференциро-
ванно- для средних (расчет-
ных) сечений рабочих лопа-
ток можно принимать i =
— ±2°; для корневых— i
< -{-12°, для наружных сече-
ний можно допускать изме-
нение i от —‘2 до —б0. Для
сопловых лопаток на расчет-
ном режиме можно допускать
углы атаки до ±10°, что
практически не будет сказы-
ваться на профильных по-
терях. Для приближенного
определения оптимального
геометрического угла входа
потока на решетку Р1л opt
в зависимости от углов pj
и Рг может служить рис.II.46.
3. Межлопаточный канал
в каждом из сечений должен
Рис II.46. Зависимость
₽1л opt 0Т ₽1 И Рз 19]
быть, по возможности, конфузорным на всем протяжении
При невозможности удовлетворить этому требованию по
прочностным или технологическим соображениям можно
допускать небольшую местную диффузорность канала
(в пределах 5%), желательно в зоне максимальной кри-
визны на выпуклой части профиля лопатки.
4. Выпуклую часть профиля следует очерчивать ли-
нией, имеющей плавные изменения кривизны, для чего
можно использовать отрезки лемнискаты Бернулли или
параболы второго порядка. При этом за узким сечением
кривизна выпуклой части профиля должна обеспечивать
угол отгиба 6Л (см. рис. II.6, б) в пределах 5—15° в зави-
симости от числа Маха 1 2 МС2. Ширину узкого сечения горла
межлопаточного канала определяют по формуле a =
= t sin Ра, где Р2 = Р2 — ДР2, а угол ДР2 можно опреде-
лить по рис. 11.24, а, в или по какой-либо из эмпирических
формул, например (11.90) или [9]
ДР, = 4,13 + 26,66сшах — 0,27595л — 4,287/.
Максимальная относительная толщина профиля
cms= cra!,Jb (см. рис. II.6, б) должна выбираться с уче-
том требований экономичности, прочности и технологич-
ности.
5. Геометрический угол а1л (Р2Л) выбирается равным
поточному углу ах (р2) или несколько меньшим (на 1—1,5°).
1 Подробнее об этом см в п IT 2
2 Меньшие значения б q при этом должны соответствовать
большим числам Маха
Некоторое увеличение а1Л (р2л) по сравнению с ах (f>2)
допускается лишь для корневых сечений лопаточных вен-
цов из-за относительно большой толщины выходных кро-
мок (см. и. II.2)1.
6. Толщина выходных кромок профилей должна быть
возможно меньшей, причем радиус ее скругления г2
(см. рис. II.6, б) рекомендуется выбирать от г.г = (0,003<-
<-0,08) сшах в корневых сечениях до г2 = (0,08-=-0,18) X
Хстах в наружных сечениях с плавным его уменьше-
нием по высоте лопатки. Для наружных сечений лопатки
Стах 0,04<-0,045. Для корневых сечений рабочих ло-
паток величина стах определяется, в первую очередь,
соображениями прочности, т. е. допустимыми напряже-
ниями растяжения, благодаря чему во многих случаях,
особенно при малых отношениях D^/l, приходится вы-
нужденно идти на увеличение стах, а следовательно, на
уменьшение относительного шага по сравнению с опти-
мальным, с соответствующим увеличением потерь.
При профилировании сопловых лопаток возникают
трудности при малых углах а1и и больших числах Мс
когда необходимо принимать малые углы <5Л, фх, ф2
(см. рис. II.6, б).
Радиус входной кромки гх (см. рис. II.6, б) прини-
мается обычно больше г2; разница между ними тем больше,
чем шире диапазон углов атаки на входе в решетку при пе-
ременных режимах работы. На величину rlopt оказывает
влияние ряд параметров, в первую очередь рхл, р,л (а1л),
Стах и г2. Для приближенной оценки выбираемого значе-
ния гг = Tj/сщах можно рекомендовать эмпирическую
формулу [9]
гх = 0,0527 sin р1л Д 0,0071 sin |32Л -J- 0,236cmax -f-
+ 0,18га — 0,053.
Наибольшее допустимое значение определяет усло-
вие, чтобы диаметр окружности, вписываемой во входную
часть межлопаточного канала, был больше (1,05-ь 1,1) а.
Углы заострения кромок на входной и выходной ча-
стях профиля <рх, ф2 (см. рис. II.6, б) зависят соответст-
венно от радиусов rx, r2, Лп. ч. от величины стах и от-
носительного ее расположения по средней дужке профиля 2:
Фх « 3,51 arctg-_Сшах/2~Г1- ;
Xfmaxin- ч — ''l
(1 Xcmax) Ьп. ч
Поскольку поставленная задача построения профилей
сопловых и рабочих лопаток должна решаться с учетом
комплекса требований экономичности, надежности и тех-
нологичности, решение по необходимости должно быть
компромиссным, т. е. оптимизированным не по какому-
либо одному из указанных требований, а по всей их сово-
купности. Именно поэтому графические или графоана-
литические методы построения профилей лопаток в конт-
рольных сечениях являются предпочтительнее аналити-
ческих методов, что в конечном счете и предопределило их
повсеместное распространение в практике проектирования
газовых турбин.
При построении решетки профилей для каждого сече-
ния необходимо установить также рациональное значение
угла установки ру (см. рис. II.6), характеризующего вза-
имное расположение входной и выходной кромок. Угол ру
является функцией ряда параметров и, в первую очередь,
углов Р1л, Р2Л, а также угла 6Л и толщины профиля сшах.
1 В ряде случаев приходится допускать большие толщины
выходной кромки, в том числе в охлаждаемых лопатках.
2 Угол <р2 не следует допускать больше 5 — 6°, чтобы не
получить заметного увеличения профильных потерь.
Для определения |3У можно использовать какую-либо
из известных эмпирических формул, например [9]
РУ = 38,82 — О,2925Р1Л + 0,9144|32Л +
+ 0,37186л -Д25,48сШах-
В первом приближении угол установки ру для сред-
них и наружных сечений лопатки можно принимать рав-
ным углу наклона вектора средней геометрической ско-
рости wOT = (wx 4- w2)/2 для корневых сечений ступени.
При заданных значениях Ру и осевой ширины решетки
В ее хорда b может быть с достаточной степенью точности
(в пределах допусков на обработку лопатки) определена
по формуле [9 ]
b = [1/sin ру 4-0,054(1 — 1/sin ру)] В.
Графические способы построения профилей
Построение лемнискатного профиля. Построение ве-
дется в следующей последовательности [56 ].
1. Проводятся две параллельные линии АВ и CD
на расстоянии В (рис. 11.47). На расстоянии шага t про-
водятся две окружности радиусом г2, касательные к АВ.
Через центры этих окружностей проводятся две прямые тп
под углом р2л; под углом ф2/2 к этим прямым проводятся
касательные к указанным окружностям.
2. Определяется ширина горла а = t sin р2; радиусом
а 4- г2 из точки О2 проводится дуга окружности, которая
ограничивает узкое сечение межлопаточного канала.
3. Выбирается угол отгиба 6Л и к линии АВ под углом
₽2л — ф2/2 + 6Л проводится касательная к дуге окружно-
сти радиуса а + г2; через точку касания Р должна пройти
линия спинки профиля.
4. Через точку пересечения q линий тп и АВ под
углом установки (Зу проводится линия до пересечения с CD.
Далее из точки Oj радиусом г1 проводится окружность,
очерчивающая переднюю кромку, касательную к CD.
Через центр этой окружности проводится линия OF под
углом [41 к CD, а затем к этой окружности проводятся две
касательные под углом фх/2 к линии OF. Точки касания g
и I к этой окружности являются начальными точками
линий, очерчивающих выпуклую и вогнутую поверхности
профиля лопатки.
5. С помощью лемнискатного лекала или кальки с вы-
черченным семейством лемнискат с соответствующим
полюсным расстоянием подбирается нужная дужка лемни-
скаты таким образом, чтобы ее прямой участок совпал с ли-
нией mfN, а сама кривая касалась дуги окружности ра-
диуса а 4- г2 в точке Р и была касательной к линии KgN,
образуя при этом требуемый угол отгиба 6Л.
Спинка профиля может очерчиваться одной или не-
сколькими лемнискатами, сопрягаемыми в точках равной
кривизны.
6. Строится вогнутая часть профиля, которая может
очерчиваться окружностью, лемнискатой, параболой или
произвольной лекальной кривой. Наиболее часто вогну-
тая часть профиля строится дугами двух окружностей.
При этом из точки Е описывается окружность диаметром
Стах, касательная к спинке профиля на расстоянии хс =
= (0,25-:-0,40) Ь (см. рис. II.6, б) от центра Ох входной
кромки. Из точки й, восстанавливается перпендикуляр
к линии mh. -Путем подбора находится радиус RB, которым
из центра О3 описывается дуга окружности, касательная
к линии mh (в точке h) и к окружности диаметром сшах-
Из точки I восстанавливается перпендикуляр к линии К1,
точка пересечения которого О', с линией О3Е будет являться
центром дуги окружности радиуса R'B, соприкасающейся
с дугой окружности радиуса RB и окружностью радиуса гх
(в-1 точке Z).
Построение профиля по дугам параболы [56, 112].
Первые четыре пункта построения профиля такие же, как
59
и в предыдущем способе. Начиная с пятого пункта пост-
роение ведется в следующей последовательности.
5. Продолжаются до взаимного пересечения в точке N
линии mf и Kg. Отрезки gN и Nf делятся на одинаковое
число равных частей, и точки деления соединяются затем
последовательно друг с другом (рис. 11.48). Огибающая
этих отрезков будет представлять собой дужку параболы,
очерчивающую спинку профиля. В случае, если дужка
этой параболы не проходит через точку Р, следует либо
тельная под углом р2С = Ргл — фг/2, причем £>2Л и ф2
определяются на основании приведенных в п. II.2 сообра-
жений. Далее с помощью лекала с переменной и монотонно
меняющейся кривизной проводят участок с2п спинки про-
филя у выходной его кромки, при этом проверяется полу-
ченное значение угла отгиба 6Л по общим рекомендациям,
приведенным выше. Из точки О2 (рис. 11.49, а, б) проводят
дугу окружности радиусом Ь — г2 и прямую O2F под углом
установки ру До пересечения с этой дугой. Из центра 0х,
изменить наклон линии mN за счет углов 6Л и ф2, либо
очерчивать спинку профиля дугами двух парабол fP и Pg,
причем каждая из них вписывается в углы, образованные
отрезками fd, dP и Pz, zg соответственно.
6. Через точку касания окружности, описанной из
центра Е радиусом сшах/2, и спинки лопатки проводят диа-
метр и нормаль, касательную к окружности в точке х, уда-
ленной от центра Ох на расстояние хс — (0,25-4-0,40) Ь.
Продолжают отрезки К1 и mh до взаимного пересечения
в точке у, после чего очерчивается вогнутая часть профиля
дугами двух парабол 1х и xh по описанному выше способу.
Построенные таким образом профили затем корректируются
с учетом перечисленных выше требований к форме межло-
паточного канала, площади поперечного сечения профиля
и расположению центра его тяжести путем варьирования
в соответствующих пределах величин Р1л, Р2Л, г, г1( г2,
Фз> ®л-
Построение профиля с помощью лекал. На предвари-
тельных этапах проектирования хорошо оправдал себя
способ построения профиля турбинной лопатки, исполь-
зующий сочетание дуг окружностей и плавных линий,
зафиксированных на специально подготовленной серии
лекал. Основным требованием при графическом построении
профиля является отсутствие скачков кривизны при со-
пряжении отдельных его участков (монотонное изменение
кривизны).
Рекомендуется следующий порядок построения про-
филя этим способом (9].
На прямой АВ (рис. 11.49, а) откладывают отрезок,
равный шагу t, из концов которого проводят две окруж-
ности радиусом г2. Из точки О2 проводят дугу окружно-
сти радиусом а + г2, к которой затем проводится каса-
60
расположенного на прямой O2F, радиусом rt проводят окру-
жность, касательную к дуге радиуса Ь — г2. Для образова-
ния входного участка спинки профиля из точки Ot
(рис. 11.49, б, в) проводят прямую под углом р1л к пря-
мой CD, параллельной АВ (переднему фронту решетки).
Проводится касательная с—с к окружности радиуса ту
под углом Ф1/2 к направлению потока на входе, и из точки
касания этой прямой с окружностью восстанавливается
перпендикуляр. На этом перпендикуляре в точке Т рас-
полагают центр дуги Дс, с помощью которой очерчивается
входная часть спинки профиля. Если не удается добиться
плавного сопряжения этой дуги с кривой с2п, то его полу-
чают варьированием угла Ру или очерчивания кривой с2п
путем использования дополнительных лекальных кривых.
Для построения вогнутой части профиля из точки f
(рис. 11.49, в, г) проводят касательную kk к окружности
радиуса гх. На перпендикуляре, восстановленном к этой
касательной из центра Оа, располагают центр дуги, кото-
рой очерчивается входной участок профиля с вогнутой
его стороны. Эта дуга должна касаться окружности ра-
диуса сшах/2, центр Е которой располагается на расстоя-
нии хс тах от входной кромки. Через центр Е и точку Т,
являющуюся центром окружности радиуса Рс, прово-
дится прямая до пересечения с прямой, перпендикуляр-
ной kk. Точка их пересечения Q и будет центром дуги
окружности радиуса RK. Дуга радиуса RK сопрягается с по-
мощью лекала с окружностью радиуса г2 на выходной кром-
ке. При этом проверяется1 допустимый угол заострения ф2/2-
1 Очевидно, что во всех случаях для соблюдения условия
сохранения ширины горла а должно соблюдаться условие
<р2 <6Л.
61
Построенные каким-либо из рассмотренных выше гра-
фических способов профили лопатки затем проверяются
на соблюдение достаточной степени конфузорности меж-
лопаточного канала. Для этого эквидистантно кривой
внутреннего профиля строится кривая на расстоянии а
(по всему контуру) и анализируется характер оставшейся
зоны с точки зрения степени ее конфузорности.
Построение профилей путем изгиба
исходного профиля
Сначала строится средняя (осевая) линия профилей
в решетке с заданными значениями углов входа рх (а2),
выхода )<»! (Р2), атаки г, поворота е = 180° — (|3Х + |32),
установки pv при заданных осевой ширине и шаге решетки
[112, 113].
В некоторых случаях в качестве осевой линии профиля
принимают дугу окружности или параболу (или их соче-
тание). В других случаях ее задают по координатам на
основании данных аналитического расчета х. Сам исходный
профиль строится по данным аналитического расчета с по-
Рис. 11.50. Исходный (эталонный) аэродинамиче-
ский профиль турбинной лопатки
следующим испытанием в аэродинамической трубе. При
его отработке стремятся получить минимальные профиль-
ные потери при малом их изменении в широком диапазоне
углов атаки.
На рис. II.50 в качестве примера приведен один из
таких исходных аэродинамических профилей, имеющий
следующие координаты [112]:
£ = 100ж/&, % . . . О 1,25 2,5 7,5 10 15 20 30
У = 100г//5, % . . . 0 1,17 1,54 1,99 2,74 3,40 3,95 4,72
£ = 100х/5, % . . . 40 50 60 70 80 90 95 100
Ц = 100Z//6, % . . . 5,00 4,76 3,70 2,51 1,42 0,85 0,72 0
Радиусы скругления входной и выходной кромок
принимаются равными: гх = (0,24-0,4) сшах 'и г2 =
= (0,054-0,08) стах у корня; гх = (0,084-0,15) стах и
г2 = (0,08-4-0,15) стах у периферии. Максимальную тол-
щину 1 2 исходный профиль обычно имеет на расстоянии
около 0,46.
При построении лопатки по рассматриваемому методу
принимаются обычно следующие-Максимальные толщины
профилей: для сопловых лопаток сШах =0,1; для рабочих
лопаток стах = 0,24-0,3 у корня и сшах = 0,044-0,05 у
периферии. Минимальная абсолютная толщина профиля
у периферии сга!П^34-4 мм.
1 Иногда координаты средней линии профиля задаются
для исходного коэффициента подъемной силы Суд. Различная
форма средней линии профиля получается уменьшением орди-
наты на отношение выбранного коэффициента Су к исход-
ному Суд.
2 Если средняя линия имеет значительную кривизну,
т. е. длина средней линии примерно на 30% больше хорды,
распределение толщины профиля задается обычно не вдоль
хорды, а вдоль средней линии профиля.
62
Закон изменения относительной толщины профиля
рабочей лопатки от корня к периферии может приниматься
или линейным, т. е.
С1 — К {г г«); К = (ск сн) (гн гк)
или экспоненциальным, т. е.
Ci = 4 (с'н/ск)('’“'’к)/(Гн~Гк)-
Тогда cmax i = cmax xfi!fK.
Для получения эффективных углов выхода потока,
равных заданным, следует изогнуть выходные кромки
профилей или несколько изменить угол их установки (5У
Аналитические методы расчета профилей
При расчетах проточной части газовых турбин с до-
статочной степенью точности может быть использована
гипотеза, когда поток в каждом цилиндрическом сечении
ступени по радиусу может рассматриваться как плоский.
Сам процесс аналитического расчета обтекания плоских
решеток (прямая задача) может быть разделен на два этапа:
1) расчет потенциального обтекания решеток идеаль-
ной жидкостью; получаемая в результате этого этапа
расчета эпюра распределения скорости по обводу профиля
позволяет провести качественный анализ течения газа при
различных режимах работы турбины и определить в первом
приближении угол выхода потока;
2) расчет обтекания с учетом влияния вязкости на рас-
пределение скоростей по профилю и угол выхода потока,
а также расчет профильных потерь по полученной на пре-
дыдущем этапе эпюре распределения скоростей (при потен-
циальном обтекании).
В теории плоских решеток рассматривается также
обратная задача, в которой при заданных распределении
скоростей вдоль профиля, длине развертки профиля и
кинематике потока на входе и выходе определяются форма
профиля и его расположение в решетке (угол ру).
Аналитические методы расчета решеток могут быть
разделены на так называемые канальные, т. е. методы рас-
чета потенциального течения идеальной жидкости в изоли-
рованном криволинейном межлопаточном канале, и
гидродинамические методы расчета обтекания плоских ре-
шеток. Последние, в свою очередь, могут быть условно
сведены в следующие три группы: 1) метод сеток; 2) метод
конформных отображений; 3) метод особенностей [9, 94]. *
Метод сеток основан на численном решении краевой
задачи для уравнения Лапласа, с помощью которого опи-
сывается плоское потенциальное течение несжимаемой
жидкости. Используя условие ортогональности линий тока
и линий одинакового потенциала, путем последовательных
приближений строят решетку профилей заданной фор-
мы [94].
В методе конформных отображений задача об обте-
кании плоской решетки профилей сводится к канонической
задаче обтекания решетки пластин, решетки кругов или
течения внутри одиночного круга.
Так, если предположить, что обтекание решетки про-
филей происходит в плоскости комплексного переменного
2 = х + iy с областью течения Gz и дана область течения
Gg через решетку круговых цилиндров единичного радиуса
с шагом, равным шагу профилей в решетке, то, обозначив
через z = £ F (Q аналитическую функцию, с помощью
которой производится однозначное взаимное конформное
отображение областей Gz и G% можно привести функцию 2,
например, к виду [87 ]
г = s + £ (с-пг") + Е
/7 = 1 /1—0
где
С-п = /р К1 И (т) di; Сп — (Л4П, kq
k
м (-ir~Wfe
2k(2k — n— 1)\2\ •
Здесь B/c — число Бернулли, а суммирование ведется от
k ~ (п + 1)/2 для нечетных значений п и k = (п + 2)/2
для четных значений п.
Разновидностью указанного метода является метод
годографа скорости [94].
В методе особенностей внутри профиля, вдоль его
средней линии помещаются особые точки (вихри, источ-
ники, стоки и т. д.), которыми индуцируется течение,
имеющее замкнутую линию тока, совпадающую с контуром
профиля. Задача при этом может быть сведена к решению
уравнений для функций тока и для потенциала [9 ].
Для функций тока после выделения имеющейся лога-
рифмической особенности в точке х - у = ц имеем
ф (х, у) = С = — (х sin — у cos + J&s +
, 1 f ... г 2л (т] ~ у)
+ (О) In Ch--------LL---------
L’
2л (g — x) 1
— cos--------------- do.
Здесь = | + w^/2 — средневектор-
ная скорость; a — скользящая координата в области G2;
JAs = tw (s.) As (21n As — 0,40369); As = As//; s; - - те-
кущая дуговая координата; L’ = L — As — участок кон-
тура с выделенной особенностью, которая, поскольку
постоянная С неизвестна, дополняется равенством Г =
= w (a) da, где Г — циркуляция скорости по обводу
L
профиля.
Указанное уравнение решается с помощью аппрокси-
мации его системой линейных алгебраических уравнений
вида
W (S) = w (s)/(ffi>co sin ртс) = w* (s) + w** (s) ctg p,
где (s) и w** (s) — относительные скорости обтекания
профиля при [Д. = л/2 и р„. 'О соответственно. После
интегрирования по контуру получим угол бесциркуля-
ционного обтекания ctg |30 = —M/N и относительную
циркуляцию
Г = 2 (Л1 + N ctg |31)/(2 N),
где
М = J w" (s) ds', N = J w** (s) ds-
L L
Для потенциала уравнение имеет вид
<р (х, у) = 2w^ (х cos + у sin -L
+ Г/<в'— I <p (о) -^-da,
L
tru Kb — значение К, соответствующее выходной кромке
профиля, причем
К =- arctg th [(л//) (т] — у)]/tg [(л//) (| — х)].
Решение указанного уравнения в рассматриваемом
конкретном случае сводится к решению системы п линей-
ных алгебраических уравнений [9]
<Р, + 2 Ж ~ Ki- /-1) = Ч ctg + 2^1 +
/
+ Ч-В
и имеет вид:
Ф (s) = Ч(х) (s) ctg (s) + Г <p(n(s);
ip (S) = (s) ctg Pi 4- ф(у) (s) | ф(Г) (s)-1— ф(г/)(з) | Г,
где и ф^ — потенциалы скоростей бесциркуляцион-
ного обтекания решетки при = 0 и — л/2 соответ-
ственно; ф(г) (s) — потенциал скорости циркуляционного
обтекания при Г = t и = 0.
Для определения Г = ctg — ctg р2, а следова-
тельно, угла выхода р2 используется дополнительное
условие о сходе потока с выходной кромки. При скруглен-
ной кромке, как это обычно имеет место в турбинных про-
филях, (tfcp/ds)s = (йф/й8)зк, где sc и sK — точки на вы-
ходной кромке профиля со стороны спинки и корыта,
соответствующие резкому падению скорости вблизи кри-
тической точки. Сравнение расчетных параметров, полу-
ченных указанным методом, с опытными данными показы-
вает их вйолне удовлетворительное совпадение [9].
Влияние сжимаемости приближенно оценивается ве-
личиной
K = 2'k\/\m — l)m-1/(/n+ l)m+1 X
X ]/(m _ U)ml[(rn — И)"1-1 (И + I)2],
где X = Ш,|СЖ — скорость условного обте-
кания рассматриваемой решетки несжимаемой жидкостью;
m = ]Д(й -j- !)/(£ — 1); U = т К(1 — X2)/(m2 —X2).
При расчете обтекания канальным методом предпо-
лагается, что распределение скоростей имеет гиперболиче-
ский характер, а линии потенциала близки к дугам окруж-
ностей. Исходное уравнение, описывающее потенциальное
течение газа в канале, имеет вид [94]
аем —(1А) (эх/а-г]) = о,
где / и 1| — дуговые координаты, отсчитываемые вдоль
линий тока и эквипотенциальных линий; 0 — угол между
касательной к линии тока и осью абсцисс.
Закон изменения скорости вдоль линии т] описывается
формулой
Х, = А/(1 4-Вт) 4-Cri2), (11.130)
где А, В, С — числовые коэффициенты.
Величина X на первой стенке определяется из урав-
б
нения расхода G = акр J р/Лт], где S — длина эквипо-
0
тенциала;
. , /, /г-1
(потенциал в этой формуле вычисляется с помощью ЭВМ),
а величина X на второй стенке определяется по формуле
(II.130).
Полученное этим методом расчета распределение дав-
лений по обводу профиля дает удовлетворительное
63
согласование с опытными данными при достаточно густых
решетках (Г С 0,7-г-0,8).
Профильные потери на трение в решетках, построен-
ных на основании аналитических методов расчета, обычно
определяются с использованием основных соотношений,
выведенных в теории пограничного слоя [9]:
Птр = 1/[ 1 +2(^М)3’26**/(^ sin 02)],
где 6*® — толщина потери импульса в пограничном слое
на выходной кромке, определяемая в зависимости от ре-
жима течения:
для ламинарного слоя (участка):
= v i/g?.
к- л w0 (s) V 1
Gi=_M4 8?[Шо(а)]4,84а;
для турбулентного слоя (участка)
8^*т = (v/^) (Gj/79,5)475 (при Re < 5-10°);
6” т = (v>0) (Gj/153,2)677 (при Re > 5 • 106).
Здесь
Gj =-------[ [^о (о)]3’8 d<y,
v[^(sK)l ’8 J
— скорость на внешней границе пограничного слоя;
sK — координата выходной кромки; т, — координата конца
ламинарного участка.
Расчет величины 6** выполняют раздельно для выпук-
лой и вогнутой частей профиля, при этом 6*® = 6**к +
+ 6®* .
1 к. с
При наличии переходного участка от ламинарного
(индекс л) к турбулентному (индекс т) пограничному
слою
где
г s
Gj = ----------т-g- —-— [ [^0 (O)5,5do:-R сл
[Юо(э)]4-5 SJ
СЛ = 1 259[ш0 (SjI)]4-5 (Re**)9710; Re** = юОл6**/У.
В этом случае для турбулентного пограничного слоя,
начинающегося после переходного участка,
{S
[ [0-0 (О)]3’8 do 4-е-
V /
где
ст = 79,5 (Re**)574 [аг0 (sT)]2,8 (ПРИ Re < 5-106);
ст = 153,2 (Re**)776 [ат0 (sT)]2,8 (при Re > 5 • 106).
Здесь зт — координата начала турбулентного участка
пограничного слоя, которая определяется в зависимости
от Pmin = Pmln/pt где р* = рх + (1/2)
64
Рассмотренный выше приближенный метод расчета
разработан в предположении, что газ несжимаем, на по-
верхности профиля нет отрывов пограничного слоя и от-
сутствует теплопередача. Учет указанных факторов дол-
жен в случае необходимости производиться с использова-
нием соответствующих полуэмпирических зависимо-
стей [42].
Построение профильной части лопатки
Необходимое количество контрольных сечений по
радиусу, для которых производится построение профилей
каким-либо из рассмотренных выше способов, опреде-
ляется как относительными, так и абсолютными размерами
профильной части лопатки и обычно составляет три—семь,
в эго число обязательно входят корневое, среднее и наруж-
ное сечения. Кроме того, с учетом применяемых техно-
логических процессов обработки строятся дополнительно
профили лопатки в двух крайних сечениях, находящихся
за пределами ее профильной части.
Корневое сечение выбирается на расстоянии 2—3 мм
от начала переходной галтели от полки к профильной
части лопатки. Относительный размер гг = гг/1, где гг —
радиус галтели, выбирается обычно в пределах 0,04—0,02
(меньшие размеры — для лопаток большей длины /).
В целях более надежного контроля точности обработки
профильной части лопатки расстояние между отдельными
сечениями не следует принимать более 25—30 мм, особенно
для сильно закрученных рабочих лопаток.
Практически проектирование профильной части ло-
патки начинается с построения решеток профилей для ее
корневого, среднего и периферийного сечений, после чего
строятся графики изменения по длине лопатки таких основ-
ных геометрических параметров решеток, как b, t, В,
г1( г2> Р1л> Ргл, Ру и ДР- Используя указанные графики,
вычерчивают или корректируют профили в остальных про-
межуточных контрольных сечениях лопатки.
Полученная в результате подобного построения гео-
метрическая форма профильной части лопатки должна
удовлетворять требованиям прочности и быть при этом
достаточно технологичной,-т. е. допускать ее изготовление
высокопроизводительными и не слишком дорогими спо-
собами. Поэтому следующим этапом построения профиль-
ной части является определение центров тяжести профилей
в контрольных сечениях и согласование их расположения
относительно оси г лопатки (рис. 11.51), что должно обе-
спечить требуемые условия прочности.
Начало координат располагают обычно в центре тя-
жести корневого сечения, а оси х, у, г ориентируют так,
как показано на рис. 11.51.
После окончательной ориентировки профилей в каж-
дом из контрольных сечений относительно осей х, у,
г и корректировки1 их геометрических параметров с точки
зрения удовлетворения требованию плавности сопряжения
по всей длине лопатки подсчитываются координаты, этих
профилей по оси у. При этом ось у делится на равные
участки, кроме входной и выходной кромок, для которых
выбираются меньшие интервалы. Так как профиль на
указанных участках имеет большую кривизну, плавность
очертания отдельных кривых проверяется дополнительно
их вычерчиванием в увеличенном масштабе (до 50 : 1).
В некоторых случаях плавность изменения кривизны
профиля выпуклой части лопатки проверяется с помощью
определения вторых разностей координат, т. е. так, чтобы
1 Корректировка координат профилей в промежуточных
контрольных сечениях может проводиться также в связи с при-
меняемыми технологическими процессами обработки профиль-
ной части лопатки, например такими, как строчечное фрезе-
рование по копирам, обкатка цилиндрическим или фасонным
режущим инструментом по одному или двум плоским копирам
и т д.
вторая производная в местах сопряжения отдельных уча-
стков не имела разрывов. Для контрольной проверки про-
фильной части лопатки иногда строят графики изменения
координаты у для одинаковых значений х в каждом из
выбранных контрольных сечений (для соответствующей
координаты z = const).
в лопатке; б — изменение геометрических параметров
решеток по оси г
В последнее время все большее распространение полу-
чают расчетные методы профилирования лопаток по их
длине с использованием ЭВМ на основе описания соответ-
ствующими математическими зависимостями контуров
выпуклой и вогнутой частей профиля, например пУтем
интерполяции граничных условий по профилям в трех
базовых сечениях (корневом, среднем и наружном), за-
данных степенными полиномами [9].
П.5. ОХЛАЖДЕНИЕ ГАЗОВЫХ ТУРБИН
Системы охлаждения деталей газовых турбин
Охлаждение деталей газовой турбины, подверженных
воздействию высоких температур, применяется для до-
стижения такого температурного уровня и перепадов
температуры в деталях, которые обеспечивают надежную
их работу на всех возможных режимах.
В качестве теплоносителей, используемых для отвода
теплоты от охлаждаемой детали, могут применяться раз-
личные газы и жидкости. Наиболее широкое распростране-
ние в современном газотурбостроении получило охлажде-
ние с помощью циклового воздуха, отбираемого из ком-
прессора и после пропуска через деталь выбрасываемого
в проточную часть — так называемое открытое воздушное
охлаждение (подробнее см. п. 1.6).
По принципу действия различают следующие способы
открытого воздушного охлаждения: внешнее—коывекшв-
ное^^лнутренцее.. к^вцктлвцощ„плщц£)чш)е_.и~ гюршгще.
Внешнее конвективное охлаждение осуществляется
обычно обдувом детали или продувкой охлаждающего
агента через щелевые зазоры между горячей и менее го-
рячей (холодной) деталями.
При внутренних конвективных способах охлаждаю-
щий агент, проходя по каналам, расположенным внутри
охлаждаемого элемента, отводит от него теплоту за счет
конвективного теплообмена со стенками.
5 Л. В. Арсеньев и др.
При пленочном и пористом охлаждении охлаждающий
агент выводится на поверхность охлаждаемого элемента,
образуя тонкий защитный холодный слой. При этом про-
исходит теплообмен между этим слоем (пленкой) и охла-
ждаемым элементом.
Пленочное охлаждение обеспечивает выдув охлади-
теля на поверхность^через систему небольших щелей или
отверстий. Создаваемая при этом на поверхности элемента
холодная пленка размывается потоком горячего газа,
поэтому при пленочном охлаждении необходимо иметь
большое количество рядов выпускных щелей (отверстий).
При охлаждении деталей проточной части газовых турбин
пленочное охлаждение обычно сочетается с конвек-
тивным.
При пористом (транспирационном) охлаждении охла-
ждающий агент, проходя через мелкие отверстия (поры)
в стенке, выдувается в пограничный слой, образуемый на
поверхности охлаждаемого элемента, обдуваемого потоком
горячего газа. Увеличение глубины охлаждения, т. е.
разности температур между газом и охлаждаемым элемен-
том, можно получить, если в качестве охлаждающего
агента использовать воду, которая при продавливании
через пористую стенку испаряется и за счет скрытой
теплоты парообразования интенсивно охлаждает деталь.
Этот метод иногда называется методом выпотевания.
В настоящее время находит применение большое ко-
личество различных систем охлаждения газовых турбин.
Их описание и анализ можно найти в работе [1161. Ниже
приводятся лишь основные конструктивные схемы охлаж-
дения сопловых и рабочих лопаток, а также дисков вы-
сокотемпературных газовых турбин.
Охлаждение сопловых лопаток. Сопловой аппарат пер-
вых ступеней турбины располагается в зоне максимальных
температур, поэтому уже при температуре газа 900—
950° С требуется его охлаждение.
При внутреннем открытом охлаждении охладитель из
лопатки выводится в проточную часть в большинстве слу-
чаев в непосредственной близости от выходной кромки (со
стороны корытца или спинки) или прямо через выходную
кромку.
Достаточно большая глубина охлаждения и сравни-
тельно малые градиенты температур могут быть получены
в дефлекторных сопловых лопатках, наиболее широко
применяемых в настоящее время. Такая лопатка представ-
ляет собою конструкцию, имеющую наружную силовую
оболочку и внутреннюю тонкостенную вставку — дефлек-
тор. В дефлекторной лопатке может быть осуществлен
струйный обдув внутренней стенки и выброс охладителя
через выходную кромку профиля. При этом движение охла-
дителя может быть как продольным, так и поперечным.
Одна из первых конструкций дефлекторной лопатки была
применена на отечественном газотурбинном двигателе
РД-20(рис. II.52, а). Примером более поздних конструкций
может служить сопловая лопатка фирмы «Дженерал-
Электрик» (рис. 11.52, б), примененная на двигателе
MS-7000 с начальной температурой газа до 1065° С.
В дефлекторных сопловых лопатках с конвективной
системой воздушного охлаждения может быть достигнуто
снижение средней температуры лопаток по сравнению
с температурой газа на 130—150° С при относительном рас-
ходе охлаждающего воздуха §охЛ 0,02.
С увеличением начальной температуры газа требуется
все большая глубина охлаждения сопловых лопаток первой
ступени турбины. При температуре газа более 1100—
1150°С необходимо дополнительно к конвективному
вводить пленочное охлаждение. На рис. 11.53, изображена
охлаждаемая лопатка ГТУ фирмы «Дженерал-Электрик»,
предназначенная для работы при температуре газа 1100° С
и выше. Здесь пленочное охлаждение применено не только
на выходной кромке, но и в зоне входной кромки со сто-
роны спинки лопатки. Струйный обдув внутренней по-
верхности профиля повышает эффективность конвективного
65
охлаждения. Подобная система охлаждения позволяет
увеличить глубину охлаждения до 200—250° С при цпхя =
= 0,0254-0,030.
Дальнейшее увеличение эффективности охлаждения
турбинных лопаток может быть достигнуто при исполь-
зовании пористого охлаждения. Конструктивно пористое
охлаждение решается по схеме гильзозых лопаток, в ко-
торых основные нагрузки воспринимает относительно
холодный несущий стержень, а тонкостенная наружная
Рис. 11.52. Сопловые лопатки дефлектор-
ного типа: а — газотурбинного двигателя
PD-20; б — двигателя MS-7000:
1 — дефлектор; 2 — наружная оболочка; 3 —
ввод охладителя, 4 — вывод охладителя
оболочка образует профильную часть (рис 11.54). Между
стержнем и оболочкой предусмотрены каналы для пропуска
охладителя.
Несмотря на более высокую эффективность пористое
охлаждение пока еще не вышло из стадии отработки опыт-
ных конструкций в авиационных ГТД. Подобное положе-
ние обусловлено сложными проблемами, возникающими
при создании таких лопаток (технология изготовления
лопаток, обеспечение работоспособности проницаемой
Рис. 11.53. Дефлекторная лопатка
с конвективно-пленочным воздушным
охлаждением
оболочки, пониженная аэродинамическая эффективность
охлаждаемой решетки профилей, повышенные требования
к чистоте охлаждающего воздуха и др.).
Охлаждение рабочих лопаток. Более сложной кон-
структивной проблемой является охлаждение рабочих
лопаток газовых турбин, которые работают при высоких
температурах в условиях значительных статических и
динамических нагрузок и переменных аэродинамических
сил. Из-за вращения ротора усложняется решение задачи
подвода охлаждающего агента, а в замкнутых системах —
и его отвода. Эти особенности приводят к большому раз-
нообразию конструктивных решений п применяемых схем
охлаждения рабочих лопаток.
Внешнее охлаждение. Наиболее часто применяют сле-
дующие три разновидности этого способа охлаждения.
1. Теплоотвод в диск от рабочих лопаток, имеющий
место в большинстве конструкций газовых турбин, по-
скольку обычно диск турбины имеет более низкую тем-
пературу, чем рабочие лопатки. Специальные мероприятия
66
по охлаждению диска, например обдув его воздухом или
продувка воздуха через замки в современных конструк-
циях, увеличивают отвод теплоты от лопаток турбины.
2. Парциальное охлаждение, которое можно организо-
вать при наличии двух рабочих тел: газа с высокой тем-
пературой, обеспечивающего выработку основной доли
полезной работы, и газа (например, циклового воздуха
или пара) с более низкой температурой, предназначенного
в основном для охлаждения рабочих лопаток. Для этих
рабочих тел в проточной части турбины выделяются два
сектора. .Проходя один сектор, лопатки нагреваются,
а другой — охлаждаются. Хотя глубина охлаждения
при этом методе может быть значительной и достигать
300—400° С [30], однако эффективность охлаждения
сравнительно невелика, так как
ходы охлаждающих агентов,
система находит ограниченное
в турбинах малой мощности).
3. Струйное охлаждение
лопаток, характеризуемое
относительной простотой. Ох-
лаждающий агент, чаще все-
го вода, подается на поверх-
ность рабочих лопаток через
систему сопел, расположен-
ных, например, в выходной
кромке сопловых лопаток. На
рабочих лопатках жидкость
испаряется и за счет этого
интенсивно их охлаждает.
При расходе охлаждающей
воды 1,5—2% температура
лопатки оказывается почти
требуются большие рас
Поэтому рассматриваемая
применение (в основном
Рис. II.54. Гильзовая ло-
патка с пористым охлаж-
дением:
1 — внутренний несущи»
стержень; 2 — тонкостенная
пористая наружная оболоч-
ка; 3 — каналы для прохо
в два раза ниже температуры
газа. Описанный способ, так
да охлаждающего агента
же как и предыдущий, применяется сравнительно редко,
в основном в турбинах вспомогательного назначения.
Внутреннее охлаждение. В большинстве случаев этот
способ охлаждения реализуется в виде систем откры-
того типа.
1. Системы охлаждения открытого типа. Впервые
внутреннее охлаждение рабочих лопаток было использо-
вано в 1942 г. на немецком ГТД ЮМО-003, а несколько
позднее на отечественном двигателе РД-20, где охлаждае-
мая пустотелая лопатка имела внутренний вставной деф-
лектор.
В охлаждаемых рабочих лопатках серийного авиа-
ционного ГТД «Спей» английской фирмы «Роллс-Ройс»
охлаждающий воздух поступает через хвостовик (ножка,)
в несколько продольных каналов эллиптического се-
чения, пройдя которые, он выбрасывается в радиальный
зазор (рис. 11.55). При начальной температуре газа
1070° С и расходе воздуха g-0XJI ж 2% такая система обес-
печивает глубину охлаждения лопаток до 220 С.
Высокой интенсивностью теплообмена характеризуется
конструкция литой лопатки двигателя «Олимп-593» фирмы
«Бристоль» (Англия). Охлаждающий тракт здесь имеет
уже 20 отверстий диаметром 1,5 мм, расположенных вдоль
пера лопатки. Охлаждающий воздух из лопатки выводится
в радиальный зазор. Подобные конструкции охлаждае-
мых лопаток использует на своих двигателях также амерч-
канская фирма «Пратт-Уиттни».
Все рассмотренные конструкции имеют продольное
течение охлаждающего воздуха в каналах лопатки. Для
таких лопаток характерна, однако, большая неравномер-
ность температур по профилю и высоте. Более равномер-
ное распределение температуры в лопатке обеспечивается
при поперечном движении охладителя, когда входная и
выходная кромки профиля могут быть охлаждены более
интенсивно. На рис. 11.56 схематически показана дефлек-
торная охлаждаемая рабочая лопатка, разработанная под
руководством К. В. Туманского [100]. Для снижения
температуры входной кромки в этой лопатке применен
струйный обдув, воздух выбрасывается через щели в вы-
ходной кромке. Эти мероприятия позволяют существенно
снизить температуру кромок и выровнять температурное
поле лопатки.
Значительные возможности воздействия на распре-
деление температур имеются в лопатках гильзовой кон-
лаждения закрытого типа. В одноконтурных системах
охладитель отбирает теплоту непосредственно у охлаждае-
мого элемента, а в двухконтурных — у промежуточного
теплоносителя, который циркулирует в охлаждаемом
Рис. 11.55. Рабочая
лопатка с продоль-
ным течением ох-
ладителя фирмы
«Роллс-Ройс» (Ан-
глия):
1 — ввод охладителя;
2 — вывод охлади-
теля
элементе.
Системы охлаждения закрытого
типа выполняются с принудитель-
ной и естественной циркуляцией
(рис. 11.57). В первом случае дви-
жение охладителя вызывается глав-
ным образом перепадом давлений,
создаваемым внешним источником
энергии, во втором случае — за
счет термосифонного эффекта. Этот
эффект создается тем, что к охла-
дителю подводится тепловой поток
от охлаждаемого элемента, который
вызывает изменение его плотности,
а поле центробежных сил обеспе-
чивает интенсивную циркуляцию.
Термосифонный эффект исполь-
зуется также в двухконтурных си-
стемах охлаждения лопаток. В этом
случае в теле лопатки 1 (рис. 11.58)
имеются глухие каналы 2, запол-
лопатка с двухкон-
турной системой
охлаждения
Рис. П.56. Рабочие лопат-
ки конструкции К. В. Ту-
манского с поперечным
движением охладителя:
1 — ввод охладителя; 2 —
вывод охладителя
ненные теплоносителем первого кон-
тура (обычно дистиллированной во-
дой или натрием). В нижней части
лопатки размещен радиатор 3, ко-
торый омывается охладителем вто-
рого контура. Во время работы турбины к перу лопатки
от горячего газа подводится теплота, а от радиатора
она отводится. При этом за счет вращения во вну-
тренних глухих каналах имеет место интенсивная есте-
ственная циркуляция охладителя первого контура (тер-
струкции, в которых более нагруженный несущий стер-
жень имеет более низкую температуру. Наружная тонко-
стенная оболочка крепится к стержню обычно в хвостовой
части лопатки и усилия от газовых сил также передает
стержню.
Для охлаждения рабочих лопаток используется также
пленочное и пористое охлаждение. Так, пленочное охлаж.
Рис. 11.57. Рабочие лопатки с системой охлаждения за-
крытого типа, а — с принудительной циркуляцией; б —
с естественной циркуляцией:
Рис. 11.59. Схемы воздушного охлаждения дисков и
роторов газовых турбин
I — зона подвода охладителя, 2 — зона отвода охладителя;
3 — разделительная йерегородка; 4 — охлаждающие каналы
дение входной кромки рабочей лопатки применено на
авиационном двигателе TF-39 фирмы «Дженерал-Элек-
трик» с начальной температурой газа 1260° С. Эта ло-
патка представляет собой многоканальную конструкцию
с выпуском воздуха через отверстия на входную кромку.
2. Системы охлаждения закрытого типа. По принципу
действия различают одно- и двухконтурные системы ох-
5*
мосифонный эффект), которая обеспечивает передачу
теплоты от пера лопатки к охладителю второго контура.
Охлаждение дисков и роторов. Диски и роторы в боль-
шинстве случаев охлаждаются с помощью циклового воз-
духа, отбираемого из компрессора. Наиболее распростра-
ненными способами охлаждения являются радиальный
обдув боковой поверхности диска (ротора) (рис. 11.59, а),
струйный обдув диска в районе хвостового соединения
рабочих лопаток (рис. 11.59, б), продувка воздуха через
67
щелевые зазоры в хвостовых соединениях рабочих лопа-
ток (рис. 11.59, в), образование пленки холодного воздуха
на внешней торцовой поверхности диска (ротора).
Газодинамический расчет охлаждаемых турбин
Рабочий процесс в охлаждаемых газовых турбинах
по сравнению с неохлаждаемыми характеризуется сле-
дующими особенностями: отводом некоторого количества
теплоты от газа к охлаждающему агенту, что обусловли-
вает соответствующее уменьшение располагаемой работы
газовой турбины; подмешиванием охлаждающего агента
в поток газа (в открытых системах); затратой части рас-
полагаемой работы газовой турбины для обеспечения цир-
куляции охлаждающего агента по тракту; возникновением
дополнительных потерь, обусловленных ухудшением
аэродинамики охлаждаемой проточной части. ,
Приближенная количественная оценка каждой из
перечисленных дополнительных составляющих потерь
рассмотрена ниже.
Потеря располагаемой работы из-за отвода части
теплоты от потока газа определяется следующим обра-
зом. Из уравнения баланса теплоты между потоками газа
и охлаждаемым элементом
С1 охл —
Лс (1 — ©ср)
1 — л'
>2
ОХЛ
—т,
— Тд
(11.133)
где Tji «з 9с. охл/^с — коэффициент, характеризующий ин-
тенсивность охлаждения сопловых лопаток.
Если лопатки имеют открытую систему охлаждения,
из-за смешения потоков газа и охладителя параметры
потока на входе в рабочее колесо будут отличаться от та-
ковых при неохлаждаемых лопатках. Так, температура
смеси на входе в рабочее колесо в рассматриваемом слу-
чае может быть приближенно подсчитана по формуле [25,
30]
Т1 СМ — Т 1н. охл [1 -|- ёохл (Тохл. вых/T 1Н. охл) ,25] X
ХО+^охл)-1, (П.134)
Сохл— G^A^- а/охл(Г* Гст) (11.131)
следует, что при заданных Gr, Т * и 7’ст величина ДТ
которая характеризует снижение работоспособности по-
тока газа из-за отвода теплоты к охлаждаемому элементу,
пропорциональна коэффициенту теплоотдачи аг и площади
поверхности ЛОхл> через которую происходит теплообмен
со стороны газа. Расход газа Gr обычно определяется из
расчета цикла ГТУ, а средняя температура охлаждаемого
элемента 7СГ — из условия обеспечения его надежной
работы (см. гл. VIII).
Поскольку при заданных значениях параметров по-
тока газа, омывающего охлаждаемый элемент, возможности
уменьшения а, ограничены, основным фактором, за счет
которого можно активно воздействовать на величину Д7Г,
является Гохл- Для охлаждаемых лопаточных венцов
требуемое уменьшение Гохл может быть реализовано сле-
дующим образом:
а) увеличением располагаемого теплового перепада
на ступень турбины, а также уменьшением степени ее
реактивности; при этом, очевидно, уменьшается число
охлаждаемых ступеней (венцов), а также длины и хорды
лопаток х;
б) увеличением относительного шага лопаток в ох-
лаждаемом венце ?охл по сравнению с неохлаждаемым,
т. е. уменьшением числа лопаток в венце;
в) нанесением жаростойких покрытий на рабочую
поверхность охлаждаемой лопатки.
Для охлаждаемого лопаточного венца работа расши-
рения газа с учетом отвода части теплоты от потока газа
к охладителю может быть подсчитана по следующим фор-
мулам 2 [30].
Для сопловых лопаток:
где
Тохл. ВЫХ = Тохл. вх + ?охл/(ср охл&хл)> §ОХЛ — G0XJi/Gr.
Абсолютная скорость смеси
С1 см = Cl (1 + Sc. охл) 1 [( Sin -|-
+ Sc. охл С1 охл sin О', охл)2 +
+ (cos + gc. охл cos ах охл)2]1/2 , (II. 135)
гДе Сюхл ~ сюхл^с1-
Угол входа потока смеси на рабочие лопатки
а1 см — arctg [(1 -|- gc. охлС1 охл X
X Sin охл/SIH <Xi)/( 1 gc. охл COS <Хг охл/COS CZl)].
(11.136)
Для рабочих лопаток:
Лр. охл •— ^р. н. йхл
р
1-Лр Р
(11.137)
/1с. охл — ^с
(11.132)
w2 охл l/"^p. охл
где лр = Pi/p2; т2 « 9р. охл/hp — коэффициент, учиты-
вающий интенсивность охлаждения рабочих лопаток;
^Icm ~ С1см + и2 — 2е1сч и cos а1охл.
Если охлаждающий агент выходит из рабочих лопа-
ток в проточную часть, смешиваясь с потоком газа, то
параметры смеси на входе в последующий лопаточный
венец могут быть подсчитаны по формулам, аналогичным
(11.134)—(11.136).
Работа и к. п. д. на окружности рабочего колеса
охлаждаемой ступени [30, 64]:
1 Применение малой или близкой к нулю степени реактив-
ности в охлаждаемых ступенях позволяет отводить большую
часть теплоты в сопловых лопатках, температура которых по
условиям прочности может быть принята более высокой, чем
рабочих лопаток.
2 При этом предполагается, что коэффициент скорости <р
н давление/? 1с не зависят от охлаждения, а теплота от газа к
лопаткам отводится равномерно вдоль канала; т — (£—!)/£,
индексы при тем. в условных обозначениях.
Т1ст. охл
hu ОХЛ — (1 + gc. охл) см COS (Zj CM ---
(1 Н- Sc. охл + Sp. охл) w2c2 см COS <х2 см; (II-138)
. Г Л / , . mCT I I „ р у
СТ I Гбс ОХЛ ОХЛ ВХ
X Ср охл! 1
Срг
" ^р. охл^охл. вхсР охл
г-г.
(11.139)
- 68
В некоторых случаях для приближенного определе-
ния к. п. д. можно использовать формулу [113]
'Пиз. ст. охл = (10 G охл) 11 “I” (2<?с. охл/с1 охл +
+ к о^/Т1)с21охл/2 +
+ (2<?р. охл/Ш2 охл + 5р. охл) Ш2 охл/2] • С11-140)
Снижение энтальпии газа на выходе из охлаждаемого
лопаточного венца вызывает уменьшение располагаемой
работы также в последующих венцах, поэтому удельная
работа и к. п. д. многоступенчатой охлаждаемой газовой
турбины могут быть определены по формулам [30]:
п
UT. ОХЛ ---
2i—1 \
1 + У] 8охл j j ^ir'CtacM i
i=l / i
1 + У i goxn J j M2ic2ucM i
,=1 / i
Пт. ox Л ^UT. ОХЛ
CpT* 1-
2n
4“ +охл [киз. охл z)
fal
(11.141)
(11.142)
где hBs. охл i — располагаемый (изоэнтропийный) перепад
охладителя, определяемый по его параметрам на входе
в z-й охлаждаемый венец и давлению на выходе из про-
точной части охлаждаемой турбины.
Потеря располагаемой работы из-за отвода части
теплоты от газа к охладителю для рационально спроекти-
рованных открытых систем воздушного охлаждения при
начальной температуре 1100—1130° С составляет 0,015—
0,020. С увеличением Tq и при использовании в качестве
охладителя жидкости указанная потеря из-за большей
глубины охлаждения лопаток может существенно увели-
читься (в два-три раза).
Затрата работы на прокачку охлаждающего агента
зависит от типа системы охлаждения и применяемого хла-
дагента. При воздушной системе охлаждения эта потеря
в общем случае представляет собой разность между ра-
ботой на сжатие соответствующего расхода воздуха в ком-
прессоре £охл и работой, производимой этим воздухом
при его введении в проточную часть турбины после про-
хождения через охлаждаемые элементы.
Потеря располагаемой работы, обусловленная отбо-
ром части циклового воздуха, сжатого в компрессоре,
может быть приближенно оценена по формуле
Д^ОХЛ. СЖ “ У. &ОХЛ Z^kZ ^РохЛ Z/^K» (11.143)
1=1
где Дрохл I — относительный перепад давлений воздуха
при его прохождении через охлаждаемый элемент; z —
число охлаждаемых элементов в турбине.
Из этой формулы следует, что при рациональном вы-
боре точки (ступени) отбора воздуха из компрессора для
подачи его к охлаждаемому элементу и конструктивном
выполнении системы охлаждения, обеспечивающем малые
гидравлические потери, величина ДйОхл. сж будет опреде-
ляться величиной gOXJ! £.
Дополнительные аэродинамические потери из-за вве-
дения охлаждения возникают вследствие ряда причин.
Наиболее существенной из них является внедрение по-
тока охлаждающего агента в основной поток газа, что
имеет место в открытых системах воздушного охлажде-
ния (например, при охлаждении дисков и роторов газо-
вых турбин путем обдува их торцовой поверхности, при
внутреннем охлаждении направляющих и рабочих лопа-
ток с выпуском охлаждающего воздуха из отверстий в про-
фильной части и у задних кромок и др.
На рис. 11.60 приведены зависимости к. п. д. тур-
бинной ступени г|ст от gOXJ1 для случаев охлаждения дис-
ков путем радиального и струйного обдува; из рисунка
следует, что аэродинамические потери, обусловленные
Рис. 11.60. Зависимость к. п. д. ступени турбины от
расхода охлаждающего воздуха при радиальном и
струйном обдуве дисков: а — струйный обдув при
готв = const и различных углах О (/ — 0 = +60°;
2 — 0 = +30°; 5 — 0 = —60°); б — радиальный
обдув различными способами (1 — без уплотнения
диска; 2 — с уплотнением диска; 3 — с гладким ко-
зырьком над диском; 4 — с козырьком над диском
с направляющими лопатками); в — сравнительные
данные по радиальному и струйному обдуву при О =
— 90° (/ — радиальный обдув; 2—4 — струйный
обдув: 2 ^отв 3 ^отв ~ 12, 4 ^отв = 4)
могут быть весьма ощутимыми [104]. При струйном обдуве
дисков указанные потери могут быть снижены за счет
соответствующего изменения угла выхода струи у
(рис. 11.60, а).
При радиальном обдуве некоторое снижение аэроди-
намических потерь может быть достигнуто установкой
специальных направляющих лопаток, позволяющих осу-
ществить безударное смешение потока охлаждающего воз-
духа с основным потоком газа на входе в проточную часть
(рис. II.60, б). Радиальный обдув всегда обеспечивает
меньшие потери по сравнению со струйным обдувом
(рис. II.60, в).
Выпуск потока охлаждающего воздуха через отвер-
стия у задних кромок лопаток в основной поток относи-
69
тельно слабо [20 , 23 , 25 , 65] влияет на профильные по-
тери §Пр. охл в лопатках (рис. 11.61).
В более развитых системах охлаждения лопаток,
например пленочной или пористой, влияние вдува ох-
лаждающего воздуха в основной поток сопровождается
более ощутимыми аэродинамическими потерями, которые
могут быть оценены с помощью соответствующих опытных
данных [30]. В лопатках газовых турбин, охлаждаемых
пропусканием хладагента по специальным каналам (по-
лостям), дополнительные аэродинамические потери мо-
гут возникать из-за утолщения профилей, главным обра-
зом в зоне выходной их кромки. Эти дополнительные по-
тери можно оценить на основании рекомендаций, изло-
женных в п. II.2.
Интенсивность охлаждения лопаток характеризуется
также отношением W = Тл!Тт, называемым иногда тем-
охлаждения при fr > 10004-1050° С можно принимать
'Похл — 0,9804-0,995.
С учетом изложенных выше соображений мощность,
развиваемую газовой турбиной с открытой системой ох-
лаждения, можно подсчитать по формуле [30]
^охл
с Т*
cpJ о
1 — 2Т г
. Т. охл
2я
“И У (£охл г^охл i)
п
'Пт. охл (^нас гйохл i) —
2гг п • \
X; ДЛут i Айт. в г И Пиех. (II. 144)
Д97'----------------------------:---------1
о 001 0,02 0,03 дох„
Рис. 11.61. Изменение профильных
потерь в охлаждаемых лопатках
пературным фактором (здесь 7’л — средняя температура
стенки лопатки; Тг — средняя температура газа, омывае-
мого лопатку). При умеренном охлаждении, когда
0,8, потери трения в пограничном слое охлаждаемых
и неохлаждаемых лопаток практически можно считать
одинаковыми. При более интенсивном охлаждении наблю-
дается увеличение профильных потерь в охлаждаемых
лопатках g!Ip. охл по сравнению с неохлаждаемыми ёпр -
Это увеличение вызвано изменением профиля скорости и
соответственно увеличением сил трения в пограничном
слое, образующемся на профиле охлаждаемой лопатки.
Так, при Т < 0,604-0,65 увеличение £Пр. охл по сравне-
нию с £Пр может достигать 30—50%, причем большие зна-
чения соответствуют рабочим лопаткам, что обусловлено
влиянием центробежных сил инерции [30]. При исполь-
зовании в расчетах коэффициентов скорости для ох-
лаждаемых воздухом лопаток, когда температурный фак-
тор Т Да 0,754-0,80, можно рекомендовать следующие
значения коэффициентов скорости: срОхл = (14- 0,995) <р
и Фохл= (0,9954-0,990) ф [42].
Охлаждение лопаток оказывает также влияние на
аэродинамические потери в проточной части газовой тур-
бины вследствие увеличения радиальных зазоров. Увели-
чение зазоров может быть достаточно точно оценено в ре-
зультате расчета температурного состояния деталей про-
точной части, а получающиеся при этом дополнительные
потери — на основании рекомендаций, приведенных
в п. II.2.
Выпуск охладителя в радиальный зазор может не-
сколько уменьшить соответствующую долю потерь, свя-
занную с его наличием [26].
Влияние увеличения относительного шага, что обычно
имеет место в венцах с охлаждаемыми лопатками, на ве-
личину коэффициента скорости ср (ф) может быть оценено
по рекомендациям п. II.2 или, в первом приближении,
по формуле [30] <Р7 = <pz opt V1 — Af2B, где Ai — (lopt —
-fl//opt; 5 = 0,4.
Все перечисленные виды дополнительных аэродинами-
ческих потерь, возникающих вследствие введения ох-
лаждения турбинной ступени, можно учесть в расчетах
с помощью коэффициента т]охл, т. е. t]CT. охл = 'Пст'Похл-
Для рационально спроектированных систем воздушного
70
где Д/гутг- — утечки рабочего тела через радиальные за-
зоры охлаждаемых сопловых и рабочих лопаток r-й сту-
пени; Д/гт. в г- — потери на трение и вентиляцию в i-й
ступени; Лохл t- = и%ых t — и^х t — работа, совершаемая
охладителем при прохождении через ступень.
В газовых турбинах с закрытой системой охлаждения
при определении А'охл надо принять gOXJI = 0.
Теплообмен в системе охлаждения
Из уравнения (11.131) можно получить, что тепловой
поток от охлаждаемого элемента qoxn . = срг.а*((Т* —
—Гст), где — приведенный коэффициент теплоотдачи.
Для оценки <7оХЛ t необходимо найти средний коэффициент
теплоотдачи с газовой стороны аг. На основании обобще-
ния большого количества опытных данных по теплообмену
в неподвижных решетках активных и реактивных профи-
Рис. 11.62. Коэффициент А в критериаль-
ном уравнении теплообмена
лей в работе [30] для определения среднего коэффи-
циента теплоотдачи рекомендуется критериальное урав-
нение
аг = 0,206 Re0’66Sr~°’58Лг/6, (11.145)
где Re = — число Рейнольдса; Ь — хорда профиля;
Sr — критерий, учитывающий поворот потока в решетке
Sr = (sin Pj/sin р2) х
X rW[/sin(P1 + р2) cos2 (Pi — Р2)/2] — 1.
Параметры потока и рабочего тела в уравнении (11.145)
определяются в сечении за решеткой. Это уравнение реко-
мендуется для использования при Re = (0,24-1,5) 10е
Ч';> 0,45. При больших числах Рейнольдса часто ис-
пользуется критериальное уравнение [30]
Nu = A Re0-68, (II. 146)
где 4= 0,074-0,11—коэффициент, зависящий от угла
поворота потока в решетке; для его более точной оценки
можно воспользоваться рис. II.62.
Уравнения (11.145) и (11.146) получены путем обра-
ботки данных опытов, проведенных при безударном обте-
кании решеток профилей. Влияние угла атаки можно учесть
с помощью коэффициента [21, 26]
е; =0,97 +0,78 (Г—0,2)2, (11.147)
где i = г/Рх — относительный угол атаки.
Уравнение (11.147) рекомендуется применять при
ReBX = (1,5=4,0) 105 и гвх/Ь = (2,3=7,3) 10“1 2. Здесь ReBX
подсчитывается по параметрам на входе в решетку, при-
чем за характерный линейный размер принимается удвоен-
ный радиус входной кромки гвх.
В условиях вращения теплообмен между газом и
профилем интенсифицируется. Влияние вращения учиты-
вается обычно поправочным коэффициентом [30, 116]
евр --- 1 _j_ 0,8 Su * , где Su = u/w2 — критерий, учиты-
вающий вращение.
Приведенные уравнения позволяют оценить тепловой
поток, отводимый от рабочего тела в охлаждаемом венце.
Требуемый расход §-охл > = б0Хл,:/<+ определяется
из уравнения теплового баланса для охлаждаемого эле-
мента:
G охлг — <7охл1 /(+охл i охл i) —
= ЙОХЛ'РоХЛ (Уст Тохл)/(ср ОХЛ i АУоХЛ l), (И. 148)
где ДТОхл i — подогрев охлаждающего воздуха при его
прохождении через рассматриваемый элемент.
Из уравнения (11.148) следует, что при заданном зна-
чении <?охл i величина б.,хл i определяется перепадом А7’Охл i-
В свою очередь, при заданных 7’сти ДУохл г величина <т0ХЛ(
зависит от геометрических и режимных характеристик
системы охлаждения.
Для приближенной оценки расхода воздуха, отбирае-
мого иа охлаждение, можно воспользоваться уравнением
130]
Soxni = kyiSfii, (11.149)
где gi = 0,015=0,025 — удельный коэффициент расхода
охладителя, определяемый конструкцией охлаждаемой
лопатки (меньшие значения соответствуют более эффек-
тивному охлаждению); 9Z= (Уг* — УСГ)/(УГ — Уохл. вх)—
относительная температура, характеризующая интенсив-
ность охлаждения; йут — 1,05=1,10 — коэффициент,
учитывающий утечки охладителя через неплотности си-
стемы.
Величина g0XJ1i определяется достаточно точно в ре-
зультате вариантных расчетов температурного состояния
рассматриваемого элемента, причем за окончательный
вариант принимается тот из них, при котором достигаются
как уровень средней температуры, так и требуемая сте-
пень равномерности ее распределения в элементе х,
обеспечивающие его надежную работу в условиях экс-
плуатации. [116].
Методы расчета теплового состояния охлаждаемых
деталей газовых турбин при стационарных и нестацио-
нарных режимах подробно изложены в специальной литера-
туре 2 [116].
Кроме теплового расчета системы охлаждения прово-
дят ее гидравлический расчет, задача которого заключается
в определении площадей проходных сечений охлаждаю-
щих каналов, обеспечивающих требуемое тепловым рас-
четом распределение охлаждающего воздуха по элементам
тракта при заданном перепаде давлений. Эти расчеты ве-
дутся обычно численным методом с использованием ЭВМ 3.
Обычно расчет охлаждаемой турбины выполняется
в два этапа. На первом этапе проводят газодинамический
расчет турбины без учета охлаждения. При этом находят
распределение параметров рабочего тела по проточной
части и геометрические характеристики лопаток. Затем
устанавливают число охлаждаемых венцов и по допустимым
температуре стенки Тст и степени неравномерности рас-
пределения температуры (уровню термических напряже-
ний) для каждого охлаждаемого венца определяют ^охл г
и йохл г- На втором этапе газодинамический расчет про-
точной части выполняют с учетом охлаждения — так,
как это показано в п. II.5.
1 Неравномерное распределение температур может вы-
звать возникновение термических напряжений, которые при
определенных условиях приводят к появлению остаточных де-
формаций и последующему разрушению детали.
2 См. также '«Руководящие указания ЦКТИ— ИТТФ».
Т. 2. Л., ЦКТИ, 1972 (вып. 29).
3 См. «Руководящие указания ЦКТИ —ИТТФ». Т. 1. Л.,
ЦКТИ, 1970 (вып. 29)1.
Глава III
ОСЕВЫЕ КОМПРЕССОРЫ
1П.1. МЕТОДЫ ГАЗОДИНАМИЧЕСКОГО РАСЧЕТА
В настоящее время в стационарных и значительной
части транспортных ГТУ применяются главным образом
осевые компрессоры. Это объясняется возможностью осе-
вых компрессоров обеспечивать большой массовый расход
воздуха и высокий к. п. д. по сравнению с компрессорами
других типов при достаточно высокой степени повышения
давления воздуха в ступени. К осевым компрессорам при
этом предъявляются требования, чтобы они имели высо-
кую экономичность и обеспечивали напор в широком диа-
пазоне физических частот вращения и расходов воздуха,
технологическую конструкцию, умеренные габариты и
массу при высокой надежности. Методика расчета и про-
ектирования компрессора должна обеспечивать выполне-
ние всех перечисленных требований.
В результате газодинамического расчета компрессора
выбираются меридиональные обводы его проточной части,
определяются число' и геометрическая форма лопаток,
обеспечивающих заданные параметры рабочего тела:
массовый расход, давление на выходе, к. п. д., запас
устойчивой работы на расчетном режиме. Необходимо
также установить связь между этими параметрами на
переменных режимах.
Таким образом, при газодинамическом расчете ком-
прессора, как и для турбины, решаются две задачи гидро-
динамики: так называемая обратная, когда заданы пара-
метры потока и требуется подобрать геометрию канала
(расчет основного режима), и прямая задача, когда задана
геометрия канала и требуется определить параметры по-
тока на разных режимах.
Учитывая, что течение реального газа через лопаточ-
ные венцы осевого компрессора представляет собой на-
столько сложное явление, что его математическое описа-
ние пока не представляется возможным, все применяемые
в настоящее время методы газодинамического расчета осе-
вых компрессоров основаны на широком использовании
экспериментальных материалов.
Метод полного моделирования основан на использо-
вании в качестве прототипов для вновь проектируемых
ГТУ существующих и успешно эксплуатируемых компрес-
соров, имеющих высокие показатели.
Метод частичного моделирования (метод изолирован-
ной ступени) основан на результатах испытаний модель-
ных ступеней и на данных исследований по влиянию раз-
личных отклонений от точного моделирования на характе-
ристики ступеней.
Третий метод расчета основан на использовании экс-
периментальных данных по исследованию плоских решеток
профилей с введением ряда поправок для учета основных
физических явлений в потоке реального газа.
Все три метода обладают определенными преимуще-
ствами и недостатками и имеют специфическую область
применения. Результаты экспериментальных исследова-
ний, полученные при разработке этих методов, дополняют
72
друг друга. В ряде случаев проточная часть компрессора
проектируется с использованием всех трех методов
Известно, что использование и перенос результатов
опытного исследования с одного объекта на другой могут
быть осуществлены на основе теории подобия [33, 89],
согласно которой течение называется подобным в тех
случаях, когда при обтекании геометрически подобных
каналов поля скоростей, давлений и температур в соот-
ветственно расположенных сечениях будут одинаковыми.
При этом должны быть одинаковыми и некоторые без-
размерные комплексы, составленные из физических ве-
личин, характеризующих процесс, и называемые опреде-
ляющими критериями подобия.
В работах [95, 112] показано, что при течении газа
с одинаковыми показателями k такими определяющими
критериями являются критерии Маха М и Рейнольдса Re.
При достаточно больших значениях числа Re (больше
3-105) его влиянием можно пренебречь; следовательно,
в этом случае необходимым и достаточным условием по-
добия потоков в проточной части турбомашины является
равенство критериев Маха:
ми = ulV'jRT; ма = сй/УTrt .
При газодинамическом расчете обычно бывают заданы
параметры р®, Tq, л*, GK, п. Должен быть обеспечен
также необходимый запас устойчивости компрессора для
расчетной частоты вращения, характеризуемый коэффи-
циентом устойчивости
ь = (як/°к)у
У K/Gk)p ’
где индекс у относится к параметрам на границе устойчи-
вости, индекс р •— в расчетной точке.
Ш.2. МЕТОД ПОЛНОГО МОДЕЛИРОВАНИЯ
При полном моделировании новая проточная часть
представляет собой выполненную в определенном мас-
штабе проточную часть существующего компрессора
(прототипа), имеющего высокие показатели по экономич-
ности и надежности. Характеристики этих проточных
частей, построенные в параметрах подобия, являются
тождественными.
Диапазон параметров GK, л*, п новых машин, созда-
ваемы^ этим методом, зависит от количества типов и пара-
метров исходных компрессоров, имеющихся в распоряже-
нии конструктора.
За истекшие 10—15 лет отечественные турбострои-
тельные заводы создали ряд высокоэффективных компрес-
соров, многие из которых могут быть использованы в ка-
честве модельных для новых разработок. На рис. Ill 1 —
III.6 в координатах л*, Gnp = GK 1/'г*/р* приведены
универсальные характеристики некоторых компрессоров
(здесь = и/]/Г*; п = п'п^, Т"' = Т*/Т*; р* =
= p*lp^, GK = GK/GK р).
Параметры, через которые выражены характеристики,
являются также параметрами подобия, так как они про-
функцией только Ма, можно получить так называемый
расходный параметр Gnp = GK КТ*/р* - f (MJ.
Таким же образом^ выражая комплекс n/VТ че-
,рез Ми, получим п/Ут = 60 1АиУ kR/(nD). Заменяя
здесь Т на Т*, получим второй параметр подобия гапр =
= я//Т* как функцию чисел Ма и М„.
Таким образом, характеристики, выраженные через
комплексы Gnp и гапр, являются универсальными, так
как режимы работы компрессоров будут подобными при
одних и тех же значениях указанных комплексов.
Если ввести понятие коэффициента моделирования —
масштаба, равного отношению m-fi = Рнат/^мод, условия
подобия турбомашин могут быть записаны в виде (индекс
нат — натура; индекс мод — модель).
^пр. нат мод! гапр нат = Ппр мод/т?ч
як. нат = як. мод> Чиз. к нат ~ 'Низ к. мод-
Используя эти условия и имея характеристику мо-
дельного компрессора, можно выбрать режим моделиро-
вания и найти коэффициент т^, умножив на который все
чертежные размеры модели, получим соответствующие
размеры проточной части вновь проектируемого компрес-
сора.
При выборе режима моделирования на характеристике
исходного компрессора намечается область, в которой
выполняются условия л; нат«Л*. мод И Яиз.к. нат ~
~'Низ к мод- В этой области должно удовлетворяться
Масштаб моделирования определяется по формуле
тК ~ Уб^пр. нат/^пр. мод • (111.2)
Однако может оказаться, что при требуемых значе-
ниях л* и к не удается одновременно обеспечить за-
данные расход и частоту вращения. Ограниченность су-
ществующего «набора» прототипов осевых компрессоров,
а также недостаток имеющейся информации не позволяют
использовать рассматриваемую методику в широком
диапазоне заданных параметров, что является ее сущест-
венным недостатком. В таком случае может быть исполь-
зован метод, базирующийся на использовании в качестве
основы проточной части натурного компрессора, отмоде-
лированного рассмотренным методом, с введением до-
полнительных предвключенных и концевых ступеней.
При этом добавляемые предвключенные ступени должны
не только позволить увеличить расход через компрессор,
но и сохранить ранее выбранный режим моделирования
несмотря на изменение абсолютных параметров воздуха
на входе в основной отсек, что приводит к необходимости
введения нового масштаба моделирования.
Если предположить, что процесс сжатия в предвклю-
ченной группе ступеней происходит по политропе со
73
&
2 /. /// // /у / X \ \^л
7 / / / //// Л005
// ''7' / /ул 76\ ОЛ 0,9 7,78\ 0,870 725 0,945 74
0 ^-75 0,6 к ^е75 \ 0,7 8,700 0,788 54
Пп^О, 373^'"
0,2 0,4 0,6 0,8 1,0 fnp
Рис. III.2 Универсальная характеристика компрессора ГТК-10 НЗЛ ^?р = 5220 обилии; Т* -
= 288 К; р” = 1,0 кгс/см2; GK 3 -= 82,4 кг/С)
!
- / аЖ уХ -
г Хх1
• / /
^5(7 \ 0.8 \дЗ 0 0>90 1; \з1,03
и,ьи, \ L. 1ПП
0,30 0, зв°л0 0.70 0,75
f 0,2 0,4 0,6 0.8 to епв
Рис. III.3. Универсальная характеристика компрессора ГТН-9 JIM3 — 4000 об/мин; 7р = 290 К; р* —
= 1,0 ktcW; GK р = 78 кг/с) Р
7'4
Z \ ////^'\
/ Z >4. z X Z /
/ Z Z / / X s 1 X / / 07
/ / / у / 0 . о<71
Z Z / / / Т^-1 /о
\ 0.9 Ю 5
* п„^0 50 0,60 \ 0,70 0,80
0.? (7.4 0,6 0.8 1.0 спр
Рис. Ш.4. Универсальная характеристика КВД ГТ-100-750 ЛМЗ (я = 4100 об/мин; Т* ~ 308 К; р* =
= 4,2 кгс/см2; GK = 432 кг/с) Р ’ Р
Рис. III.5. Универсальная характеристика КНД ГТ-100-750 ЛМЗ (лр = 3000 об/мин; Т* = 283 К; р* =
= 1,0 кгс/см2; GK р = 432 кг/с) Р
75
степенью т= 3,51)ПОл. к/(3,51)поч. к — 1), то суммарная сте-
пень повышения давления этих ступеней найдется из усло-
вия л(т-1,/т=7’0/7’1. Здесь индекс 0 соответствует усло-
виям до установки предвключенной группы ступеней,
индекс 1 — после нее. Тогда, исходя из условия подобия,
можно написать соотношения:
GK нат/^к = (Ш.З)
%ат/«мод = («;)(т-1,/т(1Ю, (Ш.4)
откуда получаются формулы для расчета коэффициента
сора, принятого за модель, построена по результатам
замеров по патрубкам компрессора.
Если полученное значение л*ат превысит заданное,
следует исключить соответствующее количество ступеней
в конце проточной части модельного компрессора. Сум-
марный к. п. д. такой комбинированной проточной части
^из. к ~ 'Низ кГ'Пиз к2 [(пк)( 1] X
X Кз К2 [("*1)<А~1)/А ~ Ч +
+ Пиз. К1 - I]}-1. (Ш.9)
Z Z
- Zi Z \ Z /Т\
Z. Z / Z / ✓ / у Z / / у М ж/ .
лХ z/"""ч / I
/ / / zS<l / / / 0,5 8 ” \?1>°о
/ / / / / 0.87 -0.65 л О,. or ?5
s 1 0.1 0.80
- Обп О.Ь V-63 0,70
п ,^0.40
0.2 0.4 0.6 0,8 10 0пр
Рис. Ш.6. Универсальная характеристика модельного компрессора МКНД-П ЛМЗ (пв =
= 13 440 об/мин; Г* = 288 К, р* = 1,033 кгс/см2; GK р = 34 кг/с)
моделирования яг£ и требуемой степени повышения дав-
ления первого отсека л*
^=[(СК.нат,Ч.мод)(т-1)/(т4-1)Х
х(«нат/«мод)Гт!1)/(3т-1); (Ш.5)
= [(GK. HaT/GK. мод) (l/42)]2m/<m41)- (Ш.6)
Заданная частота вращения проверяется по формуле
Пнат = (ш)(т~1)/(2т)Пмод ОН)- (Ш.7)
Степень повышения давления проектируемого натур-
ного компрессора
Л*ат = л^; (III .8)
причем nJ (степень повышения давления второго отсека)
следует определить, исключив потери во всасывающем
патрубке, если универсальная характеристика компрес-
Проектируя предвключенные ступени, следует иметь
в виду, что последняя ступень этой группы должна иметь
размеры, позволяющие осуществить плавный переход
к основной группе. Переходный направляющий аппарат
должен при этом переформировать поток, выходящий из
первой группы ступеней, в поток с распределением пара-
метров подобным тому, которое имело место на входе в мо-
дельный компрессор, что обычно из-за неравномерного
распределения параметров потока на выходе из предвклю-
ченной группы ступеней невыполнимо. Поэтому число
предвключенных ступеней обычно ограничивают одной-
двумя. При недостаточной степени повышения давления,
обеспечиваемой модельным компрессором, следует произ-
вести наращивание основной проточной части концевой
группой ступеней. Эти ступени рекомендуется проектиро-
вать по тем же принципам, что и исходный модельный
компрессор. Желательно, чтобы суммарная степень повы-
шения давления концевой группы ступеней не превышала,
1,4—1,5. I
III.3. МЕТОД ЧАСТИЧНОГО МОДЕЛИРОВАНИЯ
Метод частичного моделирования основан на исполь-
зовании для создания проточной части компрессора за-
ранее разработанных одиночных ступеней, характеристики
которых известны из экспериментов. Проточная часть
формируется из исходной ступени путем подрезки части
Рис. III.7. Аэродинамические характеристи-
ки модельной компрессорной ступени К-50-1
(Т; = 295 К; «н = 1504-280 м/с; d = 0,6)
--- — — граница устойчивой работы ступени
лопатки со стороны втулки или периферии или одновре-
менно с двух сторон.
Применение этого метода в известной мере ограничено
уровнем заданных параметров исходных ступеней. Кроме
того, при высоких степенях повышения давления ком-
прессора растет число ступеней и соответственно возра-
стает отклонение от точного подобия.
Вместе с тем этот метод позволяет упростить техноло-
гию изготовления лопаток и унифицировать оснастку,
т. е. удешевить производство лопаточного аппарата, что
особенно важно в условиях индивидуального и мелкосерий-
ного производства.
Рассматриваемый метод можно рекомендовать для
применения в диапазоне значений л* с 4-4-5 и «н <
С 2004-250 м/с, что при частоте вращения п =
= 3000 об/мин (50 с"1) соответствует GK С 300 кг/с.
Набор экспериментальных характеристик некоторых
исходных ступеней приведен на рис. III.7 — III. 10. Они
построены в координатах ф = Л (ф) и 1)Из. ст = /г (ф)>
где
4 = /ги з/(“п/2) l Ф = са/ин = Gk/(PF «н) •
Характеристики исходных ступеней определены по
полным параметрам на наружном диаметре £>н. Эти сту-
пени испытаны при определенных значениях d = £>вн/£>н
(где £>вн — внутренний диаметр ступени) и ин и имеют
различные законы распределения параметров потока по
высоте лопатки.
Для обеспечения равенства чисел Ми при пользовании
характеристиками определяют приведенную по темпера-
туре окружную скорость и'а = и1{угде Т’э —
температура, при которой проводились испытания ступени.
При равенстве чисел Ма обеспечивается равенство коэф-
фициентов расхода натурной ступени и исходной. Гео-
метрическое подобие ступеней при этом выдержать обычно
не удается, поскольку удлинения, зазоры, втулочные
отношения не моделируются, часть сечений лопатки у пе-
риферии или корня при подрезке удаляется. Кроме того,
Рис. III.8. Аэродинамические характеристи-
ки модельной компрессорной ступени К-70-17
(Г* = 298 К; ин = 1754-240 м/с; d = 0,6)
--- ---- граница устойчивой работы ступени
условия работы ступейи в группе отличаются от условий
работы изолированной ступени и зависят от места ее
в многоступенчатом компрессоре.
Для учета влияния всех перечисленных факторов
при расчете проточной части рассматриваемым методом
вводятся соответствующие поправки.
Расчет обычно начинают с подбора по атласу ступеней
[90] наиболее подходящего типа ступени. Для этого,
задаваясь значениями d и <р для первой ступени, опреде-
ляют окружную скорость
ин = 0,15 j/ (?к7?Г*га2/[р*Ф (1 - <IIL1°)
Если условиям технического задания удовлетворяют
несколько ступеней, то из них выбирают наиболее эф-
фективную, т. е. имеющую наибольший к. п. д. или коэф-
фициент напора.
Площади проходных сечений лопаточных венцов
зависят от типа исходных ступеней, закона распределе-
ния коэффициентов <р вдоль оси z и принятого типа про-
точной части. Выбранный закон распределения <р по сту-
пеням может существенно сказаться на размере области
оптимальных к. п. д. и на запасе устойчивости fey.
77
Можно рекомендовать следующие законы распреде-
ления ф (г).
I. ВДОЛЬ ПрОТОЧНОЙ ЧаСТИ ф = const га tPopf В этом
случае обеспечивается достаточно высокий уровень
к. п. д. в диапазоне (0,84-1,0) ии. Такой закон целесо-
образен в случае, когда от компрессора требуется обеспе-
чить наибольшую экономичность на режиме максимально
длительной нагрузки установки.
2. От первой ступени к последней коэффициент <р
возрастает при ф ф t в средних ступенях, граница
Рис III.9. Аэродинамические характеристи-
ки модельной компрессорной ступени К-50-3
(7* = 297 К; = 150-'-250 м/с; d = 0,7)
—-------граница -устойчивой работы ступени
помпажа в зоне высоких окружных скоростей при этом
смещается в область меньших расходов, что обусловлено
условиями работы последних ступеней.
3. От первой ступени к последней коэффициент ф
снижается при ф з« фор4 в средних ступенях. Для этого
закона характерно существенное расширение области
устойчивой работы при окружных скоростях, меньше
расчетных, и некоторое увеличение длины лопаток по-
следних ступеней.
Типы проточной части компрессора, которые харак-
теризуются очертанием ее меридиональных обводов и ви-
дом подрезки модельной лопатки со стороны вершины
или у корня, условно можно разделить на следующие.
I. Лопатки модельной ступени подрезаются у втулки:
£>н = const; £>вн — монотонно возрастает.
II. Лопатки модельной ступени подрезаются со сто-
роны периферии £>вп = const; DH — убывает от шупени
к ступени.
78
III. Лопатки подрезаются как у периферии, так и
у втулки: изменяются оба диаметра таким образом, что
сохраняется условие DCp = const.
IV. Модельные лопатки подрезаются с двух сторон
и смещаются или на больший диаметр (DH = const),
или на меньший (£>вн = const). Этот тип проточной части
выбирают при большом числе ступеней, когда из-за умень-
шения длины лопаток односторонняя подрезка становится
Рис. III. 10. Аэродинамические характеристики
модельной компрессорной ступени Д-02 (Г* =
= 288 К; «н = 1804-217 м/с; 0,6)
чрезмерно большой. При периферийной подрезке лопа-
ток расчетное значение окружной скорости должно для
всех ступеней приниматься не на физическом, а на расчет-
ном диаметре £>н. р.
Каждый тип проточной части имеет свои преимуще-
ства и недостатки. По сравнению с типом II аэродинами-
чески более совершенным является тип I, так как при
периферийной подрезке лопаток в корневой части сту-
пени работают наиболее густые, сильно изогнутые решетки
профилей с повышенной диффузорностью, с более высо-
кими профильными потерями. Указанный недостаток
можно устранить, перейдя к проектированию проточной
части по типу IV при £>вн = const, однако при этом при-
дется увеличить число ступеней из-за снижения окружных
скоростей от ступени к ступени. С другой стороны, про-
точная часть, выполненная по типу II, более технологична.
Схема расчета проточной части осевого компрессора
методом частичного моделирования приведена в приложе-
нии 3. Расчет проточной части компрессора рассматри-
ваемым методом проводят последовательно для каждой
ступени дважды. На первом этапе поступенчатого расчета
при заданных коэффициентах расхода п приближенно
оцененных поправочных коэффициентах определяют на-
ружные и внутренние диаметры на входе в каждую сту-
пень. Хорды лопаток определяют путем расчета на ста-
тическую и динамическую прочность. Затем строят про-
точную часть и, если по данным первого расчета ее обводы
получаются недостаточно плавными, выравнивают об-
воды. При выравнивании торцовые площади на входе
ступени могут изменяться, ввиду чего коэффициенты рас-
хода, напора и к. п. д. будут отличаться от принятых ра-
нее; кроме того, возникает необходимость изменения по-
правок на напор и к. п. д. После этого проводят второй
этап поступенчатого расчета по исправленной геометрии
канала.
Поправочные коэффициенты, учитывающие наруше-
ние геометрического подобия и взаимное влияние ступеней,
представляются в виде произведения нескольких коэффи-
циентов, каждый из которых учитывает отдельно какой-
либо из указанных факторов:
К, =-К, К К17К, -К,
ф фм фз ф/ ф дг фос>
К =К К К -К Л-К
Г) ДМ ЦЗ Г] I Г] Аг г; ос-
Здесь индексы означают: м — учет изменения напора
и к. п. д. из-за нарушения подобия, связанного с взаим-
ным влиянием ступени; з — учет различия относительных
радиальных зазоров у модели и натуры; I — учет различия
удлинений; Дг — учет типа и величины подрезки; ос —
учет различия относительных осевых зазоров у модели
и натуры.
Поправочные коэффициенты, учитывающие взаимное
влияние ступеней, принимаются равными: 7ФфМ = 0,95-ь-
-Ц 0,98; Л'пм = 0,97н-0,99 (меньшие значения рекомен-
дуются для компрессоров с числом ступеней г > 8н-9
и проточными частями, выполненными по типу II). На
нерасчетных режимах коэффициенты и следует
несколько уменьшить.
Из технологических соображений абсолютную вели-
чину радиального зазора принимают одинаковой для
группы ступеней. При этом длина лопаток уменьшается
от ступени к ступени, а следовательно, относительный
радиальный зазор бр = 6p/Z увеличивается с порядковым
номером ступени. Поскольку с увеличением бр и умень-
шением Т — lib показатели компрессорной ступени ухуд-
шаются, коэффициенты К и К- обычно находят в виде
произведения- по эмпирическим формулам:
К К ______ I — 0,045 (6р//)пат .
,|а,|:Г 1-0,045 (бр/Г)М0Д ’
к к 1 -0,024 [бр/(1-а/)]наг
лзДп7 1 -0,024 [6р/(1-а/)]МОд’
(III.И)
!
(Ш.12).
где а = b/Dn.
Увеличение радиального зазора сужает область устой-
чивой работы ступени. Поэтому при расчете характери-
стик в области, близкой к помпажу, рекомендуется умень-
шать примерно на 1,5% и добиваться, чтобы ра-
диальные зазоры у натурного компрессора были мини-
мально допустимыми по условиям обеспечения надежной
его работы.
Осевые зазоры между венцами компрессора прини-
мают обычно равными: s21 = 0,5; s22 = 0,15ч-0,20. Если
суммарный осевой зазор s2 не превышает 0,6—0,7, при-
нимают Кфос == 1,0.
Влияние подрезки ступени на ее показатели зависит
от принятого закона распределения осевых скоростей и
давлений на входе и выходе из лопаточных венцов.
На рис. III.il—III. 13 приведены зависимости коэф-
фициентов К - и К - от коэффициента расхода <р для
Рис. III. 11. Поправочный коэффициент для ступени
К-50-1: а—корневая подрезка; б — периферийная подрезка
типовых компрессорных ступеней. ''Здесь Дгн = (£>н —
Dr. р)/7Эн! Лбвн = (£%н 7ЭН. р)/Е)н. р.
Из рис. III. 13 следует, что высокий уровень к. п. д.
компрессора обеспечивается в случае когда | Дг | < 0,2.
ная подрезка
Если односторонняя подрезка ведет к превышению этой
величины, рекомендуется перейти к смещению сечений,
т. е. к организации проточной части по типу IV. При этом
ступени компрессора разбивают на группы, внутри каж-
дой из которой производят одностороннюю подрезку до
величины! Дг | = 0,1. Затем, при переходе ко второй группе
79
изменяют Ор и соответственно «р, т. е. ступень подрезается
с другой стороны, и внутри второй группы производят
одностороннюю подрезку. При двусторонней подрезке
ступени поправочные коэффициенты определяют отдельно
для каждой подрезки и в расчет вводят суммарную по-
правку
К = К . К -
фАг •ф Агн фДгвн.
ступеней К-50-1, К-50-3, К-70-17, а — корневая
подрезка; б — периферийная подрезка
При двусторонней подрезке со смещением коэф-
фициент следует принимать несколько более высо-
ким, чем при односторонней.
IH.4. РАСЧЕТ ХАРАКТЕРИСТИК КОМПРЕССОРА
При построении проточной части методом полного
моделирования характеристика компрессора известна из
результатов испытаний исходного модельного компрес-
сора. При использовании других методик необходимо
иметь расчетный метод получения характеристик компрес-
сора, и от степени его надежности будет зависеть объем
доводочных работ на вновь создаваемом компрессоре.
Разработка такого метода — весьма трудная проблема,
поскольку закономерности течения воздуха и харак-
тер изменения потерь на нерасчетных режимах очень
сложны.
Наиболее надежным является метод расчета характе-
ристик компрессора путем суммирования характеристик
отдельных ступеней с учетом искажения их на нерасчет-
ных режимах. Однако погрешность этого метода увеличи-
вается по мере отклонения режима от расчетного.
Как известно, при уменьшении расхода воздуха ниже
определенного уровня работа компрессора становится
неустойчивой. При этом поток воздуха, протекающего
через компрессор, начинает сильно пульсировать, возни-
кает вибрация и тряска компрессора. Это явление носит
название помпажа. Каждой частоте вращения соответст-
вует свое минимальное значение расхода, и линия, соеди-
няющая точки начала помпажа, называется границей
устойчивой работы компрессора (границей помпажа).
Увеличение расхода воздуха по сравнению с минимальным
возможно также до определенного предела. Степень повы-
шения давления с увеличением расхода непрерывно па-
дает, однако вначале это не сопровождается уменьше-
нием к. п. д. компрессора. Дальнейший же рост расхода
ведет к резкому падению напора и к. п. д., так что кри-
вая зависимости степени повышения давления от расхода
превращается в вертикальную прямую и расход при за-
данной частоте вращения уже увеличить не удается.
При проектировании проточной части компрессора
стремятся добиться полного соответствия между геометриеи
проточной части и геометрией потока на расчетном режиме,
однако на нерасчетных режимах отдельные ступени не-
избежно будут работать в неоптимальных условиях.
Рассмотренные ранее законы изменения ф по г на не-
расчетных режимах будут видоизменяться следующий
образом. Если <рр = ф t для всех ступеней, то при п .-з
п-р уменьшение расхода ведет к повышению (за счет
уменьшения ф-J, что вызывает падение ф2, давление за
второй ступенью также возрастает, ф3 падает еще значи-
тельнее, процесс этот интенсивно нарастает, и последние
ступени очень быстро оказываются по характеристике
исходной ступени на границе помпажа.
Таким образом, на частотах вращения, близких к лр
(принято обычно полагать п < 0,8 пр или п > пр), при
принятом законе распределения осевых скоростей (при
постоянстве пр для всех ступеней) граница устойчивой
работы определяется последними ступенями.
Если при уменьшении расхода степень повышения
давления в первой ступени все же снижается, что проис
ходит при снижении п, то помпаж возникает в средних
или первых ступенях, так как ф в последних ступенях
возрастает.
. Зону устойчивой работы при п «г пр можно, таким
образом, расширить, если принять закон возрастания <р0
от первой к последним ступеням.
Противоположная картина имеет место при падении фр
по г. при этом сужается зона устойчивой работы на
высоких частотах вращения, однако на низких частотах
зона помпажа отодвигается в область меньших рас-
ходов.
С уменьшением частоты вращения рассогласование
работы ступеней наступает очень быстро. Действительно,
если в первых ступенях ф снижается так, что они начинают
работать близко к границе устойчивой работы или дАже
в срывной зоне, то увеличение ф в последних ступенях,
которое неизбежно возникает при этом, приводит к рез-
кому падению напора и к. п. д. ступеней, так как они
начинают работать в турбинном режиме. Чем выше лк
проектируемого компрессора, тем круче характеристики
и тем быстрее наступает рассогласование работы отдель-
ных ступеней с уменьшением частоты вращения. В связи,
с этим компрессоры, имеющие лк Ю, не могут работать
при малых значениях п без специальных средств регулиро-
вания.
Поскольку надежность расчета существенно умень-
шается при отклонении режима работы компрессора от
расчетного, в настоящее время расчет характеристик ком-
прессора при п 0,8 Яр и п < 0,8 яр проводится различ-
ными методами. Так, при п > (0,80е-0,85) пр для опреде-
ления характеристик при различных расходах расчет
выполняется в той же последовательности, что и для вто-
рого поступенчатого расчета номинального режима. При
этом, задаваясь рядом значений частоты вращения п
и варьируя для каждого из них значения расхода GK,
начиная от минимального, соответствующего помпажу,
рассчитывают л* и т)из к.
Минимальное значение GK для случаев, когда помпаж
начинается в последних ступенях, определяется путем
пробных расчетов, в процессе которых проверяется то
значение GK, когда в какой-нибудь из концевых ступеней
будет достигнуто критическое (срывное) состояние потока.
При п < 0,85^-0,90, когда срывные явления возни-
кают сначала в первой ступени, минимальный расход
80
ше-
ода
ри-
ода
за-
ся
ора
ией
ме,
не-
ях.
не-
1ИМ
чет
за
чя-
зие
нке
1ри
три
ЗОЙ
шя
ас
тих
гях
крм
фр
фр
на
гах
ac-
me
но,
ют
же
п,
63’
ни
ки
чь-
юи
зть
30
нь-
от
зад-
ач-
де-
тет
то
ри
п
к,
<У-
аж
ем
то
Еей
ка.
ти-
(ОД
определяется по формуле GK min = <pyPi upFlt где <py —
значение q> на границе устойчивости’
При меньших частотах вращения первые ступени
компрессора работают в области развитых срывов, т. е. на
левой ветви их характеристик. Поскольку переход только
одной первой ступени в срывную область еще не приводит
к появлению помпажа в многоступенчатом компрессоре,
при расчете характеристик компрессора используется
левая ветвь исходной характеристики изолированной
ступени. Что касается последних ступеней, которые по-
падают при этом в область резкого снижения напора и
к п. д., то для них описанные выше методы определения
поправочных коэффициентов могут рассматриваться лишь
как сугубо приближенные.
И 1.5. МЕТОД РАСЧЕТА
ПРОТОЧНОЙ ЧАСТИ КОМПРЕССОРА
ПО РЕЗУЛЬТАТАМ ИССЛЕДОВАНИЯ
ПЛОСКИХ РЕШЕТОК ПРОФИЛЕЙ
Общие положения
Рассмотренные ранее методы расчетов, основанные
на полном или частичном моделировании, могут при-
меняться в ограниченном диапазоне параметров компрес-
соров Кроме того, использование исходной ступени одного
и того же типа для всей проточной части не всегда целе-
сообразно, так как при большом числе ступеней это
приводит к снижению эффективности всей проточной
части.
Существуют методы расчетов проточных частей ком-
прессоров, в основу которых заложен принцип проектиро-
вания каждой ступени на специально для нее заданные
параметры. В настоящем параграфе рассмотрен один из
таких методов, разработанный в авиационной промыш-
ленности.
Согласно этому методу, сначала определяют поля
скоростей во всех межвенцовых зазорах многоступенча-
того компрессора, а затем профилируют лопатки, с наи-
меньшими потерями реализующие эти поля [95].
В связи со сложностью процесса расчет полей скоро-
стей и задачу профилирования лопатки упрощают, схемати-
зируя действительный процесс на основе ряда допущений,
а в дальнейшем в расчетную схему вносят поправки, ос-
нованные на обобщении результатов экспериментальных
исследований.
При расчете действительного течения делают следую-
щие допущения, процесс является установившимся,
жидкость — идеальной и несжимаемой, а сама задача
пространственного течения сводится к двумерной, для
которой можно использовать гипотезу цилиндрических
сучений.
На первом этапе производят предварительный расчет
по среднему радиусу гср, на котором выбирают распреде-
ление по тракту основных параметров воздушного потока
(работы сжатия каждой ступени, осевых скоростей, сте-
пени реактивности, к. п. д. и др ) в зависимости от места
ступени и особенностей ее работы. На втором этапе опре-
деляют поля скоростей во всех межвенцовых зазорах по
высоте лопатки, па третьем этапе профилируют лопатки
компрессора.
Современные методы профилирования лопаток осе-
вых компрессоров базируются на данных об обтекании
воздухом плоских решеток профилей, образующихся
в плоскости развертки цилиндрических сечений на поверх-
ностях различных радиусов.
В связи с тем, что до настоящего времени не существует
эффективного метода подбора оптимальной решетки, ис-
пользуют данные экспериментальных работ по продувке
плоских диффузорных решеток профилей.
6 Л В. Арсеньев и др.
Кинематика потока в компрессорной ступени
Жидкость входит в рабочее колесо, перемещаемое
с окружной скоростью и, с абсолютной скоростью
под некоторым углом и относительной скоростью wx
(рис. III. 14). Обтекая изогнутые рабочие лопатки, по-
ток изменяет свое направление и выходит из колеса с от-
носительной скоростью ш2. Абсолютная скорость потока
за колесом с2 определяется геометрической суммой век-
Рис. III. 14. Векторная диаграмма (треугольники
скоростей) компрессорной ступени
торов w2 н и, направление потока — углом а2. Скорость
выхода из ступени с3.
При протекании потока через каналы, образованные
компрессорными решетками, изменяются не только ско-
рости, но и давления, причем обычно с3 < с2;
Ра > Pil Рз > Ра- Соотношение работы сжатия воздуха
при повышении давления в рабочем колесе и направляю-
щем аппарате зависит от типа ступени и может изменяться
в широких пределах.
Отношение работы сжатия в решетке рабочего колеса
к теоретическому напору /г),~создав*аемому ступенью, назы-
^а5ТС%^епёныо~^^ктИйнгё?ги^Т17пени В',' которая свя-
зана со скоростями с, w, и и йапорбм степени 1ц следую-
щими зависимостями:________ -______________
0 = (ffi)2~a/2)/(2Az);
О 1 — (C2U + eiu) /2',
0 = 1 — ciu/u — ht^Zu2')
(III.13)
(III.14)
(III.15)
81
Величина 0 характеризует относительную аэродина-
мическую нагруженность рабочих и направляющих реше-
ток и зависит от организации потока на входе в ступень.
Так, если поток на входе осевой, т. е. Cj = с1(2, то вектор-
ная диаграмма (треугольник скоростей) ступени имеет
Рис. III.15. Треугольники скоростей при раз-
ных значениях степени реактивности компрес-
сорной ступени: а — 0 = 0,75; б — 0 - - 0,5;
в — 0 = 1,0
вид, показанный на рис. III.15, а; при этом рабочее
колесо нагружено сильнее, а направляющий аппарат
слабее, 0 ~ 0,75.
В современных компрессорных машинах чаще при-
меняются ступени с меньшим значением 0. Отличительной
особенностью такой ступени является предварительная
закрутка в направлении вращения входящего на рабочее
колесо воздуха. Как видно из рис. III. 15, б, это приводит
к значительному увеличению скорости воздуха с2 и, сле-
довательно, к увеличению приходящейся на направляю-
щий аппарат доли общей работы сжатия, т. е. к уменьше-
нию 0. Такая схема позволяет также увеличить окружную
скорость рабочего колеса и при сохранении прежнего зна-
чения w (М^ ), а следовательно, получить больший напор
в ступени.
При 0 — 0,5 обеспечивается равное уменьшение кине-
тической энергии в рабочем колесе и направляющем ап-
парате, их треугольники скоростей становятся симметрич-
ными. Дальнейшее увеличение закрутки (с1и) или умень-
шение 0 нецелесообразно, так как это приводит к возра-
станию чисел Маха потока в направляющем аппарате
В некоторых конструкциях осевых компрессоров при-
меняются ступени с предварительной закруткой воздуха
против направления вращения (рис. III. 15, в). При этом
абсолютная скорость на выходе из рабочего колеса с2
уменьшается и падает работа сжатия, приходящаяся на
долю направляющего аппарата, т. е. увеличивается 0.
При с2 = с3 имеем 0 — 1,0. Ступени с такой степенью
реактивности рекомендуется применять при низких окруж-
ных скоростях или при возрастании темпёратуры воздуха,
когда можно увеличивать скорость и тем самым поднять
напор ступени, не опасаясь роста чисел .
Аэродинамические характеристики
плоских компрессорных решеток
Разработке теоретических методов расчета течения
несжимаемой жидкости и газа через компрессорные ре-
шетки посвящено большое количество работ, однако эти
Рис. III.16. Параметры решетки: а — про-
филя; б — компрессорной решетки
методы еще не позволяют достаточно надежно рассчитать
характеристику заданной решетки и ее геометрию, опти-
мальным образом реализующие заданный треугольник
скоростей [36, 63, 94].
В связи с этим большое внимание уделяется экспери-
ментальному исследованию решеток. Профиль компрес-
сорной решетки определяют (рис. III. 16, а) следующие
геометрические параметры: b — хорда; с — толщина;
средняя линия — геометрическое место центров вписанных
в профиль окружностей; f — максимальная стрела про-
гиба средней линии; а — расстояние от максимального
прогиба до передней кромки профиля; е — кривизна про-
филя (угол изгиба средней линии).
82
шяю-
гньше-
даую
ч зна-
напор
кине-
;м ап-
етрич-
мень-
юзра-
1рате.
। при-
здуха
этом
и с.2
;я на
'.я 9.
еныо
:руж-
?уха,
щять
В качестве исходного профиля обычно выбирают ка-
кой-либо симметричный профиль, относительные коорди-
наты которого заданы в виде функции у = f (х), где у =
= yfc, х = х!Ь-, Ушах — 1>0- Среднюю линию профиля из-
гибают или по дужке к-руга, или по отрезку параболы в за-
висимости от значения угла е.
Решетку профилей характеризуют следующие пара-
метры (рис. Ш.16, б): t— шаг; b = bit— густота ре-
шетки; Р1л; Р2Л — углы между касательными к средней
линии профиля у передней и задней кромок и фронтом
решетки; е = Р2Л — В1л; ру = е/2 + р1л — угол уста-
новки профиля; р2 — углы входа и выхода потока
в относительном движении; i = — Р1л — угол атаки;
ения
ре-
эти
Рис. Ш.17. Коэффициенты Сх и Су для ком-
прессорной решетки (b = 1,33; е= 25°; с =
= 0,1; (К- 60°);
---------= 0,7;------------М, = 0,3
1ТЬ
и-
вк
и-
,‘С-
ие
а;
к
о-
го
0-
6 — р2 — Рзл — Угол отставания потока; Д₽ = —
—Pi — Угол поворота потока в решетке Ч
При исследовании аэродинамических характеристик
плоскую решетку профилей устанавливают в аэродинами-
ческой трубе и продувают равномерным потоком при раз-
личных значениях угла атаки. При этом измеряют ве-
личины и направления скорости воздушного потока перед
и за решеткой при одновременном измерении давления
в тех же сечениях. По замерным uij, w2, Pj, строят тре-
угольники скоростей и определяют расчетным путем подъ-
емную силу Ру и сопротивление профиля Рх, характери-
зующие аэродинамическое качество решетки. Согласно
теореме Жуковского [95], имеем;
Py=-CyPm^mb/2; Px = CxPm^mb/2, (III. 16)
где рт = К PjP2 — средняя плотность потока; wm =
= (w1 + w2)/2.
Типичные результаты испытаний плоской компрес-
сорной решетки приведены на рис. III. 17, где показана
зависимость коэффициентов Сх и Су от угла атаки при
двух значениях чисел Маха.
Так как зависимость ДР от угла атаки £ имеет такой же
характер, как зависимость коэффициента С,, от I, то в даль-
нейшем при выборе решеток используют график др =
= / (i). Как видно из рис. Ш.18, с увеличением I угол
поворота Др возрастает примерно по линейному закону
до определенного значения i, после чего наступает резкое
1 Для решеток направляющего аппарата углы J3 следует
заменить на ct (см. рис. III.14).
6* *
падение Др с одновременным резким возрастанием Сх
и отрывом потока с поверхности профиля. Угол атаки,
соответствующий увеличению Сх приблизительно вдвое
по сравнению с Сх mln, называют критическим 1кр. Опти-
Рис.' III. 18. Зависимость коэффици-
ента Сх и угла поворота потока Др
от угла атаки (6 = 1,33; е = 25°; с =
= 0,1; ра= 60°)
мальный угол iopt соответствует минимальному значению
потерь Сх mln. Угол отклонения потока,- который может
быть достигнут в решетке без значительного увеличения
Рис. III. 19. Обобщенные данные резуль-
татов продувки решеток (ДРном =
= 0,8Дртах’> i — — 5 )
потерь, называют номинальным и, согласно Хоуеллу,
принимают равным Дрном =~ 0,8 Дршах [95]. Соответствую-
щий угол атаки £ном « ((кр -ф sopt)/2.
Как показали результаты испытаний большого числа
решеток, обобщенная зависимость, представленная на
рис. III. 19, справедлива как для вращающихся, так и
83
для неподвижных компрессорных решеток. Если восполь-
зоваться этим графиком и определить отношение Е —
~ д₽ном/(д₽ном)ь=1,0> то оно оказывается одинаковым
Рис. III.20. Графики для выбора требуе-
мой густоты решеток: а — Е = f (6); б —
Др = f (Р2):
-------режим !opt;------------ режим гном
(по Хоуеллу)
для каждой решетки при всех значениях р2 (штриховая
линия на рис. III.20, а).
Итак, для определения требуемой густоты решетки,
для которой АР = АРном, следует воспользоваться двумя
графиками: рис. III. 19 и III.20, а (штриховая линия).
Рис. III.21. Зависимость коэффици-
ента р от геометрических параметров
решетки
Дальнейшее уточнение рассматриваемого метода рас-
чета касается главным образом зависимостей для опреде-
ления ~Ь и Ар. В настоящее время рекомендуется в качестве
84
расчетного вместо номинального (при i = !ном) принимать
режим оптимального угла атаки (i = iopt), при котором
показатель качества решетки 1/ц = Гф/Ст максимальный.
Кривая оптимальных значений Др = f (Д2) приведена
на рис. III.20, б, соответствующие значения Е = f (i)
показаны сплошной линией на рис.III.20, а. Как видно
из графиков, при одинаковых треугольниках скоростей •
по уточненным данным решетки получаются менее гу-
стыми, чем по данным Хоуелла.
Для полного аэродинамического расчета решетки
необходимо еще определить угол отставания
я 1УТ7Г (ДР— 0 m ]ft/b /ттт
о = те V t Ь — -Д-Г------------- (III.17
1—mV t/b
где т = 0,18 + 0,23 (2а/&)2 — 0,ip2/50°; alb — отноше-
ние, определяющее расположение максимального прогиба
средней линии профиля, обычно равное 0,4—0,5. 4
Таким образом, данные продувки плоских решеток >
позволяют количественно оценить допустимые значения
углов Др и 6 при заданной густоте Ъ с учетом взаимного
влияния профилей в решетке. Эти данные позволяют также
оценить [112] потери в решетке путем определения Сх
и коэффициента Ц = СХ!СУ в зависимости от & и рт =
= (Pi + ₽3)/2 (рис. Ш.21).
С ростом чисел М-, относительного потока начинают
проявляться новые качества решетки, связанные с эф-
фектом сжимаемости. При М, >• Мкр местные скорости
на поверхности профиля и в межлопаточном канале воз-
растают до тех пор, пока средняя скорость потока в горле
канала не достигнет скорости звука, при этом = Mmax.
Потери при этом резко возрастают, а создаваемый сту-
пенью напор падает до нуля. Величина М1шах растет с ро-
стом i. При Мх < Мкр влияние на угол отклонения
потока и потери практически можно не учитывать, од
иако при М, >• Мкр угол поворота потока и к. п. д. за-
метно уменьшаются, в связи с чем при проектировании
ступени следует вводить ограничение скоростей по числу Mj
или К = f (MJ.
Связь напора и к. п. д.
ступени с параметрами решеток
Выражая относительный теоретический напор сту-
пени через проекции относительных скоростей по уравне-
нию Эйлера, т. е. / - у .
ht = ht/u2 = (wlu — w2ll)lu,
и используя векторную диаграмму элементарной компрес-
сорной ступени, можно получить зависимость
ht/Ca== sin Др/[sin р2 sin (Р2 — ДР)], (III.18)
где са = <р.
Если учесть, что на оптимальных режимах ДР
при данном значении & однозначно зависит только отР2,
и принять во внимание очевидное соотношение ctg Р2 =
= 0/га — ht/(2ca), можно получить обобщенную зависи-
мость ht!ca = I (Qlca, b) (рис. Ш.22), по которой по ис-
ходным значениям 0, са и выбранной густоте определяю!
коэффициент напора 1ц. В диапазоне 1,2 < Q!ca < 1,2/(1 +
+ 1,5 £/&) коэффициент напора практически не зависит
от степени реактивности, тогда
Мса= 1,5/(1 4-1,5//6). (III.19)
Результаты испытаний плоских решеток позволяют
проанализировать влияние величин 9, са и b на к. п д.
имать
)Т0рОМ
[ЬНЫЙ.
эедена
4(b)
ВИДНО
юстей
е гу-
щетки
компрессорной ступени. Из рис. Ш.23 [112] следует, что
Чет шах при любом значении са достигается при 0 «ь 0,5.
Увеличение Ь, позволяя увеличить напор решетки, при-
водит вместе с тем к некоторому снижению к. п, д.
юше-
огиба
петок
чения
'АНОГО
акже
(я Сх
11.17)
кают
' эф-
юсти
воз-
орле
^гпах-
сту-
с ро-
ения
ОД'
. зн-
ании
уМх
Рис. III.22. Обобщенные зависимости для
определения коэффициента напора
Для приближенной оценки коэффициента расхода са
в зависимости от 0 при минимальных потерях можно
рекомендовать формулу
сту-
вне-
рес-
.18)
Ар
*=
си-
ис-
пот
+
:ит
19)
ют
д-
Рис. III.23. Влияние коэффициента расхода,
степени реактивности и густоты решетки на
к. п. д. ступени: a — г]ст = / (0, са) (5=1,0;
7 = 1,5); б — Т)ст = f (ca, ~b) при 0 = 0,5
Поскольку при Mj As 0,7 сказывается влияние сжи-
маемости потока, рекомендуется принимать предельное
значение газодинамической функции Хпр = 0,72-4-0,75.
Изменение параметров потока
по высоте лопаток
Скорости потока на различных радиусах связаны между
собой соотношениями, которые определяются, в первую
очередь, условиями равновесия частиц при их движении
по межлопаточным каналам и в зазорах между лопаточ-
ными венцами. Аналогично рассмотренному ранее (см.
п. II.3) случаю пространственного течения газа втурбин-
но^ ступени установившееся движение в межвенцовых
зазорах ступени осевого компрессора при принятых до-
пущениях об осевой симметрии потока и отсутствии ра-
диальной составляющей скорости может быть описано
уравнением радиального равновесия.
Изменение по радиусу эффективной работы ступени
в зависимости от окружной и осевой составляющих ско-
рости потока может быть выражено уравнениями:
dht _ 1 Г 1 d [curf & д 3 .
dr 2 [ да dr + dr J ’
(III.21)
ht = u (c2U — Cm). (III.22)
Если задаться законом изменения окружной составляю-
щей скорости порадиусу, с помощью этих уравнений можно
вычислить осевые составляющие скорости на соответствую-
щем радиусе.
Законы изменения ca (г)
в компрессорных ступенях
Закон постоянства циркуляции. Наибольшее распро-
странение в практике проектирования осевых компрес-
соров получил закон, основанный на представлении о
безвихревом (потенциальном) течении воздуха в сечениях
перед и за рабочим колесом (так называемый закон по-
стоянства циркуляции), выражаемый зависимостями:
cur = const; са = const.
Работа, совершаемая потоком на всех радиусах, при
этом законе изменения си будет, очевидно, постоянной.
Коэффициент напора ht изменяется при этом обратно
пропорционально квадрату радиуса, и у лопаток с малым
втулочным отношением корневые сечения могут оказаться
перегруженными даже при умеренном значении коэффи-
циента напора в среднем сечении.
Ступени с постоянной по высоте циркуляцией характе-
ризуются существенным измерением по высоте лопатки
степени реактивности и чисел Маха на входе в рабочее
колесо и направляющий аппарат. Степень реактивности
на текущем радиусе г связана со степенью реактивности
на среднем радиусе гср зависимостью
0=1 - (1 еср) (l-d^)/(4rs), (Ш.23)
из которой следует, что чем меньше d, тем больше изме-
нение 0. Здесь г — г/гя.
Так как с увеличением 0 возрастают скорости Wj,
а с ее уменьшением — скорости с2, то при этом резко
увеличиваются числа Маха у периферии (М,) и у втулки
(М3) рабочего колеса. С уменьшением 0 уменьшается угол
установки профилей от вершины к втулке, особенно сильно
при малых значениях d, вследствие чего рабочая лопатка
получается сильно закрученной. Указанные обстоятель-
ства ограничивают применение рассматриваемого закона
для ступеней с d 0,6. Треугольники скоростей для трех
сечений лопатки, спрофилированной по этому закону,
показаны на рис. III.24.
85
Закон постоянства степени реактивности. Этот закон
характеризуется условием
0 = 1 — Сщ/и — /(2м2) = const.
Так как при этом законе осевые скорости на входе и
выходе из ступени неодинаковы, действительная степень
Рис. III.24. Треугольники скоростей при профилировании
лопаток по закону постоянства циркуляции: а — пери-
ферийное сечение; б — на среднем диаметре; в — втулоч-
ное сечение
Рис. III.25. Треугольники скоростей при профилировании лопа-
ток по закону постоянства степени реактивности: а — периферий-
ное сечение; б — на среднем диаметре; в — втулочное сечение
реактивности ступени по радиусу непостоянна, однако это
изменение незначительно.
Учитывая, что c2U = с1и — hf/u, можно получить
закон изменения окружных составляющих скорости по
радиусу перед рабочим колесом и за ним:
с1и = и (1 — 0) — hf/(2u); с2Ц = и (1 — 0) + ht/(2u),
(III.24)
причем ht (г) = const.
Лопатки, спрофилированные по этому закону, харак-
теризуются малым изменением Мх по высоте лопатки.
86
Соэтветствующие треугольники скоростей для трех сече-
ний такой ступени приведены на рис. 111.25.
Углы установки профилей по радиусу изменяются
в рассматриваемом случае заметно слабее, чем при за-
коне cur = const. Однако здесь имеет место значитель-
ное изменение осевой составляющей скорости по радиусу,
увеличивающееся с ростом ht, что ограничивает напор-
ность ступени, так как в области малых са потребуются
чрезмерно большие углы поворота потока.
Закон твердого тела. С целью увеличения напорно-
сти ступени, имеющей малое значение d, целесообразно
увеличивать напор вдоль радиуса, что позволяетэффек-
тивнес использовать повышенные окружные скорости на
периферии ступени"
При постоянстве по радиусу коэффициента напора
закрутка~ пдтока“”при условий 0 == сопзТбудет соответ^
ТгвЗвать закону ——
са/г = const,
называемому законом твердого тела.
Изменение работы ступени по радиусу при этом
ht~ht (II1.25)
Степень реактивности ступени в этом случае изменяется
также незначительно, и можно полагать, что условие
9 (г) = const практически .выполняется. Непостоянство
напора по радиусу в такой ступени, однако, создает че-
/элагоприятные условия для последующих ступеней из-за
неравномерного поля давлений, вследствие чего рекомен-
довать применение ступеней указанного типа можно только
ждагав'/ — ........ — г -I
при весьма малых d.
Комбинированный закон закрутки. В этом слу-
чае ступень имеет закрутку по радиусу, среднюю
между законами свободного вихря (cur = const) и
твердого тела (cu/r = const). Распределение с1и =
—с1и!и и c2U=c2U/u по высоте лопатки принимается
обычно в следующем виде
1 В/Г 11 с2« = 2 Ч~ В)/г2,
(II 1.26)
где коэффициенты А и В находятся из условий, что
hi (г) = const угол выхода потока у втулки
не должен превышать 90°, чтобы не получить уве-
личения гидравлических потерь в корневых сече-
ниях.
Определение
осевых составляющих скоростей по радиусу
В реальной конусной проточной части комп-
рессора поверхность тока отличается от цилиндри-
ческой и имеет кривизну в меридиональном сече-
нии. Поэтому уравнение радиального равновесия
(11.116) должно быть здесь записано в виде
(1/р) (dp/dr) = с^/г — с^тКт cos у, (III.27)
где у и Кт — угол наклона и кривизна линии тока; ось т
направлена по касательной к линии тока.
Учитывая, что ст — ca/cos у, это уравнение можно
записать в виде
Др « Дгр (С2 / г — с2 Km/cos у) (111.28)
и решать его методом последовательных приближений,
используя дополнительно уравнение неразрывности и
определяя, таким образом, на каждом радиусе значение
составляющей са.
Расчет ступени по среднему радиусу
После рассмотрения особенностей работы плоских
решеток профилей, из которых скомпонованы ступени ком-
прессора, и зависимостей, которые могут быть заложены
в расчет треугольников скоростей, становится очевидным,
что существуют оптимальные соотношения между пара-
метрами, определяющими работу ступени в зависимости
от места ее расположения в проточной части.
Анализ большого количества экспериментальных ма-
териалов по испытаниям отдельных ступеней и компрес-
соров позволяет дать рекомендации по рациональному
выбору основных параметров потока на среднем радиусе
каждой ступени, расчету параметров по высоте лопатки
и профилированию самих лопаток.
Выбор типа проточной части. Для типа I (см. стр. 78)
условие постоянства наружного диаметра DH означает,
что окружные скорости во всех ступенях, будучи макси-
мальными на периферии, на среднем диаметре возрастают
от первой ступени к последней. Все это позволяет увели-
чивать напор ступеней, а следовательно, уменьшать их
число по сравнению с другими типами проточной части.
Этот тип проточной части является предпочтительным
при требовании обеспечения высокой степени повышения
давления в компрессоре, когда нет специальных требова-
ний к конструкции ротора или когда длина лопатки по-
следней ступени еще не получается недопустимо малой.
Распределение напора по ступеням. Закон распределе-
ния выбирается из условия получения наивысшего к. п. д.
как на расчетном, так и нерасчетном режимах работы
компрессора.
На расчетном режиме наименьший к. п. д. обычно
имеют первые и последние ступени, что для первых сту-
пеней связано с большими числами М (X) и малыми d,
а для последних ступеней — со значительным искажением
поля са (г) по сравнению с расчетным, уменьшением длины
лопатки и увеличением Поэтому для увеличения общего
к. п. д. на расчетном режиме целесообразно уменьшать
напор как первых, так и последних ступеней по сравнению
с напором средних.
Если компрессор работает при п < пр, происходит
рассогласование ступеней, причем опять в ‘худшем поло-
жении оказываются первые и последние из них. Учиты-
вая вид характеристик ступени (резкое уменьшение к. п. д.
в правой ветви, т. е. при больших расходах), целесообразно
больший напор давать на ступени, расположенные в конце
проточной части. При этом уменьшение напора от сере-
дины по направлению к последним ступеням не должно
быть столь значительным, как по направлению к первым.
Максимально возможным для заданной окружной ско-
рости задается напор средних ступеней.
Практически в первых ступенях при d = 0,34-0,5
принимают коэффициент напора ht = 0,124-0,20. В по-
следующих ступенях ht увеличивают таким образом, чтобы
на среднем радиусе £ С 0,724-0,75; в последних ступе-
нях ht обычно выбирают на 10—20% ниже, чем в средних.
Следует иметь в виду, что целесообразно иметь такие коэф-
фициенты напора по ступеням компрессора, чтобы густота
решетки Ь не получалась больше 1,3.
На основании экспериментальных данных обычно
выбирают следующие значения к. п. д.: первых ступе-
ней — 0,86—0,88 (в зависимости от уровня л), средних —
0,90—0,92, последних — до 0,87.
Выбор втулочного отношения на входе в первую сту-
пень _4ПХ. Величина 4ВХ определяет допустимый уро-
вень ht и массовый расход GK. Малые значения Звх поз-
воляют при заданном расходе воздуха уменьшать диа-
метр первой ступени и всего компрессора или при задан-
ных диаметральных габаритах увеличивать GK. Однако
при этом возникает перегрузка корневых сечений (с воз
можной перекруткой потока через ось машины, т. е. (% >
> 90°), что нежелательно. Рост Ь и толщины профиля
у втулки приводят к падению Мкр, т. е. к росту потерь.
При этом резко увеличивается угол конусности проточной
части, т. е. прстранственность течения, что также вызы-
вает снижение к. п. д. В связи с этим не рекомендуется
для дозвуковых компрессоров принимать dBX С 0,454-0,5.
Для типа II проточной части (DBH = const) целесо-
образно несколько повысить rfBX, так как допустимые зна-
чения ht здесь ниже, чем при Da = const, и принимать
dBX ж- 0,6.
Изменение осевой составляющей скорости по тракту
компрессора. На входе в первую ступень составляющая са
назначается исходя из допустимого значения X, вычислен-
ного по скорости wx. Если осевая скорость изменяется
по высоте лопатки, то за расчетную величину принимается
среднерасходная скорость и предполагается, что она равна
са на среднем радиусе.
Несмотря на то что с целью увеличения напора сту-
пеней желательно иметь везде максимальное значение са,
в начале тракта его приходится ограничивать из-за роста
чисел Маха, а в конце тракта — из-за уменьшения высот
лопаток и роста потерь с выходной скоростью. Поэтому
рекомендуется плавно уменьшать уровень осевых ско-
ростей по направлению к выходу из компрессора, так
чтобы это уменьшение от одной ступени к другой не пре-
восходило 10—42 м/с.
Удельная производительность компрессора Q, рав-
ная отношению массового расхода воздуха к лобовой пло-
щади, определяемой по наружному диаметру рабочего
колеса первой ступени, Q = caBXp(l—d|x). Отсюда
следует, что для увеличения Q целесообразно увеличивать
са вх и уменьшать dBX.
Степень реактивности. Учитывая, что при 9 = 0,5
получается наиболее высокий к. п. д. и можно выбрать
"наибольшую' окружную скорость/ для первых ступеней
принимают обычно 0 « 0,5 или на среднем радиусе, или
по всей высоте лопатки. Для средних и последних ступе-
ней компрессора величину 9 следует несколько повысить.
Повышенные значения 9 целесообразно принимать для
ступеней, где местные скорости звука повышаются из-за
роста температуры и числа М (X) могут оставаться в до-
пустимых пределах при повышении а^.
Рекомендуется назначать 0 > 0,5 начиная с третьей —
пятой ступени, так чтобы прирост не превосходил 0,02—
0,03 на каждую ступень.
Коэффициенты затраченной работы КД и запаса по
расходу Ко- Коэффициентом затраченной работы (коэф-
фициентом уменьшения напора) называется отношение
Кн = hjht, где hz — коэффициент действительного на-
пора.
Отличие действительного напора от теоретического
определяется прежде всего искажением действительного
поля скоростей, вызванного трением потока о поверхности
втулки и корпуса, а также нарастанием пограничного
слоя на профильной части лопатки. Значение Кн зависит
от порядкового номера ступени в компрессоре, относитель-
ного диаметра втулки, формы меридионального сечения,
радиального зазора. На входе в первую ступень при равно-
мерном поле осевых скоростей обычно принимают Кн =
— 0,984-0,99. Вдоль проточной части величину Кн умень-
шают на 0,01—0,02 на каждую ступень, так что в послед-
них ступенях высоконапорных осевых компрессоров Кн =
= 0,86 .-0,84 В настоящее время имеется тенденция
принимать несколько большие значения Кн для послед-
них ступеней (до 0,90—0,92).
Коэффициент запаса по расходу Ко учитывает, что
часть проходного сечения занята пограничным слоем и
87
для обеспечения расчетного значения GK требуется не-
сколько увеличить проходное сечение, в связи с чем при-
нимают обычно Кв = 1,02-5-1,04, сохраняя его постоян-
ным вдоль всего тракта проточной части.
Число ступеней компрессора. Число ступеней может
быть оценено исходя из принятого значения степени по-
вышения давления средней ступени, которая для высоко-
производительных напорных дозвуковых компрессоров
обычно принимается лст ср = 1,2-н 1,25:
z = lgn*/lgn*T ср.
После ориентировочного распределения параметров
Потока по ступеням приступают к расчету проточной части
компрессора по среднему радиусу, который ведется с ис-
пользованием газодинамических функций х.
Порядок расчета. Расчет ступени по среднему радиусу
сводится к следующим операциям.
1. При заданных для первой ступени величинах d,
са, ht и 9 проводят вариантные расчеты, задаваясь рядом
значений окружной скорости ин (или диаметра Он)> а сле-
довательно, осевой скорости на среднем диаметре. Опре-
делив средний радиус 77р = у (1 + d2)/2 , окружную
составляющую абсолютной скорости
ёи = [(1-6)-Ы27ср)Рср,
а также угол входа потока в рабочее колесо ах =
= arc'tg с1и/с1а, для каждого варианта находят абсолют-
ную скорость ct = cla/sin ах, газодинамическую функцию
X = сх/18,3 ]/"7'*х и q (X) (по таблицам). После этого
проверяют принятое по уравнению неразрывности зна-
чение DH-.
рн = 1 /.... ^кут^
V т (я/4) (1 — /) pBXq (A.) sin 04 ’
(III.29)
где
т = Vk [2/(/г 4- 1)J!>//?.
Если принятое значение D-,, отличается от вычислен-
ного, расчет повторяют, изменяя значение са до сходи-
мости данных (Дс„ 0,01).
Затем рассчитывают для каждого из рассматриваемых
вариантов углы и скорости потока на входе в первую
ступень в относительном движении:
tg Pi = С1а/(гсъ — c1B); Wx = cw/sin ₽х,
После чего определяют величины:
«вх=- 20,05/ПУ(Х); MBX = w1/aBX; £ А (мвх)-
Значение 1 = f (Мвх) находят по таблицам [95 ]
и проверяют условие Хпр С 0,724-0,75.
2. После выбора окружной скорости «н и диаметра
Первой ступени выбирают тип проточной части, что поз-
воляет рассчитать окружную скорость для каждой сту-
пени.
3. Рассчитывают давление и температуру воздуха
на входе и выходе каждой i-ой ступени. По заданным для
Ступеней значениям /г/(, Khi и т]из. ст i определяют:
^из. i -
Д77 = Чз . / ^из ст () ; Ч = + ЛТ* ;
1 Подробнее об этом см в п II 2
яст, = [ * 4Аз, Дхтгг J J
A =- Рпяст i-
4. Находят общую степень повышения давления в ком-
прессоре л* — P2k,Jp*k- Если оказывается, что полученное
значение л* не равно заданному по техническим условиям,
следует или изменить число ступеней, или задаться но-
выми значениями ht по ступеням.
5. Вычисляют к. п. д. проточной части
Пиз к = л‘к[«у/г-^-1]/(Ед^)-
6. Определяют основные геометрические размеры сту-
пеней. Расчет ведут методом последовательных прибли-
жений, задаваясь и уточняя затем угол входа потока at.
Схему расчета каждой ступени см. в табл. 4.2 приложения 4
7. Строят треугольники скоростей для каждой сту-
пени — см. табл. 4.3 приложения 4.
Одновременно с расчетом по среднему радиусу сле-
дует вычертить меридиональное сечение проточной части
для проверки плавности ее очертаний, предварительно
выбрав относительные удлинения лопаток и осевые за-
зоры. 1 В дальнейшем при расчете параметров потока по
высоте лопаток возможно уточнение меридиональных очер-
таний проточной части. Это касается прежде всего группы
первых ступеней, в которых параметры потока по радиусу
изменяются наиболее интенсивно.
Расчет треугольников скоростей
по высоте лопаток
Определение окружных составляющих скорости потока
на входе и выходе из ступени (расчет закрутки потока).
В качестве предварительно выбираемого закона изменения
циркуляции в первых ступенях рекомендуется принимать
комбинированную закрутку, когда выполняются условия
(Ш-26).
По мере увеличения температуры вдоль проточной
части числа М, уменьшаются и необходимость в изменении
циркуляции по высоте отпадает. Постоянная циркуляция,
т. е. cur = const, может быть принята начиная с четвертой-
пятой ступени. Переход от резко изменяющейся циркуля-
ции в первой ступени к постоянной следует произво-
дить постепенно.
Поскольку проточная часть имеет конусное очертание,
особенно в районе первой группы ступеней^следует учиты-
вать изменение г; поэтому зависимость cu—f (г) будет
иметь вид:
с1« ~ (^г2 4-5/га) (Гъ/гх)', с%ц — Аг%(htВ)/г2,
где из условия пропорционального деления площадей
проходного сечения поверхностями тока имеем
г2 = V1 — (1 — г?) (1 — d|)/(l — d?)-
Расчетные формулы для определения коэффициентов А
и В приведены в табл. 4.4 приложения 4.
Исходя из известных для каждой ступени величин 0,
ht и d на всех заданных радиусах определяются величины
с,ц и с2и (см. табл. 4.5 приложения 4).
Расчет поля осевых скоростей по высоте лопатки.
В этом расчете можно учесть различие потерь по высоте
лопатки, что позволяет получить более достоверную кар-
тину распределения осевых скоростей.
Расчет осевой составляющей скорости са = f (г)
проводится численным интегрированием уравнения ра-
диального равновесия в форме (III.28) с использованием
уравнения неразрывности. При этом предполагается, что
величины у и Кт линейно изменяются от втулки к пери-
88
ферии, тогда на произвольном радиусе г; угол у опреде-
ляется из соотношения tg у, = аг; -ф- Ь, где константы а
и b определяются из условий:
tg Th = а + b при г —-1,0;
tg Увн = ad + b при г =~d.
Тогда
tg У/ = (tg Ун — tg Увн) + tg увн;
1 — а
Kmi = ' (Ктн Кщ вн) 4* Кт ви-
1 — d
Рекомендуемая схема численного интегрирования
приведена в табл. 4.6 приложения 4.
Для определения действительных статических пара-
метров потока необходимо знать приведенную скорость
% = Cj/Якр, т. е. знать абсолютную скорость потока. По-
скольку именно эта величина подлежит вычислению, в пер-
вом приближении принимаем значение %ср из расчета по
среднему радиусу. Затем, рассчитав скорости, по уравне-
нию неразрывности проверяем величину расхода воздуха.
Если распределение скоростей, полученное по расчету,
не обеспечивает требуемый расход, расчет повторяют,
задаваясь новым значением Хср.
Расчет углов входа и выхода потока (32, а1; а2
по высоте лопатки четвертой ступени приведен в табл. 4.7,
приложения 4. Поскольку скорости и углы потока вы-
числены для гх («!, рх) и г2 (а2, р2), для построения тре-
угольников скоростей плоских решеток необходимо, по-
строив графики а = f (г) и р = f (г), найти соответствую-
щие углы для одних и тех же значений г и вычислить Да
и ДР для таких плоских решеток.
Профилирование лопаток
Для построения рабочей поверхности лопатки обычно
задают (строят) 5—10 профилей ее сечений на различных
радиусах на равных расстояниях друг от друга в зависи-
мости от длины лопатки.
После выполнения второго этапа расчета, в результате
которого определены густоты решеток на всех радиусах
и поточные углы ах, а2, р2, можно определить угол
отставания 6 и угол атаки i, найти геометрические углы
профилей Р1л, а1л, Р2Л, а2Л, е и 0У.
Угол отставания можно определить по форм)ле(Ш.17).
Угол атаки для решеток рабочего колеса ip = 2,5blt —
— 1,5; для решеток направляющего аппарата ia =
= 2,5&/f — 3,5.
Угол установки профиля в решетке ру = е/2 -ф |31л.
Изгиб средней линии профиля выполняется по дужке
круга или по отрезку параболы.
В практике компрессоростроения разработан ряд сим-
метричных хорошо обтекаемых профилей, используемых
в качестве исходных при формировании высоконагружен-
ных лопаточных аппаратов.
Форма профиля с определенной максимальной тол-
щиной стах задается обычно в виде таблиц значений у =
= f (х), где у и х — координаты, отнесенные к максималь-
ной толщине и к хорде, являющейся осью симметрии.
Изменение толщины исходного профиля выражается
аналитически функцией у = Лг/тахх“ (1—х)^, где А,
аир — постоянные коэффициенты [19]. Варьируя эти
коэффициенты, можно получить профиль различной формы.
Максимальная толщина профиля выбирается из условий
прочности. Рекомендуется принимать свн шах = 0,12 и
сн max = 0,06, а изменение максимальной толщины по
высоте считать происходящим по линейному закону. Для
лопаток направляющих аппаратов иногда принимают
сШах = 0,08 = const.
При выборе формы исходного симметричного профиля
руководствуются главным образом значениями чисел Маха
потока, для которого предназначается профиль. Чем выше
число Маха, тем дальше от носика должна быть располо-
жена точка максимальной толщины и тем меньшую отно-
сительную-толщину должна иметь входная часть профиля.
Для широкого класса дозвуковых осевых компрессо-
ров может быть рекомендован следующий исходный сим-
метричный профиль:
У = 2,38(/тах У/ X (1 —-*)0’8-
Выбирая исходный симметричный профиль, его сред-
нюю линию изгибают так, чтобы касательные к ней на
входной и выходной кромках соответствовали рассчи-
танным углам Р1Л (а1л) и £2Л (а2л).
Построение дужки и «одевание» ее исходным профилем
можно производить графически. Для этой цели определяют
радиус кривизны дужки круга по формуле Л'д =
= Ь/ [2 sin (е/2) ], строят дужку, разбивают ее на доста-
точно большое число равных отрезков, после чего радиу-
сами, равными половине толщины исходного профиля,
«одевают» дужку. Затем плавной кривой обводят получен-
ные окружности по наружной и внутренней сторонам дуж-
ки, получая, таким образом, профиль сечения лопатки.
Координаты верхней и нижней сторон профиля определяют
графически. Поскольку указанный метод является недо-
статочно точным и непроизводительным, все большее раз-
витие получают аналитические методы расчета координат
профилей, допускающие широкое использование ЭВМ [19 ].
Глава IV
КАМЕРЫ СГОРАНИЯ
И ТЕПЛООБМЕННЫЕ АППАРАТЫ ГТУ
IV. 1. КАМЕРЫ СГОРАНИЯ
Общие сведения
Камерой сгорания называется устройство, обеспе-
чивающее повышение запаса тепловой энергии рабочего
тела в цикле ГТУ аа счет химической реакции окислении
топлива и подготовку рабочей смеси требуемой темпера-
туры для последующей ее подачи в проточную часть газо-
вой турбины.
Камера сгорания по циклу р = const представляет
собой некоторый полуогр аниченный объем, в который не-
прерывно поступают топливо и окислитель (воздух)
и из которого отводятся продукты сгорания.
Поток(рабочего тела, обычно воздуха, поступающий
в камеру сгорания, разделяется на первичный GB1, обес-
печивающий состав топливной смеси для полного ее сго-
рания, и вторичный Gb2, смешиваемый с продуктами сго-
рания для снижения их температуры до требуемого уровня.
Огневой объем камеры сгорания разделяется на зоны го-
рения и смешения.
Процесс устойчивого горения в огневой зоне камеры
обеспечивается следующими факторами: 1) подачей воз-
духа в количестве, необходимом для создания смеси нуж-
ного состава; 2) созданием нужного температурного уровня;
3) наличием зоны стабилизации фронта пламени, в которой
скорость перемещения топливно-воздушной смеси равна
скорости распространения пламени.
Для обеспечения необходимого уровня-температуры
и поля скоростей в камере сгорания организуется зона
обратных токов.
Основные элементы камер сгорания
Воздухонаправляющее устройство 1 (рис. IV. 1) служит
для распределения первичного воздуха по огневому про-
странству камеры сгорания, турбулизации воздушного
потока с целью получения лучшей топливно-воздушной
смеси, создания условий для устойчивого процесса го-
рания.
Запальное устройство 2 служит для зажигания топ-
лива (создания очага горения) в камере сгорания в момент
пуска установки.
Горелочное устройство 3 предназначено для подачи
топлива в камеру сгорания, дробления его на мелкие ча-
стицы (порции) и равномерного распределения топлива по
объему зоны горения.
Пламенная (жаровая) труба 4 служит для ограниче-
ния огневого пространства камеры сгорания и восприя-
тия тепловых нагрузок, обусловленных наличием больших
удельных тепловых потоков.
Силовой корпус 5 воспринимает силовые нагрузки, со-
здаваемые избыточным внутренним давлением в камере.
Смесители 6 перемешивают воздух с продуктами сго-
рания с целью получения на выходе из камеры сгорания
90
заданного температурного поля (по уровню средней тем-
пературы и степени неравномерности ее распределения).
Стабилизирующее устройство обеспечивает устойчи-
вость процесса горения.
Рис. VI. 1. Камера сгорания ГТУ по циклу р = const (Т —
топливо; В — воздух; В1 — первичный воздух; В2 —
вторичный воздух; ПС — продукты сгорания; ОТ — об-
ратные токи): а —• схема камеры; б — поле осевых состав-
ляющих скорости; в — поле давлений в огневой зоне
Основные характеристики камера, „рання
Коэффициент полноты сгорания топлива (иногда
называют к. п. д. камеры сгорания)
Лк. с — Q1/Q2 ~ (Q2 । Qnor) I Q4 (IV• 1)
где = Q3 4- QTOT + QB — S QnoT — количество теп-
лоты, подведенное к рабочему телу при сжигании топлива
в объеме камеры; Q2 = GTonQp — количество теплоты,
которое теоретически могло выделиться при полном сго-
рании топлива: QTOn— физическая теплота, введенная
с топливом; QB — физическая теплота, введенная с воз-
духом; 2 QnoT = Qx.n + Qm. н 4- Qo. с — суммарные по-
тери теплоты в камере (Qx. н — с химическим недожогом;
Qm. н — с механическим недожогом; Qo, с — в окружаю-
щую среду).
Обычно у современных камер сгорания во всем диапа-
зоне рабочих нагрузок ti<. с = 0,954-0,99, а на расчетных
режимах т]к. с = 0,984-0,995 (более низкие значения отно-
сятся к камерам сгорания, работающим на тяжелом жид-
ком топливе).
Относительные потери полного давления в камере
сгорания
Uc = М = (Рк - ^г)Лв, (IV.2)
где индекс 1 соответствует сечению на входе, а индекс 2 —
сечению на выходе из камеры сгорания.
Величина Др*. с учитывает все возможные потери
давления: на трение, местные потери и потери при подводе
теплоты.
Для современных конструкций камер сгорания ГТУ
?к. с ~ 0,024-0,04, для транспортных ГТУ эта величина
может повышаться до 0,05—0,06.
В качестве характеристики устойчивости процесса
горения для камеры сгорания может быть использована
так называемая срывная характеристика (рис. IV.2),
т. е. зависимость GB = f (а0бщ), где аобщ — общий коэффи-
циент избытка воздуха. Внутри кривой ACDE режимы
работы камеры сгорания являются устойчивыми [73];
участок АС этой кривой соответствует срыву факела при
богатых смесях, участок CDE— срыву факела при бедных
смесях. Лучи, выходящие из начала координат, соответ-
ствуют определенным расходам топлива GTon = const.
Срывная характеристика зависит от конструкции камеры,
температуры и давление воздуха, вида топлива и способа
его подачи.
Рис. IV.2. Срывная характеристика ка-
меры сгорания
Тепло напряженность сечения камеры сгорания (пла-
менной трубы)
UF = <?ТОП<?Х c/(PbA.c), (IV.3)
Конструкция основных элементов камер
сгорания
Воздухонаправляющие устройства разделяют на три
типа: лопаточные регистры, струйные и комбинированные
завихрители.
Простейшие регистры представляют собой кольцевую
решетку, набранную из прямых или профилированных
лопаток (рис. IV.3, а), при прохождении через которую
где Гк.с — площадь наибольшего сечения пламенной трубы.
Для камер сгорания стационарных ГТУ обычно Up =
= (5 4- 10) 10<’ккал/(м2-ч-кгс/см2), для транспортных ГТУ
она доходит до (204-25) 106 ккал/(м2-ч-кгс/см2).
Теплонапряженность объема камеры сгорания (пла-
менной трубы)
GTonQpiiK.c
Uy = ------—-----
р 1вГк .с
(IV.4)
где VK, с — объем огневой зоны пламенной трубы.
В выполненных ГТУ Uy — (3-4-100) 106 ккал/(м2 X
X ч-кгс/см2).
Неравномерность поля температур за камерой сго-
рания, характеризующая распределение температур в ра-
диальном и окружном направлениях, оценивается вели-
чиной (%)
\ = >00 (Т2*г тах - Т2*г. ср)/Г2г. ср, (IV.5)
где T?iv mdX — максимальная температура газа за каме-
рой сгорания; 7’2г ср — среднемассовая температура газа
за камерой сгорания.
Обычно Дт <: 204-30%.
Иногда за характеристику неравномерности темпе-
ратурного поля принимают величину
д; = юо (г;ггаах - ср)/(т2г. ср - ту. (iv.6)
В ряде случаев стремятся получить определенную
эпюру распределения по радиусу температур газа на вы-
ходе из камеры сгорания, повышая температуру газа у пе-
риферии лопат» с целые Увеличения запаса прочности
в опасном се сечении.
Рис. IV.3. Схемы лопаточных завихрителей
первичный воздух закручивается. В результате этой за-
крутки потока возникают центробежные силы, приводя-
щие к значительным радиальным градиентам давления
и скорости и повышающие степень турбулентности потока,
что способствует хорошему перемешиванию топлива с воз-
духом.
По способу расположения лопаток в регистре разли-
чают плоские, конические, цилиндрические и комбини-
рованные решетки (рис. 1V.3, а—д соответственно).
В многоярусных регистрах (рис. IV.3, е, ж) обычно
применяют противоположную закрутку лопаток сосед-
них ярусов.
Воздухонаправляющие устройства струйного типа
основаны на создании в зоне первичного смесеобразования
системы вихрей, способствующих перемешиванию топлива
с воздухом. Подвод воздуха в них может осуществляться
тангенциально, по кольцу, через угловой патрубок с за-
слонкой, через перфорированные стенки (рис. IV.4, а—г
соответственно).
Комбинированные воздухонаправляющие устройства
основаны на одновременном использовании регистра и
струйного подвода воздуха (рис. IV.4, д).
91
Пламенные трубы в основном различаются способом
охлаждения и могут быть разделены на следующие виды:
1) сплошная цилиндрическая обечайка, омываемая
снаружи вторичным охлаждающим воздухом (рис. IV.5, я);
Смешивающие устройства могут иметь различную
конструкцию.
В дырчатых (рис. IV.6, а) и сопловых (рис. IV.6, б)
смесителях вторичный воздух вводится через круглые или
Рис. IV.4. Схемы струй-
' ных и комбинированных
завихрителей (Т — то-
пливо; В — воздух)
2) коническая обечайка с отверстиями для пропуска
части вторичного воздуха с целью охлаждения внутренней
ее стороны (рис. IV.5, б);
3) телескопические конструкции, состоящие из не-
скольких обечаек, между которыми имеется кольцевой
овальные отверстия (сопла) в стенках пламенной трубы
таким образом, чтобы он мог достигнуть центральной части
потока продуктов сгорания. Эти смесители могут выпол-
няться двухрядными с параллельным или (реже) шахмат-
ным расположением отверстий. Дырчатые смесители с оваль-
зазор для пропуска части вторичного воздуха, охлажда-
ющего внутреннюю поверхность пламенной трубы:
а) пламенные трубы, составленные из цилиндриче-
ских обечаек без оребрения (рис. IV.5, в) или с оребрени-
ем — продольным (рис. IV.5, г) и поперечным (рис. IV.5, д');
б) чешуйчатые пламенные трубы, составленные из усе-
ченных конусов с небольшими зазорами (рис. IV.5, е);
4) двустенные трубы с использованием струйного и
заградительного способов охлаждения (рис. IV.5, ж);
5) трубы с внутренним конвективным охлаждением
закрученным потоком вторичного воздуха (рис. IV.5, з).
92
ными отверстиями и соотношением сторон 1/3—1/5 при-
меняют в пламенных трубах диаметром не менее 300 мм.
Сопловые смесители применяют в пламенных трубах с диа-
метром не менее 400 мм. Переднюю кромку сопел обычно
срезают под углом 30—45° во избежание обгорания.
Число сопел 6—12.
Лопастные (S-образные) смесители (рис. IV.6, в) при-
меняют в камерах сгорания с закрученным потоком вто-
ричного воздуха, который подхватывается на периферии
лопастями смесителя и направляется в центральную
зону, заполненную продуктами сгорания.
Рис IV.6 Схемы смесителей
------воздух,------------про-
дукты сгорания
Рис. IV 7 Камера сго-
рания с вихревым сме-
сителем
i
IV 8. Запальные
устройства
93
Вихревые смесители (рис. IV.7) устроены таким об-
разом, что из кольцевого канала охлаждающий воздух
двумя плоскими струями, вытекающими навстречу одна
другой, поступает в зону смешения. При соударении этих
струй в поперечном сечении камеры образуются четыре
вихря, центральные зоны которых из-за пониженного
давления заполняются продуктами сгорания. Интенсив-
ный массообмен внутри каждого вихря и между вихрями
приводит к выравниванию температуры продуктов сго-
рания за смесителем. Вихревые смесители с лопаточным
аппаратом находят применение в камерах сгорания с под-
водом воздуха через боковые патрубки, расположенные
в головной части камеры.
Запальные устройства электроискрового типа предста-
вляют собой электрическую свечу, между электродами
которой образуется искра с температурой 10—15 тыс. К.
От этой искры воспламеняется небольшой факел пуско-
вого топлива, а затем и основное топливо.
В качестве примера на рис. IV.8, а изображено запаль-
ное устройство, применяемое в камерах сгорания ГТУ НЗЛ.
Оно представляет собой трубу, в которой установлены авто-
мобильная свеча А16У (А14У) и газораспределительная
трубка подвода пускового газа. Воздух поступает в трубку
через систему отверстий за счет эжекции струи пуско-
вого газа.
В камерах сгорания ГТУ УТМЗ применяется запаль-
ное устройство (рис. IV.8, б) с факельными воспламени-
телями, вмонтированными в наружную часть газовой го-
релки. Воздух и топливный газ поступают в форкамеру
из примыкающих воздушной и газовой полостей через
систему отверстий. ,
К числу мероприятий по стабилизации очага горения,
применяемых в ГТУ, относятся подвод энергии извне,
термическая рециркуляция, аэродинамическая рецирку-
ляция и др. Подвод энергии извне осуществляется от де-
журной горелки или форкамеры; выходящие из них про-
дукты сгорания, нагретые до высокой температуры, по-
ступают в основную камеру, где служат источником зажи-
гания горючей смеси.
При термической рециркуляции необходимая теплота
передается потоку через специальные нагретые стержни
или стенки камеры.
При аэродинамической рециркуляции в потоке горю-
чей смеси создаются локальные участки с малыми скоро-
стями, равными скорости распространения пламени, и
зоны обратных токов, в которых нагретые продукты воз-
вращаются к корню факела из удаленных от него сечений.
Аэродинамическая рециркуляция создается обычно за-
круткой потока специальными лопаточными завихрите-
лями, установкой плохообтекаемых тел, образованием
вихрей в районе горелочного устройства и др.
Расчет основных параметров камер сгорания
Исходными данными для расчета камеры сгорания,
которые принимаются из расчета тепловой схемы ГТУ
(см. п. 1.8), являются: расход воздуха GB; параметры воз-
духа на входе в камеру сгорания — температура Т1В (/1в)
и давление р1в; температура продуктов сгорания за ка-
мерой (перед турбиной) 7’2r ™п установки и следую-
щие ее характеристики: назначение (стационарная, транс-
портная и т. д.), коэффициент потерь полного давления
£к.с, коэффициент полноты сгорания г|к. с, характе-
ристики топлива (химический состав), теплонапряженность
Up (Пу), допустимая неравномерность поля темпера-
тур Ат-
По имеющимся характеристикам топлива рассчиты-
вают низшую теплоту сгорания Qj’ и теоретическое коли-
чество воздуха Lo, необходимого для полного сгорания
топлива — см. п. 1.8 [98].
94
Расход топлива на камеру сгорания определяется
по формуле 1
Стоп — GB/(<zL0); gTon = 1/(оДо). (IV.7)
Для камеры сгорания, работающей в атмосфере влаж-
ного воздуха, может быть использована формула [98]
gTond = (1 + d)-1 [(^r - t^d = 0 + (i + d) (z*B _
- (‘2b - »'lB)d = о] [<?₽4.c - (l'*2r - ‘Тв)<7 = оГ', (IV.8)
где d — влагосодержание воздуха (масса водяного пара
в 1 кг сухого воздуха); значение Q" сдостаточной точностью
определяется по формуле (1.86). Изменение Q” для стан-
дартного углеводородного топлива в зависимости от 7’1в =
= Т^к может быть оценено по рис. IV.9 [98].
Значение gTOn d может быть также подсчитано с по-
мощью л (Г) — i — Т-функций по формуле
Stand (12в 4в)г/ {Qp Пи ,с 0 4" ^0 ^о)
х [(*2г)а = 1 — ( х1в)а = l]d +
+ £0(l+d)(/5B-<7B)rf}-i, (IV.9)
При этом
а = [5топЛ(1+й)]-1. UV. 10)
Тогда расход топлива в ГТУ можно подсчитать по
формуле
С-ТОП = ЗбОО^топЙ^В (1 Похл Syt) ’ (IV. 1 1)
где йохд определяется по рекомендациям пп. 1.6 и II.5,
a gyT — п. 11.4.
При конструировании камеры сгорания необходимо
обеспечить требуемое гидравлическое сопротивление, ко-
торое определяется уровнем скоростей воздуха и коэффи-
циентами гидравлических потерь различных ее элементов.
Подсчитав тепловые потери и разность кинетических энер-
1 Пример расчета параметров камеры сгорания стационар*
ной ГТУ приведен в приложении 5.
гий на входе и на выходе, определяют перепад статических
давлений в камере сгорания при изотермических условиях:
^Рк. с ^Рк.с ^Ртеп
(2 2 \
±1^ _ РЛ (др*х + Др,ых)) (IV 12)
где Ар* с — полное сопротивление камеры сгорания;
Ар*еп — потери полного давления при подводе теплоты;
Др*х и Др*ых — потери полного давления на дополни-
тельном входном и выходном участках камеры сгорания;
ш1в •— скорость воздуха на входе в камеру сгорания (в под-
водящей трубе), определяемая в сечении до начала раз-
ветвления тракта; ш2г — скорость газа в сечении за сме-
сителем.
Величина Ар*х — подсчитывается в тех случаях, если
заданное сопротивление Ар* включает в себя сопроти-
вление дополнительного участка до сечения, в котором
начинается распределение воздуха по трактам камеры;
АрВых — подсчитывается в тех случаях, если Дрк с вклю-
чает в себя сопротивление дополнительных участков после
смесителя камеры сгорания.
Согласно РТМ 24.022.11—74, можно считать
(р \ 2 / Т \ 2
-^\ W1B. (IV.13)
^к.с / \ '1b у 2 ’
где ?\в — площадь трубы для подвода воздуха в камеру
сгорания.
По найденному значению Дрк. с рассчитывают проход-
ные сечения и основные размеры отдельных элементов
камеры сгорания (регистра, пламенной трубы, смесителя
и других элементов) при заданном распределении потока
воздуха, причем суммарные потери давления на отдель-
ных участках, через которые проходит поток воздуха,
равны разности полных давлений на входе и выходе
из камеры сгорания, т. е.
S ДР, =Р:Х-Р Lx-
Потери давления на каждом участке (элементе) опре-
деляются суммой потерь давления на преодоление сопро-
тивления трению и местных сопротивлений:
A Pi = Артр i -ф- Дрм.с i.
Здесь
л . Л т Рщ‘
"'Ртр i — Лтр ; —g— > аРм.с i — feM.c i -—g- ’
где li—длина участка (канала), м; — эквивалентный
диаметр, d3 = 4F/PCm (F и Рсы — площадь и смоченный
периметр поперечного сечения канала); %тр — коэффициент
сопротивления трению, зависящий от относительной шеро-
ховатости стенок канала A/d0 (А — средняя высота высту-
пов шероховатости) и числа Рейнольдса Re; gM. Cj — коэф-
фициент местного сопротивления.
В кольцевых каналах принимают d, — DH — DBH,
для трубок круглого сечения d3 — d.
Для технически гладких поверхностей, т. е. для кото-
рых при заданном значении Re сопротивление еще не за-
висит от шероховатости, рекомендуются формулы:
при Re < 4-103
ZTP = 0,303/(lgRe —0,9)2; (IV. 14)
при Re = (44-100) 103
ZTp = 0,316/y^> (IV.15)
где Re = tyd3/vp; vp — коэффициент кинематической вяз-
кости воздуха при давлении pls.
Потери давления в регистрах определяются сопро-
тивлениями отдельных их участков:
дРр — (?р- вх + £р. вых -Кр.л)(Р«1х/2). (IV. 16)
Здесь
?р. вх — 1,2 (Fp. вх/г 1в 2) (1 — Fp, ВХ/Е1В);
£р. вых = 2,4 (fp. bx/Fk. с) (Fр.вх/Fp. вых — Fp. bx/Fk, с);
Г = [l~^P.K//-p.H)2]2(2-^)2tg2<p
Р’Л 4 11 — (Гр. К/Гр. L)2-m]2m ( Гр к/Гр_ н)2m
где Fp, вх и Fp, вых — площади на входе в регистр и выходе
из него (без‘учета лопаток); гр. к/гр. н — втулочное отно-
шение регистра; <р — угол выхода потока из регистра
(для плоских и плоско-конических регистров принимают
ф = 304-50°);
m — sin 2ф/(2 — уcos ф)4.
Коэффициент гидравлического сопротивления щелей
6-втщ Xj-^щ
<?в. щ
(IV.17)
где б„1щ — количество воздуха в кольцевом канале перед f
первой щелью; Е бв.щ — количество воздуха, поступаю-
щего в щели; Гщ/ и £ Fщ — площади проходных сече-
ний одной щели и суммарная всех щелей.
Если в щелях установлены гофры (оребрение), то
при определении /щ,- учитывается площадь загромо-
ждения.
При работе камеры сгорания внутренняя обечайка,
имеющая более высокую температуру, расширяется больше,
чем наружная, омываемая охлаждающим воздухом. По-
этому проходное сечение щели уменьшается на величину
JT
ДЛц. Т “ Dbh. из {[1 4“ Р (Т’в.о ---- FB, щ)]2 - 1 } ,
где Т-в. о — температура металла внутренней обечайки, К;
Тв. щ — температура воздуха в кольцевой щели, К;
Deh. из — диаметр внутренней обечайки в изотермических
условиях, м; f> — коэффициент линейного расширения
металла обечайки, который следует учитывать при расче-
тах и последующей доводке камеры сгорания.
По воздушной стороне смесителя коэффициент его
гидравлического сопротивления
£см. в — 4 [ (Еотв, см/^к. см) (ш3/ау2)0,5)0,5, (IV.18)
где FOtb. см и FK. см — площади отверстий и сечения коль-
цевого канала смесителя; w2 — скорость воздушных струй
в смесителе м/с; да3 — скорость газа за смесителем; А —
численный коэффициент, для дырчатых смесителей А =
= 3,0, для сопловых — А = 3,3.
Для дырчатых и сопловых смесителей потери стати-
ческого давления по газовой стороне
Pir - Рзг = Рз^з — Pi^i —
(^к. см/^к. с) Р2^2^вх. стр{£> а Н- , flV-19)
где индексы 1 и 3 относятся к сечениям пламенной трубы
перед и за смесителем, 2—к сечению в кольцевом канале
перед смесителем; швх. СТр — скорость втекающей струи;
а — угол наклона вектора скорости к оси отверстия, вы-
числяемый по формуле
ex = arctg (0,67^отв. см//7к. см)* (IV.20)
Потери на трение для сопловых смесителей
ДРТр =5трРз“'з/2>
95
где
?тр = (5,7 -т- 6,2) Г0ТВ. см/F К. С
Для дырчатых смесителей принимают Дртр = 0.
Рекомендуемые значения основных параметров камер
сгорания стационарных ГТУ приведены в табл. IV. 1.
производится на основе использования уравнения тепло-
вого баланса элемента стенки
<2ф. л _Ь Фф. к — Qb. к Ч- Qb. л — Qb. к Ч- Qk. к, (IV.23)
где QK. к — количество теплоты, отданной силовым кор-
пусом охлаждающему воздуху конвекцией; остальные зна-
Т а б л и ц а IV. 1. Рекомендуемые основные параметры стационарных камер сгорания
Тип камеры сгорания Топливо * Тепл ©напряженность сечения (максимальная) Up- ккал м2 • ч . кгс/см2 Диаметр пламенной трубы £>п т мм Средняя относительная длина огневой зоны (до отверстий смесителя) Lo з/D-n т Средняя относительная длина пламенной трубы Тп Т/Оп т Избыток первичного воздуха Средние скорости воздуха на выходе из воздухонаправля- ющего устройства, м/с _ Сопротивление камеры сгора- НИЯ с, % Тип смесителя
Выносная одногорелочная Газ жл жт 6 6 5,5 До 1000 2,0 2,0 2,5 2,5 2,5 3,0 1,3—1,5 1,2—1,3 1,2—1,3 50 — 60 2,0—2,5 Сопловой или дырчатый
Выносная многогорелочная Газ ЖЛ жт 8,0 8,0 7,0 Более 1000 1,3 1,3 1,5 2,0 2,0 2,5 1,3—1,5 1,2—1,3 1,2—1,3 40—50 2,0—3,0 Сопловой
Выносная многогорелочная с охлаждением закрученным потоком Газ 8,0 1000 — 1600 1,0 2,2 — 3,5 2,1 До 80 2,3 —2,8 В-ихревой
Трубчато-кольцевая и сек- ционная одногорелочная Г аз ЖЛ ЖТ 6 6 5 До 600 2,0 2,0 2,5 3,0 3,0 3,5 1,3—1,5 1,2— 1,3 1,2—1,3 50 — 60 2,0 —2,5 Сопловой илн дырчатый
Со ступенчатым подводом воздуха * Принятые обозначена Газ ЖЛ я. ЖЛ 18 — 20 18 — 20 — жидк До 500 эе легкое; 2,0 2,5 ЖТ - 3,0 3,5 жид кое 0,3 —0,5 за регистром и 1,2—1,4 за отверстиями тяжелое. 60—80 3,5—5,0 Сопловой или дырчатый
Диаметр наружного корпуса можно найти по выраже-
нию (см. РТМ 24.022.11—74)
DH. к = ]/(Г>„. т Ч- 26п. т)2 Ч- 0>785Кш~крв + 2бн. к ,
(IV.21)
где GK, к — расход воздуха в кольцевом канале между
наружным корпусом и пламенной трубой, равный GCM Т
Ч" 6охл/2 для прямоточных и GB1 0ОХл/2 для противо-
точных камер сгорания; 6П. т, 6Н. к — толщина стенки
пламенной трубы и корпуса соответственно; рв — плот-
ность воздуха на входе в смеситель. Расходы воздуха
Сохл и смеси GCM выбирают обычно по прототипу.
Проходная площадь отверстий смесителя
Ротв. см ~ к?см. в /(2рвДрк. с)- (IV.22)
Поскольку надежность работы камеры сгорания в пер-
вую очередь определяется температурным уровнем и рав-
номерностью нагрева стенки пламенной трубы, конструи-
рование камеры должно сопровождаться расчетом тем-
пературы материала ее стенки. В дальнейшем эти данные
используются для расчетов на прочность. Этот расчет
96 \
чения Qi, входящие в эту формулу могут быть подсчитаны
по следующим формулам [84].
1. Количество теплоты, отданной факелом пламенной
трубе лучеиспусканием,
Фф. Л ~ естефс(/п. т (Гф. эф — Тп. Т. ср), (IV.24)
где Со = 20, 5 кДж/(ма • ч • К4) — коэффициент лучеиспус-
кания абсолютно черного тела; е'т = 0,5 (1 ест) — при-
веденная степень черноты оболочки; ест — степень чер-
ноты поверхности материала пламенной трубы, принима-
емая равной 0,8—1,0; 8ф — условная степень черноты
факела, равная 0,07—0,10; Fn. т— внутренняя поверхность
пламенной трубы; Тф. Эф — эффективная температура
факела, в первом приближении принимаемая равной теоре-
тической температуре факела в зоне горения при а = аг;
аг — коэффициент избытка воздуха в зоне горения;
Тп. т. ср — средняя температура стенки пламенной трубы.
2. Количество теплоты, отданной факелом пламенной
трубе конвекцией,
Сф. к = «ф.п. Tfn.T Д^г.ф- (IV.25)
Здесь ДТГ. ф = Т'Г ф — Тп т; Тг ф = Т1в С (Тг ф
Т 1в) — средняя характерная температура газовоздушного
потока; С — коэффициент, равный 0,5—0,8; Тг, ф — сред-
няя температура факела; аф. п. т — коэффициент тепло-
отдачи от факела к стенке трубы [84].
/)0,82 f гг*' \ 0,35
лу _____л <Л18 Bi I ,г - Ф- |
аф. п. т V>UA)b.prp.r I g2 I у j ’
“п. т. э '
где теплоемкость срг и коэффициент динамической вязко-
сти газа щ- принимаются при температуре Тп, т; dn. т. э —
эквивалентный диаметр пламенной трубы.
3. Количество теплоты, отданной пламенной трубой
охлаждающему воздуху конвекцией,
Сз.к = «в.п.Л.тА7’п.т.ср- (IV.26)
Здесь F', — наружная поверхность пламенной трубы;
ав. л. т — коэффициент теплоотдачи от пламенной трубы
к охлаждающему воздуху; ДГп.т. ср — средняя эффек-
тивная разность температур:
o:B. п. т = NuXB/dn. т. э;
* гп__________________Т2В TtB____________
п-т'ср“ 1п[(т;.т-лв)/(т;.т-г2в)] ’
где Nu = 0,018 Re0,8; Re = w2dn. T. 3/v; ?,в — коэф-
фициент Лплопроводности воздуха при температу-
ре Тп, т; Т2В— температура, до которой нагреется
охлаждающий воздух (находится методом последо-
вательных приближений); Т'п т — температура наруж-
ной поверхности пламенной трубы,
г;.т = 7’п.т-((?ф.л+<?ф.к) M%Fn.T).
В последней формуле би/. — толщина стенки и коэф-
фициент теплопроводности материала пламенной трубы.
4. Количество теплоты, отданной пламенной трубой
охлаждающему воздуху лучеиспусканием,
<?в.л = ®пС0^.т[(^ Т)4-П], (IV.27)
где еп = (1/еп. т + 1/ек —- I)'1 — приведенная степень
черноты, в расчете обычно принимают еп = 0,67ч-0,71;
еп. 1 и ек — степень черноты наружной поверхности пла-
менной трубы и внутренней поверхности силового корпуса;
Тк = Тв + С' (Т'п т — Т1в) — температура внутренней
поверхности корпуса; С' = 0,05ч-0,2.
Входящей в формулу (IV.24) средней температурой
Т’п. т. ср в начале расчета задаются в пределах 700—850° С
в зависимости от применяемого материала и условий работы
камеры сгорания. Подставляя затем в формулы (IV.24)—
(IV.27) принятое значение следует проверить степень
сходимости условия @ф. л + 2ф. к = <2ф = Qb. к +
+ <2в.л = Qn. т- Если (фф — <2п.т)/<2ф >0,0104-0,015,
расчет следует повторить, задаваясь новыми значениями
температуры Тп. т и скорости воздуха ш2.
Рассмотренная схема приближенного расчета Тп. т
для конкретных камер сгорания обычно дополняется спе-
циальными расчетами с использованием результатов соот-
ветствующих экспериментальных исследований тепло-
обмена в камерах сгорания сходной конструкции.
IV.2. ТЕПЛООБМЕННЫЕ АППАРАТЫ ГТУ (ТОА)
Классификация теплообменных аппаратов
По назначению ТОА ГТУ разделяются на воздухо-
подогреватели, воздухоохладители, маслоохладители, се-
тевые подогреватели.воды и др., по способу передачи теп-
ла — на поверхностные и контактные.
В поверхностных теплообменных аппаратах оба тепло-
носителя или отделены один от другого твердой стенкой
(рекуператоры), или поочередно омывают одну и ту же
поверхность (регенераторы).
7 Л. В. Арсеньев и др.
В контактных теплообменных аппаратах передача
теплоты происходит при непосредственном контакте (сме-
шении) двух теплоносителей — горячего и холодного.
По схеме течения/рабочего тела ТОА разделяются на
аппараты с параллельным (прямотоком или противотоком)
и перекрестным токами. Теплообменные аппараты с пере-
крестным током разделяются, в свою очередь, на одно-
ходовые и многоходовые.
Тепловой расчет
Тепловой расчет выполняется или для определения
необходимой поверхности теплообмена ТОА, или для
установления рационального режима его работы и опре-
деления температур теплоносителей. Исходными для теп-
лового расчета ТОА являются следующие уравнения:
Q = kFMcp’, (IV.28'
Q = GlcPiV г ~ Q = GV>c О V-29)
где k — коэффициент теплопередачи; F — поверхность
теплообмена; Д1Ср— средний температурный напор;
t2, — температуры теплоносителей на входе и выходе
из теплообменного аппарата соответственно; Gx и G2 —
массовые расходы теплоносителей.
Коэффициент теплопередачи определяется по фор-
мулам:
для плоской однослойной стенки
k = (1/ах -4- 6А+1/а2)-х; (IV.30)
для плоской многослойной стенки
k — (1Sj/Zj -j- 62 -]-••• ~р 6ra/Z,t 1 /а3)-1;
(IV.31)
для однослойной трубы (отнесенной к единице длины
(IV. 32)
где а1; а2 — коэффициенты теплоотдачи от горячего тепло-
носителя к стенке и от стенки к холодному теплоносителю
соответственно; % — коэффициент теплопроводности мате-
риала стенки (трубы); 6 — толщина стенки (трубы);
Д и d2 — внутренний и наружный диаметры трубы.
Для многослойной трубы
k = ( —дуЬ In -А- -Р ~ 1П +
\ ajdj 1 2%j dx 1 2Л3 d2
dn cc2dpj.i J
(IV.33)
где dn и —• внутренний и наружный диаметры со-
ставляющих 1 труб.
Количество передаваемой теплоты для многослойной
трубы
Q = kL Mcpndcp, (IV.34)
где L — длина трубы.
При относительно малой толщине стенки многослой-
ной трубы ее длину можно определять по приближенной
формуле
Е = Q F -j— + —-) kttdzp Д/Ср).
(IV.35)
где dcp = (di + d2)/2.
97
Обычно коэффициент k определяют по отдельным уча-
сткам поверхности, а его среднее значение определяют
по формуле
*=S(^)/(2F0-
(IV.36)
С учетом загрязнения поверхности теплообмена в про-
цессе эксплуатации расчетное значение k следует умень-
шить на 15—20%.
Коэффициент теплопроводности Л различных метал-
лов, сплавов и возможных отложений на поверхностях
теплообмена имеет следующие значения, Вт/(м-°С):
Сталь углеродистая . . .
Сталь легированная . . .
Чугун .................
Латунь.................
Медь...................
Бронза ..............
Мельхиор...............
Алюминий ..............
Никель . . ............
Цинк...................
Свинец ................
Масло..................
Соль поваренная . . .
Органические отложения
накипь ................
котельная
46,5 — 58
17 — 35
62,8
87—116
149—195
35 — 46,5
29
204
58
110,5
35
0,116
1,2 —2,4
Теплопередача через оребренную поверхность
Для увеличения поверхности со стороны теплоноси-
теля с худшими теплопередающими свойствами применяют
ее продольное или поперечное оребрение.
для продольного оребрения
апр = 1,05£ра2; (IV.40}
для труб с продольным прямым оребрением [34 ]
__(nd — пр8) а2 + (2лрйр прб) агЕр
апр — (nd — Прб) (2яр/гр -J- Лрб) ’
(IV.41)
где Fp — поверхность ребер; FTp — поверхность участ-
ков труб, не занятых ребрами; F2 = F„ + FTp; Ер =
= th (mhp}/(mhp) — коэффициент эффективности ребер;
Пр — число ребер на одной трубе; d — наружный диаметр
трубы.
Использование теории подобия при
расчете ТОА
При расчетах теплоотдачи и гидравлических сопро-
тивлений в элементах ТОА ГТУ широко применяются
следующие определяющие критерии подобия: Re, Nh,
Рг, Gr и Ей.
Для вычисления этих критериев при движении тепло-
носителя внутри трубы за определяющий размер прини-
мают обычно ее внутренний диаметр, для каналов непра-
вильного и сложного сечения — эквивалентный диаметр
d3 — 4f7U, где f — площадь сечения капала для прохода
теплоносителя; U — полный периметр канала.
Рис. IV. 10. Поверхности теплообмена с трапецеидальными выступами: а — коридорное расположение
выступов; б — шахматное расположение выступов; в — шахматное расположение выступов с двусторон-
ней глубиной штамповки
Коэффициент теплопередачи через оребренную по-
верхность находят по выражениям:
для единицы основной (гладкой) поверхности
kp2 —
для единицы оребренной поверхности
i f2 6 f2 1 V1
Fj X Ft ' а2 J ’
(IV.38)
где F| и F2 — соответственно площади гладкой и оребрен-
ной поверхностей.
Формулами (IV.37) и (IV.38) можно пользоваться при
условии 0 < mhp < 0,4, где т = K2a2/(I.p6p); ftp, бр
и Лр — высота, толщина и коэффициент теплопроводности
Материала ребра. Если mftp>0,4, то в формулах (IV.37)
'> (IV.38) вместо а2 иадо подставлять хофф/щиент апр [72],
учитывающий неравномерность теплоотдачи на поверхно-
сти ребра.
Для поперечного оребрения с цилиндрическим осно-
ванием
апр = 0,85 (IV.39)
\ f2 F2 )
Значения d3 для каналов трубчатого типа различно!
формы приведены в табл. IV.2, для каналов с трепецеидаль-
ными выступами —на рис. IV. 10 и в табл. IV.3, для ка
налов волнообразного и двуугольного профилей — н;
7) *)
Рис. IV.11. Конфигурация каналов: а — волнообразной
профиля; б — двуугольного профиля
рис. IV, 11 и в табл. IV.4 и IV.5. На рис. IV. 12 и в табл. IVJ
приведены некоторые характерные формы и размеры по
верхностей с двусторонним оребрением гладкими и решет
чатыми ребрами, которые рекомендуются для создани1
компактных ТОА ГТУ.
В качестве определяющей температуры теплоносител1
в расчетах принимают обычно среднюю температуру (Ср =
98
= (t' + Г')/2, а в некоторых случаях температуру стенки
1ст. ср или температуру (tcv + <ст. Ср)/2.
Количество теплоты, передаваемой от горячего (ин-
декс 1) теплоносителя к холодному (индекс 2), пропорцио-
нально величине Д^р, называемой средним (среднелога.
Рис. IV. 12. Характерные формы и размеры оребрен-
ных поверхностей с двусторонним оребрением
рифмическим) темвературным напором. Для различных
схем течения Aicp определяется по формулам:
для прямотока
( 1 2
А^ср = [(*; - Ц - К' - ^)]/Ш ; (I V.42)
Т а б л и ц a 1V.2. Характерные размеры каналов
трубчатого типа различной формы
Форма поперечного сечения а/Ь А
Круглая труба — d 64
Эллипс (а — малая ось, b — большая ось) 0,1 0,2 0,3 0,4 0,5 0,6 1,55а 1,50а 1,44а 1,37а 1,30а 1,24а 78 76 73 70 68 66
Квадрат со стороной а а 57
Прямоугольник (а — меньшая сторона, b — большая сторона) 0,1 0,2 0,3 0,5 1,82а 1,67а 1,54а 1,33а 85 76 69 62
Равносторонний треугольник со стороной а — 0,58а 53
Равнобедренный треугочьник с основанием а и углом при вер шине р, ° 20 40 80 90 100 — 0,84а 0,70а 0,47а 0,41а 0,36а 52 54 53 52 52
Круглое кольцо шириной а — 2а 96
При течении теплоносителя в гладких прямых трубах
и каналах некруглого сечения и значениях Re = 104-т-
-4-5-106 и Рг= 0,6-ь2500 при l/d > 50 рекомендуется
применять уравнение |72]
Nu = 0,021Re°'8Pr°’43 (Рг/Ргст)0’25, (IV.45)
для противотока
А^ср = 1 (z К- G) - 0'1 - ^)]/1п -p->
4 I 2
(IV.43)
для сложных схем течения
Д/ер = [(^- Q ~ (^~ б)]/1п -V—р >
1 I ч
(IV.44)
где е — коэффициент, который можно найти из
рис. IV. 13 по значениям вспомогательных пара-
метров Р и R:
Р = (/ 2 t2)/(/ 1 — (2)j
R ~ I ^1)/(^2 b)-
В случае, если (t{ — /2) < 2,
можно использовать приближенную формулу
Дбр ~ °'5 l(z 1 — Д)].
Коэффициенты теплоотдачи определяются
режимом течения теплоносителя, его физически-
ми свойствами, конфигурацией поверхности те-
плообмена и находятся обычно из соответствую-
щих критериальных уравнений.
7*
Таблица IV 3. Характерные размеры (мм)
каналов с трапецеидальными выступами
(см. рис. IV. 10)
Форма элемента L do S, I, мм2 п Коэффи- циент кри визны
С коридорным расположением вы- ступов (см рис IV 10, а) 500 10,4 25,0 25,0 146 56,6 10,3 1,13
С шахматным рас положением высту- пов (см рис IV 10, б) 510 11,6 35,4 17,7 189 76,0 9,95 1,055
С шахматным рас положением высту- пов и двусторонней глубиной штампов- ки (см рис IV 10, в) 510 240 9,6 8,8 25,0 24,0 12,5 12,0 124 116 55,5 53,8 9,2 8,6 1,11 1,08
Примечание Здесь п — число выступов на длине L
99
Таблица IV.4. Характерные размеры (мм) каналов
волнообразного профиля (см. рис. IV. 11, а)
* K, «5 (9 + ДЛР
20,2 7,5 11,9 3 0,5 3,7 5,1 8,8 7,14 9,7 16,2 2,04 2,77 4,63
20,5 9,6 9,8 2,8 0,5 4,8 5,3 9,5 9,2 10,0 17,3 2,78 3,18 5,25
20,5 9,4 7,7 5,2 0,5 3,9 4,5 8,6 7,52 8,60 15,84 1,32 1,51 2,78
20,5 8,4 8,9 5,3 0,5 3,9 4,7 8,8 7,52 8,97 16,2 1,3 1,55 2,8
20,7 9,0 5,2 8,3 0,5 2,7 5,26 0,6
33,7 9,6 17,4 13,5 0,5 4,6 5,5 7,2 8,8 10,4 13,4 0,68 0,744 0,96
33,9 10 23,3 6,7 0,5 4,8 7,6 9,2 14,13 1,27 1,96
34,2 9,0 11,8 21,6 0,5 3,2 4, 1 5,6 6,2 7,88 10,6 0,28 0,356 0,48
40,0 12 23 16 1 7 3 13,2 9,6 5,85 0,775 0,565 0,345
где число Рг принимается при температуре теплоносителя,
а число Ргст — при температуре омываемой стенки.
Для воздуха и продуктов сгорания органического
топлива можно с достаточной точностью применять более
простое критериальное уравнение Nu = 0,018 Re0,8 [72].
При ltd < 50 в формулу (IV.45) вводится поправоч-
ный множитель — коэффициент е/ (табл. IV.7).
Для изогнутой трубы (канала) в (IV.45) вводится
поправка e# = 1 + 1,77 d/R, где /? — радиус змеевика;
d — диаметр трубы.
При продольном омывании пучка труб в формулу
(IV.45) вводится дополнительный множитель (s^/d2)0’18,
где sx и s2 — продольный и поперечный шаги труб в пучке.
За определяющий размер принимается эквивалентный диа-
метр всего канала с пучком труб, а за определяющую тем-
пературу — средняя температура теплоносителя.
При перекрестном обтекании пучков труб для треть-
его и всех последующих рядов значение Nu для жидкого
теплоносителя можно подсчитать по формулам [72]'
Для коридорных пучков труб:
Nu = O,56Re°’5Pr0,36 (Рг/Ргст)0,25 при Re < 1 • 103;
(IV.46)
Nu = 0,22Re°’65Pr°’36 (Pr/PrCT)0-25
при Re > 1 • 103;
(IV.47)
Таблица IV.5. Характерные размеры (мм) каналов
двуугольного сечения (см. рис. IV. 11, б)
SJd0 Si R r f, MM2
40 10 23,75 17,75 9,10 189
4 32 8 19,00 14,00 7,28 121
24 6 14,25 10,25 5,40 67
30 10 15 9,0 8,90 140
3 24 8 12 7,0 7,08 89
18 6 9 5,0 5,30 50
25 10 11,56 5,56 7,55 105
2,5 20 8 9,25 4,25 5,92 66
15 6 6 94 2,94 4,38 36,5
20 10 8,75 2,75 6,37 75
2 16 8 7,00 2,00 5,00 47
12 6 5,25 1,25 3,75 26,4
Примечание. Толщина листа 1 мм
для шахматных пучков труб:
Nu = 0,56Re°’5Pr°’36 (Рг/Ргст)°’25 при Re < 1-Ю3;
(IV.48)
Nu = 0,40Re°'6°Pr°-36 (Рг/Ргст)0’25 при Re > 1-Ю3-
(IV.49)
Средний коэффициент теплоотдачи всего пучка
«пуч = У,
где а. — коэффициенты теплоотдачи соответствующего
ряда труб; Ft — суммарная поверхность нагрева труб
в ряду.
Для воздуха формулы (IV.46)—(IV.49) принимают вид:
Т а б л и ц a IV.6.
Характерные размеры оребренных
поверхностей с двусторонним оребрением
(см. рис. IV. 12)
Номер поверх- ности d3, мм Толщина ребра, мм Коэффициент компактности, м2/м8
1 2,20 0,15 1490
2 2,60 1,5 1200
3 3,06 1,5 1100
4 6,16 1,5 545
5 4,40 1,5 785
6 3,64 1,5 950
7 3,08 1,5 1115
для коридорных пучков труб:
Nu = 0,49Re°’5 при Re < 1 • 103;
Nu = 0,194Re0,65 при Re > 1 • IO3)
для шахматных пучков труб:
Nu = O,49Re0,5 при Re < 1 103J
Nu = O,35Re0,60 при Re > 1 • 103.
(IV.50)
(IV.51)
(IV.52)
(IV.53)
100
г
►
? Рис IV 13 Поправочный коэффициент 8 для различных схем
течения теплоносителей при следующих значениях R
1 — 4,0, 2 — 3,0, 3 — 2,0, 4 — 1,5, 5 — 1,0, 6 — 0,8, 7 — 0,6, 5 — 04,
9 — 0,2
Если угол натекания на трубный пучок i < 90°, най-
денные из формул (IV.45)—(IV.53) значения а следует
умножить на коэффициент е,-:
i, ...»......... 90 80 70 60 50 40 30 20 10
£................ 1 1 0,98 0,94 0,88 0,78 0,67 0,52 0,42
Коэффициент теплоотдачи от воздуха к поверхности
шахматных пучков труб с наружным ленточным и шай-
бовым оребрением при поперечном их омывании потоком
определяется по формуле
K = 0;2382^^(4)-0'54(4-)-0'i4Re°.-,
(IV.54)
которая справедлива при Re = 3004- 22500; d/(=2,44-
4-9,5; hit = 0,364-5; (3 = 0,464-2,18. Здесь h — высота
ребра; t — шаг ребер; (3 = (sx — d)/(s2 — d); ег — коэф-
фициент, учитывающий влияние числа рядов труб в пуч-
ке г:
2 4 6 8 10 12
0,89 0,95 0,98 0,99 1,005 1,01
14 16 18 20 22
1,015 1,015 1,02 1,02 1,02
В формуле (IV.54) коэффициент а отнесен к площади
полной поверхности ребристых труб, физические параметры
сопротивление из-за неизотермичности течения АрИз-
В прямых трубах и каналах:
Лртр = Х,тр (Hd3) (рш2/2); (IV.58)
Лрм. с = £м. сР®2/2; (IV. 59)
/ Pi^i \
Лриз = (Pi — Рг) ^п. т + 2 g 2 / ’
(IV.60)
где /.тр — коэффициент сопротивления трению; £м. с —
коэффициент местного сопротивления; индекс 1 соответ-
ствует меньшей, а индекс 2 — большей температуре;
/гп. т — высота подъема теплоносителя.
При неизотермическом течении в прямых каналах
%тр в формуле (IV.58) подсчитывается по формулам:
для ламинарного потока
(IV .61)
для турбулентного потока
0,3164 / Ргст \1/3
Атр" Re0,25 \ Pr J ’
(IV.62)
Таблица IV.7. Поправочный коэффициент е/
Re l/d
1 2 5 10 15 20 30 40 50
b io4 1,65 1,50 1,34 1,23 1,17 1,13 1,07 1,03 1,0
2- IO4 1,51 1,40 1,27 1,18 1,13 1,10 1,05 1,02 1,0
5- I04 1,34 1,27 1,18 1,13 1,10 1,08 1,04 1,02 1,0
I • 105 1,28 1,22 1,15 1,10 1,08 1,06 1,03 1,02 1,0
1- 106 1,14 1,11 1,08 1,05 1,04 1,03 1,02 1,01 1,0
где А — коэффициент, значения которого
длц различных каналов приведены в
табл. IV.2.
' При изотермическом течении в пря-
мых каналах Лтр подсчитывается по фор-
мулам:
для ламинарного режима
X,rp = A/Re; (IV.63)
для турбулентного режима
/.тр = 0,3164/угЙё
при Re 2,2 • 103 4- 105;
(IV.64)
определяются при средней температуре потока, за опре-
деляющий размер принимается шаг ребер, скорость по-
тока определяется в узком сечении пучков.
При поверхности теплообмена, составленной из про-
фильных листов и омываемой воздухом или продуктами
сгорания при противоточном их движении, для расчетов
рекомендуется применять следующие критериальные урав-
нения [97]:
при шахматном расположении трапецеидальных вы-
ступов
' Nu = O,O83Re0,8 1 (IV.55)
в двуугольных каналах с перекрестным вводом и вы-
водом воздуха
Nu = 0,0 18Re°’8; (IV.56)
в волнообразных каналах (см. рис. IV. 11, а)
Г / d \ 0,62-1 / wd \о,7
Nu = 0,045 1 + 0,9 (-------.
L \ г +6 / J \ V /
(IV.57)
Гидравлический расчет
Суммарное гидравлическое сопротивление ТОА Ар
обычно раскладывается на отдельные составляющие:
сопротивление трению Дртр, местные сопротивления Арм. с,
102
Х,тр== 0,0032 + 0,221/Re0’237 при Re = 105 4- 108.
(IV.65)
Влияние шероховатости учитывается только при
турбулентном течении теплоносителя. Если толщина по-
граничного слоя 6* меньше средней высоты выступов ше-
роховатости А, коэффициент 7.тр подсчитывается по фор-
муле
Ктр = [1,74 + 2 lg (г/А)]~3, (IV.66)
где г — радиус трубы.
При продольном обтекании пучков труб вдоль оси
сопротивление подсчитывается по формулам для прямых
каналов.
При поперечном обтекании пучков труб коэффициент
сопротивления трению подсчитывается по формулам:
для шахматных пучков
+р = (4 + 6,6m) Re-0’28 при st/d < s2 /d;
(IV.67)
+р = (5,4 + 3,4m) Re-0,28 при sx/d > s2/d;
(IV. 68)
для коридорных пучков
7тр = (6 +9m) (S1/d)- °-28Re~°’26. (IV.69)
В формулах (IV.67)—(IV.69) скорость отнесена к уз-
кому сечению пучка, а физические параметры — к /ср;
т — число рядов в направлении потока.
При натекании потока на пучки под углом i < 90°
значения /.тр по формулам (IV.67)—(IV.69) следует умно-
жить на ер
Рис. IV. 14. Коэффициенты сопротивлени я £вх (---)
и ?вых (----) ПРИ резком сужении и расширении труб
круглого сечения:
1 — Re = 3- 103; 2 — Re = 10.10s; 3 — Re = °°
Значения коэффициента £м. с приведены в справоч-
нике [43], для некоторых наиболее характерных месг-
ных’сопротивлений можно принять следующие значения
F v
ъМ. с-
Входная или выходная камера (удар и поворот) 1,5
Поворот на 180° между ходами или секциями , , . 2,5
Поворот на 180° через колено в секциях............ 2,0
Поворот на 180° около трубной перегородки . , 1,5
Поворот на 180° в U-образной трубе................ 0,5
О'ибание трубных перегородок ......... 0,5
Вход в межтрубное пространство 1,5
Вход в трубное пространство и выход из него . . 1,0
Выход из межтрубного пространства..........* * 1,0
Поперечное омывание труб в межтрубном простран-
стве (т — число рядов труб) ..................3m
Коэффициенты местного сопротивления на входе и
выходе из трубы при внезапном расширении или сужении
потока £вх и £вых» которые являются функцией отношения
площадей /х//2 < 1, могут определяться по рис, IV. 14.
Гидравлические сопротивления поверхностей тепло-
обмена из профильных листов при противотоке определя-
ются по формулам [97]:
при шахматном расположении трепецеидальных вы-
ступов
Ар = Еио^рш2, (IV.70)
где — количество выступов по ходу потока; Еи0 —
= Eu/m == 6,9Re~0,25; Eu — критерий Эйлера; т —
количество выступов поперек потока;
в двуугольных каналах (см. рис. IV.11, б) с перекре-
стным вводом и выводом воздуха:
Лрв = °’416-^-Рв^еГ°'2; (IV.71)
A₽r=o’28-wpVrRe^0'^ <iv-72>
где индекс в соответствует воздушной, а индекс г — газо-
вой стороне; LB, Lr — длина листа по ходу воздуха и газа;
в волнообразных каналах (см. рис. IV. 11, а)
7 / 7Q)d \ —о ,3
Ар = 0,635рш24^ ( — ) х
2d \ v J
1+М2
(IV.73)
Определение мощности
для перемещения теплоносителя
Мощность для перемещения теплоносителя через ТОА
определяется по формуле
V = G Др/(3600 • 102рт]н), (IV.74)
где т]н — к. п. Д. насоса (вентилятора).
Мощность на единицу поверхности можно найти по
следующим формулам [97]:
при перекрестном движении потоков в волнообразных
каналах
No = 4,21Ец0рш3 (d/2)/(S1ip), (IV.75)
где ф = 1,05н-1,15 — коэффициент, учитывающий кри-
визну волнообразного канала; Sx — шаг ячеек;
при противоточном или прямоточном движении по-
тока в двуугольных каналах
No = 1,055g д.краЛ (IV.76)
гдсрд. к — коэффициент местного сопротивления двууголь-
ного канала.
По аналогии со степенью регенерации для воздухо-
подогревателей для воздухоохладителей вводится понятие
степени охлаждения
т]охл = (1в — 1в)/(1 в — (IV.77)
где Z,', i“ — энтальпия воздуха на входе и выходе из воз-
духоохладителя; i'w начальная энтальпия охлаждающей
воды.
Обычно Т]охл = 0,87-4-0,95. Температура воздуха
обычно принимается по соотношению t" = t'w + (10-4-
-4-15)° С.
Степень аэродинамического совершенства ТОА харак-
теризуется обычно отношением сопротивления поверхно-
сти теплообмена Дрп к суммарным потерям Дрх в си-
стеме, причем следует стремиться к соблюдению условия
Дрп T/Aps->max при Ap^-^rnin.
Степень компактности ТОА характеризуется отно-
шением F/V, где F и V — поверхность и объем теплообмен-
ника. В рекуперативных теплообменниках ГТУ обычно
FIV = 50-4-250 м3/м3.
В табл. IV.8 приведены основные характеристики
трубчатых воздухоподогревателей некоторых отечествен-
ных и зарубежных ГТУ.
103
Таблица IV.8. Основные характеристики некоторых воздухоподогревателей
отечественных и зарубежных ГТУ
Характеристика Тип ГТУ
ГТ-700-5 НЗЛ (СССР) гтк-ю, НЗЛ (СССР) ГТУ-6, (СССР) ГТУ-10 лкз (СССР) Фирма «Эйр- Прехитер» (США) Фирма «Г аррисон» (США)
Расход воздуха, кг/с 45 86 34 31,6 50
Температура продуктов сгорания, °C 462 502 — 375 448 412,5
Температура воздуха на входе, °C 175 197 — 200 214 271
Давление продуктов сгорания, кгс/см2 1,05 1,05 —- 1,117 — 1,043
Давление воздуха, кгс/см2 3,9 4,43 — 9,2 — 6,11
Мощность установки, А1Вт 4,25 10 — 4,78 5 7
Тип поверхности теплообмена < Пластинчатая (профильные листы) Трубы оре- бренные Пластинчато-ребриста я
Схема течения Противоток Перекрест- ный ток Противоток
Число ходов — — 2 3 — —
Полная поверхность теплообмена, м2 1620 3240 177 1520 1730
Степень регенерации 0,7 0,7 0,65 0,77 0,75 0,807
Сопротивление со стороны газа, % 3,27 3,4 5,55 4,36 — 2,26
Суммарные потери давления, % 5 5 11,05 5,75 2,9 3,53
Объем ТОА, м3 8,75 17,5 0,722 10 13,6 —
Масса поверхности теплообмена 1 1,5 23 — 7,05 — —
Масса теплообменника 19,2 38,7 2,4 19,6 38,8 84,5
Удельный расход металла, кг/кВт 4,53 3,67 4 4,08 7,77 12
Удельная масса, кгс/кг 427 450 261 577 1230 1690
Конструкции теплообменных аппаратов ГТУ
Воздухоподогреватели. Воздухоподогреватель ГТУ
ГТ-700-5 (НЗЛ) выполнен с перекрестным током и разде-
лен на две секции, каждая из которых составлена из трех
пакетов, заключенных в общий корпус, служащий одно-
временно газоходом. На торцах секций установлены полу-
Рис. IV. 15. Противоточный воздухонагреватель ГТУ
ГТК-5
цилиндрические крышки, служащие для компенсации пере-
пада давлений на крайние листы. Подводящий и отводя-
щий воздушные коллекторы для обеспечения герметич-
ности приварены к гребенкам (на входе и выходе) и
к корпусу.
В результате аэродинамических исследований этого
воздухонагревателя были разработаны усовершенствова-
ния, примененные в воздухоподогревателях ГТУ типа
ГТК-5 и ГТ-750-6 (НЗЛ), в которых воздушные коллек-
торы выполнены полуовальными с переменным по длине
Сечением, что позволило уменьшить массу и габариты тепло-
104
обменника (рис. IV. 15), а также снизить потери давления
со стороны воздуха.
Секция воздухоподогревателя ГТУ ГТК-10 {НЗЛ}
составлена (рис. IV. 16) из двух секций воздухоподогре-
вателя ГТК-5. Промежуток между секциями используется
как подводящий коллектор. На боковых сторонах уста-
новлены полуовальные крышки, служащие отводящими
коллекторами. На торцах также установлены полуоваль-
ные крышки, одна из которых служит для подвода воз-
духа, другая является сборным коллектором для отвода
воздуха. В коллекторах установлены направляющие про-
фильные листы, снижающие гидравлические потери и
обеспечивающие равномерную раздачу воздуха по пакетам.
В установке ГТУ-6 применен двухходовой возду-
хоподогреватель из профильных листов (рис. IV. 17).
Воздух проходит два хода по волнообразным каналам,
а продукты сгорания — один ход по двуугольным. Ка-
ждый ход выполнен в виде пакета, закрепленного в отдель-
ном корпусе при помощи гибких компенсаторов. Корпуса
обоих пакетов стянуты болтами и к ним присоединена об-
щая крышка с направляющими лопатками для перевода
воздуха из хода в ход.
Пластинчатые поверхности теплообмена воздухопо-
догревателя фирмы «Эйр-Прехшпер» (рис. IV. 18) соста-
влены из плоских листов, снабженных по обеим сторонам
корытообразными ребрами. Ребра припаяны к листам
медным припоем. По воздушной стороне к ребрам припа-
яна зигзагообразная проволока, связывающая обе стенки
воздушной ячейки, за счет чего обеспечивается прочность
конструкции и повышается интенсивность теплоотдачи
с воздушной стороны. Воздушные ячейки набраны в па-
кеты требуемого размера и приварены к коллекторам
подвода и отвода воздуха. Г аз проходит между воздушными
ячейками по прямым каналам.
Воздухоподогреватель ГТУ ГТН-9-750 {ЛМ3) вы-
полнен в двух корпусах, включенных параллельно как
по воздуху, так и по газу, с противоточным одноходовым
движением теплоносителей (рис. IV. 19). Воздух проходит
внутри трубок, а газ — в межтрубном пространстве.
Поверхность нагрева образована стальными трубами, снаб-
женными внешними продольными ребрами в виде желоб-
ков и приваренными к трубам роликовой сваркой.
Рис IV 17. Воздухоподогреватель ГТУ-6
Рис. IV 16 Противоточный воздухоподогре-
ватель ГТУ ГТ К-10
Рис IV 18 Воздухоподогреватель фирмы «Эйр-Прехитер»
1 — ребро с газовой стороны, 2 — лист, 3 — ребро с воздушной
стороны, 4 — проволока
Рис IV-21 Воздухоохладитель ГТУ‘20
f Воздух
105
Рис IV 22 Воздухоохладитель ГТУ ГТ-100 750-3
Кольцеообразная форма трубного пучка с радиальными
проходами позволяет подводить и отводить газ по всему
внутреннему и наружному контурам пучка, что обеспе-
чивает равномерное распределение потока по поверхности
нагрева. Концы труб завальцованы в двух трубных дос-
ках, к которым примыкают камеры подвода и отвода
воздуха.
В воздухоподогревателе фирмы «Эшер—Висс»
(рис. IV.20) воздух низкого давления течет внутри тру-
бок, а воздух высокого давления — в межтрубном про-
странстве. Трубки закреплены непосредственно в трубных
досках.
Воздухоохладители. В судовых установках преимуще-
ственное распространение получили воздухоохладители
с горизонтальным пучком труб, в которых по принципу
прямотока проходит вода. Примером такой конструкции
может служить воздухоохладитель ГТУ-20 (ЛКЗ) пере-
крестного типа, одноходовой по воздуху и по воде
(рис. IV.21). Поверхность теплообмена образована оваль-
ными оребренными трубками, завальцованпыми в труб-
ные доски.
Промежуточный воздухоохладитель стационарной
ГТУ типа ГТ-100-750-3 (ЛМЗ) (рис. IV.22) имеет ява кор-
пуса, включенных параллельно как по воздуху, так и по
воде. Каждый корпус состоит из двух секций: теплофика-
ционной (первой по ходу воздуха) и циркуляционной.
При отключенной теплофикации воздух охлаждается толь-
ко циркуляционной водой, подаваемой параллельно в обе
секции каждого корпуса.
Поверхности охлаждения обеих секций унифици-
рованы и образованы биметаллическими трубками с на-
ружным шайбовым оребрением, составленными из цен-
тральной томпаковой трубки и наружной алюминиевой
рубашки. К трубным доскам присоединены водяные ка-
меры, верхняя из которых снабжена патрубками для под-
вода и отвода воды.
Для улавливания капельной влаги, выделяющейся
в результате охлаждения воздуха, в корпусе воздухоохла-
дителя установлено сепарирующее устройство жалюзий-
ного типа, вода из которого стекает в корыта, объединяю-
щие отдельные группы секций, а затем отводится в сбор-
ные коллекторы.
Охлаждающая вода подводится к каждому корпусу
с внешней его стороны и через подводящий патрубок по-
ступает в верхнюю водяную камеру. По вертикально рас-
положенным трубкам вода опускается в нижнюю водяную
камеру, откуда по трубкам поднимается вновь в верхнюю
камеру и отводится через патрубок с внутренней стороны
корпуса. Верхняя водяная камера разделена перегород-
кой, разделяющей поступающую и уходящую воду.
Глава V
РЕЖИМЫ РАБОТЫ ГАЗОТУРБИННЫХ УСТАНОВОК
НА ЧАСТИЧНЫХ НАГРУЗКАХ
V.I. РАБОТА ТУРБИНЫ
НА ЧАСТИЧНЫХ НАГРУЗКАХ
Газотурбинные установки обычно эксплуатируются
в широком диапазоне изменения нагрузок, поэтому рас-
четы соответствующих режимов имеют большое значение.
Они дают возможность получить статистические характе-
ристики ГТУ, анализ которых позволяет оценить эконо-
мические показатёли различных ГТУ на частичных на-
грузках.
Расчет режимов ГТУ на частичных нагрузках и опре-
деление ее статических характеристик—'довольнотрудная
задача, поскольку приходится иметь дело с различными
тепловыми схемами, отличающимися числом основных
элементов и последовательностью их соединения. В этих
условиях для получения равновесных режимов работы,
определяющих частичные нагрузки ГТУ, необходимо уста-
новить статические характеристики отдельных элементов
(турбомашин, камер сгорания и теплообменных аппара-
тов), а затем рассмотреть возможности согласования их
работы. Эти вопросы рассмотрены ниже для всех элемен-
тов, кроме компрессора, характеристики которого при-
ведены в гл. III.
Приближенные методы расчета турбин
Расход газа через турбину при отклонении параметров
рабочего тела от их расчетных значений изменяется в ши-
роких пределах. В приближенных расчетах, когда тре-
буется быстро оцепить расход газа через турбину, приме-
няется известная формула Стодолы—Флюгеля *.
GT/GT0 = (р3/р3о) У^Ты)/Тз X
Х ^[1 “ (Рч/Рз)2],7! 1 — (Р4/Рз)о]’
ИЛИ
GT/GT0 = (Рз/Рзо) V Т30iT3 Рт/Рто, (V.1)
где Рт = ]/" 1—лД2— параметр расхода, зависящий от
степени понижения давления в турбине лг (рис. V. 1);
при лт > 6 принимают рт ~ 1.
Решение уравнения (V. 1), полученного при условии
бесконечного числа ступеней турбины и докритического
перепада на каждую ступень, тем достовернее, чем больше
число ступеней в турбине или турбинной группе. Расход
газа через турбину с любым числом ступеней можно опре-
делить по уравнению эллипса, которое можно записать
в виде [79 ]
cT = GnA/Jkx
Рзо ’ J 3
1 Здесь и далее индексом 0 обозначены параметры номи-
нального режима
108
где лкр — степень понижения давления в турбине, отве-
чающая критическому отношению давлений в одной из ее
ступеней. При лкр > лт0 и лкр > лт последний радикал
надо принимать равным единице.
Для использования уравнения (V.2) необходимо опре-
делить лкр, что обычно требует трудоемких вычислитель-
ных операций. Достаточную точность дает использование
графической зависимости лкр от степени понижения давле-
ния на расчетном режиме nj0, числа ступеней z и средней
степени реактивности по проточной части (рис. V.2) [79].
Степень реактивности здесь учитывается использованием
некоторого приведенного числа ступеней znp = z/(l — рт),
где z —' действительное число ступеней в турбине; рт —-
средняя степень реактивности ступеней турбины. При
построении графика на рис. V.2 принята равномерная раз-
бивка теплоперепада по ступеням турбины, поскольку
погрешность, вносимая этим допущением, обычно невелика.
Уравнения (V.1) и (V.2) не учитывают влияния частоты
вращения ротора на расходную характеристику турбины.
Во многих случаях эти допущения не приводят к значитель-
ным погрешностям в определении расходов, а изменение
расхода при отклонении частоты вращения не превышает
8-10%.
В случаях, когда требуются более точные результаты,
влияние частоты вращения можно учесть некоторым коэф-
фициентом kn. Тогда пропускная способность турбины
. G\ = GT0 (Р3/Р30) У^Тзо'Ts (Рт/Рто^п- (V.3)
Коэффициент kn можно найти с помощью двух соста-
вляющих k' и k”, характеризующих влияние параметра
х = и/с0 на расход через одну ступень и ряд ступеней со-
ответственно, причем kn = k' k".
Для определения k' рекомендуются формулы [79]
при средней реактивности ступеней 0—0,3
k' .= 1 4- 0,29 U.r !/Znp — 0,55) х
X Los |7х + AL'l 2L1 + 0,311; (V.4>
I. L\ xopt / 2 J )
при средней реактивности ступеней 0,3—0,6
k' = 1 +0,11 ^лт /гпр — 0,55J [cos (хл) + 1],
(V.5>
где
- = КЕА(2Ят)/]Л£ A(2tfT)]opt.
Коэффициент k" при любой степени реактивности
ступеней определяется по формуле
Г = 0,11 (лт 1/гн₽ — 0,55) [cos(xji) + 1]. (V.6)
В уравнениях (V.4)—(V.6) принято, что xopt = 0,5
для активных ступеней и х()р, = 0,75 — для реактивных.
Поскольку уравнения (V.I) и (V.2) не учитывают вли-
яния частоты вращения, ими удобно пользоваться для опре-
Рис. V.I. Параметр расхода турбины
деления степеней понижения давления в турбинах, рабо-
тающих в составе одной турбинной группы.
Если турбинная группа состоит из двух турбин, имеем:
Gt. b/Gt. во = (Рзв/Рзво) ^Т’зво/^'зв Рт. вФт. вО’
GT. h/Gt. но == (А’зк/Л’зьо) УТгна/Тзн Рт. н/Рт. но-
Учитывая условия неразрывности для рассматривае-
-мой турбинной группы, можно написать
Ят. В 1 / 1 -- 7/г. вЛт. В Рт. в _____ Рт. н
ят. во у 1—Ят. воПт.во рт. во Рт. но
(V.7)
С помощью этого уравнения для любого принятого
значения лт. в можно найти лт. н. Такое определение
удобно проводить графическим методом с помощью номо-
граммы (рис. V-З), построенной по уравнению (V.7).
Из уравнения (V.7) видно, что распределение степени
понижения давления по турбинам зависит только от от-
ношения давлений на расчетном режиме и не зависит от
уровня начальной температуры газа.
Аналогичный метод определения степени понижения
давления может быть получен и при числе турбин больше
двух. В этом случае для двух соседних турбин
Лт/ 1 /~ 1 7fT/T]T^ Рт/ _____________ Рт (14 Ъ
ят1о V 1 — Ят/оЛт/о Рт‘° (1+1)0
Задаваясь степенью понижения давления первой или
последней турбины, последовательным использованием
уравнения (V.8) или номограммы на рис. V.3, можно уста-
новить этот параметр по всем турбинам рассматриваемой
турбинной группы.
Если в составе турбинной группы имеются промежу-
точные камеры сгорания, то в уравнение для нахождения
распределения степеней понижения давления по турби-
.нам войдет отношение температур рабочего тела. Действи-
тельно, для двух турбин с камерой сгорания между ними
Тзво/Т31!О пт, в в ___ рт, н .у
Тзв/Т311 Лт. во Рт. во Рт. но
Тогда, приняв значение лт. Е, для заданных темпе-
ратур рабочего тела по уравнению (V.9) находятся Рт. н,
а затем с помощью рис. V.1 определяют лт. н.
При числе турбин больше двух расчет ведут последо-
вательно от одной турбины к другой. По полученным зна-
чениям степени понижения давления jtT/ определяют об-
щую степень понижения давления для всей турбинной
группы лт. общ = лт1лт2 . . . лгп и соответственно началь-
ное давление процесса расширения1 р3 = пт. общРт-
При наличии потерь давления между турбинами на-
чальное давление при трех, например, турбинах может быть
определено по формуле
Рз ~ .{ f ЯТ. И (Ро Арвых) ~Ь Арт. С —т. н] Лт. с
+ Арт. в-т. с} лт. в, (V.10)
или
Рз РоЛг. вЛт. сЛт. И (1 “Ь ^ВЫх)/[(1 ~ Вт. в-т. с) X
Х(1-|Т.С-Т.н)1, (V.11)
где Дрт в_т с, Дрт с_т н и Лрвых — потери давления по
тракту между турбинами высокого и среднего давления,
среднего и низкого давления и в выходном тракте соответ-
ственно; § — коэффициенты гидравлических потерь по
соответствующим трактам.
При наличии гидравлических сопротивлений между
турбинами вместо уравнения (V.8) надо пользоваться урав-
нением
1 Tj Г| Tt Рт/ (1 £.Tio) Рт (/ /)
I —- Нты^т/о Рт£о (I — Рт (£-1-1)0
(V. 12)
жения давления на расчетном режиме лт0 и приведен-
ного числа ступеней хпр
Приведенные уравнения позволяют предложить сле-
дующий порядок расчета турбинной группы:
I) произвольно принимают ряд значений степени
понижения давления первой или последней турбины;
2) по принятому значению лт с помощью уравнения
(V. 12) или номограммы на рис. V.3 (при отсутствии про-
межуточных камер сгорания) или с помощью уравнения
(V-9) (при наличии промежуточных камер сгорания)
определяют последовательно степени понижения давления
для каждой из турбин;
1 При этом предполагается, что потери давления между
отдельными турбинами (отсеками) равны нулю.
109
1
Рис. V.3. Номограмма для определения распределения степени понижения давления в турбинной группе
3) определяют общую степень понижения давления
па всю турбинную группу;
4) по какому-либо из уравнений расхода (V. 1)—(V.3)
находят расход газа через турбинную группу.
Расчет характеристик одноступенчатой
турбины
Основные соотношения. Уменьшение массовых и габа-
ритных показателей газовых турбин обычно обеспечива-
е!ся сокращением числа ступеней при росте теплоперепада
на каждую из них. Поэтому в практике газотурбострое-
ни ! широкое применение находят малоступенчаше тур-
онны в гом числе одноступенчатые.
Параметры 1 лс и лр такой турбины могут быть опре-
делены через лт с помощью степени реактивности. По-
скольку
Н-гО = срг (Т’о — Г2/); ^сО ~ срг У о* 1 и) и
^ро ~ срг {Т— T2t),
то после некоторых преобразовании можно написать:
= (V 13)
лр= (1 +ртл^гЯтртг; яс= [1 ~(1 -РгЖГ1/тг-
(V.14)
Здесь mr = (k — i)/k; Н^=1 — пт тр— относительная ра-
бота расширения в турбине. Этот параметр связан с газо-
1 Здесь и далее индекс о соответствует сотовому венцу,
индекс р — рабочему
110
динамическими функциями потока зависимостями [691
= - l)/(k -J- 1);
Ят- [М2 (k — i)/2]/[l +М2 (k— 1)/2].
Величина УЯт представляет собой относительную
скорость потока.
Относительная работа венцов:
У = (1 Рт) У', \ = Рт^тяГГ-
Расходная характеристика и к. п. д. Расход газа
через турбину, выраженный через параметры рабочего
тела на среднем диаметре,
GT = GTo (Ро/Роо) (₽с/₽со), (V-15)
где рс — параметр расхода, зависящий от степени пони-
жения давления в сопловом венце:
= ф2Йс =
(1--ф2Йс)лс
_У Ф2 п -рт)ят П -(1 -рт)ят]1/Шг ... ..
[1 — ф2 (1 — рт) Ят] лс
где ф — коэффициент скорости соплового венца.
График изменения |3 представлен на рис. V.4.
Степень реактивности на любом режиме можно полу-
чить с помощью уравнения расхода для соплового и рабо-
чего венцов: = wjvlv2. Поскольку
Wj Рт fcV2 V.
с2 I ф2 (j _ рт) J ’
V2 ____ f Pl \ _ 1—i|)2mr
Ж" — \рГ J ' ПР ’
где принято (п — 1)/п = ф2 (k — V)/k, то для одноступен-
чатой турбины на любом режиме будет справедливо урав-
нение
“/Ср
<р К1 — рт
V , . , , рт___________
COS СУт I “F Sin* "F —o~~7i ...; •—
uub U'1 / 1 1 ф2 (1 — pT)
' djc \2 sin2/ т,.— ,2 I)—фг]
. d2lp ) фа sinaf32 Н“ РЛ
(V.17)
где Ф — коэффициент скорости рабочего венца; /с и 1Р —
длины лопаток; fc и fp — площади проходных сечений
соответствующих венцов.
Если известны параметры рабочего тела на любом
режиме р*, То и р2, задана частота вращения ротора п,
то с помощью уравнения (V. 17) можно найти рт. Для
этого удобно воспользоваться графической зависимо-
стью рт = f (лт, и/с0, построенной по (V. 17) для кон-
кретной геометрии турбины.
Одноступенчатые турбины для увеличения распо-
лагаемого перепада и к. п. д. часто снабжаются диф-
фузором. В этом случае давление за проточной частью
р2Я на переменных режимах непостоянно, а зависит
от работы диффузора. Если давление за диффузором,
определяемое сопротивлением выходного тракта, обо-
значить р2 (см. рис. II.9), а располагаемый перепад
найти по р2Д, т. е. Ято = cpr7j[ 1 - (p//pM)~'”rJ, то
все полученные соотношения для одноступенчатой
турбины будут справедливы
Расход рабочего тела через диффузор 6Д =
= сд/д/и2=сд/др2/(7?72). Поскольку Т2=Т2Д[1 +
+ (^-1)Ад], то отношение расходов
Од — GpJGp,, ~
срР-2Тоо(1 -(Р2Мо(1 -фЧП1 +(11дГ- О/Ч. О
с^20Т0 ( 1 - Ч’Ч) ( 1 - А>)[ 1 + ( ЯД Г ~ 1 ) /Ч
(V.18)
где Лд = р21р2Я — степень повышения давления в диф-
фузоре; т)д — к. п. д. диффузора; сд — скорость рабочего
тела на выходе из диффузора.
Использование уравнения сплошности Од/Одо =
= GT/GT0 позволяет написать
?2д =Р2{(1-Пд) + [<Г-(1-Т)д)]0^-Х
х^5)-1/Л Г00 (1 — ф2Йс)о (1 — ф2Йр)0 Т]дРто| 1/,7’Г
V Т0 (1 — ф2йс)(1 — ф2Лр)г|д0рт J
(V.19)
где лд = р0/р2 — степень понижения давления в турбине
по давлению за диффузором.
В уравнение (V. 19) вошло отношение скоростей за
диффузором Ср!см. Принято, что Ср/см га с2/с«о, причем
+ и| — 2о>2И2 cos Рг
('^1 + U2 — 2а,2а2 COS Рг)о’
где
а-.'2 = ф ^2ртЯт0 + [2Ят0 (1 _ рт) ф2 4-Ы2 —
— 2/2Ят0 (1 — рт)ф2 uj cos a(V.20)
Уравнения (V. 19) и (V.20) позволяют на любом режиме
уточнить давление р2Д и определить характеристики тур-
бины с учетом диффузора. Поскольку эти уравнения со-
держат параметры турбины рт, Ят0, /гс и Яр, расчет про-
точной части с диффузором должен проводиться итераци-
онным методом.
Для определения к. п. д. одноступенчатой турбины
на любом режиме справедлива формула (11.67), причем
коэффициенты скорости ф и ф в этом уравнении должны
быть найдены с учетом отклонения обтекания профилей
от оптимальных условий, т. е. с учетом возможного по-
явления углов атаки в направляющей и рабочей решетках.
Порядок расчета. Рекомендуется следующий порядок
расчета одноступенчатой турбины на частичных на-
грузках.
1. Принимают новый режим работы турбины, который
задается новыми параметрами рабочего тела и TJ и ча-
стотой вращения ротора п (об/мин).
2. Для этого режима с помощью уравнения (V. 17).
или по графической зависимости, построенной для данной
турбины, определяют степень реактивности рт. Коэффи-
циенты <р и ф при этом можно считать постоянными.
3. С помощью уравнений (V. 14) находят лс и лр.
Для проверки правильности определения лс и лр можно
использовать уравнение лслр = р*/р2 = лт.
4. Определяют все элементы треугольников скоростей
и находят угол атаки i для рабочего венца. Если выбран
профиль рабочей лопатки, то по графику для этого про-
филя ф = f (г) устанавливают новое значение ф. При зна-
чительном отклонении ф от значения на номинальном ре-
жиме следует вернуться к определению рт по новому зна-
чению ф.
5. По уравнению (V.15) находят новый расход рабо-
чего тела, а затем определяют крутящий момент и мощность,
турбины. К. п. д. турбины находят с помощью уравнения
(11.67).
При наличии в турбине диффузора порядок расчета
сохраняется, но при этом необходимо использовать итера-
ционный метод. Сначала надо задаться давлением за
проточной частью турбины р2Д, а затем это давление опре-
делить по уравнению (V. 19), характеризующему работу
диффузора. По найденному значению р2Д расчет турбины
необходимо повторить.
Расчет характеристик многоступенчатой
турбины
Приближенный метод определения распределения дав-
ления по проточной части турбины. Работу i-й ступени
турбины определяют следующие характеристики
111
(рис. V.5): степень понижения давления в венцах ступени
по статическим давлениям (лА = pOi/pit-; л' £ = Рц/р^)
и по полному начальному давлению ^лс- = Рр^Рц\
яр/ = Pli^P2i)> располагаемые перепады по статическим
параметрам рабочего тела (/ic0[. = с T0(hcl; hp0- =
= cpr^Ij^pi) и 110 полным параметрам (йс0(. = cpr'Poi х
X hcl-, hci, hpOi сргТц11р[).
Рис. V.5. Работа z-й ступени многоступенча-
той турбины в i—s-диаграмме
Скорость потока на выходе из соплового венца
CU = ]/'2cpr7’oi +ММ> (Z-lj/C^pr^Oz)]-
Тогда абсолютный расход газа через сопловой венец
а _f Poi У'Р^с,+<Р/С2(/-1)/(4йрг7’ог)
Ci 1 (1-фК-Х ;
(V.21)
относительный расход газа
Gci Pai 1 / TOjO х
Gcio Poio ’ Лн
X 1 f Q ~ <Pz^cz)o ясгО
' (₽{(Лс(о+(р?ОС2 (Z—1) o/(4cpr7’ozo) (1 ~~ <№«) nci
(V.22)
Можно показать, что разность
officZ + Tjc2 (Z—1)/(4срЛог)_ д
[ф?^С1 +Ф?0с2 (Z—l)/(4cpr7’oz)]o Tzo^czo
есть величина достаточно малая [12], т. е. без большой
погрешности можно принять
____Ф^с< +Ф/С2 (Z—i)/(4Cpr7"oz) ~
[фР'сг +Ф?0с2 (Z-l)/(4Cpr7’oz)]o <pUcZO
Поэтому с достаточной для расчета точностью при-
нимают
Gcz/Gczo = (Poz/Pozo) / ЗД4 (V-23)
где
Xcl = ₽cz/₽czo- ₽cZ = УФ2^7[(! - <pXz) Я«]-
Аналогично можно показать, что для рабочего
венца [12]
^Xz+^M/(4cprM Ж» .
[<z +'P>?z/(4cpr7’iz)]o <Szo ’
и уравнение расхода будет иметь вид
Gpz/G₽zo = (Piz/Pzzo) (V-24)
где
х'р = ₽pz/₽pzo; ppz = У<z/[(l - <z) Szl-
Полагая, что = Gpt, получим
Xpi/-XCi )
или
Таким образом, для двух соседних венцов справед-
ливо уравнение
л , , , , Ч1—0,5q>2m„
^pz = ^z("cz/"czo) 1 Г> (V.25)
а для следующей пары венцов
, , z / , , ч1—0,5ф2тп
хс (Z+1) = xpi K-Hzo) ‘ Г- (V.26)
Если расчеты турбины ведутся при постоянной тепло-
емкости газа Срг, то, приняв <рг « ч|?г, можно получить
1 — 0,5<р?тг « 0,89.
При расчете распределения степени понижения дав-
ления по венцам многоступенчатой турбины по уравнениям
(V.25) и (V.26) удобно воспользоваться вспомогательными
графиками, определяющими коэффициент Р' (см. рис. V.4)
и (л /лф)0'89 (рис. V.6). Для облегчения расчетов можно
также пользоваться номограммой (рис. V.7), которая со-
стоит из четырех квадрантов. В первом квадранте по за-
данному л находят (л'/лд)0,89, во втором — произведе-
ние X' (л'/лд)0’89, в третьем — произведение Х'$’, в чет-
вертом — по параметру расхода Р' находят степень пони-
жения давления в искомом венце. При расчете следует
иметь в виду, что считаются известными степени пониже-
ния давления на расчетном режиме и коэффициенты скоро-
сти фиф.
112
Последовательность определения степеней понижения
давления в венцах турбины следующая.
1. Принимается степень понижения давления на пер-
вом (сопловом) венце л'р
Рис. V.6. Функция степени понижения давления
2. По nci находят параметр расхода Pcj (по рис. V.4
или V.7).
3. Для первого венца находят величину Хс1 = ₽cj/Pci0
(третий квадрант номограммы).
4. Определяют величину (яс1/л'1о)0’89 (по рис. V.6
или по первому квадранту номограммы).
7. По известной функции определяют степень
понижения давления во втором венце (по четвертому
квадранту номограммы или по рис. V.4).
Расчет степеней понижения давления в остальных вен-
цах аналогичен изложенному. Расчет графическим мето-
дом показан на рис. V.7 стрелками, а последовательность
операций’ указана цифрами.
Произведение полученных степеней понижения давле-
ния в венцах позволяет получить общую степень пониже-
ния давления турбины: лт = . л'п.
Определение распределения давления по проточной
части турбины с учетом скоростной составляющей. Изло-
женный выше метод расчета в силу принятого допущения
содержит некоторую погрешность. Обычно для всех рас-
четов, связанных с анализом как статических, так и дина-
мических характеристик, эта погрешность оказывается
приемлемой. Однако, если появляется- необходимость
в большей точности, можно воспользоваться другим мето-
дом расчета многоступенчатой турбины. Если выразить
скорость и объем через полные параметры на входе в ве-
нец, то расходы газа через г-й сопловой и рабочий венцы
будут определяться уравнениями:
= (Г2 V*r)
(V.27)
Рис. V.7. Номограмма для определения распределения степеней понижения давления
5. Находят А'; [с помощью уравнения (V.25) или где
по первому и второму квадрантам номограммы].
6. По найденному значению X'j и известному на
расчетном режиме параметру расхода Р'щ для второго
(рабочего) венца находят (3'j = (третий квадрант
номограммы).
8 Л. В. Арсеньев и др.
₽с(- = У ф^С(./[(1 - ф>с<)ясЯ;
₽Р1- = УЖло - ^Р<) ЯР.Ь
из
Отнеся эти расходы к соответствующим значениям
на номинальном режиме, можно получить:
Gcf/GciO = (Poi/Poto) ’yr'TOio/TOiXcl’
Gpi/Gpio = (Рц/Рцо) УТцо/тиХр1’
где Xcl — Pcz'/Pczo> Xpt = Ppz/Pp/o-
Условие равенства' расхода рабочего тела через со-
седние лопаточные венцы позволяет написать
Xpt- ^ШУн/т'0!
^С! ЯС10 (ярг/яРг)о У EU0/E0l0
Входящие в уравнение (V.28) отношения Т^/Т^
и лр£/л г можно определить через параметры соплового
венца, воспользовавшись уравнениями связи [69]:
(V.29)
1 _ ф2£ k/(k-l)
----7------‘-Х > (V.30)
Ba=(wilcifi = 1 + (“e/ci)i - 2 (%/cj); cos au. (V.31)
Тогда для двух соседних венцов [14]
2Срг = Xci (Лсг/Лс/о) (Тсг/Дсго)» (V.32)
где
k
1 — ф2/г . 1 k~1 ~'----------------—
£ -----------------1 С( 2_
Легко показать, что для следующих двух соседних
венцов (рабочего венца z-й ступени и соплового венца
i + 1-й ступени) имеет место уравнение
хс <i+D = xpi (Лрг7яРц>) (Epi/Epio)’ (V.33)
где
BPi = = 1 + («РМ)? - 2 («рДс>2)£ cos р2г
С помощью уравнений (V.32) и (V.33), приняв степень
понижения давления в первом сопловом венце, можно
определить распределение давления по проточной части
турбины. Так как в исходные уравнения входит функция В,
зависящая от отношения скоростей в венце u!clt которое
на первом этапе расчета неизвестно, то распределение да-
вления по проточной части ведется итерационным методом.
Определение степеней понижения давления в венцах
по статическим давлениям производится с помощью урав-
нений:
n'pi = npiEci’ яс (Н-D = яс (/+1)^рР fV-34>
где
fe/(fe—1)
—
Для облегчения вычислительных операций при расчете
могут быть использованы вспомогательные графики
(рис. V.8 и V.9). Рекомендуется следующий порядок рас-
чета.
1. Принимается степень понижения давления в пер-
вом сопловом венце лС1, по которой находят параметр
расхода рс1 с помощью рис. V.4 или по формуле
Pel У<1/[(1 __ ^cl) лс11 •
Коэффициенты скорости ср и ф здесь и далее на первом
этапе расчета принимаются по номинальному режиму.
2. Определяют величину XC1 = Pci/₽cio- С помощью
уравнений (V.29)—(V.31) или рис. V.8 и V.9 находят £с
и FCi- Здесь величина ВС1 соответствует параметрам номи-
нального режима.
3. По формуле (V.32) находят величину хр1, по кото-
рой определяют параметр расхода рабочего венца первой
ступени рр1 = XD1₽pl0. •
4. По известному значению рр1 с помощью рис. V.4
определяют лр1.
5. По найденному значению лр1 в последовательности,
изложенной выше, находят лС2 и так далее до последнего
венца.
6. Для определения общей степени понижения давле-
ния в турбине и распределения давления по ее проточной
части определяют степени понижения давления в венцах
по статическим давлениям, для чего используют уравне-
ния (V.34) или номограмму на рис. V.9, б. Общая степень
понижения давления в турбине = rtclnpln'2 • • • Прп-
7. Приняв pg или р2, находят давления между вен-
цами. Для турбины, расширение в которой происходит
до атмосферного давления, величина р2 известна. Тогда
начальное давление pfi = лтр2.
При наличии за турбиной диффузора давление за про-
точной частью р2Д определяют по методу, изложенному
выше.
8. По полученным данным выполняют расчет всех
параметров рабочего тела в проточной части, что дает
возможность найти углы атаки для всех профилей лопаток
114
и уточнить коэффициенты ср и ф. Здесь же уточняется и
величина В для отдельных венцов. Затем можно присту-
пить ко второму этапу расчета с новыми значениями ф,
ф и В. Последовательность этого расчета аналогична.
ь
to
и
!,
ie
з-
t.
х
!-
О
Рис. V.9. Вспомогательные
номограммы: а — функция Е; б — функция F
бочего тела по проточной части турбины. Эти перетечки
как для направляющих, так и для рабочих лопаток можно
оценить по формуле GyT = GyT0 (Grz/Gri-0), где GrJ- — рас-
S)
1,01,1 1.5 1.5 1,7 1,9Я
1,0 1? 1fi 1,6 1,8 Л
0,800
’ 10 12 1А 1,6 7,8 Л
0,1 0,15 0,2 0,25 0,58 ’ ’ ’ ’
е
л
э
с
>
I
>
Основные показатели турбины
Внутренний к. п. д. турбины зависит от потерь рас-
полагаемой работы в проточной части. На режимах ча-
стичных нагрузок эти потери меняются, поэтому меняется
и к. п. д. турбину. Деформация треугольников скоростей
по венцам турбины приводит к появлению углов атаки
при натекании потока рабочего тела на лопатки, что вы-
зывает изменение коэффициентов скорости ф и ф. Влияние
углов атаки i на величины <р и ф подробно рассмотрено
в и. II.2. Здесь можно рекомендовать эмпирическую фор-
мулу, полученную в КАИ [30]:
ф = ф0 У1 — Л I2, (V.35)
где i = (Р1о — Р1)/Рю — относительный угол атаки; ф0 —
коэффициент скорости, соответствующий условию, при
котором угол атаки отсутствует; А — постоянный коэффи-
циент; следует принимать А = 0,8 при положительных
углах атаки и Л = 0,15 — при отрицательных.
Формулу (V.35) рекомендуется применять в следую-
щих диапазонах параметров ступени и критериев М и Re:
Г= (+0,5)-Н—1,25); М<0,9; Re = (0,5 + 2,5) 106;
1 = 0,6 -0,7; (гвх/Ь0) =3 + 4%.
Значение ф0 на частичных нагрузках определяется
режимными факторами, и, в частности, основными кри-
териями подобия Re и М. Обычно частичные нагрузки свя-
заны с уменьшением Re и М по сравнению с номинальным
режимом. Поскольку для номинального режима современ-
ных газовых турбин характерны высокие значения Re (RaA
1,0-106), при которых имеет место автомодельность про-
цесса обтекания решетки, то при определении коэффици-
ентов скорости по уравнению (V.35) обычно можно при-
нимать значение ф0, соответствующее номинальному ре-
жиму. В случаях, когда частичные нагрузки характери-
зуются значительным изменением Re, выходящим за гра-
ницы автомодельности, для определания ф0 следует ис-
пользовать зависимости, приведенные в п. II.2.
При изменении параметров рабочего тела на режимах,
отличных от расчетного, будут меняться и перетечки ра-
8*
ход рабочего тела через венец, для которого определяются
перетечки. Потеря располагаемой работы для каждого
венца, связанная с перетечками рабочего тела,
Айзаз t — 0 ((jri/GriQ). (V.36)
Для определения внутреннего к. п. д. турбины на
частичных нагрузках можно рекомендовать следующий
порядок расчета. С помощью одного из изложенных в на-
стоящем параграфе методов находят распределение общей
степени понижения давления по венцам турбины. Про-
изводят полный поступенчатый расчет проточной части
итерационным способом. В первом приближении значе-
ния ф/ и ф; принимают по номинальному режийу и находят
по всем венцам углы атаки и другие параметры. Затем уточ-
няют значения <рг и ф/ и выполняют расчет проточной
части во втором приближении, которого обычно бывает
достаточно.
Затем находят потери располагаемой работы в про-
точной части, включая потери на перетечку в радиальных
зазорах венцов [по уравнению (V.36)], а также потери
на трение и вентиляцию. В заключение рассчитывают вну-
тренний к. п. д. турбины
п п
cos — и2с3 cos а2)/ — Ah3a3 t-
= —-----------------77-------m.-x ‘'°’-------- • (V-37)
В тех случаях, когда расчет характеристик турбины
на частичных нагрузках выполнен приближенным мето-
дом (без определения давлений по проточной части) или
когда достаточно приближенной оценки внутреннего к. п. д.
турбины, можно воспользоваться обобщенной зависимо-
мостью к. п. д. турбины от параметра
х = х/х0 ~
Для определения к. п. д. одноступенчатой и много-
ступенчатой турбин на частичных нагрузках можно
115
у
использовать графические зависимости (рис. V. 10), которые
хорошо аппроксимируются уравнением [79]
< % = Лто (2.0х —х2). (V.38)
Уравнение (V.38) предполагает максимальное зна-
чение к. п. д. турбины на расчетном режиме. Это обычно
имеет место для стационарных и большинства транспорт-
Рис. V.10. Изменение к. п. д.
турбины [79]:
1 — без использования выходной
скорости; 2 — с использованием вы-
ходной скорости
ных турбин. В том случае, когда на номинальном ре-
жиме Т]то < Чт max, можно воспользоваться уравнением
где
Пт ЛтО (2,Охор4 хор()/(2’0л:Ор( xopt)o’ (V.39)
Здесь индекс 0 соответствует номинальному ре-
жиму турбины, a opt — режиму Лт шах.
Момент турбины при любом режиме ее ра-
боты
М М ^т^О^ЛИтПиех .
МТ = Л4ТО -------------------, (V.40)
GT07 О0' ’тОГ!г1тОтЬлех 0
а с учетом зависимостей (V.38) и (V. 1)
Мт = Л4ТО 1/А (2,°_~х),
Р00 V Н-го Лмех о Рто
(V.41)
откуда следует, что момент турбины изменяется пропор-
ционально начальному давлению рабочего тела и в мень-
шей степени зависит от его температуры и противодавления.
Для транспортных установок большое значение имеет
изменение момента турбины в зависимости от частоты
вращения. Для этих условий при сохранении параметров
рабочего тела без изменения приближенная зависимость
для крутящего момента имеет вид
Л4Т = Л4ТО [2,0 (п/п0')] Лмех/Лмех о, (V.42)
откуда следует, что максимальный момент имеет место
при остановленном роторе (Л4шах « 2Л4т0т]мех/г|мех 0), а ма-
ксимальная частота вращения ротора — при полной
разгрузке («тах « 2га0).
Для одноступенчатой осевой турбины при докритиче-
ском расширении и постоянной степени реактивности
момент на любом режиме [53]
Мт = Мт0[ 1 + (“о - “/G)/(«lu0 - с2«о)] G2T. (V.43)
Максимальный момент одноступенчатой турбины при
заторможенном роторе
^ттах = ЧоО + ’КоК, (V.44)
где сид = (с1ы0 — с2и0)/и0 — коэффициент циркуляции
[53 ].
Эффективная мощность турбины при произвольном
режиме работы
А. (2,0-х).
Рто Пиех о
(V.45)
Механический к. п. д. турбины на частичных нагруз-
ках [79]
Пиех— 1 (1 Лмех о) (Л^то/^т) (геМо)°’ (V.46)
где а= 1,5-ь 1,8, причем большее значение принимается
при наличии за турбиной редуктора.
V.2. РАБОТА КАМЕРЫ СГОРАНИЯ
И ТЕПЛООБМЕННЫХ АППАРАТОВ
НА ЧАСТИЧНЫХ НАГРУЗКАХ
Камера сгорания
Одним из основных элементов ГТУ является камера
сгорания, обеспечивающая нагрев рабочего тела до тем-
пературы, необходимой для той или иной нагрузки уста-
новки. Уровень этой температуры на установившихся
режимах определяется уравнением теплового баланса
и зависит от коэффициента полноты сгорания т]к. с.
Величина Лк. с зависит не только от режимных фак-
торов, вида топлива и состояния проточной части камеры,
но и от особенностей ее конструкции.
_ opt
Рис. V. 11. Изменение коэффициента полноты сгорания камер
I сгорания
Обычно закон изменения Лч. с определяют экспери-
ментально при испытаниях камеры или моделируют при
подобных конструкциях.
В качестве примера на рис. V. 11 представлено изме-
нение т]к. с Для двух различных по конструкции камер
сгорания в зависимости от коэффициента избытка воздуха
а = GB/(GTOnL0). Одна камера сгорания предназначена
для работы при значительных коэффициентах избытка
воздуха (кривая 1), что обычно имеет место в установках
с регенерацией, другая — при относительно низких а
(кривая 2). Отклонение а от расчетного значения (обычно
совпадает с %pt) заметно понижает Лк с, особенно при
116
уменьшении а. При значительных отклонениях а
как в сторону обогащения состава смеси (малые os), так
и в сторону обеднения (большие а) возможно появление
неустойчивого горения и прекращение горения (бедные
или богатые срывы). В эксплуатационном диапазоне
нагрузок неустойчивое горение недопустимо.
Графическая зависимость (рис. V. 11) позволяет для
любой температуры газа Т3, необходимой для обеспече-
ния той или иной нагрузки установки, определить расход
топлива в камере сгорания ГТУ.
Другой важной характеристикой камеры, влияющей
на общие показатели установки, является ее гидравличе-
ское сопротивление. Общие потери давления в камере Лрк. с
определяются потерями на трение изотермического по-
тока Дртр из-за наличия гидравлических сопротивлений
(завихрители, каналы и т. д.) и потерями от нагрева
движущегося газа Дрн. Таким образом, Дрк. с = Дртр +
+ Дрн. Рассмотрим определение этих потерь на частичных
нагрузках.
Камера сгорания представляет собою сложную си-
стему местных сопротивлений с последовательным и па-
раллельным распределением потока. Ниже принято, что
потери трения изотермического потока отнесены к одному
характерному сечению камеры и выражаются некоторым
обобщенным коэффициентом сопротивления £тр. Тогда,
если считать характерным сечение на входе в камеру,
потери на трение при любой нагрузке Дртр = £трр2с|/2.
Отнеся эти потери к значениям на номинальном режиме
и используя уравнение сплошности, получим
дРтр — Дртро (Т21Т23) (Р20Ф2) (Gb/Gbo)2- (V.47)
Потери давления, вызванные подогревом рабочего
тела в камере сгорания [75],
ЛРн = Р2(«2/2)>с (Гз/Т’г-!), (V.48)
где к — опытный коэффициент, учитывающий неравно-
мерность полей скоростей и температур в камере сгорания.
Если принять к = const на всех нагрузках, то с уче-
том уравнения неразрывности можно написать
Л л = Лл Ту Р20 ( GB \2 Г3/Т2 — 1
Дрн Дрио гр п \ G 1 Т /Т 1 ’ (*.49)
1 20 р2 \ '-'ВО / 1 30/J 20 — 1
Таким образом, общие потери давления в камере
сгорания на любом режиме
л л ( т2 , Т3 — Т2 \ лк0 / GB \ 2
ЛРк. с — Дрк. со ( Ki ---F к2 ур----щ— ) —— (.
\ 1 20 1 30 1 20/ -~к \ '-'ВО /
(V.50)
Здесь к, = Дртр 0/Дрк. с о — коэффициент, харак-
теризующий потери на трение, выраженные в долях
от общих потерь в камере; «2 = дРно/дРк. е о — коэф-
фициент, характеризующий потери от нагрева в долях
от общих потерь. Коэффициенты Kt и к2 зависят от кон-
структивных особенностей камеры сгорания и для совре-
менных стационарных и транспортных установок состав-
ляют: = 0,654-0,7; к2= 0,3^0,35.
В тех случаях, когда потерями давления, связанными
с нагревом воздуха, можно пренебречь, общие потери
определяются только потерями на трение и для любой
нагрузки находятся по формуле
Регенератор
Заметное влияние на экономичность ГТУ при ча-
стичных нагрузках оказывает регенератор. Это влияние
характеризуется температурой воздуха на входе в ка-
меру сгорания Т5, которая на любой нагрузке опреде-
ляется уравнением Т& — Т2-^ г (Ti — Т2). Температуру
воздуха Т2 на входе в регенератор и газа Т3 находят по
соответствующим уравнениям компрессора и турбины,,
а степень регенерации г должна быть определена на
каждой нагрузке. Для этого используют общее уравнение
теплопередачи Q = kF® (где F — площадь поверхности
теплообмена; О — средняя разность температур между
газом и воздухом) и уравнение количества теплоты со
стороны воздуха Q = срвОв (Т5 — Т2). Приняв 0 =
= Т4 — Т5, можно получить известное уравнение
F — (cpBGB/k) [г/(1 — г)].
Это уравнение, написанное для двух режимов, дает фор-
мулу [57 ]
Г = Г0/[г0 -f- (1 — ro) (GB/GBo) (kg/k)]. (V.52)
Приняв для коэффициента теплопередачи прибли-
женную формулу k = агссв/(аг + <хв) и считая, что
коэффициент теплоотдачи с газовой стороны <хг и со сто-
роны воздуха ав определяется уравнением вида а =
= 0,023 (X/d) Re°’8Pr0,4, после:ряда преобразований и
упрощений, выполненных в работе [57], можно получить
уравнение
г = г0/[г0 + (1 - г0) (GB/GBO)0-2]. (V.53)
Это уравнение может быть использовано для пластин-
чатых регенераторов, которые в настоящее время при-
меняются наиболее часто.
Нетрудно видеть, что с уменьшением расхода воздуха
на частичных нагрузках степень регенерации повышается.
Влияние регенератора на показатели ГТУ при ча-
стичных нагрузках проявляется также в изменении его
гидравлического сопротивления. В зависимости от ре-
жима работы установки будет изменяться перепад давле-
ний как с воздушной стороны (Лр°ег = р2 — Рб)> так
и с газовой (Дррег=р4— рн). С воздушной стороны
общие потери давления определяются потерями на тре-
ние при адиабатном течении и потерями, вызванными
нагревом. Их определение уже было рассмотрено. Поэтому
аналогично камере сгорания для регенератора справедливо
уравнение
ДРрег = ДРрег 0 [ к1рег + к2рег (J _ у2)0 ] Х
(V.54)
як \ GB0 ]
Здесь можно принять к1рег = 0,84-0,9; к2рег = 0,14-0,2.
В некоторых случаях потерями давления из-за на-
грева можно пренебречь, а потери трения в регенераторе
и камере сгорания условно объединить. Тогда для оценки
потерь давления между компрессором и турбиной на ча-
стичной нагрузке можно использовать уравнение
ЛРк.с
— Дрк. со
1 4" Нк/’Чк ГСко
(1+Як/%)о
(V.51)
При наличии в установке регенератора температура
воздуха Т2 в (V.50) заменяется температурой Т5.
ДРк—т — ДР(к—т) 0
1 + Дк/Лк
(1 + ХГк/т]к)о
ДТко / GB \2
як \ GB0 /
(V.55)
С газовой стороны доля потерь давления из-за охлаж-
дения невелика, поэтому эти потери отдельно можно не
выделять и рассматривать их в составе общих потерь
давления выхлопной системы (см. п. V.3).
Воздухоохладитель
Воздухоохладитель влияет как на мощностные, так
и экономические показатели ГТУ. При любой его нагрузке
имеют место следующие уравнения:
Qb ~ (ТВ1 ТВ2); z
Свод = ОводСвод (ТВОД2 Т’водт),
где Св — количество теплоты, передаваемой воздухом;
Свод — количество теплоты, воспринимаемой водой.
В статических условиях Св = Свод = С = kF®. По-
скольку <хвод а,,, можно принять средний коэффициент
теплопередачи k « ав. Тогда, используя критериальное
уравнение теплообмена вида Nu = cRert и уравнение
неразрывности, приближенно можно записать
С _ Г Св ТВ1-;-7’В2 И
Со L Сво (Тв1 + rB2)oJ Оо ' ’
Приведенные уравнения позволяют рассчитать воз-
духоохладитель на переменном режиме.
также
совпа-
При расчете воздухоохладителя могут быть
использованы приближенные уравнения. Хорошее
дение с экспериментом дает уравнение [57 ]
7- т । (Тв2 Твод1)0(7’в1 Твод1)
7 вг ~ ' вод1 + — ----- 0 яд •
(V.57)
V B1— ‘ ВОД1/0/ Г'в/'-'нО,'
В работе [32] для определения температуры воздуха
за воздухоохладителем приведено другое уравнение.
Тв2 = ТВ1-------9о(ТВ1-Твод1)
бо + (1-ео) (GB/GBo)fe
где 0 ~ (Тв1 — ТВ2)/(ТВ1 — Твод1) — степень охлажде-
ния; k= 14-1,5— показатель степени.
Для транспортной ГТУ с двумя компрессорами при
переменной частоте вращения ротора компрессора низ-
кого давления можно использовать уравнение [32]
^в2 ~ ^вод! + knnl. н> (V.59)
где kn — постоянный коэффициент, определяемый рас-
четным режимом.
V.3. СОГЛАСОВАНИЕ
ПАРАМЕТРОВ ЭЛЕМЕНТОВ ГТУ
Основные уравнения
Показатели ГТУ на установившихся режимах ча-
стичных нагрузок, т. е. статические характеристики уста-
новки, определяются согласованием параметров элемен-
тов, из которых ГТУ образована. Это согласование осу-
ществляется ' решением системы уравнений, характери-
зующих совместную работу отдельных элементов. К числу
основных уравнений относятся уравнения расхода (или
сплошности), мощности и отношения давлений.
Уравнение расхода, или сплошности, показывает, что
расходы рабочего тела по всем элементам ГТУ однозначно
связаны между собой. Поэтому на каждом статическом
режиме расходы рабочего тела через элементы установки
известны.
Расход газа через турбину зависит от параметров
рабочего тела, т. е GT = f (р3, Т3, pit п) (см. п. V. 1).
Часто для получения статических характеристик ГТУ
используют приближенное уравнение расхода в виде
формулы Стодола, что значительно облегчает расчет.
Расход воздуха через компрессор также зависит от
режимных факторов и записывается при постоянных пара-
метрах наружного воздуха в виде GK = f (пк, лк). Расход
118
воздуха через компрессор обычно представляется гра-
фически в виде характеристики компрессора (см. гл. III).
Расходы рабочего тела через теплообменные аппа-
раты определяются характеристиками турбомашин.
Уравнение мощности записывается для каждого
вала установки и для статических режимов представляет
собой баланс мощности турбин, компрессоров и внешних
потребителей. Этот баланс зависит от тепловой схемы
ГТУ и рассматриваемого вала. Для турбокомпрессорного
вала, не связанного с внешним потребителем мощности,
уравнение баланса имеет вид
GT//TT]Mex - Gk7/k = О- (V.60)
Для вала ГТУ, на котором расположен внешний
потребитель, уравнение баланса мощности
От/7тт]мех — GK/7K = Ae, (V.61)
где Ne — мощность на выходном валу установки.
В случае, когда рассматривается свободный вал,
не связанный с приводом компрессора, в уравнении (V.61)
мощность компрессора отсутствует. Обычно внешний
потребитель определяет характер изменения частоты
вращения вала в зависимости от снимаемой мощности.
Так, если потребитель полезной нагрузки — генератор,
то частота вращения меняется только в пределах неравно-
мерности регулирования. Для транспортных ГТУ ди-
апазон изменения частоты вращения вала полезной мощ-
ности значительно больше и зависит от условий эксплуа-
тации.
Уравнение отношения давлений для турбомашин
характеризуется общими степенями повышения и пони-
жения давления лк. общ и лт. общ- Для идеальных уста-
новок без гидравлических сопротивлений в трактах
лк. общ — пт. общ- В реальных условиях имеют место
потери давления, и для любого режима справедливо
уравнение
^-Kl^-K2 ••• “ -И-Т1-И-Т2 ••• лтм- (V.62)
Гидравлические потери в трактах ГТУ
Потери давления в газовоздушном тракте ГТУ,
вызванные гидравлическими сопротивлениями, обычно
оцениваются величиной Др = рс, где р — характерное
давление для рассматриваемого участка; g — коэффициент
гидравлических потерь. Поскольку характерное давление
принимается в различных сечениях в зависимости от
места в схеме ГТУ, рассмотрим определение гидравличе-
ских потерь для конкретных трактов установки.
Входной тракт ГТУ. Давление перед компрессором
зависит от потерь давления во входном тракте, поскольку
Pi = рн — Дрвх, где Дрвх — потери давления во входном
тракте, вызванные наличием гидравлических сопротивле-
ний. Далее можно написать, что Дрвх = ^р^/2, где Si —
коэффициент сопротивлений во входном тракте.
Если расход воздуха через компрессор определить
приближенным уравнением [32]
GK = GK0 (рДр10) (W’25> (V.63)
то можно получить
Арвх = ДДвхо (Pi/Pio) («/«о) ’ •
Тогда на любом режиме давление перед компрессором
Pi = Рн (1 — 5вхо)/11 — ?вхо ’5)1, (V.64)
а коэффициент гидравлических потерь во входном тракте
ГТУ
U = 1 - (1 - Uo)/[1 - Ввхо (1 - «2’5)], (V.65)
ГДР ?вх о = АРвх оДн-
Для генераторных установок, работающих с постоян-
ной частотой вращения (п^'1,0), можно считать коэф-
фициент потерь давления неизменным на всех нагрузках.
От температуры засасываемого воздуха потери давле-
ния во входном тракте практически не зависят.
Тракт между компрессорами. Если потери давления
выразить через параметры воздуха перед комгрессорой
высокою давления, то для определения давления перед
этим Компрессором можно воспользоваться уравнениями,
аналогичными (V.64) и (V.65). Для этого тракта
= рзРт/У Т’з, то потери давления можно определить
по формуле
ДРвых — ДРвыхо
Рз
Рзо ^то
1 Нтот] то
(V.72)
>к, н—к в
_______1 S(K, н—к. в) О
1 &(к. Н—К. В) 0 (1 пк. в
(V.66)
(V.67)
а коэффициент гидравлических потерь — по
ёвых — ёвыхо
Рз JtT / [Зт
Рзо ЯТО \ РтО /
1 — ЯТТ[Т
1 йто^то
формуле
(V.73)
В уравнения (V.72) и (V.73) входит степень пониже-
ния давления в турбине лт, которая также зависит от
потерь давления в выхлопном тракте. Поэтому расчет
потерь в выхлопном тракте следует проводить итерацион-
ным методом. Для выхлопного тракта р4 = рн (1 + ёвых)-
_____1 ^(к и—к в) 0____
1-?(к.Н-К. в)о(1-«к.5в)
Здесь н—к. в &Рк. н-к. в/Дн-
Тракт между компрессором и турбинной группой.
Потери давления в этом тракте Дрк-т = ?к-тРзсз/2> гДе
£к_т — суммарный коэффициент сопротивлений всего
тракта; р3 и с3 — плотность и скорость рабочего тела перед
турбинной группой. Если для расхода рабочего тела
принять уравнение вида GT = рРт/1/"Т3, то потери дав-
ления в тракте между компрессором и турбинной группой
ДРК—т = ДР(к—т) о (Рз/Рзо) (Рт/Рто)-
V.4. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГТУ
Основные виды статических, характеристик ГТУ
Частичные нагрузки ГТУ характеризуются опре-
деленной совокупностью параметров. Закономерность
изменения этих параметров образует ту или иную стати-
чгскую характеристику установки; основные из них рас-
смотрены ниже.
Каждому равновесному режиму работы установки
отвечают определенные параметры рабочего тела. Сово-
‘В
будут
этом случае для любого режима работы установки
справедливы уравнения:
1 ^(к—т) О
Рз Р2 1-?(к-т)о(1-₽Жо) :
1 ^(к—т) О
(V.68)
1 1-?(к-т)о(1-₽Жо) ’
(V.69)
Здесь Рт — коэффициент, зависящий от степени пониже-
‘ния давления в турбине; при использовании формулы
Стодола Рт = У 1 — л~2; gK_T = Дрк_т/р2.
В случае, когда тракт между компрессором и турби-
ной определяется камерой сгорания и влиянием нагрева
пренебречь нельзя, потери давления следует находить по
формуле (V.50), а коэффициент гидравлических потерь —
по формуле
Рис. V.12. Универсальная характеристика компрессора
(V.70)
где коэффициенты и к2 принимаются такими же,*как
в уравнении (V.50).
Тракт между турбинами. При отсутствии промежуточ-
ной кймеры сгорания коэффициент потерь давления опре-
деляется уравнением вида (V.69). При наличии камеры
сгорания между турбинами уравнение для определения
коэффициента потерь давления будет иметь вид
~ S(t. в—т. н) 0 ( К1
>т. в—т. н
(V.71)
Здесь следует принимать Kj = 0,75+0,85; к2 = 0,15+0,25.
Тракт за турбинной группой. Здесь потери давления
Дрвых — $2Р2с2/2, где р2 и с2 — плотность и скорость
рабочего тела на выходе из турбины. Поскольку GT =
купность параметров равновесных режимов удобно на-
носить на универсальную характеристику компрессора,
которая позволяет установить ряд Особенностей работы
ГТУ. Геометрическое место точек равновесных режимов,
нанесенных на характеристику компрессора, называется
режимной (рабочей) линией. Каждая точка режимной
линии должна удовлетворять всем балансным уравнениям.
В ГТУ с одним компрессором уравнение расхода,
связывающее расходные характеристики компрессора и
турбины, и уравнение отношения давлений дают возмож-
ность нанести на характеристику компрессора (рис. V.12)
линии температур газа Та. Действительно, любая точка А
поля характеристики компрессора определяет расход
газа GT через турбину и начальное давление газа |р3 (вы-
раженное через лк). Этих параметров достаточно, чтобы
по одному из уравнений расхода газа через турбину
найти начальную температуру газа Т3.
119
Линии температур позволяют нанести на характе-
ристику компрессора линии расходов топлива GTon>
которые получены с помощью уравнений теплового баланса
камеры сгорания. В поле представленных на рис. V.12
кривых режимная линия должна удовлетворять только
одному условию — условию баланса мощности.
Расположение режимной линии зависит главным
образом от схемы установки и вида внешнего потребителя.
Например, одновальная ГТУ транспортного назначения
имеет режимную линию а—Ь, а генераторная — а—с
(рис. V. 12). На характеристике компрессора может быть
выделена зона возможного размещения режимной линии,
которая определяется условиями надежной эксплуатации
установки. Границами этой зоны являются следующие
ограничения.
1. Линия помпажа компрессора 1—I. Выход за эту
линию противопоказан из-за неустойчивой работы ком-
прессора. Допустимое минимальное приближение режим-
ной линии к границе помпажа задается коэффициен-
том запаса по помпажу (%)
Ay = [GK. рЛк. гр/(бк. гр^к. р) — 1] ЮО,
где индекс р относится к параметрам режимной линии,
Индекс гр — к границе помпажа.
Как показывает опыт эксплуатации ГТУ различного
назначения (стационарных и транспортных), для обеспе-
чения надежной работы компрессора коэффициент запаса
по помпажу должен быть не меньше 12—15%. Для боль-
шинства работающих установок fey » 20% и выше.
2. Линия предельной температуры газа 7’зпред II—II.
Превышение предельной температуры недопустимо из-за
сильного влияния температуры газа на ресурс ГТУ.
Уровень Тзпред устанавливают по температуре газа на
режиме максимальной мощности. Иногда принимают
^зпред = Тзй + (2О-Г-4О0).
3. Линия предельной частоты вращения ротора III—
III. Ограничение по гапред определяется требованиями
прочности: обычно значение «пред устанавливают на 10—
15% выше частоты вращения на номинальном режиме.
4. Линия минимальной температуры газа Tsmin
IV—IV. Эта линия связана с устойчивой работой камеры
сгорания и минимальным расходом топлива, обусловлен-
ным качеством распыливания.
5. Линия минимальной частоты вращения ротора V—V.
Обычно величина ппцп также определяется требованием
надежной работы камеры сгорания и динамической устой-
чивостью режима ГТУ.
В ГТУ с двумя и более ком прессорами выделяются
также перечисленные границы возможных режимов,
которые имеют тот же физический смысл.
Режимные характеристики определяют изменение
Основных параметров в зависимости от мощности уста-
новки. Иногда эти характеристики строят в зависимости
от частоты вращения компрессора (для однокомпрессор-
ных ГТУ). Такие характеристики дают возможность
судить ю законе изменения параметров ГТУ, в том числе
И ее экономичности с уменьшением нагрузки.
Выходные характеристики рассматриваются приме-
нительно к транспортным ГТУ. Они представляют собой
изменение крутящего момента и мощности на выходном
валу установки в зависимости от его частоты вращения.
Нанесение на эту характеристику внешнего сопротивле-
ния дает возможность судить о важных эксплуатационных
показателях, определяющих соответствие характеристик
установки переменным внешним условиям.
Для построения статических характеристик ГТУ
должны быть определены параметры статических режимов
в широком диапазоне нагрузок. Методика определения
этих параметров зависит от тепловой схемы установки и
вида потребителя, поэтому ниже рассмотрен порядок
расчета статических характеристик для различных схем
ГТУ.
120
Статические характеристики
одновальной ГТУ
При расчете частичных нагрузок должен быть опре-
делен номинальный режим и соответствующие параметры,
а также найдены характеристики всех элементов установки,
т. е. рассчитаны характеристика компрессора, показатели
турбины (GT, TjT и NT в зависимости от параметров газа
р3, Т3 и частоты вращения) и камеры сгорания. На харак-
теристике компрессора номинальная нагрузка опреде-
ляется точкой а (рис. V. 13). Вид режимной линии от
точки а зависит от внешнего потребителя.
Для генераторной ГТУ при любой нагрузке п =
== 'const. Поэтому режимная линия в этом случае имеет
Яд
Рис. V.13. Характеристика компрессора одновальной
установки при 7\ = const и рх — const
вид n — const. Уменьшение нагрузки обычно сопровож-
дается падением лк, а точки равновесных режимов будут
располагаться ниже точки а. Для определения показате-
лей ГТУ на частичной нагрузке надо на линии n = const
взять произвольную точку (например, точку 1). В этой
точке с характеристики компрессора снимаются значе-
ния GK, лк и рассчитываются показатели компрессора
(Т2, Нк, 7ИК, NK). По величине лк с помощью уравнений
(V.62) находят лт и начальное давление рабочего тела.
Рз — РнПК (1 |вх) (1 £к-т)/(1 + Sbux)-
Затем по одному из уравнений пропускной способ-
ности турбины в точке 1 определяют температуру рабочего
тела Т3 и мощность турбины. По уравнению баланса
мощности (Ут—Ук) т)мех = А'пат находят полезную мощ-
ность ГТУ, а по уравнению баланса камеры сгорания —
расход топлива. На этом расчет показателей установки
в точке 1 можно считать законченным. Затем аналогичный
расчет выполняют для точек 2, 3 и т. д. до точки С, опре-
деляющей режим холостого хода (полезная мощность
близка к нулю).
Найденные показатели позволяют для рассматривае-
мого случая построить статические характеристики ГТУ.
Режимная характеристика (рис. V. 14) включает широкий
диапазон изменения нагрузки (Ух. х ~ 0). При умень-
шении нагрузки все параметры падают, кроме расхода
воздуха, который несколько возрастает. Такая законо-
мерность указывает на то, что здесь имеет место так назы-
ваемое качественное регулирование, при котором умень-
шение мощности обеспечивается за счет понижения только
параметров рабочего тела. Такой метод регулирования
понижает эффективность теплового цикла, поэтому для
одновальной генераторной установки характерно, резкое
уменьшение ее к. п. д. с понижением нагрузки. Этим
определяется выбор режимов работы генераторной ГТУ
при эксплуатации. Обычно она работает на режимах,
близких к номинальному, а длительная работа на пони-
женных нагрузках для нее нежелательна.
Транспортная ГТУ обычно эксплуатируется при
переменной частоте вращения выходного вала, поэтому
зависимость п = f (ЛДь) определяется видом потребителя
нагрузки. Так,_для_судовой установки с винтом фикси-
рованного шага п ks для дорожной машины л ~^ф.
При расчете принято, что номинальный режим работы
Рис. V.14. Режимная характеристика одноваль-
ной генераторной ГТУ
этой установки также соответствует точке а (рис. V. 13).
Для определения режима частичной нагрузки в этом слу-
чае надо задаться произвольным значением частоты вра-
щения ротора (например, п' на рис. V. 13). На этой ча-
стоте вращения по зависимости п = f (Уэф) для данного
внешнего потребителя находится его мощность (для су-
довой установки У пот — Л^эф = Аэфоп 8). Затем на ли-
нии п' выбирают три произвольные точки Г, 2' и 3',
охватывающие значительную зону характеристики ком-
прессора. Для каждой из этих точек выполняется расчет,
аналогичный расчету для точки 1 генераторной ГТУ,
и в каждой точке находится мощность компрессора и
турбины. Равновесному режиму на линии я' = const
отвечает только та точка, в которой выполняется условие
(Ут — Ук) т)мех = Л'Пит. Для нахождения этой точки
надо построить вспомогательные графики вида Лгт — NK =
= f (лк) и У пот = f (як) = const, точка пересечения
которых / и определит равновесный режим на линии я'.
Аналогичный расчет выполняется для другой частоты
вращения и т. д. Полученные параметры ряда равновес-
ных режимов позволяют строить статические характе-
ристики установки.
Режимная линия а—b (рис. V. 13) с уменьшением
нагрузки довольно быстро приближается к границе пом-
пажа, поэтому на режиме минимальной нагрузки (точка Ь)
обычно имеет место значительная полезная мощность.
Этот режим обычно устанавливается принятым запасом
по помпажу (коэффициентом /гу).
Для одновальной транспортной ГТУ характерен
малый диапазон изменения мощности установки, а с па-
дением мощности параметры рабочего тела понижаются
(рис. V. 15, а).
Внешняя характеристика (рис. V.15, б), построенная
для крутящего момента, иллюстрирует низкое значение
коэффициента приспособляемости к = Л4шах/Л40. Расчеты
а)
Рис. V.15. Характеристики одновальной транс-
портной ГТУ: а — режимная; б — внешняя
показывают, что к= 1,1-5-1,2, что является существен-
ным недостатком при транспортном использовании одно-
вальной ГТУ. В транспортных условиях эти устайовки
могут использоваться только как однорежимные, напри-
мер, в качестве ускорительных корабельных ГТУ.
Статические характеристики
однокомпрессорной ГТУ со свободной
силовой турбиной
Рассматриваемая ГТУ состоит из двух относительно
самостоятельных элементов: турбокомпрессорного и сило-
вого блоков (свободной силовой турбины с внешним по-
требителем нагрузки). Турбокомпрессорный блок пред-
назначен для генерации рабочего тела требуемых параме-
тров, которые в силовом блоке трансформируются во внеш-
нюю (полезную) работу.
Экспериментальные исследования турбин показывают
слабое влияние частоты вращения на их пропускную спо-
собность. Эта особенность турбин значительно упрощает
121
расчет частичных нагрузок ГТУ со свободной турбиной.
В этом случае можно пренебречь влиянием режима работы
силовой турбины на турбокомпрессорный блок, который
будет определять параметры частичной нагрузки.
Расчет статических характеристик ГТУ со свободной
турбиной состоит в рассмотрении балансных уравнений для
турбокомпрессорного блока [12]. Как известно, в точке
Рис. V.16. Характеристика компрессора ГТУ со свободной силовой турбиной
равновесного режима мощность компрессорной турбины
Л'.п< равна мощности компрессора Ук, т. е.
СртОтТ'3/7ткт]ткТ1мех — CpYGt-l'
Тогда начальная температура газа на равновесном режиме
---------------------!-----. (V.74)
срт Нтк 'Птк'Пк'Пмех
Далее, имея в виду, что
Gt = ^(0 (Рз/Рзи) V7'33/Т3 (Рт/Рто) и Gk/G-y = fl,
можно написать
G 1 / Т 30 срт ЛткНкДмех Рт
Рзо Г Т1 Срк Як Н Рто
(V.75)
Зная расход воздуха и степень повышения давле-
ния лк в точке равновесного режима турбокомпрессора,
можно эту точку нанести на характеристику компрессора.
Расчет частичного режима выполняется в следующей
последовательности.
1. Выбирают произвольно степень повышения давле-
ния в компрессоре (точка 1 на рис. V. 16), обычно
меньше значения лк0 (точка а) на но-
минальной нагрузке. Этому параметру
соответствует определенное распреде-
ление степени понижения давления на
компрессорную и силовую турбины,
которое находится по одному из при-
веденных методов (см. п. V. 1).
2. С помощью уравнений (V.74)
и (V.75) находят Т3 и GT, отвечающие
равновесному режиму работы турбо-
компрессорного блока. Этот режим мо-
жно нанести на характеристику ком-
прессора (точка 1 на рис. V. 16). При
этом Т]тк и Т]к в первом приближении
можно принять по номинальному ре-
жиму, а затем уточнить их значение
и повторить расчет по уравнениям
(V.74) и (V.75). Обычно одного при-
ближения оказывается достаточно.
3. По уравнению Тза = Т3 (1 —
—НткТ]тк) находят температуру газа пе-
ред силовой турбиной. Затем, прини-
мая различные значения (Частоты вра-
щения ротора силовой турбины, опре-
деляют выходную характеристику ус-
тановки.
4. Принимают новые значения лк,
nt
лк ит. д., и для них весь цикл рас-
чета повторяется. На характеристику
компрессора наносят точки 2, 3, ...
новых равновесных режимов турбоком-
прессора, которые образуют режим-
ную линию a—Ь. Для каждой из этих
точек выполняется расчет показателей
свободной турбины.
Режимная характеристика ГТУ со
свободной турбиной, зависящая от ви-
да режимной линии на характеристике
компрессора, является при принятом
допущении об отсутствии влияния ра-
боты силовой турбины на турбокомп-
рессорный блок идентичной для генера-
торной и транспортной установок. С
уменьшением располагаемой мощности
установки, определяемой параметрами рабочего тела
и его расходом на силовую турбину, степень повыше-
ния давления и расход воздуха через компрессор пони-
жаются (рис. V.17). К. п. д. турбины в широком диапазоне
изменения располагаемой мощности меняется мало и даже
на режиме минимальной нагрузки (холостой ход) близок
к его значению на номинальном режиме. Такой характер
изменения т]тк объясняется тем, что с падением мощности
уменьшается частота вращения турбокомпрессорного блока,
а вместе с ней понижается и располагаемый теплоперепад
на компрессорной турбине. Снижение этих параметров
таково, что характеристика хтк — KS н2/(2Ятк) на
всех нагрузках остается почти постоянной.
К. п. д. компрессора меняется значительно больше.
На режимах, близких к номинальной нагрузке, величинами
может даже возрастать, что определяется выборок расчет-
ного режима. На режимах малой мощности в области по-
ниженной частоты вращения ротора компрессора наблю-
дается резкое падение к. п. д. компрессора.
122
С изменением к. п д. турбины и особенно к. п. д.
компрессора связано изменение начальной температуры
газа Т3. На режимах, близких к номинальному, когда
Нтк и т)к меняются мало, балансирование мощности на тур-
бокомпрессорном блоке сопровождается уменьшением Т3.
В зоне резкого падения г)к сначала наблюдается уменьше-
ние темпа понижения Т3, а затем могут появиться условия,
при которых баланс мощности турбокомпрессорного
а)
Чт, Ъ,
Рис. V. 17. Характеристики ГТУ со свободной
силовой "турбиной ( GTon 0> GTOn > 6’"оп >
i> GTon): а —'режимная; б — выходная
блока можно осуществить только за счет повышения Т3
(рис. V. 17, а). Таким образом, в ГТУ со свободной си-
ловой турбиной опасность перегрева появляется не только
на'режимах перегрузки, но и на режимах малой мощности,
т. е на низкой частоте вращения турбокомпрессорного
блока.
К. п. д. установки с уменьшением располагаемой
мощности падает. Однако по сравнению с одновальной
установкой относительное понижение К. п. д. здесь зна-
чительно меньше. Большая экономичность ГТУ со свобод-
ной силовой турбиной на частичных нагрузках объяс-
няется тем, что имеет место количественное регулирова-
ние мощности из-за уменьшения расхода рабочего тела.
Важным моментом для рассматриваемой установки
является выбор режима минимальной нагрузки, так как
режима холостого хода, определяемого нулевой полезной
мощностью, здесь обычно нет. При выборе этого режима
необходимо обеспечить следующие условия.
1) допустимое тепловое состояние проточной части
турбины, поскольку температура газа на режимах малой
нагрузки возрастает;
2) хорошее качество распыливания топлива, по-
скольку с уменьшением нагрузки расход топлива падает,
перепад давления топлива на форсунку уменьшается,
качество распыливания ухудшается;
3) устойчивость режима работы турбокомпрессорного
блока на минимальных нагрузках, поскольку с падением
нагрузки запас по устойчивости уменьшается.
Выходные характеристики ГТУ со свободной силовой
турбиной представляют собой обычные для турбин за-
висимости мощности и момента от частоты вращения ро-
тсфа (рис. V. 17, б). При этом каждая зависимость N =
= f (я) и М = f (п) отвечает той или иной точке на ре-
жимной линии, а располагаемой мощностью в этом случае
будет максимальная мощность, которая обеспечивается
при максимальном к. п. д. силовой турбины.
Для гсх1ерагорной I 1 У частота вращения выходного
вала остается при всех нагрузках постоянной, поэтому
к п. д. силовой турбины по мере уменьшения нагрузки
Надает.
Важным качеством рассматриваемой ГТУ при транс-
портном использовании является неуклонный рост крутя-
щего момента силовой турбины по мере уменьшения
частоты вращения выходного вала. Это значит, что чем
больше внешнее сопротивление, т. е. чем выше момент
сопротивления на выходном валу, тем больший момент
развивает турбина. Эта внутренняя приспособляемость
ГТУ к внешним условиям повышает надежность их экс-
плуатации, а применительно к дорожным машинам суще-
ственно упрощает трансмиссию.
Статические характеристики
двухкомпрессорной ГТУ
Для ГТУ с двумя компрессорами возможно различное
сочетание ее элементов. Здесь ограничимся рассмотрением
схем, которые или находят применение, или будут соз-
даны в ближайшее время. Примем, что каждый компрес-
сор приводится во вращение своей турбиной (см. рис. 1.14).
Основные различия тепловой схемы состоят в том, что
промежуточный холодильник и камера сгорания низкого
давления могут отсутствовать, а внешняя нагрузка может
сниматься с компрессорного вала низкого давления.
При расчете статических характеристик установки
считаются известными параметры номинального режима,
а также характеристики всех элементов ГТУ. Распределе-
ние степени понижения по турбинной группе рассчитано
одним из известных методов (см. п. V. 1). Номинальный
режим работы нанесен на характеристики компрессоров.
При построении режимной линии на универсальных
характеристиках компрессоров низкого (КНД) и высокого
(КВД) давления необходимо обеспечить условия равно-
весия для рассматриваемой установки. К этим условиям
относится равенство расходов (уравнение сплошности),
равенство мощностей на валах высокого и низкого давле-
ния (уравнение мощности) и баланс отношения давлении.
Эти условия надо применить к произвольно выбранному
режиму.
Можно рекомендовать следующий порядок расчета
ГТУ.
1. На характеристике КНД принимается новый рас-
ход G“p, и для него задаются тремя значениями лк нЬ
лк. Н2’ як.нз степени повышения давления (точки 1,
2 и 3 на рис. V. 18, а). Каждой из этих точек отвечает
расход воздуха через КВД (приведенные расходы G®B ь
G®p2, G°p з соответственно — рис. V. 18, б). Затем при-
нимаются три тоже произвольных значения лк. в i, як. в 2>
123
лк.вз — точки Г, 2', 3' на рис. V.18, б). Этим значениям
при G"p j соответствует на характеристике КНД точка 1,
при G®p 2 — точка 2, при G®p 3 — точка 3. Принятым
значениям отвечают для точки 1 следующие значения
общей степени повышения давления: лк. общг^^к.н Л. в i!
Рис. V.18. Характеристики компрессоров: а — КНД’
б - КВД
Пк. общ 2 ЯК. и 1ПК. в 2» ЯК. общ 3 ЯК. И 1 TtK. в 3.
Аналогичные значения лк. общ будут для точек 2 и 3.
Общая степень понижения давления в турбинной группе
ЯТ. общ як. общ''7*
2. Для каждого значения лк. общ ПРИ принятых
расходах рабочего тела по уравнению расхода через тур-
бину высокого давления (при наличии камеры сгорания
между ТВД и ТСД) или через всю турбинную группу
находится начальная температура газа Т3 перед ТВД.
Производится баланс мощности на валу высокого дав-
ления. Прежде всего необходимо установить для каждого
значения лк. общ распределение степени понижения дав-
ления по турбинам, для чего удобно пользоваться при-
ближенными методами расчета турбин. Затем для каждого
приведенного расхода КВД (G®p р G°p 2> G®p 3) строят вспо-
J24
могательные графики баланса мощности на валу
(рис. V. 19, а), и по ним для каждого значения Gnp уста-
навливают значение лк. в. р, соответствующее балансу
мощности « в р, л" в р, л™ в р на рис. V.18).
4. Балансируется мощность на валу низкого давле-
ния. Этот баланс надо находить из условия равенства
мощностей на валу высокого давления, т. е. только для
значении лк в р, ли_ в р и лк_ в . Баланс мощности здесь
также находится с помощью вспомогательного графика,
представленного на рис. V. 19, б. Таким образом, только
точка /н на характеристике КНД (см. рис. V. 18,jz) отве-
Рис. V. 19. Вспомогательные графики j
чает условию баланса мощностей как на валу низкого,
так и на валу высокого давления. Эта точка и является
точкой равновесного режима на характеристике КНД.
Для нанесения соответствующей точки на характеристику
КВД надо по л;к. н. р найти приведенный расход через
КВД G®p р. Равновесный режим на характеристике КВД
будет определяться пересечением G®p р с линией, соеди-
няющей лк в р, л" в рилкв р (точка/в на рис. V. 18, б).
Для получения режимных линий на характеристиках
компрессоров расчет надо повторить и для других рас-
ходов через КНД.
Выходные характеристики установки зависят от
работы силовой турбины, и найти их для каждого равно-
весного режима довольно просто.
Рассмотренный метод расчета относится к наиболее
сложному случаю. При отсутствии свободной силовой
турбины расчет частичных нагрузок несколько проще,
так как в этом случае режим работы вала низкого давле-
ния определен внешним потребителем нагрузки.
Для сложных схем может оказаться более предпочти-
тельным другой метод расчета частичных нагрузок, осно-
ванный на решении системы линеаризованных уравне-
ний [45].
Система исходных уравнений, отражающих свойства
установки на равновесных режимах, составляется путем-
рассмотрения отдельных аккумуляторов энергии и мате-
рии. Число и вид этих аккумуляторов, т. е. порядок си-
стемы исходных уравнений, зависит от тепловой схемы
рассматриваемой ГТУ. В состав возможных аккумулято-
ров входят аккумуляторы механической энергии 1 (ро-
торы), аккумуляторы материальной среды (газовые и
воздушные объемы) и аккумуляторы теплоты (главным
образом, камеры сгорания и регенераторы).
Для получения системы уравнений, позволяющей
провести расчет частичных нагрузок, принята схема уста-
новки, изображенная на рис. 1.14, но с подключением
потребителя к валу низкого давления (без свободной
силовой турбины). Условия равновесия элементов этой
установки имеют следующий вид [45].
Ротор турбокомпрессора высокого давления:
ЛЛ4Т. в — ДМК. в = 0;
Л*т. в = f (Рз> Тз’ Рзч’ ®в); v
Л4К. в = f (WB, р2, р1в);
а121'3 + ЙХз'Рзн Ч~ а141|,1в Ч- Я15<Рв = 0-
Ротор турбокомпрессора низкого давления:
АА4Т. „ — ДМК. „ - Л/Ипот = 0;
МТ. н — f (Рзи, Тзн, шн);
А4к. н — f (Ргн> <°н); Л4пот = f (<0H, L)',
а21'Фзн + Й22ТЗН + й2зфн + a2pp2H = а25^‘
Объем между компрессорами низкого и
давления:
AGK. н Д0к. в = 0; GK. п = f (wH, р2я)>
Gk. в — f (<ов, Р2> Pib);
G314'2H Ч- СззЧ’з Ч- ^ЗзЧЧв Ч~ а34фн Ч~ а3бфв = 0.
Объем между компрессором и турбиной
давления:
AGK. в AGT. в == 0; GT. в = / (Рз> Т3, piB)', 1
а41Фз Ч- а42фв Ч- а4зЧ'1в Ч~ а4411,4В Ч~ а45Т3 ~ 0 J
Объем между турбинами высокого и низкого давления:
AGT. в AGT. н = 0; GT. н = f (Рзн, Т’зн);
й51Фз + й52т3 + а53фзи + а5Лн = 0.
Камера сгорания высокого давления:
AQ1B AQ2B — 0’
Q1B = f (GTon. в, СОв, Рг> Р1в);
Q2B = f(₽3> Т3, р^ъУ,
«61фв Ч- а6211'3 Ч- ЯезЧЧв Ч- а64т3 Ч~ й65ф4в =
= аб6§ТОП. В-
(V.77)
высокого
(V.78)
высокого
(V.79)
(V.80)
1
(V.81)
(V.82)
Камера сгорания низкого давления:
AQih AQ2H ~ 0;
Q1H ~ f (GTon. Н> Рз> ^3> Р-1в):
Q2H — f (Рзь, Гзн);
атГФз + а72т3 Ч~ а7з4,зн + Й;Л'1 = а-зётоп. и-
Здесь постоянные коэффициенты а1х, а21, ... пред-
ставляют собой частные производные по параметрам со-
стояния соответствующих аккумуляторов, а вместо раз-
мерных параметров введены относительные величины:
ф = Ар/р'; т = ДГ/Г'; <р = Дш/ш';
&топ ~ А^топЛДоп’ L ,
... пред-
Более подробно об аккумуляторах энергии см. в гл VI.
где р', Т', ... — параметры, соответствующие известному
режиму.
В полученной системе уравнений (V.76)—(V.82) не-
известными величинами являются все параметры состоя-
ний, а также расходы топлива и нагрузка. Поскольку
для рассматриваемого случая число неизвестных на три
единицы больше числа уравнений, то для решения си-
стемы уравнений надо задаться тремя параметрами. Один
из этих параметров определяет меру изменения режима
работы установки, а два других — дополнительные экс-
плуатационные условия. Если рассматривается генера-
торная установка, то такими параметрами могут быть л,
Фн = 0 и gTon. н (или зависимость между gTon. н и gTOTI, в),
если транспортная —• X = 0, gTOn. в и gTon. н (или за-
висимость между ними).
В качестве меры изменения режима вместо X или
ётоп могут служить отклонения параметров состояния Т
ф и др., а эксплуатационные условия можно характери-
зовать связью этих величин: т3 = f (тзн); фн = f (К) и др.
Решение системы уравнений (V.76)—(V.82) позволяет
определить параметры нового режима, которые находятся
по уравнениям вида w'' = <£>^ (1 Ч~ (рн); Тд = Тз(1 Ч* т3)
и т. д., где и/, Т’3, ... я и>", Т3, ... — параметры состояния
известного и искомого режимов соответственно.
Поскольку при выводе уравнений использован метод
линеаризации, точность решения поставленной задачи
зависит от принятого диапазона изменения режима работы
установки. Для повышения точности должны задаваться
небольшие диапазоны изменения режимов, при больших
значениях можно использовать метод уточнения резуль-
татов расчета, подробно изложенный в работе [45].
В связи с некоторой погрешностью, обусловленной
линеаризацией, на новом режиме для рассмотренных
аккумуляторов будут справедливы уравнения
ДЛ4Т. в — ЛАД. в = — 6Х; AGK. в — AGT. в = — 62 и т. д.,
где 6t, 62 — погрешности расчета.
Используя для каждого аккумулятора, как и при
выводе уравнений (V.76)—(V.82), метод линеаризации,
получим систему уравнений вида
а11Фз + в12т3 Ч- Дз'Фзн Ч- а1411’1в Ч- а15*Рв = ~ (V.83)
Здесь коэффициенты a'n, а[2, ... —-те же, что и в уравне-
нии (V.76), только вычислены по производным для нового
режима работы, а переменные ф3, т3, ... представляют собой
поправки к параметрам состояния нового режима, найден-
ного решением системы (V.76)—(V.82). Тогда уточнение
параметров состояния нового режима будет определяться
уравнениями:
= Рз 0 + Ф ); Т’!’ = Тз (1 + т3) ит. д., (V.84)
где Рз, Тз — уточненные параметры нового режима.
Рекомендуется следующий порядок расчета перемен-
ных режимов с помощью линеаризованных уравнений.
1. Составляют систему линеаризованных уравнений
всех аккумуляторов энергии и материи рассматриваемой
установки. Коэффициенты уравнений а1х, а12 определяют
по параметрам известного режима.
2. Задают диапазон изменения режима параметром Л
или gTon или любым параметром состояния (<р, тит. д.).
Кроме того, принимают дополнительные эксплуатацион-
ные условия, число которых соответствует числу регули-
рующих органов установки.
3. Решением системы уравнений вида (V.76)—(V.82)
находят все безразмерные параметры состояния (ф, т
и др ). Затем по уравнениям вида о/' - <г' (1 + <рв) и г д
находят размерные параметры нового режима работы
Если приняты малые интервалы изменения режима работы
и уточнения не требуется, то на этом расчет нового
125
режима заканчивается, и для расчета другого режима его
надо повторить, приняв полученный режим за исходный.
В случае необходимости уточнения полученных ре-
зультатов расчет следует продолжить.
4. Составляют систему уравнений вида (V-76)—(V.82),
но с правой частью, определяемой величиной небаланса 6.
В этом случае нагрузка установки неизменна, поэтому
А s= °. >
5. Вычисляют коэффициенты уравнений а^, а'12, ... по
параметрам полученного в п. 3 приближенного режима.
6. Решением системы уравнений с правой частью,
полученной в п. 4, находят неизвестные ф', т' и т. д ,
по которым определяют параметры уточненного режима.
Параметры уточняют по уравнениям вида (V.84). Одного
уточнения обычно оказывается достаточно.
Улучшение статических характеристик ГТУ
за счет дополнительных регулирующих
органов
При эксплуатации ГТУ возникает ряд специальных
требований, связанных с обеспечением частичных нагру-
зок, приспособляемости к переменным атмосферным усло-
виям и маневренности. Эти требования удовлетворить
обычными средствами управления установки (топливными
органами) Не всегда удается. Тогда можно применить
Рис V.20 Режимные линии на характеристике компрес-
сора при регулируемом сопловом аппарате силовой
турбины
ab — режим при фиксированном угле установки соплового
аппарата (б = const), ас — режим п = const, ad — режим
Т3 = const
дополнительные регулирующие органы, позволяющие
улучшить эксплуатационные показатели ГТУ.
К дополнительным регулирующим органам относится
поворотный сопловой аппарат турбины, который позво-
ляет изменять ее характеристику и тем самым осуществлять
тот или иной закон частичных нагрузок. Наиболее целе-
сообразно применение такого регулирующего органа для
ГТУ со свободной силовой турбиной. Конструктивное
исполнение регулируемого соплового аппарата для тур-
бины высокого давления из-за высокой температуры газа
довольно сложно, поэтому целесообразнее устанавливать
его перед силовой турбиной.
Рассмотрим характеристики ГТУ с воздействием на
силовую турбину для двух случаев организации частичных
нагрузок с обеспечением постоянства частоты вращения
ротора турбокомпрессорного блока (я = const); с обеспе-
чением постоянства начальной температуры газа (Т3 =
= const).
Режимные линии (рис. V.20) и режимные характе-
ристики (рис V 21) соответствуют рассматриваемым слу-
чаям [15]. Осуществление частичных нагрузок по закону
Т3 = const приводит к заметному улучшению экономич-
ности установки. Однако возможность набора нагрузки
126
(приемистость установки) оказывается хуже, так как
частота вращения ротора турбокомпрессора при той же
нагрузке оказываается меньше.
С другой стороны, организация частичных нагрузок
по закону п = const обеспечивает хорошие динамические
качества (максимальная приемистость), но существенно
ухудшает" экономичность на
' частичных нагрузках.
Таким образом, при со-
пловом регулировании ГТУ
целесообразно в зависимости
от условий эксплуатации
иметь возможность устанав-
ливать закон Tg = const для
получения максимальной
экономичности, или закон
п = const для обеспечения
хороших динамических ка-
честв. В первом случае угол
установки соплового аппа-
рата 6 убывает (уменьшает-
ся проходное сечение), во
втором—возрастает.
Наряду с использова-
нием поворотных сопловых
аппаратов турбин широкие
возможности влияния на ста-
тические характеристики ус-
тановки открываются воздей-
ствием на температуру воз-
духа, забираемого компрес-
сором. Проще всего это воз-
действие обеспечивается по-
догревом воздуха, что можно
осуществлять за счет отхо-
дящей теплоты газовой тур-
бины [27 ]. При современных
условиях эксплуатации боль-
шинства ГТУ допустимо не-
посредственное смешение
продуктов-"сгорания с воз-
духом, направляемым в ком-
прессор. Простейшая схема
ГТУ с таким регулирова-
нием изображена на рис. V.22.
Топливный орган 2 обеспе-
чивает поддержание одного
из параметров установки при
любой нагрузке, например
\
\ ч
09 1
п
Gn
\
< \
Xj 4
0,2 0,4 0,6 0,8 N
частоты вращения ротора
ГТУ. Дополнительные тре-
бования обеспечивает другой
регулирующий орган — ре-
гулирующий клапан 4, дози-
рующий перепуск горячего
газа и тем самым воздейст-
вующий на температуру воз-
духа. В частности, в рас-
сматриваемой ГТУ путем ре-
гулирования температуры
воздуха на входе в компрес-
Рис. V.21. Режимные ха-
рактеристики ГТУ при
регулируемом сопловом
аппарате силовой турби-
ны (о — угол установки
соплового аппарата): q —
удельный расход теплоты
ГТУ):
------- — 6 = const,
— — — — п = coast;
— • — — — Т, = const
сор можно влиять на началь-
ную температуру газа вплоть до обеспечения по-
стоянства ее значения или изменения по заданной про-
грамме- Такой способ управления установкой может
улучшить как экономичность на частичных нагрузках,
так и динамические характеристики (маневренность) ГТУ.
В случае необходимости в рециркуляционном трубо-
проводе 3 может быть предусмотрен фильтр 1, обеспечи-
вающий необходимую чистоту подмешиваемого газа.
Реализация способа управления за счет воздействия
на температуру засасываемого воздуха отличается отно-
сительной простотой и не оказывает отрицательного влия-
ния на показатели установки на расчетном режиме.
Кроме того, существенно улучшается приспособляемость
установки к меняющимся атмосферным условиям.
При воздействии на температуру засасываемого воз-
духа не возникает опасности чрезмерного его балласти-
Рис. V.22. Схема ГТУ с воздействием на темпе-
ратуру засасываемого воздуха
рования. Расчеты показывают, что в ГТУ, выполненной
по простой тепловой схеме, при уменьшении нагрузки на
20% для обеспечения постоянства начальной температуры
газа к засасываемому воздуху необходима добавка около
4,5% отработавших газов. Такая добавка повышает тем-
пературу засасываемого воздуха приблизительно на 20° С.
В сложных схемах ГТУ достоинства рассматривае-
мого метода управления возрастают. Особенно целесооб-
разен этот метод в комбинированных установках с высо-
котемпературной газовой турбиной.
Влияние параметров наружного воздуха
на характеристики ГТУ
Одна из особенностей ГТУ — значительная чувстви-
тельность ее характеристик к изменению параметров
наружного воздуха. Поэтому анализ влияния изменения
давления и температуры воздуха перед компрессором на
работу ГТУ приобретает гораздо большее значение, чем
это имеет место в установках другого типа. Ниже
рассмотрен метод расчета основных показателей ГТУ
при изменении параметров наружного воздуха.
При выводе основных уравнений принято, что изме-
нение внешних условий происходит в пределах, не нару-
шающих условий подобия режимов работы отдельных
элементов установки, т. е. при различных параметрах
наружного воздуха можно считать постоянными следующие
величины общ! лт. общ, *Пт/*
В приведенных ниже уравнениях параметры рабочего
тела, соответствующие стандартным параметрам наруж-
ного воздуха, имеют индекс 0 (например, температура
наружного воздуха при стандартных условиях Тио).
Характеристика компрессора для учета влияния
переменности параметров на входе строится в параметрах
подобия: Gnp = GK КTuip„ — приведенный расход; лПр =
= n/VТп — приведенная частота вращения; лк — сте-
пень повышения давления. Такая характеристика яв-
ляется универсальной. Массовый расход воздуха через
компрессор при любых условиях будет GK = GK0 (рн/Рнс) X
X Тяо/Тн, а частота вращения п = п0 ]/~Тн/Тя1).
Режимная линия, нанесенная на универсальную
характеристику компрессора, не зависит от параметров
наружного воздуха, поскольку ее координатами являются
параметры подобия.
Расход через турбину при любых параметрах1 опре-
деляется выражением GT = af^p^lVT^, где а — по-
Рис V.23. Влияние параметров наружного воздуха на
характеристики ГТУ со свободной силовой турбиной:
f., а — изменение Т3, б — изменение к. п. д.:
--------7Н = 288 К;-------— 7Н = 323 К;-------------
Тн = 228 К;
1 — рИ =• 1,0; 2 — рн = 0,85; 3 — рн = 0,75
стоянная величина. Поскольку расходы через турбину
и компрессор однозначно связаны, то можно получить
уравнение
Т’з/Т’н = Т'зо/^’но — const, (V.85)
которое показывает, что температура газа перед турбиной
в каждой точке режимной линии зависит только от тем-
пературы наружного воздуха, причем чем выше темпе-
ратура воздуха Тн, тем выше Г3.
Расход топлива при всех значениях рн и Тн опре-
деляется уравнением теплового баланса камеры сгорания,
преобразование которого дает возможность получить [10]
<Зтоп/(рнКТн) = const. (V 86)
Следует отметить, что полученное уравнение является
приближенным, так как при его выводе приняты равными
- 127
теплоемкости воздуха и газа. Точные значения расхода
топлива в каждой точке следует определять по тепловому
балансу камеры сгорания.
Полезная мощность —• важный показатель установки.
Уравнение для ее определения зависит от тепловой схемы
установки, однако, для всех рассматриваемых случаев
схем ГТУ можно получить [1и]
УДРн КТн) = const. (V.87)
Влияние параметров наружного воздуха на основные
характеристики ГТУ со свободной силовой турбиной
показано на рис. V.23. Для получения одной и той же
мощности Ne при понижении Тя требуется более низкая
температура газа Т3, а понижение давления рн приводит
к росту Т3 (рис. V.23, а).
Существенное влияние параметров наружного воз-
духа на полезную мощность — одна из основных особен-
ностей газотурбинных установок. Требование надежной
работы ГТУ приводит к необходимости введения опреде-
ленных ограничений на режим предельной мощности.
Для стационарных ГТУ влияние параметров наружного
воздуха определяется прежде всего изменением его тем-
пературы Тн, поэтому ниже рассмотрено влияние этого
параметра.
При увеличении температуры Тя в рассматриваемом
подобном режиме растет и температура газа Т3. Однако
на полной нагрузке при расчетных параметрах наружного
воздуха температуру Т3 выбирают обычно максимально
допустимой для длительной работы исходя из прочност-
ных свойств применяемых материалов. Поэтому при уве-
личении температуры наружного воздуха температура
газа должна оставаться постоянной, а мощность уста-
новки при этом падает. Так, рост Тя на 10 К приводит
к падению мощности на 8—9%.
С другой стороны, понижение Тя при фиксированном
значении Т3 приводит к возрастанию мощности установки.
Обычно превышение предельной мощности недопустимо,
и в этом случае необходимо уменьшение температуры
газа Т3, которое составляет 5—6% при падении Тя на
каждые 10 К.
Для организации ограничения предельного режима
установки, согласно рассмотренной закономерности, тре-
буется вводить коррекцию в систему подачи топлива.
Расчеты показывают, что расход топлива на предельном
режиме падает как при увеличении температуры Тя,
так и при ее уменьшении. Однако уменьшение расхода
топлива при росте Тп должно быть организовано по За-
кону Т3 — const, а при падении Тя — по закону постоян-
ной мощности
Влияние параметров наружного воздуха на к. п. д.
установки иглюстрирует рис. V.23, б. При номинальной
мощности падение Т,, до 228 К увеличивает к. п. д. уста-
новки почти в 1,3 раза.
Ухудшение показателей ГТУ при повышении тем-
пературы наружного воздуха по сравнению с расчетным
ее, значением можно существенно ослабить, если исполь-
зовать форсировку установки. Наиболее целесообразной
форсировкой ГТУ является ввод пароводяного рабочего
тела в тракт высокого давления. Выполненные расчеты
и экспериментальные исследования показывают, что ввод
одного процента пароводяного тела повышает мощность
установки на 4—5%. Влияние форсировки на к. п. д.
ГТУ зависит от состояния пароводяного тела. При вводе
одного процента слабо перегретого пара к. и. д. уста-
новки возрастает на 1,0—1,5%, а при вводе неподогретой
воды — падает.
Форсировка ГТУ вводом пароводяного тела—эф-
фективное средство улучшения ее показателей, так как
позволяет сохранить расчетную мощность установки
в широком диапазоне параметров наружного воздуха.
i
f
Г лава VI
ДИНАМИЧЕСКИЕ
ХАРАКТЕРИСТИКИ ГТУ И СИСТЕМЫ
АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ,
УПРАВЛЕНИЯ И ЗАЩИТЫ
VI.1. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
Анализ статических характеристик дает возможность
выбрать рациональную программу управления ГТУ и
составить принципиальную схему их регулирования.
Для определения качественных показателей системы ре-
гулирования необходимо исследовать динамические ха-
рактеристики. Исследование этих характеристик пред-
ставляет собой динамическую задачу, и для ее решения
необходимы уравнения движения основных элементов ГТУ.
В многочисленной специальной литературе [46, 51
и др. ] показано, что ряд задач динамики решается на базе
линеаризованных дифференциальных уравнений движе-
ния. Порядок системы дифференциальных уравнений
определяется числом степеней свободы установки, которое
зависит от числа аккумуляторов энергии. В составе ГТУ
имеются следующие виды аккумуляторов:
1) механической энергии, которые представляют собой
роторы турбомашин и других элементов; их аккумулиру-
ющая способность характеризуется моментом инерции
ротора J (кгс-м2);
2) тепловой энергии, которые характеризуют накоп-
ление теплоты массой рабочего тела или элементами кон-
струкции; мерой их аккумулирующей способности яв-
ляется тепловая емкость С (кВт/кг);
3) материальной среды (рабочего тела), которые
образованы газовоздушными трактами и теплообменни-
ками; их аккумулирующая способность характеризуется
геометрическим объемом V (м3).
Ниже приведены уравнения движения основных
элементов ГТУ, которые дают возможность исследовать
динамические свойства различных установок.
Уравнения движения роторов ГТУ
В зависимости от тепловой схемы возможно различное
сочетание турбомашин, образующее роторные группы.
Для простейшей схемы уравнение движения ротора,
включающего'компрессор, турбину и потребитель энергии,
имеет вид
d(p ср
Т2 Т3 1 7\ 7’,
Tj А.
Ф1
Т’б
(VI.3)
где <р = Дсо/со; ф = Др/р; т= &.TIT — относительные
параметры установки; Л, = ДГ/L— относительное изме-
нение внешней нагрузки.
Постоянные коэффициенты Ti определяются урав-
нениями х:
Частные производные в уравнениях постоянных
коэффициентов:
д/Ит/<Эсо = — Л4т/со; д/Ит/дГ3 = 0,5Л4т/Т3;
Jdujdt = Д/Ит— Д/Ик— Д/Ипот- (VI-1)
Моменты турбины /Ит,
потребителя энергии /ИПОт
представлены следующими
компрессора А4К и внешнего
в общем случае могут быть
зависимостями:
ЗЛ4т/др3 =
= (Мм) 9 + оття7'”т/^т];
дМг/др^ =
= - (/Ит/р4) [ I / ( л2 - 1) + ттл7тт/Ят];
<WK/dp2 = (Мк/р2) («Лк КМ) +
+ (MK/GK) (dGK/dp2);
д/Ик/др1 = - (MjpJ (ткл^к/Як) +
+ (MK/GK) (аОк/дрД;
<ЭЛ4к/<Э<о = — Л4к/(о + (MK/GK) (dGK/dco);
дМк/дТ\ = /Ик/7\ + (MK/GK) (dGK/d7\).
(VI.4)
/
Мт^/т(р3, Т3, ®)> -'V— /к (Pi> Г г, р2,
А1пот — /пот А),
(VI .2)
где L — внешняя нагрузка.
Используя метод линеаризации при определении ДМ
и переходя к относительным параметрам, можно получить
дифференциальное уравнение движения в следующем виде:
9 Л В. Арсеньев и др.
Здесь расход газа через турбину определен формулой
Стодола, а его частные производные равны:
dGT/dp3 = GTp3/(p23 - pl)-, dG../d7':, = - GJT3;
dGjdPi = - GTp4/(p| - pl).
1 Здесь и далее индексом р снабжены параметры равновес-
ного режима.
129
В системе уравнений (VI.4) частные производные
расхода воздуха через компрессор (dGJdp.2 и др.) находятся
графически с помощью характеристики компрессора.
Ряд параметров в конкретных схемах ГТУ являются
постоянными величинами, поэтому их приращение отсут-
ствует. В однокомпрессорных установках, например,
принимают неизменными параметры воздуха на входе
в компрессор, в этом случае и тх в уравнении (VI.3)
будут равны нулю. Для турбины низкого давления можно
принять = 0.
Система уравнений (VI.4) предполагает в пределах
рассматриваемых отклонений постоянство к. п. д. турбо-
машины (т]т и т]к), что в окрестности равновесного режима
не приводит к заметной погрешности. Учет переменности
к. п. д. турбомашин, когда это необходимо, может быть
сделан, если известна их зависимость от параметров ра-
бочего тела.
Уравнение движения ротора (VI.3) написано в общем
виде. На его основе могуг быть получены частные случаи
уравнений роторов для различных схем ГТУ. Так, урав-
нение ротора турбокомпрессорного блока
dtywjdt = фтк/Тх ~Т Тдв/Т12 -ф-трзв/Тд,
уравнение вала свободной силовой турбины
< т/^ ~ —Фс т/^1 + тЗн/^2 + 'Фзн/Т’з
где Т' — постоянные коэффициенты вала свободной тур-
бины.
Уравнения движения аккумулятора
материальной среды
Аккумуляция материальной среды в составе ГТУ
имеет место в соответствующих объемах, которые огра-
ничены турбомашинами. Ряд таких аккумуляторов для
ГТУ рассмотрен ниже.
Газовоздушный тракт между компрессором и турбиной
в самом общем виде включает объемы регенератора, ка-
меры сгорания и тракта между компрессором и регенера-
тором. Компоновка современных Г’ТУ обычно такова, что
объемами остальных трактов можно пренебречь (см.,
например, компоновку ГТУ-20). Для этого случая урав-
нение движения имеет вид
v dpk,c <Фрег dpB
Vk- c ~~dF~ + Vper ~dT~ V" ~dT ~ Л°к - ДОт’
(VI.5)
где VK. c, Vper и VB — геометрические объемы камеры
сгорания, регенератора и воздушного тракта до регене-
ратора.
В уравнение (VI.5) могут быть включены и другие
объемы, если их размеры соизмеримы с выделенными.
Поскольку расход воздуха через компрессор в соот-
ветствии с его характеристикой при заданных параметрах
засасываемого воздуха GK = f (р2, ш), то
Дбк = (дОк/др2) Ьр2 + (5GK/5(o) Дю (VI 6)
Если параметры засасываемого воздуха переменны,
то в это уравнение надо добавить соответствующие члены.
Расход газа через турбину GT = f (р3, Т3, р4), тогда
ДОт = -^Дрз+^.Д7’з+^1-ДР1. (VI.7)
иРз и1 3 °Р4
Плотность рабочего тела на различных участках
тракта, входящую в левую часть уравнения (VI.5), при-
менительно к объемам, в которых имеет место теплообмен
с окружающей средой, следует выразить через давление
и температуру рабочего тела. Связь между этими пара-
130
метрами устанавливается уравнением Клапейрона, в ре-
зультате дифференцирования которого получим
dp = р (dp/p — dT/Т).
Этим уравнением следует пользоваться при рассмо-
трении камеры сгорания и регенератора.
Для объемов без теплообмена связь между р и пара-
метрами рабочего тела определяется политропным про-
цессом, т. е. dp = [p/(pn) ] dp, где п — показатель поли-
тропы.
Поскольку можно принять, что Дрк. с= Аррег=Дрв=
= Лр3, уравнение газовоздушного тракта между компрес-
сором и турбиной запишется в следующем виде 1.
dipg dT'! . rfTs „ di2 _
dt 1 dt 2 dt 3 dt ~
Фз I ф T3 Ф"> zVT Q\
= —(VI'8)
Здесь
VK. срк. с7’3р/(7’зр T5B)
' 1 VK. срк.с + VperPper + VbPb^
Vk. срк. с7’6р/(7’д0 4~ T3p)
+ VpeiPperVsp^T^p + (T’sp)
2 VK. cPk. с 4~ VperPper + VbPbA1
VperPper7’3p/(7’2p 4- T5p)
3 VK. cPk. c VperPper + VbPbM
VK. сРк. c 4~ VperPper “l~ VbPbM .
(dGT/dpg) p3p • (dGK/dp2) p2-p
Vк. сРк. с VperPper УвРв^
~ (двк/д<£>) <вр ’
V к. сРк. с' V регРрег 4“ V вРвД
Rs== (dGT/dTs) Тзр ;
VK. cPk. с + VрегРрег ' i ’ VВрв/И-
4 ~ (дОт/др4) pip
В тех случаях, когда один из рассмотренных объемов
отсутствует, в уравнении (VI.5) соответствующее значе-
ние V приравнивается нулю и уравнение (VI.8) упро-
щается.
Воздушный тракт между компрессорами может вклю-
чать промежуточный охладитель воздуха. Его уравнение
движения в этот случае будет VK. н-к. vdpvildt = AGK. н —
— AGK.B, или в относительных величинах
1
d''Раи ' dr1B ' dT2H
dt 1 dt 2 dt
___ 'Фгн , фн'Фз фв тхв р
^2 ^3 ^4 ^5
Здесь
/ Лв. р / ^2Н. р
7р ’ а 2 'Г 1 Т1 »
1 IB. Р Т 1 2Н. р 1 IB. р “Г 1 2Н. р
r' ___ __________Ук. Н-К. вР2Н_______ .
1 (<3GKe в др2н —- dGK, и/др2н) /?2н. р
I
С
I
}
I
А
1 При выводе уравнения (VI 8) принято, что для каждого
участка тракта характерная температура определяется как
среднеарифметическая между температурами иа входе и вы-
ходе
i-J
Г
А
Г
(
г,' Vк. н-к. вРгн . п'_______________Ук. н-к. вРгн .
2 (dGK. н/5<вн) сон. р 3 (dGK. в/др2) р2р
___ Ук. н-к. вРгн . г>'_______Ук. н-к. вРзн
4 (dGK. в/дсов) сов. р 5 (dGK. в/дТ 1в) ТjB. р
Если воздухоохладитель между компрессорами отсут-
ствует или его объем относительно мал, то изменение
состояния рабочего тела можно считать политропным,
а вместо уравнения (VI.9) записать
_ ___ Узн . Фн_____Фз______фв _ Т1В ,yj ]Q\
dt “ ~ R'l R'2 R'3 R't R's'
Тракт между турбинами может иметь существенную
аккумуляцию рабочего тела чаще всего в том случае,
когда в него включена камера сгорания. Уравнение дви-
жения этого участка тракта будет VK. cdpK. с/dt =
= AGT. в— AG,.h, или в относительных величинах
<уФот " „ t/т..,,
dt 1 dt 2 dt
__ Фзн , Фз > тз тзн (yj Щ
R'l R'2 R3 R'l '
Здесь
„ T4B. p „ R3H. p
1 T4B. P + T3H. p ’ 2 R IB. P + Tзп. P
n"________________Ук. сРзн___________ .
1 (5GT. н/^Рзн — dGt. B/5p1B) pSH. p
n" У к. сРзн . n" У К. сРзн________ .
2 (dGT. в/дрз) Р3р 3 (SGT. в/дТ3) Т3р
п” _ _______________У к. сРзн_____
4 (йОт.н/а7’зн)7’зн.р
В составе газотурбинной установки могут быть и дру-
гие объемы, являющиеся значительными аккумуляторами
рабочего тела. Для каждого из них может быть составлено
уравнение движения по методу, изложенному выше.
Однако для современных ГТУ характерны высокие
скорости и относительно малые промежуточные объемы,
поэтому влиянием аккумулирующей способности объемов
часто пренебрегают.
Уравнения движения аккумулятора
тепловой энергии
Наиболее вероятными аккумуляторами тепловой энер-
гии в составе газотурбинной установки являются камера
сгорания и регенератор.
Камера сгорания. Обычно считают, что процесс сго-
рания топлива происходит мгновенно. Если принять, что
аккумуляция тепло'ты определяется не только металлом
камеры сгорания и газохода, но и рабочим телом, сосре-
доточенным в объеме камеры, то уравнение движения
можно записать в виде
dTcp
СмеА с + №TWdt = “ А<?2’
(VI.12)
где Смет — удельная теплоемкость металла; DK, с — масса
металла камеры сгорания, газохода и направляющего
аппарата первой ступени турбины; уср — плотность
и температура газа, осредненные по камере сгорания;
Qi и Q2 — количество теплоты на входе в камеру сгорания
9*
и на выходе из нее; Тс$ с — средняя температура металла,
равная ТрР.
Пренебрегая изменением давления в пределах камеры
сгорания и предполагая, что теплообмен между рабочим
телом в камере сгорания и ее стенками происходит без
запаздывания, т. е. что температура стенки с опре-
деляется только температурой газа Т3, дифференциальное
уравнение движения камеры сгорания можно записать
в виде
dT3 —L- п ______11. , Фз , ф । gTon
dt + к-с dt 1V1 +Af2 +У3+ У4 •
(VI.13)
Здесь
_ Сметик. сТзр
1 1 ~' као2/ат3) + (5q2/5gt) (аот/аг3] тзр ;
_ ^мет-^к. с^зр
2 / Ж dGK dQ1 дт2 dQ2 dGT \ ;
k dGK др2 + дТ2 др2 dGT др3 ) Рз?
t Сметик. сТ зр
Ns = WGK) (dG:i/da) Шр :
^мет-^к. сТзр
4 (dQi/dGTon) GTOn, р
VK. сСргРзр t __________ AGTon
RCmqtDk. Зр GTOn, р
В случаях, когда тепловой инерционностью камеры
сгорания можно пренебречь,* ее уравнение будет
Т3 -- &1Фз &2ф — ^З^ТОП’
(VI.14)
где Vi/V2; k2 = k3 = A\/V4.
Регенератор. Если принять параметры рабочего тела
и его массу в регенераторе сосредоточенными, то движение
теплового аккумулятора энергии в пределах регенера-
тора можно определить следующими уравнениями:
смеАег (^регМ) = ^ег - (VI-15)
(p^/dt = AQrl - AQr2; (VI. 16)
срв^Вре/ №T?)/dt = AQB1 - AQb2. (VI. 17)
Здесь (рис. VI.1) Qrper = arfr(^p—^3 и Q«er =
= ocBFB (Fper — ^bP) — тепловые потоки через тепло-
обменные поверхности регенератора со стороны газа и
воздуха; Qrl = GrlcprT4 и Qr2 = Gr2cprT6 + аг Fr X
X (Т^р — Т’рег) — тепловые потоки со стороны газа на
входе в регенератор и на выходе из него; QB1 = GK1cpt.T 2
+ aBFB (Грег - гвр) и Qb2 = GB2cpBT5 ~ тепловые по-
токи со стороны воздуха на входе в регенератор и на вы-
ходе из Него; Урег и У®ег — объемы газовой и воздушной
полостей регенератора; смет и Орег — теплоемкость ме-
талла и масса теплопередающих поверхностей регенера-
тора; Грег — средняя температура теплопередающей по-
верхности; Твр и Твр — средние температуры газа и воз-
духа, эти температуры в дальнейшем приняты средне-
арифметическими, т. е. Твр = (Т4 Г6)/2 и Твр =
= (Т 2 + Т5)/2.
Поскольку в регенераторах современных ГТУ газовая
и воздушная тепловая аккумуляция существенно меньше
аккумуляции металла теплопередающих поверхностей,
131
ею часто пренебрегают. Тогда после перехода к относи-
тельным величинам движение теплового аккумулятора
будет определять следующая система уравнений:
(VI.18)
Лрег
dt
_ тРег . т8 т2 т5 .
V V Л?з N'5
^п'Фз 4“ ^21г3 4“ ^31г4 &41грег — &51Т6 — 0;
^Хзф 4“ ^Зз'Рз 4“ &32Т2 &42Т5 ^52Трег
^62^3 == О'
Рис. VI. 1. Принципиальная схема
регенератора
Здесь
N1 = CMeTDper/(arfr “ “.Л):
у' = 2 Смет^рег рег. р ^мет^рег Tper. р
Сйг/7 г ^4р 3 аг/"г Т ер
А4 — 2 ^мет-^рег рег. р Ac - ^мет^рег рег. р
ОСг^г 2р х* 5 “ arFr '^5Р
Ьц _ dQrl dGT dGT др3 ^зр’ ^21 = dQrl dGT dGT дТ3 Т зр!
ь __ (dQn 5Qr2 \ __ dQra
31~\дТ\ дТь)1^' " ~ ~дТ^г 1 рег' Р’
_ ( dQr2 5Gr2 dQr2 \ dQB1 dGB1
\ dGn дТв + dTl; ) 6P’ ftl2 “ dGB1 да “P’
r, _ f dQB1 5GB1 dQB2 dGB2 \
22~ugb1 dPs жг^глзр’
ь _ dQB1 _ / dQB2 dQB1 \ .
й32"^т7У2Р’ Й42~ \^77~'этГЛ5р’
ь ___ dQB1 . ь ____________ 5QB2 dGB2
52 “ атрег 1 рег- Р’ - ЖГ ЖГ1 зр-
При определении частных производных принято, что
GBx — GK; GB2 — GT; GrJ = GT; Gr2 = f (T6).
Поскольку использование уравнений регенератора
в виде (VI. 18) для исследования динамики ГТУ требует
трудоемких вычислительных операций, в ряде случаев
без большой погрешности можно принять, что аккуму-
ляция расходов воздуха и газа в пределах регенератора
не оказывает существенного влияния на его тепловое
состояние, т. е. что Grl = Gra и GB1 = GB3. Тогда два
последних уравнения в системе (VI. 18) существенно упро-
щаются и приводятся к виду:
трег — ^11г2 + &21г5> т6 — ^12грег —^22т4' (VI. 19)
Здесь
= (0.5 — рв) T2p/TFer р;
^1 = (0,5 + Рв)Т5р/Трегр;
^2 = [l/(0,5 + PB)jTper р/Т6р;
^22 = [(0.5 - рг)/(0,5 + рг)] Т4р/Т6р,
где
Рв = QB^pB/(^BAB) > Рг = ^r^Pr/l^r^r)'
Совместное решение уравнений (VI.19) и первого
уравнения системы (VI.18) приводит к уравнению реге-
нератора в следующем виде:
Nperl dT5/dt Nрег2 dx2jdt = -f- &рег2Т2 -I- ^регзП’
(VI 20)
где
Aperi — 0,5 рв, Nper2 = 0,5 p,;
*Per 1 = w; + ( 1X) (0,5 - pr)/(0,5 + pr);
*per 2 = 1M + (1M) (0.5 - PB)/(0,5 + PB);
V 3 = 1M + 0M) (0,5 + PB)/(0,5 + pr).
Поскольку величины Рв и рг обычно меньше единицы,
то коэффициент Урег 2 оказывается существенно меньшим
Vperi, поэтому в уравнении (VI.20) вторым членом в ле-
вой части в ряде случаев пренебрегают.
Для температур Т4 и Т2 имеем выражения: Т,х =
= т3 (1 — ЯтПт) И Т2 = 7\ (1 4- ЯКЛ]К), поэтому в до-
полнение к уравнению (VI.20) можно написать:
т4 = &цТз-[-г2 = ^12’Фз, (VI.21)
где
„ _ д7\ ^зр „ _ дТц Рзр __ дТ2 Pw
11 - Ж? Лр ’ 21 др3 Tip ' ~ др2 Т2Р •
Уравнения (VI.20) и (VI.21) позволяют исследовать
динамику регенератора с достаточной для практики точ-
ностью. При расчетах, требующих повышенной точности,
необходимо перейти к системе уравнений в частных про-
изводных.
Воздухоохладитель. Воздухоохладитель между ком-
прессорами также можно рассматривать как объект с со-
средоточенными параметрами. Поскольку температура
металла теплообменных поверхностей близка к температуре
охлаждающей воды и практически не меняется, учиты-
вается аккумуляция теплоты только рабочим телом,
находящимся в воздухоохладителе. Тогда уравнение
динамики теплового аккумулятора
xd(PW)M = AQB x1-AQb.x2,
ГДе Qb. х 1 = Q?BGk. нТ2н И Qb. х 2 “ £рв^к. в^хв ^^в. х X
X (Твр — Т’вод) — тепловые потоки на входе в воздухо-
охладитель и на выходе из него; Твр = 0,5 (Т2н -ф- Т1В) —
средняя температура воздуха; k и FB. х — коэффициент
теплопередачи и теплообменная поверхность.
Приняв рврТдР = PlBlRB и переходя к безразмерным
параметрам, получим
^Фхв Фхв , фн Ив _ Ч’з Фв _
dt VB. XX NB.X2 Яв. ХЗ Ав. Х4 Ав. Х5
‘ (VI.22)
132
Здесь
Срв^В.хР1В. р
X1 /?в (^Q2/dpiB dQ1/dp2ji) Pie. р
СрвУв. хР1В. р
в Х2 — RB {dQt/дая) сон. р ’
СрвУв. хР1В. р
в-хз = ет<Э2/ат1в) r1b. р;
СрвУв. хР1в. р СрвУв. xPiB.p
Е Xi = Rb (dQ2/dp2B) Рзр; 1 в-Х5 = RB (5Q2/5coB) сов •
Частные производные, определяющие коэффициенты
NB, х, находятся в соответствии с -уравнениями для Qj
и Q2. Коэффициент теплопередачи можно определять по
уравнению [57]
k = k0 (GB/GB. р)0*64 (Тв/Тв. р)0-33.
Расчеты показывают, что чаете/ тепловой аккумуля-
цией воздухоохладителя можно пренебречь [81]. Тогда
уравнение воздухоохладителя
кв. xjTib 4~ кв. хгФхв Ч- кв* хзФз kB. X4<pn 4~ kB, хвфв = 0.
(VI.23)
Здесь
_ dQ2 . . (^__д0л\о .
0T1B Т1В- Р’ *в. Х2 - др1в др№ ) р1в. р,
, _ dQ2 , _ dQz
Ав-хз_1^ГР2в-р; йв-Х4~'л57Шн-р;
__ дОг
в-Х5 = 'а^Г “в-р-
Системы дифференциальных уравнений
движения для ряда схем ГТУ
Одновальная ГТУ. При отсутствии регенератора наи-
более существенным аккумулятором энергии является
ротор, а аккумуляцией материальной среды и тепловой
энергии в камере сгорания можно обычно пренебречь.
Тогда динамические свойства такой одновальной ГТУ
будут определяться следующими уравнениями:
Jdus/dt = ДЛ4Т — ЛМК — ЛЛ4,10Т;
AGK — AGT = 0; AQi •— AQ2 = 0.
Поскольку
AfT — f (co, p3, Rg); AfK — f (co, р2У, Л4П0Т— f (co, L);
Gk — f (®, p2); Gz = f(p3, Tsy, Q1 = f(GTon, GK, T2);
Qz = f(Ts, GT),
то, переходя к безразмерным параметрам, получим:
Ri dcpldt 4~ ср ^<р2Фз = кук\
Фз 4" ^1[>2Т3 =
Т3 ^Т]Фз — ^т2ф =
(VI.24)
Значения постоянных коэффициентов здесь и далее
определяются соответствующими аккумуляторами энергии.
При наличии регенератора система уравнений, опре-
деляющая динамические свойства установки, будет иметь
вид:
Тг d(p/dt + ф — йф1т3 — £ф2ф = kKX;
R1 dty3/dt — Rj d^/dt + Ф3 — ^j<P 4~
+ ^1|)2T3 = 0’
Nt dif/dt — N2 dxjdt —
kxy^l — кр^2 ^Тзг5 = 0>
тз — k'zyh — K24> - kzx5 = &ggTon;
T4 = kZ1t3 4- &т2Фз; T2 = ^тцФз-
(VI.25)
При наличии в одновальной установке промежуточ-
ного охлаждения воздуха без регенератора уравнения,
определяющие динамику, будут иметь следующий вид.
Уравнение ротора
J dtp/dt — tk/VR — AAIr. h AAIr, b — ДА1ц0Т,
где
Мт = f (co, Рз, TУ)', Л4К. H = f(co, р2Н);
Мк. в = f (со, р2> Р1в, Rib).
Уравнение объема между компрессором высокого
давления и турбиной
AGK. в — AGT = 0,
где GK. в = f (со, р2, р1в, Т1Р).
Уравнение камеры сгорания
AQ1^AQa=O,
где Qt — f (Gzoti, GK. в, Ra); Q2 ~ f (Gt, Rg)-
Уравнение объема между компрессорами
AGK, н — AGK. в — 0»
где G,,. „=/(« р2н).
Уравнение воздухоохладителя
^Qb. XI ~~ AQb. Х2 = 0>
где <ЭВ. х г = f (Gk. н, Ran); Qb. х 2 = f (Gk. в, Rib)-
Переходя к относительным параметрам, получим:
Ri dep/dt 4- <р — ^rfqT-j — А(р2Фз 4~ ^срзФгв 4~
4“ ^<Р4Т1в — к)^,
Фз 4- ^с)>2т2 — ^фдФгв — 0;
Т3 ^"Г]Фз -- ЙТ3Ф1В = ^g^TOni ( )
Ф1в - Ч.ф + + ЧзТ1в = °;
Ив 4- ^Т1Ф1в 4~ ^г2Фз — йт3Ф = °-
В тех случаях, когда ротор является наиболее значи-
тельным аккумулятором энергии и другими аккумуля-
торами можно пренебречь, любое сочетание режимов ра-
боты определяется только двумя параметрами, например
частотой вращения ротора п и расходом топлива в ка-
мере сгорания. Тогда Л4Т == f (GTon, со) и МК = f (GTon,
со), а уравнение ротора примет вид
Тj dtp/dt 4- ф — kggmB kRk, (VI 27)
где
у. ________________ ______________________ .
1 (ЭЛ4к/асо 4- <ЭЛ4пот/5со —- 5Л1Т/Эсо) сор ’
(5VfT/dGTOn) GTOn. р
е ~ (дМк/дш 4- dMmz/d(£> — ЭЛ4т/Эсо) сор ’
(дМпот/dL} Lp
~ (ЭЛ4к/дсо 4- дМ-пот!дч> — дМх/да>) сор ‘
133
Динамическая постоянная Т lt имеющая размерность
времени, называется временем машины, а безразмерные
коэффициенты kg и k\ — коэффициентами усиления.
Время машины Т\ определяется инерционностью ротора и
характеризует собственную устойчивость установки. Для
ГТУ, равновесные режимы которой устойчивы, Тх > 0.
Коэффициенты усиления feg и устанавливают связь
между <р и gTon или К.
Частьые производные дМт/д<£> и дЛ4к/дсо, вошедшие
в определение Тх, kg и /г;., отличаются от аналогичных
выражений в системе (VI.4), поскольку эти производные
берутся при GTOrt = const и могут быть определены только
графически с помощью характеристики компрессора.
Производные dMjdGron и дМк/дйтоа находятся также
графически.
Уравнение (VI.27) предполагает независимость рас-
хода топлива <3Т0П от параметров установки. Иногда
топливный насос приводится во вращение от ротора ГТУ,
и тогда его расход будет зависеть не только от положения
регулирующего органа ш, но и от частоты вращения п,
т. е. GTOrt = f (m, со). В этом случае дифференциальное
уравнение движения ротора
T1d(fldt + (1 — ах) <р = kmii — kKK, (VI.28)
где
(амт/аотоп) (aGTon/s<o),
1 ал4к/а<о — амт/асо ’
•, _(амт/аотоп) (аотоп/ат) /нГшг<
m ~ (дМк/д® — дМт/дш) йр
Из уравнения (VI.28) видно, что зависимость расхода
топлива от частоты вращения ротора ухудшает динамиче-
ские свойства установки, уменьшая запас по саморегули-
рованию. Для устранения этого недостатка в системе
регулирования ГТУ обычно предусматривают стабили-
зацию расхода топлива, которая обеспечивается, напри-
мер, регулятором расхода топлива.
ГТУ со свободной турбиной. В установке без регене-
ратора наиболее существенными аккумуляторами энергии
являются роторы турбокомпрессорного блока и силовой
турбины. Система уравнений, определяющая динамические
свойства ГТУ, будет иметь вид:
Г1 d<pB/dt + фв — 4fjT3 — &<р2Фз
Фз — + &1[>2г3 + ^1[>3ФзН = 0;
Тз &тхФз ^ГдФзн= ^gSmn>
, , - ' (VI.29)
Л dqjdt + фн - йфт3 — Йф2ф3 —
— Чз^зн =
Фзн + + S2T3 = °-
Если между турбинами предусмотрена камера сгора-
ния, то динамические свойства будут определяться систе-
мой, включающей первые три уравнения системы (VI.29)
и еще три следующих уравнения:
Т\ d%/dt + Фв — й'фт3н — Уф2ф3н = k,y,
Фзн + ^Фз + ^2Т3 — ^фЗтЗн = 0;
т3н + ^Фзн '\2Т3 — ^г3Фз = ^g^Ton2-
(VI.30)
Для более сложных схем ГТУ уравнения движения
выводятся аналогично.
134
VI.2. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
Анализ устойчивости
Одной из основных динамических характеристик ГТУ
является устойчивость, которая определяет способность
системы самостоятельно возвращаться в равновесное
состояние. Для эксплуатации пригодны только такие
системы, которые на всех нагрузках оказываются устой-
чивыми.
Исследование устойчивости выполняется обычно ана-
литически методом малых отклонений. Сущность этого
метода состоит в том, что систему путем приложения
внешнего достаточно малого возмущения выводят из
состояния равновесия, а затем рассматривают колебания
системы под действием собственных сил около положения
равновесия. Поскольку при этом параметры установки
отклоняются от положения равновесия на малую величину,
то в пределах этих отклонений возможна линеаризация
основных зависимостей даже при их существенной не-
линейности.
Согласно постановке задачи исследований, устойчи-
вость рассматривается без внешних возмущений (изучается
движение под действием собственных сил), поэтому сов-
местное решение общей системы уравнений, описывающей
движение объекта и системы регулирования, дает харак-
теристическое уравнение вида
аошп -|- a1wn~~l 4" • • • + an-iw 4" ап = 0,
где а0, ах, ... — коэффициенты характеристического урав-
нения, зависящие от режима работы установки и системы
регулирования; w корень характеристического урав-
нения.
Характер изменения любого параметра во времени
определяется корнями характеристического уравнения,
так как
I
1
с
5
5
£
Г
J
Е
Е
С
Ь
Е
Г
В
С
с
л
т
я
в
п
в
н
н
Ф = с^е”1'' + c29eW:it + . . .;
т = скеШ1' -ф- c2te”^ + •••’>
(VI.31)
ffl со
При устойчивом равновесном состоянии значения па-
раметров, найденные по уравнениям (VI.31), с течением
времени уменьшаются и в пределе стремятся к нулю.
Устойчивое состояние будет только в том случае, если
у всех корней характеристического уравнения веществен-
ная часть — отрицательная.
Поскольку нахождение корней характеристических
уравнений высоких порядков является весьма трудоемкой
задачей, обычно используются критерии устойчивости,
определяющие знак корней по виду характеристического
уравнения или по некоторым соотношениям, составлен-
ным из коэффициентов характеристического уравнения.
В настоящее время разработаны и широко используются
как аналитические, так и графические критерии. Сущ-
ность этих критериев и методы их использования под-
робно изложены в работах [46, 51, 114 и др.]. -
В одновальной установке, динамические свойства
которой характеризуются одним аккумулятором механи-
ческой энергии, собственная устойчивость определяется
коэффициентом самовыравнивания kCB, который зависит
от частных производных моментов по угловой скорости:
kCB = дМк/да> + дМП0Т/да> — дМт,/да>.
При устойчивой работе ГТУ kCB > 0. Здесь частные
производные берутся при Grort = const, в данном слу-
чае эта величина однозначно определяет режим работы
ГТУ.
Динамический анализ ГТУ, выполненных по различ-
ным тепловым схемам, свидетельствует о наличии собствен-
ной устойчивости установок на номинальном режиме.
ч
с
ц
X
н
X
р
ц
н
д<
н
сг
У
н
в
п
м
в<
У
м
31
п<
н<
В(
Hi
Введение регенерации несколько ухудшает устойчивость
установки, однако обычно не приводит к ее нарушению.
По мере уменьшения нагрузки собственная устойчивость
ГТУ, как правило, ухудшается, и на малых нагрузках
режимы работы установки могут оказаться неустойчивыми.
Построение графика переходного процесса
Важная динамическая характеристика любой уста-
новки — переходный процесс, который определяет изме-
нение основных параметров во времени при наборе или
сбросе нагрузки. График переходного процесса позволяет
установить такие важные показатели динамических свойств
установки совместно с ее системой регулирования, как
время переходного процесса, кратковременные забросы
параметров и др.
При исследовании устойчивости обычно используют
линеаризованные уравнения, которые достаточно спра-
ведливы при малых отклонениях параметров. Линеаризо-
ванные уравнения движения часто используют при по-
строении переходных процессов и для конечных откло-
нений параметров, однако при этом имеет место погреш-
ность, которая тем больше, чем значительнее изменение
режима установки.
На переходный процесс заметное влияние оказывает
вид внешнего воздействия со стороны потребителя или
со стороны управления установкой (управляющее воздей-
ствие). Внешние воздействия могут быть заданы в виде
любой временной функции. Часто используют возмущение
типа единичного скачка (ступенчатая функция), что отра-
жает наиболее неблагоприятные условия эксплуатации.
При определении постоянных интегрирования при-
нимается тот или иной способ отсчета переменных. Если
принять начало отсчета координаты времени от устано-
вившегося положения после возмущения (новое положе-
ние равновесия), то уравнения движения принимаются
в виде однородных линейных уравнений без правой части.
В этом случае общее решение системы линейных однород-
ных уравнений по одному из параметров имеет вид
х = ^е®1-+ с2еШг'-+ .. . + . (VI.32)
Начальные значения параметров, как правило, отли-
чны от нуля и определяются величиной внешнего воздей-
ствия. Конкретные примеры построения переходных про-
цессов рассмотрены в работах [46,51].
Для получения действительного представления о пере-
ходных процессах в ГТУ при значительных изменениях
нагрузки требуется учитывать нелинейности исходных
характеристик установки, а также элементов системы
регулирования.
Одна из возможностей построения переходного про-
цесса с учетом различных нелинейностей — использова-
ние линейных уравнений на отдельных участках, в пре-
делах которых линеаризация не дает заметной погреш-
ности. Однако наиболее точный результат дает непосред-
ственное решение системы нелинейных дифференциальных
уравнений, которое обычно выполняют методами числен-
ного интегрирования. Сущность одного из методов состоит
в том, что при рассмотрении дифференциального уравнения
первого порядка dxldt = f (t, х) выбирается достаточно
малый промежуток времени, в пределах которого произ-
водную можно считать постоянной. Тогда в конце i-ro
участка по времени t параметр имеет значение х; =
= xi_t Xi-iAt. Точность этого метода тем выше, чем
меньше интервалы времени АГ Использование ЭВМ по-
зволяет принимать малые интервалы интегрирования и
получать решение с достаточной для практики точностью.
Расчет переходного процесса ГТУ с учетом нелиней-
ности основных характеристик в ряде случаев удобно про-
вести графическим методом [13]. Так, для ГТУ, выполнен-
ной по простой тепловой схеме, динамические свойства
описываются уравнением Adnldt = AM, где А = Тл/30;
AM — суммарный избыточный момент на роторе. Как
уже указывалось [см. (V-14)], избыточный момент ДЛ4
можно определить двумя параметрами: частотой враще-
ния ротора и расходом топлива, т. е. AM = f (n, GTon).
Избыточный момент на валу ротора представляет со-
бой сумму мгновенных значений моментов турбины и
компрессора, а для одновальной установки, кроме того,
и момента внешнего потребителя энергии. При достаточно
быстром и значительном изменении параметров рабочего
тела, что часто имеет место в переходных процессах ГТУ,
мгновенные значения моментов могут зависеть не только
от параметров рабочего тела, но и от аккумулирующих
свойств турбины и компрессора.
Если в турбине наблюдаются значительные измене-
ния температуры, основное влияние на величину мгно-
венного момента оказывает тепловая аккумуляция про-
точной части. Как показано в работе [32], в ГТУ, выпол-
ненной по простой схеме, мгновенный крутящий момент
турбины
Мт. ДИН = Д-т 1 + б,5ДТдин/Г3, (VI.33)
где 7ИТ — крутящий момент турбины, найденный по пара-
метрам рабочего тела без учета аккумулирующей способ-
ности проточной части турбины; ДТдин — приращение
температуры газа на выходе из турбины за счет аккуму-
лирующей способности проточной части.
При ступенчатом изменении начальной температуры
газа приближенно можно считать
АТдИн = [Гметаг/(бгСрг)1 ДГ3е (VI.34)
Здесь Гмет — площадь поверхности проточной части тур-
бины, омываемой газом; ATS — диапазон мгновенного
изменения начальной температуры газа; Т =
— D(^рГмег) — постоянная времени; Dmqt и —
масса деталей проточной части и удельная теплоемкость
металла; аг — средний коэффициент теплоотдачи по про-
точной части.
Влияние тепловой аккумуляции обычно невелико.
Так, увеличение крутящего момента ТВД установки
ГТУ-20 даже при мгновенном падении температуры газа
на 350° С в начальный момент составляет только около
2,5%. Через несколько секунд различие между ЛД.дин
и Мт исчезает совсем [32]. При разгоне этой же установки
уменьшение момента турбины составило только 0,2%.
Эти цифры показывают, что при динамических расчетах
характеристики турбины часто можно считать квазиста-
ционарными.
Влияние тепловой аккумуляции проточной части ком-
прессора при обычных темпах изменения температуры
воздуха и его расхода также невелико, а возможные от-
клонения температуры воздуха за компрессором АТДИН
не превышают 0,5—0,6% [32]. Поэтому характеристику
компрессора можно с достаточной точностью считать
квазистационарной и использовать как в статике, так и
в динамике.
При расчете переходных процессов зависимость AM =
= f (п, GTon) удобно представить в виде графика, который
иногда называют моментной характеристикой установки.
Для ГТУ, выполненой по рассматриваемой простой схеме,
такая характеристика изображена на рис. VI.2. Здесь
Д7ИТК — разность моментов турбины и компрессора;
714 пот — момент внешнего потребителя. Для одновальной
установки условие равновесного состояния ротора, опреде-
ляющего статические режимы, имеет вид ДЛ4ТК = Й4ПОТ
(точки 1, 2, 3 на рис. VI.2). Для ГТУ со свободной силовой
турбиной статические режимы лежат на оси абсцисс,
где ДЛ4ТК = 0.
Организация переходного процесса зависит от при-
нятого закона подачи топлива, который определяет вели-
чину избыточного момента на роторе. Подача топлива
135
должна'быть такой, чтобы был обеспечен необходимый
запас по помпажу и предельной температуре газа (линии //
и 111 на рис. VI.2).
Моментные характеристики удобно строить с помощью
характеристики компрессора. Для этого на ней строят
линии постоянной температуры газа перед турбиной Т.,.
Если на характеристике компрессора нанесена режимная
Рис. VI.2. Моментная характеристика ГТУ, выпол-
ненной по простой схеме:
I — момент внешнего потребителя в одновальной уста-
новке; II — граница помпажа компрессора; III — линия
предельной температуры газа Т'Зпред
линия, то при любой степени повышения давления связь
между температурой газа и расходом воздуха определяется
уравнением [13]
Gk = G„. р КТзр/73. (VI.35)
Здесь индекс р соответствует равновесному режиму, взя-
тому по режимной линии на характеристике компрессора
(см. рис. V.12).
Линии температур газа дают возможность с помощью
уравнения теплового баланса камеры сгорания нанести
Рис. VI.3. Построение переходного процесса ГТУ, выпол-
ненной по простой схеме
на характеристику компрессора линии расхода топлива
GTort, по которым и находятся крутящие моменты ком-
прессора и турбины.
Моментные характеристики (рис. VI.2) позволяют
довольно просто решить задачу построения переходного
процесса. При этом используется уравнение An/At =
= АМ/А, справедливое для достаточно малых интервалов
времени At. Здесь А = Лх/30 — постоянная для рассма-
триваемой установки величина.
Можно предложить следующий порядок расчета пе-
реходного процесса. Избыточные моменты откладывают
по оси абсцисс на расстоянии А (рис. VI.3). Координату
136
времени разбивают на интервалы At, достаточно малые
для того, чтобы принятые допущения не давали существен-
ных погрешностей. Пусть задан закон изменения расхода
топлива (рис. VI.4) в функции частоты вращения ротора
(или другого параметра). Обычно в начальный момент
времени дается мгновенный бросок по топливу AGmn =
= GTort. бр—GTOrt. х. х при неизменной частоте вращения ро-
тора. Этому броску соответствует некоторый избыточный
момент ДЛ4бр, снятый с графика на рис. VI.2. Значе-
ние AMgp откладывают на рис. VI.3 при t = 0. Через
точку A j ’проводят прямую в начало координат. Точка
пересечения этой линии с прямой Д/х будет принадлежать
Рис. VI.4. Закон подачи топлива при наборе
нагрузки ГТУ
кривой переходного процесса n=f(f), так как Апг =
= Atr (ДМбрМ). Для найденного значения пг на рис. VI.4
снимают значение GTOn х, по которому на рис. VI.2 нахо-
дят ДЛ4Х. Эту величину откладывают на рис. VI.3 при Д/х,
но не от абсциссы, а от уровня Дпх.
Дальнейшее построение проводится аналогично (см.
рис. VI.2 — VI.4). Благодаря простоте и быстроте построе-
ния может быть повышена и точность решения задачи,
так как время процесса может быть разбито на доста-
точно малые интервалы интегрирования.
Моментная характеристика позволяет довольно просто
решить задачу нахождения времени разгона установки
при любом принятом законе подачи топлива. Поскольку
t = A J dn/AM, то для определения времени переходного
П1
п2
процесса требуется найти интеграл J dra/ДМ, который
представляет собой площадь под кривой l/AM = f(ri).
Для принятого закона подачи топлива по моментной ха-
рактеристике снимают значения AM = f (п), по которым
затем строят график 1/Д7И = f (п). По этому графику
определяют площадь под кривой 1/ДЛ4, а затем находят
время разгона установки t [13].
При всех графических построениях необходимо учи-
тывать масштабные коэффициенты.
Для построения переходных процессов газотурбин-
ных установок целесообразно использовать ЭВМ, которые
существенно облегчают решение поставленной задачи.
Приемистость и останов ГТУ
Приемистость представляет собой способность уста-
новки достаточно быстро переходить с малых нагрузок
на большие.
Приемистость связана с наличием аккумуляторов
в составе установки и зависит прежде всего от их аккуму-
лирующей способности, а также условий эксплуатации.
Одновальная ГТУ для привода генератора обычно харак-
теризуется значительным аккумулированием механиче-
ской энергии в ее роторе. Однако приемистость этой уста-
новки высокая и определяется только допустимым по усло-
виям прочности темпом подъема температуры газа. Запаз-
дывание набора мощности из-за инерционности ротора
здесь отсутствует, так как установка эксплуатируется при
постоянной частоте вращения.
Влияние инерционности ротора на приемистость
можно показать на примере простой ГТУ со свободной
силовой турбиной при любом внешнем потребителе мощ-
ности [11]. Равновесные режимы турбокомпрессорного
блока наносятся на характеристику компрессора в виде
режимной линии а—b (см. рис. VI. 16). Все точки этой
линии отвечают условию равенства моментов компрессор-
ной турбины и компрессора. При уменьшении полезной
мощности, т. е. мощности силовой турбины, частота вра-
щения турбокомпрессорного блока падает. Минимальная
мощность установки, называемая режимом холостого
хода, имеет место в точке Ь (см. рис. V.16). Для повыше-
ния мощности .установки нужно увеличить частоту вра-
щения турбокомпрессора, для чего требуется создать на
его валу положительный избыточный момент. Поскольку
ротор турбокомпрессора обладает инерционностью, то
для увеличения его частоты вращения требуется время,
которое и определяет приемистость установки.
Время разгона зависит от избыточного момента на
роторе, который тем больше, чем выше начальная темпе-
ратура газа перед турбиной. Для уменьшения времени
набора мощности линия разгона, представляющая собой
геометрическое место точек совместной работы турбины
и компрессора на неустановившихся режимах, должна
располагаться как можно выше и левее режимной линии
а—b (см. рис. V.16). Положение линии разгона опреде-
ляется подачей топлива в камеру сгорания, которая дол-
жна быть организована так, чтобы исключить неустойчи-
вую работу компрессора и превышение предельно допу-
стимой температуры газа. Выбор линии разгона для раз-
личных условий эксплуатации, обеспечивающей минималь-
ное время перехода с холостого хода на полную мощность,
и обеспечение этой линии соответствующей организацией
дозировки подачи топлива при разгоне являются задачами
организации приемистости установки.
Для получения оптимальной приемистости ГТУ раз-
гон турбокомпрессора от частоты вращения холостого хода
до расчетной должен быть организован по следующим
участкам (см. рис. V.16):
1) начальный бросок (Ь—by), где повышение расхода
топлива до величины Стс,п.бр не лимитировано характе-
ристиками установки и может быть произведено практи-
чески мгновенно, если отсутствуют ограничения по тепло-
напряженности деталей;
2) граница помпажа компрессора (&>—с);
3) линия предельной температуры (с— d);
4) расход топлива, соответствующий новому режиму
(d—а), где температура газа понижается от предельно
допустимой до рабочей. Этот участок представляет собой
линию естественного разгона.
В двухкомпрессорных ГТУ время разгона обычно
лимитирует КНД, поскольку момент инерции ротора
низкого давления значительно больше, чем ротора высо-
кого давления. Поэтому рост частоты вращения КНД
встает от КВД, который, отсасывая воздух после КНД,
способствует устойчивой работе КНД. Характеристики
разгона турбокомпрессора высокого давления аналогичны
характеристикам ГТУ, выполненной по простой схеме.
Значительное улучшение приемистости газотурбин-
ных установок, выполненных по различным тепловым
схемам, достигается за счет впрыска воды или пара в тракт
высокого давления. Для примера на рис. VI.5 приведены
графики разгона ГТУ, выполненной по простой схеме
[108]. Без впрыска процесс набора нагрузки лимити-
руется скоростью подъема температуры газа и составляет
около 25 мин. Ввод воды позволяет улучшить приемистость
на 40—45%. Полное решение проблемы приемистости
может быть найдено путем ввода пара, тогда набор нагрузки
установки осуществляется практически мгновенно.'
Рис. VI.5. Характеристики разгона ГТУ,
выполненной по простой тепловой схеме:
(ky — коэффициент устойчивости компрес-
сора, определяемый границей помпажа;
d — расход воды или пара, отнесенный
к расходу воздуха):
1 — без впрыска; 2 — впрыск воды по за-
кону предельного насыщения воздуха за
компрессором; 3 —впрыск пара
(VI.36)
Для ориентировочной оценки времени набора нагру-
зки однокомпрессорной ГТУ можно воспользоваться
уравнением [79].
J (па — «в) 5860ГЯк. со (Ра — Pb)
18 600AVcp ЛЛ/срТср^к. ср
где J — момент инерции ротора; ДУСр, Нк, ср и %. Ср —
средние значения в течение переходного процесса избы-
точной мощности (кВт), изоэнтропийной работы компрес-
сора и его к. п. д.; V и Тср — объем газовоздушного тракта
между компрессором и турбиной и средняя температура
рабочего тела в этом тракте. Индексы & и а соответствуют
режимам малой и повышенной нагрузки соответственно.
Сброс нагрузки с ГТУ также осуществляется воздей-
ствием на подачу топлива, однако линия сброса нагрузки
располагается правее и ниже режимной линии а—b (см.
рис. V.16). В связи с тем, что при сбросе нагрузки нет
столь жестких ограничений, как при наборе, избыточный
момент на роторе (отрицательный) может иметь значитель-
ную величину, и время сброса нагрузки обычно меньше,
137
чем при наборе. Однако при сбросе топлива следует опа-
саться чрезмерного падения температуры рабочего тела
в камере сгорания, что может вызвать срыв факела. Сле-
дует также при уменьшении нагрузки не допускать рез-
ких падений температуры газа из-за возможности появле-
ния чрезмерных температурных напряжений в элементах
проточной части турбины. Эти напряжения могут явиться
Рис. VI.6. Принципиальная схема гидрозамедлителя:
I — рычаг управления; 2 - дроссель; 3 — сервомотор; 4 —
топливный рычаг
причиной разрушения ряда деталей турбины, в частности
лопаточного аппарата. Характеристики набора и сброса
нагрузки газотурбинных установок, выполненных по
различным тепловым схемам, приведены в работе [79].
Для организации оптимальных переходных процес-
сов в системе регулирования предусматриваются специаль-
Рис. VI.7. Принципиальная схема регулятора при-
емистости
ные устройства, обеспечивающие дозировку топлива на
переходных режимах. При наборе нагрузки используются
автоматы приемистости незамкнутого и замкнутого типов.
К первой группе относятся различные замедлители, кото-
рые осуществляют подачу топлива по заданному времен-
ному закону. Ко второй группе относятся автоматы,
организующие подачу топлива в соответствии с принятым
законом разгона установки. Эти автоматы называют регу-
ляторами приемистости.
В качестве примера автомата приемистости первой
группы на рис. VI.6 представлен гидрозамедлитель [114].
Автомат представляет собой усилительное гидравлическое
звено, в котором время сервомотора определяет темп
подачи топлива. Гидрозамедлитель устанавливается между
138
рычагом управления и топливным регулирующим орга-
ном или задатчиком пружины регулятора. Рычаг упра-
вления 1 перемещается с любой скоростью, а воздействие
на топливный орган осуществляется с выдержкой времени,
величина которой зависит от дросселей 2. Гидрозамедли-
тели довольно просты и надежны в работе, однако не могут
обеспечить оптимальную приемистость установки и поэ-
тому применяются там, где при эксплуатации не предъя-
вляют высоких требований к приемистости ГТУ.
Близкую к оптимальной организацию разгона можно
осуществить с помощью регуляторов приемистости, орга-
низующих подачу топлива по границе помпажа компрес-
сора и линии предельной температуры газа. Широкое рас-
70 4
9
Рис. VI.8. Принципиальная схема регулятора при-,
емистости упорного типа:
1 — рычаг управления; 2 — тяга; 3 — стакан; 4 — упор;
5 — регулятор приемистости; 6 — пружина; 7 — топливный
насос; 8 — дроссельный кран; 9 — регулятор расхода топ-
лива; 10 — топливо к форсункам;' 11 — подвод топлив?
пространение получили регуляторы, осуществляющие
заданный закон разгона за счет слива части топлива из
напорной магистрали (рис. VI.7). К регулятору поступают
импульсы по давлению воздуха за компрессором и давле-
нию топлива перед форсунками. Косвенно эти импульсы
характеризуют расходы топлива и воздуха. Импульс по
давлению воздуха может корректироваться дросселями 2
и 3. На статических режимах золотник 1 находится в ниж-
нем положении и не оказывает влияния на работу уста-
новки. При переходе с режима малой нагрузки на боль-
шую давление топлива растет, золотник 1 при этом под-
нимается и обеспечивает слив части топлива. За счет раз-
гона компрессора возрастает давление за компрессором р2,
а следовательно, и давление ра над мембраной 4, под дей-
ствием которого золотник перемещается вниз и прикры-
вает слив топлива. Увеличение расхода топлива при раз-
гоне происходит по мере повышения давления воздуха р2.
Возможна организация разгона установки путем ре-
гулируемого темпа перемещения органа подачи топлива
(например, дроссельного крана или задатчика основного
регулятора). В этом случае отсутствует регулируемый
слив топлива из магистрали перед форсунками и в топлив-
ную систему не вносятся дополнительные возмущения.
Принципиальная схема такого регулятора приемистости,
называемого регулятором приемистости упорного ти-
па [11], представлена на рис. VI.8, а его конструкция —
на рис. VI.9. Рычаг управления 1 (рис. VI.8) перемещается
с любой скоростью. При резком перемещении рычага 1
в сторону увеличения мощности установки тяга 2, опреде-
ляющая положение топливного регулирующего органа
Рис. VI.9. Конструкция регулятора приемистости упор-
ного типа
или настройку основного регулятора, перемещается в сто-
рону увеличения расхода топлива до тех пор, пока соеди-
ненный с тягой стакан 3 не дойдет до упора 4 поршня
Рис. VI. 10. Характеристики разгона ГТУ малой
мощности со свободной турбиной, обеспеченные ре-
гулятором приемистости упорного типа (ртоп —
давление топлива перед форсунками):
1, 2, 3 — при значениях зазора ах, а2, соответственно,
причем ах < а2 < а2
регулятора приемистости 5. Зазор а между упором 4
и стаканом 3 соответствует величине начального нерегу-
лируемого броска топлива, изменение которого может быть
произведено с любой скоростью. После постановки ста-
кана 3 на упор рычаг 1 перемещается за счет сжатия пру-
жины 6. По мере разгона двигателя растет давление воз-
духа за компрессором ра, поршень регулятора под действи-
ем этого давления перемещается, а вместе с ним переме-
щается и упор 4. В результате происходит дальнейший
разгон компрессора до выхода установки на заданный
положением рычага управления 1 режим работы.
Таким образом, разгон установки в каждый момент
времени определяется сочетанием расхода топлива и да-
вления воздуха за компрессором. Настройка регулятора
приемистости осуществляется изменением жесткости пру-
жины поршня регулятора или расходной характеристики
топливного органа, а также величиной зазора а.
Работоспособность регулятора характеризуют гра-
фики разгона ГТУ малой мощности (рис. VI.10) [11].
Изменение зазора а позволяет в широком диапазоне варьи-
ровать режимы разгона установки.
VI.3. ПУСК ГТУ
Важная динамическая характеристика газотурбинных1
установок, определяющая маневренные свойства, — про-
цесс пуска, который представляет собой вывод ГТУ на
минимальный режим устойчивой самостоятельной работы.
Большое значение для пуска имеет правильный выбор
режима холостого хода, определяемый следующими тре-
бованиями:
1) допустимым уровнем начальной температуры газа,
который не должен превышать температуру газа на номи-
нальном режиме;
2) запасом устойчивости по помпажу компрессора,
а также собственной устойчивостью установки;
3) работоспособностью камеры сгорания с точки зре-
ния устойчивости горения и качества распиливания топ-
лива.
Режим холостого хода должен отвечать условию ми-
нимальной полезной мощности установки.
Раскрутка роторов турбомашин при пуске ГТУ осу-
ществляется от посторонних источников энергии, для чего
предназначены специальные пусковые агрегаты. Выбор
типа и целесообразной мощности этого агрегата является
одной из задач расчета пусковых режимов.
Другая задача — организация процесса пуска, при
которой обеспечивается минимальное время выхода на
режим холостого хода и исключаются как помпаж компрес-
сора, так и перегрев элементов турбины. Расчет процесса
пуска и выбор его оптимальной программы сопряжены
со значительными трудностями, поскольку параметры ра-
бочего тела при пуске значительно отличаются от расчет-
ных.
В общей постановке пуск авиационных ГТУ рассмот-
рен в работах [5, 50], а сведения о пуске ГТУ общего на-
значения приведены в работах [32,79,81].
Основные типы пуско вых устройств
Электростартеры могут иметь питание как от акку-
муляторных батарей, так и от внешней электрической
сети. При батарейном питании применяются электростар-
теры постоянного тока. В этом случае в процессе пуска
регулируется частота вращения стартера, что позволяет
полнее использовать мощность пускового агрегата на
различных этапах пуска.
На рис. VI. 11 приведена принципиальная схема элек-
трической системы пуска [5], позволяющая регулировать
частоту вращения. В начальный период пуска стартер
подключается к источнику питания через пусковое со-
противление 9. При этом на стартер подается пониженное
напряжение. Затем сопротивление 9 отключается, и сила
тока в цепи стартера растет.
Батарейное питание электростартера нашло широкое
применение для пуска транспортных ГТУ, в том числе
авиационных двигателей. Основной недостаток электро-
139
стартера постоянного тока — большие габариты и масса
аккумуляторных батарей.
Для пуска транспортных ГТУ небольшой мощности
находят применение стартеры-генераторы, которые в одном
агрегате объединяют стартер и генератор. На режиме
пуска стартер-генератор работает как двигатель постоян-
ного тока с питанием от аккумуляторных батарей. После
завершения пуска установки он переводится в генератор-
ный режим и обеспечивает зарядку аккумуляторных бата-
рей и питание бортовой электрической системы.
Электростартеры переменного тока с питанием от
внешней электрической сети обычно используют для пуска
стационарных ГТУ, применяемых в электроэнергетике.
Электродвигатель обладает удовлетворительной внешней
характеристикой и может иметь значительную мощность.
Длительный опыт использования электродвигателей для
10
Рис. VI.11. Принципиальная схема электрической систе-
мы пуска:
1 — источник питания; 2 — выключатель; 3 — реле; 4 и 8 —
контакторы; 5 — пусковая кнопка, 6 — реле времени; 7 и 11 —
контакты; 9 — пусковое сопротивление, 10 — электростартер
пуска стационарных ГТУ, например ГТ-25-200 (ЛМЗ)
показал, что они являются эффективными пусковыми уст-
ройствами.
Газотурбостартер — небольшой газотурбинный дви-
гатель повышенной напряженности и малого ресурса.
Этот двигатель выполняется по двум тепловым схемам:
одновальной схеме и схеме со свободной силовой турби-
ной. В первом случае в системе редукторной передачи
устанавливается гидромуфта, которая обеспечивает тре-
буемый закон изменения крутящего момента и уменьшает
динамические нагрузки. Во втором случае свободная си-
ловая турбина позволяет в широких пределах изменять
выходную частоту вращения.
Пониженный ресурс газотурбостартера позволяет
обеспечить значительную мощность при малых габаритах
и массе.
К недостаткам газотурбостартеров относится некото-
рое усложнение пуска установки, поскольку требуется
организовать пуск самого стартера, к достоинствам —
возможность пуска ГТУ значительной мощности без
посторонних источников питания.
Турбостартеры представляют собой турбинную уста-
новку с внешним источником питания. В зависимости
от вида рабочего тела различают воздушные турбостартеры,
турбины, работающие на сжатом газе, например природ-
ном (турбодетандеры), и паровые турбостартеры.
Воздушный турбостартер обычно выполняется в виде
воздушной осевой турбины, работающей на холодном или
слабо подогретом воздухе. Этот воздух поступает из спе-
циальной системы или работающего двигателя, например
газотурбинного. Такие турбостартеры требуют значи-
тельных расходов рабочего тела, так как из-за относи-
тельно низкой температуры воздуха имеют невысокую
удельную мощность. Даже при давлениях 10—15 кгс/сма
их удельная мощность составляет только 120—150 кВт.
140
Достоинство воздушных турбостартеров — сравни-
тельно малые затраты на подготовку сжатого воздуха и
его недифицитность.
Турбодетандеры также обладают невысокой удельной
мощностью, поэтому целесообразны при наличии значи-
тельных запасов сжатого газа. Турбодетандеры нашли
широкое применение для пуска ГТУ газоперекачивающих
станций (рис. VI.12).
Паровой турбостартер представляет собой небольшую
паровую турбину, которая работает обычно с выбросом
пара в атмосферу. Этот стартер находит применение там,
где может быть обеспечено надежное снабжение паром.
Этому условию отвечают электростанции, где кроме газо-
турбинных установок имеются паровые турбины. Так,
паровой турбостартер используется для запуска газо-
турбинной установки ГТ-100-750-2 (ЛМЗ). Мощность пу-
сковой турбины 1000—1200 кВт, а общий расход пара на
пуск этой установки составляет 3 т при давлении 12 кгс/см2
и температуре 250° С [85].
Процессы, происходящие при пуске
Режимы пуска рассмотрены на примере однокомпрес-
сорной установки. Процесс пуска ГТУ разбивается на три
характерных этапа и начинается включением пускового
устройства.
На первом этапе крутящий момент генерируется
только стартером, а раскрутка ротора компрессора про-
исходит за счет пускового устройства. Крутящий момент
затрачивается на ускорение ротора и преодоление сопро-
тивлений, связанных с подачей воздуха. Газовая турбина
в этот период крутящего момента не создает. Этот этап,
который называют холодной раскруткой ротора, закан-
чивается при частоте вращения nlt составляющей 20—
25% от частоты вращения холостого хода ях х (рис. VI. 13
и VI.14).
На втором этапе начинается участие газовой турбины
в раскрутке ротора. При частоте вращения зажигается
запальное устройство и подается топливо на основные
форсунки. При этом резко возрастают начальная темпера-
тура газа и его давление, что приводит к повышению кру-
тящего момента турбины. На втором этапе пусковое устрой-
ство сопровождает турбину, поэтому общий крутящий
момент определяется суммой моментов стартера и турбины.
Второй этап заканчивается на частоте вращения п2, при
которой газовая турбина развивает достаточную для само-
стоятельной раскрутки ротора мощность.
При частоте вращения ротора п2 пусковое устройство
отключается, и дальнейший разгон ротора до частоты
вращения холостого хода пх. х, составляющий третий
этап, осуществляется только турбиной. Частота враще-
ния п2 не превышает 50—60% от значения пх. х.
Характер процесса разгона в соответствии с выделен-
ными этапами на характеристике компрессора приведен
на рис. VI. 13, а закономерность изменения крутящего
момента — на рис. VI. 14.
Процесс пуска определяется системой дифференциаль-
ных уравнений движения аккумуляторов энергии. Вид
этих аккумуляторов и их число в составе ГТУ различных
схем уже рассматривались. Поскольку основное влияние
на динамические характеристики при пуске установки
оказывает аккумуляция механической энергии, а расчеты
пусковых режимов имеют приближенный характер, влия-
нием объемов можно пренебречь. Погрешность из-за этого
невелика и даже при наличии регенерации вполне допу-
стима.
Что касается тепловой аккумуляции, то поскольку
при пуске температура рабочего тела изменяется сущест-
венно, а элементы конструкции камеры сгорания, газо-
ходов н проточной части турбины еще холодные, то часть
теплоты топлива расходуется на их нагрев. В некоторых
случаях эта теплота оказывается значительной, и ее
К- Е о
<т> sc Е
GQ
Ы
Рис VI 12. Конструкция турбодетандера НЗЛ для пуска ГТУ газоперекачивающих станций
надо учитывать при определении расхода топлива. Если
в качестве независимого параметра принять не расход
топлива GTOIS, а начальную температуру газа Т3, то раз-
гон ГТУ будет определяться только аккумулирующей
способностью ротора, а тепловой аккумулятор определит
связь между Ts и GTon-
Разгон ротора описывается уравнением
Jdm'dt = Л!П.У>+Л!Т — Мк — Л!1р, (VI.37)
где Л!п. у и Мг — крутящие моменты пускового устройства
и турбины; Л!к и Л!тр — моменты сопротивления компрес-
сора и сил трения.
Время общего разгона
t = J J Ао/ЛЛ!,
О
(VI.38)
где АЛ! — положительный избыточный момент па валу
ротора.
Для сокращения времени разгона при заданной кон-
струкции ротора следует обеспечить на всех этапах пуска
максимально возможное значение АЛ!. На его величину
в начале процесса разгона влияет мощность пускового
Рис. VI.13. Режим пуска на характеристике компрессора:
1 — линия равновесных режимов; 2 — линия холодной раскрут-
ки ротора; 3 — линия разгона по границе помпажа; 4 — линия
разгона по предельно допустимой температуре; 5 — линия раз-
гона при постоянном расходе топлива
устройства. Чем выше Vn.y> тем быстрее и надежнее осу-
ществляется процесс пуска! Однако чрезмерная мощность
пускового устройства увеличивает габариты установки
и ее весовые показатели. Поэтому одна из главных задач
расчета пуска — определение рациональной мощности
пускового устройства, которая колеблется в значительных
пределах и зависит от номинальной мощности ГТУ и
требований к скорости пуска. При мощности установки
1000—10 000 кВт мощность стартера составляет 1,5—
2% от номинальной мощности. Для ГТУ большой мощно-
сти (большее 20 000 кВт) мощность стартера уменьшается
до 1—1,5% , для ГТУ малой мощности (меньше 1000 кВт) —
увеличивается до 2,5—3%. Указанные уровни мощности
стартера являются ориентировочными и могут быть за-
метно больше при повышенных требованиях по скорости
пуска.
Другим важным фактором, влияющим на время пуска,
является выбор рационального температурного режима
пуска, который определяет характер изменения момента
турбины, а следовательно, и АЛ!. На режиме холостого
хода (рис. VI.15) температура газа существенно ниже пре-
дельно допустимой для кратковременных режимов 7’,1[ред,
обусловленной прочностью лопаток турбины. Холодный
пуск имеет место при низкой температуре Т3, которая
142
остается практически постоянной (рис. VI.15). Подача
топлива на форсунки при частоте вращения Пт сопровож-
дается повышением температуры. Ее уровень пока еще
ниже Г3пред и обычно лимитируется границей помпажа.
Для обеспечения надежного пуска и исключения помпажа
компрессора в эксплуатационных условиях уровень из-
Рис. VI-14. Характеристика моментов при
разгоне ротора:
1 — момент пускового устройства; 2 — момент
компрессора, J — момент газовой турбины; 4 —
избыточный момент ДЛ1 (в увеличенном масштабе)
менения температуры газа при разгоне по линии 3
(рис. VI. 15 и VI. 13) следует выбирать с некоторым запасом
Рис. VI. 15. Режим изменения температуры газа при
пуске:
1 — линия равновесных режимов; 2 — линия холодной рас-
крутки; 3 ~ линия разгона по границе помпажа при ky
— 10%; 4 — линия разгона по предельной температуре; 5 —
линия разгона при постоянном расходе топлива; 6 — линия
изменения температуры по границе помпажа;
------температура газа Т$‘, — — — — расход топлива
по линии 3 момент турбины растет и при некоторой ча-
стоте вращения пс оказывается равным моменту компрес-
сора. При частоте вращения п' температура газа дости-
гает предельного значения 73пред и сохраняется постоян-
ной на участке 4. Значения п’, п" и пс показаны также
на рис. VI.13 и VI.14.
Указанная закономерность изменения Тл обеспечи-
вается соответствующим законом подачи топлива. По мере
разгона ротора расход топлива GTOn растет и при частоте
вращения п" достигает значения GTon. х.х> поэтому дальней-
ший разгон и выход на режим холостого хода (пх. х,
Гзх. л происходит при GTon. х. х = const (линия 5 на
рис. VI. 15).
В некоторых случаях процесс холодной раскрутки
проходит достаточно близко от границы помпажа, поэтому
температура газа при воспламенении топлива оказывается
низкой и линия 3 на рис. VI. 15 проходит значительно пра-
вее. При таком пуске момент турбины повышается не-
значительно и процесс разгона оказывается растянутым
по времени. Для устранения этого недостатка обычно
применяют перепуск воздуха за частью ступеней компрес-
сора, для чего на компрессоре предусматривают специаль-
ный клапан. При его открытии граница помпажа пере-
мещается в сторону меньших расходов воздуха, что позво-
ляет повысить температуру газа Т3 при разгоне ротора
по линии 3.
Приведенные соображения соответствуют оптималь-
ной организации пуска при учете ограничений по предель-
ной температуре и границе помпажа компрессора. Другим
возможным ограничением допустимого броска темпера-
туры газа при зажигании топлива на частоте вращения
и темпа ее увеличения являются допустимые термические
напряжения, возникающие в наиболее напряженных де-
талях турбины (направляющие и рабочие лопатки, диски,
жаровые трубы камер сгорания и др.). Чрезмерный уро-
вень этих напряжений при многократном повторении про-
цессов пуска может привести к появлению термоусталост-
ныхьдрещин. Поэтому при организации пуска ГТУ должна
быть проведена оценка градиента температур и термиче-
ских напряжений в соответствующих элементах турбин.
Целесообразный темп увеличения температуры газа дол-
жен быть принят с учетом этих напряжений.
Пуск двухкомпрессорных ГТУ начинается с раскрутки
стартером турбокомпрессорного блока высокого давления.
Компрессор низкого давления в начальный период не
вращается, и через его проточную часть просасывается
воздух. После включения основного топлива перепад
на турбину, связанную с КНД, достигает необходимой для
вращения компрессора величины, и КНД начинает с этого
периода активно участвовать в пуске установки.
Основы расчета процесса пуска
Расчет процессов пуска ГТУ выполняют с использо-
ванием уравнения движения ротора (VI.37), которое позво-
ляет определить продолжительность пуска установки,
а такще изменение частоты вращения ротора во времени.
Ниже приведены рекомендации по определению моментов
на роторе на различных этапах пуска установки.
Крутящий момент пускового устройства зависит от
частоты вращения. Эта зависимость для применяемых
в настоящее время пусковых устройств близка к линейной
и записывается в виде Л4п.у = А40— Ьп, где Л40—'мо-
мент стартера при заторможенном роторе; Ь — коэффи-
циент, зависящий от типа пускового устройства.
При принятом законе изменения крутящего момента
максимальная мощность пускового устройства [50]
^.Утах= 1>57-10-3Ч/& (VI.39)
имеет место при частоте вращения п — М0/(2Ь).
В качестве пусковых устройств часто используют
турбины с постоянными параметрами рабочего тела (паро-
вые и воздушные турбины, газотурбостартеры со свобод-
ной турбиной и др.). Для таких пусковых устройств те-
кущий момент при одноступенчатой турбине [53]
М — G0G2 (dj/2) [clw0 — dc2!jlQ Ц-d2 (t/10 u/G)], (VI.40)
где индексом 0 обозначены параметры режима максималь-
ной мощности; G = G/Go — относительный расход рабо-
чего тела; d = d2/dt — отношение средних диаметров
(для осевой турбины обычно d = 1); d2 — средние диа-
метры облопачивания при входе в ступень и выходе из
нее.
Максимальный момент, возникающий при трогании
с места,
AIq = G0G2 (dy/2) (с1и0 — dc2U0 -|-d2ui0). (V1.41)
Момент сопротивления установки определяется пре-
жде всего моментом компрессора Л7К= GKcPB71f/K/(r)Kco),
поэтому для его нахождения требуется знание характери-
стики компрессора в области пусковых режимов. Посколь-
ку для области малых частот вращения компрессора нет
достаточно удобных методов расчета, обычно она достра-
ивается различными приближенными методами [4 и др.].
При использовании метода интерполяции на характери-
стику компрессора наносят линии постоянной температуры
газа Ta= const, по которым затем строят вспомогатель-
ные графики лк/лк.Р= Н«к/«к.р) и GK/GK.P= f(nK/nK.p).
Эти графики интерполируются в начало координат, что
позволяет в области малых частот вращения построить
линии пк = const. Для нанесения линий т]к = const
следует построить вспомогательный график т]к = f (лк)
для различных значений GK = const. Интерполяция этого
графика в начало координат позволяет провести необхо-
димые построения для определения значений т]к в области
малых расходов воздуха.
Для области малых частот вращения большое значе-
ние имеет характер протекания границы устойчивой ра-
боты компрессора. Для лк С 2 граница помпажа близка
к параболе, уравнение которой имеет вид лк — 1 =
= (GK/GK)1,8, где GK — расход воздуха через компрессор
при лк = 2 [4]. Это уравнение дает возможность построить
границу помпажа в зоне малой частоты вращения ком-
прессора.
Достроенная характеристика компрессора позволяет
в каждой точке при принятом законе разгона находить
момент компрессора.
Для определения момента компрессора при холодном
разгоне на частоту вращения холостого хода (см.
рис. VI.13) следует нанести точку D, которая принадлежит
процессу холодного разгона компрессора и может быть
определена по уравнению расхода через турбинную группу:
Gd/^kD = (GB/jtK.B) V~Тзъ!Т2о, (VI.42)
где T2d — температура воздуха за компрессором на ли-
нии холодного разгона.
Для построения линии холодного разгона следует
воспользоваться тем, что расход воздуха через компрес-
сор на пусковых режимах изменяется примерно пропор-
ционально частоте вращения. Тогда уравнение линии
холодного разгона
GK = GKDnK/nKD. (VI.43)
При организации пуска установки холодный разгон
закончится не в точке D, а в точке F при частоте вращения
(см. рис. VI.13). Положение точки F будет определяться
возможностью обеспечения устойчивого воспламенения и
сгорания топлива.
При страгивании с места момент сопротивления ока-
зывается существенно больше момента при вращении.
Для определения момента страгивания используется
уравнение [32]
Л1стр = ?трР^ш/2, (VI. 44)
где стр = 0,304-0,35 — коэффициент трения; Р — масса
ротора; dui — диаметр шейки вала.
На величину момента сопротивления оказывает влия-
ние привод вспомогательных агрегатов и трение в под-
шипниках. Как показывает опыт эксплуатации ГТУ, эти
затраты невелики и их влияние можно учесть увеличением
момента компрессора на 3—'5%.
143
Момент газовой турбины при холодной раскрутке
обычно отрицательный, так как турбина представляет
собой некоторое сопротивление, хотя и незначительное.
Положительный момент газовая турбина начинает
создавать с момента воспламенения топлива в камерах
сгорания. Затем этот момент быстро возрастает по мере
увеличения частоты вращения.
Крутящий момент газовой турбины в общем виде
МТ = GTCprT3HTTt]T!(£>. (VI.45)
Расход рабочего тела через турбины GT определяется
расходом воздуха через компрессор, так как добавка за
счет топлива невелика и при расчете пуска ее можно не
учитывать. При включении перепуска воздуха в компрес-
соре GT = GK — Опер, гДе Опер —• количество перепускае-
мого воздуха.
В одновальной ГТУ степень понижения давления лт
определяется степенью повышения давления лк, поскольку
л.т = nKv. В ГТУ с двумя и более турбинами параметр лт
зависит от распределения общей степени понижения давле-
ния между турбинами. Величину лт можно найти по урав-
нению Стодола. написанному для всех турбин. Для схем
ГТУ с двумя турбинами, когда турбина низкого давления
на первых этапах пуска неподвижна, степень понижения
давления турбины высокого давления можно найти по
уравнению [32]
(ят. в 0 (‘ ^т. в^т. в) ^х. х
где £' — коэффициент, определяемый отношением давле-
ний между турбинами; Кх. х — постоянная величина. Ко-
эффициенты I,' и Кх. х находятся по режиму холостого хода,
причем £' = р4в/Рзн-
По уравнению (VI.46) строят график лт,в = f (рзв),
с помощью которого определяют лт. в при любом зна-
чении рзв. Давление начала расширения рзв при пуске
зависит от степени повышения давления в компрессорах
и потерь давления по соответствующим трактам. Опреде-
ление этих потерь приведено в п. V.3.
На режимах пуска установки изменение к. п. д. тур-
бины определяется прежде всего отклонением параметра
х= KS и2/(2Нт) от оптимального значения. Учет влия-
ния этого отклонения, как уже указывалось в п. V. 1,
определяется коэффициентом т] = 2х — х2.
На пусковых режимах к. п.' д. турбины может заметно
ухудшаться при понижении числа Re. Для учета этого
влияния вводится коэффициент r)Re, который можно под-
считать по эмпирической формуле1 [32 ]
T)Re= 1.°-7,3-l°7(n?oRe1-1), (VI.47)
где т]10 — к. п. д. турбины на расчетном режиме.
Тогда к. п. д. турбины на пусковых режимах
т1т-К()¥1[;£. (VI. 48)
Управление пуском
Как уже указывалось, минимальные время пуска и
затраты энергии на пуск установки имеют место при под-
держании предельно допустимой температуры газа перед
турбиной на всех пусковых режимах. Эта температура
определяется прочностными свойствами материалов и
устойчивостью процессов сжатия воздуха. Поскольку
уровень температуры газа обеспечивается расходом топ-
лива, то одна из задач управления пуском состоит в орга-
низации необходимого закона подачи топлива.
1 Формула (VI 47) рекомендуется для Re > 0,1- 105.
144
Кроме организации подачи топлива при пуске ГТУ осу-
ществляются операции по включению и выключению раз-
личных элементов, работа которых строго последовательна.
ГТУ:
БУП — блок управления пуском; ТАП — топливный
автомат пуска; ГТН — главный топливный насос; ЭМК —
электромагнитный клапан; СК — стопорный клапан;
APT — автоматический распределитель топлива; Ф —
топливная форсунка; ПТН — пусковой топливный насос;
ВУ — воспламеняющее устройство; СТ — стартер; УС — ,
управляющие сигналы j
Все эти задачи решает система управления пуском, прин-
ципиальная схема одного вариант которой изображена
на рис. VI. 16. Перед пуском проверяют готовность вспо-
Рис. VI. 17. Воспламенительное устройство:
1 — соленоид; 2 — игольчатый клапан; 3 — подвод топлива,
4 — фильтр; 5 — распылитель топлива; 6 — запальная свеча,
7 — центральный электрод свечи#
могательных механизмов, после чего дается команда в блок
управления пуском (БУП). Этот блок решает логическую
задачу последовательности заданных операций.
Процесс пуска начинается включением пускового уст-
ройства, которое раскручивает ротор. При частоте враще- 1
ния пх включается пусковой топливный насос (ПТН), '
имеющий самостоятельный электрический привод, и
дается сигнал в воспламенительное устройство, одна из
конструкций которого представлена на рис. VI. 17. После
Рис. VI. 18. Топливный автомат пуска
со ступенчатым регулированием рас-
хода топлива
включения пускового насоса дается ток к соленоиду 1
и запальной свече 6. Клапан 2 открывается, и топливо,
выходящее из пусковой форсунки, поджигается от запаль-
Рис. VI. 19. Топливный автомат пуска
с плавным регулированием расхода то-
плива-
1 — плунжер, 2 —• мембрана; 3 — задающая
пружина; 4 — дроссель
ной свечи. Образовавшийся факел служит для воспламе-
нения основного топлива, поступающего через рабочую
форсунку. Воспламенительное устройство работает около
30 с, а затем БУП его отключает.
Основное топливо к рабочей форсунке поступает после
открытия электромагнитного клапана (ЭМК), сигнал на
открытие которого подается также от БУПа. Перед глав-
ной форсункой расположен автоматический распредели-
тель топлива (APT), который служит для последователь-
ного распределения топлива по каналам рабочей форсунки.
При пуске установки вплоть до режима холостого хода
APT подает топливо на один канал форсунки.
Принятый закон изменения температуры газа Ts обе-
спечивает топливный автомат пуска (ТАП), который
Рис. VI.20. Осциллограммы автоматического пуска ГТУ:
а — судовая установка ГТУ-20 [32]; б—энергетическая
установка ГТ-100 [85].
1 — включение рабочего топлива; 2 — отключение зажигания;
3 — страгивание ТКНД; 4 — отключение стартера
управляет расходом основного топлива. Наиболее простой
способ регулирования подачи топлива—регулирование
по времени с помощью замедлителей. Однако этот метод
не ведет к оптимальному разгону установки.
Оптимальный разгон можно получить, если осуще-
ствлять подачу топлива в зависимости от параметров уста-
новки. ТАП со ступенчатым регулированием расхода
топлива в зависимости от частоты вращения ротора п
показан на рис. VI. 18. При частоте вращения, соответ-
ствующей зажиганию основного топлива, от БУПа посту-
пает к ТАПу сигнал, и один из клапанов открывается.
По мере разгона ротора последовательно открываются
и два других клапана, обеспечивая ступенчатое увеличе-
ние расхода топлива в камеру сгорания. Такое регулиро-
вание разгона отличается высокой надежностью.
Рациональная организация процесса разгона уста-
новки имеет место в том случае, когда ТАП обеспечивает
10 Л. В. Арсеньев и др.
145
подачу топлива в зависимости от температуры газа. Время
разгона в этом случае будет минимальным. Однако отсут-
ствие надежных датчиков температуры, обладающих
высокой термостойкостью и приемлемой для регулирова-
ния процессов пуска инерционностью, приводит к необхо-
димости использования различных косвенных методов
определения температуры газа.
В настоящее время широкое распространение полу-
чили измерительные устройства, позволяющие контроли-
ровать температуру газа по соотношению давлений топ-
лива перед форсунками и воздуха за компрессором. Связь
между этими давлениями и температурой определяется
тем, что давления характеризуют расходы топлива и воз-
духа соответственно. На этом принципе контроля темпе-
ратуры построена работа регуляторов приемистости.
Топливный автомат пуска, основанный на этом прин-
ципе, представлен на рис. VI. 19. Количество подаваемого
к форсункам топлива определяется положением плун-
жера, управляющего сливом топлива. Это положение за-
висит от давлений топлива перед форсунками рф и воздуха
за компрессором р2, подаваемого в верхнюю полость мем-
браны, а также натяжения пружины. По мере разгона ро-
тора давление воздуха за компрессором растет и плунжер
перемещается вниз, уменьшая слив топлива. Требуемый
закон подачи топлива в камеру сгорания при пуске обе-
спечивается регулировкой натяжения пружины, а также
давления в полости над мембраной за счет подбора дрос-
селя.
В качестве примера на рис. VI.20 приведены осцил-
лограммы изменения параметров при пуске ГТУ.
VI.4. УСТРОЙСТВА ЗАЩИТЫ ГТУ
При нормальной эксплуатации ГТУ параметры влия-
ющие на надежность её работы, не должны превышать пре-
дельных значений. Однако во время эксплуатации могут
возникать случайные нежелательные состояния, связан-
ные с нарушением нормальной работы, которые могут
привести к аварии установки.
Для исключения аварийных ситуаций каждая газо-
турбинная установка снабжается устройствами защиты.
Поскольку современные ГТУ характеризуются высокими
динамическими и тепловыми нагрузками, к этим устрой-
ствам предъявляются требования высокой точности изме-
рения параметра и малой инерционности.
При нормальной эксплуатации устройства защиты не
должны оказывать никакого влияния на работу ГТУ.
Они могут проявлять себя только в тех случаях, когда
появляется опасность аварийной ситуации. Эпизодичность
работы предъявляет высокие требования к надежности
устройств защиты, поскольку вынужденный отказ в сра-
батывании может привести к аварии установки.
Устройства защиты в зависимости от принципа воздей-
ствия на объект могут быть выполнены в виде устройств
предельного (ограничительного) регулирования, при ко-
тором контролируемый параметр поддерживается на за-
данном предельном уровне, или устройств предельной
защиты (автоматы безопасности), при которой достижение
контролируемым параметром предельного уровня приводит
к экстренной остановке агрегата. В первом случае при
достижении тем или иным параметром предельного зна-
чения имеет место обычное пропорциональное регулиро-
вание с заданной статической характеристикой. Во вто-
ром случае характеристика регулирования — астатиче-
ская, что обеспечивает срабатывание устройства.
Защита по частоте вращения
Защитой от превышения частоты вращения обеспечи-
ваются все роторы установки, включая и те, частота вра-
щения которых поддерживается всережимным регулято-
ром. При достижении ротором предельной частоты вра-
щения устройство срабатывает на останов ГТУ, т. е. рабо-
тает по принципу предельной защиты.
В качестве командного органа защиты по частоте вра-
щения часто используют центробежный бойковый регуля-
тор с астатической характеристикой (рис. VI.21). При
вращении вала на боек действует центробежная сила, обу-
словленная смещением его центра тяжести от оси вращения
на величину эксцентриситета е. При п < «пред боек удер-
живается на упоре натяжением пружины. Если частота
вращения достигнет пПред, то центробежная сила и сила
натяжения пружины оказываются равными. При дальней-
шем росте частоты вращения центробежная сила растет
быстрее, чем сила натяжения пружины, и боек переходит
в другое крайнее положение, сместившись на величину а.
Рис. VI.21. Центробежный регулятор бой-
кового типа:
1 — боек; 2 — направляющая втулка; 3 —
пружина; 4 — вал турбины; 5 — заглушка
(VI.49)
При этом конец бойка, выступивший за обводы вала,
оказывает нужное воздействие на исполнительный меха-
низм, который выполнен обычно в виде рычажных соеди-
нений.
Расчет центробежного регулятора бойкового типа за-
ключается в определении начального натяга Fo и коэф-
фициента упругости k пружины. Известными при расчете
являются масса бойка, эксцентриситет е, максимальный
ход а и предельная частота вращения «пред- Для опреде-
ления Fa и k используются уравнения:
Дпах = F0 + ka’ Cmax = + а> «пред
F щах — 0,65Стах,
где Стах и Гтах — центробежная сила и сила натяжения
пружины при (Опред-
При более точных расчетах в уравнениях (VI.49)
следует учитывать центробежную силу, воздействующую
на пружину.
Для получения астатической характеристики устрой-
ства защиты может использоваться неустойчивый испол-
нительный механизм при устойчивом регуляторе скорости.
Схема предельной защиты по частоте вращения с астати-
ческим гидравлическим золотником, разработанная на
НЗЛ, показана на рис. VI.22. В качестве датчика частоты
вращения использован шестеренный насос, который вместе
с расходной шайбой генерирует импульс в виде перепада
давления. Этот перепад, пропорциональный квадрату
частоты вращения, затем используется в системе защиты.
Астатический золотник 4 при нормальной работе уста-
новки находится в нижнем положении. При повышении
146
частоты вращения до величины «пред силы, действующие
на золотник со стороны давления, и силы натяжения пру-
жины уравновешены. Дальнейший, даже незначительный
Рис VI.22. Схема предельной защиты с астатическим
золотником:
1 — шестеренный иасос; 2 — мерная шайба; 3 — регулятор
давления, 4 — астатический золотник, 5 — сервомотор бы-
строзапорного клапана
рост п приводит к перемещению золотника и открытию
сливного окна. Это вызывает падение давления в верхней
полости золотника и перемещение золотника под действием
натяжения пружины до упора.
Рис. VI.23. Принципиальная схема предельного ре-
гулирования частоты вращения транспортной одно-
компрессорной ГТУ со свободной силовой турбиной-
1,2 — датчики частоты вращения (импеллеры) турбоком-
прессорного блока и силовой турбины; 3,4 — ограничи-
тели частоты вращения турбокомпрессорного блока и си-
ловой турбины
Для транспортных ГТУ не всегда приемлемо исполь-
зование предельной защиты, так как возможны значитель-
ные кратковременные забросы частоты вращения силового
вала, вызванные эксплуатационными условиями внешнего
потребителя (например, для судовой ГТУ оголение греб-
10*
ного винта при значительном волнении моря). Поэтому
возникает необходимость в организации работы устройств
защиты по принципу предельного регулирования. На
рис. VI.23 в качестве примера приведена схема предель-
ного регулирования транспортной однокомпрессорной
ГТУ со свободной силовой турбиной.
Каждое устройство защиты настраивается на предель-
ное значение частоты вращения «пред- Ее уровень обычно
на 10—12% выше номинальной. Для вала силовой турбины
транспортной ГТУ величина /гПред обычно несколько
больше и достигает 114—115% от номинальной частоты
вращения.
Защита по начальной температуре газа
Контроль уровня начальной температуры газа в ГТУ
имеет исключительно большое значение, что связано с вы-
сокой теплонапряженностью элементов турбины. Под
начальной температурой обычно понимают среднюю тем-
пературу рабочего тела на выходе из камеры сгорания,
полученную расчетным путем с помощью уравнения тепло-
вого баланса камеры;
Т3 ~ (ФрПк ±т<ш + срвт2)/[срг 0 + Дгоп)]
Непосредственное^ измерение этой температуры Т3
представляет значительные трудности из-за неравномер-
ности температурного поля, которая может достигать
±10% от номинального уровня, нестабильности темпера-
турного поля, составляющей 40—50° С, высокого абсо-
лютного уровня температуры газа (для современных уста-
новок 900—1000° С, а в перспективе еще выше).
При разработке защиты по начальной температуре
газа следует иметь в виду ряд требований, обусловленных
условиями эксплуатации ГТУ. Температура газа должна
контролироваться с высокой точностью, поскольку для
обеспечения максимальной термической эффективности
и мощности она выбирается предельно допустимой по усло-
вию заданного ресурса. Малая тепловая инерционность
элементов камеры сгорания и лопаточного аппарата турби-
ны, особенно выходных кромок лопаток, приводит к необ-
ходимости измерения температуры газа и отработки полу-
ченного сигнала без запаздывания.
В настоящее время в энергетике находят применение
следующие основные методы непосредственного измерения
температуры рабочего тела.
1. Манометрический метод, принцип действия кото-
рого состоит в однозначной зависимости давления газа
или жидкости при постоянном объеме от их температуры.
Основными элементами схемы измерения являются конт-
рольный баллон 1, капилляр 2 и датчик 3 (рис. VI.24, а).
В зависимости от заполнения ампулы различают газовые,
жидкостные и парожидкостные датчики. В газовых дат-
чиках обычно используются инертные газы (например,
азот), которыми заполняется система под давлением 10—
15 кгс/см2. Этим методом температура измеряется надежно
и достаточно точно. Однако датчик обладает значительной
инерционностью. Здесь смещение сильфона г пропорцио
нально начальной температуре газа Т3.
2. Дилатометрический метод, использующий различия
в коэффициентах линейных расширений материалов.
Дилатометр (рис. VI.24, б) включает кварцевый стержень 1,
наружную турбку 2 и корпус 3. Различные линейные
удлинения кварцевого стержня и наружной трубки (обы-
чно никелевой) в зависимости от температуры среды явля-
ются выходным сигналом; z = f Простота дилато-
метра обеспечивает высокую надежность его работы, одна-
ко значительная инерционность датчика также ограничи-
вает применение этого метода.
3. Электрический метод с использованием различных
термопар. В зависимости от температуры (рис. VI.24, в)
147
в термопаре 1 возникает э. д. с., которая усиливается
в магнитном усилителе 2, и затем через выпрямитель 3
этот сигнал подается на электромагнитный клапан 4,
обеспечивающий срабатывание защиты. Использование
батарей параллельно включенных термопар позволяет
получить осредненное значение начальной температуры
газа. Инерционность термопар умеренная и может быть
доведена до 1—2 с. Однако с уменьшением инерционности
падает ресурс термопары, особенно при измерении высо-
ких температур газа (выше 800° С). Инерционность термо-
2. Более точный контроль за тепловым состоянием
установки дает определение начальной температуры газа
по уравнению Т3 = 3\!(\ —• //тг]т). Слабое влияние к. п. д.
турбины г]т на температуру Т3 дает возможность рассмат-
ривать зависимость Т3= f (Т4, лт) [48]. Изменение абсо-
лютного значения к. п. д. на 1% приводит к изменению
начальной температуры газа только на 1,4—1,5° С. По-
скольку к. п. д. турбины даже для широкого диапазона
нагрузок изменяется мало (обычно 2—3%), можно учесть
указанную погрешность от принятого допущения.
а)
2
Рис. VI.24 Схемы измерения
температуры газа: а — ма-
нометрический метод; б—ди-
латометрический метод; в —
электрический метод
1
1
пар в случае необходимости может быть существенно
понижена с помощью различных методов компенсации.
На этом основаны комбинированные термопары и различ-
ные компенсирующие и корректирующие устройства.
Одно из таких устройств применено в малоинерционном
регуляторе температуры, который применяет НЗЛ на
своих ГТУ.
Наряду с методами непосредственного измерения тем-
пературы газа находят применение различные косвенные
методы.
1. Некоторое распространение получил метод конт-
роля начальной температуры газа по замеру температуры
газа за турбиной. Достоинство этого метода состоит в том,
что уровень измеряемой температуры относительно невы-
сок, поэтому чувствительный элемент значительно надеж-
нее, а температурное поле за турбиной более стабильное
и равномерное. Обычно более высокие скорости газа за
турбиной увеличивают коэффициент теплоотдачи между
потоком и термопарой, что повышает быстродействие
измерителя. Однако неоднозначность зависимости началь-
ной температуры газа от температуры за турбиной при
динамических процессах ограничивает использование это-
го метода.
148
Измерение температуры Т3 по параметрам 1\ и лт
является универсальным, не зависящим ни от характе-
ристики компрессора, ни от параметров наружного воз-
духа.
Наиболее простым примером использования косвен-
ного метода измерения температуры Т3 является одно-
вальная установка В данном случае для нахождения Т3
используются два импульса (7\ и Р3), так как атмосфер-
ное давление меняется незначительно.
Конструктивное выполнение измерителя температуры
может быть различным. На рис. VI.25 приведена схема
гидравлического регулятора. Температура за турбиной
здесь измеряется манометрическим методом с помощью
ампулы 1. Давление жидкости ри в системе зависит от по-
ложения трех золотников 3, 4 и 6, связанных с чувствитель-
ными элементами температуры (2), давление Р3 (5)
и давления за турбиной Рц (7). Здесь суммирование импуль-
сов Г4, Р3 и Pi производится в гидравлической системе
с помощью дроссельных золотников, а выходным сигналом,
пропорциональным искомой температуре Т3, является
давление жидкости ри. Это давление подается в качестве
импульса в^истему автоматического регулирования (САР).
Результаты стендовых испытаний такого измерителя по-
п
р
к
н
р
п
с
с
ei
п
а
з:
С1
Р‘
н
Р<
и<
Де
ст
лт
5ТЬ
казали высокую точность его работы, что подтвердило
возможность реализации косвенного измерения начальной
температуры газа.
3. Для использования в системе защиты ГТУ пред-
ставляют также интерес методы измерения температуры
Рис. VI.25. Схема гидравлического регулятора темпера-
туры (ПП — показывающий прибор)
газа, использующие контроль давления в проточной меж-
дроссельной камере с дозированным отбором газа [81].
В зависимости от условий эксплуатации установки
устройства защиты по температуре газа могут быть орга-
низованы по принципу предельного регулирования или
предельной защиты.
Противопомпажная защита
При эксплуатации ГТУ могут возникнуть условия,
при которых компрессор попадает в неустойчивый режим
работы (помпаж). Недопустимость этого явления приводит
к необходимости предусматривать в системе регулирова-
ния устройства защиты, предотвращающие помпаж комп-
рессора: поворотные направляющие лопатки компрессора,
перепуск части воздуха за компрессором или группой
ступеней в атмосферу или на всасывание, а также совме-
стное использование этих приемов. При выпуске воздуха
его расход через компрессор или выделенную группу сту-
пеней повышается, что приводит к уменьшению углов
атаки и прекращению срыва.
При создании противопомпажной защиты возникает
задача выбора параметров для определения области неу-
стойчивой работы компрессора. Непосредственное изме-
рение параметров в момент помпажа обычно не приме-
няется, поскольку не исключает (хотя и кратковременной)
работы компрессора в помпаже. Наиболее целесообразно
использовать параметры, которые непосредственно опре-
деляют границу помпажа на универсальной характери-
стике компрессора. Для этого могут быть использованы два
любых параметра компрессора из числа следующих:
приведенный расход воздуха через компрессор GK. пр =
= GKPio 10); степень повышения давления
5ТК; приведенная частота вращения ппр = nK \^T10/Ti,
Рис. VI.26. Peiулирующие органы противопомпажной за-
щиты конструкции ЛКЗ: а — заслонка; б — клапан пере-
пуска воздуха
149
где Т10 и р10 — температура и давление воздуха на входе
в компрессор при стандартных условиях.
Приведенный расход связан довольно стабильной за-
висимостью с перепадом давления во входном патруб-
ке Др. Вблизи помпажа эта зависимости имеет вид [4]
G2K.np = (AP/Pi)(2f2/S)>
где F — площадь входного сечения компрессора; £ —
коэффициент сопротивления входного патрубка.
Эта зависимость позволяет контролировать приведен-
ный расход по отборам давления во входном патрубке.
Система защиты по помпажу обычно настраивается
на границу помпажа с некоторым запасом, оцениваемым
коэффициентом устойчивости ky 0,05.
В качестве регулирующих органов противопомпаж-
ной защиты применяют различные перепускные клапаны
и регулирующие ленты (рис. VI.26). Обычно заслонки
и клапаны имеют два рабочих положения, что не позво-
ляет регулировать количество сбрасываемого воздуха.
Возможность регулировки обеспечивает ленточный клапан.
При нормальных режимах лента затянута и перепуск
воздуха отсутствует. По мере ослабления ленты перепуск-
ные окна открываются и воздух стравливается на всасы-
вание компрессора.
На рис. VI.27 в качестве примера приведена схема
противопомпажной защиты КНД судовой установки
ГТУ-20 (ЛКЗ) [32].
VI. 5. СИСТЕМЫ
АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ГТУ
Системы регулирования ГТУ отражают их сложную
динамическую структуру. Эти системы наряду с обеспе-
чением заданного режима решают задачи безопасной и
надежной работы, поэтому в их состав включены элементы
предельного регулирования и автоматического управления.
Регулирующим органом систем регулирования ГТУ
является топливный орган, управляющий подачей топлива
в камеру сгорания. Вследствие высокой калорийности
используемого в ГТУ топлива его объемные расходы
обычно невелики, а размеры топливных клапанов и уси-
лия для их перемещения оказываются относительно не-
большими. Поэтому исполнительные механизмы не должны
развивать большие усилия и могут иметь простую кон-
струкцию.
При газообразном топливе размеры топливных кла-
панов несколько возрастают, однако усилия для их пере-
мещения не очень велики. Поэтому и в этом случае испол-
нительные механизмы системы регулирования остаются
сравнительно простыми.
Отмеченные особенности находят отражение в систе-
мах регулирования ГТУ различного назначения.
Регулирование энергетических ГТУ
Основная задача регулирования ГТУ для привода
генератора — поддержание в заданных пределах частоты
вращения генераторного вала. Поэтому командным' ор-
ганом этих систем является регулятор скорости.
Поскольку генераторная ГТУ должна работать на
одну энергетическую систему параллельно с другими агре-
г атами, в ее системе регулирования предусматривают
приспособление для изменения величины регулируемого
параметра (синхронизатор), позволяющее включать ГТУ
в энергетическую сеть и менять ее нагрузку.
Генераторные ГТУ обычно являются пиковыми уста-
новками с частыми пусками и остановами. Поэтому целе-
сообразна их полная автоматизация, в том числе и дистан-
ционное управление.
На рис. VI.28 приведена принципиальная схема си-
стемы регулирования энергетической ГТУ НЗЛ мощностью
150
12 тыс. кВт [78]. Эта ГТУ является одновальной с двумя
турбинами и двумя компрессорами. Система регулирова-
ния предусматривает работу на двух видах топлива —
жидком и газообразном. Блок 4 управляет подводом
жидкого топлива, а блок 3 — газообразного. Положением
обоих блоков управляет командный орган 6 в виде цент-
робежного регулятора скорости конструкции НЗЛ. Сле-
дящий золотник регулятора скорости имеет два дроссель-
ных окна' одно из них воздействует на давление в системе
управления жидким топливом, другое — на давление
в системе управления газообразным топливом. В сле-
;ящем золотнике предусмотрен внутренний золотник,
перемещающийся при помощи специального устройства
с ручным или дистанционным приводом. Перемещение
этого золотника определяет частоту вращения ротора
(синхронизатор). Этим же золотником обеспечивают пе-
реход с жидкого топлива на газообразное и наоборот.
Блоки 3 и 4 имеют стопорные и регулирующие кла-
паны. Для открытия стопорных клапанов необходимо
подвести масло под поршни пружинных сервомоторов.
Масло подводится контроллером 11, который служит
также и для закрытия стопорных клапанов. Быстрое
закрытие стопорных клапанов в аварийных ситуациях
достигается сбросом давления из-под поршней за счет
срабатывания электромагнитного выключателя 19 или
регулятора безопасности 20.
Управление регулирующими клапанами достигается
перемещением односторонних сервомоторов с отсечными
золотниками. Эти золотники выполнены за одно целое
с поршнем промежуточного усилителя. Изменение давле-
ния в системах управления топливом, вызванное смещением
золотника регулятора скорости, определяет перемещение
поршней сервомоторов. Обратная связь осуществляется
дроссельными золотниками выключателей, которые вос-
станавливают давление в системах управления топливом
и тем самым возвращают отсечные золотники в среднее
положение.
При наборе нахрузки подвод топлива в камеру сго-
рания зависит от давления воздуха за компрессорами.
Поэтому в блоках 3 и 4 предусмотрены сильфонные изме-
рители давления воздуха, которые при помощи золотни-
ков, движущихся внутри золотников обра1НОЙ связи,
ограничивают перемещение регулирующих клапанов. Этим
достигается ограничение расхода топлива расходом воз-
духа. Такая система выполняет задачу риулятора при-
емистости
В сооответствии с рассмотренными выше особенностями
регулирования ГТУ в рассматриваемой схеме предусмот-
рены выпускные воздушные клапаны 21 и 22 с сервомото-
рами 12 и 13. Эти клапаны обеспечивают выброс воздуха
после компрессоров высокого и низкого давления при
повышении частоты вращения за счет перемещения следя-
щего золотника регулятора скорости и при срабатывании
автомата безопасности.
К защитным устройствам относится реле осевого сдви-
га ротора 7, которое действует вследствие изменения дав-
ления в системе сливных трубопроводов. Это устройство
может давать сигнальные и управляющие импульсы.
На рис. VI.29 показана принципиальная схема дру-
гой системы регулирования — для газотурбинной уста-
новки ГТУ-6 мощностью 600 кВт [78]. Установка
также выполнена одновальной, но работает только на
жидком топливе, поэтому системы регулирования и
топливоподачи здесь более простые.
Командным органом является центробежный регуля-
тор 1 с гидравлическим золотником. Дроссельные
окна Д/ в золотнике регулятора и Д2 в главном сервомо-
торе образуют проточную систему управления топливом.
Давление масла между дросселями определяет положение
поршня главного сервомотора. При .изменении частоты
вращения дроссель Д1 изменяет давление в системе упра-
вления топливом, что вызывает смещение поршня главного
(ва-
i —
ТОМ
нем
нт
ле
ль-
еме
ш
Ик
гв^
Н’ с
ор<
пе
)0Г
гла-
имо
)ОВ
ЖИ1
рое
игх.
:чет
или
лея
ими
>лое
вле-
ием
>ние
*тся
ВОС-
ВОМ
щее
сг
1М
JMC
тни-
язи
)тим
воз
ipi
ях
VK
ото
уха
пр
5ДЯ
(НИИ
ДЕ
дав
ство
ьсы
ДРУ
гста
овка
о на
я t
уля
ьные
омо
вом
ение
ТОТЫ
пра-
вого
Рис VI 27 Конструктивная схема противопомпажной защиты
1 — командный блок, 2 — заслонка перепуска воздуха, 3 — приемный патрубок КВД, 4 — сервомотор
151
—зканнм
Рис VI 28 Принципиальная
1 — переключатель 2 — выключатель 3 — блок стопорного и регулирующего клапанов газообразного топлива, 4 —блок стопор
8 — главный масляный насос, 9 — регулятор перепада давлений, 10 — регулятор температуры с золотником, 11— пусковой кон
насоса, 16 — редукционный клапан, 17 — пусковой масляный насос, 18 — инжектор смазки 19 —электро
152
мм Линия напорного масла
»« Импульсные линии регул и
рования газообразного топлива
оосо Импульсные линии регули-
рования жидкого топлива
---- ---- воздушная линия
схема р₽гулирования ГТ 12
ного и регулирующего клапанов жидкого топлива, 5 — разгонный дроссель, 6 — регулятор скорости, 7 — реле осевого сдвига,
троллер, 12 — сервомотор с золотником выпускного клапана КВД, 13 — то же КНД, 14 — скоростной золотник, 15 — инжектор
магнитный выключатель 20 — регулятор безопасности 21, 22 — выпускные воздушные клапаны
153
\ - ..л jiijOy
Рис. VI 29. Принципиальная схема
1 — регулятор скорости; 2 — блок сервомоторов; 3 — регулятор нагрузки; 4 — редукционный клапан; 5 — противопомпажный
электромагнитов, 12 — пусковой топливный насос; 13 — ручной сливной клапан; 14 — фильтр тонкой очистки; 15 — фильтр грубой
основной топливный насос, 20 — электростартер; 21 — автомат
154
jil
'ff
I
I
e\ a
1Ы l
60
регулирования ГТУ-6
клапан, 6 — запальное устройство, 7 — форсунка, 8 — катушка, 9 — электромагнитный клапан, 10 — клапан, 11 — блок
очистки, 16 — топливный бак, 17 — электродвигатель прокрутки рогора, 18 — подкачивающий топливный насос, 19 —
безопасности, 22 — электрический выключатель
155
сервомотора. Это смещение приводит к изменению положе-
ния дросселя Д2 до восстановления нормального давления
в системе управления топливом, что является эффектом
обратной связи.
Регулирующим органом является топливная игла,
связанная с поршнем главного сервомотора. Эта игла
управляет сливом топлива из главной топливной маги-
страли, подводящей топливо к форсункам. Малые усилия
для перемещения регулирующего органа позволяют иметь
одну ступень усиления даже при дроссельном золот-
нике.
Конструкция регулятора 1 предусматривает возмож-
ность изменения частоты вращения, а также коэффициента
неравномерности. Для этого служат два концентричных
золотника, относительно которых перемещается внутрен-
ний золотник, связанный с пружинами регулятора 1.
Поступательное перемещение системы двух золотников
вызывает изменение регулируемого параметра, а поворот
одного золотника относительно другого — коэффициента
неравномерности системы. Указанное воздействие может
осуществляться как вручную, так и дистанционно с по-
мощью электропривода.
В систему регулирования включен регулятор нагру-
зки 3, который образует дополнительный импульс. Этот
регулятор также воздействует на давление в системе
управления топливом с помощью поворотного золотника.
Управляет этим золотником выявительное устройство,
расположенное в верхней части регулятора 3. Это устрой-
ство изменяет активную нагрузку генератора. В одном
корпусе с регулятором 3 расположен редукционный кла-
пан 4, обеспечивающий постоянство давления масла, под-
водимого от насоса к блоку 2.
Предельное регулирование воздействует на установку
через блок электромагнитов 11, который при срабатыва-
нии сливает масло из верхней полости сервомотора быстро-
запорного топливного клапана, расположенного в блоке
сервомоторов 2. При этом поршень сервомотора переме-
щается вверх под действием пружины и с помощью топлив-
ного клапана перекрывает подачу топлива к форсункам
ГТУ. Топливный клапан представляет собой разгружен-
ный золотник с малым перестановочным усилием.
Для защиты установки от разгона служит автомат
безопасности 21, импульс от которого передается электри-
ческому выключателю 22, связанному с блоком электро-
магнитов 11. В системе защиты предусмотрен противопом-
пажный клапан 5, которым управляет электромагнитный
элемент в соответствии с программой запуска установки.
Раскрутка ротора установки при пуске осуществляется
электростартером 20, а прокрутка при остановленном
агрегате — электродвигателем 17. Топливо к запальным
устройствам 6 в пусковой период подается пусковым
топливным насосом 12, подачей топлива управляет элек-
тромагнитный клапан 9.
Рассмотренные системы (рис. VI.28 и VI.29) предна-
значены для установок, динамические свойства которых
определяются главным образом аккумулятором механи-
ческой энергии. В связи с тем, что частота вращения под-
держивается постоянной на всех нагрузках, такие установ-
ки обладают хорошими динамическими свойствами и обыч-
но не требуют специальных устройств для их улучшения.
Рис. VI.30. Принципиальная схема
1 — регулятор скорости с пусковым устройством; 2 — гидродинамический автомат безопасности; 3 — блок стопорного и ре
и высокого давления; 7 — сервомоторное устройство выпускного воздушного клапана; 8 — сбросные воздушные клапаны;
сляный выключатель; 13 — автомат безопасности вала низкого давления; 14 — переключающий золотник; 15 — главный ма
охладитель; 20 — дроссельный клапан; 21 — инжектор насоса; 22 — пусковой масляиый насос; 23 — обратный клапан; 24 —
нитный пе
156
Регулирование ГТУ
для газоперекачивающих станций
С точки зрения работы системы автоматического регу-
лирования установки для газоперекачивающих станций
обладают следующими основными особенностями.
1. Затраты энергии на нагнетание газа от одной стан-
ции до другой в сильной степени зависят от давления пере-
качиваемого газа: чем выше давление, тем меньше затраты
энергии на перекачку газа. Поэтому задачей регулирова-
ния является поддержание на предельном уровне давле-
ния за газоперекачивающей станцией.
2. Нагнетатели газоперекачивающих станций рабо-
тают на газопровод большой протяженности (100—150 км
и больше), который обладает большой аккумулирующей
способностью. Вследствие этого изменение расхода газа
за счет потребителей вызывает плавное во времени изме-
нение давления газа за станцией. Компенсация таких
возмущений может с достаточной точностью осуществлять-
ся одним регулятором, следящим за общим давлением за
станцией. Этот регулятор должен управлять частотой
вращения нагнетателей станции, а следовательно, и мощ-
ностью агрегатов. Вместо регулятора давления может быть
применено ручное или дистанционное управление. Это
снижает уровень автоматизации, но из-за плавного ха-
рактера изменений технически осуществимо.
3. Газоперекачивающая станция оснащается, как
правило, несколькими агрегатами, работающими парал-
лельно или последовательно. Эксплуатация такого обо-
рудования требует изменения нагрузки отдельно работаю-
щих машин вплоть до включения или выключения отдель-
ных агрегатов.
Указанные особенности ГТУ для газоперекачиваю-
щих станций определяют основные элементы их систем
регулирования и управления. Каждый агрегат имеет свой
командный орган в виде регулятора скорости привод-
ного вала. Так как частота вращения приводного вала
меняется в широких пределах, то целесообразно приме-
нение гидродинамического регулятора скорости. В этом
случае задатчик частоты вращения может получить си-
гнал от общего для станции регулятора давления. При
его отсутствии частота вращения устанавливается обслу-
живающим персоналом.
Наличие свободного вала полезной мощности в рас-
сматриваемых ГТУ делает их весьма чувствительными
к разгону при сбросе нагрузки. В связи с этим помимо
основного регулирующего органа, управляющего подво-
дом топлива, применяют дополнительные средства сниже-
ния мощности, например сбросные клапаны, которые при
сбросе нагрузки выпускают воздух из компрессора в атмо-
сферу, минуя газовую турбину.
На рис. VI.30 представлена принципиальная схема
регулирования установки ГТ К-10 (НЗЛ). Командным ор-
ганом системы регулирования является регулятор ско-
рости 1, измеряющий частоту вращения силовой турбины.
Этот командный орган использует гидродинамический
принцип, получая сигнал по частоте вращения от импел-
лера 17. При изменении частоты вращения меняется да-
вление за импеллером, что приводит к перемещению золот-
ника регулятора 1. Последний через дроссельное окно
постоянного давления
Проточное масло
Масло
предельной зашиты
Моспо
предельного регулирования
Масло
от инжектора насоса
Масло
от инжектора смазки
регулирования установки ГТК-10:
гулирующего клапанов с ограничителем приемистости, 4 — регулятор давления; 5, 6 — реле осевого сдвига валов низкого
9 — скоростной золотник; 10 — расцепное устройство турбодетандера, 11 — автомат безопасности турбодетандера; 12 — ма-
сляный насос; 16 — электромагнитный выключатель, 17 — импеллер; 18— регулятор производительности насоса; 19 — масло-
регулятор давления «после себя», 25 — регулятор скорости турбодетандера; 26— клапан с сервомотором; 27 — электромаг-
реключатель
157
гасло после г/авного
Рис. VI.31. Принципиальная схема системы регулирования установки ГТ-6-750:
1 — привод клапана турбодетандера; 2< — переключатель; 3 — регулятор скорости, 4 — дифференциатор; 5 — регулятор давления газа; 6 —• стопорный клапан; 7 —
регулирующий клапан; 8 — отсечной золотник сервомотора регулирующего клапана; 9 — следящий золотник; 10 — клапан турбодетандера; 11 — регулятор соотно-
шения; 12 — противопомпажный регулятор; /3—-реле осевого сдвига вала высокого давления; 14 — противопомпажный клапан, 15 — сбросный клапан; 16 — регулятор
пуска; 17 — золотник сбросных клапанов, 18 — реле осевого сдвига силового вала; 19 — главный масляный насос; 20 — пусковой дежурный клапан; 21 — сливной зо-
лотник; 22 — регулятор давления масла; 23 — обратный клапан; 24 — золотник дистанционного ^введения защиты; 25 — аварийный насос; 26 — пусковой насос; 27 —
инжектор главного насоса; 28 — маслоохладитель; 29 — золотник автомата безопасности; 30 •— инжектор маслоохладителей
воздействует на давление масла в системе управления
топливом, что вызывает перемещение отсечного золот-
ника, расположенного в блоке клапанов 3. Работа этого
блока, включая обратную связь и регулятор приемистости,
аналогична работе схемы регулирования, показанной на
рис. VI.28.
Конструкция регулятора 1 предусматривает возмож-
ность управления частотой вращения ротора силовой тур-
бины за счет перемещения буксы регулятора, которое
может быть дистанционным или ручным.
В системе регулирования предусмотрены устройства
Другое конструктивное решение имеют системы ре-
гулирования ГТУ УТМЗ. Завод применяет гидродинамиче-
ское регулирование. В качестве чувствительных элемен-
тов используются мембранно-ленточные регуляторы да-
вления, обладающие высокой чувствительностью. В ка-
честве примера на рис. VI.31 приведена принципиальная
схема системы регулирования установки ГТ-6-750 мощ-
ностью 6000 кВт. Импульс по частоте вращения вала
ТНД генерирует главный центробежный масляный на-
сос 19. Этот импульс воспринимается регулятором ско-
рости 3 мембранно-ленточного типа. Требуемый режим ра-
Рис. VI.32. Принципиальная схема топливоподачи и регулирования транспортного ГТД:
РТБ — расходный топливный бак; ПТН — подкачивающий топливный насос; ФГО — фильтр грубой очистки; ГТН —
главный топливный насос; ФТО — фильтр тонкой очистки; ЬЗК — быстрозапориый клапан; ДК — дроссельный кран;
КРО — клапан ручного останова; APT — автоматический распределитель топлива;
1,2 — импеллеры вала высокого и низкого давления соответственно; 3 — регулятор скорости с золотником; 4 —сек-
тор газа; 5 — регулятор приемистости; 6 — сервомотор дроссельного крана; 7 — регулятор расхода топлива; 8 — серво-
мотор быстрозапорного клапана; 9 — блок защитных устройств; 10 — блок антипомпажного регулирования
предельного регулирования. Сюда относятся автоматы
безопасности вала низкого давления 13 и вала турбодетан-
дера 11, которые при срабатывании бойковых измерителей
сливают масло из системы предельного регулирования.
Для предотвращения заброса частоты вращения вала
низкого давления при сбросах нагрузки предусмотрены
выпускные клапаны с сервомоторами 7.
Для контроля осевого сдвига валов высокого и низ-
кого давления предусмотрены реле 5 и 6, которые позво-
ляют осуществлять как визуальное наблюдение, так и
воздействие на систему предельного регулирования.
Пуск установки осуществляется турбодетандером,
система управления которого включает регулятор скоро-
сти 25, клапан с сервомотором 26 и электромагнитный
переключатель 27.
Аналогичные системы регулирования НЗЛ приме-
няет и на других своих ГТУ для компрессорных стан-
ций.
боты установки определяется расходом топлива на камеры
сгорания, который зависит от открытия регулирующего
клапана 7, расположенного в топливном блоке. Регулятор
скорости 3 связан с регулирующим клапаном проточной
системы, имеющей переменное давление. Масло в проточ-
ную систему поступает из системы постоянного давления
»(4,5—5 кгещм2) через отсечной золотник 8 регулирующего
клапана. Регулятор скорости 3 имеет приспособление для
изменения частоты вращения ТНД — механизм переме-
щения сопла регулятора.
В системе регулирования предусмотрен регулятор
давления транспортируемого газа 5 также с мембранно-
ленточным чувствительным элементом. Регуляторы ско-
рости 3 и давления 5 работают только индивидуально,
и при работе одного из них другой переводится в режим
предельного регулирования.
Функции регулятора начальной температуры газа
выполняет регулятор соотношения И, управляющий по-
159
7
— V--
15
19
13
9
Ю 11
1
Стоп
___ J
16
11
14 — рукоятка
держки
перекладки;
корректора
системы
судовой
шага; 15 — кулак задания шага; 16 — ограничитель
21 20 19 18
Рис. VI 33. Принципиальная схема
регулирования и топливоподачи
ГТУ-20:
2 — импеллеры ТКНД и ТКВД соответст-
венно, 3 — ограничительный регулятор скорости
ТКНД, 4 — всережимный регулятор скорости; 5,
6 — преобразователи масло—воздух ТКВД и
ТКНД соответственно, 7 — блок коррекции по
ускорению ТКНД; 8 — объединенный штурвал
винт—газ; 9 — следящий электропривод; 10 —
кулачковый вал пульта управления; 11 — пульт
управления; 12 — клапан подачи воздуха для
задержки перекладки, 13 — баллон системы за-
шага винта; 17 — сельсин-задатчик положения лопастей;
— рукоятка ручной коррекции; 19 — задатчик частоты вращения винта; 20, 22 — задатчики частоты вращения ТКВД, 21 — на ГТД второго борТа; 23 — коррек-
тор топливоподачи, 24 - регулятор расхода топлива; 25 — распределительный клапан форсунки, 26 — форсунка, 27 — камера сгорания; 28 — ТКВД, 29 —
ХТКНД, 30 — механизм изменения шага, 31 — винт регулируемого шага; 32 — усилитель сигнала при малой частоте вращения ТКНД
я а а
Ь я 3 Ь
ложением следящего золотника 9, который определяет
темп открытия регулирующего клапана. Расход топлива
при разгоне установки увеличивается в соответствии с дав-
лением воздуха за компрессором.
Для автоматического пуска установки предусмотрены
привод клапана турбодетандера 1, управляющий клапа-
ном турбодетандера 10, и регулятор пуска 16, ограничива-
ющий подачу топлива при пуске через дежурный клапан 20.
Последовательное открытие дежурного клапана 20 и ре-
гулирующего клапана 7 осуществляется переключателем 2,
связанным с механизмом настройки регулятора скорости 3.
Для обеспечения надежного пуска установки служат
противопомпажные клапаны 14, расположенные за шестой
ступенью компрессора. Управляет этими клапанами про-
тивопомпажный регулятор 12, на который воздействует
давление воздуха за компрессором.
В качестве дополнительных регулирующих органов
на установке предусмотрены сбросные клапаны 15, ко-
торые при резком сбросе нагрузки позволяют удержать
ее на режиме холостого хода за счет сброса части воздуха
после компрессора. Клапаны открываются дифферен-
циатором 4, управляющем давлением масла в системе
пружинных сервомоторов.
Для нормальной эксплуатации установки в системе
предусмотрены защитные устройства по частоте враще-
ния ТНД, реле осевого сдвига валов высокого 13 и низ-
кого 18 давления и другие элементы.
Регулирование транспортных ГТУ
Для транспортных ГТУ характерен значительный
диапазон изменения мощности установки, что сопрово-
ждается глубоким изменением регулируемого параметра.
Поэтому в транспортных ГТУ широко используют все-
режимное регулирование.
Поскольку к этим установкам предъявляют повышен-
ные требования по маневренности, их системы регулиро-
вания обычно снабжают специальными устройствами для
организации перехода с одного режима работы на другой,
например регулятором приемистости. Кроме того, могут
быть предусмотрены дополнительные регулирующие ор-
ганы за счет соплового регулирования турбины, приме-
нения поврротных направляющих лопаток компрессора
и др.
Принципиальная схема одного из вариантов системы
топливоподачи и регулирования автомобильного ГТД
приведена на рис. VI.32. Здесь регулируемый параметр —
частота вращения выходного вала, который связан с по-
требителем мощности. Использование гидродинамичес-
кого регулятора скорости позволяет обеспечить его на-
стройку в широком диапазоне изменения регулируемого
параметра. При отклонении частоты вращения вала
низкого давления от заданного уровня регулятор 3 через
сервомотор 6 воздействует на расход топлива в камере
сгорания. Регулятор настраивается на требуемый уровень
частоты вращения сектором газа 4, изменяющим натяже-
ние пружины регулятора. Для набора нагрузки в системе
предусмотрен регулятор приемистости 5, который управ-
ляет расходом топлива в зависимости от давления воздуха
за компрессором при разгоне ротора турбокомпрессора.
В схеме предусмотрен блок защитных устройств 9, воздей-
ствующий на быстрозапорный клапан через сервомо-
тор 8.
Принципиальная схема системы регулирования судо-
вой ГТУ-20 ЛМЗ представлена на рис. VI.33 [32]. В этой
системе широко использованы пневмоэлементы, что по-
зволяет осуществить широкую унификацию узлов системы
автоматического регулирования. Всережимный регулятор
скорости 4 предназначен для поддержания заданной ча-
стоты вращения турбокомпрессора высокого давления.
Настройка этого регулятора осуществляется дистанционно
с пульта управления через пневмозадатчики 20 п 22.
Для замедления перестройки частоты вращения в команд-
ной магистрали пневмозадатчика использована емкость
с дросселем. Воздействие на частоту вращения ТКНД
осуществляется положением лопастей винта регулируе-
мого шага, что меняет момент сопротивления на гребном
валу. Предусмотрены защитные устройства по частоте
вращения валов высокого и низкого давления, по давле-
нию в системе смазки и по температуре газа за камерой
сгорания (при забросе уровня температуры до 800° С по-
дача топлива прекращается). Компрессоры ГТУ-20 имеют
систему противопомпажной защиты.
11 Л. В. Арсеньев н др.
Глава VII
й
СИСТЕМЫ ТОПЛИВОПОДАЧИ И МАСЛОСНАБЖЕНИЯ
ВСПОМОГАТЕЛЬНОЕ ОБОРУДОВАНИЕ
VII. 1. ТОПЛИВНАЯ СИСТЕМА
Топливо для ГТУ
Основными горючими элементами органического топ-
лива, используемого в ГТУ открытого цикла, являются
углерод (С) и водород (Н), которые содержатся в виде раз-
личных химических соединений, а также кислород (О),
азот (N), сера (S) и др. Техническим топливом называют
смесь различных соединений указанных элементов, а бал-
1 — легкое жидкое топливо; 2 — дизельное то-
пливо; 3 — газотурбинное топливо; 4 — мазут М 40
ластом — негорючую часть, состоящую из минеральных
неорганических включений (золы) и влаги.
По физическому состоянию все органические топлива
разделяются на газообразные, жидкие и твердые. В ста-
ционарных и транспортных ГТУ открытого цикла вслед-
ствие необходимости обеспечения высокой степени на-
дежности и долговечности (моторесурса) повсеместное
практическое применение находят высококалорийные га-
зообразные и жидкие топливах.
Основные характеристики органических топлив-.
1) удельная теплота сгорания — количество теплоты,
которое выделяется при полном сгорании единицы массы
топлива в постоянном объеме — Q®; поскольку входящая
в состав топлива вода в продуктах сгорания всегда нахо-
дится в газообразном состоянии, в расчет вводится удель-
ная теплота сгорания за вычетом той доли теплоты, кото-
1 В последнее время достигнуты определенные успехи по
сжиганию твердого топлива в ГТУ после предварительной его
газификации в газогенераторах [1271.
162
рая была затрачена на испарение воды, — низшая теплота
сгорания
2) физико-химический состав топлива, определяемый
химическим анализом. Для газообразного топлива опре-
деляют процентное содержание отдельных газов, образую-
щих газовую смесь (Н2, О2, N2, СО, СО2, СН4, тяжелые
углеводороды СпНт и др.), и содержание влаги 1F. Для
жидких топлив устанавливают процентное содержание
отдельных химических элементов (С, Н, О, N, S), а также
минеральных включений (золы) и влаги.
В ГТУ применяют следующие газообразные топлива-.
1) природный газ, состоящий в основном из метана
(СН4) с примесью углеводородов метанового ряда (этана,
пропана, бутана и др.), высших углеводородов (этилена,
пропилена и т. д.) и небольшого количества СО2, N2,
СО, Н2 и др.; для него Q” 8500 ккал/м3;
2) попутные газы, получаемые обычно как побочный
продукт при эксплуатации нефтяных месторождений и
состоящие в основном из тех же компонентов, но с боль-
шим содержанием высших углеводородов; для них Q" —
= ( 104-12) 10® ккал/м®.
3) искусственный газ, представляющий собой продукт
переработки различного сырья в промышленных процес-
сах и газогеренаторных установках (доменный, колош-
никовый, газогенераторный и др.); в его состав обычно
входят Н2, СО, СО2 и большое количество (до 50—75%) N2.
Для искусственного таза Q” = 350-4-3000 ккал/м3.
Применяемые в ГТУ жидкие топлива подразделяют
на следующие:
а) легкие, к которым относят дизельное топливо и
соляровое масло (авиационный керосин);
б) тяжелые — дистиллятные (газотурбинные) топлива
и моторное топливо, представляющее собой смесь легких
топлив с мазутом;
в) остаточное нефтяное топливо — мазуты;
г) нефть (сырая).
Наряду с низшей теплотой сгорания, содержанием
влаги и механических примесей к важнейшим характе-
ристикам жидкого топлива для ГТУ относятся следующие.
1. Вязкость, характеризующая степень текучести,
возможность перекачки и способность к распиливанию.
Вязкость 1 существенно зависит от температуры топлива,
уменьшаясь с ее повышением (рис. VII. 1) [20]. Поскольку
качественное распыливание жидкого топлива может до-
стигаться при относительно небольшой вязкости (около
6 °ВУ), из приведенных на рисунке зависимостей следует,
что для тяжелых топлив и мазутов требуется предвари-
тельный подогрев до 70—150° С перед подачей в камеру
сгорания ГТУ.
1 Вязкость жидких топлив часто измеряют в градусах
условной вязкости (°ВУ), которая связана с кинематической
вязкостью V, выраженной в см2/с, зависимостью [59] v »
= 0,07319/ВУ — 0,0631/ВУ.
2. Температура вспышки, являющаяся косвенным
показателем степени пожарной опасности топлива.
3. Температура застывания — показатель перекачи-
ваемое™ жидкого топлива по трубопроводам.
4. Зольность — основной показатель степени возмож-
ного эрозионного износа, коррозии и образования отло-
жений в проточной части газовой турбины.
Элементами, активно способствующими коррозии де-
талей проточной части из жаропрочных сплавов, являются
ванадий, сера, натрий, калий, кальций и свинец. Нали-
чие даже относительно небольших количеств указанных
элементов, особенно ванадия, в золе жидких топлив при-
водит к необходимости предварительной его подготовки
путем промывки с последующим обессоливанием, а также
введения различных антикоррозионных присадок (инги-
биторов), например каолина, ZnO, MnO, MnSO4 и других
веществ, изменяющих физико-химические свойства золо-
вых отложений в благоприятную сторону с точки зрения
возможной коррозии.
Основные характеристики жидких топлив, рекомен-
дуемых к применению в ГТУ, приведены в табл. VII. 1
(в соответствии с ГОСТ 21199—75).
Т а б л и ц а VII.1. Характеристики жидких топлив
Топливо
Характеристика Дизель- ное Г азотур- бинное Остаточ- ное (нефтя- ное)
Температура вспышки, °C Температура застыва- ния, °C Зольность, % Коксуемость, % Содержание воды, % Содержание механиче- ских примесей, % Содержание серы, % Qp, МДж/кг Кинематическая вяз- кость, Ст Содержание металлов ХЮ4, %: V Na 4- К Са РЬ 40 — 65 От —60 до —10 До 0,01 0 0 0 До 1,0 42 — 43 До 0,5 » 0,5 » 0,5 » 0,5 50—60 От —10 До 4-25 0,01 — 0,03 0,5 —2,0 До 0,5 » 0,5 0,5 —3,0 40 — 42 0,84 — 0,90 1 — 2 1 — 5 2—10 1—5 65—100 От —10 до 4~25 0,05 — 0,15 2—15 0,5 —2,0 0,05—1,0 1,0—3,0 40 — 41 0,90 — 0,98 5—150 5—10 10 2—5
Системы подачи жидкого топлива
Системы подачи предназначены для хранения опреде-
ленного количества жидкого топлива, его предваритель-
ной подготовки и подачи в камеру сгорания при массовом
расходе и параметрах, соответствующих требуемому ре-
жиму работы ГТУ.
Для образования высококачественной горючей смеси
жидкое топливо в камеру сгорания подается в мелкорас-
пыленном виде с помощью специальных устройств —
форсунок.
Топливные системы ГТУ на жидком топливе должны
обеспечивать: а) подачу к форсункам необходимого рас-
хода топлива при соответствующем давлении и темпера-
туре; б) очистку топлива от механических примесей, вы-
зывающих эрозию и загрязнение отдельных элементов
(форсунок, фильтров, насосов и т. д.); в) удаление из
топлива воды и растворенных в ней солей химических
элементов, вызывающих химическую коррозию и загряз-
нение деталей проточной части; г) прием топлива в основ-
ные цистерны и передачу его в расходные цистерны.
И*
' В зависимости от требуемых давления, расхода и сорта,
топлива для подачи жидкого топлива к форсункам при-
меняют шестеренные, винтовые или плунжерные на-
сосы.
Для транспортировки по трубопроводам и обеспече-
ния высокого качества распиливания топливо предвари-
тельно подогревают как в емкостях (баках), так и в спе-
циальных теплообменниках, греющим агентом в которых
обычно являются водяной пар, горячая вода, электриче-
ский ток, горючий газ и т. д.
Очистка топлива от механических примесей произво-
дится в фильтрах, а его обезвоживание и обессоливание —
в сепараторах или специальных фильтрах.
При использовании тяжелых жидких топлив система
топливоподачи ГТУ должна предусматривать специаль-
ные устройства для введения в топливо соответствующих
антикоррозионных присадок.
Принципиальная схема топливоподачи ГТУ, работа-
ющей на легком жидком топливе, показана на рис. VII.2
[59], а на тяжелом топливе и мазутах— на рис. VII.3 [69].
Левая верхняя часть изображенной схемы представляет
собой систему промывки и подготовки топлива, правая
верхняя часть — систему промывки легким жидким топ-
ливом, которая обеспечивает требуемую надежность пуска
агрегата.
Топливные фильтры, применяемые в ГТУ, по кон-
струкции разделяют на поверхностные и объемные. В ка-
честве фильтрующих элементов применяют металличес-
кие проволочные сетки с размером ячейки от 0,48 до 2 мкм,
искусственные ткани, термостойкую бумагу, фибру и т. д.
В некоторых конструкциях фильтрующая поверхность
образуется навивкой проволоки или ленты на ребристый
каркас.
Примерами поверхностных фильтров являются сет-
чатый фильтр (рис. VII.4), используемый для очистки топ-
лива от частиц размером до 50—100 мкм, и пластинчатый
фильтр (рис. VII.5), допускающий очистку топлива от
механических примесей с размером частиц 15—25 мкм [84].
Очистка такого фильтра производится путем поворота
пластинчатой звездочки 3 с помощью маховика или перио-
дически включаемого электродвигателя.
В объемных фильтрах отложение примесей происхо-
дит в массе фильтрующего материала, вследствие чего эти
фильтры имеют элементы разового действия, не подле-
жащие очистке. Достоинством объемных фильтров явля-
ется возможность не только очистки топлива от механи-
ческих примесей, но и отделения воды. Схематический раз-
рез одной из конструкций объемного топливного фильтра
ГТУ показан на рис. VII.6 [126].
Объемные фильтры обеспечивают очистку жидкого
топлива от твердых частиц размером до 2—7 мкм. Очистка
тяжелого жидкого топлива выполняется двухступенча-
той, причем в первой ступени удаляются механические
примеси с размером частиц более 3 мкм и отделяется сво-
бодная вода, а во второй ступени, выполненной в виде
перегородок из гидрофобного материала, .происходит
практически полное отделение эмульгированной воды.
Для непосредственной подачи к форсункам жидкого
топлива с достаточно большим избыточным давлением
(до 60 кгс/см2) используют шестеренные или винтовые
насосы. В ГТУ на легком жидком топливе широкое при-
менение находят поршневые насосы плунжерного типа
с качающейся шайбой.
Для подачи жидкого топлива в камеру сгорания наи-
более часто используют форсунки центробежного типа.
Принцип действия простейшей центробежной форсунки
(рис. VII.7, а) основан на том, что подаваемое по танген-
циальным каналам 2 в камеру 1 со скоростью ш(1 топливо
получает интенсивную закрутку wu, поэтому струя рас-
пыленного топлива выходит из сопла 3 в виде конической
пелены с центральным углом Р и центральным воздушным
шнуром радиуса гш [84]. Используя расчетную схему,
163
распределительный клапан; 10 — клапан;
сунки; 12 — основные форсунки
топлива; 9 —
Нанометр
Рис. VII.2. Принципиальная схема топливоподачи ГТУ, работающей на
легком жидком топливе:
1 — топливный бак; 2 — подкачивающий насос; 3 — отсечной кран; 4 — фильтр
грубой очистки топлива; 5 — топливный иасос низкого давления; 6 — перепуск-
ной клапан; 7 — топливный иасос высокого давления; 8 — фильтр тонкой очистки
- у/ —пусковые фор-
1 — крышка; 2
ка; 4
Рис. VI 1.4. Сетчатый топливный
фильтр:
— корпус; 3 — сет-
— каркас
м
12
13
20
РиС. VI 1.5. Пластинчатый топливный фильтр:
- маховик; 2 — корпус; 3 — пластинчатая звездочка;
4 — крестовина
Сброс шлама ?
fj отсепзрсрованной
боды
Прием
топлоба
20
J3
с’Ст-
Рис. VII.3. Принципиальная схема топливоподачи ГТУ,
работающей на тяжелом жидком топливе и мазутах:
1 — бак деэмульгатора; 2 — пресная вода; 3 — смесительная
цистерна; 4, 8 — дозирующие насосы; 5 — насос промывочной
воды; 6 ~ подогреватель; 7 — смесительный бак; 9 — в топлив-
ную цистерну; 10 — в топливную магистраль; 11 — топливная
цистерна; 12 — перекачивающий насос; 13 — подогреватель
топлива; 14 — смеситель; 15 — отстойные баки; 16 — сепара-
торы; 17 — расходная цистерна; 18 — щелевые фильтры; 19 —
подкачивающий насос; 20 — сетчатые фильтры; 21 — главный
топливный насос; 22 — подогреватель; 23 — байпасный клапан;
24 — дроссельный кран; 25, 26, 32 — отсечные краны; 27 — рас-
пределитель; 28 — основные форсунки; 29 — цистерна легкого
топлива; 30 — сетчатый фильтр; 31 — топливный насос; 33 —
пусковая форсунка; 34 — продувочный баллон
164
предложенную Г. Н. Абрамовичем [2], можно определить
расход такой форсунки по формуле [73]
^топ ~ I^^P-ron оЛ'топ1 (VI 1.1)
где Цс = 1/Р^Х2/(1 — с) 4- 1/о2 — коэффициент расхода,
а = 1 — (тш^с)2 — коэффициент живого сечения фор-
сунки; А = 7?’г|/г2т|х — геометрическая характеристика
Рис. VII.6. Объемный топливный фильтр
форсунки; г — число тангенциальных каналов; размеры
гс, гВА, R показаны на рис. VII.7, а.
Функциональная зависимость iic = f (о) имеет мак-
симум, соответствующий Цс щах = о Ко/(2 — о). Вели-
чины iic, аир являются функциями от А (рис. VII.7, б).
Угол распыливания р приближенно можно определить
по формуле
tg (р/2) = 2ИсЛ/У (1 + гш/гс)2 - 4ц242 . (VI 1.2)
Гидравлическая характеристика простой центробеж-
ной форсунки, показанная на рис. VII.7, в линией 7,
описывается формулой [84]
^топ 1/"Ртоп О'
Поскольку Р*оп max 60 ксг/см2, диапазон измене-
ния расхода топлива в ГТУ при изменении нагрузки от
нуля до полной оказывается сравнительно небольшим:
Стоп = Стоп щах/Отоп min <Зч-5.
Учитывая, что во многих случаях (например, в транс-
портных ГТУ) необходимо иметь значительно больший
диапазон изменения GTon (до 10—20 и более), в ряде слу-
чаев применяют групповые распылители, оборудованные
несколькими одноступенчатыми центробежными форсун-
ками, последовательно включаемыми в работу по мере
роста нагрузки ГТУ. Однако чаще в этих случаях приме-
няют двухступенчатые форсунки, в которых на малых
нагрузках топливо подается только через первую ступень
(линия 1 на рис. VII.7, в), а на больших — одновременно
через первую и вторую ступени. Суммарная характери-
стика GTon = f (р*ОПо) двухступенчатой форсунки изоб-
ражена на рис. VII.7, в линией abed, а ее конструкция —
на рис. VII.8, а [73]. В этой форсунке каждая из ступеней
(Z, II) имеет самостоятельные камеры закручивания, тан-
генциальные каналы и топливопроводы.
Расход топлива в одноступенчатых форсунках может
регулироваться изменением проходного сечения ее тан-
генциальных каналов, а также сливом части топлива по
перепускному каналу обратно в бак (рис. VII.8, б).
Некоторое применение в ГТУ находят также комби-
нированные пневмомеханические форсунки (рис. VI 1,8, в),
в которых за счет использования дополнительной энер-
гии вводимого сжатого воздуха оказывается возможным
существенно улучшить качество распыливания топлива
в широком диапазоне изменения его расхода. Недостат-
Рис. VII.7. Центро-
бежная форсунка: а—
схема одноступенчатой
форсунки; б — график
изменения р,, о, (5 от А
для одноступенчатой
форсунки; в — гидрав-
лическая характери-
стика одноступенчатой
и двухступенчатой фор-
сунок
ком таких форсунок является необходимость иметь авто-
номный источник сжатого воздуха высокого давления
(до 25—30 кгс/см2).
Эффективность распыливания жидкого топлива ха-
рактеризуется средним диаметром капель, который при-
ближенно может быть найден по формуле [73]
- (VI 1.3)
165
а также законом (спектром) распределения капель по их
диаметрам, приближенно определяемым уравнением [73]
5к/5к. Общ = е—°.693 (dK/dK. СР )Х. (VI 1.4)
Перед запуском ГТУ и после ее остановок все топливо-
проводы должны продуваться воздухом. На топливопро-
воде, подводящем газ к камере сгорания, необходимо
Рис. VII.8. Конструктивные схемы форсунок- а — двухступенчатая центробежная; б — одноступенчатая
с обратным сливом; в — пневмомеханическая.
1 — тангенциальные ка1Галы; 2 — камеры закручивания; 3 — сопло; 4 — каналы
Здесь Дртоп — перепад давления топлива на форсунке;
Вк — количество капель диаметром dK > dK. ср! Вк.общ —
общее количество капель; я 3.
Системы подачи газообразного топлива
Принципиальная схема топливоподачи ГТУ, рабо-
тающей на природном или попутном газе, показана на
рис. VII.9 [59]. Топливный (дожимающий) компрессор 4
необходим для создания избыточного давления газа на
входе в камеру сгорания по отношению к давлению ци-
клового воздуха (примерно на 0,2—0,5 кгс/см2). Обводная
магистраль с клапаном служит для перепуска части топ-
ливного газа на всасывание компрессора 4 на режимах
частичной нагрузки агрегата. Для повышения к. п. д.
ГТУ можно применять подогрев газа в специальном тепло-
обменнике 5 за счет использования части теплоты уходя-
щих из газовой турбины продуктов сгорания.
В системе топливоподачи должна быть предусмотрена
продувка отдельных участков топливной магистрали за
фильтрами и перед камерой сгорания через свечи с вен-
тилями. Эги свечи выводятся на наружную сторону зда-
ний на высоту около 5 м (т. е. выше его крыши).
Вследствие токсичности топливных газов необходимо
обеспечить высокую плотность всего газового тракта ГТУ.
Дожимающие компрессоры должны иметь внешние гер-
метичные уплотнения.
166
Рис. VI 1.9. Принципиальная схема топливоподачи ГТУ,
работающей на природном или попутном газе:
1 — фильтр; 2 — клапан; 3 — регулятор расхода; 4 —газовый
(дожимающий) компрессор, 5 — подогреватель; 6 —блок САР;
7 — камера сгорания
иметь автоматические запорные устройства, предохраняю-
щие газопроводы от попадания в них воздуха при ава-
рийных остановках компрессоров или падении давления
в газопроводах [59].
Необходимость перечисленных мер диктуется не только
токсичностью, но и большой взрывоопасностью смеси
горючего газа с воздухом (при содержании газа 5—14%
горелочные устройства, предназначенные для сжигания
как газообразного, так и жидкого топлива. Примеры ком-
бинированных горелок показаны на рис. VII. 11 и VII. 12.
Рис. VII-10. Газовая горелка камеры сгорания ГТ-700-5.
1 — центральная труба; 2 — кольцевая полость; 3 — завихритель; 4 — основная горелка; 5 — дежурная горелка; 6 — свеча
и температуре смеси около 300° С). Поэтому в дополнение
к указанным мерам необходимо обеспечивать хорошую
вентиляцию помещений, в которых установлены ГТУ.
Газообразное топливо подается в камеры сгорания
с помощью специальных горелочных устройств (горелок),
Рис. VII.11. Комбинированная горелка камеры сго-
рания высокого давления ГТ-100-750 (ЛМЗ):
1 — регистр; 2 — выход основного газа; 3 — выход де-
журного газа; 4 — форсунка
которые по конструкции разделяются на следующие:
регистровые; диффузионные; диффузионно-регистровые;
с раздачей горючего газа через отверстия или прямоуголь-
ные щели; струйно-стабилизаторные; многоканальные,
составленные из отдельных стабилизаторов, собранных
в секторе и устанавливаемых по фронтовому кольцу
камеры. При этом каждый сектор имеет отдельный подвод
топливного газа от общего коллектора. В качестве примера
на рис. VII. 10 показана газовая горелка камеры сгорания
приводной ГТУ ГТ-700-5 НЗЛ [55]. z
В энергетических ГТУ средней и большой мощности
асе более широкое применение находят комбинированные
VII.2. СИСТЕМА МАСЛОСНАБЖЕНИЯ
Система маслоснабжения служит для обеспечения
смазки подшипников турбомашин, зубчатых передач и
различных шарнирных соединений узлов системы автома-
тического регулирования.
Масло, подаваемое для смазки подшипников скольже-
ния турбомашин, предназначено для следующих целей:
а) уменьшения коэффициента трения между вращающимся
ротором и неподвижным подшипником, а следовательно,
уменьшения доли полезной работы, затрачиваемой на
преодоление сил трения; б) обеспечения длительной на-
дежной работы подшипников во всем диапазоне режимов
ГТУ как за счет создания масляного слоя между ротором
и подшипником, так и отвода теплоты, выделяющейся
при трении в этом масляном слое V
Масло, подаваемое для смазки зубчатых (червячных)
передач и шарнирных соединений, предназначено для
уменьшения работы трения в указанных элементах и по-
вышения их износостойкости.
При наличии гидравлической или электрогидравличе-
ской систем автоматического регулирования смазочное
масло является также рабочим телом, используемым для
передачи импульсов и функционирования элементов этой
системы.
Технические требования к смазочным маслам устанав-
ливают ГОСТ 32—74 и ГОСТ 10289—62. В табл. VII.2
приведены основные характеристики смазочных масел,
рекомендуемых к применению в стационарных и транс-
портных ГТУ [69].
Количество жидкой смазки GM, которое следует под-
вести к трущимся поверхностям, может быть приближенно
определено исходя из количества теплоты Qrp, выделяю-
щейся при трении, и допустимого нагрева смазки Д1М:
См — Qip/ (СмД^м) > • (VI1.5)
где см — средняя теплоемкость масла.
1 При наличии подшипников качения подаваемое в них
масло используется в основном для отвода теплоты, выделя-
ющейся при трении.
167
Основной газ
Рис. VII.12. Комбинированная горелка ГТУ V93 фирмы «Крафтунионверке» (ФРГ) [127]:
/ — регистр; 2 — форсунка, 3 — конус
168
Т а б л и ц а VII.2. Технические характеристики
масел для газовых турбин
Характеристика Марка масла
М22 (ГОСТ 32-74) Л22 (ТУ 38-1-01-100 — 71) Масла по ГОСТ 10289 — 62
Кинематическая вяз- кость, Ст: при 50 °C при 20 °C не более Кислотное число Зольность, %, не более Содержание примесей (водорастворимых кислот и щелочей, механических примесей, воды, серы) Температура застыва- ния, °C, не выше 20 — 23 0,02 0,005 0 — 15 20 — 23 0,05 0,005 0 — 15 7,0 —9,6 30 0,04 0,005 0 — 45
Величина Д/м определяется допустимым значением
коэффициента динамической вязкости it и стойкостью
масла против окисления, оцениваемой так называемым кис-
лотным числом \ поскольку с увеличением температуры
вязкость масла уменьшается, а склонность его к окислению
увеличивается. В ГТУ, оборудованных открытыми систе-
мами смазки, максимальная температура масла на сливе
не должна превышать 70—75° С.
Важным показателем смазочных масел является также
их зольность, характеризующаяся склонностью к образо-
ванию твердого остатка (шлама) и наличием в нем механи-
ческих примесей.
Количество теплоты QTp в первом приближении может
быть подсчитано по величине мощности, затрачиваемой
газовой турбиной на преодоление трения в опорных и
упорных подшипниках турбомашин. (При наличии редук-
тора необходимо учесть также затраты мощности на трение
в редукторе.)
В каждом из опорных подшипников скольжения за-
трата мощности
^тр.оп= п (L-ф 2а) Д1 2р<о2/ (102 о), (VI 1.6)
где L — длина шейки ротора в пределах вкладыша под-
шипника; a — ширина (вдоль оси ротора) каждого из двух
кольцевых поясков вкладыша; R — радиус окружности
вкладыша; <j = s0/R — максимальный относительный за-
зор между шейкой ротора и вкладышем; со — угловая ско-
рость вращения ротора 2.
Нагрев масла в опорном подшипнике
= 36,7 • 106 цсо/о2; (VII.7)
При нормальной работе подшипника Д1М 15° С.
В каждом из упорных подшипников турбомашины,
имеющем самоустанавливающиеся колодки, затрата мощ-
ности на трение
WTP. уп ^7’2 Р«ср. ynf у. k/S1- (VI 1.8)
1 Кислотное число измеряется количеством щелочи (КОН),
необходимой для нейтрализации кислотности заданного коли-
чества масла.
3 Наилучшую сходимость с опытом эта формула дает при
значениях L/D = 0,8^-1,0; рср == P/(LD) = 8^ 10 кг/см2 и
о « 2- 10“3, где Р — радиальная статическая нагрузка на под-
шипник; D — диаметр шейки ротора.
Здесь «ср.уп — средняя окружная скорость упорного
гребня; Ау. к — суммарная площадь упорных колодок;
sx — минимальный зазор в масляном клине на рабочих
упорных колодках,
S1 = 2,56• 102Kfу. Лу. кисг,. уп/Гос , (VII.9)
где Ly. к — ширина упорной колодки по среднему диа-
метру; Рос — осевое усилие на подшипник.
Если упорный подшипник заполнен маслом, то допол-
нительная затрата мощности на трение упорного диска
о масло
94₽Хд«3 *н.д (1 - ^у.к/f д - йдМ.д ), (VII. 10)
где Рд = f (Re) — численный коэффициент; Re ==
= Dn. pUn. д/v; £>н. д, «н. д — наружный диаметр и пери-
ферийная окружная скорость упорного диска; Гд— боко-
вая поверхность упорного диска; ЬЛ — ширина цилиндри-
ческой части упорного диска на его наружном диаметре.
В предварительных расчетах для средненагруженных
подшипников указанные значения A'Tp. Оп, Nrp. уп и Д1тр. д
могут быть определены по приближенным формулам [38]:
VTp.on~ 86О2ш (п/ЮОО)2; (VII.11)
VTp. уп^86П3ш(а/1000)2; (VII.12)
А'тр. д"- 5,07£>щ6 («/ЮОО)2,8, (VI 1.13)
где — диаметр шейки вала; п — частота вращения
ротора, об/мин.
Нагрев масла в упорном подшипнике AfM ~ 0,64рср;
при нормальной работе агрегата Д/м 10-т-15° С.
Циркуляционный расход смазочного масла можно
оценить удельным расходом ga~, при приближенных расче-
тах можно принимать ga = GM/Ne.
Действительный расход смазочного масла определяется
величиной его физических потерь (утечками во фланцевых
и ниппельных соединениях, испарением, потерями со шла-
мом и т. д.). Эти потери должны быть снижены до мини-
мума, в нормальных условиях работы ГТУ они обычно
не превышают 0,5 - 10-в кг/кДж.
Расчетное значение GM, которое определяет требуемую-
производительность маслонасоса (подробнее об этом см.
в п. VII.3), должно быть увеличено на 8—10% с учетом
расхода масла на подшипники вспомогательных механиз-
мов, шарнирные соединения и систему автоматического-
регулирования.
ГТУ оборудуется, как правило, напорными системами
смазки, в которых масло под соответствующим избыточным
давлением подается к каждому из подшипников через ка-
налы во вкладышах, снабженных дросселями, или через
форсунки. Необходимые давления и расход масла обеспе-
чиваются при нормальной работе агрегата насосом (шесте-
ренным, винтовым или центробежным).
В аварийных ситуациях, когда прекращается подача
масла от маслонасоса, используют гравитационную си-
стему смазки, в которой масло самотеком поступает из-
емкости, расположенной на некоторой высоте по отноше-
нию к подшипникам (8—10 м).
Из всех смазываемых элементов, а также из системы
регулирования масло самотеком сливается в общую ем-
кость 1. В некоторых ГТУ для отсоса масла из корпусов
подшипников используют специальные откачивающие на-
сосы (например, в ГТУ с авиационным ГТД). Необходимый
рабочий объем емкости (маслобака) может быть определен
по формуле
VM = 3,6-10WVe/(zupM), (VII.14)
1 Во многих конструкциях современных ГТУ в качестве
такой емкости используется фундаментная рама агрегата.
16$
где Рм — плотность масла; гц — кратность циркуляции
масла в системе, т. е. число полных его смен в маслобаке
в течение одного часа работы ГТУ на номинальной на-
грузке. Рекомендуется принимать: для стационарных ГТУ
гц=30-4-40; для судовых ГТУ гц= 15-4-20; для транспорт-
ных ГТУ гц = 5-4-7.
В системе маслоснабжения стационарных и судовых
ГТУ должна быть предусмотрена также отдельная емкость
для полного слива отработавшего масла.
Принципиальная схема смазки ГТУ [69] приведена
на рис. VII. 13. Наряду с уже упомянутыми элементами
Рис. VII.13. Принципиальная схема смазки
ГТУ:
1 — расходная цистерна; 2 — фильтр (магнитный);
3 — основной насос; 4 — резервный насос; 5 —
фильтр; 6 — маслоохладитель; 7 — охлаждающая
вода; 8 — гравитационная емкость; 9 — резервная
цистерна; 10 — напорная магистраль; 11 — сливная
магистраль; 12 — перекачивающий насос; 13 — се-
паратор
в указанную систему входят фильтры для очистки масла:
как на входе в насос (2), так и на выходе из него (5).
Обычно применяют фильтры поверхностного типа с филь-
трующими элементами в виде сетки, проволоки и т. п.
Иногда в качестве первой ступени применяют магнитные
фильтры.
Кроме основного насоса 3 в системе подачи масла дол-
жен быть предусмотрен резервный маслонасос 4, который
включается при падении давления масла в системе ниже
допустимого (избыточное давление 0,1 кгс/см2).
Для охлаждения напорного масла, подаваемого к под-
шипникам, в схеме предусматривают специальный тепло-
обменник, в котором в качестве охлаждающего агента ис-
пользуют циркуляционную воду, прокачиваемую насосами,
или воздух, продуваемый вентилятором.
Резервный масляный насос 4 и гравитационная ем-
кость 8 связаны с системой защиты агрегата от падения
давления масла ниже допустимого.
В некоторых случаях, например для ГТУ, располо-
женных в неотапливаемом помещении, в системе масло-
снабжения должен быть предусмотрен обогрев масла для
-обеспечения пуска установки после длительного ее оста-
нова (в расходном маслобаке или маслоподогревателе).
170
Во время пуска и останова агрегата работает пусковой
маслонасос, обеспечивающий подачу масла в систему через
обратный клапан и включаемый автоматически в зависи-
мости от давления в напорной магистрали. Пусковой насос
(обычно центробежный) приводится во вращение от элек-
тродвигателя переменногр тока. Из маслобака должен быть
предусмотрен аварийный слив по трубопроводу доста-
точно большого сечения.
В ГТУ, используемых для привода нагнетателей при-
родного газа, система маслоснабжения должна предусма-
тривать подачу масла через обратный клапан на торцовое
уплотнение нагнетателя. Загазованное масло из этого
уплотнения перед сливом в маслобак очищают в гидро-
затворе.
VII.3. ВСПОМОГАТЕЛЬНОЕ ОБОРУДОВАНИЕ
В состав вспомогательного оборудования ГТУ вклю-
чаются: фильтры для очистки воздуха, засасываемого
в компрессор; устройства для снижения уровня шума,
устройства для охлаждения и подогрева засасываемого
в компрессор воздуха; охладители смазочного масла и ох-
лаждающего воздуха, источники питания электроэнергией
для собственных нужд; противопожарная система; устрой-
ства для очистки (промывки) проточных частей компрес-
сора и турбины.
Воздухоочистительные устройства
Очистка воздуха производится для предохранения
проточных частей компрессора и турбины, а также всего
газовоздушного тракта ГТУ от вредного воздействия заса-
сываемой с воздухом естественной или промышленной
пыли, проявляющегося в образовании отложений (зано-
сах) и механическом износе (эрозии).
Попадание промышленной пыли, а также солей, со-
держащихся в морской воде, может вызвать также корро-
зию деталей проточной части. Поэтому для обеспечения
высокой степени надежности работы ГТУ к воздухоочисти-
тельным устройствам предъявляются жесткие требования
(ГОСТ 21199—75): остаточная среднегодовая запылен-
ность воздуха на входе в компрессор не должна превышать
0,3 мг/м3; а для твердых частиц размером более 20 мкм —
0,03 мг/м3; в периоды повышенной запыленности (напри-
мер, пыльных бурь в степных и пустынных районах) допу-
скается кратковременное (около 100 ч/год) увеличение кон-
центрации пыли с размерами частиц не более 30 мкм до
5 мг/м3.
В зависимости от уровня внешней запыленности при-
меняют различные типы воздухоочистительных устройств
(фильтров).
Для зон средней и высокой запыленности наиболее
рациональна двухступенчатая очистка воздуха; в качестве
первой ступени применяют инерционные фильтры жалю-
зийного или циклонного типов, а в качестве второй сту-
пени — различные типы тканевых или масляных сетчатых
фильтров.
Инерционные фильтры основаны на принципе сепара-
ции твердых частиц, увлекаемых потоком воздуха при рез-
ких его поворотах или закрутке, из-за большой разницы
в плотности. На рис. VII. 14 схематически показан инер-
ционный фильтр жалюзийного типа системы ЦКТИ. Эле-
менты собирают в общую панель стандартных размеров.
Отсепарированная пыль отсасывается специальным венти-
лятором вместе с небольшим количеством воздуха (4—6%
от общего расхода) и собирается в бункер, откуда периоди-
чески удаляется. С помощью инерционного фильтра удается
удалить из засасываемого воздуха достаточно крупные
частицы пыли (размером около 15—20 мкм).
Эффективность процесса пылеулавлива ия оцени-
вается обычно коэффициентом т]у. п == Gy. n/Gn. п, где
ой
)ез
'И-
ос
JK-
ЕТЬ
га-
1И-
13-
ое
то
ю-
го-
го
[а,
го
X-
ей
й-
с-
1Я
го
а-
)Й
о-
о-
0-
!Я
и-
ЦЯ
н-
ть
и-
у-
и-
ЦО
и-
гв
ее
ве
о-
у-
IX
а-
з-
ы
р-
е-
в.
4-
и-
я
те
ri-
le
Рис. VII.14. Инерционный фильтр жалюзийного типа:
а — элемент фильтра; б — группа элементов в сборе
Рис. VII.15. Секция рулонного фильтра фир-
мы AAF:
1 — фильтрующая ткань, 2 — барабан
Gy. п — массовый расход пыли, уловленной фильтром;
Gn. п — массовый расход пыли, поступившей в фильтр.
Для лучших конструкций инерционных фильтров
эффективность очистки от частиц пыли указанных разме-
ров весьма высока (т]у. п — 0,954-0,99).
Улавливание частиц пыли размером менее 15 мкм осу-
ществляется чаще всего с помощью тканевых фильтров
(панельных или рулонных).
На рис. VII.15 схематически показана секция рулон-
ного фильтра фирмы AAF (США), широко применяемая
в качестве второй ступени очистки для стационарных ГТУ
зарубежных фирм [127]. Фильтрующим материалом в них
является синтетическая многослойная пористая ткань,
плотность слоев которой увеличивается по ходу воздуха.
Для повышения эффективности улавливания мелкой пыли
эта ткань смачивается специальным маслом (типа висци-
нового), имеющего малую вязкость и низкую температуру
затвердевания. По мере загрязнения ткань автоматически
перематывается с верхнего (чистого) барабана на нижний.
В отечественных и зарубежных ГТУ в качестве второй
ступени очистки засасываемого воздуха находят также
применение сетчатые фильтры с неподвижными или пере-
мещаемыми панелями. Их сетки также смачиваются мас-
лом. Загрязненные сетки промываются в масляной ванне.
Эффективность улавливания мелкой пыли фильтрами
тонкой очистки может достигать значения t]v п ~ 0,9804-
4-0,995.
Устройства для глушения шума
Поскольку ГТУ являются источником вредного для
здоровья обслуживающего персонала и окружающего насе-
ления высокочастотного шума, требуется обязательная
установка специальных устройств, с помощью которых
высокий уровень внешнего шума должен быть снижен до
допустимых санитарных норм.
В местах нахождения обслуживающего персонала
допустимые уровни звукового давления и звука, создавае-
мые ГТУ, регламентируются ГОСТ 21129—75:
Среднегеометрическая ча-
стота полос, Гц ... . 63 125 250 500 1000
Уровень звукового давле
ния, дБ................. 99 92 86 83 80
Среднегеометрическая ча-
стота полос, Гц .... 2000 4000 8000 Уровень
звука
Уровень звукового давле
ния, дБ................... 78 76 74 85
В зависимости от длительности воздействия и харак-
тера шума эти значения должны корректироваться в соот-
ветствии с табл. VII.3.
В помещениях щитов управления ГТУ допустимые
уровни звукового давления и звука не должны превышать
следующих значений:
Среднегеометрическая ча-
стота полос, Гц . .
Уровень звукового давле
ния, дБ...................
Среднегеометрическая ча-
стота полос, Гц . . . .
Уровень звукового давле-
ния, дЬ................
63 125 250 500 1000
94 97 82 78 75
2000 4000 8000 Уровень
звука
73 71 70 80
Основным источником шума в ГТУ является всасывающая
часть компрессора, через которую распространяются зву-
ковые волны, возбужденные переменными аэродинамиче-
скими силами, возникающими при прохождении воздуха
через лопаточный аппарат х. Основным видом шума при
этом является так называемый сиренный шум, обусловлен-
1 Перед первой ступенью компрессора уровень звука может
достигать 130 —140 дБ.
171
ный взаимодействием неподвижного и вращающегося рядов
лопаток, через которые проходит поток воздуха. Частота
его может быть определена по формуле
Л •= ++><. р t/60, (VI 1.15)
где пк — частота вращения компрессора; zK. р — число
рабочих лопаток первой ступени компрессора; i — номер
гармоники.
Весьма эффективной для
снижения уровня шума в ок-
ружающем ГТУ пространстве
является установка решетки
из толстых пластин (рис.
VI 1.16) [127], изготавливае-
мых из пористого материала
(синтетического волокна,
войлока и т. д.) и защищае-
Вход
Т а б л и ц а VII.3.
Поправки к уровню звукового
давления, дБ
Суммарная длительность воздействия за смену (рабочий день) Характер шума, дБ
Широко- полосный Тональ- ный
От 4 до 8 ч От 1 до 4 ч От 15 мин ДО 1 ч От 5 до 15 мин Менее 5 мин 0 + 6 + 12 + 18 + 24 — 5 + 1 + 7 + 13 + 19
Рис. VII. 16 Схема шумо-
глушащего устпойства на
всасывании в компрессор
ГТУ
мого снаружи листами из перфорированного материала.
Эффект глушения шума с помощью таких пластин прибли-
женно может быть подсчитан по формуле
АТш = «зп/п/бп, (VI 1.16)
где азп — коэффициент звукопоглощения; 1п — длина
пластины; 6П — толщина пластины.
Расстояние между пластинами принимается обычно
равным (24-5) 6П.
Устройства для глушения шума часто устанавливают
также на выхлопе из турбины. Иногда над блоком турбо-
агрегатов устанавливают специальную звукоизолирую-
щую обшивку (кожух).
Устройства для охлаждения
и подогрева засасываемого воздуха
Охлаждение засасываемого в компрессор воздуха поз-
воляет увеличить удельную мощность ГТУ (до 10—12%).
Особенно эффективным оно оказывается при высоких тем-
пературах и лизкой относительной влажности в окружаю-
щей атмосфере.
Обычно воздух охлаждается путем впрыска в него
мелко распыленной воды (через форсунки), причем для
улавливания неиспарившейся влаги предусматривают уста-
новку специального сепаратора. Требования к химическому
составу впрыскиваемой воды определяются режимом ра-
боты ГТУ и ее назначением. В некоторых случаях допустим
кратковременный впрыск химически неочищенной воды.
При температуре окружающей среды около 0° С и
высокой относительной влажности возникает необходи-
мость подогрева поступающего в компрессор воздуха во
172
избежание возможного обледенения входного участка и
входного направляющего аппарата компрессора, что соз-
дает опасную ситуацию с точки зрения обеспечения надеж-
ной работы ГТУ. Подогрев может осуществляться как пере-
пуском небольшой части циклового воздуха, отбираемого
за компрессором, или продуктов сгорания на выхлопе из
ГТУ в поток засасываемого воздуха, так и пропуском подо-
гретого воздуха через лопатки входного направляющего-
аппарата компрессора. Обычно управление этими устрой-
ствами автоматизировано и включено в систему защиты
ГТУ. Подогрев засасываемого воздуха может быть целесо-
образен также для расширения диапазона регулирования
ГТУ [127].
Все перечисленные элементы, т. е. фильтры, шумоглу-
шащие и воздухоохлаждающие (подогревающие) устрой-
ства, компонуются обычно в едином блоке, устанавливае-
мом на входе в компрессор, собираемом из стандартизо-
ванных узлов и элементов и транспортируемом отдельно от
турбогруппы. Этот блок иногда называют комплексным
воздухоочистительным устройством (КВОУ).
В стационарных ГТУ большой мощности на всасыва-
нии в компрессор и выхлопе из турбины иногда устанавли-
вают специальные заслонки (жалюзи), с помощью которых
при остановке агрегата автоматически прекращается доступ
холодного воздуха из атмосферы в газовоздушный тракт,
благодаря чему уменьшаются термические напряжения
в деталях газовой турбины.
Охладители масла и охлаждающего воздуха
Смазочное масло, сливаемое из подшипников турбоаг-
регатов ГТУ, охлаждается в маслоохладителях с помощью
воды или воздуха. Для прокачки циркуляционной воды
необходимо включение в схему специального насоса (обыч-
но центробежного), а для прокачки охлаждающего воз-
духа — вентилятора с приводом от электродвигателя по-
стоянного или переменного тока.
Водяные маслоохладители имеют меньшие габариты
и массу по сравнению с воздушными, но требуют источника
водоснабжения, что может оказаться нежелательным в ряде-
случаев, например в безводных районах. Водяные масло-
охладители требуют также более частой очистки тепло-
обменной поверхности. По этой причине их обычно делают
двухсекционными, чтобы иметь возможность отключать
одну из секций для очистки без остановки ГТУ.
Теплообменная поверхность маслоохладителей фор-
мируется чаще всего из трубок с наружной оребренной
поверхностью (для интенсификации теплообмена), причем
внутри трубок обычно проходит масло, а снаружи охлаж-
дающий агент (вода или воздух).
Расход охлаждающего агента в маслоохладителе мо-
жет быть подсчитан из уравнения теплового баланса:
бохл — Ом/(Срохл А/ОХЛ) , (VII.17/
где А10хл= *2охл — 1юхл — разность температур охлажда-
ющего агента на выходе и входе в охладитель; обычно при-
нимают А/охл = 10-4-15° С; ср охл — средняя теплоемкость
охлаждающего агента.
На выходе из маслоохладителя при противоточном или
перекрестном движении температуру воды обычно прини-
мают равной /2ЭХЛ = вх — (10-4-12) °C, где /м. вх — тем'
пература масла на входе в охладитель. Отношение расхода
воды в маслоохладителе к расходу масла, называемое
кратностью охлаждения, составляет обычно 1,5—2,5.
Для повышения эффективности системы воздушного
охлаждения деталей газовой турбины, подверженных воз-
действию высоких температур, отбираемый из циклового
компрессора воздух иногда предварительно охлаждают
в специальных теплообменниках циркуляционной водой,
подаваемой самостоятельным насосом или отбираемой от
водопроводной магистрали.
Противопожарная система
Предназначена для подачи предупредительного сиг-
нала о наличии пожаро- и взрывоопасного состояния в по-
мещении, где установлена ГТУ, а также автоматического
включения устройств для быстрого тушения начавшегося
пожара.
Импульсом для подачи предупредительного сигнала
служат периодически отбираемые из различных точек по-
мещения пробы воздуха. Специальные приемники [127],
установленные в местах отбора проб, автоматически опре-
деляют содержание в воздухе газа, продуктов сгорания
топлива или масла и сопоставляют эти данные с допусти-
мыми. В качестве приемников импульса иногда служат
термопары.
Указанные системы работают обычно в трех положе-
ниях: «Спокойно», «Тревога», «Пожарная (взрыво) опас-
ность». В положении «Тревога» включаются продувочные
и дренажные устройства, в положении «Пожарная (взрыво)
опасность» — соответствующие противопожарные сред-
ства.
Автоматическое управление противопожарной систе-
мой является обычно составной частью системы автомати-
ческого управления и защиты ГТУ.
Источники питания электроэнергией
для собственных нужд
Важным составным элементом вспомогательного обо-
рудования ГТУ являются источники питания электро-
энергией для обеспечения многочисленных собственных
нужд установки- пусковых и аварийных топливных и мас-
ляных насосов, САУ, пусковых электродвигателей и др.
Питание электроэнергией для собственных нужд Г ГУ
может производиться как от внешней электросети, так и от
автономных источников- дизель генераторов, электрогене-
раторов с газотурбинным приводом аккумуляторных бата-
рей и т. п.
Затраты мощности, потребляемой вспомогательными
механизмами, определяются следующим образом.
1. На валу топливного, масляного, водяного насоса
или вентилятора
(В) = Он (в) м (РЧн (в)). (VII.18)
В случае, если запуск ГТУ производится с помощью
электродвигателя, требуемая его мощность определяется
по методике^/рассмотренной выше (см. п. 1 гл. VI).
Общую требуемую электрическую мощность для соб-
ственных нужд определяют суммированием мощностей, по-
требляемых электродвигателями кагкдого из вспомогатель-
ных механизмов, приборами и устройствами системы
АУ (КИП), с учетом коэффициентов одновременности их
использования, степени загрузки механизмов и потерь
в самих электродвигателях.
2. При наличии автономного электрогенератора для
энергоснабжения ГТУ его требуемая электрическая мощ-
ность может быть определена по формуле [69]
#э. с. н = f Кс У । Шэд(/'Пэд1 с. н> (VII 19)
V ,=1 )
где Кс ~ 1,05 — коэффициент, учитывающий потери
в электрической сети; г — число одновременно работающих
электродвигателей для привода вспомогательных меха-
низмов ГТУ; t — потребляемая мощность на валу
каждого из этих электродвигателей г; т]эд i — к- и. Д- элек-
тродвигателя; Ki — коэффициент использования электро-
двигателя, равный отношению мощности, потребляемой
вспомогательным механизмом на данном режиме, к номи-
нальной мощности электродвигателя; А'3— коэффициент
загрузки, равный отношению мощности механизма на дан-
ном режиме к его номинальной мощности, т]-.. с. н —•к- п- Д-
электрогенератора для собственных нужд.
1 Для электродвигателей, приводящих насосы (вентиля-
торы), она определяется по формуле (VII 18)
Г лава VIII
МАТЕРИАЛЫ В ГА30ТУРБ0СТР0ЕНИИ
VIH.1. МАТЕРИАЛЫ
ДЛЯ ЛОПАТОК ГАЗОВЫХ ТУРБИН
Условия эксплуатации и предъявляемые к материалам
требования. Температура металла сопловых лопаток
определяется температурой рабочего тела, омывающего
лопатки данной ступени, и системой охлаждения. Напря-
жения изгиба, возникающие под действием газового по-
тока, составляют 5—8 кгс/мм2. В перспективных высоко-
температурных мощных ГТУ эта величина повышается
до 13 кгс/мм2.
Лопатки подвергаются воздействию циклического из-
менения температуры и напряжения, соответствующего
числу пусков установки. При этом возможны температур-
ные перепады типа тепловых ударов до 400° С. В перспек-
тивных ГТУ эта величина может составить 600—700° С.
Для приводных турбин число пусков за ресурс доходит
до 200, для пиковых — до 5000 (ГОСТ 21199—75).
Лопатки подвергаются также коррозионному и эрозион-
ному воздействию потока продуктов сгорания при его ско-
рости до 700 м/с. Запыленность потока твердыми части-
цами размерами до 100 мкм может достигать концентрации
0,3 мг/м3. При неблагоприятных атмосферных условиях
эти величины могут кратковременно повышаться соответ-
ственно до 250 мкм и 2,5 мг/м3. При наличии воздухоочис-
тительных устройств запыленность газового потока не
должна превышать установленных норм (подробнее см.
в п. VII.3).
Рабочие лопатки эксплуатируются в условиях значи-
тельной разности температур металла хвостовой и профиль-
ной частей в связи с отводом теплоты в диски. Радиальный
температурный перепад может достигать 400° С. Неравно-
мерность распределения температур имеет место и в попе-
речном сечении (по профилю) лопатки при нестационарных
режимах и в связи с охлаждением.
Рабочие лопатки испытывают одновременно воздей-
ствие статических растягивающих центробежных сил, из-
гибающих сил от воздействия потока газа, динамических
вибрационных нагрузок и термических напряжений. Ди-
намические знакопеременные нагрузки достигают 5—
8 кгс/мм2. На лопатках имеются конструктивные концен-
траторы напряжения (уступы, пазы, отверстия под демп-
ферные связи и др.). Суммарные (эквивалентные) напряже-
ния в лопатках достигают обычно 16 кгс/мм2 для привод-
ных турбин мощностью до 40 МВт и 27 кгс/мм2 для пиковых
турбин мощностью 100 МВт и более. Для лопаток послед-
них ступеней с максимальной рабочей температурой про-
фильной части 650° С эти напряжения могут достигать
30—32 кгс/мм2. В перспективных высокотемпературных
ГТУ температура металла рабочих лопаток может состав-
лять 870 — 900° С. Таким температурным условиям
эксплуатации смогут удовлетворять лишь принци-
пиально новые материалы (композитные, эвтектические
и др.).
Материал для лопаток должен удовлетворять постав-
ленным требованиям по жаропрочности и жаростойкости.
174
Жаропрочность — способность материала сопротив-
ляться воздействию нагрузки при высоких температурах,
она оценивается пределом длительной прочности, преде-
лом ползучести и в некоторых случаях сопротивлением ре-
лаксации.
Предел длительной прочности c^T характеризуется
напряжением, вызывающим разрушение металла (образца)
за заданный срок т при данной температуре t. В зависи-
мости от времени, в течение* которого данное постоянное
напряжение вызывает разрушение, различают пределы
длительной прочности для значений т, равных 100, 1000,
10 000 ч и т. д. Предел длительной прочности является ос-
новной исходной характеристикой, которой руководст-
вуются при прочностных расчетах деталей, эксплуати-
руемых при высокой температуре (свыше 450—500° С).
Предел ползучести <гкт соответствует напряжению, при
котором суммарная деформация е испытуемого образца
металла за определенный промежуток времени (т = 50 4-
-г-100 000 ч) достигает некоторой величины (0,01; 0,1; 1%),
допустимой для данной детали при заданной температуре t.
Наиболее употребительной расчетной величиной является
предел ползучести, соответствующий деформации е= 1%
за 100 000 ч.
В качестве характеристики релаксационной стойкости
в турбостроении обычно принимают остаточное напряже-
ние ОдСТ, сохраняющееся в испытуемом образце через опре-
деленный период времени т (100; 1000; 10 000 ч) при дан-
ной температуре t и заданном первоначальном напряжении
(напряжении затяга), приложенном к образцу.
Материал для лопаток должен обладать запасом проч-
ности по пределу длительной прочности не менее 1,6 для
штампованных и 2,0 для литых лопаток (по отношению к
к максимальному эквивалентному напряжению при дан-
ных температуре и ресурсе). При эксплуатационной темпе-
ратуре менее 550° С для сплавов на никелевой основе и ме-
нее 400° С для хромистых нержавеющих сталей указанные
коэффициенты рассчитываются по пределу текучести ме-
талла о0,2. Для лопаток из хромистых (нержавеющих)
сталей должен быть обеспечен также запас по пределу пол-
зучести не менее 1,3 для литых лопаток и не менее 1,1 для
штампованных лопаток.
Важнейшей характеристикой металла лопаток наряду
с жаропрочностью является уровень длительной высоко-
температурной пластычнос/пы,непосредственно связанный
с работоспособностью лопаток как в стационарном, так и,
в особенности, циклически изменяющемся режиме экс-
плуатации. При испытаниях на разрыв длительностью
7 000—10 000 ч во всем диапазоне рабочих температур ре-
комендуется иметь минимальное относительное удлинение
металла 6 2,5% .
Для жаропрочных сплавов на никелевой или никель-
кобальтовой основе характеристикой работоспособности
лопаток наряду с жаропрочностью металла является
относительное удлинение при разрыве в условиях деформа-
ции с постоянной скоростью растяжения. При выборе лопа-
точных материалов желательно проведение такого испыта-
ния со скоростью растяжения 0,1% в час при температуре,
соответствующей пониженной пластичности данного ме-
талла [93]. Для сплавов указанного типа рекомендуется
проводить испытания при температуре 650—700° С. Отно-
сительное удлинение при испытаниях в таких условиях не
должно быть меньше 4,5%.
В условиях испытаний на длительную прочность
гладких цилиндрических образцов и образцов с кольцевым
надрезом (радиус скругления г = 0,15 4-0,2 мм) материал
для лопаток не должен прояв-
лять чувствительности к концен-
тратору напряжения такого ти-
па, отношение должно
быть не менее 1. Пределы дли-
тельной прочности определяются
при испытаниях длительностью
не менее 7000 ч при температу-
ре, соответствующей понижен-
ной пластичности оцениваемого
материала.
Условный предел усталости
о., материала лопаток в области
эксплуатационных температур,
определенный на базе 108 цик-
лов при соответствующей асим-
метрии цикла (статическое на-
пряжение растяжения <тс,. = 10-:-
4-20 кгс/мм2), должен быть не
менее 25 кгс/мм2 для гладких
образцов и не менее 15 кгс/мм2
для образцов с надрезом, имити-
рующим концентраторы напря-
жения в хвостовой части ло-
паток.
Жаропрочные лопаточные
материалы должны быть стой-
кими к химическому воздейст-
вию газовой среды. Они должны
обладать как удовлетворитель-
ным сопротивлением высокотем-
пературному окислению (жаро-
стойкостью), так и сопротивле-
нием высокотемпературной кор-
розии, которая развивается в присутствии в потоке газа
солей щелочных металлов, особенно натрия, а также оки-
слов ванадия.
Необходимые жаростойкость материалов и сопротив-
ление высокотемпературной коррозии могут быть обеспе-
чены регулированием и тщательным контролем химиче-
ского состава рабочего тела, оптимальным химическим
составом лопаточного материала и применением защитных
поверхностных жаростойких покрытий [НО].
При выборе материалов для лопаток должна быть про-
верена склонность их к образованию при эксплуатацион-
ных температурах нежелательных охрупчивающих о- и
р-фаз. Это фазы со сложным химическим составом и кри-
сталлическим строением типа (Cr, Mo).v (Ni, Со)р, где х и у
изменяются от 1 до 7. В с-фазе доминирующим элементом
является хром, в ц-фазе — молибден и кобальт. Эти фазы
образуются при длительном тепловом воздействии в темпе-
ратурном интервале 700—820° С при определенном сочета-
нии в сплавах легирующих элементов: хрома, молибдена,
вольфрама, кобальта. Склонное"\ сплавов к образованию
охрупчивающих фаз проявляется особенно резко при со-
держании хрома более 16%.
Важным показателем является также стабильность
свойств материала лопаток при длительных тепловых вы-
держках, имитирующих температурные условия эксплуа-
тации. Желательно, чтобы в результате старения в течение
104 ч при наименее благоприятной температуре (для спла-
вов на никелевой и никель-кобальтовой основе 500—700° С)
относительное удлинение при разрыве при комнатной тем-
пературе было бы не менее 10%, а ударная вязкость — не
менее 3 кгс/см2.
Нержавеющие стали. В турбостроении для лопаточ-
ного аппарата с температурой металла до 580° С широко
применяют хромистые (нержавеющие) стали, содержащие
12—14% Сг, в состоянии после закалки и отпуска. Они
обладают высокими коррозионной стойкостью, декремен-
том затухания и низким коэффициентом линейного расши-
Таблица VIII. 1. Механические свойства и жаропрочность сталей
на железной основе для лопаток газовых турбин (ГОСТ 19442—74)
Темпера- тура ис- %,2 ств 6. •ф ан-
пытания, °C кгс/мм2 % кгс- м/см2
20 60 80 14 45 5,5-6,5
20Х13Ш 400 46 58 16 58 20
500 42 50 28 66 23
550 38 45 32 73 22
20 68 — 80 77 — 92 17—20 56—66 8—15
15Х11МФШ 400 50 — 66 60 — 77 13—17 57 — 64 14—19
500 43-54 52 — 59 18—20 68 — 70 17 — 20
600 41—51 45 — 54 17 — 20 75 — 78 16 — 20
20 70—75 85 — 89 15—18 55 — 58 9—12
20Х12ВНМФШ 400 58 — 60 68 — 70 13—14 55 — 62 14—15
(ЭП428) 500 53 — 58 56 — 58 14—15 59 — 78 12—15
600 36 — 38 38 — 41 20 — 23 79—88 13—15
20 33 — 40 75 — 84 30 — 44 40 — 49 9—10
31Х19Н9МВБТ 1 560 21 — 26 50 — 60 26—30 40 — 47 10—11
(ЭИ572) 600 25 49 20 45 11
650 24 45 24 55 11
Примечание. Принятые об означения ов — временное сопротивление
Р азрыву (предел прочности); ба — относительное удлинение для образцов с отно-
шением рабочей длины к диаметру, равным 5; — относительное сужение попереч-
ного сечения при разрыве; он — ударная вязкость
1 Стать 31 Х19Н9МВБТ (ЭИ572) — по ГОСТ 5949—75.
рения. Высокая чистота металла и отсутствие характерных
для сталей этого типа дефектов (волосовин) обеспечиваются
при изготовлении стали способом электрошлакового пере-
плава. Для стали, выплавленной таким способом, к обо-
значению ее марки добавляется буква Ш.
Для лопаток с рабочей температурой металла до 500° С
и рабочим напряжением при ресурсе 105 ч страб <
С 10 кгс/мм2 (при 500° С) следует применять хромистую
(нержавеющую) сталь марки 20Х13Ш с КП45—КП60 V
Для лопаток с рабочей температурой 500° С и <тра(-, = 20-н
4-23 кгс/мм2 или 580° С и ораб = 104-12 кгс/мм2 рекомен-
дуются упрочненные хромистые (нержавеющие) стали
марок 15X11МФШ, 20Х12ВНМФШ (ГОСТ 5632—72;
ГОСТ 19442—74).
При рабочей температуре металла 600—650° С в от-
дельных случаях для сопловых лопаток применяют аусте-
нитную сталь с карбидным упрочнением 31Х19Н9МВБТ.
Эта марка представляет обширный класс аустенитных ста-
лей с различным уровнем прочности, в который входят мо-
дификации широко распространенной стали типа Х18Н10Т
с о0,2 = 30 кгс/мм2 (при 20° С) и более прочные стали
типа Х15Н25 и Х15Н35, дополнительно легированные Мо,
117, Ti и некоторыми другими элементами, с ов,2 до
60 кгс/мм2 (при 20° С).
1 К.П45— КП60 — категории прочности стали с минималь-
ным значением предела текучести 45 — 60 кгс/мм2.
175
Свойства сталей приведены в табл. VIII.1, VIII.2 [88]
и на рис. VIII.1, VIII.2.
Жаропрочные деформируемые сплавы. В тех случаях,
когда уровень кратковременных или длительных (жаро-
прочных) механических свойств является недостаточным,
следует применять сплавы на никелевой или никель-ко-
бальтовой основе. Сплавы этого типа получили широкое
распространение в качестве материала для лопаток газо-
Таблица VIII.2. Выносливость хромистой
(нержавеющей) стали за 107 циклов
Сталь Темпе- ратура испыта- ния, °C (Т_1$ кгс/мм2
Гладкий образец Образец с надре- зом, г— 0,5 мм
20 37 24
200 35 22
20Х13Ш 300 32 20
400 31 17
500 24 13
20 38—42 16,8
20Х12ВНМФШ 450 27 —
(ЭП428) 550 27 —
580 24 —
вых турбин в СССР и за рубежом благодаря высоким жаро-
прочным свойствам при 550—850° С.
Сплавы на указанной основе представляют собой слож-
ные многокомпонентные системы, обладающие рядом поло-
жительных качеств, позволяющих применять их при тем-
пературе металла до (0,6 4- 0,8) Тпл, где Тпл—темпера-
Рис. VIII.1. Предел ползучести нержавеющих
сталей для деформации 1% на I05 ч при раз-
личных температурах:
1 — 20Х13Ш; 2 — 15Х11МФШ; 3 — ЭП428; 4 — ЭИ572
тура плавления. Количество контролируемых легирующих
элементов доходит до 13; часть из них (Ni, Mo, W, Со, Сг,
Fe) входит в состав главным образом твердого раствора,
образующего основу сплава, другие (Ti, А1, Та, Nb) прини-
мают активное участие в образовании упрочняющих ин-
терметаллидных фаз, характерных для этих сплавов, и,
наконец, элементы С, В, Zr, Се образуют карбиды и бориды,
концентрирующиеся по границам зерен и оказывающие,
несмотря на малое содержание каждого из них, сущест-
венное влияние на свойства сплавов.
Основной упрочняющей фазой является так называе-
мая у'-фаза типа Ni3Al, в которой элементы Ti и Nb заме-
щают в различной степени А1. В этой фазе присутствуют,
замещая часть Ni, элементы Мо и W (а также Со в сплавах
на Ni—Со-основе). Количество у'-фазы зависит главным
•образом от содержания в сплаве Ti и А1. Между количе-
176
ством у'-фазы и длительной прочностью спйавов существует
непосредственная зависимость.
Следует отметить, что при выборе жаропрочных спла-
вов для лопаток ГТУ приходится учитывать ряд обстоя-
тельств, оказывающих на структуру и свойства металла
прямо противоположное влияние. Необходимость образо-
вания в сплавах все большего количества у'-фазы по мере
роста требуемой жаропрочности ограничивает содержание
хрома величиной 6—10%, так как он повышает раствори-
мость у'-фазы в матрице сплава. В то же время высокое
содержание хрома (18% и выше) является основным факто-
Рис. VIII.2. Предел длительной прочности
нержавеющих сталей при различных темпе-
ратурах: а — за 104 ч; б — за 106 ч;
1 — 20Х13Ш; 2 — 15Х11МФШ; 3 — ЭП428; 4 —
ЭИ572
ром, определяющим сопротивление сплава высокотемпе-
ратурному окислению благодаря образованию защитных
поверхностных пленок, богатых Сг2О3.
Наряду с этим повышенное содержание Сг при небла-
гоприятном сочетании с такими легирующими элементами,
как Mo, W, Al, Т1 и др. способствует возникновению слож-
ных интерметаллидных о- и ц-фаз.
Особенностью жаропрочных сплавов является то, что
под действием высокой температуры они становятся неста-
бильными системами. Присутствующие в них фазы всту-
пают во взаимодействие между собой и элементами основ-
ного твердого раствора, что приводит к изменению исход-
ной структуры и соответственно механических свойств
сплава. Торможение этих процессов, протекающих обычно
в неблагоприятном направлении, достигается рациональ-
ной технологией изготовления деталей из этих сплавов.
Принципиальными особенностями технологических
процессов применительно к сплавам на никелевой основе
являются штамповка и закалка заготовок лопаток при вы-
Рис. VIII.3. Предел длительной прочности жаропрочных
сплавов при различных температурах: а — за 104 ч; б —
за 2-104 ч;
упрочняющей сплав, повышается деформационная способ-
ность сплава и резко снижается чувствительность металла
к концентраторам напряжений.
Сплавы на никелевой и никель-кобальтовой основе
выплавляются в индукционных и вакуумно-индукционных
электрических печах, во многих случаях с последующим
вакуумно-дуговым переплавом (ВД).
В зависимости от условий эксплуатации рабочих ло-
паток (рабочие напряжения, температура металла) могут
быть применены деформируемые Сплавы ЭИ607А, ЭИ607,
ЭИ893, ЭП800ВД, ЭП783ВД, ЭИ929ВД. Сплавы указаны
в порядке возрастания уровня жаропрочности.
Расчетный ресурс для лопаток из сплавов такого типа
составляет для приводных ГТУ не менее 2-104 ч, для ГТУ,
эксплуатируемых в пиковом режиме, — не менее 1 -104 ч.
Свойства перечисленных сплавов приведены в табл. VIII.3
и на рис. VIII.3.
Жаропрочные сплавы на никелевой и никель-кобаль-
товой основе являются высоколегированными труднодефор-
мируемыми материалами. В связи с этим лопатки из спла-
вов такого типа во многих случаях изготавливают путем
точной отливки по выплавляемым моделям.
Литейные сплавы. Прогрессивным направлением
в производстве деталей из жаропрочных сплавов является
применение способа литья с направленной кристаллиза-
цией затвердевающего в форме металла. Для осуществле-
ния этого способа необходимо специальное сложное обору-
дование и хорошо отработанная технология применительно
к каждому виду изделий. Этот способ изготовления отли-
вок обеспечивает высокую плотность и повышенную жаро-
прочность металла. Длительная пластичность при этом
в 5—10 раз превышает пластичность обычных поликристал-
лических отливок. Относительное удлинение при разрыве
в условиях испытаний на длительную прочность сплава
ЖС6К с направленной кристаллизацией составляет 6—•
15% против 1,5—3,5%'для металла с обычной поликристал-
лической структурой.
Дальнейшим развитием способа изготовления отливок
с направленной кристаллизацией является производство
литых монокристаллических отливок. В металле таких
отливок практически отсутствуют межзеренные границы,
представляющие собой наиболее вероятные места возник-
новения трещин при повреждении лопаток в процессе экс-
плуатации.
Для литых высоконапряженных и высокотемператур-
ных лопаток рекомендуются сплавы ЭИ893Л, ЦЖ20,
ЖС6К (сплавы указаны в порядке возрастания жаропроч-
ности). Сплав ЭИ893Л представляет собой литейную моди-
фикацию деформируемого сплава ЭИ893. Сплав ЖС6К
имеет наиболее высокие жаропрочные свойства среди спла-
1 — ЭИ607А; 2 — ЭИ607; 3 — ЭИ893; 4 — ЭП800ВД; 5 —
ЭП783ВД; 6 — ЭП539ВД; 7 — ЭИ929ВД
ках — относительное удлинение при разрушении
Рис. VIII.4. Предел длительной прочности литейных
сплавов при различных температурах (цифры в скоб-
испытуемых образцов, %): а—за 104 ч; б—за 2-104 ч;
1 — ЭИ893Л; 2 — ЦЖ20 (за 3- 104 ч); 3 — ЖС6К, поликристаллическне отливки; 4 — ЖС6К, отливки с направлен-
ной кристаллизацией
жимы отпуска получили широкое распространение в оте-
чественной и зарубежной практике, так как при этом до-
стигается оптимальное выделение и распределение фазы,
12 л. В. Арсеньев и др.
вов на никелевой и никель-кобальтовой основе. В связи
с ликвационной неоднородностью, неизбежно присутствую-
щей в литейных сплавах и проявляющейся в обогащении
177
междендритных участков металла примесями легкоплав-
ких элементов, легирующими элементами, карбидными и
интерметаллидными фазами, при их термической обработке
применяют нагрев для последующей закалки до более вы-
Таблица VIII.3. Механические свойства жаропрочных
деформированных сплавов на никелевой и никель-кобальтовой основе
Сплав Темпе- ратура СТ0,2 ств 6s ан’
испыта- ния, °C кгс/мм2 % кге- м/см2
20 50 — 63 90—106 36 — 44 40 — 42 11-18
ХН80ТБЮА 600 40 — 50 73 — 79 45 — 43 48 — 50 —
(ЭИ607 А) 700 40—52 63—75 27—39 27 —39 —
20 65 105 24 — 30 28 — 35 10—12
ХН80ТБЮ 600 60 83 И 18
(ЭИ607) 700 50 68 7 6 —
20 48 94 38 31 7,5
ХН65В9М4ЮТР 600 40 80 29 28 —
(ЭИ893) 700 34 63 33 38 —
750 40 69 19 27 —
20 70 — 88 115—130 18 — 28 18 — 30 4 — 7
ХН65КМВЮБ 700 65 — 80 100—110 12 — 23 14 — 25 1
(ЭП800ВД) 800 65 — 75 80 — 95 8—20 12 — 22 —
850 60 — 70 70 — 80 10—20 14 — 25 —
20 80 124 15,5 20 2,5
ХН70МТФКЮ 700 75 95 28 31 —
(ЭП783ВД) 800 73 93 24 31
850 70 77 19 28 —
20 68—72 110 — 123 17 — 18 17 — 27 3,0 —4,5
ХН55ВМТФКЮР 700 59 — 63 100 20 — 22 23 — 27 .—
(ЭИ929ВД) 800 54 — 62 81 — 91 17 — 20 20 — 30 —
850 54—59 70 — 76 17 — 26 25—39 —
Т а б л и ц а VIII.4. Механические свойства литейных сплавов
на никелевой и никель-кобальтовой основе
Темпе- ратура СТ0,2 °"в ба ан,
испыта- ния, °C кгс/мм2 % кгс м/см2
ХН65В9М4ЮТ (ЭИ893Л) 20 600 650 750 800 49 — 57 53 56 53 49 68 — 73 64 64 66 56 13—18 18 10 9 11 16 — 21 32 25 17 23 И 1 1 1
ХН60МКБЮТ (ЦЖ20) 20 600 700 800 850 71 — 87 75 62 — 72 62—72 63 79—94 96 76 — 96 81—85 72 3,3—6,0 10 3,8 —8,8 6—13 7 11 14 6 — 8 10 19 2,0— 3,5 3,0 2,8
ХН65КМВЮТ (ЖС6К), гтоликри- сталлические отливки 20 800 850 900 950 82 — 95 80 — 92 80 — 85 72 — 78 50 — 58 95—110 95—100 90 — 95 80 — 82 63—67 2,5 —7,0 1,5— 1,7 1,8—1,9 2,0 —2,3 1,5 —2,1 ГО to W Ю СО О СО О © 0 дц1 0 0610$° 1,5 —3,5
ХН65КМВЮТ (ЖС6К), отливки с направленной кристаллизацией 20 900 950 82 — 90 82 58 100—110 95 67 9 — 18 7 5 13 — 25 16 3,0 —3,5
соких температур, чем для деформируемых сплавов анало-
гичного состава. Высокотемпературный нагрев оказывает
гомогенизирующее действие, благоприятствует при после-
дующем охлаждении или стабилизирующем отпуске более
равномерному распределению
выделяющихся фаз, улучшает
механические характеристики
сплава. Механические свойства
и длительная прочность литей-
ных сплавов приведены в табл.
VIII.4 и на рис. VIII.4 [70].
Литейные сплавы выплавля-
ют и разливают в вакууме. Ос-
новную часть шихты для этих
сплавов составляет металлурги-
ческая заготовка того же хими-
ческого состава, что и сплав;
шихту также следует выплавлять
в вакуумных электрических ин-
дукционных печах.
Для сопловых лопаток с ра-
бочей температурой не более
580° С при соблюдении необхо-
димого запаса прочности можно
иейользовать литейные модифи-
кации хромистых (нержавею-
щих) сталей, марки которых
приведены в табл. VIII. 1 Ли-
тые заготовки или точнолитые
лопатки поставляются по завод-
ским техническим условиям.
Для рабочих и сопловых
лопаток, изготовляемых спосо-
бами точной штамповки или от-
ливки, поверхностный обезлеги-
рованный (обезуглероженный)
слой удаляют при полировании
и шлифовании лопаток или ог-
раничивают определенной допу-
стимой толщиной в каждом кон-
кретном случае.
Во всех случаях для лопа-
ток следует выбирать наиболее
экономно легированный сплав,
так как усложнение состава
сплава может вызвать усложне-
ние производства лопаток, осо-
бые требования к их конструк-
ции и условиям эксплуатации
лопаточного аппарата.
Защитные покрытия. При
температуре металла 800° С при
сжигании чистого топлива или
720° С при сжигании топлива
с повышенным содержанием се-
ры детали из жаропрочных
сплавов нуждаются в защитных
покрытиях (при содержании
хрома в сплавах менее 2О?6)-
Особенно агрессивны продукты
сгорания топлива при наличии
в них паров солей натрия и оки-
слов ванадия.
Создание защитных покры-
тий, предназначенных для дета-
лей с длительным ресурсом, яв-
ляется сложной задачей. На-
ибольшее распространение полу-
чили защитные покрытия на ос-
нове алюминия. При темпера-
туре 950° С происходит насыще-
ние поверхности алюминием из.
178
порошка или порошковых смесей алюминия с хромом,
с кремнием, с хромом и кремнием. Возможно нанесение
защитного слоя так называемым шликерным способом,
когда раствор алюминиевого порошка наносят кистью и
затем подвергают деталь диффузионному отжигу. Защит-
ные покрытия на основе алюминия надежны в эксплуата-
ции при температуре до 950° С и продолжительности ра-
боты до 10'1 ч в атмосфере продуктов сгорания чистого
газообразного или жидкого топлива.
Для эксплуатации в условиях сжигания тяжелого топ-
лива перспективны покрытия, наносимые путем плазмен-
ного напыления смесей сложного состава Fe + Сг + А1+
+ Y; Со + Сг + Al + Y, Со + Сг + Al + Si и т. п.
Эффективно применение подслоя из платины, изолирую-
щего металл деталей от основного защитного покрытия.
Толщина слоя защитного покрытия составляет 30—60 мкм,
VIII.2. МАТЕРИАЛЫ
ДЛЯ ЛОПАТОК ОСЕВЫХ КОМПРЕССОРОВ
Рабочая температура металла первых ступеней ком-
прессора низкого давления (КНД) зависит от температуры
засасываемого атмосферного воздуха. Рабочая температура
металла лопаток последних ступеней КНД 140—180° С.
Т а б л и ц а VIII.5. Механические свойства материалов
для лопаток компрессоров
Сталь НВ СТ0,2 СТВ 6s 1|> ан> кгс. м Катего- рия проч- ности Предельная ра- бочая температу- ра металла, °C
кгс/мм2 %
Не м ?нее см2
ЭИ961Ш 3,4 —3,7 80 95 18 61 10 КП80 530
ЭП410УШ, ЭП410УВД 3,3 —3,1 100 120 15 55 12 кпюо 350
ЭП517Ш 3,4 103 108 14 55 8,5 кшоо 550
ВТ5 3,4 —3,9 65 73 8 20 5 КП65 300
ТС5 3,3 —3,7 80 86 8 20 4,0 КП80 400
ВТЗ-1 3,2 —3,7 90 100 — 120 10 25 3,0 КП90 400
Рабочая температура металла лопаток первых ступе-
ней компрессора высокого давления (КВД) 30—220° С
(30—50° С при наличии воздухоохладителя), лопаток по-
следних ступеней КВД — 320— 450° С.
Статические напряжения изгиба в направляющих ло-
патках КНД обычно составляют до 8 кгс/мм2, в рабочих
лопатках — До 6 кгс/мм2; напряжения от центробежных
сил находятся в пределах 12—22 кгс/мм5. Напряжения из-
гиба в направляющих лопатках КВД достигают 20 кгс/мм2,
в рабочих лопатках — 17 кгс/мм2; напряжения от центро-
бежных сил — 20—25 кгс/мм2. Кроме статических напря-
жений рабочие лопатки испытывают динамические напря-
жения. Направляющие и рабочие лопатки компрессоров
подвергаются, кроме того, коррозионному и эрозионному
воздействию воздушного потока.
Материал для лопаток по своим антикоррозионным
свойствам и эрозионной стойкости должен обеспечивать
возможность эксплуатации направляющих и рабочих ло-
паток компрессоров ГТУ в течение заданного ресурса без
образования повреждений, понижающих их статическую
или усталостную прочность и аэродинамические характе-
ристики. Материал для лопаток должен обладать запасом
статической прочности при рабочей температуре металла
по отношению к уровню предела текучести (nOi2) не менее
2,5. При работе лопаток в условиях ползучести запас проч-
ности по отношению к пределу ползучести должен быть не
менее 1,2.
Большинство повреждений и разрушений компрессор-
ных лопаток связано с действием динамических цикличе-
ских напряжений. Разрушения являются или чисто уста-
лостными, или начинаются из очагов эрозионного или кор-
розионного поражения и происходят при относительно
низких рабочих напряжениях. Динамические напряжения,
оказывая непосредственное разрушающее воздействие,
могут, кроме того, способствовать возникновению началь-
ных стадий коррозионного поражения, снижающего уста-
лостную прочность лопаточного материала. Поэтому важ-
нейшим требованием как к материалу, так и к лопаткам
в целом является значительное превышение уровня вынос-
ливости материала и конструктивной усталостной прочно-
сти лопаток над уровнем динамических напряжений, воз-
никающих на различных этапах эксплуатации. С учетом
этих соображений материал для рабочих компрессорных
лопаток должен обладать высокой демпфирующей способ-
ностью, которая даже при меньшем пределе выносливости
обеспечивает более надежную работу конструкции.
Для умеренно напряженных лопаток можно применять
хромистые (нержавеющие) стали типа 20Х13Ш (КП45—
КП60). Для направляющих лопаток используют литейные
модификации при обязательном условии такой степени
освоенности литейной технологии, при которой гаранти-
руются устойчивые показатели,
удовлетворяющие поставленным
требованиям. Особое внимание
следует уделять оценке уста-
лостной прочности лопаток.
Направляющие и рабочие
лопатки, для которых характе-
ристики стали указанных марок
являются недостаточными, ре-
комендуется изготавливать из
хромистой (нержавеющей) стали
повышенной прочности ЭИ961Ш
(ГОСТ 1050—74). Эта сталь
(табл. VIII.5, VIII.6) обладает
высокими демпфирующей спо-
собностью и пределом усталости,
относительно низкой чувстви-
тельностью к концентраторам
напряжений и уровню статиче-
ских напряжений, накладываю-
щихся на циклические динами-
ческие нагрузки. Для эксплуатации при более высоких
температурах (до 550° С) и напряжениях может быть
использована сталь ЭП517Ш, применяемая для ком-
прессорных лопаток с ограниченным ресурсом.
Таблица VIII.6. Механические свойства
стали ЭИ961Ш при разных температурах
Темпера- тура ис- пытания, °C Отпуск 580° С (5 ч) Отпуск 680° С (5 ч)
%,2 ств ан* кге • м СТ0,2 % й5 ан- кгс. м
кгс/мм2 % кгс/мм2 %
см2 см2
20 300 400 500 96 89 88 75 109 100 96 80 17 14 14 19 60 68 60 73 6 22 19 21 80 73 68 59 95 86 81 67 18 15 13 19 61 63 63 74 10 19 20 20
Для лопаток компрессоров, предназначенных для
эксплуатации при низкой температуре засасываемого воз-
духа без специального его подогрева, может быть исполь-
зована нержавеющая сталь 1Х15Н5Д2Т (ЭП410УШ или
ЭП410ВД; КП100) (табл. VIII.5, VIII.7) [62].
Применению стали ЭП517Ш в серийном производстве
в каждом конкретном случае должны предшествовать испы-
12*
179
Таблица VIII.7. Механические свойства стали ЭП410УШ
при разных температурах (нормализация 1000° С, 1 ч)
Темпер атура испытания, °C Отпуск 450° С (3 ч) Отпуск 600° С (3 ч)
а0,2 ств 6, °н’ кгс. м СТ0,2 ,Ств 6. ф кгс- м
кгс/мм2 % кгс/мм2 %
см2 см2
20 300 350 400 100 92 88 82 120 103 100 100 15 16 16 15 55 59 53 53 12 16 16 14 80 — 85 78 75 74 105 90 86 85 19 13 13 12 65 53 46 59 20 17 18 17
Таблица VIII.8. Механические свойства стали ЭП517Ш
при разных температурах
Темпера- тура СТ0,2 % ан,
испытания, кгс м/см2
°C кгс/мм2 %
20 95 по 17 63 7,8
600 56 59 17 74 .—,
650 47 51 17 77 —
Т а б л и ц а VIII.9. Выносливость стали
для лопаток компрессоров на базе 107 циклов
Сталь Уровень проч- ности, кгс/мм2 Тип образца Выносливость стали, кгс/мм2, при температуре испытания, °C
20 450 500 550
ЭП961Ш 105—120 Гладкий 52 46 33 30
С надрезом, г — 0,75 мм 33 28 27 25
95—100 Гладкий 50 43 — —
С надрезом, г = 0,75 мм 31 27 — —
ЭП410УШ 125—130 Гладкий 57 44 (200° С) 43 (300° С) —
С надрезом, г = 0,50 мм 42 34 40 —
95—105 Гладкий 48 43 — —
С надрезом, г = 0,50 мм 30 29 — —
ЭП517Ш 110 Гладкий 54 34 (600° С) 31 (650° С) —
С надрезом, г 0,75 мм 36 19 18 —
тания лопаточного аппарата на испы-
тательном стенде ГТУ или в эксплуа-
тационных условиях на головном аг-
регате данной серии.
Сталь ЭП517Ш — нержавеющая,
повышенной прочности, допускает ис-
пользование при длительном ресурсе,
обладает сравнительно низкими чув-
ствительностью к концентраторам на-
пряжений и коэффициентом линейного
расширения. Как и все хромистые
стали, она выплавляется способом
электрошлакового переплава (табл.
VIII.5, VIII.8).
Стали ЭП410УШ и ЭП410УВД
относятся к классу нержавеющих
мартенситостареющих сталей. Низкое
содержание углерода обеспечивает при
закалке с любой скоростью охлажде-
ния образование малоуглеродистого
мартенсита, обладающего низкой проч-
ностью и приобретающего повышенную
прочность при сохранении высоких
пластичности и ударной вязкости после
отпуска за счет дисперсионного уп-
рочнения. Уровень прочности регули-
руется температурой отпуска (450—
600° С). Присутствие в стали Си и Ti
усиливает эффект дисперсионного уп-
рочнения. Горячая пластическая де-
формация этой стали не вызывает за-
труднений, у нее отсутствует склон-
ность к трещинам при закалке; сталь
хорошо сваривается, сохраняет высо-
кую ударную вязкость до весьма низ-
кой температуры: при —60° С удар-
ная вязкость в зависимости от уровня
прочности составляет от 9 до 15 кгс/см2
против 3 кгс/см2 для стали ЭП428Ш и
7 кгс/см2 для стали ЭП961Ш.
При испытании на ударную вяз-
кость образцов с предварительно ини-
цированной трещиной за критерий
оценки переходной температуры хруп-
кости принимается значение ан. т =
= 2 кгс-м/см2. При исходной прочно-
сти о012 = 105 кгс/мм2 переходная
температура хрупкости находится ни-
же —30° С, при о012 = 85 кгс/мм2 —
ниже —70° С; для сталей ЭИ802 и
ЭП428 примерно при той же прочности
эта критическая температура смещает-
ся в область положительных значений.
В табл. VIII.9 приведены резуль-
таты испытаний стали на усталость
в условиях чистого изгиба при частоте
нагружения 100 Гц.
Декремент затухания стали
ЭП410УШ в зависимости от напряже-
ния в два—семь раз ниже, чем у стали
20X13, но в два-три раза выше, чем
у сплавов на основе титана. Эти спла-
вы обладают высокой коррозионной
стойкостью, повышенной механической
прочностью, высокой удельной проч-
ностью, более чем в два раза превы-
шающей удельную прочность хроми-
стой (нержавеющей) стали. Крити-
ческая температура хладноломко-
сти сплава ВТ5 составляет —50° С,
сплава ВТЗ-1 — ( + 120) — (+160)° С
[71].
180
Сплав ВТЗ-1 —двухфазный (а- и P-фазы), рекомен-
дуется к применению при 100—400° С, при пониженных
температурах склонен к охрупчиванию. Сплав ТС5 — од-
нофазный (a-фаза), рекомендуется для деталей с темпера-
турой 20—400° С. Сплав ВТ5 — однофазный (а-фаза),
предназначен для длительной работы при температуре не
выше 300° С, может успешно эксплуатироваться при отри-
цательной температуре. Поверхности деталей из сплавов
на основе титана должны иметь высокий класс шерохова-
тости.
Физические свойства сплавов на основе титана:
Плотность, г/см3 . . . >.(/. <3-4 7 .‘к .". . 4,4 — 4,9
Модуль нормальной упругости 10“4, кгс/мм2 1,05—1 25
Коэффициент линейного расширения а-10’ . . 8—10
Теплопроводность, кал/(см-с-°C)..............0,017 — 0,024
Теплоемкость, кал/(г °C)..................... 0,10 — 0,13
В целях повышения усталостной прочности стальных
компрессорных лопаток рекомендуется виброгалтовка
хвостовых частей и ультразвуковой способ поверхностного
механического упрочнения профильной части лопаток.
Для повышения коррозионно-эрозионной стойкости можно
применять специальные защитные покрытия, например
гальваническое никель-кадмиевое.
При изготовлении точноштампованных или точноли-
тых лопаток без механической обработки не допускается,
чтобы толщина обезлегированного (обезуглероженного)
слоя была больше толщины слоя, удаляемого при полиро-
вании лопаток.
VIH.3. МАТЕРИАЛЫ ДЛЯ, РОТОРОВ
И ДИСКОВ ГАЗОВЫХ ТУРБИН И КОМПРЕССОРОВ
В зависимости от начальной температуры газа и кон-
структивного выполнения температура центральной части
дисков или вала ротора газовых турбин составляет 230—
400° С, температура периферийной части дисков (обода
с пазами для хвостовой части лопаток) для различных сту-
пеней лопаточного аппарата колеблется от 330 до 480° С.
Температура металла роторов и дисков компрессоров
в зоне всасывания наружного воздуха Зависит от атмо-
сферных условий и может колебаться в пределах — 50° С.
При температуре наружного воздуха ниже —30° С жела-
тельно применять подогрев засасываемого воздуха, или
подогревать горячим воздухом металл ротора для под-
держания необходимого температурного запаса вязкости.
Эксплуатационная температура дисков ротора по мере
удаления их от места всасывания наружного воздуха по-
степенно повышается, при этом предельная температура
в последних ступенях зависит от конструктивной схемы
ГТУ и степени сжатия воздуха. При однокомпрессорной
схеме ГТУ температура металла диска последней ступени
может достигать 400° С. При двухкомпрессорной схеме
температурный перепад для деталей КНД составляет от
-50° С до +180° С, для деталей КВД — от 200 до 400° С.
Рабочие напряжения от центробежных сил в цен-
тральной части компрессорных дисков в зависимости от
конструктивных особенностей и номера ступени состав-
ляет 20—60 кгс/мм2.
Поковки валов, цельнокованых роторов, дисков и кон-
цевых частей роторов изготавливаются из легированных
сталей (в перспективе из сплавов на никелевой основе) и
относятся к группе заготовок с индивидуальными испыта-
ниями механических свойств.
Технологические свойства металла (деформируемость
при горячей пластической деформации, прокаливаемость,
возможность применения относительно простых приемов
термической обработки) должны обеспечивать получение
поковок, удовлетворяющих требованиям технических ус-
ловий. Соответствующие опытные заготовки должны ис-
следоваться на заводе-изготовителе. Исследования про-
водятся также в случае изменения стали или сплава, повы-
шения категории прочности, существенного изменения раз-
меров и конфигурации деталей, принципиального измене-
ния методов изготовления поковок (выплавки и разливки,
ковки, термической обработки).
Внешний вид изготовленных деталей (валов, роторов,
дисков), их макроструктура, результаты контроля травле-
нием мест, указанных на чертеже, а также ультразвуко-
вого контроля для деталей с осевым отверстием, резуль-
таты механических испытаний должны соответствовать
в каждом конкретном случае требованиям технических
условий. Определение механических свойств и остаточных
напряжений, оценка макроструктуры производятся на
образцах и темплетах, вырезанных из наиболее напряжен-
ных и наименее качественных зон, которые указаны на чер-
теже изделия. При отсутствии такой возможности должно
быть проведено исследование опытных поковок.
Шероховатость поверхности заготовок, подвергаемых
ультразвуковой дефектоскопии, должна быть не более
7?z2,5 (ГОСТ 2789—73). Для выявления дефектов (типа
трещин) заготовки подвергаются ультразвуковому кон-
тролю в нескольких направлениях. Особое внимание долж-
но быть уделено плоскости, перпендикулярной действию
наибольших растягивающих напряжений.
Для изготовления валов, роторов, дисков трубин и
компрессоров, эксплуатируемых при повышенной темпе-
ратуре в условиях, требующих повышенного сопротивле-
ния коррозии и эрозии, рекомендуются стали марок
20Х12ВНМФШ, 20Х12ВНМФВД (ГОСТ 5632—72) с пре-
делом текучести о0,2 = 60<-73 кгс/мм2. При этом следует
принять меры по обеспечению надежной работы шеек ва-
лов в подшипниках (насадные втулки, наплавка поверх-
ностного слоя и др.). Для изготовления роторных деталей,
эксплуатируемых при температуре металла не выше 300° С
(в частности, валов и дисков КНД и низкотемпературных
ступеней газовых турбин), рекомендуются легированные
конструкционные стали типа 20ХНЗМФА и 27ХНЗМ2ФА
(табл. VIII. 10, VIII.И, рис. VIII.5).
Таблица VIII. 10. Механические свойства
сталей для дисков газовых турбин
и компрессоров (образцы тангенциальные)
Сталь а0,2, кгс/мм2 %- кгс/мм2 6, % ф, % 2 X О ч и
Не мене е см2
20Х12ВНМФШ; 60 — 73 77 15 30 4,0
20Х12ВНМФВД 20ХНЗМФА 60 — 75 75 12 32 5
27ХНЗМ2ФА 70 — 85 85 13 37 6
Таблица VIII.11. Механические свойства
стали 20Х12ВНМФШ при разных температурах л
(закалка в масле 1050° С, отпуск 700° С)
Температура в» ф «н-
°C кгс/мм2 % кгс • м/см2
20 - 60 — 73 85 — 89 15—18 55 — 58 9,5—12
300 61 — 63 75 14 59 — 63 13—15
400 58 — 60 68 13 55—62 14—15
500 53 — 58 56 — 58 14 59 — 78 12—15
580 42 — 45 45 — 46 20 79 — 86 13 — 15
600 36 — 38 38—40 22 79—88 13,5—15
Применяемые для роторных деталей материалы долж-
ны обеспечивать запас прочности в наиболее напряжен-
ных элементах не менее 1,5 по пределу длительной прочно-
сти при температуре металла не ниже 450° С или по пре-
181
делу текучести при менее высокой температуре. Для хро-
мистых (нержавеющих) сталей следует учитывать запас
прочности по отношению к пределу ползучести не менее 1,1.
Для деталей с осевым отверстием допускается предельная
деформация центрального отверстия не более 0,55%.
Рис. VIII.5. Пределы длительной проч-
ности и ползучести стали
20Х12ВНМФШ (о012 = 70
<-75 кгс/мм2) при различных темпера-
турах-
1 — <7^ за 104 ч, 2 — то же за 10® ч: 3 —
ДТ
для деформации 1 % за 10® ч
В целях повышения надежности роторных деталей
следует ограничивать верхний уровень прочности хромо-
молибденованадиевых и высокохромистых сталей, так как
Рис. VIII.6. Предел
длительной прочности
сплава ЭИ698 при раз-
личных температурах.
1—за!0*ч; 2—за2-10‘ч;
3 — за 3-10* ч
повышение прочности сопровождается ростом чувствитель-
ности стали к хрупким разрушениям.
При выборе марки стали и категории ее прочности
необходимо учитывать уровень переходной температуры
хрупкости. Критерием является наличие 50% волокна в из-
ломе ударных образцов. Переходная температура хрупко-
сти (ГОСТ 4543—71) должна быть примерно на 20° С ниже
возможной минимальной температуры металла данной ро-
торной детали. В необходимых случаях рекомендуется
оценивать малоцикловую усталостную прочность на осно-
вании расчетов температурных напряжений и эксперимен-
тальных данных.
182
Для оценки сопротивления хрупким разрушениям и
определения допускаемых размеров дефектов, особенно от-
ветственных роторных деталей (валов, роторов, дисков,
соединительных муфт и т. п.), рекомендуете^ проводить
расчет критических размеров дефектов и вязкости разру-
шения Kic на основе результатов испытаний образцов с тре-
щинами [24].
Перспективным материалом для дисков стационарных
газовых турбин следует считать сплав на никелевой основе
ЭИ698 (табл. VIII. 12), применяемый в газовых турбинах
с ограниченным ресурсом.
Т а б л и ц а VIII. 12. Механические свойства
сплава ЭИ698 при разных температурах
Темпе- ратура °0,2 °в 6s •ф ан’
испыта- ния, °C кгс/мм2 % кгс - м/см2
20 70 — 77 114—118 27 — 34 29—37 9—13
500 57 — 62 100—105 29 — 33 30 — 34
600 57 — 60 97—100 28—31 28—32 ___
700 57 — 61 89 — 94 20 — 35 21—36
800 54 — 58 62 — 66 23 — 25 30 — 41 —Z —
Сплав ЭИ698 хорошо поддается горячей пластической
деформации, обладает высокими прочностными и пластиче-
скими свойствами и ударной вязкостью при комнатной и
повышенных температурах, высокой -жаропрочностью
(рис. VIII.6). Усталостная прочность на базе 107 циклов
для гладких образцов при 650 и 700°С равна 35 и 37 кгс/мм2,
для образцов с кольцевым надрезом (г = 0,75 мм) — 30 и
34 кгс/мм2 соответственно.
При выборе стали для сварных роторных деталей и
разработке технологии их сварки рекомендуется руковод-
ствоваться работами [39, 40].
Следует иметь в виду, что легированные конструкцион-
ные, нержавеющие и жаропрочные стали и сплавы имеют
повышенную чувствительность к термическому воздейст-
вию сварки и относятся к числу материалов, ограниченно
свариваемых. При сварке сталей перлитного и мартенсит-
ного классов необходимо вводить предварительный подо-
грев и подвергать сварное соединение последующей терми-
ческой обработке. Сварные соединения аустенитных сталей
и сплавов на никелевой основе обладают повышенной
склонностью к образованию трещин в условиях длительной
эксплуатации при температуре 550—600° С; кроме того,
в ряде случаев сварные соединения уступают по прочности
основному материалу, поэтому сварные стыки рекомен-
дуется располагать вне зоны действия повышенных напря-
жений.
VIII.4. МАТЕРИАЛЫ
ДЛЯ ДЕТАЛЕЙ КАМЕР СГОРАНИЯ
И ГАЗОПЛАМЕННОГО ТРАКТА
Рабочая температура металла пламенных (жаровых)
труб камер сгорания и высокотемпературных деталей газо-
пламенного тракта зависит от начальной температуры
продуктов сгорания топлива и конструкции системы охла-
ждения этих элементов. В большинстве случаев эти детали
представляют собой сварные листовые конструкции с рабо-
чей температурой металла до 750° С. Неравномерность тем-
пературы металла в деталях камеры сгорания доходит до
200° С, а перепады по длине газопламенного тракта — до
600° С. Число, частота, режимы теплосмен в этик узлах
ГТУ определяются назначением, конструкцией и режимом
работы агрегата. Материал подвергается коррозионному
воздействию продуктов сгорания топлива.
Т а б л и ц а VIII. 13. Химический состав окалиностойких сплавов
Сплав Содержание элемента, % Предель- ная тем- пература, °C (ресурс 10* ч)
С, не более Сг Мо W Ti AI Прочие элементы
ХН78 (ЭИ435) 0,12 19 — 22 — — — Не более 0,15 Ni — основа 1000
ХН75МБТЮ (ЭИ602) 0,10 19 — 22 1,8 —2,3 — 0,35 —0,75 0,35 — 0,75 Ni — основа; Nb — 0,9—1,3 950
ХН70Ю (ЭИ652) 0,10 26 — 29 — — — 2,80 — 3,50 Ni — основа; Fe — не более 4,0; С1 — не более 0,03 1200
ХН60ВТ (ЭИ868) 0,10 23,5 — \ 26,5 — 13—16 0,30 — 0,70 Не более 0,5 Ni — основа; Fe — не более 4,0 1000
ХН56ВМТЮ (ЭП199) 0,10 19 — 22 4 — 6 9—11 1,1 —1,6 2,1 —2,6 Ni — основа; В — не более 0,008 800
ХН67ВМТЮ (ЭП202) 0,10 17 — 20 4-5 4-5 2,2 —2,8 t 1,0—1,4 Ni — основа; Fe — не более 4,0 850
Детали газопламенного тракта эксплуатируются при
относительно невысоких напряжениях (<траб С 8 кгс/мм2).
При этом имеет место вибрационная нагрузка в пределах
частот от 10 до 1000 Гц, обусловленная пульсацией про-
цесса горения.
Материалы для высокотемпературных деталей газо-
пламенного тракта должны обладать необходимой жаро-
прочностью, высокой жаростой-
костью в продуктах сгорания
топлива и высокой коррозион-
ной стойкостью.
Жаростойкость таких мате-
риалов характеризуется потерей
в окалине от 0,005, до 0,01 мм
толщины детали в год. При тем-
пературе деталей 900° С и более
потери в окалине составляют
0,05—0,1 мм в год. Для повыше-
ния жаростойкости могут при-
меняться эмали, например эмаль
ЭВ-55А.
Жаропрочность материала
должна обеспечивать устойчи-
вость (сохранение формы) дета-
лей при рабочей температуре.
Запас прочности при этом по
отношению к пределу длитель-
ной прочности для заданного
ресурса должен быть не менее
1,25.
Материалы для деталей газо-
пламенного тракта должны обла-
дать удовлетворительной техно-
логичностью, позволяющей из-
готовлять гнутые или штампо-
ванные детали, а также допу-
скать применение автоматической
сварки под флюсом, аргонодуговой или контактной сварки.
Для широкого круга деталей с рабочей температурой
металла до 800° С рекомендуется сталь 12Х18Н10Т
(ГОСТ 5632—72). Для этих же целей могут быть применены
сталь 08X18IT10T (ГОСТ 9940—72), отличающаяся лучшей
свариваемостью, и сталь 20Х23Н18 (ГОСТ 5632—72).
Колебания химического состава (в пределах марочного
состава) по содержанию углерода и карбидообразующих
элементов вызывают повышенную склонность сталей этих
марок к образованию охрупчивающей о-фазы, особенно
при температуре 750—80(гС. Для предотвращения (за-
медления) образования о-фазы указанные стали должны
применяться в полностью рекристаллизованном состоянии.
Стали 12Х18Н10Т и 08Х18Н10Т могут применяться также
для облицовки внутренней поверхности корпусных деталей.
Стали 12Х18Н10Т и 08Х18Н10Т могут быть исполь-
зованы также для литых деталей топливного устройства
и газопламенного тракта. Отсутствие порога хладноломко-
сти у стали аустенитного класса позволяет применять ука-
занные материалы для деталей, эксплуатируемых при отри-
Т а б л и ц а VIII. 14. Свойства окалиностойких сплавов при разных
температурах
Сплав Темпера- тура закалки, °C (охла- ждение иа воз- духе) Темпера- тура ис- пытания, °C °В’ кгс/мм2 б6, % Технические условия
ХН78 (ЭИ435) 980—1120 20 800 70 22 30 34 ТУ 14- 1-434 — 72
ХН75МБТЮ (ЭИ602) 1050 — 1080 20 800 75 25 40 40 ЧМТУ 1-456—68
ХН70Ю (ЭИ652) 1100 20 900 75 11 25 25 ТУ 14- 1-493 — 72
ХН60ВТ (ЭИ868) 1150 20 900 75 20 40 30 ЧМТУ 1-470 — 68
ХН56ВМТЮ (ЭП199) 1150 20 800 90 40 25 ЧМТУ 1-515 — 68
ХН67ВМТЮ (ЭП202) 1150 20 850 90 25 25 ЧМТУ 1-914 — 70
цательной температуре, например для наружных деталей
топливного коллектора.
Для деталей газопламенного тракта эксплуатируемых
при более высоких температурах, могут быть применены
следующие сплавы на никелевой основе (табл. VIII. 13—
VIII. 15): ЭИ435, ЭИ602, ЭИ652, ЭИ868, ЭП199, ЭП202
(ГОСТ Г8968—73). Выбор сплава определяется условиями
эксплуатации.
Сплав ЭИ435 при умеренных напряжениях может быть
использован до рабочей температуры металла 1000° С; он
хорошо сваривается,, мало чувствителен к циклическим ус-
ловиям эксплуатации, отличается высокой стабильностью
структуры (свойств).
183
Таблица VIII. 15. Глубина
Г высокотемпературного окисления в воздушной среде
некоторых жаростойких сплавов за 104 ч
Сплав Глубина окисления, мм, при температуре, °C
800 850 900 950 1000 1100 1200
ЭИ435 0,004 0,005 0,009 0,013 0,019 0,036 0,063
ЭИ602 0,004 0,007 0,014 0,026 0,046 0,127 0,288
Сплав ЭИ602 может быть использован для более на-
пряженных деталей, но при предельных рабочих темпе-
ратурах несколько уступает сплаву ЭИ435 по окалиио-
стойкости. Сплав штампуется в холодном состоянии и сва-
ривается, хорошо сопротивляется растрескиванию, а изго-
товленные из него детали — короблению. Рекомендуется
также для внутренней облицовки корпусных деталей газо-
вых турбин с рабочей температурой 900° С.
Сплав ЭИ652 благодаря высокому содержанию хрома
и алюминия отличается высоким сопротивлением окисле-
нию и термической усталости и поэтому может применяться
для деталей с предельно высокой температурой (до 1200° С).
При сварке требуется подбор специальных режимов в за-
висимости от конструкции и назначения деталей.
Сплав ЭИ868 обладает наиболее благоприятным соче-
танием физических и технологических свойств. Отличается
хорошей штампуемостью, свариваемостью, высокой окали-
ностойкостью и сопротивлением термической усталости.
Рекомендуется также для внутренней облицовки деталей
газовых турбин с рабочей температурой до 1000° С.
Сплавы ЭП99 и ЭП202 относятся к более прочным, дис-
персионноупрочненным, сложнолегированным материалам,
которые целесообразно применять для высоконагруженных
высокотемпературных деталей (сварных диафрагм, флан-
цев и т. п.). По технологичности (штампуемости, сваривае-
мости) они уступают сплаву ЭИ868.
лей зависит от температуры газового и воздушного потоков,
конструктивного исполнения деталей, наличия охлажде-
ния или подогрева.
Химический состав, способ производства, нормы меха-
нических свойств, режимы термической обработки литых
корпусных деталей, методы контроля, а также действую-
щие стандарты и технические условия приведены в ра-
боте [88].
Для деталей с рабочей температурой от —40 до -|-350° С
при отсутствии повышенных требований к коррозионной
стойкости применяется сталь марок 20Л и 25Л
(ГОСТ 977—75). В тех случаях, когда требуется примене-
ние теплоустойчивых сталей, при рабочей температуре до
510° С рекомендуется сталь 12МХЛ, до 540° С— стали
10Х13Л или 08Х13Л, до 560° С — сталь 15Х1М1ФЛ. При
повышенных требованиях к теплоустойчивости (до 580° С)
рекомендуется сталь 15X11МФБЛ. Для деталей с повышен-
ными требованиями к жаростойкости может быть исполь-
зована сталь Х25Н13АТЛ (до 700° С), отличающаяся вы-
сокой окалиностойкостыо.
Для внутренних корпусных деталей с рабочей темпе-
ратурой металла выше 600° С (сегментные элементы ста-
Рис. VHI.7. Предел длительной прочности корпусных
литейных сталей при различных Температурах: а — за
104 ч; б — за 105 ч;
VIII.5. МАТЕРИАЛЫ
ДЛЯ ДЕТАЛЕЙ КОРПУСОВ ГАЗОВЫХ ТУРБИН
И КОМПРЕССОРОВ
I — 15Х1М1ФЛ: 2 — 15ХПМФБЛ; 3 — Х25Н13АТЛ;
4 — 10Х18Н10ТЛ; 5 - 10Х17Н10МБГ4Л (ЭИ402МЛ);
6 — 08Х16Н13М2Б (ЭИ405); 7 — 20Х23Н18 (ЭИ417);
8 — ЗХ16Н22В6Б (ЦЖ13) в кованом виде
Литые, сварнолитые, листовые сварные конструкции
корпусов газовых турбин и компрессоров подвергаются
действию умеренных статических напряжений (ораб С
С 6 кгс/мм2) от давления газовой или воздушной среды при
стационарном режиме работы и значительных цикличе-
ских температурных напряжений, возникающих как при
стационарных режимах, так и при останове или пуске ГТУ
из-за разности температур между отдельными конструктив-
ными элементами корпуса. В результате возникает опас-
ность коробления корпусных деталей, раскрытия фланце-
вых соединений и т. п. Для предотвращения этих явлений
необходимо создание благоприятного температурного ре-
жима при тщательном учете возможных термических на-
пряжений.
Рабочая температура деталей внешнего корпуса ГТУ
находится в пределах 100—540° С (за исключением необо-
греваемых деталей, температура которых зависит от тем-
пературы атмосферного воздуха). Некоторые детали (кор-
пус топливного коллектора, всасывающий патрубок КНД
и т. п.) могут иметь при эксплуатации температуру до
—50° С. Рабочая температура внутренних корпусных дета-
184
тора, обоймы разного типа и т. п.) рекомендуется аусте-
нитная сталь 10Х18Н10ТЛ (ГОСТ 2176—67) или сталь
ЭИ402МЛ (до 650° С).
Для сталей 10Х18Н10ТЛ, ЭИ402МЛ и Х25Н13АТЛ
контролируется содержание ферритной фазы, присутствие
которой в пределах 2—5% при температуре эксплуатации
отливок выше 500° Сив пределах 2—15% при меньшей
температуре обеспечивает их удовлетворительную свари-
ваемость.
При более высокой температуре металла рекомендуется
сплав ЭИ893Л [68 ]. Для внешних корпусных деталей,
к которым предъявляются требования надежной эксплуа-
тации при отрицательной температуре до —50° С, рекомен-
дуется сталь 08ГДНФЛ (ГОСТ 977—75). Критическая тем-
пература хладноломкости этой стали —75 °C. Из этой стали,
в частности, целесообразно отливать детали всасывающего
патрубка КНД.
Механические свойства указанных материалов приве-
дены в табл. VIII.16 и на рис. VIII.7.
Листовой материал, сортовой прокат и поковки для
корпусных деталей выбираются в соответствии с требова-
Таблица VIII. 16. Механические свойства литой легированной стали
при разных температурах
Сталь Темпера- тура ис- пытания, °C СТ0,2 с7в 6ъ ан’ кгс. м/см2
кгс/мм2 %
12МХЛ 20 400 550 26 24 23 45 42 38 27 20 20 52 50 52 9 8 7
15Х1М1ФЛ 20 500 600 35 26 22 58 35 24 21 24 25 65 75 90 4—16 10—13 8—10
10Х13Л 20 400 500 41—30 38 33 58—67 52 43 22 — 26 18 20 55 — 62 57 63 8—15
15Х11МФБЛ 20 400 600 ЕЭ W <О со QO 1 1 1 со 4Х О1 ЕО СО 63 — 7^2 52 — 56 32 — 40 13 — 25 13—18 20 — 27 17 — 64 50 — 60 55—84 3—10 8—14 9,5—16
Х25Н13АТЛ 20 550 650 29—33 19 17 50 — 60 40 39 28 — 45 32 29 28 — 40 43 45 5—16 17 15
08ГДНФЛ 20 35 Не ь 45 1енее 18 30 5
10Х18Н10ТЛ 20 500 700 20 — 24 19 18 50 — 67 35 23 — 26 24- 35 17 15—17 30 — 35 35 — 42 26—38 8—11 7 — 9 9
10 X 17Н10МБГ4 Л (ЭИ402МЛ) 20 500 600 750 18 — 25 14 13 13 38 — 48 32 29 20 15 — 36 20 19 33 17 — 40 28 25 58 2,5 — 9 9,5 10 10
Т абл и ц а VIII. 17. Механические свойства аустенитных сталей
для корпусных деталей при разных температурах t
Сталь Темпера- тура испыта- ния, °C СТ0,2 °в 6, ф а1Г кгс. м
КГС 'мм2 ( /о
СМ2
20 25 — 29 56 — 65 30 — 48 35 — 54 10—12
08Х16Н13М2Б 400 17—19 48 — 53 30 — 33 27-48 8—14
(ЭИ405) 500 16—18 47 — 52 31—35 28—50 10 — 20
650 15—17 41 — 45 28 — 30 34 — 46 9—16
20 31 61 — 67 29 — 35 47 — 54 14—19
20Х23Н18 400 23 55 24 — 32 39 — 45 15—17
(ЭИ417) 600 20 45 23 45 18
700 20 33 19 — 24 34 17
800 16 20 J9 —27 34 18
20 1 39 — 48 72 — 80 24 — 34 32 — 43 6—9
ЗХ16Н22В6Б 750 1 23 — 27 33 — 43 — — —
(ЦЖ13) 20 2 28 — 36 43—64 10 — 25 15 — 30 2 — 4
700 2 18 — 26 28—33 18 — 29 45 — 65 4,5 —6,8
800 2 14—20 20—26 22 — 33 47 — 66 5 — 9
1 Кованая сталь
2 Литая сталь
пиями прочности, технологично-
сти -при сварке (для сварных
деталей) и сопротивляемости
коррозии в воздушной или га-
зовой среде.
Корпусные конструкции с
рабочей температурой металла
от —20 до 4-450° С, к которым не
предъявляются специальные тре-
бования по коррозионной стойко-
сти, могут быть выполнены из
низкоуглеродистой стали, листо-
вого или фасонного проката или
поковок марок 15К или 20К
по ГОСТ 5520—69. Для деталей
с рабочей температурой металла
до 510° С применяются листовой
и сортовой прокат и поковки из
теплоустойчивой стали 12ХМ по
ЧМТУ 57-59—57, -стали 15ХМ
(ГОСТ 4543—71) или 12МХ
(ГОСТ 20072—74); при более вы-
сокой температуре металла (до
550° С) рекомендуются стали
15Х1М1Ф (по заводским техни-
ческим условиям), 09X13 (ГОСТ
5632-72) и 12Х1МФ (ГОСТ
20072—74).
Для деталей с рабочей тем-
пературой до 600° С рекоменду-
ются поковки из стали
08Х16Н13М2Б (ЭИ405) (ГОСТ
5632—72). Для деталей с рабо-
чей температурой до 800° С
(с учетом требований по проч-
ности) может применяться лист
из стали 08Х18Н10Т (ГОСТ
5582—75).
Для деталей к которым
предъявляются высокие требо-
вания по жаростойкости, реко-
мендуются листовой прокат или
поковки из стали 20Х23Н18
(ЭИ417) (ГОСТ 5632—72). Для
деталей с рабочей температурой
металла 750—800° С может быть
применена сталь ЦЖ13 в кова-
ном и литом состоянии. Свой-
ства сталей ЭИ405, ЭИ417, литой
и кованой стали ЦЖ13 приве-
дены в табл. VIII. 17 и на
рис. VIII.7.
При изготовлении сварных
деталей следует руководство-
ваться рекомендациями, изло-
женными в [40].
VIH.6. МАТЕРИАЛЫ ДЛЯ
КРЕПЕЖНЫХ ДЕТАЛЕЙ
Температура крепежных де-
талей может достигать 500° С и
выше. Отдельные резьбовые сое-
динения (болты, шпильки, гайки
внешнего корпуса компрессоров
и др.) должны обеспечивать на-
дежную эксплуатацию соедине-
ния в условиях отрицательных
температур.
185
"wiih.
Таблица VIII. 18. Механические свойства крепежных сталей при разных температурах
та %,2 % fis “н’ НВ,
2 X а> та х кгс/мм2 % см2 кгс/мм2
Н р.д
У
20 76 — 83 85 — 94 16—18 64 — 69 15—18 255 — 289
20Х1М1Ф1ТР 500 63 69 15—18 73—74 14 — 18 —
(ЭШ82) 600 47—53 48—55 15 — 20 78 15—18
650 45 — 50 47 — 52 15 — 24 78 21 —
20 67 — 82 90—100 14—18 46 — 60 6—11 262—277
2Х12ВМБФР 500 54 — 70 63 — 82 13—17 53 — 65 13—16 __
(ЭИ993) 600 41—62 44 — 70 14 — 25 60 — 79 13—18 * . .
650 40 — 58 45 — 64 16—21 65 — 78 16 — 20 —
20 85-105 105—120 10—12 10—14 3 — 4 302 — 350
10Х11Н22ТЗМР 500 75 97 12 15
(ЭИ696М) 600 74 96 10 14 —. —
700 73 95 8 12 — —
Таблица VIII.19. Сопротивление
релаксации крепежных сталей
Сталь Темпе- ратура испы- тания, °C На- чальное напря- жение СТ0, кгс/мм2 Остаточное напря- жение, кгс/мм2, за время, ч
1000 5000 10 000
25 20,7 20,0 19,4
450 30 25,0 23,8 23,2
35 28,8 27,5 27,0
25 19,3 18,2 17,4
500 30 22,8 22,0 20,7
35 26,2 25,0 24,2
20Х1М1Ф1ТР
(ЭП182)
25 15 12,4 11,0
565 30 17,5 14,3 13,0
35 19,0 — 14,5
25 14,0 11,6 8,7
580 30 15,0 « 13,0 10,5
35 17,5 13,3 11,5
25 20,5 ,
450 30 24,5 — __
35 28,0 — —
2Х 12ВМБФР 25 18,4 . -
(ЭИ993) 500 30 21,5 ——
35 25,0 — —
30 22,0 10,8 9,0
580 35 20,5 12,5 10,5
25 23,7 23,2 22,8
450 35 32,7 31,5 30,0
45 42,2 41,5 40,0
10 X11 Н22ТЗМР 25 23,0 22,8 22,6
(ЭИ696М) 500 35 32,0 31,5 31,3
45 41,2 40,7 40,0
25 11,0 10,3 7,8
650 35 18,6 12,6 8,8
45 23,0 15,7 11,5
Обязательным требованием при выборе материалов
для крепежных деталей является малая разница (не бо-
лее 10%) между коэффициентами линейного расширения
материала фланцев и крепежных деталей. Гайки следует
изготавливать из материала того же класса, что и
шпильки (болты). Твердость материала гаек должна быть
ниже твердости материала шпилек (болтов) не менее, чем
на ЯВ 12.
Материал крепежных деталей должен обладать высокой
сопротивляемостью хрупким разрушениям и малой чув-
Рис. VIII.8. Предел длительной прочности
крепежных сталей при различных температу-
рах за. 104 ч:
1 — ЭП182; 2 — ЭИ993; 3 — ЭИ696М
ствительностью к концентраторам напряжений в заданных
температурных и силовых условиях эксплуатации и необ-
ходимым уровнем сопротивления релаксации, коррозион-
ной стойкости и теплоустойчивости. В зависимости от
уровня действующих рабочих напряжений и температуры
металла рекомендуются следующие материалы: ЭП182,
20X13, 15Х11МФ, ЭП428, ЭИ993, ЭИ696М, ЭИ572.
При выборе материала для крепежных деталей сле-
дует руководствоваться требованиями ГОСТ 20700—75,
ГОСТ 18126—72, ГОСТ 1759—70. Типы и основные раз-
меры изделий — по ГОСТ 9064—75, ГОСТ 9065—75,
ГОСТ 9066—75. Механические свойства материалов, реко-
мендуемых для крепежных деталей, для которых отсутст-
вуют характеристики в приведенных ранее таблицах,
даны в табл. VIII.18 и на рис. VIII.8. Релаксационная
стойкость крепежных материалов иллюстрируется
табл. VIII. 19. Физические свойства некоторых сталей и
сплавов приведены в табл. VIII.20.
186
Таблица VIII.20. Физические свойства некоторых сталей и сплавов
Сталь Коэффициент линейного расширения а. 106, мм/(мм*°С), при температура, °C
100 200 300 400 500 600 700 800 900
25Л 11,5 12,9 13,0 13,2 13,5 — — —
15Х1М1ФЛ 12,4 12,8 13,3 13,7 14,0 14,1 — — —
10Х18Н10ТЛ 14,8 15,9 16,8 17,1 17,6 17,9 18,2 18,3 —
20X13 10,1 10,4 10,9 11,4 11,8 — —
15Х11МФ — 11,1 11,3 11,7 12,0 — 12,4 —
20Х12ВНМФШ (ЭП428) 10,0 10,5 10,7 11,0 11,2 11,6 — —
2Х12ВМБФР (ЭИ993) 11,5 11,3 11,4 Ц,8 12,0 12,2 12,1 12,6 —
31Х19Н9МВВТ (ЭИ572) — — — 16,0 16,4 16,7 16,9 17,9 —
15Х1М1Ф 11,2 11,7 12,5 13,0 13,5 13,7 — — —
20Х1М1Ф1ТР (ЭП182) 12,0 12,3 12,8 13,0 13,5 13,6 — —
Х18Н10Т 16,6 17,0 17,2 17,5 17,9 18,2 18,6 18,9 19,3
ХН78Т (ЭИ435) 12,2 13,0 13,4 13,8 14,1 14,7 15,4 15,5 —
ЭИ607, ЭИ607А — — — 14,4 14,9 15,6 16,3 —
ХН65В9М4ЮТР (ЭИ893) 11,3 — — — — — 14,4 —
ХН55ВМТФКЮР (ЭИ929ВД) 10,2 10,7 12,0 12,2 12,4 12,6 13,1 13,2 14,0
38ХНЗМФА 11,8 12,1 12,6 13,0 13,4 13,7 — — —
Сталь j Модуль нормальной упругости Е • 10“4, кгс/мм2, при температуре, °C Плот- ность, г/см3
20 100 200 300 400 500 600 700 800
л
25Л 2,17 2,07 2,01 1,96 1,87 1,78 1,72 1,52 — 7,83
15Х1М1ФЛ 2,14 — 2,05 1,99 1,91 1,81 1,65 — — 7,80
10Х18Н10ТЛ 1,70 — — 1,43 1,35 1,27 1,18 — 7,90
20X13 2,28 2,22 2,13 2,05 1,93 1,80 — — 7,75
15X11МФ 2,16 — — 2,00 1,94 1,84 1,66 — — 7,85
20Х12ВНМФШ (ЭП428) 2,28 — 2,15 2,09 1,95 1,88 1,73 1,55 — 7,85
2Х12ВМБФР (ЭИ993) 2,05 1,90 1,90 1,85 1,79 1,79 1,60 — — 7,85
31Х19Н9МВБТ (ЭИ572) 2,16 2,10 2,04 1,99 1,93 1,82 1,63 — — 7,96
15Х1М1Ф 2,15 2,12 2,08 2,02 1,94 1,83 1,70 1,53 — 7,80
20Х1М1Ф1ТР (ЭП182^ 2,02 1,98 1,93 $85 1,77 1,69 1,60 1,50 — 7,85
Х18Н10Т 2,04 — — 1,86 1,80 1,73 1,63 1,53 — 7,90
ХН78Т (ЭИ435) 2,20 2,15 2,10 2,04 2,00 1,90 1,80 — 8,00
ЭИ607, ЭИ607А 2,23 — 2,10 2,05 2,00 1,97 1,87 1,80 1,65 8,00
ХН65В9М4ЮТР (ЭИ893) 2,22 — — — — — 1,85 1,76 8,52
ХН55ВМТФКЮР (ЭИ929ВД) 2,08 — 1,95 1,86 1,80 1,70 1,60 — — 8,43
38ХНЗМФА 1,15 1,04 0,90 0,90 0,85 0,80 0,75 7,83
187
VIII.7. ПЕРСПЕКТИВНЫЕ
ЖАРОПРОЧНЫЕ МАТЕРИАЛЫ
Прй том уровне рабочих напряжений, которые имеют
место в рабочих лопатках действующих и перспективных
газовых турбин, даже наиболее жаропрочные сложнолеги-
рованные сплавы могут использоваться в стационарном
газотурбостроении только до температуры металла не выше
800—830° С. Некоторое повышение жаропрочности может
быть достигнуто дальнейшим увеличением содержания
легирующих элементов и, в первую очередь, А1 и Ti, при-
Таблица VI! 1.21. Химический состав и жаропрочность некоторых сплавов
на кобальтовой основе (США)
Сплав Содержание элемента, % Длительная проч 1 ность, кгс/мм, за ! 103 ч при 816° С
С Сг ' Ni W Та В 7г
Mar М509 0,60 21 10 7 3,5 0,01 0,50 23
Маг-М302 0,85 21 — 10 9,0 0,005 0,15 21
FSX-414 - 0,25 29 10 7 0,012 12
Х45 0,25 25 10 7 0,010 ___ 11
Haynes-1 88 0,88 22 14 — —• — 6
чем их сумма должна превышать 7—8%. Таким сплавом,
в частности, является отечественный сплав на никель-
кобальтовой основе ЭП220ВД, содержащий 3,9—4,8% А1,
2,2—2,9%Ti, 14,0—16,0% Со, 9,0—12,0% Сг. Его длитель-
ная прочность при 800° С составляет 28 кгс/мм2 за 10 000 ч
и 26 кгс/мм2 за 20 000 ч против 25 кгс/мм2 и 24 кгс/мм2
соответственно для сплава ЭИ929ВД.
Однако усложнение состава сплавов такого типа вызы-
вает существенные затруднения при горячей пластической
деформации в процессе формообразования заготовок,
в связи с чем основным направлением дальнейшего разви-
тия жаропрочных сплавов является разработка и освоение
литейных сплавов в качестве материала для сопловых ло-
паток, эксплуатируемых при высокой температуре. Специ-
фические особенности строения литейных сложнолегиро-
ванных сплавов обусловливают заметное снижение пла-
стичности и вязкости металла. Эти свойства повышаются
при отливке деталей с направленной кристаллизацией,
позволяющей применять литейные сплавы для высокона-
пряженных рабочих лопаток с длительным ресурсом.
Другой путь повышения пластичности литейных спла-
вов — дополнение основного легирующего состава ред-
кими элементами —‘ итрием (Y), рением (Re), гафнием (HI),
лантаном (La), обеспечивающими также жаростойкость
сплавов. Сплавы с повышенным содержанием гафния (1,3—
1,5%) образуют особую группу недавно разработанных
в США литейных сплавов, с успехом применяемых для
лопаток и других деталей газовых турбин благодаря повы-
шенной пластичности, выделяющей их среди лопаточных
материалов с такой же высокой степенью легирования.
В отечественной металлургии также применяются меры по
расширенному применению редких элементов в жаропроч-
ных сплавах.
Известно, что сопротивление высокотемпературной
коррозии, при котором отпадает необходимость в приме-
нении защитных жаростойких покрытий, достигается лишь
при содержании хрома 20—22%; это приобретает особое
значение при использовании тяжелых жидких топлив или
газа с повышенным содержанием серы.
Перспективными сплавами с повышенным содержа-
нием хрома, в которых не образуются охрупчивающие
фазы, являются сплавы на кобальтовой основе, имеющие
существенное преимущество по жаростойкости перед
сплавами на никелевой или никель-кобальтовой основе.
Сплавы на кобальтовой основе отличаются высокой ста-
бильностью структуры в эксплуатационных условиях и
служат хорошим материалом для статорных высокотемпе-
ратурных деталей газовых турбин с умеренными рабочими
напряжениями.
Природа упрочнения кобальтовых сплавов принци-
пиально отличается от сплавов на никелевой основе, так как
в них присутствует значительное количество карбидооб-
разующих элементов, в первую
очередь вольфрама. Жаропроч-
ность в данном случае опреде-
ляется преимущественно при-
сутствием карбидных фаз. В свя-
зи с этим содержание углерода
в литейных сплавах составляет
0,25— 1,00%. Деформируемые
кобальтовые сплавы со смешан-
ным карбидным и интерметал -
лидным упрочнением содержат
0,05—0,20% углерода.
Большинство сплавов на
кобальтовой основе содержат
10—20% никеля, что увеличи-
вает их прочность и жаропроч-
ность (табл. VIII.21).
Значительное повышение
жаропрочности сплавов может
быть достигнуто за счет так на-
зываемого механического легирования. Такие материалы
получаются путем прессования или смеси порошков особо
чистого (карбонильного) никеля и окислов некоторых
металлов, или порошков указанных окислов совместно
с порошками сплавов никеля с хромом, титаном, цирко-
Рис. VIII.9. Предел длительной прочности
дисперсноупрочненных сплавов и некоторых
обычных сплавов на никелевой и никель-кобаль-
товой основе за 103 ч:
1 — ВДУ-1, пруток; 2 — ВДУ-2, пруток; 3 — ЖС6К;
4 — ЭП220ВД; 5 — ВДУ-1, лист; 6 — ЭИ868, лист
нием, бором. После прессования материал подвергается
холодной или горячей деформации и высокотемператур-
ному отжигу.
В некоторых отраслях отечественной промышленности
находят применение сплавы ТД-никель (Ni + 2,0% ThO2),
ТД-нихром (Ni -% 20% Сг -% 2% ThO2), ВДУ-1 (Ni +
+ 2,5% ThO2), ВДУ-2 (Ni + 3% НЮ2). Замечательным
свойством этих материалов является отсутствие диффу-
зионного взаимодействия между основой сплава и упроч-
няющими материал тончайшими частицами окислов, тормо-
зящими процессы деформации под воздействием рабочих
напряжений. Сравнительные характеристики жаропроч-
ности сплавов с механическим упрочнением (дисперсно-
упрочненных) и обычных сплавов на никель-кобальтовой
основе приведены на рис. VIII.9. Как и для обычных
сплавов, жаропрочность сплавов с механическим легиро-
188
ванием повышается с усложнением их состава. Но, в отли-
чие от современных наиболее жаропрочных сплавов, содер-
жащих 10—13 легирующих элементов, новые материалы
содержат 2—6 ингредиентов. Сложное легирование обыч-
ных сплавов понижает температуру их плавления, и это
само по себе ограничивает рабочую температуру металла.
Применение легированных порошков позволяет полу-
чить материал с повышенными жаропрочностью и жаро-
стойкостью. Примером служит разработанный в США сплав
IN-853, изготавливаемый из тонких порошков карбониль-
ного никеля, металлического хрома, лигатур (Ni—Al—Ti;
Ni—Zr, Ni—В), окислов Y2O3, A12O3. Состав сплава
IN-853 (%): C —0,06; Cr — 19,7; Al — 0,88; Ti — 2,33;
B—0,07; Zr — 0,07; Y2O3 — 1,2; A1,O3 — 1,12; Ni—
основа [123].
Диспербноупрочненные сплавы имеют хорошие техно-
логические свойства, являются перспективным материалом
для листовых деталей газопламенного тракта, внутренней
облицовки корпусов ГТУ, направляющего аппарата и для
других высокотемпературных деталей.
Перспективной разновидностью материалов с механи-
ческим легированием являются волокнистые армирован-
ные композиционные материалы на основе жаростойких и
жаропрочных сплавов, упрочненных волокнами тугоплав-
ких металлов, например вольфрама или его сплавов. Глав-
ное назначение волокон состоит в том, чтобы воспринимать
основную нагрузку, тогда как металлическая матрица
передает ее волокнам и распределяет нагрузку между
волокнами. Правильным сочетанием матричного материала
и материала волокон, рациональным выбором их диаметра,
объемной доли и распределения в матрице получают ком-
позиционный материал с заданными свойствами по пла-
стичности, прочности, жаропрочности и жаростойкости.
В результате предел длительной прочности может быть
повышен по сравнению с аналогами из числа обычных
жаропрочных сплавов на 50—100%, а предельная рабочая
температура металла — на 100—200° С.
В табл. VIII.22 приведены сравнительные данные по
жаропрочности композиционного литейного сплава со
сложнолегированной матрицей на никель-кобальтовой
основе, содержащего 27% (по объему) нитей из вольфрама
с окисью тория (1—1,2%), и сплавов ЭИ929ВД и ЖС6К.
Таблица VIII.22. Сравнительные данные
по жаропрочности армированного материала
и обычных высокожаропрочных сплавов
при 900° С
Материал Предел длительной прочности, кгс/мм2, за время, ч
1000 5000
Композиционный литейный 30 25
сплав на основе ХН60КВМТБЮ (ЭП539ЛМ) ХН55ВМТФКЮГ (ЭИ929ВД) 12 8
ХН65КМВЮТ (ЖС6К) 17 13
Волокнистые композиционные сплавы могут изготав-
ливаться способом точного литья с заливкой сеток из ар-
мирующих волокон или в виде листовых заготовок из пере-
межающихся слоев тонколистового матричного сплава и
сеток из упрочняющих волокон, соединенных контактной
сваркой.
В последние годы некоторые зарубежные фирмы ведут
работы по созданию керамических деталей для наиболее
напряженных узлов транспортных и энергетических вы-
сокотемпературных газовых турбин. В качестве основного
материала для таких изделий используются порошки ни-
трида кремния, карбида кремния, нитрида бора. Детали
изготавливаются способами реактивного спекания и горя-
чего прессования. Материал отличается высокой жаро-
прочностью и может эксплуатироваться при температуре
до 1370° С.
Важной проблемой в этой области материаловедения
является преодоление высокой склонности керамических
материалов к хрупким разрушениям [128].
VIII.8. НАПРЯЖЕНИЯ
В .ОСНОВНЫХ ДЕТАЛЯХ ГТУ
При проектировании деталей основных элементов
ГТУ их газодинамические и термодинамические расчеты
обязательно должны дополняться расчетами на прочность,
в результате которых определяются действующие в этих
деталях напряжения.
Сопоставление полученных значений напряжений с до-
пускаемыми дает возможность оценить величину получае-
мых запасов прочности.
Минимальный коэффициент общего запаса прочности
определяется условиями эксплуатации (т. е. характером
нагрузки, температурным состоянием, степенью корроди-
рования и механического износа, гарантийным сроком
службы), принятой конструкцией детали, стабильностью
применяемых материалов и др.
Как правило, детали газовых турбин рассчитывают
на статическую нагрузку с помощью методов, базирую-
щихся на теории упругости, и затем сравнивают получен-
ные значения максимальных или средних напряжений
с пределами текучести (о0,2) или прочности (ов), измерен-
ными при испытаниях стандартных образцов материала 1.
Для деталей, работающих при температуре более 350—
450° С, сравнение производят со значениями пределов дли-
тельной прочности (ОдТ) и ползучести (®gT).
В некоторых специальных случаях расчеты на проч-
ность проводят с использованием методов теории пластич-
ности (например, при определении несущей способности
детали).
Динамическая прочность детали обычно оценивается
путем сравнения расчетных или экспериментальных макси-
мальных динамических напряжений с пределом усталости
(выносливости) о.!, измеренным на стандартных образцах
(гладких и надрезанных).
Ниже приведены наиболее часто применяемые при кон-
струировании формулы для расчета статических напряже-
ний, возникающих в лопатках (направляющих и рабочих),
дисках и роторах газовых турбин и осевых компрессоров.
Выводы соответствующих формул и методы расчета на
прочность деталей других элементов ГТУ (корпусов тур-
боагрегатов, камер сгорания, теплообменной аппаратуры)
приводится в специальной литературе.
Напряжения в лопатках
Напряжения от центробежных сил, действующих
в произвольном сечении по высоте лопатки переменного
профиля, не имеющей бандажной полки, находят по фор-
муле (11.109).
В корневом сечении такой лопатки напряжения будут
Равны % (к) = £ра'р (к)> гДе <% (к) = Р.ХЮср/2-- напряже-
ния у корня лопатки постоянного профиля; =
= ф Ок)р, Ocp/IpL — коэффициент разгрузки, который
можно найти по" рис. 11.33.
Напряжения от центробежных сил при наличии бан-
дажной полки определяются с учетом возникающей при
этом дополнительной центробежной силы Cg. п =
1 Сами значения максимальных напряжений определяются
с учетом их возможной концентрации, обусловленной конструк-
тивными особенностями детали.
189
- ГНШ1.1Г-
= р«2Уб. r/б. п- гДе Уб. п и Гб. п—объем и средний ра-
диус бандажной полки.
Напряжения изгиба от воздействия потока газа на ра-
бочую лопатку, не имеющую бандажной полки, на произ-
вольном радиусе [83]
Оиз (г) = М + (VII 1.1)
где = Zmin и 7,^ = Jщак —• моменты инерции се-
чения лопатки относительно главных осей инерции § и ц
Рис. VIII.10. К расчету рабочей лопатки на
прочность: а — схема лопатки; б — корневое
сечение
профиля рабочей лопатки (рис. VIII. 10); Afg и ЛЦ — изги-
бающие моменты, действующие относительно указанных
осей:
М. = sm а — М„ cos а; Л1„ = М„ cos а 4-
g ч и 1| и 1
-t- ми sin а. (VIII.2)
Напряжения изгиба достигают максимума на входной
и выходной кромках рабочей лопатки в корневом сечении
(на уровне галтели — в точках А и С). По величине этих
напряжений и рассчитывается обычно размер хорды
(осевой ширины) рабочей лопатки у ее корня.
В предварительных - расчетах можно использовать
приближенную формулу
*из.к=^«М2П-в)’ (VII 1.3)
где Z — длина лопатки; ITg_g — момент сопротивления
корневого сечения относительно оси Рщ ~ G (ст ~~
— с2ч)/гл — окружное усилие, приходящееся на одну ло-
патку; гл — число лопаток в венце.
Если центры тяжести сечений рабочей лопатки нахо-
дятся не на одном радиусе, действующие на нее центро-
бежные силы вызывают не только напряжения растяже-
ния, но и напряжения изгиба оиз. са Вследствие этого сум-
марные напряжения растяжения и изгиба, возникающие
в рабочей лопатке, могут быть выражены в следующем
виде: о2 = <тр + стиз_ г -ф оиз с, где <тиз р — напряжения
изгиба от потока газа.
Сумма оиз. г 4~ Оиз. г на расчетной частоте вращения
может быть уменьшена или даже сведена к нулю за счет
введения соответствующего эксцентриситета (рис. VIII.10),
при котором Оиз. г и стиз.г будут иметь различные знаки1.
Поэтому при определении запаса прочности рабочих лопа-
ток в приближенных расчетах часто напряжения изгиба
не принимают во внимание.
В некоторых случаях суммарные напряжения опре-
деляют по формуле = °р + 2 сиз (1 + «), в которой
с помощью коэффициента а = 0,5=0,75 учитываются до-
полнительные динамические напряжения и наличие кон-
центраторов напряжений [113].
Напряжения изгиба в сопловых (направляющих) ло-
патках, возникающие из-за воздействия потока газа, в за-
висимости от конструктивной схемы заделки лопаток опре-
деляются по формулам'
а) при односторонней (консольной) жесткой заделке —
по формуле (VIII. 1);
б) при двусторонней заделке — тоже по формуле
(VIII. 1), но при этом осевую и окружную составляющие
изгибающего момента Ма и Ми в уравнении (VIII-2) сле-
дует принимать равными:
Ма (аг) = Ри1 (ггср — г А + Qu (I — г,);
i=i
п
(гг) = У 1 Pai (г1Ср %А Qa (Z Zt),
i=l
(VIII.4)
где г(—расстояние вдоль радиуса от заделки; Pu(- nPat—
окружная и осевая составляющие усилия от давления газа
на z-й участок; Qu и Qa — окружная и осевая составляющие
силы реакции на вторую опору лопатки.
Хвостовики рабочих лопаток работают в условиях
сложнонапряженного состояния, часто в области ползуче-
сти материала. Поэтому для наиболее распространенного
типа хвостовика (торцового елочного) запасы прочности
оцениваются по нескольким видам напряжений: на смятие
рабочей поверхности зуба, на срез зуба, на его изгиб и на
разрыв хвостовика в нескольких сечениях по его высоте.
Наиболее нагруженными обычно являются первая и
последняя пары зубьев и соответствующие поперечные се-
чения хвостовика. Запасы прочности по напряжениям рас-
1 При этом на режимах, при которых частота вращений
отличается от расчетной, могут возникнуть дополнительные
напряжения изгиба, обусловленные неуравновешенным изги^
бающим моментом от центробежной силы
190
тяжения в этих сечениях подсчитывают обычно по формуле
V<4/(VP)- (VIIL5>
где Ко 1,5-ь 1,8 — коэффициент, учитывающий концен-
трацию напряжений и дополнительные напряжения изгиба
в указанных сечениях К
Неравномерное распределение температур как по
радиусу, так и по поперечному сечению (профилю) лопатки
газовой турбины вызывает появление термических напря-
жений.
Для количественной оценки суммарных напряжений
неравномерно нагретой лопатки в зоне упругих деформаций
может быть использована формула [99]
o's = Е (е — ет) = Е (е — схАГ).
Здесь Е — модуль упругости; а — коэффициент линейного
расширения; АТ — местная разность температур между
соседними волокнами; ет — температурная деформация;
8 — полная деформация, при допущении гипотезы плоских
сечений
е (?, П) = е0 — + х.я-
где х|, — составляющие упругой кривизны оси ло-
патки; е0 — деформация в начале системы координат.
Для расчетов формулу для <т„ удобно представить
в виде [99]
I V + VT ЛД + ЛД, ЛДЧ-ЛД т\
= £ —ту-т--------11 ё + J П -- 8Т .
\ --ср/ '-cpj-|-| пр с ср-Д пр /
1 (VIII.6)
Здесь введены обозначения
Л1| = j EEiydf: = — J E'e'c/df-,
cp f cp I
где f — площадь сечения лопатки.
Если модуль упругости Е можно считать постоянным
по сечению лопатки f, уравнение (VIII.6) примет вид
/V + ЛД
—
ЛД4-ЛД ЛД-ЬЛД
। £_____®Г| — Ег
' h
(VIII.7)
В случаях, когда местные суммарные напряжения
превышают предел текучести или имеет место изменение
напряжений в лопатке во времени из-за ползучести, могут
быть использованы методы расчета, изложенные в ра-
боте [99 ].
Помимо определения запасов прочности по статическим
напряжениям для лопаток газовых турбин проверяют запас
усталостной прочности Ку = овын/<Тдин, где оЕЫн — предел
выносливости материала’лопатки с учетом концентрации
напряжений, температуры и асимметрии цикла нагруже-
ния [30]; <тдьн — максимальные динамические напряже-
ния в лопатке, которые определяются при испытаниях об-
разцов с надрезом. В справочниках обычно указывается
предел выносливости при симметричном цикле нагружения
образца (CTj).
1 Окончательная проверка замкового соединения произ-
водится обычно по данным его натурных испытаний
Напряжения в дисках и роторах
В дисках, применяемых для современных конструк-
ций газовых турбин и осевых компрессоров, осевые раз-
меры по сравнению с радиальными обычно относительно
невелики, что позволяет проводить расчет возникающих
в них напряжений на основании теории тонких дисков,
в которых напряжения можно принимать равномерно рас-
пределенными по толщине.
В общем случае (произвольный профиль в меридио-
нальном сечении) диск разбивается на п участков постоян-
ной толщины, причем в середине каждого участка его ши-
Рис. VIII.11. К расчету диска на прочность
рина уп равна толщине профиля диска в этом месте
(рис. VIII.И).
Для каждого участка возникающие во вращающемся
диске радиальные (ог) и тангенциальные (оу) напряжения
могут быть определены из системы уравнений [30 ]:
ог = агог: afar, — а.С — ааТ; 1
0 (VIII 8)
^ = Mri + ₽za/t-₽cC-₽eT. J
Здесь С и Т имеют размерность напряжения; а и |3 — без-
размерные коэффициенты, значения которых в зависимости
рт отношения радиусов m = хп!хй можно найти из таблиц
или графиков в работе [30].
Для равномерно нагретого диска Т = 0. В этом случае
при последовательном переходе от одного участка к сосед-
нему на любом радиусе остаются справедливыми зависи-
мости:
®гп — АпО/1 Bn'i °tn — MnVtl Nnn ]
, , , , (VIII.9)
<!rn=An<!tl-Bn’ atn = Mnaa-Nn< J
где
°rn = ar (п-1)Уп—11Уп’
° tn = °t (n—1) + в (Уп—ifan ~~ 0 ar (n—!)•
Коэффициенты определяются последовательным рас-
чегрм по формулам [30]:
Ап = А'п_х: В = -^=1 ;
п уп п-l п Уп п 1,
^„ = m;_i + p(-^--i) л;_1;
\ Уп /
Nn = Nn-l + I1 ~ ВП-1’
x yn /
1ММГ.Э1
191
1
Ац arn^n + atn^n> ^rrfln “I- atnNn + acrfitii
M'n = $rnAn + $tnMn, N’n = trnBn + ₽/nV„ + ^n.
Для дисков без центрального отверстия (х0 = 0): Ах =
= 1; Вх = 0; Мх = 1; N± = 0.
На внутреннем радиусе диска, насаженного на вал:
Лх=0; В1=|<т,1|; Мх=1; АД = 0.
На внутреннем радиусе диска со свободным отвер-
стием' А1 = 0; Вх = 0; = 1; Vx = 0.
На внешнем радиусе диска (х = ха)
а -z ^Cl — А'а —В'
га - 2 л 2яхауа Аа t1 ^а’
где £Сг — сумма центробежных сил от профильной
части лопатки; о/, — напряжение в хвостовике и выступе
диска
071 “ (ага + (VIII 10)
Полученное значение <т/х следует подставить в си-
стему уравнений (VIII.8) для определения аг и о; на
внутреннем и внешнем радиусах каждого участка.
Напряжения на среднем радиусе каждого участка
определяются как средние арифметические значения
между <Ут (<У(п) и (f'rn (О/,,} соответственно.
При определении запасов прочности диска необхо-
димо учитывать возможность местного увеличения на-
пряжений из-за наличия различного рода концентраторов
(отверстий, пазов, щелей, выступов и т. д.).
При неравномерном распределении температуры диска
произвольного профиля в системе уравнений (VIII.8)
необходимо учитывать не только условие Т 0, но также
изменение Е, а и |1 в зависимости от температуры.
Порядок расчета диска остается таким же, как в пре-
дыдущем случае, но зависимости для otn и коэффициен-
тов Ап—Nn изменяются. Расчетные формулы для опре-
деления указанных величин можно найти в соответству-
ющей литературе [30, 83].
В’ некоторых случаях возникает необходимость опре-
деления напряжений изгиба в диске, возникающих как
из-за действия момента внешних сил, так и от неравно-
мерного распределения температуры по его ширине.
Методика таких расчетов приведена в литературе [99].
Для дисков турбин, работающих при высоких тем-
пературах (450—500° С), проводится также расчет напря-
жений с учетом пластичности и ползучести. Методика
этих расчетов изложена в работах [83, 99].
Все указанные расчеты напряжений в дисках в на-
стоящее время проводятся, как правило, с использова-
нием ЭВМ.
Расчет упругих напряжений, возникающих в расточке
цельнокованого ротора барабанного типа, применяемого
в некоторых конструкциях газовых турбин и осевых ком-
прессоров, может быть в первом приближении произ-
веден по формуле
071 = ри2 + (гг/6б) ога, (VIII И)
где г, — текущий радиус; 6g — толщина барабана.
Для цельнокованого ротора дискового типа, приме-
няемого в некоторых конструкциях газовых турбин ма-
лой и средней мощности, при t < ra (t — расстояние
между дисками, гн — наружный радиус вала) максималь-
ные упругие напряжения в расточке могут быть рассчи-
таны по методу, изложенному в работе [83].
При t > rtl расчет напряжений следует производить
по отдельным участкам, заменяя цельнокованый ротор
отдельными дисками со втулками эквивалентной длины
[83].
Расчет напряжений, возникающих в сварных роторах
газовых турбин, составленных из дисков произвольного
профиля, рекомендуется проводить по методу, изложен-
ному в работе [83].
Напряжения в статорных деталях газовых турбин
(корпуса, обоймы, фланцевые соединения), которые воз-
никают как из-за избыточного давления, так и из-за
неравномерного распределения температур (термические
напряжения), могут быть подсчитаны по соответствующим
формулам, приведенным в работах [83, 99].
Глава IX
КОНСТРУКЦИИ СОВРЕМЕННЫХ ГТУ
IX. 1. ТИПОВЫЕ КОНСТРУКТИВНЫЕ СХЕМЫ
7 Под конструктивной схемой ГТУ обычно понимают
характеристику взаимного расположения основных ее
элементов для данной тепловой схемы и принципиальное
конструктивное решение, с помощью которого это взаим-
ное расположение реализуется.
Даже при сравнительно ограниченном количестве
составных элементов в тепловой схеме ГТУ (таких, как
ступени сжатия, расширения, промежуточного охлаж-
дения и регенерации) число теоретически возможных
конструктивных схем оказывается весьма большим. Од-
нако анализ опыта отечественного и зарубежного газо-
турбостроения и результатов многочисленных технико-
экономических проработок позволяет рекомендовать ог-
раниченное количество типовых конструктивных схем
ГТУ, достаточно хорошо удовлетворяющих требованиям,
предъявляемым к агрегатам различного назначения.
В соответствии с международным стандартом ISO
рекомендуется использовать при проектировании следу-
ющие пять типовых конструктивных схем ГТУ.
Схема 1. Одновальная ГТУ простого цикла с возмож-
ной разбивкой компрессорной группы на две-три ступени
сжатия и включением соответственно одного-двух про-
межуточных охладителей (рис. IX. 1).
Схема 2. Одновальная ГТУ с регенерацией тепла ухо-
дящих газов (рис. IX.2).
Схема 3 (За—Зг). Двухвальная ГТУ с разрезным
валом, свободной силовой турбиной и устройством для
подготовки рабочего тела (газогенератором), обладающим
необходимым запасом избыточной тепловой энергии.
Газогенератор состоит из одного или нескольких комп-
рессоров для сжатия рабочего тела, устройства для его
подогрева и одной или нескольких турбин, используе-
мых для привода компрессоров. Поэтому в зависимости
от конструктивного выполнения газогенератора рассма-
триваемая схема ГТУ может иметь четыре разновидности
(рис. IX.3).
В схеме За (рис. IX.3, а) газогенератор выполняется
по простейшей конструктивной схеме, которая состоит
из компрессора, камеры сгорания и газовой турбины, при-
водящей во вращение компрессор.
В схеме 36 (рис. IX.3, б) рабочее тело подогре-
вается в специальном теплообменнике — нагревательном
устройстве (НУ) за счет передачи теплоты от внешнего
источника.
В схеме Зв (рис. IX.3, в) газогенератор кроме пере-
численных элементов включает регенератор, в котором
избыточная теплота уходящих из силовой турбины газов
используется для подогрева циклового воздуха, выходя-
щего из компрессора.
В схеме Зг (рис. IX.3, г) газогенератор выполняется
в виде двухвального турбокомпрессорного блока, в кото-
ром каждый из компрессоров приводится во вращение
самостоятельной турбиной.
Vg 13 Л. В. Арсеньев и др.
Схема 4. Двухвальная ГТУ с блокированной силовой
турбиной и свободным турбокомпрессорным валом
(рис. IX.4).
Разновидностью ее является схема, в которой ком-
прессор (КВД или КНД) разбивается на две ступени
сжатия с включением промежуточного охладителя и ре-
генератора.
Схема 5. Одновальный газотурбокомпрессор с исполь-
зованием энергетического потенциала отбираемого рабо-
Рис. IX. 1. ГТУ, типовая конструктив-
ная схема 1
чего тела (воздуха или горячего газа) для промышленных
или бытовых нужд (рис. IX.5).
Основой для выбора конструктивной схемы ГТУ
являются следующие требования технического задания,
выдаваемого заказчиком на изготовление установки:
Рис. IX.2. ГТУ, типовая конструктив-
ная схема 2
назначение установки; режимы эксплуатации; массо-
габаритные ограничения; маневренность; используемое
топливо.
Окончательно конструктивная схема выбирается по
результатам технико-экОномических расчетов, при которых
определяются суммарные годовые расчетные затраты
соответствующих вариантов с учетом необходимости обес-
печения требуемой эксплуатационной надежности и унифи-
кации создаваемой ГТУ с уже выпускающимися агрега-
тами.
При предварительном выборе конструктивной схемы
ГТУ можно руководствоваться следующими соображе-
ниями.
Для ГТУ, используемых в качестве энергетических
агрегатов для покрытия пиковых энергетических нагрузок,
193
Рис. IX 3. ГТУ, типовые конструктивные схе-
мы За—Зг
Рис. IX.4. ГТУ, типовая конструктивная
схема 4
Рис. IX.5. ГТУ, типовая конструктив-
ная схема 5
основополагающими требованиями являются хорошие
маневренные свойства, низкая стоимость установленного
киловатта при обеспечении высокой эксплуатационной
надежности. Поэтому для них наиболее предпочтитель-
ными являются схемы 1 или За.
Для ГТУ, используемых в качестве аварийного резерва,
т. е. когда число часов использования мало, но требуется
весьма высокая степень надежности при малых удельных
затратах на изготовление, монтаж и эксплуатацию, наи-
более целесообразными следует считать типовые конструк-
тивные схемы За и Зг, которые допускают использование
в качестве газогенератора авиационного ГТД.
Для стационарных ГТУ, работающих в базовом ре-
жиме, близком к номинальному, экономически оправдан-
ным является использование схем 2, Зв, 4.
Типовая схема 5 находит широкое применение в энер-
готехнологических ГТУ, используемых в химической,
нефтеперерабатывающей и металлургической отраслях
промышленности.
Транспортные ГТУ выполняются обычно по кон-
структивным схемам Зв и Зг, обеспечивающим хорошую
приспосабливаемость газотурбинного агрегата к условиям
внешней нагрузки и высокие его маневренные качества.
IX.2. ОБЩИЕ ВОПРОСЫ ПРОЕКТИРОВАНИЯ
В развитии конструкций газотурбинных установок
достаточно четко обозначаются два направления.
К первому из них могут быть отнесены конструкции
стационарных (промышленных) газовых турбин, форми- '
ровавшиеся в значительной мере под непосредственным
влиянием уже освоенных конструкций стационарных
паровых турбин, поскольку эти газовые турбины вначале
проектировались для аналогичных областей применения,
т. е. базовой или всережимной нагрузки, и изготавлива-
лись на тех же заводах, что и паровые турбины, т. е. в усло-
виях индивидуального или мелкосерийного производства.
В качестве примера можно привести стационарные
ГТУ, выпускавшиеся в 50—60-е годы зарубежными фир-
мами «Броун—Бовери», «Эшер—Висс» (Швейцария), «Ме-
трополитен-Виккерс» (Англия) и отечественными заводами
ЛМЗ (ГТ-12-3 и ГТ-25-700), НЗЛ (ГТ-700-12 и ГТ-700-4),
ХТГЗ (ГТУ-50). Для конструкции этих ГТУ были ха-
рактерны следующие основные признаки а) исполнение
каждого из элементов в отдельных корпусах с соединением
их внешними газовоздушными коммуникациями сравни-
тельно большой протяженности; б) установка корпусов
турбоагрегатов на отдельных опорах, наличие самостоя-
тельных корпусов подшипников; в) применение так назы-
ваемой подвальной компоновки элементов ГТУ с распо-
ложением турбоагрегатов на «втором этаже» на массивном
фундаменте; г) установка ГТУ в специальном здании
стационарного типа.
Технологические процессы изготовления, сборки и
монтажа таких ГТУ практически не отличались от ана-
логичных процессов для ПТУ. Длительный опыт произ-
водства и эксплуатации таких ГТУ показал несостоя-
тельность применявшихся тогда принципов проектирования
и технологии производства с точки зрения обеспечения
их конкурентоспособности, поскольку при этом не смогли
быть реализованы основные преимущества ГТУ.
По иному направлению шло развитие конструкций
авиационных и транспортных ГТУ, формировавшихся
под влиянием уже освоенного производства двигателей
внутреннего сгорания. Здесь, в частности, с самого на-
чала было характерным использование блочно-агрегат-
ного принципа проектирования, а также применение ряда
прогрессивных технологических процессов, характерных
для крупносерийного производства.
Использование принципа блочно-агрегатного или
блочного проектирования, как это будет показано ниже
194
на соответствующих примерах, позволило наилучшим
образом реализовать такие органически присущие ГТУ
преимущества по сравнению с другими типами двигателей,
как большая удельная мощность, хорошие маневренные
качества, высокая степень надежности, малые затраты на
ремонт и эксплуатацию, что имеет решающее значение для
таких областей применения, как воздушный, водный и
наземный транспорт. Именно этим обстоятельством и
объясняется неуклонное развитие указанного принципа
как на современном этапе, так и в дальнейшем.
Большие успехи, достигнутые в авиационном и
транспортном газотурбостроении, послужили мощным
побудительным толчком к пересмотру принципов проек-
тирования стационарных ГТУ со все более широким
использованием принципов блочного проектирования.
Успехи ряда таких ведущих зарубежных фирм, как
«Дженерал-Электрик» и «Вестингауз» (США), «Крафтунион-
верке» (ФРГ) и др., в области стационарного газотурбо-
строения за последние 10—12 лет объясняются широким
использованием технических достижений авиационного
газотурбостроения и в первую очередь принципа блоч-
ного проектирования
В настоящее время к реализации этого принципа в той
или иной степени перешли все зарубежные фирмы, выпу-
скающие стационарные газовые турбины, а также отече-
ственные производственные объединения, выпускающие
стационарные ГТУ
Принцип блочного проектирования ГТУ заключается
в разбивке всей установки на минимальное количество
конструктивно законченных узлов (элементов) в виде
легко поддающихся стыковке, осмотру и замене мон-
тажных блоков, вписывающихся в допустимые транспорт-
ные габариты, не превышающих допустимую грузоподъем-
ность транспортных и подъемных устройств, не подлежа-
щих разборке и не требующих подгонки, наладки и других
операций, сопутствующих обычно сборке и монтажу
агрегатов. К числу таких блоков относятся следующие.
1. Турбоагрегат, включающий в себя компрессорную
и газотурбинную группу, монтируется на общей фунда-
ментной раме, которая обычно одновременно используется
в качестве масляного бака. В указанный блок входят все
трубопроводы (коммуникации) для подачи масла, охлаж-
дающего воздуха, а также провода контрольной измери-
тельной аппаратуры. Иногда в него включаются всасыва-
ющий патрубок компрессора и выхлопной патрубок си-
ловой газовой турбины.
2. Камера сгорания, если она выполняется выносной,
например для работы на тяжелом жидком топливе. В боль-
шинстве случаев камера сгорания выполняется блочно-
секционной или кольцевой и включается в состав блока
турбоагрегатов
3. Пусковое устройство совместно с зубчатой ускори-
тельной передачей и соединительной муфтой монтируются
обычно на общей с блоком турбоагрегатов фундаментной
раме.
4. Блок полезной нагрузки (электрогенератор, цен-
тробежный нагнетатель, насос и т. д), устанавливаемый
или на общей с турбокомпрессорным блоком, или на
отдельной фундаментной раме.
5. Воздухоочистительное устройство, объединяемое
обычно с устройствами для шумоглушения на всасывании
и охлаждения или подогрева засасываемого в компрессор
воздуха.
6. Блок выхлопа из газовой турбины, объединяемый
с устройством для шумоглушения, а иногда с регенера-
тором.
7. Системы автоматического управления агрегатом
(САУ).
8. Наружная обшивка.
9. Вспомогательное оборудование масло- и воздухо-
охладители, топливные и масляные фильтры предвари-
тельной очистки и т. д.
% 13*
Число используемых блоков зависит от ряда факто-
ров, основными из которых являются единичная мощность
агрегата, конструктивная схема ГТУ, используемый вид
топлива, объем выпуска ГТУ, имеющиеся транспортные
и грузоподъемные средства.
В ГТУ малой и средней мощности в единый блок
включаются все перечисленные блоки, монтируемые на
общей раме.
В ГТУ большой мощности, особенно в стационарных
базовых агрегатах, выполненных по сложным конструк-
тивным схемам (например, по схеме 4), количество при-
меняемых блоков является наибольшим. В них часто
используют так называемый блочно-пакетный принцип.
В ГТУ большой мощности, предназначенных для работы
в качестве аварийного резерва, в отдельные блоки выде-
ляются обычно газогенераторы (часто для этой цели
используют авиационные ГТД).
ГТУ, спроектированные по блочному принципу,
обычно имеют бесподвальную компоновку с расположе-
нием рамы на массивной железобетонной плите или на
сборном каркасе.
Важным требованием, сопутствующим принципу блоч-
ного проектирования, является полная взаимозаменяе-
мость отдельных блоков при ремонтах, чему способствует
использование в них большого количества унифициро-
ванных и стандартизированных узлов и деталей. Каждый
из блоков укомплектовывается соответствующим вспомо-
гательным оборудованием и контрольно-измерительной
аппаратурой с коммуникациями, имеющими выводы и
соединительные узлы (фланцы, ниппельные соединения,
клеммники и т. Д.).
Блочный принцип проектирования предусматривает
использование специальных методов сборки, испытаний,
транспортировки, монтажа, обслуживания и ремонта
ГТУ, благодаря чему при сборке блоков сводится к ми-
нимуму количество рабочих операций и исключаются
обычно применяемые виды слесарной или механической
обработки.
Отдельные блоки и всю ГТУ под полной нагрузкой
обычно испытывают на заводе, причем все выявленные
при этом неполадки и дефекты устраняют на месте. На
место монтажа блоки транспортируются в полностью
собранном виде на раме или в жестком каркасе по желез-
ной дороге, шоссе или водным путем с использованием
большегрузных платформ, трейлеров, контейнеров и т. д.
Установка блоков на транспортные средства и монтаж
их на монтажной площадке производятся с помощью спе-
циальных приспособлений (тележек, подъемных кранов,
лебедок и т. п.). Сам монтаж блочной ГТУ сводится к ми-
нимально необходимому количеству операций, связанных
с установкой фундаментной рамы на фундамент, подсоеди-
нением коммуникаций подачи смазочного масла, топлива,
всасывания, выхлопа из ГТУ, питания собственных нужд,
полезной нагрузки и т. д. Высокая степень автоматизации,
которая обеспечивается при блочном исполнении ГТУ,
сводит их повседневное обслуживание к периодическим
визуальным осмотрам небольшим количеством персонала.
Ремонт блочных ГТУ сводится обычно к профилакти-
ческим операциям с последующей заменой соответствующих
узлов, доставляемых со склада. Консервация оборудова-
ния для таких ГТУ имеет свою специфику, заключающуюся
в применении специальных антикоррозионных покрытий,
не требующих удаления перед включением ГТУ в работу,
герметизации I внутренних полостей транспортируемых
блоков с заполнением их инертной средой (например,
азотом и т. д.).
Все это позволяет существенно повысить показатели
надежности и экономичности блочных ГТУ, а также
улучшить их общие технико-экономические показатели.
Вместе с тем проектирование ГТУ по блочному прин-
ципу предъявляет важные требования к производству
переход на новые технологические процессы изготовления,
195
комплектации, сборки, контроля, расширение коопери-
рования и т. д.
Степень реализации рассмотренного принципа блоч-
ного проектирования в современных ГТУ разлйчного
назначения рассматривается ниже на примере конструк-
ций отдельных газотурбинных агрегатов, выпускаемых
как зарубежными, так и отечественными заводами.
IX.3. конструкции
ОТДЕЛЬНЫХ ТИПОВ ГТУ
Энергетические ГТУ
Установки этого типа применяются преимущественно
в качестве агрегатов для покрытия пиковых нагрузок
и аварийного резерва для собственных нужд крупных
энергосистем, т. е. работа их происходит с частыми пу-
сками и остановами (до 500—1000 пусков в год) при отно-
сительно малом числе часов использования в течение года
(от 100 до 1500 ч/год). Диапазон единичных мощностей
таких ГТУ составляет от 1000 кВт до 100 тыс. кВт.
нагрузки и предназначены в основном для отпуска теп-
лоты и обеспечения технологического процесса сжатым
воздухом.
Ниже приведено описание конструкций некоторых,
наиболее типичных образцов энергетических ГТУ, выпу-
скаемых в настоящее время (или намечаемых к выпуску)
как отечественными заводами, так и ведущими зарубеж-
ными фирмами, их параметры даны в табл. IX. 1.
( ГТУ фирмы «Зульцер» (Швейцария) (рис. IX.6).
Эта ГТУ (модель 1) [127] выполнена по схеме 1 или 2,
с редуктором. Корпус осевого компрессора имеет гори-
зонтальный разъем. Воздух подводится к компрессору
снизу через входной односторонний патрубок с последую-
щим его поворотом на 90°. Корпус выходного диффузора
компрессора состоит из двух частей, причем одна из них
имеет вертикальный фланец, которым она связана с кор-
пусом компрессора, и кольцевой выступ для установки
промежуточного лабиринтного уплотнения.
К передней части корпуса компрессора с помощью
вертикального фланца присоединена входная часть, вы-
полненная заодно с нижней половиной корпуса переднего
Рис. IX.6. Продольный разрез ГТУ фирмы «Зульцер»
Учитывая, что решающими требованиями здесь яв-
ляются хорошая маневренность, относительно малая
стоимость установленного киловатта мощности, высокая
надежность и низкие эксплуатационные расходы, такие
ГТУ проектируют в большинстве случаев по относительно
простым схемам (схемы 1 и За).
ГТУ для привода электрогенератора находят также
применение в качестве энергоустановок вспомогательного
назначения, обеспечивающих потребность в электроэнер-
гии для каких-либо изолированных объектов (например,
морских судов), а также в качестве энергоагрегатов пере-
движных установок. Для этих ГТУ характерна работа
в диапазоне нагрузок 30—110% от номинальной при
относительно большом числе часов использования, с ча-
стыми пусками, остановами и изменением нагрузки.
Единичные мощности таких ГТУ составляют от несколь-
ких десятков киловатт до 5—10 тыс. кВт. Эти установки вы-
полняются как по схемам 1, За, Зг, так и по схемам 2 и Зв.
Быстрое развитие атомных энергетических установок,
в том числе с высокотемпературными реакторами, охлаж-
даемыми гелием, открывает перспективу применения
в них одноконтурных ГТУ, работающих по замкнутому
циклу. Эти установки проектируются, как правило, по
схеме 2, одновальными, с промежуточным охлаждением
и регенерацией.
Специфическую группу энергетических ГТУ состав-
ляют установки, работающие в технологических схемах
химических, нефтеперерабатывающих, металлургических
и других комбинатов (энерготехнологические). Они вы-
полняются обычно по схеме 5, работают в базовом режиме
196
подшипника ротора турбокомпрессорной группы.
Передний подшипник выполнен опорно-упорным. Это
значительно упрощает масляные коммуникации, умень-
шает габариты конструкции и облегчает условия работы
турбокомпрессорного вала. Масло в подшипник подается
через нижнюю опорную подушку. Слив масла осуще-
ствляется через отверстия в верхней половине корпуса.
Верхний слив масла предусмотрен для обеспечения нали-
чия масла в опорно-упорном подшипнике даже при отсут-
ствии подачи его в случае аварии в системе смазки. На пути
сливного масла установлен термодатчик, позволяющий
регистрировать уровень средней температуры масла
в подшипнике.
Выхлопная часть корпуса компрессора имеет два
патрубка для соединения с фланцами выносных камер
сгорания, расположенных вертикально.
Направляющие аппараты компрессора сварные, вы-
полнены в виде колец, имеющих горизонтальный разъем,
и установлены в кольцевых расточках промежуточного
элемента статора — обоймы. Постановка обойм несколько
увеличивает радиальные размеры корпуса, но, несмотря
на это, их применение позволяет значительно упростить
конфигурацию корпуса и произвести унификацию корпу-
сов различных компрессоров. , 1
Корпус турбины выполнен двустенным." При такой
конструкции внешняя его часть воспринимает довольно
низкую температуру, но полный перепад давлений, а вну-
тренняя — полную температуру рабочего процесса, но
не воспринимает перепада давлений. Это позволило вну-
треннюю часть корпуса изготовить тонкостенной. Для
предохранения силовой части корпуса от воздействия
высокой температуры при всех режимах работы установки
предусмотрены его воздушное охлаждение и внутренняя
тепловая изоляция.
Применение двустенного корпуса и его охлаждения
несколько усложняет конструкцию турбины, но вместе
с тем обеспечивает фиксацию размеров и формы корпуса.
Кроме того, благодаря охлаждению появилась возмож-
ность использовать для изготовления внешней части кор-
пуса менее дефицитный, а следовательно, и более дешевый
материал.
Силовая часть корпуса турбины имеет горизонталь-
ный разъем с фланцами и два кольцевых выступа для уста-
новки обоймы сопловых аппаратов.
Подвод газа к турбине осуществляется через два
патрубка с фланцами (они расположены в нижней поло-
вине корпуса), к которым присоединены корпуса камер
сгорания.
Отрицательной особенностью такой организации под-
вода газа является неравномерность параметров газа перед
турбиной. Как известно, в газовых турбинах требования
к равномерности подвода рабочего тела особенно жестки,
так как лопаточный аппарат первой ступени, определяю-
щий, как правило, работоспособность всей ГТУ, является
обычно наиболее напряженным элементом установки,
и поэтому все возможные возмущения со стороны подвода
газа стараются исключить. Применение же рассматривае-
мой конструкции подводящих патрубков оправдывается
улучшением условий работы заднего подшипника и облег-
чением доступа к подшипнику и корпусу турбины.
К заднему вертикальному фланцу корпуса турбины
крепится развитый выходной кольцевой диффузор. Вну-
тренний обтекатель этого диффузора с помощью четырех
ребер связан с внешней его обечайкой.
В передней части корпуса турбины установлена ниж-
няя половина корпуса заднего опорного подшипника
ротора. На торцах подшипника стоят маслозащигные
уплотнения, предохраняющие от растекания масла по
валу. Перед уплотнениями в нижнеи части подшипника
сделаны дренажные отверстия, обеспечивающие беспре-
пятственное удаление масла в картер.
Ротор турбокомпрессорной группы составной. Перед-
няя его часть, выполненная в виде барабана, служит для
установки рабочих лопаток компрессора, имеющих зубча-
тые хвостовики. При наборе на барабан лопатки встав-
ляются в замковые пазы и по зубчатым проточкам пере-
мещаются вдоль окружности ротора. После заводки всех
лопаток полость замкового паза заполняется замковой
вставкой, которая фиксируется двусторонним клином.
Последний зачеканивается винтом. v
Ротор газовой турбины консольного типа, он состоит
из трех дисков, соединенных с помощью центральной
стяжки со средней частью турбокомпрессорного ротора.
Центральный стяжной болт, изготовленный из высоко-
легированной стали, воспринимает значительные усилия
вследствие сильного предварительного его натяга. Под
гайку центрального болта введены пружинные элементы,
предотвращающие ослабление затяжки дисков в процессе
эксплуатации.
Передача крутящего момента от дисков производится
торцовыми треугольными шлицами — соединениями типа
«Хирт», в той или иной степени допускающими независи-
мость радиального положения сопрягаемых дисков.
Рабочие лопатки снабжены хвостовиками елочного
типа, заводка в профильные пазы дисков — торцовая.
Все лопатки застопорены во избежание их смещения
в осевом направлении. Профильная часть лопаток в верх-
нем сечении утонена, для того чтобы при возможных
задеваниях вершины о корпус исключить серьезную
поломку.
Вспомогательные механизмы установлены на перед-
13 Л В Арсеньев и др.
ней вертикальной плите, присоединенной к корпусу ком-
прессора.
Передача полезной мощности осуществляется от ро-
тора компрессора через пустотелый промежуточный вал
с помощью зубчатого соединения.
ГТУ ЕМ-27, фирма «Инглиш-Электрик» (Англия)
(рис. IX.7). Выполняется в двух модификациях: по схе-
мам За и Зв [55].
Компрессор комбинированный, имеет шесть осевых
и одну (последнюю) центробежную ступень. Входной
патрубок выполнен с осевым входом и имеет обтекатель,
связанный с корпусом четырьмя ребрами.
Направляющие лопатки осевого компрессора фикси-
руются своими хвостовиками в кольцевых пазах внутрен-
него корпуса (обоймы), имеющего горизонтальный разъем
с фланцевым соединением и устанавливаемого в расточке
наружного корпуса компрессора.
В качестве пускового устройства используется элек-
тродвигатель переменного или постоянного тока, питае-
мый от аккумуляторных батарей. За центробежным коле-
сом компрессора установлен радиально-осевой диффузор,
подающий воздух в сборную кольцевую камеру, обра-
зованную наружным и внутренним корпусами. Из этой
камеры воздух подается через общий выходной патрубок
и две наклонные трубы, снабженные гибкими компенси-
рующими элементами (сильфонами), к двум вертикальным
выносным камерам сгорания углового типа Камеры
сгорания предназначены для работы на жидком и газо-
образном топливе с автоматическим переключением с одного
вида топлива на другой во время работы агрегата.
Продукты сгорания выходят из камер в сборный
кольцевой тонкостенный коллектор, откуда они поступают
через конфузор к сегментам сопловых лопаток первой
ступени ТВД. К корпусу турбины присоединен выход-
ной осевой диффузор, к которому с помощью четырех
ребер прикреплен корпус подшипников ротора силовой
турбины. В зависимости от применяемой схемы (За или
Зв) из выхлопного патрубка продукты сгорания или вы-
брасываются в атмосферу, или предварительно проходят
через пластинчатый регенератор, смонтированный не-
посредственно на фланце выхлопного патрубка.
Корпуса компрессора и газовой турбины выполнены
без горизонтального разъема и между собой соединяются
с помощью вертикального фланца. Корпус заднего опор-
ного подшипника турбокомпрессорного вала глубоко
утоплен во входную часть корпуса турбины.
Корпус турбины опирается на две боковые шарнирные
стойки, установленные на общей фундаментной раме,
одновременно являющейся маслобаком установки. Вход-
ной патрубок компрессора имеет одну центрально распо-
ложенную опору. Ротор ТВД изготовлен составным из
поковок, соединенных с помощью вертикального фланца
и внутреннего стяжного болта, через который также осу-
ществляется подача охлаждающего воздуха, отбираемого
за пятой ступенью компрессора к дискам ТВД и ТНД.
Передний торец и периферийная часть диска, а также
внутренний подшипник ТВД охлаждаются воздухом,
отбираемым за компрессором и подаваемым по трубам
в переднюю часть корпуса турбины.
Управление ГТУ полностью автоматизировано и мо-
жет осуществляться как со щита, расположенного в не-
посредственной близости от агрегата, так и дистанционно.
Ротор турбины низкого давления, так же как и ротор
турбины высокого давления, имеет консольно располо-
женные диски, соединенные с валом. Компрессорная и
силовая турбины имеют противоположные направления
вращения, что позволяет упростить конструкцию сопло-
вых лопаток третьего ряда и увеличить пропускную спо-
собность газовой турбины при сохранении основных
геометрических размеров. Наружные части силового
корпуса турбины защищены от воздействия горячих газов
197
о
00
Таблица IX. 1. Характеристики газотурбинных установок
Фирма, страна Модель 4 Назна- чение Энергетические характеристики Компрессорный вал Силовой вал Степень повышения да- вления Температура на выхо- де, °C Число камер сгорания Расход воздуха (газа), кг/с Масса, т
Номинальная мощность, МВт ; Расход топли- 1 , кг ва >, — ! кВт.ч Максимальная мощность, МВт Число ступеней компрессора Число ступеней турбины Начальная тем- пература, °C Число ступеней : компрессора Число ступеней турбины Частота враще- ния, об/мин
«Зульцер» (Швейца- рия) «Инглиш-Электрик» (Англия) «Броун—Бовери» (Швейцария) «Дженерал-Электрик» (США) ЛМЗ (СССР) «Крафтунионвсрке» (ФРГ) «Стал^-Лаваль» (Швеция—США) AEI (Англия) УТМЗ (СССР) НЗЛ (СССР) «Вестингауз» (США) «Ингерсол — Р анд» (США) ЛКЗ (СССР) «Пратт— Уиттни» (США) «Ровер» (Англия) 1 ЕМ-2 7 ИВ MS-7001 ГТ-100-750 V-94 FT-50 (GT-200) ГТН-6 гтк-ю-з CW-352 IP-240 ГТУ-20 ST-6 2S-150 Энерге- тическая То же » » » » » Привод- ная То же » » Судовая » Автомо- бильная 3,95 / 2,63 \а ' 2,37 7 39,5 60,0 99 91 70 24,1 6,0 10 39,8 32/7 24 4,8 1,1 2 0,11 2 /0,372У 'Ц291 7 0,232 0,271 0,292 0,265 0,261 0,314 0,351 0,296 0,214 0, 176 0,183 0,308 0,291 4,17 45 74,4 107 104 82 29,7 7,2 13 50,0 46,0 26 5,8 1,8 2 6ОС+ тЩБ 13 7-,- 10 17 И 11 17 16 12 ЗОС4 -г 1ЦБ 1ЦБ 2 3 1+1 3 3 1 1 2 2 1ЦС 850 870 967 10674 750 850 9104 9504 9104 760 780 1127 750 830 10 15 17 8 1о 6 3 2 3 4 2 2 2 1 1 2 2 1 1 7300 7000 3000 3000 3600 3000 3000 3000 3000 6100 4800 5000 5250 6000 4,55 4,8 7.5 9,5 26,5 10,0 9,8 6 4,6 9,3 8,4 11,5 9 7,2 3,75 473 490 "355 447 530 396 422 347 4 450 4 410 315 541 522 497 2 2 1 10 12-4-12 2 8 8 1 1 8 1 6 2 1 35,4 19 W 227 269 443 482 327 4 161 4 45,0 89,0 112 129 62 34,2 0,95 13,5 17,9 180 267 650 301 134 6 49 56,0 92 89 201 55 30,2 0,073
Примечание. Дробными числами обозначены: в числителе — данные без регенератора, в знаменателе — с регенератором.
1 Для жидкого топпива = 10 250 ккал/кг, для газа ~ 8900 ккал/м3.
2 В тыс. л. с
’ В кг/л с ч.
4 При пиковой нагрузке.
6 Включая электрогенератор.
экраном и воздушным охлаждением. Смазочное масло
к переднему опорному подшипнику компрессора подается
через переднее ребро обтекателя, слив также осуще-
ствляется через ребро.
Рис. IX.7. Продольный разрез ГТУ ЕМ-27
Описываемая ГТУ послужила прототипом для созда-
ния установок аналогичного назначения, но большей
полезной мощности (до 7000 кВт), типа ЕМ-85, в которых
было иейользовано большое количество принципиальных
конструктивных решений. К ним прежде всего следует
отнести обойму сопловых аппаратов газовой турбины с раз-
резными сегментами, роторную группу турбокомпрессор-
ного агрегата, основные элементы системы охлаждения
и т. д.
Однако в отличие от ГТУ ЕМ-27 компрессор ЕМ-87
выполнен чисто осевого типа, т. е. без концевой центро-
бежной ступени. Это позволило применить компоновку
с одиночной камерой сгорания противоточного типа,
которая монтируется непосредственно на корпусе турбо-
13:i
агрегата. Такое конструктивное решение позволило суще-
ственно улучшить основные технико-экономические пока-
затели ГТУ и повысить ее надежность, особенно при сжи-
гании тяжелых сортов жидкого топлива.
ГТУ 11В (13В), фирма «Броун—Бовери» (Швейцария)
(рис. IX.8). Выполнена по конструктивной схеме 1 [55].
В соответствии со сложившимися у фирмы тради-
циями корпус компрессора ГТУ выполнен одностенным,
т. е. без промежуточных обойм, направляющие лопатки
установлены непосредственно в кольцевые расточки.
Корпус компрессора жестко соединен с корпусом газовой
турбины вертикальным (технологическим) фланцем. В го-
ризонтальной плоскости оба корпуса имеют общий флан-
цевый разъем. К корпусу компрессора с помощью верти-
кального фланца присоединена входная часть, которая
также имеет горизонтальный разъем, причем нижняя ее
половина отлита заодно с корпусом передних опорного
и упорного подшипников ротора турбогруппы. К осе-
радиальному диффузору компрессора с помощью фланцев
прикреплен корпус промежуточного лабиринтного уплот-
нения, который также фиксирует кольцевой входной
коллектор газовой турбины.
Йз кольцевой камеры в корпусе турбины через ниж-
ний патрубок и соединительный воздухопровод сжатый
воздух подается в выносную вертикальную камеру сго-
рания, из которой газ по внутреннему газоходу поступает
в кольцевой сборный коллектор и через кольцевой кон-
фузор попадает к первому ряду сопловых лопаток газовой
турбины.
Сопловые лопатки первого ряда газбвой турбины
литые с внутренним воздушным охлаждением. Обойма
и хвостовики сопловых лопаток остальных рядов также
охлаждаются воздухом, отбираемым за компрессором.
Ротор турбокомпрессорной группы изготовлен из
отдельных дисков сваркой. С ротором электрогенератора
ротор турбогруппы соединен промежуточным валом. Пуск
ГТУ осуществляется от возбудителя электрогенератора.
/ 199
Рабочие лопатки осевого компрессора и турбины
снабжены зубчатыми хвостовиками для тангенциальной
заводки в кольцевые пазы с последующей установкой
замковых соединений.
нейшим развитием хорошо освоенной в крупносерийном
производстве и имеющей большую наработку в эксплуа-
тационных условиях ГТУ модели MS-5001, выпускаемой
фирмой главным образом в качестве пиковых агрегатов.
Рис 1X8 Продольный разрез ГТУ 11В
Рабочие лопатки газовой турбины имеют удлиненные
хвостовики, охлаждаемые воздухом, подаваемым к ротору
от последней ступени компрессора в кольцевой промежу-
ток между ротором и экраном и последовательно проходя-
щим через щелевые зазоры в хвостовых соединениях.
Корпус турбокомпрессорной группы опирается тремя 1»| ° о ° ° » » Го~
Может служить характерным примером реализации прин-
ципа блочного проектирования ГТУ.
Осевой компрессор выполнен с односторонним боковым
или верхним подводом воздуха в сборную кольцевую
парами боковых лап на вертикальные стойки, жестко ---------
связанные с общей сварной фундаментной рамой Из этих » \А.
шести опоо четьгое являются скользящими. и л.
Рис IX.9 Продольный
Оборудование ГТУ поставляется на место монтажа
отдельными блоками. Наиболее крупным из них является
блок турбогруппы, устанавливаемый на фундаментной
раме. ГТУ 11В (13В) предназначена для работы на газо-
образном и жидком топливе (включая некоторые сорта
мазутов и дистилляты)
ГТУ MS-7001, фирма «Дженерал-Электрик» (США)
(рис. IX.9). Выполнена по схеме 1 [127]. Является даль-
200
камеру, откуда он поступает во ходную часть корпуса,
где поток поворачивается на 90° троходит через конфу-
зор ко входному поворотному н вляющему аппарату.
Ротор компрессора образова исков, соединенных
12 стяжными болтами с передне задней концевыми
частями Крутящий момент от зад1 концевой части
передается последовательно от диска к диску с помощью
торцового шлицевого соединения. Пройдя зрехрядный
спрямляющий аппарат, сжатый воздух поступает через
осевой кольцевой диффузор во внутреннюю кольцевую
полость блока секционных камер сгорания, состоящую
из 10 пламенных труб.
Сопла первой ступени газовой турбины охлаждаются
воздухом, отбираемым из кольцевой камеры корпуса
блока КС (см. рис. 11.53, б). Рабочие лопатки первой
ступени охлаждаются продувкой воздуха через радиаль-
ные сквозные каналы, как это показано на рис. 11.55.
Сопловые и рабочие лопатки изготовлены из жаропрочных
сплавов методом точного литья, причем сопловые лопатки
отливаются отдельными сегментами по четыре штуки
в каждом.
Рабочие лопатки имеют удлиненную ножку для
уменьшения возможных термических напряжений. Верх-
ние концы рабочих лопаток второй и третьей ступеней
снабжены бандажными полками с уплотняющими гре-
бешками.
Ротор газовой турбины состоит из трех дисков, двух
концевых частей и двух промежуточных колец, соединяе-
мых между собой восемью стяжными болтами. Передняя
концевая часть ротора турбины, жестко связанная с зад-
ней концевой частью ротора компрессора при помощи
фланца, имеет шейку для установки в промежуточный
опорный подшипник.
На выходе из последней ступени турбины установлен
осевой диффузор, из которого поток продуктов сгорания
поступает в выхлопную кольцевую камеру с односторон-
ним выходом, не имеющую жесткой связи с корпусом.
Турбогруппа монтируется на общей,фундаментной
раме, служащей одновременно маслобаком. На этой же
раме монтируются пусковые устройства (обычно элек-
ментной рамой ГТУ связан каркас, на котором смонти-
рована внешняя звуко- и влагоизолирующая обшивка
(кожух). Отдельными блоками на место монтажа постав-
ляются камера фильтров с шумоглушением, выхлопная
шахта с дымовой трубой и шумоглушением, а также блок
САУ. Управление и контроль за работой ГТУ полностью
автоматизированы.
ГТУ ГТ-100-750, ЛМЗ (СССР). Выполнена по схеме 4,
В этой установке, несмотря на примененную усложненную
тепловую схему (с промежуточным охлаждением воздуха
и промежуточным подогревом), довольно широко исполь-
зован принцип блочного проектирования отдельных ее
элементов и узлов [55], например блока турбокомпрес-
сорной группы ГТУ, включающей в себя КВД, КСВД
и ТВД, и объединенной конструктивно общим силовым
корпусом с КСНД и ТНД (рис. IX. 10).
Силовой корпус турбоблока сварной, имеет общий
горизонтальный разъем и два технологических вертикаль-
ных разъема. Все эти разъемы имеют фланцевые соедине-
ния. К передней части корпуса с помощью вертикального
фланца присоединена входная часть из двух половин;
нижняя половина выполнена заодно с корпусом переднего
опорно-упорного подшипника и пускового устройства
(высокооборотная паровая турбина), соединенного с по-
мощью гидравлической расцепной муфты через зубчатую
передачу с ротором компрессоров высокого давления.
Направляющие лопатки КВД, объединенные с по-
мощью сварки в направляющие аппараты (из двух половин
с горизонтальным разъемом), установлены в кольцевые
ПТ F-
------------------------------
разрез ГТУ MS 7001
тродвигатели постоянного или переменного тока), вспомо-
гательный масляный насос, маслоохладитель, масляные,
топливные фильтры и другое вспомогательное оборудо-
вание ГТУ.
Транспортировка ГТУ производится в сборе со всем
оборудованием, установленным на фундаментной раме,
но со снятыми всасывающей и выхлопной камерами.
Компоновка оборудования ГТУ бесподвальная. С фунда-
расточки обоймы, монтируемой своим гребнем в расточке
внутреннего выступа корпуса. Подобная двухстенная
конструкция, хотя и является более трудоемкой, удобна
при монтаже с точки зрения обеспечения требуемых ра-
диальных зазоров по проточной части КВД.
Через диагональный диффузор воздух поступает
в кольцевое пространство корпуса блока высокого давле
ния, в котором установлены 12 наклонно расположенных
201
QSS9
202
Mo_____ иЗОО
ные воздуховоды, подающие воз,
вертикальным камерам ы орания (
рассчитаны для работы на газообра
с переключением с одного на друго
На кольцевых внутренних реб
радиальных штифтов установлена
аппаратов компрессора, состоящая
ней из которых (по ходу воздуха)
осерадиальный диффузор с выходе
пламенных труб КСВД, объединенных общим сборным
кольцевым коллектором, откуда продукты сгорания попа
дают к сопловому аппарату первой ступени ТВД
Сопловые лопатки всех трех ступеней ТВД наби-
раются в кольцевые расточки сегментов, монтируемых,
в свою очередь, в обойму, состоящую из двух половин
и устанавливаемую своим гребнем в кольцевую расточку
выступа корпуса
Опорные подшипники роторов ТВД и ТНД установ
лены в общем корпусе блока, связанном с корпусом ТВД
вертикальным полуфланцем в нижней пловине и кольцр
вым выступом (зубом) в верхней половине Снаружи двух-
стенный корпус блока внутренних подшипников омы
вается газами высокой температуры (около 540° С) вы
ходящими из диагонального диффузора за ТВД во вну
треннюю полость корпуса блочно секционной КСНД,
которая состоит из 12 наклонно расположенных пламенных
труб имеющих выход в общий коллектор перед сопловым
аппаратом ТНД
ПодвоД и слив смазочного масла и подвод охлажда
ющего воздуха осуществляются через нижнее вертикаль
ное ребро В отличие от ТВД в ТНД сегменты с установ
ленными в них сопловыми лопатками подвешиваются
непосредственно на выступы корпуса турбины К заднему
вертикальному фланцу корпуса ТНД крепится выхлопной
патрубок с выходным диффузором и кольцевыми поворот
ными направляющими лопатками Двумя парами гори
зонтальных лап, расположенных соответственно в зоне
корпусов КСВД и КСНД, силовой корпус турбоагрегата
опирается на четыре вертикальные стойки, связанные
с фундаментом По одной паре горизонтальных лап
имеют входная и выходная части турбоблока, которыми
они также опираются на две пары вертикальных стоек
Фикспункт общего корпуса турбоагрегатов расположен
на передних лапах входной части
Ротор КВД цельнокованый, барабанного типа, с тан
генциальной заводкой рабочих лопаток Он соединен
вертикальным фланцем с промежуточной кольцевой встав-
кой, к I оторои с помощью 12 бол ов притягиваются три
диска ротора ТВД Рабочие лопатки закреплены в дисках
с помощью двухзубчиковых торцовых елочных хвосто
виков
Аналогичную конструкцию имеет ротор ТНД, со
стоящий из пяти дисков без центрального отверстия,
притягиваемых 12 болтами (стяжками) к цельнокованый
передней и задней концевым частям
Элементы ГТУ, подверженные воздействию высоких
температур (сегменты сопловых лопаток, хвостовые со
единения рабочих лопаток ТВД и ТНД, внутренний кор
пус блока внутренних подшипников, пламенные трубы
КСВД и КСНД и др ), охлаждаются воздухом, отбирае
мым за соответствующими ступенями КВД
Транспортировка оборудования к месту монтажа
ГТУ осуществляется отдельными блоками и узлами
Установка предназначена для работы на двух видах
топлива природном газе и жидком газотурбинном топ
ливе Управление ГТУ автоматизировано и может произво
диться как с местного щита, так и с центрального пульта
ГТУ V-94, фирма «Крафтунионверке» (ФРГ)
(рис IX И) Выполнена по схеме 1 [127]
Турбогруппа спроектирована по прямоточной схеме
и включает в себя 16 ступенчатый осевой компрессор и
4 ступенчатую газовую турбину
Входной патрубок компрессора выполнен кольцевым,
поток в нем поворачивается на 90°, воздух засасывается
из общей камеры (шахты)
К корпусу турбогруппы, имеющему постоянный
наружный диаметр по всей длине, с помощью вертикаль
ного фланца присоединена всасывающая камера компрес
сора и осевой диффузор турбины
Корпус lypOoipyniibi имсе1 два боковых отвода с вер
тикальными фланцами, к которым присоединены переход
ные воздуховоды, подающие воздух к двум выносным
вертикальным камерам сгорания (рис. IX. 12). Последние
рассчитаны для работы на газообразном и жидком топливе
с переключением с одного на другое во время работы ГТУ.
На кольцевых внутренних ребрах корпуса с помощью
радиальных штифтов установлена обойма направляющих
аппаратов компрессора, состоящая из трех частей, к послед-
ней из которых (по ходу воздуха) присоединен кольцевой
осерадиальный диффузор с выходом воздуха во внутрен-
радиальные уплотнения по отношению к кольцевым
поверхностям на выступах дисков газовой турбины.
Лопатки последнего (четвертого) ряда имеют бандажные
полки с радиальными уплотнениями.
Ротор турбогруппы двухопорный, составлен из от-
дельных дисков, стянутых общим центральным болтом
(стяжкой). Крутящий момент ротора передается с помощью
торцового шлицевого соединения. Сборка дискового
ротора производится в вертикальном положении с по-
Рис. IX. 12. Поперечный разрез ГТУ V-94
пюю кольцевую камеру. Передняя по ходу воздуха часть
обоймы компрессора отлита заодно с корпусом переднего
опорного и упорного подшипников.
На кольцевом выступе (ребре) корпуса установлена
обойма сопловых аппаратов газовой турбины. Продукты
сгорания к сопловому аппарату первой ступени турбины
подаются из кольцевого коллектора, к которому подходят
два боковых газохода от камер сгорания.
Корпус турбогруппы, обоймы направляющих аппа-
ратов компрессора и газовой турбины имеют общий гори-
зонтальный фланцевый разъем. Направляющие лопатки
компрессора установлены в кольцевые проточки обойм
и снабжены бандажными полками с радиальными уплот-
нениями.
Сопловые лопатки газовой турбины заведены своими
выступами в кольцевые проточки выступов обоймы и
имеют удлиненные полки, соединяющиеся последова-
тельно со смежным рядом лопаток. Нижние концы первых
трех рядов сопловых лопаток газовой турбины установ-
лены в полукольцевые коробчатые диафрагмы, имеющие
мощью специального приспособления, снабженного ги-
дравлическим прессом. Диски газовой турбины и хвосто-
вики рабочих лопаток охлаждаются продувкой воздуха
через щелевые зазоры в хвостовых соединениях. Этот
воздух подается индивидуально к каждой ступени через
расточку дисков в месте прохождения центральной стяжкц.
Корпус турбокомпрессорной группы имеет общую
сварную фундаментную раму, состоящую из соединенных
болтами трех отдельных частей и являющуюся одновре-
менно маслобаком установки. Каждая из камер сгорания
опирается на две пружинные вертикальные стойки, уста-
навливаемые непосредственно на фундамент. Сопловые
лопатки первого ряда газовой турбины охлаждаемые,
дефлекторного типа, изготавливаются точным литьем.
В последних модификациях V-94 предусмотрено охлажде-
ние воздухом рабочих лопаток первой ступени и сопловых
лопаток второго ряда газовой турбины, что позволяет
существенно повысить начальную температуру газа и
увеличить полезную мощность ГТУ соответственно до
103—110 МВт.
205
Рис. IX. 13. Продольный разрез ГТУ FT-50
Транспортировка ГТУ производится отдельными бло-
ками (корпус турбогруппы с ротором, всасывающая ка-
мера камеры сгорания, выходной диффузор, фундамент-
ная рама из трех частей и т. д.). Пуск ГТУ осуществляется
с помощью дизеля, соединенного с ротором турбоком-
прессора при помощи гидравлической муфты через
редуктор.
Все управление установкой полностью автоматизи-
ровано, в том числе предусмотрен автоматический переход
без остановки электрогенератора с режима выработки
электроэнергии на режим синхронного компенсатора
(с помощью специальной автоматически синхронизиру-
ющей муфты). ' "
ГТУ FT-50 ” (GT-200), фирма «Сталь-Лаваль»
(рис. IX. 13) (Швеция—США). Выполнена по схеме Зг.
Представляет особый интерес как энергетическая ГТУ
большой единичной мощности, спроектированная по отно-
сительно сложной конструктивной схеме (как трехвальный
агрегат) в блочно-транспортабельном исполнении [122].
Силовой корпус ГТУ составлен из пяти отдельных
блоков (модулей), соединенных между собой с помощью
вертикальных фланцев без горизонтального разъема.
Роторы турбокомпрессорных групп низкого и высо-
кого давления составные дисковые. Между дисками ком-
прессора установлены промежуточные кольца. Диски
и кольца стягиваются между собой болтами. Сборка
агрегата производится в вертикальном положении после-
довательной установкой дисков и направляющих (сопло-
вых) аппаратов компрессоров и турбин. Из семи опорных
подшипников агрегата пять расположены во внутренних
корпусах, соединенных с внешним корпусом радиальными
ребрами, через которые также подводится и сливается
смазочное масло из подшипников.
Сопловые и рабочие лопатки первой ступени турбины,
корпус газовых турбин, пламенные трубы камер сгорания
и внутренние корпуса подшипников охлаждаются воз-
духом.
Демонтаж пламенных труб камеры сгорания, коллек-
тора газа на входе в первый ряд, сопловых и рабочих
лопаток ТВД и ТСД производится путем сдвига соответ-
ствующей части корпуса вдоль оси.
Характерной особенностью конструкции FT-50 яв-
ляется осевой вход и выход, а также установка развитых
диффузоров на выходе из КВД и силовой турбины. Каж-
дая из частей корпуса имеет по две боковые опоры: перед-
ние— жесткие, остальные — подвижные (шарнирные).
Шесть из этих опор используются при монтаже агрегата.
Турбогруппа монтируется и транспортируется в соб-
ранном виде на общей сварной раме.
Энергетические ГТУ с авиационными ГТД фирмы AEI
(Англия) и «Вортингтон» (США). Выполняются обычно
по схеме За. В качестве газогенераторной группы в них
используются авиационные ГТД — или в неизменном
виде, или конвертированные для работы в наземных
условиях. Помимо переделки конструкции некоторых
узлов и деталей такое конвертирование предусматривает
иногда перевод камер сгорания на сжигание газообразного
топлива.
Так как такие ГТУ в энергетике применяются для
покрытия острых кратковременных пиков электрической
нагрузки, а также в качестве аварийно-резервных агре-
гатов для собственных нужд, требования высокой на-
дежности установки являются решающими, поэтому в та-
ких ГТУ в качестве газогенератора применяются, как
правило, новые авиационные двигатели, имеющие доста-
точно высокий моторесурс в условиях работы на само-
лете (до 6000—8000 ч/год). Поскольку при использовании
авиационных ГТД в составе энергетических агрегатов
желательно иметь максимальный моторесурс, начальная
температура газов, а иногда и частота вращения турбо-
компрессорной группы снижаются по сравнению с расчет-
ными значениями.
3
206
Примерами рассматриваемых установок могут слу-
жить энергетические ГТУ, выпускаемые фирмами AEI
(Англия) и «Вортингтон» (США). Причем первая из них
использует авиационные ГТД фирмы «Ролле—Ройс» типов
«Эвон» и «Олимп», а вторая — фирмы «Пратт—Уиттни»
типов GG3 и GG4 [127]. В этих ГТУ газогенераторная
группа для свободной силовой турбины состоит из одного
или нескольких (до восьми) авиационных ГТД
(рис. IX. 14).
Силовая турбина ГТУ фирмы «Вортингтон» выпол-
няется двухпоточной, с центральной подачей продуктов
сором и 9-ступенчатой газовой турбиной. Сжатый гелий
из компрессора в активную зону реактора подается через
кольцевое пространство между наружной и внутренней
стенками двухстенной трубы. По внутренней трубе нагре-
тый в активной зоне реактора гелий поступает во входной
патрубок газовой турбины, выполненный в виде коль-
цевой улитки. Внутренняя труба имеет уплотнения
относительно внешней трубы и снабжена компенса-
тором.
Ротор турбокомпрессорной группы изготовлен свар-
кой из отдельных дисков. Направляющие лопатки ком-
Рис. IX. 14. Схемы компоновки с авиационным
ГТД: а — один ГТД; б — два ГТД; в — четыре
ГТД; г — восемь ГТД
сгорания и выходом их через кольцевой диффузор в общий
патрубок с верхним выводом. Внутренний корпус этой
турбины и выхлопная часть имеют общий горизонтальный
фланцевый разъем. Установки рассматриваемого типа
отличает высокая степень надежности и ремонтопригод-
ности. При отработке моторесурса или выходе из строя
газогенераторная группа (авиационный ГТД) может быть
заменена в течение нескольких часов. Агрегат имеет раз-
витую САУ. Предусматривается также дистанционное
управление ГТУ по заданной программе с центрального
диспетчерского пульта.
ГТУ ЗГТУ-ЗЙО, фирма «Броун—Бовери» (Швейца-
рия—ФРГ) (рис. IX. 15). Предназначена для работы
в комплексе с высокотемпературным газоохлаждаемым
реактором на быстрых нейтронах по одноконтурной схеме.
Рабочим телом служит гелий. Единичная мощность агре-
гата 350 МВт. Температура гелия на входе в газовую
турбину 850° С, давление 60 кгс/см2. Степень повышения
давления цикла 2,8 [127].
Особенностью турбоагрегата является так называе-
мая интегральная конструктивная схема расположения
элементов в общем герметичном корпусе (капсуле). Как
следует из рис. IX. 15, ЗГТУ спроектирована в виде
одновального агрегата с 20-ступенчатым осевым компрес-
прессора и турбины смонтированы в обоймы, имеющие
горизонтальный разъем. Эти обоймы установлены своими
гребнями в кольцевые проточки корпусов.
Опорные и упорные подшипники ротора турбоком-
прессорной группы работают на жидкой синтетической
смазке. Между подшипниками и лопаточными аппаратами
компрессора (на всасывании) и турбины (на выхлопе)
установлены развитые лабиринтные уплотнения. Со сто-
роны газовой турбины ротор через промежуточный вал
соединен с ротором электрогенератора. По наружной по-
верхности промежуточного вала расположены развитые
уплотнения типа плавающих колец. В концевой части
камеры этих уплотнений предусмотрен отсос возможных
протечек, чем обеспечивается герметичность выходного
участка промежуточного вала. Между наружным герме-
тичным и внутренним силовым корпусами блока, а также
на горячих частях газовоздушного тракта предусмотрена
внутренняя тепловая изоляция.
Внешний корпус установлен в бетонной шахте. Со
стороны выхода промежуточного вала также предусмотрена
соответствующая бетонная биологическая защита. Мощ-
ность агрегата регулируется изменением начального дав-
ления гелия при постоянной его температуре на входе
в турбину.
207
Приводные ГТУ
Применяются в качестве механического привода
компрессоров и насосов, предназначенных для сжатия
и транспортировки жидких и газообразных рабочих сред,
привода буровых установок и т д
Наиболее широкое распространение среди ГТУ этого
имеет переменную частоту вращения в рабочем диапазоне
изменения мощности Ниже рассмотрены конструкции
нескольких наиболее характерных образцов приводных
ГТУ — отечественных и зарубежных
ГТУ ГТН-6, УТМЗ (СССР) (рис. IX. 16). Выпотнена
по схеме За Осевой компрессор, газовые турбины (ТВД
и ТНД) и камера сгорания скомпонованы в общем сило-
вом корпусе [85 ]
Рис IX 15 Продольный
типа получили агрегаты, приводящие во вращение центро
бежные нагнетатели природного газа на компрессорных
станциях магистральных газопроводов, а также насосы для
транспортировки нефти и нефтепродуктов
Режим нагрузки таких агрегатов характеризуется,
как правило, относительно большим числом часов исполь
зования в течение года (5500—6000 и более), редкими
пусками и остановами Требования к маневренности
менее жесткие, чем для пиковых ГТУ
Для приводных ГТУ характерен высокий коэффициент
резервирования мощности (до 30—40%), что, в свою
очередь, требует обеспечения высоких коэффициентов
оперативной готовности агрегатов 1
Полезная мощность приводных ГТУ от 2000 кВт
до 30 тыс кВт в агрегате С учетом названгых особен
ностей приводные ГТУ выполняются, как правило, по
типовым конструктивным схемам 3 В отличие от энерге
тической ГТУ, вал силовой турбины приводной ГТУ
1 Под коэффициентом оперативной готовности принято
понимать отношение времени работы агрегата и нахождения его
в резерве к календарному времени в течение года
208
Роторы турбокомпрессора и силовой турбины — цель
нокованые, составной конструкции, с опорами, разме-
щенными на гонцах Задний опорный подшипник ротора
ТВД и передний опорный подшипник ротора ТНД смок
тированы в общем корпусе (промежуточной вставке), внеш-
ний пояс которой связан с корпусом подшипников че
тырьмя радиальными ребрами
Силовой корпус агрегата изготовлен сварно штампо-
ванным, имеет общий горизонтальный фланцевый разъем
и два технологических вертикальных разъема В кольце-
вые расточки внутренних выступов корпуса установлены
обоймы направляющего аппарата компрессора и направ-
ляющего аппарата ТВД Направляющие лопатки ком-
прессора имеют призматические хвостовики, входящие
в прямоугольные пазы сегментов Сегменты с лопатками
монтируются в кольцевых проточках обойм В горизон-
тальной плоскости обоймы имеют фланцевый разъем
К переднему вертикальному фланцу крепится литая
входная часть из двух половин, нижняя из которых отлита
заодно с корпусом переднего подшипника и узлом пу-
скового устройства, в качестве которого используется
турбодетандер, работающий на природном газе. Ось
входного патрубка, расположенного в нижней половине
отливки, направлена под углом 45° к оси агрегата в целях
создания более равномерного поля скоростей на входе
во входной направляющий аппарат компрессора. На вы-
ходе из компрессора установлен радиальный диффузор,
через который сжатый воздух подается во внутреннюю
полость, образованную силовым корпусом и кольцевой
ловых аппаратов ТНД. В выхлопной части размещен осе-
радиальный выходной дифффузор. Задний опорно-упорный
подшипник ротора силовой турбины расположен в отдель-
ном корпусе, установленном на общей фундаментной
раме.
Агрегат имеет развитую систему воздушного охлаж-
дения основных узлов и деталей, подверженных воздей-
ствию высоких температур. Примененная заводом система
разрез ГТУ ЗГТУ-350
встроенной камерой сгорания. Корпус опирается лапами
на вертикальные стойки, связанные с фундаментной рамой,
являющейся одновременно маслобаком агрегата. Первич-
ный воздух через регистры подается в верхнюю часть
камеры сгорания, где установлены газовые горелки
Вторичный воздух через отверстия в пламенной трубе
поступает в нижнюю часть камеры, где смешивается
с продуктами сгорания.
Сопловые лопатки ТВД собраны в литые сегменты
(по четыре штуки в каждом сегменте), которые подвешены
на соответствующих выступах обоймы Заодно с сегмен-
тами отлиты козырьки, расположенные над вершинами
рабочих лопаток и образующие необходимые радиальные
зазоры.
Нижние концы сопловых лопаток первой ступени
ТВД имеют бандажную полку с радиальным выступом на
котором крепятся два полукольца для фиксации фигур-
ного фланца камеры сгорания.
К заднему вертикальному фланцу корпуса крепится
выхлопная часть газовой турбины, в кольцевую проточку
во внутреннем выступе которой установлена обойма соп
охлаждения обеспечила получение сравнительно низких
температур силового корпуса, обойм соплового аппарата
и роторов ТВД и ТНД, что позволило применить для их
изготовления недорогие и технологичные перлитные стали.
Указанное обстоятельство способствовало также дости-
жению высоких к. п. д. турбин (до 0,90—0,92) благодаря
стабильным и малым радиальным зазорам.
Агрегат ГТН-6 выполнен блойно транспортабельным.
Транспортировка его производится на железнодорожной
платформе или трейлере в виде собранной на фундамент-
ной раме турбогруппы при снятых входном патрубке и
выхлопной части. Управление агрегатом, включая все
пусковые операции, полностью автоматизировано.
ГТУ ГТК-10-3, НЗЛ (СССР). Выполнена по схеме Зв
На рис. IX 17 показан продольный разрез турбогруппы
агрегата [55 J
Осевой компрессор смонтирован в отдельном литом
корпусе, который жестко связан с корпусе*! газовой
турбины при помощи промежуточного элемента — литого
корпуса заднего опорного подшипника ротора турбо-
компрессора Все указанные детали имеют общий гори-
209