Управление
полетом
КОСМИЧЕСКИХ
АППАРАТОВ

УПРАВЛЕНИЕ ПОЛЕТОМ
НОСМИЧЕСНИХ
АП ПАР А ТОВ—
ПЕРЕВОД С АНГЛИЙСКОГО
ПОД РЕДАКЦИЕЙ
КАНД. ТЕХН. НАУК П. Ж. К Р И С С А
И КАНД. ТЕХН. НАУК Л. И. КУЗНЕЦОВА
ИЗДАТЕЛЬСТВО ИНОСТРАННОЙ ЛИТЕРАТУРЫ
МОСКВА 1963

АН НОТАЦИЯ
Книга посвящена важнейшим вопросам, ко¬
торые приходится решать при запуске спутников,
межпланетных ракет и научных станций: управле¬
нию полетом и положением космического аппа¬
рата в пространстве при помощи автоматических
устройств, находящихся на борту корабля, а так¬
же контролю с Земли за движением и положе¬
нием космического аппарата, измерению его тра¬
ектории.
Книга предназначена для инженеров и науч¬
ных работников, занимающихся вопросами ра¬
кетной техники, для студентов, специализирую¬
щихся в этой области, а также для офицеров
Советской Армии и слушателей военных академий.
Редакция литературы по вопросам техники

ПРЕДИСЛОВИЕ РЕДАКТОРОВ
4 октября 1957 г. запуском в СССР первого искусствен¬
ного спутника Земли открылась новая эра в развитии чело¬
вечества. Огромные успехи советской науки и техники, до¬
стигнутые в последующие годы в деле освоения космического
пространства, в особенности героические полеты первых со¬
ветских космонавтов, позволяют рассматривать дальние кос¬
мические полеты не как дело далекого, хотя и предвидимого,
будущего, а как одну из очередных задач, которые будет
с неизменным успехом решать советская наука и техника.
Осуществление дальнего космического полета — это слож¬
ная научно-техническая проблема, в решении которой прини¬
мают участие представители самых разнообразных отраслей
науки и техники. Одной из важнейших частей этой проблемы
явпяется управление полетом космических аппаратов.
Управление полетом космических аппаратов охватывает
широкий круг вопросов: выбор оптимальной траектории по¬
лета корабля и критерии этого выбора; вывод корабля на
выбранную орбиту; стабилизация положения корабля на
орбите и его ориентация в нужном направлении; навигация
корабля на курсе; посадка корабля на планету; возвращение
корабля на Землю.
Сложность задачи управления космическим кораблем, вы¬
сокие скорости кораблей, высокие точности, с которыми долж¬
но осуществляться управление, и ограниченное время для ре¬
шения навигационных задач предопределяют в процессе на¬
вигации и управления ведущую роль автоматических средств.
Все задачи управления, возникающие с момента старта ко¬
рабля до его возвращения, должны быть решены без какого-
либо участия человека. Человек должен только контролиро¬
вать работу аппаратуры.
Задача управления может быть полностью решена авто¬
матическими устройствами, находящимися на борту корабля.
В этом случае принято говорить об автономном управлении.
В ряде случаев задача управления разрешается комплексом,

6
ПРЕДИСЛОВИЕ РЕДАКТОРОВ
включающим автоматическую бортовую систему и сеть изме¬
рительных пунктов и пунктов управления, расположенных
либо на Земле, либо на специальных искусственных спутни¬
ках. Бортовая и наземная аппаратура управления космиче¬
ским полетом— это сложная и разнообразная электронная и
радиотехническая аппаратура, счетно-решающие устройства
с широким использованием самых передовых средств совре¬
менной радиоэлектроники, автоматики и техники управления
и измерения на расстоянии.
В настоящей книге, составленной по материалам, опубли¬
кованным в ряде американских периодических изданий послед¬
них лет, рассматриваются некоторые вопросы управления по¬
летом космических аппаратов. В книге использованы также
материалы VIII Международного конгресса по астронавтике
в Барселоне и IX Международного конгресса по астронавтике
в Амстердаме.
В материалах первой части книги рассматриваются прин¬
ципиальные вопросы движения корабля, расчеты движения,
формулируются требования к системам управления и
точностям измерений, рассматриваются связи между выбо¬
ром траектории полета и возможностями измерения и упра¬
вления.
Вторая часть книги посвящена вопросам космической на¬
вигации Хотя в приведенных статьях рассматриваются все
три основные фазы космического полета — выход на орбиту
(или взлет), движение по курсу и посадка, — все же основное
внимание в них уделяется задаче выбора и поддержания
курса корабля. Рассматриваются как теоретические основы на¬
вигации, так и использование различных физических явлений
для создания опорных направлений, необходимых для нави¬
гации (астронавигация, радиотехнические методы навигации,
использование инфракрасной техники и т. д.). Некоторые из
этих принципов, например радиотехнические, широко приме¬
няются в современной технике, а некоторые, использующие,
например, гравитационные силы, могут найти применение в
будущем, когда будут решены проблемы их приборной реали¬
зации.
Материалы второй части тесно связаны с материалами
третьей части, посвященной вопросам стабилизации положе¬
ния космического аппарата на орбите. Наивысшая точность
удержания заданного положения при минимальном расходе
энергии является важнейшим требованием, предъявляемым
к устройству, которое обеспечивает стабилизацию положения
корабля. Точность стабилизации и маневра положением ко¬
рабля ца орбите теснейшим образом связана с точностью

ПРЕДИСЛОВИЕ РЕДАКТОРОВ
7
автономных средств навигации на курсе и особенно при по¬
садке. Точное поддержание определенного положения корабля
в пространстве необходимо также для обеспечения научных
наблюдений и измерений, ведущихся с космического корабля
или межпланетной научной станции. В третьей части рассма¬
триваются принципы стабилизации положения корабля, воз¬
мущающие факторы, средства обеспечения стабилизации, а
также средства, при помощи которых определяются опорные
направлений.
Четвертая часть книги посвящена вопросам траекторных
измерений. Измерение траектории полета космического аппа¬
рата является одной из важнейших составляющих общей про¬
блемы управления полетом. В любой системе управления
полетом имеется канал измерения движения корабля в какой-
либо удобной для данного случая системе координат. Инфор¬
мация, получаемая в этом канале, после надлежащей обра¬
ботки в автоматических решающих устройствах используется
для выработки команд органам управления движением (кор¬
ректирующим, координатным или тормозным двигателям).
Точные измерения орбит, ведущиеся наземными контроль¬
ными пунктами, даже если они не используются непосред¬
ственно в автоматической цепи управления, имеют большое
самостоятельное значение для контроля правильности дви¬
жения корабля, точной пространственной привязки данных
научных измерений, изучения движения кораблей в сложных
системах многих тел с целью выбора наиболее удобных траек¬
торий полета.
Среди методов измерений, рассматриваемых в четвертой
части, основное место занимают допплеровские измерения
дальности и скорости, широко используемые в США для из¬
мерения траектории полета ракет и спутников.
Приведенные в книге материалы не дают полной картины
современного состояния техники управления полетом косми¬
ческих кораблей, так как не содержат данных о состоянии и
развитии этой области техники в СССР. Они не могут также
претендовать на создание полной картины современного со¬
стояния техники управления космическим полетом в США,
ибо вследствие ограниченности объема книги в нее вклю¬
чена лишь небольшая часть обширной периодической литера¬
туры, опубликованной по этому вопросу за рубежом.
Ввиду отсутствия в настоящее время капитальных трудов,
монографий или учебников, как отечественных, так и зару¬
бежных авторов, посвященных проблемам управления косми¬
ческим полетом, публикуемые в предлагаемой книге работы

8
ПРЕДИСЛОВИЕ РЕДАКТОРОВ
представляют значительный интерес для инженеров и науч¬
ных работников, занимающихся вопросами ракетной и косми¬
ческой техники, для студентов старших курсов, специализи¬
рующихся в этой области, а также для офицеров Советской
Армии и слушателей военных академий.
П. Ж. Крисс,
Л. И. Кузнецов

/. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ
ПОЛЕТОМ КОСМИЧЕСКИХ АППАРАТОВ
ОБЩИЕ ПРИНЦИПЫ НАВЕДЕНИЯ
И УПРАВЛЕНИЯ СПУТНИКАМИ И КОСМИЧЕСКИМИ
КОРАБЛЯМИ1)
Роберсон
Рассматриваются основные вопросы управления космическим кораб¬
лем. Приводятся некоторые технические и эксплуатационные требования к
системам (точность, надежность, вес, влияние внешних условий). Дается
обзор современного состояния техники наведения и управления как в от¬
ношении принципов наведения, так и в отношении способов приборной
реализации с краткими замечаниями относительно реальных систем. Ука¬
зываются проблемы, требующие особого внимания.
1.	ВВЕДЕНИЕ
Наведение и управление являются наиболее важными тех¬
ническими проблемами в астронавтике. По степени важности
они занимают второе место после проблем, связанных с созда¬
нием тяги и условий для нормальной жизнедеятельности че¬
ловека. В технической литературе эти вопросы освещены
сравнительно слабо, за исключением непосредственного при¬
ложения принципов наведения и управления к баллистиче¬
ским снарядам и к первым искусственным спутникам Земли.
В настоящей статье рассматриваются соотношения между
наведением и управлением в астронавтике, причем особое
внимание уделяется общим представлениям и теоретическим
проблемам. Обсуждаются следующие вопросы.
1.	Каковы требования к системам наведения и управления
и каково их отношение к основным задачам астронавтики?
Иначе говоря, какие требования предъявляют эти задачи
к выполняемым функциям наведения и управления, к точ¬
ности работы и к физическим характеристикам систем?
^Roberson R. Е., Ргос. IXth Intern. Astronaut. Congress, I,
PP. 25—32, 1959,

10
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
2. Какого рода систему наведения и управления пред¬
полагается применить для этих целей и как согласуются упо¬
мянутые выше требования с существующими системами и их
элементами?
3. Какие отдельные принципиальные вопросы должны при¬
влекать наше внимание?
2.	ТРЕБОВАНИЯ Н СИСТЕМАМ НАВЕДЕНИЯ И УПРАВЛЕНИЯ
Функции наведения и управления
Назначение систем наведения и управления в общих чер¬
тах общеизвестно. В основном они должны удерживать век¬
тор тяги в период активной фазы полета в таком направлении,
чтобы космический корабль двигался надлежащим образом.
(Это не значит, что корабль непременно должен двигаться
по единственной, заранее заданной траектории в космическом
пространстве.)
В статье в основном рассматриваются три физические
функции, которые могут быть объединены в единую физиче¬
скую систему или же в несколько подсистем, имеющих сла¬
бую взаимосвязь (как это часто делается в обычных систе¬
мах наведения и управления). Этими функциями являются:
1. Навигация (поскольку правильное действие космиче¬
ского корабля обычно зависит от места нахождения, скорости
и направления движения, а также от текущего времени).
2. Управление по курсу (т. е. физическое выравнивание —
уточнение вектора тяги в «правильном» направлении).
3. Обеспечение последовательности операций (например,
зажигания и отсечки двигателя).
Помимо упомянутых, имеются две тесно связанные между
собой функции, которые следует рассматривать одновременно.
К ним относится, во-первых, регулирование положения (ста¬
билизация) космического корабля во время полета с выклю¬
ченным двигателем. Эта функция может оказаться по раз¬
личным причинам связанной с назначением космического ко¬
рабля и с возможностями приборной реализации. Ко второй
функции относится обеспечение последовательности операций
бортовой аппаратуры, не связанной с навигацией и управле¬
нием. наппимер аппаратуры связи или приборов для научных
исследований.
На фиг. 1 показано несколько типичных задач астронав¬
тики, иллюстрирующих основные функции наведения и управ¬
ления. Особенно важно подчеркнуть два обстоятельства.

ЗАДА ЧИ
Фиг. 1. Типичные астронавтические задачи и функции наведения и управления.

12
I. ОБЩИН ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
Во-первых, существует по крайней мере 12 различных и отно¬
сительно независимых функций наведения, которые типичны
для задач астронавтики. Во-вторых, иногда необходимо вы¬
полнять ряд этих функций последовательно (например, осу¬
ществление межпланетного перелета связано с применением
8 таких функций).
Этот фактор, а именно ряд последовательно выполняемых
функций наведения и управления, характерный для задач
астронавтики, является, вероятно, наиболее существенным
отличием между наведением в космическом полете и наведе¬
нием при навигации вблизи Земли.
Точность
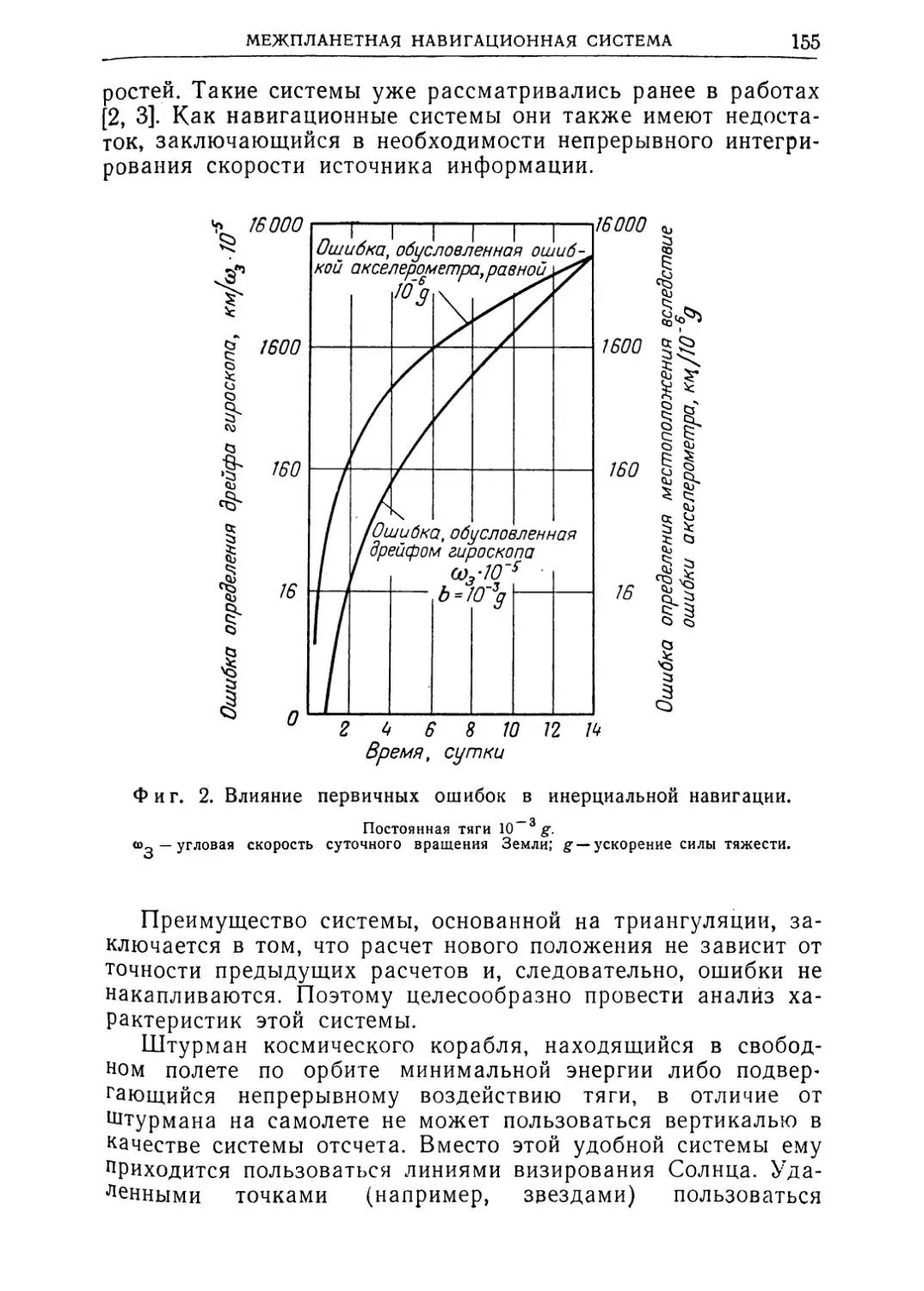
Рассмотрим требования, предъявляемые к точности систем
наведения и управления. Подробное исследование этого во¬
проса возможно было бы изложить только в отдельной статье
Ошибка в скорости (при номин. скорости 3000м/сек), м/сек
Фиг. 2. Требования к наведению для космических полетов.
для каждой из задач, поставленных перед космическим объ¬
ектом, поэтому мы ограничимся только анализом графика,
приведенного на фиг. 2.
На фиг. 2 по оси абсцисс отложена величина ошибки по
скорости, допустимая при выполнении поставленной задачи
с угловой ошибкой ориентации вектора скорости, отложенной
по оси ординат. Иначе говоря, любое сочетание ошибок по аб¬
солютной величине и угловой ориентации вектора скорости,

ОБЩИЕ ПРИНЦИПЫ НАВЕДЕНИЯ И УПРАВЛЕНИЯ
13
при котором мы попадем на ту или иную кривую, обеспечит
выполнение той функции наведения и управления, которую
представляет данная кривая.
К численным значениям, приведенным на фиг. 2, следует
относиться с осторожностью, так как при построении неко¬
торых кривых использовались довольно грубые приближения
и, кроме того, было допущено, что вблизи Земли тяга дей¬
ствует импульсами без дальнейшей коррекции курса. Это не
всегда верно для некоторых функций, представленных на
фиг. 2.
Надежность
Другой исключительно важной характеристикой системы
является ее надежность. Время полета достаточно велико, по¬
этому требования к надежности являются жесткими.
На фиг. 3 показано, что продолжительность некоторых ти¬
пичных космических полетов колеблется в пределах от 60 до
52 000 час. Чтобы иметь 50% вероятности безотказной работы
Время
часы
годы
10 7 -
- /о3
106 -
- 10г
W5 -
- 10
10*-
- 1
70J
10L
Время для
выполнения
задачи
Требуемая величина среднего срока
службы между двумя последователь¬
ными возможными отказами при
вероятности отказа
Пробный полет
на Сатурн..
Экспедиц и я
на Марс
полет
на.
олет -7
Морс I
Пробный
полет
на Луну
50%
Фиг. 3. Требования к надежности аппаратуры.
системы на протяжении всего космического полета, среднее,
время работы (или средний срок службы) системы между
двумя последовательными вероятными отказами должно быты
таким, как это показано во второй группе столбцов графика;:
Вели же вероятность появлений отказа нужно ограничить 1%,
то требования к величине среднего времени безотказной ра¬
боты между двумя последовательными вероятными отказами

14
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
значительно возрастают, как показано в третьей группе столб¬
цов графика на фиг. 3. Даже для полета на Марс в один ко¬
нец, т. е. для сравнительно простого маршрута, требование
получения вероятности отказа в 1% означает, что среднее
время безотказной работы между двумя последовательными
вероятными отказами должно составлять 600 000 час, т. е.
68 лет!
Конечно, не вся аппаратура должна работать все это
время. Предполагается, например, что система наведения
(или по крайней мере некоторые ее элементы) может быть
выключена на любой длительный период в течение свободного
полета на протяжении межпланетного рейса. Затем ее снова
можно включить во время приближения к планете, которая
является местом назначения, с тем чтобы она функциониро¬
вала на конечной стадии наведения. Но можно ли выключить
систему, оставив ее бездействующей в течение 7 или 8 месу
а затем вновь включить ее и надеяться, что она будет рабо¬
тать? По всей видимости, в настоящее время мы не в состоя¬
нии этого сделать. Итак, можно подчеркнуть, что, хотя тре¬
бования к надежности и не являются столь жесткими, как это
может показаться вначале, не оставляет сомнения, что они
достаточно строги и их выполнение представляет серьезную
проблему.
Вес
Важность габаритов и веса системы при космическом по¬
лете является очевидной. На фиг. 4 показана доля общего
веса космического корабля, приходящаяся на 1 кг аппара¬
туры для различных полетов. Цифры эти достаточно досто¬
верны, хотя многие ученые считают, что для запуска спутни¬
ков Земли возможны большие соотношения весов (например,
для спутника «Авангард» порядка 1000).
Как видно из фиг. 4, каждый дополнительный килограмм
веса аппаратуры при полете на Марс вызывает увеличение
общего веса объекта по сравнению со случаем запуска искус¬
ственного спутника Земли в 8 раз. Это означает, что работа
двигательной установки на большие дальности обходится
очень дорого.
Двигательные установки первых космических кораблей
были менее эффективными, и отношение общего веса к полез¬
ному весу у них было значительно больше.
Следует отметить также, что данные, приведенные на
фиг. 4, не дают достаточного представления о значении ма¬
лого веса систем наведения и управления.

ОБЩИЕ ПРИНЦИПЫ НАВЕДЕНИЯ И УПРАВЛЕНИЯ
15
Окружающие условия
Требования, которые накладывают условия окружающей
среды при космических полетах (например, невесомость и
вакуум), также оказывают большое влияние на приборную
реализацию систем наведения и управления. Помимо этого,
есть и другие факторы (возможно, даже более существен¬
ные). Если в качестве первичного источника энергии при кос¬
мическом полете используется атомный реактор, то влияние
Отношение общего веса космического корабля в кг на I кг
полезной нагрузки
химическое топливо;
ионная ракета.
Фиг. 4. Отношение общего веса космического корабля к весу
полезной нагрузки.
излучения на качество изоляции, смазки, на фоточувствитель-
ные элементы, оптику и полупроводники может иметь решаю¬
щее значение. Даже если в качестве источника энергии ис¬
пользовать «солнечный котел», то возникает проблема работы
аппаратуры в условиях высоких температур. Кроме того,
реальную опасность представляют замерзание оптики и попа¬
дание космической пыли. Эти требования имеют первостепен¬
ное значение и заслуживают тщательного и всеобъемлющего
анализа.
3.	ОСНОВНЫЕ ПОЛОЖЕНИЯ
Требования, связанные с назначением полета, являются
основными для всех видов подсистем. Исходя из этих требо¬
ваний, необходимо рассмотреть три фактора, определяющих

16
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
создание системы наведения и управления. Первый фактор —
это программа наведения, по которой для космического ко¬
рабля определяется, что он должен делать в любой момент
времени. Второй фактор — это схема механической реализа¬
ции, или блок-схема системы, показывающая типы элем^тов
и подсистем, которые должны выполнять работу в собтвет-
ствии со схемой их соединений. И, наконец, третий фактор —
это физическая конструкция, воплощенная в металле.
Основные положения наведения и управления для целей
астронавтики будут рассмотрены с точки зрения этих трех
факторов. Программа наведения основывается на требова¬
ниях, вытекающих из назначения полета, а также на функ¬
циях наведения и управления. Схема механической реализа¬
ции базируется на программе, а конкретная конструкция —
на схеме механической реализации.
Программа наведения
Ниже приводятся основные положения для формулирова¬
ния программы наведения.
1. Программа наведения должна быть полной. Недоста¬
точно, например, представить количественные данные для
наведения на начальном участке и в середине пути, а по по¬
воду конечной фазы ограничиться утверждением, что «вблизи
планеты, которая является местом назначения, может пона¬
добиться незначительное уточнение курса, чтобы обеспечить
точное сближение корабля». Программа должна охватывать
все требуемые функции наведения.
2. Программа наведения должна быть четкой и ясной.
3. Команды наведения должны быть однозначными.
4. Система наведения должна быть определенной и обес¬
печивать такое положение, при котором только существенное
нарушение ее работоспособности может сделать невозможным
возвращение корабля на Землю при имеющихся возможно¬
стях двигателя.
5. Программа наведения должна быть достаточно гибкой.
Отклонения и ошибки должны автоматически корректиро¬
ваться в пределах точности этой системы.
6. Система наведения должна быть простой и основы¬
ваться на простом механическом решении.
Все эти правила кажутся очевидными, однако большин¬
ство разрабатываемых систем не всегда полностью отве¬
чает им.

\
ОБЩИЕ ПРИНЦИПЫ НАВЕДЕНИЯ И УПРАВЛЕНИЯ
17
Лучше всего разработаны основные программы наведения
баллистических ракет. В наиболее распространенных в на¬
стоящее время программах используются методы возмущения;
базируясь на программированных траекториях, вносят по¬
правки на отклонения от программы таким образом, что
точка попадания на Земле остается фиксированной. Каждый
вариант аппроксимации возмущения имеет свои преимущества
и недостатки, поэтому выбор часто определяется субъектив¬
ными соображениями.
Такая же методика применяется к начальной фазе полета,
являющейся общей для всех космических полетов; задача
здесь в основном заключается в том, чтобы получить необхо¬
димый вектор скорости в конце активного участка полета.
Единственное реальное изменение заключается в самой про¬
граммированной траектории и, возможно, в требованиях
к точности.
В случае вывода спутника на орбиту за начальной фазой
разгона должна последовать конечная фаза выхода на ор¬
биту, причем обычно это происходит после определенного
периода свободного полета по восходящей траектории.
Принципы, а также практические методы вывода спутника
на орбиту хорошо изучены, и основные положения известны.
Это позволяет сделать вывод о том, что существующие про¬
граммы наведения для начальной фазы полета и для участка
с дополнительной тягой достаточно надежны, чтобы вывести
спутник на орбиту. Следует также отметить, что проблема
стабилизации спутника тщательно изучена и основные прин¬
ципы в этой области, по-видимому, отвечают необходимым
требованиям. Но не так благополучно обстоит дело для дру¬
гих рассматриваемых функций.
В некоторых случаях вообще не предполагается наведения
с Земли (например, при полете на Луну), и задача сводится
к тому, чтобы обеспечить точное вождение в начальной ста¬
дии полета и дальнейшее управление осуществлять с помощью
программирования. Однако в большинстве случаев требуется
дальнейшее наведение на среднем и конечном этапах полета.
Схемы механической реализации
Схемы механической реализации, достаточно хорошо раз¬
работанные для искусственных спутников Земли, на первый
взгляд кажутся вполне подходящими и для дальнейших при¬
менений в астронавтике. Однако предлагаемые системы неиз¬
менно ограничиваются одним способом наведения, реальность
осуществления которого из-за сложности конструкции и ее
2 Зак. 87$

18
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
веса часто вызывает серьезные сомнения. При этом авторы,
опираясь на опыт, исходят из необходимости иметь информа¬
цию об ориентации, а также некоторые сведения о скорости
или местоположении и соответствующие расчеты. Блой-схема
в таком случае составляется из подсистем таким образом,
чтобы выполнялась, каждая из этих функций.
Несомненно, однако, что если полностью сформулировать
основные программы, соответствующие назначению космиче¬
ских полетов, то в превосходных схемах механической реали¬
зации систем не будет недостатка.
Физические приборы
В литературе имеется описание целого ряда физических
приборов, предназначенных для осуществления основных из¬
мерений с целью определения ориентации, местоположения
и скорости. Многие из них являются весьма оригинальными.
Однако, за исключением баллистических ракет и искусствен¬
ных спутников, почти ничего не удалось сделать для созда¬
ния реальных конструкций.
В заключение отметим два соображения относительно со¬
временного состояния точности и надежности. К сожалению,
подробные количественные данные, относящиеся к лучшим
разработкам, которые в настоящее время могут быть исполь¬
зованы в реальных физических установках, по определенным
соображениям здесь не рассматриваются. Однако можно ут¬
верждать, что большинство задач, указанных на фиг. 2, на¬
ходится в пределах современных возможностей. Те из них,
которые требуют точного решения, определенно нуждаются
в дополнительном наведении на участке, непосредственно сле¬
дующим за начальным участком разгона. Но надо отметить,
что дополнительная фаза наведения желательна в любых слу¬
чаях, даже тогда, когда полет теоретически может быть осу¬
ществлен за счет наведения на начальном участке.
Что касается надежности, то здесь дело обстоит иначе.
Хорошо известно, что надежная, но вместе с тем достаточно
сложная электронная аппаратура имеет средний срок служ¬
бы между двумя последовательными вероятными отказами
2000—3000 час. Если сравнить эти цифры с необходимой ве¬
личиной среднего срока службы между двумя последователь¬
ными вероятными отказами при полете в один конец на
Марс, где эта величина достигает 600 000 час (при условии,
что вероятность появления отказа не превышает 1%), то ста¬
нет ясным, что между этими величинами надежности имеется
весьма ощутимый разрыв. К счастью, ситуация не является

ОБЩИЕ ПРИНЦИПЫ НАВЕДЕНИЯ И УПРАВЛЕНИЯ	19
совсе^ безнадежной. Имеются несколько факторов, выполне¬
ние крторых позволит сократить разрыв. К ним относятся:
1. Цовые принципы наведения для упрощения системы и
сокращения рабочего времени.
2. Проектирование аппаратуры с заведомо высокой на¬
дежностью за счет дублирования и коэффициентов безопас¬
ности.
3. Всесторонняя проверка аппаратуры на земле для обна¬
ружения возникающей ненадежности.
4. Системы, управляемые человеком с целью осуществле¬
ния регулировок, замены частей аппаратуры и упрощения
функций в полете.
5. Усовершенствованные двигатели для сокращения сро¬
ков выполнения поставленной задачи.
Однако эти меры не могут предохранить от всех трудно¬
стей, поэтому проблема надежности остается весьма ак¬
туальной.
4.	ПРОБЛЕМНЫЕ ВОПРОСЫ
Предыдущие замечания позволяют отметить те области,
где наведение и управление соответствуют своему назначению
и где такого соответствия еще не достигнуто.
Полное соответствие, принципиальное и физическое,
имеется для большинства запускаемых спутников Земли, за
исключением тех случаев, когда требуется исключительная
точность. В принципе указанное соответствие существует и
для первых межпланетных полетов, в которых метод наведе¬
ния остается по существу одним и тем же (регулируемый
вектор начальной скорости вблизи Земли); по-видимому, в та¬
ких задачах точность не является основной проблемой.
Существующие принципы наведения не соответствуют на¬
значению многих будущих космических полетов любой степени
сложности, и именно поэтому эта область требует немедлен¬
ного и самого широкого исследования.
Существующая аппаратура, предназначенная для наведе¬
ния и управления, значительно отстает от предъявляемых
к ней требований надежности. Необходимы новые виды фи¬
зических приборов, например приборы, использующие неко¬
торые благоприятные свойства окружающей среды. Во всяком
случае, основной проблемой наведения при космических по¬
летах представляется проблема надежности, которая должна
быть преодолена любыми средствами.
2*

ДАННЫЕ О МЕСТОПОЛОЖЕНИИ КОСМИЧЕСКОГО
КОРАБЛЯ, НЕОБХОДИМЫЕ ДЛЯ УПРАВЛЕНИЯ
ЕГО ПОЛЕТОМ В ПРОСТРАНСТВЕ ■)
Стирнс, Фрай
Динамика пространственного полета в основном зависит от двух фак¬
торов: от мощности двигателя и точности навигации. В настоящей статье
рассматривается взаимосвязь этих двух факторов, а также траектории
межпланетных полетов с различными уровнями энергии.
При современном уровне развития науки и техники первые
межпланетные летательные аппараты, очевидно, должны
двигаться по траектории с минимальной затратой энергии.
Кроме того, время запуска должно быть точно определено,
чтобы по прибытии аппарата в заранее вычисленную точку
его орбита совпадала с орбитой планеты назначения и чтобы
он мог быть «захвачен» планетой.
Траектория полета с минимальной энергией, скажем на
Венеру, представляет собой эллипс, в одном из фокусов кото¬
рого находится Солнце, в апогее — Земля в момент запуска,
а в перигее — Венера в момент прибытия (фиг. 1).
Свойства эллипса можно описать следующим образом:
Большая полуось = l/2 (Rf-\~Rn) = &\
Малая полуось = ]/RFRN — b,
где Rn и Rf — расстояния от Солнца до дальней планеты в
момент запуска (или прибытия) и до ближайшей планеты
в момент прибытия (или запуска) соответственно.
При применении такой траектории орбита космического,
корабля определяется условиями запуска и изменения могут
вноситься только во время действия тяги в течение несколь¬
ких минут. Благодаря свойствам эллипса и тому факту, что
орбита, выбранная системой наведения, должна иметь Солнце.
в одном из фокусов орбиты, можно пренебречь небольшими
погрешностями, которые при этом возникают. Такие погреш¬
ности приводят только к необходимости выполнения на ко-
*) Stearns Е. V., Frye W. Е., Space Aeronautics, 48—51 (March
1959),

ДАННЫЕ, НЕОБХОДИМЫЕ ДЛЯ УПРАВЛЕНИЯ ПОЛЕТОМ
21
нечнбм участке полета маневра, величина которого должна
соответствовать ошибке наведения.
Если же на значительной части полета могут быть исполь¬
зованы различные двигатели (солнечный, ионный, атомный
Земля
Фиг. 1. Траектория минимальной энергии от Земли до Венеры.
По такой траектории должен лететь космический корабль при современном
уровне техники.
или какой-нибудь другой), достаточно эффективные для под¬
держания необходимого уровня тяги, то траекторию космиче¬
ского корабля в этих условиях можно вычислить посредством
интегрирования дифференциального уравнения, которое сум¬
мирует ускорения, действующие на летательный аппарат:
8 = g + b,
где R — полное ускорение1); g — ускорение, вызванное грави¬
тацией, и Ь—негравитационное ускорение (обусловленное
тягой). Как только космический корабль выходит за пределы
земного притяжения, приходится учитывать влияние Солнца
(табл. 1). В настоящей статье предполагается, что, во-первых,
ускорения тяги имеют одинаковый порядок величины и, во-
вторых, они могут поддерживаться в течение времени, срав¬
нимого со временем полета.
1) Точки над символом обозначают производные по времени. — Прим.
ред.

22
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
Таблица 1
Данные о планетах
Планеты
Среднее расстояние
от Солнца
Период
орбиты,
год
Эксцен¬
триситет
орбиты
Наклон
к пло¬
скости
эклип¬
тики,
град.
Звезд¬
ная
вели¬
чина
Средняя
скорость
движения
по орбите,
км/сек
в астроно¬
мических
единицах
млн. км
Меркурий . .
0,387
57,9
0,2
0,206
7
—1,2
47,83
Венера ....
0,723
108,2
0,7
0,007
3,24
—4,4
34,99
Земля ....
1,000
149,5
1
0,017
0
—
29,76
Марс
1,524
227,8
1,9
0,093
1,51
—2,8
24,11
Юпитер . . .
5,203
777,8
11,9
0,048
1,18
—2,5
13,05
Сатурн ....
9,539
1426,6
29,5
0,056
2,29
-0,4
9,64
Уран
19,182
2869,1
84
0,047
0,46
-(-5,7
6,80
Нептун ....
30,058
4495,7
164,8
0,009
1,46
+8,8
5,43
Плутон ....
39,518
5899,1
248,4
0,249
17,09
+!5
4,73
Таблица 2
Гравитационное поле Солнца
Расстояние от
Солнца,
млн. км
Орбита
планеты
Ускорение
м/сек2
g х ю~4
228
Марс
0,0025
2,6
150
Земля
0,0060
6
129
—
0,0077
8
108
Венера
0,0115
1,19
Из табл. 1 и 2 и фиг. 2 видно, что навигацию в пределах
солнечной системы можно рассматривать (с необходимой сте¬
пенью точности) в плоскости эклиптики (орбиты Земли во¬
круг Солнца), полагая при этом, что орбиты планет (за
исключением Меркурия и Плутона) являются круговыми.
Для определения планетарных орбит и траекторий межпла¬
нетных летательных аппаратов можно применять уравнения
движения. Для целей наведения и навигации эти уравнения
особенно полезны в форме, выраженной в величинах перво¬
начального положения и скорости летательного аппарата,
когда он выходит на орбиту свободного полета.

ДАННЫЕ, НЕОБХОДИМЫЕ ДЛЯ УПРАВЛЕНИЯ ПОЛЕТОМ	23
Мы имеем следующие математические соотношения для
орбиты:
Уравнения движения
R = g; Jc+o)2a: = 0; y + ^2y=0,
где R — геоцентрический радиус-вектор; со = goRo/R3\ х и у —
составляющие вектора R; g — гравитационное ускорение, рав¬
ное RgoRo/R*-
Фиг. 2. Навигация в пределах солнечной системы.
Навигация рассматривается в плоскости вращения Земли вокруг Солнца (только Меркурий
и Плутон существенно выходят из этой плоскости).
Энергия движения
Е — GmM -i-,
где G — гравитационная постоянная; т — масса объекта, дви¬
жущегося по орбите; М — масса Солнца и а — большая по¬
луось орбиты.
Проинтегрированные уравнения движения:
r = -a(!-£2>	m
Г 1 —ecos 0 ’
x = xQ cos Ы + (sin о)^)	;	(2)
у =уо cos 0)t + (sin 0)t)	,	(3)
где е — эксцентриситет орбиты; 0 — угловое положение объек¬
та в	плоскости	орбиты; со = const; х0 и	у0	определяют	точку
входа,	а	х0	и	.у0 — скорость входа. Уравнение	(1)	содержит
потребление энергии и постоянный угловой момент. В уравне¬
ниях (2) и (3) используются начальные условия.

24
I. .ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
Эксцентриситет орбиты
где b — малая полуось.
Период орбиты
2па^2
т — Vgm ’
Угловая скорость
Q 	 (1 — £ cos 0)2
_ т (1 _ £2)3/2
Ф>Ш/ МЕЖПЛАНЕТНОГО ПОЛЕТА
Время, необходимое для межпланетного перелета с высо¬
кой энергией, зависит от программы ускорения (фиг. 3),
Максимальное расстояние
Земля-Венера
0,01%,
Минимальное
"расстояние Земля - Венера
10	15	20
Время, сутки'
3. Траекторий высокой энергии между Землей и Венерой
для различных ускорений.
Время перелета зависит также от относительного расположения обеих планет в момент
старта. Предполагается, что в течение половины пути тяга является ускоряющей, а затем
тормозящей, причем собственно ускорение действует вдоль линии полета, и что прямо¬
линейная траектория для максимального расстояния (между Землей и Венерой) не перег
секает орбиты Меркурия.
Фиг.
а также от проходимого расстояния. Последнее в свою очередь
определяется относительным расположением планет в момент
взлета (см. фиг. 1).

ДАННЫЕ, НЕОБХОДИМЫЕ ДЛЯ УПРАВЛЕНИЯ ПОЛЕТОМ
25
Полет делится на три основные фазы:
1) взлет, или выход из атмосферы Земли;
2) курс, во время которого осуществляется навигация на
огромных расстояниях в межпланетном пространстве. Пред¬
полагается, что эта фаза кончается на орбите, являющейся
орбитой спутника, который обращается вокруг планеты наз¬
начения; с этой орбиты предполагается выбрать посадочную
площадку;
Телескоп с
сервоприводом
Местная
вертикаль
Линия визирования
звезды
Вертикаль, проходящая
через звезду
- Проекция звезды
на земную сферу
Фиг. 4. Визирование звезды для получения линии положения (ЛП).
3) посадка, во время которой рассеивается большая кине¬
тическая и потенциальная энергия космического корабля, ле¬
тящего, по орбите.
В настоящей статье рассматривается проблема полета на
курсе.
Фиг. 4 иллюстрирует метод определения положения косми¬
ческого корабля относительно Земли с помощью астрономиче¬
ских приборов. При наблюдении за звездами навигатор ис¬
пользует направление силы тяжести на Земле в качестве
исходного ориентира при измерении углов подъема. Это по¬
зволяет ему следить за истинным направлением местной вер¬
тикали по мере движения корабля вокруг Земли. Для механи¬
ческого осуществления показанного треугольника необходимо
иметь: 1) устойчивую вертикаль на борту (искусственный го¬
ризонт), 2) (гиростабилизированную) систему координат,
фиксированную относительно звезд, 3) счетно-решающее
устройство и 4) каталог звезд или его эквивалент в запоми¬
нающем устройстве счетно-решающей машины.
Для межпланетного летательного аппарата определение
направления на звезду можно осущес1 вить относительно неко¬
торой опорной линии. Исходным направлением, которое

26
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
используется в данном случае, является направление гелио¬
центрической силы тяжести, которое указывается линией ви¬
зирования на Солнце.
Линии визирования на удаленные звезды не помогают на¬
вигатору при определении положения, так как в противопо¬
ложность летчику, осуществляющему полет вблизи Земли,
пилот космического летательного аппарата не «привязан»
к какой-либо сферической поверхности. При отсутствии парал¬
лакса (как это имеет место в линиях визирования удален¬
ных звезд) визированием звезд устанавливают только на¬
правление опорной линии на небесной сфере, а не положе¬
ние навигатора на этой исходной линии. За счет использова¬
ния дополнительных линий визирования звезд не удается
устранить неопределенность, так как обычно для наблюда¬
теля, расположенного в любом месте в солнечной системе,
удаленные звезды кажутся одинаковыми. Неопределенность
можно устранить следующим образом:
1) измерением угла, стягиваемого солнечным диском;
2) измерением характеристического времени и вынужден¬
ной погрешности стабилизированного индикатора гелиоцен¬
трической вертикали, определенной путем визирования
Солнца;
3) применением визирования планет и получаемого при
этом параллакса.
Первый метод не обеспечивает достаточной чувствитель¬
ности, поэтому его лучше не применять. Второй метод в прин¬
ципе пригоден для использования, однако на практике он
оказался неудобным, ибо время, необходимое для его осу¬
ществления, приблизительно равно времени обращения по
орбите. Наиболее полезным методом определения положения
в солнечной системе является применение визирования пла¬
нет.
Так как каждое визирование определяет линию в пло¬
скости эклиптики, определение положения (или точки) тре¬
бует пересечения двух известных линий. В любое время кон¬
фигурация солнечной системы известна; таким образом,
Солнце и планеты можно использовать для получения этих
линий визирования. Если следовать практике, установленной
для навигации вблизи Земли, то для определения положения
космического корабля требуются три небесных тела. При этом
точность определения местоположения зависит от расстояния,
которое отделяет космический корабль от этих небесных тел.
На фиг. 5 представлены результаты обычных вычислений.
В нашем примере (при погрешности секстанта 0,5') погреш¬
ность при измерении местоположения составит приблизи-

ДАННЫЕ, НЕОБХОДИМЫЕ ДЛЯ УПРАВЛЕНИЯ ПОЛЕТОМ	27
тельно 19000 км в направлении, перпендикулярном к линии
визирования Солнца, и ~5000 км в направлении, перпендику¬
лярном к линиям визирования двух планет.
Скорость можно определить в результате двух таких
измерений и на основании данных о затраченном времени.
/0°
40
%30
го
1,о
Линия визирования
Солнца
Линия визирования
планеты
0,1	0,4	0,6	0,8
Ошибка секстанта, 3, у гл. мин
Фиг. 5. Результаты типичных расчетов ошибки для перелета с Земли
на Венеру.
Предполагается, что корабль находится на расстоянии ^ 1 • 108 км от Солнца и среднем
расстоянии около 3 • 107 км от каждой планеты.
Однако подобное определение скорости будет неточным из-за
погрешностей, допущенных при измерении местоположения и
при определении времени между измерениями (фиг. 6). Чтобы
получить порядок величины оценки неточностей, погрешность
в скорости в результате двух последовательных измерений
была принята равной
где ос—неточность местоположения в направлении, перпен¬
дикулярном линии визирования Солнца (эта линия идет
вдоль вектора скорости), и t — промежуток времени между
измерениями. Подобно этому погрешность по курсу можно
определить так:
tgp=^.
где сп — погрешность определения местоположения в напра¬
влении, перпендикулярном линии визирования планеты, и
v — гелиоцентрическая скорость космического корабля (пер¬
пендикулярна линии, соединяющей космический корабль и
Солнце).

28
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
По прошествии 680 000 сек (~ 188,8 час) ошибки умень¬
шаются приблизительно до 1 % от разности между гелиоцен¬
трическими скоростями Земли и Венеры, или до 0,056 км/сек.
0,0010
10°
Время, сен
Фиг. 6. Точность результатов последовательных измерений
местоположения.
После 188,8 час ошибка по направлению может быть ограничена
величиной 0,5 мрад.
Приблизительно за то же время ошибки по курсу можно
уменьшить до ~0,5 мрад.
1
I
4 ^	jo	го	зо
Величина изменения курса, мрад
Фиг. 7. Расход топлива для изменения курса при активном полете
космического корабля с удельной тягой 240 сек.
Количество топлива, расходуемого при изменении курса,
можно определить, приравнивая силу тяги, полученную в ре¬
зультате сгорания топлива, к силе, необходимой для получе¬
ния изменения момента количества движения космического
корабля:
7 = wl
уд. т»

ДАННЫЕ, НЕОБХОДИМЫЕ ДЛЯ УПРАВЛЕНИЯ ПОЛЕТОМ	29
где Г —тяга, равная MVd$/dt\ w — скорость расхода топ¬
лива; /уд.т.— удельный импульс (удельная тяга); V—скорость
полета. Кривая, изображенная на фиг. 7, получена в резуль¬
тате решения дифференциального уравнения при условии, что
около 0,7% веса космического корабля необходимо исполь¬
зовать для того, чтобы внести коррекцию по курсу, равную
0,5 мрад.
ТРЕБУЕМАЯ ТОЧНОСТЬ ДАННЫХ О МЕСТОПОЛОЖЕНИИ
КОСМИЧЕСКОГО КОРАБЛЯ
Согласно грубым расчетам, приведенным выше, точность
данных о местоположении космического корабля в межпла¬
нетном путешествии имеет весьма существенное значение.
Если предположить, что на определенных интервалах расхо¬
дуется фиксированная доля / от веса космического корабля,
то полный вес можно вычислить из следующего уравнения:
1
где п — число пройденных интервалов. Для / = 0,7% и
п = 16 (соответствует 140 суткам при интервалах, равных
200 час) расход топлива равен
W = W0 \(п — 1)/] = 0,105 W0.
Это достаточно большое количество топлива, если считать,
что топливо, необходимое для посадки и для возвращения
в атмосферу, также помещается на космическом корабле.
Поскольку проблема является по существу линейной, можно
полагать, что если секстант был бы механизирован и его
погрешность сокращена до величины порядка, например, 0,05',
то величина W подобным же образом уменьшится до 0,01 W0.
Возникает вопрос, возможно ли, не изменяя курса во
время полета, корректировать его только в период непосред¬
ственного приближения к планете. Для ошибки, составляющей
1 мрад по курсу в полете на расстояние 240 000 000 км, косми¬
ческий корабль смещается с курса на 240 000 км. Если кор¬
рекция была введена з тот момент, когда до конца пути
оставалось 8 000 000 км, потребовалось бы около 40% веса
брутто космического корабля, чтобы выполнить одно это из¬
менение. С помощью новых видов топлива с гораздо более
высокой удельной тягой, конечно, удастся улучшить это поло¬
жение.

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ 7
Миккелуэйт, Томпкинс, Парк
В статье обсуждаются условия, выполнение которых обеспечивает по¬
лет к Венере по баллистической траектории. Условный случай анализа в
пространстве с двумя измерениями сравнивается с реальным случаем про¬
странства трех измерений. Определяются требования, которым необходимо
удовлетворить на конце активного участка траектории, чтобы получить
оптимальное решение проблемы управления, полезной нагрузки космиче¬
ского корабля, надежности, аэродинамических ускорений, коррекции в
середине полета и захвата летательного аппарата полем тяготения пла¬
неты-цели. Обсуждаются также вопросы, относящиеся к срокам запуска,
географической широте места старта, и проблемы, связанные с созданием
межпланетных систем связи.
ВВЕДЕНИЕ
При проектировании межпланетных объектов одна из .
основных проблем заключается в согласовании требований,
предъявляемых большой протяженностью межпланетных
баллистических траекторий и зависимостью их от малых
первоначальных возмущений. Другими словами, динамиче¬
ский и геометрический аспекты проблемы должны рассма¬
триваться в соответствии с требованиями точности. Требова¬
ния, которые предъявляются для обеспечения необходимой
скорости и управления в сочетании с техникой контроля па¬
раметров орбиты, должны рассматриваться совместно как
при проектировании космических кораблей, так и при реше¬
нии противоречия между необходимой полезной нагрузкой и
требованиями высокой точности.
Строгий анализ этой задачи в общем случае связан с
ориентацией оси вращения Земли, ориентацией плоскости
орбиты Земли и плоскостей орбит других планет и требует
в конечном итоге точного определения этих орбит. Это в зна¬
чительной степени справедливо и для околоземного спутни¬
ка. Хотя рассмотрение задачи в пространстве трех измере¬
ний обычно не является решающим фактором при проекти¬
ровании космического объекта, при расчетах полета на Луну
им не следует пренебрегать. Даже предварительный анализ
*) Mickelwait А. В., Tompkins Е. Н., Park R. A., IRE Trans,
дп Milit. Electronics, Mil-3, № 4, 149—159 (October 1959).

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ
31
межпланетных полетов показывает, что ошибка у цели с точ¬
ки зрения полезной нагрузки и точности может иметь тот же
порядок, что и рассматриваемая величина, если для упро¬
щения задачи предполагается анализировать случай двумер¬
ного пространства.
Основное внимание в настоящей статье уделяется
исключительно баллистическим полетам, т. е. полетам, при
которых орбиты за пределами окрестности Земли не коррек¬
тируются; при этом учитываются ограничения, налагаемые
существующими в настоящее время двигателями и возмож¬
ностями систем наведения. Однако очевидно, что межпланет¬
ные рейсы даже при более грубых требованиях не могут
быть успешно проведены без введения уточняющей коррек¬
ции в середине или в конце полета. Поэтому необходимо
рассмотреть некоторые траекторные характеристики, непо¬
средственно относящиеся к этим проблемам.
НИ НЕМАТИКА ДВУХ ИЗМЕРЕНИЙ
Допустим, что Земля и планета-цель движутся по круго¬
вым орбитам и что плоскости их орбит совпадают с плоско¬
стью земного экватора. Далее предположим, что объект за¬
пущен и движется в этой общей экваториальной плоскости.
Для аналитического решения сложной задачи с многими
действующими силами, обусловленными притяжением Солн¬
ца и всех планет одновременно, предположим, что орбита
космического объекта состоит из трех фаз (фиг. 1). Первая
фаза — это гипербола запуска с фокусом в центре Земли,
определяемая исключительно полем земного тяготения; вто¬
рая— эллипс с фокусом в центре Солнца, определяемый
только полем тяготения Солнца и сопрягаемый с гиперболой
запуска, и третья — аналогично первой — гипербола сближе¬
ния, в фокусе которой находится планета-цель, а параметры
определяются гравитационным полем этой планеты.
В момент запуска космический корабль, запускаемый
с Земли, движется со скоростью 30 000 м!сек вокруг Солнца.
При запусках на Венеру или Марс космический корабль по¬
кидает Землю со скоростью 10 000—12 000 м/сек относитель¬
но Земли. Во время преодоления поля земного тяготения
движение, как указывалось, происходит по гиперболе отно¬
сительно Земли. При этом к орбитальной скорости Земли
Добавляется (если запуск осуществляется в сторону Марса)
или из нее вычитается (если запуск осуществляется в сто¬
рону Венеры) только около 3000 м/сек. Хотя в принципе

а
Фиг. 1. Три фазы полета для плоской системы координат.
а —начальная гипербола относительно Земли; 6 — эллиптическая орбита вокруг Солнца;
о —гипербола сближения относительно Венеры.
Орбита космического корабля — эллипс, определяемый тяготением Солнца.
Выведение корабля на эллиптическую орбиту вокруг Солнца производится при положе¬
нии Земли, соответствующем * = 0.
т>3 — скорость Земли; v^— скорость космического корабля относительно Земли по оконча¬
нии активного участка траектории.

трехмерные межпланетные траектории
33
возможно появление значительной пространственной ошибки
за счет влияния поля тяготения Солнца (в системе двух из¬
мерений— за счет радиальной составляющей поля тяготения
Солнца), при некоторых обсуждаемых ниже ограничениях,
налагаемых на условия запуска и конца активного участка,
можно считать эту ошибку пренебрежимо малой. Поэтому
эти источники ошибок в дальнейшем не будут рассматри¬
ваться. Проблема наведения упрощается, если в конце ак¬
тивного участка выполняются определенные условия, обеспе¬
чивающие нужную скорость при переходе космического ап¬
парата в поле тяготения Солнца.
Когда же требования, диктуемые поставленной задачей,
достаточно строги, например если желательно попасть в опре¬
деленную точку Венеры, то необходимо учитывать влияние
гравитационного поля Солнца и в средней части курса для
уменьшения ошибки надо произвести коррекцию. Кроме
того, следует отметить, что недостаточно точное знание опре¬
деленных физических констант, особенно размеров солнеч¬
ной системы, приводит к неточности в определении положе¬
ния и скорости. Однако современные оценки ошибки, возни¬
кающей в результате неточного знания астрономической
единицы, показывают, что по сравнению с другими источни¬
ками ошибок ею можно пренебречь даже при вдвое боль¬
шей погрешности, чем современные погрешности в экспери¬
ментальном определении этой величины.
На фиг. 1 , а— в представлены система координат и отно¬
сительное расположение Земли и Венеры в момент старта.
Из геометрических соотношений фиг. 1 очевидно, что условия
в солнечной системе, необходимые для успешного полета,
определяются уравнением
Рс) = ®В7>С» Рс)— МЫ	О)
при r = RB,
где Si —угол в солнечной системе координат, отсчитываемый
в направлении движения космического корабля между точ¬
кой выведения и точкой встречи корабля с целью; —
средняя угловая скорость Венеры; Т — общее время полета;
02 — первоначальный базовый угол Земли относительно Ве¬
неры; г— расстояние от космического корабля до Солнца;
Яв — средний радиус орбиты Венеры.
Согласно уравнению (1), свойства траектории по окон¬
чании активного участка полета определяются исключительно
скоростью выведения в солнечной системе координат
и углом |3С между vq и радиусом, направленным на
3 Зак. 876.

34
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЁТОМ
Солнце. Предположим, что день запуска фиксирован, т. е. 02
фиксировано. Этим определяется точное функциональное
соотношение между vc и |3с- Обращаясь к фиг. 1,6, видим,
что это соотношение не может быть однозначным, т. е. воз¬
можны два значения vc и рс, допустимые для данного дня
запуска; одно значение (орбиты первого класса) соответ¬
ствует моменту встречи, когда при г = Rb космический ко¬
рабль впервые пересекает орбиту Венеры, и другое значение
(орбиты второго класса) соответствует моменту встречи,
когда корабль вторично пересекает траекторию Венеры. По
ряду причин подобная классификация орбит является полез¬
ной. При построении системы класс орбиты в значительной
мере определяет один из важных параметров системы —
расстояние при передаче информации.
Для полета по орбитам второго класса обычно тре¬
буется большее время, чем для орбиты минимальной энергии
(147 дней до Венеры и 260 дней до Марса).
Так как планета-цель в конце траектории минимальной
энергии удаляется от Земли со скоростью 18 км/сек, то отно¬
сительно небольшое изменение времени полета может ра¬
дикально уменьшить (или увеличить) расстояние связи. Так,
например, погрешность скорости выведения всего на не¬
сколько сот м/сек может изменить расстояние передачи до
50 • 106 км.
Очевидно, что наибольший эффект получается, когда
вектор v^ коллинеарен вектору скорости Земли и3 и рс =
= 90°. Если величина Voo фиксирована, а направление изме¬
няется, то Vc вращается так, что рс становится не равным
90°, и это приводит к увеличению | I (фиг. 2). Большее зна¬
чение | vq | соответствует меньшему проникновению в орбиту
Венеры. При Рс = 90° снижение | ^оо ! увеличивает | 0с | до
тех пор,, пока не совпадут две точки, в которых космический
корабль пересечет орбиту Венеры. В этом случае траектория
космического объекта касается орбиты Венеры при г = Rb
и корабль при движении от места запуска до места встречи
перемещается точно на 180° относительно Солнца (так назы¬
ваемый эллипс Хомана). Меньшие значения | 'oj и соответ¬
ствующие им меньшие начальные значения энергий дают ор¬
биту, проходящую вокруг Солнца и полностью остающуюся
внутри орбиты Земли, но не соприкасающуюся с орбитой
Венеры.
Обращаясь к выражению (1), дающему соотношения
между 02, \vc\ и Вс, видим, что если рс и \vc\ выбираются

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ
35
из условия орбиты с минимальной энергией, то время за¬
пуска определяется однозначно. Для Земли и Венеры 02 из¬
меняется примерно на сутки. Для других величин б2 при
наиболее эффективном |3с = 90° потребуются меньшие ве¬
личины \vc\y так как две точки пересечения будут удаляться
от значения 01 = 180°. При этом предполагается большее
Фиг. 2. Соотношение между
относительными скоростями кос¬
мического корабля.
Фиг. 3. Превышение скорости
в конце активного участка Да над
минимальной в зависимости от
угла Ь2.
проникновение в глубь орбиты Венеры, чем при движении
по эллипсу Хомана, и поэтому более значительное снижение
первоначальной | ас |.
На фиг. 3 показано изменение скорости относительно
требуемой для плоского эллипса Хомана ‘) при увеличении
или уменьшении угла 02 относительно 54°. Превышение ско¬
рости приводит к тому, что уменьшается число дней,
в течение которых запуск на другие планеты возможен при
ограниченных энергетических ресурсах. С другой стороны,
в силу того что угловые скорости Венеры, Земли и Марса
совершенно различны2), необходимое взаимное расположе-
1) Эллипс Хомана или орбита минимальной энергии. — Прим. ред,
) Земля: со3 = 0,986°/средние солнечные сутки;
Венера: сов == 1,600°/средние солнечные сутки;
Марс:	=	0?524°/средние	солнечные сутки,
3*

36
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
ние планет периодически повторяется с так называемым
синодическим периодом, равным для Венеры 584 дням, а для
Марса — 780 дням. Однако следует отметить, что, если учи¬
тывается положение плоскостей орбит, время повторения
одинаковых условий для запуска значительно увеличивается.
Оптимальными датами для проведения межпланетных за¬
пусков являлись 7 июня 1959 г. в сторону Венеры, 11 ок¬
тября 1960 г. в сторону Марса и 7 января 1961 г. вновь
в сторону Венеры. В эти дни в соответствии с анализом,
проведенным в системе двух измерений, имеет место угол 02,
соответствующий минимальной энергии.
Помимо экономии энергии, траектория минимальной
энергии желательна и по другим причинам. Важнейшим
требованием в большинстве случаев является либо более
длительное нахождение космического корабля в окрестности
планеты-цели, либо более медленное вхождение корабля в
атмосферу планеты-цели для уменьшения торможения и на¬
грева. В любых случаях желательно снизить скорость сбли¬
жения. Как видно из фиг. 1,в, при инерциальных скоростях
цели и космического корабля порядка 30 000 м/сек даже не¬
большие отклонения скоростей корабля v06. и планеты Vb
МОГуТ ЗНаЧИТеЛЬНО ПОВЫСИТЬ ОТНОСИТеЛЬНуЮ СКОРОСТЬ ^относит-
Поэтому тангенциальное приближение в плоскости эллипса
Хомана может дать желаемую минимальную скорость сбли¬
жения. Решение задачи на участке сближения с планетой-
целью может быть сделано более точным при использовании
условий перехода в гиперболу на этом участке. Используя
формулу сохранения накопленной энергии и выражение
угловых моментов относительно планеты-цели как единич¬
ного тела, получим соотношение между параметром встречи
6, скоростью сближения ^относит и минимальным расстоя¬
нием Д на которое корабль приближается к планете:
Параметр встречи равен величине промаха мимо цели
при отсутствии какого-либо притяжения планетой-целью.
Величина GMB является произведением универсальной
гравитационной постоянной на массу планеты-цели. Для
столкновения расстояние D должно быть равно радиусу
цели1). Для наименьшей возможной скорости сближения
9 Радиус Венеры ^ 6310 км, радиус Марса ^=3370 км,,
(2)

18000 г
22800 24000 25200 26400 27600
«£, м/сек
Фиг. 4. Коэффициент промаха db/dvc в функции от скорости
корабля для трех углов (Зс в солнечной системе координат.
м/сек
Фиг. 5. Коэффициент промаха дЬ/д$с в функции скорости корабля v
для трех значений угла £с в солнечной системе координат.

38
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
с Венерой, равной 2700 м/сек, максимально возможный
параметр столкновения равен удвоенному значению D (т. е.
действие гравитационного поля Венеры как бы удваивает ее
геометрические размеры).
Очевидно, что с этой точки зрения желательно уменьшать
^относит До минимально возможной величины.
АНАЛИЗ ЗАДАЧИ НАВЕДЕНИЯ НА ПЛОСКОСТИ
В первом приближении изучение зависимости траекто¬
рии от ошибок в конце активного участка можно провести
с помощью уравнения эллипса в солнечной системе коорди¬
нат. Из (1) получаем выражения
и
определяющие расстояние от планеты-цели до точки пересе¬
чения ее орбиты с траекторией космического корабля при
погрешностях Д^с и Дрс- Однако эта величина не является
действительной величиной промаха вследствие рассеяния
при выводе на орбиту, так как космический корабль дости¬
гает наибольшего сближения с целью обычно до или после
пересечения орбиты планеты-цели. Для оценки указанной
зависимости орбиты пригодны как изменения величины наи¬
большего сближения D, так и вариации параметра встречи
Ь. Последний употребляется чаще, так как это упрощает рас¬
четы. Если скорость сближения изменяется в небольших
пределах, можно определить максимально допустимую дис¬
персию 6, обеспечивающую успешное проведение запуска.
Выражение
Д£макс= (-^Г Д,УС) + (^Г АРс)2] k	(3)
определяет допустимую дисперсию рс и vc в пределах этого
небольшого диапазона скоростей сближения. В выражении
(3) предполагается, что Д^с и Дрс являются случайными,
независимо распределенными величинами,

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ
На фиг. 4 и 5 показано изменение так называемых коэф¬
фициентов промаха db/dvс и db/d$G при изменении условий
вывода на орбиту.
Необходимо отметить, что коэффициенты промаха
дЬ/д|Зс-^0 и db/dvс-^0 при скоростях, соответствующих ми¬
нимальной энергии. На фиг. 4 и 5 приведены кривые только
для орбит первого класса, кривые db/dv с для орбит второго
класса не имеют нуля в зависимости от скорости.
Результаты анализа в системе двух измерений не могут
быть широко использованы по двум причинам. Во-первых,
в анализе не учтено влияние угла р0 (см. фиг. 1). Как видно
из фиг. 1, изменение |Зо при прекращении работы двигателя
изменяет направление v^, но не изменяет ее величины. Од¬
нако по мере изменения направления v^ изменяется вели¬
чина как |3с, так и \vG\. Аналогично с изменением \v0\ из¬
меняется 1^1 и, следовательно, одновременно gc и \vc\.
Только тогда, когда Voo становится коллинеарным с v3, ро
и v0 непосредственно взаимодействуют с соответствующими
силами солнечной системы. Однако, как мы увидим ниже,
рассматривая траекторию в пространстве трех измерений,
очень трудно создать v^, параллельное v3, за исключением
особого случая взаимного расположения Земли и Венеры.
Во-вторых, при введении третьей степени свободы соотно¬
шения между условиями запуска и условиями выведения
усложняются. В результате четко выраженные минимумы
коэффициентов промаха выравниваются и в отдельных кон¬
кретных случаях практически исчезают совсем. Вследствие
этих недостатков анализа на плоскости необходимо ввести
третье измерение, что усложняет общие аналитические вы¬
ражения, учитывающие достаточно точное знание парамет¬
ров солнечной системы, дисперсии запуска и рассеяния при
встрече J).
АНАЛИЗ ЗАДАЧИ НАВЕДЕНИЯ В ПРОСТРАНСТВЕ
Хотя плоскости орбит Земли и Венеры наклонены друг
к Другу под очень малым углом (~ 3,4°), рассмотрение за¬
дачи в системе трех измерений для баллистических траекто¬
рии сильно влияет на энергетику, управление и характер
сближения с целью.
став^ ^олный анализ в системе двух измерений дан в работе [1], пред-
Амстердаме 25 ^30 конгРесс^ Международной федерации астронавтики в

40
I. ОВЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЁТОМ
А.	Энергетические соотношения
Допустим, что запуск произведен с начальной скоростью
v0 в системе координат S3 с началом в центре Земли (но не
вращающейся вместе с ней). Так как запуск производится
в непосредственной близости к Земле, то движение совер¬
шается вдоль гиперболической орбиты и вектор скорости по¬
степенно приближается к асимптоте этой гиперболы, а его
модуль постепенно становится равным величине Если
скорость Земли относительно Солнца v3, то сумма векторов
^оо и *з’ обозначаемая vc, является скоростью космиче¬
ского корабля в солнечной системе координат. С достаточ¬
ным приближением можно считать, что орбита объекта бу¬
дет лежать в плоскости, проходящей через вектор vc и
центр Солнца. При этом, как показано на фиг. 6, угол между
эклиптикой (плоскостью орбиты Земли) и плоскостью орби¬
ты космического корабля будет /с, а угол между vc и ра¬
диусом-вектором, направленным от космического корабля
к Солнцу, будет (Зс. Величины ис> /с и (Зс характеризуют
условия запуска космического аппарата в трехмерной сол¬
нечной системе координат.
Согласно фиг. 7, наклонные плоскости орбит Земли и Ве¬
неры пересекаются по линии АВ (линии, соединяющей точки
пересечения орбит). Сначала предположим, что угол между
этими плоскостями равен нулю, т. е. что обе орбиты распо¬
ложены в одной плоскости. Этот случай аналогичен уже опи¬
санному выше случаю пространства двух измерений, и эл¬
липс преобразования Хомана будет при 02 = 54°. Для реаль¬
ной солнечной системы угол наклона к плоскости орбиты Ве¬
неры не равен нулю, и для каждого синодического периода

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ
41
минимум энергии в пространстве двух измерений полу¬
чается при угле 02 = 54°, который может располагаться в
разных местах земной орбиты. Допустим, что при положе¬
нии Земли, изображенном на фиг.- 7, 02 = 54°. Если запуск
произведен при ic = 0°, т. е. в эклиптике, то космический
объект может достичь Венеру только в одной точке <0, —
точке пересечения траекторий на восходящей ветви, где ор¬
бита Венеры пересекает плоскость эклиптики. Однако для
Северный небесный
полюс
Фиг. 7. Трехмерное представление орбит Венеры, Земли и траектории
космического корабля.
АЛ —линия пересечения плоскостей эклиптики и орбиты Венеры; С —точка взлета;
CD — линия пересечения орбиты корабля и эклиптики; Л—точка встречи корабля с Вене¬
рой; EF — линия пересечения орбит корабля и Венеры; у — направление на точку весеннего
равноденствия; — точка пересечения на нисходящей ветви орбиты Венеры;	точка
пересечения на восходящей ветви орбиты Венеры.
такой траектории 01 намного меньше 180°, что требует боль¬
ших скоростей движения объекта и более значительных за¬
трат энергии при изменении vc и (Зс чем в случае двух из¬
мерений. Можно увеличить время полета и достигнуть Вене¬
ры в точке пересечения траекторий ^ на нисходящей ветви,
но и при этом также требуются большие затраты энергии.
Теперь рассмотрим случай, когда /с отличается от нуля,
случае двух измерений минимальная энергия затрачи¬
вается при условии, что корабль во время полета от точки
выведения до точки встречи с планетой описывает вокруг
олнца в солнечной системе координат угол, равный 180°.
зучение фиг. 7 показывает, что величина 01 = 180°

42
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
в пространстве трех измерений возможна только в том слу¬
чае, когда траектория движения проходит почти через полюс
эклиптики (/с ~ 90°), причем для осуществления полета
требуются предельно большие скорости (> 30 000 м/сек).
12 2 СО
11900
11600
11300
t
0 =180°
^ Траектории i Траектории
I типа *	//	типа
\\^32°
Рс~889
Ле-869
_L
_L
50	100	150	200
Угол 0°
_L
J
250	300
Фиг. 8. Скорость в конце активного участка v0 в зависимости
от угла 0, для различных углов вектора скорости рс (в случае
полета на Венеру в 1961 г.).
	траектории	второго	класса; 	 траектории	первого	класса.
Рассмотрим этот вопрос более подробно с точки зрения
реальных энергетических требований.
На фиг. 8 представлены скорости в конце активного
участка v0 в функции угла 0j при постоянном значении (Зс
для полета на Венеру в 1960—1961 гг. Каждая точка на
этой кривой соответствует определенным значениям {х>с, /с}
т. е. определенным датам запуска и времени полета. На
этом графике приведены следующие классификации орбит:

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ
43
Траектория I типа — для угла полета	б, 180°;
Траектория II типа — »	»	»	б, > 180°;
Траектория I класса—объект достигает Венеры при первом пересечении
ее орбиты;
Траектория II класса—объект достигает Венеры при втором пересечении
ее орбиты.
На фиг. 9 скорость v0 представлена в зависимости от
даты запуска для постоянных величин |3с. Согласно фиг. 8
и 9, в пространстве трех измерений полет	на	Венеру	с	мини¬
мальной затратой энергии в	1960—1961	гг.	приходится
12200
11900
Траектория
// типа
| 11600
11 300
Г92/
^ Огибающая минимальных I
скоростей для траекто¬
рии 1 типа
П
__1_
JL
JL
1 дек. 15дек.	1 я не.	15 ян в.	1февр. 15cpeep. 1 марта
1960 г
Дата запуска
1961г.
Фиг. 9. Скорость в конце активного участка v0 в зависимости от даты
запуска для различных углов вектора скорости рс.
 траектории
второго класса; 	 траектории	первого	класса;	—	пересечение
орбит Земли и Венеры на восходящей ветви.
на 15 января 1961 г. (т. е. через месяц после пересечения Зем¬
лей орбиты Венеры) при рс = 90° и 0,= 150°.
При этом полете v0 = 11 300 м/сек (примерно на 90 м/сек
больше абсолютной минимальной скорости в случае про¬
странства двух измерений, /С=1,Г, vc = 27 400 м/сек и
время полета tf = 126 дней. Траектория объекта наклонена
к пл°скости орбиты Венеры под углом ~ 4,3°. В день за¬
пуска Земля опережает Венеру на ~36° (вместо угла 54°,

44
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
определяемого при анализе, проведенном в случае двух из¬
мерений).
Графики фиг. 8 и 9, как и фиг. 7, показывают, что для
получения угла 01, близкого к 180°, должна быть затрачена
(Эс=58“
в,‘197' ic=-7,6‘,	в
tf=mсуток, vc=27234 м/сек, D =32-10 км
11900 b	!>	e,=	103’ic=-2,l°,iB=-2,2\
tr-95 суток, v =25710 м/сек,
4
\ 11600
b°
11 zoo
6,=172Uc=6,0°,iB*-3,Z
tf=l‘fS суток,
к,=27180 м/сек,
D=89-/06km
44 -10 km
t
9^264* ic=-0,2*
ib= J, 4 °, tf=178 суток
ту = 26010 м/сек
c D=18S-106km jo
в,=247° ic=-2,9‘, iB=3,2‘
t.=173 суток, ir=26610м/сек,
■f * C D=16S10skm
'в,=759; ic=0,6' iB=-3,9°
tf=136 суток, vc=27075м/сек,D=67-10Skm-
' / дек.	75 дек. ,	Jbhb. 15янв. 1 февр. 15февр. 1 марта
I960 г
Дата запуска
1967г
Фиг. 10. К анализу зависимости скорости в конце активного участка
от даты запуска (фиг. 9) при угле полета рс = 88°.
Дли разных точек этой кривой даны: Oj — угол в плоскости; 1q— угол между плоскостью
эклиптики и плоскостью движения космического корабля; / — угол между плоскостью
D
движения космического корабля и плоскостью орбиты Венеры; tj — время полета; vq —ско¬
рость космического корабля в солнечной системе координат; D — расстояние между Землей
и Венерой в момент наибольшего сближения космического корабля с Венерой.
значительная добавочная скорость сверх минимальной. На
фиг. 10 приведены более подробные параметры, соответ¬
ствующие нескольким точкам кривой фиг. 9 для j3c = 88°.
Рассмотрением этих точек можно начать анализ полета на
Венеру при следующих предпосылках.
1. Каждая рабочая точка на кривых определяется своими
значениями углов i. и 8, в точке пересечения орбиты Вене¬
ры. Эти углы в значительной степени определяют точность
управления траекторией и тем самым возможность успеш¬
ного осуществления полета. Они также определяют относи-

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ
45
тельную скорость сближения с Венерой и, следовательно,
требования, связанные с входом в поле тяготения планеты-
цели, встречей или посадкой.
2. Аналогично каждая точка соответствует определенной
дальности связи до момента завершения полета. Дальность
связи может изменяться от 41,5 до 250* 106 км, что в значи¬
тельной степени определяет в первые годы межпланетных
полетов возможность создания линии связи и контроля дей¬
ствительной траектории космического объекта.
3. Каждой точке соответствуют свои особые значения уг¬
лов в конце активного участка полета для данного места
запуска. Как будет показано ниже, эти углы могут быть не¬
приемлемы в силу того, что они неблагоприятно сказы¬
ваются на эффективности управления полетом на активном
участке траектории, или потому, что соответствующее им
место падения ракеты-носителя приходится на заселенные
местности.
Нельзя не отметить, что повышение скорости в конце
активного участка полета на небольшую величину по срав¬
нению с минимальной дает возможность осуществлять по¬
лет на Венеру ежегодно в течение нескольких месяцев и при
широком изменении типов траекторий в течение этого вре¬
мени. Это обстоятельство, связанное с энергетическими воз¬
можностями, следует учитывать при анализе полной си¬
стемы.
Б. Начальная часть траектории в пространстве трех
измерений
Определим энергетику полета при изменении условий в
конце активного участка траектории и покажем, как эти из¬
менения условий зависят от vc, Рс и /с, определенных
в солнечной системе координат.
При изучении энергетики полета удобно достаточно точно
установить время окончания активного участка траектории
(£о = дата + время дня) и применять следующие обозна¬
чения начальных условий (фиг. 11):
<*о — прямое восхождение1) конца активного участка;
8о склонение2) конечной точки активного участка;
*) Прямое восхождение — астрономическая долгота точки весеннего
равноденствия, которая является восходящей точкой пересечения орбиты
°Л 2?арОТНОСИТельно его кажущегося движения вокруг Земли,
плоек	ение	— астрономическая широта относительно экваториальной

46
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
го — геоцентрический радиус конечной точки активного
участка;
v0 — инерциальная скорость в конечной точке активного
участка;
Ро — угол между вектором инерциальной скорости v0 и
линией, проведенной в центр Земли;
А0—азимут v0 относительно севера, измеряемый в пло¬
скости, перпендикулярной геоцентрическому радиусу
в конечной точке активного участка.
Z Полюс
АГ р-^эклиптики
N г
Северный
экваториальный
полюс
Направление
на точку х -о-
весеннего
равноденствия
Плоскость
эклиптики
Плоскость
гиперболы
сближения
Экватор
Фиг. 11. Положение конца активного участка в геоцентрической
системе координат.
Я —точка конца активного участка; а0 —дуга BCD; К — дуга PD\ Го —длина вектора ОР;
А) —угол между плоскостью PON и плоскостью, проходящей через vQ и 0.
Эти величины при t = 0 являются начальными условиями
системы дифференциальных уравнений движения космиче¬
ского объекта и выбираются с таким расчетом, чтобы траек¬
тория прошла через точку, совпадающую с Венерой или рас¬
положенную около нее. Эти уравнения должны учитывать
сжатие Земли, притяжение Луны, Венеры и т. д. В солнеч¬
ной системе координат успешное управление может быть до¬
стигнуто воздействием на vc, рс и /с.
Пусть г0 = 6700 кму что соответствует ~ 320 км над по¬
верхностью Земли. Траектория активного участка обычно
лежит приблизительно в плоскости, проходящей через точку
запуска при старте и конечную точку активного участка в
момент времени to. Для сохранения накопленной энергии
желательно, чтобы свободный полет продолжался в этой же

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ
47
плоскости. Если выбраны протяженность активного участка
траектории, положение точки запуска и азимут Л0, то вели¬
чина So и долгота точки окончания активного участка опре¬
деляются однозначно. Прямое восхождение можно рассчи¬
тать по значениям долготы конечной точки активного участка
и момента выключения двигателей to. Остается выбрать три
параметра: азимут Л0, курсовой угол g0 и скорость в конце
активного участка Vq. На фиг. 12 показано значение А0
в функции от go Для постоянных значений скорости в конце
активного участка v0 при полете на Венеру с точкой запуска
на мысе Канаверал (шт. Флорида) 6 июня 1959 г. Эти кри¬
вые были получены с помощью счетной машины интегриро¬
ванием полного уравнения движения при начальных усло¬
виях, соответствующих полету, оканчивающемуся встречей
с Венерой. Различные точки кривых при постоянных Vo
соответствуют различным величинам ао, а следовательно,
различным временам окончания активного участка (и за¬
пуска) 1). Кривые для постоянных v0 приблизительно соответ¬
ствуют кривым при постоянных Для данной задачи и
рассматриваемого места запуска значения «возможных»
азимутов полета полностью связаны с орбитой в солнечной
системе координат и расположением планет. Кривые фиг. 12
показывают допустимые азимуты активного участка при за¬
пуске ракеты с мыса Канаверал.
Диапазон азимутов, «возможных» для выполнения поста¬
вленной задачи, должен быть сокращен с учетом проблем
безопасности, возникающих при падении на Землю отрабо¬
танных ступеней ракеты-носителя. Однако, используя «без¬
опасные» азимуты, можно получить неудовлетворительные
результаты с точки зрения энергетики, управления, дально¬
сти связи и т. д,
Эти проблемы можно проиллюстрировать на примере
возможного запуска на Марс 23 сентября 1960 г., когда
Земля находилась в точке осеннего равноденствия
(см. фиг. И). В этот день проблема полета на Марс пред¬
ставляет простую геометрическую задачу в силу того, что
при необходимой скорости угол /с = 0° и Рс = 90°. При этих
значениях /с и gc вектор v», и асимптота начальной гипер¬
болической траектории параллельны вектору скорости Земли,
а Voo и v3, определяющие движение космического объекта
по направлению к орбите Марса, суммируются. Осуществле¬
ние этих условий возможно, например, в случае полета
изм.>ПряМ0е восхожДение для фиксированной точки земной поверхности
изменяется при вращении Земли.

48
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
на север (азимут Л0 = 0°),при запуске в тот момент, когда мыс
Канаверал находится в плоскости, проходящей через ось
Земли и v3. Траектория запуска, лежащая в этой плоскости,
изображена на фиг. 13.
§ на Юг 180°
^ на Восток9О*
§М7 Север 0°
Х=77350 +
l.-ППО ТШТа“
и=77300
Траектории
II класса
70	7U	78
Ро»градусы
Фиг. 12. Зависимость азимута А0 от угла р0 для различных значений
скорости в конце активного участка vQ.
Полет на Венеру 6 июня 1959 г.; запуск с мыса Канаверал; конец активного участка
на высоте 6700 км от центра Земли
Если предположить, что активный участок покрывает 15°
земной поверхности, то для приведения Voo в положение,
параллельное v3, угол, описываемый начальной гиперболи¬
ческой частью траектории, должен быть равен 0Г = 113°.
Анализ показывает, что полет на Марс по траектории вто-

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ
рого класса с v0 « 11 500 м/сек и г0 = 6700 км может быть
осуществлен при /с = 0° и рс ^90° (эти условия обеспечи¬
вают близкое к минимальному значение Vo в системе трех
измерений для полета на Марс в 1960 г.).
Фиг. 13. Положение гиперболы запуска, находящейся в плоскости,
проходящей через вектор скорости Земли.
При данных величинах v0, г0, р0 угол 9Г можно рассчитать
по простой формуле для двух тел. Соответственно если из¬
вестны 0О, г0 и 0Г> то можно определить угол вектора скоро¬
сти р0 в конце активного участка. На фиг. 14 показаны зна¬
чения 6Г в зависимости от v0 для различных значений р0 и
Го = 6700 км. Из этого графика видно, что рассматриваемый
полет на Марс обеспечивается при £о ~ 72°.
Однако в целях повышения безопасности необходимо
увеличить азимут А0 от 0° до величины, равной, н.апример,
100—125°. Это может быть осуществлено посредством от¬
срочки запуска до тех пор, пока место запуска, перемещаясь,
по мере вращения Земли, на восток, не достигнет плоскости
начального гиперболического участка траектории (фиг. 15).
Днако при этом уменьшается 0Г и, как это видно из фиг. 14
Для постоянных значений v0y уменьшается go- Полученные
отсюда кривые р0 в функции от А0 подобны приведенным на
Фиг- 12. В действительности, однако, с целью увеличения
4 Зак. 87Q

v0, м/сек
Фиг. 14. Зависимость угла 0Г, лежащего в плоскости запуска,
от скорости в конце активного участка v0 для различных вели¬
чин Ро в конце активного участка.
Плоскость гиперболы
запуска
_ Траектория в пространстве,
описываемая мысом Канаверал
в зависимости от времени
запуска
..Экваториальная
плоскость
Фиг. 15. Вращение плоскости гиперболы запуска при изменении
времени запуска.

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ
51
эффективности энергетики полета go практически ограничена
в пределах 65—90° и действительный предел азимута имеет
место при go, не превышающих 65°.
В рассматриваемом случае при предполагаемой дате за¬
пуска требования обеспечения безопасности в заданном
районе делают запуск невозможным. Однако здесь имеется
несколько возможных решений.
1. Изменение первоначальных условий вывода в пределы
действия поля тяготения Солнца и (или) изменение даты
запуска с тем расчетом, чтобы Voo приобрело более удобное
направление. Это обычно вызывает дополнительную затрату
энергии на повышение v0 и может также привести к траекто¬
риям, нежелательным с точки зрения управления и канала
связи.
2. Запуск в более раннее время, когда плоскость траек¬
тории, проходящая через точку старта, ориентирована в на¬
правлении с северо-запада на юго-восток при направлении
запуска на юго-восток. При этом желательные величины g0
приводят к слишком большим величинам 0Г. Однако в этом
случае запуск космического корабля может производиться с
орбиты искусственного спутника, которая позволяет пройти
полпути вокруг Земли до тех пор, пока не будет обеспечена
подходящая величина 0Г. После этого последняя ступень мо¬
жет быть запущена на начальную гиперболическую часть
траектории.
3. Перемена места запуска.
Следует заметить, что некоторые или все перечисленные
варианты могут оказаться неприемлемыми. Приведенный при¬
мер только подчеркивает, что азимутальные условия запуска
могут очень сильно влиять на анализ первых межпланетных
полетов.
В.	Требования к наведению в системе трех измерений
После определения оптимальной межпланетной траекто¬
рии следует изучить ее отклонения в зависимости от вариаций
конечных условий активного участка. Это поможет устано¬
вить требования к системам наведения, действующим в тече¬
ние активного участка траектории. Но, как указывалось ра¬
нее, требования, предъявляемые к наведению, сильно зави¬
сят от выбора специальной некритичной траектории, которая
но сравнению с другими траекториями примерно в 10 раз
очУвствительна к ошибкам в задании началь^тх
условий.
4*

52
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
Оконечная (или предшествующая встрече) часть трехмер¬
ной межпланетной траектории может быть описана аналогич¬
но двумерному (плоскому) случаю. Гиперболу с центром в
планете-цели, по которой происходит сближение, можно оха¬
рактеризовать скоростью относительно этой планеты на боль¬
шом удалении от нее ^относит и параметром встречи Ь. Вектор¬
ная величина параметра встречи определяется как расстояние
Фиг. 16. Заключительная фаза сближения с планетой-целью.
наибольшего сближения, которое должно иметь место при от¬
сутствии притяжения (точнее, b является вектором, направ¬
ленным из центра планеты перпендикулярно асимптоте гипер¬
болы сближения). Таким образом, вектор b показывает на¬
правление и определяет расстояние наибольшего сближения
без учета действия гравитации планеты-цели. Чувствитель¬
ность промаха к изменению начальных условий (ао, So, |Зо, А0,
Vq, Го), заданных на Земле, может быть измерена с помощью
векторных коэффициентов промаха, определяемых следую¬
щим образом:
где j3m — коэффициент промаха полета по углам, Ат— по ази¬
муту и vm — по скорости.
Предположим, например, что оптимальной траекторией бу¬
дет та, чья асимптота проходит через точку встречи с плане¬
той (фиг. 16). Изменение |30 на 1° от номинала сдвинет траек¬

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ
53
торию относительно нуля, например, на место траектории,
обозначенной Г3. Величина рт будет служить мерой результи¬
рующего промаха (км/град).
11000	12000	13000
irQ у м/сек
11000	12000	13000
v0, м/сек
Фиг. 17. Зависимость коэффициентов промаха vm, и Ат
от величины скорости в конце активного участка v0.
Полет на Венеру 6 июня 1959 г. до прохождения Землей линии пересечения орбит.
Вернемся теперь к зависимости между (Зь и Л0, представ¬
ленной на кривых фиг. 12, и рассмотрим, как коэффициенты
промаха vm, pm и Ат изменяются для рассматриваемых точек
н^а кривых в зависимости от изменения даты запуска. На
фиг. 17 и ig приведены кривые зависимости vm, (3m и Ат от
vo для двух дат запуска на Венеру в июне 1959 г.1)
лите^ ^?ивые коэффициентов промаха были получены с помощью вычис-
Ций ,ЛЬЫ0И машины путем совместного решения системы уравнений вариа-
с нормальными уравнениями движения объекта.

54
t. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
Эти кривые скоростей соответствуют определенным вели¬
чинам Л о и ро при постоянных ао (что соответствует постоян¬
ному времени запуска) на графике |Зо в функции А0 (фиг. 12).
Расчеты, проведенные с помощью счетной машины, показы¬
вают, что обычно коэффициенты промаха, рассчитанные при
11000	12000	13000
uQt м/сек
vQ, м/сек
Ф и г. 18. Коэффициенты промаха vm, $т и Ат в зависимости
от величины скорости в конце активного участка v0.
Полет на Венеру 9 июня 1959 г. после прохождения Землей линии пересечения орбит.
постоянных значениях v0, меняются незначительно по сравне¬
нию со случаем изменения и0. Поэтому для отдельных точек
кривых Vo = const, соответствующих различным временам за¬
пуска, изменения коэффициента промаха будут малы даже
в том случае, если время запуска сдвигается на величину по¬
рядка 1 час.
Фиг. 17 и 18 дают представление о точности наведения,
требуемой при межпланетных баллистических полетах; так,

ТРЕХМЕРНЫЕ МЕЖПЛАНЕТНЫЕ ТРАЕКТОРИИ
55
типичная чувствительность к угловым ошибкам составляет от
70 ООО до 900 ООО км/град и к ошибкам по скорости — от
5900 до 118 000 км на 1 м/сек. Эта чувствительность сильно ме¬
няется в зависимости от класса орбит, скорости при запуске
ic) и отношения даты запуска к времени пересечения Зем¬
лей орбиты планеты-цели. Более того, условия некритичного
40000
5	6	7	8
Дата запуска
Максимальное значение
радиуса, начиная с которо¬
го происходит столкнове¬
ние для 1г^2700 м/сек
VМаксимальное значение
радиуса, начиная с которо¬
го происходит столкнове -
ние для	3300м/сек
Радиус Венеры
июнь 19592.
Фиг. 19. Остаточные составляющие промаха.
Полет на Венеру в июне 1959 г. Параллельные составляющие прецполагаются скомпенси¬
рованными в результате дополнительной коррекции.
запуска для v0, Р'о и А0 обычно не совпадают в одной и той
же рабочей точке на кривой, представляющей зависимость |Зо
от Л0, так что процедура оптимизации требует знания вели¬
чин каждой из ошибок при отсечке двигателя, которые систе¬
ма наведения не может устранить.
Эти исключительно высокие требования к допускам на
момент прекращения работы двигателя для межпланетных
баллистических полетов могут быть удовлетворены либо с по¬
мощью точных систем управления отсечкой, либо за счет
уточняющей коррекции по истечении. первых часов полета.
В последнем случае данные контроля траектории, полученные
в первые часы свободного полета, могут быть использованы
для точного расчета действительного положения в момент от¬
сечки двигателя, после чего требуемая коррекция может быть
определена и подана на борт космического корабля в виде
радиокоманды.
Изучение угловой ориентации векторных коэффициентов
промаха показывает, что для определенных дней и условий
в конце активного участка траектории эти векторы почти

56
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
коллинеарны. Угловые ошибки по своим проявлениям эквива¬
лентны ошибкам по скорости и могут быть скорректированы
при уточнении скорости корабля. Точность, с которой может
быть достигнута коллинеарность, существенно определяется
датой запуска. Предположим, что вектор $т образуется из
двух компонент (Зц и р параллельной и перпендикулярной
к вектору vm, а составляющая р(| устраняется с помощью уточ¬
няющей коррекции скорости. На фиг. 19 показаны вариации
Z?/w
0,2-70
\ !
Изменение lz на 1.5 м/сек ^	\	01-	/п	л	о
а	,.Поверхность Венеры
в конце активного	\	^	~J(	<	•
в конце активного
участка 0,3	0,2
0,6 05	^
на 15 м/сек на
20-й день после	НС! ?пм^сАИ
запуска	40	30-и день
0,2	0,3	Ofi-IO1
-'О,
а 'О	AS^.Ha	i5м/сек на
-0,2-l(fa&& г^Ус>^80-и день
Фиг. 20. Изменение величины и направления вектора параметра встречи
в результате действия коррекции на основном участке полета в зависи¬
мости от момента коррекции.
Полет на Венеру 8 июня 1959 г.; v<> = 11 300 м/сек; ось Г* приблизительно параллельна
плоскости эклиптики; ось Z* перпендикулярна асимптотическому вектору скорости.
остаточного промаха А^ и после уточняющей коррекции
(на 7з дугового градуса ошибки А0 и (30) в функции даты за¬
пуска для полета на Венеру в 1959 г. Точками отмечены наи¬
более коллинеарные рабочие области для каждого дня.
В дополнение к уточняющей коррекции в начале траекто¬
рии может применяться коррекция в ее средней части, причем
используются результаты длительных наблюдений за траек¬
торией. Предположим, что ось космического корабля стаби¬
лизирована в полете относительно солнечной системы коор¬
динат и что стабилизация произведена в конце активного
участка, как это, например, возможно в случае стабилизации
космического корабля с помощью вращения. Тогда вектор
Дbky представляющий собой отклонение вектора параметра
встречи от номинального значения з случае коррекции, про¬

ТРЕХМЕРНЫЕ МЁЖПЛАНЁТНЫЕ ТРАЕКТОРИИ
57
веденной в середине курса, будет вращаться в плоскости век¬
тора промаха в зависимости от момента коррекции (фиг. 20).
Мы можем разложить действие ошибки выведения на две со¬
ставляющие: параллельную vm и перпендикулярную к vm, и
устранить параллельную составляющую во время проведе¬
ния уточняющей коррекции в начале траектории, а перпенди¬
кулярную составляющую — во время уточняющей коррекции
в подходящее для этого время в середине курса.
Коррекцией в середине курса можно также устранять й
остаточную параллельную составляющую, причем в этом слу¬
чае имеется преимущество, заключающееся в значительно бо¬
лее точном знании орбиты в результате наблюдений за ней в
первые месяцы полета. Такая схема коррекции имеет то пре¬
имущество, что требует минимального количества бортового
оборудования и переносит задачу определения необходимой
коррекции на Землю с использованием уже имеющегося обо¬
рудования, необходимого для телеметрии и контроля траекто¬
рии.
выводы
На основании анализа в трехмерном пространстве проб¬
лем, связанных с межпланетными баллистическими траекто¬
риями, показано, что условное двумерное рассмотрение недо¬
статочно. Так, если сравнить фиг. 4 и 5, экстраполируя их к
условиям в конце активного участка в поле земного тяготе¬
ния с соответствующими им фиг. 17 и 18, то окажется, что
двумерный коэффициент промаха будет отличаться от трех¬
мерного в 5—10 раз. Более того, при двумерном анализе не
рассматриваются многие практические проблемы, такие, как
энергетические соотношения, безопасность запуска, скорость
сближения с целью и другие, имеющие существенное значение
для решения поставленной задачи.
В статье делается попытка показать, что при правильном
анализе траекторий, при простых способах стабилизации
космического корабля, таких, как стабилизация с помощью
вращения, и в случае применения относительно грубых си¬
стем наведения можно осуществить межпланетные запуски
космических аппаратов в дни, когда для полетов требуются
инимальные энергетические затраты. Однако если скорости
лижения с целью не являются важным условием, как это
ВатГТ в случае жесткой посадки, или если не рассматри-
являщ3аДаЧИ канала связи> т0 для запуска на Венеру
ются подходящими каждые 6 или 7 мес. синодического

э8
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
периода; подобный же период является подходящим и для
запуска на Марс. Такие траектории требуют более сложного
анализа техники наведения как на активном участке, так и
на курсе.
ЛИТЕРАТУРА
1. McGuire J. В., Smith О. К., Accuracy Requirements for Interplane¬
tary Ballistic Trajectories, Rep. TR-59-0000-00682, Space Technol,
Labs., 1959.

О РАСЧЕТАХ ОРБИТ И ПРОБЛЕМАХ
УПРАВЛЕНИЯ ДАЛЬНИМИ КОСМИЧЕСКИМИ
РАКЕТАМИ1)
К о ой
В статье рассматривается осуществление запуска дальних космических
ракет, стартующих с некоторой эллиптической орбиты и наводимых с на¬
земных станций с помощью средств радиосвязи и радиоуправления. Дает¬
ся в общем виде анализ задачи орбитальных расчетов в связи с пробле¬
мой управления космической ракетой.
ВВЕДЕНИЕ
В настоящей статье рассматривается проблема управле¬
ния дальней космической ракетой. Предположим, что эта ра¬
кета должна достигнуть области вблизи Луны или прибли¬
зиться к ней; при этом ракета вновь должна вернуться в
район Земли.
Предположим, что ракета сначала выводится на эллипти¬
ческую орбиту вокруг Земли на некотором близком расстоя¬
нии от нее и затем после некоторого времени свободного по¬
лета стартует по касательной к этой орбите. За короткий про¬
межуток времени полета на активном участке траектории
ракета в точке отсечки двигателя, имея определенную ско¬
рость, все еще будет находиться в окрестности Земли и с этой
точки начнет свой свободный дальний космический полет.
Чтобы попасть на Луну или совершить облет вблизи нее, сле¬
дует с предельной точностью определить начальное положе¬
ние в пространстве и во времени, а также начальную скорость
как по величине, так и по направлению. Преимущество эллип¬
тической орбиты, находящейся вблизи Земли, заключается
именно в том, что перед вторым стартом (по касательной
к эллиптической орбите) начальное положение и начальная
скорость могут быть определены с большой точностью по¬
средством астрономических наблюдений и расчетов и в слу¬
чае надобности может быть произведена необходимая
коррекция. При этом требуется, чтобы положение продольной
5qq J95900У ^ Ргос- IXth Intern, Astronaut. Congress, I, pp. 469^

60
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
оси ракеты- на небесной сфере можно было определить на¬
земной станцией контроля1). Поэтому на ракете, стартующей
с эллиптической орбиты вблизи Земли, должны быть уста¬
новлены телеметрическая система для передачи необходимой
информации наземным станциям, а также система радио¬
управления, которая направляла бы ось ракеты и регулиро¬
вала тягу во время разгона ракеты. Далее, очевидно, что на
активном участке траектории от Земли до промежуточной
эллиптической орбиты ракета также должна управляться. Это
управление можно осуществить либо с помощью установлен¬
ного на борту автономного автопилота, работающего в соот¬
ветствии с заданной программой, либо с помощью установки,
получающей команды через систему радиоуправления от на¬
земной станции.
Для составления принципиальной схемы управления не¬
обходимо более подробно рассмотреть движение как на ак¬
тивном, так и на пассивном участках траектории. При этом
целесообразно разбить траекторию полета ракеты на отдель¬
ные участки:
1) активный участок траектории от Земли до промежу¬
точной эллиптической орбиты;
2) промежуточное движение, происходящее по законам
Кеплера;
3) активный участок траектории после старта по каса¬
тельной к промежуточной эллиптической орбите;
4) космическую траекторию под воздействием сил тяготе¬
ния Земли, Луны и Солнца.
ПРИМЕНЯЕМЫЕ СИСТЕМЫ КООРДИНАТ
На первом активном участке траектории практически ис¬
пользуется прямоугольная система координат xyz, жестко
связанная с Землей. Пусть начало 0 этой системы (фиг. 1)
совпадает с центром Земли, а ось z — с осью суточного вра¬
щения Земли. Тогда плоскость ху будет совпадать с эквато¬
риальной плоскостью Земли. Далее, пусть xyz является вто¬
рой прямоугольной геоцентрической системой координат, ко¬
торая для t = 0 совпадает с системой xyz, но не вращается
относительно небесного пространства...
!) Здесь мы предполагаем, что направление тяги совпадает с продоль¬
ной осью.

о РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 61
Если через со обозначить угловую скорость суточного вра¬
щения Земли, то для перехода от системы хуг_ к системе хуг
можно воспользоваться следующими уравнениями (фиг. 2):
у == х cos о>/ — у sin со/;
х = х sin со/ + У cos со/	^
и для обратного перехода
х = х cos со/ —|— у sin со/;
у = — a: sin со/ + у cos со/.
(16)
Система используется для космического движения ракеты
(вне атмосферы). Обозначим через R радиус Земли, а через
2
Фиг. 1. Система координат с началом Ф иг. 2. К выводу формулы (1а)
в центре Земли.	Qcb	z	перПендиКуЛЯрна к плоскости
чертежа и направлена на наблюдателя
go — ускорение силы тяжести на поверхности Земли. Единич¬
ные векторы, направленные по осям х, у, г, обозначим через
i, j, к, а единичные векторы, направленные по осям х, у, z, —
через i, j, k.
ОПИСАНИЕ АКТИВНОГО УЧАСТКА ТРАЕКТОРИИ ВЗЛЕТА
В СИСТЕМЕ КООРДИНАТ xy_z БЕЗ УЧЕТА АЭРОДИНАМИЧЕСКИХ СИЛ
Предположим, что ракета стартует вертикально в точке
£o£?zo на поверхности Земли. Тогда R = V*о+2о+'£<>• Пред¬
положим также, что ракета состоит из четырех ступеней.
чятт1оеЛЬНЫе стУпени и «субракеты» в дальнейшем обозна-
значаютп соответствии с работой [1] (фиг. 3). Субракеты обо-
ступе™!! р™скими Цифрами IV, III II, I, а отдельные
арабскими цифрами 4, 3, 2, 1. На фиг. 3 субракета

62
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
IV представляет собой четырехступенчатую ракету с полным
запасом топлива. Предполагается, что ступени 4, 3, 2 исполь¬
зуются на взлетном участке траектории, так что на проме¬
жуточную эллиптическую орбиту выводится только субра¬
кета II, а старт с эллиптической орбиты
производит только субракета I.
Если космическая ракета должна по¬
пасть на Луну или совершить облет во¬
круг нее и если по предположению старт
с эллиптической орбиты осуществляется
по касательной к орбите под воздей¬
ствием силы тяги, постоянной по вели¬
чине и направлению, то в частном слу¬
чае плоскость эллиптической орбиты мо¬
жет совпадать с плоскостью лунной ор¬
биты. В общем случае для произвольной
точки старта на земной поверхности
взлетная траектория будет представлять
собой пространственную кривую.
Если ха, _уа, za и ха, Уа, za, значения
координат и компонент скорости *) в
начале промежуточной орбиты, то начало *ода:о_ и конец
ха, Уа, za (точка отсечки двигателя ступени 2) активного
участка траектории известны. Известно далее на¬
правление касательной к траектории в точке х0у0гоУ ибо старт
в этой точке является вертикальным, поэтому x0/~R, yo/R, z0/R
представляют собой направляющие косинусы этой касатель¬
ной. Направляющие косинусы в конечной точке взлетного
участка определяются по составляющим скорости ха, уа, zay
которые мы будем считать заданными.
С целью упрощения предположим, что аэродинамическими
силами, воздействию которых ракета подвергается при полете
в атмосфере, можно пренебречь. Тогда возможно определить
в пространстве и во времени весь активный участок взлета и
при этом удовлетворить указанным выше условиям в начале
и в конце траектории.
Обозначим координаты на активном участке взлета сле¬
дующим образом:
x = x(t),	Zj=z_(t),	(2)
где t — текущее время, a t = 0 — момент старта.
Фиг. 3. Составные
части ракеты.
/Я—полезная нагрузка..
/7
‘) Точки над символами обозначают производную по времени. — Прим.
реф.

О расчетах орбит и управлении космическими ракетами 63
Если эти выражения определены численно (в табличной
форме), то всегда возможно представить х, у и z с помощью
аппроксимирующих полиномов вида
П (t - О = (< - А) V - h) • • • V - tk-i) (* - h+i) • • • (* - in)
причем точки th (k = 1, 2, 3, ..., ti) распределены во всем ин¬
тервале времени полета по активному участку взлетной тра¬
ектории. Чем больше пу тем лучше достигаемая аппроксима¬
ция. Составляющие скорости ху у, z и составляющие ускоре-
жений (3).
Пусть т обозначает массу ракеты вместе с топливом, а
^относит — ускорение относительно системы xyz. Тогда, если
g — ускорение силы тяжести, S — тяга, v — скорость и F4 —
центробежное ускорение, то
(3)
и аналогичных выражений для у и z, где
и аналогично
1фк
ния х, у, z можно получить путем дифференцирования выра-
относит	^ I	"I	2171 (V X	т¥u
относит
ИЛИ
где Эуд — удельная тяга (тяга на единицу массы).
Отсюда
^уд=== ^ОТНОСИТ Н“ 2 (tt) X v) g	FЦ,	(4)
где
i	J	k
(о X v = О О (D f
xyz
g = — goR2 jr и Fu = m2x + jm2y + kco2z,

64	I. ОБЩЙЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЁТОМ
причем R — радиус Земли, a g0 — ускорение силы тяжести на
земной поверхности.
В проекциях выражение (4) записывается в виде
•Ч =	2*1+^2 + yJ+22),h ~ *2£,
5уд, = £ + ^*+g0R2 {х2 + yf+ zyh ~ “2У> ^	(4а)
Зул=г + &0^Z
I 60^ (JC2 + y2 г2)8/2 *
Если в выражениях (4а) x,_y,z,xyy^z^x±y±z_являются извест¬
ными функциями времени, то
^уду и ^уд*
также будут известными функциями времени:
5уд* = ^г(*). Sy*y = Fy(t), Sy^ = Fz_{t), )
5уд = /pW)7+[^Wf+[^W]2 = Fit), j (5)
Отсюда видно, что для получения нужной траектории взлета
удельная тяга в каждый момент времени должна иметь опре¬
деленную величину и направление, значения которых полу¬
чаются в том случае, если выражения (3) подставить в (4а).
Обозначим через с скорость истечения газов из сопла; то¬
гда
—=	=	W
Если двигатель работает от t = t0 до t = ti, то отношение
масс ракет в эти моменты равно
v
1 /с f F (t) dt
’ (6)
где mo обозначает начальную массу составной ракеты с топ¬
ливом, a mi — массу ракеты, когда топливо соответствующей
ступени израсходовано.
Пусть Ьвк, tti,, Ьв, — моменты прекращения работы двига¬
телей четвертой, третьей и второй ступеней ракет. Тогда со¬
ответствующие точки на орбите можно, получить из выраже¬
ний (2)./Если- г4, г3, г2 обозначают соотношения масс

о РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 65
бракет IV и III, Ш и II, II и I и если с4, с3, с2 представ¬
ит собой соответственно скорости истечения газов субра¬
кет IV, III. Н. т0> согласно формуле (6), можно записать
г4 = е 0
F (t) dt
7- J F{t)dt
C • , J
гя = е
dt
A
r2 = e B°
Введем следующие обозначения [1]:
(7)
мп
рп = -jjpi коэффициент полезной нагрузки п-й субракеты;
(8)
тк + тТ
Sn = — 	-—конструктивный коэффициент п-й ступени;
mkn
(9)
Мп — масса п-й субракеты вместе с топливом;
тк — масса конструкции п-й ступени;
т.
т — масса топлива п-й ступени.
Тогда
Мп
Мп— ТПт
(10)
Между величинами р, г и S существует следующее соотноше¬
ние:
S„-1
Рп = г„-г—р
(11)
которое можно получить из уравнений (8) — (10).
Полный коэффициент полезной нагрузки, характеризую¬
щий качество ракеты, равен
P=PiPi •••	=	(12)
ГДе обозначает полезную нагрузку субракеты I.
^ Зак. 876

66
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЁТОМ
Коэффициент полезной нагрузки для субракеты II можно
найти из формулы
(И>
где г2, г3 и г4 определяются выражениями (7). Пусть в мо¬
мент времени выключения двигателя tB^ субракета II попа¬
дает на эллиптическую орбиту, вторая ступень отделяется, а
ракета I начинает свой старт с эллиптической орбиты в мо¬
мент времени tcт. Если через tB обозначить момент времени
прекращения работы двигателя субракеты I, то для коэффи¬
циента полезной нагрузки субракеты I (отношение масс) по¬
лучим
%
LJ Fit) at
гх = е ст ,	(14)
где Ci — соответствующая скорость истечения газов из сопла.
Для полной четырехступенчатой ракеты формула коэффици¬
ента полезной нагрузки имеет вид
Р =	)	(	si-гг) ( si- г3) ( S*- г4) ’	(15)
где величины г определяются выражениями (7) и (14).
ДОМИНИРУЮЩЕЕ ВЛИЯНИЕ СН0Р0С7ЕЙ ИСТЕЧЕНИЯ
Очевидно, что сложность проблемы управления возрастает
по! мере увеличения числа ступеней ракеты. Из приведенных
выше формул следует, что минимальное число необходимых
ступеней зависит главным образом от величины скорости ис¬
течения. Для намеченной взлетной траектории активного уча¬
стка вывода на промежуточную орбиту вокруг Земли на вы¬
соте 500 км можно предположить* что
JF(t)dt^9,b км!сек (характеристическая скорость),
о
где F(t)=Syjll a tB — время работы двигателя на взлете.
Если для любой из ступеней (4, 3, 2) для скорости истечения
газов принять величину с *= 2',9' км/сек (что едва ли может
быть обеспечено химическими средствами) и S = 5 для ка¬
ждой из ступеней 4, 3, 2 (что также вряд ли возможно), то

о РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 67
соответствии с (15) получим для отношения полезной на-
грузки КО всей массе субракеты II
р - J-5/2.9 (	5-1	\»	216
г —С ^ ^ ^9,5/(2,У X 3) J —
Это значит, что для каждой тонны веса (включая топливо)
субракеты I, являющейся полезной нагрузкой субракеты II,
полный стартовый вес ракеты на Земле должен составлять
216 г.	в
Скорость спутника на промежуточной круговой орбите на
высоте 500 км составляет 7,6 км/сек. Эту скорость необходимо
увеличить до 10,6 км/сек, чтобы вывести субракету I на эл¬
липтическую орбиту с апогеем, равным расстоянию от Земли
до Луны. Предположим, что и в этой субракете может быть
получена скорость истечения с = 2,9 кн/сек. Тогда, полагая,
что промежуток времени второй фазы активного полета до¬
статочно мал (например, 2 мин), будем иметь следующее от¬
ношение масс субракеты I:
(10,6-7,6V2f9 ^ о
€	— О.
Поэтому для каждой тонны веса конструкции субракеты I
в этом случае потребуется 3 X 216 = 648 т стартового веса на
Земле. Согласно этим расчетам, /2 = 4 можно рассматривать
как минимальное число ступеней ракеты для полета к Луне
при условии, что мы располагаем только химическими сред¬
ствами. По-видимому, в этом отношении можно только на¬
деяться на увеличение скоростей истечения либо за счет хи¬
мических радикалов (реакция Н-ЬН = Н2), либо за счет
атомной энергии.
В случае применения атомной энергии использование атом¬
ного синтеза !) представляется наиболее перспективным. В ра¬
боте [2] рассматривается возможность ускорения ядер дейте¬
рия и трития в электрическом поле таким образом, чтобы, ис¬
пользуя разности масс, получить относительную скорость ме¬
жду частицами ?Н и ?Н 2). Когда эта относительная скорость
превысит некоторую величину, то при столкновении частиц
произойдет реакция слияния (синтеза) ядер, в результате об¬
разуется ядро гелия и испускается нейтрон. Тепло, выделяю¬
щееся при реакции ядерного синтеза, можно использовать для
подогрева нейтрального водорода, который должен нахо¬
диться в избытке в разрядной камере. Однако следует
9 Реакция слияния ядер. — Прим. перев.
} 1 В обозначает дейтерий, j* Н — тритий. — Прим. перев>
Ь*

68
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
заметить, что, помимо огромных трудностей, которые необхо¬
димо преодолеть при реализации этой идеи, возникает во¬
прос, как создать требуемый градиент потенциала без чрез¬
мерного увеличения мертвого груза. По-видимому, его можно
создать с помощью конвекционного тока, образуемого части-
2 з
цами iH и iH, движущимися вместе с проходящим в сопле
нейтральным водородом. Если установить кольцевой якорь
вокруг выходного отверстия сопла, то при изменениях конвек¬
ционного тока в обмотке якоря будет индуктироваться э. д. с.
Последнюю можно использовать для создания нового разряда
в камере атомного реактора и т. д. Таким путем может быть
создана изменяющаяся выхлопная струя, и лишь малая часть
энергии синтеза будет затрачена на образование рабочего
цикла. Возможно, что в цепь кольцевого якоря потребуется
включить выпрямительное устройство. Не исключено также,
что в принципе возможно реализовать подобным же образом
и синтез ядер с одинаковой массой покоя, если только мест¬
ный нагрев за счет разряда будет достаточным для возбу¬
ждения процесса.
Однако в настоящее время мы должны исходить из имею¬
щихся современных химических средств. Вероятно, лишь че¬
рез значительный период времени, после многочисленных экс¬
периментальных исследований, будет создана ракета, исполь¬
зующая энергию реакции ядерного синтеза.
ОПИСАНИЕ АКТИВНОГО УЧАСТКА ТРАЕКТОРИИ ВЗЛЕТА
В СИСТЕМЕ Х_ У_ С УЧЕТОМ АЭРОДИНАМИЧЕСКИХ СИЛ
Примем следующие обозначения:
— момент времени, с которого начинает работать рас¬
сматриваемая субракета;
М — масса субракеты с топливом в момент U\
с — скорость истечения газов из сопла в соответствующей
ступени;
S — вектор тяги;
S — численное значение тяги;
g — вектор гравитационного ускорения;
г — радиус-вектор ракеты;
(о — вектор угловой скорости суточного вращения Земли;
Fu — вектор центробежной силы;
L — векторная составляющая аэродинамической силы
(подъемная сила), перпендикулярная к г;
W — векторная составляющая аэродинамической силы
(лобовое сопротивление) в направлении —1\

о РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 69
Предположим, что вектор S совпадает с направлением
продольной оси. Тогда угол тангажа (фиг. 4) будет ра¬
вен
а = Z. (S. V).
Вектор S X v перпендикулярен к плоскости чертежа и напра¬
влен от читателя, поэтому вектор v X (S X v) совпадает по
направлению с вектором L. Абсолютная
величина вектора L зависит от a, v и от
плотности атмосферы р, которую
можно рассматривать как функцию
г = Ух? + y2 + z2- Поэтому можно за¬
писать
L = ca (a)p(r)g(w)
W = cw («) p(r) 3 (v),
где ca(a), cw(a) и 3 (v) известны из
исследований по аэродинамике, а р(г)
также можно считать известной функ¬
цией. [Если учитывать сплющенность
земного шара, то точнее записать
Дифференциальное уравнение движения субракеты в век¬
торной форме имеет вид
{M-ljsaty=
— ^ S dtJ {g + 2(v X <*>)-f-Fu} +L-(- W, (16)
to	'
где
W = — ;C,(«)p(r)SW.
Fu = iu)2^	+	k	•	0,
g = — goR2~pr', r = Vx2 -\-f-\-z2,
a = arc cosv=s=r; v =; Vx2y2z2.
= S + M —
Фиг. 4. К определе¬
нию угла подъема.
Вектор (S х v) перпенди¬
кулярен к плоскости чер¬
тежа и направлен прямо от
наблюдателя.
р = р(г) = p(xyz).]

70
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
Перепишем уравнение (16) в иной форме:
t
y[g + 2(vXft>) + F„ — г] fSdt =
to
= M(g-r) + L + W + S + 2M(vX<o) + MFu.	(16a)
Учитывая, что
i j к
SX v =
Sx Sy Sz
xyz
v X (S X v) =
ilk
x	у	z
SyZ — Szy S^x — Sxz Sxy — SyX
i j к
v X —
xyz
0	0	о»
запишем уравнение (16a) в проекциях
с {	^	(х2	+	у2	+	гг),л
2 (У
у и) -)- <о2х — х | j S dt =
:М
{-go^2-
х | —|— Sх —j— 2-М (у to) —f— A/ltsPх —f—
+
(*2 + у2 4- -2’2)8/ч
[у (5_жУ — 5у£) — £(Згх — Sj£>] С, (а) р (х, у, г) g (Ух2 + у2 + £2)
V[у (5гу—sy£)—£ (5г£—S>)J2 + [г (Sy£—S2y)—х (S^y—Syx)]2-f-
+ [£ (S*£ — Sxz) — У (Syi — S2_y)]2
XCa, (a) p (X, y, Z)%V(X2 + у2 + £2)
где
a =e arccos -
j/x2 + y2 -f- z2
Sx* 4" 5yy 4“ SgZ_
(17)
y^ + sj + sp^+f + ir2) *
Диалогичные выражения можно записать для у и г.

О РАСЧЕТАХ ОРБИТ и УПРАВЛЕНИИ КОСМИЧЕСКИМИ ракетами 71
Если в этих уравнениях величины x(t), y(t) и z(t) будут
заранее заданными функциями вида (3), то, дифференцируя,
находим х = x(t) и т. д., и х = x(t) и т. д. Вводя эти извест¬
ные функции в уравнения (17), получим
J V'S* Ч- + Sl dt — Fx (Sxi Sy, S2, t),
to
t 	.
J VS\ -\- S2y-\- S\ cit •= Fу (Sx, Sy> Sz, t),
to
t
f Vs2x-+S2y + S\ dt = F, (Sx, Sy, Sz, t).
Величины F.c, Fy и Fz могут быть вычислены для любой сово¬
купности значений SX, SV, Sz, t. Дифференцируя эти выраже¬
ния, будем иметь
dFx
dFr
+	+	4
Vsl+sl+sl
dsx
dF, ..
 L с ,
dSs
-
dSr *
dSy
dF,
• S, 4-
dSy '•'У-
dF,
dSx
*Fy.
dSг
dF.
dFx
dt
dF„
dt
dF.
dSy ^У
dt
Здесь значения частных производных SFx/dSx и т. д. и dFJdt
и т. д. могут быть вычислены для любой совокупности значе¬
нии SXl Sy, Sz, t.
Решив вышеприведенные уравнения, получим
Sx = tyx(Sxy Sy, Sz, t), Sy=tyy(Sx, Sy, S2_, t), \
S2 == ф2 (Sx, Sy, Sz, t),	j
(18)
где величины функций ф*, фу и фг_ могут быть определены для
любой совокупности значений Sx, Sv, Sz, t.
Для вертикального старта с поверхности Земли значения
S*. Syo>_ SZo, t, сох)тветствуюшие t = 0. определяются следую¬
щим, образом. При 7 = 0, на ракету действуют только силы

I. общие Принципы управления Полётом
тяги и веса, а также центробежная сила. Поэтому для t = О
получаем
^^ОТНОСИТ == So	Mg0 -|- 7WFц
или в проекциях
Мх0 = 5f0 — MgQ -=щ- -)- Мш2х0;
Му о = ^у« — м£о + ^«2у0;
^0 = Sz„ MgQ -=jr- .
Из этих выражений можно определить Sx0, Syo и SZo, если
заданы х0, у0 и г0.
Для любой субракеты можно начать расчет от начального
состояния
Sx , Sy ,	5^	,	tf0,
-/о	-/о	и
которое служит конечным состоянием предыдущей субракеты,
совершающей активный полет по взлетной траектории, с соб¬
ственным значением S(^). Поэтому для t = t0 векторное ура¬
внение (16) принимает вид
s,.+ М (г,.+2(v„ X »)+ FJ+L„+w,„
откуда
s/. —	Si.	+	2	(“	х	v,_)	—	F	J	—	L(>—W,
где
w X V/„ =
L	i	Jf
0	0	to
L к
a Af обозначает массу рассматриваемой субракеты вместе с
начальным значением массы топлива.
Из приведенных соотношений получаем
(£?.+2?o+£?.f
- 2шу<о - <Ас,о) - £f<o - Wx_u

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 73
и аналогичные выражения для Sv и Sz , в которых Lx и
— to	-to	—to
Wx обозначают выражения для совокупности величин
х , У*0*	3°’ У*0’ Zu и в К0Т0РЫХ компоненты тяги Sx, и
S2 должны быть взяты из выражений для предыдущей субра¬
кеты, в то время как 3(^)> са(а) и ^(а) относятся к после¬
дующей субракете, полученной из предыдущей при отбрасы¬
вании очередной ступени. В общем случае при скачкообраз¬
ном изменении L (а также W), обусловленном отбрасыванием
предыдущей ступени, направление S также должно получить
скачкообразное изменение, если желательно получить задан¬
ное программное движение. Но тогда условие, согласно кото¬
рому тяга должна совпадать с продольной осью, не будет вы¬
полняться. Поэтому в целях обеспечения выполнения этого
условия мы должны задать движение таким образом, чтобы
направление тяги S изменялось непрерывно при переходе от
предыдущей субракеты к последующей. Наконец, если точка,
в которой происходит прекращение работы двигателя субра¬
кеты IV, расположена достаточно высоко, то аэродинамиче¬
ские силы следует учитывать только на активном участке по¬
лета субракеты IV.
Приближенное интегрирование уравнений (18) может быть
выполнено последовательными шагами по методу Рунге —
Кутта. Приведем здесь только схему интегрирования:
kt = h-+kSx = k\ A Sy = l\ A Sz=p,
k\ = ^x(Sx9 Sy, S^j t) h\ lx = ^yKSj, Sy, St)h\
Pi — tyz fix* Sy, S^, t) h9
^2 = Ф* (s*	^ у j A,
^2 — фу	»	^У^У"*	+
Рч = Фг (S* +	>	Sy + У" »	+	y-	’	t -f у j hj
h = ф* +"У” »	$Z	“Ь'У"» ^ ■+" y) hy
h = Фу (s* + -у* Sy + ~y »	+	уг	•	t + j A,
Pz — Ф* (s* + y- ’ Sy -f- -y ,	Sz + yn ,	t + -|-) A,
k\ = tyx (Sjc H” kz> Sy + /3, S^-j-/73, t-\- ti)h,
l\ = фу (Sx -ф- k%, Sy -|- /3, S^-\-p3, t -\-h)ht
P$ = Фz (Sjf + К Sy_-f- /3, S^ +p$, t-\~ Щ hT

74
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
Численные значения величин фх, фу, фг могут быть найде¬
ны для любой совокупности переменных Sx, Sy, SZy t. Оценки
достигаемой точности расчета можно получить из данных по¬
вторного расчета с уменьшенным в два раза числом делений
на частные промежутки, когда каждый промежуток соответ¬
ствует двум промежуткам в предыдущем расчете. Величина
остаточной погрешности равняется V15 разности результатов
в обоих случаях.
Далее, если двигатель субракеты работает в интервале
времени от t = t0 до t = tu то для соотношения масс имеем
формулу	и
г =	^	.	(19)
М — у J Sdt
t
идентичную выражению (6). Поэтому можно записать
о	S	пгс	тс
F(t)=S уд = -
м~т{
Отсюда имеем
, ...w	M(t)'
где M(t) = M—f mdt. Поэтому
to
±fmdt = In *	=	ln	M
to	M	—	J	mdt	M	—/ me dt
to	и
= In -
тГ
M-— I Sdt
to

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 75
Таким образом,
ехр -‘- J F(t)dt = expin	^^
'°	М — yf$dt	M —
to	tv
и формулы (19) и (6) дают одинаковый результат.
Следовательно, если учитывать аэродинамические силы и
задавать в пространстве и времени активную траекторию с
учетом моментов отключения двигателей соответствующих
ступеней, то при подсчете коэффициента полезной нагрузки
можно воспользоваться формулами (15), (7) и (14).
Однако для того, чтобы для четырехступенчатой ра¬
кеты применять формулы (16) — (18), нужно задаться вели¬
чинами М4, с4 и \в4. Определив при интегрировании уравне¬
ний (18) в интервале от t = 0 до t = 1в функцию S = S(t)y
получим
ть< = Г S dt.
С4 J
О
Следовательно, выбрав величину тСк, определяем величину
М3 = М4 — /Пс4 — гпьЗатем снова задаемся величинами съ и
и т. д. Следуя по этому пути, найдем
М2 = Мг— тСъ — гпь,, МХ = М2 — тс, — ть2,
тр = Мх — тСх — тьг
В конечном счете можно также получить коэффициент полез¬
ной нагрузки Р = М4/тр и уравнение (15) является лишним.
Однако если аэродинамические силы оказывают влияние
только во время активного полета субракеты IV, то, опреде¬
лив г4, можно пользоваться формулой (15).
РАСЧЕТ АКТИВНОГО УЧАСТКА ТРАЕКТОРИИ ВЗЛЕТА
С УЧЕТОМ АЭРОДИНАМИЧЕСКИХ СИЛ И С ЗАДАННЫМИ ПО ОТНОШЕНИЮ
К СИСТЕМЕ х jy г ВЕЛИЧИНАМИ СОСТАВЛЯЮЩИХ ТЯГИ
Рассмотрим теперь обратную задачу получения активной
траектории взлета, если тяга S = S(t) в системе координат
*yz задана, включая моменты времени последовательного от¬
брасывания ступеней, Тогда для любой субракеты величину

/6
t. общие принципы управления полётом
* t
fsdt в выражении (17), а также величины S*, Sy и Sz мож¬
но считать известными. Поэтому	можно	написать
x = Fl(x, у,	2,	х,	у,	2,	t),
У = Р2 (х> у,	2,	х,	у,	2,	t),
z = Fz(x, у,	z,	х,	у,	г,	t).
(20)
Для каждой субракеты величины с и М, входящие в (20),
имеют различное значение. Уравнения (20) можно записать
в виде следующих совместных дифференциальных уравнений
первого порядка:
vJC = Fl(x, у,	2,	VXJ	Vy,	Vz,	t)	x = vx,
Vy = F2 (X, y,	Z,	Vx,	Vy,	Vz,	t)	y = Vy,
vz = F3(x, y,	2,	Vx,	Vy,	vz,	t)	z=vz.
(21)
Для любой субракеты можно численно проинтегрировать
уравнения (21) исходя из соответствующих начальных усло¬
вий. Если старт ракеты производится с поверхности Земли
вертикально, то функции Sx(t), Sv(t) и S2(^) для субракеты
IV (что равносильно полной четырехступенчатой ракете)
имеют вполне определенное значение, устанавливаемое доба¬
вочными условиями
Уо
So
lo
£°
"57
R
(22)
где через х0, у0 и 20 обозначены координаты точки старта.
В соотношениях (22) центробежной силой в силу ее малости
по сравнению с силой тяги пренебрегали. Для начальных ус¬
ловий по скорости
г\)* = £о = 0,	^	=	^	=	0,
^ог=£о = 0.
Таким образом, для субракеты IV начальными являются сле¬
дующие условия:
t = 0-+x0, у0, 20, i0 = 0> Уо = 0, z0 = 0.
В общем случае если t0 — момент отключения двигателя пре¬
дыдущей субракеты, для любой субракеты начальными уело-

о РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 77
виями активного участка взлетной траектории являются усло¬
вия
*о ь* Ъг *,.• Ум S.-
Для этих начальных условий путем численного интегрирова¬
ния выражений (21) находим то же решение, что и для слу¬
чая предыдущей субракеты. Выполним интегрирование выра¬
жений (21) по схеме Рунге — Кутта
At — h—> Ах = k, Ду = /, Д z = т,
AV; = p,	Avy	= q,	Дvz_=s,
^	Ч—д- ^2 Ч—з"	Н—g" ^4»	^ = 'е	А+'з^ + ’З'^з + у^4’
1	,1	.1	. 1	1 .1 ,1	. 1
т — "б /rel + "3W2 + "3 т3 + "б те4> Р — “g"Р\ I- Р2 ~~Г з’/'з + 'б'А»
1	,1	,1	, 1	1	.1 - 1	,1
9 =3'?2 + ‘3	<?3+ 6"?4>	5— -Q sl + -3-S24- -g S3H-g-S4,
kx = vji,	/j	= Vyh,	tnx	- vzh,
k2 = (v^-\-^h,	/2 = (*>, + -&-) A,	«a = («,+-§-) A,
*8=(®x+x)A» /3 = (%.H-^)^>
*4 = (®£ + /,8)А»	/4	= К + ^з)^	ffi4 = (^ + S3)ft,
p, = /7j (X, у, £, тд, “Су, г»_г, t) h,
Pi~ F
Pz~ F+ У “by* £_Ь"2?’	^z^ff’
P\~ FX(x-j-kz, у -f- /3, z + щ, Vx~\-Pz> ^у + ^з» ^“Ь^з* t-\-h)h
и аналогичные выражения для 91929394 и Si5253s4.
Расчет выполняется в следующей последовательности:
k\l\m\p\qxsu ^2/2^2^292^2, ^з/з^зРз9з5з,	Если	повто¬
рить расчет с половинным числом шагов, то Vis разности ре¬
зультатов обоих вычислений будет являться мерой точности
первого расчета.
Вообще если Sx, Sy и Sz известны, то проекции тяги на оси
системы xyzt не вращающиеся относительно небесного

78
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
пространства, находятся в соответствии с формулами (1а)
Аналогично по формулам (16) можно найти х, у, z, если х,
у и z известны.
О СТАРТЕ СУБРАНЕТЫ I ПО КАСАТЕЛЬНОЙ К ПРОМЕЖУТОЧНОЙ
ЗЛЛИПТИЧЕСНОЙ ОРБИТЕ
Пусть положение субракеты II в момент ts2 (момент от¬
ключения двигателя субракеты II) определяется точкой
ха У a za' а составляющие скорости равны ха, уа, za. С целью
упрощения примем момент времени ts7 за нулевой отсчет вре¬
мени, так что в дальнейшем будем считать 1в2 =0. Следова¬
тельно, начальное состояние (при t = 0) промежуточного кеп-
леровского движения по эллипсу будет характеризоваться ра¬
венствами
Плоскость орбиты промежуточного кеплеровского движения
дается уравнением
X (Га X veb + у (гв X V0)y + г(ra X va)z = 0,	(25)
в котором выражения (ra X v0)x, (га X va)y и (ra X Уа)гпред-
ставляют собой численные величины проекций векторного
произведения
Отсюда получаем уравнение линии пересечения плоскости ор¬
биты и плоскости экватора (плоскости ху)
Sx = Sx cos о)t — Sy sin (о/,
Sy = Sx sin Ы -+- Sy cos Ы,
(23)
ra = lxa + iya 4- kza (положение),
Va = ix'a + jya kza (скорость).
(24)
i	j	k
ra X va =	xa	ya	za
*a	Уа	Za
(26)
x(ra X Va)x + у (ra x Ve)y =
или

о РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 79
Линия (27) показана на фиг. 5, причем угол ее наклона к оси
х обозначен через %
с tg !Vg * ТаЪ
К	S	(Га	X	Va)y
или в соответствии с (26)
X = arc tg	(2Ь)
Zaxa ^cl^q,
Z
Фиг. 5. К определению угла наклона промежуточной орбиты
к плоскости экватора.
Для угла i наклона плоскости орбиты к плоскости ху имеем
cos* = Уа
I ra х Va I
или с учетом (26)
i = arc cos .	  ХдУа—УаХд	(29)
V (ХаУа — У а* а? + (хага — xaza)2 + (уага — уага)2
Единичный вектор, направленный вдоль линии узлов ОР,
равен
icos X + jsinx-	(30)
Примем в плоскости орбиты линию узлов ОР за полярную
ось, положение ракеты, двигающейся в плоскости орбиты, бу¬
дем характеризовать полярными координатами г и 0 (см.
фиг. 5). Начальное значение 0(/ = 0) определяется выраже¬

80
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
нием (30) и вектором га (24). Обозначая его через 0О, найдем
rn-fl _ 0ха + Уа + bza) (i cos у + j sin •/)
cos va —	Га
или
Хд cos X + у a Sin X
, = arc cos-
Vxl + yl + zl
Если а = L (гa, Va), ТО COS а == raVjraVa или
ХдХд + УаУа + ZgZg
а = arc cos •
(31)
V(Х1 + У2а + г1) (х2а + У2д+ Ра)
Таким образом, уравнение кеплеровского движения по эллип¬
су в соответствии с условиями для t = 0 может быть опреде¬
лено в плоскости орбиты, если принять линию узлов ОР в ка¬
честве полярной оси. Тогда, как это показано в работе [3],
1 + е cos (0 — 0О) ’
где
v\r\ sin2 а
Р2
vara sin а
V
Ulrl sin2 а
(32)
Постоянная интегрирования 0О определяется начальными
условиями при t = 0, г = га и 0 = 0а и указывает положение
перигея эллиптической орбиты. Зависимость 0 = 0o(f) дается
уравнением Кеплера [3]
t — L =
1
где
vara sin а 1^(1 — £2)
^т=/т
(to — е sin со),
6°-
. + е g 2
(33)
Постоянная интегрирования t0 находится из начальных усло¬
вий t = 0 и 8 = 0а
р2	|
<о =	—	V/;:	К=о	—	е	sin	">,=0)>
где
vara sin а У(1 — £2)3
о#=о = 2arc tg(|/~
tg
в a — «о
(34)

\ о РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 81
■4-
0з уравнения (33) видно, что t = t0 соответствует Q = 0О. По¬
этому to обозначает момент времени, в который ракета прохо¬
дит через точку перигея (при свободном промежуточном кеп-
леровском движении).
Перейдем теперь к прямоугольной системе координат.
Фиг. 6. К определению уравнений движения по промежуточной
орбите в прямоугольной системе координат.
На фиг. 6 прямоугольный треугольник с гипотенузой г и
острым углом 0 повернут вокруг линии узлов ОР в эква¬
ториальной плоскости ху. Этот треугольник в своем простран¬
ственном положении (до поворота вокруг линии ОР) состав¬
ляет с плоскостью ху угол и Непосредственно из чертежа по¬
лучим
х = г (cos б cos х — sin0 cos i sin x)>
у = r (cos 0 sin x + sin 6 cos i cos x)>
2 = r sin 0 sin /,
или в соответствии с (32)
cos 0 cos 7 — sin 0 cos i sin у
X—P 1 + e cos (0 — 0O)
  cos 0 sin x + sin 0 cos i cos /
У P	1 + e cos (0 — 0O)
sin 0 sin i
Z ~P l + ecos(6 — 0O) •
(35)
В выражениях (35) % и i суть константы, тогда как 9
является функцией t, определяемой уравнением (33). Путем
§ Зак. ш

82
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
дифференцирования из (35) получаем
х —р {[1 + е cos (0—90)] (— sin 6 cos х — cos 0 cos i sin x) +
+ (cos 0 cos x — sin 0 cos i sin x)s sin (0 — 0O)) 0 X
X [ 1 -f~ 6 cos (0 — 0O)] 2,
y=p {[1 -f- e cos (0—0O)] (—sin 0 sin x + cos 0 cos Zcosx)4“
-f- (cos 0 sin x + sin 0 cos i cos x) e sin (0 — 0O)) 0 X
X [1 s cos (0 — 0O)] 2,
z —P [1 +e cos (0 — 0O)] cos 0 sin / —J— (sin 0 sin i) e X
X sin (0 — 0O) [ 1 +ecos(0 — 0O)]-2 0-
Входящая в выражения (36) переменная 0 может быть най¬
дена непосредственно из закона Кеплера
(36)
согласно которому
г20 = ч)ага sin а,
л 	 УдГд	sin	а
(37)
В соответствии с (32) имеем
0 _ [1 + £ COS (6 — е0)]2 vara sin а
~	р2
Подставляя (37) в (36), получим х, у и z в виде функций 0
или в сочетании с (33) в виде функций t.
Теперь предположим, что в момент t = ts производится
старт по касательной к промежуточной эллиптической ор¬
бите и что на ракету действует тяга, определяемая постоян¬
ными значениями т и С\ как по величине, так и по направле¬
нию {т — масса, выраженная в единицах времени). Подста¬
вляя t = ts в (33) и (35), найдем xtg, yts, ztg. Аналогично,
подставив t = t8 в (33) и (37), найдем xis, yts, ztg. Следова¬
тельно, для направляющих косинусов тяги активного участка
траектории субракеты I можно записать
У Р( +у) +?'
f ls ls S
V *+*+*.
zh
Уx] +y} +Z2t

 РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 83
Дифференциальные уравнения движения субракеты I на этом
участке принимают вид
[Ml — m{t — ts)\x =
g0R2x	х,тс,
(уравнения для у и z аналогичны) или
g0R2x	xt	т^\
х==~ (** + У*+**)*л +Vx2t + у? +Pt Mx-m{t-ts)	(38>
*	а	'.с	1	с
(аналогичные выражения получаются для (/иг).
Обозначим кеплеровское движение, соответствующее ус¬
ловиям при t = 0 и определяемое равенствами (33), (35) —
(37), через
лг = *(/)о. У = У(А>- Z = z(t\,\
x = x{t)о, y=y(t)o, - Z = z{t)0.)
Приняв (39) за нулевое приближение, подставим его в выра¬
жение (38) и после интегрирования получим
Ж,
'	с	с	с
или
x(t) 1 *(*)»+ ^ +	^	Ct\n	(40)
f S	*S	*S
(аналогичные выражения можно получить для y(t)\ и z(t)\).
Последние уравнения определяют в первом приближении про¬
екции скорости. Чтобы найти выражения для координат пер-
Вого приближения, выражение (40) нужно проинтегрировать
6»

84
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
от ts до t. Обозначим F через t — ts\ тогда
t	v
/ = f In-и—ж'. -, dt = f ln-ду—>	=
J М, — m (t — ts)	J M, — mt
0
*'( M, \
- YMn M'	ft'
~ ln	J • / Af, \ —
1Л1, — mt')
o
t’
= t'\n M^mt, —Mxm J	—/rtf') 2A_J^^/ =
0
V
f f dt'
J Alj — mt'
Вводя для последнего интеграла обозначение Л и записав
Mi — mt' =	найдем
m	/и
Тогда
г	/'
, Г 1 и— М, da If а —	,	1 , Лу| ,
1Л = \	1 — = —2	   du	= —2(u — M1 in и)л .
1 J и	т т	т2	J и	т2 4	1	70
о	о
Следовательно,
1 = f 1п	“	1Г	—	mt^— 1п_=
— 4-г ]п Mi	Mi_	| 	Ml	|_	—.
— t{VLMx — mt'	m	— mt' '
— /V  Л 'n  L_
“ V m ) П Mx — mt' *
Итак, выражения для координат первого приближения при¬
нимают вид
x(t\ ==л;(/)о +
Н 	с-
х<] "I“У?	z<t
’ ls s s
Г/	M,	\	М,	1
[* — *»		 1птз 71	7"\—|— t — ts I
Д s т J М — m(t — ts) 1 SJ
(41)
(аналогичные выражения можно записать для y(t)\ и 2(/)().

о РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 85
Для второго приближения следует подставить первое при¬
ближение (41) в (38) и снова интегрировать от ts до t
Обозначая
и аналогичные выражения для y(t)2 и z(t)2.
Продолжая таким образом, мы можем получить и более
высокие приближения. Как только разность между двумя по¬
следовательными приближениями станет достаточно малой,
эту процедуру можно закончить. Сходимость этого процесса
будет тем сильнее, чем меньше будет интервал t—18. Если
длительность полета субракеты I по активной траектории бу¬
дет незначительной, то сходимость будет достаточной в пре¬
делах этого интервала.
С другой стороны, всегда возможно найти координаты и
скорость кеплеровского движения в некоторый момент вре¬
мени t\. Повторив изложенную выше процедуру для интер¬
вала t\ — ts, получим для координат и скорости в п-м прибли¬
жении определенные значения, обозначаемые
имеем
• где
t
(аналогичные выражения получаются для у(t)2 и z(t)2). Ин¬
тегрируя, имеем
* (t)2 = f v (t), dt +
+ xts (* — О + xt5	(43)
x (^l)n — -*'10’	У (^l)n — У 10>	z (^l)n — Zw>
x{tl)n = xlO>	y{ti)n=yw>	Z{t\)n = Z\b-

86
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
Соблюдая те же обозначения, для момента времени t = U в
кеплеровском движении будем иметь следующие соотношения:
Xl = arctg
У1QZ10  У10ZI о
г 10-*10 *^10^10
ix = arc cos
0а, = arc cos
<Xj = arc cos
•*юУю —Ую*ю
Ус*юУ io—y,o*io)2+(-*io*io—-«io^io)2+(yio-?io—Ую^о)2
jc,o cos y.i + Ую sin/.
(=0.
Vxlo + У?о + г\о
  -^io-^io T~ УюУю ~T zioz1о
V (4) + У10 + *10) (xio + У10 + г2ю)
fw = VAo + У?о + 4>- vio = VAo + У\о + zio-
-Для получения формул, аналогичных выведенным ранее,
введем новую координату времени ¥ = t— t\. Тем же путем,
как и прежде, найдем параметры кеплеровского движения,
соответствующие ¥ = 0, в прямоугольных координатах в виде
функций от ¥. Эти параметры обозначим через х(¥)о, у(¥)0,
z(¥)0. Применяя метод последовательных приближений и по¬
лагая М\ = М\ — m(t\ — ts)y получим для ^>0
хи
Сл In
м,
(44)
и аналогичные выражения для y(t') 1 и z(f)u а также
х (Ог = х (По +
К
и аналогичные выражения для y(t')\ и z{t')x. Обозначив
(45)
Sot?
х (О.
{WO,]2 + [y(Oi]2 + [^(Oi]2}“/a
для второго приближения будем иметь
х (И2 = ■») (*')i
хи
■ с. In -
м
где
V x\+fis+z\
v
7i(ni=f
М[ — mi
Ч0>
(46)

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 87
и аналогичные выражения для y(t')2 и z(t')2. Далее,
v
х {tr)2 = J т) (tf')i	+
о
У-?.+й.+^. '
1 м \ уИ
t> ! In — +/'
т I М1 — mt
4- xlQt' -(- xl0
(47)
и аналогичные выражения для y(t')2 и z(tr)2.
Продолжая эту процедуру, можно получить и более высо¬
кие приближения.
Выше мы полагали, что в любой момент времени движе¬
ния на активном участке траектории скорость не превышает
местной параболической скорости для поля земного тяготе¬
ния.
В случае лунных ракет, которые должны либо попасть в
Луну, либо совершить вокруг нее облет, это условие выпол¬
няется. Что же касается «искусственных комет», т. е. тех
случаев, когда ракета в своем конечном свободном полете
подвергается в основном действию только солнечного притя¬
жения, скорость субракеты I на некоторой части активного
участка должна превысить параболическую скорость. В этом
случае мы можем поступать следующим образом. Предполо¬
жим, что параболическая скорость достигается в момент вре¬
мени t = t2, и выберем близкие друг к другу значения t — tx
и t — t\\ так, чтобы t\ < t2 < /ц. Для интервала времени
t2 —1\ кеплеровское движение будем рассматривать как ну¬
левое приближение движения, соответствующего t = tb и при¬
меним описанный выше метод последовательных приближе¬
ний. Согласно этому способу, для некоторого момента вре¬
мени t2 получим
х2 -4- \;2	*2	_	2gpR2	_
'■	• '• К^+Д+4
= (Местная параболическая скорость)2.
В качестве нулевого приближения для метода последова¬
тельных приближений в интервале tu —12 примем кеплеров¬
ское движение, соответствующее времени t = t2. Однако в
этом случае нулевое приближение будет являться параболи¬
ческим движением. Далее, для интервала tm — где/ш > t\\,
в качестве нулевого приближения берем кеплеровское
движение, соответствующее времени t = 1ц. В этом, уже

88
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
третьем по счету, случае нулевое приближение будет являть¬
ся гиперболическим движением.
Так как для орбитальных расчетов на интервалах /ц — h
и t\\\ — t\\ эксцентриситет е кеплеровских движений, принимае¬
мых в качестве нулевых приближений, равен единице или пре¬
вышает ее, то форма кеплеровских уравнений в виде выра¬
жения (33) оказывается непригодной. Поэтому вместо (33)
используем уравнение
* vara sin а / [1 + £ cos (0 — 0О)]2 *
При е > 1 получаем [4]
j  С	dd	  С	z dz
_ J [1+£COS(0 —0О)]2 ~ J y'(z2—l)z2+2z—l ~
= —— V— l+2z + (e2 — 1)г2	*	X
е2 — 1	V	(£а—1)Т^е2 — 1
X 1п 1(е2-1)г+1 + /?^Т у —1+2г + (е2—1)2*},	(48)
где
1
z =
1 + е COS (0 — 0О) '
Следовательно, при £ > 1 уравнение (33а) принимает вид
' =	W9)
wai а sin
где
=
а 1 + 6 cos (0а — 0о) '
Далее, из уравнения (48) для случая е = 1 (параболическое
движение) получаем
= / тй=г= т {i1- У^}'■
Тогда для £ = 1
* = Valina [/(^)-Afe)l.	(50)
где	^
2 = 1 + cos (6 — 60)
И
z* = 1-1-cos (fls— 07) •	i52)

б расчетах орбит и управлений космическими ракетАмй 89
Таким образом, в случае параболического движения 0 яв¬
ляется функцией t и определяется из уравнений (50)—(52),
тогда как в случае гиперболического движения 0 как функ¬
ция t находится из уравнения (49). Далее, величина 0 как
функция t определяется из уравнения (37), a ra, va и а отно¬
сятся к рассматриваемому кеплеровскому движению.
Выше мы предполагали, что старт происходит по каса¬
тельной к промежуточной кеплеровской орбите, причем на¬
правление тяги поддерживается постоянным. При этом актив¬
ная траектория субракеты I становится плоской орбитой и
%i = Ъ а k = *•
Тем не менее для общности можно использовать трехмер¬
ную систему уравнений (38). Для случая, когда прилагается
тяга тс\, постоянная как по величине, так и по направлению,
причем направляющие косинусы имеют произвольные значе¬
ния Хи Х2 и Хз, в приведенных выше формулах можно заме¬
нить величины
КЧ+Я+Ч ’
V*)+?t+?ta ’
v*'s+k+p‘a
величийами Хи и Хз.
О РАСЧЕТЕ ПРОСТРАНСТВЕННОЙ ОРБИТЫ НОСМИЧЕСНОЙ РАНЕТЫ,
ПРЕДНАЗНАЧЕННОЙ ДЛЯ ПОПАДАНИЯ НА ЛУНУ ИЛИ ОБЛЕТА ВОКРУГ НЕЕ
Д^я космических ракет, которые должны попасть на Луну
или с о верш йтьво^ е ёГо 5 л ет, следует учитывать не только
лунное притяжение, но и воздействие Солнца, которое_имеет
тот же то	лун	ное	Тт	р	йтя жен ие.
Анализ будем производить в невращающейся геоцентриче¬
ской системе координат п р"ич’ем координаты^	Л	у	нБ1
обозначим через хл, уя, zRy а координаты центра Солнца —
через *с, уСу гс.
Если Мл и Мс — массы Луны и Солнца, а / — постоянная
тяготения, то дифференциальные уравнения движения

90
1.. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
субракеты I для свободного полета после активного участка
траектории принимают вид
г "
: х-
g0R2jc	/млхл
(*2 + у2 -f г2)*1*	(х\	+	у2л	+	Z1n)h
	тл	(хл—х)	/Мсхс
[(-^л xf + (Ул — У)2 + (гл — г)2\ (хс + Ус + гс) ’	\
/Мс(хс-х)
[(*с - х? + (Ус - У)2 + (zc ~ zf\
21*/'
(53)
и аналогично для у и z.
В этих уравнениях величины хл, ул> гл, хс, ус, гс можно
считать_известными функциями времени. ПустьТ^ О обозна-
чает начало космического полета, а хбГ У о, £о, *о, Уь z<> — на‘
чальные значения координат и составляющих скорости. Пред¬
полагается, что точка^ Хоу020 находится в непосредственной
близости от Земли.
До тех пор пока ракета находится вблизи Земли, в каче¬
стве нулевого приближения принимаем кеплеровское движе¬
ние x(t)о, y(t)о и z(t)о, предполагая, что в начальных усло¬
виях (x0yoZoX0yoZo) при t = 0 Па ракету действует только сила
притяжения Земли. В таком случае можно применить метод
последовательных приближений для интервала t\ — t и сде¬
лать переход к кеплеровскому движению, соответствующему
t = ti, а затем повторять ту же процедуру последовательных
приближений.
При выполнении этих расчетов, по мере вхождения в об¬
ласти непосредственной близости к Луне, оказывается, что в
связи со сходимостью последовательных приближений удоб¬
нее принять в качестве основного притягивающего тела Луну,
а.	Солнце и Землю считать возмущающими объектами. По¬
этому можно воспользоваться невращающейся лунной прямо-.
угольной системой координат xfy'z\ оси которой пар а л л е льн ы
осям невращающейся геоцентрической системы координат xyz.
Тогда получим следующие формулы для'ТГерёхб'да от~одной
системы координат к другой:
! *' = * —У' = У —Ул- z' = z гл
Х=х'+хл, у=у’ + ул	z=zf+zn
(54)

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 91
Если координаты центра Земли обозначить через х'ц з,
Уц.з.> К. э.*а координаты центра Солнца —через х'с, у’с, z'Ct
то дифференциальные уравнения движения в лунной
системе координау х'у'г' будут иметь вид
% _ _	f	Mn*	fMц. з.Ч з.	,
Р'Ч/Ч^Г ^	t
f Мц 3> (лГц 3 х )	/MqXq
[К 3. - *у + & 3. - У)2 + К. 3. - ОТ2	[4 + Ус +
/Мс(х с—х')
+■
[(хс-*УНУс-УУ + (гс-*УГ )
\ (55)
и аналогично для у' и zr.
Тогда в соответствии с (54) имеем 1)
Хц.з.=	ХЛ>	Уц.з.=	У Л*	Zu.3.~ ХЛ•	(56)
Далее,
хс = хс	хл*	Ус = У с	Уд9	zc	= zc~ хл%	(57)
Если выражения	(56)	и (57) подставить	в уравнение	(55),
можно получить
№д*г~	,	~
U'4/ЧЧ (Ч + уЧЧГ
	g0P2 (хл +4
[(■*л + ХУ + (Уд + уУ + (2л + г')Т
	№с (хс — хд)
[Чс - хл)2 + (Ус — Ул)2 + (zc — 2 л )T2
	/мс(хс~хл ~х')
[(*с — хл — ХУ + (Ус — Ул — У')2 + (гс — 2л — 2У\% I
+
(58)
и аналогично для у' и z
Далее, из (54) получаем
х' = х — х^ у' = у— Уя,г' = г — zn.
*) В силу того что центр Земли совпадает с началом невращающейся
геоцентрической системы координат xyz, будут иметь место следующие
равенства:
з, ^ 9> Уц. з, =	-?ц.	—-Of

92
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
Следовательно, к уравнениям (58) можно применить метод
последовательных приближений, взяв в качестве нулевого
приближения кеплеровское движение в поле лунного притя¬
жения с начальными значениями x'y'z*, x'y'z'.
При удалении на значительное расстояние от Луны (на¬
пример, в случае облета вокруг Луны) можно вновь перейти
к невращающейся геоцентрической системе координат.
Исходя из различных начальных условий, можно произ¬
вести указанные выше расчеты для исследования вопроса
о том, как наилучшим образом следует выбрать орбиту про¬
межуточного кеплеровского движения и точку на этой орбите,
которая будет служить местом старта.
РАСЧЕТ УПРАВЛЯЮЩИХ МОМЕНТОВ СИЛ ДЛЯ СТАБИЛИЗАЦИИ
РАЗЛИЧНЫХ СУБРАНЕТ
Теперь перейдем к проблеме управления. Обозначим че¬
рез XYZ вспомогательную систему осей, образуемую глав¬
ными осями инерции системы (состоящей из субракеты и
оставшегося топлива), проходящими через общий центр тя¬
жести этой системы. Пусть ось X — поперечная, ось У—нор¬
мальная, а ось Z—продольная оси.
На активном участке полета вне атмосферы уровни
жидкости в баках будут перпендикулярны а — g = SyA, где
а — вектор ускорения ракеты относительно невращающейся
геоцентрической системы координат xyz. Поэтому если S сов¬
падает с продольной осью, эти уровни жидкости, по крайней
мере на активном участке траектории вне атмосферы, будут
перпендикулярны продольной оси ракеты. Воздействие
аэродинамических сил на расположение этих уровней практи¬
чески не сказывается, так как в нижних слоях атмосферы
траектория ракеты близка к вертикали. Кроме того, всегда
возможно сохранить уровни жидкости в требуемом положе¬
нии с помощью поршней, работающих от небольшого электро¬
двигателя и оказывающих давление на жидкость.
Примем, что главные оси инерции, проходящие через мгно¬
венный центр тяжести, перемещающийся внутри ракеты в
результате выгорания топлива, всегда остаются параллель¬
ными сами себе. Предположим также, что установление по¬
ложения продольной оси относительно небесного простран¬
ства в носовой части субракеты I можно произвести с по¬
мощью гиростабилизированной системы координат xyz, при¬
чем плоскость платформы должна совпадать с плоскостью ху,
а ось z — с перпендикуляром к этой платформе. Эта материя-

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 93
лизованная прямоугольная система осей может быть в прин¬
ципе связана в начале координат О с корпусом ракеты с по¬
мощью шарового шарнира и стержня В (фиг. 7).
Система xyz сохраняет неизменное положение относи¬
тельно небесного пространства. Допустим, что она устано¬
влена таким образом, что оси х, у и z параллельны соответ¬
ствующим осям невращающейся геоцентрической системы
координат xyz, рассмотренной выше.
Шаровое сочленение в точке О может быть выполнено в
виде шарниров а и b (фиг. 8). Корпус подшипника b жестко
В
Фиг. 7. Схема шарового
сочленения.
Ф и г. 8. Шарнирное
соединение а и Ь.
Фиг. 9.
Шарнир а.
закреплен в материале плоскости ху и направлен своей осью
вдоль оси z. На конце стержня В аксиально с ним укреплена
вилка, которая может поворачиваться вокруг оси В. Она мо¬
жет также поворачиваться вокруг оси аа' (фиг. 9) шарнир¬
ного соединения а (см. фиг. 8). Ось аа' проходит через круг¬
лое отверстие стержня г. Стержень В может поворачиваться
(вместе с корпусом ракеты, который жестко связан со стерж¬
нем В) вокруг своей оси. Поэтому вся ракета может переме¬
щаться по крену, тангажу и рысканью, тогда как гиростаби-
лизированная система xyz сохраняет неизменное положение
относительно небесного пространства.
Обратимся к фиг. 7. Пусть ОР есть линия пересечения
плоскости ху с плоскостью ZOB. Тогда положение продольной
оси относительно небесного пространства определяется при
помощи углов 8 и ф, соответствующих вращающимся шарнир¬
ным соединениям а и b (см. фиг. 8). Таким образом, для
проекций тяги S, которая совпадает с продольной осью, отно¬
сительно системы xyz, а также относительно невращающейся

94
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
геоцентрической системы координат xyz имеем
SX = S sin 0 cos <р,
Sy = 5 sin б sin ср,
S, — S cos б,
откуда
ср = arctg-^Д-,
(59а)
(596)
5
б == arc cos -jr.
Так как Sx, Sy и S2 при орбитальных расчетах определяются
в виде функций t, то ф и б находят из уравнений (59); они яв¬
ляются известными функциями времени.
На фиг. 7 i, j, к обозначают единичные векторы по напра¬
влениям х, у, <г. Предположим, чго ракета управляется таким
образом, что ее поперечная ось X остается в плоскости ху и
совпадает по направлению с векторным произведением
k X S, ось У совпадает по направлению с векторным произ¬
ведением SX(kxS), а ось Z— с направлением S. Обозна¬
чим единичные векторы по направлениям X, Y и Z через V, j'
и к' соответственно. Тогда, если
есть мгновенная угловая скорость вращения ракеты относи¬
тельно мгновенного центра тяжести ракеты вместе с остав¬
шимся топливом по отношению к небесному пространству, а
В —момент количества движения, то уравнение Эйлера отно¬
сительно осей XYZ будет иметь вид
391 = 4^- + (<•> X В) + (<о х вх) + 2mkl	f	(60)
где ЭЛ — сумма действующих на ракету внешних возмущаю¬
щих моментов, a dB/dt означает производную величины В
в системе координат XYZ.
Вектор Bi означает момент количества движения при вра¬
щении насосного агрегата; этот вектор направлен по оси
тангажа (У). Величина / представляет собой расстояние от
мгновенного центра тяжести субракеты до отверстия актив¬
ного сопла, a k — экспериментальный коэффициент. Величину
массы т, расходуемую в 1 сек, можно рассматривать как
заданную функцию времени, тогда как величина скорости
расхода в уравнении (60) может быть представлена векто-
(О = 14 ¥<Оу -f- к'(Ог

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 95
ром с в направлении — к (вдоль продольной оси противопо¬
ложно действию тяги).
В уравнении (60)
(!) X В =
»Х'В' =
следовательно,
V
j'
W
шх
“у
т2
вх
sy
Вг
V
j'
W
шдг
«>у
<*>2
В,
0
0
i'
J'
к'
“у
“г
0
0
— С
i
j
0
0
	 (0
У°
О>хС
,-И*
с X («о X с) =
Уравнение (60) в проекциях имеет вид
= Вх + (оу Вг — и)гВу 2mklwxc,
к
■ с
О
г — В + (о гВх — шхВг -f
2mklwyc,
А-
X^Z I	I	(61)
mz = bz + ыхву — ibyBx — ©
Если оси XYZy которые первоначально являлись осями
тангажа, рысканья и крена, проходящими через мгновенный
центр тяжести ракеты с топливом, являются в то же времй
главными осями инерЦии ракеты совместно с топливом, то
Bx = Ixiйх, By lyio у, Bz	1zu>z*
Вх = (o/lf
(62)
где Uс, 1у и /г обозначают моменты инерции ракеты с топливом
относительно осей X, У, Z, а величины со и 1\ — угловую ско¬
рость и момент инерции ротора насосного агрегата соответ¬
ственно. Подставляя (62) в (61); получим
VyVzUz — lyy+Zmklwj'C, ,
3)1 у = /у«)у + u>zu>x (Ix — Iz) +	1	+	2ткЫус,	•	(63)
Wz = 1г<йг + «о^у (Iу — Ix) —	0)y0)/u
В соответствии с" указанными выше допущениями на основа¬
нии данных фиг. 7 получаем •

96
t. ОБЩЙЕ принципы УПРАВЛЕНИЯ ПОЛЕТОМ
Подстановка (64) в (63) дает
Ttx = 1Х$ + <р2 sin 6 cos 6 (Iz — Iy) -f- 2mklc^
ар?у = /у (4> Sin е н- <р0 cos 6) -|- <рё cos 0 (/jp — /г)+	^
-f- о>/i<p cos 0 -f- 2mklc<? sin 6,
ЗИг = Iz (cp cos 0 — <p0 sin 0) + tp0 sin 0 (Iy — Ix) — юДср sin 0.
В этих выражениях /*, ly и 1г можно считать	известными
функциями времени (выгорание топлива известно из расчета
траектории). Поэтому из (59а) находим
Sy
= откУДа
Таким образом,
(66)
Так как, согласно (596),
о S*
cos 0 = -j-,
то
• О О SSZ — SZ$
— sm0 0 = —*-03-*-
Отсюда
—	SJ	—	SS,

о расчетах орбит и управлении космическими ракетами 97
Далее, из (23) получаем
Sx = Sx cos со/ — Sy sin со/ — S^co sin со/ — Syo> cos со/,
Sy = Sx sin со/ -|- Sy cos o)/ -(- S^co cos со/ — Syсо sin со/,
откуда в соответствии с (18) имеем
Sx = [фх (S*, Sy, Sz, /) — SycoJ cos со/ —
—	Sy,	Sz,	/)-j-S^co] sin со/,
Sy = [tyx (Sx, Sy, Sz, /) — Syco] sin со/ +
+ [Ь (sx> Sy> t) H- VIC0S ы*
S2 = ^2(Sxt Sy, Sz, /).
(68)
(69)
При расчете траектории величины Sx, Sy, Sz были приняты из¬
вестными функциями времени, поэтому в соотношениях (23)
и (69) SXj Sy, S2, Sx, Sy, S2 можно считать также известными
функциями /. Следовательно, <р и 0, определяемые формулами
(66) и (67), являются известными функциями /.
Вновь дифференцируя (66) и (67) по /, найдем <р и 0, при¬
чем в полученные выражения будут входить SXy Sy, S2, кото¬
рые определяются при помощи (68)
Sx = Sx cos со/ — Sy sin со/ — s^co sin со/ — Syco cos со/ —
— S^co sin со/ — SyCO COS со/ — S^co2 COS со/ -f-
—J— Sy со2 sin со/,
и аналогичные выражения для Sy и S2.
Совместно с (18) получаем
I	I	/С	О	О	i\	I
+	S*>	S**	5Г
и аналогичные выражения для Sy и S2. Входящие в эти вы¬
ражения частные производные ctyx/dSx и т. д. могут быть
вычислены для любой совокупности значений Sx, Sy, S2, /.
Однако практичнее, по-видимому, сначала найти <р и б для
большого числа п значений th с помощью (66), (67) и (23),
Зак. 876

98
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
затем представить <р и 0 в форме полиномов вида
П <*-*<>
ft=l 1фк
ih-td
f (h)>
Hh)
(70)
(71)
и после этого путем дифференцирования этих выражений
найти ф и 0 в виде функций времени.
Для активного участка траектории вне атмосферы можно
написать
Syi = а — g,
где
а = г и g = —gQtf-L.
Проектируя на оси невращающейся геоцентрической системы
координат, получим
5УД =X + gof?.
{х2+у2 + 22)
2\9/2
*^уду — У 4* goR2
SyAz=z+g0R2
уду ^ I 6U-V (Х2_1_у2 + г2 у/г
(х3 + У2 + •г2)‘/а
По аналогии с (59а) и (596) имеем
°уду
(72)
<р = arc tgT
УД*
£
0 = arccos-^-.
•^уд
Тогда, так же как для (66) и (67), можно написать
■^уд^уду ^УДу^УДдт
5уд +Sk
5удг (^УД^УД* 5УДу^УДу "Г 5УДг^УДг) (5УД* 5УДу “I" 5уд2) 5;
(73)
(74)
(75)
'уд*
(Sy*r T 5УДи + 5удг) V 5уд+ 5УДу
(76)

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ 99
Продифференцировав (72), получим
. D2 (X* + у 2 + 3*)Ч> Х-Зх (X* + у» + Z2)'k {хх + у у + г2)
“Г 50^	(^.2	_|_	у2	_|_	г2)3	U'J
и аналогичные выражения для 5уДу и 5уд^.
С помощью (1а) и (3) х, у и 2 определяются в виде функ¬
ций времени. Подставляя выражение (3) в (1а) и дифферен¬
цируя, найдем величины
x,y,z, x,y,z, x,y,z
в виде функций времени. Применяя (72), (75) — (77), мы
получим ф и б в виде функций времени. Функции ф и б нахо¬
дятся путем дифференцирования уравнений (75) —(77) по
времени
<78>
где
А — (^уд^ + 5УДу) Р’уд^уДу + ^уд^уДу	*^УДу*^УДх	*^УДу^УДJ
2 (Sy^Sy^	5уДу5уд^) (Sy^Sy^ -(- £уДу5уДу),
в
(5уд* + Sy*y + sk)2 (5У^ + 5Уду) ’
где
В = (5уд + 5уд + 5Удг) 5уд + 5уд X
(79)
у - J~ZJ Г	->~Х	J у
X {^уд2 (Зуд^уд^. + £уду£уду + 5УД^УД<г) +
“f~ 5уд^ (б’уд^ SyJkjSyAx -|- 5уду -f- 5уДу5уду	5уд^ -|- 5удг5удг)
2 (5уд^5уд^ + SyRySyRy -j- SyRzSyz^) SyAz
(^уддг Sy*y ^yO ^уд2 ^
[*“*Удг (5Уд^удл- ^УДу^УДу “I- *^Уд2*^Удг)
(5уд* “I” ^Уду "Ь^УД2) ^уд J {^ (^удх^удх	5Уду^Уду +5УдЛдг) ^
X |/*Уд, + 5уДу + (5уд^ -f- 5уДу + 5уд2) (S^ -f 5уДу) X
-X (*5уд^уДх Ч- 5ужЛд,)} •

100
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
Далее,
SYRX = Х + g(fi2 (х2+у2 + г2)*' »	(80)
где
С — (х2 + у2 + Z2)3 [(х2 + у2 + Z2f7 X —
— Зх (х2 4- У2 4~ z2)~42 (хх 4- УУ + zz)2 —
— Зх (х2 + у2 -Ь z2)'1* (х2 +■ У2 + z2 + хх 4- уу + zz)] —
— 6 (л:2 + у2 4- z2)2 (хх 4~ УУ 4- zz) [(х2 4~ У2 4~ z2)*'7 х —
— Зх (х2 4- у2 4- z2)42 (хх 4- УУ 4- zz)];
аналогичные выражения запишем для2>уд и SyjLZ-
Величины х, у и г в выражении (80) можно найти
как функции времени путем подстановки (3) в (1а) и после¬
довательного дифференцирования по t. Тогда <р и 9 опреде¬
ляются как функции времени из (78) и (79),	а	также	(72),
(77) и (80). Резюмируя, можно сказать, что	все величины	в
правой части равенства (65) являются известными функциями
времени, поэтому управляющие моменты 2)J^, и Шг для
программного движения также будут известными функциями
времени.
ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ ПРОГРАММНЫХ УПРАВЛЯЮЩИХ
МОМЕНТОВ
Перейдем теперь к вопросу о том, каким образом могут
быть технически реализованы Wlx, 2Jiy и Ш2, представляющие
собой известные функции времени.
Можно указать следующие четыре основных метода, за¬
ключающихся в применении:
1) газовых рулей, помещенных в струю газа;
2) поворотных двигателей;
3) вспомогательных управляющих сопел;
4) вращающихся внутри ракеты масс с переменной угло¬
вой скоростью.
Последний метод, который наиболее пригоден для косми¬
ческих аппаратов с экипажем [5], в настоящей статье не рас¬
сматривается. В первых двух методах для создания упра¬
вляющих моментов предусматривается незначительное изме¬
нение направления тяги. Это приводит к некоторому откло¬
нению от принятого ранее допущения о том, что тяга совпа¬
дает е продольной осью. Правда, изменения незначительны,

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ Ю1
и при расчете траектории ими практически можно пренебречь,
однако мы предпочитаем пользоваться в дальнейшем третьим
из указанных методов, который принципиально не изменяет
ни направление тяги, ни ее величину.
На фиг. 10 можно видеть поперечное сечение ракеты и
вспомогательные сопла (отверстия). Пусть ось тангажа па¬
раллельна линии АА', а ось рыскания по курсу—линии ВВ'
(следовательно, продольная ось
перпендикулярна плоскости чер¬
тежа). Центральные линии упра¬
вляющих сопел аа' и bb' жестко
связаны и параллельны продоль¬
ной оси. Центральные линии со¬
пел рр' в среднем положении
также параллельны продольной
оси, но могут поворачиваться во¬
круг оси, параллельной оси ры¬
скания по курсу, причем если р
отклоняется влево (или вправо),
то р/ отклоняется вправо (или
влево). Ко всем соплам подво¬
дится сжатый азот (или другой
подходящий газ) из резервуара с постоянным давлением. Два
сопла bb' создают управляющий момент Шх относительно оси
тангажа, а два отверстия аа'—момент Т(у относительно оси
рыскания по курсу. Чтобы точно удовлетворить условию, со¬
гласно которому тяга ракеты направлена строго по продоль¬
ной оси и не изменяется при действии органов управления,
добавления к тяге от каждой пары сопел все время должны
быть одинаковыми. Следовательно, если питание сопла а сни¬
жается, то питание сопла а' увеличивается на ту же величину.
Этого можно добиться с помощью устройства, изображен¬
ного на фиг. 11. Когда коническая шестерня на валу серво¬
двигателя поворачивается на определенный угол, конические
зубчатые колеса I и II поворачиваются на тот же угол во
взаимно противоположных направлениях, поэтому клапаны
в отверстиях а и а' действуют также во взаимно противопо¬
ложных направлениях.
Управление относительно продольной оси может быть осу¬
ществлено двумя соплами рр' с помощью передачи вращения
такими же коническими шестернями, как и на фиг. И.
Постоянство тяги вдоль продольной оси обеспечивается
изменением тяги каждого сопла по закону S'sec^, где S' —
тяга для среднего положения сопла, а 7— угол отклонения от
среднего положения. Это может быть реализовано с помощью
I В1
I
Фиг. 10. Управляющие сопла
(схема расположения).

102
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
надлежащего клапана, приводимого в действие с помощью
шестерен, показанных на фиг. 12.
Если же на ракете имеется несколько реактивных дви¬
гателей, установленных аналогично управляющим соплам
Фиг. И. Зубчатая пере¬
дача управления вспомога¬
тельными соплами стабили¬
зации тангажа и рыскания.
Фиг. 12. Система зубчатых
шестерен передачи управления
соплами, регулирующими от¬
клонение продольной оси.
на фиг. 10, то, очевидно, управляющие связи могут быть обес¬
печены этими двигателями и от некоторых или от всех доба¬
вочных управляющих сопел можно отказаться.
ТЕЛЕМЕТРИЯ ВЕЛИЧИН 6, <р, ф и £уд
Чтобы судить о положении продольной оси ракеты в про¬
странстве, углы 0 и ф (см. фиг. 7) необходимо передавать с по¬
мощью телеметрической аппаратуры наземным командным
станциям. С этой целью можно преобразовать 0 в частоту
электромагнитного излучения с борта ракеты с помощью
установленного в точке а (см. фиг. 8) переменного конденса¬
тора, одна часть которого жестко связана со стержнем z, а
другая с развилкой В. Этот конденсатор, включенный в цепь
радиопередатчика, и определяет частоту его излучения. Ана¬
логично осуществляется телеметрия угла <р с помощью дру¬
гого переменного конденсатора, установленного в точке b
(см. фиг. 8), причем одна его часть соединена со стержнем z,
а другая — с корпусом подшипника 6, который фиксирован
в плоскости ху гиростабилизированной системы координат
xyz. Этот конденсатор включен в цепь второго генератора
электромагнитных колебаний. Вырабатываемые для телеме»
трии частоты используются либо в качестве несущей частоты

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ ЮЗ
излучения, либо служат для ее модуляции. Сигнал частоты v,
соответствующий любой из передаваемых величин, прини¬
мается и усиливается приемной схемой (фиг. 13), где две ре¬
зонансные цепи настроены на частоты vi и v2, А— якорь, a S\
и S2— обмотки возбуждения для вращения сервомотора по
часовой и против часовой стрелки. Обмотки Si и S2 питаются
пульсирующим (выпрямленным) током, когда тиратроны Т\
или Т2 запираются (якорь А питается постоянным током).
Когда vi > v > V2, то принимаемая частота практически не
оказывает влияния на резонансные цепи. Но если v увеличи¬
вается или уменьшается, то при v = vi или v = v2 один из тира'
тронов. Т\ или Г2 запирается и мотор начинает работать к
поворачивать конденсаторы С\ и С2 таким образом, что ча¬
стоты контуров vi и v2 либо увеличиваются, либо уменьшаются
и значение v снова оказывается между значениями vi и v2, т. е.
восстанавливается прежнее соотношение частот vi > v > v2,
при этом мотор опять останавливается. Таким образом, поло¬
жение мотора зависит от значения частоты v. Связав с мото¬
ром указатель (стрелку), двигающийся относительно шкалы,
мы можем получить прибор, который будет непосредственно
указывать значения угла 6 или ср. Аналогичным путем можно
осуществить телеметрию угла поворота ф, на который стер¬
жень В (см. фиг. 9) может поворачиваться в подшипнике.
Когда управление производится описанным выше способом,

104
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЁТОМ
то величина ф должна неизменно равняться нулю; если же
прибор покажет, что ф Ф 0, следует произвести измерения для
радиокоррекции.
Далее, если в некоторый момент t вследствие каких-либо
возмущений составляющие тяги Syfl отклоняются от програм¬
мных значений на величины
ASyv Д5уДу, A*Syv
то составляющие скорости будут отличаться от программных
значений в первом приближении на следующие величины:
fbSytxdt, f bSyRydt, f Д5удг dt.
Здесь интегрирование производится во всем интервале дей¬
ствия возмущения. (При этом предполагается, что указан¬
ный интервал времени достаточно мал и поле тяготения в
области, проходимой ракетой за это время, можно считать
однородным.)
Поэтому для наблюдения за движением требуется реги¬
стрировать с помощью соответствующих приборов интегралы
по времени
f Syidt, fsytdt, J Syldt.
чтобы в любой момент сравнивать их с программными зна¬
чениями. Если учесть выражения
£Удж = 5Уд sin 0 cos <Р,
5уд =Syxsin0sin«p,
5уДг =5yicos6,
то для получения этих интегралов необходимо измерить ве¬
личины 5УД с помощью телеметрических приборов. Началь¬
ное измерение 5УД в ракете можно осуществить посредством
динамометра, на который действует только эта сила тяги.
На борту космического корабля гравитационные силы урав¬
новешиваются силами инерции. Результаты измерений дина¬
мометром могут быть преобразованы в изменение емкости,
включенной в цепь генератора электромагнитных колебаний и
представлены частотой электромагнитного излучения с борта
ракеты. Принятые наземной станцией изменения излучаемой
частоты с помощью серводвигателя преобразуются в показа¬
ния прибора по схеме, приведенной на фиг. 13.
Дальнейшее использование величин 0, <р и 5УД при вычис¬
лении интегралов от составляющих удельной тяги выпол-

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ Ю5
няется по схеме, показанной на фиг. 14. Три установленных
на наземных станциях серводвигателя ^<?уд- Мн и М^ пре¬
образуют получаемую информацию б (а соответственно
sin б и cos б) и <р (а соответственно sin <р и cos <р). Серводвига¬
тель	перемещает	скользящий	контакт	по цилиндриче¬
ской обмотке сопротивления, тогда как каждый из серво¬
двигателей Af0 и УИф перемещает два контакта, скользящих
по цилиндрическим обмоткам соответствующих потенцио¬
метров. На каждый из пяти потенциометров подается по¬
стоянное напряжение, в результате чего по обмотке проте¬
кает постоянный ток.
Электрическое сопротивление вдоль обмотки потенцио¬
метра, движок которого приводится во вращение электро¬
двигателем Ms , изменяется таким образом, что падение
напряжения между зажимом « + » и скользящим контактом

106
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
пропорционально величине Буд. Для непосредственного от¬
счета величины Бул на цилиндрической поверхности корпуса
потенциометра установлена шкала, а на движке имеется
указатель. Электрическое сопротивление вдоль обмотки по¬
тенциометров, движки которых приводятся во вращение мо¬
торами УИ0 и Му, изменяется таким образом, что падение
напряжения между скользящим контактом и средней точ¬
кой обмотки потенциометра пропорционально величинам
sin 0, cos 0 и sin ф, cos ф соответственно. Если скользящий
контакт перемещается вправо от средней точки обмотки, то
разность потенциалов между скользящим контактом и сред¬
ней точкой меняет свой знак на обратный; это соответствует
изменению знака sin 0, cos 0 и sin ф, cos ф соответственно.
Следовательно, величины БУД1 sin 0, cos 0, sin cp и cos ф пред¬
ставляются в электрической форме токами /5 , /sinо, /Cos0,
/sincp, /coscp, протекающими через соответствующие обмотки че¬
тырех приборов с вращающимися катушками (рамками).
(К серводвигателям и Му могут быть добавлены указа¬
тели со шкалами, по которым можно непосредственно про¬
изводить отсчет углов 0 и ф.)
Одна из катушек каждого из упомянутых выше четырех
приборов фиксирована, тогда как другая может поворачи¬
ваться, преодолевая действие пружины, стремящейся вер¬
нуть ее в нулевое положение. Когда обе катушки находятся
под током, то электродинамический момент пропорционален
произведению величин токов в катушках и угол поворота
подвижной катушки будет мерой произведения соответствую¬
щих измеряемых величин.
На каждой подвижной катушке укреплен скользящий
контакт, показанный в виде стрелки на фиг. 14. Этот контакт
скользит по обмотке потенциометра, намотанной на сердеч¬
ник из изоляционного материала, имеющий форму дуги
окружности. К концам обмоток подключено постоянное на¬
пряжение. Если нулевое положение скользящего контакта
совпадает со средней точкой дуги, то при отклонении сколь¬
зящего контакта падение напряжения между средней точкой
обмотки и скользящим контактом будет пропорционально
произведению двух измеряемых величин. Это произведение
«преобразуется» в силу тока через катушку, на которую
действует это падение напряжения.
Произведения Бул sin 0 и 5УД cos 0 представляются в виде
пропорциональных им токов Jsyjksim> и /* cose, а произведе¬
ния (Syn sin 0) sin ф и (БуД sin 0)cos ф — пропорциональными
ИМ ТОКамИ /б'уД sin 6 sinср И /б'уд sin 0 cosf*

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ Ю7
Как видно из фиг. 14, для получения токов
^>уд sin б Sin ср И ^>уд Sin 0 coscp
последовательно включаются два прибора с подвижными ка¬
тушками, а для получения тока /$удCOs0 требуется только
одна подвижная катушка. Как видно из схемы, токи
/s sine sin ч» /syjlsin0cos<p и ISyRcosO поступают на обмотки якорей
трех электродвигателей постоянного тока, угловые скорости
которых пропорциональны токам в обмотках магнитов.
В результате углы поворота якорей двигателей, пропорцио¬
нальные интегралам
регистрируются и указываются в любой момент времени
стрелками по шкалам. Программные величины интегралов
указываются красными стрелками, которые перемещаются
посредством часового механизма. По мере того как реги¬
стрируемые величины отклоняются от программных, в авто¬
матическое радионаведение требуется введение коррекции
оператором наземной станции.
ОБ АВТОМАТИЧЕСКОМ РАДИОУПРАВЛЕНИИ ПАРАМЕТРАМИ а, 0, у И 5,
ПРОГРАММИРОВАННЫМИ ВО ВРЕМЕНИ
Обозначим положения клапанов управляющих сопел
аа', bb' и рр' через а, (3, а положение клапана, регулирую¬
щего тягу, — через б. В рассмотренных выше расчетах траек¬
тории величины а, |3, 7 и б определяются в виде заданных функ¬
ций времени. Поэтому они должны быть в каждый момент
времени замерены в ракете и преобразованы в необходимые
управляющие сигналы. Эти операции выполняются с по¬
мощью изменения частоты излучения или же частоты моду¬
ляции синусоидальных колебаний наземной контрольной
станции.
На наземной станции имеется переменный конденсатор,
включенный в схему электронного генератора колебаний и
вращаемый электродвигателем, угловая скорость которого
J SyjLzdt — J 5уд cos Qdt,

108
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
изменяется в соответствии с заданной программой посред¬
ством изменяющегося по величине напряжения. Это напря¬
жение также является заданной функцией времени. Путем
введения регулировочного сопротивления, которое может
устанавливаться вручную, можно в случае необходимости
изменять характер автоматического радиоуправления. Соот¬
ветствующий прием сигнала на ракете может быть выполнен
принципиально так, как показано на схеме фиг. 13. Если
передача производится с помощью модуляции одной и той
же несущей частоты, то для управления по а, |3, 7 и 8 тре¬
буется один радиопередатчик и соответствующий ему на
ракете один радиоприемник. Каждый серводвигатель упра¬
вляет клапанами и переменными конденсаторами С\ и С2
(см. фиг. 13), как уже было описано выше.
О НЕЙТРАЛИЗАЦИИ РЕЗКИХ (ВНЕЗАПНЫХ) ВОЗМУЩЕНИЙ
В системе управления должны предусматриваться также
средства для устранения влияния внезапных возмущений,
обусловленных, например, воздушными потоками. С этой
целью в ракете устанавливаются три скоростных гироскопа,
измеряющих угловые скорости по тангажу, курсу и крену.
Чувствительность этих гироскопов должна быть такой, что¬
бы программное движение с малыми угловыми скоростями
практически не оказывало на них влияния. При отклонениях
каждый из гироскопов поворачивает два механически свя¬
занных друг с другом конденсатора С' и С', включенных
параллельно с Ci и С2, как показано на фиг. 13. Если при
повороте С' и С' частоты vi и v2 уменьшаются и двигатель
начинает работать (при vi = v2), он поворачивает Сх и С2
в сторону увеличения vi и v2. В результате конденсаторы Сх
и С2 работают в рассматриваемой схеме как стабилизаторы
емкости, подавляющие внезапные колебания угловых ско¬
ростей.
К этому устройству могут быть добавлены датчики уско¬
рений для измерения угловых ускорений большой величины
(вызванных внезапными возмущениями). Тогда к схеме,
приведенной на фиг. 13, необходимо добавить два вращаю¬
щихся конденсатора С" и С", включаемых параллельно Сх
и С2. Эти конденсаторы (не показанные по схеме) приво¬
дятся в движение от датчиков угловых ускорений. Однако
в таком устройстве имеет место взаимное влияние скорост¬
ных гироскопов и датчиков угловых ускорений, вследствие

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ
109
чего оказывается необходимым использовать нейтрализую¬
щие устройства. В работе [6] для нейтрализации было пред¬
ложено пневматическое устройство.
РАСПРЕДЕЛЕНИЕ АППАРАТУРЫ УПРАВЛЕНИЯ ЧЕТЫРЕХСТУПЕНЧАТОЙ
РАНЕТЫ
Очевидно, что серводвигатели, соответствующие пара¬
метрам а, р, 7 и S, необходимо иметь в каждой из четырех
ступеней; поэтому в полной ракете требуется 16 таких серво¬
двигателей. Радиоприемник для приема модулирующих ча¬
стот управления va, vp, vT, v8 может быть размещен в носовой
Фиг. 15. Вариант устройства для отделения ступени
с отработанным топливом.
части субракеты I. Каждой частоте модуляции соответствует
определенная обмотка электронного устройства с управляю¬
щим серводвигателем (обмотка v на фиг. 13). При работе
данной субракеты только обмотки ведущей ступени должны
быть соединены с радиоприемником в носовой части субра¬
кеты I. В момент отделения какой-либо ступени и начала
работы следующей должны быть включены обмотки этой
последующей ступени.
Гиростабилизированная платформа (система координат
xyz) вместе с соответствующей аппаратурой (включая
радиопередающее устройство для телеметрии) может быть
размещена также в носовой части субракеты I. Отделение
ступени в точке отсечки топлива и начало работы следую¬

110
I. ОБЩИЕ ПРИНЦИПЫ УПРАВЛЕНИЯ ПОЛЕТОМ
щей ступени производится автоматически, независимо от
наземной станции управления, и может быть выполнено раз¬
личными способами. Один из возможных способов указан
на фиг. 15. Предполагается, что рассматриваемая последую¬
щая ступень имеет турбонасосный агрегат, приводимый в
действие перегретым паром, полученным при распаде Н202,
причем в качестве катализатора использован Са(Мп04)2.
На фиг. 15 показан один из топливных баков отделяющейся
ступени. На уровне жидкости находится поршень, прижимае¬
мый к ней небольшим серводвигателем р. Скользящий кон¬
такт, движущийся вместе с поршнем, замыкает цепь 7, когда
топливо выгорает. При этом включаются взрывающие
устройства а, Л и В, первое из которых служит для разделе¬
ния ступеней, второе — для открытия клапана контейнера
Н2О2 и третье — для открытия клапана контейнера с
Са(Мп04)2. Обе жидкости под давлением подаются в паро¬
генератор для запуска двигателя следующей ступени. С и
С' обозначают электрические соединения, разрываемые при
отсоединении ступени.
РАДИОТЕХНИЧЕСКИЙ СПОСОБ ОРИЕНТАЦИИ ПРОДОЛЬНОЙ ОСИ
СУБРАНЕТЫ I ПРИ ПОЛЕТЕ ПО ПРОМЕЖУТОЧНОМУ ЭЛЛИПСУ
При полете ракеты по эллипсу ее ось сохраняет то на¬
правление, которое она получила после отбрасывания второй
ступени. Поэтому прежде чем начать старт по касательной
к эллипсу, продольная ось ракеты должна принять напра¬
вление, соответствующее времени старта. Элементы эллип¬
тической орбиты с помощью астрономических наблюдений
могут быть определены с высокой степенью точности, по¬
этому необходимое направление всегда известно. Требуемая
ориентация продольной оси может быть получена с помощью
радиокоманды, подаваемой с Земли. Во время последующего
активного полета вектор S будет всегда сохранять это на¬
правление, так что 0 и <р будут постоянными. Параметры
управления a, J3, 7 и Ь также должны быть постоянными, и,
следовательно, роль наземной станции управления будет за¬
ключаться в том, чтобы поддерживать постоянными моду¬
лирующие частоты va, vp, vT, v5.
АВТОМАТИЧЕСКАЯ КОРРЕКЦИЯ ПРИ РАДИОУПРАВЛЕНИИ
Для обеспечения автоматического контроля за радио¬
управлением во время активного полета какой-либо субра¬
кеты можно на наземной станции преобразовать в электри¬

О РАСЧЕТАХ ОРБИТ И УПРАВЛЕНИИ КОСМИЧЕСКИМИ РАКЕТАМИ И1
ческие напряжения величины разности между измеренными
и программными значениями интегралов по времени от со¬
ставляющих удельной тяги. Эти напряжения вместе с напря¬
жениями, представляющими величины б, <р и ф, могут быть
введены в специальные генераторы функций, выходные на¬
пряжения которых используются для вспомогательного регу¬
лирования четырех электродвигателей. Последние поворачи¬
вают переменные конденсаторы, емкости которых опреде¬
ляют управляющие частоты модуляции. Составляющие
удельной тяги могут быть измерены непосредственно с по¬
мощью акселерометров, установленных на гироплатформе в
носовой части субракеты I, и в дальнейшем по телеметриче¬
скому каналу переданы на наземную станцию, где соответ¬
ствующие интегралы по времени снова воспроизводятся и
сравниваются с программными величинами.
ЛИТЕРАТУРА
1. Vertregt М., Calculation of Step-Rockets, Вег. V. Intern. Astronaut.
Kongrefi, S. 157, 1955.
2. Kooy .J. М., On Pelativistic Rocket Mechanics, Astronaut. Acta, 4, 31
(1957).
3. Kooy J. М., Uytenbogaart J. W., Ballistics of Future, Chapt. VI,
Haarlem, 1946.
4. Kooy J. М., Uytenbogaart J W., Ballistics of Future, Chapt. XII,
p. 412, Haarlem, 1946.
5. Kooy J. М., On Plotting Small Thrust Space Ship Orbits, in «Space-
Flight Problems», p. 107, 1953.
6. К о о у J-. М., On Automatic Internal and External Control of Long
Range Rockets, Вег. V. Intern. Astronaut. Kongrefi, p. 168, 1955.

//• АВТОНОМНАЯ НОСМИЧЕСНАЯ
НАВИГАЦИЯ
ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ
НАВИГАЦИИ >)
Шнейдер
Векторное уравнение, полученное из основных принципов механики,
описывает работу инерциальных систем навигации в любой точке простран¬
ства. Особая форма этого уравнения непосредственно применима к движе¬
нию на любой высоте и с любой скоростью над вращающейся Землей
эллиптической формы. Применимость этого уравнения иллюстрируется на
примере конкретной системы. В статье анализируются ошибки инерциаль¬
ных систем.
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
R9— экваториальный радиус эллипсоида поверхности
Земли;
/?п — полярный радиус эллипсоида поверхности Земли;
е — сжатие эллипсоида поверхности Земли;
R — вектор положения точки, проведенный из центра
Земли;
R— модуль вектора R;
срг.ц. — геоцентрическая широта;
ср — географическая широта, или просто широта;
g — вектор силы тяжести;
g0— модуль вектора g на поверхности Земли;
О — вектор напряженности гравитационного поля;
G0—модуль вектора G на поверхности Земли;
G9—величина G0 на экваторе;
Gx — составляющая вектора G, перпендикулярная к R;
<*>и. з.— вектор угловой скорости Земли относительно
инерциального пространства;
!) Schneider А. М., IRE Trans, on Aeronaut. a. Navig. Electro-
nics, ANE-G, № 3, 159-177 (September 1959).

ft *
ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ
113
^и. з. — модуль вектора <ои. 3.;
t — время;
х—переменная интегрирования по времени;
X — долгота;
Хи— инерциальная долгота;
h — высота;
йг. ц> — геоцентрическая высота;
Ли — инерциальная высота;
сри — инерциальная географическая широта;
т—рабочая масса акселерометра;
Ырв — вектор угловой скорости тела В относительно на¬
чала координат системы F;
®FBxy}t—составляющие вектора ыРВ по осям х, у, z;
f — вектор удельной силы, измеренный акселероме¬
тром (единица силы на единицу массы);
а — инерциальный вектор ускорения;
аг — измеренная величина горизонтального ускорения;
ист—индекс (в разд. 7—9), означающий истинное зна¬
чение величины; тот же символ без значка пред¬
ставляет значение этой величины, измеренное си¬
стемой (в разд. 1—6 все символы означают ис¬
тинные величины);
F, М — неподвижная и подвижная опорные системы коор-
А, В, С — произвольные векторы;
(ол — вектор угловой скорости системы координат i от¬
носительно координатной системы /;
0—угол, пройденный истинным вектором положения
на плоскости, измеренной относительно опреде¬
ленной оси;
ф— угол, пройденный контрольным вектором поло¬
жения;
/ — индекс системы координат, несущей контрольный
вектор положения;
> у, z — оси системы координат i\
* Р» Т — единичные векторы по осям х, у, z соответственно;
/—контрольная (или истинная до разд. 7) инер¬
циальная система координат;
X%Y,Z—оси системы координат /;
Ь j, k — единичные векторы по осям Я, У, Z;
$ Зак. 876,
динат с общим началом

114
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ навигация
О— индекс, означающий начальное, измеренное на по¬
верхности Земли или неизменное значение пере¬
менной величины.
ВВЕДЕНИЕ
В настоящей статье описывается метод проектирования
инерциальных систем навигации, пригодных для навигации
в любой точке пространства, причем он не зависит ни от
используемой аппаратуры, ни от выбора координатных осей.
Выводится векторное уравнение, названное «основным урав¬
нением системы» или «уравнением механизации», с помощью
которого проектируется обобщенная система инерциальной
навигации, применимая в любой точке пространства. Это
уравнение подробно рассматривается в применении к поле¬
там над Землей.
Основные уравнения систем выведены многими авторами
различными путями [1—3]. Здесь мы выведем уравнения,
используя простейшую технику векторного анализа. Этот
метод имеет следующие преимущества.
1. Метод является дедуктивным. Уравнения выводятся
непосредственно из основных принципов механики — законов
Ньютона. Он фиксирует внимание главным образом на про¬
стой физической стороне проблемы, а не на ее очень слож¬
ном механическом осуществлении.
2. Метод точен. Поскольку Земля может быть предста¬
влена твердым телом известных размеров, вращающимся
вокруг одной фиксированной в теле оси и образующим из¬
вестное гравитационное поле, то основные уравнения систе¬
мы, полученные здесь, являются точными. Эти уравнения
строго учитывают все известные усложняющие явления,
включая трехмерность Земли, ее вращение, эллиптичность,
гравитационное поле и гравитационные аномалии, а также
допускают произвольное движение объекта над любой точ¬
кой Земли, в любое время, на любой высоте и с любой ско¬
ростью.
3. Метод является общим в том смысле, что выведенные
уравнения применимы ко всем родственным системам. Эти
уравнения в простых выражениях определяют функциониро¬
вание системы и потому подчеркивают принцип действия,
который не всегда очевиден из рассмотрения конкретной
системы.
4. Проектирование системы может производиться в раз¬
ных системах координат (векторный метод). Выбор системы

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИЙ
115
координат можно рассматривать как независимую задачу,
которая решается после того, как определены функции, ко¬
торые должна выполнять система. Если метод получения
системы уравнений заранее предполагает определенную си¬
стему координат, то эта система уравнений может ока¬
заться неоптимальной.
5. Поскольку метод не зависит от аппаратуры, исполь¬
зуемой при механизации системы, он допускает свободу ее
выбора.
6. Метод дает схему систематического исследования множе¬
ства различных вариантов системы, часть которых раньше не
исследовалась, а также наиболее удобную систему координат
для анализа ошибок упрощенных систем, в которых эллиптич¬
ность, высота или другие влияния компенсированы не пол¬
ностью.
7. Наконец, при использовании этого метода простыми ло¬
гическими операциями могут быть получены условия Шулера.
Как и следовало ожидать, они появляются в одном из нормаль¬
ных видов системы, и их не нужно вводить интуитивно.
1.	АВТОНОМНАЯ НАВИГАЦИЯ
Навигация — это процесс направления движущегося объ¬
екта к месту назначения. Для выполнения навигации необ¬
ходимо знать как положение объекта, так и характер его
движения. Задача автономной навигации заключается в вы¬
полнении необходимых функций без наблюдения наземных
ориентиров или других внешних опорных пунктов. В частно¬
сти, накладывается такое ограничение, что никакие электро¬
магнитные излучения (такие, как свет, излучения звезд,
радиосигналы, сигналы радиолокационных станций, инфра¬
красные лучи и т. п.) на объекте не принимаются и с объек¬
та не излучаются.
Цель настоящей работы — получить расчетные уравнения
для системы, способной выполнять такие функции с высокой
степенью точности в течение длительного времени. Система
должна обрабатывать данные, поступающие от объекта, дви¬
жущегося совершенно произвольно в любом месте, с любой
скоростью и по любой траектории. Данные обо всех возмож¬
ных движениях должны быть правильно сгруппированы и
обработаны в целях обеспечения четкой непрерывной инфор¬
мации о положении объекта и его ориентации.
В общем случае твердое тело, движущееся в трехмерном
пространстве, обладает шестью степенями свободы. Следова¬
8*

116
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
тельно, необходимо определять шесть координат: три коор¬
динаты положения (например, широту, долготу и высоту) и
три координаты ориентации (например, курс, угол возвыше¬
ния и крен). В соответствии с этим можно предполагать, что
для выполнения такой системы необходимо иметь шесть дат¬
чиков, если каждый датчик реагирует на изменение только
одной координаты.
2.	ЧУВСТВИТЕЛЬНЫЕ ДАТЧИКИ ДЛЯ ОБНАРУтЕНИЯ ДВИЖЕНИЯ
НА ДВИЖУЩЕМСЯ ОБЪЕКТЕ
Для решения задачи автономной навигации над Землей
можно воспользоваться пассивными неинерциальными дат¬
чиками, к которым относятся измерители скорости в воздухе,
магнитные компасы и барометрические высотомеры.
Измеритель скорости в воздухе определяет движение
объекта относительно воздушных масс. Однако он не может
оценить движение воздушных масс относительно Земли (ве¬
тер), и, следовательно, выдаваемые им данные имеют огра¬
ниченную точность в тех случаях, когда он является един¬
ственным источником информации о скорости.
Магнитный компас не дает правильных показаний над
магнитными полюсами и к тому же само магнитное поле не
всегда достаточно известно. Барометрический высотомер
обеспечивает данные только по одной координате положе¬
ния, а именно по высоте, но может служить в качестве по¬
лезного дополнения к другой полностью инерциальной си¬
стеме. Возможно, что дальнейшее изучение космического
пространства вблизи Земли позволит определять положение
или скорость при прохождении объекта через один из поясов,
окружающих Землю, например пояс космических лучей, од¬
нако в настоящее время информация, имеющаяся относи¬
тельно этих поясов, недостаточна для обеспечения точной
навигации. В качестве датчиков могут быть использованы
приборы, которые по своей природе чувствительны к движе¬
нию. К таким приборам относятся гироскопы и акселеро¬
метры. Гироскопы чувствительны к вращательному движе¬
нию, которому они подвергаются; акселерометры чувстви¬
тельны к поступательному движению. Система, состоящая
из трех гироскопов и трех акселерометров, может обеспечить
информацию для определения общего движения твердого
тела.

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦЙАЛЬНОЙ НАВИГАЦИИ
117
3.	ВЛИЯНИЕ ФОРМЫ ЗЕМЛИ
Для осуществления навигации вблизи Земли важно знать
форму Земли, по отношению к которой будет определяться
положение объекта, а также ее гравитационное поле, ока¬
зывающее влияние на инерциальную систему.
Рассмотрим сначала жидкую массу, находящуюся в по¬
кое. Плотность этой массы в любой внутренней точке опре¬
деляется только расстоянием от центра. При отсутствии
внешних сил и под воздействием только сил притяже¬
ния между отдельными частицами равновесной формой этой
массы будет сфера. Если это тело вращать с постоянной
скоростью вокруг фиксированной оси, то оно примет новую
равновесную форму, симметричную относительно оси враще¬
ния, но сплющенную у полюсов и вытянутую на экваторе.
Эта форма очень близка к форме эллипсоида вращения [4].
Теорию этого явления можно использовать для определе¬
ния формы Земли. Форму Земли достаточно хорошо аппрок¬
симирует простая математическая фигура, так называемый
эллипсоид Хайфорда, который обычно используется состави¬
телями карт. Этот эллипсоид имеет следующие размеры
экваториального и полярного радиусов [5]:
R3 = 6 378 388 м,
Rn — 6 356 911, 946 м,	^
причем сплюснутость
R3 — Rn — — 1	/о\
Яэ	297 ’	W
Можно показать, что длина радиуса-вектора R из центра
в точку на поверхности эллипсоида определяется следующим
выражением:
R = R3(\—в sin2 срг ц +Слагающие высших порядков по s),
(3)
гДе Фг. ц. — геоцентрическая широта, определенная ниже.
Напряженность гравитационного поля G определяется
как гравитационная сила, действующая на единицу массы
рассматриваемого тела в данной точке пространства вслед¬
ствие притяжения между массами в выбранной инерциаль-
ной системе координат. Как показано ниже, при навигации
над Землей действующее гравитационное поле определяется
почти исключительно одной Землей. Вектор силы тяжести g,
определяемый для точки над Землей, в общем случае отли¬

118
II. АВТОНОМНАЯ космическая навигация
чается от силы притяжения. Направление вектора силы тя¬
жести называется вертикалью и определяется как постоян¬
ное направление висящего отвеса, точка опоры которого за¬
креплена на поверхности Земли. При отсутствии вращения
Земли отвес показывал бы направление напряженности гра¬
витационного поля. На вращающейся Земле он несколько
отклоняется от направления на центр Земли под действием
центростремительного ускорения.
Разница между гравитационным ускорением и ускоре¬
нием силы тяжести в любой точке представляет центростре¬
мительное ускорение
G — g = <*>и. з. X К. з. X R),	(4)
где Юи.з. —угловая скорость вращения Земли по отношению
к неподвижной звезде; R — вектор положения точки, прове¬
денный из центра Земли, или геоцентрический радиус-вектор.
Угол между направлением силы тяжести и направлением
гравитационного поля в любой точке земного шара не пре¬
вышает 6'.
Гравитационное поле вне Земли, существующее в соот¬
ветствии с известными законами теории потенциалов, пока¬
зано на фиг. 1. Если функция гравитационного потенциала

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ	119
в наружных точках выражается через сферические гармо¬
ники, то первый, наибольший по величине, член выражения
изменяется обратно пропорционально расстоянию от центра
Земли. Градиент первого члена дает радиальное гравита¬
ционное поле классической точечной массы, обратно про¬
порциональное квадрату расстояния. Следующий член, об¬
ратно пропорциональный четвертой степени расстояния, обу¬
словлен удлинением экватора Земли. Результатом влияния
Северный полюс
• Q - неподвижная точка на
поверхности Земли
g-сила тяжести („вертикаль”) в
wIE*mE*R) m04KeQ-
(р - географическая
широта точки Q
Высота точки Р
Южный полюс
Геоцентрическая
высота точки Р
Фиг. 2. Сечение Земли в плоскости меридиана.
Плечо отвеса, закрепленного неподвижно на Земле, направлено вдоль
вектора силы тяжести.
этого члена является небольшое отклонение (менее 6') век¬
тора гравитационного поля от направления к центру Земли,
как показано на фиг. 2. Очень малые члены высших порядков
характеризуют небольшие колебания поля, образующие так
называемые гравитационные аномалии. На поверхности
Земли последние вызывают отклонение вектора гравита¬
ционного поля от среднего направления на величину, не
превышающую Г, и происходят благодаря местным неодно¬
родностям в распределении массы Земли.
Если бы Земля действительно могла быть представлена
вращающимся жидким телом, то направление силы тяжести
в любой точке поверхности было бы строго перпендикулярно
поверхности. Это происходит потому, что такое же сочетание
силы притяжения и центробежной силы, которое действует
на отвес и определяет направление силы тяжести в любой
точке поверхности, действует также на частицы жидкости

120
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
и определяет форму поверхности в этой же точке. Отвес бу¬
дет указывать направление результирующей этих сил. По¬
верхность жидкости будет перпендикулярна этим силам, по¬
скольку жидкость не может иметь поверхность, наклонную
к действующим силам. Следовательно, сила тяжести будет
везде перпендикулярна поверхности. Если пренебречь ано¬
малиями и считать, что форма Земли точно представляется
Полярная ось
Долгота точки Р
Фиг. 3. Общие координаты, используемые для определения
положения относительно Земли.
эллипсоидом Хайфорда, то сила тяжести на поверхности
Земли может быть представлена вектором, перпендикуляр¬
ным к эллипсоиду.
На основании изложенного и выражения (4), которое
дает возможность найти вектор силы притяжения, зная век¬
тор силы тяжести, а также учитывая некоторые соотноше¬
ния, связанные с геометрией эллипса, можно показать, что
составляющая напряженности гравитационного поля, нор¬
мальная к геоцентрическому радиусу, проведенному в лю¬
бую точку поверхности эллипсоида, выражается следующим
образом:
Ох = | О X \ | = (2eg0 — ш2и 3 R) sin <pr.u. cos <pr- ц +
-(-Члены высших порядков по е, (5)

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ
121
где R — модуль вектора R; go— модуль вектора g на по¬
верхности эллипсоида.
Определим теперь некоторые координаты, которые пона*
добятся для описания положения данной точки по отноше¬
нию к Земле:
срг. ц. — геоцентрическая широта — угол между эквато¬
риальной плоскостью и радиусом-вектором точки,
проведенным из центра Земли;
ср—географическая широта — угол между эквато¬
риальной плоскостью и перпендикуляром к по¬
верхности эллипсоида в точке;
X—долгота — угол между Гринвичским меридианом и
меридианом точки, измеренный при движении во¬
круг полярной оси в восточном направлении;
h — высота — расстояние от точки до поверхности эл¬
липсоида, измеренное вдоль направления силы тя¬
жести;
Ар.ц. — геоцентрическая высота — расстояние от точки до
поверхности эллипсоида, измеренное вдоль гео¬
центрического радиуса, проведенного в точку из
центра эллипсоида.
Некоторые из этих величин указаны на фиг. 2 и 3.
Можно показать, что связь между геоцентрической и
географической широтами выражается следующей фор¬
мулой:
сР = сРг ц -f- 2s sin срг ц coscpr ц + Члены высших порядков по е.
(6)
4.	ИНЕРЦИАЛЬНОЕ ПРОСТРАНСТВО
Инерциальным пространством является любое простран¬
ство, в котором справедливы ньютоновские законы движе¬
ния. Поскольку действие как гироприборов, так и акселеро¬
метров основано на использовании законов Ньютона, то и
измеряемое ими движение должно быть инерциальным дви¬
жением, т. е. движением по отношению к инерциальной си¬
стеме координат. Инерциальная система координат для изу¬
чения движений над Землей имеет начало в центре Земли, при¬
чем ее оси фиксированы относительно «неподвижных звезд».
В этой системе координат необходимо учитывать только
одно гравитационное поле — поле самой Земли, поскольку
поля других небесных тел уравновешиваются ускоре¬
нием центра Земли. Существуют, правда, небольшие до¬
полнительные воздействия, обусловленные изменением поля

122
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
небесных тел в области между центром Земли и движу¬
щимся объектом, однако эти влияния незначительны (порядка
g • 10-7) и здесь не учитываются.
Введем понятие инерциального эллипсоида (не нужно
смешивать с эллипсоидом инерции, используемым в меха¬
нике). Инерциальный эллипсоид представляет воображаемое
твердое тело с размерами эллипсоида Хайфорда и центром.
Меридиан обзекта
А-долгота объекта
\ц-инерциальная долгота
Экватор	объекта
Начальный
инерциальный
меридиан
Положение Гринвичского
меридиана в момент
времени t
Фиг. 4. Инерциальная долгота.
Вид на Землю сверху вдоль полярной оси. 3 —угол, образованный вращением Земли
вокруг полярной оси. Начальный инерциальный меридиан отмечает положение Гринвичского
меридиана в инерциальном пространстве в момент / = 0.
совпадающим с центром Земли, но не вращающееся отно¬
сительно неподвижных звезд. Время между последователь¬
ными совпадениями соответствующих точек на эллипсоиде
Земли и инерциальном эллипсоиде определяет одни истин¬
ные сутки, численная величина которых равна
Истинные сутки = 23 часа 56 мин. 4,09891 сек,	(7)
если поправки на прецессию дней равноденствия добавляются
к звездным суткам.
Соответствующая угловая скорость имеет величину
сои з = 7,292116557 • 10~5 рад (сек.	(8)
Определим на инерциальном эллипсоиде северный полюс,
южный полюс, экватор, параллели, меридианы. Примем за
первый инерциальный меридиан тот, который совпадает
с Гринвичским меридианом в нулевое время (см. фиг. 11).

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ	123
Очевидно, координаты широты и высоты данной точки,
измеренные относительно эллипсоида Земли и относительно
инерциального эллипсоида, равны. Долгота требует спе¬
циального исследования. Если мы обозначим через /и —
инерциальную долготу, а через t — время, то связь между
долготой Земли и инерциальной долготой выражается сле¬
дующим образом:
l =	(9)
как показано на фиг. 4.
Поскольку инерциальные датчики измеряют движение
относительно инерциального пространства, удобно следить
за движением объекта над инерциальным эллипсоидом и
затем определять его положение над Землей с помощью
уравнения (9).
5.	ГИРОСКОП
Мы не будем рассматривать подробности конструкции и
работы гироприбора со всеми явлениями прецессии, нутации
и т. п., так как это затруднит для неспециалиста понимание
работы прибора. Мы ограничимся здесь описанием функций
идеального гироприбора и проделаем то же самое для аксе¬
лерометра в следующем разделе. Следует отметить, что
реальные гироприборы и акселерометры имеют характери¬
стики, достаточно близкие к идеальным, благодаря чему
инерциальная навигация представляет практический интерес.
Рассмотрим только гироприборы и акселерометры с од¬
ной степенью свободы. К приборам с двумя и тремя степе¬
нями свободы применима та же теория, за исключением
только деталей анализа.
Гироприбор с одной степенью свободы имеет одну ось
(закрепленную относительно корпуса), на движение вдоль
которой он реагирует. Примем без доказательства следую¬
щее положение: «Три гироприбора, закрепленных на твер¬
дом теле, могут измерять вектор угловой скорости тела отно¬
сительно инерциального пространства, выражаемый через
его составляющие по трем ортогональные осям, называемым
осями тела, фиксированным на теле и определенным соот¬
ветственно положением чувствительных осей каждого гиро¬
прибора». Выходные данные представляют собой три ска¬
лярные величины (напряжение или ток), соответственно
пропорциональные трем векторным компонентам.
Таким образом (фиг. 5), если ыРВ представляет собой уг¬
ловую скорость тела В относительно опорной системы коор*?

124
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ навигация
динат F, не вращающейся относительно инерциального
пространства, то выходными сигналами являются u>FBx, ®FBy,
®гвг* если принять ху у и z за оси тела и использовать
обозначения осей для различения соответствующих компо¬
нент.
Стабилизированной платформой называется твердое тело,
угловая скорость которого управляется независимо от вра¬
щения базы, на которой оно закреплено. Это достигается
Фиг. 5. Схема измерений с гироприбором.
Гироприбор, укрепленный на геле В, измеряет составляющие х, у, z вектора
(О —угловая скорость тела В относительно системы координат F.
креплением платформы на универсальном шарнире таким
образом, что ее можно поворачивать в любом направлении
независимо от положения базы. Гироприборы, закрепленные
на платформе, измеряют ее угловую скорость и вырабаты¬
вают сигналы для управления этой угловой скоростью. На¬
пример, может возникнуть необходимость в том, чтобы плат¬
форма имела нулевую угловую скорость относительно инер-
циального пространства. Такая платформа сохраняет неиз¬
менную ориентацию в то время, когда несущий ее объект
маневрирует, и называется инерциально-неподвижной плат¬
формой (фиг. 6).
Стабилизированную платформу также можно вращать
с определенной скоростью. Если известно, например, что
объект пролетает в северном направлении 50° широты в 1 час,
го платформу можно заставить вращаться с той же скоро¬
стью. При этом, если бы какая-то линия на платформе была
X
FB

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ
125
первоначально ориентирована вертикально, то она продол¬
жала бы оставаться вертикальной в течение всего полета.
В общем случае, чтобы заставить платформу вращаться, не¬
обходимо на каждый из трех гироприборов подать входные
1
Фиг. 6. Инерциальная невращающаяся стабилизированная платформа.
Оси платформы не вращаются относительно инерциального пространства, в то время как
самолет маневрирует (2) или движется над Землей (5).
сигналы, соответственно равные трем составляющим желае¬
мой угловой скорости по осям тела. Такие сигналы иногда
называются сигналами привода гироскопа или сигналами
управления угловой скоростью. Измерение этих сигналов оз¬
начает измерение угловой скорости платформы (см. выше).
6.	АКСЕЛЕРОМЕТР
Акселерометр состоит из рабочей (чувствительной к уско¬
рению) массы, удерживаемой пружиной, закрепленной в
корпусе, причем выходной сигнал (вырабатываемый датчи¬
ками смещения) пропорционален отклонению массы от ее
нейтрального положения в корпусе. Предполагается, что
пружина не имеет массы и развивает противодействующую
силу, пропорциональную отклонению чувствительной массы
от нейтрального положения. Акселерометр с одной степенью
свободы имеет одну ось, на движения вдоль которой он реа¬
гирует. Система с рабочей массой на пружине или любое
другое устройство для инерционного определения ускорения
одинаково хорошо реагирует и на гравитационное притяже¬
ние. Измеритель ускорения с массой на пружине, удерживае¬
мый неподвижно на Земле так, что его ось параллельна на¬
правлению гравитационного поля с напряженностью G, бу¬
дет вырабатывать выходной сигнал, который невозможно
отличить от сигнала другого идентичного измерителя уско¬
рения, чувствительная ось которого горизонтальна и который
подвержен действию ускорения G (м/сек2).

126
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ навигация
Акселерометры измеряют разность векторов
< = 0-а = <Н-дН-	О»)
где G — напряженность гравитационного поля, действующего
в даной точке выбранной инерциальной опорной системы
координат, выражаемая в единицах силы, приходящейся на
единицу массы (ускорения); а — инерциальное ускорение;
R — вектор положения акселерометра относительно начала
выбранной инерциальной опорной системы: координат*); /—
инерциальная опорная система координат.
Вектор f называется удельной силой и представляет со¬
бой силу, приходящуюся на единицу массы.
Индекс у производной по времени указывает опорную систему коорди¬
нат для дифференцирования, т. е. систему координат, в которой распола¬
гается предполагаемый наблюдатель, описывающий движение. Такие опор¬
ные системы координат должны определяться по-разному для скорости и
ускорения. Возьмем простой пример.
Пусть г будет вектор положения точки в системе координат карусели,
проведенный из начала на оси вращения. Для наблюдателя, находящегося
на карусели, этот вектор будет постоянным, следовательно, его производ¬
ная равна нулю. Однако этот же самый вектор вращается по отношению
к наблюдателю на Земле и, следовательно, для этого случая имеет произ¬
водную по времени, не равную нулю. Отсюда видно, что невозможно одно¬
значно определить скорость вектора, не задав опорную систему координат.
В общем случае векторные производные в движущихся системах коор¬
динат учитываются законом Кориолиса. Этот закон устанавливает, что
если F и М представляют «неподвижную» и «движущуюся» системы коор¬
динат с общим началом, a	угловая	скорость движущейся системы
координат по отношению к неподвижной, то соотношение между производ¬
ными любого произвольного вектора А, взятыми по отношению к двум
системам, имеет вид
и для вторых производных
)/=•= {w)ж + WFM х (*РМ х А) + mFM х А + 2<Vai X )м •
Символ &FM обозначает производную по времени угловой скорости по
отношению к движущейся или неподвижной системе координат, поскольку
1) При рассмотрении производных вектора необходимо отметить, что
первая производная вектора по времени равна скорости точки в конце
вектора, а вторая производная по времени представляет ускорение точки
при условии, что вектор всегда преобразуется так, что его начало остается
в одном месте (преобразование вектора не изменяет ни длину вектора, ни
его направление, т. е. не изменяет вектор). Для вектора положения, кото¬
рый уже имеет свое начало в фиксированной точке, первая и вторая про¬
изводные по времени представляют собой соответственно скорость и. уско¬
рение точки в конце вектора;

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИЙ	127
применение закона Кориолиса (12) к вектору показывает, что член,
содержащий векторное произведение, исчезает:
dmFM ] _(dmFM\ .	у,	_	I	Q	=	i
dt Jf~\ dt j fm ^ pm [ dt 1m	fm'
Применение закона Кориолиса к векторным производным во вращаю¬
щихся опорных системах координат более подробно рассматривается во
многих работах по векторному анализу [6]. Использование одного индекса
у второй производной, как, например, F в левой стороне второго уравне¬
ния, означает, что в обоих дифференцированиях подразумевается одна и
та же система координат.
Уравнение (10) выражает второй закон Ньютона для
чувствительной массы измерителя ускорений с тремя степе¬
нями свободы. Заметим, что вектор — f представляет силу
противодействия, приходящуюся на единицу чувствительной
массы, которую оказывает пружина для удержания чувстви¬
тельной массы в равновесии относительно корпуса. Сумма
сил, действующих на чувствительную массу —fm + mG
(сила пружины и сила гравитационного притяжения массы),
в соответствии со вторым законом Ньютона равна произве¬
дению массы на ее инерциальное ускорение.
В состоянии равновесия ускорение чувствительной массы
и ускорение корпуса равны
(с1Щ \
J j*	(11)
Отсюда непосредственно следует уравнение (10).
Таким образом, акселерометры, закрепленные на твердом
теле, измеряют вектор удельной силы, действующей на тело,
выражаемый через его составляющие по трем осям, непод¬
вижным по отношению к телу и определяемым соответ¬
ственно положением чувствительных осей каждого акселеро¬
метра. Выходные данные получаются в виде трех скалярных
величин (например, напряжений), соответственно пропор¬
циональных этим трем составляющим.
На основании изложенного можно сделать следующие
выводы:
1. Удельная сила образуется гравитационным полем и
ускорением.
2. Акселерометры измеряют удельную силу.
3. Выходные данные получаются в виде трех составляю¬
щих по осям, жестко связанным с телом.
Эти положения иллюстрируются на фиг. 7—10. Читатель
может проверить правильность уравнения (10) в каждом
отдельном случае. Третий пункт указывает, что для правиль¬
ной интерпретации показаний приборов необходимо сохранять

Корпус
Однородное гравитаци¬
онное поле, G=9, дм/сек^
Оси прибора
Линейная пружина
Фиг. 7. Реакция акселерометра, удерживаемого неподвижно
в гравитационном поле.
Некоторое тело, не показанное на фигуре (например, стол), поддерживает корпус
акселерометра неподвижным, в противном случае он начал бы падать под дей¬
ствием гравитаиионнбго поля.
Пружина и масса т находятся в установившемся состоянии покоя; пружина
отклонена от нейтрального положения. Отсчет по осям координат:
'v=°- 4=-32-
X
г?
. Отсчет''
ь'РпЧ'!-
и •' I I [О
об ill1 	^
I
iC1'
-ЛС"6 '
-2s-
Уснорение корпуса
Гчавитационное поле равно нулю
Фиг. 8. Реакция акселерометра на ускорение в пространстве,
свободном от действия силы тяжести.
Пружина и масса т находятся в установившемся состоянии покоя. Корпус имеет
ускорение 3,05 м/сек2 относительно инерциального пространства, направленное
параллельно оси у.
Отсчет по осям координат:
/»=°’ Ч	Х0'?х — °-

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ
129
неизменным направление осей акселерометра относительно
навигационной опорной системы координат. Например,
если акселерометр с одной степенью свободы жестко
связан с системой координат объекта так, что чувствитель¬
ная ось прибора направлена вдоль продольной оси объекта,
z
Фиг. 9. Реакция акселерометра на совместное воздействие притя¬
жения и ускорения.
Корпус акселерометра имеет ускорение 3,05 м/сек1 в направлении оси у. Гравита¬
ционное поле придает корпусу ускорение 9,8 м/сек2 в отрицательном направлении
оси z.
Пружина и масса т находятся в установившемся состоянии покоя.
Отчет по осям координат:
/у = -10’ /г = -32-
то акселерометр измеряет только составляющую вектора
ускорения, направленную вдоль этой оси. Это положение
иллюстрируется фиг. 10, где показано, что можно преобразо¬
вать измеренные величины (0; —8,66; 5,0), учитывая угол
30°, и получить /V = —Y = —10. Главное назначение гиро¬
приборов в инерциальной системе — давать информацию об
угловом положении осей акселерометра. Это осуществляется
измерением направления и скорости поворотов осей в про¬
странстве.
Согласно определению, опорная система координат,
жестко связанная с твердым телом, вращается, если напра¬
9 За к. 876

130
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
вление ее осей в пространстве изменяется, а начало коорди¬
нат остается в одной точке; опорная система движется по¬
ступательно, если ее начало координат перемещается, а оси
остаются параллельными своим первоначальным направле¬
ниям. В общем случае движение тела состоит из одновре¬
менных перемещений и поворотов, при этом поступательное
Оси корпуса
измерителя
ускорений
Осьх перпендикулярна к плоскости
чертежа
J Инерциалъная опорная система координат
Ось X перпендикулярна к плоскости чертежа
Фиг. 10. К измерению удельной силы.
Удельная сила измеряется составляющими по осям корпуса акселерометра. Акселе¬
рометр имеет ускорение, при котором а = j Y = у 10. Гравитационное поле равно нулю.
/* = 0; /у = - 8,66; /г=5,0.
движение начала координат образует перемещение; измене¬
ние направления осей образует вращение. Акселерометры и
гироприборы производят измерения, автоматически отделяя
перемещения от поворотов. Идеальные акселерометры изме¬
ряют перемещения (вместе с гравитационными воздействия¬
ми), не реагируя на повороты, которым они подвергаются.
Идеальные гироприборы измеряют вращение (угловую ско¬
рость), не реагируя на линейные перемещения (или на гра¬
витационное поле). Если это не оговаривается особо, то вся¬
кий раз, когда мы говорим об угловой скорости, мы будем
иметь в виду угловую скорость твердого трехмерного тела
или опорной системы координат по отношению к инерциаль-
ному пространству.
Если выходные данные трех обычных акселерометров
(измеренная удельная сила) являются единственной инер¬
циальной информацией системы о перемещениях объекта, то

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ	131
в этом случае в результатах измерений невозможно отделить
ту часть, которая определяется притяжением масс, от той
части, которая определяется ускорением !).
Пользуясь инерциальной системой, необходимо тем или
иным способом решать, какая доля определяется каким-либо
воздействием. При безупречно работающей системе никаких
затруднений не встречается. Но если в системе возможны
какие-либо ошибки, то мы можем ошибочно приписывать
какую-то часть удельной силы одному воздействию, тогда
как она является следствием другого. Это вызовет ошибки
инерциальной системы, которая может вести себя совершен¬
но неожиданным образом, как показано в разд. 9.
Иногда задают вопрос: «Если бы человек находился вну¬
три закрытой коробки в межпланетном пространстве, то ка¬
ким образом он мог бы определить, является ли простран¬
ство коробки инерциальным или нет?». Из того, что было
сказано выше, должно быть ясно, что разрешить этот вопрос
можно рядом измерений, произведенных с гироприборами и
акселерометрами. Если выходные сигналы угловой скорости
трех ортогонально расположенных гироприборов тожде¬
ственно равны нулю и если выходные сигналы системы трех
ортогонально расположенных акселерометров также тожде¬
ственно равны нулю, то систему координат коробки можно
считать инерциальным пространством, в котором не дей¬
ствует гравитационное поле.
7.	ОСНОВНОЕ УРАВНЕНИЕ ИЗМЕРИТЕЛЬНОЙ СИСТЕМЫ
Учитывая, что инерциальные датчики измеряют удельную
силу и угловую скорость, выведем уравнения навигации, со¬
держащие эти величины. Вначале необходимо ввести разли¬
чие в обозначения истинного значения величины и значения,
измеренного инерциальной системой. Для определения
истинного значения величины мы будем добавлять к обозна¬
чению индекс «ист», тогда как обозначение без индекса
будет относиться к показанию прибора или к измеренному
значению. В этом отношении новая система обозначений от¬
личается от принятой в предыдущих разделах, где такое раз¬
деление не требовалось.
Пусть опорная система координат, называемая истинной
инерциальной системой координат /ист, закреплена на инер-
!) Метод различения притяжения и ускорения инерциальными сред¬
ствами описан в работе [7].
9*

132
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
циальном эллипсоиде так, что она не может вращаться отно¬
сительно неподвижной звезды, и начало ее координат 0ИСт
находится в центре эллипсоида. Вектор положения, прове¬
денный из начала координат в точку местоположения объек¬
та, назовем истинным лектором положения RHct (фиг. И).
Предположим, что на борту движущегося объекта имеет¬
ся масштабная модель, представляющая пространствен¬
ную схему, изображенную на фиг. 11. Масштабная модель
^ист
Северный полюс
Фиг. 11. Инерциальный эллипсоид и истинная инерциальная опорная
система координат.
Все обозначения, приведенные на фигуре, представляют истинные инерциальные величины.
Эллипсоид Земли вращается около оси О Z .
называется измерительной системой, поскольку наблюдатель
внутри объекта видит на ней положение объекта. С ней
жестко связана опорная система координат, называемая из¬
мерительной инерциальной системой координат /, имеющая
свое начало 0 в точке, находящейся внутри объекта. Оси
этой системы координат первоначально ориентируются па¬
раллельно осям истинной инерциальной системы координат
и удерживаются в этом положении во время движения
объекта. По этой схеме измерительный вектор положения R
проводится из начала координат в точку пространства, опре¬
деляемую измерительной инерциальной системой координат.
Его направление должно быть таким же, как и истинного
вектора положения. Предположим, что в измерительной
инерциальной системе координат помещена масштабная мо¬
дель истинного инерциального эллипсоида, называемая из¬
мерительным инерциальным эллипсоидом. Тогда конец изме¬

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ	133
рительного вектора положения определит масштабное поло¬
жение объекта относительно измерительного инерциального
эллипсоида точно таким же образом, как конец истинного
вектора положения определяет истинное положение объекта
по отношению к истинному инерциальному эллипсоиду
(фиг. 12).
Фиг. 12. Система определения положения.
А —увеличенный вид инерциальной навигационной системы, располагаемой
внутри объекта.
В то время как объект движется в пространстве, вектор
истинного положения изменяется как по длине, так и по
направлению. Первая производная по времени этого вектора
в истинной инерциальной системе координат называется
истинной инерциальной скоростью (dRHCT/dt)IiicT, вторая про¬
изводная называется истинным инерциальным ускорением
(aPRHCT/rf/)/HCT,
Каждому движению истинного вектора положения дол¬
жно соответствовать определенное движение измерительного
вектора положения. Мы должны иметь какую-то логи¬
ческую схему для превращения измеренных инерциальными
Методами данных в правильное движение этого вектора.

134
И. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
Чтобы получить такую схему, отметим, что вторая производ¬
ная истинного вектора положения
=°-fHCT	(12)
'	/^ИСТ
соответствует формуле (10) с добавлением индекса «ист».
Если это уравнение определяет, как движется истинный век¬
тор положения, то оказывается возможным программиро¬
вать движение измерительного вектора положения в соответ¬
ствии с уравнением
(4г) = °-'-	<13>
Согласно этой формуле, измерительному вектору положе¬
ния необходимо придать ускорение относительно измеритель¬
ных инерциальных опорных осей, пропорциональное вектор¬
ной сумме двух входных сигналов, причем первый является
функцией положения, а второй непосредственно получается
из показаний акселерометра.
Гравитационное поле Земли является хорошо известной
функцией положения (см. разд. 3). Поэтому нетрудно полу¬
чить с помощью бортового счетно-решающего устройства
векторную функцию G, которая хорошо аппроксимирует
напряженность истинного гравитационного поля GHCt в дан¬
ной точке. Можно ожидать, что этот метод даст хорошие ре¬
зультаты, если навигационная система работает надлежа¬
щим образом и положение объекта хорошо известно. В связи
с этим еще раз подчеркнем, что /Ист и f дают представление
о различии между физической величиной и ее измеренным
значением и что (d2RUCT/dt2)IiicT есть истинное ускорение
объекта, тогда как (d2Rjdt2)j является ускорением, придан¬
ным вектору, который служит масштабной моделью вектора
положения системы навигации. Разница между уравнениями
(12)	и (13) состоит в том, что первое из них связывает
реальные силы с истинным движением объекта в простран¬
стве, в то время как второе выражает соотношение между
измеренными (и расчетными) силами и движением измери¬
тельного вектора положения в системе координат модели.
В силу этого выражение (13) является основным уравне¬
нием, применимым ко всем инерциальным системам опреде¬
ления положения, относящимся к рассматриваемому классу.
Нетрудно получить более удобную форму уравнения (13).
Для этого представим, что измерительный вектор положения
нашей масштабной модели закреплен на твердом теле, ко¬
торое может вращаться около начала координат измеритель-

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ	135
ной инерциальной системы координат. Повторное ориентиро¬
вание вектора выполняется сообщением телу некоторой угло¬
вой скорости. Изменение длины вектора производится
удлинением стрелки, которая совпадает с измерительным век¬
тором положения и фактически определяет его. Для удоб¬
ства введем опорную систему координат, закрепленную
координат i
Фиг. 13. Измерительная система координат срг ц.
— угловая скорость системы координат I относительно координатной системы [
на этом теле, — контрольную (измерительную) систему коор¬
динат i. Примем начало координат в точке, соответствующей
центру вращения, чтобы системы координат / и i имели
общее начало 0. Обозначим оси системы координат i через
х, у, 2, причем направление оси z выберем совпадающим
с направлением измерительного вектора положения. Пусть еди¬
ничными векторами по трем осям будут а, Р, у (фиг. 13).
При таком определении осей координат системы i вектор
R будет равен
R = T R.	(14)
Дифференцируя в системе координат £, находим, что две
первые производные также являются векторами, направлен¬
ными по оси 2
Z
г
\
(15)
(16)

136
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
где точки обозначают дифференцирование по времени, а у
является постоянным вектором в системе координат г.
При рассмотрении двух опорных систем координат — / и
i} вращающихся одна относительно другой, можно восполь¬
зоваться законом Кориолиса.
Обозначая угловую скорость системы координат i отно¬
сительно системы I через (Оц и применяя этот закон, пере¬
пишем левую сторону равенства (13) следующим образом:
(~^“). + w// X (w7i X R) + <*>/* X R +
+ 2ь)п X = Q —	(17)
Беря векторное произведение у с каждым членом этого
уравнения, получаем
тх +т [х Ып х (й,/г х R))+Y х ((0/г х R)+
+ 2TX[a)/iX(-^-)]=fXr — OXY- (18)
Этот, по-видимому сложный, результат значительно упро¬
щается, если допустить, что угловая скорость ыц не имеет
составляющих, параллельных измерительному вектору поло¬
жения. Это условие известно как «свойство инерциального
азимута» 1).
Использование этого условия представляется вполне ло¬
гичным, поскольку вращение /-й системы координат имело
целью изменить направление измерительного вектора поло¬
жения и поворот этой системы координат вокруг оси, проходя¬
щей через этот вектор, не осложняет задачи. Если наложить
это условие, то угловая скорость ыц и угловое ускорение (оц
]) Параллельные составляющие угловой скорости часто принимают не
равными нулю, так что оси стабилизированной платформы могут быть все
время направлены на восток и север. Тогда можно непосредственно инте¬
грировать скорость по широте и скорость по долготе, чтобы получить ши¬
роту и долготу. В таких системах величина этих составляющих угловой
скорости неограниченно возрастает вблизи полюсов Земли, что приводит
к ряду инструментальных проблем Полная информация о направлении на
север и восток может быть получена в инерциальной азимутальной си¬
стеме. Заметим, что векторное произведение у на единичный вектор, парал¬
лельный полярной оси Земли, образует вектор, указывающий на восток,
а векторное произведение полученного вектора на единичный вертикаль¬
ный вектор образует новый вектор, указывающий на север. Кроме того,
как указано ниже, все еще используются выходные сигналы широты и
долготы.

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ	137
будут перпендикулярны измерительному вектору положе¬
ния1). Выражая эти замечания аналитически, получаем
»/гТ= 0,	(19)
w/;-R = 0,	(20)
®/г Т=0,	(21)
i/rR = 0.	(22)
Применяя правило правой руки и учитывая геометриче¬
ские свойства векторов, в частности результат векторного
произведения ортогональных векторов, можно последова¬
тельно определить члены уравнения (18) следующим
образом:
гх(4г)=0,	(23)
т X [«О// X (w/i X R)] = 0,	(24)
Т X (ю/г X R) = R^n>	(25)
2Т X [»/, X (^)J = 2Rv>„.	(26)
Подставляя результаты (23) — (26) в выражение (18) и
разрешая уравнение относительно высших производных не¬
известной угловой скорости, получим первое из следующей
системы уравнений:
Юл = [f X т— О X Т —	(27)
R = — t’4 + Q"( + R(»,t\2,	(28)
w//-T = 0.	(19)
Второе из этих уравнений получается аналогичным обра¬
зом из выражения (17), но на этот раз скалярным умноже¬
нием на Y* Результат можно упростить и преобразовать,
чтобы получить приведенную форму. Третье уравнение (19)
выражает условие инерциального азимута.
]) Если бы угловое ускорение имело не равные нулю параллельные
составляющие, то интегрирование давало бы не равные нулю параллельные
составляющие угловой скорости, что нарушает принятое условие.

133
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
Вышеприведенные уравнения представляют собой урав¬
нения реализации инерциальной системы определения поло¬
жения 1).
Уравнение (27) является уравнением для углов. Оно по¬
казывает, как управлять ориентирующим устройством, чтобы
удерживать измерительный вектор положения все время пра¬
вильно ориентированным, так как направление этого вектора
дает возможность определить широту и долготу; уравнение
(27) можно рассматривать также как уравнение положения.
Выражение (28) является уравнением для определения
длины. Оно показывает, как изменять длину указателя,
чтобы конец измерительного вектора положения определял
правильное масштабное расстояние от центра модели Земли.
Это выражение служит для определения высоты, поэтому
его можно назвать также уравнением высот. Уравнение по¬
ложения или некоторые его видоизменения обычно реали¬
зуются в приборах. Уравнение высот реализуется только
тогда, когда требуется инерциальное определение высоты.
Каждый член в уравнении (27) имеет определенный фи¬
зический смысл. Значение наиболее важных из них можно
проиллюстрировать рассмотрением методики проектирова¬
ния инерциальной системы навигации для самолета, движу-,
щегося на постоянной высоте над сферической Землей,
имеющей радиальное гравитационное поле. При этих усло¬
виях имеем
Подставляя эти величины в (28), видим, что уравнение
реализации для системы, используемой в этих условиях,
принимает простую форму
В этом случае необходимое угловое ускорение измери¬
тельной системы координат получается как произведение
величин, стоящих в правой части уравнения.
!) Управление объектом, необходимое для прибытия к месту назначе¬
ния, основывается на знании местоположения как места назначения, так
и объекта. Первое получается неинерциальными средствами, например
предварительно заданными координатами долготы и широты. Второе полу¬
чается от системы рассматриваемого типа. О методах использования этой
информации для управления движением объекта см. в [8].
R = О,
R — R0 = const,
YX 0 = 0.
(29)
(30)
(31)
(32)

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ
139
' Удельная сила в общем случае имеет большую соста¬
вляющую, направленную вдоль истинной геоцентрической
вертикали и создаваемую в первую очередь силами притя¬
жения. Удельная сила имеет также составляющую в истин¬
ном горизонтальном направлении, которая (в этом случае)
может быть только результатом горизонтального линейного
ускорения объекта.
В результате векторного перемножения векторов боль¬
шая гравитационная составляющая должна исчезнуть (век¬
торное произведение параллельных векторов равно нулю),
а модуль произведения равен величине горизонтального
ускорения. Эта величина при делении на радиус Земли дает
правильную величину соответствующего углового ускорения
измерительного устройства. Простой результат, полученный
выше, выведенный здесь в векторной форме применительно
к движению в трех измерениях, упрощается в случае движе¬
ния на плоскости. Получаемый в этом случае результат
можно было бы иметь, вращая измерительный вектор поло¬
жения с угловым ускорением, равным измеренному линейному
горизонтальному ускорению, деленному на радиус Земли:
ё=^аг,	(33)
где 0 — угловое ускорение, которое надо придать измеритель¬
ному вектору положения (27); аг — измеренное горизонталь¬
ное ускорение.
Член, содержащий удельную силу, является, вообще го¬
воря, самым большим и самым существенным в основном
уравнении (27). Другие члены в этом уравнении предста-
вляют по существу небольшие поправки. Изменения R учи¬
тывают изменение высоты и радиуса Земли с широтой
(эллиптичность). Член G X у, представляющий программиро¬
ванную гравитационную функцию положения, является по¬
правкой на эллиптичность, необходимой вследствие того,
что гравитационное поле Земли не направлено к центру
Земли. Последний член правой части учитывает скорость
изменения высоты и скорость изменения радиуса Земли при
полете над Землей, не имеющей формы шара.
Величина программированного гравитационного члена
равна составляющей гравитационного поля, нормальной
к геоцентрическому радиусу-вектору; ее максимальное зна¬
чение составляет 0,002 величины силы тяжести на поверхно¬
сти в любой точке Земли [5]. Отметим, что именно малую
величину G X Т, а не большую величину G необходимо про¬
граммировать в любой системе, создаваемой в соответствии

140
II. АВТОНОМНАЯ космическая навигация
с уравнением механизации (27). Если гравитационные ано¬
малии достаточно хорошо известны для того, чтобы их
включить в систему, то они учитываются этим членом. Если
рассматривать выражение (13) для случая навигации над
Землей, то из принципа действия акселерометров как при¬
боров, измеряющих удельную силу, очевидно, что это урав¬
нение является исходным при проектировании инерциальной
системы навигации, работающей в любой точке простран¬
ства. В общем случае необходимо определить инерциальную
систему координат, в которой определяется положение
объекта и место назначения. Гравитационное поле, суще¬
ствующее в этой системе координат, необходимо определить
как функцию положения и времени и сохранить в системе,
где она используется для образования функции G при вве¬
дении новых данных о положении. Направление осей датчи¬
ков относительно инерциальной системы координат должно
быть известно. Измеренные величины удельной силы необ¬
ходимо обработать в соответствии с (13) для получения
ускорения при изменении положения. Ускорение в свою оче¬
редь дважды интегрируется для определения положения.
Система, спроектированная в соответствии с уравнением
(13), может быть в принципе использована для автономного
указания положения искусственного спутника Земли при
условии, что она правильно настроена и работает во время
вывода спутника на орбиту. При использовании обычных
инерциальных систем на спутнике или для космической на¬
вигации могут возникать практические трудности, обусло¬
вливаемые несовершенством оборудования и сложностью
определения расстояний и гравитационных полей в космосе
с требуемой степенью точности *). •
8.	ПОСТРОЕНИЕ ИНЕРЦИАЛЬНОЙ СИСТЕМЫ
Уравнение (27) является исходным векторным уравне¬
нием для построения инерциальной системы навигации. Оно
применимо ко всем системам, предназначаемым для навига¬
ции над Землей. Рассмотрим, как это уравнение можно
использовать для проектирования конкретной системы. Век¬
торы чаще всего механизируются посредством операций,
производимых над их скалярными компонентами. Наличие
компонент для вычислений зависит от системы опорных
!) Использование инерциальных систем на космических объектах рас¬
сматривается в работе [7].

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ	141
осей, вдоль которых векторы разлагаются. Выбор этой си¬
стемы осей, называемой расчетной опорной системой коорди¬
нат, является одной из задач, упоминаемой во введении, ко¬
торая может быть выполнена сразу после того, как получено
основное векторное уравнение. Ниже проанализируем после¬
довательность выбора одной конкретной системы координат.
Другие системы координат можно рассматривать подобным
же образом.
Система координат, выбранная в качестве опорной рас¬
четной системы, будет представлять измерительную инер-
циальную систему координат. Скалярные уравнения, которые
необходимо механизировать, легко получаются выражением
каждого вектора в уравнении (27) через его компоненты
в этой системе координат. Для выполнения этого определим
удобную систему осей и единичных . векторов следующим
образом:
Z параллельна оси вращения Земли и направлена на се¬
вер; ее единичный вектор к;
X расположена в экваториальной плоскости, пересекая
нулевой инерциальный меридиан; ее единичный вектор i;
Y расположена таким образом, что образуется правая
система ортогональных осей XYZ\ ее единичный вектор j.
Эти оси параллельны соответствующим осям Хаст Уист
ZHCT истинного инерциального эллипса на фиг. 12.
Разложение векторов на их составляющие по этим осям
производится следующим образом:
/ — Vx + j /к + K/z*	(34)
Y = hx + hy + z>	(35)
(~ж)7 = ^x	(36)
(o7/ = \wx -f- j o)K -f- ko)z,	(37)
= [~dr\ ~	(^
OXT = GX-|= (2 eg0 — mV?8)(— 'TyTz +	nxr z+k '	0)>	(39)
R = R3 (1 - e sin2 <Pr. J + К ц s /?# (1 — eT|)	hT	U,	(40)
R= — R£b • TZ • Tz + ^r.u.-	(41)
Подстановка всех выражений (34) —(41) в (27) приводит
к уравнению, в котором появляются три единичных вектора.
Приравнивая коэффициенты при каждом из этих векторов

142
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
в обеих частях уравнения, получаем следующую систему
скалярных уравнений:
°х— r [/kTz /zTIV (2££о {°21э^э)ТуТг 2/?о>Л|,
“к = Ti [/zTx — fxlz — (2е^0 — -?Л) № — 2^]>
“z — y<; 1/xTV /rTx 2/?tuz).
(42)
После интегрирования о> получаем со
t
°>x = f <°х (х) dx + “х (*о)>
to
t
(Dy = j' (i)y (t) d'Z -f- toy (t0),
to
t
°>z = f wz (x)dx + mz (to)-
(43)
Согласно закону Кориолиса для скорости изменения у»
имеем
(4г)/—(4г),+ю"х т»
(4f X = 0 -ь «>/£ X Т-
(44)
(45)
Последнее выражение следует из того, что у является
неподвижным вектором в измерительной системе координат.
Подставляя (35) — (37) в (45) и разделяя составляющие,
получаем следующую систему скалярных уравнений:
”fx — “rTz wzlr>
ir = шхТх — <°x7z>
Т z — шх7у шкТх*
(46)

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ
Интегрируя, получаем
t
lx = f Тх(х)^+Тх (4))>
I
\	1у	— f Тк(х)^х +Тк(^о)>
I	to
\	t
Т z= { Tz(x)^x + Tz(A>)-
to
Для того чтобы найти долготу и широту, достаточно
знать лишь 7. Согласно фиг. 14, геоцентрическая широта вы¬
ражается так:
?!■. Ц. = arc sin Tz-	(48)
В географическую широту она превращается с помощью
выражения (6). Из этого же чертежа видно, что инерциаль-
ная долгота равна
X„ = arctg-^.	(49)
*Х
Географическая долгота находится из инерциальной дол¬
готы с помощью формулы (9).
Для рассматриваемой системы должны быть решены сле¬
дующие уравнения: (6), (9), (40) — (43) и (46) — (49). После¬
довательность операций следующая. По известным величи¬
нам /?, 7, со и измеренным значениям удельной силы и R
с помощью (42) находятся значения со. Затем производится
интеграция (43) для получения новых величин со, которые
вместе с	7	дают	7	(46). Величины 7 в	свою	очередь	интегри¬
руются	в	соответствии с (47), образуя	новые	величины 7.
Широта и долгота рассчитываются с помощью уравнений
(6), (9), (48) и (49).
Из дальнейшего анализа видно, что ориентацию объекта
можно определить путем измерения углов осей объекта от¬
носительно контрольной инерциальной системы координат и
трансформирования результатов в систему координат север —
восток — вертикаль, направление осей которой легко полу¬
чается из исходной информации с помощью счетно-решаю¬
щего устройства. Выходные данные могут быть получены
в виде курсового угла, угла места и крена. Таким образом,
143
(47)

144
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
эта система полностью определяет положение и ориентацию
объекта.
Обратимся теперь к аппаратуре и рассмотрим устройство
элементов, которые можно использовать для проведения не-
обходимых измерений и расчетов. Прежде всего мы должны
решить, располагать ли все инерциальные элементы на кор¬
пусе объекта или на стабилизированной платформе и в слу¬
чае, если используется стабилизированная платформа, будет
Фиг. 14. К определению измерительной геоцентрической широты
и измерительной инерциальной долготы.
Y Y
?г. агс SIn h, =	'
X
ли она вращаться относительно инерциального пространства.
Не вдаваясь во все детали, произвольно выберем систему,
у которой все инерциальные элементы закреплены на стаби¬
лизированной платформе и не могут вращаться в инерциаль-
ном пространстве. Такая конструкция обладает следующими
свойствами. Система из трех ортогональных линий, прове¬
денных на платформе, представляет собой физическую реа¬
лизацию осей измерительной инерциальной системы координат
/. Линии проводятся параллельно осям истинной инерциаль¬
ной системы координат (как показано на фиг. 12) во время
первоначальной настройки и удерживаются параллельными
своему начальному положению с помощью гироприборов во
время всех последующих движений объекта. Задачей гиро-
Z

I	ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ	145
1
приборов в такой системе является лишь выполнение этой
операции. Никаких сигналов, которые нужно обрабатывать
навигационным счетно-решающим устройством, не посту¬
пает в гироприбор и не снимается с него. Акселерометры
системы можно монтировать на платформе, располагая их
чувствительные оси параллельно осям платформы. Три от¬
счета этих приборов дают три величины fx, /у и /z, необходи¬
мые при решении уравнения (42).
Дальнейший анализ уравнений, которые необходимо ин¬
струментировать, показывает, что на навигационное счетно¬
решающее устройство надо подавать следующие величины:
fx> fy> fz — измеренные значения удельной силы,
7х(0)> ТуФ)> Tz (0)—координаты исходного положения,
(юх(0), wK(0), o)z(0) — составляющие начальной скорости,
К. п.> К. п. — геоцентрическую высоту и вертикальную
скорость.
В этой системе предполагается, что данные высоты посту¬
пают от неинерциальных датчиков. Все другие величины под¬
считывает навигационное счетно-решающее устройство в соот¬
ветствии с уравнениями, приведенными выше. В качестве вы¬
ходных данных получаются широта и долгота. Схема подачи
информации показана на фиг. 15. Необходимо отметить, что
измерительный вектор положения существует только в виде
цифр в счетно-решающем устройстве; реального вектора, на¬
правленного вертикально, нет, хотя при желании его можно
легко ввести. Как и в целом ряде других задач подобного ро¬
да, можно использовать различные счетно-решающие устрой¬
ства как аналогового, так и цифрового типа. Мы не пытаемся
выбрать какую-то «лучшую» систему и ограничиваем нашу
задачу описанием нескольких интересных с инженерной точки
зрения ее характеристик.
Ранее было установлено, что инструментальные уравне¬
ния для всех других родственных систем можно получить
видоизменением используемого здесь метода. При этом необ¬
ходимо:
1) выбрать другие системы координат в качестве опор¬
ных для расчета: измерительную систему координат, систему
координат, закрепленную на объекте, и т. д.;
2) включить отличную от нуля составляющую, параллель¬
ную со/ь особенно для измерительных систем с осями север—
Запад;
3) распространить выражения (27) с помощью закона Ко¬
риолиса на другую опорную систему координат, закреплен¬
ную на Земле;
10 Зак* 876.

146
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
4)	пренебречь одним или несколькими малыми членами
и принять R за постоянную величину для получения упрощен¬
ных уравнений в тех случаях, где допустима более низкая
точность;
- Стабилизированная платформа
"Z4
Сигналы акселерометра
на счетно-решающий
прибор
Система координат I
Сигналы
акселерометра
Навигационный
счетно -решающий прибор
Контрольный
вектор
положения в
► Широта 1Иа зап0мцнаЮщее
I устройство
►Долгота J
Сигналы
измерителя
высоты
} Начальные
условия
Фиг. 15. К определению геоцентрической вертикали.
Направление геоцентрической вертикали определяется контрольным (измерительным) векто¬
ром положения R, выдаваемым счетно-решающим прибором в виде составляющих по осям
системы координат /:
*=,**+JVk*z“*(1^+JV+kTz>
Задаваемые начальные условия:
тх(0)’ “х(0)’
Ту(0), ®,(0).
Tz(0)' mz(0)*
5)	ввести другую точку в качестве начала системы коор¬
динат i, например, на линии вектора тяжести таким образом,
что у можно выбрать как вектор, направленный вдоль гео¬
графической вертикали. Это в особенности целесообразно для
систем, которые используют вектор тяжести вместо геоцен¬
трической вертикали. (Ускорения этого нового начала коор-

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ	147
динат по отношению к инерциальной системе координат сле¬
дует учитывать в том случае, если появление небольших оши¬
бок недопустимо.)
6)	Решить уравнение (13) в декартовой системе коор¬
динат.
9.	ОШИБКИ В ИНЕРЦИАЛЬНЫХ СИСТЕМАХ НАВИГАЦИИ
Легко показать, что навигационное устройство, описанное
выше, а также практически все инерциальные приборы рас¬
сматриваемого здесь класса обладают характеристикой, из¬
вестной как эффект Шулера и названной так в честь ученого,
который открыл принцип маятника с длиной подвеса, равной
радиусу Земли, и применил его для компенсации гироком¬
паса.
Эффект Шулера проявляется в виде колебаний измеритель¬
ного вектора положения относительно его правильной вели¬
чины и возрастает при определенных расстройках системы.
Сравнивая это уравнение с (12), можно показать, что коле¬
бания Шулера могут существовать во всех системах, описы¬
ваемых уравнением (13), иначе говоря, можно показать, что
колебания Шулера существуют во всех системах, построен¬
ных по методу, данному в предыдущем разделе.
В результате получено следующее соотношение:
(e-<W = (0-4Oocos(j/
Величина 0 — ф представляет собой разность углов истин¬
ного и измерительного вектора положения и, следовательно,
является ошибкой системы. Из уравнения видно, что если из¬
мерительный вектор положения первоначально не направлен
согласованно с истинным вектором положения, то он будет
совершать вокруг истинного вектора положения устойчивые
синусоидальные колебания, известные как колебания Шулера.
Период этих колебаний зависит от скорости объекта, выра¬
жаемой б (величина б находится делением инерциальной ско¬
рости на Rq). Для объектов, неподвижных относительно Зем¬
ли или двигающихся с малыми скоростями, величина б2 на¬
много меньше, чем G3//?3. В этом случае период составляет
около 84 мин. Таков же период колебаний математического
маятника длиной /?э, подвешенного в неподвижной точке па¬
раллельного гравитационного поля с напряженностью G3, что
объясняет смысл термина «маятник с длиной подвеса, равной
радиусу Земли», часто употребляемого применительно к инер-
Диальным системам навигации. Когда скорость объекта
10*

148
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
приближается к скорости спутника Земли, то S2 приближается
по величине к GJR3 и период колебаний безгранично возра¬
стает. При таких условиях данная угловая ошибка рассогла¬
сования остается постоянной по величине. Колебания Шулера
определены выше только для конкретного случая, их суще¬
ствование в более общем случае можно доказать анализом
решения уравнения (52).
Колебания Шулера могут вызываться начальным рассо¬
гласованием. Ошибки в измерении или ошибки в расчете мо¬
гут образовать новые составляющие колебания, которые
добавляются к компонентам, уже существующим в данной
системе. Фаза так же, как и амплитуда, подвергается допол¬
нительным воздействиям, и ошибки, появляющиеся в разное
время от разных источников, не обязательно накапливаются
линейно.
Оказывается невозможным надежно определять высоту
над Землей, используя лишь обычные акселерометры. Это
происходит из-за того, что система не отличает ускорение от
притяжения на выходе акселерометра. Если первоначальное
определение высоты завышено, то система будет приписывать
часть показаний акселерометра уменьшенной силе притяже¬
ния (поскольку напряженность поля уменьшается с высотой) .
и завышенному ускорению, направленному вверх. Инерциаль¬
ные приборы, измеряющие высоту, показали бы в этом слу¬
чае увеличение высоты. В то время как измеренное значение
высоты увеличивается, соответствующее значение напряжен¬
ности гравитационного поля уменьшается. Следовательно, все
большая часть выходного напряжения измерителя ускорений
будет представлена как вертикальное ускорение, приводя к
таким значениям высоты, которые бесконечно экспоненциаль¬
но возрастают, даже если объект остается неподвижным и вы¬
ходное напряжение измерителя вертикальных ускорений по¬
стоянно. Для объектов, летящих на небольшой скорости над
Землей, можно показать, что ошибка в высоте для чисто
инерциальных приборов, измеряющих высоту, имеет вид
ДЛ = (ДЛ)0 Ch]/"	(50)
где Ah — ошибка в высоте, (ДА)о — начальная величина ошиб¬
ки в высоте.
Если в этих приборах имеет место накопление, то харак¬
тер ошибок становится более сложным и их рассмотрение вы¬
ходит за рамки этой статьи.
В первом из описанных выше примеров ошибка, вызывае¬
мая начальными условиями в инерциальной навигационной

ВЕКТОРНЫЕ ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ
149
системе, изменялась синусоидально, во втором она экспонен¬
циально возрастала. С исследованием космоса и проявлением
интереса к более общим областям будет выявляться еще бо¬
лее сложный характер ошибок. Общая формула получается
при вычитании уравнения (13) из (12)
Для специального случая, когда мы учитываем только
ошибки, вызываемые начальными условиями, считаем при¬
боры совершенными (так что f является точным измеренным
значением fHcT) и допускаем, что обе системы координат I и
/ист параллельны, это уравнение упрощается
{—diT )/нст = (°н« — О).	(52)
где AR = Rhct — R — ошибка в определении положения.
Следовательно, ускорение изменения ошибки зависит от
разности между истинным гравитационным полем и его из¬
меренным значением, основанным на ошибочном определении
положения. Таким образом, мы видим, что в общем случае
изменение ошибки инерциальной системы зависит от грави¬
тационного поля, в котором она используется.
10.	ЗАКЛЮ ЧЕНИ Е
Проектирование инерциальной системы навигации в со¬
ответствии с предложенным здесь методом включает в себя
следующие этапы.
1. Первоначальный анализ уравнения реализации (27) или
одной из его видоизмененных форм. Это уравнение опреде¬
ляет, что должна делать система независимо от ее конкрет¬
ного выполнения. С помощью этого уравнения конструктор
должен произвести анализ задачи.
2. Выбор расчетной опорной системы координат. Все век¬
торы в реализации уравнений (27) разлагаются на состав¬
ляющие по осям этой системы координат. Это приводит к си¬
стеме скалярных уравнений реализации.
3. Выбор типа системы и расположения гироприборов и
акселерометров. Сигналы удельной силы, поступающие от из¬
мерителей ускорений, могут быть преобразованы для полу¬
чения составляющих, необходимых для скалярных уравнений,
полученных в предыдущем пункте. Сигналы подсчитанной

150
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
угловой скорости используются в случае необходимости как
команды для любого гироприбора.
4. Сравнение разрабатываемой конструкции системы
с другими конструкциями с точки зрения сложности и в слу¬
чае необходимости повторение всего цикла расчета.
5. Анализ ошибок системы (не описанный в настоящей ра¬
боте) и оценка всех упрощений в схеме прибора, к которым
может привести пренебрежение малыми членами.
ЛИТЕРАТУРА
1. W rig lev W., Woodbury R. В., Hovorka J., Inertial Guidance,
Inst. Aeronaut. Sci., Pap. № FF-16, January 1957.
2. Klass P., Jr., Inertial Navigation; Out of the Laboratory and Into
Missile Systems, N. Y., Aviat. Week Special Rep., 1956.
3. O’Donnell C. F., Electronic Equipment, 5, 42—49 (September 1957).
4. Darwin G. H., The Tides, Cambridge, Mass., 1898, pp. 316—333.
5. Geodesy, in «Encyclopedia Britannica», Vol. 10, pp. 127—134, 1949.
6. Coffin J. G., Vector Analysis, N. Y., 1911.
7. Crowley J. C., Kolodkin S. S., Schneider A. М., IRE Trans.
on Space Electronics a. Telemetry, SET-5, 47—54 (March 1959).
8. Schneider A. М., Instrumentation Lab. MIT, Cambridge. Mass,
Rep. № T-130, pp. 227—246, May 1957,

МЕЖПЛАНЕТНАЯ НАВИГАЦИОННАЯ СИСТЕМА *)
Стирнс
Описывается система межпланетной навигации для полета от Земли
до Венеры и дается ее обоснование. Приводятся соотношения между основ¬
ными характеристиками и механической реализацией применяемой системы.
Указывается, что приборы, использующие гироскопическую стабилизацию
при длительном полете, дают неудовлетворительную точность, а применение
системы интегрирующих акселерометров затруднительно в силу нелиней¬
ного характера задачи. Описывается система триангуляции по Солнцу и
планетам, в которой ориентация тяги обеспечивается системой счетно-ре¬
шающих устройств и акселерометров, а курс прокладывается специальным
командным счетно-решающим устройством. Приводится описание системы
и дается оценка ее качества.
Введение
В настоящей статье мы рассмотрим проблему навигации
с практической точки зрения, т. е. так, как она встает перед
экипажем космического корабля. Свойства орбит и механика
полета рассматриваться не будут, ибо они уже освещались
в литературе (см., например, [1]). Эти темы будут затраги¬
ваться лишь постольку, поскольку они необходимы для
разъяснения основной проблемы навигации.
Несмотря на то, что в первоначальных межпланетных по¬
летах, несомненно, будут использоваться орбиты минималь¬
ной энергии, эти орбиты не представляются самыми удоб¬
ными, хотя, возможно, они и наиболее эффективны. Согласно
[1], для полета по орбитам минимальной энергии требуется
наибольшее количество времени; при этом проблема навига¬
ции усложняется необходимостью управления тягой для по¬
лучения достаточной скорости в плоскости орбиты и по нор¬
мали к линии визирования Солнца.
Надо полагать, что межпланетные сообщения станут в кон¬
це концов обычным явлением; поэтому рассмотрим проблему
навигации в условиях непрерывной работы двигателя, когда
l) S t е а г n s Е. V., Ргос. IXth Intern. Astronaut Congress, I, pp. 265—
276, 1959.

152
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
время перелета можно значительно сократить и обеспечить
такое управление, которое позволит изменять задачу и место
назначения в любой момент времени полета. Основными во¬
просами, требующими решения в этом случае, являются опре¬
деление положения и расчет скорости, а также критерий для
определения курса корабля.
В качестве примера нами взят полет от Земли до Венеры,
для которого рассмотрены и оценены средства навигации, по¬
казаны некоторые детали приборов и даны их качественные
оценки. Следует подчеркнуть, что настоящая работа имеет
предварительный характер. Применяемый метод анализа ис¬
пользует только приближения первого порядка, однако, по-
видимому, он достаточен, чтобы показать относительное зна¬
чение рассматриваемых навигационных систем.
Всякий типичный перелет состоит из трех основных фаз:
взлета, полета по курсу и посадки, но, по-видимому, основ¬
ная цель настоящей работы должна заключаться в том, что¬
бы рассмотреть навигационную проблему только для участка
полета по курсу, так как именно на этой фазе перелета осу¬
ществляется навигация на огромные расстояния в межпла¬
нетном пространстве. Предполагается, что эта фаза закончит¬
ся выходом на орбиту вокруг заданной планеты, которая
является целью полета, причем с этой орбиты можно будет
провести разведку с целью выбора места посадки.
ОБЩАЯ ХАРАНТЕРИСТИНА ПОЛЕТА
При рассмотрении проблемы навигации в межпланетном
пространстве допустим, что топливо не создает каких-либо
ограничений в условиях полета и что тягой двигателя (сол¬
нечного, ионного или ядерного) на большем отрезке пути по
сравнению с притяжением Солнца (т. е. не менее 10~4 g) пре¬
небрегать нельзя. При таких условиях траектория космиче¬
ского корабля может быть получена путем интегрирования
всех ускорений, которые действуют на корабль. В дальнейшем
предполагается, что ускорение силы тяги не менее указанной
величины можно получить и поддерживать его в течение поч¬
ти всего времени.
Время, необходимое для перелета от Земли до Венеры, за¬
висит от программы работы двигателя (т. е. программного
значения ускорения) и от длины проходимого пути, который
в свою очередь определяется относительным расположением
или фазами обеих планет в момент старта. На фиг. 1 пока¬
зано максимальное и минимальнее время, требуемое для пе¬

МЕЖПЛАНЕТНАЯ НАВИГАЦИОННАЯ СИСТЕМА
153
релета от Земли к Венере, если предположить, что в первой
половине пути тяга ускоряет корабль, а во второй — замед¬
ляет его. Минимальное время перелета вычислено для слу¬
чая, когда планеты находятся в противостоянии, а максималь¬
ное рассчитано для максимальной прямолинейной траектории,
I
§
5
0
1
£
Время, сутки
суток
Орбита Земли
Орбита Венеры
Типичная траектория
полета
Орбита Меркурия
Фиг. 1. Траектории с большой затратой энергии.
Принятые допущения: 1) ускорение действует на половине пути; 2) ускорение направлено
по линии полета; 3) траектория не пересекает орбиту Меркурия.
которая не пересекает орбиту Меркурия (заштрихованная об¬
ласть является для полетов запретной). Детальный анализ
механики полета для такого рода орбит приведен в работе [9].
НАВИГАЦИЯ ПО НУРСУ
Выбор системы
При прокладке курса штурман сверяет положение кораб¬
ля и курс относительно цели и с помощью расчетных или из¬
меренных данных полета производит экстраполяцию их с тем,

154
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
чтобы определить правильность курса. Он регулирует напра¬
вление движения корабля, а иногда и скорость его до тех пор,
пока на основании расчетов не убедится в правильности курса.
Мы предлагаем наиболее прямые средства для установления
курса и обеспечения непрерывного контроля за ориентацией
вектора тяги.
Во многих отношениях навигацию по курсу на активном
участке полета можно сравнить с проблемой перехвата. К ра¬
кете необходимо приложить тягу таким образом, чтобы она
попала в предсказанное положение движущейся цели. Однако
обычная теория перехвата не эквивалентна данной задаче,
ибо, согласно этой теории, цель за время упреждения дви¬
жется без ускорений, а ускорения преследующего объекта
создаются импульсами тяги только для выполнения коррек¬
тирующего маневра. Это не соответствует случаю межпланет¬
ного полета. Благодаря действию сил притяжения Солнца
ускорения цели постоянно меняются по направлению. Кроме
того, ускорения, действующие на космический корабль, опре¬
деляются суммой переменной силы притяжения Солнца и не¬
прерывно действующей регулирующей силы тяги.
Ускорения, вызываемые притяжением Солнца, можно рас¬
считать как функции местоположения относительно Солнца,
для чего штурману необходим непрерывный график собствен¬
ного положения. Такой график можно составить при помощи
следующих хорошо известных приборов:
1) системы с интегрирующими акселерометрами (инер¬
циальный способ);
2) системы с интегрированием скорости (измеряемой по
эффекту Допплера);
3) системы определения местоположения (способ триангу¬
ляции).
Работа инерциальной системы зависит от точности измере¬
ния и интегрирования ускорений, обусловленных действием
сил негравитационного характера. Измерение ускорений дол¬
жно производиться относительно достаточно точной системы
координат. Кроме того, величину и направление силы тяже¬
сти необходимо рассчитывать непрерывно.
На фиг. 2 показаны ошибки системы, состоящей из гиро¬
скопов и акселерометров, вызванные действием первичных
ошибок этих приборов.
Система с интегрированием скорости в настоящей статье
не рассматривается, ибо при ее использовании, по-видимому,
возникают чрезвычайно трудные проблемы, касающиеся уров¬
ней мощности, отношения сигнал/шум и широкой полосы доп¬
плеровских частот, обусловленной большим диапазоном ско-

МЕЖПЛАНЕТНАЯ НАВИГАЦИОННАЯ СИСТЕМА
155
ростей. Такие системы уже рассматривались ранее в работах
[2, 3]. Как навигационные системы они также имеют недоста¬
ток, заключающийся в необходимости непрерывного интегри¬
рования скорости источника информации.
* 16000
Г
§
0
со
сз
S'
СО
§
1
съ
Qj
I
1
Ошибка, обусловленная ошиб¬
кой акселерометра равной! ^
106э \	^
1600
16
'Ошибка, обусловленная
дрейфом гироскопа
О)3'10~5
ь=ю-*9
16
2	4	6	8	10	12	/4
Время, сутки
Фиг. 2. Влияние первичных ошибок в инерциальной навигации.
Постоянная тяги 10”3 g\
— угловая скорость суточного вращения Земли; g —ускорение силы тяжести.
Преимущество системы, основанной на триангуляции, за¬
ключается в том, что расчет нового положения не зависит от
точности предыдущих расчетов и, следовательно, ошибки не
накапливаются. Поэтому целесообразно провести анализ ха¬
рактеристик этой системы.
Штурман космического корабля, находящийся в свобод¬
ном полете по орбите минимальной энергии либо подвер¬
гающийся непрерывному воздействию тяги, в отличие от
нтгурмана на самолете не может пользоваться вертикалью в
качестве системы отсчета. Вместо этой удобной системы ему
приходится пользоваться линиями визирования Солнца. Уда¬
ленными точками (например, звездами) пользоваться

156
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
невозможно, ибо они характеризуются отсутствием парал¬
лакса для линий визирования от солнечной системы. Визиро¬
вание звезд по методу, аналогичному наземной навигации,
Фиг. 3. Точность определения местоположения космической ракеты,
летящей через солнечную систему.
Ошибка визирования Солнца при расстоянии 12-107 км. Ошибка визирования планет
при расстоянии3 • 107 км.
проводить нельзя, поскольку штурман в межпланетном про¬
странстве в отличие от штурмана на самолете вблизи Земли
не находится на одном определенном расстоянии (радиус)
от центра гравитации.
Во время межпланетного путешествия человек преодоле¬
вает расстояния, которые не являются пренебрежимо малыми
по сравнению с размерами самой солнечной системы, поэтому
в этих условиях для определения положения корабля можно

МЕЖПЛАНЕТНАЯ НАВИГАЦИОННАЯ СИСТЕМА
157
использовать визирование Солнца и планет. Каждая линия
визирования находится приблизительно в плоскости эклип¬
тики, и для определения положения требуется пересечение
линий визирования двух тел (Солнца и планет), положение
которых известно для каждого момента времени.
Применяя опыт наземной навигации, штурман космиче¬
ского корабля для определения своего местоположения в сол¬
нечной системе может воспользоваться тремя такими линиями
(фиг. 3).
Плоскости орбит всех планет, за исключением Меркурия
и Плутона, наклонены к плоскости эклиптики под углом <3,5°,
поэтому навигационные расчеты можно упростить, предполо¬
жив, что движение происходит в плоскости эклиптики. Пре¬
делы влияния такого допущения, правда, можно установить
только путем более детального анализа задачи навигации,но,
по-видимому, это допущение не может иметь существенного
значения при выборе системы.
Зная текущие координаты корабля, можно путем диффе¬
ренцирования вычислить вектор скорости, который затем
можно использовать для навигации при выборе курса. Точ¬
ность расчета скорости будет зависеть от точности координат
положения и интервала времени, выбранного для дифферен¬
цирования, которыми определяется точность расчета средней
скорости. Данные на короткий отрезок времени могут быть
получены при помощи системы интегрирующих акселеромет¬
ров. Необходимый для этой цели метод описан в работе [4].
Механическая реализация системы
При рассмотрении вопроса о механической реализации на¬
вигационной системы отнесем движение космического кораб¬
ля и планеты-цели (Венера) к системе координат, которая
связана с этой планетой и во время полета не вращается
(фиг. 4). Система отсчета движется с ускорением под дей¬
ствием солнечного притяжения и позволяет рассмотреть
только относительные движения корабля и планеты. В этой
системе имеют значение ускорения, вызываемые тягой и отно¬
сительным притяжением, т. е. разностью в силе притяжения
корабля и планеты. Это существенно облегчает приборную
реализацию системы, так как тягу можно измерить, а вектор
разности притяжений есть функция положения, которая обра¬
щается в нуль, когда космический корабль достигает цели.
Анализ движения относительно этой системы отсчета и рас¬
чет вектора относительного притяжения приведен в приложе¬
нии к настоящей статье,

158
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
Определив местоположение и скорость космического ко¬
рабля относительно цели, для осуществления навигации не¬
обходимо иметь критерий для приложения тяги. Такой крите¬
рий лучше всего представить в виде математического закона,
позволяющего рассчитать величину корректирующей тяги по
имеющимся данным. Один из таких критериев будет рассмо¬
трен ниже, однако следует подчеркнуть, что он не является
оптимальным и выбран только в качестве примера.
Корабль будет двигаться по курсу встречи с целью, если
векторное произведение векторов скорости и относительного
положения обращается в нуль. При таком условии относи¬
тельная скорость двух тел будет направлена по прямой ли¬
нии, проходящей через них. Направление вектора [р X р] мо¬
жет служить осью вращения вектора силы тяги, для того что¬
бы векторы р и р совпадали. В соответствии с этим методом
управления требуется рассчитать текущие значения векторов
скорости и положения, с тем чтобы их векторное произведе¬
ние могло служить в качестве сигнала ошибки, подаваемого
на систему управления для создания относительного ускоре¬
ния. Так как усиление этой цепи слежения должно обра¬
щаться в нуль, когда расстояние до цели уменьшается до
нуля, то мы предлагаем использовать в качестве критерия
управления угловую скорость вращения космического кораб-
ля (р X р)/р2 (принятые обозначения см. в приложении).
Следует заметить, что для управления система небесной
триангуляции должна быть дополнена вспомогательной

МЕЖПЛАНЕТНАЯ НАВИГАЦИОННАЯ СИСТЕМА
159
системой, которая осуществляла бы интерполяцию получен¬
ных данных о скорости и местоположении (при коротких ин¬
тервалах времени). Вспомогательная система должна также
вырабатывать относительное ускорение, чтобы его можно было
сравнить с расчетным для создания сигнала управления.
Временной
механизм
Фиг. 5. Функциональная блок-схема системы для межпланетной навигации.
Р X Р
Угловая скорость ракеты = К—=—.
Р2
Компоненты для коррекции влияния гравитационного ускорения g:
Функциональная схема межпланетной навигационной си¬
стемы, построенной на этих принципах, показана на фиг. 5.
Она состоит из следующих основных частей.
1.	Система небесной триангуляции. Система состоит из трех
или более телескопов, которые автоматически следят за цен¬
тром диска выбранных планет; один из них предназначен для
слежения за Солнцем. Кроме того, телескопы и их следящие
системы снабжены устройствами для точного съема углов
слежения. Следует подчеркнуть, что направления этих теле¬
скопов находятся приблизительно в одной плоскости и могут
быть расположены в плоскости эклиптики. Вырабатываемый

160
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
этим прибором сигнал ошибки обеспечит полет по надлежа¬
щей орбите.
2.	Система ориентации тяги, или система акселерометров,
стабилизированных относительно расчетной системы коорди¬
нат. Акселерометры измеряют три проекции вектора силы тяги.
Солнце
4
Фиг. 6. Эскиз системы координат для ориентации тяги
и небесной триангуляции.
3. Вычислительное устройство для решения сферических
треугольников. Это устройство решает сферические треуголь¬
ники для определения положения корабля и имеет запоми¬
нающее устройство, содержащее для каждого момента вре¬
мени каталог положения планет в солнечной системе. Устрой¬
ство получает данные от систем триангуляции и ориентации
тяги и выполняет преобразование координат и расчеты ско¬
рости.
4. Навигационное командное счетно-решающее устройство.
Это устройство получает данные о местоположении и о ско¬
рости относительно цели и вырабатывает команды для ориен¬
тации вектора тяги. Эскиз системы приведен на фиг. 6.
Оценка навигационных ошибок
Ошибки, возникающие в системе небесной триангуляции,
имеют исключительно большое значение, так как они непо¬
средственно входят в ошибки определения местоположения,
а следовательно, в величину коррекции ускорения на воздей¬
ствия силы тяжести, и в ошибку определения скорости.
Для анализа этих ошибок рассмотрим 15-суточное пу¬
тешествие на Венеру на космическом корабле, тяга которого

МЕЖПЛАНЕТНАЯ НАВИГАЦИОННАЯ СИСТЁМА
161
обеспечивает ускорение 0,01 gy причем для первой половины
пути эта тяга создает ускорение корабля, а для второй —
замедление. Пройденное расстояние составляет ~5-107 км.
Основные характеристики полета приведены на фиг. 7.
Земли
///Ж
у =0,006 м/сек2
у/ Ь=±0,1 м /сек2
'/// ^	гг3= 29,3 км / сек
> А«
 иъ =35,0 км/сек
Г#
0eHH°
4	6	8	10
Время, сутки
Фиг. 7. Оценка точности системы на примере полета,
а —примерные относительные траектории; б —относительные скорости.
В первом приближении ошибки при определении положе¬
ния и скорости оцениваются [5] следующим образом (см. таб¬
лицу) .
Ошибки при определении положения появляются в резуль¬
тате ошибок в величине вектора относительного притяжения
(выражение для этого вектора приведено в приложении).
11 Зак. 876

162
ii. Автономная космическая НавйгАцМЯ
Ошибка секстанта
0,1'
0,2'
0,5'
Ошибка определения положения,
км
2400
4800
12 000
Ошибка в величине скорости *),
км/сек
0,016
0,032
0,08
Ошибка в направлении скорости,
мрад
0,5
1,0
2,5
>) Предполагается, что время усреднения составляет 1 сутки.
Если предположить, что ошибка секстанта составляет 0,2', то
ошибка в расчете ускорения притяжения равняется ~2,5 X
X Ю~6 м/сек2. В результате за одни сутки накопленная ошиб¬
ка по положению будет составлять 16 км и ошибка по скоро¬
сти — 0,3 м/сек.
Ошибки, возникающие при измерении и расчете ускоре¬
ний, существенно изменяют ориентацию силы тяги; однако су¬
ществуют способы уменьшения этих ошибок в замкнутой си¬
стеме регулирования до величины второго порядка малости.
Ошибки в ориентации относительной системы координат
должны иметь малую величину, ибо в навигационной системе
они непосредственно влияют на измерение и стабилизацию
направления действия ускорения. К дрейфу системы гироско¬
пической стабилизации предъявляются требования, которые
практически осуществить невозможно: скорость дрейфа дол¬
жна составлять не более 10-4 угловой скорости вращения
Земли, что за 15 суток полета дает ошибку 0,5°. Поэтому для
ориентации системы координат мы применяем систему небес¬
ной триангуляции, получая сигналы о местоположении для
определения ориентации относительно линии визирования
Солнца. Используя этот способ, мы при помощи секстанта с
ошибкой, не превышающей 0,2', получаем ошибку в ориента¬
ции направления начала отсчета < 0,05 мрад.
ВЫВОДЫ
На основании изложенного можно утверждать, что меж¬
планетная навигационная система описанного типа вполне
осуществима и не требует слишком высоких точностей от при¬

МЕЖПЛАНЕТНАЯ НАВИГАЦИОННАЯ СИСТЕМА
163
боров, за исключением акселерометров, точность которых дол¬
жна составлять 10~6 g. Однако для выполнения требований
динамики полета в действительности необходимы приборы с
точностью 0,1%.
Ошибки системы ограничены точностью применяемых сек¬
стантов; автоматический секстант, точность которого состав¬
ляет 0,2х, дает ошибки того же порядка величины, что и
радиус наименьшей планеты. Величины скоростей, которые
вычисляются описанным способом, составляют ~ 1 % от ор¬
битальной скорости планет.
В последующих работах по исследованию подобных си¬
стем необходимо будет определить оптимальный критерий
управления, который давал бы оптимальную эффективность
использования тяги. Следует вывести также и другой крите¬
рий управления, позволяющий осуществить условия для сво¬
бодного падения на планету назначения по так называемой
траектории спасения.
ПРИЛОЖЕНИЕ
Чтобы проанализировать относительное движение корабля
и планеты-цели (Венеры), мы выбрали систему отсчета [5],
которая связана с Венерой и не вращается, т. е. ее ориента¬
ция не меняется в течение полета (см. фиг. 4).
Кажущееся движение корабля в этой системе определяется
градиентами притяжения, негравитационными ускорениями
космического корабля и движением системы отсчета. Прово¬
димый анализ дается в соответствии с методом, приведенным
в работе [7]. Одна из интересных особенностей выбранной си¬
стемы отсчета состоит в том, что уравнения относительного
движения в этой системе имеют более простой вид, чем в
инерциальной гелиоцентрической системе отсчета. Ниже мы
ограничимся более простой задачей движения в плоскости
эклиптики. Распространение метода на движение в трехмер¬
ном пространстве, по-видимому, не представляет особых за¬
труднений.
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
R з — радиус-вектор Земли относительно Солнца;
RK — радиус-вектор космического корабля относитель¬
но Солнца;
Rb — радиус-вектор Венеры относительно Солнца;
р(х, у, z) — радиус-вектор космического корабля относитель¬
но системы отсчета, связанной с Венерой;
11*

164
П. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
х — проекция рн на ось х (перпендикулярную к осям
у и г в правой декартовой системе);
у—проекция р* на ось у (в плоскости эклиптики
в направлении гелиоцентрической вертикали в
момент вылета);
2—проекция рк на ось z (перпендикулярную к плос¬
кости эклиптики);
bx> by> bz — составляющие негравитационного ускорения по
осям х, у, 2;
шв —угловая скорость вращения Венеры по орбите;
gB—вектор солнечного притяжения на Венере;
gK — вектор солнечного притяжения на корабле;
i, j, k — единичные векторы, направленные по осям х,у,г.
Математические преобразования
Радиус-вектор космического корабля относительно вы¬
бранной системы отсчета определяется уравнением
Рк==^к «в	(Гь 1)
Дифференцируя, получаем
pK=RK-RB	(П. 2)
И
Рк = RK Rb-	(!"!• 3)
Уравнения движения космического корабля в виде, пред¬
ставленном в работе [7], получаются суммированием ускоре¬
ний, действующих на него в гелиоцентрической системе коор¬
динат
К—К+&К-	(П-4)
Аналогичное уравнение можно написать для движения Ве¬
неры относительно Солнца
Rb = Sb (Ьв = 0).	(П. 5)
В выбранной относительной системе координат движение
определяется соотношением
Рк = К - RB = bK + gK—gB.	(П. 6)
Проекции вектора gB на оси инерциальной системы коорди¬
нат, связанной с Солнцем, можно записать в виде
ёь = — £ь (l sin V i- jcos V>	(п- 7)

МЕЖПЛАНЕТНАЯ НАВИГАЦИОННАЯ СИСТЕМА
165
Силу притяжения Солнца, приложенную к космическому ко¬
раблю, можно выразить уравнениями
Заметим, что
а -_а I
Sk ёвУя1/ r ’
ёк — — ёв~Б^ (Rb + Рк)-
Rb =	('sin + J cos <V)-
(П. 8)
(П. 9)
(П. 10)
Аналогично вектор относительного притяжения определяется
выражением
(ек-8в) = -£в [‘(^f-1)sin V+
Rl
Rl
j I "75	1	)	cos	+	'	"75"x"+" j “IT У
ПО	/	D	1	n6
К	/	К
Проекции этого вектора равны
(gK — Яв)х=-ёв \ -^г*
Rb
Rl
1 ) sin <ов^
Г Rl 7 Rl
(gK — gB)y — ~ gB [^3" У “К — 1
COS d)ut
(П. 11)
(П. 12)
(П. 13)
Проекции ускорения на оси выбранной относительной системы
отсчета, определяемые из уравнения (П. 6), равны
х = ь* + (&к — ев)х>	(П. 14)
у = V+-(gK-gB)y	(И-15>
Таким образом, уравнения движения можно записать, в виде
*в
Rf
Rl
л?
(П. 16)
(П. 17)
Заметим, что эти уравнения являются нелинейными., Однако
при подходящем выборе расчетных интервалов и прц исподь

166
И. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
зовании линейной экстраполяции эти уравнения можно заме¬
нить линейными приближениями. Решениями этих уравнений
являются периодические функции с периодом ~300 суток,
аналогичным периоду Шулера в 84 мин. ^ Функция притя¬
жения (в правой части уравнения) является возмущающей
функцией, синхронизированной с движением Венеры по орбите
Фиг. 8. Параметры вырабатываемые навигационным
счетно-решающим устройством.
Частота системы и возмущающая функция показаны на
фиг. 8. Используя эти линеаризованные уравнения и их ре¬
шения, можно построить навигационную систему. Курс можно
определить, основываясь на прогнозируемой траектории.
*) Этот период играет в поле притяжения Солнца ту же роль, какую
дграет период Шулера в поле тяготения Земли. — Прим. перев.

МёжпланетНая НАвйгАцМонНАя СИСТЁМА
167
ЛИТЕРАТУРА
1 Vertregt М., Interplanetary Orbits, J. Brit. Interpl. Soc., 16, 326
(1958).
2. S о n n a b e n d D., Measurement of Velocity in Space, Proc. Am.
Astronaut. Soc., 4th Ann. Meeting, January 1958.
3. С a s t r u с с i о P. A., Communications and Navigation Techniques of
Interplanetary Travel, Trans. IRE ANE (December 4, 1957).
4. Stearns E. V., Vernon R. E., Analysis of Errors in a Second Order
Doppler Damped Accelerometer Guidance System, The Rand Corp.,
Santa Monica, Calif., July 1953.
5. S t e a г n s E. V., Interplanetary Applications of Automatic Navigation,
Proc. Am. Astronaut. Soc., 4th Ann. Meeting, January 1958.
6. McKay W., Orbital and Satellite Vehicle, Chapt. 3. Mechanics of Orbits,
Dept. Aero. Engng., MIT, August 6—17, 1956.
7. Brown S. H., Gilvary J. J., The Theory of Blind Navigation by Dy¬
namical Measurement, The Rand Corp. R-144, July 1949.
8. Riddell F.,' D e t r a R. W., Returning Alive from Space, Proc. Am.
Astronaut. Soc., 4th Ann. Meeting, January 1958.
9- Cole D. М., Minimum Time Interplanetary Orbits, Proc. Am. Astronaut.
Soc.. 4th Ann. Meeting, January 1958.

ИСПОЛЬЗОВАНИЕ АСТРОНОМИЧЕСКИХ
НАБЛЮДЕНИИ ДЛЯ КОСМИЧЕСКОЙ НАВИГАЦИИ1)
Л ар мор
Точность ориентации и следящих устройств за последние
несколько лет значительно возросла; приборные ошибки со¬
временной аппаратуры составляют ~1", температурные и
другие ограничения в конечном счете устанавливают предель¬
ную точность 0,1".
Таким образом, можно полагать, что угловые измерения
между двумя небесными телами будут ограничены точностью
0,2", или 1 мкрад. Это соответствует точности, предсказывае¬
мой создателями следящих систем за звездами. Есть все осно¬
вания полагать, что их предположения будут реализованы
в ближайшие годы, ибо навигация в межпланетном простран:
стве с помощью устройств, обеспечивающих такую точность,
вполне возможна. Однако для полной реализации таких
устройств потребуются поправки для наблюдаемых положе¬
ний звезд и планет, поскольку для обеспечения предельной
точности должны быть использованы данные с учетом вели¬
чин, которыми при наземной навигации обычно пренебре¬
гают. Кроме того, систему координат надо выбрать таким
образом, чтобы ее изменения были по возможности мини¬
мальными; это значит, что практически она должна быть не¬
подвижной. Требования по точности определения местополо¬
жения на участке полета по курсу полностью не выработаны.
Если на начальном и конечном участках полета несомненно
можно пользоваться некоторыми видами пилотажа и радио¬
навигации, то на курсе в качестве наиболее приемлемого
предусматривается использование небесных тел. Для вычис¬
лений в настоящей статье принята произвольно выбранная
относительная точность 0,001, т. е. точность оценки положе¬
ния 0,001 от кратчайшего расстояния между двумя телами
считается приемлемой. Таким образом, при полете с Земли
на Марс требуемая точность на среднем участке полета
0 Larmore L., Aero/Space Engng, 18, № 1, 37—42 (January 1959).

ИСПОЛЬЗОВАНИЕ АСТРОНОМИЧЕСКИХ НАБЛЮДЕНИЙ	169
должна составлять ~ 80 ООО км. Во многих случаях может
быть осуществлено более точное определение местоположе¬
ния и за счет этого повышена пригодность системы.
СИСТЕМЫ HOOP ДИН АТ
При выборе системы отсчета, пригодной для использова¬
ния в межпланетной навигации, ученые сталкиваются с про¬
блемой, которую многие десятилетия не могут разрешить
астрономы. Системы координат, совершенно свободной от ве¬
ковых изменений, не существует, ибо все тела, относительно
которых может быть произведен отсчет, находятся в дви¬
жении.
В экваториальной системе координат, используемой при на¬
земной навигации, видимые положения звезд изменяются
главным образом в результате прецессии точек равноден¬
ствия. Однако из-за практических соображений экваториаль¬
ная система все же используется и ежегодно вычисляются
необходимые поправки. При осуществлении навигации на
поверхности Земли с точностью 1 мкрад (~6,5 м) изменения
видимых положений звезд, вызванные прецессией, можно
вычислить почти для каждого дня.
«Неподвижная» плоскость определяется как плоскость,
проходящая через центр' масс солнечной системы и ориенти¬
рованная таким образом, что момент количества движения
солнечной системы равен нулю относительно любой из осей,
лежащих в этой плоскости. На основании принципа сохране¬
ния момента можно сделать вывод о том, что такая «непод¬
вижная» плоскость будет служить идеальной системой от¬
счета для межпланетной навигаций. Однако практически
плоскость земной орбиты (эклиптика) является вполне при¬
емлемой системой отсчета для осуществления наблюдений и
при определении местоположения. Несмотря на то что «не¬
подвижная» плоскость, очевидно, более стабильна, дополни¬
тельные исследования солнечной системы могут вызвать
изменение принятой величины наклона этой системы отсчета.
Так, например, принятая величина наклона «неподвижной»
плоскости была изменена на 1200 мкрад в связи с открытием
планеты Плутон. При выборе гелиоцентрической системы
координат с эклиптикой в качестве плоскости, от которой ве¬
дется отсчет, мы ставим себя в положение, отчасти сравнимое
с положением первых английских навигаторов, которые за
нуль долготы произвольно принимали основание своего дома.
Обычцое определение астрономической широты как углового

170
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
расстояния к северу или югу от эклиптики для межпланетной
навигации вполне приемлемо. Плоскость эклиптики накло¬
нена на 1°39' по отношению к «неподвижной» плоскости и
вращается относительно нее таким образом, что направление
линии их пересечения изменяется на 0,47" в год. Таким
образом, максимальное изменение звездной широты (склоне¬
ние), обусловленное этим эффектом, составляет ~0,07 мкрад
в год. Широтные поправки положений звезд следует вводить
примерно через каждые 10 лет.
При определении азимутального угла или астрономиче¬
ской долготы в качестве нулевой точки принята точка весен¬
него равноденствия. Поскольку эта точка смещается на
250 мкрад в год, долготные поправки положений звезд сле¬
дует вводить почти ежедневно. В связи с этим желательно
иметь более стабильное начало отсчета по долготе. Была
предложена точка земного перигелия, которая перемещается
на 55 мкрад в год. Однако более приемлемым кажется другое
предложение, когда в качестве начала отсчета по долготе
ученые предлагают использовать достаточно яркую звезду
вблизи эклиптики. Такая звезда должна быть легко опозна¬
ваема, близка к эклиптике и иметь незначительные собствен¬
ные смещения. Этим условиям удовлетворяет звезда первой
величины Спика; тангенциальная составляющая ее движения
относительно эклиптики составляет •—■ 0,1 мкрад в год. Таким
образом, введение в положение звезд поправок, обусловлен¬
ных изменениями астрономической широты и долготы, можно
осуществлять через каждые 10 лет без какой-либо чрезмерной
вычислительной работы.
Третьей координатой в этой системе может быть радиаль¬
ное расстояние от центра Солнца. Хотя Солнце перемещается
в мировом пространстве со скоростью ~18 км/сек, при меж¬
планетной навигации нет необходимости вводить соответ¬
ствующие поправки, ибо планеты участвуют в этом движении
(помимо их собственного движения вокруг Солнца).
НАВИГАЦИОННЫЕ СИСТЕМЫ
Обычная астронавигация в межпланетном пространстве
заключается в измерении угла между Солнцем и другим не¬
бесным телом. При измерении угла между Солнцем и другой
звездой геометрическим местом положений становится конус
с Солнцем в вершине. Дополнительные измерения угла Солн¬
це— звезда обеспечивают второй конус положения, а пере¬
сечение этих двух конусов дает две прямые линии положения,

ИСПОЛЬЗОВАНИЕ АСТРОНОМИЧЕСКИХ НАЁЛЮДЁНИЙ	171
как показано на фиг. 1. Следует отметить, что этот метод со¬
вершенно аналогичен обычному методу наземной астронави¬
гации, когда навигатор измеряет углы между Землей и
звездами. Пересечение конуса положения с земной поверх¬
ностью представляет собой обычный круг положения, а пере¬
сечение двух таких кругов определяет широту и долготу на¬
блюдателя. Двузначность как в наземном случае, так и в слу¬
чае солнечной системы может быть устранена с помощью
Ф и г. 1. Конусы и линии положения при межпланетной
навигации.
данных о приблизительном местоположении наблюдателя, а
конечные результаты могут быть выданы в форме поправок
к предполагаемым значениям широты и долготы. Различие
этих двух способов состоит в отношении к вопросу о времени.
В наземном случае при наблюдениях необходимо определять
время их выполнения, для того чтобы можно было учесть вра¬
щение Земли. Астрономические же координаты (широта и
долгота) могут быть определены и без учета времени, а све¬
дения о времени важны лишь для сопоставления с предпола¬
гаемым положением на орбите.
Наблюдения за звездами обеспечивают только угловые
координаты, а не расстояние до Солнца. Дополнительные на¬
блюдения третьей звезды дают лишь излишнюю информацию,
хотя ее можно использовать для исключения двузначности,

172
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
возникающей из-за двух линий положения, а также в целях
незначительного повышения точности. Радиальная коорди¬
ната может быть определена либо посредством наблюдений
за планетами, либо с помощью измерений видимого углового
диаметра Солнца. При использовании последнего метода све¬
дений о времени не требуется, но его точность в значительной
степени зависит от величины радиального расстояния.
Определение радиального расстояния посредством наблю¬
дений за планетами требует использования данных о времени
Фиг. 2. Двумерное изображение поверхностей положения, получаемых
при измерении угла между двумя телами солнечной системы.
и эфемеридах. Измерение угла планета — звезда дает тре¬
тий конус положения, который, пересекаясь с линией положе¬
ния, показанной на фиг. 1, определяет местоположение ко¬
рабля. С той же целью возможны измерения угла между
Солнцем и планетой или между планетами. В этом случае
поверхности положения не являются конусами, а предста¬
вляют собой фигуры, получающиеся при вращении кривых,
изображенных на фиг. 2, относительно линии, соединяющей
эти два тела. Угол 0 представляет собой угол между этими
двумя телами при визировании их с борта корабля.
Возможность осуществления дополнительных наблюдений
за планетами вместо использования часов весьма привлека¬
тельна. Время может быть определено на основании сведений
об эфемеридах других тел солнечной системы. Наблюдения
за Землей и Луной могут также служить этой цели, если рас¬
стояния от Земли не слишком велики и позволяют произво¬
дить измерения с достаточной точностью.
Указанные наблюдения могут производиться в самых раз¬
личных комбинациях, однако детальное рассмотрение вопроса

ИСПОЛЬЗОВАНИЕ АСТРОНОМИЧЕСКИХ НАБЛЮДЕНИЙ	1?3
показывает, что наиболее приемлемы три типа навигационных
схем:
1—а) Солнце — звезда, б) Солнце — звезда, в) угловой
диаметр Солнца;
2 — а) Солнце — звезда, б) Солнце — звезда, в)	пла¬
нета— звезда (с использованием сведений о времени и эфе¬
меридах) ;
3 — а) Солнце — звезда, б) Солнце — звезда, в)	пла¬
нета— звезда (с использованием лишь эфемерид), г)	пла¬
нета— звезда (с использованием лишь эфемерид).
ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ, ОБУСЛОВЛЕННЫЕ
ИНСТРУМЕНТАЛЬНЫМИ ОГРАНИЧЕНИЯМИ
Устройство для измерений угла между двумя небесными
объектами обычно ориентируется на центр интенсивности
излучения каждого объекта. Таким образом, изображение
объекта в виде диска или дифракционной картины от точеч¬
ного источника не вызывает особых затруднений. Допустим
Фиг. 3. Погрешность определения углового положения.
Угол пересечения равен 60°.
(согласно предположению Уилкокса), что погрешность изме¬
рений составляет 10_6 рад. Минимальная погрешность опреде¬
ления широты и долготы будет соответственно 1 мкрад. Та¬
кое положение имеет место лишь тогда, когда угол пересече¬
ния конусов составляет 90° и две образующие этих конусов,
находящиеся на этом пересечении, параллельны касательным
к широте и долготе. Во всех других случаях ошибка будет
превышать 1 мкрад. В современной аэронавигации обычно
ограничиваются углами пересечения не менее 60°, когда
используются лишь два поля обзора. Этот критерий,

174
ii. автономная космическая Навигация
по-видимому, в равной мере применим и к межпланетной на¬
вигации. В этом случае погрешность определения широты и
долготы никогда не будет больше удвоенной ошибки измере¬
ния (фиг. 3).
Для определения линейной погрешности угловую погреш¬
ность необходимо умножить на расстояние до Солнца.
В табл. 1 приведены эти величины для средних расстояний
между Солнцем и планетами.
Таблица 1
Максимальные и минимальные погрешности определения
широты и долготы положения для расстояний между
Солнцем и планетами
Планета
Среднее
радиальное
расстояние,
106 км
Минимальная
погрешность,
км (1 мкрад)
Максимальная
погрешность,
км (2 мкрад)
Меркурий
57,94
58
116
Венера
108,27
108
216
Земля
149,68
150
300
Марс
228,06
228
456
Юпитер
778,73
779
1558
Сатурн
1427,7
1428
2856
Уран
2872,4
2872
5744
Нептун
4500,8
4501
9002
Плутон
5914,8
5915
11830
Устройство, которое измеряет угол между двумя небес¬
ными телами, вероятно, невозможно использовать для изме¬
рений углового диаметра Солнца. Для этой цели лучше всего
применять какое-либо видоизменение части оборудования или
дополнение к нему, угловая точность которого будет нахо¬
диться в пределах 1 мкрад. Погрешность определения поло¬
жения, получающаяся в результате таких измерений, пропор¬
циональна квадрату расстояния от Солнца и составляет
~ 16 ООО км на орбите Земли. В табл. 2 приведены погреш¬
ности определения расстояния от Солнца, получающиеся при
измерениях такого рода.
Как и следовало ожидать, погрешность определения рас¬
стояния от Солнца таким способом значительно больше по¬
грешности определения широты или долготы. Однако вслед¬
ствие простоты вычислительных операций, независимости от
времени и ясности геометрического смысла этот метод, не¬
сомненно, найдет применение при межпланетной навигации.

ИСПОЛЬЗОВАНИЕ АСТРОНОМИЧЕСКИХ НАБЛЮДЕНИЙ	175
Табл ица 2
j
' Планета
Погрешности при
угловых измере
нилх диаметра
Солнца), км
Погрешности при
измерени v угла
планета — звезда);
угол пересечения
60°; км
Расстояние
планет от
Солнца,
108 км
Меркурий
2400
201
57,9
Венера
11000
375
108,3
Земля
16 000
520
150,0
Марс
37 000
790
228,0
Юпитер
430 000
2700
778,7
Сатурн
1450 000
4950
1427,7
Кроме того, если погрешность измерения в 1 мкрад носит слу¬
чайный характер (по закону Гаусса), то, значительно увели¬
чив время сглаживания, ее можно уменьшить.
Точность, с которой можно определить радиальное рас¬
стояние посредством измерений угла планета — звезда, зави¬
сит от расстояния до планеты и от угла пересечения кониче¬
ской поверхности с линией положения, образующейся при
двух визированиях системы Солнце — звезда.
Таким образом, для обеспечения минимальной ошибки
планета должна находиться на близком расстоянии, а угол
пересечения должен равняться 90°.
Так как расстояние до Солнца определяется посредством
визирования двух тел планета — звезда, погрешность опреде¬
ления этого расстояния будет примерно равна погрешности
в определении линии положения (ЛП), получающейся при
визировании пары Солнце — звезда, когда планета и Солнце
находятся на одинаковых расстояниях от корабля. Однако
следует отметить, что радиальная погрешность в значитель¬
ной степени зависит от угла пересечения; это обстоятельство
имеет весьма существенное значение вследствие ограничен¬
ного количества плакет, пригодных для наблюдений. На фиг. 4
приведены величины относительной погрешности в зависи¬
мости от отношения расстояния до планеты к расстоянию до
Солнца для нескольких углов пересечения. Эти прямые линии
получены из уравнения
Р А-\- COS а
где Е — отношение погрешности определения расстояния
до Солнца Др к погрешности определения линии положения

176
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
(ДЛП), а А — отношение расстояния до планеты к расстоянию
до Солнца. В табл. 2 приведены данные, относящиеся к этому
второму методу навигации, базирующемуся на использовании
расстояния планет от Солнца. Хотя сравнение погрешности
первого и второго методов показывает, что погрешности из¬
мерений пары планета — звезда меньше, следует учитывать,
Фиг. 4. Относительные погрешности определе¬
ния радиальных положений для указанных вели¬
чин угла пересечения а.
_	Расстояние от планеты
Относительное расстояние = т-	   ;
Расстояние от Солнца
Погрешность определе-
~	ния расстояния от Солнца
Относительная погрешность = -т=—-	;
Погрешность определе¬
ния ЛП от Солнца
что в этом случае имеют место систематические ошибки (эти
ошибки будут рассмотрены ниже), которые могут привести
к значительному снижению точности.
Дополнительные наблюдения за второй парой планета —
звезда в принципе могут заменить точный хронометр. Кроме
того, другие наблюдения, например затмений и очертаний
спутников, могут быть использованы для той же цели. Ана¬
лиз погрешностей для случая использования второй пары
планета — звезда не проводился, но для иллюстрации ожидае¬
мой точности можно привести следующий простой пример.
Допустим, что корабль находится между орбитами Земли и
Марса, как это показано на фиг. 5. Заданная широта и дол¬
гота устанавливают линию положения. Наблюдения вида
Земля — звезда и Марс — звезда дают конические поверх¬
ности положения, которые должны пересекать линию положе¬
ния в одной и той же точке, если точно известно время. Од-
цако, если хронометр неточен, пересечение будет таким, как

ИСПОЛЬЗОВАНИЕ АСТРОНОМИЧЕСКИХ НАБЛЮДЕНИЙ	177
Солнце
Земля '^^Посмическии^'143
корабль
\
Марс
Фиг. 5. Схема для навигации с определением местоположения
без точного хронометра.
Расстояния указаны в миллионах километров. ЛП —линия положения.
показано на фиг. 6. Поверхности положения, получающиеся
при наблюдениях вида Земля — звезда и Марс — звезда, при¬
ближаются друг к другу вдоль линии положения со скоростью
Линия полотения приизме-
' рении вида Солнце-звезда
“120 км
143 км
21,5 км!сек
24,8 км/сек
27,4 км/сек
Поверхность полотения при _
измерении вида А
Земля-звезда
Фиг. 6. Пересечение линии и поверхности положения (вклю¬
чая их ошибки) для двух измерений вида планета — звезда
без использования точного хронометра.
52 км/сек. Поскольку имеет место погрешность определения
разделяющего их расстояния, обусловленная погрешностью
измерений, то время их пересечения точно установить не
удается. В рассматриваемом примере погрешность определе¬
ния расстояния составляет 255 км} что при указанной
\% Зад. §7$,

178
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
скорости сближения дает возможную ошибку по времени
5 сек. При межпланетном полете продолжительностью не¬
сколько лет эти 5 сек составляют относительную величину
порядка 10'7. Имеющиеся в наличии лабораторные хро¬
нометры дают сведения о времени с точностью на пять или
шесть порядков выше той, которая приведена в примере.
СИСТЕМАТИЧЕСКИЕ ОШИБКИ
Проведенный выше анализ был сделан в предположении,
что погрешности определения положения появляются лишь в
результате инструментальных ограничений, другие возможные
источники ошибок игнорировались. Однако навигационным
системам, базирующимся на астрономических наблюдениях,
будут свойственны некоторые систематические ошибки.
Если величины этих ошибок известны, то их можно подать
на вход вычислительного устройства и произвести необходи¬
мую коррекцию. В тех случаях, когда величины неизвестны,
для определения конечной погрешности систематические
ошибки следует суммировать с инструментальной ошибкой.
В последующих разделах указаны три неизвестные система¬
тические ошибки и пять ошибок, которые могут быть скоррек¬
тированы.
Масштаб солнечной системы
Среди проблем межпланетной навигации наибольшее зна¬
чение имеет неизвестная систематическая ошибка, возникаю¬
щая при оценке масштаба солнечной системы в обычных еди¬
ницах. Лучше всего определять расстояния между планетами
посредством триангуляционных измерений, причем на каком-
то этапе их следует дополнить измерениями длины базовой
линии. Сочетание возможных ошибок, возникающих при опре¬
делении длины базовой линии и угловых измерениях, приво¬
дит к вероятной ошибке определения астрономической
единицы в 17 ООО км. Если сопоставить эту величину с погреш¬
ностью в 16 000 км (см. табл. 2), которая имеет место в нави¬
гационной системе при измерениях видимого углового
диаметра Солнца, то очевидно, что их значения сравнимы
между собой.
При соответствующей погрешности определения астроно¬
мической единицы первая навигационная система, по-види¬
мому, обеспечивает как простую методику измерений, так и
приемлемую точность получаемых результатов. Когда же све¬
дения q масштабе солнечной системы будут уточнены, то бу¬

ИСПОЛЬЗОВАНИЕ АСТРОНОМИЧЕСКИХ НАБЛЮДЕНИЙ	179
дет оправдано применение второй навигационной системы.
Первые межпланетные полеты могут и должны быть исполь¬
зованы для уточнения масштаба солнечной системы, по¬
скольку это имеет огромное значение не только для будущего
межпланетной навигации, но влияет также на уточнение
астрономических констант, изучаемых небесной механикой.
Вероятная ошибка установления масштаба срлнечной
системы дает погрешность, которая линейно зависит от ра¬
диального расстояния до Солнца, тогда как возможная
ошибка от измерения этого расстояния посредством первой
навигационной системы пропорциональна квадрату этого рас¬
стояния. При «земных» расстояниях эти две погрешности при¬
мерно равны. Таким образом, если при межпланетных поле¬
тах внутри земной орбиты пользоваться первой навигационной
системой, основная ошибка будет возникать из-за погрешно¬
стей масштаба солнечной системы, тогда как при полетах
к Марсу и более отдаленным планетам большая погрешность
будет связана с угловыми измерениями диаметра Солнца.
Положение планет
Следует учитывать, что, помимо возможной ошибки при
определении положения планет, связанной с погрешностями
масштаба солнечной системы, угловые положения планет не
могут быть определены совершенно точно. Частично эта
ошибка возникает при переходе от геоцентрической системы
координат к гелиоцентрической и в меньшей степени в резуль¬
тате погрешностей наблюдения и возмущений. В американ¬
ском морском ежегоднике данные о гелиоцентрическом рас¬
положении планет приводятся с точностью до О,Г', однако
в действительности наблюдаемые положения планет отли¬
чаются от указанных на величину, превышающую инструмен¬
тальную погрешность на 0,2".
Фаза планет
Прибор для измерений углов между планетами и звездами
фиксирует центр интенсивности излучения, тогда как сам по
себе объект не является точечным. Планеты, не освещенные
полностью, являются источниками излучения, для которых по¬
грешность определения угла нельзя полностью скорректиро¬
вать. Так, например, Венера при максимальном сближении
с Землей имеет угловой размер 320 мкрад. В это время пла¬
нета видна с Земли как тонкий светящийся полумесяц и
ошибка измерения может составлять —100 мкрад. Если
12*

180
11. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
ограничиться углом пересечения конусов положения равным 60°
(линия положения, получающаяся при двух измерениях вида
Солнце — звезда, пересекает поверхность положения, получае¬
мую при измерениях вида планета — звезда, под углом 60°),
то ошибка может быть существенно уменьшена, если наблю¬
дать Венеру в период ее полной фазы. Однако и в этом слу¬
чае наблюдаемое положение не будет абсолютно совпадать
с предполагаемым из-за влияний, обусловленных атмосферой
планеты и облачными образованиями, а также вследствие
отклонений от поверхности, определяемой законом Ламберта.
Большинство необходимых поправок может быть определено
заранее, но все же малая, остающаяся неизвестной, ошибка
будет превышать допустимую величину ошибки в 1 мкрад.
Аберрация света звезд
Звезда, наблюдаемая с движущейся платформы, совер¬
шает видимое угловое перемещение, которое известно под на¬
званием аберрации света звезды. Величина такого углового
смещения определяется из выражения tg Q = v/c, где v — со*
ставляющая скорости наблюдателя, перпендикулярная к на¬
правлению на звезду, с — скорость распространения света, а
0 — величина углового смещения. Для наблюдателя, находяще¬
гося на Земле, угол 0 может составлять 102 мкрад, что свиде¬
тельствует о значительной величине этой ошибки. Таким обра¬
зом, для определения положения необходимо знать скорость,
однако для осуществления достаточно точной коррекции мо¬
жет быть использована предполагаемая величина скорости.
При этом необходимо, чтобы составляющая скорости, перпен¬
дикулярная к направлению на звезду, была известна с точ¬
ностью до 0,3 км/сек и соответствующие поправки были бы
введены в счетно-решающее устройство.
Параллакс звезд
Хотя для целей навигации обычно полагают, что звезды
находятся на бесконечно далеких расстояниях, это не совсем
справедливо. Необходимые поправки могут быть сделаны на
основании измерений параллакса звезд. Параллакс звезды
есть кажущееся изменение направления на звезду при наблю¬
дениях с базовой линии, равной радиусу земной орбиты. Для
семи звезд первой величины (общее число звезд первой вели¬
чины составляет 21) коррекция на параллакс должна быть
осуществлена при навигации в пределах земной орбиты, а

ИСПОЛЬЗОВАНИЕ АСТРОНОМИЧЕСКИХ НАБЛЮДЕНИЙ	181
д^я 12 — при навигации в пределах орбиты Юпитера. Эти
поправки легко определить, исходя из предполагаемого поло¬
жения, требуемая точность оценки которого составляет
8 - 106 км для ближайшей звезды первой величины (а-Цен-
тавра).
Конечная величина скорости света
Помимо аберрации света звезд, конечная величина ско¬
рости света также приводит к возникновению систематической
ошибки, которую необходимо.скорректировать. Время прохо¬
ждения света от планеты до корабля достаточно велико (так,
например, свет пересекает земную орбиту за 1000 сек); за это
время планета успевает переместиться на значительное рас¬
стояние. Из фиг. 5 видно, что время прохождения светом
расстояния от Марса до космического корабля составляет
480 сек, за это время Марс перемещается более чем на
11 000 км. В приводимом примере время распространения
света от Земли до корабля составляет 300 сек, и за это время
Земля переместится на 9000 км. Такие поправки следует
ввести в счетно-решающее устройство, устрановленное на
борту корабля, с тем чтобы обеспечить как можно более точ¬
ный результат. Задача в этом случае значительно сложнее,
чем в двух предшествующих случаях, ибо коррекция зависит
не только от конфигурации солнечной системы в заданный
момент, но и от оцениваемого положения корабля.
Собственные движения звезд
Годичные изменения направлений на звезды на небесной
сфере, обусловленные их действительным движением, назы¬
ваются собственными движениями звезд. Величины этих пере¬
мещений достигают 51 мкрад/год. Поэтому положения звезд
могут значительно измениться даже в течение одного межпла¬
нетного перелета. Насчитывается И звезд первой величины
(из общего числа 21 звезда), собственное движение которых
превышает 1 мкрад/год, а наибольшая величина равна
18 мкрад/год для звезды а-Центавра. Таким образом, для
этой звезды необходимо производить коррекцию положения
через каждые три недели. В табл. 3 перечислены все звезды
первой величины с указанием их интенсивности (в звездных
величинах), параллакса и собственного движения. Дополни¬
тельные сведения о менее ярких звездах можно найти в лю¬
бом астрономическом каталоге.

■i 82
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
Таблица 3
Звезды первой величины, их интенсивность,
параллакс и собственное движение
Звезда
Интенсивность,
звездная
величина
Параллакс,
мкрад
Собственное
движение,
мкрад! год
Сириус
—1,58
1,9
6,6
Канопус
—0,86
0,07
0,11
а-Центавра
. 0,06
3,8
18,4
Вега
0,14
0,6
1,7
Капелла
0,21
0,35
2,2
Арктур
0,24
0,4
11,4
Ригель
0,34
0,03
0,03
Процион
0,48
1,6
1,6
Ахернар
0,60
0,25
0,5
(3-Центавра
0,86
0,08
0,2
Альтаир
0,89
1,0
3,3
Бетельгейзе
0,92
0,08
0,16
а-Креста
1,05
0,07
0,24
Альдебаран
1,06
0,3
1,0
Поллукс
1,21
0,5
3,1
Спика
1,21
0,07
0,3
Антарес
1,22
0,05
0,16
Формальгаут
1,29
0,7
1,8
Денеб
1,33
0,03
0,02
Регул
1,34
0,3
1,22
(3-Креста
1,50
0,08
0,27
ДВОЙНЫЕ ЗВЕЗДЫ
Измерительное устройство навигационной системы, опре¬
деляющее угол с точностью до 1 мкрад, вероятно, не имеет
возможности разрешить с такой же точностью близкие двой¬
ные звезды. Поэтому измерения в таком случае будут осуще¬
ствляться относительно центра интенсивности системы из двух
звезд. Среди 21 звезды первой величины имеется семь двой¬
ных звезд. Две из них будут давать ошибки, превышающие
1 мкрад. Звезда а-Креста является двойной, причем одна из
компонент ярче другой в 1,6 раза, а разделяющее их угловое
расстояние в настоящее время составляет 20 мкрад. Таким
образом, если положение определяется по более яркой компо-

ИСПОЛЬЗОВАНИЕ АСТРОНОМИЧЕСКИХ НАБЛЮДЕНИЙ	183
центе, то следует ввести коррекцию величиной 8 мкрад. Для
звезды ос-Центавра максимальное угловое расстояние, отде¬
ляющее компоненты, составляет 88 мкрад и приводит к ошиб¬
ке в 19 мкрад.
Обе компоненты двойной звезды вращаются вокруг об¬
щего центра масс. Если соотношение между массой и яр¬
костью линейно, то центр интенсивности должен совпадать
с центром масс и тогда никакой проблемы не возникает. Од¬
нако такое соотношение обычно не имеет места, поэтому в
навигационную систему необходимо вводить соответствую¬
щую коррекцию. Для звезды а-Центавра расстояние, разде¬
ляющее компоненты, постоянно увеличивается со скоростью
3 мкрад/год, что указывает на необходимость ежегодного вве¬
дения соответствующей поправки.
ЗАКЛЮ ЧЕНИЕ
Любая из трех рассмотренных навигационных систем обе¬
спечивает достаточную точность определения местоположе¬
ния при условии, что отношение требуемой точности опреде¬
ления положения к длине перелета составляет 0,001. Наиболее
точный метод определения местоположения состоит из двух
измерений вида Солнце — звезда плюс измерение вида пла¬
нета— звезда. Использование этого метода не гарантирует
навигацию в пределах земной орбиты, пока не будет уточнен
масштаб солнечной системы. Следует отметить, что рассмо¬
тренные навигационные системы широко используются в со¬
временной наземной астронавигации. Время от времени пред¬
лагаются совершенно новые принципы, согласно которым
определения местоположения не требуется. Так, например,
Геррик предлагает систему, в которой не используется мас¬
штаб солнечной системы, а важны лишь относительные рас¬
стояния между телами солнечной системы. Такая система
может быть использована не только для навигационных це¬
лей, но и для уточнения масштаба солнечной системы. Детали
других принципов навигации должны быть подвергнуты
строгому анализу, а получаемые погрешности следует сопо¬
ставить с погрешностями триангуляционных методов.

КОСМИЧЕСКАЯ НАВИГАЦИЯ И ИССЛЕДОВАНИЯ
С ПОМОЩЬЮ ИЗМЕРЕНИЯ РАЗНОСТИ СИЛ
ТЯГОТЕНИЯ1)
Кэрролл, С авет
Как известно, на физическое тело в свободном падении
действуют силы растяжения и сжатия, а также вращательные
моменты, зависящие от значения градиента поля тяготения,
ориентации и собственного вращательного движения тела.
Еще в 1765 г. применения этого явления геофизиками при¬
вели Эйлера к заключению, что Земля, рассматриваемая как
огромное твердое тело гироскопа, покачивается при наличии
момента, создаваемого градиентом поля тяготения Солнца.
Этот вывод был аналитически подтвержден в последующих
работах Лапласа (1800). Теория была обобщена для случая
Земли, которая трактовалась как упругое деформируемое
тело, подверженное явлениям растяжения и сжатия (Макс-,
велл, 1890 г.; Ньюкомб, 1892 г.; Дарвин, 1916 г.; Джеффри,
1926 г. и др.).
С 1956 г., когда это явление приобрело практическое зна¬
чение для движения космических кораблей, был опубликован
ряд статей, в которых рассматривалась проблема использо¬
вания вращательных моментов для стабилизации искусствен¬
ного спутника.
Силы растяжения и сжатия могут быть использованы при
решении проблем космической навигации, в частности для
определения местоположения, скорости и ускорения космиче¬
ского корабля, а также ускорения силы тяжести. Несмотря
на то что градиенты силы тяжести малы (порядка 10-7—
Ю~6 gs/м у поверхности Земли и 10_1°—10-9 gs/м на высоте
~60 000 км2)), были предложены различные проекты по
созданию акселерометра, работающего в диапазоне этих
ускорений.
Авторы настоящей статьи не касаются вопроса практиче¬
ской конструкции акселерометра, измеряющего разности
ускорений или градиент гравитационного поля, они рассма-
9 Carroll J., Savet P., Aero/Space Etigng., 18, N° 7, 44—47 (July
1959).
2) gs — ускорение силы тяжести у поверхности Земли.

ИСПОЛЬЗОВАНИЕ ИЗМЕРЕНИЯ РАЗНОСТИ СИЛ ТЯГОТЕНИЯ 185
тривают только возможности применения такого прибора для
космической навигации и исследовательских целей. Однако
результаты подробного анализа, проведенного в статье, по¬
зволяют вывести соотношения, которые с успехом можно при¬
менить при разработке. Имеется по крайней мере три суще¬
ственных предположения относительно применения такого
акселерометра в космической навигации и для исследователь¬
ских целей. Во-первых, он может быть применен для непре¬
рывной коррекции (удерживания) инерциальной платформы
на спутнике в точном соответствии с эквипотенциальными по¬
верхностями гравитационного поля и тем самым для опреде¬
ления текущего положения спутника относительно местной
вертикали. Более того, такое же удерживание он может вы¬
полнить относительно плоскости орбиты; в конечном итоге
может быть непосредственно получена угловая скорость дви¬
жения спутника по орбите. Отсюда следует, что если известна
гравитационная постоянная притягивающего тела, то может
быть определено и радиальное расстояние между центрами
притяжения, и, наоборот, если известно радиальное расстоя¬
ние, то может быть определена гравитационная постоянная.
Во-вторых, как дополнение к соответствующей инерциаль¬
ной системе управления при космической навигации, устрой¬
ство, определяющее градиент поля тяготения, может быть
использовано для переориентации (уточнения ориентации)
инерциальной системы, подверженной дрейфу, и тем самым
для коррекции ошибок стабилизации, определения местополо¬
жения и скорости, которые быстро накапливаются при про¬
должительном полете, характерном для космических кораб¬
лей. Возможно даже полное прекращение работы всей инер¬
циальной системы и осуществление ее переориентации в
выбранные интервалы времени.
И, в-третьих, система измерения разности гравитационных
сил может быть использована в качестве дублирующего
устройства для получения навигационных данных, что повы¬
сит общую точность системы.
СИЛЫ РАСТЯЖЕНИЯ И СЖАТИЯ, СОЗДАВАЕМЫЕ ГРАВИТАЦИЕЙ
Для того чтобы облегчить интуитивное понимание явлений
сжатия и растяжения, рассмотрим влияние сил, вызываемых
гравитацией, на массы простой конфигурации.
Точечная масса, подверженная действию центрального
поля тяготения (поля сил), при свободном падении из состоя¬
ния покоя будет перемещаться по радиальной прямой. Две

186
il. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВЙГАЦЙЯ
такие массы, одновременно начинающие свободно падать
с одной и той же сферической эквипотенциальной поверх¬
ности, столкнутся в начале координат центрального поля сил.
Предположим теперь, что две массы (Ми М2) помещены
на концах невесомого стержня L (фиг. 1). Центр тяжести
этой простой системы будет перемещаться по радиальной ли¬
нии, а каждая из масс, удерживаемая стержнем, будет дви¬
гаться по прямой траектории параллельно этой радиальной
м, мг
линии. Так как каждая масса перемещалась бы по радиаль¬
ной линии, если бы стержень не противодействовал такому
движению, то очевидно, что удерживающая каждую массу
сила (противодействующая сила) будет направлена вдоль
стержня наружу от центра тяжести и, таким образом, стер¬
жень будет испытывать сжатие.
По аналогии можно сделать заключение, что если две
массы первоначально ориентированы в радиальном направле¬
нии, как показано на фиг. 2, то масса, расположенная ближе
к центру поля тяготения, будет постоянно испытывать боль¬
шее ускорение, чем масса, расположенная за ней, и, таким
образом, расстояние между ними будет непрерывно возра¬
стать. Жесткий стержень, соединяющий обе эти массы, будет
удерживать это расстояние равным длине стержня и при этом
будет испытывать растяжение.
Е(ц ентр радиаль ~
но го поля тяготения)
Фиг. 1.
Фиг. 2.
4
Е

ИСПОЛЬЗОВАНИЕ ИЗМЕРЕНИЯ РАЗНОСТИ СИЛ ТЯГОТЕНИЯ 187
Таким образом, стержень, удерживающий систему простой
конфигурации из двух масс в свободном падении, может ис¬
пытывать либо растяжение, либо сжатие в зависимости от
ориентации стержня по отношению к направлению на центр
поля тяготения. Поскольку существует такая зависимость,
представляет интерес определить угол, при котором сжатие
или растяжение равно нулю, а в более общем случае опреде¬
лить величину сжатия в функции угла, образуемого стержнем
с направлением на центр поля тяготения.
Mi
Предположим, что две массы и соединяющий их стержень
ориентированы так, что стержень направлен под некоторым
произвольным углом а относительно направления на центр
массы Е (фиг. 3).
Из треугольников получаем
r2 = r2-\- I2 — 2rL cos а,
и
п L — г cos а
cos р2 =	  .
г\ = г2 + L2 + 2rL cos а,
L Г COS а
COS ^ =
По закону обратной пропорциональности квадрату расстоя¬
ния имеем
_ gs*2= gsR2
^1	г2 г2 + L2 + 2rL cos а
_ gsE2 __	gsR2
r\ г2 + L? — 2rL cos a ,
где R — радиус массы E (Земли). Растяжение стержня Т
определяется выражением
т =	cos Pj — m2g2 cos p2-
Если
ml — m2 = m,
то
&a = -^ = gi cos px — g2 cos p2,

188
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
что в точности представляет производную от поля тяготения
по направлению.
Для того чтобы определить производную по направлению
Да, допустим, что
Да = (& cos р, — g cos p) — (g2 cos p2 — g cos p)
и что для данной ориентации а стержня относительно местной
вертикали мы найдем величину каждого члена в скобках пу¬
тем разложения в ряд gcos|3 вблизи центра тяжести (Ц. Т.)
системы.
Таким образом, получаем выражение
о	о I Г d	(g COS Р) 1 Л Г I 1 Г	(g cos Р) 1 Л
8i cos Pj	-	g cos p = {[	y*dL P; J bL+ 2	^ P;J №},
из которого после прямого дифференцирования найдем
»«<-)•
Максимальные абсолютные значения членов ряда получаются
при а = 0	и	г = R. При	этих условиях и	при L = 0,15	м	и
R = 0,6107	м	второй член	ряда равен 0,5- 10-7gs, а третий	член
(3/8) • Ю-ч gs.
Очевидно, третьим и последующими членами можно пре¬
небречь, так как вводимая при этом ошибка не превышает
(3/8) • 10-'4 gs.
Итак,
Да = g, cos р, — g cos p = —	Д)	(1	— 3 cos2 a)
и разница ускорений силы тяжести между точечными мас¬
сами на стержне, или производная по направлению поля тя¬
готения вдоль всей длины стержня, равна
Да = — (~/r-) (т) ^ ~ 3 cos2 а)-
Растяжение равно нулю, когда А а = 0, т. е. когда
1—3 cos2 a = 0 или a = arc cos -g- ~ 54°44/. Кривые зави¬
симости Да от а показаны на фиг. 4.
Отметим, что растяжение максимально, когда точечные
массы расположены вдоль местной вертикали; сжатие мак-

ИСПОЛЬЗОВАНИЕ ИЗМЕРЕНИЯ РАЗНОСТИ СИЛ ТЯГОТЕНИЯ 189
симально, когда массы расположены на одной и той же эк¬
випотенциальной поверхности. Кроме того, величина макси-
234°W 305° 16 '
30° 60° 90° /20° 150° 180 Z10 240°270°300°330°360°
^	Угловая	ориентация	а
Фиг. 4*
мального растяжения вдвое превышает величину максималь¬
ного сжатия, и растяжение равно нулю при а = 54°44/.
РАСТЯЖЕНИЕ, ВЫЗЫВАЕМОЕ ВРАЩЕНИЕМ
Если система, состоящая из стержня с массами, вра¬
щается с некоторой угловой скоростью вокруг оси, перпен¬
дикулярной к стержню и проходящей через центр тяжести,
стержень будет испытывать растяжение, пропорциональное
сумме центробежных ускорений масс системы:
Т = mxLxyl +	■=	2mLy29
где ф — угловая скорость стержня относительно инерциаль¬
ной системы координат; 2 L — длина стержня (предпола¬
гается, что гп\ = пг2 = пг).
НАВИГАЦИЯ
Навигация в плоскости (двумерное пространство)
Предположим, что имеется прибор, способный измерять
небольшие растяжения стержня. Пусть на платформе косми¬
ческого корабля, выведенного на орбиту, смонтированы две
системы из стержней с точечными массами. Для начала
предположим, что, во-первых, притяжение между массами

190
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
каждой системы, а также между каждой из масс и распреде¬
ленной массой корабля пренебрежимо мало; во-вторых, ор¬
битальное движение происходит в плоскости и, в-третьих,
стержни остаются компланарными относительно плоскости
орбиты.
Как уже отмечалось, напряжения в стержнях возникают
в результате действия двух факторов: поля тяготения и вра¬
щения. Напряжения в стержнях определяются выражениями
Тх = — 2mL [yj (1 — 3 cos2 аг) + 2/nLy2,
Т2 = — 2mL (1 — 3 cos2a2) -|- 2mL<?2.
Если обе системы стержень—массы установлены взаимно
перпендикулярно, то
Рассмотрим следующие случаи.
1. Пусть ф — угловая скорость вращения платформы, ко¬
торая непрерывно измеряется гироскопическим устройством.
В этом случае одновременно могут быть решены два урав:
нения для определения положения платформы относительно
местной вертикали и для определения отношения g/r, про¬
порционального величине градиента поля тяготения.
2. Пусть положение платформы регулируется таким об¬
разом, чтобы поддерживалось равенство Тх = Т2. В этом
случае положение платформы относительно местной верти¬
кали можно непрерывно определять; можно будет опреде¬
лить и величину ф. Предположим, что корабль движется по
круговой орбите. Тогда, поскольку ср — угловая скорость дви¬
жения по орбите, можно определить угловую скорость спут¬
ника при его движении по орбите вокруг притягивающего
тела. Возможность распространения способа определения
величины ф на случай эллиптических орбит нуждается в до¬
полнительных вычислениях.
3. Предположим, что платформа располагается так же,
как и во втором случае, и допустим, кроме того, что расстоя¬
ние г определяется безынерционными средствами с помощью
радиолокатора. В этом случае значение g на высоте может
непрерывно вычисляться. И, наоборот, если известно значе¬
ние gy можно определить значение г.
Заметим, что во всех случаях возникает некоторая неоп¬
ределенность при определении сы, так как решение уравне¬
ний содержит тригонометрическую функцию. Однако эту

Использование измерения рАзностй сил тяготения Ш
неопределенность можно разрешить, если учесть траекторию
предшествующего этапа.
Итак, в принципе чисто инерциальными средствами можно
определить: 1) положение платформы относительно местной
вертикали, а следовательно, положение космического ко¬
рабля; 2) угловое положение спутника на орбите и 3) вели¬
чину градиента поля тяготения. Более того, при дополни¬
тельном измерении неинерциальными способами расстояния
до притягивающего тела есть возможность определить вели¬
чину гравитационного ускорения и тем самым исследовать
гравитационное поле этого тела.
Если распространить результаты, полученные выше, на
случай навигации в трехмерном пространстве, можно сделать
вывод, аналогичный случаю для плоскости. Кроме того, мож¬
но прийти к интересному заключению о том, что чисто инер¬
циальными средствами может быть определено также поло¬
жение космического корабля относительно плоскости орбиты.
Предположим, что на платформе смонтированы не два, а
три взаимно ортогональных дифференциальных акселеро¬
метра. Допустим далее, что угловые перемещения корабля
фиксируются тремя скоростными гироскопами. Тогда напря¬
жения в стержнях будут равны:
и направление текущей вертикали в каждый момент может
быть определено относительно трехгранника, образованного
тремя стержнями. Направление местной вертикали опреде¬
ляется тогда плоскостью, орбиты.
Зная направление нормали к плоскости орбиты, предпо¬
ложим, что ось вращения одного из акселерометров совпа¬
дает с направлением нормали и что весь трехгранник вра¬
щается относительно этой нормали так, чтобы поддерживать
выходные сигналы двух других дифференциальных акселеро¬
метров равными друг другу. Это эквивалентно рассмотрен¬
ному выше случаю на плоскости с теми же выводами. Од¬
нако в случае трехмерного движения мы получаем средство
для определения направления нормали к плоскости орбиты
Навигация в трехмерном пространстве
Тх = —	—3cos2 ах),

192
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
или бинормали к орбите, а также направление текущей вер¬
тикали. Таким образом, измеряя положение корабля отно¬
сительно стержней, мы можем определить ориентацию ко¬
рабля в трехмерном пространстве.
ЗАНЛЮЧЕНИЕ
Описанный выше способ определения градиента поля тя¬
готения обеспечивает средство непрерывной или периоди¬
ческой регулировки платформы таким образом, чтобы она
оставалась касательной к эквипотенциальным поверхностям.
Он также обеспечивает метод установки этой платформы от¬
носительно плоскости орбиты корабля.
Описываемая система может быть выключена в течение
любого промежутка времени без ухудшения ее последующей
работы, что чрезвычайно важно при длительных космиче¬
ских полетах из-за ограниченной мощности источников пи¬
тания; кроме того, это обеспечивает потенциальные возмож¬
ности повышения надежности системы.
Независимо от эксцентриситета орбиты появляется воз¬
можность непосредственно определить угловую скорость век¬
тора, направленного от центра притягивающего тела к спут¬
нику, а также угловую скорость спутника вокруг этого
радиуса-вектора. Более того, непосредственно могут быть
определены относительные величины радиального (г/г) и гра¬
витационного (g/r) ускорений.
Точность измерений зависит от относительной чувстви¬
тельности дифференциальных акселерометров. Ошибка в оп¬
ределении местной вертикали, выраженная в радианах, пред¬
ставляет частное от деления величины чувствительности диф¬
ференциальных акселерометров на величину градиента поля
тяготения на орбитальной высоте.
ЛИТЕРАТУРА
1. Roberson R. Е., Tatistcheff D., The Potential Energy of a Small
Rigid Body in the Gravitational Field of an Oblate Spheroid,
/. Franklin Inst., 262, № 3 (September 1956).
2. Roberson R. E., Gravitational'Torque on a Satellite Vehicle, J. Frank¬
lin Inst., 265, № 1 (January 1958).
3. О berth H., Precise Attitude Control for Artificial Satellites, Vistas
in Astronautics (Intern. Ser. of Monographs on Aeronaut. Sci. and
Space Flight, Div. VII, Astronaut. Div., Vol. I), Lnd., 1958,
pp. 217—255.
4. Growl e у J. C., Kolodkin S. S., Schneider A. М., Some Pro¬
perties of the Gravitational Field and Their Possible Application to
Space Navigation, Vth Ann. Confer. Proc., East Coast Confer, on
Aeronaut, a. Navig. Electronics, 1958.

СИСТЕМА НАВЕДЕНИЯ НА КОНЕЧНОМ УЧАСТКЕ
ВСТРЕЧИ СПУТНИКОВ 1)
Клохесс и, У и лтшайр
В настоящей статье рассматриваются вопросы сборки на орбите бес¬
пилотного корабля, составляемого из нескольких спутников, причем в мо¬
мент соединения спутников между ними должна быть обеспечена плавная
встреча. Дается вывод уравнений движения присоединяемого спутника в
относительной системе координат. Эти уравнения используются для вычис¬
ления конечной скорости при встрече по истечении интервала времени т.
Скорость периодически корректируется командной системой наведения до
момента приложения тормозного импульса при встрече. На заключитель-~
ном этапе встречи треоуется инфракрасная система наведения, которая
фактически обеспечивает физический контакт и соединение спутников. Пер¬
вым из запущенных на орбиту спутников является так называемый базо¬
вый управляющий спутник, он регулирует соединение всех остальных при¬
соединяемых спутников и имеет на борту счетно-решающее устройство,
аппаратуру для управления наведением, приборы прецизионной ориентации
и другое оборудование, необходимое для осуществления встречи. После¬
дующие присоединяемые спутники имеют систему тяги, грубую систему
регулирования по положению (систему стабилизации) и приемник команд,
а также научные приборы, размещенные для выполнения основной задачи
корабля. В статье рассматриваются:
1. Способ определения орбиты управляющего (базового) спутника и
использования ее в счетно-решающем устройстве.
2. Системы измерения и управления положением базового и присоеди¬
няемого спутников.
3. Система измерения, при помощи которой базовый спутник опреде¬
ляет относительное положение и скорость присоединяемого спутника.
4. Уравнения, которые необходимо решить для получения команд
встречи, и счетно-решающее устройство для решения этих уравнений.
5. Командная связь ог управляющего спутника к присоединяемому
спутнику, а также бортовая система управления на присоединяемом спут¬
нике.
6. Система самонаведения на этапе конечного сближения на расстоя¬
нии порядка сотен метров.
7. Описание динамики самого процесса встречи.
ВВЕДЕНИЕ
Предметом обсуждения в настоящей статье является фа¬
за «встречи» в процессе построения космической станции,
О С 1 oh ess у W. Н., Wiltshire R. S, /. Aerospace ScL, 27, № 9,
653—658 (September 1960),
13 За к, 876,

194
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
т. е. в процессе сборки на орбите большого спутника, со¬
стоящего из нескольких малых спутников. Точнее, в статье
рассматривается динамика «встречи» и аппаратура, необхо¬
димая для ее осуществления. Орбита выбирается так, чтобы
всегда получалось целое число оборотов за сутки, причем
высота орбиты не имеет строгих ограничений. Практически
из-за прецессии узлов орбиты высота ее изменяется и пло¬
скость орбиты будет через каждые сутки совпадать со стар¬
товым направлением. Последующие спутники запускаются
с интервалом в одни сутки, причем выключение двигателя
происходит так, чтобы достигнуть апогея на высоте базового
спутника. Этот маневр во времени осуществляется так, чтобы
время и положение апогея обоих спутников совпало.
СЛЕЖЕНИЕ И СТАБИЛИЗАЦИЯ
Базовый управляющий спутник запускается на круговую
орбиту. С помощью радиолокатора за ним осуществляется
слежение с Земли. Для этой цели может быть использован
радиолокатор FPS-16 (RCA), характеристики которого при¬
ведены в таблице.
Точность следящего радиолокатора FPS-15
Точность определения местоположения
Угол азимута
0,34' (среднеквадратичный)
Угол места
0,34' (среднеквадратичный)
Дальность
4,5 м (среднеквадратичная)
Точность определения скорости при усреднении данных за 20 сек
Угол азимута
0,08 угл. мин/сек
Угол места
0,08 угл. мин/сек
Дальность
0,1 м/сек
Требуемое отношение сигнал/шум, необходимое для по¬
лучения точностей, указанных в таблице, составляет при¬
мерно 15 (36 и обеспечивается бортовым передатчиком мощ¬
ностью 100 вт. Передатчик весит 4,5 кг и потребляет 25 вт
от первичного источника бортового питания.

НАВЕДЕНИЕ НА КОНЕЧНОМ УЧАСТКЕ ВСТРЕЧИ СПУТНИКОВ 195
Измеренные следящим радиолокатором величины долж¬
ны быть преобразованы из системы координат, связанной со
станцией слежения, в инерциальную систему координат.
Требуемая матрица перехода может быть легко образована
в наземном цифровом счетно-решающем устройстве, которое
используется в сочетании со следящим радиолокатором.
Необходимые для обеспечения встречи орбитальные па¬
раметры (элементы орбиты) будут передаваться на счетно¬
решающее устройство базового спутника с помощью радио¬
линии. Ширина полосы передачи может быть сужена при
использовании запоминания элементов ожидаемой орбиты в
счетно-решающем устройстве и последующей коррекции
этих величин после определения элементов действительной
орбиты.
Базовый и присоединяемый спутники распознаются по¬
средством кодированных сигналов. При этом с помощью ра¬
диолокатора FPS-16 относительное расстояние между двумя
спутниками может быть измерено с точностью до 1,5 км. Од¬
нако такая точность слежения устройства FPS-16 все еще
недостаточна для осуществления маневра встречи. Поэтому
на борту спутников для определения их относительного по¬
ложения и скорости необходимо иметь некоторые другие при¬
боры и установить также общую систему координат, отно¬
сительно которой эти величины будут измеряться.
Если предположить, что корабль, образуемый из спут¬
ников, всегда стабилизируется по местной земной верти¬
кали, то система координат будет вращающейся и будет де¬
лать один оборот за период обращения спутника.
Местная вертикаль может быть определена при помощи
инфракрасного сканирования земного диска с помощью си¬
стемы, состоящей из четырех инфракрасных телескопов,
симметрично размещенных вокруг спутника в плоскости, пер¬
пендикулярной к местной вертикали. Каждый телескоп оп¬
ределяет край земного диска, фиксируя перепад градиента
температуры между земной поверхностью и космическим
пространством, а местная вертикаль определяется биссектри¬
сами углов между противоположными парами инфракрасных
телескопов. Вращение спутника будет почти равномерным,
так как орбита выбирается близкой к круговой. Поэтому си¬
стема обнаружения горизонта будет вырабатывать только
малые отклонения величины угловой скорости вращения от
ее среднего значения.
Влияние Солнца и Луны можно устранить, так как пики
их излучения расположены на иной длине волны, чем у
Земли, и при надлежащей фильтрации система будет
13*

196
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
обнаруживать только земной диск. Кроме того, существуют
определенные зависимости углов расположения телескопов,
следящих за Землей с заданной высоты, и информация
о местной вертикали не принимается во внимание, если эти
углы выходят за пределы заданных допусков.
Влияние аномалий атмосферы и поверхности Земли при¬
водит к тому, что точность определения земного диска с по¬
мощью инфракрасных телескопов составляет около 2 мрад
на высоте 300—800 км. Если рассматривать всю систему, т. е.
телескопы, их механическую установку, системы управления
ориентацией и т. д., то точность определения местной верти¬
кали будет составлять ~0,5°.
Система управления положением спутника относительно
его центра тяжести определяется временем, в течение кото¬
рого система ориентируется, желаемой степенью точности,
допустимым весом и имеющейся электрической мощ¬
ностью.
Устройства управления базового спутника и всех после¬
дующих присоединяемых спутников оборудованы инфракрас¬
ными системами для определения местной земной вертикали,
но имеют различные характеристики при управлении.
Базовый спутник находится на орбите дольше, чем любой
присоединяемый спутник, и он призван осуществлять
ориентацию всего корабля, собираемого из нескольких спут¬
ников.
В системе управления базового спутника исподьзуются
реактивные маховики, благодаря чему устраняется необхо¬
димость применения большого количества специальных реак¬
тивных двигателей. Система реактивных маховиков лишь до¬
полняется реактивными двигателями, которые будут исполь¬
зоваться только тогда, когда мощность маховиков окажется
недостаточной или когда будет вводиться коррекция на влия¬
ние внешних моментов.
Присоединяемым спутникам ориентация необходима лишь
примерно в течение одних суток до присоединения к упра¬
вляющему спутнику. Так как их полезная нагрузка в основ¬
ном состоит из аппаратуры для научных исследований, то
имеющейся в наличии электрической мощности для реактив¬
ных маховиков будет недостаточно и при малой продолжи¬
тельности работы задача ориентации может быть лучше
обеспечена реактивными двигателями.
По результатам предварительных исследований было
установлено, что для ориентации типичного спутника (весом
~2,5 т) по местной вертикали с точностью около 0,5° си¬
стеме реактивных двигателей потребуется всего ~5 кг топ¬

НАВЕДЕНИЕ НА КОНЕЧНОМ УЧАСТКЕ ВСТРЕЧИ СПУТНИКОВ 197
лива в сутки. Необходимая тяга получается от системы, ра¬
ботающей на перекиси водорода.
Четыре присоединяемых спутника подстраиваются к базо¬
вому спутнику так, как показано на фиг. 1. На базовом спут¬
нике выбирается определенная ось, которая при помощи
гироскопического датчика угловой скорости крена ориенти¬
руется по вектору скорости. Ось 1—3 базового спутника оп¬
ределяется направлением оси гироскопического датчика уг¬
ловой скорости крена. Выходной сигнал этого гироскопа бу¬
дет равным нулю только тогда, когда ось 1—3 будет парал¬
лельна вектору скорости. Полярность сигнала угловой ско¬
рости крена определяется по полярности сигнала угловой
скорости тангажа. Однако теоретически возможно, что кур¬
совая ориентация на 180° неустойчива и будет подвержена
действию шумов системы. Базовый спутник ориентируется
так, чтобы при надлежащем курсовом положении (0°) он
оказывался направленным в сторону первого присоединяе¬
мого спутника. Присоединяемый спутник ориентируется при
помощи сигнала своего гироскопического датчика угловой
скорости крена таким образом, чтобы его продольная ось
была направлена по вектору скорости.
После того как первый присоединяемый спутник будет
подключен к базовому, последний повернется по курсу так,
чтобы его ось 2 была направлена по вектору скорости.

198
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
При этом сигналы по крену и тангажу поменяются местами и
согласование будет происходить аналогично рассмотренному
выше.
Система
координат
(земная)
Требуемое
рыскание
по курсу
Система
координат
(земная)
Система
сканирования
—Sf+
по крену
А
Угловая
.. скорость
крена
X
Ограничива¬
ющее
устройство
I
Реактивный
маховик
*
Динамика
объекта
Реактивный
двигатель
Преобразовате¬
ли угловых
скоростей
крена и
тангажа
“ I
Угловая
скорость
рыскания
Усили¬
тель^
Динамика
объекта
Реактивный
Реактивный
<—
двигатель
маховик
¥
Ограничива¬
.
ющее
устройство
-
Система
сканирования
по тангажу
Ограничива¬
ют, ее
устройство
X
Фиг. 2. Система ориентации базового спутника для типичного
составного спутника весом ^ 2500 кг.
Вес реактивных маховиков 32 кг; вес гироскопов и электронной аппаратуры 4,5 кг] вес
устройства сканирования в горизонте 14 кг; вес реактивных двигателей 27 кг; потребляемая
мощность 30 вт; объем 28 дм3.
При ориентации базового спутника для встречи третьего
и четвертого спутников знаки сигналов ошибок гироскопиче¬
ских датчиков угловой скорости крена и тангажа соответ¬
ственно изменяются. Если нужно присоединить к базовому
спутнику более четырех дополнительных спутников, сигналы
гироскопических датчиков угловой скорости крена и тангажа
уже не в состоянии обеспечить надлежащей ориентации по
курсу. Однако путем соответствующего преобразования сиг-

НАВЕДЕНИЕ НА КОНЕЧНОМ УЧАСТКЕ ВСТРЕЧИ СПУТНИКОВ 199
налов угловой скорости крена и тангажа можно достигнуть
любой ориентации по курсу. При наличии такого преоб¬
разователя базовый спутник может поворачиваться по курсу
до тех пор, пока на выходе преобразователя не выработается
нулевой сигнал (это свидетельствует о том, что корабль
достиг нужной ориентации).
■Фиг. 3. Система ориентации присоединяемого спутника для типичного
спутника весом ^ 2500 кг.
Вес реактивных двигателей 27 кг\ вес гироскопов и электронной аппаратуры 4,5 кг\ вес
устройства сканирования в горизонте 14 кг\ потребляемая мощность 30 вт\ объем 20—70 дм*.
Система ориентации управляющего базового спутника, в
которой используется система реактивных маховиков, допол¬
ненная реактивными двигателями, приведена на фиг. 2. Си¬
стема ориентации присоединяемого спутника показана на
фиг. 3. Поскольку она работает очень короткое время, в ней
используются только реактивные двигатели.
Взаимное расположение базового и присоединяемых спут¬
ников определяется назначением корабля. Их положение мо¬
жет быть таким, что продольная ось базового спутника бу¬
дет располагаться по местной вертикали, а продольные оси
присоединяемых спутников в плоскости местного горизонта и

200
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
вся система образует конструкцию, где базовый спутник иг¬
рает роль втулки, а присоединяемые спутники — роль спиц
колеса (см. фиг. 1).
После выхода каждого из спутников на орбиту они ста¬
билизируются по всем трем осям при нулевых выходных сиг¬
налах гироскопических датчиков скорости (на фиг. 2—3 при
разомкнутом Si). Будучи стабилизированным, спутник затем
начинает «искать» Землю. При замкнутом Si диск Земли об¬
наруживается при помощи горизонтальной системы сканиро¬
вания и спутник будет ориентироваться по крену и тангажу
относительно местной вертикали. После этого отработка же¬
лаемого курсового угла начинается при замыкании S2.
УПРАВЛЕНИЕ СПУТНИКАМИ ПРИ ИХ ВСТРЕЧЕ
Измерения положения и скорости производятся на борту
базового спутника и относятся к связанной с ним системе
координат. Для измерения относительного положения при¬
соединяемого спутника на базовом спутнике имеется не¬
большая бортовая радиолокационная установка. Информа¬
ция о положении в зависимости от времени подается к бор¬
товому счетно-решающему устройству для расчета относи¬
тельной скорости.
Радиолокатор, счетно-решающее устройство и приборы
для выработки команд, обеспечивающие встречу всех при¬
соединяемых спутников, размещаются на базовом спутнике,
поэтому большая часть полезной нагрузки каждого из при¬
соединяемых спутников предназначается для выполнения
других задач, связанных с назначением корабля.
Каждый из присоединяемых спутников должен быть снаб¬
жен радиолокационным маяком, с помощью которого осуще¬
ствляется точное присоединение его к базовому спутнику по¬
средством определенного разъема. Выходная импульсная
мощность маяка не превышает 500 вт. Рабочая частота сле¬
дящего радиолокатора и маяка составляет примерно
10 000 Мгц. Выбор этого диапазона обусловлен тем, что в
настоящее время подобные радиолокаторы и их антенны мо¬
гут быть сделаны очень малыми при достаточно узком луче.
Для работы на дальности порядка 300 км с существующими
радиомаяками необходимо, чтобы импульсная мощность ра¬
диолокатора составляла примерно 50 кет при средней мощ¬
ности 150 вт.
Минимальная дальность действия («мертвая зона») импуль¬
сного радиолокатора определяется длительностью импульса.

НАВЕДЕНИЕ НА КОНЕЧНОМ УЧАСТКЕ ВСТРЕЧИ СПУТНИКОВ
201
рассматриваемый здесь бортовой радиолокатор имеет дли¬
тельность импульса, равную 0,25 мксек, но так как про¬
цессы восстановления в цепях приемо-передающего и антен¬
ного трактов занимают некоторое время, то практически ми¬
нимальная рабочая дальность составит 45 м.
Определяемые наземными счетно-решающими устройст¬
вами элементы орбиты устанавливают время запуска присо¬
единяемого спутника, однако ошибки во времени, в тяге и в
системе наведения не позволяют осуществить прямую встре¬
чу спутников только по этим данным. Поэтому базовый спут¬
ник информируется о времени старта присоединяемого спут¬
ника, а также о моменте возможной их встречи. В указанное
время радиолокатор Начинает отрабатывать программу ко¬
нического сканирования для осуществления встречи с при¬
соединяемым спутником.
Радиолокатор осуществляет «захват» присоединяемого
спутника еще до выхода последнего на орбиту. При этом,
хотя радиолокатор уже захватил спутник и счетно-решаю¬
щее устройство приступило к работе, основная фаза актив¬
ного полета управляется системой наведения присоединяемого
спутника. Для управления тягой и верньерными двигателями
присоединяемого спутника используются данные, измеренные
радиолокатором, и результаты расчетов в счетно-решающем
устройстве.
Для подачи команд используется фазово-импульсная мо¬
дуляция радиолокатора. Командными сигналами для при¬
соединяемого спутника служат данные для двух углов, обра¬
зуемых вектором тяги с местной вертикалью присоединяемого
спутника, и времени работы двигателя (величина. тяги фик¬
сирована). Расчеты этих данных производятся относительно
системы координат, связанной с базовым спутником, но для
них используются углы вектора тяги присоединяемого спут¬
ника, отнесенные к его системе координат. Это возможно
потому, что в наихудшем случае разница в углах между
осями координат составляет ~5 мрад, причем по мере
сближения спутников эта разница пропорционально. умень¬
шается.
Команды присоединяемому спутнику поступают от борто¬
вого радиолокатора базового спутника, причем данные углов
тяги передаются с помощью фазово-импульсной модуляции.
Рассмотрим, например, четырехимпульсный код, показанный
на фиг. 4. Разность между первым и вторым импульсами оп¬
ределяет время, в течение которого будет приложена задан¬
ная тяга; разность между третьим и четвертым импульсами.

I4
£ ^ §
c: ^ ^
j?§ ъ
К * ^
Фиг. 4. Система передачи команд с фазово-импульсной модуляци

НАВЕДЕНИЕ НА КОНЕЧНОМ УЧАСТКЕ ВСТРЕЧИ СПУТНИКОВ 203
определяет плоскость углов, характеризующих вектор тяги,
а разность между вторым и четвертым импульсами опреде¬
ляет величину угла тяги. Временной интервал. выбирается
так, чтобы не было сомнительных случаев.
Источйик инфракрасного излучения^
на базовом спутнике
I
Матрица
Сигнал
ошибки
Преобразова¬
Управляюицие
инфракрас¬
углового
тель
—>
клапаны
ного
детектора
сопровож¬
дения
величины
тяги
по тангажу и
рысканию
i
Динамика
Силовая
спутника
<
установка
I
Присоединяемый спутник
1
Фиг. 5. Инфракрасная система самонаведения.
На последней сотне метров сближения (возможно, 60 м)
радиолокатор прекращает работу, и управление на этой ста¬
дии будет осуществляться при помощи инфракрасной следя¬
щей системы. В течение этого времени скорость уменьшается
До 3 м/сек, а за счет торможения в последние секунды сни¬
жается до 0,6 м/сек. Управление по тангажу и курсу будет
осуществляться при помощи малых верньерных двигателей

204
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
(или возможно прежних), и стабилизация системы будет про¬
исходить так, как описано выше. Инфракрасная следящая
система показана на фиг. 5.
УРАВНЕНИЯ И ДИН АМИН А ВСТРЕЧИ
Предположим, что базовый спутник выводится на круго¬
вую орбиту , радиусом г0 и движется со скоростью
v0=YGMe/rQ, а присоединяемый спутник выводится на пе¬
реходную орбиту, высота апогея которой примерно равна г0.
Предположим, далее, что встречаемый спутник достигает
апогея, несколько опередив базовый спутник, но с несколько
меньшей скоростью. Разница в скоростях может быть созда¬
на за счет включения реактивного двигателя, работа кото¬
рого затем прекращается, когда оба спутника будут нахо¬
диться на одной и той же орбите.
Процесс соединения спутников будет происходить сле¬
дующим образом. Когда движущаяся по переходной орбите
ракета оказывается в нескольких сотнях километров от ба¬
зового спутника, радиолокатор последнего захватывает ее
и счетно-решающее устройство определяет момент включения
двигателя и величину скорости, при которой должна быть
произведена его отсечка. Расчеты производятся в относи¬
тельной системе координат и направление тяги присоединяе¬
мой ракеты устанавливается также в этой системе координат.
Отсечка двигателя дается по возможности ближе к тем ус¬
ловиям, при которых через некоторый интервал времени
могла бы произойти встреча.
Сразу же после выключения двигателя вступают в дей¬
ствие небольшие верньерные двигатели (типа включ.-выкл.)
и производится коррекция, причем до встречи такая коррек¬
ция производится несколько раз. В течение этой фазы сбли¬
жения радиолокатор базового спутника следит за присоеди¬
няемым спутником, а его счетно-решающее устройство на ос¬
нове данных о местоположении в функции времени выраба¬
тывает значения относительной скорости и решает уравнения
движения для проверки соответствия процесса перехвата за¬
данной программе. Если ожидаемые ошибки становятся до¬
статочно большими, производится коррекция по скорости.
Когда расстояние между спутниками становится порядка ты¬
сячи метров, скорость с помощью тормозных двигателей сни¬
жается до 3 м/сек. На расстоянии 100 м счетно-решающее
устройство вырабатывает время встречи и за 3—5 сек до
встречи тормозные двигатели снижают скорость ракеты

НАВЕДЕНИЕ НА КОНЕЧНОМ УЧАСТКЕ ВСТРЕЧИ СПУТНИКОВ 205
до 0,6 м!сек, после чего выключаются. На этом же расстоянии
радиолокатор прекращает слежение и заменяется инфра¬
красным маяком, излучение которого направляется кониче¬
ским гнездом базового спутника. В это время в носовом ко¬
нусе присоединяемого спутника (на расстоянии до 300 м)
Круговая орбита
базового спутника
Фиг, 6. Система координат.
включается инфракрасное управляющее устройство с пас¬
сивным самонаведением, которое устанавливает нужное на¬
правление и с помощью реактивной системы управления ра¬
кетой направляет этот носовой конус в коническое гнездо,
где он механически захватывается и присоединяется к базо¬
вому спутнику.
Для выполнения этой динамической задачи необходимо
составить уравнения движения тела, приближающегося к
базовому спутнику и не имеющего больших отклонений по
скорости и координатам от базового спутника. С этой целью
мы выбираем правую систему координат (х, у, z), ось у ко¬
торой направлена по радиусу от центра Земли к базовому
спутнику, а ось z—параллельно вектору угловой скорости
вращения базового спутника вокруг Земли, т. е. перпенди¬
кулярно плоскости его орбиты в направлении вектора мо¬
мента количества движения. Тогда ось х будет касательной
к орбите и направлена (положительное направление) в сто¬
рону, противоположную движению базового спутника
(фиг. 6).

206
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
В этой системе координат имеем следующие уравнения
движения:
= х — 2 игу — ш2Х,
^-= у + 2о)Л — ш2 (у + гй),
Рг
-JL=z,
т у
где Fx> Fy, Fz содержат члены, выражающие гравитационные
силы и тягу.
Полная гравитационная сила равна
^ Земли
*2 + {У+г о)2 + *2
Для рассматриваемых значений х, у, z{Y х2-\-у2~\-z2 ^
<300 км) мы можем разложить члены, выражающие грави¬
тационные силы, в ряд по степеням У х2-]-у2-\- z2/r0 и пре¬
небречь всеми членами более высокого порядка, чем
х + У2+ z2)lrl- При этом в первом уравнении оба члена,
обозначающие центростремительные силы, исчезнут, а в ура¬
внении для у появится новый член, сходный с ними по форме.
Уравнение для z также будет содержать один член подоб¬
ного вида. Тогда уравнения примут вид
i = i-2cоу,
~~ = У + 2®х — 3 о)2у,
1*-="г+а>*г.
Анализ показывает, что
t
f (ТХх -(- Туу	ТZz) dt —
(X2 + y2+i2)+{ ^ (г2 - Зу2)
t
f Txdt = lm(x — 2<oy)ftt.

НАВЕДЕНИЕ НА КОНЕЧНОМ УЧАСТКЕ ВСТРЕЧИ СПУТНИКОВ
207
Положим, что Тх = Ту = Tz = 0. В этом случае решение за¬
пишется следующим образом:
Г У = {Ф - 3Уо) cos ^	~ sin Ы + (4у0 ~Ф) .
х = 2	—Зу0) sin ait — -^-cos wt -|- (6шу0 — 2>x^t-\-
+(*+^)-
z = Z0 COS со/ + sin со/,
где x0, yo, z0y x0i y0i z0 — начальные значения координат и со¬
ставляющих скорости по осям координат.
Плоскость орбиты присоединяемого спутника
Фиг. 7. Наклон плоскости орбиты присоединяемого спутника.
Смысл уравнения для z состоит в том, что плоскость ор¬
биты присоединяемого спутника наклонена относительно ба¬
зового спутника и совершает гармонические колебания в на¬
правлении оси z (фиг. 7)
dz Л	,	,	z0
ЧГ=°> если	^ =
или
2„акс. = V 21+{ф) '
Скорость при z = 0 составляет
фмакс. = ш |/"2'о+(^г) '
Если х0 — 2со уо Ф 0, то в уравнении для г будет иметься
слагаемое, характеризующее дрейф, которое будет наклады¬
ваться на периодическое движение по осям х, у и z. При на¬
длежащем выборе уравнений можно видеть, что траектория
движения в плоскости ху представляет собой эллипс с под¬
вижным центром или циклоиду. Однако для наших целей
достаточно	лишь показать, что	можно	выбрать	начальные

208
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
скорости Хо, уо и z0 таким образом, что для заданных х0, у0у
z0 и для требуемого момента встречи т перехват может быть
осуществлен и при надлежащем тормозном импульсе в конце
его	произойдет встреча. Пренебрегая движением по	г,	опре-
делим	начальные скорости х0, Уо так, чтобы присоединяемый
ез начало координат в момент времени
т. Тогда_получим
{.х0 х0 sin сох + у0 [бсох sin сох — 14 (1 — cos сох)]
со	Зсох Sin СОХ — 8(1 — COS сох)
Уо 	 2лг0	(1	—	cos	сох)	Уо	[4	sill	сох	— Зсох COS сох]
со	Зсох	sin сох — 8(1 — COS сох)
В пределе при т-^0 х0->	(х0/ч) и у0-> (yofr), как
это и должно быть. При выбранном т счетно-решающее уст¬
ройство вычисляет х0 и у0у и по командным линиям связи
создает с помощью реактивных и верньерных двигателей
точные условия для присоединения спутника.
Через некоторый интервал времени счетно-решающее уст¬
ройство вновь решает эти уравнения, например, для неко¬
торого момента времени т', вычисляет х0(т/) и yoi':') и, срав¬
нивая измеренные *о(т') и yo{i') с ожидаемыми вычислен¬
ными значениями, вырабатывает команды для коррекции
присоединяемого спутника. В конце операции, когда спутник
приблизится к базовому спутнику, измеренные скорости ис¬
пользуются для расчета конечного тормозного импульса, и
далее начинается процедура, описанная выше.
Начальный выбор т производится так, чтобы при доста¬
точно малой коррекции по z0 (значение которой вместе с z0
предполагается очень малым) величина z обратилась бы в
нуль в течение интервала времени, не превышающего значе¬
ния т, и движение по z прекратилось бы при помощи тор¬
мозного импульса при z—> 0. После этого ни дрейфа, ни ко¬
лебаний вдоль оси г уже не будет.
Так как угол между плоскостями орбит не должен пре
вышать 2°, то никаких затруднений в отношении выбора т
не ожидается и в дальнейшем при выборе т может быть одно
ограничение, заключающееся в том, чтобы средняя скорость
сближения составляла ~30 м/сек. Тогда при помощи тор¬
мозного импульса 225 кг в течение 30 сек скорость прибли-
' жения присоединяемой ракеты весом 2250 кг снижается до
3 м/сек (за это время ракета проходит расстояние ~500 м).
При начальном расстоянии 160 км процесс сближения бу¬
дет длиться примерно 90 мин, что составляет один период

НАВЕДЕНИЕ НА КОНЕЧНОМ УЧАСТКЕ ВСТРЕЧИ СПУТНИКОВ 209
)\
Радиолока¬
тор
обращения спутника на выбранной высоте. При выборе
^ счетно-решающее устройство производит также дополни¬
тельный расчет величины импульса для тормозного двига¬
теля и для осуществления корректирующих воздействий.
//*	Лпрма	^	С	оп 			 ^
00 О > Уо > ZD ^
j
Время
полета
до цели
Л
\
I
\ 1
i 1
X
У
Z
Запоминаю^ ее
устройство
Преобразова¬
тель
координат
х
вС п
Уо
Выработка
величин
& о? Уо*
- * ’г
Определение
скоростей
х у i
\
Сравни
г
ение
bnUfJUUIIICU
'А Счетно-решающее
^ устройство
х0-х
Уо-У
z0-z
Выработка
команд
_i
Фиг. 8. Функциональная блок-схема счетно-решающего устройства.
Если присоединяемая ракета располагает величиной им¬
пульса тяги менее полученной по расчету, то счетно-решаю-
Щее устройство «отклоняет» выбранное значение т и выдает
большее значение (которое может соответствовать, скажем,
скорости сближения 25 м/сек).
СЧЕТНО-РЕШАЮЩЕЕ УСТРОЙСТВО
Цифровое счетно-решающее устройство для выполнения
вышеупомянутых расчетов весит не более 25 кг. От радио¬
локатора к нему поступают сигналы по дальности и углам
14 Зак. 870,

210
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
в виде функций времени. При помощи преобразования коор¬
динат, дифференцирования и сглаживания это устройство
вырабатывает всю необходимую информацию, которая затем
используется в расчетах. Прежде всего устройство произ¬
водит суммирование изменений количества движения, кото¬
рые должны быть учтены при переходе к встречному сбли¬
жению со скоростью 30 м/сек. Если эти изменения оказы¬
ваются слишком большими, счетное устройство рассчитывает
новый интервал времени сближения т для скорости 25 м/сек
и т. д., пока величина т не окажется приемлемой.
После этого, используя приведенные выше уравнения, счет¬
но-решающее устройство рассчитывает значения х0 и у0 и
посылает выработанные команды на присоединяемый спут¬
ник.
Такая проверка в течение всего пути производится не¬
сколько раз, после чего делается необходимая корректиров¬
ка. Когда величина YX<1~\~V2 становится приблизительно рав¬
ной 600 м, дается тормозной импульс, который снижает ско¬
рость сближения до 3 м/сек на расстоянии 150 м. За 3 сек
до столкновения на присоединяемый спутник поступает ко¬
манда для снижения скорости до 0,6 м/сек. Блок-схема счет¬
но-решающего устройства приведена на фиг. 8.
ЗАИЛЮ ЧЕНИЕ
Резюмируем вкратце процесс осуществления встречи
спутников. Сначала на нужную орбиту выводится началь¬
ный спутник, так называемый управляющий базовый спут¬
ник, за которым производится слежение при помощи назем¬
ных радиолокаторов типа RCA AN/FPS-16. Измеренные
радиолокатором величины подаются к центральному счетно¬
решающему устройству, где определяются элементы орбиты
базового спутника. По этим данным рассчитывается время
старта второго присоединяемого спутника.
Элементы орбиты базового спутника подаются также на
его бортовое счетно-решающее устройство для использования
в расчетах маневра встречи.
Запуск присоединяемого спутника производится в тот мо¬
мент, когда плоскость орбиты базового спутника будет ком¬
планарна с плоскостью траектории второго спутника.
Неизбежные ошибки в синхронизации, тяге и системе на¬
ведения не позволяют осуществить прямую встречу. Поэтому
базовый спутник информируется о времени старта второго

НАВЕДЕНИЕ НА КОНЕЧНОМ УЧАСТКЕ ВСТРЕЧИ СПУТНИКОВ 211
сПутника и о моменте, когда бортовой радиолокатор должен
начать осуществление захвата присоединяемого спутника.
Радиолокатор производит захват последнего еще до его вы¬
хода на орбиту. С этой целью радиолокатор направляется на
присоединяемый спутник, начинает работать счетно-решаю¬
щее устройство и при помощи бортовой системы наведения
базового спутника осуществляется управление основной тя¬
гой присоединяемого спутника. Затем начинают работать
верньерные двигатели, и их тяга регулируется бортовым ра¬
диолокатором базового спутника для получения необходимой
скорости сближения. Для рассматриваемых ошибок системы
наведения, тяги и времени (момента) старта расстояние
между спутниками не будет превышать 300 км.
Радиолокатор непрерывно измеряет относительное рас¬
стояние и скорость. На основе начальных измерений счетно¬
решающее устройство определяет необходимые изменения
тяги. Результаты дальнейших измерений радиолокатора срав¬
ниваются с величинами, выработанными в счетно-решающем
устройстве для данного времени, и при наличии разности
(ошибок), если таковая имеется, начинают работать вернь¬
ерные двигатели (типа включ.-выкл.). Эта процедура по¬
вторяется до тех пор, пока расстояние между спутниками не
станет равным 600 м. В этот момент верньерные двигатели
поворачиваются на 180° и тяга действует в обратном на¬
правлении, чтобы встреча спутников произошла без столк¬
новения. С помощью счетно-решающего устройства опреде¬
ляется величина тормозного импульса, необходимого для
снижения скорости сближения до 3 м/сек за время, необхо¬
димое для прохождения расстояния ~450 м. На расстоянии
150 м начинает работать бортовая инфракрасная система
наведения присоединяемого спутника, управляемая сигна¬
лами с базового спутника.
Все команды к присоединяемому спутнику поступают от
командной системы наведения до тех пор, пока расстояние
не уменьшится до 50 м. При достижении заданного мини¬
мального расстояния включается бортовая инфракрасная си¬
стема наведения, которая определяет необходимый допол¬
нительный импульс.
За 3 сек до встречи скорость сближения снижается до
0,6 м/сек, после чего производится окончательное механиче¬
ское соединение спутников.
Л ИТЕРАТУРА
1- Siefert Н. S. (ed.), Space Technology, 1959.
14*

НАВИГАЦИОННАЯ СИСТЕМА, ОСНОВАННАЯ
НА ИСПОЛЬЗОВАНИИ СИГНАЛОВ ИСКУССТВЕННЫХ
СПУТНИКОВ, ЛЕТЯЩИХ НА БОЛЬШИХ ВЫСОТАХ1)
Муди
Применение электроники в астронавигации позволяет конструировать
системы, обеспечивающие ориентировку в пределах всей поверхности зем¬
ного шара независимо от климатических условий. Возможность использо¬
вания радиозвезд, по-видимому, исключается, однако за Солнцем и Луной
можно следить с помощью американского морского радиосекстанта
AN/SRN-4, который дает возможность производить ориентировку в огра¬
ниченном районе. Ориентация в пределах всей поверхности земного шара
может быть достигнута с помощью искусственных спутников Земли. Спут¬
ники, находящиеся на орбите, удаленной на несколько сот километров от
Земли, могут быть использованы в некоторых видах навигационных систем,
однако сложность предсказания орбиты и ограниченность района возмож¬
ной ориентации, а также сложности вычислений являются серьезными пре¬
пятствиями, которые следует преодолеть. Другим решением может быть
запуск трех или четырех спутников на орбиту с оптимальным расстоянием
от Земли 1500—20 000 км. Стабилизированная направленная антенна • с
приемником, способным принимать сигналы как от искусственных спутни¬
ков, так и от Солнца, обеспечит выполнение угловых измерений, необходи¬
мых для фиксирования положения космического корабля и для определе¬
ния направления на север. Степень сложности используемого оборудования
будет изменяться в зависимости от требований, предъявляемых к точности.
ВВЕДЕНИЕ
В настоящее время, когда искусственные спутники Земли
уже утратили свою новизну, естественно возникает вопрос
об их практическом использовании не только для научно-
исследовательских целей. Примером тому могут служить
естественные небесные тела, практическое использование ко¬
торых можно проследить на протяжении всей истории чело¬
вечества. Помимо того, что эти тела являются источниками
света и тепла, они служат другим полезным целям, в част¬
ности навигации, помогая путешественникам на земле, в
море и в воздухе при определении местоположения и напра¬
вления движения.
Астронавигация представляет интерес еще и потому, что
она может обеспечить ориентировку для определения место-
*) Moody А. В., Proc._ IRE, 48, № 4, 500—506 (April 1960)4

СИСТЕМА С ИСПОЛЬЗОВАНИЕМ ИСКУССТВЕННЫХ СПУТНИКОВ 213
положения в любой точке земного шара с одинаковой точ¬
ностью, удовлетворяя требованиям навигатора. Основной ее
недостаток — зависимость от ясной погоды, а также отсут¬
ствие достаточной базы для ориентации в горизонтальном
направлении при проведении наблюдений и необходимость
громоздких вычислений для обработки результатов наблюде¬
ний и получения с их помощью информации, характеризую¬
щей местоположение наблюдателя.
Электроника существенно облегчила решение двух по¬
следних проблем, а радиолокатор «Лоран», радиодально¬
меры различных типов, навигационная система Декка,
радиопеленгаторы и другие электронные навигационные при¬
боры в значительной степени устранили влияние климатиче¬
ских условий. Тем не менее возможность применения этих
приборов до сих пор в той или иной степени ограничивается
географическим положением, характеристиками распростра¬
нения радиоволн в пределах атмосферы с их капризами при
распространении на больших дистанциях, влиянием ионосфе¬
ры, необходимостью в международном кооперировании, ди¬
пломатическими соображениями, повреждением антенны в
результате воздействия климатических условий или действий
потенциального противника, угрозами возможных контрмер,
недостатком военной секретности, высокой стоимостью уста¬
новки и эксплуатации. Электронные приборы нашли широ¬
кое применение при создании двух превосходных систем
счисления координат местоположения: инерциальной и доп¬
плеровской. Однако они полностью неадекватны, ибо, будучи
системами счисления координат местоположения, они дают
результаты, ухудшающиеся в зависимости от времени и
пройденного расстояния.
Возможность объединения астронавигации и электроники
с целью созданця универсальных систем, работающих неза¬
висимо от климатических условий, заслуживает детального
обсуждения.
ЭЛЕКТРОННАЯ СИСТЕМА АСТРОНАВИГАЦИИ, ИСПОЛЬЗУЮЩАЯ
НЕБЕСНЫЕ ТЕЛА
Дискретные источники космической радиоэнергии, обычно
называемые радиозвездами, уже изучались с этой точки
зрения т. Угловые измерения производились обычными
способами, характерными для астронавигации. Однако сиг¬
нал, полученный от известных естественных источников, обычно
бывает слабым и быстро ослабевает по мере уменьшения

214
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
длины волны. При увеличении длины волны понижается
угловая чувствительность следящей системы. На основании
исследований, произведенных с учетом свойств приемников
и антенн, характеристик источника, ослабления сигналов
в атмосфере, а также наличия рефракции, можно сделать
вывод, что оптимальная длина волны находится около 4 сму
и для практической навигационной системы, обеспечивающей
Фиг. 1. Радиосекстант.
достаточную точность независимо от атмосферных влияний,
необходима антенна с диаметром не менее 4,5 м.
Хотя конструирование такой системы связано с большой
научно-исследовательской работой, она в конечном итоге
может быть разработана; однако, по-видимому, радиозвез¬
ды не представляют достаточно перспективной базы для со¬
здания удовлетворительной электронной системы астронави¬
гации в ближайшем будущем.
Слежение за Солнцем и Луной успешно проводилось
с помощью радиосекстанта AN/SRN-4, показанного на
фиг. 1. Были определены два оптимальных диапазона длин
волн. При X = 8,7 мм угловая чувствительность антенны за¬
данного размера относительно велика и при этом солнечная
динамическая активность не создавала помех, однако работа
системы сильно затруднялась осадками в виде дождя. При
X = 1,9 см влияние дождя было меньше и для системы потре¬

СИСТЕМА С ИСПОЛЬЗОВАНИЕМ искусственных спутников 215
бовалась антенна, размеры которой были лишь немного
больше, чем при X = 8,7 мм. При X > 2,0 см солнечная дина¬
мическая активность была достаточно велика и создавала
значительные помехи. Слежение за Луной также успешно
осуществлялось такой системой, но при этом требовалось
значительное усложнение всей системы.
Несмотря на то, что Солнце и Луна успешно исполь¬
зуются в морской навигации для определения местоположе¬
ния, они не всегда доступны для визирования. Длительность
периодов, в течение которых ни одним из них невозможно
пользоваться, возрастает по мере увеличения широты и на
полюсах достигает двух недель; в это время оба эти тела на¬
ходятся ниже линии горизонта. Поэтому следует изучить воп¬
рос о практической целесообразности использования искус¬
ственных спутников для создания системы, которая будет
удовлетворять всем требованиям навигации.
ЭЛЕКТРОННАЯ СИСТЕМА АСТРОНАВИГАЦИИ, ИСПОЛЬЗУЮЩАЯ
ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ
Рассмотрим требования, предъявляемые к искусственным
спутникам, используемым при навигации, и выясним, можно
ли осуществить эти требования при допустимых затратах.
Можно измерить следующие параметры спутника: 1) нак¬
лонную дальность и ее производные по времени; 2) высоту
и ее производные; 3) азимут и его производные.
Измерение наклонной дальности и ее производных по
времени, по существу, относится к проблеме пилотирования,
причем в этом случае определяется положение наблюдателя
относительно спутника. Наклонная дальность измеряется в
точке наибольшего сближения, причем фиксируется также
и направление на нее; в результате этих операций опреде¬
ляются координаты объекта. Местоположение объекта может
быть установлено также с помощью одновременного опреде¬
ления наклонных дальностей до двух или большего числа
спутников или с помощью текущего определения двух на¬
клонных дальностей до одного и того же спутника, произво¬
димого при различных значениях азимута.
Один из методов определения наклонной дальности со¬
стоит в прямом измерении с помощью обычной пассивной ра¬
диолокации. Однако этот метод не слишком привлекателен,
ибо его применение требует, чтобы наблюдатель, определяю¬
щий свое местоположение, пользовался передающим устрой¬
ством. Аналогичная проблема возникает также в случае

216
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
использования активного метода радиолокации, когда на бор¬
ту спутника помещается приемо-передатчик ответчика. Кроме
того, в этом случае не исключена возможность возникновения
проблемы насыщения, если ответчик спутника будет одновре¬
менно запрашиваться большим числом абонентов. Необхо¬
димо иметь в виду также, что потенциальный противник в бу¬
дущем может легко заглушить работу такой системы.
Значительно более удобным способом определения нак¬
лонной дальности является измерение допплеровского
сдвига частоты бортового передатчика спутника, рабо¬
тающего в режиме непрерывного излучения. Этот метод
успешно использовался американскими и советскими специа¬
листами для определения положения спутников с известной
точки на поверхности Земли. Изменения частоты Допплера
в любой момент времени могут быть определены, если изве¬
стно точное значение частоты передатчика. Однако если из¬
мерить и проанализировать вариации частоты Допплера, по¬
лучаемые за время прохождения сигнала со спутника в точку
измерения, то точное знание частоты передатчика не является
необходимым, по крайней мере до тех пор, пока частота
остается стабильной в течение периода измерений.
Анализ результатов измерений допплеровского сдвига
частоты с целью получения полезной информации для нави¬
гации требует применения достаточно сложной счетно-ре¬
шающей аппаратуры, а сами измерения предпочтительно
производить со спутниками, находящимися на орбитах, рас¬
положенных сравнительно близко к поверхности Земли. По
мере увеличения радиуса орбиты допплеровский эффект
уменьшается и система становится менее чувствительной
к изменениям положения наблюдателя. Если в системе не
применяется стабилизация антенной платформы или автома¬
тическое слежение объекта, то антенна должна быть доста¬
точно всенаправленной. При этом желательно использовать
относительно большие длины волн, если соответствующая
эффективная поверхность антенны будет обеспечивать полу¬
чение достаточной мощности принимаемого сигнала. Однако
по мере увеличения длины волны увеличивается вероятность
появления непредвиденных ионосферных сдвигов фазы и
влияние атмосферной рефракции, а использование в таких
случаях кратных (гармонических) частот для коррекции свя¬
зано с дополнительным усложнением системы. Для проверки
целесообразности навигационной системы, основанной на
применении эффекта Допплера, необходимо показать воз¬
можность решения упоминавшихся выше проблем и про¬
демонстрировать возможности прогнозирования орбит

СИСТЕМА С ИСПОЛЬЗОВАНИЕМ ИСКУССТВЕННЫХ СПУТНИКОВ 217
с точностью, большей чем у получаемых до сих пор
данных.
В настоящее время изучается новая возможность исполь¬
зования искусственных спутников для целей навигации, со¬
стоящая в рассмотрении последних как небесных тел и при¬
менении традиционных методов угловых измерений, исполь¬
зуемых в оптической навигации с помощью небесных тел.
В соответствии с установившейся практикой этот метод
включает измерения высоты (углового расстояния над гори¬
зонтом) двух или более небесных тел одновременно или од¬
ного небесного тела в два различных момента времени, по¬
зволяющих получить достаточные изменения азимута. Каж¬
дое такое наблюдение позволяет определять окружность
положения с центром, находящимся в точке географического
положения небесного тела (в точке земной поверхности, в ко¬
торую в данный момент проектируется небесное тело), и
радиусом, равным расстоянию от наблюдателя до зенита. Не¬
большая часть этой окружности в области, занимаемой наб¬
людателем, носит название линии Самнера, или линии поло¬
жений. Пересечение двух таких линий определяет положение
наблюдателя.
Для расстояний, на которых расположены естественные
небесные тела, изменения их видимых положений по суще¬
ству обусловлены дневным вращением Земли вокруг своей
оси. При средних высотах это обстоятельство требует нали¬
чия по крайней мере двух небесных тел для получения удо¬
влетворительных результатов. При наличии только одного
тела интервал между наблюдениями, длящимися несколько
часов, вносит неучитываемые ошибки определения, которые
могут оказаться недопустимо большими. При высоких ско¬
ростях перемещения спутников более рациональным является
метод определения текущих положений.
Одно небесное тело может обеспечить возможность астро¬
номического определения положения, если одновременно из¬
меряются любые две величины: высота, скорость изменения
высоты, азимут и скорость изменения азимута.
Методы, заключающиеся в измерении азимута и скорости
изменения последнего, практически непригодны, ибо инфор¬
мацию такого рода нельзя получить с достаточной степенью
точности. Определение же скорости изменения высоты есте¬
ственных небесных тел требует применения совершенных ме¬
тодов усреднения. И тем не менее при больших скоростях,
свойственных искусственным спутникам, этот параметр за¬
служивает тщательного рассмотрения. Одна из особенностей
использования измерений высоты и скорости изменения

218
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
последней состоит в том, что получаемые два семейства кри¬
вых будут всегда ортогональны друг другу, что является
идеальным случаем в астронавигации. Однако для удовлет¬
ворительного определения скорости изменения высоты тре¬
буется слишком большое усложнение измерительной аппа¬
ратуры.
Как известно, при использовании в навигации метода од¬
новременного измерения высот двух тел или последователь¬
ного измерения высоты одного и того же тела может быть
получена удовлетворительная навигационная система, в ко¬
торой исключается применение усложненного процесса осред¬
нения измерений. Этот метод открывает также возможность
использования таких несложных методов расчета, которые
понятны каждому навигатору. Такая методика обычно еже¬
дневно применяется в навигации с использованием естествен¬
ных небесных тел. Использование спутников для целей на¬
вигации потребует для измерения необходимых параметров
соответствующего электронного оборудования. При этом на¬
добность в анализе результатов отпадает. Расчеты, необхо¬
димые для преобразования измеренных параметров в коор¬
динаты, определяющие местонахождение наблюдателя, или
в данные, необходимые для управления, могли бы выпол¬
няться, где это необходимо, с помощью электронных прибо¬
ров, не вызывая дополнительного усложнения аппаратуры.
Хотя детали, относящиеся к точной процедуре расчетов,
а также спецификации для навигационного календаря и таб¬
лицы для прицеливания еще не разработаны, это, как нам
кажется, не представляет столь сложной проблемы по срав¬
нению с проблемами, которые были уже решены соот¬
ветствующим образом в астронавигации, использующей
естественные небесные тела. Описываемый метод является
логическим продолжением известных методов современной
астронавигации. Успех его в первую очередь зависит от воз¬
можности прогнозирования будущих положений спутников
с достаточной степенью точности, и поскольку размеры ор¬
биты не являются критичными, можно определить ее опти¬
мальные параметры. Вопросы, связанные с выбором орбиты,
подробнее обсуждаются ниже.
Если в навигации используются угловые измерения, то
с этой целью необходимо применять стабилизированные
платформы и направленные антенны. С этим связано увели¬
чение сложности и стоимости оборудования, однако никаких
серьезных технических проблем не возникает. В диапазоне
сантиметровых волн при относительно небольшой модифика¬

СИСТЕМА С ИСПОЛЬЗОВАНИЕМ ИСКУССТВЕННЫХ СПУТНИКОВ 219
ции для этих целей может быть использован радиосекстант
AN/SRN-4. В состав уже разработанной аппаратуры вхо¬
дят также достаточно хорошо стабилизированная платформа
и направленна^ антенна. Использование такой аппаратуры
избавит от необходимости проведения длительных испыта¬
ний и опытно-конструкторских работ. Указанная аппаратура
позволит использовать для целей навигации Солнце, а воз¬
можно, и Луну, расширяя тем самым диапазон применения
системы в пределах земной поверхности. Это в свою очередь
обеспечит системе дополнительные, хотя и ограниченные воз¬
можности в тех случаях, когда искусственные спутники
нельзя будет использовать по каким-либо причинам.
Применение стабилизированной платформы и направлен¬
ной антенны дает возможность использовать систему отсчета
относительно северного направления (такая возможность при
использовании других систем отсутствует). Стабилизирован¬
ная платформа и направленная антенна позволяют также уп¬
ростить аппаратуру, устанавливаемую на борту спутника.
Этот фактор очень важен, особенно если иметь в виду, что
бортовая аппаратура практически недоступна для ремонта.
ВЫБОР ОРБИТЫ
Тип навигационной системы, основанной на использова¬
нии искусственных спутников, неразрывно связан с выбором
орбиты. При этом важно иметь в виду возможность прогно¬
зирования орбиты, возможность использования системы в
различных точках земного шара и число требующихся спут¬
ников.
Возможности прогнозирования орбит искусственных спут¬
ников, запускавшихся до настоящего времени, еще не удо¬
влетворяют требованиям, предъявляемым навигацией. Пери¬
геи запущенных спутников находились на расстояниях, не
превышающих несколько сот километров от поверхности
Земли. Причины и величина возмущений таких орбит опре¬
делены еще не достаточно полно. Однако хорошо известно
что эффекты, трудно поддающиеся прогнозированию вслед¬
ствие недостатка точных сведений о гравитационном поле
Земли и изменяющихся возмущениях, создаваемых атмосфе¬
рой, представляют весьма серьезные проблемы. Специалисты
по прогнозированию орбит спутников, запущенных до настоя¬
щего времени, не высказывают никаких оптимистических пред¬
положений относительно быстрого разрешения этих проб¬
лем.

220
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
По мере увеличения размеров орбит влияние возмущаю¬
щих гравитационных и атмосферных эффектов делается не
столь заметным. Однако с увеличением радиуса орбиты воз¬
растают возмущения, вызываемые гравитационными полями
других естественных небесных тел. При очень больших зна¬
чениях радиуса эти возмущения слишком велики и трудно
поддаются прогнозированию. Это указывает на то, что
имеется некоторый промежуточный радиус, который будет
оптимальным с точки зрения возможностей прогнозирования.
Величина этого радиуса еще не установлена, однако, несом¬
ненно, он будет измеряться тысячами километров, не считая
радиуса Земли. Подобные орбиты сильно отличаются от ор¬
бит спутников, которые запускались до настоящего времени
и перигеи орбит которых находились относительно близко
к поверхности Земли. По сравнению с ними спутники, дви¬
жущиеся по оптимальной орбите, могут рассматриваться как
спутники на больших высотах.
При определении числа спутников важны размеры пло¬
щади земной поверхности, обслуживаемой одним спутником.
Спутник, находящийся на высоте 650 км от поверхности
Земли, может быть виден одновременно из различных точек,
перекрывающих площадь, которая составляет менее 5% всей
поверхности Земли. При увеличении высоты до 1600 км эта'
площадь увеличивается до 10%, при высоте 6500 км — до
25%, при высоте полета 16 000 км — до 35,5% и, наконец,
при удалении спутника в бесконечность — до 50%. На фиг. 2
показана площадь участка земной поверхности (в процен¬
тах), одновременно обслуживаемого спутником.
При решении вопроса перекрытия важно определить ши¬
рину пояса, в пределах которого может наблюдаться спутник
при его полете вокруг Земли. Для спутника, находящегося
на высоте 650 км, ширина пояса составляет ~ 45°; на вы¬
соте 1600 км ~88°; на высоте 6500 км —120°; на высоте
16 000 км ~ 143,5° и для спутника, находящегося в бесконеч¬
ности, ~180°.
При некоторых измерениях дальности ширина пояса,
в пределах которого могут эффективно производиться нави¬
гационные наблюдения, может быть несколько меньше ши¬
рины зоны прямой видимости в силу ограниченности рас¬
стояний, в пределах которых радиоизмерения наклонной
дальности обеспечивают получение удовлетворительных ре¬
зультатов.
Если используется принцип определения текущих коор¬
динат, при котором производится серия наблюдений за по¬
ложением одного и того же тела (спутника), то желательно

СИСТЕМА С ИСПОЛЬЗОВАНИЕМ ИСКУССТВЕННЫХ СПУТНИКОВ 221
рассматривать ширину пояса, в пределах которой происхо¬
дят изменения рассматриваемой угловой координаты на
заданное число градусов в течение всего полета. Если мини¬
мальное изменение азимута принимается равным 90° (причем
считается, что изменения угла на 90°, происходящие за пе¬
риод между измерениями, являются оптимальной величи¬
ной), то ширина такого пояса для спутника, находящегося
Фиг. 2. Площадь земной поверхности (в %), в пределах
которой возможно одновременное наблюдение за спутником
при различных высотах его полета.
на высоте 650 км, будет составлять 36°, для высоты
1600 км — 57°, для высоты 6400 км—101° и для высоты
16 000 км—134°. Графики на фиг. 3 показывают ширину
пояса возможных радиоизмерений, ширину пояса, в пределах
которого азимут изменяется более чем на 90°, и угол пово¬
рота Земли в течение одного оборота спутника для различ¬
ных высот.
Быстрое движение спутника, летящего на небольшой вы¬
соте, является преимуществом для любого метода, в котором
определяются производные измеряемых величин, но в то же
время предъявляет более серьезные требования к способам
измерения времени. Поэтому, для того чтобы ошибка опре¬
деления положения проекции спутника, находящегося на

222
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
высоте 650 км, не превышала 0,1', допустимая ошибка из¬
мерения времени должна быть не более 0,03 сек. По мере
увеличения высоты полета спутника допустимая ошибка из¬
мерения времени несколько увеличивается; так, при высоте
Фиг. 3. Ширина пояса видимости и величина углового
поворота Земли за один орбитальный период при различных
высотах полета спутника.
А —ширина пояса возможных радиоизмерений; В — ширина пояса, в пре¬
делах которого азимут изменяется более чем на 90°; С —угловой поворот
Земли за один орбитальный период.
полета 1600 км она составляет 0,035 сек, при высоте
6400 км — 0,067 сек и при высоте полета 16 000 км —
0,155 сек. Однако даже ошибка прогнозирования орбиты, ле¬
жащая в пределах 0,1', может оказаться слишком большой
для навигационных систем высокой точности.
Ошибка в определении высоты вносит ошибку параллак¬
са, имеющую существенное значение при угловых измере¬
ниях. Ошибка параллакса максимальна на уровне горизонта
и уменьшается до нуля в зените. Если принять ошибку па¬
раллакса равной 0,1', то допустимая точность прогнозиро¬
вания высоты будет составлять менее 800 м для спутника,

СИСТЕМА С ИСПОЛЬЗОВАНИЕМ искусственных спутников 223
летящего на высоте 650 км, несколько более 800 м — для вы¬
соты 1600 км, около 2,1 км — для высоты 6400 км и немного
более 6,5 км — для высоты 16 000 км.
Таким образом, вопросы прогнозирования положения
спутников и получение соответствующей информации об эфе¬
меридах оказываются более сложными для спутников, нахо¬
дящихся относительно близко к поверхности Земли, чем для
летящих на высоте несколько тысяч километров. Для малых
орбит (т. е. для орбит низколетящих спутников), кроме того,
возрастают требования к точности их определения.
Число спутников, необходимых для целей навигации, за¬
висит от параметров, подлежащих измерению, а также вы¬
соты полета спутника над поверхностью Земли, взаимного
расположения орбит отдельных спутников и самих спутни¬
ков, находящихся на этих орбитах; оно связано также с про¬
должительностью и частотой, с которой повторяются проме¬
жутки времени, когда невозможно производить определение
местоположения. Из геометрических соображений, рассмот¬
ренных выше, кажется очевидным, что для системы любого
типа число спутников, необходимых для того, чтобы избе¬
жать слишком длительных периодов «недоступности», тем
больше, чем ближе к поверхности Земли расположены их
орбиты. Если для системы требуется продолжительное время
наблюдения для определения местоположения, то число спут¬
ников при заданной частоте определения местоположения
должно быть больше. Максимальное число спутников тре¬
буется для систем, использующих низколетящие спутники,
когда для определения местоположения приходится исполь<
зовать весь период пребывания спутника в зоне наблюдения.
Минимальное число спутников требуется для системы, ис¬
пользующей спутники, летающие на больших высотах, и
обеспечивающие возможность непрерывного определения
местоположения наблюдателя в течение времени прохожде¬
ния спутника над горизонтом.
Число спутников, необходимых для любой системы, мож¬
но свести к минимуму при разумном выборе орбит и распо¬
ложения спутников на орбитах. Однако выбор несколько
ограничивается из-за отсутствия возможности точного вывода
спутников на предсказанную орбиту. Вследствие различия
орбит, вариации прецессии и вращения орбит можно ожи¬
дать, что планируемые соотношения положений спутников
относительно друг друга вряд ли будут достигнуты. Одним
из элементов орбиты, который можно контролировать с до¬
статочной степенью точности, является угол наклона плоско¬
сти орбиты относительно плоскости экватора. Предваритель¬

224
И. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
ное изучение показывает, что семейство орбит с постепенно
изменяющимися углами наклона лучше всего будет отвечать
требованиям, предъявляемым системами любого гипа.
Если при измерениях допустимы редко повторяющиеся
периоды недоступности длительностью в несколько минут и
случайные периоды недоступности, длящиеся более одного
часа, то, как показывают предварительные исследования,
система, основанная на использовании трех или четырех спут¬
ников, летящих на больших высотах, может обеспечить
удовлетворительное перекрытие. Последнее может быть улуч¬
шено в том случае, если система допускает также возмож¬
ность использования естественных небесных тел.
При выборе параметров орбиты весьма существенное зна¬
чение имеет проблема сопровождения. Для сопровождения
желательно использовать как оптические, так и электронные
системы. Требуемое число станций сопровождения умень¬
шается по мере увеличения высоты полета спутника, а также
района земной поверхности, с которого можно наблюдать
спутник. При высоте полета всего в несколько сот километ¬
ров и при удалении спутника на несколько десятков тысяч
километров, вследствие затруднений, связанных с предска¬
заниями природы возмущений орбиты, необходимо произво¬
дить более тщательные наблюдения за спутниками.
Пределы желательной высоты орбит еще не установлены
с достаточной определенностью; необходимо провести пред¬
варительное изучение имеющихся данных, чтобы доказать,
что оптимальные расстояния спутников от поверхности Земли
заключаются в пределах от 1600 до 19 000 км. Для этого
диапазона высот можно сконструировать систему, работаю¬
щую в коротковолновом участке сантиметровых волн, и тем
самым обеспечить возможность использования Солнца, а мо¬
жет быть, и Луны совместно с искусственными спутниками
в целях увеличения перекрытия, обеспечиваемого системой.
Такая система явилась бы естественным продолжением и
развитием уже существующих и хорошо разработанных си¬
стем.
Применение спутников, находящихся на орбитах, удален¬
ных на тысячи километров от. поверхности Земли, вероятно,
будет затруднять использование дальности и ее производных
в качестве первичной основы метода навигации с помощью
искусственных спутников. Однако в этой области имеется
так много неопределенностей, которые нуждаются в разре¬
шении, что было бы преждевременным и нереалистичным
основываться на какой-нибудь одной возможности.

СИСТЕМА С ИСПОЛЬЗОВАНИЕМ ИСКУССТВЕННЫХ СПУТНИКОВ 225
СПУТНИКИ НА ВЫСОКОЙ ОРБИТЕ
Теперь постараемся ответить на вопрос, какие же требо¬
вания должны предъявляться к спутнику на высокой орбите
при использовании его в навигационной системе, основанной
на измерениях угловых координат и, возможно, их производ¬
ных, и обеспечивающей высокую точность определения напра¬
вления на север.
Рассмотрим прежде всего соображения относительно вы¬
бора длины волны. Как отмечалось выше, использование
коротковолнового участка сантиметрового диапазона дает
возможность осуществлять навигацию по Солнцу и, возможно,
по Луне для увеличения перекрытия по сравнению с перекры¬
тием системы, основанной на использовании только искус¬
ственных спутников, и для обеспечения частичного перекры¬
тия в тех случаях, когда спутники становятся недоступными
для наблюдения. Заметим также, что соображения, относя¬
щиеся непосредственно к системе навигации при помощи
спутников, также говорят в пользу выбора коротковолнового
участка сантиметрового диапазона. На этом участке легче
обеспечивается получение соответствующей направленности
приемной антенны, без чрезмерного увеличения ее размеров
и мощности передатчика по сравнению с требованиями,
предъявляемыми в дециметровом и метровом диапазонах.
Использование коротковолнового участка сантиметрового
диапазона позволяет избежать основных трудностей распро¬
странения, связанных с нестабильностью частоты и рефрак¬
цией при прохождении сигналов через ионосферу и нижние
слои земной атмосферы. Исследования в этой области уже
дали достаточную информацию, на основании которой можно
сделать заключение, что в этом диапазоне вопросы распро¬
странения не будут столь существенными, как в том случае,
когда используются более длинные волны.
Функция передатчика, установленного на спутнике, сво¬
дится к созданию непрерывного сигнала соответствующей
мощности, необходимого для обеспечения сопровождения.
Поскольку при этом на передатчик не возлагается никаких
Дополнительных функций, то его конструкция и схема могут
быть сделаны относительно простыми, за счет чего увели¬
чивается вероятность его продолжительной и успешной ра¬
боты.
В качестве возможных источников энергии можно приме¬
нять химические и солнечные батареи, «топливные элементы»
и термоионные преобразователи, однако наиболее предпочти¬
тельной, по-видимому, является комбинация солнечных и
15 Зпк. 876

226
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
химических батарей, так как это уже проверенная комбина¬
ция. Если защитное покрытие солнечных батарей может быть,
по-видимому, снято, то это даст значительную экономию
веса. Возможно, что для использования на спутниках будут
пригодны некоторые виды атомной энергии.
Если орбита спутника будет близка к круговой и будет
поддерживаться постоянная ориентация спутника относи¬
тельно Земли, то на спутнике может быть установлена пере¬
дающая антенна с диаграммой направленности, обеспечиваю¬
щей равномерную интенсивность излучения в пределах всей
освещаемой спутником поверхности. Однако для достижения
этого требуется обеспечить условия запуска, превосходящие
пределы возможностей, ожидаемых в ближайшем будущем,
а также обеспечить стабилизацию спутника по крайней мере
по двум осям. При этом следует отметить, что даже в случае
успешного решения последней задачи применение стабилиза¬
ции приведет к усложнению аппаратуры и в результате по¬
высит вероятность ее повреждения. Наиболее реальный под¬
ход к решению вопроса состоит в использовании антенны
с диаграммой направленности, по возможности более близ¬
кой к всенаправленной. Во избежание поляризационных оши¬
бок желательно применять круговую поляризацию.
Вес передатчика, обладающего соответствующей вибро¬
устойчивостью и устойчивостью против ударных нагрузок при
запуске и сконструированного с учетом необходимости от¬
вода выделяемого при работе тепла, находится в пределах
возможностей современных бортовых приборов и, по-види¬
мому, не будет превышать 12—20 кг.
АП ПАРА ТУРА
Размеры и сложность аппаратуры в случае применения
астронавигационной системы, базирующейся на непрерывных
сигналах, получаемых от спутников, пролетающих на боль¬
ших высотах, зависит от параметров, подлежащих измере¬
нию, интервала времени между моментами определения ме¬
стоположения, требуемой точности и степени усложнения
отсчета показаний. Одна из особенностей, связанных с ис¬
пользованием сравнительно простых спутников, летящих на
высоких орбитах, состоит в том, что при одном и том же типе
излучаемых сигналов имеется широкая возможность выбора
аппаратуры, применяемой навигатором. В этом случае в со¬
став аппаратуры могут входить как относительно простые
приборы, обеспечивающие измерение высоты и азимута со

СИСТЕМА С ИСПОЛЬЗОВАНИЕМ ИСКУССТВЕННЫХ СПУТНИКОВ 227
средней точностью при ручной обработке результатов мето¬
дами, принятыми в астронавигации, так и весьма сложная
аппаратура, позволяющая получать непрерывную информа¬
цию о положении или обеспечивающая надежное управление
в соответствии с расчетной программой. Несомненно, что
с помощью такой системы удастся достигнуть требуемой точ¬
ности.
Прежде всего, вероятно, будет усовершенствован радио¬
секстант AN/SRN-4. В этом приборе имеются две важные
составные части. Одна из них — система сопровождения, со¬
стоящая из антенны и ее механизма сканирования, прием¬
ника, сервоприводов и приборов для отсчета угловых вели¬
чин. Другая часть — система стабилизации (по методу Шу¬
лера) и определения опорного направления на север.
Совершенно очевидно, что характеристики приемной си¬
стемы тесно связаны с требованиями к мощности передат¬
чика. В системах сопровождения спутников требования
к мощности передатчика могут быть сведены к минимуму
при использовании очень узкой полосы пропускания частот.
Надежные результаты следует ожидать в случае примене¬
ния приемника с системой автоматической подстройки фазы.
С другой стороны, системы, предназначенные для слежения
за положением Солнца, наоборот, требуют применения при¬
емников с очень широкой полосой пропускания. Следователь¬
но, приемник, предназначенный для сопровождения как
искусственных спутников, так и Солнца, должен работать в
режиме узкополосной системы с автоподстройкой фазы и в
режиме широкополосного радиометра. Ряд отдельных элемен¬
тов такого приемника может быть общим для обоих видов
работы. Поскольку система фазовой автоподстройки частоты
является оптимальной, рассчитанной для точного слежения
фазы приходящего сигнала, то в случае необходимости она
может обеспечить оптимальный метод выделения допплеров¬
ских сигналов. Система отсчета высоты и азимута должна
конструироваться в соответствии с требованиями точности,
предъявляемыми к каждой отдельной системе.
Как отмечалось выше, сложность 'аппаратуры, используе¬
мой при навигации, можно варьировать в широких пределах
с тем, чтобы удовлетворять различным требованиям. Про¬
стейшая аппаратура будет обеспечивать только измерение
высоты и азимута с последующим использованием получен¬
ных данных в соответствии с методами, применяемыми при
оптических методах навигации. Эта аппаратура может быть
Дополнена соответствующим счетно-решающим устройством,
обеспечивающим определение местоположения по методу
15*

228
И. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
последовательных отсчетов или одновременных наблюдений
за двумя или большим числом спутников, либо с помощью оп¬
ределения высоты и скорости изменения высоты. В течение
относительно коротких и не слишком частых периодов, когда
определение местоположения оказывается невозможным, от¬
сутствие расчетных данных можно дополнить аппроксима¬
цией графиков, простыми расчетами, расчетами с помощью
механических счетных устройств или с помощью других бо¬
лее сложных систем (таких, например, как допплеровская
или инерциальная). Многие элементы высококачественной
инерциальной системы входят как составные части в суще¬
ствующие приемные системы и системы стабилизации. Уком¬
плектованную полностью систему можно дополнить аппара¬
турой, обеспечивающей возможность управления в соответ¬
ствии с ранее заложенной программой сопровождения во
времени.
Рассматриваемую систему вполне можно использовать на
борту морских судов. Ее можно также применять на подвод¬
ных лодках; в этом случае небольшая параболическая ан¬
тенна должна периодически подниматься над поверхностью
воды на короткие интервалы времени, достаточные для оп¬
ределения местоположения. В промежутках между отсчетами
информация, относящаяся к определению местоположения,
может запоминаться с помощью высококачественной инер¬
циальной системы, установленной на подводной лодке. Опи¬
сываемую систему можно также использовать на самолетах
и даже на ракетах, но, вероятно, с некоторой потерей точно¬
сти за счет ограничений, связанных с объемом и весом на¬
вигационного оборудования.
ОСНОВНЫЕ ДОСТОИНСТВА СИСТЕМЫ НАВИГАЦИИ С ПОМОЩЬЮ СПУТНИКОВ
С ВЫСОКОЙ ОРБИТОЙ
Можно ожидать, что рассмотренная выше навигационная
система, основанная на использовании спутников с высокой
орбитой, будет иметь ряд следующих положительных
свойств.
1. Возможность независимо от погоды непрерывного оп¬
ределения местоположения с одинаковой точностью в преде¬
лах всей поверхности земного шара.
2. Непрерывное определение опорного направления на се¬
вер (независимо от погоды).
3. Разнообразие и гибкость составных частей аппара¬
туры, что дает возможность удовлетворить различным тре¬
бованиям.

СИСТЕМА С ИСПОЛЬЗОВАНИЕМ искусственных спутников 229
4. Высокая потенциальная точность.
5. Использование пассивной автономной системы, не свя¬
занной с наземными передатчиками. Для системы не тре¬
буется запроса, производимого с поверхности Земли.
6. Высокая помехозащищенность.
7. Возможность комбинированного использования искус¬
ственных спутников, по крайней мере совместно с одним не¬
бесным телом, что обеспечивает большую универсальность
системы, увеличивает перекрытие и уменьшает возможность
успешного противодействия со стороны возможного против¬
ника.
8. Максимальное использование спутников при оптималь¬
ном выборе радиусов орбит, обеспечивающих работу с наи¬
меньшим числом спутников, оборудованных простой и на¬
дежной аппаратурой.
9. Ограниченность требуемой наземной аппаратуры.
В связи с использованием высотных стабильных орбит на¬
земная аппаратура требуется только для контроля запуска,
причем она может состоять из одной радио- и трех оптиче¬
ских станций сопровождения, снабженных аппаратурой для
расчета орбиты и рассеяния. Вся аппаратура, за исключе¬
нием, пожалуй, радиостанции сопровождения, не отличается
чрезмерной сложностью.
10. Система может обеспечить кратчайший и системати¬
зированный путь развития уже разработанных методов и ап¬
паратуры.
ЛИТЕРАТУРА
1. Маг пег G. R., Automatic Radio-Celestial Navigation, /. Brit. InsU
Navig., 12, 249—259 (July — October 1959).

НАВИГАЦИЯ В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
ПРИ ПОМОЩИ ОПТИЧЕСКОЙ СИСТЕМЫ ЗАСЕЧКИ
И ИНЕРЦИАЛЬНОЙ СИСТЕМЫ ')
Кэрролл
Описываемая ниже комбинированная оптическо-инер-
циальная система может использоваться для получения ин¬
формации, необходимой при навигации между любыми двумя
точками в пространстве независимо от того, будут ли они
физическими телами или произвольными точками простран¬
ства.
Для пространственной ориентации можно пользоваться
различными физическими факторами, как, например, доста¬
точно хорошо известными местоположениями и скоростями
небесных тел.
Положения небесных тел обеспечивают устойчивую си¬
стему координат для определения скорости и местоположе¬
ния космического корабля, а также для ориентации элемен¬
тов системы навигации и наведения. Углы между двумя
парами небесных тел, непрерывно измеряемые на борту кос¬
мического корабля, достаточны для определения скорости
последнего (правда, с небольшой точностью) и его место¬
положения.
Этот метод называется навигацией методом засечек. Ме¬
тод засечек требует наличия по крайней мере трех небесных
гел, которые могут быть выбраны среди планет и Солнца.
Оптическая система засечки и инерциальная система мо¬
гут дополнять друг друга. Результаты засечки могут исполь¬
зоваться для корректировки работы инерциальной системы
и определения положения; одновременно инерциальная си¬
стема может использоваться для измерения скорости при
наведении.
ОПТИЧЕСКАЯ СИСТЕМА ЗАСЕЧКИ
Рассмотрим проблему засечки с геометрической точки
зрения (фиг. 1). Исследуем сначала задачу на плоскости,
когда три известные точки А, В и С наблюдаются из точки
9 Carroll J„ Aero/Space Engng., 18, Ns 3t 53—55, 75 (March 1959).

ИНЕРЦЙАЛЬНАЯ И ОПТИЧЕСКАЯ СИСТЕМА ЗАСЕЧКИ	231
у и измеряются углы а и р, которые вместе с известными
положениями наблюдаемых точек определяют положение
точки V. Этот так называемый метод трех точек широко ис¬
пользуется в точной топографической съемке и фотограммет¬
рии. Однако он имеет ограничения, которые зависят, во-
первых, от положения точки V относительно окружности,
проходящей через три известные точки, и, во-вторых, от
близости точки V к треугольнику, образуемому известными
Фиг. 1.
точками. Если точка V лежит на окружности, тогда ее по¬
ложение определить нельзя. Если точка значительно удалена
от треугольника или, другими словами, если углы аир неве¬
лики, то точность определения положения точки V очень
низкая. Более точное определение положения будет иметь
место в случае, когда точка лежит внутри треугольника из¬
вестных точек.
Погрешность в вычислении положения точки V для тре¬
угольника, составленного любыми тремя точками, можно оп¬
ределить, если точность измерения углов аир задана [1].
Рассмотрим одну из реальных комбинаций — положение пла¬
нет Земли, Венеры и Сатурна на 1 января 1948 г., показан¬
ное на фиг. 2. Если точка V представляет космический
корабль, то максимальная погрешность в определении поло¬
жения этой точки составит около 1300 км при ошибке измере¬
ния каждого из углов, равной 1". Если рассмотреть другую
комбинацию — Земля, Сатурн и Солнце, то максимальная
погрешность в определении положения космического корабля

232
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
составит около 1000 км при такой же ошибке измерения ка¬
ждого из углов.
Необходимо отметить, что в обоих этих примерах было
сделано предположение, не соответствующее реальной дей¬
ствительности, что три заданные точки лежат в одной пло¬
скости. Тем не менее эти примеры можно использовать для
оценки точности определения положения методом засечек.
Необходимо иметь в виду также, что определение скорости
с помощью этого метода очень неточное. Скорость космиче¬
ского корабля теоретически можно определить, зная скорость
изменения измеряемых углов. Для дальностей межпланетной
навигации и для современных скоростей космических кораб¬
лей эти скорости изменения настолько незначительны, что
будут полностью поглощаться шумами системы измерения
углов. Поэтому скорость желательно определять другими
средствами. Одним из таких средств является инерциальная
система наведения.
ИНЕРЦИАЛЬНАЯ СИСТЕМА НАВЕДЕНИЯ
Предположим, что инерциальная система навигации и на¬
ведения содержит инерциальный блок измерения1), состоя¬
1) Блок чувствительны* элементов, — Прим. перев.

ИНЕРЦИАЛЬНАЯ И ОПТИЧЕСКАЯ СИСТЕМА ЗАСЕЧКИ	233
щий из трех идеальных взаимно ортогональных акселеромет¬
ров, не вращающихся относительно инерциального простран¬
ства во время полета космического корабля (фиг. 3).
Система координат определяется направлениями осей
чувствительности акселерометров. Акселерометры измеряют
н’е гравитационные ускорения, а ускорения, возникающие
при действии тяги корабля. Гравитационные ускорения вы¬
числяют, зная положения космического корабля относитель¬
но небесных тел.
На фиг. 4 показана блок-схема инерциальной системы
наведения. Сигналы с выходов акселерометров, измеряющих
ускорения тяги, интегрируются для определения составляю¬
щих скорости. Составляющие гравитационных ускорений для
различных небесных тел вычисляются специальным счетно¬
решающим устройством, интегрируются и добавляются
к скорости тяги для получения составляющих скорости в
инерциальном пространстве.
Ошибки в определении скорости и положения (в коорди¬
натах) возникают в результате наличия погрешностей измере¬
ния ускорений акселерометрами, неточной ориентации и
дрейфа осей системы координат, а также из-за ошибок в уче¬
те гравитационных постоянных, связанных с планетами.
Ошибки учета гравитации составляют величину от малых
долей процента для Солнца, Земли и Юпитера, до 1% —для
Венеры и 20%—для Меркурия. Изменения траектории по¬
лета космического корабля, обусловленные этими ошибками,
весьма существенно зависят от близости траектории полета
к планетам. Более того, если бы эти возмущения нужно было
измерить, инерциальная система координат, состоящая из
2
2
X
Фиг. 3.

Счетно-решающие элементы
Фиг. 4. Блок-схема инерциальной системы наведения.

ИНЕРЦИАЛЬНАЯ И ОПТИЧЕСКАЯ СИСТЕМА ЗАСЕЧКИ	235
гироскопов, имела бы такой большой дрейф в течение десят¬
ков или сотен суток, необходимых для межпланетных поле¬
тов, что потребовалась бы коррекция значительных по вели¬
чине ошибок.
ИНЕРЦИАЛЬНАЯ СИСТЕМА, КОМБИНИРОВАННАЯ С ОПТИЧЕСКОЙ
СИСТЕМОЙ ЗАСЕЧКИ
Применение комбинированной системы, состоящей из
инерциальной системы и системы засечки, позволяет частич¬
но устранить указанные выше трудности. Метод засечки
Фиг. 5. Блок-схема системы засечки.
(фиг. 5) может быть использован для измерения углов за¬
сечки с целью непрерывного определения положения, а так¬
же для того, чтобы непрерывно вырабатывать пространств
венные поправки для коррекции ориентации инерциальной
системы координат. Инерциальная система используется для

236
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ НАВИГАЦИЯ
определения величины изменения тягового усилия и его на¬
правления, что необходимо для коррекции возмущений.
Начальный подъем со стартовой площадки до заданной
орбиты вокруг Солнца обеспечивается последовательным ря¬
дом фаз активного (с работающим двигателем) и свобод¬
ного полета, причем космический корабль описывает ряд
планетоцентрических орбит и, наконец, заданную гелиоцент¬
рическую орбиту. В течение времени, необходимого для на¬
чального подъема, положение и скорость корабля могут оп¬
ределяться оптически корректируемой инерциальной системой
с более высокой точностью, чем точность, достигаемая
с помощью системы засечки. Установлено, что система за¬
сечки дает погрешности определения положения в несколько
сотен км при ошибке измерения углов, равной 1". В течение
каждого часа работы оптически корректируемой инерциаль¬
ной системы ошибка определения положения составляет
малую величину. За исключением небольших коррекций ско¬
рости, которые производятся малыми и кратковременными
импульсами тяги, основная часть скорости тяги создается
работой двигателя в начале полета, когда космический ко¬
рабль подвергается влиянию гравитационных полей Земли
и Солнца, действие которых известно со сравнительно высо-.
кой степенью точности. Положение и скорость в начальной
точке заданной орбиты, определяемые инерциальной систе¬
мой, обеспечивают точную базу, относительно которой могут
быть вычислены заданные изменения параметров орбиты.
Вычислительное (счетно-решающее) устройство в системе
необходимо для выполнения следующих функций:
1) накопления необходимых для навигации данных
о Солнце и планетах;
2) выдачи команд запуска и выключения двигателя;
3) выдачи сигналов управления по тангажу, крену и рыс¬
канию;
4) переключения элементов системы засечки с одной ком¬
бинации Солнца и планет на другую.
Сложность получения команд запуска и выключения дви¬
гателя, которые должны вырабатываться в вычислителе, за¬
висит от заданной орбиты космического корабля, а также от
ряда условий в конце действия тяги. Эти условия могут
включать любую комбинацию следующих параметров ор¬
биты (фиг. 6):
1) направление линии пересечения плоскости орбиты
с эклиптикой (линия узлов);
2) угол наклона плоскости орбиты относительно эклип¬
тики (азимут);

ИНЕРЦИАЛЬНАЯ И ОПТИЧЕСКАЯ СИСТЕМА ЗАСЕЧКИ	237
угол между линией узлов и большой осью орбиты;
4)	длина большой оси;
5; эксцентриситет орбиты;
6)	время прибытия космического корабля к месту назна¬
чения:
В простейшем случае движения космического корабля по
орбите вокруг Солнца ставится только одно условие, которое
Нисходящий
узел
Линия пересечения плоскости
меридиана точки старта с
экваториальной плоскостью
Наклон плоскости орбиты к
экваториальной плоскости r ct
Линия узлов
Фиг. 6. Плоскость орбиты.
а —длина большой полуоси; (3 — угол наклона большой оси к линии узлов; 8 — угловое
положение спутника на орбите в данный момент времени.
должно удовлетворяться в конце фазы полета с тягой. В наи¬
более общем случае наведения космического корабля, когда
он должен занимать заданную точку на орбите в заданное
время, требуется одновременное удовлетворение всех шести
условий; в этом случае необходимо более сложное вычисли¬
тельное устройство. При других различных комбинациях за¬
даваемых параметров требуются вычислительные устройства
соответственно меньшей сложности.
ЗАКЛЮЧЕНИЕ
Простая оптическая система засечки может использо¬
ваться для определения положения в космическом простран¬
стве со средней точностью ~550 км на каждую секунду
ошибки угловых измерений, но с небольшой точностью

238
II. АВТОНОМНАЯ КОСМИЧЕСКАЯ навигация
/
в определении скорости. Инерциальную систему можно /при¬
менять при управлении для определения скорости с большой
точностью, но при малой точности определения положения
в течение длительных полетов. Комбинированная оптическая
система засечки совместно с инерциальной системой сочетает
достоинства обеих систем и обеспечивает возможность точ¬
ной навигации и наведения в космическом пространстве.
ЛИТЕРАТУРА
1.	Carroll J., Strength of the Three Point Resection, Photogrammetric
Engng. (September 1954).

W' СТАБИЛИЗАЦИЯ ПОЛОШЕНИЯ
\ КОСМИЧЕСКИХ АППАРАТОВ
\
\
\
\
СОВРЕМЕННОЕ СОСТОЯНИЕ ПРОБЛЕМЫ
СТАБИЛИЗАЦИИ ПОЛОЖЕНИЯ КОСМИЧЕСКОГО
КОРАБЛЯ1)
Роберсон
Решение почти каждой задачи космического полета связано с необхо¬
димостью регулировать положение космического корабля. В настоящей
статье приводится обзор проблем в области управления положением ко¬
рабля и ряда предложенных решений в этом направлении.
Проблема управления положением космического корабля
подразделяется на четыре части: 1) формулировку требова¬
ний, 2) анализ действующих моментов, 3) синтез общей
системы управления, 4) выбор физических приборов для
этой системы. Существует также проблема, связанная с ро¬
лью человека в управлении положением корабля, но этот
вопрос требует особого рассмотрения.
В числе требований, предъявляемых к системе управле¬
ния положением корабля, можно выделить функциональные
требования, физические требования и требования, предъяв¬
ляемые к характеристикам корабля. Все они, конечно, зави¬
сят от специфики назначения корабля.
Первый вопрос, связанный с функциональными требова¬
ниями, касается того, следует ли управлять стабилизацией
всего корабля в целом или только распространить эту стаби¬
лизацию на часть находящегося внутри него оборудования.
Для простых назначений, имеющих одну определенную цель,
удобно использовать неподвижно закрепленный привод и
стабилизировать всю конструкцию корабля.
С другой стороны, при многоцелевом назначении нужно
иметь в виду такие приборы, как телескопы, антенны для
связи и коллекторы солнечной радиации, причем каждый
l)	R о Ь е г s о n R. Е., Aviation Age, Re$. a. Develop. Techn. Handbook,
B-5, B-6, B-9, B-10 (1956—1959),

240 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
прибор имеет свою собственную ориентацию. В этом сдУчае
стабилизация относительно корпуса корабля кажется 0олее
естественной. Однако в некоторой мере стабилизация/ всей
конструкции требуется все же почти во всех случаях; это
необходимо для устранения перекрытия линий визирования
кораблем и для обеспечения окон для внутренних приборов
ориентации, имеющих более или менее правильное напра¬
вление.
С целью упрощения рассуждений в настоящей статье мы
ограничимся рассмотрением проблемы стабилизации всей
конструкции в целом. Допустим, что требования, предъявляе¬
мые к находящемуся внутри оборудованию, выполняются не¬
зависимо друг от друга. При этом влияние перемещения
внутреннего прибора по траектории или его вращательного
движения можно представить в виде действующего на ко¬
рабль эквивалентного возмущающего момента.
Второй важный вопрос касается установления исходного
положения, отклонения от которого должны быть измерены.
Этот вопрос также зависит от назначения корабля. Метео¬
рологический искусственный спутник или спутник, исполь¬
зуемый для уточнения карты Земли, должен иметь ось, на¬
правленную «вниз» к центру Земли. В ретрансляционном
спутнике для связи следует ориентировать антенну на опре¬
деленную точку на Земле. Космический корабль, предназна¬
ченный для исследования космических лучей или метеорных
частиц, нуждается в управлении положением, если его при¬
боры работают на солнечной энергии; в этом случае коллек¬
тор должен быть направлен на Солнце.
Даже для простого направленного «вниз» спутника выбор
исходного положения является сложной задачей [1]. Понятие
«вниз» может означать геоцентрическую, географическую,
гравитационную или какую-либо другую вертикаль, напра¬
вление «вперед» может быть в плоскости орбиты или вне
ее. Все эти вопросы зависят от характера поставленной за¬
дачи.
Основной требуемый параметр, который следует иметь в
виду, — это точность. Но при этом необходимо также учиты¬
вать, что в зависимости от поставленной задачи требования,
предъявляемые к точности, сильно меняются. При наблюде¬
ниях за погодой приемлемым является угловое отклонение
корабля на 20—30°. С другой стороны, если используется
большой установленный на спутнике телескоп для фотогра¬
фирования планет, то во время экспозиции точность его ори¬
ентации должна поддерживаться в пределах долей дуговой
секунды.

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКОГО КОРАБЛЯ	241
Большие отклонения в ориентации корабля обычно сни¬
жают эксплуатационные качества. Однако не существует оп¬
ределенной угловой точности, обеспечивающей высокое каче¬
ство системы, и в то же время любая меньшая точность
не делает систему совсем непригодной. Между точностью
стабилизации космического корабля в пространстве и его
эксплуатационными качествами существует некоторое про¬
тиворечие. Высокая точность аппаратуры достигается за
счет еефазмеров и сложности; таким образом, как правило,
нельзя ^требовать предельно достижимой точности стаби¬
лизации.
Интересно отметить, что часто это противоречие связано
с временем наблюдения, особенно для искусственных спут¬
ников. Если изменения углов ориентации корабля слишком
велики, то наблюдения следует проводить на следующей
орбите, где эти углы могут изменяться в меньших пределах.
Точная стабилизация космического корабля в пространстве
не улучшает характера получаемой информации, но ускоряет
ее получение.
Среди прочих требований к стабилизации, которые могут
быть здесь рассмотрены, особое значение имеют надежность
и срок службы. Условия космического пространства также
предъявляют свои требования к физическим элементам си¬
стемы.
Если бы не существовало моментов, действующих на кос¬
мический корабль, можно было бы придать ему желаемое
неизменное положение. В действительности неизбежны на¬
чальные угловые отклонения и начальные угловые скорости,
которые следует уменьшать. И если, как это бывает в боль¬
шинстве случаев, исходное направление не имеет постоянной
угловой скорости вращения в инерциальном пространстве, то
управляющий момент стабилизации должен прикладываться
к летательному аппарату в целях «равнения» его на исходное
направление.
В реальных случаях всегда имеются моменты, которые
стремятся нарушить стабилизацию космического корабля.
Анализ этих моментов является существенной частью проб¬
лемы, связанной со стабилизацией корабля в пространстве.
Возмущающие моменты возникают благодаря многим физи¬
ческим факторам: электрическому и магнитному полям, да¬
влению солнечной радиации и давлению радиации от самого
корабля, бомбардировке ионами, молекулами воздуха, ме¬
теорными частицами и космическими лучами, градиенту гра¬
витационного поля, внутренним подвижным элементам и эки¬
пажу корабля, неправильной ориентации тяги. Существует
16 Зак. 876,

242 HI. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
также эффективный возмущающий момент, вызываемы^ не¬
однородным вращением системы координат.	j
Ряд внутренних элементов может вызвать импульсные
моменты аналогично разрегулировке направления тягй в те¬
чение коротких периодов. Влияние начальных отклонений и
скоростей этих отклонений могут также рассматриваться как
начальные импульсы моментов. В частности, для спутников
электромагнитные моменты и моменты инерционных |сил мо¬
гут носить колебательный, причем почти (или точно! перио¬
дический, характер.	!
Многие моменты могут представлять собой случайные
функции времени, например моменты, которые вызываются
бомбардировкой частиц и некоторыми типами находящихся
на борту приводных устройств. В то же время лобовое со¬
противление воздуха, давление радиации или неправильная
ориентация направления тяги постоянно работающих дви¬
гателей с малой тягой могут вызвать появление постоянных
составляющих момента вокруг той же самой оси корабля.
Этот постоянный момент является особенно вредным, так как
он может легко насыщать систему стабилизации. Каждаяч си¬
стема управления имеет присущую ей способность накопления
импульса момента сил или момента количества движения; как
только интеграл по времени от этого момента превышает
этот уровень, система больше не может противодействовать
моменту. Система может также поддерживать только опре¬
деленный максимальный мгновенный уровень момента, а это
ведет к другому виду насыщения системы управления.
Момент, вызванный градиентами гравитационного поля,
наиболее просто описывается для искусственного спутника
Земли, конструктивно вытянутого вдоль одной оси. Грави¬
тационное поле Земли создает момент на этом спутнике и
направляет его длинную ось к центру Земли. Грубо говоря,
гравитационная сила стремится подтянуть тот конец спут¬
ника, который находится ближе к Земле, в то время как
центробежная сила стремится оттолкнуть другой его конец.
Момент, возникающий под влиянием градиента гравита¬
ционного поля, который воздействует на протяжении всего
полета удлиненного тела через изменяющееся в простран¬
стве гравитационное поле, пропорционален синусу двойного
угла между длинной осью спутника и радиальной линией ме¬
жду спутником и центром Земли. Он обычно выражается как
постоянный момент пружины для небольшого углового за¬
кручивания и измеряется в дин* см на Г разрегулировки.
Численные значения возмущающих моментов сильно за¬
висят от конфигурации летательного аппарата. Так, момент

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКОГО КОРАБЛЯ	243
от градиента гравитационного поля, который может быть
особенно важен в случае вытянутого спутника, совсем исче¬
зает, ^сли спутник имеет вид сферы. Постоянная составляю¬
щая йшента может возникнуть под влиянием давления сол¬
нечной радиации, если центр масс летательного аппарата не
проектируется в центр освещаемой площади.
Рассмотрим простой пример цилиндрического искусствен¬
ного спутника Земли, вес которого составляет -— 500 кг, плот¬
ность равна плотности спутника «Авангард», коэффициент
удлинения порядка 1:5, а высота орбиты составляет
~800 км. Момент градиента гравитационного поля для та¬
кого спутника составляет примерно 42 дин-см/град (кон¬
структор может увеличить это число до 10 000 дин - см/град
за счет удлинения спутника).
Сравним эту величину с величиной ~ 375 000 дин-см, не*
обходимой, чтобы набрать номер по телефону. Постоянный
момент такой величины совершенно перевернет спутник че¬
рез 90 сек. С другой стороны, момент, равный ~0,5 дин-см,
вызовет дрейф гироскопа с кинетическим моментом
107 г-см2/сек с угловой скоростью порядка 0,01 град/час.
Теперь предположим, что небольшой сервомотор вмонти¬
рован в спутник и развивает некоторую скорость. Как пра¬
вило, это явление может вызывать реактивный момент по¬
рядка 70 г-см за 0,02 сек. В связи с этим полная амплитуда
колебаний спутника составит ~24". Или предположим, что
внутри спутника имеется вращающийся маховик с кинетиче¬
ским моментом 107 г-см2/сек, ось вращения которого слегка
отклонена от оси тангажа спутника (номинально эта
ось направлена по нормали к орбитальной плоскости).
В результате появится крен спутника на угол порядка
7з дугового градуса на каждый градус отклонения оси вра¬
щения.
В общем можно сказать, что для ближних спутников
приемлемой конструкции важную роль играют внутренние
подвижные элементы и градиент гравитационного поля. Мо¬
менты от любого другого источника можно ограничить
величиной в пределах 10—100 дин-см.
Для отдаленных спутников и других космических кораб¬
лей действие градиента гравитационного поля значительно
ослабевает, изменяясь обратно пропорционально кубу рас¬
стояния от центра притяжения, и будет иметь место влияние
только внутренних подвижных частей.
Система стабилизации корабля состоит из трех основных
частей:
16*

244 HI. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
1) датчиков, чувствительных к положению корабля и ука¬
зывающих его изменения;
2) регулирующего фильтра или счетно-решающего устрой¬
ства, которые реагируют на воспринимаемые датчиками из¬
менения параметров и преобразуют их в управляющие сиг¬
налы.
3) исполнительных механизмов, которые создают мо¬
менты в ответ на управляющие сигналы.
Прежде всего конструктору важно получить введения
о точности стабилизации корабля и определения его скоро¬
сти, которые обеспечиваются реальными датчиками. Угловые
отклонения не могут быть использованы в качестве основных
входных сигналов до тех пор, пока не будет найден удобный
способ их измерения. Маловероятно, например, использова¬
ние угла между курсом корабля и линией, параллельной ши¬
роте; трудно представить себе прибор, который устанавли¬
вался бы сам по себе по линии, параллельной широте.
В регулирующих фильтрах особого внимания требуют их
характеристики, которые определяют передаточную функцию
между выходным сигналом датчика и входным сигналом ис¬
полнительного механизма (управляющим моментом). Если
уравнения, характеризующие положение корабля, записаны
в величинах отклонения от программного положения, то в
этих уравнениях имеются члены, представляющие управляю¬
щие моменты, которые выражены в величинах, измеряемых
датчиками (они в основном идентичны или близки к углам
отклонения). Например, управляющий момент по тангажу
может быть выбран пропорциональным угловой скорости
тангажа. Общий динамический характер эволюций корабля
описывается с помощью результирующих уравнений, что
дает возможность найти ответную реакцию корабля по поло¬
жению на любой вид возмущающего момента.
Регулирующий фильтр должен быть прост по своей
конструкции; для получения сигналов, подаваемых на испол¬
нительный механизм, должно производиться минимальное
количество вычислений. Кроме того, следует использовать
и простые приборы, которые автоматически выполняют
вычислительные функции, а также, возможно, и функции
восприятия входных величин. В качестве примера можно
привести дифференцирующий гироскоп, выходной сигнал
которого может быть послан непосредственно на вход управ¬
ляющего исполнительного механизма для демпфирования
по угловой скорости.
При выборе исполнительных механизмов существенное
внимание уделяется физическим особенностям приборов, как,

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКОГО КОРАБЛЯ 245
например, емкости запоминающего устройства на единицу
веса и эффективности использования энергии. Основные же
проблемы заключаются в выборе передаточных функций
между датчиками и исполнительными механизмами. Одна из
трудностей связана с решением вопроса, предназначена ли
эта система для сведения к минимуму постоянного рассогла¬
сования и колебаний с уменьшением пиков в переходных ре¬
жимах или же для регулирования этих параметров. Устано¬
вившееся рассогласование, например, не оказывает никакого
влияния на составление карт с помощью спутника, но имеет
большое значение при межпланетной навигации корабля, ко¬
торый постоянно приводится в движение двигателем с малой
тягой. Даже если этот вопрос решен, синтез системы упра¬
вления все еще представляет собой относительно сложную
проблему создания системы автоматического регулирования.
Уравнения эволюций корабля неизбежно включают как
зависящие от времени коэффициенты, так и нелинейные
члены, которые приобретают особое значение при определении
остаточных эволюций корабля. Существуют только два воз¬
можных пути решения этой проблемы: 1) синтез методом
последовательных приближений с помощью счетно-решаю¬
щего или моделирующего устройства; 2) обычный синтез
с помощью сервоустройств. При этом пренебрегают некото¬
рыми вызывающими сомнение величинами, и полученный ре¬
зультат используют в качестве предварительной системы, на
основании которой выясняют влияние этих не принятых во
внимание величин.
Нельзя сказать, что проблема «обычного» синтеза с по¬
мощью сервоустройств проста. Уравнения стабилизации яв¬
ляются существенно неустойчивыми, кроме тех случаев, когда
для получения необходимой стабильности используется гра¬
витационная постоянная [2], что само по себе является важ¬
ным преимуществом. Проблема заключается не в том, чтобы
получить «хорошую» характеристику от устойчивой системы,
а в том, чтобы стабилизировать эту систему.
Хотя синтез системы управления применялся в немногих
случаях, суть этой проблемы ясна. Уравнения эволюций ко¬
рабля выведены в достаточно общей форме, так что их можно
использовать при решении всех задач, связанных с запус¬
ком искусственных спутников. Методика синтеза с помощью
сервоустройств разработана достаточно детально при реше¬
нии линейных инвариантных по времени уравнений, а влия¬
ние пренебрегаемого параметрического возбуждения и нели¬
нейностей можно определить, используя счетно-решающее
устройство или метод возмущений.

246 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Существует три основных метода восприятия входных
изменяющихся параметров: инерциальный метод, метод визи¬
рования и метод использования окружающего поля. Поль¬
зуясь инерциальными методами, можно обеспечить абсолют¬
ную ориентацию посредством гиростабилизированной плат¬
формы. Это устройство рассматривается как лучшая система
координат для обеспечения кратковременной точности. Но
поскольку гироскоп подвержен дрейфу, то для получения
длительной точности наряду с гиростабилизированной плат¬
формой необходимо использовать какую-нибудь другую си¬
стему. Если вертикальная ось спутника стабилизируется
какими-либо другими дополнительными средствами, то для
восприятия рыскания вне орбитальной плоскости гироскоп
можно использовать и без платформы, в этом случае он бу¬
дет действовать аналогично гирокомпасу на Земле. Этот ме¬
тод, несмотря на все достоинства, имеет существенный недо¬
статок, заключающийся в том, что он не может различать
скорость отклонения корабля от скорости вращения основной
системы координат. Вследствие этого скорость вращения
должна определяться с помощью предварительных вычисле¬
ний или каким-нибудь другим подходящим путем.
Представляют большой интерес приборы для визирова¬
ния, особенно если возможная линия визирования находится
в простом соотношении с одной из основных осей стабилиза¬
ции. Например, можно представить себе прибор сканирова¬
ния по горизонту, который образует пучок линий визирова¬
ния по краю диска ближней планеты. Тогда средняя из этих
линий оказывается направленной к центру планеты, обеспе¬
чивая тем самым естественную вертикальную координат¬
ную ось.
В некоторых предлагаемых системах наведения луч от
космического корабля к планете, которая является местом
назначения, представляет собой естественную исходную ось.
Этот луч можно легко найти с помощью устройств слежения
за звездами. Такой вариант аналогичен случаю с антенной,
направленной на какую-нибудь точку на Земле. Здесь линия
визирования может быть установлена узким радиолучом
с Земли.
К приборам, базирующимся на измерении окружающего
поля, можно отнести, например, устройства, осуществляющие
коллимацию случайных космических лучей вблизи Земли,
для того чтобы получить исходное направление. Можно так¬
же применять устройства, использующие магнитное и грави¬
тационное поля (в последнем случае с помощью эффекта
градиента поля, уже описанного выше).

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКОГО КОРАБЛЯ	247
Для обеспечения момента управления можно использо¬
вать почти любое физическое явление, которое накладывает
возмущающий момент на корабль. Так, например, можно
возбудить большую катушку с обмоткой с тем, чтобы она
пришла во взаимодействие с магнитным полем близлежа¬
щего тела, или, например, удлинить корабль для увеличения
гравитационных моментов. Очевидно, что методы управления
могут быть самыми разнообразными. Некоторые из них не¬
удовлетворительны, поскольку достижимый уровень момента
слишком низок или потребление мощности слишком высоко;
другие ставят излишние проблемы с точки зрения приборной
реализации. В общем случае наиболее предпочтительными
являются различные инерционные методы управления
положением.
Один из простейших инерционных методов заключается
в выбрасывании вещества и использовании силы инерцион¬
ной реакции. Обычно это делается с помощью газовых реак¬
тивных струй, направляемых таким образом, чтобы обеспечить
стабилизацию вокруг всех осей тела. Именно такая система
была запланирована для корабля Х-15 фирмы «Норт Аме-
рикэн». Это устройство обеспечивает высокие уровни мо¬
мента, не требует дополнительной мощности и при всей его
простоте обладает значительной гибкостью. Однако суще¬
ствует опасность, заключающаяся в том, что газ может быть
израсходован преждевременно или по причине непредвиден¬
ных возмущений, или по недосмотру пилота. Кроме того,
остается неясным, является ли эта система наиболее эффек¬
тивной с точки зрения веса. Она, возможно, найдет приме¬
нение в ранних проектах космических кораблей, для которых
время, затрачиваемое на разработки, важнее достижения
наилучших характеристик.
Классический метод инерционного управления предста¬
вляет собой метод использования реактивных маховиков. Ма¬
ховик монтируется в корабле на фиксированных подшипни¬
ках и, получая ускорение относительно корабля, создает
реактивный момент вокруг оси вращения, который можно
использовать для управления. В качестве маховика можно
использовать ротор двигателя, а сигнал управления можно
прикладывать в виде изменения тока двигателя. Для того
чтобы обеспечить управление по трем осям тела, используют
три маховика. Эти маховики соединяются таким образом,
что если один из них, скажем маховик крена, получает уско¬
рение, то корабль испытывает воздействие по двум осям —
по оси крена и по оси рысканья. Вполне возможно, что это
Усложняет проблему сервоустройств, но в то же время

248 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
позволяет обойтись только двумя маховиками на спутнике, что
в конечном счете приводит все же к упрощению серво¬
устройств. Подводя итог, можно сказать, что этот метод,
по-видимому, является наиболее приемлемым. Конечно, су¬
ществует много других возможностей [2], но все они оказы¬
ваются более ограниченными по сравнению с рассмотрен¬
ными выше.
ЛИТЕРАТУРА
1. Roberson R. Е., Attitude Control of a Satellite Vehicle —An Outline
of the Problem, Ргос. VIIIth Intern. Astronaut. Congress, 1958.
2. Roberson R. E., A Unified Analytical Description of Satellite Attitude
Motions (available from the author).
3. Roberson R. E., Principles of Inertial Control of Satellite Attitude,
IXth Intern. Astronaut. Congress (available from the author),

ПРОБЛЕМЫ СТАБИЛИЗАЦИИ ПОЛОЖЕНИЯ СПУТНИКА1)
Роберсон
Рассматриваются основные проблемы, связанные с разработкой си¬
стемы стабилизации, а именно выбор системы координат и координатных
осей в самом корпусе летательного аппарата и характер возмущающих
моментов в системе стабилизации, оказывающих влияние на спутник. При¬
водится вывод уравнений эволюций аппарата и предлагается объяснение
синтеза системы управления. Рассматриваются также источники управляю¬
щего момента системы стабилизации, влияние конфигурации спутника и
роль чувствительных датчиков системы стабилизации.
/. ВВЕДЕНИЕ
Управление положением (стабилизация) искусственных
спутников в пространстве представляет чрезвычайно важную
проблему, широко освещаемую в литературе по астронавтике,
где рассматриваются различные случаи применения стабили¬
зации положения.
Если вопрос об эволюциях спутника рассматривается в об¬
щем виде, т. е. предъявляется общее требование, чтобы эти
эволюции были незначительными или же известными с боль¬
шой точностью, то возникает ряд сложных проблем. Услож¬
няется также и метод анализа движения.
В настоящей статье рассматриваются проблемы, возни¬
кающие в процессе изучения системы стабилизации, и указы¬
ваются области, в которых должна вестись работа над этими
проблемами.
2.	СИСТЕМЫ КООРДИНАТ
Сущность проблемы
Рассмотрим сначала вопрос о выборе системы координат.
Необходимо решить, относительно какого исходного положе¬
ния спутник должен стабилизироваться в идеальных условиях,
*) Roberson R. Е., Ргос. VHIth Intern. Astronaut. Congress,
Pp. 317—339, 1958,

250 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
другими словами, относительно какого положения следует
измерять все отклонения спутника. Конечно, исчерпывающий
ответ на этот вопрос зависит от назначения летательного
аппарата.
Если предположить, что спутник пролетает по круговой
орбите вокруг сферической поверхности Земли, то в этом
случае естественно выбирать за начальное положение верти¬
кали геоцентрическую вертикаль на спутнике, а за исходное
направление — направление вперед в орбитальной плоскости.
Однако известно, что фактической орбитой вокруг сжатой у
полюсов Земли не может быть ни круговая орбита, ни плос¬
кая и для некоторых случаев в зависимости от назначения
спутников отклонения от плоской круговой идеальной орбиты
могут быть довольно существенными.
При рассмотрении реальных случаев режима полета и на¬
значения спутников всегда может возникнуть вопрос, нет ли
других приемлемых решений и насколько хорош сделанный
выбор. Во многих случаях выбор делается интуитивно, на ос¬
нове различных определений как вертикали, так и направле¬
ния вперед, и поэтому в ряде случаев он не является опти¬
мальным. Однако ясно, что разница между этими вариан¬
тами весьма незначительна.
Последнее утверждение не означает, что проблема выбора
системы координат не заслуживает внимания. По ряду при¬
чин необходимо тщательное рассмотрение этой проблемы. Во-
первых, хорошо известно, что любая отрасль знания должна
прежде всего иметь по возможности более правильную логи¬
ческую основу. Поэтому перед тем, как перейти к рассмотре¬
нию физических систем управления, необходимо точно и ясно
определить систему координат. Во-вторых, несмотря на то,
что различие между соответствующими исходными системами
координат может быть очень незначительным, система стаби¬
лизации спутника должна постоянно корректировать это не¬
большое различие (которое она могла бы не корректировать
в ином случае) и фактическое потребление мощности может
оказаться неприемлемым. В-третьих, в некоторых случаях тре¬
буется чрезвычайно точная стабилизация (например, в слу¬
чае, когда орбита или траектория свободного полета коррек¬
тируется кратковременными импульсами тяги, направление
приложения тяги является очень критичным).
Для иллюстрации трудности простого ответа на вопрос,
какая система координат является наилучшей, приведем сле¬
дующие замечания. Допустим, что спутник не является в ди¬
намическом отношении сферическим телом и имеет «длинную
ось» (главная ось инерции, относительно которой момент

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
251
инерции является минимальным). Известно [1], что возмущаю¬
щий момент, возникающий от гравитационного поля Земли,
имеет тенденцию ориентировать спутник таким образом, что¬
бы его длинная ось была нормальна к местной гравитацион¬
ной эквипотенциальной поверхности. Более того, можно пока¬
зать, что это один из значительных (если не самый большой)
источников появления момента. Все эти факты говорят о том,
что оптимальным выбором направления вертикали будет вы¬
бор местной гравитационной вертикали, который исключает
появление любых гравитационных возмущающих моментов,
могущих увести спутник от желаемого положения по вертикали.
Однако в этом выборе есть своя отрицательная сторона, так
как для круговой орбиты (и еще больше для эллиптической
орбиты) эта гравитационная вертикаль движется с неодина¬
ковой угловой скоростью в пространстве во время обраще¬
ния спутника по орбите. Подобное обстоятельство вызывает
необходимость в создании управляющих моментов, которые
обеспечивают достаточное угловое ускорение и поддержи¬
вают ориентацию спутника относительно выбранной неравно¬
мерно вращающейся вертикали.
Возможен и обратный случай. Предположим, что исходное
направление вертикали выбирается таким образом, чтобы
вертикаль двигалась с одинаковой угловой скоростью в про¬
странстве1). Совершенно ясно, что для обеспечения нужного
положения спутника относительно равномерно вращающейся
исходной вертикали не требуется никакого момента. Однако
в этом случае исходная ось не является больше нормальной
по отношению к гравитационной эквипотенциальной поверх¬
ности летательного аппарата и последний вынужден воспри¬
нимать гравитационный возмущающий момент, который вы¬
зовет отклонения от установленного положения.
При любом другом выборе исходного направления вер¬
тикали оба упомянутых выше возмущения действуют со¬
вместно. Это обстоятельство может дать некоторые преиму¬
щества.
Выбор направления вперед является еще менее опреде¬
ленным. Несмотря на то, что это направление, как правило,
выбирают таким образом, чтобы оно было перпендикулярным
по отношению к исходному направлению вертикали, такое
требование заранее (a priori) не выдвигается. Более того,
1)	Таким исходным направлением является геоцентрическая вертикаль
в точке, которая движется по орбите со средней скоростью спутника, т. е.
с постоянной угловой скоростью, которую имел бы спутник, если бы при
той же общей энергии орбита не имела эксцентриситета.

252 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
вовсе необязательно, чтобы оно совпадало с мгновенной пло¬
скостью орбиты. Например, если бы спутник использовался
для составления карты Земли [1], то оптимальное направле¬
ние вперед находилось бы в плоскости местной геофизической
вертикали и вектора скорости спутника относительно Земли,
а не относительно инерциального пространства.
Имея в виду все эти соображения, рассмотрим вновь
вопрос об определении системы координат. Практически удоб¬
но определить целый класс «приемлемых» систем и тем са¬
мым отложить окончательный выбор. В конечном итоге по¬
следний зависит от самой постановки задачи, при этом учи¬
тываются как требования стабилизации в данном случае, так
и возможность упрощения уравнений эволюций спутника с
помощью разумного выбора. Ниже мы покажем, что в этих
уравнениях учитывается также и параметрическое возбуж¬
дение.
Основные системы координат
Пусть ЭП’З будет правой декартовой системой прямоуголь¬
ных координат, начало которой лежит в центре Земли, и
пусть ориентация осей неизменна в инерциальном простран¬
стве, а ось X расположена в направлении северного полюса
Земли. Несмотря на то, что ориентация осей X и 3 может
быть произвольная, допустим для определенности, что ось 3
направлена в точку весеннего равноденствия1). Далее допу¬
стим, что Х\ Y', Z' — такая же система, только полученная в
результате поворота системы ХХЗ на угол Л2 вокруг оси X.
Смысл обозначения, выбранного для этого угла, станет ясным
из дальнейших рассуждений. На фиг. 1 показаны обе эти си¬
стемы координат, а также взаимосвязь между ними и их от¬
ношение к Земле.
Рассмотрим плоскость, содержащую ось Z' и наклонен¬
ную к экватору Земли под углом 7 (при 0<[ тг) (фиг. 2).
Одной из важных проблем при анализе является определение
характера изменения угла Л2 при условии, что спутник дол¬
жен оставаться в пределах этой наклоненной плоскости или
поблизости от нее. Обычно говорят об «орбитальной плоско¬
сти» и об угле ^ как об «орбитальном наклоне». Когда спут¬
ник пересекает экватор с юга на север вблизи оси Z', точку
!) Точка весеннего равноденствия, обозначаемая Т\ есть та точка пе¬
ресечения на небесной сфере эклиптики и земного экватора, в которой
Солнце переходит из южного небесного полушария в северное.

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
253
пересечения этой оси с проекцией экватора на небесной сфе¬
ре принято называть «восходящим узлом»1).
Фиг. 1. Расположение систем координат ХХ8 и X'Y'Z'
относительно Земли.
Чтобы определить местонахождение искусственного
спутника относительно Земли, требуются три обобщенные
Ф и г. 2. Положение орбитальной плоскости относительно
системы координат X'Y'Z'.
— восходящий узел.
координаты. Одной из них является радиальное расстояние г
центра массы спутника от центра Земли, две другие — угловые
!) Этот восходящий узел обычно обозначается в астрономической ли¬
тературе знаком А, откуда и происходит обозначение угла широты
Заметим, что X обозначает восходящий узел Солнца во время его кажу¬
щегося обращения вокруг Земли.

254 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
координаты аир, которые выражаются через параметры орби¬
тальной плоскости. На фиг. 3 показан вид сбоку на орбиталь¬
ную плоскость, если смотреть с положительного конца оси
Z'; спутник обозначен точкой 5. Обозначим через у' ось, иду¬
щую через центр Земли и нормальную к орбитальной плоско¬
сти; ее положительное направление будет с северной стороны
этой плоскости для ^ < тс/2 и с южной стороны для ^ > тс/2.
Фиг. 3. Углы, определяющие положение (ориентацию) спутника.
Заштрихованная плоскость, представленная на фиг. 3, содер¬
жит в себе как ось у', так и спутник; она пересекает орби¬
тальную плоскость по линии, определяемой как ось г'. За по¬
ложительное направление этой оси принимается такое напра¬
вление, когда при пересечении его с лучом от центра Земли
к спутнику образуется угол <тс/2. Таким образом, угол
между плоскостью Z'yr и плоскостью y'z', обозначенный р,
дает представление об угловом перемещении спутника от вос¬
ходящего угла. Угол а, положительная величина которого из¬
меряется в плоскости y'z' так, как это показано на фиг. 3,
дает представление об отклонении спутника от орбитальной
плоскости. Ось х' дополняет оси у' и z\ определенные выше,
и образует правую систему координат.
В настоящей статье рассматриваются только такие системы
координат xyz, которые сохраняют свое положение вблизи
системы x'y'z'. Углы фь Ф2, Фз определяются с помощью по¬
казанной на фиг. 4 единичной сферы путем рассмотрения
относительного положения двух систем координат.
Для углов Ф справедливы обычные приближения, кото¬
рые имеют в виду, пользуясь выражением «малые углы»; при
этом требуется, чтобы система координат xyz оставалась

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
255
«близкой» к системе x'y'z'. Для случаев, когда это приближе¬
ние несправедливо, например когда положение должно со¬
храняться неизменным в инерциальном пространстве, можно
Фиг. 4. Расположение осей координат x'y'z' и xyz.
применять небольшое видоизменение метода. При этом пол¬
ностью сохраняются выражения для направляющих косину¬
сов, связывающих оси координат xyz с осями x'y'z' для про¬
извольных углов Фь Ф2, Фз. В этом случае, однако, может
быть желательным определение xyz непосредственно в систе¬
ме ЭПД.
Непостоянная угловая скорость системы координат
То обстоятельство, что углы фь Ф2 и Фз остаются малыми,
имеет существенное значение, потому что при этом не суще¬
ствует системы координат, которая имела бы постоянную уг¬
ловую скорость вращения в инерциальном пространстве. Это
положение доказывается следующим образом. Если xyz со¬
храняет свое положение близким к x'y'z', то относительное
положение их можно представить с помощью вектора малого
угла 1)
Ф = Ф^*' -{- Ф2Су' Фз^г'	(1)
!) ех, и т. д.— единичные векторы вдоль указанных осей.

256 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
с точностью до величин первого порядка малости:
е* = е*' + Ф3ез,' —Ф2е*',
еу = Фз^л;' -f- Су' -f- Ф^г',
е* = Ф2е*' —®iey' + e*'.
(2)
Если угловая скорость системы xyz в инерциальном простран¬
стве имеет составляющие coi, (02 и о)3 соответственно вдоль
осей х, у и z, a со*', со^', gv — составляющие относительно пер¬
воначально установленной угловой скорости при первоначаль¬
ном положении в инерциальном пространстве, то дифференци¬
рование уравнения (1) по времени даст (с точностью до вели¬
чин первого порядка малости) следующие выражения:
Теперь предположим, что coi, 002, оо3— постоянные вели¬
чины. Тогда уравнение (3) решается в квадратурах. Легко
показать, что решения <Di(0> Фг(0 и Ф3(0 включают в себя
которые неограниченно возрастают с течением времени до тех
пор, пока civ, оу, со2' не станут постоянными и в точности
равными соответственно coi, С02, со3. Однако фактически они
не могут быть постоянными. Например, величина оу в прин¬
ципе включает в себя угловую скорость спутника вокруг своей
оси, которая не является постоянной, за исключением, слу¬
чая круговой орбиты. Но круговая орбита, как известно, не
может существовать вокруг сжатой Земли. Более того, раз¬
личные возмущения орбиты вызывают небольшое вращение
линии ее узлов. Это свидетельствует о том, что в выраже¬
ниях для ыХ', (^'содержатся члены, представляющие ко¬
лебания, причем их амплитуды пропорциональны угловой ско¬
рости прецессии линии узлов.
Ясно, что все эти результаты теряют свое значение по ме¬
ре увеличения углов Фь Ф2 и Ф3, но при принятых граничных
значениях эти величины не выходят за пределы области, где
справедливы приближения для малых углов. Однако суще¬
ствует мнение, что исходная система координат отклоняется
от x'y'z' на величину, большую, чем можно допустить при
coi, со2 и со3 — const.
Ф1 —	— Ф3(^2 Фг^з — ®x’> j
Ф2 = Ф3(1)1 + 0)2 ®1<03 оу, |
Ф3 = Ф20>1 —)— Фю)2 —|— (1)3  ссг'. J
(3)
интегралы вида
о
о
о

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
257
Основной вывод, который можно сделать на основании
всех этих рассуждений, состоит в том, что мы не обладаем
свободой выбора исходной системы координат, для которой
о)ь 0)2 и о)з — постоянные величины. В связи с этим нельзя
упростить обычные уравнения эволюций объекта, заменив их
уравнениями с постоянными коэффициентами, путем соответ¬
ствующего выбора осей координат. Короче говоря, следует
примириться с существованием небольших параметрических
возбуждений в уравнениях стабилизации и ограничиться лишь
выбором членов уравнения для учета этих возбуждений.
Возможности для выбора
В табл. 1 перечисляются, правда, не полностью наиболее
приемлемые возможности как в отношении выбора направ¬
ления вертикали, так и в отношении выбора направления впе¬
ред 1).
Исходные направления вида (5, УИ), как указывалось вы¬
ше, значительно отклоняются от системы координат x'y'z'
из-за эффекта орбитальной регрессии. Они неприемлемы для
того класса систем, которые рассматриваются в настоящей
работе (даже несмотря на то, что они могли бы быть опти¬
мальными при устранении из уравнений эволюций объекта
инерционных реактивных моментов и параметрического возбу¬
ждения). Далее, если вектор скорости в направлении вперед
отклоняется от орбитальной плоскости всего на несколько ду¬
говых . секунд, то очевидно, что на практике случай (ЛУ, 1)
явно отличается от случая (ЛУ, 2) или (ЛУ, 3). Поэтому наи¬
большие возможности кроются в случаях (ЛУ, М) при ЛУ = 1,
2, 3, 4 и М = 2, 3.
Дальнейшее упрощение связано с соображениями о вы¬
полнимости датчиков. С практической точки зрения спутник
не может стабилизироваться, если не будут определены от¬
клонения от исходного положения. Любые кажущиеся пре¬
имущества от выбора такой системы координат, которая по
той или иной причине не может быть ориентирована относи¬
тельно корпуса спутника с помощью датчиков, являются ил¬
люзорными. Невозможность определения отклонений эквива¬
лентна введению моментов в уравнения эволюций объекта,
причем эти моменты не могут быть устранены с помощью
системы стабилизации. В результате будут иметь место.
*) Система, которая представляет собой особую комбинацию всех этих
возможностей, обозначается (N, М), где N — номер в таблице для верти¬
кали, а М — номер в таблице для направления вперед.
17 Зак. 876

258 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Таблица 1
Основные возможные системы координат
Вертикаль
Наименование
Определение вертикали
Геоцентрическая
Направлена вдоль геоцентрического радиуса
через летательный аппарат
Географическая
Направлена во внешнее пространство через
летательный аппарат по нормали к так на¬
зываемому международному эллипсоиду
Гравитационная
Направлена во внешнее пространство через
летательный аппарат по нормали к сглажен¬
ному эллипсоиду, являющемуся аппрокси¬
мацией эквипотенциальной поверхности гра¬
витационного поля Земли, проходящей через
летательный аппарат
Геоцентрическая для дви¬
жения со средней ско¬
ростью
Направлена во внешнее пространство вдоль
геоцентрического радиуса через точку, ко¬
торая движется со средней скоростью лета¬
тельного аппарата (в том смысле, как это
понимают в небесной механике)
Г еоцентрическая для дви¬
жения с постоянной
скоростью
Направлена во внешнее пространство вдоль
геоцентрического радиуса через точку, ко¬
торая двигалась бы со средней скоростью
летательного аппарата, если бы не было
орбитальной регрессии
Направление «вперед»
Наименование
Определение направления вперед •)
Нестандартное
Вдоль продольной скорости летательного аппа¬
рата, наблюдаемой с Земли или с плоскости
регрессии

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
259
Продолжение табл. 1
Наименование
Определение направления вперед >)
Нестандартное
Вдоль проекции направления движения, спроек¬
тированного на мгновенную орбитальную
плоскость, видимой наблюдателем, непо¬
движно стоящим на Земле непосредственно
под летательным аппаратом
Нестандартное
Вдоль проекции направления движения, спроек¬
тированного на мгновенную орбитальную
плоскость, видимой наблюдателем, находя¬
щимся в плоскости регрессии
Ч Направление «вперед» всегда лежит в плоскости, перпендикулярной к направлению
вертикали.
отклонения. Роль датчиков положения рассматривается далее
очень подробно, здесь же следует лишь отметить, что для ис¬
пользования исходного направления вперед, соответствую¬
щего случаю М = 2 следует располагать бортовыми средст¬
вами для определения рысоты, наклонения орбиты, орбиталь¬
ного периода и моментов времени, когда спутник пересекает
экватор. Во многих случаях такой комплекс данных получить
невозможно (по-видимому, М = 2 как раз является таким
случаем, которым нельзя воспользоваться на практике).
Все эти замечания могут иметь важное практическое зна¬
чение. Предположим, что при запуске спутника необходимо
сохранять направление вперед как в случае М = 2. Обычно
это сделать невозможно или по крайней мере очень трудно в
применении к случаю типа М = 3. Если практически можно
реализовать только случай М = 3, то следует принять погреш¬
ность в плоскости рыскания равной угловой разности между
направлением вперед в инерциальном пространстве и напра¬
влением вперед относительно Земли, которая составляет при¬
мерно 4° в узлах орбиты с большим наклонением и высотой
в несколько сот километров. Далее, если по соображениям
выполнимости должно быть выбрано М = 3, несмотря на то,
что оптимальным является случай М = 2, нет смысла настаи¬
вать на тщательном управлении по углу рыскания относи¬
тельно выбранного исходного направления.
17*

260 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
В общем случае можно сказать, что выбор исходного на¬
правления вперед, которое оказывается наилучшим с точки
зрения применения, является интуитивно «наиболее естест¬
венным», а именно — это горизонтальное направление впе¬
ред в мгновенной орбитальной плоскости.
Частный случай выбора исходного направления вертикали
потребует дополнительного анализа и будет определяться ха¬
рактером имеющегося датчика и величинами результирую¬
щей инерционной реакции и внешних моментов. Трудности
выбора усугубляются тем, что: 1) не существует вообще та¬
кого выбора, который упростил бы уравнения эволюций до
системы с постоянными коэффициентами; 2) ни один из воз¬
можных выборов по существу не является полностью удовле¬
творительным; 3) все неиспользуемые возможности характе¬
ризуются величинами coi, со2 и соз, описываемыми выражения¬
ми одного вида (тригонометрические ряды с небольшой
амплитудой и орбитальным периодом), члены которых, выра¬
жающие параметрическое возбуждение для четырех случаев,
не имеют заметного различия; 4) все неиспользуемые возмож¬
ности приводят к возмущающим моментам, также описывае¬
мым выражениями одного вида (тригонометрические ряды
с небольшой амплитудой, имеющие в основе орбитальный пе¬
риод). Однако для четырех случаев существуют различные
амплитуды, поэтому ни одному из них нельзя отдать предпо¬
чтения.
Формулы для углов Фь Ф2 и Ф3
Эти углы, а также составляющие угловой скорости систе¬
мы координат xyz содержатся в некоторых членах, выражаю¬
щих моменты, которые вызывают отклонения по осям (см. ни¬
же); Пиз iому полезно подробнее ознакомиться с описываю¬
щими их выражениями для различных систем координат,
предлагаемых в качестве наилучших вариантов, а именно
(N,3) при N = 1, 2, 3, 4.
Предположим, что система xyz первоначально совпадает
с системой x'y'z' и затем поворачивается на небольшой угол
е вокруг вектора в плоскости х'у\ проекции которого на эти
оси будут соответственно равны —s cos Ь и е sin 8. Четыре
оставшихся случая можно свести к следующим трем выра¬
жениям:
Фг = — е COS 8,
Ф2 = е sin 8	(4)
Ф3 = 0.
Величины е и 8 в развернутом виде даны в табл. %

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
261
Таблица 2
Значения в и 8 для различных систем отсчета вертикали ’)
—
Система отсчета вертикали
•
ь
Геоцентрическая
0
COS Y
arccos	~—
cos ks
Географическая
igg sin 2\s
COS Y
arccos	f-
cos ks
Гравитационная
tgr sin 2\s
COS Y
arccos	+
cos ls
Геоцентрическая для движения со
те
средней скоростью
<*Q t — P
T
!) и — постоянные величины, соответственно характеризующие сжатие так
называемого международного эллипсоида и гравитационную эквипотенциальную поверх¬
ность (на спутнике). Предполагается, что нуль времени соответствует моменту, когда спут¬
ник проходит через восходящий узел своей орбиты. Орбитальная частота равна ш0, а широта
спутника дается следующим выражением:
\s = sln а cos 7+cos а sin у sin р.
Угловая скорость ю системы координат xyz в инерциаль¬
ном пространстве выражается следующим образом:
о) = (uv — е cos 8)	—[— (о>у' —1“ 6 sin 8) Gy' —j— (uv — В) .	(5)
Составляющие со*, щ, со г вектора со, решенные в системе
координат xyz, имеют вид
о* = ov — е cos 8— (av — 8) е sin 8 + 0 (е2),
о)у = ay -f- е sin 8 — (av — 8) е cos 8 + 0 (е2),
о)2 = wX' — 8 — ay е cos 8 + ave sin 8 + 0(е2).
(6)
Величины (Ох', (оу' и оу можно выразить через Аа —уг¬
ловую скорость линии узлов — следующим образом:
<ох' = А2 sin 7 cosp,
оу = р + Л2 cos у,
ay — A2sin у sin p.
(7)

262 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Используя выражение для Л2, |3(0 и |3(0, данные в ра¬
боте [3], а также е, 8, взятые из табл. 2, можно найти вы¬
ражения для со*, о)у, 02 в виде функций времени или функ¬
ций р.
3.	КООРДИНАТНЫЕ ОСИ НА БОРТУ ИСКУССТВЕННОГО СПУТНИКА
Углы эволюций
С выбором координатных осей в пространстве непосред¬
ственно связан вопрос о выборе координатных осей на борту
спутника. Решение этого вопроса также зависит от способа
стабилизации корабля.
Для того чтобы показать роль координатных осей на борту
спутника, прежде всего определим ряд углов положения.
Пусть XYZ будет правой ортогональной системой осей, рас¬
положенных на борту спутника таким образом, что система
XYZ совпадает с системой xyzy когда спутник находится
в своем оптимальном или желаемом положении. Тогда лю¬
бое неоптимальное положение можно охарактеризовать
тремя углами положения 0Ь 02, 0з, которые определяют поло¬
жение системы XYZ относительно системы xyz, как показано
на единичной сфере, изображенной на фиг. 5. Углы 0Ь 02, 6з
называются соответственно углами крена, тангажа и ры¬
скания,

Таблица 3
Матрицы направляющих косинусов, определяющих взаимное
расположение систем координат x'y'z\ xyz и XYZ
А
х'
У'
г'
X
1
фз
~Ф2
У
-фз
1
ф1
Z
Ф2
-ф,
1
(Фь Ф2, Ф3—малые углы)
В
X
У
г
X
cos 02 cos 03
sin 0! sin 02 cos 03 -)-
— cos 0, sin 02 cos 03 +
+ cos 0, sin 03
+ sin 0! sin 03
Y
— cos 02 sin 03
cos 0, cos 03 —
sin 0, cos 03 +
— sin 0, sin 02 sin 03
+ cos 0, sin f,2 sin 03
Z
sin 02
— sin 0, cos 02
cos 0, cos 02
(общий случай)
С
x'
У'
г'
X
02 + 63
l—^_3-02ф2_е3Фз
03 + 0102 + 02Ф1 + Ф3
	02 + 0108 + 03ф1	Ф2
Y
	 03 + 01Ф2	 Ф3
61 + ез
1	13_3_01Ф|_0зФ3
01 + 0203 + 03Ф2 + Ф1
Z
02 + 01ф3 + Ф2
	01 + 02Ф3	 Ф1
(0ц 02> Оз. ф1> ф2> фз — малые углы)
D
X
У
Z
X
. 02 + 03
2
0102 + 03
	 02 + 0103
У
-0з
, 0? + 01
2
01 + 0203
Z
02
-01
1 0? + 022
1 2
(Gj, 02> 08 — малые углы)

264 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
В табл. 3 даны матрицы направляющих косинусов, опре¬
деляющих взаимное расположение систем координат xyz,
x'y'z' и XYZ.
Значение выбора системы координат XYZ очевидно. Углы
крена, тангажа и рыскания должны стать основными за¬
висимыми переменными, которые описывают в некотором
смысле эволюции спутника. Рассуждения не будут полными
до тех пор, пока не будет выяснен характер движения.
Главные оси спутника
Наиболее простой случай имеет место при выборе осей
системы XYZ по направлению главных осей инерции спут¬
ника. Это вполне определенная система трех осей, если
у эллипсоида инерции нет двух или трех одинаковых осей.
В последнем случае выбор может быть произвольным.
Основным преимуществом указанного выбора является
то, что некоторые возмущающие моменты (например, грави¬
тационный момент, рассматриваемый в [1], и инерционные
моменты реакции) наиболее естественно выражаются в си¬
стеме главных осей. Более того, эти оси очень часто близки
к осям физической симметрии спутника, которые предста¬
вляют собой естественную систему координат для других
возмущающих моментов.
Однако следует указать на существенный недостаток
этого выбора. В любом искусственном спутнике имеются
внутренние подвижные элементы (вращающиеся механизмы,
перемещающиеся массы, экипаж, который свободно переме¬
щается в кабине корабля, и т. д.). Таким образом, главные
оси инерции неизбежно смещаются относительно корпуса
спутника обычно на небольшие углы вокруг какого-нибудь
устойчивого (равновесного) направления. Естественно воз¬
никает вопрос, являются ли эти «блуждающие» оси теми
осями, положение которых следует регулировать.
Второе, не менее важное, обстоятельство заключается
в том, что эти главные оси являются скорее теоретическими;
они, как правило, недоступны для наблюдения, ибо их
нельзя увидеть или ощутить, и их довольно трудно опреде¬
лить для каждого отдельного случая.
Оси, жестко связанные с корпусом искусственного спутника
Оси, которые не имеют указанных выше недостатков,
представляют собой систему, жестко связанную с корпусом
корабля. Для большего удобства их следует выбирать таким

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
265
образом, чтобы они были близко расположены к главным
осям (предполагая, что последние не могут слишком далеко
отклоняться от своего среднего положения). Очевидно, что
для определения возмущающих моментов по положению,
обычно выражаемых в системе главных осей, и последую¬
щего перевода их в другую систему осей необходимо знать
взаимосвязь между этими двумя системами осей.
Основное преимущество осей, жестко связанных с корпу¬
сом, заключается в том, что задача стабилизации всегда бы¬
вает представлена в системе таких осей. Во всех случаях
применения, упомянутых выше, важно, чтобы регулировалось
положение элементов оборудования (например, ракетных
двигателей), имеющих определенную ориентацию относи¬
тельно этих осей.
В связи с этим в дальнейшем изложении оси XYZ пред¬
полагаются жестко связанными с корпусом.
Применение подвижной аппаратуры
Следует упомянуть еще один случай, когда аппаратура,
положение которой желательно регулировать (например, ан¬
тенны), не фиксируется относительно корпуса спутника,
а может поворачиваться вокруг одной или нескольких осей.
В этом случае способ управления положением не имеет отно¬
шения к осям, жестко связанным с корпусом, и можно по¬
пытаться регулировать только положение аппаратуры, пре¬
доставив корпусу поворачиваться любым образом вокруг
управляемого элемента.
Этот случай можно проанализировать аналогично преды¬
дущим, однако он более сложен, поскольку с ним связаны
дополнительные соображения. Известно, что обычно полно¬
стью игнорировать положение корпуса нельзя; какая-то часть
управления положением должна распространяться и на него.
Поэтому возникает проблема одновременного управления
положением двух или более систем координат, хотя и с раз¬
личной степенью точности.
4.	ВОЗМУЩАЮЩИЕ МОМЕНТЫ
Источники моментов
Выше мы рассматривали вопросы логического порядка —
определение соответствующих систем координат в про¬
странстве и на космическом корабле. Перейдем теперь
к анализу вопроса, имеющего физический характер, а именно

266 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
к изучению природы моментов, которые вызывают изменение
положения спутника.
Качественный характер этих моментов имеет известное
значение, так как он указывает методику проектирования
космического аппарата, предусматривающую увеличение по¬
лезных (стабилизирующих) и уменьшение нежелательных
(вызывающих отклонение) моментов. При этом их амплитуды
и зависимость от времени являются основными факторами,
определяющими проектирование системы стабилизации.
Приведем некоторые возможные источники моментов воз¬
мущения положения: 1) магнитное поле Земли; 2) электри¬
ческое поле Земли; 3) давление солнечной радиации; 4) дав¬
ление электромагнитной радиации спутника; 5) лобовое со¬
противление воздуха; 6) бомбардировка метеорными телами;
7)	бомбардировка космическим излучением; 8) гравита¬
ционные поля небесных тел; 9) неравномерное вращение
систем координат; 10) движущиеся элементы внутри спут¬
ника; 11) гравитационное поле Земли.
Большая часть всех этих моментов сильно зависит от
конфигурации спутника. Поэтому рассмотрение их в настоя¬
щей статье при отсутствии конкретной конфигурации ограни¬
чивается только общими рассуждениями. Однако даже эти
общие рассуждения имеют весьма существенное значение.
Магнитное поле Земли
Основная составляющая магнитного поля Земли на ее по¬
верхности может быть представлена диполем, располо¬
женным около центра Земли с магнитным моментом
8,1 • 1025 эл-магн. ед. Предположим, что поле на спутнике
может быть представлено тем же диполем М. Магнитная
индукция в вакууме в точке поля, которая должна быть
связана с положением спутника, выражается в единицах си¬
стемы CGS
В = —V (^1) = £ (СMX' ex' + Смуеу — 2СМг' ег>),	(8)
где Смх', Сму’у Cmz'—направляющие косинусы вектора
магнитного диполя относительно осей системы координат
x'y/z', а г измеряется от центра диполя.
Можно показать, что Смх' и Смг’ являются функциями,
отражающими процессы колебаний, содержащих частотные
составляющие соо и ш0 ± £2, где со0 — орбитальная частота и
£2 — угловая скорость вращения Земли. С другой стороны.
СМу' состоит из постоянного члена и члена, выражающего

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
267
колебания с частотой £2. Для случая эксцентрической орбиты
величина г-3 содержит составляющие с частотой па)0(п =
= 1, 2, 3). Члены, содержащие sin со0/ и cos соо^ этого источ¬
ника, будучи умноженными на соответствующие величины,
содержащиеся в Смх и СМг' , приводят в результате к воз¬
растанию малых постоянных составляющих В вдоль
осей х' и z/,
Рассмотрим сначала эффект вихревых токов. Поскольку
изменяющиеся по величине составляющие магнитного поля
существуют вдоль всех координатных осей, в проводящей
обшивке и других частях спутника индуцируются вихревые
токи. В результате взаимодействия с полем Земли они на¬
кладывают суммарный момент на спутник. Точные расчеты
этого момента очень сложны (даже если оговорена конфи¬
гурация), однако можно найти приближенный верхний предел
его, предположив, что все проводящие материалы образуют
один контур с эквивалентной площадью и сопротивлением.
В случае несферического парамагнитного тела возникает до¬
полнительный момент. Такое тело испытывает момент, стре¬
мящийся совместить его большую ось с направлением окру¬
жающего магнитного поля. Можно дать примерную оценку
величины момента, используя формулу (7) и определяя
воздействие на простой удлиненный сфероид. Момент вы¬
ражается следующим уравнением:
.	2 (р х В) (р • В)
Чл— jyj >	W
где р —вектор, величина которого зависит от объема, маг¬
нитной проницаемости и коэффициента удлинения магнит¬
ного тела, а направление совпадает с продольной осью. Не
трудно показать, что
= (2V + *V)(~ 2CMy CMz' ) ex +
+ (2рж, + 1>ж»)(2СМг,Сш,) ey, +()>*» + РУ')(2Смх'Сму')ег''
В этом уравнении произведения направляющих косинусов
Сму'СМ2' и Смх'Сму' могут быть представлены величинами
с орбитальной частотой и амплитудами (менее единицы), ко¬
торые возрастают и убывают с двойной частотой вращения
Земли. Произведение Cmx'Cmz' также колеблется с двойной
орбитальной частотой и амплитудой, которая аналогична
амплитуде других произведений. Составляющие вектора р
величины постоянные, за исключением членов, содержащих

268 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
углы эволюций; таким образом, этот возможный источник,
характеризующийся постоянным направлением, не возбуж¬
дает внешнего момента. Члены, содержащие углы эволюций,
становятся членами параметрического возбуждения в урав¬
нениях стабилизации положения.
Наконец, момент возникает и от взаимодействия поля
Земли с любым постоянным магнитом или контуром тока на
спутнике. Если известна природа этих внутренних полей,
этот эффект, по-видимому, наиболее простой для анализа.
Электрическое поле Земли
Известно, что на поверхности Земли существует радиаль¬
ное электрическое поле с примерной интенсивностью
10-2 стат. в/см. Однако никаких сведений об электрическом
поле на высотах спутника, превышающих большинство слоев
ионизированных газов атмосферы, не имеется. На этих вы¬
сотах можно ожидать существенно радиального распределе¬
ния поля, возникающего от некоторого суммарного заряда
на Земле и в ионизированных слоях.
Рассмотрим два возможных эффекта. Во-первых, если
корпус спутника не имеет сферической формы, то от окру¬
жающего электрического поля возникает момент, который
стремится ориентировать корпус вдоль поля (индуктирован¬
ный электрический эффект аналогичен указанному выше
магнитному эффекту). В радиальном поле этот эффект ка¬
чественно подобен гравитационному влиянию Земли, рассма¬
триваемому ниже. Второй эффект возникает вследствие того,
что спутник является проводником, который движется с от¬
носительно большой скоростью через магнитное поле, причем
возникает эквивалентное электрическое поле, взаимодей¬
ствующее с окружающим электрическим полем.
Предварительные грубые вычисления, выполненные авто¬
ром, показывают, что как электрическое, так и магнитное
поля, по-видимому, не вызывают образования моментов,
играющих большую роль, за исключением тех случаев, когда
на борту спутника имеется какое-либо специальное устрой¬
ство, которое намеренно или случайно увеличивает влияние
какого-либо из этих полей.
Давление солнечной радиации
Вычисление момента от давления солнечной радиации за¬
висит прежде всего от отражательной способности поверхно¬
сти спутника. Верхний предел величины таких моментов по¬
лучается, если допустить полное отражение (поглощение

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
269
равно нулю), но этот предел может быть слишком большим;
коэффициент, характеризующий величину этого момента, за¬
висит от формы поверхности и равен 2 для плоской поверх¬
ности. Однако отражательная способность поверхности зави¬
сит от степени ее окисляемости и точечной коррозии и может
оказаться очень малой.
Энергия излучения (солнечная константа) составляет
примерно 1,93 кал/см2 • мин, что соответствует давлению ра¬
диации 4,3*10-5 dunjсм2 при полном поглощении. Момент
вращения на спутнике равен произведению трех сомножите¬
лей: давления радиации, площади, освещаемой Солнцем, и
линейного расстояния между центром этой площади и проек¬
цией на нее центра масс спутника. Поэтому эта величина
очень чувствительна к форме конструкции.
Интересно отметить, что Солнце может вызвать суще¬
ственно постоянные моменты. Предположим, что положение
Солнца определяется углами Кн, Ан относительно введенных
ранее инерциальных осей XTZ следующим путем. Единичный
вектор, который определяет положение Солнца, предста¬
вляется в виде
ея = cos ^tfcos ^яе£ + cos ^я s*n Ляе9 + sin ^яе&-	(* 1)
На основании этого уравнения и взаимосвязи между осями
XTZ, xfyrzf и XYZ можно показать, что вдоль оси У (ось
тангажа) имеет место составляющая величина ея, равная
cos Хя sin Ля cos 7 + sin sin Л2 sin j —
— созХяСОзЛяСозЛазт^ + Члены, содержащие углыФ,0. (12)
Так как величины Хн, Ая и Л2 изменяются очень медленно
во времени, то составляющая, определяемая уравнением (12),
по существу является постоянной величиной. Поэтому если
произведение расстояния между центрами на упомянутую
выше спроектированную площадь имеет постоянную соста¬
вляющую в плоскости XZ, то давление солнечной радиации
вызывает существенно постоянный момент вращения вокруг
оси, нормальной к этой последней составляющей и содержа¬
щейся в плоскости XZ.
Электромагнитная радиация спутника
Если какая-либо радиация спутника, включая тепловую ра¬
диацию, является несимметричной относительно центра масс
спутника, то на борту последнего возникнет вращающий

270 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
момент. Избежать появления такого момента можно в основ¬
ном путем тщательного конструирования радиатора. Если
при мощности радиации в несколько киловатт плечо является
достаточно большим, то возникает момент, постоянная со¬
ставляющая которого при отсутствии коррекции вызовет
много осложнений.
Согласно Петерсену [4], при высоком разрежении остаточ¬
ной атмосферы на высоте полета спутника справедливо до¬
пущение свободного молекулярного течения (потока). Сред¬
няя длина свободного пробега на несколько порядков превы¬
шает размеры любого корабля обычного типа, вследствие
чего отраженные частицы оказывают пренебрежимо малое
влияние на момент вращения от встречных частиц. Если
допустить, что случайные частицы, имеющие размеры атома,
отражаются идеальным диффузным отражателем, то в соот¬
ветствии с законом Ламберта отношение числа частиц, отра¬
женных под углом к нормали, к числу частиц, отраженных
по нормали, равно косинусу угла наклона. В этих условиях
можно показать, что получающийся в результате момент бу¬
дет иметь следующий вид:
где ст — среднеквадратичная молекулярная скорость, еп —
единичный вектор в направлении нормали к элементу пло¬
щади поверхности dSt a rs—вектор от центра масс до пло¬
щади dS.
Применение этого уравнения к космическим кораблям,
обладающим некоторой внешней симметрией относительно
осей XYZ (а также относительно осей x'y'z' с точностью до
членов, имеющих порядок величин Ф и 0), обеспечивает как
постоянство аэродинамического момента вообще, так и по¬
стоянство коэффициента типа «константы для пружины».
Этот коэффициент представляет собой аэродинамический
момент, отнесенный к углу атаки, являющемуся углом тан¬
гажа 02. Соответствующий момент может стабилизироваться
или не стабилизироваться в зависимости от характера кон¬
фигурации и исходной ориентации. Постоянный момент мог
бы быть фактически устранен путем тщательного контроля
положения центра масс относительно центра давления.
Лобовое сопротивление воздуха

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
271
Бомбардировка метеорными телами
Одним из важных вопросов, проанализированных Лэнгто-
ном [5], является вопрос о том, способно ли метеорное тело
при столкновении с искусственным спутником пробить об¬
шивку корабля и вызвать повреждение системы. Однако
даже те частицы, которые не вызывают повреждения систе¬
мы и не могут проникнуть внутрь корпуса, заслуживают
внимания из-за создания импульсов моментов вращения,
прикладываемых к системе.
Не существует полностью удовлетворительной оценки ча¬
стоты импульсов момента вращения различной величины,
вызываемых метеорными телами. Это объясняется общей
неопределенностью частоты появления метеорных тел, вели¬
чины их энергии и коэффициента передачи момента при
ударе, а также распределением местного удара по некоторой
площади.
На основании сравнительно скудных сведений, имею¬
щихся по этому вопросу, можно судить, что средний момент,
возникающий от ударов метеорных тел, не слишком боль¬
шой. Даже за годовой период средний импульс, по-видимому,
составляет малую величину. Однако отдельные импульсы
определенно могут создать значительные импульсы момента,
вызывающие переходный колебательный процесс по поло¬
жению спутника, который, может оказаться более существен¬
ным по сравнению с колебаниями, возникающими от других
источников, упомянутых выше.
Мы считаем, что эта проблема заслуживает дальнейшего
изучения.
Бомбардировка космическими лучами
Согласно имеющимся в настоящее время данным о верх¬
них слоях атмосферы [6], энергия бомбардировки кос¬
мическими лучами на спутнике будет составлять
~ (2 • 109 эв/см2) /сек. Так как 1 эв = 1,59 • 10~12 эрг =
= 1,59 • 10-19 дж, то 1 • 109 эв/сек ^ 10-10 вт. Если сравнить
эти данные с результатами давления солнечной радиации,
то станет очевидным, что даже в том случае, если космиче¬
ские лучи отражаются полностью, влияние подобной бомбар¬
дировки будет незначительным по сравнению с влиянием
солнечной радиации.
Гравитационные поля небесных тел
Уравнения, которые дают представление о величине мо¬
мента вращения по осям стабилизации спутника в поле
Земли, можно использовать и для нахождения момента

272 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
от Солнца и Луны. Нетрудно показать, что последние соста¬
вляют ~ 10-9 величины момента, создаваемого Землей.
Вращение системы координат
Желаемое или исходное положение спутника не является
фиксированным в инерциальном пространстве. На исходную
систему координат обычно влияют орбитальная регрессия и
орбитальный эксцентриситет; в связи с этим возникает не¬
одинаковая угловая скорость этой системы. Таким образом,
для соответствующей ориентации спутника относительно
этой системы координат должны использоваться некоторые
управляющие моменты. Тенденция спутника отклоняться от
заданного положения показалась бы наблюдателю, находя¬
щемуся на спутнике, аналогичной отклонению/которое вы¬
зывается возмущающим моментом.
Следует напомнить, что эти так называемые моменты
реакции являются фактически эквивалентными моментами
в том смысле, что их отрицательные величины должны при¬
кладываться к спутнику для предотвращения отклонений от
исходного положения, которое подвергается действию угло¬
вых ускорений.
Для получения величин (членов), выражающих возбуж¬
дение, не требуется особого анализа, ибо они получаются
автоматически при выводе уравнений эволюций относительно
осей, жестко связанных с корпусом спутника.
Движущиеся элементы внутри спутника
В искусственном спутнике достаточно сложной конструк¬
ции имеется целый ряд подвижных элементов: вращающиеся
маховики, вибрирующие детали, циркулирующие жидкости
и пр. Движение (перемещение) всех этих деталей создает
эффективные моменты вращения на спутнике благодаря на¬
личию инерционной реакции, гироскопической связи, смеще¬
нию центра масс, смещению осей инерции и т. д. Некоторые
из этих моментов крайне малы по своей величине, другие
же могут являться очень существенными источниками воз¬
мущения положения.
Выражения для момента, создаваемого внутренними под¬
вижными элементами, даны в работе [7]. Здесь достаточно
лишь отметить, что часть этих моментов является функциями
времени, другие же представляют собой небольшие члены,
содержащие угловую скорость осей корпуса спутника, обыч¬
но с переменными коэффициентами. В связи с этим послед¬
ние фактически представляют собой величины (члены) пара¬
метрического возбуждения в уравнениях стабилизации.

\ СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА	273
Вероятно, что некоторые моменты этого типа можно
использовать в качестве управляющих моментов. Один такой
момент возникает от вращения некоторых элементов внутри
спутника с постоянной скоростью. Если момент количества
движения элемента Н (относительно корпуса спутника) по¬
стоянен, то он создает эффективный момент на спутнике
—со* X Н, где со*—угловая скорость системы координат XYZ
в инерциальном пространстве.
Гравитационное поле Земли
В работе [1] дано выражение для потенциальной функции
спутника. Пользуясь им, можно найти момент вращения
спутника, который вызывается воздействием дифференциаль¬
ного гравитационного притяжения массы различных его эле¬
ментов.
Получение указанного выражения представляет чрезвы¬
чайно сложную задачу. Если пренебречь малыми членами
второго и более высокого порядков, то остаются 27 членов,
которые отражают углы эволюций и их производные по вре¬
мени, сплющенность Земли, эллиптичность орбиты, разност¬
ные углы между осями систем координат x'y'z' и xyz, смеще¬
ния момента инерции, вызванные подвижными деталями, и
соответствующие смещения осей инерции.
Основные члены результирующего выражения имеютсле-
дующий вид:
LQ=	Зшо (IY Iz) 0i
Lо=	Зо)0 {Iх Iz)
где ©о — средняя угловая орбитальная скорость спутника,
которая является постоянной, за исключением небольших
изменений, обусловленных лобовым сопротивлением воздуха
и не учитываемых в настоящей работе. Остальные члены
представляют малые по величине возмущающие функции
времени и параметрическое возбуждение с угловыми откло¬
нениями и их производными (угловыми скоростями).
б.	УПРАВЛЕНИЕ ПОЛОЖЕНИЕМ
Уравнения эволюций (стабилизации)
Примем,	как	и ранее,	что XYZ — оси координат,	жестко
связанные со	спутником.	Предположим, что	тензор	(матри¬
ца) инерции всего космического аппарата (масса спутника,
18 з9к. т.

274 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
включая все его подвижные детали)__подраздел?яется, как
указано в [7], на постоянную величину А и переменную вели¬
чину 7. Не нарушая общности вывода, предположим, что
XYZ выбраны так* чтобы тензор для А приводился к диаго¬
нальному виду
А = 7 XQXeX + / YeYeY + 7zezez-	(15)
Допустим также, что угловая скорость со* системы XYZ в
инерциальном пространстве выражается следующим обра¬
зом:
to* = о)хех + o)Ker + o)zez.	(16)
Тогда уравнения стабилизации принимают хорошо извест¬
ную форму Эйлера
7х®х 4-(7z	7Z) (i)zcoz = Lx,
7ка)г + (7х	7Z) wxwz = Ly,	(17)
7z^z Н- (7r — 7X) (oKo)x = Z,z,
где L — полный момент, приложенный к объекту от источ¬
ников, подобных тем, которые упоминались в разд. 4.
Для того чтобы использовать эти уравнения в качестве
основы для анализа системы стабилизации, следует выра¬
зить составляющие вектора со* в зависимости от углов эво¬
люций и получить выражения в явной форме для составляю¬
щих вектора момента.
Прежде всего рассмотрим составляющие угловой скоро¬
сти со*, щ и о)2, которые в системе координат xyz в инер¬
циальном пространстве даются уравнением (6). Из фиг. 5
получаем
(О* =	—1~ ^2 COS 0jCy —j—	02 sin 0iCz —{— 0gez —j— (0,	(18)
откуда
(ox = ©i + v>x -f- o)y03 — <ог02,
0)у = ’б2	О)^03	(!)y -f- (i)201,	(19)
<0Z =	+	-
Здесь пользуемся направляющими косинусами из табл. 3,
чтобы выразить на общей основе ех, еу, ez, и ограничиваемся
рассмотрением особого случая малых углов эволюций.
Из уравнения (6) видно, что величины сох и со2 в общем
случае представляют собой малые величины, являющиеся
функциями времени или положения на орбите. Однако рели-

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА	275	•
1
чина соу содержит gv, которая включает относительно боль¬
шую орбитальную угловую скорость (о0. Определим инер¬
ционный момент реакции L/ как отрицательный по величине
момент, который должен прикладываться в целях удержа¬
ния спутника ориентированным относительно системы коор¬
динат при неоднородном движении последней.
L/ = Vх^х	ех	+	[А'Юу + (Ах — lz) “/J eY +
+ Vz^z + (!y — Ах)	(20)
Тогда уравнения стабилизации, если ограничиться членами
первого порядка для 0Ь 02, 6з и для их производных, будут
иметь следующий вид:
/x*6i-(-о)о(/к — Iz) 0i + <*>о(АхЧ“ Ах— /г)0з =
= Lx Ljx 11X ~df [(^У	<*>o) ^3	2] 4“
4" (Az — ly) [шгК + (^y — Шо)	~i“ “y^A —
— 2co0((oy — O)0) 0J),	(21)
/y02 = Ly— Liy — |/K -~jj [—
+ (Ax Iz) l°A H" Ш A — ^AT^y^l + ^у^з] } *	(22)
/z*03+^0 (ly — Ax) 03— <*>o(/xH- Iz— Iy)Ql =
= Lz LIZ |/z -jj	(°>y — шо) ®il +
H- (Jy — Ix) IK — “о) 01H- ®A + 2co0 (o)y — O)0) 03 — О)у(ог02] |. (23)
Заметим, что члены в фигурных скобках в правой части
уравнений (21) — (23) включают углы эволюций и их произ¬
водные с небольшими переменными коэффициентами. Эти
члены представляют собой параметрическое возбуждение
(обычно они пишутся в левой части уравнений). Как указы¬
валось выше, от подвижных деталей в величину L доба¬
вляется суммарное воздействие подобных параметрических
возбуждений и простых функций времени. То же справедли¬
во и для влияния дополнительного момента от гравитацион¬
ного поля Земли на величину L. Исключением является слу¬
чай, когда имеются дополнительные члены, определяемые
Уравнением (14).
Допустим, что величины LG из уравнений (14) будут до¬
бавлены в левые части уравнений (21), (22) и что управляю¬
18*

-276 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
щие моменты Lc, прикладываемые к спутнику, будут выде¬
лены из величины L. Кроме того, разобьем все оставшиеся
члены в правой части на две категории: возмущающие
функции D, коэффициенты которых зависят только от вре¬
мени, и функции параметрического возбуждения Р, коэффи¬
циенты которых включают 0i, 02, 0з, 0ь 02, 0з, а также время.
(Представим этот ряд углов и скоростей в общем виде вели¬
чиной 0.) Тогда уравнения стабилизации для малых углов
примут вид
/*01 + 4(do (1у— Iz) 01 + ^о (/x + /z— Iy) 0з =
= Lcx-{- Ах(О + Лх(0>	(24)
/г02 + Зо)о(/х—Iz)^2= Бсу-\- Оу^)-{-Ру(д, t)y (25)
/z03+ щ{1у — Ix) 03 —	Iz— Iy) 01 =
= ^cz + ^z(0 + ^z(0»	(26)
Особенно важное значение приобретают следующие свой¬
ства этих уравнений.
1. Поскольку параметрическое возбуждение возникает от
целого ряда отдельных источников, любая попытка подавить
его в одном месте вызывает появление его в другом. Таким
образом, при создании системы управления неизбежно воз¬
никают проблемы конструирования сервосистем, включаю¬
щих переменные по времени параметры системы. (В случае
больших углов эволюций возникает проблема нелинейности.)
2. За исключением членов параметрического возбужде¬
ния, движение по 02, описанное уравнением (25), является
свободным и не зависит от движений по 01 и 03, описанных
уравнениями (24) и (26). Это означает, что система управле¬
ния по оси У решает более простую задачу регу¬
лирования (поскольку Ру в действительности не исчезает).
Это также означает, что в результате наличия связи между
углами 01 и 03 достаточно ввести первичное управление
только вокруг оси X или оси Z, чтобы получить эффективное
управление вокруг обеих осей.
3. При определенных условиях главные моменты инерции
[уравнения (24) — (26)] являются стабильными (величиной
Р мы пренебрегаем). Если бы это было справедливо при на¬
личии Р, то для стабилизации спутника в желательном по¬
ложении не потребовалось бы данных об абсолютном поло¬
жении, хотя некоторые сведения об эволюции спутника все
же были бы необходимы для демпфирования. Этот вопрос
подробнее рассматривается ниже.

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
277
Иногда требуется пересмотреть уравнения (24)—(26).
Если внутри спутника существует суммарный (постоянный)
момент количества движения
Н = Нхех -|- Ну£у Н- Hz^z*
то в правой части этих уравнений имеют место существенные
по величине дополнительные члены соответственно (HY&Z —
— HZMY), {Hzu>x — Hxuz) и {Нхыу — //к(ох). Поскольку со0 суще¬
ствует в выражении для соу, составляющие Hz и Нх обусло¬
вливают постоянные моменты в уравнениях для 01 и 03. На¬
личие таких моментов для случая, когда существует средство
для их устранения, является серьезным недостатком в любой
системе стабилизации. Поэтому предполагают, что вектор Н
устанавливается, если это возможно, таким образом, чтобы
Hx = Hz = 0. В результате этого процесса члены #у(*03—
— cooQi) и Яу(0! + о)О0з) исчезают из уравнений для 01 и 03
соответственно. Объединяя оставшиеся малые члены с D и
Р, можно переписать уравнения (24) — (26) следующим
образом:
/х^ + юо [4 (Iy —	+	^i“b
+ “о dх + Az Iy Iн) = LCx + &х х> (27)
/^3 + «3 (1у — /х+/я) &з—
(Ax + 7Z IY Iн) 0Х = Lcz + Dz -\-Pz>	(28)
где IH — эквивалентный момент инерции, определяемый из
^01н = Ну-
Стабилизирующие моменты
Почти любой физический эффект, который может вызвать
моменты возмущения положения, можно рассматривать как
возможную основу для получения стабилизирующих момен¬
тов. Некоторые из этих методов нельзя признать удовлетво¬
рительными, поскольку либо достижимый уровень момента
слишком низок, либо требования по мощности слишком вы¬
соки, либо же они сопряжены с серьезными трудностями при
механической реализации.
Если детально проанализировать каждый из источников
момента, упомянутых в разд. 4, то окажется, что инерциаль-
ные методы с использованием подвижных элементов внутри
спутника являются наиболее перспективными. Для практиче¬
ского применения этих методов существует целый ряд воз¬
можностей. Одна из них, уже на протяжении многих лет

278 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
известная из литературы по астронавтике, заключается в
использовании маховиков, которые создают момент инер¬
ционной реакции при действии ускорения относительно кор¬
пуса спутника. В других методах используется гироскопиче¬
ский момент связи между вращающимся маховиком и обыч¬
ной угловой скоростью системы стабилизации спутника;
применяется также своеобразный динамический поглотитель
вибрации или гиростабилизатор. Еще один, часто упоминае¬
мый метод заключается в использовании газовых реактив¬
ных струй или в выбросе других частиц таким образом, что¬
бы к спутнику прикладывалась определенная сила. Есте¬
ственно, что в процессе его использования возможны
некоторые отклонения, обусловленные назначением и кон¬
струкцией спутника. При оценке этого метода необходимо
учитывать соотношение между весом выбрасываемого веще¬
ства и весом всей силовой установки; кроме того, следует
принимать во внимание возможность получения максималь¬
ного момента и максимального импульса момента, а также
соображения, связанные с приборной реализацией.
Характер проблемы управления не вызывает сомнения,
за исключением физического источника стабилизирующих
моментов. С помощью уравнений (25), (27), (28) следует
разработать такую систему управления, которая сможет со¬
здать момент Lc как функцию величин 01, 02, 0з, 0ь 02* 0з.
причем эволюции положения, представленные как решения
этих уравнений, останутся в известной степени незначитель¬
ными.
Принципы синтеза
При синтезе системы стабилизации основное требование
предъявляется к характеристикам этой системы. В связи
с этим следует рассмотреть следующие условия:
1) система должна быть стабильной при отсутствии D(/);
2) устойчивые колебания под влиянием параметрического
возбуждения, а также любых периодических составляющих
D должны быть «малыми»;
3) максимальные значения переходных величин аперио¬
дических составляющих D также должны быть «малыми»,
4) затухание этих переходных величин и начальных про¬
цессов должно происходить «быстро».
Первое из этих условий при отсутствии Р(0, t) предста¬
вляет собой тривиальную задачу, так как в этом случае для
обеспечения стабильности достаточны простые формы Lc-
Стабильность же параметрически возбуждаемой системы
представляет собой более тонкую и сложную задачу, поэтому

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
279
в этом случае должна быть оправдана адекватность таких
простых форм.
Указанные требования легко поддаются качественному
определению, сложнее обстоит дело с их количественным
определением. Так, например, не ясно, что означают понятия
«малый» в пп. 2 и 3 и «быстрый» в п. 4. По-видимому, еще
труднее установить относительную важность этих требова¬
ний, ибо не всегда возможно удовлетворить всем им с по¬
мощью одного и того же значения Lc. Практически дело
обстоит так, что в зависимости от точки зрения, с которой
рассматривается данный вопрос, один и тот же выбор может
либо ухудшить характеристику, либо, наоборот, улучшить
ее. Универсальный совет, который разрешил бы все эти труд¬
ности, дать невозможно. Конструктивные критерии настолько
тесно связаны со специфическим назначением спутников, что
детальное рассмотрение этого вопроса в настоящей статье не
представляется возможным.
Существует еще одна проблема, связанная с синтезом,
которая заслуживает внимания. Это вопрос о том, как сле¬
дует проводить синтез для параметрически возбуждаемой
нелинейной системы. Здесь также нельзя дать общий ответ,
но можно рекомендовать следующую концепцию (можно по¬
лагать, что последующая проверка полученных результатов
явится убедительным критерием ее справедливости).
Во-первых, следует линеаризовать уравнение стабилиза¬
ции. В настоящей статье это уже было проделано при вы¬
воде уравнений (25), (27), (28). Это ограничивает синтез
задачей малых колебаний по положению, однако не озна¬
чает, что получаемая в результате система управления обя¬
зательно имеет худшую характеристику для более значи¬
тельных колебаний по положению.
Во-вторых, надо отбросить все члены параметрического
возбуждения, оставляя уравнение с постоянными коэффи¬
циентами, которое можно легко преобразовать. Эти вполне
реальный процесс, если предположить, что подобные члены
характеризуются одним параметром малой амплитуды. Ре¬
шение нулевого порядка представляет собой решение упро¬
щенного (с постоянными коэффициентами) уравнения, полу¬
чаемого с помощью описанной методики. Решения первого
и более высокого порядков получаются из идентичных урав¬
нений с постоянными коэффициентами, в которые решения
более низкого порядка входят в качестве возмущающих чле¬
нов. Значительный интерес представляет то обстоятельство,
Что упрощение, приводящее к уравнению с постоянными
коэффициентами, устраняет все члены, содержащие бь 02, 0з,

280 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
которые характеризуют отдельную выбранную систему коор¬
динат. Поэтому выбор не следует делать до того момента,
пока не будет закончен начальный синтез.
Основное сомнение в отношении этого аргумента возни¬
кает в связи с вопросом стабильности, поскольку общеиз¬
вестно, что для таких обобщенных уравнений Хилла, которые
рассматриваются в настоящей статье, обычно существуют
ограниченные области в фазовых плоскостях параметра, для
которых имеются ограниченные решения. Однако это не
представляет очень серьезной проблемы. Обработка случая
нулевого порядка приводит в результате к созданию системы
с таким демпфированием, что при получении решений более
высокого порядка никакие резонансные эффекты не смогут
иметь места. Хотя метод возмущений не является оптималь¬
ным практическим.способом при обработке уравнений, реше¬
ние нулевого порядка дает полное представление о поведе¬
нии системы в целом.
В-третьих, следует проанализировать системы управления
так, как если бы физическая ситуация была не более слож¬
ной, чем это описывается уравнениями с постоянными коэф¬
фициентами, т. е. основная задача заключается в том, чтобы
выбрать формы и коэффициенты усиления для функций
управления. Это относится к одной из проблем синтеза сер¬
восистемы обычного типа.
После определения с помощью этого метода оптимальных
способов управления и величин параметров остается четвер¬
тый, и последний, шаг, который состоит в том, чтобы, воз¬
вратившись к нелинейным уравнениям с параметрическим
возбуждением, проверить адекватность системы с точки зре¬
ния ее свойств. Можно надеяться, что в результате предла¬
гаемой методики в большинстве случаев будет получена
удовлетворительная, если не «оптимальная», система.
Влияние конфигурации !)
Рассмотрим вкратце влияние свойств спутника, вытекаю¬
щих из его конфигурации, на проблему стабилизации. Влия¬
ние конфигурации определяется членами уравнений (24) —
(26), содержащими 1Х, 1у и Iz• Устойчивость спутника в от¬
сутствие системы управления определяется соответственно
коэффициентами при 0Ь 02 и 03. В табл. 4 приведены шесть
возможных случаев с характеристиками стабильности2). Из
]) В этом параграфе не учитывается параметрическое возбуждение.
2)	При этом предполагается, что любые два главных момента не раВ'
ры друг другу и что Ну = 0*

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
281
них имеется только один тип конфигурации, который обес¬
печивает полную стабильность. Это означает, что данная
конфигурация является наиболее логичной отправной точкой
для синтеза системы управления.
Заметим, однако, что если !х и /у становятся равными
друг другу, устойчивость по 0i и 0з теряется. Учитывая это,
легко заметить влияние члена 1Н в уравнениях (27) и (28).
Этот член позволяет устранить состояние неустойчивости
в таких случаях, когда /у < 1Х• Таким образом, для этой
цели желательно ввести внутренний кинетический момент
#у. Выбор /н не влияет на устойчивость по 02. Однако она
не может быть увеличена без дополнительной нагрузки, так
как в некоторых членах с Р имеется множитель в неявном
виде.
Значение стабилизации углового положения
Под стабилизацией положения мы подразумеваем спо¬
собность наблюдателя или приборов, установленных на
борту спутника, измерять ориентацию спутника в простран¬
стве (и, возможно, одну или несколько производных по вре¬
мени от углов ориентации). Выясним, какое значение имеет
определение положения в системе стабилизации положения.
Таблица 4
Зависимость устойчивости от конфигурации
Конфигурация
e„ es
А
А
Неустойчивая
Неустойчивая
/у < Iz < IХ
»
Устойчивая
IZ<IX<IY
Устойчивая
»
IX<lZ< *Y
Неустойчивая
IZ<IY<IX
Неустойчивая
Устойчивая
IY<IX<IZ
»
Неустойчивая
Управляющий момент Lc, вводимый в уравнения стаби¬
лизации, в общем случае должен быть функцией величин
Qi, е2, 0з, 01, 02, 0з- Но для того чтобы выработать эту функ¬
цию, необходимо получить некоторую оценку этих величин.
А это как раз те величины, которые можно получить от си¬
стемы определения положения.

282 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Для систем, определяющих угловые положения, харак¬
терны самые различные способы. В общем их можно под¬
разделить на устройства следующих видов: 1) инерциальные
(стабилизированные системы координат; дифференцирующие
гироскопы и т. д.); 2) системы с визированием небесных тел;
3) системы с использованием окружающих полей (гравита¬
ционного поля, атмосферного или магнитного поля Земли,
космических лучей, воздействующих на спутник, и т. д.);
4) визирование Земли (оптическими, радио- и др. средства¬
ми); 5) визирование с Земли. Каждый из этих методов
имеет свои преимущества и недостатки, которые следует
оценить в связи с применением спутника. Детальный обзор
различных систем определения углового положения не входит
в задачу настоящей статьи.
Существуют две основные трудности, связанные с систе¬
мами определения положения. Одна из них состоит в том,
что эти системы выполняют измерение положения, но не
дают «истинных» величин. Другими словами, при этом неиз¬
бежно существует погрешность прибора или шум, проникаю¬
щий в системы измерения и управления и проявляющийся
в качестве шумового возмущающего момента, который воз¬
буждает дополнительные эволюции.
Вторая трудность заключается в том, что измерительные
системы в общем случае измеряют не те угловые величины,
которые желательно стабилизировать. Например, вместо ве¬
личин 0ь 02, бз прибор может измерить только отклонение
оси Z от географической вертикали. Если углы 0Ь 02, 0з опре¬
деляются в системе координат с какой-либо другой верти¬
калью, например с геоцентрической вертикалью, то прежде
чем использовать измеренные данные в системе управления,
их следует преобразовать. Если не принимать это обстоя¬
тельство во внимание, то в уравнениях стабилизации по¬
являются дополнительные возмущающие члены. Если же
преобразование выполняется, то часто требуется, чтобы было
известно мгновенное текущее положение спутника для ис¬
пользования при преобразовании. Вообще говоря, преобра¬
зование вызывает дополнительные трудности и потенциаль¬
ные погрешности.
Для упрощения этих проблем рекомендуется, насколько
это возможно, обойтись без измерения углового положения.
Устойчивость при конфигурации, соответствующей случаю
Iz < Iх < /у (СМ. табл. 4), также помогает разрешить эту
проблему. Поскольку уравнения стабилизации всегда устой¬
чивы, введение сигналов 0lf 02, 0з не оказывает влияния на
устойчивость. Использование только сигналов отклонения по

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ СПУТНИКА
283
осям стабилизации, которые легко получить инерциальными
средствами внутри спутника, является вполне достаточным.
Известен ряд случаев, когда большое значение имеют не¬
зависимые измерения. Можно придать системе управления
улучшенные динамические характеристики, используя такую
систему взамен тех, которые можно получить только при
наличии конфигурации, обладающей внутренней устойчиво¬
стью. В других случаях желательно иметь независимые из¬
мерения положения для последующего создания исходного
направления, независимо от того, используется ли оно как
часть системы управления. На основании всех приведенных
соображений чувствительные к положению механизмы можно
рассматривать как один из важных видов систем стабилиза¬
ции спутников, заслуживающий подробного исследования.
ЛИТЕРАТУРА
1. Roberson R. Е., Т atistcheff D., The Potential Energy of а SmaD
Rigid Body in the Gravitational Field of an Oblate Spheroid,
/. Franklin Inst., 262, № 3, 209 (1956).
2. Havilland P. R., On Applications of the	Satellite Vehicle,	Jet Pro¬
pulsion, 26, 360, 368 (1956).
3. Roberson R. E., Orbital Behavior of Earth Satellites, J. Franklin
Inst., 264, № 3, 181; № 4, 269 (1958).
4. P	e t e г s e n N. V., Lifetimes, of Satellites in	Near-Circular	and	Elliptic
Orbits, Jet Propulsion, 26, 341, 368 (1956).
5. L	a n g t о n N. H., The Thermal Dissipation	of Meteorites	by	Bumper
Screens, Вег. V. Intern. Astronaut. Kongrefi, S. 72, 1955.
6. V a n Allen J. S., Singer S. F., Total Primary Cosmic Ray Energy
at the Geomagnetic Equator, Phys. Rev., 79, 206 (1950),
7. Roberson R. E., см. стр. 284 настоящей книги.

МОМЕНТЫ ВРАЩЕНИЯ, СОЗДАВАЕМЫЕ ДВИЖЕНИЕМ
ВНУТРИ ИСКУССТВЕННОГО СПУТНИКА1)
Роберсон
В большинстве случаев технического применения многие моменты вра¬
щения, образующиеся за счет движения частей внутри какого-либо тела,
пренебрежимо малы. Однако если это тело является спутником, то такого
рода незначительные моменты часто становятся весьма существенными и
могут даже играть доминирующую роль при возмущении стабилизации
спутника. В настоящей статье выводится полное выражение для возмущаю¬
щего момента, образующегося за счет движения тел, а также дается тол¬
кование каждому из его членов. Рассматривается система координат, ис¬
пользуемая при стабилизации спутника, и определяются моменты для трех
простых случаев.
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
ai — кажущееся ускорение вектора pt с
точки зрения наблюдателя в В0;
А — кажущееся ускорение вектора R
_ с точки зрения наблюдателя в В0;
Е—'единичный тензор (матрица);
ех, eY, ez — единичные векторы в направлении
осей координат XYZ соответственно;
ер — единичный вектор вдоль оси враще¬
ния маховика в третьем примере;
ее — единичный вектор в направлении
вибрационного движения во втором
примере;
е*,	—	единичные векторы, образующие пра¬
вую прямоугольную систему с векто¬
ром ер, который фиксируется в В0',
Н — момент количества движения си¬
стемы;
7i (i = 0, 1,	-/V)	—	тензор инерции (матрица моментов
инерции) подвижного тела В{\ каждый
момент вычисляется относительно
J) Roberson R. Е„ J. Appl. Mechu 25, JSTa 2, 196—200, 287-288
(1958).

МОМЕНТЫ ВРАЩЕНИЯ. СОЗДАВАЕМЫЕ ВНУТРИ СПУТНИКА 285
осей, параллельных осям X0Y0Z0 и
проходящих через свой собственный
центр масс;
Ipy Id — полярный и диаметральный моменты
инерции маховика в третьем примере;
Iх, 1уу Iz — диагональные составляющие матрицы
(тензора) Г в системе координат XYZ\
Jl (i = 1, 2, N) — величина тензора (матрица), опреде-
ляемая уравнением (5);
Ло — средняя величина тензора (матрицы)
__	/1 в первом примере;
К—величина тензора, определяемая урав¬
нением (6);
L — суммарный внешний момент, воздей¬
ствующий на систему;
Lр — возмущающий момент, образующийся
за счет движущихся тел;
LPX> Lpy> Lpz — составляющие вектора LP вдоль осей
XYZ;
т — полная масса системы;
Щ (* = 0, 1,	N) — масса тела В*;
N—число движущихся тел внутри корпу¬
са спутника;
R — вектор, определяющий положение
центра масс системы относительно
центра масс тела В0\
R0 — средняя величина вектора R в первом
примере;
s(t) — относительная вариация вектора Рю
в первом примере;
t — время;
V/ (/=1, 2,	N) — скорость изменения	вектора р/ во
времени с точки зрения наблюдате¬
ля в В0;
V — скорость изменения вектора R во вре¬
мени с точки зрения наблюдате¬
ля в Во;
XYZ — координатные оси в комплексном
теле (см. разд. 3);
X0YqZ0 — основные координатные оси в теле В0;
е(/) — вектор вибрационной вариации век¬
тора р2 во втором примере;
e(/)-=e0sinvf;

285 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
j(0 — переменная часть тензора (матрицы),
_ определяемая уравнением (9);
Г — постоянная часть тензора (матрицы),
определяемая уравнением (9);
Pi—вектор, определяющий положение
центра массы тела относительно
центра масс тела В0;
Рю— средняя величина вектора р! в пер¬
вом примере;
р20 — центр вибрационного движения век¬
тора р2 во втором примере;
(*)0 — угловая скорость тела В0 относитель¬
но инерциального пространства;
tot (/ = 1, 2, TV) — угловая скорость В* относительно В0;
сох, a)r, o)z — составляющие вектора со0 вдоль осей
XYZ;
Bt (/ = 0, 1, .N) — обозначение г-ro твердого тела.
Точки над вектором и тензором обозначают полные производ¬
ные по времени.
ВВЕДЕНИЕ
При рассмотрении вопроса стабилизации искусственного
спутника можно заметить, что главным источником возмуще¬
ния могут быть эффективные моменты вращения, образую¬
щиеся за счет движения тел, которые находятся внутри
спутника.
Многие небольшие по величине моменты, образующиеся
за счет внутренних тел, не учитываются при решении обыч¬
ных технических задач, касающихся конструкций с внутрен¬
ними подвижными телами. Иногда они не принимаются во
внимание из-за того, что поступательное перемещение кон¬
струкции представляет больший интерес, чем ее вращение.
Чаще это вызывается тем обстоятельством, что такие фак¬
торы, как гироскопическая связь вращающихся тел с враще¬
нием конструкции и небольшие перемещения центра масс,
осей инерции и моментов инерции тела во всей его совокуп¬
ности, образуют моменты вращения, которые являются
слишком незначительными, чтобы их учитывать по сравне¬
нию с существенными внешними моментами, воздействую¬
щими на конструкцию.
Искусственный спутник Земли представляет собой совер¬
шенно иной случай. Внешние моменты здесь, включая мо¬
менты, образующиеся за счет влияния Земли, чрезвычайно

МОМЕНТЫ ВРАЩЕНИЯ, СОЗДАВАЕМЫЕ ВНУТРИ СПУТНИКА 287
малы по сравнению с обычными техническими величи¬
нами. В этих условиях эффективный момент, образующийся
За счет движения внутренних тел, может быть значительно
большим. Такие факторы, как гироскопическая связь и сме¬
щение оси, которые обычно во внимание не принимаются,
в данном случае играют существенную роль в проблеме ди¬
намики.
В настоящей статье рассматриваются воздействующие на
спутник эффективные возмущающие моменты, которые обра¬
зуются за счет движения находящихся внутри спутника тел.
При анализе приняты следующие два основных предполо¬
жения:
1. Тело имеет поступательное перемещение и вращение,
представляющие собой заданные функции времени относи¬
тельно корпуса спутника. Случай, в котором связь между
подвижным телом и корпусом спутника имеет характер
демпфирования с помощью пружин, будет рассматриваться
отдельно.
2. Рассматривается только вращательное движение спут¬
ника около центра его массы. Это условие не является серь¬
езным ограничением, так как физическое влияние поступа¬
тельного перемещения, как правило, не представляет практи¬
ческого интереса 1).
/. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
Рассмотрим случай, когда спутник состоит из неподвиж¬
ной основной части, тела В0 с массой т0 и некоторого коли¬
чества подвижных (при индивидуальном жестком монтаже)
элементов, а именно тел Б* с массами rrii(i = 1, 2, ..., N).
Допустим, что X0Y0Zo — правая система прямоугольных коор¬
динат, жестко связанная с телом Б0 с началом в центре масс
этого основного тела и угловой скоростью (о0 в инерциаль*-
ном пространстве. Допустим, что вектор pt определяет по¬
ложение центра масс подвижного тела В* относительно
Центра масс неподвижного тела В0, а вектор о* обозначает
*) Возможность того, что поступательные движения вызывают вра¬
щательную вибрацию в подвижных телах, исключается первым предполо¬
жением. В том случае, когда возникает небольшая вибрация, которая мо¬
жет влиять на жестко закрепленное, но очень чувствительное оборудова¬
ние, допускается, что спутник выполняет роль силового или скоростного
генератора, воздействующего на аппаратуру. Однако последняя не полу*
чает ощутимого движения, которое могло бы сильно влиять на движение
спутника в целом.

288 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
угловую скорость подвижного тела В* относительно основ¬
ного тела В0- На фиг. 1 !) изображено геометрическое распо¬
ложение всех этих тел. Движение подвижных элементов от¬
носительно корпуса спутника полностью определяется функ¬
циями времени pz (/),	= 1,2, ..N).
Фиг. 1. Основное тело спутника и подвижные части (элементы).
Обозначим далее тензоры (матрицы) инерции различных
тел через /*(/ = 0, 1, ..., N), причем каждый вычисляется
относительно осей, параллельных осям X0Y0Z0 и проходящих
через свой собственный центр массы. Тогда момент количе¬
ства движения Н всего тела в целом вокруг общего центра
массы будет выражаться уравнением 2)
= А =
Н = /0 •	+ ^ + X R —
N	а N	N
—rx2W<—	0)
f = l	i-1	ivi	1
!) Следует заметить, что расположение вектора щ в центре массы.
ЦМ/ не означает прохождения мгновенной оси вращения через ее центр
массы ЦМ/.
2)	В приложении суммируются основные свойства тензоров (матриц)»
используемых в дальнейшем.

моменты вращения, создаваемые внутри спутника 289
где
N
R = iS/w^-
(2)
В этом уравнении точки обозначают истинную производ¬
ную по времени с точки зрения наблюдателя в инерциальном
пространстве.
Уравнение (1) можно значительно упростить за счет ис¬
пользования уравнения (2) и соотношения
в котором уг- — скорость изменения вектора р* по времени
с точки зрения наблюдателя в системе координат X0YqZq.
В результате получаем
центра масс тела во всей его совокупности с точки зрения
наблюдателя в В0. Тензор (матрица) /г- рассматривается как
тензор (матрица) инерции i-го тела, который вычисляется
относительно системы координат X0Y0Z0, как если бы этот
элемент был массой точки, находящейся в центре масс
комплекса. Кроме того, К представляет собой тензор (матри¬
цу) инерции, который вычисляется относительно системы
координат XqY0Zq для точки, имеющей массу, равную полной
массе тела в его совокупности, и находящейся в центре масс
этого комплексного тела.
Уравнения вращательного движения можно представить
в виде
p, = vi + ®oXpi,
(3)
н—	+	2	(А-+Л)— к\ • w0H-
N
N
+ 2А-®/+ 2«|р/X v, — mRX V, (4)
i = 1
где
А = щ(р, • PiE—PiPi)>
R=m{R- Rf—RR),
(5)
(6)
E—единичный тензор (матрица) и V — кажущаяся скорость
(7)
19 Зак. 876.

290 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
где L — суммарный внешний момент, воздействующий На
систему.
Если бы спутник был единым неподвижным телом, урав¬
нение (7) приняло бы форму
4-(F-®o) = L.	(8)
где Г — тензор (матрица) инерции с постоянными коэффи¬
циентами для отдельного тела относительно собственного
центра массы. ^Однако следует заметить, что производная
по времени от Г обычно не является нулем из-за вращения
основных векторов, относительно которых определяется Г.)
Если матрица Г при составлении по осям системы координат
XqYqZq имеет диагональную форму, то три скалярных урав¬
нения, которым соответствует уравнение (8), принимают
форму обычных уравнений Эйлера.
В связи с этим можно разделить тензор (матрицу) инер¬
ции, умноженный на вектор щ в уравнении (4), на две ча¬
сти: постоянную часть Г и переменную по времени часть
l(t); первая (Г) является матрицей с постоянными коэффи¬
циентами, а вторая (7)—с переменными коэффициентами
в уравнении
^0+ 2 Z + 2 Щ (р, • рД — р(рг) — т (R • R£ — RR). (9)
i=l	i=1
■Подобное подразделение остается все еще неясным, и в связи
с этим необходимо ввести дополнительные условия. Суще¬
ствует несколько очевидных возможностей.
1. Выбор постоянных коэффициентов как средства для
получения крайних значений (максимальных и минималь¬
ных) отклонений коэффициентов тензора (матрицы) в урав¬
нении (9).
2. Выбор постоянных коэффициентов максимальной вели¬
чины с тем, чтобы переменные части никогда не были отри¬
цательными и изменялись бы только на небольшую положи¬
тельную величину.
3. Выбор постоянных коэффициентов в качестве средних
по времени величин коэффициентов тензора (матрицы) в
уравнении (9).
Преимущество первого выбора заключается в том, что
крайние значения возмущающих моментов имеют тенденцию

МОМЕНТЫ ВРАЩЕНИЯ, СОЗДАВАЕМЫЕ ВНУТРИ СПУТНИКА 291
уменьшаться до минимума, если сделать их положительные
и отрицательные крайние значения равными по абсолютной
величине. Вторая возможность выбора позволяет получить
простое и отчетливое представление о величинах остаточных
переменных моментов (всегда положительных) и о величинах
центробежных моментов инерции. Однако третий выбор мо¬
жет иметь решающее преимущество по устранению постоян¬
ных возмущающих моментов, которые нарушают стабилиза¬
цию спутника. Например, если тело В0 имеет постоянную со¬
ставляющую угловой скорости относительно одной из коор¬
динатных осей, скажем со*, тогда составляющие постоянного
возмущающего момента возникают или за счет постоянной
величины fxz, или за счет jxy ').
В связи с этим не требуется твердого решения в отноше¬
нии того, что следует включать в 7. Но при этом необходимо
отметить, что существует три фактора, которые должны быть
включены в 7. Один из них заключается в том, что проекции
тензоров инерции внутренних движущихся элементов на оси
тела В0 являются переменными за счет членов U в уравне¬
нии (9). Подобное дополнение теряет силу, если вектор т
совпадает с осью симметрии вращения тела В{ и удерживает
фиксированную ориентацию относительно тела В0. Другой
фактор заключается в поступательном перемещении центров
масс подвижных элементов, как если бы это движение не
вызывало смещения центра масс всего комплекса. Этот фак¬
тор выражается в уравнении (9) членами	—	Р/Р/)*
Положение, при котором эти члены являются единственным
источником переменной инерции, можно представить, если
предположить, что каждое подвижное тело Вг- состоит из
двух равных точечных масс, причем величина каждой массы
составляет Ч2ти эти массы расположены как у гантели, т. е.
диаметрально противоположно относительно общего центра
масс. При этом каждая пара элементов сохраняет свою сим¬
метрию в то время, как она совершает движение, определяе¬
мое вектором р£. Эти члены не входят в величину 7, так как
Для каждого движения тела существует эквивалентное про¬
тивоположное движение, присущее другому элементу, в ре¬
зультате чего соответствующий член в уравнении (9) исче¬
зает. Третий фактор, изменяющий тензор инерции, возникает
от смещения центра масс, выраженного в уравнении (9) чле-
!) Постоянные моменты являются особенно важными из-за их тенден¬
ции к насыщению любой системы управления, которая пытается сохранить
программную стабилизацию.

292 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
ном т (R • R£ — RR). Этот эффект может быть представлен
на примере движения точечной массы т вместе с общим
центром масс спутника без учета движений отдельных тел,
вызывающих смещение вектора R.
В любом случае уравнение (7) может быть переписано
после подстановки уравнения (4) следующим образом:
г	N	N	\
~ (Г • й)0) = L —	j 7 • <1>0+ 2 Ъ ■ <•>/ 4- Yi ^PiXVi—ffiRx V f.
I	/=1	1	=	1	J
(10)
Выражение производной по времени в правой части урав¬
нения (10) может быть истолковано как момент, воздей¬
ствующий на тело В0, и, кроме того, как момент, который
исчезает, если все вспомогательные тела являются неподвиж¬
ными относительно В0. Это именно тот возмущающий мо¬
мент, который образуется за счет движения внутренних тел
и является предметом нашего анализа.
Важно отметить, что уравнение (10) можно рассматри¬
вать как векторное дифференциальное уравнение движения
для зависимой переменной соо- Однако некоторые малые
члены в правой части уравнения также содержат ю0. По¬
этому не все из них представляют собой внешние возмущаю¬
щие моменты, воздействующие на спутник. Те члены, входя¬
щие в вектор о)о, которые рассматриваются как члены пара¬
метрического возбуждения, могут, как правило, переноситься
в левую часть уравнения. Обычно невозможно провести глу¬
бокий, тщательный анализ результирующего движения, за
исключением метода возмущений и итерации или метода
числового анализа. Часто в процессе приближенного анализа
небольшие по величине члены параметрического возбуждения
могут быть оставлены в правой части уравнения; в этом слу¬
чае вектор (Оо может быть заменен приближенной функцией
времени и этот член уже рассматривается как приложенный
внешний момент. Именно по этой причине члены параметри¬
ческого возбуждения пишутся в необычной форме как воз¬
мущающие члены.
Из уравнения (10) следует также, что при наличии 1
(т. е. при наличии по крайней мере одного отличного от нуля
коэффициента, изменяющегося по времени) невозможно из¬
бежать параметрического возбуждения (как это выражается
вектором соо) при стабилизации тела В0.

МОМЕНТЫ ВРАЩЕНИЯ, СОЗДАВАЕМЫЕ ВНУТРИ СПУТНИКА 293
2.	ВОЗМУЩАЮЩИЕ МОМЕНТЫ
Члены, выражающие возмущающие моменты, могут быть
разложены в ряд следующим образом:
(	N	N	\
К = 4г U '	+	^	+	2	Xvl-mRX\}	=
\	i=1	i=l	J
= Т • »о + Т • шо + wo X Т ’ й>0 +
N	_
+ 2 (Г/ • «*>/ + Ъ ■ (й>0 X W/) + h ■ Ю/ + («о + «г) X 7г • «г —
г=1
— [7/ X (w0 + co^l со,- -f- m$i X a, -f- ml pi X (<*>0 X V;) +
+ Щ (co0 X Pi) X V/} — mR X A — mR X (<*>0 X V) —
— //г (to0 X R) X V, (11)
где 7, со, I являются производными по времени, которые бе¬
рутся только для переменных составляющих, в то время как
основные векторы определяются в инерциальной системе
координат. Другими словами, эти производные рассматри¬
ваются с точки зрения наблюдателя, который неподвижен
относительно тела В0. Кроме того, а* и А являются соответ¬
ственно кажущимися ускорениями центров масс тел и
всего тела в совокупности с точки зрения наблюдателя, ко¬
торый неподвижен относительно В0.
Можно объединить и упростить некоторые члены. В част¬
ности,
Pi X к X V,) + (»„ X Pi) X V; = Ш0 х (Pi X v4)
И
R X К X V) + K X R) X V = со0 х (R X V).
Кроме того, _	_
Ъ К X <*>,) — (7х <D0) • «о* = О
и
(/! X <*>;)• СО; = 0.
В результате получаем
Lp = Т • wo "XT *	X Т • wo +
N —	.	=5=	'	—
2 {/; • СО; + /;СО; -f- (C0Q +
w/) X /*<*>/ ~h Htfpf X a, +
i = \
+ /n;W0 x (Р/ X V;)} -/7zR x A — m'0QX (R X V).	(12)

294 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Рассмотрим последовательно каждый из этих членов:
1)	7 • о)о — инерционный реактивный момент, который
возникает за счет углового ускорения тела В0 и воздействует
на мгновенную величину остаточного (переменного) тензора
(матрицы) инерции.
7-о)о — кажущийся момент с точки зрения наблюдателя,
вращающегося вместе с телом В0, который возникает за счет
изменения по времени тензора (матрицы) инерции (по ана¬
логии с моментом, который испытывает крутящийся на
месте конькобежец, если он разводит в стороны и вытягивает
по швам руки).
3) о) X '[«о — центробежный момент, который выражает
тенденцию остаточной части тела к ориентации своей «длин¬
ной» оси (в направлении моментов инерции) вдоль вектора
угловой скорости о)0 [см. также объяснение члена 7, которое
дается _ниже].
4) U • о)г — инерционный реактивный момент за счет уг¬
лового ускорения подвижного тела В{ относительно тела BQ
с точки зрения наблюдателя, неподвижного относительно
тела Во.
5) U • о)г- — кажущийся момент, возникающий за счет- из¬
менений тензора (матрицы) инерции i-го тела с точки зрения
наблюдателя, вращающегося вместе с основным телом В0;
эти изменения вызываются изменениями в’ проекциях U на
оси тела В0.
6) сог X U •	— центробежный момент, выражающий
тенденцию подвижного тела В2- с точки зрения наблюдателя,
неподвижного относительно тела В0, к ориентации своей
«длинной» оси вдоль вектора относительно угловой скоро¬
сти соо. _	_
7) о)о X U • &i . Так как U • (о, —кажущийся момент ко¬
личества движения подвижного тела В2 за счет вращения
его вокруг собственного центра массы с точки зрения наблю¬
дателя, неподвижного относительно тела В0, то эта величина
является отрицательной величиной момента, который дол¬
жен прикладываться, чтобы вектор момента количества дви¬
жения «не отставал» от тела В0 во время вращения послед¬
него.
8) т2р;Ха2 — инерционный реактивный момент, воздей¬
ствующий на основное тело В0 за счет поступательного уско¬
рения подвижного тела В{ относительно основного тела Во•
9) m2o)o X (р/ X v2-). Так как т^р,- X v* — кажущийся
момент количества движения подвижного тела за счет

МОМЕНТЫ ВРАЩЕНИЯ, СОЗДАВАЕМЫЕ ВНУТРИ СПУТНИКА
поступательного перемещения тела В{ относительно тела В0,
то объяснение для этого члена будет аналогично данному
выше для члена 7.
10)	— mRX А - гаюо X (R X V). Если тело во всей его
совокупности рассматривается как точка с массой т, нахо¬
дящейся в центре масс этого тела, то эти члены будут ана¬
логичны членам 8 и 9 для подвижного тела Bi.
Относительно членов 8, 9 и 10 следует заметить, что на¬
чало системы координат внутри тела В0 можно определить
как точку, совпадающую с центром масс комплекса. Тогда
член 10 можно было бы опустить, а его отрицательная ве¬
личина появится в дополнениях к членам 8 и 9, так как
индекс i распространяется на все тело, .включая и В0.
Таким образом, выражение для возмущающего момента
получаем в результате следующих операций:
1) выбираем оси координат X0Y0Z0 и находим /0;
2) определяем _поступательное перемещение и вращение
тела Bi и находим /*, h и К;	_	_	_
3) определяем /0 + 2(/г- + /*) —К и разлагаем на Г +
4) определяем члены 1 —10. Ниже мы покажем, что упо¬
мянутый выше процесс должен заканчиваться.
5) находим новые координатные оси XYZ, для которых
матрица (тензор) Г приобретает диагональную форму, и
6) разлагаем вектор Lp по этим новым осям координат.
3.	ВЫБОР СИСТЕМЫ КООРДИНАТ
В конечном итоге уравнение (12) принимает скалярную
форму путем разложения его по определенным осям коор¬
динат XYZ. При этом нетрудно определить предъявляемые
к последним основные требования. Во-первых, ориентация
основного тела В0 должна задаваться непосредственно ори¬
ентацией осей XYZ. Если последние нежестко связаны с те¬
лом В0, то по крайней мере не должно быть вращения этого
тела относительно XYZ. Это требование отражает.тот факт,
что В0 представляет именно то основное тело, стабилизация
которого обычно вызывает интерес. Во-вторых, эти оси
Должны практически совпадать с главными осями комплекс¬
ного тела в целях удобства осуществления стабилизации спут¬
ника. Это требование уточняется путем определения XYZ
таким образом, чтобы постоянная часть тензора инерции Г
имела диагональную форму применительно к этим осям.

296 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
При таком выборе системы координат уравнение (10)
принимает обычную форму уравнений Эйлера. Если допу¬
стить, что	_
Г = /хехех -f- /кекек -f Izezez,	(13)
d)0 ==	-f-o)zez,	(14)
то уравнение (10) примет вид
7х0)х + (^z	Ю WyUtz	= Lx	LPX,
Iу1йу {Ix	Iz) coztox = Ly	LPY,
7z^z + (7y	Ix)	= Lz ~	LPZ.
(15)
Ориентация осей XoY0Z0 внутри тела B0 пока еще нами
точно не определена, и при формальном выводе выражений
ориентация была произвольной.
Обычным и естественным выбором является ориентация,
при которой матрица 7о имеет диагональную форму. Пред¬
положим, что это выполнено и матрица Г найдена (в общем
случае недиагональной формы относительно X0Y0Z0). Если
приравнять друг к другу оба выражения Г — одно из урав¬
нения (13) и другое, выраженное через основные векторы
в системе координат X0Y0Z0 с известными коэффициента¬
ми,— то можно воспользоваться скалярными произведениями
вида еле*, еуеу и ezez, для того чтобы полностью опреде¬
лить 1Ху /у, Iz и направляющие косинусы между двумя си¬
стемами координат. Если основная часть комплексной вели¬
чины тензора инерции совпадает с тензором инерции основного
тела В0, то составляющие матрицы Г, не расположенные по
диагонали, относительно невелики по своей величине и си¬
стемы координат XqYoZo и XYZ можно преобразовать путем
поворота на небольшой угол.
Выбор начала системы координат XYZ — вопрос менее
ясный. К счастью, он не представляет особой важности, если
мы интересуемся в основном движением системы относительно
осей стабилизации, как это имеет место в нашем анализе.
Во многих случаях вопрос о том, имеет ли система коорди¬
нат свое начало в одном или другом месте тела, не пред¬
ставляет особой важности. Однако имеются случаи, при ко¬
торых отдается предпочтение системе координат, берущей
начало в центре масс комплекса, как, например, при вычис¬
лении гравитационного и других моментов, воздействующих
на тело. В связи с этим для большей определенности допу¬
скаем, что система координат XYZ имеет начало в центре

МОМЕНТЫ ВРАЩЕНИЯ, СОЗДАВАЕМЫЕ ВНУТРИ СПУТНИКА 297
масс комплекса. Если вектор р,- рассматривается в уравнении
(12)	в системе координат XYZ, то члены 10, определенные
ранее, опускаются, но при этом предполагается, что выраже¬
ния для членов 8 и 9 справедливы как для i = 1,2, ..., N,
так и для i = 0.
4. ПРИМЕРЫ
Рассмотрим три простых примера. В более сложных слу¬
чаях алгебраические выражения значительно усложняются,
но при этом ничего нового фактически не добавляется. Воз¬
мущающий момент выражается в системе координат XqY^Zq.
Пример 1. Рассмотрим точечную массу Ви которая пере¬
мещается относительно тела В0 вдоль линии, проходящей
через центр масс комплекса. Измеряем pi от начала системы
координат XqYqZq
Pi = [1 +5(0] Рю>
где рю — среднее положение вектора pi в течение длитель¬
ного периода времени. Кроме того,
R = [1 -+- 5 (/)] R0.
В то же время
Л = 0; Л = [1 -j- s (/)]2Ую
и	_	_
K=[\+s(t)\2K0.
Кроме того, в нашем особом случае одного дополнительного
тела
Ло Ко— ^“(Рю * Рю£	РюРю)*
Тогда
Г + Т = Аз 4-	Ло + [25	(/)] ~ У10
и
7 = -542s(0 + s*(*)]710.
Так как линия движения точки В{ проходит через центр масс
комплекса и через центр масс тела В0 (в данном особом
случае), все члены 8—10 исчезают.
В связи с этим возмущающий момент может быть выра¬
жен так:
Lp =	[2s	(^) -j- s2 (^)] [Ло • woH“ <*>0 X Ло ’ <°ol +
2m0 •

298 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Вначале предполагалось, что факт прохождения линий
движения тела через центр масс комплекса может указывать
на отсутствие возмущающих моментов. Из уравнения (16)
можно видеть, что эти моменты все же существуют за счет
взаимодействия изменения момента инерции с угловой ско¬
ростью корпуса В0.
Пример 2. Рассмотрим точечную массу В2> которая испы¬
тывает продольную вибрацию при наличии небольшой ам¬
плитуды относительно неподвижной точки внутри тела В0.
Представим р2 в виде р2 = Р208 (О- И снова
/0=о, Л-/Г=-^Т2,
где
7 =з [(2р20 • е + е • е) Е — (р20е + ер20 + ее)].	(17)
Кроме того, пользуясь членами 8—10, напишем
-^|p2Xa2 + ®0X(p2Xv2)].	(18)
В этом примере основным является вопрос о том, вызывает
ли симметричное колебание суммарный эффективный мо¬
мент, воздействующий на тело В0.
Если е (tf) = e(t)ee при ее, фиксированном относительно
В о, и при e(t) = £о sin vt, то легко заметить, что члены в урав¬
нении (18) являются колебаниями со средней величиной
амплитуды, равной нулю, так что в среднем за счет этих
членов не образуется никакого момента. С другой стороны,
выражение too X v о)0 включает член — z2(t) (<*>0-ее) (со0 X ее)
Таким образом, для тела, вращающегося с постоянной ско¬
ростью, вибрация, наблюдаемая по оси, которая не парал¬
лельна и не перпендикулярна к вектору со0, возбуждает эф¬
фективный момент, приводящий к появлению дрейфа и воз¬
действующий на тело. В таком случае этот момент имеет
среднее значение по времени, не равное нулю. Следует отме¬
тить, что в член 7 • со0 также входит член е2.
Пример 3. Рассмотрим один вращающийся маховик В3.
Предположим, что он вращается вокруг своей полярной оси
ер, фиксированной относительно тела В0. Пусть эта ось про¬
ходит через центр массы маховика, положение которого
остается неизменным относительно тела В0. При данных
условиях проекции тензора /3 на оси X0Y0Z0 остаются по¬
стоянными, несмотря _на то, что они, конечно, не равны нулю.
Обе величины /3 и К являются постоянными, так как век-

МОМЕНТЫ ВРАЩЕНИЯ, СОЗДАВАЕМЫЕ ВНУТРИ СПУТНИКА 299
торы рз и R — постоянны. Таким образом, | = 0 и члены 8—
10 исчезают; т. е. за счет членов, входящих в выражение для
тензора /3, появляются только члены 4—7. Они имеют сле¬
дующие значения. Если /р— полярный и U — диаметраль¬
ный моменты инерции маховика, то
^3 = ^e„ + /deee? + /<fe4e4,	(19)
Где и eTj являются единичными векторами, перпендикуляр¬
ными к вектору ер, в результате чего векторы ер, и
образуют правую ортогональную систему. Вектор о)з = <*>3ер
и ^)3 = о)3ер; кроме того, /3 = 0. Тогда на основе этого усло¬
вия можно написать
Lр = /рш3ер + /рсо3 (w0 X е„).	(20)
Таким образом, если маховику сообщается ускорение от¬
носительно В0, то вокруг ер возникает момент. Существует
также гироскопическая связь между вращающимся махови¬
ком и вращающимся телом В0\ эта связь эквивалентна мо¬
менту, требуемому для прецессии вектора относительного
момента количества движения вращающегося маховика с уг¬
ловой скоростью вращения тела В0.
ПРИЛОЖЕНИЕ
Н ВОПРОСУ О ТЕНЗОРНЫХ ПРОИЗВЕДЕНИЯХ
Тензор D с основными векторами e»-(i = 1,2,3) опреде¬
ляется как квадратичная форма
П= 2
i.i
где dij — составляющие тензора. Если
v = 2 Vfii
i
представляет собой некоторый вектор, то мы имеем следующие
произведения:
Z) • v = 2 dijVfii

300 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Эти произведения разнятся между собой до тех пор, пока
тензор D не станет симметричным, т. е. йц = dJ2. В выраже¬
нии вида У\ • D X v2 произведение Vi -D должно быть прежде
всего использовано при получении выражения для вектора.
Затем векторное умножение используется обычным образом.
Некоторые тензоры представлены в виде совокупности двух
векторов [например, в уравнениях (5) и (6)] D = ViV2. По¬
следнее произведение должно рассматриваться как тензор,
составляющая которого ij представляет собой величину
vuv2j. Она отличается от до тех пор, пока не удовлетво¬
ряется условие v2iVu= Vnv2jy т. е. пока вектор v2 не будет
параллельным вектору
ДОПОЛНЕНИЕ
МОМЕНТЫ, ВОЗДЕЙСТВУЮЩИЕ НА СПУТНИК И ОБРАЗУЮЩИЕСЯ
ЗА СЧЕТ ДВИЖУЩИХСЯ ВНУТРИ КОРПУСА ЧАСТЕЙ
Выражения для возмущающих моментов, воздействующих
на искусственый спутник за счет внутренних подвижных эле¬
ментов, были получены путем использования в качестве
зависимой переменной величины угловой скорости о)0 основ¬
ного тела в инерциальном пространстве. Составляющие раз¬
лагались по осям XYZ, жестко связанным с телом, благодаря
чему постоянная часть тензора инерции получала диагональ¬
ную форму.
В настоящем дополнении возмущающие моменты выра¬
жаются через углы отклонения фиксированной в теле систе¬
мы координат XYZ относительно осей исходной ориентации
xyz. При этом используются составляющие вектора ©о, выра¬
жаемые через эти углы1); определяется также взаимосвязь
между XYZ и главными осями инерции X*Y*Z* всего спут¬
ника в комплексе.
ВОЗМУЩАЮЩИЕ МОМЕНТЫ
Пусть xyz — система координат, вращающаяся с угловой
скоростью <о в инерциальном пространстве. Определим углы
отклонения 0Ь 02, 0з между осями xyz и осями координат,
связанными с корпусом спутника XYZ, как показано па
фиг. 2.
*) См. стр. 249 настоящей книги. — Прим, ред±

МОМЕНТЫ ВРАЩЕНИЯ, СОЗДАВАЕМЫЕ ВНУТРИ СПУТНИКА 301
Обозначим угловую скорость системы координат XYZ
через соо и определим вектор 0 через составляющие
0 = 01еХ + 02еГ + 03eZ-
Ограничивая анализ
случаем малых углов
для величин углов
первого порядка мало¬
сти, имеем выражение
0)0 = 0" + со X 0 + о), ко¬
торое дается, как урав¬
нение (19) 1) для со¬
ставляющих2).
Выражение для воз¬
мущающего момента
за счет подвижных эле¬
ментов дается уравне¬
нием (12). Единствен¬
ными членами, которые
могут зависеть от 0 и
его производных, яв- фиг# 2. Углы отклонения по осям
ляются те, которые со-	стабилизации,
держат со0
Т • «о+Т • %+“оХт • ю0 + (1>0Х н.	(21)
N =
Здесь Н = 2^ • <*>/— кажущийся, момент количества движе¬
ния подвижных элементов с точки зрения наблюдателя
в системе координат XYZ. Обозначим оставшиеся члены
уравнения (12), которые представляют собой в чистом виде
функции времени, через D0(f)«
Подставляя выражение для соо в уравнение (21), выразим
ту часть возмущающего момента, которая содержит 0Ь 62, 0з,
в виде3)
D(0+ {?• ®' + (т + 2т X W + 2Tх Н) • 0' 4-
+ lTXw+-fXw-f(TXw)Xw + (w- liE— (1)Н)] • 0), (22)
!) См. стр. 274 настоящей книги.
2) Здесь 0' — производная по времени только от составляющих, как
если бы основной вектор был постоянным.
3) Здесь 0' и 0' — производные по времени только от составляющих,
как если бы основной вектор был постоянным.

302 ш. стабилизация положения Космических аппаратов
где
D(/) = 'f-(o + i- (i)4-(oXT'W + wXH	(23)
зависит только от движения осей xyz и внутренних элемен¬
тов, но не от движения самого спутника, а Е — единичный
тензор (матрица). При выводе уравнения (22) сохраняются
только члены первого порядка для 0 и 0'. В уравнении (22)
величина, взятая в скобки и обозначаемая через Р(0, t),
является зависимой частью возмущающего момента, полной
величиной первого порядка относительно 0, т. е. моментом
параметрического возбуждения. Полный возмущающий мо¬
мент можно представить в виде выражения LP = D0(^) +
+ D^) + Р(0, t). Таким образом, члены параметрического
возбуждения можно отделить от членов эффективного внеш¬
него возмущения и каждый из них представить в виде про¬
стого уравнения.
Для главных осей X*7*Z* матрицу Г + 7 получает диаго¬
нальную форму, при этом тензор Г имеет диагональную
форму относительно системы координат XYZ
Задача заключается в определении такого вращения системы
координат XYZ в системе координат Х*У*Z*, в результате
которого матрица Г + 7 приобретает диагональную форму
а также в определении главных моментов 0v 02> с7з- Это
хорошо известная задача, для которой уже найдены общие
решения. Одним из специальных случаев является простое
разложение на составляющие
7 = Тце^е* + Тивхвк + Ti3e*ez +	+ • • • (Ту = Т/<)-
Допустим, что 712, 723, 7з1 — малые величины по сравнению
с разностями (/1 — /2), {h — h),	—	соответственно.
В этом случае углы ф* между главными осями и осями тела
малы и имеют значения1) ф1 = 723/(/2 — /з) с точностью до
членов второго порядка малости. Кроме того,
ГЛАВНЫЕ ОСИ
Г — /i^x^X “b ^2^Y^Y “Ь ^3eze.
3czcz-
*) Аналогично для ф2 и Фз с циклической перестановкой индексов.

МОМЕНТЫ ВРАЩЕНИЯ, СОЗДАВАЕМЫЕ ВНУТРИ СПУТНИКА 303
/Для 9ч> 9 ъ имеем такую же формулу, но с циклической пе¬
рестановкой индексов.) Из этого выражения вытекают два
основных следствия. Во-первых, с помощью углов ф можно
представить недиагональные составляющие матрицы 7 в виде
членов, выраженных по осям смещения инерции, что играет
немаловажную роль в представлении физической сущности
данной проблемы. Во-вторых, уравнение (24) позволяет упро¬
стить выражения для других моментов, воздействующих на
спутник. Сюда относятся в основном гравитационные моменты,
в которые не входят величины /ь /2 и /3, но зато входят
величины 992 и 9г-
Как видно, члены параметрического возбуждения обеспе¬
чивают перекрестную связь между движениями по углам 0Ь
02 и 0з- Непосредственная связь движений (01—03) уже рас¬
сматривалась нами1), но 02 — независимое движение, за
исключением эффекта, приведенного в статье. Если 712 =
= 723 = Нх = Hz = 0, то составляющая Ру(6; t) зависит
только от 02, при этом предлагаются возможные конструктив¬
ные условия для обеспечения того, чтобы возмущения по 01
и 03 не проникали в движение по 02.
Относительно момента Di(^) следует заметить следую¬
щее: во-первых, наличие суммарного вектора Н (с теми со¬
ставляющими, которые не обращаются в нуль) неизбежно
приводит к вынужденным колебаниям в уравнениях стаби¬
лизации. Однако эти колебания могут быть сведены до ми¬
нимума путем сохранения малых значений величин Нх и #z,
если соответствующим образом вращать вектор Н на спут¬
нике. Во-вторых, путем выражения Di(£) через составляю¬
щие и отбрасывания произведений малых членов можно
показать, что составляющими у» которые в основном эффек¬
тивны в образовании внешних моментов, являются 7i2 и 723
и их производные (те же самые недостатки, что и при ука¬
занной выше связи 02 с 01 и 03). Исчезновение этих составляю¬
щих означает, что смещение осей инерции, вызванное внут¬
ренними подвижными элементами, имеет место относительно
оси У.
ЛИТЕРАТУРА
Roberson R. Е., см. стр. 249 настоящей книги.
!) См. стр. 249 настоящей книги. — Прим. ред.

ПРИНЦИПЫ ИНЕРЦИАЛЬНОЙ СТАБИЛИЗАЦИИ
ИСКУССТВЕННЫХ СПУТНИКОВ')
Роберсон
Предлагается классический способ управления положением (стабили¬
зации) спутника или космического корабля при помощи инерционного
реактивного момента вращающихся внутри спутника или космического ко¬
рабля маховиков. Даются основные аналитические выражения для управ¬
ления положением при использовании любого числа подвижных и вращаю¬
щихся элементов. Приводятся выражения для управляющих моментов и
дается формулировка задачи синтеза системы управления в виде выбора
уравнений регулирования и накладываемых физических ограничений. Рас¬
сматриваются два примера с вибрирующими массами и вращающимися
маховиками для иллюстрации задачи синтеза.
ВВЕДЕНИЕ
Для управления ориентацией спутника или космического
корабля часто предлагают использовать инерциальные сред¬
ства в виде воздействующего на корабль инерционнного
реактивного момента от ускорения некоторой массы относи¬
тельно корабля. Этот метод уже был детально освещен в ли¬
тературе по астронавтике. Так, например, в работе [1] эта
проблема описана с предельной ясностью.
Физическая реализация этого принципа возможна в раз¬
личных формах. Сюда относятся выбрасывание вещества из
корабля и использование трех двигателей на борту корабля,
активные и пассивные поглотители вибраций, активные и
пассивные гиростабилизаторы, механически ориентируемые
маховики постоянной скорости, вращение жидкости по замк¬
нутому контуру и давление излучения. Все это — инерциаль¬
ные устройства. Кроме того, возможны, конечно, способы ста¬
билизации, основанные не на инерциальных методах, а на
взаимодействии корабля с одним или несколькими видами
окружающих полей.
В работе [2] выведены выражения для реактивного инер¬
ционного момента от перемещающихся и поворачивающихся
!) Roberson R. Е,, Ргос. IXth Intern. Astronaut. Congress, Ь
pp. 33—43, 1959,

ПРИНЦИПЫ ИНЕРЦИАЛЬНОЙ СТАБИЛИЗАЦИИ СПУТНИКОВ 305
вНутри спутника элементов. При этом предполагалось, что
известен закон движения этих элементов во времени в си¬
стеме отсчета, связанной с корпусом космического корабля.
Цель настоящей статьи — рассмотреть случай, когда к
этим элементам добавляются еще один или несколько упра-
вляющих элементов.
В последующих разделах статьи выводятся выражения
для управляющих моментов и дается динамическое описание
движения системы, состоящей из собственно корабля и всех
управляющих элементов. Рассматриваются природа физиче¬
ских ограничений и сущность уравнений регулирования, ко¬
торые нужно рассматривать как часть синтеза заданной си¬
стемы. Приведены также два примера физических методов
регулирования положения. Однако здесь не рассматривается
синтез какой-либо инерциальной системы стабилизации.
Это — трудная задача (как это будет видно из дальнейшего),
и ее следует рассмотреть в отдельной работе на основе прин¬
ципов, излагаемых ниже.
Мы не рассматриваем также случаи стабилизации при
помощи реактивных струй и давления излучения, хотя они и
являются инерциальными, и ограничиваемся вопросами ста¬
билизации при помощи внутренних подвижных элементов.
Уравнения движения в рассматриваемых примерах сильно
упрощаются, если ввести параметрическое возбуждение и
другие малые члены в соответствии с принципами, изложен¬
ными в работе [3]. Это позволяет сосредоточить внимание на
основных сторонах проблемы стабилизации, не учитывая
второстепенные факторы, которые появляются при более
точном рассмотрении. Однако не следует забывать, что эти
малые факторы играют главную роль в определении точно¬
сти регулирования положения спутника. При более тщатель¬
ном рассмотрении их нужно обязательно учитывать.
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Воспользуемся обозначениями, принятыми в работе [2]
Пусть XqYqZq представляет правую ортогональную систему
координат, связанную с основным корпусом космического
корабля В0, причем начало координат находится в центре
массы этого корпуса. Ориентация осей_ выбирается так,
чтобы матрица осевого момента инерции /0 была диагональ¬
ной !).
]) Иначе говоря, чтобы оси Xq, То и Zo являлись главными осями
инерции. — Прим. перев.
20 Зак. 876

306 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Пусть pi (i =	1,2, .. N) обозначает	положение	центра
массы i-то отдельного подвижного элемента В{ относительно
системы X0Y0Zo; 0)0 — угловую скорость корабля В0 в инер¬
циальном пространстве, a	угловую скорость В{ относи-
тельно В0. Обозначим через U тензор осевого момента инер¬
ции для	Biy вычисленный относительно	осей,	проходящих
через центр массы В* и параллельных осям X0Y0ZQ.
Определим положение общего центра масс
N
R = m*i>	0)
/ = 1
где nti — масса Ви а т — общая масса корабля и всех его
частей
• ?Д— РгРг),	(2)
/(= то (R • R£ — RR)	(3)
(здесь для единичного значения величины J введен сим¬
вол Е).	_	__
Обозначим через Г и 7 соответственно постоянную и пе¬
ременную части выражения
Аз + 2^+2л—к	(4)
/ = 1	i = 1
в том смысле, как это сделано в работе [2]. Там же показано,
что возмущающий момент системы от вращающихся частей
равен
Здесь уi и V соответственно кажущиеся скорости центра
массы Bi и общего центра масс с точки зрения наблюдателя
в системе координат X0Y0Z0.
Найдем выражение для управляющего момента от вну¬
тренних подвижных частей.
УПРАВЛЯЮЩИЕ (СТАБИЛИЗИРУЮЩИЕ) МОМЕНТЫ
Добавим к N вышеупомянутым элементам, движение ко¬
торых описывается известными функциями времени,
М — N 1 элементов, предназначенных для управления.

ПРИНЦИПЫ ИНЕРЦИАЛЬНОЙ СТАБИЛИЗАЦИИ СПУТНИКОВ 307
Пусть
N
Шр — 2 щ'- Rp
/ = 1
м
тс= ^ mi’ Rс
/ = ЛЧ-1
Тогда в равенствах (3) и (5) величину R можно заменить
выражением
R=^tRc+^Rp.	(7)
Предположим, что в (7) величина Rс не имеет постоянной
составляющей. Хотя в общем случае она и существует, для
удобства ее следует отнести к величине Rp. Это обстоятель¬
ство не ограничивает общности рассуждений.
Рассмотрим выражение (4) для расширенного случая и
для новой величины К
( - _ N 2 _ )
Го+ S т, + 2 Jr- -^-(Rp • R рЕ~ Rp • Rp) +
[i = l i=1	J
( M	M	2
+	2^+2	~uT(Rc ■ Rc^— RcRc)—
L U = A4-1 l = N+1
(2RC • Rp^ RcRp RpRc j •	(8)
Обозначим через Г постоянную часть всего выражения (8),
через -у — переменную часть первого выражения в скобках,
через ф — переменную часть второго выражения в скобках.
Так же как и в работе [2], введем связанную с В0 новую си¬
стему осей XYZ, рассматриваемую далее в качестве основной
системы, ориентация которой выбирается так, чтобы матрица
Для Г была диагональной.
Полный момент от перемещающихся и управляющих
элементов определяется уравнением (5), где величина j за¬
менена на (т + Ф) и суммирование производится по всем М
и i = 1
М
1 V
:ЖГ 2
i = N+1
(б)
20*

308 Ш. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
элементам, т. е.
(	N	N
LP + LC = — ■^•{T*»o+S7|-®i + Sm»P<x vt~
{	1 = 1	1 = 1
m2	I f	M	M
~^RpXVpf~S Ъ'Ч>1+ mi?tXVi —
)	{	i	=	N+1	i	=	N+l
-^RcXVc-^^(RcXVP+RpXVc)j, (9)
В этом уравнении LP отождествляется с производной от
первого выражения в скобках, a Lc — с производной от вто¬
рого выражения в скобках. Все члены в выражении для Lc
подлежат выбору для целей управления, исключая о>о, кото¬
рый представляет собой основную зависимую переменную,
характеризующую движение спутника, а также величин RP
и VP, которые рассматриваются как заданные функции вре¬
мени. Рассуждая так же, как и при выводе уравнения (12)
в работе [2], и замечая, что
~df (Rc X Vp -f- Rp X Vc) = Re X Ap -f-
+ Rp X Ac-f-(o0 X (Rc X Vp-]- Rp X Vc), (10)
управляющий момент можно записать следующим образом:
Lo = ф • <*>0 Ф * wo “Ь wo X ф • <*>0 +
м	=
+ 2 1^/ '	‘	w/	+	K+wi)X//	•	+	X Я/ +
L=N+1
m2r
+ щюо X (р/ X v,-)}	— {Rc X Ар + со0 X (Rc X Vc)}
—-c~ P~ {Rc X Ap -f- Rp X Ac + (o0 X (Rc X Vp + Rp X Vc)} •
(П)
Здесь а*, Ac и AP — ускорения соответственно для векторов
Pi, Rc и Rp относительно системы X0YQZQ, Vc и Vp — скоро¬
сти. Точки под двойной чертой означают дифференцирование
по времени, если смотреть с точки зрения наблюдателя, на¬
ходящегося в В0.
В силу сделанного предположения (7) если все упра¬
вляющие элементы неподвижны, то Rc = 0 и Lc обращается
в нуль, как это и должно быть.

ПРИНЦИПЫ ИНЕРЦИАЛЬНОЙ СТАБИЛИЗАЦИИ спутников 309
УРАВНЕНИЯ ДВИЖЕНИЯ
Уравнения движения спутника могут быть записаны в та-
к0м же виде, как и уравнение (10) в работе [2]:
(Г * <*>о)= L Lp (со0; t) Lc,	(12)
где L — сумма всех внешних моментов, действующих на си¬
стему, и отмечена явная зависимость LP (члены параметри¬
ческого возбуждения) от соо и от времени. Величину (о0
можно выразить только через угловые скорости 0Ь 02, 0з от
желаемых значений, как это сделано в работах [3] и [4].
Проблема инерциального управления заключается в надле¬
жащем выборе Lc, чтобы этот управляющий момент обеспе¬
чивал «наилучшую компенсацию» (согласно еще не опреде¬
ленному критерию) воздействий L и LP.
Посмотрим, как это можно сделать. Осуществить упра¬
вление— это значит заставить управляющие элементы пере¬
мещаться относительно ракеты, т. е. заставить ©г и
р. (/ = N + 1, ..., М) изменяться определенным образом.
В свою очередь эти переменные можно связать с моментами
Ьг, которые создаются частями (элементами) спутника, за¬
писав уравнения динамики движения в следующем виде:
^- = L, (i = N+ 1,	М).
Н,- — h • («о0+ Wf) + Щ (рг — R) X (Рг — R),
(13)
где R определяется уравнением (7).
Будем считать, что векторные величины а>0, о)г, pt, Li
являются основными зависимыми переменными в задаче.
Они представляют 3 + 9 (М — N) зависимых скалярных пе¬
ременных. Система уравнений (13) соответствует 3(М — N)
скалярным дифференциальным уравнениям, которые связы¬
вают эти неизвестные. Присоединив к ним уравнение (12),
которое соответствует трем дополнительным скалярным
уравнениям, содержащим те же неизвестные, и используя
выражение для Lc, определяемое уравнением (11), мы полу¬
чаем всего 3 + 3 (М—N) уравнений для 3 + 9 (М—N) не¬
известных, и, следовательно, необходимо присоединить еще
6(М — N) уравнений, с тем чтобы система стала полностью
определенной. Тогда можно найти движение самого спутника
и его (М — N) управляющих элементов, а также, если мы
пожелаем, (М — N) моментов взаимодействия. (Обычно их
находить не требуется, и они исключаются, как будет
показано ниже.)

310 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Уравнения, которые делают нашу систему полной, это
такие, которые показывают, как моменты взаимодействия за¬
висят от движения спутника и от времени, и которые следо¬
вало бы назвать уравнениями регулирования (стабилиза¬
ции), а любые ограничения, которые учитываются при физи¬
ческой реализации регулирующих устройств, можно назвать
уравнениями физических ограничений. Эти уравнения, воз¬
можно, являются основными, так как они отражают заранее
выбранный нами способ механизации системы регулирова¬
ния. Например, если принято решение взять в качестве упра¬
вляющего элемента Вк электродвигатель, вращающийся
в закрепленных подшипниках относительно оси, расположен¬
ной по оси X объекта, как это предлагается в работе [1], то
в качестве физических ограничений следовало бы использо¬
вать равенства
Рк — const,	|
Кг)х = °>	|	(И)
(<лк)у = (о)K)Z	- 0,	J
где о — скорость двигателя относительно наблюдателя, нахо¬
дящегося в В0* (Напомним, что ык — угловая скорость отно¬
сительно Во-)
Следует наложить по крайней мере 3 (М — N) таких ог¬
раничений (по причине, которая будет видна ниже); число
их может быть произвольно и может достигать максималь¬
ной величины 5(М — N). Однако нельзя на один регулирую¬
щий элемент накладывать шесть скалярных ограничений,
так как это не дало бы возможности осуществить функцию
регулирования. Предположим, что наложено 3(М — N) + С
таких скалярных ограничений.
Уравнения регулирования, число которых должно быть
равно 3(М — N)—С, будут рассматриваться в следующем
разделе; здесь же мы дадим несколько предварительных по¬
яснений относительно общего подхода к решению задачи.
По-видимому, наиболее непосредственный подход к про¬
блеме заключался бы просто в написании замкнутой системы
уравнений движения объекта и регулирующих элементов
в виде
^(г.«0) = ь-ц-^Ц
ЧГ — Ч-
(15)
Можно попытаться избежать утомительных расчетов по
уравнениям (11) с заменой членов с dWi[dt выражениями,

ПРИНЦИПЫ ИНЕРЦИАЛЬНОЙ СТАБИЛИЗАЦИИ СПУТНИКОВ 311
которые в конце концов содержали бы уравнение движения
основного объекта. Однако такая процедура была бы не
совсем эквивалентной, так как уравнения (15) являются не
совсем точными выражениями. Именно, Ьс=£2Ьг-, так как Lc
содержит также члены параметрического возбуждения, ко¬
торые связаны с переменной инерцией и которые следовало
бы перенести в правую часть уравнений. Если бы это было
учтено, то в левой части уравнений (15) стояла бы скорость
изменения полного кинетического момента, который в нашей
задаче выражался бы тензором инерции с переменными
коэффициентами относительно системы XYZ.
УРАВНЕНИЯ РЕГУЛИРОВАНИЯ
Выбор уравнений регулирования представляет собой про¬
блему синтеза. Она эквивалентна нахождению L2 в виде
векторной функции от ©о, о)г, Р/ и t таким образом, чтобы
получить удовлетворительные динамические свойства систе¬
мы. Общая форма этих уравнений имеет вид
L, = f, к, в>„ Р„ о»	(16)
что соответствует 3(УИ — N) скалярным уравнениям. Так как
произвольно выбирается только 3(М — N) соотношений для
моментов, то отсюда следует, что необходимо наложить по
крайней мере 3 (М — N) физических ограничений. Если же
желательно использовать для управления элементы, вращаю¬
щиеся каждый вокруг одной оси, то нужно выбрать только
М — N соотношений для моментов и 5 (М — N) физических
ограничений.
Если после наложения всех желаемых ограничений оста¬
лось выбрать только 3 (М — N)—С соотношений для момен¬
тов, то остальные С моментов выбираются так, чтобы движе¬
ние элементов подчинялось наложенным ограничениям.
Если бы L являлось вполне заданной функцией времени,
то Li можно было выбрать также в виде функций времени
так, чтобы их суммарный эффект уравновесил внешний мо¬
мент. Однако величина L?: не является известной функцией
по следующим причинам:
1) из-за случайного характера возмущений (таких, на¬
пример, как столкновения с метеорными частицами);
2) из-за того, что современное представление о возмуще¬
ниях не адекватно определенным функциям времени.
Отсюда следует, что для создания противодействия этим
возмущениям регулирующие моменты должны зависеть от
отклонений в положении спутника (в общем случае включая

312 HI. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
производные от этих отклонений и интегралы от них), что
в действительности и имеет место. Такая зависимость может
быть записана в виде уравнений (16).
Момент LP можно компенсировать двумя способами. Так
как этот возмущающий момент обусловлен перемещающи¬
мися элементами, естественно рассмотреть компенсацию
также при помощи перемещающихся элементов. Этот способ
достаточно прост и имеет то преимущество, что влияние Lp
можно компенсировать, не прибегая к измерению отклонений
в положении. Однако исходя из соображений для энергии
или массы или же из того факта, что некоторые составляю¬
щие Lp сами предназначены для компенсации некоторых до¬
лей величины Lp, предпочтительнее рассматривать LP только
как дополнительное внешнее возбуждение, которое должно
подавляться надлежащим выбором уравнений движения ре¬
гулирующих элементов.
Неотделимым вопросом от уравнений регулирования яв¬
ляется вопрос о критерии регулирования, т. е. о том, яв¬
ляются ли выбранные L2 достаточно совершенными. В сущ¬
ности углы эволюции 0i, 02, 0з относительно исходных напра¬
влений следует сохранять по возможности малыми и согла¬
сующимися с требованиями экономики (по весу, расходу
мощности, надежности и т. д.). Некоторые требования оче¬
видны. Если уравнение (12) неустойчиво1) при отсутствии
LСу то уравнения регулирования должны обеспечить устой¬
чивость. Если движение, описываемое уравнением (12), яв¬
ляется незатухающим, затухание должно обеспечиваться
при помощи Lг (чтобы избавиться от больших начальных
условий, если нет других возмущений). По-видимому, наи¬
более важным в выборе L* является анализ практических
возможностей механизации. Однако очень трудно сформули¬
ровать критерий, который достаточно точно позволил бы вы¬
брать параметры регулирования в уравнении (16) даже
в том случае, если известна общая форма функций f*. Эта
проблема подробнее будет рассмотрена ниже, хотя для при¬
водимых примеров развернутого ответа на поставленный во¬
прос не требуется.
УРАВНОВЕШЕННЫЕ СИСТЕМЫ
Существует класс систем, для которых управляющий мо¬
мент имеет более простую форму, чем уравнение (11),
1) Такое положение может возникнуть при наличии параметрического
возбуждения от LP или же в том случае, когда L содержит дестабилизи¬
рующие члены, включающие углы эволюции.

ПРИНЦИПЫ ИНЕРЦИАЛЬНОЙ СТАБИЛИЗАЦИИ СПУТНИКОВ 313
„ричем центр масс управляющих элементов инвариантен от¬
носительно спутника. Примером могут служить маховики, вра¬
щающиеся относительно фиксированных осей и перемещаю¬
щиеся части которых уравновешиваются равными и противо¬
положно двигающимися частями. В этом случае мы полагаем
== 0, так как эта величина в уравнении (7) характеризо¬
вала перемещение центра	масс	управляющих	элементов.
Тогда
( м = =\
ф = Переменная	часть!	2 (АН-^*)!	(17)
I / =N+1	)
И
— — =	М — . ==
Lс = ф • <*>0 + ф • w0 + (о0 X ф *	<*>0	2 (А * w£ ~+~ А * ~f~
i=N\l
+ К + щ) X A * <*>, + Щ?1 X a, + mp0 X (p* XvJ). (18)
Рассмотрим в качестве иллюстрации два типа среди мно¬
жества предложенных в работе [1] устройств регулирования.
Из формы уравнения (11) видно, что эти типы устройств не
исчерпывают все возможные классы систем. Однако на этих
примерах будет раскрыт общий способ анализа подобных
систем; кроме того, они не лишены определенного интереса.
РЕГУЛИРОВАНИЕ С ВИБРИРУЮЩИМИ МАССАМИ
Рассмотрим движение двух точечных масс, находящихся
вне оси, относительно которой нужно осуществить регулиро¬
вание (стабилизацию). Пусть этой осью является ось У,
а точечными массами являются массы mN+i = mN+2 = V2W1,
причем центр масс этих точек расположен на оси У, т. е. они
образуют уравновешенную систему. Условием ограничения
колебаний Pj только относительно оси У, которое наклады¬
вается для регулирования относительно этой оси, является
равенство р4У = const; задача упрощается, если положить
эту константу равной нулю, при этом существенные особен¬
ности примера не теряются. Предположим также, что других
перемещающихся элементов не имеется. В этом случае
РлГ+1 =	P/V+2 — Р\> Av + 1 = Av+2 = Rp = Rc =0.
Если ввести для переменной части какой-либо величины
обозначение ( >, то
Ф — т\ z) (exez ezex)*

314 HI. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Следовательно,
Lc = щ£х ( (PixPiz) (^z + ^x^r) 2plzplxcoz) -f-
Щ£у {PixPlZ PizPix ~l~ (PixPiz) 03z)} +
+ ^iez { (PixPiz). (wx H- ^y°>z) 2plxplzo)x}. (19)
Предположим, что для регулирования выбрана только одна
составляющая момента (Ln+i)y=L. Ее связь с движением
элементов можно определить, найдя проекцию уравнения
(13)	на ось У:
т\ [PixPiz	PizPix* “Ь PixPiz(шх ^z) (Рх +Pz)cor +
+ 2 (PixPix-^ PizPiz) (0K_b(Piz Piz) ^x^z] =	(20)
Полученный результат (L^ + i) Ф (Lc)y на первый взгляд
может показаться удивительным, однако при этом следует
иметь в виду, что Lc включает в себя не только реакцию от
регулирующих элементов, но и члены параметрического воз¬
буждения, которые появляются из-за непостоянства инерции
системы.
Другой интересной особенностью является то, что (Lc)x
и (Lc)y отличны от нуля. Таким образом, любая попытка
использовать для регулирования устройство, подобное опи¬
санному, вносит в уравнения по крену и курсу моменты
взаимодействия. Однако для движения по тангажу вносятся
только члены второго порядка малости !). Следовательно, за¬
висимость движения по тангажу от движений по курсу и
крену достаточно слаба, и, таким образом, основное влияние
(Lс)х и (Lc)y заключается во внесении в уравнения движе¬
ний по курсу и крену членов параметрического возбуждения.
(Если pix и piz являются функциями соy, то осуществляется
косвенное взаимодействие; если же pix и piz являются функ¬
циями только времени, то и моменты будут являться момен¬
тами чистого параметрического возбуждения.)
Следующий вопрос касается числа зависимых перемен¬
ных и уравнений. Используя уравнение (17) для решения
уравнения (12), получим систему из трех уравнений с пятью
зависимыми переменными сох, соу, соz, pix, piz, в то время
как уравнение (20) содержит переменные pix, piz, сох, coy.
coz, L. Следовательно, для полного определения задачи нам
не хватает одного уравнения. Мы свободно можем наложить
*) См. явные выражения в [4] для <ох> coz> coz через углы тангажа,
курса и крена и их производные.

ПРИНЦИПЫ ИНЕРЦИАЛЬНОЙ СТАБИЛИЗАЦИИ спутников 315
физическое ограничение на геометрию траектории движения
масс, которое даст зависимость между р1Х и plz. Это условие
будет отражать только механическую реализацию, выбран¬
ную для регулирующего устройства. Уравнения (19) и (20)
можно применить к большому классу регулирующих
устройств. Наложение дополнительного ограничения на pi
сводит задачу к определению одного регулирующего устрой¬
ства.
Классическим примером инерциального управления поло¬
жением является пример падающей кошки, управляющей
своим положением при падении. Такое управление она осу¬
ществляет изменением момента инерции, выбрасывая или
убирая свои лапы, что изменяет относительное вращение
частей туловища.
Полезно также рассмотреть случай простого вибрирую¬
щего демпфера. Пусть массы, все время оставаясь на по¬
стоянном расстоянии ± а от плоскости XY, будут ограниче¬
ны в своем движении вдоль оси X только малыми расстоя¬
ниями. В этом случае pi* = е (переменная) и piz = а (по¬
стоянная). Тогда
(Lс)у = тга [е + е(о)х —(*)z)L	(21)
(Lyv+i)k ~ Щ	(^x	—	03z)4-{cl -f- e ) u>Y-f-
+ 2ssa-f- (a2 — s2) а>ха>г]. (22)
Будем придерживаться рассуждений, приведенных в дру¬
гой работе автора1), и используем из этой статьи проекцию
уравнения (12) на ось У, даваемую уравнением (25) в выра¬
жениях для отклонения по тангажу 02 и учитывающую часть
внешнего возмущающего момента, который обусловлен гра¬
витационным полем Земли. В результате будем иметь при¬
ближенно
Ву®2 {IX “— Iz) ^2 == Ly —	(23)
щ (as + a202) = L.	(24)
Здесь через со0 (не следует путать с прежним соо) обозначена
орбитальная угловая скорость спутника, а через lx, Iy, Iz—
компоненты тензора инерции при условии, что матрица имеет
Диагональную форму, обусловленную выбором осей XYZ
[см. замечания к уравнению (8)].
1) См. стр. 249 настоящей книги. — Прим. ред.

316 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Проблема заключается в выборе L в зависимости от е и
б2, чтобы получить характеристику по 02, которая имела бы
желаемую форму. Как уже отмечалось ранее, это—проблема
синтеза, которая в силу своего объема и важности может
служить темой самостоятельной работы. Однако сейчас мы
вкратце остановимся на двух возможностях.
Если 1Х > Iz, то, как видно из уравнения (23), движение
по 02 устойчивое, но не затухающее. Представим, что произ¬
веден выбор ае = С02. Это приводит к тому, что 02 удовлетво¬
ряет уравнению для простого колебательного движения. Вы¬
ражение (23) показывает также, что L = тх (С02 + а202).
Поэтому можно сказать, что если движение по тангажу
можно как-то зарегистрировать, то требуемая сила L/a, дей¬
ствующая на массы, оказывается известной и ее можно со¬
здать, используя надлежащую следящую систему.
Другая простая возможность заключается в том, чтобы
использовать пассивное взаимодействие масс со спутником,
характеризуемое следующим уравнением:
Ь = -(С^ + С2в).	(25)
При этом уравнение (24) принимает вид
тхаг -f- Схе -f- С2е = — тха2Ь2.	(26)
Система уравнений (26) и (23) будет эквивалентна ли¬
нейному дифференциальному уравнению четвертого порядка
относительно 02; выбор Сх и С2. может обеспечить необходи¬
мый вид характеристик по 02. При этом следует иметь ввиду,
что хотя величина г и исключается, но ее нельзя игнориро¬
вать, так как для выбранных С{ и С2 и 02(/) с помощью
уравнения (26) можно получить характеристику е(Ц, кото¬
рая может не соответствовать механическим ограничениям и
сделанным допущениям. Наилучший план синтеза должен
состоять в том, что сначала находится решение 02(/) и затем
вычисляется движение по е и производится оценка, удовле¬
творяет, ли оно физическим процессам.
РЕГУЛИРОВАНИЕ С ВРАЩАЮЩИМИСЯ МАХОВИНАМИ
Два маховика, элементы N + \ и N + 2, вращаются
в фиксированных подшипниках. Ось вращения одного махо¬
вика расположена вдоль оси X, и этот маховик используется
для регулирования по оси X. В аналогичных условиях рабо¬
тает и маховик для оси Z. Предположим, что оба маховика

ПРИНЦИПЫ ИНЕРЦИАЛЬНОЙ СТАБИЛИЗАЦИИ СПУТНИКОВ 317
идентичны, причем через I обозначен полярный, а через / —
экваториальный момент инерции. Предположим также, что
других вращающихся частей нет и что Rc = 0.
физические ограничения возьмем в виде уравнения (14),
где о = Ох\ Ран-2 = 0:
(a)^v+2)x = (^лг+г)}' =
(^лг+гЬ = az-
Для данного случая ф = 0
£/v+i =/exex + ‘/(eKer + ezez)^ 1	/274
^ N+2 = J (еХеХ + еУек) + ^ezeZ- J
Таким образом, из уравнения (18) получаем
Lc — ^ (ax + °Yaz) ех Н“ ^(®гах — 0}xaz) ег “W(az “y^x) ez- (28)
В уравнении (13) нас интересуют только моменты
(Ln + i)x = L\ и (Ljv + 2)z = L3, так что
^ (°х + шх)=
^ (az ~t“ ^z)= ^з*
В уравнении (28) вновь замечаем взаимосвязь движений по
X и Z с движением по У, но, как и в предыдущем примере,
она оказывается слабой. Используя методику работы [3] и
переходя к отклонениям по углам 01 и 02 относительно осей
X и Z, получаем
^x®i + 4о)о(Jy — ^)01 + шо(Ax + ^z iy) h=Lx ^(ax~b 0)y°z)>
(30)
^z*03 +	(/у — ^x) 0з — (Лс + ^z ^r) 0i = Az ^ (°z a)rax) •
(31)
Здесь имеется главная взаимосвязь движений по X и Z,
которую нельзя не учитывать. Проблема состоит в выборе
Функций L\ и L3 в зависимости от 61 и бз и их производных,
с тем чтобы решения системы уравнений (29) —(31) для 01
и б3 имели бы нужные свойства. Как можно видеть, это —
Довольно сложная задача, которую нельзя решить в данной
статье.

318 HI. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Аналогичный маховик может быть использован для регу¬
лирования относительно оси У, если, конечно, дополнить этот
маховик схемой, описанной в in. Этот способ до некоторой
степени проще, ибо он не имеет описанной выше взаимосвязи
с регулированием по X и Z, за исключением членов второго
порядка малости.
ЛИТЕРАТУРА
1. Esnault-PelterieR., L’Astronautique, Paris, 1930.
2. Roberson R. E., Torques on a Satellite Vehicle from Internal Moving
Parts. J. Appl. Mech., 25, 196 (1958). См. стр. 284 настоящей книги.
3. Roberson R. E., Attitude Control of a Satellite Vehicle — An Outline
of the Problems, см. стр. 249 настоящей книги.
4. Roberson R. E., Torques on a Satellite Vehicle from Internal Moving
Parts (Suppl.), J. Appl. Mech., 25, 281 (1958). См. стр. 300 настоящей
книги.

ДАТЧИК ПОЛОЖЕНИЯ ДЛЯ КОСМИЧЕСКИХ
КОРАБЛЕЙ')
Кендолл, С то л кап
В статье рассматриваются основные особенности конструкции датчика
положения (высотомера), который обладает достаточной компактностью
и обеспечивает необходимую надежность измерений.
Задача заключалась в разработке прибора, который обеспечивает про¬
стой способ определения вертикали с борта корабля, находящегося на ор¬
бите, на наблюдаемую с корабля планету. Эта задача была выполнена за
счет использования двух узких инфракрасных лучей, производящих непре¬
рывное сканирование. Центральная ось каждого луча вращается с по¬
стоянной угловой скоростью в плоскости, причем плоскость сканирования
одного луча перпендикулярна плоскости сканирования другого. Активный
сектор сканирования равнялся 270° для каждого луча. Когда луч пересе¬
кает поверхность планеты, уровень сигнала скачкообразно возрастает. По¬
ложение луча, соответствующее середине ступенчатого сигнала, определяет
плоскость, в которой расположен центр планеты. Пересечение двух таких
плоскостей, образуемых двумя сканирующими лучами, определяет напра¬
вление местной вертикали, опущенной на поверхность планеты. В статье
приводится детальное описание прибора.
С помощью аналогового счетно-решающего устройства можно опре¬
делять углы тангажа и крена относительно опорной вертикальной линии.
При добавлении в состав аппаратуры гироскопа с одной степенью свободы
можно получать информацию о рыскании для корабля, находящегося на
орбите.
В заключение рассматривается метод измерения высоты корабля над
планетой.
В ВЕДЕНИЕ
По мере приближения эры космических путешествий во¬
просы, связанные с управлением космическим кораблем,
усложняются и в то же время приобретают большее значе¬
ние. Первые искусственные спутники были очень простыми,
так как возможности для размещения на их борту измери¬
тельной аппаратуры были очень ограничены и вопросами
ориентации корабля почти пренебрегали. В последующие
годы определение положения космического корабля приобре¬
тало первостепенное значение не только с точки зрения зна¬
ния этого параметра, но и для управления положением ко¬
рабля. Например, если фотографировать поверхность Земли
■) Kendall P. Е., St a leu р R. Е., Proc. IRE, 48, № 4, 765—770
(April 1960).

320 ш. стабилизация положения космических аппаратов
с такого корабля, то желательно иметь возможность ориен¬
тировать фотоаппаратуру в направлении Земли в течение
длительного времени пребывания спутника на орбите.
Проблема определения положения осложняется на ко¬
рабле, вращающемся вокруг своей оси. Очень часто спутни¬
кам при запуске придается вращательное движение, имею¬
щее целью стабилизировать их положение и обеспечить по¬
стоянное направление тяги. В общем случае скорость враще¬
ния контролируется не слишком точно, однако при запуске
кораблей с человеком на борту такое вращение может быть
недопустимым; может оказаться также желательным под¬
держивать скорость вращения в пределах некоторой заранее
определенной величины. При рассмотрении проблемы разра¬
ботки прибора для определения положения, который мог бы
работать как на вращающихся, так и на стабилизированных
кораблях, было выбрано устройство, которое может работать
даже в условиях, когда скорость вращения будет достигать
60 об/мин. Диапазон измеряемых высот был выбран в пре¬
делах 270—1100 км\ измерение более значительных высот
потребовало бы уменьшения ширины луча. Прибор для опре¬
деления вертикали, описанный в настоящей статье, был
сконструирован с таким расчетом, чтобы он имел минималь¬
ный объем и мог работать в течение длительного времени,
например в течение двух лет или дольше. Имея в виду, что
описываемый прибор будет полезен для многих типов косми¬
ческих кораблей, конструкторы предусмотрели возможность
измерения различных параметров, а именно тангажа, крена
и рыскания относительно локальной вертикали, а также
определения высоты. Если измерение высоты не обязательно,
то размеры и вес прибора существенно уменьшаются. При
исключении измерения рыскания можно достигнуть еще
большего уменьшения размера и веса. Прибор выполнен в
виде блочной конструкции и поэтому допускает такие ва¬
рианты его использования.
ОПРЕДЕЛИТЕЛЬ ГОРИЗОНТА
Сканирование производится двумя узкими лучами одно¬
временно. Центральная ось каждого луча вращается с по¬
стоянной угловой скоростью в заданной плоскости, причем
плоскость вращения одного луча перпендикулярна плоскости
вращения другого. Эти плоскости, определяемые далее как пло¬
скости сканирования, фиксируются относительно оси корабля
в таком положении, чтобы линия их пересечения совпадала
с осью рыскания корабля (линией опорной вертикали).

ДАТЧИК ПОЛОЖЕНИЯ ДЛЯ КОСМИЧЕСКИХ КОРАБЛЕЙ
321
Способ определения местной вертикали поясняется на
фиг. 1, изображающей геометрическую картину типичной си¬
туации в одной из плоскостей сканирования. На чертеже по¬
казаны поперечное сечение планеты в плоскости сканирова¬
ния, линии, касательные к поверхности планеты, опорная
вертикаль корабля и ориентация сектора (90°), поясняю¬
щие образование серии периодически следующих импульсов.
Импульсы, показанные пунктиром, относятся к интервалам
Указательный
сектор (30 )
Импульсы
на выходе
детектора
Опорная
вертикаль
на космичес¬
ком корабле
f Положение космического
корабля
Т
Время
Планета
гт
Фиг. 1. Работа системы в одной плоскости сканирования.
Сканирующий луч поворачивается на 360° за Т сек.
времени, когда сканирующий находится в пределах опор¬
ного сектора, занимающего угол 90° с вершиной, располо¬
женной на опорной вертикали.
В пределах оставшихся 270° сканирующее устройство мо¬
жет принимать сигналы. Импульсы сигналов, показанные на
чертеже сплошными линиями, возникают в интервалы вре¬
мени, когда луч проходит сектор между двумя касательными
к поверхности планеты.
Угол Si представляет собой угол между опорной верти¬
калью корабля и линией, проведенной с корабля через центр
поперечного сечения планеты, т. е. угол, который должен
быть определен прибором. Он определяет положение плоско¬
сти, перпендикулярной плоскости сканирования и проходя¬
щей через центр планеты. Другая такая плоскость опреде¬
ляется с помощью второго сканирующего луча, а пересече¬
21 Зак. 876

322 HI. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
ние этих двух плоскостей определяет положение локальной
вертикали.
Очевидно, что
01 = ^(Т2 — Xj).	(1)
Углы Ti и т2— измеряемые величины, а угол 0j рассчиты¬
вается с помощью выражения (1).
При работе сканирующего устройства на его выходе воз¬
никает последовательность прямоугольных импульсов, имею¬
щих одинаковые амплитуды и длительность, равную вре¬
мени, которое требуется для прохода сканирующего луча
в секторе, равном ti. Такая последовательность импульсов
может создаваться путем включения напряжения в момент,
соответствующий заднему фронту опорного импульса, и вы¬
ключения напряжения в момент прихода переднего фронта
импульса сигнала (опорный импульс создается магнитным
датчиком механизма сканирования).
Как можно видеть,
о
= E ago5’ ’	^
где V\ — среднее значение напряжения, создаваемого после¬
довательностью импульсов, Е — амплитуда импульса.
Другая последовательность импульсов с той же амплиту¬
дой Е образуется из импульсов, длительность которых опре¬
деляется отрезком времени, заключенным между задним
фронтом импульса сигнала и передним фронтом опорного
импульса. Среднее значение напряжения этой импульсной
последовательности равно
о
V2 = Е звдб- •	(3)
Вычитая V{ из V2, находим напряжение, пропорциональ¬
ное 01. Аналогичный процесс происходит в канале, связанном
с другим сканирующим устройством, причем получаемое на¬
пряжение в этом случае будет пропорционально б2 — углу,
определяющему положение второй плоскости, в которой на¬
ходится центр планеты.
Необходимо отметить, что напряжение, пропорциональное
углу, в который вписывается поперечное сечение планеты,
может быть получено с помощью аналогичной последова¬
тельности импульсов, причем длительность каждого импуль¬
са равна длительности импульса сигнала. Этот угол, как
показано ниже, будет использован при расчете высоты по¬
лета корабля.

ДАТЧИК ПОЛОЖЕНИЯ ДЛЯ КОСМИЧЕСКИХ КОРАБЛЕЙ	323
На фиг. 2 можно видеть эскиз сканирующего устройства,
состоящего из двух оптических устройств, которые вра¬
щаются с постоянной скоростью с помощью двигателя. Для
т0го чтобы обеспечить возможность работы при вращении
корабля вокруг произвольной оси со скоростью до 1 об/сек,
такое оптическое устройство вращается со скоростью
200 об/сек.
Оптическая система состоит из плоского зеркала, отра¬
жающего инфракрасные лучи, фокусирующих линз и филь¬
тра, который обеспечивает ослабление излучений с длиной
волны X < 3 мкм. Этот фильтр служит для уменьшения влия¬
ния прямой солнечной радиации и градиентов, создаваемых
отражениями солнечного излучения от поверхности Земли.
Фокусирующие линзы представляют собой отражательный
дублет с просветленной оптикой (с антиотражательным по¬
крытием), обеспечивающей прохождение 94% излучения
с длиной волны X = 4 мкм. Как следует из спектрального
распределения излучения, отраженного от поверхности Зем¬
ли и атмосферы, рабочие колебания имеют длины волн
свыше 3 мкм.
В связи с применением высокой скорости сканирования
постоянная времени детектора должна быть относительно
малой. Кроме того, желательно использовать детектор, ко¬
торый не требовал бы охлаждения до температуры жидкого
азота. В соответствии с этими требованиями был выбран
Фиг. 2. Сканирующее устройство.
21*

324 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
индиево-сурьмяный детектор (фотоэлектромагнитного типа).
Поле зрения луча, производящего поиск, было выбрано рав¬
ным 2°. Для выполнения этого условия с оптической систе¬
мой, имеющей диаметр 24 мм и фокусное расстояние 36 мм,
потребовался детектор площадью 1 мм2 (т. е. вполне прием,
лемых размеров).
Применение метода охлаждения детектора с помощью
охлаждающего вещества на космических кораблях с боль¬
шим сроком существования представляется нерациональным,
поэтому требуются иные способы охлаждения. За пределами
атмосферы можно охлаждать детектор за счет излучения
в окружающее пространство. Для излучения служит спе¬
циальная поверхность (радиатор), термически соединенная
с детектором, причем для защиты детектора от солнечных
лучей необходимо применять заслонку с высокой отражаю¬
щей способностью, закрывающую часть излучающего радиа¬
тора, которая обращена в сторону Солнца. Естественно, что
такая заслонка должна действовать автоматически.
ОТСЛЕЖИВАНИЕ ВЕРТИКАЛИ
Для того чтобы измерить рыскание корабля, одну из
осей гироскопа с одной степенью свободы следует поддержи¬
вать параллельной направлению вертикали, опущенной
с корабля на поверхность Земли. При выполнении этого
условия наличие орбитальной угловой скорости создает мо¬
мент на роторе гироскопа, заставляющий последний отыски¬
вать положение, перпендикулярное к плоскости орбиты. Син¬
хродатчик, связанный с гироскопом, обеспечивает создание
сигнала, пропорционального углу рыскания. (Заметим, что
гироскоп должен свободно поворачиваться на 360°.)
На фиг. 3 показаны углы, необходимые для определения
положения гироскопа. Углы 0t и 02 были уже определены
выше как углы, измеренные между осями рыскания корабля
и плоскостями, проходящими через центр планеты (Земли).
Углы 01 и р необходимы для соответствующей ориентировки
гироскопа. Для облегчения расчетов линия ОЕ принимается
равной условной единице, а остальные стороны параллеле¬
пипеда определяются как функции 0Ь 02 и р. Согласно фиг. 3,
имеем
_ СА
2 ~ О А ’	(4)
tgp = tg02cos01.
Напряжения, пропорциональные 01 и 02, получаются в ка¬
налах детекторов и используются для управления контуром

ДАТЧИК ПОЛОЖЕНИЯ ДЛЯ КОСМИЧЕСКИХ КОРАБЛЕЙ	325
сервомеханической связи, обеспечивающей поддержание оси
гироскопа вдоль направления вертикали. Для этого тре¬
буется использовать двухрамочный карданный подвес с ги¬
роскопом, смонтированным на внутренней рамке подвеса.
На фиг. 4 приведена функциональная схема сервосистемы.
Для определения положения другой карданной рамки ис¬
пользуются угол 01 и обычная сервосистема.
Направление
вниз
Ось рыскания
А ШК
В
- ■*
Ось
/ Р /
крена
Ось
тангажа
Фиг. 3. Соотношения углов при слежении.
Помимо определения положения карданной рамки, серво¬
механизм, отслеживающий значения 0! по выходному сиг¬
налу, приводит в действие косинусный потенциометр.
Напряжение постоянного тока, пропорциональное 02, пре¬
образуется соответствующей пересчетной схемой в напряже¬
ние, пропорциональное tg02, которое поступает на косинус¬
ный потенциометр. На выходе потенциометра получается
напряжение, пропорциональное произведению tg 02 cos 0i.
Таким образом, сервомеханизм системы р определяет поло¬
жение оси, пропорциональное р, в соответствии с уравнением
(4). Эта ось приводит в действие сервомеханизм, обеспечи¬
вающий создание выходного сигнала и ориентировку вну¬
тренней карданной рамки карданного механизма.
Использование в цепи сервосвязи тангенсного потенцио¬
метра обратной связи на первый взгляд кажется невозмож¬
ным, поскольку известно, что tg9'Q°~ оо, Однако в тех слу¬

326 HI. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
чаях, когда величина 0! или 02 оказывается равной или пре¬
вышает 60°, нормальная цепь обратной связи сервосистемы
размыкается. В этот момент включается система запомина¬
ния скорости, служащая для отслеживания положения зем¬
ной вертикали при отсутствии сигнала со сканирующих
устройств. Функциональная схема, приведенная на фиг. 5,
показывает полную систему измерения положения корабля.
Переходные характеристики систем измерения рыскания
и тангажа в первую очередь определяются характеристиками
е = в,
<s>
\ г
Сервопри¬
вод по В,
т
I
I
I
-1
Потенциометр \
обратной связи j
о—
е*в7
Формиру¬
ющая
Ц&2 /
схема
\
■6-н
потенциометр цр
Сервопри-	„
вод по р Г J V7
о-1
Тангенсныи
потенциометр
Фиг. 4. Функциональная схема сервосистемы.
сервосистем. Для рассматриваемого случая был разработан
экспериментальный образец сервосистемы, причем результи¬
рующая петля обратной связи имитировалась с помощью
аналогового счетно-решающего устройства.
Требуемые постоянные времени переходной характери¬
стики для систем определения тангажа и крена подразуме¬
ваются идентичными, поскольку вращение корабля предпо¬
лагается в произвольном направлении. На основании этого
допущения можно считать, что сервосистема отслеживания
крена представляет наибольшие трудности с точки зрения
стабилизации, если учитывать характер обратной связи,
используемой в системе.
Результирующая переходная функция исполнительного
механизма сервосистемы (двигателя и редуктора) при усло¬
вии пренебрежения кулоновским трением имеет вид
0,156,

Линейный
потенциометр
к
о
S
Ef
«
К
•е*
К
■е-

328 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
где р — выходной угол, рад\
N—передаточное число, равное 80;
fm = 0,7 X Ю"6 — коэффициент затухания двигателя, кгм X
X сек/рад\
kx — постоянный коэффициент, характеризую-
щий момент мотора, кгм/в\.
Ет — напряжение на управляющей обмотке мо¬
тора, в.
■	р	Kv	(0,5s+ 1) (0,025 + 1)
U W ~ Ee (S) ~ s (0,1s + 1) (5s + 1) (0,002s + 1) *	W
где Ee(s)—трансформированное напряжение сигнала
ошибки.
Реакция замкнутой системы на воздействие ступенчатой
или пилообразной входной функции показана соответственно
на фиг. 6 и 7. Величина Kv в случае записей, приведенных
на фиг. 8, увеличивалась до 4800 с тем, чтобы имитировать
такие условия работы системы, когда р = 60°. Записи пока¬
зывают, что и в этом случае система все еще остается ста¬
бильной.
ИЗМЕРЕНИЕ ВЫСОТЫ
В системе, описываемой в настоящей статье, плоскости
сканирования в общем случае не проходят через центр
Земли. Следовательно, высота не может быть рассчитана
с помощью углов, определяемых вписанными хордами или
дугами.
Для измерения высоты с помощью описываемой системы
изучались различные методы. Один из методов, который
кажется нам наиболее целесообразным, рассматривается
ниже.
Из приведенного выше определения углов 0! и 02 следует,
что если один из этих углов, например 0Ь стремится к нулю,
то плоскость сканирования, в которой лежит 02, должна про¬
ходить через центр Земли. Значение угла, стягиваемого по¬
верхностью Земли в плоскости сканирования, в этот момент
может быть использовано для определения высоты полета
корабля.
Угол, стягиваемый частью окружности Земли, измеряется
с помощью селекторного устройства в момент, когда любая
из плоскостей сканирования пересекает центр Земли. Напря¬
жение, пропорциональное 0Ь управляет некоторым компара¬
тором, который создает выходной импульс при 01 = 0.

ДАТЧИК ПОЛОЖЕНИЯ ДЛЯ КОСМИЧЕСКИХ КОРАБЛЕЙ
329
Этим выходным импульсом запускается селекторное
устройство, с помощью которого напряжение, пропорцио¬
нальное |32, поступает в запоминающее устройство до тех
пор, пока существует запускающее напряжение. (|32— угол,
и
т
т
л
Н \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \V
11111 п 1111111 ш 1111111 т
UUUUUmUUUUUUU
б
//////////in in ainani if
luunlulllllUlumlU
a
Фиг. 6. Реакция сервосистемы на ступенчатую входную функцию.
р й 0°; Kv = 1200; скорость бумажной ленты 50 мм/сек', коэффициент обратной связи равен 1.
а —масштаб выходного сигнала 1 в/мм\ 6 — масштаб входного сигнала 1 в/мм\ в —масштаб
сигнала ошибки Е« 0,2 в/мм.
стягиваемый окружностью Земли в плоскости 02.) Информа¬
ция из запоминающего устройства используется для расчета
высоты. Аналогично работает и второй канал с той только
разницей, что значение |3i— угла, стягиваемого окружностью
Земли в плоскости 0ь — поступает а запоминающее устрой¬
ство в тот момент, когда 02 = 0.

330 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Угол (З1), получаемый с выхода запоминающего устрой¬
ства, используется для определения высоты с помощью схе¬
мы, показанной на фиг. 9, б. Соотношения между высотой h,
углом {3 и номинальным радиусом Земли R можно вывести,
а
Фиг. 7. Реакция сервосистемы на пилообразную входную функцию.
Kv —1200; скорость бумажной ленты 50 мм/сек; нарастание напряжения пилы 100 в/сек;
коэффциент обратной связи равен 1.
а —масштаб выходного сигнала 10 в/мм; б —масштаб входного сигнала 10 в/мм; в —масштаб
сигнала ошибки Еа 0,2 в/мм.
Hi
пользуясь фиг. 9, а. Значение sin р/2 получается с помощью
диодного формирующего устройства, а произведение
(h-\-R) sin р/2 снимается с выходного потенциометра Рь
ш
-14
шиииш
4-Ш4
-4-
Ш
Ш
б
ш тп
111II11II1II11
-j—f\
ft
тт
,
,
, |
-=4-
гН
М
$
в
1)	Р, или р2.

11! 111111!!! 11 f l 1111 l i FFFFf
Ш\Ш\
/ ШН
Ш
и
У \ \ \ \ \ \ \ \ \ \ V \-\ \ \ \ \ V \ \ \ \ \ \ \ \
Фиг. 8. Реакция сервосистемы на ступенчатую входную
функцию.
р X 60°; Kv =4800; скорость бумажной ленгы 55 мм/сек; коэффициент
обратной связи равен 1.
а —масштаб выходного сигнала 1 в/мм; б —масштаб входного сигнала 1 в/мм
Сельсин-
	/
датчик
постоянного
тока
Дифрреренциаль -
)ный сельсин
Выходной
сигнал,
пропорцио¬
нальный h
Я
Фиг. 9. К определению высоты.
а — соотношение между высотой /г, углом (3 и номинальным радиусом
Земли R; б —схема для вычисления высоты.
Точка 0 —местоположение корабля; R — номинальный радиус Земли;
точка С —центр Земли; R = {h + R) sin p/2.

332 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Это произведение затем сравнивается с постоянным напряже¬
нием, пропорциональным R. В этом случае положение оси
сервосистемы соответствует значению h + R. Дифферен¬
циальный сельсин, угол поворота выходной оси которого
пропорционален значению R> позволяет получить требуемое
значение сигнала, пропорциональное Л.
ИСТОЧНИКИ ОШИБОК
Воздействие прямой солнечной радиации на сканирую¬
щую систему может явиться причиной возникновения суще¬
ственных ошибок. Для уменьшения влияния солнечной ра¬
диации используется фиксированный фильтр, однако надо
иметь в виду, что интенсивность прямой радиации значи¬
тельно превосходит величину радиации, отраженной от Зем¬
ли. Вероятнее всего, наибольшие ошибки будут возникать
вследствие того, что прямое солнечное излучение вызовет
моментальное блокирование (парализацию) детектора. При
этом детектор не разрушится, однако он может быть пара¬
лизован в течение 1 мсек. Различие между импульсами сол¬
нечного излучения и импульсами, возникающими при возра¬
стании сигнала в момент перехода луча сканирующего
устройства из свободного пространства и встречи его с по¬
верхностью Земли, устанавливается по различной в обоих
случаях длительности импульсов. Однако если детектор ока¬
зывается парализованным в течение 1 мсек, то сканирующее
устройство оказывается ’’ослепленным” на протяжении 72°,
прежде чем чувствительность детектора будет восстановлена.
По-видимому, простых способов, позволяющих исключить
этот недостаток, нет, однако это не представляется столь
катастрофичным, как кажется на первый взгляд. Процент
времени, в течение которого Солнце появляется в поле зре¬
ния сканирующего устройства, будет сравнительно невелик
в том случае, если корабль вращается. Даже если возникают
условия, когда движение спутника происходит таким обра¬
зом, что поле зрения сканирующего устройства переме¬
щается очень медленно, то вероятность того, что Солнце по¬
падет в поле зрения, будет очень невелика.
Ошибки могут возникать также вследствие нерегулярно¬
сти поверхности Земли, влияния атмосферных слоев и облач¬
ного покрова. В целях уменьшения ошибок, связанных с эти¬
ми причинами, может потребоваться применение более ши¬
рокого луча в системе сканирования. Кроме того, влияние
вращения корабля относительно зоны сканирования может

ДАТЧИК ПОЛОЖЕНИЯ ДЛЯ КОСМИЧЕСКИХ КОРАБЛЕЙ
333
привести к усреднению этих ошибок. Указанные выше меры
(применение широкого луча и вращения) будут оказывать
лишь частичное влияние, поэтому в случае необходимости
с целью уменьшения ошибок применяется качание сканирую¬
щих плоскостей с помощью качающегося зеркала.
Для того чтобы получить представление о величине оши¬
бок, обусловленных естественными источниками, были про¬
изведены расчеты для двумерного случая при условии, что
инструментальные ошибки системы незначительны. При рас¬
четах принималось, что на одной стороне тела (планеты)
имелась выпуклость размером 0,005 /?, а другая сторона
была идеально гладкой. Результирующая ошибка в опреде¬
лении местной вертикали и расчетного значения высоты
приведена в таблице.
Высота
Погрешность по
вертикали, град.
Погрешность по
высоте
0,02/?
0,76
—0,00263/?
0,03/?
0,61
—0,00262/?
0,04/?
0,52
—0,00264/?
0,05 R
0,46
—0,00265/?
0,06 R
0,42
—0,00267/?
0,07/?
0,38
—0,00269/?
0,08/?
0,36
—0,00271 /?
0,09 R
0,34
—0,00274R
0,1/?
0,32
—0,00278/?
(Расстояния даны в долях радиуса планеты)
В указанных выше расчетах подразумевалось использова¬
ние очень узкого луча, благодаря этому ошибки, связанные
с моментом прохода луча через край профиля планеты, не
принимались во внимание. Если же луч имеет конечную ши¬
рину, то возникают дополнительные ошибки. Этот эффект
был изучен для луча, имеющего коническую форму, при сле¬
дующих допущениях:
1. В луч не поступает никакой энергии от источников,
расположенных вне луча, и чувствительность его постоянна
в пределах поля зрения.
2. Радиация от поверхности Земли равномерна.
Для установления момента, когда ось луча, выбранная
в качестве опорной линии, будет касательной к поверхности
Земли, можно применять два различных способа обработки
сигнала:

334 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
1) дифференцирование сигнала и определение точки ка¬
сания по максимуму результирующего сигнала;
2) выбор конкретного отношения сигнала к максималь¬
ному уровню для обозначения этого же момента.
Первый метод практичнее с точки зрения инструменталь¬
ного выполнения, поэтому он предпочтительнее. Ошибки рас¬
чета	высоты,	вызванные	ошибками определения	истинной
опорной	линии	касания,	при таком методе	ее	определения
могут быть рассчитаны по следующей формуле:
A h _	(а 4-1) (а + 2) а2	m
h —	2 — д(д + 2)а2	’	\<)
где Ah — ошибка определения высоты, h — истинное значе¬
ние высоты, а — половина угла луча и а = h/R — отношение
высоты к радиусу Земли.
Следует отметить, что вариации ошибок известны как
функции высоты. Следовательно, теоретически можно ком¬
пенсировать эти ошибки. Однако необходимость такой ком¬
пенсации весьма сомнительна, поскольку для значений
а > 0,1 ошибки, определяемые неоднородностями поверхно¬
сти Земли, будут значительно выше ошибок, рассчитанных
на основании формулы (7).

СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКОГО
КОРАБЛЯ ПУТЕМ ИСПОЛЬЗОВАНИЯ ДАВЛЕНИЯ
СОЛНЕЧНОЙ РАДИАЦИИ1)
Зон
Стабилизация положения космического корабля в пространстве воз¬
можна за счет использования давления солнечной радиации. Если к ко¬
раблю добавляется хвостозая поверхность флюгерного типа, то давление
солнечной радиации на этот стабилизатор (флюгер) будет противодейство¬
вать всем возмущающим моментам, вызываемым эксцентричностью грави¬
тационного поля, столкновениями с метеорными телами и давлением сол¬
нечной радиации.
Одну из сложных проблем, возникающих при проектиро¬
вании космических кораблей, которые предназначены для
длительных перелетов, представляет проблема регулирова¬
ния и стабилизации положения космического корабля для
длительного периода времени. Например, может оказаться
желательным ориентировать предназначенный для связи
искусственный спутник в заданном направлении и поддер¬
живать такое положение в довольно узких пределах. Ана¬
логично может оказаться необходимым сохранять заданное
положение при полетах к Луне или к планетам. Поэтому при
появлении возмущающих причин, обусловленных давлением
солнечной радиации или гравитационными полями, для со¬
хранения заданной ориентации нужно приложить определен¬
ный корректирующий момент. Для этого в настоящее время
обычно предполагают использовать жидкостные реактивные
двигатели2), хотя даже при наличии малых возмущений их
применение в длительном полете невозможно без больших
запасов топлива.
СИСТЕМА СТАБИЛИЗАЦИИ ПО ПОЛОЖЕНИЮ С ИСПОЛЬЗОВАНИЕМ
СОЛНЕЧНОЙ РАДИАЦИИ
Некоторые ученые в качестве активной силы для косми-
ческого корабля предлагали использовать давление солнеч¬
ной радиации, т. е. использовать так называемые солнечные
1) S oh n R., ARS Journal, 29, № 5, 371—373 (1959).
2) Даже в случае использования в системе управления маховиков кон¬
структоры применяют реактивные двигатели, которые используются для
того, чтобы избежать превышения заданного максимума скорости оборотов
маховика.

336 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
паруса [1]. Они установили, что, хотя давление солнечной
радиации мало, его достаточно для создания тяги.
Поэтому представляется вполне разумным предположе¬
ние о том, что давление солнечной радиации может успешно
использоваться и в системе стабилизации положения. Возму¬
щающие моменты (моменты от давления солнечной радиации,
гравитационных сил и столкновений с метеорными телами)
очень малы и, как будет показано ниже, имеют тот же по¬
рядок величины, что и восстанавливающий момент от давле¬
ния солнечной радиации. Указанные факторы будут рассмот¬
рены поочередно для сравнения их возмущающих моментов
с восстанавливающими моментами от давления солнечной
радиации.
ВОЗМУЩАЮЩИЙ МОМЕНТ ОТ ДАВЛЕНИЯ СОЛНЕЧНОЙ РАДИАЦИИ
Рассмотрим корабль, движущийся боковой стороной
к Солнцу при отсутствии гравитационного поля. Если центр
давления не совпадает с центром масс, то возникает возму¬
щающий момент. Корабль при этом может быть стабилизи¬
рован, если к нему добавить флюгерную поверхность, чтобы
радиация Солнца воздействовала на этот флюгер и напра¬
вляла корабль (фиг. 1).
Возмущающий момент, действующий на корабль, опреде¬
ляется выражением
= PSKx,
где Р — давление солнечной радиации; Sk — площадь, на ко¬
торую действует это давление; х—расстояние от центра
масс до центра давления.
Восстанавливающий момент от паруса тст равен
zCT — PSCTbф (для малых значений ф),
где Sст — поверхность стабилизатора; Ъ — плечо момента
стабилизатора; ф — угол рыскания по курсу, рад.
Равенство моментов дает угол рыскания по курсу ф при
равновесии
* = ТЙ- = 'Ь5°,
где численное значение получено подстановкой числовых ве¬
личин, приведенных на фиг. 1. В случае подвижной поверх¬

ИСПОЛЬЗОВАНИЕ ДАВЛЕНИЯ СОЛНЕЧНОЙ РАДИАЦИИ
337
ности угол рыскания по курсу может сохраняться равным
нулю при отклонении поверхности на угол 5, который рав¬
няется
S = 1^!L = n,50.
Гравитационные возмущающие моменты
Опрокидывающий гравитационный момент равен
, = /со2 ^1 +2-^JsinpcosP (в общем случае),
vrp '
гр •
: 3/со2 sin р cos р (для искусственного спутника),
где со — угловая скорость вращения относительно притяги¬
вающей массы, рад/сек\ г — радиус от притягивающей массы;
Фиг. 1. Использование стабилизатора с солнечным парусом при полете
к Луне.
Условия полета: масса=45 кг- сек/м] вес (на Земле)=450 /сг, лг=0,3 ж; fc = l,5 ж; 5К = 4,5 ж2;
5СТ=4,5 ж2 (2,1 х 2,1 ж); длина 4,5 ж.
/—момент инерции; р— угол наклона траектории, изме¬
ряемый относительно местного вектора гравитации, рад.
Чтобы сравнить возможность действия стабилизатора,
основанного на давлении солнечной радиации, с действием
гравитационного возмущающего момента, рассмотрим два
случая:
22 Зак. т.

338 III. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
1) корабль представляет собой спутник на орбите высо¬
той ~ 550 км\ 2) корабль летит к Луне.
В том случае, когда корабль является спутником с при¬
веденными выше характеристиками (при стабилизаторе пло¬
щадью 4,5 ж2), он способен уравновесить гравитационный
момент в наихудшем случае, когда (3 = 45°.
В случае полета к Луне конструкцию стабилизатора оста¬
вим прежней, а момент инерции увеличим в 10 раз. Необхо¬
димая для уравновешивания площадь солнечного паруса
после старта будет представлять собой некоторую функцию
Время после отсечки двигателя, мин
Фиг. 2. Требуемая площадь стабилизатора при полете к Луне.
времени, показанную на фиг. 2. Полет к Луне занимает
около 2,5 суток (3600 мин), и график представляет только
малую часть полного полета. Через 27 мин полета стабили¬
затор площадью 4,5 м2 может уравновесить все гравитацион¬
ные возмущения даже при большом моменте инерции.
При малом повороте корабля (причем в такую сторону,
чтобы его центральная линия располагалась по местной
вертикали) все моменты гравитационных сил можно исклю¬
чить. Так как особой необходимости ориентировать централь¬
ную линию вдоль траектории, по крайней мере в течение
первых часов полета, нет, то не существует причин, чтобы не
использовать солнечный стабилизатор при полете к Луне.
Если нужно принудительно держать некоторое заданное
положение, то в течение первых 30 мин полета могут быть
использованы реактивные двигатели, после чего эффектив¬
ным станет солнечный стабилизатор. Эти двигатели могут
быть небольшими по размерам и прикрепляться непосред¬
ственно к парусу. При этом основные перемещения паруса
будут также ориентировать и двигатели. Кроме того, те же
сервомеханизмы, которые используются для регулирования
паруса, могут одновременно регулировать и двигатели.

ИСПОЛЬЗОВАНИЕ ДАВЛЕНИЯ СОЛНЕЧНОЙ РАДИАЦИИ	339
Возмущения, вызванные метеорными телами
Метеорные тела также могут возмущать ориентацию ко¬
рабля, однако эти возмущения чрезвычайно малы, как об
этом можно судить по диаграмме, изображенной на фиг. 3.
(Данные по распределению частоты прохождения метеорных
тел и их величине взяты из работы Картера [2].) К счастью,
крупные метеорные тела встречаются редко и корабль может
час
Фиг. 3. Длительность времени восстановления
положения корабля в функции от промежутка вре¬
мени, прошедшего от начала полета до столкновения
с метеорными частицами (вероятность 99%).
избежать столкновения с ними. Что же касается небольших
частиц, то хотя они и встречаются чаще, но их импульсы
настолько малы, что оказывают очень небольшое возмуще¬
ние (предполагается, что столкновение с метеорными части¬
цами происходит на расстоянии около 3 ж от центра масс
корабля). Таким образом, можно сделать вывод, что метеор¬
ные частицы не создают никаких дополнительных проблем
при решении вопроса о возмущениях космического корабля.
Динамическая устойчивость
Зафиксировав стабилизатор в некотором положении
равновесия, мы получим статически устойчивый корабль, ко¬
торый динамически будет нейтральным. При возмущении
корабль в течение бесконечного времени будет совершать
колебания с амплитудой, равной удвоенной величине угла
возмущения. Это можно показать следующим образом. Из¬
быток момента равен
— /ф = хст — т„.
22*

340 ИГ. СТАБИЛИЗАЦИЯ ПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ
Обозначая начальные значения величин индексом 0, реше¬
ние для ф получаем в следующем виде (время т в сек):
ф:
— sin УА ^ + (фо—cos У At-
Va
bSc.
xSK
bSc•
где период^
2ти
~Va'
PSCTb
(квадрат собственной частоты).
Датчик скорости может быть установлен в системе регу¬
лирования для отклонения поверхности пропорционального
i: ^
§
si
5*
10	15
Время, мин
Фиг. 4. Зависимость изменения угла рыскания по
курсу от времени при возмущении на 5° (при демп¬
фировании).
скорости рыскания по курсу (S = /Сф, где К — коэффициент
пропорциональности). Тогда корабль будет задемпфирован
и будет возвращаться в положение равновесия. Если прене¬
бречь массой стабилизатора, уравнение движения принимает
вид
~y = PSCTb (ф + 8)-Р5кх.
Решая это уравнение, получаем
и _|	I	1	Ш.
1 И” /- /- ) — l J
Ф = {фо[
J I prxt I Г (Фо/г|) ~~Фо 1 pT2t
-1 Г (г2/г,)-1 \е 9
^>УА.
Типичный переходный процесс корабля, имеющего данные,
приведенные на фиг. 1, показан на фиг. 4. Как видно, в те¬
чение 12 мин корабль уменьшает начальное отклонение
с 5 до 1°,

ИСПОЛЬЗОВАНИЕ ДАВЛЕНИЯ СОЛНЕЧНОЙ РАДИАЦИИ	341
ЗАНЛЮЧЕНИЕ
Приведенные выше краткие расчеты показывают, что
солнечный флюгерный стабилизатор пригоден для ориента¬
ции корабля при его полете в солнечной системе. Хотя кор¬
ректирующие моменты, получаемые от такого стабилизатора,,
малы, они тем не менее сравнимы с внешними возмущаю¬
щими моментами.
ЛИТЕРАТУРА
1. Gar win R. L., Solar Sailing — A Practical Method of Propulsion Wi¬
thin the Solar System, Jet Propulsion, 28, № 3, 188—190 (March
1958).
2. С a r t e г L. J., Realities of Space Travel, Lnd., 1957<

IV. НОНТРОЛЬ ТРАЕНТОРИИ
НОСМИЧЕСНИХ АППАРАТОВ
РАДИОКОНТРОЛЬ ТРАЕКТОРИИ КОСМИЧЕСКИХ
АППАРАТОВ >)
Гофман
Возможности современных радиотехнических систем для контроля
траектории ограничены шириной луча антенн практически осуществимых
размеров и возможным базовым расстоянием между наземными станциями.
Естественным развитием этих систем является использование спутников
Земли, снабженных навигационным оборудованием. С целью реализации
точностей, обеспечиваемых атомными стандартами частоты, рассмотрены
импульсная и допплеровская системы. Полученные результаты сравниваются
с точки зрения точности, необходимой мощности и сложности оборудо¬
вания.
ВВЕДЕНИЕ
С развитием космической техники ракеты все глубже про¬
никают в космос. За первыми запусками высотных ракет и
искусственных спутников Земли последуют полеты к Луне и
планетам. Первой попыткой межпланетного полета будет,
вероятно, полет автоматической ракеты на Марс.
Полет ракеты с Земли на Марс можно разбить на три
основные фазы: 1) выведение на орбиту; 2) полет в средней
части траектории, являющийся основным по продолжитель¬
ности и характерный тем, что космическая ракета движется
по орбите вокруг Солнца; 3) сближение с планетой или ко¬
нечный участок, на котором космическая ракета выходит на
орбиту вокруг Марса или попадает на его поверхность.
В настоящей статье рассматриваются проблемы управле
ния в течение второй фазы полета.
Точность наведения корабля должна быть достаточной
для того, чтобы коррекция в средней фазе полета не превос-
1) Hoffmann Н., IRE Nat. Conv. Rec., 7, Pt. 5, 227—239 (March
1969).

РАДИОКОНТРОЛЬ ТРАЕКТОРИИ
343
ходила допустимую и требовала бы минимум затраты энер¬
гии, ибо основная часть энергии необходима на конечном
участке полета. Получаемое в результате увеличение отно¬
шения полезной нагрузки к полному весу горючего имеет
большое значение для космического полета. Следящие си¬
стемы, описываемые ниже, основаны на предположении, что
для обеспечения высокой точности навигации могут быть
использованы величины баз, не ограниченные размерами
Земли. Поэтому в рассматриваемые системы включены спут¬
ники Земли, несущие навигационное оборудование. Обычно
применяемая солнечная система координат (фиг. 1) имеет
начало в центре Солнца. Система координат образуется пло¬
скостью орбиты Земли (называемой плоскостью эклиптики)
и нормалью к этой плоскости из начала координат. Углы в
плоскости эклиптики обычно отсчитываются от точки весен¬
него равноденствия. Орбиты планет нашей солнечной систе¬
мы могут быть рассчитаны с высокой степенью точности по
простой теории для двух тяготеющих масс, принимая, что
планеты движутся относительно Солнца по эллиптическим
орбитам с эксцентриситетом е, причем Солнце расположено
в одном из фокусов эллипса. За исключением Плутона,
эксцентриситеты орбит планет малы, а плоскости их орбит
лишь на несколько градусов отклонены от плоскости эклип¬
тики. Космический корабль после запуска и сообщения ему
энергии, необходимой для выведения из поля земного тяго¬
тения, переходит на орбиту вокруг Солнца и движется по
ней по тем же законам, что и все планеты.

344	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Траекторией первых межпланетных ракет, запускаемых
на Марс, будет, вероятно, эллиптическая орбита Гофмана,
требующая минимальной энергии. Рассмотрим такую траек¬
торию, представляющую значительный интерес, более де¬
тально.
Для упрощения рассуждений предположим,, что:
1)	орбиты Земли и Марса лежат в плоскости эклиптики
и представляют собой окружности;
2) орбита ракеты, требующая минимальной энергии, рас¬
положена также в плоскости эклиптики;
3) ракета запускается с Земли в тот момент, когда Марс
находится впереди Земли на 44°. При движении ракеты по
указанной траектории положения ракеты и Марса совпадут
в точке М2 (фиг. 2), если принять, что
гз= 1,49494- 108 км— расстояние от Земли до Солнца;
гм = 2,28016- 108 км—расстояние от Марса до Солнца;
?3 = 0,98557ошш—угловая скорость движения Земли
вокруг Солнца;
а = 1,88755 • 108 км — половина большой оси орбиты ракеты;
е = 0,208 (эксцентриситет орбиты ракеты);
7"р=520 суток (период орбиты ракеты).

РАДИОКОНТРОЛЬ ТРАЕКТОРИИ
345
Положение (г3, ср3) Земли определяется при r3 = const
выражением
<р3 = 0,9855 • t.
Расчет положения ракеты более сложен. Положение ее
можно определить с помощью задачи двух тел и известных
постоянных, определяющих систему. Если среднее движение
п равно
2п	/1Ч
П	»	(1)
1 Р
то средняя аномалия М может быть определена как
N[ = n(t — Т0),	(2)
где Т0 — момент перехода через перигей орбиты. Так как
момент Т0 выбирается произвольно, то для анализа удобнее
положить, что Г0 = 0, тогда
N[ = nt.	(3)
Новый параметр, эксцентрическую аномалию Е (фиг. 3),
можно связать с М с помощью следующего выражения:
Е — еъхпЕ = N[ = nt.	(4)
Для малых эксцентриситетов е величина Е выражается
с помощью разложения М в ряд, причем с достаточной сте¬
пенью точности ее можно ограничить тремя членами
Е = М + е si n М е2 sin 2М.	(5)

Фиг. 4. Угол между осью ракеты и линией первоначального отсчета.
Фиг. 5. График расстояния от Земли до ракеты при полете на Марс.

РАДИОКОНТРОЛЬ ТРАЕКТОРИИ
347
Представим Е в зависимости от t, величины истинной
аномалии vp и радиуса г с помощью выражений
и
г р = а(\ —ezosE),	(7)
где гр — расстояние от ракеты до Солнца.
Как видно из фиг. 2, выражение для угла 0 будет равно
/ rn sin v„— Го sin Vo \
б = arctg -£	£	-	- j.	(8)
s \ rp cos мр — r3 cos v3 J	у >
Последовательные значения, которые принимает угол 0,
показаны на фиг. 4; они начинаются со значения, равного 90°,
слегка колеблются, затем непрерывно увеличиваются и к мо¬
менту, когда ракета достигает Марса, значение 0 становится
равным 144°.
На фиг. 5 приведен график расстояния ракеты от Земли
в функции времени полета. Эти данные показывают, что мак¬
симальное расстояние равняется 2,4 • 108 км. Расстояние от
ракеты до Земли является важным фактором, определяющим
параметры электронного оборудования, устанавливаемого на
ракете, спутниках и наземных станциях.
ИМПУЛЬСНАЯ СИСТЕМА
В этой системе (фиг. 6) передаваемые с ракеты высоко¬
частотные импульсы принимаются некоторым количеством
приемных станций. Положение ракеты может быть рассчита¬
но при условии точной привязки времени.
Расстояние S между двумя точками пространства может
быть представлено функцией времени с помощью основного
уравнения
S = ct,	(9)
где с — скорость света, t—время, необходимое радиоимпуль¬
су для прохождения расстояния S.
Если момент времени излучения радиоимпульса неизве¬
стен, то можно измерить интервал времени t\ между приемом
импульсов в разных точках Р0, ..., Р* и расстояние выразить
в декартовых координатах с помощью выражения
п — (х — Xjf -f- (у —Vif -Ь (z — ztf = с2 (t + tif,	(10)

348	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
где (х, у, z)—координаты ракеты Рр; (xit yit гг)—коорди¬
наты приемной станции Рг-; (0, 0, 0) — ведущая станция Р0;
t — время прохождения радиоимпульса от ведущей станции
до ракеты; U — интервал времени между приемом импульсов
в Р0 и Р{.
Уравнение (10) содержит четыре неизвестных: х, у, z и t.
Для определения положения ракеты Р(х, у, z) с помощью
импульсной системы такого типа необходимо иметь четыре
приемные станции и составить четыре независимых уравне¬
ния для определения всех неизвестных величин. Станция Р0
является ведущей и находится в начале системы координат.
Указанные четыре уравнения для точек Р0, Рь Р2 и Р3 имеют
следующий вид:
Рассмотрим систему приемных станций, состоящую из од¬
ной наземной станции и трех приемных станций, расположен¬
ных на спутниках (см. фиг. 6). Использование спутников по¬
зволяет: 1) увеличить величину базы системы контроля тра¬
ектории и 2) осуществлять с их помощью связь между раз¬
личными точками земной поверхности. При этом получается
полное перекрытие поверхности Земли, кроме 9° зоны около
Рр(х,у, z)
х2 + у2 + z2 — сЧ\
{х — хг)2 + (у — у i)2 + (2 — г,)2 = с2 (t + txf,
(х — x2f + (у — у2)2 + (г — г2)2 = с2 (t +12)2,
(х — х3 f 4(У — У г? + (^ — г3)2 = c2{t^r tzf.
(П)
(12)
(13)
(14)

РАДИОКОНТРОЛЬ ТРАЕКТОРИИ
349
ее полюсов (фиг. 7). Практически наземных станций должно
быть две, расположенные на обоих полюсах. Три бортовые
станции должны находиться на круговых орбитах в эквато¬
риальной плоскости с интервалом 120°. Расстояние гсп для
этих спутников должно быть равно ~42 ООО км от центра Зе¬
мли, что обеспечивает 24-часовую’синхронную с вращением
Земли орбиту (период обращения такого спутника равен од¬
ним суткам). Для наблюдателя, находящегося на Земле, этот
спутник представляется неподвижным в пространстве. Чтобы
/V
Фиг. 7. Часть земной поверхности, «освещаемой» спутником.
решить уравнения (11) — (14) применительно к нашей систе¬
ме, подставим в выражение (11) значения, даваемые (12) —
(14), и получим три независимых уравнения с четырьмя не¬
известными
/^2/2	у.2 I 2 I 2
I	I	о	/	/	*	,	I	\ У i 2 i	/л	_v
xix УсУ ziz — — с 	§	^ 	~2	’	(	^
где i = 1,2,3.
Так как
•	А+У\+А=г\а,	(16)
то можно записать
с2/2	г2
xix-!ryly-\-zlz = — c4lt +	(17)
где i — 1, 2, 3.
Полагая х, у и 2 функциями t, можем записать решение

350	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
где Д является определителем для системы трех уравнений
(17). Отсюда получаем решения для х, у и z в следующей
форме:
х = kt —J— /,
y=mt-{-n,	(19)
z=pt-\-q.
Подставляя выражения (19) в уравнение (11), получаем но¬
вое уравнение, содержащее только t:
(kt + If + (mi -f tif + (pt + qf = c2t2.	(20)
И, наконец, решая его относительно t, имеем
— 2 ijkl -j— ttiti РЯ') — Ч- Ч- РЯ)2
t =
2 (к2 + т2 + р2 — с2)
4 (к2 + т2+р2 — с2) (I2 + п2 + я2)
2 (к2 + т2+рг — с2)
(21)
Величина t должна быть действительной и больше нуля.
Подставляя ее в выражения (19), можно рассчитать вели¬
чины х, у и z.
Для упрощения расчетов систему декартовых координат
свяжем с расположением спутников, т. е. предположим, что
их положение остается фиксированным. Однако при пересчете
положения ракеты в солнечной системе координат необхо¬
димо также учитывать и тот факт, что спутники вращаются
в плоскости земного экватора и вся их конфигурация должна
быть переведена в плоскость эклиптики. Следовательно, необ¬
ходимо правильно преобразовать положение ракеты, если мы
хотим сравнить его с заранее заданным и провести необхо¬
димую коррекцию орбиты ракеты.
По двум расчетным значениям времени t0 и f с помощью
простой линейной аппроксимации можно вычислить соста¬
вляющие вектора скорости ракеты
= = (22)
t'— U ’ У —
Действительное положение ракеты во время приема им¬
пульса наземной станцией определяется следующим образом:
Xj = х —(— Vxt,
Ут = У +vyt>	(23)
zT = z-t V;t.

РАДИОКОНТРОЛЬ ТРАЕКТОРИИ
351
ДОППЛЕРОВСКАЯ СИСТЕМА
В допплеровской системе, применяемой для управления
траекторией космических кораблей, высокочастотные импуль¬
сы, излучаемые бортовым передатчиком ракеты, принимаются
определенным количеством станций, расположенных на ис¬
кусственных спутниках Зем¬
ли или на ее поверхности. На
основании данных, получен¬
ных в результате точных ча¬
стотных измерений, можно рас¬
считать положение и скорость
ракеты (фиг. 8).
По данным измерений ча¬
стоты можно определить: доп¬
плеровскую скорость или век¬
торную разность скорости ра¬
кеты vp и скорости спутника
Vi, а также нормированный
вектор расстояния г.
Уравнение для допплеров¬
ской скорости может быть по¬
лучено посредством дифферен¬
цирования по t основного ура¬
внения для дальности (10)
д (г2j) д
~ш~=ж К*—+
Спутник
, ,	чо	. /	фиг- 8. Допплеровская скорость.
-Ь(у — У if + (* — zif\• (24)
В результате дифференцирования имеем
Введем следующие обозначения:
=	—допплеровская скорость;
(25)
дх
~Ж
dt
dz
= Vt
= v.,
— составляющие скорости ракеты по осям
х, у у z\

352	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
составляющие скорости спутника по осям
хл уу 2\
направляющие косинусы по осям х, у, z.
Пользуясь этими обозначениями, запишем уравнение (25)
в более простой форме
{х — Xi) (vx — vX[) + (у — У() (Vy — Vyt) -+-
+ (Z — Zi)(Vz—Vz.) = Vhri. (26)
как постоянные системы. Если мы хотим осуществить такую
систему, установив с этой целью на ракету передатчик, рабо¬
тающий па частоте /0, то для определения шести неизвестных
потребуется минимум шесть приемных станций, измеряющих
допплеровские частоты /*.
Допплеровская скорость	связана	с	допплеровской
частотой следующим соотношением:
где с — скорость света.
Можно полагать, что непрерывный контроль траектории
в течение всех 260 дней полета не потребуется и что для кор¬
рекции траектории в средней части полета достаточно не¬
скольких измерений в день.
Анализ уравнения (26) показывает также, что оно яв¬
ляется нелинейным уравнением с шестью неизвестными и что
точно решить систему из шести таких уравнений невозможно.
Поэтому необходимо воспользоваться приближенным числен¬
ным методом, например методом последовательных прибли-
(vx — vx.) + Р, (Vy — Vy() + Ti (Vz — Vz.) = vA.
или
Уравнение (26) содержит шесть неизвестных х, у, 2, vx, v-y,
vz и 7 членов xif yiy Zi vx., vy.f vZ[ и va , рассматриваемых
(27)

РАДИОКОНТРОЛЬ ТРАЕКТОРИИ
353
жений, причем этот прием может повторяться до тех пор,
пока необходимая точность не будет достигнута. Рассмотре¬
ние различных численных методов решения показывает, что
метод Ньютона — Рафсона для совместных уравнений дает
результат после достаточно малого числа приближений.
ТРЕБОВАНИЯ Н СИСТЕМЕ
Точность измерений
Точность импульсной системы зависит от точности изме¬
рения интервалов времени приема импульсов, излучаемых
передатчиком ракеты, на приемных станциях, расположен¬
ных на спутниках, и точностью определения положения спут¬
ников относительно центра массы Земли.
Точность измерения времени зависит от двух основных
факторов:
1) точности применяемого часового механизма. На совре¬
менном этапе развития техники с помощью атомных часов
может быть достигнута точность порядка 10~п. С помощью
специальных генераторов с кварцевой стабилизацией частоты
возможно обеспечить точность порядка 10-9;
2) ширины полосы пропускания частот и отношения сиг¬
нал/шум системы. Точность определения положения спутника
в пространстве будет зависеть от точности наземной системы
контроля траектории. Если для слежения применяется опи¬
санная аппаратура, то точность также зависит от продолжи¬
тельности измерений и точности, с которой определено рас¬
положение наземных станций на поверхности Земли.
В настоящее время наибольшая точность, обеспечиваемая
в США при навигационно-геодезической съемке, составляет
~ 1 /187000. Основное предположение при геодезической
съемке состоит в том, что Земля имеет форму сплющенного
шара с неоднородной поверхностью и плотностью. Таким об¬
разом, точность системы ограничивается уже за счет этого
первоначального предположения. Системы, построенные на
базе спутников, обеспечивают более высокую степень точно¬
сти. Однако необходимо отметить, что Земля изменяет форму
в зависимости от расстояния до Солнца. Если требуется обес¬
печить максимальную точность, то точки на поверхности
Земли должны рассматриваться как изменяющиеся во вре¬
мени и должны быть рассчитаны для времени наблюдения
за ракетой. Достижимая точность системы контроля траек¬
тории будет зависеть от точности этих расчетов.
23 Зак. 876.

354	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Рассмотрим основное уравнение, полученное для импульс¬
ных систем:
(х — Xif Н- (у — у()2 + (z — zt)2 = с2 {t н- ti)2.	(28)
Если предположить, что все переменные изменяются на ма¬
лые величины, и если пренебречь составляющими второго по¬
рядка малости, то получим
(х — Xf) (Ьх — ЬХ[) + {у — yt) (8у — 8у(.)	— zt) (bz — 8гг) =■
= с2 (t -f- tt) (8/ + 8^),	(29)
где Ьх, Ъуу bz— ошибки, которые необходимо выразить в за¬
висимости от bxif btji и bzu т. е. ошибок определения постоян¬
ных системы.
Для случая четырех станций (/ = 1—4) получаем четыре
линейных уравнения, на основании решения которых могут
быть определены составляющие ошибок по ху у, z и t для
различных положений спутника и различных времен изме¬
рения.
Точность допплеровской системы зависит от того, с какой
точностью станции, расположенные на спутниках, опреде¬
ляют смещение несущей частоты, излучаемой передатчиком,
а также от того, на сколько точно известны положение и век¬
тор скорости этих спутников, измеренные в системе коорди¬
нат с началом в центре массы Земли. Эта точность зависит
также от стабильности источников излучения. Ошибка в опре¬
делении допплеровской скорости vA в зависимости от неста¬
бильности генераторов передатчика и приемника может быть
рассчитана с помощью основного допплеровского уравнения
да
где /' — значение допплеровской частоты, измеряемое на при¬
емном конце; f0 — излучаемая частота; с — скорость света;
ид — допплеровская скорость.
Отсюда
= Г1 — (/7/о)2Л ^	/31)
д L1 + (/7/о)2 J	( '
Допплеровскую ошибку 6А^Д можно определить, если изве¬
стна стабильность частоты передатчика и гетеродина прием¬
ника 6i и е2 (в %). Пусть излучаемая частота /о(1 + £i); тог'
да принимаемую частоту можно рассчитать по формуле
(32)

РАДИОКОНТРОЛЬ ТРАЕКТОРИИ
355
Точность, с которой может быть измерена /' в зависимости
от точности поддержания частоты гетеродина приемника, мо¬
жет быть рассчитана с помощью выражения
f =/о(1 +el)(l +е2) "с + ^д ’
Отсюда с точностью до величин первого порядка получаем
Х===(1+£1 + е2)1/Г| + ^ •	(34)
Величина допплеровской скорости может быть записана
в виде
и если е ~ si ~ £2, получаем выражение для ошибки
н = <35>
1 + (Ы9
Величина относительной ошибки будет равна
<36>
Для с уд
—.	(37)
Как и в импульсной системе, положение и значение век¬
тора скорости для приемных устройств, расположенных на
спутниках, также зависят от наземной системы слежения,
константы которой являются функцией расположения назем¬
ных пунктов.
Для случая расположения приемных станций на шести
спутниках (i = 1 — 6) величины ошибок по х, у, z, vx, vy, vz
могут быть определены с помощью вариаций основного доп¬
плеровского уравнения и решения всех шести детерминантов.
Мощность излучения
Обе описываемые системы — импульсная и допплеров¬
ская— используются как для связи, так и для навигации.
Передатчик ракеты в целях экономии энергии работает пе¬
риодически или включается по команде, передаваемой
с Земли. Первые передачи с ракеты, принимаемые с помощью
станций, расположенных на спутниках, используются для ус¬
23*

356	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
тановления связи и контроля траектории. Когда данные о по¬
ложении и скорости ракеты будут определены с помощью
станций, расположенных на спутниках, и переданы в счетную
машину, расположенную на Земле, на ракету направляется
наземная параболическая антенна с высоким коэффициентом
направленного действия. Повышенный коэффициент усиления
антенны позволяет увеличить скорость передачи сообщений
между ракетой и Землей.
Первый этап определения параметров рассматриваемой
системы связи заключается в расчете потерь при распростра¬
нении радиоволн в свободном пространстве по следующей
формуле:
W,„=(^rf.	(38)
где X— длина волны, излучаемой передатчиком; г — расстоя¬
ние между ракетой и Землей.
Для расчета выберем рабочую волну X = 15 см
(2000 Мац). Такая волна выгодна с точки зрения приемле¬
мых размеров антенн и прохождения через ионосферу, и, кро¬
ме того, она лежит ниже той границы, где приходится учиты¬
вать поглощение в атмосферных водяных парах.
Как это видно из фиг. 5, максимальное расстояние от
Земли, на которое может удалиться ракета в конце пути, рав¬
но 2,4-108 км. Подставляя это значение в уравнение (38), по¬
лучаем величину потерь при распространении в свободном
пространстве:
п. ==: ( 4. 2,4 • 1013 ) *
1Vc, п. = 24,6 • 1(Г28 или —266,1 дб.
Для расчета необходимой мощности передатчика имеем
основное уравнение (записанное в дб):
^пер + Опер+ Gnp+ п. — kTB'-\-N +-ДГ >	(40)
где РПер — мощность передатчика, вт\ Gneр — коэффициент
усиления передающей антенны; Gnp— коэффициент усиле¬
ния приемной антенны; k — постоянная Больцмана; Т — тем¬
пература, °К; В — ширина полосы пропускания частот прием¬
ника, гц\ N — коэффициент шума приемника; S/N — необхо¬
димое отношение сигнал/шум в приемнике.
Коэффициент шума приемной аппаратуры примем равным
6,5 дб, а окружающую температуру равной 300° К (комнат¬

РАДИОКОНТРОЛЬ ТРАЕКТОРИИ
357
ная температура). Однако в системе могут быть использо¬
ваны и более низкие температуры, легко реализуемые в кос¬
мическом пространстве, а в наземных условиях получаемые
за счет охлаждения жидким гелием. В этом случае предпола¬
гается использование квантовомеханических усилителей и
низкотемпературных кристаллических смесителей, обеспечи¬
вающих снижение необходимой мощности передатчика.
Для предварительных расчетов отношение S/N целесооб¬
разно принять равным 20 дб, а обе антенны — на ракете и
спутнике — предположить ненаправленными (Gne р= Gnp =
= 0).
Импульсная система. Предположим, что полоса пропус¬
кания приемника равна 10 Мгц. Подставляя выбранные выше
параметры в уравнение (40), получаем
Япер + 0 + 0 — 266,1 = —134 + 6,5 + 20
или
Япер = 158,6 дб, Япер = Ю15*6 вт.
Допплеровская система. Ширина полосы пропускания в
приемнике принята равной 10 гц исходя из предположения,
что в течение долей секунды не произойдет заметного изме¬
нения допплеровской частоты.
Подставляя принятые значения параметров в уравнение
(40), имеем
Япер = 98,6 дб, или Япер = 109’86 вт.
Полученная величина мощности очень велика и не может
быть	реализована в ракетных передатчиках.	Это	указывает
на необходимость применения как на ракете,	так	и	на	спут¬
нике направленных антенн с большим усилением, равным
примерно усилению 6-метровых параболических антенн. Та¬
кие антенны имеют ширину диаграммы направленности 1,7°
(по половинной мощности) и нуждаются в целеуказании, ко¬
торое может осуществляться с помощью расположенной на
Земле счетно-решающей машины.
Если принять общее усиление обеих антенн равным 79 дб
(Gnep = Gnp = 39,5 дб), требуемая мощность передатчиков
будет для импульсной системы
Япер = 79,6 дб, или Япер = 107’96 вт
и для допплеровской системы
Япер = 19,6 дб, или Япер= Ю1’96	вт.
Для импульсной системы по-прежнему остается необходи¬
мой достаточно высокая пиковая мощность, в то время как

358	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
для допплеровской системы требуется приблизительно около
100 вт.
Канал связи между ракетой и Землей может быть обеспе¬
чен с помощью наземной направленной 18-метровой антенны
с усилением 49 дб и шириной диаграммы направленности
0,59° (по половинной мощности) при условии правильной
ориентации антенны на предварительно определенное поло¬
жение ракеты. Требуемая ширина полосы пропускания в та¬
кой системе составит
20 + 39,5 + 49 — 266,1 = 1гТВ + 6,5 + 20,
kTB = —184,1, В= 100 гц.
Полученная полоса пропускания отвечает требованиям
обычной телеграфной связи. Повышение мощности на 10 дб
позволяет в 10 раз увеличить полосу пропускания.
Приемник допплеровской системы
При определении требований к допплеровскому прием¬
нику важно учесть следующее:
1. Быстрый частотный сдвиг, обусловленный движением
спутника по орбите, требует или расширения полосы пропус¬
кания, соответствующего сдвигу частоты, или применения
приемников, следящих за сдвигом несущей частоты.
2. Как показано выше, допплеровскую частоту необхо¬
димо измерять с максимально возможной точностью, так как
только при этом условии могут быть полностью использо¬
ваны преимущества этого типа систем.
Для определения допплеровского сдвига частоты, ожидае¬
мого в течение времени полета на Марс, необходимо решить
уравнение для допплеровской скорости между ракетой и Зем¬
лей и добавить допплеровские составляющие, получающиеся
за счет действия скорости спутников.
Как видно из фиг. 9, угол 0V между вектором скорости и
его тангенциальной составляющей, будет равен
0„=arctg-^-,	(41)
где г — радиальная составляющая скорости ракеты; 0 — уг¬
ловая составляющая скорости ракеты.
Общее уравнение для орбиты в задаче двух тел имеет вид
  а{\ — е2)
r ~ ~l+e cos 0 ’
(42)

РАДИОКОНТРОЛЬ ТРАЕКТОРИИ
359
где а — большая полуось орбиты. Дифференцируя его по б,
получаем
dr а( 1 — е2) е sin 0
— ~М ~~ (l+e cos 0)2
Так как
dr 	 drjdt	 _r_
dd ~	~
dQ/dt
0
(43)
(44)
то, подставляя выражения (43) и (44) в выражение (42), по¬
лучим
O0 = arctg(—|7с^).	(45>
Общее	выражение для скорости v тела на	орбите	в	задаче
двух тел имеет вид
v = Q(ml + nui)(j — ^},	(46)
где G	=	(6,67	±	0,005) • 10~8 в единицах CGS —	гравитацион¬
ная постоянная.
Для ракеты, движущейся к Марсу по орбите вокруг
Солнца,
Мс = 1,992-1033 г,
Мр = 0,
а= 1,88 • 1013 см.

360	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Земля, находящаяся на приблизительно круговой орбите
радиусом г3 = 1,49- 108 км, имеет постоянную линейную ско¬
рость, равную у3, и угловую скорость, равную *63:
/	1,49	•	108	• 2п	1П4	.	/д-
V3 = г30з = 365~Х 24— = 10,7 • 104 км/час. (47)
Фиг. 10. Изменение допплеровской скорости при полете ракеты
относительно Земли.
Как видно из фиг. 9, угол Ур между вектором vp ракеты и
вектором дальности г может определяться выражением
Vp = vp + 9ff,-0f,-e.	(48)
Учитывая, что вектор скорости Земли всегда перпендикуля¬
рен г3, получаем следующее выражение для Чг3:
\ir3 = v3 + 90° — 6.	(49)
Разность между скалярными произведениями векторов
скорости ракеты и Земли на единичный вектор г определяет

РАДИОКОНТРОЛЬ ТРАЕКТОРИИ
361
допплеровскую скорость, как это показывает следующее
уравнение:
V = Vp • г — V3	• г	(50)
или
VA = V? COS ЧГр — V3 COS ^3.
На фиг. 10 приведен график величин допплеровского сдви¬
га	при	полете	ракеты на Марс.	Максимальное	его	значение
приходится на	195-й день полета	и составляет 6,24 •	104	км/час.
Подставляя это значение в выражение (31), получаем для
частоты передатчика, равной 2000 Мгц, допплеровский сдвиг
116 064 гц. К допплеровской скорости, определяемой уравне¬
нием (50), необходимо добавить величину соответствующей
скорости спутника в единицах вектора дальности г*:
vH = (vp — v3	— vcn) • г,.	(51)
ЗАКЛЮЧЕНИЕ
В заключение приведем краткий обзор параметров им¬
пульсных и допплеровских систем в таблице.
Импульсная система
Допплеровская система
Ширина полосы
10 Мгц
10 гц
Мощность передатчика
100 кет (импульсн.)
100 вт (непрерывн.)
Диаметр антенны
6 м
6 м
Точность определения откло¬
ОД амплитуды неиска¬
Г
о
0
1
О
н
о
нения от курса
женного сигнала
Число спутников
3+1 наземная станция
6
Точность, получаемую с помощью этих двух систем, труд¬
но сравнить без числового примера, однако все же возможно
сделать некоторые общие заключения относительно точности
производимых при этом измерений. В обеих системах она
зависит от стабильности источников частоты, применяемой
Для калибровки электронных счетчиков. В импульсной си¬
стеме при малых мощностях на входе приемника точность
ограничивается временем нарастания переднего фронта им¬
пульса, который в свою очередь зависит от ширины полосы
пропускания приемника.

362	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Практическое осуществление импульсных систем более
просто по сравнению с допплеровскими, ибо при этом
1) не требуется высокой точности поддержания частоты
и, следовательно, отпадает необходимость в применении точ¬
ных маломощных генераторов с температурной стабилиза¬
цией;
2) необходимо использовать только три станции, распо¬
ложенные на спутниках, по сравнению с шестью станциями
в допплеровской системе;
3) можно использовать более простую счетную машину,
так как возможно прямое решение и не требуется последую¬
щих уточнений.
Практически допплеровские системы, по-видимому, более
пригодны для работы на больших расстояниях, а импульсные
системы следует применять на относительно коротких рас¬
стояниях, например при контроле траекторий искусственных
спутников Земли.

ТОЧНОЕ НАБЛЮДЕНИЕ ЗА КОСМИЧЕСКИМИ
КОРАБЛЯМИ РАДИОТЕХНИЧЕСКИМИ МЕТОДАМИ ')
Хэнд ел, X ё нд о р ф
При наблюдении радиотехническими методами на сантиметровых вол¬
нах можно достигнуть точности оптических систем, если известен коэффи¬
циент преломления атмосферы в местах расположения радиолокационной
станции и цели. В месте расположения станции сопровождения коэффи¬
циент преломления можно измерить; за пределами плотной атмосферы он
равен единице. Влияниями ионосферы в диапазоне сантиметровых и милли¬
метровых волн можно пренебречь Показано, кроме того, что любой пугь
распространения определенного профиля между поверхностью Земли и
целью лишь незначительно влияет на ошибки в определении расстояний и
углов. Подсчитаны и приведены пределы точности. При этих условиях мо¬
жет быть полностью использована высокая точность современного элек¬
тронного оборудования наблюдения; этот случай не распространяется на
объекты, движущиеся в атмосфере.
Точность определения углов современными радиотехниче¬
скими системами управления и сопровождения в основном
определяется отношением длины базовой линии между ан¬
тенными системами к длине волны. Используя волны санти¬
метрового и миллиметрового диапазонов и длинные базовые
линии, можно достичь любой необходимой точности.
Точность измерения расстояния зависит от точности изме¬
рения фазы сигнала на определенной частоте. Фазовый угол
на этой частоте можно выразить через соответствующий вре¬
менной интервал т, представляющий собой время распростра¬
нения радиосигнала от радиолокатора до цели и обратно.
Измеряемое расстояние находится умножением т/2 на сред¬
нюю скорость распространения радиоволн. Фазовый угол
в обычных импульсных радиолокаторах измеряется на часто¬
те повторения импульсов. Его можно также измерять на про¬
межуточной или радиочастоте.
При заданной точности измерения фазы точность измере¬
ния расстояния будет прямо пропорциональна используемой
частоте. Переходя от измерения фазы на частоте повторения
импульсов к измерениям на промежуточной или радиочас¬
тоте, можно достигнуть почти любой необходимой точности.
l) Handel P. F., Н о е n d о г f F., IRE Trans, on Milit. Electronicst
Mil.-З, № 4, 162—172 (October 1959),

364	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
При современном оборудовании можно измерять углы с точ¬
ностью до нескольких секунд и расстояния с точностью до де¬
сятков сантиметров.
Но точность, которая достигается при реальном слежении
за движущимися целями в атмосфере, ограничивается влия¬
нием условий распространения, т. е. рефракцией в плотных
слоях атмосферы. Ошибки в измерении углов и расстояний,
вызываемые изменениями коэффициента преломления по ли¬
нии распространения радиоволн, примерно на два порядка
превосходят точность системы, которая, таким образом, ни¬
когда полностью не используется. Поэтому практически не¬
целесообразно строить дорогие станции, обладающие наи¬
высшей возможной точностью.
Задача настоящей статьи заключается в том, чтобы по¬
казать, что это положение не распространяется на объекты,
движущиеся за пределами земной атмосферы. Коэффициент
преломления вдоль трассы распространения, конечно, и в
этом случае остается неопределенным. Но в месте располо¬
жения электронной системы на поверхности Земли его можно
измерить обычными методами, а в месте нахождения цели он
также известен, ибо на высотах больше 60 км его величина
отличается от единицы не более чем на 10~6.
Эффекты преломления в ионосфере не рассматриваются
в этой статье, так как можно показать, что эти влияния пре¬
небрежимо малы, если используются частоты сантиметрового
диапазона.
В дальнейшем обсуждении мы допускаем, что Земля ок¬
ружена концентрическими слоями атмосферы с постоянными
коэффициентами преломления в горизонтальном направле¬
нии. Последнее допущение вызвано тем, что измерение гра¬
диентов вдоль траектории луча практически невозможно.
Новое в нашем анализе космических траекторий заклю¬
чается в том, что мы знаем коэффициент преломления на
обоих концах пути радиолуча, в его начале на поверхности
Земли и в конце в месте нахождения цели. Как показано
ниже, можно найти семейство стандартных кривых коэффи¬
циентов преломления в функции от высоты, причем каждый
член семейства начинается с определенного коэффициента
По на поверхности Земли и на высоте 60 км отличается от
единицы не более чем на 10_6. Можно подсчитать ошибки по
углам и дальностям, определяемые этими стандартными кри¬
выми, и величины, измеренные радиолокатором сопровожде¬
ния, дополнить соответствующими поправочными членами.
Этот метод не ухудшает точности системы, ибо поправки ос¬
новываются на измеренных данных и точных расчетах.

ТОЧНОЕ НАБЛЮДЕНИЕ РАДИОТЕХНИЧЕСКИМИ МЕТОДАМИ 365
]В связи с этим возникает весьма существенный вопрос от¬
носительно величины неустранимых ошибок, которые могут
иметь место вследствие нестабильности отдельных кривых
мея^ду известными данными в начале и конце каждого на¬
правления на спутник. На фиг. 1 схематично показаны ме¬
стоположение радиолокатора и три положения спутника. Со¬
вершенно очевидно, что невозможно измерить профиль изме¬
нения коэффициентов преломления вдоль путей распростра¬
нения радиоволн между радиолокатором на Земле и всеми
Фиг. 1. Схема расположения наземного радиолокатора и искусственного
спутника.
точками Si, S2l Si вдоль траектории спутника. Метеороло¬
гические измерения рефракции в атмосфере делаются обычно
вдоль вертикальных линий, и каждое измерение требует оп¬
ределенного времени, а значения коэффициентов преломле¬
ния меняются во времени и пространстве, поэтому невозмож¬
но начертить мгновенное распределение их профилей в нуж¬
ное время.
На фиг. 2у а показаны две кривые коэффициента прелом¬
ления, соответствующие двум крайним атмосферным усло¬
виям. На поверхности Земли коэффициент в обоих случаях
одинаков, на высотах больше 70 км он близок к единице и
отличается от нее не более чем на 10_б. Кривая 1 соответ¬
ствует случаю, когда воздух на всем пути радиолуча влаж¬
ный и близок к насыщению; в случае кривой 2 предпола¬
гается, что воздух на больших высотах сухой, а на малых
высотах его влажность при приближении к Земле быстро
повышается. Подобная кривая будет иметь место также
при инверсии температуры *) в нижних слоях атмосферы.
1) Повышение температуры с увеличением высоты. — Прим. ред.

366	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
На фиг. 2,6 схематично показаны два пути распространения
луча, соответствующие двум кривым изменения коэффициен¬
та преломления. Траектория 1 имеет малую кривизну в соот¬
ветствии с более низкими градиентами коэффициента пре¬
ломления на всех высотах, тогда как траектория 2 обладает
значительной кривизной в низких слоях атмосферы, что со¬
ответствует высоким градиентам коэффициента преломле¬
ния, и очень малой кривизной в верхних слоях атмосферы,
Фиг. 2.
а. — кривые зависимости коэффициента преломления от высоты Л; б —траектории
радиолуча, соответствующие кривым а.
где градиент невелик. Обе траектории выходят из атмо¬
сферы выше 60 км как параллельные прямые линии. По¬
следнее обстоятельство лежит в основе нашего анализа. Не¬
зависимо от того, как располагаются слои атмосферы, иными
словами, независимо от характера отдельных кривых коэф¬
фициента преломления траектории радиолуча всегда выхо¬
дят из атмосферы параллельно. Обозначим ао зенитный угол,
измеренный радиолокатором, а Дон и Даг — корректируемые
ошибки на высоте 60 км, которые можно точно подсчитать,
исходя лишь из коэффициента преломления, измеренного на
поверхности Земли (п0). Обе траектории радиолуча парал¬
лельны (Доц = Да2); это означает, что для целей, удаленных
в бесконечность, остаточная (неустранимая) ошибка равна
нулю. Реальные цели не могут находиться в бесконечности,

ТОЧНОЕ НАБЛЮДЕНИЕ РАДИОТЕХНИЧЕСКИМИ МЕТОДАМИ	367
но |их высота может значительно превышать 60 км. Таким
обррзом, расчет показывает, что неустранимые ошибки
уменьшаются с увеличением расстояния. Из дальнейшего
будет видно, что для всех практических случаев они не пре¬
вышают нескольких секунд при измерении углов и соста¬
вляют ~ 1 м при измерении расстояний.
Другая картина наблюдается для целей, находящихся
внутри плотной атмосферы (см. фиг. 2). Предположим, что
цель находится на высоте 15 км. Можно видеть, что угловая
ошибка Дои резко отличается от Да2 для случая двух кривых.
Но главное в том, что ни Дои, ни Да2 не могут быть вычис¬
лены, потому что профили изменений п неизвестны. Следова¬
тельно, в случае цели, находящейся в атмосфере, Д<ц и Да2
являются не поправками, а неустранимыми ошибками значи¬
тельной величины. Современные электронные системы упра¬
вления и наблюдения обладают точностью, значительно пре¬
восходящей эти неустранимые ошибки. Следовательно, воз¬
можности систем не могут быть полностью использованы,
когда цели находятся в атмосфере. Но когда цели находятся
вне плотных слоев атмосферы, они могут быть использованы,
и нет причины, по которой электронные системы не могли
бы достичь точности оптических приборов (независимо от
погоды).
КРИВЫЕ ИЗМЕНЕНИЯ КОЭФФИЦИЕНТА ПРЕЛОМЛЕНИЯ
Коэффициент преломления п для сантиметровых и милли¬
метровых волн, проходящих через атмосферу, зависит от тем¬
пературы, давления воздуха и парциального давления паров
воды следующим образом:
v = (я — I) 10б = -£г (/> 4- -у-) ,	(1)
где с = 79° К/мбар \ Т — температура, °К; р — давление воз¬
духа, мбар; b = 4800° К; е — парциальное давление паров
воды, мбар; п — коэффициент преломления.
На фиг. 3—5 приведены зависимости коэффициентов пре¬
ломления от высоты над уровнем моря для средних, больших
и малых значений коэффициента v у поверхности Земли.
Малый коэффициент может иметь место только на высо¬
кой горе, поэтому для получения графика фиг. 4 использова¬
лись результаты метеорологического зондирования из Хол¬
ломанской базы ВВС США, причем измеренные значения
пересчитывались применительно к пику Сакраменто (3095 м

V о
К О
4 3
п м
й о
гз S
5 =
<и
л 5
н S
S
К
<D н
а м
*	я =
£2 s
^ S
. К о
Г Й О
S О
-И:
S ^
*	СП
со
m'tf

ТОЧНОЕ НАБЛЮДЕНИЕ РАДИОТЕХНИЧЕСКИМИ МЕТОДАМИ
над\уровнем моря), расположенному примерно в 15 км во¬
сточнее Холломанской базы. График средних значений v
(фиг. 3) получен в Вальпарайсо (шт. Флорида).
Зондирования для случая больших значений коэффициен¬
та преломления (фиг. 5) не проводилось. Эти кривые по¬
лучается, если допустить определенный температурный
градиент и очень высокую влажность (75—90%) на всех
высотах. Такие условия могут иметь место перед началом
тропического грозового шторма.
Величина коэффициента преломления вычислялась по из¬
меренным значениям давления, температуры, содержания па¬
ров воды и высоты с помощью формулы (1); результаты рас*
четов представлены в виде кривых а на фиг. 3—5. Во всех
трех случаях относительная влажность у поверхности Земли
равнялась 75%. Для получения кривых бис, соответствую¬
щих крайним значениям атмосферных условий при том же
значении коэффициента у поверхности Земли, предполагаем
для кривой б, что на высотах больше 300 м над поверхностью
Земли воздух влажный и близок к насыщению, а распреде¬
ление давления и температуры с высотой остается прежним.
Для кривой с, наоборот, предполагается, что воздух на вы¬
сотах свыше 300 м сухой, но быстро увлажняется по мере
уменьшения высоты, достигая у поверхности Земли влажно¬
сти 75%. Как видно из уравнения (1), те же условия будут
иметь место, когда на высоте от 0 до 300 м будет наблюдаться
инверсия температуры.
24 Зак. 87$.

370	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Кривая с на фиг. 5 выбрана специально для изучения не¬
устранимых ошибок по углам и расстояниям, вызываемых
двумя совершенно различными по характеру профилям^ из¬
менения коэффициента преломления, начинающимися с; оди¬
накового значения у поверхности Земли.	;
Кривые а и b на фиг. 3—5 были аппроксимированы экс¬
поненциальными функциями. Кривая с аппроксимирована
квадратичной параболой в своей нижней части и экспонен¬
циальной функцией в верхней части. Результаты расчета
ошибок по углам и расстояниям для восьми кривых, пока¬
занных на фиг. 3—5, приведены в табл. 1.
Таблица 1
Кривая а
Кривая b
Кривая с
Кривые а, Ь, с
м0 = 250
Да
4'43,5//
4'42,6"
444,1"
S — d
1,16 м
(фиг. 4)
Д2а
+ 0,9"
— 0,6"
Д5К
86,01 м
85,73 м
86,3 м
Д25к
4-0,46 м
— 0,06 м
О
II
СО
05
оо
Да
8'7,4"
8'3,8"
8'10,2"
S — d
0,95 м
(фиг. 3)
Д2а
4- 3,6"
— 2'8"
AsK
80,95 м
79,24 м
82 м
4- 1,72 м
— 0,86 м
о
II
05
00
Да
1048,8"
Так же, как
Ю'57,4"
S — d
0,95 м
(фиг. 5)
кривая а
Д2а
—8,6"
AsK
117 м
114 м
Д2$к
4- 3,23 м
Принятые обозначения (фиг. 6):
а = 81,75° — зенитный угол;
5 — геометрическая длина искривленной траекто¬
рии луча;
v0 = (ra-l)106;
Да — угловая поправка;
d — истинное расстояние до цели (1,460 • 103 лгж);
sK — расстояние, измеренное радиолокатором на
искривленной траектории при кажущейся ско¬
рости распространения vK = 299773,1 км/сек
(скорость распространения в вакууме £ =
— 299792,9 км/сек)',

^ ТОЧНОЕ НАБЛЮДЕНИЕ РАДИОТЕХНИЧЕСКИМИ МЕТОДАМИ 371
\
д5к±=я?— sK—поправка по дальности;
AfOC = АоС(КрИВая а) А^(криван Ь или с) НбуСТрЗНИМЗЯ уГЛОВЗЯ
ошибка;
A2Sk A-Sk (кривая а) Д«5к (кривая Ь или с) НбуСТрЗНИМЗЯ ОШИбкЗ ПО
дальности.
В табл. 1 приведены неустранимые ошибки по дальности
и по углам (Д2а и A2sK), которые происходят из-за отсутствия
данных о том, какой характер профиля коэффициента пре¬
ломления а, b или с в действительности преобладает. Вели¬
чина этих ошибок на два порядка ниже корректируемых
величин Да и ДsK.
Эти данные показывают, что нет необходимости тщатель¬
но подгонять к результатам измерений математические вы¬
ражения, экспоненциальные функции и параболы; иными
словами, точность аппроксимации на фиг. 3—5 не имеет су¬
щественного значения. Это станет ясным, если мы обратим
внимание на то, что неустранимые ошибки весьма малы, даже
если они получены в результате расчета таких разных кри¬
вых, как а, b и с, и вычислены для зенитных углов, соста¬
вляющих ~82°, т. е. на 8° выше горизонта. Это значит, что
характер распределения промежуточных слоев существенно
не влияет на измерение углов и расстояний. Определяющим
фактором является коэффициент преломления у поверхности
Земли vo, и его величина должна и может быть точно изме¬
рена в момент наблюдения и в непосредственной близости
от радиолокатора. Это положение, являющееся основным
в нашем исследовании, позволяет ввести «стандартные» про¬
фили коэффициента преломления.
С помощью уравнения (1) были рассчитаны сорок четыре
профиля, взятых для разных климатических условий и раз¬
ных зысот над уровнем моря. Для пяти из этих профилей
служба погоды США проводила индивидуальные зондиро¬
вания. Тридцать две кривые взяты из опубликованных мате¬
риалов !).
Все кривые, относящиеся к восточному побережью, а так¬
же континентальной части США и Аляски, легко аппрокси¬
мировались экспоненциальной функцией. Все кривые, отно¬
сящиеся к побережью Мексиканского залива и островов Ка-
рибского моря, имели пологий участок профиля для малых
высот. Тем не менее во всех случаях функция v = voe~h!H удо¬
влетворительно аппроксимирует профили v.
\) Из*них десять кривых взяты из «Climatic Data for White Sands
Missile Area», October 1958, двадцать две — из «Upper-Air Climatology of
the United States», U. S. Dept. Commerce, Weather Bureau, TP № 32, 1957.
24*

372	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
При вычерчивании для постоянной высоты Н величин v0,
взятых из 44 кривых, было отмечено, что все точки для Уайт
Сэндс (высота 1200 м над уровнем моря) и все точки для
побережья (высота от 0 до 7 м) расположены около прямых
линий, тогда как все другие точки разбросаны хаотично. Это
10,5
9,0
15
5,0
1 1 1 1 1 II 1 1 1 I
\
4- Определенные по кривым фиг. 3-5
-
\
о Измеренные при зондировании
ч
Л
ч
о
+
э
ЧуЛ
4
О
о
р9
5s
J.
ъ
.. Т
+
О
с
ч
+
2501 зоо 350 т т
УУРМ
Фиг. 7. Зависимость между vyp.м> и Н.
500
приводит к попытке привести все величины vo к уровню моря
с помощью следующего преобразования:
(2)
v =	9
v = (yQeh^H) е~н/н у
V — v p-h/H
— УР- м- 9
ч. — 41	р—Нъ/Н
V0  ур. МЛ' »
(3)
(4)
где vyp. м- — коэффициент преломления, приведенный к уров¬
ню моря; Я— постоянная высота, м; h — переменная высота,
м (над уровнем моря); h0 — высота места наблюдения, м
(над уровнем моря).
Результаты этих расчетов показаны на фиг. 7. Кружки
представляют собой измеренные значения, полученные при

ТОЧНОЕ НАБЛЮДЕНИЕ РАДИОТЕХНИЧЕСКИМИ МЕТОДАМИ 373
практическом зондировании; крестики определены по кри¬
вым фиг. 3—5. Через все эти точки проведена усредняющая
кривая. Пять поверок для точек, наиболее удаленных от кри¬
вой, показали, что аппроксимация при величине Я, опреде¬
ляемой усредненной кривой, лучше, чем при определении Я
по этим пяти точкам.
vo и V”
Фиг. 8. Г рафик для определения vyp# Mt и Н для стандартных кривых
при данных hQ и Y0.
Пример. Дано: А0 = 1500 м\ пй —1=280* 10“6. Тогда Н =>7395 м, Яур. м. — 1 = 344 • 10“б и по
h
приближенной формуле л0 = 1 +344е	7^.10”в,	где	А	—высота над уровнем моря.
Примем величину Я, найденную из кривой на фиг. 7, за
«стандартную» и обозначим ее Ястанд- Как видно из графика
фиг. 7, почти все точки лежат в пределах ЯСТанд = ±450 м.
Поэтому в дальнейшем мы будем считать неустранимыми
ошибками Д2а и A2sK такие ошибки, которые при одинаковой
измеренной величине vo образуются отклонением на ± 450 м
от стандартного значения Ястанд.
На фиг. 8 показано семейство стандартных кривых, полу¬
ченных с помощью уравнения (4). Для каждого vo, измерен¬
ного на высоте станции над уровнем моря Ао> соответствую¬
щее значение Я находится интерполяцией между кривыми
с различными параметрами Я. Величина vyp. м. находится
в месте пересечения выбранной кривой Я с осью абсцисс.

374	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
РАСЧЕТ ПОПРАВОК ПО УГЛУ И ДАЛЬНОСТИ
Общие уравнения
Отклонение пути распространения сантиметровых и мил¬
лиметровых волн от прямой линии при прохождении через
атмосферу может быть подсчитано с помощью закона ре¬
фракции. В своей первоначальной форме он применим
только к специальному случаю плоских поверхностей
sin ос __ п0	,-v
sin ос0 п	' '
Для наших целей его необходимо обобщить применительно
к среде с кривыми поверхностями. Такой расчет был проде¬
лан Нотом [1] и независимо Диксоном [2], которые исходили
из закона Ферма и пришли к одинаковым результатам
(см. фиг. 6):
sina   R +К	по	/гл
sin cl0 R + h	ti	' '
Из общего закона (6) нетрудно получить выражение (5),
если радиусы кривизны R + А0 и R + h считать равными бес¬
конечности, а их разность — конечной величиной, что соответ¬
ствует случаю плоскостей.
Любое измерение расстояния между точками 0 и Сп. на
фиг. 6 радиотехническими методами представляет собой из¬
мерение фазы (это может быть фаза высокой частоты, про¬
межуточной частоты или фаза частоты следования импуль¬
сов). В обычных импульсных радиолокационных станциях,
например, фазовый угол на частоте следования импульсов
измеряется между запросными импульсами передатчика и
импульсами, отраженными от цели. Если частота известна,
то фазовый угол можно выразить соответствующим времен¬
ным интервалом т, который представляет собой время рас¬
пространения фронта волны от радиолокатора до цели и об¬
ратно (время распространения в одну сторону равно т/2).
Измеряемое расстояние находится умножением т/2 на
среднюю скорость распространения сигнала и. Скорость рас¬
пространения v точно неизвестна, так как она зависит от из¬
менения коэффициента преломления вдоль траектории луча.
Для каждой системы можно, таким образом, ввести опреде¬
ленную кажущуюся скорость vKl). Измеренное значение
•) Кажущаяся скорость составляется из скорости распространения ра¬
диоволн в свободном пространстве и поправки, учитывающей состояние
среды вдоль траектории луча (ионосферная поправка). — Прим. ред.

ТОЧНОЕ НАБЛЮДЕНИЕ РАДИОТЕХНИЧЕСКИМИ МЕТОДАМИ 375
расстояния, определенное радиолокатором, представляет со¬
бой кажущееся расстояние sK, которое прошел бы фронт вол¬
ны, двигаясь с постоянной скоростью vK по траектории s
(см. фиг. 6):
— о
(7)
Если 5К измерено, a vK из¬
вестно (vK = 299773,1 км/сек),
то можно найти т/2.
Найдем длину искривленной
траектории s. Воспользуемся
с этой целью хорошо извест¬
ным выражением для скорости
распространения в среде с ко¬
эффициентом преломления п:
^  с  с
Vw п
Из фиг. 9 следует, что
dh
dS =
(8)
(9)
а из (6)
cos а =
=[,-.тЧ(4^ГШ
Ф и г. 9.
Подставляя (10) в (9), получаем
лгп
n(R + h)
ho
[п2 (R + Л)2 — п\ (R + Л0)2 sin2 а0]
К расчету
поправки.
dh,
угловой
(10)
(11)
где s — геометрическая длина искривленной траектории луча
(см. фиг. 6).
Найдем метод подсчета высоты спутника hcn, остаю¬
щуюся пока неизвестной в выражении (11).
В соответствии с (8) имеем
ds — vdt = — dt,
(12)
а из (12) и (И) находим
п* (R + h)
dt
с [п2 (R + Л)2 — п\ (/? + hQf sin2 а0]
V.
dh

376	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
т
т=4 Г-  Tdh. (13)
J W (* + Л)2 - п20 (R + hQf sin2 «о]12
Из (13) находим Лсп методами приближенного интегриро¬
вания на электронной счетной машине, поскольку все другие
величины известны (т/2 определяется выражением (7), а п —
(2) и (3)]
п = 1 +(л0— 1)£-<а-Ло)/л,
где Я определяется по графику фиг. 8 для измеренного зна¬
чения п0 и известного h0. Зная Лсп, из (11) находим 5.
Далее, мы должны определить геометрическое расстояние
(см. фиг. 6), которое является истинным расстоянием до
цели. Сторона плоского треугольника равна
d = [(/?'+ h0)2 + (R + Асп)2 - 2 (R+ h0) (R + Лсп) cos Tcnl'/a-	(14)
В	этом	уравнении	<рСп пока не известно. Для того	чтобы
найти эту величину в функции от высоты, поступаем следую¬
щим образом. Как видно из фиг. 9,
- tga • dh	/л '
^ = 4+тг-	<15)
Исключая а из (15) и (6), получаем
"с
» = Г   п°(/? + й°) si" ао	dh	П6)
Тсп J (R + h)[n*(R + hy — n20(R + ri0ysin2a0}'h ‘
П О
После этого d можно определить из (14).
Наша цель — найти поправку по дальности ДsK, которую
необходимо добавить к кажущемуся расстоянию sK) измерен¬
ному радиолокатором для нахождения истинного расстоя¬
ния d. Из (7) и (14) находим
ДsK = J-sK = l(R + hQf + {R + hsf - 2 (R + h0) X
X(/? + /tcn)coscpcn]'/! — ^VK.	(17)
Поправку по углу Да легко найти, применяя закон сину¬
сов (см. фиг. 6):
sin («0 + Да) — -R-^~d kcn sin <рсп	(18)
и
Да = arc sin ( ^ hcn sin асп^ — aQ.

ТОЧНОЕ НАБЛЮДЕНИЕ РАДИОТЕХНИЧЕСКИМИ МЕТОДАМИ 377
Расчет
Во всех практических случаях наблюдения космических
кораблей следующие величины известны из измерений:
<ик — скорость распространения с внесенной ионо¬
сферной поправкой;
й0— высота места наблюдения над уровнем мо¬
ря, м\
£>= 6371788 м—радиус Земли (сферы равного объема);
/г0=1+''о10-6 — коэффициент преломления в месте распо¬
ложения антенны радиолокатора;
а0 — кажущийся угол места, измеренный радио¬
локатором;
sK — кажущаяся дальность, измеренная радио¬
локатором;
Н и уУр.м. из фиг. 9; v из (3);
с — скорость распространения в вакууме.
В соответствии с (7) получаем
Решая (1), находим Асп методами приближенного инте¬
грирования. Затем решая последовательно (16) и (14), нахо¬
дим фсп и истинную дальность d. После этого находим по¬
правку по дальности из (17) и поправку по углу из (18).
Практически применяется несколько иной порядок рас¬
чета. Предполагают известными величины
«о:=(^-)' К R> а0- Н’ vyp.M.>	S.
Величина hcn определяется из (11), с (т/2) =с — из (13),
Фсп —из (16), d — из (14) и, наконец, Да и AsK — из (18)
и (17).
Такой порядок расчета дает возможность проконтролиро¬
вать некоторые результаты расчета, такие, как d, s и о, ко¬
торые по величине должны располагаться в приведенной по¬
следовательности, а разность s — d должна быть меньше, чем
о — 5. Кроме того, для любых v0 и ао разность о — 5 постоян¬
на, а 5 — d должна возрастать с ростом 5. Последние вели¬
чины должны уменьшаться с уменьшением ао.
Решение уравнения (И) аппроксимируется последователь¬
ным интегрированием с 1620 интервалами в каждом случае
и шириной интервала ДА = 0,61; 1,22; 2,44; 4,88; 9,76 и
19,52 м. Это дает высоту h, = 62 257 м и соответствующее sr.

378	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Отсюда для п = 1 остаток интеграла может быть легко най¬
ден; hCn затем подсчитывается из
Aon = [{S - sry + 2 (s — sr) ух + (/? + hrf\k - R,
где
А = (/? -+- hrf — По (R -f- A0)2 sin2 а.
Уравнение (13) переписывается
/г_ _
СП
4=«=/ •
ho
Этот интеграл подсчитывается тем же методом, что и вы¬
ражение (11), в той же последовательности и с той же ши¬
риной шагов. Аналогично определяется аг как величина она
высоте hT о = ог + (s — sr), поскольку при п = 1 интегралы
в (13) и (И) идентичны.
Уравнение (16) интегрируется таким же образом до вы¬
соты hr = 62 257 м и соответствующей величины. <рг на этой
высоте. Интегрирование дает
<р„ = ?, + [arc cos Мгу-Д)*».. _ arc cos ..(^jsin..] ^
Затем решаются уравнения (14), (17) и (18). Случайных
ошибок, превышающих 0,0003 м и 0,00Г', обнаружено не
было. Однако при этом могут иметь место систематические
ошибки, определяемые емкостью счетной машины. Следова¬
тельно, точность величин AsK и Да, приведенных в табл. 2,
равна двум единицам последнего разряда. Эти величины
были подсчитаны для следующих параметров:
а0 = 87,5; 85; 80; 70; 50 и 10°;
s(km)= 1520; 1370; 1220; 1070; 920; 760; 610; 460; 310;
v0 = 400; 370; 340; 310; 280;
Н(м) = Ист — 450; /Уст; /7ст + 450;
К (м) = 0.
Во всех расчетах предполагалось, что hcu^ 64 000 ж,
чтобы быть уверенным, что цель находится вне плотных сло¬
ев атмосферы.
Разности величин Да и ДsKi подсчитанные для трех раз¬
личных значений Я, определяются как Д2а и Д25к соответ¬
ственно и являются неустранимыми ошибками, вызываемыми
неопределенностью кривой коэффициента рефракции. Эти

ТОЧНОЕ НАБЛЮДЕНИЕ РАДИОТЕХНИЧЕСКИААИ МЕТОДАМИ 379
величины значительно более точные, чем Да и Д$к, так как
исчезают возможные систематические и случайные ошибки.
Величины Д2а и Д25к, приведенные в табл. 2, всегда яв
ляются наибольшими ошибками в случае, если разности для
Нот — 450 не равны.
ПРЕДЕЛЬНЫЕ ТОЧНОСТИ ЭЛЕКТРОННЫХ СИСТЕМ НАБЛЮДЕНИЯ
Как видно из табл. 2а, значительные угловые поправки
необходимо вводить при больших зенитных углах, боль¬
ших расстояниях и больших коэффициентах рефракции.
Эти поправки достигают величины свыше 20' для ао = 87°.
Фиг. 10. Угловые поправки.
При зенитных углах ао = 85° они уменьшаются примерно до
10х и при ао = 40° до величины менее V. Но даже для угла
а0 = 10° они все еще составляют 10—15", чем, конечно, нельзя
пренебречь, если точность системы лучше 2".
Неустранимые ошибки Д2а, наоборот, возрастают с умень¬
шением расстояния. Однако влияние ао и v0 на Д2а такое же,
что и на Да. Эти неустранимые ошибки имеют значительную

Таблица 2а
380
r—l
,_l
CM
CM
CO
,_l
y—t
Г-Ч
CM
а
а
о
о
о
о
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
<3
<43
о
о
о
о
0
0
©"
0"
0"
0"
0"
0"
0“
0"
0"
0"
0"
0"
о
II
ю
ю
CM
CM
05
CD
0
CM
CD
CD
LO
со
CM
0
CD
со
о
а
а
CO
со
со
CM
CO
со
со
00
CO
со
CM
CM
<3
Tt<
со"
со"
со"
00"
со"
со"
со"
со"
со"
T—1
T—4
T—1
1—1
T—1
1—1
r“l
r”‘
T—1
r—'
а
Vi
T-H
CM
CM
CO
■ _
_
ТЧ-Н
1—4
CM
CM
<3
с-
о
о
о
о
0
0
0"
0"
o"
0"
0"
о"
о"
о"
0"
0"
0"
0"
0
о
Vi
T*«
CO
CM
05
CD
CM
Ю
CO_
0
05
00
l^
ю
со
00^
CM
05
I"-
h-
CO
CD
cd"
LO
0"
05"
05"
05"
05"
05
00"
00"
CD
со
CO
CO
со
со
CO
CO
со
CO
CO
CM
CM
CM
CM
CM
CM
CM
CM
а
vi
a
*
а
Vi
Ю
CD
CD
00
©_
CO
со
CO
Th
LO
CD
p_
<3
. о
о
о
о
0
0
0"
0"
0"
0"
0"
0"
0"
0"
0"
0"
о
C»i
CM
00
Ю
is
CM
1—4
LO
is
y—4
00
05
CM
LO
00
CM
CM
о
0
05
Is"
05"
10
со"
со"
cm"
0"
ь."
cm"
Tt<
Tt<
CO
CO
со
CM
CM
CM
CM
CM
CM
CM
CM
1
a
a
*
CO
CO
CO
CO
CO
со
CO
CO
CO
CO
со
CO
00
CO
со
CO
CO
со
а
Vi
is
00
05
05
CO
CO
1
Ю
сD^
00
°l
Ю
0
1
<3
<L>
T—*
CM
CM
см"
со"
1
1—1
1-^
1—1
1—1
1
cm"
cm"
со"
1
о
8
_■
©.
4.
is
0
CO
l^
1
LO
0
0^
CO
CD_
05
1
и
lO
Tf
CN
o'
is"
00"
00"
1
05"
00"
l^."
lO
cm"
00"
cm"
со"
1
в
Vj
CM
CM
CM
CM
10
CO
CO
CM
MUH
is
is
ts
CD
1
CD
CD
CD
CD
CD
CD
CD
CD
1
с?
V»
b-
05
LO
05
CD
Ю
1
1
00
0
CM
10
05
LO
Ю
1
1
<
<43
Cj
is"
b."
00"
00“
00"
05"
0"
1
1
CD"
is."
t<
tsT
00"
05"
1
1
о
00
oo_
CM
00
CO
CO
0^
CO
II
^3
oo"
r_7
oT
со"
cm"
со"
1
1
Is"
со"
00"
cm"
со"
Г—Г
cm"
1
1
о
а
CO
со
CM
T»H
Ю
CO
СО
CM
CM
а
a
a
со
со
со
CO
CO
со
CM
1
1
CM
CM
CM
CM
CM
CM
1
1
*!
1—1
r-H
1“"1
T""
1
I
1
1—1
1—1
T~~i
1
1
а
a
Ю
о
Tt<
©„
0
0
1
1
1
CD
05
со
00
CD^
CD
1
1
1
*
CD
t^r
is"
00
00
o'
1
1
1
cm"
см"
CO
00"
10"
1
1
1
CM
CM
CM
CM
CM
CO
CM
CM
CM
CM
CM
CM
о
UO
о5
a
05
CM
00
CM
CO
lO
00
Ю
05
CD^
II
*3
03
05~
lO
00
LO
cm"
1
1
1
со"
со"
0"
2
r—7
0"
1
1
1
LO
"Sf
CM
CO
LO
Th
CO
LO
CM
а
а
<j
a
со
CM
CM
CM
CM
1
1
1
0
0
0
0
05
05
1
1
1
*1
CM
CM
CM
CM
CM
CM
1
1
1
CM
CM
CM
CM
1
1
1
о
о
о
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
CM
is
CM
Is
CM
CD
CD
CM
CM
CM
CD
CD
LO
CO
CM
0
05
IS
CD
CO
Ю
CO
CM
0
05
0
CO
«о
1—1
r“l
T”1
1—1
1 1
>
8
0
IS-
CO
о о
СО СО
См" СМ
CM СМ
СО СО
о o'
т-м 00
оо" tC
CO
со
r*l
1—1
£0
CO
Tt*"
CO
r—l
CD
CD
05
CM
to'
co“
-
00 Ol
CD (N
СМ см

381
г-*
1—1
Т—(
сч
сч
1—4
г—1
▼—1
,—1
Г-Н
1—1
г-н
сч
сч
1—4
г-н
1_Н
1-Н
г-н
т-н
г-н
сч
0,01
0,01
О
o'
о
о"
о
o'
о
о"
о
о"
о
о"
о
о"
о
о"
о
o'
о
о"
о
о"
О
о
о
©~
о
о
о
о"
о
о"
о
о"
о
о"
о
о"
о
о"
о
о"
о
о"
о
о"
ГО
O'
сч
ф
00
о
LO
ф
сч
00
сч
ю
05
00
00
со
LO
СО
05
СО
СО
<3
СЧ
СЧ
сч
’“1
о
т-н
1
1
1
r_i>
о.
о^
05
о
о
о
о
о
о
05
05
00
с. л
гч
сч
сч
сч
сч
г—1
г—•
Т-Н
1—1
г—I
1—»
Т-Н
гН
о"
о"
о"
о"
о"
о"
о"
05"
05"
of
СЧ
т—'
Г-1
Т-Н
7—‘
7—1
т—1
1—1
1—1
7—1
?-ц
т-‘
1”1
^■н
Т-Н
7—1
7—1
7—1
г—1
Г-,
сч
сч
сч
^н
^н
г-н
_
г-н
г_
Г_
1—н
сч
_Н
Г^
Г-Н
_Н
г_
^н
Т-н
Т-н
сч
о
о"
о
о
о
о
о
о
о
о
о
о
о"
о"
о"
о"
©~
о"
о"
о"
о"
о"
о"
о"
о"
1о
ф
^н
05
ю
00
ю
СО
сч
нн
О
ю
05
00
со
со
Г-Н
о
гч
1—1
1—1
о
05
ю
ю
ю
LO
ф"
ф"
'rf
со"
сч"
14-"
14."
14."
ьГ
14."
со"
со"
ф"
СЧ
СЧ
см
сч
сч
сч
7—1
7—1
1—1
г—1
7—1
Г-*
„—
ф
Ф
ф
ю
со
СО
05
со
со
со
со
ф
ю
СО
00
со
со
со
СО
со
ф
ф
со
00
о
О
о
о
о
о
о
о
о
о
о
о
о"
о"
о"
о"
о"
о"
о"
о"
о"
о"
о"
о"
о"
Ф
00
1-Н
ф
00
СО
о
14
со
оо
т—1
о
ю
о.
СО
сч
о
05
СО
ф.
сП
СП
Ю
со
о
ю
у—*
о
о
05
05
оо"
со"
со"
оо"
'ф"
со"
со"
сч"
сч"
о"
05"
со"
Т-н
LO
LO
ю
ю
ф
ф
со
со
СО
со
со
со
со
сч
сч
сч
СО
00
00
со
СО
со
сч
сч
сч
сч
сч
сч
сч
сч
сч
сч
сч
сч
сч
сч
сч
сч
сч
сч
сч
Ю
СО
00
о
сч
1
со
со
СО
ю
со
1
сч^
со.
ф.
со.
14.^
сч
1
7-4
г“|
1—1
сч
сч
сч
1
1 '
т—|
1—4
7—1
7—1
Г-н
сч"
сч"
1
1—1
Г-Н
7—1
1-Н
7-4
т-н
^н
сч"
1
°°
00
т—1
ф
00
^н
о.
ю
LO
сч
LO
сч
05
СЧ
сч
СО
05.
ф
О.
1
стГ
14."
со"
оо"
1
05"
оо"
со"
ф"
оо"
сч"
со"
1
со"
сч"
05"
СО
сч"
ь-"
оо"
1
ю
ф
1
со
со
со
СО
СО
сч
сч
1
ю
ю
ю
ф
со
СО
со
СО
СО
ю
ю
1
ю
ю
ю
ю
ю
ю
LO
ю
1
ю
LO
LO
ф
ф
ф
ф
ф
1
Ф
о
ю
СО
1
1
сч
СО
ю
со
ю
ю
со.
05.
сч
ю
Т-Н
1
1
со"
СО
Г>Г
о."
оо"
1
1
ю"
ю"
ю"
ю"
со"
со"
о-"
1
1
^ф"
-ф"
■ф"
ф"
ю"
ю"
со"
1
1
г-
оо.
СО
ю
LO
ф^
о-
о.
00.
ю
05
LO
05
СО
СО
СЯ
о
05
об'
г-Г
со"
,_г
со"
1
1
со"
сч"
оо"
Г-Г
со"
г-Г
Th"
1
со"
сч"
оо"
сч"
ф"
со"
to"
1
1
т™1'
ю
со
Ю
Tf
сч
ю
ю
ф
СО
7—1
гн
,
о
о
1
1
о
о
о
о
05
05
05
1
1
05
05
00
00
00
00
00
1
1
’—1
1—4
'—1
1
1
1
’—1
Т—1
1
1
1
1
1

00
Г-Н
00
14
00
о
СО
14
сч
05
00
о
сч
СО
со
оГ
о"
о"
,_г
1
1
1
ю"
со"
со"
со"
14."
1
1
1
сч"
со"
со"
со"
ф"
ф"
1
1
1
СЧ
сч
сч
1—1
7—1
’ 1
7—1
1—н
1 1
7"”1
-
Ф
сч
ф
сч
СО
CO. LO
,
о
СО
ф
сч
т-н
со
&
со"
со"
1
1
1
сч"
со"
,_г
со"
со"
оо"
1
1
1
со"
14."
со"
сч"
со"
со"
’ 1
1
1
On
ф
7—1
СО
сч
^н
LO
со
(М
ю
СО
00
00
O'
1
1
1
со
СО
со
ю
ю
ю
1
1
1
•ф
ф
СО
со
со
1
1
1
1
1
1
Т—Н
7—1
т—'
'И-1
1—1
7—1
1
1
1
7—1
7—1
т-н
1
1
1
8
р
О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
14
сч
СО
со
сч
O'
сч
сч
СО
СО
сч
сч
г-
сч
со
со
О
05
14
СО
ф
СО
ю
СО
сч
о*
05
СО
СО
ю
СО
сч
о
05
СО
ф
СО
т—1
1—
г_н
1—1
Т-Н
т—t
т—1
т“'
f-—
о
о
о
ф
00
СП
со
сч

Таблица 26
382
о
О
II
в
в
ч
id
<J
00 00 00 Г-1 00 ОО ОО 00 г-1
-НтНг-1(М^гНгЧгЧ(М
o' o' o' о' о-' o’4 о" о* о”
00 00 00 00 00 00 00 00 00
о* o' о" о" о*4 сГ о" о*4 о"
0,15
0,15
<
N^HOOCOfOOMCnN
oqoo^t^t^couoio^Tf1
«>г t>T ьГ t%T (>г ^
OOONCOiO^CO(N^
NrHprHHOOlNOS
оо оо О ю io ^
NNNNSNSNN
CDQONCOiO'tCOtMrH
^ T-H
°° 00
05 00
Tf rt
CN CN
o' o'
0
о
ю
II
ь
Ч
ьй
ч>
<а
N t'" »—• г—1 1—t h> 1—1 i-^ 1—t
cncncocooocncococo
o' о" cT o’4 о" о" о" о" o'
°i СЧ CN CN CN CN CN CN CN
o~ o o' o~ o~ o~ o~ o~ o~
*
Ьй
Ч>
<1
(NOCOON^THOIrH
0 0000 00 00 00 0005
iO IO ю ю' Ю iO 1C ю" iO
OlOOStOiO'tfOlMH
05 СО О О t4» i—1 00 05 00
00 00^ 05^ 05^ CO 00 t>- 00
iO lO IO Ц5 io" LO Ю iO iO
О500ЬСОЮ^СО(Мгч
0,46 95,89
0,46 85,86
/
0
о
II
«?
*>?
<1
CNiOiOCNCNiOiOiOCN
ююююююююю
о о" о" о" о~ о*4 о" о" о
050505050505050505
^ ^ ^ ^ ^ ^
o' o" o~ o" o" o~ o' o" o'4
£
<а
ЮЮ(МООГОО)О0ОО
OOOOOOr-.r-.CSI
of CN CN CN CN of of CN CN
CDOONtOiO'tOOCNrH
(N(N0)00(00(010
0_ О 05^ C5_ О О 1—1 1—1 CN
CN CN г—Г CN CN CN CN CN CN
O500NCOiO^CO(Nr-i
92.02
82.02
о
8
II
t?
Ьй
«S5
<j
о о о ов ож о о о I
1—1 1—« 1—1 1—< 1—Г 1—1 Т—• г—Г
05 05^05^0505050)005
c> o~ cT o~ o" o" o~ o~ o'4
'0,85
0,85
*
£
<
OOOOOl—1^00
00^ ОО 00 00 oq 00^ 05 о I
OONCOiO^ODCNr^
84.83
74.77
64.77
54.77
44,81
34.84
24,87
14,97
84,86
74,83
о
8
и
с?
Ч
J*
<
С— (>-*>- о- о- г— ,
^ U Jj* !_г ^ 1 1
CN CN CN CN CN CN CN ,
CO CO CO CO CO CO co
1.46
1.46
ч
id
Ч>
<
00 CN 05 о со 00 ГО
СО 00 | |
ь S ю ^ о сЗ ^
ГО N Ю Ю OO GO QO
CO 00 00 00 00 00 05 | |
CO CN ^ CO CN ^
r—. 00
CN r-^
CN CN
t-- CD
о
Ю
оо
II
«?
id
ч
<5
Ю OI !М ю ю ю ,
СО СО СО со СО СО I
CN CN CN CN CN CN 1
00 00 00 00 00 OO ,
CO CO^ CO^ 00 CO CO
CN CN CN CN CN CN
53,49 2,10
\ 43,46 1 2,13
id
Ч
<3
05 05 CN О О со
го СО ^ ^ ^ | | |
Ю ? СО сЗ ^ 1-1
CO ^ ^ ^ i-нi Is-
CO CO co CO CO Tt I I I
CN CN CN CN CN CO * 1 1
Ю ^ CO CN i-н
5*;
Ч
ооооооооо
(NNINMMO^COH
lOCOOIOQNcO'tCO
ООООООООО
(NN(NN(MCOH©rH
mcOCNOONCD^CO
о 2
Sg
£
8
О
t-T
co

383
о о
5 о о о сГ о
,о	г-н	»-«	00	04	©	Ь-
{£	p.	CD	©	tq	ч^	rf
t-'	to"	to	to	ь	^
р	CD	LO
СО 04
rf	't	^	^	^
£1 oi	oi	<n	СЧ	<n	(N
О о"	о'	о	о	о	о
с	о	4>	*-"'	00	<3*	оо
§	Ы	00	00	t^	00
©	to'	ю	Ю	©	Ю	©
{i:	CD	LO	Tt*	CO	04	1—
©©©©©©©©©
o' o' o' o' o' o' o' o' o'
©05©*—ir-t©©©^-
00	©_	LO	'ф	rf
NNNNNNNNN
O)OON0iO^fO(N^
ooooooooo
bCOONrfHQOCOlO
оо оо © go <» oo_	oo^
© © ©' © ©' © © ©' ©'
QOObCDO^COW^
(MiOiOW(N(>)lO(M(N
о' о' сГ о' о' о о' о' о
LOO’^tOOOOlOCDOO'^f
00^ t*H to, CD © tO Tf	^
t^	tC	t>T	t>T	tC tC
OOON(DiO^CO(Nh
*—•	*—1	r—I	T—<	T—I	1—<	00	t—t	1—•
(N (N	N	W	N	W	н	CN	q
о' о'	о'	о'	о'	о'	о	о'	о
N^00TfnH00i0O(N
00 00 00 00^ 00	00
to to' ©' to' to' to' to' to' to
СТ)ООЬЮЮ^СО(Мгн
C© ©	©	©	©	©	©
^ rf	't	rr	Tf	Tf	ГГ
o' o'	o'	o'	o'	o'	О
OOCOCOOOOOOOOO
o' o' o' o' o' o' o' o' o'
cooococooooooooooo
o' o' o' o' o' o' o' o' o'
T-. о CD lO
^ r"L
r-Г 04 Ol‘ of of of of
CD Ю	CO Ol	—I
cn CO
05 O
8
CT5CDONCOSWOJ
05	Q Of	05^	о	О	^	04.
«-*' 1-f	т-f of	г-н'	ci	of	of	of
05 OO	N CD	tO	Tf	CO	04	I—1
© © © 4f rf © Q N 05
05 05 05СГ505000г-н
r-T i-н' i-f i-Г r-Г of of of of
0500NC£)lO^COO)rH
О О О О О О
CDCDCDCDCDCDCDCD
о' о' о' о' о' о' о' о'
Ot^t^t^OOl'H^
N CD CD CD Ь Ь CD CD
о' о' о' о' о' о' о' о'
СО со 1—I CD со
00 00 00 00 <© О
ч^'	©
СО СО ^ СО О) Н-
OCOOO’t^cocO
00 00 00 00 00 00 G5O
г** Tf т*« rf т+н
00 4>- © ©'
rf Tf Ю
СО 04 ’—1
COOOO^TfOO
00^ 00^	00^	00_	00	СЮ	05	©_
rt*'	"Cf	rt4'	to
00 N	CO	lO	^	CO	OJ	i—•
CO CD CD CD CD
CO CO CO CO CO CO CO
CD CD CD CD CD CD <D
Ю © CO 05 CO
£f of of of Ol'
Ю rf CO 04 -
I I
05 CD CO Tf ГН ts. N
CO CO CO CO CO CO ^
О	Tt*	04	04	04	CD	04
CD	tO	©	©	tO	tO	CD
of	of	Ol'	of	of	of	Ol'
ts	CD	Ю	^	со	(N	ГЧ
СО со © О
C'f of of of
© 05 05 © © ©	,
oo^ oo_ oo oo^ oo^ co
04 Ol 04 © © ©
CO © © © CD ©
SJ SJ
s? S3 2 w*
© t- © T-H	Г-.
©^ Tf ©^ ©^ ©^ ©
'	Tt	чф
Tt © 04 »-H
s
N fs	N	©
©^ ©	©^	©^	©^	©.
©©	©	©	©	©
© 4^ CO 04 1-*
Si
55	P	о	o	©	©	©
гм	^	£4	©	i—•	©	т-н
^	О	05	С^«	©	©
О
СО
©©©©О©©©©
04	04	t"»	04	©	г—(	©	1—I
© СО 04 © 05 £"• © ^ СО
©
СО
©©©©©©©©©
040-04t^04©r-.©,—.
©©04©©t^©4f©

384	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
величину (до 0,5' при ао = 87,5 , v0 = 400 и s = 0,76 • 106 м)
для целей, появляющихся над горизонтом. Однако Д2а бы¬
стро уменьшается и падает примерно на 2—3" при ао = 80°,
менее чем до \" при ао = 70° и до ~0,01" при ао = 10°. Это
значит, что мы достигаем точности хорошей радиолокацион¬
ной системы уже при углах ао
<4 для V«sJ^
Фиг. 11. Поправ!
80°.
-1.5 0+7,5 м	0	153	м.
по дальности.
В табл. 26 показаны поправки по дальности Asl{ и оста¬
точные ошибки по дальности A2sK.
Рассмотрим сначала ошибки A2sK. Они зависят только от
ао и vo и не зависят от расстояния 5. При больших зенитных
углах ао и больших коэффициентах рефракции vo они дости¬
гают почти 3 м; при ао = 0—50° их величина составляет
~ 0,3 м и падает примерно до 0,15 м в зените.
Поправка по дальности AsK увеличивается с уменьшением
ао- Для углов ао < 80° величины AsK практически не зависят
от .vo, но они возрастают с увеличением расстояния. В первом
приближении можно считать, что в отличие от семейства кри¬
вых Да (фиг. 10) поправки AsK (фиг. 11) растут с уменьше-

ТОЧНОЕ НАБЛЮДЕНИЕ РАДИОТЁХНЙЧЕСКИМИ МЕТОДАМИ 385
нием ао и увеличением расстояния d. Это происходит потому,
что кажущаяся скорость распространения vKy принятая нами
постоянной, составляла в нашем случае 299733,1 км/сек и все
расчеты в статье основываются на этой цифре. Если ионо¬
сферная поправка имеет другую величину vK, то в (7) и (17)
необходимо изменить соответствующие числа. Если, напри¬
мер, принять vK равной скорости света в вакууме (с =
= 299792,9 км/сек), то из семейства кривых в левой части
фиг. 11 было бы видно, что ошибки Д5И увеличиваются с рос¬
том ао и уменьшением d.
Здесь снова можно видеть, что поправки по дальности
имеют порядок 100 м\ их следует учитывать для получения
точных результатов.
Результаты наших расчетов можно видеть из табл. 2а и
26. Для того чтобы получить общее представление о харак¬
тере изменения Да, Д2а, ДsK и Д2$к, данные табл. 2а и 26 при¬
ведены в виде графиков на фиг. 10 и 11. Точные величины
из этих графиков определить, конечно, трудно вследствие не¬
достаточной точности чертежа. По оси ординат на обеих фи¬
гурах отложено ао- Как видно из фиг. 10 и 11 и табл. 2а, кри¬
вые заметно расходятся только при ао > 80°.
ЗАМЕЧАНИЯ ОБ ОПТИЧЕСКОМ НАБЛЮДЕНИИ
Выше указывалось, что для внесения дополнительных уг¬
ловых поправок необходимо знать расстояние. То же самое
справедливо для оптического наблюдения искусственных
спутников Земли. На фиг. 12 показана схема наблюдения.
Спутник S' кажется совпадающим со звездой *' в направле¬
нии зенитного угла ао- Истинное положение спутника пока-
Таблица 3
Оптические поправки
Дои — Да
^ СП’
дуг. сек
10°
50°
70°
80°
0,31.106
0,33
4,0
17,1
—
0,61.10е
0,20
2,2
9,3
39,9
0,92.106
0,14
1,5
6,6
30,6
1,22 - 10е
0,11
1Д
5,3
25,9
1,53- 106
0,10
1,0
4,6
23,2
25 Зак. 876

386 iv. Контроль траектории космических аппаратов
зано в S, а истинное направление на звезду обозначено *.
Легко видеть, что поправочные углы Дасп и Да* не равны.
Разница между ними увеличивается с уменьшением расстоя¬
ния до спутника. Величина Да* является нормальной астро¬
номической поправкой на рефракцию. Для получения более
точной поправки необходимо вычесть (Да* — Да. п) из Да
Фиг. 12. Схема оптического наблюдения искусственного спутника
Земли.
Остаточная неопределенность, вызываемая неопределенно¬
стью индивидуального профиля коэффициента рефракции,
равна Д2а в табл 2а точно так же, как и для наблюдения
электронными методами.
В табл. 3 приведены необходимые поправки Да* — Дасп
в зависимости от ао и d.
ЗАКЛЮЧЕНИЕ
При наблюдении за спутниками радиотехническими мето*
дами достижима точность в несколько метров по дальности
и несколько секунд по углам. Такая точность достигается из¬
мерением коэффициента рефракции только в месте располо¬
жения радиолокатора и не требует знания этого коэффи¬

ТОЧНОЕ НАБЛЮДЕНИЕ РАДИОТЕХНИЧЕСКИМИ МЕТОДАМИ	387
циента на других участках пути распространения. Пределы
точности, определяемые условиями распространения, дости¬
гают точности лучших радиолокационных систем уже при уг¬
лах 20° над горизонтом (ао ■< 80°), если расстояние до цели
больше тысячи километров. Следовательно, необходимо со¬
средоточить внимание на создании новых радиотехнических
систем, обладающих повышенной точностью. Расстояние
должно быть известно как при радиотехническом, так и при
оптическом наблюдении для введения точных угловых попра¬
вок. В этом случае радиотехническими и оптическими мето¬
дами достигаются одинаковые точности.
ЛИТЕРАТУРА
1. Н a n d е 1 R., К п о t h е Н., The Curvature of Microwave Propagation
Through The Troposphere and the Ionospheric Layers, Holloman Air
Dev. Center, Techn. Rep. № 3, January 1956.
2. Dixon H. М., Study of Refraction Errors in Radar Propagation, White
Sands Signal Corps Agency, Techn. Rep. 18A, April 1956.
25*

ОПРЕДЕЛЕНИЕ ОРБИТЫ ПО ЧАСТОТЕ ДОППЛЕРА,
ИЗМЕРЕННОЙ ПРИ ОДНОМ ПРОХОЖДЕНИИ
ИСКУССТВЕННОГО СПУТНИКА1)
Паттон
В статье приводится описание метода определения орбиты спутника
за время одного прохождения при помощи измерения допплеровского
сдвига частоты непрерывного сигнала, излученного с Земли, отраженного
спутником и принятого одной или несколькими станциями, расположен¬
ными в разнесенных местах. Метод достаточно общий и с небольшими из¬
менениями может быть использован для измерения орбит любого типа
спутников или межконтинентальных баллистических ракет.
При расчете орбиты аппроксимация начального положения и состав¬
ляющих скорости уточняется путем последовательных дифференциальных
поправок, находимых методом средних квадратов.
Рассматривается также метод прогнозирования положения и вектора
скорости.
ВВЕДЕНИЕ
Измеряя допплеровский сдвиг частоты непрерывного сиг¬
нала, можно определить орбиту по данным, записанным в те¬
чение нескольких минут во время одного прохождения спут¬
ника. При этом не существенно, является ли источником сиг¬
нала бортовой передатчик спутника или наземная установка.
Однако поскольку в последнем случае обычно имеется воз¬
можность использовать более сложное оборудование, то это
упрощает и делает более надежными методы расчета, вклю¬
чаемые в процесс обработки данных.
Представленный здесь метод решения был развит для си¬
стем, имеющих наземный передатчик, однако его можно легко
применить в системах наблюдения за спутниками с передат¬
чиком на борту.
С небольшими изменениями метод можно использовать
цля измерения орбиты любого типа спутника или межконти-
1ентальной баллистической ракеты, так как он в основном
использует метод средних квадратов и дифференциальных
поправок.
Поскольку желательно получить быстрый и надежный
метод определения орбиты спутника по допплеровским
1)	Patton R. В., IRE Trans, on Milit. Electronics‘ МП.-4, № 2—3,
336—344 (April —July I960).

ОПРЕДЕЛЕНИЕ ОРБИТЫ ПО ЧАСТОТЕ ДОППЛЕРА
389
данным, используя минимальное количество оборудования,
то основное внимание направлено на нахождение решения
для системы данных, записанных одним приемником во вре¬
мя одного прохождения спутника.
С целью получения более строгой геометрии системы и,
следовательно, уточнения решения требование использования
лишь одного приемника было снято, однако ограничение на
использование измерений, сделанных за время одного прохо¬
ждения, было сохранено. В таких условиях наблюдение мо¬
жет производиться только в относительно короткий проме¬
жуток времени, что в свою очередь позволяет сделать следую¬
щие упрощающие допущения: во-первых, считать Землю
с точки зрения динамики сферой, хотя геометрически она рас¬
сматривается как эллипсоид; во-вторых, пренебречь, без за¬
метного снижения точности, замедлением и рефракцией в
ионосфере и атмосфере.
Это сводит проблему к определению шести параметров
кеплеровской орбиты по данным допплеровской системы с на¬
земным передатчиком. Результаты наблюдений такой систе¬
мы будут называться в этой статье «пассивными данными» в
отличие от «активных данных», получаемых от системы, ис¬
пользующей как свою составную часть бортовой передатчик.
С точки зрения обработки данных имеется несколько преиму¬
ществ в расположении передатчика на поверхности Земли.
Перечислим основные из них:
1. Если источник сигнала расположен на Земле, то легко
измерять его частоту и уходы частоты, в то время как для
любой системы, использующей бортовой передатчик, эти ве¬
личины включают дополнительные неизвестные, что значи¬
тельно ухудшает точность определения параметров орбиты.
2. Если передатчик расположен на спутнике, то для полу¬
чения надежного решения одного приемника недостаточно.
С другой стороны, часто возможны решения по пассивным
данным, полученным одним приемником, благодаря чему
можно произвести обработку, даже если несколько приемни¬
ков системы не смогли записать данные.
3. Если полностью исключить бортовое оборудование, то
надежность системы повысится.
ХАРАКТЕР ПОСТУПАЮЩИХ ДАННЫХ
Для разработки методики расчета необходимо рассмот¬
реть различные формы, в которых могут быть записаны
данные. Результаты наблюдений получаются либо в виде

390	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Сз
!
5
-7^-
допплеровской частоты, либо в виде допплеровского периода,
который легко можно превратить в частоту. Частота Допплера
в том смысле, в каком этот термин используется здесь, полу¬
чается при смешении напряжения местного гетеродина с при¬
нятым сигналом, отра¬
женным от спутника, и
используется для после¬
дующего управления вы¬
ходным напряжением раз¬
ностью частот передатчи¬
ка и местного генератора.
Если начертить график
зависимости частоты
Допплера от времени, то
получится S-образная
кривая, изображенная на
фиг. 1, а. Асимметрия
этой кривой типична для
системы, в которой на¬
земные передатчик и при¬
емник разнесены на за¬
метное расстояние, а ор¬
бита несимметрична от¬
носительно базовой ли¬
нии, соединяющей эти два
места расположения ап¬
паратуры.
Если производить из¬
мерения с небольшими
интервалами, например
через 1 сек, то получает¬
ся система данных (изо¬
браженная графически
на фиг. 1,а), годная для
подачи на вход счетной
машины. Однако для экономии мощности может оказаться
необходимым применять антенные системы, обладающие диа¬
граммой направленности в виде трех узких веерообразных
лепестков и дающие непрерывные данные, разделенные ин¬
тервалами, как показано на фиг. 1,6. Третья возможность
состоит в использовании дискретных наблюдений с равными
интервалами, как показано на фиг. 1,6. Такие данные можно
получить от системы, сканирующей небо узким веерообраз¬
ным лучом.
Время
Время
в	г
Фиг. 1. Зависимость частоты Допплера
от времени.

ОПРЕДЕЛЕНИЕ ОРБИТЫ ПО ЧАСТОТЕ ДОППЛЕРА
391
РЕШЕНИЕ
Метод решения состоит из подгонки по способу средних
квадратов рассчитанной кривой под систему измеренных зна¬
чений частоты Допплера.
Находится совместимая система поправок для шести па¬
раметров орбиты. Поправки последовательно уточняются
дифференциальной коррекцией, пока не получится полного
схождения. При этом предполагается, что спутник движется
по законам Кеплера. Уравнение для условий выхода на ор¬
биту находится разложением Тейлора около той точки, ко¬
торая характеризуется аппроксимированными величинами
шести параметров орбиты. Все члены разложения второго и
третьего порядков отбрасываются. Сходимость в сильной сте¬
пени зависит от системы параметров, которая выбирается
для определения орбиты. Не всякая система орбитальных па¬
раметров приводит к уравнениям, достаточно независимым,
чтобы допустить решение этим методом. Было установлено,
что параметры в виде составляющих положения и скорости
для данного момента времени легко приводят к сходящемуся
решению. В этом смысле весьма неудовлетворительна систе¬
ма параметров, состоящая из большой полуоси, эксцентриси¬
тета, средней аномалии за эпоху, склонения, прямого восхо¬
ждения восходящего узла и аргумента перигея.
Как было установлено ранее, результаты наблюдений бу¬
дут состоять либо из частоты Допплера в функции от вре¬
мени, либо из величин допплеровского периода, которые
можно легко превратить в частоту Допплера. С другой сто¬
роны, на вход счетной машины желательно подавать отсчет
полного числа периодов.
Если имеется запись данных за значительный период вре¬
мени, то общее число периодов можно найти простой опера¬
цией суммирования за определенные интервалы времени,
имеющие длительность несколько секунд. Если длина волны
излучаемого сигнала равна X, a Nij есть полное число перио¬
дов частоты Допплера, выделенный i-м приемником при дви¬
жении спутника за период времени от tj до tj+\, то отсюда
следует, что иц = XNij есть мера полного изменения расстоя¬
ния от передатчика до спутника и до i-го приемника за тот
же период времени. Определим gij как действительное изме¬
нение длины пути распространения радиосигнала. Из фиг. 2
следует
gij = (TSJ+1 + ед+1) - (TSj - R.Sj),	(1)

332	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
где Т — местоположение передатчика, Ri — местоположение
приемника, Sj+i — положение спутника в момент времени
tj+1 и Sj — положение спутника в момент времени tj.
В случае дискретных измерений частоты применимо тоже
определение с той разницей, что интервал времени от tj до
tj+i не превышает 1 сек.
Решение состоит в уточнении составляющих положения
и скорости, аппроксимированных для определенного момента
времени. Последний обозначается символом t0 и для удоб¬
ства принимается за время начала наблюдения.
Хотя положение системы координат, в которой опреде¬
ляются векторы положения и скорости, существенно не
влияет на сходимость, однако система координат, неподвиж¬
ная по отношению к поверхности Земли, обладает двумя зна¬
чительными преимуществами. Во-первых, функция gij не¬
сколько упрощается, если координаты мест расположения
аппаратуры не меняются во времени. Во-вторых, и это самое
главное, при таком условии можно легко изменить метод для
использования других типов измеренных данных простым из¬
менением определения функции gtj и соответственно выраже¬
ний для ее производных. Никаких дополнительных изменений
процесса балансирования, который составляет основную
часть расчета, при этом не делается.

ОПРЕДЕЛЕНИЕ ОРБИТЫ ПО ЧАСТОТЕ ДОППЛЕРА
393
Система начальных аппроксимированных значений соста¬
вляющих векторов положения и скорости определяется для
времени t0 как (*0. Уо, z0. х0, уо, г0). Опорной системой коор¬
динат является система xyz, определение которой дано ниже.
Если в разложении Тейлора вокруг точки (х0, yQ, z0, х0, у0, z0)
пренебречь членами второго и всех высших порядков, то
уравнение для условий можно записать в матричной форме
(2)
где
н
d8i
U
дхп
дуо
LV = JbX,
dgy dgti
dgij dgij
дУо
Ши.)
dz0 )’
АУ = (Д <otJ) = (vl} — gi]),
'Длг0
(3)
дх =
дУо
Д z0
Д-^о
дУо
,д20
для всех величин i и /. Следовательно, /—матрица порядка
(i • / X 6), ДК — матрица порядка (t • / X 1) и ДХ — матрица
порядка (6x1).
Так как имеется шесть неизвестных, для решения тре¬
буется минимум шесть уравнений. Практически имеется до¬
статочное количество данных для получения избыточной си¬
стемы уравнений, которые допускают решение методом наи¬
меньших квадратов
LX = (J*J)~'J*bV,	(4)
где /* — транспонированный якобиан /.
Окончательно исправленные величины начальных условий
находятся из
Х+ЬХ,
где

394	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
(Для удобства значки для указания повторения не вводятся.)
Уточненные значения X описывают начальную точку, и про¬
цесс повторяется до тех пор, пока не получится полного схо¬
ждения.
ОЦЕНКА Д V
Поскольку просто выразить функцию gij через X невоз¬
можно, оценка производится косвенным методом. Эфемерида
рассчитывается для принятых величин векторов положения
Z'
и скорости в момент времени t0. Затем с помощью выражения
(1) можно найти gij для всех величин i и /.
В процессе такого расчета целесообразно* использовать
две прямоугольные системы координат, помимо системы, при¬
вязанной к Земле и имеющей свое начало в месте располо¬
жения передатчика. Эти системы координат определяются
следующим образом (фиг. 3).

ОПРЕДЕЛЕНИЕ ОРБИТЫ ПО ЧАСТОТЕ ДОППЛЕРА
Ж
1. Система хуг представляет собой правую прямоуголь¬
ную систему координат с началом на поверхности Земли в
месте расположения передатчика. Положительная ось а на¬
правлена на юг, ось у — на восток и ось 2 — перпендикулярно
поверхности Земли.
2. Система x'y'z' является правой прямоугольной систе¬
мой координат с началом в центре Земли. Ось х' лежит в
плоскости экватора и направлена к точке весеннего равноден¬
ствия, положительное направление оси zr проходит через се¬
верный полюс. Ось у' выбирается таким образом, чтобы об¬
разовать правую систему координат.
3. Система x"y"z" подобна правой системе координат с на¬
чалом в центре Земли.
Плоскость х"у" лежит в плоскости орбиты спутника, при¬
чем положительная ось х" направлена на перигей. Положи¬
тельное направление оси z" образует с положительным на¬
правлением оси z' угол, равный углу между плоскостями ор¬
биты и экватора. Ось у" выбрана таким образом, чтобы об¬
разовать правую систему координат.
Первый шаг в этой стадии расчета состоит в определении
величин составляющих векторов начального положения и
скорости в системе координат x'y'z'. Это может быть выпол¬
нено одним поворотом и одним перемещением, не зависимыми
от времени, и, кроме того, одним поворотом, изменяющимся
со временем. Пусть Ri(a) означает матрицу поворота на угол
а вокруг i-й оси опорной системы координат. Поворот совер¬
шается таким образом, что угол положителен при вращении
в правом направлении и i = 1, 2 или 3 в зависимости от того,
совершается ли поворот вокруг оси х, у или г. Необходимое
о
Уо
=	(—	е0)	^2	(т	—	90°)
(<'
У о | = Яз(-0о)Я2(<Р-9О°)Х
U,
Ч
Р,, sin Д
Уо
+
0
. .V
Pf cosA
*0
Р9 sin Д
х0
X
Уо
+
0
+ R3 (— ®о) R2 (? — 90°)
Уо
zo.
Pv cos Д
zo
(5)
(6)

396	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
где Яз(—Во)—производная по времени от /?з(—0j) при
0j = Во; В j — правое восхождение места расположения пере¬
датчика во время tj\ ф — геодезическая широта места распо¬
ложения передатчика; — радиус-вектор, проведенный из
центра Земли в точку на ее поверхности, находящуюся на
уровне моря и имеющую широту ф; Д — разница между гео¬
дезической и геоцентрической широтами места расположения
передатчика.
Дальнейший этап расчета заключается в определении
следующих параметров орбиты:
а — большая полуось;
е — эксцентриситет;
0 — средняя аномалия за эпоху;
1 — склонение;
Q — правое восхождение восходящего узла;
со — аргумент перигея.
Эти параметры орбиты находятся из следующих уравне¬
ний:
где g — средняя гравитационная постоянная, a R — радиус
Земли, которая в следующих уравнениях предполагается сфе¬
рической:
(7)
(8)
(9)
Л/о^Х + УоУо + ^о'
ц = gR2,
где
sign (l — т) —1 ПРИ (1~:?)>0'
(13)

ОПРЕДЕЛЕНИЕ ОРБИТЫ ПО ЧАСТОТЕ ДОППЛЕРА
397
о = Eq — е sin Е0 — ntQ,
(14)
hi=y'oK — zoy'o'
(15)
fl2 - ZQX0
(16)
^3 = ХоУо У (Л)*
(17)
h = y h\ + h\ + h\.
(18)
k -±-
1 h ’
(19)
-ф
II
(20)
Ф
II
CO
(21)
7’=УА? + А|.
(22)
£
II
1
(23)
II
£
(24)
i = arc cos k3, где 0 < / < «,
(25)
х = а(о.о%Ей — e),
(26)
у = a (sin E0) Yl — e2,
(27)
r0 • N = x'jV, y^V2-
(28)
г0 X k ■ N = iV, (y0k3 20^2) H- (^o^i
(29)
«-(-I)'arc cos { i<vN)+i(r,yi«)
(30)
f 1 — sign [xz'0 + у {x'Qk2 — y^,)] \
P-\ 2 j*
2 = (—1)? arc cos Nv
(31)
где
После определения величин а, е, о, i, Q и со можно для
каждого интервала наблюдений найти gij.
Сначала определяется аномалия эксцентриситета Ej в
уравнении Кеплера
Ej — е sin Ej — ntj + о.	(32)

398	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Положение спутника в функции от времени в системе ко¬
ординат x"ynz”
f, = 2 arc tg [	tg(^)] .
rf = a( 1 — e cos Ej),
x"j — rJ cos/j,
y"j = rjsm/j.
(33)
(34)
(35)
(36)
z'j = 0 в соответствии с определением x'yV'-KoopflHHaTHoii
системы.
Преобразование в систему координат x'y'z' осуществляет¬
ся тремя поворотами
У)
/у
У j
о
(37)
X/
х)
Рт sin Д
у i
— R<2 (90° — <р) R3 (0 j)
y\
—
0
zi
z'i .
р^соэД
Положение спутника в системе координат xyz находится
г.вумя дополнительными поворотами и перемещением
(38)
Основываясь на уравнении (1), можно выразить через
координаты положения спутника в моменты времени tj и
tj+i‘
8ц = У*?л.1 + У).1 + г>,+1 +
+ V (х/+1—xif+(Уу+i—yi)2+(2/+i—zi?—
— V x) + y) 4- г* —
— V (x, — Xi)2 -4-{у, — у ^ + (Zj — zt)2.
(39)
где (Xi, уи Zi) представляют собой измеренные координаты
i-го приемника.
Окончательно Лиц определяется выражением
д Vij = vij — gu.
(40)

ОПРЕДЕЛЕНИЕ ОРБИТЫ ПО ЧАСТОТЕ ДОППЛЕРА
399
ОПРЕДЕЛЕНИЕ ЗНАЧЕИЯ J
После того как найден вектор Д1Л остается задача опре¬
деления якобиана J. Необходимое дифференцирование можно
выполнить численным способом, однако нахождение произ¬
водных из аналитических выражений сокращает время рас¬
чета и повышает точность. Учитывая, что для всех величин
i и j
допустим, что
где
j = j I gl0' SlJ' “* \
\ Xо, Уо, г0, х0, Уо, *0 / *
J=ЛЛЛЛ.
;	/	g10. ■■■’guLLy \
I Х)+V У)+\' Zj + v xj’ Zj }
(41)
yMi. ZJ+1, XJ. y}. z}\
Ji — {	a,	в,	<r, о», 0,1	)•
Л — (—/	a•’/	(43)
\ Уо» г0’ *0’ У о» 2 о /
/4 у'4-Куо.К\
\ *о> Уо» *0, *о. Уо. ^о /
Порядок вышеприведенных матриц следующий: (/*/Х 6)
для /] и (6 X 6) для /2, /з и /4.
Преимущество этого метода определения J заключается
в том, что функция gij появляется только в ]\. Следовательно,
когда решение применяется к другим типам измерений, для
правильной оценки J необходимо пересматривать только ]\.
Результаты вычислений /2 и /3 можно найти в работе [1].
НАЧАЛЬНАЯ АППРОКСИМАЦИЯ
Успех предложенного метода в первую очередь опреде¬
ляется возможностью получения совместимой системы на¬
чальных аппроксимированных значений, которые достаточно
близки к реальным величинам, чтобы процесс расчета схо¬
дился. Было установлено, что когда данные поступают от
одного приемника, то расчет сходится, если базовая линия
между приемником и передатчиком не слишком коротка и на¬
чальные значения (х0> г/о, г0, хо> Уо> %о) выбраны достаточно
точдо. Например, с базовыми линиями порядка 600 км при

400	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
наблюдениях, непрерывных или прерывистых в течение
5 мин, можно ожидать достаточно хорошей сходимости, если
ошибка в определении координат начального положения не
превосходит 90—120 км, а составляющие вектора скорости
определены с точностью 1 — 1,5 км/сек„ С другой стороны,
найдено, что для обеспечения сходимости в системе с двумя
приемниками необходимая точность в определении координат
равна 200—300 км и составляющих вектора скорости 2—
3 км/сек. Процесс расчета иногда сходится и при более зна¬
чительных начальных ошибках, однако приведенные цифры
являются пределами, в которых сходимость можно гаранти¬
ровать.
Очевидно, для успешного применения метода расчета не¬
обходим вспомогательный расчет с целью приближенного
нахождения начальных условий. Было рассмотрено несколь¬
ко вариантов таких расчетов. В наиболее предпочтительном
из них применяется аналоговая счетная машина для подгонки
рассчитанной кривой под кривую зависимости измеренной
частоты Допплера от времени. В процессе подгонки непре
рывно изменяются граничные условия дифференциального
уравнения второго порядка до тех пор, пока рассчитанная
S-образная кривая не совпадет с кривой, построенной по ре-,
зультатам наблюдений.
При составлении дифференциального уравнения орбита
считалась круговой, а Земля невращающейся. Приближенные
.начальные значения составляющих векторов положения и
скорости, которые затем служили исходными данными для
расчета, определялись по результатам процесса подгонки
кривых. Разновидностью этого метода является вычерчива¬
ние кривой по измеренным данным и отыскание соответствую¬
щей кривой в большом семействе кривых, предварительно
рассчитанных для разных круговых орбит. Оба метода наш¬
ли успешное применение.
При составлении дифференциальных уравнений, исполь¬
зуемых в процессе подгонки, будут полезны следующие опре¬
деления:
Rr — радиус-вектор, проведенный из центра Земли
в место расположения передатчика;
Tj — радиус-вектор, проведенный из центра Земли в
точку расположения спутника в момент вре
мени tj\
Ру— угол между RT и г/,
х"т, у", zT — координаты передатчика;
х", у"-, 0 — координаты спутника в момент времени

ОПРЕДЕЛЕНИЕ ОРБИТЫ ПО ЧАСТОТЕ ДОППЛЕРА
401
рj — расстояние от передатчика до спутника в момент
времени tj\
Рц—расстояние от i-rо приемника до спутника в мо¬
мент времени tj\
Н — высота спутника над поверхностью Земли;
v — скорость спутника.
Для упрощения задачи были приняты следующие допу¬
щения: 1) спутник движется по круговой кеплеровской ор¬
бите; 2) рj относительно мало в течение периода наблюдения;
3)	Земля не вращается.
Пользуясь этими допущениями, можно найти ряд полез¬
ных зависимостей (в опорной системе координат х"у"г")\
Дифференцируя дважды по времени, получаем уравнение
\Tj\=r = R + H,
где Н — постоянная;
v = nr
ПГ = \Г(x-f + iyy,
COSf}y«l,
Rr = const.
Из определения р3- следует, что
Pj= У(х";-хтТ + М-Ут)2 + (4У-	(45)
которое можно упростить так:
Р? + PjPj = v2-n2 (г» - х"4 - у"/'),
= п2(Ят • Tj),
= n2rR cosp,
Ry4
p-
Отсюда следует
(47)
26 Зак. m

402	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Подобное же выражение можно вывести для рг-у. Учитывая
определение для gijt можно записать
А — р у	А — pi
*ч*а—Г1-+-ГГ-'	<48>
где
рУ	р/у
Rv4
Первым шагом в процессе подгонки на аналоговой счет¬
ной машине является аппроксимация А} р0, p*o, ро и рг0, затем
следует расчет той кривой для g^, которая удовлетворяет ра¬
венству (48) при выполнении условий gi0 = Vi0 и gi0 = Vi0.
До получения достаточно хорошего совпадения производится
непрерывная подгонка пяти параметров. Окончательное зна¬
чение А можно использовать для нахождения скорости и,
учитывая, что орбита круговая, — высоты; последнее, однако,
для сильно эксцентричных орбит не всегда удается. Более
удобно предположить, что z0 = 0 и z0 = z, где z — высота,
найденная из эксперимента. Первое предположение является
обоснованным упрощением, тогда как второе обычно нахо¬
дится с точностью 150—300 км по характеристикам 5-образ¬
ной кривой.
В случае если в результате начальной оценки z0 сходи¬
мость не получается, можно испытать ряд значений z, не
прибегая к излишним расчетам. Начальные значения х0 и у0
находятся решением следующих уравнений:
4^+? = р2о.	I	9)
К - х$+(Уо - у О2+(г—zif=р?о- ) .
Дифференцируя pj и рц по времени для j = 0 и z0 = 0,
находим
*0*0 + УоУо ~ РоРо»	I
(x0 — xl)x0 + (y0 — yl)y0 = pl(pl0, I
которые можно решить относительно х0 и у0. На этом про¬
цесс расчета системы начальных значений заканчивается.
РЕЗУЛЬТАТЫ РАСЧЕТА
Был получен целый ряд сходящихся решений, причем на
вход счетной машины подавались как контрольные, так и
реально полученные данные. Поскольку последние предста¬

ОПРЕДЕЛЕНИЕ ОРБИТЫ ПО 4ACfOTE ДОППЛЕРА
403
вляют основной интерес, мы ограничимся обсуждением
результатов, полученных по реальным данным. Этот ме¬
тод решения был разработан специально для системы «Доп-
лок» [5].
Описываемый вариант этой допплеровской системы со¬
стоит из одного передатчика непрерывного излучения мощ¬
ностью 50 кет, расположенного в Форт Силл (шт. Оклахома),
и двух приемных станций «Доплок», одна из которых распо¬
лагалась на ракетном полигоне Уайт Сэндс и вторая в Фор¬
рест Сити (шт. Арканзас). В целях экономии мощности диа¬
грамма направленности антенны представляла собой три уз¬
ких лепестка, которые обеспечивали непрерывный прием
с интервалами, показанными на фиг. 1,6. Полученные дан¬
ные записывались одним приемником во время одного прохо¬
ждения спутника над станцией (поскольку второй приемник
в Уайт Сэндс не работал).
Помимо этих данных, приведены также параметры орби¬
ты, определенные и опубликованные Национальным упра¬
влением по космическим исследованиям (НССКК). Парамет¬
ры, полученные НССКК, были приведены ко времени работы
системы «Доплок».
Первое успешное решение по данным системы «Доплок»
было получено для 9937-го оборота третьего советского ис¬
кусственного спутника1). Результаты измерений были запи¬
саны в течение 28 сек во время приема на южный лепесток
антенной системы и в течение 7 и 12 сек во время приема на
центральный и северный лепестки с двумя перерывами в ин¬
формации по 75 сек каждый. Таким образом, данные реги¬
стрировались в течение 47 сек в интервале времени 3 мин
17 сек. Первый расчет сошелся за три повторения, дав сле¬
дующие значения составляющих векторов положения и ско¬
рости:
а = 6672 км, е = 0,0153, о = 288,04°, / = 65,37°, Q= 178,24°,
со = 104,62°.
Для сравнения использовались параметры орбиты, опуб¬
ликованные в бюллетене № 230 НССКК за 1958 г., «Дельта»
II (третий советский искусственный спутник). По этим дан¬
ным для того же времени, принятого > указанном выше ре¬
шении, был произведен расчет начальных условий, давший
следующие результаты:
а = 6615 км, е = 0,0130, о = 257,78°, I = 65,06°, Q = 178,22°,
оз = 137,95°.
!) Третий советский искусственный спутник ЗемЛи был запущен 15 мая
1958 г. — Прим. ред.
26*

404	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Сравнивая эти два решения, можно видеть достаточно
хорошее совпадение для а, е, i и Q, особенно для последних
двух. Это характерно для решения по данным одного про¬
хождения, когда эксцентриситет мал, а на вход счетной ма¬
шины подается лишь частота Допплера. При орбите, близкой
к круговой, со и а имеют менее существенные значения, чем
другие параметры, и, кроме того, более точное определение
их представляется затруднительным для любой системы. Од¬
нако благодаря малому эксцентриситету сумма со и о являет¬
ся достаточно хорошим приближением к углу, измеренному
вдоль орбиты между узловой точкой и положением спутника
в эпохальное время, и поэтому возможно сравнение двух
систем.
Сравнение результатов системы «Доплок» и НССКК для спутника
«Дискаверер» XI
Номер
оборота
а, км
е
1, град
2, град
Длитель¬
ность
измерения,
сек
Интервал
времени
наблюде¬
ния, сек
«Доплок» . . .
НССКК . . .
Разность . . .
30
6739
6744
—5
0,0295
0,0291
0,0004
80,15
80,01
0,14
215,92
215,84
0,08
35
123
«Доплок» . . .
НССКК . . .
Разность . . .
124
6625
6657
—32
0,0198
0,0203
—0,0005
80,31
80,10
0,21
207,50
207,27
0,23
44
138
«Доплок» . . .
НССКК . . .
Разность . . .
140
6662
6635
27
0,0198
0,0178
0,0020
80,44
80,10
0,34
205,22
205,78
—0,56
55 „
141
«Доплок» . . .
НССКК . . .
Разность . . .
156
6670
6614
56
0,0300
0,0148
0,0152
80,79
80,10
0,69
204,50
204,30
0,20
25
117
«Доплок» . . .
НССКК . . .
Разность . . .
165
6500
6599
—99
0,0111
0,0128
—0,0017
79,99
80,10
—0,11
203,63
203,50
0,13
49
165
«Дсплок» . . .
НССКК . . .
Разность . . .
172
6589
6586
3
0,0189
0,0111
0,0078
80,44
80,10
0,34
203,18
202,84
0,34
35
90

ОПРЕДЕЛЕНИЕ ОРБИТЫ ПО ЧАСТОТЕ ДОППЛЕРА
405
В решении по данным системы «Доплок» (со + о) = 32,66°,
тогда как данные НССКК дают 35,73°; разница между ре¬
зультатами двух систем равна 3,07°.
На основании этих результатов можно утверждать, что
если система «Доплок» имеет один приемник и производит
наблюдение за время одного прохождения, то обеспечивается
точное определение положения плоскости орбиты, достаточно
хорошее определение формы орбиты и приближенное опре¬
деление ориентации эллипса в орбитальной плоскости.
Иногда можно получить весьма точные значения а и со,
однако в общем случае описываемый упрощенный вариант
системы «Доплок» способен давать лишь приближенную
оценку этих двух величин. Поэтому при рассмотрении других
данных системы «Доплок» эти две величины исключаются.
В таблице приведены результаты для шести оборотов спут¬
ника «Дискаверер» XI, включая последний известный 172-й
оборот этого спутника. Интересно, что высота, определенная
упрощенным вариантом системы «Доплок», для этого прохо¬
ждения в момент пересечения спутником базовой линии в
89 км к западу от Форрест Сити была равна 132 км. Для
оценки результатов системы «Доплок» в таблицу включены
параметры орбиты, определенные по данным НССКК для со¬
ответствующих значений времени.
В таблице указаны также длительность измерения дан¬
ных для каждого случая и полные интервалы времени, в те¬
чение которых производилось наблюдение.
ЗАКЛЮЧЕНИЕ
Предложенный метод решения доказал свою практич¬
ность и полезность в результате многочисленных успешных
применений как с реальными, так и с контрольными данны¬
ми. Хотя были представлены результаты только для пассив¬
ного метода, с небольшими изменениями можно успешно ис¬
пользовать этот принцип и при наличии передатчика на
борту.
Процесс схождения решения требует 20—40 мин работы
на счетной машине с кодированием в десятичной системе.
Более современные машины могут выполнить тот же расчет
за 2—4 мин. Когда источником сигнала является наземный
передатчик, этот метод позволяет получить систему относи¬
тельно точных значений параметров орбиты по прерывистым
наблюдениям, проведенным одним приемником в течение
1,5—3 мин.

406	tv.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Достаточно хорошие результаты возможно получить по
наблюдениям одного приемника, хотя система с несколькими
приемниками обладает рядом существенных преимуществ.
Необходимо отметить, что решения были получены для ре¬
альных данных и что эти решения совершенно независимы от
других измерительных систем. Результаты последних исполь¬
зовались лишь для сравнения, но ни в одной фазе расчета,
давшего это решение, не применялись.
Описываемый метод является общим и поэтому не огра¬
ничивается кеплеровскими орбитами и наблюдениями часто¬
ты Допплера. Для более сложных орбит, возможно, придется
заменить аналитическое дифференцирование численным и,
конечно, будет необходимо изменить расчет для эфемерид,
однако основа решения остается той же. Если удобно исполь¬
зовать другие типы измерений, то, видоизменяя J\ и gij, мож¬
но применить этот метод для наблюдения за любыми спут¬
никами или межконтинентальными ракетами при условии, что
используются лишь кеплеровские орбиты.
ЛИТЕРАТУРА
1. Patton R. В., Jr., A Method of Solution for the Determination of Sa¬
tellite Orbital Parameters from DOPLOC Measurements, Ball. Res.
Labs., Aberdeen Proving Ground, Md., Memo. Rep. № 1237, Septem¬
ber 1959.
2. G u i e r W. H., Weiffenbach G. C., Theoretical Analysis of Doppler
Radio Signals from Earth Satellites, Appl. Phys. Lab., Silver Spring,
Md., Bumblebee Rep. № 276, April 1958.
3. D a v i s R. C., Techniques for the Statistical Analysis of Continuous-
Wave Doppler Data, US NAVORD Test Station, China-Lake, Calif.,
NAVORD Rep. № 1312, April 1951.
4. Moulton F. R., An Introduction to Celestial Mechanics, N. Y., 1902.
5. D e b e у L. G., Tracking in Space by DOPLOC. IRE Trans on Mibitary Ele¬
ctronics, MIL—4, № 2—3, 332 (1960).

ИСПОЛЬЗОВАНИЕ ИЗМЕРЕНИЙ
ДОППЛЕРОВСКОГО СДВИГА ЧАСТОТЫ СИГНАЛОВ.
ИЗЛУЧАЕМЫХ СПУТНИКАМИ ЗЕМЛИ.
I.	ЧАСТОТНЫЕ ИЗМЕРЕНИЯ НА СПУТНИКАХ1)
Лейден, Т а нцман
Рассматриваются результаты измерений частоты сигналов, излучаемых
с советских и американских искусственных спутников Земли, и приводятся
зависимости частоты от времени наблюдения во время запуска и на ор¬
бите. Описывается аппаратура, применяемая для допплеровских измере¬
ний, и обсуждаются достижимые точности измерения частоты и времени,
обеспечиваемые этой аппаратурой.
ВВЕДЕНИЕ
Ежедневно начиная с 5 октября 1957 г.2) лаборатория
связи армии США производит измерение частоты сигналов,
передаваемых с советских и американских искусственных
спутников Земли.
На большом количестве кривых изменения частоты во
времени проявляется эффект Допплера для принимаемых ра¬
диосигналов. Эти кривые получены при наблюдениях спутни¬
ков, находящихся на орбите, хотя измерения проводились для
всех американских спутников и во время их запуска. При по¬
мощи линейной аппроксимации этих кривых могут быть опре¬
делены скорость спутника и наклонные дальности.
По измеренным значениям частоты и по времени измере¬
ния можно определить орбиту спутника. Из рассмотрения
кривых, полученных в результате наблюдений за ракетами
«Авангард» и «Эксплоурер», по резким изменениям частоты
можно установить момент запуска различных ступеней, а так¬
же наличие нарушений нормального функционирования ра¬
кеты, например отказа в работе одной или нескольких сту¬
пеней.
В настоящей статье описаны различные методы измерений
частоты, которые могут быть применены для получения таких
кривых. Рассматриваемые здесь системы позволяют прово¬
!) L а у d е п О. P., Т a n z m a n Н. D,. IRE Nat. Conv. Rec., 7, Pt. 5,
54—60 (1959).
2)	Первый советский искусственный спутник Земли был запущен 4 ок¬
тября 1957 г. —Прим. ред.

408
IV. КОНТРОЛЬ ТРАЕКТОРИИ КОСМИЧЕСКИХ АППАРАТОВ
дить прямое и косвенное измерение частоты. При косвенных
измерениях неизвестной частоты принимаемого сигнала ис¬
пользуется преобразование частоты сигнала с помощью ста¬
билизированного кварцем гетеродина в более низкую частоту,
на которой и производится измерение изменений частоты во
времени. Низкочастотные колебания записывались сначала
на магнитную ленту, с которой они впоследствии воспроизво¬
дились, и измерялись с помощью осциллографа путем сравне¬
ния с частотой колебаний звукового генератора. Частоты зву¬
кового генератора и время приема на основании данных
службы времени (WWV) также автоматически записывались.
Этот метод позволяет измерить частоты с точностью ±10 гц
и время с точностью ±1,0 сек. Изменение скорости протяжки
магнитной ленты при такой системе измерений мало сказы¬
вается на точности измерений.
В статье приводятся уравнения, позволяющйе получить
аппроксимацию первого порядка для скорости и наклонных
дально-стей спутника. Для решения этих уравнений достаточ¬
но одной только информации, содержащейся в кривых зави¬
симости изменения частоты от времени.
ИЗМЕРИТЕЛЬНАЯ СИСТЕМА
Конечным результатом радионаблюдения за сигналами,
передаваемыми с борта спутников Земли и некоторых ракет,
являются кривые зависимости допплеровского сдвига часто¬
ты от времени.
Такая частотно-временная информация может быль полу¬
чена прямым измерением неизвестной принимаемой частоты
в течение всего времени приема. Это измерение может бьпь
выполнено путем непосредственной подачи напряжения при¬
нимаемого сигнала, например /= 108 Мгцу на счетчик часто¬
ты. При времени счета, равном 1 сек, частота может быть
измерена с точностью ±1 гц. Если счетчик имеет время счета,
равное 0,1 сек, то может быть реализована точность ±10 гц.
Если неизвестный сигнал переносится путем гетеродинирова-
ния в область низких частот и затем измеряется с помощью
счетчика частоты, то подобная степень точности может быть
получена только с помощью применения высокостабильного
гетеродина. Для этого типа измерений необходимо, чтобы
принимаемый сигнал имел хорошее отношение сигнал/шум.
Такая система измерений может работать только по не¬
прерывным сигналам. Короткие по длительности импульсные
сигиады, подобные тем, которые применялись ца первом

ДОППЛЕРОВСКИЙ СДВИГ ЧАСТОТЫ СИГНАЛОВ спутников, Ч. I 409
советском искусственном спутнике, с помощью такой системы
не могут быть измерены.
При косвенных измерениях неизвестная частота перено¬
сится путем гетеродинирования стабильным генератором в об¬
ласть низких (звуковых) частот, которые могут быть изме¬
рены сравнением с помощью осциллографа с частотой, да¬
ваемой стабильным звуковым генератором. Частоту звукового
Ф к г. 1. Блок-схема системы для измерения допплеровского сдвига
частоты.
генератора можно в свою очередь измерить с помощью счет¬
чика частоты. Точность измерения частоты при таком спо¬
собе достигается ±1 гц, однако здесь появляются дополни¬
тельные ошибки, вносимые оператором и достигающие не¬
скольких герц. Результирующая точность такого метода из¬
мерения лучше 10 гц. Точность измерения времени для обеих
систем, прямой и косвенной, составляет примерно ±1 сек.
При косвенном методе измерения (фиг. 1) неизвестный
сигнал на частоте 108 Мгц принимается и преобразуется в
промежуточную частоту, равную 14,4 Мгц, поступающую не¬
посредственно на радиоприемник. Стабильный сигнал с час¬
тотой 108 Мгц, даваемый эталонным кварцевым генератором,
слабо связанным со входом преобразователя, также преобра¬
зуется по частоте на 14,4 Мгц. Биение этих частот в детек¬
торной цепи приемника образует сигнал звуковой частоты,

410	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
записываемый в одном из каналов многоканального магнит¬
ного регистратора. Магнитная запись используется для обра¬
ботки результатов измерений в измерительном центре. При
этом возможно накопление данных до времени, более удоб¬
ного для обработки.
При воспроизведении с магнитной ленты звуковой сигнал
фильтруется и подается на одну пару пластин осциллографа.
На другую пару пластин поступает частота звукового гене¬
ратора, которую изменяют до тех пор, пока на экране осцил¬
лографа не получится «круг Лиссажу», свидетельствующий
о равенстве обеих частот. Неизвестный звуковой сигнал мо¬
жет быть определен посредством измерения частоты звуко¬
вого генератора путем подключения его к счетчику частоты.
В течение 1 сек, необходимой для измерения, частоту звуко¬
вого генератора можно считать неизмененной.
Метки времени, выдаваемые службой времени (WWV),
записываются по другому каналу магнитного регистратора.
Эти временные сигналы используются для эталонирования
счетчика частоты, и, таким образом, изменения скорости про¬
тяжки при записи и воспроизведении вносят лишь незначи¬
тельную ошибку при измерении частоты. При воспроизведе¬
нии результаты измерения частоты и соответствующие значе¬
ния времени автоматически записываются на бумажной ленте
с помощью печатающего цифрового устройства.
После того как результаты измерения времени и частоты
записаны с помощью печатающего цифрового устройства, на
бумажной ленте записывается от руки дополнительная ин¬
формация (название спутника, номер орбиты, время, значе¬
ние эталонной частоты и другие справочные данные). Эти
ленты в дальнейшем используются для построения зависимо¬
сти изменения частоты от времени.
Частота сигнала, принимаемого со спутника, определяется
по известным значениям частот звукового и эталонного гене¬
раторов. Полученные кривые допплеровских сдвигов частоты
могут быть использованы для определения скорости и на¬
клонной дальности.
Косвенный метод измерения частоты был использован ла¬
бораторией по двум причинам:
а) для непосредственных измерений необходим чистый
сигнал, в то время как при косвенном методе измерения ча¬
стоты могут быть проверены при наличии шумов, сравнимых
с сигналом;
б) для коротких по длительности импульсных сигналов,
подобных сигналам, передаваемым с первого советского
искусственного спутника, необходимо применять интервал

ДОППЛЕРОВСКИЙ СДВИГ ЧАСТОТЫ СИГНАЛОВ СПУТНИКОВ, Ч. I 411
измерения 0,1 сек вместо 1,0 сек, вследствие чего результи
рующая точность частотных измерений была бы снижена.
12	3
Фиг. 2. Общий вид установки для регистрации и воспроизведения
сигналов.
/ — громкоговоритель; 2 — делитель частоты; 3—усилитель громкоговорителя; 4 — 7-каналь¬
ный магнитный регистратор; 5 —счетчик частоты; 6 — счетчик времени; 7_цифровой
регистратор; 8— эталонный генератор частоты; 9 — кварцованный измеритель импульсов;
10— преобразователь частоты; 11 — приемник; 12 — осциллограф; 13 — звуковой генератор;
14 — полосовой фильтр; /5 —широкополосный усилитель; 16 — счетчик частоты.
На фиг. 2 показан общий вид регистрирующего и воспро¬
изводящего оборудования системы.
Математической основой кривых допплеровского сдвига
частоты является допплеровское уравнение
/пр	£ ^ vnp
/пер	С ± t/сц
(1)

412	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
где /пр — частота, принимаемая станцией, /пер — частота, из¬
лучаемая передатчиком спутника (предполагается постоян¬
ной), рПр — скорость приемника, vcu — скорость спутника.
Фиг. 3. Изменения допплеровской частоты при различных траекториях
спутника.
d — наклонная дальность; v — скорость спутника, г/д —составляющая скорости, направлен
ная в сторону расположения приемника или в противоположную .сторону; va~ составляю¬
щая скорости, перпендикулярная к линии, соединяющей спутник и приемную станцию.
В предположении, что упр = 0 (спутник проходит над го¬
ловой наблюдателя, и его орбита — прямая линия), уравнение
(1) можно переписать относительно скорости спутника так:
®cn = c(l—JF^-).	(2)
Формула для наклонной дальности на ближайшем участке
траектории будет следующей:
г 	 J пер сп	/о\
0	С (dfпр/^)макс
где г0 — наклонная дальность и dfnv/dt— крутизна кривой из¬
менения частоты на ближайшем участке траектории.
В этих выражениях для скорости и наклонной дальности
коэффициент рефракции среды предполагается равным

ДОППЛЕРОВСКИЙ СДВИГ ЧАСТОТЫ СИГНАЛОВ СПУТНИКОВ, Ч. I 413
единице и с — скорость света — принимается равной
300 ООО км/сек.
Допплеровская частота принимаемого сигнала изменяется
за счет изменения скорости по величине или направлению,
или одновременно по обоим. На фиг. 3 показаны две траек¬
тории прохождения спутников после их запуска с мыса Кана¬
верал. Первая траектория — это траектория спутника, запу¬
щенного в направлении на приемную станцию.
Сначала частота Допплера уменьшается по мере прибли¬
жения спутника к станции и становится равной нулю, когда
спутник проходит на минимальном расстоянии от станции
(точка В). В этой точке принимаемая частота /Пр равна частоте,
излучаемой передатчиком спутника /пер. При нормальном
прохождении спутника эта точка соответствует максималь¬
ной крутизне на допплеровской кривой, и частота понижает¬
ся в этой области кривой особенно быстро. После прохожде¬
ния спутником точки В, снова возникает частота Доппле¬
ра, и принимаемая частота уменьшается относительно часто¬
ты, излучаемой передатчиком спутника.
Вторая траектория — траектория спутника, запущенного
в стороне от станции; допплеровская составляющая скорости
всегда существует относительно этой станции.
Ускорения (за счет работы двигателя ракеты) можно от¬
мечать по значительному изменению крутизны допплеровской
кривой. Если спутник запускается вдоль первой траектории,
то при работе двигателей между точками С и В можно на¬
блюдать быстрое возрастание допплеровской частоты в связи
с возрастанием составляющей скорости, направленной на
станцию. Если же спутник движется при работающих двига¬
телях ракеты по второй траектории, то можно наблюдать
быстрое уменьшение частоты Допплера вследствие увеличе¬
ния составляющей скорости, направленной в сторону удале¬
ния от станции.
Для правильной интерпретации характера допплеровских
кривых желательно знать программу запуска спутника, что
бы связать изменения скорости с изменениями сигнала, при¬
нимаемого станциями наблюдения.
Полезными данными из программы являются: расчетная
траектория спутника (в частности, азимут и угол места точки
запуска двигателей отдельных ступеней), время работы дви¬
гателей и другая информация, связанная со скоростью движе¬
ния передатчика.
Описанный выше расчет скорости и наклонной дальности
может быть проведен, если запуск спутника был осуществлен
по направлению к приемной станции. Куда бы ни был произ¬

414	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
веден запуск в сторону от приемной станции, нуль доппле¬
ровской частоты не может быть получен и для расчета ско¬
рости понадобятся дополнительные измерения.
ИЗМЕРЕНИЯ
Измерения частоты сигналов, излучаемых передатчиком
первого советского искусственного спутника, проводились
ежедневно. В качестве примера полученной информации на
фиг. 4 показано изменение частоты во времени для близкого
прохождения спутника 18 октября 1957 г.
Среднее гринвичское время
Фиг. 4. Изменения частоты принимаемого сигнала вследствие эффекта
Допплера.
-Первый советский искусственный спутник.
/о = 1Ю7: 04; /0=40 001947, гц; крутизна 7,6 гц/сек2', орбита № 106; 18 октября 1957 г.
Информация, содержащаяся в этом графике, может быть
использована для определения скорости спутника и наклон¬
ной дальности, а также других величин, связанных с харак¬
теристикой спутника.
Данные, полученные при запуске американских искусст¬
венных спутников «Эксплоурер» и «Авангард», отчетливо по¬
казывают увеличение скорости после начала запуска. При
этом спутник проходил на высоте приблизительно 1 бЬ км над
мысом Канаверал, а сигнал принимался в Форт Монмуте.

ДОППЛЕРОВСКИЙ СДВИГ ЧАСТОТЫ СИГНАЛОВ СПУТНИКОВ, Ч. t 4i5
На фиг. 5—И видны ход запуска этих спутников и точки
включения различных ступеней ракеты-носителя.
«Эксплоурер» II. Спутник «Эксплоурер» II был запущен
5 марта 1958 г. в юго-восточном направлении от мыса Кана¬
верал (шт. Флорида), но не вышел на орбиту.
Допплеровские кривые запуска этого спутника, предста¬
вленные на фиг. 5, показывают, что сигнал с его борта при¬
нимался еще до запуска второй ступени. В момент времени
Среднее гринвичское время
Фиг. 5. Изменение частоты принимаемого сигнала при запуске спутника
«Эксплоурер» II.
Запуск спутника «Эксплоурер» И 5 марта 1958 г
1334 мин 31 сек наблюдается быстрое изменение крутизны
допплеровской кривой. Это указывает на включение второй
ступени.
Быстрое снижение частоты означает, что составляющая
ускорения, образующаяся за счет работы второй ступени, на¬
правлена в сторону удаления от станции.
В момент времени 1334 мин 41 сек имеется другое изме¬
нение крутизны допплеровской кривой. Это означает включе¬
ние третьей ступени. Дальнейшее снижение частоты, являю¬
щееся следствием сообщаемого ускорения, свидетельствует
о том, что ускорение приложено в сторону удаления от места
наблюдения.
Допплеровские кривые показывают, что четвертая ступень
не сработала. Таким образом, можно было предположить, что
спутник не вышел на орбиту из-за того, что не была достиг¬
нута необходимая скорость.

416 tv. Контроль траекторий Космических аппаратов
«Эксплоурер» III. Спутник «Эксплоурер» III был запущен
26 марта 1958 г. в юго-восточном направлении с мыса Кана¬
верал. Спутник вышел на орбиту.
Допплеровские кривые для запуска спутника «Эксплоу¬
рер» III, представленные на фиг. 6, показывают, что сигнал
с борта спутника принимался до начала работы второй сту¬
пени. В момент времени 1744 мин 23 сек произошло резкое
107 939 ООО
107 985 ООО
. 107980 ООО
| 107975 000
ё
707970 ООО
Запуск 2-й ступени
Запуск 3-й ступени
Запуск Ц-й ступени
—Выключение двигателей
№7965 ООО I	1	I	I	I	1	1	1
1792	1793	1799	1795	1796	1797	1798	1799
Среднее гринвичское время
Фиг. 6. Изменение частоты принимаемого сигнала при запуске,спутника
«Эксплоурер» III.
Запуск спутника «Эксплоурер» III 26 марта 1958 г.
изменение крутизны допплеровской кривой, свидетельствую¬
щее о запуске второй ступени. Другое резкое изменение кру¬
тизны допплеровской кривой приходится на время 1744 мин
40 сек. Оно свидетельствует о запуске третьей ступени. Третье
резкое изменение крутизны в момент времени 1744, мин ЪЪсск
указывает на запуск четвертой ступени. При запуске каждой
ступени происходит все более быстрое снижение частоты, сви¬
детельствующее о том, что ускорения направлены в сторону
от места расположения приемной станции.
«Эксплоурер» V. Спутник «Эксплоурер» V был запущен
24 августа 1958 г. в северо-восточном направлении с мыса
Канаверал. Этот спутник не вышел на орбиту.
Допплеровские кривые для данного запуска показывают,
что сигнал со спутника принимался еще до включения второй
ступени.

ДОППЛЕРОВСКИЙ СДВИГ ЧАСТОТЫ СИГНАЛОВ СПУТНИКОВ, Ч. I 417
Как видно из фиг. 7, вторая ступень включилась в момент
времени 0623 мин 24 сек, когда возникло резкое изменение
крутизны допплеровской кривой. В этой точке частота быстро
увеличивается, указывая на то, что составляющая ускорения
направлена в сторону расположения станции. Третья и чет¬
вертая ступени включились в 0623 мин 32 сек и 0623 мин
40 сек соответственно. Во время работы третьей и четвертой
0620	0621	0622	0623	062U	0625	0626'	0627
Среднее гринвичское время
Ф и г. 7. Изменение частоты принимаемого сигнала при запуске спутника
'	«Эксплоурер» V.
Запуск спутника «Эксплоурер» V 24 августа 1958 г.
ступеней частоты продолжали быстро нарастать, свидетель¬
ствуя о том, что ускорение было по-прежнему направлено
в сторону расположения станции.
При запуске второй, третьей и четвертой ступеней ско¬
рость изменения частоты была настолько велика, что изме¬
рительное оборудование не смогло его зарегистрировать. Од¬
нако в момент каждого включения имело место заметное из¬
менение звукового сигнала, по которому было определено
время включений. Это также относится к запуску спутника
«Эксплоурер» IV.
В момент времени 0623 мин 48 сек двигатель был выклю¬
чен; частота сигнала стала снижаться, так как спутник при¬
ближался к пункту наблюдения, и допплеровская частота
стала изменяться по нормальной S-образной кривой. Точка
минимального расстояния до спутника приходится на мо¬
мент времени 0625 мин 30 сек. Рассчитанная скорость в этой
27 Зак. 876

418	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
точке равнялась 7,3 км/сек\ расчетная наклонная дальность
256 км.
«Эксплоурер» IV. Спутник «Эксплоурер» IV был запущен
26 июля 1958 г. в северо-восточном направлении с мыса Ка¬
наверал. Этот спутник вышел на орбиту.
Допплеровские кривые показывают, что первый сигнал
со спутника был принят еще до запуска второй ступени. Рез¬
кое изменение крутизны кривой на фиг. 8 в точке 1506 мин
Ф й г. 8. Изменение частоты принимаемого сигнала при запуске спутника
«Эксплоурер» IV.
Запуск спутника «Эксплоурер» IV 26 июля 1958 г.
20 сек указывает на запуск второй ступени. Частота быстро
возрастает вследствие приближения объекта, и, следователь¬
но, ускорение направлено в сторону приемной станции.
Кривая показывает также моменты зажигания третьей и
четвертой ступеней.
Выключение двигателей произошло в ,момент времени
1506 мин 47 сек, на что показывает резкий излом кривой. За¬
тем частота снижается, давая нормальную S-образную допп¬
леровскую кривую, так как спутник проходил над районом
приемной станции. Время, когда спутник находился над стан¬
цией, соответствует 1508 мин 00 сек. В этой точке расчетная
скорость была равна 5,9 км/сек, а расчетная наклонная даль¬
ность — 310 км.
«Авангард» V. Спутник «Авангард» V был запущен с мыса
Канаверал в юго-восточном направлении 28 мая 1958 г. Этот
спутник не вышел на орбиту.
Выключение двигателей-
108 037 ОООг- 3апУск ** стУПвНи '
Запуск 3-й ступени —
Запуск 2- и ступени —
108 030ООО -
■0—0— 0—0
* 708029000
|
ft 108 028 ООО
с
 fo=m 028540
108027000
108 026000
1503	150Ц	1505	1506	1507	1508-	1509	1510
Среднее гринвичское время

ДОППЛЕРОВСКИЙ СДВИГ ЧАСТОТЫ СИГНАЛОВ СПУТНИКОВ, Ч. I 419
Допплеровские кривые, приведенные на фиг. 9, показы¬
вают, что сигнал наблюдался . до начала работы третьей
ступени.
В момент времени 0355 мин 47 сек крутизна допплеров¬
ской кривой резко изменяется, указывая на запуск третьей
ступени. Частота сигнала снижается, так как движение
направлено в сторону удаления от станции.
Среднее гринвичское время
Фиг. 9. Изменение частоты принимаемого сигнала при запуске спутника
«Авангард» V.
Запуск спутника «Авангард» V 23 мая 1958 г.
После выключения третьей ступени допплеровская частота
начинает увеличиваться. Это происходит в результате из¬
менения скорости спутника за счет торможения в атмосфере
Земли, при этом составляющая скорости, направленная в сто¬
рону от станции, снижается.
«Авангард» IV. Спутник «Авангард» IV был запущен с
мыса Канаверал в юго-восточном направлении 17 марта
1958 г. Этот спутник вышел на орбиту.
Допплеровские кривые показывают, что сигнал начал на¬
блюдаться еще до запуска третьей ступени (фиг. 10). В мо¬
мент времени 1225 мин 30 сек запускается третья ступень.
После этого частота быстро снижалась, указывая на то, что
составляющая ускорения направлена в сторону от приемной
станции.
В момент времени 1226 мин 18 сек крутизна допплеров¬
ской кривой резко изменяется, что указывает на выключение
двигателя третьей ступени. Наблюдаемые колебания измене¬
ний частоты в течение ~20 сек могут быть объяснены отде-
27*

Частота, ?.ц
Среднее гринвичское время
Ф и г. 10. Изменение частоты принимаемого сигнала при запуске спутника
«Авангард» IV.
Запуск спутника «Авангард» IV 17 марта 1958 г.
0845	0846	0847	0848	0849	0850	0851
Среднее гринвичское время •
Фиг. 11. Изменение частоты принимаемого сигнала при запуске косми¬
ческой ракеты «Пионер» I.
Запуск космической ракеты «Пионер» 1 11 октября 1958 г.

ДОППЛЕРОВСКИЙ СДВИГ ЧАСТОТЫ СИГНАЛОВ СПУТНИКОВ, Ч. I 421
лением спутника от ракеты-носителя. Полученные данные при
известных значениях наклонной дальности использовались
для расчета скорости спутника.
«Пионер» I. Космическая ракета «Пионер» I была запу¬
щена в сторону Луны с мыса Канаверал в северо-восточном
направлении И октября 1958 г. (фиг. 11). Ракета не вышла
на орбиту вокруг Луны, но достигла высоты 120 000 км, т. е.
более 7з расстояния между Землей и Луной.
Допплеровские кривые показывают, что в момент времени
0846 мин 31 сек происходит крутое изменение их крутизны.
Зная, что космическая ракета двигалась в это время по на¬
правлению к станции, мы могли бы за счет работы ступеней
ожидать увеличение частоты. Однако в это время ракета на¬
ходилась вблизи точки минимального расстояния от станции,
и, следовательно, быстрое снижение частоты в этой области
обусловливается обычным допплеровским сдвигом. При этом
быстрое возрастание частоты за счет ускорения было ском¬
пенсировано вследствие прохождения в области, близкой к
to значению времени. Поэтому работа третьей ступени не бы¬
ла резко выражена, и кривая не имеет обычного резкого из¬
менения.
В момент времени 0847 мин 17 сек наблюдается другое
резкое изменение крутизны, указывающее на окончание ра¬
боты третьей ступени. В этой точке космическая ракета уда¬
лялась от станции, причем скорость удаления была значи¬
тельно больше скорости при сближении, чем и объясняется
некоторое различие в общем похожих друг на друга обычных
допплеровских кривых для приближения и удаления.

ИСПОЛЬЗОВАНИЕ ИЗМЕРЕНИИ
ДОППЛЕРОВСКОГО СДВИГА ЧАСТОТЫ СИГНАЛОВ,
ИЗЛУЧАЕМЫХ СПУТНИКАМИ ЗЕМЛИ.
II.	ИЗМЕРЕНИЕ МИНИМАЛЬНОЙ НАКЛОННОЙ
ДАЛЬНОСТИ ОРБИТЫ СПУТНИКА
ДО ИЗМЕРИТЕЛЬНОГО ПУНКТА1)
Хатчинсон
Одной из самых актуальных проблем измерений траекто¬
рий спутников является точное определение положения орби¬
ты относительно точки наблюдения, расположенной на зем¬
ной поверхности. Хорошим показателем значения этой проб¬
лемы являются данные инспекции Международного геофизи¬
ческого года (МГГ) об эфемеридах спутника «3 1957» 2), где
действительная высота спутника указана с точностью до 2 км,
а табличные ‘ значения широты и долготы указаны с точностью
0,5° от действительной величины. Последняя ошибка при про¬
ектировании на поверхность Земли эквивалентна расстоянию
50 км. Очевидно, что определение наклонной дальности до
станции наблюдения является важной задачей при любых
измерениях, использующих эффект допплеровского сдвига'
частоты, будь то контроль положения спутника на орбите
или измерения с целью изучения ионосферы. Если наклонная
дальность может быть определена с достаточной степенью
точности (скажем, с точностью до 10 км) и данные об эфеме¬
ридах имеют точность, указанную ранее, то для сравнения
могут быть использованы действительные значения высоты
вместе с рассчитанной дальностью по поверхности Земли от
наблюдателя до проекции орбиты на Землю. С помощью срав¬
нения этих расстояний с предполагаемыми данными об эфе¬
меридах можно определить величину и направление коррек¬
ции эфемерид.
Таким образом, любые независимые измерения наклонной
дальности дают важную информацию для решения двух за¬
дач, а именно: коррекции орбиты и изучения эффектов пре¬
ломления в ионосфере.
В настоящей статье описывается метод измерения наклон¬
ной дальности в ближайшей к измерительному пункту точке
!) Hutchinson Н. P., IRE Nat. Conv. Rec7, Pt. 5, 61—66 (March
1959).
2) Второй советский искусственный спутник Земли был запущен
3 ноября 1957 г. — Прим. ред.

ДОППЛЕРОВСКИЙ СДВИГ ЧАСТОТЫ СИГНАЛОВ СПУТНИКОВ, Ч. II 423
траектории; кривые допплеровских сдвигов частоты, рассчи¬
танные по результатам этих измерений, и другие данные об
орбите сравниваются с наблюдениями допплеровских сдвигов
частоты, произведенными на частотах 20 и 40 Мгц при таких
же расположениях орбит. При этом сравнении отмечается
эффект рефракции в ионосфере. В заключение делается не¬
сколько замечаний о желательности применения более высо¬
ких частот для передачи сообщений со спутников, для того
Фиг. 1. Геометрические соотношения орбиты.
чтобы уничтожить нежелательные эффекты, связанные с ионо¬
сферной рефракцией.
В общем случае наземная станция наблюдения не лежит
в плоскости орбиты, а расположена несколько в стороне. По¬
этому наклонная дальность измеряется в плоскости, опреде¬
ляемой точкой наблюдения на Земле и хордой, соединяющей
две точки на участке орбиты спутника, расположенном на
наименьшем расстоянии от измерительного пункта. Таким об¬
разом, образуется треугольник с вершинами в двух точках
на орбите спутника и третьей вершиной в месте расположе¬
ния наземной станции наблюдения. Для треугольников с уг¬
лом при вершине менее 25° хорда достаточно точно аппрокси¬
мирует дугу орбиты, и это обстоятельство используется в на¬
ших расчетах.
На фиг. 1 вершина треугольника ОР\Р2 совпадает с рас¬
положением наземной станции, точки Р\ и Р2 берутся на рав¬
ных расстояниях от точки А и образуют угол (Р2ОР\), мень¬
ший 25°. Таким образом, мы имеем равнобедренный треуголь¬
ник с основанием h и высотой Н. Как отмечалось ранее, Н
представляет собой наклонную дальность до ближайшей точ
ки на орбите, т. е. расстояние, которое мы хотим определить.

424	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ.
Предположим, что точки орбиты Рь А и Р2 проходятся соот¬
ветственно в моменты времени tu tA, t2. В какой-нибудь мо¬
мент времени между tx и t2 радиальная скорость спутника vRy
направленная в сторону наблюдателя или от него, равна
Vr — t^cnsin ос, где vCu—орбитальная скорость спутника и
а — половина угла при вершине, как это показано на фиг. ).
При соответствующем выборе величины а расстояние АРХ
пропорционально Я, так как APx = Htga. Выбирая соответ¬
ствующие величины, составляем табл. 1.
Таблица I
tg а
Ар}
h
н
а, град
Sin а
0,2
0,2 Н
0,4 Н
2,5/г
11,3
0,1959
0,1
0,1//
0,2 Н
5/г
5,7
0,0993
0,05
0,05 Н
ОД Н
ЮЛ
2,9
0,050
Пользуясь этой таблицей, принимая tga равным 0,2 и
предполагая, что положение точки Р\ находится на расстоя¬
нии 0,2 Я, определим радиальную скорость спутника, которая
в этот момент будет равна 0,1959 vcu и направлена в сторону
наблюдателя. Аналогично для точки Р2 радиальная скорость
равна 0,1959 vcn, но направлена в сторону от наблюдателя.
Величина h= (t2 — ti)vCn- Зная vCUy мы можем рассчитать h
и наклонную дальность Я.
Все сказанное выше будет справедливо при условии, что
допплеровские кривые не будут зависеть от ионосферной ре¬
фракции. На фиг, 2 приведены допплеровские кривые, кото¬
рые можно рассматривать как типичные для ближайшею
участка орбиты в районе перигея. В первом приближении
скорость спутника можно рассматривать, предполагая, что
орбита является прямой линией на том участке, на котором
зарегистрирован радиосигнал. При определении скорости
спутника по наклону допплеровских кривых во время про¬
хождения спутника на минимальном расстоянии от измери¬
тельного пункта или по полному значению допплеровского
сдвига частоты при прохождении спутника полученные вели¬
чины оказываются меньше значений, рассчитанных по орби¬
тальным данным. Если скорость, рассчитанная по .орбиталь¬
ным данным, весьма близка к действительной скорости, то
величины, полученные по данным реальных допплеровских
сдвигов, существенно меняются в силу влияния-ионосферы.:и
существующей кривизны орбиты в секторе наблюдения,

ДОППЛЕРОВСКИЙ СДВИГ ЧАСТОТЫ СИГНАЛОВ СПУТНИКОВ, Ч. II 425
Поэтому при расчете необходимо учесть две поправки: одну
за счет ионосферной рефракции и другую, большую, за счет
кривизны орбиты.
В общем случае принимаемая частота равна частоте, из¬
лучённой со спутника только в точке ближайшего расстояния
до спутника. Однако, строго говоря, это верно, когда луч
(сигнал) от этой точки до наблюдателя является перпенди¬
кулярным к ионосфере и когда долгота точки наблюдения
такова, что радиальной составляющей скорости Земли можно
Фиг. 2. Типичный допплеровский сдвиг на частоте 40 Мгц.
Время наблюдения ^ 5 мня, 8 октября 1958 г. /=40 Мгц.
пренебречь. Когда же луч из точки ближайшего расстояния
до точки наблюдения проходит через ионосферу, существенно
отклоняясь от перпендикулярного к ней направления, то кри¬
вая допплеровского сдвига частоты искажается в области
прохождения через нуль, как показано на фиг. 3, где пред¬
ставлены результаты, полученные при наблюдении второго
советского искусственного спутника, запущенного в 1957 г.
Рассмотрим орбиту спутника. На фиг. 4 апогей и перигей
орбиты, близкой к круговой, лежат соответственно на высоте
200 и 1600 км над поверхностью Земли. На первый взгляд
кажется, что мы можем рассчитать и использовать среднюю
величину орбитальной скорости 0СП, зная период обращения
спутника и протяженность его орбиты. К сожалению, это не
совёем так. Применение законов Ньютона к определению
скорости на орбите дает для данного случая максимальную
скорость в перигее, равную 8,2 7сж/с^>с. В рассматриваемом
случае прохождения вблизи ’"пёрйгея, используя данные

Время, мин
Фиг. 3. Изменение частоты принимаемого сигнала от второго советского
искусственного спутника.
Время наблюдения: 8 ноября 1957 г. в 10 18 00 гражд. врем, по Гринвич, мери д. или 05 18 00
по восточному поясному времени. Обозначения: О"~40 Мгц\ х — 20 Мгц.
Фиг. 4. Эскиз орбиты спутника.
vcpeAHe7»*2 км/сек.
Частота, гц

ДОППЛЕРОВСКИЙ СДВИГ ЧАСТОТЫ СИГНАЛОВ СПУТНИКОВ, Ч. II 427
эфемерид, получаем для скорости спутника величину, равную
8,1 км! сек.
Для сравнения первоначальных данных о скорости спут¬
ника, даваемых допплеровскими измерениями (см. фиг. 3),
с теоретическими значениями скоростей, рассчитанных на
основании знания параметров орбиты, составлена табл. 2, в
которой приведены результаты, вычисленные для частот 20
и 40 Мгц как по данным допплеровского сдвига частоты, так
и по величине скорости 8,1 км/сек, рассчитанной на основа¬
нии орбитальных данных.
Таблица 2
Расчетная величина vcn для орбиты № 74 второго
советского искусственного спутника
Частота, Мгц
40,002
20,006
По величине крутизны допплеровской кри¬
вой 0» км/сек
7,90
7,73
По данным полного допплеровского сдвига
частоты, км/сек
7,61
7,43
По данным эфемерид (высота апогея и пери¬
гея, период обращения), км/сек
8,1
8,1
>) Кривая построена по результатам измерений в окрестности точки ближайшего рас¬
стояния до спутника.
Пользуясь значением скорости, рассчитанной по орбиталь¬
ным данным (8,1 км/сек) и частотному сдвигу, равному
200 гц на частоте 40 Мгц и 100 гц на частоте 20 Мгц, вели¬
чину наклонной дальности можно рассчитать по формуле
Н = 2,5 {t2 — tx) vcn,
где (t2 — )40 = 21 сек, (t2 — ^1)20 = 20 сек.
В результате расчета получаем две величины для Н: 425
и 405 км.
Теперь проверим по эфемеридам проекцию на поверхность
З^емли (фиг. 5) ближайшей орбиты, проходящей через зенит.
Расстояние от кулевой точки проекции орбиты на Землю в
точке ближайшего расстояния до спутника составляет около
200 км. Однако полагая, что высота дана в эфемеридах

428	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
(238 км) с точностью 2 км, находим, что действительная на¬
клонная дальность Н составит 415 км. Соответствующее этой
величине расстояние по Земле до точки наибольшего сбли¬
жения будет ~340 км.
Для проверки указанного метода измерений наклонной
дальности было решено рассчитать допплеровские кривые
Фиг. 5. Проекция на поверхность Земли 74-й орбиты спутника
8 октября 1958 г.
и сравнить их с результатами, полученными для эксперимен¬
тальных допплеровских сдвигов при аналогичном расположе¬
нии орбиты. При этом были получены следующие результаты:
Орбитальная скорость, км/сек	8Д
Высота спутника в точке, ближайшей к наблюда¬
телю, км	240
Наклонная дальность до точки ближайшего располо¬
жения спутника относительно наблюдателя, км . . . 415
Частота передатчика, Мгц	.-	 40
Теоретическая кривая допплеровского сдвига частоты для
спутника, движущегося по прямой линии на расстоянии
415 км от наблюдателя, представлена на фиг. 6, где по рас¬
четным величинам, отмеченным крестиками, проведена
сплошная линия. Здесь же нанесены результаты наблюдений
для 40 и 20 Мгц. Для облегчения сравнения времена прохо¬
ждения через нуль приняты одинаковыми. При расчете дан¬
ных учтено влияние скорости вращения Земли и кривизны
орбиты спутника. Эти кривые не учитывают эффекта ионо¬
сферной рефракции и эффекта изменения скорости спутника
за время прохождения им сектора наблюдения на орбите.

ДОППЛЕРОВСКИЙ СДВИГ ЧАСТОТЫ СИГНАЛОВ СПУТНИКОВ, Ч. II 429
Как видно из фиг. 6, имеет место очень хорошее совпадение
расчетных и экспериментальных данных, и, следовательно,
Фиг. 6. Расчетные значения допплеровских сдвигов частоты и экспери¬
ментальные их величины на частотах 20 и 40 Мгц.
Допплеровский сдвиг частоты вычислен для ?’сп = 8,1 км/сек.
X вычисленные данные; О экспериментальные данные на частоте 40 Мгц; □ эксперимен¬
тальные данные на^частоте 20 Мгц.
можно сделать заключение, что описанный выше метод опре¬
деления наклонной дальности может успешно применяться
на практике.

430	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Можно провести дальнейшие сравнения между расчетны¬
ми допплеровскими сдвигами и экспериментальными данны¬
ми. Для этого надо сравнить экспериментально полученный
максимальный допплеровский сдвиг с расчетным.
Расчетные максимальные допплеровские сдвиги для нуле¬
вой точки при иСп = 8,1 км!сек и частоте 40 Мац имеют сле¬
дующие значения:
Теоретический сдвиг частоты при прямолинейном про¬
хождении, гц	1080
То же с поправкой на вращение Земли, гц	1055
То же с поправкой на кривизну траектории, гц . . . 1028
Сравнивая расчетные и экспериментальные величины для
40 и 20 Мац, имеем соответственно: расчетная величина 1028
и 503 ац, экспериментальная величина 1007 и 500 ац.
С учетом инструментальной погрешности системы измере¬
ния допплеровских сдвигов, равной ±10 ац, приведенные ре¬
зультаты показывают вполне удовлетворительное совпадение
между расчетными и экспериментальными величинами.
Чтобы полностью использовать преимущества этого ме¬
тода, эффект ионосферной рефракции по пути распростране¬
ния радиоволн необходимо снизить до пренебрежимо малых-
размеров. С этой целью, и особенно для устранения влияния
спорадического слоя Е и ионизации, связанной с полярными
сияниями, необходимо использовать передатчики с частотой
1000 Мац и выше.
В заключение укажем, что при использовании достаточно
высоких частот для передачи со спутников Земли, в сочета¬
нии с более частыми допплеровскими измерениями, становится
возможным применение обсуждаемого метода для расши¬
рения и улучшения наших сведений об орбитах спутников.
Надо полагать, что этот метод использования данных орбит
и точных допплеровских измерений позволит более точно из¬
мерять наклонную дальность в точке ближайшего расстояния
между спутником и наблюдателем.
ЛИТЕРАТУРА
1.	Arendt P. R., Preliminary Results of Measurements in Doppler Shift
of Satellite Emissions, IRE Trans, Antennas a. Propagation, AP-7,
99—101 (January 1959),

АНАЛИЗ ДВИЖЕНИЯ СПУТНИКА ПО АМПЛИТУДЕ
ПРИНИМАЕМЫХ РАДИОСИГНАЛОВ1)
Вонбэн,
В статье рассматриваются изменения в принимаемом радиосигнале,
обусловленные движением спутника Земли и его вращением. В системе
координат, связанной со спутником, решается уравнение для движения
единичного вектора положения, направленного от спутника на наблюда¬
теля, и рассчитываются изменения силы сигнала, принимаемого наземной
станцией. Затем показывается, как полученные данные об изменении ве¬
личины принимаемого сигнала могут быть использованы для расчета угло¬
вых перемещений спутника в пространстве. В приводимом простом при¬
мере этот угол между нормалью к плоскости расположения турникетной
антенны спутника и некоторым фиксированным направлением в простран¬
стве определяется с помощью регистратора. Последний может работать с
антенной, имеющей как круговую, так и линейную поляризацию. Решение
рассматриваемого уравнения дает простой способ контроля работы систе¬
мы стабилизации стабилизированных спутников.
1.	ВВЕДЕНИЕ
Для спутников, несущих фотографическое оборудование,
например для наблюдений за облачным покровом, очень
важно знать положение спутника относительно некоторой
оси, фиксированной в пространстве. В настоящей статье вы¬
водится уравнение, с помощью которого положение спутника
может быть рассчитано только на основании данных, реги¬
стрируемых наземной приемной станцией.
Рассматривая только вращательное движение спутника,
автор работы [1] показал влияние этого движения на ампли¬
туду и частоту сигнала, принимаемого наземной станцией.
В настоящей статье рассматриваются уравнения, описы¬
вающие движение единичного вектора положения, направлен¬
ного на наблюдателя в системе координат спутника. Эти ура¬
внения могут быть использованы для расчета «модуляции»
радиосигнала, обусловленной вращением спутника. Показы¬
вается, как эту информацию можно использовать для опре¬
деления угловых перемещений спутника.
*) V onbun F., IRE Trans. on Milit. Electronics, МП.-4, № 2—3,
361—365 (April — July I960).

432
IV. КОНТРОЛЬ ТРАЕКТОРИИ КОСМИЧЕСКИХ АППАРАТОВ
2.	АНТЕННА СПУТНИКА
Турникетная антенна
В большинстве уже запущенных спутников для связи с на¬
земными станциями используются турникетные антенны, об¬
разованные полуволновыми диполями, питаемыми со сдвигом
фаз 90°. Преимущество антенн подобного типа заключается
в том, что их диаграмма направленности не имеет нулевых
зон, как в случае простого диполя.
В дальней зоне поле турникетной антенны может быть
рассчитано [2] на основании уравнения
Е = СР\ [.г0 X (г0 X Poi)] + ср2 [r0 X (г0 X Роа)Ь 0)
где с — величина, пропорциональная \/г — обратному рас¬
стоянию между антенной и точкой «наблюдения;
Р\ и Р2—величины моментов диполей;
Poi и Р02*— единичные векторы моментов диполей, направлен¬
ные соответственно по положительным осям X и У,
а г0— единичный вектор, направленный к наблюдателю
из антенны, находящейся в начале координат [ 1 ].
Учитывая, что для турникетной антенны р2 = jp 1 и pi = р,
получаем составляющие электрического поля в сферической
системе координат <р и О
E? = jcpe^e4a,
Еа = сре>? cos 9 • е»0,
где есро, е#0 — единичные векторы для <р и О направлений
(фиг. 1). Как видно из выражения (2), величина поля, соз¬
даваемого антенной, не зависит от угла <р.
Амплитудные изменения сигнала во времени, обусловлен¬
ные движением спутника, происходят только в зависимости
от угла -О1. Эта зависимость
COS 9 {t) = (n0 • го)	(3)
содержит информацию о движении спутника и будет исполь¬
зована в дальнейших расчетах.
Диполь
В случае когда на спутнике имеется, как это показано
пунктиром на фиг. 1, простой диполь р0, направленный по
оси г, поле в дальней зоне будет равно
Е = ср [r0 X (г0 X Р0)]	(4)

КОНТРОЛЬ по амплитуде радиосигналов
433
или в проекциях
(4а)
В этом случае, рассматривая изменения амплитуды во
времени, н'аходим, что они связаны только с углом	При
Фиг. 1. Сферические координаты поля дальней зоны турникетной
антенны.
этом для анализа изменений сигнала может быть использо
вано выражение
которое описывает поле единичного диполя в дальней зоне.
3.	ОСНОВНОЕ ДВИЖЕНИЕ ЕДИНИЧНОГО ВЕНТОРА НАБЛЮДЕНИЙ
ДЛЯ СЛУЧАЯ СЛОЖНОГО ВРАЩЕНИЯ СПУТНИКА
Изменение положения единичного вектора Го может быть
рассчитано с помощью фиг. 2.
На этой фигуре схематически представлены единичные век¬
торы дипольных моментов Poi и р02, нормаль п0 к плоскости
Z
Плоскость, касательная
\ в точке Р
Y
Е = Еь = срУ \ —cos2Ь • е&0,
28 Зак. 876.

434 IV. КОНТРОЛЬ ТРАЕКТОРИИ КОСМИЧЕСКИХ АППАРАТОВ
антенны, ось основного вращения s0, ось дополнительного
вращения h0 и вектор положения , после того как вектор г0
совершил движение в соответствии с h0 и s0.
С целью упрощения математического выражения предпо¬
ложим, что спутник неподвижен в пространстве, а единичный
вектор положения Го совершает движение.
Фиг. 2. Единичные векторы в системе координат спутника.
(h0 • г0) = cos а0; (п0 • h0) = cos р0; (s0 • h0) = cos 0О; (sj • r0) = cos (а0 —р0);
(n0 • r:) = cos 0 (0.
1. Тогда дополнительное вращение s0 вокруг h0 должно
быть заменено вращением г0 вокруг h0, в результате чего по¬
лучим (фиг. 3, а).
2. Основное вращение спутника вокруг оси s0 при фикси¬
рованном г' должно быть заменено вращением г' вокруг So,
в результате чего получим г'7 (фиг. 3,6).
Вращение одного вектора относительно другого может
быть представлено в виде
г; = (h0 • r0) (1 — cos Ш) h0 -ь r0 cos Ш + (h0 X r0) sin Qt (5)
И
Го = (S • г') (1 — COS wt*) s0 + r'0 COS <o/* -f (s0 X r0) sin Ы*.	(6)

КОНТРОЛЬ ПО АМПЛИТУДЕ РАДИОСИГНАЛОВ
435
где £2/ — угол поворота дополнительного вращения, а соt* —
угол поворота основного вращения, как показано на фиг. 3, а
и б.
Так как эти два вращательных движения взаимно незави¬
симы, то моменты вращения для угловых перемещений могут
Фиг. 3. Основное и дополнительное вращения единичного вектора
положения.
быть различными, т. е. для Qt = 0, если Q + 0. угол поворота
со/* может иметь некоторое значение, или наоборот.
При вращении г0 вокруг s0 время может быть выбрано
так, что для t*=(t — /0). h0, s0 и г0 будут компланарными
векторами, и тем самым упростится выражение для г'.
Разумеется, это условие не ограничивает общности этого
выражения для г" при постоянных значениях h0, s0 и г0. По¬
сле ряда преобразований (5) и (6) для г^' можно получить
следующее выражение:
г" = {(h0 • r0) (1 — cos Ш) (s0 • h0) + (s0 • Го) cos Ш) X
X (1 — cos о>/*) s0 + (h0 • r0) (1 — cos 2/) h0 cos Ы* +
+ r0 cos 2/ cos Ы* + (h0 X r0) sin 2/ cos o>/* -f-
+ (h0 • r0)(l cos 20 (s0 X h0) sin Ы* +
+ (s0X r0)cos 2/ sin Ы* + [s0 X (h0X r0)] sin 2/sin co/*.	(7)
Выражение (7) является основным соотношением, описы¬
вающим относительное движение единичного вектора поло¬
жения для спутника со сложным вращением. В выражении (7)
Q
б
ж*

436	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
движение спутника ограничено перемещением по неболь¬
шой дуге, в пределах которой г0 может считаться величиной
постоянной. Как можно видеть из фиг. 2, а также фиг. 3, а и
б, движение г0 по дуге, равной тг/20, не вносит большой ошиб¬
ки в результаты, даваемые уравнением (7). Таким образом,
при наклонных дальностях до спутника, составляющих
1000 км, можно рассматривать его перемещения на расстоя¬
ние — 150 км (в течение около 20 сек), не нарушая приэтом
справедливости выражения (7).
Как показано ниже, подобное малое перемещение необхо¬
димо для определения угла вращения спутника относительно
наблюдателя при его орбитальном движении.
Выражение (7), а следовательно, и выражение (3) можно
значительно упростить, если предположить, что ось вращения
s0 и нормаль к плоскости антенны совпадают, т. е.
n0 = s0>	(8)
что характерно для спутников, имеющих моменты инерции
1х = Гу<1г.
Используя выражения (3), (7) и (8), можно рассчитать
значения функции О
COS e- = (h0 • г0) (п0 • h0) (1 — cos 20 + (п0 • r0) cos 2*.	(9)
Это выражение можно, конечно, получить простым вра¬
щением г0 вокруг h0, как это было сделано для равенств (5)
и (6).
Как видно из фиг. 4,а,
(h0 • r0) = cosa0 = c1(
(п0 • h0) = cos 0о = Сч,	    \
(по * го) = cos(ao — ео) = ^1^2Н- V"l С\ 1/1— с\. } (
Подставляя выражение (10) в (9), получаем для рассма¬
триваемого частного случая
cos Ь = a+ 6 cos Ш,	(11)
где
CL — С-^ * £*2»
ь =	VT^cf.
Выражение (И) является окончательным для определе¬
ния угла О, используемого в дальнейшем для определения

КОНТРОЛЬ ПО АМПЛИТУДЕ РАДИОСИГНАЛОВ
437
угла б0, показанного на фиг. 2, 4, а и б. Заметим, что в нем
не содержится символа частоты со, обусловленной основным
Наземная '
приемная станция
О
Фиг. 4. Единичный вектор, описывающий относительное движение
нормали п0 к плоскости расположения антенны вокруг некоторой
фиксированной в пространстве оси (а); схема дополнительного
вращения спутника (б).
вращением спутника; это означает, что основное вращение
спутника в данном случае определить невозможно.
4.	СИГНАЛ, ПРИНИМАЕМЫЙ НАЗЕМНОЙ СТАНЦИЕЙ
Предположим, что на спутнике установлена турникетная
антенна и что он вращается вокруг двух осей с угловыми
частотами со и Q (см. фиг. 2 и 4).

438	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Амплитуду напряжения V принимаемого радиосигнала
можно рассчитать для двух случаев, когда основной лепесток
диаграммы направленности приемной антенны обращен вето*
рону спутника (см. фиг. 4).
Приемная антенна с линейной поляризацией
Результирующее напряжение Vc для антенны с линейной
поляризацией, представленное единичным вектором (фиг. 5),
Фиг. 5. Векторы, описывающие поле Е антенны спутника в дальней зоне,
и векторы диполей пг0 и mQ приемных антенн.
sd+6tp = T *
выражается с помощью скалярного произведения результи¬
рующего вектора электрического поля Е и ш0
l/* = G[(E^+E»).m0],	(12)
где G — общий коэффициент усиления приемной системы по
напряжению.
Из выражений (2) и фиг. 5 имеем
(е»0 • m0) = sin = о = cos 8*, \
(е* • m0) = cos \ = У1 — о2. )	^13)
Тогда принимаемое напряжение
I/ = у 1^1 — о2 + о2 cos2 (/),	(12а)
где
х = Gcp.

КОНТРОЛЬ ПО АМПЛИТУДЕ РАДИОСИГНАЛОВ
439
Приемная антенна с круговой поляризацией
Антенна с круговой поляризацией может быть выполнена
в виде двух скрещенных под углом 90° диполей или в виде
спиральной антенны. При этом величина принимаемого на¬
пряжения сигнала зависит только от напряженности прихо¬
дящего электрического поля. Таким образом,
V = G | Е | = Gcp | уе?0 4- cos Ъ •	|
или
V = х 1Л+COS2 9(0.	(14)
где
X = Gcp.
Аналогичный расчет нетрудно выполнить и для спутника
с антенной в виде диполя.
5.	ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА СПУТНИНА ЗА СЧЕТ
ДОПОЛНИТЕЛЬНОГО ВРАЩЕНИЯ НА ОСНОВЕ ЗАПИСИ СИГНАЛА,
ПРИНИМАЕМОГО НАЗЕМНОЙ СТАНЦИЕЙ
Приемная антенна с линейной поляризацией
Уравнение (12а) может быть использовано для определе¬
ния угла поворота 0О, обусловленного дополнительным вра¬
щением спутника.
Для того чтобы преобразовать (12а) для получения за¬
висимости для 8о и осо, следует предположить, что о = const.
Это предположение справедливо, если рассматривается изме¬
нение V за очень короткий промежуток времени, равный, до¬
пустим, 10—20 сек, при наклонных дальностях до спутника
1000 км и квазиэкваториальной орбите.
Причиной этого является не только постоянство rQ, как это
отмечалось ранее, но и стабильность для этих условий эф¬
фекта фарадеевского вращения [4]. Последнее является более
важным требованием, так как нельзя определить какое бы
то ни было изменение оси эллиптически поляризованного сиг¬
нала вследствие фарадеевского вращения. Однако для ква-
зиполярных орбит изменение фарадеевского вращения за пе¬
риод наблюдения при использовании антенны с линейной
поляризацией может приводить к. значительным ошибкам.

440	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Для упрощения расчетов возведем в квадрат величину V
(12а) и, подставляя (11), получим для рассматриваемой
антенны
^ = go + gi cos Ш + g2 cos 2Ш,	(126)
где
go = X2 (1 — °2) + (fl2 + j b2) X2°2.
g, = 2x2°2a ■ b,
g2-TXW.
Величины go, gi и g2 легко получаются на основании гар¬
монического анализа возведенного в квадрат напряжения при¬
нятого сигнала. Одна из возможных форм V2 представлена
sit
Фиг. 6. Прием записи наблюдаемой модуляции принимаемого сигнала
с борта вращающегося спутника.
go — средняя мощность; g{ и g2 — амплитуды первой и второй гармоник.
По оси ординат отложены относительные величины.
на фиг. 6 вместе с ее гармоническими составляющими,
определяемыми формулой (126).
Информация об угле поворота спутника 0О за счет допол¬
нительного вращения содержится в величинах а и Ь, опреде¬
ляемых выражениями (10) и (11).
Для определения четырех неизвестных %, о, а и 6 в (126)
имеются только три уравнения1). Возникает необходимость
применения второй антенны А' (регистрирующей). Предпо¬
ложим, как это показано на фиг. 5, что используется допол¬
нительный второй диполь т', перпендикулярный т0, и что
0 При расчете величины % возникают затруднения вследствие неопре¬
деленности излучаемой мощности р после запуска спутника.

КОНТРОЛЬ ПО АМПЛИТУДЕ РАДИОСИГНАЛОВ
441
приемник имеет такой же коэффициент усиления, как и в слу¬
чае приема на один диполь.
Примем (только для упрощения), что %' = х, а также
о'= (1—0*),
(15)
Как видно из (126) и (15), такая приемная станция даст две
записи
1/2 = go + £icos Qt + & cos 221,
V'2 = g'0 + g; cos 21 + g'2 cos 22/,
где
go = X2 (1 — °2) + (a2 + у &2) X2°2.
ft = 2y>2a6,
g'o = X2°2 + (a2 + 4 *2) *2 ^ — °2)*
^; = 2x2(l—o2)a6,
^ = jx2(!~°2)62.
(16)
Выходные эффекты систем А и Л' могут быть отдельно
записаны при использовании двухканальных регистраторов.
Для расчета а и b на основании выражений (16) необхо¬
димо только четыре уравнения. После простых преобразова¬
ний получаем
а— ±
Ь= ±
V 2 ft
2^2
1/2
g0 — g2 — -a(gVg2)
(17)
Угол поворота спутника 0О за счет дополнительного вра¬
щения и постоянный угол ао могут быть определены в силу
того, что значения а и 6, входящие в выражения для g0, gi и.
g2, рассчитываются на основании (17).

442	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Из (11) получаем
с2 = cos б0 = ± а | ~ (1 + а2 — Ь2) ±
± [т^+я2 — V1)— а2]/!} к>
(18)
Ci = cosа0 — ±	(1	+	а2	—	Ь2)	±
± [\{\+а2-Ь2)-а2Уу.
Приемная антенна с круговой поляризацией
В этом случае также более удобно оперировать с квадра¬
том величины принимаемого сигнала V2. На основании выра¬
жений (14) и (11) получаем выражения, подобные рассмот¬
ренным в случае антенны с линейной поляризацией:
Для определения трех неизвестных %, а и Ь имеем три
уравнения. Из (19) получаем
Выражение (18) может быть снова использовано для рас¬
чета 0о и ао соответственно. В течение необходимых для ана¬
лиза коротких интервалов записи сигнала, как указывалось
ранее, угол ао представляет собой величину, зависящую от
положения приемной станции, и является различным для
разных станций, в то время как угол 0о постоянен.
V2 = g0 + gi cos Qt + g2 cos 2 Ш,
(19)
где
go = X2 + X2(«2+-j62)-
gi - 2fab,
g2=jX2b2-
4	[	go	-	g2	-	(g?/g2)
2 g2	]'/»_
go-g2-y(g?/^)
g\/S2
(20)
b= ±

КОНТРОЛЬ ПО АМПЛИТУДЕ РАДИОСИГНАЛОВ
443
ЗАКЛЮЧЕНИЕ
Уравнение движения, записанное для единичного вектора
положения спутника со сложным вращением, является об¬
щим и может быть использовано для анализа движения раз¬
личных космических кораблей. Запись амплитуды сигнала
можно использовать для определения угла вращения спут¬
ника. Для достижения больших точностей необходимо ис¬
пользовать приемную антенну с круговой поляризацией,
в этом случае фарадеевское вращение поляризации прихо¬
дящего сигнала не влияет на работу регистратора.
ЛИТЕРАТУРА
1. Bolljahn J. Т., Effects of Satellite Spin on Ground-Received Signal,
IRE Trans. Antennas a. Propagation, AP-6, 260—267 (July 1958).
2. Stratton J A., Electromagnetic Theory, N. Y., 1941.
3. В a u e г S. (частное сообщение).
4. Daniels I., Bauer S., The Ionospheric Faraday Effect and Its Appli¬
cation, J. Franklin Inst., 267, 187—200 (March 1959),

ПРИМЕНЕНИЕ ДОППЛЕРОВСКИХ
МЕТОДОВ ИЗМЕРЕНИЙ К ЗАДАЧАМ ТЕОРИИ
ОТНОСИТЕЛЬНОСТИ, ОПРЕДЕЛЕНИЯ ТРАЕКТОРИЙ
СПУТНИКОВ И ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ1)
Ньютон
Рассматриваются вопросы точности, с которой может быть измерен
допплеровский сдвиг частоты сигнала, принятого от космического-корабля,
при условии использования на Земле атомных стандартов частоты и при¬
менения ответчика на борту корабля. Показывается возможность приме¬
нения допплеровских методов для измерения гравитационного «красного
смещения», для определения параметров орбиты космических кораблей и
измерения некоторых астрономических констант, а также для геодезиче¬
ских измерений при условии использования атомных стандартов частоты.
Показывается, что допплеровские методы могут обеспечить точность изме¬
рения, превышающую точности, существующие в этих областях в настоя¬
щее время.
ВВЕДЕНИЕ
Основные пути использования допплеровских сигналов,
получаемых от ближних искусственных спутников Земли как
для определения орбиты спутника, так и для определения
положения источника излучения были описаны ранее [1].
В предыдущей статье автора [2] рассматривался вопрос
о распространении этих общих методов для целей определе¬
ния пространственного положения межпланетных кораблей.
В настоящей статье описываются некоторые возможности
дальнейшего расширения этого метода.
Главная особенность предлагаемого метода заключается
в том, что мы пытаемся использовать всю информацию, со¬
держащуюся в допплеровском сигнале, получаемом от дви¬
жущегося передатчика. Такой подход заметно отличается от
других методов, часто применяемых при сопровождении ис¬
кусственных спутников допплеровским методом, когда доп¬
плеровская частота используется только для определения вре¬
мени и дистанции наибольшего приближения передатчика
к пункту приема (и иногда для определения скорости при¬
ближения корабля).
Поэтому мы сначала рассмотрим метод использования
прецизионных атомных стандартов частоты, а затем некоторые
9 Newton R., Proc. IRE, 48, № 4, 754—758 (April 1960).

ПРИМЕНЕНИЕ ДОППЛЕРОВСКИХ МЕТОДОВ
445
возможные применения метода для измерения явлений, вы¬
текающих из теории относительности, определения простран¬
ственного положения межпланетных кораблей, а также
для существенного уточнения астрономических данных и вы¬
полнения геодезических измерений.
ИСПОЛЬЗОВАНИЕ АТОМНЫХ СТАНДАРТОВ ЧАСТОТЫ
ПРИ ДОППЛЕРОВСКИХ ИЗМЕРЕНИЯХ
Наиболее очевидный путь использования атомных стан¬
дартов частоты при измерениях в космическом простран¬
стве — это установка атомных часов непосредственно на са¬
мом космическом корабле [3]. Однако мы опишем другой ме¬
тод, который, по-видимому, может быть реализован раньше
и с меньшими затратами.
В предлагаемом методе для облучения космического ко¬
рабля используется наземный передатчик, частота которого
стабилизирована атомными часами. Приемник, установлен¬
ный на космическом корабле, принимает сигнал, частота ко¬
торого отличается от частоты излученного сигнала на вели¬
чину допплеровского сдвига частоты. Принятый сигнал ис¬
пользуется для фазовой подстройки бортового генератора.
Затем сигнал ретранслируется бортовым генератором (при¬
чем для удобства частота ответного сигнала несколько отли¬
чается от частоты принятого сигнала) и принимается назем¬
ной станцией. В принятом сигнале также имеется доппле¬
ровский сдвиг частоты. Результирующий сигнал, содержащий
двойной допплеровский сдвиг частоты (за время пробегов
запросного и ответного сигналов), выделяется путем биений
принятого сигнала с сигналом атомного стандарта частоты.
Возможны несколько вариантов описываемого метода. При
некоторых измерениях желательно, чтобы наземный передат¬
чик и приемник находились в различных пунктах. При этом
необходимо иметь два отдельных стандарта частоты или же
обеспечить надежный метод передачи сигнала стандарта час¬
тоты с одного пункта на другой. В первом случае предел точ¬
ности ограничивается точностью используемых стандартов
частоты, а во втором — точностью системы отсчета времени
и частоты наземной линии связи. При других измерениях на¬
земный передатчик и приемник могут располагаться в одном
пункте. Это позволяет использовать только один стандарт
частоты, и точность в таком случае будет ограничиваться
только дрейфом частоты стандарта за время пробега излу¬
чаемого сигнала (туда и обратно). При работе с искусствен¬

446 lv. контроль траектории космических аппаратов
ными спутниками Земли ожидаемое время пробега сигнала
редко превышает V4 сек, и достижимая точность измерений
может быть существенно выше, чем номинальная точность
используемого стандарта частоты.
Определим более точно, что мы подразумеваем под поня¬
тием точности стандарта частоты. Предварительно отметим,
что: 1) анализируя точность рассматриваемых измерений, мы
не учитываем точность времени, указанного в эфемеридах, и
2) точность, с какой нам известна абсолютная частота стан¬
дартного генератора, не имеет значения и не является огра¬
ничивающим фактором, если стандарт частоты достаточно
стабилен для получения достоверных результатов измерения
допплеровской частоты. В рассматриваемых случаях приме¬
нения описываемого метода наблюдения производятся в те¬
чение достаточно продолжительного отрезка времени для
сглаживания кратковременных флуктуаций частоты при ста¬
тистической обработке результатов измерений. Под точностью
стандарта частоты мы подразумеваем точность, определяе¬
мую путем сравнения излученной частоты, усредненной за
отрезок времени, длящийся около часа, с частотой принятого
сигнала, имеющей почти то же значение и усредненной за
такой же период времени. Точность выражается в долях од¬
ной из двух сравниваемых частот. При таком определении
точности мы можем ожидать, что в случае использования
раздельных атомных стандартов частоты для определения
частоты излучаемого и принятого сигналов точность соста¬
вит ~ 10~10, и будет существенно лучше, чем 10~10 при исполь¬
зовании одного (общего) стандарта частоты, в тех случаях,
когда время пробега сигнала будет меньше 1 сек.
Допустим, что время пробега сигнала равно т, а отноше¬
ние девиации частоты атомного стандарта за время t к час¬
тоте, усредненной за достаточно большой отрезок времени,
равно е(t).
В этом случае ошибка измерения допплеровской частоты
за время t будет равна
В нашем анализе существенное значение имеет среднее
значение, а не среднеквадратичная величина девиации час¬
тоты за некоторый интервал времени от 0 до Т. Это среднее
значение равно
-у Iе (О — 6 (°)J*

ПРИМЕНЕНИЕ ДОППЛЕРОВСКИХ МЕТОДОВ
447
I Для атомного стандарта частоты величина, стоящая в
скобках, будет иметь порядок 10~10, а множитель т/Г — поря¬
док 10-3, поэтому в рассматриваемом случае достигается точ¬
ность порядка 10~13. Для хорошего стандарта частоты, ста¬
билизированного кварцем, соответствующая точность должна
быть лучше, чем 10-11.
В другом варианте основного метода используется либо
почти постоянная частота для излучаемого сигнала запроса,
либо применяются способы получения почти постоянной час¬
тоты ответного сигнала !).
Если на основании предварительных экспериментов доста¬
точно хорошо известна орбита корабля и положение передат¬
чика в пространстве, то можно изменять частоту излучаемого
сигнала на величину прогнозируемого допплеровского сдвига
частоты. Таким образом, частота сигнала, принимаемого на
космическом корабле, будет изменяться только в пределах
неточности предсказания допплеровского сдвига и стабиль¬
ность ответчика будет в значительной степени повышена. Та¬
кая возможность достигается ценой понижения стабильности
первоначальной излучаемой частоты. Однако общее улучше¬
ние, по-видимому, может быть получено, и в частности, в тех
случаях, когда для передачи и приема используется один
(общий) стандарт частоты.
Повышение точности определения частоты, конечно, не
может дать практического эффекта, если характеристики
всех остальных компонент системы не будут сделаны срав¬
нимыми с характеристиками стабильности частоты. В частно¬
сти, мы должны иметь возможность точно измерять время,
в течение которого частота Допплера приобретает заданное
значение; требуемая точность отсчета времени относится
к значению максимальной производной частоты Допплера по
времени. Если f — частота излучаемого сигнала и р — рас¬
стояние между передатчиком и приемником, то производная
частоты Допплера по времени будет равна
Ошибка отсчета времени bt сравнима с ошибкой, которую
мы уже определили как ошибку измерения допплеровской
частоты е/ и
bt = е/-4- — р = 4?-.
с	р
!) То есть вносится программируемая поправка на допплеровский
сдвиг частоты, возникающий при движении корабля-

448	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Минимальное требуемое значение bt получается при мак¬
симальной величине р. Значения этих величин зависят от об¬
ласти применения системы. Принимая типичные значения
р = 10 м/сек2 и е=10-11,
получаем 6/ = 3*10-4 сек. Такая точность отсчета времени
возможна при использовании атомного стандарта частоты.
Наиболее серьезная проблема, возникающая при исполь¬
зовании имеющейся точности, состоит в необходимости кор¬
рекции наблюдаемой частоты Допплера вследствие воздей¬
ствия на нее флуктуаций атмосферной и ионосферной реф¬
ракции. Многие наблюдатели сообщали о различных малых и
больших спорадических изменениях частоты сигналов, при¬
нимаемых от спутника. Такие вариации, наблюдавшиеся на
частоте 100 Мгц, встречались в диапазоне от нескольких де¬
сятых долей цикла до 10 гц и более [4]. Если для исследова¬
тельских целей возможно ограничиться данными наблюдений,
производимыми в периоды указанной минимальной вариации
ионосферы, то необходимая коррекция на рефракцию не бу¬
дет превышать одного процента.. Подобная коррекция, ве¬
роятно, может быть сделана путем использования нескольких
частот, благодаря чему из измеряемой дисперсии устраняется
влияние рефракции. В некоторых случаях можно измерить
величину эффекта Фарадея (поворот плоскости поляризации)
и оценивать величину рефракции по величине этого эффекта.
ИЗМЕРЕНИЕ РЕЛЯТИВИСГСНОГО ЭФФЕНТА
Для спутников, обращающихся по орбитам, расположен¬
ным близко от поверхности Земли, величина p/с имеет поря¬
док 10-5. Эффекты, связанные с теорией относительности
(или, как их называют, релятивистские эффекты), влияют на
величину допплеровского сдвига частоты как (p/с)2, умножен¬
ное на частоту или /• 10~10, где f — частота излучения. Если
точность измерения частоты Допплера равна е/, то мы смо¬
жем измерять релятивистские эффекты только при значениях
е<С 10"10.
Наиболее интересным релятивистским эффектом, по-ви¬
димому, является гравитационное «красное смещение». Не¬
зависимо от доступной точности «красное смещение» не мо¬
жет быть измерено в системе, использующей бортовой ответ¬
чик, поскольку гравитационный эффект сказывается как на
запросном, так и на ретранслированном ответном сигнале.

ПРИМЕНЕНИЕ ДОППЛЕРОВСКИХ МЕТОДОВ
449
j Для того чтобы измерить «красное смещение», необходи¬
мо, очевидно, иметь стабильный передатчик, установленный
ф борту спутника, причем частота этого передатчика дол¬
жна быть известна в системе отсчета спутника.
Зингер [5] в своем предложении- о методах измерения
«красного смещения», так же как авторы работы [6], пред¬
ставившие остроумный метод учета допплеровского сдвига
частоты первого порядка, очевидно, подразумевал, что атом¬
ный стандарт частоты, прокалиброванный на земле, будет со¬
хранять ту же частоту, находясь в блоке, установленном на
спутнике. Имея в виду неточность определения времени за¬
пуска, а также другие неопределенности, по-видимому, неже¬
лательно, чтобы точность эксперимента зависела от этих до¬
пущений.
Более совершенный метод используется в системе, позво¬
ляющей измерять частоту атомного стандарта во время по¬
лета способом раздельных измерений частоты и сдвига в
красном участке.
В соответствии с этим мы также предлагаем поместить
систему ответчика с атомным стандартом частоты на борту
искусственного спутника и с помощью ее определять орбиту
спутника. При этом необходимо принять, что «красное сме¬
щение» изменяет знак в зависимости от того, будет ли волна
излучения распространяться вдоль или против направления
гравитационного поля. Если известны параметры орбиты, оп¬
ределенные вышеуказанным методом, анализ допплеровского
сдвига частоты, стабилизированной с помощью атомного
стандарта частоты, даст возможность измерить совместный
сдвиг, обусловленный эффектом «красного смещения» и
сдвигом частоты стандарта. Если спутник движется по кру¬
говой орбите, оба эти сдвига будут постоянными и мы не смо¬
жем их разделить. Однако, если орбита имеет вид эллипса
с большим эксцентриситетом, можно надеяться установить
зависимость полного сдвига от величины гравитационного
потенциала и, следовательно, разделить эти два эффекта.
ОПРЕДЕЛЕНИЕ ПРОСТРАНСТВЕННОГО ПОЛОЖЕНИЯ МЕЖПЛАНЕТНЫХ
КОРАБЛЕЙ И АСТРОНОМИЧЕСКИХ ПОСТОЯННЫХ
В работе [2] точность определения пространственного по¬
ложения первых межпланетных станций с помощью доппле¬
ровских методов оценивалась как 10-5 от параметров орбиты
в конце половины дня сопровождения.
При использовании атомных стандартов частоты можно
ожидать увеличения точности до 10-7 для кратковременного
29 Зак. 876,

450	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
сопровождения и, вероятно, еще более высокой точности для
долговременного сопровождения.	,
Поскольку время пробега излучаемой волны велико, тр
использование общего (одного) стандарта частоты для на¬
земного передатчика и приемника, по-видимому, не даст бо¬
лее высокой точности по сравнению с использованием двух
раздельных стандартов частоты, хотя применение одного об¬
щего стандарта частоты более удобно. Кроме того, этот ме¬
тод имеет еще одно преимущество, состоящее в возможности
использования программного изменения частоты сигнала та¬
ким образом, чтобы частота сигнала, принимаемого на кос¬
мическом корабле, оставалась бы приблизительно постоянной.
Одним из результатов повышения точности должно быть
увеличение дальности действия станции сопровождения, вы¬
текающее из возможности уменьшения требуемой ширины
полосы пропускания, которая может быть в принципе умень¬
шена вплоть до пределов стабильности частоты принимаемого
сигнала. Если мерцания частоты, возникающие под действием
рефракции, не накладывают слишком больших ограничений,
можно, например, построить систему с полосой пропускания
0,01 гц на частоте 100 Мгц и таким образом увеличить даль¬
ность действия на неизменной базе с 50 • 106 до 500- 106 км
(при наличии на борту космического корабля передатчика,
мощность которого не превышает нескольких ватт). Однако
при этом остается неясным, можно ли достигнуть этого пре¬
дела при наличии ионосферных шумов.
Если при долговременном сопровождении точность опре¬
деления элементов орбиты довести до 10-8, то одним из ре¬
зультатов этого будет устранение необходимости отдельной
системы курсовой навигации на борту космического корабля.
Так, например, положение межпланетного корабля, отпра¬
вленного к Марсу, может быть определено вблизи от Марса
с точностью до 3,5 км, т. е. с точностью, достаточной для на¬
чала снижения, чем исключается необходимость использова¬
ния бортовой системы сопровождения корабля вплоть до
этой точки орбиты. Однако ввиду необходимой быстроты
процессов управления снижением и посадкой для этой цели,
по-видимому, потребуется применить отдельную систему.
Другой результат, вытекающий из увеличения точности,
открывает возможность уточнения значений некоторых астро¬
номических постоянных. Все величины, которые влияют на
движение корабля, движение наблюдателя или распростра¬
нение электромагнитных волн между кораблем и наблюда¬
телем, оказывают влияние и на частоту Допплера. Таким об¬
разом, измеряя частоту Допплера, мы можем измерить эти

ПРИМЕНЕНИЕ ДОППЛЕРОВСКИХ МЕТОДОВ
451
величины с точностью, которая зависит только от точности
измерения самой допплеровской частоты при условии, что
можно произвести достаточное число измерений для того, что-
б(ы выяснить, каким образом различные величины влияют на
значение допплеровской частоты. К числу таких величин
в первую очередь относятся отношение масс Солнца, Земли
и Луны, средние расстояния между ними и скорость света
в межпланетном пространстве. Если процесс сопровождения
протекает в течение нескольких месяцев, что составляет су¬
щественную часть периода обращения Меркурия или Венеры,
возможно даже получить уточненные значения их масс путем
анализа возмущений орбиты межпланетного корабля.
Геодезические данные, представляющие практическое зна¬
чение в современных условиях, можно определить с помощью
наблюдений за пространственным положением межпланетно¬
го корабля. Компоненты скорости, обусловленные движением
приемной станции вместе с поверхностью Земли благодаря
ее вращению (а следовательно, при этом движутся и гео¬
центрические координаты станции), непосредственно входят
в определяемую величину допплеровского сдвига частоты.
Если этот сдвиг частоты измеряется с точностью, равной е/,
то скорость измеряется с точностью, равной ес, что соста¬
вляет ~ 0,003 м/сек для в = 10-11. Окружная скорость на эк¬
ваторе составляет 460 м/сек, следовательно, для станции,
расположенной на экваторе, можно определить местный ра¬
диус Земли и положение приемника в направлении восток —
запад (по широте) с точностью до 40 м. Это превосходит точ¬
ность измерения, практически получаемую в некоторых об¬
ластях земного шара.
Для практической реализации в первую очередь важно,
что эти геодезические данные получаются с помощью систе¬
мы, которая полностью не зависит от аномалий гравитацион¬
ного поля Земли (поскольку она вообще не зависит замет¬
ным образом от земного поля гравитации). Во-вторых, сле¬
дует иметь в виду, что полученные данные представляют
собой непосредственные координаты приемной станции в си¬
стеме координат, начало которой находится в центре массы
Земли, а одна из осей совпадает с мгновенной осью враще¬
ния Земли. Поэтому измерения, произведенные таким спосо¬
бом, не зависят от традиционных геодезических методов, так
как они базируются на независимых принципах и, следова¬
тельно, могут служить существенным дополнением геодези¬
ческих данных.
Подобные геодезические измерения, дающие указанные
выше преимущества, можно выполнять с большей точностью
29*

452	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
при использовании допплеровских данных, получаемых от
искусственного спутника Земли, находящегося на большой
высоте. Это обстоятельство наводит на мысль о необходимо¬
сти создания геодезического спутника.
ГЕОДЕЗИЧЕСКИЙ ИСКУССТВЕННЫЙ СПУТНИК ЗЕМЛИ
Форма Земли оказывает влияние на определяемый доп¬
плеровский сдвиг частоты сигнала, получаемого от спутника,
двояким образом. Во-первых, форма Земли в соответствии
с распределением плотности определяет гравитационное по¬
ле, в котором движется спутник. Во-вторых, в чисто геомет¬
рическом смысле независимо от распределения плотности она
определяет скорость перемещения приемной станции, кото¬
рая является частью относительной скорости перемещения
пункта приема относительно пункта излучения. Поэтому же¬
лательно выполнить геодезические измерения, которые по¬
зволят разделить эти эффекты хотя бы путем устранения од¬
ного из них.
Использование космических кораблей для целей геодезии
позволяет решить задачу устранения влияния гравитацион¬
ного поля Земли, но при этом чрезмерно уменьшается чув¬
ствительность допплеровских измерений к изменениям коор¬
динат приемной станции. Спутники, обращающиеся по орби¬
там, расположенным близко от поверхности Земли, обладают
большей чувствительностью к измерениям координат, однако
имеют недостаток, состоящий в слишком.большой зависимо¬
сти орбиты как от местных гравитационных аномалий, вклю¬
чая влияния, создаваемые приливами, зависящими от вре¬
мени, так и от вариаций величины лобового сопротивления
в атмосфере [7].
Компромиссное решение заключается в использовании ор¬
бит, обеспечивающих наименьшую высоту полета спутника
при условии, что на траекторию спутника в процессе наблю¬
дений не будут оказывать влияние ни аномалии гравитаци¬
онного поля, ни флуктуации величины трения в атмосфере.
Время наблюдений должно быть порядка нескольких перио¬
дов обращения. В дальнейшем мы будем предполагать, что
высота полета должна быть близка к величине радиуса
Земли. Некоторые трудности представляет оценка требуемой
точности орбиты в целом и общей наблюдаемой картины.
Мы проделали оценку для частного случая круговой орбиты,
проходящей в районе экватора на высоте, равной радиусу
Земли, для наблюдателя, также расположенного вблизи

Применение допплеровских методов
453
экватора. Метод расчета подобен стандартному методу Нью¬
тона [2], за исключением того, чтр мы допускаем при расчете,
что среднее значение совокупности, из которой берутся вы¬
борки шумов, не равно нулю, а увеличивается равномерно от
нуля до 2е/ в течение каждого прохода спутника в районе
наблюдения. Это позволяет учесть в наблюдаемой частоте
как дрейф, так и смещение частоты. Считая ошибку в опре¬
делении локального радиуса Земли равной ср и ошибку оп¬
ределения долготы равной сд, получаем
ар = 2- 10пв м,
ад = 5 • ю12е М.
Ошибка измерения долготы приблизительно равна opsec0MaKc,
где 8Макс — максимальный угол места спутника в момент про¬
хода в районе наблюдения. Если угол 0маКс не слишком бли¬
зок к 90°, ошибка в определении долготы сравнима с ор.
Затем для е = 10-11 мы находим геоцентрические коорди¬
наты наблюдателя с точностью до нескольких метров за
один проход при условии, что точность определения ограни¬
чивается только точностью измерения частоты Допплера. По¬
скольку мы можем, по-видимому, добиться е < 10-11 и произ¬
водить наблюдения не только в течение одного прохода спут¬
ника над местом наблюдения, то можно надеяться измерить
координаты с точностью до метра или менее при условии, что
проблемы, не имеющие отношения к измерению частоты, так¬
же могут быть решены. Выше мы уже рассматривали некото¬
рые из таких проблем.
При использовании спутника, по-видимому, полез¬
но применение обоих методов: метода измерений с одним
(общим) стандартом частоты для передатчика и приемника,
находящихся в одном пункте, и метода с раздельным распо¬
ложением передающего и приемного пунктов. Первый метод
обеспечивает большую точность, второй же позволяет непо¬
средственно получить относительные координаты передатчика
и приемника и может облегчить решение некоторых вопросов.
Необходимо также иметь возможность производить измере¬
ния с борта корабля, хотя бы с некоторой потерей точности.
При этом существенно увеличиваются возможности геодези¬
ческого изучения всей поверхности земного шара.
Для поддержания почти постоянного значения частоты,
принимаемой на борту спутника, необходимо использовать
метод изменения модуляции частоты передатчика.

454	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
ЛИТЕРАТУРА
1. Guier W. Н., Weiffenbach G. С., A Satellite Doppler Navigation,
System, Proc. IRE, 48, № 4, 507 (1960).
2. Newton R. R., Tracking Objects Within the Solar System Using Only
Doppler Measurements, Proc. Xth Intern. Astronaut. Congress (в пе¬
чати).
3. Physics Today, 12, 73 (September 1959).
4. Weiffenbach G. С. (частное сообщение).
5. Singer S. F., Application of an Artificial Satellite to the Measurement
of the General Relativistic «red-shift», Phys. Rev., 104, 11 —14 (Octo¬
ber 1956).
6. В a d e s s a R. S., Kent R. L., Nowell J. C., Short-time Measure¬
ments of Time Dilation in an Earth Satellite, Phys. Rev. Lett., 3,
79—80 (July 1959).
7. King-Hele D. G., Determination of Air Density and Earth’s Gravita¬
tional Field From the Orbits of Artificial Satellites, Proc. Xth Intern.
Astronaut. Congress (в печати).

ИОНОСФЕРНОЕ МЕРЦАНИЕ ЧАСТОТЫ СИГНАЛОВ
ОТ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ >)
Хатчинсон, А рендт
При использовании метода измерений сдвига допплеровской частоты
и обычного радиолокационного метода часто наблюдаются скачки частоты
радиосигналов, излучаемых искусственными спутниками Земли. В настоя¬
щей статье приводятся результаты, полученные при использовании только
допплеровского метода. Отклонения от гладкой кривой изменения доппле¬
ровской частоты, полученные при наблюдениях отдельных спутников, дают
меру для оценки скачков частоты и указывают на неоднородность пути
сигналов, проходящих через ионосферу от спутника в точку наблюдения.
Как и следовало ожидать, такие вариации являются функцией частоты и
уменьшаются по мере увеличения частоты.
Допплеровский сдвиг частоты является в первую очередь
функцией радиальной скорости спутника по отношению к наб¬
людателю и функцией излучаемой частоты. Однако для час¬
тот, лежащих в диапазоне между 20 и несколькими сотнями
Мгц, скорость распространения волны через ионосферу зави¬
сит от коэффициента рефракции. Поэтому допплеровский
сдвиг частоты дополнительно изменяется при изменениях ко¬
эффициента рефракции или ионизации на пути распростра¬
нения волны между спутником и наблюдателем. Кроме того,
на величину допплеровского сдвига частоты влияет также
интенсивность ионизации среды, окружающей спутник. За¬
висимость наблюдаемых вариаций частоты от изменений
ионизации около спутника при прохождении последнего че¬
рез ионосферу или от изменений интегральной плотности
электронов вдоль его пути рассматривается в настоящей
статье.
Измерения частоты производились с инструментальной
точностью ± 7гц, при этом интервал измерений был равен
1 сек. В течение этого интервала производились одновремен¬
ные измерения (сравнения) частоты, излучаемой передатчи¬
ком спутника и станцией Национального бюро стандартов
(WWV). На фиг. 1 показаны отклонения наблюдаемого доп¬
плеровского сдвига частоты, записанного при наблюдениях за
i) Н u t с h i n s о n H. P., A г e n d t P. R., Proc. IRE, 48,	4,	670—671
(April 1960).

456
IV. КОНТРОЛЬ ТРАЕКТОРИИ КОСМИЧЕСКИХ АППАРАТОВ
третьим советским искусственным спутником1), от гладкой
кривой изменения частоты, проведенной через эксперимен-
Фиг. 1. Третий советский искусственный спутник, орбита № 2294,
29 октября 1958 г.
Нулевая частота —20004762 гц; нулевое время— 0428:00 ср. время по Гринвич, мерид.;
нулевая крутизна —1,3 гц/сек; излучаемая частота — 20001497 гц.
тальные точки. На фиг. 2 показаны вариации частоты 40 Мгц
(первой гармоники основной частоты), записанные при
Фиг. 2. Третий советский искусственный спутник, орбита № 2294,
29 октября 1958 г.
Нулевая частота — 40000540 гц; нулевое время —0928:36 ср. время по Гринвич, мерид.;
нулевая крутизна —3,4 гц/сек; излучаемая частота— 40001981 гц.
прохождении спутника по той же орбите. Как видно, даже на
этой частоте возникают заметные скачки частоты, проявляю¬
1) Третий советский искусственный спутник Земли был запущен 15 мая,
1958 г. — Прим. ред.

ИОНОСФЕРНОЕ МЕРЦАНИЕ ЧАСТОТЫ СИГНАЛОВ
457
щиеся в виде отклонения от гладкой кривой изменения доп¬
плеровской частоты. Переходя к диапазону 108 Мгц, мы ви¬
дим весьма гладкую кривую изменения частоты, записанную
при наблюдениях американского искусственного спутника
108031200 г
108030800-
108 030 Ш-
\
108030000-
^ \
108 029 600-
сГ	”	»
% 108 029 200-■
$
<о
^ 108 028 800 -	\
\
708028 ООО -	\
708028000-
\
108027600-	\
108027200-	\
—	Чч
108026800-
108 026 ЬОО —I |	|	| I | I I 1 I I I I I I
12	74	16	18	20	22	2Ц 26
Время, мин
Фиг. 3. Американский спутник «Эксплоурер» I, орбита № 97,
8 февраля 1958 г.
«Эксплоурер» I (фиг. 3). Центральная часть кривой совер¬
шенно гладкая, однако, как и следует ожидать, при увеличе¬
нии пути, проходимого волной, на крайних участках кривой
имеются некоторые отклонения от гладкой кривой. Орбита
этого спутника имела апогей на расстоянии 2500 км и пери¬
гей 360 км. Таким образом, большую часть времени спутник
находился в пределах ионосферы, причем длина пути в ионо¬
сфере между спутником и точкой наблюдения была несколько
меньше, чем полная толщина ионосферы в этом направлении.

458	IV.	КОНТРОЛЬ	ТРАЕКТОРИИ	КОСМИЧЕСКИХ	АППАРАТОВ
Иные условия имели место при наблюдениях за спутником
«Авангард» I, который все время находился на высоте, пре¬
вышающей нормальную высоту слоя F. Орбита этого спут¬
ника имела апогей на расстоянии 3960 км и перигей 660 кн.
На фиг. 4 заметны отклонения частоты порядка 20—25 гц,
наблюдавшиеся при записи сигналов спутника «Авангард» I,
J07998100
107998000-
'I..
* 107997900 -
Сз~
S
| 107997800 -
о
^ 107997700-
107997600-	\
4 *•
107997500-
107997UOo\	,	*
2229	25	26	27	28	29	30	31
Время
Фиг. 4. Американский спутник «Авангард» I, орбита № 128,
28 марта 1958 г.
Опорное время 22 24 : 00 (восточное поясное время).
проходившего по орбите. Состояние ионосферы во время про¬
хождения спутника было	хорошим (коэффициент	качества
был равен 7). На следующий день отмечались очень большие
кратковременные отклонения	частоты	сигналов	108	Мгц
(фиг. 5), излучаемых спутником «Авангард» I. По-видимому,
величина этих отклонений частоты превышает те значения,
которые можно было бы ожидать в результате изменений ин¬
тегральной плотности электронов в ионосфере; коэффициент
качества ионосферы и в этих случаях был «хорошим». По¬
скольку орбита этого спутника проходила на высоте, значи¬
тельно превышающей нормальную высоту слоя F, и в период
наблюдений спутник находился вблизи апогея на высоте при¬
близительно 3900 км, то можно предположить, что возникно¬
вение таких отклонений частоты было вызвано встречей спут¬
ника с облаком заряженных частиц, находящимся над ионо¬

ИОНОСФЕРНОЕ МЕРЦАНИЕ ЧАСТОТЫ СИГНАЛОВ
459
сферой. Однако для этого случая необходимо также рассмот¬
реть возможность появления на пути распространения сиг¬
налов от спутника к точке наблюдения ионизированного об¬
лака, представляющего кратковременную (3 мин) аномалию,
вызванную некоторым возмущением ионосферного слоя F.
Рассмотренные выше примеры отчетливо показывают, что
действительно имеют место значительные скачки (мерцания)
частоты сигналов спутника. Эти наблюдения соответствуют
так называемым цветовым мерцаниям сигналов, поступаю¬
щих от радиозвезд, которые были отмечены Литтлом [1].
Время
Фиг. 5. Американский спутник «Авангард» I, орбита № 138,
29 марта 1958 г.
Опорное время 22 55 : 00 (восточное поясное время).
В связи с опубликованными недавно материалами по высот¬
ным ядерным взрывам (по проекту «Аргус») были рассмот¬
рены записи допплеровских частот, полученные в этот период
с целью установить, имеет ли при этом место какое-либо си¬
стематическое явление. В качестве предварительных измере¬
ний были визуально изучены записи 89 орбит, которые после
обработки были разбиты на качественные группы, обозначае¬
мые коэффициентами (индекс мерцания) от 0 до 5, причем 0
означает полное отсутствие скачков частоты, а коэффициент
5 соответствует максимальным скачкам. Эти наблюдения
были проведены на всех орбитах третьего советского искус¬
ственного спутника на частоте 20 Мгц, на которой эффект
мерцания частоты отмечается наиболее отчетливо. На фиг. 6
приведена гистограмма распределения значений индекса мер¬
цания, измеренных в период проведения трех высотных ядер-
ных взрывов по проекту «Аргус». Отчетливо видно, что при
этом появляются систематические изменения, которые перво¬
начально дают резкое уменьшение коэффициента мерцания
допплеровских сигналов, и даже несколькими днями позже

Индекс мерцания
Индекс мерцания
Фиг. 6. Распределение индекса мерцания.
  перед взрывами; — • — во время взрывов;
  X 	 после	взрывов.
2,0 п
Аргус
1,0 -
• • •
• •
• • •• •
OS -
1 авг
i
1 сент
 1	—l	1	1	1	1	1
юоо 1200 то 1600
Номер орбиты
1 окт.
1
1800
2000
Фиг. 7. Мерцания частоты сигналов третьего советского искусственного
спутника в период проведения ядерных взрывов по проекту «Аргус»,

ИОНОСФЕРНОЕ МЕРЦАНИЕ ЧАСТОТЫ СИГНАЛОВ	,	461
показывают более низкие индексы мерцания, чем до взрывов.
Одновременно были начаты количественные измерения, при
которых использовались участки графиков, образующихся за
счет разницы между сглаженными кривыми и графиками, по¬
строенными с помощью экспериментальных точек. Для ка¬
ждой орбиты эти области измерялись в условных единицах
и результирующее число делилось на время наблюдения
(в мин).
Результаты таких расчетов приведены на фиг. 7, где дан¬
ные, относящиеся к области, лежащей слева от первой вер¬
тикальной линии, охватывают период в 18 дней до первого
взрыва, а данные справа — период 16 дней после взрыва. Из
приводимых графиков отчетливо видно, что мерцания часто¬
ты сигналов третьего советского искусственного спутника
после взрыва были, как правило, меньше, чем перед взры¬
вами.
ЛИТЕРАТУРА
j. Little G., The Jodrell Bank Program on Meteors, Aurora and Iono¬
sphere, J. Geophys. Res., 59, 152—155 (March 1954) .

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
АВТОРОВ
Арендт (А г е n d t Р, R., US Army Signal Res. a. Develop. Lab., Fort Mon¬
mouth, N. J.)
Вонбэн (V о n b u n F. O., US Army Signal Res. a. Develop. Lab., Fort
Monmouth, N. J.)
Гофман (Hoffmann H., Rome Air Develop. Center Griffiss Air Force
Base, N. Y.)
Зон (Sohn R., Space Technol. Labs., Los Angeles, Calif.)
Кендолл (Kendall P, E., Astrionics Lab., ITT Labs., Fort Wayne, Ind.)
Клохесси (Cl oh ess у W. H., Techn. Develop. Dept., Martin Co.)
Коой (Kooy J. M. J., Lector KMA, Breda, Holland),
Кэрролл (С а г г о 11 J., Am. Bosch Arma Corp.)
Лармор (Larmore L., Lockheed Aircraft Corp.)
Лейден (Layden O. F., US Army Signal Res. a. Develop. Labs., Fort
Monmouth, N. J.)
Миккельуэйт (M i с k e 1 w a i t A. B., Space Technol. Labs., Los Angeles,
Calif.)
Муди (Moody A. B., US Navy Hydrographic Office, Office of Naval Ope¬
ration, Wash.)
Ньютон (Newton R. R., Appl. Phys. Lab., John Hopkins Univ., Maryland)
Парк (Park R. A., Appl. Phys.** Lab., John Hopkins Univ., Maryland)
Паттон (Patton R. B., US Army Ballist. Res. Labs.)
Роберсон (Roberson R. E., Autonetics Div, of North American Aviation,
Inc., Dooney, Calif.)
Савет (S a v e t H., Am. Bosch Arma Corp.)
Стирнс (Stearns E., Lockheed Aircraft Corp., Sunnyvale, Calif.)
Столкап (S t a 1 с u p R. E., Astrionics Lab., ITT Labs., Fort Wayne, Ind.)
Танцман (T a n z m a n H. D., US Army Signal Res. a. Develop. Lab., Fort
Monmouth, N. J.)
Томпкинс (Tompkins E. N., Space Technol. Labs., Los Angeles, Calif.)
Уилтшайр (Wiltshire R. S., Astronaut. Sect., Martin Co.)
Фрай (Frye W., Lockheed Aircraft Corp., Sunnyvale, Calif.)
Хатчинсон (Hutchinson H. P>, US Army Signal Res. a Develop. Lab.,
Fort Monmouth, N. J.)
Хёндорф (H о e n d о г f F., AF Missile Dev. Center, Holloman AFB, N. M.)
Хэндел (Handel P. F., AF Missile Dev. Center, Holloman AFB, N. M.)
Шнейдер (Schneider A., Missile Electronics a. Control Div., RCA, Bur¬
lington)

СОДЕРЖАНИЕ
Предисловие редакторов 	   5
/. Общие принципы управления полетом
космических аппаратов
Роберсон. Общие принципы наведения и управления спутниками
и космическими кораблями 	 9
Стирнс, Фрай. Данные о местоположении космического корабля,
необходимые для управления его полетом в пространстве ...	20
Миккельуэйт, Томпкинс, Парк. Трехмерные межпланетные
траектории	 30
К о о й. О расчетах орбит и проблемах управления дальними косми¬
ческими ракетами	 59
//. Автономная космическая навигация
Шнейдер. Векторные основы инерциальной навигации	112
Стирнс. Межпланетная навигационная система	151
Л ар мор. Использование астрономических наблюдений для косми¬
ческой навигации	168
Кэрролл, Саве т. Космическая навигация и исследования с по¬
мощью измерения разности сил тяготения	184
Клохесси, Уилтшайр. Система наведения на конечном участке
встречи спутников	193
Муди. Навигационная система, основанная на использовании сиг¬
налов искусственных спутников, летящих на больших высотах 212
Кэрролл. Навигация в межпланетном пространстве при помощи
оптической системы засечки и инерциальной системы .... 230
III.	Стабилизация положения космических аппаратов
Роберсон. Современное состояние проблемы стабилизации поло¬
жения космического корабля 	239
Роберсон. Проблемы стабилизации положения спутника	249
Роберсон. Моменты вращения, создаваемые движением внутри
искусственного спутника	284
Роберсон. Принципы инерциальной стабилизации искусственных
спутников	304

464
СОДЕРЖАНИЕ
Кен до л л, Столкап. Датчик положения для космических
кораблей		 319
Зон. Стабилизация положения космического корабля путем исполь¬
зования давления солнечной радиации 	 ...	335
IV.	Контроль траектории космических аппаратов
Г о ф м а н. Радиоконтроль траектории космических	аппаратов . . . 342
Хэнде л, Хёндорф. Точное наблюдение	за	космическими кора¬
блями радиотехническими методами  	363
П а т т о н. Определение орбиты по частоте Допплера, измеренной
при одном прохождении искусственного	спутника	388
Лейден, Т а н ц м а н. Использование измерений допплеровского
сдвига частоты сигналов, излучаемых спутниками Земли.
I. Частотные измерения на спутниках	407
Хатчинсон. Использование измерений допплеровского сдвига
частоты сигналов, излучаемых спутниками Земли. II. Измере¬
ние минимальной наклонной дальности орбиты спутника до
измерительного пункта	  422
В о н б э н. Анализ движения спутника по амплитуде принимаемых
радиосигналов			431
Ньютон. Применение допплеровских методов измерений к задачам
теории относительности, определения траекторий спутников %
и геодезических измерений	.'	.	444-
Хатчинсон, Аренд т. Ионосферное мерца'ние частоты сигналов
от искусственных спутников Земли	455
Алфавитный указатель авторов	462
УПРАВЛЕНИЕ ПОЛЕТОМ КОСМИЧЕСКИХ АППАРАТОВ
Редактор Н. А. Данилов
Переплет художника А. В. Шипова. Художественный редактор Н. В. Зотова.
Технический редактор М. А. Белева
Сдано в производство 22/XI 1962 г.	Подписано	к	печати	27/V	1963	г.
Бумага 60 x 90Vi6 = 6yM. л. 14,6. Печ. л., 29,2. Уч.-изд. л. 25,2. Изд. № 20/0916. Цена 1р. 96 к.
Зак. 876
ИЗДАТЕЛЬСТВО ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва, 1-й Рижский пер., 2
Типография № 2 им. Евг. Соколовой УЦБ и ПП Ленсовнархоза
Ленинград, Измайловский пр., 29