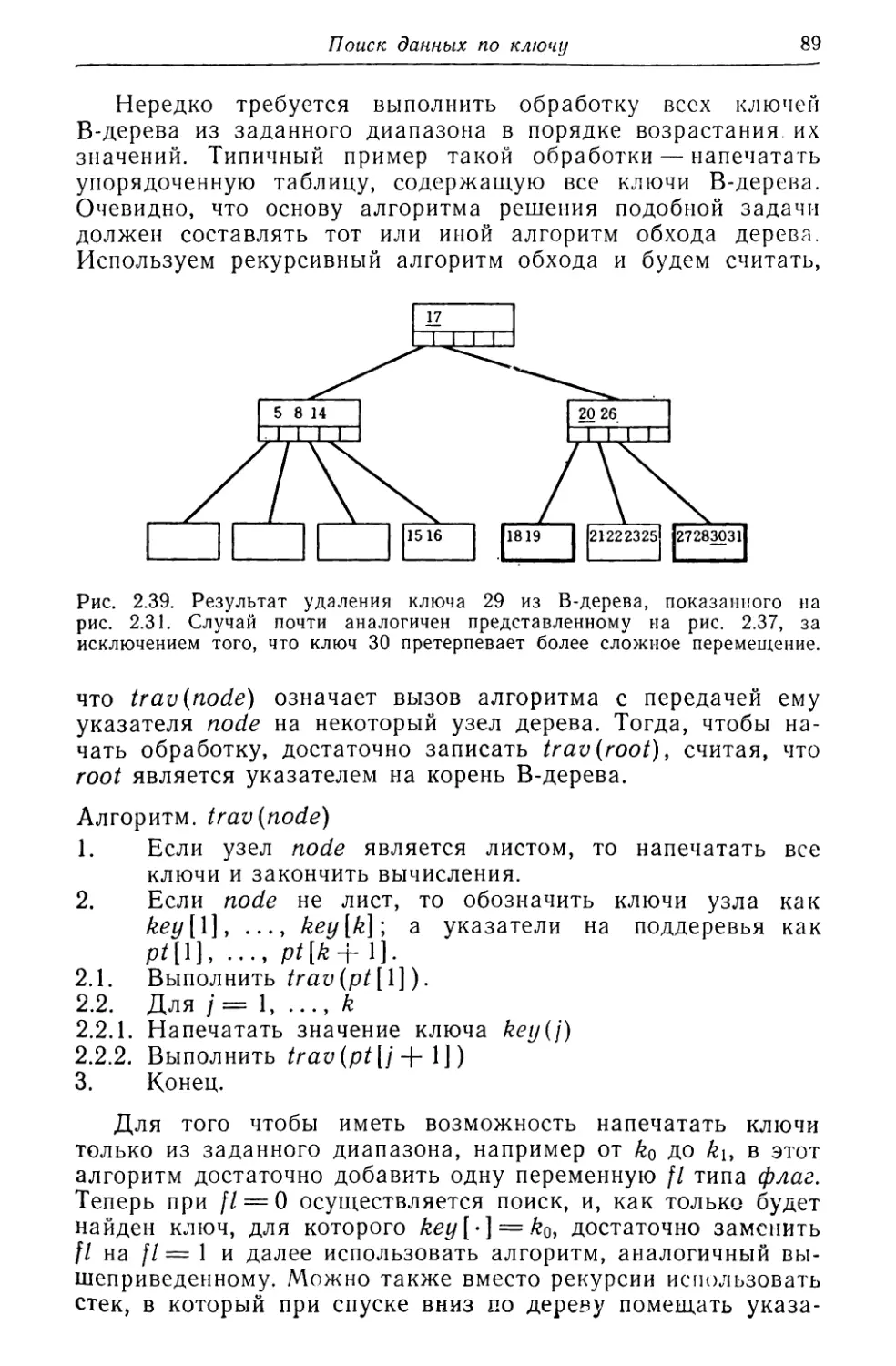
Author: Сибуя М. Ямамото Т.
Tags: компьютерные технологии программирование обработка данных вычислительная техника
Year: 1986
Text
М. Сибуя ,Т. Ямамото
АЛГОРИТМЫ
ОБРАБОТКИ
Алгоритмы обработки данных
*аишию»-11
М.Сибуя
Т. Ямамото
АЛГОРИТМЫ
ОБРАБОТКИ
ДАННЫХ
Перевод с японского
Э. К. НИКОЛАЕВОЙ
пои редакцией
канд. техн. наук В. В. ПАНФЕРОВА
МОСКВА «МИР» 1986
ББК 32.973
С 34
УДК 681.3
Сибуя М., Ямамото Т.
С 34 Алгоритмы обработки данных: Пер. с япон. — М.:
«Мир», 1986. — 218 с., ил.
В книге японских специалистов рассматриваются структуры хранения и
их отображения на память и способы динамического управления памятью.
Основное внимание уделяется вопросам использования древовидных структур
для задач поиска и сортировки. Обсуждается возможность аппаратной реали¬
зации отдельных методов сортировки.
Для научных работников и инженеров, занимающихся вычислительной
техникой.
"• ■ ебк з2'97’
Редакция литературы по информатике и робототехнике
© Иванами Сётен, 1983
© перевод на русский язык, «Мир»
1986
Предисловие редактора перевода
Книга, предлагаемая вниманию читателей, посвящена воп¬
росам структурной организации данных и методам, лежащим
в основе их обработки. Важность этой темы очевидна — ото¬
бражение на память, поиск и сортировка в той или иной
мере присутствуют во всех программах. Четкие представле¬
ния о них необходимы при решении любой задачи на ЭВМ.
В качестве концептуальной основы структурной организа¬
ции данных авторы используют понятие массива и описывают
различные способы отображения на память с позиции опера¬
ции доступа к элементам структуры. В книге рассматрива¬
ются такие фундаментальные приемы и методы нечисленного
программирования, как отображение структуры данных на
последовательную и связанную память, динамическое управ¬
ление памятью, структурная организация данных для задач
поиска и сортировки. Излагаются практически все хорошо
обоснованные методы обработки данных, для многих из них
приводятся оценки эффективности. Авторы стремятся пока¬
зать практическую направленность книги, подчеркивая, что
все рассматриваемые методы апробированы, многие широко
используются в рамках системного программного обеспече¬
ния, а некоторые уже реализованы аппаратно.
Уровень изложения материала таков, что он доступен не¬
подготовленному читателю. Книга будет полезна как инже¬
нерам, работающим над созданием практических систем, так
и студентам и аспирантам, специализирующимся в области
системного и прикладного программирования. Она может
служить хорошим введением в область нечисленных алго¬
ритмов.
Однако отметим, что материал изложен несколько кон¬
спективно. При его изучении будет полезно обратиться к не¬
которым разделам монографии Д. Кнута [1].
В заключение мне хочется поблагодарить Н. И. Ильин¬
ского и В. И. Скворцова за большую помощь, оказанную при
редактировании.
В. В. Панферов
Введение
Электронно-вычислительные машины (ЭВМ), как это сле¬
дует из названия, были разработаны в качестве машин для
вычислений. Однако в связи с расширением общественных
потребностей и соответствующим развитием техники усили¬
лась роль ЭВМ как устройства для нечисленной обработки
данных: передачи, хранения, поиска, преобразования, обра¬
ботки, связи (в том числе и связи между ЭВМ). Вместе
с этим быстро увеличивается количество данных, обрабаты¬
ваемых ЭВМ, и обычными становятся расчеты, в которых за¬
действованы объемы данных, измеряемые в таких единицах,
как гига (109) и тера (1012).
Данные, которыми оперирует машина, должны быть упо¬
рядочены и не должны представлять собой беспорядочный
набор, подобный исписанным листам бумаги, выброшенным
в корзину для мусора. Данные не только должны правильно
отражать сущность реального мира, но и форма их представ¬
ления должна быть пригодна для повседневной обработки,
например, как конторские документы для решения опреде¬
ленных задач. При упорядочении данных необходимо учиты¬
вать два аспекта: удобство использования данных человеком
и возможность их эффективной обработки машиной. Данные
вводятся в машину полуавтоматически и хранятся в ЭВМ
после соответствующей обработки. При необходимости мо¬
жет производиться их повторная обработка с выводом из
машины в виде таблицы. На всех этих этапах структура и
форма представления данных обычно различны. Так, при
вводе и выводе, например, форма представления данных
должна быть удобна для использования человеком (напри¬
мер, в графическом виде или в виде звуковой записи), а
формы данных, используемые внутри ЭВМ, — удобными для
машинной обработки
Запоминающие устройства для записи данных с течением
времени менялись. Особенно значительные изменения косну¬
лись объема памяти, в то время как логическая структура
менялась мало. Относительно быстродействующие дорогие и
обладающие небольшой емкостью запоминающие устрой¬
ства встроенные в ЭВМ, называют оперативной, внутрен¬
ней, или основной памятью. Медленнодействующие деше
вые запоминающие устройства используются в качеств*
внешней памяти, называемой также вспомогательной, или
файловой памятью, и связываются с ЭВМ через каналы. Маг-
Введение
7
нитные ленты, диски, барабаны и т. д. являются средой хра¬
нения внешних ЗУ и в большинстве случаев бывают съем¬
ными, а сами ЗУ являются при этом, в сущности, считываю-
ще-записывающими устройствами. Обращение к данным, хра¬
нящимся в оперативной памяти, может осуществляться по
мере необходимости и в требуемой последовательности. Ины¬
ми словами, возможен произвольный (случайный) доступ
к данным. В случае внешней памяти группа данных вначале
перемещается в оперативную память, только после этого про¬
изводится их обработка, т. е. для внешней памяти возможен
групповой доступ. Для данных на магнитных лентах прак¬
тически возможен только последовательный доступ — группо¬
вой доступ в направлении перемещения ленты.
Конкретная организация оперативной памяти для пользо¬
вателей ЭВМ «прозрачна», и нет большой необходимости
в понимании механизма их действия. Логически оперативная
память представляет собой множество байтов или-елов с при¬
своенными им номерами, или адресами, совокупность которых
называется адресным пространством. Даже при простой ло¬
гике доступ к внешней памяти и анализ его эффективности
оказываются сложными и зависят от характеристик машины.
При использовании виртуальной памяти, позволяющей не
вникать в различия между внешними ЗУ и ЗУ оперативной
памяти, работа пользователей ЭВМ еще более упрощается,
но еще более усложняется работа инженера, который должен
обеспечивать эффективность работы ЭВМ.
Целью настоящей книги являются рассмотрение структур
данных, используемых при обработке данных на ЭВМ, по¬
строение таких структур данных и обсуждение алгоритмов,
необходимых для их обработки.
Управление данными в своей основе относится к функциям
человека. По крайней мере правильность вводимых данных
и их полнота зависят исключительно от способностей и до¬
бросовестности человека, выполняющего эти действия. Как
же следует определять ценность однажды записанных дан¬
ных? Очевидно, что со временем ценность данных снижается.
Однако очень трудно установить единое правило, когда дан¬
ные следует удалять из информационной системы, а если их
нельзя удалять, то каким образом их переводить в архив
и т. п.
Пользователи данных обычно противятся любой попытке
удаления данных из системы, но лица, ответственные за ра¬
боту ЭВМ с финансовой стороны, безжалостно приостанав¬
ливают работы и удаляют экономически невыгодные данные.
Итак, любые данные имеют цену. Цена иных данных очень
велика, а раз так, что очевидно стремление получить эти
Данные как можно дешевле, поэтому появляются лица,
8
Введение
которые пытаются тайно копировать данные. Для надежного
полета космического корабля «Земля», например, требуется
огромное количество данных. Это потребует, очевидно, боль¬
ших затрат на сбор нужных данных любой ценой, извлече¬
ние из них необходимой информации, ее хранение, передачу
соответствующим лицам.
В этой книге не рассматривается управление данными с
точки зрения обеспечения их полноты и выбора данных для
удаления из памяти. Это, очевидно, задачи такой науки, как
статистика. Обеспечение секретности данных более тесно свя¬
зано с проблемами, обсуждаемыми в книге, но основной
темой является изучение систем, в функции которых входят
шифровка и дешифровка данных и оперирование этими дан¬
ными. Здесь рассматривается техника управления данными
не с точки зрения операций, осуществляемых человеком, а в
предположении, что данные уже введены в систему ЭВМ.
В первой главе даются общие определения основных эле¬
ментов данных и обсуждается возможность использования
структур, полученных их комбинациями. Очевидно, при этом
должны быть рассмотрены не только логические структуры —
структуры с точки зрения пользователя, но и физические
структуры, пригодные для практического использования
в ЭВМ.
Во второй главе рассматриваются древовидные структуры,
наиболее широко применяемые для представления и исполь¬
зования данных. Деревья очень хорошо подходят для описа¬
ния различных иерархических структур, просты для понима¬
ния и широко используются в различных приложениях. Кроме
того, такие структуры используют программы управления па¬
мятью операционных систем для поддержания файлов и т. д.
В этой же главе рассматриваются методы хеширования, по¬
зволяющие значительно сократить затраты времени на обра¬
ботку данных, для которых применяются совершенно другие
структуры.
В третьей главе рассматриваются наиболее простые алго¬
ритмы сортировки, обеспечивающие линейное упорядочение
данных в порядке возрастания значений ключей. Несмотря
на кажущуюся простоту сортировки, если вникать глубже и
детально проанализировать алгоритмы с точки зрения эффек¬
тивности, оказывается, что существуют проблемы, решение
Которых до сих пор не найдено.
В четвертой главе обсуждаются четыре независимые прак¬
тические проблемы. Разд. 1 посвящен методам доступа опе¬
рационных систем к виртуальной памяти, в которых исполь¬
зуются структуры В+-дерева. В разд. 2 рассматриваются
структуры данных для информационных систем типа поиска
источника (поиск по вторичному ключу). Эти структуры, упо¬
Введение
9
минавшиеся в гл. 1, рассматриваются здесь с различных сто¬
рон в конкретном применении. В разд. 3 обсуждаются осо¬
бенности представления данных, которых мы пока не каса¬
лись в предыдущих разделах книги: возможность уплотнения
данных за счет исключения избыточных элементов данных.
В разд. 4 рассматривается следующий шаг в подходе к уп¬
равлению данными — управление данными средствами аппа¬
ратного обеспечения; приведены варианты схем для сорти¬
ровки.
Поскольку отдельные аспекты, относящиеся к рассматри¬
ваемой области, обсуждаются и в специальных учебниках,
при написании данной книги авторы стремились по мере воз¬
можностей к доступному изложению материала для читате¬
лей, не являющихся специалистами в этих вопросах, учиты¬
вая важность практического применения излагаемого мате¬
риала. Недостаточность систематизации материала объясня¬
ется малочисленностью авторских сил, однако можно ожидать
расширения исследований в этой области и соответственно
притока новых исследователей.
Авторы выражают глубокую признательность членам ре¬
дакционной коллегии, рекомендовавших авторов для напи¬
сания этой книги, и редакционному отделу издательства
«Иванами Сётэн», оказывавшему самую разнообразную по¬
мощь авторам в их работе.
Май 1983 г. М. Сибуя
Т. Ямамото
Глава 1
Данные
Данные, хранящиеся в ЭВМ, представляют собой сово¬
купность нулей и единиц (битов). Биты объединяются в вось¬
мибитовые последовательности — байты, а также более длин¬
ные последовательности — слова, или длинные слова, вклю¬
чающие два и более слов. Основными последовательностями
считаются байты или слова. Каждому участку оперативной
памяти, который может вместить один байт или одно слово,
присваивается порядковый номер (адрес), и вся совокуп¬
ность адресов, предоставляемая пользователям ЭВМ, назы¬
вается адресным пространством. Какой смысл заключен в
данных, какими символами они выражены — буквенными
или цифровыми, что означает то или иное число — длину ли,
стоимость ли — все это определяется программой обработки.
В настоящее время пользователи ЭВМ подразделяют дан¬
ные, необходимые для решения практических задач, на не¬
сколько типов, связывая понятие типа не только с представ¬
лением данных в адресном пространстве, но и со способами
их обработки.
1.1. Основные типы данных
1.1.1. Элементы данных и структуры
Любое данное может быть отнесено к одному из двух
типов: основному (простому), форма представления которого
определяется структурой ЭВМ, или сложному, конструируе¬
мому пользователем для решения конкретных задач. Напри¬
мер, для нас многоугольники на плоскости — простые и
вполне понятные данные, над которыми можно выполнять
различную обработку: вычислять площадь, периметр, значе¬
ния диагоналей и углов; осуществлять перемещение, поворот
и масштабирование многоугольника на плоскости; определять
фигуры, получаемые в результате пересечения или объедине¬
ния таких многоугольников (в результате не обязательно дол¬
жен получиться многоугольник), и т. д. Каким же образом
в данном случае следует представлять многоугольники в па¬
мяти ЭВМ, чтобы иметь возможность такой обработки?
Можно воспользоваться различными способами представле¬
ния, но если абстрагироваться от них, то многоугольник сле¬
дует рассматривать как самостоятельный тип данных. Чело¬
век не может влиять на представление простых данных в ад-
Данные
11
респом пространстве. В отличие от простых представление
сложных типов данных задается человеком и образуется ком¬
бинацией простых.
Элементами данных являются символы, числа и тому по¬
добные данные, дальнейшее дробление которых не имеет
смысла. Они используются в качестве структурных элементов
сложных данных. К символам обычно относят буквы англий¬
ского алфавита, цифры, знаки, знаки азбуки «катакана»,
иероглифы, точечные знаки и т. д. Многие типы чисел хорошо
известны — натуральные, целые, десятичные числа с плаваю¬
щей точкой (вещественные числа) и т. д. Максимальное и
минимальное числа, представимые в машине, задают диапа¬
зон значений целых чисел, а также диапазон и точность
представления вещественных чисел. Целые числа из диапа¬
зона 0 и 1 часто рассматривают как значения логического
типа (переключатель, флажок). Знание физической единицы
измерения числовой величины, например длины, времени или
денежной единицы, устанавливает границы применимости
операций, что позволяет избежать многих ошибок при про¬
граммировании. Сказанное справедливо и для безразмерных
величин, если известно, какой смысл приписывает человек
обрабатываемым данным. Над целыми числами можно вы¬
полнять различные операции, отличающиеся точностью вы¬
числений, адресуемыми участками памяти и представлением.
Простая совокупность элементов данных одного типа об¬
разует массивы одномерные, двумерные и т. д. Массивы
вещественных чисел хорошо известны — это векторы, матрицы,
тензоры. Однако в обработке данных термин «массив» ис¬
пользуется в более широком смысле — просто как средство
оперирования группой данных. На практике массивами часто
называют совокупности данных двух и более типов, например
данные о продаже по месяцам, отделениям фирмы, отдель¬
ным изделиям. Отдельный элемент массива задается индек¬
сом, представляющим собой целое число или совокупность
целых чисел, указывающую местоположение элемента в мас¬
сиве. Слово языка можно представить, например, одномер¬
ным массивом букв соответствующей длины, а фразу — дву¬
мерным. Чтобы удовлетворить различным целям обработки,
слова и фразы следует рассматривать как тип данных более
высокого уровня, нежели массив символов. В японском языке
деление на слова затруднительно и требует использования
более сложного и менее очевидного способа представления
данных. Так, страницу печатного японского текста, например
эту страницу, можно представить двумерным массивом ло¬
гических величин. Для этого достаточно разбить страницу
прямоугольной сеткой на очень мелкие клетки (элементы
12
Глава 1
или ячейки изображения), такие, чтобы каждый элемент был
черным или белым. Для черно-белой фотографии потребуется
двумерный массив целых чисел, соответствующий плотностям
элементов изображения, а для цветной фотографии необхо¬
димы уже три целочисленных значения, по одному на каж¬
дый из трех основных цветов.
Разновидностями одномерных массивов являются струк¬
туры типа кольцо, стек, очередь и двусторонняя очередь.
Кольцо представляет собой одномерный массив с замкну¬
тыми концами, т. е. массив, в котором концы отсутствуют
(рис. 1.1, а). Типичным примером такой структуры является
таблица объектов, обработка которых производится путем
последовательного обхода, например входных сигналов, по¬
ступающих от терминалов, в системе с разделением времени.
И в случае когда регистрируются новые данные (п элемен¬
тов данных), которые вводятся в процесс равномерно во вре¬
мени, и в случае когда поддерживается процесс выполнения
плана, намеченного на каждый день из последующих три¬
дцати, начиная от данного дня, обычно используется кольцо.
Итак, кольцо — это такая структурная организация массива
данных, при которой целесообразнее перемещать границы
массива, оставляя неподвижными его элементы. Если органи¬
зовать кольцо неопределенной длины, то его можно исполь¬
зовать как очень гибкую структуру, в нужное место которой
можно вводить или исключать элементы данных.
Структура типа стек — это одномерный массив перемен¬
ной длины, обладающий той особенностью, что включение и
исключение элементов ограничено только одним концом мас¬
сива, называемого вершиной стека. Стек представляет собой
структуру (см. рис. 1.1,6), в которой первым обрабаты¬
вается тот элемент данных, который введен последним. Для
обработки древовидных структур, о которых речь пойдет
ниже, обычно используют рекурсивную обработку, основан¬
ную на вызове подпрограммы самой себя. При рекурсивном
вызове подпрограммы текущие значения переменных засыла¬
ются в стек и переменным присваиваются новые значения.
Обработка значений, хранящихся в стеке, может быть про¬
должена только после выхода из подпрограммы (т. е. после
завершения обработки новых значений) путем присваивания
переменным значений из стека.
Стек называли также магазинным списком, использовали
и другие названия, которые в конце концов были унифици¬
рованы. В отличие от очереди, которая будет рассмотрена
следующей, стек называли также списком, в котором первым
считается элемент, записанный последним (LIFO — last-in-
first-out list). Смысл этого названия очевиден и отражает
Данные
13
а
hi::::
ВключениеJ
Исключение
1 I 1
Н
/1
/
Исключение
-я
• I I I I
Н
| 1
IZ-CU
\
Включение
УС
1 I—
н
I I
/ /У'
Включение/
Исключение
—I I—
Н
I I
он
\
Включение
Исключение
fO^OO{Oy----COnZ~'^CO
Включение 1 Ч
Исключение Исключение
м::
н
I I—
Включение /
Исключение
Включение
Рис. 1.1. Совокупности элементов данных: а — кольцо; б — стек; в — оче¬
редь; г — двусторонняя очередь: д — двусторонняя очередь с ограничен¬
ным входом (включение данных разрешено только на одном конце); е —
двусторонняя очередь с ограниченным выходом (исключение данных раз¬
решено только на одном конце).
дисциплину обслуживания списка. В кафетериях США ис¬
пользуют посудные автоматы, называемые «Cafeteria well».
Одинаковые тарелки и чашки, точно вставленные в верти¬
кальную прорезь, поддерживаются пружиной, находящейся
на дне автомата. При заполнении прорези тарелками неза¬
висимо от их числа самая верхняя благодаря действию
14
Глава 1
пружины будет находиться на определенной высоте, удобной
для того, чтобы ее мог достать человек. Здесь как раз исполь¬
зуется принцип стека.
Структура типа очередь также представляет собой одно¬
мерный массив переменной длины и аналогична очереди лю¬
дей перед окошком кассы, торговым автоматом или телефо¬
ном-автоматом. Включение и исключение данных выполня¬
ются на разных концах массива (см. рис. 1.1,в). В отличие
от LIFO это список, в котором первым считывается элемент,
записанный первым (FIFO — first-in-first-out list). Очереди
широко используются в операционных системах, например
для организации одновременного использования устройстз
ввода-вывода многими пользователями или единственного
центрального процессора несколькими программами.
Структура, обладающая большей общностью, чем стек или
очередь, позволяющая осуществлять доступ, включение и ис¬
ключение на обоих концах массива, называется двусторонней
очередью (деком). Разновидностями двусторонней очереди
являются дек с ограниченным входом (включение допускается
только на одном конце) и дек с ограниченным выходом (ис¬
ключение допускается только на одном конце) (см. рис. 1.1, г,
а также рис. 1.10), которые с точки зрения общности зани¬
мают промежуточное положение между деком и стеком или
очередью.
Были рассмотрены три типа структур данных, которые на
логическом уровне являются просто разновидностями одно¬
мерных массивов с произвольным числом элементов. Позже
рассмотрим, как эти структуры могут быть представлены
в памяти.
Очень важной структурой, для размещения элементов ко¬
торой требуется нелинейное адресное пространство, является
дерево. Существует большое число структур данных, которые
могут быть представлены деревьями. Это и классификацион¬
ные", и иерархические, и рекурсивные структуры. В библио¬
теках книги располагают согласно классификации. Управле¬
ние предприятием имеет иерархическую структуру. Автомо¬
биль представляет собой сложный механизм и состоит из
двигателя, корпуса, электрооборудования и других узлов, ко¬
торые в свою очередь также состоят из отдельных деталей
(рекурсивная структура). Основу структуры данных, называе¬
мой деревом, как и обычного дерева, составляют «разветвле¬
ния» (только благодаря им дерево имеет «ветви» разных
порядков). Деревья состоят из данных, каждое из которых
имеет структуру дерева. В гл. 2 деревья будут рассмотрены
более детально. Для выражения более общих связей между
Данные
15
узлами (разветвлениями) используют графы или сети. При
графическом представлении узлы обозначают точками, а свя¬
зи— линиями, соединяющими две точки. В виде графов, на¬
пример, могут быть представлены дорожные сети, сети связи
и электрические схемы.
Совокупность элементов данных разного типа называют
записью. В простейшем случае запись содержит постоянное
число элементов (/ь f2j ..., fk), называемых полями. Каждое
поле fi представляет собой элемент данных определенного
типа. Практическими примерами записей могут служить на¬
кладные и прочие документы в конторских операциях; одна
(Номер-служащего-фирмы (5-значное число), фамилия-и-имя (5 иероглифи¬
ческих знаков), запись фамилии и имени знаками азбуки (10 знаков ката-
каны), дата-рождения (5-значное число), код-подразделения (3-значное
число), код-профессии (3-значное число))
Рис. 1.2. Запись основного файла «Список служащих фирмы».
накладная представляет собой отдельную запись. Пример
записи показан на рис. 1.2. Значением поля записи может
быть последовательность символов произвольной длины. В та¬
ком случае одномерный массив с произвольным числом эле¬
ментов можно представить или одним полем, или совокуп¬
ностью полей. В первом случае получим записи с полями пе¬
ременной длины, а во втором — записи с переменным числом
полей.
Совокупность записей одинаковой структуры называется
файлом. В то же время файлом называют набор данных,
представленный во внешней памяти и предназначенный для
длительного хранения и многократного использования. Для
того чтобы иметь возможность извлекать из файла отдельные
записи, каждой записи присваивают уникальный номер или
имя, которое служит ее идентификатором и располагается
в отдельном поле. Этот идентификатор называют ключом
записи. При ручной обработке в качестве ключа обычно ис¬
пользуют имя, адрес, дату или их комбинацию в форме, наи¬
более привычной для человека. Для упрощения обработки
записи обычно хранятся отсортированными по ключу — дате
или порядковому номеру дня. Символьный ключ при машин¬
ной обработке представляется последовательностью двоичных
чисел, соответствующих кодам символов ключа. Поэтому
можно считать, что ключ задан натуральным числом. Есте¬
ственно, это будет число с очень большим числом разрядов,
много большим, чем это необходимо для идентификации.
Мы рассмотрели четыре типа структур, являющихся сово¬
купностями элементов данных: массив, одномерный массив
переменной длины, дерево, запись. Более сложный тип
16
Глава 1
данных 1Может включать эти структуры в качестве элементов.
Например, элементами записи может быть массив, стек, де¬
рево и т. д. Для описания явлений реального мира, производ¬
ственных функций и т. п. используются самые различные
числовые и нечисловые данные. Возникает необходимость в
определении связей между ними и в разработке операций по
их преобразованию. Наиболее строгой формой такого описания
является алгоритм. Однако сам алгоритм во многом зависит
от того, как представлены в памяти структуры обрабатывае¬
мых данных. В свою очередь структура данных, естественно,
должна отражать структуру рассматриваемых явлений или
производственных функций, и необходимо, чтобы логические
связи между данными соответствующим образом поддержи¬
вались и на физическом уровне.
Методы представления логических связей в адресном про¬
странстве рассматриваются в следующем разделе. В заключе¬
ние в качестве подготовки к анализу этих методов обсудим
простой, но важный тип элементов данных, называемый ука¬
зателем. Значением указателя является адрес первого слова
записи или элемента данных. При этом в качестве значения
указателя может использоваться как абсолютный, так и от-,
носительный адрес (смещение по отношению к некоторому
заданному адресу). Необязательно, чтобы значение указа¬
теля было известно пользователю. Достаточно, если пользо¬
ватель понимает, па что ссылается тот или иной указатель
в каждый конкретный момент. Указатели могут использо¬
ваться и независимо, однако чаще всего указатель помещают
в одном из полей записи и используют для обозначения связи
с другими записями.
1.1.2. Представление структур
Как же реально представить в памяти структуру данных
того или иного типа? Обычно для однородных массивов по¬
стоянной длины используют последовательное представление.
В этом случае логически смежные элементы массива разме¬
щаются в физически смежных ячейках памяти. Последо¬
вательное представление нетрудно распространить и на
массивы более высокой размерности, располагая в последова¬
тельных ячейках памяти элементы массива в лексикографи¬
ческом порядке индексов (м,/2, • 4). Например, если в
случае двумерного массива через обозначим номер строки,
а через /2 — номер столбца, то массив окажется расположен¬
ным в памяти по строкам. В общем случае 6-мерному мас¬
сиву со списком индексов (о, /2, •••, ik), каждый индекс ко¬
торого принадлежит диапазону /у ^ /у ^ ги соответствует од¬
Данные
17
номерный массив, индекс которого меняется от 1 до II (г, —
— lf + 1)и может быть вычислен по формуле
1 + t (ч - h) П (Г, - h + 1), где п (ri-ll+l) = l.
/ = 1 i = /+1 i — k-\-1
Для представления одномерного массива с элементами
данных переменной длины можно или сделать их длину по¬
стоянной (из расчета на максимальную длину), добавив
в конце каждого элемента особый символ — признак конца
данного, или в начало каждого элемента ввести поле для
хранения текущей длины данного. В последнем случае утра¬
чивается возможность произвольного доступа, и каждый раз
при необходимости извлечения одного элемента приходится
прослеживать всю последовательность по порядку, начиная
с первого. Поэтому лучше подготовить отдельно одномерный
массив указателей, содержащий адреса размещения каждого
элемента. Этот метод применим для любых многомерных
массивов с элементами переменной длины и сводится к под¬
готовке массива указателей соответствующей мерности.
В случае периодического изменения числа элементов (масси¬
вов переменной длины) необходимо использовать более гиб¬
кое представление, которое рассмотрено ниже.
Можно образовать кольцо, используя для этого одномер¬
ный массив постоянной длины, при обращении к элементам
которого как только будет достигнут один конец массива,
сразу же переходить к другому концу. На базе кольца очень
просто реализовать очередь или двустороннюю очередь. Если
поддерживается баланс по числу операций включения и ис¬
ключения элементов очереди, то ячейки памяти, занятые оче¬
редью, последовательно перемещаются в направлении вклю¬
чения новых элементов. Для представления стека можно вос¬
пользоваться одномерным массивом, ограничив доступ к эле¬
ментам единственным индексом, указывающим на вершину
стека в данный момент. Нулевое значение индекса означает,
что стек пуст.
Если для представления стеков и очередей использовать
массивы с малым числом элементов, то очень велика вероят¬
ность их переполнения. Увеличение длины массивов не только
ухудшает использование памяти, но и не гарантирует от пе¬
реполнения. Если использовать массивы такой длины, чтобы
исключить возможность их переполнения, то часть памяти,
действительно занятая данными, окажется совсем небольшой.
Еще большим недостатком является то, что обработка будет
прекращена, как только переполнится хотя бы один массив,
отведенный под стек, несмотря на наличие достаточного
18
Глава 1
\л 14-»(7ТЯЧс I Ч~*~••• ~Нr I Ч-Нz I * I
£
а
Часть
мольцв
Список
свободной
памяти
B-CB-Q3-- -СИ
5
Рис. 1.3. Представление кольца и очереди с использованием указателей
(представление в связанной памяти):
а — кольцо; б — исключение из кольца (включение в кольцо). При исклю¬
чении сплошная стрелка заменяется на пунктирную, а при включении —
объема свободной памяти в других массивах. Естественно,
возникают вопросы: нельзя ли всю незанятую память, отве¬
денную для представления массивов переменной длины, ис¬
пользовать как общую; как это скажется на эффективности
использования памяти?
Эту проблему можно решить путем придания памяти
определенной структуры, связав между собой отдельные бло¬
ки (узлы) памяти с помощью указателей. Рис. 1.3, а иллю¬
стрирует идею связанного представления на примере кольца.
Прямоугольниками на рисунке показаны узлы памяти. Каж¬
дый узел состоит из двух полей. Одно поле содержит эле¬
мент или более сложную структуру данных, а другое — ука¬
затель на следующий узел. Стрелки на рисунке соответствуют
значениям указателей. Если последовательность представ¬
лена в связанной памяти, то операции включения и исклю¬
чения элементов в последовательность выполняются так, как
показано на рис. 1.3,6. Обе операции используют список
свободной памяти — при включении память занимается, а при
исключении возвращается в этот список. В любом случае
пунктирная на сплошную; в — двусторонняя очередь.
Данные
19
происходит изменение трех указателей. При этом из схемы на
рис. 1.3,6 следует, что при заданном указателе на узел, содер¬
жащий данное S, операции включения и исключения возможны
только «справа от S» и невозможны «слева от S». Операция
«исключить S» также невозможна. Одним из способов, позво¬
ляющих преодолеть эти ограничения, является использование
в каждом узле двух указателей, что будет рассмотрено ниже.
В этом случае станет возможным производить включение и
исключение справа и слева от S. Возможен и другой техни¬
чески простой прием. При необходимости «исключить узел 5»
перепишем в него данные узла, находящегося справа от S
(данное Г), а затем исключим узел справа (фактически бу¬
дет исключен узел, следующий за S,— узел, первоначально
содержавший данное Т). Аналогично может быть выполнена
и операция «включить слева от 5». Для этого вначале вклю¬
чим новый узел справа от S и перепишем в него данное 5,
затем запишем новое данное в узел, который прежде зани¬
мало данное S, и, наконец, передвинем указатель доступа
к структуре на узел, который теперь содержит данное 5.
Представление в памяти двусторонних очередей должно
обеспечить возможность доступа с обоих концов очереди. Это
может быть достигнуто использованием в каждом узле двух
указателей, как показано на рис. 1.3, в. В этом случае опе¬
рации включения и исключения потребуют изменения пяти
указателей.
Одномерный массив с возможностью его свободного изме¬
нения называется списком. Считается, что списки обеспечи¬
вают эффективное использование памяти. Надо помнить, что
для хранения указателей требуется дополнительная память,
а для работы с указателями — дополнительные операции.
Основной смысл применения указателей заключается не
столько в повышении эффективности обработки, сколько в
возможности представления более сложных структур. Ис¬
пользование указателей позволяет связывать между собой
самые разнообразные данные, что является основой представ¬
ления различных самых сложных структур, механизмов, яв¬
лений. Среди них особое место занимают сравнительно про¬
стые, но очень важные древовидные структуры. Например,
если для представления узлов бинарного дерева (см. гл. 2)
использовать записи с двумя указателями, как показано
на рис. 1.4, то можно производить обход дерева начиная от
корня в направлении концевых узлов. Операции исключения
или включения листа (концевого узла) выполняются очень
просто — изменением всего трех указателей.
В математике одним из базовых понятий является множе¬
ство. В области обработки данных операции над множествами
часто также весьма желательны. Однако представление в па¬
20
Глава 1
мяти множества, не имеющего структуры, представляет зна¬
чительную проблему, и обычно стараются обходиться без
них. Пусть, например, в трехмерном пространстве задано ко¬
нечное множество, состоящее из п точек. Как представить это
множество в памяти, чтобы иметь возможность выполнять
соответствующие операции? Если число элементов множества
постоянно и все элементы заранее известны — перенумеруем
их числами от 1 до п. Сами элементы множества — коорди¬
наты точек (Xi,yi,Zi) (/ = 1,2, ..., п) — будем хранить в мат¬
рице из (яХЗ) элементов. Тогда для представления любого
Н-Ч~Г|Гр
GaiTtjze czжш
Рис. 1.4. Представление бинарного дерева с использованием указателей.
подмножества этого множества можно воспользоваться од¬
номерным массивом из п битов (ри р2, • рп)У присваивая
pi (/-му биту) значение 1, если точка с номером / принадле¬
жит подмножеству, и 0, если не принадлежит. Такой логиче¬
ский массив обычно называют битовой картой. Операции над
множествами в таком случае сводятся к логическим опера¬
циям над соответствующими логическими массивами.
Если элементы множества заранее не известны, представ¬
ление в виде битовой карты становится невозможным. Такая
ситуация возникает, например, когда элементы множества
задаются при вводе или формируются в процессе вычислений
и передаются во внешнюю память. В этом случае приходится
хранить описание каждого элемента (обычно в виде записи),
действительно присутствующего в этом множестве, но теперь
операции над множествами потребуют поэлементного их про¬
смотра. Например, для операции пересечения надо будет
сравнивать каждый элемент одного множества со всеми эле¬
ментами другого.
Совокупность записей, принадлежащих множеству, мож¬
но разместить как в последовательной, так и в связанной па¬
мяти. При размещении в памяти множество наделяется струк¬
турой (свойственной используемой памяти), которая опреде¬
ляет способ доступа и возможные пути доступа к элементам.
В основе операций извлечения, изменения, включения и ис¬
ключения лежит операция доступа. Вторая глава посвящена
рассмотрению этих операций, составляющих основу обра¬
ботки данных.
Данные
21
1.1.3. Внутренняя и внешняя память
Выше отмечалось, что критерием выбора того или иного
способа представления данных в памяти является эффектив¬
ность доступа к данным. Доступ к данным, хранящимся во
внутренней памяти (оперативное запоминающее устройство)
ЭВМ, и к данным, хранящимся в ее внешней памяти (внеш¬
ние запоминающие устройства), имеет существенные отличия.
Объем внутренней памяти в связи с техническим прогрессом
быстро увеличивается, по той же причине еще быстрее растет
объем внешней памяти и уменьшается ее стоимость. Расши¬
ряется применение виртуальной памяти, которая позволяет
пользователям не вникать в тонкости различия между внут¬
ренней и внешней памятью; в практику стали входить такие
термины, как «адресное пространство». С ростом объемов
обрабатываемых данных использование внешней памяти ста¬
новится необходимым. Это в свою очередь требует понима¬
ния специфики использования внешней памяти и знания со¬
временного уровня ее развития.
Внутренняя (оперативная) память характеризуется сле¬
дующими особенностями:
1) Значительно меньший объем по сравнению с внешней
памятью.
2) Затраты времени на доступ к любым данным, распо¬
ложенным в любом месте памяти, одинаково малы. Если па¬
мять однородна, то не имеет значения, близко или далеко
друг от друга расположены ячейка, к которой только что
осуществлялось обращение, и ячейка, к которой будет про¬
изведено следующее обращение. В некоторых случаях целе¬
сообразно использовать в качестве внутренней памяти еще
более быструю кэш-память с последовательным доступом.
3) Затраты времени на доступ к сколь угодно большому
массиву данных много меньше или сравнимы с затратами
времени на операции по их обработке.
К внешней (вспомогательной) памяти относится память
на магнитных барабанах, дисках, лентах и других видах ЗУ.
По своим характеристикам она в значительной степени от¬
личается от внутренней памяти и обладает следующими осо¬
бенностями:
1) Большой объем, в несколько раз превышающий объем
внутренней памяти. Таким образом, для доступа ко всему
содержимому внешней памяти требуется такое время, кото¬
рым нельзя пренебречь.
2) Для того чтобы прочитать какую-то запись из внешней
памяти, необходимо: найти блок во внешней памяти, содер¬
жащий нужную запись; передать найденный блок по каналу
ввода-вывода из внешней памяти в буфер ввода-вывода
22
Глава 1
(часть оперативной памяти, выделенная специально для об¬
мена с внешней памятью); извлечь из буфера нужную запись.
При записи выполняются аналогичные действия, но в обрат¬
ном порядке — данные, подлежащие записи, сначала пересы¬
лаются в буфер, а затем поблочно передаются по каналу
ввода-вывода и записываются во внешнюю память. Для
уменьшения затрат времени на чтение разрабатываются спе¬
циальные устройства, позволяющие извлекать из внешней
памяти только необходимые данные, но широкого распростра¬
нения такие устройства пока не получили из-за своей слож¬
ности.
3) Какой метод доступа к нужному блоку внешней памяти
окажется целесообразнее — непосредственный, не зависящий
от расположения других блоков, или последовательный, в по¬
рядке их физического размещения в памяти, — зависит как
от аппаратуры, так и от операционной системы. Обычно ме¬
тоды последовательного доступа оказываются проще и тре¬
буют меньших затрат времени.
Методы доступа и способы представления данных в па¬
мяти тесно связаны между собой. Вопросы, связанные с ними,
рассматриваются в последующих главах.
1.2. Обобщенные структуры данных
Существует большое разнообразие сложных типов дан¬
ных, но исследования, проведенные на большом практическом
материале, показали, что среди них можно выделить не¬
сколько наиболее общих. В этом разделе познакомимся с не¬
которыми из них. Для каждого типа были детально исследо¬
ваны характеристики, предложен язык или подобие языка
для их машинной обработки, разработана эффективная си¬
стема операций. Здесь рассматриваются результаты этих
исследований в самом общем виде, обсуждаются не столько
специальные языки или системы для работы с такими общими
структурами данных, сколько возможность использования их
важнейших свойств в рамках универсального языка. Общие
структуры называют также моделями данных, так как они
отражают представление пользователя о данных реального
мира.
1.2.1. Отношение
Даже очень большая совокупность записей, каждая из ко¬
торых содержит п полей, всегда может быть представлена
двумерной таблицей. В общем случае можно утверждать, что
в форме таблицы можно представить самые разнообразные
данные. Это могут быть таблицы курса акций, спортивных
Данные
23
результатов, теле- или радиопрограмм и т. п. В виде таблицы,
например, можно представить данные накладных, оформляе¬
мых при конторских операциях на предприятии или между
предприятиями, данные доклада и т. д. Таблица представляет
собой достаточно общий тип данных, наиболее доступный для
понимания. Таблица, имеющая форму, показанную на
рис. 1.5, а, называется отношением. Структурно каждая стро¬
ка таблицы представляет собой запись и называется корте¬
жем, или выборкой отношения. Столбцы таблицы называют
атрибутами отношения; каждый атрибут Л/ задает область
определения элементов данных ац (i= 1, ..., m). Совокуп¬
ность данных, представленная несколькими отношениями, на¬
зывается реляционной моделью. На рис. 1.5,6 и 1.5, в пока¬
заны примеры отношений. Пример на рис. 1.2 тоже можно
считать отношением. Отношение можно рассматривать как
множество элементов (лиц, организаций, изделий, торговых
сделок, конторских операций и т. д.), свойства которых выра-.
жены значениями кортежей. Однако можно считать также,
что таблица задает связь между атрибутами (столбцами таб¬
лицы). Например, карточка каталога содержит название од¬
ной книги, имеющейся в библиотеке, но одновременно с этим
связывает между собой данные, относящиеся к автору, изда¬
тельству, области науки. По совокупности карточек можно
получить ответы на такие вопросы, как: «Какое издательство
издает массовым тиражом книги по вычислительной технике?
В какой области знаний специализируется данный автор?»
и т. д. Именно поэтому и используют термин «отношение».
Отношение а < Ь между двумя действительными числами
а и Ь определим как подмножество М ={{хуу)\ (х, у)^
eRXR уХ<у} декартова произведения RXR={(x,y);
x^Ry у е R} множества R всех действительных чисел. Те¬
перь это отношение можно записать как (а,Ь)^М. Отноше¬
ние а = Ь можно определить аналогичным образом. Говорят,
что элементы множеств А и В находятся в функциональной
зависимости, если (a,b)^G и G={(xyy)\ (х,у)^А'ХВ,
y = f{x)} являются подмножеством А X В = {(х, у); х <= Л,
i/gB}. Для обозначения этого свойства обычно используется
запись вида /: А-+В или b = f(a). Если Л ={2,3}, В =
= {1, 2, 3 ,4, 5, 6}, то отношение делимости b на а (аеД
JgB) означает, что (а, Ь) принадлежит подмножеству
А\В, содержащему {(2,2), (2,4), (2,6), (3,3), (3,6)}. Это
подмножество можно представить в виде таблицы, показан¬
ной на рис. 1.5,г. Итак, любое подмножество Ау^В является
отношением. Если подмножество конечно, то его можно пред¬
ставить в виде таблицы. Отношение R на рис. 1.5, а также
представляет собой конечное подмножество, состоящее из
иг элементов декартова произведения множеств Ах X АгХ •••
ДОХОД-ОТ-ЛРОДАЖИ ИЗДАНИЙ
в
о
сз
к»
Qj
ll
? ll
1-5 *
't § I
g Q> §
S 13 ^
<§
QQ
CSJ ^ со Оъ со
C\j CNj CN] Го
J
|§
II
l§
j
s V5
1^
& *
it
i2
%
'I
!*
4I
iй
?3
1*1
r
4
ll
Ss
iS 4
I ^
II
1
a £
1^
£«
*v ^
l!
S<*
|g
1*
1 £
t|
Й_1_
,§
ll
I
в
В
’ tt
+
В
Он
О
VO
«£)
«=5
<v
4
О
5
<*3
s
Oh
H
В
о
Он
О
E-
O
В
<u
в
Ю
. s ^
. tJ -
<N К CO
a“ S ei
7Г ® °Q
£ *■ Ш
.r S ■*
<v я
- B 1
- о £?
0
с
1
-'О
E-1
>»
VO
9S
s
3
* 3*
a
о
к
E->
О
в
в
о
с
в
а
X
Я
в
Данные
25;
... X. Ап. Например, какой смысл заключен в отношении, по¬
казанном на рис. 1.5, д? Аналогично другим типам данных
это отношение также целиком относится к расчетным таб¬
лицам.
Поясним рис. 1.5, а. Отношение может периодически ме¬
нять свое содержание и число кортежей за счет включения,
исключения или обновления данных. Все конкретные значе¬
ния атрибута не только являются элементами данных одного
типа, но имеют одинаковую семантику (например, если част¬
ное лицо будет рассматривать «доход» фирмы как собствен¬
ный «доход», получится «злоупотребление доверием»). По¬
рядок атрибутов в отношении может быть произвольным.
Обычно порядок следования атрибутов устанавливают с уче¬
том семантики отношения. Предполагается, что все кортежи
отношения различны, а порядок их следования может быть
произвольным.
Прежде чем дать определение традиционных операций
над отношениями, отметим, что результатом выполнения лю¬
бой операции является отношение, а сами операции делятся
на унарные и бинарные.
1) Операции над множествами. Пусть R и 5 — произволь¬
ные отношения, определенные на множествах Аи А2, ..., Ап.
Поскольку отношения R, S являются подмножествами декар¬
това произведения, то к ним применимы все операции над
множествами, такие, как объединение, пересечение, вычита¬
ние и т. д.
2) Прямое произведение. Пусть R и S — произвольные от¬
ношения, определенные на множествах Аь А2, ..., Ап и
Ви В2> Bk соответственно. Тогда прямое произведение
этих отношений будет подмножеством декартова произведе¬
ния А! X .. • ХАпХВ !Х ... ХВк9
R ® 5 = {(г, s) | г €= R, sg S},
где '(г, s) — кортеж, состоящий из (п + k) элементов, пред¬
ставляющий собой конкатенацию кортежа г п-й степени и
кортежа 5 k-й степени.
3) Проекция. Пусть R — произвольное отношение, опре¬
деленное на множествах Ль Л2, ..., Ап, а В — подмножество
списка атрибутов отношения R, В = Ап X Л/2Х ••• X Ajky
{/1, ..., jk} с= {1, ..., п}. Обозначим через г [Aj] /-й элемент
г-го кортежа отношения R, тогда
R [В] = {г [в] = (г [А/Ч], г [Л/2], •.., г [Ajk]); г е= R}
называется проекцией R на В. Результирующее отношение-
получается из отношения R исключением атрибутов, отлич¬
26
Глава 1
ных от Л/i, ..., Ajk. При этом также исключаются повторяю¬
щиеся кортежи для выбранных атрибутов. Например:
R: А\
А2
Л3
R [А2 X Л3]: А2
Л3
а
2
X
2
X
b
1
У
1
У
а
2
У
2
У
Ь 2 х
4) Соединение. Обозначим через 0 произвольную опера¬
цию сравнения =, Ф, >, С, Пусть отношения R и
S имеют соответственно атрибуты А и В и эти атрибуты
сравнимы. Это означает, что А и В определены на одной
области, например содержат или натуральные числа, или
действительные числа, или буквы английского алфавита (в
последнем случае 0 ограничивается только операциями =
и Ф). В этом случае R[AQB]S ={(ry s); re/?, seS,
г [Л] 0s [Б]} называют 0-соединением отношений /?, S по ат¬
рибутам Л, В. Например:
R: Ах
to
Л3
S: В,
в2
а
1
и
2
и
а
2
V
3
X
b
4
V
4
W
с
2
W
с
3
и
R [Л3 = В2] S: А,
а2
А?,
Вх
В2
R[A2>Bx]S: Л,
а2
Лз
Вх
в2
а
1
и
2
и
Ъ
4
V
2
и
с
2
W
4
W
b
4
V
3
X
с
3
и
2
и
с
3
и
2
и
При соединении в результирующем отношении образуются
пары полностью совпадающих атрибутов. Один из них можно
исключить, выполнив проекцию на список атрибутов, в кото¬
ром один из атрибутов отсутствует. Соединение, обладающее
этим свойством, называют естественным соединением. Если
0 — произвольный двухместный предикат, то можно дать бо¬
лее общее определение соединения.
5) Деление. Пусть отношения /?, S имеют общее частич¬
ное прямое произведение В = С. Обозначим через Всу Сс
Данные
27
частичные прямые произведения, не входящие в В, С соот¬
ветствующих областей определения:
ве
s:
Отношение R можно рассматривать как отображение Вс
на Bt вообще говоря, не единственное. Пусть множество ото¬
браженных значений для подмножества х элементов Вс кор¬
тежа отношения R имеет вид
g(x\ R, B) = {r[B]\ r<=R, г[Вс] = х}.
Множество, включающее все значения хаВс проекции 5
на С, S[C] (подмножество 5[ВС]),
R[B + C]S = {r [Вс); г е= /?, S [С] с= g (г [Вс]\ R, В)}
называется результатом деления отношения R на отноше¬
ние S по атрибутам В, С. Например:
R: Вх
в2
въ
S: Сх
с2
а
1
X
X
1
а
1
У
X
2
Ь
2
X
У
1
/ПВзЧ-С,^: В, В2 (R[B2XB3])[B2 + C2]S: В3
х
У
1
Результат операции представляет собой отно¬
шение, состоящее из кортежей отношения /?[BiX52], ото¬
бражение которых полностью включено в S[Ci],
6) Ограничение. Если атрибуты Л, В отношения R сравни¬
мы в том смысле, какой имелся в виду при рассмотрении
соединения, и если обозначить операцию сравнения через 8,
то выражение
R [АВВ] = {r\ r<=R> г [А] Вг [В] }
называется В-ограничением отношения R. Рассмотренное выше
8-соединение может быть выражено через операции прямого
произведения и 0-ограничения
R [ABB] S = (R&S) [ABB]
28
Глава 1
Например:
R i А\ А2 Л3 R [А2 = А3]: А\ А2 Л3 R [А2 > A^\i А\ А2 Л3
р 3 5 <733 ^64
q 3 3 г 2 2
^64
г 2 2
В заключение определим специфическое отношение-кон*
станту, содержащее всего один кортеж и один атрибут {а)\
здесь а является константой с областью определения А. Ис¬
пользуя рассмотренные операции, можно сформулировать
различные запросы к реляционной модели данных. Рассмот¬
рим примеры построения запросов к реляционной модели,
содержащей три отношения:
ДЕТАЛЬ: (номер-детали, тип)
СКЛАД: (номер-склада, место-расположения)
ХРАНЕНИЕ: (номер-детали, номер-склада)
Получить номера складов, где хранится деталь под номе¬
ром 13:
(ХРАНЕНИЕ [номер-детали = номер-детали] {13}) [номер-
склада]
Здесь {13} представляет собой отношение-константу, кон¬
станта задает номер конкретной детали из всего допустимого
множества номеров.
Получить номера складов, на которых отсутствуют детали
типа а:
(ХРАНЕНИЕ [номер-детали ф номер-детали] (ДЕТАЛЬ
[тип = тип] {а})) [номер-склада]
Определить место расположения складов, где хранятся все
детали типа а:
(СКЛАД [номер-склада = номер-склада] (ХРАНЕНИЕ [но¬
мер-детали Ч- номер-детали] (ДЕТАЛЬ [тип = тип] {а})))
[место-расположения]
1.2.2. Структуры данных и отношения
1) Массив
Отношение ДОХОД-ОТ-ПРОДАЖИ (рис. 1.5,6) имеет
следующую структуру:
(название-магазина)Х (месяц)Х (шифр-изделия)X (выручка)
Это отношение можно представить трехмерным массивом
Данные
29
данных выручка, используя в качестве индексов конкретные
значения названий магазинов, месяцев и шифров изделий.
Сечения массива выручка по магазинам показаны на
рис. 1.6. Отметим, что отношение содержит только те данные,
НАЗВАНИЕ-МАГАЗИНА НАЗВАНИЕ-МАГАЗИНА
1-я половина 2-я половина
Рис. 1.6. Представление отношения ДОХОД-ОТ-ПРОДАЖИ
(рис. 1.5, б) трехмерным массивом Выручка.
которые соответствуют конкретной выручке. Таким образом,
чтобы зафиксировать «выручку от продажи нового изделия
за конкретный месяц в конкретном магазине» в отношение
ДОХОД-ОТ-ПРОДАЖИ достаточно добавить всего одну вы¬
борку. Для представления отношения трехмерным массивом
выручка необходимо заранее знать все месяцы, названия всех
магазинов и шифры всех изделий. Если различных магазинов
и товаров много, а предполагаемый период времени продол¬
жителен, то построить трехмерный массив, который охваты¬
вал бы все эти данные, может оказаться очень сложно. По¬
этому в общем случае трудно сказать, какое представление
лучше, — все зависит от конкретных условий.
2) Иерархическая структура
Часто возникает необходимость отдельные поля записи
одного типа рассматривать как набор записей другого типа.
На рис. 1.7, а двойной рамкой выделены поля, соответствую¬
щие наборам записей, а одинарной — элементам данных.
В общем случае каждый экземпляр записи верхнего уровня
может иметь произвольное число экземпляров подчиненных
записей. Совокупность записей имеет структуру дерева, и
подчиненная запись не может существовать без своего пред¬
шественника по иерархии. Все подчиненные записи в наборе
имеют одинаковую структуру. Элементы данных, выстраи-
30
Глава 1
Иод
сотрудника
Служащие
фирма/
х
Фами¬
лия
Профес¬
сия
биогра¬
фия
Дата рож¬
дения
НаименоВа -
ние плана
ИждиВенцы
Распределение
работ
План
Имя
—1
отношения
СЛУЖАЩИЕ
ФИРМЫ
БИОГРАФИЯ
Нод-
сотрудника
Фами¬
лия
Иод-
сотрудника
Профес¬
сия
Дата -
рожд.
ПЛАН
Иод -
сотрудника
Профес¬
сия
Наименование
- плана
Распредг
работ
Родственные -
ИЖДИВЕНЦЫ
Иод-
сотрудника
Имя
1
...
1
1
Рис. 1.7. Реляционная и иерархическая модели: а — иерархический файл;
б — представление с помощью отношений.
ваясь в последовательности, образуют структуры, которые
похожи больше на аллеи (дерево с параллельными ветвями),
чем на деревья. Структуры, в которых каждая подчи¬
ненная запись имеет только одну непосредственно пред¬
шествующую запись, называются иерархическими моделями
данных.
Можно представить иерархию в виде реляционной модели,
как показано на рис. 1.7,6; число отношений в этой модели
будет равно числу элементов дерева, заключенных в двойную
рамку. В этом случае элемент данных код-сотрудника будет
ключом отношений ПЕРСОНАЛ, БИОГРАФИЯ, ИЖДИВЕН¬
ЦЫ; для отношения ПЛАН ключом будет (код-сотрудника,
профессия). Считается, что иерархическая структура проста
для понимания и подходит для описания современных орга¬
Данные
31
низаций, классификации и т. п. Реляционная модель позво¬
ляет отображать иерархическую структуру и в этом смысле
является более общей моделью.
3) Спецификация
Спецификация указывает, из каких узлов и деталей со¬
стоит механизм (такой, например, как автомобиль), и содер¬
жит основные данные для сборочного цеха. Поскольку одни
и те же детали, такие, как винты, используются практически
в каждом узле, спецификация имеет форму, показанную на
рис. 1.8, а. Собственно «деталями» в спецификации такого
вида являются только элементы Е, G, Я, F. Можно заметить,
что спецификация в виде совокупности деревьев содержит
избыточность. После объединения этих деревьев с учетом
I—
В, 2
0,1
Ej F}J.
“1
Е,3
I
С,2
Су 1 1), 1
D
~1
с, г
“I
// 1
л
ЛЛ
ДЕТАЛИ
Исход¬
ный
Порож¬
денный
• Коли¬
чество
А
В
2
А
с
1
А
Е
3
В
С
А
/
В
л
1
В
Е
2
С
£
1
с
F
3
с
9
2
л
F
1
л
И
1
ПОРОЖДЕННЫЕ
ОБЪЕКТА А
В 2
О 1
Е 3
ПОРОЖДЕННЫЕ
ОБЪЕКТА С
Летам н™“}0
£ 1
F 3
G 2
ПОРОЖДЕННЫЕ
ОбЪЕНТА В
Детали ТеТтво
С 1
Д 1
Е 2
ПОРОЖДЕННЫЕ
ОБЪЕНТА D
Детали
F
Н
Рис. 1.8. Спецификация:
а — одно из представлений спецификации: «А состоит из двух В, одного С,
трех £», ..., «D состоит из одного F, одного Я»; б — представление спе¬
цификации в виде графа; в — представление в виде одного отношения;
г — представление в виде четырех отношений, соответствующих а.
32
Глава 1
вхождения в узел более мелких узлов и деталей получится
структура, отличная от иерархической (рис. 1.8,6). Струк¬
тура, в которой любой элемент может быть связан с любым
другим элементом, называется сетью. Сетевые модели опи¬
сывают наиболее общий случай связей между данными типа
«исходный-порожденный».
Спецификация может быть представлена одним отноше¬
нием, как показано на рис. 1.8, в. Однако в этом случае за¬
просы вида «Определить количество деталей каждого типа,
входящих в узел В» сведутся к выполнению последовательно¬
сти операций естественного соединения исходного отношения
с самим собой или результатом предыдущего соединения по
атрибутам «исходный-порожденный». И так до тех пор, пока
результирующее отношение не будет содержать в атрибуте
порожденный никаких других значений, кроме Е, G, Н, F.
Рассмотренная реляционная модель не является единствен¬
ной. Список деталей можно представить и в виде четырех
отношений (рис. 1.8,г), непосредственно соответствующих
исходным деревьям (рис. 1.8, а). Но в этом случае потребу¬
ется разрешить использовать имена отношений в качестве
элементов отношений.
4) Списочная структура
Совокупность данных, структурные свойства которой огра¬
ничены лишь относительным расположением элементов, на¬
зывается списком. Список — это массив неопределенной дли¬
ны с элементами разных типов. Списочная структура пред¬
ставляет собой список, элементами которого могут быть
списки и списочные структуры. Списочная^структура является
рекурсивной структурой данных, что следует из самого опре¬
деления. Например, следующие строки:
1) {constantу pi, е)
2) (constant, {pi, 3.14), {е, 2.72))
3) {{{а, +, Ь), X, с), {{d, X, е), +, !))
являются списочными структурами. Чтобы отличить сугубо
специальный смысл слова «список» и чтобы подчеркнуть это,
обычно пишут его с большой буквы: «Список». Первая строка
представляет собой список. Вторая — списочную структуру,
так как содержит в качестве элементов два списка, {pi, 3.14)
и (е, 2.72). Первая и вторая строки являются списочными
структурами; первая состоит из трех элементов данных, а
вторая — из элемента и двух списков. Третья строка пред¬
ставляет собой арифметическое выражение {a+b)c/{de-\-f).
По определению арифметическое выражение представляет
Данные
33
собой (операнд, знак операции, операнд); операнд может
быть константой, переменной или арифметическим выраже¬
нием. Представление арифметического выражения Списком
следует из рекурсивного характера самого определения.
К операциям над списочными структурами (Списками)
относятся: исключение части Списка, и в частности одного
элемента; конкатенация (объединение) двух Списков; вклю¬
чение элемента в Список. Кроме перечисленных операций
АРИФМЕТИЧЕСКОЕ-ВЫРАЖЕНИЕ
№ формулы
1-й операнд
2-й операнд
Операция
(1)
а
ь
+
(2)
(1)
с
X
(3)
(2)
(5)
-7-
(4)
d
е
X
(5)
(4)
f
—
Рис. 1.9. Представление арифметического выражения в виде отношения.
считаются определенными и обычные операции над элемен¬
тами данных. Типичным языком, применяемым для обработки
списочных структур в ЭВМ, является Лисп. Ему посвящены
многие учебники, к которым авторы рекомендуют обратиться
при необходимости.
Списочные структуры больше подходят для обработки не¬
большого числа сложно организованных данных, чем для
обработки большого числа данных одинаковой структуры.
Таким образом, роль списочной и реляционной моделей ока¬
зывается различной. Список — очень гибкая структура, по¬
этому если он неупорядочен и сложен, то и методы обработки
такой структуры также окажутся сложными. Более удобной
для обработки будет та структура, которая больше соответ¬
ствует структуре реального объекта. В вышеприведенном
примере третья структура представляет собой одну из таких
типичных моделей, вторая структура составлена из двух мо¬
делей: (constant, <pair>, <pair>, ...), где <pair> в свою оче¬
редь представляет собой модель (буква английского алфа¬
вита, число).
Если арифметическое выражение (3) представить отноше¬
нием, то получим таблицу, показанную на рис. 1.9. Это отно¬
шение содержит данные с разными областями определения
первого и второго операндов, однако его можно считать
представлением, удобным для обработки. Здесь одна формула
соответствует одному отношению и обработка отношения
2 Зак. 127
34
Г шва 1
потребует многократного выполнения одной и той же опера¬
ции, как и в рассмотренном ранее примере спецификации, что
отличает эту обработку от обработки рассмотренных ранее
примеров отношений.
5) Массив общего вида
Наиболее общая структура данных, охватывающая все
рассмотренные ранее структуры, такие, как массив, файл,
отношение, списочная структура и т. д., называется массивом
общего вида. Таким образом, массивом общего вида называ¬
ется массив, элементы которого не обязательно относятся
к одному типу данных. Массив общего вида допускает в ка¬
честве элементов использовать другой массив общего вида.
Какие операции могут потребоваться для работы с массивами
общего вида? Естественно, в их число должны входить опе¬
рации, которые описаны выше для рассмотренных структур
данных. Однако пока трудно дать более детальные рекомен¬
дации по практической реализации этих операций и по ме¬
тодам представления массива общего вида в памяти — эти
вопросы находятся пока в стадии исследования.
1.3. Динамическое распределение памяти
1.3.1. Простые методы
В языках * программирования данные разных типов, рас¬
смотренные в разд. 1, представляются чаще не в виде кон¬
стант, а в виде переменных. В данном случае понятие «пере¬
менная» наделяется дополнительными свойствами, отлич¬
ными от привычного «изменять значение». Первое касается
использования имен в тексте программы: устанавливается,
одному или разным данным соответствуют одинаковые имена
переменных в основной программе и в подпрограмме. Обыч¬
но, если нет специального указания (по умолчанию), области
действия имен устанавливаются в соответствии с определен¬
ными соглашениями — стандартом языка. Наряду с этим су¬
ществует возможность установить области действия имен пе¬
ременных уже или шире стандартных. Второе свойство дик¬
туется необходимостью определения времени распределения
памяти для переменных: до начала выполнения программы,
в момент обращения к подпрограмме или позднее, а также
метода распределения — статического или динамического.
В дополнение к этим свойствам иногда имеется возможность
указать, когда память, выделенная для размещения перемен¬
ных, становится ненужной и может быть распределена по¬
вторно.
Данные
35
Следует ли это свойство связывать с понятием типа пере¬
менной— вопрос особый; лучше, если пользователи не будут
углубляться в этот вопрос. На практике во многих случаях
в этом нет необходимости, так как память не очень загру¬
жена. Например, из-за того, что в языке Фортран рекурсив¬
ный вызов подпрограммы не допускается, отношение между
вызывающей и вызываемой программами имеет вид типа
«исходный-порожденный», и все необходимое распределение
памяти может быть выполнено при обращении к подпро¬
грамме. Поэтому для Фортрана достаточно стекового меха¬
низма управления памятью. Если при этом необходимо выде¬
лять память и для буферов ввода-вывода, то для управления
Область памяти Вызываемые
подпрограммы
Программа^ ^ронстанты^е^мшые^^ памяти ввода-вывода
Свободная Помят для
область буферов |
овода-вы вот
г/г/м
Основная
программа
Подпро¬
грамма А
Подпро -
грамма В
Рис. 1.10. Свободная область памяти организована в виде дека.
памятью можно использовать двустороннюю очередь (см.
рис. 1.10).
В некоторых случаях не удается так просто решить про¬
блему управления памятью.
1) Бывают случаи, когда в процессе обработки данные
промежуточных расчетов оказываются многочисленными и
громоздкими; хотя эти данные уже не нужны, они продол¬
жают занимать память, в то время как появляется необхо¬
димость в размещении новых данных. Обработка списков
относится именно к такому случаю.
2) Для задач обработки данных в реальном масштабе
времени невозможно предсказать изменение объемов обра¬
батываемых данных, что необходимо учитывать при реализа¬
ции таких задач на ЭВМ.
3) Операционная система с разделением времени должна
распределять память в соответствии с требованиями пользо¬
вателей.
4) Часть внешней памяти в соответствии с требованиями
пользователей должна распределяться между постоянными
и временными файлами.
Рассмотрим коротко методы, которые применяются в этих
случаях.
В разд. 2 встречался случай, когда область памяти (пул
памяти) (все равно—внешней или оперативной), предназна¬
ченная для использования, делилась на равные блоки, ко¬
торые по мере требований предоставлялись пользователям,
причем, когда они оказывались ненужными, пользователи
2*
36
Глава 1
возвращали их обратно для повторного использования. В этом
случае список свободных блоков можно организовать в виде
стека, а для освобождения использовать метод «сбора му¬
сора». В этом методе ставшие ненужными отдельные блоки
возвращаются в память одновременно — в момент, когда спи¬
сок свободного пространства пуст. Для выявления неисполь¬
зуемых блоков достаточно исключить из всей области исполь¬
зуемые блоки. Конкретные способы выявления последних
л-\Размеи |
-ь| Размер |
Занятый
Занятый
+ 1
+ 1
Рис. 1.11. Метод управления блоками с граничными признаками. Если сво¬
бодные блоки оказываются смежными в памяти, они объединяются.
зависят от структур обрабатываемых данных и особенно Ча¬
сто обсуждаются для списочных структур (поэтому здесь эти
способы не рассматриваются). Ниже разберем случай управ¬
ления памятью для блоков разных размеров, требуемых поль¬
зователями.
Пусть вся память, подлежащая распределению, представ¬
ляет собой один блок, содержащий конечное число ячеек с
непрерывно следующими адресами. Первоначальное распре¬
деление может быть выполнено очень просто — путем после¬
довательного уменьшения первоначального блока по каждому
запросу. Когда вся память блока будет распределена, оче¬
видно, несколько блоков станут ненужными и их память мо¬
жет быть использована повторно. Однако, если операцию по¬
вторного распределения использовать многократно, свободные
блоки будут становиться все меньше и меньше, поэтому перед
повторным распределением проводится уплотнение памяти—
перемещение всех занятых блоков в последовательные ячейки
для того, чтобы всю свободную память собрать вместе в один
блок. Если область памяти имеет достаточно большие раз¬
меры, необходимость в повторных уплотнениях возникает
редко.
Однако можно избежать больших затрат времени на пе¬
ремещение данных, если во все блоки, свободные и занятые,
включить небольшую служебную информацию специально
для управления памятью. Сущность этого метода заключа¬
ется в следующем (см. рис. 1.11). Свободные блоки объедини-
Данные
37
ются ь двухсвязанный список. В начале и в конце каждого
блока хранятся логические значения, показывающие, занят
или свободен данный блок, а для свободных блоков — и их
размеры. Благодаря этому, как только находящийся в про¬
цессе использования (занятый) блок становится ненужным,
проверяется, свободны или заняты блоки, смежные с ним по
памяти; если они свободны, их можно объединить. При рас¬
пределении список свободных блоков просматривается по¬
следовательно, пока не встретится блок размера не меньше
требуемого. Как только такой блок найден, достаточно вы¬
делить из него блок требуемого размера, а из оставшейся
части образовать новый блок. Если найденный свободный
блок лишь немного больше требуемого, то лучше занять его
полностью, чем оставлять небольшой блок в списке. В про¬
тивном случае образовавшиеся в разное время маленькие
свободные блоки имеют тенденцию скапливаться в начале
списка и увеличивают время поиска. Для того чтобы избе¬
жать этого, список свободных блоков лучше организовать
в виде кольца и каждый раз операцию поиска начинать
с того места кольца, где закончилась предыдущая.
Возможности различных методов динамического управле¬
ния памятью зависят от характера распределения размеров
требуемых блоков, частоты резервирования и освобождения
(по отношению к работе, затрачиваемой на обработку дан¬
ных), разброса времени существования каждого блока. По¬
этому анализ этих методов очень сложен. Если требуются
блоки достаточно больших размеров (сравнимых с размером
пула памяти), то, естественно, легко наступит «банкротство»
(переполнение) пула. Если времена существования блоков
примерно одинаковы, то список становится близким к оче¬
реди с дисциплиной обслуживания «первым включается —
первым исключается», и тогда больших проблем не возни¬
кает. Если же времена существования блоков имеют боль¬
шой разброс и сильно смещены в сторону малых времен, то
список становится близким к стеку с дисциплиной обслужива¬
ния «последним включается — первым исключается», и в этом
случае также особых трудностей нет. Когда, несмотря на из¬
быток свободной памяти, достаточно большие блоки отсут¬
ствуют, приходится использовать уплотнение. Однако даже
полное уплотнение не гарантирует от возможного краха, если
вероятность запросов на большие блоки велика.
Если оперативная память исчерпана, часть занятых бло¬
ков можно освободить, переписав их содержимое во внешнюю
память. Однако оказывается совсем не просто определить,
какие блоки следует освобождать, но здесь эти вопросы под¬
робно обсуждаться не будут. При использовании виртуальной
38
Глава 1
памяти это производится автоматически, но появляется
другая проблема — рассредоточение активных адресов па¬
мяти, ухудшающее эффективность.
1.3.2. Метод близнецов
1) Метод близнецов с бинарным разбиением
Итак, управление памятью без ограничения на размеры
резервируемых блоков требует довольно много времени.
Если же размеры резервируемых блоков ограничить 2к (k =
= 0,1,2, ...), то работа по управлению памятью чрезвы¬
чайно упростится. Если требуемый размер блока памяти не
является степенью 2, то выделяется больший блок минималь¬
ного размера 2*. Далее, если нет свободного блока размером
2й, то блок требуемого размера получают делением большего
блока на 2,4, ... части. Для простоты примем, что размер
пула памяти равен 2п. Идея распределения памяти в методе
близнецов показана на рис. 1.12. При разделении некоторого
блока на две части полученные блоки по отношению друг
к другу называются близнецами (или братьями). Близнецы
вновь могут делиться. Свободные блоки объединяются
в списки по размерам, а головные узлы этих списков собраны
в таблицу. При резервировании блока размером Ь находят
минимальное значение /г, удовлетворяющее требованию
b ^ 2к, и начинают поиск свободного блока с k-то списка;
если окажется, что список пуст, то ищут блок размером
2*+1, 2k+2, .... Как только свободный блок будет найден, он
удаляется из списка. Если окажется, что найденный блок
больше требуемого, его делят на две части. Одну из них (од¬
ного близнеца) включают в список соответствующего раз¬
мера, а другой передают пользователю или вновь делят.
При освобождении блока проверяется состояние его близ¬
неца, и если он свободен, то вначале он исключается из
списка, а затем близнецы объединяются в один блок. Для
полученного блока снова проверяется состояние его близнеца.
Смежные по памяти блоки одинакового размера не объеди¬
няются, если они не являются близнецами. Блок, ставший
свободным, включается в соответствующий список. На
рис. 1.12,6 показано, как в случае освобождения блока раз¬
мером 1 (отмечен стрелкой) дважды производится объеди¬
нение близнецов и в результате получается блок размером 4.
Показанные слева два свободных блока размером 2 являются
смежными, но не объединяются, поскольку не являются близ¬
нецами.
Поактическая ценность метода определяется возмож¬
ностью вычисления адреса близнеца. В случае, показанном
Данные
39
Таблица головных узлов
списков свободных дУгонов
25
в
Рис. 1.12. Состояние области памяти размером 25. Распределены (предо¬
ставлены пользователю, заняты) три блока размером 22, два блока раз¬
мером 21 и один блок размером 2°. Как изменится характер распределения
в случае освобождения блока, указанного стрелкой: а — текущее состояние
памяти; занятые блоки памяти заштрихованы; б — бинарное дерево рас¬
пределения; в — битовая карта, соответствующая распределению памяти
в методе близнецов.
на рис. 1.12, пул памяти (минимальный размер блока принят
равным 1) занимает ячейки с адресами от 0 до 31. Близне¬
цом блока размером 21 (на рисунке — второй свободный
блок), начинающегося с адреса 102 в двоичной системе, будет
блок, начинающийся с адреса 1102. Вообще, для блока раз¬
мером 2*, расположенного с адреса х, близнецом будет блок,
начинающийся с адреса:
x-\-2k при х = 0 (modulo 2fe+1),
x — 2k при х=\ (modulo 2fe+1),
где a = b (modulo m) указывает на то, что (а — Ь) представ¬
ляет собой целое кратное га. Для пула памяти размером 2П
можно составить битовую карту из 2П бит и биту с номером х
присвоить значение 0 или 1 в зависимости от того, свободен
40
Глава 1
или занят блок, начинающийся с адреса х (здесь значение х
никак не связано с размером блока). На рис. 1.12,в показана
битовая карта, соответствующая распределению блоков.
2) Обобщенный метод близнецов
Ограничиваются ли возможности использования метода
близнецов исключительно блоками размером 2k (k =
= 0,1,2, ...)? Возникает вопрос: не слишком ли расточите¬
лен метод, выделяющий блок размером 2k+l вместо требуе¬
мого 2^ -f' 1 ? Один из способов улучшения метода связан с
использованием последовательности Фибоначчи для допусти¬
мых размеров блоков Li, L2, ....
1, 1,2, 3,5, 8, 13,21,34, .. ,(Lk = Lk-\ + Lk-2).
При разбиении области размера Lk на Lk-1, Lk-2 много¬
образие размеров блоков ограничено, но оказывается больше,
чем в случае последовательности 2k.
Последовательности 2k (k = 0,1,2, ...) и Фибоначчи под¬
чиняются общему правилу и могут быть представлены одним
выражением:
Lk = Lk_ i + Lk__j,
где /= 1, / = 2 соответствуют первой и второй последова¬
тельностям размеров соответственно. Однако удобно при раз
биении использовать также числовую последовательности
объединяющую обе последовательности — и 2k, и 3-2^. Эт
последовательность не может быть построена по вышеука¬
занным правилам, однако ее можно построить, используя
следующие два правила:
£=12.34 5 67 8
0) 1 1 2 4 8^ 16JS2 64 L2k-i = L2(k-i)+L2k-s
0) 1 2 3 6 12 24 48 96 L2k=L2k-i+Uk-г
Объединяя эти выражения в одно, получим
Lk — Lk-1 + L$ (&) (р (k) ^ k — 1).
Таким образом, и в случае использования обобщенного
метода близнецов управление памятью почти не отличается
от управления в методе близнецов с бинарным разбиением.
В таблицу головных узлов списков свободных блоков сле¬
дует добавить L/e, Р(£) (см. рис. 1.13, а). При разделении
блока размером Lk блок меньшего размера Lp(k) помещают,
например, слева и присваивают ему новый адрес. Кроме того,
биты разметки ab отражают местоположение блока и его
близнеца.
Для управления памятью необходимо, чтобы каждый ре¬
ально существующий блок содержал следующие данные: код
состояния блока — занят он или свободен (+, — соответ-
Данные
41
Таблца головных излов
списков свободных олоков
+ I Н \ab\
Занят
а
ab;
а~\° ~ для левого близнеца
(/ - для правого близнеца
г„значению вита а норневого 5лонаее
(при а=0)
^ значению вита Ь норневого влона(С
(при а~1)
в
Рис. 1.13. Обобщенный метод близнецов: а — вид списка свободных бло¬
ков; б — правила изменения битов разметки а, б, показывающих состоя¬
ние блока (точками отмечены блоки, входящие в состав близнецов).
ственно); k — размер блока, заданный уровнем; ab — биты
разметки блока. Биты Ь левого и правого близнецов, будучи
расположены рядом, автоматически образуют разметку ab
корневого блока (блока перед его делением на близнецов).
На рис. 1.13,6 в скобках показана разметка блоков до их
деления, и реально она не хранится.
Таким образом, в разметке ab бит а показывает, левым
или правым близнецом является блок. Бит Ь формируется
из разметки корня: бита b для левого близнеца и бита а —
для правого. При делении произвольного блока размера Lk
адрес правого близнеца будет совпадать с адресом блока,
а адрес левого близнеца будет на Lk-\ больше этого адреса.
Знание местоположения близнеца (левый или правый) по¬
зволяет сформировать бит а, а использование разметки кор¬
ня — и бит b каждого из близнецов. Поэтому в случае необ¬
ходимости процесс деления может быть продолжен до тех
пор, пока не будет получен блок требуемого размера.
При делении блока число близнецов не обязательно
должно ограничиваться двумя блоками. Можно рассмотреть
также разделение на три и более блоков.
Lk = trik + Lp (ft, и + Lp (k, 2) + • • • + L$ rk)
{Lk > L$(k, /), j — 1, 2, ..., rk).
Это потребует некоторого уточнения разметки ^блоков и
содержимого таблицы головных узлов списков. Кроме того,
42
Глава 1
наряду с данными о состоянии, размере и разметке блока
может появиться необходимость хранить номера близнецов.
Например, это целесообразно делать в случае организации бу¬
феров ввода-вывода; при этом указывают, например, дорож¬
ку диска, строку печатного текста, кадр дисплея и т. п.
1.3-3. Анализ
Сравнение методов. Ранее отмечалось, что анализ методов
динамического распределения памяти непрост, однако неко¬
торые их характеристики нам известны. Считается, что для
простых методов, описанных в разд. 1.3.1, основной характе¬
ристикой является изменение числа блоков. Обозначим число
занятых и свободных блоков через N и М соответственно и
проследим, как меняются их значения во времени. Обозначим
число занятых блоков, соседствующих по обе стороны со сво¬
бодными блоками, через Д ас занятыми блоками — через С.
Тогда число занятых блоков, соседствующих с одной стороны
с занятым, а с другой со свободным блоками, будет 2 (М —
— А) ± 1. Тогда
N = А + С + 2{М- А) = 2М- А + С.
Если предположить, что вероятность уменьшения М на 1
при освобождении блока категории А равна вероятности уве¬
личения М на 1 при освобождении блока категории С (т. е.
A/N равно C/N), то получим
N = 2M.
В методе близнецов блоки выделяются беспорядочно, что
снижает эффективность использования памяти. Это происхо¬
дит по двум причинам. Первая — это расхождение размеров
требуемого блока и блока, полученного по методу близнецов.
Вторая — появление свободных блоков при разделении. Го¬
ворят, что в первом случае имеет место внутренняя фрагмен¬
тация, а во втором — внешняя. Анализ второго случая сло¬
жен. Что касается внутренней фрагментации, то, если предпо¬
ложить, что все размеры блоков равновероятны, и провести
другие упрощения, получим результаты, которые хорошо
согласуются с результатами моделирования по методу Монте-
Карло. Поскольку блоки размером 2k + 1 требуются не слиш¬
ком часто, можно пренебречь разницей результатов внутрен¬
ней фрагментации для метода близнецов с бинарным разбие¬
нием и метода с использованием последовательности чисел
Фибоначчи или другого, более сложного метода.
Глава 2
Поиск данных по ключу
В предисловии отмечалось, что вопросы представления
данных в памяти ЭВМ тесно связаны с операциями, при по¬
мощи которых они обрабатываются. К числу таких операций
относятся выборка, изменение, включение и исключение дан¬
ных. В основе всех перечисленных операций лежит операция
доступа, которую и нельзя рассматривать независимо от спо¬
соба представления. К каким же данным, находящимся в па¬
мяти, необходимо иметь доступ? Безусловно, любое данное
в памяти должно быть доступно. Однако в задачах поиска
предполагается, что все данные хранятся в памяти с опреде¬
ленной идентификацией и, говоря о доступе, имеют в виду
прежде всего доступ к данным (называемым ключами), од¬
нозначно идентифицирующим связанные с ними совокупности
данных. В свою очередь даже ключи не обязательно должны
быть непосредственно доступными. В этой главе обсуждаются
два класса методов, реализующих доступ к данным по клю¬
чу: методы поиска по дереву и методы хеширования.
2.1. Поиск по дереву в оперативной
памяти
2.1.1. Что такое дерево?
1) Определение
Дерево является одной из самых распространенных струк¬
тур, используемых для представления данных в памяти ЭВМ.
Известно много разновидностей этой структуры и детально
изучены свойства каждой из них. Однако здесь вместо си¬
стематического изучения деревьев и их математических
свойств мы ограничимся рассмотрением главным образом де¬
ревьев, используемых для поиска данных. Вначале дадим
определение дерева.
Определение 2.1. Деревом называется конечное множе¬
ство, состоящее из одного или более элементов, называемых
узлами, таких, что:
1) Между узлами имеет место отношение типа «исход-
ный-порожденный».
2) Есть только один узел, не имеющий исходного (или
отца). Он называется корнем.
44
Глава 2
3) Все узлы, за исключением корня (существуют деревья,
состоящие из одного корня), имеют только один исходный
(одного отца); каждый узел может иметь несколько порож¬
денных (сыновей).
4) Отношение «исходный-порожденный» действует только
в одном направлении, т. е. ни один потомок некоторого узла
никогда не может стать для него предком.
Дадим рекурсивное определение дерева, эквивалентное
вышеприведенному, но более формальное. Оно является ре¬
курсивным, поскольку определение дерева производится в
терминах самих деревьев.
Определение 2.1 А. Деревом называется конечное множе¬
ство 71, состоящее из одного или более узлов, таких, что:
1) Имеется только один специально обозначенный узел
root(T), называемый корнем дерева Т.
2) Остальные узлы (исключая корень) содержатся в т
(т^О) попарно непересекающихся множествах ..., Тту
каждое из которых в свою очередь является деревом. Де¬
ревья Т1, ..., Тт называются поддеревьями данного корня
root(T).
Что же конкретно представляет собой «дерево», характе¬
ризуемое определениями 2.1 и 2.1 А? Это зависит от способа
представления структуры отношения «исходный-порожден¬
ный». На рис. 2.1 приведено несколько примеров различного
графического представления деревьев. Согласно определе¬
нию, дерево может состоять из одного узла (только корень),
однако такое дерево следует рассматривать, скорее, как ис¬
ключение. На рис. 2.1, а, б узлы показаны буквами в круж¬
ках, а отношение «исходный-порожденный» — линиями, свя¬
зывающими пары узлов. На рис. 2.1, а узлы, расположенные
выше, считаются исходными (отцами), в то время как на
рис. 2.1,6 исходными считаются узлы, расположенные ниже.
На рис. 2.1, в представлено такое же дерево, как и на
рис. 2.1, а, б, но исходными являются узлы, расположенные
слева, и связи показаны слева направо. Отношения «исход¬
ный-порожденный» могут быть представлены и без исполь¬
зования связей путем соответствующего расположения ис¬
ходного узла левее, правее, выше или ниже. К таким древо¬
видным структурам можно отнести структуру оглавления
книги: глава, раздел, подраздел. На рис. 2Л,е изображено
дерево, в котором узлы представлены графически таким об¬
разом, что узел, непосредственно содержащий в себе другие
узлы, является исходным, а узлы, непосредственно содержа¬
щиеся в другом узле, являются порожденными. Если же, на¬
оборот, узел, непосредственно содержащий в себе другие
Поиск, данных по ключу
45
(.A(B(E)(F)(G))(C)(D(HU)(K))(I)))
г д е
Рис. 2.1. Различные способы графического изображения деревьев, а — в —
изображение деревьев в виде множества узлов и связей между ними.
Корень дерева расположен: а — наверху; б—внизу; в — слева, г — е —
изображение деревьев без использования связей (теоретико-множествен¬
ная трактовка); г — вложенные множества; д — пересечение множеств;
е — вложенные скобки — структура типа (исходный (порожденный) ...
(порожденный))
узлы, считать порожденным, а содержащийся в других уз¬
лах— исходным, то получим изображение структуры, соот¬
ветствующее рис. 2.1,5, при этих условиях структуру на
рис. 2.1, г уже нельзя будет считать деревом. На рис. 2.1, е
представлена еще одна древовидная структура, в которой
порожденные узлы обозначены буквами алфавита, заключен¬
ными в скобки, и последовательно вложены в другие скобки,
в которые заключены исходные по отношению к ним узлы,
в результате чего получается графическое представление
типа (исходный (порожденный) ... (порожденный)).
Легко заметить, что структуры а и Ь на рис. 2.1 отли¬
чаются только расположением корня. Структура, представ¬
ленная на рис. 2.1,6, больше похожа на настоящее дерево.
Однако при графическом представлении оказывается удоб¬
нее рисовать дерево сверху вниз — с корня, расположенного
сверху, как показано на рис. 2.1, а.
Для узлов дерева можно дать определение уровня или
глубины. Уровень порожденного узла равен уровню его ис¬
ходного + 1. Например, если уровень корня считать равным 1,
то высота дерева на рис. 2.1, а равна 4. Удобнее, однако,
уровень корня считать равным 0.
Число порожденных отдельного узла (число поддеревьев
данного корня) называется его степенью. Узел с нулевой сте¬
пенью называют листом или концевым узлом. Максимальное
значение степени всех узлов данного дерева называется сте¬
пенью дерева. Например, степень дерева на рис. 2.1, а
равна 3.
46
Глава 2
2) Упорядоченные деревья
Если в дереве между порожденными узлами, имеющими об¬
щий исходный (в этом случае порожденные называются
братьями (или сестрами у авторов, использующих «женскую»
терминологию), или сыновьями общего отца), считается су¬
щественным их порядок, то дерево называется упорядочен¬
ным. Деревья на рис. 2.1, а, б, в, е на основании, например,
определения «первым считается узел, находящийся справа»
можно считать упорядоченными деревьями, в то время как
деревья на рис. 2.1,г и д только на основании этого правила
нельзя рассматривать как упорядоченные.
Очень важным является тот факт, что при поиске почти
во всех случаях имеют дело с упорядоченными деревьями.
Поэтому дальнейшее рассмотрение древовидных структур бу¬
дет ограничено только упорядоченными деревьями. Конкрет¬
ная форма представления отношения «исходный-порожден¬
ный» и конкретные правила, устанавливающие порядок
между поддеревьями, и их число не обязательно должны
быть одними и теми же для всего дерева. Однако на прак¬
тике обычно стараются использовать однородное представле¬
ние дерева.
3) Разновидности деревьев
Для того чтобы лучше понять смысл определения 2.1,
ослабим некотооые ограничения. Рассмотрим структуры, ко¬
торые получатся в этом случае. Например, можно снять огра¬
ничение (2) на единственность корня.
2') Имеется один или более узлов, не имеющих исходного.
Структура, соответствующая этому определению, называется
лесом. Структура, которая может иметь место в этом случае,
показана на рис. 2.2. Структура памяти часто представляет
собой именно такую структуру. Например, иерархический
файл есть не что иное, как совокупность деревьев (узлами
дерева являются записи), которую можно считать лесом.
Лес и дерево имеют глубокую связь. Если удалить у дерева
корень, то получим лес. И наоборот, если к корням леса до¬
бавим общего отца, то получим дерево.
Можно снять также ограничение (3) на единственность
исходного узла. Однако, чтобы как-то ограничить класс
о
Рис. 2.2. Лес.
Поиск данных по ключу
47
структур, получаемых в этом случае, добавим ограничение на
число связей между узлами, а также потребуем, чтобы все
узлы были связаны. Таким образом,
1") между п узлами должно иметь место п—1 связей
(п ^ 1);
2") все узлы связаны между собой.
В теории графов таким образом определенное дерево на¬
зывается свободным деревом. Пример такой структуры по¬
казан на рис. 2.3. Очевидно, что этому определению соответ¬
ствует более широкий класс древовидных структур, нежели
нашему первоначальному определению дерева.
Дерево, все узлы которого им'еют степень не больше 2,
называется бинарным деревом. Бинарное дерево особенно
часто используется при поиске данных в оперативной памяти.
Рис. 2.4. Два различных бинарных дерева, в которых узел Л — исходный
(корень), а В — порожденный.
Поскольку структура бинарного дерева наиболее проста, на
его примере мы можем хорошо усвоить базовые понятия, ка¬
сающиеся древовидной структуры. В связи с этим рассмот¬
рим эту структуру подробнее. Степень 2 означает, что для
любого узла число его порожденных (поддеревьев) состав¬
ляет 0, 1 или 2. В случае когда имеется два поддерева, очень
просто установить их порядок, назвав одно левым, а другое
правым поддеревом. И в том случае, когда имеется только
одно поддерево, можно говорить о его расположении справа
или слева. Итак, дадим, формальное определение бинарного
дерева.
Определение 2.2. Бинарное дерево представляет собой ко¬
нечное множество узлов, которое
1) или пусто,
2) или состоит из одного корня и двух бинарных деревьев,
называемых левым и правым поддеревьями этого корня.
Рис. 2.3. Свободное дерево.
2.1.2. Бинарное дерево
48
Глава 2
Это определение отличается от определения 2.1 тем, что
допускается наличие пустого дерева. Кроме того, дерево, у ко¬
торого корень имее^ только левое поддерево, и дерево, у ко-
/ХД/^х
ХШ'Ххх
Рис. 2.5. Все 14 структурно различных бинарных деревьев с четырьмя
узлами.
торого корень имеет только правое поддерево, считаются
разными, что и отражено в определении (см. рис. 2.4).
На рис. 2.5 показаны различные бинарные деревья (14 ви¬
дов), состоящие из 4 узлов.
1) Перечисление бинарных деревьев
Найдем число структурно различных бинарных деревьев.
Пусть Ьп — число различных бинарных деревьев с п узлами.
Из определения 2.2 следует, что 60 = 1 - Для п> О число
различных деревьев с k узлами в левом и n — k— 1 в правом
поддеревьях обозначим bk, bn-k-\ (£ = 0,1, ..., п—1). Та¬
ким образом, число различных бинарных деревьев с п узлами
будет
Ьфп—\ -Г- b{bn_2 “Ь ••• + bn„{b0 = bn (п^ 1).
Производящую функцию числовой последовательности Ьп
можно представить в виде
В (z) = &о "Ь b\Z “Ь *4” • • • •
Очевидно, что производящая функция удовлетворяет сле¬
дующему уравнению:
zB (z)2 s=3 В (z) — bQ = В (z) — 1.
Решая это квадратное уравнение при г = 0, zB(z)2 = 0,
В {z) = bo = 1 и учитывая, что В (0) = 1, получим
в И - ±(1 - УТ=Tz) = ) . (- 4г>") -
m > 0 m >0
= 1 + 2 + 2z2 + 5z3 + 14z4 + 42z5 + 132z6 + ....
Поиск данных по ключу
49
Коэффициент при г4 в этом выражении как раз и дает
число структурно различных бинарных деревьев из четырех
узлов. Структуры этих деревьев (14 вариантов) показаны
на рис. 2.5.
2) Поиск по бинарному дереву
Удобным методом поиска в таблице, если она не слишком
велика и число элементов фиксировано, является метод де¬
ления пополам. В качестве примера рассмотрим поиск
в табл. 2.1, в которой приведена численность населения в от¬
дельных префектурах, включая столицу, в соответствии с госу¬
дарственной переписью населения в Японии, проводившейся
в 1980 г. Таблица содержит только 15 позиций, соответ¬
ствующих численности населения для 15 префектур. Поиск
производится по коду ключа, представляющего собой назва¬
ние префектур.
Таблица 2.1. Численность населения в префектурах и столице
для 15 префектур (по государственной переписи
населения 1980 г.)
Название префектуры
(включая столицу)
Ключ
Численность населения,
десятки тыс. человек
Хоккайдо
хокаи
558
Ибараки
ихара
256
Сайтама
сайта
542
Тиба
тиха
474
Токио
тооки
1162
Канагава
канака
692
Ниигата
ниика
245
Нагано
накано
208
Сидзуока
сисуо
345
Айти
аити
622
Киото
КИОТО
253
Осака
ооса
847
Хёго
хиуко
514
Хиросима
хироси
274
Фукуока
фукуо
455
В качестве ключа взяты первые три буквы названия пре¬
фектур, записанного слоговой азбукой «катакана» (озвон¬
чение во внимание не принимается). Если представить ко¬
нечное множество в виде таблицы, упорядоченной по воз¬
растанию ключей, то появится возможность осуществлять
поиск так же, как в словаре,
50
Глава 2
Порядок
поиска
Ключ Донные
а и та
Айти
622
и зга ра
Ибарани
256
о о са
Осака
847
на на на
Канагава
692
ни о то
Киото
253
са и та
Сайтама
542
си су о
Сидзуока
345
ти ха
Тиба
474
то о ни
Токио
7762
на на но
Нагано
208
ни и на
Ниигата
245
хи у .но
Хёго
574
хи ро си
Хиросима
274
(ру ну о
Фукуока
455
хо на и
Хоккайдо
558
Рис. 2.6. Поиск ключа в таблице, составленной из названий 15 префектур
с наибольшей численностью населения: а — данные (упорядочены по пер'
вым трем буквам «катаканы»); б — бинарное дерево поиска.
Задача поиска в таблице по заданному аргументу (ключ)
поиска), который обозначен тремя первыми буквами на¬
звания, записанного «катаканой», сводится к проверке: со
держится ли в данной таблице ключ, идентичный аргу
менту. При этом порядок сравнений в зависимости (У
значения аргумента поиска указан стрелкой в столбце «По
рядок поиска» (рис. 2.6,а). Пусть, например, аргументо>
поиска является «хироси» (Хиросима). Аргумент вначале
сравнивается с ключом, находящимся в середине таблицы
т. е. восьмым ключом «тиха». Поскольку аргумент поиск
больше ключа в середине таблицы, то искомый ключ располо
Поиск данных по ключу
51
в нижней части таблицы. Теперь аргумент сравнивается
ж средним ключом нижней половины таблицы — двенадцатым
С лючом «хиуко», и так как он больше и этого ключа, то сле¬
дующее сравнение выполняется с четырнадцатым ключом
JLKyo». Поскольку аргумент меньше этого ключа, он срав¬
нивается с тринадцатым ключом «хироси», и на этом этапе
поиск заканчивается успехом. Если бы аргумент поиска имел
значение «фукуи» (Фукуи), поиск, как легко видеть, не
мог бы закончиться успешно, так как в таблице такого ключа
нет.
А что, если вместо последовательной таблицы использо¬
вать для поиска бинарное дерево, построенное так, как пока¬
зано на рис. 2.6,6? Особенностью этого бинарного дерева яв¬
ляется то, что все ключи в левом поддереве меньше, а в пра¬
вом поддереве — больше ключа корня. Правильнее сказать:
1) в каждом узле (не пустом) этого бинарного дерева
содержится по одному значению ключа,
2) для каждого узла дерева все ключи в левом поддереве
меньше, а в правом поддереве больше значения ключа дан
ного узла.
Такое бинарное дерево называют также бинарным дере-
вом поиска.
Затраты времени на поиск по бинарному дереву поиска
оказываются такими же, как и затраты времени на поиск
в упорядоченной таблице с использованием метода деления
пополам. Вначале аргумент поиска сравнивается с ключом,
находящимся в корне. Если аргумент совпадает с ключом,
поиск закончен, если же не совпадает, то в случае, когда ар¬
гумент поиска оказывается меньше ключа, поиск продолжа¬
ется в левом поддереве, а в случае, когда аргумент оказы¬
вается больше ключа, — в правом поддереве. Увеличив уро¬
вень на 1, повторяют сравнение, считая данный узел корнем.
Поиск считается неудачным, если при достижении листьев
совпадение не обнаруживается. В противном случае к этому
моменту поиск должен закончиться успехом.
Если множество ключей фиксировано, как в вышеприве¬
денном случае, то нет особого преимущества в программе,
опирающейся на использование бинарного дерева поиска.
Более выгодным, скорее, можно считать метод поиска деле¬
нием таблицы пополам, поскольку программа при этом ока¬
зывается сравнительно простой; в представлении такой струк-
гУры данных также особой сложности нет.
Однако в случае, когда множество ключей заранее неиз¬
вестно или когда это множество ключей меняется, вставки
л Удаления ключей в таблице оказываются довольно трудо¬
емкими. Более рационально использовать в таком случае би¬
нарное дерево поиска, которое позволяет значительно проще
52
Глава 2
вставлять и удалять элементы. Например, если необходимо
построить таблицу частоты использования отдельных слов
в некотором тексте на естественном языке, то для представ-
ления таблицы в памяти лучше использовать бинарное де¬
рево поиска. С другой стороны, если сравнивать поиск по
дереву с методом хеширования, который будет рассмотрен
ниже (разд. 23), то оказывается, что поиск по бинарному
дереву хотя и уступает методу хеширования в части затрат
времени на сам поиск, но имеет и свои преимущества:
сравнительно высокий коэффициент использования памяти
для размещения данных, возможность получать упорядочен¬
ный в алфавитном порядке список ключей.
3) Полностью сбалансированные деревья
Как было показано выше, число вариантов структуры
При п= 15 это число возрастает до 9 694 845. Входящая
в это число структура бинарного дерева, показанная на
рис. 2.6,6, очень специфична. Высота этого бинарного дерева
минимальна, а правое и левое поддеревья полностью сбалан¬
сированы. Такое бинарное дерево называют полностью сба¬
лансированным бинарным деревом.
В общем случае бинарное дерево с произвольным числом
узлов п (где п не обязательно равно 2k— 1) называется пол¬
ностью сбалансированным деревом, если высота левого под¬
дерева каждого узла отличается от высоты правого подде¬
рева не более чем на 1.
Если задано п различных ключей, то можно построить
столько бинарных деревьев поиска, сколько структурно раз¬
личных бинарных деревьев существует для этого п. Напри¬
мер, для п = 4 существует 14 бинарных деревьев поиска, по¬
казанных на рис. 2.7, в предположении, что ключи равны
1, 2, 3, 4. Структурно эти деревья идентичны деревьям, по¬
казанным на рис. 2.5. В соответствии с определением только
четыре структуры из этих 14 (6, е, я, п) являются полностью
сбалансированными бинарными деревьями. При п =15 среди
9 694 845 бинарных деревьев поиска будет только одно пол¬
ностью сбалансированное бинарное дерево, имеющее струк¬
туру, показанную на рис. 2.6,6. При я =16 таких деревьев
будет всего лишь 8 из 35 357 670 бинарных деревьев. Эти
примеры убедительно свидетельствуют о том, что' полностью
сбалансированные деревья крайне редки даже в случае би¬
нарных деревьев.
Если задано множество различающихся между собой клю¬
чей, то каждому бинарному дереву поиска будет соответство-
бинарного дерева с числом узлов п составляет
Поиск данных по ключу
53
рать своя процедура поиска, зависящая от характера этого
дерева. Например, бинарные деревья на рис. 2.7, а и и соот¬
ветствуют процедуре последовательного поиска в списках,
упорядоченных по убыванию и возрастанию ключей соответ¬
ственно. Деревья на рис. 2.7, д и н соответствуют процедуре
поиска в методе деления пополам, когда аргумент поиска
Рис. 2.7. Все бинарные деревья поиска с четырьмя узлами. Деревья д, е,
п, р полностью сбалансированы.
сравнивается (для четных га) с (га/2-f- 1)-м или (га/2— 1)-м
ключом соответственно. Итак, любое бинарное дерево можно
интерпретировать как соответствующее дерево поиска. По¬
этому о свойствах того или иного метода поиска можно су¬
дить по характеру реализуемого им бинарного дерева. В ка¬
честве очень простого примера попробуем подсчитать сред¬
нее число сравнений в методе деления пополам по характеру
реализуемого им полностью сбалансированного бинарного
дерева.
Высота полностью сбалансированного бинарного дерева
Для множества, содержащего п ключей, будет равна
riog2(/z+ 1)1-
Обозначение \х~\ соответствует минимальному целому числу,
большему х («потолок» х), a |_*J —максимальному целому
числу, меньшему х («пол» х) (по К. Е. Иверсону). Кроме
того, если перенумеровать узлы дерева сверху вниз и слева
направо в порядке (1), (2, 3), (4, 5, 6, 7), (8, ...), то очевид¬
но, что k-й узел будет расположен на log2(6+ 1) уровне.
Обозначим через Сп среднее число сравнений при удачном
поиске (когда аргумент поиска обязательно совпадет с од¬
ним из ключей заданного множества) в предположении, что
каждый из п ключей с равной вероятностью является
54
Глава 2
аргументом поиска. Число сравнений до совпадения аргу.
мента с ключом узла равно длине пути (числу узлов) от
корня до этого узла, т. е. уровню этого узла. Следовательно,
cn = i Z Г log, (ft+1)1. (2.1)
I < k < П
Очевидно, что правая часть этой формулы при больших
значениях п почти равна log2n. Попробуем найти ее точное
значение. Рассмотрим вначале формулу, полезную для вы¬
числения некоторых сумм, содержащих [аД:
Y, ак = пап— £ k(ak+{ — ак). (2.2)
1 < fe < ГС 1 < & < ГС
Нетрудно показать справедливость этого соотношения.
пап— Z kak+,+ £ kak =
1 <fc<rc 1 </г<гс
= пап — £ (ft — 1) а* + S kak — пап = Z ак•
1 < /г < гс 1 < /г < гс 1 < /г < гс
В свою очередь сумма ал = Tlog2(& + 1)1 представляет со¬
бой сумму первых членов ряда 1, 2, 2, 3, 3, 3, 3, 4, ... для
k = 1, 2, 3, 4, 5, 6, 7, 8, ..., и, поскольку
Г 1 (при k, равном (степени двойки) — 1)
ал+1 а£ | q (в0 всех остальных случаях),
правая часть формулы (2.2) в этом случае будет равна
«Г log2 (/i+l)l— Z (2Г — 1) =
1 <r<rIog2(«+l)i
= nriog2(n+ l)l + riog2(n+ 1)1-(2г1ов1(я+1>1- 1) =
= (я+ l)riog2(«+ l)l-2r,og!(tt+1,1+ 1.
Таким образом, формула (2.1) будет иметь вид
С - (”+ 1) Г log2 (« + 1)1-2Г 1°еП»+1)1+ | ^ ^
А каково будет среднее число сравнений в случае неудач-
ного поиска, когда аргумент не совпадает ни с одним из клю-
чей? Для этого исследуем, например, где будет заканчиваться
неудачный поиск для дерева, показанного на рис. 2.7, д. За¬
давая различные аргументы, нетрудно убедиться, что неудач¬
ный поиск всякий раз будет заканчиваться в одном из узлов
показанных на рис. 2.8 прямоугольниками. В общем случае
анализ неудачного поиска станет проще, если использовать
расширенную диаграмму бинарного дерева. Для этого всюду
где в исходном дереве (узлы которого до сих пор изобража*
Поиск данных по ключу
55
лись на рисунках кружками) имеется пустое поддерево, не¬
обходимо добавить специальный прямоугольный узел (как
на рис. 2.8). Круглые узлы бчцем называть внутренними уз-
Рис. 2.8. Расширенное дерево поиска, в котором к внутренним (помечены
кружками) добавлены внешние (помечены прямоугольниками) узлы.
Структурно оно соответствует дереву на рис. 2.7, д.
лами расширенного дерева поиска, а прямоугольные — внеш¬
ними.
Для произвольного бинарного дерева между числом пе
внешних концевых узлов и числом п внутренних узлов имеет
место простая зависимость
Сумму длин путей от корня к каждому внутреннему узлу
называют длиной внутреннего пути и обозначают 1п. Анало¬
гично сумму длин путей от корня к каждому внешнему (кон¬
цевому узлу) называют длиной внешнего пути и обозна¬
чают Еп. Между этими двумя величинами существует про¬
стая зависимость
Справедливость этой формулы может быть показана сле¬
дующим образом. Если заменить концевой узел уровня k
на внутренний узел (увеличив п на 1), то значение 1п увели¬
чится на k—1, а Еп — на 2k— (k—1) и формула получится
индукцией по числу узлов. В случае когда поиск заканчи¬
вается успехом, среднее число сравнений можно выразить
через длину внутреннего пути как Сп = {1 п/п)-\- 1.
В противном случае при условии, что частота попадания
в любой из концевых узлов от 1 до n + 1 одинакова и равна
*/(«+о, среднее число сравнений для неудачного поиска
Сражается формулой
| х<1 1 | 1<х<2|
пе = п+ 1.
Еп — In + 2 п.
гДе величина Сп определяется формулой (2.1А),
56
Глава 2
4) Представление бинарных деревьев в памяти ЭВМ
Среди бинарных деревьев полностью сбалансированные де-
ревья имеют наиболее простую структуру и могут быть пред,
ставлены в памяти ЭВМ без использования указателей. Об
этом представлении речь будет идти при рассмотрении ме¬
тода сортировки посредством дерева выбора в гл. 3.
Для того чтобы структуру произвольного бинарного дере¬
ва представить в памяти ЭВМ, необходимо как минимум сле¬
дующее:
1) Каждый узел должен содержать один ключ и два ука¬
зателя на левое и правое поддеревья.
2) Для того чтобы показать, что узел не имеет левого и
правого поддеревьев, его следует соответствующим образом
«пометить», что обычно делают путем введения вместо ука-
зателя признака его отсутствия — поля nil. Вместо этого
можно ввести указатель на некоторый специальный узел
(«сторож») и присвоить ему значение ключа, которым не
будет обладать никакой другой узел (например, использо¬
вать ключ, все биты которого равны 1). Последнее решение
позволяет в значительной мере упростить программу. Подоб¬
ные деревья называют деревьями со сторожем.
3) Чтобы сделать дерево доступным для обработки, необ¬
ходимо задать указатель на корень root. Пример такой струк¬
туры показан на рис. 2.9, а описание ее на Паскале — на
рис. 2.10.
Вышеприведенную структуру следует рассматривать не
более как схему. Например, в узле могут храниться кроме
ключа также и данные, если они имеют небольшой объем.
При большом объеме таких данных их хранят обычно от¬
дельно, а в узел включают соответствующий указатель. Ча¬
сто бывает целесообразно хранить в каждом узле не только
указатели на порожденные поддеревья, но и указатель на
исходный узел. Кроме того, для упрощения поиска жела¬
тельно иметь в каждом узле данные о числе узлов левого
поддерева:
(число узлов левого поддерева данного узла)+ 1-
Однако в связи с тем, что все эти расширения приводят не
только к увеличению занимаемого пространства памяти, но
и к усложнению операций обновления данных, необходимо
очень тщательно анализировать все плюсы и минусы в зави-
симости от того, какие данные хранятся в узле и в каком
виде, какие операции будут выполняться над деревьями, ка¬
ковы объем памяти и вычислительные ресурсы ЭВМ, которая
будет использоваться.
Поиск данных по ключу
57
£
key 1
nil | nil
hej/3
key 2
key 6
key 4
nil nil
key 5
hey 7
Р I
nil I nil
d}~
hey 6
ГГП
Рис. 2.9. Пример бинарного дерева: а — диаграмма дерева; б — пример
отображения дерева на память.
type ref = \node\
node = record key: char ;
left, right: ref
end ;
Var root: ref;
Рис. 2.10. Описание структуры дерева, показанной на рис. 2.9, на языке
Паскаль.
2.1.3. Оптимальные и случайные деревья
1) Оптимальные деревья
В предыдущем подразделе мы оценили среднее значение
числа сравнений в случае равенства частот для каждого из
ключей списка (когда поиск заканчивается удачей) и в слу¬
чае равенства частот неудачного поиска (частот реализации
любого из путей, при котором поиск заканчивается неудачей).
И без доказательства очевидно, что число сравнений при по¬
иске по полностью сбалансированному бинарному дереву бу¬
дет не больше числа сравнений при поиске по любому дру-
г°му бинарному дереву. Таким образом, полностью сбалан¬
сированное бинарное дерево представляет собой оптимальное
бинарное дерево поиска для случая, когда все ключи (аргу¬
менты) поиска равновероятны.
Однако нередки случаи, когда частоты появления ключей
Не равны между собой и при этом заранее известны. Напри-
58
Глава 2
253 345 Z08
а
5
Рис. 2.11. Оптимальные деревья поиска: а — случай удачного поиска (ча¬
стота появления ключей пропорциональна численности населения); б —
случай, охватывающий удачный и неудачный поиски (частота появления
ключей пропорциональна численности населения всех префектур).
мер, рассмотрим поиск по бинарному дереву для случая, ко¬
гда в качестве ключей используются названия префектур
рис. 2.6. а. При этом можно построить два оптимальных би¬
нарных дерева, показанные на рис. 2.11, а и б соответственно:
а) первое для случая, когда аргумент поиска обязательно
совпадает с одним из ключей списка (15 названий наиболее
важных префектур), и частоты их появления пропорциональ¬
ны численности населения соответствующих префектур (этот
частный случай соответствует удачному поиску по взвешен¬
ному дереву);
Поиск данных по ключу
59
б) второе для случая, когда в качестве аргумента поиска
может быть использовано название любой из префектур Япо¬
нии, и частоты их появления пропорциональны численности
населения соответствующих префектур (это общий случай
взвешенного дерева поиска).
Каков же алгоритм построения этих оптимальных де¬
ревьев поиска? Рассмотрим вначале случай, когда дерево
содержит четыре внутренних узла (и, следовательно, пять
внешних).
Так как значения ключей в дереве должны быть соответ¬
ствующим образом упорядочены, присвоим внутренним узлам
и К Jt м И П р
Рис. 2.12. Все структурно различные бинарные деревья поиска с четырьмя
внутренними (и пятью концевыми) узлами.
номера 1, 2, 3, 4, такие же номера присвоим и внешним
(концевым) узлам: 0, 1, 2, 3, 4. На рис. 2.12 показаны все
варианты взаимного расположения ключей в узлах, и струк¬
турно они соответствуют вариантам деревьев, показанных
на рис. 2.7, и отличаются от последних только тем, что до¬
бавлены концевые узлы. Обозначим частоту (вероятность),
с которой аргумент поиска примет значение, равное ключу
i-ro внутреннего узла (1 ^/^4), через р*, частоту (вероят¬
ность), с которой аргумент поиска окажется меньше значе¬
ния 1-го внутреннего узла (частоту неудачного поиска, завер¬
шающегося в нулевом внешнем узле), через р0, частоту (ве^
роятность), с которой аргумент поиска окажется больше зна¬
чения /-го и меньше значения (/-(- 1)-го внутреннего узла
(1^/^4) (частоту неудачного поиска, завершающегося
в i-ы внешнем узле), через qt, и частоту, с которой аргумент
окажется больше значения 4-го внутреннего узла, через р4.
Если заданы значения рь ..., р4 и q0i ..., q4) то среднее
значение (математическое ожидание) числа сравнений при
Поиске будет выражаться как
У Pi ■ (уровен @) + £ qk- (уровень m - l).
J</<4 ^ 0</г<4 1
60
Глава 2
Во второй сумме —1 говорит о том, что, хотя неудачный
поиск всегда заканчивается в одном из внешних узлов, аргу¬
мент поиска сравнивается только со значениями ключей внут¬
ренних узлов. Поэтому формулы, в которых в качестве «за¬
трат на поиск» будет принята взвешенная длина пути или
математическое ожидание числа сравнений, окажутся раз¬
ными. Будем рассматривать дальше формулу для математи¬
ческого ожидания числа сравнений. Задача состоит в опре¬
делении, какой из вариантов бинарного дерева, показанных
на рис. 2.12, минимизирует математическое ожидание числа
сравнений при поиске. Например, для бинарного дерева (г)
математическое ожидание числа сравнений будет равно
2<7о + 2/?! + Здй + Зр2 + 4^ + 4р3 + 4^3 + Я\ + Ра-
Это значение будем считать затратами на поиск по этому
бинарному дереву. Назовем эти затраты ценой дерева, а оп¬
тимальным деревом — дерево с минимальной ценой.
При таком определении оптимального дерева при подсчете
цены произвольного дерева нет необходимости требовать,
чтобы общая сумма р и q(pь •.., Рп\ ?о> . •., Цп) обяза¬
тельно равнялась единице (т. е. не обязательно для частоты
использовать нормализованное значение). Благодаря этому
появляется возможность говорить о дереве с минимальной
ценой для заданной последовательности «весов», понимая под
весом не только частоту, но и число шагов алгоритма, число
людей и т. п. Если обозначить уровень ©-го внутреннего
узла через //, а уровень |Т|-го внешнего узла — через /Л, то
затраты на поиск по дереву можно выразить формулой
S РЛ+ £ <7* (/;-!). (2.4)
КК/1 11 0 4 '
Для примера попробуем на основе вычисления цены
найти оптимальные деревья для каждой из трех комбинаций
весов:
W{ = ( 1, 1, 1, 1; 1, 1, 1, 1, 1),
W2 = (5, 3, 1, 1; 5, 1, 1, 1, 1),
Г3 = (5, 1, 4, 1; 5, 1, 1, 1, 1).
В табл. 2.2 приведены набор коэффициентов формулы
(2.4) для всех вариантов расположения узлов в дереве от а
до р на рис. 2.12 и цена каждого дерева для трех комбина¬
ций весов, которые приведены в верхней части таблицы. Для
каждой комбинации весов минимальные цены обведены круж¬
ками. Из таблицы следует, что для Wi оптимальными будут
полностью сбалансированные деревья (д), (е), (н), (/г),
Поиск данных по ключу
61
для \V2 — деревья последовательного поиска (и) и (/с) и де¬
рево (р), для Wз — единственное оптимальное дерево (р).
Таблица 2.2. Набор коэффициентов формулы (2.4) для вариантов
расположения узлов на рис. 2.12
Коэффициенты формулы (2,4) Затраты
Ьари- _
анты
распо¬
ложе¬
ния
01
07
Pi
р
Я\
Q.
Q’Л
ц.
иг.
П. 1. 1. 1;
1. 1, 1. 1-
1)
W.
(5. 3. 1. 1;
5. 1, 1. 1.
1)
W3
(5, 1. 4. 1;
5. 1, 1. 1,
1)
а
4
3
2
1
4
4
3
2
1
24
62
62
б
3
4
2
1
3
4
4
2
1
24
56
54
в
2
4
3
1
2
4
4
3
1
24
48
49
г
2
3
4
1
2
3
4
4
1
24
46
52
д
3
2
1
2
3
3
2
2
2
®
48
47
€
2
3
1
2
2
3
3
2
2
®
42
39
Ж
3
2
3
1
3
3
3
3
1
22
50
55
И
1
2
3
4
1
2
3
4
4
24
®
41
К
1
2
4
3
1
2
4
4
3
24
®
44
л
1
3
4
2
1
3
4
4
2
24
36
44
м
1
4
3
2
1
4
4
3
2
24
40
41
н
2
1
2
3
2
2
2
3
3
®
38
42
п
2
1
3
2
2
2
3
3
2
®
38
45
р
1
3
2
3
1
3
3
3
3
22
®
©
Рассмотренный метод поиска оптимальных деревьев на
основе полного перебора структур и прямого вычисления
цены имеет определенные ограничения — в частности, по мере
увеличения числа внутренних узлов экспоненциально увели¬
чивается число соответствующих им бинарных деревьев. При
больших значениях п число таких деревьев приблизительно
можно оценить по формуле Стирлинга
_1 (2ПЛ^ 4”
п + 1 \ П ) Уя п3,2
Так что практически невозможно перебрать все деревья и
выбрать из них лучшее. Очевидно, что здесь требуется совер¬
шенно другой подход.
Прежде всего попытаемся выяснить, являются ли подде¬
ревья оптимального дерева также оптимальными деревьями.
На первый взгляд это очевидно. Однако даже для одного и
того же дерева (является ли оно поддеревом большего де¬
рева или нет) значения уровней соответствующих узлов
62
Глава 2
окажутся различными. Таким образом, поскольку вклад весоа
в формуле (2.4) различен, вышеприведенное утверждение
уже не кажется столь очевидным.
Обозначим через t(i,j) поддерево оптимального дерева,
имеющего веса (рь •••. Pi+ь • • •. Pi, ■ ■ ■, Рп\ <?о <7ь
Уровни
Корень.деРева
г>—^
Рис. 2.13. t(u j)—поддерево оптимального дерева.
..., qh ..., qn), содержащее внутренние узлы (i +1) ,
... , Q) и внешние узлы jJJ, ..., |У| (рис. 2.13). Из всех
затрат на поиск по этому оптимальному дереву вклад t(i,j)
можно выразить как
- /■р‘ ('“+1‘ ~+1 «?</,к ('"+~2) “
= Ст— Р{ Pk + Z <7*} +
+ { 2 p^k + 2 ^ (^4 ~ Ь
где /т —уровень @ го корневого узла поддерева, у ;,,
Lk — уровни (g) -го внутреннего и [X]-го внешнего узлов со¬
ответственно этого поддерева.
Для узлов, образующих это поддерево, первое слагаемое
правой части формулы является константой, а второе сла¬
гаемое выражает затраты на поиск по поддереву, и, если это
поддерево является поддеревом оптимального дерева, затра¬
ты на поиск по нему будут минимальными.
Поиск данных по ключу
63
Если использовать рассмотренное выше свойство, ;о мож¬
но найти оптимальное дерево и для сравнительно больших я.
Обозначим значения, заключенные в первой и второй фигур¬
ных скобках правой части вышеприведенной формулы, отно¬
сящейся к поддереву t(i9j) оптимального дерева, через w(itj)
и c(i9j) соответственно. Теперь, если считать, что для 0^^
^ ^ п
w(i> /)= £ Pk+ Z </t (сумма весов узлов),
C{i, f)= £ pkLk+ £ qk{L'k- 1) (затраты на поиск
i+\<k<i i<*<i по поддереву),
(2.5)
то как само поддерево t{i9j), так и оба его поддерева долж¬
ны быть оптимальными деревьями, так как t(i9j) является
поддеревом оптимального дерева. Из оптимальности t(i9j)
следует, что минимально возможная цена дерева с корнем k
равна
с (i, j) = w (t, j) + rnin (C (/, k — 1) + с (k, /)) (i < j),
i<k^j
c {i9 0 = 0. (2.6)
Для нахождения оптимального дерева прежде всего по
заданным значениям весов подсчитывают полный вес w(i,j)
по формуле (2.5). Затем по формуле (2.6) вычисляют c(i9j)—
цены деревьев для j—i= 1,2, ..., п. Для этого вначале
фиксируют корень k дерева t(i9j)9 затем вычисляют значение
второго слагаемого формулы (2.6) и результат записывают
в таблицу г (i9 j).
Значения w(i,j), c(i9j) и r(i9j) для случая, когда веса
(рь р2, р3, р4; Qo, cj\9 cj2, q?,, q4) = (5, 1, 4, 1; 5, 1,1,1, 1), показа¬
ны на рис. 2.14, а — в. По найденным значениям r(iyj) можно
построить оптимальное дерево следующим образом:
1) Положить т = г(0, п). Это корень.
2) Поддеревьями дерева с корнем ® будут деревья
t(0ym—1) и t(m9n)9 а корнями этих поддеревьев оптималь¬
ного дерева будут г (0, т — 1) и г (т9 п).
3) В общем случае, если корнем поддерева t(i9j) является
узел @ , корни его правого и левого поддеревьев опреде¬
ляются как г(i9 т— 1) и r(m, /) соответственно.
Построенное по этим правилам оптимальное дерево по¬
казано на рис. 2.14, г. Оно совпадает с деревом (р), показан¬
ным на рис. 2.12.
В соответствии с вышеизложенным методом число значе¬
ний c(i9j)9 которое должно быть найдено, составляет при¬
мерно (1 /2) лг2. При этом для того, чтобы найти минимальное
64
Глава 2
**(*.>) С ( I* >)
X
0
1
2
3
4
X
0
1 2 3
4
0
5
11
13
18
20
0
0
11 16 29
36
1
1
3
8
10
1
0 3 11
16
2
X
6
8
2
0 6
11
3
1
3
3
0
3
4
1
4
0
а
6
fU,j)
0
1
2
3
4
0
0
1
1
1
1
<2
5
1
0
2
3
3
GD
5
ХГч
2
0
3
3
Т4)
Is
ч /i\
3
0
4
ш
0 ш В
1
1 1 1
4
0
г
Рис. 2.14. Построение оптимального дерева с весом (5,1,4,1; 5,1,1,1,1)
(а — в) \ г — оптимальное дерево Цифрами возле узлов показаны их веса.
значение, соответствующее формуле (2.6), необходимо ис¬
следовать примерно (1/6)п3 значений k. При этом объем па¬
мяти, необходимый для расчета, будет составлять (3/2)п2.
Таким образом, для построения оптимального дерева требу¬
ется 0(п3) единиц времени и 0(п2) объемов памяти (здесь
речь идет о временной и емкостной сложности алгоритмов,
и 0(п3) — временная, а 0(п2) — емкостная сложность рассмот¬
ренного алгоритма).
На самом деле для того, чтобы найти значение, минимизи¬
рующее второе слагаемое формулы (2.6), нет необходимости
проверять все k из диапазона i <С k ^ /, достаточно про¬
верить только k из области r(i>j—1) ^ k ^ r(i -f- 1, /). В ре¬
зультате модифицированный таким образом алгоритм потре¬
бует такого же объема памяти, как и вышеприведенный ал¬
горитм— О (я2), но зато необходимое время сократится до
О (п2). Оптимальные деревья, представленные на рис. 2.11,
получены с помощью именно такого метода.
2) Бинарные деревья поиска для данных, вводимых в случайном
порядке
До сих пор рассматривались случаи, когда все множество
ключей заранее известно, и допускалась определенная сво¬
бода в выборе конкретной структуры дерева поиска. Но ка¬
Поиск данных по ключу
65
кую структуру дерева выбрать и как ее поддерживать в тех
случаях, когда ключи задаются из некоторого допустимого
множества ключей в случайном порядке и для всех ключей,
заданных до этого момента, должен быть обеспечен поиск по
дереву?
Конечно, в случае, когда ключи вводятся в дерево в слу¬
чайном порядке, нет ничего невозможного в том, чтобы пе¬
рестраивать дерево, которое было составлено до этого мо¬
мента, и заново строить полностью сбалансированное или
оптимальное дерево. Однако если учесть требуемые для этого
затраты времени и оперативной памяти, то станет ясно, что,
за исключением отдельных особых случаев, это практически
нереально. Поэтому обычно при построении дерева стараются
сохранять, насколько возможно, прежнюю структуру дерева,
просто вставляя в него новые узлы, совершенно не перемещая
других узлов, или ограничиваться по возможности частич¬
ными изменениями для придания дереву желаемых свойств
(например, приближенной сбалансированности). Рассмотрим
свойства случайных деревьев, построенных по методу вставки
узлов без изменения ранее образованной структуры дерева.
Для вставки ключа в случайное дерево можно использо¬
вать следующий алгоритм (предполагается, что все ключи
имеют разные значения):
1. Если корень пуст, поместить в него заданный аргумент.
2. Если корень непуст, сравнить значения ключа узла с ар¬
гументом.
2.1. Если значение ключа узла больше аргумента, перейти
в левое поддерево и повторить вышеуказанные операции.
2.2. Если значение ключа узла меньше аргумента, перейти
в правое поддерево и повторить вышеуказанные опе¬
рации.
Если, используя эту процедуру, построить дерево для на¬
званий префектур, приведенных на рис. 2.6, а, вводя в него
названия префектур в порядке их географического располо¬
жения с севера на юг (как в табл. 2.1), то получится случай¬
ное дерево, показанное на рис. 2.15, а. Если же при построе¬
нии дерева вводить названия в порядке возрастания числен¬
ности населения префектур, получим дерево, показанное на
рис. 2.15 б.
Даже без внимательного анализа этих деревьев видно,
что по сравнению с полностью сбалансированным деревом,
представленным на рис. 2.6, б, структура этих деревьев много
«хуже». Если бы ключи поступали в прямом (алфавитном)
или обратном порядке возрастания значений, го дерево
стало бы «вырожденным». А если порядок поступления клю¬
чей соответствует приведенному в скобках (Айти, Хоккайдо,
3 Зак. 127
66
Глава 2
Ибараки, Фукуока, Осака, Хиросима, Канагава, Хёго, Киото,
Ниигата, Сайтама, Нагано, Сидзуока, Токио, Тиба), то полу¬
чится зигзагообразное дерево, показанное на рис. 2.15,6.
Итак, задача состоит в том, чтобы выяснить, до какой
степени можно допускать увеличение числа сравнений при
поиске со вставкой по дереву. Для этого найдем среднее
Рис. 2.15. Бинарные деревья поиска для данных, вводимых в «случайном»
порядке: а —в порядке географического расположения с севера на юг;
6 — в порядке возрастания численности населения; в — вырожденное де¬
рево.
число сравнений для случайного дерева при равенстве весов
всех п внутренних узлов.
Предположим, что каждая из п\ перестановок п различ¬
ных ключей используется с равной вероятностью для по¬
строения случайного дерева путем вставок (это не значит,
что случайное дерево в действительности строится из п\ уз¬
лов— оно содержит ровно п узлов, просто вероятности ис¬
пользования каждой из п\ перестановок равны). При задании
некоторого ключа (внутреннего узла) в качестве аргумента
поиска число сравнений, нужных для нахождения этого
ключа, на единицу больше числа сравнений, потребовав¬
шихся (в случае неудачи) при вставке этого ключа в дерево.
Среднее число сравнений Сп при удачном поиске можно вы¬
разить через среднее число сравнений С'п при неудачном
поиске, учитывая, что вероятности вставки этого ключа в пер¬
вый, второй, ..., п-й узел равны, следующим образом:
^сиросц)
а
С другой стороны, если использовать ранее полученную за-
висимость (2.3) между Сп и С'п для произвольного бинар¬
Поиск данных по ключу
67
ного дерева, получим
т. е. (п + 1) С' = 2п + 1 + С' + С' + • • • + C'n-i*
Вычитая из этого соотношения равенство
пСп-\ = 2/2 ~ 1 + С' + С' + ... + С'_2,
получим
с:=с'
Так как С' = 0, то
п п-1 1 я + 1
С'„ = 2Я„+1-2.
Таким образом,
где Нп — гармоническая постоянная, равная
Нп=1-\--^ + -о + • • • + V ~ 1°£е я + С +
2 I з • • • * I п I ^ I 12/г2 -т- • • •»
С = 0,5772 (постоянная Эйлера).
При больших п
Сп « 2 loge /г.
Если взять отношение между этим выражением и полу¬
ченным в разд. 2.1.2 средним числом сравнений для полно¬
стью сбалансированного дерева log2м, то оказывается, что
2 loge n/log2 п = 2 loge 2 == 1 >386 . . .,
т. е. число сравнений для случайного дерева в среднем всего
лишь примерно на 39 % превышает число сравнений для пол¬
ностью сбалансированного дерева и увеличивается с увели¬
чением числа узлов п всего лишь в логарифмической пропор¬
ции. Таким образом, среди случайных деревьев редко
встречаются вырожденные, а большей частью — достаточно
хорошо сбалансированные деревья; следовательно, число срав¬
нений не слишком увеличивается, если даже не пытаться пре¬
вратить случайное дерево в полностью сбалансированное.
2.1.4. Сбалансированные деревья (АВЛ-деревья)
Итак, мы выяснили, что в случае, когда ключи списка за¬
даются в случайном порядке, редко встречается необходи¬
мость искусственным путем превращать его в полностью сба¬
лансированное дерево. Однако не исключена возможность,
з*
68
Глава 2
что построенное дерево окажется вырожденным, и тогда чи¬
сло сравнений при поиске увеличится и станет пропорцио¬
нальным числу узлов п. Кроме того, может оказаться, что
предположение о полностью случайном порядке, в котором
ключи'вставляются в дерево, не соответствует реальным дан¬
ным. Таким образом, необходимо обратить внимание также
на то, что по сравнению с вышеописанным идеальным слу¬
чаем вероятность появления вырожденного дерева на прак¬
тике может оказаться много больше. А нельзя ли, используя
сравнительно простые средства и ослабив условия сбаланси¬
рованности, построить «почти сбалансированное» дерево, та¬
кое, чтобы и в самом неблагоприятном случае число сравне¬
ний при поиске (высота дерева) ограничивалось порядком
log п?
Одно из решений этой проблемы предложили два совет¬
ских математика — Г. М. Адельсон-Вельский и Е. М. Ландис.
В соответствии с их определением
Определение 2.3. Бинарное дерево называется сбаланси¬
рованным, если высота левого поддерева каждого узла отли¬
чается от высоты правого поддерева не более чем на 1.
Эти деревья называются в честь этих математи¬
ков АВЛ-деревьями, или просто сбалансированными де¬
ревьями.
Посмотрим, что включает в себя понятие сбалансирован¬
ного дерева. Ясно, что полностью сбалансированные деревья
являются частным случаем «сбалансированных деревьев» и
среди сбалансированных деревьев они являются деревьями
с минимальной высотой при заданном числе узлов. Посмот¬
рим, что представляют собой сбалансированные деревья
максимальной высоты.
Обозначим через h высоту наиболее высокого из всех воз¬
можных сбалансированных деревьев с заданным числом уз¬
лов. Очевидно, что среди сбалансированных деревьев вы¬
соты h это будет дерево с наименьшим числом узлов. Бинар¬
ное дерево, обладающее этим свойством, обозначим через 7V
Тогда одно поддерево корня, например левое, будет иметь вы¬
соту h—1. В силу определения Th можно считать, что левое
поддерево корня есть дерево Тн-\. Правое поддерево может
иметь высоту h—1 или h — 2, но, поскольку дерево должно
содержать наименьшее число узлов, следовательно, его вы¬
сота должна быть минимальной, поэтому будем считать его
деревом 7\_2. Следовательно, одно из двух поддеревьев
должно быть более высоким. Им может быть как правое, так
и левое поддерево. Ограничимся рассмотрением случая, ко¬
гда более высоким является левое поддерево.
Поиск; данных по ключу
69
Дерево Т hy обладающее такими свойствами, называется
деревом Фибоначчи высоты h. Дадим рекурсивное определе¬
ние такого дерева.
1) Пустое дерево есть дерево Фибоначчи высоты 0.
2) Дерево с одним узлом есть дерево Фибоначчи высоты 1.
3) Бинарное дерево, левое и правое поддеревья которого
являются деревьями высоты h — 1 и h — 2 (обычно деревья
Рис. 2.16. Дерево Фибоначчи. Разница в номерах узлов, проставленная на
вегвях, представляет собой последовательность чисел Фибоначчи.
перечисляют в порядке слева направо, но может быть и на¬
оборот), есть дерево Фибоначчи высоты h.
Дерево Фибоначчи высоты 6 показано на рис. 2.16.
Как ясно из сказанного выше, АВЛ-дерево высоты h есть
дерево с наименьшим числом узлов /г, высота которого почти
равна log п. Можно дать и более точную оценку h:
l,44041og2(rt + 2) —0,328 >ft>log2(n+ 1). (2.7)
Поясним это утверждение.
Правое неравенство формулы (2.7) непосредственно выте¬
кает из зависимости высоты дерева от числа узлов, то есть
высота дерева будет минимальной только в случае полностью
сбалансированного дерева. Для того чтобы показать спра¬
ведливость левого неравенства, необходимо определить зави¬
симость между высотой h дерева Фибоначчи и числом уз¬
лов tih. Из приведенного выше определения следует, что
По == 0, П[ = 1, nh = nh_x + Н~ 1 •
Отсюда и из определения последовательности Fh чисел Фи¬
боначчи имеем
= 0» == 1» Fh.= Ffi—1 Fh—2>
и можно убедиться в том, что
Пн 2 !'•
70
Глава 2
Действительно, п0 = F2 — 1=0, а
nh+ 1 “ nh + nh-1 + * = Fh + 2 + ^/1+1 — 2 + 1 = /г/г+3 — I.
Общий член последовательности чисел Фибоначчи выража¬
ется как
nh
1
(4>h+2-i>h+2)-i,
V5
где ф = (1 + У5)/2 = 1,618 ..., ф = (1 - д/5)/2=- 0,618 ....
Поскольку абсолютная величина ф меньше 1, вклад второго
члена в скобках формулы для nh меньше 1 и по мере возра¬
стания h быстро стремится к нулю. С учетом максимального
вклада члена ф можно записать
"*>-уг*Л+2-2-
Если преобразовать это выражение, прологарифмировав обе
части по основанию 2, получим
Н < Т5ёЬг1о& <"* + 2> + лёт" - 2-
Поскольку среди ABJl-деревьев с числом узлов п высота де¬
ревьев Фибоначчи оказывается наибольшей, то, заменяя в
этой формуле пн на м, получим левую часть неравенства
(2.7).
Между полностью сбалансированными деревьями и де¬
ревьями Фибоначчи располагаются самые разные сбаланси¬
рованные деревья. Дадим следующее определение «показа¬
телю сбалансированности» узлов для деревьев произвольной
структуры:
(показатель сбалансированности узла) = (высота правого
поддерева этого узла) — (высота левого поддерева этого узла)
Ясно, что в АВЛ-дереве показатель сбалансированности
всех узлов равен или —1, или 0, или +1- В полностью сба¬
лансированном дереве для всех узлов, за исключением мак¬
симум одного узла, показатель сбалансированности равен
нулю. В дереве Фибоначчи для всех узлов, за исключением
листьев, показатель сбалансированности равен + 1 или —1*
В общем случае показатели сбалансированности узлов
АВЛ-дерева могут быть разными, как показано на рис. 2.17.
Теперь попррбуем произвести вставку новых ключей
в АВЛ-дерево. Если вставку новых ключей производить в де¬
рево, показанное на рис. 2.17, то вставляемый ключ займет
место одного из внешних узлов дерева а, Ь, . . ., и, который
станет после вставки внутренним узлом дерева. При этом
могут иметь место следующие случаи:
Поиск данных по ключу
71
1) Случай с. Показатель сбалансированности улучшается.
2) Случаи A, i, /, А, /, т. Показатель сбалансированности
ухудшается, но свойства ABJI-дерева сохраняются.
3) Все остальные случаи, за исключением указанных в 1)
и 2), нарушают свойства АВЛ-дерева. Появляются узлы
Рис. 2.17. Пример АВЛ дерева. Числами в кружках (внутренних узлах)
показаны значения ключей, цифрами рядом с кружками — показатели
сбалансированности.
е показателем сбалансированности +2 или —2, и для сохра¬
нения свойства сбалансированности АВЛ-дерева потребуется
некоторая корректировка структуры дерева.
Из трех указанных выше случаев 1) и 2) проблемы не
составляют. Посмотрим, как следует изменить структуру де¬
рева в случае 3), чтобы восстановить свойство сбалансиро¬
ванности АВЛ-дерева.
Рис. 2.18. Вставка ключа «1».
Например, пусть вставляется ключ со значением «1».
Часть структуры дерева после вставки вместе с показателями
сбалансированности узлов показана на рис. 2.18, а. Здесь
показатель сбалансированности узла «4» окажется равным
—2, и условия АВЛ-дерева перестанут удовлетворяться. По¬
пробуем восстановить баланс АВЛ-дерева, производя коррек¬
тировку его структуры в пределах этого поддерева. Вместо
узла «4» корнем этого поддерева можно сделать узел «2»,
72
Глава 2
совершив поворот узлов «2» и «4» направо, как показано
стрелкой.
Что произойдет, если в исходное дерево вставить ключ не
со значением «1», а со значением «3»? В этом случае вое*
становить баланс будет несколько сложнее. Вначале повер¬
нем налево узлы «2» и «3», как показано на рис. 2.19,а, и
а б в
Рис. 2.19. Вставка ключа «3».
получим структуру, показанную на рис. 2.19,6, которая ана¬
логична структуре на рис. 2.18, а. Теперь, если узлы «3» и
«4» повернуть направо, то участок дерева окажется сбалан¬
сированным, как показано на рис. 2.19, в.
Рассмотрим теперь случай, когда производится вставка
ключа «7». В этом случае (рис. 2.20, а) вблизи вставленного
Рис. 2.20. Вставка ключа «7».
узла сбалансированность сохраняется, однако результат
вставки сказывается выше — для узла «14» показатель сба¬
лансированности становится равным —2. Поскольку при этом
узел «14» находится точно в таком же положении по отно¬
шению к узлу «10», как и узел «4» по отношению к узлу «2»
на рис. 2.18, то, если совершить аналогичный поворот на¬
право, получим сбалансированный участок, как показано на
рис. 2.20,6. Однако при этом кроме поворота, показанного
на рис. 2.18, потребуется узел «12» открепить от узла «10»
и прикрепить к узлу «14». Вставка ключа «9» приводит почти
к такому же эффекту, как и вставка ключа «7»,
Поиск данных по ключу
73
Последовательность действий при вставке ключа «И»
в дерево показана на рис. 2.21 и, по существу, аналогична
действиям, показанным на рис. 2.19; только в этом случае
также при повороте узел «11» необходимо открепить от узла
Рис. 2.21. Вставка ключа «11».
«12» и прикрепить к узлу «10». Вставка ключа «13» выпол¬
няется аналогичным образом.
Если попытаться обобщить рассмотренные случаи коррек¬
тировки структуры дерева с целью балансировки, то получим
Рис. 2.22. Случай, когда для восстановления баланса достаточно одного
поворота.
диаграммы, показанные на рис. 2.22 и 2.23. На диаграммах
прямоугольниками обозначены поддеревья, «К» помечен са¬
мый нижний узел, показатель сбалансированности которого
после вставки по абсолютной величине становится больше 1,
для узла «К» и других существенных узлов показаны значе¬
ния их показателей сбалансированности. Если после вставки
показатели сбалансированности узлов имеют одинаковый
знак и отличаются только на единицу, как для узлов «К»
и «I» на рис. 2.22, то восстановить баланс дерева можно од¬
нократным поворотом (включая одно переприкрепление под¬
дерева), при этом вставка не будет оказывать влияния на
74
Глава 2
другие участки дерева. Если же после вставки показатели
сбалансированности имеют разный знак, как для узлов «К»
и «/» на рис. 2.23 (т. е. их разница по абсолютной величине
равна 3),то можно восстановить баланс дерева двукратными
поворотами трех узлов, включая узел «У» (используя два
переприкрепления поддеревьев). В этом случае вставка так¬
же не оказывает влияния на другие участки дерева. Итак,
Рис. 2.23. Случай, когда для восстановления баланса' требуется два
поворота.
все случаи, в которых после вставки необходима дополнитель¬
ная балансировка для сохранения свойств АВЛ-дерева, огра¬
ничиваются случаями, показанными на рис. 2.22 и 2.23, и слу¬
чаями зеркального отражения этих структур. Приведенный
анализ показывает принципиальную возможность вставки
с сохранением структуры АВЛ-дерева.
Оценим эффективность поиска со вставкой, считая, что все
вставляемые ключи поступают в случайном порядке. Для
этого потребуется ответить на следующие вопросы:
1) Как зависит математическое ожидание значения вы¬
соты от общего числа узлов п в дереве?
2) Какова вероятность возникновения случаев, не требую¬
щих дополнительной балансировки, случаев, требующих од¬
нократного поворота, и случаев, требующих двукратного по¬
ворота соответственно?
3) Как зависит число операций при вставке одного узла
от длины пути, ведущего из внешнего узла вверх и от числа
узлов п в дереве?
До сих пор не удалось дать точных ответов на эти воп¬
росы. Однако сочетание некоторых теоретических рассужде¬
ний и эмпирических результатов позволяет сделать следую¬
щие утверждения.
1) Математическое ожидание значения высоты при боль¬
ших п близко к значению log2/2 + 0,25.
Поиск данных по ключу
75
2) Вероятность того, что при вставке не потребуется до¬
полнительная балансировка, потребуется однократный пово¬
рот или двукратный поворот, близка к значениям 2/3, 1/6
и 1/6 соответственно.
3) Среднее число сравнений при вставке п-то ключа в де¬
рево выражается формулой a log2 п + b (а,Ь — постоянные).
Здесь опущены теоретические выкладки, которые доказы¬
вают утверждение, что трудоемкость удаления узлов из
АВЛ-дерева также зависит от числа узлов в дереве как
log2 п. Таким образом, АВЛ-дерево представляет собой струк¬
туру, для которой любая операция: поиск, вставка и удале¬
ние ключа имеет временную сложность 0(log2n).
2.1.5. Сильно ветвящиеся деревья
1) Сильно ветвящиеся деревья
Упорядоченные деревья, имеющие степень не менее 3, на¬
зываются сильно ветвящимися деревьями. Если считать, что
степень некоторого узла равна п, то он должен содержать
(п— 1) ключей и п указателей. Схема одного из таких узлов
показана на рис. 2.24. Если (п—1) ключей в узле связать
Ключ, л-1
(П~1) ключей
77 У ка за -
спелей
Рис. 2.24. Схема узла я-арного дерева.
между собой указателями, то для представления узла потре¬
буется уже 2 (п—1) указателей. Методы, использующие та¬
кую структуру хранения деревьев в памяти, оказываются
очень гибкими с точки зрения вставки и удаления ключей,
но с точки зрения затрат на поиск, требуемого объема памяти
и т. п. уступают рассмотренным выше методам. Поэтому эту
структуру можно рекомендовать только в тех случаях, когда
степени узлов дерева или длины ключей сильно отличаются
друг от друга.
Структура сильно ветвящихся деревьев существенно отли¬
чается от структуры бинарных деревьев.
1) Степень может меняться в зависимости от узла. Если
все узлы имеют одинаковую степень пу структура называется
м-арным деревом. Примером могут служить «(3—2)-деревья»,
из каждого узла которых выходит либо 2, либо 3 ветви, или
В-деревья, о которых речь будет идти в следующем подраз¬
76
Глава 2
деле, или структуры, используемые в методах индексно-по¬
следовательной организации файла, рассматриваемые в
разд. 4.1; во всех этих деревьях степень узла п непостоянна.
2) Ключ вышерасположенного узла может совпадать
с ключом (или частью ключа) нижерасположенного узла (на¬
пример, с наибольшим).
Очевидно, для хранения и поиска данных в оперативной
памяти сильно ветвящиеся деревья не имеют больших пре¬
имуществ перед бинарными деревьями. Можно было бы счи¬
тать, что при сравнительно малой длине ключа, а также
в случаях, когда нельзя пренебречь пространством памяти,
выделяемым для размещения указателей, использование
гс-арных деревьев, для которых достаточно указателей, всего
лишь в (п-\-\)/п больше, чем ключей, окажется более эф¬
фективным по сравнению с использованием бинарных де¬
ревьев, требующих числа указателей вдвое большего, чем
число ключей. Однако анализ затрат (числа сравнений) на
поиск по дереву, содержащему N ключей, показывает, что
бинарное дерево оказывается более выгодным:
Бинарное дерево: примерно riog2Ml (точное значение: см.
формулу (2.1 А)),
ft-арное дерево: примерно (ft + 1) Гlog^ iVl.
Если же использовать слишком плотную упаковку данных
с целью экономии объема памяти, то затрудняется дополни¬
тельная балансировка, потребность в которой возникает при
вставках и удалениях ключей. Поэтому структуры сильно
ветвящихся деревьев редко обсуждаются, когда речь идет
о поиске данных в оперативной памяти. Сильно ветвящиеся
деревья оказались очень удобными для поиска во внешней
памяти, рассматриваемого в следующем разделе.
Пожалуй, единственным исключением из этого правила
является (2—3)-, или (3—2)-деревья, обладающие интерес¬
ными свойствами. Узлы дерева имеют степень 2 или 3. Они
меньше В-деревьев, более подробно рассматриваемых в сле¬
дующем разделе и называемых бинарными В-деревьями
(здесь мы ограничимся кратким знакомством с (2—3)-де¬
ревьями) .
2) (2—3)-деревья
Упорядоченное дерево, каждый узел которого содержит 2
или 3 связи, а все листья расположены на одном уровне,
называется (2—3)-деревом. Из определения следует, что узел
(2—3)-дерева может содержать один или два ключа. Пример
такого дерева показан на рис. 2.25.
Поиск данных по ключу
77
Fla рис. 2.26 показан процесс вставки в (2—3)-дерево для
случая сравнительно больших изменений. Вставляемый ключ
всегда помещается в лист, но в случае, когда лист уже со¬
держит два ключа, выполняются следующие действия. Ключ
со средним значением перемещается вверх (удаляется из ли¬
ста и включается в непосредственно предшествующий узел),
а оставшиеся ключи делятся на два узла. Если переданный
снизу ключ попадет в узел, который уже содержит два ключа,
ключ со средним значением опять перемещается вверх,
а оставшийся узел делится пополам, образуя пару одноклю¬
чевых узлов. Такой подъем по уровням может продолжаться
вплоть до корня, и если окажется, что корень содержит два
ключа, то высота дерева увеличивается на единицу. По¬
скольку (2—3)-деревья имеют большую свободу узлов, чем
АВЛ-деревья, изменение структуры затрагивают меньшую
часть дерева и расщепления узлов выполняются проще, чем
балансировка.
Удаление из (2—3)-деревьев оказывается более сложным.
В результате удаления листа может случиться, что у его ис¬
ходного узла окажется всего один порожденный. Если этот
порожденный узел содержит два ключа, то один из них пере¬
мещается в исходный, а ключ исходного может быть опущен
на место удаленного листа. В случае когда это не так, осу¬
ществляется следующая процедура.
Рис. 2.25. Пример (2—3)-дерева.
1
Рис. 2.26. Вставка в (2—3)-дерево.
78
Глава 2
Если по соседству с исходным, содержащим один ключ,
имеется узел с двумя ключами, то этот единственный ключ
перемещается на место удаленного листа. При этом произ¬
водятся перемещения вверх и вниз нескольких ключей
(рис. 2.27, а). Если по соседству с исходным узлом, со¬
держащим один ключ, имеется только одноключевой узел
(рис. 2.27,6), то два ключа опускаются, и соседние узлы
а & в
Рис. 2.27. Удаление из (2—3)-дерева. Подчеркнуты ключи, которые пере¬
мещаются (поднимаются или опускаются) по уровням дерева. ^Результа¬
том удаления ключа 9 из дерева а, имеющего соседний узел с двумя
ключами, будет дерево б. Результатом удаления ключа 6 из дерева б, не
имеющего соседнего узла с двумя ключами, будет дерево в.
объединяются. В результате у узла-предка («деда») будет
не более одного ключа; если узел-«дед» — корень, то при его
удалении уровень дерева понизится, и ключ, содержащийся в
корне, может опуститься до листа. Хотя идея перемещения
ключей по дереву при удалении достаточно проста, при напи¬
сании реальной программы могут возникнуть трудности.
Рис. 2.28. Бинарное дерево поиска, эквивалентное (2—3)-дереву на
рис. 2.26.
Если для представления узлов с двумя ключами (2—3)-де¬
рева использовать указатели, то они не будут особенно отли¬
чаться от бинарных деревьев поиска (рис. 2.28). Для этого
достаточно в каждый узел ввести флажок, чтобы отличать
«горизонтальные» указатели, связывающие первый ключ со
вторым, от «вертикальных» указателей второго ключа на
правое поддерево. При поиске нет необходимости в анализе
значения флажка (вниз или вправо) для классификации ука¬
Поиск данных по ключу
79
зателя. Изображенная на рис. 2.28 структура несимметрична
относительно левого и правого ключей узла. Для того чтобы
сделать представление симметричным, достаточно в каж¬
дый узел добавить по одному указателю: для первого (ле¬
вого) ключа ввести «вертикальный» указатель на правое
поддерево, для второго (правого) ключа ввести «горизон¬
тальный» указатель на первый (левый) ключ. В случае сим¬
метричного представления (2—3)-дерево становится анало¬
гично АВЛ-дереву.
Анализ (2—3)-деревьев также сравнительно сложен. По¬
ведение (2—3)-деревьев в среднем при случайных вставках
ключей характеризуется следующим. Если дерево содержит
п ключей, то существует ровно п + 1 путь от корня до внеш¬
него узла. При случайных вставках вероятности выбора лю¬
бого из этих путей равны. При этом среднее число внутренних
узлов при достаточно больших п лежит между 0,70л? и 0,79п.
3) /г/е-деревья
Обычно в узлах дерева поиска хранятся значения ключей,
но в случае, когда ключами являются достаточно короткие
Рис. 2.29. Список, представленный trie-
деревом.
слова, можно рассматривать каждый ключ как список букв,
а все списки вместе — как дерево поиска, структура которого
несколько отличается от рассмотренных ранее. В этой струк¬
туре узлу (/+ 1)-го уровня ставится в соответствие i-я буква
слова, так что каждый узел содержит только один символ.
Методы поиска по такому дереву часто весьма экономичны
как по памяти, так и по времени, trie—искусственно образо¬
ванное слово, представляющее собой среднюю часть слова
retrieval (поиск).
На рис. 2.29 показано дерево, построенное для 8 слов:
dig, dip, ..., due\ символ А в данном случае обозначает ко¬
нец слова. Для произвольных слов английского языка потре¬
буется 27-арное /пе-дерево. Но если различные слова пред¬
ставляют собой лишь комбинацию из одних и тех же
3—4 букв, то число разветвлений, естественно, будет очень
небольшим, trie-деревья представляют собой структуры дан¬
80
Глава 2
ных, применение которых не уступает по эффективности ме¬
тодам хеширования, которые будут рассмотрены позднее
в целях так называемой обработки слов.
2.2. Поиск по дереву во внешней памяти
Для деревьев поиска, рассмотренных в предыдущем раз¬
деле, предполагалось, что все данные располагаются в опера¬
тивной памяти, а при обсуждении преимуществ и недостатков
различных методов поиска в качестве критерия использо¬
вались затраты на доступ к данным и объем памяти, необхо¬
димый для размещения данных. Спецификой информацион¬
ных систем, однако, является то, что, во-первых, количество
данных чрезвычайно велико, в то время как частота исполь¬
зования отдельных данных невысока; во-вторых, данные хра¬
нятся не в оперативной, а в дешевой внешней памяти.
В разд. 1.1.3 были рассмотрены основные различия между
оперативной и внешней памятью. В дополнение к сказанному
отметим, что для поиска данных, хранящихся во внешней
памяти, очень важной является проблема сокращения числа
перемещений данных из внешней памяти в оперативную.
Например, в сравнении с бинарными сильно ветвящиеся
деревья окажутся более выгодными для поиска во внешней
памяти; так как их высота меньше, то при поиске потребуется
меньше обращений к внешней памяти. Число обращений
к внешней памяти можно уменьшить и в случае бинарного
дерева, если в один блок внешней памяти поместить несколь¬
ко узлов, расположенных на разных уровнях, как показано
на рис. 2.30, а. Естественно рассматривать такие структуры
как разновидность сильно ветвящихся деревьев (рис. 2.30,6).
Даже в том случае, когда в обработке участвуют только
отдельные данные, хранящиеся во внешней памяти, более
быстрым оказывается не прямой доступ к «разбросанным»
по памяти данным, а последовательный доступ к смежным
участкам. Поэтому не удивительно, что последовательный
доступ стремятся использовать всюду, где это возможно. Од¬
нако упорядоченность данных в бинарном дереве плохо со¬
ответствует порядку их расположения по адресам памяти.
В сильно ветвящихся деревьях упорядоченность ключей в де¬
реве больше соответствует их упорядоченности в простран¬
стве адресов, так как по крайней мере в каждом узле ключи
располагаются в порядке возрастания их значений.
Отсюда можно сделать вывод, что для поиска во внешней
памяти сильно ветвящиеся деревья оказываются более вы¬
годными, чем бинарные. Системное программное обеспечение
ЭВМ, включая операционные системы, использует сильно
ветвящиеся деревья для организации поиска во внешней па¬
Поиск данных по ключу
81
мяти. Выбор того или иного типа дерева зависит от особен¬
ности внешней памяти и целей поиска. Рассмотрим сравни¬
тельно недавно разработанные, но уже нашедшие широкое
ООО
ТТЛ ПЛ
о о о о о о о о о о о о о о о о о о о о о о о о
Рис. 2.30. а — группировка узлов бинарного дерева в блоки; б — сильно
ветвящееся дерево, эквивалентное бинарному дереву, показанному на
рис. 2.30, а.
применение В-деревья. С некоторыми из методов адресации
внешней памяти, использующих такие структуры данных, мы
познакомимся в разд. 4.1.
2.2.1. В-деревья
1) Определение и поиск
В-дерево имеет более сложную структуру, чем бинарное
дерево поиска. Известно несколько разновидностей этой
структуры, что расширяет диапазон практического примене¬
ния В-деревьев. Прежде всего дадим определение основной
структуры В-дерева. Расшифровка символа «В» в названии
дерева неоднозначна; это первый символ английского слова
«balanced» (сбалансированный). Данная структура разрабо¬
тана в Научно-исследовательской лаборатории фирмы «Бо¬
инг», и, наконец, авторами В-дерева являются Р. Бэйер и
Э. Мак-Крэйт, которые и дали ей это название.
В-деревом порядка п называется сильно ветвящееся де¬
рево степени 2я+1» обладающее следующими свойствами:
1) Каждый узел, за исключением корня, содержит не ме¬
нее п и не более 2п ключей.
2) Корень содержит не менее одного и не более 2п
ключей.
82
Г лава 2
3) Все листья расположены на одном уровне.
4) Каждый нелистовой узел содержит число указателей
на единицу больше числа ключей.
5) Каждый нелистовой узел содержит два списка: упоря¬
доченный по возрастанию значений список ключей и соответ¬
ствующий ему список указателей (для листовых узлов список
указателей отсутствует).
На рис. 2.31 показан пример В-дерева порядка п — 2. По¬
скольку все листья расположены на одном уровне, структура
Рис. 2.31. Пример В-дерева. Порядок п = 2. Для наглядности использо¬
ваны числовые значения ключей из диапазона 1—31. Число ключей в
корне от 1 до 4, число ключей в других узлах от 2 до 4.
напоминает больше «живую изгородь». (2—3)-дерево, рас¬
смотренное в предыдущем разделе, есть не что иное, как
В-дерево порядка п= 1. Ниже будет показано, что структура
В-дерева имеет смысл для организации поиска во внешней
памяти только при относительно больших значениях порядка
дерева, а (2—3)-деревья больше подходят для поиска в опе¬
ративной памяти. В-дерево порядка п = 2 выбрано в каче¬
стве примера только для уменьшения и упрощения рисунка.
Поскольку В-дерево является сильно ветвящимся дере¬
вом, его высота невелика, поэтому и число обращений к внеш¬
ней памяти при поиске также невелико. Кроме того:
1) сравнительно просто может быть реализован последова¬
тельный доступ, поскольку листья расположены на одном
уровне; 2) при добавлении и удалении ключей изменения
ограничиваются, как правило, одним узлом, а не затраги¬
вают всю структуру дерева, поскольку во всех узлах есть
свободные поля, максимальное число которых, за исключе¬
нием корня, составляет п = (2п)/2; 3) область влияния изме¬
нений оказывается очень узкой даже в случае, когда измене¬
ния затрагивают всю структуру дерева, так как участок, на
котором сказываются изменения, располагается между непо¬
средственным исходным и его предком. Чтобы убедиться в
справедливости перечисленных достоинств структуры В-де-
Поиск данных по ключу
83
рева, рассмотрим операции поиска, вставки и удаления
ключей.
Рассмотрим, как зависит число ключей В-дерева от его
порядка п и высоты h. Найдем сначала максимальное число
ключей N max. Очевидно, что максимальным числом узлов
такого дерева будет
1 + (2п + 1) + (2п + I)2 + ... + (2« + 1)Л 1 =
= {(2rt+ l)ft- 1}/2«.
Поскольку максимальное число ключей в каждом узле равно
2/г, то
ЛГтах = (2/г+1)Л-1.
Чтобы найти минимальное число ключей дерева Nmm,
надо знать минимально возможное число узлов такого де¬
рева. Без учета корня оно составит
2 + 2 (п + 1) + 2(п + I)2 + ... + 2 (п + 1)Л 2 =
= 2{(n+l)h-l-l}/n.
Поскольку минимально возможное число ключей в узле де-
рова равно пу то очевидно, что
ALin = 2(n+l)ft-,-l.
Следовательно, для любого В-дерева высоты h любой
ключ может быть найден не более чем за h шагов поиска.
И наоборот, В-дерево, содержащее N ключей, будет иметь
высоту h из диапазона
log2„+i (N + 1)< h < 1 + logn+l (N + 1)/2.
При больших Nun границы диапазона h почти равны
log2nN и lognN. Из табл. 2.3 следует, что при соответствую¬
щем выборе п высота дерева поиска будет небольшой даже
Таблица 2.3. Зависимость высоты В-дерева от его порядка п
и числа ключей N
'Ч'Чч\ч Число
ключей N
Порядок
п Nv
ю3
101
10s
10е
10'
10
3
4
4,5
5,6
6,7
20
2,3
3
4
4,5
6
50
2
2,3
3
3,4
4
100
2
2
3
3
4
84
Глава 2
при относительно большом файле и значение высоты мало
меняется с изменением N.
Если при поиске аргумента по В-дереву высоты h затраты
(время) на поиск в корне обозначить через Сг, затраты на
доступ к каждому из узлов, за исключением корня, и на
поиск в узлах — через С, а вероятность перехода поиска
с (i—1)-го уровня на /-й уровень — через pit то общие за¬
траты на поиск Ct будут выражаться как
Ct = СгР{ + С (р2 + рз + • • • + Ри)•
1 = р\ > р2 > ... > ph, но, поскольку общее число ключей,
содержащихся в В-дереве от корня до (/—1)-го уровня, от¬
носится к числу ключей, содержащихся на i-м уровне, как
число, заключенное между п и 2п, к единице, поиск в боль¬
шинстве случаев продолжается до листьев. Таким образом,
Pi= 1, и можно считать, что
Ct = Cr + (h- 1)С.
При больших значениях N верхний предел затрат на по¬
иск определяется как
С,<СГ + Clogn+l(N+ 1)/2,
и кажется, что чем больше п, тем лучше. Однако в действи¬
тельности с ростом п пропорционально растут затраты на
поиск в узлах, а если п превысит определенную величину, то
могут резко возрасти затраты и на доступ к поддеревьям.
Таким образом, высоту дерева не следует делать близкой
к двум за счет неограниченного увеличения степени п. Ана¬
лиз табл. 2.3 показывает, что начиная с некоторого значе¬
ния п (которое является основанием логарифма) дальнейшее
его увеличение практически не сказывается на высоте дерева.
Более того, как будет показано ниже, с ростом п растут и
затраты на вставку и удаление ключей. Здравый смысл и
практические соображения подсказывают, что значения п
следует выбирать исходя из того, чтобы узел целиком мог
быть перемещен из внешней памяти во внутреннюю (и на¬
оборот) за одну операцию ввода-вывода.
2) Вствка и удаление ключей, последовательный доступ
Для выполнения операции вставки ключа в В-дерево не¬
обходимо:
1) Убедиться в том, что аргумент поиска не совпадает ни
с одним из уже имеющихся в дереве ключей. Для этого не¬
обходимо (начиная с корня) последовательно просматривать
узлы дерева, пока не будет достигнут соответствующий лист
(неудачный поиск всегда заканчивается в листовом узле).
Поиск данных по ключу
85
2) Если лист заполнен не полностью, произвести вставку
аргумента в соответствующее место списка ключей и на этом
завершить операцию вставки (рис. 2.32).
3) Если в этом листе свободного места нет, то в резуль¬
тате вставки число ключей станет равным 2п + 1 и возникнет
Рис. 2.32. Результат вставки ключей 2 и 24 в В-дерево на рис. 2.31. По¬
казаны только ключи, имеющие отношение к процедуре вставки. Жир¬
ными линиями отмечены границы узлов в месте расщепления, подчеркнуты
вставленные ключи и поднятый ключ (ключ переноса).
ситуация переполнения. При переполнении: (п+1)-й ключ
(средний ключ списка) удалить из узла; создать новый узел
(лист) и переместить в него п ключей списка из узла, в ко¬
тором возникло переполнение; удаленный ключ вставить в
Рис. 2.33. Результат вставки ключа 12 в В-дерево, показанное на рис. 2.31.
Показаны только ключи, имеющие отношение к вставке. Жирными ли¬
ниями отмечены границы узлов в месте расщепления, подчеркнуты встав¬
ленный ключ и ключ переноса.
узел-корень переполненного узла. Таким образом, при пере¬
полнении происходит расщепление узла: образуются два но¬
вых вместо одного старого (рис. 2.32) и ключ переноса.
4) Если в результате вставки ключа переноса внутренний
узел окажется переполненным, он тоже расщепляется (при
этом половина списка ключей и списка указателей помешает¬
ся в новый узел) (рис. 2.33).
86
Глава 2
5) Если ключ переноса достигнет кормя и корень после
вставки также окажется переполненным, его тоже расщеп¬
ляют, что приводит к увеличению высоты дерева на единицу
и созданию нового корня, куда и помещается ключ переноса.
Получившиеся в результате расщепления два узла стано¬
вятся корнями поддеревьев нового корня.
Рис. 2.34. Результат удаления ключей 7 и 22 из В-дерева, показанного
на рис. 2.31. Подчеркнуты ключи, перемещенные для восстановления сба¬
лансированности после удаления.
Для выполнения операции удаления ключа необходимо
выполнить следующие действия:
1) Найти узел, содержащий ключ, который должен быть
удален. Дальнейшие действия зависят от того, содержится ли
ключ, который должен быть удален, в листе или в нелисто¬
вом узле.
2) Случай, когда ключ, который должен быть удален, на¬
ходится в листе.
2.1) Если найденный лист содержит не менее (/2+1)
ключей, то ключ просто удаляют и операцию заканчивают
(рис. 2.34).
2.2) Если в найденном листе содержится ровно п ключей,
но имется соседний лист, содержащий более п ключей, то
для сохранения равновесия достаточно выполнить перемеще¬
ние ключей из соседнего листа. Для перемещения одного
ключа из соседнего листа необходимо: удалить ключ, разде¬
ляющий списки ключей соседних листьев, из узла предыду¬
щего уровня и вставить его в лист, содержащий ключей
меньше п\ на место удаленного ключа поместить крайний (ле¬
вый или правый) ключ из соседнего листа (см. рис. 2.34).
В случае большого неравновесия числа ключей в соседних
листьях для уменьшения числа балансировок дерева при по¬
следующих удалениях лучше перемещать одновременно мак¬
симально возможное число ключей (чтобы после перемеще¬
ния число ключей в соседних листьях стало равным или при¬
мерно равным) (рис. 2.35).
Поиск данных по ключу
87
2.3) Если найденный и соседний с ним лисг содержат по
п ключей, то производят их конкатенацию — списки ключей
соседних листьев объединяются и остается один лист, а дру¬
гой уничтожается. При конкатенации листьев один из клю¬
чей предыдущего уровня, «разделявший» соседние листья,
63 65
64
65
66
67
68
69
60
61
63
64
66
67
68
69
6
60
61
Рис. 2.35. Перераспределение ключей в случае сильного нарушения баланса
после удаления. Подчеркнуты перемещенные ключи: а — до перераспреде¬
ления; б — после перераспределения.
оказывается лишним, и его необходимо переместить вниз.
На рис. 2.36 показан такой пример. Это явление (в отличие
от переполнения при вставках) можно назвать «нехваткой»
при удалении. Иногда в результате «нехватки» в узлах верх¬
него уровня число ключей может стать меньше п. Тогда для
сохранения равновесия потребуется выполнить перемещение
Рис. 2.36. Результат удаления ключа 18 из В-дерева, показанного на
рис. 2.31. Жирной линией обведен узел, полученный путем конкатенации
двух узлов. Подчеркнут ключ, опущенный из исходного.
ключей из соседнего узла того же уровня. Такой пример по¬
казан на рис. 2.37. Перемещение может потребовать удале¬
ния ключа из узла более высокого уровня, а удаление в свою
очередь — привести к ситуации нехватки на этом уровне.
Если этот процесс достигнет корня дерева — после удаления
из корня в нем не останется ключей, — то в этом случае вы¬
сота дерева уменьшится на единицу.
3) Случай, когда ключ, который должен быть удален, на¬
ходится в нелистовом узле.
88
Г лава 2
3.1) Удаляем заданный ключ и помещаем на его место
ключ, непосредственно следующий по величине за удаленным.
Узел, содержащий ключ, непосредственно следующий за уда¬
ленным, будет самым левым листом правого поддерева уда¬
ленного ключа. Чтобы найти этот узел, спускаемся вниз на
Рис. 2.37. Результат удаления ключа 31 из В-дерева, показанного на
рис. 2.31. Жирными рамками обведены узел, полученный путем конкатена¬
ции, и узел, исходный которого изменился. Подчеркнуты поднятые и опу¬
щенные ключи.
один уровень по «правому» указателю удаленного ключа, и
если это лист, то поиск закончен; в противном случае, исполь¬
зуя самый левый указатель текущего узла, спускаемся вниз
Рис. 2.38. Результат удаления ключей 8 и 20 из В-дерева, показанного
на рис. 2.31. Жирными линиями показаны пути поиска ключа, непосред¬
ственно следующего за удаленным. Подчеркнуты поднятые ключи.
по дереву до тех пор, пока не будет достигнут лист. Теперь
удаляем из листа самый левый ключ списка, который и будет
непосредственно следующим.
3.2) Последующие действия будут аналогичны удалению
ключа из листа.
На рис. 2.38 показан случай простого удаления ключей,
а на рис. 2.39 — случай, когда при удалении ключа требуется
дополнительная балансировка дерева.
Поиск данных по ключу
89
Нередко требуется выполнить обработку всех ключей
В-дерева из заданного диапазона в порядке возрастания их
значений. Типичный пример такой обработки — напечатать
упорядоченную таблицу, содержащую все ключи В-дерева.
Очевидно, что основу алгоритма решения подобной задачи
должен составлять тот или иной алгоритм обхода дерева.
Используем рекурсивный алгоритм обхода и будем считать,
Рис. 2.39. Результат удаления ключа 29 из В-дерева, показанного на
рис. 2.31. Случай почти аналогичен представленному на рис. 2.37, за
исключением того, что ключ 30 претерпевает более сложное перемещение.
что trav(node) означает вызов алгоритма с передачей ему
указателя node на некоторый узел дерева. Тогда, чтобы на¬
чать обработку, достаточно записать trav(root), считая, что
root является указателем на корень В-дерева.
Алгоритм, trav(node)
1. Если узел node является листом, то напечатать все
ключи и закончить вычисления.
2. Если node не лист, то обозначить ключи узла как
key[1], ..., key[k]\ а указатели на поддеревья как
pt[\],..., pt[k+\\.
2.1. Выполнить trav(pt[ 1]).
2.2. Для / = 1, ..., k
2.2.1. Напечатать значение ключа key(j)
2.2.2. Выполнить trav(pt[j + 1])
3. Конец.
Для того чтобы иметь возможность напечатать ключи
только из заданного диапазона, например от ko до в этот
алгоритм достаточно добавить одну переменную fl типа флаг.
Теперь при /7 = 0 осуществляется поиск, и, как только будет
найден ключ, для которого key[-] = k0, достаточно заменить
fl на fl = 1 и далее использовать алгоритм, аналогичный вы¬
шеприведенному. Можно также вместо рекурсии использовать
стек, в который при спуске вниз по дереву помещать указа¬
90
Глава 2
тели па узлы, которые еще не обработаны. При этом оче¬
видно, что максимальный размер стека не будет больше вы¬
соты В-дерева.
Поскольку большая часть ключей В-дерева содержится
в листьях, то основные затраты при работе алгоритма trav
приходятся на спуск вниз по дереву и однородную последова¬
тельную обработку ключей, расположенных в листьях. Од¬
нако нельзя пренебречь и затратами, связанными- с возвра¬
том на более высокий уровень дерева, так как для этого тре¬
буется обращение к внешней памяти. В+-дерево, рассматри¬
ваемое далее, свободно от этого недостатка и является одной
из разновидностей В-дерева.
2.2.2. Разновидности В-дерева
1) В+-дерево
Некоторые авторы рассматриваемую ниже разновидность
В-дерева называют В*-деревом, но здесь мы, следуя Д. Ко¬
меру, будем называть ее В+-деревом. В-дерево, в котором
истинные значения ключей содержатся только в листьях
(концевых узлах), будем называть В+-деревом. Во внутрен¬
них узлах В+-дерева содержатся не истинные значения клю¬
чей, а ключи-разделители, задающие диапазон изменения
ключей для поддеревьев. Во многих случаях они совпадают
с истинными значениями ключей или их частью, но, как бу¬
дет показано ниже, это вовсе не обязательно. Поскольку все
ключи расположены на одном уровне — в листьях, если свя¬
зать их указателями, то последовательный доступ станет
особенно прост при высокой скорости доступа по дереву.
Отметим, что поиск по В+-дереву всегда заканчивается
в листе; но и в В-дереве в листьях содержится большая часть
ключей, и поэтому затраты времени на поиск по В+-дереву
почти не увеличиваются даже без учета того, что сама опе¬
рация сравнения аргумента с ключом-разделителем быстрее,
чем сравнение с истинным ключом. При расщеплении листа
в результате вставки ключ из листа не удаляется, а в каче¬
стве ключа переноса используется его копия. Операция уда¬
ления из В+-дерева имеет то преимущество, что удаление
всегда производится из листа. Например, при удалении клю¬
ча 20 на рис. 2.40,6 нет необходимости в изменении ключа-
разделителя 20. Необходимость в изменении ключа-разде¬
лителя возникает только в случае нехватки, когда потребу¬
ются перестановка ключей и установление новых связей при
балансировке. Все другие операции, помимо рассмотренных
выше, выполняются аналогично операциям над В-деревьями.
Таким образом, В+-деревья во многом превосходят В-деревья;
Поиск данных по ключу
91
уступают же они В-деревьям в том, что требуют несколько
больше памяти для представления. В заключение еще раз
I ПроизВольнь/й
* доступ
■Последова¬
тельный
doctnyn —
±Н±Н±1СЬ*"-Ч±Н±
В- деребо
поиска
I Ключи w
записей
\ 14jjl 20 У 28 ЦТ
Внутренние
узлы
—Ц 16 1181 | 1*|-»[~2о] 241 27 | 14» Листья
ъ
Рис. 2.40. а — общий вид В+-дерева; б — удаление из В+-дерева: даже
при удалении ключа 20 изменения разделителя 20 не требуется.
отметим, что достоинством В+-дерева является возможность
последовательного доступа.
2) Другие изменения структуры В-дерева
Ранее отмечалось, что некоторые авторы В+-деревья на¬
зывают В*-деревьями. Однако В*- и В+-деревья не эквива¬
лентны. Структурно В*-деревья очень близки к В-деревьям
и отличаются от них только более высоким коэффициентом
использования памяти. Если для В-дерева каждый узел дол¬
жен быть заполнен ключами не менее чем наполовину, то
для В*-дерева требуется, чтобы каждый узел был заполнен
ключами не менее чем на 2/3. Чтобы и в случае переполне¬
ния при вставке обеспечить коэффициент заполнения каждого
узла не менее 2/3, необходимо вначале объединить два со¬
седних узла, расположенные на одном уровне, а затем рас¬
щепить его на три части. Если повысить коэффициент ис¬
пользования памяти, то только за счет этого можно умень¬
шить высоту дерева, а следовательно, и число шагов поиска.
Вместе с этим может оказаться, что затраты на изменение
структуры дерева при вставках и удалениях возрастут.
Мы коснулись немного структуры бора (trie-дерева), ис¬
пользуемой для поиска простых слов, когда говорили о при¬
менении сильно ветвящихся деревьев для поиска в оператив¬
ной памяти. Если слова, для которых используется такое
92
Г лава 2
дерево поиска, становятся слишком длинными, лучше исполь¬
зовать В+-дерево. Бэйер с сотрудниками назвали такое де¬
рево В-деревом с префиксом. Если список слов заранее из¬
вестен, то затраты на поиск можно уменьшить путем искус¬
ственного выбора ключа-разделителя между словами. Более
подробно об этом будет идти речь в разд. 4.1. Там же будут
рассмотрены способы реализации виртуальной памяти, ис¬
пользующие В-деревья.
2.3. Методы хеширования
2.3.1. Методы случайного упорядочения
Для повышения эффективности повседневной работы очень
важны организованность и порядок. При обработке данных
обычно также используются различные методы их упорядо¬
чения в памяти. Так, большинство рассмотренных методов
поиска базировалось на упорядочении данных в форме древо¬
видной структуры. Однако оказывается, что эффективность
поиска можно повысить, если вместо различных упорядочен¬
ных структур использовать так называемые беспорядочные
или перемешанные структуры данных. Для работы с такими
структурами и предназначены методы хеширования.
1) Организация данных
Вначале определим условия, при которых задача поиска
будет наиболее простой. Будем считать, что множество клю¬
чей невелико, все значения ключей заранее известны и на
время обработки все множество данных (или по крайней
мере данные, указывающие на расположение каждой записи
во внешней памяти) может быть размещено в оперативной
памяти. Ранее отмечалось, что на оперативную память может
быть наложена произвольная структура. Таким образом, для
данных, размещенных в оперативной памяти, можно выбрать
любую структуру, соответствующую поставленной цели. Сле¬
довательно, если имеется возможность весь файл разместить
в последовательных ячейках памяти в виде таблицы, то, зная
местоположение записи в таблице, легко определить ее ад¬
рес. Иными словами, если известно М — число записей в таб¬
лице, то каждой записи можно однозначно поставить в соот¬
ветствие некоторое положительное целое число а из диапа¬
зона О, М—1. В широком смысле это число можно рассмат¬
ривать как адрес записи. В случае если ключ k каждой от¬
дельной записи является целым неотрицательным числом, то,
как было сказано в гл. 1, его длина обычно принимается
равной стандартной длине слова или двойного слова. Оче¬
Поиск данных по ключу
93
видно, что в случае двойного слова областью определения
числового ключа будет [0,264— 1J, а область определения
буквенного ключа (при тех же условиях) будет подмноже¬
ством этой области К. Для нас прежде всего важно то, что,
хотя область определения ключа может быть очень большой,
число возможных значений К конечно (ограниченно) и это
число гораздо больше числа записей файла.
С учетом сделанных предположений задача поиска со¬
стоит в определении по заданному аргументу k^K адреса
записи a(k), содержащей заданный ключ. Требуется, чтобы
этот адрес вычислялся как можно проще и как можно быст¬
рее. Хеширование является эффективным методом решения
этой задачи. Буквально «hash» означает нарезать, измель¬
чить и перемешать что-нибудь, например нарезать мясо на
мелкие кусочки и сделать из него фарш. Почему принят та¬
кой термин, будет ясно из дальнейшего изложения. Органи¬
зация данных в виде таблицы, используемой для «вычисле¬
ния» адреса а по ключу (как непосредственно, так и косвен¬
но), называется хеш-таблицей.
На рис. 2.4, а показан пример такой таблицы: 47 назва¬
ний префектур отображены в целые числа из диапазона
[6,52]. Названия префектур записаны знаками слоговой аз¬
буки «катакана», причем знаками озвончения согласной и
знаками для выражения произношения в записях не пользо¬
вались. В качестве ключей использованы три слоговые буквы
названия. Если букв в названии было меньше трех, то спра¬
ва ключ дополнялся символом *. Каждому трехбуквенному
ключу в таблице соответствует число (последний столбец
таблицы), равное сумме трех чисел, называемых кодами пре¬
образования и приведенных для каждого слогового сочетания
в табл. 2.4,6. Поиск в такой «перемешанной» таблице можно
сделать более непосредственным и быстрым, чем поиск с ис¬
пользованием структуры дерева. Для этого достаточно по
заданному ключу К, используя коды преобразования литер
ключа, вычислить их сумму (значение хеш-функции) и взять
это значение в качестве адреса записи (a=h(k)). В по¬
строенной таблице записи перемешаны и размещены в после¬
довательных адресах. Таким образом, если число записей не¬
велико и заранее известно, то имеется возможность построить
(подобрать, найти) функцию преобразования заданного мно¬
жества ключей в различные адреса (и если возможно — в по¬
следовательные адреса). Далее будет рассмотрен более об¬
щий случай. Если число записей велико, то выявить такую
функцию h оказывается сложно, кроме того, часто само мно¬
жество ключей заранее не известно. Типичный пример —
таблица имен, используемых в программе, которая наряду
с зарезервированными словами языка программирования
94
Глава 2
Таблица 2.4, а. Отображение
47 названий
префектур в области
[6, 52]
Таблица 2.4, б. Коды
преобразования
Ключ
(сокращенное Название
название префектуры
префектуры)
Адрес
о ка я
Окаяма
6
о о и
Ойта
7
и си ка
Исикава
8
ни и ка
Ниигата
9
си ка *
Сига
10
я ма ка
Ямагата
11
ка на ка
Канагава
12
ки о то
Киото
13
хо ка и
Хоккайдо
14
о ки на
Окинава
15
то о ки
Токио
16
я ма ку
Ямагути
17
то я ма
Тояма
18
то ку си
Токусима
19
я ма на
Яманаси
20
о о са
Осака
21
ка ка ва
Кагава
22
са ка ♦
Сага
23
ва ка я
Вакаяма
24
ми я ки
Мияги
25
то ти ки
Тотиги
26
ка ко си
Кагосима
27
на ка са
Нагасаки
28
си ма нэ
Симанэ
29
на ка но
Нагано
30
ку н ма
Гумма
31
си су о
Сидзуока
32
а и ти
Айти
33
ки фу *
Г ифу
34
фу ку 0
Фукуока
35
фу ку и
Фукуи
36
фу ку си
Фукусима
37
ку ма мо
Кумамото
38
ми я са
Миядзаки
39
на ра *
Нара
40
а о мо
Аомори
41
ко у ти
Коти
42
ти ха *
Т иба
43
а ки та
Акита
44
хи у ко
Хёго
45
са и та
Сайтама
46
ми э *
Миэ
47
хи ро си
Хиросима
48
то то ри
Тоттори
49
и ва тэ
Иватэ
50
и ха ра
Ибараки
51
э хи мэ
Эхимэ
52
15
3
5
23
2
к
1
3
7
22
с
17
4
26
т
26
15
.
27
8
н
10
5
18
19
X
23
18
26
.
10
м
7
19
11
24
р
25
33
.
•
26
в
20
•
н= 17
* = 5
я = 3
Поиск данных по ключи
95
содержит идентификаторы переменных, функций и т. д., кото¬
рые программист выбирает произвольно. Нередко значения
записей, включая ключи, со временем меняются. Из сказан¬
ного следует, что как бы хорошо ни была подобрана хеш-
функция, для известного множества ключей добавление
хотя бы одного ключа может все испортить — придется за¬
ново искать хеш-функцию и заново строить таблицу. Однако
можно получить гораздо более гибкий метод, если отказаться
от идеи однозначности и рассматривать хеш-функцию просто
как функцию, рассеивающую множество ключей в множество
адресов [О, М—1]. При этом будем считать, что М всегда
больше предполагаемого числа записей и выбирается из мак¬
симально допустимого объема памяти, выделенного под хеш-
таблицу.
Отказ от требования взаимно однозначного соответствия
между ключом и адресом означает, что для различных клю¬
чей к\фк2 после вычисления хеш-функции может возникнуть
ситуация, называемая коллизией h(k\) = h(k2). Итак, для
метода хеширования главными задачами являются выбор
функции h и нахождение способов разрешения возникающих
коллизий. Говорят, что ключи k\, k2 являются синонимами
функции h, если h{k\) = h(k2).
2) Число коллизий
Прежде чем обсуждать различные методы хеширования,
рассмотрим, какова вероятность образования того или иного
числа коллизий, возникающих при случайном равномерном
распределении N ключей по М адресам. Для этого восполь¬
зуемся следующей моделью. Будем считать, что N шаров
в случайном порядке с равной вероятностью и независимо
друг от друга размещаются по М урнам. Если очередной шар
помещается не в пустую урну, будем говорить, что имеет
место коллизия. Пусть при размещении N шаров по М урнам
коллизия возникла для У шаров. Тогда после размещения
N шаров занятыми окажутся X = N—У урн. Определим
распределение вероятности случайной величины У (числа
коллизий). Для этого достаточно найти распределение слу¬
чайной величины X — числа занятых урн.
Обозначим число способов размещения N шаров по k ур¬
нам, при
Теперь можно записать соотношение для числа способов
размещения (N + 1)-го шара по k урнам. Это может осуще-
96
Глава 2
ствляться одним из двух способов: либо (УУ+1)"й шар по¬
падет в одну из k занятых ранее урн; либо (N + 1)-й шар
попадет в одну из свободных урн. Тогда ранее размещенные
N шаров должны были занимать (k— 1) урну.
Числа , удовлетворяющие (2.8) и (2.9), называются
числами Стирлинга второго рода, а последовательность та-
Число холл из и и
Рис. 2.41. Распределение вероятности числа коллизий. Число шариков
N = 50, число сосудов М = 50, 100, 200, 300.
ких чисел для всех различных N и к — подпоследователь¬
ностью Стирлинга.
Число случаев, когда при размещении N шаров занятыми
окажутся ровно k урн из М, представляет собой произведе-
— 1)(М — 2) ... (М — £+!)• Число случаев, когда при раз¬
мещении N шаров окажутся занятыми М урн, обозначим MN.
Так как все размещения N шаров по М урнам равновероят¬
ны, то распределение вероятности числа занятых урн будет
j—|—Л/j—lU—i i L_i i i i—i—l
10 15 20 25
\
число перестановок из M по k: М (М —
P,[X = k 1 =
гагчпга
(ft = 1, 2, ..., min (JV, M)).
Поиск данных по ключу
97
Поскольку сумма вероятностей выражения равна '1, по¬
ражение представить в виде суммы факториалов, то коэф¬
фициенты будут выражаться членами последовательности
Стирлинга второго рода:
Пример распределения вероятности числа коллизий
Pr [Y = k] = Pr [X = N — k] показан на рис. 2.41. Математи¬
ческое ожидание составляет М (1 — 1 /M)N — (М — N) Ф
Ф Me~N:M — (Л4 — N), а дисперсия M(l — l!Ai)N+M{M—])X
Х(1 -2/M)N — Af2(l - l/M)2N = Me-N!M(l -(M+N)e-N'M/M).
Это распределение при 1 < JV<M приближается к распре¬
делению Пуассона, а при 1 N Ф М — к нормальному рас¬
пределению.
3) Хеш-функция
При выборе хеш-функции h> отображающей множество
ключей k <= К в адреса а е [О, М — 1 ], желательно, чтобы
она не только сокращала число коллизий, но и не допускала
скучивания ключей в отдельных частях таблицы.
(1) Метод деления
В методе деления в качестве значения хеш-функции ис¬
пользуется остаток от деления ключа на некоторое целое
число М: h(k) = К mod М. Очевидно, что эффективность рас¬
сеивания ключей по таблице во многом зависит от значе¬
ния М. Так, совсем плохо, если М является степенью основа¬
ния системы счисления, так как в этом случае значением
хеш-функции будут просто младшие разряды ключа. Сказан¬
ное справедливо и для буквенных ключей. При М = 28, на¬
пример, значением хеш-функции будет последняя буква клю¬
ча. Чтобы предотвратить скучивание ключей вокруг отдель¬
ных адресов таблицы, лучше, если М будет простым числом.
Часто множества ключей представляют собой нечто вроде
арифметических прогрессий вида ХХА, ХХВ, ... или FT01,
FT02, .... Метод деления преобразует такие прогрессии в
последовательные адреса. Такую ситуацию можно считать
вполне удовлетворительной.
лучим уравнение
и если степенное вы-
(2.11)
4 Зак. 127
98
Глава 2
(2) Метод умножения
Представим k в виде двоичного числа и примем М = 2т.
Умножим дробь а на k и возьмем дробную часть числа, ко¬
торую обозначим как {&а}, а в качестве значения хеш-функ¬
ции используем т старших разрядов. Иными словами,
h(k)= LAI X {^ос} J, где [х\ —«пол» от х (наибольшее це¬
лое число, не превосходящее х). Рекомендуется в качестве
значения а использовать иррациональное число; которое близ¬
ко к длине машинного слова. Например, если взять в ка¬
честве а так называемое золотое сечение a = (V5— l)/2, то
отрезок [0,1] очень хорошо делится на {а}, {2а}, .... Од¬
ним словом, как бы мелко ни делили отрезок, длины отрез¬
ков, получающихся при разбиении, будут выражаться не бо¬
лее чем тремя различными значениями ak, ак+х, ак+2. При
последующих разбиениях отрезок длины ак делится на от¬
резки длиной ак+х, ак+2. Это свойство при использовании ме¬
тода умножения позволяет достигать хороших результатов.
Требование, чтобы при вычислении функции h(k) М = 2т,
не является обязательным. Но при а=\/М метод эквива¬
лентен методу деления.
Очень близким к методу умножения является метод «се¬
редины квадрата», в котором в качестве значения h(k) ис¬
пользуется т битов средней части квадрата ключа k2. Это
еще один из методов хеширования, но по многим параметрам
он уступает методу умножения.
(3) Преобразование системы счисления
В основе метода вычисления значения хеш-адреса лежит
преобразование значения ключа &, выраженного в одной
р-ичной системе счисления k = а0 + а\р + агР2 + , в дру¬
гую g-ичную систему счисления при ограничении 5 на поря¬
док результата: h(k) = а0 + a\q -f- ... + as~\qs~x. Здесь р
и q — положительные целые числа, такие, что р <. q. Для вы¬
числения значения функции h (k) необходимо 5 операций ум¬
ножения или деления. Следовательно, трудоемкость (число
операций) этого метода оказывается больше, чем методов
деления или умножения.
(4) Деление многочленов
Пусть k, выраженное в двоичной системе счисления, запи¬
сывается как k = 2n~xbn + ... + 26i + Ь0, и пусть М является
степенью двойки М = 2т. Представим двоичный ключ k
в виде многочлена вида k(t) = bntn-\- ... + b\t + b0l сохра¬
нив те же коэффициенты. Теперь определим остаток от деле-
Поиск данных по ключу
99
ния этого многочлена на постоянный многочлен вида c(t) =
= tm + cm-\tm~x + • • • + с it + с0. Этот остаток, опять же рас¬
сматриваемый в двоичной системе счисления, и используем
в качестве значения хеш-функции h(k). Для вычисления
остатка от деления многочленов используют полиномиальную
арифметику по модулю 2. Если в качестве c(t) выбрать про¬
стой неприводимый многочлен, то при условии близких, но не
равных ключей k\ ф k2 обязательно будет выполняться, усло¬
вие h(k\)ф h(k2). Эта функция обладает более сильным свой¬
ством рассеивания скученности в области К.
(5) Метод слияния
Рассмотренные выше методы могут быть использованы
и в случае буквенных ключей неопределенной длины. Для
этого достаточно разбить ключ на несколько отрезков (ча¬
стей) постоянной длины, а затем арифметически (логически
и т. п.) сложить значения частей. Основной недостаток этого
метода состоит в том, что он недостаточно «чувствителен»
к порядку букв в слове. Циклический сдвиг ключа позволяет
избавиться от этого недостатка. В качестве разновидности
этого метода известен подход, в котором слиянию предше¬
ствует преобразование каждой буквы ключа в двоичное чи¬
сло, а затем уже разделение числовой последовательности
на отрезки и их суммирование. Недостаток метода — необхо¬
димость преобразования в двоичную систему, что связано
с достаточно большими затратами.
Метод вычисления хеш-функции и методы вычисления по¬
следовательностей псевдослучайных чисел имеет много об¬
щего: в основе их лежат одни и те же закономерности, а при
их вычислении используются практически одни и те же про¬
стые операции. Получение очередного псевдослучайного числа
последовательности не что иное, как вычисление значения
хеш-функции от последнего (или двух последних) получен¬
ного члена последовательности. При выборе метода вычисле¬
ния хеш-функции на практике обычно отдают предпочтение
делению или умножению из-за простоты этих методов,, позво¬
ляющих производить вычисление с высокой скоростью и до¬
пускающих простую реализацию на языке высокого уровня.
Однако для аппаратной или микропрограммной реализации
хеш-функции очень хорошо подходит также метод деления
многочленов.
Для множества ключей неопределенной длины найти хеш-
функцию с идеальными свойствами практически невозможно.
Даже если представить, что такую функцию h (k) предста¬
вить удалось, то она будет взаимно однозначной не более чем
для конечного числа первых символов ключа. Однако и в
4*
100
Глава 2
этом случае можно с успехом использовать рассмотренные
выше методы, если отбросить идею однозначности и предпри¬
нять специальные меры для разрешения коллизий. Для раз¬
решения коллизий было предложено несколько методов, ко¬
торые будут рассмотрены ниже.
2.3.2. Разрешение коллизий
1) Вставка
Методы разрешения коллизий, возникающих при вставках
ключей, можно разделить на два класса: метод цепочек и
метод открытой адресации.
(1) Метод цепочек
Методом цепочек называется метод, в котором для разре¬
шения коллизий во все записи добавлены указатели, которые
используются для поддержания связанных списков (по од¬
ному на каждый возможный хеш-адрес таблицы). Сами
списки могут размещаться как в памяти, принадлежащей
хеш-таблице, так и в отдельной памяти. В первом случае
цепочки называются внутренними, а во втором — внешними.
Поиск в хеш-таблице с внешними цепочками переполнения
выполняется очень просто. После вычисления значения хеш-
функции a = h(k) задача сводится к последовательному по¬
иску в а-м списке (возможно, находящемся во внешней па¬
мяти). Внешнюю память в этом случае можно разделить на
несколько страниц так, чтобы иметь возможность хранить
все записи с ключами-синонимами на одной странице. По¬
скольку сама хеш-таблица содержит только указатели, то их
число можно сделать достаточно большим, что уменьшит ве¬
роятность возникновения коллизий. Этот метод очень хорошо
подходит при большом числе и переменной длине данных.
При добавлении новых ключей дополнительных трудностей
обычно не возникает. Если же число синонимов станет слиш¬
ком большим, можно вместо линейных списков использовать
дерево поиска (см. рис. 2.42, а). Для того чтобы более эф¬
фективно использовать память, служат хеш-таблицы с внут¬
ренними цепочками переполнения, в которых связанные спи¬
ски для синонимов по хеш-функции поддерживаются внутри
таблицы (см. рис. 2.42,6). Для поиска свободного места
в таблице можно использовать разные методы. Например,
последовательный просмотр позиций таблицы. При вставке
новых ключей появляется тенденция объединения хеш-адре¬
сов в группы, что проявляется в срастании списков. Причина
этого кроется в том, что список свободного пространства при¬
Поиск данных по ключу
101
надлежит хеш-таблице, и коллизия становится возможной не
только для ключей-синонимов по хеш-функции, но и для клю¬
чей-синонимов по списку переполнения. Таким образом, в один
список могут попасть ключи, не являющиеся синонимами по
хеш-функции, что удлиняет список. Чтобы этого избежать,
можно, например, переместить «чужой» ключ и освободить
занятое место, однако для этого требуются дополнительные
Хеш-таблица
Связанный список
Хеш-таблица
Рис. 2.42. Метод цепочек, а — внешние цепочки переполнения (списки раз¬
мещены вне хеш-таблицы); б — внутренние цепочки переполнения (списки
размещены внутри хеш-таблицы)
затраты. Итак, суть метода в том, что разрешение коллизий
происходит за счет «чужих», еще не занятых позиций хеш-
таблицы и не затрагивает других адресов. Поэтому его еще
часто называют методом срастающихся цепочек.
(2) Метод открытой адресации
Этот мотод решения проблемы коллизий состоит в том,
чтобы пользуясь каким-либо правилом, обеспечивающим пе¬
ребор всех элементов, просто просматривать один за другим
элементы хеш-таблицы. Метод аналогичен процедуре, когда
на письмо к человеку, постоянно перемещающемуся с места
на место, делают наклейки с новыми адресами, по которым
письмо пересылается вслед за адресатом. Правило поиска
свободного адреса в таблицах с внутренними цепочками пере¬
полнения показывает, что даже при отсутствии указателей
можно обеспочить реализацию одной и той же последователь¬
ности проб при поиске и вставке без просмотра всей таблицы:
1. i = 0.
2. a = hi(k).
3.1. Если а свободно, алгоритм заканчивается (если это про¬
цедура вставки, алгоритм заканчивается удачно, если это
процедура поиска, это значит, что ключа в таблице нет).
3.2. Если ключ, связанный с адресом а, равен ky алгоритм
заканчивается (если это вставка, то повторная вставка
102
Глава 2
не производится, если это поиск, алгоритм заканчивается
удачно).
4. В противном случае — коллизия. Присвоить 1 и
перейти к п. 2.
В широком смысле о представляет собой последо¬
вательность хеш-функций. Выбор их, однако, представляет
достаточно сложную проблему. Считая, что А0 является од¬
ной из ранее рассмотренных функций, обсудим, какой вид
могут иметь другие функции последовательности.
(2—1) Линейное опробование
Это простейшая схема открытой адресации, при которой
hi(k) = h0(k)-\-ci, где с — константа. Правило простое, од¬
нако, аналогично случаю срастания списков, в методе с внут¬
ренними цепочками переполнения имеется опасность образо¬
вания «первичного скучивания», при котором особенно сильно
перемешаны адреса, соответствующие этим синонимам. Для
того чтобы этого избежать, с и М должны быть взаимно про¬
стыми, а с — и не слишком малым числом. Однако в случае,
когда число ключей мало по отношению к размеру таблицы,
опасность удлинения пути поиска из-за скучивания невелика,
а то, что синонимы расположатся в физически смежных по¬
зициях, даже выгодно, например в случае использования
виртуальной памяти и т. д.
(2—2) Квадратичное опробование
Это схема открытой адресации, при которой hi(k) —
= A0(^)+c/ + d/2, где с и d — константы. Благодаря нелиней¬
ности этой адресации удается избежать увеличения числа
проб при числе синонимов более 2. Однако в случае почти
заполненной таблицы не удается избежать «вторичного ску¬
чивания» с образованием групп из последовательностей запи¬
сей, длина которых больше числа синонимов по хеш-функ¬
ции. Это связано с тем, что при большом числе ключей си¬
нонимы одной группы вступают в коллизию с другими
ключами. От этого недостатка практически свободен следую¬
щий метод, при котором последовательности проб для таких
ключей оказываются различными.
(2—3) Двойное хеширование
Это схема открытой адресации, при которой 1ц(к) —
= h0(k)+ ig(k), где g(k) — хеш-функция, почти такая же,
что и Ло, но »е эквивалентная ей. Рассмотрим различные ва¬
Поиск данных по ключу
103
рианты комбинаций h0 и g. Например, если М — простое чи¬
сло, можно рекомендовать следующие варианты соотно¬
шений:
К (k) = (k mod М) + / (1 + k mod (M — 2))
(где & mod М — остаток от деления k на М),
hi (k) = ho (k) + / (Af — h0 (k)) и др.
Во втором выражении g и h0 не являются независимыми,
что несколько ускоряет вычисления, но если ho(k) легко при¬
водит к скучиванию, то hi(k) имеет ту же тенденцию. Воз¬
можна также комбинация этого метода с методом квадратич¬
ного опробования. Если h0 и g — независимые функции, то
вероятность коллизий при двойном хешировании будет со¬
ставлять, вообще говоря, Х/М1.
При использовании методов линейного и квадратичного
опробования или двойного хеширования в случае, когда
g(k) = M — ho(k), одна и та же последовательность проб
имеет место не только для ключей-синонимов k по хеш-функ¬
ции h(k), но и для синонимов по последовательности функ¬
ций hi(k) (i= 1,2, ...) и для всех ключей, для которых най¬
дется такое /, что h0(k/) = hi(k). Сказанное справедливо и
для внутренних цепочек переполнения. Чтобы избежать
удлинения последовательности проб, возникающего в таком
случае, было предложено использовать только те хеш-функ¬
ции, на которые указывает «предсказатель». Предсказатель —
это просто некоторая величина г (обычно несколько битов),
которая вводится в хеш-таблицу и используется для управ¬
ления последовательностью проб. Для хеш-таблиц с предска¬
зателем за hi(k) следующим адресом будет hi+r(k), который
зависит от значения г и не обязательно равен hi+\(k). До¬
стоинством метода является и то, что, если длина указателя
зависит от М, длина предсказателя от М практически не за¬
висит. Метод с предсказателем не является единственным и
был рассмотрен как один из возможных подходов к решению
проблемы предупреждения скучивания.
2) Удаление и переразмещение (рехеширование)
Удаление при использовании методов хеширования, во¬
обще говоря, не является процедурой, «обратной вставке»,
поскольку при удалении нарушается связь между синони¬
мами. Чтобы этого не произошло, можно вместо ключа, став¬
шего ненужным, не производя удаления записи, вписать спе¬
циальный код, который во время опробования пропускается,
но разрешает использовать эту позицию для вставки нового
ключа. Таким образом, каждая позиция хеш-таблицы нахо-
104
Глава 2
дится в одном из грех состояний: свободном, занятом или
удаленном. Удаленные позиции при поиске рассматриваются
как занятые, а при вставках — как свободные. При использо¬
вании этого метода однажды занятая позиция не можег
стать свободной. Поэтому, несмотря на постепенное увеличе¬
ние числа удаленных позиций и снижение реального коэф¬
фициента заполнения таблицы за счет уменьшения доли за¬
нятых позиций, время поиска не уменьшается. В худшем слу¬
чае может оказаться, что почти все позиции таблицы ока¬
жутся удаленными и только немногие — занятыми, но ни одна
из удаленных не сможет стать свободной, так как это нару¬
шит связь между занятыми позициями.
Для хеш-таблиц с внешними цепочками переполнения
удаление является процедурой, обратной вставке, и выполня¬
ется аналогично операции удаления из обычного линейного
списка. Для хеш-таблиц с линейным опробованием или
с внутренними цепочками переполнения «связь» между за¬
нятыми позициями однозначна, поэтому возможны реальные
удаления. Для этого достаточно переместить содержимое
всех позиций, приндалежащих списку и следующих за уда¬
ленной. Для выявления синонимов может потребоваться по¬
вторно вычислить хеш-функцию ключей, принадлежащих
списку. Если потребовать, чтобы каждый список синонимов
обязательно начинался со «своего» хеш-адреса h0(k)y то это
позволит сократить затраты на удаление. Затраты на вставку
в этом методе будут несколько выше, так как может потре¬
боваться переместить ключ, занимавший «чужую» позицию.
Этот метод можно рекомендовать и в том случае, когда
вставки ключей в таблицу редки по сравнению с поиском.
Одной из проблем для методов хеширования является
проблема выбора размера хеш-таблицы, так как изменение
размера хотя и возможно, но очень трудоемко. Если взять
размер таблицы исходя из расчета на максимальное число
ключей, то эффективность использования памяти будет низ¬
кой, в противном случае рано или поздно наступит ее пере¬
полнение и потребуется увеличить размер таблицы. Кроме
того, для методов хеширования характерна зависимость вре¬
мени обработки от коэффициента заполнения таблицы: чем
ниже коэффициент заполнения, тем меньше времени требуют
поиск и вставка. Поэтому необходимость в увеличении раз¬
мера таблицы возникает обычно из-за резкого увеличения
времени обработки, а не физического переполнения таблицы.
Увеличение таблицы ведет за собой и изменение хеш-функ¬
ции, а поскольку новая функция перестает соответствовать
старому расположению ключей, необходимо полное перераз-
мещение ключей в расширенной таблице с использованием
Поиск данных по ключу
105
новой хеш-функции. Такое полное переразмещение называют
рехешированием, и этой работы при изменении размера таб¬
лицы избежать не удается.
Итак, каким бы ни был выбор хеш-функции, возможны
коллизии, первичные и вторичные скучивания. Это связано
с тем, что в основе хеширования лежат вероятностные зако¬
ны. В худшем случае характеристики этих методов могут
оказаться очень плохими. Поэтому особенно важно знать,
каково поведение методов хеширования в среднем.
Анализ, таким образом, сводится к вычислению среднего
значения затрат в предположении, что хеш-функция доста¬
точно хорошо распределяет значения ключей по таблице.
Обозначим через С'п среднее число проб, необходимое для
вставки (п + 1)-го ключа в таблицу, содержащую п ключей
(т. е. когда поиск заканчивается неудачей). Смысл «среднее»
предполагает, что для заданного множества ключей суще¬
ствует идеальная хеш-функция h0(k), значения которой на
отрезке [0, М— 1] независимы и имеют равномерное распре¬
деление. Иными словами, предполагается, что все Мы воз¬
можных хеш-последовательностей (аь aN) адресов а\ =
— hQ(ki), ..., aN — ho(kN), соответствующих N ключам
ku •••, kNi равновероятны (N — произвольное натуральное
число). Аналогично обозначим через Сп среднее число проб,
необходимое для нахождения ключа в таблице, содержащей
п ключей (в случае, когда поиск заканчивается удачей).
В этом случае обращение к любому из п ключей равнове¬
роятно.
Если предположить, что при вставках структура таблицы
не меняется, то средние затраты на поиск и вставку некото¬
рого определенного ключа будут одинаковы. Таким образом,
и проблема сводится к вычислению С'п.
При анализе используем следующую приближенную мо¬
дель метода открытой адресации, которую назовем идеаль¬
ным «методом равномерного хеширования (опробования)».
Он заключается в том, что при наличии в таблице п ключей
для вставки следующего ключа с равной вероятностью выби¬
рается одна из оставшихся М — п свободных позиций. На
самом деле неизвестно, как реализовать такую хеш-функцию
и как использовать ее при поиске. Такая модель принята
исключительно для упрощения анализа.
2.3.3. Анализ
106
Глава 2
Доказано, что не существует метода открытой адресации,
для которого С' для всех п меньше, чем при использовании
метода равномерного хеширования (Дж. Д. Ульман, 1972).
Кроме того, многочисленные опытные проверки показали, что
метод двойного хеширования ведет себя практически как рав¬
номерное хеширование.
Обозначим через рпг вероятность того, что для (д+1)-й
вставки при равномерном хешировании потребуется ровно
г проб. Тогда
Сп= X Грпг = (рп{ + рп2 + РпЪ + • • •) + (Рп2 + РпЪ + •••) +
1
"4“ (РпЪ “{“•••) == X Япг itfnr := Рпг "4" Рпг л-1 “Ь • • ■
1 <г</г
Поскольку имеет место свойство равенства вероятностей, то
вероятность того, что при вставке потребуется г проб, равна
вероятности (г—1)-й неудачной пробы:
я (я-1)... (я-г+ 2) ( п \1( М \ =
Ч" — М(М-\) ... (Л1-Г + 2) уг—\)/Уг—\)
/М-г+1\//М\
— 1 м-п )!\п)'
= (М+ ЩМ-п+ IX
п— 1
Тогда можно записать
с' = У (м~г +
Ln 2Д М — п
г= 1
М + 1 V 1 —M+l/tI и
Сп=——Zj Л?—Т+Т — п Wm+i — пм_п+\),
t=о
П
где Нп = X 1//.
/=1
Если через а = п/М обозначить коэффициент заполнения
хеш-таблицы, то для больших М и п формулы для С'п и Сп
можно приближенно заменить на
С = 1/(1 — а) + О (1/М),
С = (1/а) log 1/(1 — а) + О (1/М).
Найдем среднее число проб в хеш-таблице с внешними
цепочками переполнения, предполагая, что все Мп хеш-после¬
довательностей равновероятны. Обозначим через рПк вероят-
Поиск данных по ключу
107
ность того, что данный список синонимов имеет длину k. Оче¬
видно, что имеются способов фиксации положения опре¬
деленного значения в последовательности и (М—\)n~k спо¬
собов размещения других элементов. Следовательно,
(М - \)n~k
Pnk \ и ) мп
Используя Производящую функцию Pn(s)= Yj PnkSk, получим
'.<■>-£ (;)№)‘(vr-('+vr
/г=0
Тогда среднее значение числа проб при поиске можно выра¬
зить через производящую функцию и ее производные. Так,
предполагая, что неудачный поиск в списке длины k требует
k + 6^, проб, получим
с; = I (k + 6,o) рпк=р'п (1) + ра (0)=пт + (1 - (1 /М)Г
fe=0
Считая, что удачный поиск в списке длины k требует
k(k-\- 1) /2 проб, получим
k=0
Приближенно можно записать
Са = а + е~а + О (1/М),
Са == 1 + ot/2 + О (1/М).
Для анализа линейного опробования воспользуемся сле¬
дующими математическими соотношениями. Биномиальная
функция Абеля является обобщением биномиальной фор¬
мулы
(х + y)r = YJ(jk) Х(х — kzf~' (у 4- kz)r~k,
г — целое ^ 0, х ф 0, yt z — действительные числа,
которая является тождеством по трем переменным jc, у и г.
Тогда для некоторой функции s(n, х,у)у используя эту фор¬
108
Глава 2
мулу, можно записать
s(n, X, у) = Yj ( 1) (* + kf+{ (у — k)n~k~x (у — п) =
= Y, (1') х (х + к)к (у — k)n~k~[ (у-п) +
/г>0
+ П X! ( 1 _ 1 ) (х + ^ (У ~ Ь)п~к~1 (у — п) =
= х (J^jiy — п)(у — п + k)k~l (х + п — k)n~k +
к >0
+п Z ("71 )(*+*+i)ft+,(*/-6-ir^-n)=
к^О
= X (х + у)П + tlS {п — 1, X + 1, у + 1).
Далее, будем считать равновероятными все MN хеш-по¬
следовательностей (ai, ..., aN) размещения N ключей в таб¬
лице размера М. Обозначим через f(M,N) число хеш-после¬
довательностей, таких, что некоторая фиксированная позиция
в таблице будет свободна. Очевидно, что эта позиция будет
свободна с той же вероятностью, что и любая другая, тогда
f(M, N) = MN • (М — N)jM.
Число хеш-последовательностей, таких, что позиция с адре¬
сом 0 остается свободной, позиции с адресами от 1 до k —
занятыми, а позиция с адресом k + 1 —свободной, составляет
g(M, N, *) = (*)/(* + Г k)f(M-k-l, N-k).
Это выражение можно рассматривать как последовательность
различных адресов длины N, состоящую из двух последова¬
тельностей: [ljk\ и [k + 2, М—1]. Из условия симметрии
следует, что функция g будет выражаться таким образом,
где бы ни размещалась точка начала просмотра отрезка ад¬
ресов [0, й+1] (адреса рассматриваются нормализованными
к М, т. е. адреса М, М + 1, ... считаются адресами 0,1, ...).
Наконец, положим Pk равным вероятности того, что при
вставке в хеш-таблицу (N-\-\)-ro ключа понадобится ровно
(& + 1) проб. Используя выражение для gy получим
Pk^M~N(g(M, N, k) + g(M, N, k+ 1)+ ... +g(M, N, N)).
Действительно, если обозначить через а хеш-адрес (N-\- 1)-го
ключа, то Pk равно M~Nt умноженному на число хеш-после-
Поиск данных по ключу
109
Таблица 2.5. Приближенные значения среднего числа проб
Среднее
^ч. число
проб
Метод
разрешения ^ч.
коллизий
С' Сп
а а
(в случае неудачи) слУчае удачи)
Линейное опробование
Двойное хеширование
2 (* '" 1 — а') 2 (Н '(Г-а)*)
1 1 1 1
1 —а а П 1 -а
Метод внешних цепочек
Метод внутренних це¬
почек
« + е-“ 1+|
1 + -j (е2а — 1 — 2а) 1+-| + Т_(е2“-1_2а)
довательностей (аь ..., aN), таких, что в результате хеши¬
рования и линейного опробования позиции с адресами [а—
— й+1, а] окажутся занятыми, а позиция с адресом
(а — k) — свободной. Количество таких последовательностей
с занятыми позициями [а + 1, а + t] и свободной позицией
(а + t — 1) (при t = 0, 1, ...) равно ^(Af, N,k + t).
М
л'с; = м"^(Л4-1)Рй = 2](й^2)г(А1, N, k) =
=N’ *)+Е(й+1)2^(м' N’
V fe ft /
= 1/2 (MN + s (N, 1, M— 1)),
C'w= 1/2^1 + £(* + 1)^)= 1/2(1 +Qo(iW, /V- 1)),
= 1/2 (! + Z (jV^ft)<fe>) = X'2 (! + Qi N))>
( Г k \ д/(&)
где <?,(*,*) = £( ft
k
можно оценить следующим образом:
1 1 ( r +2 ^ а 1
110
Глава 2
Таким образом, приближенные значения
с:=1/2(1+ттЬг).
1/2 (l + (1 — а)2 ) ‘
В табл. 2.5 приведены приближенные формулы для среднего
числа проб, полученные Д. Е. Кнутом.
Конечно, методы разрешения коллизий отличаются не
только числом проб, но и временем выполнения пробы, тре¬
бованиями к объему памяти и эффективностью ее использо¬
вания. Однако эти различия в затратах частично компенси¬
руются, что и позволяет проводить сравнение этих методов.
2.3.4. Совершенное хеширование
В случае когда множество ключей K = {ku ..., kN} за¬
ранее известно, нельзя ли путем удачного выбора хеш-функ¬
ции сделать так, чтобы коллизий не возникало? Иными сло¬
вами, не существует ли такой «совершенной» хеш-функции Л,
которая бы для всех (/¥=/) гарантировала неравенство
h(ki)^ h(kj)? И если да, то весьма желательно, чтобы длина
таблицы была минимальной и равнялась числу ключей, т. е.
выполнялось бы условие 0 ^ h(k) ^ N — 1. Такую функцию,
обеспечивающую взаимно однозначное отображение задан¬
ного множества К в последовательности адресов {0,1, ...
..., N—1}, назовем «минимальной совершенной» хеш-функ¬
цией. В принципе таких функций может существовать сколько
угодно, однако практический интерес представляют только те
функции, которые можно вычислить так же просто, как в
рассмотренных ранее методах.
Для определения совершенной хеш-функции (не обяза¬
тельно минимальной) требуется довольно большой объем
первоначальных вычислений, пробы, ошибки и повторные вы¬
числения. Однако в некоторых случаях, таких, как обработка
ключевых (зарезервированных) слов языка программирова¬
ния или языка запросов информационной системы, имеет
смысл проделать такую работу. При этом надо быть готовым
к тому, что при изменении К придется всю работу проделать
заново.
К счастью, предложенный Дж. Джеске «метод обратных
чисел» достаточно просто позволяет построить такую мини¬
мальную совершенную функцию. Теоретической основой ме¬
тода служит следующая теорема (предполагается, что ключи
ki <= К являются числовыми и им присвоены последователь¬
ные номера в порядке возрастания значений k[<k2< ...
... < kN).
Поиск данных по ключу
111
Теорема 2.1. Выбирая соответствующим образом для за¬
данных К целые числа С, D, £, можно построить минималь¬
ную совершенную хеш-функцию вида h(k) = \_C/Dk +
+ £J (modN) (здесь, как и ранее, |_*J — «пол» х).
Для доказательства этой теоремы используем результаты
следующей вспомогательной теоремы из элементарной теории
чисел.
Вспомогательная теорема. Выбирая соответствующим об¬
разом для заданных К целые числа Z), £, можно сделать
{Dk\ + £, ..., DkN + Е) взаимно простыми (доказательство
опущено).
Действительно, поскольку на значения D, Е ограничений
нет, выберем их так, чтобы для всех ключей выполнялось
отношение Dki + Е > N. Тогда все (Dki + Е) будут больше
N, а значит, существует такая последовательность {аь ...
cln}, для каждого элемента которой
(i - 1 )(Dkt + £)< at < i (Dkt + E)>
a-t — ay- = 0 (modulo N) (1 ^i<j^N)
(здесь a = b (modulo N) означает, что а и b сравнимы по
модулю N, т. е. (a — b)—число, кратное N). Найдем С, удо¬
влетворяющее условиям
С = at (modulo N(Dkt + E)) (1 </<;V)
(существование такого С обосновывается теоремой Везу),
следовательно, С можно представить через целые числа Lг.
С = LtN {Dkt + Е) + at (1 < I < N).
Таким образом, можно записать
LCKDki + Е)j = LtN + LaiKDki + Е)J = LtN + (/ - 1) = i - 1
(modulo W)(l
что и требовалось доказать.
Эта теорема задает достаточные условия, т. е. не обяза¬
тельно требовать, чтобы (Dki-\-E) были взаимно простыми.
Вместо того, чтобы пытаться определить С аналитически,
воспользуемся следующим методом. Этот метод позволяет
найти С путем серии проб и последовательного увеличения
первоначального значения. Очевидно, что
IC/kii Ф lC/k}i (modulo ЛО (1 </< /<Л0. (2.12)
Следовательно, объем вычислений можно уменьшить, если
исключить из рассмотрения те значения, которые не могут
быть «кандидатами» в С.
Определим вначале начальное значение С0. Из свойства
монотонности ki и неравенства (2.12) следует, что
ICIkJ-lC/k^N- 1.
112
Глава 2
Минимальное значение, удовлетворяющее этому условию,
используем в качестве начального значения С:
Со= 2) k\kN/(kN — k^)\.
Далее потребуем, чтобы С было кратным какому-либо /г.
Это необходимо, так как в противном случае все С—
— lC/ki\-ki будут больше нуля, и, следовательно, найдется
хотя бы один ключ, для которого
|C/£J = |_(C — \)lkt\ (1
Практически это означает, что можно обойтись меньшим
значением С. Для того чтобы сделать С кратным какому-
либо ki, вычислим значения приращений:
г,: = С — [C/kij • kif (1</<М).
Кроме того, если существует пара (/,/), такая, что
lC/ki] = lC/kj} = п (modulo N) (0 ^ п < N),
то, если увеличить С на min (ki — riy k} — ry), это не изменит
кратности =п для другого ключа. Если таких ключей три
и более:
lC/k J = [C/kjj = [C/ktl зз ... (modulo iV),
то приращение С надо выбирать так, чтобы кратность изме¬
нилась по крайней мере для ключей
max min (kt — riy kf — rj)
i < /
(max — по всем парам, которые удовлетворяют вышеприве¬
денному выражению в группе). Необходимый для этого объем
вычислений можно существенно сократить, если в качестве
приращения С взять приращение одного из ключей с макси¬
мальным значением индексов (/,/), удовлетворяющих соот¬
ношению \_C/ki\= \_C/kj \ (modulo N). То есть определить
максимальное значение / и для него — максимальное зна¬
чение и
Эти рассуждения можно оформить в виде алгоритма, ко¬
торый и приведен ниже. Сходимость алгоритма зависит ог
исходного множества ключей. Чтобы избежать чрезвычайно
больших затрат на вычисление С и гарантировать конечность
алгоритма, в нем использовано соответствующим образом
подобранное значение Cl, являющееся предельным для С.
Алгоритм. Определение минимальной совершенной хеш-
функции методом обратных чисел
1. Положить С : = С0.
2. Определить остаток от деления [С/&г J на N для 1
^ / sc: ЛЛ Если все значения окажутся различными, закон¬
чить вычисления.
Поиск данных по ключу
ИЗ
3. Обозначить через J максимальное значение ;, такое, что
IC/ki j = lC/kf\ (modulo Л7), а через /— максимальное
значение /, удовлетворяющее выражению [С/&* J = yC/kj J
(modulo N). Положить С := С + min (ki — ru kj — о) (п =
= С — IC/kij-ki).
4. Если С < Cl, вернуться к шагу 2. В противном случае
алгоритм заканчивается неудачей.
Последовательность вычислений с помощью алгоритма для
множества из четырех взаимно не простых ключей k = {25,
41, 55 66} представлена в табл. 2.6. Для С = 123 получены
следующие значения: [C/ki] (mod 4) = 0, 3, 2, 1.
Таблица 2.6. Определение минимальной совершенной хеш-функции
[С//г. J (mod 4) для К = {25, 41, 55, 66},
С0 =4 2-25-66/41 J = 80
С = 80 С=110 С = 123
C/ki
1
3,2
5
20
4,4
10
15
4,9
2
1,9
39
2
2,6
28
13
3
3
М
25
30
0
55
2,2
4
Р2
14
52
Ь6
44
22
1,8
Последовательность вычислений для С = 80, 110, 123. Поскольку для
С =123 все значения '[.C/kiJ (mod 4) различны, вычисления заканчива¬
ются, найденное С является результатом. Волнистыми линиями подчерк¬
нуты сравнимые по модулю значения iC/kij (mod 4). Прямой линией
подчеркнуты значения приращений С на очередном шаге. Числовые значе¬
ния элементов таблицы помогут понять используемый метод вычисления С
для минимальной совершенной хеш-функции.
Очевидно, что объем вычислений быстро увеличивается
с ростом N. Это видно и на примере расчетов, приведенных
в табл. 2.6. Кроме того, если распределение значений kt на
некотором отрезке близко к равномерному, то потребуется
испытать большое число значений С, прежде чем будет по¬
лучено значение LC/kti, которое, наконец, разделит эти
ключи. Сравнительно малым числом значений С можно обой¬
тись в случае экспоненциального характера распределения
значений kt. В случае равномерного распределения ki объем
вычислений при N ^ 20 становится слишком большим.
При N ^ 20 метод становится практически неприменимым,
однако N можно уменьшить за счет разбиения множества К.
Во-первых, можно применить способ «рассечения» Д' по
114
Глава 2
Таблица 2.7. Определение минимальной совершенной хеш-функции
а) б) Код 1
Слоги
Порядковый
номер
Частотность
ка
о
и
си
я
ки
ку
то
ма
на
*
са
ти
Фу
а
У
ко
хи
ми
ва
э
та
ха
мо
ра
су
тэ
ни
нэ
но
хо
мэ
ри
ро
II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
15
10
9
8
8
7
7
7
7
6
6
5
4
4
3
3
3
3
3
3
2
2
2
2
2
а
и
У
э
о
15
3
16
21
2
к
1
6
7
.
17
с
12
4
26
т
22
13
.
27
8
н
10
28
29
30
X
23
18
14
31
м
9
19
.
32
24
в
20
.
.
.
р
25
33
34
(я
= 5, н
= 35,
* =
И)
Поиск данных по ключу
115
(см. табл. 2.4; скучиванием пренебрегаем)
в)
г) Код 2
Д)
Название
Значение
Название
Значение
префектуры
функции 1
а
и
У э
о
префектуры
функции 2
0 0 И
7
15
3
17 21
2
о ка я
6
и си ка
8
4
7 .
22
о о и
. 7
о ка я
8
к
1
и си ка
8
ка на ка
12
с
17
4
26 .
си ка =)=
10
я ма ка
15
22
13
27
8
я ма ка
11
си ка *
16
т
ка на ка
1-2
ки о то
16
н
10
28
. 29
30
ки о то
14
о о са
16
23
18
28 .
31
о ки на
16
о ки на
18
X
я ма ку
17
то ку си
19
м
7
19
. 32
24
то я ма
18
я ма ку
21
20
то ку си
19
то я ма
22
в
•
я ма на
20
ка ка ва
22
р
25
33
34
о о са
21
ка ко си
22
ка ка ва
22
Фу ку о
на ка са
23
23
(я =
3, н
= 35, *
= 5)
са ка *
ва ка я
23
24
я ма на
24
то ти ки
25
Фу ку и
24
ми я ки
26
са ка *
24
ка ко си
27
фу ку си
25
на ка са
28
ва ка я
26
то у ки
29
то ти ки
27
а и ти
31
ми я ки
30
ни и ка
32
то у ки
30
си су о
32
ки фу *
31
хо ка и
35
а и ти
31
ки фу *
37
ни и ка
32
фу ку о
37
си су о
32
Фу ку и
38
хо ка и
35
ку ма мо
38
ми я са
36
фу ку си
39
са и та
37
ми я са
39
ку ма мо
40
на ра *
40
а о мо
41
си ма нэ
40
на ка по
41
а о мо
41
си ма нэ
42
а ки та
41
а ки та
43
ти ха *
41
на ра *
46
на ка но
41
ко у тн
46
са и та
42
ти ха *
47
ми э *
45
то то рн
49
ку н ма
49
и ва тэ
50
то то ри
49
ку н ма
51
и ва тэ
50
и ха ра
51
и ха ра
51
ми э *
51
ко у ти
52
хи у ко
51
хи ро си
56
хи ро си
56
хи у ко
57
э хи мэ
71
э хи мэ
71
116
Глава 2
значениям ki. Например, в случае разбиения на два отрезка
функцию h можно представить в виде
Если N велико, можно также провести группировку ki.
Используя подходящую хеш-функцию Л0, проводим разбиение
исходного множества на / хеш-таблиц размера М (2 ^
^ М <С N), так чтобы число синонимов не превышало 15.
Далее вычислим минимальную совершенную хеш-функцию
методом обратных чисел для каждой группы синонимов:
Метод проб и ошибок для определения совершенной хеш-
функции предложен Р. Дж. Чикелли. Согласно этому методу,
h вычисляется как сумма кодов букв ключа. Обозначим че¬
рез С/ код, соответствующий /-й букве ключа k, состоящего
из / букв Li, L2, Li. Тогда можно записать
Значения C(L) для различных L не обязательно должны
быть различными, т. е. хотя все буквы множества Li, Lt
различны, среди соответствующих им кодов Си С2, ..., С/
могут быть и одинаковые. Начальный этап этого метода
(пробы) для определения С осуществляется следующим об¬
разом.
Вначале упорядочиваем буквы по частоте их использова¬
ния в словах и присваиваем им коды 0,1,2, ... начиная
с буквы, обладающей большей частотностью. Затем вычис¬
ляем значения хеш-функции для каждого ключа, используя
числовые коды букв, и упорядочиваем ключи по значениям
h(k). В случае коллизий или нарушения непрерывности зна¬
чений исследуем, не может ли функция стать минимально
совершенной, если изменить коды букв, обладающих малой
частотностью. Для слов, содержащих буквы с частотностью 1,
за счет изменения кодов этих букв удается довольно свободно
изменять h(k). Корректируя коды букв невысокой частотно¬
сти, можно довольно успешно избежать коллизий.
Именно таким образом была определена совершенная
хеш-функция для названий префектур, представленных
в табл. 2.4, в начале данного раздела. Результаты началь¬
ICJkj (mod/) (при &<£/),
I + LC2/kj (mod N — I) (при k>kj).
/-1
l = hQ(k); h (k) = £ + ICi/k] (mod N[)
h(k)=ZCi(Li).
/=1
Поиск данных по ключу
117
ного этапа метода (пробы), опирающегося па частотность
букв, собраны в табл. 2.7. Для упорядочения промежуточных
данных был применен метод диалога с ЭВМ. Можно попы¬
таться построить такую функцию, например, для названий
месяцев. Необходимые вычисления довольно просто выпол¬
нить даже вручную, без использования ЭВМ.
2.3.5. Применение хеширования
1) Поиск по части ключа
Рассмотрим случай, когда аргумент поиска не содержит
некоторых позиций, относящихся к ключу. Например, биб¬
лиотечная карточка обычно содержит такие атрибуты: автор,
название книги, издательство, год издания; когда указаны
значения всех из них, книгу легко найти. Но что, например,
надо сделать, чтобы ответить на вопрос: какие книги авто¬
ра А выпущены издательством Р? Конечно, библиотечная
карточка кроме перечисленных атрибутов обычно содержит
и регистрационный номер (т. е. номер книги на книжной
полке) — это первичный ключ, однозначно идентифицирую¬
щий запись при поиске и являющийся ее атрибутом.
Это типичный пример запроса к системе информационного
поиска (например, поиска по отношению). При этом число
записей, удовлетворяющих запросу, заранее неизвестно и мо¬
жет быть как очень большим, так и равным нулю.
Итак, пусть файл размещен во внешней памяти на маг¬
нитном барабане, диске, ленте или другом носителе и зани¬
мает несколько блоков. Очевидно, что время поиска во мно¬
гом будет зависеть от числа обращений к внешней памяти.
Для таких приложений критерием эффективности является
прежде всего число блоков файла, к которым необходимо
обратиться для ответа на поставленный вопрос.
Для простоты будем считать постоянным число элемен"
тов атрибутов т записи г = (еj, ..., ет) файла F. Каждому
атрибуту е] поставим в соответствие множество целых чисел
{О, 1, . .., v — 1}= ]£, так, что F с= Будем считать, что
файл F разделен на b = 2w блоков и w^m, b^2m. Выбе¬
рем подходящим образом хеш-функцию Л, отображающую
X™ на (1, ..., Ь}. Теперь для каждого /-го блока можно
записать: Ву = {r;rGF,A (г) = /}, при этом F = Д + . . . + Вь.
Хеш-функцию h определим следующим образом. Введем
хеш-функцию g, отображающую £ на Ь •••> — l}
(т. е. длина значения g равна \_w/m\ битов), и используем
в качестве h последовательность из m\_w/m\ битов.
h(r) = (g{ei), g(e2), g(em)).
118
Глава 2
Теперь, если задать в запросе только часть л, например
(е2, ..., ет)у то при поиске достаточно будет просмотреть все
блоки с номерами
{(fif.), g (е2). • • •. g (ej). О < gx < 2Lw,mJ}.
Обычно w является целым числом, кратным т, и поиск
по 5 атрибутам потребует обращения к 2w~s(wlm) блокам.
Значение хеш-функции h в этом случае можно рас¬
сматривать как число в смешанной системе счисления: так
как В с= Yj » |£| = t/m(l^#^i> = |£l)> т0 В имеет струк¬
туру декартова произведения В = X • • • X ГДе 12/1 =
= y(i= 1, т). В случае равновероятности всех запро¬
сов выражение для числа блоков при поиске по s атрибутам
будет иметь минимальное значение необходимого среднего
числа блоков. Реальные данные, однако, будут распределены
не так равномерно, поэтому фактическое число обращений
к блокам окажется больше и еще немного увеличится в слу¬
чае, когда w не является числом, кратным т. Из-за нерав¬
номерности данных может оказаться, что к некоторым из
Ь^2т блоков обращаются очень редко. В таких случаях-
можно в качестве значения хеш-функции h(r) использовать
только средние log2 b из w битов. Однако в наихудшем слу¬
чае это может потребовать просмотра большого числа лиш¬
них блоков.
2) Отбор с помощью хеширования
Хеширование может оказаться очень эффективным в сле¬
дующих исключительных случаях поиска. Группа ключей
(список), представляющая собой заранее выбранное относи¬
тельно малое число ключей, рассматривается как исключи¬
тельная, и мы хотим подтвердить принадлежность большей
части вновь задаваемых один за другим ключей этой исклю¬
чительной группе. Иными словами, мы хотим из очень боль¬
шого множества выбрать небольшое число исключений.
Например, можно привести такие практические случаи,
как: 1) совпадает ли группа симптомов пациента с симпто¬
мами опасного заболевания, 2) имеется ли среди перечня
старых книг инкунабула (как название инкунабулы в переч¬
не?), 3) имеется ли среди группы преступников тот, кто по¬
дозревается в особо опасном преступлении, 4) является ли
исключением правило написания дефиса в простых англий¬
ских словах и т. д.?
Обозначим через М число выделенных вначале ключей.
Будем рассматривать случай, когда М не слишком велико
и пропорционально объему памяти, но для того, чтобы раз¬
Поиск данных по ключу
119
местить все значения М ключей в оперативной памяти, их
оказывается слишком много. Если использовать дерево по¬
иска, то при поиске аргумента все равно придется обра¬
щаться к внешней памяти. При использовании хеширования
для удачного поиска также придется просматривать сами
ключи в списке, но зато для неудачного поиска можно избе¬
жать просмотра списка.
Будем считать, что для списка из М слов можно исполь¬
зовать оперативную память объема L битов (L — IM, 1 < /).
Разобьем L на X хеш-таблиц, и для каждой таблицы выбе¬
рем отдельные независимые хеш-функции /гь ..., Для
каждого ключа будем вычислять X хеш-функций Л/ (1 ^
и для ключей, содержащихся в списке, установим
X битов равными 1 и 0 — для прочих; обработку коллизий
в таблицах проводить не будем. Будем считать, что доля,
приходящаяся в каждой таблице на 1 бит, составляет р/ =
= М/(L/X) = Х/L Для таких условий проведем следующее
рассуждение, которое позднее несколько скорректируем.
Используя хеширование, проведем сравнение^списка с по¬
следовательностью Т новых ключей (слов). Обозначим число
сравнений слов со списком в случае совпадений (удачный
поиск) через 7S, а в случае отсутствия в списке (неудачный
поиск)—через Ти, Ts + Ти = Т, Ts Ти. Вычислим hj и обо¬
значим затраты на поиск по всем хеш-таблицам в оператив¬
ной памяти через Chs, а затраты на поиск во внешней памяти
при поиске элементов списка — через Сехt-
Теперь, чтобы определить, содержится ли аргумент по¬
иска в списке, необходимо последовательно вычислить X
хеш-функций. Если /г7- (/г) -я позиция хеш-таблицы содержит О,
то это означает, что в списке нет искомого аргумента, а если
она содержит 1, то вычисляем hj+\(k), и, если все пробы
hi(k)t ..., hx{k) дают результат 1, очевидно, что во внешней
памяти обнаружен весь список. Найдем сумму: 1) затрат
Ts(XChs + Cext) для случая удачи или ожидаемой величины
затрат для случая неудачи, 2) затрат 7^(1 + Pi + Р1Р2 + ...
... + pip2 + рь)Chs на хеширование и 3) затрат rupip2 ...
... p^Cext на просмотр внешней памяти. Очевидно, что затра¬
ты (3) являются определяющими, поэтому попробуем их
уменьшить.
Для этого поступим следующим образом. Меняя число X
при фиксированном L, найдем такое его значение, которое
минимизирует значение затрат (3), т. е. если задано L/M = /,
то определим Х(<1), при котором
Р1Р2 • • • Ра, ^ (V0
будет минимальным. Для этого определим граничное значе¬
ние 1(Х) для /, при котором X будет иметь оптимальное
120
Глава 2
значение:
(X/l)k<((l+ 1 )//)fc+1 <=►/<(*,+ 1)к+Ч^ = Цк).
Имеем: /(1) = 4; /(2) = 33/22 = 6,75; /(3) = 44/33 =
= 9,481, 1(1) ~ (А.+ \)е (Я —* оо)
Можно рассмотреть случай, когда возможно последова¬
тельное вычисление X хеш-функций и эти затраты Снр не за¬
висят от числа и величины таблиц. Тогда суммарные затраты
будут складываться из: Г) затрат Ти (ChP + Cext) в случае
удачи или ожидаемой величины затрат в случае неудачи,
2') затрат TuChp на хеширование и вышеуказанных за¬
трат (3). Очевидно, и в этом случае максимальный вклад
в общие затраты дает (3), а следовательно, можно исполь¬
зовать тот же метод определения X, что и выше.
Итак, при анализе предполагалось, что М слов списка,
находящегося во внешней памяти, отображалось во внутрен¬
нюю хеш-таблицу длины L/X и что вероятность того, что
таблица будет содержать 1, составляет M/(L/X) = Х/1. На
самом деле если распределение М слов в таблице L/X не
является равномерным, то коллизии будут возникать, и доля
таблиц, содержащих 1, будет меньше, чем Х/1. Однако в на¬
шем случае это даже хорошо, так как эффективность поиска
тем выше, чем меньше единиц в таблице. В том случае, ко¬
гда коллизий очень много, имеет смысл для выбора хеш-
функций hj использовать метод проб и ошибок.
3) Другие практические случаи
Эффективность вычислений является функцией времени
вычисления и используемой памяти. Часто эти параметры
взаимосвязаны, так что уменьшение одного из них приводит
к увеличению другого. Хеширование можно рассматривать
как метод, уменьшающий время поиска и рационально ис¬
пользующий память. Таким образом, в настоящее время,
когда стоимость ЗУ быстро снижается как в абсолютном,
так и в относительном смысле, наблюдается тенденция по¬
степенного расширения области применения хеширования.
Прежде всего хеширование широко используется в систе¬
мах автоматизации программирования типа Лисп. Основной
структурой хранения языка являются бинарные деревья, од¬
нако древовидная структура составляет только скелет, а весь
смысл заключен в листьях — «символах атомов». Из-за этого
приходится постоянно обращаться к сущностям, представляе¬
мым символами атомов, и ускорение этой процедуры за счет
хеширования имеет решающее значение
Поиск данных по ключу
121
В практических случаях прямого или косвенного приме¬
нения Лисп стараются, не дробя весь массив информации
до символов атомов, подвергнуть хешированию как можно
большую часть строки (последовательность символов) и тем
самым повысить эффективность.
В данном разделе были рассмотрены наиболее простые
случаи поиска по единственному ключу, который состоял из
одного или нескольких атрибутов, однако в реальных случаях
ключей может быть несколько.
Примером, когда реально используется часть ключа, яв¬
ляется давно известная ассоциативная память. В обычных ЗУ
память адресуется по местоположению — вначале формиру¬
ется адрес, а затем производится выборка содержимого па¬
мяти. Ассоциативная память адресуется по значению — со¬
держимое одного рода используется для выборки содержи¬
мого другого рода. В последнее время для обработки файлов
начинает использоваться внешняя ассоциативная память,
реализуемая средствами аппаратного обеспечения.
Примером, когда поиск осуществляется по нескольким
ключам, является совместное использование структуры типа
сбалансированного дерева с хешированием. Первая причина,
объясняющая это, заключается в том, что за счет объедине¬
ния преимуществ обоих методов оказывается возможным
либо использование хеширования для подходящей иерархии
сбалансированного дерева, либо использование сбалансиро¬
ванного дерева для представления синонимов, образующихся
при хешировании. Вторая причина заключается в том, что
хеширование, как деревья, получило достаточно широкое рас¬
пространение и оказалось эффективным методом, связываю¬
щим формальное представление сложных символьных струк¬
тур с их сущностью. Типичным примером могут служить
разреженные многомерные массивы.
В дополнение к этому отметим, что как можно большую
часть обработки, связанной с поиском, имеет смысл выпол¬
нять за счет хеширования внутри ЭВМ. В настоящее время
ведется разработка ЭВМ FLATS нового типа, которая будет
обладать для этого специальным аппаратным обеспечением.
Глава 3
Сортировка
Сортировка — это процесс целенаправленного перемеще¬
ния элементов заданной конечной последовательности, ре¬
зультатом которого является последовательность, в которой
элементы расположены в порядке возрастания (или убыва¬
ния) их значений. С самого начала истории обработки дан¬
ных с помощью ЭВМ сортировка представляла собой очень
важную задачу. Она применялась не только для обработки
данных, полностью размещаемых в оперативной памяти, но
и для обработки коммерческих данных большого объема,
записанных на внешних носителях, таких, как магнитные
ленты, при использовании оперативной памяти очень ограни¬
ченного объема.
Необходимость обработки данных все большего и боль¬
шего объема требовала расширения возможностей применяе¬
мых ЭВМ. Это привело к появлению более мощных но-'
вых устройств, используемых для хранения данных, новых
архитектур ЭВМ и как следствие к новым алгоритмам сор¬
тировки.
Сортировка имеет довольно богатую историю, задачи ее
ясны. Существует множество алгоритмов сортировки, свой¬
ства которых достаточно подробно изучены. Анализ алгорит¬
мов сортировки составляет значительный раздел науки
о компьютерах.
3.1. Внутренняя сортировка
3.3.1. Сортировка
1) Отношения порядка
Числа а и b связаны отношением порядка а ^ Ь, если
выполняются следующие условия.
(1) Рефлексивность: а ^ а.
(2) Антисимметричность: если а ^ 6, b ^ а, то а = Ь.
(3) Транзитивность: если а ^ 6, b ^ с, то а ^ с.
(4) Линейность: для произвольных а и b справедливо
а или b ^ а.
Множества чисел (натуральных, целых, рациональных,
действительных, десятичных чисел с плавающей точкой),
удовлетворяющие этим условиям, в математике называют
вполне упорядоченными.
Сортировка
123
В памяти ЭВМ цифры и буквы английского алфавита,
а также различные знаки представляются битовыми комби¬
нациями. Эти коды можно рассматривать как натуральные
числа, следовательно, и в этом случае мы имеем дело
с вполне упорядоченным множеством. Например, последо¬
вательность 0 ... 9ab ... zAB ... Z (надлежащий порядок
символов) представляет собой один из вариантов упорядоче¬
ния. В зависимости от решаемой задачи на рассматриваемом
множестве символов может оказаться целесообразным изме¬
нение заданного упорядочения, может измениться взаимное
расположение цифр, символов и букв. Всю совокупность ис¬
пользуемых букв, цифр и других знаков (символов) с учетом
их фиксированного местоположения в последовательности
называют последовательностью сопоставления, а сам набор
символов — алфавитом.
Как же определить отношение порядка для буквенных
последовательностей (слов)? Рассмотрим множество слов
длины не более k символов в некотором алфавите, содержа¬
щем п символов- Перенумеруем символы алфавита целыми
О, ..., п—1 в соответствии с последовательностью сопостав¬
ления. Теперь любое слово в алфавите можно рассматривать
как последовательность целых чисел длины k или как число
в п-ичной системе счисления из диапазона от 0 до nk—1.
Так как мы рассматриваем слова различной длины, необхо¬
димо принять некоторые соглашения, используемые при их
сравнении. Обычно при сравнении двух слов различной дли¬
ны слово меньшей длины дополняется пробелами слева (ле¬
воустановленные слова) или справа (правоустановленные
слова). Для обеспечения лексикографического упорядочения
слова при сравнении рассматриваются как левоустановлен¬
ные. С другой стороны, при расположении чисел в порядке
возрастания (или убывания) величины имеет смысл исполь¬
зовать правоустановленные слова 1).
Пример. В зависимости от способа выравнивания одно и
то же множество слов с помощью определенного нами отно¬
шения порядка может быть упорядочено по-разному:
Лексикографический порядок (лево¬
установленные слова):
1 1 О А Д
1 1 Р М А
U F О А А
А А 1 1 О
A A U F О
А 1 1 Р М
В порядке возрастания величины
(правоустановленные слова)
(Треугольником обозначена позиция пробела).
‘) Предполагается, что в последовательности сопоставления пробел
Предшествует цифрам, а цифры — буквам. — Прим. ред.
124
Глава 3
Очень сложную проблему представляет упорядочение
японских слов, записанных иероглифами. Что касается иеро¬
глифов, то интерес к последовательности их сопоставления
довольно узок. Словарь иероглифов, принятых к использова¬
нию в Японии, включая так называемые японские иероглифы,
до сих пор не составлен, но этот пробел должен, наконец,
восполнить японский промышленный стандарт «Система иеро¬
глифических знаков для обмена информацией».
Хотя сложность иероглифов и определяется прежде всего
последовательностью сопоставления, благодаря особенностям
человеческой памяти поиск по последовательности иерогли¬
фов вполне возможен глазами и не требует больших затрат
времени, но важным фактором является то, что при практи¬
ческом использовании иероглифов эти возможности поиска
нельзя распространить на машинную обработку. Многие
иероглифические слова могут быть найдены, например,
в «Большом японском словаре» в соответствии с порядком
расположения, но если неизвестно, как они читаются, то ими
нельзя пользоваться и их нельзя адекватно представить в
ЭВМ. Многие одинаковые иероглифические сочетания чита¬
ются по-разному. Японские имена и фамилии и другие соб--
ственные названия также имеют различное и очень сложное
чтение. Следует отметить, что именно такие объекты явля¬
ются наиболее часто используемыми ключами при поиске.
Если имеется одномерный массив, то, из каких бы элемен¬
тов он ни состоял, его можно рассматривать как упорядочен¬
ный по возрастанию или убыванию индекса. Если мы распо¬
ложим на бумаге двумерный массив А(/,/), то I будет пред¬
ставлять номер строки, a J — номер столбца. Если мы попы¬
таемся двумерный массив представить в виде одномерного,
то мы должны будем определить порядок строк или порядок
столбцов, в соответствии с которым и будут располагаться
элементы. В случае трехмерного массива или массива боль¬
шей размерности нам также потребуется определить порядок
изменения индекса, например слева — направо или справа —
налево. В случае представления структуры данных в адрес¬
ном пространстве обычно вводятся вполне определенные со¬
глашения о расположении элементов.
Отношение между числами, удовлетворяющее всем выше¬
приведенным условиям, за исключением условия (4) (линей¬
ность), называется отношением частичного порядка. Напри¬
мер, множество натуральных чисел 1, 2, 3, 4, 5 может быть
представлено в виде следующих последовательностей:
р{ — (31 542), р2 = (31 245), р3 = (13 542), рА = (13 245).
Сравнивая р{ и р2, можно обнаружить, что они различаются
только расположением элементов 2 и 5: в р{ эти элементы
Сортировка
125
расположены как (..5.2), а в р2 они имеют расположение
(..2.5). Таким образом, можно считать, что последователь¬
ность р2 более упорядочена по возрастанию величины своих
элементов. На множестве рассматриваемых последовательно¬
стей определим отношение порядка следующим образом.
Пусть р 1 и р2 — последовательности, различающиеся только
позициями двух элементов, причем р2 более упорядочена, чем
Рис. 3.1. Отношение частичного порядка на узлах де
рева.
рь тогда будем считать, что pi ^ р2- Очевидно, что для при¬
веденных последовательностей справедливо
Pl<P2> Pl<p3> Р2<Р4> Рз<р4-
Последовательности р2 и р3 несравнимы. Несравнимы также
непосредственно р\ и р4, тем не менее используя свойство
транзитивности, имеем р\ ^ р2, р2 ^ р4 и соответственно
Pi ^ р4. Следовательно, на рассматриваемом множестве по¬
следовательностей задано отношение частичного порядка.
Наибольшей последовательностью этого частично упорядо¬
ченного множества является последовательность (12345), а
наименьшей — (54321). Аналогично можно определить отно¬
шение частичного порядка и для последовательностей, по¬
строенных из элементов множества 1,2,3, ..., п.
В качестве другого примера рассмотрим произвольное
дерево. Определим отношение частичного порядка на множе¬
стве его узлов. Пусть а и b — узлы дерева, тогда а ^ Ьу если
а принадлежит поддереву с корнем Ь. На рис. 3.1 изображено
дерево, на узлах которого задано отношение порядка D ^ В,
Е ^ В, Н ^ £, / ^ В и т. д. Узлы В и G, С и Н и др. несо¬
поставимы. Корень дерева всегда является наибольшим эле¬
ментом. Таким образом мы определили отношение частич¬
ного порядка на множестве узлов, исходя только из их взаим¬
ного расположения в дереве, не рассматривая содержимого
узлов.
2) Сортировка
Рассмотрим элементы х\,х2у ..., хп вполне упорядоченного
множества. Последовательность таких элементов, размещен¬
ных в одномерном массиве в порядке возрастания значения
х\ ^ *2 ^ ^ хп будем называть отсортированной после¬
довательностью. Если имеется возможность переставлять
126
Г лава 3
исходную последовательность элементов в произвольном по¬
рядке (в случае, когда все х\ различны, получится п\ пере¬
становок), то процесс переразмещения элементов в от¬
сортированную последовательность называется сортировкой.
Далее для простоты ограничимся рассмотрением целых
чисел.
Пусть имеется файл, записи которого (рис. 3.2) состоят
из двух атрибутов: фамилия и возраст, причем записи рас¬
положены в алфавитном порядке по атрибуту фамилия. Пред¬
положим, что при сортировке записей в порядке увеличения
(Аоки
20)
(Ито
19)
(Ито
19)
(Кимура
19)
(Като
21)
(Симидзу
19)
(Кимура
19)
(Аоки
20)
(Сайто
20) ^
(Сайто
20)
(Симидзу
19)
(Уэно
20)
(Танака
21)
(Като
21)
(Уэно
20)
(Танака
21)
Рис. 3.2. Устойчивый алгоритм сортировки.
возраста мы хотим сохранить алфавитный порядок располо¬
жения записей внутри группы каждого возраста. Обычно
алгоритм сортировки, сохраняющий упорядоченность элемен¬
тов последовательности в каждой группе записей с одним и
тем же ключом, называют устойчивым алгоритмом. Если сор¬
тировка записей выполняется только по значениям одного
атрибута, то часто имеет смысл использовать устойчивый
алгоритм сортировки.
К сожалению, устойчивы обычно простые алгоритмы, а
сложные высокоэффективные алгоритмы, как правило, не¬
устойчивы. Например, в следующем случае алгоритм неустой¬
чив. Рассмотрим множество, состоящее из п групп чисел вида
(Xj 1, ..., XjP) (j — 1, ..., п). Отсортируем эти группы по
значениям первого элемента. Если несколько групп имеют
одинаковые значения первых элементов, отсортируем их по
вторым. Будем выполнять эти действия до тех пор, пока не
получим отсортированной последовательности п групп чисел.
Если представить дату в виде 6-разрядной числовой по¬
следовательности (например, 82 август 15 будет выглядеть
как 82, 08, 15), тогда рассмотренным способом можно отсор¬
тировать некоторое множество дат. При этом для анализа
ошибок в данных естественно использовать информацию
о диапазонах значений элементов, составляющих дату, т. е.
второй элемент содержится в интервале [1,12], а третий —
в интервале [1,31] (или в более узком интервале в зависи¬
мости от значения второго элемента).
Сортировка
127
Рассмотренным способом можно отсортировать довольно
большой массив данных. Устойчивость алгоритма можно обес¬
печить порядком рассмотрения элементов сортируемых групп:
они должны выбираться справа налево. Пример такой сорти¬
ровки приведен на рис. 3.3. Здесь сортировку обязательно
(3, 8, 7) (3, 8, 2) (4, 1, 2) (3, 2, 4)
(4, 2, 4) (4, 1, 2) (4, 2, 4) (3, 8, 2)
(3, 2, 4) =>- (4. 2, 4) (3, 2. 4) =>- (3, 8, 7)
(3, 8, 2) (3, 2, 4) (3, 8, 2) (4, 1, 2)
(4, 1, 2) (3, 8, 7) (3, 8, 7) (4, 2, 4)
Рис. 3.3. Сортировка по основанию
системы счисления с применением
устойчивого алгоритма.
надо начинать с правых элементов последовательностей, т. е.
вначале надо провести распределяющую сортировку по млад¬
шим цифрам ключей, хотя на первый взгляд кажется, что
надо поступать наоборот.
Итак, десятичное р-разрядное число можно рассматри¬
вать как группу из р элементов, полученных в результате
поразрядного разбиения. Применение к таким числам опи¬
санного выше метода сортировки называют сортировкой по
основанию системы счисления. В вычислительной технике
была целая эпоха перфокарточных систем обработки данных,
в которых применялись сейчас редко используемые перфо¬
карты. ЭВМ, входящие в эти системы, комплектовались
специальными сортирующими устройствами, которые произ¬
водили машинную сортировку перфокарт на 12 колод по
пробитой в колонне позиции (с 0 до 9 и X, Y). Это устрой¬
ство для сортировки, например, трехразрядных чисел, пред¬
ставленных в трех колонках, должно было выполнять сле¬
дующие операции: вначале произвести распределяющую
сортировку в колонках, соответствующих разряду единиц, и
разложить карты в порядке чисел, пробитых в этой колонке,
О, 1, ..., 9, затем выполнить ту же работу для колонок, со¬
ответствующих разряду десятков, а затем — разряду сотен.
После трех операций распределяющей сортировки при объ¬
единении колод карты окажутся в нужном порядке. При этом
существовала опасность того, что колоду карт, например
программы, могли по небрежности уронить и в результате
нарушить порядок перфокарт в колоде; неудобство состояло
в том, что карты должны были пробиваться в строго опре¬
деленных колонках.
Часто сортировка необходима в случаях, когда записи
файла расположены в зависимости от значений их ключей,
т. е. ключам записей предписаны определенные положения
128
Глава 3
в файле. Ниже рассмотрим случай, когда существует воз¬
можность изменить положение записи в файле вместе с клю¬
чом записи. В этом случае необходимо учитывать возмож¬
ность при заданных размерах файла, подлежащего сорти¬
ровке, его обработки только с использованием оперативной
памяти. Очевидно, что сортировка в оперативной памяти и
сортировка во внешней памяти существенно отличаются по
эффективности; будут отличаться также алгоритмы и крите¬
рии оценки алгоритмов. В следующем подразделе рассмот¬
рим только методы сортировки с использованием оператив¬
ной памяти. Ограничимся также сортировкой числовых по¬
следовательностей. В примерах будем использовать последо¬
вательность (хь ,хп) с порядком расположения элемен¬
тов 1, ..., п.
3.1.2. Методы сортировки
В повседневной деятельности, выполняя обработку раз¬
личных объектов, например документов, мы интуитивно при¬
меняем сортировку, которая основывается на том или ином
методе. Рассмотрим некоторые из них.
1) Сортировка простыми вставками
Сравним х.у и х{ и, если х{^х2, оставим их в этом порядке.
В противном случае поменяем их местами. Обозначим по-
3 15 2
4 15 2
I
3 4 5 2
i
3 4 5 2
4 '
2 3 4 5'
Рис. 3.4. Сортировка простыми вставками.
лученную в результате последовательность х\2\ х{2>. Срав¬
ним х3 с х[р и, если л;(22)^л;3, оставим этот порядок, в про¬
тивном случае передвинем xf] вправо. Сравним х3 с xf' и,
если *(2)^*3, вставим *3 на место xf\ в противном случае
подвинем х{2) вправо, а х3 вставим на место xf] и т. д.
(см. рис. 3.4).
Операции сравнения и перемещения продолжаются до
получения отсортированной последовательности. Особого вни¬
мания заслуживает случай, когда при сравнении Xk ока¬
0
4
0
3
г
0
1
0
1
0
1
Сортировка
129
зывается x{£lx^xk и ничего никуда не перемещается, и слу¬
чай, когда x\k) > xk и xk помещаются в самую левую пози¬
цию. Для упрощения правила будем считать, что и в случае
x{k-\^xk надо сДелать «пустое» перемещение. Будем счи¬
тать, что в позицию хо поставлено в качестве «сторожа» (гра¬
ничной метки начала блока информации) число, меньшее
любого из чисел хи • •., хп, с которыми можно проводить
«пустое» сравнение. Таким образом, основную операцию ал¬
горитма можно записать следующим образом.
- ( Если x[k)^xby поместить хь в (/+1)-ю
установить / — к II I к
провести сравнение ’ позицию и закончить выполнение ал-
1 горитма. В противном случае ху} под¬
винуть на (/+ 1)-ю позицию и умень¬
шить /на 1.
Операция повторяется для Л = 2,3, ..., п (см. последнюю
часть рис. 3.15).
Этот алгоритм является устойчивым алгоритмом. Если
число сравнений и перемещений разделить на минимальное
число сравнений (п—1), мы получим некоторую характери¬
стику алгоритма, называемую «числом инверсий». Для слу¬
чая, когда последовательность с самого начала отсортиро¬
вана в возрастающем порядке, число инверсий минимально
к равно 0. Если с самого начала последовательность отсор¬
тирована в убывающем порядке, число инверсий максималь¬
но и равно (п—1) п/2. Число инверсий представляет собой
шсло случаев, когда xk меньше элементов из последователь-
юсти хи •••> xk-\ для k = 2y ..., п. Предположим, что лю-
5ой порядок элементов в последовательности х\у ..., хп рав-
ювероятен. На практике последовательность обычно до
1екоторой степени упорядочена. Однако для облегчения ана-
шза обычно предполагают, что все последовательности рав-
ювероятны. Распределение числа инверсий соответствует
юэффициенту корреляции порядка, называемому в стати-
тике коэффициентом Кендэлла, свойства которого хорошо
звестны. В случае равновероятного порядка элементов в по-
ледовательности среднее значение числа инверсий является
ромежуточным между минимальным и максимальным зна-
ениями и составляет (п—1) лг/4, а дисперсия равна пг/6.
1ри использовании рассматриваемого алгоритма сортировки
случае динамического формирования элементов последова-
ельности вставки можно производить при каждом отдельном
оступлении нового (очередного) элемента.
Для алгоритма сортировки простыми вставками число
)авнений можно уменьшить. На каждом шаге Xk можно
>авнивать со значением элемента, находящегося примерно
xk с ху'
5 Зак. 127
130
Глава 3
в середине последовательности, и если хь окажется больше,
то следующее сравнение производить с элементом, находя¬
щимся примерно в середине второй половины, а если хк
окажется меньше, то сравнение производить с элементом,
находящимся примерно в середине первой половины, и т. д,
В таком случае число сравнений окажется равным n\og2n,
однако число перемещений остается прежним.
2) Сортировка простым выбором
Сравнивая между собой хи •••> хп, находим наименьшее
значение и меняем его местами с х\. Обозначим получив¬
шуюся в результате последовательность как х^К
Находим наименьшее значение среди элементов последова¬
тельности х\?], ..., х{%] и меняем его местами с лг(22). Повто¬
ряем эту операцию до конца последовательности (рис. 3.5).,
4
1
3.
х
5
2
1
3
|
1
4
5
2.
1
2
4
1
5
*
3.
1
2
3
5
4
4.
1
2
3
4
5
Рис. 3.5. Сортировка посредством простого выбора.
После (п—1) шагов сравнения и обмена получим последо-
вательность, отсортированную в возрастающем порядке.
В отличие от алгоритма сортировки простыми вставками:
в этом алгоритме операция сравнения обязательно произво¬
дится (п—1)п/2 раз. При этом необходима операция вы¬
вода наименьших значений с каждого из рассматриваемые
участков. Число операций вывода в наихудшем случае со¬
ставляет п2/4, среднее число равно /г log/г. Если сравнивать
свойства этого алгоритма со свойствами алгоритма сорти
ровки простыми вставками, то оказывается, что в случае сор
тировки простым выбором число сравнений больше, а числе
перемещений меньше. В целом большой разницы в эффек
тивности нет. Сортировка вставками больше подходит дл*
случая, когда сортируемые данные поступают последовз
тельно, а сортировка простым выбором — когда все данньк
находятся в памяти, а отсортированные данные последова
тельно выводятся.
3) Простая обменная сортировка
Просматриваем справа налево всю последовательное!'
хи ..., хп, производя при этом сравнение каждых двух со
седних элементов последовательности. Если левый элемеп
Сортировка
131
3 -
1
1
1
1
1
4 •: з .
._2_
2.
2
2
2
I*-’ 4 :
3
А
3
3
3
9 ..2
4
4
4
4
4
о
00
•5
5
5
5
5
• г
2* 8 :
9 .
•JL
6
6
6
10 ..Б**"
8 :*
9 .
• 7_
7
7
V : 10
6 : 7 :
.6-'*
10
8/
• 7***
9 ,
в.-**'
,*8_
9
8
9
5*’ б*’*
7***
10
10
10
10
из пары оказывается больше правого, меняем их местами.
Теперь элемент, имеющий наименьшее значение, находится
в самой крайней левой позиции. Если проведем ту же опера¬
цию для оставшихся (п—1) элементов, то наименьший из
этих элементов передвинется на вторую позицию слева. По¬
вторяя эту операцию для оставшихся (п — 2) элементов
и т. д., самое большее на (п—1)-м шаге убедимся, что вся
последовательность оказывает¬
ся отсортированной.
Рассмотрим пример,изобра¬
женный на рис. 3.6. Проанали¬
зируем, что получается при од¬
ном просмотре последователь¬
ности. Последовательность
хи •••> *п, представленная на
рисунке, расположена сверху
вниз. Наименьшие значения
элементов на отдельных уча¬
стках, если смотреть снизу, бу¬
дут 5, 2, 1. После первого про¬
смотра 5 «всплывает» ДО по- Рис. 3.6. Обменная сортировка,
зиции под 2, 2 — до позиции
под 1, а 1 — на самую верхнюю
позицию. Элементы, расположенные между наименьшими
значениями элементов на отдельных участках или располо¬
женные на верхнем участке, без изменения относительного
порядка опускаются на одну позицию. На 3-м шаге, как видно
из рисунка, наименьшим ключом, находящимся в процессе
перемещений, будет 6. При этом ключи от 1 до 6 уже от¬
сортированы, и на следующем шаге производится просмотр
участка с ключами, большими 6.
Этот метод назван методом «пузырька», потому что «лег¬
кие» элементы, подобно пузырькам, «всплывают» наверх.
Метод пользуется необоснованной славой из-за своего умень¬
шительно-ласкательного названия, однако по сравнению
с методом вставок и методом выбора он имеет меньшую эф¬
фективность. Число шагов просмотра с обменом оказывается
не более (п— 2), и, из-за того что «легкие» элементы всплы¬
вают по нескольку сразу, кажется, что это сильно уменьшает
затраты на сортировку. Но с другой стороны, «тяжелые»
элементы, такие, как 9, если они находятся наверху, пере¬
мещаются вниз последовательно по одной позиции при каж¬
дом шаге, что увеличивает время сортировки. Число обменов
оказывается довольно большим.
Наименьшее число обменов для получения последователь¬
ности, отсортированной в возрастающем порядке, равно 0.
Максимальное число обменов для получения последователь¬
5*
132
Глава 3
ности, отсортированной в убывающем порядке, равно (п —
— \)п/2. Среднее число обменов составляет помежуточное
значение (п— 1)/г/4. Число сравнений равно минимум (п—1),
максимум (п—1 )п/2\ первое соответствует случаю наилуч-
шего варианта числа обменов, второе — случаю наихудшего
варианта. Среднее число сравнений отклоняется от промежу¬
точного в большую сторону. Эти значения также хуже, чем
при использовании метода вставок. При использовании ме¬
тода обменной сортировки не только число сравнений оказы¬
вается несколько больше, но и число обменов оказывается не
меньше, чем число перемещений при сортировке вставками.
Если сравнивать метод обменной сортировки с сортировкой
посредством выбора, то среднее число сравнений оказывается
близким к половине, а среднее число обменов более чем
вдвое больше числа операций вывода элементов при сорти¬
ровке посредством выбора.
4) Сортировка выбором из дерева (корпоративная сортировка)
Если бинарное дерево поиска, содержащее п узлов, сба¬
лансировано, то его высота (глубина) равна l\og2{n + 1) J.
(1)22
(2)4 "(3)62
(4)23 (5)18 (6)94 (7)89
(8)45 (9)82
а
94
82.' 89
А А
45 18 62 22
А
4 23
\ 94
89 94
89 94
89 94
18 Z2
А А
23 45 62 82
А
89 94
Рис. 3.7. Корпоративная сортировка.
В случае сортировки имеет смысл также посмотреть, нель¬
зя ли в каком-либо виде использовать структуру бинарного
дерева. Методом, в котором для сортировки применяется би¬
нарное дерево, является «корпоративный», или «турнирный»,
метод сортировки. Большим преимуществом этого метода яв-
ляется то, что даже в наихудшем случае для получения от-
сортированной последовательности требуется число шагов,
пропорциональное не n2, a nlogn. Алгоритм корпоративной
сортировки не обладает свойством устойчивости.
Сортировка
133
Пусть следующие друг за другом элементы последова¬
тельности будут размещены в памяти с адреса, например,
от 1 до 9. Тогда последовательность неявно имеет структуру
бинарного дерева, представленного на рис. 3.7, а. Числа, обо¬
значенные в позициях узлов и листьев этого дерева, после
первого шага применения рассматриваемого ниже алгоритма
корпоративной сортировки займут положение, показанное на
рис. 3.7,6. В основу метода корпоративной сортировки поло¬
жено размещение сортируемой последовательности в. узлах
сбалансированного бинарного дерева. Причем в каждом узле
находится элемент последовательности, больший чем элемент,
расположенный в любом его порожденном узле. Такие де¬
ревья удобно хранить в последовательно расположенных
позициях.
На первом этапе сортировки, выполняемой корпоративным
методом, применяется следующий основной алгоритм1). Обо¬
значаем левое и правое поддеревья бинарного дерева через
Т\ и 72 соответственно и считаем, что они уже образуют «кор¬
порацию» (см. рис. 3.7, в). Если при построении 7 число, на¬
ходящееся в корне 7, больше, чем числа, находящиеся в кор¬
нях 7! и 72, оставляем этот порядок, а если меньше, то
большее из чисел меняем местами с числом, находящимся в
корне 7/. Тогда, поскольку 7* не обязательно окажется «кор¬
порацией», корень 7/ опять сравниваем с нижерасположен¬
ными узлами. Так, последовательно опуская меньшее число
ниже и ниже (или, наоборот, поднимая большее число выше
и выше), постепенно спускаемся до листа, проверяя, нет ли
меньшего числа.
Если исходный узел является 7м узлом слева на уровне
5, то его адрес определяется как / = 1 + 2 + 22 + • • • + 2s-1 +
+ t, а его порожденные, являющиеся (21— 1)-м и 2/-м узла¬
ми слева на уровне (5+ 1)> будут иметь адреса k— 1 -f- 2
+ 22 + ... + 2* + 2, — 1 = 2/ и 2/ + 1.
Итак, первый этап корпоративной сортировки связан с
построением «корпораций» для сортируемой последовательно¬
сти. Для этой цели рассмотренный алгоритм необходимо при¬
менить ко всем узлам дерева, начиная с его нижних подде¬
ревьев. Предположим, что узлы дерева размещены в элемен¬
тах памяти с адресами [1, п]. Мы можем начать обработку
с поддерева с корнем в позиции / = [п/2\. Узлы этого под¬
дерева расположены в позициях (/, п). Уменьшая / на 1 после
]) Описывается пирамидальная сортировка — одна из разновидностей
корпоративной сортировки. Сортировка выполняется в два этапа: на пер¬
вом строится «корпорация» в виде пирамиды, второй этап связан с пепо-
средственным извлечением элементов последовательности из пирамиды для
получения ее в отсортированном виде в последовательной памяти. — Прим.
Ред.
134
Глава 3
обработки очередного поддерева до тех пор, пока / не станет
равным 1, и, применяя рассмотренный алгоритм для каждого
нового выделенного поддерева, мы получим представление
последовательности в виде корпорации.
На втором этапе из «корпорации» строится отсортирован¬
ная последовательность. Вначале, поскольку наибольшее
Подпрограмма: перенос элемента х. вниз по дереву {х^ ..., хп)
представленному в последовательной памяти с адресами от 1 до п),
1.1. Если 2/ > п, алгоритм заканчивается.
1.2. При 2/ = п,
1.2.1. если х.^х^, алгоритм заканчивается;
1.2.2. если х. < хп, произвести обмен х. : = : хп и закончить алгоритм.
1.3. При 2j < п.
1.3.1. если *2/>*2/+г
то, если х2. > хпроизвести обмен
х.:=:х и положить /: = 2/, после чего возратиться в начало;
1 *1
1.3.2. если х2. < *2/+1,
то, если х21+ \ ^ */’ пРоизвести обмен
xj :==:x2j +1 и положить У':=2/+1» возратиться в начало;
1.3.3. при л:. ^ max *2/+i) закончить алгоритм.
[Построение корпорации (выстраивание в виде „корпорации44 последо¬
вательности хх, хп. Большее значение в корне).]
1. Для / = |_ J’ • * -1
1.1. опустить х. (в диапазоне л;., ..., х ).
/V ] п/
[Сортировка (извлечение из корпорации отсортированной последова¬
тельности хь ..., хп).]
1. Для i = п, п — 1, ..., 2,
1.1. произвести обмен х{ и х.,
1.2. опустить х{ (в диапазоне х{У ...,
Рис. 3.8. Алгоритм. Корпоративная сортировка.
значение находится в корне, т. е. в позиции с адресом 1, его
обменивают с числом, имеющим адрес п. Это приведет к раз¬
рушению «корпорации», поэтому ее необходимо восстановить
для еще необработанной части дерева. Для этого произво¬
дится перенос элемента из корня вниз, однако этот спуск
ограничен диапазоном адресов [1, п—1] (рис. 3.7,г). В ре¬
зультате восстановления «корпорации» в корень приходит
второе наибольшее значение; обмениваем его с числом, имею¬
щим адрес (п — 1), и поднимаем следующее наибольшее
значение из диапазона адресов [1, м — 2]. Проводя такой
подъем последовательно (п—1) раз, получим отсортирован¬
Сортировка
135
ную последовательность. Рассмотренный нами алгоритм пред¬
ставлен на рис. 3.8 (здесь а : = : b — оператор обмена значе¬
ний переменных а и Ь).
При построении отсортированной последовательности из
«корпорации» часто производятся избыточные сравнения.
Это происходит, например, если сравнительно малое число,
расположенное в позиции с адресом п, обменивается с наи¬
большим числом, расположенным в позиции с адресом 1,
Чтобы избежать избыточных сравнений, вначале содержимое
позиции с адресом 1 убирают из этой позиции и перемещают
в нее большее из значений элементов, имеющих адреса 2 и 3.
В освободившуюся позицию (узел) перемещают большее зна¬
чение из порожденных узлов, образуя новый пустой узел.
Эту операцию производят последовательно до тех пор, пока
не будет получен пустой листьевой узел из диапазона адре¬
сов [1 уп—1]. Содержимое позиции с адресом п перемеща¬
ется в пустой лист, после чего осуществляется его подъем.
Этот подъем не будет очень высоким. Однако в случае такого
усовершенствования усложнится рассмотренный алгоритм
корпоративной сортировки: изменения будут относиться к об¬
работке первой ступени «корпорации».
Корпоративный метод сортировки предполагает исполь¬
зование бинарных деревьев, однако этот метод можно рас¬
пространить и на р-арное дерево (р = 2,3, ...) (рис. 3.9).
При подъеме число, находящееся в корне, сравнивается с
максимальным значением чисел, расположенных в р порожден¬
ных узлах. Так же как и при использовании бинарного де¬
рева, можно определить адреса порожденных узлов для
исходного узла с адресом /. Адреса порожденных вершин ле¬
жат в диапазоне от (jp — р + 2) до (jp+ 1), а адрес исход¬
ного для узла с адресом j определяется как |_ (/ — 2)/р J + К
Глубина р-арного дерева для представления последователь¬
ности из п элементов равна l\ogР(п(р—l)-fl)J. Число
узлов р-арного дерева глубины h составляет (рЛ-1— 1 )/(р —
1)+ р, где (1 < <7 < Ph~1)-
Определим верхний предел затрат на корпоративную сорти¬
ровку. Для простоты будем рассматривать сбалансированные
(1)
Рис. 3.9. Корпоративная сорти¬
ровка с использованием 3-ар¬
ного дерева.
136
Глава 3
р-арные деревья. Для несбалансированных р-арных деревьев
построения аналогичны приведенным ниже. При осу¬
ществлении обмена между исходным и порожденными уз¬
лами необходимо р сравнений, поэтому число обменов со¬
ставляет самое больше 1 /р числа сравнений. Продолжая
обмены между исходными и порожденными вершинами, ино¬
гда можно выполнить k обменов, произведя (k + 2) переме¬
щений, однако эта возможность пренебрежимо мала.
При подъеме одного узла, расположенного на s-й сту¬
пени сверху, для корпорации необходимо самое большее
(h — s) обменов. Поскольку число узлов уровня корпорации
составляет ps_1, верхний предел числа обменов для всех ис¬
ходных узлов будет выражаться как
*£ .
S=1
При восстановлении после выбора наибольшего значения
в поддеревьях высоты 5 после спуска числа, находящегося
в корне, можно возвратиться на s-ю ступень. Теперь верхний
предел числа обменов для всех узлов будет выражаться как
= -JL.
Z-i н р — 1 (р — I)2 р — 1
5=1
Объединяя эти выражения, получим верхний предел числа
обменов
nh ^ п logрп.
Верхний предел числа сравнений в р раз больше этой
величины. Таким образом, верхний предел затрат на корпо¬
ративную сортировку будет составлять п log п. Определить
среднее значение затрат для выполнения корпоративной сор¬
тировки достаточно сложно. Исходя из практического опыта,
можно утверждать, что средние затраты также составляют
п log п.
Как будет зависеть верхний предел этих затрат от изме¬
нения р? Число обменов ti\ogpn снижается с увеличением р,
а число сравнений pn\ogpn с ростом р увеличивается. По¬
этому должно существовать оптимальное значение р. Примем
за единицу измерения время, необходимое для сравнения.
Тогда если для обмена требуется в а раз (а >> 1) больше
времени, то верхний предел времени будет составлять
(п log п) (р + a)/log р.
р, при котором значение этого выражения будет наимень¬
шим, определяется соотношением p(logp—l) = a, и оказы¬
Сортировка
137
вается, что может быть и так, что с увеличением а значе¬
ние р тоже увеличивается. На практике число обменов ока¬
зывается меньше числа сравнений в 1 /р раз и зависит от
разницы между средним значением и верхним предельным
значением времени вычислений и качества программы. До¬
статочно хорошей практической оценкой для р считают 3
или 4. Корпоративный метод может применяться и для дру¬
гих целей. Идеальным случаем применения рассмотренного
метода является реализация приоритетных очередей, т. е.
извлечение из некоторой неотсортированной последователь¬
ности из п элементов k первых или k-го по значению эле¬
мента.
В этом случае можно ограничиться k шагами сортировки
корпоративной последовательности. Алгоритм заканчивает
работу за k\og2n сравнений и перемещений. Для упрощен¬
ного алгоритма выбора достаточно (2п — k—\)k/2 сравнений.
При численном интегрировании по некоторой области по¬
следняя разбивается некоторым образом на участки и про¬
изводится оценка абсолютной ошибки для каждого отдель¬
ного участка разбиения. За счет увеличения числа точек
интегрирования путем выбора участка разбиения области
с наибольшей ошибкой и более детального его разбиения
можно повысить точность интегрирования. После снижения
ошибки на рассмотренном участке производят выбор участка
с наибольшей ошибкой из оставшихся. Повторяя этот про¬
цесс, можно получить корпоративную последовательность
участков разбиения области, расположенных в порядке воз¬
растания ошибки. При этом для обеспечения возможности
повышения эффективности алгоритма за счет детального
разбиения области с большим изменением функции необхо*
димо использовать подпрограмму, поддерживающую корпо¬
ративную структуру путем добавления в нее новых эле¬
ментов (в самый последний адрес) и их подъема в нуж¬
ное место.
При моделировании рассеяния частиц методом Монте-
Карло для слежения за частицами, число которых растет
в результате расщепления, используется метод, основанный
на предпочтительности более «важных» частиц, обладающих
большей энергией и меньшей вероятностью расщепления.
В этом случае также применяется корпоративный метод, бла¬
годаря которому можно осуществлять контроль за модели¬
рованием с помощью образования корпоративной структуры
с самой важной частицей в корне.
Корпоративная структура применяется также для по¬
строения начальных отрезков и в случае внешней сортировки,
Рассматриваемой в разд. 2.
138
Г лава 3
5) Метод Шелла
Метод простых вставок дает хороший эффект либо
в случае малого числа элементов сортируемой последователь¬
ности, либо в случае небольшого числа перемещений, выпол¬
няемых при сортировке. Эти особенности были использованы
при разработке аналогичного ему усовершенствованного ме¬
тода сортировки. Поясним этот метод для случая п — 8, по¬
казанного на рис. 3.10. Разобьем всю последовательность на
5 6 2 4 8 3 1 7
L L..1.T-1—-J , 1 I
5 3 1 4 8 6 2 7
1 I i-H-1-!--1 1
'1 3 2 4 5 6 8 7
I, I 1 I I I I I
Рис. 3.10. Сортировка методом Шелла.
четыре группы по два элемента в каждой, (х\, х5), (л'2> Дб),
(*з, х?) (х4, х8), и проведем сортировку в каждой из этих
групп. В результате получим последовательность х{/\ ..., xfK
Затем разобьем полученную последовательность на две груп¬
пы по четыре элемента в каждой, (х\2)> х(32), х^\ *(72)), {xS/\ х(/\
х\/\ л:(82)), и проведем сортировку в каждой из них. Полу¬
ченную в результате последовательность х\3), ..., л^3) отсор¬
тируем теперь уже всю целиком. Таким образом, метод со¬
стоит в разбиении массива на группы и в последовательном
уменьшении вдвое числа групп за счет последовательного
удвоения размера групп. Идея метода состоит в том, что при
малых размерах групп перемещаются элементы последова¬
тельности, достаточно далеко отстоящие друг от друга, а при
увеличении размера группы оказывается возможным обхо¬
диться уже более близкими перемещениями.
В рассмотренном примере п было степенью двойки, в ре¬
зультате чего величина каждого последующего шага разбие¬
ния определялась как частное от деления пополам величины
предыдущего шага: 4, 2, 1. Однако такая последовательность
шагов разбиения несущественна. Можно пользоваться любой
последовательностью, в которой последний шаг равен 1, на¬
пример последовательностью, представляющей собой нату¬
ральный ряд чисел 1 = h\ < h2 < ... < ht ^ п/2. Сорти¬
ровку в соответствующих группах (*i, *l + 2fts> •••)> (Х2у
“Х'24-hsf %2+2hs* • • •)> •• •» («£/^ — 1» ■*'2AS— 1» ^3hs—l* • • • » ) МОЖНО ПрО-
вести для s = tyt—1, ..., 1. Аналогично, положив hk=2hk-u
можно получить более рациональную последовательность ша¬
Сортировка
139
гов сортировки 1, 4, 13, 40, 121, 364, ..., полученную по
правилу hk = 3/i/e-i + 1.
Анализ этого метода, предложенного в 1959 г. Д. Л. Шел¬
лом, достаточно сложен и приводит к интересным, до конца
нерешенным математическим задачам. «Быстрая сортировка»,
которую мы рассмотрим следующей, имеет преимущества
перед этим методом и поэтому более интересна для нас.
3.1.3. «Быстрая сортировка»
Пусть задан одномерный массив (файл) или его часть
^ [/] в котором производится сравнение и обмен
элементов.
Определив некоторое значение ключа v в качестве эта¬
лона, файл можно разделить на три части со следующими
свойствами:
пусть / ^ га тогда
A[/]=^v, 1: левый подфайл;
А [га] = v : ключ-эталон
A[j\^v правый подфайл.
Ключевое значение A[m] = v занимает позицию, соответ¬
ствующую положению v в отсортированной последователь-
1. Если / < г, выполнить пункты 2 — 4, иначе закончить выполнение
алгоритма.
2. Положить v := А [/], i := / + К / : = г.
3.1. Увеличивать i на 1 до тех пор, пока A[i\ < v.
3.2. Уменьшать j на 1 до тех пор, пока A[j] > v.
4. При А [/] > v > А [/],
4.1. если / ^ /, произвести обмен A[i]: = :A[j] и перейти к шагу 3.1;
4.2. если / > /, произвести обмен А [/] : = : А [/] и закончить выполнение
алгоритма.
[Разделение на 2 подфайла закончено, / = т.
Далее применить алгоритм для левого подфайла [L j — 1] и правого
подфайла [/. г].]
Рис. 3.11. Алгоритм. „Быстрая сортировка“.
ности. Алгоритм сравнений и обменов, применяемый для опре¬
деления позиции v, повторяется для полученных отрезков
левого подфайла [I, m—lj и правого подфайла [га + 1, г].
Иными словами, алгоритм применяется рекурсивно. Для слу¬
чаев, когда v является наименьшим значением отрезка А [/]
или его наибольшим значением, левый или правый подфайл
может исчезнуть, т. е. общая длина левого и правого подфай-
лов должна быть по крайней мере на единицу меньше длины
140
Глава 3
исходного файла. Таким образом, последовательность ока¬
жется отсортированной, когда подфайлы будут обработаны.
Такое разбиение файлов на два подфайла осуществля¬
ется с помощью алгоритма, представленного на рис. 3.11.
Предположим, что Л[ 1 ] = v — наибольшее значение ключа
файла. В этом случае на шаге 3.1 алгоритм может не закон¬
читься со значением i = r + 1. Для нормальной работы алго¬
ритма при пустом правом подфайле необходимо выполнение
м
Б, М7 , М, М Б, Бу . . . , 5, М
а
больше V М, v Б, ...,Б меньше V
3
Рис. 3.12. Последний шаг деления пополам с использованием v при «быст¬
рой сортировке».
условия Л[/]^Л[г+1] Аналогичные рассуж¬
дения можно провести и для случая пустого левого под¬
файла. Для обеспечения корректности алгоритма можно
ввести понятие «сторож», определяемое как наибольшее воз¬
можное значение ключа файла и связываемое с г + 1-м эле¬
ментом. Например, для Л[1], ..., Л [iV] сторожем будет эле¬
мент Л [jV -j— 1].
Если все значения Л [/] (/ ^ / ^ г) различны, то при вы¬
полнении последнего шага алгоритма будет иметь место си¬
туация, показанная на рис. 3.12, а. Буквы М и Б обозначают
меньшие v и большие v соответственно. В результате при
/ = /+ 1 придется переходить к шагу 4.2. При наличии среди
^(/) (7+1 ^ ^ О значений, равных v, если они при этом
находятся в позициях отсортированного участка, будет иметь
место ситуация, показанная на рис. 3.12,6. При этом в слу¬
чае i = / + 2 надо переходить к шагу 4.2, и в результате
обмена с Л [1] окажется, что Л[/] = Л[/+ l] = v.
Если в шагах 3.1 и 3.2 знаки строгого неравенства <, >
заменить на ^ соответственно, то, очевидно, можно из¬
бежать ненужных сравнений и тем повысить эффективность
Сортировка
141
метода. Но, если это сделать, то в случае равенства всех
А(/) в пп- 3.1 и 3.2 алгоритма для v получим некорректные
значения i и /. Ненужных сравнений удается избежать с по¬
мощью метода, описанного ниже.
На рис. 3.13 представлен случай последовательности из
15 одноразрядных чисел. Волнистой линией подчеркнуты
значения, которые перемещаются в позиции, отмеченные
693147180559945с»
1 brzzr-j- j : 1 '
X X
д
5
3
1 4
4 1
5
0
(6)
8
9
9
7
9
00
Дч
0
3
1 4
4 (5)
5
5
2
8
9
0
7
9
оо
Дч
0
(1)
3 4
4 2
5
5
2
8
9
9
7
9
оо
0
(1)
А 4
4 2
5
5
2
8
9
9
7
9
оо
2
1
2
А
4 2
5
5
2
8
9
9
7
9
оо
2
2
2
2 (4)
4 1
2
5
2
8
9
9
7
9
оо
0
1
1
3 4
4 5
(5)
5
2
JL
9
9
7
9
00
0
1
1
3 4
4 5
5
5
6
7
(8)
2
9
9
оо
0
1
1
3 4
4 5
5
5
б
7
8
9
(9)
9
00
Рис. 3.13. Пример быстрой сортировки.
скобками ( ). Сплошной линией подчеркнуты элементы, за¬
нявшие окончательные положения. На рисунке подробно по¬
казано, как производятся обмены при начальном разбиении
только на три подфайла.
Если в файле много одинаковых ключей, то для того,
чтобы избежать ненужных обменов, вначале просматриваем
файл слева и убеждаемся, что имеется по меньшей мере два
отличающихся друг от друга элемента. Обозначим больший
из них через v и будем считать левым подфайлом последова¬
тельность значений, не достигающих значения v, а правым
подфайлом — последовательность значений, превышающих
значение v. Поскольку левый и правый подфайлы непусты,
действительно имеет место разделение файла на два под¬
файла (см. рис. 3.14).
Для анализа свойств быстрой сортировки будем считать,
что все элементы файла длины п различны; время обработки
при условии равной вероятности всех п\ возможных вариан¬
тов порядка расположения обозначим через Т(п). Будем
также считать, что любой из п элементов может быть клю¬
чевым. Под ключевым значением здесь понимается значение
элемента последовательности (файла), управляющего раз¬
биением.
142
Глава 3
Затраты на разделение файла на 3 подфайла пропорцио¬
нальны п\ число сравнений равно я, а число обменов в сред¬
нем составляет около я/6. Для простоты будем считать, что
ключ также входит в левый или правый подфайл. Тогда
1. Если / < г, выполнить пункты 2 — 5, иначе закончить выполнение
алгоритма.
2.1. Если А [/] = ... =А[г] (при просмотре все элементы оказываются
одинаковыми), закончить выполнение алгоритма.
2.2. Если А [/] = ... = A [s — 1] < A [s] (обнаружено число, большее чем
А [/], то i := s + 1,
2.3. если А [/] = ... = А [5 — 1] > A [s] (обнаружено число, меньшее чем
А [/], то произвести обмен А [I] : = : A [s], / := s + 1, s := / + 1-
3. Положить v := A [s], j : = г.
4.1. Увеличивать i на 1 до тех пор, пока A[i\ < v.
4.2. Уменьшать / на 1 до тех пор, пока А [у] ^ v.
5. При А [/] ^ v > А [/],
5.1. если i < /, произвести обмен А [г] :=: А [/] и перейти к шагу 4;
5.2. если i > /, произвести обмен A\s]:=:A[j] и закончить выполнение
алгоритма
[Применить алгоритм для отрезков [/, / — 1 ] и [/, г].]
Рис. 3.14. Улучшенный алгоритм быстрой сортировки.
Т (п) определяется следующим асимптотическим выраже¬
нием:
п—1 п—1
T(n) = l/n X {Т {т.) + Т (п — m)} + ап — 2/п £ Т(пг) + ап,
m=1 m=1
ИЛИ
Я—I
пТ(п) = ап2 + 2 X Т(т).
т~ 1
Если вычесть это выражение из (я + 1 )Т (п+ 1) = а (п + I)2 +
п
+ 2 Yj Т (m)y получим
m= 1
Т (п + 1) Т (п) , ^ 2/г + 1
п + 2 п + 1 {п + 1) (п + 2) *
Г (п) V 2/г —
а Z W+TT+с=а (3//-1 - н»> +с'-
п+ 1
fc=l
Поскольку Нп = 1 + 1/2 + ... + 1/я ~ /г log /г,
Г (/г) « 2ая log п.
В среднем скорость сортировки будет порядка О(п log п),
однако в наихудшем случае она будет составлять О (я)2. Та¬
кое положение будет возникать в случае, когда последова¬
тельность отсортирована с самого начала. При этом разделе-
Сортировка
143
ние обычно производится на отрезки длиной 1 и (п— 1), 1 и
(п — 2) , поэтому затраты на сортировку пропорциональны
п + (п—1)+ ... 1 = п(п + 1)/2. Если последовательность в
самом деле расположена в обратном порядке, производятся
обмены. Далее сортировка выполняется аналогично рассмот¬
ренному ранее случаю.
Метод этот можно улучшить, если в качестве ключа v не
выбирать при разделении на подфайлы ни одного из двух
крайних значений. Для этого из файла выбирают случайным
образом три элемента и в качестве v принимают или значе¬
ние среднего из этих элементов, или среднее значение для
этих трех элементов. Если предположить, что элементы после¬
довательности расположены до некоторой степени случайно,
сортировка будет наиболее неэффективна, когда элементы
последовательности оказываются частично отсортированными
в порядке, близком к обратному. Для улучшения характерис¬
тики алгоритма в этом случае в качестве трех элементов,
определяющих значение v, выбирают обычно два крайних
и один средний элементы файла.
Благодаря такому усовершенствованию понижается ве¬
роятность несбалансированного разделения файла. Однако,
хотя и с очень малой вероятностью, все еще может иметь
место случай очень большой несбалансированности при раз¬
делении. Если имеется опасение возникновения такого наи¬
худшего случая, то его можно избежать переходом к методу
сортировки с использованием корпоративной структуры после
того, как число шагов разделения достигнет определенного
уровня.
Для повышения эффективности быстрой сортировки
можно, не применяя рекурсивной процедуры к ставшему ко¬
ротким подфайлу, перейти к методу простых вставок или
методу сортировки посредством выбора. В частности, если
использовать метод сортировки простыми вставками, то отпа¬
дет необходимость в рекурсивном вызове подпрограммы ме¬
тода простых вставок для каждого подфайла. Ставший корот¬
ким подфайл не сортируется методом быстрой сортировки.
То есть рекурсивная процедура применяется только для ле¬
вого или правого подфайла, длина которого не менее опреде¬
ленной границы. Короткие подфайлы можно сортировать
методом простых вставок. Экспериментально найденные зна¬
чения нижнего предела длины подфайлов для применения
быстрой сортировки составляют по сообщениям от 7 до 16,
оптимальное значение равно 10.
Рекурсивный вызов подпрограммы в некоторых языках
программирования невозможен, но и в том случае, когда он
возможен, эффективность применения рекурсии может быть
Недостаточно высокой. Бывает также, что рекурсивный вызов
144
Глава 3
подпрограммы необходим для части левого или правого под-
файла, а для оставшейся части необязателен. Этого можно
достигнуть, используя вместо рекурсивного вызова стек. Если
пространство памяти, отводимое под стек, невелико, лучше
вначале поднимать короткий подфайл. Если левый подфайл
всегда обладает приоритетом, то в стек можно отправлять
только левые крайние позиции оставшегося правого под-
файла.
SUBROUTINE FSQS(X, N)
REAL X(N + 1),T
INTEGER L, R, STACK(20)
* FAILSAFE QUICKSORT/PARTITION BY MEAN OF THREE
L = 1
R = N
* SET A LIMIT TO THE STACK DEPTH
IPMAX = 4
NMAX = 16
10 IF(N .GT. NMAX) THEN
IPMAX = IPMAX+ 1
NMAX = NMAX+2
GOTO 10
ENDIF
IPMAX = 3+IPMAX/2
* CHECK NECESSITY OF PARTITION
IP - 0
20 IF(R-L .LE. 10) GOTO 50
IF(IP .EQ. IPMAX) THEN
CALL HEAP(X, L, R)
GOTO 50
ENDIF
* PARTITION
T = (X(L) + X((L + R)/2) + X(R))/3.0
I = L — 1
j = R +1
30 1 = 1 + 1
IF(X(I) .LT. T) GOTO 30
40 J = J-1
IF(X(J) .GT. T) GOTO 40
IF(I .LT. J) THEN
XX = X(I)
X(I) = X(J)
X(J) = XX
GOTO 30
ELSE IF(I .EQ. J) THEN
J = J-l
ENDIF
1P = IP + 1
STACK(IP) = R
R = J
GOTO 20
Рис. 3.15. Программа надежной быстрой сортировки на языке Фортран 77,
Сортировка
145
* AFTER SORTING A BLOCK
50 IF(IP .EQ. 0) GOTO 60
IF(STACK(IP) ,EQ. 0) THEN
IP = IP-1
GOTO 50
ENDIF
L = R4-1
R = STACK(IP)
STACK(IP) = 0
GOTO 20
* SIMPLE INSERTION/LARGER NUMBERS IN RIGHT
60 CONTINUE
DO 80 К = N-l, 1, -1
X(N + 1) = X(K)
M = K + l
70 IF(X(M) .LT. X(N + 1)) THEN
X(M-l) = X(M)
M = M + l
GOTO 70
ENDIF
X(M-l) = X(N + 1)
80 CONTINUE
RETURN
END
Рис. 3.15. (Продолжение.)
На рис. 3.15 представлена программа на языке FORT¬
RAN 77, реализующая рассмотренные выше модификации.
Эту программу несколько усовершенствовали А. Нодзаки
и Т. Сугимото и назвали ее программой «надежности быстрой
сортировки». CALL HEAP (X, L, Р) в программе означает
вызов подпрограммы сортировки с использованием корпора¬
тивной структуры для массива X(L), X(L-f-l), ..., X(R).
Например, в работе С. Окома (1982 г.) в качестве ключа v
принято среднее значение трех чисел: двух крайних и одного
среднего в файле, а разбиение файла проведено не на три
подфайла, как выполнялось выше, а на два. Если все три
числа не равны между собой, то, поскольку меньшие значе¬
ния меньше v, а большие значения больше v, ни один из
двух подфайлов непуст. В случае равенства всех трех чисел
по меньшей мере одно из них войдет в левый подфайл, а дру¬
гое войдет в правый подфайл, поэтому опять-таки ни один
из подфайлов не будет пуст.
3.1.4. Другие методы сортировки
Благодаря усовершенствованию методов корпоративной
сортировки и быстрой сортировки затраты на сортировку
Даже для наихудшего случая удалось сделать не более
146
Г лава 3
п log п. А нельзя ли получить метод, с помощью которого это
значение можно было бы сделать еще меньшим? Ответом
может быть и да, и нет.
В рассуждениях, приведенных выше, предполагалось, что
все ключи вполне упорядочены и что производится сравнение
их свойств со средней эффективностью при равной вероятно¬
сти п\ возможных вариантов расположения ключей в после¬
довательности. Смысл первого предположения заключается
в том, что определение большего (или меньшего) из двух
ключей производится
только в результате срав¬
нения их величин. Сорти¬
ровка рассматривается
как процедура, эквива¬
лентная определению то¬
го, которому из лг! вариан¬
тов расположения ключей
соответствует заданный
вариант расположения.
При одном сравнении оп¬
ределяют, какой из двух
групп п\/2 вариантов рас¬
положения ключей при¬
надлежит заданная последовательность ключей; при двух
сравнениях полученное множество вариантов еще раз де¬
лится пополам. Если продолжать разделение вариантов попо¬
лам до h сравнений, то число возможных разделений будет
составлять число 2Н\ количество листьев полного бинарного
дерева высоты h. Значение h определяется условием 2Н ^ п\
Если использовать формулу Стирлинга, то получим
h ^ log2n! — п Iog2 я + (1/2) log2(2jm) — п log2e
(см. разд. 3.3.1).
Однако если ввести некоторую дисциплину выбора значе¬
ний ключей, то возможно улучшение этой оценки. Одним из
примеров может служить метод сортировки по основанию
системы счисления, приведенный в разд. 3.1.1.
Если известно, что ключи представляют собой т-разряд-
ные числа в р-ичной системе счисления, то, как было сказано
выше, распределение элементов последовательности по р груп¬
пам производится в соответствии со значениями ключей в со¬
ответствующих разрядах начиная с младшего разряда 0, 1, ...
р—1. Используя списки для представления групп, полу¬
чим структуру, показанную на рис. 3.16. При распределении
каждый элемент помещается в конец списка, определяемого
анализируемым разрядом. Для этой цели для каждого списка
вводится указатель на его конец. После распределения эле-
Распре деле - Распределены е
ние^ указа те- указателей
лей на начало на конец
0 н-ав-ш*—a
1 EHIIZb 0
p-iB-DZb в
Рис. 3.16. Первый шаг алгоритма сорти¬
ровки по основанию системы счисления.
Разделение разряда единиц.
Сортировка
147
ментов последовательности по значениям младшего разряда
ключей по р спискам полученные списки объединяются в один
посредством следующей процедуры: поле указателя по¬
следнего элемента списка устанавливается на головной эле¬
мент следующего списка. Эта процедура выполняется для всех
списков, кроме последнего. Таким образом, конец списка
для 0 соединяется с началом списка для 1, конец для 1 —
с началом для 2 и т. д. Указатели на начала и концы всех
списков, кроме списка для 0 и списка для р, сбрасываются.
Для списка 0 сбрасывается указатель на конец, а для списка
р сбрасывается указатель на начало. Очередная фаза рас¬
пределения осуществляется по следующему разряду значений
элементов по новым р спискам. Таким образом, за га распре¬
делений и связываний получится отсортированная последо¬
вательность. Поскольку для каждого разряда производится
/г-операций, то всего будет проделано пгп операций.
Если производить распределение элементов по группам от
О до р2— 1, анализируя каждый раз по два разряда, то общие
затраты можно сократить до шп/2 операций, а при выборе
по три или четыре разряда их можно было бы сократить еще
более значительно. Однако это лимитируется возрастанием
затрат, связанным с увеличением числа пар указателей на
начало и конец от р до р2 и р3, а также с ограничениями на
объем памяти. Таким образом, если допускается использо¬
вание рт ячеек памяти и если нет дублирования ключей,
то возможна сортировка без операции сравнения. При
этом необходим возврат в исходное состояние всех рт ячеек
памяти в процессе перехода от одной фазы сортировки
к другой.
Если ключи являются действительными числами, то прин¬
ципиально возможно применение метода сортировки по осно¬
ванию системы счисления. В случае ограниченной точности
также при использовании метода сортировки по основанию
системы счисления га оказывается слишком большим. Однако
если известно, что распределение значений ключей относи¬
тельно равномерно, то возможно применение следующего
метода, близкого к методу сортировки по основанию системы
счисления.
Определяют минимальное значение а и максимальное
значение Ь элементов х} (1 ^ j ^ п) и для каждого х\ вы¬
числяют kj = 1 + L (Л — 1) (*/ “ а)/(Ь — а) J (1 ^ kj ^ п) -
Определяем
Cj = „число а при ka — /“ (1
С j — 2^ са9 Cq — 0, Сп fit
а = 1
148
Г лава 3
и вводим Xj в специальный файл Y, представленный на
отрезке [Ckj_{ + U Ckj\ (длиной cfe/). Файл Y сортируем с по¬
мощью метода простых вставок.
Если max Cj велико, т. е. если х\ имеют в целом равномер¬
ное распределение, то можно отсортировать только подфайлы
файлы Y, для чего метод сортировки простыми вставками
оказывается достаточно быстрым.
Благодаря использованию 3п дополнительных ячеек па¬
мяти для размещения помимо Х\ еще и kj из файлов Y и С/
при условии равномерности распределения х\ можно добиться
улучшения, обеспечивающего затраты меньше чем n\ogn.
Это чрезвычайно жесткие условия, однако следующий
подход обеспечивает равномерность распределения. Имеется
файл, представляющий собой последовательность /V записей.
Для того чтобы проанализировать его, извлечем из него слу¬
чайным образом п записей. Для этого выберем случайным
образом из множества {1, 2, N} п чисел без дублирова¬
ния. Расположим выбранные числа в отсортированном
порядке (удобно выбирать записи с номерами, представляю¬
щими собой отсортированную последовательность). Суще¬
ствует несколько способов составления таких групп случай¬
ных чисел, однако, если n, N очень велики и при этом п2 ^ N,
эффективным является следующий способ. Случайным обра¬
зом производят выборку п чисел, имеющих равномерное рас¬
пределение на отрезке [1 ,N), сортируют их указанным мето¬
дом, фиксируя число возникновения коллизий с. При условии
n2^N ожидаемое число коллизий будет не больше 1. Де¬
лают выборку с новых чисел из отрезка [1, N]. Новые слу¬
чайные числа сортируют методом простых вставок и прове¬
ряют, нет ли дублирования с элементами сделанной перед
этим выборки. Когда число вновь выбранных отсортирован¬
ных элементов достигнет пу объединим две группы получен¬
ных чисел в одну. В процессе объединения исключим повто¬
ряющиеся элементы. Используя этот метод, можно добиться
поставленной цели: уменьшения затрат на сортировку.
3.2. Сортировка во внешней памяти
3.2.1. Внешняя сортировка
1) Особенности внешней сортировки
В предыдущем разделе мы рассмотрели внутреннюю сор¬
тировку, которая проводилась для данных, размещенных
в оперативной (главной) памяти ЭВМ, путем осуществления
операций сравнения больших элементов с меньшими и их пе¬
Сортировка
149
ремещений, а также обменов, обрабатывая элементы один
за другим (не параллельно) и постепенно приводя последова¬
тельность к упорядоченной. В данном разделе рассмотрим сор¬
тировку, которая производится для последовательностей за¬
писей, хранящихся в файлах с последовательным доступом,
расположенных на запоминающих устройствах внешней па¬
мяти, таких, как магнитные диски и магнитные ленты.
Заданные последовательности записей, т. е. сортируемые
файлы, имеют обычно объем значительно больший, чем объем
доступной оперативной памяти.
Для выполнения внешней сортировки производятся сле¬
дующие операции:
(1) Находят нужный блок во внешней памяти. Для этого
перемещают считывающую головку или подматывают маг¬
нитную ленту.1)
(2) Производят считывание и передачу данных по каналу
ввода-вывода в оперативную память.
(3) В оперативной памяти осуществляют операции срав¬
нения и перемещения.
(4) Выполняют запись во внешнюю память в соответствии
с пп. (1) и (2).
При выборе того или другого алгоритма сортировки необ¬
ходимо учитывать следующие параметры:
(а) объем оперативной памяти, используемой в качестве
рабочей области;
(б) тип, число, объем ЗУ внешней памяти, используемых
в качестве рабочей области;
(в) число каналов ввода-вывода;
(г) число и длина записей;
(д) время выполнения операций в оперативной памяти.
Поскольку операции, выполняемые в оперативной памяти
для сортировки, сравнительно просты, эффективность сорти¬
ровки будет определяться в основном операциями ввода-вы¬
вода, время выполнения которых существенно больше. Именно
в этом заключается основное отличие внешней сортировки.
В алгоритмах, которые будут рассмотрены ниже, все вводи¬
мые данные вновь выводятся, поэтому сравнительный вес
ввода и вывода одинаков, однако ввод оказывается важнее:
обработка данных не начнется, пока данные не будут соот¬
ветствующим образом подобраны. При использовании мето¬
дов доступа операционной системы операции (1) — (4) могут
*) Под временем перемещения считывающей головки автор понимает,
но-видимому, не только время подвода головок, но и задержку от вра¬
щения, а также время прохода межблочного промежутка. Для магнитных
лент оно соответствует только времени прохода межблочного промежут-
Ка- — Прим. ред.
150
Глава 3
производиться параллельно, однако при этом необходимо пра-
вильно распределять время, требуемое на каждую из опера¬
ций. Эффективность такого подхода будет рассмотрена ниже.
2) Применение метода сортировки по основанию системы счисления
Для того чтобы выяснить разницу между внутренней сор¬
тировкой и внешней сортировкой, рассмотрим метод сорти¬
ровки по основанию системы счисления в применении к внеш¬
ней сортировке. Для сортировки последовательности /п-раз~
рядных ключей при достаточном объеме памяти можно, как
отмечалось ранее, проводить сортировку, не прибегая к опе¬
рации сравнения с помощью распределения записей по рт
отдельным блокам. Если речь идет о внешней памяти, ее
обычно достаточно, и при условии, что в рт блоках не содер¬
жится повторяющихся ключей, этот метод может показаться
эффективным. Кажется, что он может обеспечить затраты на
сортировку, составляющие примерно п единиц времени. Од¬
нако на самом деле эффективность этого метода низка из-за
затрат на слияние, о котором речь пойдет ниже.
3) Разделение ключей и записей
Рассмотрим случай, когда ключи файла отделяются от
соответствующих записей. Несмотря на значительную длину
записи, ключи могут оказаться достаточно короткими. Нельзя
ли при сортировке больших массивов данных, используя это
свойство, сократить физические перемещения массива запи¬
сей? Иными словами, построить небольшие записи, состоящие
из пар (номер позиции в исходном файле, значение ключа),
расположить эти пары в порядке размещения исходных запи¬
сей в файле, а затем отсортировать по значениям ключей.
Очевидно, в таком случае часто возможна сортировка и с ис¬
пользованием только оперативной памяти. Как же использо¬
вать результаты этой сортировки? Например, если необходимо
выбрать только по 10 записей старших и младших значении
в отсортированном порядке, то такой метод вполне приемлем,
Однако для сортировки всего файла он практически неприго¬
ден, поскольку потребует слишком большого количества счи¬
тываний блоков, содержащих записи исходного файла.
После сортировки пар (номер позиции в исходном файле,
значение ключа) значения ключей можно заменить на по¬
следовательные целые, определяющие порядок следования
ключей в отсортированном файле. Еще раз отсортируем полу¬
ченный файл по номерам позиций исходного файла. В резуль¬
тате получаем описание порядка расстановки записей исход¬
ного файла для приведения его к отсортированному виду.
Сортировка
151
Посмотрим еще раз, возможно ли применение такого под¬
хода. Опуская теоретические выкладки, положим, что общее
число записей составляет п, в один блок вводится b записей,
в оперативную память вводится m блоков; тогда оказывается
необходимым самое меньшее (п log2 b)/т считываний блоков,
откуда следует, что метод практически неприменим.
3.2.2. Отрезки и слияние отрезков
1) Отрезки
Выберем как можно более длинные участки, представляю¬
щие собой отсортированные последовательности вида ak ^
^ cik+1 ^ ^ я/-1 в конечной числовой последова¬
тельности а\у а,2, ап. Эти участки назовем отрезками. Точ¬
нее, это будут возрастающие отрезки. Рассмотрим пример
5 6 2 4 8 9 3 1 7
Рис. 3.17. Отрезки.
числовой последовательности приведений на рис. 3.17. Под¬
черкнутые участки представляют собой отрезки длиной 2, 4,
1, 2. Отсортированная последовательность состоит из одного
отрезка длиной /г, а последовательность, отсортированная
в обратном порядке, состоит из п отрезков длиной 1.
Пусть дана последовательность а\, а2у ап различных
чисел. Можно показать, что при равновероятности п\ возмож¬
ных вариантов расположения элементов этой последователь¬
ности среднее значение числа отрезков равно (п + 1)/2.
Это следует из того, что математическое ожидание числа
отрезков длиной не менее р будет составлять
при р = 1 число отрезков равно (п -f- 1) /2.
Ожидаемое значение длин отрезков зависит от начальной
позиции отрезков в последовательности, однако можно счи¬
тать, что оно равно примерно 2. Это можно предположить по
выражению для ожидаемого значения числа отрезков.
2) Слияние отрезков
Обсудим далее слияние, при помощи которого при задан¬
ных отрезках ключей записей файла путем их объединения
°бразуют один более длинный отрезок, Прежде всего рас«
152
Глава 3
смотрим простой случай, когда два отрезка входят в различ¬
ные файлы. При этом производят сравнение начальных эле¬
ментов каждого из отрезков: меньший элемент выводят, а на
место выведенного вводят следующий за выведенным элемент.
Этот элемент становится новым начальным элементом соот¬
ветствующего отрезка. Эту операцию повторяют до тех пор,
пока один из отрезков не закончится; оставшиеся элементы
другого отрезка выводят, не изменяя порядка (рис. 3.18).
Обобщая эту схему двухпутевого слияния, можно получить
р-путевое слияние для отрезков, размещенных в р файлах
(р > 2) Для р-путевого слияния может быть применен сле¬
дующий базовый алгоритм.
Алгоритм, р-путевое слияние
1. Установить число отрезков г \ = р.
2. Повторять следующие операции до тех пор, пока г не бу¬
дет равным 1.
2.1. Вывести наименьший из начальных элементов оставшихся
г отрезков, ввести следующий элемент в отрезок с наи¬
меньшим значением элемента.
2.2. Если отрезок, из которого выбрать элемент, станет пус¬
тым, запомнить этот факт и уменьшить г на 1.
3. Если г станет равным 1, вывести оставшийся отрезок, не
изменяя порядка расположения его элементов, закончить
выполнение алгоритма.
Каким же образом мы практически осуществляем шаги
2.1 и 2.2 рассмотренного алгоритма? Прежде всего при вы¬
полнении шага 2.1 каждый раз производятся конкретные
затраты на поиск наименьшего значения и не используется
результат предыдущего сравнения. Если использовать корпо¬
ративную структуру, рассмотренную в предыдущем разделе,
то можно выполнить всю работу за log2p сравнений. С дру¬
гой стороны, в корпоративную структуру должны входить не
только значения ключей, но и указатели на отрезки, из кото¬
рых они выбраны. Другими словами, встраивая номера от¬
резков в корпоративную структуру, косвенно осуществляют
операцию сравнения. Таким образом, преимущества метода
с использованием корпоративной структуры невелики.
Для запоминания номера закончившегося отрезка (шаг
2.2) можно использовать одномерный массив длиной р, фик¬
2 4 5 6 8
56
2 4 8 9
Рис. 3.18. Двухпутевое слияние.
Сортировка
153*
сируя в нем номера оставшихся г отрезков. Используя эти
номера, можно косвенно установить и адреса отрезков.
Вернемся к двухпутевому слиянию и попробуем распро¬
странить его на случай, когда в каждом из двух вводных
файлов имеется по нескольку отрезков. При этом независимо>
Рис. 3.19. Слияние файлов, содержащих несколько отрезков.
от числа отрезков в обоих файлах слияние будет произво¬
диться только в один отрезок.
Алгоритм. Слияние отрезков двух файлов
1. Считать начальные элементы каждого файла. Если одиц
из отрезков является последним в файле, перейти к об¬
работке конца файла.
2. Повторять до окончания какого-либо из отрезков.
2.1. Сравнить два элемента и вывести тот, который не
больше.
2.2. Считать следующий элемент файла, элемент которого
был выведен.
2.2.1. Если конец отрезка не достигнут, перейти к шагу 2.1.
2.2.2. Если достигнут конец отрезка, выводить элементы дру¬
гого файла до окончания отрезка и перейти к шагу 1.
ся отрезки (хотя бы один), производить ввод и вывод
элементов этих отрезков без изменения порядка распо¬
ложения элементов, закончить выполнение алгоритма.
В отличие от предыдущего в рассмотренном алгоритме не¬
обходимо обнаружение конца отрезка. Это можно сделать
различными способами:
(1) Ключ выведенной записи сравнивают с ключом сле¬
дующей записи. Если значение ключа новой записи меньше,
то отрезок закончен (рис. 3.19, а).
(2) В качестве метки, указывающей на конец отрезка,
вставляют специальный ключ, в качестве которого выбирают
число, не входящее в диапазон значений ключа. Как только
будет введено это значение, конец отрезка достигнут. При
а
2 4 5 6 8 9 оо 1 3 7 оо <
5 б оо 3 оо
2 4 8 9 оо 1 3 7 оо
5
1 2 3 5 6 7
2 3 6 9|
1 5 7|
2 911 7(
3 6 j 51
( 9|6|1|5'
I 2 j 3 J 71
8
3. (Обработка конца файла). Если в другом файле имеют-
154
Г лава 3
использовании этого метода необходимо обязательно убе-
диться в том, что выбранный признак конца отрезка не вхо¬
дит в диапазон значений ключа (рис. 3.19,6).
(3) Отрезки в файлах делают фиксированной длины.
В заключение рассмотрим еще один метод. Не обращая
внимания на содержимое заданного исходного файла, его
рассматривают как составленный из отрезков длиной 1. Раз¬
деляя этот файл на два подфайла и производя их слияние,
получают отрезки длиной 2. Повторяя эту операцию, доводят
длину отрезков до 2* (к = 0, 1, 2, ...). Если при этом длина
файла п не является степенью 2, то по окончании слияния
последний отрезок будет иметь избыток элементов, равный
n-г 2k. На рис. 3.19,в показан пример, в котором для про¬
стоты в качестве файла использовано семь одноразрядных
чисел.
Обычно при двухпутевом слиянии из 2г отрезков средней
длины / получают г отрезков средней длины 2/, т. е. если
начинают с отрезков длиной 1, то для получения длины от¬
резка 210 = 1024 потребуется десять слияний, поэтому при
внешней сортировке необходимо начинать с файла, содержа¬
щего самые длинные отрезки. Структуру таких начальных
отрезков обсудим позднее.
Внешняя сортировка с помощью многофазного слияния
осуществляется следующим образом.
Алгоритм. Внешняя сортировка слиянием
1. Используя оперативную память, сформировать как можно
более длинные начальные отрезки из элементов заданного
файла; распределить их подходящим образом на несколько
файлов.
2. Сформировать более длинные отрезки путем слияния от¬
резков нескольких файлов; вторично распределить их под¬
ходящим образом по нескольким файлам. Повторять эту
операцию.
3. Если в конце образуется один отрезок, закончить сорти¬
ровку.
На шаге 2 имеется несколько вариантов распределения
отрезков по нескольким файлам. В следующем подразделе
обсудим три таких варианта.
3.2.3. Алгоритм сортировки слиянием
I) Сортировка сбалансированным слиянием
Наиболее простым методом сортировки, предполагающем
многократные распределения и слияния отрезков, является
метод сортировки сбалансированным слиянием. В качестве
Сортировка
155
буферов ввода и вывода используется р файлов (р = 2). При¬
мер сортировки с помощью этого метода для р — 2 и 11 на¬
чальных отрезков А, В, ..., К представлен в табл. 3.1.
В самом начале, формируя начальные отрезки из элемен¬
тов файла F1, переписываем их в файлы F3 и F4. Поскольку
число отрезков перед началом операции неизвестно, для сба¬
лансированности отрезки Л, В, ... записывают в F3, F4 попе¬
ременно. Если считывание в обратном порядке с магнитных
лент невозможно, то ленты, на которых находятся файлы
F3, F4, необходимо перемотать обратно. Если файлы F3, F4
размещены на магнитных дисках, то этих проблем не возни¬
кает. Далее отрезки файлов F3, F4 сливают и вновь в про¬
цессе слияния попеременно записывают, формируя новые
отрезки, в файлы FI, F2. При сортировке большого числа
записей исходный файл целесообразно сохранить, поэтому
файл F1 должен быть пятым по счету файлом, но мы пред¬
ставляем его как F1, подразумевая под этим одну и ту же за¬
писывающую аппаратуру и среду записи для исходного и про¬
межуточного файлов. Через (АВ) в таблице обозначен резуль¬
тат слияния отрезков Л, В. Естественно, это не значит, что
в АВ за отрезком А следует отрезок В. Аналогичное замеча¬
ние справедливо и для (ABCD) и т. п. В представленном
в таблице случае длины отрезков здесь одинаковы. Длины
отрезков, образованных в результате последующих распре¬
делений и слияний, выражены в таблице в длинах начальных
отрезков. Например, 2*3 означает три отрезка длиной 2 каж¬
дый; 4* 1 + 3*1 означает, что к одному отрезку длиной 4 до¬
бавлен один отрезок длиной 3 и т. д.
Возможны ли распределения и слияния для файлов F1,
F2, F3 с использованием только трех магнитных лент? Это
возможно. Начальные отрезки распределяют в файлы F2, F3
и сливают в файл F1. Затем полученные отрезки можно снова
распределить по файлам F2, F3, однако это приведет к из¬
лишним копированиям. Количество копирований можно су¬
щественно сократить с помощью следующего приема. По¬
скольку число отрезков после слияния определяется числом
начальных отрезков и в файл F2 переносится только половина
отрезков файла F1, тогда оставшиеся отрезки файлов F1
и F2 можно слить и перенести в файл F3.
Что же получится, если повторять р-путевое слияние, ис¬
пользуя 2р файлов и распределение по р файлам? Обозначим
через г число начальных отрезков. Тогда операции распреде¬
ления и слияния закончатся за HogpKI шагов. Например,
в табл. 3.2 представлен случай р = 3, г = 25. На каждом
Шаге число вводимых и выводимых записей постоянно, и не¬
обходимо однократное считывание каждого файла ввода и
однократное формирование каждого файла вывода. Таким
Таблица 3.1. Сортировка сбалансированным слиянием. р = 2, двухпутевое слияние с использованием 4 файлов
156
Глава 3
S Н П
* х 5 £
S s £ а)
s ^ 5. Р*
(1) О) г- н
О Л 03
а 9" СП 5
g.8 8.2
ы ® <и 5
е 5 2 S
Я П '
(П 55 ™
Я
Ч л
Ф н
Ч О
си
СХ X
К 3
О,
о-
я
о
Я
а
Ю X
- ь
§
S'
к
я
ф
t; и
5 О
* Й
<1) со
а. ф
е о*
5 й
со О
a
+ ^
СМ О
с —
О
со к,
■ СЦ
см ^
S'
я
о
я
a
Т
- !<
+ Q
- О
•i «5
я
я
я
я
ч
и
(ABCDEFGH) (IJK) (ABCDEFGHIJK)
Сортировка
157
образом, если увеличивать р, то, поскольку число шагов равно
logp это приведет к уменьшению числа шагов и соответ¬
ственно к уменьшению числа операций ввода-вывода. Дей¬
ствительно ли это так? Для данного случая это справедливо,
однако, когда р возрастает в процессе сортировки, проблема
оказывается несколько сложнее. Трудности, связанные с этим,
рассматриваются при обсуждении эффективности внешней
сортировки.
2) Сортировка многофазным слиянием
Обязательно ли для р-путевого слияния использование
2р файлов? При сбалансированном распределении это дей¬
ствительно так: каждый отрезок каждого из р файлов вы¬
вода формируется из отрезков р файлов ввода. Если распре¬
деление отрезков каждого из файлов соответствующим обра¬
зом не сбалансировано и освободившийся файл ввода заме¬
няется на файл вывода, то р-путевое слияние можно провести
с помощью (р + 1) файлов.
Таблица 3.2. Сортировка сбалансированным слиянием
(случай р = 3, число файлов 6)
Распределение отрезков по файлам
Число
перемещаемых
записей
Шаг
FI F2 F3 F4
F5 F6
Операция
(за единицу
измерения
принят
начальный
отрезок)
0
— - - 1 • 25
— —
—
—
1
1
00
00
О)
■
Распределение
начальных
отрезков
25
2
- - - 3-3
3-3 3-2+1
Распределение
слитых
25
отрезков
3
9-1 9 • 1 7 • 1 -
— —
Распределение
слитых
отрезков
25
4
- — -25-1
— —
Слияние
25
В табл. 3.3 представлен процесс сортировки 4-путевым
слиянием 49 начальных отрезков при использовании 5 фай-
158
Глава 3
лов. В самом начале производится распределение по файлам
FI — F4 по 15, 14, 12, 8 отрезков соответственно. Почему вы¬
брано такое распределение, будет обсуждено позже. Произ¬
водя слияние этих отрезков в файл F5, получим 8 отрезков
длиной 4 (считая за единицу измерения длину начального
отрезка), а файл F4 свободным. В файлах FI — F3 остаются
по 7, 6, 4 начальных отрезков. Теперь произведем слияние
отрезков из файлов FI — F3 и файла F5 и выведем их
в файл F4. Теперь получим четыре отрезка длиной 7 и сво¬
бодный файл F3. Повторяя эту операцию, на 5-м шаге будем
иметь в файлах F2 — F5 по одному отрезку длиной 25, 13,
7, 4; после их слияния сортировка завершится. В этом методе
все операции представляют собой только операции слияния,
а распределение осуществляется только за счет замены файла
вывода.
Таблица 3.3. Сортировка многофазным слиянием (случай р = 4,
число файлов 5)
Распределение отрезков по файлам
Число
перемещаемых
записей•
Шаг
F1
F2
F3
F4
F5
Операция
(за единицу
измерения
принят
начальный
отрезок)
0
1 -49
1
1 .15
1 . 14
1 • 12
1 • 8
Распределение
начальных
отрезков
49
2
1-7
1 *6
1 -4
—
00
Слияние
32
3
1 ‘3
1-2
—
7-4
4-4
»
28
4
1 • 1
—
13-2
7-2
to
»
26
5
—
25-1
13-1
7-1
4-1
»
25
6
49 • 1
» 49
Итого: 209
В отличие от уже рассмотренного метода сортировки сба¬
лансированным слиянием и метода сортировки каскадным
слиянием, который мы обсудим позже, сортировка многофаз¬
ным слиянием требует перемещения всех записей только при
начальном распределении и самом последнем слиянии. При
всех остальных операциях перемещение всех записей необя¬
зательно. Количество практически перемещаемых записей
постепенно убывает, и непосредственно перед тем, как число
отрезков в каждом файле станет равным 1, почти во всех
файлах окажется по два отрезка, поэтому перемещается
Сортировка
159
только около половины записей. (При р — 2,3 число переме-
щаемых записей не будет характеризоваться монотонным
убыванием и до половины не уменьшится.)
В этом примере файл вывода образуется проходом от F5
к F1, а сортировка 49 отрезков завершается на 6( = р + 2)
шаге, включая также и начальное распределение. Рассмотрим
следующий пример. Термин «многофазный» отражает тот
факт, что разные файлы ввода могут заканчиваться на раз¬
ных шагах и проход этих файлов может осуществляться па¬
раллельно.
В этом методе при р = 2 может быть использовано мак¬
симальное число файлов, равное 3. В табл. 3.4 представлен
процесс сортировки многофазным слиянием при распределе¬
нии 21 начального отрезка между файлами FI, F2 по 13 и 8.
В этом случае длина и число отрезков первой половины ша¬
гов симметричны длине и числу отрезков второй половины
шагов.
Таблица 3.4. Сортировка многофазным слиянием (случай числа
файлов, равного 3)
Шаг
Распределение отрезков
по файлам
Операция
Число
перемещаемых
записей
(за единицу
измерения
принят
начальный
отрезок)
F1
F2
F3
0
1 .21
1
1 • 13
1 • 8
—
Распределение началь¬
21
2
1-5
00
см
ных отрезков
Слияние
16
3
—
3-5
2-3
»
15
4
5-3
3-2
—
»
15
5
5 ♦ 1
—
см
00
»
16
6
—
13 . 1
8-1
»
13
7
21 • 1
—
—
»
21
Таким образом, чтобы определить число начальных отрез¬
ков и способ их распределения, для рационального осуществ¬
ления сортировки будем рассматривать только число отрезков
из нижней части табл. 3.4. Для того чтобы в самом конце
число отрезков в файлах FI, F2 составляло (1, 0), число
отрезков в файлах F2, F3 на предшествующем шаге должно
составлять (1, 1), а в файлах F3, F1 на еще более раннем
Шаге — (2, 1), т. е. число отрезков в файлах в соответствии
160
Глава 3
с порядком их прохода должно составлять
(1,0), (1,1), (2,1), (3,2), (5,3), (8,5), (13,8),....
Если записать пару п-го шага (ЬП9ап), то будем иметь
bn+\ — bn + ап+j =bn = b 1_] + ап_{ = ап + ап_ и
иными словами, если записать последовательность чисел
Фибоначчи F0 = 0, Т7, = 1, Fn+\ = Fn + Fn_u то (Ь„ап) =
= (Fn^Fn_,) (« = 1,2,...). Fn = (Г-(1 -ф)пУ V5, ф =
= (У5+1)/2, и при представлении ^ как F„_, + Fn_2
можно использовать Fn^i/Fn « <j> — 1 =0,618. Случай, когда
число начальных отрезков не равно /%*, будет рассмотрен
позже.
Посмотрим, что будет при р > 2. Рассмотрим в обратном
порядке строки табл. 3.3, построенной для 4-путевого слия¬
ния. Для каждой строки построим четверку чисел, соответ¬
ствующую количеству отрезков в файлах, вовлеченных в
слияние:
(1, 0, 0, 0), (1, 1, 1, 1), (2, 2, 2, 1),
(4, 4, 3, 2), (8, 7, 6, 4), (15, 14, 12, 8),
(29, 27, 23, 15), (56, 52, 44, 29), ....
Если обозначить группу из четырех элементов п-го шага че¬
рез (dn, Сп9 Ъп, ап), то
dn+1 == dn + crt, сп+1 == dn -f- bПУ bп+j = dn -j- CLnt
&п+1 == dn == dn_ j сn_ j = un -f- dn_2 + bn_2==
= + dn_з -f art_3 = + art-1 + an_2 +
Определим последовательность чисел Фибоначчи 4-го по¬
рядка:
F<4» = /?<«> = F24) = 0, F'34) = 1,
Fall = fn’ + F{*L 1 + F(4i2 + П41з (n - 3,4, ...),
тогда
n /7(4)
Un — г /i+ i,
и /7(4) I n(4)
On — rn+1 + Г n >
л /7(4) I 17(4) I p(4)
Cn — Г n+1 "T" * n ~T Г n-1,
Л /7(4) 1 /7(4) I n( 4) I n(4)
an + bn + cn + da = 4 Fnh + 8 F(? + 2/^1, + F(„4i2.
Таким образом, если заданы ап + bn + сп + dn начальных от¬
резков, то, распределяя эти отрезки на 4 файла по an, bn>
Сортировка
161
Спу dn отрезков, после 4-путевого слияния за п шагов полу¬
чим отсортированную последовательность.
В общем случае последовательность чисел Фибоначчи р-то
порядка определяется как
pip) pip) pip) п pip) i
r0 Г1 ••• —Гр-2 и, Гр- 1 1,
piP) piP) I piP) I I piP)
Гп+1 —Г n -j- Г n-\ -p rn-p+i.
В соответствии с этим р-путевое слияние с использованием
р + 1 файлов сформирует отсортированную последователь¬
ность за п шагов при числе начальных отрезков
hP) = pF{np)+p-з + • • • + 2^1, + F[nPU
пэсле распределения этих отрезков на р файлов по
р(р) , f(p) _L f(p) f(p) _|_ _ _1_ f(p) _|_ p(p)
ti+p—3* n+p—3 ~ n+p — 4’ * n+p—3 ' ’ ’ ' n— 1 ‘ n — 2*
В табл. 3.5 приведены числа начальных отрезков i{?\ для
которых осуществляется „полное" р-путевое слияние.
Обычно число начальных отрезков неопределенно и зави¬
сит не только от сортируемых данных, то и от того, с помощью
какого алгоритма они получены. Более того, даже когда число
начальных отрезков известно, оно не совпадает со значениями
из табл. 3.5. Для приведения числа начальных отрезков сор¬
тируемого файла к значениям таблицы вводится соответ¬
ствующее число фиктивных отрезков (нулевой длины), рас¬
полагаемых в начале файлов. В примере, приведенном
в табл. 3.6 для р = 4 при числе начальных отрезков, рав¬
ном 44, производится их распределение по файлам FI—F4
как можно равномернее с добавлением пяти недостающих
фиктивных отрезков, которые распределяются по файлам
FI — F4 как 1, 1, 1, 2. Далее сортировка выполняется так
же, как и для полного числа начальных отрезков. С шага 3
фиктивные отрезки исчезают и их влияние отражается только
в существовании более коротких отрезков.
При сортировке многофазным слиянием на каждом шаге
имеются записи и отрезки, над которыми не производится ни¬
каких операций (сравнения, перемещения). Таким образом,
число шагов, на которых разные начальные отрезки подвер¬
гаются определенным операциям, оказывается неодинаковым.
В случае когда используются фиктивные отрезки, эффектив¬
ность алгоритма оказывается выше, если фиктивные отрезки
распределяются по позициям начальных отрезков, операции
над которыми производятся за большее число шагов. Можно
было бы привести причины, по которым при начальном рас¬
пределении фиктивные отрезки лучше располагать в начале
файлов. Однако для этого потребуется более детальное об¬
суждение оптимального распределения фиктивных отрезков,
но из-за недостатка места мы его опускаем.
6 Зак. 127
Таблица 3.5. Полное число начальных отрезков г = при котором возможна сортировка р-путевым слиянием
за п шагов. В скобках приведено полное число перемещений записей, соответствующих начальным
отрезкам и обозначаемое через и
162
Глава 3
Сортировка
163
Рассмотрим случай, когда при начальном распределении
отрезков их общее количество неизвестно. В этом случае на
каждом шаге распределения пересчитывается соответствую¬
щая текущему количеству распределенных отрезков последо¬
вательность (dn, сп, Ьп, CLn) чисел Фибоначчи. Отличие реаль¬
ного распределения по окончании файла ввода от распреде¬
ления Фибоначчи и будет определять число фиктивных от¬
резков для каждого файла 1).
Если сортировка многофазным слиянием осуществляется
с использованием магнитных лент, часто значительные за¬
держки связаны с большим числом перемоток, выполняемых
лентопротяжными устройствами. Так, например, необходима
перемотка, чтобы один-единственный файл вывода на послед¬
нем шаге сделать файлом ввода. При сбалансированном
слиянии перематывают 2р файлов одновременно; бывает и
так, что производится перемотка 1 /р части всех файлов, но
в этом случае необходимо перематывать файлы ввода, кото¬
рые составляют по меньшей мере 1/2 всех файлов. Что ка¬
сается освободившейся ленты ввода, то при необходимости
ее также приходится перематывать для использования в ка¬
честве ленты вывода.
Если мы хотим сэкономить время, которое тратится на
перемотку, то для р-путевого слияния следует использовать
р + З файла: один из них находится в процессе перемотки
в результате вывода, другой — в процессе перемотки как
освободившийся файл ввода. Таким образом, число обраба¬
тываемых записей на первом шаге будет составлять не более
половины всех записей. Число отрезков в файлах оказыва¬
ется близким к числу элементов в последовательности чисел
Фибоначчи, но все-таки отличается от него и представляет
собой числовую последовательность, удовлетворяющую ре¬
куррентному выражению ап+\ = ап-\ + ... + Чтобы
отсортировать начальные отрезки одинаковой длины таким
усовершенствованным способом, требуется больше шагов, но
в целом меньше операций перемещений, чем при обычном
многофазном (р-путевом) слиянии.
3) Сортировка каскадным слиянием
Метод сортировки каскадным слиянием очень похож на
метод сортировки многофазным слиянием. Особенностью
О Этот метод распределения, когда отрезки поочередно распределяют¬
ся по файлам в соответствии с некоторой процедурой, управляемой пере¬
считываемой последовательностью Фибоначчи, получил название горизон¬
тального расширения. (Алгоритм такого распределения см., например,
•Ц* Кнут. Искусство программирования для ЭВМ, М., Мир, т. 3, с. 322. —
Прим. ред.)
6*
Таблица 3.6. Сортировка многофазным слиянием (случай недостающего числа начальных отрезков)
164
Глава 3
5⧑£няг
и a S SaS ^ И
Ка)ЕЗТ?4>о,ЯО.
• я о
X
3
Ч> д
к Л
Ж с;
о> Л
ч Ж
О)
ж
ж
к
ж
*5
U
+
ю
CD
+
_Н ТГ
СЧ
СО **
+
'Ж
о
+
СЧ
+
I +
I +
сч
N.
+
сч
CD
+
СО
сч
1
+
сч
СП
сч
1
сч
со
1
_1
Jh
1
Сортировка
165
26-
166
Глава 3
этого метода является то, что при его применении произво¬
дится не только точное распределение, но и изменение коли¬
чества путей слияния.
В табл. 3.7 показан процесс сортировки для 85 начальных
отрезков при использовании 5 файлов, как в случае табл. 3.6.
При начальном распределении числа отрезков между файла¬
ми FI — F4 — 30, 26, 19, 10, процесс их 4-путевого слияния
в 10 отрезков файла F5 длиной 4 производится аналогично
случаю табл. 3.6. На этом аналогия кончается.
Затем проводят 3-путевое слияние оставшихся отрезков
файлов FI — F3 в файл F4, не производя 4-путевого слия¬
ния, после чего 2-путевое слияние отрезков, оставшихся в
файлах FI—F2, в файл F3, и затем для большей ясности
копируют оставшиеся отрезки файла F1 в файл F2. В конце
концов большая часть содержимого файлов FI — F4 каскад¬
ным образом сольется в файлы F2 — F5. Если повторить эту
процедуру дважды, можно получить по одному отрезку в
файлах F2 — F5 и 4-путевым слиянием завершить сорти¬
ровку. Этот метод не имеет особых преимуществ перед мето¬
дом сортировки многофазным слиянием. На самом деле при
р> 6 метод каскадного слияния при сортировке одинако¬
вого числа начальных отрезков оказывается несколько вы¬
годнее метода многофазного слияния с точки зрения общего
числа выполняемых операций. Однако выигрыш не слишком
велик.
4) Способы подготовки начальных отрезков
При сортировке слиянием чем меньше начальное число
отрезков, тем меньше операций в целом на нее потребуется.
Иными словами, лучше, если длина начальных отрезков бу
дет как можно больше. Каким образом при использовании
ограниченной оперативной памяти сформировать длинные
отрезки?
Первым приходит в голову способ, при котором из файла
ввода в оперативную память переносят как можно больше
записей, сортируют их одним из методов внутренней сорти¬
ровки, описанных в предыдущем разделе, например методом
быстрой сортировки, а затем выводят (рис. 3.20). Преимуще¬
ством этого способа является то, что независимо от размера,
заключительного отрезка, начальные отрезки будут иметь
одинаковую длину. Это свойство позволяет несколько упрос¬
тить программу сортировки.
Однако если в оперативной памяти нельзя использовать
более М ячеек, то, надо полагать, рассмотренным способом
нельзя сформировать отрезок длиной больше М. Пусть за¬
Сортировка
167
дана последовательность 2-разрядных целых чисел, как по¬
казано на рис. 3.21, и ее надо отсортировать в оперативной
памяти объема М = 3. Осуществляют вывод наименьшего
значения после сортировки трех чисел, вводят следующую
запись и снова сортируют. Выводят наименьшее значение из
Рис. 3.20. Формирование начальных отрезков. «Групповая» система.
полученной отсортированной в оперативной памяти последо¬
вательности, если оно больше выведенного в предыдущем
шаге. Повторяя эту операцию, проводим через оперативную
Изменение в оперативной память
М=3. Подчеркнутое значение вы¬
водится, на ее о место вводится
другое
Файл ввода 78, 45,72, 59, 20, 43, 85, 33,92, 81, 34,85, 16, 49,61, •
Конец первого отрезка.
Файл вывода
78 45 72
78 59 72
78 20 72
78 20 43
85 20 43
33 20 43
33 92 42
81 92 43
81 92 34
85 92 34
16 — 34 Конец второго отрезка
16 49 34
45. 59.72, 78, 85 | 20, 33, 43, 81, 85, 92 | 16, —
Рис. 3.21. Формирование начальных отрезков (непрерывная система).
Формируются отрезки длины 5, 6, ... в оперативной памяти объема
М = 3.
память весь первый начальный отрезок, признаком оконча¬
ния отрезка будет служить размещение в оперативной па¬
мяти только чисел, значения которых меньше, чем последнее
выведенное число. Далее вновь выводим наименьшее число
из находящихся в оперативной памяти и т. д. Минимальная
Алина отрезка, кроме последнего, будет не меньше М.
168
Глава 3
В рассматриваемом методе построения отрезков удобно
использовать корпоративную структуру. В этом случае ал¬
горитм будет выглядеть следующим образом.
Алгоритм. Формирование начальных отрезков
1. Построить корпоративную структуру с меньшим значе¬
нием в корне.
2. Вывести корень.
3. Ввести следующую запись и выбрать значение ключа.
4.1. Если оно больше последнего выведенного значения, по¬
местить его в корень.
4.2.1. В противном случае: если корпоративная структура не¬
пуста, то последний элемент поместить в корень, а вве¬
денный элемент поместить в последнюю позицию; диа¬
пазон адресов корпоративной структуры уменьшить
на 1.
4.2.2. Если корпоративная структура пуста, то завершить об¬
работку отрезка и возвратиться к шагу 1.
5. Восстановить корпоративную структуру и перейти
к шагу 2.
При такой непрерывной системе в памяти, содержащей-
М записей, можно формировать начальные отрезки средней
длины 2М. Здесь предполагается, что последовательность
значений ключей в файле ввода случайна.
Попробуем содержательно рассмотреть это свойство. Зна¬
чения ключей, вводимые из файла ввода, распределены более
или менее случайно. Распределение же выводимых значений
смещено от меньших к большим. Можно провести аналогию
с процессом фракционирования сырой нефти, представляю¬
щей собой смесь легких и тяжелых фракций, в колонне фрак¬
ционирования: в колонну вводится смесь всех фракций от
легких до тяжелых и с той же скоростью, с которой вводится
нефть, выводятся отдельные фракции, начиная с самой тя¬
желой и кончая самой легкой (рис. 3.22). Колонна непре¬
рывно работает в таком режиме. Если ввод производится
равномерно, а смещение позиций вывода будет происходить
с постоянной скоростью, то распределение качества фрак¬
ционируемой нефти будет соответствовать уменьшению с по¬
стоянным наклоном за один временной цикл от выбранной
текущей точки. Таким образом, количество нефти, выводимой
за один временной цикл (т. е. длина отрезка), составляет
полное количество нефти, находящееся в данный момент
в колонне, плюс половина количества нефти, введенного в ко¬
лонну в течение одного временного цикла, т. е. количество,
равное количеству нефти, находящемуся в колонне в данный
момент. Иными словами, за один временной цикл выводится
количество нефти, вдвое большее находящегося в колонне
Сортировка
169
в данный момент, т. е. двойной объем фракционирующей ко¬
лонны.
Если использовать в качестве модели такого «нефтяного
резервуара» не только оперативную, но и внешнюю память,
то можно еще больше увеличить среднюю длину отрезка.
Иными словами, если вводится ключ, меньший чем послед¬
ний выведенный, то его можно, не задерживая в оперативной
Рис. 3.22. Формирование начальных отрезков (непрерывная система).
памяти, поместить в некоторый файл во внешней памяти.
Благодаря этому увеличивается пространство памяти, ис¬
пользуемое для текущего отрезка. При формировании сле¬
дующего отрезка порция нефти вводится в начало отрезка из
этого нефтяного резервуара. Если положить, что объем М'
нефтяного резервуара равен Му то по аналогии с проведен¬
ным выше рассуждением можно вычислить, что среднее зна¬
чение длины отрезка будет равно еМ (где е — основание на¬
турального логарифма). Однако в этом случае требуются
большие дополнительные затраты, связанные с операциями
ввода в «резервуар» и операциями вывода из «резервуара».
3.2.4. Эффективность внешней сортировки
1) Мультипрограммирование
Выше обсуждалась проблема, касающаяся определения
числа операций для отдельных записей или начальных от¬
резков при внешней сортировке слиянием. В вычислительных
системах с мультипрограммной обработкой потери времени,
обусловленные ожиданием выполнения операций ввода-вы¬
170
Г лава 3
вода, могу'1 быть существенно снижены. Это является важ¬
ным фактором. В соответствии с этим кажется, что при
использовании любой схемы слияния в среде с мультипрограм¬
мированием — сбалансированного, многофазного, каскадно¬
го— по мере увеличения р в р-путевом слиянии эффектив¬
ность должна повышаться. Так ли это на самом деле? При
размещении файлов на магнитных лентах количество файлов
(одновременно обрабатываемых) естественно ограничивается
числом доступных лентопротяжных устройств. Размещение
данных на магнитных дисках позволяет увеличить число фай¬
лов, однако и в этом случае необходимо учитывать реальные
ограничения на размеры внешней памяти. При любой схеме
слияния, за исключением сбалансированного, число отрезков
в обрабатываемом файле изменяется, да и с самого начала
длины отрезков обычно неодинаковы. В связи с этим файлы,
используемые при сортировке, необходимо делать достаточно
большими.
Эффективность мультипрограммирования во многом опре¬
деляется объемом оперативной памяти. Примем за единицу
объема данных, вводимых в оперативную память и выводи¬
мых из нее, один блок. Разобьем оперативную память на
р + 1 равных блоков: р блоков используем для ввода и один
блок — для вывода. Значительное увеличение р приведет
к уменьшению размера блока, что в свою очередь потребует
выполнения большего количества операций ввода-вывода,
увеличения времени перемещения считывающих головок и
как следствие замедлит процесс сортировки.
Обозначим полное число литер в сортируемом файле че¬
рез L, размер оперативной памяти в литерах через М, длину
блока в литерах через В = М/(р-Ь 1). Число блоков, нахо¬
дящихся в процессе ввода-вывода на первом шаге выполне¬
ния алгоритма сортировки, будет составлять L/B=(p-1-
+ 1)L/M. При сбалансированном слиянии, обозначая через
г число начальных отрезков, число операций ввода-вывода
блоков при слиянии на шаге logpr можно выразить как
(log, г) ЦВ = (L log r/M) . ({р + 1 )/log р).
(х-}-\)/\ ogpX принимает наименьшее значение при х9 рав¬
ном примерно 3,6. Исходя из этого, в качестве наиболее эф¬
фективного значения р следует принять р = 4. При много¬
фазном и каскадном слиянии влияние р оценить несколько
сложнее, однако общий характер зависимости не меняется.
Как будет показано ниже, в случае использования буфери¬
зации в процессе обработки оказывается 2(р+1) блоков,
поэтому В = М/2(р -±- 1). В приведенной ранее формуле для
В М заменяется на М/2, однако это не влияет на способ
выбора р.
Сортировка
171
Для более точного анализа необходим учет всех допол¬
нительных факторов, таких, как вспомогательные ЗУ и ка¬
налы связи, однако для практических целей достаточно, как
правило, следующей оценки.
Если при р-путевом сбалансированном слиянии, рассмот¬
ренном выше, блоки достаточно велики, время перемещения
считывающей головки и время обработки, приходящиеся на
одну литеру, равны. Проанализируем время, необходимое на
7(2в+/9)
Рис. 3.23. Оптимизация процесса слия¬
ния. Коэффициент а: 3-3 + 2-2 + 2-2 +
+ 4 • 2 + 7-2 = 39, коэффициент р:
3 + 2 + 2 + 44-7 = 18.
ввод и обработку данных на шаге 1 обработки. Обозначим
время перемещения считывающей головки через 5, время
ввода и обработки, приходящееся на одну литеру, — через т.
Тогда затраты будут составлять
s-^ + mL = s(p + l)-^- + mL = L(p + + + + m)=L(ap+p),
где a, Р— положительные константы. Предположим, что об¬
работка начинается сразу после окончания ввода. При этом
даже если пренебречь временем, требуемым на операцию
сравнения, это скажется только на значении р, а вид
формулы не изменится. Кроме того, если предположить
дополнительно, что вывод осуществляется параллельно
с операцией сравнения, вид формулы все равно останется
прежним.
Анализируя вид полученной формулы, рассмотрим опти¬
мизацию процесса слияния при заданных аир. Изобразим
р-путевое слияние в виде дерева, как показано на рис. 3.23
(листья представляют собой начальные отрезки одинаковой
длины). Сопоставленное с каждым узлом значение выражает
затраты (число перемещений) на данном шаге алгоритма.
Общие затраты на сортировку составляют сумму значений
всех узлов, к которой добавляются затраты на начальное
распределение. Таким образом, коэффициенты при а, р опре¬
деляются только структурой дерева: при р длиной внешнего
пути дерева, а при а длиной степенного пути дерева, опреде¬
ляемой как сумма произведений по всем внутренним узлам
степени внутреннего узла на число листьев поддерева с кор¬
172
Глава 3
нем в данном узле. При заданных аир можно рассмотреть
задачу построения дерева, обеспечивающего минимальные за¬
траты на слияние. Решение этой задачи здесь опускается.
2) Область буферной памяти
Для уменьшения времени сортировки можно совместить
выполнение ввода данных и их обработку в оперативной па¬
мяти. Это достигается за счет организации области буфер¬
ной памяти для ввода, содержащей буферы (блоки), коли¬
чество которых превосходит количество обрабатываемых
файлов. Введение дополнительных буферов ввода позволяет
обеспечить так называемую опережающую буферизацию: ко
времени окончания обработки одного блока заканчивается
ввод в другой буфер следующего, так что потерь времени на
ожидание ввода не возникает. Сколько же необходимо иметь
буферов? Если,число буферов будет велико, величина одного
буфера и соответственно блока должна уменьшиться и, как
отмечалось выше, возрастут накладные расходы, связанные
с увеличением количества перемещений считывающей голов¬
ки 1}. Посмотрим, какими минимальными затратами можно
обойтись для слияния р очень длинных отрезков, состоящих
из большого числа блоков.
Прежде всего предположим, что ввод записей, составляю¬
щих один блок, операции сравнения и вывод этих записей
производятся с одинаковой скоростью. В противном случае
ввод необходимых данных будет задерживаться, вызывая
соответственно и задержку обработки уже введенных данных.
Для вывода обычно достаточно двух буферов. В то время как
в один буфер размещаются результаты слияния, содержимое
другого буфера выводится. Ко времени заполнения первого
буфера должно заканчиваться освобождение второго. То же
самое справедливо и в отношении ввода; ясно, что при на¬
ших предположениях для каждого файла ввода потребуется
использование двух буферов. Иными словами, если при слия¬
нии одних блоков производится считывание других блоков,
то к моменту, когда заканчивается обработка первых, долж¬
но заканчиваться также и считывание других. Однако это
рассуждение предполагает, что используется достаточное ко¬
личество каналов ввода-вывода и что требуемые каналы
свободны в требуемое время. Ниже мы покажем, что если
правильно выбрать порядок файлов ввода, то можно пре¬
красно обойтись даже одним каналом. На рис. 3.24 приведен
пример для р = 4.
*) Увеличение количества межблочных промежутков на носителях дан¬
ных. — Прим. ред.
Сортировка
173
Рассмотрим случай ввода блоков в р буферов, соответ¬
ствующих р файлам, начиная с момента начала слияния.
Предположим, записи, принадлежащие р блокам (по одному
из каждого файла ввода), находятся в области буферной
памяти. При операции слияния необходимо вначале произ¬
водить считывание блока, следующего за первым освободив¬
шимся блоком, а при исчерпании текущего отрезка — считы¬
вание следующего отрезка. Аналогично можно показать, что
если в момент окончания считывания одного блока начина¬
ется считывание наименьшего файла, последняя запись те¬
кущего буфера которого имеет наименьший ключ среди по¬
следних записей текущих буферов, то не будет ожидания
ввода для 2р буферов.
Рассмотрим вначале случай, когда существуют файлы
ввода, содержащие более двух блоков, в которых еще не на¬
чата операция сравнения (см. рис. 3.24, а). Для последнего
ключа kA2 второго блока одного из таких файлов РА произво¬
дятся сравнения перед считыванием 3-го блока. Значения
последних ключей kc\, kD\ файлов Fc и FD, содержащих
только блоки, в которых начата операция сравнения, должны
быть больше значения ключа kA2• Иными словами, окончание
обработки текущих блоков файлов Fc и FD производится
после окончания обработки 2-го блока файла FA. Таким об¬
разом, если в момент, показанный на рис. 3.24, а, следующим
считывается файл с наименьшим значением из kA$y kB2, &сь
£di, то не производится затрат времени на ожидание ввода.
В противном случае, как показано на рис. 3.24,6, произ¬
водится разделение на группу а файлов, содержащих в бу¬
ферной области только один блок, в котором не начата опера¬
ция сравнения, и группу р файлов, содержащих в буферной
области только блоки, в которых начата операция сравне¬
ния. Если обозначить (число записей в обрабатываемых бло¬
ках) -f- (число записей в одном блоке) через bA, bB, fee, bo,
то, поскольку полное число записей содержится в р блоках,
имеем
X h+ X bll = p — Ct = p.
Аеа це (3
Здесь а, р— количества файлов в группе а и группе р соот¬
ветственно. Таким- образом, для произвольного случая
5>* + &в = р- X 6Ц>Р-(Р - 1)=1.
Л<=а (х ф 0
Поскольку к моменту окончания обработки текущего блока
файла Fо выполняется условие k$\>ku (Х^а), должна
быть полностью закончена обработка первого блока файла
^е, и вышеприведенная формула показывает, что сумма чи¬
сел этих записей превышает число записей, содержащихся
174
Глава 3
j?a | ищ1 уттшшц
kBi квг
jrg |
ка
Fc I **4
*01
Ft, I Щ
кс 1» *oi > клг
а
Ьл кА1 кАг
ЬВ кдх кв1
Гв | ШЩ
Ьс кс I
Р | У////////////Щ
t>D к о I
fd | ^
h
*j41 kAi
Fa I \щ •
Fb | ша^ р
ус | ШЩ .
*01
fd I Щ
kj11. кв 1, ка < коI < к442, квг, кСг
в
Рис. 3.24. Ввод для р путевого слияния с использованием 2р буферов.
Случай р = 4. Отрезками показаны буфера; штриховкой показаны необ¬
работанные части буферов. Данные из буфера выводятся слева, а — слу¬
чай, когда отдельные файлы используют не менее двух блоков; б—случай,
когда каждый из а файлов использует более одного блока, а каждый из
р файлов использует ровно один блок; в — состояние, в котором необхо¬
димы 2р буферов.
в одном блоке. Таким образом, если в момент, показанный
на рис. 3.24,6, следующим считывается блок файла с наи¬
меньшим значением из &Л2> кв2> &сь kD\, то затраты времени
на ожидание ввода отсутствуют.
Итак, в любом из случаев, показанных на рис. 3.24, а, б,
из какого бы файла ни считывался следующим блок, в мо¬
мент окончания считывания нового вводного блока опять
возникают условия, показанные на одном из рис. 3.24, а
или б, или заканчивается отрезок какого-либо файла. В слу¬
чае, показанном на рис. 3.24, в (здесь изображен момент
окончания считывания 2-го блока одного из файлов FAi FB}
Сортировка
175
fc)y необходимо начать считывание следующего блока фай¬
ла FDy т. е. в любом случае необходимо 2р буферов.
3) Виртуальная память
Широкое распространение в архитектуре современных
ЭВМ получила виртуальная память. Можно ли в случае
большого виртуального адресного пространства ограничиться
использованием методов сортировки в оперативной памяти,
описанных в разд. 1, или и здесь необходим переход к внеш¬
ней сортировке?
Виртуальная память отличается от других видов памяти
как поддерживающей аппаратурой, так и операционной си¬
стемой, под управлением которой осуществляется работа
с ней. Во-первых, даже при внутренней сортировке в вирту¬
альной памяти реальная обработка выполняется с использо¬
ванием внешней памяти, поэтому необходимо учитывать ее
влияние — неизбежные при этом затраты на запись и считы¬
вание. И наоборот, считывание и запись при внешней сорти¬
ровке почти идентичны перемещениям записей в виртуальной
памяти. Из соображений практического удобства обычно го¬
раздо охотнее используют внутреннюю сортировку. При этом
важным фактором, влияющим на эффективность, является
интенсивность использования массы сильно различающихся
'адресов за сравнительно короткие временные интервалы.
С этой точки зрения в среде виртуальной памяти быстрая
сортировка оказывается лучше корпоративной. При подъеме
значений в случае корпоративной сортировки адреса ключей,
вовлекаемых в сравнения, изменяются с большим прираще¬
нием, что может привести к большему количеству странич¬
ных обменов. При быстрой сортировке на каждом шаге
сравнение и обмен производят для ключей с адресами, плавно
изменяющимися от обоих концов к центру. За счет этого при
быстрой сортировке сравнение и обмен, как правило, произ¬
водятся в относительно узком диапазоне.
Если в среде виртуальной памяти используется внешняя
сортировка, управляемая прикладной программой, имеет
смысл практически используемое пространство памяти орга¬
низовать в реальной, а не в виртуальной памяти. Во всяком
случае для внешней сортировки должен обеспечиваться до¬
статочный объем реальной памяти. Если это требование не
выполняется, использование виртуальной памяти может при¬
вести к заметному снижению эффективности сортировки.
3.3. Объем вычислений при сортировке
В предыдущих разделах рассматривались различные ал¬
горитмы сортировки и оценивался объем вычислений для
этих алгоритмов. Чтобы оценить затраты на сортировку клю¬
176
Глава 3
чей п записей, исследовали, в какой функциональной зави¬
симости от п находится число «однократных операций», т. е.
число необходимых сравнений, обменов, операций вывода и
ввода и т. д. Смысл оценки различных алгоритмов заклю¬
чался в нахождении их усредненных характеристик. Иссле¬
дуем теперь предельные значения затрат при использовании
разных алгоритмов.
3.3.1. Минимальное число сравнений
Прежде всего оценим число необходимых операций
сравнения, не накладывая ограничений на число перемеще¬
ний или обменов, а также на объем памяти. Рассмотрим слу¬
чай, когда определение большего или меньшего из двух эле¬
ментов производится только с помощью сравнения их между
собой. При этом исключим из рассмотрения сортировку по
основаниям систем счисления, рассмотренную в разд. 3.2.4.
Там уже отмечалось, что необходимое число сравнений для
сортировки по основаниям систем счисления составляет
riog2 п!"|.
Рассмотрим сравнения четырех взаимно отличающихся
чисел а, 6, с, d {п = 4). На рис. 3.25 для обозначения а <Ь
используется а-^Ь. На рис. 3.25, а приведена только 1/4 всех
4! =24 случаев сравнения, затем показано, что имеет место
обмен между а и Ьу с и d и отсортированная последователь¬
ность получается в результате пяти сравнений. На шаге 3
сравниваются два больших элемента. Дальнейшее выполне¬
ние процедуры можно было бы осуществить и сравнением
меньших элементов. А может быть, на шаге 3 надо сравни¬
вать больший элемент с меньшим? Как можно видеть на
рис. 3.25,6, сортировка пятью сравнениями обеспечивается
только в первом случае, а остальные два потребуют боль¬
шего числа сравнений.
Итак, для ответа на вопрос «Каково минимальное число
сравнений?» необходимо определить минимальное число срав¬
нений для наихудшего случая. Для этого следует всячески из¬
бегать случаев благоприятного решения. Если уже определен
порядок элементов при трех первых сравнениях, последую¬
щее сравнение проведем, используя результаты первых трех,
методом деления пополам от середины. При сравнении пяти
различных чисел а, 6, с, d, е для чисел а, Ьу с, d до шага 3
процедура соответствует показанной на рис. 3.25, а. Если,
например, в результате окажется, что a-+b-^dy c-*dy то
дальше надо вначале е сравнить с d, а затем с каким-то из
элементов a, d и определить, куда должен быть вставлен
элемент е в последовательности a-^b^-d (а может быть,
до или после нее). Затем двумя сравнениями определим,
Сортировка
177
Рис. 3.25. Последовательность сравнения четырех чисел а, Ь, с, d\ а — сор
тировка пятью сравнениями; б — сортировка шестью сравнениями.
в какой из отрезков меньше d (длины 3 или 2) в этой после¬
довательности надо вставить с, ив результате получим от¬
сортированную последовательность за семь сравнений.
Как правило, высокую эффективность обеспечивает так
называемый метод сортировки вставками и слиянием Фор¬
да— Джонсона. В этом методе сочетаются слияния и вставки.
Алгоритм сортировки вставками и слиянием в рекурсивном
виде представлен на рис. 3.26.
Алгоритм. Сортировка слиянием со вставками
1. Формируя из п чисел \_п/2\ пар, произвести сравнения
в парах. Если п нечетно, то один элемент не участвует
в сравнениях.
2. Отсортировать вставками и слиянием \п/2\ больших
элементов пар, найденных на шаге 1. Результат предста¬
вить в виде, показанном на рис. 3.26(1). Если п нечетно,
взять в качестве конца половины последовательности
/г/2 т *
178
Глава 3
3.1. Сравнить Ьъ с последовательностью Ь\-+- а\-+ а2. Если
сравнение начинается с а\> результат может быть полу¬
чен двумя сравнениями. В полученной последовательно¬
сти вставить Ь2 на отрезке меньше а2. Вставка будет вы¬
полнена за два сравнения. Представить результат в виде
диаграммы, показанной на рис. 3.26(2).
3.2. Сравнить 65 (см. рис. 3.26(2)) с последовательностью
С\ —>■ ... ->с6->а4 длины 7 = 23—1. Вставка будет вы-
‘A-i/Sj (6rn/20
/■ ; ч Самое болыиее 2 вставки
' v1~‘>C2~^C3^ C4~,>C5~,>C6~H>jHJ~y5~yeT в последовательность длины 7
bi 65 Ьб •••
Самое большее 6
вставок в после-
Аб 67 6в 69 *f. 6u - доватемность
длинь( /в
(И) х\~* хг~*"' o-tk + \-~ а{ +2'-* "а,. -
/ • / /
i|* + l .btb + 2 ••• Ь (4.1
Рис. 3.26. Алгоритм сортировки вставками и слиянием.
полнена за три сравнения. Сравнить 64 с отрезком мень¬
ше а4 полученной последовательности. Если длина этого
участка 7 или 6, то на вставку потребуется три сравне¬
ния. Представить результат в виде диаграммы, показан¬
ной на рис. 3.26(3).
3.3. Далее за четыре сравнения вставить Ь\\ (а не Ь7)
в нужное место последовательности d\-> ...
аб -> ... ->аю длины 15 = 24 — 1. Элементы &ю, Ь9,
..., b6 вставляются также за четыре сравнения (каж¬
дый в нужное место последовательности длины 15).
[Обобщая 3.1—3.3, определим шаг З./е, для кото¬
рого представим последовательность натуральных чисел
(/*)“ как t\ == 1, tk_x + lk = 2k (k = 1, 2, ...). Тогда 2tk +
+ (//c+i — tk — 1) = 2k — 1 {k — \y 2, ...). При выполнении
шагов 3.1—3.3 bt , btk_u bt +x в указанном по¬
рядке сравнивают с последовательностью длины макси¬
мум 2k+{ — 1 (k= 1, 2, 3). Длина отсортированной части
последовательности, полученной в результате трех ша¬
гов, составляет 2/fe+1+l.]
3.&. Результат (k— 1) повторения шага 3 представить в виде
диаграммы, показанной на рис. 3.26 (k). Здесь в верх¬
нем ряду приведена последовательность до min (tk+u
Сортировка
170
/г/2 J). Провести сравнение с последовательностью длины
максимум 2k — 1 элементов, уменьшая значение индекса
на 1, начиная с btk+{ (если в процессе сравнения ряд
окажется законченным, то начиная с Ьгп/21 или л/2 j)-
[Обобщением шага 3 алгоритма является „шаг 3.k для
6 = 1, 2, ... повторять до завершения сортировки".]
Итак, в случае использования метода сортировки встав¬
ками и слиянием обозначим число сравнений при сортировке
п элементов (чисел) через F(n). На шаге 1 число сравнений
составляет |_дг/2J , на шаге 2 — F(ln/2])t на шаге 3.6—
самое большее (k-\-\)(tk+\— tk)\ если обозначить т =
=Гя/2]< tk+1, то число сравнений на шаге 3.6 составляет
(6 + 1) im — tk)- На шаге 3 число сравнений равно
2 (/ "Ь (*/+i */) + (& + 1) (w — tk) =
= (6 -f- l)m — (tk + • • • + t[ + 1).
Поскольку
tk = 2k -tk_{ = 2k -2k~l + ... +(-l)ft-2° = (2ft+1 + (-l)*)/3,
то при tk <C Г я/2] ^ tk+1 в конце концов получим
F (п) = ln/2} + F (L/z/2J) + (6 + 1) Гя/2] - L2fe+2/3J.
Это выражение несколько громоздко, однако после простых
преобразований получим
F (п) — F (п — 1) == flog2 (3/4«)1,
откуда
F(n)= Z riog2(3/4fe)l.
К Л <п
Если попробуем провести вычисления F(u) для оптималь¬
ной сортировки вставками и слиянием, окажется, что F(n)
совпадет с нижним пределом числа сравнений для 2^п^11,
равному Tlog2^!]1). Понятно, что при достаточно большом п
метод вставок и слияний окажется очень эффективным, од¬
нако в каком диапазоне расположены наилучшие значения
F(n)y а также каково отношение наименьшего числа сравне¬
ний к полному числу п — эти проблемы остаются неразре¬
шенными.
*) Алгоритм оптимален также и при 20 ^ п ^ 21 (см. Д. Кнут. Ис¬
кусство программирования для ЭВМ, М., Мир, 1978, т. 3, с. 226. — Прим.
Ред.
180
Глава 3
3.3.2. Сортировка с использованием специальных
структур
Другим методом оценки объема вычислений при сорти¬
ровке является оценка того, насколько длинными числовыми
последовательностями оперируют при осуществлении сорти¬
ровки в случае использования специальных структур памяти.
В качестве конкретного примера рассмотрим- переформиро¬
вание товарных поездов на сортировочной станции железной
Запасной путь
\ -
fly.т/ь -«—► Основной путь Путь
выезда подъезда
а
Рис. 3.27. Переформирование товарного поезда с помощью запасного пути:
а — в — две параллельные очереди; г — стек.
дороги. На обычной станции в наиболее простых случаях ис¬
пользуется запасной путь (см. рис. 3.27, а). Если предполо¬
жить, что все товарные вагоны самоходны в любом направ¬
лении и что имеется достаточно длинный запасной путь, поезд
можно переформировать, отсортировав вагоны в любом по¬
рядке. Распределение вагонов с пути подъезда па замаспой
путь и параллельный ему основной путь соответствует рас¬
пределению начальных отрезков, затем двухпутевым слия¬
нием вагоны попадают на путь выезда; далее вагоны возвра¬
щаются обратно с распределением на запасной и основной
пути; если эту операцию повторять, она будет соответство¬
вать сортировке со сбалансированным слиянием.
Если движение будет возможно только в одну сторону,
провести сортировку только одним двухпутевым слиянием
не удается, но если через такую станцию пропускать поезд
k раз, то можно провести слияние 2k начальных отрезков, не
увеличивая и не уменьшая по пути число вагонов. Если рас¬
сматривать это с точки зрения структур памяти ЭВМ, то
можно назвать это структурой, связывающей две параллель¬
ные очереди с k последовательностями (см. рис. 3.27,6).
Сортировка
181
Рассмотрим случай тупикового запасного пути, обеспечи¬
вающего возможность возвращения на путь подъезда. При
этих предположениях оказывается так же, как и в вышеопи¬
санном случае, возможным вначале распределение, а затем
слияние (см. рис. 3.27, в). Ситуация существенно изменится,
если с запасного пути нельзя будет возвращаться на путь
подъезда (см. рис. 3.27,г). Для этой конфигурации слияние
в общем случае невозможно. Например, невозможно отсор¬
тировать последовательность вида (2, 4, 1, 3). Невозможно
также отсортировать последовательность длины 3 (2, 3, 1),
в то время как последовательность (1, 2, 6, 3, 4, 5) сорти¬
руется. Возможно также отсортировать последовательность,
в которой возрастающий отрезок следует после убывающего.
Рассмотренная структура, организованная в памяти ЭВМ,
получила название стек.
Обобщая последние два случая, введем понятие сети,
узлы которой рассматриваются как очереди, стеки, деки,
ограниченные деки. При этом связи между узлами сети имеют
только одно направление, в сети также отсутствуют кольца.
Можно считать, что на входе и на выходе сети организованы
очереди. Очередь на входе представляет собой числовую по¬
следовательность, элементы которой поступают в сеть. В ре¬
зультате прохода элементов по сети на выходе образуется
очередь, представляющая собой отсортированную последова¬
тельность. Здесь, в отличие от случаев, рассмотренных в 3.3.1,
достаточно просто определить необходимое число сравнений.
Если предположить, что порядок заданной числовой последо¬
вательности известен, как и при переформировании товарного
поезда, то можно найти оптимальный способ перемещения
ее элементов. При ограничениях, наложенных на вид и число
перемещений, задача сводится к определению длины или
сложности последовательности, которую можно отсортиро¬
вать.
В качестве простого примера рассмотрим k параллельных
очередей. Последовательность очередей не имеет смысла.
Обозначим через d(a) максимальную длину убывающей по¬
следовательности a,ix > cii2 > ... в числовой последователь¬
ности а = {а)п{ взаимно различных чисел.
Теорема 3.1. Необходимым и достаточным условием воз¬
можности сортировки а элементов в k параллельных очередях
является условие d(ci)^k.
Доказательство. Возможность такой сортировки можно
доказать с помощью существования (построения) конкрет¬
ного алгоритма. Присвоим очередям номера от 1 до k.
1. Для i = 1, ..., п\
182
Глава 3
1.1. для /' = 1, . . ., k\
1.1.1. если /-я очередь пуста или ее последний элемент мень-
me di, добавить at в /-ю очередь.
Поскольку начало каждой очереди представляет собой
убывающую подпоследовательность элементов а, то, если
d(a)^k, можно образовать самое большее k возрастающих
отрезков. При их слиянии получим отсортированную после-
довательность. Если d(a)>ky то при распределении элемен¬
тов а по всем очередям будут иметь место очереди, имеющие
обратный порядок, си > aj (i < /). Отсортировать такие оче¬
реди невозможно. На этом доказательство можно считать
законченным. *
Таким образом, для k параллельных очередей нельзя по¬
лучить последовательность, отсортированную в обратном по¬
рядке (k + 1, k, ..., 2,1) длины k + 1.
Аналогичное доказательство можно провести и для k па¬
раллельных стеков. Если минимальное значение числовой
последовательности а находится в самом ее конце, то все
элементы, кроме последнего, необходимо ввести в стек. При
слиянии с использованием параллельных стеков сортировку
осуществляют, вводя в стек убывающие отрезки. Алгоритм
такой сортировки аналогичен алгоритму, использовавшемуся
для доказательства вышеприведенной теоремы, надо только,
чтобы вывод в результате сравнения на шаге 1.1.1 был об¬
ратным. Если обозначить через Ца) длину самой длинной
возрастающей подпоследовательности последовательности а,
то можно сформулировать следующую теорему.
Теорема 3.2. Поскольку все элементы а входят в k па¬
раллельных стеков, необходимым и достаточным условием
возможности их сортировки является ia ^ k.
Следствие. Сортировка числовой последовательности
(2,3, ..., k + 2,1) длины Н2 в 4 параллельных стеках
невозможна.
Последовательное соединение двух стеков резко услож¬
няет задачу. Становится неясным, что же можно отсортиро¬
вать в такой структуре. Например, любую числовую последо¬
вательность длины 6 можно отсортировать, но, если ее длина
оказывается равна 7, например (2, 4, 3, 5, 7, 6, 1), ее сорти¬
ровка становится невозможной. Обобщая эти рассуждения,
определим нижний предел числовой последовательности,
которую можно отсортировать в k последовательных
стеках.
Теорема 3.3. В k последовательных стеках можно отсор¬
тировать последовательность длины по меньшей мере 6*2А~2.
Сортировка
183
Доказательство. Если считать, что числовая последова¬
тельность максимальной длины l(k) может быть вся отсор¬
тирована в k стеках, то должно выполняться условие:
l(k + 1) ^ 2l(k). На самом деле если половину входной чис¬
ловой последовательности при обратном порядке расположе¬
ния в k стеках ввести в последний стек, то из этого стека
можно вывести один возрастающий отрезок, а оставшаяся
половина входной числовой последовательности размещается
в k стеках в прямом порядке. В результате слияния содер¬
жимого k стеков с отрезком последнего стека на выходе по¬
лучается отсортированная последовательность. Поскольку мы
исходили из очевидного 1(2) = 6, теорема доказана.
Для нахождения верхнего предела длины последователь¬
ности, для которой возможна сортировка, под несколько
иным углом зрения рассматривается следующая задача. По¬
пробуем определить варианты а(1) порядка расположения
элементов последовательности, гарантирующие возможность
получения отсортированной последовательности длины I
с использованием одного стека. Поскольку упорядоченную
последовательность с помощью обратных операций можно
превратить в исходную, а(1) есть не что иное, как число по¬
следовательностей длины /, только эти последовательности
и могут быть отсортированы в одном стеке. Если обозначить
операцию включения числа в стек через D, а операцию ис¬
ключения из стека через — U, то перестановка элементов чис¬
ловой последовательности длины / будет представляться по¬
следовательностью I элементов D и / элементов U. Например,
при 1 = 4 будет DDDUUDUU и т. п. Все эти последователь-
стеке операция извлечения не имеет смысла. Иными слова¬
ми, если считать число вхождений элементов D и U в после¬
довательность слова, то текущее число элементов U не мо¬
жет быть больше текущего числа элементов D. Например,
рассмотрим такую некорректную последовательность, как
DDUUUDDU. На участке, где U превышает D, если смот¬
реть слева, заменим элементы U на D, а элементы D этой
подпоследовательности — на U. Для вышеприведенного при¬
мера получим UUDDDDDU. Подчеркнутый участок является
участком обмена. В результате сформировала последователь¬
ность с числом (/+ 1) элементов D и числом (/— 1) элемен¬
тов U. И наоборот, если была задана последовательность
с числом (/+1) элементов D и числом (/—1) элементов U,
то, производя обмен U и D на участке, где число D пре¬
вышает число элементов U, если считать справа в левой под¬
последовательности (не считая этого D), получим некоррект¬
ности элементов D, U имеют
однако при пустом
184
Глава 3
ную последовательность. Таким образом, число операций,
приводящих к удобным последовательностям, составляет
(21Л-( 21 ) & (2/>!
V I ) \l—l) /!(/+!)!'
Пусть заданы две взаимно различных удобных последователь¬
ности элементов D, U. Поскольку на участке, где возникает
различие элементов, если просматривать эти две последова¬
тельности слева, операции будут различными, то различными
должны быть и элементы на выходе. Если последователь¬
ности элементов D и U различны, то, поскольку различны
соответствующие последовательности на выходе, вышеприве¬
денная формула может рассматриваться как выражение для
искомого а(1).
Теорема 3.4. Число последовательностей длины 1У которые
могут быть отсортированы в k последовательных стеках, со¬
ставляет максимум (a(l))k.
Доказательство. Вторично введем отсортированную после¬
довательность и посмотрим, каким будет ее порядок. После¬
довательность, которая может образоваться после прохожде¬
ния одного стека, будет иметь вид а(1). Если в результате
еще одного пропускания через стек полученной последова¬
тельности появится возможность образования на выходе та¬
кой же последовательности, которая была на входе, то бу¬
дем иметь максимум (а(1))2 вариантов. Продолжая анало¬
гичную процедуру, получим доказательство теорем.
Наоборот, для того чтобы отсортировать все числовые
последовательности длины /, должно выполняться условие
(а (п))к ^ п\ <=> k ^ log n\j\og а (п).
Так как а (п) = (2п)\/{п\(п + 1)0> используя формулу Стир¬
линга, получим правое неравенство в следующем виде:
k^(n+ 1) log — /г — 1 + 1/2 log п (п + 1) + log 4л ^
~ 1/2 log2 /г, (п-> оо),
что и является нижним пределом.
С другой стороны, верхний предел необходимого числа
стеков, как следует из теоремы 3.3, составляет
3 • 2к~х ^ п <=> k ^ log2 п — log2 3 + 1.
При п —оо верхний и нижний пределы отличаются друг
от друга в два раза, но точный предел неизвестен. Расчет
для дека еще сложнее. В заключение отметим, что один дек
менее эффективен, чем два последовательных стека. В одном
деке не могут быть отсортированы даже все последователь¬
ности длины 5. Например, не может быть отсортирована по¬
следовательность (2, 4, 3, 5, 1),
Глава 4
Практические аспекты
обработки данных
В гл. 1—3 были изложены базовые понятия и алгоритмы,
составляющие основу информатики. В практической работе,
связанной с обработкой данных, эти понятия и алгоритмы
являются фундаментом, на котором строится решение той
или иной задачи. В данной главе обсуждаются четыре такие
задачи из области практической обработки данных.
4.1. Методы доступа к внешней памяти
4.1.1. Методы доступа, реализуемые операционной
системой
Если рассматривать организацию и механизмы обмена
данными между внешней и основной памятью с точки зре¬
ния архитектуры системы управления вводом-выводом, то
последние можно разделить на следующие три основных
типа:
(1) Система непосредственного управления устройствами
ввода-вывода.
(2) Система управления устройствами ввода-вывода с по¬
мощью каналов ввода-вывода.
(3) Система с использованием процессоров баз дан¬
ных.
В системах первого типа управление внешними устрой¬
ствами осуществляется центральным процессором с исполь¬
зованием ряда регистров и линий управления. Такая система
применяется в малогабаритных специальных системах обра¬
ботки данных. Системы третьего типа в настоящее время
представляют предмет научных исследований и разработок,
однако частично уже реализованы. Кратко подобные системы
рассматриваются в разд. 4 данной главы. Основное внимание
в этой главе уделено системам второго типа.
С другой стороны, если рассматривать внешнюю память
с точки зрения прикладного или системного программного
обеспечения, то можно выделить следующие основные эле¬
менты:
(4) отдельные устройства;
(5) файлы или наборы данных;
(5.1) физические блоки или физические записи, представ¬
ляющие собой единицы обмена данными при использовании
микрокоманд READ/WRITE ассемблера;
186
Глава 4
(5.2) логические записи или кортежи, представляющие
собой отдельные считываемые и записываемые элементы дан¬
ных при использовании микрокоманд GET/PUT ассемблера.
Рассматриваемые в этой главе в качестве примеров ме¬
тоды доступа являются методами доступа операционной си¬
стемы (сокращенно ОС) широко распространенных больших
ЭВМ фирмы ИБМ, в частности виртуальный последователь¬
ный метод доступа VSAM.
Обсуждаемые здесь методы доступа в узком смысле пред¬
ставляют собой группу программ операционной системы,
основное назначение которых состоит в реализации запросов
на ввод-вывод, определяемых в программе пользователя мак¬
рокомандами чтения READ/GET либо записи данных
WRITE/PUT, в построении необходимых для этого программ
канала и управляющих блоков, а также инициировании про¬
цесса ввода-вывода.
В ранних вычислительных машинах ввод-вывод данных
осуществлялся центральным процессором, что заставляло его
функционировать во многих случаях со скоростью работы
устройств ввода-вывода. Для компенсации этого различия
стали использоваться каналы ввода-вывода, которые управ-'
ляют потоком данных между основной памятью и устрой¬
ствами ввода-вывода, обеспечивая центральному процессору
возможность работать одновременно с выполнением операций
ввода-вывода. Канал ввода-вывода, по существу, представ¬
ляет собой некоторую вычислительную машину, управляю¬
щую работой внешних устройств с помощью программ ка¬
нала. Так как функционирование центрального процессора и
обработка ввода-вывода протекают асинхронно, то вся управ¬
ляющая информация, требуемая для организации ввода-вы¬
вода, содержится в ряде управляющих блоков и таблиц,
которые сложным образом связаны между собой. Непосред¬
ственное выполнение операций обмена осуществляется спе¬
циальным компонентом ОС — супервизором ввода-вывода
(рис. 4.1). Методы доступа — это программы ОС, обеспечи¬
вающие связь между программами пользователей и супер¬
визором ввода-вывода. Если осуществить вызов супервизора
ввода-вывода, непосредственно записывая программу канала
в программе пользователя, можно выполнять ввод-вывод, не
прибегая к методам доступа, но в больших системах этот спо¬
соб используется редко.
Совокупность логически связанных полей данных назы¬
вается логической записью. Одна или несколько логических
записей образуют блок, являющийся физической единицей
данных и называемый иногда физической записью. Операции
ввода-вывода выполняются на уровне блоков, а не на уровне
логических записей. Процесс объединения логических записей
Практические аспекты обработки данных 187
Рис. 4.1. Методы доступа.
в блок называется блокированием, и, наоборот, процесс раз¬
биения считанного блока на отдельные логические записи
называется деблокированием. Область основной памяти, ис¬
пользуемая при обмене данными между внешней и оператив¬
ной памятью, называется буфером. Совокупность буферов
образует буферный пул. Процесс управления буферным пу¬
лом, осуществляемый при выполнении операций ввода-вы¬
вода, называется буферизацией. Блокирование, деблокирова¬
ние и буферизация входят в состав функций методов доступа.
4.1.2. ISAM (индексно-последовательный метод
доступа)
К основным методам доступа относятся методы последо¬
вательного доступа SAM, прямого доступа DAM, индексно-
последовательного доступа ISAM и др. Наиболее близким
к ISAM является виртуально-последовательный метод до¬
ступа VSAM. Наборы данных с индексно-последовательной
организацией (наборы данных ISAM) располагаются в ос¬
новном на магнитных дисках. Доступ к записям этих наборов
осуществляется двояко: прямой доступ по значению ключа
и последовательный доступ в порядке возрастания значений
их ключей. Можно выполнить последовательную обработку
188
Глава 4
либо всего набора данных, либо его части в пределах задан¬
ного диапазона значений ключей.
Наборы данных ISAM можно представить в виде древо¬
видной структуры определенной высоты. В примере, показан¬
ном на рис. 4.2, высота дерева равна 3, листьевые вершины
дерева соответствуют дорожкам магнитного диска.
Каждая дорожка диска может содержать несколько запи¬
сей, р каждой из которых в определенном месте (в данном
Адрес
диска
Индекс
ООО
\п\но\ |z \ZZ0\
цилиндров
110
; \т 1 \f\nz\ \h\u3\ \п\т |
Индекс
дорожек
111
112
113
11*1
И 1
- IM -ч
и 1 и ••••
1М 1
14 IN
■JM
Дорожка
Дорожка
Дорожка
Дорожка
Основная
, область
напяти
Ключ
Запись
Рис. 4.2. Организация файла в методе доступа ISAM.
случае в начале) указывается ключ записи. Узлы, непосред¬
ственно предшествующие листьям, соответствуют индексу
дорожки. Каждой занятой дорожке цилиндра в индексе до¬
рожек соответствует один элемент, содержащий адрес до¬
рожки и значение ключа последней записи на этой дорожке.
При заполнении записями очередной дорожки диска проис¬
ходит формирование нового элемента индекса дорожек и осу¬
ществляется переход на следующую дорожку.
После того как будут составлены элементы индекса для
всех дорожек первого цилиндра, по аналогии с индексом до¬
рожек составляется индекс цилиндров. Значением элемента
индексов цилиндров являются адрес цилиндра и значение
ключа последней записи этого цилиндра.
Организация обработки переполнения дорожек здесь не
рассматривается. Однако можно предположить, что для на¬
боров данных ISAM будут иметь место следующие проблемы:
(1) возникнут трудности, если максимальная длина запи¬
си превысит длину одной дорожки диска;
(2) трудно сформировать набор данных, располагаю*
щийся на дисках разного типа;
Практические аспекты обработки данных
189
(3) при большом количестве добавлений в набор данных
новых записей значительно усложняется его структура и сни¬
жается эффективность поиска и использования пространства
памяти.
4.1.3. VSAM (виртуальный метод доступа)
Метод VSAM имеет много общего с вышеописанным ме¬
тодом ISAM, однако лишен присущих ему недостатков. В ме¬
тоде VSAM среди используемых структур данных выделяют
область индексов и область данных (рис. 4.3).
Область индексов представляет собой организованную
в виде В+-дерева совокупность ключей. В листьевых верши¬
нах В+-дерева содержатся все ключи, составляющие дерево
I»,
8*
*>+
«ьоо
СА
СА
Рис. 4.3. Организация файла в методе доступа VSAM.
и упорядоченные в порядке возрастания их значений. Листье¬
вые вершины связываются между собой с использованием
указателей. Использование В+-дерева обеспечивает выполне¬
ние сравнительно небольшого числа шагов поиска записей
и связанных с этим операций ввода-вывода. При этом встав¬
ки и удаления записей чаще всего не оказывают влияния на
структуру В+-дерева, а в тех случаях, когда оно имеет место,
диапазон его воздействия сравнительно узок.
Благодаря таким свойствам VSAM эффективность как
прямого, так и последовательного доступов оказывается вы¬
сокой. Когда ключ представляется буквенно-цифровыми сим¬
волами, то поиск данных по начальным символам ключа на¬
190
Глава 4
зывают поиском по родовому ключу. В данном случае, тре¬
бующем одновременного использования прямого и последо¬
вательного доступов, VSAM дает особенно хороший ре¬
зультат.
В методе доступа VSAM существуют управляемые обла¬
сти, разделенные на управляемые интервалы. Подобно ме¬
тоду ISAM, в котором на каждый цилиндр имеется один
индекс дорожек, в методе VSAM на каждую .управляемую
область имеется один индекс управляемых интервалов. Каж¬
дый индекс управляемых интервалов соответствует листьевой
вершине В+-дерева индексов и называется набором указате¬
лей. В нем содержатся максимальные значения ключа для
каждого управляемого интервала и указатель на соответ¬
ствующий интервал. Вершины В+-дерева, расположенные
уровнем выше листьевых вершин, содержат максимальные
значения ключа для каждой управляемой области и указа¬
тель на соответствующий данной области набор указателей
(рис. 4.3).
На одной дорожке диска могут располагаться несколько
управляемых интервалов, в то же время один управляемый
интервал может занимать несколько дорожек. Максимальная
длина интервала не должна превышать размера одного ци¬
линдра. Управляемый интервал является единицей обмена
при операциях ввода-вывода. Отличительной чертой органи¬
зации VSAM является ее независимость от типа внешнего
ЗУ прямого доступа. В связи с этим такая организация по¬
зволяет определять размер управляемого интервала с уче¬
том распределения длин записей данных и возможностей
доступа и подходит для хранения и поиска данных пере¬
менной длины, включая длинные записи, как в системах по¬
иска данных, использующих для записи ключей естественные
языки.
Рассмотрим способы уплотнения данных, используемые
для VSAM, с целью экономии пространства памяти.
Например, пусть имеется список ключей ABIKO,
AKASHI, ..., BEPPU, представленный в первой колонке
табл. 4.1. Для каждого из ключей определим F — размер со¬
кращения, L — длину сокращенного значения, а также зна¬
чение сокращенного ключа следующим образом:
(1) Выбираем строку таблицы и сравниваем представлен¬
ный в ней ключ с ключом в предыдущей строке, определяя
позицию Р первой отличной литеры ключа в выбранной
строке. Полагаем F = P— 1.
(2) Сравниваем выбранный ключ с ключом в последую¬
щей строке и определяем позицию N первой отличной литеры
выбранного ключа.
Практические аспекты обработки данных
191
(3) Если P^.Nt записываем в качестве значения сокра¬
щенного ключа литеры выбранного ключа с Р-й до N-Pi по¬
зиций; полагаем L = N + 1 — Р.
(4) При Р > N сокращенные ключи в память не записы¬
ваем; полагаем L = 0.
Теперь индекс наряду с указателями будет содержать со¬
ответствующие значения F, L и сокращенных ключей.
Таблица 4.1. Метод уплотнения индексов
Список ключей
p
N
F
L
Сокращенный ключ
ABIKO
1
2
0
2
AB
AKASHI
2
3
1
2
KA
AKIBA
3
4
2
2
IB
AKITA
4
2
3
0
ARIMA
2
2
1
1
R
AT AMI
2
3
1
2
ТА
ATSUGI
3
5
2
3
SUG
ATSUTA
5
1
4
0
BEPPU
1
1
0
1
В
Если обозначить через A(j) (j = 1, m) j-ю литеру
аргумента поиска, а через E(k) (fe=l, ..., L) — fe-ю литеру
сокращенного ключа рассматриваемой строки, то можно вы¬
полнить поиск заданного аргумента по сокращенным ключам.
Алгоритм
1. Положить j:=k:= 1. Начать со строки с подходящим
индексом.
2. При / = Е + 1»
2.1. если L = 0, это искомый аргумент.
2.2. Если A(j) = E(k)t повторять следующую процедуру.
2.2.1. Если fe = L, это искомый аргумент.
2.2.2. Если fee L, увеличить j и k на 1 и возвратиться в
шаг 2.2.
2.3. Если A(j)> E(k), переместиться на следующую стро¬
ку, положить fe:=l и, не изменяя /, возвратиться в
шаг 2.
2.4. Если А(/)< £(fe), это искомый аргумент.
3. Если j > F + 1, это искомый аргумент.
4. Если j <С F -f-1, переместиться на следующую строку,
положить fe:=l и, не изменяя /, вернуться в начало.
Пример поиска аргумента «ATSUGI» с помощью приве¬
денного алгоритма показан в табл. 4.2.
192
Глава 4
Таблица 4.2. Метод поиска в сокращенном индексе
(случай A = «ATSUGI»)
Содержимое индекса
Конечное
положение
F
L
сокращенный ключ
/
k
шаг алгоритма
0
2
АВ
1
1
2.2.2
0
2
АВ
2
2
2.3
1
2
КА
2
1
2.3
2
2
IB
2
1
3
3
0
2
1
3
1
1
R
2
1
2.3
1
2
ТА
3
2
2.3
2
3
SUG
5
3
2.2.1
4.2. Структура памяти и поиск данных
Пусть искомые данные представляют собой отдельные не¬
связанные между собой записи набора данных, размещен¬
ного на внешнем ЗУ. Ключ, о котором шла речь в разд. 1.1.1,
однозначно идентифицирующий запись, будем называть пер¬
вичным ключом. В качестве первичного ключа может слу¬
жить либо идентификационный код, либо некоторая совокуп¬
ность полей записи, обладающая свойством однозначной
идентификации записи. Использование идентификационного
кода бывает затруднено из-за отсутствия в нем какой-либо
семантики, характеризующей свойства идентифицируемого
объекта.
Для больших баз данных часто бывает трудно или вообще
невозможно выбрать в качестве первичного ключа совокуп¬
ность полей записи. В этом случае, чтобы не увеличивать
длину идентификационного кода, придавая ему требуемый
смысл для поиска записей, используют другие поля записи,
выступающие в роли вторичного ключа. Значения вторичного
ключа не обязательно должны быть уникальными для каж¬
дой записи. Часто записи могут иметь одинаковые значения
вторичного ключа.
Наиболее простым случаем поиска является поиск одной
записи с заданным значением первичного ключа. Результа¬
том поиска является вся запись или ее часть, например по¬
иск чертежа по заданному номеру чертежа, поиск стоимости
акций по заданному названию фирмы и т. д. Такая система
называется системой поиска с простым запросом.
Поиск данных, при котором определяется множество запи¬
сей, соответствующих заданному значению одного или не-
Практические аспекты обработки данных
193
скольких вторичных ключей, и предоставление пользователю
их необходимой части называются поиском источника. Мно¬
гие системы поиска можно отнести к системам поиска источ¬
ника. Это не только так называемый поиск литературного
источника, как в случае поиска статьи в журнале или па¬
тента, но и поиск по библиотечному каталогу, позволяющий
осуществлять поиск по сочетанию «фамилия автора — год из¬
дания» или «название издательства — заголовок» и т. д.
4.2.1. Доступ к записям по ключам
Поскольку между первичным ключом и записью суще¬
ствует взаимно однозначное соответствие, в системе поиска
Инвертированный индекс
ЁЭчги
(ЗЭ-шппз
Рис. 4.4. Система инвертированных индексов.
с простым запросом можно использовать любой способ орга¬
низации наборов данных и любой метод доступа из упомяну¬
тых в разд. 4.1. На практике этот выбор определяется диапа¬
зоном значений ключей, количеством записей, характером
поиска (в частности, необходим ли, например, поиск по родо¬
вым ключам).
Методы доступа к записям по вторичным ключам исполь¬
зуют три основных типа организации данных: инвертирован¬
ную, с использованием битовых карт, мультисписочную.
В инвертированной организации (рис. 4.4) для каждого
вторичного ключа создается индекс, в котором для каждого
значения ключа задается отсортированный список указателей
на записи основного файла, содержащие данное значение
ключа. Инвертированные индексы записываются в отдель¬
ный набор данных. При этом указатели не обязательно опре¬
7 Зак. 127
194
Глава 4
деляют адрес записи, они могут, например, указывать значе¬
ние первичного ключа.
Система инвертированных индексов оказывается чрезвы¬
чайно удобной при поиске среди большого объема данных
благодаря следующим своим особенностям.
1) Возможность получения за одно или малое число обра¬
щений к внешней памяти вне зависимости от объема данных
и о ю 1
Рис. 4.5. Инвертированный список,
списка указателей записей, удовлетворяющих произвольным
значениям вторичных ключей.
2) Отсутствие необходимости доступа к основному набору
данных при обработке сложных условий поиска за счет за¬
мены сложных логических операций над значениями вторич¬
ных ключей простыми операциями слияния инвертированных
списков.
3) Область памяти, используемая для индексов, зависит
от длины указателей и частоты их появления, но обычно
меньше, чем при использовании других способов организации.
Таким образом, использование инвертированных индексов
позволяет обеспечить поиск среди данных большого объема,
за исключением очень небольшого числа случаев.
К недостаткам этой системы относятся довольно большие
затраты времени на составление инвертированных индексов
и их обновление, причем эти затраты возрастают с увеличе¬
нием объема базы данных. Поэтому для очень больших баз
данных часто может оказаться лучшим последовательный до¬
ступ, при котором используют, например, специальные аппа¬
ратные средства для ускорения выборки данных посредством
выполнения параллельных операций поиска и чтения записей.
Можно привести пример системы обработки сложных запро¬
Практические аспекты обработки данных
195
сов к базе данных, содержащей на диске примерно 5 млн.
записей химических соединений, с использованием пяти спе¬
циальных управляющих оконечных устройств.
При использовании битовых карт (рис. 4.5) для каждого
значения вторичного ключа записей основного набора дан¬
ных записывается последовательность битов. Длина последо¬
вательности битов равна чис¬
лу записей. Таким образом,
каждый бит этой последова¬
тельности соответствует од¬
ной записи. Бит записи, со¬
держащей заданное значе¬
ние вторичного ключа, уста¬
навливается в единицу, в
противном случае — в нуль.
При использовании бито¬
вых карт последовательность
битов, соответствующая
каждому значению вторич¬
ного ключа, имеет постоян¬
ную длину, что делает удоб¬
ным выполнение логических
операций над ними, в част¬
ности операции конъюнк¬
ции. Достаточно просто мо¬
жет быть достигнута высо¬
кая эффективность про¬
грамм поиска и управления
индексом. В связи с этим
битовые карты часто исполь¬
зуются для поиска в сравнительно небольших файлах с не¬
большим числом различных вторичных ключей. Достоинством
является и сравнительная простота обновления индексов при
вставках записей. Однако по мере увеличения числа записей
длина битовой строки увеличивается, а при возрастании числа
вторичных ключей большинство битов становятся нулевыми
(что по смыслу эквивалентно «не существуют»). Все это ве¬
дет к снижению эффективности метода для больших баз
данных.
Мультисписочная организация (рис. 4.6) представляет со¬
бой организацию, в которой для каждого значения вторич¬
ного ключа основного набора данных составляется цепочка
связанных указателями записей, содержащих заданное зна¬
чение вторичного ключа. Заметим, что каждая запись может
участвовать в нескольких связанных списках, максимальное
число которых определяет количество полей записи. Про¬
смотр цепочки записей связан с выполнением операций ввода
Рис. 4.6. Мультисписочная организа^
ция.
7*
196
Глава 4
из внешной памяти. В противоположность этому при исполь¬
зовании системы инвертированных индексов число обраще¬
ний к инвертированным спискам может быть пропорциональ¬
ным числу вторичных ключей. Вследствие этого применение
мультисписочной структуры ограничивается файлами неболь¬
шого размера, но преимуществом являются гибкость и про¬
стота обновления записей.
4.2.2. Структура записи основного файла
Из предыдущего подраздела следует, что при поиске дан¬
ных в базах данных большого размера обычно применяется
система инвертированных
индексов. На рис. 4.4 пред¬
ставлена всего лишь общая
~П модель такой системы, а
— конкретная структура памя-
JL ти зависит от характера дан-
^ ных, размещаемых в памя¬
ти. В свою очередь структу¬
ра памяти каждой записи
_ зависит от характера эле¬
ментов данных, включаемых
в запись.
(1) В зависимости от
применений число различ-
— ных элементов в базе дан¬
ных может достигать по
меньшей мере 100, а в неко-
loro торых случаях превышает и
1000. Например, рассмотрим
базу данных научно-техни¬
ческой литературы. Если рассматривать эти данные только
с точки зрения авторов, то необходимо различать литератур¬
ные источники, имеющие одного автора и автора-организа-
цию, авторов отдельных статей и составителей отдельных
изданий или сборников статей, в случае переводного источ¬
ника — переводчика и т. д. Обычно в изданиях указаны, кроме
того, авторы иллюстраций и фотографий. То же самое отно¬
сится и к названиям. Существуют названия статей, отдель¬
ных изданий или основные названия журналов, их подзаго¬
ловки, названия выпусков, симпозиумов, конференций и т. п.,
заголовки переводов.
(2) Большинство таких элементов данных имеют неопре¬
деленную длину и неопределенную частоту появления, при¬
чем бывает трудно установить верхнюю границу длины или
верхнюю границу числа появлений. Обычно количество, дли¬
Рис. 4.7. Структура записи глав
файла.
Практические аспекты обработки данных
197
на и частота появления различных данных имеют некоторые
усредненные оценки. Однако среди большого числа источни¬
ков часто встречаются сочетания особенно отличающихся
друг от друга данных. Максимальная длина имени человека,
максимальная длина заголовка, верхний предел числа авто¬
ров и т. д., если их не ограничить каким-либо способом, на¬
пример, меткой могут иметь чрезвычайно большие значения.
В связи с этим записи в основном наборе данных часто
представляются в виде данных с меткой (как показано на
рис. 4.7). В некоторых случаях для записи метки используют
десятичные цифры и буквы (база данных библиотеки кон¬
гресса США), но в большинстве случаев метка имеет бинар¬
ное значение (база данных для статей по химии).
4.2.3. Структура файла с инвертированным индексом
Влияние, которое оказывает характер вторичных ключей
на структуру памяти файла с инвертированными индексами,
можно формулировать следующим образом:
(1) В качестве значений вторичного ключа могут исполь¬
зоваться слова или фразы естественного языка, за исключе¬
нием некоторых слов, не употребляемых в качестве значений
ключей, к которым относятся артикли, предлоги и т. д. Од¬
нако в этом случае число различных значений вторичных
ключей очень велико (например, 100 000) и, кроме того, ме¬
няется с каждым обновлением.
(2) Естественно, что списки указателей для каждого зна¬
чения вторичного ключа (инвертированные списки) имеют
переменную длину, причем такие списки перемешаны: среди
большого числа коротких списков изредка встречаются очень
длинные, что обусловливает неравномерность их статистиче¬
ского распределения. Например, среди множества немецких
слов, согласно известному экспериментальному закону Зип-
фа, примерно 50 % всех слов появляется всего один раз
(длина инвертированного списка равна единице), причем
это практически не зависит от мощности множества. Слова,
появляющиеся два раза, составляют примерно 1/4 всех слов;
слова, появляющиеся п раз, будут составлять не более 1/п2
всех слов. С другой стороны, наибольшая частота появления
всех слов, естественно, пропорциональна величине множества,
однако слова с высокой частотностью появляются всего лишь
один раз на 10 литературных источников. Поэтому для базы
данных, включающей 1 млн. литературных источников, мак¬
симальная длина инвертированного списка будет составлять
100 тыс.
(3) А нельзя ли избежать этой проблемы, если вместо
множества значений вторичных ключей, состоящего из эле¬
198
Глава 4
ментов (слов) естественного языка, использовать множество
кодов равномерно распределенных по содержанию литера¬
турных источников и, присвоив такой код каждой записи,
воспользоваться им как вторичным ключом? Под равномер¬
ным понимается такое распределение, при котором каждое
значение кода присваивается примерно одинаковому числу
литературных источников. Этот метод время от времени пы¬
тались использовать со времен озобретения ЭВМ. Однако
на практике оказывается, что такую систему равномерного
распределения кода очень трудно поддерживать на протяже¬
нии длительного времени. Это происходит потому, что с те¬
чением времени данные меняются и первоначально равно¬
мерное распределение перестает соответствовать реальному.
Сказанное в одинаковой мере справедливо как для распре¬
деления символов и цифр, так и для распределения слов
и фраз. В конце концов не удается сохранить равномерность
распределения без изменения значений кодов.
(4) При осуществлении доступа по вторичным ключам,
содержащим элементы естественного языка, используются
такие средства, как составление производных слов, спрягае¬
мых форм и т. д. Поэтому очень часто бывает необходим
поиск по совпадению начала слов, или поиск по определен¬
ному диапазону значений аргументов.
Подводя итог вышесказанному, можно сделать вывод
о том, что в файлах с инвертированными индексами при ис¬
пользовании системы поиска источника в базах данных боль¬
шого объема возможны записи переменной длины, причем
максимальная длина записи может быть чрезвычайно боль¬
шой. При этом прежде всего следует постараться уменьшить
затраты на хранение и поиск коротких записей, так как
именно они составляют большую часть всех записей. Кроме
того, необходимо удешевить прямой доступ, обеспечивающий
полное совпадение аргументов поиска, и индексно-последова¬
тельный доступ по заданному диапазону значений аргумен¬
тов. Это наводит на мысль об использовании структур, по¬
добных VSAM. В реальных системах используют различные
структуры хранения, ориентированные как на использование
VSAM, так и ISAM, которые в конечном счете достаточно
близки между собой.
4.3. Уплотнение данных
Несмотря на значительное удешевление памяти, исполь¬
зуемой для хранения и обработки больших объемов данных,
вопросы уплотнения (сжатия) данных не теряют своей акту¬
альности. Во многих случаях уплотнение позволяет обрабаты¬
вать еще большие объемы данных. Уплотнение необходимо
Практические аспекты обработки данных
199
также и при передаче данных для повышения скорости и
экономичности передачи. При обработке графической инфор¬
мации объем данных также оказывается очень большим. По¬
этому и в этом случае уплотнение данных может оказаться
очень полезным. Уплотнение данных приводит к существен¬
ной экономии памяти. Известны различные методы уплотне¬
ния данных.
Прежде всего обратим внимание на то, что возможность
уплотнения данных связана с их избыточностью и что эффек¬
тивность соответствующего метода уплотнения зависит от
характера данных. Для случайных данных (отсутствует ка¬
кая-либо закономерность в распределении множества значе¬
ний), как, например, при бинарном представлении чисел, по¬
лученных при измерении белого шума, уплотнение невозмож¬
но. Обычно данные не являются случайными, а подчинены
определенным правилам, их смысл понятен человеку с пер¬
вого взгляда, они обладают достаточно большой избыточ¬
ностью. Например, известно, что различные английские тек¬
сты могут быть сравнительно просто сокращены (уплотнены)
на 1/3—1/4 с сохранением смысла. Избыточность устраняет
двусмысленность, защищает от ошибок, обеспечивает лег¬
кость исправления ошибок в случае их появления. Однако
все эти преимущества в результате уплотнения данных могут
быть утрачены. Следует также учитывать затраты на обра¬
ботку, связанные с уплотнением и последующим восстанов¬
лением данных, однако эти аспекты здесь обсуждаться не
будут.
4.3.1. Кодирование
Пусть названия 15 префектур расположены в порядке
убывания численности населения, как показано в табл. 4.3,
и записаны кодом составленным из трех слогов слоговой
Исходные данные (А) о о с а <ру ну о те у ни си су о на на ко то у ни ни и на хи ро си хо цу нсС
Локированные данные (а) о еру то си на то ни хи ро хо
(5) 001010010001101000110001111010110101
(В) 10110000010000011000110010000010001
Рис. 4.8. Примеры различных способов уплотнения исходных данных.
азбуки «катакана». Пусть в случайной выборке ki оказались
расположенными в порядке, показанном на рис. 4.8(A), и бу¬
дем считать, что частота появления pi каждого из ki пропор¬
циональна численности населения т соответствующей пре¬
фектуры, т. е. другие названия не появляются. В этом случае
данные уже до некоторой степени уплотнены, так как ki
получены из полных названий префектур..
200
Глава 4
Если один слог катаканы записать восемью битами, то для
каждого ki потребуется 24 бита, и ясно, что можно провести
дальнейшее уплотнение. Рассмотрим несколько простых ме¬
тодов, подходящих для этой цели.
а) Проанализировав трехслоговые коды префектур, мож¬
но заметить, что все они, кроме двух, различаются по пер¬
вому слогу. Более того, коды, имеющие одинаковые первые
слоги, различаются вторыми слогами: «хи ро» и «хи ё». В со¬
ответствии с этим коды двух названий префектур представим
двумя слогами, а коды остальных названий — одним слогом
(кодирование, допускающее возможность декодирования в
нужное время). Можно было бы использовать в качестве
кодов для этих двух префектур и слоги «ро» и «ё», так как
ни «ро», ни «ё» не появляются в качестве первого слога для
других префектур. Если один слог представляется восемью
битами, то в первом случае (два слога) код записывается
как 8,8 бит, а во втором случае (один слог)—как 8 бит.
Таблица 4.3. Кодирование названий префектур. Частотность
использования исходного кода пропорциональна
численности населения (предполагается, что другие
названия префектур, кроме представленных в таблице,
не используются. Варианты кодирования а — в поясняются
в тексте; см. табл. 2.1, 2.4)
Исходный
код
k{
Числ, насел.
(10 тыс. чел.)
ni
Частотность
Варианты кодирования
Pi
а
б
в
то у ки
1162
0,156
ТО
0001
001
о о са
847
0,114
О
0010
101
ка на ка
692
0,093
ка
ООП
110
а и ти
622
0,084
а
0100
111
хо цу ка
558
0,075
хо
0101
0001
са и та
542
0,073
са
0110
оюо
хи ё у
514
0,069
хи ё
0111
0101
ти ха
474
0,063
ти
1000
0111
фу ку о
455
0,061
фу
1001
1000
си су 0
345
0,046
си
1010
00000
хи ро си
274
0,037
хи ро
1011
00001
и ха ра
256
0,034
и
1100
01100
ки ё у
253
0,034
к и
1101
01101
ни и ка
254
0,033
ни
1110
10010
на ка но
208
0,028
на
1111
10011
б) Поскольку рассматривается всего 15 названий префек¬
тур, то, присваивая им последовательные номера, можно про¬
Практические аспекты обработки данных
201
извести их кодирование 4-разрядными двоичными числами,
т. е. длина кода, соответствующего каждому ki, составит
4 бит.
в) Для представления ki кодом переменной длины можно
использовать кодирование Хафмана. Средняя длина кода в
этом случае составляет
3 X (0,156 + 0,114 + 0,093 + 0,084) +
+ 4 X (0,075 + 0,073 + 0,069 + 0,063 + 0,061) +
+ 5 X (0,046 + 0,037 + 0,034 + 0,034 + 0,033 + 0,028) »
« 3,765 (бит)
В нашем случае длина исходных данных (одно из назва¬
ний префектур) ограничена тремя слогами и кодирование
Хафмана приведет к наибольшему уплотнению. Дальнейшее
уплотнение невозможно. Однако в случае непрерывного пред¬
ставления данных, как на рис. 4.8(A), кодирование для каж¬
дого названия префектуры не производится, а последова¬
тельно кодируются различные сочетания слогов. В результате
такого кодирования средняя длина кода будет еще меньше
15
— Z Pi l°g2 Pi « 3.73 (бит).
На практике используется большое число разнообразных ко¬
дов. Способы кодирования также весьма различны, поскольку
они зависят как от частотности, так и от независимости ко¬
дируемых данных.
4.3.2. Уплотнение данных в естественных языках
Частотность отдельных элементов в текстах на естествен¬
ных языках зависит от того, насколько эти элементы подчи¬
няются закону статистического распределения, от трудности
выборки, человека, пользующегося языком, и целей кодиро¬
вания, от эпохи и т. д. В силу перечисленных факторов часто
невозможно точно определить частотность отдельных элемен¬
тов. Например, если рассматривать частотность отдельных
букв английского алфавита в тексте, то известно, что Е имеет
максимальную частотность, Т — частотность, следующую за
частотностью Е, далее идут А или О, а затем I или N, а час¬
тотность появления других букв зависит от характера анали¬
зируемых текстов. Исследовалась также частотность сочета¬
ний из двух, трех и более букв. Если использовать марков¬
скую модель для анализа текстов на естественном языке, го
можно получить некоторые оценки длины кода для кодиро¬
вания слов.
202
Глава 4
На основе использования этой модели получены следую¬
щие оценки для кодирования одного слова английского тек¬
ста: 11,8 бит и 9,8 бит. Кроме того, известно, что при кодиро¬
вании на одну букву в английском тексте приходится от 1
до 2 бит. Если эти значения сопоставить с обсуждавшимся
уже значением 8 бит на один знак азбуки (слоговой), то и
здесь можно ожидать аналогичных результатов. В связи
с постоянным увеличением объема доступной оперативной
памяти улучшаются и условия кодирования и обработки ко¬
дированных данных. Это связано прежде всего с возмож¬
ностью более эффективной организации словарей, исполь¬
зуемых для кодирования и декодирования. Для кодирования
и уплотнения информации в японском языке предложено не¬
сколько методов. Однако здесь мы рассмотрим некоторые
методы, которые предназначены для уплотнения главным об¬
разом текстов английского языка.
(1) Выбирая только слова с высокой частотностью вхож¬
дения в различные фразы, производят их кодирование. Этот
метод может, например, применяться для кодированного
представления диагностических сообщений компилятора.
(2) Сокращение слов за счет выделения основы слова,
исключения гласных и т. д. Такой способ кодирования слов
может привести к кодам из 4—5 согласных. Однако с увели¬
чением объема кодируемых данных потери информации при
использовании этого метода становятся слишком большими,
отсюда и проблематичность его применения для уплотнения
данных.
(3) Получение кода переменной длины с ограничителем.
При кодировании Хафмана все коды оказываются перемен¬
ной длины, что очень затрудняет обработку. При использова¬
нии данного метода можно выбирать коды, длина которых
кратна некоторому целому, например 8, т. е. можно рассмат¬
ривать коды длиной 8, 16 бит и т. д. При таком подходе
слова сортируют в порядке уменьшения частотности их ис¬
пользования, а затем кодируют следующим образом. Слова,
занимающие в отсортированной последовательности с 1-й по
128-ю позиции (27 слов), кодируют 8-битовыми кодами, со
129-й по 16 512-ю позиции (214 слов)—16-битовыми, а с
16 513-й по 2 113 664-ю позиции (221 слов) — 24-битовыми. Для
слов, закодированных с помощью 8 бит, первый бит устанав¬
ливают равным единице; для слов, закодированных 16 бит,
первый бит устанавливают равным нулю, а 9-й бит — единице
для слов, закодированных 24 бит, 1-й и 9-й биты полагают
равными нулю, а 17-й бит — единице. Остальные биты соот¬
ветствуют порядковому номеру слова в отсортированной по¬
следовательности (рис. 4.9). Коэффициент уплотнения, кото¬
рый может быть достигнут при использовании этого метода,
Практические аспекты обработки данных
203
примерно на 20 % ниже, чем при кодировании Хафмана, т. е.
здесь коэффициент уплотнения также сравнительно высок и
метод может быть реализован достаточно эффективно на
большинстве ЭВМ с адресацией памяти до байта. Следует
заметить, что использование этого метода предполагает, как
правило, хранение в оперативной памяти списка слов как для
Шкала кодиро¬
вания
Рис. 4.9. Уплотнение с ис¬
пользованием кодов пере¬
менной длины с ограниче¬
нием. Длины кодов ограни¬
чены и равны 8, 16, 24 бит.
кодирования, так и для декодирования. Именно это на прак¬
тике и определяет верхнюю границу числа кодируемых слов.
4.3.3. Кодирование длин серий и другие методы
В случаях когда данные обладают высокой избыточ¬
ностью, выражающейся в частом появлении серий с одина¬
ковой длиной кода (при малом разнообразии кодов), доволь¬
но просто можно достичь высокого уплотнения с помощью
кодирования не самих серий, а их длин. Этот метод назы¬
вается методом кодирования длин серий. Для файлов вво¬
да-вывода с записями фиксированной длины (например,
перфокарточные файлы или файлы печати) можно получить
довольно высокое уплотнение, выполняя такое кодирование
только лишь для пробелов.
Если данные во времени изменяются медленно, можно
ограничиться передачей в память не абсолютных значений
данных, а их изменений; таким образом, при кодировании
можно обойтись меньшими длинами кодов. Исследуя законы
статистического распределения изменений, можно прогнозиро¬
вать будущие значения по имеющимся данным, а если в ка¬
честве данных рассматривать отклонение от прогнозируемой
величины, то можно еще больше уменьшить избыточность.
Дискретизированный звук (голос, музыка) также можно
уплотнить с помощью кодирования. При кодировании голоса
нельзя ожидать полного восстановления после декодирования,
204
Глава 4
т. е. звуковые гона искажаются. Однако за счет кодирования
до предельного уровня понимаемости речи удается достичь
высокого коэффициента уплотнения.
4.4. Параллельная аппаратная сортировка
Если обработка данных производится параллельно, то
естественно ожидать сокращения времени и повышения эф¬
фективности обработки. Уже давно применяется, например,
параллельная работа внешних ЗУ и центрального процес¬
сора. Здесь мы познакомимся с некоторыми методами не
однородной, а параллельной обработки, реализуемой сред¬
ствами аппаратного обеспечения. Методы параллельной обра¬
ботки начали изучаться сравнительно давно прежде всего из-
за различных ограничений; в частности, со стороны аппарат¬
ного обеспечения и за исключением некоторых специальных
случаев на практике они почти не применялись. Однако в по¬
следнее время в связи с постепенным переходом на инте¬
гральные схемы и их удешевление методам параллельной
обработки вообще и параллельной сортировке в частности
стали придавать серьезное значение. Далее рассматриваются
некоторые подходы использования параллельной обработки
при сортировке данных.
4.4.1. Сеть сортировки из компараторов
с двумя входами
Пусть имеется схема (компаратор с двумя входами), ко¬
торая при сравнении двух различных К\ и /(2, поступивших
на входы, выводит их в порядке возрастания значений
(рис. 4.10). Используя эту элементарную схему, как пока¬
зано на рис. 4.11, а, можно построить сеть для сортировки
четырех вводимых элементов, например, методом простых
вставок. Традиционное изображение сети компараторов по¬
казано на рис. 4.11, б.
На рис. 4.12, а изображена сеть для сортировки четырех
вводимых элементов методом простых обменов, Однако с уче¬
том возможности параллельной обработки эту сеть можно
еще упростить. Сеть после такого упрощения приведена на
рис. 4.12,6. Сети, представленные на рис. 4.12, не являются
совершенно одинаковыми — время, требуемое на обработку
в случае б, меньше. Если принять за единицу времени время
работы одного компаратора, то в случае а для сортировки
потребуется 6 единиц времени, а в случае б — 5 единиц.
Возвращаясь немного назад, можно отметить, что парал¬
лельная обработка возможна также и для сети на рис. 4.11,6.
Таким образом, и в случае параллельной обработки метод
Практические аспекты обработки данных
205
простых вставок и метод простых обменов оказываются экви¬
валентными.
Сеть для сортировки четырех элементов может быть и
другой. На рис. 4.13, а — в, например, приведены также сети
tfi-
Кг-
-V
-Кг
Кх' = Ки К2' = Кг (К^К2)
Kl, = K2t Кг' = кх {Кх>Кг)
Рис. 4.10. Компаратор с двумя входами: Ки Кг— входы, К\, К2—вы¬
ходы.
Кг-
*з-
КА-
-К/
К2
Кг9
к;
a S
Рис. 4.11. Сеть сортировки из компараторов с двумя входами.
для сортировки четырех элементов. Однако убедиться в ра¬
ботоспособности сети не всегда легко. Если проверять все ва¬
рианты упорядочения входных данных, то потребуется рас¬
смотреть работу каждой сети для 4! = 24 различных случаев.
Такая проверка приемлема для четырех входов, однако при
Рис. 4.12. а — сеть сортировки —г — —
методом простых обменов; б —
сеть для параллельной обра- .
ботки. а 6
большом числе входов она практически неосуществима. Для
облегчения проверки может быть использована следующая
теорема (приводится без доказательства).
Теорема 4.1. Если сеть компараторов с п входами сорти¬
рует в неубывающем порядке все 2п различных последова¬
тельностей длины п, составленных только из нуля и единицы,
то эта сеть сортирует произвольные последовательности дли¬
ны п.
Таким образом, в случае п = 4 требуется проверить по¬
следовательности на выходе для 16 входных последователь¬
206
Глава 4
ностей (0, 0, 0, 0), (О, О, О, 1), (О, О, 1, 0), (О, 1, 0, 0), ...
(1, 1, 1, 1). Не проверяя, можно видеть, что из всех
16 последовательностей к наиболее отсортированным в не¬
убывающем порядке относятся следующие: (0, 0, 0, 0),
(0, 0, 0, 1), (0, 0, 1, 1), (0, 1, 1, 1), (1, 1, 1, 1). Эти последо¬
вательности явно не требуют перестановок. Для оставшихся
11 вариантов можно провести проверку.
Если провести сравнение для четырех сетей, представлен¬
ных на рис. 4.12,6 и 4.13, а — в, по затратам, включающим
а 6 S
Рис. 4.13. Различные варианты сети для сортировки четырех элементов из
компараторов с двумя входами.
сложность схемы (число компараторов) и время, требуемое
на сортировку, то получим данные табл. 4.4, из которых
видно, что сеть рис. 4.13, в оказывается наиболее эффек¬
тивной.
Таблица 4.4. Затраты на сортировку для различных сетей
компараторов с двумя входами
Но можно ли назвать эту сеть вообще наиболее эффек¬
тивной? Иными словами, существует ли сеть с меньшим чис¬
лом компараторов (не более четырех) или сеть, требующая
меньшего времени на сортировку (не более двух)? Каковы
вообще наименьшее число необходимых компараторов S(n)
и наименьшее значение требуемого времени Т(п) для сети
с п входами?
Простейший анализ показывает, что при п — 4 и по числу
компараторов, и по требуемому времени наилучшей будет
сеть, для которой S(n)> 4, Т(п)'>2, т. е. сеть, представлен¬
ная на рис. 4.13, в. Но при увеличении значения п определе¬
ние лучшей сети превращается в достаточно трудную про¬
Практические аспекты обработки данных
207
блему. До п = 8 значения §(п) и Т(п) найдены; они пред¬
ставлены в табл. 4.5. Для п> 8 достоверные значения 5 (я)
и Т(п) до сих пор не определены.
Таблица 4.5. Минимальные значения затрат в зависимости от числа
входов сети n-S (п) — наименьшее число компараторов,
Т (п) — наименьшее значение времени, требуемого
на сортировку (значения для п > 8 неизвестны)
2 3 4 5 6 7 8
§ (я)
1
3
5
9
12
16
19
Т (п)
1
3
3
5
5
6
6
Для случая п — 4 5(/г) и Т(п) оказались оптимальными
для одной и той же сети, но в общем случае сеть с наимень¬
шим числом компараторов не обязательно совпадает с сетью
с наименьшим временем, требуемым на операцию сортировки.
4.4.2. Сети сортировки и логические запоминающие
устройства
Можно построить сеть сортировки, используя в качестве
элементов не компараторы с двумя входами (2-сортировщи¬
ки), а устройства, осуществляющие сортировку большего
числа вводимых данных. Например,
на рис. 4.14 показана сеть для сорти¬
ровки 9 элементов, построенная из
3-сортировщиков.
Сортировку, которая могла бы осу¬
ществляться сетями такого типа, вы¬
полняет так называемый интеллекту¬
альный диск (LIM) или логическое за¬
поминающее устройство (ЛЗУ). ЛЗУ
представляет собой диск с логической
схемой, включенной между головками
считывания/записи магнитного диска,
которая осуществляет сравнительно
сложные операции с данными на са¬
мом диске, не передавая их для обработки в центральный
процессор. В зависимости от назначения ЛЗУ могут быть
различной сложности. Так, давно уже ведутся исследования
по их использованию для сортировки и поиска.
1
2
3
4
5
6
7 L
8
9
Рис. 4.14. Сеть из 3-сор¬
тировщиков.
208
Глава 4
На рис. 4.15 показан пример такого ЛЗУ, имеющего очень
простое устройство. На каждую дорожку диска имеются две
раздельные головки — считывающая и записывающая. Дан¬
ное со считывающей головки анализируется логической схе¬
мой и при необходимости заносится в небольшую локальную
память (например, регистр). Диск между тем вращается, и
анализ заканчивается как раз к моменту прохождения под
записывающей головкой текущей записи, так что, если потре¬
буется запись ранее считанных данных, все уже подготовлено
R\ Ri /?з Ri R$ R& Rj
У = — 3 _ __ _3 1 4 5 9 2 6
У = — 2 _ j_2 4 5 9 2 6
У=-1 _ 1 1 _4_ 5' 9 2 6
y=o A 3 A A 9 2 6
У = 1 1 ± 4 5_ _9 2 6
У=2 1 325496
У = 3 1 3 2 _5_ 4 6_.9
У = 4 1 3 2 5 _4 6 _9
У = 5 1 .3 2 5 4 A 9
j = 6 1 3 2 5 4 6 _9_
У — — 3 _ _ A. 3 2 5 4 6 9
У = — 2 _ AA 2 5 4 6 9
J = - 1 1 1 5 4 6 9 Рис. 4.16. Последователь¬
нее) A 2 11 4 6 9 ность сортировки для ЛЗУ
y = i 1 2 з 4 5 6 г9 с тремя головками.
для этого. Итак, предположим, что на дорожке этого диска
размещены N записей (например, N = 7) Ru R2, ..., /?w;
в этом порядке они проходят под считывающей головкой. Ло¬
гическая схема обычно производит сравнение п записей, опре¬
деляемых относительным положением. Например, в случае,
показанном на рис. 4.16, при п = 3 это будут только что
считанная запись [fti = l], запись, считанная на одну пози¬
цию раньше [/i2 = 2], и запись, считанная еще раньше перед
Практические аспекты обработки данных
209
последней с пропуском одной позиции [Л3 = 4]. Если эти п
записей не отсортированы, то они сортируются, и, когда пер¬
вая из этих записей окажется под записывающей головкой,
осуществляется запись. Этот процесс можно рассмотреть и
на модели, показанной на рис. 4.17. ЗУ имеет три головки
считывания/записи, которые расположены с установленными
промежутками, занимая в целом четыре позиции. Для них
используется следующая логика сортировки: записи, находя¬
щиеся под головками, сравниваются и при необходимости
Рис. 4Л7. Логическое ЗУ с
тремя головками для считы¬
вания/записи.
переставляются. Если для поворота диска использовать тер¬
мин «прогон», а для промежутка между записывающей го¬
ловкой и первой буквой на диске — термин «шаг», то каж¬
дый прогон составит N -f п—1 шагов. На шаге / при j —
= 1—я, 2 — п, ..., N—1 окажется отсортированной после¬
довательность записей Rj+hx> R /+А2» •••> Я/+л ■ Если / + Л*
меньше единицы или больше N, то запись Rj+hk не рассма¬
тривается.
Посмотрим теперь, какими должны быть условия, чтобы
за несколько прогонов с помощью этого ЛЗУ отсортировать
всю дорожку. И каково должно быть расположение головок
считывания/записи для того, чтобы получить отсортирован¬
ную последовательность за один прогон. Опуская доказатель¬
ства, приведем только выводы.
(1) При соседнем расположении любых двух головок счи¬
тывания/записи (для любого k из выполняется
условие h[k+ 1 ] = h[k\-\- 1) любая последовательность обя¬
зательно будет отсортирована за конечное число прогонов.
В наиболее простом случае достаточно двух рядом располо¬
женных головок считывания/записи; в этом случае ЛЗУ реа¬
лизует метод простых обменов.
(2) В случае когда нет рядом расположенных головок
считывания/записи (для всех k из 1 ^ k < m выполняется
условие h [k + 1 ] ^ h [k\ -f- 2), отсортированную последова¬
тельность удается получить не всегда. Если для 1 ^ k < m
210
Глава 4
выполняется условие h [k + 1] ^ h [k] -f- k при N^n—1, то
можно получить отсортированную последовательность не бо¬
лее чем за Г (N— 1 )/(п— 1)1 прогонов.
(3) Можно получить отсортированную последовательность
за один прогон для N = m(m—1)/2+1 записей, если ис¬
пользовать следующее расположение головок:
(huh2,h3, hm) = (1, 2, 4, 7, 11, т(т— 1)/2+ 1).
Такие логические ЗУ, использующие память с зарядовой
связью, на пузырьковых доменах и т. п., активно исследуются
с точки зрения применения их в так называемых «машинах
баз данных».
Литература
Ко всей книге:
1. Knuth D. Е., The Art of Computer Programming, Vol. 1, Fundamental
Algorithms, 2nd ed., 1981, Vol. 3, Sorting and Searching, Addison-Wes-
ley, 1973. [Имеется перевод: Кнут Д., Искусство программирования
для ЭВМ. В 3-х тт. Т. 1. Основные алгоритмы. — М.: Мир, 1976. Т. 3.
Поиск и сортировка. — М.: Мир, 1978.1
2. Aho А. V., Hopcroft J. Е., Ullman J. D., Data Structures and Algo¬
rithms, Addison-Wesley, 1983.
3. Aho A. V., Hopcroft J. E., Ullman J. D., The Design and Analysis of
Computer Algorithms, Addison-Wesley, 1976. [Имеется перевод: Axo A.,
Хопкрофт Дж., Ульман Дж., Построение и анализ вычислительных
алгоритмов. — М.: Мир, 1979.]
4. Wirth N., Algorithms + Data Structures = Programs, Prentice-Hall, 1976.
[Имеется перевод: Вирт H., Алгоритмы + структуры данных = про¬
граммы.— М.: Мир, 1985.]
5. Reingold Е. М., Hansen W. J., Data Structures, Little Brown and Co.,
1983.
К главе 1:
К разделу 1.2:
6. Date J., An Introduction to Database Systems, 3rd ed., Addison-Wesley,
1981. [Имеется перевод: Дейт К., Введение в системы баз данных.—
М.: Наука, 1980.]
7. Borkin S. A., Data Models: A. Semantic Approach for Database Systems,
MIT Press, 1980.
8. Ullman J. D., Principles of Data Systems, Computer Science Press,
1982. [Имеется перевод: Ульман Дж., Основы систем баз данных.—
М.: Финансы и статистика, 1983.]
9. Wiederhold G., Database Design, McGraw-Hill, 1982.
10 Ghandour Z., Mczei J., General arrays, operators and functions, IBM J.
Res. Develop., 17, 335—352 (1973).
К разделу 1.2.3:
11. Peterson J. L., Norman T. A., Buddy systems, Comm. ACM, 20, 421 —
431 (1977).
12. Russell D. L., Internal fragmentation in a class of buddy systems,
SLAM J. Computing, 6, 607—621 (1977).
К главе 2:
К разделу 2.2.1:
13. Yao A. Chi-Chih, On random 2—3 trees, Acta Informatica, 9, 159—170
(1978).
К разделу 2.2.2:
14. Comer D., The ubiquitous В-tree, Computing Surveys, 11,121 —137 (1979).
К разделу 2.2.3:
15. Maurer W. D., Lewis T. G. Hash Table methods, Computing Surveys,
7, 5—19 (1975).
16. Knott G. D., Hashing functions, The Computer Journal, 18, 265—278
(1975).
212
Литература
17. Vitter J. S., Implementations for coalesced hashing, Comm. ACM. 25,
911—926 (1982).
18. Нисихара С., Хлгивара X., Метод открытого хеширования с предска¬
зателем, Дзёхо сёри, 15, 510—515 (1974).
19. Jaeschke G., Reciprocal hashing: a method for generating minimal per¬
fect hashing functions, Comm. ACM, 24, 829—833 (1981).
К главе 3:
20. Lorin H., Sorting and Sorting Systems, Addison-Wesley, 1975.
К разделу 3.1:
21. Okoma S., Generalized heapsort, в Dembinski P. (ed.), Mathematical
Foundations of Computer Science, Lecture Notes in Computer Science,
88, Springer-Verlag, 439—451 (1980).
22. Kahaner D. K., FORTRAN implementation of heap programs for effi¬
cient table maintenance, ACM Transactions on Mathematical Software,
6, 444—449 (1980). (Collected Algorithms from ACM, Algorithm 561.)
23. Sedgewick R., Implementing quicksort programs, Comm. ACM, 21, 847—
857 (1978).
24. Нодзаки А., Сугимото Т., Надежная быстрая сортировка, Дзёхо сёри
гаккай ромбун си, 21, 164—166 (1980).
К разделу 3.3:
25. Tarjan R., Sorting using network of queues and stacks, Jour. ACM, 19,
341—346 (1972).
26. Imamiya A., Nozaki A., Generating and sorting permutations -using
restricted deques, Information Processing in Japan, 17, 1128—1134
(1977).
27. Nozaki A., Sorting using networks of deques, Jour. Computer and Sy¬
stem Sciences, 19, 309—315 (1979).
28. Нодзаки А., Сортировка с использованием деков, Дзёхо сёри гаккай
ромбун си, 21, 76—78 (1980).
29. Нодзаки А., Сортировка с помощью параллельно расположенных де¬
ков, Дзёхо сёри гаккай ромбун си, 22, 274—276 (1981).
К главе 4:
К разделу 4.4.1:
30. Donovan J. J., Systems programming, McGraw-Hill, 1972. [Имеется
перевод: Донован Дж., Системное программирование. — М.: Мир, 1975.}
31. Martin J., Computer Data — Base Organizations, 2nd ed., Prentice-Hall,
1977. [Имеется перевод: Мартин Дж., Организация баз данных в вы¬
числительных системах. — М.: Мир, 1980.]
32. Wagner R. Е., Indexing design considerations, IBM Systems J., 12,
351—367 (1973).
33. Heaps H. S., Information Retrieval: Computational and Theoretical as¬
pects, Academic Press, 1978.
34. Rijsbergen C. J. van, Information Retrieval, 2nd ed., Butterworths, 1979.
К разделу 4.4.3:
35. Standish T. A., Data Structure Techniques, Addison-Wesley, 1980.
36. Уэмура Т., Маэгава М., Машины для баз данных, Сборник докладов
по обработке данных Научного общества обработки данных, 1980.
Предметный указатель
АВЛ-дерево 68
Адрес 10
— абсолютный 16
— «близнеца» 38, 40
— относительный ‘•'б
Адресное пространство 7, 10
Алгоритм быстрой сортировки 139
улучшенный 142
— вставки в дерево 65
— корпоративной сортировки 134
— поиска по сокращенному клю¬
чу 191
— распечатки ключей В-дерева 89
— совершенного хеширования 112
— сортировки слиянием 152—154
— формирования начальных от¬
резков 168
Байт 10
Бинарное дерево 47, 51
АВЛ-дерево 71
оптимальное 57, 60
перечисление деревьев 48
поиска 51
расширенное 55
— — сбалансированное 52
— — случайное 65
Фибоначчи 69
Бит 10
— разметки 41
Битовая карта 20, 194
«Близнецы» двоичные 38
— фибоначчиевы 40
Блок памяти 18
Буфер 21, 172
Буферный пулл 187
Вершина стека 12
Виртуальная память 21
Вставка в АВЛ-дерево 70
— — бинарное дерево 51, 65
В-дерево 84
(2—3)-дерево 77
Выборка отношения 23
Высота дерева 45
АВЛ-дерева 69
— — полностью сбалансирован¬
ного 53
— — Фибоначчи 70
— В-дерева 83
— я-арного дерева 76
Граф 14
Данное сложное 10
— элементарное 11
Дек 14
Декартово произведение 23
Дерева длина взвешенного пути
63
внешнего пути 55
внутреннего пути 55
степенного пути 171
Дерево 14, 43, 44
— бинарное 47
— графическое представление 45
— расширенное 54
— свободное 47
— связанное представление 19, 51
56
— со «сторожем» 56
Дерево поиска 41
АВЛ-дерево 68
бинарное 49, 51
сбалансированное 57
сильноветвящееся 75
214
Предметный указатель
— — случайное 65
Фибоначчи 69
В-дерево 81
В+-дерево 91
с префиксом 92
(2—3)-дерево 76
trie-дерево 207
Диск ителлектуальный 207—209
Доступ к памяти 7
— операция 20, 43
— по В+-дереву 90
последовательный 90
Запись 15
Запрос 28
Иерархическая модель 29
Инверсия 129
Индекс 11, 189
— дорожки 188
— массива 11
— инвертированный 193
— цилидра 188
Интеллектуальный диск 207—209
Карта битовая 20, 194
Ключ вторичный 192
— записи 15
— первичный 192
— переноса 85, 90
— поиска 49
— разделитель 90
Коллизия 95, 100
Кольцо 12
Компаратор 204
Кортеж 23
Лес из деревьев 46
Лист дерева 45
Массив И, 28
— общего вида 34
— однородный 16
— сечение 29
Метод доступа 186
виртуальный 189
индексно-последовательный
187
по вторичным ключам 193
Множество 19
— вполне упорядоченное 122
— операции над множествами
25—28
Модель данных 22
иерархическая 29
общего вида (массив) 34
реляционная 23
сетевая 32
списочная 32
Мультисписок 195
Операции над деревьями 51—90
вставки 51, 65, 70, 77, 84
поиска 51, 76, 79, 82, 90
удаления 77, 86, 90
отношениями 25—27
деление 27
проекция 25
прямое произведение 25
соединение 26
0.соединение 26
©-ограничение 27
Отношение 22
— порядка 122, 124
ма множестве узлов 125
Отрезки 151
— слияние отрезков 151
— способы подготовки 166
— фибоначчиевы 160
— фиктивные 161
Очередь двусторонняя (дек) 14
— типа FIFO 14
LIFO (стек) 12
Память буферная 21, 172, 187
— виртуальная 21, 175
— внешняя 6, 21
—оперативная (внутренняя) 6,21
*— перемешанная (см. хеширова-
Предметный указатель
215
ние) 92
■— последовательная 16
— связанная 18
— управление 34
динамическое 35—42
статическое 34
Поле записи 15
Поиск по вторичному ключу 195
— во внешней памяти 80—92
— источника 193
— в оперативной памяти 43—80
— с простым запросом 192
Поиск по дереву 51, 76
— по В-дереву 82
В+-дереву 90
(2—3)-дереву 79
trie-дереву 79
— в упорядоченной таблице 49
хеш-таблице 92
Последовательность более упорядо¬
ченная 125
— отсортированная 125
— сопоставления 123
Программа быстрой сортировки 144
— рекурсивная 12
Проекция 25
Пространство адресов 7, 10
Путь доступа 20
Пулл буферный 187
Разрешение коллизий 100—103
методом цепочек 100
открытой адресацией 101 —
103
сравнение методов 105
Распределение отрезков начальное
160, 163
— памяти динамическое 34—41
с граничными признаками
36
* в методе «близнецов» 38
фибоначчиево 40
Реляционная модель 23
Рехеширование 103
Сетевая модель 32
Сеть 14
— сортировки 204
Сечение массива 29
Сжатие данных (см. уплотнение)
Скучивание при хешировании 102
Слово машинное 10
двойное 10
— правоустановлепное 123
— левоустановленное 123
Случайное дерево 65
Стек 12
Сортировка 122, 126
— аппаратная 204—210
— внутренняя 128—148
быстрая 139
вставками 128
выбором 130
из дерева 132
корпоративая 132
методом «пузырька» 131
пирамидальная 133
распределяющая 127
Шелла 128
— внешняя 148—175
— -— вставками и слиянием 177
каскадная 163
многофазная 157
распределяющая 150
р-путевым слиянием 155, 174
— с использованием стеков 182
Список 19, 32
— свободных блоков 37, 39
Степень дерева 45
— узла 45
Сравнимость последовательностей
125
«Сторож» 56, 129
Тип данных 10, 34
простой 10
указатель 16
сложный 10
дерево 14
запись 15
кольцо 12
очередь 14
стек 12
216
Предметный указатель
Удаление из В-дерева 86
— из В+-дерева 90
(2—3)-дерева 77
Узел 14
— дерева внешний 55
внутренний 55
концевой 45
— «сторож» 56, 129
Узлы «близнецы» 38
Указатель 16
— доступа 18
Уплотнение данных 190, 198
кодированием 198—204
длин серий 203
кодом постоянной длины 200
переменной длины 201
с ограничителем 203
Упорядоченность лексикографиче¬
ская 123
Управление памятью динамическое
35
в методе с граничными
признаками 36
бинарных близнецов 38
фибоначчиевых близне¬
цов 40
статическое 34
Уровень дерева 45
Файл 15
Фибоначчиевые «близнецы» 40
— дерево 69
— отрезки 160
— последовательность 69
— число 70
Хафмана кодирование 93
Хеширование 93
— во внешней памяти 117—120
поиск по части ключа
117
— методом деления 97
многочленов 98
преобразования системы счис¬
ления 98
слияния 98
умножения 98
— разрешение коллизий 100—103
— рехеширование (переразмеще-
пие) 103, 105
— совершенное 110, 112
методом проб и ошибок 116
— срастание списков 100
— среднее число проб 109
— удаление ключа 103—105
Цена дерева 60
Число инверсий 129
— узлов в АВЛ-дереве 69
В-дереве 83
Содержание
Предисловие редактора перевода 5
Введение . 6
Глава 1. Данные .10
1.1. Основные типы данных 10
1.1 Л. Элементы данных и структуры 10
1.1.2. Представление структур 16
1Л.З. Внутренняя и внешняя память 21
1.2. Обобщенные структуры данных 22
1.2.1. Отношение 22
1.2.2. Структуры данных и отношения 28
1.3. Динамическое распределение памяти 34
1.3.1. Простые методы 34
1.3.2. Метод близнецов 38
1.3.3. Анализ 42
Глава 2. Поиск данных по ключу . « * . .... 43
2.1. Поиск по дереву в оперативной памяти 43
2.1.1. Что такое дерево? 43
2.1.2. Бинарное дерево .... 47
2.1.3. Оптимальные и случайные деревья 57
2.1.4. Сбалансированные деревья (АВЛ-деревья) 67
2.1.5. Сильно ветвящиеся деревья 75
2.2. Поиск по дереву во внешней памяти ... 80
2.2.1. В-деревья .81
2.2.2. Разновидности В-дерева .90
2.3. Методы хеширования .92
2.3.1. Методы случайного упорядочения .92
2.3.2. Разрешение коллизий .100
2.3.3. Анализ ... . 105
2.3.4. Совершенное хеширование .110
2.3.5. Применение хеширования 117
Глава 3. Сортировка . 122
3.1. Внутренняя сортировка 122
3.1.1. Сортировка 122
3.1.2. Методы сортировки 128
3.1.3. «Быстрая сортировка» 139
3.1.4. Другие методы сортировки 145
3.2. Сортировка во внешней памяти 143
3.2.1. Внешняя сортировка 148
3.2.2. Отрезки и слияние отрезков 151
3.2.3. Алгоритм сортировки слиянием 154
3.2.4. Эффективность внешней сортировки 169
3.3. Объем вычислений при сортировке 175
3.3.1. Минимальное число сравнений . 176
3.3.2. Сортировка с использованием специальных структур . . 180
'218
Содержание
Глава 4. Практические аспекты обработки данных .
4.1. Методы доступа к внешней памяти . . .
4.1.1. Методы доступа, реализуемые операционной системой
4.1.2. ISAM (индексно-последовательный метод доступа) . .
4.1.3. VSAM (виртуальный метод доступа)
4.2. Структура памяти и поиск данных
4.2.1. Доступ к записям по ключам ...
4.2.2. Структура записи основного файла
4.2.3. Структура файла с инвертированным индексом . . . .
4.3. Уплотнение данных . .
4.3.1. Кодирование
4.3.2. Уплотнение данных в естественных языках
4.3.3. Кодирование длин серий и другие методы
4.4. Параллельная аппаратная сортировка
4.4.1. Сеть сортировки из компараторов с двумя входами
4.4.2. Сети сортировки и логические запоминающие устройства
Литература
Предметный указатель
185
185
185
187
189
192
193
196
197
198
199
201
203
204
204
207
211
213
Содержание
217
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее оформле¬
нии, качестве перевода и другие просим присылать по
адресу: 129820, Москва, И-110, ГСП, 1-й Рижский пер.,
д. 2, изд-во «Мир».
МОНОГРАФИЯ
Масааки Сибуя, Такэо Ямамото
АЛГОРИТМЫ ОБРАБОТКИ ДАННЫХ
Научный редактор Т. Н. Шестакова
Мл. научный редактор В. IT. Соколова
Художник А. В. Захаров
Художественный редактор Н. М. Иванов
Технический редактор Н. И. Манохина
Корректор Н. В. Андреева
И Б № 5485
Сдано в набор28.03.86. Подписано к печати 16.09.86. Фор¬
мат 60X907i6. Бумага кн.-журн. имп. Печать высокая.
Гарнитура литературная. Объем 7,00 бум. л. Уел. печ.
л. 14,00. Уел. кр.-отт. 14,25. Уч.-изд. л. 12,81.
Изд . № 6/4067. Тираж 15 000 экз. Зак. 127. Цена I р.
ИЗДАТЕЛЬСТВО «МИР» 129820, ГСП, Москва, И-110,
l-й Рижский пер., 2
Ленинградская типография № 2 головное предприятие
ордена Трудового Красного Знамени Ленинградского
объединения «Техническая книга» им. Евгении Соколо¬
вой Союзполиграфпрома при Государственном комитете
СССР по делам издательств, полиграфии и книжной
торговли. 198052, г. Ленинград, Л-52, Измайловский про¬
спект. 29.
В 1986 году издательство «Мир» выпустит
следующие книги:
Компьютеры: Справочное руководство. В 3-х томах.
Пер. с англ./Под ред. Г. Хелмса. —М.: Мир, 1986
(И кв.). — 77 л., ил. — 5 р. за комплект, 50 000 экз.
Том I — 24 л., 1 р. 60 к.; том 2 — 27 л., 1 р. 70 к.,
том 3 — 26 л., 1 р. 70 к.
Охватывает основные проблемы построения ком¬
пьютеров, периферийного оборудования и соответ¬
ствующего программного обеспечения. Дано описа¬
ние и сравнение диалоговых языков Бейсик, АПЛ и
алгоритмических Кобол, Фортран, ПЛ/1, Паскаль,
а также принципов организации программного обес¬
печения на базе языка ассемблера. Приведено пол¬
ное программное обеспечение микропроцессорных
систем Интел 8080 и 8085. В качестве примеров
рассмотрены применения микрокомпьютеров в сред¬
ствах машинной графики, устройствах для распо¬
знавания речи и робототехнических системах.
Для инженеров, работающих с вычислительной
техникой, и студентов соответствующих специально¬
стей вузов.
Нагао М., Катаяма Т., Уэмура С. Структуры и ба¬
зы данных: Пер. с япон. — М.: Мир, 1986 (III кв.).—
14 л., ил. — 1 р. 10 к. 15 000 экз.
Излагаются теоретические основы построения
структур и методы проектирования баз данных, по¬
лучившие широкое распространение в Японии, что
представляет значительный интерес в свете созда¬
ния микрокомпьютеров пятого поколения. Рассма¬
триваются аспекты построения структур баз дан¬
ных абстрактного типа. Большая часть книги по¬
священа современным способам проектирования
баз данных по концепции «сущность — свойство —
отношение». Все конкретные примеры даются на
языке Паскаль. Выдвигается концепция независи¬
мости базы данных от вида примера.
Для научных работников и инженеров, зани¬
мающихся созданием систем программного обеспе¬
чения.
В 1987 году издательство «Мир» выпустит
следующие книги:
Наука и техника в картинках*
Издание подобного рода предпринимается в
СССР впервые. Хотя оно и относится к категории
книг в картинках, но повествует о серьезных во¬
просах науки и техники. Предлагая советскому чи¬
тателю две такие книги, издательство исходило из
того, что во Франции, где эти книги увидели свет,
они пользуются большой популярностью. Можно
предположить, что найдена удачная форма озна¬
комления широкого круга специалистов со смежны¬
ми областями знаний.
Стюарт И. Тайны катастрофы: Пер. с франц. — М.:
Мир, 1987 (II кв.) —11л. ил.—(В пер.)’ 80 к.,
75 000 экз.
Имя автора хорошо известно советскому чита¬
телю по монографии «Теория катастроф», написан¬
ной им совместно с Т. Постоном (М.: Мир, 1980).
Данная книга посвящена изложению основных по¬
ложений и практических применений теории ката¬
строф в занимательной форме, чему способствуют
многочисленные забавные иллюстрации.
Для специалистов, работающих в различных об¬
ластях науки и техники и в народном хозяйстве, а
также для студентов вузов.
Пети Ж.-П. О чем мечтают роботы?: Пер. с
франц.— М.: Мир, 1987 (II кв.).— 12 л., ил.—
85 к., 75 000 экз.
Оригинальное изложение основных тенденций
развития роботов с программным управлением,
адаптацией и элементами искусственного интел¬
лекта, построенное на многочисленных забавных
иллюстрациях. Однако такая занимательность по¬
дачи материала не означает элементарности содер¬
жания. Например, автор вводит читателя в мир
основополагающих идей Н. Винера и Дж. фон
Неймана, на основе которых в ближайшие годы
будут создаваться сложные робототехнические ком¬
плексы.
Для специалистов, занимающихся созданием и
применением роботов в народном хозяйстве, а так¬
же для студентов вузов соответствующего профиля.
1 руб.