В.Д.Могилевский
Наведение
баллистических
летательных
аппаратов

В. Д. МОГИЛЕВСКИЙ
НАВЕДЕНИЕ
БАЛЛИСТИЧЕСКИХ
ЛЕТАТЕЛЬНЫХ
АППАРАТОВ
Москва
«МАШИНОСТРОЕНИЕ»
1976

УДК 629.76.001.2
Рецензент канд. техн. наук А. И. Шеховцев
Могилевский В. Д. Наведение баллистических летательных аппаратов.
М., «Машиностроение», 1976, 208 с.
В книге рассмотрены основы недавно сформировавшейся теории наведе¬
ния летательных аппаратов с баллистическим участком полета. Теория наве¬
дения охватывает комплекс проблем, связанных с оптимальным управлением
движением центра масс широкого класса объектов: ракет-носителей, балли¬
стических ракет, управляемых космических аппаратов. Задача управления
заключается в такой организации движения объекта на активном участке,
которая обеспечила бы требуемые свойства последующей баллистической
траектории. Исходя из этого в книге дана характеристика задачи наведения
и приведены математические формы описания концевых условий управления,
выполнение которых означает необходимость перехода к баллистической
фазе полета для успешного решения задачи наведения. Далее рассмотрено
построение оптимального (по минимуму расхода топлива) управления выве¬
дением ракет-носителей и баллистических ракет и управления сближением
космических аппаратов. В заключение освещен вопрос управления выключе¬
нием двигательной установки на базе информации об истинных параметрах
движения. При использовании автономных систем управления для получе¬
ния последних необходимо привлекать навигационные алгоритмы, которые
также кратко описаны в книге.
Книга предназначена для научных работников и инженеров, а также
может быть полезна аспирантам и студентам старших курсов соответствую¬
щей специальности.
Ил. 69, список лит. 173 назв.
31904-208
ж	208-76	©Издательство	«Машиностроение»,	1976	г.
038(01)-76

ПРЕДИСЛОВИЕ
Характерной чертой развития теории и прикладных исследо¬
ваний является возникновение в какой-то момент времени воз¬
можности и необходимости обобщить результаты разработок
более или менее разнородных задач на базе единого подхода.
Такое состояние, по-видимому, характерно в настоящее время
для достаточно широкого круга проблем управления движением
центра масс летательных аппаратов, имеющих баллистическую
фазу полета. Указанное свойство распространяется на управле¬
ние выведением ракет-носителей и баллистических ракет, а так¬
же управление маневром космических аппаратов. Основа общно¬
сти состоит в формальной трактовке задач данного типа как
задач с подвижным правым концом фазовой траектории. По¬
движность левого конца траектории не меняет смысла решения
и лишь усложняет процедуру его отыскания.
Возможность использования единой методологии позволяет
установить характерные черты решений отдельных задач, вза¬
имно обогатить частные исследования, наконец, ориентировать
теорию в направлении разработки конкретных методов синтеза.
При отыскании оптимального (или близкого к нему) реше¬
ния, справедливого для целой совокупности задач, как правило,
не удается получить алгоритм, который мог бы реально претен¬
довать на реализацию. Причина подобного разрыва заключает¬
ся в сложности математической модели объекта, ограниченнос¬
ти методов синтеза и специфике технических требований. Для
представления алгоритма оптимального управления в обозри¬
мом виде приходится прибегать к сравнительно серьезным
упрощениям. Однако при достаточно корректных допущениях в
полученных результатах можно выявить структуру решения, что
позволяет сделать поиск технически реализуемых алгоритмов
более целенаправленным, а также уменьшить вес эвристики при
разработке законов управления.
Предлагаемая книга является попыткой систематизирован¬
ного изложения основных вопросов теории наведения: именно
этот термин можно считать установившимся для определения
задачи оптимального управления движением центра масс лета¬
тельного аппарата с баллистическим этапом полета. Цель кни¬
ги— описать круг задач теории наведения, изучить облик си¬
стем наведения, разработать базовые алгоритмы наведения.
3

Для этого, в первую очередь, следует сформулировать и
математически описать задачу наведения (гл. 1). Управление
движением осуществляется на активном участке полета и пре¬
кращается в момент, когда параметры движения соответствуют
последующему баллистическому движению с требуемыми свой¬
ствами. Поэтому в гл. 2 формализуется баллистическое движе¬
ние для определения семейства попадающих траекторий, т. е.
траекторий с заданными характеристиками (разд. 2.3 написан
К. Р. Разиным и А. В. Костровым). В 3 и 4-й главах соответст¬
венно рассматриваются задачи формирования оптимального и
близкого к нему управления на этапе выведения ракет-носите¬
лей, баллистических ракет и маневра космических аппаратов
для сближения. Последняя, 5-я глава посвящена построению
алгоритмов фиксации момента выключения двигателя, что со¬
ответствует удовлетворению условий, определяющих принад*
лежность траектории семейству попадающих.
Автор с удовольствием пользуется возможностью выразить
глубокую признательность коллегам за внимательное отноше¬
ние к работе, а также матери Е. М. Ершовой, помощь которой
трудно переоценить.

ВВЕДЕНИЕ
Человечество за всю свою историю еще не сталкивалось с
такой колоссальной по масштабам, безгранично комплексной,
конгломеративной по своей сути проблемой, каковую представ¬
ляют космонавтика и ракетодинамика. Для их развития потре¬
бовалось объединить творческие усилия специалистов в области
теории управления и баллистики, астрономии и радиоэлектро¬
ники, материаловедения и механики, химии и физики, медицины
и психологии и многих, многих других. Освоение космического
пространства и перспективы решения этой задачи — одно из
наиболее ярких проявлений научно-технической революции.
Отечественное ракетостроение прошло грандиозный путь от
первых работ К. Э. Циолковского, в которых точность (матема¬
тических формулировок изящно переплеталась с плодами науч¬
ной интуиции автора, до первого искусственного спутника, пер¬
вого полета космонавта Ю. А. Гагарина, орбитальных станций
и межпланетных кораблей. Эти успехи следует расценивать как
определенные промежуточные результаты гармонического раз¬
вития большого числа самостоятельных направлений науки и
техники. Диалектика процесса формирования научных дости¬
жений, разработки и реализации конструкторских решений при¬
вела к тесному взаимодействию ранее обособленных научных
дисциплин, их взаимообогащению, необходимости решать тео¬
ретические проблемы с учетом возможностей технического во¬
площения этих решений.
Более того, потребности практики заставили критически пе¬
ресмотреть традиционные подходы и методы исследования,
обусловили появление фундаментальных научных результатов.
К числу последних можно отнести, например, широко исполь¬
зуемый метод оптимизации, созданный школой Л. С. Понтряги-
на (принцип максимума) и возникший при исследовании задачи
управления объектом с рулями, имеющими естественные огра¬
ничения по углу поворота.
Одним из научных направлений, окончательно сформировав¬
шимся в последнее десятилетие, является теория наведения
баллистических летательных аппаратов. Под теорией наведения
будем понимать управление движением центра масс летатель¬
ных аппаратов, имеющих наряду с активным (управляемым)
5

еще и баллистический участок движения, в результате чего»
обеспечивается решение поставленной задачи. Активных и пас¬
сивных участков может быть несколько и они могут чередовать¬
ся друг с другом.
Отметим, что в широком смысле под управлением понимают
специальным образом сконструированное целенаправленное
воздействие на объект. В такое определение можно включить*
например, изменение конструкции объекта, настройку парамет¬
ров системы управления и т. д. Далее под управлением пони¬
мается силовое воздействие на объект, приводящее к изменению
параметров его движения.
Процесс становления теории наведения знаменовался появ¬
лением большого числа фундаментальных работ известных уче¬
ных: А. Ю. Ишл и некого, Н. Н. Красовского, Д. Е. Охоцимского*
А. М. Летова, В. М. Пономарева, Р. Бэттина, А. Брайсона,
Д. Лоудена, не говоря уже об огромном количестве публикаций
в периодической литературе. Однако внимание, проявленное
исследователями к той или иной области познания, еще не сви¬
детельствует о появлении нового обособленного научного
направления, науки. В качестве признаков «замкнутости»
научного направления, определяющих его единство с ранее
образовавшимися направлениями и отличия от них, по-видимо¬
му, могут выступать:
— объект изучения;
— цель и прикладное значение исследований;
— методы исследований.
Кратко охарактеризуем содержание этих признаков с пози¬
ции теории наведения.
Объект изучения. Как следует из определения теории наве¬
дения, объектом в общем случае является управляемое движе¬
ние центра масс летательного аппарата, выполняющего постав¬
ленную задачу. К числу последних можно отнести управление
движением ракеты-носителя (PH) для выведения ее последней
ступени (космического аппарата) на орбиту с требуемыми па¬
раметрами, управление переходом аппарата с одной орбиты на
другую, управление движением космического аппарата (КА) в
интересах встречи с другими КА, управление движением балли¬
стической ракеты (БР) и другие случаи. На движение этого
класса объектов существенно влияют внешние силы — аэроди¬
намические, если рассматривается движение в атмосфере, и гра¬
витационные. Обеспечение же требуемых свойств движения до¬
стигается за счет управляющей силы—тяги реактивных двига¬
телей или аэродинамических рулей. Во время полета (в общем
случае пространственного) объект находится под воздействием
всех этих сил, выделить эффект от действия какой-либо из них
не удается. Все это приводит к тому, что формализованная мо¬
дель объекта, представляющая собой с известной степенью до¬
стоверности объективное отражение свойств движения летатель-
6

аого аппарата (ЛА), является весьма сложной. Трудность ее
изучения усугубляется развитой системой кинематических соот¬
ношений, определяющих взаимосвязь параметров движения с
координатами, измеряемыми чувствительными элементами.
Следует подчеркнуть отличие в подходе к составлению мате¬
матической модели объекта для анализа его движения и син¬
теза управления. В первом случае, исследуемом баллистикой
и теорией полета, управляющее воздействие считается извест¬
ным; требуется найти траекторию движения и законы измене¬
ния кинематических параметров. Для этого необходимо как
можно точнее учесть все факторы, сказывающиеся на движении
объекта. При синтезе управления (эта задача является основ¬
ной для теории наведения) использовать полную систему диф¬
ференциальных и алгебраических уравнений, описывающих
движение, невозможно и нерационально. Во-первых, детальное
описание движения чрезвычайно затрудняет синтез даже при
применении ЦВМ и препятствует осмыслению и анализу ре¬
зультатов. Во-вторых, условия полета заранее трудно предска¬
зать, поэтому скрупулезность при формализации иногда просто
бессмысленна.
Упрощение математической модели должно быть адекватно
цели синтеза и отвечать совокупности допущений, характерных
для реального движения.
Общность в подходе к формированию модели движения с
позиций теории полета и теории наведения заключается в пред¬
положении известной зависимости сил, действующих на объект,
от характера движения. Изучением последней занимаются не¬
бесная механика и аэродинамика совместно с теорией конст¬
рукции ЛА и их двигательных установок.
Цель и прикладное значение исследований. Отличительным
признаком рассматриваемого класса ЛА является наличие двух
характерных этапов движения:	управляемого	(активного)	и
баллистического (пассивного). На первом этапе (их так же, как
и пассивных, может быть несколько, но для простоты далее бу¬
дем исходить из наличия лишь одного активного и одного пас¬
сивного участков) происходит целенаправленное движение ЛА
при использовании системы управляющих сил, воздействующих
на объект, наряду с совокупностью внешних сил, зависящих от
условий движения. В момент окончания активного участка дей¬
ствие управляющих сил прекращается и объект совершает даль¬
нейшее движение по инерции. На характер изменения парамет¬
ров движения объекта на баллистическом участке влияют
внешние силы, основной из которых является сила гравитацион¬
ного притяжения, а если рассматривается участок полета в
плотных слоях атмосферы, то и аэродинамическая сила.
Известно, что требуемые свойства полета ЛА могут быть
достигнуты, во-первых, выбором соответствующих начальных
условий движения (например, назначением определенного мо¬
7

мента запуска PH или момента начала работы двигательной
установки КА при старте с околоземной орбиты), во-вторых,
организацией системы сил, действующих на объект. Благодаря
зтаму возможности видоизменения характера движения у ЛА
рассматриваемого класса оказываются чрезвычайно широкими.
Очевидно, что выполнению задачи полета соответствует в
общем случае бесконечное число траекторий, определяемых
бесконечным разнообразием законов управления, реализуемых
на активном участке. Следуя терминологии, применяемой в бал¬
листике, совокупность баллистических траекторий, удовлетво¬
ряющую задачам полета, будем называть попадающими траек¬
ториями.
Правый конец семейства попадающих баллистических траек¬
торий характеризуется условиями задачи полета, а совокуп¬
ность параметров движения на левом конце траектории можно
описать некоторой математической зависимостью, определяю¬
щей принадлежность траектории множеству попадающих. Та¬
кая зависимость, называемая граничными или концевыми усло¬
виями (с точки зрения предшествующего активного этапа
движения), представляет собой условия прекращения управ¬
ляющего воздействия на объект с тем, чтобы последующее бал¬
листическое движение привело к выполнению задачи полета.
Граничные условия есть совокупность некоторых соотношений,
устанавливающих связь между параметрами движения ЛА в
момент окончания активного участка и параметрами движения
в конце баллистического участка. Формализованную задачу
полета будем называть условиями встречи.
Таким образом, к параметрам движения ЛА в начале и кон¬
це баллистического участка предъявляются особые требования.
Требования на правом конце (условия встречи) определяют за¬
дачу полета, а на левом конце (концевые или граничные усло¬
вия) описывают семейство попадающих траекторий.
Тогда задачу теории наведения можно трактовать как на¬
хождение такого управления, воздействующего на ЛА, которое
обеспечило бы оптимальное, в определенном смысле наилучшее
выполнение концевых условий за время активного этапа движе¬
ния, а значит, и условий встречи. При этом следует учесть, что
в общем случае выбор указанного управления стеснен различ¬
ными ограничениями энергетического, конструктивного и друго¬
го характера. Существенным является требование реализуемо¬
сти, возможности конструктивного воплощения разработанного
алгоритма управления в системе наведения.
Что касается прикладной направленности теории наведения,
то достаточно сказать, что в систему управления (СУ) ЛА
рассматриваемого класса обязательно входит в качестве состав¬
ной части система наведения как материализованный результат
применения теории наведения к решению конкретной задачи
управления движением центра масс данного типа ЛА.
8

Методы исследования. Из сказанного очевидно, что для оты¬
скания оптимального управления в задаче наведения следует
использовать все многообразие методов, которыми располагает
современная теория оптимизации. Характерной особенностью
математической постановки задачи наведения является то, что
она принадлежит классу задач с подвижным правым концом
фазовой траектории, перемещение которого лимитируется гра¬
ничными условиями. Это обстоятельство приводит к тому, что
результат синтеза оптимального управления можно получить в
виде алгоритма, имеющего итерационный характер и ограничен¬
ную сходимость, оценить которую заранее весьма затрудни¬
тельно. Такие свойства решения вступают в явное противоречие
с требованием простоты реализации алгоритма управления, что
вынуждает заниматься поиском форм управления, близких
к оптимальным и одновременно удобных для конструктивного
воплощения. Необходимость принимать во внимание это про¬
тиворечие при построении систем наведения составляет харак¬
терную особенность теории наведения и заставляет широко при¬
влекать различные методы синтеза, обеспечивающие нахожде¬
ние управлений, близких к оптимальным.
Подводя итог сказанному относительно теории наведения,
можно указать на следующие характерные черты:
— объектом исследований для теории наведения является
управляемое движение центра масс ЛА, имеющего наряду с ак¬
тивным участком еще и пассивный, баллистический участок;
— формализованная постановка задачи нахождения опти¬
мального управления относится к классу краевых задач с по¬
движным правым концом, перемещение которого стеснено гра¬
ничными условиями;
— в силу прикладной ориентации теории наведения, направ¬
ленной на разработку систем наведения, при получении алго¬
ритмов оптимального управления необходимо принимать во
внимание возможность их последующей конструктивной реали¬
зации.
Характеристику теории наведения нельзя считать полной,
если не раскрыть механизм формирования управления и крите¬
рия оценки качества решения задач исследуемого класса. Вна¬
чале остановимся на понятии управления.
Оптимизацию управления, строго говоря, можно проводить
лишь тогда, когда известны условия движения объекта на всем
участке управления. Во время полета наиболее целесообразно
получать информацию об условиях движения, изучая поведение
объекта и его реакции на внешние воздействия. Такая форма
анализа условий движения является наиболее естественной, так
как исключает необходимость трудно реализуемого процесса
измерения непосредственно внешних сил. В качестве объектив¬
ного показателя условий движения выступает вектор истинного
9

ускорения объекта как геометрическая сумма вектора гравита-
ционного ускорения и вектора кажущегося ускорения.
Рационально, по крайней мере на этапе решения фун¬
даментальных задач теории наведения, вектор кажущегося
ускорения отождествлять с управлением. Если за управляющее-
воздействие принять вектор кажущегося ускорения как таковой,
то задача оптимизации управления сводится к тому, чтобы наи¬
лучшим образом распорядиться ориентацией и величиной этого
вектора. Но, с одной стороны, при движении в плотных слоях
атмосферы во время выведения JIA или его посадки на Землю
величина аэродинамических сил изменяется в широком диапазо¬
не и зависит от траектории и углового положения объекта.
С другой стороны, сила тяги реактивного двигателя может ре¬
гулироваться в сравнительно узких пределах из-за необходи¬
мости сохранения соотношения между окислителем и горючим,
близкого к расчетному, а в двигателях на твердом топливе-
практически управление тягой в настоящее время исключено.
По этим причинам задача управления величиной кажущегося
ускорения представляется несколько искусственной. Более ши¬
рокие возможности для проектирования ЛА открываются при
управлении только ориентацией вектора кажущегося ускорения,,
направляющий орт которого для PH и БР фактически определя¬
ет положение продольной оси. В предлагаемой работе принята
именно такая трактовка управления. Тем не менее, следует от¬
давать отчет, что минимальное значение критерия, полученное
в результате оптимизации ориентации вектора кажущегося
ускорения, может быть уменьшено, если предположить допусти¬
мость регулирования и модуля этого вектора.
При стремлении разработать наилучшую в известном смысле
систему целесообразно в качестве критерия оптимальности при¬
нять характеристику, наиболее полно описывающую назначение-
этой системы. Но при создании систем наведения количество
частных показателей, которые и составляют характеристику си¬
стемы, весьма велико. Поэтому при теоретической проработ¬
ке системы выделяют наиболее существенный показатель,,
адекватный требованиям к системе, и в процессе оптимизации
достигают его экстремального значения. В качестве такого кри¬
терия можно было бы принять показатель точности системы на¬
ведения, выразив его через характеристики, описывающие сто¬
хастический характер реальных условий полета и зависящие
от управления.
Однако современное состояние теории синтеза управления*
оптимального по статическому критерию, для нелинейных
объектов (именно к такому классу принадлежат объекты тео¬
рии наведения) таково, что не дает возможность получить
решение задачи в общей постановке. Поэтому приходится
формулировать задачу как детерминированную и управление
синтезировать с «запасом», ориентируясь на наихудшие условия
ю

движения. Требование увеличения точности наведения остается
определяющим при разработке систем. Оно удовлетворяется
специальными мерами, проводимыми в двух направлениях.
Во-первых, входная информация, носящая статистический
характер, подвергается обработке для получения оптимальных
оценок измеряемых координат, а при синтезе управления пред¬
полагается, что все помехи отфильтрованы. Справедливость та¬
кой декомпозиции доказана только для линейных систем, но
естественность подхода делает его весьма привлекательным
для инженерной практики.
Во-вторых, точность наведения ЛА зависит от строгости
удовлетворения концевым условиям в момент начала баллисти¬
ческой фазы полета. При получении концевых условий необхо¬
димо возможно полнее учитывать все факторы, сказывающиеся
на баллистическом движении объекта, для исключения методиче¬
ских ошибок наведения. В то же время на этапе активного
участка можно использовать упрощенные модели: допущения
при формализации движения проявятся на величине достигну¬
того критерия оптимальности, но не приведут к уменьшению
точности при строгом выполнении концевых условий.
В качестве критерия оптимальности в задачах наведения
может быть с успехом применена длительность активного
участка: чем быстрее достигает ЛА концевых условий, тем ка¬
чественнее система наведения. Так как на активном участке по
•его определению двигатель работает непрерывно, то нетрудно
связать указанный критерий с количеством топлива, израсходо¬
ванного для достижения концевых условий. Экономное расходо¬
вание топлива позволяет увеличить полезную нагрузку или сни¬
зить стартовый вес объекта, или, наконец, расширить диапазон
возможностей данного типа ЛА.
Итак, рассмотренные особенности постановки и решения за¬
дач теории наведения свидетельствуют о необходимости обосно¬
ванного выбора рационального метода синтеза из арсенала из¬
вестных, о необходимости трансформировать общие процедуры
применительно к специфике задачи, наконец, о целесообразнос¬
ти разработки специальных методов для формирования опти¬
мального управления. Тем не менее, даже при корректном син¬
тезе не следует надеяться на возможность получения алгорит¬
мов, которые могли быть реализованы в системе управления без
существенной доработки. Построение реальных алгоритмов та¬
ких сложных систем основано на дальнейшем изучении конкрет¬
ной задачи, широком использовании вычислительной техники,
позволяющей учесть особенности движения и проанализировать
различные алгоритмы управления, а также на умении проекти¬
ровщика привлекать опыт решения аналогичных задач, интуи¬
цию и здравый смысл.

ГЛАВА 1
ПОСТАНОВКА ЗАДАЧИ НАВЕДЕНИЯ
1.1.	Объект управления
При математическом описании объекта управления и разра¬
ботке модели его движения обычно устанавливают:
1) динамические свойства объекта, т. е. реакцию объекта на
действие всей совокупности входных сигналов — управлений и
внешних воздействий или возмущений;
2) характер информации о параметрах движения объекта,,
которая может быть получена с помощью системы чувствитель¬
ных элементов (измерителей);
3) ограничения и другие специфические требования, предъ¬
являемые к движению объекта.
В состав объекта управления включают и неизменяемую
часть системы, которая не подвергается синтезу, но необходима
для работоспособности системы. В системах управления неиз¬
меняемую часть составляют измерители и исполнительные орга¬
ны, выбор которых может быть ограничен образцами, изготов¬
ляемыми промышленностью, или спроектированные специально
для данного объекта.
Динамические свойства объекта характеризуют зависимость
выходной величины х от входных величин управления и и по¬
мехи z. Так как эти величины обычно являются функциями не¬
зависимого переменного времени, то зависимость между этими
функциями в общем случае определяется оператором вида
x(t) = F[u(t\ z{t\ t].	(1. 1)
Функции, входящие в (1.1), суть векторы соответствующей раз¬
мерности, определенные в некоторой эвклидовой системе
x(*)={*i(0. ■**(*). •••, xa(t)}, u(t)=[uх(<), и2(0, •••. «г(*)Ь
z(t)={z1{t), z2{t), ..., ^(г1)}.	(1-2)
Более конкретной формой представления соотношения (1.1)
является запись в виде векторного дифференциального уравне¬
ния в форме Коши:
x(*) = f[x(*), и(/), z(t), t\,	(1.3)
12

где f — я-мерная вектор-функция, кусочно-непрерывная или
непрерывная по всей совокупности аргументов, принадлежащих
области задания xgX, ugU, zgZ, и определенная на интер¬
вале
Если f является аналитической функцией, т. е. ее каждая
скалярная компонента разлагается в абсолютно сходящийся
степенной ряд в окрестности каждой точки x(t)>	П» то
уравнение (1.3) можно подвергнуть линеаризации при малых
отклонениях выходной координаты от ее программного, заранее
известного значения хпр(0- Линеаризованная модель объекта
(1.3) имеет вид
у (/) = А (0 у (0 + в (0 Ли (/) + с (t) z (t),	(1.4)
где	Аи(*)=и(^)	—и|ф(^); УМ=х(*)—хпр(/);
А (г1), В(7), С(7)—матрицы соответствующей размерности, вычис¬
ленные для х=хпр (t); u=unp (t):
A{t)=^-(ty,	C(0 = -^-(0-
ox	dn	dz
Решение уравнения (1.3) при известном законе изменения и (/)
и z (t) записывается как
t
х(/) = хн + f f (х, u, z, t)dt, xH = x(0,	(1.5)
К
а для соотношения (1.4)
t
x(0=Y (*)xH + Y {t) Y_1(t)B(t) Au(t)fl?t -f-
>h
+ J Y(<)Y->(T)C(t)z(t)rft,	(1.6)
^ H
где Y (^)— фундаментальная матрица решений однородной
системы
Y(0 = A(*)Y(*).
Если рассматривается движение объекта с «замороженными»
коэффициентами, величина которых в выражении (1.4) фикси¬
рована в некоторый момент времени (стационарный объект),
то для нахождения его реакции широко используются оператор¬
ные методы.
При формализации объекта обычно возникает ситуация, при
которой выходные координаты, характеризующие движение
объекта, не совпадают с параметрами, измеряемыми чувстви¬
тельными элементами. В общем случае число скалярных состав¬
ляющих х (t) больше измеренных. Тогда для формирования
13

управления приходится решать задачу восстановления недо¬
стающих координат по наблюдаемым значениям переменных х
(задача идентификации) или строить управление в условиях
недостаточности информации о параметрах движения. Пусть из¬
меренные параметры движения характеризуются ^-мерным век¬
тором х*(Л= (х*(Л, x\{t), ...,	Тогда связь х (t) с х* (t)
можно представить через некоторый непрерывный оператор R,
имеющий обратный R-1:
x*(t) = R[x(/), t],	(1.7)
называемый кинематическим. Примером сложной и развитой
структуры оператора R может служить определение параметров
движения ЛА при математическом моделировании инерциаль-
ного базиса пб показаниям акселерометров и датчиков угловых
скоростей [5]. В частных случаях R вырождается в матрицу, на¬
пример, при несовпадении осей чувствительности измерителей
с координатной системой, в которой фиксируется движение
объекта.
Потребность в решении задачи идентификации возникает
также тогда, когда для построения управления необходима ин¬
формация о высших производных, непосредственное измерение
которых обычно сопряжено с серьезными техническими затруд¬
нениями.
Следует подчеркнуть, что выбор системы координат, в кото-'
рой фиксируется состояние объекта, и математической модели
описания его движения является далеко не однозначной зада¬
чей. Представление движения специальной математической
формой, обоснование и выбор системы рациональных допуще¬
ний представляют собой специфичную проблему, которую надо
решать с позиций адекватности ее целям синтеза. Корректное
решение проблемы в значительной степени определяет успех
синтеза управления. Высказать же какие-либо общие рекомен¬
дации в этом отношении затруднительно.
В баллистике и теории полета для описания движения цент¬
ра масс ЛА используется несколько систем координат, которые
можно классифицировать по следующим признакам:
а) начало отсчета (начало системы координат может сов¬
падать с центром притяжения; с точкой старта БР или PH; с
центром масс одного из КА);
б) характер перемещения осей системы (инерциальная си¬
стема, оси которой могут перемещаться плоскопараллельно, не
вращаясь относительно пространства звезд; связанная система,
которая участвует в суточном вращении Земли или обращается
вместе с КА по орбите, имея относительно нее или Земли опре¬
деленную ориентацию).
На данном этапе изложения введем две системы координат:
связанную геоцентрическую 0TXV oYr.cZT,r и абсолютную (инер-
ииальную) геоцентрическую ОДг.аУг.Дг.а. Ось ОгУг.с ориенти¬
14

руется по вектору угловой скорости вращения Земли и направле¬
на в сторону Северного полюса, оси ОгХг.с, OrZr.c лежат в плоско¬
сти экватора, при этом часто оси ОДг.с придают определенное
положение, связывая ее с 'меридианом точки старта или Грин¬
вичским меридианом. Ось OrZr.c дополняет систему до правой.
Система 0Дг.аУг.а2г.а до момента начала отсчета (например,
момента старта tH) может совпадать с 0Дг.сУг.с2г.с, а в tH ее по¬
ложение фиксируется в инерциальном пространстве. Ориента¬
ция оси ОтХг.а иногда связана с линией узлов орбиты или точкой
весеннего равноденствия. Строгая определенность в задании си¬
стем координат пока не обязательна, она будет вводиться по
мере необходимости.
В абсолютной системе координат запишем уравнения движе¬
ния центра масс ЛА, который представляет собой материальную
точку с массой mtf), равной массе ЛА. В соответствии с первым
законом динамики — законом Ньютона
m(^)r(/) = 2F^)-	И-8)
i
eft Г
где г (t) =	 —вторая производная по времени от радиуса-
dfi
вектора г (£), фиксирующего положение центра масс в
ОгХг а?гг aZr а; У Fi —сумма сил, действующих на ЛА и при-
i
ложенных в центре масс. К числу сил, определяющих движе¬
ние ЛА, относят: суммарную аэродинамическую силу R, возни¬
кающую при перемещении ЛА в атмосфере; силу тяги реактив¬
ного двигателя Р, включая и силу, создаваемую управляющими
органами; силу притяжения Q, проявляющуюся согласно закону
всемирного тяготения.
В соответствии с последним величина и направление силы Q
зависит от положения точки относительно притягивающего тела,
т. е. представляет собой функцию радиуса-вектора g(f)> харак¬
теризующего координаты центра масс в связанной системе
ОД.с^г.Л.с- Одним из центральных положений теории притяже¬
ния является тот факт, что силу притяжения, действующую на
единицу массы, можно представить как градиент некоторой сило¬
вой функции U(q), т. е.
—77rQ[p(*)] = grad£/[pi*)],	(1-9)
m(t)
а значит, U (q) есть потенциал * векторного поля	Послед¬
няя вектор-функция имеет смысл ускорения, создаваемого силой
притяжения.
* Строго говоря, потенциал имеет знак, обратный силовой функции;
ниже функции U рассматривается только как положительная и на нее рас¬
пространяются оба термина.
15

Тогда (1.8) можно записать в виде
rV) = w(*) + grad£/[(p(/)],	(1.10)
где w(^) = —-—	[R(0 + P(^)1 —кажущееся	ускорение центра
/71 (^)
масс, т. е. ускорение, которое получает материальная точка при
действии на нее всех сил негравитационного происхождения.
Трудность использования этого соотношения заключается в
представлении в разных системах координат абсолютного
ускорения г	и	ускорения силы притяжения,	которую несложно
преодолеть, устанавливая соотношение
р(/) = А(/)г(0,	(1-11)
cosS3(^ — tn)
0 -
-sin 2„(/ —
A)
где
А(/) =
0
1
0
sin 23(* — t„)
0
cos23(^ —
A)
— матрица перехода от 0TXT,cYT^cZrtC к 0TXT^YT^Zr^ при выполне¬
нии предположения о совпадении этих систем до f=fH; £23=
= const — угловая скорость
вращения Земли (рис. 1.1).
С учетом последнего соотноше¬
ния (1.10) можно представить
к а. к
г (/) = w (/)-}-grad U [г [t), t\.
(1. 12)
Отсюда видно, что ускорение
силы притяжения, определяе¬
мое в инерциальной системе ко¬
ординат, в общем случае зави¬
сит не только от координат
центра масс в этой системе, но
и явно от времени, что являет¬
ся следствием вращения Земли
з принятой системе отсчета.
Однако	явная зависимость
ускорения от времени исчезает
для простых моделей гравитационного поля, таких как плоско¬
параллельное, сферическое векторное поле, для которых дейст¬
вие силы	притяжения	зависит	только от	удаления от центра
притяжения.
На основании уравнения (1.10) можно построить функцио¬
нальную	схему	математической модели	движения центра
масс JIA (рис. 1.2). На рисунке обозначено Р = и показано,
Рис. 1.1.
16

что суммарная аэродинамическая сила зависит от параметров
движения г (t), г (£). Фактически же оператор R в значительной
мере зависит еще и от характеристик ЛА (массовых, инерцион¬
ных, геометрических) и определяется движением объекта отно¬
сительно центра масс. Именно через этот оператор, как будет
показано, проникают в тракт управления различные возмущения,
имеющие размерность моментов и сказывающиеся на движении
центра масс.
grad U
Рис. 1.2.
В баллистике и теории полета часто используются уравнения
движения центра масс ЛА, записанные в связанной системе коор¬
динат. Эти уравнения можно получить на основе выражения
(1.10), учитывая лишь, что система координат участвует в суточ¬
ном вращении Земли.
Известно, что вектор абсолютного ускорения точки (в абсо¬
лютной системе координат) равен сумме вектора переносного
ускорения апер (ускорения точки, неизменно связанной с подвиж¬
ной системой), вектора относительного ускорения а0Тн (ускорения
в подвижной системе) и вектора кориолисова ускорения аКОр, т. е.
З-а ^нер ^-отн^кор*	О*	1^)
Слагаемые (1.13) представляются в виде
&пср=£23Х (£23Xq) ; аотн = р; aKop = 2Q3Xp,
где р(^), p(/f), p(t) —параметры движения в связанной систе¬
ме координат. Тогда аналогично уравнению (1.8) можно за¬
писать
m{t){ а„еР + аотн + акор)=Р + R + Q
или
m(/)p(*) = P + R + Q + FIiep + FKop,
где
^пер	^ ^нер’ FKOp	^	(0 ^кор*
17

Равнодействующая, слагающаяся из силы притяжения Q и
силы инерции переносного ускорения из-за вращения Земли,
называется силой тяжести
для которой аналогично соотношению (1.9) существует потен¬
циал V (q) векторного поля тяжести. Окончательно можно за¬
писать
m(/)p(/) = P-{-R^- G (р) — 2m(/)(i?3Xp и
или
P(0 = w(0 + gradl/(p)-2(Q3Xp).	(1.	14;
Применение той или иной формы описания движения опреде¬
ляется содержанием конкретной задачи. Следует лишь отметить,
что в уравнении (1.14)
присутствует дополни¬
тельное слагаемое по
сравнению с формой
(1.12), но несколько про¬
ще учитывается влияние
гравитационного поля.
Если система управления
автономная и имеет инер-
циальные измерители, то
удобнее пользоваться
(1. 12), хотя в этом случае
необходимо учесть вра¬
щение Земли, когда цель
полета каким-либо образом соотносится с земной поверх¬
ностью.
Как уже отмечалось во введении, широкий круг задач кос¬
монавтики связан с необходимостью изучения движения двух
объектов, находящихся в определенных взаимоотношениях. На
первый план при этом выступает исследование их относитель¬
ного движения, математическая модель которого и составляет
объект управления.
В системе OvXT^YT^ZT^ положение аппаратов фиксируется
ri(/) и г2{t) (рис. 1.3,а), а значит, расстояние между ними (век¬
тор дальности)
D (0 = r1(/) —r2(/).	(1.	15)
Вводится понятие относительной скорости
Уотн (*0 — D (0 — Г, (/) — Г4 (я.	(1-	16)
18

Тогда уравнение относительного движения можно представить
в виде
vim.(0 =D(/) = w1(/) — w3 (0 + grad £/[!■!(/), t\ — gradi/[r2(0, Ф
(1. 17)
Весьма распространено описание движения JIA в некоторой под¬
вижной системе OcXcYcZc, перемещающейся относительно
О г X г а YT hZ г а (см. рис. 1.3,6). На основании правил дифферен¬
цирования вектора, отнесенного к подвижной системе, с учетом
уравнения (1.8) имеем
mi?L = mfo + D + iXD + ®X(®XD) + 2«oXD] + P + R+Q,
сit2
а значит, уравнение движения
-^==r0+D-{-<oXD-|-<i>X (wXD)X2wXD-}-w-|-gi'ad U (г> ^)»
dt2
(1.18)
где со, со — угловая скорость и угловое ускорение подвижной сис¬
темы координат OcXcYcZc. Такая форма описания движения
широко используется для исследования относительного движе¬
ния КА. Она чрезвычайно удобна, когда рассматривается отно¬
сительное движение объекта, положение которого фиксируется
вектором D(£), а перемещение подвижной системы известно:
система OcXcYcZc связана с КА, обращающимся по определен¬
ной орбите [96]. Последнее означает, что известны законы изме¬
нения г0(/), to(t) и их производные, а это дает возможность ус¬
тановить зависимость D(0 от параметров орбиты и кажущегося
ускорения w (£).
Таким образом, движение центра масс ЛА, описываемое
уравнениями (1.1), (1.3) или (1.4), для решения какой-либо кон¬
кретной задачи представляется одной из форм векторного диф¬
ференциального уравнения второго порядка—(1.12),	(1.14),
(1.17)	или (1.18). Эти уравнения и представляют собой матема¬
тическую модель объекта управления в задачах наведения.
На параметры движения центра масс в процессе постановки
задачи наведения или ее решения могут быть наложены неко¬
торые ограничения. Так, возможно предъявление особых требо¬
ваний, во-первых, к начальному или конечному состоянию объ¬
екта, заданных, например, в форме неравенств
G„[x (/„)]< 0, От[х(Г)]<0;	(1.19)
во-вторых, системой условий вида
С?Лх(0]<0,	Т], i= 1, 2, ..., 5	(1.20)
ограничиваются некоторые комбинации переменных или абсо¬
лютные значения отдельных переменных:
|л:/(ЛКХ, О = const, /=1, 2, ...,	11. 21)
19

Наконец, в-третьих, могут быть сформулированы требования к
промежуточному состоянию объекта управления в виде
N[x(tj)] = 0, t^[tH,T]	(1.22а)
ИЛИ
x(tj) = Cj.	(1.226)
Для полного описания движения такого сложного объекта,
каким является ЛА, разумеется, необходимо принимать во вни¬
мание его угловое движение и движение относительно центра
масс. Этому сложному специфичному вопросу посвящено боль¬
шое количество публикаций, например [1, 85, 123]. Однако при
решении задач баллистики [8] пренебрегают колебаниями объек¬
та относительно центра масс, поскольку они слабо влияют на
движение центра масс при наличии качественной системы авто¬
матической стабилизации этих колебаний; аналогичный подход
повсеместно используется далее.
1.2.	Способы формирования управляющих
связей
Цель управления движением обследуемого класса объектов,
поведение которых описывается векторным дифференциальным
уравнением второго порядка—(1.12), (1.14), (1.17) или (1.18),
состоит в достижении таких параметров конца активного участ-'
ка, сочетание которых обеспечило бы выполнение задачи полета
при последующем баллистическом движении. Другими словами,
в результате воздействия управления на объект должны быть
получены соответствующие r(7K) = rK, г(7к) = гк. Подставив их
в уравнения баллистического движения в качестве начальных
условий и проинтегрировав эти уравнения, достигаем цели.
Целенаправленность силового воздействия (управление) для
таких объектов обычно обеспечивается регулированием вектора
кажущегося ускорения
/72(0
который удобно представить в виде двух сомножителей
vr(t) = w (/)w0(/), | w° (/) | = 1.	(1.24)
На безатмосферном участке траектории управление формирует¬
ся изменением вектора тяги P(t), а на атмосферном — в этом
участвует и вектор суммарной аэродинамической силы R(0-
Простейший способ достижения необходимых rK, rK=vK при
соблюдении равенства начальных условий расчетным состоит
в обеспечении программного изменения всех функций, образую¬
щих правую часть дифференциальных уравнений, описывающих
20

движение объекта, т. е. w(f) и grad [U(г, t)]. Тогда^ будут изме¬
няться по заранее рассчитанной программе и г(Д, г(/). При вы¬
полнении этого условия систему наведения можно было бы
строить по принципу разомкнутой системы автоматического ре¬
гулирования: вводить в систему программу, определяющую из¬
менение w(/), и в заранее известный момент времени выключить
двигатель Р(/)=0 для t^tK. Однако реализация такой прос¬
тейшей системы наталкивается на недостаточность априорной
информации о характере сил, действующих на объект.
В реальных условиях движения объект находится под дей¬
ствием сил, отличных от заранее рассчитанных. Эти разностные
силы интерпретируют как проявление некоторых случайных
возмущений.
Кратко рассмотрим природу этих возмущений. Сила грави¬
тационного притяжения описывается весьма сложными соотно¬
шениями [42], которые преднамеренно существенно упрощают
при расчете программного движения [8]. Поэтому, даже если
обеспечивается движение центра масс ЛА по заранее рассчитан¬
ной траектории, г(£)=гпр(0> реальное проявление гравитации
отличается от программного. Возмущения по линии аэродинами¬
ческой силы обусловлены, во-первых, отклонением свойств
атмосферы от модельных (действие ветра, отличия в плотности
атмосферы) и, во-вторых, несовпадением геометрических, весо¬
вых, инерционных характеристик объекта с эталонными, приня¬
тыми при расчетах. Сила тяги реактивного двигателя также
отличается от предполагаемой ввиду технологических ошибок,
ошибок сборки, отклонений в производственном процессе изго¬
товления топлива и т. д. Наконец, добиться идеального управле¬
ния также невозможно из-за ошибок, свойственных самой
системе управления. Последние возмущения, с точки зрения
управления, являются внутренними, а перечисленные ранее —
внешними. Однако проявляется действие этих возмущений
одинаково: оно приводит к отклонению траектории от про¬
граммной.
Тогда, учитывая реальные условия полета, можно опреде¬
лить назначение системы наведения как выполнение поставлен¬
ной цели автоматического управления полетом (наведения) в
условиях действия возмущений.
Для того чтобы осуществить наведение при наличии возму¬
щений, действующих на объект управления, на последний необ¬
ходимо наложить управляющие связи, т. е. некоторые ограниче¬
ния, которые не позволяют материальной системе занимать
произвольное положение в пространстве и иметь произвольные
скорости. Тогда систему наведения следует интерпретировать*
как материальное воплощение всей совокупности управляющих
связей. Объект, охваченный управляющими связями, представ¬
ляет собой замкнутую систему автоматического управления со
21

всеми ее преимуществами, которые так ярко проявляются при
действии возмущений.
Для выявления структуры связей рассмотрим наиболее рас*
пространенное программное управление [44, 55]. В этом случае
перед системой наведения ставится задача удержания центра
масс на некоторой программной траектории, которая представ¬
ляет собой кривую при сохранении скорости, равной расчетной.
В аналитической механике принято называть программу жест¬
кой, если число управляющих связей равно числу степеней сво¬
боды [53], в нашем случае трем.
Следует оговорить, что с точки зрения управления с помощью
обратных связей необходимо регулировать шесть параметров
движения: три проекции г и три проекции г, которые однознач¬
но определяют баллистическое движение. Таким образом, коли¬
чество управляющих связей должно быть в два раза больше
числа степеней свободы пли равно числу переменных, полностью
описывающих движение. С другой стороны, можно ограничить¬
ся учетом трех управляющих связей, но при этом рассматривать
их как определенные интегро-дифференциальные соотношения,
реализация которых в контуре управления необходима для ка¬
чественного управления.'
Вполне очевидно, что управлять в общем случае пространст¬
венным движением ЛА с помощью какой-либо одной связи не
представляется возможным. Поэтому задачу управления движе¬
нием сложных объектов делят на возможно большее число част¬
ных задач, каждую из которых решает специально синтезиро¬
ванная управляющая связь. Качество управления в значительной
мере зависит от успеха проведения декомпозиции и от возмож¬
ностей технической реализации частного алгоритма.
Как уже указывалось, фиксация положения центра масс су¬
щественно зависит от выбора системы координат, которая в зна¬
чительной мере определяет состав управляющих связей, их свой¬
ства и степень простоты их технической реализации.
Вначале рассмотрим инерциальную прямоугольную декарто¬
ву систему координат, связанную с точкой старта ОсХс.aZc.aZc.a
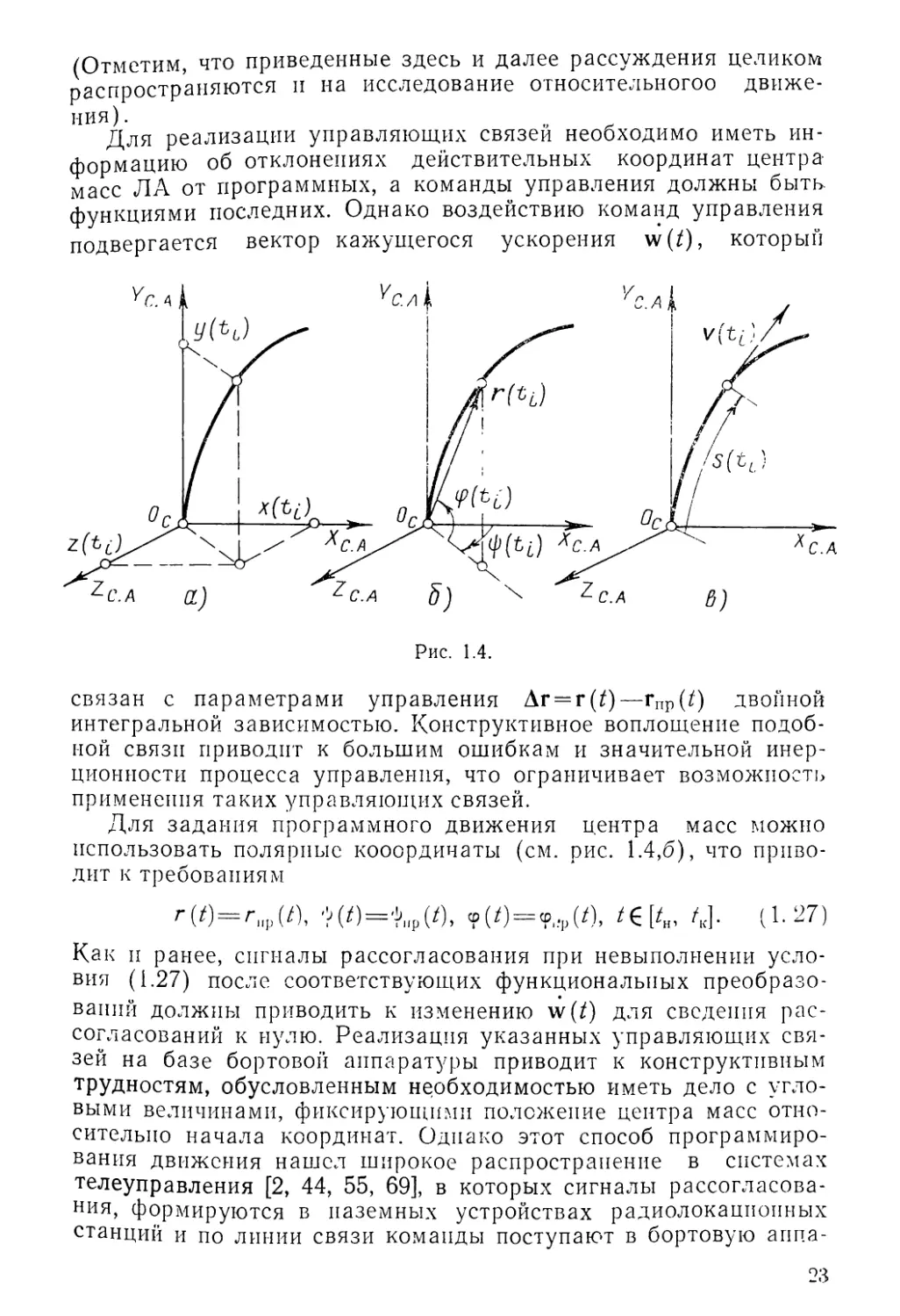
(рис. 1.4,а), где ОДс.а направлена в сторону цели, ОсКс.а сов¬
падает с местной вертикалью, a OcZc.a дополняет систему до
правой. В этой системе программную траекторию можно задать
соотношениями
X=xup{t), у = уар(0, Z = zuf(t),	(1.25)
а для обеспечения движения центра масс по программной тра¬
ектории следует сформировать управляющие связи, которые
обеспечивали бы близость действительных координат програм¬
мным в каждый момент времени:
ГС) = 1\гр(^. ИЛИ
x(t)=xap(t), y(t) = yup(t), z(/) = Ziip(^ t£\tK, g, (1.26)
где /к — момент окончания активного участка.

(Отметим, что приведенные здесь и далее рассуждения целиком
распространяются и на исследование относительногоо движе¬
ния).	u
Для реализации управляющих связей неооходимо иметь ин¬
формацию об отклонениях действительных координат центра
масс ЛА от программных, а команды управления должны быть,
функциями последних. Однако воздействию команд управления
подвергается вектор кажущегося ускорения w (t), который
Рис. 1.4.
связан с параметрами управления Дг = г(£)—гпр(£) двойной
интегральной зависимостью. Конструктивное воплощение подоб¬
ной связи приводит к большим ошибкам и значительной инер¬
ционности процесса управления, что ограничивает возможность
применения таких управляющих связей.
Для задания программного движения центра масс можно
использовать полярные кооордичаты (см. рис. 1.4,6), что приво¬
дит к требованиям
r(t) = rlip(t\ 'Д/)=4,ф(/), ср(/) = ср|ф(Л, /€[*„, А]-	(1-27)
Как и ранее, сигналы рассогласования при невыполнении усло¬
вия (1.27) после соответствующих функциональных преобразо¬
ваний должны приводить к изменению w(f) для сведения рас¬
согласований к нулю. Реализация указанных управляющих свя¬
зей на базе бортовой аппаратуры приводит к конструктивным
трудностям, обусловленным необходимостью иметь дело с угло¬
выми величинами, фиксирующими положение центра масс отно¬
сительно начала координат. Однако этот способ программиро¬
вания движения нашел широкое распространение в системах
телеуправления [2, 44, 55, 69], в которых сигналы рассогласова¬
ния, формируются в наземных устройствах радиолокационных
станций и по линии связи команды поступают в бортовую агша-

ратуру СУ ЛА. Для БР автономные системы, т. е. системы, в
которых вся необходимая для управления информация выраба¬
тывается на борту объекта, имеют ряд преимуществ по сравне¬
нию с радиотехническими [4].
Наконец, возможно использование параметрического способа
задания программной траектории и на этой основе формирова¬
ния управляющих связей. В параметрической форме программ¬
ная траектория имеет вид
Г = Г,гр (5), г (s)=x (s) i + у (s) j + Z (s) k,
или
x=x(s), y = y(s), z=z(s),
t
где	5	=	f	[x2	+	у2 + z2] V2 dt.
Любую гладкую кривую можно интерпретировать как совокуп¬
ность касательных, проведенных через все точки этой кривой,
если последнюю рассматривать как интегральную кривую неко¬
торого дифференциального уравнения с непрерывной правой
частью. Тогда, определив касательную r(/)=v(f) в некоторый
произвольный момент ti^[tn, Т] и зафиксировав точку траекто-.
рии, через которую она проведена, дугой Si = s {U), можно за¬
писать программную траекторию (см. рис. 1.4,в) как
v(0 = v,„(/),	(1.30а)
s(t) = sup(i).	(1.306)
С учетом требований (1.29) очевидно, что для обеспечения
движения центра масс по программной траектории достаточно
качественного выполнения (1.30а).
Последний способ задания программного движения нашел
наиболее широкое распространение для формирования управля¬
ющих связей автономных СУ БР и PH, что обусловлено просто¬
той конструктивной реализации управляющих связей.
Кратко охарактеризуем состав и алгоритмы управляющих
связей при параметрическом способе задания программной тра¬
ектории. Каждая управляющая связь, будь то отдельный авто¬
мат системы управления или в этом принимает участие элек¬
тронная	вычислительная машина (ЭВМ),	реализуется по
принципу	замкнутой	системы управления.	В	состав	управляю¬
щей связи входит один или несколько измерителей, устройство
преобразования и усиления сигналов (эта функция может быть
возложена на ЭВМ) и управляющие органы для прямого или
косвенного воздействия па объект управления.
(1.28)
(1.29)
24

Информацию для управления движением центра масс
в автономной системе доставляют акселерометры, фиксиру¬
ющие величину проекции кажущегося ускорения w(/) на свою
ось чувствительности. Последние для полноты измерений долж¬
ны образовывать некоторый базис (а, |э, у) в инерциальной сис¬
теме отсчета 0АлаУа2а (рис. 1.5), который связан с ней через
матрицу перехода
[A-aKaZJ = B[a, В, у].
Если движение запрограммировано в той же системе, то анало¬
гично преобразуется замеренная информация
[wx, wy, wz\ = Б [wa, тор, Wt\.	(1-31)
Так как при программировании движения используются истин¬
ные параметры, то для формирования управления, вообще гово¬
ря, необходимо решить задачу нави¬
гации: по замеренному кажущемуся
ускорению w(t) определить истинные
параметры движения v(/) и r(t).
Следует отметить, что при форми¬
ровании измерительного базиса обыч¬
но стремятся минимизировать инстру¬
ментальные ошибки акселерометров.
Это достигается изучением их дина¬
мических свойств, свойств стаби¬
лизированного основания, на кото¬
ром они располагаются, и режимов	Рис- 1-5.
полета ЛА.
Для управления боковым движением (в простейшем случае
движение на участке управления происходит в заранее выбран¬
ной плоскости стрельбы) используется информация о боковой
составляющей ускорения vz(t). Движение будет происходить по
программной траектории, если выполнить требование vz(t)~
= ^znP(O' в частном случае у2Пр(/)=0. Для увеличения точнос¬
ти управления целесообразно потребовать z(t)=zuv(t) или
z(t) =гпр(0 =0. Система, реализующая указанные соотноше¬
ния, называется системой бокового управления или боковой
стабилизации, если программные значения равны нулю.
Чтобы обеспечить необходимую ориентацию вектора скорос¬
ти v°(t), |v°(£)| = l, в систему управления должна быть введе¬
на соответствующая информация v°p(^). Тогда при появлении
составляющих вектора скорости, ориентированных по нормали
к программному положению касательной v° система управ¬
ления должна выработать команду на деформацию траектории,
при которой эти составляющие становились бы равными нулю.
Таким образом, в состав СУ должна входить система нормаль¬
ной стабилизации.
25

Указанные две системы обеспечивают при качественном
функционировании требуемую ориентацию вектора скорости.
Для выполнения требования (1.30а) необходимо сформировать
управляющую связь по величине скорости. Система, обеспечи¬
вающая и(0=ипр(0> называется системой регулирования ско¬
рости. (Если управлению подвергается w(t) по информации от
датчиков кажущейся скорости, то соответственно изменяется и
название системы — система регулирования кажущейся скорос¬
ти). Эта система управляет продольным движением объекта и
при наличии рассогласования Av(t) должна оказать воздействие
па двигательную установку объекта.
Системы бокового, нормального и продольного управления
для выработки команд управления используют информацию о
векторе скорости, представленную в виде составляющих по осям
трехгранника, связанного с центром масс и перемещающегося
вдоль программной траектории. Аналогично формируются и не¬
зависимые друг от друга управляющие воздействия. Можно за¬
давать движение, программируя составляющие скорости в инер-
циалыюй системе, однако сформированные команды управления
следует распределять по соответствующим каналам силового
воздействия. Так что в любом случае возникает необходимость
в пересчете информации из системы координат измерителей в
связанную с объектом систему координат, в которой функциони¬
руют управляющие органы. Одновременно следует решать
задачу определения рассогласования программных и действи¬
тельных значений параметров движения, чтобы на этой основе
Еыработать команды управления.
Рассмотренные три управляющие связи воздействуют не¬
посредственно на параметры движения центра масс объекта:
вектор скорости его движения, а значит, и координаты. Однако
при решении задачи качественного управления движением цент¬
ра масс важная роль принадлежит и связям, контролирующим
угловое движение объекта, т. е. его движение относительно цент¬
ра масс.
Физически попятно, что для отработки команд управления
движения центра масс необходима определенная угловая ориен¬
тация корпуса летательного аппарата, так как основная управ¬
ляющая сила объектов исследуемого класса — сила тяги —
создается реактивным двигателем, перемещения которого отно¬
сительно корпуса, в общем случае, ограничены. Гораздо целесооб¬
разнее ликвидировать действие возмущений в «зародыше» (пока
они еще не привели к боковым и нормальным перегрузкам),
сохраняя требуемое угловое положение объекта. Этого же тре¬
бует и ограниченная конструктивная прочность ЛА: при боль¬
ших перегрузках корпус может деформироваться или даже раз¬
рушиться.
Аналогично дело обстоит с вводом программы в контур
управления: ее можно задавать в виде программного положения
26

вектора скорости, но по указанным причинам это отрицательно
скажется на качестве управления. Рациональнее программиро¬
вать положение продольной оси объекта. Эта задача решается
применением автомата угловой стабилизации, который поддер¬
живает равными программным значения трех угловых координат
(углов тангажа, рыскания и вращения или крена), определяю¬
щих положение объекта относительно центра масс в ннерциаль-
ной системе отсчета.
Рис. 1.6.
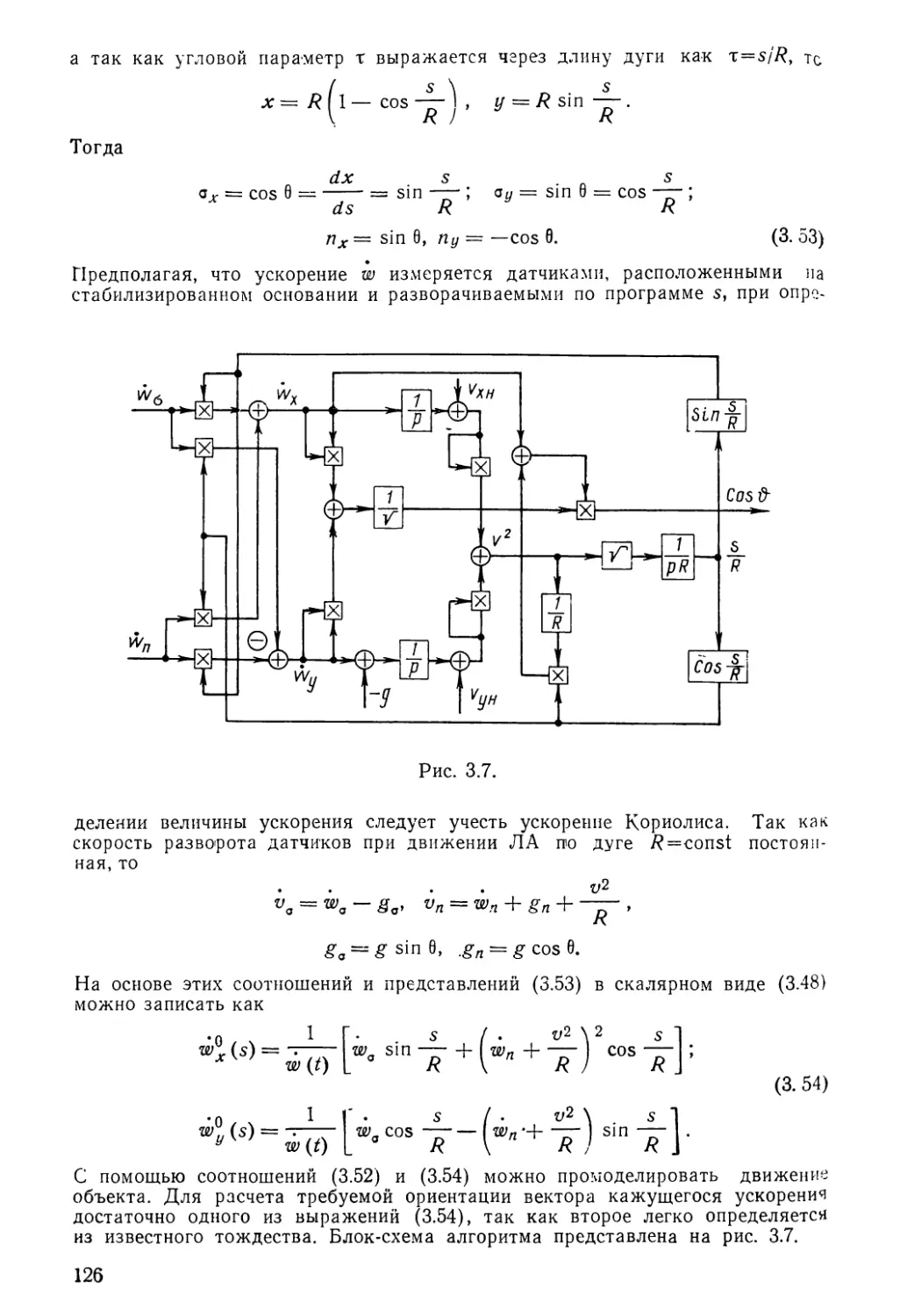
На рис. 1.6 представлена одна из возможных разновиднос¬
тей — упрошенная структурная схема линеаризованной модели
движения объекта в вертикальной плоскости без учета силы,
создаваемой рулевыми органами, и при пренебрежении пзгибны-
ми колебаниями и колебаниями жидкого наполнителя [123].
Обозначения на рисунке: Я*, М*в— привеченные возмущающие си¬
ла и момент;	М*-с—управляющие моменты, создаваемые
командами по каналу тангажа автомата угловой стабилизации
п системой нормальной стабилизации центра масс; $ — угол
тангажа; vn — проекция v(/) на нормаль к траектории; ЯуЛг—-
проекция управляющей силы на нормаль; Кс(р), КлЛр)—пере¬
даточные функции уравнений сил и моментов: С^, Съ-ъ— пере¬
даточные коэффициенты.
Представленная структура дает две возможности ввода
управления в контур: программируется либо vu(t)y либо ft (t).
Предположим, что в первом случае отсутствует угловая стаби¬
лизация, т. е. КАуС(Р)~0. Тогда Мв прямо проникает в траьл
управления движением центра масс и возникает трудность обес¬
печения устойчивости из-за статической неустойчивости объекта
(р) и положительной обратной связи контура, создаваемого
уравнением сил. При введении контура угловой стабилизации
появляется средство борьбы с неустойчивостью из-за Км (р) и
действием Мв{р). Однако если задаться целью полностью ис¬
ключить влияние М*(р) на контур, то это потребовало бы бес¬
конечно увеличить К л у ci что не дает возможности стабилизиро¬
вать движение центра масс. Поэтому в системах управления
программируют угол положения продольной оси ФПр(0> а
^аус(р) выбирают из условия обеспечения качественной стаби¬
27

лизации углового движения и возможности отработки команд
управления движением центра масс.
Момент достижения концевых условий, обеспечивающих тре¬
буемые свойства последующего баллистического движения, фик¬
сирует автомат управления выключением двигателя (управле¬
ние дальностью). Последний вырабатывает команду на выклю¬
чение двигательной установки, а значит, определяет переход к
баллистической фазе движения. По принципу работы этот авто¬
мат следует отнести к классу разомкнутых систем управления,
он оказывает однократное управляющее воздействие на движе¬
ние ЛА.
Итак, система управления представляет собой реализацию
совокупности управляющих связей, функционально необходимых
для: поддержания заданной ориентации объекта относительно
центра масс; стабилизации требуемого положения вектора ско¬
рости; регулирования величины скорости в соответствии с про¬
граммой; выключения двигательной установки в момент дости¬
жения требуемых граничных условий. Система управления мо¬
жет включать и другие управляющие связи, например, обеспе¬
чивающие одновременное израсходование компонентов топлива,
синхронизацию опорожнения топлива, если объект имеет боль¬
шое количество баков с топливом и др.
1.3.	Принципы программирования движения
Если структура объекта управления позволяет наложить на
его движение управляющие связи, которые контролируют изме¬
нение всех параметров движения г(£) и г(/), то наиболее просто
реализуется принцип жесткого программирования. Этот принцип
составляет идея предварительного, до начала движения, состав¬
ления априорной модели движения с разработкой программы
управления. После этого программные значения параметров
движения в виде задания вводятся в контур управления, а на
систему возлагается задача отработки этих программ в реаль¬
ных условиях полета. Функциональная схема реализации жест¬
кой программы показана на рис. 1.7.
Структура управления в этом случае
и(0 = ипр(Я+дя(0,
где unv(t)—программное управление; Au(t) вырабатывается
системой в процессе полета по информации об отклонении пара¬
метров движения от программных значений и направлено на
парирование возмущений и в итоге на стабилизацию параметров
движения относительно программных. Следует отметить, что
«жесткость» программы проявляется в ее зависимости от одного
переменного—времени и отсутствии возможности изменить про¬
грамму в реальных условиях полета, отличающихся от априор¬
ных, принятых при программировании движения. Достоинством
28

этой классической схемы управления движением JIA является
простота технической реализации, при которой все управляющие
связи строятся по схеме систем программного управления или
стабилизации.
При нахождении программы движения принципиально дос¬
таточно на траектории такого сочетания r(t) и r(f), которые бы
при подстановке в качестве начальных условий в уравнения
баллистического движения, например (1.10), в результате по¬
следующего интегрирования привели бы к выполнению задачи
11 программы
Программное устройстбо
Механизм
ббода программы
Устройстбо запомина-
ния программы
К5
Контур отработки программы
Измеритель
рассогласобания
Устройстбо бы радо тки
команд упрабления
Рулебое
устройстбо
Объект
упрабления
Рис. 1.7.
полета, т. е. принадлежали бы концевым условиям. Однако по¬
добный произвол кажущийся, так как выбор программы сущест¬
венно ограничен необходимостью удовлетворения многочислен¬
ным требованиям:	допустимости	перегрузок, эффективности
рулевых органов, ограничениями по тепловому режиму, мини¬
мальным расходом топлива и т. д. С учетом этих соображений
построены сложные методы расчета программы полета, которые
относятся к сфере баллистики [8].
Концепция жесткого управления по своей сути достаточно
ограничена и в ряде практически важных ситуаций применение
ее затруднительно. В качестве примеров рассмотрим ряд слу¬
чаев.
Неполная совокупность управляющих свя¬
зей. Принципиальная особенность реактивных двигателей на
твердом топливе состоит в отсутствии возможности регулировать
тягу двигателя [107]. Тогда задание жесткой программы разворо¬
та в плоскости стрельбы без удовлетворения v(t) ^ vnv(t) при¬
водит к существенным отклонениям действительной траектории
от программной. В силу этого условия полета значительно отли¬
чаются от рассчитанных заранее, что приводит к усложнению
алгоритмов управления и особенно к трудностям определения
момента выключения двигателя.
29

Большие внешние возмущения. Большими следует
называть возмущения, которые не удается скомпенсировать сис¬
темой управления данной структуры, что сказывается на изме¬
нении параметров движения, отличающихся от расчетных на¬
столько, что не может быть принята линеаризованная модель
движения. Одним из характерных примеров является выход из
строя одного из многочисленных двигателей тяжелых PH. Тогда
топлива на борту достаточно для выведения КА, но динамика
движения объекта не будет совпадать с априорной, а значит,
жесткое программирование станет неэффективным.
Отличие начальных условий. Такая ситуация воз¬
никает при старте КА с промежуточной орбиты или решении за¬
дачи посадки, когда не удается точно обеспечить равенство на¬
чальных условий движения программным. Сложность подготов¬
ки к старту PH затрудняет их запуск в заранее рассчитанный
момент времени, а это приводит к изменению относительного
положения небесных тел и точки старта. В этих случаях также
применение предварительно вычисленной временной программы
может привести к недопустимым ошибкам движения.
Рассмотренные примеры можно обобщить и утверждать, что
в том случае, когда мала достоверность априорной информа¬
ции о начальных условиях или условиях полета с высоким
уровнем внешних возмущений, использование жестких программ
становится нецелесообразным.
Более рациональной следует считать систему наведения, в ко¬
торой в той или иной математической форме задается цель
управления (движения), а программа требуемого движения
определяется непосредственно во время полета на основе
информации об условиях движения [154, 159]. При более узком
подходе от системы можно потребовать возможности ввода
коррекций, соответствующих отклонениям условий полета от
программных, рассчитанных заранее. Другими словами, в осно¬
ву формирования алгоритма наведения необходимо положить
принцип самонастройки, дающий возможность соответствующим
образом реагировать на изменение внешних условий.
Принцип управления, при котором программа требуемого
движения определяется во время полета на основе информации
о текущих параметрах движения и цели управления, называют
управлением по свободной программе или принципом свободно¬
го программирования.
Функциональная схема реализации свободной программы
представлена на рис. 1.8. Отличие ее от традиционной заключа¬
ется в наличии дополнительной связи, образующей контур вы¬
работки программы (w° — орт, определяющий ориентацию про¬
дольной оси объекта).
Несомненным достоинством свободного программирования
является высокий уровень формализации задачи, заключаю¬
щийся в том, что для наведения необходимо знать текущие усло¬
30

вия управляемого движения (их можно рассматривать как на¬
чальные для последующего полета), цель управления и совокуп¬
ность ограничений, которым должна удовлетворять траектория.
Столь же велики и недостатки метода, требующего по сути ре¬
шения задачи расчета программы непосредственно во время по¬
лета, используя априорную информацию об условиях движения,
но с экстраполяцией этих условий на меньший интервал време¬
ни: от текущего момента до конца участка управления. Все это
приводит к образованию весьма высоких требований к вычисли¬
телю— но быстродействию, объему памяти, разрядности.
Рис. 1.8.
Предпринималась попытка применить подобный принцип
[158] при разработке системы наведения «Сатурн» (метод на¬
страивающейся траектории»), однако, судя по принятому ва¬
рианту [69, 122, 145], это предложение реализовать не удалось.
Положительные стороны и недостатки полярных принципов
жесткого и свободного программирования движения стимулиро¬
вало большое количество работ, в которых рассмотрены различ¬
ные пути получения промежуточных по своей идеологии алго¬
ритмов, обладающих большей гибкостью по сравнению с «жест¬
ким» управлением и более просто реализуемые, чем метод
свободного программирования. К числу решений, которые в той
или иной мере могут быть использованы в качестве алгоритмов
управления, следует отнести применение градиентного метода
[21, 129], трактовку задачи наведения как проблемы финитного,
терминального управления [77, 99], использование функций вли¬
яния (сопряженной переменной) для синтеза [70, 135, 149, 157]
и различные эвристические подходы [10, 69, 96]. Некоторые из
этих решений будут проанализированы по ходу изложения мате¬
риала.
Существенным недостатком жесткого и свободного програм¬
мирования является представление управления в функции вре¬
мени: u = и (/), т. е. в виде программы управления. Поэтому на¬
рушение априорных условий, для которых рассчитывалась
программа, требует или ее пересчета, или ведет к ошибкам уп¬
равления. Гораздо более рациональным было бы представление
управления в виде закона, т. е. как функции измеренных пара¬
31

метров движения u=u[x (/)]. Подобное соотношение устанавли¬
вает прямую связь между управлением и сигналами от чувстви¬
тельных элементов, легко реализуется и не базируется на экстра¬
поляции условий движения в оставшийся интервал управляемо¬
го полета, а значит, не требует расчета будущего управления.
Однако современные математические методы позволяют найти
закон управления лишь для простейших задач, для которых при¬
менимы методы аналитического конструирования [73].
Для решения задач наведения, где объект имеет сравнитель¬
но развитую структуру, поиск законов управления состоит в раз¬
работке так называемых параметрических программ, представ¬
ляющих по сути зависимость, аналогичную закону управления,
но в значительной мере основанных на эвристическом подходе.
Параметрические программы реализуют принцип гибкого про¬
граммирования.
Использование принципа гибкого программирования приво¬
дит к формированию управляющих связей вида u = u[x(^)], обес¬
печивающих сближение действительной траектории движения
и программной, рассчитанной заранее, когда применение жест¬
кого программирования становится нецелесообразным (мала
достоверность априорной информации, необходимой для реали¬
зации последнего принципа).
Из рассмотренных трех принципов программирования дви¬
жения в задачах наведения ниже будут исследоваться два
последних: принцип свободного и гибкого программирования.
Расчет программы требуемого движения принадлежит области
теории полета и баллистики, поэтому не относится к тематике
данной книги (будем предполагать программное движение из¬
вестным). Стабилизация движения ЛА относительно програм¬
много, если выполняются все необходимые допущения, традици-
онна и успешно решается методами классической теории авто¬
матического управления.
1.4.	Критерии оптимальности.
Граничные условия
При разработке любой системы управления, в частности сис¬
темы наведения, естественно стремление сделать ее наилучшей
в каком-либо смысле, т. е. оптимальной. Создание оптимальной
(или близкой к ней) системы подразумевает синтез такой систе¬
мы, в процессе функционирования которой обеспечивалось бы
экстремальное значение некоторого показателя качества работы
этой системы, критерия. Критерий должен отражать основное
назначение системы и характеризовать эффективность выполне¬
ния поставленных перед ней задач. Чем полнее критерий описы¬
вает назначение системы, тем выше его практическая ценность.
Однако далеко не во всех случаях удается математически сфор¬
мулировать указанные требования.
32

Для сложных систем с большим количеством разнородных
критериев в качестве показателя часто принимают какую-либо
основную характеристику и синтезируют систему, добиваясь эк¬
стремального значения этой характеристики. Разработанную
систему проверяют с целью определения остальных показателей
качества и при необходимости корректируют характеристики
системы для удовлетворения требований, предъявляемых к дру¬
гим показателям.
Эффективность систе¬
мы характеризуется неко¬
торым числовым показа¬
телем /, который требует¬
ся в результате синтеза
обратить в минимум или
максимум.
С позиций общей по¬
становки задачи в про¬
странстве X (1.2) зада¬
ется непрерывный функционал f, который определен на движе¬
ниях системы и порождает функционал /, определяемый для
ugU как
f(/4i) = /(u),	(1.32)
а в качестве оптимального и0Пт^И применяется управление,
удовлетворяющее
/(uonT)=extr/(u).
ueu
Процесс синтеза иллюстрируется рис. 1.9. Определяя реак¬
цию системы на совокупность начальных условий и внешних
возмущений, находим значение выбранного критерия. По из¬
вестному значению I в соответствии с методом оптимизации
осуществляется направленное воздействие на систему (ее дина¬
мические характеристики, структуру, параметры), которое дол¬
жно привести к достижению экстремума критерия.
Из рисунка видно, что / зависит от двух видов факторов:
— от заданных характеристик системы, не подвергающихся
оптимизации, которые будем описывать вектором a={ai, ct2,...};
— от вектора управления u={ab и2,..., иг}. Векторы и и a
могут быть как функциями, так и числами:
/=/(и, а).	(1.33)
Вообще говоря, J зависит от начального состояния объекта хн
и от входной информации (в том числе и от внешних возмуще¬
ний), но этот факт обычно в критерии не находит отражения,
так как система должна функционировать в целом диапазоне
условий.
Воздейстдие
Процедура
синтеза
Входная
	э
информа¬
ция
Синтезируемая
Выходные
<Рарпироданцр\
система
параметры
критерия j
Рис. 1.9.
2	3953
33

В процессе синтеза системы требуется достигнуть, например,
•Лип = max/(и, «)=/(иапт, «).	(1.34)
1	иеи
Следует отметить, что, как правило, существующие методы
нахождения экстремумов позволяют найти один экстремум в об¬
ласти U. Если в этой области имеется несколько экстремумов
(многоэкстремальиая задача), то определение глобального (на¬
пример, наибольшего из нескольких максимумов) — проблема
сложная, непреодолимая без существенного усложнения вычис¬
лений.
Ранее указывалось, что для сложных систем существует це¬
лая совокупность характеристик /г-, i= 1, 2,..., описывающих ка¬
чество их работы. Например, J\ — точность работы системы;
/2 — стоимость разработки, изготовления и эксплуатации; /з—
надежность и т. д. Зная величины этих показателей, можно со¬
ставить полное представление о системе. Однако для синтеза,
объективной оценки и сравнения систем необходимо иметь еди¬
ный показатель. Объединить отдельные показатели в единый
обобщенный критерий можно следующим образом:
1) строится обобщенный критерий в виде аддитивной формы
/=2/Л,	(1.35)
i
представляющий наиболее простую математическую структуру,
однако возникает задача задания весовых коэффициентов сг-;
2) можно выделить какой-нибудь основной показатель, на¬
пример /ь и в результате синтеза обеспечивать его экстремаль¬
ное значение, а на остальные наложить ограничения
(1.36)
где величина в правых частях обусловлена техническим зада¬
нием;
3) еслц в системе имеются случайные процессы, то за обоб¬
щенный критерий можно принять вероятность Р удовлетворения
всем техническим требованиям:
/ = P[/l^/Tp; J2	^2тр’ ^З^^Зтр» •••]•	(1.37)
По приведенным способам формирования обобщенного кри¬
терия следует сделать ряд замечаний.
1.' Попытка с единых позиций оценить систему всегда имеет
элемент субъективизма, который проявляется либо при назначе¬
нии весовых коэффициентов, либо при задании требуемых гра¬
ничных значений отдельных показателей. Чтобы уменьшить не¬
определенность, необходимо хорошо представлять условия
работы будущей системы и перспективы развития техники.
Иначе,, если требования будут завышены, их не удается удов¬
34'

летворить вообще или только после длительной проработки сис¬
темы Если требования низкие, то возникает вопрос об актуаль¬
ности создания такой системы.
2 Использовать единый критерий при разработке системы
удается далеко не всегда. Причина заключается в отсутствии
однозначной зависимости частных показателей от искомой вели¬
чины—оптимального управления. Действительно, трудно анали¬
тически описать влияние управления, например, на надежность
системы, ее весовые или габаритные характеристики, так как
прямая связь между ними или не просматривается, или ее мож¬
но установить только после изготовления макета.
3. При использовании обобщенного критерия возникает опас¬
ность компенсации положительных свойств системы отрицатель¬
ными ввиду того, что частные критерии имеют алгебраический
характер: положительные характеризуют свойства системы, ко¬
торые целесообразно увеличивать, а отрицательные — умень¬
шать. Тогда максимизация может быть проведена, например,
созданием системы с низкими показателями точности, но высо¬
кой надежностью. Это вынуждает контролировать тенденции
изменения отдельных составляющих критерия в процессе
синтеза.
В силу указанных причин при технической разработке сис¬
тем наведения обычно используют простые критерии, включаю¬
щие лишь основное требование к системе. Следует указать на
перспективность синтеза по обобщенным критериям, основы те¬
ории которого в настоящее время только закладываются [34, 124].
Одним из основных признаков классификации критериев
является гипотеза об условиях работы системы, качество работы
которой оценивает принятый показатель. Объективно любая сис¬
тема работает в условиях неопределенности, источником кото¬
рой являются ошибки при математическом описании системы,
постулировании условий ее работы и реализации системы. Одна¬
ко уровни неопределенности могут быть различными. Наихудшим
вариантом, с точки зрения системы, является случай, когда ни¬
чего неизвестно о входной информации и внешних условиях.
Более естественной считается постановка, при которой имеется
некоторая априорная информация о вероятностных характерис¬
тиках полезных сигналов и помех, полученная при эксперимен¬
те или накопленная при изучении аналогичных систем. Наконец,
может быть принята гипотеза о наличии полной информации —
детерминированный случай.
Детерминированный подход нашел широкое распространение
при построении систем наведения ЛА. При синтезе систем наве¬
дения часто исходят из максимального уровня действующих воз¬
мущений, т. е. из детерминистской постановки. Статистические
методы синтеза на современном этапе не дают возможности ре¬
шить в полном объеме задачу наведения; это более подробно
будет пояснено далее.
2*
35

Итак, для класса детерминированных систем распространен¬
ным критерием является соотношение вида
Л(и, хн, /н, Т\=К(хк, n+J ^[х(4 U(/), t\dt. (1.38)
'н
Достоинство критерия состоит в том, что он характеризует не
только качество конечного состояния (первое слагаемое), но
и процесс перехода из начального состояния в конечное. Та или
иная оценка акцентируется введением весового коэффициента.
При синтезе можно использовать отдельно каждое из слага¬
емых:
Л[и(/), Хн, /„, 7’]=ЛГ[хк(и, хн, /„, Т), 7'];	(1.39)
Л[ц(/), Хн, /н, л = | £[х(/), и(/), t\dt.	(1.40)
Вид функционала критерия составляет один из признаков
классификации задачи вариационном исчислении: (1.Э8) —за¬
дача Больца; (1.39) —задача Майера; (1.40) —задача Лагран¬
жа.
Наряду с требованием достижения экстремума критерия в
практике синтеза могут встречаться дополнительные ограниче¬
ния вида
т
j 7V[x(0, u(*), i\ const,	(1-41)
например, ограничение количества топлива, которое может быть
затрачено на маневрирование. Иногда требование типа (1.41)
называют дисциплинирующим критерием, а вариационную за¬
дачу, содержащую .подобное условие, относят к классу изопери¬
метр ических.
Если система предназначена для определенных математиче¬
ских преобразований над входным сигналом, например, следя¬
щая система или система стабилизации, то мерой качества ее
работы может служить интегральная оценка
[I	)1/р
Л=|| |A(/)|^/j .	(1.42)
где р — целые числа; р^1; A(t) — вектор ошибки системы как
разность между требуемымм и действительным выходными сиг¬
налами.
Более подробно критерии качества исследования систем ав¬
томатического регулирования изложены в работе [12]. В моно¬
графии [36] рассмотрены показатели, характеризующие каче-
36

ство процесса управления движением КА, снабженных двигате¬
лями малой тяги.
В статистической постановке, когда функция А (г)—стацио¬
нарный случайный процесс, удобной и наиболее простой мерой
оценки качества системы может служить величина средней
квадратичной ошибки
( Т )1/2
/Б=11т|^ А2(^)Л| = »[Д(*)].	(1.43)
При оценке систем управления важно не только иметь све¬
дения о возможных разбросах выходной ошибки, мерилом чего
является а, но и о величине математического ожидания. Поэто¬
му большей общностью обладает критерий, представляющий не¬
которую функцию а и математического ожидания Л4[Д(£)]:
/,=5(Л4[А(*)], *[Д(*)]).	(1.44)
В частном случае из выражения (1.44) следует (распростра¬
ненный критерий, определяющий вероятность невыхода ошибки
за фиксированные границы допуска, если ошибка распределена
по нормальному закону (D — дисперсия):
Сч
J,=P(Cl<| д I <г2)=(2я£2)-1/2 jexp[-(л1~д)2~ rfA. (1.45)
Ci
Для оценки качества нелинейных и нестационарных систем
используются непосредственно (результаты наблюдения за пове¬
дением выходных координат. Кроме математического ожидания
и кор/реляционных функций, критерием в этом случае служат
моменты высших порядков:
*2, .... *п)=М[У(а К (*„)] =
оо оо
= J — j У1У2-Уп/п(Уи У г, —, y„)dyidy2...dyn, (1.46)
— ОО —ОО
п_мерная плотность вероятности случайной функции
Применение более общих критериев, основанных на введении
функции потерь (ом., например, [92]), при синтезе оптимального
управления в задаче наведения связано с большими математи¬
ческими и вычислительными трудностями, а поэтому не находит
широкого распространения.
Следует особо отметить класс задач ,по исследованию кон¬
фликтных ситуаций, возникающих при анализе наведения объ-
37

ектов ic противоположными интересами [30, 58, 60]. Мерой каче¬
ства управления в этом случае служит минимаксный показатель
y8 = min max/8(u, v),	(1-47)
V	u
где Js— величина выбранного показателя, зависящая от приме¬
ненной каждым из соперников стратегий поведения и(£) и v(^).
Сделаем два замечания относительно математической структу¬
ры приведенных показателей качества.
1. Критерии в задачах теории наведения, как правило^ пред¬
ставляют собой функционалы. Однако возможны случаи, в кото¬
рых управление характеризуется как совокупность констант,,
целенаправленный выбор которых и доставляет критерию экст¬
ремум. Примером этого может служить система с известной
структурой, когда в процессе -синтеза следует найти ряд неиз¬
вестных параметров этой структуры. Тогда в качестве показате¬
ля выступает критериальная функция, заданная в некоторой до¬
пустимой области изменения своих аргументов — параметров
системы.
2. С точки зрения оптимизации наибольший интерес пред¬
ставляют показатели, записанные в квадратичной форме. При¬
мером может служить второй центральный момент ошибки си¬
стемы или выражение
y9= f W*[M{t), x{t)\dt,
U72=xrAx + xrBu-{-urBx-f urCu,	(1.48)
где А, В, С — положительно определенные матрицы соответст¬
вующих размерностей, а индекс «Г» означает применение опе¬
рации транспонирования.
Для того чтобы оценка свойств системы была объективной,
мерой чего является критерий, любая форма его-записи должна
содержать в себе информацию не только об изменении управле¬
ния на интервале регулирования, но и о конечном и начальном
состоянии системы. В системах наведения используются различ¬
ные способы задания граничных состояний системы в зависимо¬
сти от конкретной физической сущности задачи.
Простейший способ заключается в фиксации граничных ус¬
ловий— задача с закрепленными концами. К такому случаю
можно свести задачу стрельбы БР, когда задаются координаты
точек старта и цели, или управление движением PH при опреде¬
ленных параметрах конца участка выведения.
К числу простейших относится также вариант, когда допу¬
скается произвольное положение объекта в момент окончания
управления tK (задача со свободным правым концом). При этом
выделяют случай фиксированной длительности участка управ-
38

ления tK—tn (задача с закрепленным .временем). Последнее ог¬
раничение достаточно естественно: оно существует объективно
ввиду конечного запаса топлива на борту ЛА. Задача со свобод¬
ным правым концом относится к числу модельных и не имеет
практического аналога.
Наиболее общим случаем задания граничных условии явля¬
ются задачи с подвижными концами (левым, если допускается
вариация начальных	условий, и правым, если	ограничения на¬
ложены на конечные	условия движения). Физически	это	означа¬
ет, что граничное состояние системы определено с точностью до
выполнения некоторых соотношений, называемых граничными
условиями, например
SH[x(4), *J = 0,	(1.49а)
5к(хк, у = 0.	(1.496)
В рамках удовлетворения этих уравнений допустимо любое
начальное или (конечное состояние системы. Например:
если известно, что имеется (подвижный комплекс, который
может произвести запуск БР с любой тонки определенного уча¬
стка поверхности, то уравнение '.поверхности можно трактовать
как граничные условия, наложенные на левый конец;
так как каждой наземной цели соответствует бесконечное
множество попадающих траекторий, то математическое описа¬
ние -параметров движения центра масс в момент окончания ак¬
тивного участка, охватывающее все попадающие траектории,
составляет граничное условие, наложенное на правый конец.
Таким образом, задачу с фиксированными концами (опреде¬
лены точки старта и цели) можно трансформировать в задачу с
подвижным правым концом. Такое преобразование становится
допустимым, если ввести промежуточный этап—конец активно¬
го участка — и применительно к этому моменту математически
формализовать множество попадающих траекторий.
Следует особо оговорить, что граничных условий может быть
несколько. Если их число равно числу параметров, полностью
описывающих движение, и уравнения типа (1.49), задающие эти
условия, имеют совместное решение, то «подвижность» конца
пропадает. Более наглядно это будет показано в следующем
разделе.
1.5.	Геометрическая интерпретация задачи
наведения
Требование наглядности математических результатов всегда
бьгло и остается весьма важным, особенно для последующего
практического приложения теории к .конкретным техническим
разработкам. В теории.оптимального управления, наряду с изу¬
чением различных частных случаев и математических примеров,
39

применяется геометрическая интерпретация поведения управля¬
емого объекта с помощью фазового пространства, которое для
дискретных систем часто называют пространством состояний.
Основы такого подхода были заложены при исследовании нели¬
нейных систем и получили дальнейшее распространение в рабо¬
тах А. А. Фельдбаума (114], В. Г. Болтянского [17], Дж. Лейт¬
мана [70].
Фазовое пространство представляет собой я-мерное вектор¬
ное пространство, образованное координатами, полностью опи¬
сывающими движение объекта. Для класса задач, составляю¬
щих теорию наведения, движение объекта управления описы¬
вается векторным дифференциальным уравнением второго
порядка (см. разд. 1.1), поэтому размерность фазового прост¬
ранства равна шести, т. е.
Если же наряду с движением центра масс изучается угловое
движение объекта, то размерность X увеличивается до девяти
(x7=ft) х8=ф, *9=y)> а Учет упругих колебаний корпуса и коле¬
баний жидкого наполнителя приводит к дальнейшему расшире¬
нию пространства на число, равное количеству дополнительных
степеней свободы.
Изменение во времени переменных (1.50) соответствует пе¬
ремещению в X некоторой изображающей точки, фиксируемой
вектором x(/)gX, ,по траектории, называемой фазовой (рис.
1.10). Следует отметить, что фазовая траектория может исхо¬
дить из начала координат или из некоторой х(/н)=хн в зави¬
симости от системы отсчета, используемой для описания дви¬
жения. В дальнейшем для простоты будем рассматривать
только первый вариант, если это не сказывается на строгости
рассуждений.
Рис. 1.10.
Рис. 1.11.
Х= \х1=гх, х2=гу, х3=гг, xt=rx=vx,
xb=ry=vy, X9 = r\ = Vt}.
(1.50)
40

Фазовое (Пространство иногда удобно расширять, включая в
него дополнительные координаты. Так, в (неавтономных систе¬
мах, правая часть которых явно зависит от времени (1.3), в
качестве дополнительной координаты рассматривают независи¬
мое переменное и тем самым система формально становится
автономной. Большую наглядность приобретает задача оптимиза¬
ции, если пространство X дополнить координатой, имеющей раз¬
мерность критерия оптимальности. Тогда проекция векторов
начального и конечного состояния системы на эту ось позволяет
судить о качестве управления (рис. 1.11). Таким образом, в от¬
дельных случаях для иллюстрации задачи наведения бывает
удобно привлекать 8-мерное пространство X**; если в X вклю¬
чается время, то пространства будем обозначать X*.
В соответствии с правилами, векторного исчисления фазовая
скорость движения изображающей точки в X есть вектор х, ори¬
ентированный по касательной к траектории.
Основу геометрической интерпретации задачи наведения сос¬
тавляет возможность наглядного отображения в фазовом прост¬
ранстве граничных условий, так как параметры, полностью оп¬
ределяющие движение центра масс JIA, как раз и являются ко¬
ординатными осями X. Тогда концевое условие, как математиче¬
ское описание совокупности попадающих траекторий, записанное
в виде 5к(хк)=0, можно трактовать как гиперповерхность,
заданную неявной формой. Эта гиперповерхность зависит
от ряда параметров, например, координат цели гц, устанавли¬
вающих соответствие семейства попадающих траекторий с за¬
данной целью; некоторых констант, определяющих заданные
свойства траектории баллистического движения, таких, как вы¬
сота орбиты, размеры апогея или перигея, угловые координаты
и т. д.; фиксированных временных интервалов — длительность
активного участка tK—tHi время достижения какой-либо фикси¬
рованной точки в процессе баллистического движения tB—tH>
где tB—момент встречи, и др. Таким образом, уравнение, задаю¬
щее гиперповерхность концевых условий, может быть записано
как
*sK(xK) q)=o,	(1.51)
где^ q — вектор параметров, доставляющий семейству траекто¬
рий требуемые свойства.
Очевидно, далеко не всегда разнообразные требования, кото¬
рые могут быть сформулированы при постановке задачи наведе¬
ния, удается представить в виде одного уравнения типа (1.51).
Следует ожидать появления в процессе формализации некото¬
рой группы соотношений, каждое из которых определяет одно
или несколько требуемых свойств:
S/K(xK, q) = 0, /= 1, 2, ..., г.	(1.52)
41

Если эти условия не противоречивы, то они образуют в X -систе¬
му пересекающихся гиперповерхностей, а результат их пересе¬
чения есть гиперповерхность размерности п—г. Отсюда ясно,
что в 6-мерном пространстве X не может быть удовлетворено
больше шести условий одновременно.
Для получения единой формы вида (1.51) уравнения (1.52)
можно записать в лагранжевой форме
5к(хк, q)=SlK(xK, q)+2XA+i.K(xK,q)-	(1-53)
/-1
В каждом Si могут присутствовать отдельные составляющие
общего вектора q.
В задачах рассматриваемого класса гиперповерхности 5гк
обычно представляют собой гладкие многообразия: их градиен¬
ты grad SiK линейно незави¬
симы.
Итак, варьируя каким-либо
образом определенную опор¬
ную траекторию, получим мно¬
жество возмущенных траекто¬
рий, которые пусть оканчи¬
ваются на SK. Это означает,,
что данное множество являет¬
ся попадающим. При этом SK
может иметь размерность
меньше размерности X (рис.
1.12).
Один из способов формиро¬
вания множества возмущен¬
ных траекторий состоит в варь¬
ировании управления. Переби¬
рая последовательно все уп¬
равления из допустимой обла¬
сти u(/)gU и строя для каждого из них фазовую траекторию,,
получим указанное множество. При этом можно учесть все огра¬
ничения, наложенные как на управление, так и на характер из¬
менения параметров движения — фазовых координат. Для каж¬
дой из точек фазовой траектории будем вычислять значение
критерия оптимальности
i), У(/2), ..., J{tt\ ..., J{tK\
где tK — пода не определено. Таким образом, получим совокуп¬
ность траекторий для каждого /g[fH, ^к], причем любая точка
траектории отвечает конкретному значению J. В силу непрерыв¬
ной зависимости х(/) и / от измеримого управления, имеющего
•компактное замыкание [98], множество варьированных траекто-
42

оий образуют тело в X. Граничная (поверхность этого тела обра¬
зована множествам векторов х[^-, /(**)], которое при выполнении
a допущений [29], обычно справедливых для большинства за¬
дач наведения, является выпуклым и, замкнутым. Следуя опре¬
делению [114], последнюю гиперповерхность Д)[х(^), /(^)] бу¬
дем называть изофункциональной.
Когда критерий оптимальности есть время (задача быстро¬
действия), Ki представляет собой изохронную поверхность, ог¬
раничивающую множество достижимости фазового простран¬
ства X, т. е. геометрическое место точек, которое может быть до¬
стигнуто изображающей точкой за интервал U—tH.
Итак, принадлежность х(^)е/Сгс=Х свидетельствует о нали¬
чии наилучшего в определенном смысле управления и*(£), обес¬
печивающего движение изображающей точки по данной фазо¬
вой траектории, которая привела к наибольшему расширению
тела в фиксированном направлении. Если бы другое управление
дало приращение телу в том же направлении при
Ли* (^)]=Ли** (^)L то именно эту граничную точку следовало
бы включить в Kit а х[и*(/*), /<] стала бы внутренней точкой
тела.
Варьируя длительность управления ti9 i= 1, 2,..., k, получим
семейство выпуклых, непересекающихся гиперповерхностей Ки
вложенных друг в друга. Наличие точек пересечения х[^,
./(г*)]=х[^, J(tj)] означало бы, что одну и ту же точку фазово¬
го пространства X можно достичь за разное время и с различ¬
ными значения /. Но тогда (пусть ti<c.tj, /(^г) <.J(tj)) возникает
обоснованное недоумение: почему за время бt=tj—U не уда¬
лось достичь некоторого' приращения фазовой траектории 6х=
= х(^)—x(U) с одновременным увеличением показателя опти¬
мальности б J=J(tj)—
Остановимся теперь на выяснении механизма взаимодей¬
ствия изофункциональной поверхности К(t) и гиперповерхности
концевых условий (1.51). Рассмотрим более общий случай, ког¬
да (1.51) явно зависит от времени:
Sk(xk, q, t)=0.	(1.54)
Физически это означает, что для удовлетворения концевых у.с-
ловий не безразличен момент их выполнения. Реально причиной
нестационарности 5К может быть изменение экстраполирован¬
ного (на интервал оставшегося времени полета на активном и
пассивном участках) положения цели в системе координат* в ко¬
торой фиксируются фазовые переменные.
С течением времени	У	гиперповерхность	5К	деформи¬
руется, изменяя свое положение в фазовом пространстве X. Од¬
новременно перемещается в X и изофункциональная гиперпо¬
верхность K(t), причем последнее является в итоге результатом
Действия управления. При правильно организованном наведе¬
43

нии 'расстояние между SK и К начинает уменьшаться, свидетель-
ствуя о приближении значений параметров движения к желае¬
мым (рис. 1.13). Наконец, в какой-то момент у этих двух поверх¬
ностей окажется общая точка. Наличие точки .касания SK и К—
весьма важный фактор, который определяет: 1) существование
оптимальной траектории хОПт(0> а значит, и оптимального уп¬
равления и0цт (0, обеспечивающего выполнение концевых усло¬
вий при экстремальном значении критерия; 2) окончание ак¬
тивного участка (t=tK), так как
именно в этот момент следует пре¬
кратить управление.
Математически условие касания,
гиперповерхностей запишется как
£gradSK(xK, q, ^^gradVC^),
(1.55)
где с — некоторая константа, знак
которой можно установить из ана¬
лиза выпуклости обеих гиперпо¬
верхностей.
Возможен случай, когда увеличе¬
ния размеров гипертела и перемеще¬
ние K{t) прекращаются в неко¬
торый момент, что может быть
обусловлено, например, полным:
выгоранием топлива. Это означает, что поставленная задача
наведения не может быть выполнена при использовании дан¬
ного типа ЛА.
На основе этого качественного анализа легко сформулиро-
вать другую задачу: при заданных характеристиках объекта оп¬
ределить его предельные возможности, например, для PH наи¬
большую высоту круговой орбиты или максимальный разворот
плоскости орбиты КА; для БР — максимальный угол входа в.
плотные слои атмосферы при фиксированной дальности и т. д.
Такая задача решается нахождением предельной изофункци-
ональной поверхности /Спред, отвечающей максимальной дли¬
тельности участка управления при форсированном режиме по¬
лета, и установлением предельных возможностей из анализа SKy
имеющей точку касания с /Спред. И в этом случае условие (1.55)
дает возможность выделить оптимальные х(^) и и(^) из всего
множества допустимых траекторий и управлений.
Понятие гиперповерхности концевых условий 5K(xK, q, t)
можно распространить и на баллистическое движение. Действи¬
тельно, рассматривая совокупность попадающих траекторий при
/е(хк, q, t), можно в каждый момент времени описать геомет¬
рическое место точек фазового пространства X, которое образу¬
ет параметры движения центров масс объектов, движущихся по
Рис. 1.13.
44

указанным траекториям. Это и будет гиперповерхность, задан¬
ная уравнением
S [х(/), q, /]=0, /€[4, У-
Таким образом, в момент t=tK гиперповерхность 5(х, q, t)
отделяется от концевого многообразия 5К (хк, q, t) и переме¬
щается в фазовом пространстве, характеризуя изменение пара¬
метров баллистического движения семейства попадающих
траекторий во времени (рис. 1.14).
Уточним поведение щели в фазовом пространстве X и выте¬
кающую отсюда картину фазового движения по» попадающим
траекториям. В начале предполо¬
жим, что известны положения цели,
не перемещающейся в системе ко¬
ординат, в которой измеряются эле¬
менты фазового движения, т. е. цель
задана вектором Хц={гхц, Гу ц> ^ц}*
Тогда в фазовом пространстве поло¬
жение цели описывается гиперпло¬
скостью, проведенной через хц^Х и
параллельной остальным координат¬
ным осям. Эта гиперплоскость опи¬
сывает целевое многообразие 5Ц, т. е.
характеризует параметры допусти¬
мого движения центра масс JIA в момент встречи с целью.
В данном случае отсутствует ограничение на скорость встречи с
целью.
Если скорость встречи с целью ограничена, например, усло¬
вием ув£='[оВтт, ^втах], то из целевого многообразия выделяется
часть гиперплоскости, удовлетворяющая указанному условию.
Может быть случай, когда 5Ц превращается в точку в X, т. е. на
все фазовые координаты наложены жесткие требования. Приме¬
ром может служить требование встречи двух КА в заданной точ¬
ке пространства с нулевой скоростью (мягкий контакт).
Возможна ситуация, когда координаты цели меняются во
времени, например уточняется экстраполированное положение
Цели (КА, с которым необходимо состыковать управляемый
объект), или цель совершает движение (перемещение наземной
ВДли в инерщиальной системе отсчета в задачах возвращения
КА на Землю или стрельбы БР). Это адекватно перемещению
целевого многообразия в X.
Таким образом, на этапе баллистического движения изменя¬
ется размерность гиперповерхности попадающих траекторий
н?’	от	6—г,	где г—число условий, задающих 5К, до 3
при фиксированных координатах цели или даже до. 1, если фик¬
сирована скорость встречи. Характер деформации показан на
45

В фазовом пространстве может быть дана наглядная геомет¬
рическая трактовка отдельных технических задач, возникающих
при формировании проблемы наведения. Кратко рассмотрим
некоторые из них.
1. Протяженность SK в X не беспредельна. Ее ограничивают,
в первую очередь, энергетические, маневренные, конструктив¬
ные параметры конкретного типа ЛА. При заданных параметрах
границы 5К определяются величинами гц и q. Если варьировать
этими величинами, то диапазону изменения гц и q в X будет
представление о технических возможностях исследуемого типа
ЛА, об «узких местах» системы.
2. В задачах наведения часто возникает потребность в кор¬
рекции движения, ликвидации накопленных ошибок, например
при межпланетных перелетах. Это эквивалентно необходимости
перевести изображающую точку с некоторой 5(х', q', t'), кото¬
рой принадлежит эта точка, на другую 5(х//, q", i"). Предпола¬
гая импульсный характер управляющего воздействия в X, мож¬
но построить гипертело Г, образованное указанными поверхно¬
стями, а боковые грани суть цилиндрические поверхности, об¬
разующие которых параллельны осям x4 = fXy х$ = гу, Xe = rz. Если
управление непрерывно, то в процессе коррекции изменяется
иг(/),а значит, боковые грани не являются цилиндрами. Объем
тела Т при фиксированных гц' и гц" характеризует энергетиче¬
ские затраты на маневрирование. При ограниченных энергоза¬
пасах или наличии других ограничений на управление, очевид¬
но, некоторое множество точек 5(х, q(rn'), t) не может быть
приведено на S(x, q(r//), t).
3. Перемещение гиперповерхности попадающих траекторий
S (х, q, t) отвечает определенной математической -модели дви¬
жения, например кеплеровской теории. При изменении условий
движения нарушается и фазовый портрет, так как изменяется
модель объекта. Если на этапе спуска можно осуществлять уп-
Рис. 1.15.
соответствовать некоторое ги¬
пертело R, внешняя поверх¬
ность которого образована по¬
верхностью 5К, отвечающей
верхнему пределу диапазона,
а внутренняя — нижнему (рис.
1.	15). Поперечные размеры R
также зависят от принятого
метода управления, ошибок на¬
ведения, комплекса действую¬
щих возмущений, так как эти
факторы определяют возмож¬
ность достижения изображаю¬
щей точкой той или иной точки
5KciX. Построение R и изуче¬
ние его позволяет составить
46

павление (коррекцию движения), то это приводит к расширению
области .попадающих траекторий. Размеры деформации зави¬
сят от величины и эффективности управления, а также от мо¬
мента начала маневра tM. При	получается	семей¬
ство выпуклых и замкнутых фазовых подпространств, вложен¬
ных друг ;в друга.
Следует отметить естественную ограниченность иллюстриро¬
вания многомерной задачи в трехмерном пространстве. Этим
объясняется наличие общих объемов, пересечений тел на от¬
дельных рисунках для различных семейств попадающих траек¬
торий. В действительности положение изображающей точки в
X однозначно определяет траекторию баллистического движе¬
ния.
Таким образом, привлечение фазового пространства позво¬
ляет наглядно проиллюстрировать большинство задач теории
наведения и составить не только качественное представление об
их решении, но и получить количественные оценки, имеющие
практическое значение, привлечением численных методов.

ГЛАВА 2
ФОРМАЛИЗАЦИЯ
БАЛЛИСТИЧЕСКОГО ДВИЖЕНИЯ
2.1.	Модели гравитационного поля
Для интегрирования уравнений движения (1.12), (1.14),
(1.17)	или (1.18) необходимо задать конкретный вид потен¬
циала поля тяготения t/[{>(0L являющегося наиболее удобной
для описания движения математической формой представления
закона всемирного тяготения. В общем случае потенциал притя¬
жения некоторого тела Т в декартовой системе координат
OXYZ с началом в произвольно выбранной точке и с неизвест¬
ным направлением осей записывается как
U(x, y,'z)=f \	(2.1)
<Г)
где dm—элемент массы тела; х, у, z — координаты точки, в ко¬
торой определяется потенциал; s — расстояние частицы тела
с массой dm до точки (х, у, z)\ f — постоянная всемирного тяго¬
тения. Интегрирование ведется по всей массе тела.
Величина потенциала, очевидно, зависит от формы тела,
от его внутреннего строения (распределения массы), а также
от положения системы координат относительно тела. Не менее
очевидно, что вычислить (2. 1) в элементарных функциях
в общем случае невозможно. Разработка методов приближен¬
ного представления и вычисления (2.1), изучение свойств
U(q) составляет содержание теории притяжения (см., напри-
мер, [42]).
Изучение поля тяготения Земли, особенно в околоземном
пространстве, когда приходится принимать во внимание ее раз¬
меры,— очень сложная задача, если учитывать сложную форму
этой планеты и неоднородность распределения массы. Одной из
наиболее общих математических форм описания земного потен¬
48

циала тяготения является его представление в виде ряда по
сферическим функциям
оо оо
U(Q, <р, *)=/ У,	cosk\-\-Bnk sin AX],
(2.2)
где
^	2	(n	—	k)\
®k (n + A) I
\ (q')7* (s*n C0S
(T)
(eWCsin^sin^rfm, 8ft=|2’*=0
(« + *>М	(l,	£>0
суть постоянные, зависящие от формы и распределения масс Г;
q, ф, Я — сферические координаты точки, в которой вычис¬
ляется потенциал; переменные со штрихом опреде¬
ляют точку внутри Г;
P£ft)(sincp)—присоединенная функция Лежандра степени п и
порядка А.
Последние выражаются через многочлены Лежандра
P<0)(sin ср):
^*р(°) /sin ф\
pm (sin ср) = (1 — sin2ср)*/2	-	?}-,
п	d	sin	<p*
Я») (sin 9)=—— d"(sin2?-1)n.	(2.3)
nl2n	sin	<рл
Аналогично можно записать разложение U по функциям декар¬
товых координат путем перехода к последним от сферических.
Использование выражений (2.2) и (2.3) для анализа движе¬
ния или синтеза управления сопряжено с большими аналитиче¬
скими и вычислительными трудностями. Поэтому для практи¬
ческого приложения, во-первых, переходят от бесконечных
рядов к конечным и, во-вторых, привлекают ряд гипотез, хорошо
согласующихся с практикой.
Так, предположим, что Земля обладает геометрической и
механической (*в смысле распределения масс) симметрией.
Тогда центр симметрии тела является центром масс, а линии
пересечения плоскостей симметрии совпадают с главными цент¬
ральными осями инерции. Если при этом поместить начало ко¬
ординат в центре масс, а за оси системы координат
^rXTtCYTmCZT,c выбрать главные центральные оси инерции, то [42]
в выражение (2.2) входят только члены разложения с п=2А,
2,...
Другим важным случаем является наличие у тела геометри¬
ческой и механической симметрии относительно оси, т. е. внеш¬
49

няя поверхность тела есть поверхность вращения. Если указан¬
ную ось принять за аппликату, то все коэффициенты Апь,
Bnhy k>0 равны нулю и разложение (2.2) принимает вид
У(*	(2.4,
л-0
При распределении массы симметрично относительно плоско¬
сти, перпендикулярной оси вращения, и соответствующем рас¬
положении системы координат в соотношении (2.4) присутст¬
вуют только четные члены разложения.
Так как принятое описание потенциала тяготения является
аддитивной формой, то в качестве первого приближения (может
быть (принят случай п = 0, & = 0, что соответствует сферической
форме Земли с однородной массой (сферическая модель Земли).
Тогда составляющую
(2.5)
q q q
называют потенциалом основной силы притяжения (М — масса
Земли, д0 — геопостоянная).
В качестве следующего приближения используют эллипсоид
вращения также с равномерно распределенной внутри него мас¬
сой, что приводит к необходимости учета последующих членов
разложения (2.4):
?)=£Л>(р)-Ь^2(6» ?) + ^4(б» ?) + ••• =
=J7+^rT(3sin2tp_1)+irT^5sin4tp-30sin2cp+3)+-.
(2.6)
где ф — геоцентрическая широта в системе OrXr.cYr,cZT,с.
При дальнейшем уточнении потенциала притяжения возни¬
кает дилемма (между увеличением длины ряда (2.6) и перехо¬
дом к более сложной фигуре Земли для учета долготного изме¬
нения потенциала. Простейшей формой учета неравномерного
распределения массы вокруг центра Земли (нарушение осесим-
метричности) является представление потенциала в виде
U(Q, ь X)=^+^^ + C-25)JL(3sin«9-l)+
+ -|-(С — 4)3cos2cpcos2X j,	(2.7)
где А, В, С — соответственно главные центральные моменты
инерпии Земли относительно осей системы 0Дг.сУг.с2г.с'Д — дол¬
гота. Однако в технических исследованиях предпочтение от¬
дается (2.6) и считается, что учет двух (максимум четырех)
50

членов разложения вполне обеспечивает требуемую точность
описания поля тяготения Земли [8, 25, 88, 153].
Применение той или иной модели гравитационного поля за¬
висит от необходимой точности решения задачи, а также от
длительности интервала, на котором интегрируют уравнения
движения: чем больше интервал, там больше накапливаемые
ошибки. Если модель используется для решения задачи навига¬
ции, то определяющим является чувствительность измерителей
параметров движения—для измерителей малой точности неце¬
лесообразно привлекать развитую модель потенциала тяготе¬
ния, также недопустимо и обратное.
В разд. 1.1 указывалось, что ускорение силы притяжения
равно градиенту силовой функции этого поля. В соответствии
с правилами вычисления градиента величина проекции ускоре¬
ния силы притяжения g на некоторое направление, фиксируемое
•ортом с0,
^=^=c?grad£/(c).	(2.8)
Координаты градиента записываются:
в декартовой системе
gradUM=f..+^.j+f-k,	(2.9)
в системе сферических координат
grad£/(p)=-f^ee+-!-^-eT+—1	-f-e,,	(2.10)
дд	q д<?	q	cos <р д\
где i, j, k; eQ, e?9 e* — орты систем координат.
Тогда
g=£ J + gyi+Szk=+g?e?+gxex	(2.11)
и для ряда (2.6) можно записать
gQ=—§—т^3 sin2<p~J)—^гт(35 sin4(p-30 sin2?+3);
(2. 12)
3 sin <р coscp-|—^(120 sin3<p coscp —60 sin cpcoscp);
для разложения (2.7) имеем
gQ =—X_L^ + C-25)-i-(3sin2cp-l) +
-j—^-(C — A) 3 cos2 cp cos 2X j;	(2. 13)
— [A-\-C — 25)3 sin <p cos cp — (C — A ) 3 sin cpcoscp cos 2X|;
gx= —^-(C — Л) 3 cos cp sin 2X.
51

Аналогичные рассуждения можно провести для потенциала
силы тяжести V(q) = U{q) + Уц(о), где Уц(д) —потенциал цент¬
робежной силы, вызванной 'вращением Земли вокруг своей оси.
В прямоугольных геоцентрических координат Кц=-у- (**2 + z2),
а в сферических	2gQ2	cos2	ср, откуда легко определить
дополнительную силу тяжести как поправку к силе притяжения.
Итак, приведенные соотношения дают возможность проин¬
тегрировать уравнения баллистического движения центра масс
ЛА, если зивестны начальные условия и механизм воздействия
на объект аэродинамических сил. Если же дополнительно изве¬
стен и закон управления, то можно рассчитать и активный уча¬
сток траектории. Однако существует и другой путь, позволяю¬
щий в ряде случаев определить параметры движения более
просто. В отличие от «силовой» или ньютоновской схемы послед¬
ний принято называть «энергетической» схемой.
Основы «энергетической» схемы были заложены еще Лейб¬
ницем, который в отличие от Ньютона, фиксирующего действие
силы импульсом, предложил характеризовать действие силы не¬
которым динамическим показателем (живой силой) пропорцио¬
нальной кинетической энергии. В дальнейшем состав этих пока¬
зателей был расширен введением понятия потенциальной энер¬
гии, и механика получила понятия, столь широко используемые
в настоящее время.
Позднее Эйлер и Лагранж сформулировали принцип наи¬
меньшего действия, а Гамильтон и Остроградский расширили
его. Смысл принципа заключается в том, что природой в каче¬
стве траектории выбирается та, для которой минимально «дейст¬
вие»— интеграл по времени от кинетической энергии. На базе
этого принципа формируются теоремы о кинетическом моменте
и энергии.
Применяя последние к исходному уравнению (1.8) и допу¬
ская наличие ньютоновского потенциала (2.5), можно получить
первые интегралы (1.8), которые представляют собой аналити¬
ческие формы характеристик кеплеровых траекторий (совокуп¬
ность первых интегралов составляет общий интеграл уравнений
движения [41]). Далее эти показатели будут широко исполь¬
зоваться.
2.2.	Концевые условия выведения
(кеплеровы движения)
Концевые условия выведения представляют собой математи¬
ческое описание совокупности баллистических траекторий,
удовлетворяющих поставленной задаче полета, например, выве¬
дение ЛА на орбиту с заданными свойствами, спуск с орбиты
и достижение фиксированной точки на поверхности Земли, попа¬
52

дание БР в цель. В общем виде граничные условия представ-
лены уравнением (1.54).
Из разд. 2.1 ясно, что поле притяжения Земли описывается
достаточно сложно, однако ряд обстоятельств позволяет исполь¬
зовать'простую модель (2.5). Во-первых, простота представле¬
ния гравитационного (воздействия дает возможность записать
концевые условия без каких-либо последующих упрощений
в аналитической форме, что представляет известный методиче¬
ский интерес. Во-вторых, такого рода
граничные условия с успехом могут
быть применены для синтеза оптималь¬
ного управления на активном участке
траектории, а для определения момен¬
та выключения двигательной установ¬
ки следует применять более точные
соотношения. Ошибка при использова¬
нии сферической модели Земли для
формирования алгоритма управления
выключением двигателя'при дальности
(6—8)103 км может составить 10—
12 км [88]. Наконец, в-третьих, можно
расширить область применения конце¬
вых условий, .полученных из paccMOi-
рения кеплерова движения, введением	рис	2.1.
аддитивных составляющих, учитываю¬
щих несферичность Земли [87, 152, 153].
Первое концевое условие SiK(xK, q, /к) =0 сформулируем как
требование прохождения баллистической треактории через не¬
которую точку, фиксируемую радиусом-вектором гц в некоторой
инерциальной системе координат.
Из кеплеровой теории известно, что любая траектория или
орбита являются коническим сечением, которое в полярных ко¬
ординатах имеет вид
(2. 14)
1+6 COS & ’
где р — фокальный параметр; е — эксцентриситет; ft— истинная
аномалия отсчитывается от перигея орбиты.
Задача заключается в установлении зависимости на классе
кривых (2. 14) между текущими параметрами движения центра
масс r(£), r(^) = \{t) и точкой гц. Такая зависимость как раз
и является описанием семейства баллистических попадающих
траекторий: если в процессе активного участка управления бу-
Дут достигнуты г (t), г (£), удовлетворяющие искомой зависи¬
мости, то это признак принадлежности данной траектории семей-
ству попадающих при прекращении управляющего воздействия
в этот момент времени.
53

Рассмотрим эллипс (е<\) в некоторой инерциальной гео¬
центрической системе координат ОДг.аУг.а, произвольно ориен¬
тированный в плоскости большого круга; начало системы сов¬
падает с фокусом эллипса (рис. 2.1). Единственным условием,
наложенным на ориентацию и параметры эллипса, является
прохождение его через конец гц, т. е.
1 + е cos (*о 4- <рц)
(2. 15)
а уравнение эллипса в соответствии с введенными обозначе¬
ниями
r(t)=	S.	.	(2.16)
1 + е cos [»0 + f (01
Из выражений (2.15) и (2.16) исключим произвольную вели¬
чину ■до, определяющую положение ОгХт.аУг.а. Тогда соотношение
(2.15) примет вид
г„=
или
e=^l+ecos ^<рц —<p + arccos-£—1
P=ra\	cos(tpu—<р) —е	I —sin(cp„-cp)
(2.17)
Это соотношение представляет зависимость между параметрами
эллипса и заданной точкой гц и, вообще говоря, может рассмат¬
риваться как концевое условие. Подвергнем уравнение (2.17)
некоторым преобразованиям для увеличения физической нагляд¬
ности и удобства применения. Для этого перейдем от канониче¬
ской формы к параметрам движения ЛА.
Используем известные соотношения
Р =—,	,	(2.18)
Яо	Яо
где а — удвоенная скорость, c=rXv;
f*=nl+ho\	(2.19)
где h = v2 —	—интеграл энергии; f — модуль вектора Лап¬
ласа.
Тогда
-11/2
е=|" 1 +-у r2v2 sin2d(v2-2
(2.20)
•54

■и .подстановка .в уравнение (2.17) дает
_i_ r2x>2 sin20=гц ( 1 -f (— rv2 sin2	0— 1)	cos (<рц—<p) —
«0	V \Я0
 — sin (срц— ср) jV2|~ 1-|—l—r2v2 sin20 (v2 — 2я0—^ —
Г r2l/2 sin 2 0	-|2-|1/2|
I я0 Г J J Г
После несложных преобразований с учетом знака для нисходя¬
щей ветви траектории
— r2fo2 sin2 0=гц[ 1 — cos (срц—ср)-]—— rv2	sin	©sin(cpu— ? + ©)]•
Ло	L	л0
(2.21)
Теперь перейдем от сферических координат к декартовым, для
чего запишем ряд очевидных соотношений:
ra=(xl+yl)1/2; г=(л:2+у7/2; t.=(i2 +у2)1/2;
I vXr\=rv sinQ=xy — xy; rv=rv cosQ=xx-\-yy;
lrXra|=rrusin (<fa-<?)=xya-xny;
rr„=rr„ cos (cp„- T)=xxn+yya.	(2.22)
Применив представления (2.22) к (2.21), будем иметь
(ху - ху) [х (у -уа)-у(х- *„)] - я„ Ух2а+У2аХ
+ УУп
X
l/^u + S/u) ix2+V2)
(2.23)
Это соотношение определяет эллиптическую траекторию, прохо¬
дящую через точки (х, у) и (хц, г/ц), иначе представляет собой
неявную форму задания семейства траекторий, у которых
имеется одна общая точка (лтц, уц). Величина отклонения функ¬
ции от нуля может служить мерой ошибки удовлетворения
УСЛОВИЯ Г (tB) = Гц.
В векторной форме первое концевое условие можно пред¬
ставить как
51к=(ГкХГк)[ГкХ(Гк-гц)]-я0гцГ 1—(2.24)
L ГК^Ц J
Отметим, что соотношение (2.24) характеризует все семейство
попадающих траекторий в рамках допущения о гравитационном
воздействии. Рассмотрение плоской задачи естественно, так как
псе баллистические траектории располагаются в плоскости боль¬
55

шого круга, проходящей через гц и центр притяжения. Роль век¬
тора q [см. соотношение (1.54)] в выражении (2.24) выполняет
величина гц. При ликвидации индекса «к» в (2.24) последнее
определяет изменение параметров движения семейства попадаю¬
щих траекторий на интервале [tK, tB].
Однако выполнение условия (2.24) обеспечивает решение
поставленной задачи наведения лишь в том случае, если цель
наведения (гц) сохраняет неизменным свое положение в инер-
циальном пространстве во время баллистического движения
или, совершая собственное движение,
переместится в эту точку. Простейшей яв¬
ляется ситуация, при которой известен за¬
кон перемещения цели гц(0, например,
орбитальное движение или участие цели
в суточном вращении Земли. При этом не¬
обходимо найти траекторию движения це¬
ли и установить ее местоположение в мо¬
мент tB. Если цель расположена на по¬
верхности Земли, то ее премещение за
время полета tB — tK определяется как
(1.11)
Гц(0=А(/в-^гц(£).	(2-25)
Итак, приведенные рассуждения сви¬
детельствуют о необходимости учета ин¬
тервала tB — tH при формировании гра¬
ничных условий наведения, так как SiK = 0 справедливо для
Гц=Гц(^в). Поэтому второе концевое условие представляет собой
неявную форму задания длительности баллистического участка
при известных параметрах конца активного участка и его дли¬
тельности.
Для получения S2K привлечем уравнение Кеплера
я1/2а-з/2y-tB)=E-esinE,	(2. 26)
где а — большая полуось эллипса; tu — время прохождения пе¬
ригея; Е—^эксцентрическая аномалия	(рис.	2.2).	Оно	связы¬
вает время, отсчитываемое от момента прохождения перигея,
с изменением эксцентрической аномалии.
Тогда, зафиксировав положение принадлежащих эллипсу
радиусов векторов гц(*в) и rK = r(fK), можем записать
4— к= {к— к)— {к— О,
а значит,
Еа-sin ЕК).	(2. 27)
Используем уравнение эллиптической орбиты <в виде
a — r=aecosE	(2.28)
56

и учтем, что
а=—?—.	(2.29)
1 — е2	к
Тогда, принимая во внимание величины Ек и из равенства
(2.28) следует
sin£-““[i_(isr!)T' (Z30)
Исключая величину а с помощью подстановки соотношения
(2.29) и учитывая формулы (2.18) и (2.20), после несложных
преобразований с использованием представления (2.30) будем
иметь
e(sin £в—sin £,()=—— (2	«кУ^Х
Я0 \ гк )
X |2jt0r„^l —	— rKt>Ksin20Icy/2-|-rK't»Kcos0Kj .	(2.31)
При получении этого соотношения параметры эллипса выража¬
лись через параметры движения в точке К—гк, vK и 0К. Теперь
нетрудно определить значения эксцентрических аномалий, вос¬
пользовавшись соотношениями (2.30) и применив представления
(2.18), (2.20) и (2.29):
Ек= arcsin ^я§ — (2 -jb- — г£)	sin20Kj_1/2	X
X [2fK-v^rKvKcos 0к}-яо;
6B= — arcsin ^ я2 — ^2 -52.— Пкj r2n2 sin2 0Kj 1/2 X
X (2 ^ -«*)* [2я0гц(1 - I^+rlvl-rlvl sin20K j} . (2.32)
Подстановка выражений (2.31) и (2.32) в соотношение (2.27)
с учетом представлений (2.18), (2.20) и (2.29) дает возмож¬
ность записать уравнение
*.-4= (2	{|2я0гц(l — -^-)+г2п2-г2п2 sin20Kj1/2+
+ rKvK cos 0к| -f Я0 (2 -p. —	[2яв	—	arcsin	X
X {[«J- (2	+2sina0K]-1/2
57

(2.33)
которое представляет собой зависимость длительности пассив¬
ного участка от параметров движения в момент выключения
двигателя rK, vK и координат цели гц(^в), т. е. является вторым
концевым условием. В векторной форме S2K имеет вид
Иногда бывает удобно фиксировать не координаты цели ра¬
диусом-вектором гц, а величину линейной дальности L, которая
представляет собой длину трассы баллистического участка как
проекцию траектории на сферу Земли. Следует помнить, что при
любом из этих способов задания положения цели автоматиче¬
ски определяется плоскость, в которой происходит баллистиче¬
ское движение: она является плоскостью большого круга и про¬
ходит через гк, центр притяжения и гц.
Для кеплеровых движений L находится как
где R3 — радиус сферической Земли; Ф—центральный угол, со¬
ставленный векторами, определяющими начальную и конечную
точки траектории (угловая дальность полета). Обозначим угло¬
вую дальность баллистического движения ФБ (угол между гк
и гц). В работе [95] приведена формула для вычисления этого
угла:
S2K=tB-tK-(2 -SL	1	||2я0гц	(1 -	-г*г£-
- (гк X vKf]1/2+rKvK} + я0(2	[2*о	-
— arcsin
(2.34)
(2. 35)
58

Тогда после очевидных преобразований можно записать
3>j.=2arctg{/w^ sin 0к[2ЯоГц—2гцгкт>2 sin 0К—
\ г“
Если на активном участке отсутствует боковой маневр, т. е.
движение происходит в той же плоскости большого круга, что
и на баллистическом участке, то можно определить полную ли¬
нейную дальность от точки начала движения гн, введя угловую
дальность участка управления ФА:
Тогда в качестве концевого условия можно использовать соот
ношение
где Z.P — требуемая или расчетная дальность.
В качестве составляющих q (1.51) следует рассматривать вели¬
чины Z.P, гц.
Важным показателем наведения, особенно при возвращении
КА из межпланетного или околоземного полета, является угол
входа в плотные слои атмосферы, который также можно интер¬
претировать как концевое условие этапа управления. Восполь¬
зовавшись постоянством секторной скорости (второй закон Кеп¬
лера) , запишем
где индекс «вх» — значение параметра движения в момент
входа, который определяется как достижение центром масс ЛА
плотных слоев атмосферы, высота которых фиксируется вели¬
чиной гвх. Если величина овх не является критичной, то ее можно
исключить подстановкой
Фв=ФА-|-Ф.б, —Я,(ФА + Ф5).
S3K=Lf - R3 [Фл + 2arctg ([гцнк |гк X vk|] [2я0гц- 2гцнк |гк X vj -
-(rK-ra) ^к|гк X vk|] 1 Гctg 0K-j- /ctg2 0К + Гк ■	[2я0гц-
\	'и
\ ц
(2.39)
и окончательно получим
0ax=arcsln |rKrBX vK sin 0K [®*+2я0 ^— J-j J 1/2 j .
59

Концевое условие, наложенное на величину 0ВХ, можно запи¬
сать как	!
-S4k=0bPx- arcsin Jr-1 |rKXvK| [®*+2я„ (“"'“)]-1/2}==a t2'40)
Приведенные концевые условия регламентируют заключи¬
тельный участок баллистического движения вблизи точки
встречи. Однако с помощью
чения, выраженные в форме концевых условий. Например, со¬
отношение (2. 20) можно записать как
Аналогично нетрудно предъявить требования к угловой ориен¬
тации орбиты.
Разумеется, приведенные соотношения не исчерпывают весь
класс задач, которые могут быть поставлены при формулировке
проблемы наведения. Наиболее распространена ситуация, когда
в процессе управления необходимо удовлетворить ряд требова¬
ний таких, как, например, фиксированная ориентация круговой
орбиты заданной высоты; соблюдение режима перегрузок на
этапе спуска и т. д. Следует подчеркнуть, что рассмотренные ус¬
ловия могут применяться как для выведения КА и управления
движением БР, так и в задачах коррекции движения для дефор¬
мации орбит, организации спуска и других. В частных случаях
требуется уточнять понятие цели и применять соответствующие
способы ее фиксации. Учитывая разнообразие возможных конце¬
вых условий, что обусловлено широким диапазоном требований»
v(t)	rK, vK можно придать необходл-
4	мые свойства самой орбите. Из *
'	вестно, что кеплеровское дви-
(	жение определяют шесть неза-
^	висимых произвольных посто¬
янных [41]: долгота восходя¬
щего узла Q, наклонение
орбиты /, угловое расстояние
перицентра от восходящего уз¬
ла со, истинная аномалия Ф и
уже известные р и е( рис. 2.3).
На каждую из этих величин
могут быть наложены ограни-
концевых условий особой орга¬
низацией параметров движения
Рис. 2.3.
1 — X v*>2 (2—— z>2V1/2=0	(2.41)
Jtn V гк к!
ло V ''к
или на базе выражений (2.18)
(2. 42)
£0

предъявляемых к управлению в задаче наведения, очевидно,
нецелесообразно пытаться охватить все возможные случаи. Ана¬
лиз каждой конкретной задачи позволит построить соответству¬
ющие концевые условия. С этой точки зрения, материал парагра¬
фа можно рассматривать как методический.
2.3.	Концевые условия выведения с учетом
нецентральности гравитационного поля
Если анализ поставленной задачи показывает недостаточную
точность описания движения в рамках кеплеровой схемы, то сле¬
дует привлечь более полную модель гравитационного поля.
В дальнейшем в этом параграфе используется представление по¬
тенциала поля притяжения в форме (2.6), ограничившись второй
зональной гармоникой. За¬
дача получения концевых
условий формулируется так
же, как и в разд. 2.2. Кон¬
цевое многообразие харак¬
теризует требования про¬
хождения баллистической
траектории через точку
в инерциальном простран¬
стве (накладываются усло¬
вия на боковое и продоль¬
ное движение) или точку,
участвующую в суточном
вращении Земли (следует
дополнительно учесть время
полета).	Рис. 2.4.
Как указывалось, дви¬
жение материальной точки
может описываться с использованием «силовой» схемы. Тогда
учет возмущающих сил, обусловленных нецентральностью поля,
приводит к уравнениям Клеро — Лапласа. Линеаризация их по¬
зволяет получить лишь в квадратурах отклонения параметров,
вызванные действием возмущающих сил. Примененный ниже
«энергетический» подход позволил выразить указанные откло¬
нения через элементарные функции. Смысл «энергетической»
схемы заключается в введении обобщенных координат в уравне¬
ния, выражающие принцип Даламбера в системе консерватив¬
ных сил, что приводит к уравнениям Лагранжа второго
рода [24].
В качестве исходной системы отсчета, в которой определя¬
ется движение материальной точки, принимается инерциальная
геоцентрическая система координат 0Дг.бУг.б2г.б (рис. 2.4),
связанная с началом пассивного участка. Ось ОгУг.б проходит
через точку К\ ось ОтХт.б лежит в плоскости, проходящей через
61

vK, и направлена в сторону движения; ось OrZr.6 дополняет
систему до правой. Положение материальной точки определяет¬
ся тремя сферическими координатами г, г], £. Угол г] характери¬
зует угловое удаление точки в плоскости ОДг.бУг.б от оси ОгУг.б.
Угол £ фиксирует боковое отклонение точки от плоскости
ОтХг.бУг.б- Принимая в качестве обобщенных координат г, г) и
выразим кинетическую энергию точки через обобщенные ско¬
рости и координаты. Тогда для лагранжиана будем иметь сле¬
дующее выражение:
характеризует потенциал, учитывающий первую степень поляр¬
ного сжатия. Это отклонение значительно меньше основно¬
го ньютоновского потенциала, что позволяет в дальнейшем при¬
нять р в качестве малого параметра.
В соответствии с уравнением Лагранжа 2-го рода необходи¬
мо найти частные производные от функции (2.43) по обобщен¬
ным координатам и обобщенным скоростям. В результате урав¬
нения примут вид:
Эта система обыкновенных дифференциальных уравнений опи¬
сывает движение материальной точки на пассивном участке.
Вообще говоря, система не позволяет строго получить первые
и вторые интегралы. Интегрировать систему можно только чис¬
ленными методами. Однако в настоящее время известно доволь¬
но много различных математических приемов определения приб¬
лиженных решений. Заметим, что правые части дифференциаль¬
ных уравнений линейно зависят от малого параметра. Это позво¬
лит, как увидим, применить метод Пуанкаре.
Для получения аналитического решения проделаем ряд пре¬
образований. Введем переменные и и о:
где [1= — ^- = 0,5413-1(У~3 — безразмерный параметр, который
 si
г3
г
(2.45)
62

и в полученной системе уравнений (2.44) перейдем от незави¬
симой переменной t к независимой переменной г] с помощью ра¬
венства
dt=-^~ .	(2.46)
Оц2
После подстановки выражений (2.45) и (2.46) в уравнения
(2.44) получим
d [ rfS \ ,	.	„	„	6|мх0ЯзИ	.
— о— -j-° sin jcos? =	sin	«р	cos<p;
di\ \ dt\ )	a
— (acos2$)=—6|iJt°^stt sin <f cos <p — ;	(2.47)
d"t[	q	dti
dt _	1
dti o(i)) «2(тi)
Для интегрирования системы необходимо задать шесть началь¬
ных условий, например, для т]=0 задаются ик, —, $к, —, ок,
dt\	di\
tK. Входящие в правые части дифференциальных уравнений
(2.47) величины sin <р, cos<p— и cos<p — преобразуем с помощью
d\	d'fi
соотношения, полученного из элементарного свойства сфериче¬
ского треугольника (см. рис. 2.4):
sin <р= sin £ cos i -f- cos £ sin i sin y,
откуда
cos cp — = cos £ cos i — sin £ sin i sin y;
T dt
<2-48)
COS CD— = cos 5 sin i cosy,
dr\
где i — наклонение орбиты;
у — угловая дальность, отсчитываемая от линии узлов.
Для сохранения единой системы отсчета (от оси ОгУг.б) пред¬
ставим угол у в виде
7=^ + 4,
где г]1—угол, отсчитываемый от линии узлов до оси ОгУг.б, опре¬
деляется из начальных условий.
63

Решение нелинейных дифференциальных уравнений получим,
используя асимптотические методы теории дифференциальных
уравнений. Воспользуемся методом разложения решения в ряды,
расположенные по степеням малого параметра и являющиеся
частным случаем асимптотических рядов Пуанкаре. Будем сле¬
довать методу Ляпунова — Пуанкаре. Представим искомые
функции в виде рядов:
«(л)=21аЧ-(т1)>
J- О
?(Ч)=2	(2.49)
)- о
ОО
•(Л)=2 рЧ(Л)-
}- о
Четвертое уравнение системы (2.47) пока не решается. Его ре¬
шение будет получено в конце параграфа. В общем случае
асимптотическое свойство рядов вида (2.49) состоит в том, что
при (1=0 они описывают движение объекта, обычно называемое
невозмущенным (в нашем случае в центральном гравитацион¬
ном поле). В этом случае |0(г])=0. Фиксируя определенное
количество членов в разложении (2.49), будем решать задачу
с определенной степенью точности, зависящей, естественно, от
величины | (lx |. Можно говорить о приближениях первом, вто¬
ром и т. д. в зависимости от того, сколькими членами ограничи¬
ваются в разложениях. Практически не пользуются более чем
вторым приближением.
Механизм получения соответствующего приближения состоит
в следующем. В правых частях уравнений (2.47) заменяются
тригонометрические функции подстановкой соотношений (2.48),
а вместо аргументов используются их представления (2.49). За¬
тем приравниваются коэффициенты при одинаковых степенях р.
В результате имеем следующую систему уравнений для опреде¬
ления решения нулевого приближения:
d2u0
d-тр
а — —
0 — „2
°0
^=0;
d-q
$о=0
(2.50)
64

(2.51)
и первого приближения
«! = ЗЯ°23“0 [ 1 — 3 sin2 / sin2 (л + Л1)] —
rfV	О0
1	do i	dtiQ e
Og	(IQ	rfl) rfT]
^Y + ?x=—sin 2/ sin (Л + Лх);
dr?	c0
rfCj	ЗЯ0Л3Ц0	•	2 •	•	О Лп	I m
—-=	5—	sin2*	sin 2(л+Лх).
rfT)	C0
Решение нулевого приближения системы (2.50) известно:
Ио=-т- [1 + есо8(л„+Л)];
°о	(2.52)
а0 = const,
где г)п определяется из начальных условий.
Не останавливаясь на способах решения системы линейных
неоднородных дифференциальных уравнений с постоянными ко-1
эффициентами, приведем решение в конечном виде. Заметим, что
интегрирование первого уравнения (2.51) возможно лишь после
того, как будет проинтегрировано третье уравнение. В результа¬
те
■ 1
Их(Л)=Л 2	/Л + &21+1 COS/Л) +
_/-0
"Т2^2/+2 s*n -/'Л-j-&2у+з cos У'Л)1,	(2. 53)
J-1	J
где Л1=_1 ;
«о
6, = 1	— -f- sin 2 /1	- h — cos(2Лх + 2ли) +
+ cos 2л, + е cos (2л, + Лп) + -у- соз (2лх + Л„) —е2 j ;
 1- sin2ij cos л„; b3=e(l ^-sin2/j sin л„;
—{b3+2£e + 3&g- j-401O); ^5= (^1 + ^7+^9 + ^u);
з 3953	65-

~ sin2 /) sin 2Л„+-^- sin2 /^1	sin	2^;
—f"(1 — 'f’sin2/) cos2t1“—rsin2/( *+7^cos 21,1
esin2/ sin (2Лх-|гЛп);
-Й- t> sin2
24
~~^e sin2/cos(2%+Лп);
sin2 / sin (21^ -f 2ti„);
— sin2 / cos (2iii + 2л„);
^ Л' {a2l sin /л+a2l+1 cos /rj) -f
' 1
Мл)=л2
_/-0
2
+2 {a2}+2 sin УЛ+Оу+8 cos /Л)
я	ЗядЛ2	sin	2i
Да= Ц :
a±=e sin (Лх —Л„);
02 = sin Лх!
a3= — cos rjxi
a4= cos Лх -f -усоз^х+ль);
ab=-e sin (ti1_fin)+-|- sin (Лх+Л„);
ae =	1-	cos(,n1 + ri1));
«7= — -J- sin (Лх+Л„);
' 1
«X (Л)=Аь . 2 Л'(сгг sin /Л + %+1 cos/ti) +
J-0
+ 2 ^+2 sin •/tl + ^+3 cos УЛ)!
/-1	J
(2.54)
(2.55)
(2.56)
(2.57)

cx=\cos 2r>i+-§-cos (2t>i+Пв)+cos (2Tii+Tin);
сг=-~ sin (2ть-л„);
са= — cos (2т]4 лп),
с4=-^-sin 2%;	(2.58)
сь= cos 2^;
Сл=—— sin (г^+Лп);
О
С,= ^COS (2tU + 4„),
-Ф
_	sin	фк	• _	1	°омк
где	T|i	=	arcsin —; rin^arccos—
sin i	в	[	Яо
Полученное решение системы уравнений позволяет перейти
к формированию аналитических концевых условий. Предвари¬
тельно определим целевое множество на правом конце баллисти¬
ческой траектории. Как и ранее, будем считать, что задача на¬
ведения успешно решена, если траектория проходит через неко¬
торую точку, фиксированную,# принятой системе отсчета радиу¬
сом- вектором гц:
5к=гц-гп(гк, vK, 4-0=0.	(2.59)
Целесообразно в общем случае в качестве составляющих векто¬
ра Гц принять следующие координаты:
Гц={|гц|, Фтр, Лтр},	(2.60|
где Фтр — требуемая угловая дальность;
^4тр — требуемое угловое боковое отклонение.
Тогда с учетом представления (2.60) векторное концевое соот¬
ношение можно заменить тремя скалярными:
5К |Гц1	|l\i (Гк>	4)| = ^к(Гю VK, Гц, tB	/н)^0,
*^1к= ^тр	® (Гк»	VK, tB	^н)==^1к(Гк> ^к, Гц, tB	^н)==®»	(2.61)
^2к- АТр	A (rK,	vK, tB	tH) 5гк (гк,- vk, гк, tB	^н)=0,
Удовлетворение которым означает выполнение трех условий: пе¬
ресечение траектории движения материальной точки с поверх¬
ностью заданного радиуса на заданном угловом удалении и при
требуемом отклонении.
3*	*	67

Введем инерциальную геоцентрическую систему координат,
в которой зафиксируем гц. Положение ее осей видно из рис. 2.5.
Введение такой системы координат позволит упростить вывод
концевых условий. Учесть перемещение цели за время tB—
можно в абсолютной системе координат, а влияние сил, действу¬
ющих на материальную точку, — в начальных условиях движе¬
ния. Представление гц в виде (2.60) позволяет в дальнейшем
учитывать только два скалярных соотношения (2.61), так как
модуль гц входит в Sik и Sac
Рис. 2.5.
Перейдем к формированию первого концевого условия. Зна¬
чение дальности пассивного участка Ф(гк, vK, гц) представим
в виде дальности, определяемой движением в центральном поле,
и первого приближения отклонения дальности, вызванного уче¬
том нецентральное™ поля
Ф = Ф9 + рФ1.	(2.62)
Для определения (Dj воспользуемся первым уравнением систе¬
мы (2.49) при г)=Ф, ограничившись членом первого приближе¬
ния
и(Ф)=в,(Ф)+1«*1(Ф#)=Яд,	(2.63)
где
Па==~ы'
Подставим в ряд (2.63) выражение (2.62) и разложим левую
часть полученного уравнения в ряд Тейлора относительно Ф0,
ограничившись линейными членами ряда. В результате получим
Фх=иц. (2.64)
6S

g вЬ1ражении (2.64) последний член суммы представляет собой
величину второго порядка — малости, а и0(Фо) ~иц. Учитывая
зТ0? запишем интересующее нас соотношение
Ф1=-
«1 (Фр)
ди0
дт] ф0
Тогда первое концевое условие оудет иметь вид
С	_лч	I	№(Фр)
*^1к Фтр Фк Ф0~Г
(2. 65)
где Фк — дальность управляемого участка.
Опуская ряд преобразований, приведем его в окончательном
виде:
SlK  Фтр
Зр-Яо^з
■arctg
хк
Ук
■ arccos — — и„ — 1) — arccos
е \я0
^-4+
^1 + Wo sin Фо + М>0 C°S Фо+ 2 (^2;+2 sin J®0+hj+3 со$ УФо)
:	  J.
°0 (cos Чп sin Ф0 + sin Т]„ cos Ф0)
=0,
(2. 66)
где коэффициенты Ьи 62... определяются соотношениями (2.54).
В общем случае полученного концевого условия для решения
ряда задач еще недостаточно, так как вектор гц может не лежать
в плоскости, определяемой начальными условиями движения.
Это вызывает необходимость в формировании
второго концевого условия, определяющего
ориентацию плоскости стрельбы. Рассмотрим
плоскость ZOX (рис. 2.6) принятой системы
координат. В момент tH ориентация вектора
гц= {хц, уЦу 2Ц} определяется углом Лтр. В мо¬
мент fK ориентация плоскости пассивного уча¬
стка траектории характеризуется углом Ак.
Для получения второго концевого условия
з аналитическом виде воспользуемся уравне¬
нием прямой в полярных координатах (ом.
рис. 2.6). Тогда в принятых обозначениях
Уравнение прямой КЦ в полярных координа¬
тах будет иметь вид

или, переходя к углам Лк и Лтр, получим
Q =	 .
cos (Лтр—Лк)
С другой стороны, р определяется соотношением
Q=V (*ц—гк?+(•*« -
Приравнивая правые части последних двух соотношений после
ряда несложных преобразований, получим интересующее нас
соотношение в виде
Лт =arccos . . - Zix~7.Zk- [-arctg^""^ .
if (2u	*к)2	*+*	(**ц	*к)2	**ц	*k
Выполнение этого соотношения обеспечивает пересечение балли¬
стической траектории с точкой Ц, если движение в плоскости
ZOX будет происходить по линии КЦ. В действительности, вви¬
ду нецентральности гравитационного поля плоскость траектории
отклонится на угол £, определяемый соотношением (2.55). С уче¬
том сказанного второе концевое условие будет иметь вид
^2к = ^тр — arccos	*чо~*,К	'	so~ ~ arctg
V (*ц — г к)2 + (-Кц — *к)2	-*ц	—	Хк
Зр-Яд/?2 sin 21
ч
ах 4- агФ0 sin Ф0+д3Ф0 cos Ф0+
2
+ 2 («у+«sin У® о+а2;+3 cos /Фо = 0.	(2.67)
1
где аи о,2... определяются соотношением (2.56).
Таким образом, получены концевые условия, при удовлетво¬
рении которым дальнейшее баллистическое движение в нецен¬
тральном гравитационном поле обеспечит пересечение траекто¬
рии с заданным вектором гц.
Концевые условия (2.66) и (2.67) могут быть значительна
упрощены. В. частности, практически без потери точности можно
рекомендовать пренебрежение некоторыми членами в коэффици¬
ентах bi. Можно так же исследовать влияние каждого из чле¬
нов, стоящих под знаком 2. В этом случае необходимо оценить
методическую ошибку, вызванную отбрасыванием того или ино¬
го количества членов.
Для учета эффектов от вращения Земли кратко остановимся
на. определении полного времени полета /в—^н. Представим его
в виде суммы
==
70

Зремя полета на управляемом участке tK считаем известным.
Задача определения времени полета на пассивном участке
.сводится к решению последнего уравнения системы (2.47)
dt-
dri
а (т)) «2 (т))
Это уравнение с разделяющимися переменными будем интегри¬
ровать на отрезке от 0 до Ф, где Ф определяется соотношени¬
ем (2. 62). Тогда
ф^+цф,
t = i d1i
J «(ч)**2^) *
Разложим подынтегральную функцию по степеням малого
параметра р, ограничившись членами 1-го порядка. Тогда
Ф0 + и.Фх
/= Г (	1	р	2“1(1|)	р	31	\dn—
J	у “о (Ч) °о (Ч)	«О l1)) °о(1)) «о (Ч) °о I1)) /
\ [ «о (I) «о (I)
О
Ф0 + ^Ф1 ^
I «ОО))'
фп L
«iQ])
«о (ч) ®о (i)
«о (ч) «о (ч)
«о (ч)
(ч
2ai(4)
»1 (Ч)
о (ч) «О (ч)
«О (ч) °о (ч)
dr\. (2.68)
Разложив последний интеграл в ряд и сохранив только члены
первого порядка, получим
Ф0+^ф1
' '	1	-I»,
ф.
«о
«L
4-
J
О (ч) °о (ч)
1
«О (ч) °о (ч)
1
«О (ч) °о (ч)
(Ч)
°1 (ч)
«о (Ч)°0(Ч)
2«1(Ч)
«о(ч)°о(ч)
«1 (л)
■[*
«О (ч) «О (ч)
2«i(4)
“о (Ч) °о (Ч)
а1 (ч)
о (ч) °0 (ч)
«о (ч) °0 (ч)
dr\ =
P®!.	(2.69)
Таким образом, в соответствии с выражениями (2.68) и (2.69)
время движения по эллиптической траектории определяется вы¬
ражением (2.34), а первое приближение соотношением
ix-
“о (ч) °о (Ч)
2ц1(1)	,
*о(ч)°о(ч)	«о(ч)°о(ч)
Щ—\ dx\, (2. 70)
71

№ (Фо) 4
которое можно несколько детализировать:

Яд е sin (Ф0 + In) [I + е cos (Ф0 + дп)]2
 Мз) 4V мз) (2>71)
J t1 + е C0S (‘П+'Пп)]3	Яд J [1 + б cos (Т) + *Г]п)]2
Все величины, входящие в (2.71), известны. Для получения U
в явном виде следует разложить знаменатели подынтегральных
выражений в ряд и ограничиться числом членов, удовлетворяю¬
щих требуемой точности. После некоторых тригонометрических
преобразований интегралы берутся в элементарных функциях.
2.4.	Методика применения концевых условий выведения
Ранее отмечалось, что расширение совокупности концевых
условий приводит к уменьшению размерности граничного много¬
образия SK, если условия совместны. Тем самым накладываются
дополнительные ограничения на область допустимых значений
гк, гк, что иногда существенно усложняет задачу наведения во¬
обще и использование концевых условий в частности.
Характерным примером является задача выведения, когда
целевое многообразие явно зависит от времени, т. е. перемеща¬
ется в фазовом пространстве, образованном параметрами дви¬
жения, измеренными в инерциальной системе координат. Рас¬
смотрим взаимосвязь концевых условий S\K (или 53к) и S2K>
необходимость изучения которой возникает при наведении на
цель, закон перемещения которой в инерциальном пространстве
известен, а ограничения на скорость встречи отсутствуют. Дей¬
ствительно, выполнение условий перехода к баллистическому
движению зависит от положения цели, а последнее, в свою оче¬
редь, связано с длительностью полета,	которая однозначна
определяется параметрами конца активного участка. В общем
виде условия (2.24) можно записать как
SlK=SlK[rK, гк, гц(0]	(2.72)
или для простейшего случая участия цели в суточном вращении
Земли с учетом перехода (2.25)
51к=51к [гк, гк, А(/„-Огц(*„)].	(2. 73)
Второе концевое условие (2.34) можно представить как
S2k=S2k [гк, гк, г„(/в),	(2.74)
Если бы удалось разрешить последнее соотношение относитель¬
но tB:
t.=S£[rK, гк, гц (*„)],	(2.75)
72

t0 задача получения единого концевого условия была бы решена
п0дстановкой (2.75) в (2.73):
SlK=SlK [rK, rK, {A (Sto [гк, гк, гц (*„)]) — 4) гц(/„)],	(2.76)
так как известно именно rn(tH). Однако в явном виде осущест-
вить обратное преобразование (2.75) невозможно, поэтому вмес¬
то использования (2.76) приходится применять итерационное
согласование (2.72) и (2.74). Далее более подробно рассмотрим
сущность этого.
Введем несколько систем координат. Во-первых, определим
систему, связанную с инерциальным базисом, в котором прово¬
дят измерения при помощи бортовых инерциальных датчиков.
Эта система OrXTMYTMZTM имеет начало в центре притяжения,
ОгУг.и проходит через точку старта, ОДг.и параллельна каса¬
тельной к сфере в этой точке и совпадает с направлением поле¬
та, ОДг.и дополняет систему до правой (рис. 2.7). Во-вторых,
введем инерциальную геоцентрическую систему, характеризую¬
щую баллистический этап полета ОДг.бУгДг.б (рис. 2.8): ОДг.б
совпадает с гк; ОДг.б совпадает с плоскостью большого круга,
в которой происходит движение, a OrZr.б дополняет систему до
правой. Если активный участок есть плоская кривая, то ОДг.Дг.и
и ОДг.бУг.б совпадают, а ОгУг.б смещена на угол Фа относитель¬
но ОгУг.и. Связь этих систем определяется простым соотношени¬
ем Дг.б, Уг.б, 2г.б) =ВДг.и, Уг.и, Zr.il)
, ®a = arctg-^ft. (2.77)
г (^н) Г к
cos
Фа '
— sin
Фа
0
в=
sin
Фа
cos
Фа
0
0
0
1
73

Переход от стартовой инерциальной системы OrXT.aYT.nZr.v.
к абсолютной геоцентрической 0TXT.aYr.3ZT.& описывается
(Хтм, YTM, ZTM)=Y{Xuz, Км, Zr<1);
Г=
• sin Аа cos X
— cos Ай sin В0 cos X cos Л0 cos В0
cos В0 cos X
-f sin A0 sin B0 cos X — sin A0 cos B0 — cos Л0 cos X
sin B0 cos B0 sin X
(2. 78),
где 50=фо — геодезическая широта точки старта; Ло — азимут;
Я — широта (см. рис. 2.7).
Условие того, что плоскость баллистического движения есть.
плоскость большого круга, ма¬
тематически можно предста¬
вить как
(г« ХОгц(/.)=0.	(2.79)
На основе этого соотношения
следует в общем случае опре¬
делить ориентацию осей си¬
стемы 0Дг.бУг.б2г.б относитель¬
но ОДг.аУг.а^г.а- Будем считать
заданной ориентацию ортов ia,
ja, ка системы ОДг.аУг.а^г.а
(рис. 2.9). Тогда, считая из¬
вестными Гк, гк, Гц(^в), МОЖНО
определить орты системы
^г-^чг.бУг.б-^г.б как
1б=л’бХкб; 36=—; k6=rL777$^T.	(2.80)
Гк	|гц	(/в)	X	ГК|
Определим взаимное положение систем ОДг. б^г.б2г.б и
ОДг.а^г.а^г.а углами Эйлера:
— угол нутации $=arccos ;
— угол прецессии d>=arccos 2^-; п° = —а-х кб ;
К	t,no	|ка х кб|
— угол чистого вращения <p=arccos .	(2.81)
Тогда переход от OrZr-aKr-aZr<a к OrA'rj5Kr.6Zr 6
есть
(Z,6Kr.6Zr.6)= ДД,аКг.а, ZM).
74

д=
lx т1 пх
1-2 т, л.
(2.82)
/д /Ид «з	/д	SiSg.
m1=s2^,3 — c1c2s3;	«3= — s^;	cx=cos&;	sx = sin &;
^2=52^з + с1с2сз;	ft2=SiC3;	c2=cos4i;	s2 = sin<)i;
m3 —	^’3==^i»	Сз== coscp,	<Sg;— sin cp,
Пусть координаты точки старта и цели определены в связан¬
ной системе координат OrXr,cYrxZr.c. Положение этой системы
.фиксируется в начальный момент времени /=^н, ориентация ее
осей для f>^H сохраняется неизменной и совпадает с ОДг.аУг.а2т.а.
Зная г(^н) и Гц(^н), с помощью (1.11) легко определить положе¬
ние этих радиусов-векторов в любой момент времени.
Дальнейшее решение задачи согласования концевых условий
наталкивается на трудность определения положения системы
■ОДг.бУг.б^г.б, в которой по сути записаны концевые условия. Для
построения последовательного приближения необходимо вос¬
пользоваться гипотезой программного движения первого приб¬
лижения на участке управления. Допустим, что в общем случае
JIA совершает некоторый пространственный маневр на активном
участке, окончание которого определяет положение системы
ОДг.б^г.б^г.б в соответствии с условием (2.79). Тогда становится
известным положение этой системы относительно OrXr.ayr.aZr.a
(2.82) и с учетом заданных свойств маневра находится положе¬
ние системы ОДг.иТг.Дг.и (2.78).
Так как параметры программного движения предполагаются
заданными, то можно найти фазовые координаты J1A в момент
выключения двигателя, например, из условия SlK=0, а затем,
используя (2.34), вычислить tB. После этого с помощью (1.11),
зная Гц(^н), можно определить гц(/в) и сравнить положение
последнего с точкой пересечения траектории со сферой Земли.
При несовпадении координат, очевидно, необходима коррекция
в программном движении, которая может относиться как к из¬
менению маневра относительно плоскости ОгХг.иУг.и, так и де¬
формации траектории в этой плоскости. Коррекция программы,
таким образом, может привести к изменению ориентации плос¬
кости ОДг.бУг.б- Для разработки алгоритма такой процедуры
и обеспечения ее качественной сходимости следует разработать
механизм, реализующий воздействие на многочисленные пара¬
метры управляемого движения в зависимости от отклонения
условий встречи от требуемых. Подобного рода задачу в общей
Постановке формализовать с необходимой степенью детализа¬
ции, очевидно, невозможно.
Существенную помощь при изучении проблемы может ока¬
зать предположение о стабилизации бокового движения J1A.
75

Выполнение этого допущения приводит к совпадению плоское-
тей ОДг.иУг.и и ОДг.бУг.б и означает, что центр масс ЛА может
совершать только плоское движение. Тогда системы OrXT.KYr.KZT,lt
и ОДг.бП.б^г.б оказываются связанными простым соотношением
(2.77) и задача наведения сводится к нахождению программы
движения в плоскости ОДг.Л.и (в баллистике — плоскость
стрельбы), приводящей к одновременному удовлетворению усло¬
вия (2.24) и (2.34).
Определение множества программных траекторий, обеспечи¬
вающих одновременное выполнение концевых условий, по срав¬
нению с предыдущим случаем упрощается. Выбирается некото¬
рое значение tBM и на основании известного гц(^н) находится
Гц(^в), а значит, фиксируется положение системы OvXT^YT^ZT^y
в которой записаны концевые условия. Принимается некоторое
программное управляемое движение и параметры гк, гк отыски¬
ваются из интегрирования траектории активного участка при
SiK=0. При их подстановке в S2K=0 вычисляется /в(2) и весь
процесс повторяется. Сходимость процедуры может быть улуч¬
шена привлечением специальных приемов, например, формиро¬
вания градиента в пространстве параметров, определяющих
ориентацию ОДг.б^г.б^г.б (А0) и траекторию управляемого дви¬
жения.
В заключение параграфа сделаем несколько замечаний.
1. Задача согласования концевых условий вылилась, как и
следовало ожидать, в определение допустимых гк, гк. В отличие
от модельных постановок при рассмотрении частных концевых
условий возникла необходимость в расширении схемы до про¬
странственной и привлечении программного движения на актив¬
ном участке с известными свойствами. Последнее является прин¬
ципиальным, так как в общем случае удовлетворение первому
концевому условию вовсе не означает одновременного выполне¬
ния второго.
2. Явно просматриваются два средства обеспечения одновре¬
менного прихода в точку встречи ЛА и цели: выбором соответ¬
ствующей плоскости стрельбы (или плоскости прицеливания)
или маневром в плоскости стрельбы при фиксации последней-
Этот вопрос еще будет обсуждаться позднее.
3. При совпадении плоскостей ОДг.и^г.и и ОДг.б^г.б (стаби¬
лизация движения относительно этих плоскостей) можно исклю¬
чить зависимость Д от гк, гк построением матрицы
(ХтЛ, К,б) Zr.6)=E(Zr.aKr.aZr.a)
с помощью изменения (2.80):
(2. 83)
при сохранении (2.8U) и (2.32)
76

2.	5. Уравнения относительного движения
в абсолютной системе координат
В предыдущих параграфах этой главы изучалось баллисти¬
ческое движение одного объекта в гравитационном поле Земли.
Теперь перейдем к рассмотрению специфичной задачи исследо¬
вания относительного движения двух КА, обращающихся по
орбитам.
В разд. 1.1 приведены уравнения относительного движения
в геоцентрической, системе ОДг.аУг.а£г.а (1-17) и подвижной сис¬
теме координат OcXcYcZc (1.18). Остановимся на более деталь¬
ном описании первого случая.
Предварительно отметим, что при исследовании относитель¬
ного движения объектов, как правило, можно использовать более
грубую модель поля притяжения, чем при изучении движения
одного баллистического объекта. Это объясняется тем, что на
относительное движение влияет лишь разность действия поля на
оба объекта. Если же расстояние между объектами (разность
высот) мало и исследуемый интервал полета также невелик, то
какой бы сложной ни была принята модель, на относительном
движении это не скажется, а значит, можно рассматривать это
движение как происходящее в бессиловом поле. Такой подход
наблюдается в большинстве работ по исследованию управления
сближением [18, 27, 173 и др.]. Для большинства задач синтеза
оптимального управления при наведении вполне достаточно
представления Земли в виде сферы. Эта гипотеза широко также
применяется при решении технических задач [10, 68, 69, 164].
Уравнение (1.17) для баллистического движения обоих КА
можно записать в виде
v0TH (t) = Aw+g [rx (*), t\ — g [r2 [t)J],	(2.84)
где Aw — вектор кажущегося ускорения, обусловленного возму¬
щениями (отклонением формы Земли от принятой модели, воз¬
действием атмосферы, Солнца и др.). Принимая в качестве по¬
тенциала силы притяжения представление (2.5), получим выра¬
жение для гравитационной составляющей относительной ско¬
рости:
Г? (О г°(0
r*(0	r\(t)
АV (0= 5 (g [ri(0]-g[rs(011^= —я0 \
Га(0=Гг(0г1(0, r2(t)=r°2(t)r2{t), |r°|=l.
dt, (2.85)
Для интегрирования последнего следует раскрыть зависимость
радиуса-вектора, определяющего положение КА, от времени.
К сожалению, в конечном виде такую связь установить невоз-
77

можно; она выражается лишь через систему трансцендентных
уравнений.
Действительно, изменение радиуса-вектора в рамках эллип¬
тической теории характеризуется соотношением (2.14). Для того
чтобы получить уравне¬
ние связи между истин¬
ной аномалией и време¬
нем, следует уравнение
(2.26) дополнить соотно¬
шением [41]
Рис. 2.10.
*-НЙ)‘М.
(2. 86)
т. е. связь между i и #
выражается через экс¬
центрическую анома¬
лию Е.
Характер изменения ориентации г(/), который определяется
4>ртом г°(£), выражается в системе ортов, связанных с орбитой
(рис. 2.10), f°, т|°,
аде	>г°=г$т;, f=-я0—+ (vX с),	(2.87)
/	\с Х/|	Г
f — вектор Лапласа [41] и r(t) перемещается от f° к г\° по крат¬
чайшему пути при движении точки по орбите. Тогда
г° (/) = f° cos 0 -f rj° sin ft
(2. 88)
или окончательно с учетом соотношений (2.18) и (2.20) можно
представить изменение радиуса-вектора как функцию от истин¬
ной аномалии и начальных условий
г(Ъ)=г*(&)/■(&)=
(гн X Ун)2 (1° COS ft 4- *J° sin ft)
Ло 4" [я? + (гн х VH)2 (vl—2 "j 1 cos ft
(2. 89)
Система (2.26), (2.86) и (2.89) дает возможность проинтегриро¬
вать (2.85) и получить изменение во времени относительной
скорости, обусловленной неодинаковым действием поля притя¬
жения на оба объекта. Трудность решения такой задачи очевид¬
на, особенно если учесть, что все уравнения, кроме (2.85), необ¬
ходимо решать дважды для каждого объекта.
Естественньщ рпороб преодоления подобной трудности за¬
ключается в поисках приближенного решения, в частности, раз¬
ложения g[r(/)] в РЯД относительно г2(0» что допустимо ввиду
78

D<^r\, Г2 [25, 144]. Тогда, рассматривая ускорение притяжения
как векторную функцию точки, можно записать
б [fi W]=б [га W+D (0] = б [г* W] + (D grad) grad U [г* (*)] -f
+ -у (D • grad)2 grad U [r2 (■*)].	(2. 90)
Удерживая два члена разложения после вычисления градиента
для (2.5), будем иметь
бЫО]—бЫ0]=-
Яо
^ Яг
-	2	3
г2 г2
(2.91)
По сравнению с уравнением (2.85) налицо существенное упро¬
щение описания разностного гравитационного воздействия, тем
не менее аналитическое решение уравнения (2.84) при Aw(/)=i
= 0 невозможно. Решение получается достаточно наглядным
при выполнении допущений о малости угла некомпланарности
между обеими орбитами и близости орбиты, относительно кото¬
рой производится разложение в ряд, к круговой.
На основе разложения (2.91) Е. Гильберт [142] и его после¬
дователи разработали математический аппарат анализа относи¬
тельного движения с помощью круговых диаграмм, который
представляет дальнейшее развитие орбитальных годографов
У. Р. Гамильтона. Суть метода заключается в переходе к новым
нормализованным координатам и получении решения на классе
периодических функций. Метбд позволяет осуществлять и син¬
тез управляющих воздействий*. обеспечивающих требуемые па¬
раметры орбиты. Особенно наглядным получается решение при
импульсной коррекции, когда не происходят позиционные изме¬
нения.
В настоящее время широкое применение получила формали¬
зация движения в орбитальной системе координат (1.18). В этой
системе компактно записываются уравнения относительного
движения, удобно линеаризуется гравитационное воздействие,
легко переходить к фазовым координатам и, наконец, наглядно
интерпретируются условия наведения как достижение начала
координат. Указанные достоинства нашли свое отражение при
решении большого количества теоретических и технических за¬
дач [72, 96, 136, 137, 148]. Более того, осуществленные советские
и американские проекты сближающихся КА основаны на исполь¬
зовании именно этой системы координат. Вывод и анализ урав¬
нений движения в орбитальной системе координат можно найти
в [10, 69, 96].
Как отмечалось ранее, выбор той или иной системы коорди¬
нат должен быть взаимосвязан с системой измерителей. В про¬
тивном случае можно ожидать появления весьма развитого ки¬
нематического оператора (1.7) и усложнения алгоритма обра¬
79

ботки информации. С этой точки зрения орбитальная система
координат удобна, если измерители расположены на объекте,
совершающем орбитальное движение; система управления этого
объекта вырабатывает команды на маневрирование, передаю¬
щиеся по радиолинии связи на сближаемый КА. Однако возмож¬
но исходить из расположения измерителей на маневрирующем
КА, бортовая система которого формирует команды управления
на основе наблюдения за объектом, обращающимся по орбите.
Такой подход встречается в ряде работ [50, 165] и в настоящее
время отмечается усиление тенденции выбора системы коорди¬
нат не только с точки зрения простоты анализа относительного
движения, но и с учетом построения алгоритмов управления
[33, 100, 108]. В принципе сформулированную задачу можно ре¬
шать и в орбитальной системе, но при этом существенно-услож¬
нится алгоритм управления, в который войдут угловые коорди¬
наты ввиду необходимости перехода от орбитальной системы к
геоцентрической и далее к системе координат измерителей.
Следует отметить, что формализацию движения на базе
уравнения (2.85) удобно применять при использовании инфор¬
мации от наземных станций наблюдения, система координат ко¬
торых простыми соотношениями связана с геоцентрической сис¬
темой.
Обратимся к описанию движения в абсолютной системе ко¬
ординат.
Представим относительную скорость (1.16) в виде
v0thW=Vi„—v2H-f Av(0,	(2.92)
где vH—v2h — вектор разности скоростей 1-го и 2-го КА в неко¬
торое	причем	при/^/н	Vih—v2H=const; Av(/, tn) —поправ¬
ка за счет неодинакового действия поля притяжения — см. (2.85).
Определив относительную скорость таким образом, мы рас¬
сматриваем относительное движение как сумму двух движений:
движения в однородном поле с ViH—v2H=const и движения, обу¬
словленного разным действием поля на объекты.
Подобный подход справедлив и для отдельной точки, обра¬
щающейся по орбите:
v(*)=r(*) = vu(0+v_(0,	(2.93)
где для конкретности vn=const отнесено к моменту прохожде¬
ния перигея, а
t	t
v~{t)=\&\r{t)\dt=-n^±MLdt.	(2.94)
о	о
Обратим внимание на представление секторной скорости в виде
c = rv sin 0=г2— или dt = —db.	(2.95)
dt	с	v	'
80

что дает возможность
dt db
которое можно записать как —=—
Г2 с
представить уравнение (2.94) с подстановкой разложения (2.88)
как
(2.96)
в предположении использования связи (2.26), (2.86).
Выражения (2.93) и (2.96) дают полное представление об
изменении скорости объекта, которое легко иллюстрируется гра-
Рис. 2.12.
фически с помощью годографа (рис. 2.11). Радиус окружности
равен Ло/с. Годограф описывает изменение скорости для любых
орбит. Так, при
е=0, vn=^-\ е< 1, 'Уп<2 — ; е=1, v„=2
Л0 .
Л0
Годограф может найти применение для тех же задач анализа и
синтеза, что и годограф Гильберта.
Если за начальный момент принять t=tu¥= 0, то
v~(^> 4)=“"” [f°(sin fr— sin ftj— yj°(cos fr — cos ®H)],	(2.	97)
с
где 'О’н — истинная аномалия в t=tK. Соответствующий годограф
представлен на рис. 2.12.
Теперь можно записать соотношения для относительного дви¬
жения (2.92). Из уравнений (2.85) и (2.94) следует
Av=Av1^ — Av2_;
81

с использованием (2.97) для обоих объектов можно записать
AV(*. Q-— я„(— [f х (sin — sin &lH) — ^(cos^ — cos&lH)] —
I C\
—J- [fa(sin &2—sin &2h)— vj2(cos&2 — cos»2h)]J , (2.98)
где 'Ог отсчитываются от соответствующего f/° i-и орбиты.
Более общий случай представляется как требование запи¬
сать уравнения относительного движения в системе координат,
орты которой повернуты на угол Фн относительно {f°, ч0}. Также
возможна ситуация, когда параметры движения фиксируются
не в перигее, а в некоторый to¥=tH. Примером может служить
случай измерения с Земли параметров JIA в t=U и необходи¬
мостью анализировать процесс сближения с момента /н. Рис. 2.13
дает представление о взаимном расположении ортов одного объ¬
екта, аналогичная картина будет и для другого. Для этих усло¬
вий опишем характер изменения относительной скорости.
Итак, в t=t0 известны v1(/0)=v10 и v20. В t=tn
Vi(^„)=v10 + Av1(4, t0);
to)= —— [fi(sir. »lH— sin &„) —>ji(cos&lH—cos&0)] (2.99)
С
и аналогично
V2(4) = v20 + Av2(/H) /0).
Система ортов (f2, 4S) связана с (f°, rj0} соотношением
f°=f2 cos &н — rj° sin &н; >20=4н sin &H -f cos &H.	(2.	100)
82

Тогда на основе (2.92) с использованием (2.99) и (2.100) мож¬
но записать
Ду(/, О=я0 f— [f?. sin (&х- &1н)- пЪ (cos (Ь,-&1н)- 1]] -
—i-[f2°„ sin(&2-&2H)-T&{cos(&2-&2H)-l}]} . (2. 101в)
Соотношения (2.101) и (2.99) являются наиболее общими в при¬
нятой схеме формализации. Годограф изменения скорости одно¬
го КА представлен на рис. 2.14.
Другим параметром, описывающим процесс относительного
движения, является вектор дальности D(£). Очевидно,
Начальную дальность можно представить, используя (1.15),
(2.14) и (2.88) в виде
D (0 = DH = fl (П0 + Д COS V)-1 (f? COS »1H+ 1J? sin &lH) -
— Л (я0+/2 cos ^2H)—1 (f° cos &2H + 42 sin &2H).	(2.	103)
DH=с? (я0+Д cos &1н)-г fi„ — cl (n0-)-/2 cos f2H. (2.104)
He повторяя только что проведенных преобразований, сразу за
пишем
При расчете D(/) так же, как и ранее, необходимо привлекать
уравнения связи истинной аномалии с временем.
В заключение параграфа опишем орбитальные движения
обоих КА в единой системе координат. При этом будет следовать
концепции расположения измерителей на борту аппарата с ин¬
дексом «2». Тогда задача сводится к нахождению матрицы пе¬
рехода от {f 1, yji} к {f2, 42} и записи полученных уравнений
в этой системе.
С учетом некомпланарности орбит введем третий орт х°> об¬
разующий с известными правую тройку.
^отн(^>	AV	(/?,	ta)y
v0(4)=viH—v2H=const при />/н;
(2.101а)
(2. 1016)
t
(2. 102)
н
Переходя к ортам {fн, 4°) для каждого из объектов, получим
D W=D (»lt &2)=с? (jto+Д cos ^)-i [f?H cos (^ - &1н)+
+ 41н sin (»х - »1н)] - С2 (я0 + Д cos
х [f2°„ COS (*,-»*)+4* sin (»2-»2H)]-	(2-	105)
S3

На рис. 2.15 показана ориентация орбит обоих КА. Введем мат¬
рицу И как определяющую связь систем {f°, >j°, X0} и {f?, ij?, х?)
и аналогично матрицу К для второго объекта. Оси координат
будем соответственно обозначать ОгХт У? Z\ , ОтХ\т Y\TZ^T и
otxIyIzIt.
Тогда
(*?, У?, Z°r) = U(X°lr, У°1г, Z?r)7	(2.106)
Рис. 2.15.
где И определяется эйлеровскими углами, причем
Ci~cos i, с2—— sin 2,	c3=sinu),
s1==sin/, s2=cos2,	s3=cosu).	(2.107)
Аналогично записывается матрица К. В итоге
(Ч, У°т, Z°T) = ttrK(xi,	У°2г, Zi)	(2.108)
и требуется найти указанную матрицу ИТК = Л.
После ряда преобразований будем иметь
/is
/22
/32
л=
mis
m2 2
ms s
/*is
/*22
/*32
/2Я =/i1>/ia>+mj l)mJa>+«J1>«ia>;
84

ОТИ=/М> + т^тР + пРпР; т3,=	#>	+ тРт|2) +
«H=/J1)/i2) + mi1)mi2) + 41)«i2);
Л8«=/М> + т£М2) + /Л£2),
где верхний индекс означает номер КА, а
/х— — sin (u>-|-0)sin 2 — cos/cos(a)-f-fr)cos2;
/2=sin 2 cos (a) 4-&) — cos/cos 2 sin (u>-(-&);
/3=sin i cos 2,
m^sin (a)4-^)cos2 — cos/cos(a) + ft)sin 2;	(2.	109)
m2= — cos(u)-j-ft) cos 2 — cos i sin (w-f^) sin 2;
m3=sin/sin2; /i1=sin i cos (w-]-&);
n2 = s\n i sin (o)-f- 2); /&3 = cos/.
На этой	основе можно записать основные результаты	этого	па¬
раграфа	в	системе {f2н, Ч2н, Х2н}* Так, используя	формулы
(2Л09), представим соотношения (2.101 в) в виде
Av (t, tH)= - я0 (— sin (»! — »te) + — [cos (ftj - &„) - 1] -
{ С1	С1
 sin (&2 — &2H)j f2°„- Я0 (— sin (&! — &lH) +
C2	)	I Cl
+ — [COS(0-1 — ftlH)— 1]]^2н+Я0	sin (®1—®ih) +
C\	I	[	Cl
, n2Z
.	L[cos(^-&lH)-l] x°2H.	(2.110)
С1	J
В	общем	случае	при	задании	Vio, v2o и /о¥=^н,	определив	форму
V1H=+ Ъц7}1„; v2n=v2fi°2H 4- гзд2„,
вместо (2.101,6) можно записать
vo (A.)= {hiv-if — П\svl7l — v2/) f2„ — {las'Vxf—tlsnV^ + v2J r)2„ +
X2h-	(2.111)
Подвергнув	(2.103)	и (2.105)	аналогичным преобразованиям, по¬
лучим
Dh=IK + /icos&ih)-1 къс\ — (я0 + /2cos &.J-1 c2]f2„ +
+ (n0 + /iCOS&lH)~1^JlCl1l2H— (Яо + /х COS ^J-1/3Sc?X2H; (2. 112)
85

D (/)= {(я0+/х cos ftj-1 cj [In cos — »lH) — tin sin (&x—&1и)] —
— (яо+/a cos &a)-1 & cos (&a — &2h)} *2h —
— {(ло+ficos &x)_1 C1 [^32 COS (&x — &lH) — tin sin — &lH)] +
"Г(Яо ~ /2 cos ^г)—1 COS (^2 — &2„)} ri2il"b
+ {(Яо + fl COS &l)_1 c\ln COS (»! — &lH) — «22 sin — &lH)) X2k-
(2. 113)
Возможен случай, когда положение орбит не фиксируется в
ОДг.а^г.а2г.а, а указывается их относительное положение с по¬
мощью углов Эйлера между
ОД1гУlrZlr и ОДггУ2Д2Г (рис.
2.16). Тогда матрица перехода
упрощается
м ^1г» *1Р,
1 =
Л'(*2Г,
Угг> -^2г)>
^1
т1 п1
II
II
ч
к
т2 «2
(2. 114)
к
т3 «з
и вместо выражений (2.110) и
(2.113) имеем
Av(*, *„)= —я0{— sin (^1 —^i„)+—[cos(»! — »!„)—1] —
( С1	Cl
sin (&2— &2н)) f0
Sin (»!-&!„) [cOS^-ftJ- 1] +
C2 J	I	Cl	Сi
cos (S2- Э2н) j ^
C2
2°„-Я0 Sin {bt- K)-^ [COS (&!-»!„)- 1]) X2H J
I ^1	С1	J
(2. 115)
D (Ю = ((«о+Л cos &J-1 c\ [k cos (&x - &lH) - l2 sin (»x - &lH)] —
— (Я0 + /2 COS a2)-1 cl COS (&2 — &2H)} f2H —
— 1(Я0 + fl cos &J-1 c\ [Щ cos (&! — &lH) — m2 sin (&2 — &lH)] +
+(я0+/а cos &2)_1 cl cos (d2 — &2H)} VJ2H+
4-{(no+/1cos&1)ci[«1cos(ai —&1H) —«2sin(&x —»1и)]} Х2н- (2. 116)
Следует отметить, что ориентация системы координат, связанной
со вторым объектом, отвечает естественному положению ортов
на момент tH и в дальнейшем при t"^tH сохраняется, т. е. пере¬
мещается поступательно вместе с этим КА.
«б

2.6.	Уравнения относительного движения в связанной
системе координат
В предыдущем параграфе основные усилия были направлены
на изучение механизма гравитационного воздействия на КА в
рамках модели сферической Земли. Ниже будем предполагать*
что характер действующих на объекты сил (гравитационных*
возмущений или создаваемых при управлении) нам известен*
т. е. известен закон изменения вектора скорости каждого КА*
а задачу будем видеть в получении кинематических соотноше¬
ний, определяющих изменение во времени параметров относи¬
тельного движения (1.16)—Voth (0 > D(0-
Итак, движение каждого объекта характеризуется vi(^) и
v2(£). Положение обоих векторов будем описывать в произволь¬
но ориентированных инерциальных системах координат 0\X\Y\Z\
и 02Х2Y2Z2, связанных с центрами масс каждого из объектов
углами Эйлера 0Ь ф>1 и 02, фг (рис. 2.17). При этом одноименные
оси систем взаимно параллельны. Относительное положение цент¬
ров масс определяется вектором дальности D(/), ориентация ко¬
торого в O2X2Y2Z2 фиксируется углами р, и Я.
Для составления уравнений относительного движения опреде¬
лим проекции соответствующих векторов скорости на плоскость*
перпендикулярную D(^). При этом в последующих выкладках
опустим индекс у v(£), так как все рассуждения справедливы
для обоих объектов с точностью до знака, который будет учтен
ниже.
Представим D(^) в виде
D(t) = D°(t)D(t), |D°(0|=1.	(2.117)
87

Тогда, разлагая v(/) на два вектора, — совпадающего с направ¬
лением D(0 и ему перпендикулярного (рис. 2.18), запишем со¬
ответственно
L=:(vD°)D°,
DQ X (у X Р°)
— vDo
(2. 118)
(2. 119)
■где М лежит в плоскости S, перпендикулярной D(£). Далее про¬
ведем плоскость R через D0 и единичный вектор j оси О2У2, кото¬
рая при пересечении с плоскостью S дает след РР (см. рис. 2.18).
Второе опорное направление получим, проведя линию КК через
начало D0 в плоскости S перпендикулярно PP. Отметим, что КК
есть след пересечения плоско¬
стей S и O2X2Z2. Теперь можно
однозначно определить углы % и
jul, фиксирующие вектор D(£):
jli — угол, отсчитываемый в поло¬
жительном направлении (против
часовой стрелки) в плоскости R от
следа пересечения этой плоскости
плоскостью 02X2Z2 до продолже¬
ния D; X — угол, отсчитываемый
в положительном направлении
в плоскости 02X2Z2 от оси 02Х2
до следа пересечения этой плоско¬
сти с плоскостью R.
Для определения закона изменения D(t) разложим вектор
М на два: один по направлению КК (К), а другой по направле¬
нию РР (Р) — рис. 2. 19. Орты к0, р° применительно к случаю,
изображенному на рисунке, суть
D°Xj . D0_ D0 X КО _ DO X (DO X j)
Рис. 2.19.
к°=
|D°X j|
po Dq X KQ
|D°Xj|
|D°Xj|
или
/С = М-К°
D° X (v X D°) D° X j
P = M‘P°:
vDO
DQ X (v X DQ)
vDQ
|D° X j|
D° X (D° X j)
|D° X j|
(2. 120)
(2. 121)
Из рис. 2.18 видно, что проекции Vi(0 и \2(t) на направление D
вызывают изменение модуля, т. е.
D(0=LaC0—Ь.0),
(2. 122)
а проекции скорости на РР приводят к повороту D(/) в плос¬
кости R:
(2. 123)
*8

с учетом направления положительного отсчета угла р. Проекции
скорости на КК обеспечивают поворот D в плоскости, проведен¬
ной через D и К, что отличается от вращения следа в плоскости
O2X2Y, фиксируемого углом Я. Чтобы записать закон изменения
%, следует определить проекцию D на плоскость O2X2Z2. Исполь¬
зуя формулы, аналогичные (2.119) и (2.120), можно записать
D[jX |5Г$Тг]^-*‘'	(2Л24>
Теперь, чтобы получить уравнения относительного движения,,
запишем	в	скалярной форме и раскроем соотношения (2.118)
и (2.	120)	—	(2. 124). Представим
v=vxi -f Vyj -j- vzk;	(2. 125)
DO = Doi + DOj+jDok.
Так как
L = vD° = vxD°-l-v1,D°-{-vzDl	(2.126)
TO
M = v — LD° = [vx — vx (D®)2 — VyD®D°y — vzD°xD°zj i -f-
+ [Vy-vxD0Dl-vy(Dl)*-vzD°D0] j +
+ [vz-vxD0xD°-VyDlD0-vz(D°zy] k	(2.127)
и на основании соотношения (2.120) с подстановкой выражений
(2.125) и (2.127) получим
K=(-vxD°z-\-vzD°x) [(D“)2 + (£>z)2p.	(2. 128)
Аналогично соотношение (2.121) с учетом представлений (2.125)
и (2.127) дает
р=	Vy {DVf-Vy {Diy+vzD°yD?[ [(D°)2+
(2. 129)
Раскрывая левую часть уравнения (2.124), будем иметь
D	j]=D	[W+Wf2.	(2.130)
Конкретизируем полученные векторные соотношения и запишем
их в полярной системе координат. Проекции векторов v и D
суть
vx=v cos 0 cos ф; ^ sin 0; vz= — v cos 0 sin ф;
£)0 = cos(i, cosX; D°y = sin ц; D°z— — cos [a sin К
89

В результате подстановки этих формул в соотношения (2.126),
(2.128) и (2.129) получим
К— —■о cos 0 sin (<]> — X);	(2.131а)
P = v [cos 0cos(<]> — X) sin [x — sin 6 cos|x];	(2. 1316)
L—v [cos 6 cos(]j — X) cos [xsin 0sin [x],	(2. 131b)
а выражение (2.130) равно ZXcosp. При использовании пред¬
ставления (2.131) вместо (2.122) — (2.124) с учетом индексов
«1» и «2» можно записать
D(t)=v1(if) [cos 02 cos (фх — X) cos |х -j- sin бх sin jx] —
— v2(t) [cos 02 cos(4>a — X) cos[x-[- sin 02 sin jx]; (2. 132)
D{t)^.{t)=v1{t) [sin 02 cos jx — cos 0X cos(фх — X) sin (xj —
— i)2(i■) [sin 02 cos |x — cos 02 cos(<]Xj —X) sin (x[;	(2.	133)
D(t)\(t) — v1{t)cos 0X sin (<!>! — X)esc[x — v2(^)cos 02 sin (ф2 — X) esc jx.
(2. 134)
Приведенные уравнения представляют собой кинематические
уравнения относительного движения, записанные в инерциаль-
ной системе координат. Для того чтобы рассчитать траекторию
относительного движения, необходимо, кроме начальных усло¬
вий, знать законы изменения Vi(£) и v2(/)-
Если исследуется относительное движение в системе коорди¬
нат, например второго КА, и известен характер изменения отно¬
сительной скорости (1.16), то уравнения упрощаются:
D(^)==tjoth(*!)[cos0cos(i{i — X) cos [х-f-sin 0sin [x];	(2.135)
D(t)y.(t)=v0TH(t) [sin 0cosp. — cos0cos(tb — X) sin (*]; (2. 136)
D(t)X(t)=vOTH(t)cos 0 sin (ф — X)csc[x,	(2.	137)
где 0, ф — углы, определяющие ориентацию vOTh(0 (cm.
рис. 2.17).
Следует указать, что в результате интегрирования приведен¬
ных систем дифференциальных уравнений находятся параметры,
характеризующие относительное перемещение обоих объектов
—D(t), X(t), р(0- Именно эти величины (или их производные)
наиболее просто измеряются с помощью бортовых средств [55,
69, 26].
Из уравнений (2.132) — (2.134) легко получить распростра¬
ненные кинематические соотношения для плоского движения.
90

Так, при наложении условия 0 = р=О будем иметь уравнения,
характеризующие движение в горизонтальной плоскости:
D{t)=v1(t) cos — X) — z>2 (t) cos (<J»2—X);
£)(jf)X(/l)=Di(/f) sin (4»i —X)—г»2(^) sin (ф2—X),	(2.	138)
а из условия ф=Х=0
D (t)=(t) cos (0X — (л) —1>2 (t) cos (02—[a);
£)(^)n(^)='yi(^) sin (0i — p) — vz{t) sin (02 — «■).	(2.	139)
2.7.	Концевые условия сближения
При изучении задачи сближения (именно для ее решения
привлекаются уравнения относительного движения) смысл кон-
цевых условий остается таким же, как и при исследовании рас¬
смотренных задач выведения, спуска и коррекции траекторий
или орбит, фиксируемых в абсолютной системе координат. Иначе
концевые условия представляют собой формализованный при¬
знак, определяющий принадлежность траектории семейству по¬
падающих. Напомним, что в термин «попадающая траектория»
вкладывается смысл удовлетворения траекторией некоторых
требований, сформулированных при постановке задачи наведе¬
ния. К числу последних, как уже указывалось, в задаче сближе¬
ния относятся требование фиксированного минимального или
нулевого расстояния между аппаратами в заранее заданный или
неопределенный момент времени и условие на требуемую ско¬
рость встречи, которая в зависимости от характера решаемой
задачи может быть равна нулю (мягкий контакт) или подобное
ограничение не принципиально (жесткий контакт).
Остановимся вначале на первом условии как основном для
задачи сближения (задача выполнения мягкого контакта обычно
решается выведением КА на траекторию встречи и ликвидацией
относительной скорости импульсным воздействием тяги не¬
посредственно перед контактом).
В задачах управления относительным движением принято
называть промахом минимальное расстояние между двумя объ¬
ектами на исследуемом интервале времени, т. е. вектор промаха
определяют как
A = minD(rf), t$ [4, Т\.	(2.140)
Практически же интервал ограничен моментом встречи
A=D(*B),	(2.141)
а движение на интервале jYB, Л обычно внимания не привлекает.
Исследование на минимум вектор-функции (2.140) сопряже¬
но с вычислительными трудностями и требует использования
91

итерационных процедур. Поэтому целесообразно найти какие-
либо аналитические формы, представления этой зависимости.
Отметим, что в большинстве практических случаев достаточ¬
но ограничиться скалярным представлением промаха. Если так,
то необходимым условием экстремума функции дальности явля¬
ется D(tB)= 0. Так как в общем случае относительная скорость
в этот момент времени не равна нулю, то для момента пролета
(при D = 0 — момент встречи) характерно
cos 0(4) cos [4 (4) — cos |J. (*:„)+sin 0(4) sin [1 (4)=0, (2. 142)
что следует из уравнения (2.135). Из рассмотрения соотноше¬
ния (2.131в) очевидно, что это означает равенство нулю состав-
.ляющей относительной скорости, перпендикулярной вектору
дальности. Последнее имеет вполне понятный физический смысл.
Однако выражение (2.142) не может быть использовано в ка¬
честве концевого условия, так как характеризует момент дости¬
жения минимальной дальности, но не несет информации о па¬
раметрах движения в конце участка управления, которые долж¬
ны быть достигнуты с тем, чтобы последующее баллистическое
движение привело к требуемым условиям встречи. Момент встре¬
чи целесообразно определять условием
D(4)vOTH(4) = 0.	(2.143)
Принимая	гипотезу	сферической Земли, на основании	(2.102)
с учетом (2.101) можно записать
А = D (4)	+ (*» ■- Q v0 + JAv (0 dt,	(2. 144)
'к
где индекс «к», как и в разд. 2.2, относится к моменту прекра¬
щения управления и началу баллистического движения.
Последнее соотношение достаточно просто рассчитывается,
если известно tBy нахождение которого и представляет основные
трудности.
Для детализации	условия (2.143) учтем	представления
(2.101) и (2.102). Тогда
I\vo + (tB “ 4) vo 4~ DKAv (tB) -j- (tB — tK) v0 Av (YB) -f-
ie
+ [v0 + Av(4)] j \v(t)dt=0.	(2.	145)
Представим векторы, входящие в (2.145), в виде
ок=ад°н+^к2Л20н+адн;
v0 = ^oif2„ + «мЧан + «А;
(2. 146)
92

Av= Д^н+	Д®85Са
'2н
в системе ортов второго КА, фиксируемых в момент начала бал¬
листического движения (по аналогии с обозначениями ортов
в разд. 2.5 сохранен индекс «н»). Величины отдельных состав¬
ляющих легко найти из сравнения (2.146) с (2.110), (2.111) и
(2.112). Тогда подстановка разложения (2.146) в (2.145) дает
уравнение, которое достаточно просто алгоритмируется:
Acl^oi + £^2^02 + ^КЗ^ОЗ “К А “ А) « "t" ^02 "Ь ^оз) "Г
“h[^Ki“b(4”“ 4)^01]	(4)4_[^к2"Ь(^в”“4)<г;02]	а^2(4)4~
+ Ркз + (А-4)^оз] A^3(4)+Ki+ A^i(4)] j 4®1(<)Л +
ьЛ
+ [^024~ А^2(4)] J А^2W~г[^оз~t~ A^3(4)]J L^{t)dt=0. (2. 147)
*к	*к
При той же подстановке в выражение (2. 144) имеем
А = j^DKl-f-(4“4)^oi+1 A^i(0^| fi>H +
+ £Д<2 + (А — 4) ^02 + J А'Уг (0^j Лгн "Ь
Ч-^кз~h(^в — ^к)^оз + J ATJ3(^)a^j %2Н*	(2*	148)
Таким образом, для расчета величины промаха по известным
начальным значениям параметров движения следует знать ве¬
личину /в.	Для	упрощения вычислений точные (в	рамках допу¬
щения	о	поле притяжения) соотношения (2.147)	и	(2.148) за¬
меним приближенными.
Наиболее грубое приближение, отвечающее плоскопараллель¬
ному полю, дает возможность записать выражения, прямо сле¬
дующие из соотношений (2.147) и (2.148) при условии Av(0=0:
4=“ТГ: A=DK+^-^)v0.	(2.149)
Если движение задается в полярной системе координат и про¬
исходит в плоскости, то имеем
д^^Л^к+^к^к)-172,	(2.150)
93

а при выполнении допущения DKpK<^DK получаем формулу,,
имеющую широкое распространение в инженерной практике
В статье [104] в предположении равномерного и прямолиней¬
ного движения Объектов приведено выражение для определения
#в при отсутствии информации о Д а лишь на основе измерения
D и D.
При более строгом подходе следует в какой-либо мере учиты¬
вать различное действие поля притяжения на объекты. Основ¬
ная трудность при использовании формул (2.147) и (2.148) за-
дартный способ упрощения расчетов состоит в представлении
этих выражений в виде отрезка какого-либо ряда.
В качестве простейшего рассмотрим возможность аппрокси¬
мации Av(£) рядом Маклорена, ограничившись первыми тремя
членами, и учтем, что Av(/K) =0:
Тогда для нулевого приближения имеем случай, приведенный
выше, а для 2-го приближения вместо соотношений (2.147) и
(2.148)	можем записать
(4 — Q* + 5 (tB—/к)4 AvKAvK -j- 2 (tB—tK)z (3дт;к + 4v0 д vK) -f-
+ 6 (tB—/K)2 (3AvKv0 -f- DKAvK) -f- 12 (tB—tK) (tjq + DkAvk) -f-
где все функции определены на момент tK.
' Некоторая трудность возникает при расчете частных произ¬
водных от Av(/) по времени. Это объясняется тем, что факти¬
чески Av(/) зависит от истинной аномалии (2.110), а для на¬
хождения производных по времени следует привлечь зависимос¬
ти (2.26) и (2.86). Методика получения подобных производных
достаточно хорошо известна, например [85]. После громоздких,
94
[55, 61]:
(2. 151)
ключается в необходимости
к
Ду(г)=(г-уДу(У+-^-02АУ(гк).	(2.	152)
+ 12DKy0=0;
(2. 153)
A=DK+ft.-*K)	+	(2.154)

но несложных преобразований в предположении круговой орби¬
ты первого КА будем иметь:
д*,= -я0
\ С\	(?2	'
д Vy— Jt0
С1
д„,=	»,_4;
с 1	С?
д;,=-„0(-^*;+л ф
\ С\	C<i	J
д£, = -я0 (-^L 4?+-L «I) ;	(2.	155)
\ С1	Со	'
С1	С2
; •	_	шзе	<?2.
&vz= — я0
ci
f iC-Г' f£ -i^-+ £	;
2	\	db	)	\ dE2 1 d£	дЬ2)
£=яо/2 [af (l-e2 cos fj]-1:
  1 /1~Ь g2\ffi sin f?2K/2 _
<?£2	2 U—e2/ cos3£2k/2 ’
Ё = — Я0е2 sin	И*72 (1 —e2 cos A'2k)]_1;
52£   1 sin &2k/2
<9»2	2	cos3 92k/2
Приведенные формулы позволяют определить момент встречи из
решения полинома 5-го порядка (2.153) и найти величину про¬
маха (2.154) по известным начальным условиям баллистическо¬
го относительного движения.
Однако аппроксимация Av(/) рядом Маклорена представля¬
ет в известном смысле достаточно ограниченный подход. Дело
в том, что при больших tB—изменение Av(f) отвечает перио¬
дическому процессу или их совокупности. Сравнительно точная
аппроксимация такой кривой рядом Маклорена связана с необ¬
ходимостью сохранения большого числа членов ряда. В силу
этого целесообразно аппроксимировать, Av(/) рядом экспонент,
95

имеющим структуру, больше отвечающую характеру исходной
функции:
полиномом наилучшего приближения.
Необходимым и достаточным условием того, что некоторый
полином
(Ci — действительные числа) является полиномом наилучшего
приближения,формулирует теорема Хаара [13]. Эта теорема тре¬
бует, чтобы фг(х) образовывали систему Чебышева. В свою оче¬
редь, для доказательства последнего следует использовать тео¬
рему [13], гарантирующую образование системы Чебышева в
случае, если ф(х) п раз дифференцируемы в области задания
и вронскиан W этой системы не равен нулю, при всех k=l, 2,..., п.
Вронскиан для рассматриваемой системы есть
(__ 1 )*+i\ье-и (__ i ^+i2k\ke-m	(__ i ykkx-ke-k\t
Последовательными преобразованиями данного определителя
можно показать, что определитель Вронского для принятого ви¬
да координатных функций приводится к определителю Вандер-
монда. В результате решения последнего вронскиан записывает¬
ся в виде
Таким образом, неравенство нулю вронскиана (2.157) для всех
k и составляет условие аппроксимации Av(/) полиномом наилуч¬
шего приближения (2.156).
ду(0 = 2Ак(1-е-ш).
k
(2.156)
Установим условия, при выполнении которых этот ряд является
п
ф(*)=2*л>/ (■*)
cpi	<р2	...	<рЛ
Ь	?2	•"	?*
W («Pi, ?а,-.?*) =
1~е~х/
Xe~xt
\ — е~т
2\e~2Xi
1 — е~ш
( —1)!
(2. 157)

При решении задачи отыскания неизвестных в разложении
(2.156) ввиду отсутствия точных сведений о характере измене¬
ния \v(t) в реальных условиях и необходимости обеспечить
интегральное приближение к аппроксимируемой зависимости ра¬
ционально использовать критерий среднего квадратичного при¬
ближения, т. е. отыскивать К и из условия
(векторные обозначения в последних выражениях использованы
лишь для сокращения записи).
Величина tB должна удовлетворять уравнению
X [v0 + Aa + A2-e-X(,--('‘)(A1 + Aae-X(,-+<K))] = 0> (2. 159)
Итак, в качестве концевых условий в задаче сближения выступа¬
ют соотношения (2.144) и (2.145), или (2.147) и (2.148), или
(2.149)—*(2.151), или (2.153) и (2.154), или, наконец, (2.159) и
(2.160). В общем случае концевые условия можно записать с
неявной форме
дХ дАх дАг	дАп
Для нахождения неизвестных при «=2 имеем систему
дА„
«В
f [Av(t) - Aj (1 - e~xt)- A,(1 - e~2X<)] (1 - е~ш) dt=0;
(2. 158)
J^K+(v0+A1 + A2)(4— tK)—	x~^~e	X<<B	^
а величина промаха находится как
А— DK-|-(v0-]-A1-)-A2)(4—4) —•^■А2 + -^-А1(е Х(<в <к)— 1).
(2. 160)
Six Рк, tK, tB, v0K, Av(^k, 7b)] = 0;
“-*2к Рк, ^к» ^bi v0K, Av (7К, г?в)] = 0.
(2. 161)
4	3953
97

Второе концевое условие необходимо для отыскания tB, поэтому
если можно из него выразить iB в явном виде
t.=S£ [tK DK> v0K, Av(/J],
TO
(2. 162)
т. e. наблюдается полная аналогия с формулировкой задачи уп¬
равления выведением (см. разд. 2.2). Однако получить /в как
функцию начальных условий в явном виде можно лишь для су¬
щественно упрощенной модели поля приближения. При более
строгом подходе следует использовать два условия типа (2.161).
Следует отметить, что при точном выполнении 1-го концево¬
го условия (равенства нулю промаха) 2-е условие не дает воз¬
можности найти /в из-за превращения базисного соотношения
(2.143) в тождество.
Однако при расчетах на ЭВМ реального движения такой
случай обычно не наблюдается из-за вычислительных и методи¬
ческих ошибок.
Дополнительно прокомментируем концевые условия, полу¬
ченные при допущении об однородности поля притяжения. Усло¬
вие, записанное в виде (2.149), означает совпадение по направ¬
лению векторов DK и VoK. Величина /в—tK (длительность баллис¬
тического движения) является параметром и его конкретному
значению отвечает своя траектория. Значение этого параметра
может быть задано. Если требование на /в—tK отсутствует, то
можно записать концевое условие в другом виде
для получения которого достаточно спроектировать векторную
запись (2.149) на инерциальные оси и исключить параметр. Вы¬
полнение условия (2.163) означает коллинеарность входящих
в него векторов, но не содержит требования их противополож¬
ной ориентации. Поэтому его можно использовать, когда требуе¬
мая ориентация векторов DK, v0K гарантируется, например, управ¬
лением на предшествующем этапе движения.
Аналогичный смысл имеет требование
которое получается из соотношения (2.150) и может быть ис¬
пользовано при задании движения в полярных координатах.
9а
VokXDk = 0.
(2. 163)
hc = °>
(2. 164)

Для выполнения мягкого контакта следует потребовать
Voth(*b)=0, D(O-0.	(2.165)
Возможность использования баллистического этапа движения
при этом отсутствует, так как выключать двигатель необходимо
при vOTii=0, но тогда не будет изменяться дальность. В техни¬
ческих задачах может быть наложено ограничение на относи¬
тельную скорость в момент встречи (или ему непосредственно
предшествующий) с тем, чтобы импульсным воздействием ском¬
пенсировать оставшуюся скорость и перейти к этапу причалива¬
ния [10, 69].
4*

ГЛАВА 3
УПРАВЛЕНИЕ ВЫВЕДЕНИЕМ
3.1. Анализ постановок задач и некоторых методов
синтеза оптимального управления
Многообразие задач синтеза оптимального управления мож¬
но достаточно четко разделить .на две группы: отработка задан¬
ного входного воздействия (рис. 3.1, а) и отработка начальных
условий (рис. 3.1, б).
в)
Рис. 3.1.
Формулировка .первой ,в значительной мере основана на за¬
даче Винера—Колмогорова и состоит в следующем. Известен
класс входных полезных сигналов хВх(0> комбинируемых опре¬
деленным образом с помехой z(t) с заданными статистическими
свойствами. Известно требуемое преобразование (оператор Я),
которое должно быть осуществлено с полезным сигналом. Сле¬
дует найти оператор системы Ф, обеспечивающий экстремум по¬
казателя качества (1.43) — (1.46), формируемый оператором W.
Использование такой постановки задачи для наведения JIA в
значительной мере ограничено необходимостью знать класс
входных сигналов и оператор Я. Обычно решение легко полу¬
чить для достаточно простых задач слежения, фильтрации, экст¬
раполяции, но в задаче наведения именно- в определении этого
оператора и состоит цель исследования. Попытки применить та¬
100

ку.ю постановку к синтезу оптимального управления движением,
например [102, 168], значительного успеха не принесли из-за
серьезности сделанных допущений.
В настоящее -время в трудах В. С. Пугачева, Н. Н. Красов-
ского, А. М. Летова, А. В. Солодова, Р. Бэттина, Р. Калмана и
др. разработаны эффективные методы -синтеза оптимальных по
статистическому критерию систем на класс линейных операто¬
ров. Для нелинейных систем общего решения не существует, а
для определения характеристик выходного сигнала используют¬
ся различные методы приближения нелинейных операторов к
линейным и методы аппроксимации.
Вторая (постановка задачи обычно базируется на детермини¬
стском подходе, соответствующими принимаются и критерии:
(1.38) — (1.40), (1.42). При этом известна математическая мо¬
дель объекта управления F, совокупность внешних воз-мущений,
начальные и конечные условия; требуется найти оператор вы¬
работки управляющего -воздействия Р, -обеспечивающего экстре¬
мальное достижение конечных условий. Развитие этого направ¬
ления связано с работами Л. С. Понтрягина и его 'коллег,
В. И. Зубова, В. Ф. Кротова, В. М. Пономарева и др. Данная
постановка отвечает принципу свободного программирования
управляемого движения.
Итак, при решении задачи наведения естественно стремле¬
ние сформулировать ее так, чтобы сделать адекватной реаль¬
ным условиям, т. е. привлечь статистическую модель. Однако
существующие -методы не позволяют в этих условиях в полном
объеме решить задачу синтеза оптимального управления.
Большую помощь при разработке алгоритмов -систем управ¬
ления движением ЛА оказывает теорема о декомпозиции [147,
172]. Эта теорема, строго говоря, применимая для стационарных
линейных систем с квадратичным критерием качества и нор¬
мальным распределением входных сигналов, утверждает воз¬
можность раздельного решения задач оптимальной обработки
входной информации и синтеза закона управления в предполо¬
жении о детерминированном характере входных воздействий.
В целом ряде работ [14, 15, 111] получены обобщающие ре¬
зультаты о возможном разделении задач обработки и управле¬
ния при ограничении управляющего воздействия, функционале
общего вида и определенной нелинейности объекта. Хотя рас¬
пространить результаты на общий случай нельзя, однако усмат¬
ривается возможность раздельного проектирования алгоритмов
обработки и формирования управляющего сигнала. Это предпо¬
ложение широко используется в практике синтеза, например
[7, 10, 35, 55, 63,161], и делает более правомочным детерминиро¬
ванный подход при работе системы в условиях возмущений. Ин¬
тересные результаты приведены в работе [163], где показано, что
при незначительной неопределенности фазовых координат объ¬
101

екта и ограниченном управлении оптимальный регулятор имеет
нелинейную структуру. По .мере ро.ста неопределенности в систе¬
ме регулятор приближается к линейному.
Другой путь, упрощающий процедуру синтеза и дающий воз¬
можность привлечь статистические методы, уже давно нашел
практическое применение и получил законченность в труде (96].
Суть его заключается в разделении процедуры синтеза на два
последовательных этапа. На первом этапе синтезируется опти¬
мальная программа управления методами классического вариа¬
ционного исчисления или его современными модификациями.
Решение состоит в нахождении
и.,..т(*) = и|1р(Хн, Хк, 0; Х0Пт(Л = Х](р [u01(T(£), t\.
На втором этапе в предположении милости действующих возму¬
щений линеаризируется движение, и оптимальный закон управ¬
ления отыскивается на базе линейной модели, которая позволя¬
ет пронести синтез закона управления (функция ф.азовых коор¬
динат), оптимального по статистическому критерию
АиЦ1|.г(Дх, *0 = Аи011Т ^хн, — (/), Дх (О, П ,
df
где Лх (0 = х(^)—х1ф(0; -—(О-матрица частных производных,
UX
вычисленная вдоль програм-
ной траектории.
Математически это можно представить, если разложить fu
(1.32) в ряд Тейлора и ограничиться двумя членами:
f (ulip + Au) = ^(ulip)+ Auf'u1?p.
Тогда, предполагая F в ('1.32) аддитивным, можно принять его
различным для каждого из слагаемых. Например, для определе¬
ния ипр использовать критерий энергетических затрат, а для
Ли — точности.
Такого рода подход весьма продуктивен для широкого круга
задач наведения, что подтверждается как отечественными (4, 7,
94], так и зарубежными [91, 102, 132, 139, 168] исследованиями.
Однако подобные решения обладают и известной ограниченно¬
стью. Так, .при необходимости изменения программной траекто¬
рии всю задачу приходится решать заново, включая, строго го¬
воря, и синтез оптимального регулятора Au(Ах, t), свойства ко¬
торого зависят от программы движения. Подход может оказать¬
ся недостаточно эффективным, когда действие комплекса воз¬
мущений столь велико, что не выполняется гипотеза о малости
отклонений возмущенной траектории от программной, на основе
которого синтезируется закон управления. Наконец, для ряда
задач наведения, как справедливо показано в работах [96, 127,
10?

141], необходимость -синтеза .последовательно программы и зако¬
на управления вообще спорна. К такому «классу задач относит¬
ся управление сближением КА или управление 'маневром при
спуске с орбиты. В этом случае из-за большого допустимого
разброса начальных условий невозможно заранее найти про¬
грамму управления, и процесс управления должен быть опера¬
тивным на основе анализа текущей информации.
С формальной точки зрения проблема оптимизации системы
заключается в отыскании управления, .которое обеспечивает
экстремум функционалу — показателю качества работы этой
системы (1.34). Возможность решения этой задачи основана на
предварительном установлении математической модели систе¬
мы, выборе критерия и наличии экстремума в области допу¬
стимых управлений. Если эти предположения выполнены' и
функционал (функция) дифференцируемы, то необходимым ус¬
ловием существования экстремума является равенство нулю
градиента критерия в некоторой точке ueU, которая называет¬
ся стационарной или особой
grad/(u) = 0,	(3.1)
или
dJ _ 0
да i	ди2	даг	’
Это условие выделяет лишь локальные экстремумы и если их
несколько, то задача определения глобального экстремума пере¬
растает в отдельную проблему, разрешимую, как правило, лишь
•с помощью вычислительных методов.
Использование (3.1) не дает возможности установить, явля¬
ется ли обнаруженный экстремум максимумом или минимумом,
для чего следует привлекать достаточные условия. В техниче¬
ских задачах вид экстремума часто становится ясным непосред¬
ственно из смысла задачи. Однако привлечение достаточных ус¬
ловий имеет самостоятельное значение, так как позволяет убе¬
диться в наличии решения, а значит, проверить корректность
постановки задачи. В качестве достаточных условий обычно вы¬
ступает значение второго дифференциала функционала в стаци¬
онарной точке d2J (и) или совокупность вторых частных произ-
Приведенны-е необходимые и достаточные условия являются
общими, однако- их применение для решения практических за¬
дач ограничено двумя факторами. Во-первых, далеко не всегда,
справедли'вочпредположсние о расположении экстремума внутри
допустимой области управления. Во-вторых, в ряде случаев сос-.
тавляет трудность представление критерия в форме, в которой
103

роль независимого переменного игра-ет управление. Как уже яс¬
но из описания объекта управления, весьма -сложно записать в;
явном виде связь между фазовыми переменными и. управлением
с тем, чтобы выразить критерий 'как аналитическую зависимость
от управления. В противном случае использование условий (3.1)
затруднено.
Наконец, применение необходимых и достаточных усло¬
вий будет более продуктивным, если их -конкретизировать
для узких постановок задач. При подобной детализации
возникают ,не только разнообразные рецепты для решения тога
или иного класса задач, но и различные математические ме¬
тоды.
Естественно, в объеме одного параграфа н-ет смысла пытать¬
ся охватить весь арсенал методов, которыми располагает совре¬
менная теория оптимизации. Поставим более скромную цель —
определить область применения и решению задачи наведения
оонсеных ефсрмироваЕШихея направлений теории и весьма
кратко- изложить суть методов, которые в той или иной степени
будут применяться ниже.
Для изучения тесрии оптимального управления можно реко¬
мендовать обобщающие работы [9, 65], а для уяснения основно¬
го содержания распространенных методов —[28, 92, 118], в -каж¬
дой из которых читатель найдет обширную библиографию.
Существующие методы решения задач оптимального- управ¬
ления можно условно разделить на три основные группы:
— формализм Лагранжа и принцип максимума Понтрягина,
— формализм Гамильтона—Якоби и принцип оптимальности
Веллмана;
— алгоритмические методы синтеза.
К формализму Лагранжа в первую очередь относится клас¬
сическое вариационное исчисление.
Основная задача вариационного исчисления (задача Лаг¬
ранжа) заключается в нахождении экстремума функционала
К этому виду приводится критерий (1.40) при подстановке
(1.1), когда известен комплекс действующих возмущений. При
этом обычно предполагается непрерывность .подынтегральной
функции по совокупности ее аргументов, а также существова¬
ние и непрерывность ее частных производных до 3-го по¬
рядка.
Необходимые условия экстремума -получаются из обращения
в нуль первой вариации функционала — линейной, по отноше¬
(3.2)
н
104

нию к (приращению аргумента 6и(/), -части дриращения функ¬
ционала 6J (и):
Lu-^Li. = 0,	(3.3)
1 dt i
где
Lu =-£-L(u, й, t), L- =-^-L{u, й,t)
1 dui	ui	dUi
— известные уравнения Эйлера—Лагранжа. Особенностью по¬
лучения этих уравнений является предположение о том, что/при
варьировании' функция u(£)+6u(£) ,не достигает границы допу¬
стимой области, а значит, экстремум лежит внутри этой обла¬
сти. Заметим, что о помощью специальных приемов [71, 84, 114]
в отдельных случаях можно применить -вариационное исчисле¬
ние и для замкнутых областей аргумента.
Если решение и(/) содержит угловые точки (и терпит раз¬
рыв), то в точках излома должны выполняться дополнительные
условия Вейерштрасса—Эрдмана.
Каждое уравнение (3.3) —дифференциальное уравнение
второго порядка, поэтому его решение зависит от двух произ¬
вольных постоянных, для определения которых надо иметь два
условия. В задачах с закрепленными концами в роли последних
выступают фиксированные начальные и конечные значения пе¬
ременных, а в задачах с подвижными концами произвольные
постоянные находятся на базе условий трансверсальности (см.
далее).
Как уже говорилось, далеко не всегда удается свести оптими¬
зацию к поиску экстремума функционала, заданного на множе¬
стве управлений. Если фазовую переменную из функционала
исключить нельзя, то говорят, что на функции, от которых зави¬
сит функционал, наложены связи — уравнения, описывающие
динамику объекта. Если соотношение (1.1) записать в неявном
виде
F,(x,M)=0, i=l,2,...,s,	(3.4)
то доказывается, что задачу на условный экстремум (опреде¬
ление экстремума при наличии связей) можно свести к задаче
на безусловный экстремум формированием
+	(3.5)
/= 1
где Xi(t) —множители Лагранжа, и применением к этому функ¬
ционалу уравнений (3.3). Уравнений типа (3.3), дополненных
(3.4) совместно с граничными условиями, достаточно для опре¬
деления UonT'(0 и Xi(t).
Задача оптимизации при использовании классического вари¬
ационного исчисления или других методов не обязательно фор¬
105

мулируется как проблема отыскания оптимального управления-
С той же правомочностью она может ставиться 1как нахождение
оптимальной траектории хопт(0 —экстремали. Если известно-
иОПт(0» то определение хопт(0 не вызывает затруднений: для
этого следует использовать уравнения движения объекта (1.5)
или (1.6). Обратная задача обычно решается сложнее, хотя-
принципиальных трудностей не вызывает. Она. формулируется
следующим образом. Требуется отыскать экстремум функцио¬
нала
*к
J= j Z,(x, х, t)dt	(3. 6)
в предположениях, приведенных ранее. Уравнения Эйлера —
Лагранжа для (3.6) имеют вид
L..- + L.-A.	(3.7,
Таким образом, для нахождения решения задачи в той или
иной форме надо решить систему дифференциальных уравнений
(3.3)	или (3.7). К сожалению, далеко не всегда эти уравнения
решаются в аналитических функциях, поэтому большое значе¬
ние приобретают методы (точные или приближенные) получе¬
ния решения.
Одним из таких направлений можно считать метод канони¬
ческих преобразований, которые интерпретируют'ся как особые
преобразования системы координат, удовлетворяющие специаль¬
ным условиям [24]. Переход к каноническим уравнениям произ¬
водится введением новых неизвестных
■М0=-Г-,	(3-8)
дх[
дх[дхк
, i, k=l,2,...,n
что дает возможность, если матрица
неособенная, выразить
■*Н*)=<рЛх(*).Ф(0.Ф	(3-9>
Гамильтонианом для функционала (3.6) называют функцию от
х(0> Ф(0> t виДа
П
Н (х, ф, t)= L (х, х, ^)-j- ^ Xt	x,x,t).	(3.	10)
Тогда имеют место соотношения
Ь = ~гг~,	(3.11а>
OXi
Xi=¥r, t = l,2,...,n,	(3.116)
106

которые представляют каноническую или гамильтонову форму
записи уравнений Эйлера—Лагранжа. Характерной особенно¬
стью! этой системы является сохранение постоянного значения
Я вдоль оптимальной траектории, определяемой уравнениями
(3.7) или (3.11), поэтому Я есть первый интеграл системы. Это
свойство может фигурировать в качестве признака экстремали.
Принцип максимума Л. С. Понтрягина имеет более широкую
область применения, нежели классическое вариационное исчис¬
ление, так как справедлив и для замкнутой области управления.
Вообще говоря, принцип максимума определяет необходимые
условия оптимальности, а достаточность доказана только для
линейных систем. Но в работе [17] показано, что принцип мак¬
симума весьма близок к достаточным условиям и для нелиней¬
ных систем, если для последних удается осуществить оптимиза¬
цию.
Постановка задачи при использовании принципа максимума
хорошо согласуется с практикой. Динамика объекта описыва¬
ется уравнением (1.3), z(t) известно, a fi непрерывны по сово¬
купности всех аргументов и непрерывно дифференцируемы по
фазовым переменным. Автономность системы при явной зависи¬
мости правой части (1.3) от времени достигается формальным
введением новой переменной xn+i = t. Допустимая область уп¬
равления замкнута |и(/)|^1 и образована кусочно-непрерыв¬
ными функциями (разрывы первого рода). При этом если из¬
вестны начальные условия, то система ('1.3) имеет единственное
решение при заданном u(t).
Рассматривается решение задачи Лагранжа, т. е. отыскива¬
ется экстремум (1.40). Предполагается, что L непрерывно диф¬
ференцируема по совокупности всех аргументов, изменяющих¬
ся в допустимой области. При L= 1 имеет место задача об оп¬
тимальном быстродействии. Фазовое пространство расширяется
введением новой переменной
что позволяет записать уравнения объекта в обобщенном виде,
рассматривая совместно (1.3) и (3.12), а если необходимо, то и
(я+1)-ю координату.
Тогда задача оптимизации формулируется как нахождение
управления иОПт(0^и, ПРИ котором решения системы (1.3),
(3.12)	при фиксированных начальных условиях Xi(tn)=xiUf
i= 1, 2, .. ., п дает наименьшее значение *о(^к)«
Для оптимизации вводится вектор-функция сопряженной пе¬
ременной ф(/) = {фо(0> 'ФДО»---» фп(0} в соответствии с урав¬
нением (3.11):
x0{t) = L{x, u)=/0(x, u),
(3. 12)
(3. 13)
107

и гамильтониан записывается аналогично' (3.10):
tf(i|>tx,u)=4>(0f(*).	(3.14)
Система линейных дифференциальных уравнений (3.13) имеет
единственное решение при любых начальных условиях для ф,
если каким-либо образом выбрано u(^)^U ,и для него вычисле¬
но х(0-
Принцип максимума формулируется -следующим образом'.
Для достижения экстремума функционала (1.40) необходимо»
существование такой ненулевой непрерывной функции Ф(0>
соответствующей x(f) и u(t), что пр.и любом	/к] функция
Я (г!?, х, и) переменного u^U до-стигает в точке и максимума
Н [Ч> (t\ X (0, uorrT (*)] = max Н [i|з {t), х {t), u (*)].	(3. 15)
ueu
В конечный момент времени t=tK:
to(y<0,//№(/K), x(tK), uK(/)] = 0.	(3. 16)
Кроме того, если ф(£), x(t), u(t) удовлетворяют системе (3.11) с
учетом (1.3), то функции ф0 (0 и Я(ф, х, и0Пт) являются посто¬
янными на в-сем интервале времени и (3.16) можно '.проверять
для любого	Q.
Для открытого множества U, что отвечает задачам класси¬
ческого вариационного .исчисления, достижение максимума Я
(3.15) соответствует выполнению
—=0.	(3.17)
dui
При подвижности концов фазовой траектории, стесненной
(1.51), привлекаются условия трансверсальности, имеющие наг¬
лядную геометрическую интерпретацию: вектор-функция ip(t) в.
tH или должна быть ортогональна касательной гиперплоско¬
сти, проведенной через точку пересечения фазовой траектории
с 5К, т. е.
Ч>(*«)=gradS*.	(3.18)
Если концевые условия задаются в виде (1.52), то ф(^к) долж¬
на быть ортогональна их линейной комбинации:
444)=gradSlK + 2 \ grad5i+1,K.	(3.19)
/= 1
Для оптимизации в соответствии с принципом максимума
требуется решить систему 2\п дифференциальных уравнений
(1.3),	(3.13)	и	найти г функций uionT(t). Для	вычисления	послед¬
них имеется	г	конечных соотношений (3.15)	или	(3.17),	поэтому
можно ожидать, что все функции будут определены, если изве¬
108

стны 2lп начальных условий для соответствующих /систем диф¬
ференциальных уравнений (1.3) и (3.13). Так как Н является
линейной и однородной функцией ф(0> то последнюю достаточ¬
но определить с точностью до постоянного множителя. Это дает
право утверждать, что для /получения решения (fK предполага¬
ется .известным) необходимо задать (2п—1) начальное условие.
Фазовые координаты начала процесса хн, как правило, из¬
меряются и известны, поэтому проблема сводится к определе¬
нию ф(^н). Обычно условия, которые бы определили ф(/н), от¬
сутствуют и их следует найти из рассмотрения правого кон(ца
фазовой траектории — для задачи с подвижным правым концом
это соотношение (3.18) или (3.19). Таким образом, задача опти¬
мизации имеет характер краевой или является задачей с разде¬
ленными условиями. Решение краевой задачи обычно сопровож¬
дается трудностями, разрешимыми лишь вычислениями.
Однако для одного класса задач можно получить решение в
явном виде и(£)=К(Ох(0> гДе МО—действительная сим¬
метричная матрица., без решения краевой задачи [9, 70, 73]. Этот
класс составляют системы, заданные линейными уравнениями
(1.4), оптимизируемые по квадратичному критерию типа (L48).
Наиболее ярким представителем второй группы методов, от¬
носящихся к формализму Гамильтона—Якоби, является метод
динамического программирования Р. Веллмана. При использо¬
вании метода принято различать его применение к непрерывным
и дискретным системам. Если для дискретных систем строгость
обоснования метода не вызывает сомнений, то применительно
к непрерывным системам динамическое программирование но¬
сит элемент эвристического подхода из-за серьезности сделан¬
ных предположений [17]. Возможность получения оптимального
решения сложных динамических задач в значительной мере за¬
висит от характеристик используемой ЭВМ, так как требует
большого расхода памяти. Последнее обусловлено необходимо¬
стью построения и запоминания поля экстремалей. Действен¬
ным средством борьбы с «проклятием размерности» служит
метод аппроксимации решений промежуточных этапов, который
позволяет получить решение в форме закона управления. Дина¬
мическое программирование используется и применительно к
задачам наведения, пр.и этом наиболее эффективным оказалось
его применение для синтеза оптимального импульсного управле¬
ния движением КА [2, 25, 33].
Существенным обобщением метода Веллмана является метод,
предложенный В. Ф. Кротовым [62, 63] и основанный на доопре¬
делении достаточных условий оптимальности. Метод позволяет
решить ряд практически важных задач динамики полета, приво¬
дящих к особому управлению и скользящим режимам. Труд¬
ность использования метода состоит в конструировании особой
функции, относительно которого нет строгих рекомендаций.
109

В работах Н. Н. Краеовского> [59, 60] развевается метод син¬
теза оптимальных управлений при известной импульсной пере¬
ходной матриц-е решения. Управление должно принадлежать
некоторому функциональному пространству, которое является
сопряженным .пространству, где норма оператора на классе им¬
пульсных переходных функций есть критерий оптимальности.
Достоинство метода заключается в простоте решения задачи
синтеза на классе линейных систем и применимости его к синте¬
зу управления в игровых задачах. Некоторая ограниченность
состоит в трудности подбора пространства, где .критерий экви¬
валентен норме оператора, для сложных показателей качества,
а также малой эффективности подхода при синтезе управления
для нелинейных объектов.
Перейдем к краткому обследованию алгоритмических мето¬
дов. Само это понятие возникло недавно, впервые, по-видимому,
в работе {117], и объединяет способы синтеза, которые в итоге
дают алгоритм, последующая реализация которого обеспечива¬
ет решение задачи. Обычно решение достигается итерационным
путем на основе широкого применения ЭВМ. В настоящее вре¬
мя затруднительно классифицировать алгоритмические методы
ввиду становления этого -направления, поэтому ограничимся пе¬
речислением и краткой характеристикой отдельных научных ре¬
зультатов.
К числу наиболее развитых следует отнести проекционные
методы. В их основе лежит идея О1 предварительной аппроксима¬
ции исходного функционального уравнения и последующем точ¬
ном решении его аппроксимирующего аналога. В технических
приложениях проекционные методы чаще называют прямыми и
их разновидности (метод Ритца, Бубнова—Галерки,на, Эйлера,
Канторовича и др.) широко используются в практике синтеза.
Идея прямых методов заключается в замене вариационной
задачи задачей отыскания экстремума функции конечного числа
переменных. Последний находится привлечением градиентного
подхода, методами линейного или нелинейного программирова¬
ния.
Пусть требуется найти минимум некоторого функционала,
имеющего точную нижнюю грань
inf [и* (*)] = т > — оо,
и, кроме того, удается выделить некоторую последовательность
функции {ик(0Ь £=/1> 2,. . ., которая дает
lim J [uK{t)\ — m.	(3. 20)
Тогда часто обнаруживается, что эта минимизирующая после¬
довательность сходится к некоторой функции u(t), причем
J(ii) = m,	(3.21)
110

и определение минимума функционала сводится к определению
последовательности {^к}-
Предположим u(t) найдено и эту функцию можно разло¬
жить в некоторый ряд
где <pj(0 —известные функции (координатные).
Тогда, птобы найти u(t), необходимо вычислить .коэффици¬
енты a,j. При подстановке (3.22) функционал превращается в
функцию бесконечного числа переменных aj, /=О, 1, 2,..., в
пространстве которых следует найти минимум.
Однако несмотря на кажущуюся простоту прямых методов,
их применение связано с рядом трудностей. Во-первых, при ре¬
шении прикладных задач следует ограничить бесконечный ряд
(3.22), что в общем случае приводит к потере точности решения.
Точность решения также зависит от вида .координатных функ¬
ций. Обычно к системе {<pj(0} предъявляется требование полно¬
ты, т. е. система должна позволить аппроксимировать решение
с любой, наперед заданной точностью. Условия полноты зави¬
сят от класса функций и вида функционала (48, 82].
Во-вторых, оптимальное решение находится подстановкой
(3.22) в показатель качества и последующим вычислением сово¬
купности коэффициентов {flj}, отвечающих его экстремуму. Эту
операцию можно осуществлять привлечением необходимых ус¬
ловий (3.1). Для существования решения обычно требуется диф¬
ференцируемость и линейная независимость координатных
функций. Но отыскание оптимального решения из системы
(3.1)	—задача далеко не тривиальная, поэтому иногда бывает
удобнее воспользоваться градиентными методами для нахож¬
дения экстремума функционала в пространстве вещественных
переменных.
Большая группа алгоритмических методов основана на идее
определения экстремума функционала непосредственно в про¬
странстве управлений. Выбрав в качестве начального прибли¬
жения некоторое u0<=\Jy используется метод наискорейшего спу¬
ска (подъема), метод градиента или их модификация для после¬
дующего улучшения управления, принимаемого за начальное.
В результате получается минимизирующая последовательность
u0, Ui, u2..., которой отвечает
Формирование указанного направления связано с работами
[64, 84, 125, 135, 149]. В дальнейшем эти методы подвергались
незначительным изменениям и получили широкое распростране¬
ние. В их основе лежит весьма плодотворная идея об использо¬
оо
(3. 22)
У(и0)>У(и1)>У(и,)>...
111

вании сопряженной системы (3.13), позволяющей связать вари¬
ацию фазовых .координат 6х(^к) ,с текущей вариацией управле¬
ния 6и(/). Это позволяет вьцразить изменение функционала кри¬
терия через приращение вектора управления. Действительно,
умножая (1.4) на ф(0 и (3.13), записанное для объекта (1.4),
на у (t), после суммирования левых и правых частей получим
-^(Фу)=Виф.
at
Предположив нулевые начальные условия у(^н)=0, можно за¬
писать последнее .соотношение в интегральной форме
Ф(ОУ (4)=-|К(Виф)^.
С другой стороны, вариацию функционала вида (1.39) можно
представить как
8/=^к)у(а
ду
а использование условия (3.18) позволяет записать
\3p(tK) = dK/dу или #У=*(/к)у(<|С)-
Тогда в итоге
*к
gy = —j (Виф)Л.	(3.23)
Это соотношение позволяет строить итерационные процедуры
оптимизации для широкого класса задач [35, 71]. На каждой
итерации управление должно находиться из условия наиболь¬
шей деформации критерия в сторону его- экстремума. Условие
выбора оптимального управления — maxBmf совпадает с требо¬
ванием принципа максимума для линейной (или линеаризован¬
ной) системы.
В последние годы повышенное внимание было обращено на
привлечение функционального анализа .к исследованию необхо¬
димых условий экстремума и формирования итерационных про¬
цедур, приводящих к выполнению указанных условий [37, 38, 45,
52, 101, 110]. Продуктивность подобного подхода несомненна и
от этого направления следует ожидать важных результатов,
особенно для формирования алгоритмов определения оптималь¬
ного управления сложными объектами, к категории которых
относится и класс задач наведения. Однако этой группе мето¬
дов присущ недостаток, характерный для большинства методов
синтеза: результатом синтеза является построение программы
управления.
112

Наконец, ,к алгоритмическим методам .синтеза можно отне¬
сти поиск экстремума критерия с помощью линейного или нели¬
нейного программирования, когда удается прямо .связать крите¬
рий со -структурой или (совокупностью параметров системы. За¬
дача синтеза формулируется следующим образом: даны урав¬
нения объекта и структура регулятора или алгоритма управле¬
ния -с неизвестными параметрами, область -существования ко¬
торых стеснена дополнительными условиями. Параметры надо
выбрать так, чтобы система обладала экстремальными свойст¬
вами '[56, 97, 109]. Такой подход эффективен для решения .инже¬
нерных задач при заданной структуре регулятора. Но экстре¬
мум в этом случае достигается «с точностью до -структуры», в
выборе которой могут -быть заложены предпосылки, существен¬
но удаляющие систему от экстремальной. Выбрать структуру
обоснованно и строго невозможно.
3.2.	Определение оптимальной программы управления
выведением
Примем в качестве 'математической модели объекта управ¬
ления (1.12), которое в форме Коши можно записать
r(t) = v(t);	(3.24а)
v (t) = w (t) -f grad U.	(3. 246)
Ниже будем	предполагать, что в представлении вектора .кажу¬
щегося ускорения (1.24) модуль вектора w(t) есть известная
заранее или измеряемая функция времени, а неизвестным яв¬
ляется орт w°(/), выбором которого и надлежит придать дви¬
жению экстремальные свойства. В принципе можно сформули¬
ровать и решить задачу определения оптимальной программы
изменения величины w(t). Но реализация этой программы тре¬
бует создания	дополнительной управляющей	связи,	включаю¬
щей в свой состав двигательную установку, что приводит к до¬
полнительным аппаратурным трудностям. С другой стороны,
Двигатели на твердом топливе с трудом поддаются регулировке
и, как будет показано в этой главе, отсутствует принципиальная
необходимость в регулировке тяги двигателя.
Задачу будем решать в предположении выполнения двух до¬
пущений, .которые, с одной стороны, достаточно отвечают реаль¬
ным условиям, а с другой, — призваны сделать решение задачи
обозримым.
Во-первых, будем предполагать, что движение происходит
На безатмосферном участке, т. .е. кажущееся ускорение создает¬
ся только тягой двигателя (1.23). Справедливость этого допуще¬
ния основана на том, что Р (/)	(t).
113

Во-вто.рых, будем решать задачу 'без учета ограничений на
скорость изменения положения продольной оси, которые сущест¬
венны при формировании программы начального участка поле¬
та (1, 8, 79]. Таким образом, сделанные допущения ограничива¬
ют применимость результатов к этапу полета в атмосфере, од¬
нако не настолько, что'бы дискредитировать постановку задачи:
они практически всегда используются при аналогичных иссле¬
дованиях [46, 63, 74].
Если пренебречь боковыми составляющими вектора тяги,
вызванными эксцентриситетом и действием рулевых органов, то
•при сделанных допущениях орт w° фиксирует положение про¬
дольной оси JIA, вдоль которой действует тяга двигателя.
В качестве критерия оптимальности примем количество из¬
расходованного топлива для выполнения цели управления, фор¬
мально представленной в виде заданной совокупности концевых
условий. Смысл этого распространенного критерия заключается
в возможности расширить диапазон условий встречи (например,
увеличить высоту круговой орбиты, на которую должен быть
выведен КА) при сохранении полезной нагрузки или увеличении
последней при фиксированном диапазоне условий.
Уместно подчеркнуть, что мероприятия, направленные на
точность решения задачи, целесообразно- организовывать в двух
направлениях. Во-первых, включением в состав концевых усло¬
вий требований к траектории, от которых зависят характеристи¬
ки рассеивания, например, на угол входа в плотные слои атмо¬
сферы при управлении спуском КА, и удовлетворением этих тре¬
бований в процессе управления на активном участке движения
[151, 162, 170]. Во-вторых, на показатели точности существенно
влияют ошибки при определении момента выполнения ксецевых
условий (своевременное выключение двигателя). Меры борьбы
с методическими ошибками такого рода будут рассмотрены в
гл. 5, а инструментальные ошибки составляют предмет отдель¬
ного изучения.
Итак, величина израсходованного топлива
лК .
М = ^ т (t)dt,	(3. 25)
гн
где m(t) —секундный расход массы топлива (горючего и
окислителя). При известных и стабильных характе¬
ристиках двигателя (3.25) превращается в функцию
верхнего предела интегрирования, если пренебречь
до,стартовыми, расходами.
Тогда критерием оптимальности становится быстродействие
А = АК(/)],	(3.26)
114

а задача -синтеза состоит в нахожденяя оптимального значения
w°(0> обеспечивающего быстрейшее выполнение к-онцевых ус¬
ловий.
В соответствии с выражением (3.14) введем #=^f, где век¬
тор фазовой скорости f на основании уравнений (3.24)
f = tffi.fal = {'"jc,ww°x + gx,ww°y\-gy,ww°z + gz}, (3.27)
а ф есть решение (3.13). Важным свойством функции сопряжен¬
ной переменной является тот факт, что она равна градиенту изо-
хроны: ф(/) = grad K{t). Принцип максимума утверждает необ¬
ходимость такой ориентации f, чтобы его проекция на градиент
K(t) была максимальной, т. е. выбором w°(£), входящего в соот¬
ношение (3.27), следует удерживать величину (3.14) на верхней
грани.
Решение уравнений (3.13) -позволяет найти ф(/)> а значит,
применяя процедуру оптимизации, определить w°onT(/). Сфор¬
мировать правую часть (3.13) не .составляет труда, но для ин¬
тегрирования системы требуется знать ф(/н). Информация о на¬
чальном значении ф(/) отсутствует и известно лишь ее конечное
значение, задаваемое условиями трансверсальности
iH4) = gradSK,	(3.28^
что и определяет краевой характер решаемой задачи.
Сравнивая условие (3.28) с требованием текущей ориента¬
ции ф(£)> легко заключить, что выход изображающей точки на
5К сопровождается касанием K(t) и SK(t) (см. разд. 1.6). При.
фиксации гц(/в) однозначно определяется SK(t) и задача сво¬
дится к определению управления, которое реализует фазовую
траекторию, проходящую через точку касания в некоторый мо¬
мент tK. Если же задано tUl то задача состоит в отыскании каса¬
тельной к K(t) гиперповерхности концевых условий и соответ¬
ствующего управления и траектории, В этом состоит однотип¬
ность решения двух задач, на которую указано' в разд. 1.6.
Можно записать
+	(3.29)
обратив внимание на то, что для дальнейшего использования в
представлении (3.29) можно ограничиться одной составляющей
f, а именно f2, которая зависит от w°.
Так как фактически w°(/) в данной постановке не ограничен,
то экстремум Н лежит внутри открытой области допустимых
Управлений и требование принципа -максимума может быть
представлено в виде (3.17). Тогда с учетом соотношения (3.29)
115

можно записать (Необходимые условия для определения опти¬
мального управления
=	(3.30)
rfwO Y у у rfwO	1
Последний -сомножитель, вообще говоря, является тензором, но
так как изменению подвергается лишь направление дифферен¬
цируемого вектора, то (3.30) можно записать как
= ф (/) 'w (/) [(доо grad) w° (/)] = 0,
rfw0
a	(w°grad)	w°	= —,	(3.31)
R
где n — единичный вектор главной нормали, R — радиус кри¬
визны.
Определение пи R связывает¬
ся с некоторой линией, которую
описывает при виртуальных пе¬
ремещениях w°(/). Подстановка
соотношения (3.31) в условие
(3.30) дает
W (t)
пф(*!) = 0,
(3. 32)
что /может -быть выполнено только при ортогональности п и ^
На рис. 3.2 изображен w°, через конец которого проведена пер¬
пендикулярная ему плоскость N. Варьирование w°(/) заключа¬
ется в формировании w° + 6w°, причем 6w° лежит в плоскости N
в силу ограниченности его величины. Вектор п, следовательно,
также принадлежит N как перпендикуляр к касательной кри¬
вой, описываемой w° при варьировании. Из этого следует вывод
о совпадении по .направлению векторов ф(/) и w°(0, т. -е.
WOiit(0— •	(3.33)
1Ф (01
Важно отметить, что оптимальная ориентация орта кажущего¬
ся ускорения явно не зависит от модели гравитационного поля.
116

Итак, задача отыскания оптимального управления, а значит,
и оптимальной траектории, заключается в интегрировании сис¬
темы
r(0=v(/); v(0=®(/)-J^r + g[r(/),/I,	(3.34)
It (01
6 Vj
*w~23-crwo-
/-1
где
х = {гЛ, Гд, rz, vx, Vg, vz};
t = {vx,vy,vz,w-^+gx\ W-^ + gy, w^-+gz
при начальных условиях x(tH) = {rxH, r№ rZH, vxlJ, vyHf vZH} и ус¬
ловиях на правом конце ф(£к) = grad SK. Если граничных усло¬
вий несколько, то следует привлекать (3.19).
Детализируем запись системы сопряженных уравнений при¬
менительно к уравнениям (3.24). Представим
Ф(*)={«М0, «Ы0, trz(t),	«ЫО, кл*)и
где индексы у .составляющих определяются проекцией вектора
фазовых координат, с которыми они сопряжены. Тогда система
(3.13) примет вид
~ (k)+>l”k$k) +	;
к Ш+♦-£(£)+f~k(k) ■■ (3-“>
^-^к{к)^к^кЛк.
Из рассмотрения системы видно, что для ее решения требу¬
ется, во-первых, выбрать конкретную модель гравитационного
поля и, во-вторых, задать совокупность граничных условий, оп¬
ределяющих значение на правом .конце траектории. Для выяв¬
ления структуры решения рассмотрим пример.
Пример. Разберем случай плоскопараллельного поля тяготения, т. е.
dU dU	dU
u = —grv, а значит,	— = — = 0;	—	=	-g
dr x dr z	dr	у
и все вторые производные равны нулю. Обращаясь к уравнениям (3.3:5),
ьмеем
\гх = Ьу = Ьг = = 0. \vx = -Фгл.	= —Фг!/. Фvz = —Фrz>
117

интегрирование которых с учетом условий трансверсальности дает
(О
dSK	dSK
^(0==^. ф„(0 = '
dr*	дгу
dSK	dSK
tyvx (0 = “7	+	(^к	О
dS*
0rz
i/vy (t) = -
\vz (0 =
акд
dSK
dvy
dSK
dv.
+ (*K -0
"Г (^K	 0
C>ri/
JSk_
drz
(3.36)
причем все производные вычислены для момента t—-(K. Тогда
шхопт
Г dSK	dSK
= te + (^-<)
dSK	ч	dSK	12
- + (,'-')57Г]
+
+
dSK	dSKV	Г	dSK
'>1гГР
£0®
//ОПТ
ч-
dSK 12 г^5к	^5k-12w1/2
* 0 _
^гопт
+
[dS±
[dvy
dSK
dvz
dSк
<?r2
t[£+«■-*>£]
+
1/2
Отметим, что для формирования оптимального направления вектора кажу¬
щегося ускорения привлекаются те составляющие ф(0» которые сопряжены
с проекциями фазовой скорости, зависящими от управления — аналогия с
(3.29 j.
Сходные результаты были получены в ряде работ [150, 155].
Для рассматриваемого случая выведем концевое условие, предполагая,
что движение объекта происходит в одной плоскости, а система координат
ориентирована так, что vz=rz=0. Для записи условия проинтегрируем урав¬
нения движения на пассивном участке
и получим
гх = 0. "г у = ~g
Vx (t — *к) = VX {tK)> Vy (t — tK) = Vy (tK) — g(t—tKy,
rx (t t\d = r x (^k) 4“ {t ^k) vx (^k)» r У if ^k) =
— Гу (^к) + (t — ^k) vy (tx) 4“ g (t — ^k)2.
■Обозначив длительность баллистического движения через т,
из условия
г у (^к Ч- тО = 0;
определим его
т = — (vyK + у v] + 2gryK). -
СГ	V	*
•118

Считая Гц=гл(/к + т), можно записать величину дальности
Гп = О-к + ~ (уук + Vv2yK + 2^к),
§
а само концевое условие примет вид
5к — Г*к—4“ Kk + T^W)-	(3.38)
Тогда
и подстановка в соотношения (3.37) дает возможность после некоторых пре¬
образований выразить
Подобные результаты были получены ранее [46, 90, 141, 150] для различ¬
ных способов фиксации правого конца траектории.
Итак, формулы (3.39) (позволяют вычислить wonT(^) = const,,
но само направление является функцией параметров конца ак¬
тивного участка. При этом краевая задача выступает® наиболее
упрощенном виде.
Прямой метод решения такой задачи заключается в следу¬
ющем. На основании ориентировочных данных или интуитивных
представлений задаются Wx{w°y сразу же находится из извест¬
ного тождества направляющих косинусов (w°x)2(w°y)2 = \) и
интегрируется (3.24) вплоть до выполнения условия (3.38). По¬
лученные значения гк и vK позволяют вычислить уравнение
(3.39) и повторить процедуру, не гарантируя сходимость, до>
стабилизации решения.
Когда модель гравитационного поля более сложная, для ре¬
шения краевой задачи следует привлечь специальные приемы
Ранее указывалось на серьезные трудности, возникающие
при попытке возложить на БЦВМ реализацию приведенных ал¬
горитмов для определения программы движения во время поле¬
та. Сейчас возможно сделать это более аргументировано:
1)	алгоритм управления вилиочает как неотъемлемую часть
краевую задачу. Существующие методычне только не гаранти¬
руют достижение требуемой точности за фиксированное число
Итераций для широкого диапазона начальных условий, но в об¬
щем случае не дают возможности утверждать наличие сходя¬
щегося решения. Сходимость процесса в значительной мере за-
(3. 39)
[84].
119-

висит от успешного выбора 1-го приближения. Последнее можно
отыскать, привлекая систему допущений, например, о ха-
рактере управляющего усилия (импульсная или постоянная
сила тяги [117]), о модели гравитационного толя и др.;
2)	само решение имеет вид программы управления WonT(£),
рассчитанной для известных условий движения — характера
внешних возмущений, сил притяжения и движущего усилия.
Тогда, если хоть одно из перечисленных воздействий отличает¬
ся от априорно известного, требуется достаточно часто обнов¬
лять информацию об изменении текущих параметров движения
и задаваться моделью последующих условий полета. При этом
текущие параметры принимаются за начальные условия и вновь
рассчитывается программа движения. Стремление приблизить
траекторию к оптимальной вынуждает чаще обновлять инфор¬
мацию об условиях полета, что ведет к загрузке ЭВМ, но не га¬
рантирует желаемого результата из-за возможных ошибок при
экстраполяции условий полета. Тем не менее оптимальное реше¬
ние дает возможность строить эвристические алгоритмы анало¬
гичной структуры и, что не менее важно, сравнивать различные
•алгоритмы и оценивать их близость к оптимальному.
Одним из распространенных способов борьбы с указанными
недостатками является формирование алгоритма, сохраняюще¬
го структуру оптимального управления и имеющего аддитивные
поправки, найденные итерационным образом из анализа усло¬
вий движения. Такова идеология управления движением ракеты
«Сатурн-5» на этапе выведения [69]. Этот подход прорабаты¬
вался теоретически в ряде работ [3, 76, 134], где показана его
высокая эффективность.
Другой путь состоит в запоминании совокупности констант
[2, 26], описывающих допустимое семейство возможных законов
управления. Тогда идентификацией условий движения (выбира¬
ется соответствующая группа констант, характеризующая наи¬
лучший закон управления. Аналогичная концепция заложена в
методе Х-матричного управления [19, 134], который основан на
подборе переменных коэффициентов из условия наиболее эко¬
номного использования управляющего воздействия.
3.3.	Синтез однопараметрических законов управления
Недостатков, присущих оптимальным программам управле¬
ния, вообще говоря, лишены оптимальные законы управления,
представленные в виде u=u[x(/)]. Однако, как уже пояснялось,
синтез такого управления разработан лишь для узкого класса
систем.
Для формирования закона управления выведением сузим
постановку задачи. Будем предполагать, что известна надле¬
жащим образом обоснованная программа управления и соот¬
ветствующая ей фазовая траектория для априорно заданного
120

комплекса внешних воздействий и силы тяти. Зададим-ся целью
сформировать такую управляющую связь, которая обеспечила
бы приближение действительной фазовой траектории к програм¬
мной при наличии существенных отклонений условий полета от
известных заранее.
Задача управления движением изображающей тонки вблизи
фазовой траектории, принятой за программную^ или требуемую*
достаточно широко представлена в литературе [11, 80, 81, 83,
86]. Синтез проводится для линейных систем, как правило, для
квадратичного критерия оптимальности, правый конец траекто¬
рии фиксирован. В качестве метода решения применяется дина¬
мическое программирование и .принцип максимума. Трудность
реализации разработанных решений, кроме их сложной алго¬
ритмизации, заклюнается в представлении управления в виде
функции времени. В рамках линейной модели движения при
учете стохастических условий полета задача синтеза оптималь¬
ного однопараметрического закона управления для широкого
класса объектов решена в работе [96].
При выполнении предположения о нерегулируемой тяге
двигателя, разбросы которой могут быть настолько велики, что
нарушается линейность модели объекта, очевидно, невозможно
решить задачу управления в полном объеме, как сведение к ну¬
лю вариаций фазовых координат на интервале	/к]
|Ах(/) | = |хпр(<)—х(/) |, xgX* или в момент t=tK. В этих усло¬
виях целесообразно использовать в качестве аргумента управ¬
ления какой-либо параметр движения или сформированную
функцию от группы параметров — и = и(^г) или u = u[s(^i)] с
тем, чтобы наложить управляющую связь на некоторые, наибо¬
лее критичные фазовые координаты. Тогда можно говорить о ста¬
билизации отдельных изопараметрических вариаций фазовых
кс-ординат Axj(s)—>Т), в то время как другие составляющие фа¬
зового вектора будут иметь конечные отклонения, которые сле¬
дует расценивать как методические ошибки.
Роль управления на этапе выведения в исследуемой модели
играет ориентация продольной оси ЛА или направление вектора
кажущегося ускорения. Тогда в общем случае задача состоит в
формировании зависимости w° = w°[s(^)], которая должна
Удовлетворять требованиям, предъявляемым к этапу выведения.
В основу этих требований можно положить идею «кривого ору¬
дийного ствола», т. е. обеспечения сохранения геометрической
формы траектории, а значит, и программной ориентации векто¬
ра скорости при допустимых отклонениях нерегулируемой вели¬
чины —модуля скорости. При такой постановке задачи стаби¬
лизируется положение вектора скорости на заключительной фа¬
зе выведения, что весьма важно для точного управления выклю¬
чением двигателя; как правило, невелики утлы атаки, что суще¬
ственно с точки зрения динамики полета [8], и упрощается ре-
121

шение .навигационной задачи ввиду возможности использования
более грубой модели ноля притяжения.
Математически требование сохранения геометрической фор¬
мы траектории выражается следующим образом. В предполо¬
жении движения, происходящего в одной плоскости, пусть най¬
дены соотношения rx=rxu])(s) и ry = ryTlv(s). Тогда, исключая
параметр s из этих зависимостей, можно записать инвариант¬
ное (по отношению ко «времени) выражение
гу~гупу{гх).	(3.40)
Сохранение этой связи на интервале t^[tlu tK] и будет озна¬
чать движение по .программной траектории в смысле первых
трех координат фазового пространства (1.50). При этом к па¬
раметру 5 предъявляется требование непрерывности и монотон¬
ности.
Простейшим примером такой параметрической управляю¬
щей связи является зависимость [93]
w° = w101p(Tj) или & = &1|р(^)	(3.41)
для .плоскости траектории, которая образуется при исключении
' времени из зависимостей О=ОПр(0» у = упР(0 (рис. 3.3). Из
рассмотрения рисунка нетрудно установить, что при отклонении
скорости движения от программной наблюдается «вариация ско¬
рости изменения угла тангажа:	при v(t)>vuv(t) происходит
более быстрый программный разворот объекта в плоскости по¬
лета (ср. .положение точек 4', 4*' и 4", 4*"). Благодаря этому в
пространстве (координат) производится сближение действи-
122

тельной траектории с программной; при жестком (программиро¬
вании разворота '0,=фпр(/) трубка возможных траекторий име¬
ла бы большие габариты (рис. 3.4). На рисунке показана также
деформация возможной области выключения двигателя: умень¬
шаются поперечные размеры области, но увеличиваются про¬
дольные. Это обстоятельство дает возможность более просто
сформировать алгоритм управления
выключением двигателя.
Другой способ построения гиб¬
кой управляющей связи базируется
на параметрическом задании про¬
граммного движения (см. разд. 1.2),
а в качестве параметра выступает
длина дуги 5, пройденная центром
масс по траектории [162]. Программ¬
ную траекторию в инерциальной си¬
стеме отсчета описывает зависи¬
мость
r(0=r[s(0]	(3.42)
или
v(t) = r(t) = — s = sa = v<s, (3. 43)
ds
где a— орт касательной v = vo.
Дифференцирование по времени (3.
шеиие
*	* I *	|	do
v = va<j -j- na = цса -р v —
ds
где п — орт нормали, R — радиус кривизны, —касательная
составляющая ускорения. Представив v = v°v, |v°|=l, будем
иметь
^0 = _Д(^а+ТП)’ г, = |‘г,2 + ^1/2.	(3.45)
Теперь определим инварианты траектории, т. е. условия, вы¬
полнение которых обеспечит движение центра масс ЛА по про¬
граммной траектории, фиксированной в пространстве коорди¬
нат, в условиях действия возмущений. В число возмущений бу¬
дем включать воздействия, приводимые к вариациям вектора
Ускорения. При наличии таких воздействий и отсутствии регу¬
лятора скорости, очевидно, невозможно добиться s(t)=snp(t)y
однако (3.40) будет выполнено, если потребовать
»(s) = «..p(s).	(3-46)
н так как a(s)n(s)=0, то тем самым обеспечивается опреде¬
ленная ориентация и n (s).
hr
'/л/ '/	06л	а	с	ть	при
V/
Область боз/www
zo дыклмченця дби-
гателя
Рис. 3.4.
г
43) дает известное соотно-
s = t)aa + -^ п,	(3.44)
н
123

Итак, для удержания центра масс программной траектории
необходимо сохранять программное значение орта касательной
как функции длины дуги. Тогда (3.45) позволяет вычислить тре¬
буемую ориентацию вектора ускорения, при этом допускается
должна подвергаться ориентация вектора кажущегося ускоре¬
ния, то на основании
Последнее в целях наглядности можно представить в двух фор¬
мах:
Если траектория программного движения задана уравнени¬
ем ry=F(rx), то для вычисления (3.48) или (3.49) можно рас¬
считать угол между a(s) и осью абсцисс 0(5) и радиус кривиз¬
ны R(s) по формулам
При этом следует найти соответствие частных производных ду¬
ге (1.29), запомнить эту зависимость и воспроизводить резуль¬
тат при расчете требуемого орта кажущегося ускорения.
На рис. 3.5 и 3.6 приведены графики, иллюстрирующие ха¬
рактер изменения нормированных зависимостей s(t), R(s) для
которые соответственно имеют индексы один и два штриха.
Таким образом, для реализации приведенного алгоритма не¬
обходимо использовать два ортогональных измерителя ускоре¬
ния, расположенных на стабилизированном н инерщиальном
пространстве основании. Оси чувствительности измерителей мо¬
гут быть неподвижны в этом пространстве (тогда необходимо
пересчитывать их показания для определения величины, входя-
124
изменение величин v(t) и v(t). Так как программированию
I v	*
w = VQ<3 -) n — g
R
можно записать
w
-®(в)=-Л— f W.(*)<j(sH
w(t) L
(s)-g(r)]-	(3.47)
R(s)
=~/~i\ & (*)9 (s)+vn W n (s) - g (r)]; 3
w (t)
-g(r)];8	(3.48)
(s)-g(r)].	(3.49)
программного движения и случаев	(0>	^	(0	<	^пр	W	»

щей в алгоритм управления) или разворачивать по программе
0 функции s.
Для иллюстрации структуры решения рассмотрим пример.
Пример. Обследуем задачу программирования движения центра масс
ДА в плоскопараллельном гравитационном поле, причем зададим траекторию
требуемого движения аналитической формой, а именно, движение должно
лроисходить по дуге окружности.
Рис- З-5-	Рис.	3.6.
Запишем соотношения, характеризующие движение центра масс:
ix = w(t)w°x(t); by(t)=w(t)wl(t) — g\
v(*)= [ 'v\ (t) + 'v\ (0]1/2;
v (0 = [vl (0 + v] (0]1/2; S (t) == J V (0 dt.	(3.	52)
0
Параметрическая форма задания программной траектории (окружность со сме¬
ненным цетром) есть
х = R (1 — cos и), у = R sin и,
125

а так как угловой параметр т выражается через длину дуги как t=s/7?, тс
х = R ^1 — cos -~ \ , у = R sin	.
Тогда
ах = cos 0 =	=	sin ; Qy = sin 0 = cos —■;
ds	R	R
nx = sin 0, ny = —cos 0.	(3.	53}
Предполагая, что ускорение w измеряется датчиками, расположенными на
стабилизированном основании и разворачиваемыми по программе s, при опре¬
делении величины ускорения следует учесть ускорение Кориолиса. Так как
скорость разворота датчиков при движении Л А по дуге /?=const постоян¬
ная, то
V2
Va = Wa — 8а* Vn = Wn + gn +	,
£ sin 0, ,gn — g cos 0.
На основе этих соотношений и представлений (3.53) в скалярном виде (3.48)
можно записать как
(s)-[*'■si" ~к+('"+тУ’■т lH'■
(3. 54)
•!(s)" iW [”*“s т~ К+ т)si" т] ■■
С помощью соотношений (3.52) и (3.54) можно промоделировать движение
объекта. Для расчета требуемой ориентации вектора кажущегося ускорения
достаточно одного из выражений (3.54), так как второе легко определяется
из известного тождества. Блок-схема алгоритма представлена на рис. 3.7.
126

Если измерения осуществляются в иперичальном базисе, то (3.49) с уче¬
том (3.53) принимает вид
Для построения алгоритмов требуется приблизительно одинаковое число ма¬
тематических операций. Недостатком последнего алгоритма является необхо¬
димость возведения в высокую степень параметров движения. Однако выра¬
жения (3.54) требуют учета кориолпсова ускорения, а также программирова¬
ния разворота акселерометров, что может вызвать затруднения при сложной
форме траектории. Следует также отметить, что для реализации алгоритма
необходима информация об истинных параметрах движения.
3.4.	Синтез многопараметрических законов управления
Необходимо отдавать себе отчет, что классификация законов
управления на одно- и многопараметрические, наметившаяся
в названии разд. 3.3 и 3.4, в значительной мере условная: обос¬
нованно можно утверждать, что аргумент рассмотренных зако¬
нов управления (скорость или интеграл от нее) следует тракто¬
вать как функцию нескольких фазовых переменных, а значит,
отнести эти законы к классу многопараметрических. Однако:
1)	предлагаемые классификационные признаки практически
всегда можно оспаривать или дополнять; 2) понятие однопара¬
метрических законов или программ есть понятие сложившееся,
достаточно указать на работу [96], где при синтезе не делается
различий между аргументами — время или параметр движения;
3)	синтез однопараметрических законов существенно отличается
от синтеза многопараметрических конструкций и решения для
общего случая пока не найдено. Поэтому, говоря о многопара¬
метрических законах, в настоящем разделе в термин «параметр»
вкладывается смысл константы, характеристики закона управле¬
ния, а не кинематического параметра, фазовой переменной.
Из сказанного очевидно, что для синтеза многопараметричес¬
ких законов используется проекционный подход. Нечто анало¬
гичное часто применяется в баллистике для учета влияния на
динамику движения различных возмущающих факторов, см.,
например, [8]. Итак, представим вектор управления w°(/) в ска¬
лярной форме
или i = x, уу г, а координатные функции удовлетворяют требо¬
ванию полноты (см. разд. 3.1). Зависимость верхнего предела
суммирования от i свидетельствует о возможности изменения
Длины ряда при аппроксимации отдельных составляющих век¬
(3.55)
m(i)
®2/(0=2	/=1,	2,	з,
(3. 56)
127

тора управления; в дальнейшем для сокращения записи эту за-
висимость отображать не будем.
Результат интегрирования (3.24) до t=tK с учетом обозна-
чений фазовых координат (1.50) можно записать как
'к t
dU
i—1, 2, 3...лГ/(4)—■*/н + -*/+з,н(*к”“*н) + ^ ^ ~~dx7^
*н 'н
*к *
j j w(t)w°i{t)df\
'к
j=4, 5, 6...Xj(tK)=xjH-\- ^
‘0
+ j w{t)Wi[t)dt.	(3.57)
Подставив в уравнения (3.57) управление, записанное в форме
(3.56), получим граничные значения фазовых координат, кото-
рые для простоты обращения с ними представим в обобщенном
виде
х1я, tK, Cj, cpj{tK), j w(t)d?J,
s=l, 2,	6;	j— 1, 2, m; 1=1, 2, 3.	(3.53)
Упрощение записи интегральных членов является, как это будет
видно далее, допустимым, а само их наличие принципиально.
Найденные выражения (3.58) позволяют найти новое представ¬
ление общего уравнения концевых условий (1.51):
SK(xH, tK, cJt cpj(tK), j w{t)dt^ = 0.	(3. 59;
Таким образом, установлена естественная зависимость кон¬
цевых условий от начального состояния системы, параметров
управления и энерговооруженности объекта.
Теперь задачу определения оптимального закона управления
можно рассматривать как отыскание некоторой совокупности
{Cj}, которая обеспечит выход изображающей точки на 5К за
кратчайшее время. Особо подчеркнем, что изменение w(t) пред¬
полагается известным (детерминированным) на данном этапе
решения. Последнее позволяет ограничиться в простейшей по¬
становке учетом 51к для расчета оптимальной траектории. Дей¬
128

ствительно, при полной априорной информации каждому хк бу¬
дет отвечать определенная баллистическая траектория с извест¬
ной длительностью движения. Тогда на основании предваритель¬
ного решения задачи прицеливания (см. разд. 2.4) можно обес¬
печить решение задачи наведения —г(^в)=гц(^в) или других
условий встречи при известной траектории движения в упреж¬
денную точку.
Так как SlK играет роль неявной формы задания tK от искомой
совокупности {с7}—в самом деле, {Cj\ однозначно определяет
траекторию, а значит, и момент достижения граничных условий,
то для определения минимального значения tK следует восполь¬
зоваться необходимыми условиями экстремума (3.1):
Естественно, эти условия пригодны для отыскания экстремаль¬
ных параметров закона управления, если экстремум функции в
пространстве {с?} располагается внутри допустимой области
или область определения неограничена, а функция выпукла.
Если же экстремум находится на границе, то для его отыскания
необходимо привлечь методы градиента. Вполне допустимо, что
последние окажутся более эффективными во всех случаях, осо¬
бенно при большой размерности пространства параметров.
Если рассматривается движение, происходящее в одной из
плоскостей инерциальной.системы координат (например, качест¬
венная боковая стабилизация движения), то целесообразнее
перейти от направляющих косинусов w*, Wz к углу, фик¬
сирующему ориентацию вектора тяги 0. Тогда вместо уравнений
(3.57)	можно записать
dS\K __ foiK
dsiK .
(3. 60а)
(3. 606)
дс1 дс2
*к t
-х1н~т{^к~ ^н)^4н+ \ \ ——dt2\ w [t) cos Ь [t)dt2\
J .) dx i	J	j
*^2к	О	ХЪн	T~	J	^	dt	"t"	^	J	(ОЖч
Xsin b{t)dt2\
(3.61)
к
x4k=x4h -\- Г dU dt \ w (t) cos ft (t)dt',
J dxx
H
H
5	3953
129

а вектор управления вместо (3.56) будет выражаться более
просто
т
0(0 = 2	(3-	62)
У-i
Детализируем первую группу соотношений (3.60):
<?5ik	^	aste	^	ае	а
/=»! ,2,4,5
дс,-	dxj	дв	дсi
/ = 1,2,4,5
Всю систему (3.60) в общем виде можно представить как
tfpU, <7, *к. ТуСО. j «»(0^) = 0;	(З.бЗа'!
S1K |*н, Cj, tK, С?J (tK), j w (t) dtj = 0.	(3.	636)
Система включает (m+1) уравнений и позволяет найти все
(га+1) неизвестные: tl{, си С2, —,ст, т. е. полностью определена.
Приведенные рассуждения распространяются и на случай
более сложного описания совокупности граничных условий, ко¬
торую следует представить в форме (1.53). Пространство пара¬
метров при этом расширяется за счет введенных множителей
Лагранжа. Аналогично следует поступать и при необходимости
оптимизации по более сложному критерию: выразить функцио¬
нал через совокупность искомых параметров подстановкой в
уравнения (3.57) или (3.61), записанных для текущего момента
времени, и включить его в концевое условие через множители
Лагранжа. Другими словами, и в этом случае задача состоит
в нахождении условного экстремума функции конечного числа
переменных.
Итак, решение в форме (3.60) или (3.63) позволяет найти
совокупность констант {с.,}, обеспечивающих оптимальное
управление движением. Управление зависит от хп, вида коорди¬
натных функций, концевых условий, модели поля притяжения
и закона изменения кажущегося ускорения. Если последний
известен, то аппроксимация управления рядом с неизвестными
параметрами, как этого и следовало ожидать, дает возможность
свести вариационную задачу к задаче отыскания экстремума
в пространстве конечного числа неизвестных. Иначе, упрощается
процедура отыскания решения, близкого (с точностью до аппрок¬
симации) к оптимальному, однако сохраняется требование на¬
личия информации о законе изменения кажущегося ускорения
на оставшемся интервале движения. Механизм вычисления
управления в принципе остается таким же, как и при реализации
130

результатов решения вариационной задачи: вычисляется опти¬
мальная совокупность {cj опт} для данного t на основе модели
изменения w(t) на [t, tK], через некоторое время вычисления по¬
вторяются при уточненной модели изменения w(t) и новых на¬
чальных условиях и т. д.
В разд. 3.2 говорилось о возможности построения метода
управления при сохранении структуры оптимального решения
и использовании поправок, вычисляемых итерационно. Харак¬
терным примером является алгоритм управления выведением
ракеты-носителя «Сатурн-5», принцип построения которого за¬
ключается в следующем.
Известно, что в простейшем случае управления движением
в плоскопараллельном поле задача сводится к краевой и сос¬
тоит в нахождении оптимальной ориентации вектора кажущего¬
ся ускорения (3.39). Для общего случая оптимальная ориентация
последнего переменна во времени (3.33). Для управления дви¬
жением ракеты «Сатурн-5» принят следующий алгоритм:
tg » = tg&011т-{К-k,t)~»011Т-kx4-k2t,	(3. 64)
где Фонт==const — оптимальный угол ориентации продольной оси
ракеты.
Итак, управление по своей структуре является оптимальным
для более общего случая, нежели плоскопараллельное поле.
Оптимальный угол Фонт можно вычислить при использовании
этого упрощающего предположения и зафиксировав правый ко¬
нец траектории (например, по вектору конечной скорости и вы¬
соте), что дает возможность сразу рассчитать (3.39). Разумеет¬
ся, при этом должен быть известен закон изменения кажущегося
ускорения на всем участке движения [t, /к].
Для определения параметров закона управления ku k2 выра¬
жение (3.64) подставляют в уравнения движения (3.61), что
позволяет выразить
Гк = гк(^(гк), К К)\ vK=vK(4, g(rK), къ kb)
и найти константы из условия обеспечения требуемых парамет¬
ров конца активного участка. Алгоритм решения имеет итера¬
ционный характер и основан на экстраполяции параметров дви¬
жения для уточняемого закона изменения кажущегося ускоре¬
ния и эффекта от действия гравитационного поля с учетом не-
сферичности Земли с точностью до второй зональной гармоники.
Недостатками такого решения являются, во-первых, его форма
в виде функции времени заданного вида с неизвестными пара¬
метрами и, во-вторых, применимость решения к узкому классу
задач с закрепленным правым концом.
Покажем, что на основе многопараметрического закона
управления (3.56) или (3.62) можно получить алгоритм, лишен¬
ный в принципе указанных недостатков.
5*
131

Предварительно сделаем одно важное знамечание. Ранее в
этом параграфе решалась задача отыскания {сг}, отвечающей
экстремальному значению критерия. Можно изменить постановку
задачи и считать известной программную траекторию или управ¬
ление. Если известно управление, то совокупность {cj} следует
определять из условия наилучшей аппроксимации рядом . (3.56)
или (3.62) заданного управления. Когда задана траектория,
мерой достижения экстремума является близость полученной
траектории, отвечающей некоторой {Cj}, программной. Та:кая
постановка более характерна для технического проектирования
Рис. 3.8.
алгоритмов системы управления, так как программное движение
рассчитывается специалистами по теории полета. Итак, будем
считать известной {с?-р}, которая обеспечивает требуемое движе¬
ние с выводом изображающей точки на гиперповерхности Sl4-
в расчетную точку хкеХ*. Реальное движение отличается о г
расчетного из-за действия возмущений, которые так же, как и
в разд. 3.3, будем считать приведенными к вариации кажущегося
ускорения. Задача заключается в отысканий такой новой сово¬
купности {с7}, которой бы отвечала скорректированная траекто¬
рия, проходящая через множество SI{, образованное пересечением
S2-Kc:X*. Тем самым решается задача нахождения механизма
воздействия на траекторию управляемого движения, которая в
итоге должна обеспечить баллистическому движению требуемые
свойства по информации о конечном состоянии объекта.
Будем полагать, что новая (искомая) совокупность отлича¬
ется аддитивной добавкой, т. е. если представить {cj} как вектор
с в соответствующем m-мерном пространстве, то
с = ср + 8с,	(3.65)
где
С= {Су}, сР = {сР}, 8с=(8с;.), j — 1, 2, т.
В результате синтеза следует найти (рис. 3.8)
8c = /7(5W),	(3.66)
где 8w = wnp(/) — w(/)—приведенное возмущение.
Тогда при реализации управляющей связи вида (3.66) сис¬
тема будет обладать инвариантными свойствами (в смысле вы¬
132

полнения граничных условий) к возмущениям по кажущемуся
ускорению. Строгость инвариантности зависит от точности опре¬
деления (3.66) и степени приближения решения, полученного на
основе прямого метода, к точному. Более того, интуитивно ясно,
что такого рода решение будет в определенной степени (с точ¬
ностью до переходных процессов) отвечать экстремальному, так
как в силу непрерывности (3.66) появлению 6w будет однознач¬
но соответствовать некоторое 6с, приводящее к минимально не¬
обходимой деформации траектории, требуемой для выполне¬
ния граничных условий.
В последующем для конкретности будем полагать, что 5h
образовано пересечением S[u и S2к- Для нахождения (3.66) под¬
вергнем линеаризации (3.63). При этом учтем, что
1) при данном составе Sin задача управления состоит в одно*
временном выполнении Sin=S2n = 0 или в предположении дви¬
жения в одной плоскости: в t=tK должно быть
4~ ^АУТ + ^ПУТ = 4 (^АУТ = 4“ 4> 4гУТ = 4 ~ 4)>
т. е. фиксируется общая длительность полета;
2) нормальные по отношению к плоскости движения возму¬
щения парируются системой боковой стабилизации, а приведен¬
ное возмущение, на борьбу с которым ориентирован рассматри¬
ваемый алгоритм, расположено в плоскости движения, т. е.
Sw (/) = bwj (/) i + bw2 (4 j,	(3.	67)
где \, j — орты системы OvXT^YT^ZT^ (см. рис. 2.7). Эти обстоя¬
тельства фактически означают, что управление призвано дефор¬
мировать траекторию в плоскости стрельбы, оставив последнюю
неизменной. Аналогичный подход к формированию управления
предлагается в работе [146], алгоритм управления строится из
эвристических соображений.
Система уравнений, полученная при линеаризации выраже¬
ний (3.63), имеет вид
Х-^8щ£=0;	(3.686)
dws
^аут + ^пут=0, /7=1, 2, ..., m, i= 1, 2, 4, 5.	(3. 63в)
Выполнение последнего требования наряду с условием SlK=0
гарантирует стабилизацию длительности полета.
133

По системе (3.68) сделаем два замечания.
1. Линеаризации не подвергается соотношение (3.63б), так
как в противном случае вместе с (3.63 а) образуется тривиаль¬
ное решение. Смысл этого заключается в том, что окончание
активного участка производится по выполнению S\K=0.
2. При линеаризации вырьируется w{t)y которое входит через
интегральные зависимости в концевые значения фазовых коор¬
динат (3.58), а значит, и в граничные условия (3.59). Поэтому
в (3.68) входят интегральные вариации кажущегося ускорения,
что отмечено звездочками в индексе.
Итак, имеем линейную алгебраическую систему (т+2) урав¬
нений, которая позволяет найти 8с={8с1,	...,
^пут- Искомая зависимость (3.66) выродилась в линейную:
ml’ ^АУТ»
bci = kilbw\-\-k12bw2.
(3. 69)
Методическую ошибку можно оценить либо учетом вторых
членов разложения и последующим расчетом траектории, либо
анализом возмущенной траектории, найденной с применением
полного алгоритма (3.63).
Детализируем результат (3.69), пользуясь правилами реше¬
ния линейных уравнений. Определитель (3.68) есть
D--
а/?1
dRr
dRr
dRr
0
дс 1
dc2
дст
<^АУТ
dRm
dRm
dRm
dRm
0
дс\
dc2
dcn
dt АУТ
dSriK
dS2K
dS2 к
dS2K
dS2K
(3. 70)
дс\ дс2	дст dtAyT dtnyj
0	0	Oil
Алгебраическое дополнение D1{ (k — номер столбца) получается
заменой соответствующего столбца столбцом правой части —
двойные суммы в (3.68).
Тогда	bcf	=—.	(3.71)
j D
Для приведения соотношения (3.71) к виду (3.69) следует раз¬
ложить каждый дополнительный определитель по элементам
столбца. Известно, что
/72 + 2
DK = 2 *я*Ая*	(3-72)
<7=1
134

где aq к — элемент k-то столбца q-й строки; Адк — соответствую¬
щее алгебраическое дополнение. Элементы k-то столбца суть
* .*	dRv	dxt	*	•*	dR*>	1	о
7i 	;	bw2 7 ,~2	г-.	P=l,	2,	•••,	tn,
Jam &xi dwi	^m	&xt	dw2
г=1, 2, 4, 5.
Zjk dxt dw±	dxt	*Ja
Тогда выражение (3.72) можно записать как
т+2	т+2
Ас = 8®*2	+	Я?кЛ?К)
Я -1	<?~1
^£7
^<7 к „ ияК
V=73T’
или окончательно
ос.
1ш+2	/71+2	-■
8^; \Ja;KA?K+8a>2^a'gK^?Kj,
(3. 73)
что и является искомой зависимостью, а при сопоставлении с вы¬
ражением (3.69) находятся константы.
При реализации полученного алгоритма для вычисления по¬
правок к коэффициентам ряда, аппроксимирующего требуемое
управление, необходимо знать интегральные вариации бw*.
Определение последних связано с экстраполяцией приведенных
возмущений на интервал [г, £к], т. е. начиная с текущего момента
до окончания управления. При этом задача приобретает дуаль¬
ный характер: увеличение интервала экстраполяции, вообще
говоря, приближает решение к оптимальному, но может привес¬
ти к росту ошибок и, как следствие, к необоснованным маневрам
на траектории. Нижняя грань интервала определяется быстро¬
действием системы и допустимой максимальной величиной ин¬
тегральной вариации. Вообще, следует подчеркнуть необходи¬
мость технической проработки задачи экстраполяции возмущений
и их последствий для реализации оптимальных или близких к
ним алгоритмов управления.
В заключение приведем методический пример, иллюстриру¬
ющий некоторые аспекты построения рассмотренных алгоритмов.
Пример. Примем допущения, использованные в примерах разд. 3.2 и 3.3.
В качестве концевого условия можно использовать (3.38), на основе ко¬
135

торого будем решать задачу максимизации дальности. Соотношения (3.61)
запишем в виде
/к /	tK	t	щ
Гхк = § J W (0 cos 9(t)dfi; r,jK=\ f w (/) sin 6 (/) dfi— — (tK— <„)2;
<H 'h
(3. 74)
'.к.	'к.
Wjck = j w (0 cos 6 (0 dt, vyK = jw (t) sin 0 (7) d/ — (tK — tH) g.
Так как при использованных допущениях максимум дальности достигается
при f)=const (3.39), го ряд (3.62) вырождается: i)=ci, ф!(^) = 1. Для прос¬
тоты вычислений положим w (t) = const.
Тогда
Гхк =	(4	—	4)2	W cos съ гУк = -	(*к — *н)2 (W sin Cl — g);
VXK = (*к — *н) W cos Cl,	^K=(^	sinci-4	(4—	*h).
Найдем частные производные, входящие в * соотношения (3.63). При этом
учтем, что первые сомножители (3.63а) получены ранее [см. (3.38)]. Вторые
сомножители имеют вид	'
дгхк	1	.	dvXK
—— = —— (*к — tHy*w sin си -— = —(iK—tH)w sin ch
и сi	z	ocj
d/\yK 1	.n	•	di/wK
-r— = — (4 — *h)2	W cos	Cl,	——	=	(4 — to)	W COS	С1.
C/Ci Z	(7^1
Тогда соотношение (3.63a) принимает вид
1	1	.	.	_1/9 w
—— sin сi — — w cos2 сi [оу sin ci (ze> sin ci — g)]	1 — -— (sin2 c\ — cos2 Ci) —
z	z	g
— ~—[w sin ci (w sin c\—£)]""'1^2+w2 cos2 Ci sin ci[w sin сДоу cos c\—^)]—1/2=(>
g
или после ряда преобразований
(п sin ci + [(и sin ci)2 — n sin ci]1/2^h cos 2ci + -y- sin ci^ —
— n cos 2ci == 0,	(3.	75)
где	n = w/g.
Линеаризация последнего соотношения дает возможность получить аналог
(3.68а)
50 = Sc 1 = — |sin с 1 cos 2ci + sin cij (2 [(/г sin ci)2 — n sin Ci]1^2 +
+ 2n sin ci — 1) + 2 cos 2ci [(n sin ci)2 — n sin c{\1^ (n sin ci +
+ [(/г sin c{)2—n sin Ci]1^2) — cos 2ci [(n sinci)2— n sin Ci]1//2j X
136

X |л cos c\ ^/z cos 2ci -f- — sin Cij (2 [(n sin C\)2—n sin Ci]1/2+2/zsin c\— 1) -b
-j- 2 [(/z sin ci)2— n sin c\]^2 (n sin c\ + [(л sin Ci)2 — n sin Ci]1/2) ^-^-cos C\—
— 2n sin 2c\) -f- 2n sin 2c\ [(л sin Ci)2 — n sin ci]1^2! bn. (3. 76}
Рис. 3.9.
Результаты расчета (3.75) совпали с результатами решения вариационной за¬
дачи [74]. Они представлены на рис. 3.9.

ГЛАВА 4
УПРАВЛЕНИЕ СБЛИЖЕНИЕМ
4.1.	Анализ методов управления
сближением
Задача управления сближением с точки зрения ее постанов¬
ки и формализации имеет много общего с задачей управления
выведением, что обусловлено принадлежностью обеих к классу
задач, составляющих теорию наведения. Естественно, что эта
общность распространяется и на методы синтеза оптимального
или близкого к нему управ тения.
Далее в основном будем рассматривать управление
относительным движением, которое формируется на основании
информации о параметрах этого движения, т. е. оставаясь в рам¬
ках модели, описанной в разд. 2.5, 2.6. Тогда алгоритмы управле-'
ния могут реализоваться на базе бортовой аппаратуры или на¬
земными средствами, на которые поступает информация об отно¬
сительном движении, измеренная бортовыми датчиками и пере¬
данная по радиолинии связи или вычисленная на основании
данных от наземного измерительного комплекса. Для последую¬
щего изложения принципиален не способ получения информации
и место размещения вычислительного устройства, а характер
информации от измерителей, фиксирующих изменение парамет¬
ров относительного движения.
Задача управления сближением возникла давно как необхо¬
димость организации встречи судов и наведения истребителя
на бомбардировщик. Алгоритмы управления в 40—50-х годах
получили название методов наведения и приобрели свою совре¬
менную трактовку несколько позднее, при создании систем про¬
тивовоздушной и противоракетной обороны. В этот период были
сформулированы и обследованы многочисленные методы наведе¬
ния: метод погони, параллельного сближения, пропорциональ¬
ной навигации и их модификации [16, 61]. Использование на
-современном этапе методов наведения для задач управления
сближением КА ограничено, хотя такие возможности просматри¬
ваются [27, 54, 131]. Ограниченность применения методов наве¬
дения для рассматриваемого круга задач вызвана следующими
причинами:
138

— в основе методов наведения лежит требование создания
возможно меньших боковых и нормальных перегрузок, необходи¬
мых для маневра встречи с целью, перемещающейся в соответст¬
вии с определенной заранее гипотезой: равномерное или равно¬
ускоренное движение по траектории с фиксированной крутизной.
Выполнение этого требования гарантирует необходимый мини¬
мум динамической ошибки как составляющей промаха, образо¬
вывающегося при наведении на цель, маневр уклонения которой
от встречи близок к принятой гипотезе. Однако при управлении
в космосе величина перегрузки, как правило, не является пока¬
зателем промаха, так как объект сближения обычно не соверша¬
ет энергичного маневра и атмосфера отсутствует;
— простота их реализации как с точки зрения используемой
информации, так и элементарной формульной зависимости меж¬
ду измерительными сигналами и командами управления. Мето¬
ды наведения можно отнести к категории эвристических законов
управления, не обеспечивающих оптимальных свойств процесса
сближения, хотя в некоторых случаях достаточно близких к ним
[18, 143]. Интересно отметить, что в ряде американских обзоров
недавнего времени [33, 103], посвященных анализу перспектив
синтеза систем управления ЛА, настойчиво рекомендуется боль¬
ше внимания уделять разработке оптимальных решений, даже
если они не могут быть реализованы. Авторы выступают против
эвристических решений, главным достоинством которых являет¬
ся простота реализации;
— методы наведения предполагают непрерывное силовое
воздействие на объект управления до момента встречи с целью.
Качественно новая постановка задачи управления сближением
КА заключается в управлении вплоть до выполнения известных
граничных условий с последующим выключением двигателя и
полете по баллистической траектории (с предусмотрением воз¬
можности ее коррекции) до момента встречи. В этом полная
аналогия с задачей управления выведением.
Одним из способов улучшения управления, задаваемого ме¬
тодом наведения, является оптимизация некоторых коэффициен¬
тов, входящих в уравнение метода [4, 160]. Дальнейшим развити¬
ем подобного подхода можно считать разработку параметричес¬
ких программ заданной структуры, в которых роль независимой
переменной играет дальность, ее производная или угловая ско¬
рость вектора дальности (линии визирования) [39, 69, 96]. Иног¬
да в качестве переменной предлагается использовать истинную
аномалию, фазовый угол и разность высот [139, 166]. Обычно вид
закона управления выбирается таким, чтобы можно было полу¬
чить решение уравнений относительного движения в квадрату¬
рах, при этом рассматривается плоское движение в однородном
поле. Тогда задача сводится к отысканию констант, которые
находятся из условия достижения экстремума критерия. Струк¬
139

тура параметрической программы может выбираться из условия
совпадения фазовой траектории с оптимальной, найденной на
основе решения экстремальной задачи.
Существенное достоинство методов наведения и параметри¬
ческих программ состоит в удобстве реализации таких алгорит¬
мов, обусловленном прямой зависимостью управления от не¬
посредственно измеряемых параметров относительного движе¬
ния. Это качество является принципиальным ввиду необходимос¬
ти оперативного управления при сближении для широкого диа¬
пазона начальных условий, который может быть весьма прибли¬
зительно описан априорно. В этом заключается отличие от
управления полетом PH и БР, для которых целевое многообра¬
зие обычно известно с высокой степенью достоверности. Указан¬
ная особенность определяет специфику синтеза алгоритмов
управления сближением и в значительной мере предопределяет
выбор математического аппарата. В частности, как справедливо
отмечалось в работах [96, 127, 141], при управлении сближением
практически исключена возможность использования оптималь¬
ной опорной траектории. В этом смысле реализация законов
управления чрезвычайно удобна, однако не следует забывать,
что за привлечение эвристического подхода приходится платить
отклонением от экстремума критерия, а именно — дополнитель¬
ными расходами топлива.
Стремление создать оптимальный регулятор заставляет обра¬
щаться к классическим методам вариационного исчисления и его
модификациям. Решения, полученные на их основе, обладают
всеми указанными ранее недостатками. Традиционными остают¬
ся и пути борьбы с последними, используемые при синтезе алго¬
ритмов управления сближением. Так, в работе [26] предлагает¬
ся множество оптимальных программ аппроксимировать
совокупностью констант, каждая группа которых отнесена к
соответствующему диапазону начальных условий. Использование
сопряженной переменной для определения текущей вариации
управления обследуется в трудах [2, 157]. В ряде работ для на¬
хождения величины близкого к оптимальному управления при¬
влекается градиентный метод [21, 133, 164]. В соответствии с ним
управление в каждый момент времени выбирается из условия
наибольшей деформации граничного условия, в роли которого
выступает величина промаха, возникающего при прекращении
управления в данный момент. В качестве частного решения по¬
лучен результат об ориентации вектора тяги по нормали к век¬
тору дальности в плоскости, проходящей через последний вектор
и вектор относительной скорости.
К последнему направлению примыкают методы синтеза, ба¬
зирующиеся на определении требуемой скорости, необходимой
для выполнения встречи [165, 169]. По своей идеологии они ничем
не отличаются от аналогичных построений при формировании
140

управления для БР и PH. При вычислении требуемой скорости
используются статистические оценки вектора промаха.
Следует указать, что идея определения требуемой скорости
глубоко прорабатывалась для широкого класса задач, в том чис¬
ле и задач сближения. Для последних требуемое приращение
скорости находится на основе изучения динамики взаимного
орбитального движения двух объектов. Величина приращения
должна быть минимальной, а само приращение должно быть
ориентировано в таком направлении и такой величины, чтобы
обеспечить перевод управляемого КА на одну или несколько про¬
межуточных орбит, а затем на требуемую, по которой обра¬
щается цель. Характерным условием для такого рассмотрения
является допущение об импульсном изменении скорости (дли¬
тельность приложения силового воздействия много меньше вре¬
мени полета).
Наиболее обстоятельно подобного рода решения описаны
в работах [10, 25, 69]. Однако при построении алгоритмов пред¬
полагается наличие полной информации об эфемеридах обоих
объектов, которые наиболее просто фиксируются в геоцентриче¬
ской системе координат, и не принимаются во внимание возмож¬
ности использования бортовых измерителей. Последнее отличает
постановку задачи, принятую в данном изложении.
Остановимся подробнее на роли статистических методов при
описании и решении задачи оптимального управления сближе¬
нием. Вообще говоря, рассматриваемая проблема требует более
глубокого изучения стохастического характера информации, по¬
ступающей от измерителей, нежели задача наведения БР или
PH. Это обусловлено определением в процессе управления пара¬
метров относительного движения, которые непосредственно за¬
висят от характеристик движения цели. Такого рода информация
получается с помощью радиоизмерений с органически присущи¬
ми им помехами. При измерении параметров движения PH или
БР информация поступает от бортовых измерителей, сигналы
которых имеют достаточно ограниченную структуру. Погрешнос¬
ти в этом случае характеризуются гораздо лучшим приближени¬
ем апостериорной информации к априорной.
Однако широкому привлечению статистических методов к
синтезу оптимального управления препятствует ограниченная
возможность их применения для нелинейных объектов, что ха¬
рактерно для задач сближения.
Существенные результаты получены при допущении о линей¬
ности модели объекта и импульсном характере силового воздей¬
ствия [25, 74, 94, 100, 167]. Такие предположения позволяют
широко использовать принцип декомпозиции и хорошо согласу¬
ются с реальными условиями межпланетных перелетов. Управ¬
ление при этом рассматривается как вектор с составляющими:
величина, момент приложения, ориентация вектора тяги. В ка¬
141

честве критерия используется форма вида (1.38), позволяющая
учесть как точность решения задачи, так и необходимые энерге¬
тические затраты. Основной метод синтеза — динамическое про¬
граммирование; используются и локально-оптимальные эвристи¬
ческие программы [49, 112]. Наиболее глубоко синтез рассмотрен
в работах [25, 68].
Аналогично исследовалось и управление сближением, несмот¬
ря на ограниченность подобного подхода, вызванного предполо¬
жением о линейности модели [18, 36]. Если же в модели учитыва¬
ется линейная составляющая гравитационного ускорения (при
описании движения в орбитальной системе координат), то опти¬
мальное решение имеет вид алгоритма, непременным элементом
которого является краевая задача [46, 137, 159]. Недостатки та¬
кого рода алгоритма уже обсуждались.
Подводя итог анализу методов управления сближением,
можно отметить, что, судя по известной нам литературе, пробле¬
мой остается разработка алгоритмов, обеспечивающих оператив¬
ное определение оптимального управления для широкого диапа¬
зона начальных условий, когда относительное гравитационное
ускорение существенно влияет на динамику сближения:	при
больших относительных расстояниях между объектами и дли¬
тельных интервалах полета до встречи. В опубликованных ра¬
ботах, исключая общие решения импульсного управления пере¬
ходом с орбиты на орбиту, выходящих за рамки рассматривае¬
мой проблематики, приводятся эвристические программы даль¬
него сближения, не претендующие на оптимальность. Так, в [69]
описывается метод опорных точек и способ привязки трассы к
опорным пунктам в интересах организации управления сближе¬
нием; в [127] излагается метод «переменной точки», предназна¬
ченный для быстрого изменения программы полета. Метод бази¬
руется на использовании самонаведения, не привязан к номи¬
нальной траектории и учитывает изменение эфемерид цели за
время полета управляемого КА.
Однако алгоритм управления включает ряд подпрограмм
(планирования полета, навигации, наведения), которые не яв¬
ляются оптимальными ввиду использования эвристических
принципов.
Мы не останавливались на классификации систем и методов
управления сближением, принципах получения информации,
вопросах формирования управляющих усилий и других, так как
предполагается, что заинтересованный читатель найдет ответы
на свои вопросы в соответствующей литературе {4, 35, 61, 96].
На основании рассмотрения особенностей задачи управления
сближением в исследуемой постановке можно утверждать, что
она укладывается в рамки теории наведения и при ее решении
уместно применять методы синтеза, характерные для управления
движением PH и БР.
142

4.2.	Особенности формализации задачи сближения
для целей синтеза
Как и в предыдущей главе, задача заключается в отыскании
оптимальной программы (или закона управления) изменения
орта кажущегося ускорения w2nT. В качестве критерия оптималь¬
ности аналогично примем величину топлива, которую надо из¬
расходовать для достижения некоторых граничных условий.
Предполагая известными характеристики двигательной установ¬
ки, этот критерий сводится к быстродействию (3.26).
Допустим, что один из аппаратов не маневрирует (wi(/)=0)
и обращается по стабильной орбите. Тогда уравнения относи¬
тельного движения в абсолютной системе координат (1.16),
(1.17), можно записать в форме Коши:
DW = v0TH(*);	(4.1а)
v0TH(^)=w(/!) + gradf/[r1(/!), t] — gradU [r2(^), г!],	(4.16)
где w(t) =—w2(t)—кажущееся ускорение, возникающее при
управлении (работе двигательной установки). Если управление
началось в / —/п и закончилось в t=tK, то с учетом (2.101)
Voth(Ao ^н) — V0 (0"f I* w(0^ + Av(/K, *н)>	(4.2)
'н
где Av(^K> tB) определяется соотношением (2.85). Очевидна за¬
висимость Av от г2(t), который изменяется при сближении:
*к t
г2(0 = г2(^н)“Ь(4~~^н)г2(^н)+ f j* [grad£/(r2(£), ^) + w (t)]dt2. (4.3)
i t
*н н
Таким образом, для построения траектории относительного дви¬
жения на этапе активного участка (управления) необходимо
проинтегрировать уравнения (4.1). При этом действие управ¬
ления проявляется двояко: 1) ускорение от действия управле¬
ния прямо сказывается на величине относительной скорости
(4.1 б); 2) управление вызывает деформацию траектории, а зна¬
чит, и изменение гравитационного воздействия, что также при¬
водит к вариации параметров относительного движения.
Второе обстоятельство существенно усложняет описание от¬
носительного движения на этапе коррекции, так как исключает
возможность использования конечных аналитических соотноше¬
ний и заставляет обращаться к интегрированию уравнений вида
(1.12), (1.14) или (1.18).
143

Представим разность гравитационных воздействий в виде
Ag(/‘)=grad6r[r1(^), t\ — gradf/[r2(^), ^]=Aga(^) + Agp(/),	(4.4)
где составляющей Aga(0 отвечает баллистическое движение
управляемого аппарата с начальными условиями г2(/н), г2(7н).
Второе слагаемое разложения (4.4) характеризует изменение
относительного ускорения силы притяжения, обусловленное ма¬
невром. Тогда, принимая во внимание только линейные члены,
можно записать
(*)==1П7Г'	(4-5)
^1*2 (0 dw (t)
где все производные берутся относительно невозмущенной тра¬
ектории при t^[tUy Гк].
В процессе синтеза будем полагать, что Agp(/) = 0, тем са¬
мым будем считать справедливым допущение об одинаковом
действии гравитационного поля на КА, летящий по невозмущен¬
ной (баллистической) и возмущенной управлением траекториям.
Такое допущение достаточно справедливо, так как по характе¬
ру своего появления ^-составляющую можно рассматривать как
малую величину 2-го порядка по сравнению с а-составляющей.
Допущение выполняется тем точнее, чем меньше интервал кор¬
рекции и тяга двигательной установки. Далее будем считать
Ag(0 = Aga(0 при t^[tn, /к]- Тогда для этого временного интер¬
вала можно записать вместо (4.1):
t
^Отн [U О— vo (0~b Av {t,	(t)dt\	(4.6)
t
D(^> ^h) = D(4) + (^~4) уо(0 + j Av(t)dt-\-
+ j(W(/)^2,	(4.7)
'h
где Av(£) находится по формуле (2.98),	(2.101), (2.110) или
(2.115) в зависимости от способа фиксации начальных условий.
Отметим, что при использовании допущения о сохранении
в процессе управления закона изменения гравитационной состав¬
ляющей относительной скорости в качестве единственной причи¬
ны, вызывающей отклонение относительной скорости от закона
ее изменения, отвечающего баллистическому движению, на этом
этапе принимается управляющее ускорение. Тем самым под¬
тверждается, что управление проявляется в изменении ранее
считавшейся постоянной составляющей относительной скорости:
v0=Vih—v2ii [см. отношение (2.92)].
144

Итак, при известном законе изменения кажущегося ускоре¬
ния \v(t) = v/0(t)w(t) подобный подход позволяет применять мо¬
дель относительного движения, разработанную в гл. 2, для рас¬
чета траектории на этапе коррекции. Однако остается открытым
вопрос об определении новых начальных
условий для последующего вычисления бал¬
листической траектории после выполнения
граничных условий управления. Перейдем
к рассмотрению этих алгоритмов.
Алгоритм расчета начальных условий.
Пусть начальное положение объектов за¬
дается в геоцентрической системе ОДгУДг
относительно некоторой точки, принадлежа¬
щей оси ОгУг. Известны радиус-вектор этой
точки г={0, г, 0} и скорость ее движения	2г
v={^a;, vy, 0}. Параметры движения обоих
объектов определены приращениями коор¬
динат и скорости к соответствующим пара¬
метрам указанной точки:
Агх = {а:х, уъ zx.}, Аг2 = {д:2, у2, z2},
Av1 = {иъ Wy\, Av2= {tt2,	w2}.
(4.8)
Системы координат, соотнесенные к центрам масс обоих объек¬
тов, целесообразно ориентировать таким образом, чтобы их век¬
торы скоростей лежали в плоскостях ОДцТ^ и ОД2гУгг
(рис. 4.1). Тогда в начальный момент времени параметры дви¬
жения в системе ОДгУДг определятся как
Г|н={*1, r + Уг, zx}; vlH = {vx-(-и1, vy-\-v2, w,};
г2н=(^2, r-\-y2, z2}; v2H={;i)_l. + a2, vy-\-v2, w2}.	(4.9)
На базе имеющейся информации можно найти взаимное по¬
ложение систем координат ОДДДг и OvX\TY\TZ\T, ОД2гУ2Д2г,
а также 0TX\TY\TZiT и ОгХ2гУ2Д2г. Примем систему отсчета углов
такой же, как и представлена на рис. 2.16. Зная начальное поло¬
жение объектов (4.9) и условие ориентации векторов скорости
в плоскостях ОД, У достаточно просто определить углы 0, ф, <р
построением вектора удвоенной секторной скорости c=rXv.
Действительно, линия пересечения плоскостей ОДУ любой из
двух совместно рассматриваемых систем координат фиксируется
вектором
Vap = c<,Xcp,	(4.10)
где индексы «а» и «|3» соответствуют требуемому сочетанию ве¬
личины:
Cl = rlHXvlH> С2 = Г2нХ V2H> c = rXv-
6	3953
145

Тогда
6=arccos—sUL; 6 = arccos-~ g--;	(4.11)
coP$	rPvaP
raVa3
cp = arccos	—.
'’Лр
Для определенности присвоим матрицам Д, характеризующим
взаимное положение систем координат (2.114) или (2.82), соот¬
ветствующие обозначения:
Д—переход от OvXlvYlvZlv к OrAT2rK2rZ2r; Д1 —от OrXrYrZr к
ОгХ1гУ lrZlr\ Д2 от OrXrYrZr к OrX2rY2rZ2r.
Параметры орбит каждого из объектов находятся по формулам:
р— (2.18); е— (2.20), истинная аномалия Ф — из (2.14) с под¬
становкой в них скалярных соотношений (4.9).
Следует напомнить, что при составлении программ для ЦВМ
необходимо учесть ограниченность обратных функций, так как
главные значения (4.11) определены в пределах 0—2к. Поэтому
для нахождения возможных отрицательных величин углов це
лесообразно сформулировать дополнительные условия, которые
можно получить из изучения относительного движения.
Алгоритм перехода от баллистического движения к управля¬
емому и обратно. Согласно принятому подходу относительное
движение определяется в системе координат управляемого (вто¬
рого) КА (см. разд. 2.5—2.7). Ранее на ориентацию связанных
с центрами масс системами координат 0\XiYiZ{ и O2X2Y2Z2 ни¬
каких ограничений не накладывалось. Однако, как это будет ясно
из последующего, в ряде случаев удается достигнуть известных
преимуществ (простоты алгоритмов управления) при особом
расположении системы O2X2Y2Z2, а именно — совпадении оси
02Х2 с вектором дальности.
Введем связанную с центром масс второго КА систему коор¬
динат с индексом «у» в знак того, что в этой системе осуществля¬
ется управление— 02А'2уУ2у^2у. Известно (см. разд. 2.6, рис. 2.17)
что в системе O2X2Y2Z2 вектор дальности D фиксируется углами
X и ц. Предположим, что ориентация 02A2Y2Z2 совпадает с
OrA2rY2rZ2r в t=tH=0, и установим связь
№у>	Z2y) = ЩХ*	z2)-	(4.	12)
На рис. 4.2 показана последовательность поворотов при установ¬
лении взаимного расположения систем координат; система
является промежуточной и определяет ориента¬
цию — D. Несложно установить, что
— COS X COS {J*
— sin {x
sin X cos{x
м=
cos X sin *j.
—-COS{J.
—■ sin X sin [x
sin X
0
cosX
146

а углы, входящие в матрицу, вычисляются через проекции век¬
тора дальности в системе O2X2Y2Z2 следующим образом:
я —arctg-^Ц Dx>0;
Dx
-arctg^, £>,<0;
Dr
(j.=
я — arcsin —- , Dx *> 0;
D
-arcsin -5*-, Dx<0.
(4. 14)
Теперь можно сформулировать последовательность операций
пои расчете управляемого и неуправляемого движения КА.
Пока предположим, что исследование относительного движе¬
ния начинается с момента ^н=0, соответствующего начальным
условиям, определенным ранее.
В этот же момент начинается управ¬
ление движением второго КА, кото¬
рое фиксируется в системе
О2Х2У Y 2у^2у- Вычислив изменение
параметров движения 1-го КА за
время tK в геоцентрической системе
OvX\TY\TZ\v и результат воздействия
управления на параметры 2-го КА,
можно найти вариации параметров
обоих КА, чтобы затем воспользо¬
ваться алгоритмом расчета началь¬
ных условий последующего балли¬
стического движения. При этом тре¬
буется пересчитать указанные ва¬
риации из системы 02X2yY2yZ2y в
ОгХ2т К>г^2г И ИЗ OrXirYir/ir В
OrXrYrZr. Такую процедуру следует применять столько раз,
сколько участков управления насчитывает этап сближения. Бо¬
лее детально рассмотрим этот переход.
В общем случае, который рассмотрен в разд. 2.5, возможна
фиксация начальных условий относительного движения до мо¬
мента начала управления tu в t=t0<tH. Тогда на момент tH бу¬
дут иметь место значения v0, D и Av, не равные нулю и опреде¬
ленные в системе O2X2Y2Z2. Если это так, то следует воспользо¬
ваться переходом (4.12) и записать в O2X2-3Y23Z2-3
v0H = Mv0: Dh = MD; Avh = MAv.
(4. 15)
Принимая во внимание допущение А^р=0 и учитывая, что сис¬
тема O2X23Y2-3Z2-3 не изменяет ориентацию своих осей при
^['н, fK], нетрудно вычислить значения параметров (4.15) на
момент
v0(O = v0K; 0(г‘к)=С>к; Av(^)=AvK,
(4. 16)
6*
147-'

привлекая (4.7) и соответствующие формулы для нахождения
Av(/). Величина tK находится из факта удовлетворения приня¬
тым граничным условиям.
Обратимся к анализу движения 1-го КА на интервале [/н, ^к]
(рис. 4.3).	Известно,	что движение происходит в	плоскости
ОД1гУ1г.	Для	того	чтобы определить поворот системы на угол
Фу, соответствующий /к—^н, вокруг оси OrZir, необходимо по из¬
вестным параметрам орбиты вычислить эксцентрическую ано¬
малию ЕНу воспользовавшись 1-м соот¬
ношением (2.30). Тогда из (2.27) лег¬
ко найти Ек (индексы Е отвечают ин¬
дексации времени), а	значит, и
г 1 (^к)-= г 1К. Подстановка в	(2.37) дает
возможность вычислить Фу. Величина
скорости v 1к вычисляется	по (2.39),
а его ориентация находится из условия
постоянства секторной скорости. По¬
лученных данных достаточно для опре¬
деления приращения координат и ско¬
рости
Аг1к г1к г1н {Д-х^, Дz/j, 0},
Av1k = v1k-v1h={a«1, дг»!, 0}	(4.	17)
в системе 0TX\TY\TZ\T.
Если предположение об исследовании относительного движе¬
ния начиная с ta считается недопустимым, то аналогичную про¬
цедуру следует повторить для 2-го КА и для обоих объектов
рассчитать приращения вида (4.17) для соответствующего мо¬
мента времени. При этом следует учесть изменение матриц
А Дь Д2 цз-за изменения углов ф и ф соответственно ФУ1 и ФУ2-
Несколько сложнее дело обстоит с нахождением вариаций
параметров движения 2-го КА, полученным за интервал управ¬
ления, что объясняется наличием информации лишь об относи¬
тельном движении в процессе интегрирования управляемого дви¬
жения.
Из уравнения (4.6) Следует
*1ГЛ
tr, L1T
Рис. 4.3.
к
V2 (А) = VlK — V0 — AvK — j w {t)dt
(4. 18)
в системе OrX2гУгг^г- Формула для приращения скорости с уче¬
том принятых допущений имеет вид

Учитывая, что 1-е слагаемое правой части определяется в
OrXirYirZir, а последние — в 02X2yY2yZ2y, можно записать
Приращение для координаты 2-го КА определяется на основе
уравнения (4.7), а именно:
в системе ОДггКгг^гг, а в системе 0TXvYTZT можно записать:
Эти приращения параметров движения, если есть необходимость
в расчете последующего баллистического движения, следует ис¬
пользовать в качестве новых вариаций для определения началь¬
ных условий вместо (4.8) и повторить вычисления в соответст¬
вии с алгоритмами расчета начальных условий.
4.3.	Определение оптимальной программы управления
сближением
В соответствии с проведенной формализацией процесса сбли¬
жения и принятой системой допущений объект управления опи¬
сывается уравнениями
записанными в произвольно ориентированной инерциальной сис¬
теме координат O2X2Y2Z2. По аналогии с постановкой задачи
вых условий (2.161) и минимум функционала (3.26) при исполь¬
зующихся предположениях о характере работы двигательной
установки. Для последующего рассмотрения примем концевые
условия в достаточно общей форме (2.144), (2.145).	}
к
(4. 19)
О
Тогда
Аг2к = ДгАг1к — AD
(4. 20)
Ari=A[AriK={A^i, Дуг дгх};
Аг2=Д£Аг.2к = {\х2, Ду2, дг2);
Ау1=Д[Ау1к={дм1, д©!, AWj};
А у2=Д£Ау2к = {ди2, Д1>2, дт2).
(4.21)
DW = voW + Av(*0, v0(t)=w(t),	4],	(4.22)
управления выведением требуется найти WonT(0> w(/)=w°(£)®>(*),
w°(jf)|=l, обеспечивающее достижение некоторых конце-
149

Введем фазовый вектор x(/)gX:
xWHAr. Dy, Dz\ V0xt voy, v0z)
и для единства индексации обозначим
bv(t) = {Avx(t)=h1, дvy(t)=h2, дvz(t)=hz)\
w0(*) = {«,°(*)=ai) w°y{t)=a2, да°(г?)=йз}.	(4.23)
Для простоты последующей записи примем /н=0. Тогда уравне¬
ния движения и концевые условия примут вид
х2=хь + А2, Хз=лгв + Л3;	(4.24)
л:x=wux, xb = wu2, хe=wu3\
‘в
*^1К = -*1к “Ь ~"Ь ^h1(t)dt:= 0,	tK,
'к
'в
З'гк = х2к“Ь^охы<J h2{t)dt = 0,
*к
'в
^зк=л:зк_1-^охбк'Т j* h3(t)dt=0,	(4.25)
<к
^4к = Х1кХ4к + х2кХ6к + ХзЛк + t<S (Х4К + Х5К + Хбк) Т
xlKh\K~\~ X2Kfl2K -(- ^зк^Зк-Ь ^0 {.Х4к^1к~\~ ХЬк^2к “Ь ^вк^Зк) ""Ь
<„	tR
■"Н^псТ-^к) ^ h1{t)dt-\-(h2K-\-x^ | h2{t)dt-f-
*к	*к
"Н^зк-Ь^вк) j h3(t)dt=0.
<к
Применяя принцип максимума, получим
Н = ФЛ + Ф**в + Фз^в + • 4«1 + Фб«2 + 4 6«3;	(4. 26)
4i(*1) = c1, фг(/) = г2, <]>3(/) = с3,
Ф4^=44к + (^-0^1. Ф5(« = Ф5к + (^-0с..	(4.27)
Фв (0 = Фвк + Кк ~ 0 Г3>
где сь Сг, Сз — некоторые константы.
150

Условия трансверсальности для вектора сопряженной пере¬
менной запишутся как
'hK=gradS1*+ 2 A;--igrad SjK,	(4.28)
j-2
где kj-\ — константы.
Расшифровывая это уравнение для (4.25), будем иметь
S 1к= 1 “Ь А3 (^4к “Ь^1к)> V2k = ^1 “Г h (^бкН-^гк)'
1'зк — ^2 4~ А3 (-^вк “Ь ^зк)>
: 4к — *о I A3
'твк = AjA + h
Фвк—k%t0-\-k.
-^Ik 1 ^^0^"4к I- ^0^1к I j* hx(t)dt
'к
'в
-*-2к4""Уо-^-бк“Ь^о^2к“h j" h2{t)dt
К
хзк~Ь 2^0л:6к-|-/0/г3к-)- J h3(t)dt
(4. 29)
а значит, проекции вектора сопряженной переменной (4.27) мож¬
но представить как
Ф1 (0 = ^1= I + M^k + ^Ik);
^2 (0	^2	==	Aj	“1"	К	(Л^бК	~\~ ^2к)»
1 3 W == ^3 == ^2 “Ь А3 ("Ак “Ь ^Зк)>
A W= [ 1 + А3 (Ак + М А — t) -(- ta k3 [л:1к -(-10 (2х4к-j- h.lK) -)-
+ J hi(t)dt];
‘к
i»(0 = [Ai + A3(^бк + Агк)] A — 0 + AA +
<B	1
+ A3 [•д<:2к + ^о12л:бк + A2K)-f- J h2{t)dt ;
'к	-I
Ч'в (0 — [^2 "Г A3 (Ак + А3к)] (tK — t) -j- k2tQ-f-
(4. 30)
4" A3
<B 1
•*:зк-Мо(2.Квк + А3к)-|-1 /г3(г1)аУ|.
151

Тогда
Н =... + Ф4«14- ф6И2 + '\U3
' — ... 4“#i j[l +^3(-*4k + ^1k)] (4“0 + ^O~h^3
4~^ik)4~ j hx{t)dt
■*1к4“4>(2-*4к4“
4~ и2 {[^1 4" h (ХЬк 4" *2к)] ( А 0 4~ Vo 4~
Г	*в
4- kA -^2к4"^о(2-^6к4"^2к)4“| fl2{t)dt
L	tK
4"йз
^2 4" (-*вк 4" V X
Х(А—0 4-Vo 4-^3
в
-^Зк 4" U (^Ок 4" ^Зк) 4" J fl3{t)dt
,	(4.31)
где многоточием обозначены члены, не зависящие от управле¬
ния, а значит, и не определяющие его.
Рассмотрение выражения (4.31) дает возможность сделать
вывод, что условие оптимальности будет удовлетворено, если
w°(/) будет коллинеарен вектору, проекции которого содержат¬
ся в фигурных скобках. Обозначив последние через t/b f/2,
получим
^Ioiit {t) = (Wxom{t)= ±	#2опт (^“^опт (0 = ±	(4.32)
Язопт(0=^2опт(/)=±^ u=(Ut+ui+uiy/*.
u,
и
Дополнив соотношения (4.32) граничными условиями (4.25) и
результатами интегрирования (4.22):
1к t
•*ik=-*ih+4-*4h+ j h1{t)dt+J ^w{t)ulom{t)df\
*к	*к	t
х2к х2н4~4“ J h2(f)dt-\- J j* w (t)и2опт (4 dfi,
о	oo
*к	^	f
д:3к = -х:3н4"^к^:бн~4 J ^3 (0 ^4“ j* I ^(О^Золт	(4.33)
*^4к == *^4н 4~ J ^	^1опт (^) dtf
1 0
•^бк ~-^бн 4~~ (* ^ (0 ^2опт (0
0
** = •*«> +jw(0»«o»r (*)<**.
152

получим полную систему из 13 уравнений для определения неиз¬
вестных
' ^1опт W* ^2опт(0» ^Зоит(^)»	^2>	Ag, -^Iki Х2к> -^Зю -^4k* *^6k» -^вк*
Недостающее уравнение представляет собой известное соотноше-
з
ние для направляющих косинусов — ^ и2=1.
i-1
Итак, рассматривая полученное решение, можно сделать
вывод, что, во-первых, оптимальное управление является функ¬
цией времени. Во-вторых, благодаря линейному характеру урав¬
нений, описывающих объект управления, удалось разрешить в
квадратурах уравнения для сопряженной переменной. Это об¬
стоятельство дало возможность свести краевую задачу к наибо¬
лее простому виду, а именно, к отысканию в процессе ее реше¬
ния совокупности констант — ku k2, k$. Тогда можно представить
-следующую последовательность действий при отыскании опти¬
мального управления. Выбирается начальная совокупность k['\
х1к> •••’ хбк}> ^7) и для известного закона изменения
h\{t), h2(t), А3(0 вычисляется оптимальное управление (4.32).
С этими значениями входят в соотношения (4.33) и рассчитыва¬
ют их до выполнения граничных условий (4.25). На основании
сравнения полученных данных о концевых значениях параметров
движения с принятой начальной совокупностью производят кор¬
рекцию исходных условий и повторяют процедуру вплоть до
совпадения с требуемой точностью начальных условий с конеч¬
ными. Однако заранее нельзя сказать что-либо определенное о
сходимости вычислительной процедуры. Это заставляет попы¬
таться избавиться от итерационного характера решения.
Естественный способ получения упрощенных решений — при¬
менение более серьезных допущений о характере воздействия
поля тяготения. Такой путь, как уже отмечалось ранее, приводит
к потерям в значении показателя оптимальности. Точность же
решения задачи управления не пострадает, если подобные допу¬
щения не использовать при конструировании граничных условий,
которое осуществить со всей тщательностью.
Примем гипотезу о движении обоих КА в плоскопараллель¬
ном поле тяготения. Тогда для фиксации конца процесса сбли¬
жения достаточно привлечь концевые условия в форме (2.149).
Наличие явного выражения tB через параметры движений дает
возможность ограничиться только одним векторным условием
S* =	“Ь ^0-^4к = 0,	S2k = Х2к “1“ ^0*^бк = 0 >
^зк=^к“Мол:вк=0>	(4*	34)
где U=tB—tK является параметром, на который могут быть на¬
ложены определенные требования.
153

Применение условий трансверсальности дает
4,lK===l> ^2k==^T> Фзк==^2» ^4k==^0» ,|'бк== ^1^0» 1)вк==^2^0
и на основании (4.27) имеем
Ф4(0=^-*,	№)=&-t)k* (4.35)
Тогда подстановка в (4.31) позволяет записать
Н = . .	(tB—0(й1“Ь^1И2"Ь^2Из)»
а это означает, что оптимальным будет управление, коллинеар-
ное вектору k= {1, ku k2}, т. е.
йюпт(0=±~5 ^2опт(^)=±~’
(4. 36;
и3тп({)=±	k={\ + k\+kl)Xft.
к
Вид соотношений показывает, что при сделанном предположении
оптимальным будет постоянное направление силового воздейст¬
вия (управление). Совместно с уравнениями (4.33) и (4.34) пос¬
ледние соотношения образуют систему, решение которой позво¬
ляет определить оптимальное управление. Само решение отли¬
чается от предыдущего случая меньшим количеством констант,
которые надо находить в процессе согласования концевых усло¬
вий с начальными.
Получим оптимальное управление для (2.163) с целью ана¬
лиза влияния на структуре решения концевых условий, которые
справедливы для аналогичных допущений. В скалярной форме
^1к = -^2к-^4к	^1к^бк“^»	^2к = -^1к-^6к	‘	(4. 37,
*^3к = -^Зк-^бк -^2к*^6к = 0,
однако эта система является зависимой, поэтому для дальней¬
шего достаточно принимать во внимание два условия, напри¬
мер, первые. Тогда изменение сопряженной переменной будет
характеризоваться соотношениями
Ф1К=— -*Бк + £*вю Ф2К = *4К* Фзк=—
^4к	*^2к	^-^Зю Фбк	^1ю Фбк==^'*^1ю
ф4 (*)=*2к — kx3K + {tK-1) (kxSK — xbK);
Фб(^==	•*'1к-Ь(^к	^)^4к»
%(t) = kxlK — (tK — t)kx^
а гамильтониан запишется в форме
Н ...-)- [х2к kx3K -)- (tK t) (kx$K хбк)] -J-
4~#2 [ -^Ik + (^к 0 ^4k] "j" ^3	(^к	0	kX^к]*	(4.	38,
154

^аким образом, оптимальное управление определяется вектором
с проекциями, заключенными в квадратные скобки. Каждая
проекция имеет две составляющие: постоянную и линейно зави¬
сящую от времени. Вектор с такими проекциями будет иметь не¬
зависимую во времени ориентацию, если составляющие проекций
ззаимно пропорциональны, т. е.
*2к—£*зк __ *1к kXiK
х5к. &*бк х4к
Привлекая условия (4.37), нетрудно показать, что эта пропор¬
ция сводится к тождеству, т. е. оптимальная ориентация векто¬
ра кажущегося ускорения постоянна. Само оптимальное управ¬
ление характеризуется выражениями
Wx опт = #1опт = i (*^2к ^Зк) [*1К ( 1 ~\~ &Т “1“ {Х2к ^Зк)2]	^2»
w°y опт=и2опт = + xlK [xiK (1 -(- kf -f- (х2к — kx3K)2] 1/2;	(4.39)
опт = U3onT = + kXlK [xiK ( 1 + kf -(- (Х2к — kX3Kf\ 1/2,
которые, дополненные соотношениями (4.33) и (4.37), образуют
полную систему.
Итак, в отличие от рассмотренных ранее случаев полученное
оптимальное управление является явной функцией фазовых ко¬
ординат и одной константы, что облегчает решение краевой за¬
дачи. Этот факт подтверждает критичность решения от конце¬
вых условий и свидетельствует о необходимости тщательного
обоснования вида граничных условий при постановке задачи
оптимизации.
Особенно наглядно выявляется структура решения при рас¬
смотрении плоского движения, например, л;3=л;6=0. Тогда до¬
статочно использовать только 5iK и выражения (4.39) принима¬
ют вид
±	г=	±	;	<4-	^
Ух\К + Д&	Ас
Х\К	Рх	к
°к
и2опт=+ „1К , = +
Или, если принять во внимание, что DK=toVок> то
а — -и v°y к •	и  Т V°XK
•^lonT Ш	>	и'2опт	I
^Ок	^Ок
т- е. оптимальная ориентация вектора тяги определяется отно¬
шением отдельных проекций концевых значений параметров дви¬
жения к их полным величинам.
155

4.4.	Синтез оптимального закона управления
сближением
Как видно из предыдущего раздела, использование упрощаю-
щего допущения о действии гравитационного поля дало, возмож¬
ность несколько упростить решение (вместо 13 неизвестных для
системы (4.25) в случаях (4.34) и (4.37) необходимо отыскивать
соответственно 12 и 11) и сделать его более наглядным, однако
не позволило представить оптимальное управление как функ¬
цию начальных условий относительного движения и парамет¬
ров объекта управления. Попытаемся синтезировать оптималь¬
ный закон управления сближением для концевых условий (4.34)
и (4.37), используя информацию о структуре управления, а имен¬
но тот факт, что оптимальное управление есть величина посто¬
янная. Подход к решению основан на привлечении проекционно¬
го метода, применявшегося в предыдущей главе.
Выразим концевые условия (4.34) через начальные условия
движения и управления подстановкой в них (4.33) с учетом до¬
пущения о действии притяжения (h=0). Получим
*к .	*к	t
0 0 0
*к .	*k	*
^2к=х2н~^гt0u2 j* w (^) dt-\-u2 j* j* w{t)df\ (4.41)
6	oo
*K .	*K	t
53k=.£gH 4“ -^бн^в 4“ j* w (t) dt-\-ti% j* j* w (t) dt,
0 0 0
S^K = U\-\-ii2-\-u^—1 = 0.	(4.42)
Требуется определить щ, u2, мз> tK, причем tB = t0 + tK. Как и ра¬
нее, длительность участка коррекции можно рассматривать как
неявную функцию от управления и именно эту зависимость вы¬
ражают соотношения (4.41) и (4.42). Тогда для отыскания ^Кшш
и соответствующих щ 0пт, и2 опт, опт необходимо потребовать
равенства нулю частных производных от линейной формы
^1к К$2к + V>3k ^4к*	,	(4-	43)
В соответствии с правилами определения экстремума неявной
функции такую систему уравнений следует дополнить концевы¬
156

ми условиями. Итак, экстремальные значения неизвестных нахо¬
дятся из системы
dSlK	| -ч	^2к	I	\ dS%K	I	  fj.
—	г Л1	“д	г 2 ~	г Лз
Otl\	OU\	OU\	OUi
dSlK	j ^	dS<2K	j	^	I ^ d«S4K	q.
dti2 1 du,2 2 du,2 3 du2 ’	(4.	44)
dSlK	I	^*^2k	I d«S3K	i л dS4K	~
“X	Г Л1	”X	Г	2 ~	Г A3 “	—
dtt3	OU3	OUs	ou3
*-*1к(^к»	^1»	^2» ^3)	^ 2 k == *^3к == *^4 к	0.
Из первых трех уравнений можно записать
A	Ai.4	\2А
Ыл=—; й2=^—-—; ич=—-—,
1	2Х3	2Х3	3	2А3
*к.	*к1	(4-	45)
A = t0 ^w(t)dt-\-^ ^w{t)dt2.
о	0	0
Эти выражения следует подставить в последние соотношения
(4.44) и тогда 5г к становятся функциями Х1-Т-Х4, tK.
В результате некоторых преобразований можно получить
уравнение для нахождения tK:
(■*1н Ч~ ^4н)2 + (х2н Т" ^5н)2 + (^Зн “f ^вХ6нТ = ^2,
откуда
(*4н+*5н+*6н) 1 ^*^4н ^5н “f~ Y«^6h i
± [(а*4н + P*fa + Y*6„)2 ~ (а2 + Р2 + Y2 - А2) (^н+^и+л^)] ^л
Последнее в итоге можно представить как функцию параметров
движения в достаточно компактном виде
/к=	{^2oh	+	DhVoh	±	[АЧ\-(ОнХ	VJ2]1/2}.	(4.46)
Однако записать решение в явной форме на базе (4.46) нельзя,
так как A=A(tK). Для простейшего случая w = a = const, а вмес¬
то уравнения (4.46) имеем
■f-4+a%4+a%242-^H(^0 + y2 + 2(DHv0H) (*„+*„)-
- 4- [(*>и X v1)H)2 + (DHv0Hf] =0.	(4.47)
Он
157

После нахождения tK из трансцендентного уравнения (4.46)
или приближений, построенных на его основе, легко определяют¬
ся неопределенные коэффициенты
\	х2н + ^в-^бн .	  -^Зн	+	^в-^бн	.
—  » ^2  ’
х1н ”h ^в*^4н	х1н	+	^в-^4н
Х3=.	—	,	(4.48)
2 (-^1н 4~ ^в-*4н)
после чего оптимальное управление находится по (4.45).
Итак, задачу определения оптимального управления можно
разбить на две: 1) вычисление длительности участка коррекции
tK на основе информации о начальных условиях и известном
законе изменения кажущегося ускорения—(4.46); 2) нахожде¬
ние 11опт по формулам (4.48), (4.45). Таким образом, удалось
синтезировать оптимальный закон управления исключением про¬
цедуры решения краевой задачи на основе использования све¬
дений о структуре оптимального решения. Наибольшую, но пре¬
одолимую трудность в полученном алгоритме отыскания и0Пт
представляет нахождение решения трансцендентного уравнения
(4.46).
Теперь перейдем к исследованию решения для граничных ус¬
ловий (4.37). Для получения оптимального управления привле¬
чем методику, изложенную ранее. Необходимые условия экстре¬
мума в данном случае будут иметь вид
б	6
1 — 3) Y*Jl!.**LL+	ifLJS4- Х2-^ = 0, s=l, 2, 3;
jbddxi к dus	dxt	к	dus	'	das
<-i	t-i
4—5) SlK(tK, иъ u2, u3)=S2K{tK, иъ иъ и3) = 0;	(4.49)
5)	S3K=tii-\-u.2-\-itz— 1 = 0
— система из уравнений для нахождения шести неизвестных tK,
Щ, и2, U3, %и %2.
Первые три уравнения представляются как
<к	tK е	t	i
1)	х*	j w{t)dt — хЪк II да(г() Л'2 + Х1 jc6k j	j w {t ) Lie- —
0 0
t
о 0
— д:3к w{t)dt
-1_2Х2й1 — 0;
t
2)	xiK j jw{t)dt2 — xlKj w(t)dt-\-2\2u2=0;

После подстановки в эти соотношения (4.33) с учетом последних
трех уравнений (4.49) будет иметь нелинейную алгебраическую
систему для определения искомых параметров:
1) 2Х.2й! — xbHF + \x6HF -f х.2аЕ — \х3нЕ = 0;
2) 2Х2и2 — х1яЕ 4- xisF=0;
3) 2Х2и3 — \xiHF 4- 'кх1нЕ = 0;
4) (х2нЕ - х6иЕ) их + (xiHF - х1яЕ) и2+х2нл:4н - л:1нл:Бн=0;
5) (-*внF ~ xSnE )и1 + {х1иЕ- xiHF) и3 4- л;1нл:вн - x3HxiH=0;
6) — 1=0,
В итоге после несложных, но весьма объемных преобразований
можно получить выражения для отыскания управления
А = {(а2 4- р2 4- у2) [а2 (р2 4- q2) 4- {§р — у?)2]}
а = Сл;1н+х:4н, Р=Сл2н4-х:5н, У = Слг3н+х:вн;	(4.5 1
Трудность анализа и применения приведенных соотношений
заключается не только в их сложной функциональной зависимо¬
сти, но и в том, что а, р, у зависят от величины С, которая опре¬
деляется характеристиками объекта и tK. Поэтому задача опре¬
деления и0пт> как и в предыдущем случае, должна решаться в
два этапа: 1) вычисляется tKy для чего в соотношения (4.51)
подставляются выражения (4.52) и результаты используются
для нахождения tu из тождества, образованного формулами
где
о
о о
#1онт— +
«гопт = + А (№р—у2я—«V),
«зонт = ± А (Vvq — fp — а2р),
(4. 5 0
где
Р -К ] н*Кби -Кзн-К4н> Я -Kih-Кбн -К2н-К4н'
Т" + Г«2(Р2 + <72) + (Рр- yq)tnj2
*	~	[	а2	(а2	+	р	+	у2)
(4. 53)
159

(4.53), ТК' = ТК"; 2) по формулам (4.50) определяется иопт с уче¬
том соотношений (4.51) и (4.52).
Использование алгоритмов (4.45), (4.46), (4.48) или (4.50) —
(4.53) зависит от специфики решаемой задачи, которая находит
отражение в принятой системе граничных условий (см. разд.
2.7). С точки зрения сложности вычислений указанные алгорит¬
мы приблизительно эквивалентны.
Решение остается прежним, но алгоритм значительно упроща¬
ется при разбиении пространственной задачи на две плоские.
Так, для исследования движения в вертикальной плоскости сис¬
темы O2X2Y2Z2 достаточно положить p = q = 0. Тогда
Илоп1 = + г — ^ i #2опт== 4- г	——	» ^К 4“	>	-= • (4. 54)
10ПТ	/а2+р2	2о,,т	-/а2	+	р2	~/а2+р2	V	'
Аналогично получаются формулы и для горизонтального дви¬
жения в плоскости O2X2Z2.
С учетом кинематических соотношений (см. разд. 2.6) выра¬
жения (4.54) можно записать в виде
•0	„	-т CDH sin (i.H	+ Vi	sin 0i — v2h	sin	02h .
Wxom = UlonT= 4-
1/(CD„ + D„)2 + (Dh(1„)2
'0	,	CD„	COS	(X„	+	Vi	COS	01	—	V2„	COS	02h
Wu —"	“	1
(4. 55)
V (CD„ + D„)2 + (D^Hf
T"	DlK*
•* K“
/(CDh + DhF + IDhjIh)2'
Трудность реализации алгоритма (4.55), (4.52), (4.53) опреде¬
ляется необходимостью измерения ориентации векторов D и V.
Для ликвидации этого недостатка потребуем, чтобы в момент
начала коррекции /н=0 ось 02Х2 системы O2X2Y2Z2, на ориента¬
цию которой ранее никаких ограничений не накладывалось,
совпадала с линией визирования — вектором DH (в последую¬
щем, при	как	и	ранее,	система	O2X2Y2Z2	сохраняет	ориен¬
тацию своих осей). При выполнении этого условия Ян = р,н = 0,
а соотношения (4.55) преобразуются к виду
опт
Y (СО„ + Д,)2 + (D„(iH)2
«**= ± Ср-+Д =-:	(4.56)
г (^Z)H 4~ DH) + (Z)hH*h)
'г1*  ,	М*н	(CDH)2
1 к— х
V(67)Н 4- Z)J2 4- (Z^hM-h)2 *
Реализация последнего алгоритма, с точки зрения необходимой
информации, не представляет затруднений: измерение дальности,
160

скорости ее изменения и угловой скорости линии визирования
являются обычными процедурами при построении систем управ¬
ления сближением.
Наличие двух знаков в выражениях (4.56) и ранее объясня¬
ется существованием двух видов управления, реализующих
траектории сближения и расхождения КА, так как граничные
условия не содержат конкретизирующего требования. Для вы¬
бора знака, соответствующего сближению, можно использовать
следующее рассуждение. С учетом предположения о совпадении
в начальный момент времени оси О^Х2 с D„ из соотношений
(2Л39) и (4.6) для / = 0+следует
°+
о
Так как величина интеграла существенно положительна, а ко¬
нечная цель управления состоит в сведении к нулю рп, то следует
потребовать, чтобы знак гиу° совпадал со знаком ин,
т. е. sign «j°=sign <хн и sign^ = — sign txH.
При решении пространственной задачи с произвольной ори¬
ентацией системы координат знаки направляющих косинусов
необходимо выбирать из анализа уравнений относительного
движения (2.133) и (2.134), где в правой части уравнений долж¬
но быть учтено наличие управления. Части уравнения, завися¬
щие от управления, должны иметь знаки, противоположные зна¬
ку суммы членов, определяемых начальными условиями. Огово¬
рим, что подобная рекомендация справедлива только для моно¬
тонного характера изменения р(/) и выполнения условия D(t)<
<0.
Замкнутый контур управления сближением, реализующий
•алгоритм (4.56), (4.52), (4.53), представлен на рис. 4.4. Инфор¬
мация о параметрах относительного движения £>, Z), (х, изме¬
ренная с помощью чувствительных элементов, поступает в вы¬
числительное устройство. Последнее, если управляющее усилие
создается двигательной установкой, неподвижно закрепленной
на КА, выдает величину требуемого угла разворота 0Тр в сис¬
тему ориентации. Когда разность между действительным и тре¬
буемым значениям этого угла станет достаточно малой, включа¬
ется двигатель коррекции и его ориентация в процессе работы
сохраняется неизменной. Момент прекращения работы двигателя
определяется, например, из условия p(/)^const. При наличии
•ошибок, циркулирующих в контуре управления, коррекции мо¬
гут повторяться.
161

Отметим, что для импульсного управления из соотношений
(4.52), (4.53) и (4.55) легко показать, что
С = оо, 7’к=0, w°=0, да°= + 1, w°=± 1.	(4.57)
Это означает, что в рамках сделанных допущений оптимальный
импульс приращения скорости должен быть ориентирован в пло¬
скости, перпендикулярной вектору дальности.
Итак, удалось получить алгоритм оптимального по расходу
энергии управления сближением в форме закона управления,
т. е. функцию измеряемых
параметров. Этому способ¬
ствовали, во-первых, допу¬
щение об одинаковом дейст¬
вии гравитационного поля
на оба объекта, во-вторых,
выявление структуры управ¬
ления с помощью принципа
максимума: сохранение ори¬
ентации вектора управления
в инерциальном простран¬
стве на интервале коррек¬
ции. Тот факт, что примене¬
ние принципа максимума по¬
зволило установить общие
свойства оптимального уп¬
равления, но не позволило
избежать краевой задачи,
по-видимому, свидетельст¬
вует о скрытых возможно¬
стях метода, в частности,
при использовании сопря¬
женной переменной.
В заключение раздела остановимся на некоторых результа¬
тах вычислительного эксперимента, построенного на рассмот¬
ренных алгоритмах. Обследовалось решение задачи управления
сближением в одной плоскости; само управление вычислялось по
формулам (4.52), (4.53), (4.56). Были приняты меры к учету
неодинакового действия гравитационного поля на оба объекта
при расчете траекторий относительного движения. Ставилась
задача построить быстро сходящуюся итерационную процедуру,
которая позволяла бы распространить частные решения, полу¬
ченные при упрощенной модели притяжения, на более общие
условия. С этой целью привлекались концевые условия (4.25),
при использовании которых наибольшую трудность составляет
расчет tB—задаваемого 54к. Последняя обусловлена необходи¬
мостью вычисления гравитационной составляющей относитель¬
ной скорости и интегралов от нее, отвечающих траектории
сближения.
Параметры движе¬
ния 1-го к А
Рис. 4.4.
162

Итерационный процесс вычисления траектории встречи стро¬
ился следующим образом. С помощью SiK и S2k (4.25) формиро¬
валась выпуклая форма
[<в	р г	<в	1г
+	^к)^4к+J hx{t)dt -f- х2к(tB tK)XjKI h2{t)dt ,
<K	J L	<K	J
(4.58)
достижение минимума которой свидетельствовало о необходи¬
мости прекращения управления. Величина tB—tK находилась с
/ ^ Ю , м
лг W3м
Рис. 4.5.
Рис. 4.6.
помощью достаточно «грубого» соотношения, следующего из
(2.149):
X2 4-х2 V/2
х ^ -4- х^
4к ' 5к
интегралы в выражении (4.58) определялись как
j hi(t)dt=j hi_1{t)dt—[hi{t)
tK	0	0
(t) dt,
(4. 59)
(4. 60)
где i — номер итерации при вычислении каждой проекции
Av(/).
После расчета начальных условий и необходимых преобразо¬
ваний систем координат (см. разд. 4.2) интегрировалась траек¬
тория активного участка (4.33) при наличии оптимального уп-
163

равления (4.52), (4.53), (4.56). На каждом шаге вычислений’
рассчитывались отношения (4.59), (4.60) и за tK принималось те¬
кущее t вплоть до достижения минимума (4.58). В качестве пер¬
вой итерации принималась траектория неуправляемого движения
и в памяти ЦВМ хранились вычисленные для нее значения.
Результаты вычислений траекторий относительного движении
для различных вариантов начальных условий приведены на
рис. 4.5 и 4.6. Из графиков видно, что при увеличении начальных:
рассогласований незначительно растет число итераций, необхо¬
димых для определения траектории встречи. На рис. 4.7 приве¬
дены зависимости изменения гравитационной составляющей от¬
носительной скорости (первая цифра—номер варианта, вторая—
номер итерации).
о
200 Ш 600	800	1000	t, с
Рис. 4.7.

ГЛАВА 5
УПРАВЛЕНИЕ ВЫКЛЮЧЕНИЕМ
ДВИГАТЕЛЯ
5.1. Задача автономной навигации
Условием качественного управления движением ЛА являет¬
ся наличие информации об истинных значениях .параметров
движения — радиусе-векторе центра ма-сс и векторе -скорости,
определенных в той системе координат, в которой отроится уп¬
равление. Аналогично дело обстоит и -с управлением выключе¬
нием двигателя: факт выполнения .граничных условий можно
установить, располагая лишь указанными данными.
Следует отметить, что в частном случае программного управ¬
ления можно довольствоваться требованием удовлетворитель¬
ного функционирования совокупности управляющих связей, наз¬
начение которых удерживать значения параметров движения
близкими к программным. Если эта совокупность полная и уро¬
вень внешних воздействий и ошибок системы управления не пре¬
вышает допустимый, то непосредственного использования ин¬
формации о фазовом состоянии объекта при формировании уп¬
равления можно' избежать предварительным учетом ее на этапе
расчета программы движения и ограничиться измерением ли¬
нейных вариаций кажущихся параметров. Однако подобный
подход, ка.к уже отмечалось ранее, имеет естественную ограни¬
ченность, присущую принципу жесткого программирования, и
не отвечает тенденции увеличения точности управления совре¬
менных систем.
Совокупность вопросов, связанных с определением истинных
параметров движения центра масс движущегося объекта по ре¬
зультатам наблюдений и измерений, составляет задачу навига¬
ции.
Такое определение принято в отечественной литературе в от¬
личие от некоторых американских публикаций, где понятие на¬
вигация дополнительно включает вопросы нахождения траекто¬
рии, приводящей в пункт назначения.
Основной классификационный признак подразделения сис¬
тем навигации заключается в способе получения информации,
165

используемой для вычисления фазовых .координат объекта. В со¬
ответствии с этим системы подразделяются н.а автономные и
неавтономные. В -первых для определения сведений о состоянии
объекта .привлекается информация от аппаратуры, находящей¬
ся на борту ЛА и не фиксирующей сигналов от внешних истоп¬
ников информации. В неавтономных системах используется
внешняя навигационная информация от наземных .радиотехни¬
ческих, оптических и каких-либо других систем или от наблюде¬
ния за естественными факторами: гравитационное или маг¬
нитное поле Земли, положение планет и др. Широкое распрост¬
ранение получают и комбинированные системы, представляю¬
щие собой сочетание указанных двух классов.
Автономные системы навигации, как и автономные системы
управления общего назначения, имеют ряд достоинств — абсо¬
лютная защищенность от внешних помех и отсутствие ограниче¬
ний на вид маневра объекта. Неавтономные системы могут .кон¬
курировать с автономными по таким показателям как простота
конструкции, точность, возможность использования во время
длительного полета. Для комбинированных систем характерно
органическое сочетание достоинств обоих видов систем. Под¬
робную классификацию навигационных систем с обоснованием
цринцила их работы можно найти в р-аботе [106].
Для объектов рассматриваемого класса наибольший интерес
представляют автономные системы, точнее инерциальные сис¬
темы навигации, составляющие основную подгруппу автоном¬
ных систем. Принцип инерциальной навигации заключается в
нахождении параметров абсолютного движения ЛА (в инерци-
нльной системе координат) на основе показаний акселеромет¬
ров (ньютонометров). Инерциальные навигационные системы
работают по принципу моделирования основного соотношения
динамики — .первого закона Ньютона (1.10). С помощью аксе¬
лерометров на борту ЛА получается информация о кажущемся
ускорении как реакции объекта на действие всех сил негравита¬
ционного происхождения. Математическим моделированием ус¬
корения сил притяжения формируется правая часть (1.10), а. не¬
обходимые для управления фазовые координаты получаются
одно- или двухкратным интегрированием этого уравнения. По¬
этому общая блок-схема системы инерциальной -нанигации име¬
ет вид системы с обратной связью, (рис. 5.1). Сравнение струк¬
тур, представленных на рис. 1.2 и 5.1, позволяет увидеть в блок-
схеме системы навигации именно модель основного контура
движения центра масс ЛА.
Целесообразность использования в СУ объектов данного
класса принципов инерциальной навигации объясняется нали¬
чием общих измерительных элементов и удобством применения
системы именно на участке активного движения, где определя¬
ющую роль в динамике движения играет кажущееся ускорение.
166

На этапе баллистического полета на вход инерциальной систе¬
мы информация о движении не поступает, и работа системы на¬
вигации сводится к функцинированию контура обратной связи.
Отсюда следует ожидать появления быстрорастущих погрешно¬
стей в вычислении вектора скорости и местоположения объекта
ввиду неизбежных ошибок в определении начальных условий
баллистического движения и допущений при формировании мо¬
дели поля гравитации. Если существует потребность в точном
определении параметров баллистического движения большой
Пт
1 w
Днселерометры j—
ГСП
Вычисление
$м
■ r(t)
■ Г It}
Рис. 5.1.
продолжительности, то целесообразно привлечение источников
внешней информации для коррекции показаний инерциальной
системы навигации.
Перейдем к изложению принципа построения инерциальной
системы навигации. Сделаем ряд предположений:	1)	совокуп¬
ность 'бортовых акселерометров позволяет измерить вектор ка¬
жущегося ускорения w. Для конкретности примем, что оси чув¬
ствительности измерителей образуют ортогональный трехгран¬
ник приборной системы координат с центром в корпусе объекта
OiJnEnZn. Если измерительный базис системы не ортогональ¬
ный, то допустим пересчет показаний акселерометров (или ре¬
зультата обработки этих показаний) в ортогональный базис;
2)	каждый акселерометр точно фиксирует проекцию кажущего¬
ся ускорения на его ось чувствительности, при этом динамика
акселерометра во внимание не принимается, в частности, не учи¬
тывается перемещение инерциальной массы относительно точки
0А в процессе измерения. Тем самым предполагается, что про¬
цесс измерения происходит идеально точно.
Уравнение (1.10) можно записать в виде
riW = w(0 + g[p!W]	(5.1)
и отметить, что гД/) —вектор, фиксирующий положение точки
01 в инерциальной геоцентрической системе координат
ОДг.а^г.а^г.а; дифференцирование в (5.1) абсолютное, т. е. урав¬
нение определяет абсолютное ускорение точки Oi в указанной
системе; (/)—' вектор, определяющий положение Оь в некоторой
связанной с Землей системе координат, например 0ГХГ)СУГ.С2Г.С,
167

участвующей в суточном вращении. Решение навигационного
уравнения (5.1) вначале рассмотрим в предположении сохране¬
ния неизменной ориентации в инерциальном -пространстве трех¬
гранника приборной системы координат OiXn.a^n.a^n,a- Это соот¬
ветствует расположению акселерометров на гиростабилизиро-
ванной платформе (ГСП), удерживающей свою ориентацию в
инерциальном пространстве. Можно также допустить, что оси
О^п.аГд.а^п.а параллельны одноименным осям системы
ОДг.а^г.а^т.а (если это не так, то нетрудно осуществить требуе¬
мое .преобразование координат). Тогда интегрирование уравне¬
ния (5.1) дает
Таким образом, для вычисления координат центра масс ЛА (с
точностью до» расстояния между центром 'масс и точкой ОД тре¬
буется знать начальные условия
диус-вектор А г (рис. 5.2), т. е. r = ri + Ar. Тогда, принимая за
ускорение и скорость движения центра масс результаты реше¬
ния уравнения (5.1), следует сознавать, что при этом допу-
скорректировать при наличии информации о перемещении
центра масс в процессе полета Аг(/) для жесткого объекта. Если
же объект упругий, то получение такой информации практиче¬
ски невозможно и для более точного определения скорости
и ускорения целесообразно размещать измерители вблизи
центра масс. В дальнейшем будем полагать, что это требование
выполнено, тем самым можно опустить индекс «1» в уравнениях
(5.1) и (5.2). Скорость движения центра масс выражается как
ГщП ционного поля и установить связь
между инерциальной и связанной
системами координат типа (1. 11)
для вычисления ускорения земного
притяжения.
Определим возможность получе¬
ния информации о скорости и уско¬
рении движения центра масс на базе
уравнения (5.1). Для этого учтем,
что положение центра масс объекта
О0 связано с точкой 0{ через ра-
движения, вычисленные в инер¬
циальной системе гД^н) и гД£н),
принять некоторую модель гравита-
Рис. 5.2.
скаются ошибки, равные Дг и Дг. Эти погрешности нетрудно
t
г (/)—г (4) +j (w W + £ [р (Oil dt- »	(5.3)
168

В соотношения (5.2) и (5.3) входит ускорение силы земно¬
го .притяжения, которое записывается в связанной системе ко¬
ординат. Если считать поле тяготения сферическим (2.5), то
гравитационное ускорение зависит лишь от удаленности центра
масс объекта от центра притяжения:
g(p)=g(r)=--^-	(5.4)
и не зависит от взаимного расположения объекта и Земли. Это
позволяет ограничиться в данном случае соотношениями (5.2) и
(5.4) для решения навигационной задачи. Аналогичная картина
будет иметь место и для формы Земли, симметричной относи¬
тельно оси вращения (эллипсоид вращения).
При использовании более точных форм описания потенциала
поля притяжения, например (2.7), следует учитывать тот факт,
что ускорение силы притяжения задано в связанной системе
координат и действие поля зависит от сферических координат
объекта. Переход от связанной системы к инерциальной опреде¬
ляется соотношением (1.11), использование которого приводит
к явной зависимости от времени ускорения силы притяжения
(1.12). Связь между сферическими геоцентрическими координа¬
тами, в которых записаны составляющие g(p, ср, X), и прямо¬
угольными в системе 0TXTXYT^CZT}C устанавливается зависимо¬
стями
QX^=Q cos ср COS X, Qy=Q sin ср, q2=q coscp sin X,
cp = arcsin ; X=arctg —, q = V q*+60+6*-
Q	Qz
Когда плоскость OrAr.cZr.c совпадает с плоскостью экватора, а
ось ОДг.с лежит в плоскости гринвического меридиана, то ср и X
суть соответственно'геоцентрические широта и долгота.
Если задача навигации решается в прямоугольной системе
координат, то целесообразно воспользоваться соотношениями
go* = gQ cosAcoscp-g>sin Сp + gx COS ср sin X;
gQy = ge cos X sin <p + gvc°s<p + gx sin cp sin X;	(5.	6)
gQz = gQ sin X—gx cos X,
которые позволяют от составляющих ускорения в сферической
системе координат (2.12), (2.13) перейти к проекциям в прямо¬
угольной связанной системе.
Итак, подведем итог проведенным рассуждениям. Рассмот¬
рен случай измерения вектора кажущегося ускорения акселеро¬
метрами, расположенными на основании, стабилизированном в
инерциально.м пространстве. Для простоты предположили, что
одноименные оси систем ^1-Ап.з.Ед ^ и ОрАр.&Тр.э/^г.а взаимно
параллельны. Тогда использование соотношений (5.2) и (5.3)
169

позволяет вычислить фазовые координаты движения объекта.
Для определения .гравитационного ускорения, потенциал кото¬
рого злдан в общем виде (2.7), необходимо от (5.3) о помощью
(1.11) найти радиус-вектор, фиксирующий положение центра
масс в связанной сферической системе q= {q, ср, К}, и вычислить
составляющие ускорения силы притяжения в сферической сис¬
теме (2.13). Затем на основании (5.6) определить g(e) в сис¬
теме OrXr>cyr.cZr>c, далее использовать обратное преобразование
(1.11), что дает возможность представить g[r(t), t] и тем самым
замкнуть контур обратной связи. Схема рассуждений графиче¬
ски представлена на рис. 5.3.
г
Рис. 5.3.
Отметим, что преобразование из прямоугольной системы ко¬
ординат в сферическую и обратно связано только с формой
представления £(д) в виде (2.13). Это преобразование исключа¬
ется, если гравитационное ускорение представлено через проек¬
ции на оси системы ОДг.сУг.Дг.с- Так, выражение для потенци¬
ала притяжения, записанное при тех же предположениях, что и
(2.7), как функция прямоугольных координат имеет вид
U=Jf + i (A + B+C-3J),
у=Л(т),+в(т),+с(т)!’	<57>
А, В, С — главные центральные .моменты инерции Земли;
/ — момент инерции относительно оси, совпадающей с
вектором q.
Или
откуда
U(QX> Qy> Qz) —	[(^Ч~^ — 2A)-j-
-{-(A -[-C — 2A —2C)qI],
^=^=-^l + ^l(5 + C-2A)-5-^X
dQx	Q3	Q5	2q7
X [(В~\~С — 2A)qx-\-(A-\-C — 25)	-{-(5-)-A — 2C)qI\;
170

^=£=-’мг+1^-(А+с-'2в]-5-ёг X
dQy	Q3	Q5	2Q7
X [(Я + С-2Л)е*+(Л+С-2Д)с* + (Я + Л^2С)о*];	<5.8)
g-QZ = _^.= -^ + ^(5 + A-2C)-5-^X
dpz	Q3	Q5	2Q7
Х[(5 + С-2ЛЩ + (А + С-2£)д2„-Н£ + Л-2С)е*].
Е.сли не учитывается неравномерность распределения массы
Земли вокруг оси вращения, то исчезает зависимость от дол-го-
5Ln(t~tH)Q3
Рис. 5.4.
ты в выражении для «потенциала (2.6) или (2.7), что. позволяет
использовать (2.12) при работе со сферической системой коор¬
динат.
Аналогичное предположение приводит к упрощению со¬
отношений (5.8) ввиду выполнения условия А = С. Блок-схема
вычислительного .алгоритма обратной связи (расчет ускорения
силы земного притяжения) для А = С при использовании систе¬
мы координат 0TXTCYT'CZTC представлена на рис. 5.4.
Построение вычислителя существенно облегчается ггри
переходе к упрощенной модели гравитационного поля. Так,
171

для сферической модели уравнение (Ъ. 3) можно записать
в виде
t
(г2+Л2)3'2 dt — W*
(5.9)
Яр Гу
« + ’\Г
■dt=w,—r,(Q
в предположении движения, совершаемого вдоль параллели
(составляющая -г учитывается аналогично).
Блок-схема решения навигационной задачи для этого случая
изображена на рис. 5.5.
Дальнейшее упрощение в
решении навигационной зада¬
чи может быть произведено
л wy
лгх
4гхн
1
1
1
1
7
7
Р
Р
Р
Рис. 5.6.
путем использования предположения о близости траектории
движения ЛА к программной, рассчитанной заранее. Предполо¬
жив степень близости настолько большой, что справедлива ли¬
неаризация ускорения силы притяжения, будем иметь
t	t
Дг* + \ 1Г£д'УИ + \ -^ЬГуМ=№0х-ьгхуя)\
J or х	J	or у
(5. 10)
Art/“h^ кгдгydt—MWy ДгД/н),
dgy
172,

де
Дг.г (*) = гх (0 - гл.,.р (*); *дгу (t) = гу (/) - гуп[> (/);
bwx(t) = wx{()-wx пр (t); д Wy{t) = w„{t) — wg пр (О;
dgx
дгх
•(*) = я0
г2 - 2г2
У	X
(г2 + г2 )^2 ’	<?Г4
dgtj	rjr	^Г!1
{£) О / 2 ,	„2	\5/2
dgx
дги
(0=
(0=
44+ 4)5
ЗЯрГ ХГ у
(4 + 4)5/2'
Значения частных производных вычисляются относительно
программной траектории и могут быть .введены в память БЦВМ
предварительно, до начала полета. Блок-схема решения -приве¬
дена на рис. 5.6.
Рис. 5.7.
Наионед, записанный выше алгоритм может быть представ¬
лен в еще более простом виде в результате линеаризации не от¬
носительно программной траектории движения, а относительно
некоторой точки с фиксированными координатами, принадле¬
жащей этой траектории. Например, приняв ry=R0, гх=0, из
уравнений (5.10) получим
dgx _ До __ go . dgx _ dgy _n. dgy
Ro '	'
dr г
dr a
dr.
dr,i
-2
JtQ
p3
= 2
go
Ro
Блок-схемы каналов решения задачи изображены на рис. 5.7.
В заключение отметим, что алгоритмы вычисления
гравитационного ускорения в общей схеме решения навигацион¬
ной задачи выступает в роли -положительной обратной .связи.
Это вселяет серьезные опасения в устойчивости всей вычисли¬
тельной процедуры. От такого рода схем также следует ожидать
существенного роста ошибок определения координат, обуслов¬
ленных погрешностями измерений.
5.2. Решение навигационной задачи при математическом
моделировании инерциального базиса
Одним из наиболее «узких» мест инерциальных систем наве¬
дения является гиро-стабилизированная платформа (ГСП),
173

предназначенная для физического моделирования инерциальной
систем,ы координат на борту JIA. Этот прибор оказывает серь¬
езное -сдерживающее влияние на дальнейшее -совершенствование
систем наведения, что обусловлено -самим .принципом его постро¬
ения. ГСП представляет собой сложный прецезионный электро¬
механический прибор, в значительной мере определяющий точ¬
ность наведения. При разработке и изготовлении ГСП большое
внимание требуется уделять мерам по -снижению трения в осях
подвеса, узлах съема информации и энергопитания; трудно обес¬
печить температурный режим работы прибора; из-за .карданова
подвеса даже небольшое увеличение габаритов элементов при¬
водит к значительному увеличению объема ГСП. Наконец, ГСП
потребляет много энергии, имеет большой вес и габариты (осо¬
бенно по сравнению с вычислительной аппаратурой), сложна и
дорога в производстве.
По этим причинам в последние 10 лет обострился интерес к
созданию эквивалента ГСП, обеспечивающего информацию об
ориентации инерциального базиса. Для создания такого эквива¬
лента требуется состав измерительной аппаратуры, традицион¬
ный для систем наведения — а-селерометры и датчики угловой
скорости (ДУС). Показания этих «приборов необходимо-подвер¬
гать достаточно сложным математическим преобразованиям,
поэтому математическое моделирование инердиального базиса
невозможно без развитой бортовой вычислительной техники.
Кроме того, для успешного построения инерциального базиса от
акселерометров и ДУС требуется высокая точность, очевидно,
существенно выше, чем для формирования команд управления,
так как ошибки .в определении инерциального базиса немедлен¬
но сказываются на ошибках получения фазовых координат [32,.
113].
Совокупность измерителей, необходимая для математическо¬
го моделирования инерциального базиса, располагается жестко
на объекте. Систему управления, в задачу которой входит про¬
ведение указанного моделирования, принято называть басплат-
форменной инерциальной системой (БИС). Такие системы обла¬
дают рядом достоинств по -сравнению ,с системами с ГСП [80]:
простота эксплуатации, малый вес и габариты, более простая
механическая часть системы, отсутствие эффекта складывания
рамок карданова подвеса и допустимость работы в условиях
больших перегрузок.
Приступим к изложению принципа работы БИС. Наиболее
полно этот вопрос освещен в работе [5]. Будем видеть задачу в
определении ф.азовых координат центра масс объекта в системе
ОДг.аГг.а^г.а или OrAr>cFr>cZr.c, считая известной начальную ори¬
ентацию приборной системы координат	жестко	свя¬
занной с объектом. Относительно акселерометров используем
допущения, принятые в предыдущем параграфе.
174

Для увеличения наглядности изложения введем еще одну
систему координат 0ГХГ.ПУГ>П2Г.П с .началом в центре притяжения,
оси которой параллельны соответствующим осям системы
OiXnynZn. В этой системе положение центра масс объекта фик¬
сируется радиусом-вектором
r' =xK-{~yLJrz^in	(5.11)
где in, jn, kn — орты системы 0Дг.пУг.п2г.п. Относительно системы
ОДг.аУг.а ^г.а система ОДг.пУгДг-п вращается с угловой скоро¬
стью со, которая имеет в 0ДГ.ПУГ.П2Г.П проекции со*, соу, coz.
Запишем выражение для абсолютной производной вектора
скорости в системе координат 0ГХГ.ПУГ.П2Г.П, для чего продиффе¬
ренцируем представление (5.-11). Будем иметь
rfr-=v=^ill+^j„+—к |1+х^+г/^+^-
dt	dt	'	dt	‘	dt	1	dt	dt	dt
= r' + »Xr' ® = “>A + ®i.jn + ffl*kI1.	(5.12)
Так как дифференцирование ведется в подвижной системе ко¬
ординат, то следует различать абсолютную производную от ло¬
кальной: первое слагаемое правой части уравнения (5.12) есть
локальная производная, т. е. .выражение скорости движения цен¬
тра масс ЛА в предположении постоянной ориентации системы
ОДг.пУг,Дг.п (точка над символом в данном параграфе означа¬
ет локальную производную).
Выражение для ускорения получим дифференцированием
уравнения (5.12):
d2r 	 d2x	.	, d2y	.	| d2z	^	,	dx	d\n	,	dy	tfj„	,	dz	dkn ,
dt2 ~~ dt2	n	dt2	Jl1 ^ dt2	If	dt	dt	'	dt	dt	'	dt	dt
+“X
Первая тру-ппа слагаемых правой части представляет собой вто¬
рую локальную производную радиуса-вектора г', вторая груп¬
па есть ооХг' (по аналогии с (5. 12), см., например, [57]); послед¬
нюю с учетом уравнения (5.12) можно представить как со X ~ •
dt
Итак,
•—т=г, + 0)Х r'	+ wX r' + wX ~	>
dt2	4	|	I	dt
но нетрудно убедиться, что первые три члена есть локальная
производная
r4“Xr4«Xr' = f(r' + ®Xf') = v.
dt
175

Тогда окончательно
(5. 13)
Таким образом, соотношения (5.11), (5.12) и (5ЛЗ) описывают
изменения радиуса-вектора и его производных в системе коор¬
динат ОДг.пУг.п^г.п. Левые части уравнений (5.12) и (5ЛЗ) .суть
производные в абсолютной системе координат ОДг.аУг.а^г_а, по¬
этому уравнения фактически устанавливают связь между дви¬
жением в инерциальной системе и в приборной, жестко соеди¬
ненной с объектом.
Подставим уравнение (5.13) в (5.1) и разрешим результат*
а также уравнение (5.12), относительно локальных производ¬
ных:
Если распространить на совокупность ДУС предположения, при¬
нятые для акселерометров, и считать, что g(g) задано в системе
ОДг.пЕг.Дг.п как функция координат и в конечном итоге вре¬
мени, то последнюю систему можно проинтегрировать и запи¬
сать текущие значения векторов скорости и местоположения*
представленные в связанной системе координат OrXTnYTJIZTmll:
Для их вычисления требуется знать, кроме g(t), соответствую¬
щие начальные значения и значения векторов кажущегося уско¬
рения и угловой скорости движения объекта, фиксируемые дат¬
чиками СУ.
Относительно вычисления g(/) в системе ОДг.Дг.Дг.п можно
провести рассуждения, аналогичные изложенным в предыдущем
разделе: если модель поля принята в виде (5.4), то проблемы
с интегрированием (5.15) нет. Если же действие силы тяготения
зависит от положения объекта в системе ОДг.Дг.Дг.с, то для
решения задачи навигации дополнительно следует установить
взаимосвязи между системами ОДг.Дг.Дг.п и ОДг.аЕгДг.а или
непосредственно с системой ОДг.сУг.Дгс. Другими словами,
следующая задача состоит в определении ориентации системы
ОДг.Дг.Дг.п относительно системы ОДг.аУгДг.а на основании
известного начального положения первой и измеряемого в про¬
цессе движения вектора со.
v = w — соХ v4-g(p),
г' = V— to X г'-
(5. 14)
v(0=v(O+J [w(0—»(0Х v(0+8(0]
(5. 15)
t
г' {t)=г' (0+ j lv (0—»(0 Xг' (01dt-
176

Для фиксации взаимного положения систем ОДг.п^г.п^г.п w
ОДг.а^г.а^г.а могут быть использованы различные параметры:
направляющие косинусы, углы Эйлера, параометры Кейли-Клей¬
на или Родрига—Гамильтона. Рассмотрим вначале решение за¬
дачи для направляющих косинусов.
Пусть ориентация системы координат 0Дг.пГг.п2г.п относи¬
тельно OrZr.ayr.aZr.a характеризуется матрицей направляющих,
косинусов
^11 ^12
(хтл, утл, ггл)=Щхт.„, уr,„ zrM\ н=
А13
сх21 а2
Qqi а«,
или
*а = ац»1г+ «121, + «13k..i
ja = а21',г “Ь a22jllC a23kiP
ка = а31'н + аз2Г + аззк..-
; (5. 16)
(5. 17)
В соответствии с -правилом дифференцирования в -подвижной
системе координат ,по аналогии с (5.12) можно записать
-^r=i'a+“X 'а! -^ = ja+»Xj.; ^ = ka + ®Xka- (5.18)
at	at	at
Но система OrZr.ayr.aZr.a не меняет своей ориентации, а потому
абсолютные производньке ее ортов повремени равны нулю, сле¬
довательно, уравнения (5.18) можно переписать и получить
уравнения Пуассона:
i'a + 0) X >а = °; ja + «XJa = 0, ka + ft)Xka = 0.	(5.19)i
Данные уравнения позволяют определить ориентацию си¬
стемы OrZr.ayr.aZr.a на основании информации о векторе1
угловой скорости а) и начальном положении системы относи¬
тельно OpZp л Ур .nZp л.
iaW = Ja(0+J [*а(0Х®(0]^.
t
J'a 00 = J'a Ю + j [Ja 00 X « (01 dt-	(5. 20)
,|?H
M0=MO+( [ka(0X©(0]^:
К
Подставляя в уравнения (5.20) соотношения (5.17), учитывая
представление а) (5Л2) и приравнивая члены в правой и левой
части с -одинаковыми ортами, получим 9 скалярных уравнений'
3953
177

для определения Н. Запишем первое из -них, а остальные полу¬
чаются цикличным смещением индексов:
<Хц(гО = ац(4) + j [an(t)uz(t)—als{t)wy{t)]dt. (5.21)
'н
Отметим, что точно, таким же образом, используя уравнения
Пуассона, можно найти матрицу А, определяющую взаимосвязь
систем 0Дг.сУг.с2г.с и ОДг.а^г.а^г.а- Для этого в уравнениях
(5.19) достаточно (вместо <о подставить вектор угловой скорости
вращения Земли Й3.
Начальные
ус поЬия
Рис. 5.8.
Теперь нетрудно записать переход от связаннбй с Землей
системы координат к приборной, связанной с объектом и рас¬
положенными на нем измерителями, для чего следует восполь¬
зоваться соотношениями (1.12) и (5.16):
(Хм, Утл, ггл) = АН (Хгл, Уг.п, Zr.n).	(5.	22)
Известные свойства этого перехода дают возможность, как и в
предыдущем р.азделе, пересчитать ускорение силы земного при¬
тяжения, заданного в системе ОДг.сУг.Дг,с, ,в систему
0Дг.п^г.п2г.п, а именно это и необходимо для интегрирования
системы (5.15). Для определения параметров движения в абсо¬
лютной системе следует результаты интегрирования трансфор¬
мировать, используя обратную матрицу Н-1. Если же требуется
записать фазовые координаты в системе координат ОДг.Дг.Дг.с,
то переход задается матрицей
Блок-схема вычислительного алгоритма представлена на рис.
5.8. Выходная информация о параметрах движения отсчитыва¬
ется в инерциальной системе координат. Данные ДУС использу¬
ются, ©о-первых, для определения матрицы перехода (5.16),
во-.вторых, при .вычислении подынтегральной функции (5.15).
178

По изложенному материалу сделаем дв.а замечания.
1. Состав измерителей (акселерометры и датчики угловой
скорости), кроме задачи навигации, участвуют и в решении за¬
дачи наведения. Наличие информации о проекциях .вектора уг¬
ловой -скорости н,а связанную с объектом .систему координат
позволяет решить задачу стабилизации объекта относительно
центра масс.
2. Рассмотренный алгоритм математического моделирования
инерциального базиса является далеко не единственным. Так,
существуют разнообразные возможности по решению основного
навигационного уравнения (5.1) в различных системах коорди¬
нат. Например, показания акселерометров могут сразу пересчи¬
тываться в инерциальную систему координат с по,мощью (5.16)
для того, 'чтобы в последующем воспользоваться соотношения¬
ми, приведенными в разд. 5.1.
Против применения этого способа имеется .аргумент: величи¬
на кажущегося ускорения достаточно быстро изменяется, поэто¬
му производить с ней математические операции целесообразно
после интегрирования. Другим способом решения задачи может
явиться алгоритм, построенный на проведении первого интегри¬
рования в приборной системе координат с последующим пере¬
счетом данных в инерциальную систему и проведения в ней вто¬
рого интегрирования. Иной способ записи уравнений (5.1-5) при¬
водит к построению другой вычислительной процедуры. А имен¬
но— детализация (5.13) дает известное уравнение для пред¬
ставления вектора абсолютного ускорения точки в качестве сум¬
мы векторов переносного*, относительного и ускорения Кориоли-
са [на базе этого записано соотношение (1.16)]:
■^ = f + »Хг' + 2» X г' + Ю х (® X г')-
Использование уравнения (5.1) и последующее интегрирование
дает
Г' (/)=Г' (О + С [w (г1) - ю X Г' — 2й) X г' — «> X (ю X Г') + £
К
г' (0=(^н) Ч- 4)г (О
+ f f IwW—wXr' — 2wXi:-<‘)X(‘»XO+g^)]^-
к к
Общая блок-схема вычислительного алгоритма представлена на
рис. 5.9. Построение БИС при таком способе решения задачи
навигации для различных систем координат, связанных ,с Зем¬
лей, обстоятельно исследовано в работах [87, 105].
Наконец, вычислительный алгоритм существенно зависит от
способа определения ориентации системы координат
7*
179

OA.nWr.n в системе 0TXT^Yv^ZT^. Как указывалось, для. этого
могут быть применены различные группы параметров, к крат¬
кому рассмотрению которых мы сейчас и перейдем.
Вначале остановимся на углах Эйлера и будем видеть зада¬
чу в получении соотношений, связывающих измеряемые ДУС про¬
екции вектора угловой скорости вращения объекта с величина¬
ми этих углов. Как и ранее, введем последовательность эйле-
ровских поворотов, показанную на рис. 5.10. Угловое рассогла¬
сование систем координат обусловлено вращением с угловой
скоростью о) системы 0ДГ.ПУГ.П2Г.П относительно системы
0гХг.аУг.а2г.а. Поэтому можно записать
где ia, ja, ka— орты системы OrAr.ayr.aZr.a. Тогда проекции угло¬
вой скорости в связанной системе координат можно представить
как
Проекции о на оси системы 0Дг.аУг>а2г.а получаются аналогич¬
но, как скалярные произведения o>ia; o>ja; o>ka.
1 ДУС \^-Л*{Вычис/1ениеШ\1\Вь1числениеЩ\^
Рис. 5.9.
^ гя
Г. А
ГЯ
Рис. 5.10.
(5. 23)
сох = ам1Г=ф sin ft cos ср — ft sin ср;
a)y = cojn=i cos & + ср;
co2 = o)kn=i sin ft sin cp —|— ft cos cp,
-откуда несложно получить и обратные зависимости:
sin &
(5. 24)
ft= — сох sin ср —|—	cos ср;
ср = 03^ — (со^ COS ср -|- (Оz sin ср) ctg ft.
<180

Итак, .получили систему нелинейных дифференциальных
■уравнений (6.24), интегрирование которой-позволяет вычислить
значения углов Эйлера по измеренным проекциям угловой ско¬
рости в связанной с объектом системе координат. Нелинейность
-системы затрудняет ее интегрирование. Кроме того, углы Эйле¬
ра дают недостаточно информации для однозначного определе¬
ния углового -положения объекта, обусловленное вырождением
кинематических уравнений (эффект складывания рамо-к карда¬
нов а подвеса).
Другой совокупностью величин, фиксирующих -пространст¬
венную ориентацию тела, являются параметры Родрига-Гамиль-
тона. Эти .параметры представляют .собой группу нормирован-
з
ных величин Х0, К, кз, 2	^	’	характеризующих	проекции
/=о
вектора конечного поворота подвижной системы координат от¬
носительно неподвижной на оси последней. Иначе, пусть поло¬
жение оси, вращение подвижной системы 0Дг.п^г.п2г.п относи¬
тельно которой приводит к некоторому рассогласованию, харак¬
теризуется углами а, р, у в системе 0Дг.аКг.а2г.а, а само враще¬
ние тела (системы Orir.nWr.n) измеряется углом %. Тогда па¬
раметры Родрига-Гамильтона определяются через введенные
углы следующим образом [75]:
a1 = cos a sin	X2 = cos[3 sin	X3 = cosy sin	X0-=cos-^-,
а матрица (5.16) через эти параметры выражается так:
_.-к2
0 . 2 Д1 3
2 (—-(- Х2Х3)
2(У» + ХЛ)
н=
+ ^2
2(—Х0Х2 -|- ХгХ3)
2 ( —XQX3 ~\~ КЮ
2(Х0Х2 + Х1Х3)
^0 + ^1 _ *2 — ^3
Система дифференциальных уравнений для определения пара¬
метров Родрига-Гамильтона по известным проекциям со на оси
ОДг.п^г.п^г.п имеет вид
2Х0 = — ((o2Xj -f- сохХ2 -j- ^г/Х3);
2Х1 = со2Х0-[-соуХ2 — со^Х3;	(5.26)
2Х2 = со^Х0 -|- со2Х3 — о)^;
2Xg = соу\coxXx — согХ2.
Интегрирование этой системы с последующим вычислением
(5.25) и (5.26) дает возможность найти взаимное положение
систем координат.
Параметры Кейли-Клейна также предназначены для фикса¬
ции поворота тела относительно неподвижной системы отсчета
181

и представляют -собой комплексные комбинации .параметров
Р одр иг а - Г а м ил ьто н а [75]:
а —	Р——У — ^2 + ^1’ ^	\	(5.27)
а их выражения через углы Эйлера имеют вид
6 + ср	ф-ср
$	2	о •	• $	2
a = cos — е ; p = *sin — е ;
2 2
(5. 28)
2
Для .вычисления параметров Кейли-Клейна по измеренным про¬
екциям вектора -скорости на о-си системы OjX^Y^nZ^ служит
система дифференциальных уравнений
Отсюда видно, что система распадается на две системы линей¬
ных уравнений первого порядка одинаковой структуры, что су¬
щественно облегчает ее интегрирование. Нахождение этих па¬
раметров дает возможность отыскать зависимости, обратные за¬
висимостям (5.28) или (5.27), и .в последнем случае определить
матрицу (5.25), а значит, и (5.16).
Подробнее с указанными параметрами и их применением
для определения ориентации объекта и оптимальным управле¬
нием пространственным угловым движением можно ознакомить¬
ся в работе [20].
В заключение отметим, что привлечение того или иного спо¬
соба формализации углового движения тела должно обеспечить,
во-первых, однозначную фиксацию его положения (чего нельзя
достигнуть при использовании углов Эйлера), во-вторых, позво¬
лить с наименьшими машинными затратами проинтегрировать
систему уравнений, связывающих изменение того или иного па¬
раметра с вектором угловой скорости поворота тела, фиксируе¬
мым измерителями. По оценке, приведенной в работе [89], наибо¬
лее просто реализуются машинные алгоритмы при использова¬
нии аппарата направляющих косинусов, далее идут параметры
Кейли-Клейна.
(5.29)
182

5.3.	Формирование упрощенных методов управления
выключением двигательной установки
Решение навигационной задачи позволяет найти истинные
параметры движения J1A (фазовые координаты) с точностью,
обусловленной методическими погрешностями из-за использо¬
вания упрощенной модели поля притяжения и инструменталь¬
ными ошибками, вызванными ограниченной точностью измери¬
телей и погрешностями вычислений. Для управления движени¬
ем JIA на активном участке, как уже указывалось ранее, можно
пойти на снижение относительно предельной точности определе¬
ния фазовых координат, так как при правильно построенных ал¬
горитмах управления это приведет лишь к потерям в критерии
оптимальности, заложенном в .процедуру отыскания оптималь¬
ных управлений. Возможно более высокая точность вычисления
параметров движения требуется при определении факта дости¬
жения изображающей точкой гиперповерхности концевых усло¬
вий. Ошибки решения навигационной задачи при этом немедлен¬
но приведут к сшибкам в определении 'момента выключения
двигательной установки, что скажется на точности выполнения
условий встречи, будь то сближение двух КА, выведение PH на
орбиту с требуемыми свойствами или встреча опускаемого КА
(головной части БР) с поверхностью Земли. Именно точное
выполнение концевых условий гарантирует принадлежность
баллистической траектории семейству попадающих.
Точность наведения зависит не только от строгости решения
навигационной задачи и своевременности выключения двига¬
тельной установки, но и от совокупности допущений, использу¬
емых при формализации баллистического движения и описания
семейства попадающих траекторий. В первую очередь причиной
последнего являются упрощения при анализе условий движения,
в частности, при выборе модели гравитационного поля или огра¬
ниченный учет атмосферных воздействий на заключительном
этапе полета в околоземном пространстве. Однако, как следует
из гл. 2, даже использование достаточно серьезных допущений
указанного типа приводит к столь сложному описанию концево¬
го многообразия, что констатация факта удовлетворения этих
концевых условий требует больших вычислительных возможно¬
стей, которые у бортовой аппаратуры достаточно ограничены.
Следует дополнительно учесть, что от ЭВМ требуется не только
проведение вычислений в реальном времени, но и экстраполяция
значений параметров движения .на интервал расчета концевого
условия или его упрощенного аналога, чтобы не допустить за¬
паздывания при формировании команды на выключение двига¬
теля. Чисто технические трудности реализации сложных вычис¬
лительных процедур при определении граничных условий дела¬
ют необходимым формирование упрощенных зависимостей, ха¬
рактеризующих принадлежность баллистической траектории се-
183

мейству попадающих. Умеет,но также отметить, что подобный
подход тем более правомочен, чем меньше отклонение действи¬
тельной фазовой траектории от программной в момент выключе¬
ния двигателя.
Как всегда в .подобных случаях, рациональным способом по¬
лучения упрощенных зависимостей является метод аппроксима¬
ции. Задача состоит в формировании зависимостей, с требуемой
точностью1 аппроксимирующих многомерную гиперповерхность
5К, вычисление которых должно (быть существенно проще, не¬
жели расчет полных соотношений. Тривиальный подход состоит
в следующем. Для построения аппроксимационного аналога на
гиперповерхности концевых условий фиксируют точку xkpgSk,
соответствующую расчетным условиям выключения двигателя
или центру допустимой области пучка фазовых траекторий ак¬
тивного участка. Относительно этой точки SK раскладывают в
ряд Тейлора, ограничиваясь, например, членами второго поряд¬
ка. Аппроксимирующая форма характеризуется уравнением
У jf(y-£-)'sJ^^-^i=0’	<5-30>
7 = 1	V i=i 1 J
которое описывает гиперповерхность второго порядка. Частные
производные вычисляются в х£, а дл:/=л:Р — xt. Разложение.
(5.30) включает 28 членов, поэтому увеличение порядка гипер¬
поверхности, по-видимому, нецелесообразно ввиду его громозд¬
кости и трудности расчета ва.риадий высокого порядка. Следует
отметить, что влияние различных частных производных на точ¬
ность аппроксимации неодинаково. В конечном итоге вес каж¬
дой производной зависит от структуры гиперповерхности конце¬
вых условий.
Другим способо-м построения приближений является аппрок¬
симация SK совокупностью касательных гиперплоскостей, по¬
строенных относительно группы расчетных точек xpz£Sk.
Совокупность гиперплоскостей записывается следующим обра¬
зом:
7
1=1'2"-’р’ (5-31)
/=1 1
где кХц=хри — хп, а частные производные вычисляются в каж¬
дой из расчетных точек. Этот способ отличается меньшим объ¬
емом вычислений по сравнению с (5.32), однако возникает до¬
полнительная задача выявления принадлежности фазового век¬
тора соответствующей подобл.асти, которой отвечает определен¬
ная совокупность частных производных. Разумеется, подобный
подход может быть использован при аппроксимации подоблас¬
тей 5К поверхностями второго порядка (5.30).
184

В предыдущих .случаях использовались фиксированные зна-
чения частных .производных, вычисленные заранее в 'некоторой
точке «программной траектории-, принадлежащей SK. Пр.и .нали¬
чии аналитического представления концевого многообразия эту
ограниченность можно ликвидировать вычислением во время
активного участка, точнее —его заключительной фазы, указан¬
ных частных производных. Такой подход позволяет существен¬
но ослабить требование .на близость действительной траектории
к программной или даже во¬
обще снять его.
Каким бы способом ни ап¬
проксимировалось концевое
многообразие, следует оценить
выбранный способ и выявить
влияние ошибок аппроксима¬
ции на точность решения зада¬
чи наведения. Некоторые кон¬
цевые условия непосредствен¬
но связаны -с показателем
качества наведения, например,
при управлении сближением
в качестве концевого условия
использовалось требование об¬
ращения в нуль промаха. В этом случае ошибки аппроксимации
позволяют сразу же определить величину промаха. Больше рас¬
пространена ситуация, при которой не удается по ошибкам апп¬
роксимации немедленно установить методическую ошибку наве¬
дения. Остановимся на таком случае более подробно.
На рис. 5.11 в -пространстве X* изображены дв.е гиперповерх¬
ности!: 5K(xK, q) и ее аппроксимирующий аналог 5K'(xK, q). Эти
поверхности имеют общую -касательную точку х£ , отвечающую
программной траектории хпр(/). В действительности движение
и-зображающей точки происходит по возмущенной траектории
х(/) и двигатель выключается по достижении гилерпо-верхности
*^к (хк> ч), так ка.к именно этот алгоритм реализован в бортовой
СУ. Но через точку xkgSk'(xk, q), очевидно, (можно провести не¬
которую гиперповерхность SK(xK, q'). Это означает, что реально
из-за ошибок аплрО'Ксимании и несовпадения действительной
траектории с программной вектор параметров q, фиксирующий
требуемые свойства семейства попадающих траекторий, будет
отличаться от желаемого (q'^q). Например, пусть зада¬
чей наведения является достижение на этапе баллистического
движения точки, заданной и системе ОгХг.аУг.а4а радиусом-
вектором гц и принадлежащей земной поверхности. Для опреде¬
ления величины/ методической ошибки Агц=гц—гц' следует при¬
влечь первое концевое условие 51к(хк, гц')=0, которым необхо¬
димо воспользоваться для определения векторной величины
Рис. 5.11.
185

АГц={Дл:ц, Луц}. Для ее однозначного1 вычисления можно ис¬
пользовать очевидное соотношение (хц')2+ (уц')2=Д32, где R3 —
радиус Земли.
В общем случае задача определения вариаций параметров
орбитального движения по известным возмущениям начальных
условий всесторонне обследована, особе ни о в рамках линейной
теории.
Проведенные рассуждения позволяют выявить структуру
формирования методических ошибок наведения. Фактически в.се
составляющие погрешностей отдельных управляющих связей
(будь то инструментальные ошибки или методические) приво¬
дят к отклонению действительной фазовой траектории от прог¬
раммной. Методические ошибки управляющих связей появля¬
ются в результате неполного парирования внешних возмущений,
что обусловлено ограниченным качеством законов управления,
например, .низким порядком .астатизма. Такого рода отклонение
не дает ошибки в решении задачи наведения, если используется
точное описание семейства попадающих траекторий. Однако
из-за допущений, сделанных при формализации баллистиче¬
ского движения, а также из-за применения аплроксимационных
форм возникает методическая ошибка. Величина ее будет тем
больше, чем больше вариации фазовых координат в точке вык¬
лючения движения xkgX*. Эту жесткую- связь между качеством,
управления на активном участке и допустимой степенью- упро¬
щения алгоритмов управления выключением двигателя обяза¬
тельно приходится учитывать при разработке алгоритмов и ана-
л из е точное ти у п р авя е н и я.
Ранее в этом параграфе мы исходили из рассмотрения обоб¬
щенного концевого условия 5К, в то время как в общем случае
SK есть результат совместного удовлетворения группы требова¬
ний: 5К= {51к П 52к П.. .П 5Кг}. При построении а-ппроксим ани¬
онной формы каждое из SiK следует подвергнуть соответствую¬
щему преобразованию и результирующая совокупность, допус¬
кающая совместные решения, будет играть роль приближенно¬
го аналога. Было бы рациональнее аппроксимировать результат
пересечения отдельных гиперповерхностей, но сделать это невоз¬
можно. Поэтому при определении момента выключения двига¬
теля (как однократного управления баллистическим движе¬
нием) используют факт достижения изображающей точкой ка¬
кого-либо основного концевого условия, а одновременного удов¬
летворения других условий достигают соответствующим управ¬
лением движением на предшествующем этапе полета.
Например, при выведении ракеты-ноейтеля «Сатурн-5» в ка¬
честве основных требований приняты условия достижения про¬
граммных ук и zK (и их производных) в системе координат выве¬
дения, а проекции параметров движения на направление х кор¬
ректируются опосредственно. Основным условием выключения
186

движения БР является достижение заданной дальности полета,
а в качестве дополнительного выступает величина требуемого
бокового отклонения. В группе алгоритмов наведения по требу¬
емой скорости (например, [93]) в качестве основного граничного
условия выступает требование достижения в конце активного
участка требуемой скорости, -при этом указывается на/ возмож¬
ность лоявления дополнительных условий, как-то:	скорость
встречи с делью, угол входа в /плотные слон атмосферы, суммар¬
ное время полета и др.
При необходимости одновременного удовлетворения несколь¬
ким концевым условиям :мож,но конструировать управление дви¬
жением исходя, например, из следующей концепции:	потребо¬
вать выполнение дополнительных условий начиная с некоторого
мо-мента tj* —Т и до £к. Если привлечь геометрическую интерпре¬
тацию решения задачи управления, то это будет означать необ¬
ходимость удерживать в интервале [t* —Г, £к] изображающую
точку на гиперповерхности, образованной пересечением допол¬
нительных условий, ,и ждать удовлетворения основного условия,
что является сигналом необходимости выключить двигатель. Та¬
кой -подход представляет наиболее «бездумную» политику, а по¬
тому сопряжен с рядом трудностей.
Во-первых, подобное решение далеко не оптимально в смыс¬
ле экономного расхода топлива. Действительно, возьмем случай
управления движением Б‘Р. В соответствии со .смыслом решения
к началу указанного интервала времени боковое отклонение у
цели должно быть скомпенсировано и удерживаться вблизи тре¬
буемой величины. Экстраполированное боковое отклонение дол¬
жно определяться на основе правила: «если в данный момент
достигнута требуемая дальность, а значит, выключен двигатель,
то таким и будет отклонение». Теперь представим, что БР ле¬
тит точно- по программной траектории. При этом в момент
tK=tv все условия будут выполнены, но в системе подобная ин¬
формация отсутствует, поэтому он-a будет производить воздей¬
ствие на объект в интервале —Ту £к], чего не требуется по
условиям полета.
Во-вторых, заранее трудно определить величину Т. С одной
стороны, стремление избежать избыточного маневрирования за¬
ставляет уменьшать ее значение, но с другой стороны, этому
препятствуют ограниченное быстродействие -объекта по углово¬
му движению и необходимость принимать во- внимание разбро¬
сы параметров движения и характеристик двигательной уста¬
новки.
Наконец, в-третьих, перевод изображающей точки на гипер¬
поверхность дополнительных условий и удержание на ней свя¬
заны с энергичным маневрированием. Все переходные процессы в
динамике движения центра масс должны быть закончены к мо¬
менту /к- Все это затрудняет организацию движения на самом
187

ответственном (в .смысле удовлетворения требованиям ,по- точ¬
ности) участке полета.
Большинство из -перечисленных -проблем отпадает при экст¬
раполяции изменения параметров движения на .интервале
[tк —Т, /к]. Действительно, при введении какого-либо управле¬
ния первого приближения и возможности описать изменение
фазовых координат до момента tK при этом управлении нетруд¬
но определить необходимую коррекцию управления из условия
одновременного выполнения всех граничных условий в момент
выключения двигателя. Именно такая идея заложена в конструк¬
цию управления выведением PH «Сатурн-5», а также использу¬
ется в р.азд. 3.4.
При допущении о малости отклонений действительного дви¬
жения относительного программного для формирования алго¬
ритма управления достаточно информации о t^. В этом случае в
качестве аргумента корректирующего управления целесообраз¬
но применить величину отклонения от нуля основного концево¬
го условия, по которому включается двигатель, например 51к.
Дополнительное концевое условие несложно параметризовать —
представить в виде SiK(S\K) и сформировать вариацию'
д5/ K — SiK (SlK) —	(51к). Последняя несет информацию о ха¬
рактере изменения граничного условия относительно программ¬
ного как функция основного- концевого- условия. Корректирую¬
щее управление может быть построено- как Дц=М5г-к(51к), где
k — -коэффициент пропорциональности. Оно должно обеспечить
сведение к нулю ASiK в момент Sik(^k)='0. Такая конструкция
позволяет избежать избыточного маневрирования на траекто¬
рии благодаря учету расчетного значения дополнительного кон¬
цевого условия, отвечающего текущему 51к, и сводит задачу уп¬
равления к терминальной: процесс регулирования должен быть
закончен к моменту равенства аргумента нулю. Подход, близ¬
кий к изложенному, рассматривается в трудах [115, 146].
При построении упрощенных методов управления выключе¬
нием двигателя и управления, обеспечивающего одновременное
выполнение нескольких концевых условий, весьма рационально
применение геометрической интерпретации. Так как наглядность
изучения семимерного пространства весьма относительна, то
прибегают к построению' сечений SK плоскостью, параллельной
двум выбранным координатным осям и проходящей через Хк
[47,87]. Так, при -сечении SlK (разд. 2.2 и 2.3) принято различать
изоскороотную характеристику (рис. 5.12, а) и годограф требу¬
емых скоростей (рис. 5.12, б). Первая есть геометрическое мес¬
то радиуса-вектора, фиксирующего положение центра мас-с в
t=tK, которое соответствует семейству попадающих траекторий
при условии гк = г £. Годограф требуемых скоростей характеризу¬
ет возможное изменение вектора скорости -попадающих траек¬
188

торий при выполнении гк=г£ . Изменение q приводит к смеще¬
нию и деформации изображенных кривых.
Выделим на обоих годографах фазовые координаты, соответ¬
ствующие программному движению xJc^SK. Тогда исполь¬
зование только линейной части- разложения (5.30) означает ап¬
проксимацию 51к гиперплоскостью, следом которой являются
касательные на рис. 5.12, проходящие через г£, г£ . Удержание
квадратичных членов соответствует аппроксимации годогр.афоБ
параболой. Небольшие перемещения гк и гк относительно рас¬
четной точки по касательным, очевидно, не приведут к сущест¬
венным методическим ошибкам. Наоборот, следует ожидать по¬
явления ошибок, если вариации Агк и Агк будут ориентированы
по нормали к годографу. Эти направления фиксируются соот¬
ветственно. углами pi
Большой интерес представляет рассмотрение в трехмерном
пространстве (скоростей или координат) двух граничных усло¬
вий. На рис. 5,13 в пространстве гк изображено два концевых
условия 51к и 52к. Касательная к линии их пересечения, прове¬
денная через точку г£ = у£, описывается уравнением
^Чдгк 	 к		 ^zk
(5. 32)
Введем ор,т т, |т|=1, совпадающий с касательной, и определим
направления быстрейшего изменения 51к и 52к как градиенты
dSu'
dSXK dSu
dS ik
dSlK
I ^
l ^
I^Co
1 7-
dvyK dvZK
dvZK
foXK
dvXK dvyK
д $2k
dS2K dS2K
d S2k d S2k
dvyк dvZK
dvZK
6VXK
dVxK дну#
N = gradSlK = №, dSlK
I dvx
M = grad S2
. | dS2K
I dvx
dvy
д$2к
dvu
dv2
dS2K
dvz
(5. 33)
189

Тогда можно ввести еще два орта, фиксирующих направления
максимального увеличения 51к нри выполнении S2k=0 (орт и
наибольшего роста S2K при условии SiK = 0 (орт а). Использо¬
вание одного и того же обозначения на рис. 5.12 и 5.13 можно
считать оправданным, так как оно характеризует направление
скорейшего роста 51к, хотя в последнем случае учитывается до¬
полнительное условие 52к=|0. Формально орты можно опреде¬
лить следующим образом:
x=jttxN_. x=_LXM_; q = _Nx*_.	(5.34)
|MXN|	h	X	M|	|N	X	x|	V
Аналогично вводятся критические направления и в пространст¬
ве координат.
Ценность подобных представлений заключается в демонстра¬
ции возможности изменения одного из граничных условий при
сохранении другого формированием приращений в скорости и
координатах в строго фиксированных направлениях. Такого ро¬
да интерпретация справедлива лишь для малых окрестностей
вокруг точки, принятой за опорную. При наличии аналитиче¬
ских выражений для концевых условий область возможного ана¬
лиза расширяется.
5.4.	Линейные методы управления выключением двигателя
Линейные методы управления выключением двигателя осно¬
ваны на разложении 5К в ряд Тейлора относительно х£ и удер¬
жании линейных членов. Эти методы самые простые, легко' реа¬
лизуются и, как уже указывалось, могут удовлетворять требо¬
ваниям по точности, при .малых отклонениях параметров конца
активного участка от расчетных. Область применения линейных
методов может быть расширена при использовании переменных
во времени производных, рассчитываемых во время полета, или
190

введением в память БЦБМ совокупности производных, отвеча¬
ющих группе опорных точек.
Линейные методы управления формируются на базе разло¬
жения (5.30):
где /=1, 2,..., г — количество концевых условий, определяю¬
щих граничное многообразие; Дх* = х? (tl)—Xi(tK)\ производные
вычислены при хк=х£.
При управлении, движением БР применяются два основных
концевых условия, характеризующих дальность и боковое отк¬
лонение точки падения. Соответственно их линейные представ¬
ления:
Последний случай в предположении наличия на борту информа¬
ции о кажущихся параметрах движения (отсутствует решение
навигационной задачи) всесторонне обследован в работах [47,
67]. Особенность такого рода решения заключается в необходи¬
мости перехода от полных вариаций, фигурирующих в соотно¬
шениях (5.35), (5.36), к изохронным, что позволяет ограничить¬
ся информацией от акселерометров, без ее последующей обра¬
ботки при качественной работе системы управляющих связей,
обеспечивающих близость траектории к программной.
В принципе структура алгоритмов управления при переходе
к истинным параметр-ам движения и их вариациям не изменит¬
ся. Такого рода алгоритмы обладают большей точностью в си¬
лу того, что концевые условия, строго говоря, выражаются че¬
рез фазовые координаты, определенные в инерциальной системе
отсчета. Однако необходимость решения навигационной задачи
усложняет структуру алгоритмов СУ, чего в ряде случаев мож¬
но избежать.
Как уже неоднократно отмечалось, для удобства организа¬
ции управления целесообразно .представлять пространственное
движение как сумму движений в ортогональных плоскостях и
рассматривать отдельно поведение проекций параметров движе¬
ний — -составляющих фазовых координат. Тогда, предполагая
вариации параметров движения малыми, а именно для этого
(5. 35)
7
(5. 36)
7
191

случая и «справедливы линейные методы, очевидно, возможно
разбить совокупность граничных условий на две группы:
dS j к
^ Дг, + — Дгу + ^ дг», +	Lvy + Ц* М=0;	(5.	37а)
дгх	дгу	dvx	dvy	dt
dSjK	dSjK	,	r\	/с	Q7^\
——Дгг + —!—	—— Д^=0,	(5.376)
orz	ovz	ot
т. e. пренебречь перекрестными связями, каналов ,и выделить
боковое дбижение. Если этого сделать нельзя, то последующие
выкладки много терянот в наглядности, хотя наличие в разложе¬
нии (5.35) всех «вариаций принципиальных затруднений при. реа¬
лизации не вызовет. Справедливость представления (5.37) для
управления движением БР показана в р,аботах [67, 105].
Соотношение (5.37 а) называют основным баллистическим
уравнением и на eiro основе строят нелинейные методы управ¬
ления выключением двигателя.
При формировании методов управления целесообразно их
классифицировать «по. следующим признакам:
— по точности аппроксимации SK можно различать линейные
методы и нелинейные, включающие, кроме линейных, и после¬
дующие члены разложения SK в -ряд Тейлора. Линейные методы
могут быть полными или неполными. Последние в отличие от
полных содержат не все вариации фазовых координат, умножен¬
ные на соответствующие 'частные производные;
— по количеству проекций вектора кажущегося ускорения
(или скорости), измеренных чувствительными элементами и ис¬
пользуемых для формирования метода управления. Могут быть
одно-, двух- и трехкоординатные методы управления. При этом
следует учитывать, что количество измерителей , может быть
больше числа координат, участвующих в формировании коман¬
ды на выключение двигателя. После измерений показания «аксе¬
лерометров «преобразуются для создания в общем случае неор¬
тогонального измерительного базиса;
— по виду информации, используемой «для расчета алгорит¬
ма управления, можно рассматривать методы, учитывающие ус¬
корение, скорость, координату и их комбинации. Данная класси¬
фикация может быть расширена включением в нее .признаков,
касающихся конструктивного воплощения метода; например,
тип примененных акселерометров, способ реализации- вычисли¬
тельного устройства и др.
Рассмотрим несколько характерных линейных методов уп¬
равления для уяснения способа их формирования.
Метод управления при ортогональных измерителях (х—у).
Уравнение метода получается непосредственно из разложения
192

<5.37а). Подставим вариации параметров движения и пере¬
группируем члены. Будем иметь
+^,	+!^	,<^ =
дгх	дгу	dvx	dvy	dt
=^rpj_^rp_i_^£iJ$t)P_L^ij<	.(5.38)
drx x	dry lJ	dvx x	dvy lJ	dt
В правой части -содержатся члены, которые могут быть опреде¬
лены заранее, для .программного' движения. Тогда, определяя во
время полета текущее значение управляющей функции
®(/)==^£iK	, djh*	, dSu	, а5(к	, dSu	5 39.
w	drx X 1	dry У	1	dvx X	1	dvy У ^ dt	V	'
команду на .выключение двигателя следует подать при выполне¬
нии равенства
Ф(У=ФР(/Р)/Фр(/Р)=^гР+^гР + ^-кг;Р+^т;Р+^/Р,
дгх л or у у	dvx л dvy у	dt
что свидетельствует о достижении изображающей точкой
аппроксимирующей гиперплоскости, проходящей через
х£ = {г*0, гР, V?, т;р, /Р).
К 1 X1 </’ Jf’ г/ ’ к/
Рис. 5.14.
Блок-схема реализации метода изображена на рис. 5.14. Для
выработки команды на выключение двигателя требуется инфор¬
мация о .проекции истинного ускорения движения ЛА на оси
О^Х, OiY инерциальной системы координат (если используется
информация о скорости, то первые интеграторы излишни), в ко¬
торой вычислены частные производные и Фр. В соответствии с
классификацией .метод относится к разряду неполных линейных
двухкоординатных методов с использованием информации об
ускорении (скорости) движения центра масс ЛА.
Метод управления при неортогональных измерителях (к—
р). Переход к ,н-е орто-гон а ль но му .измерительному базису позво¬
193

ляет уменьшить число/ интеграторов. Введем два вектора част¬
ных производных
Гу. —.проекции параметров движения на инерциальные нап¬
равления, зафиксированные соответственно углами % и ц (рис.
5.15). Для того чтобы представить выражение (5.41) в приня¬
той форме [67], следует его пронормировать относительно коэф¬
фициента Р:
Кроме того, для простоты реализации рационально уменьшить
величину интегрального слагаемого переходом к вариации от¬
носительно программы —	Д^|=	—	v™? (t). Соответст¬
венно необходимо скорректировать и расчетное значение управ¬
ляющей функции .представлением
(5. 40)
и учтем, что r= {rx, ry}, v= {vx, vy}.
Тогда соотношение (3.39) можно записать в виде
® = Pv + Qr+^ = P®x + Q/v+5!!f4	(5.41)
ot	ot
где
0 а)
Рис. 5.15.
о
(5.42)

Подстановка в соотношение (5. 42) дает
t
ф.(0 = ®х(*) + * f Дv^t)dt+ft,
(5.43)
фр =-^—k у>Р[t)dt + k ^Vnv{t)dt.
0	<K
Второе слагаемое Ф£ вычисляется заранее, а последнее /пред¬
ставляет составляющую методической ошибки, вызванную раз¬
бросом времени выключения двигателя относительно расчет¬
ного значения.
/р
Рис. 5.16.
Блок-схема (реализации метода представлена на рис. 5.16, от¬
куда видно уменьшение количества интеграторов на один по
сравнению с предыдущим методом.
Направления % и р имеют достаточно .наглядный физический
смысл-. Действительно, векторы Р и Q суть градиенты «годогра¬
фа требуемых скоростей и изоскоростной характеристики и оп¬
ределяют наиболее критичные, с точки зрения появления оши¬
бок выполнения концевых условий, направления. Зная анали¬
тическое выражение для SiK и расчетные значения параметров
движения Хк , нетрудно определить Vp и все величины, опреде¬
ляющие метод управления.
Данный метод относится к тому же классу, что и «х—у», но
отличается от него неортогональностью измерительного базиса.
Метод управления с программным разворотом датчика уско¬
рения (х).
Пусть в качестве информации, используемой при вычислении
основного баллистического уравнения (5.39), фигурируют про¬
екции вектора ускорения vx{t) и vy(t). Тогда с применением
известной формулы Коши преобразования двойного интеграла
195

в простой, содержащий верхний предел в .виде параметра в
подынтегральном выражении, можно выразить значения пара¬
метров движения, входящих в соотношение (5.39), через
vx(t), vy(t) в следующем виде:
rx(.t)=\ f	(t~x)vx{x)dx;	=	J Vx{t)dt.
ООО	О
(5. 44)
t	t
ry{t)= f {t—x)vy{x)dt\ vy(t)=^ vy(t)dt.
o	o
Подстановка в разложение (5.37 а) дает
0
(S'45)
которое можно преобразовать к виду
t
Ф(/)=^/+^ [k(t)V(T)]rfT,	(5.46)
О
где
к(т) = /(*-т)^ + ^5; {t-х)д-^д-^\
{	дгх	dvx
,х wx	dry dvy)
v(t) = K(t), ®„(t)}.
Иначе соотношение (5.46) можно записать аналогично (5.41):
dSlK .
Ф{*)=-^(+'\к{х)Ьх (x)dx,	(5.47)
о
где
у (т) = arete dSiK/dl’У + (^ — т) dSi}Jdry
dSiK/dvx+(t-%)dSiKldrx ’•
a vx —проекция истинного ускорения на некоторое направле¬
ние в инерщиальном пространстве переменное во времени и оп¬
ределяемое программным изменением угла %(t).
Таким образом, уравнение метода управления (5.47) пока¬
зывает возможность его реализации с помощью измерения толь¬
ко одной проекции ускорения на переменное направление [47].
Блок-схема реализации алгоритма управления показана на рис.
5.17.
196

В соответствии с приведенной классификацией метод отно¬
сится к групле неполных линейных однокоординатных методов с
использованием информации об ускорении.
Метод управления с неор7огональными измерителями уско¬
рения (V—j/).
Уравнение (5.45) по сути представляет собой управляющую
функцию двухкоординатного метода с измерителями ускорения,
оси чувствительности которых ориентированы по осям прямо-
Рис. 5.17.
Рис. 5.18.
угольной инерциальной системы координат. Его можно перепи¬
сать в виде
t
K(T)^(t) + «i/('r)^!/(t)]flfT-	(5-48>
о
Однако известно1 [31, 87], что для уменьшения погрешностей из¬
мерений акселерометрами оси их чувствительности следует рас¬
полагать в некоторых направлениях, зависящих от динамики
ГСП и режима полета. Поэтому рассмотрим случай ориентации
датчиков ускорений под некоторыми углами X' и р/ к горизон¬
ту (рис. 5.18) и .н,айдем управляющую1 функцию на основе (5.48)
длн этого случая.
Акселерометры выдают информацию (после решения нави¬
гационной задачи) об изменениях проекций ускорения ^х(0>-
v^t), которые связаны с vx(t) и vy(t) уравнениями
vx = —Т7 ^ - Vy te Г ’ Vy= —t—г Vp - vx с tg p'r,
COS A	Sin [A
откуда
tgX' .	ctg(A'	.
‘	—	 Vu.	  —	V\
cos X sin ix' **	•	sinfx' cosX'
v r =	  ;	vu =	  ,
|1 — tg X' ctg fx'	1	—	tgX'	ctgfx'
197

а подстановка в (5.48) дает
Ф(/)=“!!* + ! { +
dt 1 — tgX'ctgfi' J ILcos X	cos	X	J
о
+ f ЦЩ. - rtx (t)	V, (t)\ dx.	(5. 49)
I sin fl'	sin	fl' J J
Использование (5.45) дает возможность в окончательном виде
записать
t
\ (5-50)
о
где из'сравнения с (5.49) следует
«x(t) = «x. + t/lx,=—L7r[f£iS + <ffi£“Ctg|*'(fi5 + /fi5)l“
cos X \_dvx дгх	\	dv	у	dr	у	j \
— X ( 1	dSiK	ctgfj/	•
\ cos X' drx	cos X' dry /
sin fl' L dvy	dry	\	dvx	drx J	J
 ^ f 1 dSlK	 tg X'	dSiK\ e
\sinfi' dry	sinfi'	drx) ’
k= 1	,
1 — tg X' ctg p'
т. e. fix(t), rtf,(x) так же, как и пх(х), пу(х), меняются по линей¬
ному закону, чего и следовало ожидать ,в силу линейности пре¬
образования.
nju(t)
W)
Рис. 5.19.
Блок-схема .реализации метода по.казана на рис. 5.19. Отли¬
чие классифицирующих признаков метода от предыдущего
только в том, что он двухкоординатный.
198

Следует подчеркнуть, что все рассмотренные методы с точ¬
ки зрения методической .погрешности эквивалентны, так как ба¬
зируются на одном исходном уравнении (5.38), -полученном иа
(5.37 а). Состав линейных методов управления выключением
двигателя можно было бы расширить, используя другое пред¬
ставление входной информации, новые измерительные базисы
и, наконец, упрощая представленные зависимости. Для вынесе¬
ния окончательного- суждения о качестве метода следует оце¬
нить не только методические, но и инструментальные ошибки,
определить возможности технической реализации на базе ана¬
лиза аппаратуры, входящей в со1став системы управления и т. д.

СПИСОК ЛИТЕРАТУРЫ
1. Абгарян К. А., Рапопорт И. М. Динамика ракет. М., «Машиностроение»,
1969, 378 с.
2. Алексеев К. Б., Бебенин Г. Г., Ярошевский В. А. Маневрирование кос¬
мических аппаратов. М., «Машиностроение», 1970, 418 с.
3. Алешков Ю. 3. Метод последовательных приближений для решения
вариационных задач механики полета. — «Автоматика и телемеханика» (А и
Т) '1965, № 10, с. 1657—1662.
4. Алешков Ю. 3., Баранов А. Ю., Хоменюк В. В. Решение некоторых за¬
дач механики полета —-А и Т., 1967, ]МЬ 6, с. 43—'50.
5. Андреев В. Д. Теория инерциальной навигации Т. 1, 2, М., «Наука»,
1966, 579 с, 647 с..
6. Андреев Н. И. Корреляционная теория статистически оптимальных сис¬
тем. М., «Наука», 1966, 454 с.
7. Андреевский В. В. Динамика спуска КА на Землю. М., «Машинострое¬
ние», 19Б6, 232 с.
8. Аппазов Р. Ф., Лавров С. С., Мишин В. П. Баллистика управляемых ра¬
кет дальнего действия. М., «Наука», 1966, 307 с.
9. Атанс М., Фалб П. Оптимальное управление. М., «Машиностроение»,
1968, 764 с.
10. Балахонцев В. Г., Иванов В. А., Шабанов В. И. Сближение в космосе.
Воениздат, 1973, 240 с.
11. Барабашин Е. А. О приближенном осуществлении движения по за¬
данной траектории.—А и Т, 1961, № 6, с. 857—864.
12. Барковский В. В., Захаров В. Н., Шаталов А. С. Методы синтеза
систем управления. М., «Машиностроение», 1969, 327 с.
13. Березин И. С., Жидков Н. П. Методы вычислений, т. I. М., «Наука»,
1966, 632 с.
14. Богуславский И. А. Об уравнениях стохастического управления.—
А и Т, 1966, № 11.
15. Богуславский И. А. Методы навигации и управления по неполной
статистической информации. М., «Машиностроение», 1970, 256 с.
16. Боднер В. А. Системы управления летательными аппаратами. М., «Ма¬
шиностроение», 1973, 504 с.
17. Болтянский В. Г. Математические методы оптимального управления.
М., «Наука», 1966, 307 с.
18. Брайсон. Линейное управление с обратной связью для оптимальных
задач перехвата, встречи и мягкой посадки. — «Ракетная техника и космонав¬
тика (РТ и К) 1965, № 8, с. 228—234.
19. Брайсон, Дэнхем. Принципы систем наведения КА, возвращающегося
в атмосферу со сверхзвуковой скоростью при использовании подъемной си¬
лы.— «Ракетная техника» (РТ), 1962, № 6, с. 171—180.
20. Бранец В. Н., Шмыглевский И. П. Применение кватернионов в зада¬
чах ориентации твердого тела. М., «Наука», 1973, 319 с.
21. Бреквелл, Танг, Смит. Приложение непрерывных и дискретных стра¬
тегий теории минимальных затрат к наведению межпланетного аппарата. —
РТ и К, 1965, № 5, с. 137—И41.
200

22. Браш, Рид. Оперативный метод выбора программы управления угло¬
вым движением ракет-носителей. — «Вопросы ракетной техники» (ВРТ), 1973г
X* 4, с. 57—68.
23. Бусленко Н. П., Калашников В. В., Коваленко И. Н. Лекции по тео-
рии сложных систем.—-'«Сов. радио», 1973, 439 с.
24. Бутенин Н. В. Введение в аналитическую механику. М., «Шука»,
1971, 264 с.
25. Бэтгин Р. Наведение в космосе. М., «Машиностроение», 1966, 447 с.
26. Ванс. Реализация режима оптимального адаптивного наведения. —
РТ и К, 1965, № 1, с. 218—222.
27. Вебер, Бонфанти. Нелинейный метод наведения при перехвате. —
ВРТ, 1972, № 3, с. 71—76.
28. Вентцель Е. С. Исследование операций. — «Сов. радио», 1972, 551 с.
29. Габасов Р., Кириллова Ф. М. Качественная теория оптимальных про-
цесоь. М., «Наука», 1971, 507 с.
30. Гаврилов В. М. Оптимальные процессы в конфликтных ситуациях.—
«Сов. радио», 1969, 160 с.
31. Ганкель, Ван-дер-Стойн. Оптимизация ориентации акселерометров.—
ВРТ, 1967, № 4, с. 76—97.
32. Гелб, Саутерленд мл. Способы уменьшения ошибок бесплатформенных
систем, вызванных ошибками гиротахометров. — ВРТ, 1969, № 6, с. 58—91.
33. Гобец, Долл. Обзор импульсных траекторий. — РТ и К, 1969, № 5,
с. 3—12.
34. Гороховик В. В. К проблеме векторной оптимизации. — «Известия
АН СССР. Техническая кибернетика» (ТК) 1972, № 6., с. 63—71.
35. Г'родзовский Г. А., Иванов Ю. Н., Токарев В. В. Механика космичес¬
кого полета. М., «Наука», 1966, 680 с.
36. Данхем, Спейр. Оптимальная программа измерения и коррекции ско¬
рости для наведения на среднем участке траектории. — РТ и К, 1964, № 5,
с. 87—94.
37. Демьянов В. Ф., Малоземов В. Н. Введение в минимакс. М., «Наука»,
1972, 366 с.
38. Демьянов В. Ф., Рубинов А. М. Приближенные методы решения
экстремальных задач. Изд. ЛГУ, 1968, 180 с.
39. Джонсон, Леондес, Пейн. Обобщенный линейный закон для космичес¬
ких летательных аппаратов. — РТ и К, '1968, № 5.
40. Дмитриевский А. А. Внешняя баллистика. М., «Машиностроение»,
1972, 583 с.
41. Дубошин Г. Н. Небесная механика. Основные задачи и методы.
ГИФМЛ, 1963, 586 с.
42. Дубошин Г. Н. Теория притяжения. ГИФМЛ, 1961, 288 с.
43. Дэнхем, Моухен. Выбор параметров траектории, максимизирующих
вероятность успеха полета. — РТ и К, 1966, № 7, с. 181 — 187.
44. Жакой А. М., Пигулевский Ф. А. Управление баллистическими ракета¬
ми. Военнздат, 1965, 277 с.
45. Заборски Дж., Горман Д. Управление с помощью функционального
разложения Лагранжа. — «Труды III ИФАК». Сек. 18, ст. 18Е, 17 с.
46. Исаев В. К. Принцип максимума Понтрягина Л. С. и динамическое
программирование тяги ракет.—А и Т, 1961, № 8, с. 1164—1172.
47. Ишлинский А. Ю. Инерциальное управление БР. М., «Наука», 1968,
142 с.
48. Канторович Л. В., Крылов В. И. Приближенные методы высшего ана¬
лиза. ГИФМЛ, 1962, 708 с.
49. Керкендаль, Пфейфер. Анализ методов программирования многонм-
пульсных траекторий. — ВРТ, 1965, JVT® 6, с. 114—126.
50. Кидд, Соул. Конечные маневры спутников для встречи на восходя¬
щей траектории. — РТ, 1962, № 1, с. 75—91.
51. Кириллова Л. С. Задача об оптимизации конечного состояния регули¬
руемой системы. — А и Т, 1962, № 12, с. 2157—2162.
201

52. Кирин Н. Е. Вычислительные методы теории оптимального управле¬
ния. Изд. ЛГУ, 1968, 143 с.
53. Коренев Г. В. Введение в механику управляемого тела. М., «Наука»,
1969, 568 с.
54. «Космические траектории». Сб. ИЛ, 1963, 243 с.
5э. Кочетков В. Т., Половко А. М., Пономарев В. М. Теория систем теле¬
управления и самонаведения ракет. М., «Наука», 1964, 536 с.
56. Кочетков В. Т., Поцелуев А. В. О синтезе оптимальных нелинейных
систем управления по критерию максимума вероятности.—ТК, 1966, № 4,
с: 170—174.
57. Кочин Н. Е. Векторное исчисление и начала тензорного исчисления.
М., «Наука», 1965, 426 с.
58. Крапивин В. Ф. Теоретико-игровые методы синтеза сложных систем в
конфликтной ситуации. М.,—«Сов. радио», 1972, 192 с.
59. Красовский Н. Н. Теория управляемого движения. М., «Наука», 1968,
475 с.
60. Красовский Н. Н. Игровые задачи о встречи движений. М., «Наука»,
1970, 420 с.
61. Кринецкий Е. И. Системы самонаведения. М., «Машиностроение»,
1970, 236 с.
62. Кротов В. Ф., Букреев В. Г,. Гурман В. И. Новые методы вариацион¬
ного исчисления в динамике полета. М., «Машиностроение», 1969, 288 с.
63. Кротов В. Ф., Гурман В. И. Методы и задачи оптимального управле¬
ния. М., «Наука», 1973, 446 с.
64. Крылов И. А., Черноусько Ф. JI. О методе последовательных прибли¬
жений для решения задач оптимального управления. — ЖВМ и МФ, 1962,
№ 6, с. 128—137.
65. Кузин Н. Т. Основы кибернетики. М., «Энергия», 1973, 503 с.
66. Лейб Д. М. Одна задача многоразовой коррекции движения. — ТК,
1972, № 4, с. 20—26.
67. Лебедев А. А., Герасюта Н. Ф. Баллистика ракет. М., «Машинострое¬
ние», 1969, 244 с.
68. Лебедев А. А., Красильщиков М. Н., Малышев В. В. Оптимальное
управление движением космических летательных аппаратов. М., «Машино¬
строение», 1974, 199 с.
69. Лебедев А. А., Соколов В. Б. Встреча на орбите. М., «Машинострое¬
ние», 1970, 366 с.
70. Лейтман Д. Введение в теорию оптимального управления. М., «Нау¬
ка», 1968, 190 с.
71. Лейтман Д. и др. Методы оптимизации с приложением к механике
космического поле! а. М., «Наука», 1965, 538 с.
72. Леондес К. Т. и др. Управление космическими летательными аппара¬
тами. М., «Машиностроение», 1967, 324 с.
73. Летов А. М. Динамика полета и управление. М., «Наука», 1969, 359 с.
74. Лоуден Д. Ф. Оптимальные траектории для космической навигации.
«Мир», 1966, 152 с.
75. Лурье А. И. Аналитическая механика. ГИФМЛ, 1961, 824 с.
76. Льюоллен, Тэпли, Уильямс. Итерационная процедура для непрямых
методов оптимизации траекторий.— РТ и К, 1968, № 3, с. 212—222.
77. Медичи Дж. С., Ньюстад Л. У. Применение оптимального управления
к наведению на среднем участке траектории. Труды II ИФАК, «Наука», 1965,
с. 91—106.
78. Мессарович М. и др. Общая теория систем. «Мир», 1966, 187 с.
79. Микишев Г. Н., Рабинович Б. И. Динамика твердого тела с полостя¬
ми, частично заполненными жидкостью. М., «Машиностроение», 1968, 532 с.
80. Мильштейн Г. Н. Об оптимальном осуществлении траекторий. — А и
Т, 1965, № 4, с. 621—628.
81. Миронов В. И. Стабилизация движения нелинейных систем по задан¬
ной траектории. — ТК, 1968, № 4, с. 137—143.
202

82. Михлин С. Г. Численная реализация вариационных методов. М., «На¬
ука», 1966, 432 с.
83. Мишулина О. А. Синтез оптимальной системы управления с заданным
фазовым движением в условиях помех. — А и Т, 1973, № 9, с. 33—39.
84. Моисеев Н. Н. Численные методы в теории оптимальных систем. М.,
«Наука», 1971, 424 с.
"85. Новоселов В. С. Аналитическая теория оптимизации в гравитацион¬
ных полях. Изд. ЛГУ, 1972, 317 с.
86. Нгуен Тхань Банг. Метод последовательного приближения для реше¬
ния одной задачи оптимального приближения. — А и Т, 1969, № 6, с. 29—36.
87. О’Доннел К. Ф. и др. Инерциальная навигация. Анализ и проекти¬
рование. М., «Наука», 1969, 592 с.
88. Остославский И. В., Стражева И. В. Динамика полета. М., «Машино¬
строение», 1969, 449 с.
89. Оттен. Инерциальные навигационные системы без ГСП. — ВРТ, 1967,
№ 12, с. 68—86.
90. Охоцимский Д. Е., Энеев Т. М. Некоторые вариационные задачи, свя¬
занные с запуском ИСЗ. — УФН 1957, т. 63 вып. 1а, с. 5—33.
91. Паевонски, Вудроу. Задача пространственной оптимальной по быстро¬
действию встречи. — РТ и К, 1966, № 12, с. 180—190.
92. Пашкеев С. Д., Минязов Р. И., Могилевский В. Д. Машинные методы-
оптимизации в технике связи. М., «Связь», 1975, 347 с.
93. Питтман Д. и др. Инерциальные системы управления, Воениздат,
1964, 454 с.
94. Платонов А. К. Исследование корректирующих маневров в межпла¬
нетных перелетах.—■ «Космические исследования» (КИ), Ю66, вып. 5, с. 618—
624.
95. Погорелов Д. А. Теория кеплеровских движений летательных аппара¬
тов. — ФМ, 1961, 107 с.
96. Пономарев В. М. Теория управления движением КА. М., «Наука»,
1965, 455 с.
97. Пономарев В. М. Метод последовательной оптимизации в задачах
управления. — ТК, 1967, № 2, с. 3—10.
98. Понтрягин J1. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф.
Математическая теория оптимальных процессов. ГИФМЛ, 1961, 392 с.
99. Пфейфер. Метод оптимизации терминального управления для актив¬
ных участков траекторий. — РТ и К, 1966, № 2, с. 202—212.
100. Пфейфер. Метод расчета многократно корректируемых траекторий,
основанный на динамическом программировании. — РТ и К, 1965,	№	9,
с. 138—141.
101. Растригин J1. А. Системы экстремального регулирования. М., «Нау¬
ка», 1974, 630 с.
102. Ришел. Оптимальное наведение ракеты воздух — поверхность. —
ВРТ, 1968, № 9, с. 72—88.
103. Робинсон. Обзор методов проектирования управления полетом.—
ВРТ, 1969, № 9,110, с. 68—69, 71—90.
104. Роулинг. Пассивное определение промаха. — РТ и К, 1968, № 8,
с. 203—205.
105. Савант С. Дж., Ховард Р., Соллоуай С., Савант С. А. Принципы
инерциальной навигации. «Мир», 1965, 355 с.
106. Селезнев В. П. Навигационные устройства. М., «Машиностроение»,
1974, 600 с.
107. Синюков А. М., Волков J1. И., Львов А. И., Шишкевич А. М. Бал¬
листическая ракета на твердом топливе. Воениздат, 1972.
108. Соколов В. Б., Иващенко О. И. Исследование относительного дви¬
жения спутников методом обобщенных параметров. — КИ. 1969, вып. 5, с.
667—6716.
203

109. Спейер Дж., Келли Г. и др. Метод проекции ускоренного градиента
и его использование для оптимизации траекторий ракет. — В кн: Управление
в космосе, т. 1, «Наука», 1972, с. 60—69.
110. Спиди К., Браун Р., Гудвин Дж. Теория управления. «Мир», 1973,
248 с.
111. Стратонович P. J1. Новейшее развитие методов динамического про¬
граммирования и их применение для синтеза оптимальных систем. — «Труды
II Конгресса ИФАК». «Наука», 1965, с. 120—121.
112. Танг. Оптимальная стратегия дискретного управления для межпла¬
нетной навигации. — ВРТ, 1966, № 5, с. 68—81.
113. Томпсон, Унгер. Характеристики инерциальных чувствительных эле¬
ментов бескарданных систем. — ВРТ, 1967, № 5, 6, с. 60—74.
114. Федьдбаум А. А. Основы теории оптимальных автоматических систем.
ГИФМЛ, 1963, 552 с.
Иб.Флауэс. Уравнение наведения для КА ОАО, ATS, «Маринер».— ВРТ,
1970, № 1, с. 64—68.
116. Фридлендер Г. О. Инерциальные системы навигации. ГИФМЛ, 1961,
154 с.
117. Хенделсмен. Оптимизация траектории полета в безводушном про¬
странстве с постоянной тягой при использовании импульсных траекторий в
качестве начального приближения. — РТ и К, 1966, № 6, с. 151—160.
118. Цлаф JI. Я. Вариационное исчисление и интегральные уравнения. М.,
«Наука», 1966, 176 с.
119. Цыпкин Я. 3. Адаптация и обучение в автоматических системах. М.,
«Наука», 1968, 399 с.
120. Чандлер, Смит. Итеративное наведение ракет. — ВРТ, 1967, № 12,
с. 55—68.
121. Чернецкий В. И. Анализ точности нелинейных систем управления. М.,
«Машиностроение», 1968, 247 с.
122. Чэнг С. С. JI. Видоизмененный принцип максимума для оптималь¬
ных систем с ограниченными фазовыми координатами. — «Труды II Конгрес¬
са ИФАК», «Наука», 1965, с. 131—140.
123. Шаталов А. С. Летательный аппарат как объект управления. М.,
«Машиностроение», 1974, 239 с.
124. Шапот д. в. О построении критериев качества технических объек¬
тов. — ТК, 1971, ДЬ 6, с. 53—61.
125. Шатровский JI. И. Об одном численном методе задачи оптимального
управления. — ЖВМ и МФ, 1962, № 2, с. 141—146.
126. Шварцбейн, Джерстен, Смит. Точное аналитическое решение урав¬
нений задачи встречи. — ВРТ, 1965, № 6, с. 65—86.
127. Шнейдер, Кейп, Кемил. Последние достижения в области управле¬
ния по методу переменной точки для космической встречи и спасения — РТ
и К, 1967, № 12, с. 43—51.
128. Элдин X. А. Управление траекторией в задачах встречи на орбите
с использованием методов регуляризации. — В кн.: Управление в космосе, т. 2,
«Наука», 1972, с. 243—253.
129. Энеев Т. М. О применении градиентного метода в задачах теории
оптимального управления — КИ, 1966, вып. 5, с. 687—692.
130. Alfriend К. Т., Kashiwagi I. Minimum time orbital rendezvous between
neighboring elHptical orbits. J. Opt. Theory and Appl. 4, N 4, 1969, p. 260—276.
131. Brainin S. М., Me Chee R. B. Optimal biased proportional navigation,
IEEE Trans. Autom. Contr, 13, N 4, 1968, p. 440—442.
132. Breakwell J. V., Tung F., Smith R. R. Application of the continious and
descrete strategies of minimum effort theory of interplanetory guidance, AIAA
Jorn. 3, may 1965, p. 903—907.
133. Breakwell J. V. A double singular problem in optimal interplanetory
guidance. «J. Soc. Ind. and Appl. Math.» N 6, 1965, p. 71—77.
204

134. Bryson A. E., Denham W. F. Multivariable terminal control for mean
square deviation from a nominal path, Proc. Simp, on Vechicle Systems optirn.
nov. 28—29, 1961. N 4, p. 416—433.
135. Bryson A. E., Carrol F. Т., Mikami K-, Denham W. F. Determination
of the lift or a drag programm that minimizes re-entry heating with acceleration
or range constraints using a satellite descent computation procedure XXIX Con¬
gress IAS. N. — Y., 1960, p. 454—462.
136. Cera J. Branched trajectories optimization by the projected gradient
technique, AIAA paper N 917, 1969, p. 1—10.
137. Chamberlini J. A., Rose J. T. Gemini rendezvous programm, J. Spacecr.
And Rock., N 1, 1964, p. 74—81.
138. Dahlard L. Application of Pontryagin‘s maximum principle in determing
the optimum control of a variable-mass vechicle, Progr. Astr. and Rock. N-Y —
L Acad. Press, 1962, p. 121—134.
139. Euler E. A. Optimal low-thrust rendezvous control, AIAA Jorn. N 6,
1969, p. 1140—1144.
140. Fried B. D., Richardson J. Optimal rocket trajectories, Jorn. Appl. Ph.
N 8, 1956, p. 187—195.
141. Fusca J. A. Catching a satellite. «Space /Aeron», 44, N 4, 1965, p. 84—
91.
142. Gilbert E. O. Orbit control and analysis technique for equatorial
24-hours satellites, Space Techn. Lab. STL/TN—6—27149, p. 1—58.
143. Ho Y. C., Brison A. E., Baron C. Differential games and optimal
trajectories, IEEE Trans, on Autom. Cont. N 4 oct. 1965, p. 47—56.
144. Hord R. A. Realative motion in the terminal phase of the interception
of satellite or a ballistic missile, NASA TN—4399, 1956, p. 1—79.
145. Horn H. Т., Chandler D. C., Buckelev V. L. Iterative guidance applied
to generalized missions, J. Spacecr. and Rock. 6. N 1, 1969, p. 4—8.
146. Itow. H., Tushie J. E. P—matrix guidance, J. Spacecr. and Rock. N 3,
1966, p. 34—45.
147. Joseph P.	D., Tou J. T. On linear	control	theory,	IEEE	Trane.	Appl.
And. Ind. 80/sept.	1961, p. 193—196.
148. Kahne S.	J. Optimal cooperative	state	rendezvous	and	Pontryagin‘s
maximus principle,	Intern. J. Contr. 2, N 5,	1965,	p.	218—231.
149. Kelly H. J. Gradient theory of optimal flight paths ARS Jorn. 30, 1960.
p. 28—59.
150. Leitman G. On a class of variational problems in rocket flight, Journ.
Aero/Space N 9, 1959, p. 586—591.
151. Leondes С. Т., Volgenau E. Improvment of missile and space vechicle
accuracy bv trajectory optimization, J. Spacecr. and Rock., 4, 1967, p. 1609—
1612.
152. Levine S. A. Explict guidance for an oblate gravitational field,
J. Spacecr. and Rock., N 7, 1966, p. 175—184.
153.	Longman R. W. Short term bounds for the effect of oblateness	on
ballistic	trajectories, J. Spacecr. and Rock., N 11, 1972, p. 17—22.
154.	Lovingood J. A., Blair J. C., Geissler E. O. Shuttle ascent guidance	and
control, Astronaut, and Aeronaut., N 2, 1972, p. 66—70.
155. Lowden D. Dynamic problems of interplanetory flight, Aeronautical
Quart. Vol. 6. 1955.
156. Lowden D. Optimal rocket trajectory of an earth satellite, Jet Prop.
N 6, 1957, p. 98—111.
157. Melborne W. G. Space flight optimisation. «Proc. NASA Univ. Conf.
Sci. and	Techn. Space Explorat.» Chicago, 1962, p. 173—178.
158.	Miner W. E., Schneider D. H., Brand N. J. Pathadaptive mode	for
guiding space flight vechicles, Progr. Astr. And. Rock. Vol. 8. N—Y—L. Acad.
Press, 1962, p. 184—191.
159. Neustadt L. W. A general theory of minimum fuel space trajectories,
J. Soc. Ind. and Appl. Math. A3, N 2, 1965, p. 317—356.
205

160. O’Brien R. М., Sivers R. F. Optimization of guidance lows to achieve
orbital rendezvous with a propulsion system of only moderate throattlability,
AIAA/ION Guidance Control Cond. Minneapolis ang. 16—18. 1965, p. 270—277.
161. Pfeifer C. Some theoretical considerations arising in guidance analysis,
N—Y. Amar. Asts. Soc., N—Y, 1964, p. 79—87.
162. Rosenbaum R. The reduction of	launch vechicle	injection	errors	by
trajectory shaping, AIAA Paper, 1970, N	1078, p. 1—10.
163. Rosenbrock H. H. The formulation of optimal control with an applica¬
tion of large systems, Automatica I, N 4, 1963, p. 37—42.
164. Savage P. G. Terminal prediction guidance, AIAA/ION Guidance Con¬
trol Conf. Minneapolis aug. 16—18, 1965, p. 398—407.
165.	Schwarzbein Z. E., Gersten	R. H., Smith G. E. An	exact	closedform
solution	to the rendezvous problem,	Advance in the Astr.	Sci. Vol. 16, 1963,
p. 143—149.
166. Shen C. N., Gelon W. S. Analytic guidance and control of low thrust
rendezvous, AIAA Paper N 862, 1968, p. 1—11.
167. Smith G. L. Multivariable linear filter theory applied to space vechicle
guidance, J. Soc. Ind. And Appl. Math. A	2, N 1, 1964, p.	19—32.
168. Soong Т. Т., Pfeifer C. G. Unified guidance analysis in	design	of
space trajectories, J. Spacecr. And Rock. 3, N 1, 1966, p. 98—103.
169.	Vaccaro P. J., Kirby M. J.	Rendezvous guidance of	lifting	aerospace
vechicle,	J. Spacecr. And Rock. 2. N	5, 1965, p. 705—711.
170. Watson J. W., Stubbernd A. R. Atmospheric entry employing range
sensitivity, J. Spacecr. and Rock., N 5, 1968, p. 983—984.
171. Wingrove R. C. A survey of atmpsphere reentry guidance	and	control
methods, IAS Paper N 63—86, 1963, p. 1—39.
172. Wonhem W. M. Stochastic problem in optimal control,	IEEE	Intern.
Conv. Rec., march 1963. p. 317—332.
173. Zee Ch. H. Finite-thrust explict guidance low for nearly circular
orbital rendezvous, Jor. of Spacecr. and Rock. N. 1, 1967, p. 79—87.

ОГЛАВЛЕНИЕ
Стр.
Предисловие . .	  3
Введение 	 5
Глава 1. Постановка задачи наведения	  12
1.1. Объект управления	 12
1.2. Способы формирования управляющих связей	 20
1.3. Принципы программирования движения	 28
1.4. Критерии оптимальности. Граничные условия	 32
1.5. Геометрическая интерпретация задачи наведения	 39
Глава 2. Формализация баллистического движения	 48
2.1. Модели гравитационного поля	 48
2.2. Концевые условия выведения (кеплеровы движения) ....	52
2.3. Концевые условия выведения с учетом нецентральности гравита¬
ционного поля	 61
■2.4. Методика применения концевых условий выведения	 72
2.5. Уравнения относительного движения в абсолютной системе ко¬
ординат 	 77
2.6. Уравнения относительного движения в связанной системе ко¬
ординат 	 87
2.7. Концевые условия сближения	 91
Глава 3. Управление выведением	  100
3.1. Анализ постановок задач и некоторых методов синтеза опти¬
мального управления	 100
3.2. Определение оптимальной программы управления выведением .	113
3.3. Синтез однопараметрических законов управления	 120
3.4. Синтез многопараметрических законов управления	127
Глава 4. Управление сближением	 138
4.1. Анализ методов управления сближением	 1,38
4.2. Особенности формализации задачи сближения для целей синтеза	143
4.3. Определение оптимальной программы управления сближением	149
4.4. Синтез оптимального закона управления сближением ....	156
Глава 5. Управление выключением двигателя	 165
5.1. Задача автономной навигации	  165
5.2. Решение навигационной задачи при математическом моделирова¬
нии инерциального базиса 	 173
5.3. Формирование упрощенных методов управления выключением
двигательной установки	 183
5.4. Линейные методы управления выключением двигателя ....	190
Список литературы	 200

Вадим Дмитриевич Могилевский
НАВЕДЕНИЕ БАЛЛИСТИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Редактор издательства С. И. Виноградская
Технический редактор А. Я. Дудинская	Художник Л. С. Вендров
Корректор Л. Е. Хохлова
Сдано в набор 8/IX 1975 г. Подписано к печати 22/XII 1975 г.	Т—18284
Формат 60X90716	Бумага	№ 1	Печ.	л.	13,0	Уч.-изд. л. 12,3
Цена 1 р. 24 к.	Тираж	1600	экз.	Изд.	зак.	350
Издательство «Машиностроение», 107885, Б-78, 1-й Басманный пер., 3.
Московская типография № 8 Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли
Хохловский пер., 7. Тип. зак. 3953

Цена 1 p. 24 к.